Автор: Аксенова М.Д. Володин В.А.
Теги: издания для определенного назначения математика справочные издания по математике энциклопедия для детей
ISBN: 5-94623-072-7
Год: 2003
Текст
ГЕНЕРАЛЬНЫЙ ДИРЕ КТОР
Георrий Хромов
ГЛАВНЫЙ РЕДАКТОР
Мориом Аксен ова
ГЛАВНЫЙ ХУДОЖНИК
Е11ено Дукельскоя
МЕТОДОЛОГИЧЕСКИЙ И ОТВЕТСТВЕННЫЙ РЕДАКТОР ТОМА
Виктор Володин
НАУЧНЫЕ РЕДАКТОРЫ РАЗДЕЛОВ ТОМА
[Анатолий Савин~ Изабелла Башмакова, Владимир Болн1нский,
Николай Долбили11, Владимир Дубровский, Владимир Тихомиров
МАТЕМАТИКА
УДl< 087.5:51(031)
1ШК 22. lя2
э68
ISBN 5-94623-072-7 ('r. 11)
rSBN 5-94623-001-8
I СЕS -,-N-т-ЕR-N-л-т1-о-,-л-L_c_E_-.;т_R_E_o_F_E_Du_c_л_т_1o_N_л_L_s_v-sт-E-~,-s-11e-rs-1 ••~ :иr.,,
МЕЖnУ Н АРО!\Н ЫЙ UЕНТР ОБУЧЛЮШИХ СИСТЕМ 1 ЩОСI .~~f.~~:'"
CENTRE PHERNAТIONЛL OES SYSTEMCS D' LDUCATION 1CISf1 ••~::0'~3"
.
_1v_т_н_н_Nr1_т_1_o_v_л1_E_s_z_i:_N_r_н_t_.~1_F_u_R_л_u_~_в1_1_D_11_N_a_s5_Y_s_т_E.1_1E_11z_л_s1 .__•·_•u_.~_д_:'._"_,
~
О IESCO
МЕЖДУНАРОДНАЯ КА.ФЕдРА- СЕ"JЪ UNESCO/JCES
"TILY.HИЧRCKO.li' И ГТРОФl!СС:ИОНА/ТЬНО.Е 06РА30МНИЕ
и лодrо1 ·овт« I«ЛРОВ'·
Рекол~еидовшю Ali!Ж<h111ajюд11ы/vt це1тц1ш1 иб1·чшищ11х ~11~mt'..1t
(МЦОС) 11,1w.:11а)рю/юд1юй 1.;афейриi1 tt'fflЫ(J ЮНЕСКО/!IЩОС а ка11(!01·1ос·
. J' 'lt'mllNU IIOCUбUЛ
Сер ия «Эпц.uю&011едил dlUI дenU'l/л реКf.J.1t1е11доваиаДеппрта.меи-
1110.м обj?свпватш1ы·1ы.х 11рогрс.1.лt~r" стrшдt.1{!111(111 оfi1цего nfipr1,юr1a111rл .1111 -
нистерстеа пбра10пания. l'occulrc'!<:oi1. r/>f!6e;xщu11.
JI К'Oll'J91)C(' JIUЛ)'ЧU1J'Ю 1.7 -lli?:J' Юда Ш(')ЩJЩЮ,(;Л'IХ! om·,щ)11Netl/U! //fJaf{йia-f
нtЩ>а:)Jсдrто диrию.мо.;11 0111 :!':J.()3.99 .1t1.11учrиий 1-1.1дame.;1ы,"Kllll ,фое-J..'111
год(1 для детей и юно~иестtш.
Оргко..111и1rи:т Х1 i\1JQc-л:vвcl(Qf1 Ме Ji{·u1111ap()mюil 1>.·11и >и.11тi я/мтрл:11, l е
11ералы1ая дupe11.1{UJ1.межi>J11шр1х)пы,\1,1щж ''-7'·"' аып11аао11: 11я;.нщjхж11п
грааили uздcrmc.nw:1;oe обr..ёд111п111/.U' //(Jafиfi,a, · 1)11ш1rнщ11 r11110.:.'.00.9R1.;с1л·
t10бед11 111 Ш1Я в 1111м1гНU1{ШI «Ca11iьth •.ttaccoвый иознавате..r~ы1ый 1tро
ект. 1998».
: ~а ptL'ljJafim пху нq) 1ч1щ~.иш11оr>11 чео·ой i\'OI ц(l:'l11 <''и 11:и11ж ·ш1шt уцl!бн111.."<:
,ШlJ'lliJ}Jlltl 'Шfl фJ'НOtlЩ11iJ/JtlЛЫltl}l Ji"IJOl/.1f/.I)/ Lli/)11)1 •• }нz/1/h.' 'lШIL'йШI rlФI rlt:mvй··
нt1 гра:ж:дена 1zpe..t1ueii ЛреJ 11 денп111 Рисси йf.:кой Фе<)еjJац~ш
в (.IOЛQC11lll обра_ювтт.11 .J(I 200 1 год.
Энциююпедия для детей. Т 11. М:rтсмат\'ОСJ / Гл:~в. peri..
~6Н М . Д Аксё~-юв~l ; м.сrод. и отв (X'.n;. В. А l3оn<щи11. - М.: А.ванта+,
2003. -
6НН с.: ил.
ISBN 5-Ч-·Н>25-07 2-7 (т 1 1)
{:,BN 5-9 1613 -001 -8
Н '1'с)ме • Ма 1емати:~\<1• t't:рин •<:)нц111u1опс:дшJ щ1я детей• t:OJ\<::pжa-rcя
сведения 1н.1 с;1м.ым раз ным раздс11ам соuреме111 юй м;11·ема1ню1 - как
ш<..'Тючё 1-1111.1м в Шl(()J1 ь11ую про1·рамму. так и 13ыхо11.ящ1~ !\t з:~ сё р:~мки. ~~то
и спраnоч 1юе ПО('СJбие JVl fl lLПЮЛЫ·I ИIЮВ, и популя1:тая KH llГ:I JVlfl ЧTCfl llfJ_
которую отт1чJют полн()та с<щсржаню1идскту1111 ост 1,11~i1южсн1н1 . Ав
тnrы статей - RС/\)'lЦИс учёныс, СJnытн ыt: 1 ю11}·лир11 :1аторы и 11rх; 1 щд;1-
ватели. Я ркие и красочные: 1m11 юсrр:.1 11ии. схемы. rраф11ки пробуждают
ин·1уиц11ю и вообр:.tже 11 иt:. 1 1<.:стр:.~я мозаика щшмсроu, зад.1ч 11 формул
сю1ан ыв:.tется в единую к:1 рт111-1 у неликонеп11оi1 , с1тюй 1юй и 11еисчерпа
е.•юй ll:l )'KИ Матем'!тшсн.
УДК 087.5:51(031)
ББК 22.1я2
~Нз;щ·1·СJ 1 1,с кий 11е1 п·р "А n.шта+" • 1111JJЯето1 11 р:1 nообл .щ.1 1слсм н:1 CТ()fl щl'
го н11~.1111-1я Использом111 ·1с 11:щ:~11 ия 1111слом irn11 mof>nli его ч:1сти бс;1 r;1з
ретпе111ш ~ и·щатсл1,скоrо нснтр;:~ ,.Ав:нпа +"• мсчёт 0·1·нетственнuсть
R С{)()ТJ3СТС1"С\Ш С ДС:ЙСТRУIОЩНМ '! ;il<OHO/\a' l'f'Лl>Пl\0~1.
К ЧИТАТЕЛЮ
Чтu даж1 матема·1·нка людям' Заче,"1 её н:ч.rчать?
Когда она родИJ 1 ась и что явизюсь пр11чи1ю 1:-r
t:ё 1ю1 1-1икновения? Д3лайтt; гюrоАuрим обо
11сём этом.
Часто можно пrючесть, что математит<:а 1юз
пшшаnглубокойдревностииз практиче-
с к их потребностей людей. 110 поводу древ
ности математ~шн 11иicru спорить нс будет, а вот
о том, что же 11обудило тод<:>й с:ю заниматься,
сущестRуt~т и друl'Ос мнение. Согласно ему, ма
тематика , так жt как поэзия, живuш1сь , музык::~ ,
театр и вообще - 11скусство, б1,1 ла вызвана к
жизни д у х n в н ы м J1 потреfiностям11 чело
пека. его, быть может 11е до конца осознанным
ещё, стремлением 1< познанию и красоте.
В 11с-гории науки пр1111ято наз ывать первым
математиком Фалеса - гречес1юго h'J'ПЦа , пу
тешестве1шию.1 'И фшюсофа (он родился n VII в.
до 11. э.). Конечно. существуют более рашше
египетские н вавилонские псточrrики. содер
жаuще р<t::~нообразные <~рифметичс::скис и гео
"1етрич ес кнс снеденю1. но в них 1-н:"1 · даже
намЕка на доказатсльстна. Ф:Jлtсу же прнписы
АШОТ 11ервые матема1 · нч<.;с1:<11е т с о р е м ы.
Кстати, Фалес 1-1с б~.~л толысо ~ ч1.-tс1ъ1м ~ матема
тиком, 011 реша11 ~1 прикладные эадачи. Изме
рив тент, от е!'иnетской пирамид1)1 и тен 11 от
ш еста н нримснин свои теоремы о 1101~обиrr, он
ВЫЧ11СJIНЛ ИЫСU'lу 11ирамщ.1,ы . Так, по Л(Тен,щ.:.
родю1ась наша наука.
В 11режние времена , вnло1ъ до конца XlX сто
летия, Ntатематнкой занималио. немногие. Сей
час ей IЮ('RЯЩаЮ'!'ЖИЗ!Тl1) \ССЯТl<J.1,;] IЮ:1М()Жl-Ю, 11
сот н и тысяч людей. Одних 1щол'нош~яст nрн
кладпой аспект математики, других - её пнуг
решIЯЯ кра<:ота 11 гарМОilНЯ , а Тf)еТЬИХ nриnле
кает и то и другое.
Связь матРмПИКИ и кr<кnты nO-ttonnмy пrояв11л~сь в хх в"
щrдi! f\ыл11 открыть~ 11ес.Юычны~ м~ t\:MJ 1нческие обь~кты -
фрд ктал~,1 .
5
К читателю
Геометрия е<.ть поз нание всего суш1:~го.
Платон
Маrематика... выявляет порядок, симметрию и
011ре.t.еl\ённость, а это - важнейшl-'е виль~ r1рекрас
ноrо.
Аристотель
В огромном саду 1 еометрии каждый 11айдет букет
себе по вкусу.
Лавил Гильберт
Математик, который не есть отчасти поэт, не будет
11икогла подль111ным математиком.
Карл Вейерштрасс
Числа 11е управляют миром , 110 показывают , как
управляется мир.
Иоганн Вольфганг Гете
Вдохновение нужнп в геометрии, как и в поэзии.
Алехсанлр Сергеевич Пушкин
•·Красотй? К;шая может быn, t<расота в м::пе
мапшс? - недоумёшю с11рuс11т учс11111<, 11е пu
люби1:1шш'1 сщ(.· ::~тuт прсдмL01·. - Искусстr.ю
-
совсем лру1ое дело!" И ,цейе1·ви·.1·сл~,но, нспом
ннм шекслирояско1т> l'э млста, е1·п потрясен11е
и1·рой актёра, кuторый ~н А 1 .1мыпи~с 1 111оl1 (."r·рз
ст 1 1 так rюf(пял 11'УХ свО1'1 ло стюе1'i мечты". l I всё
из -:'lа чет? Из-:1а Ге 1<убы! Что ему Гекуба. что
011 Гекубе, чтоб о ней рыл:пъ?». Мы не удивля
емся, •по чслпnека заставляет nосхнщатися п
рыдатL волшебная с1rла 11с1<усства .
Но послу1 11аем рассказ Тtру1·ого чслоnе1<а, со
време111 шка llleкc1rнpa . об 11стор 1 1н с1юс1·0 от
крытия: «Восемь мссяцсJJ тому 11азад ПCJX:J(O
.\lной fiлt'снул псрныl1 луч <:1кvга, з;1 тр 1 1 месsщ:1
ующсл }1 /\C lll"11, 1l~llIOHCJ \. coиcc:vt IJl'/PUIIO я смог
увтщеть луче:iарт юе сот 11 \С". Я пох~1т11л золо-г1.1 е
сосу;1ы е 1 ·иптш 1, чтобы со:щать из 1111х хр<1м мо
е.м:у божеству вщ1.rш от 11ределов Errinтa ... Жрс-
61111 брошен . Я нншу оюю к11111)·. Прочтёто1 ли
она мои,чи соnрсме1шикам1111лт1 по·1·омством -
мне всё р~1нно - опа п~1 йдt'·1· своего ч11татеJШ .
PaJl:JC Госпо;1ь 1)01· нс ждал 1 11 ссtъ тысяч лет со
:J<:р1 щтеш1 С1:ю<:1·u ·1·1.юренюl? ~ . 1\то пишст это
восторжен ноl' 11ш·ж11111е' 11 с1·1·0 n po11 :io111лu?
П111uет нслию1l1 учё111>111, которFМ1 всю ж11·J111,
характери:ювал ссбн тш1ьк<1 одним слшюм -
,\1атем:1тнк: «Ma1l1ema1ikl1" Jol1a1111es Kcplc1- .;
-
«Ма темэ·1·r1к Иол11111 1<е11ж:р». :~rели11(е, пред
ставшее перед ш1м, - пе те:пралытые пrщж1ст
кн, а сама Rселе1шая. храпящан м11ожес11ю тайн .
И однэ иэ них 11 результате тнта11нческ11х уси
лиr1 Кеплера вдруг отr<рылэсь ему. Тс11срь 011а
изнестна всему культурному мнру как трсп1l1
:~:шо11 Ке11лсра· к11:щрат отношсш 1я 1rсрнодон
обраще11ия д11ух ш1:111ет ранен 1-.--у()у отношс НJ1я
; 1л 1 1н бш1 ы1111х пш 1 уоссл их орб1п. J\i!oж1ro с11ро
<.:итп, 11торя Гамлету: «Ч то e. -. - ry ор61 пы . чтобы так
1111копа1ъ:.-·>. 011ie1 1 1аходим у 11ру1·01·0 вст 1ко1·0
мысJ 111т~щ Алuбt:рта Э1'111111тсй11а: «Ощущенне
тайны - наиболее прекрасное 11з доступных
н;:~м переж1 mа~п1i1. l"l мешю это чунстnо стоит у
колыбели 11с'Гпmюrо нскусстnа 11 настоящс~"1
11аую1». lle H<.:t'JЧ /l.атю 11с11ытать это счасrъе. э1·от
1юстоrr 3r11тtJ1я .\111роздаrrня а страсть тяорца,
но 11х 11 ро11схож;(сн1к· то Жl.', 11·1·0 у актёра ,
ры1 (а1ощс1'0 о Гt:кубt:: нспос1·1 LЖиJ\10е с1ю 1'1с1'тю
чсловска - с1 ремж:н~1с к 1ю;~11~111ию ~1 1юсх11ще-
11иl' 1·jpмo111 1eli.
Н() матсмат1 11<:1 - ::J'J'O не тnJ11>1<0 1:1дохнове-
1 11 rе т1юр 1 юв 11 nосх11ще11не тех. к·1·0 спщ·оfiс11
оце1111 ·1 ь1\,\ ДОСТНЖСШ1Н. F.:f 1 1cтopll)I \[;IПOЛtlella
.
'
"_
-
Cuop!!'Vll:' ft11 J s1 мJП' 'Уlапн.~ 1 фоrм~1ruвJл.1с ь 11p11'Yl('f)1tu ·IOU (1(•· 1
ТО\i У к.НdЛ в rm'Лd\ r.~.1<111ея, Кеплера , (Юйrен(",l, 1IЫ<П()К.3 ,
Л1:nб11<ш.1. мл оры(• с tр1!'1или сь попнчь J<1кu ны д~>1А<t:f1и1111С!бt.•от'
rел А в 1846 г уже 6ла rnдdрЯ мнем,т1кЕ' fiыла nткrыта nл.1нt>т~
Н~111у11 , КО!Ор ую tllclЧdЛd ~bl Чlit.,ИЛll. d fl()T O \i об 11 <1ру>КИЛl l ilcl Гll'fk•
и Т(рамат1rчсскими событнями. 1lередт<о псрnо
открыватсшr опереж;u1и сnоё время и нс встре
чали rюнима11ш1 у совреме11н11кон. Так было с
открьп·исм в ХГХ 1:1. нсснклидо1юЛ 1·еомt:трии
-
од1111м из фун11.амснталы 1ых дос1нжег1и~l 11ауки,
которое стшю ос1 ю1юй 1v1я всей соврсмс1 n юй
физнки; вьщающ11йся русски11 уqё 1п)rй Николай
Иш111онич Лобачевский умер 11 е 11рнз 11а 1н1ым и
11еоценё111IЬL"1. Боязrн, быть пепо1шты:N1 остапо
вила rтеро nсли1<ого Г:.~.усса, который 11е рискнул
прс/\ать глас~ юсти свои ш::следо.ва11ия; гепналъ
ный нен1·ерский м:~тс.\1 l1°1 ·ик Янош Больяй 1ш
ш 11 ; ю1 рассунка от тнжёлых пережннан11й.
ТL'псрь nрI1шло нремн сказать о том, что же
дзла матсма· г r1к:~ ч1::1Ю1iечеству . Мно1·и<:' круп
не1~пш 1 е учё11 ы е (сренн них Жо:~еф Фур1.t: 11
Лll[JH Пуан~<аре) видели с.:ё гщ1ш1ую 3адачу 11
С'()f1.Сйст1ши обыгспепию :1а1<01 Юli 11р 1 ~роды . Га
шrлсю при11адлежат замечателы 1ы е слоRа: "вс
л11кая юш1·а 1 1рнроды наткана я:1ыком .\1ате
~1атиюr». Uдох11оnс:ш-1ы ."1 сторо11ни1<ом этой
к01ще11ц11и н1tilяется оли11 нз I<руnнейшнх ма-
Нщ"ол.Jи Ие.~но~;и •1
Лnna• t(:IUf кии
К читателю
· 1·емз·1·111<01i соnреме1 нюсти - Вл:щпмир Игорс
Rич Артюльд. Он даже как-то написал, что «,чз
тематика - часть физиюн.
С01~ремеппая м.~тсиатиl<а сформнровал:кь
прпмерно ·100 ле-1 тому наза;1 Rтру;\ах Г:.u1и11ся ,
Кеплера, Гюйгенса , Н1,ютuна, Jlсйб 11 и~1а , nд1 1нм
11з осно1111ых стимулов для которых было по
стичь ЗаКОНl>I f\RllЖCHl lH П.:Л. В тrуд::tХ ЭТИХ
уч ёных '11~\Тем:пнка 11фи:зн~<:а ка1< бы сливалис1,
rюедт ю. Сою:1 математпкн и 11ау1< о природе
припёс самые яркие плоды в начале ХХ n. Тогда
родилнсь 1еория от11ос1rrелыюсrн п t<n~штовая
меха1 шка.
Математичсt:кие кор~-ш 01с:цнал ы-ю~'1 тео
рии от110сительности вскрыл НЫ/\::ttuщийся
немецкий J\1 u·1·см;1 '111 к Гсрма11 Мш1ковскr·1i1 ,
уl'та1юнин11111й сё 1 ·лубоча 1!л 1 ую свя:~ь с гсо
мстрис i1 Лобачепского. Это стало тр11умфО.\1\
матсмати1си: чисто теоре1 · 11ческне построеIJия
мзтематик;:~ 1 1е~: 1 ст111 1те11ы ю 01<а:'lалпсь язьп\ом,
на 1<отором написана юrига Природы. Имена
Гаусса. Gольяя r1 Лобаченского произносятся
тепер1, кан: нмена героев. Квантован мсх;11111ка
базировалась 11а родившемсs1 н начаJ1е ХХ 1~ .
фушщиоштьном ана1шзt:, что стало ещё 011.ной
победой ма ·1'ематическо1~1 на ую 1 . R н:1111с нремн
м:1тем •1т11 ка 11 тсоретнческ:l}I физ11ка в1юнь пt:
режнн~1ют 11ermo)\ интенпrвно1·0 t:блнжtн11я.
О11на1<0 11р11ложе1 mн матем::1·1·111<1 1 11е- rнра 1 11-1 -
чиваются 11и1111) фн:ш1юй. С Л'VШ п" со премён
:?йлера п Лагранжа, мате\.1аn11\а служит ба:юй
л:ля тнтжсттсртrьrх паук. Все крупные тех1ш•1е
скне ,rщстижешш - от строительства зданий 11
мостоu до расl\репощс11ия атомной энсрпш,
сверхзвуковой авнацин н косм 1 NССТ<их 1ю.11ё
тов - были бы нснозможны бс:J м;:псмат11кн .
Гер\.\с1Н М1 IHM!6( ~111~ .
7
К читателю
8
.•.Внешний мир навязывает нам своими ре<1льными
фактами новые вопросы и открывает 11ам новые
области математического знания И в npouecce
включения этих 1ювых обласrей знания в uapcrвo
чистой мысли мы часто нахолим ответы на с.тарые
нере1J.Jt'нные проблемы и таким путем наилучшим
образом продвигаем вnер~лсrарыетеории . На этой
постоянно nовторяюwейся и сменяюшейся и гре
межлу мышt1ением и опытом, мне кажется, и осно
ваны те много•1исленные и поражаюшие аналогии
и та кажушаяся nредусrановленная гармония. ко
торые математик так часто обнаруживает в задс;~чах,
методах и понятиях различных областей зн ания .
Лавиd Гильберт
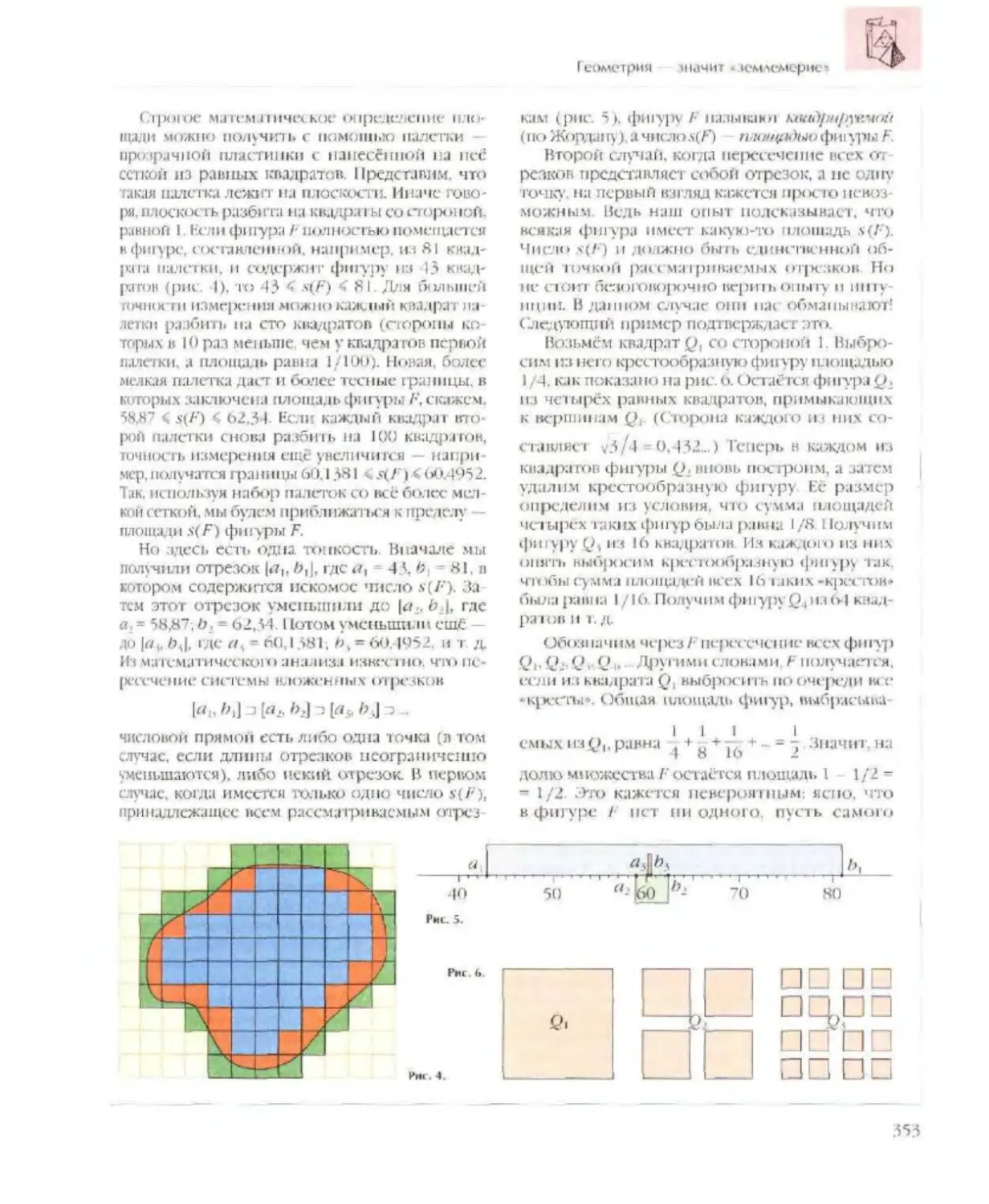
Стрм1~ша одного 1н nерв1.о1х учеб11иков по 1.1атема тике
Hd руге кпм яо~ык е - •Арифмеrи"и • /\ . Ф Маrн~шщrо 170 J r .
!1отре6 1 юс1ъ рсш::1ть эти rрандио:шые задачи
привела к созданию комш,ютерuв, и на наших
глазах лроисходит новш1 техническая н и1-1фор
мацнон 1 1ая революция Наше нремя - t~ериод
11ени!{а11н() 1'0 расцве-1·а математики Достwже
rтпя ХХ века 1ю меш, 111 ей ;\1ере спnост~н1имы с
результатами нсеr() преншествующеrо 11ернода
её раз1щтил - отФалесадо11::1чала хх: столетня.
А чнсло ещё не раскрытых тайн неисчерпаемо.
Людей, для котuрых знание матем;~тикн
явпяется прuфессиональ~ юй nотрсб11ос·1 ью, с
каждым годом С1jнОJштся нсё больше. Но нуж
но ли )1'./ IЛЪ м:псм;~тнке всех? Сомне111rя в не
обход11мостн 1 1 е тOJJ 1~кu ма1е м а1 1 1 ческого, 1 1и
И.. более ПJIJrOKO, 11ауч110ГО ОбраЗОНЭНИЯ UОО6-
Ще время от t1ремени к~.сска ~зыn~нотся н разно -
•.. Я преЖде всего хочу говорить об истине на.уч
ной; но вместе с тем я хочу говорить и об истине
моральной, no отношенVlю к которой то, 1.\10
зовётся сnравелливостью, есть только один из
видов ... я не могу отделять их, и те, которые любят
олну, не могут не любить другую. Лля того чтобы
найти од11у, так же как и лля того, чтобы найти
другую, нужно постаратьо1 полностью освоболить
душу от r1релубежления и присrрастия. нужно ло
СТ\1\r11уть абсолютной истинности. Эти оба рода 1-1с
ти~1ы, однажлы открытые, nриволят нас в олинако
вое восхишение; и та и другая, лишь только их
усмотре/\и, сиs:~ют одним и тем же светом, так что
нужно или вилеть их, или закрыть глаза. 1Нако1 reu,
обе они и привлек ают нас, и уско/\ьзают от на с;
они никогла не фиксирова11ы жестко : К<>rда кто
~111будь подумает, •1то достиг ~1х, - сейчас же уви
дит, что еше нужно илти, и тот, кто стремится по
стичь их, осуЖАён никогда не знать п окоя.
Анри Пуанкаре
Математика играет весь.\i1а сушествен н ую роль в
формировании нашего духовного облика. Занятие
математикой - полобно мифотворчеству. литера
туре или музыке - :по Од1-1а ю H.lt.tбoлce nрис.уwих
человеку областей его творческой деятел.ьности, в
которой проявляется его человеческая суw11ость,
стремление к интеллектуальной сфере жи":Jни, явля
юшейся олн им из проявлений мировой гармо1111и.
Герман Вейль
об раз 11ых дис1сусонхх как в России. так и за её
rrреf(елами. При этом считаете}\. что обнзателп-
1-гым для всех должно быть 1 1ишь гуманитарное
образование. Один известный журналист, на
прнмср, как-то сказал: «Каким только мусором
нс забивали нам 1 ·о;юf}у учителя! Что, какая
часть того, чем мучюш нас учнт<.:ля и мучают
теnер1, наших детей , с1·одилась нам в жизнн ,
для /~ела, Д.НЯ JIЮбви?". Нетру;~но ло1·ал:.11ъся, ЧТ()
11од ~м учи1тлямн ~ 0 11 подразумевVJ прежде
nсего учитепе~I математики .
Но нет отдельной rуманитар1юй ку11мур1.1 .
Есть общечеловеческая кулы·ура, и с,rща ли не
основ11ым звеном в ней являются достижен ия
пауки. II свозмож1 ю рассматриnать историю
человечества только как историю царей и пол
ко ною tев, войн, рсволюцю1 и реформ , Ht' зuт
раrивзя истории Культуры , нстuрнп Илей ,
высших взлётов Разума.
H:i вопрuс «ддя че1·0 11 зучают математику?•
замечателы ю от ветил ещё в хпr н. английский
философ и естествоиспытатель Роджер Бэкnн:
.-тот, кто не знает математики , не может ус~пать
никакой другой науки и 71аже не может обнару
жип, с1юсго невежества».
Отметим и ещt: одну, особую роль мзтсма
тики как дисцю ~; 1 ин ы, развивающей и 1rтсллск
'1уал hн ые и творчесю.1е способности человека.
Лучшего средства дня цх совершенстнона н ия
пока не найдено.
к с1итателю
Математический язык удивитель но хоро шо приспо
соблен АЛЯ формулировки ф изи ческих законов.
Это чудесный дар, который мы не п он имаем и ко
торого не зас.'\уживаем. Нам остается ли шь благо
дарить за него судьбу и надеяться, что и в своих
будуших исследованиях мы сможем по-прежнему
пользоваться им. Мы думаем, что сфера его при
менимости (хорошо это или плохо) будет неп рерыв
но возрастать, при нося нам не только радость, 1 ю
и новые rолоrюлом ные проблемы .. .
. ..Вел и кий математи к rюлностью владеет всем арсе
налом лоп устнмых приёмов мышления и, действуя
подчас весьма рискован но, балансирует на самой
грани допустимого. Уже одно то, с1то его безрас
судсrво не завело его в пучину противореч ий, само
по себе чудо. Трудно поверить, что дарви новский
проuесс естесrвешюго отбора довел 1-1 аше мышле
н и е до такой степен и совершенсrва , которой о но,
суля no всему, обладает .
Юджин Вигнер,
лауреат Нобелевско/1 премии по физике
Этот том <;ЭJIЦJ·1 клоnсдии для детей., призв:u 1
внести вас в таинственный и прекрасный мир
математики. Хотим 11ожелать нашим ч.итате
;rям, чтобы они научились н е только нзвлекать
11()} 1ь:зу из заннти й математикой, но 11 носхн
щаться сё красотой.
История математики
г---
СТАРИННЫЕ СИСТЕМЫ ЗАПИСИ ЧИСЕЛ
12
Памят1, чеповечестна не сохранила. недо1 1есла
до ш~с ИJ\l(Я изобретателя 1<олеса или гончар
ного крута. Это и нсуд11вителыто: более J О тыс.
лет прошло с тех пор. ю1к .rrтодн вссрьёз завя
JIИсь землелслием, скотоводством и производ
ством простейших товаров. Назвать же имя
1·енил, нпсрныс з~щавше1·об1 вопросом "скол~
ко7 •>, тем более неnозможнu.
В каменном веке, коrда люди собнра11и
плоды' ЛОНI IJJИ рыбу и охотились [ 1а жи ВО'П lblX,
потреб~ юсть в счёте 1ю~i1 нrкла так же естествен
но, ю1к н потребность в добьrnаrши оr11я. Об
этом свилстельствуют находки археологов на
стояrшах первобытных людей. 1-Jапример, n
19:)7 r. в Вестонице (Моравия) на У~есте одной
нз т:н<Их стоянок ш1 йден<1. волчы1 кость с 55
глубокими зарубками . Позже в других мсст~L'I.
учёные 11ахо11.илн стоJlь же древние к:~ме1-111ые
1 1 редметы сточками и чёрточками~ с 1 ·рупплро
ванr1ымп по три 1 ~ли по 1rя·1ъ. Т<tкая система
записи чнсе.11 называете>~ еди1-tuчиой, та 1< как
любое чнсло в 1rеИ образуется путём повторе
' 1ия одного з1 1 ака, симнолизирующего е;"(ини
цу. Груш 1 ировкн и вспомогательные зна,1ки
нспользуrо·тся лишь для облеrче 1 1ия восприя
тия больших чисС'л.
Едиюrч.ная система с ч исления пср1юбыт
l1ЫХ лю11,ей, рнсоватuнх палочки на стсн;1х
neщcpht нли дела1:нш1х зарубкн н::~ костях жн-
1ют11ых н нстк<lх деревьев, rrc :забыта и в наш.и
/\Н.И. К::~ к узнать, на каком курсе учнтсн курсант
военнш ·о училища? Сосч11тайте, сколько по
лосок 11аш1 1то на рукаве ero му 1 тл.ира. О l{ОЛИ
честве самопётоu протrшника, сбитых асом n
во:1дуuшых боях, говорит число звё:щочек, па
рнсованных на фюзеляже его самолёта.
llоmтучпо сч11тать предметы удобно то1да,
ко 1 ·ла их не очень м1101·0. Псресчитынать же
такнм образом бoJJьULиe соно/\упности с~<учно
и утомнп:J1ьнu, Lюэтому 1ю:~никла иде}I объ
t;-1,иня1ъ <::диницы н группы. Появился счёт пя
тёрками, дес}lтками, двадщ.1тками - по коли
чесrву nальцеu рук н но1· ~cчei·ofIOJ(:H.
ИЕРОГЛИФИ Ч ЕСКАЯ СИСТЕМА
ЛРЕВНИХ ЕГИПТЯН
Около .3 - 2,5 тыс. лет до 1ю1юi1 эры ;~ревн11с
е1·и11тяне 11р11думали свою числону10 систсму. В
ней ключевые числа: 1, 10, 100 и т. д. - 11зобра
жалис1, спе1~иальными :1нач 1<а ми - 11ерогm·1-
ф:н.ш. Еги11тяне nысеюшн их щ1 сте1 tах но1ре
балы 1ых ~<амер, m1 салнтросrнико13ым пером 1 1 а
с 1ш·1·ках 1raшrpyca.
Д;ш затки чнсел онн утютребюти следую
щ:ие иероrл 11ф 1,1 :
rr1~11)._
\!' :О
1()
Вес остальные числ:.~ состанлял 11 с ь и з этнх ю1ю
чсuых при помrнц11 опеrщш1 сложе1шя. IIа
пrнмер, :запис1 .
расшифровьшалась так: две тыся'-IН. трн сотни,
два деснтка 11 L11 ссть единит~.
l.3елищ1н<~ числа, занис;ш1-ю.1·0ни<:'рогт1ф11-
ческой системе . нс :зависит от ·1·01·0, fl каком
норя/11<е расrтоложены состан;тнющне с1·п :1на
ю1. Д~1же если зап 11сать их с11р:.1к<1 11алс110, один
под друпrм ю11 1 вперемешку - число от этоr 'u
не н:..-1 ."1ен11тся.
В рез~·льi"ате упро 1 цешнr и стнлизаций от
пероrлифов поз)l.нее щювэошт1 условные зна
ки, облегчающие письмо от рука. Они легли 13
ocrroвy так пазьmаемш·о 11ератичс<.:кого письма
(от греч. « ИСратш<ОС? - •·сnяще11ны1·н). Эту с 1 1-
стему :..-iaпиCJI ч11сел моЖJ-ю uбt 1ар)')1шть в более
по3дн. 1tх с1 ·1шетскнх п~1 пнрусах.
Уцслелн два м:1тсматнческих папируса, 11ас
крывающис тайну древю..:египстского счёта.
Один И3 11их 11азва11 <- Г1а11 1,1русом Pai1t1/1,a~, 11py-
rm"i - ~москопским» (1 ю,1tpon1 ice ()6 этим 1 ·t>1ю
ри.·1·ся н ста·1ъе ~древшui Ег~mе'Т'»).
РИ МСКИЕ UИФРЫ
Среди м н ожества нероrлиф11чесю 1х систем
сч11с11е 1 пш, которые сущестrюnали n раз11ыс
време 1 1а у разных пародов, только одна 1rсполь
зуется до пrх nor. Её цифры знакомы всем,
хотя им уже окОJю :г. '5 тысячедетий. Эти цифры
всrреч:~ются ш1 циферблатах часов, фронтонах
е1·ари1:1ных 11 современных зданий, Ш!NtяТ-
Старинные системы записи чисел
~
EU.l(!J
н 11 ках, е1гани1цх книг. Ну IOJllCYHO же, rсч1.
идёт о р1 IMCKOIJ CI ICl'CMC C'-lHCJleпviя.
Нелr.зя ска:3ать, ч~ ·о лремя совсем не косну
лось of1111-11<a римских цифр. Еслн б ы жлтель
Древнс::го Рима захотел прочитать число, обо
значающее дату открытия ста1щ 1 щ метро «Рим
с 1<ан·> н Москве, то 011 оказался 6hl n нснмонср
ном затруднении. Причина R том, Ч'IО тол1,ко
зн аки l, У , Х с течением нрсмепи не претерпе
ли какнх-либо изменений . Друп 1 е же цr1фры в
дрt 1 11 юсти 1 1:юбраж;u111с1, н1 ia че.
Учёныс 11 rедnола1·ают, что пер1ю 11 ачwыю
иерог11иф для числа 1()() имел н1 1л пучка из
трёх чёрточек наnо!(обие русской б),СВЫ Ж а
для числа 50 - шщ верхней ПОЛО!ШIIЮI ЭТОЙ
буквы: '\V. 13 далыrсйшем nослсд11 ю'1 11ерогm1ф
nостепеш ю трапсформировался n з1 rак L: '\V -7
-4 \J.J -7
.. .L
--) L. А <щсло 100 ст:.1щ1 060::1нач.1·1ъ
буююй С (от начальн ой букны шLтинскu1·u
оюн;1 сепtшn - <.с_~го" ).
Симиол ы μ,;ш ч1ке1 1 500 1·1 1OOU тdкжс про
шт 1;v1и · 1 ·сJ1 ьнvю энолюц11ю. В 1 1ачаж: для ч 1 ru1<1
1ООО 11рименя~п 1сь значю 1 Ф, <О, 0), -h . На1rр11мср ,
1 1 а титулuном листе ю-1ип1«Рассужде1 1 11е оме
ТО!\С» нзвестrrого фра11цузскоrо математика и
философа Рене ДСJ\арта , издаи ной в 16.17 r"
указана дата ФРсхххv 1 1. il этой загшси наряду с
уже известными п:.tм цифрам 11 l, V, Х. С исподь
зонаны старинные римскне иероглифы. Ф =
= l ООО, Р = 500. 1IришсдJНнt'1 1 м на сме н у ::111ак~1
М и О нро11:ю 1 шш uт нач:шьньrл. букн л::~т1 1н
скнх слон 111i1Je - .;·1·ыся •1:н и der1нmille
-
<-ПО
лон 1 11-1:~ ты сячи~, <· ПЯ"I ьсот».
Древниt: римюr 1 1 t: ,\1or·m1 ныр:1:~1пъ од11 1 1м
знаком 11 ч11сла болыJJе тыотчи. Та!\, ллл числа
1О ООО omf приме11ящ1 :тачок r.4-\ а для ч11сла
l 00 0()0 - rll~ . Крайrше дужки в последнем
иеро1·лнфе со nремснем сомкнулись в «арку»
@, с..-1·аншую прообразом спсци;и1ьной рамоч
ки: П. Цифра, 1 юмсщёш 1 :ш 1:1 такую рамuчку,
ум 1 южаласh 11:1 НЮ UUO. Заш1съ 1Х1, т;~ю1м обра
:юм, пpt'/J.C'I :1нлнла число 1 ООО ООО.
В СрL'д11ис века эта тр:щиция лолучил;з свое
образное продолже11 11с Для то1·0 чтобы указат1"
что чJ 1 сло следует ум11ожа1ъ 11а 1ООО, сверл}' над
11 им сганш111 чёрточку. На 1 1р11 мер, за111к 1, iVv1
обозначала число 4 1()()() + 6 = 4006.
К;щ ЧJ1r.~ть римские ц11фры? О111ю из правил
записи римских чисел гласит: «Если боль
шая цифра стоит перед ;\1С r rьшсй. то ош 1 скла
дьш~1ются, CCJI H Жt MCl!Ь Ш :UI C'J 'OllT перед бOJlh
шtй (в этом случае ме1.-1ьшан ц11фра нс мuжет
[_)
l.;.f
История м.:11 сматики
IJOl:!'l'()J1ЯTl;(.'fl), Т() MC.:lfbltlaн 13ЫЧI!Тается И:'! 60111,-
WC.:lt» кпrнмсру,Vll= '> +l+1=7;lX=1о -1=
= t) 1lот.;,~у н сь э·111м нранююм. можно рассч11 -
1 ·а 1ъ. н 1.:1 ком 1оду u·1·щ)ыщ1с1> ст,шция метр о
"r 11жl\a)! ·.>' МСМХ С\1 = 1()()\) + ( 1()()() - 100) +
+(1()()- 1о)+') =199'>.
R 11:111111 11 1111 любую 1 1::1 рr1м сю 1л цифр 3<tнрt:
щаетсн 1:1111 1 lъ1 н:пъ в 0;11юм ч11сле бо.:~ес.: трс:.'х
р.1 з ПOi\f)HJ!. R с11я.i11 с э 111 м выраженш1 \.' Ll l l,
ХХХХ 11 ·1 п сч 11 тзютсн некорре1<111Ы .\.1J1 Одна
ко дрс11111 н: р11мляr rc о nодоб1 юм оrран 1 1 че-111 11 1
н11чс.:1'0 11с nc;1a. 111 11 чпс;ю 199'5 скорее всего
:за11 1 ка.t111 бы так .\Ш CCCCLX..XXXV.
l 'uлпкu что .\IЫ столю 1у:шс ь с любоnыт11ь1:11
фl·но,н:11оч 11 •·общl·ствс» рнмсюrх чпссл. раз-
рс.· 11111н цифрач 1шр111 1 чикам прн ~сборке-• нu-
1.l hLЛ ч11 сl"1 нс тол 1.ко складыnатъс1L, 110 11 выч 1 1 -
та·1 hCH, мы 'l'C .:\\ С:!МЫ~\ Jl lllШ L'lli р11мсы1е ЧJIСЛЭ
<>ННО/'() l l:i 11ажн1,1'\ \\,l'l'C\1,ITl l'I CCКIIX СВО J)СТН -
е, 11 1 11<.-11 1с.· 11н ос.-111 1 1рс.:1(сгзнлс1111я Что теперь ~tе
шает, 11 з1 1р11,1 ср. ~:11 11 кt1т 1, да·1у отк рытня <.-га11 -
1~1-rи м с-1 ро • Р11чска.и» как /'V1Y~1, 11т1 как \11)\'[),
111111 ещЕ11сr 1юлы.;11м 1 r ,"(ру 1'11\111 спосо6а~111 ;.
Ес111 1 11ро<1н;1л 11 з 11ровз т1, м1южество ст:~
ршшых 1t CO ll\)tMC I П llo!X 11адп11се(t \)ll\\CKl\~111
1~'1фраr.ш, 1о можt ю v6сд1111,ся, что авторы, cт::i
p:t't'<.:JI 1 . 1 10СК(),\1П()!101141 КШI I C этн цнфры в ЧI кла.
11р11 ; ~с рж1 1наm кh к:1ю 1 х-то т 1 егт1 спых ттр;~т1л .
Н о с.:д 111 lhl X 11 1 1t"J'1<11x 11р11нц11п ов :;1;im1c11 р11м
сю1х ЧJtl't:J 1 ; ~о с 11х 1юr т:ж 11 нt.: выработаrю.
Су щес·1· 11у11 >· 1 1111111 п 1111 тсрссныt 11ре;(1южен11я
Тш<, сопрсмс-11 111.111 :1~1 cpr11<a11 cк 11 r'1 учё ный Ст 11 -
nе11 Шн а р11ма11 11рсJ ~Л~11·ает Междуна rо;\ 11ыl1
ста 1 щарт р11м(ю1х ч11сел (ISRN - T111em:.1Lioпal
Stan<.tart J{o 111an NL1111 c r 41ls), в ocrro ne 1.;оторо 1 ·u
ДUJIЖC.: 11 ЛСЖ:.11Ъ СIЮД H~J спец11альпо ПO,'l,Oopa11 -
l lhlX 11\1 IJJ<:CTll ПpJ11ТIJI
l:.tlll l в 1.1 ;>..OTllТ{.' :J< lfllll'ЫH.l 'l'b р11мсю1е 'ШCJia
··~·К, Ч 'I о()ы он 11 1ю:ш< к 1hIO COUTl.!CTCTIIOB:.tЛ ll
11ока с.:щс.: н с.: )~1·нс.:рждt 1 11ю~1 у мсжду11аrод1юму
CT:ll 1/~.1р1~, '1'0 11 '- ) ·10\1 l l0\10ЖC' I llpl IВCДCllJl:IЯ
:~,1~с1, ~;1бт 111:1.
Ol>U~l l.\Ч.Ш IНЕ ЧПСЕЛ
Pl LЧСЮ 1~11 1 Цl IФРЛ:'- IИ
1 •д111uщы / ~С'СЯ'I IOI
1
1
1() х
211
2() 'СХ
,) 111
ю ххх
4IV
1()
XI.
')\
')() L
() YI
()() 1.Х
7 \111
70 LXX
н \.'111 fIO r.xx:x
9lX
~ю хе
COTlll f
Тысяч1 1
100с1000м
2()() се 2()()() 1Y\ l\I
500 ссс ~()()() ммм
!()() СО
' )(j() L)
()()() Т1С
7UO JJCC
R<IO ПС:СС
1)()() см 1
()на 11() i!IOJIЖ"I u6o:m;IЧll'I h 1 юбuс Ч11С!IО от 1
/\О ~<)<)() С11ач.1. 1:1 .1.1111111111 ic ч 11 ию ка к uб1>1 'НЮ.
в ;:t~OllllЧI IOJ I C lll ll'\ll' . ~а1 с:ч
:~:1я 1~11фр l 10-
HЩll.X н paJpя, t.1\: 1ЫL>IЧ, lO'lt"ll. 1 !С'lЯТКОН IJ l":t11-
llJIЦ, по таолr щt· 11щ1'1с:рптс соо 1 нетсгнующу10
кодоn)1О 1р\•1111у. Н.1пр1шеr>. вот 1.;:щ fiy:te-1 вы-
1шщt1'1, ч11с:ю ~i)t)<) 1'1J\l.\KMXC:lX.
О ЧЁМ МОГУТ РАССКАЗАТЬ
ЧИСЛИТЕЛЬНЫЕ
Числительные - слова, обозначаюшис количествu
или порядок предметов при счете, - появились в
те 11е за памяп1ы е времена, когда числам на•1али
давать назв ани я. Прислушайтесь к числительным
русского языка - они могут расска1а1 ь о себе мно
го интересного .
По-вилимuму, число 4 когда -то игра ло осuбую
роль . Спе1Jиалисты полdГают, что в глубокой лрРвно
сти 01 ю служило своеобразн ым рубежом, отделяюшим
числа, у которых уже имелись собствен~1ые на"Jв<111ия
(олин, лва, три, четыре), от безликого и безымя~нюго
м1южества чисел, скрывавш11хся пол понятием «м~ю-
lic1111 же гrонадоб11·1-01 :1:mисатr. число в ript: -
/\t:лax MИЛJll!O l l<I, '1'0 ДJ I Я R l .ЩСЛСНИЯ ЗН<JК()ВОЙ
rруппы тыснч можно иоспольаовап.ся 1 1ад
счюч1ю й чёрточкой или же пометит~, группу
тысяч маленькой подстрочной буквоИ т , rra -
11pн:viep, 273 847 = CCLXXlll1111JCCCXl.VL1 (наrю
мним, что т - нерван буква л:п ш 1ско1·0 CJIORa
11ullt: - <- тыаrча" ). Так тuжt: nрш-1ято былu запи
сыва 1ь римские:: числа fl сгарш-rу.
ЛРУГИЕ ИЕРОГЛИФИЧЕС КИЕ
СИСТЕМЫ
Кроме спrпстскоii и rшмс1сой к пероглифиче:
скпм системам чисел опюсятся фш шкийская,
nальм11рс 1<ая, критская, сиршlск:u~, 1 ·рсчесю1я
:tтпIЧсская, шш Герuц и а н uна (нме1111( 1 нз сооб
щешш J'P:.!MM;l'1 '11Ka l"<::rюд11ан;J, ЖllIOllC l'O IIO Ll -
ПL .в1:1.• залаююt:нро11еt1скнс ш:тuр11ки к1н~рныс
узнаш 1 о её сущестиок;u;ии). Известны также
с·1 арnк~па liская , rт:1 ро111 щ11 ЙС'I<ая, ~щтекска>J
r1срuглифиче:с1<11е с~1с 1 е,"1ы. В них, как и в е1 н -
Старинныi:' <ист~мы {,·1 ПИ( 11 ч1кt>л
ГО•. Вероятно, у наших дам•ких предков «мно1 о» обо
знач ало любое кпличество больше чет1>1рёх. Посмот
рите, какие окончания у сущеспsительных в сочета
нии с лрев11сйшими чиt.лительными: две коровы, три
коровы, четыр!:' кopntJы . Но уже начиная с пяти и далее
сушествителы1ы е меняют окончания: пять коров,
шесть коров.
Особняком в ряду числит/i'лhных rго ит и «сорок » .
Оно явнп не похоже на слова, обозначаюшие назва
ния десятков: «двалuать•, "тридuать•, " пятьдесят•. По
всей ВИдИl\1\ОСПI, слово !<СО РОК» дошло ло l ldC как ПJ
MflТb о бытовавшей в стар ину системе счисления с
ос1 юв;шиС'м 40. Теперь о ней 11апоми11ает лишь рус
ское устаревшее числи тельн ое «сорок сороков•: со
рок сороков uерквей, с,орок со1.юков Вt"яких небылиu...
11етс1юй 11 p11мCI<(Jf1 снстем:1х, 111ю1~ятся ключе
вые числа, для обозначеr~ия 1юторых прпме
rтяrотся спецшты1ыс исро 1 ·л11фы. llce О<.J.аль
ные числа обра:~уются приттисыnа1шем с той
ИЛ ! ! ннuй ("f'O/)Uflbl КЛIОЧС.ЕЮl'О ЧIKJ!:I друп1х
ю 1 ючсв1.1х ч1 1с1:11 , нозможнu t' нскотuрым11 по
вторе111tям11
Jlюnопытнu ОТМСТJПЪ, что у MIЮГIIX наро
доnдпя C)003 1IaЧt:IJllЯ ЧllCJ1:1 1 Пр 1 1J\1СНЯЛСЯ OДIIH
11тот же с11м1юл - вертикальн:нr чёрточка. Это
ClMOt /~ре 1111 ее '"1И('JIO в 11CJ пр11 1 1 ЧCJIO llC'ЧCC'l li::I.
()1ю 1юз1 11 1юю 1 1 з простоl1 ч ср'11,1 11а земле, 11з
~1арубю1 на дереве илн тюс'п1.
АЛФАВИТНЫЕ СИСТЕМ Ы
1l арщ~у с 1н:ро1 J 111tj:шчсскнм11 н ;~рt:ш юст1 1 ш1 1 -
роко пр11мс11ял1къ <:11сн:мh1, 1:1 юнорых ч11 01 а
н:юGражаткъ бую1ам11 :1лф;ншт~1 . Имt:111 ю т;1-
кой быпа 1 · речес1<ая алф~1ннтна11 нум~рац1 1 я,
nrтучттmая название 1юн11чсской Ола смt:
шша аттическую систему в IП в. ~о 11 э. в~1есте
1')
1(1
Ис-rори~ матеман1ки
с хрие1·1 r<i нст1юм 1·1 т 1 с1,меrнюстыо эта нуме
рацю1 пришла к славюrам - сначала к южным,
а потом и 1( rЮСТ()ЧНЫМ .
Ниже 1 1рт.ше!(ены изображения 27 бую~ сла
uю1скоrо алфавита с их число~ыми зн3чения
ми. ,Dщ1 обозначення чисел н~щ буквами сверху
стаRr 1лся специаль11ый значок ...
-
титло. (Сам
алф~1вJ1т здесь лредставлеп нс 1ют-юстью, 1 1 а
пример, отсутстuуют буква Б - «бую1" 11 неко
торые другие .)
Едиrrицы
Десятки
Сот1 rи
...
r
~
1G\
10[
!00 р
"
...
f,
2G
20к
200
3f
.)О
..
л
.)00 f
д
•'
"
4
40 Л\.
400 у
в
.-
5
50н
500 ф
..
~
6$
60а
600 х
7j
70"
70() w
о
вй
80 ri
800 w
9 .$.
90
...
900 ft
ч
С помощыо этой таблицы можно ле1·ко за
mкатьлюбuс Цt'JIOe число 0·1· 1до999 включи
тслыю , например:
н~ Ы'rИ а
'5 '5
.288
уЧй
49R
Числа 100(), 200() и т. д. наши пре,~ки заnи
сынали теми же буквами, что 1, 2, "" но слена
1шизу с1·авнл11 опознавательный з11<.ш тысяч:
). = 1ООО, "G == 2000, ". ·j'- =9000.
ДесятJ<И тысяч т;u(ЖС отмеч:~т1сь первыми бук
вами алфав11та, но уже без т11тл:.1, 11 букnы обtю
диJшсь кружком:
@=1О00(),@ =20ООО,." @ =9()ООО.
Сотни 1ысяч кюбражались 1 юхо.жим обр~1 зо1v1,
но кружок сюrадыва1 1 и из точек
А= lUOООО, 6 =200ООО,." .О· =900ООО
Наконец, ,"1ишп1uны отмеч.а.J шс 1~ кр}?Кочком ~1э
чср п JЧt:h.
{А}= 10()0()00,{с) =2 ООО ООО, ."
''•""
f /11
{~;~ = С) ()()() ()()(),
Чнсл:-1, которые обuзн;.rч~111сh букnамл в кру
жочках, точках н чёрточках, 11мст1 <.'11<.:циат.-
111,1~ 11<431\:.tl H·LЯ:
@ - ~тьм~1,>, А
-
«ЛС 1'нО11о); (i•.'J - «JТеодр"
~"...
Кзк бvдст Вh11·лн;~ст1, 'П 1 сло 4 210 ООО n ста
рославя~ско1"1 нумсрац~ ш? Поскольку 4 l О" =
,,",,,
~
,.\
®
""~.А},2· 1О = Е,1 1О = А.следовательно,
421оouo- это~I!.в@.
'• •·'
Олнсаrшая выше нумсрацин rюлучюш на-
зnан11е 'малое 'ШСЛО?. В 1н~й uтчётливu 11росту·
11аю·1· зачатки lЮЗШ ~HOHL-Юi"L С И СТt'МЫ , посколь
ку ДШI ОбО::!ЮIЧСН l lЯ еДИНIЩ f1aЗllЬIX [)<!Зр}:[ДОА
приме.1:1нютс51 одни и те же сим1юJ1 ы.
13 одной 1rз сла вянских ру1<011Т1Сетl XYlI в.
упоминается и другая с11с1 ем2 - «болъшое
ЧИСЛО». илн «IJeJHIKOe ЧИСЛО» . Наэваrшя боль
ш их ч rкt:..rr 11 ней строятся на основе любоnыт·
I IOI'() nриёма - «ВОЗЬМИ С'ГОJ!ЬКО по СТОЛЬКО».
весь м а uерояпю ::шrмспюн.:1111юrо у Архимеда
Первоначально число l O'' объявлsк~тся тмюli .
затем ·1 ьма тем, т. е. J U 1 ~, пшNчает наз13а1111е ле
г1ю11: лепюп пегионов, ·г. е. ·1OJ4, получает н:.~-
®
-''i -
...
~
l\
"l\ -
-
-
.
.
...
~
", .,,"
Т1,м.1
Ле{'ио11
Ле"дf1
nщхш
Ко:ю11а
10"
101~
10~1
j()IH
J о4')
-
'Т
з\
'
'
""
<1щ ЕЖf сч11т11t1 с"' доrтJ ·гыс...члн 11 ~;ош7'
npon.&~· ~CIHl)\J: 'l;lr.r~ ЦЫФ~j"l1\\ll •
"
..........
'
&TOf/,111 _?Gf4 'IHf~"Л •
~
•1
10
100
100-О
10.РОО
100000
JOCOOOO
JOOQQ!)OO
toaaooooo
) OQ0.,00-0 .000
!
... .
"~ C'l'O Tl,;CA\Lll?: •
J.
,
,
"•I TLl<A\ЧJW ·n .1CA .ljlrn
~ ·n,;r...цn; т1.:САЦl!Н
" '• ("fO т1,;c-o.t1r1. rbl<R>ЦJfll•
kJ
t
,
'
тъ~r....цю. 1~. 1с.щ~ т~t
C"'lf.101 • н,111 ТЛ\1/ •
тprri11 ~"fAJ" ·
'
'Х,
\"''
'
?С
К\\1\Жl\!,1 '1\IC .rь ксr... €VfWt\!.t fU.\\CKH •
Infl(rvуVI\'IIvшJXх
"&lд€s3 11.о.1
А+
Х{
,J)
Сrр<1 1-11ш.1
1н pyccкuru
уч1:'!1ника
.1рифмf'1ики
1699 r
знанислепдр; а лсuдр J1eo;~po1:J, т. е. 1 0·1н, имену
t"Тся вup01-tu.м. Вороны обозначались букваJ"ш.
обрамлён 1 тыми кружочком 11з крестиков: 1:~:·.
Следующий рубеж, 1() 1
'
1
• назып:шся 11;щюдий .
На ней ~сrютыкаJ111сь», и счёт окончательно пре
рывался ~ ~...и более cero несrь '-lеловеческому
уму разумевати». Колода обозначалась так: Д.
Похожие снстеJ.11ы счислснщ1, в которых
букnы алфавита по совместительству юодра
батьшашr» цифрами , использок:шись в <..~1·ари
ну у :~рабов, еврее.в, гrуэин, армян .
С'..лавянская нумерация просущестковала /\0
конца XVll столеп~я. rюка :вм<.:сте с реформа
i\Н1 Петра Т в Россию из Европы нt пришла по
з и1 ~ионная лесятичная система счислсJ-1ин, ко
торой мы поm,зуемся и сейчас.
ШЕСТИЛЕСЯТЕРИЧНАЯ
(ВАВИЛОНСКАЯ) СИСТЕМА
Записи чисел в алфавитной нумс:рацни полу
ч:\ются более короткими, чем в иероглифиче
ской . Но и у той и у другой сист·tмы представ
леr tия чисе.~1 есrь один весьма сущесгве111 1 ый
неrюс-1·ато1<: арифмtтические дейстL1ия над та
кими ч11с!lами - занятие кесьма трудоёмкое.
Этого неудобства нет у no3uцuo1mыx систем.
Старинные системы записи чисел
Идея nрипи:сьrnать цифрам разные вСJшч1111ы в
~ависи:мости от того, какую поз1щию они за
нимают к ~аписи ч11сла . впервые поя.вилась в
Ш ты ся челетии ;ю 11. э н Месопотамни (Между
речье) у дрснне 1 ·0 талантли1юго наро~~1 - шуме
ров. От 1 1их она 11ерешла к наr~илонянам - 110-
вым хозяенам Мсж;..1,уречья, rючсму и 1юu 1 ла в
ИСТ(}f)ИЮ как навилонска)f система счисления .
До t1зс дошли сотни тыся.ч обожжёпных
глиняных таб.rrич-ек с письме11ами древних
вавило1 тн. Простейшими цифрами в их систе
ме служили два знака : вертикальный K.flИLJ Т для
обозначения 1 11 rорнзо11тальны 11 клин ( - ДJlЯ.
l О. LJ ис; 1 а от 1 до '59 :з~111 нсы.н:urись с помощью
этих ;~вух знаков, как н обыч~-юй иеро1'.l 1ифн
ческой си стеме ·
rr=2,<:т = 11,<<< =30.
Число 60 спона обозначалось тем же знач
ком. '-lто и 1, т е. т . Таким же образом записы
вались и все другие стеле1:и 60: :S6<IO = 60!,
216 О()()=6U~и т.д.
На этих примерах видно, как R вавилонской
системе прелстанляли раJлич 1 1ыс числ::~ :
т<: п
<«ТП«
72=1 •6()+12,
20()() = 33 ()() + 20.
Однако из-за отсугствия нуля эта система за
nи.сн была не()днозна41ю.й. 11 зависимости от
контекста одпа 11 та же запас r , могла о:зна-
чатъ ч11сло 72, илн 4 320 = 1 6<i+l2 (>0
1
,
или11/., = 1 60°+12 601ит.д.
Шестилссят<.:ричная снстема. широ
ко 11рименЯJ 1 ась н астрономическн.х
расчётах вплоть ло эпохи Возрождс
н ия. Им:енно ею 1юльзовался во 11 н.
1 ·р~ческ 1-1 й матсма·1·1 1 к и аt"r·роном t(JJ
нии таблицы синусов, 7\ре1шеи- t'J ~ ~
шей ИЗ [(ОШедuшх ДО нас.
{
.
_
Кла 1щий Пт011емей при состав~е~
Г. ~."/М
...,.-= 1-..1
......"
.
.
-,.. ,_,,__
17
~
а'"'{Ю
Исrор~1я матема 1ики
IH
СЧЁТ И UИФРЫ ИНЛЕЙUЕВ МАЙЯ
Индеl1сю1й 11арод маf1я. обнтающий иа т~:ррн
т<>р1111 ЦентрЗJJьной Лмср11ю1, в т~ ачалс:: 1ю1юii
эры прсдставтrл числа примерно так, как и
древннt шумсры. Майя 11зобре.rтн похожую чt1 -
слоную систему, по с 11рул1мн ос1 юва1-~11Яl\П:1 -
шпсрич110-д13адцатср11ч1тую Лростсnшнr-1и
цпфрами у н11х были чёрточки и точки, ко·1·0 -
рым11 за111·1СЫf\аJ111с" ч11сла от 1 до 19. Точкам11
они обознач:шн сю11шцы пт 1 /{О 4 . чёрточ-
1ю(1 -
') К примеру, зa11irc 1, .:..:.:. пзнач~~ж1 число
R, а· ··· - ч11010 19.
Осr-юп11ую рот. 13 с11ст<:ме майя 11rрала «ис
кажётша>J ·> двал1 ~атер11ч11аи с1к'Iема сч1 1 слс11шr.
!:ели ва1шлонскан снстема ос1юn~ш:~ 11а разт 1ч-
11ых сп:11е 11ях числа 60, то\' майя так11мп ю110-
чеnым1 1 ЧИCJl;\MII BЫCTYП<IJl;I 20. 18 20, li::i . 20! ,
1
1
.
•
18 2() ,18·20 ит.лПризаписr1числацифры-
кир1111 ч11кн :~а1111сывал 11 сь 0J111 a 1юд друr' ой,
ИЗ ИСТОРИ И UИФР
Время изменило внешний облик uифр. Если в Xl l в.
uифры огубар», п рименявшиеся о мавританских госу
дарсrвах, им~ли следуюший вид:
2
345
7
89о
G18?о
то уже в 1480 г. в книге «Зеркало Вселенной~ аиrли
чанина Каксто~1а 01-iи изображаются rак:
1z3
И лишь в 1 'J22 r. в книrе итальянuа Тонпалля рни
принимают более-менее современныи вид:
I'L)f)с7g
о
Л1Обопыт110, что в Индии uифры тоже видоизме
нились и к 11ачалу ХХ в. выглядели так:
1-~~8-Ч(б т { о
Начиная с XVl в., кuгла в Европ~ уже бь1ло развито
книптечатание, многие хуложн11ки работали над со
зданием раз~юобразных типографских шрифтов, 1·1а.д
формой букв и uифр. Они старались придать им при
ятный лл11 глаза вид. Но история ш1фр на этом не кон-
r1р11чt;м ст:.~рше1'1 ян1 1н11ас1-> н~рхннн 1т.11фр<1. 1la-
.: ..:. .: .:
щ111мt:р, 3а11нсь :· · в с 11 стсмс майя 11рсдстан -
-
-
л.ялачислоl9 JlL20-t- 13 Ш+11=7111
(IЮNН:: рю1у1ы КJIЮЧСНЫС Ч11СЖt)
/l,llя обоз 1тачс1шл11ую1 мшЪ1 11 р1rмен>1Jш з11 :.ш,
11;шом11пающий полуз~Н<рытый глаз: <Ш>. Так.
:~arnкh <Ы> 1-11,rражала число 2 · 20 + О = 40
ПОЗИUИОННАЯ
ЛЕСЯТИЧНАЯ СИСТЕМА
Дрсш 1еС1111ая НЗRСС'1 '11'1 Я :3а1 1и сь в IЮЗНЦl!ОIПIОЙ
/(еся·1 1 1ЧJюl1 системе обнаружеIIа u И11д1111 11
датируется ')()') r. ПояnлснJJе хорошо з11;~комо
rо нам пуш1 было подготовлено системамн
CЧILCJIClllIЯ , l rзд~шна Пp!u\.fCHЯJШЛI.iVIJICЯ rrc толь
ко в И.1:-щи11 , ~ю 11 н Дрешrем К11тае. 11 :-э111х <:та -
чае rся . Например, совсем 11еда1.:111 0 в ряде Cl ра11 стали
ислоль:ю~ать такую .1.~nись:
Чем ·ни uифры лучше обычных? А 'Тем, •1то у четных
Llифр ~хвостики " идут вверх, а у неч ётных - вниз.
Теперь труднее спутать, скажем. 2 и 5 . Прс:шда, это
нововведРние широко не привило с1,. А вот начерта
ние uифр, которое знакомо кажлому ·
о123чs6l8g
·)Ти uифры можно видеть на микрокалькулятора х и
ручных ·)Лектронных часах. С nомошью ~1аЬора из семи
отрезкоо улаётся досrаточ110 « узнаваемо » изобра-~и 1ь
кажду10 И3 леопи uифр.
[ше одно и ·юбражение uифр, связанное с потреб-
1юстями техники, можно 11а1.1п1 на обороте почтово
го ко11верта:
о127чs6rв9
Здесь в написании uифр участвуют уже девять от
rезков . Uифрь1 прсдна'.\на•1 ены лля электронной ма
шины, сортируюшей коррс с по1 1 де11uию . Жирные
черто•1к11 Нdд и11дск сом 11а ко11вертс 11уж11ь1 лля того,
ч гuбы машинс1 tмor ла ~очно настроюьr.я на наткан
ный vтправителем индекс:
р111111ых сие~ емах для ;~ан иен одшта1со1ю 1 ·0
числа сд1ш1щ. десяпшв, сотсп wш тысяч 11с
пользовались одrrи и те же сI1мnолы, по до
ттол1mтслы то rюме<-1алос1,, n каком раэря/1,е 01111
стuят. Гlостсn<:нно Ja ,'v1t'т1ш11, ч'1·u даже ecm1
нс указынать 11м е на р:.~зрндов, то ч11сло всf
rdюю можно nро1111тать, так как у каж;~о 1 ·0
разря;tа есть своё о~юсщочтюс мсс1·0" - пuз1 ·1-
1t11я . А есл11 поэ1щ11я пуста», то t:ё нужно поме-
1·1гrъ спец~ 1ал ыi ы м з1 1::1 чком - нуJ 1ём. R 11ОС$/1,НИХ
nаnт~ло11сю1х текстах с тал 1ю.нв.тшться такой
з нак, однако н кохще чrкла его 111шоrда не ста-
1шщ1. Лишь n ИпJ(иr1 в lX в . нуль окончателы-ю
l:т.:1ри1-111ыс <. 11<. темы з;:щнсн чи<.l:'Л
,Аь.
8'.i(!J
;~а ш1J1 оюt: место 1~ нумер;щ1111, котор:н1 рас11ро
стр:11шлас 1 , зан:·м гю nсел1у миру.
И11дийская 11} мер;щия прJ1111ла crrз чала в
арабс1<ие страны, а затем и в :~ападную Европу.
О не11 подробно рассказал среднеазиатс101й ма
тематик алъ-Хорсзми. Простые н удобныl' пра
вил:_~ слож<:нш1 11выч11тан11л скот, уго,11но боль
JJ 1их ЧJ,н.:с.:л , З;.1 1 rисанны.х н 1юз11цишn юй с 1 1с1:ем<:.
сделали её особ<.:нно 1юпут1рной. А .поскuл1>ку
труд <uн,-Хорезми был написан на общем дю1
мусулыv1аn скm·о мира }J:'!ыкс.:: - ар~16ском. то ;3а
инднйстюй 11умера~т;пей н Еврппс ::1акре11ш10с1,
1tеnрашшыrое 11 а:1в::шш~ - «арабск<1.н ».
20
Истприя математики
МАТЕМАТИКА ЛРЕВНЕГО ВОСТОКА
ЛРЕВНИЙ ЕГИПЕТ
CaNiыe ранние математические тексты, извест-
11ые в наши ДJ 1и, оставили ~ве великие циви
.rtизации древности - Еп-mет и Месопотамия,
или Междуречье. l1ме11но там появились лер
ныс матсмат.иqескне задачи, решения которых
требовала rюнседненная ж11знь. Нсдь ненозмож
но без расчётон построи1ъ зд~u-~ие, будь то ве
л ичестве1111ы:й дворец или простой сю1ад дл.я
зерна. И как гюделнть землю между родствен-
1111 кам и." прибыт, между торговцами , 11айт1-1
праnильн1,1й путь n пустын е и;ш н морс, ео1и
вы не знакомы с прапилами счёта?
Несколы<о тысячелетнй кул~,тура Египта
развивалась бса каких бы то ни было внешних
nлияний, и именно 3ТИМ обънсниетсн сё само
бытrюсть. ~'pouer rь дpenr rсегилетской математи
ки был дшюлыю Rысок. Дреннис греки, до
стижения которых лежат н основе сонрсмсн ной
нзуки, считали себя ученика мн египтин. Вот как
нисал об этом в V в. дон. э. знаменитый грече
ский историк Геродот:
~,оп и [е1·иnстские жрецы] говорили, <tто 11арь
разf\ели11 землю между nсемн епштянамн , ,п;ав
каждому по раГ11юму прямоуt ·ол ьr-юму участку:
из этого 011 со:щал себе Д()ходы, np1 rказан еже
го11по н1юс11ть налог. Есю1 же от какоrо-н 11 будь
11адела река отнимала что-11нбудь, то владелец,
приходя к r(арю, сообщал о rтроисшедшем. Царr,
же посылал людей , которыедоЛЖJ-JЫ был~~ осмо
треть учасl'Ок зсм1 1и и 11змсрнт1, , 11а скот,ко он
ст~щ мены11е, чтобы вл;щелец н1 юсю 1 с остан-
111сйся 111ющз/(И н:тог, про11ор1\иО1i.:-lJ1ы 1 ый усrа
новлснному. Мне кажется . ч1-о так и fiылз и зоб
ретена rеоме-1 рия , кu·1-орая :.~атем из Египта бьта
перевесе~ 1 а n Элл:щу» .
ПЕРВЫЕ УЧЕБНИКИ
Общсствсrшос устройство Древнего Епшта
н:с менялось н течс1:шс дuт ·ого времени. Сохра
ннл ись без нзменен11й и 11аучныt :ш:н-11ш, JЮ
этому сс rоднн учёным O' - it'Ht.> трудно точно
определить /t<ITY TOl' O или ИHOl 'LI O'ГKpnlTliЯ.
К тому же исто чников. no которым можно су
ди1ъ об уровне м атема·л1чсских ~iна11ий 1tрев-
ннх с:ги1 1 тян, со нсс:м rieмнo r·o. Назовём са м ые
и:щестпые пз н их.
Во -первьlJ{, это nanиpyc Райщщ, назnа~-шьн1
так по 1Lvre1 ш своего первого ВJщдсльuа. Он был
11аiще11 в J858 г.. расш11фронап н нздан 13 1870 J'.
Ру1<оn 1 кь пре)].ставляла собой узкую (3.3 см) н
Jl.JIИH I JYIO (5,25 м:) rюлосу п::~ 1 1ируса , <.:Оде ржа
щую H·I :{ад<1чи. Теперь одна часть п:1 пнруса
хран11тся 1:1 Британско м музее п Лонлоне , а
дру1'ая 11ахою 1·1·сн н Ныn-йпркс.
Ro-Rтnpыx, так назыиаемый Москоrккий
na1111pyc - e rn n декабрt.:: 1888 г. приобрёл в
JJyкcope русткий египтолог Владимир Семё1ю -
1111ч Голсн111цсв. Сейч~с папирус при надлежат
l'осу;щрствею-юму музею изобразитс.rть ных ис
ку<.:ств имени А. С. П ушкина . Этот с:виток wrи
нoi1 5..+4 ми rпирююй 8 см вклю ч ает 25 задач.
Пщ Ptl J,~ 11олс 1 1(• 10"' кол~1че<. 1в..~ н.•рн,J Eri..1111. •1 tt<t1H п ,,тул·ка
Околfl 2040- 171\'i п· дон '
М<П~матика Лревнеrо Восток;)
И н~шопец, •Кожаный сnиток егип етской
математики», с болъшнм трудо м распрямлён
пый в 1927 г и во мноl'Ом проливший свет на
арифметические знан11я егиr~тян. Ны11е он
хра1.1 ится в Брнта 11 ском музее.
Эти рукош 1 с11 относнтся к эпохе Срсдне1'0
1 \Ц>ства (XX-X\ТII вн. ло н . э.) . Московский па
пирус б~.111 п среtшсаr 1 11 ею·1м учепиком между
1800 н 1600 1·с. до 11. э. с более древнего текста.
примерно 1900 r. до 1t. э. А п апирус Райнда пе
рсшrсал писец Л.,'{мсс около 1650 r. до н. э.
Автор ори г инала 11еизRестсн, устано влено
лишь, ч·~·о тскс 1· созд~1нался во второй по1юn11 -
пе XlX н. дон . э . ~кож:.~.ный <.:В иток? датирует<.:я
XlX-XVlll вв. до н.:::)
Пnдобн ые пап11русы, 1 ю-пн;(имому, служ11л 1 J
сное гп рnда учеtlник:1 м 11 . КаТ< СJ{а::тю в руrюпи
си Ахмсса, ока nосвюцена <-сонсрrненному н
ос1-юн;пелы юму исСJrедощнтю() всех ве111ей, 1ю-
11им ани.ю их су~цr-юс1·и, шхн-1анню их тайн". Так
в ы соко ценились в те далёк.1е nремена мате.ма
·rнческис знания! 13 папирусах есть зад~1 чи на
вы числение - образцы выпош1с 1 1ю1 арифмети
ческих опера ций, задас~и щ1 раздел имущества.
ш1 нахождение объёма амбара или корзины,
площади поля и т. д. Длs~ ко1'0 же nредна~тач.а
лнсь такие учебники?
Папирус Ра.йн/{а з:1канч1ш:tстся такнм 11 сло
н:1ми: •Ло 11 и r·мов, мы 111 ет\ иы r 1а.11ыва1I <.:орныс
траны зэсnежо; ПOJfyчaf1 обнлы1ую пряжу. П ро-
01 у бт·а Ра ·1·епла, ветра 11 высо1<0'1 rю;{111". По
э·сому 11 екоторые 1ксле~о11атсm 1 реш11л11, что
свиток адресован зе.чледел~,цам. Однако м 1 ю-
1нс из содсржащпхсн в 11ём задач i\OIICC нс11)'Ж
r 1ъ1 крсстьшmну. l3 с~·рапе фараоноn была
особал 1'р:тпа 111Uдer'1, которой требов<111.ись
11одобные :5H3III 1 Н , - ЭТО lllK I \1.1
. Пнс< .:ц - /~OJJЖ
H OCTh отвстстненн<1л и uесьма лривилс1 ·нро
н;1ннам . Он обнзан был 06J1;щ~r1ъ са ."1ьш11 разно
uбрззными ма·1 ·с:::м:.п11чесю1i"111 1 rаны1<ам1 1 , чтобы
11сэ труда рз:-1рсш11· 1·ь любую з:тачу.
МЕТОЛЫ ВЫЧИСЛЕН И Й
Вес пран11ла cчi..~:.t дрснптLх египтян щ:новыва
лн<.ъ на умс:нш 1 скла/1,ы и~пъ 11 иыч 1 1·1 ·ать, удва -
11 Rать числа н ДО I ЮJJЮПЪ J(pun 11 / \U е')\ИНl l ЦЫ.
Умножение [1;\с1 1 еннс: сною 1л11 к сложе1111ю
11рк по....ющ1 1 acoбolr опера11111 1
-
мно1·ократ
Е1ОГО удвоения ю11-1 раад 1юе11ня ч11сс.r1. Вы1 ·11н
дt:Лп т:~кис р::к·qёты ;щnол1.но громозл.J<О.
2l
22
История м;пем;з тики
1n1 \1
~
-
l 'МI!
---
.
11
~р
.JlfJI
1
"\
р
,
~
Er11neтcкft e 11'1фры " ч 11ела .
Дш1 лробей были с11еппалы U> te обоз~ 1 ачсп ия.
Е1'иnтm 1е использоnали дроби вида 1/н, где п -
натуральное ч нсло. Такие л;роби наз ьшаются
ал.иквотиы.лш. Едипствепная неалиюютпая
л;робь, 1сото рую « признав;ши» египетские ма
тематики, - это 2/:,. Иног)"(а вместо дсле:ння
1
т : п производили у~vшожспие т · -
. Дпя этого
п.
прим<:: •iЯли специ~\ю,ные таблицы . Haf(o ска-
з:пъ, что нейств11}1 с дrюбям и состанлнди uсо
бе1-1 нос1ъ е~·ипстской арифметики, 1:1 которой
самые rrростые 11ычис; 1 еrrия порой пf)еL1ращ::J.
лис r, R сложt1ые задаl..fи.
Сравнительно rтебольuюй круг задач в еги
петских папирусах сводится к решению лро
стейших уравнений с одним неизвестным, н.а
nример 33-я задача из шшируса Рай11да: « lleкoe
колнчество, ei·o 2/3, с.1·0 l /2 и eJ 'O J /7, сложен-
1 1 1 ,тс нмс:о·е , 11.ают ~7 . Какоrю э· 1 ·0 1шm1честАо?•>.
Ответ 1(> .:/.1~ ззш1снr n эщ11<1ютн1.1хдробях:
1
1
1
16+-+ - - +--.
56 679 776
П рн решении подоб11ых ]адач мя 11е11зnест
н о1 ·0 IICI IOJIKIORaJlll CllCЦH:IЛhl-tЫil 11ер01'11Иф со
:! f !~I ЧСНИ<.:М QKy•t:!». В 3;(Д~Ч'1Х nro ~K}'' t y», rкша-
CMhlX t.:JJ,ИНЫ.М Mlvl'OДOM, можнu усмотрt:1 ъ 3~1 -
Ч:!'l'КН :1111·сбры к;.~к н~ую1 об ур; 111нсн11н х.
R t'J 1tnt: 1 ·cю1x11 :ш11русах 1:1стрtчаются ·1акжt.:
~~а;1ач1 ·1 на :1р11фмстическую t1 J 't.;ОL\1t.:трнчсскую
rrро1т>есси11. что ещё раз nодчёркинаст 11е · юль
ко пр::11<тическrп1, 1ю11теореrпчесю1i1 характеr
μperшci'1 матема1'ики.
ГЕОМЕТРИЯ СТРАНЫ ПИРАМИД
Пораз11тслыю, 1ю 11 рн дово11ънu 11р11м н· 1·т 1ннuй.
11 громоз1 1ко1'1 арнфмстнке е1·111rтянt: с:мш·1111
HUOllTl>CH :Ш;./ЧИТt!JЪНЫХ услtХОВ R l'еОМСТрНИ.
Онн умсл11точ1ю11аходн1· ь 111юп\:ц1ь 1юля пря
"юутлы ю~1. треу 1'01 1ы юй и · 1 ·рапе:цневнд1 юй
формы.
Известпо, что в серслине 1 тысячелетия
до 11. э. для постросrнш прямого уг.r1а сrпптяне
tю1uльзоваJн 1 вtрёвку, раздслёнпую уалаr-ш тrа
12 p:tBllhL'{ ч:.~стс.;й Ко1щы всрёвки связьш11ш н
з:псм натн1·1шали t:ё на трн кuлыwка. ~ели сто
роны 0111осились как.). "1: S, 10 гюлучала1 пря
моутльный ч1еуголы-111к и это - едшrс:твсн
НЫJI прямоуголы1ый треу1 uльн11к, 1ю·1орь11-1
3н~1!1и uДрl:Rнсм Епште. Е папирусах не1 :задач,
как -т1fi() связютт11 ,1 х с теоремоil Пифа1·()ра ,
Х()'!'Я Д() расшнфроuки .математических текстон
существовало мнение, что древние сги11·1.шrе
были с 11сй знакомы.
Важным дос1·1~же1шс:м 1·еом.стрич.еской на
ую1 t'1·1штян былu оче 1 rъ хuрошсе пр11ближс
ю1t: числа тт, которое rюлучаетсн из формулhl
юш площа;\11 кру1·а дна метра tl:
5 = (d-icli=(l- i)2d
2
•
Этомуправплу из SО- й змачи папируса Райнла
ссютветствуп значение тт = .. .J .(8/9) z "" 3,160<:/.
Однако каким образом сrю 1тяпе получали
саму формулу, rп ко1-rтекс1·а псяс~ ю.
Матем ,н ика Лревнt:>1 о Востока
~
S!JШ
:-;;:---; :-~·~··' ~~~
~-
--
-
-~
-~_- ~- -~ ~··_-::.: .
-~
...
"~
.... -
~-----
~1
В Московском п'1.пирусе еnъ ещё ощта 1 11tте
ресная :Jадача: вычисляется поnерхност1, кор
зи111>1 «С отверстием 4
1
/J» · Исследователи толку
ют сё по -рю1 юму. поскольку n текс1·с 11с укаэа~ ю.
какuй формы бьuш 1<орз11на. llо nce схu,цятся ~ю
м1Jсн111-1 , что 11 ::1/\lТь ;1,.11н чнсл:1 л nерёто1 ·1·u Жl'
самое nрнближённuс :тачс11ис "-l(R/9)~. Замс
п1м , что 1ш Rcё .V! Древнем Востокl' пr)lj 111,11111 -
слсн~щх нсnоль'юRаJ ЮСh .~н.t•1с11~н:: тt = .~ Цаж<.:
в Библии есть ука3ание 11а 11с1'0 Так что R этом
OTll()ШeJllJИ CГИll 'l'ЯJJC 11ам1101 () опсредш111 11ру-
1·ие 11арщ1ы.
Среди простра11стпенных тел самым (< еr11-
пстским» ~южпо считаn, нирамит, ведь имен
но такую форму имеют :щ:.~мен11тыс усшrат,
ницы фараuнuн. Так нот. сжазываl"t'СJI. кроме
объёмон куба , r1араллелс 11 1нrеда . r1р11змы 11
ЦИJIННдра e1·1111ТHll<: ум<.:ли l:IЫЧllCЛ>ITb объём
усечённоi1 1трам1щы, н оснокн111ях которой
лежат ква~ра·11,1 со сторо11ам11 п. ~1 h , :~ нысо·1 ·~1
ран11а h. От 1 11r11 .'ll1снял11 формулу
\f ::((/~+C/h+f')L)fl
3
23
История математики
О ФОРМУЛЕ П ЛОШАЛИ
ЧЕТЫРЁХУГОЛЬНИКА
В папирусе Райнла приводится
такое правило для вычисления
площади произвольного четырех
угольн ика ; полу сумму лли 1-1 двух
противоположных сторон ч еты
рехугольника умножить на полу
сумму длин двух других сторон.
Разумеется, оно пояснял1>сь на
примере, а не с помошью фор
мулы, как на рис. 1 .
Но это правило невер1-ю! Лаже
для парамелограмма оно не дает
игтинного значения п лощади. Ведь
если изготовить шарнирный пря
моугольн~1к (рис. 2), а затем сжать
его так, чтобы uн превратился в
КАК МОГЛО ПОЯВИТЬСЯ
ПЕРВОЕ ПРИБЛИЖЕН И Е
ЧИСЛА п
Чтобы понять, каким обра·юм древ
ниt! учёные получили тот или иной
результат, нужно постараться пред
ставить себя на их мсL те, т. е. по
пытаться реши ть поставленную :1а
лачу, исполь•уя только знания и
приемы вычислений того времени.
Именно так поступают иссле1юва
тели стариttных тек( тов. однако
решения , которые им удается
найти, вовсе не обя зательно не
самые». ОчР.нь часто д/\Я одной
задачи премагается несколько воз
можных вариа н тов решеt 1ия -
реконструкuии. Каждый внравЕ:' от
дать прелпоспение оыюму из спо
собов, 1ю 1111кто 11с может утверж
дать, что име1 lllO им ~1 ПОЛЬ3\)IЫЛИСЬ
в лрев11ости.
По поводу формулы пло шали
круга HJM кажется весьма правдо
подоG1-юй гипотеза автора много
чиLЛенных кни1 1ю истории мате
матики А . Е. Раик; плошадь круга
диаме гра cf Lpa вн11вается с пло-
параллелограмм, то длины сторон
не изменsпся, а плошаль умень
шитсs1. Вообше, для любого четы
рёхугольника со стороt1амиа, Ь, с,
d имеет место неравенство
Рис. 1.
s.;: а+с b+d
2
2
S=fJ...±. .f . .b+d
2
2
с
шалью описан1юго вокруг него
квадрата, из которого по очерели
удаляются малые квадраты со сто-
1
1
ронами бd и gd.
cf
(/
В наших обозt1аче11иях вычис
ления булут выглядеть так. Н пер
вом приближении площадь круга 5
равна разности между плошалью
квадрата со стороной d и суммар
ной плошалью четырt:'х малых к1:1ал-
1
ратов А со стороной 6d:
В равенство оно преврашается
тол1,ко дЛЯ прямоугольника. Иначе
гuворя, еrи11етское правило с11 ра
велливо \и то не точно, а лишь
приближенно), когда четырехуголь-
1-1 и к мало отличается от прямо
уголы-~ика. По-виы1мому, имен110
такую форму имело большинство
земельных участков египтян, и лля
1-1их ошибка, заключённая в :пом
оравиле, была нсзначителы-~а.
Лалее 1н получе1111ой олошали
нужно вычесть nл1)шаль вщ ьми
l
квадратов В со стороной 9 cf , и
тогда nлошадь круга будет при
ближен1ю рав11а LЛедуюшему 1:1ы
раж е нию:
-~[1-~)dl =[1-~yd2•
В польз у излuжен~юи здесь ги
потезы свидетельствуют аналогич
ные вычисления в однои из 1алач
Московског о папируса , где пред
лага1::тс~ <..осчит..~ть
(1-~)-~(1-_! _)'
999
Эта формула считается высшим 11остиже1 т ем
дреш-rеегнпетс 1юй математики.
Подnедём итог. Математика в Дреnне.~1 Епш
тс представляла собой совокупность знаний,
между которыми ещё нс существовало четких
МЕЖЛУРЕЧЬЕ
Первые очаги кулътуры Дреянсй Месппотами11
(Междуре'!Ъя) 1юз11икли на берегу Персидско
го залива. Именно здесь, в дельте Тигра а Ев
фрата, 13 IV тысячелетии дон. э. жилп шумеры;
они построили города Ур, Урук (под НJvн:щ·м
Эрtх он угю мнн.~стся н Бибюн1). Л~11'а111 и Ларс<t.
Севернее жили сеNшты-аккадцы, гщ11:1ны м ro-
[IO/\OM которых был Аккад.
Ужt> в серещ. 11-1с IV ·1ъкя чслетия лu н. ~. н
Шумере сущес-1·tю1~апа nисьме1 п юст1 .. Мзтери
алом !(ЛЯ пио,ма вначале служили каме1-н-1 ые н
гmшшrые плитки. На ШIХ острым предметом
вьщараnывали надписи. Затем писать стали на
сырой глине бамбуковыми 11ли костяными па
лочками, после чего плитку высуrm1щmи или
обжигали При надавлннанrш палочка остав
ш111а на 1·1niнe след в R1-ще ю1ин::1, и онредсJiён-
1-1ый набоr Т<.lКИХ КJIИJ-JЪCB служил для перС/\:1-
ЧJJ того 11ЛН нноrо ПОНЯТ:ILЯ .
ло.1 nш u~ llt'flCl l Иlbl!l•IКll ддНЬ ИJ IJX8d' ll:HHUI u ( СЛ('НЩI. Р(!льеф
д~l•pu.1 r111 1d~<'pИf>,1 ~ f IИI Н'Ш1" Vll lj Д(I 11 э
Матем.:пика Лревнеrо Востока
~
c:tl~
1-ран1щ. Э10 были правила для реше11ня 1<()11
крстных задач, имеnших практическое значе
ние. И лишь постепенно, o(ie1 11, и о ч е llь медлен
но, задачи начади обобщаться и приобретап,
более абстрактны~:: черты .
Во II тысн челе-1 и11 ;~о 11. ::>. rюnые племена
семитпв. пришедшие с занада, стали хозяева
ми Междуречья. 31\СС~. сложилио, две мощные
державы - Ассирия на севере (сё стол ицей
была Н1·1нен~н1) и Ван1шония на ю1·с (с1·олиц<1
Ванилон) . Шумер()<Jккадское письмо 61,uю ::!а
имсттюнано ванило1-1янам11 и ассир11йцамн, а
также соседнпми народами - ХL'1там11 , перса
ми н урарту (1rрею<амн армя11).
JlOLЛC арХСШЮГНЧССКИХ ИЗЫСКаl 111Й 1-1 серею1-
11е X I X в. КЛИIЮПИСllЫС ГЛИILЯIIЫ<С табллчки в
огромных колнчестnах стали пос1упат1, в Енро
пу. Так, в 1849- 1850 rr. 13 развалинах l l и~1евии
обнаружили дворцовую бибm10тску, а в 18Я г
открыли 61 16J11ЮТСК)-' Ашmурбанип:vщ ассирий
ского царя, ~rраrшвшего в \ГН в. до н . э.13 Британ
ском музее (J l oi щон) храннтсн 2U тыс. таблнчt:к
н :{ этих раскопок Все1 ·0 же в 111ире насчнтынJ
ется ()КОЛО '500 тыс. ю1111-ютк1-1111х табличек
КАК ВОЗНИКЛА ШЕСТИЛЕСЯТЕРИЧНАЯ
СИСТЕМА СЧИСЛЕНИЯ
Шестилесятеричная система счислениs~, rю-вилим(}
му, сложилась п ри торговых сделках между двумя
древ1iими народами Месопотамии - шумерами и
аккалuами. У шумеров «де~tсж11ои сди11иuей » с11у
жим мина - кучка серебра. Это была круп н аs~
сумма, и при продаже 11едорогих товаров ее обыч
нu де11и11и пополам. а каЖАую половиttу - еше на
три ча<-.ти, так что шестая ч<1сть мины широко ис
пользовалась пр1~ расчётах. У .жкалuев в ходу была
своя монета - шеккель. При сделках между шумера
ми и аккалuамt1 шестая часть мины приравнивалась
к 1О шеккелям, т. е. мина составляла 60 шеккелей.
В результате появил11сь з11аки лля чи сел 1, 1О,
bl), 600, 3600. Это произоШl\О окu110 5 тыl. лет
назад. З 11 аки выдавливалиеt, тупым конuом палоч
ки дм1 письма на глиняных табм~чках. Позл11ее онн
превратились в к11инья и уголки.
26
История математики
Н Навшюrн.:ком царстnс nссми рас• 1ётами за
нимались шкцы, кu·1 орыt прншщлt:жали 1с
нысшему сослон1 1ю. Нередко сыновья uр,шитt
лей и::1б11р:uш ~ту проф<:ссшо. Школа , ГJ\С uбу
чалнсь шrсцы. называлась ~дом т::tбличекь ~пн
сец должен уметь писа·1·ь понятно, хорошо
:~1 1э·1 ь счёт, уме-1ьмежевал_,1емт1 , [Jримирsпъ
споря~щтх», - mтсал олиn пз учстпю11 сnое
му друrу. Дrш таких школ прсд11а::1пачалт1сь
специальные J\1атематические ·1 абличю1. Тек
сты па них можно раздстпъ IJa }\na класс:.1.
·1 ·аблицы и з;щачники.
Широкое:: нрименен11е различных
1'абли1t - характернаи uсuбенност1,
в;ншло 11 скоl1 матемзтню1. Кро,...н:
таблиц умножс:ння были <:щётаб -
111щы ю1ащх1то11 llaтypam.11ыx
ч1rсел , кубов, квадrат11ых кор-
11ей (в шсспще<:ятсричных дробях) и даже таб
mщы ЧJКt:Л ю1;~а п1
+1/ 1.Jтuбы раздtшпъ <nн:ло
т на 'ilICJIO 11, в:ш11лоня1-н.: IKL:ГNI брал11 ЧНСJ Ю
п' = 1/п, обрзтнос дели·~ ~лю, 11 ум1 юж:~лн 1п
И1м1•рf' Н'1Е'
терр11тори11
~е"'ельноr u у~Ja( 1Kd
в Умме
(МС'жлуре"!Ье)
Гли11я11 ая табл11чка .
ш1 п'. 1юэтому бъmо много та.блиц обратных
nеличин . Та кой под,\:од к делению сохраюu1сн
и в современ ной мат<::матнке. на11 р11 м t: р н
шн ебре м:при1l-
Что к:tса~ 1 сн тскстоп-з;щачннкок . с амы м
ую-1ш1тсльным оказалось ·1
·0 , что боm.шннс·1 ·ао
з;щач сноднтся к ре111 е 11ню кА :Щр:п11ы х ура1те
нигl . Эт() 1 юразителыюс открытие 1ю:шол1.uто
от1 1ес111 ртrщстrие алгебры 11е к V в. до т1. э., как
полаrалн прежде, а к ХVШ n.110 п. э" т. е. 11а 11
веков н азад. Но об этом чугь п озже.
КАКИЕ ЗАдАЧИ
РЕШАЛИ В ВАВИЛОНЕ~
Сред и Аычиоп1тtл 1>11ых :~ад~~ч на клн 1 юnи с 1 1ых
таблн чках встречаются :~ал::~ч и н а ар1 1фмет11 -
чес 1ш е 11 геометрически~ про1 ·ресси н , ттред
стаrтения о которых у вавилонян были более
раэвиты, чем у египтян. М етоды решения в ос
но1шом ош 1ралнсь на 1щси пропорц1 юн;:urыrоfI
1авис11мосп1 и с редн с 1 ·0 арифметичес кого. Ва
в11лонсю1с 1111с~~ы з11 :1ли нра.вшю су мм11рuв<1-
.1шя п ч1 1 ено н арифмет11чсско 1'111 ро1·рссс11и:
s·
_ п (а1+а")
'11 -
2
.
U юш1ю1111с1 1 ых текстах. содtрж:по1 11 ерные
змачп rra проценты - ведь Ваннлон стоял 11:1
пересечении то рговьrх пуrсй. и :щесь рано 110-
явнлис ь денежные з на кн и креди1 . Было у
вавштотrн 11 пр авило д;r_я 11р11 6л ижёпно го
вычислс1 111Я кв;щратных кортrсй.
Математика Лр~внего ВостокJ
~
Ell.l{]]
КАК ВАВИЛОНЯНЕ РЕШМИ
КВАЛРАТНЫЕ УРАВНЕНИЯ
Hi!. одной из клинописных табличек Janиca1-1 a такая
Задt1ча: • Множимое и м1 южитель 2; 30». Речь в 11 си
ил~т u лвух Аjа и м н о обратных всличи11ах х и у
(ху = 1), сумма которых равна 2; 10, т. е 2 +
+ 30/60 = 2,5. Таким образом, ученику для реше -
11 ия прсллагается система, кurupyю 1;1 сонременной
символике можно .:1аписать к<1к
гдеа=2,5, Ь =1.
{
Xi у= с:!,
ху=Ь,
Лалее в тексте табли чки ука3ывается, какие опе
раuии нужно nрод~лать. чтобы получ ить ответ.
Ниже привеле но решение вавилс1нСК()ГО F1ыч11см1-
теля. Оно сопровожлается лоой 11 ым перевплом -
записью да11 11ых и опера uи й ll десян1ч ~ю и по1иuи
он ной СУJстеме и ~с\ПИlЫО дейnвий 1:1 (Оl:!ременных
буквс1тых 0601 наче ниях:
«На O;JO умножь: 2, 5
1
а
2= 1,25
-
1; 15».
2
«1; 11 на 1i15
1,251,21 =
а
~=(~)l
-
умножь:
= 1,5625
2
1; 33, 45».
« 1 вычти отсюла: l ,S625- 1 =
(1')' -ь
О; 33, 45».
= 0,5625
" L\то на что надо \i(), '1625 =
г;--;~-
ум1 южить, чтобы
= 0,75
~(~) - /}
получить
О; В. 4Я»
r
1,25+0,75=2
1•
(<О;45к1;15
.1
")
прибав~:.:
2+v(2) - h=x
2 - множимое».
110;45от 1;15
1,25 - 0,75=
~-Д~J -/J = y
вычти: О; 30 -
= 0,5
обратное».
Очевидно, что дае тс я ре uепт для реше ния квал
раnюrо урае11ени~1 z 1 JL + Ь = О, к которому соо
лится с истема i•). Никаких пояснений в тексте 11е 1.
а то, что этот алгоритм н осит Оfiший характt>р, ил
люстрируется больш им ч ислом олнотипных задач.
28
История математики
I>олыпое число зада ч снодится к ур:н111е11и
ям ш ш системам уравпеню1 первой и второГ1
стеnе11ей. И."\': записывали без симво.1юв, в сnо
ей особо(r терминологии. Раз 1 ·<.шор11ым nзыком
ванююнян 61,u1 аккадский , 1 ю н науке в каче
стве тсрмннон они упо· 1·ре6J1 яnи 111умерошс
С'ЛОl:!а. КЭЖ/\ОС 11 3 таких СЛОR и:юбражаJЮСЬ од
ннм знаком и потому н ьщел нлось в общем тек
сте на фоне бoJJ ee по:зднеrо п о nроисхожде-
1rию CJIO l;OJIO ГO ГП·IСl>М:1.
Искусство ре ш ения ура1311е1шй .n.ости 1·1ю
высоко го уровня DХVШ n. .n.o н. э., u эпоху наря
Х;~ммураnи. Обычно в задачах требовалосъ
найти <>дли ну·> и « ширину» и;ш «м 11 ожимое» и
«ш-южитслr.», дnя котор1.1х были сформулиро
ва1-11.1 ра:шн ч ны<:: условия. Про11·знс.:дениедлины
11 ШТ!рtЛ lbl l I MCHOB::tЛOCЬ «ПJТОЩ::tДЬЮ» . в З<J,Т\ач а х,
снодящ11хся к кубическим ура rиrсн иям (а б ыл11
11 такrrс!), 1юн н1rялос1, третье 11еизnсстное -
~ 1·луб111rа », 11 nроизаедешrе nccx трёх пс:лич11н
называлось ~объёмом»
Хотя тсрмтюлогия указывает ш1 гсоме-1 ри
чеоюе пр ои схожлеJJие задач, для вавило11 я11
:;)ТО были прежде всего просто числа. вот по
чему они свuбоднu складъшали дли ну с пло
щадью 11 т п. В дрсю 1 е1 рсчсской м:lтсматике
( 11 с::щёдолгое времи 1t0сле) это1·uдt:.11ать было
нельзи.
Существовал 11 ,'\руl'Ой 1·1ш :1зщ1LJ , такжt: тр<::
бсащвнrий разни'НLИ ангебра11•tесю11х мс:тодов. -
1 1 ео 11ределё птrые ура 1з нения (таr< 11 азыв;-11отся
ypaIJнe111 щ в которых дне нm 1более 11 е .изнест
ны<:: nелнч~шы) Вот сам 1.1l1 древний п з наме
нитыil приме р нео11ределёштого уравнс: пшr:
(*)
Во мнш·нх клино писных т<::кстах речь ндёт
о ре 111 е нни ЭТО\'() У\J<Н~ненин в р;.1 1\нонаньных
ЧI ю1ах (.\".у, z) - ПО:'!ДI ICC нх стми 11азы 11;\'l 'h ~ 11 н
фа гогюны ми тройками~. lle совсем ясно, знали
B~1Jll I ЛO l IЯHC о()щне формулы CI о решt:ННЯ HJIH
пет, rщ11ако многие таю"е троfпш и"1 Сtыли нз
nсстны, напри.мер (.), 4 , '5), (), 12, 13), (_8 . 1'), 17)
11 др. Сохра1шлась даже табл и на р::щио11алы 1ы х
~ 11 ифагоровых трое~<", 1ю ю~ю1~1 обрJзом она
быж\ получе.11а, Qnрсделёшю сказат~, нель:~я.
Древние нан1111 011я11с рассматрнвалп ещё
0,111 ю неuп ре/~t"л<.'н нuе ур:шш:·1111с :
Его paц1ю 11aJJLiHbl<.: rс111е1 111н (ll, l', /./')образуют
"l 'a 1\ 11<1. :зынас м ы е «Н:l ВИЛОНСКI IC 'l' J)OЙ К11•1.
Это урат 1е 11ие таюке пмееr 1·еометrическую
природу. Оно возшшло nри ре 1 u енип за,Т\ачи,
часто nстречающсйсн й вав ~ионских текстах:
рассечь дашrую тр:шсцию на ,1'ne рав11овели -
1ше части 11рямu 11. 11 ар~L1IЛ<::J1ыюй· uсtювюшю
( ри с 1). Ес:J1и обоз11;~чн1 ь нижнее 01.:нон:шис
буквой //, н~::рх 1 rc:c - и, а ра:1JJ,<.:ля ющую пр>1-
мую - и1, то нетрудно н1щс·1·ь, что для 1111х
В..-111илоtк1<J~ f \111fs;tнaя 1 1.•ЬМ•"•К'I.\, с.одср А-.dШdЯ rеuме 1 р11ч<:< кие
~dЛi!'llI 1~.1•1Jl\C>11 1щ и•1PM'Tll!1 Л() 11 ,_ 1\1ыдр.зт l<lд'1 1111lol)\
f><HмepurJ nuделен HJ р:tз~ 11•111ы(' ф1н уры. плошаль коюрых
Y ' IPHHI( ЛОЛ~( ·Н ВIM 't \llC 'Л ИTt,1
и будет справедливо у'рав1 reшre (**). Вавило11ю 1е
умел~ 1 паходи1ъ бескопечно много решенпй
этого ураnпення.
Они также знали, что решения ураnпений
(~) и (**) свюаны Мl'жду собой: <::СJ 1и (х, у, .z') -
корни ураш-н:н~.-01 ("), то и= .'С - у. l' = х + у,
ll' = z - корни уr:ш1-1с1-1ия (**).
Т<1ковы дuст11жсн1tЯ древних ванилою1н 11
а.~н·ебре. И.х успехи в геометрии быпи скром -
11ее и от11осш1ись в гrервую очереN, к измере-
1шю nростеfiши."Х фнгур. Наряду с тсю1 фигу
рами, которые встреч<VIИС& н геометри ческкх
задачах еrиnтя11, - кубом, параллелепи 11едом,
11ризмой, цилиндром - вав.~.шоrtянс изучал11
некоторые правильные многоу1·олышки, сег
мент кру1·а, усе::чён.ный конус. lkронтно. было
и з в<:стнп пр;~вило /\ЛЯ вычисленнн объё.\НI
усечi::нноС1 гrирамиды. Дrшну окружности rа с
счит111в;~ли , утр;н-JRая J(Иаметр , т. е. для тт браш-1
з 11аче1111е 3. С тем же значением п 011реде:лял11
площад•• т<руга.
Одним из самых замечательных геомет
рических открытий было появлс1 ше. и притом
для общего случ<щ теоремы, которую впослед
стш1и стал11 на~1ыватh тt:оремой Пифагора.
Вщ: рт1ыс uна встречается в КJ111но11ис1-1ь~х тек
стах кремё11 царн Хаммураш1.
***
Т:ш же как и н Древнем Египте, L~ Междуречье
математические тексты излагались д01 ·мати-
ЛРЕВНИЙ КИТАЙ
Наиболее ранние из дошедшнх до нас китай
сю-~х мате матических текстов от н uсятсн к кон
цуJтысячелетия т~о н.э.Во11в /Щ н о.были
1~а11исан ы математико -астро1-1ш.1ичссю1й чТрак
тат об измерителъном шесте~ и «М<Пt'м<1тика R
дсвят11 ю1и1'ах» Поаю-rее, уже н VП 11" оба сочи-
11 ения вошли R сбарш-1к «десять ютассичесю1х
трактатов», который 11зучали в течение многих
столетий. Сборник в1<лючал и другие труды:
~трактат о морс1<ом остроне ~ Лrо Хуэя (111 п.) с
задачами на оnрсдсле1-те расстояний до r1сдо
СJуш1ых предметов и их размtроR; «Математи
ческий трактат» Сунь-цзы (Ш н.), содсржа щ11й
м:.~тсмат11qеские тttблицы , арифметические и
1·еометрич:сские зад~1чи , зада чи на системы 1Lи-
Мс1тематика Лpco1 rcro Uостока
~
ElfJ®
чески. Все 11рав11щ1 были сное1·0 ро1 1а рецепта
IvlИ (дeл:ilt раз, делай два, делаfr три ) , которые
пе обсуж,щишсь. ll строго нерархичсских и ;1ес
nотичсстшх государствах rосrюдствовал аnто
рнт:.~рный склад мы1111 1 сн 1tя . Учёrrым 11с nрихо
/\илось отст<'шватъ сною 11 равоту. доказыnать
11 ст1 -1111 юс1ъ резуJ1ьтатон доно;щми разума. что.
конечно , сдерж11н<1ло развитие 11~1у1<11 .
И ·1·tм нс менее открытня, едела 1111ы е м~пс
мат1 1 ками Межr~урсчы1, 1 юражают аюнм разма
хом. Ведь 11мет 11 ю з;1есь пояшшас1, пераая 1ю:т-
1J,Ио1111ая система счисления, и в rrтore тех 1 1ика
вычислений оказала<.ъ л:аже выше, чем у греков.
Здесь nn epRыe быш1 разработана алгебра ли
нейных и 1<n<t,"tpaп1ыx уравнений и рассмот
рены 11ервые нсопрс11слённые уравнения, воз
никшие из 1 ·еомстр 1rчсскпх зздач Такан тtсная
снязь гепметричесюrх з<!дач с ал 1'еброй н тео
рией чнсел - одна 11:1 особенностей в:.~нююн
скай матt:матию1.
Древ11ие греки н<1чпнали сван нсс1 1t:дова.ния
с тех проfiлем, кпторые занимали нан11 1ю1 rян.
Наnилонские традиции можно лроследнть n
работах Герона и Днофаrrта, а ещё лозд11ее -
у :шь-Хорсзми и других основателей ал1·ебра
ич<::ской ш1юлы стран арабскuго Восто1<а. ll ре
обр:1зование: матсматик11 113 совокупности
отдельных расчётов и пrавил в стройную ло-
1 · 11ческую систему, в кпторой эти nrнёмы в
правила nолучилн стрn1 ·ое пбоснова1-шс , ста
лп 1 ·лаш1ым дwом а11т11ч 11 uL'{ учёных.
нtйных уравнений: анонимный «Математнчс
скнй трактат пят11 ведомстн~ с задачами 11рш<
тиче('ко1·0 со;~сржания .
Оснонны111 IJ::l)"IHЫM тру11 ом бhlJJ;J v Матс
матика 1~ девяти кни1·ах;.. Она nредназнач :ш:.tс1,
29
30
История "1атематики
длн всех, 1<0му трсбоватк1, м;-~тсматнческ11 с
зна11ня : 1tЛЯ :;еМJ1С1\1ерон, нпженеров , чиноRни
ков, торго1щсн. По c111tecтRy, это сборник JJ:i 246
задач без нн<щных текстов и 11рею~эрител1,1-1 1 ,1х
разъяс11е11 ил. Каж/\Ы И ра~ ш 1:.1 чале фор,v1у111 1 ру
ется з~1нача. затем сопбщастсн отвtт и н сжатп1'1
формt: ук<1:11.1 н:зетсн сппсоf) реше11 ин.
АРИФМЕТИКА
С 1лубокой древ11ост11 счi.'т в Китае вели дссят
Т«t~rи. Примерно с IV н. l\O н. э. стали счнт:пь с
помощью с11t.: 1 t 1.1альных паJючск. О11и fiыл11 в
ходу на 11ротнжени11 более 11плу1пр:о1 тыснч лс:т.
Палuчки р:.tсюrадыв<~ли 11а счётной доске, кото
р;~я. к<1к полагают, была ра:з111 11 юиа11а 11а строки
н столfiц1)1 . ЕсJ1и как()й-то разряд н ч и сле отсу1·
ст1юш1л. то соответствующая ячейка ос1·Jвалас1,
пустой. Т~Н< что юттайская 11умерацня с по
мощью счёт1 1 ых п:1лочск - дрещ 1 ей'шая иэ дсся
т1 1 ч11 ых позици01ш ь1х систем.
I< lll в. дu н. э. уста ~ toв1mach и )Ч))'I Шt срорма
обо:щачении ч~ а сел - исро 1 'J1ифнче'ск::~я При
З~Ш.ИС\1 ч [ 1(..'Jla, СОСТОЯЩС l'О, 11апр1rмер, 1 t:~ тыснч,
ситсн . леснткпв н сдт 11-rц , сначала :за11нсыпш111
ч11с1 ю тысяч, затем 01ра1:1а 1 1лн снизу иеро 1 ·
J 11tф , обо:та ч::tющиi1 тыся чу, чнсJю сотен, :~а
ним - нероп1иф, обозначающий сотню, число
дtсят 1юн, знак десяти и, наконец. чнсло е1~и-
111п{.
Таблицу умножения от l х 1 /{О 9 х ~) эауч11 -
в::tлн 11аизусть. Ее декламироnаm1 юш даже
распеват1 ш1 уроках . Был1 1 11 др)т 1 1с числовыс
табшщы, нклю 1 1 ~шшнс: npu1r:>Rcl\CllJ1Я кв~щра
ток. кубов и ·~стнёртых с1 ·с11с11сй.
Лю Хvэи .
И:щав11а в l<11тat· бь1 J 111 И3Rt'стны 1tp()611
J lекотuрыс имс.1111 ;рже свон н:.1Звання . По110-
в11на 11а:~ыв:1л:tеь <,бан1' '" тpL"l'I• - ~ш:.ю б::~нл->
(•м~1J1::111 1 ю1ют111э » ) , /tве треп ~ - ~тай 6:.1111. "
(<,бо11 1,111а.я 11олпuи11а» ). ГТо:щпее пш11111Jюо, спе
l{Тiалы юе 1 1 а 11 ме1 юв::шпе для четвёртоl1 час
п1 - «слабая по.'!ошп~а». I lользоnалас1. п деся
т1 I ЧIJЬJMII дробя."JИ.
При реше11нн за,11ач порой прихо/1,тmось от
мс1-11,111сго колич<.:стна 0· 1 ·н11м:1· 1 ъ большее. Так
IIO JJ В. ДО Н. Э. 1IOHВ11Jll'IC11t)T[)I11 ~aTCJ! Ы-11'!(;: ЧIIСЛ:1 .
На счётно 1~1 NJCKC 11х ныдслялr 1 t1аJ1uчкам11
T\P)'l'v1·0 цнета 11т1 фор:-.11>1 , а 1-1 руко 1 п1си -
/tру 1 ·1 1 м 1 1 чсрютам11 11; 111 косu 1\ чt:ртu1'1. 0 1р11 -
цзтет,ныс чнсл;1 1 1а:з111нал11съ «фу». а 1ЮJЮЖ11 -
тсль11ые - « чжэн». Постепен110 ч11 сла «фу» ста
т ·~ 11 столковьш::tть как долг, недостаток.
Вщ:дение отр11цатсльных чисел и правил их
сложения 11 вычитатшя можно счнтат1, одп.им
из самых круш1ы.х uткрыт1·11-1 к 1 rтайс.кнх
учfных. В 1 ·речсскuй м · 1 ·1 ·смап 1 ке это с;tслал
/t11nфант н ссрсю1не 111 в.. и лн1111, 11 Vll н. отrнr
цателъю,rс чнсла поя 1iюн10, 11 111 щ11йско 1l ма
·1ематике .
АЛ ГЕБ РА И ТЕОРИЯ ЧИСЕЛ
В трактате «М:tтемат1ша в девят11 кн~rгах-> объ
яс1шется, как извлечь квадратный н куб11че
ски 1'i корни с помuщыо формуJ111t квадрат:~ и
куба суммы днух ч1 ю..:л. Пuсколы,~· ю1таl!скнс
м:~тсм:пию 1нсю 1счi.:'1· 11::1 доске. 11.х о юсоб 11мс-л
некотuры<.: осоt.11::111юсп 1 . Позжс: (HI был обоб
щё11 лля случая тобо1·0 i<oprrя п 1юобщt: д;LЯ
числсн1юго реше1111.н ура1те1шя 11-\1 с 1 ·с 1 1с1111 .
Метсщ nOJ l)'ЧШJ 113 зnа11ис "тя 1 тъ-юа111," (бу1шат,
тю - « 1 1ебео 11,111 элемент->) - так юпа!1 11,ы 060-
~шачат1 1 1ен:~nесптую вt:J1ичш 1 у. В1 10СJ 1 с::;1ствш 1
метол «тmп,-юа11 ь» р::~зш11п1 п разработ11ш 1<11 -
тайские алгебраисты Xll l-XIV нв. (В Европе н
XlX n. 011 ст;щ извсстсн ка1< мс· 1·0/\ Руффнни
Гор11сра.)
Дпя рсшсн11.я с1н.·тсмы /1 1 шнейных уравнt.:-
1IИЙ(.'17Ht'J1знс с~1·н ЫMll 11p11Ml'1fЯJll'H Ml"I'(.)) \ «фан
LJЭH '), 1l азн~ll ШС 03HaЧ:tl'T <- НЫСГ['!<Шнаннс ЧJICCJI
1Ю l\JICTKa,\,\ » ( ra:~yмee'l'CSI, I ТЗ CЧL:T1 t0i'1 ДОС!<е) .
Этот ;щ·тu;~ 11а 1 юмш1:icr дейстшrя с матр1щ:-lМ11
II опреде.r11 IТСЛЯМП . 13 Европе 11ервыт~r ПО/\ХОД 1\
реше1 1 1r10 снстсмы линей ~ 1ых ураnr1спш"1 nстре
'-1ается: у Леонардо IIJ 1 з at 1 ci.;01·0 (1202 r.), а Э<П ем
у Джероламо L<ардатю ( 1'5 ·15 1'. ) .
Из За/(ЗУ , от.носящихся к тсорпи ·спксл, сле
дует }11Ом.»н уть кл:ксич<::скую задачу нз послсд
нсfJ кнш·н « М~1·1·сматическо1·0 трактата·, Сунь
цзы: «Имеются ВСЩJ!. ЧНСJЮ IJ X t-ICHЗll<.'CI HO. HCJ IИ
считать 1 1х 'l'f){)ЙКам11, то остаток 2; еслн счи
тать нх ш1тё1жзм 11 , то ос1 ·аток 3: сст1 сч 11 та ть
их семёр rсзм11, то остаток 2. С1 1р :~ш и вае·1·ся :
С1\011ы<0 нещей?J) . Ины:мн слоnамп, требуетсн
11айтн чнсло, кото рое при делешш 11~1 3, <) п 7
даёт соответстnсrшо остатки 2, :1 " 2. Искомое
qпсло - 2J
Вс;сьма возмож н о, что задача более дрсвпс-
1·0 нронсхож.це1шя [1 в «Матсмат11 ку R деннти
KHl l f':IX » нс ПOШ/JI~I 1ютому, что н е IJOJ(OITTЛa Н11
к О}\1 ЮЙ теме сё rазделов. и у Сунь-цз ы задач :~
та 1ю1 п ·п 111 а - ед1111сгпст rая. Кстати , она был :~
шнрпко и:1вестна в нарrте и бла~·одарн совпа
де1111ю нмён служила примером осоfюй муJl
рости n()лко1юдца Сунь-цз ы.
Общее пр~шило решения подо611ых задач
сформу11J.о1ро1:1 а1ю нс было. <.Jно nояnлието1
ШIШЬ ДС(;ЯТЬ t:ТUЛ<.;:'ГИЙ с1 1уст.н у Ц11нь Ц:но-шао
н lTO •дс1:1ят11 кюн·ах 110 математик<.:.> (X!fl н.).
Термн 11 ы, R Нсдё1-1ные 11м" заимствованы из
сада·1·<.~m,1юй терми н оло1·ии конфуц11а1 1 с кu/'1
•Кн 11 г11 перемен» (УШ-VП 1ш. 1т..о н. ?!.). R ос1 ю-
11е г~щан и я леж:1J10 11редска:1а1111<:: сульбы по
с1·еблн м ·1 · ысячел истппка, IШТ()рт.rе расю1ад ы
n.tлщъ произвольным об разом па отдслы1 ы с
груды. 13 р<::зультатс .ма r-rипуляцнй с этими па
лочкам11 .и 1юз ш1к11~1 уnомяrтутая теорети ко
ч11словая зада ча. с 1<0тороl1 Цю11, Цзю -шао
11;\ЧИIТ:tСТ Llюё COЧl'JHt'HИt'. отдавая д;шь IICO-
кoнфy циal JCTl:I~·'. (Остал 1,ные зада<ш нз теории
чисt=.11 уже н е свя:iан ы с l 'аJ(3 11.и ямн; 0 11 11 ноз
н11к;u1 н н пс1 ю 11н ом п р11 сос_~ганлсю t 11 к~1л t11-
/Щ>СЙ .)
В Евро11с эта же ззJ.1,ача 11р111ююпся Лсонар
f(() П11:1',mсюrм, встречаетсн н од1101I нr1:~ан·п 111-
ской рукот:rси XlV 1:1. , н н еме цких р)'1<0П1к11ых
ар ифметика." ХV в. и n русских математнческнх
рvко nнся...'\': Х\:'11 в. Общий метол: 1хщсн1ш так11х
'iадач был нно~ 1, разработ~tн Лсо нарл;ом Эйле
ром в 17·IO t '" и K;i рлом l'ауссом в 1801 г.
ГЕОМЕТРИЯ
fс()метр11н n Древнем Китае 11 е р;1~ви11ас1, 11 са
~юстояте)Jы tую 11 аут(у, к:ш ::>то пр он :юшло 11
Древпеif Грец11и. J3 11ерво1t юшrс «Maтc J\l a·1 111< 11
IJДCHflTll l(!IШ ':lX? Пр!tnО,r:(ЛТСЯ ОТДСJIЬНЫС правила
Ма 1ема тика Лревнего Востока
11змер<::1 rия площадей 11 рнмоу1 ·олышка, трс
уrолы ш1щ трапеции, кольца, круга, е1·0 сектора
и ссrмс;11т;1. 13 1ш1·uй кн..ш·с рассматрrшаются объ
ёмы нрямого п:1раю1слс111111сда с квадратным
OCIIO\\<IHHCM. lljJ$\MЫe при :iМЫ с тр~.111\.:J~СИД~\JlЬ
ным н тр~у1·ольным оснона1-111нм11 . п 1 1р:~м11 ;1 ы с
ква11ратн ым и ll j)Я M OYl'OJUoHЫM OCI юна 1111 НМ11 11
дру п1~ п::ометричссюrе ф 1 11ур1·,1
Co1·Jt:J с1ю <·Трактату об тrзмеритеJt ы юr-1 шес
те'>, тс()рсма Пнфаt·ора для ча стного случая -
nртvюу1·олыюго трсуrольшно со сторо11ами :),
..+, S - была 11звестна за 1100летдо п. э., адля
общего с; 1 уч:1я - в VT н. до н э. Доказатсл~,ство
осно1:1 ьша 1юс1, на ра:.1611с1-11111 ющдрат а. по
с11:юс нн ого на сумме 1<~1'/'t'TOB 11ря..,ю у 1 ·ольно1·0
ЗАЛАЧИ НА ТЕОРЕМУ ПИФАГОРА
Вот з..~дача о и з девятои кни1 и « Математ ики в девя
ти книгах » : « Имt>ется водоем со стороной в 1 чжан
(= 1Очи). В L1ентрР его растет камыш , которыи высту
пает над вuдой на 1 чи . Если потянуть кам1>1ш к берt!-
1у, то он как раз кщ:нt?т< я его. СпрашивJt:тrs1: какова
глубин:э волы и какова ллина камNШ<З~» .
Если обозн<l'1ить глубину воды черезх. то по
лучим прямоугольный треугольник, олин ка 1е1 ко
торого епь х, второй равен 5, а гипптенуза х + 1.
По теореме Пиф:эгор:э легко вычислить, что глубина
воды составляет 12 чи, а ллина камыша - 13 ч11.
Приведем 1ад3чу 13 из той же книги: «Имеется
бамбук высспой в 1 чжан (=1 О чи) . Вершину его
соп1ули так, что она касается земли на расстu янии
3 чи от корня. Спраш11вается: какuва высо1а после
сгиба ни11? ».
Применяя к прямоугольному треугольни ку те
орему Пифагор а, получ~1м , чтu высота бамбука
посл~ СГl'!ба11ия равна 4 11 / 2n чи.
;)l
История математики
треуголы-rиr<а, на 1юсемr, треуголы-1 ш<о 11, рав
ных между соб()й, н на маленький 1ша11рат со
стороной, равной разности r<атетоu.
Легко заметип" что большо11 квадрат на сто
роне а + Ь составлен из кв<1драта на стороне:: с
и четырех прлмо-утолы1ых треу 1·ш 1 ью1К.ОВ с ка
тстамн а и Ь, а значит,
(а+ь/-=с~+2аЬ.
С другой стороны, па ::пом же чертеже нетру71-
1 ю разглядет 11 и доказательство и звестного во
нсех дрс::нних цив1-1лr1з:о11\1н1х ал 1тбраическо1·0
тождеств;:~
>
>
'
(а +Ь)-=а-+ь- +2ah,
откуда следуе-1·. ч ·r·о
с.!.= с12 + /J:!..
Этот вариант реконструrщи 1 1 докааательства
приrщцлс1ю1т известному математику Б. д Ван
дер-Вардену. Замстнм, что существуют и друп1с::.
***
Вплоть до xrv н. математика н Китае ра:.щи-на
лась как сис 1·сма стrоги:х праRил , предна~1-1а
че1шых дт:r решения :~~щач по ::1рифмет1 1 ке ,
алгебре и геометрии. Китайская маr~·ем:пика
rre была изолирована от науюr Индии, Средней
Аэии, стран Блюю-1е1 о и Среднего Востока, что
подтвt:рждается сходством многи:х задач и
общностью Mt:TO/\Ofl их рt:шсния . Через =~ти
страны матсматию1 Кит:1я оказала влияние на
мзтематику среднсвско1ю 11 Еврuпы. Однако
м11оrие открытня r<итайсю 1 х учёных С1али нз
оес~·1 1ы 11 Енроттс уже noCJ1e то r·о. как свропс~:-щы
пришли к 1111м саrvюстонтелыю.
АНТИЧНАЯ МАТЕМАТИКА
ФАЛЕС И ПЕРВЫЕ ДОКАЗАТЕЛЬСТВА
ПоЖ'JJtуй, }lату поя1:шс1-1ня маТС'v\атики к;1к 11:1-
~-кн МОЖШ) OTT[lL'f\CЛJITb ДОВО!IЫЮ тuчно - \! /В.
/\О н. э. На 11pn·1яже1-11111 20-30 прсдыдущ11 х
веков н;~роды ;1.pem 1е1 о Вое.тока сдел:1л11 нема
ло о·nч1ы·1 нi1 n арнфмет111\е, 1 ·ео1\1стрm1 н эс~ро-
1юм1ш. тю сдшюi1 матем::пнчсской I1аук11 01111
нс создали. Грс1~а,·1 же это удапuс1, н те'-1ешrе
одног о с1 олепш, что ло сил пор кажется чудом.
l la полтора l"I Шlетия раньше - н ccpCi\IШe
VIJI в. до н ::i. - 1 ·рск11 ш~рсж11 J 111 насн.>ЯЩ)'Ю
ку11ь·1 урную pc.:t\OJll(ЩI llO. у HlL'\ llШIНI I JICSI сноi1
;iлt.j1:iк11·1 , 11 ю 11очанп111Л глас~ 1ыс буквы . То1 J \:J Жt'
()1,1л~1 со:ц1,а1 11.1 1юЭ\ 11,1 ~ иm1.t;lЭ » 11 <·()JJ, 11ccc}J·>
Гомеро1~ск11i1 :"llIOl 1ю. 1110111гл 11рLюб1_ц11л101 к
ку.'11.~)ре ~кем , ;\аже 11с·1 ·рамот11ым. Re,(1, ст~1х11
11струю ю RЫ'УЧПТL r1:111зус·11,. В ту же :=юnху 110: 1-
1111юп1 Олr1м111111сю1с..: игры. На них каждыс
чстыре 1·ода встрсчат1с1, шшболсс aкт1lli1iыe 1J
11pocncщc1111h1L' 1р,tжда11с rоро;щн <Jлла,r(ы (таrс
11:1::н,111ал11 с1~с.нu рuд11ну самп r1к·ю1).
<..: ссрсд1 шы \.·11 1
11. дон. э ()ыtтро росло
ЧJJLJIO 1OpOJ \011, РСО()с1 шо Н ЗЯ ~1С JpCIOJX r<OJI0-
111 IЯЛ . R !IOHCK<!X новых 'i('~ll'}ll>. пr111 ( ЩНЪIХ ДllЯ
ССЛЬСК()!'() хu:ш\1С111::1 . CQ'l' H\I l'С•Н.:Й пcpcпpailJIЯ
J lllCb ia мuрс 11 ССЛJJЛ11tъ 1ю н<:сму нобl'рсжью
Срсд111смщJ1 о 11 Чср11и1·0 морсt'1 - р>щом с ~н.:
cr11ur'v111 <·нарнар~1м11 -> ~;)Jш шrы ·шакомшшсь с
кут.турnй соссд1111х 11арщtов. уч11л~1С11 у 1111х 11
сами пытат1п. уч1пr, нх. /К111е:111 горо;кюrх
респубJJ 111< - П()Л11СОI3
-
еЖС{\1 ICBI Ю Обсулщалн
па улн.Цах 11 площ~1х uce nолноваnuше 11х rю
просы: от Dидов 11<.1 Урожаl1 н тн.: трое1н111
uкрсс."п 1ых варnаμон до rювосте~\ пр1 шс~ёш !bL'\
'{ас:::1ж11м11 К)-пцам1r
C:-t м hl(;" 11 H 'J'(;"j)t'Cll hl(;' l l:JIН.:C l ' I ш J] р1 IXO/ (l IЛ 11 11:J
l'OCYf \<I рстн Бm 1ж11tтu Восток;~ - Ji1 11п·1 :1 н Лс
снрш 1. ;1 ПОСЛ(:' J'HOt'Jl ll Aн.:1 tp1 1йt:KU l'(J [\'1(lCTK'1 -
1-1:-111 <щt'1111н1шс\<.:10 ш1щ~.снш1Ванн, ю11r1r111 М11 -
f(Ш1. 13 cepe!ll111e \/111. i \tJ r1 . .:1 . 1ке :о1· 111 3t'MJ111 r10-
п.1лн П()/1. власт1. nе1ков, 1щт ор1>1t' yC'l ·a1 Юti11ю1
Г1р0L11IЫЙ ~tпр в сuоей (JГf)OMIIOil !IМПср1111 .
Tcnc..:pi, м1ю111е лю6озн:пелы rыс элт.111ы 11~1 e
J111 воз можr10ст1, бсзопас~ ro rr)- 1ешествоnать по
зсмш1м llcpc11дc1<<J1'1 державы: О/\1111 - с торго -
11ы ,,111 1l(.'Jш ч11 "~ру1 ш.: - н н.1;1;с;1у;с 11prio()1r t1111 ,ciJ
К VlyдpOC'J'IJ l'l 'flll IЯH 11 11aН1IJ l()l-OIH
31
Иt тория матем.пики
<J);iл er 1равюрu
Hd \1!>ЛИ XVlll 8
Вср 1 1уrтпкь /\омо1\ такпй 11у·1·е111ес"п~еr 1 1п11<
Rcerл;a rю:~буждал Ж111юf' J1ю601щтст1ю соrраж
,rщн. Но не JIO 11сём ему nсрили 11а слово. ll<1 -
п рш•1ер. от1 rоnорил, будто n ёпште стоят
рукопюрl!Ыt' ХШJМЫ llЗ K<IJ\!JIЯ rробIIИЦЫ
.Щ->t:Нl-HIX царсl1 - BbKOTOIJ в 20() 1/JШ 5UU лuк
тсй. 1lсужt:ш1 011 сам 1вмсрил 11х выt:uту? К;:~
ю1м пбра:юм' Пус1ъ :щкажст, что его слова -
нра1ща! И сщё: он ска:.щл, •1то мудрые t:Г1tптя11с
)":VICJOT nrt:,JJ.CKa:'la'l'I_, срок будуЩС l 'О ЗaTMl' I HIH
Лу11ы 11111 1Спm щ::~. Пус1ъ пбъяс111 п. как от t11 этn
лелатот! И 1шгда мы у111щ11м nчере,11,1юе затмс-
1ше 13 нашем 1·ородс'
Ви,1п1мо. перnым нз rреков. кто научнлся
убсднтслыю отвечать на подобные вопросы,
был Фалес .Милетский.
Фалсс (OKOJIO 625 - OKOJlO 5·17 до н. э.)
роюшсн и вырос н 1uрсщс М 11лt:те (л.rенней.шем
1·речес ком цснтрt 1~ Мащ)i1А:шн),1~оэтш.1у его
и на:.ihrнают Фалесом М 1 шетским. На собстнен-
1 юм корабле. rружённuм l'речсскнм11 ·1оаара
мн, Фалес плавал по Сре;~иземном:у моrю Осо
бе нпо удачно он нё.11 торгrmлю плиnковым
маслом, чем нажил огромное состшшие. Бы
вал Фалсс в Епштс, Ассирии, l3aвrrлo 11e. где по
знакомился с м атематикой и астро rтомисй .
Именно этим наукам он посnя щал с 1юё сво
бодное время. Кроме того, он был философом.
:-iакон одэтелем. Е1 ·0 считают псрRым 11 ~~ семи
Rсликих мудрецон древности - оснонателей
греческой 1<у11ьтур 1,1 н науки.
R ')8'5 г. тr.о п. з. Фалсс пре.дсказ::~л сол11еч1юе
затмение. В то nре.мя шла 1юй 1 щ 11, 1щг1~а npek
сказание сбылось ( <·11.ет-11) преврап 1лся в ночь",
по словам исто рю<а Геродота) , воины в страхе
поброса.'ти оружие 11 ра:.iбсжал1къ . Затмt.:111 1 е
быдо раl'цснснu как 11μ~:1~знамснu11анис, и
11u 1·11 щ прскр:1т11л:1<.'h
J !о ttl' астро1юм11>1. а матсм<iтнка ст;uш лю-
611мым эа1~нтнсм Фалtса . ()н 6ыJ 1 11ер111,1м. кто
1тач;111 дока. J ы 11ат11 11екс1л >рые 1 ·еометр1.1ческнс
1 1 ре;tл()же1тя, ЧП) прсnраттшо rt:o:v1eтp1rю
11з свода практпческк'( праиил в nодт11-1ную
11а~1~·.
J\110:,ю то СIЩЛЬЮ) угодно ра:{ убсжда'lЪСЯ П)тём
нзмсрсн~J!"t, ч•1·u J(H:t 1н.:рт11~.:а ; 1 ы-1 ых у1·ла раш1ы
межлу собоl1 . I::сш 1 OJ\I rн 11:-i ш 1 х со;~ерж11т 60°.
то н ,i1py1лi'J 't'C >Же. CCJ\11 н OДl-IOM 12° )О', то 11 н
другом стшр-.кu жс, 11 т. J\. Но 1щру1· /J.JIH очень
малсны;11х углт1, которые ·1 ·руд1ю 11змер11тъ .
:'JTO 1 1 е- т;:~к? 0 ;11 rако ~м():1р1пелыюе рассужлс-
11не - nьшод (шш , как "чы те11ср1~ 1·01юр11:v1 .
до1сазате.11ьсшо) позJJОJJЯет у11зсрждат1,, что этот
фак1 верен веста и щ1я всех утлов.
J<аю1м же обра~юм проводнл Фалсс l'BOII
док;t:iатеды:тиа~ Д.нл ::Jтo!t цслн он 1 1 c1ю11hJOВ:.l.'l
~движ<.::111 1 н". Есл 1 1 J(BC ф111 ·уры ПJчни со1:1мtт
тятся дру1· с друго.'\1 rюсрс.;дсттюм /\НТ 1жс1тт1я, то
:-'JTII фill~'PЫ 0/\1!1-\aIOШl>I, рав11ы
Иrvt<.::1-JJJO таю1~1 П)~l't'l1 Ф:~лес дnк:~зал rя,1
псрнт.1 х ·1спрем 1·еоме-1·р1111 . F.cm 1 п;юскос1ъ по
вер11у1·1, как тнёрдое 1~елое 1юкруг 11ското1ю!1
точrо1 О па пол-оборота (lHO"), го луч ОА
nере 1'щё·1 n его продолжсrmс UC. J ! о тогда ясно.
что стороны од1ю 1 ·0 и~i двух вt:ртllкальных
углов как раз перейдут в стороны друсоl'О. т. е.
:1ти два у1 ·;ш соимесштся Знач11т. вср·1нк;uтыrыс
уты раины ( рнс. 1) . ' l't:\1 ж<: с1 юсобом Фалс:с
нuка:з;ш , что днамстр дt.::.111п кrу1' попuлам, т. с:.
дна полукруга р:.шн 1 ,1 м~жлу co()ofi.
Ko 1 1eчJJO. те 1 1ер1,, 1.:ог/(а с ге()метрпет1 знаком
каждый шко11п1 1 1 1 к, кажется-. ЧТ() nсё это абсо
лтот1rо очсRrrд1ю. Однако до Фалеса доказа
тельств просто не сущеспю1:шю! Точно так же
ИЫI'JIЯДl!Т совершенно еСТССТJ3СШIЫМ, ЧТО гон
чар делает ~.;руглый сосуд, пользуясь нращаю-
в
Р1к. 1.
Рис. 2.
щ11\1t :.1 ~ 1om11\01-1 . Но человек, котоμый первым
llj)ll1I\ м.1.1 .но, 111 l t: IКЯЮ IX сом1-1енпt 1, CUBl'f)IllHJI
1e1111,1JIЫIOl' ОП<рып 1 е.
Ф.1лсс д<жаз,ш раnе1ктво упюn 1tp11 ос 1юна-
111 r11 ращ юбt:дрс11нuго трс}толы-шка. А р~1ссуж
;1ал 011 так ра1шобс;~рс11н1,u'1 •1рсу1·олы111к c 11м
ML"1pir< Jl'l I OTH ()l'J ITCJI 1>1-1 0 (1 11е:сект рт1сы y 1·11:J 11р11
н1.:р111н1н.:, а з11:1чит, 11рн псре1·ибан1111 чсртt'жа
rro Ci1ю:t 1\'I рщт у 1·лы 11ри оснон:111ии сон п~щут
(!HI( 2)
< >н ) ст:11ю 1 111л 11 оюm 11 з прпзн~шоu ра
11с1н 111.1 1 ·рс::у 1 ·ол1 .11шюn: еслл ,тша треуголыпша
11ж·ют р.1n11ую сторону и дна раrшых )Тл~1 . np11 -
.1e1Jющ1 1х 1\ э·1 0 11 стороне ( рнс -~). то эт1 1 трс
~тuлы шю 1 p .tl!l!(,I , l lo пр~д<ШИЮ, он 11p1tMCllH.'t
А11т11чн.::~я мaтe.vtd r11ка
ПОI Щ/11.111.11', чтобы oпpe;\C!lllTb p:IClTOffill lC ДО
IIO\X\\)JLЯ !} море
11 )' 11. 1'0 JIC'll IO. llЗДО ОТ\\СТI!ТЬ ТО yTRt'pЛ\,.'ll
IIJIC. r.:uтopoc мы 11 сеl1ч.1с н:1зын;1см 1 1..·orc.\щi1
Ф.1:1сс:1 t.:C.'111 н.1 п, 1нu i1 <. юроне ~т;1а от.1t)Ж111ъ
р:1нньн: 01·1к·~ю1 :1 3:tтсч Чl'рсз концы эт11:s от
рс ih:OH llj)OHl'< · 1
·11
ll:IJ>:ill!JC. lhfll>IC 11ря .\J ЫС, J u 11:1
нторо1·1 е1оронс)1 ла 1 1р11 псресечс111 111 с эт11'111
11p:.1~11>\\\ll \<'\КЖt: обра:~ую 1 ся fЩШIЪIС '\1eiK,\Y (0-
f)()JI отрt":Н\11 ( р11с -4) KaI< ;щказыnал теорему
Ф.tлt>с, мшыю толыю дога;1ыnаться. l \ o- nr1д11 -
J\I0~1)', oir 11 здес1. 1юль:.юва11ся тем же 11р11:та-
1,ом r:ше11C1'13:l ·1рl'угол h l uшо н.
"'...*
Т:1ю1м 06р;1 .юм, Ф;шl'с 111х: 11ратш1 J\{lCIНllOIO 11
снящсr 11 ry10учСностr,нr1р1.:;1мет с 11оро н и ;~ока
"1:1·1·с111,(."1'н l /скушё11 н 1,1е li с 11nр·пнн~ ы х сос1 ж·~а ·
111\Н ~ 1j)tКll щ· .1нал11 ; 1ото 1'1 П()j)Т>! СЛОЖ IIЫХ 1111 ·
1е-л, 1 t.:ктуалы11.1 '\ 11гр 11ро11е ш:~х,1ат С лёгrюf1
р) ю1 Фалес<I гс()метрня оказалась 1 1ервоt1 та
1,ой 1н·роf1. Вскоре он~1 ста.1а почl"7пым за11.и
n1с;\1, 1<ак бы 11:н.1.1 ю11аnьным I:ШДv\t спорта -
-~
В".Lf!J
История математики
нараnне с ттолитико\1 или Ол~тмпнйск11м 11 ю·
рэмr~. В геометрии rтояш111ись мастера. кото
рые nрсвзошлн Фалеса н па'-rали открьшатъ
такие математические истнны. ~юторые даж:е
нс сrщтtсь их прсдшест.вснш 1 кам .
ПИФАГОР И ЕГО ШКОЛА
Be;i 1.1ю1l1 дрс111 1 е 1т>еческ111-1 учё11ыГ1 Пнфагор
ролнлся 11а ое1poneСамое АVI в до 11. э. В ~ю
:юдОLl'И побыnал в Еrиnте, где yчи.rrcJ1 у жре
цов. Говорят, что ori был допущен в сокровен
ные свяпrт1ща Пгнnта, посстнл халдеnсюrх
мудре 1 tов 11 псрсJJ,1\СТШХ магов, Ок01ю 5:$0 г
до 11. э. Пифагор пcpcexa.rr н l<рото н
-
r-речс
скую ко1юmnо н LОжно 1i Итал1tи , 1'дс основал
так 11азь111асмыli п11ф;11·ореltекнl1 сою:з (шн1
крптонскос братство). В сферу 11 1-11еrн.~со н
чле 1 юв сою:-1а нхо11нл1-1 на~rч1 1 ые исследонапня,
рел 11 г r юзпо-философсю1е иска 11ия, 1юлит11 -
ческа~J деятелыюС'1 1,. Онн вели суровьп1 образ
П>~фагор
1 f'•IRk•p.1
11~ п~r~1нно11
•11•11и
В 1юt~1· иже 1 L1-111 Вселсююл чt'rез математи
ку п1·ром 1-1 1.1i1 ша 1· нпсрёд сделзл Пнфа 1'ор. 011
первым ;i;:~меп1 л, ЧТ<) с 11ла п tдн1 1 ст1~0 1rаую 1 ос
нова н ы 11а работе с идеалыrымн объе1стам11
llanpимep, прямая линня - это пе тетнва на
тянутого лука 11 нс луч cIЗera: осдь они имеют
11сбuлыную ю11щпну, а т1ния тuл щиr 1ы не пмс:
ет. То же относитсн к 1·сомстр 11 чеошй 1 1 1юско
стт 1 и nоверхнос11 1 волы н споко 1'i1ю.\11 о::н.:рс
илн к ч 11слу '1 [1 пят11 пальцам на руке. Илсаль-
1 1 ые nбъскты (буд1. Т() чнслз 11лн ф1 пуры) встре
чаются тоm, rю н r.1 атема ·п 1чсском рассужд<::ни1 1
И только /~ля них верны строгие 11ауч11ые выrю
ды! Поэтому мзтемат1 1 1<а 5Шлястсn как бы «вто
рым зрением" человека : она открывает раэуму
идеальн ы е объеk"'ГЫ, 1огд:~ как обычные чувства
1'оворт· нам и своikтв;1х прпролных тел.
ж11:~ни , rrревыше nct1'('> 11сш 1m 1са мообл:цщ11 rre .
смелос 1 ъ и коллектниную лr 1 сц ш 1Jппту. Ппфа
rорейцы жилн вместе, у 11нх было со~месгно\
Нi\1)'Щес1 во, и даже сван открытия онн счита
;т общим достолш1е.,1 .
Дся'1·сльнос1 ь сою3а была u.кружс.на тайной,
rюэтому ннк~1х т<:кстut1 от раш-111х 11ифаrо
ре 1!1\ен нс остшюсь. Крощ.· ·1or·o, 110 TJ1:.lД\11(l t H.
0 1111 вес открыт 1 1н r1рн1111 <.: 1,111ат1 П1 1фдгору, ()
котором уже 11р11 ж113н11 XO/(llJНI 11е 1 ·ен!(ы. Кто
на самом деж: я 11; 1 нстс я автором тп1·0 1111и тю
гп реэул~,п1та, пеи:ше ст1ю.
Пифзгорей~1ы 11азывал 1 1 собстnс111 1 ые исс.11е
~ова.~111я <· математ;н, ч·1 о 0:1пачаст <- Ш1ую 1», 1.1
делилп 11х на четыре части : арпфметику. rео
метршо, ::1строноыню 11 гармоншо (уче1 шс и
музыке). Гл;:~вrюй сч11л1л:1сь ар 1 1фметшс.1 -
наук:~ о ч 1 1сш1х. 11менно 011а т:ж;и 1 а 11основе11
1·еомстр1r11, н ;,~стрт-юм 1111 , 11 1'аrмо111111.
АРИ ФМЕТИКА
Ilнфа('()рей11ы nредсташ1ялн ~1 1 1 сла как сово
~-..-у111 юстн точек образующих н:ометрнчсс 1ш~
копфш·) ращ11 1 - r1Jподоб 1н: р~JСутrка из 1<а
\rсшкоn па зс,,тс. Т;,~ю1111 обр:1зо11·1 . 110д LШС
ло.ч ОIШ I IOJ(p:!З\'\11t.: Ha.'llr f,\.UНJЖ<.:CTHO t.:ДllJ-11\Ц'>
(1/1(!•1 . "-ар 1 ттмt)с.») 11 11r11 ~>нан:11111 тол ы<о J(C..'lnte
Ф11гурнt.1f' •ои< Лd . 1рруruл 1,~1ые, квадратные.
nрямоу1 ольныt:. пятиугольные.
tюложительпые (т. е. 1tатурады1ыt:) числа.
разделяя их на чётпые и нечёт11ые. (ILозже
I1'1ато11 говорил, trтo арифмепша есть учение
о чётнuм и нечётпом.)
П11фа1·орейцы доказали псрn-у10 теорему те
ори 11 rtелимост и: 1tроизв1:дение двух чисел
чi:'THOTO l '[J.<11 1 Т'ОЛЫ<U'l'О!Ла, КОt'Да чётнопо кр:.~й
ней чср<.: одно 11з ннх_ О11н постаннлн такжt"
задачу п r1ахожденн11 совершенных чисеJ1, т. t:.
члсел , ран~ rы х сумме своих 11<:.л 11т<.:л е1~1 (см
с1·атыо «Соверш енн ые и дружестне111 1ь1t: чисжн).
Ед11ю1щ1 с читалас ь педслимоr1, у 1 1 её 1te быпо
~доле11» . Uместо этого rrифагоре1'п1ы расс~1атрн
валн ОТI10шс1шя (т. е. про порции ) целых <rnccл.
1{ пр11мсру, они мопш сказать, что 2 точно так
относится к 3. как ' ' к 6. Говоря современным
языком. 0 111-1 построи ли теор ию раци о 11аm,нf,1х
чисел как теорию пар. Её и зложе ние дошло до
1-1ас в «Началах? Евюв1;~~1 (111 в. до н. э.).
ГЕОМЕТРИЯ
Остаётся 1Lеизuестным, сколько и ю1ю 1е имен-
110 аксиомы положили ранние пифагорс~щы n
ос нову свосl1 геомеrрип, 110 nce ою1 относи
лись к ш1;,~1-1нм е 1 рин 11рямоли нейпых ф11tур.
Изуча 1шс1> свu й стн а трtугольн111<ов, прям о
у1·u11ьнико1:1. нараллелuграммuн 11 дру1·их шюt
кнх ф111'ур, сравниналнсь 11х шю11(:J)\I1 . Пен ч~uю
их 01с:тему зю1нv~i1 докззательст1ю з 11ам1::нитоl1
l'еорсмы П11фа1·ора, котор<UJ до этш·о 6ы11а 11.J-
вест11а лишь как факт для некоторых: частных
случаеn. Трудно переоцеIJ итт, з11аче 11не тео
ремы Пнфагора (см. статью «Тr>еуголъник, nро
стеl1шш·1 и 11 сисчерпаемый» ). J::ё обобщение
и сспщня лежит в основе определения: всех
ме1 р 11ч есю-1 х 1 1ростра11ств.
Мож.но утверж;1~1ть. что и в стерсометрнн
nифа 1·орс:1lцы дuсп11 ·m1 .ш:Jчнтелы-1ы х успехов.
По сtнще1 t'ЛhСтву грсчсскот нстори ка и фн
лософа 'i/ н. П рrжл~1 . нмt:нно uн11 Л()стr1)ю1н
ш1·1ъ правилыrых м1юсо 1ранннков: тетраэдр,
Анти1.1ная матем;ника
куб, оr<та эдр, дсщекаэ1~р, 1 1 косаэдр (см. стат1.ю
"Мrюгогра1 шию1" ). Правда , м1 юп1с соuремен
ны е исследователи сч.итают, что ll11фa1·opy
бьuш и:шестны ли1m, куб, тетраэдр 11 додекаэдр.
а uктаЭ/\Р 11 11косаэдр открыл Тсэт(;т Афш-кю1й
(IV в. до 11. э.) , таю1нтливы l1 уч е ник пифаго
рейца Феодора К11ре1 1 ско 1'0 н Плато 1 1:1.
АСТРОНОМИЯ И ГАРМОНИЯ
Пифагорейцы считали. что Зс~шя имеет форму
шара и наход 1 пся в центре Вселенной: ведь нет
нн ка.ю...L'\: оснований, чтобы uна бьmа смещена
и л н R ы'шнуrа .в ка1<ую-то о;сну сторону. Сотщс
же.Лу11;1и11нтh11J1анет (Меркурий , Нснсра. Марс,
Юпитер и Сат~'{J н ) днажутся 1юкр ~т Земли Рж·
стuн11ия от них до нашей rJ.1Ja11eты таковы , что
т1и как бы состаяляют ссмне1·р}'11r 1 ую <1рфу, 11
при их дR и же 11ш1 11озн 11к ает прекрасна я му
зыка - музыка сфер. Оf>ыч но люд11 нс слышат
её из-за суеты жиз1-m, и лшuь после смерти не
которы е из !Jl[X смогут шклаюпъся ею. А Пи
фа1·ор слыш;ш се и прн жизни.
llифilrop l му.1ыкальнuй шкмой. <'Ppr11 м~'н1 фpf't ~11 Р,1фнл11
• AфliH(KJll IJJKOЛ,1 •. l'i 11 Г.
Истор~1я математики
ТЕЭТЕТ
Теэтет, молодой афинский матl:'
матик, имел 11еобык~юве~111ые спо
собности и при лом был ве<.ьм..~
скромен 11 лружелюfiен. Великий
философ Сократ говорил, что Те
этет несо1V1нснно прослuвится , ко
гд;:~ достигн ет возмужания. Н о его
жизнь оборвалась рано. В 369 1.
дон. э. ТсэтС'т был смертель110 ра
не11 на поле брани под Коринфом.
Умираюшеr о героя 11риое.ми в Афи
ны и пели хвалебный г имн о том,
как храбро он бился в сражении.
Несмотря rtJ 11едоl\rую жиз11ь,
Теэтет оставил глубокий Сl\ед в
науке. Он развиА учение о «Соиз
меримости• и лал •\ОказатеАьст1ю
тстра:Jдр и лолека:>Лр) бым1 изу
чены nифаrорейuам11, а два послел
~1их (октюлр 11 11косаэлр), nо-вили
мому, OtKpьtA Т~.:нет.
ирраuиональности чисел ~2, , 3
и других, причём как в алгt>браи
ческой, так и в геометрическои
форме. Это былu совсршен~ю но
вое направление в математике.
Теэтету при1~амежит и зас-луга
завершения учения о правильных
мноrогранниках. Их на3ывакл- так
же nАатnновым11 телами , хотя их
открыл не Платон. Три ю них (куб,
Стро11 арфы доmксн был подчиняться 3ако-
11а.\1 арШj)~1('1 ИК.И. в чаСТН()СТИ. к~к ()ОНар~жи
JШ п11фа 1 ·орейцы, так1tе муз1,1ка111,н1,н: нн·1 ·ср
н::u1ы , как 01<1"-lв:-1 , ю1и 1 1'1";.i и кв;1 рта . соnтнетствуют
:знучанню 11::irы од1111~1 ковn 11атяr1 утых струн ,
д;111нh1 кот()рых находятся в отношен11и 1 • 2,
2:.~н3. ..J.
Rce :<1тн от!\рытш1 н привели rn1фarnpefщcв
к ·11f{ee о том, что «Rсё есп, ч~ 1сло», т. с. :1аковы
прнроды - не что шюе , как закон ы целых
чисел 11 их отношений.
ОТКРЫТИЕ ИРРАUИОНАЛЬНОСТИ
Кпачале пифагоrейцы пол:11 ·а1ш. что отноше
ш 1я л юбых физнчсских 1JЛJ1 гсомстр11чсск11х
lleJlllЧl!ll МОЖJ 10 1З!~!ра:з11·1ъ ()'f'IIOШCliШ:l."11-111е,1 1ых
ч11сел. в ЧаС"ПЮСТl f. ШПI CЧIITЗЛII, что nce от
резки сонзмеrr 1 мы, т. е. 1с1коnы бы шr бьuш два
отрс:зка .1В и CD. <...-ущестnует такой отрезок е.
который целое ч11СJю раз укнадьшаетсн каr< по
длиr 1 е А О, так и по длине CD, а ЗIJачит, rсомст
р11ю можно свести к арифметике.
Однако uскоре ш1фагорейцы сдеш1J11I oт
K(JhLT11c, которое перевернуло все и.х взгляды:
он 11 жжазали, что отr rошспис ,r1rтa гонат r к сто
р(!Не к1:1адрата нельзя выра::н-п ь от1rошенпем
l\CЛhl'< чисе ; 1.
П<х1же fi1,uш 11а1~ще11ы н J(pyr' 11e несои :з."1ери
мыс отрсэю1. R сщстноrтп , Ф<:одuр Ю1рснсктri1
обш1ружнл, что сторон 1,1 кн:щратон с пm 1щадя
мн :), '),6, 7 ,R, 1О, 11, 12. 1~. 1-t, 1 '>11естrзмеримы
со сторо1юй ед11 1 111ч1юrо кв:щрат:-1 Л Te:::i-reт
/\Ol<(IJaл, что если nлоща71ъ кналрата выражается
любым целы.ч 1Iекnадрат11ым чнСJЮ!'-'1 N , то сто
рон а е1'0 1 тссои~1мсрн:ма с с,г1иrпще11. Нны~1и
слона~1и, было усr:шовлепо: сели .'V Фа;, то \ ~ \ i
нс 1:1ыр:::t;.к:н:тс.н ннкаю1м р:ш,1 ·юнат, 1 1h1 ,\1 ч 1 1с
лом - он ирр:щ1ю11~uтс11 (см сгатыо «Ирf1:1t\1ю-
11 алы1ые ч1 ~ела ~).
И тогда нре111 1 е1 ·речесю1е м 1 .1сл1 rтел11 .1:11<.• rю
чнш1, что ар11фмет11к;:~ 11~ может служ11 1 1, ос1 ю
uoil для ~·еометри11. Геометр1 1ч есю1с 1iem 1ч и1 11.1,
решилн ош1 , 11меют более общую прнроду. че.ч
ч1rсла и 1rx отrюшешш. Jначит, в основу мате
мат11ю·1 следует полож11т1, rеоУ1стр1по!
ГЕОМЕТРИЧЕСКАЯ АЛГЕБРА И ПОНЯТИЕ БЕСКОНЕЧНОСТИ
Геометрическое облачеш rе придало м:пемати
ке 11еобыююuе1шую красоту и ~101юш111юсть.
У•1ение о решени:и уравтrениН ла п сама ариф
Уlетика приобрели rсоыстричсскую фор :му
Именно .!еамет/mЧl'СJШй tl.llгuбjюй назьшасм
мы теперь 1 у ч;:rс1ъ а11п1ч1 юf1 математ11ки. 1<() -
торан затптмалась нсч11слсrшем отрt:эков н
площадей.
Осrювы этой 11ауJ<и был11 изJ1оже11ы е «На
ча11ах" ~ню1 н1щ. Там рассматр1111аются uтре:жи
и опрt.:Дl'ШlЮТСЯ арнф.Мt'ТIТЧССЮll' ()ПСр<ЩШ!
шщ 1111м11. 1-lанрнмср, f\t1a uтр<.:::Н<:t складышuш,
11р11станляя 0;(111-1 к 1\rугuму, кы<1итал11 , у611рая
11:~ 60Л11!1Il'J'O ОТ[)l'З Ка Ч:1С'l1>, р:1rшую J\•\C!IЫJICMY.
ПрО11зве;(е111 r ем f(вух отрс:.~ков Н d:lЫВ<!лся пo
crpocrn rr.rlr 1rэ 1шх прямоуr·олыпrк, трёх отре1-
1шв - пpm.юyroJf ы 1ый параллеж:mmсrr,.
Разумееrся, rrc 11~re110 смысла rоворитr:, о сло
же1111н пря ,'>Ю)ТОm,rтию1 11 отре1к::1. Поэтому пс-
1 шслс:шrс. оrrрсделёнrюс 11 1 ·ео.~v1с трнчсской
t.tJJ r'cбpl'. бьuю ктупе нчаты.м». Псрн~·ю с-rупL'нь
(."О<."J'а кюшн u· 1·рсзк~ 1, вторую - 11лощ: 1;tн, тр<.:
·r ыu - с >бъ<:м ы . О 11po11.3f\tJLl' HIНI ч:<:"t' h1pi:'x 11
fiOJICl' отрезков речи нс шло, BCJL I> НСКО:З\·ЮЖJ 1О
11рс,~сгаn~пь r\m 1ypy, имеющую более трi.'х 11~
щ:рс1111й. И11стrумс1 1 тзмн, с 1юм о 1ц1>Ю 1ш·1·ор1,1х
р:1:1рсшалос1, 11 ро/\tдьrвать rюс.:троt'11ия n rсоJ1.1 е1 ·
рнческой :lЛГсбрс, стат~ ц нрку.тл, 11 J 111ш:·йкd.
J3 первом же предложении ~порой юшги
• llачал·) даrто гео.четрнчсское дока3~1 тсл1,спю
распрсJ1ел 1 пслыюr ·о (,1.1,истrнбут1·1нно1·0) :за
кона умножения: L:сл11 11 рнмоу1·ш11>1-1 1 1к 1 ю
стросн 1-1:i отрсзках а 11 /) ( рнс. 1) 11 ()/tн r1 и::~
н11Л, скажtм а, р:1Ссечёr 1 на час 1·11 а= а, + а~+
+...+UmТО
r1!1=(а,+а2+...+С111)Ь= t11h+tl2IJ+...+Cl,/J.
Перехоf( к гепметр11L1tскому языку по:шолнл
uперJЗые л.ою:tзать 11 некоторые алгебра~ 1чесю1с
тождества, н:шримср в~см 1!зnссп-1~10,форr-1улу
КR:~лрата суммы (а+ /J) " =а · 1- 2a/J + ь- (рве. 2).
Oi.i~m щно, что п:юща;\h квадрата, 11остросн
нот 11а ,~, орсн-1с а -1 fJ. склщ\ы нас-1 сн 11 :~ шющ:t
дс~'1 ;~ 1~ух кв:~др:П(Jll ( 11:1 сторо 11 с: п 11 e1·opo11t: !?),
:J таюкt ,'\Н~'Х 11p>H•I0Yl'OЛЫlllK(JK, llOL'l'J10l'llHЫX
11:1 11их. Пр11 чём спраnеюн11юсrь тожцеС'nsа
;о·:шовлепа rr,11н нюбых а п Ь 11ез:1вист1мо о 1· 11х
ко111<ретных ГКЛllЧ[Нl и ОТ того. COllЗMtpIIMЫ
01111 нт r нет.
З:иачи. экшшалептные ю~адратным ~1Jанш:
шrям , ·~·шоке: полvчпJ111 1 ·еоыстрпчt'скую форму
(/
аЬ
/)
/1 аЬ
(. /11
Ри~. 1.
f't1L. 2 .
Античная Mcl 1· ~матик;1
11
~:)!X'll"" "
1fi1mtl11ш1 J~ro No1!• dladqti <:< ('IJ(ID ""'•нлшn
1npf.i fi r:t'qt1U cntl)u;,\ (1.tiUCfiJ (ltJJdt \Nufu\I~' ir.co .
ФЭ1~ Lн1а,а.ь.01111 1а 111.0.с.-:.1.tl~.d b.Ot.QI;' .'йо~ q;,f11q ~i
tl'lt fiX W·~a.b.111(cqot11 <:1.с .ь.f.t\\llii (l'\ lн-1qD'fщ11t (~ Фr11101
11:11 \11:11Пti!t~q; tжr;n1m p;iп1>11n qб va~:i111 PQ.tdx!.olk1w- .c .s ., ,{t.b (qщJ.1
11J11ur.:1.c.t' b .f .6!111tcrlu111<JtUf,t <~tn.;.a;.b.(tl.fQ3 p p:..:1mfT.amqь М <т«t/ •
ftit.l.•111 tot111n.a.ь.щuб"qD(u q.~1"11.k .11.1 ur1•11CCJ \;t6t.•.t.иq1 tr.k .1 о.Ь .
1щJ6f1н~шшict.<1.ti 1p('C.-'6(J.,k .юo111111\ir<N ~.h qg.11u~-a.b &n011111'8'
ст1d qr.k . t .. alt .IUt t'\4U3'o.~pJt« \\':1;dr( pюpo(11n1t1.
1J:>:"P"fino ".
fo<r1tt111C'a tn t'IЩl~'Wt'1!0tU11~ 1Jlt1~ qt\fitiq: ~rшu t~
001Mlt<'tntn .rrё cquit <Тltb~q<~C<Jmt dnld< p:lr
1·
1 111ulrt.wш.
°1P':"poMto · - 4
Э fi.it}lf f&llt"ll~tf} VШI~ blfUC'ltOll11tlud Q"l:t:tlDCПI ron°i
c1p(J f1r-.c:quu i: Ь1очcr i)C("m\1muJq; rt!Gl l~tpl:\ f11tc.
r1"1al1tт;s btt! JE.-1~('( ma111fclt Uf q, i ot 4'ft 'i .1tl) \1u' IDQ
rk1roQIHtG t1Шf11(1('Т ft\\\(~rncdi.11 (ш1t SПlbC quзdr>atC'.
([!:';t111<11"'J.Jl,b.t1rP1''11i ·1.ai.c~.b.t toltoq•ф11drtl11n1 rmuз
11.Ь. щrJ1t1 a!~J.Юu", qa1'!:.Jtц_'r OU4n11nli11car1nn .a.t. r.~.(.oor10 а~ q.6
f.r r:tronu • 1 11J:н-а.;: 1.11..it1л-Jш:r,,.lmoo111'°Jt~dt.ttьn1 ,11'"~' ~orr~:11шm f11q\
c.d.b.c.qtl3dn1U l1n<(.,t Ь,tщ ad&1 1r,sJn1 s;1101 11мi(~·o"id1i at1tt1i ь1r..tt1116 1111((
!i.ft11.UGf'i).ti С. q~Г:ш1111 Ьосщ6,i11qu.Юшо «fСПр!О p:Ch!ll.чam Cl!lfl'IClrU
ь..<t•..:а 1'-U llC ll),] , cd11(11111pc:rpc11da..1i11r<m (1)~Jttkmr1 . a ь.i;i11Cf1.l.\'J .k ."p'1 t .k
-r~IJ.mCml b.J! . , . i-. dut3nt ffq)qi10 roomjr1111нnuroJ.'t't,J p11ntto.f r:oФltJn
{.~.('-11JtJ1 11Jnrc(11\.(.: .с ь.qui.f.t:i.<.Ь.11' r:od1Jt'3n' f:rq)quo tcntmтjrt рй-:rо
5.~r:od1Nj.t,d.'1iu~J h.- : : .i:.d. ffq;od k.frq;шaooolзttl'\1 ,d.(л.c.b m•1•
~~.d.r~Ь.fi111rcqnai1.1~dUfJ>CY.s p:u111 сн10 aiis!Ja.(.d.ь. 't.t.~.d.щ1itcs:-: qt
0.t1s1il1~.r.dt rмu~ <nt ~.~:..р:нn1 flctqj щr:m1-J1tto.!rL'l'ft, .f~dc 143rk псr1
~u~:qiз11:;u!o:ai.t .d.ь.-:..c.ь.-J cщ1rщJ1aзu rct1 1.qiwLe rocбd1e1nn.~9 ~
11tl Cl'\f WJl~\(n(q;<f.l~IUC~a!lёi'iofqm rr.n1.b.(.d.1.b.d.f.~.}i. f,d,f .k,d.J, ПК
dli.1ag f(:m n'»O C·6.f'~18nt.J.j.1.S, Ь..timtЦl11:ik!I, (1m1IUCГ Cillt'I)) .f .4. 't .11 .b.
pзnr6c.f.Ьл.l>.d..11(1.\\(.t\,1.k d qlШ,\"fr2rj)t'Cl:m:i(p~l(1cn1.<a.b!J f.1 .t,
tf,f>.t tO ~uadr3r11.z"\~101J1~(\IJJi1r.Jruщ,'3.b.f.g.qнitqutdr~cLi ~n«:.·~.b.!011
lt'1 fй0~1"~q.цdтiЩ)q1Xr$1i)r1n1amo1!ш~~r1mt ~1dr..at:iD\1.ir1ri11
1.t1юn:1n '3.с.-:.с.ь -:«oooЬooft1Niltm(n11Sqooii v:11*~·pdoaf« .t.tJ11
~.c.pJra p~OQQГ11uщ щ:Oni.<IЭ!ttcrt'tr lioo:1.~.b. Vt P~i o.щft t11 <1,, .t . .< .b\
ь~
[[]•
'
•
о
.~:•
<
'
l~n~a'\,)Tfl ,'\bl 1нп 61tПрн6) T IHHH.I '- 1lt V'\НiОЖЕ't-ЩЯ н cJ•opr-.1)' i\til
1ш,1л рм.~ t.v~щы "''10.\ом геометр11ческст ,~л гt>оры.
1. t{KMI.\. < Нс1'1.!Лс1> И$,\,11111Р 111\.! r .
; 111ронку. Реч 1 . li 1111х 11ш;1 о f 1 1pr1Jroжe 11111 1 пло
ща,11;е1~1 ,). Р:1со1этр11 1 1э1111 тprr п 111 а т:tю 1х :-~ад:lч:
1) преобр;.~зовать /\а1 111ыf1 прямп) 1-с>JLьшп< в
кв;.щрат, т. с:. ре1111нь урзвпсrще .У2
= a[J (пара
болпческая :iадача );
J.) пр 1 т.1ож11ть r< 1(3111ЮМУ отрезку а прямо
у1•олышк :1~щ;~н1 юfr rшощ:.1;l 11 S так. ч:тоб 1,1 •! 1l'до
с 1 ·:1ток» был l<Ba/lPCl'f "OM: x(rf -
.\') = S (эю11 11 п·11-
чсскам :~а;1:1ч<1.):
;1) при;юж1лъ к ;рннсщу и1рсзку tl 11pммu
~TOJL'1!Lll l\ :J:.If(3111Юi"l J[Jf()llla/ \11s · 1:Jl\,ч106 1,1 <' JIЭ
быТ(Ж ·> был 1ш:1r\р:1том: .:\'(n + х) = S ( 1·1тrтepoo
mrL1cc1~u1 :iа11ач:1).
С 1 юио111ыо циркуля 11 тше1'пш можно ре
ша11. за;tач н, :жшшале 1 1т1 rыс ю1адра·11 rьщ уран
нl' 1-11 mм. ИМt:ЮlЩIМ дсйсТВ I ПС.'IЫIЫil ПOJIOЖll
l'C.'lhHЫЙ корt:н1,_ Те ж<: мс..:тu;(ы познот1ют
pt:11taп, Jaд;JЧJI, CBOJl,)LЩIJt'(Я к IIOCJICД()B,l 'l'CJl l>HU
CТll Hl'CKUJlhКllX 1ш:щрат11ых ур:1нr·1<.·1111!1, в ко
., opor1 коэффr11 \llCH 'IЪI К: l Ж!\01'0 O()C.!JC/ lY1011\L'l 1)
ур~11111еrп 1 я :з:ншсят от кор1161 11pt'д1.11\yr1 \е1 ·о.
Очс 1 11, скоро поннт111сь 11 др) 1 · 11е :~ад:.1чтr: 06
уд1:юеrrни куба, о тр11сскщн1 уела, о тшадратуре
кру1·а (см. статыо ,:1·рн:ш~1ме1111тыс :1алач~1 древ-
1юсти " ). Jдссь гсометрIJчсск;~я аш·ебр;t 01<аза
пась 6CCCll.'Jh1i;\. Одпак(.) уже CLMJI IЮПЫТЮJ
г
История ман'ма1ики
реши1 ь эт11 з:-~дач11 привели к nыдающпмся
рсзут.татам. Упомянем лишь. что пр 11 1 1сслс
дова111 ш заμаt.ш об у;~носнн11 куб:J были откры
ты кuннчсскш.: сечс1щя - 11овые, чрезныча1~1-
нu нажныс крr 1 1-1ые, нашсд ш нс бт-1 статсльное
11риме11ен J1 е н ;1стр()11ом1-111 ю1е тысячи Л(:Т
спустя (см. е1 ·атью "Замеч::1 ·1е1111 1 1ые кр1нJые»).
Неразреш 1rJ\10cт1) :11t:~менитых за11ач дреrн rостн
смrт11-1 доказа 1·1, тnJ 1 ько в XlX в.
ПОСТИЖЕНИЕ БЕСКОНЕЧНОГО
Нместе с открытием 11есонзмср11мьLх вел11чrш в
l 'JХ'ЧСС КОЙ ма·1·с\1.ап1ке IIOЯBJ I JIOCb l lOJ-IЯTИ~ ficc-
KOllCЧ! IОСП1 Трудн ости, СПЯ:1ан Hbll' с ЭTll м nо
ня 1 ·нсм. 1Jрн вел н к 1·лубо1ю.му 1<ри:-11-1су а1пич 1 юй
м<Jтема·1·11ю1 ::1тС16ыла первая большая буря, по
трнс 11 1ан ещё 11е окрепшее здание 11:-~ую 1. В об
су'lrсдетше nюпочились ф11лософы всех школ 11
11алравле 11и.й: от Л11а1<с1гора н Дсмокрнта до
Лрис-1 0·1·елн. Софисты (профсссиошшы1ыс учи
теля философии), I<Отuрых Платон окрсст 1 111
МСJ1Ю11'11И тор1·01:1ц;1 мн ИCTИ I IOll, CДCJl;\JIJJ ...JТИ во
просы оченn rюнулнрнымн.
В<.:l(рыть 11,сйстн11тсnьныс тру7~;носп1, т~1ящ11-
сся н поня·1 1 1>1х 1-11:: преры1ню1 ·0 11бесконеч11ого,
и тем самым показать, ско111 . 11есоверте 1 н 1 1,1
ещё бытr 11rедст:-~ нлеm'1Я о них. удалось 3сно
пу ЭлсfrскоJ1.1у (около 49U-око.rю -J. -)0 до н. э ).
сформут1rовавшсмх их n виде парадоксоn. нли
cmopuii (греч. «апор 1 rя•1 - «трудпостм, «бсзыс
ходтюст1.») Вот уже более 25 веков ош-1 при
влск:нот внимапнс мат1:мат11 кон и ф1щософон.
:Jснон был любимым учеником Лармеtш
J\а - ~·лавы шкu1rъ1 ~ле;.~тов (no н~J ЗВ:J.нню ro-
Зt•tщн -Элещ ~''"'
1р.шю1ы 1ьОЬ r
рода Элея), кo-ropыff nсрnым т~ачал строить
фнлософшо 11а ос11ов~ лопrческих рассу'А<f\С -
1шй Дрсв1шс счптали Парменида родо11ачаль-
1-111ком 1ю1 ·ню-1 Элсаты nостояrпю пол r,зо1-1:1-
лнс 1, докаэ;1тс11ы:тна ч11 11 утём 11 р111:1ед~ 1 iИЯ
к абсурду. Так 11ос1упал 11 З<.:но н , призн~нный
з ;~ м <~стсрскnс нлаJ\ен не дна11ект1 1 кой •·лву
н:-1 1 ,11нн1 ».
R J(JX'R 1юr"1 11 6ы1ю 11·~вест1 f() бол~е сорока
апорий 3сrюн:1, но пас же л.п 111ло всеГ'О девюъ.
Самыми знамешrтым11 являются четыре а110-
rии ДВИЖСIПIЯ, •ДИХОТОМИЯ», «А.хиЛЛеС 11 чере
паха ·), <· Стрела» в •Стад1юн", rюторые форrv1 у
л 11руст 11 11< );чю6но nбС)'Ж/\аст в сrюс:й «Ф 1 111 о<С»
Ар1l(.' 1 '( >Tt::JJ />.
Своим зl1орням .1е 1 1011 Пf)И/\ал ярко ныра
же 1 11. 11.1l1 (l) 1 1Зf-ГЧCCl\Hll смысл: он l-1~1J1paв111t 1 1 Х
ПрОТИВ 1ЮЗМОЖ! IOCTJ.I ДПI rже1 П I H. Н() 11едl• ДFН IЖС
ПИС тел пpOllC'XO/HIT ежею1е 11 110 11:1 f l ~U I ИX
глазах! U чЕ.м же '"ело? Очстп, остроум~ ю раз
мышления на эту тему а:~ложил в пс()олы пом
стпхотnорешш Ллеl\с:нщр Сер 1·еев11ч Пушюш.
Вот как он прсдст:шил слор двух мыст1тслс~"1
/\рсmюс-11 1 - Зенона 11 J~iю r ·e н:i :
Дв11же11ы1 щ•m. осазал .Л~)·дрец брадатый.
Др) •юti CШJJ/ 1-/(/Jl / .( ( 111(1.7 пре(} IJU.M
. \"(J('IUJ11l1.
Сши~нее бы не .~юг 011 возразитъ;
XlШ/tUЛU i:JC(! Ш1'/i:J(!1)] 3tlMblc;!l()(:/({1J/Ыzl.
Но, госноr)(/, :шби1л11ый CJ~J' Ч(l1t Cl!1'i
Дj~)1Юй 11/JШUJ/J NCI 11flAIЯ1П'h .1111-il:' 11/J/180д/1111:
Ведt. к.аж:r)ь11/ f)eнt, преа налt11 сш1нце xщ)um,
Ойщт:п .11( прав у11ря.мы1/ Гапl(.m!1!.
Об 11 1епрннятой н 1 ·рс ческой мап.:матнке
стала точю1 3рен11я, 1:1пtрвые в ы сказаннан ф11-
лософом АнаксаJ'()р0~1 (V В. ДО I J. Э.) . 011 пrо
IЮ~гл:кил. что • н >vtaJ юм Hl' существует 11 ~шмеш.-
1 1 1 е 1 ·0, гю nce1~1a естт, сщё мснпu1с<.>>. R рс~)J1hт:1те
11елення отрез1<а 11re1·; \a 1'1удут 11ОЛ)"-1<l'п,01 отре~
ки, которые по-прсжнсчу остаютсн /\еmшы
м11 ВСЛИЧIП ! ;:JJ\11!, и таr<иr-1 11у1ём мы l!ИКО J ·д,1
не доlщё_r..1 ДО llCДCЛlli\.lblX •Iасттщ. ~ТО ОЗШ!Чае1 ,
спо 0·1 резок ш: <.:остонт 11:.i точек, а ест 1, «rеомет
ри ческое место » точек
l l oш.1c основы маТС\1:11·~·1 кн - общее учс111rс
об 0'1 HOIJJCH.llJIX 11C'l'fl<H'llC методы пpcJ~l:Jlhl-lf>IX
11ереходоu - былн со:щ:~ны Ендоксом К1-11щ
скт1м (около 40R- n1<0JIO 3'>') N> 11. э.).
Еn,ТJ,окс б1.1л 1 1 е толыт 1 ·е 11 1 1 а11ы11>1\1 матсма
тиком, по 11 вы/1.зющ11мся зсrро 1 юмом. 1ео1·ра
фом . врачом. фшюсофnl\'1 11 ора 1ором. 011
АПОРИИ ЗЕНОНА
дихотомия (рассечение n оnолам).движушееся тело
t111 когда 11 е достигн ет KOtll.LJ пути, поскольку сначала
оно должно дойти до середины пути, по1ом - лосе
реди ны ост;:~тка и так далее. 3 начит, прежде чем
лоити до конца, 0 110 долж1ю «отсчитать» бескон еч
rюе число сереы1 н , а следовател ы1 0, до конца дой1и
ему не удастся.
И ногда этот парадокс пытаются обы1снить тем,
что сумма всех пройденных расстоян и й представля
ет< обой хотя и бесконечный, но всё же сходяший ся
ряд (с.м. статью « Чи 1ловые ряды•):
Американский математик Герман Вейль, чтобы
пояс 11и ть, в чём именно здесь состоит труд ность ,
привёл тако и 11ример. Представим себе вычислитель
ную машину, которая выПоl\няет первую операuию
за 1/2 м11н, вторую- за 1/4 м11н, третью-за 1/8 мин
и т. д. Такая машина моглil бы к конuу первой ми
нуты р~>шить, t1ап рим ер, вели кую теорему Ферма. Но
ясно, что работа над построе нием подобной машины
обречена на неудJчу. Так п оч ему же тогда тело смо
жет достигнуть конuа п ути, отсч итав бесконечное
множество 1ерели н ?
Ахимес и черепаха. Быстрuнuгий Ахиллес 11икогда
не лоt онит черепаху, если даст ~й хоп1 бы малень
кую фору. Ведь пока он пробежит расстояние форы,
чере паха уnолзёт на другое расстояние, и пока Ахил-
1юд1~лся в Книдс (на ю r ·о-з:~паде МаJюй А3и11)
и ркс н молодnст1·1 гюбr,лзал по мноп1х l~гран:~х_
tl;1 С11цит щ оп учился мещщ1111е, а п Грецт1
юучал мате.\1атику под р)'1<0Аол:с·тпом 1.;ру1111е1<1-
шеrо учё1юго то1·0 времснп Архнта Таре11· 1 -
скоrо И если Фещtора Кире11с1юго и Теэте·1 а
\ЮЖНО было бы 11азват1. алгебраистами, то Лр
х11т и Еnдокс :3анимались 1адачам11. 1<отор ы е
ССl 'ОДНЯ прю IЯТО (JТН()СИТ'f, к "1tаТематнческо.му
анализу .
1<.ндоксу было немногнм бот.нrс f\н::щцати.
кшд:~ ()Н прие.:х;u1 п Афины - 1'J l :tR11ый кулh
турный цсн·1р I'реции Г::1·0, как 11 \1но111х дру-
1 и х мо110д1>1х людей, пр11nлек;1т1 :~11аме11 1пш1
Лкаf\смия I l лато 1 ra, на дверях которой быщ1
высечена тщrтись: <Да 11е nойдёт СЮ/1,а пс зпа
ющ11й геометрии». В Лкадем 1 ш ш11роко обсуж
д:~лисъ ос1ю1111ыt' проблемы ~rа\'Т<И и филосо
фии. Именно :3/tt<.:I> Евдокс 3аиптсрссовался
Ан 1ичная математика
!\ее добежит до этого места, она уnолJет еше дальше ,
и 1.1к до беско н ечно сти.
В эн; и <I пории помимо того же затрудне11ия со
с-чита нной беско11еч1 юсти есть еше одно. Пусть н.:1-
чальное расстояние форы - а, и пусть Ахиллес
бежит в k раз быстрее ч е р епахи. Ко гда Ах~1Ллес
пройдет р асстояни е а, черепаха отползёт 11а a/k,
а когда Ахилле< п окроет 11 это расстоя н ие, череr1аха
пролвинется еше наа/k~, и т. д . Предположим, что в
какой-то момент Ахи ллес догонит •1ерепаху. Запи
шем путь Ахиллеса
5 =а;-~+~+
"
kk2
и путь черепахи
аа
а
s.,=т+k1 +kl+
Кажлому отрезку пути , пройде1 11;ом у Лхиллесuм , со
uтветпвует отрезок п ути черепахи. Поэтому к мо
менту встречи Ахиллес долже н п ройти «СТОl\ько Же»
отрезков, сколько и черепаха. С другои сгороны , к,1ж
дому отрезку, 11ро йдеt11юму чср ст1хой, можно сопо
ставить равный ем у по велич ине отрезок пути Ахил -
1\€\<1 Н о кроме них Ахиллесу нужно преололеть еш ё
один оrрез<>к ллины а, т . с. 011 должен пробежать на
оли н отрезок больше, чем черепаха. Если количео·во
oтpe'IKOR, прuйленное последней, равно п, то nолу
чаем,чтоп+1=п.
Парадокс о том, что « часть равна uелому», стал
в посl\едСТвии предметом ра .iмышлений Галилея, Ни
колая Кузанского и м ногих других учё 11ы х, которые
даВ<1Ли эrому парадоксу различные объясне11~1я.
:3Эда ч ей, постанлсш юй Пт1тоном · скш ~струп
rоват1, MOДCJlh, А KO'l'Oj1<JIJ С ПОМОЩЬЮ ранно
МСрН ых i-. :py1' 0 111 .1 х днижений сфер М( JЖJ 1< >ПыЛ< >
/\рх11т Тарентски11.
f f liШ~lfJ<I J ()(111 1
.:.\ J
·12
И< тоrия 'vldT~MdTИKl1
6 1.1 110J1} 1 111·1ъ l:\Ct: rнщимые дш~же1111н С.отща.
Лу1 1 ы 11 11т11 н.:т, - н yc11cr111 ю сё рстrпrл. Вс1шрl'
F.в:tOKl Ot'H()K;Lll coбcTl:JCI 111уто 11:~учную IТТТ<О.'1)'
в К11 !1 11\t:. н:1 южнu \1 1юбсрсжье М рз \\Opr ю1·п
чорх Там ..ке 61.ща 11щ· 1·р< н.:на обссрватор ня ,
псрnзя n :~лл:це.
Uдн,11<0 11:tп60J1et: 1·11убою н: 1-1сс:J1с,щн:11111я
Ещ.1окс:1 0·1 J юснтсх 1< 06J1:ti.-1 ·11, котор:.J>I тс1 1 L·рь
на:.н.1вастся внеде1 11 н.·м 11 ::J 11 aJ111з бесконечно
м:ш ых нсщ tчш r. Ilo q.щ~стDу, or1 пос1ро11;~ 11с.:р
В}Ю к щ: тор111 1 т1::ор11юдс1ктнн·1е:1ыю1п ч11с11а
('1еор11н 1<1·11 ioшe111 1 lr ) 11cu щал \1спщ 1rcчtpnы
n::i1111я "0·1оры'1 1ю.r1ь Juкал о1 np11 выч1к. 1 е11111 1
П.'lOЩ:l/tl'il кp1 11IOЛllHl'ilfl l,1' ф111·ур. ~)ТОТ мето, 1
по:ш().111111 с 1 por·o с:ощ:р 111 а 1·1, 11рсдслы 1ыс П<.:)Х:
хою.1 ~1 l- 1·a11 пс 1ю1юl1 а11т11ч 1 шl1 тсор1111 щх·д<:
лов Надо с1<ааат1 •. что 0 ·1крr.1тыс 11а рубеже
Л'\· 11 Х\1 111110. !\1e'I'()/(11I 111 IH:' l'(X1ЛЬHOI'() 1IСЧ ll('!ll '-
HllSI устуnJ .1и по cтporncпr ме~ону Fкюжс.1 .
С1 [10Г11t: ЖС МСТО.J,Ы ПОЯ\311Л11Сu illlllll• 11 '\IX 11.
•"*
Геоr-н.:тр11 1 1 cl t-;:.!» ;u11·<.:6p:1, 1ruJншrщ1ш::J) 1 11:1 r 1ер
вых 11Ор:1х 110JIJ'Ч1 1·1·h Gom, 11111 <.: п рсимущсстnа
пере,~ ч l ICJIOIIOll :1Jll 't:'t)po1'1 B:tHI IЛOШlll. 13 опр<.:
.J.еJ1ё11111.111 мn\1е11т стаJ1,1 1ор\юз 1п ь pa:и.il 1п re
:нrrнч11oir мJтс.чат11юr . 011:1. rю,'{обнv 11;~нц11рю,
сковьш::~ла её ж~шо1·1 ор1·:11111 ·з м н .\Н~ 111:1ла l'~'Y
11ра111L11>1ю расти. Н:.~чат1, хптя бы с 1·01 ·0 , ч 1·0
ур:ш11сшш чствертоi1 степе ш1 11 в1,m1t: J \:tЖ<.:
нс рассм:1·1р11uалнсь. 13 1 ·<.:о.ме1 рнчес~ш1·1 :11 11 ·еб
ре нс 61.11ю места 11ля uтpr lll~Пслы rыл c111 ccn.
llt' п торн уже о м1 шмых. l lco(lxo..::rr-r.чo t)ы;ю от
ка~а 11>(.'Я ( 1'( Гl'OMl"l'PI IЧ<.:CKOl 'O stзыка 11 ис1,;ат1,
1ювы11 , 11n. 1ee ot>щ11l1 11 l>олес п16ю 1 1! . l'Jкo1'1
язы1< ()1,1.'1 11аiщс;;т 1 то. 11.ко в 11cpRыt: нек.1 нuнui1
эры н ·юоху эт 1111111 :1,1а.
ПЛАТQN
AJ<A6HMIA
ЭПОХА ЭЛЛИНИЗМА И ЗАКАТ АНТИЧНОСТИ
Новая .-н н 1x:i :tJ 1·п1 щюi1 11сторшr - эпоха элл~1-
н 1 1.1.ч:1 - 11aч:u1ach с за 1юсв:1н111'1 Ллександр:~ Ма
Kt:ДOIН:KOIO В :).)2 -. 11:'> 1'1'. /(() 1-1 . Э. OI I 1101<0р11Л
t1·1111ет. R::~ш 1 1ю1111ю, Пср<'1110, Со1·;.щ:шv. u:1кт
р1110 11 д..1.ж<.: чаt.'Тu И11н1111 П оен~ С.\t<.:рт11 А. н:к
с.1ндр.1 u1 рочнан 11ч11ер11н рас11зласh. Е1 о 110!1-
коиuАltЫ раздсл~1.rt11 \1<'it<;!) собоi1 ззиоёка11ны<:
c1·p;.t 1rы : h1·11ncт vl<З:J:lлcя под nл:1ст1.10 Пл 1л<.:
мс.:ск. 11 Мссо1юта:v11111 ~1 <..:11р1 1 и с 1:~л11 11р:~1111 ·1ъ
С<:;1с11К11/t1.1 , н \.1,1 Kt:/(Uн1111 Л1п111·011 11 <:1011р<.:
ем1 111 к 11 .J t: 1ж<.: в . tOJ11111c.: 1'111 ,1.1 пpanи.rr11 греческr1е
ЮlЯ:11»1. 3аКОГJЧIL'l:.кь :iJ IJlllll11(.TllLll'CJ~;.ш эгюх.1 в
!>О-х 1·1 :io н :с.э. юн ·, 1:1 1 • 1 · 1111с.:т - 11ослс:111ня
rpCЧC C1'<UI l\OJI OllШI 11о~-;ор11,1сн (111 ч. шна \I
~1pah."lt'p1юf! чt'рто11 +1011 :-тол11 61.1.•ю llU/\-
ражаннс 1ю11111сю 1"'1 ( 1·рс.:Ч<:l к~ 1\1) оi1р,1·щ:1 ~1 нu
вс<.:м - 11 11с1<усстне. 11:1) i(t' , 1<у; 11.1 уре
1 ·ос~11:1р
с·1·нс1 111 ы\·1 я:!ыком. :1:111ачт1т,11 я:1ы1<()м н:1ую1 11
культур 1.1 nо11сю11у быJJ r·pcчccrшi1. Учёные
те11ерь легко об щалшъ и rюс11ршшмали тра
д1щии. сохрашшurиесн в науке ра:-шых стран,
ранее обособлен11 ых.
Цар1, n·1·ш1емс1v1 1 Сотt::р 11р:1вил El'Иll'J'() M 1:\
.101-283 1т до н ::J Свuсй CT!JJ1и1 tei1 он 11збр:ш
город. OCI IOHaHHhlJI к .~31 г. ДО н . э АлtкСаНДf)()Л1
~1аке11.0Е1О< 1-1м 11 на:зн~н1 1 1ыii Ji с 1 ·0 ч1.:с1ъ Алсксан
щ1 11 tl1. Здесь ПтоJJемсй ос 1·10нал 1v1усейо 1 1 (хр:.1.11.1
чу:1 11 окроnrпе;1ы 111ц п ау1< 11 11CJ<yccтn ). ста а
шиii ЦСJJТром 11аучrюй мысли ЭЛОХJI ЭJIJШ IШ:1иа.
13 сос1 ан Муссйона в.ходила 11601~атсf11n ая Алек
сuщр1tйская би блиотека, 1ха считыu:11:1шая око;ю
7U() тыс TOMOfl ( C l.ШTJ(OR) . Е~ ocrюny. 1ю преда
нию. tо<.:т~шнл: 1 б 116шют1.:ка дри<.:то·1·еля. Имен
rю ею; ~;~ стрсм11 1 11 rс 1, Ж3Ж/t)'щ11 с знашrй .'vluлu
/IЫC JHO/ \H со нсе 1 ·0 MJJpa
В IП-П 1ш. дон. э. особе11 1ю 61,1C1JX) ра:~1111-
r1а.·111с1>'ючные 11;-~ укн. И :по 11еуднnнтслы1 0, пп
сколы<у IJ Т() нремя Жl1JIII и TR()[JШ I И ГС I ПН!,
11ме1 1а 1юторы.х н:шсс-rны 1J uеках, - F.вюшд, Ар
химед, Лполло1шй . 13сс крулпейшис учёные, за
нсю1ючсн11см Архимеда, работали 1·0 1 да в Ллс1<
сандр ш 1.
Ен клид б ы J I совремt'1111иком Лтолсмеs~ 1.
И это, rюж~1луr1 , всё, ч-~о досто верно о нём
11авест 11 0. Нет с1:1сдс1111й о том, uткуда 0 11 бы.11
ро,(ОМ, r·дс l I у кого уч ш101 Кос-кrо и з и сторикон
11ayic11даже11ред 1 юлагал, ч·1 о имя ЕнКJJИ/\ елу-жи
ло nсеRдо1 111мом лля 1-руппы алекс:шдрийскнх
матемаr1 1ков (подобно тому, 1~к фра 1 щузскпi'1
матемаr11к 1l икотi Gyp6~1к~r или руссю1й писа
тель Козь.\1а Прут1<01J лвлялис1, J шшь ВЪL\11,1шлен
ными персонажами . з~1 кuторымн скрываласr,
1 1<.:л:н1 rp)11П<I анторов ) О; 1нако у шн.: нет о<.:нu-
1!:111ю·1 сом ненат 1,01 н ·1ом, что Енкт щ peu1 ы-1 u
Еuкл11д. 1 pttBfl'Jf)il ft(1 ,"едt1
П1mмРfНЮ X\lllJ в
АI ПИЧНJЯ Мс1ТСматнка
~
8'J.(]_J
существо пал, как пс сом~ 1ев:~лш::ь R з'го~1 и по
зю 1ейшне греческие учё 1 1 ые.
Н оюrом нз сnоих соч1шс1 1 ш'~ r lапп Лле1,с:11т
дрнйсютП ( 111 1:1) изображаt:1 Еnюнщ:~ как чс
лuнека ИCJ<ЛIOЧllTC!lЬIIO ЧС<.:'L'Н01'0, TllXOl'O н
скром11оrо. чуждо1·<1 ·1 · щс::славня 11 э 1·011зма. Он
нако R нооросах, кас1.10щ11х ся нзучснш1 ,'vt~1-
· 1·е;ч:.~тню1 , 011 П 1,1 л li яысше~'1 с 1 ·L'псн11 сср 1 .ё~1<:н
1r C'l'po1·.
Как coofi 111acт пстор111< 11 ф1июсоф
Прокл (V 11.), одпажJ\Ы царь Птш1емс::i1 спрос~ 1J1
Нвклида, пелюs1 ли найти более коро·1 ·ю1fr 11 ме
нее у·1·ом1пслыrы~'1 11уть к 1пучс1111ю п:<1мстр1нr.
чtм шту,~ровашrс <·H::tt 1 :ш~. Учё11т.п'1 см<::Jю от
нстил: «В гсо,н::трин пет 11а1х:кой доро 1·11!» Дру-
1·011 11сторичсск~1й :шекдuт rюв(хтвуст о том.
что Oi \1 IH IOI Юllta, 11:sуч1ш первое прсДJЮЖСНJIС
"J-Iaчa11~. cпpOCllJI у ПBК!lll/~3 : «А что н CMOI')' ~.1<1-
JXIOO'Г~ITh. выуч11в нсё это'·• . То г.п.з Енктщ нознаJ 1
раб::~ 11 ска:зал: "ДаГ1 ему трл обола, т::1 к 1с1к бе11-
1IЯжка хочет з~1рJбота·11 • дспьг11 сноим уче11н
е~1». (060J1 - мелкая серебряная мо 1 1с::та.)
Евкш-1д - ;штор «Наqал•
-
юrиги. 11ережнл -
111сй бoJJee двух ·п,rсячел<.:т1 rй. lle будет r1pe) ве
nнчt1шсм сказать, что по нс11 уч11л 11сь матсча
т11к 11 нссх вр<.:мён н наро11uн. И до си.х 110μ ..:Jта
у1\ 11 внтСJ 1ьн ая ю1111 ·а не ~-1ратнла с.1юсго Jначс
ния . Со;1сржзнне et: ;1: 1J 1 еко 11с исч<:μ1 1 ынае1·сs1
:--1.rтсме1 1тар11ой 1 ·ео'v1етр11ci1 . 3/(L'l'h 1нщ 1-юд1 1 то1
1пиг болсt' ч ем .)()()-летнему разк11т11ю :111п 1ч-
1101'1~1а·1·ем~1тию 111 1 1месте с те."1 С< >:щаётся проч
ная ба:1а дш1 дальней шнх 11ссш~доnа111-111. Прокл
ут1:1ерждал , что , составляя ··Начала", L:вкmщ
"r1ю1ючнл в шrх ~шогое пз Enдoi.\ca. усоnершс11 -
с:тnов;1л :vшoroc нз Теэтета и дал 11еопроr1ерж11-
мыс дсжаз;~тсльсrва того, что его предшсствст1 -
1111к~111окаэал11111:строго*. И хотя матсм:1т1~1к;1 со
F1ремё1 1 Е.вклиr1а IJЗMCIТ\1Jl;]Ch OЧl'lll> С\.1ЛЬНО. 1 1 а
11pcrvюжc111·1>-J ~ начал» нее послед) ющ11t матс
ма J 'И КИ CCЫJJЭJll1CI> как на llCЧTO око11ча'J'СJТnНО
уста1ю1щсн 1 rое. (Ппдробнее об ~то'v1 юаор н тся
n статт,е ~ ,. Нзчал а" ЕRюшда·>.)
Истприя мdтематики
Hu <>Н:.tчала» - нс ед11нстнен 11ый труд Eнк
JI11Jta. Ему прнна.шrежш 1и также ~данные·>. J10-
щ>m~яющис « Нач<111<1 ~; ~се ченне ка 1-ю11~1~ ('1-рак
тат гю тсор11н музык и) ; утt:рян 1 tый труд о
конических ссчсн11ях <-Геометрпческне- месrа
на гюверхноеп+>; · 1 -рактат о лслс11н11 c/)l(ryp, со
хранившийся ли1пъ n араf>ском нереrюl(с; «По
рпзмьr·> («Следствия»), о которых свидетель
ствуют Лрокл и Папп, а кроме тоrо, тракта1ы
по оптике, механике rr ~1 стр01-юмни.
Друп1м ныдающимся учё1 1 ым эпох 11 эл1111-
н11Jма бьш Арх.имен, о жизн 11 которur·о сложе
но 1rсмало J1e1·cн;t. Т 1юрчест1ю этого 1·е::ннн на
доm·ис века опрс11слшю С)'/11,бу н ауки, а тем са
мым и судьбу ЧСЛОRечсtтна.
Н есмотря на r·лубо1шй интерес Архнме/tа r<
1-юпросам меха 11 ики, гидростатики, оптики, ос-
1ювн ьhVI делом его жизни была математика_
По слоnам зш1 мешпого историка Плутарха
( 1- 11 rш ). учёный был простu одержим t:ю.
часто :~абывал о шrщt: н с0Rер111сшю не з.~
боп 1 лсн о себе. Его м;псм :.1т11ческие труды -
, и зме ре1-111с круг.~ ·~. «0 шаре и 1 t11лr 11 1дре?, «Ис
• 11 1слсни<.: песчинок» н др. - 1юражают орип1-
налы-юстыо мысли, мастероюй техникой вы
чнсле11 иС1 и стро1·остыо дою1зательсп1. Кроме
того. математичес 1<ие резулы а·1 ы Архимеда
11зложены в е1·0 письмах к александрийским
учё ным . и 1<аждое письмо ттрсдставm1ет собой
за1<01 1ч сш1ый научный мемуар.
Нскuторые сочин ения Архимеда сохран11-
т1сь тuлько в арабском 11ере 1ю.це ба 1 ·щщскurо
учёно1'0 lX R. Сабита нбн Kypf1ЪL Это «Ле .\11 .\1\ЪI->.
«0 семиу1·011ы-1нке» и <.<О касающихся кру1'ах».
В ~ле ммах ·> с.:ред 1 1 1tруп1х задач 1rзла 1'аетсн
реше1111е зздач 11 о ·1рисею ~нп углэ с 1юмощыо
А[)Хl~МЕ'Д
Ан П1'111Ыl1 рt•ль.::ф
Собрм1 ие tоч11fщнии Аμхим~АJ.
IHM HHOE' В Ьа <l'Лf' 11 1'>44 Г
пставки (см ста·1но «Трп з 11;1меrт1ъте ~1адачu
,'J,peniюcт1 1 "). R сочш1е 11и11 «О семиутолы1111<е•
расс"'1атр1 шаетсн задача, экDiшале11тпая ~611-
чсскому ypa13JICillПO. В CГlHCI<C COЧИIICШIII Ap-
XllMeдa, известных арабам_ упом.ш1астся таюке
тра1<.1ат <'О пар:uшслы-1ых лшшJIХ~. ilозмож1ю.
Архимед был Оf(ним J.IЗ ltt'pвыx уч ёных, 1 1ы тав-
1ш-1 хся ;~оказать rLЯтыl! поС"rул:п Евктща (с.м
статью <-Гсомстр1 1я Лобачевского").
На116олее важе11 nклад Архимеда в ту область
математики , которая тепср11 1 1:азывается интег
ральным 11счисле 1шем. Его и сследова1шя по
IЗЫЧИСЛСIППО ПЛ()Щаде 11: плоских фш) р и объ
ёмоn тел. к сожален1110. не получили развитня
в древности. Человечество дважды открьншю
длн себя Архнмеда, н r1нажды учёные n 1 ,1талнсь
продвинутьtя щ1лы1r<.:. В первый раз это про
изошло в Сре;~ние века на ар:.~бско.м Впстоке.
B(J второ!"1 - в Европ<:" Л'VТ-ХУl l 1щ Jlyчwt: всслJ
о значении е1 ·0 pafioт с1<а:1ал од11н 11з создате
лей ;~иф<.}х:ре1щ11 а.11ыюrо 1 1r 11 пегралыюго11с
чиспе1111н - Готфрид llиJ1ы·елт.м Лейбшщ
<·ll11J·Jмt1тeлыt0 читан соч 1 111енш1 Архимеда,
перестаёmь удивлятъся всем новейшим откры
тиям: геоме-~ pon·> . (См также статью "Арх нмед».)
Третий из вслию-~х греческих математиков
ЭLIOXH ЭЛЛIIIШЗМа - АПОЛЛОLIНЙ РО/lИЛСЯ R
городе П ер 1':1 н M:iлol1 Азн11. О нремс1111 его ж11з
Н11 иl\1сются прот111юречивые св 1 1детсльств;1.
Некоторые иссле/1оватслн полаr:нот, что Алол
;ю ний ро;t1шсн uкuло 260 1' . ;юн. э .. 11 ес:т1. ос-
11011<1ния СЧll'l':пъ. Ч' I о около 170 Г. 1\0 11 . З. он
ещё был жив.
Расцвет деятелыюс1·11 учёпого пришёлся на
копеu Ш в до 11. э .. 1<огда он работал в Алексан
дрии. 13 э1·ом городе проuша бол~.лrая часть его
ж11з1 п1. Сюда Аполлон11й приехал юнuше11.
З/(есь учился у м.ате.v1:.1т11ко1:1 шкuлы Еккmщ:1, ;1
затем 11репо.~аnал ~~атсматmсу. В предисловии
к ncpnoй юшгс <·Конических сеченн11 " А1ю11-
1юний сообщает, что начатh р::~боту над этим
сочинением его побудил 1·еометр 1lаnкратес,
которыir слушал с1·0 лсю~и1 1 в Алскс1ндрн11.
По-в11;~имому, позже Лполлоний переехал 11
Гfсргам - кру1111еИ11111й куm,тур 11ы й це11тр Ма
жн'1 Лзи11. В библиотеке Пергама храшшось до
2()0 1ыс. cnrптcon; по количеству ру1<0писей она
уступала ш1шь Алеr<сандри.Иской бнблиотеt{С.
Более всего Аполлотrиfr извссгсп свuи~1 тру
дом « Котшчсскис ссчсшrя» в восьми кнш·ах.
1Jсрвыс четырt: кн111·и дошни до на11111х днt:й в
оригинале.:, следующие три - в ::~рабском пе
рсrюде Саб11та иб11 Курры, нось,v1ая же книга
утерю1а. В с1юём трактате Аполлониii постро-
1111 Jакuнче111rую ' L'ео рию 1<рнвых второго по
рн11ка (т. е. окружности, эллипса. параболы и
1 ·1111ерб()ЛЫ~ см. также статью «За мечательные
Т JC;r Q..Vl 1 X't". LLNT1$il,\(I
Opmf.'<rDo<'\JfftuiPЬ.l*i:Ьun•
'""""'u B•pull""' м,,...,.р,.;
airiurt) Vmcwn\Marh.t,nю.;:
'~1а1шакr Aшum 1n V1Ьс
V nкt1 Lcl.. "tan:n РuЫ;,
cum.Dt(i/uo m 1.3
"'1um Tndut1,_
.l(Nouнcrlro
p<dl>.
П1•ршя· 11t·ч .1 111<11' и 1ла1111f• Аn олло11ия , rnдl? pЖilWl'P л,п11нr~ии
ne~IIOll К<>нИч е1 к>1х ,·е• 1ениl1 >. fkнt<u1111 1'i \ 7 г
f
Античн<1я математика
Llертеж н3 11змн1111
«K01t111 1t:'CK •1 X ff.?Ч(! lll1\1»
Аnnл лоння . Бол онь11
1~ы, г
крнвыс->) , 11 зложнн её 11е ·1 ·оnы<0 без ал1 ·ебра11че
Сf(НХ спм1юло n. но лаже: Ek1 пспользовз11 1 rя
таюrх пmштнй, как « 11олм н «Отрrщзтелы1ая
величи11а», неизuес1ных то1·да 1реческ0Гr мате
матш<с. tlcc доказательства Аполлония 1rысют
чисто геометрический характер, 11 в это.v~
смысле е1 ·о работу можно сч 11та· 1·h Hh1c111<.:i'I 1·uч
кой, кот< 1рой дос.~1· 111·ла 1 · речес1<ая 1 ·еоме·1р11-
ческая :шгеfiра .
И3учатr. кон11ческис ссчсюLЯ в ГpCllИll нач::t
т1 в rv FI. до н . э Их ()ТКрып МСНСХ..\1 , учен11к
Е 1щокс1, 11р11 1ю11ы· 1 ·ке рен1н · 1ъ ;~:.~дач) уд1юе 1 н1я
куба. Он представил их к~ш ссчс 1шя пря.мо
уrоль11ого, тупоу1·0:1ыюю 11остроугопы101·0 ко
нусоn вращення плоскостью. псрттепдикуляр
т юй образующей. лпоmю11иi1 n своей книге дал
более общ<.:с стсрсомстр11чсс1юс опрсдслс1 rис
ко11нчесю1х сечен11!1. Во-1 1 ерных , uн рассм:пр11 -
11;u1 rrрш1:щолы 1ы Г1 крутоной конус. Во-вторых.
уч 11тывал one его полости, что поз 1юлялп 11зу
ч и·1ъ обе не1·1111 1·1 rперболы И l 1:i ко11е1 l, 011 про
нолт 1л сечен11я mюскос1·ып, рас 1 юлnже111юi1 под
лю(iым углом к образующе 1'1.
О11ре;~елиn 11 1юстро11н тр11 1<()111 1ч <.:сю1х сс
чеrшя. лпошюний 11сследова 11 их ос1юв~1ые
свойстnа. асимптоты, касатслы1ыс. фокусы.
сопряжё1111ьн:: ДИ:IМt"lрЫ 11 '1' . д . к COЖ::tJICIU1IO.
методы нсследuвюiю1 кривьL\':. создаш1ыс А.!1011-
лонием. в дрс.:вности не 11uJJyLJИ J Ш раз1шпш.
хотя ШUIO'IЪ до H<IЧ(lJJ;\ v tl. cTU 't'p)'Цhl нзучал 11 11
KOM.\1CllTИp()t1:1 Jll·I Са~111 K()llllЧC:'CIOlt;" Ct'ЧCllllЯ
ПJlll'vtt>ня1111 J 1н1111, дт1 рс111сн11я куf111чt:ск11х
ур~щ11е1111Г1 . Так что теор11ю 1\01111чесю 1х се ч е
11111! Аrю1 11ю11l11! спзщ1; 1 ~ажщгп ;~п того, к;н; пщ1
оказалась пе()()ходимой.
Только в XVII в. Репе Декарт. Пм:::р Ферм~.
Исаак 11 ЪIOTO ll 11 1\ругие г1ёrrые обратнлr 1 с1.
46
История матсм.:1тики
к rабот:1м AГIOJIJl()l lll>I , СамСJе ll lllfXЖOC' пр11ме-
1re1111e ·1·еор ин ко 1 rпческих ссчс1mй п ттучт 1ла li
мехат1ке 11 астрономни. И01·аш1 Кеплс:r уста
тюви.rr, что планеты Солнечной сr 1 сте~tы д1ш
жутсн 110э; 1ш 111сам, в од1юи 113 фокусоn которых
находится <..олтще. Галилео Г;vншей показал, что
в пустоте бrошсш1n1й ю1J\н.:т, (ил н снаряд) буде~·
JJeтeтh LIO 11арабо.11с А в RO-x 1·1
·
Иса:н< IJыото11
СОЗ.' \:!Л CBOI·! зна \\СН 1IТЫС «М:.1 тсмз ·1 1 1ч есю I C 1-1а
ч:v1а 11::iтyp:u1t>1roй ф11:юсс1фт111•>. 1 н;~посрс;~сrщ:н-
1ю O ГIИj):IR(.Ъ H:.t рсзу.11ътз.ты ЛТТОЛ!ТО!-1 1 1>1.
ПОСЛЕЛНИЙ ПОЛЬЁМ
АНТИЧНОЙ МАТЕМАТИКИ
Творчс:ство Евклнд:.1 , Аrхнмс:ди 11 Аrщ: 1 1ю1-111н
было вершш-1о~'J 1'р еч~с коl1 м~пем:пик11 . Ис
слс11овання. 1 1ро1юд1rвш 11 ео1
в последу1ощ11е /\па столс:тия.
не выхоJ 1ию1 11 з 1<ру1 ·а 11роблем.
которые (ШП к-1учат 1. Н11 но
вых 1 rдей, ни новых теор11 й
IIC ТТОЯПЛЯЛОСI>. f l есомнен1 ю,
~то б1.1ло сRяз:1 н< >11 t' 1ю;11 1·1·1 1 чесю >й <>nст:11 ~он-
1<а1\ с 1<л а; \1.1 на11111с:1'1ся 11 м t 1пс.
Уже с 1ю111l<I Tll п. дп r1. :"'>. 11ач:-1m 1с1, заноева ·
те:1ь11ые войны pн~L'IШI. Экшюм 1 rческан 11 куль
тур 11 ая жиз111, 11 1-речесю1х колошIЯХ замерла .
Измученные стра11,анш1м11, люди п отш rуднсь к
рслш' ш1 , которая обе щала друrую, лучшую
жпзнь. Абстрактное мышлеrше, лоrичсск 11 е
р:Кс)'ЖЛС l ll!Я OTOЛRllHYЛИCI> Н~ нтоrой IJ!!:.tH
П-l fШ. дон. э. ст:v111 нрсмс11t:м с 1·рсмl[тель-
1юсп IIO:lBl>l1Нet111Я P 1t M:1 . В :'1>0 - х 1'1. ДО 11. d . пало
ПOCЛf'[\IJe e 11 :1 ЭJIJll !llJI C'l ' ИЧt"' C l<ll X l'OC)'/\:t[1CTB -
Египет 11 был:~ ос1юва 11 а Р1tмск:н1 1 ш11ер11я. tl rе
эультате жиэ11ь 6ыn ш11 х грсческ11 х коло1111И ко
ре~ 1н ы:-..1о6разои 1. 1зме1 11 и:~.с~.. С одтюй стороны,
прскратилнсь rазоритслыtыс rюi111t.1 и 11 рнмой
p:1::16u1\ <:JKUHOM I I Чt:<.:кuc I IOJIOЖl'HИl' стало fioлee
устойч1шh1м . Но с /\ру1·ой - эшшн1ктичсские
1 ·осуцарстна 1 ю1·t:рш 11 1 са ."1uстоя 1 ·сm,нuс.~1·ь 11 . по
uбраз11ом) ныражс 11111t> 1Jл~тарха , ж1 1 ·1t:1111 по
сгоя 111ю сознавал11. что н~щ и х 1 ·01ювам 11 за1 1 е
сё11 «римский сап т·"·
И .всё же греческая кулыура ожнвала. Ко11ец
1-11 88 . обычно называют «гречtсю 1м nозрож
деттием~. так как в это время творит ~ такие вели
rшс ппсатсли, ка~< Пл)-rарх 11' Лук 11 :11 1 . ~стестRс11-
ные науки таюкс испытьш:ти под1.ём. В первые
нска ноноll эры АJ1ександрия оставалась науч
ным и куль·1ур11 ым ц~ 1 t'1 ром дренн~1'0 мир;1.. Рrш
НllКОГД<! не м ог ср~ШШIТЬ СЯ с не1-1 в этом
ОТНОПIСН 1111. Он СЛ~IВНЛС}I CBOl IMИ поэта
ми, и стор 11к ам11 , юристами, но так 11
11е r 1р11общ11лс>11<1·J 1убн11:.1м :--:1ллн1rско й
ш1учпоlr мысли.
1:3 1 n. n Алекс<нщртш работал пре1<рас-
11ый матс матllк 11 тал:штлт1Dый ннже
нер-изобрt~татсль Геро н , 1<оторый 01· крьш
ГI:<)МЕТРИЯ РИМСКИХ
ЗЕМЛЕМЕРОВ
Согл.!< но лревн11м м ифам, окружа
юш11й чслове~..сJ м11р вuзн11~.. 1:1 неiа
ПсJ\1Ятt1ые врt·\1t• на пос ре~и бсско
неч11u rо ~1 жуткого хаоса В uтл~1ч щ~
m >..юса, в котором 1н:1 ;1 акu н ов1
~111r упuрядuс1 с11 В 1~см, во первы >.,
Cl.11> щ•нтрал1>НrlЯ TO'IKJ -
• пуп
зt•мм1 Во- вторых , в м11ре сстt.
ВЫЛ('Лt' I 1 ные 11.lПрdВЛl'НИЯ. в ropи -
10 tlTJЛbHUЙ /I ЛОСКОСIИ ~то ЛИ llИ И
се1.н.: р-1С1r и 1.~пал-восток. обр.1 -
~уюш11е крест 11 разби ва1ошие пло<
кnсть 11а 4 чао11
Э1и дрсвнt!~ш1ие и простейшие
геuметри ч еск 11 е предс:: 1 а в ле~1ия
на11(Юl\Се ПОЛllО ИСПU/\Ь·Ювам1 в
Лреn11е"' Р~1мс НапримРр, .\лsi га
д..~1 1 ия по полету пти u ри..,ск и с
..+.рl'ш>1 '1ыслен 1ю раэб11оалн 11etio
на 1части ЛИН11\.IМИ <.CBt:p-tOГ и зз
n,,д оuсток Затем пар:~ллель110
ГЛi\OllblM /I Иll ИllM • ПрО ВОЫ1ЛИ » BTU-
po< rt-11енные так что вс<: нt!бо 011..1
шва лпсь 110д1:лс11 ным Нс1 равные
квадраты. н.1 (1люд ая за пс-реме
ШCtt Иt'\o\ ппш И"! ОдtЮ ГО квадрата
в \рути, онн по определе н ны"'
прав и лам ИL t uлк овывал и волю
Ю1111 1 с.:р,1
По тому же принuипу р11млs~не
ра'iЬив;:~ли на чс1сти свои поля. На
поле отмеча11и uентраль ную точ ку,
чер<:з кото рую перп ендикуляр1ю
друг лругу проклад ывали дее глав -
ныс дорu1 ~· - kardo max1mL1'>
(с CLUt'J)cl нс~ ю1 ) 11 clec um.:inus nы
х11щ1~ (( воспж.1 на запад), со11.ра
шенно КМ 11 ОМ . 3.:~тсм nс~ раллель
н о ГЛс)Ul/ЫМ дорог il\1 черЕ'i r<'IBHЬIC
patt r ш1н~1я п роводим1 rp.:i 11 иuы ,
раlдРЛЯRШ 11Е' ПОЛ(' на СИСП.'\1У КВсlд
р а тов . )111 кu.:~дμ.п ы 11d 'iьt 1ылись
uе11тур ия\'1~1 . l dкую ЖI' сетку р~1...1
ляttt:• 1н ПО'\ЬЗовал11 при fJJ 1бив"е
военнЬI'< лarcpNt и про~кп1ровс~
ню1 1юоь1х 1upuдoo.
В 1-1 1вв.1 р.1н иuь1 Р11мскои им
пер и и 11.олоссilльно раLш~1р~1лись.
r 3Jхва• 1 с>н~1ых земель и i t оняли
nр~Ж l/ ИХ BЛdд('l\ l>llHB, и гоrула р
ственные ·~емлРмеры п р11сту 1 1ам 1 к
свое~~ работе Упорно н .-.1с.:тол ич
но разби вая nuлc.: 1ы uентур 1·111, о н~1
не п1.юrто 0Оо.т,1чали гр;111иuы
влJде ю11с1 , ~ю олнпвре,1сн 1 ю ycrd
HclBЛllR.lЛll на ЗС'IАЛС nорядо", ( хол
ныи с 1«:м, что был нз небе -
в оби 1с.:ли <амс 11 с) Юп итер.:~.
l la колон~1 а11ыtы'< зем11ях n рак
тич11ы с и хоэяиL твенные р11м"IЯНР
ввом1л11 п1Стему коорди 11 <1т, оче11 ь
похожу ю 11 а rп време11ныс.: п рямо-
,сtвюкущую силу пара. ll 1<0r-щc нск~1 ·1ам жил ма
те,1:1·1 11 к 11 астроно;\t Ме11ела11, сuздан:Jt ь си
стечы 1еож.·тр1111 и тр11rотюме:1 р1 111 на <.фсре -
первоf1 11~:сню11 111ово~'1 rеометрнп (см с-1 ·атью
~Ф11 rvры 11:1 с фере~) Во II в. знаме1штыl1 алек
с:шдр111fсю1!1 аст1юном 11 матсматнJ\ К,1авд1 1f1
Птолсмей соз, ~ал rс..:о цс111 ричсскую м олслh
~щр:t. просущсt-1·1юна 111 11 ую до XV- XVl 1111.
В ~рудах этнх уче н ых: )ЖС н аметилась те11 -
,'1.сн1~11 я поворота к выч 11с.1нтс"'Jh 1t Оl1 ма 1е.мати
кс:, рас 11111рс:1ш ю п о11ят11я ч.и сл а , отказу от rео
"lетр11чс..:скuй :.tJtгсбры. Особе11н о нрко новое
напрз1111 с1 111с 11μонв1 шос~, в пюрчееmс вс..rшчай
шего ат ·сбра1 1с 1-:.1 Д1 юфа 11та Алекса~ 1др1 11"1 ского.
которы 1~1 п01южил нач ало двум наукам ал гебре
лffh
c:D.LfJJ
_J L_J ;SL_I L_J
] ГsDll§~ rпп"I
~!~ UKI
KAR UO ~ MAXIMl lS
] ГsDil:srю 1
1
f )()ll
J[fuJ~~~("1 ~
·по
ш1vпп1 rю1
П(ll ~CKll С1\11
\Jl'1Пр.~лы1с111 чс1пь P""' 'nrn nu \11 <
IH"HT) р11я,111. лля f<(I орых УКd33НЫ и~
коорл 1111 мы с 11cno111. 11111 .111 1>1 <''1 1н1 м( f(l1X
u нфр 111 11 ( tll<IJ<lllH·H~IЯ о.з н ачDЮТ
(.)(.) tclextrJ (\rcun1an 1\
t r1p.11:1.1 о т ОМ,
sn •sttlt''' ·' tll'~UПIJl\il - C'\PBil ОТ n м
U li. !ulнa ka rd1nt>m ·1 ш11·рх т li.M
(К (с illol k,щl11\l'П\) - IJНl11 ()Т КМ
уrолы1ы <: ( декарншы) коорм1 наты
11.i плuLкuст11 . Кс~жла11 uентурия 11а
п ом• кол ировалась лву."1я •t иi 11,1м и.
По н11м вл,1делсu мur легко 01 ыt
катъ 11а плане t1ю11 участо~.. Отли
чне этоГ1 с исте~1ы от лекартооо~1 со
стоs~м.1 ЛltШЬ в том, 'ITO римЛЯНf'
не знал11 отриuатt:льных чи<ел. Он11
~1 CПOЛbJUBdM1 выражен 1111 rЛL'IЗJ от
ом" - справа ()Т DM), «BllИJ uт
км. - «Восрх 01 КМ».
C~t''"l roptJдlKUГO ПOCl.'Лl.'fllt Я 113
рукоП 11(1 t fHIM( t<ИХ lf'M l\(''IC:f)Uf) .
В11м1ы r 11.1вныt• лороrн CP/Jf'('l--l()Г
" заnал-!l()(то...
"-1 7
48
История матемалщи
н днофапто ву апашпу. Ему суждено было стзт1,
последним великим математико;у1 древ Jiости.
После Д1 юфанта работалн только более или
менее:: тал~штшmыс ко:ммсrгrаторы.
Христиа.гК"J'l:Ю, возникшее в 11ервых веках
НОIЮЙ :::>phl, ныс 1 ущию 11 ро· 1 · и в ЯJ ЫЧ ССКОЙ K}'Jlh-
тypы IJ науки ВJtаст:итсли .\1Ир~1 - р 11мляне так
же не 1юuщрнлн з:,~нятнf1 <J.бстрактной наукой.
Но 11 к стот, небла~ ·о приятнnй оnстановке алtк
сш щри йскэя ш коJ1а 11 росущест1ю 1{а11 а с:щё око
ло трёх веков. В III- IIачале IV в. в Александрии
жил и работал замечательный учёный Ilапп. Его
труд « Математнческое собраll ие" rюказывает,
что 011 был прскр<1спъrм знатоком к.пассичсской
:шп1ч110й г<:омстрии. n КОI ЩС l'v' в. Хрисп 1 аI1 -
скан Церковь начала ор 1 ·ан11:юнанное 11асту11-
л1.:1111е 11а 11а)'ку. В .~91 г. была сожжена :шачи
тельнзя ч асть Алсксандр11йской 6IIблиотсю 1 .
Остав ш иt.:ся pyкo{ll JCH продолжшm ун 1 1чтож;пъ
11 а лrотяже1111н более ·1 ·рёх столети l1.
« НАЧАЛА » ЕВКЛИЛА
.Быть мож<..'т, Евклид и не принадлежит к числу
таких но~заторон н ма·1·1.:ма·1' икt:. как Ф:!)1ес 1111и
Af)XI 1Мt:Д. Но он. кне НСЯК() l 'О сом 1te l-fl1.Я, я НЮU!СЯ
нспрснзоlfдённым с 1 1стt.:м:пт 1 :>атuром, ттед::1го
гом 11 1101 1 уляриз;~тором 11аую1 . Спш1мr 1 учеб-
11111<амl1 ('J'. е. ю1111·а:v1 и, сnста11ннш1.1l\н1 ern <-На
чзлз->) ЕиКJнщ охватщJ нrю :"IJ 1 eмt1 1 таr 11 ую
ы:пематику :-эпохн Платова.
«J!ача1 1 а» (др}той переnод названия - «:С:IЛе
мспты ~) прсл.ставлнют собой з~шсршсш-1 1.: це
лого ряда нс дошt'дшнх до нас .\1атсмат 11 чссю L~
прон:~нсдtшн1. Например, в шпой кнш·е ~·На
чал» и~1л: 11 ·астся т1.:orm1 отно111ени/'1 по Ен)\ОК
су, в десятш·1 кнн 1 ·с - теория иr1хщипнальных
RCJll1Ч[ I H пп Тt:этсту, 13 тр11н::Щl(<IТОЙ - теоrня
гt[): 1 BllJIЫ1 "1Х 'V11101 '0 1 'рЗ1111111(0 1\ · 1·з ЮКе llOCXOД}l -
11 \:1.Я 1< Теэте- 1 у.
Р:пумсстсн, Тiзлагая откrытия Тсэтстз. En -
,1 10 1<c:1 и другах свошс прсдшсствспликов, Ешс
лr щ добавнл мr ю1·0 нового, дал нол11ые дока
зательства того, что нс было ок01 1 L1атслыrо
уста 1 ювленр pa11ct Петь в ~ началах» н 11екотu
р1,1<.: Н :tХО/\К11, нr l/(HMU 11p11н~ljl) I CЖ<l ll \ ll C с~1 мому
~l\IOlll/\Y· 0 /\11 :.1 11 :3 11 ;.~и болсс яр1<ИХ l'al<~ I X 1I~IXO
ДOI\ -
·1 ·copt1'-'ta о бссконсчност11 множества
11рос1ъгх ч1 1 с<:л (см. статыо « Пrостыt: числа ·>) .
Из учён"'х конца lV н . ~южно назвать Теона
Александрийского TI его ДОЧI> r1111атию - 11ер-
11ую n истории женщину-математика. rнпа
т1 1 я - ;mтор коммсн·1 арнсн к работа м Аlюшю
ния 11 Диофшп~1 :;)т;:~ ;iамсчателы 1 ая жен 1ц ин ;1
сла н11лась умом и красноречнем. О её трап~ че
ской су;\ьбt на11щ:аны нсторичt.:сю 1 1.: романы .
В 41S 1·. Гипатня 6 ы ла рзс"l ·ер:~з 11з тол 1юй фа 11 а
т11ков-христна11 за то, что нс хотела порыRат1,
с я~ычестnом .
В V в. учёныс пою1,11ал н Ллекса 1 тдр1110 н nе
реезж<ши в Афш 1ы 3дссь работал 11 poкri (410-
485) , ксrюμы l1 оставил коммснта р11и к первой
юш ге <- 1l ачал"' F.11ю11~ди и кратю 111об::~ор 1 ктu
р1 ш геометrи11 ()Т Фзлtса до Енкп 1 ща , В VI n.
1юсл~днне 11з н1::лию1л комме 1 rтатоrоt\ - Евто
ю~й r1С11м11лr1ю11\ 1 1з1·1 1а1111ые 11:1 Лф1111, 11ъ111уж
дсны nылrт пересет r т~.ся в Ирз 11 Л1 1 т11 ч 11аи
наука и т~71ЬТ)11:1 угасли вместе с п ~ белью ncer()
а 1п·н~п юго общестна.
СОЛЕРЖАНИЕ (( НАЧАЛ » ЕВКЛИдА
« Нач ала» состоs1т из три надuати кн~1г. Первы е четы
ре посвяшены геометрии 1;а п лоскосr и. КаЖАую к11и
гу Евклид начинает с определений, но, кроме этого,
nервой книге предшеству ют пять а кс и ом и п осту
латов, сред1<1 которых 1·1uход11тся знаменитый nsный
no( тулат о па ра ллельны х линия х.
Затем в 1к ниге изла гается п ланиметр и я п рямоли
нейн ых фигур; устанавливаются основные свойства
треугольни ков, параллелограммо в. тра п еuи й. Ве1;ча
ют кн11гу теорема Пифагора и обратнuе ей преы.о
жение - треугольник, коадрат одной и• сторон ко
торого ра вен сумме квадратов двух дру r·и х сторон,
nр я моуrол ьны й.
Вп 11 к ниге изла гаются основы геометрической
алгебры.
К11ига 111 посвяшена свойсгвам кру1 а, его каса-
1 ельных и хо рд - воп росам, которые Gыли исследо
ваны Гиппократом Хиосским lV в. ло н. э.) илн ранее.
В IV книге строятся правильные п-уголь11ики при
11 =3, 4, 5. 1(), 15. Исключительно изяшнuе rюстрое
ниt" пrавильногп 15-угольни ка при надлежит самому
Евклиду.
Кttига V сuлuржит об шую теори ю отноu.1N111 и вели
чин no Е13дсЖ( у. Многие современt1ыс yчt:!tlыe счита
ют ее первой теорией действител ьного числа, во мн о
гом напоминаюше>й теорию сече11и~1 Лелекинда,
CO.iдclll H YIO В XJ X В.
В VIкни1 е Евклид излаrа~т уче~1ис о rюдобии. Он
nриме~1яет это учение к .:1адачам. которые можно
Несколько слон о ТО\1, как 1юегрое11 ы <-ll;1-
ч:.1л:1». Слслун л01·ичсской системе снос1·0 уч11-
теля Арщтотсля, Евк.тш;\ 1 1 ытаt:тся i\·1·1ъ :.1кснn
~1;п11 чсскос и:'!.lюжс:ние 1'с:Омстрн 1 1. Это \южно
ПШ!l'l l lЛ h CJll'f\}'IOЩH!\1 о6р:~зом.
F.слн р:ксмотрет1, /\OI01 :-i a 1 ·с::лъс1· 1ю ттекото
ро1'1 теорем ы, т мож110 ушr,1е."1Ъ те 6олс:с про
r·1ые ф:н<1'ы. с nомо щ ыо которых оно п о
строено. Эт11 nросг ые факты, н сво ю очсрсю"
вьпскают И:3 сщё более 11росты х факто11 11 т. )\.
BЫ I IOЛIIllГI тако iт :lH:IЛl!J /.~JlЯ BCt: X Tt'opt:м l'l '0-
. 11e1p 1111. ;v1ы 11uлуч1 1 м l'писок 11ростt:й u11 1 .\ фаr-
ток. облад:о~ ю1 щ1х CJl{::f\y к111 lнм11 с1юl1с·1 н:1м1 1: но-
111.::рJ-1ых, u1-11 1сок~ршен1 ю «оч ев~ 11тны " 11 потому
НL"1рt:бу кл 1 tо к:.1 з:~тельс1 f\3, 3 во - вто рых, 11 э 11 11х
\Юil\IIO m .rпес 1·н. ил.я о()ратт1ы м путём. BL.C тео
ремы rеометрпн Такие r1ростсl1шне факты 1т;:~
зы 1шотся акс 1 юмам 1r, d все осталыrыс фаюъ1
rеометр11 н явля ются теорсN1 а.ч11 . н ка.1.кдую тt
орему мо:;юю доказатъ с помощью аксном 11
Античная математн ка
свести к решен ию различных типов квадратных урав
нений.
Книги Vll- IX посвяшены ар11фметике, т. е. тео
рии uслых и раuиональных чисел (она была известн;:~
пифагорейuам не пщднее V в. до 11. э .). П<>мимо тео
рем, относяшихся к сло жению и умн ожению uелы х
ч11сел и их отt-юшени~, в них рассматриваются и воп
росы теории чисел: вводится алгоритм Евк11ида, изла
га к 1тся основы теарии делимосл~ Uf'лы х чисел, дока
зывается знаменитая теорема Евклида о том, что
просты х чисел беско11ечно много.
В книге Х на основании учения о uелых и рашю
нальн ых числах Евклид, следуя Теэтету, лает класси
фикаuию квадратичных ирра uиональностеА, возн и
каюших при решеi"I ИИ uепос1ек квадратных уравнении.
Кн ига XI п освяшен а стереометри и . Она содержит
основные теорем1,1 о прямых и nлоскLн.:тях в 1 р~хмер
ном простра11стве, задачи на построение (например,
как опустить r1ерnе11дикуляр из да ~11юй точки 11а
данную nлоL кость), а та кже теnрем ы о тnм, при каких
условиях параллелепипед и призма могут имегь
рав1-1ые объёмы .
В книге Xll с помошью метода исчерпывания Ев
L\Окса лок .ны ваю1·ся теорем ы о том. что отношенщ~
плошалей кругов равно отноше1111ю кос1Аратоо их
диа~1етров1 J отно ш ен и е объемов ша ров равно опю
шен и ю кубов их ди аметров .
В книге Xlll излагается учение о правильных мно
гСJгр.знниках· как их мо;.t<,1-ю пострQить, как нанти
д!\И llУ их ребер . зн ая радиус оn иса11111.>й сфе ры, и nо
•1ему лμугих nрав11льн ых тf'л не сушепвует.
ра 11ес уст:~1 гоклс11ных теорем. Т:~ю 1 м 061x1~JOl\1 ,
всё Зi\ан ис 1·сомстрш 1сто1 1т 11:1 фун/\<~ме нтс 11з
не6ш1ы1ю1·0 '-!1 1сп:1 акс1 юм.
F.1щm1л ра:l11 1 1'-! зл а кс1том1 .1 и посгулат1.1. Г10-
сrулат:~ м11 0 11 1 1ззы 1цл требощнпrя, кото рымп
слелуст рУrюn<1дстnонзться np11 гсо метр 1 r че
сю1х построеrrнях. H:.inp11мep. одш1 нз посп·
:1атов 1·ласrтт, что «1 1з любого цс11тра любы."•
p1t1.\II)'COM можно ош1сат1, окружность ~. Срсд11
пос·1 улаток. сформул11рuкш111 ых Нв1,л1щом.
бьL11и и такие: "Lkpc:3 ДНt:' точю1 можно 11рож:с
т1 1 нрнмую~: <1JJ,1~e 11рнмыс 11<: \101ут 3;Jк,11< 1ч 1пъ
JJростр:~н стна >:> (Э'l'О можно ГЮl lЯ'IЪ l'i/I(. ЧТО l:CЛI!
i \l:lt' прямыt: l1мекп дне nбщне точкr1. тn 0 1111
J\Олжны соn11асть) 11 11р.
с ЛO! IHТI IЯ~IH делn 06сто11т a11aJТ O ГlJЧllO .
К r1р1 1м еру, о круж1 ю('"Гr, опрелсляется как п:'о
мстрическое место точек JI3 пл оскостн, от
сншщrIX от панной TOЧKll () (1\<.'HT IXI) на дан
ш.к: рассr·uннис 1-.
Таю1м обра:юм . чтоб1,1 да·1·1,
49
Ипор1,1я м,11 ема ги к и
[вкл11д , l't'\Ы'ф pdtютi..i J\11дрt'д 1 1 " .мно Около 1 ~34- 1341.11 г
()1 1 ре;\епеш 1с окруж1юс1· 1 1. rта,1\О :шать. что т~1 -
1<ое ,,то чка», "расстоmше», <-nлоскос·rъ» 11 т. д.
13 KOJ ще 1\ОТ!ЦОВ можно IJi.tЛeлIITЬ lICбO!LbWUe
ч1тсло нз116опее 11рuсп,гх понятий. с 1ю,,·10 11 \ 1,rо
котоrых 011pl'дt."JШ 1и1·ся все ос1·:uн,ю,1с 1юня ·1 'J ~я
«Лсрвонач:т1,ные·• же поннт11н нас·1·011ы<о 11рос
т1,1 11 ИCll Ы , ЧТО 1IX )'Жl' Н(' 'l'pc()ye'l'CH ОПрС{l.СЛЯТ I>.
Впрочем , Енюнщ 11 1:: хи1·сл ! КТ:.Jнш11ъ fieз
t н 1гк·1\<:лс 111 1н даже 11ростсl11нr 1 е 1ю11нтпя. Т<tк, он
1 1111J1ет: '·Точк~1 есть то, что 1 1е 1 тмсст частей".
O,r\11ако нсяс110, что оз11ачаст ~ нс нмt'ть частей».
(Скорее все 1·0 U1щлиi1хочет11росто пояст11пь.
что rео."1етр1 rчсская точка не имеет р:~змсров)
llеудатпслыю. что это тумашюс 0 11рсдслс н1 тс
lВК!lИД 11111 '/J,t' /t;!J ll>l lН: нс l!CПOJlhЗycт
11нтерСС1 Ю Пj)rJCJLCДl1 '1'1>, Ка 1( IIr!)IIOДЯTCЯ В
<' !!:~чала х» самые нервы<.: л.ок::~за·1 сльстна. П о
Е11 ю 1иду.лкс ф111·уры 11азываютсн ранным11 , t'C!llJ
OJJll чогут быт1. «СОВ\1\С ЩСНЫ•> HCt'Mll C IIO ИMJI
точкам11 ('1'. е. 11 ерсм1::щан од11) фигуру ка!\
п1ё1щос ц<.:лос, мож1 ю ТОЧ1JО наложить её на
вторую фшуру). 1lo Еnюшд не опрслслщ:т. что
эш1ч11т <,совм<.:ст111ЪУ , Таким образом. его «011ре
деле 1 rнс.:» равенеl'!~:.t фигур па с;.1"чо.м дс;1 с t:с1ъ
обр;uц<:: 1ш<:: к 1L:.t11н.:rv1) IЮ13ССДН:<::J:Н-Ю МУ ()IJ Ы'l'Y· к
ш.:p<::MCll\{;Hl·llO тел "К:ll{ ' l'Нё/)Д<Н'О Цt::JШ\ '0->. Да-
:lt't:. l ' ШJMOIЦl,10 . -:J' l 'O l 'O HH lj)t: /\e.IJ <::l lll И'> hHКilll!l
Д< )~<азыRа<.:т прн:1нак~ 1 раве11п в~1 трсуголын1ков
R ПОСЛt';\)'IОЩL 1х же raccyЖJ\t:HШIX <111 ()ол i>ltl('
11 <:: 11 {JJI 1 .эуетсн налnжс 11 11t:м ф 1 11 ·) р. ;1 ссылается
на уже сформулиров~т 11ыс прrr:шаю1 равепсти~
треуrоль ш11<он. 1Iапртrмср , чтобы i\0 1\азатr,
равеJ1ст1ю 1-тлоп при ос 1юв::~111111 раnrю6ед·
рст шого тре~то.r1ьн rтка, Еnюшд провод1 1т бис
с<::ктрнсу у1·11;1 11р11 всршпне и 1юказ111на е1, что
IIOJl)'ЧCHl!ЫC < )JОЛС>IНН-/Ю / » р:1н 11 ы I IO пс:рно.\•1)
11р 11 :~11аку. А 11оскот,ку 1~ ран11п1 х трt')ТОJ 1ы111-
к;,~х-1юJющ1111<ах 11рп·1·11н р:нн-11 11х сторо11 лежат
р~ш111,1t: ут.·1ы. С'J1е1юв: 1тс;1 ы ю. )Тл ы 11р11 nc11or.:1 ·
111111 11cxnJJ,1югo треу1ол1.11111<:.з р;ншы (рпс. 1)
R r\слом тnореш 1 е Ен1сл1т1р веm 1<-1естве11 1 ю
Со:щ:ншан 11ч с1ктсма нзложе111ш 1·со мстр1ш
быт~ 11асголъко xuporтr~1. что прос.ущсо·13она.1:1
более двух тысяч лет. Впл о1ъ до ХХ стuж"1'1 1н в
странах Енро1 1п1 (в том ч.1клс н l'occ1 11 1) 1·со~н:.:т
р 1 110 н 111кол:е~х 11rL·1ю1 1a11a.1 111 11 0 псрско;1ам 11m 1
llO l l)'JJ Hp HЫM 06рабu1 K:IM rBКJllЩtll:IЫЛ <· HaчaJI ->
Но 1IOCЛt:Д)'IOЩ I IC IJUK()Jll'l l l IЯ ~1атем;J'l 1 1кон
l lt:: liO 1кём ClJГЛ:.1Ш~UlJ ICl1 с CI 1 стс:.юi1 а.КСПОJ\1 11
О11ре; 1елстнrf1 Евю11щ;1 11 JlblT:lЛllCb ее ул~'ЧШIЛЪ.
Наттр 1 ~мер, аксиома о том. что псе прямые ~тm,1
рzшпы меж;\у coбofi, 01Gtэаласъ пе11уж1 юГ1: тго
пред;южеrщ с удалnсь доказат1, т.:ак теорему
исх одя п:i остат, ны х акспом
Поднер 1·1111 ch с< >Мш.:шно 11н еко·1·орыt: r1py 1'11e
акс1юмы 11 1шстул:~ты rнкJ111л:.1 Осоfk:нное
НС:)'/ !< )J\JIC''J'B<>peн 1 IC всс1:1 1;1 1\ЫЗЪIR:Ш l IЯ'J'ЫJI П< )Cl)'-
JL;J· 1, утнерж; 1ан11111l1 : tтл 11 д,Кt" 11rнu.1ыс. 11~pt"' Ce·
::>·" rNr.11;:оuь
У.111гл пr.рв"JJ,
l}<'~н r.rг~ri.t ),·~ ,,n щ;.1tmЪ [/111~ ·..~"Ъ
11 )'1'.-\Х}1.т. 1.11j(}'14',\fl f11t.~ \'t 11 Q0}11f1J,1-.'Ъ
!·1 1 уrа'Ъ •11)M'•'\.' 1111 u·1r..1~Ъ J !.J ';il." I C
<J n.t 11.\\сл•••рч•t-11:0.Ъ и11.1.ЪJ111 ., 1t11•Ъ t·:i-
" .., ,, 1(\111 3o~t1 nl '· .-.~rf1 1 ~1,1
~1м' q>,-rJfU ,..111·1()
У' U/\•iH ~' l tt"l r 1_)'Mlf • 11111: Гшr~ n'mL. щ«t(A/lt .\ HЫ~l
t111i•\1"y 1,.._щ 11.н.jh 11н1 tt~f-'·\.\CAЩ'f•:l\:"1.i.'81 .11\1 -1
ш.1•1)",1;с: - n\,_ cv1 Q~•l\l'•H•1l1 (ltfc''ll11
• 1q1•1)р.1Ь
triнi1r11J','\111111.·";~1 "n:--.ч• n th!'il'. н~rrн "r ! JJ 1 t 1 't 1 -
ivmlo Н• 1 11'1{С :. r
"._ . 1 \'1 на1т"n.Л~ f (f11 nr(;r Цf\·
1tyll'I mv П Allfl){<MY rlllf('jt'~W.
rн 1·1· яко;.1Ъ '1 ·rr-vr·" \l 1fr; J; 11rnмnyr" 1
1 10~1li. ""' .11,н'11 Cl\'>K' ~nто ро1 1 r.р~
м11му у 1"у npoт1 ruA'l\ >r-пЪ p.нtril>
FCT~ nрнчы, ъ ..1nухЪ fOK'JfЪ К11.1)р1"·
'IЛ~IU ЧllHO
l l t'jJIIOI ' рус ('"1~
IПдJН\11:' • I 1,J•<~Л•
l•ЭЛt'Mt'll!l)fl n l
Е JK/\11Л<l. 17jq г.
LA+LB< 180 '
.,.
.,.
.,.
чённNt т1х~·1·ы.:й. обра:>уют 1ю одну стuр(Jну от
трt"гы:й ЩJ.И ,\1UЙ 1шутрен11не у1·J1ы. сумма кото
рh1Х Mt:HCC Дli)'X прямых )'l'Jl(Щ '1'0 1 1рп 11р()ДОЛ
жс:нии ~-1'их Т(Нух 1 1рямых 0 1111 1н.:ттреметю 11е
ресекуте>1 , причём пме111 ю с той стороны от
тре-1' 1)ей 11 рдмой. 1·де сумма олносторошпrх
утлон .менее 180° (рнс. 2).
Об этом постулате уже нельзя сказать «ОН
столь прост н очен 1-1деп, что пс требует до
казатСJ1ьства ·>, нс праRла л 1 1~ liсть н 1·еомtтр1ш
'1<.:uремы, котор 1,1с 1:1ыражают 1 ·ораз;ю болс:е
пр<КТЫС и OЧCBИJ\HhlC 1·~011,1стричсски ф:!КТЫ,
АРХ ИМЕЛ
Нссо~шс11 1 ю, Архнмсд (О1<01ю 287-2 12
дон э.) - CIM hU1 гсниалы1ы1'1 учёный Дренней
Гр<::цин . Он сто1л н 0;1ном ряду с Ныотш [(),\1,
Гаус~.:ом, uйлс1х>м, Лоб<1че1:1~.:ю 1м н 11руп1мн
вслича(11.11нмп м;.~·1·см<~т11ками всех нрсмi:н. E1·u
Тр)'l\Ы n ос нящtны 11t тш1ько матtматш<t . Он
сдеш1л замечательные спl\ры·1 ш:1 н мt:ха11шсt.
хорошо знал астро110,,шю, оптику, rи;т,равлпку
J1 был JIOИCTJШe легендарной ЛJ IЧI ЮСТЫО ,
Сь111 астронома Фпдия, написаnшет соч1ше-
11не о ниаметрах С:олнца и Луны, Архимед
родился и жю1 в гре• 1 еском гoporte Сиракузы па
ОЩ1mн1,1, Он б ыJ 1 11r116лижён ко двору цар>1 Г11-
l'рона 11 н l:J'O CЫH<.t-HaCЛ<.:JtH11Ka.
Хорuшо известен rассказ о жертвен нuм
11t:нце Гперо11:i. Арх 11 мс;~;у nпруч11л11 11poncp1 1 ·1ъ
честност 1, ю11еп 11ра 11опрсJ\елнть, СJ\tлаи иенсц
нз ч1 1<.то1·0 золота ит-1 с примесями друг11х ме
талжн1 п r1e-1
· лн ю ~у тр и 11ero пуетт. О;\нажл1,1,
размышляя об этом, Архимед 1101·руз11J1ся в
1ш111у и заметил, что nытссне 1 шая его телом
вод;~ пролнл:~сь через край. Гсrrнал.ыюrо учёпо-
1·0 тут же осс~-шла яркая пдея, и с кр1шом «Эв
rика. энрнка!» (Т. С, «1l :н.uёл,11<1111/::Л~») ОН, IOJK был
H::l l'OJI, брос 1 JЛСЯ проАОJ~ПТ!, экспtр1 I MCH'I' ,
Антич~ I JЯ мат<:?матик.:~
н~11р11мt:р 'l'еl)ремз о Т()м, ч·1'() n ра1шо6е,л,ре11-
1 юм треуrолынше у1·лы пр11 пстювании равны.
Неудпnит<::лы ю. что на протнже11т 1иекоn м~ю
rие матсм::1тш01 nытаJ111С1> доказать пятый nо
е1улат Евклида как теорему.
Былп найдспы и друпк формулнровю·r это 11
i!КСIЮЯЫ, КО'!'ОрЫС выражаюто1 11\i<JЧ(' , IIO Э.l<'IШ -
1:\~VleH'l'HЫ пятом у пос.-1-ул:пу, О,цна И:3 ннл таt;шщ:
чt.:ре:~ точк~. 11<.: прш 1 ;.щле.жащую 11анной пrя
мо(r, мож1roлровесп1 'J'Om,кo одну 11рнму10, 11:i -
pam1eJ1ы-ryю датюй (т. с . 1н: щ;ресекающу1ося
с ней). Име111101зтакпl1 tlIOP;\1t пршюдптсн аксп
ома па 1хщлеJГL1 юстп в совреме1 шых Шl\OJJЫ 1ых
Уче61 шках.
Но М()Ж!IО ЛI I ДОК;t:~:.~тъ ПЯTblfl постулат с
помощью остальных аксно;\J? Нс1т да, то эта
аю:1ю.,1а 1 1 с i-ryжiia, т. с. 11зJю.жсн11с 1·еомстрr·111
\ЮЖНО СДСЛU'I Ъ более ЩХJСl'ЫМ. А <.:CJUI 1!СТ ?" ()·1 -
1\СТИ'lЪ на ЗТО'J' IIOll[IOC VIЗTC,l\!:JTJ !КН смо1·m1 J I HШh
через дне 1 ъ1ся ч 1·1 лет после Евюшда (Ct\1. ст:пъю
"Геометр~ 1я Л обз чеrкко1·0~ ) .
Иде.:я ЛрхнмсJ\:1 0•1снh проста. Тело, погру
ж<::н1 юе н 1:ю11у, вытесняет стш1ько ж1111кuст11,
каков объё,,1 само1'u тела . Тlоместн 1кнен, R
Ц11/1111-1Дf1ИЧССКИЙ СОС)Д С BOHOJI, МОЖНО 011рС
дели-~ъ. какuс КОЛНЧССТВ{) ЖllДl.IOC'll l uн HЫTt'C
HJ 1т. т. t. уз1 ~ ать его объём.. А з1 i:iя объём и R~зае
с11в ве 11 ец. леl"КО nыч1rслит~. удельную м~кс~ .
Это и даст возможность установ rп·ь 11стr111у:
ве,111, золото - очень тяжёлыit мет;:~лл. а более
,0,рх»М<'А Г1мnюра
(" а HTllЧ t IOI О <tЗUUfJilЖCHИl'I
()коле"> "\Vll l в
')1
,Аъ.
CZ'.l(]J
История математики
'52
лёrкис примес11 , и тем более пустоты, уrv1ень
шают удельную массу изделия.
Но Архимед на этом не остано1шлся. В тру-
1\е «О пщшающихтелах» он сформулировал за
кон, который гласит: ~тело, rюгружёштое u·
жию<0с1ъ, теряет в сноём весе столько, кm<ов
вес вытесненной жидкости». Закон Архшv1е/\а
являе;rся (наряду с другими, позже открытыми
фаtпами) основой гидравлнки - науки, нзуча
ю1цей зеiконы днижения 1·r равновесия жидко
стей . Именно этот закон объясняет, почему
стальной шар (без пустот) тонет в воl\е, тогда
ЮН\. дсревя/lнос тело всплывает. В первом слу
чае вес нытеснеr11 юй 1юды меньше веса самого
urapa, т. е. архимедова « Ныталки:nающая» сил~1
педоСТ3ТОЧJ 1а для того, чтобы удержать его 1ia
поверхности. А тяжело rружённый корабль,
корпус которого сделан из металла, не тонет,
погружаясь только до так назъшас.мой nатер
;ш ни и . Поскольку внутри !\Орлуса корабля
много 11ространстна, заполненного воздухо.и,
сре; \11яя удельная масса судна мснhlл е плотно-
сrи вuды и вытал1швающая сила удерживает
егu н;~ плаву. З<~кон ApX1'L"tcдa объясняет также,
почему воздушный шар , заполне1-пrьui тёnлым
воздухом или газом , которьпl лс1·чс воздуха
(~=юдородом , гелием) , улетает ввысь.
Знание пщранлию·1 rю:толнло Архимеду
нзобrести вшповui1 1-1асос r~ю1 вык<1чи1:1ання
воды. Такой насос (1<охля) до педащ 1 его време-
1щ применялся па испанс1шх 11 мексиканских
серебряных руд11111<ах.
И:> курса физики всем знакомо Архиме,цово
пр:ншло рыч:н·;~. Со1·ласно пред<1нию. учёный
про11 :шёс крыжн11 ю фразу: <Дайте мне то<IК)'
опоры, и я подниму Землю' ~. Конечно. Архи
~1ед нмел в rшду пр11мене11не рыча1~а . но, nрн
мо о<аже;ч, 011 был несколько самоу13сре11: кро
ме точки опоры ему п rычаг понадобился бы
совершенно фанl'астнче('кий - 11евеJюя·11 ю
д.rrинный и прп этом 1rесrибжмый с_-герже1гь.
Достонерю,1с факты п мrю1'очнсле1шыс ле
генды тrюрят о том, ч·1·0 Архи,\tед изобрёл
немаJЮ интерес11ьLх машнн и присnособл ений.
Цар11 Гиерон приказал построи1ъ огромный
корабm; «Сиракосия» . Но он был так тяжёл, что
множестnо вои11оn не смогmf даже сдвш·1уrь eJ ·o
с места. Тогда Архимед скопсгруироRал мсха
н1пм , который nоз1юлил сделат ь это О1' Н ОМ)'
человеку. Царп сам спустил корабль на воду и в
вocroprc закричал: ~01 •нынс, что бы 1 1 и сказал
наш Архимед, мы всё будем сч11·1-а·1ъ ис1·и 1 шым! ».
Архимед был семидеся·1·илетним стариком,
1ю1·да римт1 11е осадили ег() родной гоrод С11-
ра1'"}'ЗЫ. Чтобы помочь жителям в обороне, оп
изобретал военные машины. Мощные ката
пулыъ1 метали тяжёлые камни: на римские ле
гионы, а более лёгкие обрушивали н ;,~ враг.~
целый град ядер. Специальные береговые кpa
HhI. 1юзвы111авшн ес51 над крепuсr:ными с1'енu"'н1 ,
поднимали крюка.ми корабли римлян и опро
кидывал и 1. 1х. Р11мский тюеначальн~rк Марцс::лл,
r~едоволы1ый сrюими 1юе1111ымн и11женерами,
nосх1·111lался Арлvrмедом, который «черпал море
римскими кораблями». А легионеры в панr-ше
разбеr;шись, когда из-за r·ородской стены по
казывалась ка.юш-ннбудь nсрё.вка или бревно:
•Архимед придумал rrо.вую машнну на нашу
11ш11бель!->.
t..(тобы отразить ttаnадение болыuо1 ·0 рам
с кого корабля, Архимед заставил 1·ре ч еск11.х
1юигюв до блеска отполировать мt:т·аJ1лические
щил,1 , а затем выстро 1·пъся 1що.~1, береrа.. По е 1 ·0
указа~ 1ию воины сфокусиронали С())шечные
Jiучи от щито-в в одной точке на борту корабля.
Деревянная обшивка судна IIarpeлacь до высо
r<ой температуры и вспыхнул:~ - на 1<ораблс
начался пожар.
Но дла само 1 ·0 учёного все эти военные
изобретения были лишь н езначительными
11 рактическими приложениями его н;.~учных
открытий. Кроме правила рычага и закона о
ныталкивающей силе, заставляющей тела пла
нюъ, Архимед создал уче 11 ие о центр:Iх тяжес111
'fел и с его помощью доказаJt ·1·еорему о меди
анах треу1•ол ьника , которую теперь называют
его именем.
АрхИJ\'tед рассуждал ·rак Поместим три рав
ные массы в вершинах треугольника АВС, и
пусть О - центр тяжести этих масс, т. е" еслн
110;\11ере-тъ треу1·ольн ик н ~той точке, он бущ:т
находиться н равновесии (рис. 1). Теперь
nеренесём дне нз этих масс в середю-tу ссют
ветствующей сто роны ВС. "! '. е. R точку, явпяю
щуюся цеатром тяжести этих двух масс. В ре
:~ультате положение общего центра тяжести
Анти чная математика
всех трёх масс не изменитсн (рис. 2). Но зато
стш ювится ясным, что точка () находится н;1
медrrанс АЛ-1 и делит её в отнош<.:11ин 2 : J
(сч11т~ш от нерШ1 1 ннА). Tu же рассу-жденне при
мсю1м:о 11 к любоf1 другой меднане. А знач11т,
все три медианы проходят через точt-..'У О. Так
Архи мед доказал. что н любом треуrоJ1ьникс
мед11а11ы пересекаются в сщноf'I точке (r \ei-rтpc
т51жссти треугольника).
Архимед наmёл и ряд других геометриче
ских nримс11е1 rнй своей тсорю 1це1 iтpun тяже
сти: он р:!ссказал u них в труде «О равновесии
тюских фигур''·
Hu самые замсч;.пельныс м::~тематнчесю1С
открыпнt Аrх11мед.а сн>1з:.1ны с его мстодам11
вычнсн ени.н тющадей 1·1объёмов. Эт11 мст<щы
фа 1<тичссю 1 прсдносхити1111 l.'~дею ннтегриро
вания - за 18 веков /(О того, "ак дт 1 ффере111 щ
:шьное и 1-ште1·ралыюе исчисление 61,mo rю
строено liыотоном и Лейбни 1 ~ем!
I lрименяя метод Евдо.кса, Архнмед nычнслил
площадь 11роизволыю1·0 сегмента параболы. В
CORpeMCIIHJ,JX 0ООЗН3ЧСНИЯХ ЭТИ раСС)'ЖДСНИЯ
можно изJюж1пь следующим образом.
Рассмотрим сс1·мент парабОJLЫ , uтсекаемьuvJ
от этQ.й кривой хор;\Ой АС, и пусть 11рямая,
параллелы 1ая хорде, кз саетс.» ш~раболы н точ
ке В (рис. 3). Треу1'0льни 1< АВС ме11 ы11е 110 шю
щади, чем рассматриRаемый сегмент тtрабол~-.1.
Возьмём тепер1, на параболе ещё две точки G,
Н, которые проектируются в середины отрез
ков AD и DC. Доб:ши.в к треуголышку AJJC тре
угольники ABG, вен, мы получим многоуголь
пиклс;внс, который по шющади более близок
к сеrмеюу параболы . Теnерп можнu на хордах
AG, СВ, ВН, НС 1 юстро 1нь новые треу1 ·uльники
·А Рис.1.
53
54
Истnрия математики
(с трсты:l1 нершшю~'1 нrt параболе) 11 т д. В
рс:iультатс: N\Ы будс:м нсё болс:е точнu у:н~анаТh
шющаr1 1 , сеrм<::нта параболы .
А ;-щлыIJс Архимед лрu1юю11 сноп замеча
тельные 11::1ыскаюrя. 011 нычнсляет плnщади
тюлучающr1хся м1ю1·оуrольникпв (таких, как
АСВНС и тюсз1едующтте) и фаю·11чесю r 1rахп1~1 1 т
nре/(ел, к которому стремятся :=~ти площаюr. т. е.
нахол;ит п1ют;а;~ь сегме11та параболы. Окюы
вается. она составляет 2/3 от площади нарал
пелогр~м.ма АЕРС.
::>тот результат Архимел получае1· дпумя с110-
соб:1.мн . 8 пср1юм он 11сп011к~ус:т учение о
центрах 'Г>J.Жести · к;Lк бы р<1зре~:.1ет се1 ·м~:нт па
раболы на тuнкне нертикальныс пnлоски 1r,
смещая llX, 11<.IХОДНТ пе11тры TIOKCCTll IIOJIOCOK в
псрно 1 1::1чал~,ном 1-1 смещённОJ\1 положе 1 rш1х,
уrа111ювешиная с помощью рычага сегмент
параболы н 1-1екоторый треугольник Второй
способ - чпсто выч 1 клнтельный
-
даёт вы
раженле nлощаде1'1 вписанных в сегмент мно
rоуголышков с помощью формулы
1
)2
~-~
1
...
5(L+~ +...+/1)- п +11. +(J+.t.+ ...+11)
РазумеС'f'ся, Архимсн пр1 rнодит её в словесной
формулировке
Разрез:шне на по1 юсю1 , нт1 сло1 1 , Арх11мед
применнет 1·акже д1 1 я вычисле1 1 11я 06'1,ё,"та н
nоnерхrюстн тара, объёма и поверх~юстп
urapoвo r·o слrщ объёма параболоида nращепия
и других тел (рис. .+).
Архимеду пр1шадлсжит ещё много замеча
телы 1 ых 1·еометр11чсских открытнЛ ()11 на
учплся выч 1 1слять сторо11ы шшсанного сем11-
у 1 ·от,н11ка; / (ОК;J.З:JЛ , что H<JKJIOHHOC c<:Ч<::ltl-Je
конуса 11рсдста.вляст собо11 эллvrпс. Формулу
Н;JХОЖ/\СНШi l IJIOIT(aДИ. ·1-реугоm,ника 110 ДЛ\.'ГН::lМ
е го стuро11 :
Рис. 4.
S = ,/ р( р-а)(р- b)(J1- с:.)
Pite. 5 . Aμx11м eлnR.i
t llНj.JdЛb
[ vH?fПb Архн.,.l"л .1 . Копня XVlll и. 1 римrкш1 "tн.1ик1t 11в
называют фор.му.'Iой Герона, тю Архимед з11ал
её раньше.
Кроме то го, Арх 11МС/\ ПОС1 p01 IJI сnпрал ь, H<l-
Зhl f\~1 IOЩ)'IO("}J тcncph el'(> именем (рис i) Им
уст;11 юв1 1егю , что сслн JJpsi \t ~1я нр:ш.щется рав
ном ерно нокр,11 · 11екоторо1'1 свпеlJ точю1 n, а но
этоn прямо!~ раnномср1ю дR11жетсн 'ючка , то
она uп 1 кывае-r спнраI11,_ )],J1я этоl1 с11щ1алн Ар
хнме;~ nывел угалне~ш<' н полярных кппрдll
н:пах, 11ашёл тсасательную n произuОJ[Ы-Юй точ
ке, вычнслил площадь между дuумя радиусами
и между дnумя в11тт<амп. 011 описал т:uоке рнд
мехаш1чс:ских примснсr шй такоf1 cr111pam1
ll1пt'Jx·c 110. ч10 Арх11мсд снач<lла нс даnал
/(OK;J1aTCJlbCTll, T<IK как ЖCJl<JJ I , чтобы <· К:I Ж/ \hlll
м.3 1 емапrк имеJ1 у11овольстние самш:тшпельно
11 олуч11ть этот рсзулъта'J ">. Более то1·0, он любил
ОЗ<!./1,<1.Ч/11\аП, CROllX ·jaШ1CTHllKOI~. пр11n:11:тяя Нt'
которые 11енсрные у1 верж;,t.:111щ •·N• бы тот, кто
бу; \еТ уверЯ'JЪ беэ )\OKaЗ<lП.:Jl/)CT.R::I. ЧТО ОН все ОТ-
1\рЫЛ сам. rютталс я 6ы n 1юnvптку, утнерж; 1ая без
ос11опания , что 11а111ёл то, чего 1 1 сльэя найти".
Древние 1'рею1 nокрынал11 стол сухим песком
и на ::JТUl-i <-rrecчaнu1·1 но<.:ке" дел;.ин1 liСртсжн За
т:.~кнм столом и силе; ~ Арх1 1 ме;1, углу61 1 ённыГ1 н
CB()JJ MЪICJll -1 , кпгд:1 OД I LH и;-J ГJИМСК11.Х HO l lHOA,
СJюм1 11тп1х сппрт 1-1вле н1-1t' 1 ·ре1<ов , ворнался 1<
нему. «Не CN1t:й 1poran, мон чертежн~ ,, - за -
1..:рнчал учё11h11'1 . Легионер вскипел. Лере;' ни:1-1
был враг, yi mчтожа.вшн(1 рнмс1ше кораблн, со-
J,. \311JllllЙ ;'ЩСЮfС MЗllllJIIЬГ. Т<о·1·орыс ;'\1е'!';.1ЛИ КЗ~l
rrп и у6 1тщ1т 1 его тонар1шJ.сl1. И, 11еомпря 1 1~1
·шпрет военачаJ1ы1ш<а Марцелла. 011 прон:шл
старика мечом. Обтщаясь 1.:р оn ыо, Архпмед
упал 1ia свои чсрп.:жи, Н<Хiможно содсржав шш.:
ещt о;~.но научно<.: отк р1,r· 1·11 е...
« АРИФМЕТИКА » ЛИОФАНТА
Дп 11 :i tШL~ J\11e(1 дошлн два nронзведсп11н Дш)
фанта, оба 1 1 с 1101шостыо. :)то «Арифметика•
(шес11> 1<1 11 11· нз тринадuат11) и uтрьшю 1 из тра к
тата <· О ~шоrоуголъпых ч.ислах?. 1:-Lu о са ~юм
авторе 1 1 е:: 11~~ВС(vгно 1 юЧ'!11 н11чс 1·0 Фr:н-щузский
1кторJ1к м:1тс,\1 :Т11 1ки Поль Т: 1 ннср11 , t>СНоRывз
нсь на косвс11ныхдзш1ых, опредслr 1 J 1, чтоДио
с!шrrжru~ k ct:re1t1 1нс lll в. n11.нa1<CJ учёные ~ r юхн
Возрож11с11ня, n·1 ·к rыя11111е coч1111e 1 rrrя Д110-
фанта в 6иnmютеке 8 3T~n<a 1 1а, оттюс 1 1ли время
ею ж11:ши J< серед1111 с 1.1 в. Сохранило1 1·екст
эm1тафи11 ( па11писи lla 11адгробrrом к~1м1н:). нз
KOTOr()fT МОЖНО IIЗПЛеУ.Ь IЮС -КаКИС СRt'ДС:ШIЯ:
ПрахД1тфстта г;ю6111ш,а 1101\ошп:
диrшсь l!tf - и каме1tь
J~) 1cJpы11 U<.'Л:J'CCIJl(JQ,;lt C!ZO Cl\(LЖY!J/1
усоптеги (U'JL.
Волр1/ богои июсп~1 110 часть .11(uзни
()/-/ 11/ЮЖ'Шl jJe(iё11J\IJ.M .
и )Щ111 >н1 1 ну 11/ l!CHIO(/ RCYnf.щ miu1.
с 1~,1 1mх:о.м на ll(l!JCa.\".
Т11.1111л-о лmн:~:'ш С(:'()U1ная, с шн)ругот
mt оfiручuли1.
С ·llt!IO nmJU1 лет щювсдя .
cыlfa до.ждш1СJ1 .ч11дрсt(.
7'с.иы~о 1юлжиз1-tи отцовс1\оii
воз.любле1111ы1/ сын его 11/JШICLlЛ -
Uтнлт 011 был 11 опща pa11н&t"r
_.1юг 1 и11 )li сmщ1!.
Два.>1сды дtю гш)а рос)итш1ъ ш1Jшкиr:мu1
JYlЯ:J/CIШf! горl!.
Тут и у1ш()ел 11/NйeJ1 .J1с11.ан11
llt!ЧtlЛЫIOzi C(l(}f!Lf.
Д<Х'Т:П'() • 1н о pбltll'f'I, yp:i ш ICHI lt:' 1н:рАо й сте 11 е-
1111 с O/\flllM не11:~uсстным - 11 мы у:тасм. что
Д1юфант 11rюЖ11л fЧ 1·ола.
Е 1·0 ~ Ариф м е·т· ика<> стат~ rюuоротным пунк
·1·ом в 1х1зmп111 1 злсебры11 теорпн ч1кt:Л. Имен -
А нп1 ч нd1 1 мате"1мпик<1
~то проrtзошл(I u 212 r. до 1r. .- > ••Марцелл np1 1-
каJ:.т с почссп1м11 похоро111 rт1, Лрхимедз , а на
~101плыюй плпте иэобра:нлъ цн.11и11др 11 н1ш
сан ны11 в н<"тu шар. Такхотt:л сам учёньнl , 110-
скою,ку оче 11ь 1·ор,t1 1л ся открыты \1 11м сщ>тно-
1нсн1 1 см объёмов ::>т1 1 х фигур - 3: 2.
110 :щссь nропзошсл Ol<Ol l Ч:lTCЛЫIЫ fl (УПШ:3 от
rеомстрr JLJt:cкolr :-1лп::бры. Бпанщаря б) кнс111101't
снмнuюшt' Д1юф~111 та ал1тбра uбрt.:ла ноныl1
ш:1ык, i ·opa.31\0 Guлct: ш1t.:р;п 1 11111ы1'1 11 у, 1,06 1-1ыl1 .
•1см я::1ык гt::o,'ll1cтp1J11 (см . ста тыо "f1ткде1111с (iук
кс шюfr с11.,шо.rттrю r ·•).
«Ар11фмет11ка" -- ::>то 1н:: тсnрет1 1с~ сско~ прn-
11:шс,1е 1 11 1е, ка1' «l l aчaл::t» r:1щл11rta 1ип1 " Ке> 1111 чс
с 1ше се че~ пш-> Лпо.11.rюrmя. :)то с6о ршп' : sадзч
(nce t·o 1rx t 8<)). каж,:1::ш н:~ r.:oтopurx с1 r :.16жlт1а
ОД !lИМ llJIИ llCCKOJlbКlL'\Ш рt:ШСПШI М\1 и нco6-
XO,l.11Lt\1ЫMl'I II05JCIICHl151,'vllf,
в н.:Nалс Сl:Ю<.:ГО ~ ·руда /~1 юфа~rт 1IOMCCTl lJI
кр~ткое вве11.<.:н11с. ста 111нее 1 н: рны~1 11з.южс нн
см ()С Н ОН алтс:бр1,1. В НёМ СТрСШТСН l IOJll' ra 1~1 I0-
1J:IJ111H ЫX ЧJ I CCJI 11 BBOДL l 'J'(' Я fiуккс 1 111:1н C l 1MПO
Jll lK<I. Та .\1 же <lюрму1 111руюто11 1раш1ла1161сп111~1
с м1ю1'о ч ; 1 ~пам 11 11 :-1)ar111e11шr~11 1 Цх.1з:-· отnо
р11м сл, чн-, ап:~лн;з ре111е1 шf1 ~1а1tач по. пюляет
0611аружr пь 13 •·Лр11фмст 1 1ке·• 60_1ее шнрокие
тсорет11ческнt: ос 1 10uа1ш:я, чем те, 1-\ОТ()р ы е
>wrю пз1южс:ны но ввсдещщ Пре)fщс всего это
опюс 1 11·ся к ч н слоно1I обл:1ст1 1 .
l l 3!1UMHIJ.\1, что R КJl:lCt:JIЧCCKOi'I а1 1 тr 1ч но~'r
.'lll :t'ГCM:lТJIKC: ч11слам1 1 113:1ЫR:JЛ ll CI> М !-I ОЖССТВ ;]
t:/\lfНJЩ, '1'. с:. ТОJ.IЫШ на тураЛh НЫ С Ч!LCJ l :l
Дно
ф~IJIТ же Х/)ТН 11 ) \:1 t ·1 cн1pe.r\CJICH I Jt: Ч11 СJ 1 ~1 [((tl{
мнnжс:стRа е; ~нннr1 , 1 ю н;J 11ротнже 1 н 1 11 всех
КllНГ !1 ~1:11>111аст r<аждос l lOJIOЖllH'J lul IOC p:lЦIIO
нали1ю с решение сnо их з:щач словом «ч11сло ».
()д 11 аr<о д:1я построе11ил :тгсбры Ol\IlHX
толы<о полож1 пе.'1Ь1n,1х дробс~'t 11едостаточт10.
11 Цtюф:шт делает рспн пе.r1ы1ыi1 шаг Rnoд1 rт
отр 1щатсJп,ные чнсла. Дrrя :о~того он выбнр:н:т
Ml~I'C>/\, l IЗHCCTI IЫJI TCГIC:/)h как :1 кс 1 юмaTl·l'l t'CIO ltf:
01 1 0 1 1рс;1<:11нt:т 1юш,111 ofiъtж1·, которы i'r 1~а:зы-
1:$~1ет < НС/~<х·т~п·ком», и фор .чул11рует пран11ла
11c1lcтm 1 r1 с 1111 1>1. Диофант 1 111 шtт: « Недостаток
у1V1ножс:111 rыlr 11;.i НС/1,остатоt<, д:lёт 11 :~л ичяе ;
11едоста·1·ок же:, ''м1южс 11 1 11,1 й п:.t н;.1m1ч 11е, даёт
.
.
56
Исrория математики
Лиофант.
11 сдостuток » 3то « 11раашю з 11;.iкrm·> мы .vrожем
зa11JJca ·11, так:
(-)х(-) =(+),
(-)х(+)=(-).
Прашmа СЛОЖСНllН 1r IЗЫЧIIТан11н / (}!}1 110ВЫХ
чи<.:сл Д11офu н·1· 1-r<: 1r:1ла1 ·аt:т , он просто пол ь
зуетсн 1rм11 в с1ю11х книr·uх И. всё же отршtа
·1e.Jl hHl>l t: числ::~ Днофа 11 т 11р11м еняст тол~)ко 1~
nрuмс::жу·1очных выч. и слсниях . а в качест в е
рс шенш1 НСt: ГД~I выб11ра е1 ПOЛOЖllTeJll>IIOC р:i
Ц I ЮН:!ЛЫЮе ЧИ СЛО.
В 1~реf1!1оже1ш01'1 Диофантом буквешюй сим
волике примечательно то. что кроме знака для
И3д<IНИР
Nлр~1фмt! I Иti.И \
Лиофанта
Ба·1ель 1:i75 r
11е и::.11:1сстнuй нелн ч1111ы н1юдятсн обuз нач с::ню1
для nер кы х шести сС с1·спс нсй . к::~к пшюж и
телhНЪLХ. т~1к н uтрю~<1телы1ых То естьлля Д1ю
ф;~нт:.1 эти вt:личн111,1 11е 11мскл п::оме'rр11ческо
го см 1>1 ст1. как было ра11ы11е. С:формуm1рошш
11раrнта умтюжс.:аия с1е11е1rей п еп звестного 11
rте1щ специ::tлы1ые з 1такн для равенства - 1cr
( 11 ,1ч .~лы1ые буквы грсчес1<01·0 слова <-ПСОС " -
« раu11ый ») и нсопред<::лё11тюrо квадр:.1та - О ,
Днофант внерные н м:1тсматикс IЮJ1учает воз
можно с·1ъ зап 11 сыва 11> 11J;ll\ 11 c r111я н111 1 01стсмы
урав11сгшй. l<ан счно, е1·0 форма заш1 с 11 1111 -
скuлыш нс 1юход11т 11 ::1 сонремснную, ОД11:1 ко ~1 о
настоящие уращ 1 е 11ня. щ,щt:11я10щ11еся н тексте
т<1к же, ка ~< в 11ынеппшх м ;1те\1атических ра60-
п1х . Собственно говоря, /\() Диофанта 1rи1<::tю1х
уравнений - 1111 опредслёшrых, 1111 пеопрсдс
лёшLЬLХ. - просто 11 е быJJо Рассматр1 шались за
дачи, 1соторыс мы те11ерь м ожем свес.-r·и к уран-
1 1с1 1иям, и не болt'с топ)
Наконец, но нвелс11111 1 Диофант форУ1ул11ру
ет дна uснош 1ых 11 рани;1 ~1 11pt.:c >nразонан1 1 я ~·ра 11-
1rс11 и(1 1rранило 11t:ре1юса члена ура1шеr 111я 11з
одной части н ;1руrую с uбратr1ым ~паком и
пр;lВ ило Щ) 1113е11епия пu.п,об11ы,-.. членов Вп о
сле,цс 1 в r1 и этп правила ста11н нзвестны п од
арабскпми назв:н шями "ат,-джебр" и <«Uiь-t-ч
кабала -> (см статью "Страпы :-~рабского Вос
то ка")
По<.:кольку <·Арнфметнка ·, - это сбор нпк
задач. можtт с.:л<Jжнп,с.:я вп еча1·;tе нн е. что Д1 ю
ф ~шт разμаботал остроуi\1ные 11р~ 1 ё мы !J.ШJ
рtшенни частны х сл~ чаен. но не создал общt-
1·u метода. Однако при 1ш1 1:м .tт1:льно м чтени11
можно у6сд1 1т1,ся· 1·щатсл1.ю,1й подбпр 11 про
дума111юе рас положе1ш е зада ч напраnлеrrы 11:1
·10, чтобы проиллюстрировать применение
rшпm-те определённых общих .методов.
В п ервой ю1нrе решаютсн определённыс
у равнения п ервой u второй сте пен ей, нu
все остальные кнн1· и пос вящены реше ни ю
всопределtнны х ураннени 1"i 1·1 с и стем т~1ких
уравкеннй Тщатсл ы-ю разб11рая решен11я Ди ·
офанта, можн о у1шдстh , что 0 11 фактичсск11
доказынаст слс;\ующую взж11 ую теорему · если
уравнение второ1'1 сте 11ени с J\ПУ1"1я 11е11з11ес1 -
ными и с ра1~11rнrалы1ым11 1<оэффитщептами
имеет хотя бы одно рац1юпалыюе решение.
то это уравнение имеет бесконечное м1южс
ство таки"'1: реше1шii. Более того, зпачсш 1с нс11з
вестных х и у можно задат~, раци ональны.мн
функциями от одного пара м етра: .-х: = <p (k),
у<= ljl(k). Для уравнений оыше второй степени
этu }"J 'Rержденис неверно.
Диuф~11-1т 1юл. ноt.:тью nроа11ализнровш1
нсопределённые уrаннсния Rторой стспе 11н с
двумя нсшmсстными .Для реше 1 1ия ураннt.:ний
11 систем более нысою-~х стспенс~'1 он р:'lз рабо
тал ещё более тоJ 11<ие н сложные методы , 1<0-
·1·орые привлекали в11има 1 rи е м110 1 ·их сF1ропей
с1<их математиков Нового временн Од1п1м из
этих методов решается самая извест~тая задача
Д11офшпа: «Зада rшый квадрат разложит~, на
дnа квадрата•). Двепадц;пь ве1<оn спустя р:1з
мы 1 11лсню1 над ней побудишт фратщузск01·0
матСУtатика Г11,сра Фе рма сформулировап, его
Античная математика
знаменитую теорему (см. статью « Rели1<ая те
орема Ферма»)
Труды Диофанта и.мели фу11даменталыюе
значение для развития ал~·ебры и теории ч11сел.
r: ил1е 11 ем это1·0 учё.но 1'0 свя::!ано rюяк11ение а
развитие алгебранче::ской 1·еомстри 11. г~робж:ма
ми которой вrюа1е;\ствю·1 занималиСh Л ео н:Jрд
Эйлер, Каrл Якоби 1,1 дру гне а1поры . Н:щболее
тубокое применение методы Диофанта 1-1 ашл1-1
в рабптах ~амечателы-ю 1 'О математи1<а ко1-ш.<1
ХIХ- начала Х)С n. Л11р11 Пуанкаре. На oc1rone
этих методоu строится арифметиI<а ат·е6раи
чссюIХ криDых - область, иптс1 1 сиu1ю разви
н~нощаяся в конце ХХ столетня
История матf'ман1 к~i
СРЕЛНИЕ BEl<A И ВОЗРОЖЛЕНИЕ
СРЕЛНЕВЕКОВАЯ ИНЛИЯ
Уже н ссредш1е 111 тысяч<..:л1.."гин .цо н. э в доли -
11с реки И нд сущсспюв~1л~1 р;1Jнитш1 цн1шли
:~ац11н. Об уровн<.: знаний Т()Й д~~лёкой энохн
MOЖl-IO судJIТЬ 11() (1<.:З)'JlhТ:пам арХСОЛ()Г11ЧС
СJНIХ иэысканиl1 . l la11pнм.tp , пр11 расконк:ах
Gы;1н 11ай;~е11ы обломок: .rн 111 eilю 1с делс:1111нми
и древнейшие в мире иr рJJIЬ ные костп кубн
ческой формы. На каж,f"\ОЙ стороне ямочт<ам11
обоз~ rачены ч исла от 0,11 ro1··0 до шес1 и. Тор
гош~ы тех далёких времен ттолr.зоuал11сь ка
мсшrыми п1ря,\111 различной вслич1111 1,1 . Архе
оло 1 ·11 uбна р-ужили болън юс ч11с1ю прсдмстоn
1 11х1ш-rлыrо!1 1 ·сомстричсской формы Дю1 1ю
строt.:ния сжруж1 юс-r<::1'111нд11йцы, 110-нид1 1мu-
1\.'fУ, применяли и1-1 струмент, похож1 rl1 на соврс
ме1шый циркуль.
М 1 rо 1 ·ие черты роднят 1(1 1 щ111нза1 0 11о)(ОJ1J1ны
Иr ща с други.м11 J(pe1-1 11им и куль~1Jамп - Ег1"11 r-
том и государствами Меж:1уречr,я. !)езде во:-1-
шп<~Ши одппаковые 11роблсмьJ. приходилось
делать расчL'ты ттри стронтельствс ;щорпов.
XPJMOB, ЖИJIШJ..J,, складов /\JHI зерна, BOCIUILIX
укrсш1с1-1нй, 01 1рсдслять r::i·Jмcpы и очертания
по;1е11, учитывать кот1чест1ю матсрпалов и
протlуктон - словом, решхтъ схожие матема
п 1 чt:скнс з адас1 11.
Ro 11 - 1 'J'ЫСЯЧСJIСТ!!ЯХ ДО 11 . :7. ПОЯВIIЛJIС Ь
рСЛ111'НОЗНО-фшюсофск1'1С КНИПJ - ВС'/\Ы ( <iЗl-!a
HI 1и» ). Од1111 11з раз/\СJЮВ Вt'д1 11·1скоl1т1тсратуры
1 1а:з ыnался <-illy.111,();1 -C)тp:1 » ( <·Пр;шт ита верёнr<Н,>)
?}тот 1 ракrат, сост~rще111 1 1.1l1 11 V11 - \i вn. /\() 11 э.,
С()держ11т праnнла и:i ,V1epe111111 (.." пом()щ1.ю 1зе
рёню 1, 11р11ме1 шемыс пр~ 1С1-рс:1 11·1 c.1ucтne жерт
nенпых алтаре1'i и храмов.
В 11срвыс века по1ю1'! эры полш1лис1, аст
роrюми ч сск:нс 11 м,1 тt:матичссю 1 е 1руды - cид
/JX:JH' I ы ( "' Y 'ICl-11 I И» ). Фаюы, IBЛOЖClll-lbll' н llt'pвыx
сиддха1-пах, :{~t11м с·1 ·1юваны у дрснн 1 1х tрсков
Труд •Пут 1с;1-с11ю~хаt1та -> нришкыкжтся aJl(:K-
c:11 щрийtкому :ктрш-н >.">1~ ЛауJ1осу. О ~·р~чt::ском
происхожде1tнн с1111дстсл1,с-1 ·ку~т 11 11::1 :танш.:
«Ромака-сиддхалт:.~ " (жнтелt1~1 Восточно1' 1 Р11~1 -
С1<ой империи часто назыnали ро.чеями) . 13 спд
дх<нп·ах нспользова 1 1ы некоторые греческие
термины Впрочсi\1. лаучные связн И1щ11н 111'ре
цш1 сущсст~tша:ш сщt n ::111т11чньн.: времtпа.
В Среднt r<" века рабатат 1 н1111 111у1скис мате
мап1ки 11 :.1стrоrюмы Лр11збх;.iта (V- Vl вв.) ,
БрахмагУnта (Vll в.), Магаш1ра (IX 11.), Шртiдхара
(lX- X вn.), I.>x:icкapa (Xll в.), Н11лака1па (XV-
XVI вв.).
Бш1ьw11непю трактатов 1111f\11йцев 11<1п1.ка-
110 н<1caнcr<pr1те - я::;ыке наую·•. ко· 1 ·uр ый абъе
дш1ю1 ученых. 1·онорнкшнх на разных наре
чшrх М11ог·нс труны r1з;юже111>1 FI с·rи хах, r~ я
того чтnбы пrаннла можно 61 .1110 з<1учн1:1а1ъ
наизус1ъ. Науч.11ые текоъ1 обычно сопровож
дались 1ю;(f"Юбн1.rми 1<омме11тариямн, где каж
дое nraf\ПJIO ТЩЗТСЛЫЮ ОбЪЯСНЯЛОСЬ.
ИНЛИЙСКИЙ СЧЁТ
С 11peвr-rtl1111 нx 11ре,,,1ё н в И11;~ии 11римснялась
f\ССЯТИЧJ l :JЯ 01стема счнслсння. .Цля СДИJ 1111\ су
ЩССТfЮН:.11111 спс.: 1\11~uтr.1 rые :·1н:н:и. а десятки н
сот11н заrтнс ынал и теми же 1\ифраJ\нt, 1то li
друmй rю:~vщии. Памимо цифровых у чисел
были и словесные обозначепня. Tar<. нут, обо-
111:1чали слоn:~ми «нусто1т». «нtбо» илн ~д ыра»;
ед1111ицу - н:.~зnаниями единичных предметов :
•Луна->, «Jемля->: дnойку - назв::tниями n.~рньос
пред~н:тоn: <-бди:нrс1\n1->, « глаза·>, «1юз;1ри·>.
•губы') 11 т. д.
Имс11110 01' 1шд111kкой IIOЗ!ll\llOHJ-Юii нумс
рацшr прон :юшла прнпычнан 1~ам система
Средние BE'Kil и ВозрожлениС'
~
EDJ®
сч1 1 сле 1111я . И11,'iпГтr\111 рдра(Jп· 1·ал11 nр~11111ла
ар11фметичепшх детrсттшfi. ос1юва1111ые на
этоl! нумерацшr (первым 11х применил Ар11~1б
хата) . Оrш умелн ск.1аf\Ы1Jать. ш.1читат1" умно
жать, !(СJ 11 ггь, вознод11ть LНICMI в ю3:щрат н куб.
изнпекать к~адр~1т11111<.: н К)16Нчt'сю1с корни. .!3н
rю11с:йцы ll:1З l1IH<llO'I' Цttфры ОТ() ДО q :.1paбCIOL
Ml ·I , т:~к как 3а1 •1м с.~гвон;1лн 1 1х) арабов. Но с:1,111
арабы 1 1м еную1 ~тн цнфры ннд.ийскнм11 . :1
ар11фмст11ку, uс1юн;11111)'1О 11t1 дс:сяпrчrrой от
стеме. - ПIТА11йошм счётом
Арифметические правила шщ11йцев м:1ло
чем отличались от 11равIJл , изучаемых соuрс
,"rе 1шыми школышками.13от 1car< f)хаскара от1 -
сал операцию сJюжс1шя: «Сложи ц11фры , сто
ящнс н:t ОДН!IХ 11 тех же пo:нrttlIOШIЫX •ЧCel'~IX ,
в r1рямом 11ш1 06р:1т1-юм порню<с" (11р1111rямом
nоря;tкс сложеш 1 е нач1111;1ется с сд 1 н1н1\, пр11
обrа·1·1-юм - со с1·аршнх pa:irя/ЩR). Д6rстR 1 1е
1-11.1чнтаrrия Бх:н: к.арэ \н1ре1tслю 1 так: <· R1.1ч1п·:11: 1
ч 11сла 11 соответстшш с нх 1ю:нщ1юшu,1мп ме
стами R прямом IIJJИ обрат-~ юм поряд1<е». А пра
n11ла для сложешrя. вычнтапш1 и )'Мrюжещrя
дробей такuвы: «После прш:!t'flеттшr дробей к
общему знаменателю с:лож 11 Чil('JlПTCJllI»; <.По
сле nр11не1tеюrя /tроб<::й к общему з наменап.:
лю СJlедуст юять p:1:311UC'IЪ между ЧТICJl ft'l'C)l}l
MlH; (< ПpoI LЯl:!C/(CHlle ЧI ICJIHTCJlt:Й , /tСлё ш юс H~I
1 1рои3вед<::ннс з 11 амсна·1·сле~'1, с.:с1ь рсзульт:)'1·
ум1южспп>J двух 11т1 болt:с Л!Х>беl!».
59
60
История математики
Н;J.чи н ая <.: VII J:J. и1щийск1 1 е математик 11
nользов~uшсъ отрш ~атсльным11 чио1::~м11. Пшю
ж1 1 тсльные чис;1а они 11азыпали <>дхана» или
~с13а » ( «иму1цСС1'fЮ»), а 0·1·ри ца1·елы rые - ~pm ta»
11J111 «КJJ.tайя» («долг"). 13ра.'Смагугrта, приводя
прашша арифметических действий пад отри
цательпым:н Lrислам:и, ещё пе отмечает двузнач
пост1, квадратного корня. но Магавпра в IX в.
уже указывает на неё.
АЛГЕБРА И ТЕОРИЯ ЧИСЕЛ
Индпйские математик~ 1СОЗJЩ.J111 развитую атееi
ранческую символику. R Индии пrrepnыe nояви
лнсr. rкоб1.1е знаки для .мтюrнх неизпестных
величи11, свобо;щого члена ура 1ч-rення. степе
ней, основных арнфмет1 ·rчес.:кнх дейстшrй. Болъ
шm 1ство симrюлон предст:1влю 111 собой первые
слоги сапскритских терминов. Наnрнмер, не11з
вестну10 величину ~11-1ди 11цы называли ~·й:.~в:~т
тават» (<.С-Т'ОЛl>КО-СКОJIЬКО») , сё обС1Зllач~иш cлo
l'QM «й:н. Если неизвестных было несколыш, то
11м дапали наимепова111ш разл11ч1 1 ых цне ·тв·
чёр11ый - •кал(.(IСа», голубой
-
«т-rилака», жё.:1 -
тыИ - «nита1<а о)
-
и эаписыnал11 слогами ~ка».
<НIИ», «ПН» И Т. П.
Индиl1с1ше математики достигли больших
успехов в решении задач, свя:3аш1ых с алгеб
раичеСКИJ\оШ вычиСJ1е н ю1 ми. Ариабхата ое1·а .1шл
зад~tчи, сводящ 11есн к ре1щ:ниНJ линейного
~'ра1:1нения с одним не11звестным. У МасавирьL
Бха<:к:.~ры и /фу1 · 11х учёных есть з~щ::~чи. прино
днщ11е к систем:1м линейных уравнений с нс
<.:колькими нси~1.Аест11ым1 1 . Вот одна нз эадач
Ма1 ·аF1иры: «CT()J1.i'v10CTЬ 9 лимонов и 7 ЛССIIЫХ
яблок равна 107; стоимость 7 т-1монов и 9 лес
ных яблок равна 1О l. О математик, быстро ш1-
зовн м не цепу лимона и лесного яблока».
Задача при.1ющп к системе двух линейпьrх
урав нений с п:вумя н еизнес-1· ными:
{9х +7у=107,
7х + 9)'= 101.
Метод решения, изложеш rый Магавирой, не от
личается от современного способа решения
с помощью уравнивания коэффнциентов.
Бхаскара nрс:длш·ает т~u<ую з<щачу: «Од1ш
имеет :IOU монет и 6 лошадей; дру1·ой имеет
1О таких лошадей, но у него недостаfт l 00 мо-
нет. Оба оди11аково богаты. КаТ<оuа uена лоша
ди?" . УСJюние ныражас::тся ур:шш:-ш1см
6х+.30()= 1Ох- 100.
Отсюда Бх~ккара нахот~ит, что JIOШ<l,L\I> стоит
100 мо11ет.
Задачи на ква~ратные ур<11..1не 1 шя ес1ъ уже в
«Ш)'Льба-сугре», где прrmедены ур:пше 11 ия п11да
а;;/ = IJ, ах
2
+х=/-;.
О;\нако их решеюш :-..1ы впервые встречае:-1 у
Ариабхаты. Этu :заJ~ачн на СJ ЮЖные проценты
п на нахождение ч1кщ1 членов арифметиче
скuй прогрессии . Бхаск::~rа рассм~принал спс
ц11алы ю лодобранныс ур;~внсн~rя третье!~ 11
четRёртоii сте11е11е1\ целоч11ст.:: н н ые КС1рнн
которых он ва..'i:сщнл путём неслож11ых лреоб
разоват111й.
Итщийсюrс матемзт11ки усnеш110 решали
нсопредслё1шыс урав1rе1rня, r(оторые rюз1шка
т1 в ::н:тpOHOJ\·HNeCКllX задачах. в OTJllJЧИC от
Диоф;1нта. искавшс1 ·1) любые рацио113Льные
корни, 1 1н;(ийцы далн способ ре111ения неопре
деJ1ё1111ы.х ур:шнсннй в целых п01южнтеJ1ы1ых
ч11слах . Л1111ей11ое ур:шн.сн1-1 с в целых ч11слах с
[(Тlумя 1-1ензt1еС'l'l 1ы мн
ах+!:> =~} '
приnодит уже Ариабхата. но более подробно о
нё,\1 рассrGtзывают в своих сочш rешшх .l.5рах
ма~у11та 11. Бхаскара .
1.kршин<~ достижений шщийс.:ю1Х .\ilа1·ем<Jт11 -
кон н тсоrи1 ·1 ч11сел - ретс11не в целых 1юло
ж11тельных чнслах нсопрсi(t:JJённ01·u )'равне-
11ня второй степени с ;~нумя нt:извt'стны.м11
axl+fJ=):2,
rде а - целое число , не являющееся квадра
том. Эт() уравнение рассматртrRалн Браы.ш
гупта и Бхаскара , который ш1 примерах изло
ж~;.ш метод, 11азываемый теперь циклическюt
Позже в E~pu.11e этим уравнением занимались
П. Ферм.~, JI. Эйлер, )К л. л~нранж. Метод на·
хождения nолн.01'0 ре111ен11я , открытый Лагран·
жем. в 1769 1·" близок к шщ 11 йскому.
Арнфме•п1чсскис и 1'сомстr 1 rчески.е про-
1'рес'Сии за11имали видное место R индийской
математике. Некоторые задзчи очень извест
ны, к примеру задача о награде за изобрете
ние шахмат, которая сводится к пахожле нию
суммы геометрической прогрессии со знаме
нателем 2. Суммирование числовых рядов ин·
тересо11а.1ю многих индийских математнков
(см. ста1ъю ~числовые ряды»). Ар1 1 абхата при
nодит прав~ща суммирования рядов треутоль
ных чнсел, натуральн ых кn::~дратоu и кубов, а
Маrавира - правила сумми роnани я рядов
квадратов и кубов членов арифметической
11ро 1 рес<..:ии
БоJ 1 ыnой интерес 11н; \ 11й1\ ы проявляли к
комбин~1торнкt:. Вот, например, задача Ма1·а
виры: ~о /\руг, 1-ш:юв11 'fИCJIO р;!ЗJГН Ч J-fЫХ uжcpc
Лllit. которые можно получить из брш1лнантоu,
сапф11р()1:1. изумрудов. коrх1 1 1 ;ю 11 и жемчугов».
А уШридхары 11р1 1 но1iи·1·ся такая задача: <.Повар
готовнт рззл11чпые блюда с шестью вкусовы
мн оттепк::~мн : острым, горьким, в.яжущпм, ютс
лы.'.1, солё11ы.'-1. слащшм. Друг, с1<ажи, каково
чнсло 1:1сех разноnид1 юстсй·1.
ГЕОМЕТРИЯ
311а1 tнн н открытия 1rнщп~tскнх математиКОli 11
rео~1 етрн11 скромнtе, чем 11 арнфмет1 1 ке, алгеб
ре и теории ч11сел. Спеr~иалъныхсочт-шений по
r·еометрщ1 в Индии пе было, эти сведения со-
Инл1111rк~1й "э11уrкр1<nт XVI в.. кпш1я матРм,п 1 1ч~·<"ко 1 1
рукоnиl" Бхаск.~ры
Средние века и Возрожлен ие
общалис1, 11 ар11фN1етических тракгатах нли в
а риф.метн ч еских разделах сочипе11 и 1! по зст
роном 1111.
Геометрические теоремы r1 р1шодил11сь без
доказательСТ13. Обычно ЭТО был только чсrтёж
со с;юном «смотри». Лшuъ в редких случанх t1·0
сопровождали кр~1 ·1 ·ю1с 1 юя<.:11е11ин. I Iо-1:11щ11мо
му, доказате.11ы"1на учащимс51 сообщались уст
но. В геометр11ческнх :~~щачах 1:1опросы чаще
вct."ro Сt.юд 1-1ю 1 сь к иьrчrклснням 11 гораз1ю
ре.же - к построен11нм .
СаJ1-1 ьн:: ра1111ие сведе1111н о 1юз11а1 1 115!Х н11яrrй
цев в обласп... геометрии содержатся n руковод
стnс по постройке алтзрей н храмов - <·Шу111.ба
сутрс<> Храмы ВОЗ!ЮД11ЛИ, П ОДЧ l fl l ЯЯСЬ рл,11у
правил: здапнл должны были иметь в основа
ниях опрсдслешrьrе фнгуры и бьпь сорнентн
рон:шы no странам С1~ст:1. ДrLЯ :;i·r ·o1·0 требовалось
у\1енне стрuи'IЪ прямой ~1·ш1. ю~адр:п, nрнмо
у1·оnы tые треу1·ольннки. сторон1>1 которых вы
ражаются це.1 1 ым11 чrкламн . Н1-щпr~щы эналн. как
tюстронть ква;\р:-tт, р<11Jно11е;1 ики~1 11 рямо~1 ·олt,
нюq:, и кнадра 'I'. 1IJ ЮЩЭДI> J(()ТО\)()Г() 1<рат11а ТТЛ()
щади данного тrnа,11р~па. Отnравпой точ1юй м1 ю
п r х построений служила теорема 1Iпфагора .
Пхаскара приnодпт дою1~штсльст1ю :.,~то11 тео
ремы в виде чертежа с: 11адшкыо: <· С.\1отри·>
ТРИГОНОМЕТ РИ Я
На ра:ш11т1 1е ас1рп1юм 1 п 1 в И1 1;11111, пп- nт111нмп
му, оказали u11 1 iя 1 111e труды Птолемся, кот()рые
1 шдийцы nреобразоnалп n спстему расчёт11ых
п1хtвш1. Глаш1ым их достнжеш 1 ем стала заме-
11 :.1 хорд синусамп. ЧТО ПОЗRОЛI I ЛО JЗ JЮДИТЪ
()1
,Аtъ.
EUL[!J
История математики
62
р;~зл11ч1tые фупю~ш1. сnя:зат1ые со сторо 1 1ам11
11 уt·лаып пряl\Ю)ТОЛЫЮl·о треугольника. Таким
образом в Иr-щш1 бьшо положено rr<tt 1 aлo три
го 1 10метри11 как учсншо о тр11гоном<.тр 1 1чс
ск.1-L-... ве1н1чинах.
!1нднйс1ше ученые тн11,;.юн:.1 J 111<.ъ ра:3.11ичны
м1 1 триrонометр11ЧССК11l\11 1 COOTHOL 11 t:L 1 11Я.\'I И. 1-S
ТОМ ЧIIC!IC Н TCMIJ, "()'t'OГf• I C fl СОl!()СМСННОЙ фор
;\-1С Rыражаются как
siп1ц +co.s~o: = 1.
c;in а= cos (90°- а).
si11 {а± Р> = .sin <.У. со-, р ±со::. п ·siп~.
l111дий1~ы тшокс знал 11 фор~1улы для rq)атн1.1х
у1лов si!i 110., cos 1ю., 1·нс 11 = 2., 3. -\, 5.
Тр111 ·ономстрин г1собход1 1м;,~ N•Я астроно
J\Н1чссю1х μасч.ётон, которые оформляются в
н~1дс т;.~бm1ц. Псрн:нr ·1абтща с 1111усов 11мсетси
1:1 «С)Т>ЬН -сщv~х;штс» п у Лриабхаты. О11а прп
nеде11<'1 qерсз 3"4<>'. Позю~ее учt:11ыс состз~шли
более подробные т::~бшщы: вапрнмер, Бхасr<ара
nр1шоднт табщщу cшrycon через 1°.
10ж1ю 1111юrrк1ш~ математики в X\f l n. доби
ш1с1, больших успе:хов в области суммнрона-
СТРАНЫ АРАБСКОГО ВОСТОКА
Kom<J. н (>22 1·. 11рор<ж Мухаммел бежал 1 1з Мск
ю.1 И С'ТЭЛ nрОПОНедоnать ПСЛЗJ\1 (араб «ПО1Юр-
1ЮСТЬ•>), ещё ничто не нредвещало •'Рsrдущего
трнумфа IIOBOЙ реJJИl'ИИ и ИСЛ<LЫСКОЙ государ
ствс111юс·1·11. Ilo уже к нас~алу \TlJI 11. арабские х~1-
лифы (прсс.мнню1 11ророка) покорили огром
ную территорию от Псн11.жаба и Хорс:зм<1 H<I
щ >с1 ·оке до Геркулесовых стол бон ( Гнбралтар
скш·о 1 1ролина) 11 а западе. Псрныс халнфы не
жалсж<utн с11е1·ску10 1<yJll>1ypv 11на\'Ку, н том ч1 кщ·
мaтe1v1<1'1'J.JJ<y. Л вот халифы нторой ;'(и 11ас-гии .
ЛГ>6ас1 щов, - a.flli- Maнcп) и Харун ар-Ра11тд (l'а
рун аm гt>ашпд, :шакоиый всем no ска:-~ка!\1 <:Гы
снчи и ощю11 ночи"), 1·л:убо1ю y'R3Ж<l.fl учёпость,
стал11 11ригла111атr, 1> liа 1 ·щщ ино;~емлых мудре
цов. В 1Х-Х нн. на щх1бскнй я:~ъrк б1,1л1111ерt:нt:
/ (С ны ос1юm1ыс нрошшt:;(сния Енкли,тщ, Архн
МС/Щ, Аполло1 шя, Герона, Птш1<::мс:я 11 Диоф:~нт:~.
В VL1L-1X kB. в Арабском хал11фатс уже
пользоналн<.ъ 11ндн[iско(J лссw1·1 1ч 11от'r поз11-
111ю11нuт'1 с 1 ктемот'1. Трактат «0() и11ди~'1ском
шш бес1ш печ 11ых чтrслоных ря,_1он. По-ю 111rrчо·
му, O!ll1 3:1JП IM ~IЛ11Cb ЭTlfMll l!ССЛС,Т(ОВа1шлм11,
ко1·да rтсюm11 способы 1.:1ыч1rслен11я более точ
ных значсню1 ч11сла п. l lнлака11т~1 с110вссно
!1рt·шол11т ttpaш ша разложен~ tя аркташ·снс1 11
бсск011ечны~-1 С"1·епен11u 11 ря;1. Л в аншшмнuм
трактате ~карlНi~ш<1щ1х:п11 ,, (<.ТL"хш 1ка вn1чнСJ1с
ннй ->) л;1ны 11p;ш1m:J раз.гюжсн11я сшJуса 11 ко·
с1-11 ryca в ()с:ско11еч1 tыt: стспе 1 1111,1е ряды. Нрю~о
ска:-~ать, ч то RЕвроnе " 1юдо611 ы м результатам
подошли JllJmJ, в Л"VН -ХУШ вв. Так ряды Д}IЯ
синуса и косинуса nыве:л И. liьюто11 около
1666 r., а ряд арктанrе1ка бьur 11a\'iдeJ-1 Дж. l'ре
гор111.:1167] г. н Г.li.Лсi'iбн 1 щсмв 167:31·.
***
В \:JП в. учёные стран Ьл11ж1rt.то 11 Срсr1нс1·0
Вооока позна1<ом 1 m11сь с ·1 рудам11 и 1 1диlкюL'<
матем ал 1кон 11 ::~п ро1 юмоn 11 11ере::всл11 11 х на
арабсюri1 нз 1 ,1к. 13 серс;~111 1е IX fl. срсд IIеа:нrат·
ский учё11ый аль-Хорсзм11 н:~пис~ сочи11е1111е
<>Об 1п 1дш1с1ш;11 стrёте». После того как арабсю rе
трактаты 61,1m1 ш:рсвсдсны на латы11ь, многие
И/1;~11 ИlJДllЙСКИХ матем;~тнкu.в CT:.tml ДUL'ТОЯIШ ·
ем сиропейсrюй. а. затем i1 мирuвой на уки.
счётс-> - 11ервы!1 араt1с 1шй тру;1, н котором
F1С"1·речается 1ювая 111щ11l1скал нумерация. Его
наткал uыдающтпlся учtпый Мух~1мме,\ бен
Муса аль-Хорезм 11 щшмерно в 825 г. В XII в.
юп-1гу 11 сревсл1 1 на л;пынь. И 1юск<.тьку н !iнро
ну деся·11 1ч ню1 с 11 стсма пр 1 rшл:1 чсрс' :~р:.tбов,
сё <.:тшш 11аз1"1н:пь 3(Х~бсюJй. Прав1rла деf1стню1
с /(ССЯТ l!ЧllЫМИ Чl l CJШMll IIOJJyчшrи назь<11111е
«алгоритм-> Это слоно про1 1 схо;111т от латнн
скоfl формы пмет111 з;11)-Хорез1v111 .
Учёпые арабского 'Востока был1 1 в ос1юn·
1юм астрономами. С !Х в. n Лрабс 1юм халифа·
те начала складываться сrюеобраз 1 rал матема
п 1 чсс1<ая культура. Здесь ~стоды 1 ·rсчсской
матсм.атшш пр1L"1ешшись для рсшс1 11 1я астро·
1юмпчс:ских за;щч.11м<:нно nотребнuстп :~стро-
1юмш1 и np1 шел и к буr1юму ра зш 1л 1ю алгебры
11'J р11гонометрш1
Ос1юRы ап!'ебры кdк 11ауки 3:1лож 11п труд
:ть-Хоrс::1м11 ·f<таб аль-лж~()р валт,- ... 1укабала1
( • Кшrга () nосстаноnле 1 11111 п пр()т1-11ю1юст:.~nле·
Средние B€:'KJ и Возрожлt'llИ~
111111 »). Сло1ю «ал1.-;ркебр>} R матем::пической
11и'rt:paтy1Je арабского lЗостоI<а означало 11ерс-
11с(е1ше отрнцателыюго члена из одной частн
ур:шнсш 1я в другую, чтобы нолучптт, н обеих
час1н.л полож1п слыrыс члены; u-1сюд<J 11 11ро-
11зо1шю н:1 ·ша11не наую1 - алr·tбра. <·А.111,-мука
бала~ 11 сренодито1 как "сраннсннс~, "nрот11вu-
1юставлс11"н.:,,: с ·1 ·0 1 1ки зрс11 11н матсм:.1т11ю1 это
orrepJцшr 11r11всдr:ю1я по;(обных чле1юв н
оnсих частнх ) р:шнсm 1н.
J>ешение ю1адра·1'11ых, кубпчесю1х н 11еопрс
делётrых ураnr 1 ешн\ 1 1 зшн:чсrш е корнс1I ·1рс
т1,ей, ЧL'Тflёpтofl 11 nюой сте11 с11сй сталн ос11ов-
11ьrм11 дост11жснням 1 1 арабской алгебры. llp11
рсu1<::1111и ур:шJ 1сн11i1 11с1ю1tьзонат 1 сh ар11фмс
т1 fl-JC<..:КI1<.' 11 l 'COMCT[JI 1Чt::СЮ Н..: МСТОJ(Ы .
Алп.:6р~11·1ч ссю1й тракта·~ :шь-Хоре.1м 11 был
СОС'J ':шлсн как p~XOflOДCTll(J /1,ШI pt:lllCI !ИН пр:.11<
т1rчео01х :щп.ач. 1юз1п1к:н1Lш1х. 11,111ример. 11р11
разделе 11аслс1к·1· ва (М~ cyJ1 ьманс1юе право
А/\Ь-ХОРЕЗМИ
РоЖдение матем« гию1 и п ер1:1ые её
шаги 1,пра1:н:~дли1ю t вязывают с
именами учёных Лрев1·н:•й Греuии.
Но случалось и ТJк, что свет зна
ний шел ю Азии, .:1аставляя улив
ляты я Европу. Вем1к 1:1клад в срел
невекоаую науку Мухам.... ела {)ен
Мусы аль-Хорезми (787- око.ло
85()}. Кстати, в самом t!ro име ни
содержится опрелелён ная инфор
маuия: Мухаммед, сын Мусы из
Хорезма.
Хоре:-~м - земля древняя. За
тысячу лет до новой эры там уже
был 11 пострuены магистральн~..1е
просительны~ ка11алы и искус11ые
ирри гаuионные сооруже ния. Надо
полаr.~ть, именно потребность в
точном сельскохозяи<..-твенном ка
лендdре, в регулирова1 1 ии стока
волы и планировани11 поливных
земель э.:ктавила хорезмuев разв и
вать математику и астрономию с
особым усердием.
IX век стал временем п одли 1i-
1юrо расцвета науки в Сред11ей
Азии. Именно тогда nыли состав
ле11ы первые тригонометричесю1е
и астро 11омические табли uы, про
ве.ьсны и;1мерения величины
Земли, строились обс-срватор11и,
появились научные трулы по геп
граф~1и и первые гео1·рафическне
карты. По'lтому 11 ель3я сказать,
ЧТ() rlЛb-X opeJM И был ()ЛИНОК В
своf'м отечестве, - 110 он был 11 а
ГОЛОВУ IЗl>IШC МНОГИХ.
О его детских и ю1·юшеских
rпдах, учёбе 11 учителях свелений
не сохранилось. И1вестно, •по
околп 81f)1. проrвеш/:lн11ый халиф
аль-Мамун пригласил аль-Хорезми
( коrорый к тому времени уже з<J
воевал ttаучный авторитет и хо
рошо знал основные 1руды уче ных
древней Греuии, Индии, Ирана) в
Багдад. Там аль-Хо резм11 возгла
вил библиотеку Лuма Мудрости
(сеrолня мы на:1~dл11 бы его t\ка
демl'tеи 11аук). Пол его нач алом
в библиотеке переводили трул1>1
Птuлемея, Енкм1 ла, Ар11гrотt>ля,
д1юфанта, Герона. Он работал в
окружении 1:1слуших учё11ых Вос
тока, которых собрал у себя х;миф
аль-Мамун.
Аль-Хорезми - автор олиннал
uат~1 работ; шесть из них лошли ло
на< в арабском ори rин;;~ле, три -
в пер еводах и пересказах , а лве, к
сожале11ию, были утеряю.~. Наи
больший ин1 ерес представляют
трактаты аль- Хоре·i."1и по ,1рифме
тике и аr\ гебре.
Арифметически и тракта 1 13
ори1 инале не солранился. В Xll f:I.
в Испании его перевели на латынь,
~атем в XIV в перепи сали, и елин
t твенгrый ·ж.iемпляр этой руко
писи находится ныне в Ан1 лии, 13
библиnтt'ке Ke'vlfipилжc:кnrn у11и
верситета. Как озаглави" тракт.:~т
ав1 ор- неиз вестн о, .:1а переводом
же 1акрепилось назва ние «06 ин
диС1ском счете•.
Но если в арифмстиче<..ком
трактdте аль-Хоре.:1ми главным об
р:~зом проп аг.:1нли ров ал достижf:'
ни11 ИНДИЙ СК ИХ матемJТ11КОВ, ТО
алгебраический его трактат «К11 и
га о восrтановлении и противо по
ставле11ии )) - сочи нен и е совс.:р-
шенно оригиналЫJUl'. Лрев11ис 1re·
~..и шли от rеоме1·рии к алгебре,
аль -Хорсзми использует гсомет
рию для иллюстраuии с.ловес 1-1ы х
алrебраичепих правил, которые
для него первичны . Истор11к Ибн
Халду11 ~в Туниса писал в XIV в.,
ч то ~кн ~t га аль-Хuрсзми о шести
типах аl\ге6ра1~ческих зала<t при
надлежит к числу лу<twих кн11г, <"о
ста 1менныл в ::пои области».
Митематичео.ие труды алt.-Хо
ре.,,м и высоко uuене-ны во всем
мире. В 11 45 г. алrебраическии
трактат был п~рсослен н,1 латынь,
в 1 В42 1. сделан его перевод на
франuузrкий язык, в 1Н57 - на
немеuкий, потом на Jttt м1йский , а
в ХХ в. ;пи сочи не11 ия опублико
ваны на русском Я '{ЫКе.
Вnрочсм, ал~..-Хорезми зани
мался не только матсм.пико~::-1. В
< пио:е t:-ro основных работ 1на
чится и трактат по астрономии , в
ко1ором 0 11 иtслсдует движс1-1и е
Солнuа, Луны и пяти пла11ет, ла(!Т
пrав~1ла измер<:'ния геnrрафичР
ских широт и долгот, оnрелсляет
размеры солнеч н о~ о лиска, рас
скёнывает о солнечных и лунных
1атмениял .
Лруrая раб(П;~ аль- Хорезми -
« Книга кар1 и ны Земли• - труд
географический . В нем л.1ны ко
орли1-1аты 2402 пу1-1кто 1з ЗС'М J·JОИ
поuсрхности и нJлuже н.1 uри 1 ~1-
Н<1льная 1ео1 рафическ.~я СИ( 1ема
с уч~>том климатическю. зон . К сп
жалснию, эта книга не 61->jла 11з
вес:тна европсйuам, 1ю t?c JI 1 ачс
н ие для развитин географии н а
Восток!:' очень велико.
История матема г и к и
п редусматривало тота сложную систему на
слсдова1 rнн, в соответствии с которой мно rо
числс 1ш ыс родст~'lе н никн умерше го 11олжны
были п олучить CJ:IOI() /ЮЛЮ в ЗШ:ШСИМОСТИ ОТ
степе~ 1 и родеrва.)
Аль-Хо резм.и дал классификацию ли 1 1ейных
и кn;щр::~тных ураu 11 е11и~1 н с п особы и х реше-
1 1ия. Общее решение квал;рат1 ют ураш rеrшя он
не рассматрю1ал. Во-первых, его не шrтересо
вали уравпе ~ шя. у которьL'с не было ни од но1·0
положительного корня. А no - nтopьi.", он ста
рался записать уравнен ие т.~к, чтобы вес еп)
члены выс тупали н к::~честве сла гаемы х, а не ны
читасмых. Поэтому ;~ль-Хорсзмн рассм;~трннал
отд<.~лnнu 111 ссть R1rдou ур~шнений, к которым
путём алгебра ~ 1ческих п реобра :юJ:1а1 ~и 11 сnо
дятся /IР}ггт 1 с уранне н ин:
1) их-= !1:х (в терминологии aJ 1ь-Хорезми -
«квал;рат,ы рзu11 ы ко рням»);
2) а:-.::-= с ( «КВадраn,1 равн ы числу»);
3) tL"< ;= с («кор ни р аnн ы числу»);
4) а.'1:- + Ь:х = с (~квадраты и корн и ран ны
ч.нслу» );
5) o:\·J +с= /JX (« кш1 драты н чнсла 1х1 в1-1ы
корням~);
,
6) lxx +с= ах- («к()рн11 н чнсJ1::t равны квад
ратам ~).
Здесьа,fJ,с>а.
Помимо ат·ебраического способа нахож
дения корпя уршшения аль-Хорезми обыч но
предлагал и 1·ео:мстрнческий. Нот, 11апримс р,
nссьма изя щ ное геометрическое рt'ше ни е
ур.uшс 1 шя
х2
+ lOx= 39,
(*)
ОТ'НОСЯЩСJ'ОСЯ К -1·-МУ ТИП)'.
Рисуеrся квад р:п, сторона котuрОJ'() оfi()з11а
чаетсн неI1з1к:ст1 юй не111 1 чн110!1 х. ПJ1()Щадь та
коr() кщ~.щхпа х.!. На сторшт::~х кnадрата стро
mся четыре прнмоу1 ·опь1 ш ка со СТ()ронамн .\" 11
lU/ 4, а в углах - четыре квадрата со сторо11ой
IU/ 4 (рнс. 1 ). То1·да площадь каждо1 ·0 из 110-
10
строенных 11рямоусоль111rкut1 будет -:Jx , ;1
сумма 11х ПJ IOЩ::t/leJI 10.У. Пщ)Щ::t/\h каж;lо 1·0 11:J
чс-1ырёх yl'Jlo1:1ы х квадратон равна 100/ 16 = 6 ,Yi,
а 11х сумма 100/ 4 = 2'5 . Ecm-1 сложит~ . шющад11
кн:tдрата (х2) 11 четырёх 11рямоугnлт,н 1 1кuR
( 1Ох). то получнтся выражен не. стоя"ще~ в лt
нot'r чаС'l·и ур:~ннсння (*) , т. е. суммарная 11ло
щаДЕ, ршш:1 59 Отсtода нахою1м, что площадь
бол ьшого ква,тtрата :)9 + 2') = 64, а его сторона
соответс-rне нr ю 8. ~ то же время из ч ертежа
следует, что С1'орону больто1 ·0 к н:щрата мож
но выразить как сумму х+ 2 10/~1. Пр11рав-
1111в::1я:х+ 2- 10/.:1 = 8, rюлучасм х = 3.
Другой ара6ски.й математик. аль-КарадЖJ 1
(? -1 016), 11ред1ю ч итал ариф м ети ч ески~ ме
тоды решепня я1аn 11 е 11и й Его эаслуга n том,
что он ввёл бескопечпо м1 ю1·0 положителы1ъ1х
и отрицателы-1ых сте пеней неизвестных 11
арифмети ч<.:скис опсрац 1 1и над многочле1 r ами
(пращ~tt. нри делении огра ничивался лить
деленнсм мно 1 ·очлсна на одночnе н ). Однако
ал ь- Карадж11 нс б ыли чужды 11 гсометр1rческие
мето/\ Ы . ТТрнведём эле1·а 1 rтное гсомстрич<::скu
аm'ебрзич еское дuказательстно формулы сум
мы кубов натуралы 1 ых чисел (у аль - Кара/\ЖJt
ll = 10):
1\+2'+5'+ 1:1+...+п\=
= (1+2+.3 -j4+...+н/.
Р:ксматривается кнадрат АВСD со стороной,
равнойсумме 1+2+3+...J +...+ll (JlИC.2).
В квадрате Rьщелнетсн уто:нж BB'C'D'DC, такоi1,
ч1п DD' =В.В'= п . ТТлощ:.Iдь ~~·1·п1 ·а уголка, p~1111 1 aJ1
сумме площадей прямор· m1ы111кпн D'ПСЕ 11
R'FCB м.нпус плn 111аJ11, квадрата CFCE. пре;1с·1-ал
ляется разностью
2r1(1+2+5+4+...+11)- 11.!..
Преобразуя этu выр<lжепиt" с 1юмuщыо фор
мулы ДJШ суммы apиф.tv!(.'TИЧCCKU IJ 11ро1-ресс1ш
1+2+3+4+...+п=п(n+1)/2.rюлуч;н:\1
2n(l+2+:i+ 1+ .. +n)-N~ =
= ln _11_(~1_1 _
.... _
!-'-
)
2
Дзлсс рассматривается кна,цр;п , Ш'СD'.
13 нём ·1·а.кжс выделяется )TO!IOJ< B'B"C'/J"D'C',
])
Fс
D'
С'Е
х1
!Ох
-zr·
D"
С"
6 1'4
А
В"В'в
Рис. 1.
Р11 г. 2.
~
81~ История математики
66
Рнt. З.
11е n1>1JIO, :1a1111CJ1 урап11е11111'1 11 НЗЛОЖ<::l 11-Н.: re:1ym,-
TaTOR оставалпст. с1юж11r.1м11 11 11еуноб11ым11 .
Очень важны псслсдоватшя ара6сю 1х учё
ных u 0611асти 1·еоме11)1111, в частности ра\1оты,
поснлщёш1ые док;-~з:~тельстuу пятого постулап
~Rютида о п3раллслы1ых. Разу:-.1сется, псе rюпыт
ю 1 доказ:t1 ь пятый постулат бьин обречены на
1н:у) \<11 1у, нu 01-111 110/\1·0·1·uн111111 1ючву для 1юсл е
дующих иссл<::/\он;11111i1 ~11ро11е1kкнх математ11-
ков 11 В К.ОНеЧ 110М 1IТОП: ДJ IЯ OTKpЫ'l'I IЯ В Х rX Н
н<.:с:ню.LИ/\ОВhl х 1·сомстр1 tit ( с,..,1. с r·атью ~ Гсо.УlеТ'
рня Лобачевс:1ю1·0~). Kpo:vi1.: тоr·о. про11схо;\111ю
СРЕДНЕВЕКОВАЯ ЕВРОПА
r1:ш.::н<1 тнор1\<Ж антнчной ма·r·с,1:1·1·11ки - 1111-
фаt'ора, !::вю111д:1, Арх11ме1 1:1 - зте1 к:1;~..:,т1ый, l lo
11011po()yi"11 e HCIIOJIHllЛb X()l'>I ()ы ОДНОJ '() 11:~ eн
(lUПt:ЙCКIJX .У1зтсм:~1·11ков С:rсднснсковья, tJ н~к
скорее 11eei·n пост111~ нс'1· нсу;1ач:~ А пr11ч11н .1 нот
11 чём. 11 Сре;11111е 11ек~1 (ко11е1 \ \' -
Х\'ш1)11Енрс>-
пе формируется нн:щ отлт rчтrая от а т1тич1-ют1
снстема цеш юстей. !iё основу уже не сосrавля
ст r<улr,т паутш. 1lом1.1слы людеl1 обращены
к Богу , Цсрюш, соnсрт епстnоRанпю J\уш11
У большшк"гва в; r шпслы п,rх: богосл:оnов н ~1ыс
J 111теле 1'1 то1 ·0 крс:-.1сн11 н с на(1т11 размышJ1ен11й
() \•1:l'!'t'Ma'J 11ке 11 ее pomL в M11(1t°. СХ()/\НЫХ 1!0
глуб111-1с с 1рсчсскr1мн образцз.v~11.
И вес же н сред~ 1енсконо1'1 Европе нс забыли
1ю111юстыо о ~11 1аче11111r м<пе..,,1ат11ю1. В VГ н. Фла
в11(1 Кзссиоf(ор. п;.1,1111 11 з 1юсJ1е;~111 1х образо
ва1111ых р11мт111, ос1юн:1 ·1еJ1ь хр11стиа11ско1 'О
моттастыря тта лаnшсrюм :~ападс. 1'\Срзтrул пред
ставать Б01 ·а-Твор ца в образе 1 ·еометра В е/'О
трактате «l lастаnлст111я n науках Божсстnспнr.1х
п чсловсчссюDС» глав:~ о геометрии открыва
ется заспшом, который в вольном псрсложениа
;тучm так: • Теперь 1н.:рейдём к нзложснию
H<llШПЛCllllt: 1 ·еоме-1р11че.сю 1 .х фat('IOH, КIПt>рЫt'
111юследстnпп быт~ осоз11а111.1ка1\11rеwюже1111я
::iIOШllaЛelITJIЫe ПЯТОМ) постулату. TaIOtMH nre,.r1 ·
ЛОЖСНТТЯМIТ JffiJIHIOTCЯ, 11::tпр11мер, утверждеш1я
о сущt("l'1:Юн~шш1 лараллс:.11огра.мма и прямоу
rолh1-111к:.~, кuторыt' 6:t1'}.J,aдcrш r1 матсмап1к Сабит
11611 Kyrpa (8.)6-9U 1) 11снuньзоиал для доказа
тt:J1nс·1·н:.~ 11ято1'0 1юt~1ул:1·1·:.~ А 01V1ap Xaйsl\t 111жа-
3ыаал СГU l·IC.X()/\H и;~ ~ l 'J-\C(lЖ/~CHI rя· <·ECJLll }\НС
11рн .\1ые 11rи6т1жаются 11гу1· к дру1·у, то 01-111 обя
:1атслыю ,1ол;юrы псрсссч-1.сн·>.
Ара6с!(ие м:~тематиrш впервые rпучили rке
тр11го1 юме1 р11чесю1е фушщш1 и сосr.ш1mи н6-
лицы оптусоn углоn с промежутком u 1U', прн
чё."'1 с пор.1:-штслыrоr'r точrrостыо - до 1/60·1
.
~ помощью тр111·ш юметричсских футrю~иr'1 они
llCCJICДOB:IJlll COOTJIOJll<..'llllН МСЖJ\У е~-оронам 11 11
у1·лам11 треугштъннков. To!tbKP ЭТJ 1тrеу1плы111юr
11;1х<щ11т1<.ъ нс на 11лоскост11 , а на повер:-.1юсти
сферы. f'<Шt:t: 1ю110611ым11 1юпрос1м11 зан1ш:~
лно. Мевел:Н'! (1о. )11 К'1:11щ11f1 Ilтoлeмeir (lJ n.)
-
со.щатеmr сфсрнчсскоi1 тр111'0 1юметрш1.
bor-Tвopeu
к.н~ Г{•ометр
rеомстртr. Ст1детельств:.1мн 11реnп11х п ерсю1-
110, что J()шrтер в дся11нях CJIOJIX nоступас1 как
П.'О.\н.:тр. 1-k знаю. л;остойно лн это nохnалы шur
llOJJIЩШIIЩ IIO 01111 OCMCЛILJIIICb СI<; 1 зат 1., что
Ю11 1 гrср на нсu<: пюр11т no;\0{)1ro 1·<:0.\ileтpy.
р11сующем~ ф111уры 11<1 р:1<.:кра1 11 е11но1"т 11ыm1 .
11uкрын::но111с~"1 1·сомстр11ческую цоску. Так~ rc
peчLI. еслн 11Х с ДOJJЖHOII ()ГOLIO[>l<O(I о·r·нссги !(
Т1ю1щу, 1к·смо1унJ.t:'МУ Госно((у, мо1·ш1 бы, по.жа
луй. COO'J'BC.:TC'l'ПOli:.lTI> I I CTL HTe - Bt::Лh Сшпан
Tpomta постунает, еслн доз.волепо буде-г 1·< .11<
выразпться, как геометр, ко1да пр1щ2ёт Сволм
•r ·1юрснпям оnредслё111-1ую форму 1r Rriд . Откуд<1
слсдуL"I', что всt:, что правильно р<~сполаr<.tетсн
н обтщас.:1 .зако нчснн остыо фор~1. может бь11ъ
Ш"L{aЧt' L IO ЭТОй дщ:ЦllrтJl\IHO.Й».
Уе.рберт и3 Орийака
(Папа Ci1JlЪ~ecтpJI)
о
оо
l р<?л1ще века и 1:!01ро~е1ще
По-R1~дr1мо:\\у, те же сооf>раже11 11я 1:щ(тоm<
нут 1 неr<ОтQрых cpc1ri;f1eвeт<onыx ху;~ож11и1ю11 к
rreo61,1чrroi1 m~ee: нзобраз~пъ Tuoprщ с 01-ром
ным ЦI!рh.·улем , 2 /.НIOJД:I с HCCl.ЧII I1ЛII ПJJ(.)TlНЩ
IO I M )Tom.1-11rкo"'1 в рук:Jх . 1ro подобных мш111-
атюр <:СJхраю1лось uче111, м<1ло. БшIЬu1и11ст1.ю ж<.:
ж 1 1шJ1111сцt~11 нс ()ралн н :~ сс6я смслостъ ююж11'1·1,
в рую1 Твор1 ~а 1111струмсю ы - ведh 1-t}.. 11с1юль
·ю на1111с огр:11111чи11аJю Er·o 1к-смо1ущt'ст 1ю.
МАТЕМАТИЧЕСКИЕ ТРАКТАТЫ
РАННЕГО СРЕЛНЕВЕКОВЬЯ
r;цш1·шс матбrатшш в Ра .нлем Ср~д-
11<.:t~скuнь<.: (до Xtt в.) нач~ tнююсъ с
ПОС'l 'L'Ш: Н НО!'( 1 OCtIO(.'J-НJH :1нт11ч 1-JО(1
:- . \<1 t<.:ма·1·11чс t'1<ой куn1,туры R мо-
1l:l("l'l>IJJЯX MHПl'CJКp:t'J'H(I 11ert:п11c1.1-
fl(\J1J\ 11 11:Jуч:1ли .~1щ111<т)11ед1 1ч е
сю11! тракт:п i\1ap1111:iнa Ка;1 еллы
"о браюхочета1пш Фплтюп 111 11
Мсрю•рия" (\1 в.) , а также труды
Аш1ция Ма11111шТорю"ата Cenepн1 ra
Бо:щия (около -HI0 - )2.:J.).
И:ннщ пс1х1 lюэцш1 6лсстя-
щс1·0 (."l'I JJJllCTa, 11:.iBCC'ЛIOJ'O (.)(:нo нa
TCJll>HhlM :н1:11111см :н-1тнчнm'1 11а
ую1, - HЫlll!IJ 1 Л:ITIJHCIO IC пepcBO/(f1I
,п.вух фу11л:1мс111·аJ1ы1ых 1-речсск11х
\
1
1
1
J
,Аь_
~ Иr гория матt>матию1
Пер1:вuл . н ,1•1,11\0 [t1клилJ 111 •оfiр,1нн11 rn•1инен1111 Г.nэu11я.
Издание 1499 г
68
трактатов: .н1аJ\·tс111п·ых «Ha •I:tл" Евклтща и .-На
станлешт в арr1ф,"1е1111<е» t 1 ео1111фа юреl'щ:~ 1111-
комаха пз Гсrаст.1 ( J- Jl rш.) Псрсвон "J-Jачал•,
во;~.\Юж1ю. был частнч11ы,\1. И:~ м 1 101·очш.:ле11-
н ых 1·1с1·оч ни ~..:он Бо::н tнй ·1·а кже се К"1·ан1111 _11:1'1 '1 -1 н
ску1О KO.\.lll l JJIЯЦ IJ IO <·] laCT:JBJI Cl ll l l' 11 музыке•
(Ком1111шщ11еi1 назынастся 1 1rю 1 1анслен11с. сn
ст;.111лt: 11н< >L' ~i;1 11t'рt:рабпта11н1>1л фра1 · ме11то11
Ч)')ЮIX СОЧ!111е111111 ) в 11е1'1 1{ COO'l 1\e'I t"1·1111и (
rреческоi1 траl\1щие1:1 i\-rу:1ыка трактовалась как
ма·1 еман·1с1ес 1<м1 д11сц 1 111.1 1н1 r::t.
В коп цс V11 1n. тю рол~, фра111<оn Карл 1 Всл11 -
ю 1Т-1 обр:.~пш шп 1~1 ~шис 11а бсдс:твсшюс поло
жс::ш1t: с 11:1уч.<.:1шс.\1 11:1ук в варв: 1рскuм св<я:м
отt:чсствс. <..; пр11с у щl'1'1 сму энсрr11сi1 I<ap!1
11.\НЛСЯ :~:1 rс.:форму 06р:1:юн:1t111Я 11 flf)CЖ/\C BCl'! 'O
распорн ;\)!ЛСЯ !IС1Тра111т·1ъ на ПСТIС)Щ~ Л)'ЧlШL'\
текстов лttп r11скуто Б r 1 П111110 11 fio1·ocл)?KefJ11ыe
ю1111 1 1 P:.iз r,JCюm::iя т~110 1 е теl\ст1.1, :i тэюке учеб -
1 1 ию ( Л3ТИ1 I CJ(()(J 1p::t~IM:1Tl!l(JJ, i\1()JJЗX l l часто JJЗ
талюшаЛJJСЬ 11а ру1шш 1 с11 :111н1ч11ых автороn.
01:111 были носл'lнце111.1 пронзnсдс1111ямп Всрп1-
m~я и Горащщ Овндня 11 Ц1щсрона. llач.иная с
lX u. (::~то BJJl'ИЯ [ l;.J:3ЬJHaю·1 ~кЩ.IOJ I Ш tl 'C'IOl~I IЮЗ
рткденt l l'\1·•) 1rpOIL::!Hl'/J.C Hl!}I HCJlllKHX p r JMЩ I H
CTlJHJl l l н:1 l lOJll<:IX VIUH:1cтыpci..:11x 61t6J1110'lt.:I\
1»щом со Свнщ<.::1111ым 1111с:11111см 11 1руд.шн
Отцон Цсрюш. Трактаты J)оэл11н по ар11фмст11-
ке бы1111 1'0 1~да оче11 r, r1онут1р11 ы ~ l :шеС"1 но око
JЮ J ')() СПИ("ТШR I>C>:~ 1 i:пc1юf1 <· Лр1fф\1СТl-ТКТI•
Л юбопытпо, что Оl\Ш1 rп богато пллюстрпро
в.ш ньL'\ рукопнсей lX в. при11адлежала nнр<)
К.tрла llemн<o1·0 - 1<орото l<apJJy Лысому. Он
оеrаnил по~1с11ш на её полях.
Иная сую,ба ож~ 1)1<1ж1 Gоэ1tt1с11 r 1 срснод .1 1а
ч ;.1л.} .t:ню11 1 11а З11ач11тслh11ая час~ h это1·0 тр:1к
·rа·1·:1 'l':J ll HCTBC lllt ЫM 06ра:ю_11.1 llCЧC~Нl.l 11:1 110:1я
:1рсния сщё в Ран1-н.:м Срс;~нсвс ковьс. Ос1·авшу
тоо1 час1ъ - определенr 1 я, пос 1 у.11аты, :скс110 .\1ьr
и формуJ1нро 1 11т r1pe; 1m>жe1111i1 11:1 11ер11ыл
чегырёх ктrпг - псполкюnал1111с как са·"lосто
ятелыюе прои:шеде1 ше, :i юш осноо у для нк
назьшаем.ьL\: флорилео1i1 (от лат. floгilegL1s -
~со611рающ11й 1~nеточ11ый нскrар ~ ). Флорпле-
1'11SI - это нечто nродс моз:нп:л, сложс111 ю 1·1 нз
~ 11 tтсрсо Lых фрш мен·1 он текстов. Дне нанболс:е
11:шсст11ы е флорнле1н11 , сос1·аи11е111 1 ые н rx 11
Xl 1ш.. под11ис1ны 1rмснсм само го Боэц11я. хо·1~
сдна ли н;.1половину прин:.tдлt:ж зт tто 11еру
В n рочt:м. такоi1 под1ю1· - янлеt 111е обыч1 юе для
ш1т1 1УЕюстн 11 Средненекоm.я. Не 11адеясь 11::1 то.
ЧТО Ю{ детище будет СО:'Ч>апеrю ДЛЯ ПОТОМКО}j,
/..дr.\ 1 ВРлик1111, ко1юл1> фра11ко11. 11 "nepa1op
tея wt•111юй 1'11мtко11 им11<>1н111 .
lft'J\OTOp1.1c ;i llП>рьт ГЮ/ \Ш 1 сыn3111 [ cn011 'J'PY/1.J.J
llt'.'1111\И\,1\ llMC\13.i\!H. T ':lK, J\(} Ш\ШИХ )Ш~Й J\ОШJШ
сш1сю 1 соч1·1 11ешт й nсендо-Аристотели, 11ct'n.n;o -
Л.nryrn111a н др.
Rсrсr~нсксковых l't:uмcтpнs1x П('СIЩU-ЬОЭI ~' lli
ыы Bllt:pвыc CЛIJIJ<IIKacмcя со С'Lр~1111-11,1м НШI С-
11ш.:м. совср1ш:"·нно 1 1 сТ1JJ111'111ым дю1 ю 1 ж·с11чс
скоЛ грс 1 1сскоl1 "1:rтемат11кн. Высок:н1 эллнн
ска и на~·к:r llCOЖH/\<IHHO OK<IЗЫB:Jt:l'OJ cpt:/1.11
тсксr'Ов зсмJ1е\1t'рнп1·(' солержанпя, которые
tpt' i-\11 1Юо\1ще СКЛОННЫ (11,1 mт ВЫ 1IОС111Ъ :Ja nre-
/LeJlbl м;пем:пнк11 Гсометрт~я F.: 1нr:.11ma ·1 еряет
свою счю 1 ·ост1,, J(о1сазател 1,стnа теорем 11счез:1 -
ют. :1 trx \1есто :~ан11мают ссылюr щ1 формы
по;1сf1 (кру1·..1юс, треугоm,1юt'. квадратное 11 т. д.)
11 формулы NШ выч11слсш1я 11х шющадеЛ То.
11p()TllB чсr·о так B03(1<tЖ:tJ l ll J\[\CHIJCJ'Pl'ЧCCIOlt'
учL~ны<: - н~1ру1 1 н:: 1 111с ис:рарх1111 н ()бж1сп1 зн:-~-
1шя , - свср1н111юс1" Стро1·остh 11 ч11стота 11аую1
fiыm 1оскнс:р11снh1 .
( релние вt->к;~ и Возр0Ждt:>11ие
Последстn~ш этоrо oкa:i:JЛJ 1 с 1 , для геометрии
кат:ктрофичесю 1м11. Вот пр11мср тш·о, т<ак 110-
ш1м:~лся в гксвдо Бu:-)ЦIJCШ)L'{ 1·сол.н.?-тр11ях в·1·0-
роiт 11uстула ·1 · Евю111/1а. согщ1с110 котором у
нснкую 11рнму 10 11ин11 10 можно щ:о 1ран1 1 • 1 енно
1 1rк>;1олжа · 1 · 1,. Есл и гтрt:/\С'l'авлнть 111 rнию ка"
1ран1111у уч: 1 стка 11а пuлс , то она, сстtе1·вс:111ю.
11l' "10Жt:'I' быт1) бecr<01 1 eч1-1oli. что nrю·1·1шоре
ч 11'1· Rнкл идоnу 1юсrул::пу Гсоме·1·ры Ра 1111еги
Сре1 111свеrтвья ш .1ходплп r 1з з:пру/\11еrшя сле
дующнм образом. 0 11 11 сч1пали, чтu в постула
те μ~чъ 1-1дё1· о nродолже11111:1 11с rю 11pяJ\Юll. а
" вбок", п n своих рукоптrсях обычно 1шюск·1·
rнрокшш ЭТU 3 :1MIOIYTOi1 Л()М:tНОЙ
«РЕН ЕССАНС Xll ВЕКА»
И ГЕОМЕТРИ Я
f-l(m;m во1111а псрс1юдоn дре111 1егрсчесю rx ру1,о
пнсс1'1 u ]апа,.1,1юi1 Г.::нроnе nри штю, на XJJ в.
:·}10 nрсм.н ш1зывают «ренессансом (uозрождс-
1 тпс,..1) ХН nека». vL\\сн1ю то1да во~1н 1 1ю1 1 1 пер
вые с в ропсiтс..:ю lt' ушшеро1п:ты. t'о:танавшнссн
обычно н;1 базе крул11ы.х к:н/х:д ралы1ых ш1шл .
Как 11п 1л ьдш 1срL·д11с:в<.:кон.ы х рс:месл<.:1-1 ни1шв.
у1 11 шсрс1 1 тсты 11аход1 1 111JС1, под nuкрпш1·1·сль
ст1юм C l:H.TCКllX 11 l(CJЖORHЫX н<.:рарх11н 11не з;1-
!1r lCCJ I И от про11:тола фсо11ало11. H:шl1oJJct: 11:i -
нecп-1r.rc 113 утtинерстrтетnн ТОГ() нr>eMCIJl.I -
Партксю1Г1 (Copi1n1111a)11 ()ксфорнсю1й. а т::rк
жс Бплопсю1й 11 Падуа11скпй. lltpnыe два Сiы:ш
особс11110 зттаменнт1,1 Сl3011.ч11 богосл.01.кюr:vтп
факультетами и факультетами «11скусст~», на
которhl Х изуча; 11 1 ф 1 1 1юсо ф1 r ю 11 матсматнчt..:
ск11.с: 1 1а~'1<11. в XII к. в1 1 сr11пк· 11щ1111 1 J 1 1 tc1, rюлныt:
11<1:1· щ-1.скt1е пс;рс1Ю/\Ы " tL~l'taл » Евю 1 1 ща. нntпол-
11<.:: 11н 1,1е с ар:16скш·о. Исчс~JJО "нарнаrскос• 11ро
ЧТl'н11t..: кл:зсс1rчl'скr 1 х Тl'кстон. Ою1:11.;о сама
ндс:н общнос1 ·11 гсометр1111 11 11ра"·1·нче<.:К11х
1 1 р 11 L'vю 1i 11амсре 1 1111-1 остал:кь 11 11рrшсла t< по
яnле11шо пово1·0 ра:1дела матемзтпю1 т~ш тrа
зыnасмой nrщ11,тичес1.:.ой геи..метр1111.
n тра1<татзх но nра 1пнчсской гсометrпт~
nроблс:.ч ы ~1 змсре111rя полt:~"1 н<.:t: бсты11с ус.ту
п:.~т-1 Мt'с.~го эа;~ач:tм 11а нахож;~енис расстош 11111
)\() 1-K'(\OC'I '} l ll JЫ X r1peд;.1cTOf\ (C:1Mll ;:)Tll :1:.~ 11ач11
ROCXO[ \lllll l [{ r11мсю 1 м llCTO ЧHJIK:lM) . Mcтo;~n l llX
решсн 11я KllOЛHC OTl:lt'Ч~1Jlll Щ)lfHJ~lJП:lм п:OJ\1e'l '
pr111 ~BKltlЩa. H ~trlбOJICe llC!HtC'f'НhHvlll llЗ T:'llOIX
· 1р:н,та·1тш l1ыт1 тру,Г(ы мСJнахэ-l)ене,Г(т1к1 1 rт11\:1
f\1·0 Сс11 - Викторс1ют (?- 1 L ~l1 ), в1~1дато11~егосл
7()
Иrтория ,1,1атематики
Гуго (рн
В>1кrо1кки.:1
R кpvrv rr1011x
уч1е1111ков
\1 .1pи1111 ,tst
КНЮ~Нi\Я
,\1 ~ 1HJ1,J rtu p .t
11·1~1льян скп 1·0 матс.-.,1а·1·11к:1 Лt:uнар710 П11:~а1-1ск< )-
1·0 , 1 1 :шсстно 1 ·0 также 1юд 11ме11е.\1 Ф11бо1-1:1чч11.
11ар1-1жско 1"0 матсчатнка 1111р11;\rюр1ю1·u астро-
1101·а Д()ме111-11т / \е К'!аRаз 1 ю (XJV н. ) ~ 1 ба 1<:111:тра
меющш1ы Н11 1<0л~ IП1<жt~ (Лv· к), рабптан111t-1л
в Jl1юш::.
11-ужно ск;:~зать, что срелпевскоn~,тм ш1,от1-
рам премудростн нра!(Тической геометрии
дав~шись с больш11м трулом. Чертежн, сопро
вождающне Тt'Орсмы. IIal1,o было за1ю мншпь
Вот ::JTO и с1·анонrvюсь ю1.\1нсм пr<.·тк11онсн и н
;urя уч.ащихо.1 , которым прuщс 6ьто :~а 1вср-
Рис. 1.
С 1p.11111u.1 "J ,1льUtJ\«1 1:!нлл,1ра
t.'Оннl:' кур.1 Гпри~1)~1т"лы1~я nр11Р~ 1 111я
0.iшt'll ( оiюр,1 ll 1\11t\H{'
литт, 11аизусп, 11есколысо стр~111нц латиш.:кого
текста, щ:жсли rюспрои :шссти по паi"mти чер
тёж. Ikдь люди тогда 1ючти Н<:' сталюшат1сь в
CBO(;'l! Ж l l:..SHl1 с таю 1 м11 nпннТННМ IJ , !(;}К lL'Jall
иm1 чсртёж. ныпоттсr 1 ныl1 н масштабt'. Как
r·пнорят 11стпршш. 0 1111 ЖIIJIИ «В м 11 рс пр116ли·
Jи·1·е111.1 юс1 "' " 11 нмс С'1'СJ 11 змеrе1 lllЯ 11 вычсрчи ·
натrют н1ч11ых 1 ·епмс-гр 11 ч<.:ск11х форм доноль
ствоnалттс1. и-х сл СJ11ес11ым1 1 оmкапиямтf. Чтобы
11адёж11ее Зtl!IОМIППЪ ТОТ 1 1.'Ш ИllОЙ чертёж из
« ll ачал" Еnютпда. ученики прндумывалп им
с 1v1ешные . :мп оми11ающ11сся на:шашш вро,1е
« К)'р~1нuй лапы», •OCJll IH()I'() MOC'l':J. • 11Jlll <ХВОСТ:!
11аш11111а .- (р 1 1с. 1).
Остаётся :i:.Jl'~I Jtкo li , от-кудэ чсрпал11 з н:1н1tя
по гсомс.~1р1 111 с ред11енС'коныt: архr1тскторы 11
стрrн-пе.:111 1 ·0·1 ·11чt:скпх соб()rюв, вeJ tl> m11 1. по
nидпмому, 11е 1юсе 11 tалн yr шnерсптt'Т()R, Скорее
uсего секреты зо,'('i 11 .х uереданалпсь от мастера
к учеш шу и не подлежал~ 1 раз!'J1ашеншо. 04'~·
nттдтю, поэтому от т<.:х nрсмё11 до нас лоспн
не дошло арл"1ттскrурных альбомов. которы~ч11
так богата 1юследу1тцая эrюх:1 Возрождеюrn.
Ед1шстве 1 11юе исключеннс - чулом уr (елещ11 11 й
:~льбом арх1Iтек·1урных ззрнстюк, пр 11 над.11е
жавuп 11'i некоему Виллаrу д'()ннс:куру. 011 д:п11-
руС'1·ся np11.vrcpнo 12;is r·.
Полторы стrан 1щы
1rс 1 1ещре11ur чсrтсжамп <' по;(1 1ио1мr1 н<1 m 1кар
.~иl!ском лш1лекте старофранпу:к1<оf'О яэ 1,1 ка,
разънсшuощимп их смысл. Расшнфровать «гсо
'-'tстр1 1 ю" Uшшара д·оштскура нещюсто д:1же
историюм арх 1 пе1('1у11ы.
АРИФМЕТИКА НА АБАl<Е
В Срсднщ: нск:1 бор1.б~· за право называться
м::1·1·ема·11 1чl'Скоl1 н~1у 1юl1 1юнt:JШ nр;,~кт1 гка счёта.
Так, с 1<О1 ща Х 11. ост ювным рукоuодством 110
арифметике 01уж11л трактат «О пран11J1 ax аба
ка " учё1 юго монаха l 'ерберта нэ Орайзк:J (око-
1ю 940- 1()():) ). ст::ш щ сго 1шослс;1стn~ш Па ной
РимсюL\1 С11л1,пестрuм 11.
Абт,- - это прост<:lн 1 н::е счi:'т11ос прп способ
!1е1 ll-l t (СМ. СТ~IТЫО <· Чe'l' hlj)(' Jtc:i'I CTIOШ :~р пф
Mt."l'JJIOJ->). L\тобы 11 1хr\с'l'анr1ть себе, к:1к о н вы
глядел. Д()стато ч но 1к1юмн11т1, русск11е счt:ты.
У<" 1 ·ройс:тво аnака Гcpfiep·1·;:i 1 1 ескоm)ко r1 нос Он
llCЛOЛliЗ()Щ.I JI 11 l(:lЧt:CTRC Вl1IЧJJCЛИTe'J I 111 !111.Х ЭЛС
МСНТОR ЖеТОl!Ы с 11ане<:'ёпны~н~ 11 а 1111х 1~нфра·
ми от 1 !\О 9. Раскла;\ывая жето11ы на а(')а\\е, Гер
бер·1 чо1· нзображ:~ть 11ззт1ч11ые на·1-у11ал.ыrые
Пv11t1
(>tльвестр 11
1 Ге-рt1ср1
•н Ор•1>1а.ка) .
1р.1в~1р.1
на 11ep<>~t
1мfie111.1
1 l\\рв11ньяр.1
ч11СJ1а 1юч·1 11 т;ш Жl' , ка" мы 11р ед<~ 1 ·а11J1яем 1rx н
АL'ся·1·1 1 ч 1юй rю~шцнон ной c 1 icтe.v1e. Тош,кu .вм<:
сто нули 0 11 брал п устой жетон
Ноный аб<JК н1>н:л бш 11,шое прс1f\1)'1JJ,ee1 ·щ>.11<.1
11t-м \10Ж1-f() было ум 1южат1, 11 1..1е.111п1,. (Ста ры1'1
р 11 :-.1о:нй ;t6ак бы.'1 Щ1\ ICl10l.OGЛC!1 к OCIIOl\HOM
ДТIЯ C.'IOЖellHH И BЬJLHJТaJIШl. ) Уд06СТ130 С Чсrа 11 ;1
абаке состояло n том, что ОН :.1аt<СИl\1:1ЛЫIО
':9 •
f,
~( Т1'>'> ~
c;Jf ~;
\.,J,al 1~
""fnt(
f"лr .r,.,,. ,
11
~.r 1
'f"
"
,r
'
r .,.
(8'18/' с.у~~\) 1
--~
~-· -- .xi• ii. t
...
-
...
t
~....
Cf 111
с
хJ....х
~
Б 1..
ь....- l
v
dl"/~
v
l~
--
--
_.
ь
~~ъ~ъь
-
~L 1~ 1&~
~t-
!.!\
i
:tON 11 \ сеl >.Х'1 11_,....'>
1)'
11ь
"'
-
--
»L) ~
;l.XU> IY ~
1у
с'У ,'ОС/
J(lt,
:а «\., ёёL ~~
1
1
С ~е"а ,1tы1о. ,1 Герберта
ра:11·руж;1л лачнп,· lll•IЧl l CJLCllllЯ f\L'JlllCb IJOЧТll
аnтом::tт11чtтю 1 , 11 е тр<=6011а1юс1, :1а1юм11н:пь
допол 111 1 1 е:1ыrыс: рззрню.1 11р11 у·~нюже111111 11
уидьшат1, частllое пр11 деле 111 111 llромсжу·юч
пыс рсзул 1.,т;~ты обычно зашкыв~1т1 на nоско-
1:1~ ю таблs1чю· (цсру) m 160 11редстаnллли D шще
кuмбшr:щшr т1льцсн Надо отмеппь, LJТO па .1а
т1 шскuм Зшrадt: сущсс1·1юв;Uiа 1х1знн ·1·ан система
11редС'l'<ШJН.:н1т ЧШ.'LJI н:1 IJШIЬЦ<!Х и1.о 9l)99). Она
01 1 11с.1 н;1 1:1 1·ракт;..j 1 ·с Бс11ы ) tостогюч.1 ~11но1'0
(OIIOJI() (173- Ol<OJIO 7.~5) •. () счёте lipt:.\ ll'J\11 '>.
гтосnи щё111 юм р:кчёту 1щеl1 Пасх~ 1 Oчt'Jll> П()
чоrала пр 1 1 1i1>1ЧI1c:.rseпш1 ., 11 1·а бтща ум1 южt'-
11ш1, сост:шлетпrан ещё в 4-17 1 рнмюн111ном
Ни1пор~1ем
Остаётсн за1·адкой. 1<;11< у l 'ерберта ро,Г(rrлась
tЩ(.'}1 е1 ·<.щ ь yдuri1 1ш ·o абака с мсчены,\lн жсто
нам 11 0 ) \I JH CpLJ\l l t:BCKUKhU~I а1:1тор. Щ1;tНДа . CU-
oбщal'J, 11'1'0 "Герберт JIOX I ITI !JI абаl< у с1ра1 \J I H ».
г. с. у арабпя ;L61стн111 елы ю . li м ш~одое111 011
11ронеJ1 некоторое нрсм? н Ис11:1нско1'1 м::~ркс
\погра11 11ч щн1 с араба.-.ш 1·е рр!1торнн) О; ~нако
не док::~:~атю. что у самих apafю1i в те вреi'1 е 1 L3
с~1.цес1 вова.1 та кой аб:ш
Пор•pt'r Ьt.'л~1 дut 1 ог111ч 1 e1111u1 о 11 1 к1111 1 " ,() t чl' 1l' 1o1μt•,1t·н~1
Пdрю+:. и~,~аниР 1r, p7 г
71
72
Имя Герберта нз Орнйака - э;шсчател ы ю 1 ·0
математика 11 11су'томимого церковно-пол11т 1 1-
'IеС1<0 1 ·u дентош - было (Жрркс110 01·ромt 1 ьнv1
KOЛI I ЧC('' l 'HOM l'Jl yXOH н J!Cl'CHД. Его даже обшп Щ
Jll! \{ чс.рноюt1ТiКШ I \\ <.:IIOlllCHHHX l' JJ ,bHJIOJIOM. в
н:1рнарсю·1l1 кск с у1tо1юльп·внt:м сочнн н л11 нс-
6ыш щ 111 о че11n некt, ум<:тшк:м ум1-1 ожать 11дел 1 1ть
болы1гне •1и сла, и:11·0·1·а 11тпъ <·1·онорнщ 11 с 1 ·шш-
111,1", :туrюn(')й ~ффе 1,· 1 · 1<0·1 ·np111x со:1л.:111;uкя, по
в1111 1 1мому, силой пара, и n poчrre 11е ме 11 ее ~·;~1 1 -
вrrтелытыс вещи.
l'ербсрту 11рипщ:ыщ11от сщё одн о наж11ое
азобрс...:тс 11 нс (tшро чем, 0110 сп~ло нзnсстrю уже
поон.: c...:ru пн.:рт11). ~тu н;ктuлы1;u1 ИJ'[XI no:t 11а
:1в:.~шн.:м ~r11тмuмах ~.-н1 ·>, что uзнач:.~ст «бнтва
ч 1 н.:с...:л». ИгроН!JС поле ритмом~1х11н наnом 11 1-1а-
1ю шахма· 11 юе. И1· р~!, оснона н нан на з11э11ш1
npocrcй r 1111x сво l ктн чнсел 11 нх11ро1 1 зн<:.:1~ен 1 1lr .
11 TtЧ~III JC СС!VГИ l'ICJШR служrт::~ 11ре 11ОСХ()ДJJЫМ
1ше1\е~шем в арифметику, гrр111н 1 1-1 ая 11 аныю 1
работы с ЧHCJI :lMH .
С 11ач~и1а Xll в. в Европ<.: стала рас11ростра
rrят1.01 :Ja11м("1 ·к011:11-шая у арабов по:.шцио ппая
дс<.:ят1·11111 аи с 11 сгс\1а счнс11снш1. Однако у1111 -
всrх: 1Пt."1·сю tl' l tpoфeccopa НС 11 pOЯBJJ.ЯJlll К ней
о<.:0601 ·011нтерсс1 _11рсr~лочнт~н1 11 :и1 ;н«t'l'h 111 1фа-
1·uр<.:r~н: ку10 ар 11 фмстнку 11.11 11 1 1 раннла абака.
С ч 11таетсн, ч·1·п 1 1ерпымr 1 110-11ас 1 ·онщсму оцен11-
1111 у;(оfiст1ю ;1ра6скоl1 ц нф 1 1 рн нт:щыf 1 1сюн::
ку 11 1 1,1,J. llовая I[)'111срэ 1 ~1ш п р ижнлас1, в ку11ече
с1<0тr среде Италии н в ремеслснпых rоролах
Ю:iк1юй l 'срмашш на 11злё·1·е С:ред 11еnекопы1, R
Xl\1 - XV nn. Коммсрсаптам бо1·зтьL\. тор 1 ·овых
crpa1J осuб<.: н1-ю часто пр1 1ходmнхъ сосrамятт,
KCKCCJI Я, С'М.С'l'Ы , НЫЧIТ<.'JIЯ 'I '/, CJIOЖl-ll> lt: 1 1роценты
Дсся1т1 ч1 rая с1 ~ стема окончателы ю vгвepJ\J 1ж1с1,
11 С:нрпне, ко 1 ·да вмс.:сто доrю 1 ·ос1·оя щс1·0 не р 1«1-
мс1па (в ыдеJJа 11 1ю1'1 ·1 ·01-1коl1 кож 1 1) 1юнн11лась
6011С'е /\е111ё11зн Г1ума 1 ·а, 1 1 а которui1 мож н о бь1 ло
прт 1 :шод1пъ ар11фмет 1 1,1еск 11 е расчёты . Но
Ntжe развнтие ю 1111 оп<: ч атюшя нс смогло пол -
1юстью nытсснитr. счёт на :~баке.
МАТЕ МАТИ КА
И НАУКА О ЛВИЖЕНИИ
Oi1t10 1 1 з 1~а11более прш ·1шалънъ1-х J1.Ост1 1 жсн11й
C[JL'/( f-ICBC t<OBO(I ммсm1 - мзтем~'l 1!Ч t:СК;\Я тсо
рня ,~впж<:m 1 я. Начш 1 ан с XII н. н Екрnпу посп.:-
11е111 ю, через переводы с арабсrю 1'0, ст;u11 1 11ро
rшк.1.ТЬ идеп Ар1 ~стотею1 Хоп1 са);! Аристотель
11o:ipaжt.tл протпn ITCTIOJl b :'IOl\'11111>1 ,\1:1Tt'MaT\ l "IC-
CIO!.'< ме·l'ОдО.1:! в фll3 1 1J(C, IIML'IПIO пр11 ()CMЫ CJle
IIШI его ПJ'(с1'1 11а ла·1·ш1ском ~~ападс н nо:щнюrа
у1r11 к:l.'lь11:ш в сно61 ро!(С rrayкa о 1~н 11же11ш1
По-11~н.:тонщсму <..трьёзное ра:~витис оп:t
rюлуч1и1: 1 11 XI\' 11 :>->т: 1 наука 11 мtJ1a две uсобсн
ноеr11. Прежде все 1 ·0, 11 Ар 1 1с1·0·1·ст,, 11 средне
некоm.rс учi.lны<.: ПOHHM~IЛl l IH)ДДHl l ЖL'lllleм 1\СЯ
кос 11з~1е 1 1е11 н<: m юбщ<:: 0·1 11 ;н. 1 снсннн цкет:з 11
п:~мnсратуры ло 1 юя11ле11ня 11 уr1ичтожсн1 1 н
всщсtr. r! о это1'1 11р11чине одно и то же лопrrю
м~тсматнческое построеrше, скажем теоrпя
нро11орцш1, исnол1.зоnалос 1, д1 1 н оn11са1шя
таю1х ра:JJ11Ilшыхш1;к·ш1й. как прuстра11стnсн
нос ПL:рсмс11 ~сн1 н:, μаснμсделснш.· <-теплоты» 11
qхшюда» 1~ орг:111и1мl' чсло вск:1 (тu1ла это была
oc110ua ·1·еореп 1 чсско(1 мсд1щ1шы), 11дажс .пля
осмыс; 1е 111 1>1 <• неликоr'1 1~<:111 1 бы·111н» , простнрав-
111сйся пт Божесл-1е 1 11 юп) со 1 1сршснсп1а через
ат 11 ·с.:лоn 11 чслоnска ло 11еж 11 11oi1 11 р 11рuды.
Дру1 ·:ш особешюст1, срс~нсnек()Jюй тепр 1111
дшDкспшr состояла в том. что 11аблrодс111ш п::~,1
прнродоn не ш ·ралн в пcrl рсmаrощей роли.
Часто о н и давалl! ШШ1Ь псрвы 1'i толчо1< к раз
~1ьш 1лt.' 1111 }щ. а :3аТс,\1 мысJlЬ уносш1 ась в облает~,
чш..:тnl1 11ш ·11ю1. Taкofr сrюсоб ш.:слсдонапия
1-(;[:3ЫК:~лся CXOЛ:lCТI JJ-\()Й (0'1' l/JeЧ. * СХUЛасти
КОС? - <· J[JJ\OЛl1HJ,Jli », «учёныll ·~)
Мате:1..,-3т 1 1чес~ше мо;1ел 1111н 1 1жсн 1 rя 11с1ю1!h
.юнались !(ЛЯ ()ор1,6ы с :ктр()JЮ\'11ей. Так, фр~~н-
СР ЕЛНЕВЕКОВЫЕ
СХОЛАСТЫ П РОТИВ
АН Т ИЧНЫХ ФИЛОСОФОВ
Средневеко вы е уч ёные -схол;э< rы
использов;зл и математически е рас
суждения лля опровержения фи110-
софс к~1 х доктrин античнuсти, и
прежде всеrо утвf'рж.ления Дем о
критLI о том, что uc.b состоит из
ан)мо в . Ан глийски й схоласт Томас
Бrалва рдин критиковал эту точ ку
эрс11ия слелуюшим обра зом.
10 rоч ек ди аметра 1:юсс1анов 11м
пер п ен дикуляры , которые пере
(.скут окружность в 20 точкJХ . По
лус1ается, что длин а окр уж 1-юс.ти
влвое больше диаметμJ, 1110 , е< rе
ствен 1 ю, ош11боч 11 0. « Об 1том, -
т1шет Брад1:1арди11, - з11ают
не только математи ки, но и плот
ники, каме~1шики и другие м;;~с
тсри , опыт кото р ы х показыв ает
лож11ость подоб1-1о r<1 заклюс1е1-1ия• .
мых Оуде·т п олько ЖЕ.', Lкол1>ко 1о
ответствуюши х перпенл11куляров
в прямоуголь11икс САГ[, а по дли
не о ни прееосхt,ля т э ги перпе нди
куляры в отношенииСС: СА Если
nлощ.1ли состоя т из ли нии, то во1 -
11 икае 1 111ютивор~ч ие: 11 ардл11ело
грамм больше равного ему п рямо
у~-t)/\hНИК:'I в се : СА р<н П рич l:'м,
выхолит , чем оrтрее угол п ир.злле
лоrрамм.:~, тем больше 1.:1 о пло
Ш<lдЬ, что, КОНЕ-'ЧН(), Нt'81.:'рно.
Е(.ли 11ри1·1ять, •1то всяк,н1
непrе рывнаЯ l:lеЛИЧИllд - ЛИtl И Я,
плоская фиrура Иl\И теАо - сосю-
11т из кон еч но го ч11с11а атомов-то
чек, то н еизбежно прон1 вореч и е.
Лейп 1-1и тельно, п рЕ'.лn олuжим, что
•1и сло точек на н е котором отр~:з ке
ко11е•1но и рав1-ю, скажем, 1О. По
строим на э1·ом отрезке как 1-1а
диаметре окружность. В каждой и-~
А ~ют ка ким Р<Н'< ужден ием он
опрове ргал кон цспUИ J(), со глас но
которои 1 1е п р ерыuная величи 11 J
состоит из бесконечtю1·0 чи< ла 1 ю
леi\имых точ~к .
Известно, что параллелограмм
равновелик прs1мо у rольн и ку с те
М~1 же ()( новаНИЕ-'М и ВЫСОТОЙ . П ро
ведем в па раллелограммеСGК[ от
всех то•1ек опюва1 1ия С[ «вес пря
мые» к тuчкам 11ротивополож11ой
rтороны СК 11а ра ллельн о ГС. Пря-
цукю 1й схол:н:т Н11кол:I Орсо\1 (около 1.)23-
1 .)~2.) рt::юнн о пол :.~гал, Ч' НJ если ш,1fip:i · 11, лкt
C'He'J llJJ a , '1() Jlt'(lШJ'l'JJOCTb TOJ'\). ЧТt) t)' J' l-IOIГТC I l t 1 е
Н\ LКоросте11 б~'дl'Т р;1 1 ~1 rо11::1лы1ым ч11слом,
11нч-rож 1 ю мала. А коль с коро шю 1{ыр;ur.;аетса
чткло.м 11рраш-юналы1ым. то два сnспш~1 rrн -
1<0111а 11 е понторнт cnoe1·0 нач алыюJ'о n ол ожс
шш н:~ небе. и, значит. астролоп-rя пс может
61,п ь ТОЧI ЮЙ 11аукой.
В н :111 6ол <.х: 110лr юм ющс ма тсм:1 ·1· 1r че<: к:.1я
тсuр 1 н1 /\н1-1жс11ня 11зл ожс 11 а н <- К11 1 1п.:- в ьтчнс.11с-
1 1т~, " ~~н1 11нйскr)J'() сх1 таст:1 Р11чарда Суа йно.ед~1
11 tpyna' Орсма. ИJ1ея :Jаключаl'тся 1:1 том, что61,1
•качtстна» 1rреr~мсто11, 11 в част1 юLТН скорос-11.
дш1же1 11 tн, н:101.iражат1, •~tрt:1камн прям о!~ . ко
торыеотюrадьшаю·1 сн пер11.е1 щш<уляр11от1r rип,
06о:~т1<1ч ающе й uремя или 1х1сс'('Оя 11ис. Если на
r·opн ю r 1т~LJU,1 юй л ишш отмеч~uш nрс.чя. то по
луч;~лся рисунок, rюхожИJ'r на соnрсмснп_ь1l1
1раф11к :шзисимосrи скорост11 от врс\1сш1. Рас
стоян1 1с. про 1'11 1сн 1 юс телом за uн рсю:пСш11-,1 ~-1
11ptмl'1111ш't 11 ро м <.:ж~·пж, r1р<::) ~ст::штr л а ф1 r rypa,
построс 1111 ая на nc1 1нрсмс1 1н Н:шр11 м ср, к слу
чаеДШ!ЖСНJ !Н с ПОСТОН! !!!От'! с1<0ростыо З'l'О был
t1pR\юy 1опыrш<, 11 случае р ав ноус 1ю реш ю 1 ·0 нлн
ра вr ю:~а."1ею1сш ю1·0 двнжешtя - 11рямоуt n1n., -
m,rfr трс)тол ышк и ·г. д. ПОJГ'} чшшшесп ф1 f111)Ы
исследо вали ~1атемат1 1 чссюr.
Ор<.: м дока:-iыв:ut. что тющ~щ1. r rpнмoy1·om,-
1юго T J'l"Yl' <))11-,l JПK:J. 11 pt.:дcra KJ!>I ю ЩlTtJ pa}j-
1-юycкope11rro<.: f(t111жt'1r1 re. рав11<-1 п;юща101 1tри
МО)ТОJ 11,ш11с1 с тем же ОСПО11:-1 11ИС:'\'( и В,'\ВОе
меr 1ьшсi1 высотт"1, че.м у ·1 реуголr,r11ша. (; точ
Кlf зреlIНЯ мел:ншют это 02начало. чтu путь,
проlще н11ы1~1 тс~ло м 11рн ра11 1 JОус r<орс 11 пом
дю1жсш1и, раnсн щn 11, которо<.: он о прошло бы
:3:1то ж<.: нремя, д1н 11·:шсь со CJк·д1 1ci"1 скоростью
Чср<::.~ 2"5 n J1<:т ·1
·0 •11 юс д1.ж:1:~а·1·ельс1·1ю /(,1 1111< >r ·o
I IO.ll OЖC l!! JЯ /(::IC'I Г:mruн:r> r~I Jll lJl!;' J\ KO' l< Jp 1, 11'1 11
11р11?v1ен1 1·1 сго к 0111ка1 111н' пю()О)\1н11 о 11<1.'tl·-
1111>1 'l'<.:Jt;J IJ l l )'L-Г<П't'
1\11.1 пр11нетr ДОС'"l :lТОЧl!О !![IOC'IOil Пj)H\ltp.
Но схоласп.1 3аш1ман11сt. 11 бощ:е t py1(1LЫ \.t11
п роблсмам11. Прсдполож11 м. что 11e1.:t) r·o μoc
·1<.:ло .щнжется в те ч е ни е отре.ша n рсме 1 ш.
рав11 оrо 1. <:о с кuрщ:тыu 1. J:tTl'M в TC'Lt' I шe
npc.\H.'IIИ 1/2 cu Cl\OpOC'lЫО !. , в п: ч сшr<.:
щх·мс1ш 1/-1 = 1/ 2! - со скоμостыu ~. 11 тсчс-
,
~
11щ· врсмс1111 1/t5 = 1/1.
-
со скорtк"11-,ю 1111 ;~.
КакоС1 11}' 1ь 11μ0 1'щё·1 'lt:JI< 1 за арс,н1 _ ра тюt: 2·1
(3;\ес1, оощеt: нрt'мя д 1ш же 11т1 CL~r r, су~-1 ,1 ;1 ()с:- с
ко 11е ч 1то 1·0 ч 1кл:1 чле 11 он rc-n:v1eтpп чecrш lr прn
111
rp<.:c:c111 1с основа1111см 1/ 2: 1+1 +
2
!+)7+.=2.)
И ш: будет лп э·1 от путъ вообще бесконечным ?
7~
Исrория м.:~ 1~мат11ки
Со1:1рt:мt:нныl1 \1а·1·<.:м;.1т11к ска :~;ш бы . что
пуп~, пр1 ) lI/~(.'111 /0\1)' TL~110i\1 , {:()( >TBCTl'Т R)'CT ВСJПl
ч1111а. 11ре;к" 1<НJ.11е1111~1Я l1ескоr1еч11ым рядом
1>l
1
1
]+21+.., 2'+4.21+')21+...
Этот ряд паТJ,о спзчзлз псслс;~;оnатr. 1ra сходп
ыос1 Ь, J [ еслп 011 СХОДЛЩИllСЯ - ПОПЬ\1 JТЬСЯ
нa{JTlJ t:J 'O JH:ICJ(:'HIJC' .
Opt.:"1 рж:с ужнал нначс. Как 1111; 11-ю 11:.1 11рс; \
.·1оженно1·0 11м ч ертежа (рпс. 2). сумм:J рнд:~
п рt.:7\ст:шляс:тся ка к площ:щ1, ПОТ\ бс.:сконсчнul1
Сl)'Пt:11ч~~·101'1 : 1111 mt>l-1 , 1~:щстроt:11110\i 11ад отрt::i-
1ш;ч АВ = 2. Rысот:~ каждоrr <•ступены<rr·' посто
янш1 11 равна 1. Ширнна ступенек убьmаст в
гео :v1етр11ческой л рогрессш1 с o cr юва1 шем l / 2
Jатсм Opc:vi рассматривжт прямоуголышк с
нькотоfl 1, 1юс-1 роенный на 1·ор11зонталыюм
отрс~кс СЛ = 2 . ПJJощ~щь ::>TOl'U 11рн\1оу 1'олышка
рав11а 2. 0 ·1 р<.::.ю1< CD разб1шастся, 11ач11ная от
точкн С, на отрсзю1, длш 1а ко1орых \'бымает по
'
'
\
1
•
закону l, 1/ 2. 1;2-, l / 2 , 1/ 2 .... расоютрсt-11-юму
111.1 11 1 е. Черt:.1 кп1111,ы :1' 11 1х 0 ·1ре:жо11 Орем 11рп
Fю1111т nсртmс1лып,1с .m.пнтн тэк. чтп nрямп
уг()лы шк ока:-1ьшаt:тся состамеmп,n.1 и:i ()сско
неч.tю1 о ч.ас11а пря~юугО.'lЫlИКОВ Е, F. с; н т. Д"
площади которых образуют nсё ту же 1 ео-
Рис 2
G
--
F
Е
.А
л
шс
1J
мстр1 ·1 чсс кую 11po 1'pL'cc:11 ю. д~1J1<:с:: он за щ: • 1ает.
чтu часть с1·упс11 ч:1·1 <)\t ф111уры. но3ны 111:1 ю111анс}I
над JICp:tIOll «CT~'llCHhKOIJ », r.остш1 ·1 111 T:JКJIX же
тuч110 прямоугольн 1 1коn Е. Р. (/ 11 т д. Поск()льку
су.ч~1:1 111юща)1е~'1 Е ...t. - Р + <7 + ." = 2, ;J 1що1ц;щ1,
псрноii ступснъкr1 тзюке раш 01стся 2, то оnщая
11лпщадь nод С'Jупенчатой mшпей будет равпа 4.
Так IТ\'Тём 11е~.:ложт1ых гео:v~етр11ческих рассуж-
1\етшй в Сре;111сnсков1.с до 1.;азт.mалн некоторые
теоре .мы ма·1ема111ческо1·0 анализа.
11 нее же срсднеRсконhlе теuр1111 д 1шжешtя
бьиш скорсс 1rо1 ·нко-ф11лософс.:кт.11 1 , 11сжслн
матс"1::1т11чссюш11. I3с11ь в тt: щк· м1..:11а, ка1< 11 н
а1 1 ·1·t1ч 1 юстн, мате.v1атнк:J t' ll \ё не (i1 ,1л;1 оторRана
nт 1<улr,1ур1.1 l')M:!lll-1'1~lp1юй и l lt'}'ДHIHГl'tЛMIO,
что сре11н мате:v1 а·1 11l{Ofl Сред~ 1 е11е 1<0вr»1 пс-1реча
лос1, немало тсоло1 ·0 11 ({)01 ·ос1ю11011 ). Тешю1 ·ом
бr,1 л ;нт 1 иltс 1шй схоласт Томас Iiрад.nардш1
(около 12\JO - l _~._~LJ). J3 трааа:пс "о Божсстuс11-
1ю~'1 1rрич1 1 не» он первым нысказал .\IIЫСЛЬ ото~~ .
что J1рuстран<:." 1·1ю, в кuторо<: 1ю 1 ·ружён шtш
м11р, беско11е•1но. Эта нс11р11с:мл<:>v1ан длн ;.~н п1ч -
11ос1 н 11 Срс; ~ Е I Cl.JCKOHЫI J IДСЯ В1IОСJН~/К'ТНI11 1 СЫГ·
p~I J l : I ПаЖI!\ 1() ГЮЛЬ 11 paJRI I T I 111 l'RpOПCllCKOi1
'1ыслн. Она n кош:чном ито1·е npIJнcлa к uтож
/(1.:с·1ш1сн1 1ю 6ескош:ч1ю1·0. 0;1норо; 1н о1·0 про
стμанстн:1 с атрибуто,\1 1)01·. 1 иm1 )~ажt с с:1м11\1
Бо1 O\t. Р~1 :-1ру111 ш1 ;,tнт11ч11 ьн.: и срс;1ненсконыс
1rонят11я о Космосе, он:~ пр0Jю;ю1n:111угь }IOllЫVI
11ар,:1м - нсбесrюl1 .\1ех:~н111<е 11 мзте\1<1тнче
СК(щу ;tнаю 1зу Л'\7111;
Е11\ё о;щп пример - теолог 11 матс;v1атнк
карднлал Ннколаft Куза11сю111 (1-Ю 1-1464),
который ттервым ввfл n матсматнку понятш~
6CC!<OJICЧIIO малой 11 01.:СК()[ IСЧН О болы11uй
1к·m1ч11н. I< ним он прншё:1. р:1зl\1ы111лян 11:щ за -
Сред11ИР l:IE:'Kil и RtН\ЮЖлt'НШ~
~
а~
дачб1 о кв;1лратурl' кру1·:1 11 н:щ ·1·солоr11чес 1<0!'1
11ро611с\ЮЙ 0·1ношен1 щ в KU'J'( 1ром rt~LXOJ(H'l'бJ
ьо1· 11 со:~лан11ыr1 Им l«JC\IOC.
Была J11f срсд11снсковая н;~~·к:~ о д1111жсн1111
1111с,т\Теч1.:l1 матtм:~т1 rчect<nг<) СС"1·есгво111:1 ния
Ноrюгп нrс),1е1111? Ил~ 1 же R XV[J CTOJl~TIПI 11/Ю
llЗОШЛа революция:, н ходе· которой нонан
11аую1, оm1раясь на образны l'pt:чecкor1 "'fатема
пшн, 1Т прсжле 13ССГО на труды lICПOIIЯTOГO в
Среднсвс:1<о~ьс Архимеда, отброс11л:1 за непу-А<
ноС'rъю схож1сп1ческ11с тепри11/ Об ..,;том до
снх пор спорят 1rстор11ю1 1rаую1
ЛЕОНАРЛО ПИЗАНСКИЙ И ЕГО ВРЕМЯ
Срс,1н совремсшппюв е.му 11е было р:11шых ll в
nосле,"(ующвс трн столе·rш1 11ельзя 113зu:1т~, 1111
одного учёноrо такого ;часштзба. Тnорчестnо
Леон:1рдо Il11занскоrо (l lH0-121()) ока:{аJю рс-
11шощеt: ю1ш11111t: на ра~щи·1·11е ат·ебры l1 теu
р1ш 1111се.r1. 11 част1юеп1 на 1ксш:~;~.uка11ня таю1х
~1атс:мат11кон. /'\:JK Франсу:~ Внст t1 Пьер Ферма
Леонардо род11ли1 и бш1ы1юм 11·1·алыu1СЮ->\1
1·ор1·оком 1 ·ородс -р<.х: 11у6.rш1\е Пн:1е. Е1·и Ч(IСТО
11а;млают Фr-1{)011ачч11. т. е. сы11 Бопачч1 1 (Доб
рого). 1l:н:тонщая el'O фам1 uнrл. гrо-впли;-.юму,
ьш·оmю. llo кpJйL1ef1 мере так он rюнменован
в ;ште о покуш((.: :.1е;\11ш, которую совсршJL'1 гто
...1uвt:решюстн для сnосго родстнснннка.
Отс1~ Лсощ1рдо 61,щ ноп\.)llусом респуб:111-
к11 П11э;1 Ikкop(: rrocлc ртк.це111 1 я сына e r· o 1ю
с11:1. 111 со служеб1 1ы\1 11оручсн11t:м 1:1 1:>удж11
(11ынс Ллж11р), 1'1\С' 011 ныполш1:1 t>б>1:1.о;11-11-юст1 1,
бтлю 1е 1<конL·улн:ю t,v1. Ко~ да Лсонаrщо 11сп ол -
1111J1<Хъ 12. Jteт. oтt:r\ liЫ:-J11aл er·o к себе, чтоб1,1
поз11;1ком111ъ с дещ1 м ~1. n пер в)10 очере,11, с ком
мерчсс~<н1'1ш расс1ётамн. Вес этн сnеденшт со
общает сам Леонардо n преднслошш I< ф)1rда
мснталыю.,1у труду «Книга абака».
Лсоrзардо rту1·ешсстнов;.~л r ru 1:\п 1rгry. Си р1 rи,
Грt:щш. С1щ1т1111 11 1Iрuнансу и вt:щс <.т:~рался
ПCJЗH:JKUMll'l'hO.l с fJ<l:JJlllЧllЫJ\111 с1шсоб~t\1 11 C1lL'1 ':t
1111ачш1а\111 ал1 сбры. Он убсл1тся. что техника
счС:.:та IIO ДCOl'f 'I JЧHOJI ПОЗ) ll(J ЮНJ-!ОЙ CJ 1сте:-.н:~
11::iм11oro пре1юсход11т все друп 1 е.
Нер1rуnш 1 ю, n П1 1 .зу, Лепн:~рг~:о серъёз1 ю :1а
нллся матем:.~тшю11. Он nо:l11аком11лсл с «На<1а
ламн» Евюш11а н. спс1111111ш эп1 з11а11ия с тем,
что уз11~1л от ар;~бских у•1Еных. состав1rл n
1202 г. «Кinrry абаr<а·> 11астонщую эт11\111сю-
1тедто ~1атс,,1ат11•11.:с1\11х :нrаtшй с1·0 :·>nохн
:37'ССЬ проян.11:~ас1, нысо1<:ш одарён1юст1, автора:
"f'P\rд Jku11;1pдu Ш' ~ЧCI-Jil'H:l'Kaя KOMll!IЛЯJtlТЯ. а
1·лубоко лро11ум:ШНОl' н К() MIIOJ'OM OJ111П!ll;]Jlf)
нщ: пго11:шс;~сн11с. В нём рассма· 1р11н;,~ 1( н·с.я но
rчюсы ;UIJ't:бpы, ГС<1МСТJ11111 11 'J 'C 'O{J l111 ЧI llTЛ.
Имснrю н :'>тоi1 кн1п·с rзпсрныt~ пр111нщ11тся
ре111етrне ~1звестнот1 за1t:~ч11 о K[IOJ1irкюc С11ра
п 11 н1ается. сколыш пар кролпков ро11:т ся в год
от оюrой rrapы. t:слн кажюш ттар:1 прmюс!Iт
ежемсс~шо по паре. сrюсоб 1ю\1 н сnою очередь
через .\1ССЯЦ к р.1З)IШ()ЖСШПО. 11 сели HII OJ{H:l
пара не гrо1 ·ибпст. Ответ даi.:тсн суммой ряN1
1+1+.?.i 3+"\+н+". +111.к~1жды\'1член
;.1·1·01 ·0 f1ЯJt:I. H:JЧI 1Н:JЯ (' трС'ТЫ.'J'О, янляt~1·с.я С~'\1-
мш'j ЛН)';'\. 11pt:Jth!/t)'IЦHX:
П<ХJТС/"(Оli::1Телыюст1, {liп l в на.11>11ег·1шt~Ч C"l';'\!ЛI
на.11,шать nослсдоnатслыюст1,ю Ф116011аччл
(см. статью «Лослсло11атслыюеrr1») .
В 122:\ ·1" Леонардо пuсвятнл 13торuс изда
нщ: ::Пой ю1 1 1гн свuс,чу другу М111<сж· Скuтто -
11μндrюрнuму :1стrоному 1 1 астrолшу11.щ1ср:1-
тuра Фр11дрнх:1 11, гому са,чому, кuтuporo 110-
гом Да11 гс уrнн1ш-1с1 в <-Ьожсствс11ноi1 кu:v1t:
/ \1 IIH (Данте ПОМССГI L'J l'l 'O н J:IO(ЪMOJJ t<pyt ала.
в ЧС'!'Вёр·1'ыГ1 ров. f\местс с ;tруп1м1 1 пf'iма11щн -
1самr1, вr.r11анавm11м:и себя за ттрпr11г~;~1·н:~лет1:
А следую1.цт'i, .·тют худобш1тi,
811а11ся ,Нтсе:лf! Сл:оп тт 11 fiш1ы111t~t
н (Ю,11/((е()JtЫ..У llЛJ'ltlllЯX llOLflltfla'lCЯ дrЖ<Jlf)
76
История математики
Эт() посnящс 1ш с говорит о близости Лео
пардо к с1щиm1йскоi\1у11вору Фрндр1L'Сl 11 Шт~1 -
уфе11а, перnого пз просnсщtrшых дссшу1 он
l+Т<IЛИИ, К()Торыми l!ПOCJJCДL'l'.IШ l1 бьщо Т:1К
богато Возрождснш: llo дажt' в ·ю сvронос
время Фридр 1 е{ сумел nрuслан 1.1·гnся особо~'1 Жl..'
с· 1·окоl~1ыо. P:tC('l\:lЗЫJl<lJI J 1, бу/\Т() 011 raзpC1113JI
Щ10НО/\11Тh анатом ~IЧССКНС l·ICCЛl:J\1 )H~I н IOI 11 ~1
жн 1~1,1х 111одях - осужде11r 1ы х 11rесту1111и1<ал.
Пр11 а·1 ом 011 1 юкро11 11те;н.ст1ю1'lа;1 литературе
11 11эу1«1 м и сумел сж р~rж тпт, себя учсттымп и
философами.
Связu Леонардо с блестящим ощнлийсютм
:~вором nссьма прнмсчатслыш. Ведь через Си
ц11т1ю 11 Исп:шшо За11адная Енро1 1 а позна
комилась с арабской наукu11 Но. в 0·1·1111ч 11 с <J'I
J/l<.:11a11и11, H:J C! Щ l l JIH11 nЫJlll И llCllOCpeДC l 'HeJ 1-
llhH.: ко11т~11<1ъ 1 с '">JJJIH нскоlr наукой. Дело нто~•.
Ч'l'О ос1 рон с /\JJCHHCЙlllllX 11рс.чен ЯRШIЛОI l 'j)t'-
чсской KOJIOllHt:Гf С 601':.JTh \Mlt K)Jll,1)p11bl1\Jll
1·0 1ю1\<l мн. Элли~ rская тра.п;пция сохр:,шилась и
п осле Jавоеn:нпrя его ртr.млятшми (коI1ец lJl в.
.п;о 11. э. ). Сар,щrшы (арабы) иысадюшсь 11<1 Сн
циmш в 827 1·. и к 878 1'. заnер111 1 1лн её по1\оре -
1111е. Их вытес11илн оттуда порм:шпы (1060-
1092 1'1.) . которыt' 11 uснонат 1 С 11ц1111ийскос
K()p011C HC'l'B0. K~I K : tр:.16Ы, 'l':JK И 110f1М:.!ШIЫ l]J1()-
H BШUl H ptJ l ll l 'HO.Нl}"IO ·1ep1 t11M OCTh, llOЭ'l'OM}'
11а острове ИCll<JBCДOH:.JЛHCI> XjJlll"Т'H<IHCKaя r1
мусу111,манск<1я рслнги1·1 и были n хrщу ·1 р1.1
языкз: 1 ·речесю.11!, л:п1 11 ю<ий и арабсю 1й. Учё -
Фр"др11х 11
Шт,1уф<"н
V\и 1 111.i1юpd
Xlll и
ные мо1·1 111 сноnrт 1 ю общат1,сн, обме111 1 ваться
з11атпшм11 .
Ilpff дворе Фридриха устра11ват1сь наусшые
днснуты. lla одном нз 11 1iX придворный фшю
соф магистр И.ога1111 Г1алсрмсrшй nрсдлож11.1
Лсопар/~о !l11защ; 1<ому два вопро<.:а, 1юторыс в
со нрсменных обозначен~ 1нх н 1,11 ·1 1 1щн ·1· так:
1) н:1iп1 1 корень урав11с1111я
,.\'\ + 2.\) + 10.\' = 20.
(*)
2) 11а1:пи р:щ1 юнат.1 11.l l' rешсш 1 я с11стемы
уращ re1111й
{
:\'
2
+5=1/.
х2- '5 =1r
с··)
Леонардо прuвi::'л ·1щатсльныс 1 кслсдо1ш-шя
o6CIJX 3адач 11 наr lllCIJI ,ЦНС К11111'11 - < · [lilCTUK» JI
•K llJI!'~) KB:.l)\f1~1TOH» {llЛIJ ~ J\11н1 ·; 1 {) ю~;щр:1т11ых
ч11слах ·>) ( 122'5 1· . ). пос1н1щён 11ы с 11х рс1 1 1с11ню
Хотя обе: раб01 ы и:щаны т111 ю1т>:.1фс1<1 1 ."1 сно
собом '1·олы.;о 1~ J 862 1·, ма 1е.1атикам сре;1 11 еве·
коиой Енро11ы 01 111 6ш11 1 лоро11ю11знес1·11ы .
В первоiI кшrге Леонардо уста11овал. что
корень уравнепня (*) 11е является ни целым
ч11сло.м, rrrr дробью Orr таюкс 11с может 11мсть
1шд , 11. 'n+,m ш111 \11 - vт. Н:11ю11ец,Лео-
1rардо ВЫЧllСЛИ.'1 сго с ТОЧН!1СТЬЮ ДО шестого
1rrе спщссятср 1тчн о1·0 :.~ттака :
,\' = 1;22.7, ..+2, .1:).4. .ю
(здсс1, TOLIK<I с запятой отдемrет пелущ часть от
npo61шi1, :1 :;;шнтыс - ШС("1•идсо1терпчныс
р;1:Jрнды). Каким сrюсобом было полуL1t1Н> это
значсн11е, 110 c~tx пор <JСТ:rётсн 1н.:11з1:1ееrным
Rт()rую '{а/1:1чу. постанлtнную ИО1 ·:н1ном
Гl:111ср1\tс101м , Леон~1 р.до нcc.r1t'J10RaJr в <·К 11нге
ккадратоА~ . В конце ко11цо11 011 r1:ш1ёJ1 ответ, 110
;~то щ· сам()е 1щ1т-юе.
Разм ышлетrия ir;щ зтой Jа11ачей nрнuелп
его к юраздо более пr1терссном:у rю11росу: ка
ю1е значс rшя tvюжст 11ри1111м:1т1, 1:1ыраже11пс
4Jщ(f/ - </)? J!совардо заюночил , что нрн
цcJJ ых р н tJ u110 не можеr· быть кв:щратом. По
сут11 это ут11ерж11ен11е :-IKRHH:lJJCHTHO HC'Jll LКOIJ
теоrсме Феμма для Чt:'1ъёрт1'1х стсnснеi\. Таки~~
nбра:юм, ЧаСТlfЫЙ случай Ht'ЛHKOfl тсоrе~11,1
Фсrма бы11 откр1.1т :Ja 400 лег ; 1n Ферма! Ол1 щ
ко локазат1. е1'0 Лео11ар/\О 11t' улалось.
***
В nрсднслот ш к « Кшrгс к1.1адратов,• Лео11ар110
п11сал:
•Когда, u знам<:юп't.:1'1шиf1 кювn 1 ·uсшщ11н
Фр111чJ11х, м:11·ис'1·р Доминик nр1шёл м<:ш1 в
П11зс к 1ю1·ам Ва11н: 1·u вt:J111честн~1, м:.irr1Cтp
Ио1'анн П::~лерлкки11. 11сгrt:г1ш мt:ня. 11ре~1,Jшжнл
м11е вон рос, о ко'rоро:-.1 я на 1111 шу 1111жt.: 11 кп
торыi1 lll' Mt:JICC OTI юсип:-я к 1t:0\1CTpl Гl l , чем
Срелние ве1<d ~' Во~рожден11е
к чнслам. а именно 11айти 1.;Rадр:.пнос ·1~1CJIO.
1<оторос, будучт1 увслJ 1чс1ю шш умt:11ьп1ено
на 1 1н ·1ъ, вснк 1 1й раз 1юрождш10 бы кналратное
ЧIJСЛО
Посл е размышлсннн н~щ рt.:нте1111см .-~то го
1ю11ро<.:а, 1ттuрое я уже н;.1шё.r~ , )1 y1111l\CJ1 _ что
ИCTOЧlll!IOI Э'lОГО pt:111C I Jl l }f лежат во MHOl' l lX
вещ:L-х. которые ОТ!IОСЯТСЯ к ЮЗЗ/1,ратш,1~1 'ПJ С
ла.ч са мн по <"еое 11 н их 0·11 юuтс1 t11и пру~· к
другу. l\роме ·гоrо, узнав нз р:1 згоно роn н Пизе
11 ;~ру1·их, которые дош11и до меня 11 з нi\mера
торско1'О NIOpa, что 13ащс н<::личество собла1'u
Rоли 1ю 11рочее1ъ 1<н111·у, которую я 11anиc:u1 о
ч11с.т1:.L'<, 1-1 чтп Ему 111 ю1·д~1 ;~оставляет у;10 1ю11 ь
ст·н1 ic слытать 11 :>я щ1 ~ыс р:1 ссуждс 1н1я . от1 юся
щ11сся к 1 ·с()мстри11 , я нс110.ч11r111 о Rorrpocc. ко
тnрыlf }f сформу•лпронал 11 котор 1 м'r uы.11 м11е
предложен при Нашем дnоре Ваmт1м фююсо
фом. Я юял этот rюпрос n качесше темы н ттред
прпr шл состаuлс1111е 11:1стонщсi1 работы, кото
рую рсшнл назв~п. ,,1\шт гой о к1:1адратных
числах" Тс11ерь л t1ропту B;.imc11 сшкхuдтпt..:Jrь-
1-юстн н том. <.:нуч ас, 1..:сл11 кнш ·а <.:UJ~<:rж11т чтu
лнбо б<Jлсс 1Jл11 ме11сс 1.1срнос 11 11co(Jxtщ11,YtoC.
так как 11очн11тr, обо нсём 11 1-11 -1 н чём нс uш11-
баться оюйет'Ненно nпжt.ттвс1п-1< ):viy~·мy бuж:l'.
чсJ1·1 чел онеческо му. 11 11е·г н11ко1 ·0. к1·0 снобо
; 1е1 r от 11t:,rtостатков 11 сrюсобен у•1естъ всi::·>.
ЭПОХА ВОЗРОЖЛЕНИЯ: СЛАВНЫЕ ОТКРЫТИЯ
Эпохо 1I По:3рож;~сюш, илн Рс11ссса11са , r1рн11я
rо CЧH'l';l'IЪ XV-XVJ вн., К() l '/Щ но МНОl'ИХ снро
nеЙ.СК~IХ сгра1 1 ах стаJ 1 тюзрuждатnся ·1'm nысо
ю1й уровспь кут,1уры, KOTOj)J)I Й C)'ЩCCТ IIOR <Ul в
а1-1'r11чноl1 Грс 1 111и. Ра1-11 ,щс, чем 11 дру1'их Сl [Х1-
нах, - н XIII- XIV 1щ - Rо~~ртме1111с 11ачалос1)
в Италии, наиболее развитой и R зко1юмиче
с1<0м, н в культуртюм оп-тоше11ии. К то,\1у же н
снду географического положения Италия была
связующим :1веном между Западом 11 Востоко.УL
НоRые всян1-ш отра~шшсь в творчестве всю 1ких
мастсрuн· н поэзии и прозе Динтt Ал1uъерн,
Джонашrи Боккаччо 11 Фрап'!сско Пстраркн, в
жнн()nнси Джотт, Лсо11ардо да Винч11 и Рафа
эля \.а1пн. в прекрасных скулыl'lурах Мнксла 1 1-
джело Буп11арроп1 11 Бснвенутn Чеm 11 11 rи. Все
01111 верили n безrра1111чш,те возмnж.110<.:т~ 1чело
века, его волю и разум: r:шдели в нём венец тво-
рt.:ннн . ~" 1·нt'рж;1:ш в 1-щсал !'~1р1.ю1111чноl1 i 1т1:1ор
ческuй J JНЧНО('ТИ.
Эпоха Во:~рождсння стала 11 э11пхоl1 Вею ·1к11.х
гсогр<1с]шчесю1х открытнЛ. В 1-192 1·.
Хр11сто
фuр Колумб rУ!'крыJ1 Амер11ку. в f ') 19 - 1')2 \ rт.
Фер11ап M:-IГCJIJl::ll! совеr ши11 К}))ТОСНСТrюе пу
те111естш1е. Вот кзк ппс;1л об этом яркий пред
стаrнпель Возрождения nрач, математик и фи
лософ Джероламо Кард:ню:
«JJ роднлся n тuм веке, ко1·да бъv1 открыт
несь :3емной шар. тогда как в ;фев1юсти было
извсст1ю mш11, Нl'М1ю 1 ·ш1о1 бол<.:с uдной с1'0 трс
т11 . " Есть ли что-лr 160 бuлсе у;,тшнтсm,ноt:, чем
nирот1::лн11ю1 11 человеческ:~н \.1ш11111я (·1 · е.
артнлJJернн. - ПptrJJ·t. ред.) , которая траздо
011acr1ce мол11нн rтeПoжrrтeJ1t:lf. f-le уJ11олчу л 11
о теnе, пет 1ки(1 м~1пп1·1·, о тебе, nс;1ущсм 1ra c П< >
беэnрежпым мор.нм n темноте 1ючп DO время
77
78
История математик~~
ужас.11сi1ших бурь в далекие неnедомые края'
Прибавим 1< ::Jтому еще четnёртое откр1,пие -
нзoбpl'TCHllt: KHI (J'Оllt:ч.папня COJД<llПIOC pvl(.1 -
M I 1 люд<:й, щ1 1 rд~N1з1111щ; 1ix 1енис'vl . Оно сош~р
н11чает с Божссг11сю 1ым11 чул.<::са.чи. 1160 чс ~·а Жl'
t:щё нед(Jстаёт нам кро.\1с tJвл::~дсш 1я 11eбoVI' »
1111е 1ресrесю1е р~кошк11 11"1е111ю учё11ые 1311
эаптип сохрJ11и:ш для ш.:сх послсдующах поrю·
лс1шfl бссцс1Шf)t' 1рсчсскос нuu1t'Д1Jt' , которо<.
н l't' Ht'CI IOKOl IHblt' нμс\\С:Н:t 1!1 ((JJIl lt: \1()1JIO p.IJ/\l'
шпь судьбу дрс1~нсюпаi1Lю1л 1рактатов по "1:1
тс'11:п икс (по повсл<.:нJJю импср;пора Ц11111, Ш1 1
Х\.111-.т~.11ш11111ыл11 L1>)10Ke111 .1п21 .~ 1 дп 11 ::i)
В Сред111 re ве1<а 01\ 1 111м 11з крупнсйш11х на
учпых rt<:r пр() в Евроrщ бш1а В и зз1 пня Сюда
съе.1жаJшс~.. ~·чёные из ра'11 r1,1x стр:н 1 чтпnы пе
решкьшатr, , нзучат1, п rшммептирова~ъ древ
R 11011Lк1х со101 1111коn гтрот11n ·Г\11пк В11з,111
тшr сnл11:пrл:к1, с Bc11c:r(11cfr. В те времена вене
ц11а11ские корJ6Л11 борозд11ли морн. н боr;пыс
ЖИВОПИСЬ И ГЕОМЕТРИЯ
Пр11мерно с Xll l в. худож11ики (сре
ди 11их. италья1·rеu Лжотто ди Бон
доне) н.:tчали ~кrпериментировать с
изображением простра нства Они
·<Создавали» живописное nростран
сню, И3М(!НЯЯ р.нмсры фи1·ур, ра< •
полагая по определ~нным прави
лам Jлемснты архнтектуры . детали
ландшафта.
В то время на латинrком Запа
ле rтали популярными трактаты по
опп1ке и в частности труд «Пер-
спектива» польского ученоrо Uе
лека в~1 тело (около 1225 - около
1280) В нем описание оптических
экспериментов сочеталосt. с изло
жением 11выс шей математики» 1ш1
эпохи· фрагме1~тов «l-laч;iл. Евк
Ntлa, «Ко 1-1ическ~1х. сече1-1ии » Лпол
лония и «Гlер('пt:-к·1111:1ы» с11мбскогu
математика Х XI вв. И()н аль Хаи
сама IАльгазе>на\ Интерес к гео!'v1ет
рии пространства в ко11еч11ом ~по
ге привел к т крытию в живопиr11
линеи 11 0~1 перrпективы r единои
ГОЧКU~1 СХОдJ. (ТОЧI 1ее rказать "\ТОТ
прием был переоткрыт поскольку
им вла.лели ешё древние греки )
В XV в итальянскии архитектор
и скульптор Фнлиппо Брущ:ллсс
ю1 наnи<.dл мн, к.~1пины t в~1лdми
Фl\оренни1~ при~f'НИR 1аконы пер
СПСК1ИВЫ к СОЖJl\е11ию эти рабо
ты Н!:' сохранились. Истnрики спо
рят о тnм обладал ли Брунелле< ки
недЮА<ИНllЫМ11 ПOJI 1а1 IИЯ~И в м,1те
матикс и других науках Если так
то е1 о картины прсдrтавляли со-
С тp.111•1uJ
11з Руковолсrва
К "1 lM~pe1 Н1Ю
А ,\н1р1>ра
Нюрнб~;-рг
1525 г
Тро1ша Фрt·~к,1
Мазаччо
вroGope
Санта Мария
Новема
Ф\Opl'HIJl1Я
1425-142611
бои <ложнеишие геометрические
поrтроРния [сть и другое мне>ние:
Брунеллески вначале писал кар
ти11ы 11а зеркале обводя и рас
краL11ивая отражения Именно по
натолкнуло Е'ГО н а мысль о пер
спективном сокра шснии архитек
тур11ых фСJрм Вскоре у него по
яв"'м1сь ученики 11 nослело1:1атели
В их числе - друг Брунеллески ж~1
вопип•u МJJаччо Его кисти пр~1-
наллс'жит монуме11тальнос па11~ю
< Троиuа• во флоренл1йско11 uер
кви С.1нта Мария 1lовелла где
Х}'дUЖllИК nримt:llИЛ ед1111ую точку
сход,1 ухолиших в 1лyfi~111y м1ни11
Страстнt.1м энтузиастом перспек
тивы был и П<.1олu У•1 челло.
Прdкп1чР< кvкJ п:ометр1·110 и.~у
чали отложив на время кисти 11
кр.:к~-.и . вел11ча11шис художн11кн 11
теоретики искvrства Лестарло Аа
В11нчи и Алпбрех.т Люрер Они И<
пользnflали гео"1етриче<"кую тРхн11
ку в приложении к теории п ропор
uий и перспективы в ж~11юпи<.н
r:унцы Город:~ дoжt:lr nem1 ож1шлсr~ную тор -
1·овлю с по1лоу,ым 1 1 ~·орода:--ш l>m1ж11сго Вос
'J(Жа. Поон.: падсн11я 1\онстаrттшюполн 13 1-iS:'> 1·.
ученые, ра6от;,tнw11с т;1м. стал11 11срсс::!жать 1 1а
З;1ria;~. Так научный мнр Екропы по~1-1а1юм 1 1 J IС){
({) M I HJГl1:'>111 IOJ;ll'CllЧt::CКll .\11-1 трудами ПIJ м:1тс
мат1-JКl: 11<1 1 рс ч ескuм J-1.11.1кL:.
Одн:11<0 1 1 ауч 11 ыt: :ша 11 1щ р~КЩ)1>сtраш1з 1 1-1с1,
.\ IeJ1.J1t:111 ю. ма·1·t;,ч<1т1 •К) пре1 юдаnаJ/11 в ~~н 1вt:р
снтеrах, которые тог[(а 11~Lхо11.11 1шсь под покро
r.итет,ст1юм ЦерК13и. Её нерзрл·н стар;.11шсь со
хр:~rнпь срсдневсконыс предстаrшспш1 о ~шр<:
11прот1~1111л11с1,1юэраст,1 ющс~1)' wншт111ю 11аую1.
\( ·1·Gиу же уч<:ньн.: uбычнu рлбuта: ш 1'· u,цшюч-
1<.) 1lc быmJ научных об щt:стн 11 журнаJ1о н, м~1-
теs1:1111ю 1 не вс.:лл 11 ;1у чн ой щ:рсшн:ю1. Состон
11:1 жзлнван1,е у 1<<1КШ'{)·Ниб~д1> 1\\t'Het-·1<1·1 ·. 1 11 1 ю
('ТШ11-1но 01 rасансъ апастr. 11 1r1::мююс 1 1" м;нема
тнк ренпшю oбc;:pcraJJ своr 1откры·1· 1 1я.
Хар;щтерпая нриме1· а того нрб1<.:1н1 - нdуч
пые тур1111ры. Победа в таком турш rрс 1юроi1
стапоuш1ась реш:но щ им событие~t lJ ж11з11и .
Побсдптслю доставал:.~<.:~-. нс тонько 01ана, 110 11
кру11но<: [\<.: 1-н.:жно<.: 1юJ1 1аrражде11н<:, а ч:кто 11
весьма ны1·од1-юе пр111·лзшенис на работу.
В ссрсд11ш; XV к быJю l!:юбрстсrю ю-шrопс:
чата111 1 l', н знання сг:uт1 1 дос1упны 6онсс uшро
К()М} кр~ту :~юдеr'1 Хm·н 11ауч 11 ыс:: соч1111еI-mя
нс по11ал11 n ч 11 сло 11ервых 11ес1ат11ых юш1, нсё
же к копщ' Х\/ n. в Европе у-л<с полшrm 1сь "ком
мерчrска н ар1 1фметш\а'' (1478 г.). «H:.P·t;:iлa» Еn-
1@ща (1482 t'.) в латшн..:ком переводе Камшн1~1
!Jаваррскuго. сдслантrом в ХШ в" и " ~умма з11а-
11н l1 ~ ( 1~9-1 1·) учё1 юго мо11:оса-фраrщ11скаш \а
Лую LПаqrнш. В Х\1 1 н . напе::чатаны ·1·pyrlы А1 юп
;юн1нt 11 Аr-~шмt:да. Кн.11п1 н~1 т1ты1ш мог про
ч11тt1 ·1 ь /tJлско не каждый. поэтому Пачо111r,
l'шшлсlt 11 Д<..:кз р1 С(.)3!ШТСПЫЮ Пl!C<}JLlt своп
μэбтъ1 11а •·р:tзrо 11орных» яаы1шх - r 1 ' 1(1;11,я 1 1 -
с1<0:У1 11 фра 1щуэском.
«Сумма зт~а 111 1й" итзлып 1ца Паqшш сопер
жала нсё, что тогда знаm1 по ар11фметпкс, ал геб
ре, rco~1eтp111 r й триrономстри1L В этом труде,
R L1аспюстн, была поmюстыо вос проИЗll<:дена
•Кн111 ·а абака» Леон ардо П нза нского. В 1<0111 (е
рп:щсла, лосвящё 1 1нu 1 ·0 аJл ·ебранч<:ск11м уран
r~енш1:v~ Пачл1ш за.\1сти11 , что /J.'I~ рсшсння ку
бичесюtх уран н е тr й <·искусстrю алгебры сщ~
кс ;1а;ю способа , I<a к нс на 11 способ к на,!\ратур r,,
круга". Ero сл она rюспуж111111 оюеоб ра:щ ым
вызовом для следующе1·0 поколе1 щя алrебра 1 1-
сrов. Молzет бы1ъ, вперв ые после «С рсднеnеко -
С релн 11 е века и l:kнрожлсн 1н•
~
E"ll.l(IO
f\YKA ПАЧО/\И
Лука П а•юли (t>k.oлo 1445 около 1514) был круп -
11 ейшим Сfjрuпейским алгебрсtи t:тuм XV u . Он
рuлилс:я в мес. 1 ечке Бор го-Сан-Сепuль~<ро в Uент
ральнои ИталиИI, учился в Болон с 1<ом ун иверп1те
rе. Па•юли ста!\ профессором ма 1 ематики и пре
nолав;1л в Риме, H eanoлt>, Миланf', <Dлорt>нш1 и,
Болонье .
В Мила н е 011 подружился с вылаюш~1мся хулож-
1-1икuм и ученым /\ео11ардо да Ви11 чи. П С' настоя
нию Леонардо r.; 14q7 1. Пачом1 написал к ни гу «0
Божественнои про порu11 и. (её печ.:~тное излан ие
вышло в Вен еФ1и в 1509 г.) . Са.\о\ /\ео11арло 1:1ы пол
нил иллюстра u ии лля этой книги, в том ч исле
59 изображе ний многоrра ню1ков.
Но самым --с нам('ниты м сочин е11~1 ем П ачол11
стала (< Сумм а з нан и й 1ю арифметике, геометрии.
отношс11иям и проnор uионалыюсти» (1487 г.).
Книга была напечатан;:~ в Венеции в 1494 г.
Лука П.эчuли. Карп 111.1 щ•11Jвес:т 1 ю1 о Х\'дu:>1.н11к а J 49 i; r .
rюй с11я чюf>} еоро п еiiцы осо"ша.; 1 11, qто м~1.10
только следовать класснчtс 1ш .ч образцам н
прилежно усватmать аr 1111чщ1ю 11ау1<у. пора по
иыта1ъся создап.. что -то новое, 11epcwai-rry-п,
1'раrшrщ , )'l<аз:н ш ые ю1 ;1сс11камн. 11 это 1rм уда
лось. Ит:1щ,янсю1с матс.-.1ап тк11 XVl н. 1 1аш 1 ш
форму1 1n1 1шрнс 1! :.ыr·L:fip::1.11чecк11x уравнен ~ 1i1
трет ьей 11 чстн~ртоГ1 степе ~ 1~f1 11 те.\1 c1мJ1J '\1
решт11 1 зада ч у, котор;l я н~~ протяжс 111 rн мло
п 1 х пеков rLрсr~стап11 н11ас1, учё11 ы м нсра:~рсш11-
мой. В<1т п очеУ1у Л-VТ столетне 1ю 1111ю н 11сто
р 1110 м атемат11 1<11 как J'leк алгебры.
79
_,Аъ_
Cll.lfl!
История м<~тем.:пики
СЕ КРЕТНЫЕ ФОРМУЛЫ
1 1~·р1ыя 1тр.11, цu,1
,('ум\\Ы 1Н.1 Н '111 »
Л 1 1,1ч1 1л1-1 Bt•Ht! UИ>t
~l~t\.lHllP 11..! ! 1
В м ате матике то 1·0 вре мени от рнц;tтслы1ые
сrпсла е щё не ПОЛ)'ЧI1л11 <· праu 1·ражл:п 1 ства ·}. Их
нс.:пользовали при решении урашн:ш1й только
н щюмсжуточ ных рзсчётах, IIO (;'(Jlll ИCl\OMЫJl
коре нь or<:tэыв:ctJtcЯ отр пца1·сльным чнслоы, то
CЧlIТJJIOCh. что yp:lBHCl-H fl' кuр1 I СЙ l [(..' нrvtceт. Д.1 1 я
тu1 ·0 чтобы научнтьсн рсш:пьлюf>ос куб 11ч сс кш:
\'IXlllHCHl1C, MЗTtM(l'l'Hl<l ·I ДОJ lЖН1>1 fi1,L1llf :1! 1 ~1ТЬ , как
рс111а1п1пr тр 11 ра:~ных т11па ypamre11иrr:
.\'~+fJX = Cj,
х1=рх+ tf.
\
.\' + f/ =р.х,
где р, (/ - rю1южитслы1ые LШCm1. Исторшr от
крытия qюрму11 корней эт1 rx урав 11с 1 1ий полна
драм ат11:.1м а. 11 1rтрш', коварства 11 оfiмана.
П <.:рным ус 11 еха 1 \uбилсн профессор Боло11-
ско 1 '(1 унипсrн.: 1 пста С1\1ш 1 ю11 Дал 1) Фсрро
( 1"-165- .1526). Ha,11u сказат11. что n Л'V-XVJ 1ш.
Болонскиii уmrвсрс~пет был 011;Т 1и :ч из с;.1,чых
11з1:1ест11 1 .1 х у1шверситетоn Enponы. В рз з 1юс
время его студе нтами б ыл11 Jly1<a Пачолн, Аль
брехт Дюрер 11 Ннколай Коперник. В 1'11.:; г.
д{LЛL, Фсррu 11ашёл рсшс1ше уравн е ния вида
х +р.,. = t/, но, щ) обычаю то1'0 нремени. н<:
011ублико1шл е1·0, а хранил в тайне. Рукоп ись с
н.з1 южt:11Ие.:'.1 :'Jтo1 ·u uтк рытш1 Д~mь Фt:рр< >пе ре-
1~ш 1 с 1юсму >ят10 и nрtемни~:--у по к:.~фtдре Ан -
1-111б:Jле дt~лла J lанс. Хотя впоследс" 1·нm1 рукопись
11айт11 11е yдaJJO('I•. с он р с.:-IСПТIИЮ 1 )'Чtf IOI'() 1111·
1ю1да IJe осп:~рнnашr с1·0 пр1юр11тета, 11 во м1ю-
1 ·их матсматп ч есю 1х соч1111с111 1лх X\TJ n. rч шю ю
встрс:тить уном11на 11ис () ,,правшrс ДаJ11, Фсрро-> .
И::1щ.:сп 1ы f1нт:шы1нс ю 11'1 11 стuрт u<м~1тсмап1-
ки У. Фор 1и наJываст 11мс11а t:щё двух чt:Jюnск,
ко 1·орыс энаJ111 с п1 н:об ,Ц:ui ь Фсрро: это лnоря·
HI IH пo~Hlt:O UOJIOJll'Tl 11 11Лll 1 '0 1 11 ltJ Мар11н Дt:ЛI>
Ф 1 .()рt:, уче1-шк прш/х:ссор3 Дэ.111, Фсрро. После
смерт1 1 сrюе1"< 1учr 1·1·ею1 /\СЛ 1, Ф1,оре rюл 1,:1()11ался
С()общёrшым ему сскре-1 ом. 6. 1аго;р ря чему
r юбсждал н а r1 ауч11ьLх турнпрах.
НИККО/\О ТАРТА/\ЬЯ
Н астоя шмr его фа'v1илия - Фонт.:~на. Прозвише
ТJрталья (нJика») Никколо получ ил, когда l'Мубыло
шесть лет . 011 вместе с родственниками спасался в
11еркви от фр::~нuу ·кк и х -1авоеват('лей, осам1вш их
его ролно~1 город Брешу. Свяшен11ы ~' 1тЕч 11~ . ол11а
ко, не уберегли от несчастья : Ни кколо был тяжело
pat 1е11 в горта нь и 11 а всю жиз нь U(:TJЛ< ~1 1аи кой.
Ма/\ ьч ~1к р(К в бедной семь(;', ра но остс1лся (\€'~
()ТIJJ . Мать нс могла плат~нь 1а обуч\:' 1111е сына, П ()
этому в школе Никк олu успел в ы учить лишь поло
вину <IЛфсlВИ Г, \ , И ВСЕ' Жt> (,Tpl'MЛC I IИЕ' К '1 Ht~H l•IS!M И
н еоuыкнш~ен н ая твёрлость хар<1ктера проявились
>'Же в лстствl'. Тарталья нс толL>ко самостоятель~ю
11ауч ил<..я читать и писать, нu и сумt!л при обрvсти
большие П(ннания 11 ма 1 Рма 1·и ке и мf'х,1нике. Вnо
слРлствии 011 созл<:tл 1аме ч ательныи лля свое го
времени трuктат «Новая наукJ • . в котором р ас
е мотрел р.нлич н ые воnр0< ы меха11ики 1 в том ч исле
расчёт тrаекторий сн.зрялов.
Н11кколо
Тарталья
И вот R J ~) "> г. дедь Фьоре uызвал 11а состнза-
11 пе з11аме1111то1·0 матем.атюса 1tию<оло Тар -
1м1ью (о коло 14()()-t 557). Тарталы1, у:шаn. что
дет, Фьорс обладаеr· сt:кретuм Сцитюна д~u11,
Фсрро, за rrccкuл hKO ю 1el1 /\О ·1 урннра cyмt:J1 с1-
мuе1·онтс::лы-ю открыть (j10р .\.1улу корней и O/tcp-
ж;u1 1 юбс11у За два ч:rса он репл rл нее ~s~щ~1чи дtл1,
Фьnрс:. Протишл 1к же, nu слон;~м са .нот Т;.~рта
nы1. ш: спра1н111ся ни с о;~ной. дзже 11з 1·ех, кuто
rыс MOI' бы pCIТI! пъ по 11р<Н1илу Д;;JЛf> Фсрро
Череэ лень после тур1шра Тарталья репшл
также ураrпте.1-шt: nида х' == рх + cf. Это было
вел11ча iiшнм оп<рытисм. К учёному nр1 шша
слава, c 1·u пршж1mаш 1 прс 1 юдавать н Верону,
J.k1H.:llИIO, Пы1 чеJщу, Брешу. Но пубm1коват1,
пю11 формулы Тарталы1 не стал. Пuчсму' Во~
можно, 11р11ч1 1 на был:-1 нот н чё.ч .
Куfiнчсскпе ура втте1111е первого т11 щ1, т. е.
уrмине1111е
_\J + px=q.
1'
'\
с 1юмощыu nпдст:11-1оню1 х = 1,U - vиТ:-~рт~1лья
(вслед за Д;:~ль Фсрро) с1юдш1 к квадратнО.'-'1)'
yp<tB !lt'I IJIIO
.!
(р)'
и-чи. -
.1
=О.
Дискрими на.1 п ::>1·{ н·о ур;нше1п 1 >1
ПОЛОЖИТСЛСН, И ПОЭТОМ)' 0110 1IMCCT 0,ЦШ I flO-
JIOЖJl'l'tJ IЫIЫЙ корень.
,Ш~х решения ур;,~внс11ш1 нщр
х1=рх+ц
~
;
'l'арталыr решил с;(слатL зэмепу .i .: = ' 11+\1 •
Со01·нс·1·ствснно ш1 JJ<)Jlyчrrл кRа;~ратное ура11-
вс1111 е
>
fJ
()
~
tГ- tjlf+ °'Т =О,
/\ llCKPHMlllJШl 'I' кuторu 1 ·0
чnжетбытr, ка1< поJюжите11ытъLч. такп отр1 11tа
'l'е.'lы-1ым. В 1 ·ом случае, коща 011 отрицателен
Средние века и ВозрожлРние
(т'1к 11азываемыi 1 nапршюдUt11ыt/ с.лучаil), метод
Тарт:1.11ы1 «не работад», хотя кубнческос ура11-
1-1е1шс и IIMCЛO peшt:IIИC.
Имс::н110 :,)Та 'l'РУ/tность стал::~ камнем 11рс
·1·ю ювсн ия для rsccx учс2н ых . Т.tрталья, rю-н11/(1 1 -
мому. 11с: хотел nубт 1кок1ть свою формулу /(О
тех пор, пока окончатсJ 1 ы-ю не р<J::Jберt:тся с
11е11ривuд11мым случ;.~ем.
Тем щ1сме11ем ещё 11ри жиз11и ТЩ"Jтзльи с:1 -
мое важное cro откры·1 не у1<рас :ило юшгу
другш·о человека. А случилось это так
В l 536 г. Джероламо Ка рдан о, 1-отоnя к изг~:а
нию сочинение «Практика арифме 1 ·1·1ю-т», уэ1 1:.и1
о сущестнованин ~ 11 рав11ла Даль Фсрро». НJ нест
ного /lH)'M ученым - Ннкколо Тарт~u 11,с 11 Ан
тонио дсль Фьорс. Карл<1но 1н111нл, ч · 1 0 ~сJ ш
)/lJСтся 011убт 1 ко11а·11, этпт ре;{ул 11·1·а·1 в с1юей
юп11 ·е, то с;1а 1{а бyrte1 ему 0Пес 11ече11з Однакп
11се ПО\\ЫТКИ сзмому ПЗl~i'ПI ре111е1ше Ol<ЗЗM IKh
безуспе1ш1ы.\.1И. Тоща он задум~JЛ выuснать сст<
рет у Тарnтьи И nот, после долл1х. )топоров и
увсщеnа1шй, в марте 1S:S9 г. Тарталья, nрсдва
рнтелыю нзнв с Карда.но юrнтву н с раэглашать
это 1'0 открыт1ш 11 /(:~же заншфроnать с1·0 так,
CARDANI
A H:S MAGNA
Alt l ТНМ.НТ 1~1f: .
Scu L11\<;:r ч1.1aclra1;н\t::t Cap1tulol'L1111 ,
& чu.нlra~111t.1 QQ;rllюnun1.
1'RОOLМ1VМ
AD R {) l'l/11 /i'l'l' J\1 .1J(C/lf.NТfT"'f,
l 'p[ropum ""'!' i•"tir .ltpнHrt
"1а5·:. '"'1 С) ·~" '·· !(1. /'ir1 1·, ...."
, , 1, .•.,,,1t ,.,.,.м (
.r.
а •1-. ..
•
•
-
.Jм •
.t
.....--
:t1
L
,
,Ji,
"
1
t:"
"
......
• ,.... . ::;:;:-: ". "";r;
1."" 111
'1
•
,,'".'"
1 .J,
".
1i.,1 " ~ 11~-1..11,01 ; \;111··.r•rr1 1c ' - 'I '•'"" '
... ,"
_,/,,·111tftJ'.Z:
1111rV1r"
~·._."
Первая rтра 1 111ua
тp ,l KTdTd
« В<'ЛИКОf'
Иt.t{ y(( IHtli
111 nол11ого
с оt>рани11
< t•'IИHl 'lllH1
д.,., Карыно
81
82
История математики
чтобы никто не смог прочитать напr1санн ое ,
передал ему «Стихотворный алгорити ·> ре
шения.
13скорс после этого самому т:1ж1нтт1н()му
уче1-1нку 1<~1 рr~ано - Лудо1шко Фсррари ( 1'1 2 2 -
1')(>')) удалое~, наfiтп с 1 юсоб реше ния ура кнс-
1111я чет11ер·1011 стt1 1 tнн. Жt11а11нt Карн<~но
оnуб.11иконат~. таю 1 е 111.щаю щ11 еси re:-iyJll)l'3 'J'bl
ЛЖЕРОЛАМО КАРЛАНО
ЛЖер оламо Кардано ( 1501 - 1576) был ~ктинным
сыном :юохи Возрожления, воплотившим как хоро
шие, так и дурные стороны с1юе1 о времени. С юно
пи джС>роламо пбуревала жажда славь~ « Uель, к
которой s1 стремиЛ<·я, - писал он на склоне лет в
автобио1·раф~1и, - заключалась в увековечива11ии
моего имени, поскольку я мог этого до<.тиrнуть, а
вовсе не в богатстве или п раздности , не в почестях,
lie в высоких дО/\ЖtЮСiЯХ, lie во ВЛdLТИ". »
Кардано nuлучил мелиuинское образование и
всю жизн ь занимался вра•1ебной практикои. Одна
ко, как многи е учёные эпохи Возрождения , он 1ю
ограничивал себя лишь од1 юй областью 1-Jауки: Кu.р
дано вошел в историю как математик , философ,
естествои с пьпат~ль и изобретатель. Суш~ствует
леге нда, булто он составил свой гороскоп и п ред
сказал , что умрет 21 сентября 1576 1- .
дабы под
держать собственную славу астролога , к назначен
НО"vlу сроку он уморил себя голодом. Лаже если этот
рассказ и вымышле 111-tый , суть характера Карда1ю
передана очень верно.
(;:~мой и з вестнои к~1игои Кард;:~ но стал трактат
1 ю ал1 eGpt: под названием • Великое иtкуtсrво 11 1
опуОликованный в 1545 г. Книга содержала фор
мулы ре шения кубического урdвнения - секрет
Лал1, Фе рrо и Тартальи.
джерола"о Кард.~но.
стало JJpocтo I:Н:'преодолнмы.м. l< то му же в
l '542 1'. 1\Щ)/(3.Н U 11 Ферр:~ри кстрС'1' 1 IJll ICb с ДС.'U1:1
ltaвc, который охотrю пcж::t:{:!JJ 1·ос1·ям рукоn11сь
снос1 ·0 тсстн с -зансл ю Г1 фор~1у11nй. 31 1::~ч11т, сё
мож~ ю было у:111:i·11, 1 1е 1·ш11.кп пт Tapт:JJJы11 Кэр
дано ре11111л . чтп 11'\1еет 11р:ню 11:1ру11111·1ъ Jl:ll 111ую
Тартальс клятnу, 11 RЮТЮЧllЛ RСё ему llЗBCC'Tl!Oe
11 со6стве11щ10 юш1 ·у.
Наrю отмстить. что чест1. 11е11 1 1ю1х открьJ'Тiн1
Карда1ю отд:ш нмс1шо тем mодям, которые се
заслуж111н1 011 11ис~и 1 .
•·Н 11:111н: неm1кое вр<::-н1 С1 l1 1 n1юн Jl:1JJ1, Фер
ро откrыл rlюрмул): "Kyfi ксщ11 ш1юс вещь
р~кны чнслу". ~то был о 1юнсп11-1t: rtpt:кp.tcнoe
открытие Так 1(ак 11олоб11оt 11 с.кусс1 rю прt'вос
ходr 1т nсё человечес1юе остро~'м 11 е 11 всю яс-
1юс1ъ ума с.мернюго. то 1::1 ·0 iryж11 0 расо1атр11·
Rэт1 , как подарок небесвого прои:схожде1шя. а
также способrюст1, силы ума. Это настолько
слашюс: открытпt, что от того, кто мог его до
ст1 1 1'H)" I h, ,\>ЮЖНО ожнд:tть . Ч'I'() 01-1 ДUC'l'Jll'Ht'I'
всс1·0 Co1tcp111 1ч<1J1 с L111 ,- . .1 , 1111ю<0J Ю Таrталы1 11з
Г1рс1н11, наш друг, liудучн ны::1н:11-1 на сос1·и зан11с
учс:н 1 1ко .ч Даю, Фtрро 110 11м1.:н11 Ан·1он1ю Мэ
рш1 Флоридо. ре11111л , д::11.l1.1 r1e бr.1 ·1ъ rюбt:Ж.'\tli·
НЫМ , ту же Ca/\J)'IO проб;1 е му 11 IIOCJll.. ' (\Ш\П\ 1\
просъб псрс[(а.rт её мн е. Я был внелё11 в зз блуж
де 11 1 te словамн Луки Пзчолн, который гоuорш1.
что rrcт общего рсrпсшш т~нюrо ураnне111щ 11,
так 1<ак я обш.щ~LГI ужt MllOГHMIT, MllO IO СIМИМ
с.цел:~ш1ыи11ОТiфЫТШL\111, я11с uтч:швался ш111-
та то, ч1.:1·с1 н не cмtJt 1ккать. О;~нако ко1да 11
получ11л эту 1'л :шу 11 дtJбр:11н.:м до t:ё рt:шен1щ
то н у1ч·JДСЛ , что с сё IЮ.\10ЩЬЮ MCJЖllO }v\J юrое
е щё сделап_" 11 уже с 11стыше11тю1'1 у в ерен-
1-юсrыо n ('fiOИX СlfЛЗХ я nрн Jr('CЛe/1,0ПЗlll!JI ()Т
крыл 11am,11cfm1 cc, чз стыо с:,1 м, ч:ктыn с Лудn·
т 1ко Феррарл, моп м бъmттшм учс1n11юи".
Т~1рТ'1.ЛЪЯ СЧёЛ Себн ОСКОрблёш I ЫМ, !! раэра
:-!НЛСЯ ск;11r,'щл. В тсчсm 1 с тр<:х лет 011 11 Л~довн
ко Ферраr11. вставший 11а 3ащиту с воего учи·
тсля . uб~н.' нин~иr11сь ру1·а'J'!.:11 ьн.ым11111~сьм:t,щj 11
nамфл t:там11 . И tсл 1111 1х:ж;к научнан IШJLt',\ШK:t
в<:лас ь 11:1 J1:J'1ъш11, то 1·с 1н: рь об:.~ ~штор:.~ 1·1 '3.Jt;11'~t·
JUI CJIOII МЫ СЛJI нз <- L 1 ap( ЩJIOM ~ }!;-JЬJ KC. .Вен Ита·
JН-f}J_ с 111 l'l't'j)tC()M CЛ t:/ lHJl(I 3:.J ра:.нн гп ll'M t'ОбЬI·
т11й. Сам же Карла1ю от )'Ч::~стнн н ;(11С'куссш1
отказался. <- 1<ак дворянrш отка: 1апся бы от дуэлн
с 11ростошодшюм~.
Точку n этом споре nостаннл тур1111р :-.1 ежду
Тартальсй п Фcprar11 Оп состоял ся l О аrнуста
1">4Н 1·. н Мш1ане , родн ол1 1·uроде Кардано н
Фсррарн. Gоль ш1шспю ~рнтеJit'Й, конечно же.
1ющ.1,ержива111 1 l'н.uс t·о .3t' ~u 1 нк~с Как rutctн 1юзд
J1t:C Т<tрталь>J, «для меня стало яt:нu, что \1Оё н:~
v1cpt1 1нt· убс,11 1те11ыю 1·rнюр1 1ть перед тшнюй
1 н::ос~·щсствимо. r1 так l\ar< я нач :u1 сн1 аса1ъо1
худ111е1·0. то 11а с.г~едующнi1 деr11" H t' ска::1а 1~ 11и
кт1у 1 1н слоnа, уехал 1 ю друго~'1 д()роге в Бре
шу". Ло(Jед1 1телем был 06ъявлс:11 Фсррари. по
скольку er () со 11е ршп; поки11 у.r1 «Поле боя».
Да.11ы 1еr'ш1ая жнз 1 11, Феррари сложиJiась удач
но: 011 п олу• 1ил ,\НЮГО лсстньL'i. предложе ни й 11
ныбр;~л самое Hhll 'OДHOC IП них. 13ОС<..'МЬ лет он
вn:ллающл 11~1Ло 1 ·оrюс 1:1едо.мство R 11рош 1111 ~ 111Т
.'vl all'lyя. ! ЮТОМ CT:Ul профсссорш.1 \1;1 '1'С М :1ТИЮI
В nOJl()f ICKOM )'Н 1rнcrcиTCTt'.
Ннктn пз участ1-н1коR этn~1 1ктор1 111 бС>лылс
пе C,'\en:m 11шса юrх м а·1 е 1"1атнчсс 1с нх открытп!1 .
О6ъясп ит1, непр1шо1\и мыi1. случ:н'1 JСубическо
го ураn11с11ия удзлосr, Раффаэле Бомбе.rнш.
ПОЯВЛЕ Н ИЕ МНИМЫХ ЧИСЕЛ
Рафс!ЫЭ.'J t: nO\.lбCi!ЛH ( 1'526 - 1') ..,2) б ыл IH·1жe
lll:JJ 0\1-l 't 1ДfXIПJl1 1 K0!\1 11 прщ:ланился 11 ро,11но 1!
Итаю 1н работа >ПI по с >суше ~ 111 ю болот в ж.:с
течке В:ть-дн-К1>я11 а (Дот п 1а Болот) в 1'549-
1')')1 11. В снобоююе н ре м я оп ::1;1111 1 малс.sт м а
·сем;~тпч сск11 ми 11сследоnа 1ш ям п . К J '>50 1'.
lJочбеJши :1а коrrчлл нервый nзр1 1а 1п· с nосго со
ч 1шс:11 ш1 «Алгебра,>. t lро.:~.олжая ра боту над
кнпгой, 0 11 отыскал в бибш ютске Ватик:нт а
•1·речсскос С()Ч1 1 не1 шс по этш1 дасц1н 1;11ше.
<.·ост:111л<: н нuс 11сю 1.>1 Л н uфан 1 ·0 :-.1 Ллекса J щ рн й
сю 1м."•. llахсщка прон:шела н:~ не1·0 с11т,ное
llllt"Ч~ITJICHlle. (."Чтобы 0601·а11-1т1) ~11 1[) 'J':lКllM
:за.,1е ч ателr,ныvt r1ро1 1 :з 1к:лсп ием, 1 1.зят 1cr> м r.1 :-ia
перевод н п ерепели шп1, юmг 11з семи, 1щтп
рые пе б1.111н персr.е~ены до этого", - ттнсал
i)0,\10CЛJI Н.
Под nJ1ш1J11 км Диофантuвой «Лр11фмсп1ки»
Gомбслли кuре1ш ым образо м ттср сра бот<.1 л
еrюю рукош1с1" ню1ючиn н нсё lil.1 з;1д;,~ч11 Ди
офан·1·а. Но 11с тu;1ько ;;:адачн 11 нх rс111сн1.LЯ
1 юра:.11 1лн Gомбеллн . CtюcuCi 1шсдс н11я н м атс
\1ал1ку новых ВL:лич1111 - отриц;.1тсл1,1-1ых
'-IИCeJI - вот что бьuю важ1 IЫ М ,'1,ПЯ нсгп 1 fk;~ь
11мс111 ю ·1·аким ()аразпм, чистп акс11омапrче
с1ш, м())ю ю определ~ 11 1, 11е толыш птрш ~а тел1,-
11ые. 1ю п 1\И'1·11е чпсл;,~ . И Боибелл1-1 перnы.м
ввёл n алгебру м 1 mмые нслиL1ш1 ы (см . статыо
«Зачем 1 1 ~ж1-1ы новые чи<.'ла? ·>)
L' .1:1\ LG E BRA
OPERA
D1 R.•нsL8онанt1da BoJosna
Diш(; >n rre LiЬri.
C•• l~i•.ltrм}iипо J..fe poi.J 'llmirttn prrfi1t11
rogmшm<d.//~1,"1<•1ltll'Ar1,,.,11<~.
C..n 1•n • T•11 0I• copi or• d<lkmi1<ri<1 cЪc
in clf• й comcngono.
1о/• hor• '*ltm ) ltntfm <f'U' ЛN"1.jii
Jm A ftlfyfttnt .
lN BOLOG NA,
l'cr G1ouann•RaG1, i\\ L> l.XXIX.
Соп l•tZti," dt' S11;щ 1et1 ,
д!1ь_
с=и~
Г11~ул1>ны11 лщ 1
BT(lf'< .11 U '1 iЛ<l>IИЯ
"ллгебr • ~·
r ь11м(>1елл•·•
Бо J.~ОНЬ\1 l 'i7<11
C 11 ;1чaJ 1 :.i он, кзк н Дrюф;шт, ,\ал 011рt'/\t:лс
н11 е 0·1·р1 11 tатслы,1 ым чнст1м (1юторыс нее м::~
тсм<1т1 1 ю1 ТОГО вpcivH..'llll CЧ llT:J.111 1 <')JOЖ H l>l 1\ll 1 4 ) 11
уст:нюв11л 111х1щ 1л:,~ обращt' 1 11 1 я с н1 1 м 11 Кна,п.
р:п11 ыl1 1<0 рснь 1 1 з 0·1 р 1 щателы10 1 ·0 чrклз, к~н;
заметил Бомбелли, не J\Южет.бьгп, 1111 положп
тел ьны.м, нп отр1 щатепы 1 ым числом. То 1'да 01 1
пред.'lожнл назвать эти ~юные. «софнста<rе-
t:ю:1с• Ч HCJI U «ПЛЮС<JМ 11 :1 МIПТ)'С'1" ( +\'- J ). fIOl'/\3
ИХ ll'(ЖI IO 11p116ЗH;l}l'J'I>, 11 «МНТJУСОМ 11:1 i\1IПT)C3»
(-\-\ ). когд::~ 11.'( llY)IO IO BЫЧllT:t'l'l1.
В со крl' .\.\е 1111ой :.im ·e()pc, н 1юдя ,\11-11 rмy 1<J с;~11-
ш11 \у, матt:\1'1 ' 1 ~ 11<11 гово рят· 1· П yL·1·n С \'щестнуст
1re 1..;m·npoc ч 1 1с1ю, которnе 11 р1 1 тю:{ведетш в
ю~:;щр::1·1· рзвпястсн - J. Оно <1удет 11а~\ЫН~п 1,сн
:--11111.мoir еюпшце ir i. То есть i 2
=-
1, и, следова-
телы ю, по оr1 реж:лt'111 1 ю, i = ,_1 "· Т<::~к 1нщ 1 1,\:1.
опреде.11е 1 ш<.: м1 11 1моli едшп щ ы эа 11роrпедш 11е
·НЮ лет 1ю суп~ 11е 113менr~лос~,, а :,~р11фме1 11-
ч.ескпс 11е(r ств11я с 11еГ1 щюпэнодятся 11 :чет ю
та к. как эт<J делал Бомбслл 1 t в XVI в.
Н 11какш·n 1 ·еомстр11 ч еск< 11·0 обос1ю1{а Н11н
~ юным ч1 rсла:>v1 Бnмбt'11Л11 1 1е д:-tвал. ()п ~х1 ссма·1·
р~m:-1л 1 1х к;1к формаю.1r1>1с спмrю111.1 . о котn рых
1шчсrп 11е 1 1:1весттю. кроме опреде.11ё1111 ых 1 1 м
11 рап11л. I I Jiмешю с 11 п,,ющью зт11х ч1кс:л е~1 у
у,'\аJтосъ объяс н пт1,. rючсм:у ,1\аже в том случае,
84
-
История матем<1т11ки
ко1·;~:.~ в фор"1улах 1юр11еl1 1<уб11чес1<01 о уrх11111 е-
1111я 1юд :~1 i;1 ко.:.1 квадрат~ ю1 о корпя стоит от
ртп,ателы юе число ('1 J1\ что этот 1<0ренъ вро,'\е
бы н 11е сущсстnу<.:т). ур;шнспне нсе-·1 ак11 ИJ1-1еет
11ейстщпелыюе μtшение.
Мшrмыс ч11сла, нведённыс Бомбешш. более
двух столL·тш1 вос11р11н11м:1m 1 с1, J11нш. как ~доб-
ныс CI IMKOJIЫ. Ма 1ем:~ J IJKJI П[1ИMt'l IЯJll I llX R прu·
\1ежуто•11 rых 111,1 клщ~ках . но дю1 pe3yJt 1r1 .!'Га 1к"
П\JЛ l1ЗOliaJ I l1 ТОЛЫ(() <·1 1ас1·оя щш.: -> - 1'eЙCTl111'1'eJ1L··
ные члсла. Липть в 11::~чJле XJX в., после:: того ка~<
~ r<o/ю.riь математиков» Гаусс npc!(Jloж11n нагляд
ную гсометрн•1ескую ш1терпретацшо комплекс-
11ых чпссл, 01111 пол:у·ч11л11 « 11pitн.11ражд.шства~.
РОЖЛЕНИЕ БУКВЕННОЙ СИМВОЛИКИ
Не1юзмож1 ю лредстаоить себе математику ()еэ
спе r,т1алы 11>1х обозначе11ий. Мы насто.rrъко пр11-
выю1и 1< 1шм. что порой нс можем 1'ОКазат1"
не прнбеган к Сl11\11юл<11v1, 11ростейшие тш1щесп3а
Соз11:~тслсм аJ11'ебра1тческо1'r снмно1шки по 11ра
ву считается фр:НЩ)"1СК1111 математ11к Фр:.~нсуа
Ви ет. СRон нде~1(}J1 нэлтю1J1 но "нne,r1e11111-1 Rа~1з
т1тнческос llCl<}'CCTIIO» ( J ')<) 1 t' .), которое долж
но было с1атъ началом всео61'смлющего трак
тата по ~u1гсбрс. Внс:т пис:-tл: «Искуtтт1ю, кuтupu<.:
<DPAHCYA ВИЕТ
Фраtку<1 Виет ( 1 'i40- I bD ~}
родился в городке Фонте1-1е-ле
Ко1п прuвинuии Пуату, недалеко
от Jнаменитой крепuс:ти /\а-Ро-
1t1 ель. Сын прокурора, Виет полу
чи/\ юридическпе оnра1ован11е и
начал адвокатскую практику в род
Н()М городе . Но вскоре он стал
секретарем и домашним учитеАем
в дuме 31ытного дворя11ина-гу ге
но rа де Партеt1ей. (Гугеtюты -
послеловатеАИ к аАьви ни1м а, одно
го из основных течений Реформа
uи и Uеркви.) Тогдil Виет очень
)'Влекси изучением астрономии и
триго1юметрии и м1же not\yчиt\
~1екотuрые важные резуАьтаты. На
примеμ, 11 н сумел представить
c,1n пх и cos 11,\ в виде многпчм•нов
отsinхиcosх.
В 1571 г. Виет переехал в Па ·
риж, где возоG 1ювил адвокатrкую
практику, а позже стал советником
nарАамснта в Gрета11и. З11;:~1<омство
с Ген рихом Наваррским, будушим
королём Франuии Генμихом JV,
помогло Виету за нять видную при
дворную должность - То:\ЙНОГО со
ветн ика - с начала при королс Гсн
рихе 111, а затем 11 при Генрихе IV.
JJ 11:ш:11 ·J10, нов о шш. по кpaй!lcil \1Срс, настuль
кu 11с1юрчснu времеш:м и искажено ш1иян11е.'1
Ол1111м 11з самых .:1<\мс•чатсльныл
достижении Виста ~1а кщюлсulкuи
Сl\ужбе UЫЛд p a:iraдK'1 шифра, R
котором на сч иты валоrь Волее
500 знаков, менявшихся врем>~ 01
1Jрсмс11и. Этим шифром п оль:юва
лись недруги франuуккого короля
в Нидерм.1ндах для переписки с ис
n<Н1t.ким дDuром. Хотя франuузы
часто перехватывали п1~rьм.1 из Ис
пан ии , раrшифровать их никто 11е -
мог. И только Вист быстро нашел
Кl\ЮЧ. ПоJже И\П..tнuы обвиняли
Генриха IV в том, что у него на
rAyжfiE" состоит сам льявол.
Виет жил в :тоху кровопрu
литных религиu.iных войн. Нет с ве
дении о том, 1<3ТОl\ИКОМ он бЬI/\ ~il\И
гугенотом. И1веrт1~0 только, ч го
по 11апш111ию яpt,ix католиков п:>р
uогов де Гиюв ero отар а н или от
должности в ко1ш.;- 1584 г. /\ишь
после разрыва кuрuли l де г~1Jами ,
в н..~чале 1SR9 1 ., он вновь fiыA
приглаш ё н ко двору.
Четыре года оп,\АЫ <.жа.1<1лись
11собычайtю плодотворными дмt
ВиЕ>та. МатЕ>ма rикёl аала его еди н
ствен ной страrт1,ю, он работал са
мо1абос 11 но. По р,ксказам Lо1:1ре
Мt!н11икuв, Вие1 мог 11рuсиживdть ы
пис ьменным (талом по трое rуток
подряд, только иногда эабываясь
Lнu м на 11 ескuл ько минут. Именно
тor,~i\ он начал f)оАьшой труд, коп1 -
рь1 и назвал "Искусс тво анализа ,
И/\И Новая алгебра». Несмотря на
огромноt' жемние и упор11ы1~ -~аня
тия , книгу В111н Rr·1• Жt' не завершил.
l lo ГАав1юс было написа110. И Jто
главное u11рсдем1ло р<1зЕ1и rие 1:1се11
м,1тематики Нового времени.
Фра нсуа В~1ет
Лнтnгrа•l111я 1 rr,111к1p t~ Х\1 1 t<
11<1рнарон, что н счёJJ 11ужны~1 1tр 1щ:лъ t:.\ty со
всrшен1ю НОНЫЙ ВН[\" .». Хотя Cll.\lf\()J!1 1K:I В11ст:1
обладала 11<:кtУl'Оf1Ы.\1И н<:.цостатк:11.н1. Tt.\1 Ht'
:.-1е11(.'(.; ЭТО бhlJ I ОГ[ЮМI IЫl~J шаt' вnерёд. А 1Ю1' щх·н-
1111е ,\1атt:м:~таюr вполне обходилпrп без бу1<
пенных обозтrаче 1шй и специалы 1ы х пр::~внл
011erшroFJa111 ш с 1 111м н. Наверное, будс:т rю11ез
по вернуться назад и посмотреть, каt\ 1 юявилпс 1 ,
первые .\JЮ'с,чаттrческш: :шак11.
СИМВОЛ ЛЛЯ НЕИЗВЕСТНОЙ
ВЕЛИЧИНЫ
Уже li rаботах Гt:рона 1'\.11екса 1 щр11йс1шго (Т Н.)
11 в М11ч11гапском 11апирусе (ll в.) можно наiiт11
с1тец11алы1ь11l зшпс для 11еиЗI3ССТI ЮЙ ВСЛИЧИI lbl.
Это бу1<11а грсчес1ш1·0 алфаnита .;
-
«кшщсв:.1л
сшжt», r1c ШJ1.свш:u1 ч11слово1 ·u :~11аченш1. Сле
дующий н 1 а~· в со:ща 1-пщ а;н·сбранч.сс.:коr'1 с1 1м
щ>Л11ки С/Lt'Л:щ Д11офа1 rт Ллсксu 1 1/1р111!сю11'1 -
llOl'ЛCДHllЙ BCJJJ!IOIЙ м:псматик :ll-IЛJ 1 1110CTll (Cvt.
ст~·тъю «"Лр11фмст1 1кJ" Д1юфа1 1Та») . nо;1роГ1тюс
() rшсаннс ~юных обозначсннl1 vчёпыif 11()-
месп ш в<1 вnс/1,е11и11 к cn()eii :шаме1111той «Лрпф
мстm<е». Там 011 rrprmёл 01мвоm,т дня 11сиэ
веспюго. шестп cro положrпелыrых 11 шести
отр1щ1телы1h1х. степе~ ~ей. J также 11равппа г~ей
ствш'f с 11нм~r.
Ilo тр:щнr о ш того нрсме1н 1, J\IO! ш~rно~'1 сте
nсн11 Нt'и:т<хтной неm1чнны Д11офан ·1· 11 с пш1ь
:юк:1Л знак;. :1 ) ~JНI ()С'l':U!ЬНЫХ C'l'C!ll'HCI\ - <:u-
кращен11н от 11.х 1· рс::чсскнх на~щ:н-шr1:
х" - t.." (81)vсхμн; - «Сила•, <-Стспе1 11·,•);
х' - к'' (кuРос;
-
«куб»);
х1
-
л"л (ouvaμoouvo.μ1.;
-
«ющtрэто
кuадрат~ );
.л5 - ~" К (o,)vaμ ок-Uрос; - "ко;щрато-.куб» );
l)
\1
'п. '( .t
-
б
х - к К (1пJ1Juru"щ - «куоо-ку )~).
()тр111 t;!ТСЛЫ IЫС сте 1 ICI IJ 1 Д~юфа1 ('[' ОЛ\Х'ДС'
ЛЯ!I каК1\fЮ611 с ч1тст-rгслем 1 11 знаменателем,
равным сО()'1' нетст11ующ6i 1юложптелы юй стс
ттени. Для 0·1рицатею,11ых cтe11er- 1 cl1 был ·1·акжс
нnедё11 особый знак х, 1<0тор1,1й доfiавю1лся
спрала c1icpxy т< си~волу по1юж1пслыюй стс
nc1111 . Н :шрим.ер, х ~ в обоз11:.~чеп1 1 я.х Диофа1 п:t
fJЫFЛЯДJIT KaJ( д"~ .
Был у Днофаптз и энак юш нсизnестного n
нупевой стс 11 сни - М, в котор1.1й вошли 11срвыс
две букны l'рсчсского слова •· 1\юнаr » - <-l'/\11-
Средние векJ и Возрождение
д!1h
EU~
lllll l'1». JJ.1 1 otj1~111т нс OTOЖ/\CC'l ' BJIНJI t:J'O с: Ч11СЛОМ
1. Поско.1 11>1<.у в •· Лрифl\11.'Тt1Кt ·• нет сnе1н 1 ат.1-11.1х
:m:1 ко1i ;ин июже111 rя 1r умr юже1111.fl, оче 11 t> к1жеп
11орядок 3:.i1111cr1 стсnе1111 неи:шестrю 1«) и 1<оэф
qнщ11е1 1·1~1: :1j энаком степени вссmа следовал
ко::>ффтщне11т, так что с11м1юл М выполнял ещё
и з 11 1коrаздел11тслыrуто ф~.1шциrо.
л вот дш1 uщ.:р:щш1 нычнтаmнr Д11офа11т
ВВёЛ 311:11< lfl. В f1C:ЗyЛbT;l'l'C Jl(HIHllЛ~I Cb BOЗVlOЖ-
1-IOL"l '/ , .)~IПI ICl1I нать [):l:ЗJ ll IЧHЪIC l\1Jl()Г{)ЧJ1Cflbl • cнa
Ч:lJJ 3 11cpcЧllCJ IHJ11fCf, f-ICl' IIOЛOЖITTCЛl1llЫC члены ,
а после :-111ак:.1 lfl - все отrн1tа·1 ·елыrые.
Исrюm1:1уя Аместп этша ра 11еrк111а первые
щ1е (Jуквы c.iю 1ia юос; (<· нСОС·• «р:шныir» >,Д1ю
фаr1т заг,шсыnал r1 }1)аnнешш. Напрнмер, урав -
11е1rисх'= !.
-
х n з::шиси J~иофа 1rта ш.rглщ..tсло
бы так;
к~ сшJМ~l l\ ф
(буквам а. 11~н1·rсчсскоi1 алфав11т1-ю~'1 11умсrх1 -
цш1 отвсч:1т1 знач1.:ш 1 я 1 тr 2).
llocлe з ака·1 ·а ar 1т11ч 1,ю~'1 матс:-.1зтr 11<11 1~с;нтр
:111ш 1нй nеремсст1111сн на Востпк. 3дсс1" благо
!l,арн тryJ1.a ~11 арабсютх учёш,rх, алсебра nьщею1-
лас1, в сампстоятелытуто об;~асп, матем~1 т111ш.
На арабском Воспже впервые стал11 1ют,зо
ваться десятнчпоi1 поз1·щ1юшюЛ с11с:тс,чой
счн.с1!сtшя . занмстnоnа11нuй нз Н1щш1. tta араб
сю 1f-r }131,1 к былн 11ерсвсдс1-11.1 мно1 ·11<:: 1'реч.ссю IL'
11 r1нднйсн:J1с: ·1·срм11ны , но от бу.кксн11ыл обо
~{11а Ч<:HHJJ l ICI IЗRCCTI 111.!Л матем:tТI fl:(] 1(Уl 'Ка :Jалнсь
11 11а3ыкаш1 1\Х СЛОRЗМI\ . H:-tЩllil\\t:\l . aJ11>-Xupc:>-
l\1H все 1\СЛНЧJ lllbl. с KfYl'OpЫ.\tJ 1 l'M~ 1Гj)l ·IXOJ\ШIOCl1
н мс1ъ J\t":JI(). 1х1з 1 1ет 1л на тр 1 r ви/~:а: 11е1 1 :тсс1 -
rюе - «джп:~р·~ ( «1юрен1»>) пли « ШaiI ·> ( <· вещь» );
квадрат неи:шсстного - " '"1зл» («вмущеrтпо" );
с1юбодпыi 1 члеп - "дархе.ч» ( <- серебряная мо
J 1 е-1·а»). Позже Абу Kaмll.'l J1:i:m:iл третью степень
<- 1с:~'б" (<-куб·>).
Отк:~зш3шис1,от аш·сбра11чсско1·1 снмвош1ю1,
арабские ~1а 'ге,\11а ·1·11 ю1 сдслал11 ur;iг 11:r~ад 110
Cf1:1Rllt:HH/O с rpt:Чl'CIOIMlf учёнЫ,\1111 .
АЛГЕБРАИЧЕСКАЯ СИМВОЛИКА
МАТЕМАТИКОВ
СРЕЛНЕВЕКОВОй ЕВРОПЫ
С дост1DКе1шлм 1 r ~1рабсrюй алгебры свроnсй
сю1х уl1ёных гюзнаком1111 Лсон;1рдо Пrrз:111-
ск 111~1 !\суд11н11т<:=11ын; , что оснuнные ·1·срм11ны
85
~
&"®
История мLtтематики
Sб
t ювоrо ип.:тсства бшrи пеrеnсдены с арабско -
1·0 языка. Но при персrюде 11а итальянсю 11:r гю
лучал11сь слова. Ш\LПIJ1 ;tющиеся на одну и 1у же
букву: COS:l ( ~ ВСЩI»> ), сспsо (<'ИМУЩСL"ГВО~) п CllbO
(«куб"). Внднмо, поэтuм у 11·1·;.и1ы1н<.:кие алгсбра-
11<.:ть1 uбu:>на чали сте11е1111 11 е11 зке<.:тнu1 ·о д1:1умя
11ерны м 11 бую\а ми соот1iстс 1 кующего слuна. T;tк.
в нсданно найден1-юм 1'[хtктатс Маэстро )К11т ю
«Во1~росы ~u11·сбрые> ( l 3R4 1.) х - э·r·u со" xL -
се.,.'\: - u.t.,x
1
-
и:•. cli се. (се пsо di сепsо - 1• кнал
рато- r<валр::1т" ).
Ш колы алгебраистов воз~ ~икали 11е только n
Италии, lJO и в Гер ."'1ашrn . Ита.rтыmское слово
cosa (nроизноопся «коза·') :щссь преnрат ююс 1,
в Со~ ( «косе») , п потому нсмецю-rх алгсбраистоn
назьш,tЛI! <-КОСС ИСТ~МИ». а RRсдекныс Н.МН 060-
:щ ач с 11 ия - «косснч сскн.\ш•. l l t:p1:1ым в Гер ма
нн11 J1t.·кцин по <tlll'c()pc ст<~л ч итатh урожс11е1 ~
Чехии Ян Вндма 1 1 (Н6()-11ач:ию XYJ R.) . В с1 о
учебнике <·Быстрый и кр.~си11ый счё·1 r~ля 1кс 1 ·0
купечества» ( 1489 r.) nперnые пш1111 111нс1•. 1 11:.~ки
оюже1-шя и выч ита1 rия , которые нсполъзрот ;~о
снх поr: вместо символар (отит. piti - «плюс»)
о п использов ал знак +, J вместо гn (от ит.
шсnо - «мн~rус»)
-
нривычIIыfr -
Наиболее изnестным коссис-rом был Адам
PIIзe ( 1489- 15'59) В сноё м) чсбннке ~со ~*, так
11 нс нап еч<~ташюм, Рt 1 зе nоместш1 болhwую
таблш~у косси чесю1л обоз начений , которы е
впослсдст1ш11 11 с11ользоuал Л. Ф. Магн111~ю1(1 в
п<:>р воri росс11йской <•Арнф метикс:» (1703 г.).
J
1
Стр:~н 1щы •Ар11 ф~1ети к11 . /\. Ф маrниuкого l 70J г.
Лла"' Рюе Гр,1вюрJ 11а дl':J<' fl~" ыноRо 01.:р~шенная 15j0 г
Нсмсuю1 е ;:~лгебр:шсты того npcJ\1c11и стре
мились со1<ратнть ч1к;ю с нмволов и nnссти
едшюобр аз1 rыс обозпаче ш1я Большую роль в
этом сыr·μала кII11ra J\1лхсля 11lт1 н.рс:1ш ч flол ная
аrифмt:ТI IKa -> ( 154-1 1'.) .
Изоб рет~11 11с к11 .11сопсчатани}1 окззшш 01 -
ромrюt" пл 11янис на нею снрстейскую культу
ру, 11 п частнос.тr1 на разв 11 т1tе математики.
f'укоr111<.ны>1
3К\t'\о\П/\11р
учС'61111Кд
А Р111е •Со~'
В •111слс 11ср1:1ых опубтжонаш 1ы х матем:1т11qс
ск11:х соч11нсн нli бьта •Сумма :шашл"r п о ар 1 1ф
~1tтнкс, геометрии, 0· 1·ношСНl'ШМ и пропор1 \И
<>на1 1hнос1·11 <> J!ук11 r1ачолr1, 11 <:1·0 обоз1-1аqе1111я
ГЮЛ)'Чили 1ш1рокос рас11рос1· раш~1111с. Ою 1 ако
fiылн 1rc оче11 11 удоб11 ы , н потому N1атем:пи ю r
П[Ю/Г.Шlжали rтп<2т1, более простую снсте м у
()(iQ;Щ:lЧёШ I Й.
Фр:11щуз бз1<.1.11~шр м<::диt~иr1ы Нт1кола Шюке
U - ОI\ОЛО J ')()() 1·.) предложил собстnенпы ii
вар11;1нт: пока :iатсль степени он 11ис:-1л мелкrr~
шр11фтuм ок:р~у 11 справа от коэффтщиснта.
Напр11мер, l 2x н :5а 1 1ио1 Шюке выглядело ка к
12 1. Кроме ·m1·0, Ulю ке смс1ю ннё11 н с1:1ою с11м
кuлик-у нс толt>КО 11 у11е1юй (/ \JНI с нu бuд ных
~!JICl lOH }1ХШН<.:Н11Й). НО 11. OTpИ l\:}'J'CJIЫ lЬIЙ I IOKa-
o
8\ -1
6)
-
:~атслъ. оыраже1111е ..'С
·7Х
= ') ">.'\: - рн 11::юора-
-
8~
71 111
••
-62
зш1оытак:" . по~пюжстнюс на
,д:~е·1 ,J »,
Ту же идею иснользовал в xv1 в. италr»щец
Раффаэлс Бомбеллн н с1.юей ,A.rJгeбrt". Нсизnс
спюе 011 об<ннаtfал спсннальным с11МJюлом 1.
а его стсш.:ни - символаыи 1, , j_ , ." Обозначс.::
н11я 60J\1nt:ЛЛJt ()l\;JЗ:.VIl'I Hj lИJIHl1C ir 11а алгс6р:~ 1 .r
чсскую сrrмволику ш1дtр1 1 а11;(ско1·u i\1атсмат1 1 к~1
Снмо11<1 сп~в нн а ( 1'i...\8-1620). 011 нс TOJl11KU
ВВёЛ IJОХ()ЖИе OnO~IHaЧt:Hll>I /l,JНI L:ТelJt ll eй ()/\НО
Г() нсн:-1Rест 1 ю1 ·0 - (D, ф, G), .."но и распрост
р;1н1rл их па стспе11п нтпро1·0 11е~ 1 знtстноJ·о -
sec. ф, sec. @ , sec. (j), .. "а таюкс трен,ет - 1е1·. ф,
/Ш: ф, /f!1'. (3), ."
ПЕРВОЕ БУКВЕ ННО Е ИСЧИСЛЕНИЕ
Дпя соз1 1анин бук нс 1-1н о 1 '0 псчислсн 1 1.и остана
Jюс ь с1tе11ал. еди 11ст1~енн1.1 й, но 11рш щ 1 шиал 1,
но ~юnый 111 аг - t111еС'п1 06о::~н;.~чсн1tя нс тш111кn
;и1я 11еи:шест1 юrо и e1·n сте1 1 е11е1\ 1ю 1-1 д.rш1rapз
\te-гron. Это и сделал Фра11су2 Виет в т1х1кrате
• Вnеде11ие в ::шалит11ческос 11скусrтнn,>. (Виет
стрем11лся со:щатъ тюnую науку, которую назы
вал а11<11111ти ч<.:сю1м искусством. Она должна
была обла;1а· 1ъ строюстью гсо.1\.К"Iрии и оттсра
ти1ш<х1·ыо iш 1 ·сбры. Перед т:1кой на}1Юй, 1<ак по
т1 1·а.11 Вист, нt: MOl'Jla бы устон·1ъ нн uдна зад<~ча.)
Сво ~о ноную сим1:1оm 1чt:скую ш 11 ·<.:бру (lugis ti -
ca speciosa) В1 1 ет 11 рот11вогтоставлнл прежней
ащебрс - чнсло1юй (logi~tica 11L1111 ею~а). Учё
ный с ч1 1 таJ1, что только псрnая - ;по аJ11 •ебра в
собсrвсшюм смысле, т~ 1< как по:пюляет 0 1 1ер11-
ровать с цслымн кпассами вещей. llторая же есть
арифмtти.ка, о п ср11рующая просю числамн.
Средние века и Возрождение
Прежде че.'11 рассУ..ззьшзт1, ч11тателю об арпф
М<.."п1чссю 1 х дсйстсш~х с классамн, Виет 13 пол
ном соответс.:тв11и с rсометр:ичсской а.r1п;бро-И
,r1 рсвних rреков разделил щ.:с возможные всшr
чнг1ы 1сш ступснн. 1\ 1rep1юlr сту11е 1 ш 0 11 0·1·н('с
«71,JПIНЫ\ ИЛИ ВеJШ4 1111Ы О/\Н ОГО ll :iMC[)l:H llЯ , K0-
'1'0p11le можно сю1ад ы1:1лъ н выч.ит~тn - 11з болh-
11161 ме11 1. шую. Й реiуmп·атс ЭTllX /ЩУХ OПCpa l \llJI
получится Re.r111ч1 111 a '1·0 11 же: ступе1ш. По ecm1
11ереы 1южити две Rcшrqи1Jы 11 ерuой ступснп, то
рсзул 1,татом будет уже ~площадr>" - ве11и•11ша
второf1 стуnсшr, или nеличнна двух 11змсрст ш й.
Следую щей ступенью , ес1·ественпо, были
юбъём ы ~. Н отли чие от греческих ма- 1·ематнкоn
в~н~т 11(.' щ:та н он н лс н 1-1:.1 первых тrёх сту 11 с нн.х,
а по111ёл 1-1;u1h1L1e - JJX у нс1·0 бесконечн о м11ого.
Вэ'1'Ом исч11слсн11и нажсн 11ршп..1,11л одноро1 1но
стн: МОЖ IТО СКJ13ДЫtl3 '!Ъ ll nычнтатт. ЛИl lJ l1 Вt.11\1-
ЧИШ1l 0[\ПОй ступ е нн. llp11 у1ЧI ЮЖС llНТ1 Be.llllЧJН IЫ
ступеш 1 /1 на nс:тпчи11у сту11ени т получ~пся
nсличиrrа ступеrш 11 + т. Раз,r~ет 1·1ъ же их ~юж-
110, толы<о если 11 > т. Результ:.~т такого де1!ств 1 rя
бу11е1· 11р инадлtжать егупснн п - т.
:1ате м Вист обозначш1 все нст1ч 1-1ны буква
ми алфаннт:J. Поскольку величи н ы быв~1 ют 1:1з
нсстным11 t1 н е 11:;Неl"1 ·1-11.1м11 , то ДJJЯ обозн ачсн~н1
11tрвых он кыбрш1 сш ·ласю.t(' В. С, О. .." а ;1,.1н1
вторых - гласные А. Е, 1, .. (Сегодня м1,1 060~-~на
час:v1 11 арзме-1ры задачJJ, как праншю, 11 ервым11
буквами л~тинскоrо алфа1~ 1-па а, fJ, с, .." а 1rе11:1 -
nестные - буквами иэ ко1-щз алфаnита
-
x ,y, z.)
IN ARTEM ANALYT TCEM
t)лfi()(,,_
'Dc Dtjmtmt &'r ullf#/llfXrA•d.Jfit.rJ <;- "''l'f'-'"'',.."
Zщ,Jt04,
tл1'v~ 1.
П•!rRilЯ пr;~н1шi1
гр.~кг.н а Ф. Ви~ 1 а
• Beo;,лt'1t>1t·
1'1 dl·t алнп1че<..кое
ИL"-YLL llIO ". lур11н
15!)1 г.
87
,Аiъ.
a'Jl{!J
История математики
НАУЧНЫЙ ВЫЗОВ ВАН 1-'ОМЕНА
С имен~м Франсуа Виета cвs1зJ1-t0 1-1есколько замеча
тельны х истоμий. Вот одна и.з н~1х .
Оы1аЖАы в ноябре 15q4 г. при дворе Генрю"а IV
нидерландский посланник рассказал об изееснюй
задаче з 11аме нитого матемап1ка Адрисна ван Ромена
(1561-1 Ы SJ. Это был вызов математикам всего
мира. Речь шла о решении уравнс11ия 4 5-й сте пени
45х- 379')х1 +9534х~ - ". -
12300x3q + 945х• 1 -
-
45х41
+X
4
s =а,
В спиLке тех, кому слеловало направить его науч
н ый вызов, ван Ромен не указал 11и ол1ю го франuуза,
и посланник заметил, что , по -видимому, во Фра1шии
нет математиков. «Но ПО4ему же? - во .~ра:.ил ко
роль. - У меня есть математик, и весьма выдаюший
ся ». И он посла л за Виетом.
Тепе рь В1rет смог залис ын атъ ур:~нненин
нс тпл1око с кш1кретными ч11слш1ым н ~т:.~ченн
ям11 , но и с параметрам11, ·1 . с::. 1~с::лыс KJJaccы :~а
лач, К<1ТОрые МОЖНО рс 111 ап, С IЮМ()ЩЫО ОД НОГО
правила, не забынаи , 1.:оне<пю, о гrрt11щи11е сщ
нородности. Например, уравнение.\} + 5Вх = D
у 1:)11ета uы1лядсло бы так:
А c:ubus + В р!апо 3 in А aequшi 1J solido.
З.п,ес 1о А cubus означает третыо степень нси з
всстно1'0 А , В plano - <18 плоское», D solido -
«ТСЛО 0 1>.
Но что особе~ ню нажно, помимо ураю 1с1 rий
те J1 ер1, можно 6 1ошо :iа11исы1~а1ъ 11 формулы.
Один коренt, Вист н ашёл сразу же, а на слелую
шее утро представил ешё 22 решения уравне11ия. Как
же ему удалось Lделать это так быстро?
Лело в том, что, занимаясь разложен~1емsin пх в
cos пх по степеням siп х и cos х, Виетустанов11л связь
некоторых алгебраических урае 1-1е 11 ий и задачи о
дслt:нии угла на ранные части. Он увидел, что прел
лuженное з нач еж1е параметра а является сторо1юй
вписанно го в круг правильного 15 -угольника , т. е.
хордой, стягиваюшей дуrу е 24° . Коэффиuиенты nри
х45, x•J, .", х показывали, что речь идёт о делени 11
это го угла на 45 равных частей, зн ач ит, одно из реше
ний преАЛо женнu го ураsнения
2
.
240 2.40
SIП- -
=SIП-.
2. 45
15
Остальны е п оложителы1ые решения будут иметь в~tд
2~in(120+п.360oJ· п = 1, 2, ""22.
45
Ешё 22 решения - отриuателы1ые, и, по традиL111и
то1 о времени , Виет их не У4ИТЬ18ал.
Ответ Виета был оскоре опубликован и при11ес
учёному мировую славу.
Bt:J(ь математ.иче<.:кш: форМ}'J 1ы - это нс толr.,
ко сокр:.~щённан З:\JШСЬ теоr<:м . Гл:~ннuс :{aIOllO·
чается н том, что н:1;~ формулами М( )ЖН О 11ро-
1 1.з11одmъ (тер:~ ц1 ш 111юл учат~, ноАыl' lj юr 1v1>·, tы
и rопттю111е11ни . T:i ю 1м пбра:юм , n}·кnенн оl' Lrc-
ч11cлcrrн c тто з1юляет :'lамс1-тт1, ча с·rъ рассуждс-
1шй меха1нтч еским11 о пера11.11ям11 ( 1 11.1 ю1~щ
ю1ми) . Как говор11л Лейбшщ, о по " Р::t з 1гуж<1 ет
воображе1 ше".
Сейчас нам трудн о 11редсташтть м;пе мат11-
ку без формуд, но 11ме1 11ю тако11 он:~ бьшt1 до
811 ета . I Iоследн11й (,штрих» з.п,есr, доба1шл уже n
Х\ТП в. Реве Дск~1рт к скосй <·Геомстр11н» - 011
отк:~зался от принц~rлэ сщнороююст11 .
НОВОЕ ВРЕМЯ
~
81~
СТАНОВЛЕНИЕ МАТЕМАТИЧЕСКОГО АНАЛИЗА
Со врсмёв <нrтичr-Ю(ТИ учёные пыт:шись н.ай
ш методы ]{Ь1чис.11снш1 площадей кр11волн
не11ных фн1-ур 11об·~,ёмо1{ тел враще11ш1 К КОIТ
цу XVI 11. к ЭTllM З~IД:JЧ<1М l(Oб:ll:!И!LПCJ> l-IOBhl.C
-
110с1тюсн1 1с касзтслъных к кр1шым, разложс
t1ие фуt1ю\11й н rнщы 11С();щани~ 1юrар 11фмон"
Замечателы ю то, что, несмотря 11а раз11006ра
з11 е з:щач и 1юноввсr~е1111!1, все ошr оказзт 1сь
•1 резвыч:~йrю тесно сnяз:111ы меж11у собой.
АНМИТИЧЕСКАЯ ГЕОМЕТРИЯ
Одно 11 :~ к~1ж.нейш их дщ"1·ижент-:-1 1-lоного щх·
\1ени - co:~f\:11-IИ.t:: ::1щv1ити.4еской 1 ·сомстрии.
С1ю 11м рожден1-1t:м OHJ. обяз:.1н;1 дRум круп 1 Jс й-
11111м фр;11-щуэсю 1м математ11ка.'vl XVТI в. - n 1)е
ру Феrм<1 (160 l -1665) и Рс:11е Декарту (l '596-
165U). О ни леэаrшс им о друт от друг:1 н
одновреысшю начали разрабатывать ос1юt1ы
это!'i новой матема11-1чес/\ой дисщюю111ы.
В 1656 r Ферма налпсал <:татыо <-Dneдcmн~
в изуч<..·нщ· пл оских и ·1 ·tлесных l\fCCT». Говоря
о "тюо:их. и. телесных местах", 011 исходнn И:-$
античной классифик:щнн криnых , которыt'
л одразделяю1сt> на шюскне (лрямыс 11 окруж-
1юст11), тслс::с rrыс (эллипсы. пщх16олы 11 ги1н::р-
6олы) и 111л 1сй11ы с {кр1шыс, определяемые ки
н емат11ч сс. ю1). Ферма :1.ал 1·е()месрr1чt:ское
1тре1(стаnлс11ие нх1т 1еrшя с !(Н)'МН переме1111ы
ми с JIOMOПJ,ЫO I<ОСО~ТОЛЫ!ЫХ rюорд1111::~·1" ()rr
Щ)()Из1ю11ыrо nыбирал начало 1<0ор,'\ш1ат и
проIЮ/\Ил от 11cro ось ::~бсцнсс Ордип:па, 11:~
к1юпённатт 11(),11, некоторым факс11роuа1tr1ым уг
лом, ОДlШ.М CBOJIM КОНЛ,ОМ CJ(0ffi>31IJLa 110 OCJ1
абсцисс, в то нрем.н как 1пороf1 t:ё конt:ц 0 11и
сын;ш с1м~ кривую. Т~ншм обр::~ :.юм Ферма rю
каза;~, что крн11·м1, котора}1 '>:!/~а\:то1 кu:-~др<~.т
ньrм уран~ 1 е 1111 ем . ~C'J'f) KOl-JJ1Ч<.:l'KOC <..'СЧ~ НI Н.' -
эюшпс. па р<1бола ил.и гипербола . Сущсст11<.:н-
11ым r1 едостатком с:го под'\О,rJ.:.1 было то, что 011,
как н Ф. 13нет, продолжал прндерживатьсн
античного правилз ОJщ.ороююстн. Т~ш. антич
ная N1aтeNraнrкa уста11:J вливала соответствие
между операцией сложtrшя н он<Ладъша 1rнсм
0·1рсзков - сл~1 гае.'>1ых ндоm, прямой лшнш.
89
А-=-.
&1i]J
Истор1-1 я математи1<и
Итак, желая решить какую-нибудь задачу, следует
сперва её рассматривать решенной и да гь назва
ния всем ли11иям, которые представляются необ
ходимыми лля ее решения, притом 1-~еиз1:1естным так
же, как известным. Затем, не проводя различия
меЖАу этими известными и неи'lвестны'Аи л11ния
ми, нуж110 обозреть труыюсть, следуя тому поряд
ку, который показывает наиболее естественным
образом, как они tваимно зависят друг от друга,
до тех пор, пока не будет найдено средство выра
"lить од11у и ту же величи~1у двояким образом: :но
то, что н азывается уравнением, ибо члены, полу
ченные одним из этих способов, равны членам, по
лученным другим_
GГ.ОМГ:ТRrА.
il
R[1'Л1·О DГ~СЛ1~ТrS
Лnno 16J7 Galli~~odi"1nunцumn
Сuм Nотн
r ;_оR! M11Nl>J (J[ 'J,J"/fr'N f ,
l•t1oril •t.fi-Jc..,llkш'IJt~,
la ~i...ш.м.m.,&,_ct\Q_
n!sШallrlц
q.r.r ",,.. _, ,, .
111\1'11'11~'>f"11оо11N,
~i....._.. ...,...._....,.i.м..ьu...
~.~-
Lw••·~· а...,•• оа. •••
Е.х OAic1n' 1<> 'N N1 М \ 1ц,
CI~ 13С: Жl.&Х•
<)()
Ренедекарт
'
"' ~U1e1.11·"rюn .i ''- t .I
-<,•
W
"*1nltl\~1um Jc - "• ~
\.'tf1 kи и1р1t111 о:р" ztnrn' ll 1l•nr 11· (" qo.1)•1\
fLi1
•,VQl>ll tkJo1>1 1 t ,, (1)" J)(J nlt1(e( ()-111 . lll ILJ..;I !~-
C.: J &: 1IJ.:11 1tllJl1 nt N
rl) )\ н••"1..
Jt111 t: ,,,a .J11(4,," ~r1
,.,
•11111111t.\ ·e-
1.ir f111·1~ rl.t:IШI ,lcr." k
J
''' ~(1 111
d:Lmcti:J'( u ~Li'-'f-... $. ~
н11,,
JmC'жD-\ .
. i-r
r
~"
J\].t/J.1 G L. "
.l ft.t'C1•1t1L с , ,.
., -fi
Титульны11 ЛИ(Т и с тr~ниuа
•1 ~ КНИI И р Лскарт,1
"•11~
, J t;>uщ•1 /')'1R • И3дание 1u4CJ Г
Рис. 1.
ГРnмРтри<tР ( кая
11111 Cf) l lfJCTdU'1Я
vмнnж Рния
110Дt'1o.dp1y
Зл<"с 1, 1RE1 =,,/,
Умноже:ниt:' же 11ре,r~;стаRляли ка1< r юстроенне
прямо} 1·олы1икз со сторонами , р::шными со
м пожптслкм~, ·1 . е. произnсдспне дuух длил
было uещ1с1m10й другого рода - площадью
« Введентrс» Ферма , дош·ое нрсмя остававше
еся n р)1<оmки , 11 е нашло ·1
·01 ·0 широкого рас -
1 1ространеющ какое получш1 а « ['сuметри1н Де
кар·1 а, 11::11~анн ан в 1637 L'. Это nр11ложе11ие к
ф 1 1лософскому тр~1ктату ~Р<1Ссуж11сн 1 1е u мето
де•> должно было сл~')ю 1 ·1ъ матсмаrлческой ил
Jtюстра r 1нсй 1::1·0 ,...,1етодолопrческнх 11рн1111и:пов.
На само ,ч дeJJe <- Геометрия» ОТJ(рьи1а ноиую
страш1щ 11 математике и име; 1 а фу1щал1с11таль
L1Ое значение совершенно пе~аrшсимо O'J' ф11 -
лософш1 Фратщузсюн1 .чатема·rm< 1 т истор ик
науки Миm<:ль Шаль рuннu чr.:рез два столетня
1 1 щ:ле ооубликuнаная ~ гсометр1-ш·> 1111сщ что
представлс:нш1 , н ней р;.~:ш11·1 ые. яш1>1 ютсн «ж~rъ
.VJH , rюяюн:шшfl НК'>J и.1 свеr 6е:3 vrатср11 ~. 11 :1столь
ко OH l l JJt: JlOXOЖlf Н~! прс.::ж1пою MЭ 'I CJl.l ::ITHК)'.
Декарт rтреодолt:л 1 1 е;1остэток :н-1ал~1 ·1 11 че
ской 1·ео:-1е·1р1 111 Ферма . Он 1юr\азал. что если
выбра11а едиюща дшшы, то ncc велпчш1ы вне
заннс11мости от 11х размертюстн (длiшы, nло
щают, объёмы) ""югут бытъ прс11стаuлены оди
ш1ковым образом, а LL.\1t'HHO с 1юмо щыо соот
нстствующсго 0·1
.резка. Тс 11 срь умложен11с11 вес
ост;шьные ариф:-.н: 1· 11ческ11с /(Сl1ствия д~tвamt
ВСJ11,1чнну, ОJ~1Юр(ЩН)'Ю с ИCX()) \I IЬIJVLl l (рис 1).
Поэтому, 11:111рниср, к::~ждому 0·1ре:3ку .'\"и мно
l'Очлену Р(.х) с ра111ю11:IJ1ы 1ыми кuэфф1·щнен
· 1·зм11 можно 1 юста111 1ть n соотв~тстnие l\pyrori
отrсзоку = Р(х). Это утнерж,Т\еш н: п составля
ет ocнvny 1·<.·омс.'ТТ)нн Дс1<щла, ю.У1·орая v.. конце
Х\'Ш н была на::.~вана аншштичf:'l..:Кuй. Интерес
но. Ч'J'U 'l'OЧllO T;JKOt' Же UПfX~) ~C.JJeH ll<.: J J1 1 1 фMC
Tl 14t:CК\·1X опсрац11й над u·1-резкам н ~стреч~н.:тся
1:1 J\ ' к1 11 11·t: <·Алr<:бры» Р. Бомбеттп. 1tamt c1 111 юй
JJ 1'1'50 1·. 11ire 11 убл ит юн ал п1 еii си ,110 11:Jчала ХХ '"
К(:тат11. н " Ге.омсrрни" соп,ср~u1ись ~ др~тие
IЮIЮ6ВСДе11ня. Н:~ пример, И.\1СНIЮ Декар·r СТ<IЛ
обпзш1чLт, не 11зnесш ыс тюследнпми буквами
латинс"о1·0 алфавита (х, у. z), а коэффнци
еlJ'l'Ы - ттсрными ((.t, Ь, с, d".) . 011 т<1кже внёJ1 11ри -
v
1
'
вwчную лам заrшсь с.-1·спе н си. х· , :v и т. д.
ОТКРЫТИЕ ЛОГАРИФМОВ
Пол1..1тю 1 С0П()('1 "<1ВИТЪ МНОЖСС1'13У чисел шща
1О' м 1 южест 1ю соотnетствую щих· пок;~зателей
степенн х мы Ш\ходим 13 XVI в. у немецкого rv1а
тематиl(а Михсш1 Штнфсля. Важ~юстr, тa_l(oro
1юдхода NJЯ uракп 1 к11 nыч 11слс пий дuст:tточно
1к11а. Есш •111сну r1.·" сuu·11'l<::теп~ует 1юказатеш,
)'
\
1
\"+ 1
х, а ЧllСЛ)' (l - у, ТО прон~ВСДСJJНЮ а· . (,{.
={(
будет отвечать сумм:~ х +у. т. <::. ум1-южсю1с
можно ззменить оюжсние~л. что было да13нсй
\1сч·1nй нссх 11 ы чнс1 111тсJ1е 1·1. Чтобы ef осущt
стR~п1" трсбовалос1, соста 1111·1· 1 , точ 11 ыс таб
ли1\ы, n которых содержались бы вес 1tеобхо
димые дашrые. Этот о r·ромный труд оказался
ло сплам шоттшдско.му мате,,1атику Джону
lleнepy <1') '50 - 1617).
Работа f-l eпepa 1 юд названш:м 1·Опнсаш 1 с
\'ДШШТСJI hНОЙ таб; r HЦhl ло1·ар 1 1фмок• llOH l:!Ш/Ж' I,
н tc1t4 г В L619 1·., у-..кt' после смерти автора,
011уf!лнкона 1 ю <-ТТостrюснне уд11нJ 1 · 1 ·ел 1 ,ной таб-
Лжnн 1tеп ер.
Huuo~ вр~мя
~
~~
р
/~
,_______
'\1'(1нf\'(/[~у~[
CANO=- < IS l'JE~CRIPТTO.
."
l'Ц,-t"<:f•J.'No"f""
.,...,.,_".....
n~bf,~-::;l.t"•/dw d-
A~ x \noQЩWt
l.&r~ A.L"t\'b6'1nt Nt--
"
Apud Ba11h.Vinccn 1 iн111.
.·
Т И 1у111,11 ь11i Л11< 1
ке 11н 11Лж. 1tc.~11Qpa
"' <>nнса1 1 ~1~
улщ 1 щ'f'ЛЬ Н ()I(
la(!Л l-!UЫ
лu1-ариф,юF1•
Издание 1(,20 1
шщы лo1".1pirфi\IOU» , me объясш1Lvrся нршщт1
ло1 ·:~рифмнчсошх табш щ. 11uмt:щfн11ых 1111t:р-
11ой ю1 1 н·е. В N.:Сtс11штt:лыю<.:т11 1пор~щ юш1·а
былз 1-1ап1 1 с1нз ра!l ьше псрtюl! , r1, 1НJ- в11,111мо
му. у-же к l 59LI r·_
Нспсr 11л~щсл ттр11нц1нюм об
рз:Ю\"\аншt логарифмо~ (ctv1_ стз:rыо ~.3немt:11-
тарные фу11кц11и н нх свойсгвэ») Ht"зamrc11м()
от Не11ера в 1620 r. ,-~ 11 алогт1ч11ьrе , хо· 1 ·н и ме11ее
сонершс 1 шые таб !шц1.1 ЛОL щ111фмоn оnуб:шко
шш ТТIDейцарсюп'i мате.м:tтик и астроном Иобсг
Бюр rи в юrпге «Табл11цы ар нфмстичсс1юr'1 н
rеом.етрическоit нрогрес<.:иtt»,
1lc11cp состав;mл табл~ щы мя · 1·р11го 1 ю~н::три
чесю·L': HЫЧJi('Jl~l-\l 'IЙ, а /(JI}\ дру1· 11 л jl:JCЧt"l 'Oll ШН\
fir.щи неуr~обны Учёный хорошо пони.мал эт(),
и совершс11с.-пюF1:111 не снсгем ы JIOJ ·::~рнфмпв <~га -
1ю R дат,ней шем общt>й заfютuй Пещ·р;1 11 t'ГО
др)Та 01\СфОрL!.СК()ГО нrюфессорз Ге 1 tpH Брщ'(:;J..
В l б24 1'. Брr 1 1У осуществпл заду,1:.1111юе нмr~
улучшение. Оп оnубликовал СJЗОЮ «Лоrарнфмн
ческую ар 1 tфмет1-tку», в которой содержа1шсь
табл нцы дсснтн:чных логарнфмок
ВЫЧИСЛЕНИЕ ПЛОШАдЕЙ
R а11п 1 чносп 1 н:ншыс 11 111х рс:~у111.>1 «1тпн о ш,тч.11с-
1 1t11ин площаде 1;-r ра:м1rчп 1 .1 х фпгуr дост11r
Архимед. В Honoe вреr..щ эта :1:1д;1ча, которую
на:1 ывали задачей лУ1аr)ратуры, привлекала
шшма11 ие мuоп 1.л учё 11ьrх. Так, 1 ·1 огаш 1 Кеплер
прн выnоде второго з::~кон:~ двvDксrпrя планет
91
~
ED.l(!j
История ма1 см.:пики
Тн ЕОRЕ МА. III.
Cyl111dri vcroad Par·allelcpipedшn colпnшa1·cre
ll:a11gulшu xg;al шrn, ciuod Cylindп co1·pus fi:nпg1r
qu:нJraщ fim l)afibus¶Hclls larcri!Jщ, 1·at10efl:ca-
dc111, ciu:i:: сн c 1Jli ad quad.ratu11н:11'cumfcriptu111, l1oc
elreadt:mqнx 11. :id ' 4'·
f(f,. ,.,, ..
/1J.
Vrcniro CD CvHndrica ЬзGнir.
culari• •d ЛВ quad;1нum circom(cri.
ршm, 11~ Cfcorpos Cyllodrl,adЛE
c o rpus paral!clcpJpedi rcfungufi, fсц
c olumnz•
. Afclt: dcSpb:tra& Cylindro .
CyJmdcr сшm & соlшnпа ~que·
ol u!untluc vcluti quxdam plana cor-
pora1a:acc1du111igi1urill1~ cadcmqui
pJan1J,
Вз-
ТНЕ О-
(,тpatH1UJ IH КН11П1 и Кеплер,1 , н,щ,1я C l\'f>l'OMl.' 1 1)1·1~ Bl1Hllbl)(
/10•1<>11 " И1л,111и Р 1(i1 q r
попытался Rыч нслн1ъ nжщ ~;:щ r , эnn 111 1·1· 11 чес 1ю-
1·0 rе1ппра. сю1адывая радиусы-веJ(Торы, как
если t'lы шп r были «отрезка1"Ш», 1-h\1еющнм11 ·1ол
щпну. Профессор математшш Боло1 1 rкoro у1 ш
верснтета, мона,'i: орден а исронимнтоn Бона
вентура Юшальер11 (1 '59Н-16'П) в сочшrешш
«Геометрия, изложс1-111::~н 1-юным с1юсобом нр11
помощи неделнмых не 1 1рерь11.шоrо» дал с11стс
мат1 1 • 1 сскоt' 11з1южс1-п1с: своего 11счнслсн11я бсс
ко1 1 сч110 м:тых ( 1lод бесконечно малы ."пr в то
В!JС:\1Я IIOHllMaJl l l не1-:ие неJ 1 11ч111 1 ы, l<O'l'Of)Ыt'
Mt:l lbНlt: любоl1 KOHt:ЧJJOJI ВСЛИЧIПIЫ, тю всё же
11е pam rы 11ул ю.) C.omacIJo Кавальерн, любую
плоскую фигуру можпо рассJ1.1атр1 mать r<ar< со
.вокуш !ОСТЬ параю1 ельных лшшй JIЛИ COBOKyТI
l IOCTJ, ~<СЛСJЮ13». IIOT<Jpыe 0(."J,ШJUIC'l' JLЮШЯ, пс
рсдnигаяс1. параллсл1.нu C:.tl\I01'1 себе (рнс. 2)
Аш11ю п :rч1ю д~1t'гся лрещ:тавлсн 1 1с и телах: он 1 1
обра3уются нри двнженни плоскос:те(L 1 lеоют
ря 11~1 ·1 о что к~ш :шьеrю вшщсл am·cnp:.н гчссю 1-
Рис. 2. l lло 11ыли ф1.1rур J:H(,r 11 AlJC. н ОТНОПIП. Я ~.;1к < ВСе ,,ИН'1'1 >1,
ПfШНJЛЛt>ЖЩIИ<' )ТИМ rj)l1гypdм . Lсм1 RS = NO, Г/-1 = ао
TV =11(.j и r л , тu nлош ,1д11 фигур равны .
Рщ·унnк 11~ ~ ()nО1тnв о G~ К.1FЧ1льt>ри
~н1 мстода\1\11 , свою «Гсомстр11ю 1 1с,Т(еJ111мых ~ он
спз11:пеm.1 ю 11 :шож11л на я3ыкс сню1идовnil
геометр11ческоi 1 ат·еnrы . сч11тан, что такnм
обра:юм до61 шастся бплы 11cr'1 строгое~ 11 И:~-1~
этого 01·р~111нчения 011 получил кnадра~1)ы сте·
псшюl! фупrщлн у= .\'
11
(т. е . шющад11 под
~·рафиком кривой) только для 11 = 1 11 11 == 2.
11оскш11,ку ужt: 11μ11 n = 2 t:му ЩJИXUДIJЛ()L h
П()ЛЬЭ(.Ш<IТЫ:~1 npeд<."l 'ttH; J(.:Hl1CM u трСх.\1ерных
н.:лах . Е 1'0 др)'I 11) чсннк Эна1щжсл1н:та Торр11 -
челm1 ( 1(10R - I () 17) Bl>IЧIIOlllЛ в 1() 1: 1 1' ТIО ж
Т(Щу KaRaлi,ep11 ofJ·1.ё ,\1 ·1ем1, 1ю1 1уч:зющt'1 ос~
вращсппс:\-1 рат юrторп1111еi1 1·1>111epfJoJJ1,1 :\у = сг
вокруг осп (~)"
Метод Каu~шьер11 раэш1л аш т 1Лсю 1й ;\·1атема
тик, профсс-сор Оксфорi~ского у11 1 шерситс:т:1
Джон Вал.1111с (1616-1 70 .7>). OLI псрсвёл rpo-
M<XIJ\IOJ<: l'(.'UMCTJJHЧl'CIOI(.' I IOC'l 'pOCHl l }J н:\ ШЫК
ар11ф.-.1С1 НЮ! В <ч\рнфМt:Тl l КС nt'C:KOH<.'ЧHOПJ•
( 10'5 '5 1'.) B~IJIЛllC НЫЧНСЛllЛ ШЮЩа/~Ь 1ю: 1 гр,1ф11·
ком пока~5<1Тt'Л r.г-юй фуню 1н 11 у = х
11
нс тот.1ю
llJIЯ 1 rат)ра.111.r1ых р. 1 ю таюке ;111я 1ю1 1 ожитt~'IU
ных и отр1щатслы1ых ра1~1ю11алы1ых 1юr<з:1:не
лей. Рассматривая шющадь кр)та е111ш11ч1юrо
pa,1\lfyca, четнёрт;:щ час-11.> 1ю1орой па юыке со ·
врсмстюй матсматию1 Dыр:~жаетсн ю 1тегра110'1
1
f''
1t
\1-.'У' (/_\' =4'
(1
Валю н." получт1 прс,ГJ,ст:1влсн11с ч1 ICJl<I .:.J /тт в вrще
бс::ско11еч1 ю1 о 11ро11 .тс11с:1111я .
-1 -~3·5·"17799
-
-
тт !.4-Н-1(>НH-LO
Иным путё.С\1 шш1 фршщу-зсюrс матемапrк11
Фсрм;1, н,шр11.\1ер, находил площадь фттры
11сщ крнноi'1 . н1111L'ы.в:1н в неё такие nrямо1тол1~·
111 1 ю1, шющал11 KO'lupыx ссктавшuш бссконсч·
ну 1и убыи~1 1tнцун> 1·еомtтр11чс::скую 11рu1·ресе11 ю
Посколы;у сrтособ вычпсл<:нин суммы ::нoi'I
1 1ро1 ресс1111 ()1,1л уже нзнесн::11, pt:1L1eн11c :3:щачн
CR();\IOIOCl1 1{ IIOl!Ct.:~ llОДХОДНЩеl'() ():IЭtlJГt'Hll>l.
Nkтол 1ша11ра11т> и::1учал н 11ру1·ой э11аче1ш
·1 ый фра1щу1скиf1 иа·гематr.ш и фп::1ик - Блез
Паскат. ( 162'-i - 16С)2) 13 работе 16'59 г 011
выскаэ:ш сообrажсвис, что прн nычrrсле11 1 ш
rию111:111е11 о;~ни бесконечно .\1;шы<.' могут заме·
llЯТЬСЯ ;1руг11 \111, 11 Ч:JCTH<JC'l'l'I , малую /J,)'l 'Y крн
иой 01i сч1 rтал рашю1-1 малому отрезку касатель
ной. Тру/ \ П:~скаля ока:ц.11 ocofioc нm1я1111е на
ЛеГ1(} 1 11ща, 1«поры~'1 прочёл с1·0 н IC)7~ '"
РАЗЛОЖЕНИЕ ФУНКUИЙ В РЯЛЬI
:3:щ:.tч:.t о нычисленш 1 площадс~-1 ою.1~~аш1с1. тс:-с-
1ю свюанш нl с разложенrJем функцнй 1:1 ряды.
Так, У11лы1f..1 брс')ункер ( 1620-lbl:Ч) , nервы(r
1 1 pe:m;(c 1 1т Ло 11донско1·0 королевского nбт.ест
ва. 011 рсл1::11ял 1.11ю11 tад 1, 1юл г иt1 ербшн )lt <l) :J к·1 11 -
чесю1 как пpeдt"JJ 111ш са11 нr,1х прямоутопы·1111шв,
а т:щже К<Н• nре;1ел вписа нны х треутолnr1иков.
Дая 11epB()I'() случан ()Н Ш))I)iЧИЛ. ЧТ()
1
.
1
1
1
S= 112 =-- +-
-
+--+ .
.,
l-2
.1
4с;6
г:1е.) - искомая mющадь. Броункер н~ёл эту
фор1\1улу нс позднее Jб'i7 1·.. но опублт1конал сё
ТОЛЫ<О в 1668 1' . 3/tCCh егп oпept?JЩJI 11таЛhЯН
СКl lЙ м~псмзт1rк Пhетро МенJ'о11и ( 1625- 1686),
кuторы1'1 11рнвёл этот ря/t в « fl:1чaл:Jx 11и;101юй
1·eoмe1'/)l'!l 1 » ( 1659 г.). В 1668 г. 11 еме 11ю 1~'r м:lтс
матик Н111юлаус Кауфмз 11 (около 16 20 - l blP),
р:~ботаuшп!I тогда n Ло11,11011е 11 более нзвест-
11ыi1 под m1Т1ши3ироnа1шым 11ме11ем Меркатор.
шmечатал n с1юсй книге ~11огарифмотех1п1ка·>
ра:тожс1 те
х~ х' х-1
Jл(l+x) =х --+ 2 --+ . _ ('")
2;)
-t
для :ш;Jчс1111i1 х == 0. J н 0,2. При х= 1 ;~:н1ны1'1
j11Ц CUl3ПЩ~:lt:T С j)<LЗЛOЖl'J IИС,\.1 o p OyJ IKCp<t -
нt:()f1хо;(11мп , 111111ь пр1111t:ст11 к обще:-1 ~· эпамс-
11ат<:то стоящ11е в 1 1ём разнос·~ lJ.
Новоf' время
Эти дО<."rижс11 1 ш ш,1знат 1 шпрою1\1 отюш1' к
среде ан1 ·;ш1kк1JХ ~1а1'1.:мат11ков. Ват111с , н част
ност11 , 3aмeTH.i l. Ч'!'() CXOJ~ll MOCIЪ рщ~а (*) 11:1ру
ш:1стся, сс1111 .У > 1, 11 11ашёл р:!эложt:m 1 с ll рнд
д11и функцю r
1
111
1-.У .
Далы1ейпн1 й JJ\)OL' pecc 11 этом 11 a npauлcш1J1
сuлза1 1 с именем замечатслыю1·0 шотланнско
го математика 11 астро1-10.м:1 /])I«.:ймса Гре1·uрн
(16.)8-16/)). В 1667 1' . 0 111-!<IJl/ I C:!JI [)аботу ()
кна;цхпурс кр у 1·а и 1н111.:рбш1ы , н 1\отороС1 щ;-
1юль:юнал 1'5<.;ско н сч 11 ыс схолн 11111сся рялы. Грс-
1·ори едва 1111 нt: псрuым устаJ 101l1 1J1 чё·1·кuе
pa:3JIHЧlle м<.:жду СХUД}IЩ l/ ,Ч/101 тr р:tСХО/\Я ЩJJ
мися ряд<1м11. В т~ругом своём труде. «У11ивеr
сальн зя 1 ·еомет р11я ". 01 1 прннёл гн1/t пра1.шл
выч 1клсн1ш ллощмей под. r<р11вым11 н об·.ьё:мов
тел. обр:.~зуюпщхся !!р1 1 .вращсшш данных
I< р ивых. Рс:1ульта·1 ъ1 , ттолучс.ю1ы<.: Гр<.:1 ·ор11 , ос-
1·авал 1к1, Ht:JI3HeCJ'J-IЫMJJ HI IJ10'1'1, ДО J9 39 1'. , ко 1 ·;~:1
1111ерныс 6ыт1 о п убm1кованы е 1 ·0 п1 1t· п~1а 11
руко1111с11. Ок;.~залuсь. что ~rчQны r~1 щх~ю.юсх 11-
тш1 мн<>1'11 е открыт1 1 я в теоr1111 ч11сел 1r кана
т1:i<.:. ТI:.inp11111ep, 011 .н 1 : 1л o\11 r\ <.:e р :1зложt:>1 111 с
днучJfен;1 ( 1 + .\:)
111
,а·1
·:1кже р:1 эло же111 re, к< rmp< ><:
1ю:1,ri;1-1et: стало 11 .тес' п 10 как fЩд Teirлopa (с~1.
статью •·Сте11е11r1ые ряд1м). н ч~1 ст1юсти рн,т~;ы
для та1rге11са, cer<at 1c:J 11 аркт;u 11·снсt.
ЗАдАЧА О ПРОВЕЛЕНИИ
КАСАТЕЛЬНОЙ К КРИВОЙ
Ro 1п·ороr'1 ч<."гнерт11 Х\ТТJ 1~. 11p11tтa111,11f;e н1-111-
маr 11 rc N1:псм:п11 кон 11ач:т:.1 п р1 t11ж:к:1т1, :~a/\:.t ча
о 11рuвсдс1 111и ка спслы 11.1 х..
О11т11ч~ск11е 1 1соrе;1ов:11 r1 1>i /l,Lf\apт:1 11р11 ве1111
его ктакоir nроGлемс: рассч1rтат1, форму J1 111пы
с да1 111ым фоК\пrым р<~сс:тт111ием . i\1J атематн
ческ11 это требоrшше эюншале1111ю обр:пrюi1
Jад:~ чс nocтpoerrrrя касатслыrо lr - 11ахождеrп1rо
кrmюй, нормаль к которо l1 обладает 11<.:кото
ры1.r зщ.рнны.ч сво~'н..т1юы (нсно. что норl\tаль
11 кaC:tTC:JIЫI ШJ в:~аим1ю oлpc;(L'.IOI IOTJIPYl'/ ( iJ~T:I).
ff.eк:1p·1· рсш11.1 1 ::~а1 1ач~ о m 111 :к·, а т~Н<"~С прс:;1л о
:ж1rл пбщ1 1 П мс-m;\ 1юстрос нш1 нор ."1 :ше i1 ( 11 ка
с~т..:; 11,11ых) к крнным. 011 быJJ )'rrpoщ<:11 r-111;~ер
лаJ1дским м<1 ·1·е.чап 1 ко"" 11ог:н11юм ГyJ tN· 11 в
э·1 о."1ycrн1cp 1 J1e 1 1ст~ю1щ1 нюм вл;tе оrтубт11Юн:!11
11 иалашш « Гсометрнн·• Де1<,1рт:t 16'59 1·. Кл ш· а
дf!ь_
EUJ(!J
История мат~мJ.1 ню1
11ы1111 1 а н ;1атинскuм 11срс1юдс с коммсt 1 та рня
"'11 ;1руtп1 о н~щсрлан;1скоr·о учё 1 ю1 ·с1 - Франса
нэ н Схотt.:на .
М1.:·1·щ~ Де1<аrта годился только л.ля <1л~"ебр::~и
чес ю1х (с1м Д1.:к:1р'J' 11а:1ынал 11.л 1 ·еометрически
м11) r<p11nt.LX .
·1 . е. д;1н 1<р1111ых. ураnнепиямн
которых яu;rяются ~uюгочлены ко1 1 ечrюЛ сте
пе~ ш. l lo существуют и неалrебраrтчесютс кри
вые, FJапрпмер цикло1ща - траскторня. кото
рую пр11 вращет 1ни 1.:олсса описыв: 1 ет точк:1 ,
находящащ:я 11 а его ободt'. Профессор Пар11:.к
ско1 ·0 кор011 свск01·0 кuллсжа Ж1111ь Роfiерваль
( l (')()2-1б75) ра~р',161>тал11ру1 ·с.нl мстол. рассмат
р1 IR:J Я кр 11 ну10 юж траекн1р11ю /\ННЖСI Lll Я 'IОЧJ(И.
Еп~ё Га11илей , 1.J :~уч:о~я дннже11не с11аряла ,
бро 111 е1r1ю1 ·0 rorнr :н>r-1тал ы ю, /(О 1«1.1 ал, что
м1·1 юветтая скоросп, ч :кпщы пбусловлена её
учас ти ем u Jtli)'X ие::~аткимых двнжениях -
раnномсрном движении по горизонт;ши и
раnIТО)'СТ(Орешюм cepTПKdJТLIIOM падt:ШШ ILOД
действием сш1ы тяжсстн. И ссл11дш 1женне точ
ю1 t:l'Tb рtзультат СЛОЖСI uш двух ДНИЖСНJ 1(1, тu
касатслы-1ш1 рас11ола1 ·аtтсн по напr:шлс111110
су.-.1 ,-.1 ;1р1юi1 скu1хкт1 1 (р 1 1с..)).Именно этn co-
nnpaжc1111e llCПOЛbЗOH;UJI I Н 0/1,1-Ю 11 ТО Жt: UJIC'MH,
н J 6-1 -1 1·" Тnрричслли 11 Роберuаль. Тпррт 1ч ел
: 111 11пстрптт кас1тtm .1 1ую 1< 11 apafioлc, а Р()бер-
()
J'
Рис. З. Провt>ден11е
кa( JTeЛt>HOll к Пс1рi100Л(',
коюр м1 яuл1-1 е rся
1f)cl t't\ l ()l)lt(:•й IPЛcl,
ljpoш('tlHClГO гор11 HIHlil.'\11111}
с,орость в точке л1
с кмлываt>тся 1н скорост11
p~l!HOM! :j>IIO I О д1J11Жt'111 1Я !Ю
1 1>р11 1011т.1м1 v - MN 11
скоросп 1паления Дt = MS .
Их Гf'Щ<1' 1J)11ЧС'ская сумма
л IV Л<1 С'Т IЫП[JJBЛ< 01!'1 t'
к~JL <' r<-•лt-.1н1й.
11~1J11, - к 1 \11кrю1 1/ \t: 11 некоторым J\py1·11~1 11с: 1л-
1 ·ебра1 1ч еским крнн1,1м.
С поr1стсом тако1·0 пп11оже 11ин кзсате.т,1ю1'r.
в котором 0 11 а 11араллелыта осп абсцисс, тесно
спязана задача нахождения ,..,1акснмума rrлrr
м111шмума фушщиr1. Bnep3i,1c эту сш1зь обпа·
ружил Ферма в работе « Метод отысканшr м:~к
с~1 .\1у м ок н МИ1Шl\·1)ТМОВ». Она опублнкuнана u
1679 1·., уже после с.мсрт1 1 учС: 1-ю1 ·0, 1 ю н c p~/\t.'
фран~\узских i\1ап: м:пиков получ.нла 11 акест
носп, 11<1 1 ю1шска раньrпс.
Реч1, 1 11ла о следующей эада ч е: 11м еется 0·1 -
ре:ю1< {{аннон ДJllfI-lbl /); треl1уе1·ся rаздетпъ его
па две част11 'r':l.f(~li\1 образом . чтобы ор1:1:1ма , ос-
11оuан11ем 1<отщюl1 служиr квадрат со сторо1 юJI
а, равной ncpвofi с1аст11 отрезка. а высотой -
втu р:ш чаL1" 1, отрезка (т. е /J - а). 11мt.r1 :1 макс11 -
l\1:tл 1,н ы й объ61 ( рнс 4). Без какuт бы 1·0 н~1
бшю /\(Ж:J:iатсльства 11;1н обоснс.т:t1 11 rя Фе рма
ll CIJOJ1Ь30BaJI 11p11i.::\>1, paBll()('llJJЫLЫil 11ЫЧIJ CJ IC
IJJIIO 11ро 11 з кою-юй :
1
.
((.·~: + /1) - }(.'\')
"
1111 .
/
: ./ (.\;).
h->1)
,
а затеl\.~ - 11рирзF11mnатппо этой пронзвод11ой
/(нулю.
Рис 4. \,1,ыч1
Феf)мd д,н~
oтrt'~'" , \ { =/J
LГ(! надо рс1Jдсл~ щ
t l 11 ЛАС> Ч1I С-П.I
АВ=а"'ВС =Ь-а
1,\ КИ \.\ o op.1 ·IO'vL,
•1тоt>ы о6ы •м
прймо.-~ 11 Р" """·
1нofip.1>1.P.HHOll
1 ы рщу11кС', fi1н
М.1К( f1'-l~ .\ b Hhl\1
СОЗЛАНИЕ ЛИФФЕРЕНUИА/\ЬНОГО
И ИНТЕГРАЛЬНОГО И СЧИС/\ЕНИЯ.
НЬЮТОН И /\ЕЙБНИU
Несмотря на то что 11 ныч11 СJ 1 сн1tсм площ;щсй
п<щ кривымJ 1 , ti ;;~щзчам11 на провсдс1111с ююt·
'Гtл ы11.1х к кр11в1,1м учi.'11111<:" :1:.J[ J1J м :1л11Ch / (01ю1111·
по f(a rmo, 01-111 нсё ещё 11е уС' матртшалн Ш[КЗ
кой сняз~1 межлу /(В)'?v!Я :;)TJI.'>Ш процед)'рамн
То·1 пс менее связь эта 11мсла фундамснталь·
пос :ш:~чсние , та 1.; 1<ак ~1,азыв~1 ла на общнiJ
характер анализа бссконсч110 м::tлыл. Псрl!ЫМ
Ч l.'ЛClHt'KOM, сумсвшнм это обнар)'ЖJl'IЪ, б ыл
И.с;1~1к Б::~рроу ( 1 6;IO- J б77) .
В 166.1 1. н;,~ срt"дс1·ва некоего Генрн Лукас:1
н колле/(ЖС Сю1то1) Тро111 (Ы (Тр1 ~r 1 ити-ко11лс; (ж)
в Ксмбрнджс был;~ учрсж;~е 1 1а кафедра мат<:м~J
тики. и занял tё 33-нt1· н 11i·\ Исаак Барроу ,
весьма одарё 1Тн ы й учё 1 Th1i1. зпа:вш11й математи
ку стол~, же хорошо, ка.к и богосл онне и дрен-
1111е языю1 . В 1670 r. Барроу 011убm1ковал cno11
•Лскцин по геометрии». где показал . что ()пе
рац1111 ~rахш1щения площади п ттроведе r rня ка
с;1тслыю/1 }1вляютси взаи.мпu обратным и.
н J.\;lJlЫ ICJJll lt м pa3RHT111J [·1нтс1 · рал hHOI'{) 11
д11фференщ1<1ЛhНU1'О llCЧ I !CЛel l\ J}j 1'.%\ВШl~ роль
11ршщц.1н,;:ж:нта дн)·~~ ксликим учёным - а 1-rглн
ч:~нrrну ИСЭ:11\')' Ныотону ( 1643-172 . 7) 11 н см.цу
Гптфр 1 11'у Rr 1111,rcл1>M)' Лейбн ицу ( 1646- 17 16).
Ныото1 1 был самоучкой в матем ат11ке, 1JO С<l
моучкой rепиалъны м . Ког,п;а он, став с·1удентом
Кембр11джского унинсрситета, mrepnыe nрншёл
на эт<замен по математике, выяснилось. что Ев
к.r 1 ида, по которому учили r1 ~1-IИRCJX11'1't.'Тc. OJJ
нс знает, но зато з-нако~1 с.: ~ геомстр11сй» Де
карта. В к01 ще кокцон экзаме11 он Rьщержал -
экз;1ме11~пuр, сам Исаак Ба рроу, 1 юдосто1 11 1с·1·ву
оценил е 1'() матеv1а·1·11 ч сское нарованис. к тому
времс11н Н ыт он прn чёл нс ТОJ 11 ,ко Де1сартз, но
т:акже Ва.1mт 1са 11 Схnте 11;1 11 уже почу11ст1ювал
ПК)'С к 1\.1атематически!'.·f nроблсмам.
И<.1.JК н1.ю 1 u11 П11ртрет ИJ 111л.1ння < О1 1 тики • 1740 1,
Нuвое врt:>мя
13скоре Лш·лню ПОСТПГЛ О ('Tp:.!ШJJCJC 6ед
СТТШе - эпидемия Ч)'i'1Ы. Ушн;ерснтст 11а врс.ми
закры-'1 01, и Н 1,ют011 почтн два года пронfл в
сrюё,\1\ 1юмсс1 ·ьс Вуле1'ор11в 1·рt1фствс Л11нкол 1,н-
1J1ир. Эти l'OJ(Ы ок:валнсь лля не1·0 уюrн11тсльно
1 1лолотвор 1 тым11. По:щнес 011 нс1юм1шал: "13 11:1-
ч:~лс 166') 1·. я открыл МСТО/( 11р11бт1жё 1111ых
JJЛ/~OFI 11 [ [раншrо /l,JIH СВt'ДСН ня тобой стспсн 11
тобоrо 6111юма т< так11м рн; 1,аl\1. 13 м:~е тш·о Жt'
ro,11,a я ОТJ(р1>1л метод 1<:1сатсл1>1 1 1,1х Гpe 1 ·np1r 11
Слюэ•l, а u ноябре - прямоi1 метод флнжо1И". и
в слс;1ующб1 гощ u !ltac я уже имел n рас 11 оря
же11ин обрзт11ьп·1 ~tетод флюкс111r....lkё это нро
н:ютпло в дnа чумных год:.1. 1(>6'5 11 J666. Ибо в
:-по вре!\tн н наход1щся в на1шучшсм 11,ля откры
тшi во::iрастс и ,.'.\yм:ur о матсма ·1 ·11кс 11 ф 1 1жк·о
ф11н бот,шt:. чс~·1 кш·да-л1160 1ю:..1жс ~.
Л рямсн'т мето11, фл 1шсс1 п'r. а которо/\ 1 1 01юр1-1т
Н ыото11. - не что 11ное. как д 1-1tj1фсрснц 1 1 р<1в:1-
11111::. соо·1 ·встст11ен rro обратн L,111 .четод фJ1101<
сий - шпегр11рощ.11111е (см. ст:1 п,ю «Что 1·акое
математ11ческий ан~1з»). 1:3последсттпr 01 1на
писал работу под 11азват111ем «Метод флюксий
r·1бесконечных рядов», тю пр11 ж11:3I111 ош1так11
11с бы!!а 11апеч~1 тшта: в 1756 г. онубтнюван сё
ан1·;111Оскнй щ:рt'.1щд, а opш·1rпVIыrыfr J 1ап111 -
ск11й текс1 у1ш,Ц<:Л снtт m111 1 ь н 177() 1'.
.l lepe~1e111rыc веJ 11 1чнны .~:. у, :: Ilьютон 11:о1 -
з 1 ,1нал флюснтй:11н, т. е. «текущ11 ,ч и ·> (от лат.
nll~ - «ТеКу»), ;.! « О:ОрОСТН, С КОТО/)ЫМН КЗЖ)\Шi
флюе1rта увелнчнвается в снлу пnрОЖJ"(ающе
го J (tШЖCТll·fH ", - ф11юксиям1 1 . О1ш обп.н-1~1 1.J:.1-
лисL теми же буквам11, 110 с п;ч rшй вверху:
Ист ория матем,~тики
JJJ11m1/r.t1i~ J.r 111 ,fj,f ,ul.11.
Х t 1L 1...с' 111t1t11C1\J dct. Q1:111nщ6 fof1JCJ1t~>\ 1..'c!\-& -d3rc tai:.t
rimtia J:\.dc:!';1щш.:nt reutCJ•f .:Z r r• _ ,. _' t' . c(\ion di:(IJllCliь, t1~1111 ,jq_p11•
11с1 11.Je.linuut"tlJ '")CH•t'\ i;Li; 11.110, clk • (1111 r e o n 1111u1-IJC 'r.)l;(!t ~'-'IJ·
roc1\I~) ((ln1 ('(i•шuc: !, _ "' \f~ttG'~ dt: Jcu r Flu, o ')U Л1.i.""f1J11fc-nч:11• .
Х 1V• .i;, drinc !с prndш1d.: 1" ~lefrr.:..: ~щ мс tJ1.ш1111J U.J .:.
fi'l1.nrn1 rctнr.: " • c \.lt .н11 :.:, !i t1• rr-pr~ l\_-.~f~ 1., ; 11 1mu :11.1 d'urн:
Q-~..w.tё ~.Jcli:o1~i:\uc " ~ Lt\ ~"t1щ" 1"1; 1.1. ., ~u.~t~ : • 1
, т,.k\-w.'\
tepr~knt~ ylf ~1~1-., 11..11 1 p 1n:c q\lc:~ , р, .ot•, ;и fощ cl1~u 11.t
~OllHl.М:8 1 f 1 1·,~
.х \f. rwa ОО1к ~JU-' k' ll~.11J1cш1 trid"Щ.~ ;._ , • 1~ (о м IC$ ас"
c cft1 -> "• аи .l.'.l:\1111.111a11of1'1 1 n 1fcl11\·11к11-r 1)1. ll(t '' ~n ~ ,,~щit t. f. l l )i = Ф •
tcs ..: ~ ·"' pcm)an : k5 1л&:ti1~11n ~nt 1•tn1, 1nttrv.il.;. dr 1е1щ., 1) l'lщ
tjll<: «t Qu:inшO " N f -»1•1-U .д~ 1f'!!t.:t1J~ll11! ar.d1.li11 .11!ie 11 pi:tit &
tam., d ;:o,,-1.1.'1uн~nt x+~• & у +;-, , & p~r oauf.!°'1.l)C n• fEqu~ti("I
qa1t.n '""J!:'OWI~ ct1• r11ut iq1Ji:mf't1t IJ. ll ct:irtt•11 .ka t)uJ111u-6 f ·\ucl•
ш,-(',-1pmw:tA- I" lk li!.11(1" С'!НС ~-;.-~" 6;. r+ ; , tOU' 11dfi.tщ-ц
'1tlC:rltrC: Jt 6' J • Olnfi (Щ f~Uf fu!J6i1Ut'f" \l.\IU Ц 1~1С i::qu -a-nQl1
• -+,;• & )'+;11, .цt1t1J ii: •« у
Х V J. $ .Qir di)!'lc l'E:pr.at~U dмn.ic quc:lcьn111c .1 - .t"~+ l-lff
_
, , g;;O JC (11bllui:c ,· + U P'Y.11 ~,&y-a..ju po11".Yi .:.с1·м
Стри11иud
и 3 фра 1шу ккоrо
11JД<IШIЯ • Метод3
флюк< ~,й и
бесконечных рялов , ,
ltме ржашая
объяснение
tlJJИI I Шll lOH
д11ффt'/)! •НШt~ЛЬНОГ(I
И С '-IИt..Л Е' t-1\.IЯ ,
П<1р11ж. 1740 г.
.\:,у, z. Ныотu 1 r таюкс рассмзтр1 шал « моме1 rты
фJ1юкс11й » (в совремешюll тсрмююлогни диф
фереrщизлы). т. с. нt1111чнны xo.yo,zo, 1де о -
бссКОllСЧЛ() M:lЛUC K<JЛllЧC<."П~<J.
Н качестве ал!'оритмз щ1фферс 1 щ 1 1рон:~нш1
Н1,ютuн 11споm,зонал ту же процедуру , ч.то 11
Ферма пр11 отыска 11 11и NJЗ 1<симумо11 н ми1111му
\ЮR функцнlr . Нзпр11;\·1ер, выч1rсJ1>01 1 1 рm 1 :знод-
11у1n (флнжс1110) от х-, оп ттоступтrл бт.r так:
(х+i·o)t _ .\.~
()
х! + 2..'\:\:о + .\'о.\:о - х~ _ )
."
-
-\.\,
(}
причём чле1 1ы, нключающ11е:: и н C'L't:Пt:Hll выше
п<:'рвой, он просто отбр~1сы11:.1л . ~ нбо 11х "южно
считать за нич·1·n 110 сран11t.::11шо <.: 11 ру 1'1 1ми •.
Точно так же: можно IЮЛ)'Чнть формулы прu
н :шuю1ых н /IJIЯ стс:11ен<.:й нынн.: нторuй . Дли
д 11фферс 1 щ11роuаJ1ш1 фу111щин с р:щнкалаvнr н
!\[1Обям VI Н 1 ,юто11 ИС ПОЛllЗОПЭЛ liCПOMOI а·1 ·ен1,-
11ы е 11ере,"1е1 шые, :i для не ;шгебр.нтчсских функ-
1\нi1 - раз11ожеш1е в бесконечные rяды.
В «Мето!(е флюксн11 ~ чётко сформУш1рованы
обе :}адачи нс'-пtслснпя бсскuпсчтю малых:
1. l lo 1tа11ному С<.ЮТНОШСНЮО между <..jJЛIO
CLIТ;IMИ опрсщ:лнть COOTH() l llt.::HИ(; м ежду lj.IJIIOK-
CliЯMl'l.
1 . П о H:llНIOMY yp::ШHCHllIO , СО/\С'рЖаЩС.\1)'
фл1окс1111, 1 1 а~1т11 с оотпоше1111с ~1СЖТ\ У флю
е нтаМLI .
Яс 1ю , что п пepnol1 за,Г\:.~чс реч1, J.Jдёт о ;1иф
фере111 ~111хт;1111 IИ. и мы ~гже шщели, как Н ьютон
сё рсrпзст. Что кас::~стся nтороП, то дать общ11 l 1
ме::пщ ш1тсrр11ров:нпш yp:tвпcrшir n то nрсмя
11е представшuюсь 1юзыож1 1 ым. И nсё жс llыото
нуу{(алось н;1йт1 1 формулы ;v r я большо(1 1·ру1111ы
!!НТtтрал о в , С<Щ срж~IЩI IX 11pp<11\l1UHUЛl>l-IO("l'И .
Все .~т11 открыт11я 6h1JН1 нуж11ы учёному
HL: ca.'Vlll ло сс:бе. а / 1,ЛЯ [Х'IПСН\НI ГJ laHHOJI ::1~1Д~
ч11 - t.о~щ;11 нш 1ю1юl1 ф11 з ню1 . Е1·0 осгюшщil
1·ру;1 - «Матеl\1атичсскпс начала 11::~турат, 1ю1'1
фплософин" ( 16t{7) 1щ.ёт м•пем:~тнческое до1\;1·
зательстnо того фзrпа, что есш1 траекторня
орбиты 1шанеты есть rщппчсское сечение
(эlUIТrnc. п;~рабола ини пtпср б оJ ~а) , то сила пр11 -
тяжешш м<::ЖJtУ ш~анt:· 1·ой 11 Солнцем обр:tтrю
11ро11()рцнональна расстоя11ню меж;tу нш111
(закон все .\111р1 юrо 1·яготсн11я). 3,1'\l'Ch жt: f-l ыо
гон прнн<.:1 1 реше 11 щ' f\.11 ю 1 ·нх з::щач , прt.:ж.тав
люш11 LX суп ~ествс1 п rые математ11чесю 1е труд~ ю
сти , таю1х, ка1\ о6ъясш:ш rc пр~ шн11011, ос1 юпы
теор~ ш ;,вr-1же1 ~нл JI vны, проблема притяжения
массиш1ых сфер и т. п. Uсrrошюму содерж:ншю
к11ипт предпослана н1юднш г ча<.~гь, 1дс: нзло
:жсна теория npcЛL'ЛUf\. Францу:кк11i1 матем:1·1·1щ
L'ийО.\1 де Jlошпалъ , 1<uторый в 16()6 1·. 011убл11-
ков:u 1 11срныii учс6н11к rш 1 1 сч11слс 1 111ю бс:скu-
11сч1ю.'v1<.1лых,11 прсд11с1юmш к нему ш1сш. •1то
R кншт Ньютп 1 1э «."есtъ 11оч·111 все, что 11ред
с1·ат1яе·1 спбой это исчнслс1ттн.:" .
Соч1111е11ия Ньютона по матсмат11кс увн;tе·
ли сnет только н ХVШ столет1111. хотя ocrюn
ш,rc рс:~упътаты о п получшt в ЫJ-х tт. ХVП n
Од11:1ко iюe- LIТO бьuто пзвсстпо его 1<0Jme1 ·;:iм 11з
ш 1 ссм. Так, нско·юрые свои рс:~упьтаты в а11а
J1 11зс: Ньютон сооnщнл Ле f1 nн1щу 11 1676 1'.
ко1·да тот уже сам прнш<.:л к открыт11ю д11ффе
рt1-щи:u11,нпго ll интсгр ~uгьнш ·о нсч11сл<:н11я
Лсйб11н11 со:тал исч11слснис бесконеч11 0
м:и1ых сонср111е111 ю 1 1 езап~кн мо от Ныо'l'Она н
аернод между 167j и 1(,7() rr. На 11em llfXJ11 :l 11e-
m1 бnJ11,11юе 1111е•~атле11ие математнчес1rnс ра
бmъr Паскаля, в особенности то, как н од1Iой
rо<ФР"' '''~"'~' 1
l\1·H(HIИL1. j
ю ~:~дач с 11\1()1\СД(;НЩ:М касате-1 1 ыюй он 11(.' I ЮЮ,
зовал ·1 рtугол:.ьн ик обра:ю ваю 11,1й скоm, у1 ·одно
i\laJIJ,JM l l UТ(X'ЗK~IMl l л:v, ду, лs (р 1 fl' ')) . )1,руr·~1 м
JICf'() 1 IH/,J К( >М ,\•J;JTCi\1 ат1 IЧtC/(()1'0 IЩOXHOl~Ct-J 11н
Лей6н1·11 \~~ был~~. как 01 1са,ч 11риз11:т:111. а1 1ат1-
'пf•1ес1<<tн п:оме· 1 р 11 н Де 1<аrта Н рабnт1,\ nалл~ \Cl
11 Мер1«1 торз о рндах. Уже в началt с1юей работы
Лей611и 1 ~ вnёл термин «фу11 rщю1 » и ппдуч 11л
р:1 зложе111 1 е ар1стJr 11 ·епса, а с его пом ощью - рпд
п
111
-
= 1--+- -
-+ ".
,,
.~57
11:.Jнt'c1 11 ы 1J 11ы11с !{:tк рн;t Jl616mщ:i . Тrеуп)J1ь-
1111к cu стuрш 1:1м11 ti\' . ф1, ilz (<·хаr:1ктср1tCП I' 1<.:
сю1l1 ") 011 p :tCCMJTPI IH:IJJ как 1IJ IC'11'Y·\1CI JT но
('Т\Ю'.:111 rn .:ас1·1 с:;11 ы юй дня :-1ад<1 ч ca!\IOI'() 06щс1·()
тщэ. С 1rомпщып :это1·0 Ж<:' треупшы11п<а Лсr'1 6-
111щ n 167:'> r. устано 1 111л для сrаспю1·0 случ~1 л
n:~аим1ю пбrат11ый характер onep;щнlf. r 1 а
зв;1 пных им влос11сдстrш11 диффtреrщиrова
ннем '1 ш-псrриро 1~:лшем.
В октнбре J675 r'. сдел;Шh! пер н ыс u1а1 ·н rJO
COЗ/\ CIHl l IO H<.'ЧllCJI CHHH - Н J1YKШll ·I CЯX JICJ16 -
ШЩa ПОННШНОТСН ОС! ЮННЫt: !IOHJ.!'l' HH , IШО/1ЯТСЯ
ш1сr;~щш 11 симнолы . Н аконс1~. летоr-1 1(i77 1'. в
от1~~те Ньют·ону на tго второе 1шс1->мо Леl161 1 ш\
СО()бщ11; 1 np:Jmrm1 щ.1ффеrс 1 ЩНJХ'J 11з r 111я прт1 з
веде11ия (э пмешrо d(.л:у) =ycLY + .л:t{)') r1стс 11еп 11.
а ~";lюке cпocofJ, пrнме~шя которы!'r 11ет нужды
освобождаться от нрр;щи()нальпосте(f, ю1к это
1'\елалн математики прежде , а ~юж.но вро11:>.nо
дить дифференцн:роnашrс пепосрсдс'1'всн1rо.
:3дссь же впервые понвr тся тер,"1 r-ш ~;1"иффсrен-
1111:~лhное ур~1 ннсн11е ».
Свш1 ре3уm>1·:1ты Леfrбн ин отrубт 1конал л ншь
1\ 16R41· 11<1 стра11и1~ах журнащ1 ~лс 1 <1 eп1ditoп.1111 »
(•.ТJ1}Лht учf111.1 Х») А короткой стат1)е, 1ю·1·nр<1н
1fмtла. однако, ~11Югозна ч ителыюс 1 1а:шание:
•Новый ~te-1·011 макс.имумоR и .мш rимумов. а так-
J:."'
в
HOHOI-' 8рt' .\1Я
Рнс 5.
,, Л,1р.1 ю ернt п1чеrк1 1 11
r p<'y1 11~"""""'
(l()p,\ '()[! ,НЩЩt С ~..()ЛЬ
VI IJЛI t{) !\\il.ЛM\l& i
;>TPP'lk '1M11 Л \ - t/.. ,
ЛI:['f.., ,\,= /С.
же к;~сп l'JJI,ныx. для юл орого 1 1с служат пpLI 1ят
стн 1 1<::у1 llH щ106111,1е, ШI llf)\)al~ЩHIЗ Jl\,H\\lC \\ё:Jlll
ЧJllТЫ , и ncnfiы{I /\Л Н ~T()J'() рпд llCЧTfCJlё: l t llЯ ·>.
~ осоf>ый рО,'\ исч11С.'1е1 1 1rя " - это, кmrecn ю, ;п 1 ф
фсре11циалыюе исчисле1те. Лейбт 1 1щ пр1111од1 rт
в ста·1ъс пrос1сi-1 шпе rrрав1ша ю1фферс1щ11ро
иа11ия. устанавнива<:: 1· ра~.11ичис межну }.1:1кснмv
,\Ю .М Н \11-!HllMY\IOM f\/)J IH0/1 JI /(:ll:T Гlj): I Bll JI(! J\]IJI
опрс:д<:ЛСННЯ TOЧKll lll'J1CI 11ба. с ЗТОГ() М()1\1СНТ(!
н;~ч111-1а1:тся <>ф111~налы 1 ая 11стор11я .мшпе.мати
'1~(-л-ого CIHtlЛU.ЗCI .
Г1rклепукнц11е с1·0 ст;п, 1>11 . печзтаншнL~С)J в
тnм iК<:' журпа; 1с с Lbl~() по 1(><)7 1·.. бы! IН 1юсня·
щсны ра:щичным 11робле;,1ам ашu 1 н:{а. в ч:~ст
I ЮСТ\1 нorrpoc~LM нrпerpaJir.IJ()ГO lfCЧllCJICHHЯ
(этот Тt'рмиrт также nринад.rтеж1 п Лейбшщу).
llanpнмcp. в ст~t·rъс l 6<J-1 г. уста1-~авщша;цсь
свя::Jь между 111J·1 ·<.:гр;шом п 1 1 ро н звод1ю1·1. лрн
чём проИЗIЮ/ \Н~lЯ p:.tCCM:J 'J'PШ\;u1:1 cь К'11-> танl'L'НС
) гла t1аклон::1 к:1с:пс.г1ы юй к пен а6С"ц11сс.
Jif lтледо11а 1111я Лсйбн1 1 1 \<! н .~нач И'l 't'лы 10!1 C'l't'·
ненн 011ре11еннли ра:щ~-ннс метож,н анал11за R
конт1111с11т<1Л ы-1 т1 Еnропе. Сре;1 1 I е1·0 1н >СЛеf(СJ11 ;1-
телей 11 ~1:юнём 6ра·п1ен Ио1юп 1<1 н Яко():~ Ikpriyn-
mт. Пьера На р и11ьошt и Гнйома l\e Лошпаля.
ИДЕАЛЬНЫЙ МАТЕМАТИК - ЛЕОНАРЛ ЭЙЛЕР
XVI 11 о·ш 1е1· 11с - нCJ\OJtl' ИЙ щ;к l l pocv.l'1дcн11s1
меЖ/()' .~похамJJ жестокой 1r ~тсрпимости. Все
го лшг11, :ia 111с:с1ъ 11е1· /\О рожления Лсон;~рн:.1
Эйжрэ ( 1707- 178.:3) u Бtр.rтн11с была пубт 1 ч-
1ю сожжст 1 ;1 П()Следшrя ве/(ЬМ~I- А ч<:ре:з ПJ tX"TTJ
лет посяе его смер1и.тю1ыл'1 1уш1 Вел нЕан фран
цузская ревоюотt11я .
:')Й111.:ру 1ю~е\JЮ: он ро;~Ш\СЯ l~ ,Y1<1J1CllbKOЙ Т\ 1-
ХОЙ fЛн6щар11и, куд:.1 сп вcci'r Евро 1 1ы пр1 1 е:i
жалп м~1 стс:rа lJ уч~т1ыl'. нс желаш r 111t' тр:п ·1 н1,
,'\l);]1·оцет11юе нрсмн на 1·раж/~а11с1< 1 н:: смуты 11 ; 11 1
рслнгнозные расnри. Так нересслнлась в ero
родной Базель Н'3 Гш1лшщш·1 сем~,я l)ерну;mн -
упнкалъпое соэnсз,J.ие rrаучных талантт-1 по
9Н
Ипория мэтематики
Г.~ \t", \ b 1f)cllllO('lol 17 6 1 1
главе с братьямн Якобом н Иогашюм. Вокруг
братьев Берпуллн с1юж11ло1 саь1ыl1 нр1шй ма
те~tатичесю 111к ружок,11 на пnл1:1ска Ьазел1, ст:u1
треты•1м 1ю важности матсмат11ческ1 rм цен
тром Европы 1 юслс ГL1р11жа 11 Лондона, где уже
11роцнстат1 акадt,\111 1 11 наук КаЖJ(ЫЙ l'O/J, J-1 кrуж
кс решалис~, трун11ыс 11 увJJеТ\<1телы1ыс :1адачт 1,
а 1ш смену им пст<1ш1л1 1 новые .
Поступиn n Базел~,ский утпшерситет, Эйлер
слушал лс1щни Иоганна Бер нулли н подру
жиле>~ с его сы1товьям11 - Ннколас:м н Дантш
лом. Но когда учёнън: орлята ~юдросли, выяс11и-
1юсь, что 11 Швt"йц<1р1rи не хвап1т м<:::ста д1ш 11х
собс_;·нсш tых 1·нс~щ. З:1то н далёкой Россш1 1ю
замью1у Петра 1.и по проекту Лейбн1ща13 1724 r'
был<t учреждена Пете рбургсю:~н А:к:щемня наук
Русских учёных 11е хватало, и трое друз<::й -
Леонард Эйл<::р и братья Да111 1 нл и Н111<олай Бер
нулт 1 отпр<1 н илт 1сь Т)'да А поис~<ах с чае1ъя и на
учн ых подвигов.
Чем только не пришлось за11нматься Эйлеру
на ноnом месте' Он обраб:пывал данные вес-
)J\11:.0 'i))i"\..1 '. .'V\>i "'i\cf)~'1'-V1 ""-~"-~>'t:\''""' \ \'\ \\'lR:>f\~'°1':\
эrу 01 ромнvю р,1боrу в оди11очкv) . 0 1t расшнф·
ровывал перехвас1е1шые ююстра 1 111ые д1111 1юма·
111чесю1с дсш:ш11 (оказалось. что с де1ш1фрой·
кой м.атематики спр.шлmотся быстрее 11 лучше
прочи,""< С1Jе1\налистон) . Он обучал .молодых мо·
ряков вш.:ш ей м:1·1ема·1·ике, ;1с'1'роном 11н, а так·
же о<.:11сшзм 1щр ~1 блсс·1·рое 1 1ии 11 упр:~Rлен11я
гтарусным t:удном n 11п·ш1п 11 н буrю А <::щё со·
ст::~илял т:абJ 11 щы. 11еобход 11мы<.: /(ЛЯ рJсчёта
артню1ер1 rrrcrюrr стрельбы и табл rrr(Ы дmrА<еrшя
Луны (ведь 11 щ1лы1ем 11лаваш ш Луна чаоо за
меняла часы nри 011редслеш111 долготы)
Только гс1шй мо1· 'Ja этнм11 трудам 11 не за
быть о большой пауке Эйлер 11 был гсщ1ем З3
[ 1.J Лt.'Т сносr·о пср1ю1'0 прt:бысатu1я н Росош
(1727- 1 7~111'1 '.) 0 11 ycщ:J I l[~IЩI C:l'IЪ 11еркы11 R
мир е учеб ник 110 ·1·сщк·т11чсскоС1 механике
С.1 11~1 - flетерб)'Р' . Гравюр.1 XVlll в .
(,llL" }'Чlf'l.h Жt: cтy;leJITOK 11() CJIOЖlll>l:vl l{JlllJ':.1~1
Ныто11а!) , а также курс м:пемат1rческо~'11raR11-
1a101111 1."11 югпе нр)'ГИС труды. Пт1сал Эйлер лег
ко 11 быстро, простым н ПО!\ЯТ11ЫМ Я'\ЫКОМ .
Сто:11.> же быстро он ouлaдc:n;v1 нопъщ11 языка
м11. по nкуса кл11п:ратуре ш: имел. Матс~·1а11ша
по1 ·1 ш1щmа нес Cl'O нрсмя н снnы.
В 26 лет !'Э 1l лср~1 и:.~бралн росс1-11~1ски1'<1 :1каж:
\1иком. а чсре:-1 носем1, J 1 ст 011 nсрсех:1л 11:.1 П е
тt.:рG~·р1 ·~1 и Берт 1н. В чём /lсло? Тшr пко ч'ю за
вt:ршшюсь [\<1рствt)В<1нrн.: Анны Иоан1-юш1ы, 11
во:юб1юн 11ла сь чсхарла днnр1ювь1 х псре1юро
·пж n11ш1 ко Эйлера Э'l'С) вnр>1мую l(e [\:JJ.:aлoct»
('l[JIT:l'l'l>OJ v JICMцe .\.'l» fl П етербур 1 е было безо
П:!СlЮ 11 престшкrю, а учёньLх- немцеn ценили
ш вес золот;~. 110 оп \1Же по•1увствоnал себя од-
1111,"1 пз с 1 1лънсйшrrх "'tатсматикоn Еnропы -
11 uдpyr заметил. что здесь CJ\1Y нс с ке,.-.1 па
р:шных по1·онори1ъ о cnoc1~1 науке. Пrиезжая
11НОС1 р;.11-111;,~я ,\.IQJ IOftfЖf, 1IOBЗJX>CJit'ЩI 11 !lибо nu-
IOll·ryлa д11 кую, п1 1 асную Россию, 111-1 60 погрязла
в мелкоr:1 ·1екущсlr р:1nоте Л ncpRoe nоко11епнс
уче11ых-росси~н сщё 111.: выросЛL> . (Вспомним,
чтп ЛомпносrJ11 нахо;\ило1 'H>rl(a 11::1 учёбе 11
Теrмз11нн . ) Эйнер pe111111r переелатr, туда, где
1ш<~ш науч11ых J\искусснй был шшы111е. 011
яыбр:т Пср.1п111 - там молодоf1 король Фрнд
р11х Il рсrш JЛ созд;~ть 1тау'-111 ый центр не слабее
пар11жскоrо .
J(1лср п роuсл к licp.11ш1c чет нерп, иска
(с 17.с/ 1 по 1766 г.) и t:ЧИT<IJI э ПI ГО/\1•1 Jl}'ЧНIHM11
н своей ЖllЗllll. у 11е!'О ннонь ПOSШIUIOl'h МJЮГ()
дру:1с~'1-~11 1С::r 1ых, в IIX ч11слс прсз1щснт Бср
:1инск(н'1 акздемтт 11 аук ТТ1,ер Лу11 М()ро ;1е Мо
nсртю1 '1 ( l 69R- l 7"59) Физ111< 11 rет·раф, n11
проnернл r·ипоте:зу Ныпто11а п сплюс11утостн
зе,,нюгn 1u apa nn:.лe полюсоn. Л;1я этог() 011 пз
·'н.:рял дт11 ry градус:~ мс:р1щаапа п Jlзплаr 1;щи.
Новое время
н то вреr"l.Н как е1·и коллеги выполняли ·1у же
работу в Н1жной Амернке. Мопе1т1 юн решил
n рсf\зойтн Н ью·гона, откр r.111 1ювый мэтемзти
чесr<иii :>а rюн прнроды - приr-щ~ш наимень
шего дейстr~ин, которы.11 выделяет трае.к-тории
rеалыюrо [\nижепия тел (11а11ри:мср, 01<руж
тюсть и параболу) из огромного множества
rюобра:~им1,L~ траекторий.
11/\Сн Мопертюи была хороша, но её матс
м ат11 ческ~н~ су 1ъ ок~~зал:кь оченп сложной, и
нотрсбовалась помощь 3йж:ра. Тот понял, что
нок1,1й закон относится к област11 иарl!~Lцtюн-
1-101·0 11L ч1 кления. Эfrлер coзr~aJ1 это 11счнсле1111<::
11 1740-t 1т. Пр1шц11n М о1 к·ртюи стал пдн11м 11з
11ерnых 11рпложе11иl1 1 юnой 11аую1. К нему
·:iйJJ(~p сделал замечателr,ное добаuле1П1 е. 011
заметнл. ч'f'о естестnеrшыс мате.маттrческие
услоиия ,/'\оn.ускают траектории не только м11 -
1шма ; 1 ыюго, 110 и максималыю1 ·0 дейстuия.
Пращ\;\, в Mt'X<tliикe этн ,\ilаю.:vtмумы гючему-то
нс 11аблl(щаютос но 1З 1~руг1х 06J1астях ф11з 1 1-
ю 1- h-1·0т1ас1 ·'
Д1)1'а; 1ка П 1111ера 11()/~TRcp/~1mac1,11t11.111, в кон
це Л'Х 11•• кот;:~ ф11з11ки н<tчз;1и нзуча ·1ъ нера11-
1юнссныt' снстем 1.1. спосо(тые 11зме11н1ъ своё
с1 тюеrше и з1ко11ы с1юеrо rюведс1111я. Ока:за
ЛСКh, что '1 ::tкнс nерехо11.ы, nырзжаюm~н:-ся R
и:~мснеш-ш СП!'-1мс.-триi 1 спстемы..ГJ)'lJШC nсего
01 t11сьmато·1 ся траектор11ями экстрс:малыюrо
(n часпюсти, макснмалыюr ·о) дейс·1·ш1я.
Эйш~р заm1мался самым11 разными проблс
мамн. и почт11 нcx:r;ia - ус 11 еш110. Напрпмt'р,
захотелось ему 11ере11ссти нее мет<щы м:~тема
т1 1 чсско1·0 анат1 :i:1 на фу нкцни, за~н1сящ11с от
ком1111t 1<сны>. ncpcмer1н1i1x , 11 он создал ·1 ·ео
рню элементарных фу11к11ттй 1юмлщ·ксrюrо
Пhtep Ау11 Мнро
д.., \\0111ер 1KJll
С)С)
Истприн м.1Т(:'МJ г и к~1
/\P(\H,1p t.
::1<t\<" P
Пщ>1рр 1
1моu1ы
) X 1-1HЛM1tllH.1
С.еред1tна
\Vlll в
ll(:peмt'H!-101 '0. l lu 11 y1·нo К Ы ЯСНJ IJIOt:b. у 1() 1юк;1 -
j;JТ(;'Jt1,н:н 1 фун1-щин (:-;кс1юн<..:нта) l l с 1 1 нусо11л:~
t.yrъ J\11<..: с."1011011ы ол.1 ro11 мt:лалн . Это пыража
<:тся фо р .,tулой
(!
11
= ('()~t+i'>i11t.
которая гt:ок:.~зывас1 01 np11 по м ощ~( с1·ене1 шых
рядоо
llo коль скоро экспонента п сюrусоrща
•'Сёстры.- , волткает з.tысчатt'лы-шя сннзь _,1tж
ду •шслам 11 е (ос1юв;,~н11<..:\1 с:tм 1,1:< удобных :ю
гаршрмов) J11t (OTШ.>JJJCIJJJL:.M ДJLJ JllЫ ОК!1УЖНО-
ll\TRODUCTJO
IN ANALTSIN
1NfJN J TORu~L
1. L 01'1ПJ\ RDO rut..FRO , .
PrtfiJёn 'Rp BJ\a. OL ltffWSlt d 4lllitм1AI•
~-.ЮМ//llllfftlfJ !'J.Тa.OJ'OLIT41)tA
.
w..
r1\;
1,JlJ~'us
AVS~"i N A
~w-J Al.t.t . t "t u 11 1"11-.нн1. 8<н1н~Dt 1 i. Si. .o.a.
100
L11!11< 1'!(J~1l~
"r''г r-1~tмuц
810 1 ~' '!l<IH!lt. 1 • -
"''~
"." ....,1
,,,..
•;•
,."
.• •"
",1 ,." .." (>.
".
,,.""~,..,,~. t..lo
'f~~::-;:.1.::~:~··:~·::""""
11
1,
:~.~"" •_..__:._u.,:~.:'j . ... .
lLl t yAt·ltt..lй Л"ll
11 nРрв.1 я (' TIJ<lHlllJJ kH111 ll
Л .::1i1л1:!р,1 "Bu(!д(!ltltt!
fi dtt,J ЛIH {H"'t. K Olt t"ЧHt'>IX "·
1;-4в ,
сп·1 к ; (11 ; 1 \1С1·μ~) Т lоскольк~ нррац1ю 1 1а:1шос1ь
{;' )_(()К;1:·11,ш:1L:ТСН (. ран1-111 · 1·с; 11, н о 11pUL'1'U (уж очень
}/(OUllhli'I рнл1-11/JI+l/21+ l/jl 1- l'XO[\lllCЯ
1< :')ТОМ} Чll СТ\' ). то, нal1l'[11-10l'. 'l 'OT же 11 )'1'1> 11[)11·
вс,11ёт 11 1' /(0 1\;'JЗ3Te,11>t~I ну 1 1 ppa 1~I JO H <1Jlbl-IOCTLJ п
О,11;1 rако. " пусть '\.1ОЛОЛ111 \" м ~п ел1:1 · 1~1ю1 одо.1с11п·
эту дреш 11ою проблслrу. аЭйл(>ру cm111h1 ужедос
таточrю ! Так рассуд1 1J 1 учёны!1 - н нс ош 11 6ся·
в 1766 1·. Иога1111 l 'c 11 p 11x Jlзмберт нашёл до1<а
J~1·1·с~11ьст 1ю 11ррац11ш 1алы юст~ 1 л .
'!'о же бhlJIU с нсJ 111 кu!1 'l<:u p<..:мuf1 Фсрщ1
УсJ1ы111ав о 11cl1 . Эl~лср p<.:11111 J1сам носст:11юu11ть
)r1pa ч l'111Joc: дока:~а'1·t:J1ьстно Вскu рс u11 11μ 11шt:л
к ~ 1 <..:-1 оду cnyL к:с к.tк 11 Ф<.рм:1 Hl'\\lJ\1 p:1111,111t:
(С,\1. статыо <- lk.-11 1кая т<:прс:ма Фc:pvi.J») llfIOHe·
р1111 е1·0 длн п e 11t:11c-i1 ~ 11 1, ::Эi 111с:р (1бра'111лся к
следующе."1У щюс1 сшуnою.i~Пс..:лю -
'1 "1\т llCJ3·
fl\1I0111 З<t'l'ру..:~.11ешш. 11 0 1l OCT,11Jll. I ' 'JTY Tt'M~ М()·
.1(.)/\Ы~I I!LCЛC!\(Щ<ITC.1HM.
В л:омстршr Эlпсра 1штсрссошJ11 1 11е столь·
кu ноные ф.~ю ы. сколько общ 11 с тсоро1 ы
щ: ую1~1;\ ыв:11011\нссн в 1ю 1 ·ма' 1 '11ку t:нк"111;щ fl<J·
11p l·J1'v1C p. ' 1l'орсма () Cl:SH ~Ш .Чt:ЛЩу Ч ll C!l:I Mll нt:р·
l11HH , рё6t:р н 1р анс[j HЫII) KJlOI () ~ )) I Ol'Ol'paн-
111\Ka: R - Р
-1 Г - 2. :'1т~· формулу J1ш1 l:Ще
Деt<:1р·1, 110 llt'<X~1-:1 1111л L'fдoкэ :ЫTCJlhCTH:I :>111лер
легко 11 з111ё.1 1 / \<Ж:вз·1·еJ1 1,с1 ·tю. а т ютом .1а1lумш1ся·
еслп фор:v1ула t:npaвc11,.rrтrRa f\IOI 1 кел в1.111~клыл
тс11, то ч&ё же своr1ство онз nьrр,1ж.1ет·, bl()жei
б ыть. свойство сферы. в котор)1О можно 11е
фор.м11ровать любой вытrу1<Лыi1 :многогр.uш r !К?
Т01д:~ 1 ·р,1 н11 превратятся n «стра 111,1" , а рёбра -
R «1ран1щы ». Есл 11 так. то формул,1 в 11ядш 1 <'пра-
1:1сдш 1в:1 /l.JlЯ "Ка рт·>, нансс(:н1-11,1х на дру1 ·ис ЗJ)t·
КН~'ГЫ С ГIOHl'P'<l-l()CTI 1 R роде тор:1 llЛJJ кр<.: 11) \(;, IЯ
llp0 11t'rкa Jl(Ж:1:1ала: /JЛЯ Hl'IШTOjlblX '· l\Э f' I " 1Щ
тре п 1,1р;111<е1 11tе IЗ - Р + Г пр11н1:~маl'Т :111аче·
11 ие О. ~1 11::i 1<ре11де11е - :н1::tчtm1~
-2 Но t((Ж:I·
ч ать эп1 равенств:~ ,'J/Hl всех rсзrт 1 1~111:11111111 s 1 ш
нерх11остях ~)ИJ1ер пе су:v1ел п опят~. щ·та1111J1
рсшснпс проблс~1ы п о·юмкам . Удзча 11p11uuтa n
l 89U-c lT к А11р11 I lу:шкщх:..
В l 766 1. Лсоп:1рд Эiш<..:р покинул ficp.rш11 [J
ксрнулсSJ н Рuссшо. Новая россш1с1с1я 11мперэ·
тр1111,<1 Пк:1·1 t:р111-1а lT . не мка n u 11ро11схождс1111ю.
1tpeJ \J l <JЖllJШ У' 1 ~1 IO:VJ) 1ораЗ[\О JIY ' 11111 н.: ~ СЛОВJ IЯ
Жll Зllll, Ч (;,'v] TL', ЧТО пpL'/(OCTaHJIЯ!J CIIOJl!\I ;1 к:ще
~1111('1М ску11011.11ы1I и к:111р1 1~н1ыl1 Фр 1 щрш: 11.
Надн италась старосп" JL()Э'I O ,\t) :)(1, 1 с-р co1·mt·
силен. Тесrюс оащс 1-11 1 с с J 1 ,1у ч1101~1 м оJЮ/\ёжью
е1·0 ~-же 11е увле1\;m о. Он хоте.'! усп"т1 , 11з1юж111ъ
rra бумаге бесч11сле1 1 t 1ы е открьп 11н 11 .10ГJ.\КН
кото р1.1е осеш rлн с 1 ·0 в <-Золо'l}'ТО•> 6ерлшrску10
нору. Тружкnосuбность 11 1щох1 юnст 111 е э'Гоrо
че.rювека поrа:m' 1 ·сльны: вес п:!уч1tыс жyr11::111h 1
Евро11ы 1юст<нн1 11 0 1н:ча· 1 · алJ 1 н оRые сп1·1ъ11
~)йлсра, 11тем н t: менее.: м1 ro1·1rc t.:I' () труды так 11
1 1е ~1{11дсm 1 свет прн жнз111J :штора.
Rc кopt· rroCJ tc 11t:pct':Щa в Пе-1 ·с:рбур1' учё 1 ют
1ю1х1:~11; 1а слt:потэ . liеукрот1 1 мый старс 1 ~ про
;1олж:~11 раб(У\':пь - J\11IO'OH3'\'n C'TaThll \'\ КННПI.
Н так до caмolr смерти, rюторая пост1 т1а el'O
т 77- м году жи:щп и 11а 16-м го:1у слепоты.
За rою.1 пребьша ш ш Эйлера в россиi 1ской
CI ОJШЦС вокруг HtTO выросла Ш::Т<.:рбур 1'СКШJ
ма·1·с.•-~:-~т11чсская 1шшш1 , более ч с:.:м на п олот 1 ну
сщто}jвшая ~в русею 1х учёных. Тогла ЖС' :~авс.::r
uшлась 11)•6J11 1к;щ11я 1'J1ан1 юй с1·0 тrшлоr1 1 1 1 об
1 l овое врt>мя
OCIJOB~IX диффсрС!П~lt<lJIЫЮ ГО н н11те 1 ·1х1лыю1 ·0
нсчисж:пия (no 11ей почт~ 1столетне уч11m 1сь ncc
свро1н::йскис матем.:1тню1) . О11а выгодно от1ш
чалась 11 от -. IJa<-1;ш,> Е11кл 1 ща.11 от <·М:.пе,\1:.1т11чс
ск1 1х нач~ш шJ·1урат,ной фrmucuф 1 111 ~ 1 ! 1 .к>тона.
Воз 11с; (я tw1poй 1юс зда н не ма·1·с.:ма· 1 ·11чес1<О1'0 аны-
1 1 11 з :1 от самого фущщмснта , nluн:p нс y6r~u1 т<.:
леса н .11есп111цы , по кспорым <)Н сам 11:16нр~u1ся
1< с 1юнм О'l' l<j">ытиям. М 1 юп 1 е крас11ные н1>1·:щкн
н 1 1~1чалы1ые r 1ле11 дока:1атсm,0·11 coxpa1Je11 1.1 11
тексте. несмотря 1 ra СО/l;Сржащ 11еся n т 1х ош116 -
ю:1, - u поучение все.ч 1 1 аследш1кам Эйлеровой
мыслн. lkрвый учебник, алрссова1шыf1 нс rю
слс;~оnа·1·слям, а псслсдuliатсдям - тако1ю :.1аrк
щаш1с Лсuнарда ~)йт: ра и нссй :-:111охт1 Прuсвс
щсн1111 1 ·рядущим Нt'Ка .ч 11 11 арuд:.1м.
XIX ВЕК: ОСВОЕНИЕ АБСТРАКТНОГО
ОТКРЫТИЯ ГАУССА, АБЕJ\Я И ГAJ\УА
Есл11 н ·1 ·еч.е1 шс 1\1НОп1х столетий алгебра за
ннм;.~.11 ~н.ъ рсшеннс~1 уравнсш1 !'i , то в XL'\. в. ct
l \l'JIЫO е1·алu 1 1зуче 1 1щ: <1JJL'<:6p:111ч<.:c1<11x струк
тур. Этпт 1-ювый ур< >нt:нь аборак 1 ( 1 1и сш1 зан н
нсрвую очередь с работам~ 1 1:1ет нщ1·0 нсмс:1 t-
1ш1·0 ,\1 а·1·с: •-:~:.~тrп<з К1 рла Фрнл. rн :-<а Г<t усе а
( 1777 - 1~')')).Его заJ1.1ечательныf1 тру;( "Лрнф
щ:·шчссю"!с исс;1едон<tпия~. ()11у6лП\\()11<.1ш1ый n
1iIO1 l '. , ознаменовзл рожле 1 1 1 1е соnрсме111 юй
•\l<l'fC,\.laTI 1КН.
Га\·сс L1сслсдо 11ал зада~r, 11а;\ котороiТ труд11 -
.11 ш.ъ
1.: щС ма·1·t ,чат11к11 Дре1шсl1 Грсц1ш: ка1<0с
Кар., Фр..,дри\ Гаусс.
ЧllCJIO стор он ,~ОЛЖС:Il ИМСТJ, 11рав1 IЛ Ы rыi1 Иl IО
ГО)ТОЛЬНJП;, чтобы el'O м ожпо бь1J10 п остр оить
с помощью цнркулн и 1ш 1 1сйюL? Древние грск11
умели строttтъ М!ЮГОУL'ОJLЫШКН с чи.сно м сто
рон 1.
-1
.
5. 6, 8. 1О. 1). Uнн :шат 1также. спо.
l l MCH 11ран1шы1ы1'1 MH< ) l'O)'ГOЛЫ 111K, Jlt.:l'K() уююн·1·1,
ч11с1ю е1 о стnрон. А но:3 .ч ожно ш 1 пострш:111к·
r(ирку:1ем 11 JIHllCl-fKOJI Mll(JJ 'O)TOЛЬI 11 11\ОН с 7. 9 ,
1 l , 13 rтopnнa'Vlir' БОJ1ее ;tв:'х тыс}JсL л ет \1атс
i\1:1 ·п1ю1 пс 111()\'Л\1 (Y\'\\CTHTl1 Щ) ЭТlУГ Т\011\)ОС.
:Ю марта j7C)() 1'. , за МС СЯI UlO CllOCГO 19-J1 ет11Я,
Г;~усс сл:сJ1ал о чеш. n;iж11)10 :~аш1с1 . 11 /(11ешшкс.
Е.\1)" 'm:1Jюсь дсжаза·1ъ . что с по~ющыо цнрку11 я
11 лш1с~'1 ю1 строJiтся 11ранш1ы 1 ыiт 1 7 -у1·олы1ш;:.
в '1'0 врС\1 Я юноша ГIOC'J')'llaJI R l 'ё'l"l 'llНl"CIJ CIOllf
ун11нс1х1 1Т<."l' 11 tщ~ 11t рс11111;1, чс~1у 1юсннппъ
ж11знr, - "1:1·1·смат11кс 11л11 ф11лшю11111 Uткры
т11с:, сня :!аннос с rrр:т11л1>11ым 1 7-у1 ·011 ы1111<ом ,
Oll[)CДC!IJ IJI() t: l'O RЫ6Ор 11 п щ н.:3у м:1тe'l1 : Пll l\l I.
В "Лр11фме' 1· 11чt'сю1х 11СС.!1 елоR:11п1ях " Г: 1усс
сформу.rтирон;-1 1 1 теорсJ1.1у: ес1111 /1 - 11р остос
ч11с.11п 1111 - 1 = р,р2 ."р,. сст1, ра:~11ожс11J1е ч11сJ1а
11 - 1 11а простые м1юж11тсm1 , то рсшсr 1 1 1с ypJn
нения х " - 1 = () своюттсл к рсшсттю /..~ урав
нс1птr1 сп::ш~ш:й fJ 1, р:.· ".. Р1.:· В частностн , ссл11
1l - 1 = l"', уран~ ICIII!l' .'>.'
11
-
1 = uCBO/~ll'l'Cll к це
почке кваJ1.rатных. ура1111сни~"t.
/1,лн на1·ш1; 11юст1 1 11ринс1tём такоl1 11р11мср:
5
.
,j
\
'
х - 1=(.У- l)(X +х +х-+х+1)=0.
10~
Ип·ория м<~т~матики
IJIS•zl' IH1·10NH$
ARTTHMETICAE
Ll,StAE
ОТh'уда
Х-\=()llЛH
·1>11у~ы1ы~1 \>11 1
nepвnro 111л.1ния
~11111 И К Ф l,tyll,I
~ Ap11cf>м~л 1чert1.11E--
11tt л~·л/нs.111ия)
Ле11щ111г l IIO 1 г.
х1+х'+х!+х+ 1=О.
Последнее ур:~ннснис ра:3J\с..:J1нм на х!·
'
11о
x~+x+I+-+-~
х .,.~
Прои:теля- замену
11 3:tMCTИl'I, ЧТО
1
z=.:'(+-
\:'
'
'
1
z-= x- +-,+1.
~·-
""
nолучпм N!Я z ураu11е11ие
z!+z- 1=О.
;\ /\ЛЯ .\' ИЗ (*) уравнснпс
х~- z:\·+1=U.
(*)
Реше1111е уршше1шя х5
-
1 = () сксдснu к решс
ш 1ю дnух квадрат1 1 ьLх ура1шсш 1 1-1 и o,1нu1·u m1-
11сt"пюго.
Ypallнcю1t:х1-- 1=О('!'. с. 11- 1 = 2'
1
) oю
J\t 1тся к чстырl:м кн~щратным ур::т1 1 е11ням. и, слс
донателыю, 1 1 rан1 1 1 1 ы1ыf1 1 7 -у(олы111к можно
посчю 1 IТL с 1ю.vющью 1\1 1 ркулп 11 mrнсйю1. Гаусс
дuкаэал. что в том случае, кut /\a ра зложснщ:
ч11с: 1;L ll - 1 содержнт множ11тсл 1 1 , отличные
от 2, ураnнс1-111сх" - 1 =О 1-н::m,Jя скесп 1 к1\епuч-
102
К<: квадратных урав11с.:ннi1. Л з11ачнт. 1 тевозмож
r ю /l<.:J 1 <:1шe окружнuсти 11а 7. 1 1, l .l, 19 частеiJ.
~лр 1 1фмет11чссю н..: 1кслсдоn:.1 т1я" стат~ на
сгш1 ы ю!1 KHI ll'UiJ M:1T<:M:JTI lKUll XlX 13. lkнь :щссь
cn;~epжaЛIICb l l t: ТОЛl>КО }/рюн; pt::.iyJ IL>T3T bl , но 11
rю111,1!1 матс,1ат11чесю 1!1 ш 111ар:1 г нля нсслеяо
nат 1 ия ат·еnра 1 1чсс~<11х урат-1с1шr1
llапомl!нм , ч ·1 ·0 сщё матема·1·11юt Дрепнего
Междуречья р1ел11 решат~ , Юi:.tЩJ;tт11ые ур::11111е-
11ия, а в XVl н. n ИТ'JЛIJИ были 11::11\~е1 1 ы фор;ч~лы
дт1 корней урш.з11е::1111й трс1ъеi1 н четвёрто1· 1 l-гt-
1 1 снt:1I. Пuщ:ю1 фор.,1ул /\ЛЯ ура1шеш 1 lr пятой
< "l 'l'П<:н1 1 11 ньнщ; уснеха 11с нме;ш В l 77() г.
фр:.1111tу:.кю111 .ча1·см;1т111< >Кспс.:ф Лу 11 Jlа1р;шж
( 1756-JRJ.)) к р:16оте •P:t:Jмыш;1еш1>1 об ;1л1·е6-
ра 11 чl'с ком p<:LIJt: 1 1н1r у1х1 к11е1-1 1 1l1-> кр11т11 1 1t:.'ск11
псресмсп 'рел 1к<.: су11tеств) 1011t11t: мс.:тод1.1 [1<.:111t:-
1шя )1Xtm1e 1111!1 11ерnых че·1·ырfх c1·L:пe-11e1't, что
бы ПOILЯTu, поче.v1у l lll o;t11 11 11.3 lll!X 11(; Г()/lllTOJ
мя ур:.11ше1шй плтоi1 стеn~.;нн. Ла 1 р~шж н11ер
выс рассматривал rруп11у подста110110 1-: корпсй
ура.1шсrпн1 (см. статью ,, 1·ру1 1 nы » ), указа ~\, lJTO
т~uрин IIOДCT;JJIO I IOK ЯНilЯСТСЯ <- l!C'l'l l НLIOiI ~ICT::t
фн:ШJ<OCI рсшсшrя ураннс1-111й».
В J А24-1826 1·1 · молодой 11орnсжск111! учс-
11ыl1 Нш1ы: Хснр1 1 к Абст, ( 180l-ltiL9) .:~.uка
:1ал, чтu 06щt:t'1 формуJ1ы J1,J1я р<:шсн11я ура11не-
11иl1 степсн11 11 :;;,. :; 11t сущсс·1·кует Лр11 это.\1
11екотпрые ур::ннrснпя \Ю1·р· бытh ре11н::111,1 11
радикалах.. а друп1е нет, n 182С) \',. 11<:::'\адолгп до
свое i1 бе:шречс111ю1'1 смсртТI. Лnелr1 опуf>л111ю
nал •Мемуа.р об ою-юм особом классе алrс6ра
нчески разреuшмых ~'ра13не 1 шf1» . Н ьше 11х ва
·.~ываю1 :lf)слсны1,ш ур;ш11сшшм11.
l louыe круш1ые отт<рыт1 ш u :.tJU"c6pc С/tелал
моло:~;от·1 фр;шцузсю1й уч<.: 1 rы1'1 Эuарш"г Г;шуз
Нилы. Хенр11к Лоель .
Memoir в
l c t 6qr1ationJ at s~briques
. , , ,. 6./ofi•\11!1'0 1 "roшi""'81• i•" 1tнt1.t." 4• rеч..-111.-.. ьblta'lir
ф,, 01111(11!f11t•~<tl
Ga r1•11tt\1&
O• lir-1,,,., .1•" tlt••_ . l"H
lftt,.
« Ме"1уар об uл1 ю"'
oco6o\t tUн-lrCP
алг~орм 1ч<"ски
f) rl iiJt'Шll\llol X
YJJ~ 8H E'Hl111
Н Х: Аб"""
И1л,1ние 1R24 г
(1811- 1 ~ ."il) Развивая lЩCII лагра rrжа, Гаусса
нАбt'!IЯ. 0 11 1юстаниJ1 и блесп1ще решил :заf(ачу
о 'l'OM, KdK по ннл;у yp:iю-t('H l l}I .\·
11
+a1Xl/-I+."+
+{/" 1-' + а"= о 0 11рС/\СЛИТЬ, pcш~lC'f'CJI ЛJI оно н
ра;1ю<ш 1::~х ('1. t . существует т1 форr-.1у;1~1 кор11tй
да1 llIOГ() )1)аf111е11ш1 ). Д11н знm> 011 JШtЛ ГЮПЯ-ПIН
лшш 11 rр~тmы по/~;ста1101ю1< 1юр 11е1:1 ура1111сrшя,
те мешнощнх прав11лыю сп1р::щ1ю11алы1ьrх со
отrюше1шi 1 между корнями~. cтanrmtt." oci юш rы
ми в теории l 'алуа. Dнар11с1 Галуа пог11б н;~ ;~;уэл 11
n .Ю ж:'l. Свои рс:1ут.таты оп очень I<P<.11 ко из
ложиJ1 11 ;1нух м с чуарах 1~ .-юг. и в mtеьмс. н ;111и
rа1111ом н 1юч1, nc rк·1\ 1юс; 11шкuм.
Потрсбонашкь дсопнJ 1 е1 · 11и , • 1 · 1·uбы тсорш1
Гал~'а ст:u1а 1юняп1 а м:пt::матш<ам. О нt.:й рас
rказ;v1 в 187() 1· фран11узск~ нl уч~11ы~'1 Кам11m>
Н овое время
Жuрдан в «Трактате о 11 0/\С'rанов ка х 11 алгеб рз -
11чсс1шх ур:1внснш1х->. 1Jo м~рс то1·0 как н ;m1·сб
ре происхо,п;r 11ги нзмснсн11J-1 . с11з 1iа Г:туз росла.
В 18SЧ 1 а111 m1i1cю п'i мзте м атик Лрту[> Кэли
( 1821 - 189'5) ; 1ш1 общtt' опредслсшн.: 1·руппы
как конечного м 1 10жес·1 ва объе ктов пр оиз -
1юлыюй природы с :-iaj\a1 11 1ым за ко 11ом 1<ом
nо:J1щ1нт, который удовл етво ря ет услониям
ассоц~rат1rnностн, С) ществоваr шя е;пrю1цы 11
од11о:шач11 ой ра з ре11111мости уравш.'11нй а.\= /J,
J'CI. = /? ДдЯ ЛЮбЬL'{ С/ И lJ. [-{ 18<)8 1' l!С.МеЦI<НЙ
учёнш'1 Генр11х Вебер (1842 - 1 У 1 5) ссl.ЮРМ)'ЛИ
rюкзл :JКСИШ,\:JТl-1 Чt'CKU{; 01 1() l'ДеЛСН1 lC 1'/)УП IJ Ы ,
Создатсл "1 теор~ 111 гру пп исходиш1 из про
блемы раэреш1 ~мости в ради кал.ах ат·сnранчс
с1ю1 -с> урав11<::ННЯ 11 1•1 :ЗУЧ~IЛ11 J'Л;HlllЫM оnр<~:юм
rpy11111.1 1юд<.та11()пок еп) кор11сй. Те 11 е р1) же
группы 11грают ~цжr1е1~1шую роль тю ч1ю 1 ·н х
областн.х Шl)lШ: fl тепр 11н /Щ ффереrщнальных
уравнений (rpynпi...i Jlи). н фи:щкс (группа Л о
ре~-ща), в геометрии (rр-у 1шы прсобразонаt111fi).
«ВООБРАЖАЕМ ЫЕ » ГЕОМЕТРИИ
И·1ак. в x rx Г!. ~1лп.:бр<1 нес 60JIЫ lle ;1 бс грап1ро
наJ 1 :1СI> от 1 1р11 г:нщ1,1 н:.!учз см ых оnъе1пов. CтoJrh
же p eu<>JllOl\l lOJ ll l l1IC ll:iMCHC!ll IH llj)Ol ICXOДJtJll 111
n гсомстрт1. 0 1111 с11я:з:-~1-11,1 с JТ\1er1:iм11 К Ф. Га
уссз, Н. И. Ло6ачеrsсJ<сн о, Я БолLяя 11 Б. Р11ма 1 1:1
(см. статыо « Гео.метрIIя Лобачсвс~со1 о").
Jlocлc того ка1< n 111 в. до 1r. .:> Евю1нл т1зло
жи 11 CIJC'I сму ;!!\СНОМ rеомстр11 11 , Hl11 1.\1:tl1Ht:
учi..' ны х 1~ '1 '(.' ЧСI ШС MHOГllX CTOJ I C'J.'llЙ было 11~1
111хшлс1-rо на : 1кс110м у о 11араJUlслы-н,1х , кuторую
назhrваю·1таюке1шт1>Jл.t 1rос1ула·tом. 01.1 ,11:J 11 :J et.'
И<..тор11я мdТt'мд ·1 ики
фор_муm1ронок зnучнт так через точку Al, лежа
щую J:\1-H: прнмол АВ, н 11лоскос'1·и АВМ можно
пронсс1·н толыш одну нрямую, параллелы 1 уюА.Н
Ма·1·с.\1а· 1·11 ю·1 е~ремндись либо за_11>1снить акс1ю
_\1у () пaraлЛt'Jll,HЫX ООЛС:С 11рОСТОЙ , И11'1 ')'ИТНА I Ю
яс1 юй , ли()о /(01<a:Jaтr> её как теорему, 011и р:шсп
H;J ЛРУ l 'Иt аКСИО :\1 1 >( <- НЗЧЭJI·>, nри этом 1шлот1, до
Х1Х к 11икrо пе С()М11енался 1 ш r. \К' 1·и~шост11
П>fТОГО постулат~~ . ни в том , <ПО СlЗЮlИДОRа
геометрия C}\ИllCTUeIIIIO UO:ЗMOЖii<lH. JIИ п том,
<по orra ошкьшает реалы 1 ыi1 фи:шчсский мпр.
Гаусс обратился к теорш1 rrа раллеJ 1ьн ых в
1792 1'. С11а•1щ 1 а он напе suн:я 1\(Жазать 1 ш 1нй
тюстулат. но зэтсм нrи111ёJ1кмыСJ11 1 о1юсr· рос
н 1 111 11овuй 1 ·соме;:тр1111. которую на:тал Нt'ев
кл1щово.й. Н 18 ! 7 1· в щ1ном и:r гrнсем учfныl1
11р11:.шался : «Я 11 рнхожу всё 60J1et к убсж;\е1н110,
что пеобходимосJЪ пашсr:-1 1 ·еомстр 11и нс мо
жет быть доказана». Во обнародоватъ эти идеи
он не репптся и:! боязни быт ь петтонятым.
l·aycc не опублнхонал ш-1 один из сuои:х резуль
татов. хо·1·н 11:{ его n11ct.\t и личных бума~· нпДiю,
что он ра:чх1бо·1·ал оснонныt: положения нt:ен
юш;.1овой 1·ео метr 1 1 и.
Т1юр 1 ~ам1·1 новой п.:ометрнн ст:ши также 11ро
фсссор Ю1з:1нск01 ·0yr 11-rнсрс~п·t:та Н нкощ1:й Ивэ
но1mч Лобзчt:пскш'r ( 1792- 18">(>) п Нt:t·11 ·ерский
мате1щ1 тик Я-110 11 1 Болынl (Бой~ш) ( 1802- 186()).
R отш1-с.11 1 е от Гаусса они стремились рзсnро
стра11нт1, свои идеи, 110 болы 11 ннство матема -
111ков тогда сщё не были Ротоны irx воспритшть.
Рсзудьтаты Я нош~1 Болыrя бьши сжато изло
жены в 18.52 г. Е пршюжснии к ю.шгс с1·0 отца,
Ф;1ркаш;1 Болыш. Тру;\ Н. Бол.ьш1 " Гlршюж.снис,
содсрж:~щеt: науку о 11ространстrк: , абсо;uотно
l l("ITll-11l)'IO, НС З:llШCЯll\)'IO O'L' IКТИННРСТГI llJlll
:южности X l акс 1 юм1>1 FRКJ1нда ( ч тп а p1·iu1·i
н1 L1'n1лa рс:ше1 1 0 OhlТ I > 11t: может)» обыч1 ю KPJ'l-
кo 11:ззы11ают «Аnпе 1 щш<с,, (.1шт. <·прш1ожстr11е»).
Прочпт;~н это соч1 1 1 1е1шс, Г;~усс натп r сал cnoe-
" f)' учешrку. мат<::мат~rку Герли:шу: "Я считаю
MOJIOДOI о r<::OMe'I ра фон UOflbllЯ ГСI 111ем псрно1'1
nеш 1чины». О1111а 1ю н шк1.ме к Ф. БоJ1ьшо оп
ото:шался о соч1шс111ш Яноша l'оразлu сдt:р
жанн<:t>: <ТСГlt'рь кос- 1 1 то о работе Tl:IOCJ'() <.'ЬLIOJ..
Есю1 Jr начну с того, 11то ;j'r ·y ра6оту нс д01 1жсн
XH:tЛllTh, ТО ТЫ. КСН-IСЧНО, Jl:t Ml'HOl:Sl:ll l fC 11О[><l
ЗJIШЬСЯ, ни /Jl l aчe н не М(IГ)'; XH::tJlll'IЪ сё 3 11 ач111ю
бы хнал~пь с:11vю1·0 с.:сбн· uсё t:ОJ\ержа11нс сочи -
11еtл1я. н уть, по l(CYIO[)OMY 'ПЮЙ Cbll l 1 юmёл, 11
ре:-1ульта1ъ1. которые 01 1получил, п очтн сплоm1,
со впадают с моими собст13е 1 п л .1м11 достнжени-
1()4
ЯM l l, которые ЧЖ"ПIЧНО нмсют ДШ31ЮСТЬ 30-
~') Л<:'! "'· l le IJ;JЙ)\Я IIOДf\Cj)ЖКll у СОRрс:мс 1 !H l lKOB,
Я. Больяй 11ерсстал эа 111t,\~аться м: 1 ·1·ем:УJ 1rкul1 .
Оп ) J\1cp н СОС'l'ОШ 11111 1 ·лубок<11'1 / (спрс.:ссн11 ;;1
несколько лет д< >TO l'O, как нсевr<.rrндона 1·еомст
р1 1 я nо.1 1 у'Ч1 1ла 1кео!1щсе t1рнзнз 1 11rе.
Лобаче11ский н~ 1ерные 011убт1кп11а11 рс:1ут,
таты своих 1·еомстрнческих 1кслсдоиаш1й 11
1829 г. в работе «О 11ачалах геометрии» . Зате~1
0 11 ра:ш 1 ш;v1 ::>111 ИftCH во M I IOJ'ШC трудах, IIЗДll
вan u11 rхся нс только rш русском . но 11 н~1 фран
цу:кком 11 11t'мсцком я::~ыках. Учены~-1 смс1ю
11ис1л о тuм, что тrарн/\У с 1·сомстр 1 1с(r Е1:1юп1;(;.1
cyr1(cL~r· кyt'т нру1 ·ая 1 ·t'uмстр1 1 я. кm·оrую он 11э
з.1:1ал вuображаt'мой . Jl11шь 01 1 ыт, счнтал 0 11. ~ю
жст rеш HTl1. Ка К;lЯ 113 1·еомеrри 11 J HvJC:tT MeC"IO В
ре:.tльном 1 ~ростра1 1 c1·uc.
Птъ1й пооу.1 1 ат Евклида Лобачево:11й аа
мt>шщ следу10щ11м: сели дана прнмая AIJ н
LLe лежащая ШI IICЙ ТОЧI<а Ji, '!'О LJCpcз точку .ни
плоскости AH,\J можн о провести две nряь·LЫС.
пара1 111слы1ьн.:АВ. Ilринсдf.м 1 1ссколько тсuрсм
1 ·сометр1н 1 J10\1ачснсю..J1·{):
Сумма у1·1юн трсу1 ·олы-1 1 1ка меJ 1 ы11с J8()0 Она
11ЗМl'1 1 я<::тся пр11 псрсхо;~е от од1юго тр~уголь-
11ика 1с другому
Не существует 1111 o,r\rюi"i нaphl 1юдо61щх
треуr·олы п1 ков.
Нс через каждые три то<1ю1. 11с лежащпе 11а
прям.ой, можно провести окрулшостъ.
Не Сущсст~ует IIИ одного ттрш,юуголышка.
DOOBPд,/ltAI:M A.Я
:1!}
Г Е О МЕТРlЯ.
\'/
Т11Тум.нt.1 и
\~IL-Г Ktllll JI
1-1 И. Л<!б,JЧt-'R • 1,111< 1
, Воо бр.:~ж.1t· ,4,151
1etJMl'l р11я ' K<13d1t1,
1835 г.
:7 ·1
·11 у·1·ш·рж;1сню1 к:.~ :~ат1сп сощJсмс::н 1 111кам
ст11~ш1тыми , Не",Jн.:п 1.1ми Круr1не 1~ш1ие "1й.Тt:М<Уп1-
ки Росс1111 - М. R. Оt-1ро1радсю1й и В. Я f)ут1-
к<>nскнй выс1·}"Пи;1п нрот~.ш 1ю 1юй rе()ме·1 р 1111 .
Кр11п1 •1еоюе (1Т1 юнн::1111е r<o1mcr несщ),,1ило Ло
баrrенского. J kнзирая на отрицатею,11ыс per(e11 -
з111i , 11жмешк11 , о н продо11жал и<.:сж:,!\оваш1я .
LJoc;1c С\1ерп1 Гаусса были 11зданы n11сьма, в
которых 011 н:;лагзл с 1юн нз1·яяr~ы н а нсевюн r-
дову гео метрию 11 тюсторжсн1ш п1зын;11 1 ся о
со ч1111сюшхЛ06ачснско1 ·0. Н:.~лрнмср, н I R·16 1'.
Г'~l)'С:.:С' 111 ICШI OДf I01\.l)' И:1 ЩJузс 1'1: «Ло()аче 11L1\J 11'1
тш1кус·1 · о 11редм сте r<ак :н1атrж , в 1rст1 1 1 11 ю
1·ео:v~етричсошм ;1уле. Я с ч11'1:но ссб>1 of> >1 :1a11-
111.r :v1 06рапп1, Uавн.: в 1 rима1111е ш1 юш 1у "Гео
метр11чесю 1 е нсследоnаrшл rю теор1п 1 парал
лелы1ых 1ш1111i1 ", чтс11 1 к· которой нспремсшю
при11еl'fт ~ам бол1>111ос )'ДOIIOЛl>C.'TBHt"» .
!jш1ч '.нн; 11е<::1Sкп~щока !'<.:'Оме1·р 1щ ю1 зан:1сь
<.:IOIJ IIO!I. к ко·1·оrо11 ОПl'LС:!Н фа Н'J'~I СТИЧ<.:С.КI 1й м 11 р.
Где 11р11мсюн:тси эта 1 ·<.:u мстрин?Нt: содt.:ржнт ли
0 11:~ nро·1· 11 rюрtчи11? Творцы нoun il t·сомt:три11
счm ·<1т1, что ма·1ема1't1чесю1 е :1 бс1·ракцт111олж-
1 tьr выражать реалып,те свойства окружающего
'111ра. 11 на ()стющ11ша опытов 11ал.еялись отв<:>
11-пъ на ноnрос. к:шона rеометрш1 фн:шческоп)
простр;111С'111а. Лобачевский, н.нтример, запялся
неnосрс11ствс 1111ым измерением «космУ1 чссю1х
трсугольн 1 ткоn», раL'сч11тьшан с: IГО.\Ющr,ю дан
f{ЬJХ ;1стршюм11н 1 юказа ·1 ъ, что cy~'<ta 11х уиюн
не р:шн~1 18()0
,
0;\н~ко вп;: сп·юю11с1·111 я 1У1 1R0°
окд;1J11 1 сь R J1рсдслах точнпст11 11<1блюде н11й .
Toma учё1:-1h1й выска :1;u r пре11полож<.:1111е, чтn tто
1сометр11я ()JJ11c1,inae1 · м 11 кром1 1р.
Впоследст1шп мате,,,.1а·1·r 1 rп1 рс1111rm1 11р<1бле
му 1штерттре:тацш1 t1еевюп1д01кн't rеометр1-1 11 , а
ф11зr r ю1 ш: попыовали сё рсзулы·аты в своих
псслсдоnа11инх. И что примсчатслыю, н осно
ве ~ювых ндс~: 1 лежал;~ теория повсрхrюстсf 1,
сuзда11 11ая Гауссом.
l'aycC .\ltfl(JГU JICT :;al-IIJMaЛCH l 'l'OДC:J ! l <:'(J: пro
JIO/(llЛ 1'соr~с.ш ч ескую съёмку Ганновt.:rско1·0
корош:rктн:.1, 11:~м<2рял )~у!')' мL:р1щи:111:1. ()1-1 прга -
1111зовh шал rюлспыс 11змерс11ня. сам и 11ох ~rча
ствоu:lл, выrют1ял трудоёмюrе иыч11слtю1я.
В рс:-~улптатс 0 11 ()'r·крыл 1ювыl1 ра~щсл мэ·1 ·сJ\1:1 -
ш 1ш - шrу~рс11111ою гсо.-.-rстршо понерл1 юстей.
l\ 1828 1'. Гаусс оtrубюпювал «Об щие нссле7'О
вання о кривых nоверхлостях~ . где 1.1 11срвые
бьuю введено п о11ятис 1·ауссовой криnн:шы .
Исслсдо ванил ravcca нротщлжилФсрдш rанд
Гu1·;1н601щч М11ню~111, ( 1H06-1RH5). ро<тн~1-
Houoc uрсмн
,Аь_
EDJ(!!
J\111 хаил Н;н 11лы11-нtч
()п рогралс ~•111 .
cюrfr м;1тсматн1< , нс:мец по пронсхождешно.
работ;~вшю1 вДсрnт<.' (пы1 1 е Та рту). Оп 11эучил
IIOIIHTИ<.: К\)ИВИ:3НЫ П()BCpxrIOl."IЪ , крини::.ш',l К()
торо 1'1 р:шн;~ н~·лю, сс· 1 ъ простая 111111 11Jо 1 ·нутан
НJIC)CKUC'l'I>. Jloнt.:pXHOC'IЪ. KJ1 J I HJ 1 :н1;.1 KU'l' l )j.)OЙ
ПL>CJ 'O}l l IJ l a J 1 ПOJIOЖ1ITC:J!l1H:! , МС)ЖС'I' nЫ'ГЬ H;JJl(J-
Жt:H:.1 11<1 111:.ip. М1 1 н;(111 11" рассмотрсJ1 по11tрл
ЕЮС'LЪ 11oc1·mr~11 юй отр11ttа'L'е; 1 ы1ой крr-11шз1н.1 -
так щ1зыnаемую псс: н,~осферу - 11 11 а1 11 ел трп -
1·01ю:мс·1·р11чеl.'ю1<.: соотщ)111сн11я н т р еу гол:u
r 1 ию1х на этой поверхностн.
Юtк сжазалось, Лобачсвскrrй в юшге f Нооб
р:,~жас .м ;:~.я геометрия " вынел ,~ля чху1·ол ы шков
те же с:tмыс трагиномстрr :1 ческис формулы , что
11 Ми1-1днв1 · д;1s1 треу 1·0J 1ы~нксщ на 11сt1»дщ:фсре.
tlo <:JJ aчa11:i \'Чtныс не Jа.щ~н1л11 Э'1 ш·о сон11аде
ння . Чсрс:~ ~·;1-юr·о Jll"I . н 1!'36R 1·, н:1 11<.:1·0 1 >6рат11л
11н нман 11с 11·1·а,1ыrнск11 !'1 мзтсматнк Э\·дж<.:111 ю
Rem»r'J):iмн ( 1R~-1- 1900) 11 /(O /\a :1aJJ . чтn l'COM e"l -
pr1н orpa11 11 ч<.:111 ю lr ч:~п· н 11лоскос"1· 11 Лоб;~ч<.:1{·
оюго спраиедт 1щ1 ;~ля rю::n;1осфер1 ,, Р:1:тык11с ·
~шя , да11 11ыс Белътра;ч 1 1, помоr'JIП поr1~п 1. п
лрн :нr:пъ 11есuктпщоR\' J ·ео метршо.
fkp11xapд Рт'rматr ( 1826- 1Н66), матс\1а1т1к 1 1 з
Гt'рм;шлт1 , перстёл от IJ зучс:r шл 1юверх1юстеi1
l\ JI C:.:CЛCД(JВ:Шl l IO rrpocтp a!ICTB. В J IIOJH: Н)-1 1 1'. ~
['ёт 1·1н 1 н~1кком у 111н~чхнтt"1·1;: 13 r1 р 1 к~"1·с1·1ш11
Гаусса он лроч11·гал л<.:кц 11ю ,. о 1·111ю·1 <.::JаХ, 1 1 с
жащ JJ х в ос111 >ва1 1 1111 1т uмtтр 1111". Глу6окис 11
смел ые \llЫCJ llJ P 1 1мat-1:t. 1 1зложенн ы е очt.:1-1ь сж:~
тп, соврt'ме11J1ию1HnL·np 1 п 1н 1111 11 е сра:зу. Лскц11н
была опубл11ков:.ша 11ш111, в l~bl~ г" 1юсж~ с1 0
смер·1' 11 . 1lонят11е кр1ш 1 1:111 1 .1 пр оп· ра 11 ст11а
у Рнма11а - это обобщсшн: л.1уссо 1юlr кри
в 11 3ньr д.11я п о uсрх.rюсти. Обращепне кr 1 in11зr1ы
в .н ут, во нсех точ:ках характсрн:3ует е 13кл11до11u
1()5
л!Jъ.
& l(!J
Исrория математ ики
простр:.~н<:тво. Гt:OJ\tC'tp11я двущ.·р 11 01·r> 11110стра 11 -
сг к ,1 <.: rюt•1·о н111 юй п олож .1-пе11 ы ю11 крнпн з 1 юi'i
сов1 [;1;щt"J' с 1 ·eaмt.:·rr11eil 11а сфере, а гео .v~етрrтя
111юс1 р:11тс тn:1 с 1юстояшюй отриr~ател ы юй
1<р11щп1юй - с 1·епмстrией. Лоба ,1 евс1ш rо.
Открытня Гаусса,Лобачеnскоrо. Рамана з 11а
ме 1 юкш11 собой реuолю11ию в о6ш~стн чсловс
ческоr1 мъкли - nрсобраэованн<.: ф11знчесю 1 х
воззрс1111й на 11ространство и нрс~tя Уже R н а
чале хх: в. в · 1рула,'< А. Эйнштейна, А Пуанкаре,
1'. М111-1ковско 1 ·0 6ь1J1а со:щ:ша с r1сц~1ат,ная тео
рш1 O'l'llOCI LTCJI 1.11ости, а та кжс уст:н IOBJJCHa сё
с кюь с 1 ·с< >:-..1стрl1сй Лобачснскою. R 191 6 1·. ~й 11 -
ппсй 11 1юс1·ронл ОU Щ)'Ю теорию OTI IOCI ITCЛ!J
HOCTl I, OCIIORЫЩlЯCI• 11(1 работах Гауссl! о югут
ре 111 1ei"i гео!'vlетрин nоF1срх11остей п нсполь:зун
'1 ;-~тем:~.т11ческшl :1 пттар:п 1 ·еоV[етрш1 P11Jv1ai1:1 .
« ЭР/\АНГЕНСКАЯ ПРОГРАММА »
К/\ЕЙНА
Ещi:: 11 f~ре1шс!1 Грс1~1111 была 11:3 11сст11а сфср11-
чсо-:~н11·coмC'lptiя, к юлороr1 пр111Ю)\m1и з;.ща
ЧIJ астро 1 юм1 1н . Состаuле11ие 1·еографичtс1<11л
кзрт трсбоn;uто 11а~'1т1 1 сnосо6ы о·~оnражсшп'1
,-.Jm 1и11 соп1'а [ l a JJJюскость. Художшпш. архнтек
·юр 1.1. 1шже1 rеры ра:~рабатын<lЛи правш1а 11ер
спскпrны. II 1822 г. Жа1 [ l31 жrop По11сс:ле ( 1788-
t 867). фрапцузскш'1 матс~1атпк 11 1шжс11 ер ,
опубшшовап •Тра ктат о t 1 μ0<.:к· 11 ш 1т ых сно1'1-
ств,1х фи1 ·ур;; Он 11сслсно1~ал сtю iкт ва , • 11сна
ру111:1см ы с 11р1 -1 11роскт11rонанr ги ~ . Нс1ю. что
;\J llJНЫ IJ )'l 'Jrh1 н 11роскц нн ,\ Hl' COX (X!IНllOTCЯ , но
'l'ОЧКН , ЛСЖ~Ш\И (.' на OДHOII примой. Ta t-. :OH1>1'\1( 1 1-1
(1ста10тся . t 1 ересекающ11 ео1 1 1рямыс ос'1·аюто1
1U6
нсрссскаю щимис:я . Та.к во::!н11кла 11дс:я щх:ледо·
наТh с войс:тва ф111ур. 1111 на р11а11тньк: (Нl'llЗ\\СН
ные) опюс11п:л 1t110 проскт11ров:11-1 11н.
После та1·0 ка1< fi ыло rюказ:шп. что rt.:омст·
р111'1 Е11кл 11да 11 Лоfiаче11оюгп ран ~ 10nр<11111ы, на·
:1рел:1 псобход1 l\IOC'l 'I• }\:1т1 , кл:1сс 11 ф1 11<ац1 1ю всех
сущсствующ11 х 1 ·ет.,1С1]1Ичесю 1 х 01Стем. Эту за·
да ч у реш 11л 11еме1 1 1сий матсма1r1к Фел11кс l<лей11
(18-J.9 - 192')) _
Сво 1 J иыс1ш l{лci-111 выск~1:1ал в 1872 г Вету·
нан н должпость 11рофессора Эрла н1 ·l' 11 с:кого
ун11ш:рс11тс..:та. о н 1 1рочнт:ш J [скц11ю •Cpaнш1-
't'l'J1hl юс обu::!рс..:1-1 11 (:' 11онейш11х J 'COM t"Г(1 11ЧCCIO-L\
1 н:слс1tован1 11~1Q. н з:нестн~·ю п о; ~ 11а~{н~11111ем ~?1р
т1н1 ·с1 1 ск:н1 11р о1·рамма-> .
По Клс1111у, ;1л н 11ос1рпеп1 1я ·1иi1 11J111 1111oi'I
r·ео метр1111 1 1уж1ю1адзть м11ожесmо эле~1е 11тов
11 I 'py1111y прео6 разон:~. 1 1нi1. Задач:J I·еометр1ш
состоит в пзучеш ш тех от11 оше1111i1 чежду эле
мепта.ч11, которые остаютс.н 1111 nариа11т11ы\111
np11 всех прсобразован1 шх J \анно~'1 групны. lla·
нр11м1:·р. rCO);It~тp11111i НЮ\Н/\а нзучае1"t l' l'JIOf1erna
фн1ур. которы<.' остаются н с:: 11 :1мс111 1 ы,ч1 1 11р11
ДKHЖCHllИ. llo CCTh 11 друтне НllДЫ ll'(),\lll'Tp11чe
CKИ X rrpcofipa ~ю.1:1:11-11 111. ко1 1фоrмны<.:, нt:прерын·
Н111t:. т 111сr1ныс 11 т. д В 1<n11формно11 1 ·еомет·
rнн1 н сслс1tуются 11реоб ра:юпа 1111я , которые
11ерсВОf1.ЯТ кру1 ·11 н "РУПI и сохрт 1я ют~тт,1. То
поло 1·ия ~1 зучаст вепрерыn11ыс преобразооа-
11ш1, аффшш:~.я 1·еомстр11я - m 111cf1m,1c nрсоб·
разоn анин. Клс1'i1 1 :i:tмcпur. чта свюшдовы
дш1жс1-U 1я, nрсо6р:t:юван 1 rн ПО/\О61щ аффuн-
11ые . 11роскпшньн:.:. кuнформ11ыс врсuбра:юва·
1-11 Ш 11 1 IC<::HIO ll1/\UllЫ /\ Ш IЖC HJ IЯ оnр~1:1уют 1руr111ы,
eCЛL I C ЧlfT;ITh 11\)0ll ЗKl:[\Clllll'M нвух 11рсuбра:Ю·
в;~ ннi1 результат п ос11е,.ща::~т~.:лыю1·СJ 111.ню1111е·
11ня да1-Jных пр~::обrазонат1й.
Про 1рамl\1а Клей11а осущсс1111 1J1а 1ю1Jыi1с1111·
1·е;1 l!Л гсбры. 111·еометрпп. та1< ч·1·0 в ХХ в. 11за11·
!IIOЩIOI 111 IOIOllelП l l: этих ДlJСl\1111ЛИ11 стало ещё
более ГЛУбОI<ИМ.
Ра3работанпая Кле.\1 нам 1'лас:с 11фнкацил
1 ·со.метрщl пс BКJIIOY.:IJI;.! в l't:бя ф\'Н)J.:t~IСН'1'<1ЛЪ·
ные и11еи Римана. Кле йн 11:.1~ LitlJl 1·pyt1 11f,1 1 1 рсо~
ра~юн:н шй . Рнма н же в1 це.1 1 цс; 1 h 1·со,1етrю11 в
н :{уЧtННН 11 po<.T(1:llfCTll. 1-l :! ОС Н< ШС Cl'O щ:следО·
ван11й в хх li . н 1\1атс:щ1•пщу l lOШJll 1M<:'l'p l·I Чl'C KllC
и·1
·n1 ю1юп-1чсс 1<не 11 рпстра11ства, l1ш 1 C()1Jtan
фу11ю1т1011:1111.11ыil ан ;.1л11.1 - ра;щел мат~ чаш
ю1. n 1<0торn,,1 о(i()(>щаются ос 1 юн~тые операцmJ
;\1 атема ти чсского анализа: прсf(сльпые пере
хо,11ы, д11ффере 1 ЩfJ ponaп11с. ш 1те 1·р 11ро11анrr~
Новое оремя
НИКОЛАЙ ИВАНОВИЧ ЛОБАЧЕВСКИЙ
!lтшлай Ип:11rо~пч Ло6;;1че13с1щi1 родrшся п
l 7<)2 1'. 1 iнж1т~м ! lон1·ородс. Ко1·да .м;шъч1 шу
б1>uю дс: 1ш·1ъ лет. <..:с м ьн лерL'ехала в K:1Ja1Ih.
Здt.:сJ, ll1 1 кo11a>J u 1 1pe;te_1 11 1л1 r в r ·11м 1r :1:н1ю <·На
ка~Снныr'1 сч<:т··
R 1R07 г. \ L\-, 1t:'1·1 11 н1 1-\ 1 1коJ1:1й Ло(')~1чснсю1i1
rт:1л ст~дt.:нтом КазанскС>1·0 ун1rнcpc t 1те1«1 .. кото
ры!1 открылсн т11111. ;щумя 1 ·олам11 pairee. Т:1м
rtpcпoдan;vщ nчспь хороттшс м::~тем:~ттнш, сре
д1 1 ш1х - профессор Маμтин Фё1101 юв 1-1ч:
(Нога1ш М;1 рт1 ш Кр11стна11) Партельс, бт тзко
зн:1кочы11 с сам.нм L'ауссом. Прс11одаватсю1
nыде11.ял~ 1 на 1\урсе двух студентов. .Иrшrа Сн
'юн.она (нnослt.:дстю 11 1 он стал J 1 рофс-ссором
Каэанско1 ·о у1ШHl'\ll'I1тст:1) н 1tJ.н<o!faЯ Лоб а ч<.:в
скш·о. в ОТ'1ЫВl' Дl'Ка11а, ЩJC,ЦCTaШICHIJOl\1 R
IRl2 1'., 1 ·0 1юр1щосh: "хотн Снмонон хоро 1 1ю
ос11едr1;1.1лё1-1 R м:1темаn 1 чtтк 1 1х на~гк:~х, щ1нако
Лоб:1че1кю 1 1t нрсrюсходнт. особенlю R 1ю 11 -
росах то11юtх».Дска11 ут 11 шсрснте1·а с<штал. что
Лобачеосю r i! «П будущем пе сможет ост;~ться
неnрослаnлс111 rыи».
Кар1,ера Jlоб~ · 1евско1·0 разшшалас~, стреми
тслыю В НН-1- г. по рскоме~rд:щ1111 13артсльса
его утнер;щл 11 <IДЪIOJIKTOM ( t ЮМОЩ НИКОМ про
фессора). а чс.:рс::.~ дна 1·о;р. R нозрастr; 2.) ж:т,
\\Ыбр~IJШ экстраор,л;и 11 :.1рным 11rюt\х:е<.:ором (со
от1:1стстну1:т /lOJJЖI юсти дшtt:нта) . В J 822 t. Ло
бачевсю 1 (1 п·~т ор;о-1нар11ы .v~ прuфt:ссо рuм.
С1111сок курсов. которыt: 0 11 1 1 рочнтал н пер
вые 10 - 12 . Jtcт сrюей ПСJ\~rог' 1 ческо~1 /°'\б1Тель
носп1. со~ерж1п более десm'ка 11ан."1е1 юнаний.
н"~•Jл<н• ив.нюии,,
ЛorJa 1ct о(м10
~">то теория ч11сс:.'Т (по ! 'ауссу). тюск~ш 11 сфе
р11ческая тр1н·оном<::трня. ~111~1л~1т11чсская и 11а
чч)'J'атс:льная J '<;U,МС'Гр11Я, :н::трОНОМIIЯ, диффс
р<:НЦИ:lJI ЬНОС Н llJ-l'l'l'l'/);!Jt bHO(.' ПCЧllCJil'fJ I IC: .
ф1·13НК:J . C'l :l'l 'l t Ka 11 Дl lH:tl\.1ИK;J 11 )!р. К~Н< ВJЩНМ.
,\\\)Jl\ЩОЙ профtТСt)р 1\ \ 1'\ 'ШI леющ11 llC 'l 'OJl1>KO
11() разЛТ!Чlff>l .\1 оСiJJЖ'ТИ\ 1 M:J 'J't 'M<!Tl·fK l l , fJO 11 по
ф1 1:1111<t: 11 <1стро1юм 1 111 Он 61,1J1 оч.с 1 11, прш1 еж-
11 ым .' l eI\l'opo,1.
ОД1 1 аЖ,J\Ы н кх~э1ккпi1 ),Шперс11Те'I лр11111ЛЭ
~rнструкцrш. утпсрж/.1,ёr 1 шн1 нмператором Алек
сандром 1: <·llpoфeccop теорет~ 1ч ескоii н 011ыт-
11о l1 фн :шкн обнэ,1н во псt ГIPO'l'f!Жl'I ll JC кпха
оюс1 '0 укаэыв:1·1ъ 11а 11ремудрое1ъ Пожню 11 01 ·ра
н11 ч е 11 нлсть на1ш1х ч у1:1ст1:1 11 оруднй 1vrя нозt1а
н11я нспрсст;1юю окр)!",кающ11х 11ас чуд<:с~. J:lpя_.t
лr1 Ji116.1чс1кю1й, которы !'1ч11·1·ш1 в то крсмн курс
~тспrетческая 11практ1 rчесrшя ф1 rянка», c11c;~o-
11:u1 :3ТС1М~ rтpt;'l,l lИ:C:iH\.110.
К ТО'\1.)' 11ре."1сш1 011 уже тр11 года. 11ачттая с
1Hl7-1·0. работал 1 1:.iлo11110i1 11~:1·1рудней11 1 1 1х про
бле.\f - доrса:1атсльспюм пятого постулата Ен
клнда о параллелы~ыл. ! l-a ле 1щня:х 01 1 расскз
зывад студентам о попытках жжа:1ать, что Lrcpcз
точ ку 1:111 е прямой можно лронест1 1 сдm tС."!'нс:н
ную 11 рнмую, 11ap:11111c:J1 ьную Ci i. 1\.11 IOJ'l le 11 :.!НССТ
\l Ые математики исслс;\ощu11111ро611с .му11и·1 ()1 't)
1юстулат:1 . но но нес врс.\Jс11а немало было н
;.1мби 1 (JJоз11ых невежд, которые хи:1т:1л11с1. :!<1 .'IT~
Э~l/\:1Ч) ТОЛhКО гю·r ому. что сЕ форм~·mrронк;r
бьm:1 ;~:ост) н11а каж,ному. Лобач.е1ккнi~ 11р11;\<111а;1
ei1особое:: :з1rачетн:. 0 11 ш1с::.1л, ч·1·0 :3;щача о nз
ралдслытых предст:mляет собой •ч1уд1юсть. J\t>
ci 1x: пор 11еnо6едш.1ую. 110 ~~ежду 1см заключ::~
ющую 13 себе 1-н.1·ш1ы Ощ)•1·1 ~тель11ые. вне ucmzo -
1·0 сом пешш. н столь важные !ИН! пеJ1ей наую1.
что н1 1 как н е могут быт1, обоfr;1с11ы".
В н ~1чалt: J1обачевскн{J 11 ос1у 1 1ал к;~к t l 6011ь
t1J1ш L~пю J\py1·11x матсматнюж, ·1· е. нскаJ1 ;юка
за· 1·сл1,стRn CYI пр<Н IГIШпt о. '1\IЮ LM путём 01 l
НЫНL'Л МIЮЖССТНО утнерЖДL'НI 1(1, l ICJ<O'l'0[1ЫC 1rэ
I JJIX Н Ы l'ШЩСЛН . MUf 'h:() 1·онорн. Lvгр:11-11ю, Н() rн...
КП1\.\Оi 'О 1 1рот1. 1 Н<Jrн::~ннt 1''аК 11 Н<: 1IOJ1\''-ll IJH 1(.]J.
U l~lj r. 011 пршнС:л к ~tыс1ш о педсжазуе.юс
т11 1штu1·0 постулат;~ 11 о нозможност11 1ю1юfJ
1·со1Ч<:"Трин. Болt.:с тш·о. J!оба чеnсю 111 понял, '1то
:.:~та •·!:юображасмая" 1·со"1стр11я, 1. 1есмотрн на
11с11 1·)и1~ыч1юеп, се сонсржан11я. к пр11н1\11п с
нс может бытп 0 11ровср1 ·11ута 11~1ш 11 :- .1 01 1ытом
107
Истор~1s~ матсм;пию1
0\1111.1 '. 1 TO P CI O \1 О li\.l IВCii \l'O YHJI-
ШWC!lTJ:..TI
18З~
1. DAYJ:U
UC]')'П.t EIOX.
JJ,~fi'!f.I 1t~1.J.c:-st1.G '1 11н1 ''" Гco"«mrl" 111 rог" n :r·
r:i ~>l>i\U J('\o. f<,V 1•t1 :ir. •
111•! •1• IМ.1 1!!&11 1Н." l>t~ 1Jl'l.<>L+.-~1t·
""''' 11. 1~щ('1М1'1 " "'_ .l , . 1a;11 \:f• ,P•'~'ri. L.t.11.111.1•, v:;,. 111• ,.
!l•••t"JU),•• 1 _...,,1,.1.i. . 1t.1111.,
"'-''•1.i...11J,1 "'-"'"" '"Ч"J•
) 't:.1111щ,, •н11<1 lo'l.(l.c ,JllJJ . ,C . llнl.lli"l1':'t'J. сЩ" l.ltJi'!r.. \10 -
"
с•1.1с11 1110.1 S1~11111ro1, ll"liloVl')lt/ :ir. ,;i.111•1-ta jj<Jo.1& .lo.Mf:tl:I
tl ILOllllll!} r.I шн.J.~11..)11 1•11~<1\l loO ~p,r1i~r. "Qil ll'l t<1foIOl'I.
"
1lt•fJll<lll 1 1 j)<IHl\U,\
p.Jl><>I hl
11 И 1\ОбдЧРВtКОГО
« Нош.•1 с 1t.JЧdлL1
гео"етрнн •,
LJГIVUЛllKШ!.1H I IUЙ
в ·«Учены>. запио(,1>.
K.1 {.illt Kuto
униRРf)( IПPTil .
1835 1
13 ф<:врале 1R2()1 ·" ко 1 ·цз Лоба•1е- 11с~о1й 1 1 ;~1 1н
сал псрnую работу об открытии 11овоf1 гсо
мстр 1ш и передал её 11ес1<0льюL~'1 профессорам
)1пшерс1пет::t, ответа от колле1· не последоuз
ло. А сама работа вскоре был;:~ утеря11а.
В l 82t) г. журнал <·К:~.запсrшй всспшю> опуб
ликовал сочш 1с:11ие Лобачевского о неевю11що-
1юl1 l'COMC'l'()I 111. в ОТ:JЫНС H ~l H C l 'O 11 31\C:(" J'f-IЫl'J ма
тсм:1т11к :.J 1<адс1vшк М. В. Остроградсю1!1 1 111с111:
«А нтор, 1ю-в1щнмом1. з;щ:шо1целью 1 111с:пъта
ю1м обр~1зом. чтобы его нст,зя 6 1,~ло понн•1ъ.
0JI i \OCTI 11 ' CIIOCil 1\tJ1 Н: nOJJЫHa>J Ч:lСIЪ Ю !lll'IJ
ос- 1·з;1:.1с 1 , сто1 11, же 11 е 1 fз1-1ес1· 1·ю1·1 11/ IH ме11н. ка1<
cCJUI бы я ш 1коr·да ие видел её».
1·е1шi 1 все1 ·.ца 011ережает сноё время. Через
~U --IO лет пояRятся работы, н н:оторых бущ.-т
док~1:{а110, что l'сомстрия Лобачснс 1щ 1 ·0 <.:толь
же пр:~во •\1ср~ 1а, как и 1·еометр 11я tню1 1 111а, 11 t:i..;
О'1·крf,1 ·1 ·1 1<.: - важный 111а 1 · 1-1<1П}"l'lf1\ nо1-111 .,1а1-1 11 ю
<>Kj)}'}K:J10 11~e1п 11 ас мнра. Jll> в ко1ще 20-х 1·1 .
XIX к. Лобаче1кк11r1 ока:J:mсн н очсн 1, сложном
llO:J()ЖCJ-11111. f.1 ·0 НС Гl()lil'IM:.JJ111 11 fl;lЖ{:' ocyжr\<1JП I
луч11111е м;1 '1 't:\1:Jт 11 к и ·1 ·() 1'0 11 реме111 1 , ~;:ол 11е1·1 1
ЩIП.~Jl l l 113('.Vle' lllЛl lll Ыe, а 1I0p()l1 ос 1<ор611те;1ы 1 ые
от.1ывы о его работе. Это было настоящее тrс-
11ьпа1ше х;1ра1пера учё1ю1·0 . Лобаченсю 1 (1 е
чсстыо его nьщсржал. э~1 ncpnoli: бол ьшой
ста1ъ~й псклсдоваrш новые работы на ту же
тему. н этом он pCWJITCJlbHO OTJIИЧ::IJl<..'Я от дру -
1'01 '0 пср1юо·1 · крыт1атсля 1 1ccnклr 1 j\onof1 гco
J\•t<: 1p111 1- Га усс:1 (< Кородь мaTC.\1.l'l'J 1КОВ» OKOJIO
108
_1 0 лет з~11111малс>1 ·1enp11ei1 11ара11!Телы1ых п
прпшёл к выводу о праnомсрпост1 1 11ссRкющо
uоl! 1·еометр1ш. 110 так 11 не 011Убт1кt1в~л с1ю11
рсзулr,таты.
Однако Гаусс сы1 рал важную роль н сд1111-
с1 ·кснном 11р11 :ж.и~ненно:.1 1 1р11:таю111 научных
э:н:11 у1 · Лuбач~нско 1 ·u. в 1 l:Ц2 1·. 11 ~·•кuJtaй 11вано
н~ 1ч iiыл 11 :~6ра1 1 ч11с11\)М-К( )ррt>СПl}IЩ~1 1том Гё'1·
T I IH l' CHCKOI '() учёно1 ·о 06.щеL·1·ва (ак:JДС~1J IJ 1 н:~у к)
Реше11ие n() нзбра1 1 r 1и 1 1дн 111юм 1юд1 11 1 с:1ныt·~1·
'vПIM Гауссом.
Обра т~ 1м ш шжнше 11:1 ответ Лобаче1юi0ГС
Га уссу· <Лроснпе мле. '-По я так доЛl'о 1<0ле·
баJJсн с ответом. :зJIOJ ю; 1 уч 11ш'1 1юж.1р ~·орода
отnстсгвсп :.1а это: этот послс1щ 11й расстроил
мш: :щорон ье ". обрсменrш ,vн.:нн сщt массой
особых <.:1rужсl>1 1 ых :3абот-> Учс11ом\1 сообщаю~
об нзб раннн с1 ·0 члсно,ч ан·1·щштс'1 11с 1\111е1·0
н<1учно1·0 сообщссJ на. ;1 ему нско 1 ·1\:1 O'I ~сп1·r·ь
и:{-за п<~жара 11 1 ·ор1щ<: В 11111·1,мt' р:ккрыкается
Па\.\яr 1 щк Aofi.J'lt?HtKOмy в К.-1 ы11и
ещё 01111а с1 ·о~нш;11111L111oc 1 ·11 ЛобачснскuпJ. Jl.с1~1-
стн11тсл1.1 ш. м: 1тсм:.1т~ 1ч<.:с1<1 11'1талант 11 нсобык -
1 1оrк1 11 l:l}I crp:iC'l'lfOC' I ,, н OTI f() lllCI 11111 к 1 1:1 укс co-
ЧC"J ;JJIHCI> у JILTO (.' Иh l COIO l 1\I 1 1рс/\(.~1 · анлс н1н.·м об
общеС'ПSС I 1l юм /\OЛJ't.
Уже112<. -
~О-лст11ем 1Ю:1расте Jl~)6aчt:11Cю1iJ
.1:н1t:дова11 0Gс1.;рнатор 1 iсй. был лек;нюм l\ШТс:
ж1т11ческоr·о факу11ьтста. Многие годы 0 11 во:1-
г;1мшлл ут 1 111>срси '1·с1·с:к,·ю бнбшюте к у. 11 0 -
нш.1:1я. J\ah'YIO нажную r>оль u 06разон;ши11
ш·рас·1· бr16тютска. Лuбачетккиfl с:щш1 R Гl с
·1·ч')бур1', чтобы Jшч нu от6 1 ·1 рат1, 11 зак;т1 атъ кнн
r 11 К:1к пренсс,1атсm, стгннrте;1ыю 1 ·0 КОJ\1Итtта
у1111Rс 1х·11тста . т 1 ру1-юrю;щ.11 с1·р01 1 тсл1,с1·щ ) i\1
ноных учсf)ных кор11усо11.
В 1К1 7 1'. Ло6~1чc: 1KK(JJ'<1 11 :с1\lр;1лт 1 рс:1-;тором
K1;iarrc1<01 пу1111нсрс 11·1 t"1·a . R1 юследстш11 1 m r пс
rе11 ;161 11х1 лся Ш1 ЭТ)' [\ОЛЖ I ЮСТЬ 111 естr, раз JI
oc'l<1IOJ1Cя ректором в тсчен11с lO ле1'. На этом
посту J lобачсвсю1l1 э11ерr1 1ч1 rо 11 коипетеr 1ттю
з:11ш,v1 ~L1СЯ 6yкnaJJЪLIO всем: учt:бно i'! н лауч1юй
работu 1\ фт 1н:шса мн. стрu11тс!lы·1 ·во.\·t. Осоnсн-
ХХ ВЕК
НА РУБЕЖЕ ВЕКОВ
8 августа 1900 г. па Втором Между11аро,тl1юм
мате;чатн че:ском кош·р~ссс u Ларшю.: nыcтynaJI
Датщ Гильберт - 0111ш из вет1чаi1щ1 rх матс
ч:тrков всех времен. а то 1 ·1"щ молодой профt.т
сор 11 ~~ Гё'1·1·и .111 ·t.:на. Сной :311·,1мб111'1ъ1(1 J\1жл:17\,
11001ящё нный м ;1 тсмат 11чссю 1 м проблс.\1:1,v1, 011
нач:L'J CIOB;tM l t: ~ К'I\) 113 11:1 с tн: XOTt' . JI бы 1 1р нот
крьп 11 ;1анссу. :{:. -t кин1рой скр ы·1 о наше ()уд} 1цес
чтобы хоть 0,1.J.JI ГIM IJ;Jj 'Jl}J;~()M про111 IKH)'TIJв 11 pt:J\
CTOЯЩl lt: усгrехн на 111с:го :J 1lаН11>1 и таl111 ы е 1 -о
разщ1тш1 li ближайшт 1 е с1·оле-тя?».
Тогда. на 1юроге ХХ в" оглядывансъ на ве~<
~11111ув11н 1 й, ;vюж110 бЫЛО пrсдС'l'<l13JШТЬ t: ебе
бу~1це<.' Je~1111 прскр~1 с11ым. Казал()СJ,, что па
стущет эра блз годсrктння 11 pa~i~r;o.1a . А ссгод1 вт
мы, к;1к 1·1 lf:JJlll г прс:;\11.1ССТНСН1П ·I КИ сто Jll'T па:1 :1Д,
брщ:Jем в:5 1 'JIНi\ 1-1:1 11р01J1ею 11 ее t" 1·oлt.: · 1 ·11e . Ч то
tЩДll.\ol М hl T\l f\\?
НJдt:Ж/\Ы н а !)л;11л1 1 е11ств11t не оt 1р ;11щ~1-
т 1п, - н хх неке быт) MJ юго '/'(l;./ l'~IY.CCKOIO: Н11
сче.ч 11с ср:-11ш1 ~ мое взр11;1рс1'по. оскупе шrс 11р 1 r-
РО/\Ы. отр:~11лс11 111,1е рек11 1-r 11ы сох11тн~~ \1О рн .
Нот 1е. вр~мя
но ·r ру;11 ю 11р1ш1лось во 1:1рсл111 xo:rcp1юi1 эшr-
11см1111 1~.)-) )'. 1 1}'IIO~U Jll~ ' l 'OЛ> 1 южа 1 >:1 lH12 1'.
В lК-1(> 1·.
11:1аLт11 укол 11111 1 Лоб;тчснскоr о с
11ш1ж 1 1ост11 рсктр:~. U ян юре 18'12 1°. ~мер L'J 'o
стар11 111!1 сы11 . ,\·l:1·1·tp11:u 1ы юс 11 0,юже11 11с се: мы 1
с1:р1.ё.1110 ух~ i\11111тюс1" Нез~ЩО.'11 ·0 J\O 01tрт11 Нн
колаir 1111~1110111-1<1 гю· 1 с:ря.11 . 1рст 1 е. Послс:~11юю
работу « П а11гс()Ме1рт1н -> (греч.сскзя пр 1. 1стаnка
"11ari-" озт 1 ачает <- всё». , nсеоб щш'1 "). нриурочсн
вую к '50-лстню Казанпюr·о уш1не1х1 1 · 1·ета . 011
про;111кто11а ;1 ою 11 ,ч <.:1'удс11та .ч буд)ЧlJ у,кс со
1:1<.'с,,·1 слt:п ы .\1 . У м<:р Лоn:tчевсю 11~1 в 1i:S"i6 1' .
в lf;.28 l' f!( ) C'l~Ч:llO 1 1<:-рной ( '()j\() J~ ЩllHЫ СВ()С[ '(!
рскторстна Лоnа чсвсю11'1 про11:111ёс ст:111111~ н1
гю·1·ом з11:1мст 11но~т реч~.. "() важ 1r eйm11" ттре/\
мстах TIOCJJIП'<IYIШI-' . н 1 1 ет1 0 11 . fl Ч~KTIJOCTl l . сrс1 -
зап: чПр11rv1еры научают нуч111е. нсжеnп 1·0:1ко
ваш тя н ю111п1 ". )1(11:JJ11, ll11 ко:1ан l! нз11<)tн 1 ч.а
J Jобачсnск.ого са .ч ,1 н1шястсн : 1з~1 с.'L1ателъным
11 р11 мсром спужсн 1IЯ O'l'l"ЧC'CTBY ll [ 1 ~1 yicc .
rт:~нержеш1с мор;иш , чудошrщ111.1t: лр сс1упле
шrя, 1·еrютшд. rрнбы :п·омт,тх п:;рыuоn. 11епре
кратц:нощт1еся rюС шы." 13сё 61.ию. :-по пра1щ;-~. Но
11е вся нр:Ш/\:t. ЭТ()Т nет< - Jt чудо1111щ ны r'1 н
вслнкпй од 1 юnрr:мс1 11 rо.
ДJ1н на\'1<1·1 Х,'{ нск бы11 нст1ю1м. Д<хт1 1же1 шя
м ~пем:п11ю1 11 ;;э· 1 ом l"'l'\ .)Jlt'Ti111 . нож:шу\1 . 11pt:11ot'-
xo/\}1T нсС ТО, Ч 'l'U CCJ ~/\ ;\Ht 1 :1<1 111 Jt') \lllCl-l'НYKHЦJll'
Дll<:: Тl1I СИЧТI Лt'Т .
RоС1можпы ра:.н·I Ыt' точю r :чх: 111 1я 11;1 c,'v1hr cл
~3:н-1нтvн1 матсм:1·1·1 1 коi1. Н ХlЛ н . 1ю:{1 1 11к снор
между N~у~1н : н-1<1ме 1. 11пым11 уч~ны~ш - фран
Щ':'!сю 1 м м~1 тем:1' L'Т11<0 .v1 >Кn:~сфом Ф)р1 .е 11 11с
м.с 1 \тшм - К:.tр1ю11-1 Якоби. Фур11е счнт:1J 1, ч·1 ·0
цt:зть матсм.::п11кт 1- се щеiiсnюла11, объяс- 11с111 110
лрнроды . Якоби о·r·всча.01. Ч'Н) сё rtел1, - щю
славлять LJ<:лoвeчecюftl ра:1уи. l3 nр.нrщ11 ш:,
МОЖНО прн :шат1, лp;-irlOlT О6ОТI.\, 11 0 . кrюме
то 1 ·0, 1tt'JJЬIO матемаТIIЧl'СКНХ 11<.:С.'1С) \ОВ::111111·1 л
ПОСJIСД\111 (' тр 11 СТШ!i.."1'1\Н fн,JП!I 11 p<tl<T\IЧC(.' K \ !C
лр нл оже н нн - 11нженср.ныс.: . 1\011 1.." 1·μ~ ктuμсю1с .
::JK() l·J0\111Ч e<.:Юl(' 11 ИllЫ<.:. H~JJШJ-I C I (. l\l:l'l 'l'~l :I TJIK,I
во нее Rрсме1 ш ока:1ы нала нJ 11 ш11 rIL' t 1:1ф11лосr >ф
C'l\()t" ОСJ\ 1 1.тсле1111с мнра .
1()l)
Иггория математики
Матсматнчсск;tя 11:1у1'а ХХ <."1·олt:1· 11я 111x>cл:.i-
1шJJ ~1 c 1, 11:.i всех :-:Jт11х 11а 11равле1 шях .
МАТЕМАТИЧЕСКИЕ ШКО/\Ы
13 первой половине ХХ n. м;~те.матшса разшша
лась ~·11ан11ым образом п 1r ;щио11алы-1ых рамках.
Ве,1}'щую ролт" как и в предыдущем столст1ш"
11гралн фршщу:ккая 11 немецкая математиче
<..:кнс UJKUJJЫ, JIO в м1 1pu11u<.: <.:UOOЩ<..:CTHU м;1Т<..:
м;п 1 1ков уж<..: акт11111ю включаm1сь t1'1-;ыья11ск11е.
не ш·t:рсю1 е, :1встр11йсю1с. шксдск 1 1с учёныс
Ещё tl сt:рсд111-1с xrx Н. обра:юв:urась росс11(1ская ,
в nсновном петербурr·ская, школа Птшrшись
первые кру1111 1.1 е математики 11а А!'.1 ер11ка11с1<nм
1ю1тт1птсптс, формировалась польская мюсма
т11чс.-ская ш1ю1ш .
I3 д:mьнейшем :v~атемат111са стала nр11обрс
т:~ть черты иптс:ртщпон:шыюй 11аую1 Н:.~чала
осущссгnляться :v~ыс1ь Гш1ьбtрта о том , Ч'!u .шш
M:.1'1'(.',\1aП JK<t R(;'(:t, куm,турны(r ,\111[> пrt) \СТ:ШЛЯ
t.:'1' собо11 с:щ11 rую с1рану.
ЭнnJI IO l lJ 110 наую 1 НСIЮЗ \ЮЖНО 11fЮСЛС.-ЛI IT!>,
нс коснун11111с1, · г1юrчt:(" 1 к1 кр~тr1н.:й1 1н1 х, наи
болl'1.: F1m1ятt::лы 1r.1х учё111.1 >.. Н:~:зонём 11ме 1 1а
ма 1t"м:1л1ко1-1, 1 11ра 1т11 1 х н111111ую рот> 1:1 nep1юl1
1ю, 1 ов~ Пlе ХХ столетия.
Особым авторнтето.м польз оuался Даrшд
Гш1ьберт ( 1862- J94:)). 1lсмстn<ую матсщ1ти
чсску10 rтn<олу прсдсr..1впяли и такие выд;нощие
ся учёныс, как Гер.чан Вейль ( 1885-1955), Фl'
ликс Кпt::йн (1849- '19 2')), Герман 1\!l инкuвскн1I
( 186~J-J 90CJ), :;"Jммн !!Етеr (lR82- lC).- 1'1), Фс
л11кс Х~)'С/lОрф ( 1SбЯ-1942).
Ф[1<1Н1lуз Жrот. Лr1р11 П у:ткаре ( 1854 -
l C) l 2) - одн1111:> ue1нi ч эi'i1_1_11 tx 11ауч11ых 1е11иен
ucex 11ремё11 . После ТТуа1н;аре 11анбплт.rннм
ант()рнтетом среди математпков Фраrщrш
полr..:ктался Ж:Н< Адамар ( 11565-1<)63). 13 чнсле
.выдаюЩJ1хо1 фра 1 щузсю 1 х матсматrнюв нужно
11а зnатr, Эмиля Борс:ля ( 1871 - 1956), Жш1а Гас
тон;~ Дарбу ( 18Ll2 -l<Jl 7). Эл11 Жозефа Картана
( lR(')<)-1951),АнриЛеона Лебс1·а ( 1ю::;-1941 ).
ПолSJ Монтслн ( 1t376-l У75), Э,\ 111Лн П1 1 к:1р:1
( 1856-1 У-11 )
И1:11 1h>1НLкую м~1тсмат11чt:скую 111колу пpt:/\
l-1 :.~нлялн В нто 8()m»1·epp~1 ( 1860 - 19-Ю) 11 Тул -
ЛllO Ле1111-Ч1111~1та (187:)- 19-J .1). IТIRC[\C KV"IO
-
М:11'1 1 ус l'ёст::~ М 1-1паr-Лёффлср (18..J.6 - l<J27) п
:-Эp rrr< Ив~1r Фредголь;ч ( 18(J6- l 927). а11пш!1-
скую - 1·одфр 1 1 Л:~ролд Хардн ( 18 77- 19..J.7),
110
л,1 111 ри•i Федоров "0 1l1ороR.
Джон Иден:юr Лнтлuуд ( 1RR)-1 С)77), Бtртран
Р<1ссел ( 187 2- 1970), русскую - Ллексстдр
Мих:li11ювнч Ляrrутюв (18')7- 191R) т 1 Л1т,~реf1
Лrтдрссnич Маркпn ( 18'56 - 1<)22), амсрпк:ш
скуто - Джордж Дейшщ Бирю ·оф ( 188'-i - l ()+!)
11 Осн:11 1 ;\ В~блсп ( J88/J J \.)()()) .
Слtдует с:ка:за·1ь. что и н 1н.:рвuй 11олu.1шш·
СТО.!ГСТ~IЯ Мl)ЖН() KhЩC:ll J'J 'I> дна 11ер1ю.ца - ДО 11
ПОСЛ(.' 11с.-рпо1'1 м11ронuй H()JI Hbl 191-1-1918 1'1'
Лосле войн 1 .1 прощ·лол11 .. 1а смена поколt:н1н1.
1щ·1·01х1н :~;пронул.1 11рсж;..1.с нсс1·0 фр: 11 щу.il'К)'Ю
пп<0лу. Фаптисты. прнr11с1111111с.- к нл:ктн в Гср\1а
шш, ра:з1ром1 1 m 1 11емец1\)1011аук1. J\.11 кн·о т<1ю11 1·
тшых молол:т.тх )1.ЦТСМ<IТПКОП пз Еnротты псrе
схали n Америку, п там 11ачалн формироnат1,ся
rювыс матсматичесю1е ШI(Олы и 11аrтравлt1шя .
llеобыч:ti11ю1·0 расц11е·1·а достt 11 ·nа москов
ск:нt м:1тем:.rnrчсская школа 13 .1>0-с 1т. она.
nС:З)1СЛОН l-Ю, 3<1 НЮ1а J lll/(11p)'IOЩtC I IOЛOЖCHllt Ji
~шрс. Её ос1юн;пслям11 Gы1111 Д.1\.111·1·р11~'1 Фёдо-
ни~о"i111 Hll~O.\aC'OllЧ 1\VЗllfl
f)()1щч f. 1 ·арш1 ( 18()9-193 1) и Нн1<опаИ Нн1<а
лаен11ч Лузнr1 ( I R8~-19')0).
НАУЧНЫЕ НАПРАВЛЕНИЯ
В МАТЕМАТИКЕ ХХ ВЕ КА
Г l рс11ст~шлс:н11<..: о том , .каки е на11равл сн ия 11рсоб
тщ;~л и к матсм;пикс 11ач:;~ла )(Х в.. ,да(,;т сr1и сок
ссю~и й на нсторичсском Парижс ком кош·рсс
сt. ~:Это чет ыре основные се ю ~111 1~ ар11ti>мст1н~а и
а.; 11·ебра: анал11з; 1·еомеrр11я; механпка 11 матс:м;1 -
п1чсс1са н фпз r ша, а т;нокс сщё дnс: история п
611блиоrраф11я: преподавание и методол огия.
Об п:!ме 11еш 1лх, произошедпrнх с тех лор
n 11ауке, с1шдстет,стuует псрс• 1 е1 1и сс1щиi1 сов рl'
ж.·1пrых тю ш:рсссов: ма·1·с:матиqсt:к;н1 ;ю1·ика 11
uс.: н ования м;.1 ·1·ематию1 ; а;11 ·сбра: тt:ор11н чис<::л:
1·ео1--11.:трин; топu1юt·ин; аю·<..:браис1t:скан 1 ·<.:u:..1ет
р11}1 : ком11лсксный анuлн з: r · ryп111,1 Ли и · 1·со р11н
ГIГJCl LCT::ш11c 1111i'1 ; ВСЩtТТАСННЫй н фyню1110LJ:.tJ l l1-
{11>1Й ан:т и з; теорш1 в<..:рою·щ 1c1·cr1 н м;1:п.:м:~т11 -
чес1<ан ст:1т1кттrка: ; 111ффсрс1 11 tи ..-.лы rыс п)а 1111е-
1шя с частr1 ыr.ш про 11 зuод11ымн; обыкновстпrые
д11фференп11алы 1 ы е у1Хшнения; математическая
фнзнr<а; ч.ислетшые иетощ,1 и теория о ычпсл е-
1 пrif: дискретная м:пем.атика п кш.1бит1аториrс.1:
~1атсматичес кш.: :~спскты ш1фор ~tа'L'НКН; принu
же н ю1 матсма · 1· 11ки к ш.:'ф11зичесю.1Nt н:~укам; н с-
1 щ111н математ11к11; 11ре1юдаван ис ,,1:~тем:1т~1ю1.
Мно 1 · 11<..: 1 1 з 1-1азн:J11ных pa·щt'JIOR м ~пемат 1·1 К11
fЮЗ н11ю11 1 1шн офuрм11т 1сь F\ ХХ в. На рубсжс
ХIХ-ХХ Htl. rюдл1111 сь 'J'РИ тшпра11J1е1 1 11я , KO' l'O-
[Шl\1 суж;~t'НО fi1.IЛ() с 1,1ГJХIТЪ flЫ)ЩЮЩуюси рот,
11 истор ии матемап1ю1: фуню~rю11алы r ый а 11а
лиз. тополоrия 11 теория функцпi'I.
Фун1щион альны:й анализ. I:::щi: в ХУШ в.
были разработаны методы рснн:н ия систем
л111н: l111ых ураш-н.: н11й . В 1(0 1 щс Х!Х 11. обн ару
жс1-1 ы :.111:1 лоп 1и мt'ж,11у тспр11t:1'1 с1 1 стсм 111 1-
нrйных ур:нн-1сн11С1 ко11счно1·0 ч1 1сла 11ере
ме1111ых и 11х бссконс ч1юм<.:р11ых ~1н:1лu1тнs -
т111с i111ы х 1 11п·е1·р:mы-1ых уравнс1111i 1 .
Рс 111:11ощ11й 111;,~г сдсл:111 wв<::дскн~'i ма·1·~ма1·1·11'
Нвар Фре11,1 ·ол и~1 в 1900 г. Пр 1 1мешш метпды
rе111е111ш с и стем шшеfшых ураrнrсш1й н пе
рейдя к нредl'Л)'. 0 11 11аш<:л ус1101шя разреш11-
мuстн 1r алгоритмы решений уранш: 1шй шща
11
.\"(/)-АfJ((t, t )X('t' )C/1' =у(!),
({
Новое время
д!Jh
С?О4Ш
Это послуА<ИJЮ (~П IMYJJOJV\ 1< raз raf'O'!'Kl: тсори1 {,
1ю·гор:н1 соч L-та.11 :1 11 <.:l'бС ~J 1емt:нты аm·ебры 11
>'еометри11 , 1ю u бсс1сп1 1 еч11омер J rых пр остр:.1 н
ствах. Так пш1~н1пся лu1-1rJй11ы1/ ф)111л.·ц~m1Lш1ь
ны1! т1ализ.
Rажны:ч разделом фушщ1то11аJ1ыюrо ан;:~
лп:;а стала теория квад11:1тнчных форм. начала
которо~-т З<1Jrожш1 l'1щь6срт. Со нокуш юсть всех
функцнlr с н1-1·1·с1 ·рирусм ы м ю~~щратом
/1
Jx~(t)dt <=
tl
получ ш1а 11а :;ваш 1е гил ьберт оrю Щюстра11-
с11uю (ci.( обозначают /.~). Нш,с; 1 сдстнш1 теор11я
юз:tJ \р: 1· 1 11чпыл ф{)рм в п1m,fk:ртовых 11 μос-1р~т
ст13ах П()СJ1ужнл;.1 M:t'l'CM~ITI IЧl' CKOt'I ба зой д.'Jjj
к1:1а1tтснюй мехаt1нкн.
Тоrю;1огия . T~ fl.\H-IH «'l'Ol lOJ' O l 'l ljj" можt:т бы ·1·1,
отнссё11 к д11ум р;1:·щела-. 1 м:1темат1 1~-;и. От ry то
п о;ю гшо, ро1юш1 ч<и1ыm ко.ч которой был Пр11 -
каре, долгое время 11азыо;vш мJ..мби11стшр;т/1.
]а дру1·ой . у псто ков которой стоял 11емец1..:11~'1
учё1 п,1(1 Георг К:;~нтор ( 1845 - P)J S), закреm r
лось назnа1 1 и е общей 11лн mt!орет11ко-"111юJ1се
ствен нтi .
1\омб 11натор11 :1jj ·1·опо1ю1·ш1 - ра:щс;r 1·со
мс:тр1 t1 1. О1 1 а 1t:'!уч а ет с во1kтна 1 ·со:\1С"1'р 1 1чссю ·1.х
ф111ур , ос·1 ·3ющисся 11 ен зм сн11ым11 npt1 1:1.з:1нм
но О/( 1 Ю:'j1-13ч 1 1 1,1х 11 ~-1 с 11рсрыв ны х о'l·оn ра жс
н 11я х. /'1,t)JIГ'oc нремя то n01ю 111я 1юспр 1 11111мш1:1с1,
1.;;н..; п<~уТ\а , далёкая от жн ;ш11, пр11:111:-1ш1ая m11ш.
" пр ославшrт1, человсчесю1й рз~\1111 " . Но н
11ашс время выяс11шюсь, что она имеет с:.11110е
lt•op1 К.1111ор .
111
Истори я ,.,,1атсм;~л 1 к 11
rIJBel\ ( Ppr <' !'!JllЧ
Л'\РКС it111~po в.
НС! юcpt:/~CTBCll ( Юt: оттю 111 е1 111е (( OnЪHC'llt'JJllIO
устройства МНJЮ:'!~а11 1 ш.
~)(Jщая ·1·01юлопнr лр11м1,псtст к теор1111 м но
жеств 11 ,1сжи· 1 в ucпon:i r н ш .чатсма·лоо 1. Это
:11.:стюм:п 11'-н::с к:нг теорIIя . прнзнаш r~ш 1J <-'l'!lcдo
н;пъ такп с 1юняпrя. I(;JK - 1 1рсдсл ", «CXUД1Lмoc·1 ·h·'·
" 1к· 11рерывнос·1·1", 11 ·1
·.
11. Оснсж ы :11<с1юмат1 1ю1
TOПOJ IOl 'I [L[('CK(}l'O 1 1pucтra1 l l"11!a б hlЛН ЗJЛОЖСНЫ
Фс; шксом Хаус;tорфuм 11 ~-1::~ 11t'р 1 11<:ны роо: 111'1-
ск~ 1 м м:1· 1 ·с;;1ат1 r к<>м J! ;нuюм Cerm: eвi1чc:v1 AJtt'K-
c:11 IH[J< IНhlM ( J 8t)(1- I C)ii2).
Теория функций. U ШlLJaлc века фра1щу:1
А11р>1 JJ e6cr :1аверши.11 п остроеш 1 с тсор1ш ме ры
н пттте1·рщюшr1 11 1я. 13 Xl.X n. 1кл<::д за О. Коши п
.LJ. 1:'11ма11о м ш 1тсrрал
,,
f/(.\' )CL\·
(/
щ.1н11м:ш 1 1 как 1 1ре;~ел р н м:.t1юш,1х су'\1 ~. За
11р11f>J111жё 1 111ое :-1 наче11 11е 11 нте1 '[)ал:1 бра11н 111,1-
р;.~же11ш1 R1 1да
11
I,лс,,н.v, - .У,_ 1 ).
1дс.\'1 -
11екоторая точка отрезка /х, 1. x, I, о =
= .\',, < х1 < ... <. .У,, 1 <.1:11 = /J - раз611е1111с отрезка
11нте1·рщюш11 1 ия \а, tJ \.
Лl:бtт ст: 1л rюсту1шт 1 , нн:~ чс. Он p~i:j611вa 11
irл: ''"YL'r.1 ·~ifY~ 1•1.},.t,/,'.'L ~ ·ь. 1\"1'-}tJ '\Y\'.//\•-'1_t1'a{1\ ' '\ f\'J ..!"\_'<'2''.4'\1\'' 4• • < . .
<. 1', 1 < у, < .... MOTIIl\l·IPYЯ Э'l'О тем. Ч'l'О ДЛЯ рзз
rывпоiI ф)•llKЦill I,{HeHOЗMOЖ!IO l\Ыб\Х.\\\, ТОЧКУ
.\',. кuто рая а;tс1<ва-11. ю <-Предст~шюrла» аы фу1 ш
ц11ю 11а 0 ·1р<::л-.:е jx1 1. х,). Jlo если фунющя ;~о
е1·аточтю сложна. то .v1 1южества Е, нз ос1 1 :16с
ПIн.:с. ДЛЯ ~LYП.>pbL'< Yr- I <, ./\.\:) <у,. MO!') ' I' бh!ТЬ
112
yc· 1poc11hl H(>ChM::J 11p11 •1 y;l.)ll llIO. 1т ч ·1 п()1, 1 JIOC'll)O-
IПЪ ·1·сор1110 1J 1 1тс1·р1 tpo11:11 11 1н 1·1t:об.хою 1мо ()ыло
НЭЧ.:1.'LЪ ( meo/Jl.111 Ш!jJЫ. '1' t'. Jl;.!)'Ч lf 'J ы·н 11 :1 \J CJЖIЪ
r':iкr1c м11ижсстна. ::)·1
·0 c;~~J1ЭJ111 l)opc. 11 , 11JlL:()e1
М ера мrюжесл~а Е (с~с1жем.. 11 а отре:ше 10. Jj)
опрслеляется следующ11 м о6рззом. Н 1 rж 111ою
грань сумм щшн н11тtтр:L'ЮТ\ 1юкры11ающ11х Е.
rтазо..uём вl!jJ.Y1-t01! .мcpotl Н. J:kpx1 1ю1 мер;~ ощх~
дслсна .ЦjШ шобо1 ·u 11-uюжсс1·на.1'1пожt:ешо Е 11а
зы н а<:то1 lf3..~юри.мьн1 по Jil!бe?_J '. t:сл11 сум ~1 а
lll'(1X 1-н.: й Мt:ры :"!ТО!'( ) м 1I OЖCC'l ШI 11 Rt:px11 c1' 1
меры Cl'() i \O/IOЛllCHШ! (!Ю OTl-!OllJCllJIIO" огрl':l
ку (U, ll) раы1а C/\J 1111щс. 1'(JJ'дa вс.:рх11ю10 меру Е
11a:J1,1 в:нот .мероi1 Лебеиt 11,1 11ожес1 ·н~ Е 11 п\10:111;-~
ч:1 ЮТ П1(:S Е.
Ри .v1:шоnы су.чмы для вы • 1 ис 1е111ш 111гr<:rp;:iлa
1kбе1 · :~aMClШ.JJ C)ГMM:JMl1 НJЦа
I Т\,шс:-.А,,
1·де т~, - lll'K(Yl'Up:1н точю1 0·1·р<':ща [ J', 1
• l',l Он
кссhм :1 ныра:-1 1 1п:1 1 ы10о х:1рактср1 1:ю11ап 11 рс: 1 1му
щсстни сщ ,с1п ме-1·ода. ~в мет1щl' Ко1 1111. - 11 11
ст Лсбе1. - оперируrот т;.11, , 1<:i 1< [(ел:-tет :~Т()
l l t'() I J l 1l'ГПЫЙ ю1е::рк, J<()'l'Opblfl IIO/ ~(' Чl lТЫB:'l e'I' М(] ·
11е·1 1.1 11 крl:д~ п 1 1ыс 6иле 11,1 ссюбра:шо ТО1\1 у, ка1<
0 1111 1юпадаются 1юд ру1<у. Тогда ка!\ мы опери
руем, ка к опыт11ы:i 1 н иетол.пчоый клерк l'OHO ·
ря щиi1 : у мсIJ я rпes Е 1 монс:.т по 01tтюму фрашт.
сп)ящнх 1хшс~F1, у ,чспя 111ск Е~ монет но д~3
фpaI1 1<:.t, стоящнх 2 х mcs Е!. у меня 1щ.:s п, мо
нс:т но 1IН' l'h ф\)аL 1 кон, с:.vrо н щш< '5 х mc~ ,";. Ltтo-
1·<>,у мс:.:нн1хшс"f,1+2 х111с:-.1~':.+'iхпк·-,Е;+
фра1-1 ко11. Конечн о, r1тот и 11 р)то 11 ю1ерю 1 111т
дут к 0;(1 юму п тrJ~·1 y же pcэy.r11>1<J·1 у. HrJ в случае
сумм 11сдсm1м 1.1х, чпсло которых 6ес коне<11Ю.
раз~ 11щ~ 1lB}:\ ~1 tт(щов ка111 rт~mы1э·), llа ба:1е 1 ео
рпи меры ро,rщ.rюсь 11 оное пащхтлепие в тео
рн н фушщш'1 - лum~рl!цесл:ал теория фу111щшi
Тр а1 1сформ11роваласJ, в тсорпs1 м1южссн1
Трп фр~111цу:кю1х учi.;ныл - Борет,, Лсбс1· 11
Ре не Лу и J-;1::1p - :зэложш 1 1J ос1 ю 11:1н1 ш r)l!оф1т
т11вной IШIO/JllUЛ1.IIO)l((!C11 Ж 'L '. с . теор1 1 11 ЧJ IC J[ O ·
l~ Ы Х Мl·!ОЖ.е\Т\~.
R 20-с п·. нсдущан рш1u в тсор1111 ф~ ню 1 111'1
?<..::'iY.::u·1д~t ·L'. 'fJ~''-'-·6.~J'ii1 ·шк\.>nс. 1,0 l\ J\IYIO 11ptдl 1·а11·
тrлп Н. ll. Лу:нш 11 его уче1111юr: П. С. Ллt:кс:111-
1\РО'<'•, Н . К. Пaplt:\. А. Н. Конмоrорсн~. Д. ~- Ме11ь·
шоn, М. Я . Суст-ш, А Я. Хт1чш1.
Раз.вптис а бстрактных разделов матем:~·
тики Стрс:.\щ:1шс 11р1к.л аtш 1· ь чt.:. IO\\l' 'lt:t:ю11'
разу,,1 ,\lf;1f)п11н,wн:1ло усилия .~ti'i'O.' liX,., м1.·о,• их
j'чё111.1х . Внрочем, 1н.:рС!'•СО 0110 утю;tшю их 11
rакпс ,"\ебр11. которые почт~ 1 11 е н.мст1 сопрп-
1\uс11ове~шlт с реальностью.
н ПС'рной П()ЛОНИl!t' хх н. нo:ШJJК.'I~I концсл
ЦJIЯ аксио~1атнчсскогu ностроt'нш1 всей матс
щ1·шки. Со1'л;ю-ю этой концеп1tнi1. lJ<.) с1ю 11а"'
ак;111<::.ш ка А11/\Рl'Я l-11 1кол ;н:кн чэ Кол мu1 орона
(190:\ - l987), '< Н OCl-IOHC t .K<.:it 1' 1;,l"J l'.\.la'J'Ш<ll ЛСЖJ l'J'
Yl lLT:JH 'l't:Ория МНОЖt.:СТ!З» - духовно<:: / \C'J 'IJ J(lt;
1«:ор1 ·~1 Кантора. J\11ю1·11м 1<а ::J :~лось, что 61 1аг0/\~1ря
11сиедо11а1О1яl\1 Ка1 1тора математ1ша 1 1олж11а
61.i .r1,1с t:п п f"юлсс стройной н с~ю юй - состоя-
1ше. которпе Г11льберт 11аэк1л «раем». Koi; ta 06-
11 аруж11лщъ пр отшюр~::чнн u теории мtюжссгn
~1 мат<:м.~тнки C1':v111 выражат1, COJ' - 'J 11е11ия R c:1м1L'i:
et 1к1юват1нх . Г1rльбср·1· 1юскл11кнул : « !1111шму
11с д,1нu 1п1·11а·1ъ нас 11.> кантuрu.нсю}J'(.> рая~ ~-
Раэ 1111 · 1 · нt: аксиом:~т11 чес ко1 ·u мстсщз 1ю1 ·рt:60-
1шю кр1r·1· 1 1чс.с ю 1 11с:рсс"ю' 1·рl"ть оснон-а1-11, щ на
которы е оп11рал:.1с ь мате1ч :пн1<:1 K1)JI •\.1UJ ' OP<J11
JlllC':-t!1 : «\lp11 IHК:TJ10l'llШI 061ш 1р11ых 11 Н110ГЩ1
11ес1,"1:1 a6C'rpaкr 1 11.1x теорий, охватывающих,
rюии.чо тех ча стных случаен, которые п.rнте1111
Г\ 11л со:~,"\;пrню, 01тюм111.1й матсрнаJ 1, получаю -
1щ1й КОВК\)i;;ТПЫС lф\!МСНС1НШ JIИШ\," 11ерсш.:1'-
11шс десяп1ж.:тнi1, ждать пспосредст1к:111тых сн1·-
1ылuв о 11сдuстаточ1 ю\1 коррс1пнuст11 теор и 11
ПС'ЛhЗ!I . ВМСС]'(} ~ТОП.) llj)HXU[(ИTCЯ оnр<1ща IЪСЯ КО
1ю.: \\у llaKOПЛCJJJ[()l\;\Y uпьпу работы Yt'JIUllCЧC
cкol1 ~1ы с, 111, котС)рый как p:t3 11 суммнрустся R
ныраб:пын:н:: мых 1н>сгr::псr1но науюн't трсnо11а-
11шrх к " L"1 р< н·ос1·1 !'. доrса:1атс::m,с1 'Г1».
Гr1.11.берт СО:iJЦЛ ;1J(C I IO i\1;) ' 1'f IKY ЭЛСМСI п ap1юir
1·с::омстр1111 , ;i Колмогоров - тсор1111. веронт110-
стс l1 Ст:11ш р:.1зшша1ъсп мног11е др5т11с Jкс1ю
матпчесю1е п.:uрпн.
ll коrще 5U -x гг. гру1ш;~ фран1~узсютх .мате
машкuв. вые 1 '\1 111шшн:< н 11ечатн 1ю,~ 11сt:в1101-11 ·1-
мо:-.-1 Н11кол:i 1->°урбаю'1, оf1ъс;1 1·1н1rщ11_:ь 11 жстнш11
l lUC' l'PO l lTЬ KCfO ~1:1'L'(;' .\'1:ITI1 ку 1[;1 а K~HOM<l 'J'l I чсско 1"1
оо ювt.:. Ф)о 1~даl\1ентом с.11уж1111:-1 тсорня множесп1 .
3л 1::;-. 1 сгр0111101
пср~ыJ·1 этаж у1юрядоч~.:1111 ые
с·1·ру1<тур1>1, '1! 11·е\1ра. общая ·1 ·ополnпщ теор~ rн
11сры. По-1 ом сле; щваJЮ ноз1н:·сги nтCJpCJ1i эт:1Ж,
r.·1e ('OC/tltllЯЛПCЬ бы струКТ)1JЫ - :шгсбр:.111•1е
:к11е, 1·еомс-rрическш: и 1'. н"
-
состашшющие
ntр1ш й этаж. :·)та по11ытка осталась 11сзавершL·н
иО1\ так каr< сама цст" 1 10-вrщимому, бъша ую
m1чн~1.
R 2U-<:: IТ. JIL'U6ЫIOIOKtlll-I01'0 \):IЗBll'l'lfИ до
=т111ж1 ;;m ·сбра , нрои :щ шла :ш 1 ·сбранз<11 щя ма-
1 loooc орсмя
Лн11рt·i1111щм ,11·ш1•<
Колмоrо роs
'J 'CM:t'l'llIOI . C:p<:J\11 тех, K'J'() н :{H ;IЧl'l'l 'CJll>HOO м<:рl'
с11особс1·кока.11 :-~тому 111хщсссу , t 1 :що н:1.:~на · 1ъ
нсмсц1«J1'<J матt:мt1·1 · 1·1к::1 Змм11 Нёп:р 11 ее учс-
1111к::1 1·01u1:1 t t/ tl (:1 fia 1т1 '(;'Jl<I Л<.:1 l / \t:рт~1Ra11-,tt:p-Bap
/ (t:Jta ( 19();1 - 1996).
МАТЕМАТИКА И ФИЗИКА
В конц<:: Xl.X n. каза:юсь, что фи зика
-
:1аuер-
1ш:~1mая облает~, з11ш111й. Р~1сска::~ываrот. что
некай ющ.>llL:t обрат~ u1сн к мэтру (на стан~ в 1ку)
с пrосьбuй о 11а11утстн1111 - он хоп.:л стать ф1J
з11ко,ч. //о мэтr OTBC'l 'HJI , Ч'JО у t\Jl!ЗJIКI 1 1н:т гrcr
(ПCl<TIJВ: 11а почт11бс:юблач1шм11сбс 0·1·крыт1,1х
llC'I llH HIЩllJ,I ЛllШЬ / \Ua [ I CбOJIЫUIIX обл :~чка -
0111,1 ·1
· 1'v1а ~'1 1<сл псо 11а ((Jtl 1tока:~ал 11с:-.1;1в11с1шост1,
скорост11 света ()·1· /(Виже11ю1 :kмт1 . Пр1Lм.
ред.) 11:-~а1ю 1 1ы11:1.11учсния. Скоро 01111 рассеются,
н в фпз111<е нечего 6)7\СТ делать.
Через нс.:сколько лет 1 1з ~1срво1·0 об11ач1<а
рuдиласт, с11~цнал~.11:ш тсор11н uт1юс11тслыю
стн, а 11.:~ втuро1·0 - ккантован мt:хаtшка .
Ct 1 сц11а : 1ы1ан 1с.;орня 0·1 ·нос11тсл ы-юс 1 11 cu-
:3:\<tнa к 1905-1906 rт. усшшнм1·1 Альсk:rта ?Юн -
111· 1-еl1на ( 1А7С)-19'55) 11 Пуанкаре. Устроl1стно
ф11 :111чсощ1 ·0 :v1ира, 011исы~асм о1 о .- f1 011 те1)р11-
tl1, Gы1 10 оче111, 11 t:пр1н11,1ч11 ы VJ . 01 ю r1ротинорс:
ч11Jю · 1.·с:м 11 pt:ДC'l'~lliJH; IПIHJl.I, /..0'1ЛрЫt" 11ыр;1б:п1.1
валпс1, па nротяже11ш1 пос1 1t:t1шх тrёх ueкon.
Чct·u стон·~, нанрнмер, ч1арадокс 61111:~ш: цо в+ .
Один и з 1шх жиnёт 11;1 Земле, а другой отправ
ш1<:тсл в тщошчсскос путешествие па свt'рх
скоростной ракt.:тс. l3ер1 1 уш 111 1с 1, 11а:~а/\ 1ючти
11с 11:з1v1<:1-~нuш11мсн, всС:· так11м же Н)НЫ~t. ка1\ в мo
Mt:H'I' ст;~рта, 011 :~:1 ст;1ёт с воt1·0 (1рат;:~ 1 ·nубою1м
lH
История математики
ЖюАь Анри Пу~ н карр
l~1·ари ком - ведь nрсм:я на Земл е и в космиче
ской ракете текло по-ра:шо му.
1! о коr.п. а 061-1аруж.илась снязь спе циальнuй
тсо рнн относитt:ль 1-юсти с 1·сомстрпt:й Лuба
ченскоrо, это кдох1 ювилu м<1тема11,1 ков: теория,
1 1 редс1 авляншаяся многим абсурдной заумью,
Bfl.pyr оI<азалась пежа щей в основа 111 111 uсего
мнро :ща тrя.
Через десять лет :7йmuтей11 создал общую
теорию относителыю сти , 1<ото рая полностью
разрушила представл е1ше о « Плос 1<0м» мире .
Геометрия мира предсгала «искрнвлёпrюй» и
снН::!<1нной с: тя 1 ·отен11см . Пок:~ з:шия 11риборов,
сонер шнв111и х rтуть от одной точки н дру 1 ую,
как ныясн.илuсь, тюлжн1,1 завн сеть от траекто
rни J\f\ИЖС ННЯ Паралле.11ы-ше пс.rе н есе 1 IИ<:' на
1-1 ск rнил Е ннn~ х поверхностях опре11 еляето1
одннм н з tJаж11ейших понятнй 1·еоме1rни -
свл:тостью. 0110 было п 1х:дметом изучения
геш.1етров итальm·1ской тттколы - Леви-Чивита
и др. Всё это повлекло за собой интенсишюе
развитие 1-еоl\1етрии в 20-е и 30-е rr.
Тогда же научны й мир ожидал и другой
« 11ruк ~ - рuждсние квантовой механики. Ру
шился сщн н 1·13 H <:З hl бЛC MhLXДOT(}JJ поры баС'l'И
о н он на уч ног о мнровпззрсния - прю-щ1 1 11
детерм1 1низм::1, т. е. nредск:~зуемости будущею
по пр ошлому. Выяснилось, что мнкром11р
неnрелсказуем . В ссютвстствии с при1щmюм
неопределёштост и мы 11 е можем точно уз1 1 э·1ъ
од11оnреме11110 н пол ожение элеме нтарп о f\
частн!(ы и сё скорость. Это казалос1, неnероят
ным даже такому rcr rнro, как Эйнштейн, - од
ному из ОСНОВОПОЛОЖIIИI<ОD квантовой теории.
~ я нс нер ю .в Бо1·а, иrрающе1·0 н кост~», -
н с уставал п о вторять он.
114
т~1к случн 1 юсь. чт11ма· 1·с мат11ческис основа
нш1 к1:1а1п·о вой мсханюш были с:озданы Гнль
бертом и е 1·0 ПОСЛС.:/\01'\аТСJl>IМ И ll C.::.J;Jll;OJIГO ДО
рожде 11ня само~! t 1 аук11 . В ч<1сп-юст11 . Г11т.бt:р
тоnа теория бесконс чrтомер11ьLх кпадrаптч11ых
фо рм помогла установитъ рав1t0с 1rлыrость
двух 1юдходов к о rтнса нию микр омира - ма
тричной механики Гейзенберга и вотю1юlr ме
хашш:и Wpi.:1~11н1·t'pa .
в 190'5 1' :;)r1 нш ·1·е йн uпубликовал тrи рабu
ты . Ою1а была посвящен~• спе r tи ал ы-ю й теор1111
от1-юс11теJJы-1ос_-г и. !\ругая - кна11·1·01ю1'1 механ11 -
к<::, ЧХ0Тl>Я -
'1еОр1·111 броуН<.>RСКОГО /~111-IЖ<::HJ 1Я
О первых ,11вух пробпемах уже rr>1юр 1-1лос1"
тепер1,, peLJЬ пойдёт о трет1.е н .
Математическую теорию б роу 1 ~овского
дnижет-п-ш построил Колмогоров. 13 пей nоссо
t'ди11илт 1 сь тео рия теплоты, пачат~u1 11 сслс1ю
кшия.ми Фурье, Т(;орю1 броут10Rско 1'u дш1.же
н11н Эйнштейна - с~юлухuвс:кого, со;9щ11нш1
ими на фн::sичсском уровне, и ре::iульт:пы тео
рии вероят1юстсl1 , нач:.11ю которым положи
Jllt M<tfЖOn и Rи1 1ер.
Высокого ~1Jоnня достит ·л<t теория урав 11е
ний с частнымн гrрон:1tю; 11 11 .1ми. Пуант<а ре 1111-
сал: «Каждая физическая тео р1ш . п<нюnа~1у
освещает уравне ния. Без ;:,ти х теорий мы
н е зналн бы, что та кое ураu11ения в ч астных
проиэво; tны х•. Прониюювспис мз тематики в
различные обласvr'и мс::ханики и физнки шло
широким фронтом . Уч ёные-ма тсматики 11ри
нимал11 активное уч<1стие 1:! р;вработке м но
гих фн з ичt:t:КИХ тсо р11й - турбуJ 1 t:нт н ост11
с nерх прОВО,!\ИМОСТИ 11 др.
МАТЕМАТИКА
И ВОЕН НО-ПРОМЫШЛЕН Н ЫЙ
КОМ ПЛЕКС
Матсм~1 тнка }"Jастновал:~ ин т;.~ю 1х дб1 н1 шх нека
котоrые п о11нсли человечество к rранн всем11р·
ной катастрr>фы. О1·ром1юс ч1 1 слn учёных я
разных п·ра 1 1 ах 11ринюш учасп-t~ R11рu 1 раммах
110 СОЗД:.111ИЮ IIOFleЙt llllX сrедСТП 1юоруже 1 1 11.я 11
веде1 1 ия военных дейстnиi1 .
Потреб11осп 1 самолётостроспия пр иоел н li
развитшо аэродинамrпси и появле11и ю n m<ra-
лc всI<а теорин полёта. Среди ю1а сси 1юn это11
науки - «0тс1 1 русской :~виаци 11 » 11. I::. ЖуТ<ов·
ский и его 11осле;1он ап::ли - С. А Ча 1 1лыt·1 щ
1.1 . 13. Голубев и др. Длн создання те:орш1 rюлёта
ош1 прнмс н яли н шттенснв1ю разnивзлп тсо
р11ю фу11кц11Г1 ком1~лс1,сного переменного.
С..:о стропп.'ЛЬСТJЮМ IЩЦВОДНОГО 11 ПОДIЮДJЮ
\'U t\11ют~ были с.вя :>.:11-1ы фу1 1J\аме11т;u~ъные до
ст1гжсt 111я н обп:к~1·1 1 теор1111 кор~1бля (А. 1-1 Кры
лов), гироскошн1 (А. Ю И1 11 тшскнй), ра:тнт11с
г·сnрин )'C'l'OЙЧ l·IJIOC"ПI , ме'J'ОД()В RЫЧНСJ1ени1I .
Н1111ер и Копмогорт1 :1ан 1-1 ~1ат rс1, ,\11rог11мн
пр 11ложепннми теор 11 н нероят1юстей, R ч :кт-
1юстн утtранлением ар·r·илперийсrшм с>п1ём и
nроблема ,\1и бомбометания. Из nотрсf1 1 юсте 1'1
11шфроnк11 секретных сообщений 11 эффск-пт
1юi 1 псрсд:.~чи их по как~Uiам сш1зи nырос со
вер 1 uешrо новы 11 ра~дсл матс~1атики - meoprm
11нфор.мmр1U (К \Uе нно11). сонсршс1-1стnоuалась
11 1·сорин конирона 11 ин . КО11с·1·руи рова ние раке· r·
{\а11ы-1с1·0 дсйстния с1·имуниrокало развит11е
оп·п1м:.~лh1юго ут1ранлс11ия (Л . С. Понтряги11 .
Р Бt:.ш r ;11:.1 1 Т) и мнопrх друтнх p<1З/\t:JIOB прш<Ла/t-
11ой п ч1к·тоИ м::~те,,1атнюr. Г1рЛ1<.1!<1/1,t1ая м:.<тема
тпка обслужнн;vrа и ~томную про 1·рам .v1у.
Лроп~rюстоя 1 ше дnух со1tиалы 1 ых систем
привело к невилашюму развитию техпнки и в
конt:чном ито1 ·с - к и11форм;щионному взры
ву, выз нш 11-юму коиrrhlотернз:щисй . Роль матс
,\lатикон к pa~raбu·r·кc 11 сuзданн11 n l'рных ком
пыотсрuн н1.::сьма 11(.'лнка.
МАТЕМАТИКА И НАУЧНОЕ
МИРОВОЗЗРЕНИЕ
Неличие ХХ столетrщ в часn-юсти, 1:1 том, что
01ю нарушило, изме1шло, преобразовало п очти
нес 11редставлсния челоне ч сства об окружаю-
Новое орсмя
Щс\1 мире. И здесJ, л1атсмат111ш сы 1 ·ра;1.~ вы,rр
ющуюся роль .
В 11 ачалt: века казалос~. - 11ау1<а fi.rшзка к
оn'Ьлс11е1mю картт1 1.r мирозда 1 ннr . Учё11ые
были Уflерепы в том, что м1tр nпзнаnаем , что
.l:k-cJ 1 e1111aн суrцествует вечrrо. что она пе имеет
ни начала, /Н I l\OtlЦ<l 11.И во Bj)CMCIIJt. ШI u 11ро
стра 11 ст~е . Земля, счпт:~ли они, образоnа;1 ась
естественным 11утём. естественным путем во3-
н111.<л:t на нсй жизнь 11 н ходе естест1к:нноrо
р: 1 :.т11т1 1я она ,r\ост1 н·ла щ.:сго то1·0, что открыто
пер<::/\ нашнм llЗ()ром.
Однакп 0()11(:1 н ·rтпрт1 относнтст.1-1остн
Зйнr11те1"111а пr1 1 11слз к развитию .космологии. к
теорн1 1 Болr,шого В:1рыва - пачэль11оli точки
отсчёт:1 ж11 31111 lkелеш rой . Лростраrк1'во Rсе
лешю11 О1<азалось ограниче11 ным, хотя и рас
пrпртощимся.
В больш1111сrне теорий о происхождешш
Солнечной с11стсмh1 обнаружилпсь глубоюrс
ИЗЪЯНЫ. \.':щ{: f>OJJCC ' \'~\HllC'TBCHHhlM ~Ыl'JIЯДl'\T
IЮЯllJJ(.'ltHC ЖИЗt-111 на Зt:,\.1ЛС н сё ЭВ{)ЛЮJ \1 !Я , 11ро
исхождс 1 r нс чел о нека. Нз месте пошатну11-
uн1хо1 TI pyXH)'llllLllX П[)CДCT::JRJICHHJI Об }'C 'Tr>OJ1-
Cl'HC Rce;1e-11нoi1 сонреме1111ыс учсныt' пытаются
соэ7(;.п11 р<щиоrrат rстнч ескую версию мирозда
шщ хотя уnереmюсти в ус 11ехе у 11их 1 ·ора :то
менъше, ч ем быJ ю у 1юr<олс11ия 11х уч11те.11~й .
l3cp11ёмся к вопросу о дстерм11ш1зме. Оо юn
но11 тезис постн ыотоноnской н:~турф 1 rлосо
фш1 состшm D том. <rто мир управляется диф
ференцш1 лы-1ы мн урав111.:н1шм11, 1111ачс 1·01юря ,
01 1 rюлнос·1·ыо пред с казусм . Гlослу111айте:: , на
пр11мср, t1ьср;.1 Симона JТанпаса: .-,Ум , кт·орому
fiЬJJll.J nы 1I Э llCCТ.l I Ы ДЛЯ КС!ЖДОГО /\aHHOl'O МО
ме11 ·га вес с11лы _ ОЛ}Wевляю 11п 1 е пр 11[Ю!\У, 11 от-
1юс11телыюе 11оложеш 1 е 1ксх tё составных
частеf1, еслп бы n11.обаrюк 011 оказался / \r JСТатuч
но обш 11рпым. чтобы подчш1иТh эти да11 11 ые
анализу. - он обнял бы в одпой фopl\-ty.rte
дш1жс11ю1 вслнчай1uихтел l3селс11 н ой наряду с
движениями лс1 ·чаftших атомов: 1rc щ_'ТаJЮ<.:1> бы
н1 1 <1егu, ч'1·0 бызю бы для него недостunср110, и
будущее 'J'~ll< же, каr< 1-1 прошс.:ю 11 ес. 1 1рС/(Ст~1л о
бы \IC}ll:;'/\ CJ'O ВЗО[ЮМ ».
Ro npcмtн:.i Ла11J 1 aca Ш'ром1 1 ыlr мнр представ
лялся 1щрст1юм Поря11.ка, 1~ нём всё нр~дt:к<tзус
мо, nrСД()ПрсдеЛСllО, И ТОЛЬКО ШIЧ 'l'ОЖllЫЙ J(ЛО
ЧОК этого мнра зашrмала « прот11 1юпр:ав 1 1ая ->
область, где утверждал себя Хаос, - азартные
1rгры Пасr<аль, Ферма, Я . Бернулли н сам Лаплас
uписади первые законы случая.
115
Иrrория матt>митики
Жюль Анр11 1 1 у.111к ,1рt•
стаrтпюм - ведь время 11а Земле и в космнче
ской ракете текло 1ю -раэ1 юму.
1Jo кота обнаружилась связь специалr..rюй
теории относит<:лыюсти с геометрией Лоба
чевского. это ндою-ютmо математиков: теория,
1 1рсдставлянrш1яся мJ-ю1·им абсурдной зау м1,10,
BJtpyг ОК:133Л3.СЬ m::ж:1111сй R OCJJOBЭllИИ всего
м11роздан11я .
Черсз десять лет ЭйнштсЛн создал общую
теор~ 1ю от1юс1 1'1·елы-юст11 , которая поm юстъю
ра:зруш11ла представление о ~ 1 тлоскnм» мире.
Геометрия мира 11редс1·ала «тrскривлёпной~ и
свлэаш-юИ с тя готением. Показа ния приборов.
совершивших путь от од1 юй точю1 в другую,
к;щ выяснилось, доджны зависеть от траекго
рии движения . Параллельное перенесение на
нскривJ 1 ённых nовсрх 1 юстях 01 1р едет1етсн
олннм и :~ важнейших 1юнн·1·ю) 1·еометр1ш -
сн~зностыо. Оно было 11ред м етом изучения
геометро 11 ит:з11ыrнской школы - Ле1т-Чивнта
[r др Всё э·1·0 1ювлекло з(! соб()й 1111те11сн ш юе
ра::mитне геомеrрш1 11 20-е 11 30-е п.
Tor,1,a же 11 ауч 11 ый мнр ожидал 1-1 другой
« ШО!\ •> - рождение квантовой механики. Ру
шился одm 1 и:з незыблемых до той поры басти
онов научного мировоззре ния - принцип
детер.м11низ ма, т. с. предс казуемости будущс1'0
по 11 ро1111юму 13ыясншюсь , что мокром1 1 р
11сnрСf(СКазусм. в COO'l'RCTCTl\llИ с пpHHl(ИflOM
нсопрсделё нтюстн мы не можем точн о узнат1.
од11овреме1 11 ю н положение элементарной
части~ (Ы и сё скорое1ъ. Это казалос~. певеронт
ным даже такому r·етпо. как Эйн штейн , - од-
1юму из ОСНОВОПОЛОЖ l lИКОВ квантовой теори и.
«Я 11е ве рю й Бога, играющего в кости•>, -
не уставdЛ повторять о н .
114
Так l'J IYЧ.11JLOCI>. ЧТ<J матсм;~т 1 IЧ {:(.'!{НС ОС НОН3-
НШI квантmюй механ 11 ю1 были со.:щаны Г11J1 ь
бt:ртом 11 ето после11m1а · 1 ·е11>1мн нсза,r~,ш11'0 до
рож,це1111я са моl 1 1-1аую r . Н час·тност11. Г11J11,бер
това теорпя бесконечномерных r<naдpaтrrЧ1rыx
форм помоJ ·ла устанонип, рав11осплыюст1,
ДRух 110,ri,xoл:on r< опи сашпо микромира - ма
трично й м<.:ханню1 Геl1з<.:нбсрга и тюm юnof1 мс
хаш 1ки Шр~д11н 1 ·ср:~ .
В 1905 1·. :;1r1ш1y1·1.::i:-111 tшубл 11.конап тр 11 р:160-
ты Одна была посня Щl"На спе1 ~11 ~u 11,1 юit теор111 1
ОТН(1ситс.rгьносп 1 ,дру 1 ·;:~}! - квантшюй м ехан и
ке, 1т>еты1 - ·1·еор1 1 и броу110 1ккого ;~н11жrн11я.
() nepnr.1x двух проблемах уже 1'0 1 1орнлос1"
теперь реЧ1, пойдёт о третьей .
Математи<-1ес1сую теорию броуновского
дшfжсшrя построш1 Кuлмо1·ороn. 13 ней nоссо
едш1шшtъ теорня те1шuты , начатая исслсдо
вш шями Фурье, тсор11я брuутювского дв11жс
н ш1 Эй н111тс:й 11 а - С"юлуховскш·о, сu:.ща111 r ая
имн на фи :шчссr<ом уроRнс, t1 резу111.т:1ты т~:о
р1111 вероятностей. начало которым положи
ли Мар1ю11 и Rи1 1ер.
Высо1<ого уроrнrя досп1гла '1 ·еорШ1 yraD11e -
1rи:й с частными проиэnодт1ыми . 1lуа11каре1111-
с:зл: <- Каждая физичес1<зя теория... п о - 1ю1юму
освещает ура!311ения. Без ;:,тих теорий мы
н е з нали бы. '-ПО такое уравнения в частных
произ1юдных~ . Про н11ю-ювс rrие матсмап1ю1 в
различные области мех;1ш1ки и физики шло
ши роким фрuнтом . Уч ё ны е-математики 11 ри
нимаJ1и активнuе участие н разрабuткс м 1-ю
t'ИХ фн з 11чсских тсорпй - турбулент1 юс·1 11.
снерхnрО!'IО/~имлс-п1 н д р.
МАТЕМАТИКА
И ВОЕННО-ПРОМЫ ШЛЕНН ЫЙ
КОМПЛ ЕКС
Математика участвонала н Rтаких r1е>1н пях века.
котор ы е подвели челuвечестнu к 1'ра1 ш ш::ем 1 1р·
ной катастрофы. О1 · р()м1юе ч-1 1 сло учёr11,1 х н
раз1rыхе1-р;н1<1х при 1 rю111 уч аст11е н [ 1 роtраммах
1ю со:1да 1 тию 11 овей ш11х сре11сп~ нооружt11ия ~1
Rсдс11ия военных действий .
llотребпостп самолётостроешш прилел11 к
paзDlfTllIO аэродипамm<и и rюявлешuо u 1~а•1а
лс пека теории полёта. Среди класс11коn этой
пауки - «0те1 ~ русской а ни ац1ш,) Н. Е. Жу}{ОВ·
с ки й и е1 ·0 1 юс.:11едо 1~~1тели - С. А. Ч.аплыnщ
13. В l'олубсв и др. Длн со:щан~m тсорш1 попtта
0111·1 11р1 ·1мснял 11 п шrтсш..:1 шно разн 1 ш;JJш тео
рию фуr llЩI JJJ KO,\l!ПJICl<CI (()!'() 11еремt:н H()J 'О.
Со строJ JTl'Jlьcтвuм 1 1 ~щ1юд1 ю1·0 о лоднuдно
го флота быт 1 свнз~н 1 ы фу11дамснт;lЛьНые до
с~·ижсrшя и област11 тсорнн кор:.rблн (А. К. Кры
жш), 1·ирnс 1юпr 11 1 (Л. 1-0. Итлт rсr<ий), разuнтие
теор1111 устойчиnос-·ги, мепщов JЗычпсленr 1r'f.
Uиттеr 11 К()nмог()роn ~аннмзлнсь м1ю 1·има
nр111южешшмн теории вероят11остей, в част-
1юст11 уnраnление м артиллери-йсrшм оrнём н
пробпем:н.~н бо.мбометзшrn. Из по1·rкбно(тсй.
шнфро.кю-1 секретных сообщt' 1-ги 1"1 и эффектив
но11 псrсда4Н JIX ПО K:lH:lЛ:ti\1 СВНЗИ вырос CO-
кep111Cl-\llO ноный р:щц~1 М<IТСМ~IТИКИ - 1·neo/ЩJJ
инфо(J.лш111111 (К Ulc 1 1нш 1). соRерmенствонал~н.:f,
и теорнн kл;111ронан1нс Конструир0Rан1·1<:: р:~кс.·т
д;1ш.11\:\'() дейt"r1~115\ сти м уJI 11 ров~ло развитие
оптнмалы юго )r11раш1ен 11я (Л. С. Понтря rин,
Р. Пеллмап) и м 1 юги.х[(р-~тнх раз;tелов прнклап:
ной 11 чнС'10\1м:псмати1ш. 1 Iр11кладп~я матема
тнка обаrул~11в:иа г1 атш.нrую програМ).f}'.
1Iропmостолr шс: двух соцпалыu)rх С1 ~стем
11р11uсло к нсш щанному ра:.1внтшо тсхш~кп ин
конечном rrт01·c - к ш-1фоrм:щ1юНiюму ВЗ[>hl
иу. вызванному компh}tУJ'ер1 1 за1щеЛ. Ро11.ь м;1тс
мат1-1ков к разработке 11созд;1нии 11ерRых ком-
1тыотtра11 Ht:ChMЗ BCJI 111<3.
МАТЕМАТИКА И НАУЧНОЕ
МИРОВОЗЗРЕН ИЕ
Всm~чис ХХ сталс.тия , в часпюС1'11, в том, что
оно 11арушило, 1 1змсюr1ю, nрсобразовало почти
все прсд(~r:шления чслонс:чества об окружаю-
1-fовое орещ1
-~
~L(!J
щсм м 11ре. И здесь мате,vr<1'1'1'П<'1 сы1·ра1 1а 11ы;tа
ющуюс}j роль.
В начапс век:~ ка:~алосъ - наука блнзка 1<
объяснению картш 1 ы мирu:щ:нrпя . У ч еные
были уверены н том, ч.то мир лоз 11авасм, что
Вс<"·л1.::1-ш~ш сущесшует 1~еч1-ю, ч·1·0 она не им1::ст
н11 начшш, 1·11 -1 конца 1 1н tю нрсi\1<.:11и , 11и н 11ро
странстве. Зе111ля, счнталн они, образuвалзсr,
естественным путём, естест1:1ен111,1м П)rt·ём nоз
ннкла на не~1 ж11э 1 11. и 1~ хсте естестве ~ 11ю1·0
ра::~11J1тня она /\Ост1гг11а всего ·roro. ч·ю открытп
перед нашнм. н:юром.
Однако общая тсорт~я отпосителыюсти
Эfi 1 шпеfщ;1 nриnеда к разnиnно ~юсмо;югии, 1<
теории Нолыпого Вэр.ыва - началън оil точю-t
отсчёта ж 1 rзнн Вссл<.;Ш-юi1. l Ipoc1·p:111cтнu Все
лс-нной OJ\;.iз::uюc1, огра1111чснт1ым, хотя 11 рас-
1 r 1иряю 1ц имся
В большинстве теорий о про11схожJJ.сI11ш
Сот-1ечной с11сп::мы обн:1руж1uнкъ глубою1с
1п r .яны . Ещё более ·1·~111нсп~еrrнъrм выr·ляJ\и ·г
1юн1111с11 1 1е жrr:JJ(H на 3eмJre н её ~нолюцня, 11ро
исхож.дешrс челоnека. На месте noшaт11yn
rn11xo1 и рухнувших представлеш1ii об устрой
сnзе Вселешюй соuрем:снвыеуч.6тые пытаютсн
создат1, р;.~ 1.1,Ионалнстнчсскую .версию мирозда
ния, хотя уnерснrюсти в успехе у ш 1х гораздо
меньше, чем бьJJю у п<ж<.mсния 11х у чнтелей..
Вернёмо1 к вопросуощ:т~рмнннз м с. Оснон-
1 юй тез 1к 1юс.:тныlУ1'uнонс1юi1 натурфщюсо
фин сое1·ш1J 1 в том что м11р управляется днф
ферсн1tн:1лhным11 уравне111,1 ямн, нн:1чс го1юря,
он 11от юс1ыо прt'лска:зуt'М. TTocлy11 ra ilтe, 11а
пример, Пьера Симощ1 Лапласа· «Ум, которому
быт1 бы аэnсстны длJ/ каждого щшrю1·0 мо
мента все: сиJТы, одушевляющие прщюду. н от
ноо пслы юе rюJюжсние всех её состаnных
частей, еслп бы uдобавок он оказаJ1ся дос1·~точ -
1ю обшнрным, чтобы 1юдчш11пъ эти даю 1 ыс
:ш:1т-гзу, - он об11яп бы 11 одной фopмyJJt:
дrн 1 жс.:1шн1:1t:1111ч;1Л111нх тел Rссл енной 11:1рялу с
дв 1 rмсниям11 лс1чай111их атомоо; 11е ост~шось бы
н11чс1 ·0, что было бы для 1-tcro 11с;щстонеrно , н
будущее так Жt', как 1r прnшс]\шсе, предсr:тп
бr.r перед с1·0 в:юром».
Во врсме11а Лапласа огромны.И мир предста u-
ляло1 Ilарством Порядка, в нём всё nрсдсI\азус
мо, пре;юnредслеrю. И только нпчтоЖJrr.rй юю
чок этого .мира :~анимала <•противонравmtя?
uбпасть, где уr·нсржд:т себя. Х:юс, - азартные
И1ры . Ласк:'.lль, Ферма, Я. Бер11ую1и н сам Ла111шс
опие:u1и 11~рвые законы сJJучая.
11 ')
Иtтория математики
ЛлеКСi\Ндр м1,1хм1лов11ч
л~тунсщ,
Но." облас1ъ Х:.юса расш11рял:~с1" 1fау1<з а слу
ч:н11 ю:vi - теория 1~e/юяm1LrJu11uй
-
ра: ш1mалась
11 кре11лJ. В ХХ n. 1ю J\IJl(m"Jм 6лаr()д.tря усншшм
П. Л . Чсf>ыm~ва, л. М. Л~rл ,·1юва, Л . л. Маркоuа.
С. Н. .Dtрнштейн:-t и А. 11. r<:олмоrороАа от око 11 -
чатсл 1 , н о оформил.tсь 11 стал.t :1 ,шимать всf
6ольшсl' M(X'l'U !:) 'j'UJIKU.В<IHИH 11р11р01~ы . I::щС I ТU.IJ
BL'K:l назад казаJlо(.ъ, чтu 1~<1рс·1 1 10 Х:юс: 1 11 1t:~р
спю Пuр sщка п u край 11 ti1 o\lt'pt <.:О И. {J\\t'р11мы
лру1·(.' лру 1 ом. Но к llЭШt: время 1\] Jj()J 'ИC учёныс
11сповс.:.:дую· 1 но:13ренr t l'. Y", j {l' 11 ря мо 11ротн нопо
:южнос н1,н >Т< >I-H >-ла пласопскому, Y"l 'Пt[lЖ/Laя, •по
1ке eC'I ь Х<юс. и у 1111!1. 1tm1э·1·01·0 епъ м11оrо oc-
1ю1ia11r1!1.
R -Ю-с п·. родилос 1, [f0130e направление н
;11~1т~матике - теория ~шформацин . Амер11ю111 -
скш·1 учёный IJ орберт tlнщ:р ( 18()4 196 1)
nклточпл тсоршо 1шфо рJ.1:щ1 111 в божт общ) ю
научную д1кц1- 1ru111ну. ко·1·орую он н.1;.1в:1 11 1m-
бejmenm~o{1 (г/Jеч. " 1 ~скус<." 11ю yнp::iв1Lt.'111lЯ")
116
Рож; tс.:1111с этой пауки т:шжс спя :~:шо с ооrы<.
ж: 1111 с.:м J\ш01·11х фшюсофсю1х 1<01щс 1 щнй. н
lf{ll'Ж/\L' HCC l 'U С l l(JH~ITl l CJ\ I COJHilHШI hЫJl,1 111,1-
CKa.~;.i 11<1 ~1/\бl -" 10/(l'JIJ 1рш~а1111}1 чеJН HIC'lt:Cl{()l 'O
Cn:1 1r:i 1г11я _ Но:iможностh со:щан11я 11екусс1 нс.:н-
11ых t'YЩl'CTH, o6J l 3/\alOЩHX MЫlllJ\Clllll:~1. -
одш1 из r1 робщ·м 1I01io1:1 филосафии. 1 ю:-1 1 1111<
шейnко1щеХХн.
И JТаконец, оди 11 11:1 кр::tеуголы 1ых кампtir
фшюсофш1 начала не1<а - сама 1щея Jюз11.1 -
н;~с.: ,,юсп1 м11ра. по - ш l/llL\1 0мy, тожt: разруш<.:11а
Uo всяко.;1 ст·час, uршщшш:u1ьн;т ш~ р:t3ре-
1ш1мос1ъ 11μ06J1t'\IЫ "разрс 11111 ..,,юсп 1 ВС(.'Х 11ро
блt:'vР nыла ус1 :IHOШ lt'Jl :l В :Ю -1..· 11 ' l\)l'YllJ!\I
Гtд<:Jlt'l\I ( 1906 - 197Н). :1кс 1р11Г1сю l:\'l м:1 1·сл1::~ 111 -
1юм. :'11\1 111 ·р1 1 р(нi;1Нш11.\t 11оз;t11сс 11 CUTA
НЕКОТО РЫЕ МАТЕМАТИЧЕСКИЕ
ПРОБЛЕМl::~I И ИХ j-JfWEHИE
« Нt:нu:.;1\1ож1то отри~ lа1ъ глубокое :~1 rачсшrс. ко
l'Орое l lMt'IO'I OIJj.Jl'Дt'Jlt:HHhlt: 11po6J1C\1J,I Д.1111 11pu-
1'1:R IJЖCH[I!/ матема·1·11чс:.:ско1'1 11аук11 1юобr 1 ~<.:. 11
важную рот" кuтuрую 01 111 1 11 ·р~щл к paб<Yl 'l'
()1:дcЛbll()l(J l l CCJ l (. 'Jl()l\;1•1t:JI H » -
Э'l ll tJl()К:I ['11Jlb-
l)ep·1 llj)OI r:{н(;с ко HC'I у1lll'J'CJIbllOll Ч.ll 111 CHOL:J'()
; (ОI<Л;Ща, тюсвн щё111 IOIЛ формут lj)OJ\l\~IM .матt:
ма гичесю 1х 11робJ1ем.
ХХ век }'H<tcлt.:,'l.O fiil!l от n рошл i.rx 11ремс11
11сс1<олъко ncm 1к1 rx проблс\1. С:1м;u1 сгар.1я 11.1
лпх, поставлешrан в XVll в., ~ тсо1х:ма <l>ep:--1.1 о
11t'pa3pt'1Шli\1 0CTИ 11 1raтypaJJ 1,1 !ЫХ ЧllСЛах Д llO
ф<l l l'l'Ol!:t НХШ ll С 1111Я .\'
11
+)'
11
-z''прпJJ>2Двt
3На .чснНТhl С г1роблс,11,1 - ГonhJ\6,1x.1 11 ~!'1.11<.:р,1 -
н TL'op1111 ч11се:r 11р1 1111л1 1 11.~ Х\' 111 11 Rср1 ю J111,
дd1:111л Гильоt-μ1 .
что К:tЖДОt: на·Г)1Х11ГЫ·Юt: Ч\/СJЮ, 60J 1ы 11et 6, t:CTb
сумм;:~ ·~-рёх npocтr.tx ? С этим во11росом в 1742 г.
Х. 1·от,дбах обрэтился к Л. !)йлеру. Эйлер же
за.•1етил. что длн o-rneт:i на nоста1шс1шый во
пр()с досгаточ1-ю ,~юказать, что каждое чётное
ЧJICJIO является су.:v~мой двух J1poc.rыx.
И:1 пробл<:"1 X JX н. нанболсе 11звестна 11ро-
6лсма ко1 1т1JJ1уума, 110с1·аю1е1-mаи l<антором : су
ществ>'<.:'!' ли такое множсстно, которое можно
ю:1ш.11 ю ол1 юз1 tачно отобра:тть в сдr 1ннчный
OT[>e:\<JK , НО пр11 ЭТОМ еЮ·11 1 11ЧНЫЙ отре:Ю.К
11сm,зн f13;m~пю однпз11ач110 0·1·06ра:нлъ fl это
м~южесттю?
('и.rп.берт сформулировШl 2) проблемы, ко
торые, rю ei-o м11е11и10, доюю1ы быm1 опреде
лш·1, nерс11ективы матсматшш в ХХ 11. Во мrю
пrх нопросах оп окаэ:шся хорошшv1 прnвщщсм,
но в нескот,ких снучанх r1н·1у1 щr~н нз мет ша
С,\1у. Как лрантю, это быJJо напрJJмую с1:.шзано
с Т<.: .м ~Ql l'l'llMlfC'f 'llЧCCIOTM» RЗ l'JUЩOM н ;1 М~!р. о
котором уже твор111юсr" Сною убсж.;~ённ остh
111 rerJl'pa1 шчснных Rоэможностях ч..еловсчс ско
rо разум:.~ Г~rт,бсрт выразил н афор11зме «Мы
XOT\tM Зlll1.T I>, мы бу!\еМ з11а1ъ" .
Оста1юш1мсл лш нь па некоторых пробле
мах l'шн.берт:~. На первом месте в его списке
стояла проблема ковтrшуума. Обращаясь к 11ei'1,
Ги.%6<.:р"J псход11л нз возможr rестн её разрсше
н~ш н ту 11лн 1шую сторону: да или не:т. llo
к1,1нс1111sюс1" ч· 1·0 она нс может бы·1 ъ J:-111 дока
:1:~щ1 , 11и т1ровtрп1 уrа мстuдамvt д1ат~матнч<.:
ско i'r 1ю1·11ю1 н r1дной общспр11нято11 акс1Lома
тичес 1·;0\·1 ·1·соrшей 'шожсс.:тв. То, 1..1то еС: н1::ль:1я
011 ронер п ryтr" лпкаэал п 19 ~() 1- . Гё;1ел ь. а обрат
ную 'reorcмy - 11 19(1:1> 1·. 3мер11к;-~псю111 ма"1•е
,\1:111ш Пол Коэrт (родился n 1Q34 J• ) .
Уверсшюсть n том, что I<аJКДая опrеделёп
пая м~1тс~атJJческ::~я вроблсма flепремснно
должна нмеп> решеrл re, лоб)'днла Гал ьбер·1·;~
1юсп1щ11"h п 10- ю проблему .-УJ(азат1, способ.
llf>JI I Ю\ЮЩ r r которого 1юзможr ю после кuпеч-
1ю1'u числ:.~ оr1еращ1й усrа1юв11·1ъ, разре1uимо
.1Н ЩIHll<Jl' ypaBllCHl!e 13 ltСЛЫХ f1aЦ110lf;JJlbl!ЫX
ч11ст1х» . Иначе 1()-я 11робл~м:r формут1rуется
Новое время
так: дока:3ат1.., что С}'l.Цсствуе·r аm ·ор ит.1v1, кото
рый 110 данному мн огочлену ;; от п г~ере
м.енных с целым~ r коэфф~ щ11ентаJ\·Ш рнспозIIа
вал 6ы, имеет ур:11ше,н11с Р =О целоч1к'J1<.: 1 1ныс
корн.и 11m1 нет. U 1970 r· .
IОрн1'1 Вл;щнм11ров1·1ч
МатннсеmР 1 (роютсн в 19-1
.7
1· .) устаtювш1, что
требуемОl'О ;u 11 ·орнтма нс существует.
rнльберт 6ш1 настсжыю у1~ерс11, ч·1·0 фу11к-
1tю1 трёх nерсме:нных устроены слож 11 ее, чем
фут11щи1 rлnух нереме1шых. что 111>1С1<З :з:lJ1 таr<у ю
гнпотезу: нскоторзя ко11J(рет11ая фупкцнл 1рёх
nере:мешrых 11епредставима в rнщс суnерпозrт
ции непрерывных фупкцш'1 ДВ)"'Х псремешп,1х
(13-я 11роблсма). Её онроверrли в 195 7 г. Кол
м<хоров н В1t:~дп~шр Игорс:nич Л.р~юнь/l, (ро
д11лся :в J 9.)7 1'. ) . Ок;:~~алосъ, что с помо щью
'1OJIhK() ОД! \ОЙ, 11 1lp11TOM 11ростей шей , фуню \1 \И
;tвух ПCfXM t lfHЫ X с:).·,у) ~.\"+у 11 Нt:Прерыиных
фр1кцнй о.п:ноi1 персмсн1-юl1 .мuж1ю носстано
АИ'IЪ любую ф)'lfЮА 1 1ю 11 пС[)(:,ченных.
Пробл ем:~ Фе:рма б ьи1а разрешена н 199') '"
(см. статыо <·Вет 1кан ·1·еu рем<1 Фt'рма·>) . Проб
лема Гоm,.п:бзхз ок:lзалас1. <· почт~,,, ре1u ё1 нюi1
в 19:Р L'. Ива.1ТО~1. 1\1атвееnтtчем Urп югра.д()ным
( l891 - 198:)), кuторыfr доказал, что J1юбое до
статочно l><шьшос на1)11хu1ыюе чпсло предста
в ~ 1м о сум...мой трёх прсктых. П роблсма Эflllcp;i
1ктал:1съ 1н::ра:.1рсurёююl1 и 11 1шш1с ХХ в.
Числа
АЗБУКА СЧЕТА
ПОЗИUИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ
ПокуттатеJ1JJ. нриходя в иа 1 ·а:шп . видит товары
самой разной стоимостн - есть о~rеаь дешё
вые, есть неrrо.мсрrю дороr11с. Чтоб ы у11рос111ть
расчёты пр11 покупке, Цс: нтралытый баr-11< вы
пускает дtш.:жныс зн;ак11 различ1-ю1·u достоин
ства. Кu 1 ·да фото1·р:зф J1ш1 ап·1·tк:Jр1, / LJIЯ r~р1л·о
тпнл е н 1111 нтжного ему р<1стнор.1 нзнешив::tет
порош кн , он 1 1 сгют,зуст спt:ци:~льные ап1ек:~р
ск1-1е весы 11 11а(юр 1 '11рек р:вной "'ассы То ч но
тз к же Т1З базов1.1 х ::JJ1eмe1 1'1 ()П, НЛI 1 КЛJОЧt:ВЫХ
ч11сел, с1тюнтся любая числовая с11стема .
Если пrи взвеш1ша1шн порош1<а ~ттекаръ
положил 11::1 ч~1 шу nccon дnе rиpLкr1 по 'Ю 1 , одну
ПфьJ<у в ') 1· r1 одну гирьку в 2 г, то nec порошка
составил2 '501·+1 '51·+1·21=107г.Iloи
сама запись ч 1 1 сла 107 сш1зана со спt:циалыюй
ч11ою1.юй б::t:юй, а имен~ ю 1, 1О, 100, ." Так,
1~ифр: 1 1 3:1) \аёт ЧllCJIO COTCJ-1, () - ЧllCJIO J~есят
ков. 7 - чнс;ю ени 11111 \. Эт.:м1,;нты ч ислоноГ1
f)аз ы. 11лн кпючеnые ч11сJ1а, u l((llнюм случае
11рс:1,с.-1·;шля ют собой степе~ 111 д.есн· 1 1 1
1=10°, 1о=н)', 1()()= н/1ООО=1()'ит.д.
120
В JLеоп ·н,шой системе всего лесят1, цнфr; О,
1, 2, :'), 4, S, 6, 7, 8, 9. Говорят также. что эти
цифры представляют coбofi коэфф1щ11енты
разпоже1шя :!;ща11110rо числа по степеня.ч 10. а
само число 10 н.t~{wвакп ос1ю(iа!ШС.М системы
СЧИСЛСНIШ. ~ tkc» цнфры R i(eCHTI ILHIOЙ заш1сн
числа 011рслеляется её П< )з1щис1!. ч t:м дш1ьшl
отстоrrт .п.;.~нная поз1щ1tя т крайне1 '0 11р~1нш·о
ра:~ряд~1 ед111-1тщ, тем большую ч·0111щ н ос1ъ~ 11
<· АСС» она нмее1 Поэт()му пр 1 н-1 ятзя снстсж1
.3агшс1 1 чн сел пазываето1 Оесятич11ий 111л1111,11-
тию1i с"сте.мой счиспе1111я.
Пытлrmый читатель ~шраве спросит~,: а поче
му u качестnс ба зоnых LJ11Ce11 выбираются сте
пе1-11 1 11ме11110 числа 1Ut 1l елъзя лн воспот,зо
n;пr,ся сте11сш1ми друго 1 ·0 числа, наnрлмер
пятёрки или ;щойкн?
,'vl ожно. 1{ 11р11мсру, р~1:тожс н1 1с ч 1 1сла I U7
ло степеням пятерки Rhll 'ЛЯ/\11·1 · ·1 ак:
107=4 52
+15
1
+2.5°,
а по степе11.ям двойкII следующим о6р::~:юм :
JU7=1.i'+1.1'+lJ 21+J 1.' +() 2L+
+1 11
+12'
1
В 11~р1ю.м <-.:луч',н.· множ1·пс:1 им 11 1 1 р11 <.:1'(.:11е 1. 1и х
1~1.к1упают11,11фрr.т из 11абора О, 1,2, 5, 4, 110 вто
ром - 1·~1ю1х ц11фр всего пне: О п 1.
6.ВО ИЧНАЯ СИСТЕМА СЧИСЛ ЕНИЯ
Прuч11таr'r· 1·с шуточное c:1 ·11XO'J'1101x~1 r 11t' А. Lj. Ст:1-
рJ1 ков;1 <Л<.::oбыJ<J HJl!C H H:нr /~СJ:!ОЧКа •:
Ezi бы.по тысяча сто лет.
Она в сто rrf!/жый ;..:ласе :'(.одила,
Н пор11и/юлС' 110 сто юн 1г 1юс11.11t1 -
Во! -тт 11рши)а. с1 11 е fi/ }l:'(1.
К()гr)а, пычя f)есят11п:11 ног.
О11а 111{1гапа 1 ю йо;югс,
3а 11111/ асегда t7С'.>1шл 1це11т1
С m)1ш·11 х1юсто...н, 3а11ю сто1югиt't.
О11а ловила 11дJ1ц)ы1/ з~1·1,·
Сво1Lми (>1?слтыо yzuaмu.
11 дr:сять загирелы:~: PJ 'h.'
Портфель и пиводт.;, дер;1сшти.
lt деот1.ь mёiN1ю -cu11ux гл<.t.1
Расс.мтn/н1.8алli .м1 1р 1фивыч1-ю."
Но cmmtf!m всё С(Jщ:е.111 обычньнt,
Кигда ппit.мёп~е н:аm fюсскаJ
Ра::11·;щ;пъ :~агадку поэта IJ aм номожет слсдую
щс:с: 11 ,16люде111 1с:. Uыш1 шt: м уnшмшутыс в l"J11-
хuтвuре111111 числ:~: 1, 10. IUO, IOL, l l OU. Легко
1:1 \1C'J 111'h. • по нес OH!l 3:1 ПI [CЫB:.JIOTCJI с 110-
\HlЩl>IO JJИlllh двух цJiфр: О 11 \ . Может б1.п1,_
здсс 11 Jаш1 1 фронано pa:11roжcr 1 иt" ч11сел по сп:~ -
11е11я~1 днот1 1<1-1? Пр()иери'''
1-Етr бы.1() 1100 лет»: 1 21
+122+О21
+
+О i' = 12 . :~1 1 а<л11, e1-f t)ы1ю 12 ле-1-.
«Онз в 101-й 1<ласс ходш1:1»: 1 1-!. +О 21+
+ 1 2'' = S. З11ачнт, она хоюта fl ') -11 класс Н
т:н< далее. Дс ikтннтслмю , IТOJJ}'Ч a(."1'01 со всем
обычная 1<:1μпша . А помо1·ш1 11:.tr.·1дво11ч11ая с11 -
<.:тем:1 СЧ.НСJ I СНИЛ.
Итак.1 1 о:щц1 ю1 11 1ш1 с11с 1 ·с масч1 1 слс111т. н ко
торо1! н качсегнс 6;1~он~,1 х ч1 JCCJ1 в1.1i111ранпс}1
cтi.: 1rt 11 11 ч 11 сла 2, 11а: 1ынаето1 ()rю11чГ10[1 гю3 11ц11 -
m11ю(i п1ппе.~юй cчuc;1J:!ll11Я. Чтобы рi1-v1и ч пт1 ,
ч11сла. :-~а1шса111 1ыс в р;~:тых спстемах сч11сле-
111щ IJX :J;I J(JП()Ч:JIOT в с 1юбю1, а в11и:~у СПJХ! Щl )1\3.-
зьгваю·1 ос1 юuаш·1е системы сч1 1 слс.:IПIЯ. H:mpL 1-
мep, з~п1rсь ( 1HI0)2 озп;tчае1'"rо же са .чос •нкло.
чтп 11 ;{;,1.1 1 1 1 с11 ( 12) 11). Поскольку все м1,1 110 ; 11 ,:{у
tмсн J\t:OП'l\Ч.HOll CIK'\'t:MO~\ СЧllСЛС'Ю !Я, '\'О J\t:CИ
ТJ IЧHOe ос1 ю11ан~:1е 061,1 ч1ю r1e ук:1:~ы r1асто1·
(1100)! = 12.
Чтобы rю1шти с1 ихотrюрсrте u 1 1собьпаю
пеш ю 1) деночке, п ришлосr, перс.:nссп 1 ч11сла 1 1з
двонч r юй с.:исте~ы в дс.:сятичную. 1lссложrю
п роиз вс.:ст11 и обратную uпср:щ шо: :{;щ~шнос
Дl'CЯ 'l 'l·J Чl! OC Чl!СЛU i1pC:IO""l aВJ ITl1 13 /~ПU! I Ч J Ю\1
ш1 ;~е. Пустп трсбуtтсн Нt'р<.:1.1сстн н ;~1ю 1 1ч11~'н1
с 11стсму ч11с110 HJO. Вообраз 11 м, что :за пш-:упку
н ма1 ·::1:111не 11)rж1-ю уплатит~, 1О() дснсж111,1 х с;11 1-
11 11ц, :i н нашt:м рас 1 юряже1ш11 1 1 мсс·1с}1 слсду
ющ111'iнаборК}11Юр· l.2, -! .А, IC), Ч.(>...J , l2S, ...
F.стестnеr 11 ю, отсчёт y;~ofi11ee 11;з.ч;пъ с сампr'1
кру111 юi'! к~ пюр1.1 u Щ)С/'\елах 100. :~атем 1юз1,мЬ1
CJ I CД}'IOШ,)10 ПО,.J.ХО/\Я Щ)'Ю ДJIЯ 11а6о р;1 1 1уж110!1
ср.1мы lI т. д. В m ·o 1·c .: паша "бухг алтер1ш » 11р11-
ыст 1шд: 64 + 32 + .cJ = 1OU. l lo лоскот.К) вес.: c11:t -
1·:ic .v1 1,1c - ! 1(' что l IHOC. как CTCl!t:III! /{l:IO IJIO I . ' 1'()
(1
;
i
Mn1T~IKЖCl1MCC.:~I ] ()U=2 + 2 + 2 -= (J1001()0) 1 .
на 11 р: 1 KTJLI(~ 11срс1ю;t Чl-JC('JI 11.{ ) \l'OJTJ 1'1JН>il
C' ll l~1 ·cмы CЧllCJICllHЯ н ,tl"IO l lЧll}H) удибщ:с 11 ро-
11:,110J \1лъ методом 1\елен 1 1 я Бу;\ем J\t:..:11 п ·1,, 1кх~ )Д-
1юt: ч исло, а ·1 ·акж е 1 юлучаю 11 1 1 1ес-я н r1po1 tl'CCt'
J teлcrrин частные:- 1 1а 2. 110 тех 1юр. 11 ока в 11'1 ·ore
пс 1 юлу·ч11 м 1 Прr1 это~1 от,це.1 1ыю бу;1,е;-.1 он1е
ч:пь 1 1р()МСЖуто чт1ыс остатк1 1 , ка к J](Ж;1 .J;1 r ю
121
Чщлt.1
1111жс Ч11 и 10 о()р:~ ·юн.1111 tO(' 1JOU lt:)tl11 ш ч~r с 11 1ы ч
1 11 ос1 ;п K; lf\'111 . l l C[X'ЧltCJ ll'HH l,J;\111 Lll[l.IH. I Н.IЛС-
1\\\, \>~ ;\\.:'\' IKKO\\IM•\
lL
'50 l1
'50 2')
о 2·1
1
1()() = ( 1100 1()()),
Л,1ю11ч11ан. LHC'I емJ СЧI 1 сле11ия CTJ.'Тd ОДПТIVJ !Н
l IL'TOKOB rтро 11.юше,1шt;й u ~х в. 1·pal11lIIOЗ!LOlf
1ю мпьютер11ой ренолюшш . Тех1111 1 1сс101 ri;вc
122
ЗАЛАЧА О РАЗ Н ОВ ЕСАХ
Соврем1;:нныС;: продав u ы уже ttастолько пр1шыкм1 к
элек трон 11 ым несам ч10 ~t e пред< т;1 вл11к)т 1 ef>t-> , как
бы Oll И ВЗВЕ'ШИВJЛИ ТОВар r ПОМОШЬЮ Пif1b piHHOBe
сов. Тем 11е менее Htl μы~1кJх и t1 небольших маг.э
~инах лосих rюр можно Астретиrь Rt'CЫ простеише~t
ко 11струкuи11 ГJк что ст;~ри н ная задача о р;вновесах
l'ШС' 11<: совtt:м пuн:р~1ла .:~к;уJльность А история её
ГdКОНд .
Почти 400 лет н.1зал но Франuии жил Клод Гаспар
Б.:~ше де МсJири <lК с11искавшии rебс славу позтJ и
тш1коrо ш:•11 ителя мате.\ытики . Bu 1.пuром изда11~1и его
cбop t tttKd « ПрИЯIНЫt' и lа н им,1ТРЛhН Ые 3<:1Лс:JЧ11 * есть
и тако:~я какое 11 .:~именьшее чиrло гирь потребуется
для ювсшив<lния любого прсд1v1ета. масса которого
равна uслому числу фу11тов от 1 до 40~
Ок<ПЫR<l ется , Е:'l'ЛИ гирьки r;:11реш;:~етп1 склалы
ват~, только 11а од11у ч<1 111 у RecnA, тп достаточно за па
стись шестью раJ11uвес<1ми , масс.ы ко1орых чщлен 110
ра1:1ны uелым rтепЕ:'ням лвоики : ·1, 2, 4, R, 1n, 12. Бо
лее того, тех же гирек хвати т для взвеш и ва н ия всех
пр!:'д1v1СЮ1;i MJ( rои до f)-1 фунтов . По•1 ему(
Лd по тои ..+.t · прич 11 н1::, по которои шссrи таков
достаточно лля ~dnиси люГ>о го 11 а 1 ур<~льного чи( ·ла о 1
1 до 63 о лвоич1юи с.истс'vlе счислt:·ttшt . Аtt ,)ЛОГИЯ
J/ШСЬ ПOЛlliHI . Mi.lC.C.e п1рьки отвсчас ·r «ПUЗ~t Шl()llllЫИ
l:!t:'C » шнμры в Лl:IОИЧН()И ЫГIИСИ ЧИ! ла, fJt:'ll1€HИIO по
ложи ть гир1>ку н.:~ Аеrы - 11ифра 1 в rоответrтвую
шси 110зиuщ 1 реше11ию нс ~1спользов'1ть гирьку -
uифрс1 О . Например двоичная зап ись числа 6 - это
11 О З н а 1 1ит, для уравновеши1:1ания 1 ру~,1 VlclCToй
6 фунтов liJ другую чашу в<:>со11 11уж110 положить гирь
ки о 4 н 2 фут а. Наибольшее Ж\:' 'tи<.лu, кu 1opuc
о+о=о
охо=о
о+1
1
о)(1=о
\ ,\Q\\1 UЬ'
1+о=1
1хо=о
t .\ O ..+ilЧ lllЯ
11 \'V.HO:».eHllЯ
1+1=10
1х1=1
l\ЕИ1н~1ных
4111 (: \
1~11фры 1юс11рт1 .1 11ес·1 1 1 11ростп: 1 прпхо1 11 1 1
101< n поm.ттро 1ю,7111 1 шотюм ·~ж: мс11п.• О - 1ок
нс прохо,.(IП . Сtк 10J111ш1 -темt:н1·а <- 11rюхо4ш
'l 'OK • 11 · 11 1: 1l j)OXOIOIТ ТОК > .ЧОIТТ С~Н~!IЯТЬ др)Т
/\Р) 1·:1 :~а OYl'ttЬ коро1 кис11ро~·н.::жу1·ю r нрсмснн -
Ml l JJJJllOHHЫC' 1-10, 111 CCК: I JДhl ~)r ·u 110:.!IIOJlllCT 1rро-
11:шол11т1, ~1р1 rфмст1l'll'Cю1с ; ~<:l1 t-т1 ш н:I/ \ ;~вш 1ч -
111 .1м11 чtн:л.l\JJI с lll' l [\IOH~p11ol1 (1\ОрОС'IЫО .
Тl() сра11rн.'н11ю l 1ромо:-111,к11~111 г.1.6т11 tам1 1
, .ЧП(JЖ<:ПШI ll L.'IOЖt:Jflf}J ЧtlleJJ 11 / \t:C >i 1 1 1ч1101'1 C'll -
C'I ече 1 ·аб,11щы ОIОЖС111 1 Н 11" ~ MllOЖCllШI /ПЮ
в дВШIЧllОИ СИСТС'Мl' l<JflИlbllJt.l\:'TCЯ l помuшыо LUec н1
.{llCIMJU, -
)ТО\11·1111)=6.3
А тuпt'рь предположим, •1то п1рьки р;нрешJеТ<'R
кло:~сть Н<1 обе чаши uer oв Любопыпю . что в такои
llULтJно1:1к е 1алача о pa:i t ювссах встречается еше у
италын1< ко1 о 'vtа тематика Леонардо Пи.:1анского (Фи
Ьона11чиJ - 1а •1етыре столсп1я до Ме1ири.жа 1
Понj') п ю, ' I TO в 1тuм случае можr ю uбuитись лажи
ме~н,ши"1 шбором разновесов· 1r , , q и 27 фунтов .
Так, в<1вешина$1 тово:~р в ''° фу 11 т()в, все эт11 гир~,ки по
ложим 11;:1 вторую •1ашу весов, '1 для взвеш~ 1 ва11ия
11рслм1:т,1 u 25 фу11тоu гирьку Mil<Loи J фунта ~тус
rимнаоднуснимчашувеrовидвегирьки- в1и27
фунтов - HJ другую
Н Пi1f1'111V п1р11 11М<1~1 1 фt1рчу ' IJШIЖ '1 6i<.ЛсlдЬl13i.1ЛЩ \,
друг в друга . ка" ..,,преш к11
ПОЧЁМ КИ/\0 БАЙТОВ?
Ссrолня комnьютероV1 никс1го не уд11R11шh. Прш1лёт
ешt' 11смного t:sрt>мени, и для вrе>-. п,111ут привыч
ным~• такие слов.:~, как «килuб,1йт», « ,-.1сгабайт»,
« п1га6,1йТ» ... Что они 03начают{
В соАрем енноИ мате.,,1атике С'\ТЬ такпи ра~дел -
1еор1 1я информ;ш~~11. Эта ICO\)\l\S\, в ч1.1с11юсти, опре
леляе1 с11оспб Иiмерения ком1чества информа1J 1 1и
11 Ры111иuу и1мерения н;э1ывэет « hИТ». А fiаит - это
1JULl'\•1 ь б11тов. Терминами « 611т" и « б,1йн широа<<1
1юль1укпся npor р.1мм~1пъ1 и Lnl'ш1aлиL 1ы по ш1ф
рпв1т тех11ике. У н их даже е< 11, шутмшая no1тюр~.;<1
., з.:1 од1111 ба нт восе"~ 1, б~нов л;эют ".
ПриL тавка же • кило- " tзCC'vl хuрошо 1нJкuм<1.
Он..~ ш1 t<tЧ ,lt'T 1ысячу: кщоrрамм - тыо1ча rр<ш
'юв, 1<илометр - тысячJ метров. Учёные и инже -
11еры, имеюшие дt'ло с болы11им11 велич1111ами, иС·
поль;1укн также пристс.1uк н «ме г а- » (миллион) ,
" rиril-» (миллиарл) и 1. л.
Проrр;:щмисты тоже оперируют большими ' 1 И( -
лами . И он и использую ~ прист,10ки « Кило -», • Mt:'-
ra -», «1иrd-», но, как 11и cтp<t t11 101 в другим ~ 11ачении.
Программ 1ктское «К11ло- » чуть 6ольше об ы• 1ного.
Пр11 •1и1юи тому двоичнdЯ систе1v1а счисле 1111я. Всм.
в ней «круглыми» числами являются не сrспсн11
лес ятки, а стеnен и лвойки. Аот и поы>Врали Т;.'lкие
пеnt:' 11 и 1 1 исл,1 2, которые лу• 1 ше всего соотвf'тству
ют обшеnри нятому смыслу JПI >-. приставок. Поэто
\\У nр11мс н ительно к компьютерам н с~ш и приставк 11
означают·
кило- 2 111 = 1024,
мf'ra- 2ш =1024! = 1 048 '>7f"
ГИГJ- zin =10241 = 1 07\ 741 824.
11чных чнсел .ч1 ~пиа·1 rop 1 11>1. Бш 1 t<=' тон), У·"" ю
же111н:: на 1 1юоf> 11•с не 1\1е1шст ч1 1 сж1 . По~то~1у,
ч1оfн,1 щ:рем 1 южJпь лва :-шогораэрндr 1 ых /'(ВО-
1\ч111>rл. ч 1 1сна, дост;нuчпо 11сс~юны<0 раз сдш1
Н)"l 1· верхшri 1 (()И!IОЖПТель на СООТНСТСТВу10-
ЩСС l\OЛl l ЧCC.-lBO ра .фЯДОВ [IJICIIO и cyM .\'11 1pOH.t'l I>
L{CC rюлучснныс ч1кла
Uш.:ра 1 ~1 11 111ростс\1 11111 е , и KOM l\bl(.)'ICj) HЫIIOJl
rrщ.:·1 llX бt.:{)'ITPCЧllO. l lu ll f-IOГ/\,I в ~ 1 .lllll ll Jl' 11ро-
11СЛО/l1П какой- 11 116"~ / lЬ cбolt 11m1 1 1 роrр~1 _11;1 ма -
:1:щанис комныотt:ру 11а li1>tl 1t )J1 11 c11 11 t: расчё
юи - сО/\ерж11' 1' РIП1 1 6ку Тог,'\а 11ро1ра.\1~111ст;.t1'1
nр1 1 лон1по1 1 1ept:rrponepiпь себя и 1ш,чm,ютер.
позтому бсэ :111а1 IНЯ IЗCCJI КОМ! 1 ыотсрной K)'XIТJ I,
· с1ряп:11ощеl 1 " л1ю11ч~rые чнсла, хорошс .ч\ сш:
1lH:lilllC'1"\' 1 1 111{ак нс 0601'пш:ь.
СЧЁТ ЛЮЖИНАМИ
Г< Лll /'J()l\ЬltJ111\1 П3ЛЫ.t('М рую1 COCЧ llTJTI, •111сло ф.1
л,111r на други х пальu .~х ·ло11 руки , то мы щ1лучим
·12 - JсlМl'Чспслыюt• ЧИlЛU, столп же пuпуляр11о с в
н!:'которых !:'нропеиских стрJнах , к,1к и •111•ло 1О.
Можс•т быть, ')Тои поnуляр1 юсп1 11С>м.~лп c11ocofi-
<тuовалu сuои с твu чи с "а 12 бс~ осн1 KJ л<•м1 rься
11а2,l,411Ы
Группы no 12 nрt>дметnв име11овались дюжин;:~
м11 (лат. duuclt:c1m , фр. rlouzai11c , 11т . clozzi11a , <1нг;1.
(i uд:п). Люжи11а дюжю 1 с щ тавляла грщ с lt:1 u/3 м
lll:'pl:'tiOдt' t H1:'"1t:'Ul<OГ() - « UОЛЬWОЙ » ) , <1 ЛК)Ж11Нс1
гроссов
м.ксу.
Лtс1с 1 1алuап,ричными дрс;бями n uльiU!}аЛиLь
t>Wt' др1-1нниt.: рн.\.\Мlнf' Лроf1ь 1/ 12 ри>v1лян~> на :{nt
В<IЛИ унL1ие~1. У{а1<они1ъ лвеналL1.нер11чную с 1кте
му - сс1ёт ДЮ:.+.1111.JМИ И rro cCiJ.\IИ - П l,IТёlЛСЯ ШАС'Л
( кии корпл1, K<lfJЛ Xll ( rот сам1.>1й, коruрогп py<-t к11с
воИ(к,1ра1гром11л1111ол 1 lолг.щои в 170'1 г.1 . В 8'.0 H-
ue XV\1 1 8 . 11лея 11С'ре>ход::111d двс-11алl1,пернч11ую сн
стему всерьёз обt ужлс1ла(ь r?U Фр<шuи и .
Влияю1 е Lf~H л,1 12 щцушаl'ГО1ва 1 1гло-<1мt>JJИ8'..1н
ской системt;' линеиных мер, в которои 1 фут
(10,48 см) р;~Аен 12 дюи~1<1м, 1 лю11м - 12 л~111иям,
а 1ли1 1~1я - 6 тuчкам. Миu1-ис пр(:-'дметы пугови uw,
платки, куриные яиuа и 1. п. - в .~апал1юевроnеА
ских странах ло сих п ор n род<Jются люжи11ам 11 .
12~
Числ<1
ПОЗ ИUИОННЫЕ СИСТЕМЫ
С ПРОИЗВО/\L-:>НЫМ ОСНОВАНИЕМ
лнnп, сТ :тачеmrт'1. О. 1rл11 1. 11m 1 2, -· ·
11л11(/-1
:1аыстиr>1 . ч1 о u случае d > 1(} пр111'ё 101 11 р1 щу
\11,шат1, 1.ювые с1 1 .vнюлы д.1я 1~11фр.
мы 11р11ш,1к.;111 к .'J,(::l'Я'l'l \LUJl)iJ снс~н:мt: l'ЧI l (.'Лt:Ш IJ.I .
Компыот<.:ру как 11 L'J 11,:3~1 лучнн.: 1 ю;\ход1 п· дно-
1J ЧJ 1.tя CHCT<.;M:.i. l l o 111 1()1}\;1 мо1ут<>К:t3<!ТЬ01 yдufi
HЫMll c1 1 cтt::\1hl с дру1 · 1 1м11 nc 1ю11a11 1tJ.1\111 . С ч ет
на ЛЮЖIГНЫ rtpl'K[J<It'Hhll:I ТОМ) 11рнмер. ~дес1.
ч1к,ю 11;·J J.1 f)а·~з - l~1e 11e1111 -сшсла 12.
)L'IЯ ШlХОЖДСПIIЯ llH фp 'lllCJl ::J. llO задаrшому
ч1rслуN 1 J uснuнан шо с/ мшюю к<Jспол1,:юn:1тьсл
l '<:'M Жl' C I I UL'U601'1, Ч'l'U 11 11рн у1 IJI:!T<:: сум.:v~ы ДClltl'
К [Xl3. "1<:' f K' i\' p y (')лc:lt . О h'O 'l'UfJUM l 'lHIOp11ЛOCb
p;i н1,111с Сна ч:т: 1 н:1л.0) 1ят с~1мос: ()( >J1ы 1 ю<.: ба:ю
нос: ЧНСЛО с/11, НС 11 рl'НОСХОДНЩ<:'<:' ,\.' . ~;J ' l <: 'M Ч I ЮЮ
''
f'I
/ v :1ет1·1 11а r; , li ре:~ут,т~1 ·1 ·t" Ч l..'1 о rюлуч:нот 11с-
В о6щс;ч же случае nрсдС'1а1111'1ъ 11ро11зuот,-
1юс: <шою "\ в снстеме сч11слст111я с з:щат 1 ым
ос 1 юн:.~1111ем du311aчae· 1 :sаш ~сагь <::10 в штде
полrюе чж·ттюс а,, п остаток 1~1 1• т. е.
,\'= а11d"+г"1•
\,
1"
//1
11
1
,
=n11 t +а11 1с/ +".+a~r, +п1 с +п,1•
Остаток 1·11 1 уже :- .1c111.rrJC ба.ю1ю1·0 ~шсл.t ci'.
поэтому дсл11м 1·11 1 на с/'
11
п получ:tс\1 не1ю"1-
1·,щ: с/ - любое целое ч11с1ю, боn ынес tJ\J 111и 1 \Ы .
Коэфф~ 11 \llL'I rты t10, с1 1 , • , tt" на:{hlflаютсн r 11·1фра
~111 в c/-11ч1-1< >fr :~а1 111 с 11 ,\' 0111 1 \101·~т пр111т11мат1.
нос час1·нос п11 1 11 остаток г" !·
ИГРА «UЗЯНЬШИUЗЬ11}
И ЧИСЛА ФИБОНАЧЧVI
в П ()ЗИ UИ()Н НЫ Х СИ\Т~мах счисле
ния ~1Ы фиксируем некоторпе ос
нu1;1 а 11и ~ - uелос пuложи1ельное
чи< ло 1/ - и раtсм;прива ем базис,
составленный из с тепенеи qтoro
числа: d 0
,
d1, d
2
,
••"
d", ... А ЧП)
будет, е<.:ли в кач естве базиса вы
брать не геометриче1 кую прогрес
\ИЮ, а любую nоследооат('льность
ВОЗрастаЮЩИХ HJTyp.ЭAb Hl,J J( "IИСеЛ
1/о=l <q1<(/~< ...< ч11< ...{Име~1-
но таким обпбшё н н ым базисом
поi\1.,зовались, 11апри"'ер, инлейuы
ма йя (1...м. с.татью ~ стuрин~1ые си
стемы 'апи< и чисел»). В их t иrтe'l!lc
\ЧИСЛС1111Яq 11 = 1, (/1 =20,q]= 1Bq,,
q,=20q!.q"=20с7,ит.л.
Люuопытным r1римером t.исте
мы сч ислt-ния < обобшенным ба
J 1ком явмюто1 Фибона•1чиева си
с-1 ~мс1 Lчис.лс:ния. В tieи в качестве
fi;ни< ных ч11п:•л бi>pyi ('Я чиt .ла по
rлеловатеАь~юсти Фибоначчи : 1, 2,
) , 5, 13. 13, 21 ...., IJ KOГUJJOl·I каж
дЫИ член, н ач ин ая с треть!!го, ра
вен суммt> лвух прелылу ши х члРнов
(см. стат~..ю « П ослсдовательносп1 ») .
При октеме lЧИLЛе 11 ия с б.ви
tом1,2,З, 'i,а,1'3, "вкачегпщ
11ифр дпст;~точно иметь то.л.ыю О
и 1. Еы1ниu.:1 в rе ервом (кр;:щ 1юм
пр,нюм) ра:1рнле 06<>'1начаст 1, во
ВТt)ром - 2 , в трЕ>тм,•м - ~. в чет
вертом- 5,впятом - 8ит.д.
Правла, за пис~.. числа в тако11 систе
ме булет неоднозна чной . Н а при
мер, ч1кло 5 =2 + 3 может быть
Jап~ка1 ю как 1 1О и 1ООО. Чтобы ю
Ьежа 1ь та кой нtюлнознач ности,
достаточно лс1говор ит ьо1 ~1е стu
в и т ь рялом л1:1е ели11и uы. Тuгла
кажлое натураль н о<' число в Фи6о
наччиевои системе счисления 1апи
сывается еы1нстве11 11ым обрюом.
0=0
1=1
:.1 =1U
3=100
4=l01
'i = 1ООО
6=1001
7=1010
н = 10000
9 = 10001
10 =1()()1(')
11=101uo
12 = 10101
1i =100000
14 = 10()()01
15 = 100010
1б = 100100
и1.л.
рill.( мотrим />Л НУ КИТ(IЙС КУК)
игру - «UЗЯНЬШИШЫ» в qтой игре
два игрока по очереди бl'рут кJм-
11и ю лвух куч<::к 1а один ра::1 мож
но А'IЯ ТЬ 11 1ofioe ЧИС'ЛО К'1МНС'Й и i
однои кучки ил 11 noponнy и з обе
их. ВыигрываN тот, кто з<1бираС'т
по' лелние ка мни , тем с..~мым ли
шая партнер а возможно\ти rде
Аат~.. ход.
/.
-
с· 1111+1·
11- I
-
111-I G
11
[сАИ проанал11зировать эту игру
лля небольших зна• 1ени й ч исла ка~1-
~1ей в кучках, то получим, что начи
наю ший ее п рои грывае1, есл11 в
кучк<1х будут та кие колиL~ества кам
неи: О и О (:это uчсвилно\; 1 и 2,
1и5;4и7;6и10;8и·11;9и15.
В этой последов;пель 1ю\ти n.1p
ч исел кажлос мс 11 ьшее ч ~кло 11dры
является наим!:'н ьши м число."' ' сшt:>
н е ПОЯАИВ111ИМСН В пrелылушю,
п арах. А вот закu 11 образован 11 я
бuльшсrо чи сла со верше11110 11eno·
н ятен. Н о л<1вай1f' ~.т ишем ·ни
п ары чиrел в Фибоначч1~е1юи t1к
теме С"IИСЛС llИЯ .
Пdре <0; 11> соответсrвует <0; 0>,
< 1;2>
< 1;10>,
<3;5> -
< 100; 1000>,
<4;7> -<101;1010>,
<б; 10> -
< 1()() 1 ; 10010>,
<3; 13> - < 10000, 100000>,
<9; 15> - < 10001; 100010>
Теп ерь уже виыю, что большее
Ч IКЛО п олучаете я из MC'llbWCГO ДО·
баАЛ!:! Н ИеМ н уля в KO HIJE' ч~1rл~ .
Попробуите само\Т()Ятельно выяс:-
111пь, почему имс11110 ')Пi п,1ры •1и
lСА ЯIЗЛЮОТlЯ п роиг рыш 11ы м11 лля
НIГО, К1 О Н.-1ЧИ11<1СТ ИI ру, а :ЫОЛНО
06ос н ов,1ть их свя.:1ь с ФибонJ11ч11
СВОИ O ll ТСМОИ СЧ ИСЛС ll ИЯ.
Пос.-1·~1 1 ,ш 1ю;106ным об ра:ю:-1 11 ; ~алее , в ко11 11с
KOIЩОI\ " l!hlOL'pC.:M • '11 ICJIO /\О K{Jf! l(;J, l IOJJ) Ч1113 110-
llYTlIO 11абоr ц11фр а11• с111_1•••, а1• 011
Н_а 11р.t 1\1 1 1кс ш1 1х·;\с1 1я ·11, с/- 11чные 1 1>1фр1 .1
Чlll'! l ~1N. 1 1 ач111 IШI С() CJ арте 1 ()р<.1Эj)Я/\;\.1 1е О Ч С I 11>
удоб1 rо. ДIЯ .Э'J'O(J ЦC.:Jll I обыч 1 ю пр1IМt:ПЯ1-0 1' i \P} -
r oi1 способ. IТре;1стаrн r.м число ,'v в н1rдс 11щх1 -
же11ия. пс содержащ<:: го сн~пс11 е1'1:
,\ ~По+ с/((11 + с/(а2 +с/(". +ct(a11 1 + da,,) ..)))
Отсю,1.1 нm11 ю, что 1111фр1,1 а,1, f/ 1, r1~·" ,а" .' -'IOl'\"I'
быт~. 11:11\:-11 .:111,1 1 н1t:J1t:до 1\а· 1т.11ыю, н.ач1 1 1-1,1>1 с
мJ1ад111е1·0 р~1 .iрн ; 1.1 , в рсзуш,т;11 с <.' J IL'J\) 1ощ~ 1 ·u
MIIOI T )IЩll UK! ! l'O 11 /)ОЦt' ССа:
НАЗВАНИЯ БОЛЬШИХ ЧИСЕЛ
Чнс.rю ~ нем<:1 ( пpo11 Jr 1 ссё·1 ка.~-: «цвай" (пш11ета1
Z\YCt) . а111 Jll lЧ:llllI!I
-
K~ll< «ТУ" (f'VU) . Л НОТ ЧJICJIO
1ООО \\(jU и русский. 11нt:мсн.1 _1 ·.11н ·я1 1 ча1 1111-11-1:.1-
эовут 0/1,llH;.JKOHO
-
MllJJJll IO l I.
Лю(iо1 ll>ITH:J 11стор1 ш ч 1ICJI ИTCJlhl 1()1'О "/\'lllJl-
Лl IO l I» R 12711· 11<.:11с111,1:1нс1шi1 ку11с11 ;\t\арко
Поло о·п 1р;1111 що1 н 11ал i: 1<и i1 и :-1.11 ·а;1о ч 1rr,r11 Кн-
1·1111 П\'1 1, в Кн·1·а11 лсжзл чсре-1 мнсн·не п р.11 rы
Всрнуnшип, домоi1 поч·1·и чсрt>З чствср1ъ нск.1.
он нс персс-1 аuал оосторгзт~,сн ) ш 1;~е 1 шым11
чудеса.\1!l. 13 Cl' O рсч11 10 »L дело слыmалос1,;
•Мш1лиот 1 е _ .\ПJJIJНIOfle -> Слово «mille" ( «ты
сяча ~) было 11звсстно еще• в Дрен ~ 1е.'\1 J->11мс. Сло-
11t.:\.\1ю <м1шн1юнс". которы\\ отн: 1жны 1·1 1 1у1'\:
шес1нс1 11111к H:J :.$nJKa.IJ тыс нч у ' IЪI О!Ч, JIPUЧH()
r1р11с1мю к Мар1щ Пот) С:онрс:чсн1 1ню 1 t1рu
·шал11 е1 о J\'\Щжо 1\1lилmюr1<:.
( JJOIIO • .\1 1-IЛЛ ll :IPJ\> ; И}I H ::l. -\1\ JJ -IJJ)J Ч l lCJla
1ООО ООО ООО 11мс<.:т фрат 1у:зское 11ро 1 к;-.;ожле
шн:· Е1·ос1 11 юш1 ,,1 - •'O llJJJШOП ·> Ilр11сташ«1 <·бн-»
nо-ла1ъ11111 оз 11 ,1ч;Jст «ДJюйrюИ » - к тыснче 1\а1<
бы присоСJu111нюrся л.ва .-ва1·о нч 11ка-> п о три
нуля. Далее на:ш:ш11я чисел обраэуюн:я от ;1 а
п шск11 х нан'v!с1юнш111!1 кuш1ч~сша т; 1ких 1· на-
1·онq111юн..,, ЛJ' l•ЩLП ШН.'МЫХ c11paR: 1:
1 ООО ООО noo 00() - тр1111.'111(111,
1 ()()() ()()() 00() ООО()()() - IO:laJ\ГИЛJ IH OH,
1 0()0 ООО ООО О()() ()ОО ООО - кв11н·r·11лт 11 11 1
На:1ват1я ч 11се;1 в11лот1, /(() 1()('
1
с 21 •nа1·оr1чн-
1юм » пpr11ieдcr11,1 11 тafi11иr1c li К(J!Ще сr·аты·r. Ja-
_,1eт1;re . что количестrю "ваго1 rlШJ<aв " 11а е11н-
111щу больше л;~ тнн ского числ:.~, звучащего н
(/11 р;.ш1ю ос·1 ;\Tl\Y () r Дl'ЛLНИЯ ,\ н:1 [.(,
а 1 рав1-юос1 ·:1ткуо·1дсл<.:1 r11н11 ; 1 с/11t.: 1 юmю1 ·0
Ч:IC'TIJOJ 'O, l l ШIY 'll:llHO l 'O ll;t llJX~Дbl /\YЩ<.: .\f ll l :t l t:,
0 11 равr ю ос1 :~тку t!'1J\t:Jlt't11rн 11;1 c/ 11er1{)JI1ю1 о
Ч .J C" l lIOJ 'O. fl()Jl~Чt°lllIOJO на ltpt.:/.\Ы, \}'11\C:M ш:11е
Тп. ЧП) чr1с.1ю ,\' в d- 1r l11юfr с1ктt:\1е счнс:1е
пт1н выр,tжастсн цнфр;1ми а11, с1,1 1• ", с111• з:шп
сыв. 1 ется так -
1\' = (tf" {{" 1 " tl1Clo),1 ·
11,шμrнн: р . 26 700 = ( l LOlO()<J()JO()J 100)2
= (1 .~l.:i300)~.
1Jа зна 11111r. l.kдь "состав" 11;1ча; 1 фор.чироnа 1ьсл
llC с «T<.:llJ!OBO:Зa » - С,Щ IIИЧЮ I , а ()'1 CЦCflКI 1i-Т(,'11-
JН\1\О:З,\» С ОДГ\ll\\ « 1-1<1\ '0llЧ l lK0 \1 '> - Тl>IО!ЧИ
126
Числil
СКОЛЬКО ПЕСЧИНОК ВО ВСЕЛЕННОЙ~
Стои1 М'<.1З 11<1я ropa вь1 ( GTo l>I в тысячу локтен. Раз в
lЫ<"яч у l\E' I nрнлет,1l'т k ней м,1ле111.>к<1я 111 11чка и ТР'tит
l t\Uй Kl\1<18 о ~е вершину Kor/\.! 1IH<I LTUЧИl" t\LIO 1ору Д\)
Ol1t01ы111111, nрРi1лет пер1ыя rекунлJ Bl''lll<JCl"и
6опоч11ая му.цюсть
Песчинка и lkеленная. Крупиuа мироздания на ми
зи1 ше ребе~ 1ка и бездо111 tыс, беспредельные пр()сторы
Ku<.мucd ... Можно ли одно измерять другим?
«н~т! » -
OTOC"lilЛИ древние. Ottи считали, ЧТО
размеры Вселс1111ой неимоверно огромны и никаки
ми доrrупными 1110с.0Gами их не оuенить и не и.-1ме
рить. Это и 11 е мудрено, ведь лля практиче1. ких 11ужл
они вполне обходились небольшими числами. Все
ленная же - нечт() 11еобъятное, 1-1 еиз мер~1мо е, гюrло
wаюwее в себе все и вся. Разве можно к неи подхо
дить с обычными мерками?
«Л<l !• -
раздался гол uг Арх имела, 1ениальноrо
ученого лревнопи. В его сочинении « Псаммит • (•Ис
числение песчинок») есть описание чисел, которые
позволяют оuенить фантастиче с ю1 огромную вели
чину - ч~кло мельчайших песчинок, какое п отребо
оалос~. бы, чтобы заполнить все простра1-1ство Все
ленной, весь мир, представляемый древними греками.
Архимед начал « П саммит» с краткого астрономи
ческого экскурса. Ин заметил, что, по мнению боль
шинств.:~ астрономов, Вселенная имеет форму шара, в
uентре которого находится iемля, а ралнус его равен
расстоянию между uентрами Земли и Солнuа. Арис
тарх же Самосский, по свидетельству Архимеда, при
держив<1лся другой гипотезы: 0 11 предполагал, что « Не
подвижные 111езлы и Солнuе находятся в покое , а
Земля обрашается вокруг СолнLtа по окружности кру
га, rа<П()ложенного посередине между Солнuем и 11('-
ПОдОИЖl·IЫМИ звездами». При этом расстояние от
Сол1ша ло неподвижных звезд оче11ь велико. Хотя Ар
химед не говорил, какои модели мира придерживался
( ам, но л<tнные о размерах Вселенной он fipaл у Лрис
тарха, потому что у того « мир 1-uра3до (юльше, чем
пnлаrают обы чно • . Лиаметр Вселеннои Архимед по
ложил равнь1м 10 11стадиям, что составляет примерно
2 световых гола. А песчинки, пu Лрхимеду, таки е ми
ниатюр1-1ые, что в одном маковом зернышке их помес
тилас~, бы uелая мириада - ю•. Результат оказался
не столь уж запрелелы1ым лля человеческого понима
ния. Наш совремt:'нник Jаписал бы его как единицу
с бJ нулями.
Но как обозначить это число? Ведь ни деопич
ной позиuионноИ системы , ни 1акой улобной формы
записи с помошью степеней во времена Архимеда не
было. Тогда 011 разрабо1ал систему 11аиме1юва11ий
больших чисел, отправляясь от мириало-мириалы -
числа 106
= l<IO ООО ООО. Числа от l до 108
-1 он на-
1вал •Первыми»>. Мириало-мирнала стала единиuей
«чисел вторых». 1016 - ед11ниuей «чисел тре1 ьих~
и т. д. вплоть до чи<.ла 1ofl
111 1
'
10011 1
"'
111
' - ели11 иuы • чисел
мириадо-мири.:1лныхu. Так удалось поим е 1юв ать
числа в диапаJоt1е 01 1 ло IО 11111"
111
t1<мю - 1. Но Лрхиме
<\У и этого пока:~ало1 ь мало. Нее эти числа nн обьели
нил в «Первый период» и далее переш ёл ко второму,
третьему ... м11р~1ало -мириалному периодам . Такю.1
образом. названия получили числа 13 огромном д11апа
зоне - о г 1до1oм nnnnnl1 oм 04' 0 11"" - 1. Если за11и1ать
верениuу uифр последнего числа н<1 Gумажнuй лен
те, отволя на каждую u~1фру по 5 мм, то мина этой
ленты~ несколько ра.з превы сит ра1меры н аше й 11ла
ttетно й системы! (Сс1ма11 отдаленная от Сол нца пла
нета - Плутон - име:.>-ет средний радиус орбиты око
ло G млрд км.) Лля сравнения <кажем , что лля записи
ч1кл.:1. выражаюwего количество пес•1инок 1J Архиме
дu1юи Вссле11ной, хватило бы 32 см.
J\юбо11ытнu срав11ить оuснку Арх11меда с данными
tuвременной астрофи-1ики . С~.>.rолня ученые полагакп.
•по во Вселенной количf'сrво ·мементарных ча стиu ,
из которых состоят ато"1ы вешеств<>, н е больше, чем
1083• Известная н;~м часть В селе 111 юй может быть по
мешена в куб с ребром длиной 40 млрд светов ых лет.
Если заполн~1ть его кубиками с ребром 10 - 11 мм (каж
лыИ такой кубик ме1 tьше прптова или нейтрона - jЛе
ментарной частиuы вешепва), то обшее число этих
крохотных кубиков окаж ~тся меньше юн; .
Такая с истем:~ 1~аз ва11ш1 бол~,шнх чнсел
пришrт;:~ 110чти rю всех сnрс>пtйских cтpaIIax
11 в Сослинfнных JUтатах Лмерию r А жл во
Фр;1нцни 11 XV н. посчит;иrн, что <-ва1·он•11tК» и :i
1рёх 11улей 01ишко ."1 мзл. и помест11ли FI одн11
•t.1a/'OJIЧИK>1 ШСС'IЪ JIYJJCЙ. В rУКОПИСlЮМ l:ОЧИ
НСНJТ!f 110 эprrфмt"J ' HKe JIJIOI ICl\OГO нр:.~ча Нн
ко:r<i JПюке м 1.1 наход1-н"1 слона «6ию111сн 1 " ,
"'1рилл~ЮН " И 'J'. Д ., KOTOpl>! ,"ПI 011 06О~!Нача;1
втору1п, ·1·ретыо н 11оследующие степени ,_\fИЛ
mюна, т. е. чиспа 1 ooouuu 2
= t 000000 пооооо,
l OUUUOO ~ = 1 000000 OOUUOU 000000 11 т. д. Эта
тради1~ия до сих пор сохраrrилась в Гсрма1111и
11 Ангтrн. Сами же фра1щузы с серсд riны
XVH в. ст~u1и 1х1з.це)15ПЪ ч1кла на периоды по
1·ри ЦI rфphl в r<:IЖ/(OM вместо WCCTJ 1. J .I СЛОН()
<-611ЛЛТЮН • Г!ОЛУЧИJЮ \' НИХ :m;lЧtllJIC:: 1()'1_
,
'
Наэнания бплыпнх ч11сел привлекают 1111н
~1аш1е м атематиков ин 11а111и дни. Лрофсссор
Стзr1сjюrщс1юrа у11иnерсптета (США) До11аль11
Э Кнут посч11тал, ч10 в траднциошп,1 х сис
темах наэва11ия щш чисел <· р~кходу10тся» сm1ш
ком расточитслыю. Предстаним на м1шуш:у.
что мы у.мtсм н;.~зынать тою,кu числа н пpt
ДCJ tax от 1 ;~u .100 . Уже это1·0 небш11,11ю1·0
ЧИСМ-«ВЕ/\ИКАНЫ»
Математикам приходится иметь дело с гораздо
большими числами, чем физикам и астрономам.
В науке (J числе различных комбинаuий - комби
наторике - числа-«великаны» вс~речаются бук-
13ально 11а кажлом шагу.
Огром1-1 ые •1исла возн~1 кают и при оuенке веро
ятностеи редких событий. Например, всрояпю\ть
rого, что обезьяна, бессистемно nарабаняшая по
клавишuм nишушей Мi:lшинки , случайно напечата
ет шекспировского « Гамлета», можно оuени1ь при
мерно как один шанс из Jl)m.xю = 10 41 1'8~ (~лесь прt"д
полаrается , что на машинке 35 клавиш, а текст
- Гамлета» с:остоит из 27 тыс. символов}.
Большие числа - •1асгые гости в таком раJделе
vtатематики, как теория ч и сел. Известно, что любое
чиrло, nревышаюшее величину N =3
3
" ' >1Ol11>J~;~ю,
может быть выражено в вид!' rуммы трех простых
чисел. Сра3у же возникает вопрос: обl\адают ли
этим свuйством все числil, меньшие No Увы. мош
нейшей электронно-вычислителы1ой машине 1ы
проверку э1ого свойс1ва лля кажлого натуральнот
числа от 1 до N потребуется время, во много раз
превосхоляшее предполагаемый 1юзраст Вселен
ной, котuрый оuенивается менее чем в 10 16 секунд.
Л.1fivк,1 < чti 1а
1\АТИ Н СКИ[
КОЛИЧЕСТВЕННЫЕ ЧИCl\ИTEJ\bHIJIE
Число НаJва11и(•
Прои.тuш1..:11иt·
1
LIПLl'i
унус
"
dщJ
луо
"'
tre~, lr1a
тре r, ; rm<i
IV
qual\Lюr
кв,птуор
v
qL1t11(1ue
KBИ l llФ~
VI
~ех
<РКС
Vll
o::ept en1
Сf>ПТем
V lll
octo
ОКН)
IX
11ovem
HUl:H-.' M
х
de-rem
'
деu ем
XI
uпclt->< 1111
у11деш1м
Xll
duodc cim
дуодеuим
Xlll
trerlccim
трt·леuим
XIV
qu.illuorde\I m кватту?рлеuим
xv
quiпclecim
KB11Hдt'Ul1M
XVI
~etJec1m
(('Дt:UИМ
XVll 1,ept en<i e( im
СЕ'птенл~uим
Х\1111 dLюdev1g i пti
'
луодсОИГl>IН ТИ
Х!Х
undevig111t1
у11дсв~1гинти
хх
v1gi11 t i
8VHIHTl1
6J1'ажа з 11а1111~'1 ) ~ост:почно, чтобы 11щ1 ,'11сн о
в:.~ 1·ь все ч11сJ1з от 1 11.0 9999 После;1нее ч 11ою
можrю назвать "/tевя посто /~сnять co·1"eIJ де
ВЯН(}СТО l\СШ:1Ть•) . Точно так же. если вслед ~а
л.ре1:1 1шмн грека.мн число 1О ООО 11азва1ъ ''-~ш
рпа11ой-1, далее ~же можно поиме11оватъ все
ч.11сла от 1 до 10' . 1l аnрнмер, чнс..rrо 9l)l)9 <) 1)t)9
назо1:1t'м «дс 1шносто левнть сотС:'н девяносто
ДСIШ1Ъ \1Нри:щ )tCШIHOCT() /\СННТЬ сотсн деюню
стu ДСl:IЯ'IЪ ».
ОБШЕПРИНЯТЫЕ НАЗВАНИЯ
БОЛЬШИХ ЧИСЕ/\
103
тысяча
10"'
у1·1леuимио11
106
МИl\ЛИОН
\ ()JЧ луолеuилл11011
10• ·'
109 миллиаrл, биллион
тредеuилли о н
10 1~ триллиuн
i о• · кв,1ттуордсш1лл1 ю11
1() 1;
квалрИl\ЛИ(Н\
1о•• КtlИНД('l.IИЛl\ИО\ \
1013 КВИНТИЛl\ИОН
1(1 11 rедЕ'Ш IЛЛИОН
10~ 1
секстилл1101-1
10·•
сеп1 леuиллиu 1 1
1014 сеrПИЛNЮН
·1О"' дyUдt'IJИI 11Н ТИЛЛ11U11
102 7 о ктиллион
1 uы> у11леви 1-ин rнллион
101n 1IОllИЛЛИОН
10" 1 вип111т11лли о 11
1OJJ леuилмюн
127
Слсдую щ1 J "' 1ю 11coбxoJ \l l O\IOC111 н;.~:ш анным
ч11сж>м N)JlЖH< >быть 1О>!. Д :;:)_ К1ry· 1·111х·11;1ш·аст
/l,. l !JI llCI'() 11:.l 'iH:tHlll' « Mll.'lbIOIJ" '·Од1нжор1;·нн 1 ,1с
C.'IOKa. L1:1J lр11.чtр .,NI l IJI r,ю1н.-р·' - обЛ:1/\:1Те11h Mll-
itl1l! J!ll\()ГO состошпш, также (1ы111 1 бы удобны н
о\-iраще1111 IJ ·>,
ОП1СЧ~IСТ ()J I , Л,61 ст11~ )-1 'l'ОЧ 1IП
так же н J \il.rтee. мы 1<аждый pa:i 6~·;\<..:"1 1tэна· 1 1,
1ювос 11а:таrп1с чнс; 1 у, 1 1редстаuляющl'N1у co6of1
1.;11:i,i.paт прсдылущс1·0 п;че 1юна111юго LlJtcлa .
.'Гю60 11ыт110, •по 6m13кал 1цс.sт пр11 образо-
1щ111ш llOJl(H'O llJ\ll'HUl\:111 HUl'U ЧIJCJJa vб рать
Cl'())lhKO 1]() Cl'( Jclbl{O» -
вt- l'P l'Ч:tl'TCH н старш1-
1ю~'1 1 1 у.,,н:р:щ 1 01 славян (см. е1·:1·1·ыо •Ст:1р 111111ы с
Clll''l'l ' Mbl :~:tl lllCJ I ЧIJCLJI" ). ;J l'Щё p:111t>llLC - 11
:1ршl1,1с·1 1 1чесю1л 11 сс1 1едою1111ях Лрх11мс1р.
ra'{ \1 ы111лян о с 1 юсоi1а х 0()0:~11ачс1111я бот.-
11111 х чr1сел. Кщт в 1<)77 r. nостронл п rстсму ,,1;1 -
тс~ 1а111ЧСС!О1Х CH ,\HIO!Юll, с помощью котороf1
шюс.•1едст1ш11 была ш1спспа са)11~ш 60.1[1,шая и:1
I<ОГЛ<НI ~ 1 00 нс.трСLЫJ3ШIIХСН n ~1атем;1'1' 11 чесюrх
,цою1~i;~тсm.стн:1-: констант - так 11аJыn;1~~-юе
ч 11 сло l'рэ,,сма И.1-:;;1 сно<..:f'1 нсобыюювеrшой
1 ·ro~10:;1tK< )cr 11 (>нn 11е може 1 6ы·11, ныр:1;кено
11нач.t.' к:1к 11осре1~<."1 ном особ 1,1 х от1спt.:,1ы1ых
К< )нстр~'кrt1 11'т. Rот :~ж·с1. 11 1 1р 11 гщ1,11л:н.:п <1~1 -ню11-
11t"ван с1ктсча С'l l \Нюлов, 11редложе1111;1я Кну
то ,,1. :?·~от ре:1)лuтат :1:Jm1~1;icт no;tofJ:1ro11(ee ему
nочётт юс мес·1 ·0 н К1111н.- ре1.:ордов Гm 111ecr;1.
./) :}:JIOJ[(\ЧCI lllC llCЛl,:1}1 11е) гюмянут:u () таю1л
•ВI fCOI CTCMJ 1ыл ~ 11а :3н а1111нх 'lL ICCЛ" J(:IJ..: " l 'VГОЛ»
JtJ' •
"
Д'1Я ЧllC.'1:.1 ) () 11 <- 1 'у 1 "OJl l IJI CKC •) - "!.1,JШ сшс.11;1 \ (j n
(11'111
...
сте11е1111 Г)ТUЛ: 1О' . О; 11. 1а~1щи1 а.чер11к;шсю111
1\1атс"'1ат 1 1к ~ю1арл К:1снср ста :~ 1ш11ысю ш:т.
корп 1КОС 11 .l:~i'
1111
0 Mllll ;llOlll,<:TCЯ CJ [()H!) Jt;IЯ !1.lЗB:l-
1 111я ч11 сл:t 1О . 011 сnроп 1л сноеrл /\еюп 1и1с1-
1 1сгп П!lе\1Яl шик,1, как ()ы 011на:т~uт ::Jтn ч1к,10,
11 то1 ответил: "L 'у1·011 " .
ЧЕТЫРЕ ДЕЙСТВИЯ АРИФМЕТИКИ
С/\ОЖЕНИЕ И ВЫЧИТАНИЕ
Ч11сла 61,1111 r rтр1щума111.1 , 1ю; 11.м11. ч·1 0()1.1 0()0:11tа
ч ат1 . коm 1ч есr·но 11ред;-.1етов: о ре.'1 fl 1шлча 1 rt:,
мtm1<c>n :1t:р 1 та п амбаре. 011е ц u стадt. Но этн
вел11ч1 шы 11с ппстоя11111.1 - 1ют 1чеспю 11редме
тов то уnет 1ч1 шалось, то у:v1с1 1ы11алос1" поэто
му nажпо 6ыщ1 уметь скнадьшлъ 11 вычптатъ.
Ко1 ·1.1,;1 ч11с:л:1 6ыл1 1 1н:n<ш1,11111м11. ::>то / \<:! 1;июсъ
11 J1< IC 1'( > pt lC<Нl:!Л Н Чё.:р·1 ОЧ КН на /J.l:j)CHt:, i;tВЯ3 Ы
на1111 \.it:.•11<11 11а 1н.: рt11к<::. Пас:\.:т пас1 ·ул стадо
< н1сr\, 11:1 ~юнее" у 1 1е1·11 нt:р(:пка , а 1-1:1 всμС::нкс
tтолпко у~стщн, с 1<0!1ыю овец н cт:tf\l'. Р<щ11 лсн
~т 1 L~ 11 ок - пастух завязал е11\ё од1111 у:-~с.:тж. У'1<1 -
щш н1 1ю.1 1ю1 д.uух оuс:ц - ра:тsт:~ал 11n;1 узеm,;1.
Вмссю 11срёню1 часто нспuпь:.ю11;,~1ш жпвоir
«nыч1 1 сл 11тельныir прибор" - nалы1ы. Об ы•11 ю
11мсшю тt1к считают .малы шJI. Большого тру;1а
сто 1 п пpcilO/tJ R<iTC ! IH\1 отуч1 пь ш.:рвоклассrт
кон от тако1·0 счt:-1 ·:1 11 11р11уч 11ть к усп юму счi..~'Г)'
•н y\t<..:• О;t11::1ко на116шн.:с стоГ1ю1 е 11р(х\011ж; 1-
н1т сч1 1т~т1-> 11:.1 1 шлы \:.tХ.1'Срж: 1 рую 1 н карJ\\: 1нах ,
ч тобы Н<.: BllДeJI учи·1ет1 с\ 0/\1111 llt"]lBOIVL:.tCCllllK
склаr1,ын:11r ч1кла, тщ1,я 11 а ц11фер()Jшт часо 11.
с р::!:тнтнем ЦИВПЛ.ПЗЭI\1-Н-1 1fQ}J li)J}IJll ICl1 1x 1:s-
ЛIIЧT1l,JC nриёмы с чёта. 0 1111 6ыл.J1 нсобхоюrмы
11 к~тщам, и р<.:.месле11111.11<ам, 11 тоrд:~шним
128
<- б:J l·Л<llp;tM " - j)()C' I OHll l llK: l1\\. 0/1.H:tKO 11 1.. 'K\'t:C'l '-
H\}.\1 счёт:1 1v1:1;1,C ' , 11 r 11<: 1ч1юп 1с ДJш pacчf· r 011 11 р11-
пж:к:!Л11 с пе11.11 ;элы ю оf>учс-11111,1х лн >11cl1 - счi..;· 1 -
ч1 1 кn11 . Прс:дстаnьте. что rш 0 1.::13:i;1 11c1, 11 Дрс11нс~1
Рпмс 1 т 11~1:.1 с.r1едует с;юж1Lп" 11 аттр11~1ер. ч11 сщ1
cxxxrx 1( CCCXLlV. ЧТ() вы ()у71,стс ЛСЖI 1ъ? 1\11-
несню. сrтачала гrсрспншете r1 x пр1rвычттым11
/\ЛЯ себн ц~1фрамп: 1_~ч 11 -1++. ~ 1 ю·1·о м 6у;~ете
СЮl~!ДЫНа·11, так, как учt l.JlJI н lUKOЛt .
Л как это l'/\l'J 1 :1л f>ы р 1 1мсю111 счСтч11к~ 'J'oч
llO т:1 к же. хотя 11H/\r 1l1ск.1я 1to~-1 1.11 t1101111:1 я с1 1 стс
,\.1 а сч11с 1 t:111 rн 11р11111ла к Е11рш1~ 11 ;1мщ) 1 •0 1юз
жс. ;'1.с110 11 том, что т:1ко(1 11с1к1ш:.1, с• 1Стч11к
< 'Ч'lf~l'l'Tlll"IT 1 1е ~:H lllCl>ll\:НI ЧllC.rl: I , ~1 < 11')M0Щhl0
C llOC:l'O cчtTI IOl 'O 1111С'1руме 11 т:1 ;1(i:11<:1.
1 Jt)aл· - это i\Oc1c 1 с 11роре:1:11111ы ,,111 11 1 н:1'1
же11обам11. Чтобы слож 1 п t, l _)() 11 :)-1 -1, счётчтrк
с11а~1ала обо:шачаст н;~ аб;:ше 't11с.гю 1:)9. Для
этого 011 укладывает па ш1ж 11см жёлобе <) 1<;1-
мс шков. 11а следующем - ) камспп<а 11 од 1 111
камешскю1 ~щt..,,1· н трс·1·11 1'1 жё;юб. (•Ка.м<..:шск·} по
л:.1ты1 111 c .1lct1!t11'; отсю;1:1и11рш1зо 1111ю на:знаюн:
сонр<..:МС I 11 IOl'O ЭJ l (.'[(TPOJ 11 IОГ'О счётч1ш~1 - <1\;~Л11-
кулнтор". ) F.сю1 как1J1·0-то р;1;зрщ\а н ч11елс 11с1,
то пустует н COOTIJt:TC'l'll}'IOЩllfl Жt.'JI060 1(. Н<:
1 1р:нща ЛII. это ПОШЮСТl1Ю COl!Jla/ pt'I с CORpl'-
:'.•1CППltf:Ч нр 1 шцшюм зamrcrr ч11сс11?
А 11зльше? Дальше счётч.ик кладё·1 1:1 послед
ний желобак к името111,имся там 9 каметкам ещё
4, затем снимэет orry.n .a t О камешков, оставляя
лишь 3. и t каме шек кла}\ёт во второй жёлоб.
Потом до6<1wrяет ещё 4 кJмt:шка (в рсзул hтатс
та~t оказывается. 8 камешков) и заканчикает
вычисщ:11ин, доб<шляя в третий жёJ106 3 ка
мешк<1. Тсщ:р1) каме111кн 1-1;.1 /tоскс ппказывают
чнсло 483.
Этот ~вы чиСJ1и·1·елы-1ый прибпр" вам что-·го
11апомннает? Ну ка11ечно же, добрые с1·арые
С'l(ёт1.1 Только в счётах вместо камешк<.т - дере
вюшые 111ари1ш, на11иза11ные на пrоволоку. Рус
сю1е счёты отличаются. от западноевропейских
тем, что па первых по десять шариков n рнду, а
Шt вторЬL'Х - по де13ять. Любопытно, что в Евро
пе их и по ce1"i день 1 1 азы.1:1:нот ~абак·>.
Счёт ы использовались :и ш1 Востоке - в
К11тас и Япш-шн. У китайских счётов суан-т.1н
щ1 каждо1) проволочке не по дсся'rъ шар111<оu и
нс по девт ь. а по семь, причём дnе 1юсточrси
отделены от остальных 11яти . Каждая из ЭTIIX
доух косточек ():'\начает пять единиц дашюго
разряда. Такое усо.всршенствоnаннс позnо1rnст
уменьшить t~исло .косточек в счётах.
Ещё совсем неданно в бух.1·алтсрннх учреж
ден11й и лредприятий нt:прерынно знуч<tли
щелчки 11ерt:брасываемых на сч~т:п' косточек.
Au Яnонни 11 н Н<lШИ днн J1ровuдятся сорса1ю-
1:ш111я 110 скоростн счёта мс:жду людьми, 11оору
же11111.1ми srпо11скнми счётамн соро6а11, и опе
раторам.и вычислительных мапшп. Причём,
1<ак правило, nобе11щают вычиспители на счё
Т-JХ. Ведь чтобы машина начала считать, для нсё
надо состакнть nрограм,"1у!
С:чстh1 суа1 1 -пан как будто с1кцналыю 11rш
сrюсоблены к римской записн чисел. Это не
уднвнтел1>но. ведь и то и друJ·ое rюзннкло r1з
«ГJаJн,цевой системы»: пять палыtеR - кос1 ·о чка
слева или uифра V, ещё пять пальцев - 11торая
косточка слсяа и затем пеrехо/~ 11 единицу сле
т1ощего разряда - 1:\Сё K<IJ( В pИMCKOii ЗаТТИС11 .
Мож110 даже усовершенстnоn:пь суан-пан по
аналогии с западноевропейскими счётами: вме
сто r~яти 1<осточск с11рава ocтaвi-rrr, только четы
ре. ;,i вместо / ~кух косточек слека - ли1uь u.цну
Псрехон 11а поз111.1,ионную 1tссяти 1 111ую си
стему счисления 11озвш 11;ш сqита·1ъ б~з абак::~.
Такая запис1) чисел получила назван11е «и ндий
сю1й счёт», поскольку и цифры, и r1ра1:1ила дей
СТJJИЙ поя~шткъ впервые t3 Ин,тrии. Изменения
коснулись и абака: вместо камешков в желоба
Азбука счета
AiJaк lвверху ! . русские счеты . сущ-пан .
АЛЬ-ХОРЕЗМИ ОБ И НДИЙСКОМ СЧЁТЕ
Если ты хочешь прибавить число к числу или отнять
число от числа, поставь оба числа в два ряда, т. е.
одно пол другим, и пусть будет разряд елиниu пол
разрядом единиu и разряд десятков под разрядом
десятков. Если захочешь сложить оба числа, т. е.
прибавить омю к другому, то прибавь каждый
разряд к разряду тоrо же рода, который нал ним,
т. е. елиниuы к единиuам, десятки к десяткам. Если
в каком-нибудь из разрядов, т. е. в разряде единиu,
или десятков, или каком-нибудь другом, соберется
десять, ставь вместо ttиx еди 11 и uу и выдвигай ее в
верхний рял, т. е. если ты имеешь в первом разря
де, который есть разряд единиL1, десять, еделай из
н~1х ~диниuу и rюлн1>1ми ее в разряд десятков, и там
она будет означать десять. Если от числа осталось
что-нибудь, что ниже десяти, или если само число
ниже десяти, оставь его в том же разряде. А если
11ичего не осганется, поставь кружок. чтобы разряд
не был пуст; но пусть будет в нем кружок, который
займёт его, чтобы не случилось так, что, если он
будет nуст, разряды уменьшатся и второй будет
принят за первый, и так ты обманешься в своем
числе. То же самое ты сделаешь во всех разрядах.
129
Числа
\тapLIHHhlrt f11tMI ''"'" ·1() ,;~
<.:тш1и у1vтады в:.1ть жеюны с 11:1mк~1нным11 н:~
н11х н11фрами. Эт1 1 жето11 ~-.1 на1ынзлlf(Ъ •·апек
сы·, Но абак с ;11 1 t'ксзм11 нс вылсржал 11с111,1 ·1 ·а
нш1 временем tJ был Jабыт.
УМНОЖЕНИЕ
Умножсrтпе ч11сеJ1 сейчас и :3}rча 1т 1:1 ш:·рнuм
1<лассс школы А 1ют в Средние 1:1ск:1 совсем
не.мнu1·ие владст1 нскусспюм ум 1 юж<:1 шя . Рс.J\
ю 1С1 а р1-н.:тuкра·1 мо1· пох Rа статьоr зна н нем та()
л1 щы ум 1-rожс11 ия, д:~жс ccm r он щю11 ч11J1 евро-
11сfiскнt'1 у11нверс11тст.
~а тыо1чслст1 1 я раз1'111т11 н м:псматию 1 было
1 1 11 111 1уман о м1южес·1 · 1ю сппсобов рнюже1111н
чисел . Нталы111сю1й математн к Лука Ilачоли 11
своём трактате «Сумма з напш1 по ар11фмет11ке,
оттю шсш~ям и пропорц11011алы-юс1' 11 » ( I'-19LJ 1· )
прнводит rюссмь ра:-1Jшчны.х мсто1юn ум 1 юже-
1шя. Uди11 IП них IIOC ll'I' H<J ЗR3111tC ~ рсвно с1 ъ.
ю 1и решет чат ое умноже ние~
CJ1a•1aJ1a р11сустся 1 1рнмоу1 ·оm,ник. ра:зде.11ё 1 1-
нhп-1 н <1. квадраты , 1 1р1 1чСм р<tзмеры сторо11 пря
мо;.1т111ышка соотнетствуrот чнслу десяп 1L111ы~
з11а1<011 у множl 1 мо1·0 11 ,\111 южrпеля. Затем квад
ратпы<:: ю1 е-1 ки пелятся по дш11· она11и, 11 «" п о
лучае-1 с н ~<артин ка , п охожая ш1 ретётчатые
ставн1 1 -жалю:ш. - 1111шст Пачоли
-
Таю1с
ставш 1 вешались 11а окна всне11нанск 1 1х / \омон.
мсшан ут-1•п 1ьu"1 прuхuжим в 1 1деть с1 щнщих у
окон ;1а .м н MOH~IXHHh ~.
11еrемножнм эн1 -"1 сносоnо м чпсл~1 l 99R 11
987. Дл11 Э1'01 'l) З;JIШШСМ нвер:ку ·габ111 щ1.1 число
9fP, а СJ 1 ева - J998, как 1ю1<а:1аrю на рпс. 1.
но
Т<.' 1 н.:-р1, в "аж; \ 1,в'1 ква/1ратик nп11111e .\i1 111х) 11з·
1iCJ\t..:1 шc 1 111фр-с.:о.\н1шю 1 телеИ, расnоложе1111ых
п од1юi1строке 1 1 н одном столбце с этим кнад
ратшюм.Дссятки распола1 ·;uшся в ннжнемтре·
угuлышкс, а сдш-111111.1 - в верю н.: м. ЛoL'JJt: то1·0
~"ш нее 1·реу1 ·ш 1hн11 ю1 ::;апол11е11ы. цнфры н ю~х
сю1а;\ы ваютс..я вдоль каждоf1д11~11 ·онат 1. Р<.;зуль
тзты з:зш 1 сываются L'Пp:tп:t н с11 11 :~~ от таб
шщы - 111.туч;н.:"J <..Я 1 97 2 ()2()
3то·1 с1юсоf} 1 111чу1ъ ттt xyA\t. чем оnщеnr11-
ш1тыс1. 011 даже: проще. 1юс1<оm,ку n клетк11
таf>.rп1цы З<ШОСЯ'1СЯ •шсла прям о нз габлицы
умноженш1 без 0,1~.поврсмс 1 11ю1·0 сложения,
прнсутсrнующс 1 о в о J1-щар·1 ном м етоде Затем
остаL"тL'я 1олько нрш 1з н<х.·п 1 С.:Jюже нис.
Дpy1 ·ui'I с 1 юсuб 11 :1:iы на~· 1 с.:н ~ ма;11:1-1 ьк111·1 ~1a
I\IШ«> Сн: 1ч :зла, как \111>1 11 гтрнт,1t<.' 1 ~1. одно ч11сло
::1а 1111с 1 м1ж·тся по11дру11щ. 1ю ::1ате'V1цнфр1.111rrx
нc1 ·0 ч11сла п ооч.ерё;\J ю ~ м 1 южаются 11~1 1 111ж1 1ее
ч11сло. r1р11ч ё м 11ач1шают с цпфр 1.1 ст:~ршеJ'()
ра зр»/\а н н:а:лтый р:зз добаuшr ют 1 1уж1ю<: чнсл()
пулсir
На p 1rc. L пока:~аtю у\1t-южсн11е чассл 1tJЧ8 11
t)t\7 ЭТН.\·1 способu \1 l~ 1 ·0 прсt 1м ущес11ю в ·1·0,,·1 ,
что уже с ctмu1 ·0 начала 01tре;1с1~яютсн щ1 фры
старшнх разря;юв. <1 это ()ыв:н."т нажно. сст111
трсбvстся fiыcтro оцсн 1 п 1, 11<:J 111ч1-111у Ос 1-:u1ь-
11ые шест~-. приё,\101\ пп11с~11 1111>1х Пачпт1 , также
оr1нр~1ются 11 ;:1 :з11а11ие табтщы ум1юже1 1ия
От 1ако n Рпссr ш среди крестьm 1некоторых
1·уберн11iт б ыл распрос1 ра11ё!I способ, котоrьu'1
нс требовал знания всей таблицы умножения
0 11 получ11л 11 азва 1 rис ~ русошй крес-1 ы111 с1шй
способ умrюжешш~. Здt'с1, нсобход11мо бьL'Jо
m 1шь умен~ 1е умножа·1ъ 11дсл1 1·1ъ ч1 ~ела на 2 Пе-
ЗАКОНЫ С/\ОЖЕНИЯ И УМНОЖЕНИЯ
Переместительный (коммутативный):
а+Ь=Ь+а,
аЬ =Ьа.
Сочетс1тельный (ассош1ативныйi:
(а+Ь)+с=а+(Ь+с),
(аЬ)с=а(Ьс).
Распределительн ый (дистрибупшныi'\):
а(Ь+с)=аЬ+ас,
(Ь+с)а =Ьа+са.
Правила Л/\1'1 11ум1:
а+О=а,
а+ (-а)= О.
Правилu ЛJ\Я елини uы : а 1 =а.
Азбука счета
9~РООО
9
888~00
Рис. 1. У'1Н1Jже11щ• • 1>1t:ел 911 7 11 1'198 мР1 олuм • Jll 'IJH U< 11> •
ре,..шожим сщt ра~ числа 987 11 1998 Э'I'I 1м пю
собом
Н:ш 1 1шем одно 1 1:~ ч11сеJ1 сJ1ещ1. а н·1 uрое -
справа rта од 1 юй егрочке Ле вuс чнслп будем
пе.rщ·п> 1 1 а 2, з 1 1 rа1юе - ум1-южа·г1. 1ra 2 н резут,
татhl зат1сынат1. в еюлб 1 1к (рлс.:'>)
Ест~ 11 ри ]\елешш 13оэ1 t1 11ше·1· uстз·1·ок (· 1
-.
е.
дет1м:ое окажетсн нсчётпым числом), то он
987
1998
- 193
3~)96
246
79q2
123
1'59R4
61
:) 1G68
50-
6 :N36-
1')
127872
7
2')'5744
~
51148~
1022()76
1972026
Рис. 3. Умножег1 ие чисел <J8 7
11 19'11.\ • русLк "м кр«пьянск'щ
с11псобо" '.
88830
7896
}<)12026
Рис. 2. У'lнс>.+;ег111r ч•Кf'\ 1'J98 11 '1 8 7
·\.\eTOЛf),,i « V1dЛ< 1HbKJ.1~f l rl \1U1'»
0·1·брасыв~1е1ся Ум1южсш 1 с 11дслс:нис н<~ 1. лро
АОllЖаt:м дn тс:х LLop, по~t слсна не uстанt:н: н l
Затем нычсрк 1 н:м те стрuчю1 столб11 1<он. н
кuтпрых слена стоят чётные ч11сж1 . Те1 ~ерь сло
ж 1 1~1 остаR 1ш1<.:ся ч11сnа в 11раном с1•олfiце -
11C)Jlyчr 1 м 1 CJ72 02(). Это 11 есть щю 1 1звс;\с1111с
nереМJ10жае~1ых чисел.
Почему да 1 ш ый способ даёт верный резуль
т·Jт' Оказывается, oir нспосре~стве 1 шо сюrзан
с прсдставлеrпrем оf(ного нз сомножителей, а
именно первого. в д1ю 1 rч1юй системе счисле
ния (см. с1 ·;пъю fПОз{·Щиuнныс снсте.мы сч1 1 -
слсн11я»):9~7=J z''+1.2н+1·2-+J i'+
+()·2;t}2'
1
+1·2'+()·2~+l 2.
1
+1 i'Есл11
тс::пср r. ум 1 южнт1. этu ныраж<.:н11е на l 99R, то
nолуч11м 1·102297()+1 511 ЧВR+1·2')5 74-t +
+1·127R71+()·С>:1936+1 3196S+1·159R4+
+О 7991+1 599(1+ 1 19'Ж~аметьте,что
м ножнтелъ О стопт как раз 11ерtд 1·ем 1 1 ч11сш1 -
t'v1и, которые были uычеркнуты в правом стол
бике!
~крестьянсю11'1 способ~ ....юж<:т 1ющхшнп,ся
тем , кто нс м ла/J,ах с табл11цt:~"1 ум 1 южс1r1ш ,
п ра нд:~. З/tССЬ прнхою ITCH JJPO J !ЗlЮДН'J'Ь больше
сложснн rl. nf(1 1 aкo таnm,щу ум1юж<.:ння все же
стп11·1· выучить. Ну 11е хвата·1ъся же за ю1ршщ::н11
13J
• Числа
и бумагу, чтобы выяснить, сколько будуr сто
ить 7 пирожков ло 80 копеек за ш·rуку!
ДЕЛЕНИЕ
Хотя умножен ие в старину и считалось нелёr
ким делом, однако деление бьmо ещё сложнее.
В Италии до сих пор сохранилась поговорка
«Трудное дело деление,}. Так обычно говорят,
когда оказываются 11ерс::д почти неразрешимой
проблемой . В Сре}lние века шодей, умевших
произ.1юдить деление, можно было пересчитать
чуть ли не по пальцам. Их уважительно назы
вали ~магистрами деления». Они переезжали из
города в город по 1 .1риглашениям куп цов, же
лавших 11ривести n порядrж СRОИ счета .
Методов деления было придумано немало.
Монах-математик Герберт, будущий Папа Рим
ский Снлызестр II, привёл в с1юих сочинениях
несколъко способов деления на абаке. При
:=пом он придерживался таких принципов:
-
как мшю-ю меньше применЯ1ъ таблицу
умножения, в частности не использова1ъ умно
жение в у~1е двузначных чисел на uднозн::~чные;
-
избе 1'ать вычитаниr1. заменяя их сложе
ния.мн ;
-
работа должна вы 1юлняться ~штом:пичес
ки, без nporiepo1< , при которых тоже могут по
явит1,ся ошиб1<и.
Такие строгие ограничения он ввёл, учиты
вая, скоm, неграмотны были мо Liахи, произво
/\](НШrие вычисления. Почти ш1кrо из них не
знал таблицы умпожt:ния. Но в итоге пр:шю1а
Герберта оказались настолько с;южнымн, что
пе были понятны тщже самым при ле жным
счётчикам-аб;111истам . Ко1·да R Европе по
я.вю~ся арабский способ деления , основа1-н-11,1й
на 1 1 ринятой сейчас позиционной дссятнчной
системе сч.исле 1 rия, он получил 11азва11ие «зо
лотое деJ1е11ие". Им мы гюлuзуемся и по сей
деш" Л метод Герберта стали па.:~ьша.ть «желсз -
1 1ы м ;~елепием». Кроме этих способов были и
!(ругне. Например, рзс1mадывалн делитель ш1
множители, а затем последовательно делили
делимое на эти числа . При этом дш1 деле ния
на однознtt 'Jн ы е числа сущесттювал специаль
ный метод.
Долгое время в Европе конкурировал11, два
способа деления: «Золотое деление-> и (•1'алера~.
Прежде всего напомним npaвиJta «золотого
деления» . Разделим 987 654 1-1а 346 (рис. 4).
132
Сначала нахuднм наибольшее целое чнсло,
которое, будучи умноженным на 346, окажется
меньше, чем 987. Такое число - 2 , оно и будет
первой цифрой час 1·ного Затем в ум ~ умножа
ем 34(> 1·1а 2, результат записьтаем псщ первы
ми тремя цифрами депимоrо и производим
вычитание. Потом к получе1-пюму чис.лу при
m1сываем следующую цифру делимого и про ·
должаем процесс, повторяя те же деr1ствия .
Второй способ итаm,я~щы ш1эы1шш1 «Гале
ра» из-за того , что после окuнчания иыч11слс
ннй цифры располагаются в ввж· фигуры, на
поминающей это гребное судно. Уангт1чан он
известен как «метод зачерю1ваю-~й·>, r юскuльку
здесь посгояmю приходится зачёркиuать циф
ры. Лу1<а Пачоли счи1ал этот способ са мым
быстрым. Может быть, кто-то из читателей
решит пользоваться именно им.
Метод « галера-> отли•1ается от «Золотого
делення·~ тем, что в нём нет ум1южсш1я в уме
многозначного числа на однозначное. Оно за
меняется нескольким.и у.множеншrми однп
знач.ных чисел на однозначные и вычитания
ми получ енных результатов по очереди.
Итак, тrсбустся р~1~·mел~пь 987 654 на 346
З::~пишем J1~Jн1мое, а 11од н11м дет,1тет•. Спра6з
01 ДCJIИMO l'O ПОС'l'аRИМ скобку, за l(()TOJ10Й 6у,71ем
nоснедоиателыю з<1пнсывать цифры частпоrо.
Как и при обычном делен ии. подбором нахо
дим первую цифру частного, 13 дашюм сл~чае
2. 3аписываем её (рис. '5, а).
Теперь умножаем первую цифру де;штел.я,
3, 11а 2 и результат нычптаем из перво~"r 1~ифры
дслим01·0. РаЗН()СТь 9 - 5 2 = .) за~rисыв:~ем
сверху, над цифрой 9, после чего зачёркнш~см
Рис. 4. делен11е
числ~ YIP 654 ~•а >46
Ml;'Tn/\OM •Зn/\ОЩГ()
дeЛl'l'llts-4 ~
3
;Ю
987654 (2
987654 (2
987614 (2
346
346
346
а
б
в
]
'/.
.38
2<)
29
'/.9~
;)05
Ы15
3рsв
~'~7654 (2
987654 (28 9§"П954 (28
346
3466
М66
:$4
г
.4
34е
11
п
)'
Цl
_,,..
!Л~
$$"1
Z9РЛ
~051'\
30~~0
9~7654 (285 98 654 (2854 170
346Ц)
34~~~(')
~16
Рис. 5. Леленне
H:J
3444
числа С)87 654
.'{
1fi
на 346 методом
)#(
3
•r31\E~f'3> .
о"<t\О
,.... _
С]\ \Г\ \D
~.\('00\О\О
"<""> 00 N") V°', r-- '.0
......
N\/")С]\о00~
N ;.,-, С\
""
'
"
Лзбука счета
цифру 9 и цифру 3 в делителе - они уже
«вышли нз игры ~ (рис. 5, б)
Переходим конторой r\ифрс делителя - 4 .
Умножаем сё на 2 и полученное произве11е1-ше
8 вычитаем из числа 38, которое сто11т над этой
цнфроlr делителя . В данном случае достатuч
но зачерю 1у1ъ цифру 8 и над ней 11а111 1сат11 О.
Tenep1, можно зачерю rу1ъ п r\11фру 4 в дел11Те
ле (рис. '), в).
Переходим к rrоследней цифре делателя -
6 . Умножаем её на 2 и вычитаем из числа 307,
образовавшегося свер:лrу 1юслс предыдущего
~таrш. Так как :Ю7 - 6 2 = 295, то зачёркиваем
307 и пишем над 11им 295 (р11с. 5, г)
После всех этих опер:ш.ий 1~ифры ш:~ерху
рис. 5, г можно прочитат1, как ЧИСJIО 295 654,
К()Торое получает ся нри «ЗОЛ()ТОМ делешш»
после первого вычитанv~я.
Теперь снова пишем внизу число 346 1tu<,
как это нзображс:но на рrн.:. 5, д, н подбираем
вторую цифру частного. Эт<' цифра 8. Записы
ваем сё 11 11оследов:~телыrо вычитаем из числа
2956 цифры '-ШCJla ,)46, ум11оженные на 8 11
"1""
~ Н'1
~ «"'>
("<"")
"
'
Рис. 6. В результате делен~1я
\Н:ОТС)Д()М •Галt'ра " nr)paзyeтrsi
фигура, наnо'1ннакнuая лолку,
а черточки г1ревр<1u1аю rcsi в весла
133
ЧИС/\i)
соотuстстнующ11м обр:азом С/\НI 111у1 ые. Получа
ем Т(), ЧТО f!:З<JбражtНО На ()ИС. ') , е.
В зто"1случае1 1 езачёркнугые цифры вверху
состаплmот Ч11сло 1Н R'5~. Это же число полу
чилось после второго nычнта1 Lия прн «:юлотом
дсл~юш". что и нсудишпельно .
Продолжая этот пронссс (р11с. 5, ж:. з), по
лучаем окончатель ный рt:зульт~1·1·; 28">-1 и 170 н
ос.~1·:1ткt: .
Ес1111 nонерн)r1ъ 11ос11еднт1й рнсунок на 90•.
то 1 111фры обра3уют ф11rуру, 11 ;нюм1111ающую
ДЕЛИТСЯ ИЛИ НЕ ДЕЛИТСЯ?
Иногда возш-шаст сптуа11 ия , ко1·да нужно
быс 1· ро определить, делится 0;1 1 ю ч11с1ю на
;1ру1·ос irm1 н ет. Пред1юложим. яы ку11ш1н в м;1-
1·аз1шс .i 1 tастика , 6 каран11анн.:~'1 r,1 9 0;1ина
ксжh1х тстра/\Сf\ а 11ро11зпец 1 ·0 11орит: ,,с нас ;1а
покупку дсся'rъ рублей », Даже нс :нrая точ ной
1т,е111,1 ncжynr<н, мпж1 ю сразу по1шти, что прп-
1\анец rт1116ся. Вед r> нто1·011ая стои_\ЮСть обя
:зательно доmкпа /\елиться п а :), r ю ш1 1О руб
леfr , 1ш 1000 копеек на 3 нс делятся.
К~11< у:щ:пь, делится m1 одно щкло на другое ,
нс прибегая к трад1щ 1 ю111юму ,r~.слс 1 1 и ю «у1·011 -
ком»? Дпя нс:большнх дсm 1.те11еl1 С) щ~ствуют
11рос1ъ1 е, леr·ко за1юм 11 нi1ющ11сся 11 р1вн:~кн.
Признак делимости на 2. Ч1 rсло н лс:1111·1·01
нз 2 в l'O!vl н только А Т() ,\1\ CJ 1yч.;.ie, t:CЛll t:l'O 110-
СJН:'Д/LЯЯ цифра Дt:ЛИТСЯ па 2.
Признак делямостн на 4. Число /7 ,дешпся
на 4 в то.ми только в том случае, если на 4
делится ч11ою, обра:юв~1шюс 113 двух после]\
'ШХ ц11фр ЧHCJia f1 .
Призна1' делимосп~ на 8. Ч 1 к1ю п де;н 1то1
на8втоиитольковтомслучае,еслина8
дслнтоr трехзнаLJнuе чнсло, обра,юв~нп·rtх: 11з
трёх гюслепн нх 1 1,11 фр чr 1 сл~1 п
llр1 ше1~ ём при мер: делимосп. ч1rсла
199 6J 9 971 998 на 2 определнется 11111J1r-. по од
ной e r"o последней щ1фре Я (11а 2 1~е.~t11тсн); 11 а
4 - rю,щ1ум 1юследним 1.1,нфра?>11 (9Н н е делится
тrа 4): на Я - по чнслу <)98 (11а 8 не делнтся;
впроче"'1, это уже следует rrз того факта, что
1.JИСЛО 199 619 l)71 998 нс дслuтся на - ~).
Есл н вниматслыю pacL \Ютрстh 11ризна1ш
деш·L.\ЮСт11 на 2, 4, 8, то мож1 ю 11а1·п11 признак
делиJ\1ос·1·и на 2"' (ni = 1 , 2, 3, 4 , .. .). Ч11сло 11
1.Ч
лодку 11лн корабль. а 11а11111 ч ёрточю1 сл r шаются
в сплош1 1ые т 1н1111. похож~1с на длншrыс нёсла
r-алер1.1 (рис 6).
Этот меТ<J/1, J)()i \llЛC» н И 1 щи11, orгyr1a через
;~рабские страны ов 11протпш n Enrorтy. Пrзвда,
у 1-щдий.цен в результате делеmrя тпшаю 1 х !{()·
р<~блrшов пс получалось. Ведь u то время on11
нс 1юльзо1:1а;шсь для вычпслсmп1 бумагой . а
1 r11салн на дощечках. которые былп по1<рыты
1IЫЛЫО НЛI 1 песком. ll,\lfCCTO 'f'UI'{) чтобы :-i:tчёp
IO·lllaTu т111фры , онн 1rx прос1 ·0 стира111 1 .
делнтся на 2"' u том 11 только n том случае, еслп
на .!.
111
дс1штся т-:шаLшос число, которое обра
зую·~· т 1 юслс;1н11х 1111фр ч11сла п.
Дсйствителы IO, }ICXO/\HOC ч И('JIO п MUiКllO
прсдст:ши1ъ 111-11 1;1с сум мы двух сл:н·аемых О/\НО-
1·0, O l<:lJ IЧ l lП3IOШ,<:: l 'OCЯ 1ll ll )'JНI Mll, 11 друТ'Оl'О, Q(i-
paзonaнrюm тrэ т после,:J.11 н_~ 1 1нфр ч11сла 11. llt:p-
noe слагаемое ,1е.rrится 11:i 10 111
• ::i :'lltaч1п . 11:1 2"'.
1юск011Ьку 101
"
='5т1.
111
• Т:жим обра:юм . 11011r<1c
о ДCJIИMUCJ'l I на 2"' ИСХОДllОГО чпсла вссщ:ло за
ВIIСИТ от ДСЛИМОСТТI 11а 2"' B'f 'OPOl'O сл:.н·аемого.
Признак деЛИ!\tО<-"ТИ на 5. Ч нсло 11 ,11ет1тся
11:.1 5 н том и толr,кu R том слу'Iае. если его по
следr 1яя 11,ифра О 1 1ли ')_
Признак делимости чисда 1l на степе1IЬ
шrтёрки 5"' (т = 1 , 2, 3, ... ) схож с 11р11:.тако.ч
; ~eJ IНMOCll l Ч[JСJШ /1 Н:.1 степень ДFЮЙКН 2111
• ::Jто
вполпе естестве11110, tieJ\1>J \e.J111тem1 2 н 5 1 1 1·р:~
ют соuершеш ю од 11ш1ко в)1О рою, n 06разоиа-
11ин оснонашLЯ десяти чIJОй сnстсмы счио 1е
юш- •-шсла10=2 ).
.Возь:мём какос - rrибудь крупюс числ о. 11 а-
11р11 мер 20. Еслн от ЧIIСЛа 20 ОТНЯТЬ цнфру его
несяткun - 1. , то в реJуJJьтате rюлучнтсл чпс:ю
18, дсшrщсеся на 9 Jlc 1 ·кo проверrлъ. что ::~то
Cf\O(lCТIIO BЬJЛOJll-Шe'I'(..'}f 11 /\ЛЯ др~т11х ЧI ICl'JI: 10,
.~(), . 1(), .. " 90. Е 1'0 такжt: можно р:.1спростран11ть
и 11а бопее 1<рупны<.: круr·лые чнсла. ).1,еГ1<.v1·щ1-
тслы·ю, еслп от ч 11сл:1 т r<i' (:щ1::с1, /11 11 k -
натуральные) отнять qисло т, то JЮJ 1 уч1rтсп
/;!
(•
т1U-т =т ·(JО-1),1.е.чиою,завс,1nмо
делящееся на 9. ncдr> сомножитель 1Ok - l в
десятичной по;;~1щ1юr11юй системе заn11сывает
сн од н11мн дсвнткам11 Это наблюлсннс пшю
жет пам обпс 1 юнат1, пр11 з нак дс; ш.мосп1 на 9.
СТАР И Н НАЯ ВОСТОЧ НАЯ ПРИ ТЧА
давным-дав н о жил-был старик, который,
умирая, оставил своим трем сыновьям 1 9 вср
бл~олов. Он з;:~nешал сt<1ршему сыну поло
еину, среднему - четв<:i ртую •1асть , а мл<1д
шему - пятую. Не суме в найти решени s~
самостоятельно (ведь зада •1 а в «uелых вер
блюдах • реше~1ия не 11меет), братья обрати
лись к мулрtш у.
- О мудреu! - ска~ал старший брат.
-
Отеu остilвил нам 19 вербl\юдов и вel\el\
разделить между собой: старш ему- полови
ну, сред нему - четве рть, младшему - пятую
часть. Но 19 не делится ни на 2, н11 на 4, ни
на 'i. Можешь ли ты, о лостопочтенный,
помочь нашему горю, ибо мы хотим выпол
нить волю отuа?
-
Нет ничего npowe, -
ответил им мул
реu. - Возьмите моего верблюда 11 ~•ыне
дQМОЙ.
Братья дома легко разделили 20 верблю
лов пополам, на 4 и ~1а 5. С1арши и брат rюl\у
ч11Л 10, средний - 5, а младший- 4 верnлю
м. При этом олин верблюд остался (1О + 5 +
+4 = 19) . Раздосадова нн ые, брат1>я вернулись
к мулреuу 11 nожаловалщ ь:
-
О мулреu, оп ять мы не выполнили волю
01ua~ Вот лот вербl\ЮА - 1\ИUJНиИ .
-
Это не ли w tщй, - сказал мулреu,
-
это мой верОлюд. Верните ег() и иди тf' ламой.
[Jризнак делимости на 9. Ч r~ ело 11 дс::т rтся
на 9 n том r1 Т()11пко в том случае, есл 1 1 су.,1м:.~
ет ц11фр делнто1 1 1 ~ С)
/L1я докз:ытелъст13;.~ этого 11рн :m:1ка вспl)м
шш. что mобое н~1 1111аm,нnе LПJСло /1 мшюю
оредс1·авнтъ u nirдe С\'ММЫ f !ССКО!ТЪКТ l.Х 1(руг.'1ЪТЛ
чисел - дсся'Т1Ю11, сотен и т. l\.
-
н, nо:1~юж1 то.
какого-то КОJ\ИЧ<:С'l'ЩI С/\ШШЦ. Например, ЧИС!IО
'iU - это 5 сотен, 2. десю'ка н 2. <.:диннцы. Со
с-1·:1nляющж.: этого числ~r можно с1·ру1111нро1.-1ать
rr по-друl'Ому. Выделим в отделы rую 1·pytmy сум
чу нссх ц11фр ч11с11::~ ).12 () + !. + 2"" С>) То1'д;1
срс:д11 оставшихся сл:н·аемых окаж~" J'СЯ кру1 ·111,rе
Ч I ICJl:t С ВЫЧt::'ГОМ «/!:111И » ( ')i}() -
.:; =-J.9'5:.Ш - 2 =
= 18), уплаrа кото1к>1u1 .пелает rrx кр:.~т 11 ым11 О.
i\от более форм<.tЛьпос обопюв~ш 1 1е это1 о
рзссуждеш~я. L\нcJ1o
11 "" Hi'nл.+ 1</ 1
nk. 1+ +10111+111).
l'/tCllo, 11 L•/1;·...• 171• -
Ц1 1 фрЫ В Д(.'01'1'1 IЧll0,\1 rrrt-; \-
CT:Jl\ЛCHl ll I ЧlllЛ;/ JI. З~IЛIJШС1\\ Н HJ ЩС С}"\1МЬI
ll =[llk+ f/k 1+ .. +111 1-1111] +[( 10.11- l)ll1c +
t-L
+(]() - 1)111--1+ ... + (1() - l)ll,]
Перна~ Ю},щратная скобка u щ1:1в01'1 час1 п
это1 ·0 раве11стн::1 - нс с~то 11но е, к<~к сумма
r~11фр Ll[IC'l'~I IZ , а вторая - всё, что O('T~l!l.CTCf).
после вычета су~·1м ы цифр~ это чпсло занеr~,о
\Юдетrтся 11а l).
1'~1ю1,., образu.,1 дею 1 мос ·1ъ на 9 ч1к11а 11 всс
цсJ10 :iaHH Cl lT ()'J /(С Лl!МОСПI ll:J <) суммы е!'О
1111фр. 1<:11'01"1ос1·атuк 11р1 1 дс..:J1с 1 11111 на 9 / \:Jёт э·1 :1
С~'мма. •1·ако(1 ост;l'lок 11р11 ;1еле11 1 111 на 9 /\;J ~· r
ч1к1ю11, 11 1 1:юfiорот. :1амет11 м. ч ю мы гюл~ ч1u111
;рже более сш 1 ыюе. че1v1 трсбо1щщ)С'1 ,, утвt:рж
дс ш 1е, н:-1 которt)Н> вытскаL"'l' сформу.1шро11ю 1-
ный nы1uc признак 11ел11мост11 а:л 9 (11р113на~<
13')
Числа
соответствует t.:лучаю, кu 1 да указаrшые остат
ки равны нулю). Бuлее тuro, из не1·0 же вып;ка
ет 11 признак дсл~1мосп1 на .) .
Признак делимо сти на 3. Число п делится
на 3 в том и толыю А том случае, если сумма
е 1·0 цифр дели•rся па 3.
У пр11знаков делимости па .3 п па 9 есп. np11 -
мечателыu,1е особенности. Они могут приме
няться многократно: спасrала к самому числу,
потом к сумме е1·0 цифр. зате:м к сумме цифр
1юлуч<::ШJО['О числа и т. д" 11ока нач::шыюс,
скоJiь бы ни было оrрuмное, чш..:Jю посте11ен
но н е «снернt.:,·ся » в одну-едю IC.V['Beн ную цифру.
Лус..ть, 11апрнмер, нуА<но уз нать, де.11 итс я ли
на 9 число, соста нл е ннос 1:1:; 1998 сднннц:
11 ... J 1. Сумма его r~ифр рав11а 1998. Послетн::е
число /\елнтся ш1 9, поскольку сумма его цифr
1+9+9 +8 =27делитсяна9.Значит,11исход
ное чнсло также делится па 9.
Заметнм, что в процtссс подсчёта суммы
цифр девятки можно не учитывать, так что
делнмость числа 1998 на 9 своднтсн к вонросу
о деш1мuсти на 9 чи сла 1 + 8. отнет 11:i кото
рый очсвиде 11 .
Коl\l\бинируя уже изtJест11ые признаки дели
мости, можно уэнать, f\елится ; 1 и ,ца~ 11 юе число
на 6. Дш1 этоrо ашJ одповремешю 11.отк1 ю
делиться 11 на 2, и на :) . СJJедоватепыю, IIaдo
пр11Nенить два при :.шака: признат< делимости
ш1 2 и признак ,целимостн на :). Ашиюп1ч1Iо
выводятся 1 1 рИЗНС!Кll ДеJIИМОС!'И на 12, 15, 18 и
друп 1с состав1 1 ые чис11а.
Признак Пас.каля. Ф1х11-щузски~'1 матtма
тик, фи зик и философ :ХVП в. Блс:с~ Паскаль он
Н<!ЖДЫ :Jадало1 1ю1 1росом: ч·ю будt=т, t=сли в деся-
1.36
Блез Пагкаль. ГравюрJ
ИJ 1- 1u юма cot>paнщ~
C'O'IИHel<>IЙ . 177q r.
тичном разложсIIИИ на·турального числа 11 =
k
k1
= lUnk+10 n1.-.-~+". + Н)111+п0всестепени
десят1ш - 1() 1
, 1IY, .. " 1О'"' - в:шть и заме~штr. на
остатки m 1, m J, .", m k, пuлучающн<::ся нрн Д(;Ле
нюr эпrх степеней на нското рос ф11ксиро~ан
нос число rn? ()казьшается, в рсзульт:1Тl' такой
замены образуется ЧJ 1 слп р = m knk + т1г 1nk-t +
+ ... + т1111 + п0, которое даёт точно такой же
остаток при делении на т , ЧТ(J и '-П rСЛ() 11. В этом
и состоит сутъ приз11аI<а, описа1111ого Паскалб1
в работе «Особенности делимости чисел'"
Убедимся ll tГ() CЩXШ<.:)J,JШ.IIO<.:Tl l. Для этого
каждую стt:п е1 11, нес11тк11 1О' в дсслти'-шом
ра :ы uженнн ч11стt 11 прt/tстаним в .1:11щt 10' =
= q,nz + ni,, J'J(C: q, -
неL1шшое час·п-юс 0·1 · дt:ле
нпя 1О'нзт(i= 1, 2..". k).Мы гrолучнм
п= (lf;гm+mk)n1г+(q,нnt +mk 1)н,._1+." +
+ (q1m+ n·t,)1l1 +llo= mk1tk+ mk-11l1н +." +
+m11l1+по+(q1n1+q2n!+". +qk11k)m=
= Р+(q1n1+cu12+". +q,;2")m.
Отсюда н~щно, что чна1а "· и р r1p1 1 делен.ни11:1
т дают с_щ11н и тот же остаток
На 11ракп-1кс.: r1но1·да бывает удо611 ес неко
торые н с~ пстаткоп т ,, 1п 1, "" m k 3амснять соот
петствующими <-r 1е1щс1·а· 1·1<ам1r » 11рн ;эрн.: нш11;а
т - 1 1риз11ак Паск~1ля и в этом C'J1yч;ie остаётся
в силе. Замстпм также, что если о процессе 110-
следоnателы нн·о дслсшrя чисел 10, 102, 10.1
и т. д. на т на очередном, i-м шаге уже 11айдс11
остато1< т, uт деж:ния 1О' на т, то для нахож
дения слслующ<.:1'0 остатка 111 11 1 им можно
чу;\ес н ым 06pa:~oN1 вuсrют,зuкаться . И3ба
внться от 1 шш11их громоздких выкладоl\ 1юз1ю
ляе-г такое полез~ юе ·1ождество:
10"
1
= JO·10' = 10·(q,tn+"п,)=IOq,m+10т,.
/·Ч
Из 11ero видно, что числа 1О н 1От, имеют
одн11ако.1;1ые оспrп<и от деления IJa т. А по
скольку чиСJю 1Um, нри большом i и пе очеJJь
бОЛЬШОМ 1n l'ОраЗДО fvltHЬШe <ШСЛа 10'-I, ЯСНО.
что следующий остатuк т,+ 1 следует опрсдсля1ъ
именно ло числу 1От,.
Признак дели мост.и на 7 . Llиain /1 делт·tя
Fla 7 1~ том и тол~,ко 1} том случае, если 11 :1 7
делитсячислор=п0+3n1+2п.!.- (п:. +.3п.1+
+ 2п,) + ... (здесь, как и ранее, nU> 111, n2, ."
-
цифры едюпщ, десятков, сотен" . ЧJ rсла п).
Убедиться в этом нам поможет униnерсат,
ный признак Гlаскаля. Последователы-ю находя
ост;r1·ю1 1 111и недостатки при делении Ч!fСсл 1О,
10!. IO s.."пат = 7. имеем
1о
7+3,т1=
.1;
Н)m1=
-J. 7+2,т2= 2;
1()111!= ) ·7- 1, т~= -1;
1()1/'f1 = -1 '7-.~.т, = -.1;
10т1 = -..J
.7
-
2,JJ15= - 2;
10т,=-3 ·7+1,т(,= 1;
1От1,= J
·7+3,т7=3
:и т. /~.
С11с11<mа·1·елыю, Lt'Yt cлn п ;~аёт ·га кой же остаток
пр11 делеr-ши на 7. что и число р.
Так, например, ч и:сло 1999 не делится на 7,
посколъкуна7 неделитсяч.ислор= 9 +:1> 9+
+21)-1= ").1.
Признакделимостина 11. Ч 11с1юпдслит
ся н:1 11 в том и только в том случае. если сумма
<.:Гu цнфр, СТО}IЩИх на нечётных местах, отли
ча t.'тся от суммы цифр. стоящих на ч ётн ы х
мссrах , 1ra пелнчину. кратную 11.
Дтr 11оказате11ьстnа :-ia мет~ 1м, что чнсJ1а 1О,
102
, 1()\ .", ]ok при делепип 1та ll дают 1re110-
k ...
cn1Th1·1н остатки - 1, 1, - 1, 1, "" (- 1).Следова-
телыю, ло признаку Пасr<аля, оронзвольное
натуральное число п при делешш на 11 даёт
т:1.ко1"1жеостаток,Ч'l'О ичисло 111) - n1+п, - 11~+
.
-
+." + (- 1) 11"' . Те11ерь ост;~лось толькu з амегить.
что 1юс; 1с:д rн:с выражен не лре;1ег~1 Rлнtт собой
p:JЗllO<."JЪ двух cy/' .l\J\,\ ц11фр ЧliCJ l a 1'l , С'l'ОЯЩИХ на
чётных 11 1 1еч<::тных местах:
(п0+п~+n-J+".)
-
(n1 +111 +11~ + .").
На11р11мер, чпс.тю 1969 делитсн на 11, п отому
чтодля 11ero эта разпост1" а именно 18 - 7 = 11 ,
делится на J 1.
Првзнак делимости на 13. Число 11 ,целит
сн на 13 в тuм и только н том случ11е, когда на 1:)
/\елнтся число l, 1101rучсrшое нз него :~а ч ёрки
F1а11исм последней 1 1 ифры и 11рибавлением к по
лучснrюму числу учет1к:рённо1·0 :тачt;ния этой
цнфры. Напри111 ер, число п = ">2 деJ1ится на 13,
таккак~шслоl=5+4·2 = 13/J,елитсяrra13.
ОТРИUАТЕЛЬНЫЕ ЧИСЛА
Об отр~-щатепы-tых числах, т. е. числах, мень
ших , чем О, математики знали ещё 2 тыс. лет
назад. Уrюминание об отрицателы-1 ы х числах
встречается. 13 восьмой книге древнекитайского
Азбука счётJ
Предс'1·ави·м чисJю tl 11 виде 1Оа + Ь. Заметим,
что11= IОа+Ь = l0(a + ~h) - 39h= 10/ - 13·.:)Ь,
L"де l = с( + 4Ь. Отсюца следует. что ч.нсла п н l 11а
Н делятся шш не делятся од11оnремеrшо.
За немногочислеlшыми и простыми исклю
чепиями . число / в несколько раз .мtныпе 1Iс
хuд1ю 1'0 чнс){а п. Число 11 как бы псреда ёт эста
фетную 11 а1ючку с1ю<.::му меньшему сuбрату:
мш1 , узнайте, дсли·1·01 л~ 11::1 t;!> м ой r-.ш:1)\111нй
бр;п, ;1 тоr·да уж у:тастс н о()о мне. Понторня
;1,.1 1н ч нсл:t / процещrру с зачёрю шание1'-1 1юсп~/(
нсй ннфрьJ п прибавлением уче-rnсрё111юй
этой 1~rrфры к ре~-~улътату, мож1ю перейти к en tё
ме11ьшсму числу н т. /t. В конце концоD п олу
чится такое м~1ленькое число, делнмосп, кото
ро1 ·u 11а Jj очевидна. Так, проделав эту опера
цию над Ч J JCЛUM 1.()02, получим
2()02-7208-752-7]3.
31Jач11т, чнсло 2on2 дсm п•ся 11а 1.) .
Существует со нершс 111 tn :.Jамечательный
призr 1а1< делимост11, кnтnрыi1 n ра1111ой мере n·r -
11осится 11 •< ч.нслу 7, и к числу L1. Г,олее того,
его с таким же уснехом можно пр11мснить и 1<
ч ислу 13! Эти чудеса лод стать nолшебствам.
ОПИСJ.ННЫМ в сказках .:гыснчн н ОДНОЙ НОЧИ»,
Это и нcyJ\l'J нительно, нс.ц ь 1001 = 7 · 11
· 13.
НаСщём OCT<JTКl ·J ( шrн lfC/ \UCTaтю1) ОТ .ЦeJJe
HY!H "4исел IOs. !(/', .", 10 1k н~~ 1001 :
1о\ =1'l001-1
т=-1.
\
~
'
1
'
1()т=1о.(-1)=-1 .1001+l,тJ= 1;
11
~.
-
1От1=1О·1=1·1()()1-1,
m,=-1
Поэтому лрп делении на l 00 l число п даёт
такойжеостаток,что пЧJtслоС/= 110 - п, +п~ -
( j)~·
"
-
п~+." + -
11~" где 111), п,. п2, ." -
трехзначные
ч исла, обознач~нощне еди н ицы, тысяч11 , мнл-
1шоr 1 ы 11 т. д. в числе п. Следовательно, число
п ДЕ/lИТСН 1-1::! 7, 11 Ш!И l.3 , CCJJl l на 7. 1 j ИJllJ
1;, ; ~слитен q . Напрнмер , 11;1 7 дели·1·ся чис;ю
п=2016,таккаквэтомслучаеq=14.
трактата <-Математнка в r~еняти книгах->, Их рас
сматривал Д11офант, живший в Греции в ПI в. Их
зн~ши индийцы (Брахмагупта, VП н.), ими поль
зовались арз.бские математики (Абу-л-Вафа,
137
Числа
г
1
____.
Береж"'шый хозянн лолА<е t1 хорошо ~нать 1«1к раJмер своего
И\1)'Шеrrва. т.зк ~· ( оои ЛОЛР-1 . J 1,1 (1 дВОЙllU~1 tty x1 ...~л 1 ~рИЯ ·•
СЛVЖ11Т XOJIOlllPll llЛ\ЮСТр.111111:>11 /)ЛЯ nоложитf:льных
и u т риu,н елы1ых чис~л
J
Х в.). Нес 01 11 1называли их с;ю.ном, которос о:ш~1 -
ча.rю ~дош·~. чiсдостатсж» , н отJ 111 ч 11е u·1 ~ нму
щ<:ств~1 » -
rю1 юж11те;1 h1-1or·o ч 1 1 сл а . 1JpJJ этом
речь 11е 1кс1да шла о /\l'Hr1гax нт 1 товаре.
В пракп 1ку отр11щ1телы 1ые ч1-1CJI<1 BXOi\Hm 1с
бuлr11111 1м тру11ом, чере~с1 ·1 абу - « 1 1еш,:3и». С н t>
з аr r амятн 1 ,1 х нрс:мен сущсспюnало 11р~ннr1ю ·
пет.~я Аl>ГЧI I Тй' IЪ бот,шее L!ИСЛО 1-CJ MCHIJ UJCГO.
Это npanmю вос nритrим алось rсак 1шо1ше есте
стnешюе и разум11ое: 11у р:.tзвс можтrо щюисаТL
nыраже111 1е а - Ь. есни 1.11:>1 :шас тс, что а мсrп,
шс, чем Ь? 01(rтзт<0 пасталu вре~щ когда подоб
ный :~~шрст стал обрсмс111 1те1 1 1,1-11,1м , а 11отом 11
npucтu нс:11р11е1\IJ1смыи. Пш1 нлс:111 1 с о 1 ·р 1-н~а-
1·е; 1ьных ч1 r сс.:11 отк ры ло J\O [IO l'Y к соз1~:11-н 1 ю
~u1 п:бры.
rассмотрю...1 . наггримс.:р, та 1<ую зада чу: "ябло-
1<0нлимш1 вмсстс стоят 3 рублн. а ?! нблока и 2
л11~ю11а о·оят 7 py611t:i 1 Н а о:олъко н блоко
дороже лимона?~. Ео 1 и обозшt<п гrь искомую
вет ~чину через х, а сто им ость 111 1111 0 1ia через у.
то rюлу'-шм дnз уравнения.:
{(Х+)')+)' = _\
_)(х+у)+2у = 7 .
Рl'шив эту снс~·е::му, н айдtм , что х = - 1 рубт1, а
.-по :1н<~ч1 1 т, ч'п> яfiлоко не i\Ороже, ;,i дешенJ1е
н::~ l рубJLь. Точно так же, есл и np1r ре111етн 1
;за:~а ч и, скажем, о днух тrутннка.х получается, что
первый пr1-п11ёл из ттупrпа А в пункт В на -2 часа
раньше, че м второй, п онятн о, что 011 nришё.11
на 2 часа 1 юJж<.: второго. Если бы мы 1 1е 11ользо
н:11111сь отр 111 ~:.1телht-1 ыми щ 1 с1~1 .мн, то пр11utгюсь
бы uмссто 0111ю1I :3Щ\а ч1 1 решать две: в од 11оi1
м1.r прсдпола1·:vш бы. 'r то nt.:rныil nут11 11к 11р11-
111 ё11 ра r11,ше, а но нтпроЛ - что раньше nr1ш1сл
nтпрп{1 тту'1'1111к
П олnлеттп с отр11 11,ател ы11>1 х ч1 1 сt:л пр 1~нод11-
;ю и к довольно nарадоксалы1ым с11ту:щ ш1 м
Скажите, пожа!I\· йста. какое ч11сло вююе бnт,
шс, чс:м - . .+? М1юпн.: ;v1 пювешю отuечают: «J\1 11 -
нус восемь». А разве -Н больше. че.1 -·Р l3 от-
11t"1' н а это ВUJ[Хtж<:ни<.: об ычно r·оворят: ц"J'оrда
м1 шу<: дна->. J lu, пот~ум:.ш , откюываются и от та
ко1 ·о 0·1 кета I<акс..> 1~1 Жt: uт1к··1 кс1.х:н? 1Jшс:uщ1·1 1
Вс~ дело в тпм , что ПОНЯТI 1е ~ н11ное \Jол ЫllC~ ОJ1-
реде: 1 ялось llИJlll> ДJIЯ ПОJIОЖJrТСЛЬНЫХ ЧllCCJI, :1
для ОТ)ТИТ\аТе.'ТЫ IЫХ ero 1 1уж 11 011 11 60 011р еделтъ
заново, либо вообще нс 1 кпот,зппат1"
Конечно же, отр1щателы п,1е ч11сла 11р116.нщ
лн забот :-..1:пемат11кам. Прн11пос1.,, вnод1 1 т~, 1ю
Rыс огра1шчсш 1я. Так, запре щалнсь отрнца
Т<.::11 hH hlt" ч11с1ш под энака.VJJ r кв~1драт1 юго корllЯ
11лш· :чшфма . :•)'1 ·0нсу)(l1н 1 1те.1ы-ю. Ведь, 11апр11 -
мср, н звле чь кв:1,црат11ыi1 корень H:.i ч 11с1 1а -J
-
ЭН:! Ч 11Т найТJJ такое ЧИСЛ() .У, КЩ1/ЧХIТ которо1·0
равс-н -1 : х: = -1 . А квадр:л :\CilCTH I ITCJll>l-IOl·o
Чll CJJa l l t' может (J 1.r т 1 . отr1щатсльнЫ .\1 . А11::1 ло
пrчrю, найти J101-а р11фм 110 ос1-1овэю 1 ю а ч11сm
- 1 означает найп r т:шое ч1 ~ело .х·, что
а'=-1.прн~Jёма>О.
Но ct' > О для любого де!1стшпелыю го ч11 сла .\'.
И всё же. когда говорят. • по 11 еJ1ьзя извлечь
кна; 1рат11ыrl кuрень 11:3 отрицатслыюго числа,
а Таf(ЖС н:.IЙTll ло1·:1р 11 фм uтp 1 1 r\;ITeJlh l IO!'O YllC·
ла. /\елают бол ь111ую 011ш бку. Выс111 аи ·"' атс
м:ника уч11т, что таю 1е кор1111 11 ло 1 ; 1 р11фмы
су щес•1·11уют. Пj)~Щ'\а. ОНИ ЯВЛНЮТСЯ уже.: JJC J\eil-
CTB llTCЛ ЫJЫ ML I , ~t ком111н::ксн~.1м11 ч11слам11 (см
статью <>Зачем irpю-L ьr 1ювые числ::~ ? ») .
ПРАВИЛА СЛОЖЕНИЯ И УМНОЖЕНИ Я
ОТРИ UАТЕЛЬНЫХ ЧИ С ЕЛ
Правила сложения: а+ (-Ь) =а - Ь,
а-(-Ь)=а+Ь,
а-а= О.
Правила умножения: а (-Ь) = (-а)Ь = -аЬ,
(-а) (-Ь) = аЬ.
ПРОUЕНТЫ
Мrюго ли соли н ,\щрскоfl воле? Этот во11рос
мож1ю понпмать по-р а:3тюму. НапрИ:\1Ср, сколт,
t'О 1>есит RСЯ соль, растворён11ая в морях 11 окс
:~нах? А можно 11 так: сколr,ко соли прихо;\нтся
11а ведро z-юрской воды? Чтобы С>ТР.СТИ'\Ъ н~ пер
вый вопрос, ;щстаточ1 ю ю11'1т 1 1 ответ 1-1а нторой
11 ещё уз11атh, скш1ько кёдср тю1~ы содержится 1\
.v10рю: н океанах.
Жителю nриморст<оr'о города или посёлr<а
на второй nопрос отnет1 1 ть С()ВСе;ч нетрудно.
АзбукJ счёта
Для ;поrо 1rу:;юю пабрать ведро морской воды ,
поставить его на ОJ'Онь и греть. пок;1 вся вода
не nыкипит , а затем !3:3I1есит1 , останшуюся на
дне сопь. J lo можно ли у1·нержлать, что у С()СС,д~1
1юлучнтся столько же? Веронтнес все1'<\ нет. А
клруг с1·0 ксдро окажется fioлt>we И Jl!f мсныт1с
либ() налито 01ю будет более иm1 менее пол -
110' В резул1.-1·ате сосед буде-1· вы11ар 1 111:п1. /(ру
готl объём nоды, а потому у него ос-1·а11ется
другое КОШIЧССl'ВО соли.
229
11эСJ1tдопмiл ,1r·ь, со.1с
\ J!ИПIЬ пебо.!lъш.iя: 1шлебавiu, on, 3 ,oo/G
'НОСТЬ ХО'J'Оры.хъ ~OC'J'.llracrъ ТQДJ,Г.Q 3,30/G
.<\ЩС :ыевьше. BвyтP6ЯUiJJ щ1рн Go.11.e
~~ft.•Jзe)ШOB море aoдep:i:..u'l"ь оть 3.8
(uъ rорышх-ъ бacceiiuaxъ 00.11:-
Числа
Такffм оfiразом, наша мера солёности - ко
личество соли на fle~po воды - окаэалась не
удачной. Нозьмём друrуто меру - кош~чt::ство
сош1 на 1<Илограмм расшора. То есть ~о кипя
чения раствор нужно взnссип,, а потом нес ло
лучен:н0.й соли рn:.щелить rr~t ncc раствора.
Пусть 1к:с pa<..~rrюp:l 8,4 ю', а нес соли 1.1 г. Вы
чнсляем : 21/8,4 = 5/2 1' р~1мм:с1 соли на кило
грамм раствора . Если опыт повторитh, то ошпъ
получнто~ ПО Ч'ГИ ТdКая же ВСЛИЧIШ3.
Но почему rрамм1.1 на кило1·рамм, ::l нс 1~с 1 тт
неры 11а тонну или фунты па пуд? Давай·1·е-ка
будем с ч итати в ~·раммах па грамм. flocr{()111~кy
в 1шлоrрамме 1ООО 1· , то и ре:.~улътат nудет в
1ООО раз .11.1сньшс: 5 / 2000 = l /400. Тот же ответ
получится, если мы буд<:м сч итати число тонн
соли в тонне р;н::т1юра ю 11 1 11удов в пуде.
Подходящ:u~ мера н:.1й11ена, но вот за11ись...
Скажите, какое число nольше; 11 / 1002 ил и
12/1090? Сразу и не гюймёшь, нужно считатr"
Куд:t легче срав1шнат1, десятнчн ы с дробн!
Дроб1.О,010~)7 меньше, че.v1 (),01 JOl, fl(rтму что
число С/1.ИllИЦ, десятых и сотых у 1:-IИХ Of\ИJ!a
кono, а число тысячных у uторой больше. Удоб
но? Конечно. Решено: буJI.ем записывать резуль
тат не uбыкновснной, а дсся-тичной дробью.
Каза1юс1, бы, зачем столько премудростей
ради к<1кой-то мпрской во;1ы? 1ly а если вужt ю
точно зна1ъ содержание металла в ру11с, жира R
молоке , химических веществ в }[екарстве? Ведь
задача та же сам.ая.
Ит:tк, мы доrоворилис 1, заnисынатr, ответ в
1111де десятичной дроби. А с какой ·1·очно~..."'1ъю?
С nомnщью каранд:ш 1~1 и бума!'и J\IIОЖllО/\елить
даже ;ю м~rллнардных дш1ей , но отhуда беруп:и
сам~1 нсхо11111.1 с:: числа? Есл11 весы в маrаанне
поназьш:нот ">20 r, то в дейстн 1не21-юсти 11ред
мст может uесить 11 S1S, и )24 r, а двести-триста
лет назад точность necon была ещё меньше.
Поэтому и всличиrrу содержания одного ве
ще<.."Тн:.1 !:{ дру1·ом имело смысл рассм:~триnап, с
то• 11 юстью ло nерных двух цпфр после J;:шятоli:
0 ,27; 0 ,64; OJ7, 1. е, 27 l'uтых, 64 сотых, .~7 сu1ых.
Rnт мы и прнптл11 к nfIOZ{eJtma.м. потuму • по
n rтере1юде с ла·1ъ11111 pro ccntl1m - « Сотая
час'Тъ». С.ущестuует и специ3Ль11ая заш 1 сь: 27 ~"
б4 9\,, ~7 9<,. ГоRорят , кm'да-то у 11аборщ1 1 ка сло
малась литера, n рсзул~,тате чего 1юз пю< этот
причудливый знак %, призш1н11ый затем во
н<..:tм м_и ре. Запись оттrотений стала удобнее,
нсчезлн нуJJь и заrшт<u1. а символ % сразу у:ка
зыв~1 tт, ЧТО псрсд Н:1МИ ОТIЮСИ 'l'еJ.1ь н ;н1 Вt'JШ
ЧН/-1<1, а н.е 1 р:.1ммы, т 1тры, рубJ ш ш1и метр 1.1 .
flро 1 ~снты fiыш1 r 1 звестны r-1 ндийц::~м ещё t!
V сто11е 1 ·ии. Это нсудивитеJ1ыю, потому что в
И ндии с давних 1юр счёт в~:лся n десят11ч1юй
системе. В Еврсте десятич111~1е дроби n ояnн
щ1сь толы<о спустя тысячелетне, их вnёл шщер
лапдский учёный Симон Стетнш .
Со временем люди научшшсъ извлекать из
всщее1 · ва комш..>щ.: 1 пъ1, состаuю1ющис n,кяч-
1-JЬtе ~от 1 от неса с:1м01·0 ве::щес'ГН<! . 1'0 1 ·д;1. чтобы
не вводить нули н запятую, т. е. не t 1ис1тh 0,6 ~'6.
•
1
п р н думали новую 1 1сл11чнну - 11роми11ле
-
тысячную долю, которую обо:тачилн 1У.111, а 1Jме
сто (),6 % ст::~ли п 1ка1ъ 6 1Yr111 .
ВОЗВЕДЕНИЕ В СТЕПЕНЬ И ИЗВЛЕЧЕНИЕ КОРНЯ
Первыми в списке:; арифjv1етw1еских действий
иду1· сложение , вы чнтание , умножение и неле
ние. Во:теде11ие tl сте11t11ь и извлечен ие кор 11 }1
иногда называют пятой и ш естой оnерат ~иямн.
Представление о вознедении r-1 с1·слень как
о самостоятельной опера 1 ~и и у м атемап1ков
сложилос1, не сразу, хотя зада ч и па вычисле
ние степеней всгречаются n са мых древних ма
тематических текстах (см. статьи «Дреnннй
Египет~, ~междуречье»).
14U
Своеобrазно онисывает первые на1У})алъ
ные степени чисел Диоф<1нт Александрийский
в своей зж1 м е н итой «Арифмет11 ке,>:
« В се числа , 1~к ты зпасш1" состоят из 11еко
торо 1 '0 количества ед11н1щ; ясн о, что 0 11 и про
должаются, увст1чнная.с1. до бесконсч1юст11.
Так пот, среди них находятся :
квадраты, получающиеся от умножсн11я 1-1е
которо1·0 ч11ст1 само 1'0 н:~ себя; это же •mс1ю
наз ы вается стороной квадрата,
затем кубы, получающиеся: от умножения
квадратов на их сторону.
далее квад рата-квадраты - от уJ1.шоже 1 111я
квадратов С<lмих на себя.,
/\алее кв~щрато-кубы, nолучаIОщиеся от умно
жения ква/\рата на куб его сторu н ы,
далее куб о -кубы - от умноже ния куб()11
самих на L'Сбя».
Одним из первых, J('f0 о I<ОНЦС xvr - начале
XVU 11. предприннл ша ги к построению совре
менной теории степеней, был нидерландский
математик Си мон Стевин. Он обо:шачал неиз
вестную величину кружком О , а внуrри его ука
зы ва;т n оказате;1и с-гепени . IJanpимep, Ф, Ф , Ф в
ет за писи обоз rта•rади х, х , х. Сте 1ч111 отверг
Дипфа11товы составные выражения «к вадра то
кnадрат», " квадрато -куб» и предложил называтr,
степени по их показателям - чствёртой , пятой
и т. д. Современное обозначение степеней а2,
~
r1, ... мы ш.1ходнм у Ре не Декарта.
***
Опер:ш.ию во:1оеденнн в с.·те11<::11ь естественн о
0 11 редел1-пъ по ана;юr·и и <.:операцией умноже
ню1. В с::~мом деле, если многократ11ое сложе
ние СJТ\Н1-1аковых чисел заме няется пдним i~ей
ствием -умножен ием:
а+а+". +а =а·п,
~
11 j1J'i
то гтодобным же образом можr ю объеднни·гь
J.I умноже ние одинаковых сшсел :
а·а· ... ·а= al/.
~
11(1.11
П()следнее раnенство - пе что ш юе. K'.aI< опре
деление п-й степетш числа а. При этом а на
зывается ос11.ова1-1ие,;~1 cmeneтtu, а п - её потса
.'lаmеле.м.
Степени с натуральными 11 оказ;пелям 11 об
Л<t/\ают свойствами , которые л еr'ко 11ро верить:
при перемножении двух степеней
одного и того же числа .кх показате
ли с:кладываJ01·ся:
(*)
~ при деле1ши двух степеней одного
\.( и то1·0 же числа а # О их показатели
вычитаются:
11
!!:__= а" -"'
а"'
("*)
Во нторо,'111 с1юйст1-1е JJрел.полаrаетсн, что п > т.
Д11н 1 1раверки Jщста·r«">чн u кажд~'Ю степе н.ь
записать 1'1 виде произRеде1 1ня одтrа1ювы х со
множителей. Появление условия а --F О лcrl\o
Азбука с•1ёта
ФОРМУЛЫ ВОЗВЕдЕНИЯ В СТЕ П ЕНЬ
Определения:
а0
=1
а"=а·а·
1пР"
а"":;-
а"
п
д"'=~
Свойства:
а
(n>О);
(а~О,п>О);
(т;1: О, а> О).
(!\ГаJ =а;~ = а (а>О).
объя с11ит1·.: 11а rrуль л.еmп1, 11ельзл . Л tKYI' огр;1-
ш1че1rие п > т вызы вает Ч}"11спю неудовле·1·1ю
рённост11, не правда ли? Нельзн ли без пего
обойтись?
Заметим, что при т ~ п u левой части ра
венства (**) получается nполне осмысленное
Rыражсннс:
11 11·' ·1
__ .......____
(./,
11
аа'"
(/
=
=
l
=_1
_
, CCJlИ l/'l > rl,
ат а·а·... а а·а·.., а
а'" -11
'---v- - --'
щ р.1J
т //[)';l 't
и
и"--;;; = 1,еслн т = /1.
а
Это позволнеt· н а м расrrтирить опер:.щию 1:1оз
Rсдсн 1н1 н стс1 1 снь нз спучай н улСiю1·0 1-11111 uт
рнц:зтслhНОJ 'О 1 юка:!атслл . !<стати , расnрос1'р~1 -
не1111е привычных 0 11 ерац11й на 11ct новые 11
нов ые област11 - очень удоб 11 ый приём, r юзnо
ляющий расшнрить сферу nр11ме11ения разра
ботанных рат ree методов.
Итак по о прелеле11шо, полож11м
ан= l (а:;t: О);
1
и11
=-
(а*(),11 >О).
а"
Таю1м обра зом, оnерацин во:щенс::ння н сте 11 ен ь
()lfределе на для нсех 1~СJ1ых пок::~::1атt:.11ей . Пр11
это м ра1-1е 11 сrпа (*)и(**) rкталr rсь в силе 11 бе:з
Hl
Числа
дос~дного orpa1-11JL1eн11я п > т. L<расшю, про
сто 11 удобно!
А что буде~, если выраж<.:1-111е а", в свою очс
рс;~ь, 1~ознс<.-г11 n степень т? Воспользовзвш11сь
0 11 ре.целе1-те: ,"1 сте щ;11 11
(а")'"=с1"·с~" ·". ·а" ,
-v-
11/ Р·"
11р11меrш м формулу(''):
ll!Jlt --1 11
а'1•(lJ} "• • а" =а //•1'·•
1
= а"т_
nJ p.t of
То сс·1 ъ
при возведении степени в степень
показатели перемножаются:
(***)
Извлечение корпя определяют ка1< опера
цшо, об ратную 1юзвсдени10 н степень. qто это
Jн~1ч1п - «обратн)11О~f 1<01щ1 требуется нозвес
т11 ЧllСЛ<) tl R(.'TCILCltЫl, 1'() само чн сло 11 покаЗ<l
телh С1'епс1111 считаются ю1нными, а х = а" -
11скомой келичлноfl. Обrхзт11ан З::!дача - Е1 ай
·1 · 11 такое ч11сло х, Jt-я t'тс 1 1снь которого равна
да111 юму ч1 1 с.гrу а:
t'сшепне этоr'i з:~дачи 11 называется иза.лача1tи
L~м коршz п- 11 степени 1rз чпсла а:
_.,,,. ='Z.a.
1Iоскu111,к\' '""tl 1нус 11а м11нус /(аёт 11люс» , то
'
11
'
11 ·с
·
о
х- = (-х)- ~ J. Гlоэ1·ому 1 1р 11 (,/ < 11ЗRЛСЧЬ ко-
реш) чt:тно(r степени 11с удаё'1'ся., ::i при а >О
1 1м еются сраэу il,fla l<opшt. от:rrи чаю щнеся толь
ко знаком. Д;r я ОП[1СJtслёшюстн полагают, что
..~апись 21{1 а обоэначзст лuлuжнтельный корень
(cro <.:щё н:вынают ар11фмстичсск им). Второй
1.J• '
кореш, - зто
-
<Jа.
Е<.'1111 01 ·1х111нч 1 1ть рассмотрение только по
_110Жl1т1.:л ы~ым11 оенона н~н1 м.н, то опер~щии воз
нс11,енш1 R·11-10 стс11<::11ь и н~ш1сч.ення корня п- й
стt::пс1 rи становн·1·сн вза нмно <>бр<J ТН 1.1м 11 . T<iK,
возие;~н чи<.'ло !i во nтпрую ст~пснъ, получил1 9,
а если нз 9 1 ·1звлечь юзадр:1п1ый коре11 1 " ·1 ·0
снова получптся :) . 13 общем случае
il,
U•'
J1
( г-)''
-
\et =а н \(,/ =а.
142
КАК ПОЯВИ ЛСЯ ЗНАЧОК КОРН Я
Вначале погuвuрим о самом tлове ,,корень•. Кро
ме прям о го , биuлогическо гu значения: «кuре~tп
дерева», « корень зуба» - у него имеется и мета
форический, иносказат12ль1-1ый смысl\: «коре нь Зl\3»,
"РОдов ы ~ корttи » . Крылатое 1нречение Ко1ьмы
Пrуткова «Зри в корень!» пр и зывает к 1юстиже
н11ю сут11 , первоосновы, пер13опричины проблемы.
В древней И~tL\ИИ неизвестное имсновалос.:ь
<< мула », что оз начает «начало», «о<· нов а 11 Иt?», «ко
рень (дере ва) )) . Арабы дм1 эти х uелей использова
ли слово «джизр " с тем же значен ием. Евроnсйuы
1-1еревели его 1ш ла1ынь как radix - •Ко ре11ь ». Та11.
воз н ик математическ и й термин • радикал ». С этим
назва нием связан и пр11выч 11ый н ам значок кор11я
J.А история его такова.
На протяжен ии нескольк11 х веков математики
вслед за Леонардо Пи:~а1 кким 1<вадра 1ный корень
обозначали знаком~ (сокрашенис от смJва radix).
Постепе нн о R. превратилось в стrоч ную букву r.
IJ книге по алгебре Кристпфа Рудольфа - первом
руководстве подобного рода, наnиса11 1 юм на н е
меuком языке (1525 г.), - вместо r исоолыуеп я
значок У. Этот символ уже похож на тот, которым
nпль"lуемся и мы. С9вр~менную 3апись корней
'
1
J1 "р
разныхстеnе1·1ей- ~ ,~ , ". -
мы находим у гол-
ландского математикс~ Альбера Жирара. А горизон
rалы 1ую черту над выр ажен и ем под радикалом ввёл
в 1&37 r. Рене Лекар•.
Изnлече1111е корпя служнт как 61,1 зерк111Ь
ным отражс 1ш ем возведения n с·1-епень . и 1 1~
t>борот. Но великое чу;10 математию"' состо11т
в ТО,\1, 11'1'0 оба ЭТIIХ /\<:ЙСТННS! МОЖI!<) тракто
в;пh". как 01(1 ю. Для это1 '0 1 1 уж1-10 сдс11;&·1 ъ 1.:щё
'mлъко од1 1н ш~н·: расrтространит1, опер:11 ~11ю
11озt1едс:1 п ~я в стс 11 с11 1, 11:1 ;:i,po61 1ыс показ<1теш 1.
11
Что такое а"'? )J.a11ai-iтc r1<н1робус."1 форм~u1ь-
1ю воз1:1ее1·н ~т<J выраже 1 п1с в стс11е1 11. т, нос
поль:юnа1н11н с 1. раненст1ю.111 (***):
З1ш ч11т, ЧllCJIO а"' <::стссгвен1-ю пон 1 1м~пъ как
J<Орень 111-й стспснн из ч1 1 сла с/':
11
am = '~а".
Это н t:с1ъ 011ре;~1::лсние дробно~'~ степе~ 111. Так
иы 111cC'lyt0 01н.:рзц1110-нзнпечеrше корни rюл -
1юс·п)1u свеп 11 к пятоi1 - nозве; tепию 11степе~ 11.:
СРЕЛНИЕ ЗНАЧЕНИЯ
Ко1да 1 ·mюр>1·1· <'срслн~ 1 (i 1.юзрас1-. , ~сrедн111'1
rюс1' ·1, "cpc111111f1 ааработок" , всем поня·1· 1 ю, о
чём 11дёт рtчъ. В матсмат 1 11се же рассматринз
ется м1южеС'11щ разлн•пiых «срет1нх», поэтr>
чу все1 ·ла нуж1 ro угпч1 ~ять. какое 11 мсJ 11 ю «C'pcrt -
11ee" 11,\·tCIOT А 1111ду.
В са~юм общем смысл.с среднее значенне
11ес1юльюхх ч1Kt'J1 - это 11скоторuс ч.исло, :{а
к1110чённоt' МСЖ/tу нa~'VJCHl>Ш l l.J\oJ и H3И60Лl>IHIIM:
113 них.
Для /\НУХ 11(.)ЛОЖllТСЛЬНЫХ ЧIIССЛ а 11 /J ЧJЩL'
всс1'0 рассм::~тр11нают
среднее ориф.~zетичеоте
а+Ь
111= - -.
2
средuС'е гao.i\tempu •1еское
1
g=vаь.
среднее ?t1j1люн11чf!сл·vе
2
2а!;
//::::-- = -
-
]1a+/J
-
+-
(/ /?
Можно 1нж:1:i:пъ. что :-пн срС/\НИе :.sначения
удnRлtтноря f()'I' 1-rtp:нн:1-tc1·!'a "''
'
2afJ
1
а+Ь " 'а.!. +lэ
2
-
-
~ 'VCllJ~ -- "'
1
,
и.rтн
a+fJ
.2
~2
пр11чс~ы :{1 1:1 к ранс1 н.:тна дос-1·1н·астся 1111ш 1, в с1 1 у
ч:н.: а= tJ.
С рс.:; (1111с значсння ч зсто встречаются в
гс:омстр1t11 11 ал 1 ·ебрс. На~1римср. катет прямо
}ТОJ1ыюrо ·1 рt:у1'оm,11ика ранt:11 срt:д11сму 1·с:о-
А3букJ с чет ц
~сrкэлы r< )С отражс1111t: c1111m )С 1. <.: 0'1р:1л<;н:, 11.щ
объскгом. J.1, ны ходит, нсt:го у 11::tc не 11Jt:cт1" ;i
пнть ар11ф.v1етпчесю1х J\Cf1 cтm11~1 .
метрнческому 1 •1-нютснры 11 nросю~ 1 111 :')T()J'O
K<ITL'TЗ 1r::i 1 ' 1IПO'l'el1y:-iy. л 1-\i>! COTa 11рn~юу1 ·011ы 1 (1-
1·0 треуrоl)ыпr1<з JJроведёттая к rнпоте~rузе ,
сст1, cpeJ1.1 1ee rеометричес1юе прое1щий нате
тоn 11а пшотенуэу ( р11с. 1).
Рис.1. " = ~1а,;/1=/:;,. /J
.
с
/1
В люfюй трапс1~1111с<к 1 юнапш1мна11 /?от
ре:юк. параллелыrый осtюnапаям. копцы като
р()rО лежат па боковых сторо11ах.
-
раnен среднему арифмстпческом~ оспо
в:н-шй . сслн он соединяет серсд11ны боко.l:!ых
сторон (рнс. 2):
MN "' а+/>:
1.
Рис. 2.
/\П КО ПК /\1\
-+-=-1
-
:
оll'\6!\В
А/3
= АН = 1, ('l\ЬlUBdП'ЛbllU,
1'0 =~
,1)11.
-
parie11 срс1111ему rармот rчес1юму ос11онэ -
11У1i1, tcm1 1 1 рохсщит через точку перссече1тя
дпаголалеИ (рис 2):
Ю,= 2ufJ ;
а1-Ь
раnсн срс.:ннему 1·сом с:тр1 1ч сскому ос1 ю
на н1 1й, ест ~ ;~слит тр:э 11 е1\ 11ю lia /\ВС тр ;нн.:ц1111.
110;\обн ые r.н.'ЖJtY coбolr (рис. 3 ):
'
Е!:=\п/J.
1-1 :\
14'-1
Числа
в
ь
а
A---------' D
Рнt:. З. .i!_ = EF.
[[ь
следов.~ rсльно,
EF = ../аЬ.
-
раnен среднему квадрати•шому основа
ний, сели делит трапецию на две трапе ци.и
р:ншой площади (рис. 4 ) :
Отрезки а. s, т, g, 11, Ь при а > Ь ~кета бу,11ут
располагаться 1J том порядке, я каком здесь :1а-
11исаны. Ко11счrю, это следуе1 · 11~ нсраве11стн
между средними. Но гораздо и11терес11ее уста -
1юшпп, что nорядок име1шо пu<ов, из 1 ·ео мет
р11ческих соображсIIий (полробуйте, это лег
ко!) и тt:м самым доказать ~1л геб ранческие
нера вен<.~1'щ1.
А fIOT несколько примерон .из алгебrы. Ос-
1 ювное снойство, которое определяет арифме
тн ческую 11ро1рессию и объя сняетеё на:.ш:тн<::,
с:остонт в том. что 1<аждый члеп nporpecc1 111 ,
пачш1ая со второго, равен среднему арифме
тичес1<0му соседних членов. Аналогично, в
геометрической прогрессии с положител 1,ны
ми членами каждый члс11 прогрессии, начиная
со нторо r ·о, равен среднему гсомстрическо...,1у
'
'
'
'
'
'
,,
1
'•
'
1
1
'
So
ь
s
s
а
1
Р11 с. 4.
'
'
1
50 +25 =(~)~
1
1
5(1
/)
51~:5 =(Р~/):
'
t.ледов1(_1 1- елы-1(J ,
2(pt~' )l -1=Ы)'
'
1'
,,РО2=,i·-
>-
'
2
сuс:едних чле1Ю1i (С;\-! . ст:пъю «Арифмет1 1ч сскЗJ1
и геометрическая пр0t·рессни»). ТТоследоu:.~
телы-юс1ъ чисел 1, J/2. 1/3, ... , l / n , ... обрjзова11:1
так, что каждый её Lшен, начиная Ct1 uтoporo,
равен сре;, н ему гармоническому сосед 1111 х
членов. Эта последоватслыrость и составлен
н ый изеёчле1ювря;t 1+1/2 -+ 1/3+ ... + 1/11 +".
на зываются гармсшнчесю:.1ми (см. статью •По
следов:о~тельности .~).
Арифметическое, геометрическое и 1·армо
г1ическое средние ;~нзче 1r11 я были ~1з1зест11ы
ещё античL1Ьuv1 матем.~ти1G.1м. Эти сред11ие свя
заны с теорией пропорций, котор<i}J лежала в
осноDе дрсвпеrреческого учения о музыке,
геометрической теории чисел, а 110:1же - тео
рии площа11ей и конических ссчеIIИ Й.
И з неракенства м<.:ж.ду средннм геометр11-
ч ес ким н средн11м арифметичесю r м
г- Cl+ь
;Jab<.
2
следует теорема:
Произведение двух положитеJIЪнъrх
велwrин при постоmmой сумме при·
ни.мает наибольшее значение в слу·
чае равенства этих величин ; сумма
двух положительных величин при
постоянном произведеоии прини
мает наимены11ее з начени е, ко1·да
слаrаемые равны.
Применив эту теорел-rу, мож1iо, п::11 rримср,
доказать, что из всех прнмоуголышков с задан
ным щ:рl'•.метром н:шболыпую площадь 1rмсст
квадрат и 11з всех прямоу1 ·ол ьннков с :зад;~:нноil
шю1щ11t 1,ю наиме11ьши1'1 псрнметр таюl(е 1ше
ет кнатtр:н.
Ддя п пС11ю.ж1пс.r11,ных чис~л а 1 , а~...., а" 11х
срt:д1111м арифме·1·11чс:ски;v1 называется число
П1+а.,+". +(/11
п1=
-
11
средшu.1 ~·еомстричссю L\11 - число
средним l'ЗРМОНИЧL:СК11М - число
l:J = ____1
_1_
_
_
11
1•
-
+- + ...+
а1 t.ll
а"
КАК ПОСТРОИТЬ СРЕЛНИЕ ЗНАЧЕНИЯ
В антич н ой математи ке, по преимушеству геометри
ческой , большое внимание уделялось построен иям с
помощью uиркуля и ли11ейки. Было принято несколь
ко с пособов построения средних по двум да н ны м от
резкам а и Ь. В « Математ ическом собрании» Пап па
Александрийского (111 вJ - своде достижени й древ
негреческой математики - при ведены различн ы е по
строен~1я средн их зна,1ений no методам его п редще
ственн иков, дано также описание построени я трёх
средних на оыюй фигуре.
Вот одн(J и :3 возмож ны х построений всех ч еты рёх
средних значений. На прямой отложим смежные 01' -
резки АМ"' а и МВ= Ь. Н а О1'резке АВ как н а диамет
рt• построим окруж ность с uентром О; ~ё радиус
а+Ь
-
2
-
равен среднему арифметическuму отрезков.
В точке М п роведём перпенди куляр МС к п ря
мой АВ. Треугольн ик ОСМ прямоугольный . По ню
ремеПифагора,СМ1 = ОС2 - ОМ1,ноОС=ОА,
значит,СМ1=ОА2- ОМ1=(ОА+ОМ)(ОА-ОМ) =
""ЛМ МВ= аЬ . Отсюда СМ= .Jab - среднее геu
метрическое.
К ОС 1юстроим nерпеНАикуляр MN. Из п одобия
треу1 ольн икuв CMN и СОМ следует, что CN : СМ =
СМ1 2аЬ
=СМ:ОС,01к,удаCN= СС = --
l - среднее rap-
J
а+J
моническое.
l'редннм кн~щратнчным - 4ИС!Ю
~·
}
1
Cli+Cli+".+а.~
s;:: \'
1
2
Как 11 в случае двух чисел, эти среднне зна
ч:ення удовлетворmот нераве1IСтuам
h<g~т~s,
н кo·t·up1->Lx. знак равсн.стна досnн·астса тогд:t н
только ·1·огда, ког11а а1 = а2 = ... =а" .
Рассматр1шаю·1·ся также ювеишн:нъи1 средние
чисел и1.al, "" tt11 с Rесами р,, р1, .." р11, оnреде-
1шем1,1е формулой
Р1а1 +P2al +". +Рпа"
р,+Р1+". +.р"
(*)
Азбука счёт<J
Из прямоугольtюrо треугольн ика DMO, в кото-
а+Ь
а-Ь
ромOD= -
2
-
иОМ=-
2
-, находим ОМ: DM=
t
/аl+Ь2
= vOlY+OM ,т.е. ОМ= ~--
2- - срелнееквал-
рати ч ное.
В прямоуголь ном треугольнике катет мен ьше гиnо
Г а+Ь
тенузы, поэтомуСМ< ОС, т. е. vab < -
2
-; CN <СМ,
2аЬ Гяhь
а+Ь ~а1+ь2
т.е. --Ь<~а ;00<ОМ,т.е.__< .
_
_
_
.
а+
2
2
Если длины отрезков а и Ь равны, то точки О и М
сов п адают и все нерав~ttства переходят в равенсгва.
А
..
.
D
в
Такое r 1 а:3нани:с объяснне1·сн п1х.1с·1·ой м<..:ха
нической моделью: если а 1 , tll, ." , а11 - .коорди
наты к<Jких-тu п материзльных то ч ек, а /1 1,jJl· ""
р11 - их массы , то среднее взвеше 1 1ное (*)есть
коорд1,шатз нх 1\ентра масс
Можно привести н другой пример. Пусть а 1 ,
а2 , .. " а,1 - экспертные оценки 11е~<оторой вели
чины, ар 1 , р,!., ""р" - степени нашегодонеrшл
к соотве"J'Ствующим оце1щам (или экспертам,
и,.;, выс~~завшим) . Тогда среднее взвешенное -
это сумм:lрная оценк;э, нычнсленнан таю1м об
разом , чтобhl мнення более надёжных ~кснер
тов «nереве111нвали ~ .мнения менее надёжных.
ВзRсше:нные средние э11:1чс1111я. ш1tроко 11рн
меняются в теории вершrr· 1-юстей, 11матсмат1·J
ческой С1·атнстнке при обр<~ботке результатон
набmодений или измерений.
Числ.:1
UЕ/\ЫЕ ЧИ СЛА
ПРОСТЫЕ ЧИСЛА
КJж,цос тпуралыюе ч11 ою, большее е;111н1щ1.1,
делнтся 1ю кrюй11еr1 мере н.1 1 111а ч11сщ1· на 1 11
11:.i самп се() н F.сли mr 11;1 1<а1ю<' /tр~тос нату
ралыюе т.нкло 0 1ю наце.rю не делится, ·ю на
зыnается просmь1А1, а если у 11ero имею·1-ся ещё
юнще-то целые дешrтсли, то состсюны111. Eл1r-
1111Y.i<a же нс сч11тается ни пр<ктым чнслом. 1ш
сос1ав11ым. ilOL\t:мy?" Об этом рt:Ч.1> впсрс]lи (см.
<..~r;пью ~осноRная теор<..·,,,,rа арнф,..,1етнки,> ).
Не большу ю <·коллекц 1 1Ю? простых чисел
нам поможет сос1 авить стзр1111ный способ.
придум:тный ещё R Ш 11. до 11. : =! . Эратnсфсно,"1
Кпре11ским, храпнте.rтем э11амс1111·1 ·0Г1 Алексап
др11Г1с1<0й библио·гек11.
Вhm11шем нескплько rюлрлд 1111,уЩнх чнсел ,
начшrая с 1. (рнс. 1). Двойку О'Т'берём n свою
коллекцию, а остальные числа, кратные 2,
з;1черкнём. Ближайшим нсзачёрк:пуrым числом
бутr.ет :). Возьмём в коллекцию и e1·u, а все uс
тальныс ч1-1с11а. кратные.\ зачсрЮ:itМ. Прн этом
окажется, что некоторые чнсл~1 }'Же Выли ны
qеркн~rъ1 раньше. к:-~к, н:шрнмер, 6, 12 н др .
Слсду1:ощеt: 1tзнмс11ы11ее неза чёркнутщ.: чrк-
1-46
Jю - зтu ') Бсрi.:м щ1тСрку . :э ое1 ·:1л111-Jыс: ч11сJщ
кр:и·н1,1t' '5 . 1а чёркJ1наt.:м Пон1·о ряя :'.11') 11 1ю
I\С/()р~ · CIIO/!a 11 СНОВ~4, 1\\Ы в коrщс КОl·ЩОВ ,(О-
6исмсн Т()п1 ч то 11 е.1<1чёr к11 у1ыУ111 ос.:та нутси
ОДllИ Jlllilll> прос1ъ1е ЧИС'JJЗ - OH JI CJIOH H() про
ССЯЛНСI> сквозь решето. Поэтом~· таl(ОЙ способ
и 11олучш1 назnа rше .-решето Эратосфеп<1"
Можно лл. nторя поэту, сказать, что простых
ч11ссл столько, ~о..:олько звё:.щ 11а rrcб<.:, сколько
рыб в воде•? Отu<:"1 н;~хо,цнм н дсш1тоf1 юшгс
знаменнто1'0 соч11 не1111я Енкл 11да «1lач:~ла• -
11еmенно1·0 памятника /1,рсннсrо мира. Д1цд
ца·гая теорема н этni1 ю-шге уr·всрждает· ~пер·
nых (Щ)()С1'1,1 х) чисеJJ cyщt.:c11.1yci больше лю·
fю.r ·n ~:казатюrо ч1кла нх•>
Рис. 1. Pewf'Тo ")ратпrфt• н,1
Hor 1нжа:1а·1ельоnо этоr1 теоремы Предпо
ложим , что существует некое нанбольшсс про
стое чпсло Р. Torд:i nерсм .1 юж11м вес 11рос1ыс
•1нсла, н~1•11ш ан с 2. 111\011ч:.~нР, 11 увелич1 1м тю
луче::шюе 11ро11:>11ед~.:11 11е на е1111н1щу: 2 · ~ · ') · 7 х
х f1+ 1= М Ест1 •111с1юМсоставно<:. гu оно
ДOJJЖI ro l I MC'I 1> 1ю краr"11-н.~ r1 ~1сре однн ЩIOLTOJJ
/\<.:Л111 <.:ль. Н о :-эт11м f\<::тп елсм нt: можtт 61.11ъ 1111
одно 11J прос~ых чисел 2, 3. 5.
. . Р, 1IOC1\0J!i>K\1
пр11 1~t.:л е11rш J1l ~1 :1 каждое нз 11их получаем в
U !!лые числа
БЛИЗНЕUЫ
двс;1 nрость1х числ'1, кuтоμые отл11ч<1ютс~ 11а 2, ка"
5 и 7, 11 и l !, 17 ~1 191 получ11Ли образное назва
ние 11 близнеuы». Любоnьтю, что в на-туральном
ряду имеется даже •тройня » - :~то числJ З , 5, 7.
Ну а t'колt.ко вссгu С'ушеrтвуст близнеuuв - со
време 1 ~ной науке неизвестно
Ч11с-"а близнеuы 11з з<:~дан н ой таблиuы чиt ел
можно прщ:(;'ив.нь, слегка «Подправив )> решето
Эратосфена. Если лля к<.1.жлого вычеркнуто~ о спо
собом Эратоrфена чиrлdn вычеркнуть также число
п - 2, то в таблиuе ост;~нутся л11шь такие чием р.
лля которых число р + 2 тоже простое. В пределах
перFюй сотни близнеuы - это {Лелуюшие пары
чисел: (3, 'i), (5, i), (11, 1 З), (17. 19), (29, 31), (41 ,
4 3), (,)9, б1), (71 , 73).
По мере улален11я от нуля бли 'IHCuoв становится
6<:е меньше и меньше, хоп~ исследован11я, прuво
t.11мые •в глубоком ч 11слщюм космосе», продолжа
ю~ выявлять эн1 замечателы~ые11 загадочные пары.
Н а 19q11 г. рекордсме11ам11 С"ч1нались бl\И3н~uы
242 20С1 083 2J8 880 ± 1, найден н ые, естественно, с
помощью эвм.
Бм1Знеuы могут соб11раться в скопления, обра
зуячетверки вила (n-4,п - 'l,п +2, п +4),напри
мер(5,7,11,13)или(11,13,17,19).Какмного
таких ско пле~1нй - тоже пока неизвестно.
OC'Lv..tтт<:c 1. Слсдов;.1.тtлън.о, ч LICJIO М JLибu С!МО
простuе, т160 ю::лится на лростuе чнсло. боль
шее Р. Значит, прс.n.nолож~;ниt'. ч•1•0 существует
1-1;.~нбuльшее 11ростое число Р. некерно и мнл
жееrно простых чисел бсс 1<0нсчно
ПРОСТОЕ ИЛИ СОСТАВНОЫ
Не о всs~ком числе моЖJю сразу сказать, простое
оно или составное. Во:;ьмём, паuрнмер, число
1999. Е<.:ли нет 11од рукой спе циаль ных слра
вочныхтабли.ц ~Ull1 ll ()MOЩHИK<!-KO MПl>JOTepa. Т()
11ридётся вспомнить о старом, но надёжном
рсщет<.: Эратосфена Однакп не рспектнва ~~а-
1-J.Яться одн ообр<~з 1ю- скучн ым выч<::ркнн:~ниt'м
длннно1·0 ряда чисел нескопько удручает I<o-
1-reqнo , число 1999 ещё н е стоЛL1 вел ико, чтоб1.1
с трудом nросетъся сквозь это решето, по на
его примере поучительно рассмотреть дей
ствие другого инструмента
Итю<, в качестве лредлолагаемых дслител~11
1999 <- приглашаются? 1rач:альные простые числа.
147
Числа
г:=-----
При этом чнс110 2 можно не брать - яс1 ю, что
1999 на него нс делится. Простейшие призна
ю·• дели.1>юстн (см. статью (;Делится или IJe де
лится?») позволяют сранкитсльно быстро от
вергнуть н другие ~кандидатуры»::>, 5, 7, l l, l:).
Проверяем следующее просгое число, 17, -
не
подходит. Проверяем 19 - тоже не годится .
Л 23?.. С каждой fювой попыткой надежда на
быстрый успех иtчезает. Скоды'о же чисел
ка1 щндатон 11ам нуж1 ю перебрать, чтобы дой·1·н
до 1999?!
Стоп! А зачем, собственно, доходить до са
мой вершины? Заl3етной цели можно достичь
и пройдя через межгорный перевал, ведь если
чнсло п р;шво лрои~недению двух натураль
ных чисел, то по крайней мере одно нз ннх нс:
больше, чем {п . Ст:шо быть, .на числа-ка1rд11-
латы. бuльшие , rz , .можно просто не обращатn
внимания. Пос1<0льку 44 < .,.
11999< 45, то про-
148
аер1пь осrалос1, сп всем нем 1юrоч11сел - нсе1·0
лишь 2.3, 29, ~1 . 37, 41 , 43. Как по~<азывает про·
верка, ни одно из них не подходит. СлеJ1ова·
телыю, число 1999 - простое.
Этот приём, отме ченный сщё Леонардо
Пизанским , хотя и ~·скоряет поиск воз.можны.х
делителей данного ЧJ-tела п, всё же оставляет
много ругинной работh1, если число ДОВОJ{ьно
большое. Такую работу лучше всего п ерело·
ж:~ 1ть на плечи компьютера.
Если мы воз1,мём 11ауrад какое-нибу/\Ъ до
статочно большое нюуралы-юе число, то с боль·
шой nероятностыо оно окажется составным.
Это 11~удивителыю. Ведь по мере уд<1Ления 11
бескон.ечность решето Эратосфена становится
ч.аще. а значит, простые чисщ1 встречаются всё
реже и реже А нельзя ли придумать такой. метод,
который для под<1вляющего большинства со
ставш~tх чисеJt сравнительно просто п озволял
бы уста1-юви1ъ, что 01111 составные? Toma в ос-
U~л ьrе Ч ~IС:Ла
-1
ПЕРВЫЕ 320 ПРОСТЫХ ЧИСЕЛ И 6/\ИЗНЕUЫ СРЕЛИ НИХ
2
ф
Щ)
©23
®37
®47
53
©
@7q
83
211
223
aEJ233
~257
~GID293
307
~331
337
©353
359
367
373
379
383
389
397
401
409
419
421
31
433
439
443
449
457
~467
479
487
491
499
503
509
GlD541
547
557
563
@577
587
593
(ill)607
6'13
СШ)
631
©647
~673
677
683
691
701
709
719
727
733
739
743
751
757
761
769
773
та11шихся со мнительны х случаю' мы могли бы
воспользоваться трудоёмким с пособом, рас
смотренным выше. Всё равно в среднем noлy
LJ>UJacь бы значителъ.н:~я эконо мия сил.
К с частью, такой способ существует. Пусть
п > 2 - на1ураль ное числ о, 11ростоту которо-
1·0 требуется уст;шов и ть. Последовзтt:J1ьно
выч ислим з1-1ач ен11я ku, k 1, "" k,н по следую
щей схеме:
k(1 =l,
k -{2k1, если2k, < п,
1
+
1- 2k, - п н 11рот11вном случае ,
rдсi=О.l,2,.."п - 2.Теперь,еслиk".1~1,ч1к1ю
'11 точно составное. Если же k 11_, = 1, то вопрос
uс·1·аётся открытым: чнсло п может оказаться
как 11ро стым , т;~к н состанны м .
Секрет это1·0 метода впт в ч ём. Оказывается ,
ЧИСЛ() k"_, будет ~1а 111-ю 1 в том н T()JJЬKO 11 том
случае, кnг!(а 2"
-
1 делится на п. Согласно
же малой теореме ФерJ\11а, ecm1 п > 2 простое,
то 211
-
1
-
1 делится на п. Но нс нсеrда наобо
рот. 1la этот счет даже ~1звестна одна поуч11 -
тсльная история.
1549
1553
1559
1567
1571
1579
1583
1597
1777
1783
~1801
1811
1823
, 831
1847
186 1
1867
1973
1979
1987
1993
@;)
2003
2011
20 17
Экспериментиру>~ с числамн вида 211
-
2,
древнекитайские математики заметали: если
11 простое, то 2'
1
-
2 дсmпся на п, а если со
стаонос - то не делится , и таI< для всех 11 о·г 2
до .100. Они по<.:читали, что это1·0 достаточ
но - кедь число 2~
1
ю действительно впечатля
ет оюей величнной: для е1·0 записи требуется
90 цифр! И они сдел;.1J11 1 вывод, что это прави
JЮ вы полняется всегда. На са м ом деле }"А<С
число 34 1 = 11 · 3 1 наруmает его. Древне
китайским математикам не хв:пипо совсем
н емного терпения, чтобы в своих экспери
ме1-ттах дойти 1'0 это rо числа.
ОХОТА ЗА П РОСТ Ы МИ ЧИСММИ
Первую 11звес1·ную нам таблнцу простых чисел
составил нта11ьянский матем ~1 тш< Пы:тrю Ан
тонио Катальд11 в 160) r. Она охва'Jынала все
простые числа от 2 до 74.- 1.
В 1770 r. немецкий мате м атик Ио1 ·а 111 т Ген
рих Ламберт опубликовал таnлн11.у 11аимен11-
ших делителей всех чисел, не превосходящ1 ix
102 ООО и не делящ11хся на 1., .:$, 5. Rлож11u в этот
труд поистине колоссальные усил ия, Ламберт
1-19
Числа
гара11т11ровал: бессмертие то.му, кто доведёт таб
лину делителей до милm1011а. На е 1·0 призыв от-
1ши~шулись многие вычислители.
К середине XIX в. у-лес былтr составлены таб
тщы на11меньших деru·rтеней нt: только 11ер
воrо миллиона. нn и следующ11х. вплоть до
девятою. В это же время в прессе появились
сСJобщения, которые предс1·авлялись :..Jбсолют
но ф:-1нтастичесю 1 ми: в Венскую академию по
ступило сем~, болыннх томо1~ ру1юписньLх таб-
111щ ~ Велиюrй канон делителей всех •mсел,
которые не делятся па 2, 3 и '5, и простых чисел
между ними до 100 330 201». Автором это го
труда был Якуб Филипп Кулик. профессор
высшей матсмати.1ш Пражсr<оrо уни.верснтета.
В дальнейшем поиски простых чисел уже н<:
носили характера массоной охоты, с которой
можно с равнить состав11е1 1 нс табли1 ~. а пренра
тились в целенапр;:нv1е1111ый отбор отделt.11ых
предстаюпелей. У охопппюн за числами болr,
шt: все1·0 поnуJJярны простЬtе чнсла Мерсеr-ша .
О11и названы в честь французского учёноrо
Марена Мерсенна, сыгравшего 13 X\t lll в. видную
роль 13 становлении свронейской пауки (см. еiа
тьи "Совершенные и дружественные числа»,
"Ч нсж1 Мсрсснн:1: заблужле1rия и рекор;~ы.,.).
ЗАКОН РАСП РЕЛЕЛЕ Н ИЯ
ПРОСТЫХ ЧИСЕЛ
Некоторые 11редсrавле11ия о распределении
простых чrкел имели уже дrеюrие греки. Из
1101<азательства r:вклида следует, например, что
они не собраны вм<::сте, а разбросаны no всей
числовой оси. Но как чж:то?
В l 84 5 г. французский математик Жозеф
Бертран, исследуя таблицу прuстых ч11сел в
промежуl'ке от l дu 6 ООО ООО. 0611::~ружил, что
М<::ЖJ~У ЧJICЛ:JJ\<НI п 11 2п - 2, щеп > 3, содержится
110 кр<~йнсй мереод1ю г1ростое число. В1юслел
ств 1ш э·го сt1ойство получюю 11 аз"Аание nocnzi• -
лmna Бертрана. хотя самому Бертрану обос
но 11ат1> его та1< и не удалось. Доказал его в
1852 r. русский математик Пафнуrш1 Львович
Чебышёв. Из результатов Ч:ебышёnа следовала
н более точная оценка. Таким образом, даже
среди очень больших чи сел простые числа не
так уж редки .
С другой стороны" существуют nромсжутки,
1н<J1юч ающне тысячи. милпионы, миллиарды и
Lб ще какое у 1 ·од~ю большое 1юли. чеспю
1')0
подряд стоятr\их натуралъных чисел , среди
котор.ьrх 11ел1,зя найти ни одно1·0 простого'
В самом деле, зад~шшись 11ро11 ::нюлh11ьrм боль
шнм 11:.tтуральным ч 1 1сrюм k, постро11м ряд
ч1кслk!+2,k! +3..", k!+k(здесьk!=1·2·3
.
k).
Каждое из эт11х ч 11сt:л состаш юе. Н:тример,
число k! + т l\!:ЛИ'ГСЯ 11а т. поскольку k! 1~ел 11тся
на nz п са.мо 1п дел11тся на ш.
Если рассматр1-mать фушщию тт(х), -выража
ющую кот1чество простых чисел, ме11ьшнх
или рав11ых х, то пр11 псбОJ 1ь шнх значснияхх
бросается в глаза её нере1у.rшрностъ. Од11ако
стоит только уменьшнть мас111таб графика в
нескоmко тыс.s1ч раз, н нашему в:~ору 11ред<.1· а-
11ет кр;н:ивал 1шавн:.~я линю~ (рис. 2). Это сле
Т(уе>г отнести к числу YJ'HBИ'l 'eJrг, 1 tейшнх фак
тпв математики .
Пятнадцатилетний Карл Гаусс зан~ 1теrесо
вался ·1 ·абJ 1 11цаi\1и простых чисел, помещённы
ми В fЮТ\ареrпюй ему «Таблице лorarиф,\1QB•J.
1lытт нюму уму открылся замечатслы 1ый ,~ште
матический закон: ф)'111щия тс(х) с ростом apry-
20
15
10
5
. "\'
Рис. 2. Г1ы фики
о
50
100
фу11кш111 Jri~·)
в р.н11ых
.-...кшт~бах.
6000
5000
4000
~ООО
2000
1ООО
20000
40000
х
о 10000
30000
50000
че11та х ПjХll<Т1ТЧески не О'lJШЧ~К"ТСЯ от фр11<
ЦJ111 х/ 111 х Ссйч<tс этu·1 ф<tкr носит 11азuа1111с
ЗCIК.Ofla рас11редши!11uя простых ц11сШl Сосной
С1'11t:ннш1 J'L:HllH,\IJ прозорлшю<.vIЫО Гаусс у111щ<::.1 1
Э'J'UT ~{:.IKUH, но найти 1к:ские ap1y;-.-1t.' l-\TЫ ) \JIЯ Cl'O
06ос1-1он:11111я ему было нс суж11сно.
В 181 2 1 Гlаф11ут11й Лыюв11ч Чебышев rюк:а
зал, что 11ре; 1ел от1ю 111 ет1 1 ~н тт(х): "v/lп х r1p11 х --+ <)()
1н.: маже·1 0·1·т 1ч ~tтhСЯ от еnн1 1н~ .t.ы. Останалосr,
только доказать, что такой пре,rtел действите; 1ь-
но с.:у:rт\ествуст. Э·ю сделали в 1Н96 r Жзк Адамар
11 нt:зав11с 1 rмо от него Ла Валлс Пуссен . В с.ноё.\1
;~оказатслъс·1·не ~·чё11ы<: uшrра111къ н:1 р<::.iуль
таты нt·мсц1ш1·0 ма · 1·с.мат111<а l:i t:pнx:1p/\:t Р11ма11а ,
11олучсш1ые 11м 1:1 , к;1 ~~алось бы. очень ;1ал~ко\1
от T<.:Up J111 ЧI J('С:Л обл3С'1' Н матсм аТIIЮ·I - IJ 'l'<::O-
p 1111 функцп'1 К()м11.гн..: кс~ют nсреме111ю1·0 . BO'I ·
так yc 11J1 юrм1r м1ю1· их мате .V1атикоR 11 хаос е
рзспрс"-елеш1я простых чнссл была обнару
:>J.:сна с 1<рытая rарJЧонш1.
СОВЕРШЕННЫЕ И ЛРУЖЕСТВЕННЫЕ ЧИСЛА
СТРОГИЕ КАНОНЫ СОВЕРШЕН СТВА
О юерш<'1t1-1ыми 1 1а з 1.1 в~1юто1 чнсла, рав1 rые сум
ме сrюнх собстве1111ых делителей (т. е. ucex
делителе й , включая e,r(muщy и нсюпочм само
ч1~сло) . Та1ювы , напрю,1ср, числа 6 п 18, по
с1<О:1Ькуv=1+2+j,28=l+2+4~7+1-1.
Jlюд11 обрат11 т1 н а НIIX п1111ма.нш: оч<.:ньдашю.
дrе111 1 с1.:т1.шетская мера дл11ны локо1ъ содер
жала 28 н:шьцск В Древнем Рнмс сущестrювал
обычай отнодить ш1 пира х шеста<.: место са
мьL"' знатным 11 почё-111ым гостям. С()нсрте11 -
На руке Святого { и~< r.i
шесть nэльuев, Фрагмент
карп111ы Р,1фа)11Я
• СИl(С"'Н1Н<'К3!1 M<ll'>QHH<I•
11515-l'il'Jrг!
нымн чис;1 ами унJ1екали с 1, 11нфаrоре~:щы -
rюслсr1она ·1 ·е.rrи ппюл ы дреrнr егречс скоrо ма!'е
м~п нка Пнф~н·оrа.
Одна нэ теорем n дсвят011 кн 11 гс Нвклидовых
,.Jlачал" гюсвящс1rа замсчате; 1ыюму с1юl1ству
сu13сршс::1111ы.х чш.:с::л. открытому . как пола1·аюt ,
уче1111к: 1м11ll иф:11'uра: 1::сл11ч 11с;юр=1 + 2 + i +
211 2птl l
)"
+ ..+
=
-
r1pucтoc, 'ГО чт IСЛО ~ /J COBt:p-
IUCHHoe П сnраве,цлнRости "J ю го утнсrжденш1
можно уб~д1 пъся , расс мотрек l'CC собс1 ~:;с11ны е
'.
>"р·1)1 )">"'J
l
дел111ел11 чнсJ1.1 _
.
.
,~.
,.."~,_
-
,
l (211
i
1
-
I).
.:.j (211
•
1
-
1), .." 2"-I (21111
-
[)-Н
11 одсч:итаn их сумму. Jlравнло .tвКJ11 ща nозво
muю древнегреческому математику 1l ико.ч<~л-у
п з Герасы (l- 11 вв. ) найти такие совершенные
~тела, I<ак 6, 28, 496. 8128 (при п = 1. 2, LI. 6).
ПосJ1едующ11с С'tолстн}j uка::J:uпкъ не столп уро
жай11ымн на нaXOJ\кlt Оч ерс/\НUе, ш1•1·о е п u
счt:ту совеrшснное ч1кло .1 ., 5 '1 0 3.)6 (11 = 12)
было обнаруже1 ют н111, н XV R.
Яркая ст ра 1 tJщa н п сторин С()вер 111 <.:1111ых
чнсел Сtiнзапа с 11ме11ем фра 1 щузс ко т про п()
liедникз н учёrюГ() Марена Мерсепна . 1\1~nучая
обществеш rая деят<::JТЫ юс1 ь не ме шаJiа патеру
заниматься математикой. Н е1·0 сrесть про<.:тыс
<nкла шщаМ" = 21' -
1 nрн прос1·1,1хр былн на
:шаны нростымн числам11 Мерсс:нна . По 11р~1-
1ншу ЕRю1нщ1 , каждое: 11 рос·1 ·ое чнсл о м1, 011ре
деляс:т со11ср1t1сн1101: число .1!1, • 21'
1
Сам McpC<::HJ-1 заяв11л , что очеrедныс flrt:'l~ r· 1.
ст1ер111енных чнсел после 33 5'10 3 36 соотnет
ствуют чнсла.м,\117, м1", м,,, /\11,-. 1VJ11~ и МJ'Р·до
сих пор остаётся ~1аrздкой. чем 011 рукооод
стnовался, называя этот ряд. Оказалось. что
Мсрсенн ошибся в двух случаях нз шести.
Числа Л11,- и М1 " - со(1<1нные, п, следоватеJ1ыю,
1') 1
1~)
)~
Числа
ШЕСТЬСОТ ШЕСТЬДЕСЯТ ШЕСТЬ
Здесь мудрость. Кто "мее1 ум, тот сочти число
зверя , ибо это чиt:/\О человеческое, число i:>ro ш е{ТЬ·
сот шестьдесят wесть.
Откровение V/оJнна Богоrлова (AmЖJ/\иncнr)
1J. 18
П « Вой не и мире» Л. Н . Толстого есть эпизод, когда
Пьер счел «uифир~1 ый вее» Наполеона равным
числу зверя - 666, подогнал наn1о1сание свое1·0
имени под такой же, увидел в том знамение и
решился идти убивать Бонапарта. Не поленитесь
перепроверить арифметику Пьера - возможно,
это подскажет прич ину его 11еудачи.
Число же и в самом леле необычное. Вот лишь
некоторые из его удивительных арифмети ческих
свойств:
-
чи сло зверя есть сумма квадратов первых
семи простых:
ббб=2l+у+51+7
2
+11
2
+1у+172
;
-
число зверя есть сумма первых 36 нату
ральных:
-
число зверя есть разность и сумма шестых
сте п еней первы х трех натуральных:
666=1
6
-
2°+з~;
-
число зверя можно записать девятью uифра
ми двумя способами в их возрастаюшем порядке и
лишь одним - в убываюшем порялке:
666=1+2+3+4+567+89=123+456+78+9,
666=9+87+6+543+21.
Число вида 2', содержашее в своей зап~1 си число
666, называется апокалиптическим , а чиrло, имею
шее в своей записи ровно 666 з наков, - числом
Апокалипсиса.
соответств'·1ощие нм числа Л1 · 2..'
1 111еямя·
J
/'
ются со11срш с:rшыми .
Все совершенные числа, которые можно
1-:1айти rю правилу Енкли;щ чё·1'ные. А существу
ют ли нечётныс совеrшенные чнсжl? До сих пор
это некзнсстно , хотя мнш·очисле1111ые исследо
ваш1я , uы 1 ю11ненны е R Х:Х в" свидетельствуют·
если такие числа и сущестиуют, то они должны
подчиняться многочислеппым «хи·rрым » ус~о
nиям. Совреме11ный немец~<ий математик Валь
тер Боро как-то сrсазал: «Работы, nосuящёпные
нечётньн.1 совершснаым числам , наnомипают
охоту за призр аком: нш<.то никогда его не видел ,
110 npuвt:дt:нu много остроумных ис.:сл<:Дов:uпm
того , как он не может вы 1'ЛЯl\t:Т I»>.
УЗЫ ЛРУЖБЫ В МИРЕ ЧИСЕЛ
Два натуральных числа т и п наз ываются
дру.жеспюениы~wи , если сумма собстuе1111ых
делителей т ранна п , а сумма собственных
дел11телей п р авна т.
И стория /~ру--местне нных чнсел теря ется в
глубине векш~ По св1щетельству аю· 11чно1·0
философа Ямнлихз (ПI - lV нн ) , Rелию rr:\ Пи
фа 1 ·ор на вопрос, кою сл едует с читать свон м
1(1Jугом, ОТАетил: «TO I '(), кто ЯJ3ЛЯt'ТСЯ MUl lM ВТО·
рымЯ, как ~шсла 220 н 28Ф>. ПpnRep111·e, 11 ожа·
луйста, что числа 220 н 284 дружественные.
Для нахождения дружественных ч исел
арабский учё1rъпi Сабит ибн Курра (IX в.) пред
;южил хитроум11ый с пособ. задавшись на1)•·
ра J 1 ьнn1м числом п , tюдсчитать вспомо га
тельные ВСЛИЧIН·lЫ р = 5 . 2
11
-
1
-1.q =3.2
11
-
1
9 2)11-1
нt·=
-
-
1. Если окажется, что числа р, q,
r 11ростые, то1·да числа А =2
11
/Щ11В=211
1· дру
жестnев 11 ые.
Ilифа1·орощ1 пара 220 и 284 получается. 110
этому методу при п = 2 . С..JJедую щую пару чи
сел - 17 296 и 18 416 - обнаружили нсз:rnи
симо друг от друга марокканский учёный Ибн
апь-БаJJна и три С!'олетия cnycпr француз Пьер
Ферма. R этом слу1.-1ае п = 4 . Третью nзру
-
<.)363584и9437056(прип=7) - указал n
1638 г. Рене Декарт. Дальнейшие попытки най
ти дружественные пары при небольших зна
с1сния..~ ·п к успеху не прmюдят. Более ТОТ'О, спо
соб Сабпта 116н Курры не nыя1vmет н11 011ной
ноной п<~ры нружсственных ч.исел, есш1 п уве
личивать до 20 ООО! Нс)'"'..кели дружественные
-г11сла - алмазы-самородки и для подсчёта нх
пар м11огонато даже пальцев од11ой руки?
В l 747-1750 rт. Леоr 1 ард Эйлер пропёл у11и
каm,11ы е числовые «расколки» . 01-1 при;~умаJI
Uелы е •1 иtла
ор11гт-~алы-1ыt методы поис1<а r1 обнаружш1 сра
:1у 6 1 но вую пару /1,р~.r,кес-1·всrшых чис~11 . Примt
чатс.~1ыю, что среди 1111х оказа.11нс1, и 11ечётные
числа:696J5и 114983'15; 8763.J и 12024045.
Сейчас из.Rесттю около 1100 пар др~жествеш1ьL"\
чисел . Любопытно, что в 1866 '" италыrnсJ<ИЙ
L1tкольннк 1J. Паг :1юшн (однофам11лсн велико-
1·0 скр11п ~1сlа) 11 :ш1ёл 11ару др)'"'А<ественных чисел
1184 н 12 10, которую 1ке, н том числ е и 1::1ьщаю
щисся математики. проrлядtли !
Rот пары дружестве1111ых чнсен и 11редслзх
100 ОСЮ:
220
l 184
2 620
5 020
6 232
10 744
12 285
17 296
63 020
66 928
67 ()t)')
6() 61 ')
79 750
284,
1 210.
2 924,
5 564,
6 ?>68,
10 856,
14 '195 ,
18416,
76 084,
66 <)92,
71 14'5,
87 633,
88 730.
Дружественные числ<.1 прu;щлж.~ют скр1,1-
вать м1южt:стнu тайн. Jiс1ъ ли смсшанныt: 11;,~ры
у которых О/\НО чи сло ч ётное, ~~ дру1·ое -
нечётное? Существуе·1· ли общая формула ,
огr1 1 сы Rающ::~я все дружестnенные ш1ры? Ко-
11ечпо нли беско11еч1ю число такнх 11ар? На эти
и другие во11росы ответы пока нс 11аГщены.
ЧИСЛА МЕРСЕННА : ЗАБЛУЖЛЕНИЯ И РЕКОРЛЫ
Леrк() убед иться, gтn еслн число п сост:шное,
то чнс;ю 211
-
1 тпже состаr111ос . В сам ом деле,
2"- l=2'''-1=(2k)/-1=
= (lk- l)(i~<f-1)+2"(/l) + ". +l).
llr111oть до 1S36 J'. было распространено
мнс1111е, чтu верно н обратное, т. е. простота 11
влсчёт ::1а собой простоту 2 11
-
1, покJ У11/\;ш
р11кус Per11yc нс отмет11л, что 2 11 - 1 = 20L17 =
= 2:7> 89. Ою-1:1ко длительный псрно11; лрамап1 -
чесю 1х ::1абл~ж,l\ею1й был ещё впереди . Нз по-
роге ХVП С"t't>Летия Пы:тро Антuн1ю Ката11ьд1r
[ '1'
.
1L)
проRсрнл , что 2 ·
-
1н2 -Jс~р1ъпростые
ЧНСШI, н ГЮЗIЮЛ:ИJ/ себе утверж,1:~а·1ъ, что 2'
1
-
1
простотаюке при п= 2:\ 29, 31, 37. В 16401'.
П ьер Ферма уста1101ш:1, что д!lя 23 и :) 7 это
утвержде ние II e веrню, <• в 17 38 r . Ле()11ард
uйлср показал его ошибочность дпя 29, но под
тnерднл ИСТJШIЮСТЬ длн 3 1.
Тем nремснсм ri 1644 I'. французскиfr монах
учёный Мар~н Мерсен11 заяnил , что L1исла 2" -
-
1просты11р1111 = 2, ."\, 5,7. 1.3, 17, 19, .'Sl,67.
127 , 257 11 не лросты Пf1 11 ОСТ:lЛЬl!Ы Х ~14 проСТh!Х
Llи сла
н. мt11ы11 1 1х 257. Но 11с этнм 11ред1ю11ткением
11 е 060ШJIOC I) бt:З КОЛЛIIЗИЙ. Хотя кое- чего
монах АС'ё-таки ;к1стн1" eC.'I II число 2 11
-
1 прос
тое, его называют числам Мерсетш.
Заблуждение Ме1хспна продержалось до
188:) r " когда русскнй священник Иван М11хсс
ю 1 ч Пt:р вуш1ш дока:3ал, что чнСJю i'
1
-
J прос
тое, <t не::нь 6 1 нt зн ::~ч_илось в сп иске М срсснн а.
С дру1·ой r..-l'Орон ы, уже я ХХ н. было 11<1й/\t:1 ю,
что ЧIJCШI i'" - l и 26~ - 1СОСТ~1RНЫе П01с1 11е
и:..~ всстн о, бескон е чн о m 1 кол ичестяо ч~1 сел
Mep cerr1ra, а ясt, что 11 айдены, приве,це 1 1ы 11и жt.
ЧИСЛА МЕРСЕННА. ТАБЛИUА РЕКОРЛОВ
Номер п
Год
Номер
п
Год
числа
числа
1
2-
19
4253 1961
2
3-
20
4423 1961
3
5-
21
9689 1963
4
7-
22
9941 1963
5
13 1456
23
11213 1963
6
17 1588
24
19937 1971
7
19 1588
25
21701 1978
8
31 1772
26
23209 1979
9
61 1883
27
44497 1979
10
89 1911
28
86243 1982
11
107 1914
29
110503 1988
12
127 1876
30
132049 1983
13 521 1952
31
216091 1985
14
607 1952
32
7568 39 1992
15 1279 1952
33
859433 1994
16 2203 195 2
34
1257787 1996
17 2281 1952
35
1398269 1996
18 3217 1957
?
2976221 1997
154
Табю.11 \3 шжа:~ы вае-1, скол 1. 1
·11 }'боко :'l:t6луж
да.r1 с.н •·кrёст1 1 ьп'1 оте 1 1, ~ ?!тих з;1м еч~1тt"льных
1-uксл .
И::~ uбщстсu рстичссю 1х фа ктов о чнслах
Mc r ce1ша (IЗKCCTHU HCMHUl'UC. Напри мер, если
11=3 (inod '~)простое, тu 2
11
-
l делнтся r щ 211+
+ l тогда 11 только то1")1.а, кuгда 2. 11 + l 11росто.
И мееrся также общ11ir кр11тср 11 й - 1·ак на·
:i ы naeм ыlJ тес~ Люка - Лсмсра: для не ч ё·пюrо
11 числ о 2" - 1 просто тm ·Jщ 1r только тor;ia,
т<аrда S(n - 1) делится 11а 2..
11
-
1. r,r1,e
S(l) = 4,
S(n+l)=S(11)J- !..
Реко рды в по11ске ч11сел Мерсенна теnсрь
ста т1·г ком пыuтсры. r1 га к бу;.(С'J ;ю ·1 ех пор. 1 юк;1
п е появятся теоре- 1 11ческ и с рсзул ьтаты об об·
щих :~ако 1 юмер1 юеt'ЯХ /tJTЯ :-JTJIX Ч НСС'Л
Кто (1ьнтрееl
ЧИСМФЕРМА
В одном и1 своих писем к Марену Мерсе нн у Пьер
Ферма высказал предположе~н1е, чтn числа вида 2n + 1
обязательно простые, если п - степень двойки. Он
проверил это лляп = 1, 2, 4, 8 и 1Ь. Ф~:рмс1 также :тал,
что если пне степе11ь двойки, то чиrло2" + 1 НЕ' прос
тое. Числа вила 'f" + 1стали на:.~ ыватьчи<.Лами Ферма.
Гипотеза Ферма прожила более ста лет - до тех
пор, пока в 1732 г . /\еонард Эйлер не nпказал, что
2л+1=4294967297=641 67СЮ417.
Все дальней ш ие проверенные числа Ферма тuже
ока:iались состав н ыми, так что естественно возникает
***
По формуле <..уммы 11 членов rеоv~етрической
нро1 ·ресси11 ,
')" -1
1+2+". + 21t-!. +zu-J = .:;--- = 2
11
-
1.
2-1
(}1скща 1нщ11n : чисщ.1 Мерсенна естъ не •пп
н1-юе, к;щ прос1·1-.1е суммы <-шенов геометриче
ской п рогресспи с основанием 2. Но почему
б ы нам не обратнтъся к прогрессиям с иным
основап1 1ем?
Обобщёtmы.м •щс.ла.м Мерс.:енна будем назы
нать пр<к~1ое значt'ние суммы членов 1 ·со~1 ет
рической 11ро1·рессии с оснон~1 ние м а·
)
t.i''- 1
1+а+а- +... +а"-
1
= ---
а-1
Яс110, что м 1 южест1ю 11сех обобщёш rых чисел
Мерсешта совпадает со м 1 южестnом ucex не-
UелыР числа
прелположе~1ие, п ря'vlо противоположное исхоыюму:
а не ко нечно ли коли чес тво п ростых среди чисел
Ферма'
Известны достаточно обшие свойпва чи<.ел Фер
ма . Н апример, любые два числсl Феμма в~аим110
просты. Карл Гаусс доказал, что п равильныйп-уrоль
ник строится при помо ши uиркуля f1 м11-1 ейкf1 тогда 11
только тогда, когдd число его сторонn = 2" р1 р1 ." р,,
где все простые числа р, имеют вид i ' + 1. Среди
первых 1ООО значений таких п всего 54.
Обшетеоретическую значимость чисел Ферма для
и'\учения простых обусловливает слелуюшая теорема:
Если а ~ 2 и числоаn + 1 простое, тоа чётно и
n=2т.
ч<::n 1 ых простых, посколы<у если р простое 11
р>2,то
(р-2)р (jJ- 1/-1
jJ=
=
.
р-2
(/J- 1)- 1
Te11epL1 каждый может самостоятель но 11с
сле110J'lать и 11ычисю1·1 1-. новые, свон собстне 1 т
ные числа Мерсе1111а. Rот 1 1 ~ч::uю табJ1 1 щы, а
продолжение - :за вами.
а"-1
а п, прн которых чнсл;з --- пр()ст 1,1
a-l
3 :),7,15.71,."
42.
'5 3.7, 11, 15.-П, ...
() 2,3,7,29, ."
7 5.].),,
83.
ОСНОВНАЯ ТЕОРЕМА АРИФМЕТИКИ
Почему простые числа иногд::~ имскуют ч 1 к
л:ами-~кирnичи-ками»? Потому. что любое со
став н ое чJкло Jlcrкo строитсн из 11рос1ъ1х <:
110м о щыо ум 1южt 111-1я. Напрн ,"rер , составное
число 1998 можно соорудить из чисел-«кир
ПИ\.IИКОВ» 2, 3, 37 таким об ра:3UМ:
1998= 2
.1>
.1..3..)7.
Тенерь легко объяснить. почему l н е с ч нт:1-
ется прост 1.1 м число м . Единицз ш ·рает точно
такую же роль при ум 1южt:н~1и , как нулh - пrи
<.:!Южснии: сколько нн ум11ожай 11а едини1\у, ни
чего не изменится. Раскладывая чи сло 1998 11а
простые множители , м ожно было бы з:ти сат1,
1998=1 2 .:.)
.3
.
3.
-1>7.или1998= J .1 2х
х3·j
·3
37, или ещё бесчислеrшым мт-юже
стном стюсобоn. Какой из 1шх правильный? Да
любой Ведь по суп1 оrти ни чем 11е 01личаются
По:::>тому лучше до 1 ·овориться раз и навсегла . что
единнца нахсщнтсн на особом положеш111
1'5'5
Чи сла
Ci 1rавеN11ша теорема, 1ю1<аза·1 ел1,ство кото
рой, несмотрн 11 а 1Jсю её естестRе1 шость, тре
бует определёнпой изобретатслы-юсп1:
Любое Jiатуральное число ", > 1 либо
само является простым, либо пред
ставляется в виде произведения
простых чисел. Разложение числа
на простые множители единствен
но, если не обращать вни~1ания ка
порядок следования сомножителей.
Это уrверж;\ение 1ЮJ!"учило название ОС/ юв1юi1
теоре.J11ы apuifJ.Мemщru.
Воспользовавшись обозначением степени,
разложс11ис числа 1998 на простые множите-
i\юuue чиtлu л~160 LaVlo являетrя 1 1 рос1ы"•
лиf10 nрРлrга вляе т(·я в в~1де r1р(н-t Зl:l~дt!1н1я простых ч"tсел.
156
т1 можно записать как 21· 3' · 371. То•1но так
же nри разложении 11ро11зuолы-юго натураль
ного числа 11 один аков ые простые множюелн
можно собирать н R1ще степеней и запнс ы11ат1"
(*)
l"дt Р1,Р2 • ".,jJ~. - различные простые м1южите
ли числа п, r1ричём числu р 1 нходит а.1 раз, p1 -
a.i раз 11T . fl. Если все простые qислар 1 ,р~. .-, р1
н этой формуле ныс-1раиваются в порядке воз
раста 1тия:р1 <р2 < ". <Р1г. то '1·акое р:!зложен11с
назыяается к,а1 юничеСl\.U.М.
Ка~-юниqестюе разложение чнсла - сноеоб
разное «досье», из кптороrо мnжт-ю извлечь
массу любопытных сRедений об этом числе.
СКОЛЬКО ЛЕЛИТЕ/\ЕЙ У ЧИС/\Ап (
Подсчитывать котrчt:ство де.r11 псле r1 у неболь·
ших ч11сел не соста13J!Яет особого труд:~ Так, ~
чнсла 2 nсего два дt~шrтелн: 1 11 2; у числа 6 по
больше: J, 2, 3, 6; а uo"I", скажем, у числа 180 11х
уже18:1,2,3,4,5,6,9,10,12,15,1R,20,30.36,
4 5, 60 , 90, НЮ. А если исследуемое число 12 ещё
боm,ше? Выписывать все его делители не оче111>
привлекательное занятие . Этот кропотливый
труд можн о облегчить. если uбратпть внн
ма1ше 11а кано1-1нческое раз~uжс:ние числа п.
Например. запись 180 = 2- · .1 -
· 5 на блюдатель-
1-юму 1кследонателю показывает. что нроиз
tЮJ 1uны й дслитvrь чн.сла 180 может бытn обра
зона JJ JIИШI> следvющ1-1ми СОМНОЖ ИТСШ/М[l: i',
21
,2
2
, 3u.3
1
,3
1
,'5
11
:s1
• Пр и этом каж ;~ый изтрёх
nариантов степеней 2 может сочетаться с 11ю
бым из трёх вариантов степе ней .~ и с любым
из двух nариантов степеней 5. Всего разшrчпых
комбинаций может быть 3 · 3 · 2 = 18. Имеrшо
это чнсло и было ранее получено другим, .'1е
нее эко н о мичным способом.
Итак, если в 1<:1но ническое ра зложен11е (•)
11ei:<o·ropoc nростое число р нход11Jт в с1 с11сш1
о:, то п делится на все сте 11еLI.и f> от О ;~о а_ р°,
р 1 , ""p(J.. Поэтому делителей. н которых учасгRу·
ет только OДJJO ЭТ() ПfЮСТОе ЧИСJ Ю р, име~тся
ровно а+ 1.
В делителях п IIa r<аждое из а 1 + 1 значений
степеней числа р 1 может прнходитъся любое
ИJ а1 + 1 значеII пй стененей р4, на к:~ждое 11з
которых , н свою uчepe/th. может прих.од1пь ся
любое 11 :з а~+ 1 нозмпж11ых :~нач е н 111I степе
ней числа Р~ 11 т. Jt. Поэтому •(n) - ofiщt:c ко-
11ичс::ст1ю ;~слителсй числа /1 - зада ётся фuр
М\'JЮй:
t(н) = (о: ,+ 1)(о:! + l)."(o:k+ 1).
Фу11кщт 't (n) имеет характер неоnъезжен-
1юго мустанга. Она может скол ь yroДI ю высоко
вздыматься- вверх, при этом всякий раз, когда
11 СТСIН.Оf\ИТСЯ простым числом, функция воз
вра1щ1 ется к двойке. Однако при всех стран -
1-юеr·ях и причу1'ах • (n) её <>близкая родстнен
н rща ~, функция
't~Р (п) = _!_ ('t(l) + 1:(2) + ... + -т:(п)).
п
ведёт себя впол не «блаrообра;то и чишю». Не
меню r й математик Петер Густав Лежён Дн рих
ле показал, ~по •ч, (n) с хорошей ·1·о ч11остью
можно нриблизить н~пурал ьным логарифмом
от числа п, а точнее:
•cp(n)=Jnп+(2С- 1)+е,,,
ще С= 0,577216... -
постоянная Эйлеrа и сла
гаемое е" бысr~ро стремится к нулю с рос1·ом п.
15
J2
9
G
3
о
20406080JOO120140
Функш1я ~(n) и ei! • ближая родственниuа • t q,(n).
ЧЕМУ РАВНА
СУММА ЛЕЛИТЕЛЕЙ ЧИСЛА п?
Для nодсчёта суммы [IСJrитслей числа, предстаn
лею ЮГО В КаНОНИЧеСКОМ разложении (•), ВКJ IЮ
чая 1 и само число п, можно ВОСПОЛl>ЗОН~IТЬСЯ
формулой
р«•,,_
1Р~'т1_1
а(11)= .;...;.
1
---
----
р,-1 !~-l
установленной за.\fеqателъным а11глийск:им ма
тсма·r·иком ХУП в. Джоном Валлнсом. Дтш вывода
её заметим, что делителями п будут все чис
JШ ннда р: 1 Pl2 ... р~" 1·де 1 юказатель степе ни t 1
Ut:лыt• числа
КАНОНИЧЕСКОЕ РАЗЛОЖЕНИЕ
ПЕРВЫХ 150 ЧИСЕЛ
1
1
51 з.17
2
2
52 22
•13
3
3
53 53
4
2!
54 2.33
5
5
55 5.11
6
2·3
56 21
·7
7
7
57 3.19
8
2j
58 2.29
9
32
59 59
10 2·5
60 zi.з.5
11 11
61 61
12 22·3
62 2.31
13 13
63 32.7
14 2-7
64 2&
15 3.5
65 5·13
16 24
66 2·J 11
17 17
67 67
18 2.32
68 21.17
19 19
69 3.23
20 22•5
70 2·5 ·7
21 3.7
71
71
22 2.11
72 2~.32
23 23
73 73
24 21
·3
74 2.37
25 52
75 J.51
26 2.13
76 2~.19
27 31
77 7.11
28 22
·7
78 2.3 .13
29 29
79 79
30 2·3·5
80 2~.5
31 31
81 3~
32 25
82 2.41
33 3.11
83 83
34 2.17
84 21•з.7
35 5.7
85 5.17
36 22. 32
86 2.43
37 37
87 3.29
38 2.19
88 21
•11
39 313
89 89
40 23
•5
90 2.З2.5
41 41
91 7.13
42 2 ·3·7
92 22•23
43 43
93 3.31
44 22•11
94 2.47
45 31
·5
95 519
46 2.23
96 25.з
47 47
97 97
48 2~.3
98 272
49 72
99 У·11
50 2.5i
100 22.52
101
102
103
104
105
106
107
106
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
12&
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
101
2.3 .17
103
23
·
13
3.5.7
2.53
107
22.31
109
2511
3. 37
247
113
2 3.19
5. 23
22 29
31
•13
2. 59
7.17
2J 3.5
111
2. 61
341
21.31
5з
232•7
127
21
з. 43
2.5 13
131
22•3 .11
7.19
267
з3.5
23•17
137
2.3 .23
139
22
•5·7
3.47
2.71
11 13
24.31
5. 29
2. 73
з.72
2l-37
149
2.з.52
157
Числа
Из всех п рпблем, рассматриваемых в математике,
J 1ет т.:~к их, котарые сч итались бы в н.:~стояшее время
более бесплодными и лишён 1iыми прелложен~1 й,
чем проблемы, кас.аю шиесS\ природы чисел 1~ их
лелителей." В этом отношении нынешние матема
тики сильно отлиLtаются от древ н их, прилававших
горазлu большее ;на ч е11ие исслелова11 иям такого
рола ... Кроме то го, что отыС"к<1 н ие истины само по
себе казалось им nохваль~1ым и достойным челове
ческого nоэнаню1 , древние хорошо чувствовали,
ч10 при этом замечатель н ым обр,tзом развивается
изобретательность и перед челnвечt-ским разумом
рilскрываю тся новые возможности решать сложные
з.tдачи ... Математика, верояnю, никогда 11е до
стигла бы такой стеnе н ~1 соверш енсп1а, есл и бы
древн ие не п освят1>1ли столько сил развити ю во
просов, кuторь~м1-1 сеrолня бо"ьwинство пренебре
гает из-за их м н имой бесплол1юсти.
Леонард Эt::tЛер
пробегает вес з11ачсrн1Я от О rr.o а, , пою1за· 1 ·ель
степени t ! - t1CC зн.1чс1шя 0·1 · О до а~ 11т д Сум
му ВССХ Т:JКИХ ЧИСl'.11 Ml1J IЮЛУЧИМ , CCJ!H p3CK[JO-
<..:M скобки 11 прои~не; 1еню1
(1+р,+...+р~')(1+р~ +.+J1;)".
." (1+Pk+...+Pl'),
а саму формулу Валлнса - если зашIШем каж
дое нз ныражсJп rй в круглых скобках по фор
муле суммы копеч 1 юrо чпсла члсrюn геомет
рической прогрессин,
Для п римера найдём сумму делителей ч 11сла
20()0=21 5~:
J' -1 5.J
-
1
cr(20UU):::: -- -
-
-
= :) l 1'56:::: -t836.
2-15-1
.
-
Получит~, это з начение неrюсредст11е111-ю, т. е.
опре11.ел.нв с11ача1 1 а все ,11;елители чн СJ1з 2000, а
затем подсчитав их cyМl'llfy, было бы гораздо
сложнее.
СКО/\ЬКО НАТУРА/\ЬНЫХ ЧИСЕ/\,
НЕ ПРЕВОСХОЛЯШИХ п ,
ВЗАИМНО ПРОСТЫ С n (
Чтобы 0 11 ределит1, кол ичество таких чисел -
обозначим его через <p(n), -
можно восп оль
зо паться уже :ш акомым нам математи ческим
инструментом - реn1етом Э ратосфена. t>a c-
158
/\еонард
)/оtлер.
Портр~т
rпбоn,1
Э Хандманна.
17% r
Сf\ЮТрим 1ЮСЛСДQR:t'l'елы f()i.. "l'h нaтyp:lJI hНЬIХ чи
сел от 1до п = р;'1J1; ".р;:•. Вычеркнем 11з нее
f\CC ч 11сла , KOTOf)bll: /~СJIЯТСЯ на /J 1 T:i кнх Чl!ССЛ
будет ро11нu 11/fJ 1 Ос1·анстся /1 - 11/р, чисел, 11е
дtлнщн.хся нар , Теперь из оставншхся ч_11сел
вычt:ркне"1 псt: дслящ11е<:я 11зр~, - их G)/~ст
Остапетсн
11
Jl- -
/J1
---·
Продол:жая ТЗJ<1 1 м же образо,\1 <·nросеиu:пы
числа, кратные р,, р 1••••• Pk· в конце концов
прrщём к формуле
q>(n)=n ( i --
1
)(1-.2._J ... (1--
1
J·
р,
Pz
/Jk
Н аr 1 рнмер, дли нзхож.;\еш~я количества на
тур<~льных чнсел, мсныJ11-1х 2000 н в~анмно
11рпстых (" 2()()() = 2 1 5 1
, /\ЫЧИСЛЯСМ
<р(2000) = 2000( l -n( 1-* J;:; 800.
Фу,rкция <р(п) называется функцпей Эйлера.
Именно OII открът ее в 1763 г.
U f'Лbl l-' Ч~lt'Лс1
АРИФМЕТИКА ОСТАТКОВ И ТЕОРИЯ СРАВНЕНИЙ
н ОД! юй 1r3 С ЦСI/ С:К:IЗЮ' «AJ111 Ca н с_:тра 1-1 (.' Ч)'/ \l'С»
з:~м<.:чатl'l1hHOI'<> ан 1 ·д11 1'к:ко1·0 1 111са·1 с:11я 11 ма·1·с
чат11 к<1 J lыш 1с:1 l("1ppo. 1,1a (ЗТО ЛНТС'{Х!Т)Т>Нl>I Й
1 1сс1щ01 rнм Чаrлза Лату1 щжа Дlщжсо11: 1 ) t:С"П•
3:~банн ыl1 :71111зо;\. Лл нс:~. М арто11с 10 1 i1 1ая ц 11
nолна н щ11 к ведут све"1·ск~·ю 6ece1iY :13 ч аем :
<·Пе р111 ,1\1 :--1a ronop11л Болвапщ11к
К:шос Сt:ГОДШI Чl!СЛО~ - CI J POCllЛ 0 11 , ТЮ
Dорачиuаясь к Лл 11сс 11 ш,rшrмая 1 в кармана
часы Он с: тр<.:1101•с н'1 1JOl'JJЯ/l<.'JI 1 1а 1 11 1х, 1ю·1 рнt 11
11 р11лож11л к у·ху.
i\т1сз П! )Д~"'1 а, ~;1 11 l>ТНt~п1л а.
-
Ч е-111ёртое.
-
Отст::нот 11:1 .~ва ю н1 . - IO/\OXJ rул Г>ол в;ш-
ЩJШ:>.
Может б ыть, н:~ ш со uре.че 111111 к. 11 збало u:ш -
1rы1'i чудссамп :1лсктрош rю 1, в rсплнкс Бо..'ш;~11-
щнка 11 1к· наlщё·1 1111чс1·0 стра1 нюr·о. 0;\нако
ФОРМУЛА ВЕЧНОГО КАЛЕНЛАРЯ
Ka~Ot:, Mfll\blf:, }' lldC ТЫСЯЧе 1eTbt: t /iJ дВОр!i'l
Б Пдстернак
Можете: ли в ы отв ет ить, 11а ка кой день недели придетс я
день BdШer o рождения, скажем, черf':1 пять лет~ Jто
несложно вычислить. Тут, f..aK и во многю. других
слу•~аях , п ригодится умен ие рассчитыва ть остат ки .
М ы приведём универсальн ую формулу . пригс1дн ую
длs~ определения дня недели люfJой даты в любом сто
летии . Пусть п - 11омер дня недели в следую щем по
рялке: О - воскресе~1ье. 1 - понедельник, 2 - втор
ник, -~ - среда, 4 - четверг, 5 - пятниuа, 6 -
суббота; d - число месяна (дата); т - номер меrяuа,
если 1 1ач11нать счет с марта: 1 - март, 2 - апрель".
12 - февраль (такая нумсраuия помогает при вывод~>
формулы уrтранить неудобство, с вsпанное с п еремен
ным количест13ОМ дней в феврале). далее, пусть у -
это номер гола о столетии , с - колич ество стuлетий с
учётом то1 о, что ин1:1арь считаетси 1 1-м, а февраль -
12-м меся uем предыдушего года . ( К при меру, если речь
идёт о 2000 г., то лля даты, прихолящейся на январь
или февраль, следует счи тать у = 99, с= 19, а дМI даты ,
прихоля шейся на другие месяuы, у= О. с= 20.)
В этих обоз начени ях формула мя нахожлен ия дня
недел и такова: п - остаток от деле11ия 11а 7 числа W,
где
w=d+[
1~-lJ+у+[~]+[%]-2с.
Квадратн ы е скобки здесь обозн;~чают так н азы ваемую
uелую часть числа, i .e. на~1большее ueлue число, 11е
превuс:ходя wее данное число . Например, [3,4] = 3,
1-З,14] =- 4, IЗI = з.
даже если W принимает отриuателы·юе з 1-1ач ен ие,
остаток 11 от его делени я н а 7 всё равно должен быть
больше или равен нулю. Например, лля В марта 2000 г.
W=-25=7 (-4)+3.Поэтому11=3,т.е.этосреда.
1~9
щ; следует забывать, ЧТО R XfX В" КОГ/\а была
написана эта юш 1 ·а. часы в большинстве своём
1ююшына 1111 лиш1, доJ1и суток, выраженные в
часах 11 минутах
Ситу~~ ция с repoя ,vm R Стране чу;~сс В/\руг
cтaJta .действи· r·еm, 1 ю актуалыюй 11 а поро1·е
XXI 1-s · мы 11е знаем, 1<a r< nере:нести на круг
ПI тыоrчелетия внутреютие хронометры мил
лионов компьютеров.
*"*
Представьте себе такую С1-11уацию. Однажды
утром вам звонит дру1· и <:ообщает: «Сегодня н
десят 1, ноль-1юль я выезжаю , встречай мой
поезд через /lеня 1-юсто восемь часов». Когда вам
нужн о прийти ю1 вокз<1Л? В 98 часо'В укладыRа
е·1·ся тюm ю1~е1111ых 4 C)r m 1<, да сщё 2 часа будет
в оста11<е. Rот и получается, что ны встрстнтсс1,
спустя 4 сут()к в 12 ч:~сов.
В другой раз 13Ы сами 11адумаете 11аnестить
старого друга и предварительно, 3а 45 суток,
закажете билет В какой день недели состоится
11ред1ю11а1·•н::мый ныез;\, если бнлет за1<азыва
сто1 н нон еделышк' Неделя - это 7 суток. Раз
делив 4 5 11а 7, получим в остатке 3 - ноэтому
ны отбываете в четвер1 '.
Н;1родная мущххтъ 1·ласит ~остат1<и сл:1rt-
1<и ·~. llрr 1 ведёшrые примеры показьшают, •-по
остатки, nош1маемыс в матtматичсском смыс
ле, nорой иl'рают весьма важ11ую poJJь, t1ыяf!J 1 я~
закономерности повтортощихся, перно~иче
ских процессов.
«КЛАССОВОЕ РАССЛО ЕНИЕ »
Если юят1, какое-либо натур;~льное чиою 111, то
при делtнш1 на нег() других целых чисел воз
можно т раз11кчr1ых остатков: О, l, 2, .., т - J .
Те числа, которые при делении на т дают оди-
11а1ювые остатt<и , объединим в оди11 ю1асс- Ита1<,
«С точки зрения числа m » все целые числа
разбиваются на т различных классов. Очевид
но, что чем больше само т, тем обширнее набор
классов. Так, при т = 1 получаем всего О/'\ИП
IOJacc - класс целых чисел; при т = 2 - дnа
класса: чётные и нечётные cu-1c11::1 и т. д.
Учёт ~1<J1ассовой структуры общества» целых
чисел бьшает полезен nrи решении некоторых
задач, 1rапример такой: требуется док:Iзать, что
п~и прОИЗ130JIЫ-ЮМ целом OCIIOL1a1r1 1 н п ЧИСJЮ
п: - 11 делится 1ra 6.
160
В этос~ беrконечной tr111рали два ч11сла ра с11uложе11ы о~а uлоюи
оr;: рн1кальной nрямои тогл11 и только тогда, когл.1 t)н11 л.1 001
одинаковые остатки nри .•елt>нии н.1 11
о
'
-
п Rыраже н11и п - 1z, вынесем 11 за скоnки, а
то, чтu останется, ~аз1южим ,11 0 формудс ра~-1-
1 юсти кr1::\лратов: п - п ; n\п- - 1) ; r1(n.
-
1)х
х (11 + L), ~111и (ll - 1)11(11 + 1). Это произведе11не
трех послсдоватсль11ых 1\eJIJ,JX с1исел , которые
при де.'lени11 ш1 ) дают различны е ос1·атю1. Сле
,\оватслыю, одно из них обязательно делится
ш1 :) 11 по крайней мере одно - на 1.. Зrтачнт, nсё
лрощвсдеш1с делится на 6 = 2 :) (ведь чнсла 2
и :S между собой юаимпо просr1.1 ) .
Имея о ч исле 11 дополюпель 1 rу~о информ а
цшо, к пр11меrу з11ая , что 1z, нечётн ое. мы мuг·
ш1 бы \1твсржцать нс: что бuл ынеt:, а именно что
.
"
ч11сло п - п делится н~1 12 11 даже H<J 24. (Пo-
11roбyliтt: uбос.н овать это самостоятель н о.)
Дпн ·1·01·0 ч.тоб1>1 сформировать отряд чисел
нз 11редставитслей всех KJJaccoн. п о рож,цёштых
11 етюторы м числом т. соверrпепно 11еобя
затсш.rю брать т носледоватет,ных целых
чисел. Для этой цели MOl')'T под о йтп и по
следонательныс члены <~рифметнческой про
rрссс 1т
п.п+d,п+2d,"., п+(т- l)d.
(")
еСJ 1 и только cl взаимно пrосто с т. Де.йст1:1и
теm.1 ю, расе м отрнм ра::~ность k-го и /-r ·o чи сел
11осле1\011з·1·еJ1 ы 10с1·и (*): cl(k - l ). Поскольку с/
113<1ш.шо просто с т, :i 11г - t I<т, то d(k - !)
11е делится на 111. :1ш1чит, сре; 1и чле нон :п()й
после,11о nателы-юсти нет двух, дающих пдина
коnыс остатки при делении на т. Татшм обра
за~~, послсдователы юсть включает пре)1стави
телсй нсех классов, порождё н.ных Lшслом т.
Иэ 11оказа ннш·о утвtрждсння следует, в
Ч:1С'IHUCTll, что ССЛIТ числа т. 11 п JЗЗЮIМНО
проеп.1 , то чл е ны 1юсле)1ов~1тельностн
ll, 2п. 3п..", (т - 1)11. т11
;~ают полны!~ 11збор остатков 11р11 дслсни11 на
т: от О TI.O т - 1 . Чтпбы в :;этом убс1~1ттьсн , до
rтаточ1 ю u последователыюст11 (*) положит~,
с/= 11.
Этот результат можно проиллюстрировать
гео~1ст рнчсски, как это сделал француэски й
мап:матш< н физик Лу11 Пуансо. Пронумеруем
вср1111 1ны вьшуююrо т- уголъrнп<а •шс;~ами от
U до т - 1. Отnр:.1~v 1ш1сь от 1саr<0й -либо вср
ши1 1ы . будем переход 1r1·1ъ к 11ру1·им. его верш 11-
на.м, 110 11<:: JI07'JJЯ/t, ;,i с Ш:J J 'O M п , т. t:. 11р011у с каи
llO /1 - ] 'J'()Чt:K. в том cJJy чae, КОГ/\<1 11 RЭ:!ИМ-
1 Ю 11росго с т. будут пройдены нее н<:ршины:
О.1.2, "" т - i ,прежд,ечеммысновапопадём
Uелые числа
н исходную точку (рис. 1). А ecm r 11ит11е nза-
11мн о 11росты, то мы прой.дём только через
m./n из них, ~·деD - 11апбояь111нй общий дсли
телh чисел 11 и т. (рис. 2).
Р•1с. 1. Прu 11ущ•руl!м sерш11ны ч11rлами 0 1 О дот - 1
11, nтправлЯЯ( 1. r) 'I ~.JКОЙ-ЛL\00 верш ИНhl h\rдe\.\ 111.'рl!ХОдИl ь к
лμу1 им еершина\1 t шэго,1п Er1111п11 т вза имно пропь~, 10
t1улу• про йдены вrе вРрш ~il"iЫ, прt•ждt• Ч(.>М +\1ы 1:ншАь пe1 n"1.дl!"--t в
ИСХОЛНУЮ ТОЧКУ !Зд('(Ь m = (/, /1 = 4 1.
г
Рис. 2. [{ли чиtJ\а п н т не ~:ваимно прпс 1ы{т ='!, n =J), тu мы
nро~:м.ём толь ко через m / D верu1L1н. глt! О - на 1·1бо11 ьш11и об111и й
Д(~Л~IТР.ЛЬ 11 И nl
Ч~н Л.l
СРАВНЕНИЯ ПО МОЛУ!\Ю
И ИХ СВОЙСТВА
T(J' I ф:1кт. что чнсл;1 а и /J 1r:.1CHJ'I' 01 \1111~11\ОКЫL'
остатк11 11р11 деле111н1 11а натур<1лr,нос ч11ию т.
нс:\1сr1ю1й м::~темат111< Карл Фр11лр11х Г<1усс
11 pe;\J10Жl!J1 :~аmкывзп. так: а = f-J (mocl m)
(ч 11тае-1·ся: «а сраш шмо с IJ по молулю т"). :')Та
:1::~ш1с1, 1~азыuаетс;1 cpamu11ш<.1.Jt.f. Вот nрпмсры
ср:ншеш1й: -LI =1 (тое! 7): 1{)97 =l (шоd -~):
t>k + 1 =1 (rнocl 8), ~·дс: k - целое.
) 1,ля то1 ·0 чтобы убсд11ты:я в с равrшмостп
двух ЧI!СС.'1 ({ 11 /J 11() .vюдулю 1/J , COBC<:'.)'l нс обя
затслыrо lJ;I XOi \1 l'lЪ O C'l ':JTIOI () 1 /\CJ 1L'H1 lЛ на т
К:tЖ) \01'0 11 3 HllX. ДOCl:JTOЧJIO pacc,'v\OTpl'Th llX
[):!:Л \ОС'IЪ:
,1'.; а"'Ь(n1odт)втомитольков'l'Ом
l~' случае, когда а - IJ делится па т.
СраВI 1е1 IПЯ: обт 1аруж11 на ют CUOJICl'ШI, во MI ю -
1·ом похож.нс на свойс,.-тn~1 раненстн. Раненслш
можно сю1~1ды13:1ть дру1· с другом. умпожать,
1\ЫЧlГТ:IТI> U)\HU И~ J\μy1'0L'O - 1:\ pe:{yJIЪT;tTC ПОЛ)'
ЧIIТСЯ вL:rнос р:.1ксне1· 1ю. То же саl>юс сорансд
ш 1но 11 Д)l}I cr:1Bl l l:HHЙ.
.~. Если nрон:звоm.иыс целые числа tt,
1~1 Ь, с, d TЗJ(OBI>J , что tl сраnниl\1'0 с Ь, а с
сраDИИМО с d по модулю т, 'J'O по
:"Jтому же модушо сравпимы чис;1а
и-t-сиЬ
-t-d,а-сиЬ
-
d,асиIJd.
Эп r сrюйстnа легко ;щк:\зать, ес1111 1:1место
cp;i rч 1 е1 11 111 расс.,,,ютрсть соопк"Гств~'1ощис раз
rюстr1 . Дuкажсм , на11р11мср , пос.rн:ю1сс свой
ство. Пусп, п =/J (m<xl 111) н с= cl (incк! m). Тогда
п - /? дс1111тсfl 11а /11 11 с - с/ лс11 ~п·с;1 на т. По
ско;1ьку же си; - /){/::. а(с - d) +tl(a - IJ). то 11
ttC - fJcf 1~сmпп1 11:1т. Зн:1 ч11т, ис = htl (пюс.1 m).
что 11 треоС>11а 1 юс 1. ;1ока:3ат1"
О11срацr 1я нС>.111ене1111н н 1штураm,11 ую с.тс
т::н 1, снодrrтся r' м11оrо~ср:п1юму уо\11южению,
i IOЭT()MY
ьd
k
k
Еслиа s (mo т) , тоиа = Ь (modm).
.lleDyю 11 нравую част11 равснстnа мож110
paз,ri;emnъ на сщну 11 ту же вс:ш1чш~у, отличную
от пуля Cu сран11сн 1в1м11 так 11осгу11атъ. 1юоб
щс 1 '01Юр>J , Нt::ЛЬЭН 0ДJl:JK()
lbl
:f.._ .
Если числа с и т взаЮ\-tно прост1)} и
·k~ ас= Ьс (mo(f т), то fl =Ь (mod т).
С дry1·<1f1 cтurur·thl , Обе Ч~ICTJI cpanrrCIШЯ
1\,·юж1 1 0раз, ~сJ1r1·1 h на од110 11 то же ч 11с1 ю одно
нrеме11 1 ю С MUДYJil'M :
.~~ ЕСJШ ас = /Jc (шоd те), •1·0 а= Ь (шоd 111).
~[
:-311аЯ CJ:IO{IC'Ш'1 cramICTПIЙ, :VТ())Кf Ю Cy11.1,eC' 1'Re1t-
lIO упрощатr. сложные ар11фчетичесю1с nы ·
кпадю 1. ко1да 1rac 1п1тсрссует толъI<о остаток от
,r~;еле 1111н на нсrшторос число т. Неди u это~
случае н любо~~ ш 11 ·сбравчсском nыраже1 11 ш.
получс1111ом HJ 1~с:лых ч11сел с помощью опс
р;11 ~н~'1 l'JIOЖ~JlllH. BЫЧlf'f':lllШf 11 ум 11 uжсшщ
·"'IOЖ l lO Э:li\1l'li l lTI> ЭTll Чlll'Jla 1LX ост:1 тк: 1мн 0'1 '
;~t:лс.:ннн 11::1 111 . не 1 1 змt:11яя рl'эут,тата.
Н:111рнмер, 1" с1ъ 1 1 eofixo1 111м.u \1:н-1ать , к:iкoi"i
"
;
" ) 1t1t)""'
•
осга пJ.К даст число _ 11р11 /\t:: 1t:.111111 на 7 . Ре-
1111п1, э·1у задачу "в лоб·· лоrюлыю тру; \1Ю. Вы
руч;1ст теорая сраннешrй:
2'. ,.,- =(2~)0('5 · 2~ = 1°''~ 4 =4(1ПОСI 7).
Отnет: -~.
дитан J :iдac1a: требуется рсплпr. в ценю;
LJИCШtX .~·.у ур:1ннсн1 1 t
7.х: - 2 ~)'::. ] (')() 7
Ч тоf) ы н:~б<J1111ТЫ" Я от слаг: 1 смо 1·0 7.У, сr:ш
НН.\\ ЛС11~'10 н llJXll!yIO Lf<ICTll этого уранне1t1 1 f! IJO
,\10/1.)"ЛЮ 7 :
- 2у =.!. (inod 7).
так как 7х=О (111od 7). -2>,у=-.!.у (nюd 7),а
l <)<)7 =2 ( 111ocl 7 ) Ilocкo.rrы;y .1 J1 7 наашш о
п.рост~..1, .v1ъr можем домrюжтпъ обе част1111олу·
чешюrо сраннснш1 на ;):
-~1 · =6 (mutl 7).
л ОТСЮ/\~1 . )'ЧlfThlH,IH , Ч'IО -6_1' =у (mod 7), 110 ·
J l \'Чae.\1
.J' :: (1 (IШKI 7).
~Ha Ч\IT,J' ::. 6 + 7А>, !'/lC' k - люfiос l\CJIOC ЧJIC:IO.
l lодст:113ИВ шн"щсшюс nыраже 1111 е щ 1н у 1111с:ход·
rюс yp::inr 1e1111 e. rюлучаем 7х - 2:)(71? + 6) = l9m
н ваходп~1. что х ::. :Ю'5 + .!.5k. Отвеr :
{х ::. 30~+ 2,)k.
у=()+ 7k,
l'Дt: k - JIIOnOt: J~l'.'Юt: Ч11С:J Ю.
КАК СОСТАВ ИТЬ РАСПИСАНИЕ ТУРНИРN
Пр~поло:>ким, в LПорти в1юм соревновании учJс1ву
ют N кома11д и лля выявлен ия поОслит1::ля кажлая и 1
них должна сыгр.пь по одной игре с кажлой другои
командпи. Жел,пельнn составить расnи с;:~ ние тур1 1 ира
т<1к, ч тобы у команд не было лиш1-1~1х и простоев ~> . И в
'!Том нам поможет теория сrавнен 11й .
Лотвор11мся считать ч исло N четным . Если ")то
нt так, то лобав 11м олну фиктиuную ком<111ду -
«HГPil " L ~1 ей будет прирt1в1-1иваться для когu к вы11уж
ленному, а лля кu1 о к ~а< луженному отдыху . Кажлои
команд!' присвоим 1юмер в турнирнш1 т.-~бл иuс:х = l 1
}, .."N
1, N.
Р;н <мо1 рим 11t"1н11>1t' N - 1 команл . В l<CJ l.\t'(IBe
nарт11ера кома нды с номером л наз11ачим в r-м туре
(r=1, .2, ..., N
1) кuма11ду с номером у, удовлепю
р11кнuнм УLЛОВНЯМ
{х+у=r(mocl (N- 1)),
,\:Fу.
(овnмение номеров х 11у п р11 выполнени11 ср:1вне
ниs1 >. +у= r (mocl !N 1}) IЮЗ'V\ОЖНО только в том слу
чае, еLли 2'< "' r (111щJ (N - 1)) . А ло, в свою очср~дь,
ВСН\ЮЖНО, когда
Тl'о р11ю с р:~ш 1сн11!1 чож 11 0 11 р11 '1снк1 h 11 ;~юr
11(10HCJЖI 1слож ны' J рнфме1 ·11ЧС(. 1..:11 х p:tL чi."J '(JН.
Лрс, tпо.rюж 11 м , 111.1гюлr1е1ю умножс1 11 1е-; J <.)()7 х
Х 19<)9 = :) t)<) 1 00:). Ср~lПТ П IM обе ЧаС.~ГIJ 1ЮЛ)'Чt' Н-
110\'О p3H<::!l<.TI\~\ IIO модулю 9. З·1·0 ЛСП\О C1\eJ1:1'\ \, ,
по:ш1)ЯС.ь тем, что само чr1с1ю и сумма е 1 п
цнфр ГJСсца срашшмы 1 ю ~ю;\улю <) (См . ста
тыо <Дt'mпся н.111 11 е дсл r rтсн~ " ). 13 даш ю111 слу-
НЕОПРЕЛЕЛЁННЫЕ УРАВНЕНИЯ
Обд}мыnа>t ре 1щ:ш н:· лю60 1'1 эа1 1:1чп, tKt:'J /ta по
.1ез1ю обращ:лъ 11 11 1 1мапие 11а то. какн е 11 11et'1
пспn,1ьзуются ве; 111 ч.rшы. МО Г}'I 1111 om1 6 1л ·1)
11ещ::11М•ш ? Полож1 1 ·1 е11ы1ы.\ш1 1л11 отрrщат~т.
ны.ч1е До11ускается ли н 0·1·ветt' оrром11ое чною
11m1, 11аобоrют. чересчур :чаленькос? Даже ма
лu:ща<111т<.:; 1 ы:1 ая дст:1.11 1, 1юмогаст 1tc ·t·о:IЬко 11с
ю1юч11·1 1, 01111 1 6ку в р<.:111t:н1ш ::J:щач11. но 11 ш1f1 -
т1 1 с:tщ> рс:uн.· 1-11 1 t.:. Убс11 11 J\1(.'}1 н::Jтом 11а пр1 шер<:
Дсн1устнм, в акв:1r11}"'.Н-' ЖllB)"I ' о<.: 1, :-.1111-1 01 · 11 11
~юrо;щ· :1111:3/(hl. у ()(Ъ,\.lllHO l 'Ot\
-
по 8 lIOl', ;.i у
UелыР чsкла
r
rtN- 1
х =2 при че:>тно"1 r, >. =
2
при ll(!ч ётном r.
В таком <..лучас лля комilндыл в качесrве партне
ра н.нна•111.v1 команду с но""ерuмN.
ТJк будут выполнены вrе 11еобхолимы<:> условия
1ур1-1ира:
1. В nдном туrе ра 1ны1· команды имею·r ра ·{н ы"
партн ёров.
2. Любая комJ.11дJ в р.1 .с1ныл тур,1х игр,1е т с р.1;!НЫ
м и п арт11<'рами.
3. По завершении N - 1 тур.э кажлая ко\<а1;Лd сыг
рает (. К<!ЖдО И.
Вот как выr лямп туμ11ир11,1я Tc\(JM1UJ для Ше( ти
уча{'ТНИ!'()\) .
r?~l 1 2#'} 1 4 .".)~~
15+4б21.{
265432~1
3215634
-
4.
4 116r15j42
1
15.4 32_~5
H t1 пересечrти и г-й <троки ил-го croлl>11<1 < гощ 11омер
шртн ера, с которым ксщ,1нла .\ играет в r-м туре.
ч:1с сран н с:1111<.: о ка :3аJ1 <КЪ н снсрны:-1. 199 ~ х
х 19CJC):X 1=~(111щl9) а:) t)<) J ()(J:\= ""' (motl lJ).
111ач 1 п, н 111 ,1 ч1rс1сн1шх ест~. ш111 1 \)к:1 Дс1· 1с1 н11 -
телыю, 1 1рэ11 11.•11,11ы~'1 отнет - :) L)L)2 00.i.
1! о1к:~ же \~<l"v1с:1~нуе1·11мl.:'1· 1, 1> ннду: 110; \06н-.~я
проверr(Э хотя 11 llПМОЖСТ 110 \11 IOП I X с. 1уч:1н'
uб11а ружнт~., ош116 1<)-, сщнако пе 1 ·:1ра11п1рует t:f
OTC~'I СТШ lЯ.
\:IOPCKllX :~нёзд - l lO с.;, 'fkt'l'O l<OHL'ЧHtll tt'll 11;/-
СЧТ!ТЫIJаt'ТСЯ 59. Ско.11 1 , 1<0 в :1 ю1а р11~ \1С 1\JOj)l к11.\.
ЖНIКП I 1ых?
На 1 1cpl3ыlr взuш;\ 1-::1 жс.:·J·о1. что в .1,1;1.tчt" 11t:
лватаст ,'\~1111LЬL'<. Еслн. 11а11р11мr.:р. чс:рез :\· u\10
:тач1пъ количество :\юрсю1х звё:~д. :1 через!' -
uсь,\ш 1 юrон, тu у<.:лонне з:1д:~ч11поз воляет1rаш1 -
с: 1· 1ъ O..'J,J ю 1,.'/1.ll не1·1к·ш юс) ра IШСШН.:: ')_у + ку -
.N.
Такие:: ур.шн сннл 11 спс.1<:1\IЫ уравш.:т111й , н кото
рых чнс:по 11t:н :mL:стных 11рсн1,1111:1с·1 ч11с, н1 уран
HClll J{J , lla:31>1:К~l IO'l 'L 'H l/('(Jll/)(:'{)f~'li!Jlllbl.'1111
ЧИС/\J
У t>с ьми11uнщ -11U В 1ю1 . у мuрс.ких звезд - по 5 Сколько
в .:ноыr11у\1(' ,юрских "'"'вnт н ых. 1?с1111 вrern коне•11юстей - i9'
3а;четп.-.1. что кот 1 честно >к 11 1-10· 1 ·111.1х 11е мо
жет измеряться т-1ецеm,тм1r ипи отр 1 щателы r ы
м11 веm 1чтrа~rи. СлсJ1оватслыю, ecm1х - целое
нсотрицатслыюс число, то и
.39- 5х
у= ---
8
,ГJ;ОJГЛ<НО 6ЫТI• Цt'ЛЫМ 1 1 неОТf)НЦ::педЫ1ым. Аз11а
ЧI 1т. ну-мно, чтобы выражение .~9 - Sx lieз ост::~т
ка де:н11юс11 1 1а 8. Простой перебор нарна~-ггоR
показывает, что это всх1моЖJ ю толыю при.\·= 3.
Отсюда у = 1.
Перебор nа р иантоn. ттриме т 1ё 1 ть111 ш1м1 1
здес1" пс очень удобен в задачах с большими
ч1 1словым11 д:l1111ым11. Гораздо луо.1ше 1юс1юль
зоваться общ1 L'\1 методом, rюторьп1 древrтсю 1-
;~и 1lскис м<1то1 :.1тики J 1 а:iыв~ш11.методйм pacce-
lttJaJtuя шш .1ие11юдо.111 cr~J 'C'fCCl.
КАК РЕШАТЬ УРАВНЕНИЯ
ПЕРВ О Й СТЕПЕНИ
Дpeurшfr реце11т решео~1 я в 1\елых ч 11 слах
нео11ределё11но го ураnненпя 11ер rю11 степен и
ах+Ьу==с
(*)
с иэвестными целым 1 1 коэффиц11ентамн а, Ь и
с р::~зберсм на nrим<.:rc уже знакомого нам
уrа 1ше11ия
16-1
Sx+8у=39.
Bt,J\1e rк~м не11;111еепюе, 11меющее 1 1 :1име1 1 ьшнй
К()Эфф1щие 11 '1 '. И ПЫf)а~НМ его через дf)УТ'ОС
1 1 е1-1~.11ес~·1 юе:
39-RJ'
~-
.
.
-
5
Тепсrь ~ыделим целую час·rъ:
.+ -:) )'
.х=7 - 1 •+-----
-
')
Всё число f1у11ет 1\ел.ым, ecmr целым окажется
з11ачеп:ие (-t
-
3, 11)/ 5. :~то возмож~ юлишь тоJДа,
коrда число 4 - -~У без ОСТЗТJ\а j\eJП I TCЯ llЭ 5
Внодя дuполю1Т<..'JIЫJУЮ цслоч11слешrу10 пере
менную z. rюследнес ус;ю1ше запишем в внде
4 - :\у= 5z. Мы нр11шли к уранненшо т;:шого же
п1па , как и исходное, н u уж<.: с мспьшими ко
эффиц1 1 1;:11т: 1 мtt. Решать ~1 ·0 теперь нужно от
tюс 1 1тt.:.1тьнr> 11ерсмс нн ы.х у и z.
П рощ)!lжаем дейе1·1ю13::1ть нсё П<J тому жt:
пршщиnу:
~1-Sz
1- 2z
J'=---= 1 -z + --
-
~
:1
11,ля того чтобы у 01<.азалос 1, целым, пеобходп
мо, чтобы число 1 - lz бс:-1 остатка делr1лось
на j: 1 - 2z = ,71-1 ( т-шRь янсдена допол1111тель
ная nсрс"-'н..: 11 н"'я и, гтр1 1 нимающая тот-.ко пелые
;1н~1чсння) . ОтсюJ1:1 по уже: uтraбoтarшofI схе
ме 1юлучаем
1-511 1 -и
Z=---=- - - ll
2
1.
.
Пр()должпм". Чиспо z f>удст 1~СJ1ым, если ч11сло
1- и бе:> остатк,1 делнтся на 2: 1 - и= 21>, 1·дс
z; - пронзuолыюе целое. Отсю;\а и = 1 - 21 1
Дробей бол~,птс нет. спуск закопчен.
Осталось теперь 6лаl"ополуч1ю •rюμняться
вверх ». Выр~1 :.тм 1 1ерсз псрсмсш rую 11 сначала
Z, ПОТОМ _1' И , H<JK(J l-H:~ I \, .У:
z=31•- l,
у=:) - )/',
:\'= .)+81'.
Фор~;rы х = : .) + 8и. у= :3 - 51' прс11.ст::1нт1ют
общее реше1ше исходпого ')'[):Jн11ею 1я в щ:лых
чпсла,"·
А если нас ннтересутот только неотрица
тtльные целые числа, то среди всех целы.\
решений нужно выбрать т;,~кне. для которых
Х ~ IJ,J ~ () 11, C'l'aJIO 6h1Th,
{
_)+8L1~0,
:)-)l'), о.
-;:c-
2z+3и=1
J
~11:'ТUд lПу<.ка
((щ~1естно ~пп тrеране11стна .11.юryr nыпт11 ~яться
лиш1. при u = (). В этом случае х = :'>,у= ;).
Пршнщаясь за ттm1сю1 решения нео11редt"
лёшюго ура1Знення (*), мы предполагали, что
целочнсленнос реше1ше у нсrо непремешю
есть. А rкег,ца ли это т<~к? Если коэфф1щиснты
а, /J. с т:1 ковы, чтu лев;:ш чаоъ уравненю1 делит
<.:я на некоторое чисJю, а 11равая - нет. то решс
ю1l1 данноt" ураннсн11с не нмеет. Более точно·
11сопрет1с11ённое урз1шс1 rис пср1юй степе ни ('")
с целым1 1 коэфф 1щ11снтами а, Ь, с разрсrш1мо
n целых ч11СJ1ах то1да и только то 1 да, ко 1 ·да сво
бод11ыИ ЧЛt:Il С ДCJlVITCЯ lia 11а116ОЛЪППП"1 оnщнi 1
делителn чнсел а и f).
УРАВН ЕНИЯ ВТОРОЙ СТЕПЕНИ
Неопрtдслённые уравнсн:юr ч астu называют
диофtщтовы.м11 уравненuн.ми - по имени no-
l'ж·:1нc1·u J:1елико 1 ·0 мат<:матнка а11·1·ичнос·1·и Дио
фант<t Алсксандрнйскоr·u (JII в.). В дошед111 1 1х до
нас шести КНИl'ах <-А рнфм етнки » Л:нофанта сu-
1 lеrжится 18<) задач с рсшснияrvщ н пояснения
ми. П.озн<1КОМИМСЯ с CJДJIO!r из НИХ: <~адз1 111ый
Kliai1paт разложит~, на }l.Ra квадрата».
Эта задача эквивалентна урашrетrю Rторой
степени x t +у~ = aL с пеи:~несrными х н у nрн
задан ном з нзче1тии параметра а (у Диофап-
Uелые числ<.'1
T(I - целпм или р::щио 11 алы-ГО\1). Просте1:11нщ:
ретпе11ня данrтоrо ур;1в11ен11я n олуч ::н(пся прн
нулевом :~11ачепии OJl. 1ro1 ·n 11.1 11с 11 ~ 1iес1 · 11ых.
Другие решения Диофапт пщет. вьmолняя щщ
становку
у=lгх-а.
1дс /г - произвольное рацион:иы-I uс число.
в рt:З\1Льт:пс ) fCXO)l, HUe ура11 1 1с11ие:= пр1 llЮДПТСЯ
к нитt)• (lгх - а)
2
+х
2
= t/, откуда после 11реоб
разоьзн11й получаются рзциm-1 ;JJ1ьныс вырзже-
1-1 ш1 для 11е11звест11ых х и у
2k
k2
-
1
"Х' =а--- 1' =а --
.
k1+1' -
k~+'1•
Способ ,ll.иофанта позволяет находиТl, так
пазыв;:~емые пифагоровы mpoi-1~u чисел -
наборы целых чисел х. у, z, .выражающих
длины стороt1 nрямоу1 ·ол ыюrо треугольника.
т. е. удо.влствоrнющнх уравнению х! + у1 = z~.
llрвмер такой трu~ки - числа 3. 4 . 5.
З:нrн 1 uем неопре,г~;е; 1 ённос )rрав 1 1с1-те x i +
+ )'2
= z2 В BJIJIC
приме1шм 1< нему приве)1.ё1-111ые выше расс)"л<
деш·tя Диофанта и получим выrажешш
165
DIOPHANTI
АL!!ХАN11R1N1
Rcruin A11rlinн:11 carur11
Ulmfrx.
tpюrt11юm 1 tluu .1tltr(r .1 111111.. _nr Sr 11а1.1~
J.IAXJЯI , :' 1 1( t:(JPl({\ЩJ cl\ J
111#.tl'l tH t
Itcн't t.нir ' fll! t1'1 11c11.11 P dt.1tJ(1 ),J>
Jш 4\~~il1'mt;,~J1·
о;". ",o,-1uЛ~t1,rr"4 uf11::... , ," lf. " lAf..j/Jup:-' . J?".
#a'~·-•l•tll•;l'o>'•··~·~.;м..
А (.t1~ Vн. " -.r."'o Л<•Jt~"'"i"r"<l !•M1Ь 01r
L<111 •(1(.f..lctt •n 6.С:<.1111'1 ,.., .1111 lot••
1·1.J"нi,".' "~11"",, .tol ,,' '·
..
flJt~,.J ,""('frL.• 11 ov1•t"; . ,, -,""'1•.rr1o:t.*'
11А<1L(!..Е
l't" J."~j,_ 1 1 \' ,'1 (,,,f.;(1:-1v" ,
«)/l <o.IJt. Alf !l'l"tt . "
;~ Тt LXXY
х l.k
1' 1?.
2
-
1
-= ---·
..:.,_ =---·
Zk1
+1
1и1 улыtы1.1 л11п
.,дрнфмРrики"
Лиоф.~111d
157\1
1 1 ·ю(iы 11~н1111 ре111е11нс n целых ч11 слах. nOJJO-
ж1 r.ч /? = т/11, rJ(c т. 11 - 11ро11зnолы1ые целые,
11 ?" о ToГJ(~I
.У
.!.т11 ·1·
'
}
JIГ-п-
;__ =
---
-
-
:::: --, ---, .
z т-+11· z
'
'
llГ + 11-
11 можно н:1ять х = !.11111,у = т
2
-
n
2
,z=т
2
+11
2
.
0/\оло 1б.10 r'. ш:ревод "Арнфмеr trкrl" поп:т
в p)IOI 1:1ыда1u11t<:мусн французскому м:1тс .ча· 111 -
1\У Пьер~ Фt:р ."1.:1 Бессмс.:р'1 ный ' t'PYlt Дr1офа11та
1цохн(1нг1; 1 Ферма на оче-111. то~п.;ис н глубокне
теорс-· 1 ·11 1ю-чнсловые 11ccлc,ri;on:ш1 LН . R ч;~стпо с-
111, 1tJ(Я тто сто11ам Дтюфапта, Ферма доказш1.
что н::~туралыюе чнсло а тorJ(a н только тor,ri;a
предстаnн'ю n uиде суммы двух кщщратов
х: +у с 1к1IЬ1.,111 х II.J'. когда вес uμостыс :ц:лн
тслr1 а. д:нощи:е npr-r лс:псшш на 4 остаток .$,
nходят в с-1 в 'fёт11ой сп:ш.:1-111. Он таюкс нaw<.:JJ
фuμмулу [1,ЛЯ KOJlllЧl'CTBa р:1 3Л11Ч НЫХ 11ар (Х, _)')
таю1х 1 111ссл
111:11111с.:1111то\1 стал;~ 11 :1алача Фt:р\1а . 1111!\1t -
щt1111ан !IM К3К KOM\ICHTap11)1 1!;1 тюлях l(l l lJl .11
Д1юф;!J1·1·а: <·Н:11'11•11 примоуголыn.n~i ·трt'у1·0.111.1 1 1тк
н чт 1с1тзх, г11пт е11уза которого была Пы кn:1f(
рл о м , а также 1т cy>vrмa сюрон rтрп щжмо1ч
166
у1 ·, 1 е·>. ~'1т:1 : 1ад:~ч:1 ofi и11.1ск:~111111 т.1ю ' ·" 1111ф аrо
роnых 1рое!\ х, у. z. что дл1111~1 п шотепузы z и
cy,\L\1tt JtJ 11Л1 т.;атетов .\· + \' щк~,1с:ташшю1 собой
пол11ыс кuадр;пы , имсс1 6есr:о11сч1щ м11ОJО
рсшс1н1l1 . М111111ма.r1ьныс 11э ШL~ - это чнс.~:t,
найдс1111ыс Фсrша. х = ~1 56'5 1Н6 017 76 1, у=
= 1 U616'52 .!.~); ')20. z =Ч 6R7 JL>86 10 lH9(3,'\eCh
z=216-'5О17'riх+у=2:П.2 1592).
n·p11\н.:ч:~тt'лы 1:1 сую.ба сщi.; од1101·0 нсш1ре
; 1слt:111101 ·11 ур:111не1111я .
ФИГУРЫ С UЕЛОЧИСЛЕННЫМИ
МИНАМИ )ЛСМЕНТОВ
Сушепвуют nрямоу1ольнь11~ треугольн11ки с 1щл о·
1 нкле1111ыми дли нами сторон . А есть ли лруrне
фигуры(. dНJЛОП1ЧllЫМИ С!JОИСТ Вами?
Ока '{ЫВfl~Т< я, tiыоакп г~рямоуrольныс паралле
лепипеды , у которых 11 ллины рi>бер , и лли11d д11аrо
нал11 выражаются ц~лL,i'Vlи числами. Uл1111 и11н1х -
Г1i1p<1Ml:'Л<~n~1r1eл с рёбрJми 4, 6 н 12, El п" 1,1кжс
r1рямоуголы1ые nаралл!-'лf'n11пt>лы, у котор ы х ребра
и лиnго11<1м1 бокавых гран<:'й имеют ueлoч иrлt'tiH}'IO
длину. Этому условию, например, удовлетворяет
ПCIJ1<!Mt-'Лf'ПИllt'д < длИНс1МИ f)ef>E'p 44, 11 7 И 240 .
Олн,1ко 11е111нРстно, сушеству('т ли прялюуrольный
пар.:~мел~пипед . у которого дли11ы и ребер, и соб
ст-венной дИ<\Г()ltdЛИ , и дИдl UНdЛСЙ ГJJdltCЙ вырi1)1..с1 ·
,\l lCb бы Ш:' /\ЫМI\ ЧИ( Лс1М•1.
Уt>11611тl.'лЫоы11 чРт1>1рехуr()ль1шк , nо"у• 1енны1 1 11з с л()А( l'ННЬ'~
u~ll'lTe п1noн•11yJ,l·\t" д1.1ух ол•111,1коuых 11ps.мuytul\ы1ыx
тpt•vгoлl>Ш•KOFJ с лл1111.1~111t10po11 ~ 10, 11\11. \ ЯJ. В<<' (•го
t 10ро111,1 , лн.зго11.1л11, рJЛ1 1 уп.1 р.1~.\'1•1н1.о1х un11с.1нных 11
nnиc .JШfbl)\ ""РУ'А(Н (]..-ТЕ'И , ра1 \ТО Я1111R \1Е'1hду llf'НТfbl\1 11 ~тщ
щ,румностРi1 . м!':>1;ду Т()Чкам11 ка lдн11~1 о~-.ружностеи to
стор() 11амн 11 д11~гонdЛЯ\.\11- uслые чи сла
13 с1щё 1~рсмя Ар.х.1·1:-.1сд сост~шнл :~ад~1чу u
быках четырёх ,..,1:о1стс1\ которые: пасл11с1, н
ЧСТЫрt:Х LТадал. ПDПН:IДJIС'ЖЗIНШtХ 6огу COJJHЩ1
Ге:тосу. R AI 1де с·1·нхот1юр1 юго постш 11я 011
отпр;1f\ил её Эратосфену К11ре11с1юму. Защ1ча
с1юд11тсл к урав11ешrю х~ -
..+ 72') 4<J4 у1 == 1.
Общее; тюш1честrю быко11 выр:~ж:н.:тся числом
поряl{Ка 7 7()(J 1()· щ,, 11 . Та кос стадо стари к l'с
тюс нс смог бы разместить пе тоm,ко n пре
дет1х с.1юсi1: nотlшны - Com 1сч1 юl1 с1ктсl\1ы,
IIO и в rра1-111щ1х вссй y,\1(J:.:ip1I Tt'JlЬJ юli 13Ct'Щ;'I l -
11un. По-шщ111\1ому, лукан11л АрхJiмсл" посыла}]
свщ:,\1)' UШIOJ lt:llTY npaKTJJЧl:CIO 1Нt:разрсш11мую
зад:~ чу 11 обращано, к rн:му со cлoи:lYIII:
J!(Л/.111/Ы .91110 llClltд('JIUЬ. t~)'.Jl(rJCll1/JCIЖ!Ц.
умом IIO/ШCl\111-/)'H,
11 (;M0.110!11/'h tl70ЧHU llCl,IНClll'l11
КU)f(с)пго (;/J1(1дП ЧllCJIO.
То yxm)u, 1юзzоfн)иншись побеr)пi1,
11 ~J'l)em считаться.
Что rl .=тюй л~1·1)(юо1111 ты
исё до л·mщr-111ревао111ёл.
З;1 ур:шнешк·м ннда
.Х2
-
С~)'~= /
UC'i\bll' Ч11Сi\.)
:·1·1\ер;1ююс1> 11:13в~1нне <·ур:шн<·1 111е П<:: 1л51 " 110
11 -"1е1 111 >v1э ·1·с-\1атнк;1 Джона Пе11т1 , i-;o 1оро .ч~·
Эl1J 1 ep ОШI 1боч110 ПDI 111 l tCa.il 0/\1 f l t 11.1 СПО('О(/011
t:г() решен ш1. Ферч::~ у1'1сл решать ,Г\аl 11н1с )·р~111
11енне в l~елых чнслзл. Л по:~л;нсе 1:1ыя\1ш_~ юсь,
что с этоl1 :i:.1/1:1чei1 спраnлн:кя сщё н XIJ в. 1тт1 -
д1 нkкий математик ьхаскар:~. од.~ 1:1ко его мспщ
ост;uтся п:-~укс 1rсизвестсн.
lkonpcj\t:J1~1шыc ура~:нн~11ш1 второi1 С'П.'
ПС! 111 С ДВ)'МЯ HCИЗBC.:CTJ-IJ,J\Ш В 11:111111 Дllll llC-
CJIC/J.Oll:1HЫ пол1юстыо. Соврсмс1 11 1ыс ,,1стоды
позво11яют ппрсдслнть все рс:шсн11я такнх
уратн~внfi. если он11 сущсствуют, т1бn nбо
с1-юва1•1, отС)ТС'1·в11с решс:1111!1. Од11ако с уран
нс1111нми выше второlr степени дело п()стт11
1 ·ораз;10 сложнее.
Одпа 11:-1 :знаметn rтых проnлем Д::in11;p Гат,
бсрта, сформршров~шпых ш1 11 Меж.1()'Народ-
1юм конгрессе ч:~тем,гпrкuн в llарижс u 19()() r"
заюпочалась в слсду~ощсм: пус1ъ лапо 11ропз -
00J1ыюс ююфш1тоnо уравпс111 IL'; требуется у1<а
зать общий .\fС"1·од, <..'J 1 сдуя 1<oтopo.rv1y можно
было бhl за кш 1 с:чнос ч11с1ю ша 1 ·ок у:Jнать, 11 \·1с
ст ОНО f)CUICHHe Н Ц(.'ЛЫХ YHCJJ:IX IUlll llL'T.
R 1970 1'. лсн1rн 1р:щсю1т'1 м : 1·1смат1tк Юр11l1
Вл:щнм1·1ршшч Матн>1сеш 1ч дсжа.зэл. что ·1'.1ко-
1·0 общего .ме"1'ода нс су 1цс;СтАуег.
167
Чи сла
ВЕЛИКАЯ ТЕОРЕМА ФЕРМА
ЗА ГАЛОЧ Н ОЕ УТВЕРЖЛЕНИЕ
Эту тeopCJ\.fY Пr,ep Ферма записал т ra поля х вто
рой ю1игн «Арифметики» Диофапт~ напротив
задачи 8, которая гласит: «Заданный кнадрат
разложить на два квадрата». И н аче ronopя, нри
данном t l требуется решить в р:щиональных
числа,-х ур~t вненне
)'
l
Х-+JГ=Cl.
Ферма заметил: <· Н ельзя разложить ни куб на два
куба, ни ющт1рато-кнадрат 11 а два кнадр~tто - квад
рат::t, 11 вообще нmсакую сгепент, m.1111e квадрата
и до бесконечности нельзя разложип. на две
сгепе 11и с тем же показателе м. Я открыл этому
поистине чудесное до1\азателъспю, но поля эти
для не1'0 слишком узки ·>.
168
Др)'тими слu вам11 ,
Неоnр сделённое уравнение
Х"+у"=Z"
при п ~ 3 не и меет рациональных
решенийх,у,z,таких,чтох,у,z*О.
Быть может, потомство будет признательно мне за
то, что я доказал ему, что древние не всё знали, и
это может проникнуть в соз на ние тех, которы е п ри
лут после ме1iя АЛЯ передачи факела сыновьям...
Пьер Ферма
Это утtрЖJtенис 11 сс1 ь неJrи1«1я. ил и по
след няя, теоре).13 Ф ерма, ;~оказателъсттю 1<()ТО
рой математики- н е кали nолее :)50 лет.
Сам Ферма оста1шл / (оказательство всл~шоf1
теоремы только для п = 4. 1:3 J7 _18 г_ это1 случаfl
теоремы nновь доказал Jl eot 1ард Э 11лер, 110 про
шл о е щё 30 лет, прежде чем он сумслдатьдо1<а
:~ателье1 ·1ю /VIЯ /1 = . 3. Поэн~1ком1 1 в11rись с ндся
ми этих J(оказательств, мы увrщ н м, 1rочему
д<жаз~1 1·е.ньство ;1,ля ч стнёртых степепеi! было
намного легче, че."1 для кубо в.
МЕТОЛ БЕСКОНЕЧНОГО СПУСКА
J-Jачнём со случая п = 2, так как он nонадобнтся
в далы1сйшсм. П ост<олъку любую тро 1lку рацио
налы1ьL':. чисел, удоnлстnорнющих урав11ешпо
'
}
J
х- +у- =z,
можно преврат11ть в 11ел ыс:.: числа умножением
на их общи й зн аменател ь, достаточно petШJТJ,
данное уравнение 11 цсльгх числах. О том, как
::JT() делае-1 ся, расск:1зано в о атье <,Неоттрсдс
лёппъте ура111-rе11 1 1 я <>. Напомним рс;~ут. 1 ат: вся
кое целочислетп-rос реmеш1е уравнения Ферма
для п = 2 ."-Южно заm 1сатъ R в~ще
х=Р
2
-
с/,у=2.pcj, z =;/ +q
2
,
~дер и q - произrюлъные целые ч 1 rсла. пrшчЬ1
при всенозмо:жных в:~<1имло 11рuстых р и Cf по-
МАЛАЯ ТЕОР Е МА ФЕРМА
Малой теоремой Ф ерма н аз ывают слслуюшее
утвержление:
Если число а не лелится на простое число
р, то суwествует такой показатель Л, что
а1· - 1 делится нар, причём Л. является лели·
телем р - 1 . В частности, аР-
1
- 1 всегда де
лится на р.
Эта теорема - основная во всей элементарноj.i
теори и чисел. /\ео1-1 арл Эйлер 1-1 аше/\ для нее не
скол ько раз/\и ч ных доказательств. Кроме того, он
обоб шил малую теорему для случа я , когдар пред
ставляет собо~1 не простое, а любое uелое числu,
вз аим но простое с а.
луч;1то1 нес реше11ю1 ураннення с »~:шмно про
с1ъ1ма х н у.
::Jти фоj1мулы былн 11з13есгн ы ещё пифа1 ·о
рей ца м. н tю1·о м у за11 :-1на е."rые rrмн тройки
чиселnбhlч1ю на:1ьmают т1фаrоро 1~ымп . Сама>1
1гз всстная нз 11нх (:), 4, S) nолучаето1 11ри р = 2,
q=1.Ест,~жеположитьр = .1,q = 2,то 11айдём
ещё одtю логrулярrюе в дреnт-юсrи ~1сшение -
(S,12,J:J).
Тж11м образом, при 11 = 2 . уравнснне Ферма
имеет беско11сч11 0 11.1ного решений, а при 11 > 2,
как он угве рждал, - ни одного!
Вею1кая теорем а Фе рма связа на со многи
ми матем:1тич ескпии теориями , о которых речь
впеrеди . Сейчас с кажем только, что сам Ферма
знал о её свя:ш с задачей о площади цслочис-
11ен~юго прнмоу1 ·олы-юrо тре}толъни 1<а. Одно
изеrозамеча~тий к,Циофа1п()вой «Арифметике»
гла сит: «Площа1'l• прямоуrолыюго треуголь
ника n tшслах (т. е. со сторонами, длш1ы кото
рых - целые числа.
-
llpu.м. ред. ) не может
быть квадратом (це.1101·0 числа) ?. Ферма пока
зал з;т:м. Ч'I'О это уrнсрждение э книвале1пно
великой теореме для п = L~, и дсжаз:т с1·0.
Дсй ствитет,но, пусть дан прямоуrоль11ый
треутоль ник, к:петы х, у и 1·илотенуза z кото
ро1rJ 1~ело числс 1 r11 1 .1е. И пусть его площадь
l
s=-
.'\1'
2.
-
кпадрзт цел оrо числа. Предположим, что х и
у вэаимно просты (иначе можно со.кратить чис
ла .\у. а в;честе с ними и z на наибольший об
щиi1 делительхи у) . Тогда с учётои формул для
Пифагоровы троики
Uелые числа
Ме1 uл беrконР•1но1 о • nvrкa
169
11
пиф:11·оровых троек S = /НJ(JJ ' - с/), где р, ц и
pl-с/
-
вза1t"11ю простые: числа. 110 ccлrr
пр о 1пнсдспис пссколью1 х l{J:111мно 11ро<.:тых
MHUЖllTCJICЙ ракно к1:1;щр<1'IУ, ТО 11 кажды 1I f·l :3
'"l 't·11x м 110ж11 · 1· слей /\олжен бы1ъ кн:1дратол1 :
jJ=1/ .ц=~~,;/-r/= ·/,г.е.а·
1
-
~·1 =у-. Итак,
сст 1 Г1п1 п римо~толъны й треvтлы 1и к, рассмат
р 1 1наем1,1 !'1 в зад<1 ч с, сущtеmовал. то мож1 ю 6шю
f>ы ~гка :~а · 1· 1, ;\ве четнёр·1·1,1е степени (целых чи
сел), раз 1 юсть 1<отор1~1х равнялась бы кnадрату.
Ферма доказал , что это невозможно. И, ~mач1п,
тем более не1ЮЗ;\Ю)ЮЮ, чтобы такая разность
была р :нша четnёртой стенени, а ::1то 11 е<.:ть
)-Тв<.:рждс1 rис нсл111ю1'1 тсорt:мы fVlH 11 = LI. Ею дu-
1<а ::1атсJ1ьст1:10 - с.ц1 шственное rютюе теорстн
ко-ч 1 1СJ ювuс /\01,аз;п<:J11,стно Ферма , которос
доuvю до н:1ш1 1 х д нсl1. Здео. ()11 щ111;\·1е 1 111л 110-
кый мощны(~ м~год - .м!!mад бесл·тщч1 югп ( 11т 1
щущреде.пё1аюю) 1.:nyCJca. Псшснпм н.г1сю :ппт
метn[(а на rтр 1 1мере 11:н11е i1 задачи.
H:tf(O л()ка;~ать пснпзможность раuе11ства
.\' 1
+ )'1
= z2 .Предполш·аем обрат~юс: оrю вr,mол
няется /lllЯ 1\СЛЫХ rт01юж 1 1те.11ьных LJJ K'C:'Л х 1 , у 1 .
.z-1
.
Что бы провести спуск , до'Ка:Jьш а <..:.\1 , ч ·1 ·0
расс:чатр 1 ш:~емо.чу ура ннен 11 ю oбн:JaT<.:JlhHU
будет у,1.юю 1 <::твu рять 11 д rулн1 тро11 ка 1\CJtыx
ГТОЛОЖИ'l'С)) ьн ых чl !Cl'Jl Х2. J' L• z ~· на11f)ол ьшсе 11З
которых (z~) мс11ыJ1l' 11а116олыrr<..:го lt З чнссл
пср1юl1 тро1lкн (z 1) . От1юс11те111) 1 ю 1 101ю 1 ·0
реше 1 111я можно пронt"сти то же рассужлснпс
11 о·п,1 ска·1 ·1, тре·гhЮ трuйку ~шсел х.1.у,, z ,, глс
z, < z 2• Н, 1<ат< m 1сал Ферма, «так 1юстоm11ю до
6еою 1rсчтюстr1 Gу[(ем ТJаходить целые •шсла,
~1еrIЬш11е предыдущих. Но :~то псвозмшкrю, так
к::11~ ccлrr дало r<аtюе -либо целое чнсJЮ (Ферма
подра::~умсвал, что O IIO П()Jl<)ЖT l1't:JTЫIOC. - ! !ри.'11.
ред.) , то не сущr::стнуст ()сскпщ: ч1юстr1 1\с.:лых
ЧllССЛ, MCHbШllX СГО ».
Ферма }'l' Асрж;1:1л , что псе сnш1 ,заJ\1счатсль
ные теоремы относ11'J'ел ы ю чнсел 0 11 доказал
1-1 ~ 1 ен1 ю ::7Т 11 м мет()дом . Мс.-гол; спуска и сеrпдт 1я
нrр~ет fю11ьшую рот. 1~ те()рии ч.исел.
ВЕЛИКАЯ ТЕОРЕМА ФЕРМА дJ\Я п = 4
Ферма дал бс:1упрсчпое f\Оказатею,ство с1юе11
Tt'Opt'MЫ ДJШ П = 4, НО ДОК~1 :1:1Т<:ЛЬС1ТЮ Э frл с р<.1
исн<:е 11 короче . Поэтому рассмптрнм здесь
I IMCH!IO Cl'O .
Пус-1ъ мы 1 1з111ли т11ml1<v чисел х. 1', z , ;~ля
1
1
,
•)l
'
,
-
'
которыхх +у = z-. 1m11 (х-) +Су')- =z-. Вое-
170
1 Ю.'JIJЗ уемся фор:v1уламп для шrфагпро11ых тро
ек. ПО.'Т)'Чтrм
х2
= pJ. - (/.у.: =2Jщ,z=;/ +с/.
Можно сч1л:лъ. что чr1cJ1~1 .\· 11 у, :1 :Jначнт. u
ч11слар 11 tf t:1за11."1ш111росты с. Тснла, 1юскодьК\'
1·
2
= 2.рц
чt:тно, .У2 J\ш1ж110 быть J н.:чl'тны~1 Но
:\...! = р
2
-
с/, CЛt'ДOH;J.'J'l'JlЬHO. fJ 11 {/ - ЧI JСЛ~
раз 1 юl 1 <.Jёт1 юс1 · 11. 11р11чёJ\1 р должно 6ытг, Нl'
чёпrыl\I, а cz чёт11ым. Дейстnнтел ы ю. ю1:щр:п
•rётного числа деш1тся на 4, а юзадрат t1ечёт-
1roro пр11 1'·1слс 1 ПIJТ на -J . даёт остаток 1 (та1< 1<ai<
(21 i 1)2
= 4/J. + 41 + 1). llоэтому если быр бьшо
..
"
)
четным LIИ<.:110.:-.1, а С/ нечетным, то разностьр· -
-
(./11л.н.>лабы н1щ4k- l,т,t:.ш:могла бы быт1,
квадратом ( вt:;~ь кн:щраты np11 f\<:Лсн1111 н:1 ·1
д:.tют в остатке ТОЛl>КО О 1 11ш l ) . Мы ЮЮtiь тюлv-
J
'
·'
4
ЧНЛII "111lф:lJ'Op0110» )'l):IП l-ICHl!C:X- + ч-= fi " -
11
с учёто,1 T()J'O . чт() q чёпю, можем 3аш 1 с:пь его
рстс111ш n niщc
)1
))
х=,.--
s.q=2п;,р= ,.-
+.с
1J осколькух 11 (/ вз;~имно просты ( ш~аче х 11
)
)'- = 2.JЩ llMtJШ бы общий ~ШОЖIJТСЛЬ) , LJИСЛа }'
.
)
,
11sтакже нзаимно п росты. l lр 11 этом J'S (1~ +s·) =
= /-Ji// !. = 1,! / 4 - кнадрат, следоватс:rь1rо. оба эт11х
ч11с11<1 11 .11нсло У2 + s! дш 1жны быть кн:щратаюt
1·= <i.s=~
2
•,.!+s
2
= у. l l:1й1~r::нa 1rон<1 и трш1ка
ч н сел - .Г1.. р. у. удон~rепюряющ~~я тш1~ же урав
~rе11ию С( + р"' = у-. Ее 11aJ1()cmы11ee ч11 ою ркнь
птеZ:/' = / +s
2
= р<р.!+(i=z<z.!..
Тем еамы:v~ мы осущест 1:1111111 с 1 1ус1( и нсле,'\
ЗJ Ферма н Эйлером .:11ожем :1аю1юч 111 1), ч·1·0
тcopcvra доказана.
ВЕЛИКАЯ ТЕОРЕМА ФЕРМА
дJ\Я п = 3: ПРОРЫВ ЭЙЛЕРА
Т1..:орсму Ферма тин 11 =
. 3 з~-1лер ;юкaJ:J JJ в
l 76R !'. Д,т1 ЭТО('() потре6lm:1лас г , CORCJ1ШCll HO
НОRЗЯ Н)'\Сй. и C0("\'0:.IJ I;:\ 011 <1 н том . чтоб1,1 11р11
ИССЛС,Т'{ОRаrrии f\ОПр()С()Н of! об 1,1ч111,1х 1\t'ЛЫХ
чпслах прпмсrтятr, :- .1 1 11 1rv11>1e 11ыраже1111я rшда
п+/Jv
0
-
n, 1·де а. IJ - 11t:J1ыc, а 11>О.(Ото\.f,ка
кой. смысл 1:1юшдьш:1стся в nыражс1 шя с коршr·
Mll Н3 oтp rtl \(l'l'CJl bHbL'{ ЧllCCJI . см. главу <•КОМТТ·
ле 1<с 11ыс числа·> . ) Э 1lлер так пнсал об этом
Ж. л. л~11ра11жу: . я был ВОС ХllГl\ён l3:1ш11м Мс·
'l'O/ \OM 11р11менсн11и 11рр:11\1ю 11:1лы 1ы. х 11 даже
MllllMЫX ЧllC~JI 11 T O ll ЧЭСП I :!H:JJll l Зa, кoтop<lJI
ИЛЕЯ дОКАЗАТЕ/\ЬСТВА НЕ/\ИКОЙ
ТЕОРЕМЫ ФЕРМА д/\Я 11=3
Требустrя дока~,1ть, что нсопрел\"лс111 Ю!' уμа внf:'нис
(*}
не 11меет uслых пилuжительных pt:>we 11 ий. Лока.-~а
тельспю булем пронолить метоло'vl сnуск.-1.
Предположим , что урJвне1111е (*) ~1мес т рсше -
11ие (.\,у, zJ. докажем 1uгла. что 0110 имt'ет и другое
pewL'H11~ (х,, у,, L 1), ме11ьwее nep1юro (т. "'· н,1иGоль
wсе нз чисел х,, у,, 7 1 \1еньше наибольшего из х, у,
LI. От (х 1 , у,, z ,) тем же рассуждс11ием переидсм к
tx1. У2. Zz) и т. л. Но сушt::ствует лишь конечнuе число
uелых положительных ч11(ел, мРньших данного.
311ач11т, 11ачальное предположение не вер 1 ю.
Итак, nycтt.. сушествует рсшеш1е(х, у. z). Чис.ла
!(, у, z будем полагать взаи'vlно простыми. Тогда
яrно, что два 1н ни>< лолжны быть нечl:'тными, а одно
чепшм. Пусть х и у будут нечетными, а z чётным
(иf1<1че, сели чt~тно х, будем вести р<1ссужде11 ие 01-
нос итРльно разности куfiов х3 = z
1
-
у' ил11, есм1
с1етно у, - урав11ения у1 = z 1 - х1). Положим р "'
=(х+у)/2,q =(х-у)/2,откуда '1::;р+q,у =р -q.
Чи< ла μ и ч должны быть разной челюrти. После
nоытановки в уравнение ("') имеем
'(!+у1
= 2р(р1 + 1q2):: L'.
Тс~к KdK L - четное, а pJ + Jq~ - Нt'чётное число,
то z' делится 11а 8 11 р должно быть чётным. Слслов.:~
тсflьно, cr - нсчётнос. З.1мст•1м также, что числuμ ~1
р1 + Jq 1 мuгут иметь только олин обwий множитель -
чнсло З. Эйлер расrматривает nС>этому лв<~ случая:
1) р не делитсн 11<1 З,
2) р делится на 3.
Мы остановимся только на первом< лучае, так как
второй легко к 1~сму свод ится.
относится t< UДШL\11 TI >ЛЬК<J рац1 юr l :lЛbHbL\I\ чис
л:~м. Вuт у-,,к<;: несколько лет, как у мt:11н 11ш1 в11-
л 11сь сходные 11де11". опублшщпан здесь (в Poc-
шrr. - При.м.. /11::д.) r юлную алгеnру 11а русскоl\1
яз1.1r<с, я rюдробнп излт10 m н не й зтот спос?б,
н я показал, ч:ю для ре111е1ши Ураnне11ин ~\·- +
'
'J
'
л
.
+ 11у- = (р- + nq· ) достаточ 1 ю реши1ъ следую -
щее уравнение: х + у~п = (р +<J\
1
-11 )А».
13 своём доказ~тсльстне Эйлер рассмотрел
выражения ви11,а а = а+ l7 J-3 . И ·1ут он сJ1,ел~1л
е ще одш1 шаr· чре:шыч:н1но1I н:1Ж.1-юст1 1: 11ере-
11ёс на этн кыражснан с1юйст1:1а целых ч 11ссл.
Что :'~то :1н:1чнт? Д~1я 061,rчныл 11t.11ыл ч11 се11 су-
Итак, Ч11('Ла р и q В'i,1имно просты, кроме того,
р •tётное, а q нечёт 11ое , 1ю rюскольку р нс делитсS1
Hd 3, з11ачи1 , числuμ и ре+ 3q ' в.~аимнu 11росты.
Лля проведения лалы1ейшего лока~тельств<~ Jй
лер делает смелый шаг - р.нмгаст р 1 + 3q: на
м1юж11тели : р' +3Cf ! = (p+Cf\1- 3)(p - C/\' -3). И ли
м1юж1пели 011 рассматривас:-т, к<1к если бы они
Gыли UCflЫMll числами . В част~ юсти, пuсколь11.у
(
1
'
2pf>+qv ~){μ-ч\-3)=L ивсемножителивзаим-
110 просrы, Эилер пол.~гает
·~
~
г-
2р=1, pH/\-3=(r+s., .- J J
1
1
'
p-qv-З=(r-.s-V-3) ·
Возведя / ±_.,, - 3 в куб и принимuя, •1то (J-3)·' =-J,
UH ПО/\ yчdel
р =r(r - 3s)(1 + 3s),
q=J~(r+~нr-s).
Зде<..ь r, s - числа ра.з1юи •1ет1юс1 11 , пр11• 1i:'м, как
нетf)удно видеть, число r должно быть ч ётн ым, d s
нечёт11ым .
С другой сrороны, 2р: f\ Т.1.!. 21·(1 - Зs\ (1+3s) =
= f! . BLe множители в.:1аим1ю просты, тогда Кilжды1-1
И '{ н11х об~нан ()ыть кубом:
r+Зs=g J .r-Ъ=h J .
Азначит.2r=/1J+S' = /
3
•
Мы получ11л1-1 HOF.\01:' решение и; _t .: , 1) уравнен11я
(*).меньшее первого~, у, z). Спуск ОLушеGвлен, и
случай 1 дока'!а11. Тс1ким образом, можно утверж
дать, •по уравнен11е Ферма лля п = 1 н е имеет
IJE'Лl>l)I. ПОЛОЖИТt"ЛЬНЬIХ реше>нии.
щ<xтnyl''J' бш·атая арнф.мсппсt: н.х можн о не
только складьшать. вы • 11 пать 11 )'1\11 JU:ж:~ть, ере
/ 1,11 H I JX .МОЖJЮ НhЩСЛ11 '1Ъ t.:ДllH l lHY. прос тые
Чl 1сл:1. В:{al!MI !() пrостыс HaI<Olll:I ~. cпp:iut.:ДJl l IН;t
фу'Н1~аме11талы-1:1я тсuрема об с щ rю:3Н ач1юст11
ра:ш оже 11ня лю601·0 чщ: на R щ1()11 з нс1~сш1с
r1ростых м 1 южн·1·слсr'1. Пола!'а.1 11 , ч· 1 о )~а11ньн:
cnor1 cт11t1 nрнсущ11 толысо ч 1 1слам 11:~туралы н 1-
го [)ЯДа 1. 2, :). ".И Ч'l'О ПОНЯ'Пtе « 1\СЛОС Чl lC.'IO"
не допускает шш:н-\оrо обобще1 шя. 31!лер щ1с/\-
11оложи .•1. что чпслз m1да а= а + /J v-5 обла,~а
ют таюIИI 1же СНОЙСТН:l:\'1( 1 : срсд 1 r ШIХ тоже (;'(. 'T I>
лp<X:'l 'hlC, ДJIH l!JIX с11р:1нс::д1111н :5aKUJ-I ()Jl НU:3Нач
ности ра:тожс1111я на пpo c 1· t-.1l' мно;ю1тс11н .
171
Числа
Исходя из этого, оп 11 доказал велнкуrо теоре
му ЯТIЯ 11 = 5. Однако обос11овьшат1, сrюи nред
положс111н1 Эйлер не стал. Эти вопrюсы nнош.
нст:u1и 11ере11 м~1 темат11камн RX IX н. - и опять
в свюн с Д(Ж.азательстRом 'rеоремы Ферма.
ВЕЛИКАЯ ТЕОРЕМА И ТЕОРИЯ
АЛГЕБРАИЧЕСКИХ ЧИСЕЛ
1 марта 1847 i·. и~шсспrый фра11пузский мате
матик и физик Габриель Ламе доложил на за
ссдашш Пар11жской академ.и1111аук новое лока
:i~tтслы.:тво вс:ликой теоремы. Пр.и :·пом он
011с:рнровал числами вцпа
/Jo + bt~ +/)2~l+ ." +/J,__lc,л-I,
(*)
где /71 -
''елые, ::t ~ - n·!·1111ч 1 юе 0·1 1 комплскс-
1юе ч11с1ю, такое, что ~· = 1 . Отмет11м. что при
Л. = 3 ч1~сла Ламе содержат те, котпрые приме
нил: Эйлер. Действительно, ~ ~ - 1 = (~ - 1) х
х (~2
+~+1),но~*1,значит.~l+~+1=О,
откуда
-
l±v-3
~1,2= 2
.
В своём доказ:~тельстве Ламе исхоr1ил из ·1 ·01·0.
что для чисел вид<J (*) спранещ1 ины нее :~ако11ы
обычной арифме·1 ·11ки, в чае1 ·нос'1·11 :-~акон одно
:~начности rазложения t ia пrппъ1е множители .
Л.р)'ГОЙ И:1всстпый францу:~скнй м.<пематик.
Жозеф Лиу.вилль, за.четил: «".сделанные по111,1т
ки (т. е. до1<азатсльст130 Ламе. - При.м. ред.) по
казали мне, ~1то сначала нужно было установить
для ко}.lmлексных чисел теорему, аналогичную
элементарному предположению о том, что
нроизнедение может бnl'IЪ тоnько одним спо
собом разложено на простые м 1 южите11и. Ана
шrз Ламе то111,ко yтncpдJJJI меня в этом мнении.
Нет ли туг лаку 11 ы, котор)'Ю н:.tдо за1ю11ни·1 ъ1».
Затронутые 1юnрпсы от1юсятся к :~рифмt:
тике алгебраических чисел , т е. чисел , яnтт
юrцихся корнями уравнснпй с целыми коэф
фи11ие1тгами (см. статью «Транспетщентпые
числа» ). Благодаря замеча11ию Лиуuилля этот
раздел матсматик11 почтп год находился в
центре нн 1н"1 ан11я французских ученых. Им
усиленно з: 1н11ма1111сh 11 сам Ламе. и Пьер Вант
цет" и д:~же вел нки й Оrюстен Коши. Нпо
слс111.~r·тш 11 их исследования. r1р11нс.111 r к форми
рованию пu11я·п1я кольца - мзте ,\.1~пическо1'0
172
пбъе1\1·а. в котором в самом пбщем 1111де отра
жены сnойстоа целых чпсел по от110111е11ию
к сложению и умножению.
Uюrако вернёмся в 1847 г. Той же весrюй
немецкий математ11к Эрнст Кум.мер СQОбщил
в 11исы11с к Л11>'вш1лю u свuём удив1пСJ1ыюм
откrы·1·11н. Оказалось, что ~{~1 кон ол.нuз начно
сп1 (1а:ЗЛОЖСНllЯ на простые MIIOЖ I TTCJIJI /t!lJI
ЧИССЛ !:!НДЭ е). ПООбще l'ОНОрЯ, НС НМеет мест::~.
Пr>н этом Куммер у!'Очшт само поннт11с про
стого числа .
Натуральные простые числа можно охарак·
теризоват1, любым аз двух свойс.."Тв:
1) шш неразложимы о произведение дnух
множи·rелей, OTJШLUJЫX ОТ СДИllИНЫ;
1) если проrrзнеденl'lе аЬ дC'JIИTUJ на простое
число р, то по кpa rlнcfl мере пдш1 из сомнож11-
телей лопжен [\елиться нз р.
Обычно нерuое из этих свойств прш1имают
за опрслелепие 11росто1·0 ч11сла , а нторос дока
зьшают.
Кум мер уст:шовил. что чпсла тщца (*) мо1уr
обладать свойством 1. но 11е иметь с1юйстш1 2.
Как же такое rюзможно? Пр:инедём nrocтoil
пример. nричtм с самыми обычными цеm,1ми
qисламн.
Предста1шм, что у нас сеть только чё111ые
числа Тогда числа 2, 6. 1О. Н, ". будут « про
стым и» на основании с1юйстщ1 1 (О/tин н~ их
делнтеле~-1 нечетный, и мы ei·n 11е рассматри
ваем). Н() СIЮЙСТIЮ 2 для них не HЫIIOJIHIJtTCJ!.
Например, 6() = 2 3() = 6 · 1О, J'. е. 1 1 роиз1:1еж-
11ис: 6 · 10 делится на * t•ростое» чнсло 30, но
)f)нrт Кум"rр
Uелые ч1-1сла
ш 1 оди11 нз сомнож11телеГ1 11а не::го не дсл11тся .
Чиаю 60 здесь разложеrю 11а «простые» мно
ж1гrелт1 двумя раз 1 1ым11 спасобам и. Д11н ч исел
в1ща (*):заметить псодноз11ач11остъ ра:11южс 1 111>1
11а простые быдо 'fl)}'д IIO. так как она впервые
06 11 аружищ1 стся толы<О при Л. = 23.
бы дuбавить нeюrir аналог нсчёт11ых чис<.:J 1 . то
о.ц 1 юз начность разложе11I1я на простые мноЖJ 1-
тели nыла бы посстанонле11а. :;:эрнст Т<уммер так
и пос~угтил. В L1е.цё111 n,rc rrм 11оuые пnъскты 01 1
1 1азш1Л идеалыrымп множителями 11 с ~'\ 11п
мощью дока:-~ал великую теорему для обшир1 ю
го юrасса простых показателей п. Од11:11<0 дт;э
зать теор<.:~fУ n обще."• виде не смог. Зато его
Прпмср с чёттп,~ми сll1сдами подсказывает
l':Jкую идею: если к чйслам вид;-1 (*) .мы сумели
«ПОС/\ЕдНИЙ ШТУРМ»
ВЕЛИКОЙ ТЕОРЕМЫ
ФЕРМА
Конеu ХХ в. ознаменовался для
математиков настояшей сенсаu и
ей: попытки доказать великую те
орему Ферма нако неu-то уве11ча
лись усп ехом!
Летом 1995 г. в одном из веду
ш~1 х математических журналuв -
«Анналы математики ~ - было
опубликова но полное до казатель
ство теоремы. Разбитое на две ста
тьи, 0110 за н яло весь номер - в
обшей сложности более 1 00 стра
ниu. Основная часть доказатель
ства п ри н адлежала 42-леп1 ему
английскому математику Эндрю
Уайлсу, профессору П ри нсто н ско
го универсюета (С Ш А}, « штурмо
вавшему» з н аменитую п роблему
почти десять лет. На последнем
лапе к рабые подключился Ричард
Тейлор, профессор Оксфордского
Эндрю Уайлс .
у н1-1верситета. 0~1 noмor устранить
пробеt\Ы, 1-1мевшиеся в первона
чал ыюм доказотельстве Уайлса.
Это первоначал ь ное доказа
тельство Уайt\С 1нложил 23 июня
1993 г. в uикле лекuий, прочи
танных им в Институте мJтем;пи
ческих наук имен и Исаака Нью
тона в Кембридже. Оно явилось
п лодом нап ряженной затворниче
ской работы . По пр изнанию Уайл
са, никто, кроме его жены, не знал,
что он работает в этой области.
Идеи Уайлса от1рал1-1сь на за
мечатель н ую связь межлу уравне
нием Фермах"+ у"= Ln и элли пти
ческ и м и кривыми, задаваемыми
уравнени ем
у2=х(х -а")(х
-
с")
("')
(впервые на не!? обратил внимание
франuузскии математик Ив Элле
гарш в 1970 г.J. Ранее, в 1955 г"
яrюнский математик Ютака Тани
яма сформулировал в виде гипо
тезы одно свойство множества
элли птических кривых -так 11азы
ваему ю модуляр ность. В 1 qв5 г.
немеuкий учёный Герхард Фрей
п редположил, что и з справедливо
сти этой гипотезы для кри вых ("')
можно вы вести теорему Ферма, а
в 1986 г. американеu Кеннет Ри
бет дока3ал предположен ие Фрея.
Таким образом, чтоб ы доказать те
орему Ферма, оставалось толь ко
найти доказательство гипотезы
Тани~мы . Имен но оно и было из
ложе н о Уайлсом в кембриАЖских
лекuиях.
Н и кто не ожидал такой смело
сти от малоизвестного матема
ти ка. Сп еu 1-1алисты взял ись за тша
тельную п росерку доказательства
Уайлс<1. И ч ере3 н есколько меся-
uев \как не ра:> уже бывало в исто
ри и доказательства вел и кой тео
ремы) он и обнаруж ~1ЛИ в работе
Уайлса пробелы. Но в uелом его
идеи были признаны глубокими,
красивым и и современными.
Уаилс пр ин ялся исправлять до
казательство. П рошел почти тл, и
в августе 1<J94-гn о н был nриглс:~
ш ен на 0•1ерелной МеЖдуН<1род
ныи математический кuн1· ресс в
Uюрихе. Матемап~ческий мир с
нетер п ением ждал его доклада.
Уайлс, конечно же, хотел завер
шить доказательство к моменту
своего высту плен и я, но не успе
вал. Коллеги видели, как д.:~же Пf:'
ред самым докладом о н продолжал
работать, сидя на ступеньках ря
дом с ,1удиторией. И когда, подняв
шись 11а кафедру, Уайлt пюбшил
замершему в ожидании залу, что
пока не обладает полным дОКд
зательстеом, ему друж но ~аа пло
дировали.
Однако уже 19 сентября
1994 г., всего через месяu после
к0t1 гресса, Уайлса, по его словам,
озарила ключевая 11дея, которая
и позволила ему (вместе с при
глашён н ым к сотруы1и•1еству
Тейлором) 1эосnол 1iить нако н еu
имевшийся пробел. На этот раз
доказа тельство выдержало все са
м ые <.кру п улез 11 ые проверки и
было опубликовано. Так заверши
лась 350-летняя история доказа
тельства вели кой теоремы.
А мо1 ло ли дока мтельство са
мого Ферма (если таковое суше
ствовJло} быть аналогично уа йл
совскому{ Вот мнение Уi!йлса на
этот счет: «Ферма не мог распо
лагать таким доказательством. Это
доказательство двадuатого векJ».
17~
ЧислСJ
11у 1 ъ 1юс·1 · р()е1111н ар 11ф мет 1 1к11 члсел mI ,'1,3. (*)
llОЛУЧИЛ R XrX (Т()ЛСТ1111 ПЛ(){J,0Т1Юр r юе rаэви
ТТ!С. Лрнф:v~стнку самых общих колец аЛ1·ебра11 -
ческ11х ч 11 се11 11ез:11.нк 1 1.чо друг от 11 рут<1 ТТ<>
стро11л11 руссю tf1 .>1аТ(.:мат11к К И. Золотарёв IJ
11t'мсцкис:: :v1ат~ма·1·11ю1 Л . Кронсю:р ll Ю. В. Р. л:с
ш.:кш щ l !OCJll'ДH ~ 111 н нёл н ;IJIJ'<.:бpy 1IOIШ(;' н:~ж
НЬIС 06·1.скты - 11,'(('<!ЛЪI.
И ВСЁ-ТАКИ О НА ЛОl<АЗА НА!
R ХХ 1-1 . 6ыла ()611аружепа связь вешшоir тео
ремы с быстро раз1шнающейся .чатем:~т1 J<1 е
ской тt:орпей - аю·ебра 11чес((оi1 геометр~ 1сfт.
И.>н:нно н ра.,,1ках :·ппй тсор1111 11 1'1ы. 1 NК:ТIП'·
11~т ) с11ех . Rкл:щ 11 дnr<J1:пem.cr 1ю теnре'ш
Ферм:~ 111 rесп и r1ескпт,1ш м:~тематr 11ю11. rю Т()Ч·
](\' ПОСТ~ННIЛ u 19')'1 1-.
а11ГЛIIЙСЮIir ученый
Зндрю Yaiiлc. Доказ~1тст,стно У:1iшса чрезвы-
11:11' 1110 С.:Л ОЖ!IОС. ()110 CBON ITCЯ (( рс11н::11и10 ОД
llОЙ з ада'-11 1 об :-.шшrnТIILI<.:cю1x кр11вых, т с
aлt·cбp;ШLICCIOJX кр111:1ых трсты.:fl ("J'C ГIC'HH.
lkлr 1 кJя т<:орt'\1а Фt'рма 11ос11т 1,.н< 6~д·1·() бы
част1 11,1 i1 харз1пер. Н а 11 nп 1,1п.:1 1 её /1,01.:аза·
тет.с·1 · 1iа о\1()1 ·:~ 1 ш1 11 ,\1атем:1тr11.;) 1 юны\111 r11teя·
MIJ. Mt:TOll.;l\Ш. тco pШIMII. в :-пом IJ состопт
лсnреходящt'<:: :Ш'1ЧС:JIШ: Bt'ЛllKOJI 1't'Opt:.\.JЬJ .
Леис 1в11rЕ>лы1ые •1исла
ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА
РАUИОНАЛЬНЫЕ ЧИСЛА
R со 1<ровr1щ 1 н 11\с эа11н.м;1 · 1е;11,1-ю 1 о м~1темаТ1 1 -
ческо1 о фо111>1<1юра ес1 · 1, так;~я за/\;~ча · <1Бут1 ,1лка
С ПfЮбt<ОJГ С'Г()1 1'1 ' 11 МОПtТ, 11р11ч ёМ бу1'ЫЛl(;J f Г~I
1()монет, ~< >роже 1 1 rюf>ю1 . <:кол ы<0 стn1 1 1· прnб
к:1?• Прелесть этоff задачн в том. что, 11е долго
ду~1ая. f\Ce даю·1 0113СТ: « Пробка СТО!ТТ OД II)' мо
нету~. И, к01 1сч1 ro же, 0111116аются! 1lст<о·1 орыс,
сделав пройерку н убеднnшисъ 13 сносй 011шб
ке, '1)'1' же i:tЯRJUUoт , что з:щача вnйсе rr t 11мес1 ·
рс::шс1111н. Дсйt:'I't:ШТ(.'J IЫ-ю, эта з:щ:1ча н<: р<::ша
стсJ1 н целых ч л слах. 110 за 1о существуют дроб
ные Чf'ICЛ:l, ПОJl,ХUДЯl.ЦИ С /~ЛЯ с:ё ре111сн1нt: Дl:СЯТI>
С Щ)J\()11\IHO\.t МОНС.:1' С'П)\1'\' б)"ГЫJ\1\<1, И П()Jl:VЩ··
11r-rы - 1 1робка
А дре11 1 юстн к г, ет,1м и /\робн1,щ ч1 rс.r1 :01м
()ТJJOC 11m1c1 , nо-ра:щому: 11рс,r~,nпчтс1 11 1н быю1 11а
стороне целых чпсел. <•ЕСJш ты з :~хочешь ,'\С
л11ть ед11ш11.w. математшш nысмсю·1 тебя 11 ш:
поз волят это делать», - ппсал осповатсл1,
афшrскоfJ Акадс.ми11 1lлатон. llo НС вес нрс1шс-
1·рсt1ссю1е математ11кн со1·лашал11сь с П1 1 ,1·1 о
ном. С /\po6J-Jм 11 свободно обращ:tлись Лр:ш
~·IС/\ 11 ГLро11 Алскса1щрийсю11·1. ftaжc П11ф:11ор,
C<J с11нще1111 1 .1ч тр<::псТ()м олюс11вr111 1lr си r-: 11:1 -
T}1XIJ11,111 .1м ч11слам, cu:1;i,a11aи теор 1 по i\tуэыкаm.-
1юf1 1111(;urы. сн>~эал nС 1Г( JП111,1 е му:l 1.1 1->ал1>111.1с 1111 -
терnалы с дробш,п1. Лраrща , сам 11 ,, по ш1 п1с::~1
дро611 П1rфагор1 1 е1 о учешлш не по.%ЗОJJJд1Кь
011!1 ЛОЗIЮЛЯЛIJ себе l 'OВ(>pll'IЬ ЛllШЬ 06 O'l'llO-
ПICl-ШЯX целых чш.:с::1.
Л106011ьп1rо, что но .шюJ 11л снр01 1 сlкю1х
)'ЧС6ннк;1х ар11фмtтш.т1 X\!lJI н. ра:-:,г1сл с ; 1ро
бнм11 IIOMC Щ,\Лll ({ K<.HH.:tt К11111 '\1 . Ан1·1 111С1 сю 11'1
1 1\tlTOH tll 11()380ЛНР1 Л~l\11ТЬ ( 't\~IHlllJ\
17)
Числа
~АВИМдЕЙСТВИЙ СдРОБЯМИ
Сокраше1-1 ие:
таа
m·Ь =Ь,еслит;tО.
а с ad+cb
Сложение и вычитание: Ь+d = Ь d
асаd-c·b
b-d=ьd
Умножение и деление:
асс1с
ь·""d=ьd'
асa·d
:-
=--
ьdьс.
nрос11ет1 1тет, }1,жо11 Керсн н 1 1 редис1 юш 1 н 1<
16 - му и зrr.апию «Арнфмен11<и» У11111 ета (Ло11-
доп, 17 :35 г.) объясняет этот обычай та1<: «Дня
удобства и в ш 1тересах тех уч:1щнхся, которые
х:отят ознакомитr,ся с ар11ф»•1етиl{ОЙ лишь на
столько, насколько опа полезна при дснежпых
расчетах. .:.J.ю1 тор1 ·uвли 11 др~т11х подобных
11р 1 11южсн11й ... ·1 ·с 11 срь даётсн 11pucтue н щ)л<:з-
1юе н~1Jюженнс ар 1 1фмст1 1ю1 1 ~СJ1ы:< чисе; 1 рань
Шt:, чем ( )'t'Kpын:IC'I ся ) \ОС!) 11 к Kf))'TЪJM путям
дfюП<.:11, пr11 RI1дс которhlх некоторые ) чащ11-
еся гrрl(ходя·1· n такое:: унын1н::. что останав
ливаются и fюсклицают: "No)1) plL1s Llltгa (лтп
"rшчсrо более сверх··. - Пр11.м.ред.), ;1а;н.ше м1,1
!!<:: пойдём! ''».
Тем примечательнее, что одн11 и:} первых
известных нам математических трудов наqа
нался Шvl CHHO с упражш::пий II::t ДСIIСТВНЯ с
J\робям11.
АЛИКВОТНЫЕ ДРОБИ
Так 11 а:-~ываемый па~ 111рус Рай11да - :·1то 11rе::нн:с
сгипстскиt'1 матсматичесюrй теl(СТ, 11 ере1 1и сз1 1 -
11ый около 1650 г. тю н. э. ппсrщм Ахмесом (сч.
статью «Древний Египет») . Н пём расс матрина
лис~, лишь дроби, ~шслители которых раш 1и1 1.
Исключение сделано только для д роби. 2/3.
Дроби вида 1/п (где 11 - патуральнос число),
которп1м с 1 ·и11·п1нс отдавали предпочтение,
1:1 со крсмсн 1 юй матемитикс им.е нуЮ'J'СЯ ат1~
вопты.м.и (cYI .llt/.'IU. al i чLюt
-
«НееколhК()<) ) .
Чтобы прсдста1:1ить какое-либо число н 1шдl'
суммы <11mюю·1·ны х дрuб<.:й, порой 11р11хuд11-
176
лосъ 11рш1R1шть незаурядную изоб рстатель
ноt'ТЪ. Скажс,·1 , ч11сло 2/4:) в 11аш1русс выра·
жснu так:
2
11
]1
-=-+-+- -+ --.
·15 42 Н6 12<) :Ю1
Лроиз1юди1ъ арифметичесю. 1е дейстш1я 11ад
члсламп, nсякиtr раз раскпадьшая их в сумм}
долей сд11111щы , очень пеудобно. Имеет л11 при·
страст11е е::1 ·1шп1н к алнюютным дробям какое·
либо объяс 1н: 1111е:> Р<.1сс.:мотри11 1 такую задачу:
«Ра:щст1ть 7 хщ:бов меЖ/\У 8 mодьм 1 ·1».
Сuнрсмснны~"1 школышк скорее нсс1·() ре·
п 11111 бы за;р чу так: на[(о ра~-1резать каж,r1ый хлеб
на 8 рэн 111,1.х частей 11 1«1ждому ч<::лонtку дать
по одпой части 1>Т кaжll;oro хлеба. А 1ю·1 к:J1< Э1';1
зал,ача реше11а у Ахмеса ПоскОJlЬК")'
7111
-=-+-+-·
н1.1н
К.ж р.пле111н1, 7 хлебов 11,1 8 р.ш 11u1х чс11 1(•11 ?
Т() каждому 11(.'Jl()U(.'Ky н ужно Nl'l'Ь по П OJIOl:ШJ IC.
четнерт11 11 носhму 111кl" XJ1e::na. И ест·1 11:1111 ему
школ1.11 1 1ку пр11шлс )с ь б hl сделать 49 ра зре:юн.
ТО AXMt'CY
-
11<.: t:J 'O J 7. "1'. С . t'l 'llПC'l 'CIO IJI СПОL'ОО
ПОЧТ I 1 11 !> раэа ЭKOltOMl!Ч 11ес.
Ш ЕСТИЛЕСЯТЕРИЧ Н Ы Е
И ЛВ ЕНАЛUАТЕРИЧНЫЕ ЛРОБИ
Вссь.'-1:1 11скус ны в обр:~щснн1 1 с дробнми 6 ыт1
КШНJЮllЯНС' . llСnолъ:ю~ан 1 ш 1 с llll'C'l 'HJ\CCЯTCPll'l
нyю с11стс '"} сч 11слс 11 ин. 1 JоСJ 1е;\0Rателы·юс-rъ 11
OC I !()B:J.TCJ ll>HOCTn , с которым l L ЖI ITCJ!l l j"f_peв нc
l'U Меж:1урсч bll СОЗ/\а B:J.Jll I свпю ЧJ ICJIOвyro C I 1('-
те.\1у, вы з1 .r вают 1юсх 11111е11 щ:: 111~ст11десятер1 rч
ное освопаш1е 0 1111рзспро страт1т1 11 е толыю
11:1 цсльн:: натур3Ль11ыс чнсла, 110 и 113 лробп.
Дпс11:щца1 ервч 11ы с ,цро611 по~·чнлн рас
простра11е11ис u Дрсш1см Рнмс. М<:л11ую J\Юнс
ту, а uпоследсrnю1 единицу веса - асс p1tNUlЯ
нt дстши на 12 равных частей - унцнй.
В 111 ко;1:1х Дрt:Ннt.'1·0 Р11м;.1 11ы•шсле ш1н 1\1 с l(!)О
бями у; к·1ш1 юс ь ocofiuc в1-u-1мэнн е. В<· 1Jаук<: по
эз1ш" Гор~ш.юl 1trиво/\ 11 тта1шй .ц11<1 ло1 · учJ 1т<:Jш
l учс1111коJ11 :
~си11 Альбшю.' ch:t.u1cu _м не: есл11 А·rы. tмнвши
llЯlilb J'l·tЦШI,
В111ЧmеJн ой11у, чти осmанется/" - ·1'рt:>т1,я
чисm1) асса·>. - <- / !релjюсно.'
П11 1 -асс({
1/ 1.! (/('( '(/,
1( ../ - ((l..UI
1/; l/t(,{/
1~1 '. ты и.м.е11ы! сво{J 11<: fJacm/)(fm11111ь!
А l!C'IU Щm(iови..11
}{ 11/Jl.!.>IO·U/J\/ !/}t/}lfl :1/Ы OUfl;I '. Чll/() бyйl:! lll
11с1Сго?~ -
'"Jf(J. 'mm11N1 ·•.
~к ннди :--1. юньrй р11млш11111 у11.~ело 1 1ьmо1шш1
,'\еlrстrнш с ,1 11ена,1щ1те р11ч11ыМJ r Jфобячн:
')11:;
J
1
12-12 =3: l2+12;l
ПОНЯТИЕ РАUИОНА/\l~ного ЧИСЛА
С 1,1 н Лm,61111:.1 м о1 · () 1,1 11001~~л<11т1, ;1остоl1 н 1,1м
n ри ;v1ером епропl:l11 t:IM Сре;l,11 евеков ья, 1.;< 'то ·
рыс даже rюлтора тысячелетття сrтус 1 ·я n 11el!
С'ПJJШХ с дрООЯ;\-111 усматр1шат 1 11 С33)'ГШ/\ l lОС'
11скусстuо. 1Iапр11 ме р, Jl)'KY J l ачош 1, пpenoд;i
вanшet·v м:.tтс~1атш<у в Перудже, 1l еаполе. M1t-
J 1;шc, Флорснцш 1, Р11м t' 11 !kнецr ш. птыю с,v1у
щ:.uю упuтрсблt"111 1с: cJJOJ3З ~у мн ожс: 1111с " 110
(у1·1 шше1 н1ю к 11робям , 1ю1 д<1 11ро11:~нсдt'1111с ока -
3ы налос1, !llCJ IЫJJ t' J\1HOЖ H"l '{.'Лt,>tl.
С умножс1 1 11с::\1 щю6е\1 с вя::1а11а ~1 дру1 · зя
СМ Ы СJI ОВ:н1 'l'[l)'l~llOCTb Умнож11ть ЧИСЛ() н.;1 на
турат,1 юt: n о, н ra чаt:т взнть е1 ·о н 1<::tчс:с 1 ·1 11.: спа
п.1емого 11pa :i.1ю11 с·1 1111ка1щго 01ыс1 1 ~1 с.:к.r 1 ~1;(ы
ва1 ь ЧТ()-ТО, ш1nршv1ср. . 2 /5 ра:1а. Как же следует
пошrма 1ъ слова •·У·"пrожнт1, 1ы .!. /'!'1» ? Сов рt;~1 сн
пыi'i ш1юлынш с.:кажС1'': ··Ум 1южr 1 т1, на 2/5 оз 1 rа
част t~:нпъ два ра 3~1 третью часть" .
с H::IMCIICl:-IИCM 11 p:t CШ l lj)C:IIHt',\1 значст 111fl
1 ·с рм111ю11 м ы tталю1ваl"\1l'н. r1 н дру1·11хслучан'. ,
нa .IJ р11м ер BBONI ( >Tpl 1ц;,l'J'CJl .bl lbll' ЧI I CJJ:J. l l OH)'! 'l '-
нn . что от 2 >1 б11ок 11 сль:jн от 11ят1; ;1нблсжа.1ю
f\M e(. "l'c:' l ' Т<.::\1 тс:мпср:-1т~11а МОЖt'Т yMl'HhlШ l'f 'l1CH
с .2 1'ра;1:·со 11 на ~ 1 'ра11.уса. !7то мы носпр 111111-
м:~ ем сстс::с·1·11е-1 111 0.
rt·1 ·aк. j)UЦll()Jt(Иblfbl.Шf Ч71СЛС!41/t ll:l ~ulВ<1 10"ITSI
<шсла шща т (п , r;t.e т, 11целы<.:: 1111 ;to О. Ес11.1111 = 1.
рациоr1алыюе qнс110 т/11 ЯRJшется 1\елыи.
llo,1'(061ro то~;у каr< u 06ласт 1 1 все.х це.'Тых
чисел оnераrлщ u ычJtт:11п~я nр1юб рстаст LВ\111 -
ство JJt:oгpaн..ИLJCHl-J()J) ~~ЫПОJШI IМOCTI r: 1):! любо
\'!) 1\t:ЛШ'(.) ЧllCJ\a М(.)Жl \(.) !3ЫЧС<..:ТЬ J tю бо<..: Цl'JIOL'
ЧJJ CЛU - в обл;1ст11 paЦ!IUH:lЛhl-I ЬJX Ч11Ct:JI Нt:О-
1 ·рзш 1ч с111 1ую нып ол111 1мость 11 р1 ю6 рст;н:т 01Jt"-
r~щ11я /\CJJt: l IШJ ВС,1'\Ь П()Дt:ЛI ш одну дроб 1. Ш1
друтую. мы ош1л, nол~'ч11м 11роб1•. ЕJ111нствс11-
тrое тн.:ю1юч е 1111е - 11 у:11.: 1 1а не1'0 лел11тh 11ельзн
Числ.з
Так~ 1м обр~1:юм, coR<::pшa>i тобь1е:: :ч1нфме::
·1·11чссю 1 е дt:l1спmя (СJюжt:нr1е. вычи· 1~11н<:, ум-
1юже1 гне 11 /(Слtпие) на11 р:11 t~юналы1ы~1н чнс
л:-1м 1 1, .чы пе liЫХ()ДИ.ч эа npcдt:Jrы :'>тнх ч1н::еrr.
Т~1 кое множество чнссл, 11а кот()ром :1аданы ncc
четыре арнфметнчсские оnерацин и 01 ш пе
uьшодят эа нредсm,1 этого мrюжестnа, ш1зы
нается пола.114.
Почс~1у же II)'Лh находптся ~ra особо."'1 поло
жоши? Дело н то~1 . что, хоп1 бы однажды разр<:
щ11н /\е.J1сн1 1с 11~1 1 1у.111,, мы f\ПOCJICДeJ ' RИII /(01\Жf-IЫ
б1,11ъ 1 ·0·1·опы к разт1ч1Lым ~ чу;tссам» . С t'l."ажсм,
сократ11в в обс 1 rx ч астях 1н:р1 юго равенства
() 1=О· 2 11уJ1ь, 1юлу~нм 1= 2, 11 так можно
бу/\е'f' «,;J.(Ж;J3"111G 1"1»' ncf что угО,'1,1 IO.
ЛЕСЯТИЧНЫЕ ЛРОБИ
Н 11.irm1 дю1 pC,'\IIO rют,з~1отся обытшоненпыю 1
,\ро6я.ч11 , 11рсдпочнтают дtcя·1·11щп,1t. llu нсдь ш.'
1кякую обыкно в~.:1-111ую дробг. ~южно 11 рслставтъ
fl к1ще 1шнt:чно1J 11есятнчно~"1 дрu61 ·1 Т;;~к. чтобы н
в1111t лссятн 1 1ноr't дроби 3:11111с;;~ть 1/7. понащ>-
611тся 6сско11счнос число знакnв: О. J-128671
Почему же тодн 1rcpt:rrrлr1 <ТГ обыкr-ю11е11ных
Л,ро661 1( /K'CЯTlfCJ llbl;l-1 ? Да ПОТОМ}'. Ч"'J'() /\еЙС 'ПН IЯ
с 1111мн бопее простые. oco\1cJ 111 0 сложt:111 1 е 11
вычнта1ше. Сложи.ч дроби .1/ '>0 п 7/ 40. С..:11 <~чала
11уж110 найтп 11анмепьшее обrпс:е i-.:paтrioe их
3113.'vleIТaTCJitfl (ЭТО Чl!ОЮ 200), потом раз.11е;ш1ъ
ею па 50 11 результат (чпсло -4) умножить JТа
LfПCЛIIT<:'.'J h 1-1 знаме натель первой дробн. Полу-
178
чае1 ·ся 12/lUO. По·r ·ом 11ано ра:щсm1т1, .ЩОна40
11 частнnL· (ч1 1 с110 '1) Y"IJIOЖll'l'h н;1 чн с.r11m::лы1
~{На чt:нате11ь нторой :ч-щ611 . ТТОll}'Чаt:тся 35/200
i\•1ы П!) 1 1ВСЛ11 дро()н К оnщем~ :ЗH<IM eH:lTC!IIO
Тш1ы<о ·1·е1 ~ ерь мы мnжс~1 слож11·1ъ чтю111те.111
и получн1ъ отnет· -47 / 200 А еслrт зтп дроби
представ11-гь в десят11ч1101'1 за n11сн: -~/ 50 = 0 .06
7 / 40 =О, L7"), cyмtv1 a находится мпюuе11110 -эrс
O.J5S. l(o oe<Irro же, ~111сло 1/ 7 приходится за,
m1сынат1, ш 1шь с нскоторо~1 точностью.11аnри·
мер 0, 1 1.) JIJfll O,J cll87. но ведь 1-\ жи:т и все
l1\.1ее::т пюн пpe;1eJlh l TOЧJIOCTIJ,
Сс1·0;111я мni 1ют,~tус·"кя дссят11ч11ым11 дробя·
ми сс1те1·нснно 11 С1ю1)одно. Ою 1 ::~ко то. что к:J·
жегся естсстне1 111 ым нам, служ1шо 1-1ас1·оящш1
1<змне;\1 пре1· 1<1юnст11 1н 11ля y'-lf111,1x Сред11еве·
коnья . В :J;шад1юi1 Нnропе XVl в. nместе с широ·
ко расnростр~шённой део1 т11 q110 1'1 систем0!1
предстаnленш1 целых чисел n расчётах nовсю
/JУ rrp11мt1 tя.тmс1, шсепщссятср11чныс .rJ.роби. DOC·
ХО~ЯЩllС сщi: к дрс:ш тс:й трад1ЩИ1 1 В~IВНЛОПШ I
llош1; 106 1 шо1 с в<:т:щй ум н11/\L'рл:шдско1·01-1:1те
матика Симuна Стt:н111-1а . 1 1тобы 11р 111к~е1·11 з~ш1сБ
11 1\ел ых . 11 ;ц10бных ч 11 ceJ1 н 1::д1 Jну10 с и стему llo·
HH) \ l lMOMy. 'l'ОЛЧКОМ к открыт 1-110 )\t'б!ТJIЧНЫХ
дpuut:r'r дш1 Стс:нrлrа rюсп)жr11 111 t·ot·r·;шntнныe
им таi1л1щъ1 слож11ых 11 rт1е11тон. R J 585 1'. о н
о нуб11 нкоR:ш ю 11 1Г)' «Л.t:оп 1111 а". в l\C>' f'OJIOll объяс-
1111л десн·1·11чпыс дробп. Обо.111аченшr Стешша
нс от.rш ч::1Л11съ сонертс11с·1·uо,ч. так же как 11 обо
з rrа чеш 1я его коллег п после1"юн:~те.1е11 Вот ка!\
01111 зап нсат1 бы •щсло 3.1 -41 '>:
_1,®I Ф-\ Ф J Ф')@
()111Ill(\'
}11l')
. ) Ll.±l2
(С <..:тсвшr),
(Й. Х. Бс~'1<.:р),
(А. Жирар).
Л11ш1, в 11cpвoii чстнt:рт11 Л'VШ н. дробны~
ч11с11а стал11 за 11 1кыпат1. с 11 омuщъю nrocтoii
11есятичпо 11 тоЧ1ш. R 11е1штоrr, 1 х страна.'<, u в
ч асnюстн н Росснн. вместо точ1<и 11с пОJIЬЗ)~О11
эапятую. Её вnёл 1 1 смецк11й математ111< Георг
Андреас Бёк;1ер n lbl>l г.
КОН Е ЧНЫЕ И ПЕРИОДИЧ ЕСКИЕ
ЛЕСЯТИЧНЫЕ ЛРОБИ
Д.rн1 "1 ого чтобы какую-ш rбо обыкнщеннуt0
дроб1. m / n :J~IП!IC;)'J Ъ н Н!Щt" 1\L'C>ITJ!YHOЙ, ДОст:f
TOЧllO HOCЛO.'JJ,ЗOli:JTI>t.:я школыrым (110СО6())!
деления "у1 ·олко,·м. U одних случая..х та1\ое де;1е
rше заnсршнтся за кош:'ч1юе чнс;ю операци й.
и мы получнм конечную десят11чную д.роб 1,:
5/25::::: 0 . 12; н друт11х - 11роцс:с.:с деления бу;\СТ
f\eCKOHt'Чl:'fl : l/j =' 0 , .-1:)j;)" . IV10Жtf0 ЛИ l1pt:/J.CK3-
:J:ITb ::rт з~1ра нсе пu н11;n· 1~роб11 111/ 11? Ока:.~ына
стся , t:слн н раз1южснни чнст1 /1 на простые
мнuжнт<2ш встрсчаютсн только чнсла 2 н 5, то
ДtCWП I ч Hd}I дробь будt"I 1\01lt'ЧIТ()(t; f\ Пj10THFll I O M
С'J1учас в деся'пrч 1 юм разлпже1пn 1 обяэателыю
воз~ 111ю1ет пер1 юд~-Nески поn'Горmощаяся ГР)·ТJ
па ц11фр - гrс111юд.
llyc-rъ t1:-1сется перисщпческан дссятнчпан
дробь U, J l)l)819t)8l998." El' за1шсывают сщё п
так Щ 1998). указывая нифрьr ш::р11ода в круг
лых скобках. М.шrаю 1111 представить сё н юще
1н: которо 1'1 обыкноне1 rнoll ;1роб1 r? Замет~ 1.\1. что
сс;111 ~1ы умножим д~1н11у ю 1~роб1, на 10000 (т. с.
11 срс11ссi.:м з:шятую н:1 LJ :1н:1к::1 1щр:ню) 11 от1ш
мсм l 99R. то у H~IC ()ПЯ1Ъ обр;~зу<:-тся /(l)Oб J, та-
1\()ПJ Жf' 1111;\а. Обоз11ачнn et: чере:1 х. поJ 1 ~rч11м
:1)а1шение 10000.У - 1')CJ8 = х, OТIC)'f\a
1998 222
.У=-- =--.
999') l 111
То·1· же самыi1 рсзут,тат получится. сс11и па
щ:ходную [(робь n~1·1ш11у1ъ 1<ar< на сумму бсско
нt:чно убh1в:.~ющеi! 1 ·сuме1рнчt"скuй лрu1·рессн11
с 11 ;1ч:шы1ым ч11сном U. 1998 11 J11а,.,,1е 11атслсм
1/ 100011 (C\t . CI'::JTl>J{j ~Ар нфМС."1'1t4t't:Кая н J't 'O -
i\1C'1р1 1 чсск:н1 пр<л11ссс111-1 ·>).
Ещё 11 <: HO ll ШКОЛ l1НЫС J 'U/\Ы 1lt'M<..:J \Кlll[ А1~1 'Гt:
манrк Т<арл Фр11;1р1 1 х Г<~усс эа,г1.а.r 1 ся вопросом :
че:\1) рав11а ;(лн1 1 а пср1юда лро6н 1/р, ccJrH р -
11ростое чпсло, о·ошчrтое от 2 н ')? В теории
чнсел сеть тcopezv1a (мал-ан тсоре:1ш Ферм-а),
которая утнсрждаст, 'IТО для тако1·0 простого
ЧПСЛа fJ раЗНОСТJ, 101'
1
-
1 ДСЩIТСЯ 11;1 j}, ПОЭТО-
ИРРАUИОНАЛЬНЫЕ ЧИСЛА
Мы :ш~1e'vl, что 1н.:которые 1хщ11 01 1 ~u1ы 11лс ч1н.:ла
выраж;.1юто1 беС' r<0 не ч11ыми пер1юпичесюrмн
деопич11ы:v111 дробя.ми, как, 11 а прнмер. ч11сло
l/ l99H = О, 000'500'500';00." Но ничто не мешает
rюобразит1, и чпсло, u десятислюм разложенни
"оторого не обнаружщ~ается ннкако1·0 псрнода.
Такие •шел::~ 1-1юыnаются 1rррац1юuш1ы-1.ыл'111.
Дейt.ТВИl С:'ЛЬНЫt' чиrл.:~
му можно запнсатL 1о 1' 1
= fJ/..?+l,гдеk- ~rе1ю
торое натуралпное ч11с;ю. 0·1·с1011а l //J 1о'' 1
=
= k + 1/р. :J это (Уiнач:1е'l', что CCЛll в ДC<:ЯTIJ'l
J юlr /1,роб1 1 1/jJ t1е1х·мсст11ть ·за11ятую к:1 jJ - 1
Зll:LJ.\0 1~ вправо,'!'() l/OJIYЧllTCЯ LJllCJIO с TOJI Жl'
c::iмoi'i ;1робноl1 "Чае1·ыо. Сле;нш:пель110. ч11с!ю
.fJ - 1 кр:п1 ю : \:11111е 11errю/ \:1. Пр11 ~н:юн1 п.: же
р<1ссужденrrя, \ЮЖ1 ю уточ1шт1,· ) \Лill t:l ncp1 ю/~а
pan11::i trarrмeнъшer.ry з11 аче rшю 1-, такому. "ЧТО
1о'· - 1 дслrпбr нар.
ссл11 мы рассмотрим такпе числ::~, как 1/ 6 =
= 0 ,1666.", 7/!>О= 0,2.:'>.:'>.~"" то 0611аруж1 rм. что
псрно1' 11а1.Jи~тается 11е сраз~ после зa1mтot'r.1Io
чему это щю1rсходит! Ока:Jьшастсн, LJJICTO т:
р1ющ1 ческис ДССЯТ I LЧl lЫС р:1:.! ! ЮЖL'НШ1, Т. с. та
юн: , н кu·1·оrых пер110,111:1ч 1 шастся сраз~ 110с.'Н:
:iiHIЯ' I O!"t. llШШJlllIO'l'CИ Jlllllll> 11 Tt:X CJ l}nl~ШX. KOL'Д<I
:JIJ:JMCH::IT(:Лh п ITCCOKfXl 'l 11 .'IH )(1дроn11 //l /11 Ht: нс
ЛJl'J'CЯ ШI .2 Т1 H:J ">.
JVf Ы KOCI l)'JШCI, JШlll Ь 1Jl[ЧTOЖllU M<!JIOil Ч-;Jl"l 11
раз11ообраэ1-1еi11rп1х своJ°1с тв рзцно 11а л 1,1 1 1,1 х
чщ:ел MlIOl'Jf<: 1L'\ :JjГадюt в С ОСТО>1 1 11111 рас
крыть вы самп . Для этогп вам потребуются
шшть ручка, бумага и 11е.маого у11орстnа .
ИСТОРИЯ « НЕРАЗУМНЫХ » ЧИСЕЛ
Ис-1·орпя 11рра1 що11<1 ; 11.~ны х ЧJКС"д восхО/(НТ t(
уд1 1 витслыюму отщл.rт1 rю rшф::11'орейнев е1 цс
u \Т] н. до JТ. э. А 11ачалось всё с npocтoro, к:1:~'1 -
нос 1~ 61 .1, 1.юnро<.:а. какнм числом н1,1р.1жае1 ся
д:нrна дна1·ш 1 ал11 квадрата со сторо1rой l?
17<.)
Числа
Дш11·01 1 ат. раз61шает кна/1,рат 11а дnа О/\IПJа
коnых Щ)ШvЮ}ТОлы1ых ·грсуголы нша. n каждом
нз которых 011а выполняет рот, ттшотенузы.
Поэтому, как следует 1 1 з теоремы П1 1 фагора ,
:
J
)
'
щн 11-1;1 диа1·онаJ 111 кв;щрата равна vl- +1 - =112 .
Сра:~у же rюэникает соблазн достать микрокаль
кулятор 11 нажать r<..ТJаnпшу изнлечения квадрат -
1юго корнн. Н а табло мы увидим 1.- 11 12 1
_) ) .Бо
лее (.'0Вершсш1ый IOIJI hl<)'ЛЯТОр, Hbl 1IOJll IПIOЩIO~I
ныч1н.:лс1111я с высокой точностью, 1 1с.н:ажет
1,414213562 .~7} А с 1ю~ющыи мощ н ого соврс-
,-
МСН I ЮГО ко~шью·1·ср;.1 -v2 МОЖJЮ Hh!Ч!-ICJUl1Ъ с
точ1юстью /l.O сотен, ·1ъ1о~ч, мнллионоn :1наков
лослс эапятпй. Но даж!:' с.:амьтй nыс(жn 11 ронзно
,11ггелы1ый KOMllnIO'J'ep, CKO!ll> б ы , \ОЛГО ()11 1111
rх1бота11, 1111коr.п;а пе сможе; 11и рассчитат1, nce
,..1еопич1 rыt цнфры ч1 1Сn'1 \'1, тш обнаружнть в
1mx какой-11 иf>о период.
и ХОП! у Пи фа /'011<1 1-1 его учен 11 IIOR ком 111>10 -
Гt()<l 1 1е было. обас11оват 1 этат факт юv1е 1 1но
0111 1. Пифатрей11;ъ1 ДОI\а:1ал тт, что у диаго на ли
1.;вал;рата и cro t.·то1ю11ы общей 1черы (т. t. т:U<o
ro отреэ"а, JСоторый целое число раз отклады
nалсн бы н на диагонали, 11 на стороне) не ст
ществуст. Следовательно, отноптснш:' их дли11 -
число "' 2 - пспь:ш выразить ОТIЮШСН llС.М ш:
которь1 х [\СЛЬL'{ ЧИССJ / 111 IJ 17. А КО.% скоро это
так добаnнм мы, дссят11ч1юс р:1ЗJюже11не УJ[СЛа
\ i 2 не 0611аrУ'лш1:шtт 1111какой p<.:тy.riнr)J)oii зако
но.V1ср1юсп 1.
()ткrыв 1-ю1:11>1i 1 матсN1:-tтJ1 чесю1й объt:кт, 1111
фаrорt1щы 1 1рт 1 rнт 1 в rюл 1юе :1амешатет,ство.
В ос r юне осеоf; щей 1·армотп ш м11ра. сч11 тали
опи, должны лежать целые числа н их отно
ше11ш1. Нтп(аких друr11х чисел они 1 1 е знали.
../2
18()
Длнн а л~1~11 UHtlЛt.1
._Bdдpc:} l c:I
tu LГt1р11но•1 1 -
Ч'1(i\0
иμр,шиональн()(·
П О СЛЕДАМ
ОТКРЫТИЯ ПИФАГОРЕЙUЕВ
Как Л0Кс1Зать, что ЧИLЛV v2 иррашюналыю? Пред.
положим, су ш ествует rаu иональное чисАо m/n,
такое, что m/ п = f2 . Лробь т/п будем считать не
сократимо(-1 (ведь сократимую дробь всегда можно
привести к несократимому виду). Возвеля обе части
равен ства в квадра т, 11олучим ml = 2п•. Отсюда
заключаем, чтn т - ч исло чётноf', т. е. т = 2k.
П оэтому т ! = 4k· 11, следовательно, 4k2 =ln1, им1
2k2 = nl. Но тоrла получается, что и п также число
четное, а этого быть не может, поrкоАьку дробь
т/п несократима. Воз1-1икает п ротиворечие.
Остаётся сделать ВЬ!вод, •1то 11аше предположе
ние 11евер1-ю и раuион01лы-юго чи сла т/11, paвttoro
..J2, не сушес-твует.
И вдруt' :па гармония рv1пнтся - cyщecrn;1CYr
uеличт шы, которые отпошеш 1см 1 клых чисел
о при11цнае нс являются!
() пережитом учсrшка,\1И П11фагора смяте-
1ши свидетсльстврот дрстшс легенды. Он11
дср:жали пюё открытие n <.:tкрстс. U,ц н ако Гrш-
1 1.а с и з J\!tет:нюнта р:.1З1'ласш1 nю,r~нм ~у-'ж:кную1
тзй 1 1у сутл,<..:ствов:шшr нссuJ1змеrш.1ых вt::лн
ч11н, и 1l t:бo пок<1рало сн •: 0 1-1 утонул п морс во
время rптurма.
Пn дrугоl1 л1:те1 ще, наклнк::~н 11а ~ ·плову Г1m
ш1са нссчжтhя, т1ф::~горсйцы сам11 nыршшещ
Сlfi\Ш<m 11 ческую l\tOГJ 1 лу, «1<ак будто 11 екогдз
бьш ш иr'r пх товарищ н самом деле у111ёл из зем
ноrl жи~ши», - тах т кал античный фнлософ
Ямnлих. Впрочем. n это трудно повср1пъ. nедъ
члс пы ш1фагорсйскu 1 ·0 союза всегда слав~ишсь
вз~шмоuы ручкой н креnю1 м11 у3ами др)жбы.
По11ятия ~ р;11~1-юн:.JЛы1ыil• 11 <·нрр:.щнон;и1ь-
1-1ый • I LC I Ю.'11,:.юн~ш )Ж(' П латон н JtJIЭЛO l 'C (• Гоq
) \ арстно·>. р~1 с.:суждая u с.:швмср11мост11 д11а
rонат1 Ю3:1драта 11 e1 ·u стороны. Rстречаются
ОН/ r 11 н Д~CHTL}l~I KH I 11 е ··Начап ~ RBКJll l/ (;l. в пере
т ще с л~1тh1н11 слово <-iп:11io1 1 ali :-." tJЗ11зчаеr~не
ра;~умншl». Jlюfiопытно, ч·1·0 11 срс11.11енекоuой
Европе 11а 1щчу с jпari o 11a li.'> в ходу был еще 11
другой термин - st1tdнs
-
« l".'1)'Xoi1" вл 11 те
мой~. Судя по тако:-.1)· 11аз 1,шmю, матсмаn~кам
С ред11еве1<ооья 11ррацно11альпыс чпсла пред
ставт1л11съ чем-то настолькu 1н.:сураз11ым, 'fГО
букналыю «HIL RЫСК:1::Sать. HIJ H"1 C.ll)'lll3Tb>.
Г1юn.ir pa1rл,jr 11л люд11~1 vж,1< ную таину cyшerTBQf!d H11я
1 1сtоИJ"1 t.: р11мых uрм1 •щ11 - 11 Hf'\)t) nuкарало Р1 о
Лс-иствителы I Ы<' ч исла
РАUИОНМЬНО
ИЛИ ИРРАUИОНМЬНО~
Если числа а и /) раuиональны иЬ не uелое, то аь-
в бол17ш11нстве случаев число ирраuионалыюе. lia-
'
пример, а= 2, Ь = 1/2, тогда а"= 21 ~ J2 .А 1-~аобо-
рот! Сушествуют ли такие и рраu ион альн ые числа
а и Ь, что число а"раuио11ально?
докажем , •1то он и суwествуют. Возьмем •1 11сло
(,!2)" . Рашюнально ли оно~ Сразу и не скажешь,
неп r~н ятно лаже, как выясню ь природу этот числа.
Однако да ва й те ра ссмотр и м об~> возможности.
Если 11аше ч11<..ло t = (\ 2}'
2
раuиОН<lльно, зна
чит, оно и есть ~1скомое. Ну а если число с ирра-
ц110~1 ально ? Тогда во'!велём его в сте п ень v2 и по
лучим числu d:
гl = с'1 =((,2)'!( =( \2r =2 .
Выходит, числоd llC' только rаuио н аль~юс. 1 ю даже
uелое. Поэтому если с ирраuионалыю. ro искомы
ми Ч11(Л(IМИ ()удут
а=С,Ь=\
0
2.
Итак. мы 11е 11ашли ирраuионалt>llЫХ •1исел а и
/,, дЛЯ которых ч исло а0 является раuио11альным,
но доl'а"!ал и , что 1акие 'i И(ла сушествуют. Лля ма
тематики подобное положен ие ти п ич н о Очень
•1асто бывает важно убелиться в tу шсствовани1-1
обьекта с нужными Lвой ст1:1ами, Ht:> и нтересуясь при
этом ко н кретными примерам и .
Но 1~ер1 1 Ь101 к 11.ре1111 п.11,r rpe1<:iм . У11 и111 1е1ш~
н 11,осща. с которыми оп11 1шачалс 1.юспр1п шли
нрраI\Иональные числа, тшоследстшш смспн
лись интересом и пристальным щrnмaJ m<:м J(
JJOBЬJ.м .матсмат.нчссю1м объсrпа.м. Фсщюр Кн
рснсю·нi н IV n. до JL э. l\UIOt3:.iл прр;щиu1 ~ал ь-
Г.1
'
'
;
ностьчисел \3. vS, v6, \7. \8, v1U, ,.11 ,
\12, \13. , 1Ч, ,15.аегuучс1ткТсэтстuбо
снонал нррациощ1л 1,носТh rкt::x ч нсt.J 1 111-щ;~ \ N ,
1·де N - целое ч и сло, нс ннлs1 ющсесн точ11ым
кн;щратом Те::Jтст 11 ;1 ~том 11 е ост::~ 1 ювн 11 ся,
ПОЗД/lt:t: ОН докаЗ:lЛ , ЧН) ирр::щ1 IO I l<!Jtl>J-!Ы вес
'\r
чипrа в1 ща ,.N , 1 ·,цс N - целое, нс яшIЯющсеся
то чн ым кубом , а также рассмотрел ир)l<11t1-1 0-
н:шьностн нн1щ \ J\f+N . v Af+\1\', ..,, ,н,;v .
181
ЧИ('ЛJ
ПoJLh:Jyяc1, 011реле11е1 1и ем, 11р1х11 ~1ю11ал"'1ыt'
ЧI н.:ла MOЖllO соl111рат1, из T\l'CЯ'l'llЧI ll>IX цнфр,
как н1·рушю1 11 з !(Сталей дето<n 1'() 1ю11С'трук-
1·ор:1. Нужпо эаботнться m11111, о тоi\·1. чтобы
появле11не ц11фр 11с плдчтпrялоо" шшако1"'r пс
риод11ч1юс'Г11. Так. 11ррацио11ат,~rым 6удст
чнс1ю , 11зо6ражёшюе дlтяп1ч110(1 дробью
U,1О1001()()()1 О"" .1:1 ко·1·орuй сд1 ш1щ:.1 шкж:ж>
nатслыю вcтpc'-1at"1 'csi чt=pt::~ одну. днс. тр11 по
Jиц1в1 и '1 './\. , IU IИ YJ IC:JIO О, 12.Ч56789 L011l2 .1 !У ""
11 .'~Cl'SП 11чной 3;1111к11 которо1 ·0 1юслс :3<!ПЯТО(t
тщr}щ 1юмс1г~~1ются псе 11атуrальныс ч1tела
Г<JраJ; ю слож11ее 6 1.~нает )'\ок:1эа· 1 '" что 11е1ю
тор:.~н эа11а1111ая ч11сювэ.я 1<0пстру 1щ11н 11реrtста11 -
лж··1 собой 11мс11110 нррац~ю11алытос ч1rс1ю
Бш1111шfх трудов, 11апрпмср, сто1rло обосно
п:1·п, ~1ррац1ю11алыюсть таких з1ш\!еmпых по
стоянных, ~<ат< ЧllСЛО 1t = 5, 14 l '5927"" ЧHCJlO
с-
.! . ..7 182818." А 1ют u кuпс·т;11пе ~·:>йлсра
С= lim(l+ 1/2+ 1/:1+."+1/n - Jлn), прпбли-
11 ••"
ЖСШf() ра.ннuГ10,577216. ПОК:1 (на l l)97 1.) Jl('Jlb3}1
ска:3аТh 1111ч 1.:1·<1 011рсдслён1~uсu. Рац1юналы1~1
011а 11 л11 11~.:т - это сщё лрс1к-1uнт ныясюлъ.
ПРИБЛИЖЕНИЕ
ИРРАUИОНАЛЬНЫХ ЧИСЕЛ
РАUИОНАЛЬНЫМИ
LL:i [Ючто1ю1'1 коррсс11онде111(11П адрес ука:3ына
ется послсдоватt'J1ьнu: снач;ш:~ с1·рана , потом
кpail (обл:ктh), 1'uрод, ушща,;~ul\1, квщл11ра Т:-~к
Жt' 11 MtTTOlIOJIOЖCH l IC ЛJОО( )J ' () нррац1 юнаЛЫТ( , _
Ht\ llt••f f OHIH'1 to.1;pflt-'t.ГliH(Лt:-'ltUJtИ ~1лр' '(
ук.1lь1в.1~>тся nncлсловательно. ..
1l)2
1'0 ЧI l('Л~J J1:1 ЧI 1ию1ю1"1 OCI1можтю у:ш~п J; с нро·
н:шолы юi1 точ1 юстыо . рассматр1шан ра з ное
кол11чество [tифр после запятой у 11ре;~стаnля
ющеti его д<::ся·1·ич1ю1'1 11ро611. Т;ш. д1юбн 1..+ .
l.41 ; 1,-11-1: ."п озволяют u прсдсшпъ , ·2 с точ-
1юстыо до десятых, СО1ЪIХ, ТЫСНЧllЬL'\. 11 т. д. К:vк
дое 113 ЭTIIX Ч!IССЛ рац1ю11а.11h l ЮС. 11 мы. таю1м
образо,-.1 , получаl'м 11р116.111ж~1111е 11рр:щ110-
налы J()J'O '- l llCJ ia \ 2 flOCJJ (',{OKa f 'eJI Ы·ЮС'l'ЫО ра-
1\l !ОНаЛЫ-IЫ Х.
Лтобоt" 11рра1111011:~л~.нос ч11сло ~южно с
про1 I3В<)JI ы юli TOЧIIO(Tbl() n р! I OJШ:il 1т1, 1юсле
довател 1) 1юсrыо рацао 1 1:1ль11ых, nо с колы~·
1юсле.rцше •·весьма шют1 ю ... р:.1сш)ш11·:~ются на
CJIICЛOHOЙ OCll: между каждЫМ\1 /\Hy .чst f1:ЩИ()·
НШlhНЫМИ ЧllCJia.'vlll IК't'l'/\a 1rм.е10 ·1с>1 11 дру1 ·ие
ра1 \1 юнальныt' ч.ш.:л а . Ест 1 нзн·1ъ, к нрн ~1еру,
ере, \11ес щшф,~с·111 чсскоt' /tнух 11р<н1 :; нш11,ных
p:ЩLIOН.aJIЫ·I Ы '- ЧI JCCJI, 1\IОЖН() ПШl~'Чll 'l 1> (1:!ЦIЮ·
налы-юс ч1 ~ело , р~кпол;1г:1 ющеt·си ,,1ежду ннч11.
11 ОЭТ()\1У «C:JM< >1 '() \).'JI J Зl<.01'0» p:lltJIOH:IJ111ll ()l'O
чиС'ла I< да11 1 юм~ иррационально .чу ire с~ще
ствует
l l ах<щнт1, тrскоторые пр11ближстr11я ква1~
рат11ых кпрнсй нз про11зrюлыrых чнс<:.'1 р1ел11
уже дрст ше nавшюняне - 06 этом сш щетель
ств~1от к:шrюппс11ыс та6л11<-uш. составлснrn.1с за
н~.:скuлько столс·1·111'1 щJ новой эры С1юсuб на ·
ХОЖ!(С I IИЯ 11р11блнжс111111 \ 2 ( 11 р1 IТ( )М Н;\11.11уч111 1 L\
11rш ,r1;:1нн ом :н1 ~1м е 11:пслс) :$Н<1.•111 t:11.1,ё 1111евнне
1'рсю 1. ()11 Сiьш 01111с:1 н Тсо1том С:м~1р1кю1м (1Т в.).
М:~тсмас11ю1 Нонш 'о нреме11 1 1 nостан11ла но
вые нопросы Ес111:1:~ф111\('11ропат1, з11:.~ме11;1·1'ель
11 у ri.poб11 т/п, то можп о иск:~ть 11:111.rтучпте
ттр116лиже1111я 1< заr~.ап1юм7 11ррац1юналыюму
с~ислу и · срС1'П так11х рац1ю11алы1ых ч11сел. }
котор1.1х :Jнаме11ател1. меньше шш раоен n
Може'г показатъся. что тоq1юсть ЩJJ 1 бтrжепия
прн этом бу1'<.."Г 1ICBt'J ШK:l - Ч'l'О-1 '0 !.!роде HCJlll·
чнны 1/11. Ока:-~ываеt·с.н. ою r:1кu, что сущее1'В)'·
ют 1 ·аюн.: рационат,ные 11рнбл11жснш1 111 / 11 к
ч11слу li'. ,для ко·1·ор1,1х точ1. юе1ъ пр116;11rжен11я
L! сто. ТЫС>JЧ}' . MllJUJllOll ра :~ лучнн.: !
В ХТХ н. нt: .\1сцю1й .ч:Пt:.\1ат111< l le-1cp Густзв
Лежё~ 1 Д11р 11 хлс:: 1юка:-~аJ1, ч·1·0 срсд11 пр 1 1бт1же·
11111~1 какш ·о -J111()0 нрра11;1юш1лы101·0 ч1ю1~ и·
ра11;ио11:.urы rымri rнrл:а 111/п встречаю·гся числа.
отстоящщ· от 11• r1c только :-.1е11ьше, чс,1 п:~ l/11.
но даже меньше, чем на 1/п:.. В д;u1ьнеi1шем
результат Д1 1р1 1хле ус 1 rттш1 нсмt'цю1\1 \lатеча·
t'HK Адольф 1·урк111l 11 фр:11-щузс ю1r"1 учёны l1
Э.\ШJJ11 Борсль. Они JlOKa:>~ш 11. что дт1 то601·0
1 1rр;~нщ>н;u1ьно1·0 числа и• сущ<:ттн~ ст беско
нечно ~шо1 ·0 пр116J 1 иже111111 m/n, / lШI котор11 1 х
HЫIIOJJllHCTCH llt:paнt:HCTBO /u· -т/пl < l/(t/ \s),
пр 1 1чё;..1 Чll<.'JIO \с, Г1 этой фоrл~ущ.: НС: МОЖ<:"f
nы1ъ YRt:Jll IЧl'H()
РАUИО НА/\ЬНЫЕ +
ИР РАUИО НА/\ЬНЫ Е
Р:щ1юн аль1 1ы<.· 11 11рр<1ц11011:1л111-1ы1; ч11с.!1~1 11.\1сс
'J еоnраэуют м1-южестно r)~йс11ю11тш1ьных •шсt'л.
Пос11юе- 11 нс: системы ;~е l1стн1пс11 1,111.1-; 1.11 1 сен
было ~Jавср 111е1 ю талыш RX IX столетни ~сшшя
~ш Ю. lJ. Р Де111:ю 1нда, l' Кантора. К Т. 13. 13сйер
штра rса 11 ,1.\Р)ТШ< матемапшсш.
Образом соuокутюстн ,цсйстrнпеJ 1 ыLых
чнсел является nр1Lчая. Прот1едfы на шюскост11
прямую. ныбсрс.'\1 на нсй две тuчю1, и пусть
одна 11э 1111х и :.юбражаt:т н у'Jlь, а друrан - ед11-
тщу Откланыяая еди1111ч11ы~'1 отrсзок н обе
сторt)l-(Ы от нуля. полу•шм 11зобrаж1:: 1 1111: на
лря .чоi1 Jt<.·лых чисел {т}. Раэдс.тп 1м ед1111 11 ч111.1й
отрс.шк погюлзм н , пткл:щьшая его н обе сто-
роны. попуч11"1 и:.ю6r:1жсннс ч11се: 1 {т/2}. ~а-
1ем р:.~·щсл1т\1 отре:юк на :S, · 1, '5 ...., 11 ч:1с1·с11
11 т. д" б~ДС:V\ ()ТК,1Зj\ЫН:l'IЪ отрl'.Зl<\1 )!Jl\11-IOll l/ n
н лплуч.tть 11зобрхкения чисел {т/11}.
Но 1кё равно таким образом 11ам пе у/tастся
Jапол11 1 1ть всю пряi\1уЮ. Всдь ясно. что сел~ 1 от
ложить от нутt 0· 1·рсэок, ранныrr J~HJ. 1·011am 1
кв:tJtрат;1 со сrорuной 1, то консц это ~ ·о отрез к~~
не со1ш;~дёт нн с ою·юr"i и:'! построс1111ых намн
р;щ1ю11:1111.ных 1·очск. Ч11сл() -v 2 м ожно t1рсд
ста1111т.ь себе 1<а1< "щель" между рацпональны
ю1числ:~щ1 llемснки 1'1 '1атсм;1т 1 1 к IОлпус В11ль-
1·е.JJ1>м Рнх:~р,1\ Дедеюл-11~ в.често слова ~щел ь·)
\ТТ<Уrрсбш1 термшf «сечеl!ие». Чrк;ю , 2 рассе-
ЕО1111111/l IЬIil
отре.юл·
1
'
1
~~~
·11/2 -1
1/2 ()1111/2~/,1 11/1 1. 21/2 5
Лt:>йсгвитс:Аьныt:> ч1н ла
Патуралыше :
1,.
. 1 .., '"'!,
Целые::
_J 1.О.12
Дробн ые:
"
~.
-
Рацпона..·1ы1ые :
-"'
-2, -1,0.1
).
Иррациональные
-· ,,
~.i· о J2.~. !), J)(>( 5(J) ri др
-.
-
Алrебрю1чсские:
Траисцсu ·
KOJ1 1111 \'j).I HHl'l!llЙ ~;11/Ц
~ентпые:
{f,,"\.JI + ({JI- _\" '/,'
' + +{/1.\'+(/, =о.
t!, ~ 11др
IЛt' (!1 -
1\СЛЫt' <J!Jt .IJ
Дейстн11тслы1ые
l •1r1t•l\U rия ле~к тв11 1ел.~ 1-11..rл ч~кс·'
каст рац1юналы 11,Je чш:ла на :1нс: ч;1ст11
те.
1<вадрат которых м<.:пыuе 2. п те, ю~:щр:п кото
rых 6UJ1ЬШС 2. J3UT T:I Кlli\.\lt (}(!(}('КJll/дUi:Jbl.\ll/ C(l-
l/~/11/>lM/.I IJ IШПOЛl lHl.:"l'CH .\lllOЖCCIHtJ j):tl\llU-
H;:JJJЬHЫX ч11сс11. Tt:n<.:pь пря .,1ш1 ока~~ывастся
заrюлш:1 пJUil - K3ЖJJ,()JI сё 1'( !ЧКС C'l':JB!JT(Я J! cu-
OTllC l'CTBI IC 11еко1ирос • ll ТC 1IO
Карл Теодор 13 1 шы сл1,"11k11срштрасс пошёл
rю дру1 ому пут11: uмс.:сгr> сече1111(1 п 11 р;1 со1ат
рнn:о1л 11n::1р астаю11 \r re т ·ра1тче1 11 1т.rt шкледr>11а
тслыюс·п1 рацио11алъны.х ч11Сt.'1 (с.м. стап.ю
<•Последоn:,~тсл ыюспr" ). Каждая 11з 1111х прсл
стаnляла uno:пrc оnределёшюе 1 1 рр~щ 1 ю11алыюс
•111сло. li~np11.\1Cp. вы •шсляя пос!1едов:пслыю
/lCCЯТl lЧ l lblt: :иrаю1 '\ 2. \1Ы ПОЛ)'ЧllМ прс11t-1·~111лн
Ю1Цj f(.} ЭТ() ЧllL'JIU UОСЛС){UВатслыюсть { l; 1.4:
1. -1 1 ; 1,"11·1; 1.+142; f.
Д11н дt:i"I<.'TB I ПT.'IЫIЫ.X Чl l CCJ I 11p1! X()ДllTCH :Ja-
11.01\0 011pt:J.lt:J I ЯTI> 011ерац~ 111 C.'10Жt:Jtl HI , НЫЧI П ':J
Hl'l$1, )'M I ЮЖСI \\'\}\ 11 }IСЛСУ\\Н\ ( К[Ю\1С неле11ш1 Н:1
11)71Ь). ();Щlf П:l СГЮС<16011 -
' R:1H'l'l1 11рсrкт:.1н, 1я10 -
щне каждое 1 1 з чпсел ан !J послсдоnателы шr
т1 1 { а"} и {/Jп}, а затем состаnrп1, последот1 -
тслыюстп {а11 + /J"}. {а,1 - /J11 }, {a11h11 } 11 {а"/Ь,1}
(в п оследнем случае среди Ь11 LJe долж1 ю f>ып,
нулей). Этн послсдовзтелыюстr-1 щ1сдста Lш1·
ЧllCJI;[ а +ь, (./ - ь. а/) 11 (f/U.
Построенны е таким способом ч1 1 сл:1 обра
зуют поле (кстат11, этот 1·срщ1н ннё.J1 1 1 мl'н~-ю
-~C)l.CKJJJ щ), а с учЕтом TOl'O , что ) \Юl Н1 !)( ()1 rpt-
/ \eЛt:HЫ ()'f1:-IO l11tl-l lJЯ "6ОЛЫUt:» 11 "\lCI ! l>llll" • , -
- 'lli
неf11ю ,1•1ю/JЯ()очеmюf! пrие.
Числа
UЕПНЫЕ ЛРОБИ
Просктпроnщикам зубчатых колёс хорошо
:шакома т;1 кая :~адача. Пред положим. требуется
ско1:н.:трунровать зубч атую передачу пз лвух
1ш.:стсрёнок с от~-юшсш1см у 1 ·1юньL'С скоростей
нrащс1111я (1ю::.~фф1щ 11 снтом 11еμе) \ач1 1 ), близ-
/
ю1м к '2 . Посколы<у чнсло это иррациошvп,-
110. то tll1K~IIO I M l(ОJ 1е• 1 ным l(OJIИЧeC'l' l\OЛ-1 :.Jубы: в
на 11 1сстt:р н ях нслыт добнт1,сн ·1 ·01·0, чтобы ко
эфф 111 \11сн·1 · псрс/~ач11 ранняло1 ему 1:1 точнос
т11 . Это можно С/\ел:лъ ли1n1, с болы11е(1 1 1т1
меt 11 .шeii степе ~ 1 ыо 11р116т1же11шi.
Взиn. 1<пр 1Jмсру, па большо1'1 шестерёш<е l+
зубьсн. а на маленькой. 10, получ11м коэффи
ц1 1снт 1 1средачн /.г = 1.-1. Это 1 ·рубос 11р 1 16ш~же-
тп1с к , 2. Еслп же па fюлыной бУ71е:г 14 1-1 -2 :iуба.
а 11а малс::11ы<0i1 1 О ООО, то прибл11жсн 1 н: полу
чпто1 более точ 1 1ым: k = 1,41-k~. В 11 р1 111 ц 1 111е,
увел11ч11вая ч11сло :1у61.ев как 11а ол:тюй, так и 1 тз
11pyroli шестерёнке, можно добтъсн сколь
)'ГО/\ТТО xopowcro nр~~блшке 1 1ия коэфф1щ11е11тз
nсрсдач11 к q11с:ту .,,·2 . О[\накu рост коm 1 честна
:\у6ьс11 всдёт 1<y}.~CI 1ьшс1 шю нх р:1змсrюн 11. слс
; \()Н~УсJ11,1-ю. \\ 1ю· 1 ере 11 роч кост11 .
Возю1кае 1· во1 1 рос: нельзя щ1 подобμа1ъ та
к11с кuJ 111чсстnа /11 11 /1 зуб 1,св на шсс"['срt:нках ,
чтобы отrю п тс111н.: т/11 хорu 11 ю пр11бm 1 жшю
,·2 11 вместе сТб1 чтобы ч11сш1 тнпбылисрав-
11итслы ю 11с()ольшпм 1 т? Замс."r1 Hvl. что число /1
сонсс\1 нс обязана бhl'l'h с1·с 1 1сныо 1О.
Простой способ пахож,т~:стптя ;i;poncт1 с нс-
6оль ш 1 1м1 1 :11та ме1 s:~тештми , которые IVlЯ любо-
го нецелого числа даАал11 бы е1·0 хорошее прн
ближен11с. 11рсдлагастся в тcopmI цеп н ых
,r~:робей. с ШIM l l .'vlЫ сс 11час JJ ПОЗТ l ~Н<ОМВ~ЮI
КАНОНИЧЕСКИЕ UЕПНЫЕ ДРОБИ
Цеп н ые (л,ругпе 11 з:н~:.11 111е - 11 епrеrыв11ыс)
дrобr 1 nпсряыс пояnил11с 1 . fl XVl 11. Кщю1m
чеС11.:ая цеm tafl r)робь - :пп п 1t1раже 1 rrre 111 щ:~
Uo +-------
о,+ ---
Cl.+
-
а~+ ...
l'J\<.: ({() - лю()ос ЦCJl()C ЧI JCJIO. (/ ,, С1 2. (/ \ , ...,
-
J teJ1ыe lЮ-1южи·1·ел ы-rые: ( натур~l!lьныс) ч11сл:1 ,
назы\\зе~~1.1е 11е1юл11.ыми 1.tt1c1n11ы.м11 11л11 эле
..щ?11mшни дarшofi
/1.р()6И. R :ыn11с1 1 мост11 tл l<O-
JI и чеrтвэ эп 1 х Э.'Iбн~птов ра:~лттч атот ко11еч11ыr
и бесконечны е цепные !(!"Юбн. Н апр1 1 мер. неп·
11 ым1 1 дробнмн буд.)'1 таю:н:: выр.1жеrпш:
1
l+-
2'
1
l
\+- -
}+----- 1+----
1'
l
.
l
2+
2+
1+
)
,
1
l+1
1+ --
.
-~+ ...
1+ "'
I l cpuыe дн::~ 1 11х·,1~ст~шпяют cono1I конечные цеп
ные /\робн, ;1 rюо1ед111 1е - бес1юr1ечш,1е.
Дrт того чтобы цсш 1 ыс дроб11 не оста1111сь
лн 1111 . 1ср<кшюli м11темат11ческой 1<01 1 стр)1<1 \11ей,
в::~ж110 научпться решать два т ш 1:~ :-~адач:
UL•п 11 ыL• 1.1р• •• 1н у< 1μ11"ны
H.1nn,1nf\1 1e матреше~
в ~HdM(...11.1Г<·л~·f1•н ·11t'ЛН( I\~
Лf)Пhl< ( 1t!Н!.\ « 11J) ЯЧР rся »
ut•r1нaя дрuuь .
1) дана цсшУJЯ дробъ. требуе-~ся (Ш\Хдслит1,
tc 3на• rсн t re:
2) дано ,гtсlrспштеJ 1 ыюс ч1 rсло. трсбуето1
f ЮС l'[IOIJTh ("OO'l'Bl"l'C l 'HYIOЩ)'IO Це! 111 ую /\/)001>.
КАК ОПРЕЛЕЛ ИТ Ь
ЗНАЧЕНИЕ UЕПНОЙ ЛРОБИ
Есш ценная дроб1, конечна, то зад::~ча с1юднтся
ки111ъ 1< более ш1и менее -~ру,:щС:м 1юму вычнс
лс1 шю, а рсзут,тат nрсдс~·;:ш;u1<:>т собой р~щио
шшы юс число. Совсем друго<:> дело. когда она
бес.:кuнс 1 1на ..
Irpи6ЛJ JJI J TCЛbHUl' 311::1 ЧL"Lll l t: бt:CKUHC' I HUll
ка1юm1ческо11 цt:п r-юй rtpu611 можно поучить,
t:CJШ <· nрtВ[Хп1 1тм сё н ко1н:ч11у10. т с:. отбро
с11·11, ,, х r1 ()C' 11r К»:
17
1+------= ] +---- = -
)112'
2+
)1
-
+)
-
+
_+
2+~
flp1 1этом чем больше <-rгажсй • \1Ы оrта1щм, ·~ем
точнс<.: бу/tст рtзулптат. Но ·1ar:oe ре 1 ш:1 r нс вряд
mr гюнран1 rтся математ11кам .
[ fio j~itur frattio e jufrno di
юntiвue fratt:i. qц:i: libct • 6с
l cfignata.
Сцm igi tur conltct, rcc epta
11cthodo, r cd11aionr m inllit11i
po!fc ad Ьаас • od uai,
!....! ( d
"
•
-
t ...
" У 7_.,.с,
~
4·
"
-=-
"'
"
.!_Ь
•#
"'t:=ъ+" ~-
~!_. f =~rJ,.d~')' _
11.;у .i.r+by+"~,_
!-Ьс
=
n~d+нl·~•B'YJI
" Т -:у ; ьиt"JZ11+,,,(iTГilt"~ ,,.;.
"
Фра r·\11·1н ( тr.~ HllUhl IH КН11Пt Лжо11J IЗалЛJ-1( il
·Ар1>ф~!.'Нt1(;.) tJetKOl\t:ЧIK!IO • t • [JUb\lt:He нн•=~
11епн ы\ лробе 11 1I• 'itн
Лейс.твнтеАьнь1е чисм1
Иногда 11айтн зн~че.1111е цешюй 71робl1 по
могает уд;.tч~юс riaблro11e111-re. ll:тршч<.:р, в RЫ
ражспип
1
! +------
2+ ---
1
2+
1.+
."
:нrамеп::~тель нервой дробн А точ 1юсп 1 на е/~;11-
111 щу болыпс всего выражешur ·
!.+---
,- =1+[1+ 1
2+ --
2+ --
2+ -·
2+ ".
Пр r п-JЯR 11о<О,\1ую вел11ч11ну ::ia х. ПОЛ) чнм )ГаR-
11е111 н:-
1
.'\'=1+--, 11ю1 х(1+х)=(1+.х)+1,
l+x
0·1·ку; ~~1 х~=2, ~1 х=± \ 2 Отр 1 ща·1 ·с:льны111шrен1,
яшю нс 110;\хо1 щ·1 . Отбр:кывасм с1·0 11 оконча
'п:~л ы;о ттолучае.'v1
1
г-
1+- - ----= ~2
2+
21
+>
-+ ".
Л 1rалопrчпо, 061 1 а руж1111:1ем , что дро6 1,
l+----
1+
1 +."
'
ран11э 1-шслуФилня Ф=(\ '5 - 1)/2 (см. статью
<·Ч11сла Фидия 11 зол отое сечен не?)
ТакоJ1 приём 1rо;11юJнп п11рс1tсл11тп 3 11~1че1-111с:
л юб()й 11ернод11 ческо!i цспноii дро61 1 . Нужно
ОТМе'ППl>, что 11еrгюд1-1чtткос IIOH'l 'OJ1Clfl l t: 1-н::
П()Jll\l>I X частных CflOJ I C'J'ПClfH(} IKt:M 11ppa 1\IIO-
IТЗЛbl-f l,J/'vl ч11сла:v~. которые ннлнютс.я кор11ямп
квадратт1ыхура1111е1 1111'1 с целыми коэффиц11е11-
тамн. - и только I'fм. Этот фаю доказал n
177() г. nы,цающиl!ся фр;11щузск11i1 математнк п
мсхапиJ< Жозеф Луп Лагранж.
Пока 11с r J :шсспю, есrъ mr к~1ю1с -тrбо зако-
11омсрности н стр~ ктуре r 1е11ных дробсi1 ;1,1 1н
1RS
Чи<ла
KO(JJ Jt::il мт l()ГOЧJIC: l IUH бuлt:<.: llЫCUКI I X СТСП<.: t l<.: J'r.
Этз n6ласть матсма·1 1 1 ю 1 остаётся т1,рытn i1 J tЛЯ
IJCCЛЦ\ПR;\Hllil [ 1, Ю Н IСЧIЮ же. /J.ЛЯ uткрыт нlr .
КАК ПОСТРОИТЬ UЕПН У Ю ЛРОБЬ
Р:.~зложе1ше u ка1101111 t1ескую це1111ую дроб1,
пронзтют,поrо лсйстrн 1тслы10rо •nтсла - это
однообра:шый nрощ:сс:. ко·юрый <.:ост01 1т ш
днух мнсяuкр:1·1·нu 11он· 1·оряю щ11хсн 11 чер<.:; 1ую-
111нхсн J1py1· с JIJl)TOM )\CilCTHIJtt: ~1rолуч<.: J 111Я )(()-
ст: 1 тка~ 11«06 1х11 цсн11я ос.~1·атка». Рассмотр11:.1 е1 ·0
н:.1 1 1 р11\1с1х· ч11сла 1997 /3 l.
Снач :u1:1 ll !)t'JJ.CTaшtяeм ЧI I СЛО н BHJ\t' C)'Шv'lf il
11.<.:m 1!"1 чat:l'll (дпс1 ·:п'l\а} 11 11.рп(-н ю11 (<К'1 ·а 1 ·1\а):
t997=6~1+1.1
:Н
:S i'
Ес.1п остато(( отт1чсп от пуля. 1<а1-: n ла т том
слу•цс, то его можно 3аписать в в11дс дроби
t
51
/ l _) (обращение остатка). Пр11чём знаме на-
тель это11 дроби всегдз бо.· ~ьше едюшцы .
186
'Гс:n1.::р 1, т<.: же: д61 стщ щ 11рuдслыв:н~м уже с
'IJ ICЛOM .~ 1/ 1.):
а :1начпт.
51
')
1
-= 2+-=2+--
15
13
15 5.
1997
1
-·-=б·I+
.:Н
)1
-
~
t 3.::;
Прuнолжан d'1·0· 1 11 pouccc. н ко1-ще кшщон
1 юлуч11.\1
1997
- - =&l +-----
jl
)
-
+
2+
l+
ti
1
2
Для н ррацно1ылыю 1·0 ч ш:ла процесс его
р:1з;южс н ин 11 цс.: 11н ую ;~роб 1, 11 рuдuлжастсн бсс
юн~t:ч110. lJo 11 R :'J 1·ом случ;н: 1111ш·д;~ можно
ощх:дст 1 1ъ внд , 1.робt 1 РасСJ1.ю·1 р н ч н кзчссr·ве
пр11,\1ера чнсJю v
1
'"J = 2. 236". Его це.'Т:lЯ часть -
~
2. слсдоватслыю, остаток \15 -1 . После об-
ращения остатка 1:1ыражсштс nршшмаст в11д
.
t
y"i;;; 2 +
.
i (vs -2)
Умножим ч11сл11тсль 11:ша;-..к II атслъ ш rутрс 1111ей
,цр()n11 на ~"> + .!. :
1
{5 =2 +----- )+-------
1(\''') -2)--
\1'5 +2
(vS -2)(\1') + 2)
По фopo\-t~:rie раэ 1 юстт 1 квадратоn.
(,s -2)(..;~ +2) =5-2~ =1.
llо:-пому
-
)1
,,')= +---
-
2+ v"5
Есш 1 11 11р~ню~1 ч:itJ,'11 111ю1ед11е!1 форму.'IЬ1
полставнтъ вместо ,·'J С'1. ,,1у сё «бескш 1 еч1 юе
ЧI ICJIO раа~. ' 1'() лолуч1 IM
,:; =1+-------
~+
~1+
-1+
ПОЛХОЛЯШИЕ ЛРОБ И
llroнecc пос1роспия 1<aiютr11чeo:nl1 1\e1 11rof1
il.J1t >6H wн1 пронз1юлы ЮЛ) чис,а <Х чож1 ю 060-
рна·11 . 11а к.1ком -то ш:1 1'е. 11 пол:уч1.rrся та" тrазы-
ШПНЫЕ ЛРОБИ И КАЛЕНЛАРЬ
• Лс11ь 11 ночь - сутк11 прочь)) , " Зи'vlа и лсто
-
гола
11сту1) ... С незап.~мsпных 1:1рсме~1 люли полметили, •по
важнейш~1(.' tпрсзки вμемен11 - гол и сутки
-
опре
деляк>Т('~J рdми •1 ными природными пpnuecca'vlи. Ол-
11а кu в том , что год 11е и>меряется ц(•лым чи,лuм су
ток, они разобралис ь лалеко нс rpa'!y. Но нель есл11
1вмерsпь гол 1н:~лым количеством суток, то п остепен
но 11абегут (ил11 убегут) « лиu1 н11с » секунды , минуты,
ч.~сы. которые (0 вре'vlс11ем составят д11и, 11сдt·ли f1
меошы. Так оно и прои-!оwло.
В 4(, г. н. }. Юли й Uе.{арь поставил перед у•1 ё11ыми
i.Злачу и1б::1виться от ош ибок в к;:~лсндаре. По 11рс.д
лr>А<t~нию алеКСdНдри йского clCTJJO I ШMJ Созигена 0 11
ввел rакуК> <.истему: КdЖЛЫй четвертыи год лолжен
быть на 1 сутки больше, чем обычный гол, состоя
ший И1 365 суток. (Вrюс.лелстви и Л/\Иltными, или висu
косными, стали rч и тать голы, номер которых лелится
HJ 4J В честь Юлия Uезаря этот календарь стали на-
1ывать Ю/\Иа 1~ ским. Но и он был не GeJy1 1peчe1 1 -
ср..:лнsт Л/\И 1·1 а юли ан с кого гола больше истинной 11 а
11 "тнут 14 секунл.
Следующую реформу календаря в [вропе прел
nри11ял П ;:1 11а Римскии Григорий Xlll в 1582 г., когдil
расхожление межлу истинным и юлиа нским голо'v1 сn
стJвило 1О лней. Он осущестnил проект, п рсдЛожен-
11ы11 ита11ы1 н ским врачом и математиком Ауилжи Аи-
11110. Этот каленларь, которым пuль:{уютс я <t'Ичас и в
России, стали на'{ыеать григори:з нск им.
В григориа11ском кале11даре сохраняется черело
вание простых и високосных лет, но оно лопuлнsн:•тся
правилом: если номер гола сжан ч ива~:>тся лвy'v1SI н у
лями, а число сотен не делится на 4, то этот год -
простой (голы 1700, 1800. 1900-и - простые, iJ год
2000-й - високосный). По григор11а н скому ка
"енАарю средн яя Л/\Ина гол.а составляет 365 суток
5 ч<:1сnв 4<} минут 12 секунд, что на 26 секунд больше
11сн1111юи. Такая точность вполне приемлема, ведь
ЛЕ:.'нстшп('льные числ.:~
n:1смая пm)хойЯ1ца>1 1)/юб1J. Это·1 · ·п:рм 1 1 11 п<1-
ш1шкя щ: L.1yчai"11 10 п11,r~,хою1щ11с J\JX>a 11 деi1-
ств111елыю ОЧtШ , хлrо 111 О •· IЮДХОД}JТ» /\ЛЯ 11 [1 11 -
6Л11жсr 1ш1 ч исеJ1. Судите с:t:-.н1. сел 11 1 1 epen11L-.1тr,
1ю;\ХU.ЦНЩ)'Ю дробь в nпf(e о быююв<:шюi1 11с
сократ 11\ю l1 дpo6JJ jJ / cJ. то o rт:i б)дС'1 отлнчаться
()'1' ч11 t". 1:1 сх не 6UJ1ьwt, чем па 1 /с/. 11 \1CllhlllC,
ЧL М люi1 :1.и / \ру1 ·а~1 06h1 ~ 1-юве11ная J (j)( >61, cu :ma-
\1l'H<JTLлeм. не 11]1<..'BOCXU/~HЩJ l\1 tj Т:1 ю1м оnrа
:юм, 1\аждан 11з 1 10;\Х( щнщ 11 л 1tpoi1cl1: \ai:"1 н :~том
смысле т r з т~л~'ч11 1 ее 11 рн('iлт1жс:шrс
:7то сn01kпю пеп 111.1s ; 1роб<:f1 поз 1юл не 1
peLШ rтr, залачу о 111 естерё' 11 ках, ттост:.~nлст111)Ю
ош ибка n 1 сутки пр1 1 дан н ой сисгvмС' наОРжит пр11-
мерно "1<1 ВОО лет.
д<'\В,) ИТС СНГЛЯl l СМ 11.:t проблему ка11е11д,1ря с точкн
зре 11ия теuрии uеп111>1>. лроСiРй. В1>1раз11м лл 1111у голи в
(ут ках и 11релгrав11м ну вел11ч11ну 1:1 1:111ле 1Jemю11
лроб11:
1 ГОЛ=165, 142199... :: Н1 'i+ -------<у л ж .
4
7+
1+
3 +...
П ослслова ГVЛЬНОСl"Ь ПОдХОд\1Ш11Х дpotie11 Л/\Я неt'
TilKOl:ld:
г..3651.1'r: 7 • 11:г:8.н.~31.
Jб:>, . -,
11.1-,
J1 J:J- ,
1u.1--,
4
2Ч
ii
12Н
Как.:~я 11..s :них лробеи в.:ам болыuс 11равится~
Возьмем ~65 У" В ..пuм случа~ 3<1 4 год,1 набега
ет 1 « лишний » дРнь - 11 мы получаt•м К>Л11анс h.Ий
калс11ларь .
Во1ь,~ём 365 %. Теперь ы Н годil 11 uбе гает
8 « ЛИШllИХ ~ дней , и но - к<1ленлар1" пре,~ЛОЖf'ННЫЙ
в 1079 г. п ерсидским матем<~тиком и по·пnм Ома
рам Х.:~иямом О н лаже то•111сс 1р14гоrиа11ского
А 4;!< ли 1:1ыбрать пuлхuляшую дробь 365 'Yi ", 1 то по
луч11м ( ооrкетс твук)WИй ей к.1ленд..~рь ф<1нт<1п ИЧl:'
скои точнпсти , по которо<v1у сре!днs~я лли н а гола 1111wL,
на 1 секу11ду будt:п 11реоышать 1к rи~1 ную! В 1864 г.
профеuор ЛЕ-μп тско го унив(•рсит~ r<1 (ныне 1 артус -
кий) Иог;~н н Генrих Медм'р прсллож11л с ХХ в ввести
такuи каленЛL1рь в Росси~1. В 11е.,1 пришлоrь бы к,1ж
дыс 128 л~т пропуr К.ЗТI> ОдИН АИ( ОКU(. 1 IЫЙ год, ('('ЛИ
виt окос ные 1оды отсчитывать по п ринят< >й тоrд,1 юли
анской <"истеме. Проuслура простая. но... То 111 1в силу
обы·1 ~ю1 о конссрвапt.jма, то ли по лру1 им пр11чи11ам
лот кале 11до:1рь рсКl l f)ОСТранения Ht:' получил.
lIO
к начале сп1т ы r. Рассмотрпм rюдходящпе 1'\РО
Г111 / 1,,.l lJI ЧIJCJl:I
\2=1+----
1
2+ --
2+ ...
Буl(см /(е11ствооа1ъ гюследонатслыю:
1+_.!_= 2=1,5:
22
,
1
7
l+--=-=l 1·
1 .:;
'
1
2+-
2
1
1711(.
+----=- ='1)()".
l
12
2+ --
)1
~+
2
Уже пнтал по счёту дроб ь
<)IJ/70 =
1 .~11 428">7 ...
-
конк:ур иру<:>т 1 ю гочностп с
i tpo61,ю 1"11 12/ ЮООО. с 1юмоLцьнJ ~:uтuрой мы
к11ачале пы'1:vшсь npнбm13JJ'1ь ко:-1ффиц11е11т
пepc;~: IЧ ll днул шссн.:рёrюк, ::1 ЧILСЛ НТСЛЬ 1·1 3Жl
мснатеJIЬ прн ЭТОМ llO Ч'l' H 11 1so раз MClll>llJC!
Т:.~ю 1м обра:юм, 11.v1есто шсстерё1нж с нс1юоб
рз:т м 1,1м чпслом зубьеu - 14 142 11 1()ООО -
можrю обойпtе ь п шюлпе 1 1 рне!lшсмым нх ко-
лuчество:v~ - 99 11 70.
·
ОБОБШЁННЫЕ UЕПНЫЕ дРОБИ
Сто 11т ю 1111ь отк:.~ з;л ъся от требсша1111я . чтобы в
ЧНСЛИТСJНIХ <- ,\1НОl'ОЭТ:.IЖСК'> посеJIЯЛJ ICl> 11СКШО
ЧJ.rl'СЛЫ!О енин ~-LЧКН, и мы получим l\()ИЫЙ Т1'Ш
:1рнф м ст11ческоri ~застрой1Си • - обобЩёlf.nЫе
1~emtыl! йро()u :
/.J t
Clн+ ---......:...---
h!
ь~
а,+--
188
-
а~+".
1'/\<:: а0,а1•и~, .;h1, Ь2,h1,".
-
1 \елы<.: числа.
Coxp<i l-LЯЯ Flt-l tШlle<:: СХ()Д(.~гно со CBOИMII кa
H OHl l Ч<::CIO IMlf протО'I н11ам11, 0606 1_цё 1111ы е l\Cil-
llЫ C ,1\рО611 нсё Жt: 01'JlllЧ ~I IO'l'CЯ от HllX: 1 1рt:J\СТ<1-
1шть к~кое -лт 1 60 дt:liствителы юе чнсГJо н ни;,е
11с1<а1юш1ческо1·1 1\е rш о й дJюб 1 1 ·1еперь ~юж110
уже IIC Ci'\ l'll ICTlK'III IЫM способо:\J .
Так, ч1кло \ ~ нмеет раэложешш
·1+_ ___! ___
2
L+ --- --
l+
1
1
l+--
l,+ ."
2+
2- ------
.i-
.i-1
-~-
...
ll ,1\.11 rnжeci IIO дру 1 JIX.
2
)
2 +---
2+ ..
Rrюnщe . с 6сско11еч111.1 мн обnбщЕнным н
цеmтым11 дрпбями сле,цует обраща ·1ъсн кр:1йне
осторож но. И 11а'1t: можrrо и « 11 1 1 ужу сссп1». Рас
смотрим, напр1гv1ер, uыражепт 1 е
1=-2-
3- 1.
~CJ ll I 1 13 ~llJMCI l:IT<::Jlt' ~aMCHifТt> ШI ЭКВIШалс 11т-
2
Jl()t пыражtН1 1t: :) - 1 . то I ШJJYЧHM
(_ Ut:L KUll t:Ч>IЫ ~lll UUUOШl'll llbl\1 11 11(11Hbl"1H дрош1м 11
нvж1ю оf1р,1 uы 1ьLя кр<111нс> U( 1 орожно
2
1=----
2
3--
.
3-1
ГГоитортm зту операцию по от~ютпснито к по
иоft е,7111шще. стонщей в :шамспатсле. 11 П()
ступая далее подобным обра:юм, мы построим
6еско11еч11ую цепную дlХ>бь:
2
1= -----
2
.1-
...
2
')-
.
3- ...
С дру1 ·0~1 CT()pmrы, дe(rerRyя точ1ю та~< же.
мож1ю nредсташпь в виде беско1-1сч1юlf цетт
ноИ дроби Чl!СЛО 2:
АЛГОРИТМ ЕВКЛИЛА
Ко1 ·д;1 .мы 11меем деJЮ (" О,Т\НОрон 1 (bli\tII пrслмс
г:ш11, то чэстп возг111каст вuпrос: которыГI 1 1 э
н11х f\олы11с? Какое ябJJоко 11а ()лкщс с:1мос
()оды1юе? Каю11-1 1·opo,r\ боль111е: Сн-1кт-Петеr-
6) р1 шш Екатсршrб)1JГ? Ес.1111 11 меетсн 1111а от
ре:щ;~, Т() 11еслОЖ!lО UЫЯС"тrитr" 1<31\0lr из IIИX
бо!lьше. Но намного трудrтее скаэать. к;~1юво от-
11оше1ше длпп этrтх отре~ков, или, друп1м11
слоnамн, во сколько pa:-i одш1 больше друтоrо.
Чтобы ответить на этот вопрос, нужно наl1-
т11 un11o •ю N(!j~J' ОТf)t":н<01:1 а rr Ь (ест·1 таконан
сущ<::стнуе1'), т. е. ·1~кой отрезок, который Цl'Л<1<::
ч11 с1ю pa:-i) клаr1ыRался бы к~1к 1--1~1 отрезке а, т~1 к
11 н ~1 отрс:1кt Ь. Для удобств~~ 11m'111ы этих отрез-
fJ
/?
/)
,-
1
г1
{/
(/
,"
,.
1
Риt.. 1. ()11р/:'Л(;'Л( 'l lИ(' оf°iШ РЙ
MPf1bl 0Tf1P3 K()R а " h
Леиl тви 1елы-1ые LJИ<-Лil
2
.!.
1
2=--=---- - ... -
------
3-2
)
)----
•
_)
-
2
'
2
::-- ----
2
.)- --
5-
."
Что же uыходнт~ 1lостросппыс псптrыс дро-
611 равны ,rt;p)т !{ругу, слсдоватслыю. равны 11
числа, из которьп~ они 1юлучены, ·L . <:: . 1 = 2 .
Парадокс~
***
Д.ш1 цепных дробей нr.т просты.х 11 уноt1111,1х
пpaRllЛ R!1!ПOJIHl'HffЯ :1p11 фмt:TL I ЧC:Cl\llX ; 1~1'1 -
сп1111"i. тем 11е менее 011и 11зхоf(ят у,r(ачпое Щ)Il
,\1eJ 1 е1111е Ro многпх теоретических нсследо
nашrях 11 пр11кла r111ых за; 1 ачах. напри~ср в
зад<~чах 1 1 e6cc1юfl мсхаrп-1кп
кон также будем обозн~1чат1, букнамн а 1-1 /J_ Очt'
ю1,-1но, ЧТ() в CJl)'Ч:lC, KOl'Д<I С( = /7, общсl1 мepOtl
СЛ)ТЖJIТ Jll{)OOЙ 11:1 Д31 11 1ЫХ О'l'ре:жов. 1lo ~ \Oll)C
·1 ·11i\J , а > /J (рис. 1 J. Тпгл;~ :-.южлл отложить от
резоl\ /; па отре:нсе а макс11.чалыюе ч1 1 с1ю раз.
l2сл11 отрезо1< с1 11счсрпастся 1 \слыл1 rшm1чс
ствоы отрезкоn h. то отрезок Ь Jf бул;ст 11х 11:.111 -
большеJ'i общей мерой. Rпол11с nерояпю, одна
ко, что отрс:юк /J нс уложится н:1 отрезке о
целое чrrс1ю раз и uc 1 ·:.1нt:' 1 '01 1-н:бо11ы11о~'1 ~ ~·со
чск-> 1-1
_r.ст сстн е н1ю ' 1·еп срь
11 <.:t' n 11с 11 ыт:J.ТL1 н ка-
11<.х"1'.кt: общей !\1Cphl отрсэков а 11 h. О11 11с1'ктви
·1·с11ь1-10 ПO/\OIJJ\l:T на ЭТ) рот~. tCJlll 1\tлое ЧIJCJIO
раз умссrитсн на отре~ке f7. Ест r же щш этом
UПЯТ I; получ.им O C'J':.l'J 'Ol< 1·~, 'J'O Ll :l сленующt.:м
11Ja1~e бу;\е.ч ис11ы·1·ына'п1 отрезок 1·. ! .J по ~~,кс по
оттюrнетппо к отрезку1·1 и т. д. Ес,-ш в KOJ ще кон
цов получится та1юй отрезок J/" J<оторыJ'1 цс.1ос
число раз ОТJЮЖНТСН (\ прс/{ЫЛ,УЩСМ оста·шс 1·!,- 1,
то он и будет общсf1 мерой всех отрс;:{1<0в . 12сли
же ~тот про11ссс rшкогда нс :~акш1L1и1·сн, тu об
щей меры у отрс3кш1а11 /.J не с у щсствуст - 0 1111
неСОUЗ.Н<!/Лf.МЫ.
То·1 жс метод i\1< >ЖН( > 11р111У1сн 11ть нс к< 1трез
к~1м, ::i к цслд1м ч11сл~1м . Тота рсч1, 110!'1 11ет о 11ан
nш1ы11с~ общем l \t'ЛHTl:JIC ЧJ rct:л (/и /J Bo:'I J11\1ё ."1 ,
11:1пrтм<:р. а = 2()()0, 11 = :\(10. Пр11 :~·гпм м1.1 1ю
следона '1'еJ11,1ю 11 плуч1rм
189
Чи< л<1
~OПD ;3EiD · 5~i?DD
ЗБD=ШJ · 1• IБD
21J[]=IБD . 1~чо
lбD=ЧD ·Ч
2()00 = 560
.:; + .ZOU;
-юо=:юо 1+160;
200=16() l+-Ю;
160 = ..f() -+.
0·1·сю.-1:1 заю1юЧ:J.l' М , чтu н~нrбол1,ш11~'i общнй
J\t::Лll ' I L'Л b ЧllCCJI 2000 11 _)()(J раве 1-1 40
IJrн:рвыс..: этот мето;\ упuмянуr а «1l ачалах »
Енкл нда, п о чему 11вошё1 1н11етрню rюд E1;r:ma-
н11l'м ~шu·ор 1пм Е1:1ю11ща ~. Э<1т 1ш е,ч tто с nо
мощыu Ц(;JIOLJIO I paнt:: H CTl:I:
и=/J/11+1·,:
fJ = г1112 1 !".:.:
1"1 : 1·~n~+I';;
1~. 1 = l 'r.J/J..o
-
1·
.Vlз этой цепочки сра1шитс::m,1ю легко полу
ч.1стся прс.:.1став:1с::111тс чпс1а a / IJ n вtl/1C 1<ЗJЮ
н 1 1ч<:скuir цcru юt'1 .:.1роб11 (см. статию «Цt:шrые
;{рuб1 '").
(/
,.
-
= //! +.....!.. = ll + --- = п, +-----
/>
/J
1·.
/·/,+ -
1·,
= 11, + --------
Вuт ·1ак ат·ор1 ,... ,, Енкл (IJJ.:I нl'ожн;~ан но ок;1 -
~аi 1 ся <..' l lЯ:З<.lHHh!M с llCП lllolMll дробя.м1 1
ЧИСЛА ФИЛИЯ И ЗОЛОТОЕ СЕЧЕНИЕ
l 1.Jпш<011счтr;~я зuезд:~ - пентаграмма
-
nccr71a
прrтnле1.<а.11а вш 1 мат111е тодеu соnсрmе 11 ством
формы ПIIфа!'Орсйцы нмсшю её ныбра:ш си:-·1 -
вшюм с 1юсго союз:~. Она же сч11т;_~лась а.мулс-
1·uм :щоровыс И в наши д1ш гнп11ко нсчная
:щс:з;~а красуt.:тбt 11:.t фл<1.1 ';.~х н 1·t:pf1ax. м HOL'll X
Cl'JX! 11 В Чt:.'v\ ЖС СС 11 ()1 Ш]l(::Ка'l'СЛЪНОСТЬ?
Ле;ю в HJM, что в этой ф1 1 1 уrх: н~1 блюдастся
У/l.IШIПС:ЛЫ-Юе !IOC''l'OЯIKTIIO ОТН()J11е1111 й состав
ляющих её отрсзкоn. Вз1·11 ю 1 ю·с па рпс. 1: труд-
1топо1-1ернть.1юAD.АС =АС:CD=АВ:ВС=
=.. -- lD .АЕ "'АН: ЕС. Полъзуясh с 1 1:1~метрпей з nез/tы.
этот ряд раnспстн можно с::щё тюлго 11rюдолжа1ъ.
Рассмотрпи no:\pOб llee п~рвос равенство.
Точl(а С 11ел lJТ отрс:юк AJ) 11:1 две 11сраnные
ч:кт11, 11 болы11ая часть так от1-юснта1 к мсаь-
111 с 1\ как вс::о, отрезuк - к 6011 ы11 е ~·1 часта.
А чсму равно это отно111сн11е~ Чтобы 11 айт11 еп>.
Щ)!JМем [1.:11шу отрезка АЛ Ja tt, отреяк:1 АС -
:1а{}.ТаккакСП=и- /},тоа:/J=IJ:(а - 17).rшн
190
а1,,,a!J+h
2
• Раз;~; е!1иu обе част11 r1з 172 11 обо:ша
чrш ист<омое опюшс1тне a / IJ 6ую:ю1'1 Ф, лолу
ч1 L\1 уравнсrшс
F.
Р11 с 1 . П11 1нt.1 Jflt'Ч t1.1si Н1<'111•1
111•11 1 ,1г1ы~1м.1 R • 1111'1 ф111) ре
l l ~l>ЛIOЛd!:!T(Я УЫIВИГ('!\ЬНО~ 11U("ГО!!НСТВО ОТН<)ШμН\111 (1Гр('ЗhОВ
lлt>сьА// А( :А( (/)=АН ВС-=АП 1\1 =АЕ Е( 11r д
ф2=ф-! 1,
(*)
JIM<.:IUЩt:C С1'"\ 11Н С1l~С:ННЫЙ ПОЛОЖllТСЛЫJЫ(J KO-
pt:IH1 Ф = (v~ + 1)/2 = J ,б \ 8034... Часто рассмат
рш1:11от нс: О'ГНОШСНТН:: болыut:го <Hpt:JK:I к
м<.:ньшс"1у, а обратную 11t:лr1ч1111у - от 1 юн1е1111е
мс:н1,шt:П> птре:~1-:а к бом.111ему 1/Ф. F:го 060-
з11ачают бую.юй (j>. 11 оно ра11110 ( \15 - 1)/2 =
=0 ,618 О:Н... (Кстати, ~порой корень уравнення
(•) - ЭТО
- <[>.)
Ф 11 <р - прописнш1 и строчн;.tн фuрt·4Ы 1·μе
чсскоi'i буквы. ,. фи->. Таксх: обuзн:1чен11е 11рннs1-
то 11 чt:е1ъ дре1:1н е1 ·μеческо1·0 ску11 ы пора Ф1110 щ
жиншlТО 11 \' н. ;~u 11.э. Фню1й руко1ю1t1 111 егро11-
Т<:.'1ьст1юм ч1~tма ТТ:tрфснон в Афннах. в 11ро-
1юр1tш1х .--:1того х1х1м а м1югократтю прис) ·1 ·с 1 ·ну
ет чtн.~Jю <р (р11с. 2).
Rы , 1ш11еч1ю, о6раптп тптмаппс тrа то, что
:~нач:еншr чпссл Ф 11 <р от.'шча101·ся только пер
во1'i цпфрой. Этот факт заложен в са.мо.м урав
нении ДJШ 1.fИСЛа Ф ("'). Разделим его па Ф:
Ф=l+l/Ф=1+q>,
откуда вндно , что числа Ф 11 <р разл 11 ч<1ются
ров~ю на 1.
f<е1·ат~1 . сели то же ураш1е1 rне прсобrхщютъ
в Ф =.,/1+ Ф , то, заменив Ф 11од корнем на
.----
'
1
"1+Ф . nплучим, что Ф =\'l +,,1+Ф .Понторяя
::ny процс:дуру еще 11 ещё раз , 11 так да беско
r1счност11, 111.~педем формупу
1r1
1
Ф = \l+\l+vl+ v l+
Ес:тъ с щё одна красив:.ш формула:
1
Ф=l+---
1+-l -
1+...
Риl. 2. R 11rш1101 ш11ях
Парфенона '11-iогократно
П[>11ГVТП Rvf'I •tИ\ Л\) 1r
rr
'
Лt>~ктвин~льные числа
Она ншrучаетсн. есл11 13 прсобразоnаJПЮJ\I ypan-
11ен11и Ф = 1 + 1/Ф замсш1ть Ф 13 :~на.\н:1~ателе на
это же выра:жсш 1с:
1
Ф= L+--
1'
1+
ф
а :затем бес1<011еч.1 ю 11 рпдnJ 1,;кат1, этт 11 рпцесс.
Как же ра:-111:ет пn птрезот< n птrтоmсппп Ф?
Такое построеrше с ПО;\.Ющью циркуля 11 ли
нt: 11ю1 описано уже в зпамснптых " н ачал:~х"
Нв.к.тща. Оно пок~з;шо на рис. 5. С11;.~ч:.111а к от
резку АВ восст~шов~ rм псрпе1 rд1 nсулнр ВС, длш 1а
которш ·о равна 1ю1ювине д1шны отрезка АВ.
Затем прсте::д(:м отрезок АС - ::зто 1·1111отс 11уз~t
треугш1ы 1нкаАВС. ц~шее 11:юбраз1 rм две окр)Ж-
1IOCTI1 : <тну с центром А ТОЧКt с ]1 IJ:lJtllYCOl\1
BG, а вторую - с нt:11тром Li тпчкеrl 11 ра,' (11усо.м
AN, гдеN - точка 11ересечt"111н1 11epнoi"i сн<р)Ж
Рис. З. Золu10('1 tL"lt111иl'
urpeJк,1.,,,8, вып олненное
с nомошью 11иркул11 и
л"1 1 е~:11<и.
а("\/5- 1)
2
а
с
а
2
в
тюсти с очх:;iком !\С. Точка .lf. н которо1'1 1порая
окружпост1. п<::ресек::~е-1· отренж АВ. дел~ 1 т е1 ·0 11
о·тошешшФ,т.е.AJ!:МВ= Ф.
Соразмерность. uыражаемая ч11слом Ф, 1io
свндетt.1ьству мноп1х нсследоватслсr1. 11ан60 -
лее 11ршттпа для глаза. Лсопардо да В1111чн сч11
T:!JI. ЧТl) 1щcaл1.IILIC пропорц11и ЧС!ЮАСЧССIЮl "О
тст1 /\OJDКJIЫ быть свя3:Шы с LШCJIOM Ф. Дслс-
1-111с отре::зка н отно111ен1 111 Фон назн;u1 .зо. 1юmы.л1
U:'Чl:'"'l-t.Ut::.м. Ятот тсрм1111 сохр:11111 :1ся 110 11;~ш11х
т1ей . в э1юху Boзpo:ж;tc!JIJ}j :юлотос CCЧCIJl[L'
бьию очень 11оr1улнрно срсю1 Х) 11ожник1)Н.
скулы1торпн 11 арх11тскторп11 . H;Jr1p11мcp. 11
бOЛЫl!lll IC'l "liC Ж\ llIOI lllC I \l )IX 11<.:llЭ:.1Жt'l
0
I Л\11 IШI r·о
р11зо11та 11еJ1ит 1ю: ю1·1 ю 1ю 1~1.1о·пе н т·1 ю1 11е
нrпт. блrвком 1< Ф. А выбнr:ш ра:-1мсры са:--юi1
картшrы. старалнсь, чтобы от11оше1111е шир1J
ны к высоте тоже равшшос1, Ф. Ta1юir прям о
у1 '0,11-~н 11 к ст;:~т1 на зыnать •·золотым">.
ECJlll от vЭ ОЛОТОГ О прямоугольшща., от
реза l'h квадрат , ·1 ·0 UI IЯ"I ь l IOJIYЧ НТО! «З{)JIQ 'l"Otl
191
Числа
11рямО)·Толы111 1<». 11 так .можно ттролплж:~ть до
()ес1ю1 1 еч1юсп1. H::i p~te. 1 в1tдно, •1 то t>сл1 1 про
вtтти ю 1 а1·n11алп пср 1 ю 1·0 11 1поро1 п 11рямо
~толыппшn, 1·0 точка их пересечеш1л О Пудет
прr11rаддежать всс:--1 ПOJJ) чаемым <-:юлотым прл
моуголышкаJ\1->.
----ер ----
1
!~·--------- Ф---------Г
Рис. 4. « 1i)ЛUГcJl-I примоу1олЬНL1К>J 1CЛtl Ul' l lt'fO C)lf)( 1 J., lh КАалр(_tТ ;
оnя r ь о• rа1<Ртс Р ";.~олото>1 nрямt>уго ~ьнщ"" 11 по1 11рс щРr <
'1ож11u прuдuлж,111> UPtкu11~ч1ю . Л ди,111J11,J'1И первu1 о•• 11101>01 <)
Пf)Я'юу rnл1,1tИh. ПН 11t'f>t'IP~yтп1 8 1t1чм•О , ~,.отор.>Я tiyм•1
t lf.1Иlldдл< •,i.,,пь в<..rм получ,\t''1ЫМ <золuтым пря~юугuльн111--ам.
f>азуиt>стся, быоает н •<Ю.rтотой треугол.ыпш:»,
На p1IC. 1 это ршшобе,'\ре1111ые трсуrолы11rюr
FEC. ЕАС 11 НЕС, у которых оттюшеш1с щпrпы
боко1юl! стороны к ДJIИIIC оспоn;н 111.н р:шнястоr
Ф. Одно и:{ :{а~н:чатl'льных cвoflcтn т;.~кш·о трс
у t·ш1пн11ка состо11т в ·rом , что длш1ы биссе:к1-
р11с у1·1шн 11р11 L:rn nснон:11111н р:.~нны J.1.JШ ll<: ca-
;vю r ·o оснонан11я (pJ1c 5).
192
Ес-1· 1" 11 ~~юлотой кубоид" - это J1рямоугот,
rrыl1 nарэю1tлеппn ед с рёбрам11 т1л н1 юй Ф, l ~1 q>.
Рис. 5. • Зo,шruer
r рl· у 111,,ь 1•иК• ЛЛ11111,1
(JН(.сектр1к у1 лщ1 пр11 его
j)( Н П8.1 1·ШИ J)rlt3HЬI лл~1нt·
самого <>< нuнания
Площа11 1, <:гu 1ювсрхност11 paнrra -~Ф. ;\ д11аго·
11а111, - 2 (вы ~то мuжt>тl' прuнс.:μ11ть ). Отсюда
слсдуе1·, ч ГО OJШC]J 111:01НОКр)1' J l t:ГlJ сф<.:ра llMC-
CT рад11ус J. 11 , знач1п, cf: площа; \ь р:шна -111
По:поl\1уот1ю111е1111е пrн1срх1юсп1 этоf1 сферы
к повер:х1юстп «зшю·1 л1·0 кyf>ntщ<l» ранt-ю Jt Ф.
Чис;ю Ф оказалос1, 1ес1 ю сnлзэ 11111,1 м с после·
дов:пс:1ыюстыо Ф11бона,1чи: 1. t , 2.. ) . - 1. R. 1~. ."
н которой каждыf! члt>lf. 1та,11шая с трс1ъет.
rащ: н су,\1мс двух прсдыдущ11х (см. статью " по
следок1тt·л ьнос·1 ·11·1). В ч:1стнос1·и, 11-я степень
чщ:ла Ф нырзжастсн з;.1,,кчат<::,1nной фщшуло11
Ф"1
-
1)
= :z(u11,1+ ;" .
l/~t' а" - 11 -е ч11с1ю Ф116011:~чч11, :1/J11 -
11- й члс::н
последонате.1ыюrп 1 1..~. -t , 7 . l l, JR. 29, ., стрu·
ящеlrся по тому же прrп ш,1111)'. что и П()СJ 1 е,щ·
u:~телыюс1ъ Ф116011ачLпt.
Лt"1.11«1рдо .л.1 В1111•~н и1 1юлсm8J<\ • 1<1~11 1 ш1 1f.1ey1 u .~ьн11к
в кпм11о~нш111 <1\01"11 {HJ'1e1<111 "11 •i\А..о~пнм," ,
ТРАНСUЕНЛЕНТНЫЕ ЧИСЛА
Выражение •транс11е11де1п1юе чпс1ю') 1 1 :шер -
11я1<а слышали nce В ш1щле обычно сообщают,
ЧТО те и е - тrанс1 \ендептrп.1е LJИСЖ1. Олнако
что это значит - пе 1<аждьu'I пот1И1'11ает.
Латинское слово «rranscendeлtiS» можно пс
рсв<.:сти как ~потусторонний». Каким же обра
зом это сдово, стою, любимое ф~11юсофам1-1 ,
11роникло в матtматнку? Неужели 11 ~лес~, сеть
сной «Потусторо111111й мир»? И что н таком слу
чае математ11ки полразумевают под •посюеr·о
роню1ми» числами?
Если отrалкиuат1,сн пт 11атур<VТЪных чис..:ел 1,
2. 3... .,то с помощью qетr,трёх арифметических
действий - с1ю.жею1н, выч1гrа11ия, умножения
и делеrшя - получаются все рациональные
числа, 11 только они. Поэтому рациональные
числа с полным праrюм ,vюгли бы называтъся
~арифметическими».
Добывив опер<1 1\ию шш11ечения кор 1rя п- й
степени, можно nолуч;пъ <:щё и дру1·11с чнс11а,
11алримср:
1997
1~1998+ffl99
1'\[~)7 + 1w.f; ~ 2000
.
Доказано, что любое такое число является кор
нем того или шюrо алгебраического ураю-ю -
1шл с цсльrми коэффициент:щи, т. е. ураннс
ния ви.ца
/1
••и- 1
.
_О
а"х +а11_1"" +... +а,х+а0-
,
t'дt все а, - целые. Поэтому естественно было
назRать эти числа алrебраическиМl'I.
Итак, алгебраические числа - ЭТ() числа,
которые являются корнями а11гебраических
уравнений с целыми коэффиr~иентами. Имен
но их математm<И и считают «посюсторотш
ми», обычными .
Правда. в ХГХ в выяс ни лось. что далеко не
все корни аш·сбраичесю1х урав11 е11.ий удаётся
выразить с nомо1 цью че1ъ1рёх арнфмети чесю1х
действий и нзвлечення корня (см. сга 'п1ю
~Ур;шнсн:ия высоких стсnене11v). К пpi-Lvrepy,
ураn11ение
х~-4х-2=О
не имеет решения «Б радикалах». Так что сооб
щсСТ13о алгебраических чисел оказалось устро
tнным гораздо сложт 1ес, чем полагали слачаJJа.
Леиl тв~пелы-1ыс числа
Слuво olra11" Pnclenl1 s• мож110 nере1юп11 ....1к .~ н.ну1 торu11нftн >
ПРЕОЛОЛЕНИЕ МАГИИ КРУГА
Более дnух с nолон11ной тыс.нчс:летиf1 наз<~д
древнсrрсческш:: матем<пик11 з;:щались целью
построит1.> квадрат, р:н111овелr1ки11 данному
кругу (т. е. имеющий ту же 1иющ:1ДJ1), пр11чём
неnреме111Jо mmн, uнркулем 11 л11нет11<0й . Они
счнталп, что ·тлъко r\1 1 ркуль и 11111 rе~ша у11омс:т
nоряю1 божссТDеш1ым ка11011ам кр:1соты и 1·ар
мопии. н отвергали геомстричесюfе 11острое
пня с испол1>зоваписм друтих шктрументов
(см. егатью ·Три :тамс:11н·1ые ::1:.щач11 древнос
ти") Мно 1 ·очнслс:н н 1,1t бr::зус11еш1 Thlt поныткн
ре1uнть э·1у задачу щ к.1,щдратуре кру1 'а,> 11остс:
пенно сюю1 1или учёных к r.1ыcлri , •по она нооб
ще неразрешима. Но «склоняться ~ ещ~ нt: :та
чи1' «доказат 1,·>.
Решпть ~адачу о кв:щрату11е ~<руга - з·1 о то
же само<::. что 1юстро1л и nтрсзок дJ11rной -!п.
Ведь квадрат, ностроеш-~ый на т~шом отрезке,
будс1• r1меть ллощадь, ранную 7t , т. <.: . площади
193
ч~кла
К11адр.пура круга - lалача с мноrовековои 1кторие>1 .
круг<~, rад 1•1ус которого - с:дин 1ща. в то же
11ремя нее нос1 рое1111я с 1юмо щ1,ю цщж:уля и
J11 11 tе 1~ши, если их гrеренестп на алrебраичесю.~й
>1зык, сnодятся r< nьшолпеншо чсrырёх арпф
мет11ческнх деiкпш!J 11 11з1течеш 1 ю квадрат-
11ых 1\ор11eii. Так что norrpoc состоит n том ,
\ЮЖНО лп с ПОМО IДЪЮ этих пяти опсрациl!
вътра:шть •n1сло rr:.
n 1882 ['. Ht:MCЦКJlll M:l'l'<.:M:l'l'llK l(apJI Ферд 1 1-
11;1н1tЛШl/\t:МаН ) \UКа:3:.1J 1 , что Ч l lCJJO 7t'l'pa11c 1 teн
Дt:HT I ю 11, следона ·~·сл hНП , нс только не 11 редст::1-
н11.\Н >с ПOMOUtl•IO I03aдpaT l lblX р<!Д1 11{ЗЛОВ, нон
тюобще не -..юж~1 · fiыть кuрнем 1 111како 1 ·0 алге
Г1р:111чес1ю1т> ур::111не11ш1 с цет,1мн ко:"1ффицн
<.:11·1·ами. Та1< бш1а 11останлепа точка н м1ю 1 ·о не
ковой исторни эадачн о квадратуре круга.
l9-I
НЕСЧ ЁТНАЯ РАТЬ
!(ому-то 1 юкажетсs1 , что тр;,1нсцt: н дснтных
•111<.:<:л - ~кот 11а11J 1 :.1к:.vн>. пда е - вот и всс 1, <-ПО
тусторон1-11 1 1'1 м11р'>. На саыом деле это не так
В опrс/tслё1 11 юм смысm:: тр:.1 1 rсщ~ 1 щс:н11 rых ч н
сс:л ;.(аже бол ы 1Je, чем tuJJ ебра 11 чесю:1х: есш 1 по
сJ1еJ11 1 ие можно «проr 1 умеровать" , т. е 1<аждому
;,j)lГсбrаическому числу поставпть в соотне-1 ·
ст1ше отдельное натуральное чнсло. то трапе -
t(е1щ<.: 1 1 · 1нЫl' ч11с11а тако10 пересqёта 11е но11ус
кают - 11л 11есчL;т11ая рат 1,!
Еще н 17LЦ г. Леон~~ рд ;;юлер ны;\н1 1 нул 1'111ю
тезу, что ч11с;1а 111щd \оg.,Ь nо'1т11 11ри 11сех p:l·
цио11алы1ых а и /н1е мо 1 ут бы·1•1, корнямл м1ю·
го~ше11013 с цел.1,11,ш коэффн1tr1е11тамн 13 1844 r.
французский (11атематик Жо:зсф Л1-1у1111лль тю·
строил первые примеры ·1 ра11сце11дстrтных
ч11<.:сл. ПоJlь~унсь рецептом Лиувилт1, такие
ч11сла cт:im1 uбнаружннать н другие: Nатем~1т11-
ки. ]{ кпнцу XIX н }')Kt: fiыл:1 лока:.1:1н:~ J'JIПOTCЗa
Э!iлера. а Карл Всйсрштrасс обосновал транс
це 1 ще11т11псrъ чr~ссл .-,iпа IL сом'.t. rюч111 дпя всех
алгеГlра r 1чесю1х а:.
Выступая n 1900 r. 11;:1 11 J\.Jеждународном тсон-
1 ·рессе математшюn, Даnптr. Гильnерт сформу-
1шровал 2.) проблемы, которые XIX nск остав-
1рансuенле11тных чисел - 11~сче1 11.н~ рать
пял n наслсдстrю грядущему столе1·юо. Седьмая
проблема касалась доказате.т1ьстRа тра11С1 tсн
центности чисел вида а11, 1'/(е а - отличное от
О и l ~mrебраичсст<ое чис1 ю, <i ~ - 3.J1r·е::браl1-
чсское ЧНСJЮ, нс НВЛЯЮЩССОI рац1101 raJIЫJЫM.
число 1t
0'ШОШtПИе ДJJИНЫ ОКр)'ЖНОСТИ К её ДИаМеТ
ру - величина посто.11ннан и не ::1:.~1шс 1 1т от
разиеров окружноеп-1. ч1,н:ло, выр:.1ж;о~ющее это
отношение , принято обозн<lчать 1 ·речсс1юй
буквой л ( ~ 111н) - щ:рно11 букtюй слова «пери
ферия~ (гjжч. «с.жружнлсть»). Оnще}Ш)треби
-гельным такое обоз~ 1ачепт.-rе стало с середины
XVIU в. Число л выражается бесконечной пе
nериnдичсстюй десятичной дробью п приблн
жённо расно 3, 141 592653589...
В глубокой древности считалось, LJTO окруж
иос1ъ poJ3HO в .3 раза /\Линнее диаметра Эти
сведения содержатся в клнноrmсных таблич
ках Древнего Междуречья . Та.кос же значение
можно извлечь и з текста Библии: <, И с;1слаJ1
Лсйстш11~1\ьные числа
В 1954 1'. сс;\ьмую 11ро6Лб1)' Г1rльбсрта 11сзави
симо друг от друга рt.:шшш сонетскнй матсма
н1к Але1<санлр Ос111юв11ч Гс11пфо1щ 11 немец
ки.(! учё1-11>1[1 Teor~op Шн:~йт~;с р. 1шн·1· 11срдиn
птотезу о тра11сцендспт1юс1 и чисел ц11•
m1тое из м ею·1 море. - от края его до края ero
ДССЯТh JIOKГel\ - СОIЧ'СМ 1ч1углос . . 1·1 снурок в
·1рп;щать локте1'1 обн11мал сг·о кру1·ом " (.) Цар.
7. 23). Итак, перnы~1 прибл11же1111 ем ч11сJ 1а л
было 1. Од1тко уже но П 1ъ1ся чслt"п 111 110 11 э
математики Дрсвщто Е1 илта на ходнл н более
КАК ЗАПОМНИ1Ь
ПЕРВЫЕ UИФРЫ ЧИСЛАл
Три nервые uифры '*1Сла л = 3, 14 ... заnом11и ть со
всем несложно. А дЛs\ 3аnомнна1 1 ия большего числа
знаков сушесrвуют З<бавные поrоворк11 и ст11х11.
Например, такие :
Нуж но только rюс·.ара rься
И запомнить все юк есть:
Три, че тырнадuать, пятнадиать,
лсвяностQ два и ш(сть.
С. БJбров. «Волшебный лвурог »
Тот, кто выучит это че·веросrишие, всегда сможет
назвать восемь знаков числа 7t: .{, 1415926...
В слелуюших фраз.э< знаки числа 7t можно оп ре~
делить по количеству tукв в кажлом слове:
«Что я з11аю о круг.~х~» (n"' 3,141 fi);
«Вот и знаю я чисю, именуемое Пи. - Моло
деu!» (ТL"' 3,1415927};
«Уч и и знай в чи,ле извеснюм Ja uифрой
uифру, как удачу при.чечать» (л"' З, 14159265359).
Поrоворку «Что~ ~аю о круrах~» nреАЛожил
заме•1ательн ый nоnуля;:и затор ~1ауки Яков Исидо·
рО!'!ИЧ Перельман. Уч.~гель од1 юй из московсю1х
школ придумал строку. «Это я знаю и помн ю пре
крас1-Ю », а его учени1Jасочинила забавное nролол
жение: « Пи многие з~1а(и мне ли шни, напрщ;ны».
Это двустишие позволsn восстановить 12 uифр .
А так выглядит 101 з-1ак числа л без округления:
з, 14159 265358979313846 26433 83279 5021:18
4 19716939937510 53209 74944 59230 7Bl64
0621:16 20899 8628) 34825 3 4211 70679.
Ч11( Лil
то·. ое от1ю 111t·1 111е. В 11~1111 1 pyct> Ра~'1н1\3, кото
рый ~'ат11руt..."1 Сн 11р11(),11131 1тельно 16')() r до н. ::J.,
;.V1Я Чll('Jl.I те 11/)llHV,'(l l I CЯ :.тачt:нщ: (16/t>( lJ
деся1 llЧIIO M 11p 116л11Жl'll ll ll ЭТО 3.16.
(. VJ 11 :,п н. -+ .чатс111ат п чес1'ая наук<~ стре
"11 11<;>.1t.1ю ра:1ш111алась вДре1111сй Грецш 1 . J lм с11-
1 ю дре 1111 еrречссю 1 с геометры eep oro ,rщ1<аза
,ш. что i\JП 11 1а OЩ/)'Жt IOCтrf проrюрцион~uIЬ11а её
д11амс1 ру (1- 2rrR, Н - рад11ус окружностн, /
её д1ш 1 1.J ), а шющ:щь круг:~ р:~пна по1юн11н<:
nро11::111сдсн1 1н ДJ11 11 1t-.1 окр~rжное1·и и рзд11ус:~:
~·=~/ N= п.N1
.
2
.
':fп 1нок:1 :1а·1 e.r 11,c"111:1 11 р1 шнсыва ют Евдоксу К11 11;'
скому 11 Лрх11м е11у.
l96
ФОРМУЛ ЧУЛНЫХ СОВЕР Ш Е Н СТВО...
С чи<лом n cusiзa1ю множество красивых формул:
-
г1
3.-,~ 12+212. 2+]_ ']_+1 12 /2+...
1t
~2\22~2'22\22'2
'2
lt 22446681
2"'1"335 5 7 7j
ir
1111
- = 1+-;+,- i--y+,..~".
6
'l345
к!-
1111
-
;; 1+-
, +,+,+-,•".
8
зs-7-9'
(Ф. Виет),
(Лж. Вамис),
(Л. Эйл€!р),
(Л. Эйлер)
(многоточ и е 'Jдеrь 01начает что выстраивать число
RЫЕ' ко11rтрук11ии следует ПfОдолжать и дальше).
Сеть еше тaKc1SI формула
11r.
тт - 2~ 1 3~2 v2+\2+"+J2+.JЗ ,k}2. (*)
[ели предыдущ и е форму:.11 обосновываются в со
м1д11ых курсах матсмати•ескоrо анализа, io для
ВЫl.Юда ПОСЛСдtlСГО COOTllOU.<!HИЯ досrаточно сведениА,
почерпнутых и~ станлартюrо школьного учебн~1ка.
Как и1вестно, пери"'етр тисанного в окружность
диаметром 1 правильного n-угольн11ка выч11сляется
по фор,1улс
180°
Р~ -п 3П-n-.
.о
Удud11еая чfte\o
L 111/IOll np.1R11\Ыlbl\
BПIK.J>t HЫ'I:
\.~НО ГО\ Г( •ЛhHlil\f,B f
,н,.....-нсJ 1 ·юлучtlТt..
ВСЕ' OOM't' 11 fJllЛt-i'
Тf)•tHt)t,• ЛidЧ(•tнtt'
~111( '\а п
13 1111'1 ДU 11, ::1. c\f">XJIMCД Н СОЧIНIСШШ «()() 111-
MC(1Cllll ll кру1·а" 1~ыч11с11нл периметры впи
са111 1 1.1 х н окруж11сн..·т1, н 011исанных сжопо
11('ё праn11111,111.1х MIIOl'O)'ГOJIЫIИKOH - 0'1' 6- ~о
При больших з11ачеt1иях 11 псримс1р Pn приЬлн
з11rельно равен чиtлу n. Положим п = 3 2k, тогла
р" = 3 2k'> I П 60/2~. (flHYC угла 60/i' >.,ЮЖНО выраЗf1ТЬ
по-другому, если ВОСПОl\ЬЗОВаться ТОЖде<:ТВdМft дЛЯ
тригонометрических фуt1кuии noлoBftHнoro аргумента:
г.--
1
Ct
1- СО!> а
а '1+СО!>а
'itn2=\/2•cos2=v2
для различных :iначен~1 й k нахоли,1
/..
-
1:
k =1:
k= 3:
k:
ЫJ"
si11
в
60~ 1/ ~-
cos -
=- "2." \2+,/з.
н2t
'
'
б()С1r {- ==-~
~·n y = 2 ,2-,2..-\l2~." +.Jз
t IМ>'"......,.
Отсюда уже НЕ'ПОС:рt>дrrвен но nолучае,1формулу1•) .
96-у~'<mышка. Тuю1м образом пн усnн·ю RШJ, что
LПfC.'10 л :-~акл ючстю .1:1 пределах 0·1 · 3 111- 1 до -1 У-,
т. i.: j,JLl08 <л <.1,1-128. Значt:ние 3У- дu c1ix
1юр счr 1тастся шюлнс хоrюш11м npr16JI11жeн11-
l:M чисrа 1t !\ЛЯ ПJ11·Н<Ла1'НЬIХ :-{:JД~IЧ fit>ЛC e 'J'()Ч-
1юе пр11блтке1111е 3 1/i~o (л ~ 3, 14166) нашёл
значе11 1 1ты 1'i астро1юм, создатель три 1 ·ономет
рrш Кл;1Rд11!'1 Птолсмсй (11 в.), но шю 11с 1101111ю
н ynm реблсн 11е.
Ин1111й1~ы11ttрабы1юJ1агат 1, что л = \
1
1О. Этп
11 r:~чt:пие приводит инлнйс 1<нй vtате ма·1 нк VIТ к
Гiр11 хма1упта. Кита 1lские учёт 11 .1 е н Ш n. исгюn~.-
юнал н fl.IIЯ 7t значс.:ннс :)~0 , которое хуже при
бннжt:пия Лрхимед:1 В тюнце У в. Ц:~у Чу11 Чжи
1 юлуч11.'1 г1р~16m 1жс11ис .1'55/11) (n: ~ 3, 1"11 '5917).
Онп осталось 1rеизнеLПю cnpo11ейцам и было
в1ювь 11айде110 1 шдерландским матемапшом
Лдр11апо.ч Л11то11исом литпь н l '585 г.
К ктщу Л'VI н. н еnронейско1I матемап1 кс
сфо рмнроnались 110ш1тт 1 я ращюпаm,J 1 1 ,1х и
11рра1(11011альпых чисел. Хотя .м~ютпе быJJи
убеждены, что чтrс;ю 7t - ирращюIIалыюе.
дока:3::п1) этого ~шкrо ие мог ll то же время не
которые .У~атематнки продолжали заниматься
вычлс;1енш:м числа 7t. ll ндсрла1-щсю1й учёпый
Лудольф ва 1-1 r~ейш::н в 161 .:; 1- .
щ1111ё11 для него
32 11ра.1шлы I ЫХ ;~eCЯTl·IЧH l,\X 3Нак::~, ЭТ() 11рнб;ш
же11щ: назык:.1лн лудольфовым ч11 с1ю~v1
С ра:)вит11см м~1тс:м:гп 1 ческu 1·0 ~~нaJJн~:i с 1·0
Ml:TCJ/\Ы r 1 ачалн прНJ\1ешпъся 1J для 011рсде11е-
11ия числа п. R этом при11имал11 участие nt>Чтt·J
nce и з вестные математик н: Ф. Rнет, Х. Гюй1·е 1 1с,
Дж. Валлис, Г. В. Лейбниц, Л. Эйлер. Они полу
чаю~ различные выражен ия для л Dвиде беско -
11ечноrо произведения, суммы ряда, бес1юнеч -
11ой лро611.
Например, Готфриf\ Внльгслт,м Л<.:йбru щ n
167·1 1·. устагюн нл следующую формулу
1t
]11
-= 1- -+ ---+".
4
3')7'
вырэжающую ч1 1 сно n/4 кат< сумму ряда (см.
ст;пыо "ч и еловые ряды"). Однако этот rяд схо
дится очспъ медлеrпю. Чтобы вычис;ш1ъ тт с
точностью до ,i\есятн з11а1<ов, nотрtбощuюсь бы ,
как пок<1з:.1; 1 Исаат< H t~ю·1 ·01 r, 11айп1 сумму') млрд
ч11сел 11 эатра ·1·и ·1ъ на это около тыо1чи лет нс
прt рывной работы.
Лt:и(тв11тельные чи сла
J101-щон сю 1й мате;:мат 11к Джон М э-ч 1 1н в
1706 г" 11рнме11ян нсскл11 ы<0 ра :-1 формулу
х+ J'
arc1g х + a1·ctg 11 = a1·ctg --
·-.
.
1-.'\.у
получил ВЫ [ЩЖСI rие
lt
Подста1 ю13ка н нс1·0 :.i1·c1g 1= -
н рядов /(11я
4
1~1'1
-
,н-ctg х (arctgx=x--x + -.х --х · +".) пр11-
3
57
1юдит 1<фор,чул е
~= 4(.! __1 +-1 -".) -
4
5 )·)'
') ')~
(
l
1
l
1
-
2:N-32:N'+52:)<}- ".)·
1\улольф в;:~11 U f'•1M'н 1ю мегоду Архимt'л,1 умы 11u,1л Чl.f{'ЛQ гтор1111
вписанных и оnиtанных \1ноrоуrоль ннков Так он вычщ ·мол
12 десятнч11ы.'< знак;~ •jи tл~ 11 , nuтр~п1 в на зто мнuгrJ ле г
Л,1льн еишi1я 11стор11s1 Аыч 11 r~\ени я чи\ла n: наn()мин.-1ет
tnо рншны ~ сорt•в>юв,111" я, ко1 д<I 10 nлин, HJ лру1 uй rn11p 1п"1P1 1
вырыв ,1 етп1 вперРд, пал,1е т, вс1ает 11 с навои п1лои устр<'мл я еТ< я
к n об<::д~
197
Числа
кото1х1я r10 с11х 11ор счнтастся от юй и:~ луч
ших для приближё111 юrо uычнсления л. Чтобы
вайтr r те же десять точных зт r аков. потребуется
всею нсо<алLко часов руLпюго счёта. Сам Джо11
М :-)ч11н Rычис;шл 1t со 100 нсрны.ми знаками.
В 1766 1'. ~-11,:мецr<.н 1':i матем~п11к Ио1~1 нн Лам
берт строго ;~ока з:щ 11 ррацион алыюсrъ чнсла
n: чнс1ю n: 11 е можеr б ыть предста1;1ле11 0 про
ст 1>1м1,1 r1poб}IMH. JQ K бы l lП быJП,1 ВСЛИЮ•I чи сл и
тель 11 :шаменатст,, И тем Lte менее нстория
чнсла тт 11а этом 11е эат<ОJ 1чпласт•.
В ко11цс XIX к профессор Мюпхспст<аго утти
верс11тета Карл Фердина 1щ Лш щема11 докааал,
что к - число трат 1сцсндеrrrпое, т. е. 0 110 не шз
лястся корнем пнка1<01'0 <Uiгсбраичсского ураn
нения а"х:'' + а11 1х" 1
+",+а1.V+а0=Осцелыми
ко:::!ффиц1-1 снт.~ми. Er«> дою1за телы:тво nuст<1ви
ло точку н ~rстории древней шей l'>t~1тем:п ич.е
ской Jадачи о квадратуре круга (см . статью «Три
з 11амс:ннтые з~ща чи дре н~ юсти»). Н а протяжении
т1.1 снчелетнн о на нс 11омаnалас~, усиJtн.им мате
матиков, н ю.1р аже 1111е «к.в::щратура круга» даже
стало синонимо м нсразрептимой п роблемы.
«З~т1r1о чное упорство» ::~той :;адачи, как оказа
лось, сnязано именно с природой числа 1t.
В память об открытии трансцендентности
числа 1t 1:1 :;;але пер ед матс:матической аудито-
ЧИСЛОе
Число е ~ 2,7 182818.284'19 - сщна нз нажней
ших постояmn,rх н математике. По определе
ншо, 0110 раnпо пределу последовательности
:х:" ::: (1+ _!_) /1
п
при нсо 1 ·р;~н и ченнuм 1::1озрастаню1 п. Обозна
чение е внёл Л еон.ар;~ Эйлер н 1736 г. Он вычис
лr1л псрные 2 .) з 11ак::~ э·1·0 1·0 числа н деся'п,1чной
:'!~IПИСИ.
С rюсо б :зада нин числа е прекрас но иллюст
р11руе-1 · ·1 ·п·1 · наж11ый для иатсматики факт. что
мпоrне чпсла мтуr быть определены шlШЪ как
п ределы некоторых rюследонателыюстей. Что
бы доказать существова1шс предела у послсдо
вателыюсти (*),прежде всего устанавливают,
что она мопотоrта (х" > х"_1 11ри всех п) и
огран 11чена (2 <Хп < .1 при всех 11). По теореме
198
ПРОСТЫЕ И тт
Рас<:мотрим бесконечное произведе~1и е дробей
23571113
-·-·-·-·-
·-
·
12661014
Здесь в числителях стоят все n ро{.тые числа, а зна
менатели отличаются от них на един и uу. При этом
знаменатель больше числителя, если тот имеет вид
4п + 1, и ме11ьше - в nротивtюм случае.
Леонард Эйлер локазал, что это бесконеч ное
!t
1'1ро изееде ние равtю 2, т. е . отtюше11ию дм1t11>1 по·
луокружности к её диаметру.
рн сй Мюн хенского ун нRерс и:тета б ыл установ·
лен бюст Линдемана. l l a пост:,~менте под ero
именем нзоб ражён круг, 11 ересечённый квад
ратом рапной площади , внутри к()торого на
черта r ra букоа л.
13 наше время с помощью ЭВМ число л
вычислено с миллионами пр ашmыrых знаков
после запятой. Но такая точность не Щl)Юtа нн
13 каких вычислениях и предстаuляет скорее
технический , чем научный интерес.
Вейерштрасса, ecJiи последопа·1·елыюсть мшю·
тонна и ограничена, то опа схо[( ится, т е. су
щестuует число , к которому стремятся члены
этой лоследователыюс1и при стремлетmи /1 к
бесконечr юстн (см. статью « Предел nоследо·
ватСЛЪIIОСТИ» ).
Разлагая выражение для х" п о формуле
б.инuм :.~ Ньютu на, можно доказ;~1 ъ, что число
е явл яется тrре1~елом и ;,ругой последонатель·
НОСТ[1:
11
1
s 11 = l +-+-+ ... +-,те.
!! 2!
п!
e=liшs" = 1+l+l+."+J..+ . ..
n-• -
1! 2!
п!
Здесьk!=1 ·2 ·3 · ... · k (t.fитается:«kфактори
ат ), Эта формула более удобна для расчётон
при 011ределен ш1 числа е, так как, найдя зна·
ч<:шн:: s11 • J.J.JТll вычислс 111 1я слс; ~ую щ еr'о з н а ч е
rrшr 1-~адо нобав 1 пь к 11реды;1ущсму ч r 1слу лн 1 11ь
одно <.:ла 1·:1емое :
l
s1"1=s11+
.
(11+ 1)!
Уже npr1 н = !()сумма s" отт1чается от истrш
ного з11а•1е1шя числа е меньш~. '-1ем rra j 10-
11
•
поэтому s 10 даёт лрибш1жеr111е ч11сла е с семью
праш 1лы 1 ымн зr 1 ак:u\Н1.
Ч11сло (! - 1Ippa 1\нон ал t>ное 11трансце1 1ж::11т
rюе. Доказ;1·1·с;1ы~1но 1 р:н 1 с1 \сндентнuстr 1 • 11 1с11а
е нnерю,1с д:ш фр:.шцу:кюtй м:~тематпк ш~1рЛ1>
Эрм11т 11187.11· .
Число е 11rрает особую rою, н математ11че
сr<0м ;1нат1зе. По1<::1з:1· r ·ст,11а>1 фу1-rкщш с ос 1 ю-
11аш1е ,\1 е, на:{ъпшемая aкcnolle11moй, - уд:пви
теJ1ь11 ая фушщия, про.и:тодная которой равна
ей сам01"1·
,
(е') =ех.
ЗАдАЧА О РОСТОВШИКЕ
Представителю з наменитой швейuарской династии
матемаr\1\ков Якобу Бернуми nри1~аллежит идея сле
дую 1 111"й ".Jадачи.
Некий ростовшик дал взаймы кynuy апрелелён
ную сумму денег с условием, что чере1 год тот вернет
3аем в двукрат1юм размере. Когда купеu в следую
ший ра;{ обратился к нему с просьбой дать денег, рос
товщик изменил условия договора: за первые полгола
nоАЛежа щая вuзt1рату сумма возрастет в полтора
раза, а 110 истече11ии второй полови11ы срока вновь
образованная сумма увеличится ешё в полтора раза .
Ростовш~1к рассчи;ал, что таким образом он nовы
сиr nерD011ачальную сумму займа в 9/4 раза, что,
безусловно, выгоднее двукратного увеличения.
Постепенно в rолое.е ростовwика сложилсй еще
более хитрый план: сумму, поАЛежащую возврату,
увем1чивать непрерывно. А именtю: весь срок, на
который купuу ол<1лживаются деньги, разлелить на
большое чи сло 11 равнь1х промежутков. По истечении
кажлого nромежутка сумма долrn долж11а возрастать
в 1 + l/11 раз. Так что к окончанию срока nервона
чальныи заем увеличится в (1 + 1/п)" раз. « Наверное,
:по оче1 1ь большое число », - подумал ростовщик.
Korдd эту формулу вывел лля себя купеu, 011 рассу
дил нк: «С одной cтupoнhl, nоказат1=ль стеnени 11 ,
уееличиваясь, тянет за собой в бесконечность всю
степень, поскольку основание её, 1 + 1/ п, больше еди
ни1Jы. Казалось бы, непрерывное прирашение д.олrа
в конне конuов выльется в колоссальную денеж ~1ую
3
2 ,'i
2
15
0.5
о
Леиств 1нсль11ые •1исла
'"
N,...._,
1
--(",
~1
~-N
2~45
N
11\ 1'·
\/"\
"'
1/"\
N
c-:i ,._~"
678С)1()11
сумму - сверхприбыль для ростовщика и соответ
пве11но сверхубы1ок лля менн. Но, с другой сторон1>1,
хотя основание 1 + 1/п и больше единиuы, с увеличе
нием 11 01-10 все сrремитель11ее к 11еи приближаек~ .
А эту упрямую uифру в какую степень н~• возводи,
всё рав1ю лишь ~>линиuу получишь ... » .
На самом деле выражение (1 + 1/п)" с роrтом п
стремито1 к числу е = 2 , 718281828459045... , 11азы
ваемому также .1йлеровым числом. Это олна и.:1 самых
замечательных математ1~ческих констант, основани~
щtтурального ло1-.:~рифма.
Первые з11аки числа е запомt1ить несложно: два,
за11»тая, семь, год рождения Льва Толстого - два
раза , сорок пять , девяносто, сорок nять.
1<)С)
200
Числа
Логарифмнческал фушщия с ос11ола 1 1ием е
назыnастся 1ютура.лы1ым логариф.мо.м и обо
значается ln х. Её nро11зnодная вычисляется по
сле/\ующе::му правилу:
ЛОКАЗАТЕЛЬСТВО
ИРРАUИОНАЛЬНОСТИ чием е
Число е- 1 допускает разложение в ряд:
1
111
е =1--+- - -+".
1!2!З!
Обозначим первые п + 1 чле11ов ряда через ап:
(Х=1-2.+_..!._ -
_..!._ + ". + (-1)п
"
1!2!З!
п!'
а бесконечный «ХВОСТ» через 1'311 :
(-1)" t 1
~"=(n+1)!+...
Если абсолютные зна•1 ения знакочередуюшегося
ряда монотш11t0 убывают, то остаток по абсолют
ной величине меньше его первого члена:
(•)
Поло.жим а11 =п!а.т Ь" =п!/311 • Пользуясь неравен
ством (*), находим, что ап - натуральное число, а
О < (-1)"-
1
bn<_!_l
.
п+
Отсюда вытекает, что 11и п ри каком п число
п!е-1 =а"+ Ь" не является uелым. Поэтому число Ve,
а з11ачит. и самое не являются рациональными.
'
1
(ln х) =;:-.
а производные показательной функции а~ 11
логарифмической фушщии log"x онре::дсля
ютсн 110 формулам
'
(а') =a"lna,
1
1
(logax) =- -
x lnu
Эйлер обнарУ'жил связь между трнrономет
ричссю1ми функцшtми и экспонентой с млн
Jvtым показателем :
ШlИ
е'х= cosх+1si11.~:,
е•~-e-L•
sinx=----
21
ПРЕКРАСНЫЙ СОЮЗ
•Судьбы» двух констант - тт и е - тесно перелле
лись. Эту пару, стоящую в одной формуле, можно
встретить в сам ых разных областях математики
в теории чисел, теории р51дов, теории дифференuи
альных уравнений, теории вероятностей.
Вот, например, формула, открытая индийским
математиком Сринивасой Рамануд.жаном. Если
то
Ь=-------
1+------
2
1+ -----
3
1+
4
1+ --
1+ ...
~
а+Ь=~Т.
Эту формулу. без всяких сомнений , можно отнестч
к шедеврам математики. Ни беско~1еч11ый ряд, ни
uеnная дробь в /\евой ее части в отдельности не
выражаются через числа тт и е, а в сумме они дают
такую поразительную комбинацию!
Из этих формул вытекает замечательное
равенство
е'" +1 =0,
J<Оторое связывает числа О, 1, а, 1t и мнимую еди
щщу i.
Даж<:: немн01·ие привсдёrтые :3Д<::Сь примеры
локазывают, что ч.11сло е встреч:аетсн в самых
разных разделах высшей мате.матики.1<онстан
·1у е иногда без достаточных на то оснований
Лействнтельные числа
называют 11еп<::ровым числом - по имени
изобретателя логарифмов шотландского мат<::
матика Джона Неттера. Действительно, при по
строении таблиц логарифмов, 011убликоnан
ных в 1614 r. , в качестве ос1тонания Непер
использовал число o,9999999Looooooo, очень
близкое к числу J /е. Однако следует иметъ в
виду, что понятие предела , с ттомощьrо кото
рого определяется число е, во времена Ненера
н мат<::матике ещё не сформировалось.
Числа
КОМПЛЕКСНЫЕ ЧИ СЛА
ЗАЧЕМ НУЖНЫ НОВЫЕ ЧИСЛА?
Когда мы слышим слово «ЧИСЛО->, то па ум преж
де всего nриходят натуральные числа : 1, 2..), ...
Их мы используем для пересчёта разнооб
разнn1х лредметов 13сли натуралr)ных ч.11сел
оказывается недостаточно, nрибегзсм к лро
бям, а точнее - к рационаныrым числам. И то,
как правило, пе тю всем , а лишъ 1< тем , которые
выражаются ко11еч11ыми десятичпы_ми дробя
ми. Уж их-то вполне хnатает для повсед11еrшых
нужд. Конечные десятичн:ые дроби nозволню1
фиксировать результаты всевозможных изме
рений с произвольной точностыо. Чего же ещё
ждать от чисел?
Но нот нам говорят, что сущесrвуют несо
измеримые величины. Например , лиаго:налъ
квздрата несоизмсри·ма с е1·0 стороной, 'Т'. с. от-
ношение их дли~-1 -
. J2 - не является р:щио
валыrым qис;ю.м, хотя и может с люб()й н~пе
рёд зада1шой точ1юс1 ыо быт1, приближено
рациональными числами. И тогда становится
понятно, что проще признать эти новые , ир
рациональные числа , 'Iем кажд~1й ра3 вместu
202
~решим ур::tвпспне х2
= 2 ·~ гоnорить «1-1айдём та
кое х, ч1"06ы х2 отлпчалось от 2 пе более, чем
Н'1 такую-то величину».
Построе111-юе таким образом сообщество -
мнuжество действ11тельных чисел - уже ке
только удm1J1етrюряет 11ашим гrракт11чсским по
требностям , 1ю и обладает nттрС/\СЛённой тсо
ретнчесr<ой rinm ютой 01 ю nозволяе'J форму
лировать разнообразные заJ1ачи , с1ююпь 11х к
уравнениям 11 решать, не боясь впасть в пр()
тююречис. Конечно, и З/\ССЬ ес1 ь свои праnила
и ограничения . Нельзя, например, делить на
нуль, нслкт извлечь корень ч.ётной степе1111 из
отриц;,пелы-ю1 ·0 числа и т. д Однако прав11ла
эти, несложны е, и сслн им стро1 ·0 следовать, то
всё бут\ет в порядке. .
_
Но всё ли' Рассмотрим такой пример: (~'1
можно счита1ъ равным н 1, 11 -1, а oпp<..:J\eJIН'IЪ
<'f-1 невозможно. С другой стороны. что такое
1/6! Это то же самое, "П'l._ 2/12. Однако c,v-1 =
=(-1) 1 '~ (-1)2; 1! = 12..}( - 1) 2 = 12Jt, а послеμний
корень можно извлечь!
•Заn~тный • коре нь.
Вот ещё один пример:
(-1)2
== с-1)2= с-1)2 =cJ=-1>'·
"[1]4
Но если квадратного корнн из -1 не существу
ет, то и его чствёртой степени не существует.
Значит. - 1 нельзя возвести даже в квадрат?
Кому-то покажется, что всё это не настоя
щие противоречия. Можно на.1тожи1ъ дополни
тельн ые запреты на действия с числами, и по
добные ситуации больше не 1юзникнут. По
всегда ли разумны запреты? Представ1/1-е себе,
что 11екоторые зада ч и яес1>ма успешно реша
ются только с наруuтеrшем о пределёш-юго за
прета, и ни1<аI< не удаётся найти «зат<шшого»
способа их решения. Не стоит ли в таком
случае отказаться от ограничения, ставшего
слишком обременительным? Именно это nро
ИЗОlШЮ в сrюё время с запретом извлекать квад
ратный корень из отрицательных величин нри
решении так называемого неп р иводимого
случая кубнч.еского уравнения.
НЕПРИВОЛИМЫЙ елУЧАЙ
КУБИЧЕСКОГО УРАВНЕНИЯ
Подобно тому как для решения квадрапю1·0
уравнения существует общая формула , выра
жающая корн.и уравнснI-1я через его коэффи
циенты, аналогичная формула есть и для ку-
Комплексные числа
б.ичсского уравнения (см. статью «Кубнчсскне
уравнения»). Она Н:!зывается формулой Карда
но - 110 имени математш<а , 011ерnые её опу
бликовавrпе 1·0. Но, к примеру, для уравнения
х~= 30х+ 36
формула I<ардано даёт
х=~18+~-676 +\{is-[
-676.
Под 1шадратr1ь1м корнем здесь оrс1 залось отри
пател ьное число. В то же время уравнение име
еr решение х = 6 - это легко проверить.
Однако предположим на секунду, что коr11и
из отрицательных чисел существуют. Тогда ,
сели 11аучиться изuле1<ать кубические корпи нз
.--
выражений вида А+ у -В (см . статыо «Возведе -
ние в степень и н:щлечение корпя из ком
плексного числа»), можно будет вычислить
VW+~-676 и Vis -~-676. Мы получим 3+
+.J-1 и 3- J-1. n самом деле, возвсдём в t<уб
выражение 3 + ~ , восnользоnавшись форму
лой(а+Ь)3= а3+3alb+!JabL+ь~:
сз+н)~ = 27+'!l .9.-Г-~ +3·3-С..Г-1)2 +
+с н)-s =27 -9+(27-1),/ -1 =
= 1 в+26Г-l = 18+ ~-676.
Аналогично, (3-f. -I)' = 18- -}-676. !!оэтому
х= Viв+ ~-676 +·Vis - ~-676 =
= (3+J- 1)+(3--Г-1)=6.
Как в.иди:м" «странные» корни успешно сокра
щаются. То есть мы рt"шалн обычное уравне
ние II н~шли корень - обычное дейсТRотсль
ное (и даже н:~тура.пьное) число. Ilo JVlЯ этого
в проме)l...уrочных ныкладках нам пришлось
опер11:ровать «trсобычнымн» чн<.:11<tми. И са мое
главное - никаким l\ругим: способом , за ис
ключением разве 'IТО угмывания, это решение
получить не удаётся!
Теперь у вас сст:ь три пути:
-
безоговорочно следовать уста 1 ювленн.ым
за11ретам и отю1затьсн от 1ювых 1 ~риобретений,
т. е. считать, что н11како1·0 метода решенин
20=)
Числа
[3 npouecce решр ни51 мы >~сnольз0t1<1лн • не<.ушествvюшиt' uбъекты. но в и1t)re он~1 успеш11п ( окрспил 1кь.
11е11р111юди.моrо случая 1'.)!бическо1 ·0 ур:шнетr11н
у пас нет;
-
«с прятать 1·олоnу в 1 11:;сок», т. с. каждый p:.i:~,
р~:;шая ураннения, 11р11 переходе к .цсйl-rнию с
выражс11 иями вида J-Л 1·онор11ть « 1-пй11н11·1·е!»,
а возвращаясь *На законную uочву•;, лсжпь ющ,
что н1rчс1·0 нс произunию;
-
KOJIЪ скоро м 1,1 допустили n пр()МСЖ)'Т() Ч
тrые Rыкладки объсюъ1 rю1юй п1л-rро~м. всерьё:-~
:-~апяться пх изучением : дать опре,11елсние , ис
следовать свойстnа, научиться nъшоmш1ъ ар1rф
метнческие операции.
Хотя 11 не сразу, по II конечном 1по1 ·е мате
матюш ныбрш1и трети 1'1 путь. И бьтн нозна
rраждс:ны: ~странные-> корнн нaL1J J 111 н1нрокоt::
применение в электрт·1.:хннке, аэроюrн;.~мике
и другнх областях знаний
ЛЕЙСТВИТЕЛЬНО Е +МНИМОЕ =
КОМПЛЕКСНОЕ
Итак, кроме привычных действитслыrhLХ (бук
в;шыю - <·реально C)rщec1·Ryющi-L'\") '-Шсел нам
приходптсн рассматрищl'l'h еще чнсла шща f -A ,
где А - rю; 1 шю1телыюс действительное число
Что это J::t чис11а, как и~ f ПОтрш·ать руками·; -
всё ::J'L'O 1юпросы, не имсющиt:: ответ~. Мы про
сто доrонорил псь сч ит::~·1ъ, что онн есть. И нпuл
нс сеJ·есrненно. что такие числа были 11аэ наны
.лt нu.,нылtu, ·1 ' . е. <· нереал ыrымн >}.
l lo кое-что о м1 шмых числах мы всё же зна
ем. Например, что при нознедс11ии n Кl:!адрат
204
они дают отрицателы rые числ:.~. Далее, поr1<от,
ку-А=А·(- l).то\-А=,А,'-1,а \1
.tl - это
обыч1 roe ;~с 1:1стнител 1,1 ю~:; чJrс;ю. 311~1•111т, любое
м11имое ЧIKJIO можно получ11 '1 j, l!CXOJ\H 11:-1 t/\JIH-
cтricшюro ~11111мm·о •нtсла \' - 1 , есл11 ум11ож~пъ
его на подходящее деi1стш1телыюе lШCJIO. Та ·
кии образом. в:-v1есто безбреж1ю1·0 оке;ша тап11 -
ст.нсн11ых объе1.:·1·ов мы 11У1ее,.,,1 0μ111r- сди11стве11-
11ый нс11р11вычrr1>1й объект. все же о<.Т<L'IЫ 1ые
строятсн с 1юмощью 011 ер:.1ции умножсшu1. <.;о
r1шо1тссь, с т~ко11с11ту;щщ'l1 11рнм11rнться уже
1·ора:що лс 1 ч1::
Число \1-1. ш ·р::~ющсс rш1ь "Cl'p011TCJll>ll01'0
бllOI\<t» в м11ре МIШМЫХ Чl1Ct'!I. /\:l:1ЫВЗЮ'f' ." 1 1/U-
КОЕ-ЧТО О КВАДРАТНОМ УРАВНЕНИИ
Если вам скажут: «Квадратное уравнение, дискри
минант которого меньше н ум1 , не имеет решения ».
можете блеснуть -_,рули uи ей, уточнив: « Нс имеет в
действительных числах, в комплексных же 11меет
uелы х два&. Рассмотрим ТJкос уравне11ис :
х2- 2х+5=U.
\•)
По обшей формуле находим
1-
/.
х,~=1±vl2
-s =l±v-4 .
Здесь дискриминант П =- 4 отри uателен. Однако
знакомство с комплексными ч ислами юбавит вас
ОТ ЛИШНИХ СОМНNIИЙ :
Х1.1=1± ~·-4 = 1 ±2~- 1 =1± 2i.
Таким образом. уравнение (*) имеет два ком
плекс1-1ых кuрня: х1 = l + 2i, х2 =l - 2i.
,1юй ffдll11/1Цf1й и 110 t1ре,r1..тн>жсш1ю Лt:онард:J
Эйлеrа оnоз ш1чают букно1:1 i (от лат. itn<1gina -
riL1s - •мн1 rмыJI->). Основное свойсТRО м111-1мn(1
едш11щы н1,~раж~1ется 11рость1м р:ше11ст11ом:
/=-).
Одш~1-ю, r<ак nодсr<изыnает оuъп решения ку
бическнх уравнс1 шй, кроме действительных и
мшrмьL" ч11сс-л нам nри.ходJ 1то1 рассматрин:~ть
Комnлекеt 1ые чнсла
ТаКЖС: ЧHCJl~ RLЩa Л -t \
1
- В , К<1ТО[)ЫС Гf(1C/1,CTaH
JПllOT собой C}"•IM)' дt:С1с.тв11тслыю1 ·0 н мн11мо 1·0.
Таю-1с числа ~1Ме11у1о'Т-с>1 комm1t'КСнъ1мн, т. е. со
с1·авными.
А теперь. суммируя всё ска::~аш-юе, сqюrму
л11русм накош:ц определение комплеI<сного
чнсл~r : х:о.мn1и•r.-с11ым •щс;юм 11а::~ывастся выра
жсн11с внда а + Ьi, еде ан Ь - щ.:йствнте1сы1ые
ч1 1 сла , :i i - .v~н11м:т сдr11-11rца .
СВОЙСТВА КОМПЛЕКСНЫХ ЧИСЕЛ
В кожтскс1юм числе nrщa
z=а+Ы.
,
(*)
l'Дf.' tl 11 f) - ) \eJ1C'l'RHTt:Л Ы11>Je '-!11СЛа , а i = \'-1
-
мнt1мая е;щ[{ица. сла1·~смое а 1tазьшаетса (}еf/
ствите.:1ыюt! •юс:тыо, з сла~·ас~1ое fJi - л111U
.~1ой 'lастью. Дс:r"1ствитслы1~10 ч.:.1сть с1 п кuэф
фиц11 с11т /? 11р11нято обо~{начю·1, ~·ак
а=R(· .z.Ь =r111z.
Пплу<1:.1стся, что любое дti1c11штелы юе ч11с
ло - это такое комплексное чнсло. i'<Ш1 ·1мая
часть которого ра.1:3на lJ)'JIIO, ш1щх1мср:
О=О+Oi,1 =I+Oi11т.п.
Мнимое же число - :-:)'!'О 1 ·аюJе ком11лскснщ·
ЧllСЛО, у которо1·0 J-1улю р::шна /\с~'J СТВ11ТСЛЫШЯ
чае1ъ. а мн11мая часть отт1•11-1а от 11'у·ля , R ч~1 ст
ност11:
i=О+Ii.
Ко:-mпекс~1ые чт~сла мткrю ovra11.ыnaт1, н пе
ре.~нюл«пь точно так же. r\ак это делают с
алгебра~ JЧССI<ИИИ 11ыраже1 ШЮlfИ. Прн ЭТОМ пр11-
вычлыс зш<оны сложения и ум1южс11н11 - со
чстатс.r1ы1ыfl ( ассоцна11ш11ый), псрсмtс'r 'итель
ный (КО.\1му1·атик11ы!J) , распрс;\ел11телы1ыi1
tю1стр116ут111шый) - остаюто1 1:1 с 11ле:
Особое значещн: нуля 11 едпшп1ы также со.л."}Jа
няется:
де йL"I"вител ьна.n
чаС'J·ь
z-1()=z,z,()=(),z 'J =z.
Рпль же м 1111моr'1 сщ 11 нщr,1 i сонерпrеm ю особэя
t1 не пмсе-1· a11aJl()Г()11 n •·об1,1ч1юй~ ::1рифме-1·ищ~:
,1
( '))
,-=
-
/-=
-
1.
1lонятня « больше » н «.меньше » в област11
I<OM!IJICKClll>IX чисел тсршо·1 BCllKHЙ смысл. l lа
нр11мср. 1-н;льзн ска:ш·1 ь, что болыuс: 5 + 6i нли
6 + '5i. Мuжно лш11ь срив1-11шэт1, no отдслышс
·111 /\L'JIC'l'BИTCJIЫ1ую 11 мнимую част11 .
СЛОЖЕНИЕ, ВЫЧИТАНИЕ,
УМНОЖЕНИЕ
I1ро11зводя арпфметнчесю1е операции с дей
стщпслы1ыми ч11сл;1.м11, мы нс сом11евае мсн.
что ~ и1·оге тоже получится /\(:: йствитслыюе
Числа
чнсло (исключение составлнет деле11ие на
нут,). Переходя к комплексным числам, нуж
но убедиться в том, что арифметические отте
раци н над ними порождают толы<о 1<омплскс
ные '-:lисла. Это значит, что результат 11юбой
ар11фметической опера~ ~ии )\ОJLЖен быть пред
ст;1влен в стандартной форме (*).
Нач~rём сосложения. Пустьz 1 =а+hi иz2 =
= с+ di. Тогда
z1+zl=(а+Ьi)+(с+di)=(а+с)+(Ь+c/)i.
То с<..""Ть сумма двух комплексных чисел сеть
комш1екснос число, дейстнителт,ная часть ко
торого равна <.:уммс дсйствитслы 1 ы.х частей
этIIх чисел, а мним;,~я часrь - сумме их мнимых
частей.
Аналогично можно найти р:вность двух
комплекс~ rы.х чисел:
z1- z·2 =(а+Ы) -(с+di)=(а-с)+(h-d)i.
Перейдём к умножению. Зто тоже 11етруд
но, сели механичесI<И раскрыть скобки и во
врСJ\Ш вспомнить, что i " = - l :
z 1 • z.!. =(а+ Ьi) ·(с+dt") =ас+bci+ acli +l1di2=
=ас+IJci + adi- hd.=(ас
-
b(J) + (Ьс + ad)i.
Таким образом, сумму. р<~зноеrъ и произ
Rе~е1 rие люб1>1х двух ком 1щt:ксных чисел нам
уд~vтось представить в форме (*). Нес~<олькп
сложнее с оператщей деления. Камень пре
ткновения - коМIUiексный :'lнаменателпдробн:
Z1 а+Ы
-=--·
Дш1 того чтобы обратить er 'o в действитель
ный, придt1-'ся предпрИНЯТh /\OllOJll-IИTCJlbHOe
исследона 11 t-Le.
КОМПЛЕКСНО-СОПРЯЖЁННЫЕ
ЧИСЛА
Обычно Мiшмую единицу i определтот IC:tI<
кnа/\ре~тный корень из числа - 1. 1!о т<акой из
двух1 Сказать «1101rож 11тельный~ нельэя , nе; 1ь
понятия НЮJIОЖИТСJIЫIЫЙ'> и «0'1'рищ~тельныИ»
/\JIЯ мнимых чисел нс определены ... Это напо
минает казусные рассу,кдения Марка Тщ~на:
одш 1нз двух бпиз11ецов у1:онул, а второй ·1 ·ак и
не понял, h"ТО же утонул - or1 сам или его брат.
206
У к.iждuru комnлl.:'кtного ч11сла есть 1.uои • !Jл11.1неu• .
К сч~к1ъю, выясняется, что беспокоиться не о
чем. Ропь i и -i в сообщесше 1<0мплексных
чисел аfiсолют1rо с11мметрич11а: i и -i
-
два
равноправных r<ор11я нз - 1 . Эта симметрtu~
приводит к тому, что у каждо1·0 комплексного
числа z = а + Ы имеется «близнец» z =с1- Ы.
Такие «бл11зпецы" назывшотся ко.мплексгю
со11ряJ1сёнными итr просто сопряжё1ты.ми
чиСJ1ами. (В том случае, r<0Г'J\<1 Ь =О. т с. z -
дейстнительное число, оно янляетс.я со11ряжён
ным самому себе: z =z .)
К.омr~лексно-tопряжёш 1ые числа облздают
пнтеrесными свойствами. Прежде 1ксго, 1тх
сумма и прrн-tз1~еденr1 t: являются /(ействrпель
ными числами. В самом деле,
z+z=(а+Ы)+(а-Ы) =2а,
-
(h'
ь· ' ь'·'
'ь'
Z ·Z = .а+ t)(a- t.)=СГ- -1- = tГ+
-.
Выражение ti + Ь
2
немецкий ученый Карл
Фридрих Гаусс назвал нормой комплскснurо
числа а + l'Ji, а кв:щратныИ корень из нормы
(точнее, его nоложите.rrt>ное з11аче1 rие) гю пред
ложению французского м :пематйка 01'юстена
Коши стали имепоnа·1ъ .мОО)Иlем комплексного
числа. Обозначают его чаще всего букnой п1т1
знаком абсолютной величины: r = izl = !сн b1j =
=bl+ Ь2 • Отсюда легко получить сле1~ующее
свойство сопряжён1-1ых чисел: их 1юрмh1 11мо·
дули 11сс1'да равны между собой А щюанализи·
ровав формулы суммы, ра з ности н щюизf1еде·
н1щ можно доказать и лругие сrю!Iства:
ЛЕЛЕНИЕ КОМПЛЕКСНЫХ ЧИСЕЛ
Tcncp1, несложно спран 1 1ться и с делением ком
плексrrьL'< чнссл. Чтобы 11 р11вестн •щсткuе
z1 а+fп'
-
=--
к с1 ·а 1щартному виду (*), пужrrо и:збавитъся
от МПИМ()Й едиНИ l (Ы R знамеrr~пеле. Для ЭТ()ГО
домножпм числитель н знамепа те.rп, нз ч нс-
1ю, сопряжёшюе ЗI1а"11енатслю, с - di (всдL про-
11звсдс1ше комплскс1ю ~со11ряжёш 1ых ч11сСJ1 -
чнс;ю дсйстnитслькое) . В (Х.:зулhтате получ11м
Ком плекс н ые ч исла
z , а+ Ы (а+ Ьi)(c-di)
-::: --=
=
zl с+ di (с+ cli)(c - di)
ил11 короче
= (ac+bd)+(bc - ad)i =
cl +d2
(ctc +bd) (Ьс- ad).
=
)'+
'
'
1,
с+ r1-
с~+(1-
Z1
Z 1Z2
-
=--
·
zl lzl1.!
***
Возможно, кому-то 1·ромС>здю 1е сjюрмулы ум 1 ю
ження п /\еJJения 11а и другие свпйстна 1<омтт
де 1<спых чнсел пока:жуrся сm 1ш ком с1южт1ыми
и даже ис~.усствеш1ы:ми. В таком случае. чтобы
рассмотренньн: понятия стал1 1 вполне наrляд-
1-11.1ми . И.\1сст смысл гюзнакuмит 1,ся с rсомст
р1 1 чсс~<сн'1 1 iнтernpeт:.iц11clr KOMTIJ!t:KCHЫX ЧНСt.11.
ГЕОМЕТРИЯ КОМПЛЕКСНЫХ ЧИСЕЛ
Наглядно предстат пъ м1111мыс числа впе рnыс
попытался ещё в ХVП в. :.шглпйскнй учёш,п'1
Джон Валлнс. Он прсмагал ра:1т1ч11ые вари
анты, и од1 ш из них выглядел так: мнимое
Чl-IСЛО -~ = j l · (-1) 11ре1к~1·аRЛЯС'I' cof1or1 срен
н.ее1·соJ\IСТр!1Ч еСКОС мсжлу 1 и -l . Ст:д()ватсль-
1
1ю, ~- 1 есть сторона 1шадрата, ращ юuелшшrо
пrs~мпугс))lы 1 нку со cтoprmaмir 1 н - 1. С:ер 1.<::э-
1ю1 ·0 ()'ГJVIИТ<а у сопрс:мст п тп 1<()11 ндсн BaлJ111c:i
пе вызнал н.
R 1799 '" датс1шй ма·гематик Кас11ар Tkcccm.
предложил простую гео,-.,1етричссК)1О шпер
nретацию 1<омплекс1Lых чисел, однако е 1 ·0
работа ОС1'алась 11еза.\1ечсшюl1. Ли шь через три
дс:сятка лет Карл Фртщрих Гаусс вы 11 устпл в
свет труд (Теория б r шн:щратных вьtчс1·ов v, в
кuтuром дал такое же 1·еuмtтр 11 чсское прс; 1 -
сташ1е11ие комплексных чисел, 1с:1к 11 Вссссш,_
Идея Вссселя н Гаусс<'\ настолько прозрач на,
чтп nстаётся ·1·олhко уднв.11яться , поче м у ни кто
ю учfных ТJе додум:тся до 11её раньше. А сn
сто11Т 011а в слепующем.
ЛВЕ ОСИ И КОМПЛЕКСНАЯ
плоскость
Действитслыiые ч11сла удобно представлять n
н11де точек н<1 чнсловuй оси. 1lадо лm1.1ь вы
бр::~тh 11ач;,11ю коор/\ИНат (нуленую ·~·очку) , rю
лпжнтt:льное н:нrр :1 нлt:н11е 11 t::юн-шцу и :щере
ння, и тu 1·да любому 1 1t:11ств11тt"J11>1-1ому ч нслу
булс:т COOTBC"l 'CTHOB<ITb ~:ДИJ IC' l ' Ht::l l l l;tЯ точ K~I
чт 1 сJюной оси, и 11::106орот: ю1жщJri точке -
дейстnите.rrьное чнс.rю.
Точно та~< же, точ1<ам 1 1 ш1 чнслп1юi 1 ос 1 1 ,
мож110 изобразнть и чисто м~шмые ч11сла bl:
точке с 1<оординатой Ь будет отве ч ать число
Ы,аумножитьЬпа;леп:опвуме.Такчто
ч 11 словая ось шюлнс прпrолна для представ
лс1111я r1дейст 1штеш,ных, и м1 1 11мых чнссл. l lo
только 11<.' о;1нонремеш-101 Значит, чтuбhJ олr ю-
11рt::мсн1-ю изо\1ражатъ дейстRительныс н мни
мые ч нсла , нуж1ю в:зя.ть ср;1:>у дне оси. 1I азовём
их соотnстстве 1 шп дeйcmfltmu-.nыmй осып н
.-~ttlu.мoil осыо и расnлложнм перпе 1 щ11куляр1ю
ll)7
Числа
две осн -лРис:тви~-сльн;н1 н "н11м<1Я - раrполо"'ены
n ерnс нл11кул11р11u .
друг другу - так, чтобы они пересеклись 13 ну
лсrюй точке. ~ этом и состояла основная идея.
Бесселя и Гаусса. Дня оnредслённости в.ьrберем
1юложитt:льное панравление дейстnитслыюй
оси впрано, а мнимой. оси - вверх. Едшпща
же 11змерен11я (масштаб) 110 обеим осям пусть
будет одна и та же.
Итак, R нзшсй 1'еометрнческой 1штерпрета
ции м11нмые ч11сла «рас положе ны перпенди
кулярно» дt:ffстннтелы1ым. Ну а r<nмпле1<с11ые?
Они ~размещаютсн» по всей nлоскостн, n ко
·1·ороf1 лежат ч.исловые оси. Выберем на плос-
1сости произвольную то'П{)' и спроектируем её
па этн оси. Допустим, проекция точки на дей
ствителы rую ось имеет координату а, на мни
мую ось - координату lJ (рис. 1). Будем счи
тат 1, эту точку и:юбражt:J 1ием r<омллсксного
ч1н.:л ;~ а + Ьi. Телерь можно смело утверждзть,
1? ----------------.та+Ы
а
Рис. 1.
что каждой точке 11лос1щсти соответствует
ол1 ю JЗполне оnре.п.елённое комллексное число.
Вер1 ю и обрат~ юе: каждому комллекснО.\1}'
числу а+ ы СООТRетствуе·1 ' Oll:IIЗ точ1<а ПЛОСКО·
сти. Такнм образом, между точкамй плосt<0С111
и комnле1<сными числами существует взаимно
однозначное сuотnетстnие.
КОМПЛЕКСНОЕ ЧИСЛО КАК ВЕКТОР
Соединим riaчaлn координат и точку, изобра
жающую комплексное число а + hi, наnрав
ленным отрезком - вектором, как показано
на рис. 1. Что это .л,аёт? От<азьrnается , очень
многое.
Прежде всегu, теперь можно наглядно пред
ставить операци1-1сложения11 вычитания r<OM·
11нск<.:ны.к чис:е11. Изuбразнм комплексные чис
ла z, и z 2 в нидс двух вектора~ . З:пем построим
на н11х rutpaллe;I01'pai'.1M. Вектор, соед 11няющнй
н.~чало 1<оорд1111ат с че-rI1ёртой nершиной п:~·
раллело1·рамма, в точ1юст·и соответствует ком
плексному числу, раrтому сум.ме z1 +z2 (ри с. 2).
А чтобы предстаDитъ разность двух комnлекс
ных чисел, достаточ1 ю за~\1енитъ второй нектор
противололожrю направленным. Или иначе;
вектор, идущ:ий от Zz к z 1, надо перенести 11 на
ч.ало кооrю-1нат (рис. 3).
Д;~лее, число О - это нуль-вектор, а кш1-
r:и1ексно-со1 rряжённыс числа - векторы, сим·
метрнч1 rыс от1юсите;тьно1\ейстnитv1hНОй оси.
Н2конец, м ожно BЫЧИCJIJ.-JTh длину ВСh'ТОра,
соотnетствутощеr() комплексному ч_нслу z=a+
+ lJ/. Воспользуемся /VШ это1'() теоремой Пифа
гора. Из рнс. 1 понятно, что длина nектора есть
Рис. 2.
--
-
--
-
-
-
-
-
----- -
----- ---
J
208
Рис. 3.
д.~11н а г1111отс11 у:11.1 п ря моу 1 ·ол ы юн> • 1 ·рсу1 ш1 п
пшiа с катетами " 11 /J, по:~ТОJ\1~ 0 1J:1 раноа
'ict!+ Ь1 . а это МОi\уль комплею:~rю1·п ч11сла z
Таким обрззо ~1 ,
длина вектора, соо"·ветст:ву1011~еrо
KO~UUJ CI<CHOMY числу z, равна eJ' O
модулю 1z1-
Комn\!!кr но-rо11 р>1АЕ'нны е '111\llil 11 1оiiр,1жакпrя вектnр,1м11 ,
С11"щ'rр11ч11ы"и от1<0l <11 елыю де1ктвителы10>1 001
l<омПЛ!-'КСНЫе 1 IИСЛJ
Примсш1м этот результат 1~ I'COJ\1e-tpнчcc1<0l 1
1штсрпр стацш1 СJЮЖСТIШJ KUMШICKCI!Ы X Чll<.:<.:л.
Поскuньку любан сторо11а чх:у1'ОJ1ЬШШа Jll' 1lpt'-
HOCXOJ(l l'I' сумl\lЫ /(Вух друп IX, C!ll'/(UH:l l l:JlbllO,
lz1 +z~l ~lz1 l + lz~l.J t:
~г модуль суммь1 КОМПЛСIССJJЫХ ЧJIССЛ
Lro.
пе превосходит С}'l"JМЫ их модулей.
АРГУМЕНТ комплексного числА
Как 11 :mt'ct но, 1к·ю ·ор 0 11pcдt:J111 L~1·cн нс lOJthIO.J
JVlltllt>CI, нu II н:111p~1 Ш1l'llll C1\1 Ч1061,J l'l 'O ::!<IJJ.a 'lh ,
можно llCIIOJibЭORal h ytoJJ Мl'Ж/СУ ГIOJIOЖ.l l'l'l'Лh
llЫM напрJи11е11иtм дс~'к·11-111'1'ел ы нн1 ос11 11 11a-
npaНJ1e11 нtм nскте>ра. 11< 1 это1 ·0 1н:r1()(таточ1 ю.
tlо:1ьмёi\1 71ва сопряженных ко.11.шл:експы х чнсла
z =а+hi и z =а-Ы. На щюскостн 01111 11·ю
бражаются всктора,,111, с11ммстр1rч11ым11 отrто
сптслыто действ1пслыюf1 ос11(рпс.4). 11рнчi..'.\J
у1 ·11ы мсжJ\У ним~ 1 и дсI1с1 ·ш 1·1·сm,ной осыо рак
г1ы l1011учае1 ·ся, что, ~н:.н1 нел11чнну у1Jш, Mhl нсi..1
l'Щё 11е в с()стянш 1 ныбr;лъ однР 11 ·~ J\11\"\ 1юд
х01~.ящ1 L'-' 11зпранлен1111
-
/')
-
--------
-
_
z=п+/Ji
1
1(/
1
1
1
'
'i=e1-bl
l'ис. 4.
130 J1:16ежш 111е этой 11еощк,'\с11ё111юс 111
шюдяг 1юшпнt' тщравлешrя 1rз,1сре11ия у1ла 11
как следствие - uтр11цате.·лы1ьк углы. t:стт пр11
и:-1 мсрс1 шн у1 ла ~rы nннже~кн <п по110жн 1·сль
H()I о ll~lnpaHJ ICHШI ЧIJCЛ()JIUll uсн протrтn ч:1со
кой с 1рстш. .:JHa чен 11с ~т11:1 О)/\СМ с~нпал, 11 0-
J10ЖllTl'J11,н hl '-'t, а t'CJll I 1ю часuвой <.трl41 Kl' -
то
отр1ща · 1 ·{.') 11,ным R та~ю\1 сJ1учж.: для •11к11:..1 z на
/)JJ(. ..\ )TOJI llOЛOЖll'l'CJICll , а )VНI Z - ()l'j)llJl.ll'i.>
ле11. 3'1п1 yron 11а:~1.tвают ар,~1ии:'1111т.л1 r-;< щ 1u 1 е1.;е-
1ю1 ·п ч11ст1 и обо:тачi3ютта1<: <р = ~iгgz. О(J 1,1ч1ю
01 1 н~мер}lе1ся нс 11 rрадус~1х , а в ра1\11ап:1х
.209
Итак, мы н~1учнm1съ одпозпачно задавать
наnракщ:н11е вtктnра. llo ое1·алась дру1·ан нt-
01~юз11ачностъ: одному 11 тому же напраю1с
н ию вектора сои~·вегстну1~т вовсе 11 е е;~1111 стве11-
111,1 l1 аргуме1 rт.
Предположим, прн сrгсчёте yl'J1a прот1-ш часо-
13Ой стрелки аргумент раке 11 тт/4. Но 11ичто не
мешает отсчитывать угол н по часовой стрет<е.
То1·да. совершив почти полный оборот (2rt),
получим - (2rr - n/4) =
- 7rt/4. Можно разnптъ
эту идею 11 к всличи11 с утла добавить (или от
нят~,) какое угод1ю целое ч11 с.rю оборотоf\, что
всрнё-1· вектор в то же 1 юложенис. Посколы<у
од ин оборот - это 2n, то t\CJIOe число оборо
тrн1 - это 2тсk, где /г
-
11рои з1юJ 1ьн ое целое
чнсло. Выходит, еслн <р - аргумент комплекс
ного числа z, то с ралным пра1юм мож r ю счи
тать аргуме1 1'1'Ш'1 и mобое из бескопсчпого ко
ли ~1естu:~ значет 1 й, определяемых по формуле
<р+ 2тtk (k =О, ±1, ±2, ...).
Как быть с этой м1югозтшчпостыо( Нс уста-
1-юв1 1тh ли 1 ·р;1ни11ы для аргумента, считаядопу
с1·11мым1 ·[ ш 11J1ь такие е1·0 значенш1 , которые
лежат. скажем, в прсж:лах от -л до те или от ()
до 2п' Но, оказывается , это нсу11оf>но 1ю другим
соображt11ия,.,,1 (см. статью "возвсдсн11с в стс
пе11ь и иэш1ече1-1ие корня нз комnлtкс1-юго
числа»). Приходится см1 1р111ъся с тем, что каж
дому комплексному числу соотRетсmуст еди11-
сше1 шый модуль, но бесконечное кол11чество
арrумснтон. А для нуля арrумеIJтом юшяется
вообще произвольное чис1ю.
Тсш:рh ком11лексное число можно опрсдс
мпъ не только парой 1шордижl'I', но и 1ю-дру1·0-
му: парой модулп - :.Jр1умснт. И встаёт нuвый
вопrос: кзк от от-юго спщ:оf>а nерей.тн к дру1·0-
му rr ююборот? Здесь нам на помощп 11рихо
д11т ·1ри1 ·онометрня.
ТРИГОНОМЕТРИЧЕСКАЯ ФОРМА
ЗАПИСИ КОМПАЕКСНЬ/Х ЧИСЕА
Возьмt;м произвольное комплексное чнсло . 'Z =
= а + Ь1 11 изобразнм его в виде вектора ОМ на
ко:v~nлсксной плос1юс11i (рис. 5). ПустьN - llpo-
cкroLЯ точю1 М на дейсткительную ось. В пря
моугот1ном трсу1 'олы-1ике OM~V ДJIШ 1Ъ1 ~тетов
ON и NM ра1111ы соо'1·вС'1·ственно а 11 h, а длпна
,--
гипотенузы ОМ равна lzl = yal + ь~ . Из три-
rо~юметрни известно, что отно11 1 tнне 1vн11-1ы
210
о
а = Jzlcos<р
,м
1
1
: Ь =lzlsirнp
1
N
Рис. 5.
к:-пета к Д)lf'IHC 1·н1ютенузы ранняется коСШI)'()'
прилс:жащс:1·u у1'ла и синусу протищ1леж;~ще 1'0.
Сленовательно,
а= Rez =1z1 cos(f>,
!J=!111z=1z1 ·sin<р,
где <р - арrуме11т комплексного числа z. 1'аю1~1
образом.
z= lzl·(cos<р+isiп<р).
l{о 11 сч 1IO. три 1'01юметrн 1 1ескан форма за пи
си ком11лекс1 IOl'O ЧI \СЛ:1 Bhll'JISl/\11'1' l 'J10M<1З/\KO nn
сравнению с 11риныч.1юl1. Но давайте rюнробу
см r1 срсмншкнтъ JIRa компJн.:ксных ч11сла, запн·
санных и триго11омс::трнчtско1'1 форме: z 1:::
=
lz11(cos q>1 + i si11 <р,) 11 z~ = lz~1(cos1Р2+
+ i sin <р 2) . Всё сноднтсл к элеме11тарномv рас
крьтrшо скобок с последующей заменой i1 rra -1
z, z~ = lz1 l lzJl(cosq> 1 +isiл<p1 )(cosq:i2 +
+isiп <р2)= lz1llz2l[(oJs<р1соь<pl -
-
sin <р1sin <р!) +i (sin<р1 cus<p_i +sin <PLcos cp1)J
В крутлых скобках 11етру/\НО уанать выражеи11я
мя косинус:.~ н сннуt.:а суммы J\Ryx утлон . По
этому
z, · Zt = lz1l lz~llcn~(q>1 + cpl) + isiп (Q>1 +qil)J.
Неож11даннъrй и красиDьu-1 результат:
при умцожении комплексных чисел
их ~1одули необходимо пере~mо·
жить, а аргументы - СЛОЖИ'IЪ.
flструдно доказать, что
при делении необходимо 11роиз»ес·
ти обрати.ые операции: нодешm
модули и вычесть аргуl\tепты.
Отсющ1 нытекаст 1·еометрическшl смысл
011ераций умножения и деJ1ення комш1ексных
ЧИСе.11:
-
при ум 1южепии 1ra 1<омпле1<с1 юе число z =
= lzl (cos tp + / sio <р) вектор, соответствующий
множимому, нужно растянуть n 1z 1раз и повер
Н)ТЬ на угол q> (рис. 6);
-
11 ри ДСТIСНИИ вектор, СUОТВ<:ТСТRующий
делимому, надо сж<1ть в 1z 1раз и tювер11уть Eta
)TOJl -q>.
К:Jк мы убедились, триrономе1· ричстка.я
форма ;шгrиси комплексного •тела 11е менее
полеэ1-1з , чем обычная. Вопрос лr-11ш> в том, ко1'да
какую ю 11их удобнее nрим:енлт~,. При сложе
пин и вычи'fа11ш1 легче оперировать комплекс
ным '111с.rюм в виде суммы действи·гслыюii и
М1111мой частей. l!u если ре'-!Ь идёт об ум11ожс-
11ии и де.т1с1ши, 11реимущсств;:~ тр11гонuметри
ческоrо 11редстамения неоспоримы .
о
КомnАексные чисАа
Рис. б.
ВОЗВЕДЕНИЕ В СТЕПЕНЬ И ИЗВЛЕЧЕНИЕ КОРНЯ
ИЗ КОМПЛЕКСНОГО ЧИСЛА
Триrовометрическая форма записи комплекс
пых чвсел удоб на при возведении в степень и
измечснии корней. Попробуем вuзnести в на
туральную сл:пенh п комплексное '-n1сло
z= r(cos<р+siл<р).
Зд1:с1, У - мо,f\уль к0Jvшлексн01·0 ЧHCJia z, а q> -
его <1.ргумснт. Возоед<:ние R натуралы1ую сте
лень п можно заме~ ш·1ъ многократным ('l'ОЧ-
11ее, п-крат11ым) перемно.жением одm 1ак0Rых
ч11сел. Прп nереi\шоженин, как нам и:шесrнn,
модули умножаются, а аргументы складьmа
ются, поэтому модуль полученного в итоге
числа будет равен 11' , а аргу мент n<p.
Можно бьшо бы взять в качес_-твс ар1умснта
11исла z не q>, а К'Jкое-то друюе значение , отли
чающееся от q> на " целое число оборотов». на
nрю1ер q> + 27t. 13 зтом случае аргумент числа z"
равнялся бы n<p + 2rtn. По сути ;1е; 1 а это ниче1·0
не меняет, ведь si11 х и cos х - 2п-периоднчс
ские функции. Итак,
11· (cos q> + i sin q>)]11
= r''(cos n<p + i sin mp).
Это выражение пазьшается форл~)'.ЛОU 1Нуав
ра - в честь аиrлийского математик<~ Лбра
хама де Myanpa, открьшше1·0 её в 17()11«
Прн умножении и деле11ии a.rryмellT 1<С1м
плексного числа всдёт себя точно так же. как и
показатель степени. Действнтелъпо, 11ра ум110-
жени11 аргументы склад ьшатотся. при Д<:')ltнни
нычитшuтсн. Поч.ему бы н таком случае не лрсд
ПС>1южнть, что
cos ч> + / siл <р ==A<i>,
1 ·деЛ - не~<оторос r.~нс1ю, прнчём одно нто же
lVIЯ нсех значе11ий ф. Леонард Эйлер показал н
1743 1·. , что таким чпслом ямясrся А= е'. 3део>
е = 2,71828." -
:н·1аме11итое число Эi'"lllepa, а i -
мнимая ед:ишща. Та 1< что справедлива cjjop.11~)иa
Эйлера:
<!"1' = cos <р+isi11 <р.
Фuрмула вtсьма любопытная. 1lодстанив в
нес::<р=7tн уч1лъ1Rая, ч1·0cos7t= - 1,аsin7t=О,
получнм у;1иш1телhное <.:оотн оше ш1е меж;1у
пятhю сам.ымн полулярнымн 11 матсматн1<с кон
сrа11тами: пулём, едитщей, МJшмоИ <::11н11иче 1~1.
а 'Гdr<же замечательными ч1 1 слами е и тт:
е"'+1=О.
Ото р~шепсттю во все времена nызывало nос
торжснные отклики. По словам изnеспrоrо
211
Ч11сла
ФОРМУМ МУАВРА И ТРИГОНОМЕТРИЯ
С помошью формулы Муавра можно быстро вывес
ти тригонометрические формулы си нуса и кос и
нуса кратных углов (лвойно1 u, 1 рои ного и т. д.).
К примеру, пусть п = 2:
(cos<Р+isiпq>)'=cos2q>+isio2q>.
Ра<.:крыв скобки в левой ч асти, после 11риведе11ия
rюлобных членов имut>м
(coslо.р- sin2<р)+i 2sinq>cosq>=cos2q>+isiп2q>.
Прир<1вниваf1 по отл~льности действительные и
мнимые части , полу•1 аем сразу две формулы - для
кос и11уса и си11ус;а двойного угла:
cos 21р = cos~о.р - sinlер,
sin2<р=2stnч>cos<р.
Точно так же легко 11айти формулы дм1 тройно
rо угла. Теперь неудивительно, что комплексные
числа нашли ши рокое применен ие при описан и и
период1<1ческих проut:ссов, н<~ пример в uеп ях пе
ременного тока (см. статью " Комплексные ч 11сла и
электротехник.~•).
кораблестроителя ri математика :шадемика
Алексея Ннr<оласо 1 1ча Крылова, в 11ём таш1 -
сrnсш rы м образом 1юссоедш111;11къ чнсла, сим-
1юзшзl!рующ11е ;1р11фметнку (U и 1), :V1гебру (i),
ана1111 з (1:') н 1·еомстршо (1t).
С помощыо форму.r1ы Эйлера rю1 1учсtСМ crr1ё
0 / \IIO, ОЧСНh I<Оl\1Пактнос прсJ \СТ3ШI С1111е ком-
11лсксно 1··0 чнсла:
Оно 11а: 1ывается экспrтеm~lю.лыю{1 формой
лрелставлешш. Если же шщо€1рать такое дсй
стu1пелытое и , что 1· = е
11
(и дошюю быть р:~шю
1 1 зтуралыюму логарнфму числ;:~ J~ u = ln 1·) . то
получим
z = е"""~.
Тt:11 ерп можно 11 :~RJICЧh 1r:.11111 сла z коrс111, н-11
CTCIICHИ (// - нaтyp;.I J ll>f-l{}t' ):
1
1/~
(
)
'\1п/'Р = (п_,"Р )-;; = 1 ·
11
v11 =
11
,'r cos ~+i~iп ~
11
1/.
Та1.;11м обра зом. пр11 п:шлечешш ко рш1 нату
рал ы Юrl СТСПСIПf 1/ Н3 модуля 11адо lfЗnJ1eч1, ЭТОТ
KOJX~lll> ()OЬIЧllbl .'VI с11 особо м, получ~ш ПOJIOЖ.11 -
l 'CJIЫIOC ч11 ('J Ю , ;1 <lj)I)'МCIIТ поделнть на /1. Но,
212
В JlrlM r,JHt'tlr l l:IP r ~Н1НП HPI I Н Ы\1 oi 1(1.Э-iОМ H0Cft l~.Лl111'1'\'-1( 1) 1111( ,\ J,
('1~м1юл~1 111руюш11е ар11фмеп1 ку, а \Гебру. анализ 11 геощ;тр1 1ю
КАК ПОЛУЧИ ТЬ ФОРМУЛУ ЭЙ/\ЕРА
Извест но, что функuии ьi n х, cos х и /:1 можно nрел
ставить степf'н н ым и рядами (см . статью ц СтРПf'Н·
~tые ряды » ):
.
х~х~л7
s1nx = ,, ---;-- ---+ ... ,
3!517!
л.1 х~ xr,
COSX= 1-- +
-
-
-
+
2!4!6!
х1
.YJ х•
е' = l +x +21+зт+41+ ...
В nослед11юю формулу вместох п од<.тавим 1х:
"
.
).,>
.х1
... ..
\;
il"
(.'
= 1+IX---1-+-+ 1--- ..
2!
З! 4!
'i!
6!
Ср.~в11ивая пи отделыюсп1 дейсrвитель11ую н м 1 111-
мую части этой формулы r рмами лля коо 1 нуса и
синуса, полу•1аем, что
1::!" =cusх+isi11х.
Используя формулу ЭйлерСI, мож11О предложить
новы ~ определе11ия для фу1-~кuий s111x и со~ х (втuм
числе действительного аргумента):
е"-е"
sinx=---
li
е'"+ен
cosx= ----
2
И:i данных формул можнn вывести все- обыч ны~
свойства этих тригоном етрических функuий .
IIOCKOJJЫ<Y аргуме11'1' KOMПJICKCH(} I '() ЧHCJl:J 01 rре
Дl'Лён с тnч1 IOCTl>IO /(О 21Ik, 11;.~ряду с <р мы f\OJIЖ
llbl рап:МОТре'l 1> ·1·аJ<ЖС llCe arl')'MCHTЫ BIJД<J <р +
+ 2тсk, те А.1 - целое. Т:11< rr пос1у 1 111м:
"- ,1"', 2"" 1
пГ[ (q:i 1.тсk) . . (<Р 2ттk)]
vr·e
='1·С!)~
-
+--+1ып-+
--
.
11
J'l
11
/7
Мы видим. что раэл~rЧJ1ым k =О, 1, .", 11 - 1 со
от1~t:1·е1·вую·1 ра:mи чныс 11е кр:пные 2л аргумен-
1ы З1-1ач11т. при изнлс:ченпи кор11н на·1ура.11ыщй
11-й сте11е1ш 11мсстся 11 з11ачсний корня н р:с~ з
ность между «сосе,r~.ним 11·) :ша чс1111яJ;ш :-~ргумсн
та ра11ш1 1.тr/п (на r1rc. l да111 1 рш11ср7\ЛЯ п = 6).
Рис. 1.
Jlтак, любо<.: комплеКСiiLН.~ (в том ч11CJL<.: дей
стn11тt:.11ь1-юе) 4 1ICJIO ILMCCT [1011НО 11 КОМПЛt:КС
НЫ Х корней n-i'i степе1111. Рассмотр11м, н:шрJJ
мер,z = 1. l l ач11ём с кн:щрат1 юго корня (п = 2):
~l
2тсk . . 2тсk
-1~ ••
-/,
\ =C():i --+ /5111 -- = COSн.К+1-'11111.л!
2
2
'
rде k =О нr1t1 l . Получаем дв~1 кор1ш :
1)со<;()t /siлU=1+1 О=1,
2)COS1t+i<;1Птt= -1+i·() = -1 .
[)f)3 OHli !\CllCTBHT(;'Jl bHЫe, пр11чём 11ме11но Tt: .
каторьLх 11 cлcдoR:lJIO ожпдат1;
Случ:в·1 п = 3 11н тсгк:с 11еt:·
\1
2тtk . . 2ттk
v1=cos -
-
+1sш --.
~
:)
КомплРКСt 1ие чиrла
Пр11 k =О, 1 11 2 11мееj'1 три кпр1н1·
1)cos()+i~inО=1+i·О =1,
1
2)
Zл: . 2тс
1 .v5
со~- -t/sш-
=--+L-
3
3
22'
3
-+п .. 4п
1 .v:S
)COS- +tS\11-
=---l
-
.
.3
3
22
Псрный н:~ них обычны~'~ дсl1ствн·1·елы-1ы~"1
кубнчссю 11' 1 корень нз 1. Друп,н:: же r1н~1 Н(;' столь
пч.енщtн ы (рис 2). JJ,ля про1:1ерк11 возвсдём .хотя
бы n;1ш 1 11з них н куб. скажем 11торо 1i:
'
1
1
]1
'
2'
1
= - (9-1)=1.
8.
Рис. 2.
llp11 нзнлсчt.: 1 11111 корня 1-ii с-1 епеш 1 п олуч:~
с:м1, - 1,i,- iнт.[I,.
Д:ш потюты следует расою·1реть сщё слу
чаl1 l<OMШICKCJIOГO ЧllСЛа с нсну:н:вым ар1·умс11
том. И:·шлечём. 1< прим еру, коадратныi1 корень
11~ -1 Здесь модул ь 1х1 r1c11 1, а ар 1~1мспт 1t. !Io
формул<.:
v-=-i' =cns(%+nk)+isiп(~+л*}
k = () н J, nолучаетси дн:~ корнн· i и -1.
Чис/\а
г
УРАВНЕНИЯ И НЕРАВЕНСТВА
ОТ АРИФМЕТИКИ К АЛГЕБРЕ
ТАЙ НОЕ СТАНОВИТСЯ ЯВНЫМ
Пrелстав1)те, ч·1·0 1~ оqень лёпюм - праь."ТИЧе
ски невсС'омом - кошельке содержится какое
то количестnо монет одинакового досrоинсrва.
Как уз11ат1,, сколько монет в кошельке, не за
гmщывая внутрь? Естn очень нростой с11особ:
ноложнм ко шслёк на щ1ну чашу рычажных ве
сов и уравновеснм е 1-·о монетками на другой
чаше (рис. 1). Сколько монет дпя этого потре
буется - столько же их и н кошельке.
214
Рис. 1. l nомошью
ры•ыжнь1х в<>сnв мnжнn
узнаrь, сколько "'01t eT08'
лежит о кошельке
Исnыта1111ый измерите;1ьньr.й ннструм е1:1r
11родаtщои, хн.миксщ и :штекарей прпхо;щr 1:1а
ПОМОПl.n и fl чуть 60J1ee CJl()ЖltOM случае: пусть
на лeRmi чаше находящихся fl ра 1товеси11
весов лежат кошелёк с неизвестным числш1
монет 1r ещё '5 монет рядом с ним , а 11а правой
чаше - 15 точно таюrх же монеток. Для того
чтобы у:щать, сколько монет в кошельке, сни
мем по 5 монет с обеих чаш - равновесие пр11
этом н е нару ш ится (рис. 2). СJ1едователь1:10,
внутри кошепька 10 монет.
Рис. 2. Е(л11 r обеи1
•1аш <:н~tЬ ОАИН3 КО~
ко11нчество мш1сrок
рдВН ОВеt.не
fl{' 11 аруш~пся .
Ал1>-Хорt>3МИ uдн11м 1н первых 'тал о()раша·1ь<.я с уравне~1;1ям11 так .
K<IK TOproвeu Оuрзшае1с-R (_ ры• 1ажНЫ'1'4 ВеС.lМИ.
В те далёкие време11а, ко1да мудрецы впер
uые стали задумыват1,ся о равенствах, содержа
щ11х неизвестные величины, Тlаверное, ещё нс
было ш1 м()пет. ни 1<ошеJ1ьков. Но эато были
кучи, а татою: горшки, t<орзнны. которые пре
красно 1юдходили на роль тайников-храни
лищ, вмсщающнх 11с11зnестпое количество
прсдмеruк. (;Ищется .куча, которая BJVtetтe с
дв~мя тр<~ТЯМИ её, ПОЛОВИ ! ЮЙ 11 ()ДJ ЮЙ седьмой
составт1ет 37".», -
поуч~ш во П ·1ътсячСJJ<::тии Jtu
ноJЮй эры сгипстсю1й пr1се 1 (Ахмсс. В древних
м:пематнчес 1н 1 х задачах Междуреч ья, Индии,
К11тая, Грецин 1-1 е1 rзвестr 1 ые велпчю-11:>1 выраж::~
ли число павлинов n саду, коли чество быков в
стаде, спвокуnr-юсть вещей, учитываемых при
разделе им:ущестна. Хорошо обучеюrые науке
сqёта писцы, чmюв11ию1 и nосвящёщrые в тай
ные зн:ншя жрецы довольно успсrшю снрав
лялись с такими задач~~ ми.
Дошедшие ДО H::JC источники CRl.--IДCTeJlЬCTBy
IOT, что 11рсв11ие учёныс владели какнми-то об
щими приt:мам11 решс 1 1ия задач с непзвестны
мн величинами. Однако ни п 0;1 1 юм 11:-tш1русс,
1ш в одной 1·11и11я1-юй таблич1<е не дано опиrа
ш1я этих пр 11ёмоJJ. Лт·оры лишь изpt;fl.1<a с11аб
жал11 свон чнслоnые 11ы101адю1 Сhу'11ь~ми ком
~1е1пар11.ями пmа: «Смотри!», «Делай так!», «Ты
пра1.1ильно 11ашёл" . В этом смысле нсюпоче
нием является «Арифметика" греческого м.~те
ма'l'иl.<а Диофанта Александрийского (Ш в. ) -
собрание защ1ч на сост;.ншенне ур:шнсний с си
сrематичссю1м нзложениt.:м нх решений.
Однако перным руководстном по ре1щ:ншо
задач, rюлучн~шим широкую известность, стал
труд ба1·дадс1<ОГ() учё r юго IX n. Мухам.меда бсн
Му\ы ащ,-Хоре~\ми.. Слово "аль-,цжебр•} и:-1 iipaб
cкoro пазва~1ш1 это1·0 1"/JaI<1·aтa - «Кнтаб аль
джебр валъ-мукабала'> (<>Книга о восст~новле-
Уравнения и 11С'равенггвл
--i
".Я составил книгу о восстановлении
~1 противопоставлении, заключаюшую
в себе простые и сложные вопросы
арифметики, ибо это необходимо
люлям при дележе наследств, состав
ле1·1ии за вещаний , разделе имушесrва
и в судебны)( де/\ах, в торговле и все
возможных сделках, а также при из
мере1·1ии земе/\ь , проведе~1ии t<анаАов,
в инженерном искусстве и прочих
разновидностях подобных дел.
Аль-Хорезми
нии и прот.иrю1юставлею11н) - со временем
нрсвратилос1, 11 хороню знакомое всем слово
<· а.11гебра", а само сочинение :зль-Хорезм11 по
служило оmравной точкой 1:1 становлетн1и па
ую 1 о решении ураrшещпi.
Алъ-Хорезмн одним из первых стал обра
щаться с уравнениями так, как торго1:1ец обра
щастсн с рыча>юrыми весами. Пусть, на~rримср,
имеется ра венстно 5х - 16 == 20 - Чх. Считая ,
что оно ::~адаёт раююнесне 11<:которых 1рузuв
на чашах 1:1ecol3, торrонец вправе закл10<111ть,
что равенство нс изменитсн, ecJ111 он 11::i обе
lf~Ш IH добанит одно 11 ТО же КОЛИЧ\..:СТВ():
было
добавил
стало
'5х- 16=20- Чх,
+16+16,
'5х
= 36- 4х.
Лослс этой за 1шш-юй операции прибавления
одинаковых колнчеств число 16 исчезло аз
левой части 11схuд1юго раве11G-тва, эато со зна
ком плюс оно воэ1111кло (восстановилось) в
11раrю1~1 части. Точ.но так же ш1 обе чаши весов
можно 1~об~шить од110 и то же коm1чеС1'RО 4х:
было
5:\· =36 - 4х,
добавил + 4х
+ 4:\':,
стало
9х=36.
Опятъ И:I npano1) част11 raneнcтna nъч)~Же11нс
4х п роп:lЛо, а n левой части оrю 1юсс1·аноюr
лось со знаком rшюс. И:) полученного просто
го раIJенства t)x = 36 уже легко вычислить, что
х= L\.
Восстановл~нием ( «аль-джебр») аль- Хорез
м и 11~1зы~ал операцию нскнючения нз uбtих
частей уравнt:ния вычитаемых членон путём
доба1:1J1ения пропнюrюложных по :шаку. Про
т1·11юпостав11ение (<-~11)-мукаб:u1а») - это сокра
щение "R часrях уравненин одн1 1 з1<0Rых ч11етюn.
1
1
\
1
l
1
1
215
Ч11сл..~
Rзгля11. на ур:1ннс:1-шс как rra ра1:1свспю гру-
3()11 11 :1 весах, на обе1 1х чашах которых можно
11рn11 :~нсщ 11 ·1ъ од~ 111а ко вые прt:обраЗ()L1аш 1я ,
ока:-~ался очс 1п1 nлn11.nтnnp111.1м. Рэn11ые 1<nm 1-
чества можно не тпт,тш гrрrrбамя'fъ 1< nбеим
частя ~ч уравнешш иди вычитать из них. Ра
венство нс нарушится и тог1щ когда обе части
у.ч ножа ютея ш1.и делятся на одно а то же 'Iисло
(раз~ мс<:"1'сs1 , сс;ш оно нt нуль) . Главный прш1-
1 1,1rп · с:слн нан 1хн1нh1ми кшrнчс.:еt'l:\амн нро1в
вест11 ою111аковыс 11.сйсrвнj-1, то н рсзу111,т:1тс
снон;1 1ю11учато1 р;_~нные кп;1 11ч ес·1·н;1 - с:т:1л
СJН Jсо()ра:нюй <-воmL1сбной палоч ко1!», кото
рую об11ар)Ж11; 1 и 11думчиш.1е чнтател11 руко
rюл:стnа :111r,- Хорезм11. Ою 1а ко « 11алоч кoll" э·1·ой
пужтю П()ЛЬ:101l3ТЪОI с OCTOj)OЖIIOCTl>JO (см.
статью •·Несколько coneтon начинающим вол
птсбr шкам, нли Как решать ураn11еш1я» ).
ВМЕСТО ЧИСЕЛ - БУКВЫ
в COЧl lll Cl ll'llf aJJJ,-Xopcз:vш 11(::1!:.>ВССТНЫ(;' HCJlll-
Чlll-lbl, так же как 11 вес со11у·1 ·ствую1ц11с вык11:.1д
ю1 11 11ре()()р;~:1011а11ия ур:нн1е1111i1, 11ыражт11-1с1.
словссrю. Т;:нюй ст11m, 11:-111оже11ия, ха ра1<тер
ный для раннего этапа разnптпя алгебры, 11с
торш<и науки называют р11тор11чесю1:м (тrаппм-
1шм. что р11тор11к:~ - 1~скусспю красrюречнл).
l lo11ыi'i встпшй прорыn в алгебре сnязап с
т 1 менсм французского учё1юго Л'VI в. Фр;шсуа
В1 ~ста. Он п е рвым нз математиков ввёл буквен-
11 ые обоз11ачснrщ дm1 кu~фф1 щ11снтов уравнс
н11я 11 нс11:·11к:ст11ых всm1чи11. А тра/1и r1ие1-1 обо
:лrачатъ 11е11звегг11ыс вел11ч1шы 1юслсдтшм11
букн;~м11 л:,~тннско 1 ·0 алфан 1па (х.у 11ли z) мы
~16
обяз:шы соnтечестнет 111 1 1К)' R11ета - Рене Де
каrту (СМ. СТ:JП1Ю «РШКJ1е111rе ауrше 11 1юi1 СЩ1·
BOJIИКll'' ).
И:юt1ретение 1311ет~ позвол11ло гораздо леr
че 11зхсщ111ъ с::~мые общие решешш для м110-
п1х похожих одна 11а другую задач. Прсдполо·
жим, со ста нщ1н. находящейся в 160 км от
Мос1~вы, в 11:шравлен1111 от стотщы выезжает
посэд С() скоростыо RS км/ч. Через какое.: врб~я
uн окажется на pac·(~1·n}tн1 11 1 ')()0 км т· Москкы?
Как 11змсн1пся рсшсн11с. есл11 пое:щ отпр:штr·
етс}t со с·1·а 1щ11 н. уд:1лё111 юl1 на 39'1 км от сто
т Щhl , ;_i с1<орост 1, егп 1 1ннже11 ня 7() 1.:м/ч? Эт11
;1не :1:щ<tч11 отличаются лишь исхо!(rтыми дан·
111,1м11, поэтому л:опускают :1апист, условrtя в
nбщем виде. Нсл11 поезд отправляется 11з П)~n(·
та, р::~споло;ке1 пroro в а км 0·1 "\1осквы.1.1 проти·
вополо.жную от нсё сторо11у со скоростью
l ' КМ/Ч. '1'0 ДJIH 'l'UI '(), чтобы достичь раССl'()ЯНИЯ
ь км 01' CTOЛlll\hf, ему ПОН<L/\Об!IТСН Rрсм111
Условие: выраж;1 ен:я ур;1внениt:м
а-1 z•/=h.
Решая э'L'О у1х11111е1111е 0·1·1юо 1т~л ы-10 н1::1 ~:шест·
но1·0 /, н::~хоμим
/J-a
!=--.
/'
Это общая формула . котор:~я охnатыв:~ет ncr
частн1.н: случп11 ЩIЯ конкретных чпсловых m
рамстрон а. /1, '" Наnр11мер, 1юла1 ·ан tt = 1 60кv
Ь = 5UO км. l' = 8'5 км/ч, получ:1ем
'500 - 160 -1
l=
= (ч)
85
.
Есзп1жt:а= 395км,Ь= '500км,/· = 701<м/ч.10
'500-395 1-с)
l=
=
)Ч,
70
'
Формула одна, а решсн11я разные. Лонстн.не
«м;:немат июt - :сно искусство лаRа '1 '1) разлнч
пым вещам ()ДНО и то же наз1:1аt111е>>. Этот остр<1-
у.'1ный и rлубоrшй афоризм принадлежит Апрн
Пуанкаре, создателю многих современных об
:~астсй математики. В работе «Н.аука и метод"
Пуанкаре особо выделял спосо611щ:ть учёноrо
не прuсто вищ::ть 1·олые факты..1 за~лядьшат1,
ruраздо 1 ·лубже - позн:н~ать дyury Ф:t"-"Т'О1:1, 11rю-
11зводить uбобщсюrя: ~1 lрuстым примt:рuм
яв.'lяется алгебраическая формуnа, которая даёт
шм решение ucex численных з::~дач опрсдслён-
1ю1 ·0 типа, та1< что достаточно лишь заменить
букnы •шСJrами. Благnдаря такот1 формуле
ат·ебраичест<ое вычислсгше, однажды nыпол
нешюе, и:-~батшт нас от необходнмости повто
рятr, без конца всё новые 11 rюныс численные
ВЫКJШДКИ».
Слова Пуанкарt: необычайн о актуальны в
на111 ~с.::1< всеобщего триумфа ком11ьютерной
техншш. Умницы-компьютеры науч11лн сь 1ю
н11ма1ъ язык алгсбранчесюt:к фuрмул н спо
соб11ы пер~::рабатыиат1J (т. с. нычис1m'п, по этим
форму11ам) оrромные м:зссивы чпслопых дан
rrых. Нужло только тто[(бира·1 1. и вво[(НТh 1 1 сход
ные числа, чтобы получать готовые ответы.
РАВЕНСТВА, ВЕРНЫЕ ВСЕГЛА
Есть в языке формул 011но прекр::~сное свой
ство - 1<р~1ткость. Напrимср. 11еремести.тель -
1tый зи1сон сложения: ~от перемены мест ела-
1·а1::мых сумма пс меняется» - выражается ла
ко1-111чным тождестном
(1+h=1?+ ti.
Ти.ж:десmв(Мt в м атематике и::~зывают равс11-
ство, вер\lое при нюб1,1х зн<\чею1ях nходяш,нх
в его состав nерем.ешrых.
1:3 руках у;-.1елоrо вычисmнеля тождес1·1ю ста
тюnится таким же чудесным штструмеrпом, кат.:
скрипка н руках музь~канта-nиртуоза. П) С1Ъ, на
нримср, требуется вычисл11ть сумму 2:$ + 12 +
+ 17 + 28 Воспользуемся тем, что слагаемые
MOЖllO Мt:НИТЬ MCCT:JMI 1. ~Т:.1 сумма равна l:S +
+17+_"J.,2+28=40+60=ню.
З,1.~ссь неявно 1кпользова нu н ещё 01~но наж
r1еiш1сс.:: правнло алгсбра11чt:сютх прс обра:юва-
1111й - сичетателыtый зако1-l cлr )Жt: I шя:
(а+/?)+с=а+(fJ+с)
Сlюбю1 у:каз1,mают порядок, в ко·1 ором про11 з -
1юдято1 операr~ин: в первую очередь выполня
ются действия внутри скобок, 11 n J(аль11ейшпх
13ычислсниях уч~ ствует только их результат.
Соч<:.:татсльный закон уl'Верждаст. что пpll сло
жt.: ни н пор1щuк действи1·1 не важен. Что бы
быстрсt: п одсчитатh су,.,,1 му , 1шдu замен~ rть nо
с11едонательные сложсн.ия ((23 + 32) + 17) + 28
таю1м: (23 + 17) + (32 + 28).
Оба закона, псремесп1тсльныi1 11 сочета
тельный, выnот1яются 11 для умноже11нн:
ah=ba,
(аЬ) с= а (Ьс).
Ою1ако для самых уднвитсльпых 11 красивых
аm·ебр:тчсскнх <-фокусо в » требуется ю~;щеть
217
Числа
распредели те.лы1ы.м закО1юм, который соеди -
1-шет две операции - умножение и сложение:
а(Ь+с)=аЬ+ас
R математиче:::сюrх ныкладюх этот з;.~ кон прн
меняется пи-разному. Если выражение а (Ь +с)
требуется заменить ранным ем.у выраже1-1исм
аЬ + ас, то говпрят, ч1·0 следует раскрыть скоб
ю1, т е. умножитr. а на h, а 11а с и слпжить полу
че1 ш1.1е ре;~ультаты. Глав1юс при этом - не за-
6ьшат1" что стоящий за скобкой множитель, как
предупредительный официант, обслуживает
всех юшентов, находящихся в ограниченном
скобками зале. В силу nереместителыюго за
конаумноженияа(t;+с) =(Ь+с)а,'l.е.не
важно, с какой Сl'Орины с1·оит «оф1щиан·н , -
результат обслуживания буJ 1ст ощ1н 11 тот же
Когда ныраже11 ие cth +ас заменяется на равное
ему а (Ь +с), 1·овоrят, что пере.ме1J1tая t1 пы1ю
с11тся за скобки. Такое преобра:юванпе потю
ляет сэкотю.мить на одной арифметиче ской
операции: вместо двух умноженнй аЬ и ас н
сложения аЬ +ас достаточно один р~1з слож1-гг1>
величины (Ь +с) и один раз умножить а на по
лученный рсзул1,тат.
Выведем с помощью этих законо"Н О/\НО 1~1з
самых главных н полезных ал1·ебраических
соотношений - формулу квадрата суммы:
'
l
~
(а+Ь)"=а +2.аЬ+fJ-,
TUНI, ЧТО ТО же самое,
(а+fJ) (а+Ь)=al+2ci/'J+1}.
Скобки, стоящие в левой части этого равенства ,
подсказьmают нам носпользоваться распрсде -
1штелы1ым за 1<01юм: х (У+ z) = - 'JI + xz. Нужно
только ~прю·ласить актёрОВ?: 11а роль у назн:1-
чим а, poлt-. z попросим исполнить Ь, а рольх -
218
Мнuж11т е11ь .1а с коб~оit,
КдК nреду nред1пе11ьныи
оф11ш-ыю, ofit 11ужив.э е г
всех KllИf'HTOB
в 11гран11•1ен~юм tкобками
з~ле.
скобку (а+ /J) Такой приём пазынается 1юд
стащншой. Ныпол11иn подстапоnку, получим
(а+Ь)(а+Ь)=(а+Ь)а+(а+Ь)IJ.
Вновь раскроем скобю 1н 11р11ведём 1юдобныс:
~
"
2
l
,
(а+Ь)-=а-+/Ja+ah+h =а +2аЬ+ь·.
Р11сунок 3 объясняе:::т геометр11чсскиf1 смысл
этой формулы 1 1а ~нзыке» площадей пря.мо
у1·олышко1J и квадратоn. Именно на таком
яз1,ше изъяснялись мате.чатики до изобретения
бyкnernroтl с 1IМвошши, да и сейчас его 01толос
ки слышатся, r<огда мы называем вторую 11
третью степени квадратом н кубом. Не правда
ли, оп прост и нагляд<::н. Но только до тех пор.
IJO.К:t И фОрМ}'ЛЫ ДОСТ~JТОЧНО flJ)OCThl . В .U.peBHll.X
l> аЬ
Ь2
аа!.аЬ
ь
Рис. 3.
текстах, описыв<~ющих решснпя более слож
ных задач, порой 1.юсх1 1щают не столько сами
рсшення, сколько с п особносr1, автuрон сочн
ннть , а их читателе!~ - носr~р~1нr1матt-. этн
г·ро мо:щкие оп11са11ия. Вnт [IОчему введенне
букв дало eroлr, мощ11ъ1~:1 'l'OJJчoк разннтшо ма
тем::~пгческой IТаукп.
Форму11а r<nадрата суммы - o,~r-ra из фор;1tул
сощющё111юго у.м1юJ1сеuия, которые должен
знатъ 1~аждый школьник Вес оrш легко uьшо
дятся из свойств сложения и умножения. Вот
IIX ПОЛIТЬПl перечень:
(а+Ь/=с/+2alJ+Ь
1
,
'
о
l.
(а-h)-=а-
-
2.аЬ+/J;
(Cl- Ь)(а+Ь)=а.!.- li;
~
~
'
'
'1
(а+IJ)=а+)а'Ь+::ia1)-+IJ =
=а' + Ь{+ )аЬ (а+ IJ);
)
1
1-
;
~1h')
2
~
(а- Ь
-
а-ja +:;аЬ-h
=
""а1- h1
+3а/?(а-h);
1(,
ь
J
1
{
(аf-r?) се-а +ь-)=а +/');
(а- h)(а2
+аЬ+h
2
)=а1
-
/Jj .
В с..·таТЫtХ этого раздела вы унидит<-', какю1 у;щви·
тельная с1т~1 :~аключенз в этIL"'{ равенствах. КШ(
JfORKO ОНИ рзfiотают 11\)11 (1ешенпи ур~ВНеl-IИЙ
Уравнения и нЕ>равенства
НЕСКОЛЬКО СОВЕТОВ НАЧИНАЮШИМ ВОЛШЕБНИКАМ,
ИЛИ КАК РЕШАТЬ УРАВНЕНИЯ
Од11н начинающий волшебник, герой шуточ
ной песенки, неумело обращался с заютинани
яии , в результате вместо грозы у не~·о получи
лась коза, а вместо у11ога - слон Чтобы решить
уравненне, тоже бывает l!f'ЖHO совершить ряд
пре11ра1ц<::1-1ий (алгебраических 11реобразова
ний), и делать это следует очеп 1> осмотрител1,-
110 Например, решая ура1:1ненис х
2
= х, мтюю
было бы рассудить так: «Это урашrепие суще
ствсmю упростится, если обе его частн поде
лить на одно и то же число х. Мы cpa:.:iy полу
чи~ ответ х = 1~. На самом дtле , стар::~нсь
•нзбанитъся от все1 ·0 лишнего~, мы допустили
бы шш1fiку, ;i именно потеряли е щ ё одно 1;~
коннос решение х =О. В задач ни ках по ~~л1 ·сб
ре 11 э1~амснацио1111ых билетах шкопы1ико.в и
<1битурие11тон LJacтo подстерегаю1 1rодобнъrе
ловушки. l(:]J( же в них нс попасть?
Прежде всего нужно чётко пони.мать, чем в ы
занимаетесь , когда решаете уравнение.
Нач•н·мюшие волшебники иногла
неумело обрашаютrя r заt<ливаниями .
ЧТО ЗНАЧИТ «Р ЕШИТЬ УРАВНЕНИЕ»
УравнениШ!'t с однu.N1 неизвестн.ьиw 11азывается
з::~пис1, nида А(х) = В(:х') , в которойА(х) и В(х) -
выражсн.ия от НСИЗВССТ/ ЮГО .У. в эти 131•1[ХlЖСН11Я
пом~ 1м о чисел, з11ако11 арифме-1'ических 011ерз
цпй 11 обо:шачепий функций мoryr вхою1т1, и
другнс буквы , 1<0торые обознзчают перемен
ные, наэываемые параметрами.
Обласпzыо опреде.леlluя уравнения (иногда
говорят - обласп, допустимых значений не
известного) н;~зывается множестно нсех знач е
ний х. нри которых олре,r~;слены обе час'~ 11
ура1:1ненин.
Ku/mi!-м, илн /Jeu,1t'1tиe.м, ур:.11.шения н:выва
е-1 с.я знач.ен11е 11еизвест1101 ·0, при rюдt~1·;н-ювке
которого в ypaвrre1 ше получается верное чис
ловое равенство. Решить уравнение - значит
найти все его корни или доказап" что их пет.
Есть несколько видов уравнений, которые
решаются по готовым формулам.. Это линей
ное и квадратное ура13нения, а 1 ·::~юкс ураввс
н ия видаj(.х) =а, 1·де.( - о;~на 11з ст<1.н;~аrтп111х
функций (степеннаи шш показательн<1и функ
ция , J1оrарифм , сш1ус, кос1111ус, тан1'ен с И JПJ
котангенс). Таю1е уrавнсния считаются про
стейшими. Например, коре1-11, ур:н111ения .х' =а
~Г
R
ранен va, корень уравн ения log~ х =а есть 3 ,
а уравнение соо; х = а решается по фоrмуле
х=±arccosа+Ъtn,1·деп.=О,±\,±2, ... Суще
ствует формула и для кубического уμавнепия,
но его к простейшю.1 пе относят.
Так вот, главная задача uри рсшенин любо
го ураннс:ния - снсс1и его к простейw11м.
КАК УПРОСТИТЬ УРАВНЕНИЕ
Два осtюв11ых способа упрощения ураm1е-
11ий - это заме1tа переJ1~етюй и раз.ло.ж:е1tuе
1ta J1.~1-ю:жите.ли.
Например, биквадратное уравнение х4
+
+ах~+ Ь := О сводится к квадратному зам<::
н ой J' =xl, а три1·онометричсское уравнение
2cos-х+cosх- 1=О - з<1менойу=cusх. Rооб
ще, если ны сумели заr1 нспъ уrавнение в виде:
219
Числа
F(/(x)) = О, cдeJla i:1·1•e замену у=j(x). Рсппm, л;ва
уравrrешщ F(y) =О иf(:Х:) = у, почти все1'Да про
ще. чем одно данное.
Разложить уравне1шс на м1южитош - :ша
ч.ит прсдставить сто в шmcj(x) g(x) = U . Такое
уравнсtu1с можно :iаме1111ть совокупнuстhю
,'\вух ураннен11й:f(х) =О и .q(., -x:) =О Множеством
рt:ше111пl исхол;нuго уравнсння буr1ст объсдн
не1-ше множестн реше11и(1 :=~тих днух бuлсс
rrростых. Правда , :щссъ спрятана т 1 CJДJ 1а 11з 1ю
в1111ек. При замене од1101 о урашrешш двумя мо
жет растт1рwпся область определешш задач11:
первое уравнение определено на пересеченин
облас1·ей онределе1 пш/иg, а совокуm юсть ,71нух
уравнеш11'J: - на объединении. Так. ур~шнсrшс
-fxcx + 1) = U имttт толыщ одшт корень (х = О).
етюкушюстъ же ура1111е11н~1 vX = () 11 х + 1 =
=0-/tНЭ(Х=0llХ= -1).
Рассмптрнм уравнение
х;- .~х
-
2 =О.
Один: корень легко угадать. х = - 1 . Как пайтп
остальные? Можно докаэать, что t:с;ш х0 - ко
рень м11огочле1rа Р(х), ·1 ·0 этот мно1·очлсн
делится пах - х0, т. с. разлагается на множнте
ли, однн и:i которых л - х0 (ЭТО с11енс: 1 ·шн.: нз
теоре м ы Бсзу). Вьшолн11м это разложение -
НЫI 1ессм из JICHOЙ части м НОЖИТt:ЛЪ х + 1.
При решении уравнении метоtФм lА<:'дС! в~т "..,,, у1 11uявн1 i..t я
110сrоruнни1? корни По;пому 1а1н:>рш3 1щu11м ~ТдПС>м являf'тr я
проверка всел найден н ых реше11и'1 nун!м их 1юлст<11юоки
">~гхолнщ• vrJннРн11.-
220
• Я r<:O!J 1юродил,
н 11·011 " уtiьк1 '
~
.;
)
l
'
}
х-.3х
-
2=х +х-- :\·- -
;,х- 2 =х-(х+1)-
-
(х.'!+.х)-2х - 2 =(х+1)(х~- :\· 2)
Uбратт1те вшLчание на 11с1юльС1уемый прп :этФt
ттриё:-.1 - 11р1 1 банленне 11 13ыч11тзш1е одного н
того же выражснпя (... + .\ '! - х
2
".). ~)'JO'L нею1т
рый , но очень полсзпьтт~1 прпём 11ос11т шyr.111-
Roe назн:т11с · ~1етод Тараса Бульбы» (вспомни
те: «Я тебя порою1л, н ·1·сбн .11 убью! ·)) . Ну :1
дальше остаётся rсши·1ъ кR;11чхп·1 юе урав1-1ен11е
Таконы r·лавныс с1юсобы упrощс 1 1ш1 . О11на
ко дог<1д::1 ·1 ·1,ся, каf..-ую 1rмснно замену C'JlCJ \Ye'f
ттрименн11) 1-1щ1 ка1< разложнтh на множнтелrr
копкрепюе ураnнение, 11оро(1 быпает очен1>
трудно. Успех здесь завнспт от ~ 1 тз 1 111н стан·
дартпых формул, 011ыта, смек:uuш и в болылой
мере - от удачп.
«КТО-ТО ТЕРЯЕТ, КТО-ТО НАХОЛИТ»
Допусrим. вы nр11[J.умал11 , к:~к упrюс~ и1ъ ур:ш
.rr ение . Теперь слеmет провсст11 прсобразова-
1 1 ия так. чтобы 11збеж::J'ГI> потери рсr11сниl1111111
приобрстсння л11111н11х кор1161. Внед<::м ti связи
с эти~1 важные определения.
Уравнеппе У1 называется с11едствие11,.1 ур:.tв·
неuня У 1 , если любой корень У 1 явпяетен111\ор
нем У.!; 3аш1сын~1ют это так У 1 ==) У2•
Ура ннен 1-1}1 на3ы н:нотси рс1и11и(.:илы1ы,1111
(У 1 ~ уJ н Т()М случае, КОl').Щ MHOЖCCJ' B:l их 1\Ор·
не11 сов11адаю1
с /'ОЧКl l зpt:! ll lЯ ЛOI'Т I КIJ реше1-uш <Х:ТЬ два
пут11: л11бп вы [\опускаете переходы к слсдст1ш
ям, л11бп делаете тот,ко рав1-юс1rлытыс перс
хuды. Тре1ъесо не дано: если на одном 1 1 :з
::Jтt1noв появилось уравпепr1е, тrе янпяющееся
следствием предътдущего, :нтачит, 111,1 безвоз
nратпо уrеряли какой-то корень.
Сравним два рсmстшя уравнения
~х+l=х-1.
(*)
Любоt' ч11с1ю, утtонлетвuряю1ц<:с 11ан1-юму урав
нен ню, удовлет1юряст н уравнснню. по1 1учен -
11ому 1 юсJ 1 е впзвененнн с1·0 R кв<11tрат:
.х+ 1 =.'С! - 2.У+ 1.
)то К113дратное ураnттеппс - следсти11е 11сход-
11ого. Его т<орни х1 = О 11 х2 = :). Подсrаноnт<а
11х u ур:.шнснис С') показывает. что первый ко
рень носторонш 111: оп даёт 11cncp1 юс равенство
1 = - 1 . Нторой корень 1 1ровсрку вьщсрж11наст.
Итак, пеrвый пут1, - RhlHC}\CHJ l e CJJCДCTJШiJ и
11ронерка нссх 11011уче1 шых корней
Пnсмотр11м. 1(;11( ПЫl 'ЛЯ/ \l lТ нторuс rсше1н1е:
,
jx+l=(x - 1/.
vx+l=.\:-1~
<::)
.\'- l?--о
[х_: - .)х+ 2= О. j[х=5.
~•
(::;>
.\'= о.
lx >1
.\:~ J
~.X=_l.
Ф111·ур11ая скuбк;,~ - :.т;,~к с11Lmел1ы . 011а пок;,~
зыв:J.ст, qто 11 уж1 ю бр::1·1·1.~ нерtсtчс:1-шс r-1ножест11
рt:шеrшй охваченных ею ура1ще1111й 11 rrсра
ве 11 ств. Квадратная скобка - з11а1< c uuo11)'JJJIO-
cmu - означает объед 1 шсrпrс реше1 1 1111.
Поясним толыю первый переход, осталы1ые
оче1нщны . Исходное урав11ен11е н/1.1еет вид
11 = lJ,1·де А= I~+ 1, В = х - 1. Чтобы 11з()з1шться
от раю1ка11а, 1юз1юд11м обе част в КRадрат. Этот
п<:рсхо)~ 11er:~ внос 1·1J 1 сн. поскольку равен стно
.4~ =В
2
HhШOЛШJe'l'CSJ уж<: в JI Юбоы из двух CJJ)-
Ч;JCH: А = В r1 А = -В. (Имен 110 н·1·opul1, ~l lОсто
рон 11 н й~ случ::~й н ,1\ал нам лиш~-ш~"i корен1,
.r1 = О 11 первом ре 111 е11 ин.) Чтобы обсспсч 1л·1,
рэиноснльность, нмо 1\0 Iюm r1 1'1'eJt1>1~< > потребо
n:пъ, чтобы выражения Ан В бынн од1н 1ro :щака.
По оnределе1 п 110 1mадратr юго корня, А > О, по
это.,.rу и накладьmается усло1ше В = х - 1 ~ О.
Ура внения и неrаненствd
1'.1л11 н.1л 11 0 1оч·д, l l t't 11и~•ш1111 с1юl\олу
( l'l.Мllll('Г() в НРМ д.+.ннн~ .
Сле!\ует помнить . что пр11 11 :~6аF1лсю111 от
р:щ111<ала 11ас ГГOf\CTC[Jl:n:ieт ещё <JД11а опасность:
рап1111рнетсн обткт1, опрс1\елен11я ур<1в1 1 с1111я .
Рад111\аЛ - ЭТ() с1юе 1 ·n rода сосуд, cтeCH>JIOЩllJI
сnободу сидящего н 11ём лж111111з (под зпа:rюм
корпя rтс могут стоять отрющтслы 1 ые велп
чи 11 ы). fсла р;щн1<ал исче:-~аст, пж111ш оыръша
стся наружу и может noзJJomrть себе такое, о
1 1ём раньше 011 мог толы<о мс'lтать. К прнмсру,
нuз<щця обс.- части ~1)а1ше1шя ~ :У-.)= ~l - .Y n
квадрат, получае ,..,, ура 1111е11r1с х -
.:)= 1 -х,ею111-
С"rвешrыlI коре~ п, которо1·0 х = 2 - пnсторо11-
1111й, п отому ч то rrc ri:-.oд11т в облас·n, 0 11 ре1 1е; 1е
тmя псход1ю1·0 уравнения. Rообще, прн з:~мс11с
ныражt:н11я (vfcx) )~ 11а/(х) к уранн~ншо 11:.~до
пр 1 11111сать услош1(:'.{(х) ~ U. ДJ1н н>а1шс 1 111н (*)
таю 1м услоннсм было 6h1.\' + 1 ~ О. Мы t:l'O ону
сп 11111, потому что 01-10 выпот 1яl'тсн антомат11-
чесю1, и снлу рав~нстна .У + 1 = (х - 1)~•
Та ю1м обр~1:юм, су1ъ J.порп1 ·0 пу1·11 рсше
н11н - ~iemm)a fJt1юшо1.11ьных 11ере.\:одов
-
ll
1·пм , чтобы цено!'1 доnоm 1 нтель11ы х yu10F111й 1r
ра('смотре 11 и я от11,с.J11,ных: случаев п()ес1н.~ч11т1,
нertf)HK()('\IOl~eLl l lOCIЪ МН< IЖt:Ства ре111<:: 1 111й .
Бесспорно, пеrвое ре11 1 ение урзвпеш1я (*)
выглядит проще. Но п само уран11ение оч:епъ
221
Числа
пр()стое. А nедь бывают ;1адач~-У, n которых
отсеять лшuпие кор1-111 едва ли не слож нее, чем
найти 1пс К 1 1сдостаткам метода рав1юсилы 1 ых
псреходо1:1 отнесём то, что уравнение пост<::11с1-1-
но .начин~~е'I' ~ке-гв 1 1ты.:я<> и обр<tстать условия
ми , за которыми непросто услет~и·1ъ. Hu в то же
RpeMJ.t мы п онимаем, в каком м ест<:: 11ас МОЖL'Т
ож.щ{аТh ловуш 1<а, и лучше контролируем ход
решения.
Есть ещё один арrумент R по11ьзу метода
равнос:илы1ых переходов - и пожалуй, rлаn -
11ый. Только так можно решать неравенств::~
(нроверить рсшсr-ше нсравепстnа подстановкой
просто н евозможно). На ш совет - научитесь
этому методу и пош,зуйтесh им нсегда, ~а искто
чен11ем, быть может, самых простых случаев.
Для это 1'О нужно знать причин ы , 1ю кото
рым р;;н11юсюu>1 юсть может нарушиться. По
смотрим, r<:ш обыч.110 11реобразуют уравнения
и чем ::>ти п реобразования ч.реш~ты.
АЛГЕБРАИЧЕСКИЕ « РИФЫ »
Когд:-~ вы п ри бавл н с-1 ·е к обеим частям урав
нения число, то ре 111 снютм , коне ч но, ни что
не уrрожаст. Но если это н с число, а функция,
1 1а11рим.ер l/x, будьте на с~ ску: уравнение х =О
имеет оди11 корень - О, а уравнениех + 1/х =
= J/х корней не имеет! При прибавлешш функ
ции может нарушиться область онредеJtен ия
~1)а11.11ения. Если он а расширяется, 11 ри 11иши
тс к уравнеIJию соответстnующее о rраниче
ние, а если сужается, проверьте, не я.в.т.rяются
ли 1щрн н ми уравнения точки , где функция
не определена.
То же самое от1 юсито1 и к умножению. J<ро
ме то1'О, здесь к решениям урав н ении м01уг
J(обавитт,ся те зна ч ен ия неизвестной, которr.1с
обращают множитель в нуль. Ну-.м:но провер1лъ,
не дают т1 01rн лиш11нх корней.
Выражение, вхо,тщщее n ypan11e111re , мтюю
заменять на тождественно равное. 3)1ecr- .
надо
учитыnать, что бывают два в ида тожтr.еств.
Абсолютным тождество./11 называют равен
ство А =В, в котором выражения А и В имеют
одип:жовую область определения и ч исле~ 1но
раины 11р11 нсех зн~Jчениях переменных из
этоn области. Это, например, формулы сокра
щёшюrо умножения или формупы сложе11ия
длн си11уса и коси 11ус:!. Таким.и тождест11ами
пользуйтесь без orrac1<и. Но ес1ъ тождестnа и
222
Пр11меняя "обе11м частям уравнениR ш1ну и ту же функuню,
оtiычно рас1ужлают так· •~ел" а =Ь, i o 11 /(а)= 111J) , _Hn
с11едует nо~1нюь, что оfiратное, к сожалению, не В('еrда верно.
шюrо ро,1\а, 1<ai< упомянутое nыше раоенство
('"'А)1
= А илиIg~=lg.х+lgу.Внихоблаrп1
определения частей различны , как нравило,
одна со,1\ержитсн в дру1·ой (х и у к ле ной ч<~t.ти
тождества с 1ю 1'ариф.мом - любые числа од-
1юго знака, в пр:нюй - толыю положитель
ные). Та1<ие ·1 ·ождtс1·на называются оm//.оси
пzелъ1tы.ми, J1 1< 11им по1п-юс1ъю применимы
паши замечания об изменtнии обласn1 опре
деления.
Наконец, применяя 1< обеим частям ураш-те
ния одну пту же фушщию. nы таю1<е р1 1 ск-уете
нотерять корни. Ведь если функция определена
н е всюду. то область определения уравне ния
может сузиться. С другой стороны, есJ 1 и функ
ция.((:~) не нзаимно однозн;JЧН:J, ·1
·. е. р:н1енство
. f(x,) = j(xl) ВОЗМОЖJ-Ю и 11 рн Х1 *Х2, то г~ри 11е
реход<.: от уравнения А= IJ кf(А) =/(В) м<щ1 ·
n()яю-1т1,ся гюсн1ронниt' кор1111. Ос1 юпной (11 нз
практике по чт11 единст1Jенный) прн.мер такой
функции -/(х) = х~. н вы знаете, ка" <-подстра
ховаться» в этом случае.
В учебниках и пособиях ;vтя поступающих в
вузы приводится м 1 юго стандартных схем paв
f-IOCИJJhHblX преобразований, 1-1:шр 1 шер избав
ления от радикалов в уравнениях. Но можно
обойтись и оrщнм коротким советом: буд1:.те
начеку 11 ри любом измененнп nбласти опрене
J1t 1-1пя и проверяйте обратнмосrъ 11среходоR'
КВАЛРАТНЫЕ УРАВНЕНИЯ
К11адра·п LЫМ 11а~1ьшается уравнение тща
u,-...·
2
+Ь:х:+с=О,
цс а, Ь, с - дейст1:1итсл1>ные ч и сла и с1 *О. Если
а= 1, то 1<11адра11 1 uс уранн<.:нне н:.~зынают прu
ведённым" если а '# l - непринедён:ным.
Вг1 ер1~ыс кнанратноt ураннею1с сумели p<::-
w11Th матема'Гнt<иДрсн11е1·0 Еrн 1 1та. В 0;11юм нз
ма1ематичесю1х паnнрусов содержится задач<~:
•Найт11 сrоро11ы: полн, имею щего форм.у прн
мо}толы 1 иr<а, есл11 ero ллощадь 12, а 3/ 4 ЩIИПЫ
равны ш11р.1-ше». Рассмотрим сё.
Пусть х - длнпа поля. Тогда 3х/'1
-
е1·0
шнрю1а,S= 3х.!/4 - площ;щь. Лолучилос.:ь ква;1-
ра'1·нос ура н нснне
3х2 =12.
-J.
R r1аш1русе дано прапилодля его решсшн~: <· Ра:1-
11е.>111 12 11 ~1 :$/4».
12:l=l2·i=l6.
4
j
11тai<,xJ = 16. <-Д~~ина по; ш paвlia Ф>
-
ука:яшu 1:1
паr 11 rрусс.
1!ро шлн TЫCЯ' J t:JIC'l'llJI. l! :~лгебр}' IIOШЛll от
р1Щ:1ТСЛhНЫе числа. Решая уравнс1111с х~ = 16,
мы получаем }.\l!:I ч исла: х1 = 4, х1 = -rl. Разуме-
УрJВ•JСния и 11срJве1 1 ства
ется, n епrпстско11 задаче 11 мы прншти бы
х = 4, таIС как дли1 1а поля может бьгп. тот, ко
1 10Л()ЖИТСЛЪНШ1 ве1111 чиной.
Огромный 1ш1 1· нпсрёд rю сра вн<.:ншо с ма
тематиками Е1 ·и r1 та С7'<::11али учё11 ыс М ежду
рс:ч ьи. Они ш11 шш пр:ншло длJJ решения пр 1 1 -
11е[1.ёНJ IOl' O квадратtю1 ·0 ураш н::Нl 1я
х~+р.?.:+q=О,
['Дер и q - любые дейсrrнtтельные числа.
В одной из вавилонски:х задач таюке требо
валось определить длину 11рямоу~·ольпо1·0 поля
(обозначим <::ё х) н с1·0 ширину (1'): «Сзюжив
длину 11 ;~ве шир и ны прнмпу1 ·uлh1ю 1 ·0 1 юлн , r~u
луч ишь 14, а ПJlO Щ;IДI> IIOJIЯ 24 J !a JJД\·1 сго (.~J'O
pt) Hbl'I. Сuс1 ·аuим с11 СТL'му ур:11~н е1·1 иi'1 :
fx+2y = 1·1,
l·''' == 24.
Из nтoporo уравнения находим у= 24/х н под
ставляем n первое уравпеrн rс:
х+4Н==14.
х
Отсю.п;а получаем кв::щра 1·1юс ур;шнсни<.:
х2
-
Цх+48= О.
12.
-$
ЧислJ
,lJ;lЯ t'J 'O [К"Шl'Ш IЯ приб<ШI IM К Rblf1aЖL'HlllO Х~ -
-
14.\' 11 ексrтрое число , чтпбы 11011учнт1. 1ю11 -
11 hJ fl J<ВЗJЧ1ЗТ:
х2
-
J'-l"i;· -
х2
-
2.·7 ·~,.=.х·~-2 ·7 ",.+7~-7
2
=
=(Х-7)2
-
49.
Tcn<.:ph ураннсю1с мuжнu ::~ат1сат1, так:
('\' - 7/- 49+L18=0.ИJll•I
(Х- 7)2
=1.
Мы прншли к квадратному ураnнешпо, кото
рое ум<::.1ш решать и египтяне. 1Le зная отри
цателыlЬL'С чисел, древние математнют получа
лих- 7 =1,х ==8.Слсдоватслыю,у == 24/8= .1.
То ес1ь дш1.на 1ю1ш ранна 8, а 1111 rр11на .).
ЗАдАЧА О СТАЕ ОБЕЗЬЯН
Состr~вив квалратн ое уравнение, решите древне инлий скую
зал,1чу о стае обезьян.
224
Ответ:
х, =16,
Х1=48.
Rообщt жt· кналратноt уравнl'Нl 1с (.У - 7/ =
1 и1'>1ее-1 /tli3 кор 11 я ·
1)х- 7 =1,отку,1\ах =R,у=3;
2)х-7 = - 1,откудах =G,y=24/6= -\..
ФОРМУЛА ВИЕТА
Покаже,\1 , как м ожно на~'iт11 формулу для реше
ншr любо r ·о приведi::нного квщ1ратноrо ураR-
11 е11ня
'
.х-+рх+q=О.
Запишем фор.•4улу юзадрата сум.1\11.ы:
(а+l:J)!= al+ 2a1J+Ь
2
11 заменим н 11ей а 11 ;.1 .:t·:
С'-"+Ь)!=х
2
+Ь.:h+ /1
2
(*'J
Сраrтим гюлучс1111ut выражсн1 1с с 11а111им урав·
11е1 1 1-1ем . Нетруд1 ю эаметить, ч·1оес;ш1101южить
/J = р/2, то левая часть уравнения (*) fiyЛe1' от·
ЛИЧа'I ЬСЯ 0·1 llOJJIIOJ 'O квадрата (*") только по
СТОЯНIЮI1. Это паблюле1шс п 01~сказывае; oc-
11 onrryю идею рсшспня. В уравнсшт ("') нужно
В ЫД<.:ЛИТЬ ПОЛil:ЫЙ квадрат;
(х+~)1 =.У2 +рх+/~~ '
а то, что ост:111етсн, т. t. пы1х1жение (- jJ~/4 +ц).
nере11есп-1 r1 11 р:н,у1() часп •. После этurо }"pIOI·
11 еJ1ие (*) прнмет н11л
Jicнo, что ю1 при каком х выраж.ешrс (х + pjl)1
не может бhпъ отрищ~тел ьным. О1сдоn:1тельно,
если р2/4 - q < О, то квад1х1·1·ное уранненне не
имеет дсйстн11тсльных корнеi1 . Пусть р2/4-
-
cz > О. То1 да, извлекая юшдрат1 1ы й rшрс111, нз
1юсJ1еднего ура1111е111 ~я, 1юJ 1 учаем
р
р!
х+-=±i--c1
2
~41
'
откуда окончательно находим два корня :
11Л11 , в сокращt.:нном ВН/\С,
Эту фор;11улу rrазывают формулой Вzюта - по
именп фра11цузского математика 1<011щ1 XYl n"
Rнёсше 1'0 значительный вклад u станuиление
алтсбраическuй с 11мнол11ки (см. ст;1· 1 ъю <Эпоха
13шрож;~ею tН: СJ1а 1н-tы1:: открыт~ !Я») -
ДИСКР ИМИНАНТ
КВАд РАТНОГО УРАВНЕНИЯ
Rп1 ражепне. стоящее в формуле В 11ета под зна
l(ОМ корня, называют дискр 11.,~,1ш1а1тю.м (от
лтп. discriminans - «р:.tэделяющш1" , « раз11ич<1 -
ющнй?) и обозш1ча10·1· бую:Ю1°1 D. Д11я нашсто
приrн:дённогu квадратнul'о уr<ш не нн .я
р2
D=4-c1.
Дt:йст1ттелы-ю, r1p11 рс 111 ет 111 и кnад,ра11 1 ых ура1~
r 1ен1 1!'1 пмеет смысл различат~, три c.riy\.\:UI - в :~а-
1111снмости от :ш:ша ,'\искрrrмннант<~. Гlри D < О
ура 1шеrшс rre имеет корней. ПриD >О оrю име
ет дnа разтrчпых корня х 1 и"'--~, котор ые нахо
дят по формуле Вн~а. Что же будет, ссл111J = ()~
В этом случ ае ч = р -/...1, 1н..·в;~я часть ураR 1 1tнш1
(*) прtдставляст собой nо1шый квадрат
[:r+~)! =O,
Ура13нсния 11 ~1ср.:1вснстоа
тэк Ч'J'() UHO 11мс:ет O/l.1 11 1
- t:J\l ll lC'I вс:н ный l<Upc 11 1>
х = -р/2. Формут1 Виста 11 этом с11учае 11зёт
т. е. олрс11~ляемыс ею два корня совпа,тщют
(гонорнт также, что ур<1внс:1111t нмсст дву1ч)41·1·
ный кuрень)
ТЕОРЕМА ВИЕТА
С 1юмо111,ыо вве,1ё1 111оrо 1J м буквснтюJ'О 1кч11с
ле11ня Франсуа Вист не толь.ко эаrтсал в об
щtм виде формулы /l.ЛЯ корне rl юзадранюrо
уравнения, но rr rrащёл n ыражение для J{ОЭф
фи 1 lНСнтов ура 1ш с111 ш через его кuрн11 , котu
рое сейчас 11 ;1зынаетсн llU!UfJl!.MOli Ви(-)та:
Если .х 1 и .\: 2 - :ко1эни: квадратного
уравнения х2
+рх+q=О,тох1+Xz=
=-р, ах1";л·l =q.
Т.i)'Квет-юе щ:числеш1с позволяет 1'1.СЖа:-~ы
вать теоремы с помощью ал 1"ебра~rческ~L'< пре
()()разований. Мы :-mаем, что при D ~ О корни
квадрапюго уравнення 11аходятсн по фор,,1у;1с
р
,-
\' ---+,о
.
IJ-
2-
.
1'с:псрь ДOCT;ITOЧllU аккуратно BhJТIUJIHII'IЪ '1 .l -
r тбра11чt..:ские прt.:обра :юв:11н 1 я - 11 теорема
Виста будет Д(Ж<1зана:
ЗАдАЧА
ИЗ ВАВИЛОНСКОЙ
ТАБЛ ИЧКИ
во второе уравнение, раскроем
С1<06ю1, приведем подобные. П олу
чится квадраmое уравне11ие
Используя формулу у ::: 27 - > ..
вычисляем ши рину поля;
У1=27-15=12,
• Я сложил длину и ш ири11у, полу
чил 27 . Избыто1< длины над шири ·
ной я прибавил к плошали поля и
получил 183. Найди ллину, шири ·
11у и плошадь ».
Пусть х - д/\ина, у- ширина.
П()лучаем систему уравнений
{х+у=27,
(х- у)+ху =1В3.
Из первого уравнения 11аходим у:::
= 27 - х. Полсrавим это выр<:1жен~1е
х1- 29х+21О=О.
Вычислим дискрими11а1н:
D=(-
29
)
1
-
2 10= .В4I _ 210=_!_,
2
4
4
И накuнеu, найдем корни:
291
X 1i =-т±2;х1 = 15,х~ = 14.
Итак, мы получили два различных
значе ни я лля длины поля: 15 и 14.
У2=27- 14=13
И СГU П/\С)Ш.lдt.:
S1= 15·12 =180,
51=14 1з =182.
Лреuний матема1 ~1к ldкже 110-
лучил в npouecce вы 1 1 ислений чие
м15и14.Ноонвзялдлядлины
1олько 15 и ~1аписал, что исти1111ая
ширина 12, а площадь 180. Мы же
н.зшли еше ()д 110 решенис-: ллин.э 14,
ширина 1 З, ГIЛОШадЬ 182.
225
Числа
КА К ОГОРОДИТЬ
НАИБОЛЬШИ Й
УЧАСТОК ЗЕМЛИ(
Подставив это значеыие в форму
лу ПЛ(IWdдИ, ПОЛУЧИМ
х,+~.
ч иr11им пn форму11~ Xn =2""·
ОтсюдаХо=Ь,У1)=J и5=18.
Итак, размРры площадк и: длина
6 м, шири1~а 3 м, nлошадь 18 м1•
Имеется стрuител ы-1ы и ма·rер и ал,
ю которого можн о постро ить 'lil -
бop ллиной 12 м. Мы хотим огоро
дить п ри ле1 аюwую к дому п рямо
угольную плошал ку на иfiольш !:й
пло шад 1~. Каковы её размеры?
5=х((1-~)=- ~J + 6х
Перед н.:~м и ур<1в нен ~н:! параболы,
ветви кnторой нап равле н ы вниз.
Нужно определить такое х, при
котором S пр и11 ~1мает наибол 1,ш ее
{Начени~,>.
5
5 = ~(6-f]
Пусть ,\ - лли11а nлошалки,у
ш1-1ри11а, 5 = ху- ее плошаль. Со
ставляем урав н ение
Сначал<l 11а илё.'м точк и п сресе
чения п11раболы с осью ;~бсu нсс .
Лля это го реш им КВdдр<~тное урав-
х+2у= 12,
не ние
из ко1ороrо н аходим
х
х·
hx--=О.
2
у =(>-2-
Егокорни~1= О 11х2=12. 3dтем
абсuисrу верш ин ь1 п араболы о ы -
х +.'\:,= --+\1D + --- '!D = - /J
(р1.)(р iJ
1
-
2
2
'
;/- [р2 J
= -=i-- ~- {j
= Cf·
Обратим n11им::1111тс сщё ш1 одно 1 штсрсс н щ:
соопюшс111 1с - д11скр1 1мш1:~нт уравнения ра
вен кв;щрату ра:шоспr е1·0 корней: IJ = (х1 - х1)~.
Из теоремы В11 ста ны·1·е 1<<.1ет, что при венt:11-
ны~'1 1<вадрат 11 ыrl трёхчле н с корням н х 1 11 х2
мож1iо :заJJис:1ть в н1 щс (х - х 1 )(х - хJ.Действи
тсльнu, раскрыва я скобю 1 r~ э·1'о м проиэве;1е
нtн1, п олуч;.:~ем выраже 11 ие
)
l
.--
-
(.У1+х!)х+х1х1=х +рх+q.
И п ~юбор(П. это разложе 11не 11а множ11тели
:.южно использоnать для доказатсльств<.1 тсо ~
ремы Виста без вычислен ий. В с11vюм деле,
пусть дан 1шадратныlr трёхчле11 х~ + рх + q. а
х1и.\', - e t·o кuр11 и. Замс:ч~1см. чтu
\Х - .'>:\)(х
-
xJ=х~ -(х1+х~):У+x1xL
есть 11р1 1 недённый квадr<.1тнwт·1 трi..:хчлt:н с тсмr 1
же корням11 х1 11 .'\:2, что и данн1.1 й. Ра:шость днух
трЕхчленон ра нн <l
226
Этол 1·1.11ейная фупк1 01яотнос 1 rтелыrо.'\:. Пр 1 1чём
поскольку оба многочлена обр::~щаются :А н1rлъ
к точка х .-х· 1 11х.!, то 11 нх разтюст1, (**") обращ~
стся 11 ную, в тех же точ1<а-.~. Д11я т шсй1юй футrк·
(~111 1 ЭТО BU:3MOЖI IO ТUЛЫ(() в том случ:.~с, сели она
ЭКЗАМЕНАUИОННАЯ ЗАЛАЧА
Эту задачу прелл.1гал и решить п ос 1·уn,1 юшим в Мое·.
ковск ий ун и верситет н а физ 14 чески й факультет.
Урав11<!ние
ах2+Ьх+2=О,
где а <О, имеет одним и:1 своих кор 11ей ч исло .{ .
РР.шитс уравнен ие
ах~+Ьх1+2=О.
Решение. П римен и м теорему Виета к первому
2
2
уравнению:х1•>-2 =а-. Так какх1=.3,то Х1=1а
и, следовательно , x l <О. Обоз11ач им х1 = (, тоrда
второе уравн ение пр и мет вид
at2+Ьс+2=О.
Сравн и в это уравн ение с исходным, получ11м
2
t1=З;11=За,t2<О.
Уч1-1тывая, чтохl = r, з 11 ачеt1 ие l l отбрасываем, а из
равенства 11 = 3 находим х1 =- З .
Ответ:х1! =±"'13.
ТОЖJLl'("1 · ненно рав 11 <1 нулю. ОтсJО/\:1 н h1тскает, чтu
fJ: -( х, + .У2), а t/ = х1х~, т. с. теорем~~ Виета.
Это рассуждсннс, каt< н самутсщх:муВнста,
можно Ofi()б tЦH'tЪ 1 1~{ м Н()Г()чле11ы п юбо 11 СТ<:'
пе11и:
,fd Коэффициент при х"-1 в м11ОГО'-1Ле
'k-I не степени 11 равен суъ1ме ero " кор -
11ей со 311а1<ом минус, а свободный
член - произведению всех 1<0рнсй и
•шсла ( -1)".
НЕП РИ ВЕЛЁННО Е УРАВНЕНИЕ
Непрнuснё111 юе ю_1адратнос ура 1111еш 1t"
1
ах-+IJ.\·+с=U, а--FU,
после де11сш1л на а превращается в привсдён -
1юе уравнен~ rc
)ьс
Х" +-Х+-=0,
а
а
дЛJ! КО'mрою у нас уже есть формула . llоэтому
его корнн -
1~
'
Хи =-
2: ±~±(;у :
1,
-h± vb- - -Juc
2а
Днскрнмипапт это1 ·0 уравпення D = hJ - -+ас.
Теорема Виста д;ш 11епрнnсдё1шо1·0 ураnне-
1rпя звуч~1т так:
1
f!,,-
Если х1 и х2 - :корни квадратного
'k" уравнения ах
2
+Ьх+с=О,тох1+.х2=
= - Ь/а, а х1·х2=c/tl.
В рассказе о кналрат1Ю 1\1 ур:-1-внсr1ни мы
paCCNl:l'IPИR::tJlll TOJll1KO ;~ейстнитеJI Ы·I ЫС кор1 IИ.
Но н области комплексных чисел нсё обсrо11т
даже проще: ШОбое KRaf\p:lПIOe )11ШН·ТС!1Ие t1Me-
<:T два корня, Р.озмож1ю соrн~а,цающих (при
lJ = О). llpи отр ицательном 7щскримшта11те
корнп будут сопряжёнными 1юмnлексным 1 1
чш:лами. /(оказ:~тельстnо 11 нывод формул со
хrанн ютсн бс::! RС51КИХ ИЗМ<.:Нt:ННЙ. Более '1'01'0 ,
11 формуJ1ы для кор11е 11, 11 ·1·еоре::,•1а llиетз остd
ются в силе для к1:1адр:.~т1 1 ых ур:11:1не1111(1 с про
шrю11ьнъ1м.1 1 ко.V1пл~ксным 1 1 коэффицне11там.п.
В этом случ~н::: , ; IJ н~що пош1ма ·1ъ к;~к любu 1!
11:Jдвух 1юм.ллекстrых корней из числа D.
Уравне11ия и н~μавс11пщ1
УРАВНЕНИЯ, СВОЛИМ Ы Е
К КВАЛРАТНЫМ
К квадратным уравнен иям привоыпся биквалрат
ные уравнения, r. е. уравнения вила
.1х·1
i- Ьх2 +с= О.
Лействительно, сделав Jаменухl =у, получим квад
ратное уравнение
<1YL +Ьу+с=О,
найлём его кор~rи У1 и У11 а Ji.!Тем и корни перво
ttачального уравнения Х1 i =.!:~у 1 , х 1 4 = ± ~уJ .
Ясно, что сред~., зна1.1ений у 1 и Yl моrут бы rь и отри
uательные, и комплексные числа, а дсйггвите11пные
1начения х возможны лишь при положительных зна
чениях у.
Примене1тый здесь метод может быть исполь
зuван более широко.
Задача 1 . Решить уравнение4 ' -
.:!·2' '
1
16 =О.
[ели сдел<1ть .здмену 2' = у, то мы вновь придем
к квадратному уравне11ию
yL- бу - 16;::; 0.
Его коr)~IИ у , = R 11 у,= -2. Первый корень лаёт урав
не11ие 2' = 8 , откуда х =3, а второй коре11ь - урав
нение 2' =-2, которuе 1 1е имеет реше11ия в дсАпви
тельн ых числах .
Зал.ача 2. Р<'шитп уравне11ие cos 2 '< + J siп х =2.
IЗыразим cos 2х через si" х 11 пuдставим е урав
неt1ис:
1-2~in2x+~si11х=2, 11л"'
2sin!х-3sinх+1=а.
Теперь замени м siп х на у, чтобы nолу1.1ить для у
квадратное ура1:1нение:
2у1
-
Зу+ 1 =О.
Корнями :Jтого уравнения являются У1 = 1/2. у1 : 1.
Осталось реш ить nростеишиетриго1~ометрическ11t:.'
урав нения
.
1
SIПX= -
И Sil1Х=\.
2
Первое из них лаёт множество решений
х" =(-1)" .!: + пп,
6
где п - п роизвольное uелое • 1 исло , второе уравне
ние.- множество решений
х =~+2пп
п2
.
?.2 7
Числа
КУБИЧЕСКИЕ УРАВНЕНИЯ
Если кnа)lратные уравненшJ умели реш:tть сщё
математ11ю-1 Ва1н11юн н11 н Дрсшн.-:~-r И н)\ 1111 . то
ку611ческн<.:, т. с. ур:1 кнl'ная нида
ах~+fx>/ +сх+tl=О,г;1еci*О,
ОК<l:{<JЛИСЬ <·Крепким opeLIJK().М'>. в KOl l t(e xv 1~.
1 1рофессор математию1 n университетах Р11ма
и Милана Лука Гlачол.и в своём з 11амешпом
уч<:б ню<е «Сумма знаний по ариф~1ет11ке, 1·ео
ме-1 рии, отношенням 11 пропорrт,ионалыюсти »
задачу о нахождении общtто мстода для рсmс
ния кубических уранне н 1 t.й стшшл в один ряд
с задасн.: й о кнадра'1урс крута. И щ;ё же усю1ш1 -
м11 ит~11t1»1 н ск11х а111 ·сбра и сто к такой мс·1·0;~
вскоре бьш 11айде11.
НАЧНЁМ С УПРОШЕНИЯ
Ecm1 кубнческос ураnнсшrс общего внда
1
'
ш.: + /J.x· -
+сх+rl=О,1деа~О,
раздеш11Ъ на а, то кuэффиц11ент пр11.х~ сташ:т
ранен 1. llо:этому в ;1а_r1ы-1е й 111 е."1 буд~::м нсхоДiпь
11з уравненин
228
~
'
х +р;у-+.Qx+R=U.
(')
Так же как н nснож: решения ква;(ра ·1 н 01·u) рав-
11 е1111я J1t:ж11т формула кн~щ1х1та суммы . рсше
н 1-1е кубнчtско1·0 ~г;111нсн11я 0 1111р ае1 01 н:.1 фор
мулу куба сумм ы :
(а+Ь)'=с/+~a
1
h+3а/?!.+h~.
Чтоб ы нс путаться n rсоэфф1щиентах, :~алн.:нпм
здесь а 111 х 11 псрсгруптт11руем c11a1 ·3e,'-tьre:
'
'
,
.
)
'
(,\'+/J) =.\' +2>hX"+){J"X +Ь.
(•*)
Мы виднм , чтu 11:1;1,л~:жащ1щ выбором /J , а 11мс11-
1ю 11::н1в /J = Р/3, можно до()шъся 101 о. ч·1 0
нравая часл, ~Т()1"1 формут ,1 будет отл 11чагhСЯ
от Jtcвolr част11 ура11 1н.:: 1шя (*) толпко коэфф11-
11,1 1 снто~1 прн х I! сnобrщ 11ым чле1юм . Сл11жш1
ура11 1 1е1 1 шr (* ) и (**) и прпnеll.ёМ подоб11ые·
(.У+Ь)'+(Q- .~Ь!)х+N- IJ'=О.
Есл 11 здесь сделать за.ме ну у = х + IJ, получим
rсуб пческuе ура вн еrш с оп10с1rтслыю )' без
Lrлc11aс / :
/+PJ'+q=O.
Итак мы гнжа . J~1ли, что в ку611чсском ура 11нt:-
1-11 1 и (*) с rтомощыо 1юдходящtl1 п одстановю 1
можно н збаtJ н:t 1)ся т ЧJ1с11а , содсржащ<.то ква/\·
1х1·1· .н t1 1 эnесттюго. По::п ому ·1 ·е1 1 еμь будем ре
ш а·1ъ уравнен ие nада
х'+рх+q= U.
(***)
ФОРМУЛА КАРЛАНО
Данай·1·е е 1.цё p::t:.! обра' 1'11 мся ~ фо риущ; ~<уб~
суммы, н о за п1 11.нем её 1111аче:
;
)
1
(а+h) =С1 +!?+3a!J(a+Ь).
Ср;1пннте С'1ТУ за111к 1, с ура11 11е 1 нн::м ( ***) и no·
1 1 \)Об}'Й'l "t ycтaJIOFIИ'fЪ CFIЯЗI> между J 111.M !I. Даже
с 1юдо:азкой это непросто. На11п о· ща'п, долж
ное математтл<ам эпохи Uозрождеrrпя , rern 1o1в·
ш11м кубическое урав11с11и е, rre вщщея бу1-: ое11·
IIOЙ СИМfЮЛ ИКО I). 11одст;uшм: в н:нuу формул~
x=a + I?:
х1 =а
1
+11 1+ .)аЬх. 1ш и
:х-5
-
3аЬх- (а~+1?1) =О
Теперь уже Яl'НО: для то~ ·о. чтобы 11а йт11 1<орс11 n
ураuнснт1н (***). /tостаточ110 рсш11·1ъ систему
)1p~Ш\IClll'!JI
{а'+ 11' = -tf,
11ЛJ ·I
.~Cl/J= - fJ.
а'+11' =-(f,
;
a'h'=-(;}
11 (jзять к кэчествс х сvмм\' а 11 h .'Заме~ шй и= а ~.
;
,
.
1' = {J эта l'ИСТс:=ма прНВ(ЩJ ITOI к СОRсем про-
стому внду:
Д:шьшс )ложно дейеrвовать во-разному, но Rce
•JtOpOl 'JJ-> llj)ИRC'Д)' I ' к 0/tHOMY и тому же ква ;1р::~т
ночу ураRненню. На11р11мер, согласно теореме
Внt'та, суУ~ма кop11eii пр11недён1-ю 1 ·0 1шадр;~т1 ю
го у1х111нснш1 раnт 1 <1 ко:-1ффицr1СПту нри х со
знаком .\.пrнус, :1 произ11едсние - cnofinднoмy
чле11у (см. статыо «Кnадр:~тные ураnнеш-rя»).
Отсюда следует, LПО и и l' -
I(орни ураr111ения
111· (/!- (р/3)~=О.
Вьшншсм эти кор1-ш:
1--_-
,
·'
t )= - q±1(!1)+(./JJ
•-
2~2
3
Перtмсr:-тые а 1t Ь равны 1:-.-уб11ческнм кор11ям
ю t1 1112, :1 искомое ре 111 е1 ше ку6нческого 111~ш
не1 шя (**") - сумме этпх корпсй:
1--1-2
~1---~
'
x=~1-g_+ '(:i) .Jр) ;-~ _g__ 1(:!..) +(р)
2v2l.~~2\2
.3
Этц формущ1 11змсст1 ra как фор.i1,1ула f(ajJдrmo
(С\1. cт:.tThIO «Эrюха Возрожденнн: славны<.: от
КJ.Ш Т1 !Я ").
РЕШАЕМ УРАВ НЕНИ Я
Прежде чем посмотреть пd формулу Карпапо
в работе , поясним , как по одному кор11ю
ку611чсс1<01·0 ураннсния (''•*) найти друп1с его
корн1 1 , если ош1 есть.
Урдв11<.>1111я и 11еравенства
Пусть 11зF1ест1ю. что 11а1пе ypaвll(:t-111e ~~мест
корс111, fl. Тоr.п:а ен> лсnую часг1. мшюто разло
ЖИ 'l'J> ШI т111ейный II квадр:ПIIЬПJ MllШIO I TeJll1.
Дс:лается это очеI1ь просто. Подставляем н урав
псf1не выражение свободно1·0 члсп:1 через ко
рснт,CJ= -
!1~ - pl1 11 пользуемся фuμмyлui'J
ра:щuсти кубон:
1
\
.
,
1
()=х· -h +р:>.:-ph=(х -h)(x~+!1х+h-)+
+р(::.: - /1) = (Х - /1)(Х
2
+ft\"+f12+р).
Тенсръ мож110 решнтт. 1.;1:1адрат~ юе ~11anr 1 e1 ше
х2+llУ+112+fJ=()
и ш1йт11 осталыrые кор1111 дашюго куб11чес1ю
rо vравнсrшя.
Итак, мы но всеору·;к111-1 и. казалось бы . 1vю
жем справнться с люnым куб11чссютм ур:~нис
ннем . Дава1\тс 1юпробуем снои снлы.
l. НаЧJ1ём с урав11е11ня
х'+6х- 2=О.
Подставляем в формулу Kap~aIJo р = 6 и q = - 2
и после 1 1cc.rroжIIыx сокращсr111i1 получаем от-
нет: :,· = \ -=i' - ~2. Что ж, фnp:vryлa вnш111е снм11а
т1 1ч11ая. Т()лыю перслекr~ша оыrюсить мrюж~1-
тель х - (\.' 4 - · 't/2) из лcnofi части ур<Jвнсшш 11
решать <кт~юш,ссся кнадратнос ур:шнt..:нас {.'О
"е1ра111ны.\Ш » 1<оэфф1щнснтамн !JJШ выч11слсш1н
других корней нс очснь-тu вдохнuнлнс::т. Одна
ко, 11рнсмuтре1шrнсь к ураш-rс111110 нн11.ч:1 ·1·с;1ь-
1 1 ес, \ЮЖНО успокоиться: фу11Ю\llЯ H JICBt >iJ ЧЖ'Тll
~·
... ,
1
;...
'С)
+
. \.·
Рис. 1. Гr;~ф1"
функ1J1111
)' =;\ +r,,-2
nepect:'" ''ic 1 01 ь
~нJt Ulr$l t ~ ()Лt-1()11
1 0'11<("
"\
1
-1 \"2
2:Ю
Чиrла
с1·ропJ rюзрж:таст и 11отому может обр~1щзтьо1
L! 11у1111 тш1ы<0 одш r раз (J1 11 c. 1). З нач~ 1т, найдсн-
1юе Чt1CJIO - eдl 'lll C'J'Bt: l lJ!bl[J дe1rCl'RИ'ГeJJl1llЫЙ ко
рень ур авпею нr.
2. Следующий пример
-
)1):11ше1шс
х3+).х-~=О.
Фор\·1у11а Кар;1анu ;~ает х = \}2 + \;') + \12- \':; .
l<ак 11 й llРСЛ Ы[(у11\ем nримере, i\IЫ DllД I I M, ' -l TO
этuт корень едш L<.:твс1шый. llо не ауж110 обла
дать сверх.11роницательнuстью, чтобы, 1·ющя ш1
урав н с::нщ:, угадать t: 1'0 кuрснь: х = L. Прнхо
дитсн пр11з 11 ать, чтu фuрмула выfl,ала обыч н ую
единицу в тз 1шм п ри чудл н вом ииде. Между
проч11м, упро<.:т 1 1ть это rро.моздкос, но нс
111 1шё111 юе 11 :знщест11а 11ыраже1111е ат ·ебрJ 11ч е
сюл.н 1 11рсобразоватtюrми rre удаётся - куби
чсстшс пр раr\иопалыюспr в пём пеустр :н rимы.
3. 1ly а теперь щпьмём ур~шпспие. :~авсдомо
11 ..,,1 еющсе тр11 дt 11ст1:1итеды1ых кuршL Соста.~шть
cru лt: 1 кu - просто пер<:м 1 южим тр 1 1 скобки
и11/\а х - h . J -ly-" A<I-IO только поззботиться. ч тобы
суммз ко рн ей равнялась нулю, ведь, 110 об щс!1
теорсмt: В11ста, она отлич ается от коэффици
ента щ1в х2 топько :sнако~с Самый nросто11
11аб()р таких 1<()p11ei'1 - ::~то О. 1 и -1 (р 11с. 2).
Пртrмепп'\if формулу Кар,'\аТiо к у1)а~шеr 1ию
X(.Y
-
l)(x+1)=0. HJllf х'-.У=О.
Полагаяuнейр= - 1иС/=О. получаем
1
г
х-~,1v '\
.1J/
-
-
\''!-/гт'i-v-/J7.
х
Рис. 2.
Yp.J011eн"t:'
х(х- 1}(х+11=()
ИМСt,.\ 1 tpH
де11rТВИТРl\Ь Н~~ х
кuр11и: -1, (} и 1.
Соо11Je1сl Lit-t 1но
график функu'lн
У='Х(Х - 1)()1+ 11
ПPpli'<'PK;Jel OCL>
,1бlU 11l(. Н 1f)PX
ТПЧКi!Х,
110,'1 :{J1:.1к( )\1 кш1д [хt1 т юго корня rюнвилось от
рнцатслыюе чиою. Та1<0е быш1 tт 11 при рсшt
н1111 кк;щрат11 ы х ура1те 1111!1 . Но кн адр:~тное
ур:.~в11ет 1 е в этом случае нс имеет дейст111 1 -
тельных т<орней. а у кубl1ческого их цeJJЬL'i: трн!
Более тщателы1ыi1 анализ rюкttзывает, что
мы пол али в этv ЛOB\'IIШV пс СЛ'?Ча йпо. Ураnпе-
о\
,J
•
"
)
11.ие .\' + рх + С/ = О К\tест три действительных
1юрпя тоr·да н тол1->ко тu1 ·да. ко1да .ныраженне
Л = (q/2)J + (jl/ .~)
1
1юд к~;;.щратным кор 1 н.:м в
формуJ 1 е Кардано 0·1 ·р1-щ:-пел ыю (р11с. .) . п).
!:ели д > О , то д<::rk"гR 1 ггельный корt:нh ОД[[Н
(р1к..\ б),аесл1rд= О,тонхдв::~ (одн1111:1111гх-
1н~укратн.1->пl). з;~ исюrюче111 1 е~1 с,1 1 учан р =с]= О,
коrд::~ rкс трп корня сливаются .
КУБИЧЕСКИЕ УРАВНЕНИЯ
И КОМПЛ ЕКСНЫЕ ЧИСЛА
О1учай д < О, 11:зз ы l:!:зе1•1ый 1сtеnр11вт1uмы.м, до
стаRил н смюю хлопот псрнооткрывзтслям фор
мул решс 1111я куб11ческ11.х ура111 те 1111 й. Ещt: бы,
ведь 01-111 с трудом допускали даже отр1щатель
ныс ч11сла! (Джероламо Кзрда1 ю 11 азьш::~11 11х
«чисто ложпы~п t», а комплексные ч 11сл::t - «ltO·
истине софистичесю rми~.) Однако стоит при-
11ят1. 1юзе11ожность сущеспювання корней из от
рицателыrых ч11ссл и опрсдслёrпrыс пра111rла
обращеш ш с ним11, как любое квадрат~ юе урав
нение получит два корнн. а формулы Кардано
,1\адут пранил1>нh1 t :!начення дсйс·1·ни·1·е; 11,ны.х
корней и в 11 tt1rнводн.\Ю1\J случа е (это откры
·1
·11<: сде::лал 11ослсдоватсл1-> Кардана - Рафф:1 э
ле Бомбt:ш111). С:дt1же;v1 , если R 11 римерс ::) прн-
~г-
"'~
,,-
МСПТ!Тh равс:.:нстrю \1
-ct = - ,'а к ч11сJ1у а= \'-1,
пш1уч~ 1 .\1 верный корен1, УJlаннен ия: .'У= О.
KoJJь скоро иы решили выйти 1.1 область
комплскспых чисел, н адо учитыватr, и то, что
здесь у любОJ 'О нснулс1:101 '0 числа С("IЪ дRа квад
ратных и три кубн чссках корня. Если rюдст;1в
лять ncc эт11 зн.ачсн.ия в формулу Кардана, со
держащую дщ1 1шадрат11ых радш<ала (-..}д) 11
два кубических { V- ц/ 2 ± ~ д ), вьu~~лет 1\елых 36
случttе1:1! Пранипо нычнспсния ве рных значе-
1111 й кор11ей 11 11епр1 1 1юдимпм случа е неслож-
1ю: щтщшая 11ерпому куб11чесr<ому рад 1 1к:u11·
три возможных :mэ чеrrин. R качестве соптвет
СТR)r~ощих зш.~ чсний нторпт 11 а1~0 брал . кт1-
пле1<с1 ю-сопряжёrшые числа. Другнi\lш слоnа-
м11, трп ,тtсйстnнтелы1ых корпн уравнения
равны уд1.юсшrым дсi1стnителъ1Lыи частям
трёх nоз.vюжных зш1 чс1rnй первого слагаемо-
1·0 нhlр:1же 11ня \ 1-c,J / l. +, л.
Интересно, а нслюя ли ныраз нть эт11 щJ1 -
ст1штсль11ыt част11 нспосрсдстнешю через кu
эфф1щ11енты р 11 q, 11е пр11бtгая к пзвлсчсю 1ю
кopнL:lt из I<()Мплекс11ых чисел ? nк::~з11юс1), что
1ю11ы·11<11 вывести такое nыражение стrпnз 11р11-
Rа71ят". r< пепр 1 шодимому случаю кубнчсс1<()ГО
yμani rc1 rпя.
Таю1м образом , сслп 11се три корнн ~р:11ше
ш1я - деiн.твитtлы 1ыс числа (самы1'1 как будто
бы хоро ш111~1 случ: 1JJ) , то выразнть их через ко
эфф1щ1rенты уран1-1t'н11я с r юмuщью <1стырёх
:1р11фм ет11 ЧССКJ IX опера l (llJI 11 LI ЗJ~Jl t: Чt: l I ня кuр
неi1 'l'()JIЬKO 11 3 ДС::ЙLТШJТСЛЬНЫХ ЧJ I CCJI нсвоэ
можно Са:.1а :1ащ1ча 11росто нынулт 1ла \1атсма
т111ши rюi1ти папеrекор пюнм 1 1 rедст:нvн~нr1ям
и же11з11ням п вnестп в обнход 1юн1,1е - стра11 -
11ые, rш окnзаuшнеся столь полс;нrымп, - кпм
n.1ексные числа. Отмстим, что ко11це XVI в.
Франсуа В11ет, 1юспольэов~шшись формулоl1
со::. .)с:р = -+со::. -s <р - 3cos <р, нашёл рсшсттис ;1,ля
11cпpr-1130/1I I MOJ'O CJJYY~UJ в ТjШl'ОНОМСТ(1ИЧССЮIХ
функциях. По существу, это решt'ние эквнва
лс н ·1 · но 11знлече1-шю кубичес ких корней ~-rз
ко~1 ш1ексш,J){ ч исе::л.
Уравнения и неравенстоа
у
д>U
)'= -jJX- 'f
а
Рщ" 3. Kytm•1 eL кoe ур,ш1 1Р11ие• ' ' + 11л + r1 = 1~ моА<11О ripi.:дl r,111и11.
в виде кJ =-р~ CJ. Отrк1д,1 В'1д110, •11·0 кор11ям vр,1 в11t"·11и11 t1улуг
rrютветrтвnвнь aor1J11rrы тn«ек nPrPrP<1Pн 1 1я двух гr.1ф11кnе
у= л' и у= -рх -ч L( Аи :. < О, и '1ее" тр1о1 де>1сте11тельных
кс;>рня , есл11 j >О од111 1
Допустн н 1<0~111л екс111.rе ч 11сла, можн u н~нlт11
по формуле Карда~ ю три ре111е1111я К)·бнчtт1щ-
1·0 уrа1теuия и в случае ол;1югп де~"тстнr 1тет,-
1 10го кор11я (~na /\py1 ·r1x будут со пряжёшrыын
комплек<.:11ымп чпст1ми), и 13 случае ко.чн
лексных коэфф~-щисптоn ура1ше11ая. И 11 усть
практическое значе1шс эп1х формул 11евет1 -
ко - труднu r1t'p t oцt1-ш1ъ тот мо щный 111\1 -
пульс, КО'f'()РЫЙ ОШI )(:!ЛИ p:13HllTИIO соврс.чен-
1ЮЙ :11 11 'С6ры .
УРАВНЕНИЯ ЧЕТВЁРТОЙ СТЕПЕНИ
:Vlетод решенш1 уравщ:ни11 чстnёртой степени
11а111сл n Х\'l в. Лудовико Фсррарп , учсни1< Дже
роламо Карда но. Он так и на%1ш1стся - .'жтюд
Феррари.
Как и 11р1 1 рс111е11ии кубическо 1 ·0 11 кнадрат
но1·0 ура1шс1-rий, н урзвнс1111и чt=т13ёртой l~l'<::
n<.:н11
х1+рх~+q.\) +1~У+s=()
,>юж11 0 и:iбавиться от члена р.у' нодстаноnкuй
х = у - р/-+. Ilоэтому будем счптатъ, что коэф
фнциепт пр11 кубе 1 1е11звестного равен нулю:
.\'·I+Clv''/+h.Y -1 С=U.
Идея Фср11ар11 сuс·1 ·шша в том, чтобы пред
ставить ура1шеr111е н виле А 2
=13
2
,
1·.це лев;u1
)
час-1 ъ - кнадр;л · 1:1ырзженю1 А= :х·- + s, <!правая
часть - квадрат л1шеИ.1ю1·0 выражеrшя В от х,
1юе>фф1щиспты 1<отороrо заш1сят от s. П осле
э·1·ого останется рсптт11ъ дnа кн~щратrrых ур:ш-
11е1 1.1-ш:.1l ~ В иА = -В. Конечно. т:щое nредстаn
лсние nозможно только прн спсциал ыюм
выбор~ Л:lр:.~м стра s. У;\061 ю взятr, s н 111 щс
а/2 + /, тота ур:.1нн:сн11t' 11 ерепн1щ:тся так
(
,
CI)
2
,
(
t1'!. )
x-+
2 + t =2t.-c-f1x+ t
2
+ut-c+-
1
(*)
П ра r{а» часть этого ураnпеш1я - 10i::t/ \[Xt '1 ' 11ы1'1
трёхчлс11 от х. Полным кuадрато м оп будет
тогда, ко 1 да его дискриминант ра ве1 r 1rулю, т. с.
D=h!. -
4-J.t (r~+at-c+~:)=o.1ш11
231
Чи сла
Графи~..11 фу11кu~1И у = (1О+ 2< )'(
1
+ Вх + <" - 5 111я1 р.1зм1чнt..1х s
1
"
J
l
/J- = ll\4Г +4at +а - -1с).
Это у1х1 пнt.:нне 11азы ваетсярезольвеюпным (т. с.
« разреш::~ ющ.11.vt») ()т1-юсит~:;лы-ю t оно куб~ 1ч е
с1<0е, и формула Кард:ню (см. еr·атыо «Кубиче
сю1е ураnтrе1111л») позволяет найтп какой
нибунъ его корень t0• При t = t11 правая •1астъ
уравuешш (*) пршшмает nид
(
(? )l
210 х--.- '
411)
а сами уравне111 ·1е с1юдится к двум r<ва11р~1т11ым:
Их кop rr11 и дают nce решения исходного урав
r1енш1_
Решим для пр имера уравнение
х1
-
1OxJ-8х+5=О.
2:)2
Эдесь удобнее будет uосл олъзо11ат1,ся 11 е
готовыми формулами, а с;.1мо.й идеей решен11я.
Перепишем уравпещте в виде
х1
= 10.Y..t+8.У- 5
б
~
)1.
)
н до ;11шм к ооr:им чаСТЯ\1 в ыр:~жr:н11е ~sx +s- ,
ч тобы в левой часп1 образовался п ол ный квад
рат:
(х2+s/=(1О+2s).x
1
+8х+s2- ')
Теперь прир ::ш пяем к rry7пO дисщ1 11 мшш1тпра-
1юii часrп уравнс~шя:
16 - (10 + 2s)(S2
-
))=0,
шш, пос_:щ; уLLрощсн 11я ,
s
1
+SsJ-Ss- 33=О.
Один из корней 1юлучсюю1 ·0 уран11еш1я •V(()Ж·
it o уга;\~·11-. перебрав дсл нт еш 1 стюбодноrо
чле1 1::~: s0 = - 3. П осле подстано11к:н этоп) з11аче
ния пол учим ) равнение
1.
)
)
J
(х - :i)-=4x- +8x+4=4(x+ 1) ~ ,
откуда :r.·
2
-
3 = ±2(х + J ). Корни обраэова~
ши хся квадратных ур:~в неннй - х 1 2 = 1± \6
и Х:1 4 = - \ ± ~2. Р:1зумсстся, в общем случае :.ю-
1-·ут 1 юлуч11ться и комплексные корни .
у
х
Кпрн1щ
уvав нен~1я
х =1ох· +в~ -s
соu т всн- тзу~<п
11fir11 Иl(l>1 1UЧI'~
nРреLРче ння
лвух график ов
Уравнения и нt::равенства
УРАВНЕНИЯ ВЫСОКИХ СТЕПЕНЕЙ
РАЗРЕШИМОСТЬ В РАЛИКМАХ
Формуна корней квадратного ур:ншения из
вестна с незапамятных nремён, а u XV! в. италh
янские аЛl'ебраисты решили n р~щикала.," ураn
ненил трс1ъсй и четвёртой степеней. Таким
образом , было уста1 ювлено, ч1'0 корни любо
го yp:H!l l t:HИЯ не выгпс четнёртой CTC ll C HИ
выражаются чt:рсэ коэффи 1 \иенты ур::шнения
формулой, в которой ИCllOl!bЗ~'lO'l'CЯ 'l'ОЛЬКО
четыре <1риф,v1ети"Ческие опер:.щ 1-tи (слшкенне,
вычнта1-1ие, умrюже ние. ~еJiенис) и нзrтече1 irre
r<орней с тепени, не nреnышающей степень
\'Равнения. Более того, nce уравнения даююй
стеттени п (п -~ 4) можно «ОбслужИ1ъ» одной
общей формуной. При подстатювке в неё 1<0-
эффи щ1енто1:1 ураннения nолучнм 1кс кор
н11 - и действитель ные, 11 комнлексные.
1lосле этого ест<.:стлеюю J:I03HHI< вопрос : а
есп.т1 nохl1жие об щи е формулы для решеню1
уравнений J1ятой степени н выше ? Ответ на
него с мо1· 11ай·t·и норвежсю1й математнк Нит,с
ХеприкАбелъ в начале XIX в. Чугъ paI IЫJJC знл
резулътат бьт ука:~ан, но недостаточно обосно
в;т итальянцем. Паоло Руффи1-ш. Тео рема
Лбеля-Руффини звучит таt<:
!:: " Общее уравнение степени ti при
i,{ п ~ 5 неразрешимо в радикалах.
Таки'\1 обрззом, общей формулы , r~рн:мсни
мой ко всем ураш rеrrиям д~ю-юй с1·епе11и п ~ '5,
не Lу~дестnует. Однако это 11е значит, что 11етюз
мож110 рстить в ра/1,НКалах те ит.1 и111..rе часпn,1е
шцы уравнений высоких степеней. Сам Абель
нашёл такое решение дтr широкого класса ураn
нений произnолъно высокой стеnстrи - тат< на
зыиаемhiх абслсных уравн еш 111. Теорема Абс::ля
Руффи11и н~:: нс.к11ючает ;щже и того, что тшрни
к<1ЖJ\01·0 конкретно1 ·0 аm·ебраич~ского ура внс
ншз мож110 заш1 сатъ чере:J ст коэфф1·щиенты
с Ш)мощью знаков Glрифметических операцпй
11 rа;~икалоп, в частности, что любое ат·ебраи
ческQе qнсло, 1'. е. корень урав 1 1ения внда
с целыми коэффициентами, можно выразитъ
в радикалах через р;щиональные числа. На са
~юм дeJJe т:~кос выражение сущестnует далеко
f / С НСеJ 'Щ1 Это следует 113 теоrин разрешимпсти
а.;1гебраических yp:lm 1ет1й, rюcтpo~Ifl юl1 ны
дзюп.1.ючtся фра1п:~,узс1<им математиком 31~<1.
ристом l'алуа в его <- Мемуаре об условиях разре-
1ш1мости ураnнеш1й в ради1'алах» ( 18:1> .L г .:
оnубликован n 1846 г.).
Подчсрю-!ём, что н прикладных за;щчах нас
11н тересую·1· только прнбл ижён11 ые з1-1ач~::н11.я
кпрнсй ypaRF-reню1. Поэ·1 ·о му ef'O разрсmJJ.мос-гь
в радикалах здесh обыч1 ю ро!111 нс и1·р.~ст. Им е
ются с11еци::тьные вычис11и'гс; 1ьны е методы,
1ю;~nоляющне на~1·m кор1111 тобою уравнения
с любой 11 эперед задашюr1точ1юстhю,1шчу-1 ·h
не меньшей, чем дают вычисл.ешm по ~·отовым
формуJiам.
УРАВНЕ НИЯ , КОТОРЫЕ РЕШАЮТСЯ
Хотя уравнения Rысокнх степеней в <16щем
случае нер;.1зрсшнмы в радикалах, щ1 и фор
мулы Каrда1ю и Фсррари ДJlЯ ураннен 1~й тре
т1,ей и чет11ёртой степеней н 1нколt" не прохо
дят, в у чеб1 шках по алгебре, на вС1")1тr1телы 1ы х
эк:~аменах в 111к1·итугы нrюrда 11с1речаютс.я зэ
да 'lИ, где требуется решить уравJJепия вьrше
второй стеттеr r и. ОбычIIо их спеuиалъно под
бирают так. чтоб ы корни r1')aвнc111·rn можно
быно Шtйти с помощью н екоторых элеме 1 t-
тар1 rых приемов.
Паоло rуффини
Числа
В ocr" те сщ110 1 ·п н:-1 ·1 ·:1ю 1 х п рнёмnв J1ежнт те
орем::~ () p:i 1 tiю11ал ы 1 ~.rх rюр11ях J\11 юго члена:
«
Если несо1<рати~хая дробь p / q явлл -
!fг".
п
~ ется корнем многочдеца Р(х) = а"х +
t~1 ·ap 1111-11i ко:эффнц1 1 е1 п lC()Topol'O ранен 1, •к:JJ I·
!\Иf\атамн» \1улут /(t:lllJТt:JТ!f ч1 1 сла - 2 . Их вссто
четыре: 1, - 1, 2 н -2 Пра не 1 жа по1<:1С1ы11~н~·1. что
кор11ем я Г1ляется тплы<о от ю н:1 зпrх чисел
Хо= -2
11- 1
ф
+а"_р"!С +." +al'"!C+а0сцелымикuэ -
фицнентами, то её числитель р явш•
етоr делителем свободного qлена а0,
а знаменатель q - делителем старше
го коэффициента а".
Если ОД1111 карет" 11аfще11, MOЖIJO ЛОШ IЗJПЪ
c1·t: 11 t:нh уравнения. <..:огласно теореме 1.iезу.
«
остаток от деления мноrоqлена Р (х)
!С'(
'k, на двучлен х - с равен Р(с), т. с.
Р(х)= (х - с)Q(x) +Р(с).
Д;~и дпказатею1стnа ,пnстат()чтю пnдстаnип.
в урашrе 1 ше P(.v.:) = () х = р/с/ п умножить Ч'аn
венис на с/'. Лолучнм
Из теоремы 11егюсредстне 1 1 1 ю след)е'• , что
1J
11- 1
111
11
u
а"р +а11 1Р q+ ... +a1pq +aoq =
.
1J...,
если с - корень мноrочлена Р(х).
!d то много~шен делится на х - с, т. е.
Вес слагаемые в левоil <1ас·1 ·и, кромс rюслсдне-
1·0. делятся нар, 1ю:::1то"'у н u 1,ct" щ:лн ·1 ·ся н <1 р. 3
1юскuльку q 11 р - взаим 1 10 простыt: чнсла , р
НВJ I И СТСЯ /tCJllJ'["(;:ЛC<VI {/()· Дока~1ап.:лытно для l/
:11 ~~ию1 н чн о"
Р(х) = (х - c)Q(x). rде Q(x) - много
член степени , на 1 меньше.И, че1'1Р (х).
Прuлuлжая на11 1 п р11м<.:р. ныне(СVI 1tз м но
l'()ЧJГt1-1а
с ГЮМОЩ!11О ~-пoii Tt:Opt'Mf)J МОЖI lCJ liЭ !1Tн все
ра ЦL J()J JaJI hl 1ые l<ОрНИ }11аRНеППЛ С ЦСЛЬL\111 КО
эффrщие1 ТТамТ1 нспытапие.м конечного числа
«ю.m11.птtатоn ·>. На гrрн мер, для }11а 1шеr шя
Р(х)=х~+).:\.2+х- 2
1\.11южитет1 х - Х1 1 = ,,. + 2. Чтобы н::1й11 1 част~ roe
Q(.'1.'), мшкrю ВЫПОЛН1'1ТТ1 ,Г\СЛенпе ")'ГШП(();\I ·>, к:i r,
по казано на рщ:. 1. Но есть и более простой
слособ. Он станет понятен и::~ примера:
234
х' + 1.-х.2 + .'1.·
-
2=О,
АЛГЕБРАИЧЕСКИЕ
УРАВ НЕН ИЯ
И ГРУППЫ ГАЛУА
Теория Галуа позволяет выяснить
для любого ко нкретного уравне
ния, рt:шается ли о~ю в радикалах .
Для этого данному уравнению со
поставляется некоторая груп па пе
рес-та 1-ювок его кор1·1ей (см . статью
« Группы•; само понят ие « группа»
было придума но Галуа имен но лля
1>1 сследова ния уравнс11и й). Важ1 ю,
что эту группу, 11азываемую сей час
группой Галуа, можно определить,
не вычисляя корней урав 11 ения,
только по его коJффиuи ентам.
Галуа уt'та н овил связь межлу
разрешимостью алгебраического
уравнения в радикалах и особым
свойством групп ы это го уравне
н ия, которое также было на.:1ВсJНО
разрешимостью . В Ltаснюст11, лю
бая коммутативная группа разрс·
шима. Если коэффиuиенты уравне
н ия ра 11 иональны и его левая •1асть
не р.:~злагается на множители с
раuиона/\ьными к1пффиuиентам и
(не приволима), то "но урав~1ение
разрешимо в ралик'1лах то1 д<:l и
тuлько тогда , когда разреш~1"1а его
группа Галу<t.
Например, уравне ние х~
-
4х + 2 =О имеет пять различ11ых
корней. Хотя они нам неизвестны,
можно пока .ыть, чтu группа Г<1лу<1
да11ноrо уравнения совпадает с
группой всех перестановок его
пяти корней - 'Э10 с"1мая 1<бол ь
шм1» из возмпжных групr~ для
уравнен и й пятои степени. Лока
зывается, что эта груп п а нераз
ре шима. Следовательно, корни
даtтого урав 11 е ния не выраж.:~
ются о радикала х, а з11ачит, и об
шей формулы лля решен и я урав
не11ий пятой сте пени в радикала х
11е с.ушествуе·r.
у
у=\,-4х+2
'(
-2
23
-2
-3
-4
К<1к видно ю этого графlfк~. уравненНf
,, " - 4л +2=ОимеРтде11пшлt>льные
реше11 ия Их мож110 выч11слить с любо>
точнопию. однако в ра.шкалал они
не выражаются.
х~+.3х1+х-21х+2
-
х'+2х2
х2+х- J
х2 +х
-х2 +2х
-х- 2
-
-х- 2
о
Рис. 1. /\t>лен ие
мнuro•1лt- 11 .:i
~1 у гnлком »
\
>
'
,
l
Р(х)= .\· +3х-+.\" - 2 =(х +2:х·-)+(х +2х)-
-
(.\·+ 2)=(х+2)(х!+х - 1).
t~перь остаётся решить кnадр::~т1юс.: урав11 етш е
х· + :>..:
-
1 = О. El'O корн:и:
-1±';'5
Х1> =
.
·-
2
Еснн у многочнена с п.елыми коэффицнен
там11 р:щио1rалы1ы-" корней не 01<азалось, мож
но попробовать р:~зложить его па множители
меньше1'1 CTCTTCI!ll с Цt.11.ЫМИ !(ОЭффvЩИСl!Т<IМll.
Расоютр11м. например, ура 1ш<::11ие
х·1
-
Ъ:1 - 8.:х:
-
.) =О.
Прс:дсrавим ле вую ч<~стъ н виде про11зве11сн 1 1н
двух кна; ~ратн ых трёхч ленов с нс.:11знt'ст11ымн
(неопределёr 11 rымн) 1<о:=~ффнние11тами:
4
?
о
')
')
х-2.х"
-
ах- 3=(х-+а~\·+Ь)(:х:-+рх+q).
Раскроем скобю 1 R правой часп1 и прнведём
подобные:
х4 - 2.У!
-
8х-3=х
1
+ (а+р)х' +
+(Ь +ар+CJ)X1+(сщ+l1p)x+bCf.
Теперь. пr1 1 rанн11ная коэфф 11щ1снты 11рн одн
t~акоr1ь1Х степе н ях х в обеих часткх , tюnучим
с1 1стему уравнсшл:1
а+р=О,
fJ+ар+q=-2 .
tl,(,/+bfJ= - 8,
htf := -3.
По пытка решить эту систему fl общем в1 ще
вернула бы 11;ic назад, к рсrое 1 rню исходносо
\'j:ХJ.В11сння. Но целые кор11и, если ош 1 суще
ствуют, нетрудно 11аГrrи и подбором. Не огра-
1шч11вая общности , можно счнтать, что h ~ q,
ю1да последнее ураrн 1е1 ше rюказывает , что
над() рассмотреть лиnrъ два варианта: Ь = 3,
Уравнеt·1ия и н€'рnвенпва
ц = -1 и Ь;: 1, (1 = - :) ПOJ\C'\",\ВЛilll :~ти пары :~на
ченнй н остальные ур::шненю1 , убежд;1 с:мб1. что
гн~рнзя из них даё1 искомое р<1:1ложени е: х'1
-
2
)
.
'
-
2х-8х - 3 =(х"+2х+:))(х-- 2х - 1).Э·гот
способ рещен ня ур<trтений 11~~ зыRаетсн .мепю
да,:и llеrтреде.лётtы:х: л:оэфф1щt1еllnюа.
Ес;ли уrаш1еш-rе 1-1~1еет вид P(Q(x)) =О, l'де Р
11 Q - -"Пюrочлены, то замена у = Q(x) сrюдит
сго решешн: к реше1Iиюдnух ураш1сн11й мсш.-
1ш1..х. стспен.ей: Р()') = О и Q(x) ;: у. 3амсн:~ ис
полhзуется , н часп-юст11, при рс111снш1 611-
кн::~лратных уранненнl1 .
Более 11нтереспый случай - во:иратные
уравF-r еш1я, т. с. ур;~впення чётной стс 11 е1111
н которых 1<оэфф11щ1е1пы. од1 111аtюво отстоя
щие от 1<01що11. раnны: а!..11 : a(I, а 'ri-1 : а1 тr т. д.
Такое уравнение сnодится к ур~.шпе111110 nдnoe
мсrп,mей степстш делением 11а :х" 11 послещ'ю
щей заме~юйу= х ± 1j.x.
Расомпрнм, н;шримср. ураю l l'HИt:
.х:1 + ах' + (J:I'.-" +ах+ 1 =О.
nодслив е1·0 н~1 х1 (что закон110. так к::~к х = О
не ятJлястсн корнем) , r1rтучасм
>
(,/
1-
х-+а.":+lJ+- + - =о
хх2
Замет11.'Vl. что
(
1Jl
>
1
х+-
::= х- +-,+l
х
:г
Поэтому нсю1чнJ1а у=_\: + 1/х удонлетвuряе·1
ЮJ<tдратному урав11с11ию
/ +С1:1'+h- 2=О,
pf1111 111 которое можнл найти .'\· и:~ ~rавнс1111я
х--ух+1==О.
При ре111снин во:~врат~rых урав11е1 шl1 ()олее
высою1х степеней обычно исполuзуют 1от
ф:шт, что выражение xk + l/xk при любом k
можно представить как ,-..шогочлен стспен 1 r k
оту=х+1/х.
On L1сан11ыс з11.с:сь ар11ём ы нсrюльзуются 11р11
1~сслсд0Rан1111 (н комплексных ч 1 1сл::~х) У[)аннс
ння деления кр;.та 11а 11ятh чзстей:
.л5- 1=о.
Ураnне1 1 не шt~ыnзетсн так потому, что ест 1crr>
корпи отметить rта 1<()мплеtсстюl1 плостюст11. то
235
Числа
OIIH ПОПЗ[{}'Т Н 1~ершш1 ы Пf)ЗВ!!Л/1 1 101 '0 Ш!'l'Н
УГОЛЬlIИКЗ, вписанного в едиш-1'-шую окруж
ность. прнqём одпот1 из nе рши11 будет то•-ша с
коордш1атам11 ( l ; О) (рис. 2). Испот,зуя трию
нuме.:трнчс<..:коt: щх:дст~1 нлt:н ие комШit:к<.:1 юго
ч11С!т ~1 (с м . статью <-Геом етр ия комлж::ксных
ч11сеJ19 ), ;:}TJ1кор н и м.ожгю за ш 1 с: 1т1, следую щнм
образом:
2(k- l)1t " .
2(k- l)л:
Zм=СО5 S +1SIП
<)
, k =1,2, .\4,) ,
Среди ш1х находится п едннствеrшый дсйсгви
тслы1ый: коре11ьz1 = cos О +i siп () = 1.Спраши
вается" можно т 1 выра:щть осталы 1ыс rюрни в
ращ 1калах?
Попробуt:м это сдt:штть. l lоскольку Oftl 11-1 ко
рень, х = 1 , нам изnt:стсн , лоннзнм степе нь
ураnнсння, ны1юся 11з его ле1ю 1'1 частн двучлс 11
х- 1:
_,_
5- 1=(х - 1)(х'1+х:~+х2+.'\:+1).
Остаётся урав11 етшс
х4+xi+~..J+х+1=U.
0110 возвратное, а таю,1с уравнс rшя мы решать
у.чес::м. Делпм его на х-:
)
])
х-+..х+1+- + - , =0
хх-
Подстанлясм z = х + lj.Y:
z1+z- 1=о.
Ко р1ш этого КВ3/(рат ного уравнения:
-1 ±~ -1 ±,/'5
Z12=
2
=
2.
Дщ1 "\' поnу<1аем уравнст1с
Рис. 2.
236
'
.~·-- ZJ,l · .\:+1=0.J1JJJJ
2х2 - (-1± ,/s}: +2 =О.
Отсюда
.
-
-
l± f?±\
1
6±2.\
1
"5-16
.\)''.
-
=
-"~·'
-1
-
1± ,/5 ±i ~10±2~'5
--1
Таким обра:ю м, 11 ~шJе ypam rc 1111 e ;~011\'Cl\atт
решение в ра/{икалэ х, и даже в ква11ра т 11 ых
радик;:u1ах. 1lоследнсе озна чает, что праrшлыrыil
пятиуг олы-rик можно пост ро 11т1, с помощью
ц11ркуля и 1ш11сir1ш (см. статью <{'сометрпчесю1е
п острое н ~ JЛ ,)). Б< >лес тu 1 ·0, полученные фuрмулы
ука3ывают и конкретныi1 способ: прсжле 1:1се1·0
надо постро 11ть отрезки" рав11ые действнтель·
llbl.\1 и ,\.IНИМЫМ частям КОМШl СКС НЫ Х чисел .х, . а
з:пем точки с CUOTRCTCТ'f\YIOЩllMH кuорд11на'1'а ·
ми - orrи и будуг нерптипами пят11у1·оm.1-111ка.
l !0J1110e реше1ше задач и о n острое 111111 r1p a·
вилы1ых м ногоугол ьrппюв, т. е. о ра:1ре тшюс·
ти в квадрат11ых р~ш<алах уравL1е1111я делстrnя
круга п-й степени, дал Карл Фрпдрих l'aycc .
ОС Н ОВНАЯ ТЕОРЕМА АЛГЕБРЫ
Итак, мы рассмо·1·релн rю11рос о выражен1111
кпр11 ей ал 1 ·ебраичсскn1·0 ураш-н.: н1 u1 в р~щ11ка
лах" Л 11се1ла ли ч~ст1. что 11ыража'1ъ->? Всякое m1
алrебраичсстще )1)а11 11 еш rе имеет хатя 6111 одr1н
1<о рен 1,? Когда реч1, ндёт только о дсikтв11 ·
тельных 1<ор11ях уравнс11 11я с 11сйстн11 тельны ·
мп 1<0эффицие11тами. их м ожет и 11е ()ыт1,_ как
у кн;щратпо го уравJJ ення с отр11ца тель11ым
;~1 1 скр им11н антом. l10 со111 до11усп г1ъ KO}JlllJieк
cныe кор11и. то у J 1ю601·0 1<В:t/~ [Xl'l' 1-ю1·0 уравнс
н11я - как с /(еi1ств11тсль ным н, так 11 с кo~ш
Jle KCНl>JM'1 ко~фс\11щнс1п:\МН - их l\CCl'JP po!!HI)
/.1,на с уч ётuм к1х1тно<..тJ.1 " Это провсrяетсн 11 ря·
мой rю; 1ста1ю11кой п знест1 ю 1 ·0 в ыражснJJя ,J,.rtя
корней (фо рм упы Виста) n ура11 11 е 1111 с. Точн()
таJ< же формут,1 кор11ей уравне11лй тре·1ъей н
чстnёртой сте1 re1 re f 1по1сазыnа ют, что эти урав
нения вссгд~1 нмсют соотщ:тстnсшю т ри и че
тыре комш1еко1ых кор1-ш.Дш1 ypanнc1mfi более
Hh!COIOiX С"l'енсней, ЮН< мы ВИДС::Лll, общ 1 1с фор
му1 1ы отсу1·стнуют. Тем н с менее спрпвсдлнщ
CЛCJ\ytOll \~HJ тещх.:ма:
Любое алх·ебраическое уравневие с
хомпл ехсными коэффициента,'1.И ,
т. е. уравне11ие Р(х) = О, 1'де Р(х) -
мноrочлен: , и ~1 е ет хотя бь1 од ин
J<O~пJЛeKCJI:ЬIЙ корень .
Этп (·чтr стая теорема сущестnоnаш rя ». Она
нс объясаяС'т, как наrпн корень, а л11шь угnер
ждаст, что оп есть. Ее rrазывшот ооютюfl m<!o-
pe.,нoli Сf.Лгебры. Конечно, с тех пор как теорема
пол~ ч.ила такое на :.т :ши t', м еrоды ш1гебры
ушл~~ далеко н1 1 срi.:;д 11 н.t ОL"ран11ч11н:11uтся 1 к
<.'JJt'!\О Н~11-шс.:м тuлыю аш ·сбранчссю-rх ур;.~нне
н ш1. Поэтому ·1·1:::п~:рь это на:т:н-111е с корее 11ань
11с1 оричес кой тр:.~д1щи11.
Есл 11 Р"(х) - м1ю1·очлс11 степени /1 11 .У 1 -
ет кореJJ ь, It али ч и:е которого обеспеч 1 mается
осtювной · 1·ео ремой ал гебры, то, no уnо~1яну
том у pa1Iee следстnюо иэ теоремы Бсзу, Р11 (.У) =
= (х - х1)Р1, 1(х), где Р11 1(х) - многочлен стс
пеннп- 1.Всвоюочередь,Р" 1(Х)=(х - хl)х
хР11 2(х), где х2 - корень Р" 1(.\ :), <i Р11 J(x) -
\1 H0t'()ЧJ!t: H CTCПCHl.J n - 2 .
Продолжая ~тот процесс, qсрез п шагоR по
луч1 1>1 разложение мно1'очлtнаРпСХ') на лш 1 ей
ные множ 11тели:
/?11(х) = а(х- Х1) (х- .х~) ." (:х: - х11).
Некото рые из ш 1х могут по вторяться. n этом
с:тучае говорят, что стоя щее n ш IХ число .">:.:1
-
кратный корень многочл~11 а Рп(Х) , а кшшче
спю повторений r rаз ьшается крат~юс1ъю этого
корнд И:~ ПОJI)"-Jешю 1 ·0 разложсннн 1шд 1 ю, что
•
любое алгебраическое уравнение 1~-й
!t'./
k<>
сте пени имее'l' ровно 1i ко~ПU1 екс11ых
корней, если сч1-1та·rь последние
с учётом кратности.
()сrюв 11 ая теорема ал~·ебры n 11epnыe была
nысказана n ХVП столетии D формулировке,
нес кол ыю отл11 ч 1юй от соn ремс111юй. Рене
Декарт говорил . что чнсло корней алгебра
ического урав нения совпадает с • числом tто
11змср<::ний » ( 1б!У 7 r.) . Первое. не совсем стро-
1 ·ос ;щк азательство тсор<:: м ы принадлежит
Фrхн·щу:зскому мt:ханику н матt:м::~тику ж~ну
Лсrо11у Д'Аламбсру (17Lf6 1· .). ТТозд 11еt' птшr 1 -
m 1сь .11.оказател 1..>ст1:1а Эйлера (он же ~~тq1 1 нл
фор мумrрп.вку •георемы) и друп1х мате.мати
КОli, но сrтершеп1 ю строгое показатещ.ство
nпсрвые !(а11 Гаусс.
УраF1не11ия и 11ераве нства
КОРНИ МНОГОЧ/\ЕНА
С ЛЕЙСТВИТЕ /\Ь НЫ МИ
КОЭФФИUИЕНТАМИ
Жан Ло.>ро 11
д . А\л,щ! •!!р
Если nce коэфс]:н щненты мнuгочJ 1 ена Р(.'\:) дс!r
ств11'1'е; 1 1,ны , 'го вмесп: с любым t't'o ком-
11лt'кс11 ым кuр11ем а = tt + hi к:орнсм будет '1·:1 к
же коt.1шлексно-сопряжё1 1 1-юе число (i = а - i/J.
~группировал соотв<.'Тс1·ву1о щ ие скобюr в раз
ложени и м но rо•1ле11а, получпм квадратный
трёхчлсII с действительными коэффицие11та
ии п отриц~тельным диск рими11аато м (его
корrш м н имые):
(х-а)(х-а)=.:\.· 2 - (а+а)х + а а=
С..ледователuт ю,
тобой многочлен степенп 11 с дей
ствительным.и ко э фф 11циентами
раскладывается в произведение дей
ствительных многочл енов степени
не выше 2.
Разложим, н:шрим~р , 1\tН О1'очле 11
Р(х) =х·1
+1
на дейстшпельны е 1\П-юж11тv1н, и<.:11ользуи е го
компле 1<с1юе ра зложеннс.
2:Р
ЧислLI
Knpr r и уrаrтення х 1
+ 1 = О лсrк() тrаi1п1, :'lа
мрттrв rкхп~юе уравнение на два IФадрапrых:
х-=±i.Итак,
Дпя пары комп; 1 екс1-ю-сопрнжённых корней
1+i
1-/
Х1=--=-И Х? = -;=-
~2
-
v'2
СИСТЕМЫ УРАВНЕНИЙ
Во мrюгнх задачах бl,J B:teт нужно н::tйтн не
сколько HCI IЗBt:CТllЫX вслич l ll J' 311 ая' что J\P}'ГI IC,
образона.нньн: с itx помощью нс1111ч1шы (фу 11 к-
1~ш1 от нсrrзRС(~r·ных) равны дру r· другу нлr1 к;:~
КIL'<1-то ;р1шы.ч велr1чюrам. Рассмотр11м про
стl1 1 1 р~1мер.
Пря~1оуголr, 1-1 ый участок земли площа,1\ЬЮ
2-ЮО м - пюроже11 забором щ1ш юf1 1()0 м. Най
т11дш111у и 1н11рr111у участка.
11меем(х-х1)(.х-х2) = х2- v
0
2x + 1. Ашuюп1ч·
1ю, для tiторой пuры
-
1+i
-
1-i
Х1 =--их1 =~
\
0
2
"12
11мtсм (х-х1)(х -
.\·1) =х~ +-!2х+1. В ито1·е
1IOJI)"-:tae:.ч ра:иожсш rc
х 1 +1=(х2 -,LY+lXx..: +,·'2х + 1) .
Обозначнм длш rу участка через х, а ш11р11-
11 у - через у. Из ус11овш1 зада ч11 следует, что s
и у 0;~1 юврсм<.:ннu удоR11ет1юряют двум р<1ВСН·
CTH;:J...'vl, ИЛИ. к;~к 1 1(11 1НЯТ() 1·овuр11 ·1 ъ, Cl l C'l'eмc: И3
л.иух уравнсн1 1й :
{2х + 2у =200,
.\)' = 2400 '
Разделам обе част11 первого }1Хtю rения 11 а 2 11
nы разнм одно аз д13ух 11еизnесп1ых, rrапрпмер
J'. через другое:_) ' = 100 - х. Те11ерь можно под
ст.~витh это выражение во второе ураnне1ше
вместu у 11 1юлуч1 rтп квадратное уравнсtшс с
од11им 11е11звестным х (этот снособ решс11и~
так н 11а:зыв~1 е::тся - .метuд пuдстанивкu) :
X(l00-. :\)=2-J00, HЛll .Y~ - J()0x+24()0=0.
Решив его, 11·аходим :\; 1= 6(), :\·2
= 40 11 за1·см со·
отвегстврощпе значеrшя у: у 1 = t .10, у2 = 60 . Та·
ким образои. система имеет ,ri;вa «симме·1 -
рнч1LЫХ»решення:х=60,у =40пх= 40,у =60
Это и 1 rеудивителыю. ведь сама система сим·
мстрична - она нс меняется при замене х паJ
1r наоборот. Однако, наэв~ш длину участк:~ х. а
111н рш1у у, мы нешнп н;,~1южшш н;~ не1пвсст·
ные е щё о;сно услов11е: .У ~ у (дтша не меньше
шприны) . П():1Тому н:.s l~H)'X решеннй оставля·
ем одно: ДJшн::~ .У= 6() ,\-1 , ш11r 11ш1 у= 4U ~1 . Фак·
тически ~;1m ·~бр:шчсскоl1 моделью ~ н~tшей зз·
дачи явл~ется с н стема и:с1 д 1'lу"Х ур:н11-1 ен11й 11
одноr() неравенства.
llозможные orpaIIИЧCJ-IIIЯ-HCpaRCHCTF!Э ll}'Ж·
1ю иметь в виду всегда, когда nы решаете эа,дз·
чи на составле11ие с11стем уравнений. Но nc1
же ~лаю-Юt' - решить сами уравне1111я. О мето·
дах. которьн.: 11рн этом прнменяютоr. ;111ы и
р~tсскажем.
Начнfм с ш1рс;клс:ннfJ. Систе"мтi урсюнl!
нтi на:iынаетсн набuр llJ нескольк11х (болы 1 1с
uд1ю1 ·0) >'r:.шненнй, соед11нё111-11,rх фш·~ рноЛ
с кuб1юl1. Фнтптая скобк:J означает. ч·10 нее
~paннeJJllH С 1 1СТСМЫ ДОJ I ЖНЫ llЫ I ЮЛНЯТЫ"'Я ( )/J,JI0 -
11peщ.:н11и. Соптпстствс 1 11 rп реиюнliе.л·t снстемы
уращн::ниf1наз1 ,тае-1'ся1кю01f1 н:)fiop :.н-1 а'-1ен1 1 Г1
11е11звеспrы.х, лрн лодстапонкс которцхn урав
нешш с11стемы осе ош1 одпонрб1ешю прсвр:~
щаются в ж:рпые чисJ1овые раненстuа. Таким
образа.и, мrюжсство рсшс1111й састстчы - это
п ересечение .-,,шожестn рсптен11й всех сё урав
неннu. :1 рСШIТТЪ CVlCTCi\1y - Jl-!:.lЧJIT ЩjlvlTH ЭТО
псрссечс 1111е ш111 показат1, , что 01 -ю пусто, т с.
реше1шг'1 нет. В последнем случае снстсм:~ на
зьшжто1 1и:>соа;и ест ноi.1.
Н:.~до сказать, чтп бынаю1· н таю1с: з~щачи, в
которых требуется 1 1а\lти об1,едине 1 ~нс реше-
11 11 й llесколышх датп 1 ых yparн-remri1, т. е все
з rrачешш не11звест11ьос 06р3щающие в равен
ство хотя бы од1 ю из них. Н этом случас rово
рнт о сов(жупноспш уравщ•11mi. Д11я 060::11 rачt'
нин со.коr;ул ности исrюm,зуют кв~щр<tпrую
1..'J<Обку:
[/(х,у)= О.
д(х,у) =О,
Но 1~ерпёмся 1< С>~стемам. Чнсло 1 1 с:изнtст-
11ых. входя щ1 ~х в ураnненпн с11с1·с:мы, ;\fOЖcr
быт~, н больше, 11 меньше чнсла ypan11e1111i:--1;
быв;нот. наnрнмер, системы с о,rщнм 11елзвест
ню1. Одн~'ко на уроках математики чаще пр11-
ло;\11тся ~ 1ме1ъ дс;ю с систсмамп. в которых
LJJ ICJlO Htl rзнестных н ура HHCJ 11 1й ON 1ШIКОВ(),
В 11екотuрых заJ~ачах бывает дuст~1 тuч110
тоm,ко нссJ 1 е[l.ов::1· 1 ъ с1 rстему, т. е. 011rсдс111 пъ,
1rмеет т 1 он :] рсше11I1я , конс.;чrю ит1 бсск01 1 сч-
1JCJ ~111ожество pe111er 1ил т-r 1·. 11 .
Ca.VJ ыe nрост 1,1е урав11е11ня - лине1~11rые.
И самые простые систе11-1ы - это юrне1··mые си
сте:чы уравнений. Они замечатст .ны ·1 ем, что
доnусI<ают нот юс нсследов:1 1ше 11 решеш 1 е,
nрJJчём с помо щ ью од них только элсмен
тар 1 Jых 3J11't'6р:шчссю1х прсобразt>наннй. Д.11я
днух 11 трёх ш:: ре,vн:нных их умеJ 111 реш~пъ у".>кс
чат1:м а·111ю1 Nlсждурсчья 11 Древнс1·0 Кнта.н.
Сэтн\111 с11стсмзы11 мы и познакuмимся n Пt'р-
11~ ю очерс:11ь
Ур.:~внения и нсраве1 1ства
АИНЕЙНЫЕ СИСТЕМЫ УРАВНЕНИЙ
Итак, система уращ 1спий пазьшается лшte{o юй,
ест 1uна содержит тот,кu первые степени 11е -
11з1к·с1ных . Мстсщ рсшеш 1н miнelш hJX систем,
1юторы 11 мы p<!CCvl(Yl'(JlL.' vl , ) IJBCCl'CII как .M<'JJ?Oд
ГLIJ'CCa.
lТусть 11 ан;.~ снс1 ·с\1:J JIЗ ·1рёх у1хншснн 11 с
·1рсмя не11энсс1·11ымн .
/х+)'+ :::=0.
1
x+2y+.)z = 2 ,
.У- )'
=
1
Вычтем первое уратшспне 11з второ1·0 (т. е пр11-
ра н11яем р:1 знос1 ·1, .тн::вых частс11 к ра:3носп 1r1 р:1 -
н1>1х), ~1 ~{:JTCM 11з тpeтr,crn:
j.\' ·f- )' +
.z=о'
y+2z=l"
-2у-Z=1.
0~1еrн~д110, что любое решент:.- 11схо,шюf1 си
стемы будет удоолетRорять 11 nолучешюй п:~
нсё ноnой системе. 1lаоборот. от 1ю1юii си
стс~ы можно nсрну1ъсл к старой, добав11в ттер
нut \r ра1шснш:: к двум др~тнм, поэтому любое
решсш 1е ноноi1 с110'<.::мы у;1uю 1 с·1·воряет т1 11с
ход1юli. В реJульт~те:: мы NК'1·н1·nи наж11оf1
ЦtJIИ - ИСЮJЮЧИЛ11 х li:3 нторого 11 'l'JJC 'ГbCl 'O
ура1шен111(, кот< >рък: 'гсrrерь можно рассматμ11-
1:Ja·1ь 1((1 /{ отделъ 1tу10 СИ<.'ТСМ~' 113 днул ~'r ~· KI ICHI 111
с ;~uумн l ICП:'!JieCTI ll>JMT I.
Далее, нсключн:.1 у пз тpe-J'L.ero ура1J11сп1щ
вычитая нз него второе, умпожtшюе 11:1 -2 .
Пол.уч11"1 1:исн:~1у грсуrолыю1·0 Bill\~ с тем же
мrтож.естном решешл\ что 11 у 1Jpt'д1.щyщeii. а
значит, ну исходпт't системы:
I
X+)'+ z =O,
)'+lz = l.,
jz=5.
Из noCJlt'J\1-тe1 ·0 у1хшнет 1 я нахrщ 1 1 ,\.1 z== ::C,f.1 Под
ста11ин :это ;111аче1111с 'fl() второе yp:.H 'lrie1-111L' , 11~1-
ХО!\ИМ у = -4/:1. На1ю1rен, подставшгсм у 11 z в
первое уран11епне н получаем х = - 1/ ).
Методом Га)'Сса можно peuiaтi, .11нr1ей11ыс
систе.чы с тобы... ,,1 число:.1 1 1снзвссп1ых п уран
нештй. Стта<1ала уран11с11ия за1111еывают ·гак
чтобы неи:Jнестныс п них шлп н од1 юм 11 том
же пuряr~кt:, одвнаконые нс11звее1ныс 1ю н<.тх
Числа
урап11е1 111нх стояли в од н ом стол6не 11 чтобы
[1ер1юе п ензвест1 юе ттр11 суrствонаrю ТJ первом
ураn пенrш. Возможно, для этого прндётся
переставить ураl311е1111я илп ш:известные n тшх
(одповрсменно 1ю всех) . Это может нс полу
читься в ед11нс~1·всшюм случае - коr·да вес уран
нснш1 11м еют вид О= Ь. Но тогда сразу можно
сказать, что лнбо система нс нмсет решен11й
(Cl'Лll хотн бы Оf\ на нз правых ч.<~с1 ·е(1 не нулъ) ,
ш1()0 любо~'~ набор ;1 н <~ чен11i'1 1rен:тсст11 1.1 х
является её рсшст1ем (если н пр~н~ы е части
нулен 1,1 е). Этот случай мы уnомш щем 11 е нз
чре:-~мерно1·0 недантизма, а потому, что он мо
жет встретиться в в ходе реше 1Iия «1юрмал~,
ноi1» с виду системы.
На следующем птаrс мы 1 кю1ючасм псрное
нсизвсстнuс из всех 1юслсд111ощ11х урав~ 1 е1 1 11й,
вычитая т1з ю1х первое уравнсннс, умножен
ное па соотвстстnующ нй множ11те11ь. После
эгого мыслсннn вычёрюIRаем пер1юс уршше
н 1 1с, повторяем всю процедуру с ост;~ншеt'1 оr
С ! JCTCMOI\ li 1юторо~'1 ! 1а OillIO ур<.1.ВI 1е1 ' [!С н OДIIO
неизвестное ме1Jы 11с. И действуем так до тех
пор, пока ест~, что исю1юqатъ. Если система
<-хо rю ш ая» (математики говорят •Неnырож
деtша~1» ). то в конце коf.щов мы нрндём к тре
уrолыюй сис1·сме. в которой nослс~11ее урав
пс1шснмествндaz=Ь,rrteа=t:: О. аz-
последнее 11еизвсст1-1ое. Остаётся ттолучнть из
него z , а :~атсм пройти вес уравнения в обрат
rюм порндке и последоватст.н ымн подста нов
ками найт1,1 ОС1':1Лью,1е 11еи знест J-Jые. Н ~·1·ом
случае систем а имеет единстnсшюе ре111енис .
Но н е всегда 0111каппый ашоритм рсшешш
:-~ака11чивается сто т, же 1·ладко, кzu( н предыду-
а
у
/ .-•
х
"
/
щем nрпмере. Заменим в пашей системе по
следнее урав1 1енис:
j-":+ у+ z=O,
х+2у+;)z=2.
Sx+7у+9.z = 1.
Исключая .л;. получнм
jx+у+z=O.
y + 2z=2,
2y+4z= 4.
Те11ерь исюuочаему нз последнсго ур:ннн:нш1:
J
X+J'+Z=0..
)'+2z=2
-
,
0=0.
В резуль·1 ·ате последIIее ураnпеппе фактическн
исчс: зло - што выпол1rяется при всех :нтаче
ниях неизвестных. Мrюжеслю pcшcrшli это/1
системы бес 1<онечно: z можно з:щана ·1 · h прот
вопыю,IIO.1' =2 -2zи.У=z- 2llOCJieэтого
01 1р сr(Сл я ются одно;щачнu. Рсшсн11ям11 си
стем ы яв1шюто1 нее тройюr ч 1 н:t:J1 ви.ца (z - 2:
2 - 2z; z). 1'дс z - про 11 зно11ь11ое ч11 с1ю.
Возможна н друга н ситуация . Снстема
1
.1 ·+ 1'+ z=n.
:\·+2у+3z=2.
'ix+7у+9z=5
методом Гаусса приводптся т< виду
б
)'
'
8
q
i-
/
у-х~1
Ly-2..t =2
Рис. 1. Лля двух ур<1внении r двумя не1~J ве1 гны\\11 возможны тр11 <..луч<.111: имеется елнн<.. пщ;~но<: р!:'шен ~1е (прямые щ•р<:< екd1U1 ся).
peWt'H~t \i1 11е 1 ( прямые ni1.раллРл1... 11ы), рсшf.~ний. f)P( конечно много ( 11fJЯ1'.1ы~ ( онп 11л.~ют) .
2-Ю
f.'7+J'+ z == O.
1
у+а~2 ,
0== 1.
Очевидно. ~1то решеннй 0 11 а не имеет.
Л11ней11ые ст::темы можно рассматриnать и
с rеuмстричсской точ.ки зрения. В случж дР.ух
ПСИ:.Jl:Н:~СТI 1ых граф 1ш JI 111-ICi!HUl 'O ypaвIICH ия 114
коорд1 ~натной J 1лuскости - nрям:1и. По:-.1· 1 ·0."1у
ре 1111пь с~1стсму т1нсйных ураннсниГ1 с дну.'УtЯ
ве11:.Jвсl~rным11 - :н1::~чнт 11a{rr11 общ11 е точкп
1-tе.:кольких прнмых ( рнс. 1). Дпя двух yp;iRнe
н11i1 В()Змож11ы тр1 1 случая: прямые псрес~к:J
ются (едm-1с·п1 ен 11ле решен ие), п араллель11ы
(pe111e 1-mf1 пет). соnпа;\ают (решспий бесконеч
но JЧ!-ЮГО).
Jlипеfн юе урав1 rепис с тремя 1 1ензвестr 1ыи11
задаёт плоскость в трехмерном простр:шствс.
Гlлоскостн, отвечающие уравнениям нашей
перной систсмы, пересекаются в сщной точке.
()11н моr·ут т:.~кжс 11ерссск::пъся по общей пrя
~ЮЙ, как во второй с1 tетсме, или ае имеп, 1-111
одной общей точки, как втрет1,ей. Наконе1(, Rce
ч)lr ттлnскостн мо1у1 · спrт::ща·1ъ. Н этом СЛ}'чае
j'ра1Н те111 I Я СНСТt:МЫ О'ГЛИЧЭЮТОJ J(pyr ()Т f(py1'a
только постоянным мr южи ·1:елсм.
Кроме метода Гаусса r:::стъ 11 другне способы
решсп11н лпней н ых систем. В н ате время
методы ре шен ия линейных снстсм. nрпобрсл11
особую в;.tжность в стт:ш с задачами матсма
шчс:скuй экономики. Обычно т:1 кис за,цач11
снодятсн 1" JlllHt:ftHЫM t:11стем:1м с ()l'(JOMHhlM
чнсJ JО\1 1 1 1;:изнееrн ых.
ОБ ШИ Е ПРИНUИПЫ
РЕШЕНИЯ СИСТЕМ
fJернёмся к системам общего Dнда. Дне ст rc1 ем ы
ур:ш11 r:::ний от одних и тех же переменных 11а
зываются равносuлы 1 ЫJ11~и 111111 эк:вllва1еН1n11ы -
11U. ссз1и множества IL'r решений сон11:щают, т. е.
любое решен~ 1 е первой снегемы яш1нетсs1 рс
шенщ:м нтпрой, IJ наuбnрот. В м есто з:щ:J111-ю~'i
си с1тмы урзвнений можно реп1ать любую
f)<1RHOCl!Лhll)'IO СЙ.
(>'ществует рял: 11peonra зuna1 п rй уранне111 гй,
при которых получе11ная новая снсте...,1а ос~ ·а
ётся равт-10сит,1юй т 1 сход~юй . Этн nрео6ра:ю-
1.шшя делаются с таким расчё'rом, ЧТ()аы до
биться главного - вывести иэ ~ашюй системы
Ур.:~внег111я и г1cpaue11crJ:Ja
сщну ИJIH H<.:CKOJlhJ<O систем с MCJll>lllllM ЧИСЛО\1
11еи:шесп 1 ых. Конеч110, )'Р<шнс11иi1 н ноных с1 1 -
стемах ДОЛЖllО бы · п, f\ОС'П!ТОЧНО для того.
0по61.1 их 1'v\ОЖНО быJ Ю реаmть . ПOC J lt" ЭТОl'()
процесс попторяется. по для меныш-rх с1 ~стем.
в 1поrе обысшо прнходим 1\ YP<JJ3JICl111IO с
одним 11еи~nест ным, решаем ero. затем rю
слсдо~>атсл ь•ю подставляем t:\ U рнп n другие
уравнения. Именно так мы решал11 лннеГшые
C J JCTt:.\llЬI . Пr:.~1ща , на rrp11 .\ '1Cpc 'l 'l"X Ж(' СПСТСМ
IШДl-10, Ч'l'О I JJIO l 'Д;.t FIЬl).(CJlllTЬ yp<iBIН.' HIJC С UДJll1J\1
f·I C:l l ЗH(;TTHЫM н пр11н1щпс нено;нvlОЖ l-tО - J'Ol/(;J
решсн~rя выr:оtжзю · 1·ся ч:ерсз 1te<.:кoJ11,кu пронз
FЮЛJ,ных пэраметрон. Но в шкпт.ных з:щачах
этnт С!I)'Ча 1"1 nоч·п1пе1ктречасrся, i1 мы к нему
больше во:тращэ·1ъся 11е 6р(ем.
JJpи преобразопа11пях с11стема ."'tожст " н<::1 -
.н1пьсn·>, преnр~щатъся u СОRОКу'Пность нескоJLь
ких снс1·с!\11 причё,ч 1<уравпспням могут добаf\
лятьсн нсраnснств:1 , ограннчннающне область
нх дейсткия. И ноп~а ест1, С!\11"1сл пр111-1сст11 в
жсртну р3 HH UCИJI hl-IOC'IЪ и З;J MCI JЯ 'JЪ уранне1111}1
11а 1rx СJJ<::/~ст 1тн, с тем что6n1 11 .1 ~алhнс 1'1111е~1 от
сент1, 11осторо11нне кор11и. 8:Jж1-ю вним~1тс.r1h
Н() С!IСДIЛЪ зэ тем, как млжст llЗMCJ-lI I ThCH мно
жеспю реш<.;ниi1 пр 11 1 1реобразС>u::~н11ях.
Ч::~ще всего дю1 умен:ьшенпя ч11сла не11:~
nсстr r ых применяются дuа менща: метот( пnд
становюr, который был нсnоль:юuаrr при рсше
шш задачи об участке в начале статьн, н..метод
llCICf/10t/t!1ll/Я 11L'l!З6t!CJJ1J/bl).;, когда IJCCl\OЛl>KO
у1хш11сн11й комбшrнруют таким обрдом, •rто
бы какоt.:-·1·0 нсн:;нсспю<.; сократшюсь lТак
работает мета;( Гаусса) . Hu 1 1р 1 1мсн11ть эт11
методы обычно .'>южно 1п 1 1 11 ь после: соотнст
ст11у1uщеl1 nод1·0·1'онки системы .
Какие же прсоf)разо11анш1 во:~мож11ы без
[>IICK<l 11р1юбресп1 л11шю 1 е нл11. что е1нС.: Х)"'tК<:.
1ютернл, 11ужr 1ые реп 1 е1 1 1тя?
1. Любое уравнение снстемы мтю ю ПО/\
в~рп1у-rь 11реобраэов::ш11ю, кот орое ттеренод~п
е1·0 u рашrоснлыюе ураш 1ст11tе ; напрн.\1Lр, !IJ)11-
бав11ть к обс11м qастям уравпе111 rя ощю 11 то же
ЧJ IСЛО ШILJ умножнть обе части H:l ОДНО 11 то же
ненулевое число. В :щ:;сти чш.:ла :щссь мо;кш)
нзнть фуг1кщ1ю, сс;1н эта шн:::ра1\ 1 Н1 не и:3мснн
ет обла<.:1ъ 011рсдt:лt1111я ~·равнсншJ (в с1учас
yM t lOЖC l lIOJ) 11 (/>)'Ht:Jl( I Я llt' OnJJ:HЦaCTCH В ну11ь.
2. К с11с·1·с:ме мож1щ 11рн11нсать любое cL;
CJIC[(CJ ' IШC, и Е1аоборот, t:CJll 1 к~ J<Ot'-ЛI tбо ура R-
непие системыявлж:тся СJ1Сl\С'Тнием С>стат,н1,1х .
его мож1 ю Rычерюrут~.,.
2·+J
Чиr,'\а
Напр 1 1мср, к с11с1еме
{/(.\",_)')=О,
g(x.y) = U
.\ЮЖНО ,Г(обаnить сё следстu11е - ур:ншение
/ {х, у) + k.p, (х, у) =О. А нз 11олученноf1 системы
!лх.у) = u,
д(х,у)= О,
.f(x.y)+k.L((x.y) = U
;vюж110 )'д;.IJill 'I ь 11epU()l: yp:tRHCJ-IHC IIЛI I , при k :/=
:1= () , 1порое, 1ю·1·ому что uба 011 11 , оч евидно. сле
дуют из ~nyx {\руrих. Огсюда - трет11е праnшю.
3. Любое урав11еш1е с11стс:v1ы можно заме
н1пt. 11а его сумму с любым дру1·им \rраш1е11и
см, ум1южс11ным на nроизJЗолыюс число. Это
прсобра:юван11е - осповпос в методе Гаусса .
01·p~1t-1!'l'J11MC}J тремя правилами. хсrп1 есть 11
дру 1 ·11 с (так, пр11 соответствующих 0 1 ·u1юрках
уран~ 1ен 1m с1 ~стемы моЖJ ю nсрем.1 южатъ ).
ТТосмО'lр11м, как дейстнуют эт11 пр:1А1mа 11р11
ре111е 111111 к011 крет1 ю1~1 системы. ( n рещюже11-
111>1 й 01ocofi может пок:~заты.:я неопт11\1Зл1,11ым,
1ю 011 1юучт1телсп n дру1 ·ом смысл.е.) 11ус1 ъ 11адо
ретюъ спстему 11з днух ураш 1е1111й
fx+y=a.
l·\1' = {J.
Вuзвсдём R кн:~драт первое )1);шпс1ше:
xl +2..'\т+)'.! = а.!.
(*)
Это прсобrа:.юв;1 1 llJ C' ш:ранносшrьно. так как
получс1 1 1 ю .чу ура1шсн11ю с ранны ,,1 успехом
от11ечают и решения уравнения .\·+у= -а. 11 0
МОЖI 1О 11plt COCДИJIИT/) у1х1111 1 е11не (*) к 1 1 аше1~1
системе в качестuе СJ 1 едс1·11 н я. Вычтем нз }1)ав
нешur (*)второе уравнение системы, у-мпожеп
пое 11а 4:
.\". ~
-
2.\J' + у
1
=(х-у)
1
=с/' - 4/J, юш
r1 :~;~ме1111м этим ураннсн 1 1ем второе, :1 :.1атсм
выбрuс 11 м вс11омо1·ателыюс ур3в1-1ение (*),
сле11l-п111е 11epuoгn:
jx+.1' =tl.
'
1
х-у =±,·а--4/J.
Замстптс, ЧТ(J ППСЛЩ~НL'С: yp:1нн<..:Hlll: - ;')Т() на
сам< 1м дeJte со11оку1111ост1, ,цвух уран11е1111(1: со
:~1 1 акам11 11mnc 11м1111ус. Теперr. можно юятъ по
лусумму и nолура:нюсть r1хшне 1 шй снстемы.
В резушл·::~те приходим 1< ~ормулс .~ля корней
квад р:пrюго ypanrrcrrия х- - а:>.:+ /J = U. " кото
рому сводится :.~ад:tча :
Система же имеет нна решешщ отлнчающнеся
перестшю11коi1: (х, у) = (х1 , .х!) 111111 (х~,.\'1 ).
Дна важr 1ы х прнёма упрощения ~1х111нс111 1i1 -
р:1зложепис па м11ожител11 11 :замена перемс11-
11ой (см. статью ~нес1<олы<о coneтon 11ачиrшо
шнм Rол111сб11икам. ш1н К:.~к рс:шать урште
ния») - н ри,\1еняю·1·01 11 11ри реrш:н и~ 1с1н..тем.
На 1 1римс:р. сс;ш ~ с 1 к"1·емс
!;\'~ +J: =2 '
.У+у-=2
вычес1·1, 11ерное ~·раА1 re1 rщ" r 1э нторпго, получн\1
jx2
+y=2.
t
))
Х-)1-х-+)1- =()
.
-
'
ИЛ!I, П()СЛС ра:.~ложспnл 11:.t MIIOЖllTCЛ I J второго
ур~шнtння,
j".1 ' )'=,
.\.. т"
L.,
\с.1:- J')(l-. '\· -у) = О.
/\ ;::эт3 с1-1сте:-.1а р~кпадэется на со1101~111юсть
двух с11с1·ем
{.\:~+у== 2.
х-.J' =.о.
{х1+J'=2.
1-х-у=iJ.
решаемьL': бе:з ucoбu1'(J ·1 ру;1а .
Систсма НИ{ \а
{х' +)'' =а,
.\.у= fJ
1юзнИ1<:ает при решсш·ш кубиqеского ураш 1е11ня
n o методу Кардано (см. ст:.lтыо "Кубические
ураш1ешtя»). 1Jосле возведения обеих частей
'
второго уnаннения R кvб опа замс1юй и= х , с=
'
•t"
,
=у с1юднтсн к стоnь знакомой нам снстемс;
{и+ l' =а,
Ull = h~.
Метщ~: заменъr nеремен 1 юй особею-ю часто
примепя<->тся при решении систем уравпеш1й
РЕШЕНИЕ НЕРАВЕНСТВ
Дня J1Юбh1Х днух разЛl·I ЧlfЫХ ЧllССЛ ан h ВЪIПОJl-
11яется одно из нвух услови11 : 111160 а боJLьше h
(а> /1), т160 а меныuе f1 (а <h). Если 11мссто
ч11ссл с1 и Ь в:1srrь ш,1раже111шА(х) 1i В(х) \>Т пе
ремеmюй х, то соо1'1юшеш 1е между их число
nым11 эначешшмн будет з;шисетъ от того. ка
кое чнсло подст:шля.ется вместо х. l:3озникает
задача: найти все значениях, которые пр1 1 нод
ста 11овю:: n заrшсьА(х) > В(х) превращают её в
верное Lшсло.~юе нср;шенс1·во. Эт:,~ запись на
зывается 11еравенствам с ненз нест.ным .х, а ис
комы е значенин х - 1::го реиил-tшuии. Nlеняя в
нер:.шенстж: знак, 11олучнм е щё О)1 НН 1:нщ стро
юю 11сравенств<t -А(х) < Н(х) (что ра nносиш,
но В(х) > А(.х)) 11 /~ fla п1111.;~ нестрогих нера
r1е11стn - А (х) ~ В(.х) и: А(х) ~ В(х).
В качестве перного, п ростейшего примера
реш11м лuней1tое неравепстuо
Sx+.3>:Sx+7.
Сна•1ала вычтем 1 rз обе11х час-1·ей 3.У + )·
2х >4.
За мст11м, что :-этот переход нВJ IЯ(.'ТСЯ раю-юсиль
ным, т. е. не ~rзме ннет множеств() рсшс1111й не
равенства. Он 01111раеrся н~\ одно из важ1-1ей-
1ш 1х СIЮЙСТН ч 1IСЛОВ Ы Х нера t1e1 ICTR:
Д~Iя любых действительнъrх чисел а ,
Ьисеслиа>Ь,тоа+с>Ь+с.
Если .:х·11 - решение д:н-1ного неравенства, то,
добавляя к обеим частя.,v~ число с= - (3х0 + .?),
получим , что .\ ·0 удовле1·воряет 11 uеравенстnу
.2..-
0 >4. Разумеется, верно и обр:~ '1·ное. Пользу
ясь друrпм свойстном 11 ер;:~вс 1 1стя,
... .
•r =[
l(\l еслиа>Ьис>О,тоас>Ьс,
Уравн е~-1ия и нерав~нLтва
с тр:шс1 \<.:rще11 тнымн функцшrми (ло1·ар11фма
мr 1 . 110ка:$а1'СЛЪlЮ(( н тpHL'OH0\1t:TpИЧCCKllMlt
функ1\иям11 ; см. стат1,ю •nл<..:м<..:нт:~рные функ
ц 1,1и н нх снойс>гв;н). Одн ~ню 11 общем случае -
в~адtlчах. но:31шкающнх 11а r 1 ра1пикс, - ренrат 1,
таю1е системы fн ,1н аt:т оче 1 rt> слож1 ю. Для этих
за;рч часто прихоr~итсл ис1юль::юи:1ть методы
щ:т:бпижёштых uычисле1 1 ш~1.
разделим обе части на 2 (иначе 1·оворя, умно
жим па с = 1 /2). Получнм
х>2.
TaKИ i'Vl обра:юм, 1\СХОДIЮС неr:шенство вернu
для 11екоторurо х = х0 то1'/tа н то:rько тur·да,
кш·д;~ х0 > 2. А нес: .множ<..:с.~пю pc1t1 <..:11нlr 11.:з. 1111 0 1·0
11ер<1ве 11сл~·,~ на ч1кл0tюй осн rtр<..:д("1 ·ав1~яеr·ся
Л}'"ЧОМ ( 2; оо).
Теперь репшм л·аадрат1юс 1 1 ера11сr1ст1ю
axl +Ь.\·+с>О.Г/~еа;еО.
Рассмотри.~'Vl днскр1u'v!1111аr 1т 1) = /J
1
-
..+ас квад
ратного трёхчш:на q(x) = axJ + /Jx + с. Допус
т11м сначала, что D >U, т. <..: . ц(.\·) 11мест дна
кuрнн - -'1 и х!, пr11чём х, <х~ ТОГ/{~1 (см.
статью •Квал.ратные урав11еню1?) нсра11е11ст1ю
'VIOЖllO за п нсать в воде
243
Числd
)'
D>O
у
J'
п<о
у=11.r'+lJ.\'+с
+
+
х
.\:
х
о
()
х, = ·'-'2
о
а
б
в
P1te. 1. Кв.1лrм1 lto<' Hl!JJd lll:lfc 1IJU ,ix· + Ьх + t > IJ , 1N' ,, > О При О > <l решсн11~·" 11 cpdi;t•t l L"1 >1U/\Я~ 1 (Я 11t\ьелнн~>н11f' дFl}'X •'\'Чf'и
(- " ,: ,, )u (;. , ; ~t Пр~1 О=О решРНИР - в<11•н1словdЯ rарЯ'>lt.ЗЯ. крометочкаа\=х, =- ,,,. При{) <U- 1к~ •щслоо,1я 11рям,1я
Слу•1.-1.n .t < () pr, C( 'v\.JТfH1B'-1(_)Tf51(iH-.:IЛft l 11••нrJ, -ГCJЛl>k(J IJP IBlt П 1Jр.1t)ОЛ fiyлy1 11 -.1прс.t1JЛ< 111ы в1111 .,
Здесь пр11 х < .х·, оба 11ыражt:1шя R скобках от
рнцатслы-1ы, 11ри .\" 1 < х <.х~ псрRос отрицатеm.
но, а второе 1ю1южr 1 тс:лы-ю, а пр11 х > х~ 0\13
llOJIOЖИTCЛl>l lbl. По?>тому 11р11 а> о МIЮЖССТПО
рсшениii 11a w ero нep<JRcrrcтna - 3То объед11-
11е11ие двух лучей: (- оо; Х1) U (Х!; оо) (рис. 1. а). а
нри а< U- интервал (х1 ; х,).
Случай n =О. когдах 1 = :х.~ 11 q(x) =а(:>.: - х,)"~.
расс:матри вается аналогнчпо. Еслп же D < О. то
ф~·нкция С/(.'\") имеt:т один и тот же знак на все 1'1
)lt:lll"l'HИTt:)lhl IOil 11рЯМО(J (рис. l, б. в). в .ЭТОМ
ле1 ' КС1 убещ JТhСЯ, н1>11\С:J1 ня и;, (j(X) 1юл нъu:\ кв~;t
рат. как лprt pc11 1 t:111п 1 кнщратно1·0 ураннсння:
(](.\')=а((.\"+.!!._)" +~]-
1.а -~tГ
Очешщ110, что з наl\ выражения в правой част11
совnаджт со знаком а, т е. функция q(x) поло
житслы та при а> !J и отр1щателы1а прп п <О
Ито1· наше1·0 ма11снhкого ис:следовашrя под.ве
r1Ь1 н сле11.ую щ<.:й ·1абшщс.
Pewt:н иt: 11ер::ще 1 ктfiа
Днс:-кr 11 r.uш:шт
a'!t·L+/Jx+с>Оnри
а>()
а<О
[)>u
( -""'; ..\'1) U (Х~; 00)
(.\"1, Х1)
D=O
( - оо; .х-1 ) U (Х2; оо) Решений нет
D <()
(-оо: «>)
Рt'нн:r 1ий 11ет
Т;~к же рс111аются 11сrхшеш:тво q(x) <О и н с
стро 1 ·1rс ткр:шt:11с-1 н:э С/(Х) ~ U. q(x) ~ (J
Кn::щр;п 1юе 11 ерапенстт-ю мтю ю рсmать 11
н11аче. КRа/1.ратнчпая ф~1rкп,1ш q(x) 11епреры1ша
rra псей ч11словой прямой. Наt'ЛJЩНО это оз11э
чает. что её график - параболу
-
можно
1rа <rсртить, нс отрывая карандаша от б~·мап1
(точ11 ос опредеш.:н.ш: см. в статье «Фунtщ1щ 11е
прсрыв11ые 11 разрынньн~~ ). Поэтому сст 1 на
~ ·рафике t:сть точка ннжс uc11Ох 11 точха nьш1с
ос н их. ТО он JIOJ IЖC H пересечь ось между ЭТН:Мll
ючкам1-1 (рис 2). Гоноря бш 1 сс стrого.
Фун1<ция, непрерывная на каком
либо проме:жугке и принимающая п
двух ero точках значения развых
знаков, обязательно обращается в
нуль .между этим.и точкаъш.
Это угвсрждсю1с назьш астсн mC'ofJe.11.юП о 11ро
.мю11.уточно.м зна четт 11дuказ1,~нас:тся в ~-1:.те
ма п1чtском а налнзс.
J'
()
РиL. 2. Еtл11
на граф11кf'
Hl'l IP'"I ""~111IЙ
функш111 r11 ., ·} епь
1 очt.. ~1 HJ-1*-.t- ()(.Н <А'
И 1()"1 1<а НЫШ(' 1·11·ц
l)\, ТО "1еЖЛу
~тt1ми 1оч ка,щ
1 р.1фи к лолжен
Гl('Р()С€'Ч1:1 ось
Итак, 1rрн D <О функц11я q(:x) Н)1J 1er1 не [IМе
ет. R этпм c.rryчae tiecr, её rrаф rтк J1ежнт пu од r 1у
сrорш1у от оси аfJсцисс. т. с. q(:\·) н.v1ест один и
тот же ~шак гю всех точк(lх. Наnри:чер, CJ(O) = с,
так •1то знак с.1(-..:) на всей прямой совпадает со
знаком свободного член:.~ с. Ещё можно з:.~ме
тт1ть, что при достаточно больших .У абсо
лютная ве;шчина выражсr-шя а:'/ больше абсо
лютной величины l:Jx +с, 11 пQтомv знак С/(.У)
'
,
со1ш:щаст со знзком а.х-, т е. со :ш~псом а.! lрн
JJ > О корни q(x) рззб11в~1 ют ось абсцнсс 11.::i трн
прСJмежу·1 ·ка. ( - оо; х,), (х,; .\'2) !/ (Х1; оо). На K::IЖ
JtO\•J 11:1 них q(x) сохраш1 егз 11 ак, причём 1ra дuух
краr111 нх, бескоrrеч ных н 11тер11алах CJ1-1сопгr:ща
сr со зп~ком ct, з 11з сред~ tем шперн:ше - про
швопол:ожен. (Дейстшпельпо, n сереюшс
.:1:·1 +х,
/;
сре;\не 1 ·0 11нтерн:u1а. точкt:
-
=--
з на-
2
21.1'
.
D
qe1н1cq(x) равrю -
4а .) Отсюда нноrн, 1юлуча-
е.ч r1р1шс;\ё1Jную p;mce табJГицу.
Э'га ндея рt=шсння пр11меним<1 к любому нс
раве11ству внд:1/(.У) > ()или/(.\) < ()с не11рср1,1в-
11ой фунющей/(х) . Нуж 1ю тоJ1ыщ у'Чеоъ. что
функт~юt /(х) J1.-Юже1· бъ1·1ъ оттрt:дсле1 1 а и 11е 11а
всей числовой прямой. Мы нa..'CO,ri;н.vr обJt~стт,
определения fix) и корпи у11авнеш,ш f(x) = О,
определяем з11~u< фуню.(ШJ п::~ каждом из ш1тср-
15алон, tr:t кСJторыс кuрпи разб11в::.tю·1· обл.~сть
онр е11елен11я (эт11 з1шкн постоянны, 110 теоре
\I С о 1 1ромсжутuчном значс1-1ю1 ). н выбнраси
111-1тсрвалы с нуж11ым ~11-1:аком. Прн рс111~111111
не<.v1-ро1·01 ·0 нер:н~енства Jtx) > О 11ли /(.'\')~О к
l!nТбранным Нll'J't:pB::tЛ<IM надо l l[JHC()t:Дl·IHHTh
11 у_·ш фу11101и11. Что(')ы rн1реf\е.rп 1т 1 , З1fаю1 фу11к
пш1 па интеrвалах-, мож1 ю юя·1ъ на каж/\ОМ и:~
них 110 точке и вычнслит1. :шаче11ияj(х) т-1 этих
точт(ах. Дру1·ой путь - пайтн знак 1 ra I<аком-то
одном ш1тернале 11 проследнтъ, как он пзме
няется при переходе через коrщы иr1тср1.1алов.
Р<.:шим ·1акпм сщкобом 1-н.:рзненстнu
!(•) _(Х
-
2)(Х+1) ()
.\.
-
;:>
•
х-1
Его облас1ъ определения - множество всех
X;t 1, Т. С. OnЪC/,IНICHllC лучеr"i ( - оо; 1) 11 (l ; оо).
Нул11 фу1П1.'Т \ИТJ j(x) raзnиJJaГ()'I' ЭТО множесТRО
!J a че-1 ыре щ10~1ежуrка: (- оо;
-
1).( -1;1),(1;2)
и (l ; оо) . Пра перехо.п,е через каждьпu1 11з концов
да11ных промежуткоn - точl<н
-
1.1и2
-
ровно одна аз скобок меняет знак. Значит, 13
каждой из этих точек мет ut<::тor ~шак нссй пс -
Ура о11с1-1ия и 1к•рJве1-1<тоа
у
,_ (x- l)(Y+2)
J-
,\'- 1
. '\'
(" :!1(•т!)
Рис. З. HP p.1Ht't tПRO ·
> О HMl'C'1 < Л<'ду~ 11 11c-•r r,1•1J1N111r
\-1
\'с Н, 1! v(l, ~·1.
пой <1;,~стн. Найдём з11~11< футткцтr 113 ою юм 11з
лроме::жупшв. Напр11меr, очсшщ1ю, •тто/(х) > о
1 1 рнх =:$из промсжутк,;,~ (2: = ). Т<.:11срь щ:но. что
./~."'\') >он np11х Е (-1 : 1),а H:t N~YX ;~ру1·11х 11ро-
МСЖ)r1·ках/(.У) <О. Отсюда отке1 : х Е (-1: 1) u
u (2: =)(рис..)) .
Если 6ы мы решали н<.:с1го1·ое н1::равс11стно
j(.'I.') >n. то н отнетt: 1юлуч11л11 б1t1 м1южсст1ю
.хЕl- !"l)1-.J r2~ ()<)) . Т{)4Ка
.'\ ' = ! ltCl<JIIOЧaeтcя 11:\
мтюжестt3а рсшетшi1, так как oJia 11е вход1п в
область опред<:ле1шя фушщи11j(\').
Такой ~1Стод решсп 1ш пера uенств называ
сто1 л1с>11юдо.м lmmервалов. l lo сущсстnу, 011
~юз1юш1с·1· свсс1·и решение нсране1к1·ваЛх) > О
к рс11 1ению ураннеш 1 я /(.У)= О Чаще ncero стu
прнменяют, r<огд::~ /(х) 11pc;~cт:11.1IOJC't ' со бой т -
ноше::н11е дну-х м1-ю1·очлс1 юн, которые: удаl:тся
paЗJIOЖlfTI) 11<1 M I IOЖH l 'tJlll Если ЭТО pa:-!ЛllЧIJf,Jl"
ю1неl1ные множнтсл1-1 , т<1 з 1 rак:и 11з НJ 1тср1:1ал а :х
чеrе,11:уются . Но так бl>J 11ает 11е нcem~t. Н апр~ 1-
иер. ЛСRаН Ч~JС'l'Ь 11ераве1 I С'ГП(t
(Х- l)!(.\'+1)>0
обр;1щаети1в11улL в точ1\е .>.: = l. rю з т1<1J\ в это l1
точ1~t: нс меютст (р11с. 4 ). Пр11 этом з11аче1111с
х = l кс~ раыю исюLючзt:тсн нз мтюжсства
pt:we1111й, ПOCKOJil>KY 11t:paвt:1 I CТIIO стрр1·uс. От
вет:(-1;1)u(1;=).
Другой r1аж11ейшнй метод решс1111Я 11сра
ве1 rстт1 - .метr1д раm-юс1w1)ных 11peofi/ю3r11:шm1t'1 .
при КОТ()Р()М Д~HllIOC 11еране11ст1ю с lIOMUЩL1IO
сер1 ш ат ·ебра11 чссюrх npeonpaзoв;i ш 1(1. нс 11:-1 -
мешнощих .мrюжестRо рсmеш1й. препращается
в комбиII~щшо простеiшшх 11ераве11ств n11да
2-15
Числа
.У > а, х " Ь 11 т. н. Прt>дставлt:нис u нём даёт
пр1шсдё1-1нос в 1-1;,iч1u1e статы 1 решс1111е ли11ей-
1юго неравенства. Об этом методе пр11менн
тслыю к уравнениям подробно рассказано в
статье «Н<:тколr,ко советов 11ачи11ающи~1 1:1011 -
шеn11ш<ам, ILIНI Как рсш;JТЪ уратшения~. Поэто
му здесь ос1·а1юн1 1 мся только па особстптостях,
отлпчаютц11х реwен11е 11ераненств от rешешш
урашrеш1 й.
Прежде всего подчерютём, что при решении
11(:равснстn р:шносилъность t1срехuдов - тре
бов:ш11е непреложное. Ведь. в u·1·1шч ие:: от урав
нен11я , множество решешн1 неравt:нства обыч
но бесконечно. 11 отсе>1ть посторо1111ие корни
rюдстанuвкой 1111сходнос нераRснстно 11росто
НСАОЗМОЖНО.
Доб:шлt:111 1 t: к обt:им частям пераnенства или
вычнтз11ие нз 1111х какой.-либо функции, а так
же заме~ 1а выраже11ий 11а тождествешю рав11ые
-
г-
r
(скажем. \' А vВ на ..,f АВ) не влияют, консчпо,
1-Ja з11ак 11ер:.:~т::нстRа, 110 могут измспить его
область определения.
При умн.оженнн обеих частей 11ерзне11стна
на фу»кцию}(х) надо следить не только за об
л:зстью опре1~елсний, но 11 эа знаком этой функ
ции. В области, гне /(:х) > О, :знак неравенства
после умножсння сохраняется; там, 1-де/~1.:) <О,
01 1 ме11яется 11а прот 11 пополож11ый, а пули
фупrщнн следует 11рш1ер1пь отдельпо.
Осо6ан зккур;п1юс1ъ нужна. когда берётся
одна и та же фут нщия .f(.х) от обеих •1астей не
равенства. Из неравенства А(х) > В(х) полу
чится пераnепстnо.f(А(х)) > .!(В(х)), только сели
)(х) - MQIIOTOIIIIO возра<..:Т<IЮIЩОI функц1щ
011ре,целёш~ая для всех ре щ е11иi1 ИСХО/\НОГО не-
у
о
Рис. 4. MнnЖf' (TnC> рРш1·ний нf'ра~Рнс-тва (л 1J'( x + J \ > О
СОСТО11Т IH обь~ИltNН1Я двух 001\a(lt'Й: (-1; 1 /•. .J \1 ; " .) .
2-16
раве:нс:ша . Есл11 j(x) убыnает, знак нераuенства
~ перt:Rtрнётся ~: ./(А(х)) <.f(B(x)). Л если/(~) не
MOJIOTOHIJ<"IЯ функцня (напримср,J(х) = х-), ТО
область её опредсЛ<: ния прнхсщится раз61шать
r1a участки возрастзн11я и убьшания 11 на каж
дом рассма·1рнвать неравенство отделы ю.
Решнм 11ераuет 1ст1ю
..J.\:+1>х-1.
(')
Чтобы избаииться от rадтшала, 11адо обе части
возвести в 1шадрат. Однако функция у = :х~ не
.жшотонна: 011а возрастает пр 1 r х ~ О 11 убыва·
ет 1rри х ~О. Леная часть нашего нepaneнcrn:i
неотрицu·1·сJ 1ьна в области определения (т. с.
пр11 .У.+ 1 >О) , 11р;1наи жt: 11 риннмаt:т любые
:~нз ч с ния . Пnэтому следует рассмотрсп, ;1на
случан::х- 1~() и.У- 1<О. В псрвом оrучж
фуню1ия у = х2 нозрас·1·;;1ет 11 11ерапе11с·~1ю (*)
раnносилъно нер;н1енстRу х + 1 > (х - 1)- . (Пр11
заме11еиыражешш (~х+1)2 пах+! облает~,
определения расш11рястся , но это 11е нарушает
равное ил ьности, нотому что для всех рсшсниI1
:х:+l >("-' - l)1~О.) Bu нтuрuм случа<:: но вteii
обл:.~сп1 определения нераненспю (*) ны11uл·
нястоJ автоматичесю1 (лсвая час1ъ нсотр1ща·
тtm,н<J , nр3ню1 отрицат~лы 1 а) . Вот краткая за·
п 11сь решения :
,Jx+l>x-1<=:>
[{
XL- 3.Х<0.
<:::>
.х> 1,
~
-1<х<1
{·~+1>(.Х' - l)L,
х-1~О,
{·~+ 1~ О,
.Х-1<()
. :=>
[
l<х<,)
.
.
~-1~.'\'<3.
-1<·" <1
На1юм11им , что ф11гурю,1с скобки обозначают
системы (R данном случае - нераненстR), :1
квадратные - сотюкупност11. Первый и тав·
ный шаг :щссь можно немного у11ростить 11
представить в общем виде так:
Аналогнчные схемы по.11ез110 состакнтъ и J.VIЯ
дrугнх п1п ов не.:равенств с радикала мн .
у
2-
-
2
2
Рис. 5. Рt>шением неμавРн<тв~
..r:;-;1 > >( - 1
явл~ етrя nолуннтС?р 1J,1л 1-1: Н.
А тепе рь лр.иведём дру1 ·ос рсшс111 rc нсра
всне111а (*). В нt:.м и~поЛI·•:..~уен.:я :~амс1 1 а нсрс-
.
п
>
мt1111011. усгh у= \'Х+ 1. то1·да .х =у-
-
1 11 11с-
раве11ство станов нтся кnадрапп,тм:
Ур11внРнш1 и нераве нства
у-
.J' - 2<О.
Множестно его решеш1Л - 11 1 1тервал - 1 < у < 2.
Подсташ1м сюда х:
-
1 <\.\:°+l<2.
С у 1 1 ёто"1 обла сти u11ределсн11л 1101tуч1 1 м
()<..'\"+ ]<._J ,НЛI1
-1~х<3.
Можно решить это нераве пстnо и .чсто;'(ом
ннтерва.rто n (рнс <; ). Нди11ствс11ныi1 кореш,
соотвстстuующсго ура 1шешrn "У .У + 1 = .У - 1 . рав
т-1ы!I 3 (см . статью • Н сско:~ь кu сонс тон 11ач11-
1rзющ11 м 1юJ1шсб 1 111ка111 , 1 tл 11 Как решал. ур:нн1е-
1111я~ ) . pa:.i\)rinae·1обл:кн n11редс1 1сrп rя .\" ~ - 1 rra
,ri;na 11ромежутТ<а : [- 1: ) ) 11 (3; "°) . R:шn. к 11р1 1,1ер~ ,
.:\: = О 11 .1:· ~ 8. 11аlmём, что rr:.i пер1ю;11 пптернале
11ep aвe11 crno выполняется. а 11<1 втором 11ет.
ЧислJ
ПЕРЕБОР ВАРИАНТОВ
« ОСОБАЯ ПРИМЕТА » КОМБИНАТОРНЫХ ЗАЛАЧ
В з 1 тамеш-ггой бзсне Крылова «КRартет" <- про
кJзтпща Марты ш к.1, Осёл. Козёл .rц косола пый
Мишка-> устроили mобот.1·1 11ьn1 экспср11ме1п :
UtШ ш:сЛСДОВ:lJIН l>JIШШ IIe ВЗ::IИJ\1. НОГО расп оло
ЖСН I JЯ муз ыКJНТОН H~I K<IY.t 'CTBQ IJ('ll()JIHC:HHЯ. и
<.:ел11 бы 11с вмc111~UIC>J Сшюнс1\ ) частнню1 кнар
гс::т.1 , нанср1юе, п<.:рспроnон;urн бы нtе во:3мож-
111.1е п.~рнан 1ы Задад 1 1мс11 вшчю<-ом сколько
су1 цес-1 нуL"'Г способов. чтобы рассадJ 1т1" напр11-
.\1ср R (Щ1111 рял, четырёх музr.rка 1лон7
Дpyrot1 случJй . Bocr1e-1ы l'i Маяковсю 1,\1 '·J\Ю
лоткастыfi, серпастый·• соnетскнй пас п орт
имел серию 1-1помер, состоящш: в обше!1 слож
ности IIЗ трёх с1астсй
1) IIСкоторос ч.11сло, заm1с;шнос р пмскимн
ц~ 1 фрам11.
2) дне русею 1с букnы ~
3) шес1ъ :1рабских ц11фр.
l-\:mp1т>v1cp, IХ- РГ No 062993 rззумеето1 . нес 11ac-
nop 1·а дш1жн ы 11меть ра~111 ыс нО,\1t[>.1 Сколько
:vюже 1 fi1,л 1, разтrч 1 1111х 11 :Jcпop-ron?
Треп.я с 11туац11л. Н ас 11 р1 11 жнпают сы1р<~·1ь
u Л.отто-М1rллио11 . Суть rтгры в 1ом. что нуж 1 ю
218
t1 з -19 rюмepo ti ут::щать 6. 1ю·1·орыс пыпе111ут но
время т1rража. ,Тi,J1я учаегпя в 111 ре сле,Т\Ует нри
обресш спецналыrую картоЧК) и вы ч срю 1 )1Ъ
в ней 6 любых юзадра·1 он, пропумеро1:1а 1 шых
ч ~1 слами от 1 до -J.9 . Чтобы nы н1 Р<Пъ наверняка,
можнu было бы J~1ГJ •1<."111с ь таюн1 ко111·1 ч<..:стnо:ч
к:чпочек какое нt<.>бход11мо JJ.,IЯ вы чёркин:tн1 1я
6 номеров щ; смн воз:.южным 1 r способами.
(":fюлпко ~·111х оюсоnuн'
Обш,<::с у нсех трёх эадач то, 'П'() ~.1 х ре111ени
е.,1 заннмается отдеJ1ьная обласv1· ь математики,
называемая коJ..~бинатори"'ой. •Особая np1-t -
ПЕРЕСТАНОВКИ
Пусr·п 11меется 11объс1~то1:1, 11tпажно каюLх, т шrь
бы всt они разли ч ал н сь между собой: ю 111пт,
детские ~-.-убнки нm 1 музыканты крылонс1<01'()
~ к11арте-1·а». Мыслетю рассr::шим их n ряд и та
кое упорндоче шюс расположение объектов
назовём перестаиовкоli. Попытаемся ответитт,
rra вопрос: с1<олъко Dctro nозможно n ереста 1ю
во1< из п nрсдмстов:> Число пс::рtстанuвuк обо
значают Р,1 1 нодч ёрюш:~ н тем самым , чтu оно
зависит от коли ч ест1:1;:~ прсдмето к п.
Попытаемся найти Р11 с н ач•,1ла длн нсбот.,
пn 1 х п. Есл11 п = 1, т. е. 11мсстся од н11-сд1111стве 11-
ный 1 1рсдмет, то су1_11сстнуL"Т и од и 1-1 -с:ди нстпс:н
ный способ el'O рассrанотш. Поэтому Р, = l.
Возь."1ём п = 2. Сразу понятно, что Р2 == 2, по
скольку два предмета (назооё.м их А п Б) мож
но расставить двумя разпичпымн способами:
АБ и БА. Попробуем рассуждать несколы<О
ш1аче: первый 11рсдмt'1' (А) устанuвнм нen o
!UJIIЖHO, а второй ( Б) бу;~ем 6 1 1рн1 1 ажиf\атп~ к
не.чу. Безусловно, 06'11ект Б можно 1юставить
анбо c11ept:l\И, либо сзади 01· А, СJ 11.:до ватс;1ы ю,
'ШСЛr> n ереста 1 Ю FЮК Р2 вд1юt: больше, чем Р1 ,
т.с.Р2==Р1•2 =1 ·2.Доnавимтепtрьтретий
предмет В. К каждой И:i п с рестатю 1юк л.пух
объектоn А и Б мож1ю пристронть трети([
nре;\мет тремя различными сnособами: nоста
внть его спереди, между ними либо сзади. Пе
реста новка АБ , таким образом, порождает три
псреста110 1жи: ВАБ, АDБ и АБВ, nерсстаноnка
БА - таюке трн: DБА, БВА и БАВ, 11 nce ло
:тучивш и.еся тесть rtерестановuк - разные.
Отсюда1,~=Pl ·3 =1 ·2
· .).
Вообще, 11з каждо1:-1 персстановю 1н - 1 пред-
11етоu моЖJ ю п оJ 1 )rчить п д01юлн11·1 ·ельн ых пе
рестэr ювок, доба 1шяя п - й предмет 111 160 спе
ред11 , лнбо с~ади, лнбо между ниеющимися
преf(метами (между п - 1 nредметами суще
ствует/1 - 2промежу1·1<:1: l +1+п- 2
-
вот и
выходит ровно n). Стало быть, при переходе
от /1 - 1 к 11 предметам количtстnо псрестапо
вок унеличн нается 1:1 п рuз . Поэтому общая фор
мула будет ·1·;.~кой:
Перебор вариа11тов
мета-> кпмбн11:пор111.1х з:щач - вuнрос, который
всеrд:а можно сформул11ропат 1, так. чтuбы uн
начи11ался оюnами: «Cкo111-.ю·L;vtH с~:юсоб.~мн" .» .
\
'
'
1
'
'
п-1
"
/
,/
1Jl
/
Из кмкдnи nереrrа1ювк~111 - 1 nрС'лмето[I можно получитьп
перестановок п прелмеп>в. лоб.iвляя п-11 npeд\tl:'T либо сnеред1 1,
м1бо сз,1д.., , л1160 межлу имеюшимиlЯ nрелмет;~ми.
Р"=12 -)
· ... · п;::п!.
l3осклищпел1,ным знаком (в ·"l<ITC.l\ll:пш<e 0 11
на ~~ьшается факторипло.м) nрннято uбо~на
ч:~ть нрои3L'.едение всех 11;1·1·ypa.irt.ны1' ч11ссп от
] /tO n f\КЛЮЧИТеJJЫ·Ю.
Мы не просто 1:1ы нел 11 формулу, но од 1 1ОRре
ме 1 11 ю указат 1 способ, как 11ол)''ЧI1Тu ncc 1юэ
м:ож 11111с переста11овю1. На;~о отметн1ъ, что он
"алеко не еm·шстнеш-rы\:1. Нанрим1;:р, В(е 11с:rе
ста110Rки можно получить И:i пача11ыюй, по
очерёдно меняя м естами coce,r\rшe объсюъr :
АБВ-4АВБ-)ВАБ-)ВБА-4БВА-)БАВ.
РЕШЕНИЕ ЗАдАЧИ О КВА РТЕТЕ
Ч етыре rо ре - музык;.111т<1 11:3 бас н и Кр1,11юnа
долr·о пер~саж1шал11сь с места 11 а место. В ход<.:
Э'f() \'О <>т1юрчсско1·0 поисК<t» OcёJI внёс пред1ю
жеште: «Мы, верно. уж 1юла;~11м, ~сою, рядом С»
ДСМ» . Попробовали - rre r юмопю. Но n рщ1-тn
мтюю сесrь по-разному! Давайте оnределим
ч11 сло возможm,rх перестановок Эдесь /1 ::= . 4,
поэтом:у с пособо\3 "усесться чшпю в ряд·, н ме-
етснР.1:=4!=J •2 ·3 ·11=2LJ.
249
Чиr м1
Добавим. что для ретепия некоторых: зад;:~.ч
приходится применять и,~ею переста1ювоr\ не
u <-ч11стом" Jщl\e, а с п оправк:-tми . До11устим. глаn
н ыiт ф~штор, uлияющиf1 на т<ачсстnо игры, -
это соседи каж,дого музыканта, и нс нажнu, кто
из ю 1х спр~ша. а кто слс::к1. Лр и таком услов1111
пс::рест;ш онк;~ <-Марты111ка , Осёл, l<n:~ёл, Мшнка»
экю 1налснтна зсркалы-10-с им мстрич нn l1: "Ми~н
ка, Кnзёл, Осёл, Марты111ка». Понятно, что в этом
случае пес Р 1 нар11антон раJбиваются 1r:i 1.1ары
рашюэ11ач11ых 11срсст;н-ю1юк. И если 11 з каж,цот1
11;.~ры оставить 110 0;~1юi1 нерестаrювкс, то об
щее число раз111 1ч ающихся вариа11тов будет
Р4/2 = 24/2 = 12.
Теперт, nрСl\Ставим , •по музыканты сели нс
в ряд. а по круrу. 13 этом случае можно рассуж
д~1ть так: н каждом из вариантов прuну м еруе м
всех участников но ч:ковоеt стрслю.:, 11ачи 11::1н ,
ск:~же.м.. с Осла . Н ра:3л11ч 11ы х перест:товк:~х
к:~ж/\Ый муз ыка нт, К()11~::чно, должен 1 1 мет1,
разн 1м:.: 11омсrа. Только у одно1·0 нэ них -
Осла - fiудет rюстоннн ы й 11омеr 1. Зп:~чит,
OCi'ЗJIOCh nронумерова1ъ ра~1ич1 rы ми способа-
l';O
мн толы<о троих. llоэто му здесь чнсло 1юз
мож11ых перестановок - Р~ = !i! =6 .
ПЕРЕСТАНОВКИ С ПОВТОР Е НИЯМИ
Есть особы~-1 (11 очень и:Jжны111) 1шд nсрсс1·а
новок - 1U!jJ~cmcu-tOIO·\U с noшno/U!HШJ.MU. в Hll"X
сре;\и 11роч1 rx уч:~стнуют прсдмеrы. I1ер:.1злпчн
м ые межлу собой, - «бm1э 1tt:1\Ы •>. 3,-~мена Ol\llO·
го «близнеца" /\l)у1·им не nр тнюлнт 1\ rroвoi1
расстановке. П редположим. что. отчанв11111съ,
наши муэьша 1пы решил 11 соз~ать вместо rшар·
тста симфоничесюrй оркестр. Для этого Мар·
тышка 11ривела с собой сщt 1 '5 Мщтгышек.
Осi:л - е щё 20 Ослов, Козi.:л - 1О Козлон, шшJЬ
МИШК;J поленился и OC'l':IJICЯ н OJtlH·IOЧt:CTHe.
Выясн11м , сколькими сrюсоб:~м1 1 можно расса
/\И'IЪ l'IX 11 ряд.
Воз1,мём любую прm1:нюлы гую р;,~сст:11 ю11-
куrкех1С>+21+ 11+ 1=49муэыr<a11то11.Ес1111
бы «блиэ 11 ецон» н 11х числ е ire оказалось, то
перест:11ю1юк 6 ыл() бы 49!. Н о вот cpeдrt шrх
1юяR1rдось 16 О!{шrакоnых Мартыа1ек Нс тро
гая остадытых звереi1, а меняя м естами лтпнь
Мартыщек нсемн возмоiю rими способаr-н-r (а нх
будет 16!). получим вро!{е бы новые персс1·а
новки, но те11еръ уже нер:.1зличнJ1.-1ые. То есть
каждые 161 с1 ·арых 11ер<.::стан01юк лреобразу
юто1 н одну гюную и общее число 11tрес.·ганu-
1юк уменъша~тся R 16! раз. ОчеRнд1 ю, ·1·~ же ис
тор11я 11 с Ослами , и с Козла.ми (лнш1» Мt=две1tь
П()·11rсж11ему однн). В 11тоrе количес·п~о 11tре
стат-юноr< окажется р:1вны .11,;1
49!
16!.21!.11!.
Медведя мы н суч111ъ1вали , r ю, дабы не 1rару111ать
едшюобразl'Ш, добавим и е 1 ·0, т. с. лотtслим уr<а
з:шное выражение ещё на J ! = 1, что 1rичсго нс
~tсняет. А за п11сынатh это принято так:
Р
491
"' 1.4. 1и~~.
16~1·11·1 = lfi!·2IЧIH! .
Обратите щ rимание 11а горизо11та11 ы тую чер·1у
нцл букnой Р: с её помощью отли чают слу~1ай с
повторениями от обычных пеrеС'1~,шовок
Нетрmно получить и общую формулу для
случая, когда имеется /1 rрулп «бmrзш.:цо1н. со
Сl'Ь>1щих COOTBt"ГCTBCIJHO из k, , k~, "" )е// нсраз
JIJ/qнмых 11ре.цмtтuв:
(k 1 +/г2 +",+kп)!
~.1k. l.t" :
-'---------'-
k1!k.!! ... k/J!
Множество факториалов в этой формул~ ко1'0-
то может смутиТt" Н о ti комб:инатоμиr<е факто
рнал - •1астый rосгь, даже хозяин. К спжале
rшю. на ка11ькуляторе фу11кцил «факториат
обычно ОТС)'l'Ствует. поэтому при практических
расчt:тах приходится последовательно умно
жа·1ъ натура;1ьные числ<~. Занятие довольно
трулоёмкое - 1юпrюбуйтс, напр.им ер, вьгчис
ЛИТh Ч9 1 • Однако, ко 1 ·ю1 нс требуетсн ;1бсолют
ной точ.1юlти, !(ЛЯ болылих п можно с успехом
~1СЛ()Jн,;юnат1, фt>рмулу, 1<оторую нывел RЛ'VШ в.
11ютла111tский математик Джеймс Ст11рли1-1г:
()
1/
11
г
п!= е
.y21tl1,
Она прнмсчатtл.ъна пе тодько высокой точ
носrъю (уже np1111=10 ноrрешностъ м<::нее 1 '.Уо) ,
110 11 неожиданным присутствием дnух за м е
чат<:льных ц1.кел: числа Эйнера е = 2,71828." в
Перебор вариантов
ire меr 1 ее знаменитого л = ;), 1.Ч 1)9". (см. статы1
"числа тt», « Число е»). А 11роизF1еС'1· 11 11ычислс-
11ия по формуле Стт 1рmшга па хо1)()шсм l(а.111,
кутпоре t ie составляет труда.
251
Числа
РАЗМЕШЕНИЯ
И1ю 1 ·да бывает нужно 11з п 1н.-1еющихся различ
ных uбъсr<Тов отобrать произвольные т штук
(т i>; 12) 11 rасrюлож11ть их lj некотором поряд
ке. К:1ждое такое упорядоч енное расположение
назынастся /1аз.1и,еzцение.vи. Сколr,ко сущесr·нует
р:~:iмещепиli при :~адзшrых ·11 и т1 О r<азьшаетсх,
ответ мож1 ю /\ат11, ос1 юв ыnаясь па :нrатп-пr пе
реста 1 ювок
Обозна•шм 11с1сомое число .л;:'. Сначала
~юзьмём любую перестановку всех /1 объе1пов
11 рассмотри !l'r первые т И:3 них. Они образуют
разме щение т объектов из п И l\1сющихся, то 1 ·да
к:1к после11 ние п - т оnъектон сонер ш енно не
ш r инют н~j это размещен нс, как их ни псрсст:ш
ляй. Но этн п - т «хностоных» объектов мо1 у1
быть перс:станле11ы Р11_111 с1 юсобами. З 11 ачит, каж
дому разме ще1 1 ию мож110 <- 11р н1 r1 r 11ъ» Р"_,,, раз
личн'l-,!Х «XIIOC.TO\ '\», Ч\0 110\Х'>ЖJ\,'ает СТQТТЪК() же
перестановок всех п объектов. Общее число пе
рестановок ncex объектов Р" в та1<0.м случае рав-
1 ю произвсдсшпо ИСI<Омоr·о л::' ч:исла и Р,н":
!',, = л::'
Р,,_т.
Отсюда
р
п•
л::' = __
"_=
----
р/1 111 (11- m)! ·
Предnuл<>жим, что прохол•rт !iекнй конкурс r 8учd{1ник,щн
Олновре,1е ннu n puouли 1 cw u11кгори1 1 а : нужно уr,1л<нь1
КТ() JaCtмt'T u KUt tкypLe 1, 2 и )-е Mf'Пil . { КОЛЬК(J Btt'Гl>
<. ушс>ствуе1 вариантов ni RРтnв' О•1t·011111ю, ч 1n t1'Kt) Mf!f'
KOl\>iчeгrno равно •111tлу размешею1И и~ 8 пс~ .~
А~-~:;87Ь=336.
1l а;ю с1<азать, что некоторые сле1'ствия из этой
формуды до1юлыю неuжнданны" .
ЕСТЬ ЛИ У НУЛЯ ФАКТОРИАЛ?
Как nы думаете, сколы<I1ми сппсоf>ам11 можн()
выбрап, () 061 .сктоR r1з п r rмеюm;пхот. ющ
другими словами, сколькими способамr 1 мож
но не выбрать ни одного объекта? Uопрос. 1\О
неУно. странный, но формально получается
А') = 11!
=11!=1
11
(11- U)! п! .
П ()ж~1луй. это Jю1·11 ч нп· есть едннстRснныл спо
С()б не выf1рать ни одного объекта 11з 1·1 нмею
щихся - Н11ЧtГО Ht Дt:J l aTh.
~ТО\)()Й t\()\\\)ОС '. С\<()П11l<ИМН С\\ОСо6ами мож
I ТО сrtелап, упорЯ!\очс 1 ш ы i\ выбор 11:1 п объек
тов"_ осех п? Поступаем так: выбираем л10бой
объект, рядом с ним размещаем второй, потом
трt:тий и т ;i, . II олучается обыкноиеш 1 ая п ер е
становка всех п объекто13. I I ч11сло такнх пере
ста 1-ю1юк Р11 = п!. С дру1 ·ой сторо11ы , согласно
наrщсш юfт фор:\1улс, ·-это же число равннется
А11 = 11!
n!
11
(n- n)! О!
Пшrвнлосh новое выр:1же1111е ()! (ф:-~ктор~rал мы
011pei\eJJял11 только для натураль11 ы х ч1 1 сел),
Предположим, ч·1 ·п О! - это ка1юе-то 1 1еизвест-
1юе ч1 1 с1ю , и 1 1 ай,f\ём его н1 равенств:~ л:: = Р,,,
Тогда п!/О! = п!, откуда О! = 1, т. е . факториал
пуля равен единице (хотя казалось, ч го это не_,
прсмешю должен б ьпь нуль) . Факrориi111 нуля
во:шикает в самых раз н ых комб1111атор11ых
задачах. 1ю везде 11 всегда его пр 111111 маю1
равrrым сдrrнице.
РАЗМЕШЕНИЯ С ПОВТОРЕНИЯМИ
Пом1 1 мо обыч11ых размеще 1 111й быnают 11раз,
л·~еще1tиЯ с поатореттми (ТО"ШО так же. J{ЗХ
персстаrюшш) . Пусть имеется 11 разлнчнш
объектов. .Выберем из них ;п шrук,действуяпа
следующему nршщи11у. Возr.,.мём любой. но~
будем устанаnmшать его в какой-то рнд, аЩ»i
сто залишсм под номером 1 е1·0 н;.~знанне,с:JNo
Кажлыn объе~1 после • Исnол ь·юеания • возврJw~J.ется обратно
и v.o,;.er f>ыть • И<:шм~ шван. 11nвторнn.
же объект после этого nернём к осталыrы .>vL За
тем опять нз ncex п объсктоn Rьrбсрем оди11 (в
том ч11сле, возможпо, 11 тот, который был толь
ко что взя·1·) , за11ншсм его назв~1 ние, поисти1:1
ном еро м 2, и с:нова нернём объек.vr обратно И
так.далее, 11ока не понучнм т шtзRа1п1й.. Раз>v1с
щешrя с понторениямн обозначаются Л,~1•
ОпрсдСJ1итh это число неслож1 ю. н~1 1 1срвом
месте п с1тиск~ можеr находи·1ъси л юбо!I И:'! /1
объек1он, нз uтором - тоже любой:, и 1ш тре
тъем, и н:1 ч:с1 вёртом... n общем, пз кажд()м .
Поэто."'1У чнс.ло размещетu1 с nонтореrшями
выр.tжается формулой
л,;" =п":
Зам<1'Им, что здесь,11,оnуег~rм случай. кor)\<i т > 11,
т е 11ыбр:нн 1ых объсктон болыuе, ч~м их всего
11.,11еt:тся Это щ::уд11в11 •rелыю· к:.~ждый объек-1
nосл:е " нсnо11ьзоJ~а11ия> возвращается обратно 11
1южет быть •·11сrю;1ьзоnа11-> поuтортю.
РЕШЕНИЕ ЗАЛАЧИ О ПАСПОРТАХ
Давайте определим, сколько может быть пас
портов советского образца с различными Сl'
рия,\.1 1 1 и номе рами, сели зафиксировать рим
скиt ц11фрt>1 серн и. Ое1'акнся J\l~e русские буквы
СОЧЕТАНИЯ
В 11екоторых :задачах п о комбинаторике
не нмсет значения порядок расположения
uбъекrоn в той нли иной со1301<утпюсти. Важно
Перебор uариантов
и шсс1 ь арабсюt х цифр. Рассrvютрим букны 11
цифры отдель110.
Буквы. В русс1<ом алфавите :):) бу1Фы Н:Jм
нуж1 ю выбрать любые две, 11р11 этом 011и могут
оказэться н одшr~1ковыми. 01<..'до вателы-ю, 11м~
ет место размещени е с повторен1шмн, где
11=33ит=2:;ц"=3У =1089,
Цифры. Здесь выбr 1 р~1ется ( 11 опятh с по
нторе11иями) т == 6 ц1 ·1 фр r1з t1 = 1()но:~ м оЖJ 1ых.
Д•JН Э'l'Ol'O CC'l 'I " А~;) = 106 CПOCOOOfl.
И·ror: пос1со11ысу каждую 11ару букв можно
сое,~шштт, с любой шестёрrю!"1 цифр, то воз
можно сущеспюuапие ;ц~ А~п = :3~z IU(' =
= 1 089 UUU ООО nаспортоu, нмеющих о,rцш н те
же рнмсrшс.- цифры серин, - больше ми.ruшар
да1 Ну а сели потрсбонать, чтобы JЗ ка11щом но
мере 11 букны , и 1~ифры быmJ разJ111чт 1 ыми , -
скол1,ко тогда 11олуч11тсн 11 асnоrто в ' З1~ссn
вместо размеще ний с понторсн 11J1м1111ужно1-1с-
1юлъзо11ать обычные р:.~змещения ГТоэто~ч' от
вет таков:
)3!
LU!
331 1О!
=
0:3-2)! (1О-6)! .)1! · -J.!
.
Сделайте 11ыч11слс1111я са ми и сра вните nолу
чеш rый результат с предыдущим . ЧнСJю зна
чит~лыiо уменьшилос!'>, 11t: nр~1вл.<1 ;ш~
липrr, то, 1<::1кие 11 меr 11 ю ;.,ле мептr,1 её составля
ют. К примеру, прет~.стаnнм себе штсолы 1 ыl1
класс. который прншёл n спортзал. Школы шю r
2'5:~
254
Числа
КОМПОЗИUИИ И РАЗБИЕНИЯ
Р аз611вuт~, 11а отдельные част1-1 можно нс толькu мно
жества, но даже числа. Рассмотрим натураль ное, т . е.
uелое и положительное, числоn; его можно предста
в~1ть в в иде суммы нату ральных чисел раз~ 1 ыми спо
собами, напр имер:
4= 1+1+1+1= 1+ 1 +2= 1+2+1 =2+1+1
=2+2=1+3=3+ 1 =4.
Скольк им и способами мож~ю представить п роиз
вольнuе натуральнuе п в виде суммы из k н ату
ральных сла гаемых? Подска'\ку дает дре внегреч еский
математи к Лиофант Алексаt-tлрийский; од1-1 а из его
книг начи1iается фразой: «Ть1. конеч 110. знаешь, что
каждое uелое есrь просто не1<.оторое коли чество еди
ниu » . Вот и изобразим числоп в виде совокупности
п елин иu:
111...1.
А теперь расставим k - 1 вертико:~льных палочек в п -
-
·1 промежутков меЖАу этими елиниuами так, что бы
две палочки не попадали в олин промежуток:
11... 111". 11 1.. .11" . 1.
У нас получилось ровноk гpynn, в кажлой из которы х
сnдерж1пся некоторое натуро:~льное чи сло единиu
т,(i= 1, ""k), r. е. п прелставле~ю в виде суммыk
слагаемых: п = 111 1 + т1 + ". + mA. А скuлькими сrюtо
бами можнn осуществить такую расстановку, мы уже
Jнаем - это число сочетан и й из п - 1 элеме нтов
(промежутков) rю k - l (Па/\ОЧСК\, Т. е . С~-:.
Такие предста6/\е11и я числа уn орядочен 11 ыми сум·
мами сл<~гаемых ~1азываются композициями. В атлн
чие от композ~ш ии раэбиt>ние чи сла есть eru предсrав
ление неупорялоченно11 суммои слагаемых, например.
4=1+1+1+1=1+1+2=·1+3=2+2=4.
Разбиений, как о~tлим, меньше. чем комnо1~шиИ.
А вот удобная тuч 11а я формула лля их числа неи3-
вестна. Индийск и й матемап1к Сри нив;~са Рамануд·
жан и его английский комега Готфри Харолл Хары1
t-овмсстно получили первые приближс1111ые формулы
ллs~ Rл - количества всех во:~можных разбиени 11
числа п. Простеишая и1 этих формул выглядит так:
1 к111
Rn ~ -,_-е \J
4 v3п
1000
i
CfoO 1
16.н 1
ro2f
to.:f
+:t
JOO
:оо
,,.
rr
JO
;<>
1"
tql
1"'
Сколькими способами можно nредстав11ть л.н 11юс • 111сло в в1ы1
t.уммы рJJлич11ых натуральных! С1ра ниuа из книп1
Якоба Ьеорнумн ~ис.;усrпl() nрелl'\с'lлОж!'нии • 171 \ 1
"101·у·1· выегроитьсJ1 в 1uсrх"нгу, а мшу1· бс1·;111>
1'Jtc 111 нrало, rrpыJ·a1ъ, .к:увы ркат1,с>1, стонтh н.э
тлояе, лазать 1ю к:Jнату- всё равно они ост:~-
11утся 1ем же с;.1мым м11ожестном учсн11кон
1\Лзсс1. Tenepr~ часть Ir:l них nсреве;~ём н сосед
нее помещение, где им т:ноке до~nоляется
беJ ЗТ!>, П/)ЫГаТr, И Т. Д. Т~u<ая ВЫбОрка ЗJJ<::Ме!ПОВ,
при которой их поrядок соuсршсщю неважен.
11,1зывастся сочшпаNиu.м. Число вссво3можпьL'С
сочстани 11 113 Jl элс.--~снтов пот обозначзстся
с;,п. flc>11poaycм 1-1:.IIJTll ЭТО ЧИСЛО
Ьудсм oct ювываться н:;~ тол1 , что нам 11зн<::ст-
110. 1-1:.i р<i:-1мсще~п1ях и переtтанонках. С11<1ч;1.11а
нз 11 элемс1~тон 1>ьщслl'1м какш.--т1бо m энемен
тои с ~'Чёто,\1 очер~д1юст11 uыбора. Это - р:1:зме
щсш1е. н чиою таких размеще 1 шй л:;1 , Очещ щ-
1ю, что разлт1°1ные размещет 1 я, в которые
nходят те же объекты. 1ю в ином порят~ке, будут
соответствоn~пь одному сочетанию (r1ед1, п со
четании порядок роли 11с играет) Друт11ми сло
n,t,\Ш. любая псреста~ юnка выбранных т :~ле
ме11то1i 1юрuжд:н::1 1·0 же: самос сuчtта нис. Но
l';JKHX 11ерес1·;.~новок !',,,. ГIОЭТ().J\1}' Ч l lCJIO Cl)ЧC
T:lHТICt нз 11 элtментов по т в Р", раз мс:ныпе
ч11rла р:1змс:щс11111\ ·1. е.
lll
ст11
"' r1.::' =(n- m)1
Р,11
т!
m!(n - m)!
Jt!
Uбратнте впнманне на сrюеобразную снммет
ршо э·юй формулы: сели заменить т пап - т,
получится то же самое, только ф;штор11алы n
знзме 1-ттеле поменяются .v1ест:~ми. Отсюда слс
,1,)'С'I замсчатею,нле свойство сочетан11й .
Перебор 1мриdнтов
Объясняс.:тся это n росто· каждому сочсташно нз
т отобр:н 1ных эл<.:мснтов nссгда соuтвстсmуст
сочетание 11з п - т ост:tнu 11 1хся. Так что ·v~ож-
1 ю с самого 11ачала 1·01юр11·1·h 11с о 11ыдсл <::н и11 т
об-1,с1< 1·он 11;J 11 , а () ра:~б11с11нн множt:ства нс
хо;ц 1ых н элс.:.ме 11т()11 (11э11римср, тех Жl' шко111.
ш11юn) 11:i лве част11 - щ) т 11 Jl - 111 11 каждой
(тчещ)Rек- вOДJllТЗ:1Л,а/1- т
-
в /\Р}Тnй).
По11ытаемся тсnеръ ответнт1, 11:1 слсдующ1 !Й
1.юnрос. CKOЛl>IШMII сnособам11 11 ШКОЛЫ ll Н<ОD
мшу1· ра :щслиться по t з:.~л:ам так, чтобы в пep
IIOJ'. -t з~uн: оказШЮСh т, ШКОJIЫ I ИКОD, !Ю nтором
11·1~ 1r ·1 -д.. 1·де m 1 + m~+ ... + m,=11? Обо:{начпм
l\Cl<OMOt: чнсло чсрtз с;;11 111
'
1111
• К: 11 < CI'(.) 1юлу
ч111 ь? С11ач;~л:1 11:3 uбщсr'о кuлнчсстн:1 11 н1коль-
1111кон 131,1;1<::.лим 111 1, потом и:-1 п - т 1(к-1·акшихся
т2 11 т. /\" следоватсJJьно,
( -.n1
1
111,
'11
С"''n- m 1
С"''
"'
п т1-ш"- -nlt 1
т11 111/ "т,!·
У11111:1итеJ1 1,но· ~отя мы 11с.: рассматрн11ал11 н1ща
ю1х п ерестановок 1t все: шкuлышю 1 заnедоr.ш
р~1зныс . тем не менеt: выведена формула. точно
ПОН'l'Ор>!ЮЩ:.IЯ формулу /l,JIЯ YH<.' J l;t l ll'JX'C'l 'a!IOUOK
с ПОК'Т'ОрСНllЯ,\11 L А нс(: )\CJIU в том. Ч'J'f) да11ную
аа;1~1чу можно траr<ТОНа'IЪ ДIЮЯКО с OДH()t't СJ'()
ро 1 1ы, мы распредетн::.м nтJн-1чающнхся друг от
лруга пn<0лы11що11 11<1 зал ам . Тог/~.а ттолуч;нотси
сочетания. Но оп 11пrе,ч с итуа1 ~ию по-;~.рутму·
мы J{<J.f< бы 11аспредсляем срс:цн 111ко111,н1 1 1юн
билеты в разны е залы. 1lрнчём биле'1ЪJ н оди н
зал пеuтт1чиV1ы друг от друга. :?то уже пере
стан.онкн (билстоn срс;~.и пuстрос1 шьL"'\. в рRд
школы111кон) с гювторсния"1н.
ЗАЛАЧА О /\ОТТО-МИМИОН
Сlшт.ко кар ~ o<it:к Л11по-М 111111 11011 11ужJ10 ку-
11111Ъ 1-1 З~IJJOЛI IJ 111" '-f T()fibl 11а ТIИХ ок:1эат IC'b нес
тшмfн 1 н<1ц1 1 и 1 ю 6 номеров rтз 49 11оамож111.1х'
Понятно, что колт 1 чес11ю карточ~:к 1х~н1 ю ч11слу
сочета1шlr из 49 элемептоn по 6, т. С'.
С'' - 491
'" - 6!·Ч:-S!
<1 ::1То сис1 ·аш1яе1 · 1ючт11 J-1 млн_ Можно с;tелать
нын<1д: /1.лн решrнзац 1 1н 1юдобной 11дt'11 уже н~що
быть м11люю11ср<1м! Но 11 н этом случш:~ раэ-
60 1 ·атсть fiудст трудн<1, поскоm,ку вьн1 1 ·рыш
Числа
-г.- •
-
111 х
-
·· ><Х!
-
)(1 )( ,,
-
•
••
JdПO\HPHHdЯ
1<ар1очк,1
Лотто-М11мион .
пс фпкснрин:т и в каждом тираж(; на пр11:ю
вой фо1щ OTIIOJ( HTCH ЛHIUI~ ч асть собра нной ОТ
11родаж 1 1 билетов суммы.
лоnробуем ответи ·п> ещё на несколы{() во
просов. ДonycTl!M, МЫ КУПИЛИ С'.~9 Ka[Yl"OЧeJ.; 11
вес 1rx по-разному заполт~или. После тиража()
t:Ч<H-'Tm 1въrх помероn окажется толпко на одной
1rз 1111х. Но n Лотто-Мил.1111011 выиrрывают н
кар>rочюr с совпаr~ением 5 и даже 4 номеров.
Сколько lL"'\?
Есш1 на карточке у1·адано 5 номеров, это
значит, что из 6 выпавших номеров здесь мо
гут быть вычеркнуты любые 5. а 11з осталы-1.ых
"13 - т1шь l. Поэтому чнс;ю способnв у1 ·адать
-
G'~ G'1 Т
" но~1ероR равно 1, ·
1 .~ · очно т.~к же карто-
чек с совпа;_1еrt11ем 4 1юмерон буде-1· с~ .cf~.
Наконец. на С~\ 1<арточках не сжажется ни од
ного нып:шшего номера. Кстати, это болытте
или мerrыne половины от количества всех куп
J1е11111.1х 1<арточек? Попробуйте сначала угадат~",
а потом проверьте себя.
СОЧЕТАНИЯ С ПОВТОРЕНИЯМИ
И щ:рсстанонюr, 11 раамсщсния могут бьпъ с
1юнторе11иями. Имеет смысл гоnоритъ 11 о соче
ттшя.",с с повторе11иями. Из м1южес1 на, содер
жащего п предметов. возьмём один nроизвот,-
11ы й, защ:сём е1·0 .u с11исок, ноа 1 е че1·0 верt 1 ё.м
обрат~ ю. За·1·ем точно так же 11ыберем ещё оди11
объект 11 т. д" rюка 11 с11иске не окажетсн т 11а -
1 1 мснованm! (Среди !!ИХ могут быть И ОДИПаКО-
256
вые). Приrп\11rшалr.11ое nтлич11е от ра:-~меще1~11\1
с rю11торt11ияУш заключается в TOJ\1, что в ,ri;a 11·
11ом случае элементы списка не нр.1еруются.
Например. спис1<И « А, Б, А, 1·" 11 <- 13, Г. А, А» счита
ются одинакоными. Попробуем 1ш1ти чнслu ё~"
сочетаний с повторения.ми 1-в п элемс::11тов no
т. Дпя ::1того пr 1 щс.:тся прuявитъ uпрслслtнную
изобрстателыюсть. С',лсдите в11нмателъно.
Прои зволь но пронумеруем элементы 11с
ход1юго м~южеств:~ числам11 от 1 до 11. Пусть в
какое-то 11з ттолуче111п.1х сочетатшй no1uлo k1
элементnв под номером 1, k 2 элсмс t 1тов ПО/\ 110-
мером 2, " ., k 11 элементов под 11омером 11. Что
можно сказать обо всех этих ч11слах k,? Ясно,
чтосуммаk1+k~+". +k11 = т (nед1, в списке
все~-о т об•ьектовt) .
Теперь и зоб рази:-1 это сuчtт:~н 1 1е в виде
цеuочки н ~i нулей .11 еднннц. Ел11ш1щ1 здесь
будет обоз н<1чать каждый отдельный эле,\.lент
сочtтання. а 11у111, - с11мволн:~11ровать гр:тнцу
межлу 1·ру111 1 ам1 ·1 ЭJ1ементон, соn·1·ветствующ11х
соседним k1• Ecm·1некоторое k1: О, т. е. элеме11·
·1 ·пв с 1юмером i в сш 1 ске нет, то в соответсrву·
ющем месте цепочюr окажутся два morpa·
НИЧНЫХ -> пуля подряд.
Итак, з;.~писъmао1: спачала ki едш-шц, затем
один нуль, после этогоk~сдшнщ 11 с1юв:~ нуль..
k11• 1 едшmц11 от1тп нуль, наконец, k11 едшнщ
и всё.
Поскольку сумма всех k, равн;~ т, в по
строенной цспочкс содержится т ед11н1щ Ну·
лей же 1t - 1. Так что нся 1~епочка сuстоит
НЗ17+/11 - 1ЦItфр.
ПодRедём итог. Каждому возможпnму сnпс·
1<у 1юс1·а uле1 ш в соответствие 11екоторан цепоч·
ка 11:{ нулей и единиц длиной /1 + т - 1. При
этом еслп /Щtl списка о,1J,ин;:щоnы, то 11 цепочки
получатся од1шакоnымп. Верно 11 обраnюе:
каждой ценочке соответствует опрсдслёнпЪ11!
список Haripи."1ep, 1 ~с 1 ючю.1 1111 OU IOLO гово
рит нам. что 1J списке - четыrе ::Jлеме1т
номер 1, ни одно со э1н.:мента ном ер 2, по од·
11ому элементу номер 3 н LI 11 н1 1 одно!'() эле,
мента номер 5. Таким образом, зздача свелась
к поиску отnета па nопрое: с.колы<о можно со·
егаш 1т1) различных цепочек длтю\"1 11 + т-1
ffЗnzедншщип- 1нулей?Аэтонечтонн~
как число перестановок с повторешшм1111зт
r-rуле:й и /2 - 1 едишщ. т. е. Р111, " 1• Поэтоыу
(11+т-1)!
11~(11 - 1)!
И 1·:1к, фоrмулы щтя 11еrест:шоnuк, р:1зме1цс:ннй
11 сочстанJJй (с 1юи'юрениямн 11 без) обн;1ру
жин~1ют TCCI 1ую связ1, МСЖ/J,У OC I IOIJHЫ!\111 ГIOll H-
БИНОМ НЬЮТОНА
~ал гебре дnно; 1 ыю часто 11 рихою,1тся козкп
д11·1ъ 1:1е1 ·еr1сг1 ь11.13учлен а+ /1. Н сларом каж;\ы/'1
111коJ1ы-1ик зауч11Rаст н~н т:~ус1·1. формулы ква;\
рт1~111 куба суммы двух чисел. 1lомн1 1те, <>~tlЗJ\
paт перво1·0 чнсл:з 1 щюс у1 11 юс:тпюе 11рон :~всде-
1111е".» 11 ·1. д.? А11 а1юпrч 11 ая формула , 110 уже для
пrю 11 з13ол 1.1 юго11 > О на~{ынается бш1амам Jlыо
шона, хотя и была 11зв<:ст11а зщ~.ош·о до него.
(Слово « би110м » п псрсrюдс с латы1111 о:шачает
•дnучJ1е11 ».) Фоrмуш1 эта 11меет 11 рямос от110 1 11е
нис к комбнн;,~тор 11 ке.
Дпя у;1обс1·11а ~' kЫражен 1 111 (t1 + l?)
11
1:1n11 1tте~1
f/' за скобю1 11 обu:1нач11м a/h 'Jercз .\". Получа-
тннмн кuмби11атор 1 1ки . Э 1•1 1 формулы состан
.rн1ю·1· с1юего род:~ ~1 зfiуку комбнн ~пuрнкн , 1ю
ско11ы<у нз 11нх ос11опэгю решсн11е 60111)11111н
ства mкол:ьных комбнrrаторпых зада ч.
етси 1711
(.\: + 1)'
1
.
На Rремн забу;\с11,1 11ро множ11-
теm, 1711 н бу; \с.м 11ск~1т1, фоrмулу /(JIЯ (:'· + 1/ .
Нстру;\но /(<1Г«IJ(a'1·ucя , что после р:~с1<р1.1тн>J ско
бок nep<.: .,r\ 1 1 ам11 пpeJ1cra 1 1ет м 1 ю1·очле1 1 н-й стt
nе11и. HyiIOIO ·1 ·олыю опре;\елптr, коэффит111 -
еrпы пр11 раэл1Iч 11 ых степенях х.
Поступ 11м С'1С/1,ующ1111.1 обр:.tЗОJ\1. Вытшн: м
прои:1всll,еш1с 1 1 з rт скобсж (х + 1):
(.'\"+ 1)(Х+ l)(-'t+ 1)." (.У+ 1).
l'<:'1 н:pn раскроем скuбюt, но 1 1 rн ::этом 1 1с б)дсм
11р 11во1\ить 1юдобны~ члс11ы. Напрнмср:
)
'
(Х+1( =(.\'+ 1)(Х+1)=х-+Х+Х+(~
'•
(х+l) = (х+ l)(x+ l)(x+ L)=
= х'+х
2
+.У!+х+х
2
+х+х+1 пт.д.
Есrсстnенrю, rе::1ультат 11редстзвляет co бoii
сумму l(~ШНХ-ТО C'l'CПCIJC(I ,'> . .' ( 11 ТОМ ЧIJСЛС 11 11}' -
JlCBOЙ, Т. С, 1).
lJ:~конец, соберём щ:с х rro 0111шакоJ3ыJ'1 стt:-
11 сням н 1юJ 1 уч 11 м м1101'очлен n- lт сте11енн уже н
11р1 шыч11ом kll)(C'. Ясно, что коэффшщент пр11
::-/" бу;1ет ранен ко1 1нчссr'ну слэ 1 ·асмых "\
111
н 1н.~р-
1ю11ача1 1 1,1юм , 11~пр1111е1~<.:11 1 ю~1 шще. Сконuко
их? !iщё 11е :тая, как отuе111ть 11а :')'ГОТ rюпрос,
МЫ )'ЖС Ч)'J:JСТвуем, ЧТQ перед 11ам11 KOl\1б11Щl
TOJl11'1H з~ща •ta".
БИН ОМИ М ЬНЫЕ К ОЭФФИUИЕНТЫ
И СОЧЕТАНИЯ
После r1сrсмножсния п скобок (х + 1) любая
ПОЯВ 111JШ:.IЯСН сrспе1-11, х JJOЗHIJl(J]:l IOJJ< про11звс
/1,СIТJ1е ll COM I J(JЖllH::Л<:: r1 по сщ 1 юму ОТ К<IЖ
дой CKOnКl l. Н() 11Се COM I IOЖ l l'l'Cffi1 раl!ПЫ ЛllбО
х, лпбо 1. )J;m пшт мешщ m - I1 степени х необ
ходимо, ч:тобы rrpи перемножении ровно пз т
скобок были взяты сом.ножптели .х. а нз остал1.
ныхн-тскобок
-
1. Сколышмн способ:~ми
:vюж1ю выбр;1· 1ъ т обы;К"1·ов (к дашюм случж·
257
1
'-
Числа
ТаЬн1а
Com~in111ioшtm , /(и Numerorиm FigNr 4NrHm.
Exp1J11elu1 Com6iшtJiм11m.
11t1 11. 1ш.r1~v. 1vr.1v11.1vш.11х. 1х. 1хт.1 xr1.
1.1!1!olololol olо! ololololо
iз..ll1l1Jol ol ol ol ol olо/о!olо
~.].IТ!Г2Tllol ol olо/ о[ olololо
~-4.lf!-I31JIrlolololо!ololо1о
§r.!1114161411/01ol ololololо
~6.1'115110!10/ rl11olо/о/о[ol0
;. 7.f:rl6/1rГzolrrl 61 11 ol ol olо! 0
~-з:н117Izl1н1н1111 7I 11 о1о1о1о
~ 9.l/1IS/28 I f61 701 561 2-81 81 -cl о1 oj О
•~ 10.ll1/9116I 84 l1.2ь1126 I 841 з61 9111 i;,I о
rт.111(io/4r 1110121QJ2p.l21011zol -4r , -10Гi1 о
12~1/ 11z1/ rr /r6r/нo/46.z/46.zl но/16-r·/ rr / 11 1 1
ТаОл1ю J 11и 11омиJАь ных к1JJфф11UиР 11rое 113 кн11r11 Якоб01
Бернуми "Ио<у е,(' 11ю 11f.1едположениИ •. 171 3 1.
скоfiсж) из 11 возможных? Или, другимн слова
ми. 1<аконо с111сло сочетаний пз п элементон по
т' Ответ мы знаем: с;:1 • Итак раскрыв нес скоб
I<И. ПОлучТТМ с::' CJ1araeMЫX, paBHbLX Х
111
, И, ЗНа
ЧИТ, после приведения подобных членов коэф
ф1щ11ент 11р11 :х:"' равt:в с;;1 • П о::этому
(.'\" + 1) 11
= c::xll i- c::- 1
xr1-I +с:: ~.\: 11-~ i-
G• l. G·t1
+". + ,:,л+·11 .
Так как чнсла с;;1 яв1~.яются коэффициентами
в формуJJе би:по!\.tа Ньютона, опи назыnа.ются
бипо.миалыtыми к;озффицuетпа;11и. Попробуй
те выписат1) формулы б~нома (х + 1)
11
для не
которых кон кретrrых зна чений х, н~ арю.tер
для х =о, ±1, ±2, ±1/2.
Нетрудно вывести подобную формулу 1111.ля
(и + Ь)". rLало только всnом1-1ить, что a./h = х н
(а + Ь)" = 1/'(х + 1)". В резут,тате получим
(а+ l:J)11
= С"а" + С"-Jа11- 1ь +С" 1а'.,_2Ь2 +
"
1/.
fl
+ ". + с,~аь"-
1
+ с::ь".
Проверш.1 данную формулу для п = :?:
(а+fJ)' = С_~а' +Cta;.h t-(.'_~abl +С~
1
1/'.
Поскольку
с!=С.~1=~=1ис:=с11= _i._ = 3
'
'
3!·0!
'
2!.J! • '
слсдовател ыю,
258
-
ЗН:!КОМая формул~ куба )\B)'4!1Cll:.I!
Фuрму11<1 бннuма НЫОТОJ ta ПОЗНОЛЯе'I' обна
ружнтh важную за1:1нснмос1·1, между бн1-юJ.щаль
ными коэф1шщ1снтаин . Р:ксмотрим фпрмулу
для (х+ 1)"
1
•
Чt:му равен 1ю~ффиц11trl'I' 11 р11
х"' н ? Яспо, Ч'J'О это с:::71 • с друm.й стороны,
1111
(х + 1) мшю ю получить, умножив формулу
для (х + 1)" [!а (.х + 1). Тогда (m + 1)-я стеле11ь
числах может быть п олучена 11ибо прн умно
жении слага<.:мо!'О с;;1х"
1
на х, л1160 uμ11 умно-
,.-·щ +t JIH]
(·п
l••ф
жен.и11 \," х
на . . . о::этому коэ<~:- 1щнент
c;;~~l t R формул<..: /(ЛЯ ~Х + 1)
11 1 ДОЛЖСll бЫТЬ
[XШCIJ сумме: с::' И с::'+ ,Т. С.
(")
ТРЕУГОЛЬНИК ПАСКАЛЯ
Формула (*) п озволяет довол ьн о лешо посrро
ить табт,щу биномиальных коэфф1щиснтов.
не Rы11исляя их 1 ю отд<::л ьн ости с 11uмощью
н!
громоздкой формулы '(
)'. Н ачнём с
т. п-т.
тuro. что Rышrшем в одну строку бесконечное
ЧI IСЛО 11:ущ; 1:1 н 1'0Jli>1(0 одну един~-щу с реди llИ:X:
оооо
оооо
Ниже СОЗ/\адиь1 вторую строку чисел, за1111сы
nая между каждыми двумя ч11сJ1ами n е рво11
строкп 11х сумму. Затем под ~порой егрокой
запи111ем по тем же 11раш,u1ам третью, че1·Rёр·
туюИТ.Д.:
о()оо
()ооо
ооо
1оооо
о()о
21о()о
о()1331о()о
оо
464]о()
u15101051оо
lJ161')20156
о
721.35.352171о
С м отрите, как стрем1 rтельно увеличин;1ются
н<:нуленые ч:1. 1с1 1а, распш1заясь .н~11х1 1ю и вле110'
Чтобы на1 ·тщнее прL:дста..вить резуm,тат, со
тр6·1 все t1 ym1 , а строки 11ро11умсруtм, 11ачш1ая
с 1tуля (рнс. 1).
Впервые этот цифроrюй тре)толы шк под
робно описал французский математик Блеэ
Паскаль в своём "Тра1<тате об арнфметнческом
Гleppfiop вариантов
Рис. 1. Трtуго~ьн11к П;~r~,м11
Числа
ТРЕУГОЛЬНОЕ РЕШЕТО
о1
1
111
2
112l
3
11331
4
11-i6-i
5
115
6
7
8
9
10
11
12
о1234;67891011
Злесь rрl:'уrольн и к П аскаля и 'юбрi.iжен нес колько
НЕ'Оfiыч ным обра:юм. Во-пе рвых , строки сдви н уты
i JK, что первые :элементы образуют месенку» со сту
n еньк.~ми размсро....1 в лоа шага. Во-вторых, те эле
мент ы, которые делятся на номер своей строки k, от
ме'1е 11ы зелёным uостом, а те, которые не л<.·м1тся на
k,-
крас ным.
Нако н еu, с:толбu ы также были пронумерова н ы
числами О, 11 2, ... При этом цвета ис п ол1,1овал ись по
tледуюшему r1рин uип у: если все эле ме нты таког о
«Сдви11утого » треугольн ика Паскаля, t нт ш ие в k-м
треу1 ·ш1ы11 1ке-> (ОL1 уб1111конан н !(')()') 1'.) . С тех
nur OJJ так и 113ЗЫ8астсн - 111/JГ!)'lH//h////h- Пас
л:алн. Н 1;;ско; 1 t.ко нные riарна11ты Э'f"nr~r т:~блн 1(11 1
былн 11з 11еС'т11ы 1-пат)mп1у Н1 1ююло Ta pт::im1c,
п ерсидс 1<0му поэту и учё~-юму Омару Хай яму,
ю1· 1·айо<им и 1 11 щт 1 rкким матсматнкэм.
В треутолы 11 ше Паскаля п -я строка содержит
-
фф
сп с.·1 .2
G'/J
онномнальн1,1с коэ и11ие11ты ,", 11 , с"'". , ' " .
Это следует из фо рмуJ1Ь1 (*), которан примс11и
тслы 10 к пuс.:троеш-ю 11 табш,ще uз 1тач ает, что
каждое LH ICJIO ранно С}'Ммс днух иы1uестон щ11х.
Трс:уrолы111к Паскали u611алает мнuжсспюм
заме чательных с 1юйств. Напр11 мср, сумма ч1 1 -
сел 11-й срuк11 трсуголышка раш1 а 211
•
Чтобы
1~( 1 казал, это, доста·юч1 то рассмотрt~ть 6111юм,
у кот()роrо а= /1 = 1. С ощ ю1I стороны , оп раве11
2" , а с 11ругой - сумме нсех 6ппомиалы1ых ко
эффициеrпоn этой строки.
2()()
Дру 1·ос свойство: тсоличестгю псчётных сш
сс:л .13 п - й стро1<с rк<.тда равно сте 1 1t:1 rи двойю1 .
1
lU1051
)1615.201561
117..п35.352171
11 8 28567056288
1 1 9 3684126126
11 1045120
11 11
12131415161718192021222.~
полбuс, зел~ныt:', то k - номер стол61J.э
-
тоже
1еленый; есЛ11 хотя бы олин 'Эl\емент в столбuе крас-
11ый, -т 1-1 номер этого столбuа крас11ы~.1. (,)собым11
слу•1аs1 ми остамкt. 1 1 срв ыс два c-ruлбua.
Вы у::~наете "lеле НЫ(:> номера столбuов? Ла, это nr.ю
сты е чисl\а, и только они !
Самое уди ни rcлt.1 юе то, чтu, несмотря н а Gолес ч1щ
трёхв екову к1 историю rреугольн11к<1 Паскаля, f'1 ·0 rвнзь
с простыми числами обн<1ружилась лишь в ХХ в"
причt:•м Сl\у•1айно. Её открыли в 1972 г. Г. В. MJ1111 11
Л. Ш е нкс, отлажива$1 прогрdМму ~1.1 компьютер<:.
-
2"'
/,
f)()J tee TOl' (J, 011() [l~I кн о . 1';'\t: !?.
-
ч 1ICJIO Cl\llНll tl
н ДIIOl·IЧll()Й Э ~IПllC'l l ЧIJСЛа 11 . llзпр11мср, 5-я
строка силс:рж1 1 ·1 · ч11сла 1. ~. 1п. in. S, 1, среди
t<пторых 4 11 с-чёттщх. R то же 11ремя число Sв
дrюн"п ю1~1 о ~стеме сч исле1 п1я ~а1 1 НС'1>1п~1стся как
10 1. Число 1 01 СО!\ержнт1. ед1 11 пщы, 11 21=4.
Дою1за·1ъ это с войство l'OPilЗ/10 С.'ТОЖl\СС. ЧС~I
псрrюс. ~ели читатель 1 юзьмётся за дока:~атсль
<:пю• .1ют пuдска:жа : строки 110;~ 11ом<:рам11 2'" -
-
1, I ЛС /17 - 11атуралы10t: , COCT()JIT ТШIЫ(Q JJJ
нсчётных 1 1иссл .
J:щё от11ю свойстно трсу~ ·с mы1 11 ка Il аска;н~
в каж,тщЛ строке.: сумма ч11ссл , стоящ 11 х щ
н<::чёл 1ых .местах, p::i вна сум мс ч1 ~ сел, стоящ1Lt
11а ч ётттых местах. Чтобы yne11,11т1,01 н :ппм. рас
смотрите бином, у t<()торого rt = 1, fJ = - 1. Кро ·
ме то1'0, сел и 110.мер строю~ - простое ч.11с.10,
то все числа в строке, з::~ r1ст<люче1rием дuух
крайних е;\1 11 шц, делятся 11;i 11омср строкtJ .ДО·
ка:.iать это Т()Жt: Н t:СЛОЖJ ю.
ЗАЛАЧИ ПО КОМБИНАТОРИКЕ
Прн ptr11cш11 1 комби11атор1i 1 11х :Jа;~ач очс r-11,
r~ажпо умело приме~шть нзвестные формуны.
rro ещё nажнее уметь комбинаторно рассу?к
даrъ, 0611аружиG<НJ n необозримом rта нсрвыИ
нзгля[(мrюжсстnе 1шрнантов впутрсшшй норя
до1' и простоту. Хорошей ю1люстр;щней к ска-
3:шном} .можс:т служит~, класс ~ 1 ческ.ая задача о
разбисн ин 111юскост11 11рямыми.
ЗАЛАЧА О РАЗБ ИЕНИИ
ПЛОСКОСТИ П РЯМ ЫМИ
На сколько частей разбивают ллос1<ость п пря
мых, ес,11 и н 1 п<аки.е две 11з них не параллельны 11
11 ик:1ю1с три нс проходят через одну точку?
Попробуем сIIачала найпr O'l1!C'l' НJ Ш небш rь
lllИХ п При п = 1 шюскос1ъ ок:~жс:1'СЯ разбитой
н:~ две ч:1с·1·11 (обознач1 1 м это т:1к: .\. ·1
= 2), пrи
п= 2.
-
1-1а ч~тыре (х2 = 4). Слсду rощсс зrrачс
нис - х1 = 7 (рис. 1). Проnе,цём сщё одну 11ря
~rую. T)"l' же .1юзнr1кает со,"п-тешrс: а rre бу11ет 111-1
число ч астей завнсетr, o·r· рас1юложе 11тт чет-
1\фтоll 11р1rмой от1-юсителыю первых трёх'
В са~юм деле, четвёртая прям;:ш может пеrесечь
образованный тремя предыдутщ 1 i\Ш треу1·оль
щ1к (рнс. 2)\ 110 может и обойти е1·0 (рис. 5).
К счастью, ч1 r сло частей в обоих случаях од11-
на 1<0во: х 1 = 1 1. Построив лятую прямую, обна
ру,ки _-.,1, что рсзуm>r ·ат отпъ 11 с за.вис 1 тт от в~а
им1101·r> распшюжtн ия прямых и .~·5 = 16. Но
рис) 1юк бу11ет ужс бу1шалы ю за1·ромож.r-1ён 11ря
мымrr, так что 1rр~щётся оrраrrичrгп,ся пятыr>
11 tрnым11 значения.ми: 2, ~1 , 7, 11 , 16.
Перебор вариJнтов
Обратите внимание : раз1юсти сосед1шх
чисел предстаnлшот собоt1 поснедоnатеньпые
на тураль11ые числа, нач r шая с :!.. Деl1сТ1Зитсль-
110,~1 -2 =l,7-4=3,11-7=4,16-11=5.
Получается, ч'r'о очередная , п-н 110 счёту прям;:ur
yнcJI]'ILJ I JR;te'l ЧIН:ЛО НМСН111..ИХСЯ }(() это~·о L1(1СТей
ронно ri :r 1l. Д:шаirтс убед11мся, что тзк будет
HCCJ 'Д;l.
Предположим. qто п - 1 1tрямъr.х ужt: ссгь и
мы nро1юднм е щё о,Т(11у, ш1чи1-1ан rв беско11еч-
1 юсm. Новая ттрнмая ИJ(ё'1 · по отюй из облас
тей, на которые уже бьmа разделена плоскость.
lio вот она встрстит1 сь с t«tкoji -тo прямой - и
эта областr. ра:{билась надвое. т. е. tюявш1ась
ещё одна ч:1сть. Прнм:ш нпёт далы11е по оче
р'едrюi\ област11 и, встретившись со сж.:дующсй
примой , разлСJш~т 11:Jд1юе и :~ту обл~1с1ъ. Ч:.н:
тс\'1 опн'1ъ стало щ1 ()ДН)' болыuе. 'Таю~м обра
зом _ rrовая пrям~нr rrерсссчётся по од r юму rазу
со rкемн п - 1 1 rrямыми , и np11 столююпснии
с 1юслещ 1еi1, (11 - l)-(1, tн1сло час1·ей~еJ 111чится
тоже нз 11 - 1. Но 11а зтом пря.\ilая нс обрыва
ется: «распростин 111 исм с послед~ 1 е11 нз <· ста
рьrх» nрям1,1 х, она режет очередную область,
уходя в беско11сч 1 юс1ъ.
Итак, п -я 11рямая дс:й:ствнтельпо увелич11в;1ет
ч11сло частей на п, т. с . для любого 11 > 1 спр::~
ведшrно равенстRо .У11 = .'\·" _
1+ п. Остаётся 11ай
тт1 формулу для х" н зани~11мостr1 от n . Испьп :.1 -
е.м фор.vrулу вида х11= t.т-+Ьп + с, Г/\С а,/J, с -
какие-то неи:~всстные пак:~ ч11сл ~1 . Их 11ужно
1юдобра ·1·ь тате. чтобы nы1 юлпял1 rсь дn::i услот rя:
1)Х11-
.\11_1 = f1(ll>J),
2)х1=2.
261
1...j И(/\ё\
Перебор вариантов
Посrсольку
>
х11_ 1 =а(п - J) ~ +b(n-1)+,·=
:= (t.:n/+Ь11+с)- 2tm- (!>- а) =
ЗАЛАЧА О РАЗБИЕНИИ
ПРОСТРАНСТВА ПЛОСКОСТЯМИ
=х,,-2ст
-
(IJ - а).
11з r1срво 1'0 услов11я tюлучж:м, что ;~mt любu 1 ·u
п > 1 ДOJlЖIIO RЫl!ОЛJ-IЯТЬСЯ равенство 2аи + (/J -
-
а) = 11. Это nозможно , тол1,1<0 1.:сли 2а = 1 11
Ь- с1= о.:~начит. ({ = ь = 1/2. ПОЭ'l"ОМ:'Х11 = 1z1;2 +
+ n(2 +с. Из второго уою1шя ('ле;\ует. что х1 =
=i -/2+ J/2+с=2.откуд:.~с =1.Окончательно
Те 11 ерь можно рассмотреп" и 11ространсгвен-
1 1ый нар11аt 1т ::;той эа;щч11 : требустс}! вhшсн11·1ъ.
на скоm,ко 1 .1 астс1I (оfiознач11м 1rxy") разб11на
ю·г пространl-1·но п плоскостс/1, если вик:1юrc
i\Ht: из 111 1 х 11с пзраллст.111.1. 1 шк.:щие тр11 не
пересекаютсн по од11оr1 прямой 11 вш<:акпс
'-Jетыре 11е проходят через одну ·1 ·оч1су.
х,, =!!!:_+!!.+1=п! -t п+2
Допуспrм. 11 плоскостсJ) уже имеется 11 rrро
с.:транство раз6 11то па у11 частсf1 . 1lровСJ\ём сщё
одну 1mоскос1·11 - (11 + 1) - ю. Ка.ждан 11э р:1нее
22
1
МЕЛАНХОЛИЯ И МАГИЯ
В КВАдРАТЕ
На известной гравюре « Меланхо
/\НЯ » (1514 г.) 1ierv1euкuгo худож~1ика
Альfiрехта Люрера nрисутству"т
од11н замечатРльныи математиче
ск11й объ!?кт. Это кr;мрат, ра3битыl71
на клетки , 13 которые вписаны чис
ла. Не-rрудно убедиться, что они
уловлеТВ()ряют ср,1зу 11ескольким
услuвиям:
-
если сложить вrе числа R
каждой строке,
-
если сложить все числа в
каЖдОМ СТОl\бUе,
-
если lЛОЖИТЬ все ЧИСЛd в
.м~ух диагоналях,
l'U все эти суммы окажутся равны
одному и тому же числу. Удиrзи
те11ьны~1 квадрат! Такие квадраты
вазываются магическими.
Хотите 11 аучит~,ся строить ма
ги•1еские квадраты rколь угодно
большого размера~ Пожалуиста.
Исnоль:1уем метод, описанный сто-
11етием nозж.е, в Н112 г., франuуз
ским математиком Клодом Баше
де Мезириаком. (Русский перевод
его кни1·и издан в Петербурге в
1877 г. под названием « И гры и ·-1а
дачи, основ:~н11ые на математике» . )
Магическ и й квадрат удоб 1·ю
строить на бумаге в клетку. Пуггь
п - нечетное число, и нужно по
строить квадрат п ><пс L1ислами от
1 ло ni. действуем поэтапно.
1. Все числа от 1 до п2 запиrы
васм 13 клеточки 110 диагонали (по
п чисел в ряд), чтобы оnразовался
диаго11альный квадрат.
2. Вылеляем в erCJ uе11тре квад
рат п х п. :)то и есrь ос нова (t:>ше
не все клетки за полнен ы) будуше
го магическоrо квалрат.з .
5
4
10
:3
9
1:;
2
8
14 2U
1
7
13 19 2'5
6121824
11
17 2?>
16 22
21
1. Каждый наХtмяшийt я вне
uентраль ного квадрата чиlлово11
«уголок• аккуратно переносим
внугрь - к пр()тивополож1-юй по
роне квадрата. Чисr\а ·них « угол
ков• должн~..1 заполнить все пустые
клетки.
Магический кrзt1др;п nuпроен.
Теперь можно проверить, что в
таком ма гическом квадрате п х п
из первых п 1 натуральных чисел
сумма ч11сел по каждой ли11ии
(строка, столбеu, диагональ) в точ
ности равна
с2,
(11' +1)11
-
"-'-\ = -
---'--
п
2
Магическии кв<~драт послужил
предвес т 11иком рождс11ня о•н:• нь
важного liаправления в комби
наторике. Оно рассматривает так
называемые ~очные схемы , т. е.
таблиuы ИJ <.истем чисел и11и мно
жепв, котоrыt> удовлf'творяют ол
новременно большому количеству
очень жестких условий. Настоль
ко жестких, что, как правило, речь
идет уже не о перечислении всн
можных вариантов, но о самом су
шествова~1ии такой схемы.
'J 16922]'5
20821142
72513119
2'-1 12
')
186
]14J7102:3
26.)
• Чиrла
гrюстроенныхш:юскостей пересекаетсясней
no какой-лнбо прямой, и эти п 11рямых разби
Rа~от новую плоскость на :х11 частеfr. Л каждая
из этих частей плоскости дел и ·~· 11екоторую
ранее ~отреза 11 11ую» областт, прос.,траш.:твз 11з
две ч асп 1 . То ест1. (п + 1)-я плоскость увелич11-
nает число частей ровно на х11• llоэтому y 11i 1 =
=у"+ х11=у"+ (п2
+ 11 + 2)/2. 1rоскольку, кроме
того, у 1 = 2, flCJIO. что данная формула 1юзво
ляе1· uычислить у" для любо1·0 скош. угодно
большого п. Можно 11олучить н ю111ое выраже
ш1еу11 чере3 п, если по аналоги1,\с nрс!~ыдущей
зал::~Уей иск:.~ть у11 в 1шде у11 = ап + tиz- +сп+ d.
ПрпRО/~им резу; 1ьтат:
У11 =
п\+'5n+6
6
ОБОБШЁ Н НЫЙ ФАКТОРИАЛ
И ЧИСЛА КАТА/\АНА
на окру-;КНости з;щан ы 2п точек. Скот,ким11
способам11 их можно попарно соеднннть с
помо щь ю н отрезков, чтобr,J 1111Ка1<не два от
резк::~ не пересекались?
Обоз на чи м искомпе число способов через
z". Прt1~по1ЮЖ Л1\ что значения z 1, z 2• •", z" из
nест11ы, попытаемся найти Z//+t· Расположим на
окружности Цп + 1) точек и выберем любую из
них (точка Л на рис. 4 ). Её можно соединит~. с
любой из осталь11ых то чек При этом провсдён
нан хорда ра:юбьёт остан111ис::сн точки на две
группы . Точки , nрин::щлежащ11е ра зн ым r· руп
пам, соелиннть нельзя - отрезок непременно
перессчёт тоm,ко что проuедё1111ую хорду. Зна
'U!Т, остаL'-1 ся как-·1 '() coeдrrrrитr, точки п 1<:1ждой
группе между соt1пй Но если число точеJ< 11
Рис. 4.
1·руппах 11 ечётное, то 11рокести отр езки нс
удастся - одной точке не хватит пары. Слсло
ватсльно, точку А мож11О соединять нс с каждой
и:1 прочих точе 1<, а через одну - т;Jк, чтобы о
1 - й н 2-й группах оказалось соотnетствешю О и
2пточек;2и2п- 2;4и'!.п-4;...;211иО.Еслив
одной из групп О точек, то всё многообразие
соед1111е11ий дают 211 точек другой группы , и их
число равно z11• Ес111 же в одной группе 1.т ~ О
ТОЧС:'К, а в другой 2(11 - in) * о, '! '() число 1Ю3-
м ожных соединений ста1-юRится рав11ым zщz"_111 •
Отсюда получ аем выражение для Z11+ 1:
Ис11ользуя данпую формулу, можно, на
чишtя с z 1 = 1, вычис..чrrп, первые несколr,ко ЗJ 1а
чениit z 11:
Z1=] +1=2,
z~=2+ 1 J +·2= 5,
Z.1 =5+1·2+2·1+5""14,
Z;= ]4+1 5+2·2+5·J+14=42.
Эт11 •шсла 11 ХV1Л u. рассм:привал Леонард
Эйлер, правда н связи с conerшe111 ю другой за
дачей. 0 11 подобрал (как сам пр11з11ался, с бот,
ш11м трудом) формулу для z":
(417. -2) !!!!
z= ~---'-
,,
(n+ 1)! ·
В числителе дроби сто11т так на:.1ыш1емый
vбобщi!н:ныu фаюпириап . Поясним :о~то.
Выражение k! означает, что llеремножаются
nce натурпль11ые ч11сл:1 подр5щ и н:1и болы 11101
из сомножитслеli равен k Rыраже11ш: kll озш1 -
част, что пеrем11пжаются н;пуральные чнсла
через од1 ю и папб ольшнй сом 1 южитет. таюке
рэnетт k . Таким обр;:~зом, если k чётное, то k'!
есть про изnеде1111е всех чётпых чпсел, 1 1е nре
nыmающих k (k!! = 2 4
k); если же Jг
вечётное , то это произв<::де 11ие .ucex 11счёт11ых
чисел, 11с превышающнх k (k'! = l · . -1 ". k) Ана
логично. t'CJIH IIO CJН.: ч 1 1сла pac 1 IOJIOЖCHU тр1 1
BOCKЛllЩITCJlbHhТX 3н~1 ка , ТО IIСj)С::!\НЮЖается
каждое третье число . а ест 1 чстhlре - каждое
четвёртос. Лрнменнтt:лыю к нашему случаю
lfMCC!\1 (411- 2)!!!! = 2 (1 ]() · ."
·
(1\ГI - 2).
З 11 <1я формупу, 11аЙ) \t:1111у 10 3йJ1сро;11, мож1ю
попытзться доказать её с11 ра веллr пюсть (по·
пробуй·1·е сделат1, ::это). Кст:п1 1, чпсла z 11 rюн11J111-
ются в самых ра31 1 ых комбннаторных задачах.
Их принято тt:зышпь чuс.ла;.,ш Каталс111а -
в честь бслы·11йско1·0 матсматнка XlX. в., хотя
Эl1лср открыл нх раньше
ГРИБЫ И ЗНАКОМСТВА
А" А, образуют выпук11ый четырех
уго11ьник;
Теорема. Среди 11юбых nяти rрибов
в 11ery найдутся четыре в верши нах
выnукll(>Ю четыреху rо11ьника.
Рассмотрим на плоскости пять
тос1екА1, Л1, ••., А5 и выберем и1 них
лее, а име нно те, которые удале 11ы
лруr от дpyrJ. на наибольшее и з
всех возможных п оп арrtых рассто
яt1ий . Пусть :поА1 и А 2 • П остро~1м
лва равновеликих круга, как пок а
за110 ниже.
Поопределеt1ию отрезкаА1А2, все
опальные точки -А1, А4 и As -
долж ны располагаться исключи
тель~ю в области пересечения эrих
лвух кругов. Тут возмож ны не
сколько елуча ев.
1. Сушествуют точ ки по разные
сторон ы отрезка A1Al 1 н о тог да
четырёхуголь ник А 1А ,А 2А11 rде
А. - любая точка из верхней об
hасти, а А, -любая точка из ниж
ней обмети, является выпуклым.
2 .Точки А ,, А11 А~ лt>жат по
ом~у сторону отрезкаА 1 А 1- И здесь
u свою очеред~, возможны лuа ва
р11ант,1 ·
а! наилётся примаи Л А1, пере
сс>каюшая прямую А ,А ~ вн е от
резка A1Ai1 но тогда точки А1,Al
б) в альтернатив ном случае
либо точки А1, А 1, А4 А5, либо точ
ки А1, А3, А4 А~ образуют выпук
лый четырt~хугольник.
Оказывается, если вы захоти
те гар а нтирова нно найп1 выпук
лый пятиу гольник, то по1-ребуется
перебрать уже девять точек. По
пробуйте дока зать ло самостоя
тель~ю.
Вообwе,пустt>N,0 ,- на име11 t>
wее число точек плоскости, среди
которых гарантированн о суш е
ствует выпуклый п-угольник. Име
ется гипотеза, ч то
N<111=2"~+1,
но это t'ШС lie локаза110. К этой
rеомеrр ич~ской ·~nдаче тес но при
мыкает следу 1щнан.
***
Сред!~ люf>ь~х трех ч11ловек 1iаи
ду1< я лвut: олноru 1юла .
Нироаная мудрQt:ть
Теорема. Среди любы х шести ч ~
ловек оЬя·\ательно най t..утrя либо
трое поп,)р1 ю зником ы х, либо трое
попарно н еJ11аком ~,1х.
Пf'ребор Rари аюов
Вста нем 11tз то•1ку зрения любо
го из выбранных шести человек: он
RtАдит nерел собой пи теrых, к не
которым из 11их у 11его одно отно
шение (например. з~1акомы), а к
ооальным, слелп вате11ь но, лругое
(не1накомы). Ясно, что И"I пs~ти
всегда нtзйлуrся трое, к которым
его отношени!-' оли11 а ково. Ло пус
тим, пни ему знакомы. Если среди
эти х тро1·1х и меется п ара зн акомых
друг с другом , то требуемый «тре
уголь ник ~ людей с одним отно
шением друг к другу пбнаружен.
Если же такой пары среди них н е-г,
значит, все трое t1ез 11 акомы - и
опять-таки решение на йдQНо.
Важно птметить, что в данной
задс1че выбор не менее ш естерых
человек сушестве11. Так, среди пя
ти человЕ'К может сложиться сле
дуюшая к;~ ртин а зн акомств (чёр
н ое) и нез накомсrв (красное}.
З десь, к;:~к видим , НЕ'Т ни черного,
ни красного треугольника и, таким
образом, ни трех п о парно ЗНJ
комых , 11и трёх nопар1·ю нез11а
комых. Поэтому шестерка явля ется
экстрем<1льной (в да1111ом случае -
11а11меньшt'И возможной) характе·
ри стикuй, nри которой выnолня«>т
ся требуемое свой ство, как и N1n1 в
1адаче о rриб<1х.
Задача о з 11 акuмствах ПОАО
жила начало н овому н<1правле1"111Ю
в комбинаторике - теории 1-' ам
сея. Олна и-1 базов,ых ;,1адач :пuй
теории - о п реы•лен ие наимt-нь-
111еrо 411{'1\8 1\Ю де й "1," ,, 113 КОТО
р1>1Х всегда можно оыбратt> либо п
попарtю знакомых, либо п 11опар
но не• накомых. Уаанtн~лено , что
R'",= 18, но далы-~ейшие точные
з1 1ачения R101 11N1звес.1 ны.
26~
Числа
ГРАФЫ
Всем 11зн<:::с1·1 t< >. что C'JIOtIO «граф» о:ш<1ч:н.:т ;~нu
rн 11ски й т1-пул, HtlllpИNlt:p граф ЛсR HllKOJl<IC-
f!IJЧ Т()}( Сf'() Й J\ ROT Н J\\a'J CM<l'ГI11\C г}Jarj3nи H<IЗЫ
flaIOT r 1 абор тпчск , нскоторые 11з кrнорых
сосдтптетты лнr1т1ми. Точки ш.1снуются Repюu-
Рис. 2. Г енеалогическое древо .
266
нами 1·рафа. а отрезки - рi!бралш На р11с. 1
нзuбр<1жён 1·раф, хорошо зтrатюмыi1 москш 1 чам
Э·~о схема МlК'ко 1-1ского метро: всрш111 1 ы - ко
нечные ст;,~1 11 \111111 сп1 нцш1 пересадок, рёбра
п~~п1 , сuеднняющ11с эти ст:тц 1 ш. Нз рис 1 вы
11ид1пе е11\ё uднн 1 ·rаф - ч:.~сть гснсаJ ю 1·иче
скою J1pe 1-1a 1·рафа Л. Н. Толстum. ~дссь нср
ши11ы - nредкп ттнсатеJ1я 1 ::i рёбр:з пuка:шв11-
ют роде·~ ве т шые связи между 11ими.
Основы теоршr 1 рафоn как математ11чес1юй
науки заложил в J 7 36 г. Леонар[I. Эйлер. рас
сматривая задачу о кётп1rсберrсю1х мостах.
ЗАЛАЧА
О КЁ НИГСБЕР ГСКИХ МОСТАХ
I>ыrнш1й Кё1 1 н1·с()е(lJ ( 1 1ынt: Калининград) p:J C·
положен па реке Преrелh В r1реде11а х l'Орода
рс1<а омывает два острова . С берегоn 1r:-i ост
ров:.t бьши псрекиrrугы .fl.ЮСты. Старые i\IOC11A
не сохраниттсь , 110 осталась карта гoporta, 1'де
uни 11зображс11ы. Кёнитсберt·цы предлага.1111
приt:зжим 01tдующую ~1адачу: пройти 110 uсем
мостам и нерну1ъсн в t1:.~чш1ы1ый пункт, nри
чём на каждом мосту СJ1t'/(о в:1ло 1юбьш:пъ толь-
1т nдиIJ раз.
Проl'уля•гься по городсю1м МQСТ:1м прt:дло
жилТt 11 :::>i\леру. После бсзуспсш11011 попыткн
совершитъ нужный о6хо;( он 11ачсрт11л упро·
щенную схему мостоn. Получ1u1оr 1 ·раф. вер·
шш1ы которого - •1аст11 города, разделё1111 ые
рt:кой, а рёбр;~ - мосты (рис. 5).
Прежде ч.ем uбост юnатr, не1юзмож1юстьтре
буемu!'о маршру1·а. Эйлер рассмотрел и другую,
nолее слож ную кар·1у (рнс. ' 1) В 11топ; он доказал
общее угвержде11ие· J \JШ тu1·u чтобы мшю ю бьшо
обойти вес рёбра r-рафа по 01~1юму paJy 11 вср
нутъся fl нсход11~'Ю вс:-р11_шну, нсобход1rмо 11 до·
статочно flы 1ют1еш гя слсдующих двух уоюв111t
1) и:-~ любоi1 вер 1111111 1)1 1 -раф;~ ;1олжсн с~ щt
ствоuатъ пугь по СП) рёбрам 1~ любую l\ру1ую
1Зсрш 1 rну (1рафы, удовлетворяющие ~1'0,\t)' трс·
бов~1нию, назьшаются связными);
2) н з каждой вершины 1\ОЛЖIЮ DЫХОДl!ТЬ
чётt юе КОШIЧСС'l'/.Ю рёбер.
Замк11уrый 1 1уть , 11роходлщий по одному
разу JIO всем рёбрзм 1р:1фа. называют с тех пор
.~fиероны.м чuклом .
с
а
P1tc. 1. Мое 1ы Кен"гсберг.i Р11 сv1юк 1н собр,1ння
тч1111е1 111й А Jйлсра (,1 ) 11 cuorB('I < 1иуюш 11111 1ыф ~1}
Еслн 0·1·брос 1 1ть условие nоз.вращення 13 ~к
ход11)'IО nершшrу, то можнодопуспrтr, налпчт r е
дnул вершин, из которых выходrп псчё11юс
колнчество рёбер. В этом случ~1с r-1 :1 1 11нrа·1 ъ
,\в r1же111rс слсдуt:т с OJ\I roil 11з этих J{нух нt.'рш1111 ,
11 заю1нч11н~1·r1, - н другоl1.
Возмож 1 ю, мноп1м чю·атсmJ.м подобно1·0
род;~ за,'\ач.1 1 зн::шомы ещё 1ю :ih')'ptraл:iм "М)р
зилка" 111111 «Весёльте картш1ю1». Там г1рсдл::~ 1 ·а
лось начер1'ить как~10-нибудь фигуру, не отры
вая карандаша от бумагн 1r не nротюдя дnажды
rю одной линип. На рис. '5 и 6 приnедены две
т:~ю1е фигуры. Первая нз них назыnае1ся «Саб
ли !\f:11·0.\1eт:-J». в ней C}'l l {CCTB}'CT эйлерuв ЦIIКЛ,
так1<ак из шест11 всршнн графа вьLход1,rr чt.:·1·1 юе
чнс.rю рёбер Втор:tя фт·ура - «Раслсчатаннuе
шrсп"Ш* - имеет /tRc 11ершш1ы (ннжтtе), нз
котпры:х выход11т нечётнос коn11чествп рёfн::р
Пrш1ому rнсунок 1rужнп 1-1 ачнна1 r. с ОДl ЮЙ К1
111ix, а 1с1 другой - зака1 rч1шат1"
Л как же обсттrт !{ело С' r<ё11игсберrсю 1 мн
иосrам11? Эдесь пр 1 1 каждой из четыр~х вершr111
11еl1ет11ое число рёбср, тш< что нет не только
P~1 t. 5.
Рис. 6.
ПерЕ'бор наризнн>в
Р11с. 4.
эйлсро11а цнкпа. rю н путп 1 rз одтюП всрт 1 шы
n другую, прохuдящсr·о по nссм рёбрам графа.
Карту, 11зображён11ую rш p1 1L' .: .\, 1ю11робуйтс
11роа1 1 ;.u111знроиать c;J,\10CT(JH TCЛ ьно.
ГРАФЫ ИЗОМОРФНЫЕ И ПЛОСКИЕ
В J 8S9 г. am·Jшiкю1i1 1'Iатематпк Уильям Га
мнnьтол выпустн,1 u прода.;ку rолоnоло мку О11а
щк~лставляла собой дсрсuяш1ьrй додекаэ;tр
( 12-r·р~шншс) . u нсрruннах которого вбиты 1 ноз
дшш (рис. .., ) Kaж"r:i:шr 11з 20 nершин бы11::~ nомс
ч«.::на назн;uшем oд1io1·u н :~ крупr1 1,rх 1 ·u род ()в
мнра - Дl:J111. 1:>рю<.:<.:ен1" К.н1то1-1 11 '1. J\ . Требо
валось налтн :за,\11ю1угый путь. 11ruхою1щ1111 по
рёбра .\1 до;1t.:к~1.::щ,ра 11 n<юнол)jющнй rюбывать
R к~жл.01:1 t:1'0 flершш1е 110 од1н1му разу. Тlугь
CJ!tДO RaJIO ОТ,\lеЧЗТh с IЮМ ОЩЫО 11J11ypa, за -
1tеП!l»я е го за rrю :щ н кн.
Игрушка 11е нмела такой ПОП)'J1яр1юС'r 11, ка
кой ещё недавно пол1.зовалсн «кубнк Ру611ка " ,
но uста1:нш;,~ след n м::~тс~атнке. Зам.кн:утый П)ТJ,
Рис. 7.
267
nn рёбрам графа. прохо11ящ11й rю одному раэу
через все нершш1ы, называют гам1.t.11ы 110новы.м
цш.:Тfп.м. В отлич1 1 е от эйлеμо.ва ц11кл :.1 услuш1я
су щеСТl:IОВ3 1 ШЯ 11:1 11p01 ·JЗB<J.llhHO'vt гр :.~ф с 1·:1-
MИЛ l{l 'OHOn:1 1\ИКЛ:J /\()сих пор не ycт:H JOllJ I C'flbl .
1!.сли пос·1 ·::~в 1 пь проволо чны1:1 ; 10 ; 1ei<:l;)J\P 11 ;1
111юскость. а зате~1 1юr1 нест11 исrочш 1t< с ве 1·:а
бm1эко к 11ентру его nерх11ей 1 ·ра1ш ( pIIc. R) , то
1 1рое 1щ1111-тс:11и pf.6ep на ПЛОСt<ОС'IЪ СОСТ:l13ЯТ
Т'раф, 1f:'\обрзжё1111ы(1 ш1 рпс. 9. Красш,1м 11вс
·mм пт.мече 11 rамшrьтоrюn r1ню1. На рис. lU по
каз аны графы, 1юлуче1111ыс татшм ж<.: uбразо.м
1 1~1 о<:талы 1 ых чстырёх пр:ш11ль11ых м11т·о1'ран
rшков. llопытайтссь найти нJ ю1л 1амнльто
ноnы цию1ы.
К;~к ни;1нu из п р11мсра с проекциям11. свой
стк;t tрафа 11~ мeJIJ.ll()'JПJ с И:1М<.:НСIП IСМ П()Л()
женш1 с:1'0 нt.:рш11н, нс зав1 1ся·1· от 1·01·0, какими
Pitt. 9.
ИМСТ!IТО ЛIJ!ШН.'\111 вершш 1 ы С'ОС/ (ИН t НЫ . Дна
графа, и:юбrажённые н а р1к. 11, н этом смыс
ле О[\Н Н;tкок ы : у них OДJll f::IKClll()(: ЧJJCJIO нcpLllИIJ,
и еош две вtрш111-л,1 LЩноrо графа соединеuы
ребром, то нершн н ы нторurо графа , имеющие
тс:- же:: н омtра . также сос:; 11ш е111.1 ребром Это
заме чаннс б()лее стро1·0 формушrрустся так:
два 1 ·рафа 1rаэьmаются и:ю.морф11ыми (от фС'I.
•пзос,) - ",хш11ыи ~ н "морфе·>
-
«mщ», "ФОР·
ма»), если между их nсршнн:.tмt L мткно уста-
1rоюпь взаимно од1ю:ша ч нис сuuтвстств11е ,
при котором вершшшм, сосю 111 е1111ы м. рсбrом,
соотвстстnуrот нершнны . таюю..: С()ед111-1снныс
рс..:брuм . l'рафы 11:1 р11с. 12 тоже нзоморфны. Or-
f\l
'\
/\
'~\"d)
\1~/ P>t c. 1!.
M(;Tlu•1 . •пu } uд1 ю 1 ·0 Н3 них нcкuтopt,Jt' μёбра
1н.~ рсо.: каются, у второ1 ·о же.: таю rx Пl'fX:<.:c.:чt.:1-11 111
Н(.'Т А BCCГJ\:t Jll I гrаф МОЖНО JI:io6p:1:1 1 1Т I> 11 :t
nш>скос111 так, чтобы его рёбра нс: псрссск:1 -
111JС1,1 С1к:1~-1ывэетсн , 1 1е·1 ·. l 'рафы.11/1 » 1ю·1 пр 1 .1 х :'JT()
B().1\J()if<I Ю, 11/:l:ll>ffi'1ТOTCЯ IUIOC/\:11., Hll
P:icc'vlrпp11м пn~1 1·рафа. которые «ПС )l\.'Щ~ы
nаюто1" r1a пл\ккость беэ пересtче1111я рёбер.
П е рвыi1 11э 1шх - 1·раф с 1штъю всршннам11,
1\:tЖДЫl ;\Ж: П :J которых <:OCДlllICi lt.I rt..:6p01\1. Та
коll 1р,1ф назынаl"1'с..:>1 1юю1ын (р 1 1с. 1:)).
Bтupoil гр:1ф, с 111ес1 1.10 нср11111н:1.м11 11 ; \t'-
ю1 1·1.ю pёfip:lNH I (рщ: l '-1) , 11ос1 1т 11:дна1111е •·до
м11ю l - ко1юдцы·'. 0 1-ю 11рон :югш10 от старт 1-
нolr з:щ:-~ ЧI l-l'()J]( )В()JJOMIOI.
В трёх 11:1()у 1 111\Зх :.ю 1 л11 ·11юе ; (руэе~"1 . ()кож>
11\ ,'\()МIПЮП ТТ:1ХО,'"( 1 ТЛО(Ъ трп колщщ:1: Of\ПI I с
Рис. 14 .
солё1юl1 1кщпй, 11·1·оrх>й - со с11:1/( 1юй. а ·1·ре
тнй - с пресной. Н о од нажды дру:1ья nоссори
m1сь, д:~ так, 'ITO 11 шщеть д руг друга 11е хоте!ш.
И реш11л11 01 111 лo-110QO.'-'IY проложип. трошш
ю1 от домоn к колод1 (ам, чтобы пх путн пс пс
рссск:ишсь Как :~то сделать~ lla рис. 1"5 прове
дено воссм1. нз дскнл 1 тро11ннuк , нu 1 1ро ксс..:тн
дсвнту ю у·же 111:: удаё·1·сн
Полhск11!'1 матсматнк Каз 11 мсж Кур:.tтовсю 11!
ус1·зноm1Л , что н1гкаю1х приющn11алы-ю rп-rъгх
11t 111юсю 1х 1р<.1фо 1 1 1 1е сущсстнует. То'"'П 1tc, tсл н
1раф "11е у1<1 1 а;~ 1,~вае-101 » 11а 11лоскост1" то 1{ t 1ё,"1
•сид11т» по краf!пей мере ОТ\1 IП пз этнх дnух
графов (поm 1ый граф с пя1ъю вер ш шш~ш нл н
•,~;омшш - кололлы ·~) , бып, может с допол11и
тслы1ыМJ1 вершшr:LМи на рёбрах.
l l1юсю1е 1рафы обладают м 1югн ми 1u псрес
ным11 ско~'1с1 нам11. Так, Э(1J1ер обнаружил 11ро
стую сю1з1, между кш1ичес~г 1юм верш1111 (В), ко
лrrчсс1·1юм рёбср (Р) 1-1 KOJll l ЧCCTIIOM Ч3СТt"Й (Г) ,
на кт орыс 1·рж\1 ра:щелнет плоскuстт,.
В-Р+Г=2.
Ес.1111 вспомнить, как с помощью лампочюr
с1рошкн шюский 1·раф, изо1чорфный 1·рафу.
Пf'pf'I шр вариантпв
P11t. 15.
сос1·0.нщсму 11з перш~ 111 11рl:бср131,,111~·юш1 о м1 ю
гоrрашпн;:а , то легко тто пяn" что эта фо рмула
нср11;1 длн любон> НЫП)'l'-11()1'0 МНО I'Огра1 !111П<:I ,
11p 1 1чf,'vt /3 11 р - Hl-l()Kh K()Jll l ЧCt:'IB:l нер11 111 11 JI
pi.'ncp,а/· -
ч11010 1pa11cl1м1101·ш'р;-ш 1 1111<а . :;)•1от
фак· 1 , к~1к н<.:давно 11ынсш1. 1оtъ. был 11 :нк:с1с11
сщё Гене Лекар't').
ГРАФЫ ИГР
I la рнс. 16 11зображс11а mахматн:~я м111пr-дос 1<:~
размером _) х _) кпеnш, а на 11ef1 четыре l\O LIЯ -
два белых II два чёр11ых . За,11ач:1 псрсстаn11ть
фшуры так чтобы uдшrаковыс кuшr оказались
в 11рот11 1ю1 t0Jюж1-1ых y t'Jtах J\OCКI 1( р11с. 17). Пе
ремещать llX MOЖllO 'J'QJll,KO хсщом 11l~IXM:JTll<J
ГO r<OJ1н rt 11слъ:sя ста ш 1т1. фигуру 1-1~1 у-жс :1а 1 1я
тос полt:.
Все 1ю11ытю .1 со11ер1шпъ т:1 ~-у10 11срtста1юн
ку терш1т 1rеула чу. Почему?
ДаnМrте 11ачертн:-1 граф no:1;vюЖJ1ьLx Х(ЩОВ
коней по доске (рнс. 18). Затем постро11м 11зо
морф1 п,пl ему граф без самопсрссечсниlr n!{nyx
вар11 антах· 11а одном UTMC'ПL"-t псрво 11а ч~L'!Ы юс
000~
~~~QJ
Р•1 С. 16.
Рщ:. 17.
Рис. 18.
269
Числ<~
ГJ( )J ЮЖ<:1111с: ко 1J ей, з на д(1у 1 ·ом - трl'i)ус:мое
(р1н:. 19, и, б). Вот теnс:р11 1 юшпнu , почс:му
задача нс реш:1ется. Днижс:н 11с 1ю 1 t6i ло графу
оз 11ач:н-·1 nсрехпды в сосе;1 11н е вср111111rы , и пе
рейти из перnо:й позицш1 во вторую 1Iевозмож
но бс::1 «nсрескока" через коня JI,pyтoro цнста.
Этот Жt' граф rюмог:~ст решить и ещё одну
3адачу. Н нс!I трсбустсл нэ положс:н.ия, показан
н01·0 на р 11 с. 16, :1;1 11 а 11 ме11ыпе::с количс:сnю
хо/].ов неrс:вс..:ст11 кuией в положе11 ие , н:юG ра
жённос 11а р11 с 20, т. е . помс:11ять мес-1·амн
чEpH hJX 11 ntлых. Внош. обрат11мся к р11с. 19, CI.
Яс11 0, что ф11 1 уры лолжны дrн rrатr,сн по :">тому
грзфу в од ном 11 том же 11а11раоле11и11, 11 каж,r~;о
му 1<011ю придётс>~ сдс:ла.т1, рошю 4 хода, т. е.
всего по1 rадобится 16 ходов.
••
~ 62J
l'н с. 19.
Рнс. 20.
Вообще, граф игры - это 1 ·раф, нсршнны
1юторого - ситуацни, нозшшающне п процес
се 1 П'ры. а рl'бра связьшаrот вер1шшу с теми вер
ШИ1-Iами -снтуац1 rям11 , которые мor ')!J' сложит1,с.н
после o чepcJ~HO L 'O хо;р. Так, в пцхм:~тах [I З на
чал ы-юй Л OЗli l (1 11'1 ПCJ1Bh1NI ходом можно 1ЮJJ)'
'-\ИТЬ 20 1юзиций : каждая nешкз может пойти
нэ oдi-r y или ;~нс клетки впсрёд, н ю1ж; 1ыi1 кu1 11,
мпжr::т поf1ти 11а uдно тrз ; 111ух поле й . После хо; 1а
чёр11ых число возможпых познций стаrю uнтся
раuпым 20 10 = 400 и в }'!;ЗЛЫ 1ейшем быстро
уuел11чиnйется. Это обстоятельство 11 стало ос
тюо1юй труд11остью при созд<11шп ruax1"1aтrrыx
программ .
Чтобы 61111Жt познакоми1ъся с 1 vа фом и1 ·ры ,
р <1<.:смотрим 11rμy с не60J11"шв м кu11и4еством
но3мuж 1-1ых си'rу<11111й. Пуе1ъ на столе лежит 5
<.:п11чек JJ,1юt.: 1 11 ·р<жо11 по очерСf\11 берут 1 нш 1 2
сп 11чк~1 . Выигрывает тот , кто забирас:т по
следнюю .
Нарисуем граф нссnозмож1тых продолжс-
1шй игры (рис. 21 ). Видно, что после nсрв01·0
хода на столе ос та L'тся 3 шш 4 сn11чю1. Если
тот, кто 11ачи нает. оставит на еrол е 3 спички.
то оп 13Ыl:'tграст: nедь е го партнёр вынужден
бунет ост:ншть 1 или 2 спички, которьн:: нач и-
27U
Р11с. 21.
fl:шший 11 заб<.'рёт на следую щем ход) . Ест1 же
лачинающ11й Нl 'Р) О<.."Гаш1·1 ·1сп1р1ю1 . то 01 1прu
и~ ·раt:т. так как партнёр, в:~ян 1 с 1111чку. uста1шт
t'MY .1, что. K~IK ,' 1.lhl уже К11/\СЛ I 1, вс.цёт к про111·
р1>11ну 1н'рок;1 , дслающr:: 1 ·0 о черt·д 11оl1 ход Ко
нечr ю же, в·трой 11ггюк мажет оста1т·п, 2 сп11ч
ки и ту, · же nрон.1 · р~т1,, 110 11 аJ\б1· 1'ъсs1 11<! это 11е
прихою п сн . Мож110 сдела11, вынод: 11ач1шаю
щш1 прои 1-рываст, если и схо;( 1 Юе числа с nн
че1< делится на ), и nыш·рьшас· 1· в осталъ~ 1ых
случаях, ост~шляя 1Jар-пrёру вся 1<Lrй раз колпче
ст1:Ю сшrче!{, кото рое ; 1с:.~1ится на .J.
Граф м ожно сuстав11·1ъ о для 111 ·ры •Крес1·11-
ю·н-1 ш 111ю t o>. 1IpoatJdЛI 1з 11 poll<1B tто, мы убедимся.
что 11ри 11 р;1ни11ь н ой и1 ·ре 11:1ртию всс1 ·; ~а мож-
1ю С Rсстн к ничьей Разумеется, ::>тот l'рафбуде'\
несколько бол~)шс. чем r ·p::iф дш1 т ·р ы в с1 н1чкн.
БРОЛЯЧИЕ ТОРГОВ UЫ
И ЖЕЛЕЗНЫЕ ЛОРОГИ
Одна нз кл;.tсснчсс 1шх задач теоршr графов
на:Jr-,шается «З а;щ че::й коммшюяжёра" J.-UШ "з;1-
дач.ей о бродн•н:: м торговце» .
пrедста BI 1м себе TOPl 'O HOl'O ttrt:нтa , который
) \ШIЖСН 11uбыв;лъ н Нt::СКОJТЬКИХ l'Ородзх 11 кt:р·
11ут1,01 uбр;п 1ю. И знt'с1·110. 1<а кис /(Оро 1 · и соеди
няют эти 1 ·о рола и каковы р<1ссгоя 1 шя м<.:Жд)'
11ими n o этим догю 1'ам (рнс. 2 2). Н}гжпо uыбрать
самы й корон.:нй маршрут. Это ~rже 11е •11гrv
mсчная" зада ча . l laнpи.rv1 cp, 1ю.цителт. пос~товоrо
аJЗтомо61 1;ш, вьп шмающий nнсьма 11з тдтгкоn,
оч.ень хоте11 бы з11ат1, t< р атчайuшй маршруr. К'ак
и нодитель грузовика, р~звозящн й товары по
киоскам Л рештпъ эту :Jа11ачу оче 1 11, 1 1е1 tp<Jc1о,
особе 1 11 ю 1<01да число вершнн графа нел11 1ю.
Rот другая зада•щ в некотором смысле про
тиuополож1111я задаче коммиnояжёра. llредпо
лагастсн rтролож11 ть железную дороrу, которая
соеди~ 1 11т 1 1ес кол nко кру1 1 ных1·ородuн. Дня л ю
бой пары городов и звест н а сто11rуюс·1· 1, r 1 ро
кладк1111у1·11 между ними Тр<::буется н ~tйти нан
болес Jtс ш ён ый вар 1 r<~нт стронтеJ1ьства.
И.нтсрссно, Ч'l'О а111·ор11тм 11ахождс:r 1 ия UПТ11-
М:!ЛЫЮ1 '0 варпанта строительства /Ю FЮ11 1,1ю
ripoc1 · (че 1 л нельзн сказать о других :1а,1~чах
теории графов) . П родемонстрнруе.м его на
«ТРЕБУЮТСЯ. "
ТРЕБУЮТСЯ .. .
ТРЕБУЮТСЯ " .>)
рёбрам~1 . Такие графы называются
АВУАОЛЫI ЫМИ. двудuлы-1 ым явля
РТСЯ и граф «до мики - кололuы.».
Предсrаuим себе, ч то ор га н изу
етrя географ ическая экс п едиu и я
на острова Тихого оке<1на. В ее
состав кроме началь н ика лолжн ы
войти три географа, п о в.:1р, ра
дист, врач и техник. Уч аствовать
в зкспелиции из ьяв или жела н ие
десять человек , пр ичем кажлый
владеет олно и или 1-1есколькими из
этих профессий. Вrегла ли началь-
1тк :жспедиuии сможе т из такой
гру11пы набрать нуж11 ых ему спе
uиалистов?
Нарисуем граф, у которого лве
группы вер ш ин : лесять соответ
ствуют претенле нта м и семь -
должностям. Рёбрам и соединим
вершинь1 претенлентов с верwина
"'IИ ~1х спеuи.:1лыюстей (р11с. 1).
Казалось бы, есё в п орялке, 11а
кажл()е место есть канлилат . Ол
нако впечатление это обманчиво.
Посмотрите: на должность врача
~1м еется лишь олин прете н дент
(No '\),разумеется, он её и займёт .
Но тогда на три места географов
останутся только лва п рете~ 1ле1 гrа .
Таким образом, ~1з этой группы же
лающих не удастся собрать коман
ду ::>кспелиu и~1.
Мы ра ссмотрели спец и фиче
ский граф. Его вf'ршины распала
ются на два множества, такие, что
вершины одного и того же мно
жества не соеди нены межлу собой
Теперь заглянем на биржу тру
ла. С юла приш ли семь человек. Им
прелложили де< ять рабочих мест
по тем сп е uиальностям, которыми
~rеограф
*rеаграф
~Географ
~Bji(/LI
1?Рас}ист
~~~'Р
Тl'.\'Н//Л
l'нс. 1.
Перебор вариа~-пов
011 и владеют. С1 юв.:1 1-1 .:1рисусм дву
дольный 1раф соответствия людей
и их профессий (рис. 2). Это1 граф
похож на прелылуший, только лю
ли и вака 1-1 сии поме~1 яли сь ме<..l'а
ми. Смuгут ли всt> (;ем~ро получить
работу по спеш~альностиг
'1r111та:ж:11ш,
Рис. 2.
271
271.
ЗЛЛАЧА О ЧЕТ ЫРЁХ КРАСКАХ
В нимательно рассматривая географи ческую карту,
можно 3аметить, что кроме графов, изображаюших
железные 11ли шоссейные лорог1.1, есть еще один -
граф, состоящий ю гра1 1иu между странами (облас
н1111111, районами) (рис 1). Сам и грани uы служат реб
р::~ми, а вершин.Jми )ТОго графа являются точ ки, о
котvрых сходятся гра~1 иuы грех или более стран.
Задача, о которой мы хuтим расскdзать, Вl:'дет
свою истор ию с 1852 г. Uлнажл ы англи искю1 студент
Френсис Гутри раскра ш ив;~л карту Вел икобритани и
Каждое графство 01·1 в ыделял u ветом. К сожален и ю,
выбор красок у него был невелик, и приходилось их
ис п ользова ть п овторно. 1утр и старался , чтобы лв<~
грJфства, имсю ш ие общи й участок гра н иuы, бы ли
окраш~ны в ра.т ы е uвета. Это за н яти е зап;;1вило его
залуматьсн о том, какоr·о наимен1>ше 1 о числа красок
достаточ~ю для раскрашив<tния любои карты. Гутри
счит<.1л, •но с1 етырех красок всегда хвати т, 1-ю лока-
3ать это нР мог. Проблема некоторое в ремя ак1 и вно
обсужлалась среди ло ндонских студентов, а потом о
неи забыли. В 1879 г. известный ан гли ~1ск 1.1 й матема
п1к Артур Кэли опубликов<.1л эту lмачу в первом томе
« Трудов Королевско 1 0 1еографическоrо обшес1вd» ,
и 0 11<1 п олуч ила широкую изв<.>спюсть.
Cu временем и нтерес к «проблеме ч е гырех кра
сок>~ рос, но он а н1;> помавалась усили ям лаже ныд..Jю-
Р11с. 1.
щ~1хся математиков . В 1890 г. англи иск11и математик
Перси Хивуд доказ,м, с1тu пяти красок хв<пн1 дt\Я
раскра ши вания люGои карты. В '1968 г. б1>1 ло лока1а
н о, что карту, на которои обоз начено меньше 40 стран,
всеrдJ можно раlкрасить с помошью четырех красок.
Нdк0tнщ, в 1976 г. америкdнские математики Кен
нет Аппель и Вольфганг Хакен решили эту ~ада<1у с
п омошью ком п ьютера. Они ра1били 8С(' карты на
2000 птов Компьютер по сосrавленнои ими про
грамме исlлеловал. может ли в раl<.ма тр~1 ваемом
типе карт н айнкь такая, лл~ которой недостаточно
1 1 етырёх краrок. С тремя типам11 карт компьютер не
сп рав11лrя, и над ними r1ришлось потруди1 ься самим
математикам. Получив ответ « н ет~ лля всех lO!IO
типов, исслелователи объя вили, 1 1то проблема четы
рех крас..ок решена. Почтовое отделение при универ
rитете, в котuром работали Ап пель и Хакс11 , в тот ле11ь
гас и ло марки на письмах штем п елем со слоr~ам11:
« Ч еты рёх красок достаточно».
Задачу о четырёх кр.:~сках можно предс.;тавюь 11
несколько и 11 ачf1 • Рас<.мотr им для прои3 вольной
к;~рты следуюши й граф: его верши н ы - стол~шы госу
дарств, а рёбр<1 м и связа н ы те из 1 1их, чьи государства
им<:КJТ общий учасrок r раниuы (рис. 2). для гюлучеli·
ного графсi задача формул11руето1 так: раскрасить
его вершины , используя только четыре краски, чmбы
при этом любые две верш и ны, котuрь1е <.оединены
ребр()м, были р ащого uвета .
Р"с. 2.
пр11мсре дороги, сое;пшяющей nят1 , городон:
А , В, С, .и н Е. Стоимость нрокладки 11ути между
К;\Ждой 11<1рой ruрож.ш указана в таблнцс, а
р::.~с1юложснне 1 ·ородон - 1-1~1 карте (рщ: 25)
С.нзчала стронм ту дорту. котор~ш нмсе·1
тш,vн::ньшую с_~гоимость. В нашем случае это
щ1р11 1 rу1" /З - Е. Теггсrь на.йдём '-'Э1"rую дe rJ.ri: H}'IO
л11 1 нпо, с()еди 11 яющую горпд В ню1 Ei с как11м-
АвсDЕ
l'и 1... 2З.
А
1,5122,5
в 1,5
1,2 3 0,8
с11,2
1.1 0,9
D231,1
2,7
Е') ,..
.... ,) 0,8 0,9 2,7
то из ()CTЭJll>l lblX !'ОРСЩОf!. э·1·0 пут 1, между Е и с.
Включаем его в схему. ДаJ1ее лостуnас:м анало
rнч1ю - шцсм самый ,f\ен 1ёnый rн 11уrей, со
е,:rшшющих о,ТJ,шт из городов В, С. F, с одн им 11:1
ост:mшихся - А нли D. Это дорога между С 1r А.
Осталось поf\ключ нть 1< желсз 11 одоrож11ой
С<."П 1гоrод П. Дсшснлс нее го соедннит1, <:то с С.
Пu.rr>·чнм есть, и:юбражt:f-шую на рнс 21.J.
Оп11с;111ный аm·ор11тм ОТН ОС! I ТСЛ к К:1ТС1'()
рни «Жадных»: н::~ каждом ш~1ге мы выбнра<::м
самое /~ешёtюе ЩJО/\онжс.ннс. пути. Дrш да1111ой
задач11 011 nодходнт K:ll< нt:л 1,зя лучше. Но в
Перебор вариа нтов
л\ уп
~
~
'
D (Q,
Рис. 24.
1\ругих случаях "ж:щ11п1е " ат ор11тi\.11,1 мпгут нt:
дана1ъ 011п1маm.1юе решет1е, 11:111ример в .з:~
даче кп.r"~м1.шшrжёра. Если :здсо) с с1 мо 1 ·u 11ачала
выбир;.пь наиболее «[(ешёные" элеме11ты, т. е.
I<ратчайnшс р<.!ССТОЯIПНI. пе l·ICI<JПO'-lel!O, t.П () в
конце 1 1 ридётся воспо.ru..зоваться оче1 11, ~доро
г11м 11 ~ - д;111 н~n,1м11, 1r общая д11ш 1 а марuтр~~га
ок:~жс::тся C)"Щt::CTRl'J 11 IU llhl Ш t: олтимнлы Юil,
НАПРАВЛЕННЫЕ ГРАФЫ
Во Мiюrих случаях пр11 ме11е111~я rрафон рёбра.
соеднняюпще верш1шы, 11мсю1 чёт1ш выра
же нное наттравлеш1е. Так, 11:1 гр:~фах 1·с11еало
гнчсск.1-L'\: дсревr>ев 11апраnлеrше, есrестnст шо,
идёт от родителей к детям . f!оэтому ш1 фраг
менте rенсал01·ичсско1·0 ,f\рсва (рнс. 2')). те
буююй А1 обоз1-1~Р 1е1 1 ы J\1 ужч 1 111ы. а буквой\~." -
женщины. 11ИJ\11м. что у су11ружеской 11~1ры М 1
н 1f'J сс1ъ сын, но у супруга - ещё двос детей
(дс1:1очка 11 ма1rьч111<) от пер 1ю1·u брак;.~ с t\'11
1о
Nf ,,
Рис. 25.
27.:S
Числа
В графах игр рёбра тоже часто бынают 11а
праuлеш1ыми: если из познт~ии Р 1 можно nе
рс:йти к по::~1щ11и P J, ю 11е всеI"Да нз ттозищ 1 и Р1
можно нсрну1ъся к позицин Р 1 .
Графом является и система ушщ rорода. Его
вер1111шы - 11J ющади н перекрё<.тки, а рёбр::~
-
ули1 ~ы . В боль ших го рон::~х на некоторых ут·1-
цах уста наш вrнается односто ронн ее ;щ1 tжснне
F:стсстве11Jrо, ч то такой срафдшпкен имстL. на
пра11лешrые рёбра. То 1 да утrц ы с д вусl'О рон
ним движением можно обп;н-rач11т1. парам11
рёбср с 11рппшоположпыми напраnлевиями.
Графы, n которых uce рёбра имеют наnраn
лсния, н:вьшаются орграфа.ми. Нз них удобно
рассматр 11нать ра зл ичны <:: трансп ортны е 3ада
чи. На11рим<::р, м ежду 1'орnдам11 А 11 В им<::стся
сС1·1, f~opor, и н~• некоторых из ни х дR 1 1же1-:1и<::
од1 юстороннее (рис. 26). Кроме тu1 ·0, :~~щана
пропускI1ая сrюсобность каждой 7щроги, сю1 -
жем fi тысячах машин в час. Т101 1 робусм отвс
тип, на вопрос: како й максимальный ноток
машин возможенизА вВи изВ вА?
Как видим, хотя из А может выезжать в час
7 тыс. машин, но В"Ъехап, n В в ч:ас смогут лишь
Строите,11,,;люn 1 _ ·
.\ л:.ла1Jк11
,\Jо11111аЖ UIU!ll
Рис. 26.
4 тыс. и:J них. Несложно 11ровtр 1 лъ, •-rто •1тыс
ма шин н час остал ы-r ые дорогн в состошrnн
t 1ролустить .
С друго1! стороны, из В н А MOJ ")ГI' выехать
3 тыс. машин в час, однако въехат1, в А за час
смогу~· ;~ишь 2 тыс. Поток в 2 тыс. ма шин из В в
А остальны е /J;Opon1. каr< не-груNю убед иться,
также смогут пронуст ип"
Ус:трийст11и
ll1Юrt'IU
Ри4:. 27.
1,щn.?(l/J(//fa 1.. , ~ ~~\'Ж!сшенпш
11 mфе1.;,р1тшй
_....:'_н!}----:'1о; r - - ·
--
-
-
: 20,:
L
274
//
1-
·, П0<1 вп11
"
/.vи11пно11~'t1
,_______. .
"),~'
t
< / 't . -ll'h .11/1)()- + ( j 0, Э.'li!hШpO
• ~прудпванил
,:)/f(!pШu
Пpoк..mrtw
( \О ; Лпд11ГJд
газп
/'
:, 14 .1 Г/jЮliдШ)К(/
".... _ ,,.
uoiJonpnвtJда
Усттют.:а
l(./J(){!Ь/.\'
Jt:татжко
те.11е1ртюв
оо
оо00
о00
tcJш гр:.~ф лоро1· более сложен, то н::~ йтн
решеннс }'Жt' нс так жтко. Были 11рщ1ум~1 ны
' 1il l'Oj)J1'1':\-11>1, ПО:'lfЮJНIЮЩНе С П ОМОЩЬЮ l<OM -
flЬIOTepa ш1и без ие1·0 О1 1ре/1,елитt. м а1<симал1,
но RО3можный аото к меж.rw любым~ 1днумя нср
шина.\Ш о р1 ·рафа, ест 1 указа на nро11ускн:н1
сrтособность каждого из е1·0 рёбср.
Вотещё одно r1 рнмененне ор1рафа . При со
:таn11с rrин бсщыuих пrосктоn, содержащих
DаЗЛТ1LJПЫС ВНДL! р<16от, часто ВОЗIШЮI СТ ситун
Ц11Я , ко1·,r1а ·1у нлн 11ную р;1 6оту можно нач ать
1111шь по око11ч ::~нин л.ругнх. Тэк, при строн-
1·ельствс дома 11елъзя пр~ 1ступ1 11ъ к отдслоч 11ым
μ:~ботам , 1юка нс RОЗRенены стены, ·и 11сл1.зн
вФво11,нть сте ны до ую1<щки: фундим<.:нта По
:11с1tu 11ате111 .нос1ъ p::tбO'I' 11зображается п нr-ще
:)p1p::iф;:i (рис. 27). Зж:сь вер11л 1 11ы
-
прот1 :з nо
~имые работы (с указание м их щхщплжитель
ности). а стрелк11 указыnают, какие из них мо-
П~ребор вариантов
1yr вьтолняться только по оr<ончании 11реды-
11ущ11х. Такие о μграфы lI:.13ЫВаютоr се-тевы.1v1u
грщfтками. Они прн мtюно·1·с.fj при ш1а 11нрu
нан 1 п1 дсятелыю(.w1 ·н пренпрнs~тия
Напри.мер, зная дату нач:u1<t стро1-1тенпс 1 ·ва
11 время, необходн ..,,юс щш в ьтал1 rсшш !QЖДОй
работы, можтю 1:1ыясннт1,, к какому сроку сле
дует поднезт.и матсрrrалы r1 m1 приrл;к 1 лъ бр11-
гады с пе1 ~иалистов: nло1'mшов , маляров , элект
риков и т. д. Чтобы олреде11ить общее время
стро нтелт.еrна, нужно найти самrый продоmки
тельвый n утъ n o рёбрам орграфа - or1 назы
Р.;1стся критическим. путё.м. Продол:ж.итсл.ь
tюсть 11угн - это сумма про11олжн.тснън.остей
работ, находящихся на этол.t пути .
Сстс11 1.1 е t' рафи кн r,1 с п ол 1.зуют 11с только
стронтс:ли. тю 11 1<011с~ рукторы машин с бuт,
т1;rм количеспюм узлrн~ и деталей, д нспетч~ры
Же/IеЗПЫХ доро1· и MI югне друп 1 е CileJ \И aJIИCГhl .
Фигуры
~
Г ,.-----~--~~~
ГЕОМЕТРИЯ НА ПЛОСКОСТИ
ТРЕУГОЛЬНИК, ПРОСТЕЙШИЙ И НЕИСЧЕРПАЕМЫЙ
Дреннс1·р<::ческий 11с:тор1 1 к L1е rю;ют останн:1
описание то1 ·0, как t: l'иn тянс посJ 1с.: каж;(Оl'О
разт-ша Нил:J ~{а ново ра::~ м ечали шюдородныс
уч:к-1 ки его берt1·ов, с которых ушла 1Ю/\а. По
Геродоту, с з·го1·0 п началась 1 ·еомстр1 1 я - <<:~ем
лсмерне" (0·1 греч. «гео» - «эемля» J
·1 <-метрео•} -
«измеряю»).
Дрешше :1емлемеры RЫпоm шли 1 ·еоме1 ри
ческr,tе rюстроен rш, измеряли NoИны и шюща
ди; астролопr рассчитывали раслолож<:нис нс
бесн ьrх CReтиJJ - всё это требовало весьма
обширных rю::~наннй о с1-1uйс:твах плоских н
11ростр:шстве111 1ых фигур, и в первую очередь
() трсуголън и ке.
Знакомый всс::м трсу1'0JJъник rю rтрану t'ЧИ
тается прос1 ·сйшей пз фн1'ур; 11 юб<1я 11лпсю1я,
·1. е. nросп1рающаяся в двух изм~;::рениях, фи
гура /Щлжш1 содержать хотя бы трй то <rки,
не лежащие па одной прямой. Еспи сосдишпъ
эти TO•!IOI nопар1ю npЯMUJiИHCЙllЫMИ u·1резка
ми, то rтосгроеrrная фr·-rгур<1 и будет тре~толь
н.икuм. Так же называют и заключённую вну1 ·
ри обра:.ювавшl:юсл контура часть плоскосn 1.
278
ЭЛЕМЕНТЫ ТРЕУГОЛЬНИКА
Оснон1 tым11 эJ1емс1-1тами трtу1·uл1>н 1tка АВС яв
ляютсн вер111 1 1ны - · 1очк11 А, В и С: старины
-
отр<:эю1 а == ВС, fJ =AC и с=АВ. соtди1 1яю1щ 1е
nepJJJ rп-rы: у1·л ы, обраэова.1 11-1ые тремя riapa~ш
сторо11. Углы часто обозначают так же. 1.;ак и
верu н ~ны. - 6}1снамиг!.1J и С (рис 1). Кроме этих
осrю1шых элем-сптов в треу1·ольш1ке расо1аr
rжв:нот Идрупrс О'1 реЗКИ. обладШОЩВС IJl!Tepec·
HhlMИ с1юйства.м11 , nрсждl: все1 ·0 средние юшиu.
ме1щаны , 6исt'екгр 1 н.:ы н высоты (μ11с 2, а)
Срщ)ние л1тии - это uтрезю 1, соед~ 1няющне
сср~днны д 1"ух стuрон. Три с рс;1нне ш1н 1·1ич)е
угольннка образуют ·•nписан~-1ы й·} в нt1 ·0 трt'
угоJLы-11·1 1<, 11азь11~аемь11'r серед~птым.
J\!/ейиаиы (от .тщт. 111edi ;1 11 a - «сре;\няя» )
-
отрезки, соеюпшющие вершины треуголышк-а
с серединами протнвополож11ых сторон.
Биссектрисам.и (от лат. bts - «дважды• и
sccu - « ( J:.tсссю1ю») назыr1ают заключёrпrые
внуrр11 трl:}ТГОЛЬНИJ<а uтрезю1 прнмых, которые
l\СЛ Н Т лоnолам t:ro у1·лы.
(, moj>oни
а/
r11e. 1
. з""·"енты трС'угольн11к.1
Рис. 2. 1.)"'сч,пЕ>л1,1 н.1 с
Л>tllllИ в тре\'1 (МЬШIКЕ'
flucce"/\,mfiuca
Вытты nрсдста.нлякн собой nеμ11бщнкут1 -
rы. nг1уще1111ые 11:1 l'lepmт 1 i-r трСуГОJIЫПП<а 11а
про·1 1111ополож11ыс стпроп 1,1. Точка пересече
ния высоты со сторопоi1 трсу1·опыrика назы
вается oc11oвamr(u11. высvты. С:СJш одпн и:; упrо11
при стороне треугольника тулой, то сшущсн
ная ш1 неё нысота надает на прu11олжст 111с сто
роны (р11с. 2, б).
l lазн::ШIIЯ ЭJ I CMCHTOB тrсуrОЛЫПIК;.J - ВС<.:Х
cro ()тrсзков н углон - в то же время яnляются
и 11;~зrш 1111ям11 их uелич1 1 11{так , 11::~ттrи;,1ер, вме
сто ~длин;:~ 611ссектр1кы равна a't) говорят про
сто ~писссктриса ран 11 ;1 а;;).
ВИЛЫ ТРЕУГО!\ЬН ИКО В
Лри ОПрt:/tеЛt'НИИ IШД;t ТрС)'l 'ОЛЬНИК:! )'ЧlfTh!H:l
IO'I величины е 1·0 уrлон 1-1 нали ч ие равных сто
ро11. По первому из ::эт~1х при::такuн ·1'Реуголh
н11ю1 /ttлят н~1 оспz/юугольн:ые -у ннх 11(:с уr ·лы
осгры~. Jlj)J/МO..'YlOЛ'tйtЫI! - с 11рямым уr·лом 11
тупоуголь11ые - \ •1упым у1 ·1 ю;11.1 (рис. 3). У 1110-
боrо треуrолы шка сумма уrло13 равп<1. развёр
нутому }ТЛу, ИJ!И lfIOc., а ЛОТОМ)' ТОЛЬКО ОДИН
из ero углов может нс быть ()Стрым.
Сторо ны пря м:оуrолы юго треу 1 ·олы 1и ка
имеют особые назвапия: сторона, лежащая на
против nrнмого угла, н~з 1,шается гипотенузой ,
:1две ;фуt·нс сторС> 11 ы - л·amf!ma11-ш.
По наш1чию рав 11 ых сторон ра~.11ич<1ют три
вида треу1пльннков (рис. 4). У равн.остор(m-
11u~: (шrн правилыtы.х) трсуrот,ников tiCe три
стороны раRны. Ра.вн.обедренн:ь~е треуrтп.нv1-
ки имеют л1с1е рапные сrоро 11 ы; эти сторо~-11>1
называют бокоnыми, а третью сторону - ос
поnанисм. Все остальные трсуrольнитш -
ратостороню 1е.
Те же виды nолуч аютсд, если сравшш:пъ тре
)ТОJ1ы1ики по сте11ени их симметричности. Вы-
Геометрия на плоскости
а
с
б
ПЫCOJUCl -
ptЖCJ\.1 из бума1'1-1 ;~ва абсотот1 t<J Ol\H I 1 ai<onыx
треуголы-т~н«1. Если они разносторо11ш1 е, то и:х
можно будет точно сонместнть .~р~т с др~тш1
1r.ишъ од1 шм-с,тщнствсппым сnособом. есюt о шt
раn~-юб <.:дрснньн: - то днумн, а если раююl~ю
ро111 111е -
·r·u 1нсстыо с11uсобам11 . (Чтuбы nра
иил ы ю нодсчитать споt:обы, 1ш .чет 1,тt' вер
тины треу1-олы 1 иков букн:1мн и лрослсд1пс, как
0 1 1н совмещаются.)
Раnносторо11н~rе треу1'nльники , по сун\е
сту. nce пд1шакопы - 01111 и;-.1еют <щ11у и ту же
фnprvry и могут отличатт,сн др)'т С>Т друга 1 1 и1ш.
размераt.п 1 . Рашюаедрст111ые же треутолыштси
оказъшаются той очень УJ1.О6 1 юй стуnенъкой,
на I<оторую нетрудно подняться, когда толы<о
только приступают к изучению rеомстрн11. А с
этой ступснr,ки уже открьшастся воз можность
/\алп11ей11Jе1 ·0 fl.Н l·J)кенин rшерё/t.
Ckm/IO.)'I011ы11>1i.t ПjJящ~1 ·гилыщП
Ри<:. З. Вилы тре>'гuл ьников пu u r нщu ен щu ~углам
1'аш юоrюрт m 111/
( llfJCШtl!lЫ-f.blfl)
Рпу1щбедр!!1111щi
1
Ра.з1mс111u/л1111щf1
Рис. 4 . Вил 1; треv1 олt,н11ков no uтнош ...нию к порu нам
279
Фигуры
РАВНОБЕЛРЕННЫЙ ТРЕУГО!\Ы IИК
В 0:111011 н:i 11 с рны х ·1·со рсм <· Начал" ~uю11щ:1
п1 ю р\1уш1рон:з 110 Ot'lf()f\lf ()l' CBOJICTBO р:~шю
6<:дrснно1·u трс~тш11,1111ка: у1лы 1Jp11 е 1'0 ос но
ван111 1 p:mrrы.
Дor<a:З:J'leJlliCTIIO :'ПOir тсоrсмы Пр11П11 <.ЪIВ:t
ЮТ t\)a.ГJccy М11л<.·тско.му, ж11 11Ш<.:\I} за :111;1 11е1<~1
,'\О ~uюшда. HПOCЛC,l\CTШ llI тt:upeм~I IIOJ l)'Чll J la
11а з вшше Prms asi1ю11m1, что 11а ла·1ын1 1 о.-1 н: 1 -
'-Iает." «:-.юст ослоn~. Оf>ъясняют такое н:1 :ша 1 111с,
с: O,l\ IIOfl сто роны , тем, LJ'l'O чсртёж, исп ш11,:ю
ва1шый Еню 1 1 1; 1ом ;1,.1 111 ct: ; 1ок:1:1ат~лм.-1·11:1, 11 :11 ю
\t1 1н <1ст мuе1·11к, :1 <. /\ру r·ой
-
м 1 Jе1111с ,\1, будто
ТО.1 1 hKO OCJI ы нс \\()( ~-1· этот ~10CTJtK 11ере iп11
(p tк. ')). ( Br 1J)()Ч<:\1 н соврсме ш юм 3111·m1l1C •<O'I
я:-1ыкс л ат1111скос 111,11ыж1;::11111.:: •·ролs a~ i 11011.1111"
~ 1нп~бJ!Яt'ТОI 11 l lt:'CIIOJI "''° llf \ОМ см ысщ: 1\.11 '
• <. уро1юе 1 кnыта 1111 с с посо61 юстсП нсu11 ы 1·но
rо человека·>.)
Обыч1 ю ДJТЯ ,l\О1Сазат<:льст11а р авен<.~1·на )Tm н1
11р11 ос1юва1111 1 1 рав 1 ю6<.:дрсн 1 JОП) трt.уrо11ы 111ка
11сполr..эуют <.то <: 1/\1ме1·μ 11ч н1 )Ст1" Трt·ул Jm,r 111к
.\ЮЖI Ю nсрснсрну1·1. 11 11:1 J IOЖIJTl1 IJ ;{ Ct'ri}.I '1':11<, Ч'/'()
кailv1:1я 1 1 з боко ны:-. с1·оро 11 со1ща;1еv1· с ;1ругоi1~
то1л:~ 11 ~т.1ы нр11 ос 11 онu н1111 сов~rсстятсн дру1·
с ,\р} 1ом. Ikpн :t 11 oi'ip:iт1 ~ан ·J'ео рема.:
1
, ,,,
Еслн уг11 ы при осповании трсуrол ь
"'
ника равны , то ou равнобедренный .
Ри<..5. • Мо< 1о!лшн
2110
Та1Сим обра:юм. 1х1 вс11с·1щ) )TЛO JJ 11р11 oc11ona
11ш1 треу1·ою, 1 11 1 1<:.i
это ll/Jll3Jtaк:. т. с. доста
точное услоrшс то1 ·0, что 01 1 раннобс; 1рс 11111,1i1
Есть н дp)'TII l' nр11з11ак11. l l u 11 pн~1cp, трt:
польш~к б)м<."1 p:11111oik·, 11x·1111ы:.1, сс,11 1 лю()ы<.:
два нз 1·рёх uтрс3ко11 - \\l:'д11:111:i . ныс01;1 11 ,111
611сс<:ктр11с:l . 11p011c, 1i.·111 11,1с к основа11 1110. ра1111ы
Вт сщё тр11 np11 111:1ка:
Если n рав нобедренном треутолыш·
ке равны дnе ~1ед11аны, или две вы·
соты, или две биссектрисы , то та1сой
треу1·олы1и1с рашюбедре1пrый.
Первые два nр11з1 1 ака д<.ж:~з 1.1ваютсн 11рое1 0.
О,1нзко пск:л<:д11111'1 . 11 , 111 тсорс'1 ) u · ю,1, ч 1 отрс
,· 1·0:1ышк. 1l\1CJ()Щll11 :tв<.· 1х11ш ыt: 6 11 cct:i-'1 р11сы,
SIHЛSIC'l'CSI pa111106l0JЧX'l ll lhll\1, ,щк:взть :tоно. 1 111ю
lllOЖllO ';) 1() ·1:11' н:1:11,1 нас111~1я тсщ1см.1 lll н:i1-
нcra - Лсмуt :1 . 1111 н:p t:C ll O, Ч'I'() с. Л. Ле\l}С
ост;~лся 11 11 l~1·opr111 м ~1тсм,1 т11ю1 нсключте111:.-
11<11ю·1·ому, что в 1Н40 1'. nр 1 ктш шве!щар с1<0-
му 1 ·еомtтру Я r<()6у Штсfшсру ш1съмо с прос~,·
1>011 11::1т1, rеомстр11чео;ое дока~атс111,стnо
дJшюго факта.
ПРИЗНАКИ
РАВЕНСТВА ТРЕ УГОЛ ЬНИКО В
Трс~т();1ьн11к11 .\Rc: 11 1118 1<.' 1 11 ~1ЭЫ1i:.IЮтся рап·
Jll>l.JНI (. есл11 0111 ( lli\1t'IO 1 соо l l!CTCТfiCJIIIO р:.1n11ыс
сю ро11ы 11 }ТЛЫ, т. с. rторона,· lВ р::нша сторо11е
1l1R 1• угол пр11 uep1111 11 1e zl 11ep1Joro трсугот,т111к~
раnсн }Тлу пр11 пер 1111111 е . 11 11тоrюrо треуrол~,
llИK;l и ' 1 д. ото рав 1 IOC I 1.1(,( 1О СЛl'д)'IОЩСМ V <>Прt·
/tелс111110, пр11щ.:1111м ому к;1ю6ым ф111 урам ·11\'·
1толышю1 раВI[Ы, если сущестнует движе
шrе. щ:рсводящсс од1 ш u:; п11х u другоf1.
Равснстnо двух трсугш1ышкоn. т. с. ncc.'i: J.1X
ШССТIJ ОСНОВ\IЫХ ::JJICMC I Л'<JH, МОЖ!I() l::!bШCCТll 113
ране~ 1стrш 1icкn юр ы х трёх :::JJн:мt:нтон. Соuтвст
ств}'!UЩllt' 1со рсмы 11а:зык1ютс>1 11ри:т:1кам11
ране t1 ства грсуголы-1111ш11. Пр11всдём тр 11таю1х
OCI IOВIIJ>lX пр 1 t :l ll :lKa.
П ервыf1 приз11з1<:
Если у двух т1Jеуrольни1юв равны
две стороны и угол, заюпочённы:й
между НИ!\-IИ , то эти треугольнИim
равны.
Это оз1 1 ач~1 ст. что р~tкны 1 1х ·1·1х:·1ы1 с 1 ·орш1ы 11
прнт.:жащ11с: к нн ."1 у1 ·11ы .
Rтopo il 11р 1 1:т:1к:
1'-,"
Треугольники равны, CCJ1 и сторова и
lr~ прилежащие 1< ней углы одного тре
уголью1ка равны стороне и приле
жащим к пей углам другого.
Гl рс;1а н11е , д<К'1 ·онср11ость котори1·0 нря7' т1
\tOЖIIO 11ровср и1 ь, свя :3ывает д01с:1з;.~тельстnо
Э1'0 1 ·0 ф:1кт:1 с им енем Ф:шс:с.1.
Тrстнй 1 1111 1знак:
Если стороны доух '1'реуrо11ы1иков
соотве'J·ствеп110 равны, то ра1н1 ы и
сами треуrольники.
Помвмо трёх ос1 ювных нри:ша1<0в равен
ства трсугол ы·tин:оn можпо указать немало
цр}1 ·11х. Как прав 11 ло. два трсуголь11ика равны ,
CCJl!I у l lllX p:tBJIЫ любые тр11 СООТВ(''l'СТ1:1ующ11х
Э!ICMl'1 J'l'a, 1 1рнчём 11С 00.>J:!~IТСЛЬНО то.111,кu сто
роны 11уr·лы. 1l o да 111 юс у·1·нер)К/\сн1н: с 11равед
!1 шю 11с ncc1·; 1,a. На пример, "1 1рн:{11:.~к » 1х1н<:11(.т11:.1
трtуго111>11нко11 11 0 двум с.vl'Оронам 11 углу, JIСЖ:.t
щему папро·1 · 11в оююй и:з них. 11ен~рс11. О;~ 11 ако
ecmJ 11знест r ю. что стор011а, про·пшолсжащэя
расо1атр 1 шаемому )ТЛ)', 11е меньше др;тоГ1 сто
роны, 1·0 треу1·опышю 1 равны, что сJLедует нз
рпс. 6, 1шщостр11 r1rтоще1 ·0построеш1с треуюлъ
н11к:1 110 эп1м э11смс11там.
;J;.t 1и 1х1нс11е1 ·на 11рнмоугот.ных трсу 1·uлыш
ков /\()CT~l'l'OЧ НО II0'1pL'6UН:-ITh f)<I HCHC'J 'Ha JI ЮбЫХ
;\НУХ ЭЛСМС I ITUH ( 1 10мr 1м о []JlЯMOl 'O у1·л:1) , C:CJll I
\rп·я бы uд11н 1 1:111 1 1х - сторон::~_ Все.то 11олуч:1-
ется пят 1 , р:1зл~1 ч11ых 1rри~~1 1 аков: н::шр1rмср. 110
гсомстри я l IJ П/\ОСКОСТИ
f'11t . (). l lu1 1fHH'l111(. '
1рРvrnлынн~.1
ПО l IOJ>llllд\\ ;\[/
11В('l'tVIЛ\'А.
0,\1\ОМу \!:~ кtlTC'\'()H \\ 1·111 юте11узt:, N~YM K<!Tl' 1ам.
1·1 11 ютtпу~1с 11 ()ДПОМ) 1 1:~ OCTj)l>IX )Т.1!011 11 ' 1' , /\.
СУММА УГ/\ОВ ТРЕУГО/\ЬНИКА
Нели н качсств<.: ·1 рёх элс.мс1 1тов пршr:щолыю-
1·0 трt'ут·ш1ы-111к.:.1 н:шт1, с 1 ·0 у1·11ы. тu Н< )ЭHJJJ<Ж" I '
(.' ( )J:!Cl'M 11.ру1·: 1н с нту::~ ЦJ I H: С)'11 (l'C'l 'HYt.:'1 (it,:l'](( )l J(. '
1J-
1-1() м110 1 ·0ш н1:.1р110 нt:раю11>1\. трсу1·олы 111 ков с
)ТJ1ам 11, ранным11 ~п1а ,\1 д~1111 ю1·0 ·1 ·1х:у 1 ·0;11,1111к:1.
fkлu в т()м, ч·1·0, :~ 11ая тр 11 у1·ла, Mhl 11а ('а1>1ом
J\eJJt зпае.\11 ·1·олько ;1 11:1 11с:1ав 11 с 1 1м 1,1х :::JJ1e.\1e11т:.1
трсу1·олышка: р;:шепство двух пар уmов д11ух
треуr олы rшюв гарантирует paнe11crno нх трс
ты1х углов. :':)тот фаю · сж~дует нз уже )'11Ом11-
11авшсйся теоремы о суммL'уrло11·1рсуголыш 1<:.1:
,f;. / У любоrо треуrолыrи1.:а сумма у1'ло в
'ld равна развёрнутому углу, .или НЮ0 •
Tc()pciV!:a о сум~н:.: у11ю11 трсу 1 ·uJ11,н11ка была
н:щссп 1 <:1 п11qx11 ·orcli1.1,;tм, 110 кра\шсй мере Jl.ЛЯ
l IJXllllUll1l IOI '() тpey1 '0J111 I [Jll(a. 0111 1A 1 >1K0ДJ l!J[I сё ~1:1
того факта, ' 1' 10 ПЛОСК()("IЪ МОЖ I Ю 1IOl\p11l' l 'f • l:~a
MOCTIТTI>) рав11ым 1 1 п1хш11лы1ьL"Ш треуголы11-11\а
м11 бе::~ пrобелов 11 перекрыт1rf1. ::>то 11ср110 11 для
трсу1·олы11п{о11 про11зnо.11ыюi1 формы (р11с. 7).
J:) любом рле 06раз1rтощейсл треуп>лыюi1 сет
ки сходится шсс 1ъ углоn, срсдн тсоторых 1шж
/\ы l1 у1 ·011 ·1·рсуп>11ы r 11ю1 встре ч ается рон 1 ю два
ра : \:1. Т~IКИМ об [ХIЗОМ, cy.\11M~I llC<.:X ЭТИХ fll CC'l'IJ
:тлон,'1'. с. У/\НОС111 rая сумма :гглон тrcyrom.11 1 11\~I .
р:щ11э llOJJIIOMY y1·J1y - 5Ы) ".
Рщ:. 7.
281
Фигуры
В нс:ксУгорых случаях вместо теоремы о сум
.\1С у1·1 юв удобнеt: ~r<.:1ю11пзонать 1х1внuс1 1 1 1ьrюе
cl1 своСктно Rнлш11.его угле~ треуt·олы111ка . т. е.
утла, обр:1:юпанно 1 ·0 стороной 11 про; ~олже
т~11 ем дру 1'ОЙ стпро 111,1 .
R
Внепший утол треу~·ольиика равен
сумме двух внутренних углов,
не смежных с ним (рис. 8).
1
1
Рис. 8. Внешн1>111 угол
rр t'уго ~ ытка
1
1
с----- -- -
Теорема о сумме углов треу1·олы~ика
факт. хар:нпсрны i1 И"-Iешю l\ЛЯ еnюшдовой
геометр1:ш Н~шримср . на поверхности ш ара
сумма угла.в треутольтшка может nри11иматr,
разные:шачс: 1 1ия, но ксе1·да болы11ис 180°. Кро
ме тот, д;ш тре}тол ы111 кон на сф~рс спраНС!\-
111113 лраз нак ра1:1енстна rю трё.м у1·лам (см.
статью <-Фнгуры на сфере~) .
ПРИЗНАКИ ПОЛОБИЯ
l'оuорнт, что треу1·олышю1 шщобны, если 11 х
углы соответствсн110 раввы, з сто роны nропор
цио11ал ы~1 ы. Каждый из двух подо611ых трсуголь
ншшв МО)JШО г1 срсвести в другой отображс ~rи
tм , при КОтоrом 1.JCC ра СС'l'ОЯНИЯ IВМС Н ЯЮТС.Н В
однн~Jковос чи сло раз. (Это свойство опредслн
ст 1юдобне 11рои :нюлы;ых фигур.)
Тlростсrш1и й случай подобия возникает,
ког/р в трсу1'ОJ11J11ике пpoROi~Я't' среднюю лп-
11ию. Отрс:засмый ею мале 1 1ький треу1 ·олы 1 ик
имеет те же углы п вдвое ме11 1,шпе стороны,
"Iем исходный (pl-'\C. 9). И3 :~тоrо снедует тtо
рем::~ о средней тнrии треугольника:
Средняя линюr треутольника, кото
рая соединяет cro боковые стороны,
равна половине основания и парал
лельна ему.
Подобие треуmJ11>1 1иков можно уста~ ювить
с помощью трёх ттрнзнако н, которые соотuет
с:твуют np1 ~ :зна кам равенства треу1·олышков:
282
Рис. 9. 1 1шr~м•
(J с релнеи м1 1н11
l"fJPYГOЛЫlttKtl
Треv r·о льникf1
118 1( 1иА(К
nuлotJНы
Два треугольпи1.:а подобны: 1) если
01ш имеют по равному углу и отно ·
шсния заюпоча.ющих его cтopoIJ рав·
ны; 2) если их соответственные уrлы
равны (достаточно равенства двух
пар ут·лов); 3) если их соотвстс:rвен·
ные стороны uропорционалъны.
Эти ттрн з11аки часто 1 1римt:ш1ю·1·сн u Д<.Ж:l·
зательств:.~х теорем, в том чпсле теорем о за ·
мечательных точках и Jшниях трсуrот,шn<а.
ЗАМЕЧАТЕЛЬНЫ Е ТОЧКИ ,
ПРЯМЫЕ И ОКРУЖНОСТИ
Описанная окружность. Так называют
сжружность, 11рохоJ 1н щу~о ч ерез нс<: трн Rер
ши11ы трсутольннк~1. ЕЕ цс:1 11р обf,1чно обо:~на·
ч<tют буквой О. а р:щнус !< (рнс. 1О). Чтоt1ы
убедиться в том , что такая сжружност1, существу
ет а яuляется е.~инсп:~ешюй для любо1·0 l'ре
уголы-шка, обратите вш-1 ма1111е: центр И -
общая nершина трёх раш юбедрешrых треуrоль·
нико.в , осноnаrшя rюторых - сторо11ы дашюrо
треуголы-11-~ка. Высоты ::эт1 1 х треугольников, ону
щсн н ые 11 ::1 осноr1t1 н1rя , служ.тг однонремен110 и
их мсдна11ам11, Таким об ра:ю~т , центр оnнс:ш·
1юй окружное~ и лежит н:~ 1 1 t:рl'сс.:чении трех
11ер111:::ндикуляров к сторон:.~м трсу1 'ольника,
проведё1111ы.х 11 их серею шах. Они так 11 t1азы-
11аются - ceper)ll1mыe периещ)uлуляры. И обрат·
110: поскольку IШЖJ\ЫЙ нз трёх серсдишrых пер
пстщикуляров к сторонам треуголыrm<:а состоит
из точе1<, раrнюудалё1п1ых от концов стороны,
к которой 011 пр оведён, тоLша пересечснllя
любых двух из них 11аходитсл на оди11;11<0вом
расс1·оннш1 0'1' ксех тrёх вершин, а :н-1ачит, ле
жи·r н<~ третьем 11ерnен/1,икулнре.
Итак. серединные 11ерпен/1,икуляры к сторо
нам 11 юбо!'о трt.:утольника пересск2юто1 к одно11
точке - це 1 1'1·ре оттис~tн1-юй вощ1уг него or<pfAi·
ности. В остроу1·о.rJ ыюм треуrолыН1ке центр
OПIICll lllOi'f пкруж~ ЮС'f'И леж 11т LlllYIPI f е1 ·п, н 11рн
~оу1 nт.1 1 nм - 11а г11 nоте1rу:>е, а ут}rnоуrолыю -
1·n 'fllC:rгoЛЫ ll П\a - ПIIC СГО.
Биссектрисы, вписанная и вневписа:~пIЫе
окружности. В1шсат-юй 0Кj~/ 1.J1сностыо трс
)ТОЛЬJшка наз ьшаегся окр:~;Ю-Jос1ъ, касающ:н101
вС<:'Х <.:J'O <."1'opu11 (рис 11 ). /~ ругнми слона.v1 н ,
цtнтр / 11n11c1111 юй uкруж1 юо·11 уд;urё11 от всt:х
тр~х <.:торо н трсу 1 ·0.гн,ннк:~ н<t одно 11 тu же
расстuя11не 1-, ра1111ое её рад11усу. М 1южес•1·1ю ·1 ·0 -
ч е1< ti1 1 ~-11)11 тре~rсолыrнка, раАrюу;1алё1 п11,1 х от
дн:х егn сторон , есть биссеr<трнса )Тла, оfiра
:юnюпюго этю.ш сторо11а~ш. llоэтому док:~эать,
qтu шшс;uшая u треу1·оnын1к 01<р}ЖI юс11, суще
стuует п опа е,~ипствстшая. можно так ж.с. как
бьшо сдс11ано в случае UJ 1исан ной uкру·..кност11,
'J'UJIЫ<O p:tBl IOY/\4/lё l 11 юсть 1\CJ 1·1p::i сжруж1 IOC'l'~J
от нер1ш111 н;що ~;1м<.:11ить р:шноу;~алённостыо
от сторон, а середин ныс 11ср11сндикуляры -
б11ссскrр1 1 сами. По путно уст::н-1аплнн~1 ето1 . что
вес трн б 1 rcct 1«1 ·pиc11J имеют eд1111C'1 ' tlt 1 11 1 yю
общро точку - 1\с1ттр /.
Три окружностн, каждая нз которых каса
ется о,ц1юй сторо11ы (сн::~ружи) и 11родоюкеш1i·1
двух I~pyr1 1x сторон трсуголы1ю<а (рпс. 11),
11:1ЗЫВ'1IОТ<.:я (j/((!(J1lltCaJ!JlЫ.MU. Центр В IIСВПИ-
R
~--/
l)и с. 10. Ct:pt! ы11 111i.te
Пf'J1Пl''ftl\11KyMIJ1t.1
\
~• оnщ~нн,н~ окружность .
\
)
Рис. 11.
Ьиссектрисы
И HГl~1{<cltllliHI
окружность.
1
Геометрия 11J плоскости
са 1 (IЮЙ окружJJОСТН JICЖIJT 11а пс:рtССЧСНИJI
fil1CCeJ(TpHCl1I O/~lIOI'() Bll)~1·pe1111e J'() ~TJt:l И nиC
CCKTpIIC IШCllНПIX )ТЛОП при [{Вух JЧ)~Tl lX Rep -
Шll!lax. Т<1к11.м образом, шесть биссектрис трс
~толы rш<а трн шrутрспrпк п три впс1шпrс
пересекаются по три в чt:тыр<::х точках -
центра х 1-шисанно~'1 11 трfх iшев1111са1шых
окруж11( ICTl'i'I .
Высоты . ТТрямhlс , со,r\сржащ11с выl'оп.1 трс
у 1 ·()J 1 111111 ка. нсе1·д;1 11ересею110·1·01 в од1 юй ' 1 лч 1.;е.
r1азыnасмоi1 сп1 о/mюце11т/ю н. 13 остроугштъ
rюм трсуголънш<с ортоцентр лсж 1 1т rшутрп
тре1толышка (рпс. l:). с1), и прямоу1·одыюм
-
corina,ri;aeт с нероr111rой прямого yrJJa, а R тупо
угольном - находится вне трсуголышка п:1 пс
рсссчсн1111 11ро;ю11жсю 1lr высuт (р11с 1 .~. б).
Нсш1 jj - о ртоцеllтр l'PC)'['(JJIЫJИK~1 AJJC, '! '(1
1110():1>1 11:i чстwрёх ·1·очс1< А, В, С J1 !1 }j 11лястсн
орто 1 ~<.:нтром трсу1·ольнr1ка, обр~1 зо 1{:1нн оп)
Tp<.:~tfl J\ру1 ·1 r ми точкам1r .
Докзжем, что орто це-1пр треу1·оm.1111 ка су
щсствует. H;,i р11с. 14 треуголып ш АВС: - это
середшшый треу1·о;tьшш д;ш.1\1JJ 1 С1 ; з11а •111т, вы-
соты 11ер.rюго треуrолы 1ию1 nнляются сереf\и11-
пымн псрпсндиf(уляра ми второго. Отстюnатсль
по, оrш псрссск;нотся в центре ll ош1с;ншоl1
(
А
в
/
/
Рис. l.l .
Вn>tеанная
1
Н HHl1HI H11 ,1 J IHЫE.-'
окруЖНОСТfl
l1
1
1
2Н3
Фи гуры
l'1к. 13. Пp1otJ E'l t rr
треугuлы11 1 ~,1 -
б
1111 к<:1 , об рJ зок1ш ю1 ·0 осr10nа1111ям 1 1 11ысо1 . Or-
cю,ri:a СЛС,'(}'СТ. Ч'J о O!lll 11меют об щую ТОЧI\)'.
М с,1~иа н ы. Можно до ка~~ать. чт1 ! точка JJ. распо-
1южен1 tаи 1нrутr1 1 тр1:у 1 ·ш 11,н11ка А/5С, ;1сж11т на
~1l'Л llaHl', llJ10K~) \{;1 IJ l()Й J< tтo pu 1 ll' 8(.' TOl'/\;J 11
'Г()_llf,KO TПГft;J, KO l') \a П! ЮIЦ:!/\11 'l 'J1 l'Yl '()Jl l 1HllKOJJ
"'--_J...J...________;,,...(.
}JrllJ н J>/\ C 1x1 пrri.r (Jll 1с. 15. п). Исхnю1 1 1.~ :с1·1·<>п> 11
Ри<.. 14.
0tю1ю нтпрrн·о треутолышка (1круж 1 юст1 1 , 11
:пот I lCHтp соnп:щаст с о ртоцентром трс:уголь -
1шка 1ШС.
Р 1 ку1 юн: 11. помогает вьшсстн теорему о вы
сотзх и з теоремы о б нсссктрпсах. Постюmжу
6псссктр11сы смсж11 1,1 х у1·1ю1:1 1:1:3а11м110 псрпсп
/\llК~лнр1LЬ1 , ll:I pHC)'lll<C любо lvl 0:3 l\Cll'l'POH чс:
тыр<.~х окружr-юстс 1v1 (н нен1 11 1саt 111 ых 11 ш111с 11 1-
1юl1 ) }jJl)J}\C:'l'CЯ op' l 'O l \l'HTP!JM ' l ' [X'Yl't>J l bl-lllK: l с
к1.:р1ш IH:IMJI в трёх других ЦСI ПJXIX, а ТОЧКI 1Л, в
11 Сслv-жат оснона1н.1J1м11 с 1 ·0 ш,1сот. Мткн о как
бы "lltрсщ:· рнутъ -> ;;,то набЛЮi~е1111 е 11 J \()К:t:зат1 "
ЧТО Bl>IC'O'l'Ы 1 1poи з 110J11_1IIOL O тpt:~TOЛbllf[](a -
6rrсс{;ктр1 кы ортоп1р1;:у,'1Иышка. ·1 . е. 1т)(::уголь-
28..J.
р:ксуж;1~н1 ' 1':11< же, 1<: 11{ 11р 1 1 ;н н1::1 ~1атсл ьст11:1:х ·1 ео
рем О 6 r tCC'C l\Т()IТC~I X 11 Ce()eJ\llШlЫX Ш::рnеJЩП-
1\УЛЯрах '1реу1·0J r ы11ша, убежласмся n том. чтон
медна п ы пср<.:ССТ(аrотся н од но ~'i точке - :\1
(р11с. 1"5, б), пrн 1 ч61 вес три треу1'ОJ1Ь1ш1сt,МАВ,
,\/ !3С 11 МСА, lL.\1<:ю1 р:tвl!ую пло1 1 1:11t1" 1 1т 1 μанно
вслт 1 к11 r;oлt.:c тu1 ·0, н любом трс.::у1 ·олhн 11кс
точкам детrт кажну 10 мt.:; 1r1a11~ н 0; 1но,1 11 1·оч
жt: от1 r<J 111 cн 11 11 l.: 1. сч 11таи 0· 1 nep1111 1111.1 .
И11·1·ерес1 юе сво r'1стnо точкп nср есече 11ш1
\1С/\1-1;111 сш1 ;~:1110 с <l111:11rчесю1 1\\ по 1 тт 1 1ем l \t"l lT·
р а масс. Оказынасто1 . сст 1 1юместrпъ n nc p·
1111шы треунтынrка p:.inrrыc мас сы. ·1·0 1 1 х цеrrтр
nоnадёт 1 1ме1 1110 в эту точку.
l'ис. 15 . Мелнаны треvго111.1111к,1
Цсптр р:нты х масс 111н>1 ·1 р 11аэыn:ш)1 l\ell'I ·
рпидом . Иисr 1110 по:~1 ому rоно рн·1. ч то точ ка
пс:р сссчс 1111н ме11, 1rан - це1m1/ющ) трсугпль-
1 шка. 13 этоfr же: точ 1<с расгrол:11 ·ж·тсн и центр
масс щ.1но1ю.u.ш >fl треуголыюit 1 1J rаст11н к11 Есш
n о;щб н ую 1щастшшу ш>ст;шн1· 1 , н:~ буланку так,
Ч1( 1nы (\(' l '(JI 1(' 11( \CJI C) \IJt'Jl 1юпа:10 ' f( !'1110 11 1\СНТ
р<)) 1/\. '1 '0 Шt:JCTJ l IJJCI ny,f\CT 11;1 ХО/1,1 П l1бl К р:ШI lO·
вссr 11 1. Л1рfiопытно, что l\t:t1• 1p \Т:1 сс пртю:юч
н<)1'0 '1()<.")·l 'OJI"'IOI'() f(( >l Пура С( )ВП;щ:1ет с ;\()~l'{)(J
точтют'1 - с 11,е 11· 1р«щ 1111r 1 сн111 ой <жруж11пс п r
его ccpc; 1111 11 ro 1·0 1 ·рl:)Т<1: 11,1111к~1.
Пря м:ая Эйлера. Леоl!ар,11 :7йлс р с; ю1:~11 це
лы~'~ ряд ~~амсчатст,111,1х oтr<p1 ,п 11t'r 1:11·сомстr1111
трсу 1 ·ш 1 h1-тка J J.,шрнмср, 011 ,'1сжазал, что r 1с11-
·tронл.1'1 любm·о трсу1 ·ш 1hншс1 11сж_11т 11:1 отрсз
r<с мсж;1у цснтроf\ 1 ()с.то 011 1 1 с,11 111 0 1'1 окружно
е ~ 11 11 ортоцс: 11т ро м ll ~1 :1с1 111т :-этот отрс:юк R
от1rошс11r111 О/\/ : .l/fl = 1 · 2 11ря ман ()Н на:i1,1в:1-
Рtк. 16.
'
-
1
1--
,',1i~~~
о1
1
/,
~
tIOJ 11рямой Эй11с:ра [(а1 111<хо треу1 ·оm,тнша
( рнС' 16 ). Попробуйте дока:J::1 ·1 ь теорем у () пря
моir Эitлера, лользулси рве. 14.
Изоrона~rьные точки. J:kть н другая 1111т<::
рtснш1 1:1::\Ш IMOCBK!b М<.:ЖJ\У орто ~ ~<:!·Пром 11 1\<..:Н
трuм оrшснпюй окружност11 ·1рt>у1 ·011ы 1 11ка .
Можно rюк~tзать. чтu
Прямые, си.l\1метр1:1•U1.Ь1е высо1'а.l\t от
носительно соответству-Jо1цнх бис
сектрис, проходят чере:1 центр опи
санной окруж~юсти,
т. с. содержат сё радИ\rс 1,1 ( рнс. 17). <..:11равсдлн на
11 более общая теорема·
а Если три 11чямые, проведённые из
1'?'1
J;
1,.
вершин треугольника. пересекаюта1
в одной точке, ·ro и прямые , сим11-1ет
ричt1ы е им О'l'l(UСИТеЛ1.но СООТDСТ
С'J'В)'IОЦ~ИХ биссе1<трис, тоже прохо
МП через одну и ту же тоЧJ<у.
Пщ106ныс дnе точ1<и т r азьшаются изого11апы1ы
шt Та~<им образом, ортоr~ентр трсуголышк;~
нзо1uналс 11 центру una<.:<1.шiпr·1 uкружнос1 а.
Рис. 17. ()p rouL•НТfl /-/
IJJt'YIO\bHHlo.<1
11~01 011,1лl'н u e1 11 ру ()
01 1 щанно11
11... ру"'1ю1 1 11
в,
А
Гt:омt·rрия 1·1<1 пло< кщ rи
Рис . 18. (, 1tмел11dны
11 IO"'IKJ. ЛРму~1н~1
в
0 1 ра;11 т от1юс~пt:л 1.н о 6нс<.:сктр1 rc трсупт 1, -
111 rк:t СОО'IВt'ТСГПую1щ 1 е ~·1C'7'1 1 :1 111 tl , ll()Jlyч ;1ют IIO-
DUi e за.мечатс.11ы1ыс лшши - ClLllUJ<)иrmы. Точ1с1 /.
'L" псрссечешнr 11азыuастсн moчл-rJit }/(~"11 ·тщ
трt'у1·ш1ы п 11<а . Она яn:ше1 ся l \CI прОТ17'О \1 трс
уто11ы шкаr1 1 /З 1 С1, обра:ювашюrо её нросю(J uuч11
11 <1 стороны ис.:хuднот трсуюлъrrиr<а (р 11 <.: l Н).
Окружность девят11 точек. IJpu; 1011ж:ш раl'
суждс- 11 Ш! , CIOI Зll 111111!<..: с Г1 рямоir :-эr:i,1t:pa , MOЖllO
J \Ш<<l:-J<ITI>. ЧТО
~ . Середины сторт-1 тt>еуr·олъюоса (точ-
r {\f. I<И / , 5 И 7), ОСИОВаНИЯ е1·0 ВЫСОТ
(точки 2 , 4 и 8) и середины отрезков
o'l· вершин до ортоцентра (точки 3,
6 н 9) лежат на одной 01сруж.1юсти
(ри:с. 19).
t:c:e р~диу<.: р:111сн 11())(()1\ННС р:щ11ус.1 OIJJJ(.';IHH()(J
OKf))'ЖllOCTl l . <1 Цl'НТр Р !ТСЖ ll Т I ЮC<..:pC}(ll J I (;'
отрезка ОН. Окруж1нк-гъ 1; 11аэ h1наетсн окруж
fl( JL°'ТЫО девнт11 тпчек , нл н ( 11<рv-жн< 1пъю ~-)1'1лср: 1 ,
~1 J 1 И окруж1 1щ.:1ъю Фе::lrсрба .-...:1 - 11 0 11м<..:н11
Карла Фсйсрбаха, nрон1. 11п~нал1.1ю1 ·0 уч 1 1теля
м:.~тсма·1 нюr п:-1 1 ·срма11ю1 , родного Gpa r·a фтю
соф:.~ ЛI<.щrн1га Фсйсрбаха. К. Фс1'1србах открыл
Р11С. ·19.
()~ pyЖ I IO!Th
Л('''"ll i.t t• •ч~к
28'5
Фигуры
РиL 20. Окружногrь
Llf'f!RT 't ТО'< <> ~ кJсается
Чl'11.1р Р'- 1жруж>ю пt •и .
1\
/
\
!'
\
1·
',
/"'///
\/
r
~''
'
'
\
еще ОДlЮ, самое yдiJJ:!ИTeJIF>HOC СIЮЙСТНО ;.)ТОЙ
окруж1юс1·и: она кас::tстся четырёх окру--..кнос
теr1 треу1·ольн1 1 ка - вnис1нной и трёх ш rепm1 -
са н ных (рнс 20).
Точки Жерrолна Ji Наrеля. Можно доказать,
что ч)п отрезка, сосдинmощие вершин ы тре
угольника с точками, n которых впислн ш1я ~
него окружrrость касается соотnетствешю
протиrюrюложных нсршипам сторо1 1 . 1 1сресс
каются в 01тной точ кс.f (рис 2 1). Она н~1з ы вn
ется тuчкой. Жергuнна.
ОтрсзюJ, соею 1 няющие каждую из верш и н
трсуrолы 11 1ка с то ч кой , в кот()рой противопо
ложная сторона к:~сается СО()тnстст11ующс.й
вневшrсанной окружrюс1·и, ~"оже пересекаются
n ()fl:ТЮЙ точке N - то·чке Нагеля. Она инте
ресна тем, что отрезок NI, где 1 - центр или-
Рис. 21 . То'tки
Жep1011tia '' Наr ел.1
286
----
\
------~ ',,
санной окруж1юст1 1, проход • 1т через центрощ
м треуrолышка и /~СЛНТСЯ им в ОТll<)ШСШЩ
.l'v:H :;Н/= 2:1(рве. 2J).
Теорема Ч.евы . Пrю 1 е такоr·о 1t:10611л ю1 т~:оре~
о трёх прнi\1ых. 11рохо; 1ящих черt:{ ою-~у Т()ЧJ\)',
ВО3Нl 1 К1е'Т' во11рос- Ht:T !111 [{;)КОГО -ТО общет спо
соба J\01\Ззы1щтr) э 1шюrп'л thte )rrвсржде111ш?Та-
1<ой с п особ дейст1:н1телыю есть . Ern н:~шёл
итаJrьянскпй геометр .и мехз11икДжова1 11 111 Чева.
13ыберем~ на сторонах ВС, С4 пАВ тре)толь
rrикаАВС точкпА1.В, t1 С1 н соедш1им 11х пря
мым11 с протикоположнымн вер 1 11 1 1ж1м1 1. Такие
11 рям 1 .1 е называют прямымн Чсвы 11111 1 че виа
нами. Тtор~ма ЧсRы 1·ласнт tрнс. 22, а):
i~ Ес11н 'l'ри ч евианы nересекаются в
kc,
одной точ1<е, то отношения, .в кото·
рых их ОСНОDания Л р в] и С1 делят
стороны треуrоль:ника , удовлетворя
ют раDенству
ВА. 'свl АС. =1.
С)
А1С В1А С1В
Д:H-IН<Jt: соотношение будет нъ1 п0J шя1ъси 11
тш·да, 1югд:~ точка п t:рссечения п рямых лежлт
вне трсуrо л~. н11к::~ юш нес они параллельны
При этом две из трёх ·ючек!11, 81н С1 11ахо
/\ятся 1 1 а про1101~же11нях сторо п треуголъннка
(рис. 22, б, в). R таком случ:~е rоворнт, что ос
нования чен.нан депят эти стороны n СО()Тnет·
стt~ ующих оп10 111 е 1 1иях в 11 ешннм образом
Справедлива и обр:~тная теорема:
Еслиточ ки А 1 , В1 и С1 напрямы.х, оrра·
ничивающих треуrольникАВС. удов·
ле·rворяют условию Чевы , nричЬ1
собственно на его сторов ах лежат все
три либо ровно одна из них, то coor·
ветствующие чевианы nересека10·rся
в одной точке или параллельны.
Из зтой теоремы можно в ывести нее при·
ведённыс выше утвержде н ия о пересечении
трёх прнмых в треугольнике.
Теорем:а Менел ал. П ри обсуж;~еюш теоре·
мы Чевы мы полчёркинали, что на сторонах
треугольнrrк:а 1 1 сж<1т либо нее три ос~-юванщ
чениан , либо только одно из 11 пх. Без э·1 ой oro-
tюpi<и можно попастt. t1 услоRия друтой КЛ~\С·
в
Рнс. 22. Теоремы
Чt•oi; (,1 rs).
М~НРЛi\ Я и 11 их
11μ11м~1-1е1JИС'
А
к бне<:ектrис ~м !л) .
А
с
А1В
с11ческо~"1 теоремы , нпсящей имя ;~рс:н н е 1т>ечес
ко1'0 математика 11 астроно м а Ме нелая Алек
сандрийского (I-П в н.) :
Если стороны ВС, СА и АВ треуголь
ника АВС или их продолжения nере
сека~отс.я не1юторой прямой в TO'-m:ax
А1, В1 и С1 соотnе.тстnе11но, то выnол-
1шетсл соотношение(*) (рис. 22, г).
Uбратная теорс:ма также сор;.~нсдлина. При
этом ротшо одна либо нес три точки лежат на
продолжениях сторон треугольника.
Для примера прпмсним теоремы Чсвы 11 Ме
нелая к биссектрисам внуrренних и вн~шних
углов треуrолы rика. Соглас1 ю и з вест1 юму свой
ству, биссе1пр иса AD треугольни ка АВС делит
сторону ВС на части, пропор циональные при
лежащим к ним сторонам: BD/ DC = ВА/АС. То же
верно и для бнсссктрисы.АЕ ( рис. 22, д) :ВЕ/ЕС=
=ВА/АС. Подставляя эти равс11с113а для соотвс..-т
с111ующих биссектрис в теорему Чевы, получим
уже з11акомую нам теорему о том, что три ннут
ренние или одна вну1·ренняя и две внешнне 61-1с
Сеf\·три с ы (т. е. биссектрис ы внеш н их углов)
пересекаются в одной точке. А и з теорем ы J\'lе
нелая а11алогич1·ю ~з ыте 1<ает, что ос 1 ювания од-
1юй внешней и двух внутренних биссектрис,
проведённых из раз ных вершин, лежат па од
ной прямой.
Теорема Морлел. Эта краси вая теорема бьmа
сфо рмулирована в ко1.-ще XlX столетня амери
канrtем Фрэнком Морлее м.
llронедём mj)UCl:!К,117/.JUCЫ )'l"JIOR T{ll:Y l 'UЛh
llИK~I - 11 рямые, кот<1рые делят у1'лы на трн
равные части. Отметим точки 11ересеч ения 11ар
тр нсектрис, прrmежащи,°" к каж,т~:ой из сторо1 1
треугольника (рис. 23). Отмеченные точк11
бу;1;ут нерпптами правильного треугольниI<а.
l'ис. 23. 1 (!Орем,1
Mopl\C>t
Воистину геометрия треугольника 11енсс1ер
пае.ма, еслн такая жсмчужи11а мо гл:~ сохра
ниться не:-1амес1ешюй па протяжении более
чем дnух тыснчеж:тий!
ТЕОРЕМА ПИФАГОРА
Фо рмулы , связывающие между собой ) (111-1ны
отрезков, ПJЮЩЗJ(11 , 11еJ1 1-1ч.1111ы у1·;юв 11 фи1-урах,
11азышнот ,'v/еmрическuми сотп1юшения.м11. И
пожалуй, самое знаменитое из таких соотио
шепий - теорема Пифагора. Она устанавли
вает прос1ую зависимость между сто ро11ам1 1
11рямоугольно1·0 треу1·ольника:
Квадрат гипотенуз ы равен сумме
квадратов катетов.
287
Фигуры
.
-
011cm lпl>сщщ1 p1opofi1щn.
1fЬ1opolirio .44 .
в
1й ontni rriansolo 1·(cf\IJ1gulo q1111dr1Jn1111 q;)ti rarcre rc
f
"
cco1111511lo oppolico 111 tentcnplo ouao oclcriЬif cq11ii ё
1)t1оЬщ; qu11dr11tis qut~ t>n~b'i' rd1q111s tltfttibus со111
fmbunmr.
C:5it rna11suluв.11.b.c.<01us 011S!Jluз.aJlt rc((us olco <r quadr111
rii latcris .b .c.cquii с quadraro.e .b.i quedr11ro.в.c.Г1I fumptiв..Quadrobo gl>c<
1т1а l1Шt'Q fu1 ooctтl11a P<(d mils:firq; qdrв1fi.b.c.(11~ticш1.b.c.d.c.i qdrarii .ь.
IJ.fUP.fidro .Ь. f .\j.\1 . 'Z qdrвni .o.c.ft1P.ftilC\J . S,c.b.k.\IЬ U1J11(0.11.rccro OU CQ lld b.if
i).d.c. ЬЗfi) lnll,P~tiqdralt IТCG11t1(;1B J.a.\ ccjdt!m!G \>triq; IOtCfl.b .d . 7.C.c .q fc
са.Ь.с i p1icto.n1л fPOtbani(l\l!.o.dл.в.c.1rёq5 о tJuoЬ 9 rd1qt:l'i1Jli6 rnaqli q(uc
b. i .c .ouci ad 0110011115\0011uo!I qdraro;: mio~ oш>tJ l1iss fc 111rf((n1ce icro ipfli
Фр~Г\1 РНТ ДС11\<1 j,JТPЛ,.,CТRJ
l •• up~\1bl 1lщlJ,11 <1р,1 ~~K.\ltд.
«t l11 Ч c.11'rl 1 И -\J\,1H~1t ' J11811
Предстз 1ш·1ь <:сбе .эту тсоре-~1у отлелыю от
ИМСТll 1 UeJUfKOl'0 1·rека уже Ш.'ВОJМОЖ110, IIO на
самом лсле соотношеIIис, тю·1·о рос 01ra утuерж
даст. было 11зnеспю дрешшм мат<.:.'-'l:tтшщм :~а
м1ю1·0 веков до П11фагор<1. О наибоJ 1 ес 11~шсс.· 1·
ном частном с11vчае тсор<.:мы - ~е 1·1111 етском
·1pcv1·011ы 111 кс-> l'(.) сторонам 11 :). ~1 11 ~ (:) _: + ...'/ _: =
~/
.
= )-)
-
l 'Шюрнтсн х 11агп·1русс , кuторы1J 1к" 1 ·0-
рнк~J ()T IЩC}l'I ПГН1бШIЗИ'l'еЛ11НU К 2()()\) 1'. ДП Н :'1 .
То же сот 1101нс11и е встречается н i 1a t~а111-1 1ю11 -
сю 1 х Кlll!ТIOПllCIIЬL'{ табJ LНУКаХ, ll 1\Щ)СRТ·1 екитай
сю 1х. 11 в древ1 1е1111,1\нйс ю1х тра1С1 <1т:tх (см ста
тьи «Дрешuп·1 Еr11пет~ , « Межд'i'РС'Н>е·>, «Дрсщшй
Кнтаf1 ". «С ред1н.:вс ковая И1щш1 ») . Однако в ("О-
МЕТРИЧЕСКИЕ СООТНОШЕНИЯ
В ТРЕУГОЛЬНИКЕ
ОбознJ.чим в 1-реуrолы·1ике АВС его стороны как а,
Ь, с; углы - А, В, С; выl.01у, опушен ную и~ верши~1ы
А, - h ,,; медиану- щ,; бип t•ктрису- IJ; ра лиусъ1
вп~канн ои и оп11са1111ой окруж ностей - соответ
ствен1ю r и R; nолуnериметр-р; плош<1дь-5.
Лля 11рямоугольно1 о треутльникаАВС (с п рямым
углом С) вер11ы соотно шения :
с1 =а 2 + h 1 (теорема Пифагора ),
а=с!.iпА =ссо~81
а==htgА==ЬctgВ,
1'= (а+Ь-с)/2.
Лля прои зво льн ого же треуголы111ка вер11ь1 сле
дуюшие соо 1нош ения :
С~= а!+ /Ji - 2af> lOS С (тео рема косинусов),
с1
ь
(
--=-= --=2R
siпЛ siпB siпC
( а ус иле н ная~ теорема си11усов),
11р1.:ме1111or1 11СТ()рн11 ма 1 ·емат11ю Lсч11"1-астся , что
11метю Пнфаr()р /tал его 11 ервое ; 101- 11чесю 1
стройное /~оказ:~тсльсt'uо.
Справедш 1во 11 ушеrжлешrе, обра 1110<: тео
реме I Jпфагора:
~-/ Если е:rороны треут~лъ1~r ка Jдовле:r·
'!!-:. воря_ют равеНС1'ВУ а- + ь· = С , ТО Э1'0Т
треуголъник прлмоугоm.ный.
ДеГ1с1·ннтслы ю, <::СЛI 1 'f :ll<OC р<1в е1 ICl'IIO ВЫПОЛ·
ня ето1 щ1н ка 1ю1·о-то треу1OJ 1ы-1111':.1 . ·1о он 6y11e-r
р;.1не~-1 П() ·1·р~;-.1 <.."Т()f)ОНаМ Пj)»Mt ))1'0Jlblll}MY 1'\">е
уголышку с кзтетамн а п h.
А
ь
с
1
1
аЬс
5 ,,. -а/1 =- al?smC =-:
2JL
4R
=2R2 sinA s1nB si11 С=2 гр,
2
5 = Jр(р - а)(р- IJ)(p - с) (формула Герона),
т}=(2Ь~+2с1- а2)/4,
2bccosA 2
l ,=---
--
h+c
А
вс
в
Геомеrрия н.1 ПМ)( КО<Ти
1Jлагод,1ря Н)М)' что тсорсм'1 Пифагора nо
зволяе'1 ЩJX0/1,ll'IЪ /VШНУ отр~зr<:;~ (ПТПОТС I J)ЗЫ),
не ызмс:рян егu нс 1 юс р<:дствснпu, она как бы
пткрынае 1 пут.h <.: llpJJMOIJ н;1 ШIUCI<OC1 ь, с flЛOC
KOCTIJ в 'J рсХ •\1(.'{11-ЮС прос1 p:JH(_V[ 'f\П 11 ;tальшс -
н мнотмсрные пrостр"1 н ст11: 1 . Этт 1м опрсд<.:J1я
е-1ся сё 11с1<111оч1пслы-r;.~я наж 1 юст1, для 1·самст
рии н м.псм::~тпк 1 1 в целом.
U некотором смысле n теоре.:-.tс llпфагорJ ,
l~Ш u JСрнс, закточс1 1 ;i no1 еnюшдоnа пла1111мет
рня. Вспом.шРvl форr4у;1у щш рас(.'тояшtя между
·1·uчкам 1 1./I(.\' 1 ; у1 ) 11 Л(xJ.J'1 ) в декартовых коор-
ЧЕТЫРЕ ДО КАЗАТЕЛЬ СТВА
ТЕОРЕМЫ ПИФАГОРА
ro врем!::'11 Пифагора появилось
несколько сотен лока ·-1а тель ств его
~наменито й теоремы, так что она
даже по п .зла в Книгу рекордов
Гиннесса. Однако при11uипиалыю
различных 11л~;И в эт и х дuказа
rельствах и с пользуется сравн и
rельно немно го .
В « На чалах. Евклида теnрема
д;н1а в следуюwеi1 формулировке:
nлошаль к~эалрата , поn-рое111юго
на rи11отенузе, равна сумме nлоwа
дей К13i1.Лратuв, пострае 1111ы х на 1ч1-
тетах. Суть лоеол ыю сложного
доказательства состоит в том , что
больш~t й квалрат предстает в в и де
сумvtы лву.х чисrt:'й, рав но великих
ме11~1.11им квадратам. Н о можно и
npuпo разреjать п ерв ый квадрд т
11а т;1кис куски, и з котор ых состав-
1\ЯЮТСЯ два других квадрата. Олно
нз подобных локазательств привt>
лено на p•tc. 1 . [ro называют « шар -
111-1рнь1м •. потому •1то зде<.1> меня
ют своё положение только лве
•1.~пи, равные и с хоыюму тре
угольнику, причем они как бы при
креплены к остальной фигуре н.~
шарн11рах , вокруr ко1'орых повора
'IИ В.:tются.
Лру гои чисто геометрический
cnocuб прямого локазательства те
орс\1ь1 П ~tф<:\ГОра - Ht:' разрезание,
э доnолнен иР квадратов ло равных
фигур равными же фигурами . Ри
сунок 2 •~мюстрирует лока~ателt•
ство т,111.ого типа , данное Аеонардо
ьа Винчи. ( Попробуйте восстан(1-
0и гь егu по чертежу.)
В <лелую ш е й груп п е лока.:sа
т~льств т1ш ре....1ы Пифагор <1 исполь
зуются ф()рмулt.t для вычисления
ди11:пах. АВ=\(Х2-
.'\·1)~ +()'2 - у1/ ~ 0;~1ro1'1
сторп ны_ это просто тсор<.:ма Пнфа1 ·ора д1 1я
треуго11ы111к:-1 с 1·н11отену:юИ АВ 11 катетал111 .
,,,,'-~\
,,
t\
,,. ., ,..-
,\
Cei'"' ---' ' -- ----- ;' \
Рис. 1.
Рис. 2.
1
\
1
1
\
плошали, т. е. геuме rрия в них с<>
чета етсн с алгеброй. Олно И3 та"их
дока1ательств при веденп в тр;жта
те инд\liи ского мате>v1а тю<а Xll в .
Бхаскары . Оно JН.:1ме11ито тем, что
весь тексr к черт~жу (рис. 3) со
сто ит 10 ели н стве~1~юго слова
«Смuтри!». Историки с.читают, что
Бхаскара выражал плошаль с !
квадрата, построенного на гипоте
нузе, к<lк сумму плоwалсй ч етырех
треугольников 4(JЬ/2) и плошади
квалрата со стороной, равной рэJ
~юсти катетов (а - 1>)! , т. е.
•
alJ ( /)'
с·= 4-+а-) -
2
(.
с
с
Рис;. J.
ь
Рис. 4.
Поtле у проше ния ?ТО р<tвt'н
(ТВо п реврашdетсs~ в ~нdкомую
формулу J
1
+Ь
2
= с1.
В ряде локазатсльстl) ис11ол1:.эу
ется подобие ·1·реу1олы1иков. Во 1,
возможнu. 11а~1бuле~ Хdрактернuе
из таких лока зателЬ(ТR. Высота ,
оnушен ная на rи1ю1ен у3у , ра'\бн
в.эет дJн ны и п рямоугnльный тре
уголыIИК ПЛОWJДИ s11а дВJ ему по
лобных с 11лоша,лями5 , и 5t, (рис. 4).
При ::эrом его с-rороны оказыва
ютсн гнп оте11у:ым и rpcx rpeyr оль
ни ков. Плошали треугольников от
ноLятся, как квалраты пю: пnрон :
S,,:51,:5=а~:Ь~:cl.НоS,+5,,== 5.
Следовательно, а ' + Ь ' =с~ .
Фигуры
п.1 раш1с'Jt hным 11 оснм коор;~н нат (11х /\л н 11 ы
р:~нны 1.\.'2 - x 1111 ly2 -у11 ) llo, с дf)Yt'()ll стщю 1 1ы,
t:CJlll CЧHT:l'l'b нары ЧllCeJ! (.Х; у) тnчка.'-111 llJIOC-
IШCTll. то1·1~;;~ ;;iт~r формула у-же >1нлясто1 uпр<.:ю>
Лt'lflTt:\1 paCCTШ!llJI}\ , ll:1 11 eё МШКIЮ JI Ы ReCl'И Асе
1IO l IЯ 'l'I Щ t t eГIOCpe,l\C'rReT 11 ТО О П ре,71еляе:-.1ые ЧС[)еЗ
paCCT()Я I TJIЯ, - Т::IКТ I С, r.;ат< рзве l!СТВО и подобие
фНГ)ТJ. Или, например, окружность. О11а опре
де.1яется t<Ш< множество пар чисел (.\::у), для
которt.1х
1';\с (.\'0:.11( ,)
-
1н: 1юторая ~ад:ншая тичк:~ (центр
окруж ностн)
Можно ппрс11сл11т1, 1r пес друп r е 1 ·с-оме 1 ·р11 -
чсские rюr~ят11я н тер.vтпэх рэсстотпп'т: n част-
1юст11, nтре:юr< 118 - :">то мпожестnо таких то
чt:к С, что r!C + СВ = АВ. л стоит доб:шюъ ещё
0;1пу коорд11) ~ату z 11 соотuетстнующее слагае
мое (z1 - z 1)- н формулу расстояrrия
-
11мыn
трёхмсрлом nростраш"-твс. Подобным же об
ра:юм 1·с.::омстр 1 1ч<.:скан l " J ру1лура н1ю; 111 тсн к
нространс1· нах 11юбu11 , J~аж<.: бссконеч1ю\1
paЗ ,\lll'JJl-Юl"l 'I J.
Тсщ:к·ма 1l 11ф:11 ·ор: 1 ЛСЖJJТ к OCI JOHt: MI IO l'llX
бшн.т общ11х Mt:'l'PHЧCCКl·L'( CO()Tl-IOIПC H l-lll H;J
11J юс1шстн tJ н щюс1р:1нстнt. R знач 1 1тt;J11,1юrl
м<.:рt: 11:1 11t~ оm 1 растt'я 11 ·1р111 ·0 1 10метр 1 н1 : нeJtl>
11аж11еГ1шее тр1 1 1·0 1 юметrичсстюс тож.11сс тrю
cos~с1.+ si112а= 1 - ~то та же 'Т'сорсма П11фа
гора, :iаm rсаппая в дJ1)Т<>М виде.
Н ЕРАВЕНСТВО ТРЕУГО/\ЬНИКА.
КААССИЧ ЕСКИ Е ЭКСТРЕМАЛЬНЫ Е
ЗАЛА ЧИ
ti 1 ·еомстр11и тpcyJ'OJLhHllKa CCTh H<.:Cl<ШlhKO :1a-
MCЧ:!Tl:JIJ • Hl>l:X ~ад::rч о п:1нбот.ш11х 11 11а11v1e1111-
11 11 1х з11аче111 1 ях сняза1111ых с т1м величи r т, без
rютпрых расска;~ п трсуrо.rrыпшс бу,11ст пе п ол-
11r,1м . При рептепни таю 1 х :1а11ач r т:.i первыlr пла11
выступэют соот11оше1шя между эле111е11 т;~,>vш
треуптышка, выр:1жаемые не ра.nенстnам1 1 .
Неравенство треуrольника. ::>тu нсрансн
ст1ю утнсрждаст , чтu ка ждая cтupor 1 а трсу1 ·uл п
ш 1ка MCHl\l llC С}'J\1 МЫ /tB)'X /\PYl' JIX CJ'() сторон.
Пр 1 1 <:<хтuш1е11н11 савремет111ых курсов 1·соме1-
р1111 ш.:ранснс1 но трс:уталh н нк;r часто ню1ю-
290
ч ается n систему аJ(СНОЫ. т. с. nршшмается
бс:{ дока:{:птльства , хо1я в «! lачалах" Ев1iЛида
это теорема. в f\:tЧt'C'l'HC :IJ'CJIOMhl оно FIК.ШО
чае·1·сн 11 Cfl IН.:СЖ 0('1 IOl! l I ых (.'l.!Ol:H." l'B р:Н:С.-1'0·
т1т 1 !1: расстояние между днумя точка, 11-1 нс
болы11с сум .v11,1 рассннrн111'1 11'1' ннх 110 лю()оИ
тре1ъеi1 'J'()ЧКI r
И :1 1repa ве1 1 rтнэ тpeyrn111, 1 пш:-~ следует. что
отрс:юк является кр:пча1 1 шсй н:i лиш 1 l1, сас;~н
шuощнх две ТОЧЮL И.чешю это С!ЮЙСТВО ис
пuльзустся прн рстпстrr пт двух класснчссю rхэкс·
трсм:~лы rых задач 1r:> н:ом<.:тршr трсуп.>11Ьш1к.1
Задача Фаныню. Трсбустсн u1111с1ть трсу1·оль-
1шк м 1 п1 1 111·1 алыюн.J 11ср11мс:тра 111ta1111ыr1 uстро
уr·ольный трсупты-~ик :Jта задача наэывастся
:~ал.ачсi1 Фаны11ю - но 11мс:111 111т;1л 1 .ю~сr<о 1 ома·
тема·~ ика. 011уfi.111нт11а11 ш е1 ·() 11 l 7"i"i 1·. её a11aJU1·
тичес 1юе реше:нпе. ~lскnмым треуrnm,п11ко\!
НССГfР llyJ \CT ортотрс~Т()ЛЫ 111К ( [1 1!С. 2+).
.7тот ре:iуm,тат MOЖIIO ПОЯСJ 11 пь с помощью
:3аконоu ф11з11ки . Вспомним. что высоты тре
у1·uлышка являются биссскгрпсам11 орто·грt>
у1·олы1ика. Ин аче 1·шюря . юобыс д13<.: сюроиы
01У1·отр<.:угольнпка образуют равные углы со
cтopOJ-IOJJ I JCXO..JHOl'O TIJC}'l 'OJJЫШK: I . 11роходя·
щс!"t ч срсJ 11л общую н<.:р11111ну. J lu::>тu:v1y JJYIJ
света (ш111 \1ш1ьн 1-щ11ыl1 ш ~1 р),11ущснныl1 н,юль
Р11с. 24.
>рнJ 1111 , 1 '\tt1~1"'
1).) .\;.··t,1 t_J ,\'-tb~H"
uop' 1111.1 1)р· 1 1'' "tK~)1·0.'1 1 ,н 111\:1, отр:1жаяп, o·r · сто
рон •\)О.'111 1 110 1 '()" ·r·11cyнJ,IUТ flll(;) ll C()()TBCTCTlll[JJ
l "\:Н\( н Ю'-1"~ 1 ·0J 1 панешш раве11 yr11~ очхtж.ещш».
!1у,1ст р~1:1 :1а рдо.ч обе~ ·;лъ о ртотрсутлы шк по
11~р11щ•тr\. т е н<.:р1 1 мt;1р ортотрсуrолыпrка 11
t'l J f, 1 р.н:юор1 ш '!';\КОГО Л) ча..1 Clll 'T, I'ак 113J!t.:C'l ' -
1!0, р.1с11рос·1рJ11яется по 1-:ратча1'1шс .\1у 11у1·11
l lщ:с1·ся 1.:щt: o.i.11a, ~tех: 11-111 •1сска}\·>, 11111·cp-
npll:щm1 1:1д. 1• 111 Фа11ы1но. l lyc11, 1рс)то, 11,1111к
t,ll'Jl.lll 111 11ро1юло1.:11, 1 1р 11 ч(:.\1 на к:ик,,1у10 е10
оорон~ 11:1,к·1·0 .\IJ.ll'Hh юн: ко, 11>1lо. Чере:~ ~-:0.11.
ц.111po,~t. 1 :1 11:1п111~ 1.1и 11111h l пруж11111;:~\\11
\rш 2:;;,) К:1ю)с 1111,южсн11е она ~а1·1~1ё1. коrнз
t'OiM1tTCИ \1,lh:(l ll\1.t. lbl ю. l'CJП I CЧIIТ'J 1·ь. что n Cl!-
t н·щ· 11t.~r 1pt·111m" !-:011сч1ю. ю положс111н.:. пр11
f\оторо.ч ct· /l.' 1 1 11 1;1 ,-.11 1111 r;\1а. 1ы ш. Уч11тыn.1я. что
с~ чм:~ t 11.1 . ,\t'iктвутощш; 11а 1~J;1-,юе кол1,цо в
01IOllЧ:!1ClblHl\1 11(J:юже111111 JНl'Ш, pJ13H~ 11~ 1110.
JICTP\'ДllO 111.1ч11с.111ть. '!ТО отрl'ЗКI\ r!JJ"l 11 ()ун~ 1'
соста11,1н 1 1. раш 11.1 с ~1· 1ы с ссн1·1вL" l\." 1 'ну11нц11,111
t•1·opo1!.l l\l ll тpl')'I '())\ hl 111 ка. ()'J'I'~ ;р LJ <.:1Гt:1~~ t:'I. Ч' I '!)
н 1 1·11, оt."р:ну<.: 1 о р 1·11 l'JX'} 1·, 1. 1ьr 111 к.
1\0l lC' lll! I т, 11<()1 '() j>O/\:J p:tl 'C)ilЩl'H I J}l l l C \IO l )"I '
tJ1}"11\ l I J'l1 l 'l'() \ 'll' 'I Jll 1 1 1 l'CЮ1 \11 1 1\( )1\;l:!;П l'. 'l l 1lTllJ М 11,
1(() 0 1111 JI( )\)< ltl l f( ЦCl<:I il.Н-l:lНJ ' I . [1l'llle 1lllt' '1~1 t:IЧT I .
ТОЧhа Фер~1а -Торричедд.и. :.:-) 1·;i ТРЧК:1 н трс
ут.11. 1111кс t m1·1J11.1 с нчсна.\111 сра:1у 1 pfx
fll•l;t.11oщ1Jxo1 )'Чё11ых прот.1ого. 13ттс рньн:о нсl1
п11юr 11.юс1,, 1\ раfют~1х фp:.iшty:к1'oru ).1ал.:ча
т111\:1 111,l 'pa Фсрча. который pl'ш:L1 за,~ач~ о
чt·стtню:10жсн11 1 1 n трl'\ 1о.'1ы111кс "шс т:1ко11
ТОЧКll 1 'ITO l'Y\\ \\,1 /·.-1 + гв 1' гс· сё р:н:с1·оя 1111l1
~с) HlplUl lll \)1,111;1 1)1,1 \11111111\.1:1.'LЫ!OI!.
Ш11L·iщap1.·1-11i1 l'L'0\1l' I р Яко~') Штс\111ер р.к
с~1:1 1 р1111а:1 1) же 11pcн1.1l'\I\ н неско;rr,кп более
oi1ЩL'.\I н1 l /\L', 011 111. 1 т:.r1ки 11,111 п1 кра 1ч:1iптl) ю сеп.
;topor·. tot"J\1111> 11 oщ1 1 x lp11 ~~1к1а Ока.1ык1стся.
f L'0\11>T[Jll~ Н,1 П I\()( J..<)( 111
что T:Ll<:tJI C<:'l I• nсё p:t BI 1О долж 11а COCl 'OHTI> 11:3
трi.:х С.:\0/~Я Щll ХСЯ 11 <ЩIJO l'l l'()lf)(l' rtpЯ !IJO.'ll l
!H.:1'1 11 ыx /lO\IOI'. 11\)JI Чl',\\ О,'(11. 1 Jl:J :-ITl l ,\. ;1,оро 1 · ,\1(]-
;кс· 1 сж.1·1N:н н 1 0•1к~ (к<11< 11 н :i;Ц:jчс Фt· р ~ 1 :1) В
та1ш1'1 фор\1~ ;111ронкс. 1ю р<с . (. 1 я прш1:то.11->110-
1·0 ч 11 с11:1 1 1~1 1 "'1'()1~ 1:1;1ача 11р1нн)рс 1 .1с· 1· 11 ч11с·10
11р;ш·1 ·1 1•1t·скоt . н1a•1l'111tl'. Н:111р11~1ер. t:ё 11р11хо ·
1\1 11·01 рL·111.1т1, 11р11 11р<ж.1:цкl~ 1.::1~1t::~ы1ых ccтeit
Фигуры
Разрабо111110 несколько Jлгоритмов nocrpo-
e11ш1 кратчай1 1 тх <.х:те11 дш1 да111юго р;.~сnшю
же1111я сосд~ 11 rясмых пунктов. Но эта задача име
ет 11спр11ятную особе1111ость: с ув<::личенисм
ч11сла 1 1 унктuн чрешычаl1но б1,1стро но:~р:~стаст
К0!111ЧССТНО опера~ \l l Й , Нh!ПОЛIIЯСМЫХ КОМ11ЫОТС
ром 11ри её рс111сни11, - как 11оказатст1ная фу111<-
1\1 IЯ пт ч11сл~ пунктон. В итоге f\аже 11 :1 сверх
мощных ком111>1отерах З;,t 1 1p11eм11e.'Vloe nрсмя
у1\:1ётся ре11111п1 задачу толыю тuтя дnух-трёх
11еопкоrs точек. Чтобы улучпшть 11~1еющисся
:1лгор11т~1ы, матемап пш и сегодня продолжают
11сследоuап, структуру кратчайших сетей.
Ф11з1 lЧескую модель ДJШ peu1e1nrя класси че
сrюй за;1ачи Ферма можно сделать так н<tрису
см треугольник на к:.1кой-ш16удь / \Оске, 1юбьём
гво:щию 1 в е1·0 верш~ ~на.х. перекинем через каж
дыiJ ГIЮ~-\/(НК ннть с OДHH:tKOHbL\1. 1 'РУЗОМ на КО/ 1-
ll(~ 11, наконец, свяжем сuободные кuн11ы 1 11 пеl1
к о/~ 1 1н узел (рис. 26). Ко1·да 1·py-J 1.1 будут о·mу-
1 нены. 01111 ш1· 1 ·я11ут нити. Пр 1 1 этом обща я
;v11 111a 0· 1 11естrых частей нн 1 ·е11стаrтст11а116оль-
11 1 ей, а сум.м.а рассто.яш~й от узл;:~ до rвоз;'\ll-
1\Он - нанменьшей. Слсдователь110, узел уста
rю1щтся u искомой точке. Посколы;.у 11а 1 1е1·0
6~·т.-1· действоnать три рав и ые r10 nслич1ш<:: и
ура1:нюпеши вающш: дру1· д руг;,~ сплы, 11а11ран
лс1шыс BДOJl b нитей, УГJ I Ы мс::жду НИТИМ11 )\OJIЖ
llЬl быть р<Jвны Таким обра:юм , l~l'Opo 1 1ы трс
у1·ш1ьн11ка будут в1~дны нз точю1Р 1юд ран нымI 1
(нu 120°) у1 ·лзми.
Точку треугольника. Iюложенис rютopoii
yдoBJICTкop~t~T ЭТ l 11"1 yCJIORI LЯМ, ПОСТJ1()И J 1 итал 1.
МНОГОУГОЛЬНИКИ
J.:сли последовательно на,1сртить шt шюскосn 1
1rссколъко отр(::;jков так, чтобы каждый сле,'(у
ющий 1-~а~шналсн там, 1 ·щ:: кон~шстся предыду
щнй, то нолучитсялол1днtmл1.гния. Сами отрс:~
ю1 называются сё 3вl!НЬH.Atll, а 1 1х концы -
i:5&p1111maмu. Когда последняя всрu111на ломаной
сонпадаст с перпой, то 1 ·0Rорят, чтn 11ома11 ая
..за.1111.:1~1 ·п·zс1, а еслп лома11а51 сама себн 1 1с п ересе
•<эс:т, ·1
·n 011з rrа;1ь111ается прпспю1{ (рнс. 1. а).
Простая :1амк11у1·ая ломаная разб 1 шает пло
скость rr a две такие частн (области). что из
произ.волыюй точю1 одно1'1 области .v.10,юю
прой·r11 в J<a 1~10 угодно точку той же обласп1.
292
Рис. 27. l очкd
Torr11• 1t>л.\11.
я11сю 1 й учёный Эв;1нr~жсл11с·1 ·а Торр 1 1ч<:ллt1. 11з
вес·1 ·11ыJ'r как нзобрет:пе)1 1, ртуrтюГ<) барометра.
Такая точка cyщeL~гвye1 " 1·m 1 hlIO Rтрсу1 ·олън11ках
с )'ГJ\<IM\1. 11 е r1ре11ОСХО/\ЯТП.ПМI I 110'', 11 ('()1111'1).lа
ст с '1 ·очкой Ферма. Однако с:1ма з:щзча Фер\tЭ
имеет rс шеш 1е и коl'Да одш r rrз уrлов треуrоль·
пика больше 12U". В этом случае точка 1; соnпа
даст с вершптюй тупого у1·ш1.
Точку Торр 1 1чсщ1и можно 1юлу•штr, так: по
<.трu11м 11а стор()нах тре-утольн11к:1 вне <:ГО пра
rш11ъпыс трсу1·01lЬн11к1 1 (рис. 27) и соедш1ю1
отре:щом каж.;\ую вер111н1 1 у исходно1 ·0 · ~рсу 1 'ОЛh
ш1к<1 с всрш1 1 1юй 11р<шн111,ного тrе~1·ш1ы111к;~,
ПOC'l'JlO<:HIIOГO на П[IOTlll\0 1 IOJJOЖ I IOIJ егоронс
П олученные отре:нш p:1R111>1, обр;~зуют др~т с
дру 1·ом раRны~ )ТЛ Ы (1 ю (10 °) 11 пересекаются 11
omюr~ точке 'f' -
точке Торричеллн .
11<: щж.идш1 с.::ё, а любой п:~1·h в то ч ку дpy1 ·uf1 об
ла.сти обязатслы ю псрсссчёт лом:1ную. Дока
за·1ъ столh, казалось бы, очс:mщ 1 юс )rl'нсrжде·
Hllt' COHCCJ\I Ht.: просто . Это было C/\CJl;JHO (ддя
более общс1·0 случая) лишt• 11 1RR2 1·. фр:1нцу з ·
скнм 1'vtатсмат11 1шм Кам1 1 11ем Жор;\а1юм
OдJJa 11з двух областей. з<1.даваемых 1 1 1юстоf1
замю 1ymi r ломаной, все 1 ·щ1 конечна. а другая
просп rрается 6еско11счно далtко . 1lерв: ю на
зывают 1111утре1mс>й. а втору10 - rmeumeil об
л(./стыо Л(.J.;~t(IJlOй.
Простую з:1.мхнутую ;юм:-JН)'Ю вместе с rё
1111yч)(~I ll ltJ106JJ<IC'l'J,IO нa :5ЫH:.JIO'J'_,Щl(J,'{~)'lШlbl/U·
а
Рис. 1.
HHf (j)llC. J, 6'). э~r'llM Ж~ CJIOIIOM Ч;JСТО 0()031 L<1 -
ч;1101 н саму зt1мЮ1)r1ую JЮ,\1~1ную - к:tк прп
с1ую. так п самоттересекающуюся (1J1 1c. 1, в). з
rюpot'r 11 произnолытую областh, 1ратща кота-
1ю~"r состоит 11з пескольюrх отреэкпн (рис. 1. г).
3венья лома11ой mн 1ш1 , ограпичпnающсй
~ню1·оу1·олы1ик, назыnшотся его cmQ/I01taм!I. а
все ос1·ал 1,ные отрезки. сос.:дипяющие вершины
м1rогоу1 ·олы:~нка, - его Пш1.го11алями. Ясно, что
число сторон м 1-ю 1'оу1'0;11,ннка ранно чнслу er ·o
кср 1 1111н, 11т1 , иначе 1·оворя,у1·лов. А rютому :v1но-
1 ·пу1 ·олы1ик сп eropu1-1a1>111 н •1 зывастся п-у1·оm,-
1u·1 ко.-,,1 . Rеличин::I Yl'Jltl пrн rк~р111ннс многоу1·олr1 -
l[ИК:J., т. с. угла между сторпнами, ныхщ1ящими
11:-1 з·юй nep111 ины , измеряется н1;щутр1 1 -> ф111'уры
(r>11 c. 2). Таким обра:юм. н птли ч ие от yl'Jla мсж-
11)' лучами, пршшмающсго :шачеrтr 1н от () до
180°, \'ГОЛ м1югоvrолы1.и ка может изменяться от
Uдо ~60° (шщ ~ радш11пю1"r мере, от О до 2it).
(.)д11а 1\О 11меется важный класс многоуголы 1и
кол, углы кuторых всегда I1 e болыпс разnёрну
того. Это ны1 ~}1КJ1ые .Аl'ногоуголытки.
ВИЛЫ МНОГОУ ГО/\ЬНИКОВ
М1 ююуrолыптк пазпшается иь1J1уклы м, сслr 1011
леж11·1· по одну сторону от тобой прямой . со
деrжащей е 1 ·0 сторону. Все треу1 ·0J 1ы1нки вы
пуклы. ~1 м1юr·оуrо;1ыrики с бОЛLШ llМ Ч! IСЛОМ
сторон мо1у1· быть как выпукrrым.и (рнс. l, а),
та1\ 11 1-1евьшуI01ымн (рас. 1, б. 2).
Друrо(1 нажный щт:ш:ш. по которому вы
дtля10·1 в1 11i t,1 \'1Но 1 ·оу1·011Ь 1шкuв, - это палнчнс
р:пных ·1·н1юн с:11мметр~н\ ш1 1 1 са.чuсовмсщс
нш·r. 1'асс11-10трнм с этОJ-r точк1 ·1 зрсн11я в 1щы
чстырёху1 ·оm.ннкок (рис. :\ ).
Tpr1 вида че-1·1.1рёхупты-11 1ков име1от тот . ко
од1 ry си:мметри 1\ ): 11аfш11ж!л< 1г/JсLил1 - це11·1·рзт,-
1ю- сн мметричс11: <)елыпоид - с~1ммстриче11
ОТНОСl !ТеЛЫЮ O / \IIO(f IO I Эl '() l l(.IJIH: /)ctffllOfi<nCaЯ
Гсометр~я 1-1а плоскости
г
Рис. 2.
т/1mи'ция - п r мметрична u·1'1юс11т<.:льнп ли
т111 , СU<.:JiННЯЮЩСЙ C~jl~Ю l l lbl ос11ов;1н11!1 .
Есп1 чt:·1•1,1рё::хугш11>нню1. н~1е101ц11е двt: ос11
снмметрн tr. После1t1111е оnяз<rтелы ю 11ер11е1 щr1-
куляр11ы, а тпчка нх 11ересече1111я является 1~е1 1 -
тром си.мметрю1 четырёхуrол1,,11нка. Это ро.мб
и ~7/JЯ.ivtОуго.пыш1\-.
В 11ерво.и осн с11.ммстр1 ш -
диагопал rr, rю втором - средннс т 11 п111 .
Наконец, камьп·-1 ст·1м мстр11с111ыл ~ чстырёх
у1 ·011Ьн11к- квадрат - обладает кссмп уже па
:3ван11ым 11 т111 1ам11 снммстрнЛ , ;J кро,\1с то1·0 ,
спнмсщастся с Сl,\ШМ cnб<>l"1 11р11 rroвopoт;.ix 11:1
у 1 ·лы , кр:пные 90°, 1:нжру1· общ~lr точкн cr·o
четырёх осей снммстр 1 н 1 .
Вообще, имLтто1 несколь1<0 раэ11ых, но р<1н
гюси11 r) 111.1 х усло111rн, нсобхrщнм 1.1х и доста
точных п;ля тп1 ·0. чтобы четырёл1тол1>111\1\ 11р11 -
надлежал к даТ\IЮ,\f)' 1ш,riy. ()111ю11 з rш х бсрётсн
за определение вида. а ост::иJы 1 ыс ста~ ювят01 его
призпат<ам 11. В школыrьL-х. учсбrшках nнды четы
рёх.угольшшоn oбЫLJIJO определяются чере:з
{ fClj)ClЛЖ?Л()lj)Ш•t.,11
!Zl\I1
-
!
f'etвнnrinium
111pc111ei(ШI
1
/j\
Prшii
п1т.~1(о •га'1ышк
!<всu>ртп
,.____._~,
'
1~~
-
:~~- -
,
1'
,''
'
П/>rlll. ШШThl((IЯ
111/Jll!U'ЦllЯ
Рис. :J.
Фигуμы
ИЗ ПОМЕТРИИ ЧСТЫРЁХУГ()ЛЬl IИКА
Геометрия •ютырсхугол1>11ика нс менеl' бuгатJ , L1ем
1l'Uметрия трс•у1·ольш1ка. Вот 11сс~<олькu фактов , Ji.1-
мt-•ч;11f>,\bHЫ\ Т("vl, что они ( ВЯ":\с\НЫ <: ~1ME:'H.-IM11 лнух
велик11х учt•11ых.
Прuдuлжи.'l.1 сторо11ы чс·1 ырехугольн~1ка ЛВСО.
То1 де. с~р~t>и11а L отр~.~к.~, со~L\ИННК>Шl'Гl1 1очки Е и
г Пf>рРсеЧ(;'НИЯ 11родолжении проТИRОПОЛОЖНЫХ i'ТO
putt. и ссрсди1щ М и N диагоналси ск'п..tрехуголь -
1111ка будут лL·ж..~ т ь 11а uл11ой прямоil. 01~,1 на.Jы
н.1t-тu1 nrялюи 1ау< Cd. Если 1:.1 четырt>хугольник
RП11ra11a окружнпсть. то H<i лои же прям(Нi\ лежит
и <.•ё UL'tпp О (теорема Нью 1 uна~.
Теперь Gудем поочер~лно выб11рс1ть и.~ че·1 ырёл
прямых, огра11ичиваюших четырехугоАьник, любые
три и строи r1.о TULtKt.1 п ересече11ю1 вькот обрJзо
в<11111ых ими 1 рсу 1 uл~..11~1 ков . Полу·н~н 11 ые четыре
!ОЧКИ (Hci рИ( УНКЕ:' ГIOKd .ic1Hbl ЛВI:' - Р ЛАЯ дАВГ И
()для дВС[) также лежат 11 .:1 ол1юй прямой , npичi?'l.1
u11J псрпсr 1ы11<уляр 11 J мрямuи Гаус. са.
lf
1
11
,,
fI
fI
1
1
11
D
11
11
1
,
11
1
•
L
А
<..' 1юf1 L1ri:11rx стоrхн 1 н )ТЛ011. Нзпр 1 1мер, ро\1{) -
че-1 ырёхутолытик с р;:~н11ы.\>111 с1·огюн::tм1 1 . r1ря
:1.юуr()л 1.11111 -;
-
ЧСТЫ[JёХуf ·0111 ,1J llK С ра В11Т1J\1 1 1
(прff.\1ЫМП) уrлам11. а пар;~ттслоrр:1мм - четы
рёлJ.то11ы 1ш.:, у которого проппюполож11ые
сто ро ны пар:~л:1сльпы . Пр11 таком способе
1Шf1С.:,'\СЛС1 \1\}1 11 ар;шж.·лограi\1му ПОМН1\Ю ЦСllТ
ралыюй сr~мметрни ~ра:чхшастсн» 1 1ие-1ъ 11
, 1ру1 · щ.~ C:lJ\!(ICOHM(;' ll \CHИЯ , так что poмfi 11 11рн-
~1о у1'u: 1ышк с.:та1юш1тсн с.:1·0 ч:.1ст111>1м11 и1учая
\1И. а 1<11:щрат ЯВ.'lЯ(.'ТСИ ро мбом 11 Пр}1\1U\'1'0ЛЬ
Н 1 1КО.Ч O/tl 1онрС .\1.С.:Ш IO.
ЕС.'111 ) ЧC'l'1,1pCЛ~'l'OJIЫIJll<:.t 'f()_lf ,KO одна пар:1
l l<lp:tJJЛ<.~.riы IЫХ 11J10'1'111IOllOJ IOЖHhl .\. c1 ·opu11 , 1'0 UH
н .t :ihl liaeтo1 111/ ю llf1t~11eft . Tp:i пс.:ц1 щ у ~шторой
lll'П:tp~IЛЛC'.'IJ,ll l 1le (fi< IKOHhl e) с l'Oj)<lllbl p:tRllЫ ,
1r\1<.:1 t)'(ТСЯ j)tlmюiJoл ·m/. Еот ю1эсс11ф r 11111 ро1шть
ЧC'l'l1Ip6..)TO.'lЪIJJII<П по 11р11:шаку ('11 \1 \.le' I /1111 !, то
ш.- р.~т юбокан тр.1 псцr rя 11с ны~е:шется в 01;{е.•1ь·
11ыl1 н1ц. Ht.' . как п про11зво11ы1ьп'1 чстырёх)Т<ЫЬ·
J П I К. \ЮЖНО COB~ICCTII'l11 CaJll} с co6ol1 Cf{ll!ICTBeLI-
llblM L·1нк·обом. llt случ ;1iто с:юном "1Т>апецня·1
в Щ)о1111 1 ом 060~1на LJ<IJ Ш :110601·1 '-l<.:"1ырL'х~тол~,
нщс п11шч11ьн'1от11:1ралл<.:ЛJН рамма .
С:рсдн мно1 ·оу1 ·011ы111ков с ч11с:ю .ч сторон
бот,1 1 1с че·11,1 рfх ri зm.:мснтар1юt'1 1·с::о,,1е1р1111 ны·
i (t.'IЯIOT lljJ(.f(lfl. '/(11/lllf' . НJl() t'(~ J'гШ lblf fl/\ 'fl . у HTIX все
Сl'Ор011Ы 11псе )"l'Jll1I p:llll 11>1 ~1СЖ;1у (()()1 }Jf tрис ~)
Пран11лы1ыс ~пюго)то111,111uш nccrrp ш111 1 ~клые.
по с1щсстuуют и са;\юпсресекающ11сся :~:~чк11~·-
1ъ1е !JO.\.l~IIIЫC, 11 .\lеЮЩИ(.' р~ШllЫС ЗJIC!lbЛ и )Т.1Ы.
Фr1гуры гакого шrrta назыuаются пр:~ш1.%11ЬL\fН
: шёз[l.Чаты 'Ш ~11ю1·о~толы1111.-а~ш IL'Ш пол11гра.ч
мам~.1. 1 ю ана1 101·ш1 с пснтат·μаммш'~ - пrх1n11ль·
110/'r ш1·1·1 1ко 1 н::ч11ой :шсэдо1'1 (11 :ю6раж<.'11:1 1шуr
р11пран11лыю1'01ш·1·щтолы111ка на μнс.:.")).
Любо\1 111хш11111>1-1ы~'1 ~1110 1 'оу1·0111,1111к. выпук·
лы~'1 H!llt ~{f\ёJ/(Ч:J l'Ьll\ .\Н>ЖIЮ H;tJIOЖll'l'b сам на
ссб}J ·1 ·~11\, <поб1,1 011на 11 :i ц 11ух 11ро11 :ню. 1 ыю З:I·
ланн 1 )1х сюрт r совп::~ла с /ЦJ~ 1·oi1: ·1 ·0 жс верно
11.ля тобых 1 t li~ :- ..
~го н~р1ш111. И 06рат 1. ю: мно1·0·
y(OJlbJIITК. обл:ц~а IOЩll t'1 06тrм 1 1 Э'l \ I Ml l ClIOJ)·
стна \1J 1. 11раш 1л~..пыfi. Но С) щеспзу:ют r1сп1хн1~t·1ь-
11ые ~[JI()Г()~TOJll1l I\ !Ю 1. у которЪL\: Та!\Ое CBOЙCTllO
спрансд;шво толыю JUТЯ сторон, как у ромба.
ПЛII TOJlbKO для вc.:ru1111I. ((,\К у llj)ЯЩ)\'ГОЛЫШКа.
1·1M.Ct:'l'CH 211 С!Юс<Jб()В l'UBM<:'C'l'llТЬ правилъ·
ный 11-~1/'0J!hHHK сам с собоt'1 : I ЮЛОR!Ша 113
н11х - 1юнороты нui-:py 1 · OJ(tJOй 11тui1 же тощ..11,
Рис. . +.
'-
.'
'-
1/
-·
-·-·~:~?i:_
_
--
/ i°'·,
/
.
.
/!\
1
его центра. н;,~ у1·лы, кратн hl с 560"/п, вт{)рая nо
.'lоюша -11 симметрий <У! ' 1 юснтс11ьно 11рям ы х.
сос;( 1 1ннющ11х це11тр с нер ш1 н1;1 мн н серед~ 111;1-
мн сторон.
Центр 11ра1111льно1п м1югоуголы-111ка ранно
удалён от нее'< cro стоrо 1 J 11 от нсех верш нн,
поэто'IУ 0 11 служ 1 тт 01 ~1 юнре~н:ннu це11трсн1
щнr сз rнюй п опнса1 11 ю~1 окруж1юс1 ·е й мпого
уrот. 1·1 1 1ю1 (р ис. 6). Пернметр (сумма длш1 сто
ро 11 ) п раrншыю1·0 п-утолышка при :'!адашюм
ч11сле сторон п ааиболсс близок к мине е1·0
описа1 11 юй окружности среди 13сех вштсшных
n неё 11-у 1 олы шкоn: таким же свойством 011 06-
лад;1ст 11 по UТНОШСIП Т Ю к IШИСШТIОЙ окружно
СТIL Поскол~,ку HЫЧllCJICIJ11C }~JIИНЫ сжружност11
счнтаJJось 1~ лрс нн ости всс пм а нажной з:1ла ч<.:й ,
м 1 ruru усилий было затрачено на то, чтобы на
учиться оцен11вать пср11метр nпнс:111нон) n 1-н:ё
прав11льно1л J\11JОГО)'ГОЛЫ111Ка лр11 /tOC'l";}TIJЧllП
оольп 111 х н. Оспбс:шю преус11ел в этом Арх11-
мед (см. статыо <-<1кrужност1. 11 l(py1·" ) .
Rпрочем, правиm,m,1е м1101·оуголы111ки при -
1V1екали ш mма 1ще ,цреш rcгpcLJecю 1Х учё11 ых за
.1о лr о до Архим с;~а . l lифагорсй:цы. .u филосо
фии которых числа и 1 ·ралн главную роль,
п ридавали uчс:нь болr..шuс :шачсrrпс :-$ад:1че о
делении окружност 111т:.1 ра1шые час.:ти. т. с. о ~ю
строс 11 ш1 11ранилы-ю1·0 ип 11 сан н 01·0 м 1 101·u
~·тлмн1ка В ~l laч:inax» ЕнКJШJtа пр111юдятся
п острщ: r 1ш1 с гюмощ.ыо ~tнркул>J 11 .1 1 ш1с(1к~ 1
nр;шг1льных м1тогuу1·онпн1 rr<oп с ЧJ ~ сло м стоrон
()·~· трех до 111естн, <1 также r1т·1 rад1tат11угоJ1 ы r~ ~ка.
З111м П( ютсд11нм осабсннп н 11 ·1 ·еrх:со11ал 1rc1,: со
глас1 го r1змtреtпнт:-.1 лреюu~х астро 1 юм.оn. уrол
11аклошt п.rюскости эклиnтпю1 к экnатору раu
няжя 1/ 1') ПОЛIIОГО у1·11а, т. с. L4 '' (ПСТШIIЮС зпа
ЧtШIС чуть ме11ьпrс - 25°27'). Задача о по
стросrпш 11 μавилыrых мно1·оуголы 1н ков была
1ю:uюстыо р<:шсна лпшь ;tна ·1ъ1сячелстr1я снустя
(('М. ст~tтыо <- Гсuметр11ч<.:скr1с 11остроенин ").
Рис.>.
Р11 с. Ь.
гt'ОМ!"Трия н,1 ПЛ()( КО( 1 и
ТЕОРЕМА О СУММЕ
УГЛОВ МНОГОУГОЛЬНИКА
Любой: мю H'O)T<JJll,1-11 1к ле1 · ко ра :щст 1 т1. н:1
1:11>1 IТ~ГJ<Jll,lt: м HOl '()~TU!l hH ню f ; ;~mr dTOI"(} Д( JC' I : ~точ
но 1 1родолж~ 1тh нее ei ·o стороны и рз:чlСэ:tтh ф11-
1уру нл())11, 11олучс1111ы.-.: 11рнмых (рис. 7. tl). Раз
бнп" м1юго}ТnJ1ыrик тта выпуклые t.tacт11 ,,южпо
и так, чтобы вер шины nп:х кускоu соnп а,1~ю 1 с
его nершннами. Н сnою о чсрс/~1,. из выпуклого
м1югоуго11ыrика 111rчего 1 1е стоит сделаn, трс
ун;лыппщ - если, 11априJ\·1ер. провести ~ке
;ща1·011шш нз одноl! верпти111>1 (р11с. 7, б). С·1с
до 11:1·1'СJ1ьно, шuбu rl МНШ'О)ТОЛl>НИК в l<OIIЦC тшн
цои J\Южнu ра:~б11т1. н а трсупJл 1,1 1н ю 1 . что ок:~
:3Ыnастся полс:лтым пр11 ип1 nпдс р;~эл~1 •1111.1\.
Cl:IOi"fCTH MHOГO)' l '()Jlbl ll fK(IB . Н~н1 6ОЛСС 11 3BCCTJI0t"
иэ ~ТIIX свойс-1 в -
· 1 <:optм::t () с~ м \К: }TJIOH ,\1 1Ю
r•оугол ы 1 11ка.
На рис.. 7, б ныпую11>1l 1 11- уголы111к р:1эГ1т1т rra
11-
. !. треуrолышка. Сумма TIX у1·:юn ramr::t С)'М
мс )-ТЛОВ п-уголы 11 ща. llo. как 1 1зnсо1ю, сумма
углон каждого трсуголы шк<! сост:.1 мяс·L 180".
Т:аю1м образом, сум.\1а yrлon тобоrо выщ1<JЮ
rо 11-уr'()ЛЪШШа paulla (Jl - 2) НЮ<>. IIЛII. n pJ.Дll
a HHO IJ мере, (11 - 2)тt. Ilр 1 т:-tt'чатt.:лы10. '-По
сумма у 1'1 юв нс :~: 111 1 к'1 1 ·1· от <.рорм ы ~11-югоу1·01 11,
н11ю1; сущсс·1·нснно л11 111 ь ч11с110 с1 ·0 сторон. Uо.i
можно. прнчн 11а ~тоr·о ста 11ст понят~ tt:c . ест ~
рассмотrсть н11t'шнт1L· у 1·1 1п1 11-уголы111ка. ·1 с
yгJJJ>J , сvтсжн ыс с т1у1рснн1t ,\IИ.
Оt10!1дt:м мн о1·(,~тол ын1к Hfltнll• 1 ·ран111(1.1 ,
11ачаn с каr<nl1 - нибулъ точю1 11а его стороне 11
nер11увш11сь n ту же точhу. П ока мы 11,с~ём по
стороне. наr1равлстптс 11аше 1 ·0 днпжеш~я 11с мс-
11.яется, а n каждой nсрш1ше мы повора ч1шасу1
на угол, ратrый внсппrему углу n это1'i вepшir
rrc (р11с. ~). u 1<01щс пути мы двнжс.мся n то;11 ;кс
11;1прак11сню1, n котором <."Т'ар· 1·uнал11 Т:1ю1 ч
'
Р1н:. 7.
'
'
'
'
'
'
'
'
'
'
'
29')
Фигуры
Рис. 8.
образо м, за nр~мя обхода наnравление нашсг()
двнжсш rл соnершает один полный оборот. а
это значит, что сумма у1 ·11011 всех отдельных
понорото.н н вершинах , т. с. сумма ннешшrх
у1·лон Ml IОl 'О)'!'()ЛЬНИКа, равн:1 27t 11 нс з:нш сит
11с ·1·0111,ко от фирмы многоутолы1нка, но 1-1 от
ч 11сл~1 его сторон!
Конечно, тот же ре~утrг;1т слелуст из Т('()
ремы а с~мм~ уГJюf!. Дейстн 11 1·е111,1ю, сумма
nнеттттrего и впуrре1111е1 ·0 углов при т<ажлпй вер
шине раnпа ·л:. Зт~ачит, сложив ncc такие сумм 1 .1
в 11-уголытикс, мы па.'1уч1 1м птс. тогда па nпепнте
углы будет пр11хо,11ит1 .от птс - (11 - 2)тт = 2. тr.
Т:.1 же формул;~ для суммы утлоn cпpaueДJtиna
11 для нсnыrтуюп.rх м 1 ю1·01тольш11щв (без само-
1rсрессчсннй) Чтобы )1Оказать это, нужно
разбr r·тъ ди;н·ошurям11 произвольный 11-у1·оль -
11н1-: 11;.1 ныr1уклыс многоу1·ш 1 1> 11нк1-1 .
КАК НАЙТИ П/\ОШАЛЬ
МНОГОУГОЛЬНИКА
Площал 1, паралле1101· рамма вычисляется 1ro
формулам
S=a!Jsiлa= ah.
1лс с1 - е1·0 основашн.:, Ь
-
боковая с1·оро11а.
о:. - угол мс:жду HIL\Ш, 11 - 1~ысота (рис 9. а)
1JJющa/\h тр<111~ции
S = a+/Jh,
2
Г)l,е С/ l·! f) - её ()CI IOR:1HI IJJ', /1 - RЫСОТЭ (рис. 9 . б).
Ее-ли J~a1rы дщ11 ·пнал1т е и/1 1 y1·n;1 с1. между
пн1,пr, тп плпща;~h 1tроизво.тrьпого четырёх
у1 олыппо 11аходят по формуле
~ =~<tl si11a.
В частr юстн. площа11ъ ромба равна полулро-
11з1>сдсш1ю его /1,Иаrоналей:
{'1
•
.) = -l'/.
2
Площадь пр<1н3нолыю1·0 ч.стырЕху1·u;11,ника
можно FП1rраз1 пъ черt:~ его стороны о , fJ. с 11 с/н
сумму qJ Щl[)Ы l lJlOTllROПOJIOЖHhL'-; ~TJ IOJ\:
1
S~ \~<.р-а)(jJ- fJ)(fJ- с)(р-d)-abcciсоь!t.
гдер - пол)тrср1 1м етр четырtл"утолышка .
ГIJJощ:щь кшrсашшго n 01<р)rА(Н.ОСть чсrы
рё:хугш1ы111ка (ер= 180": см. статыо <·Окружность
и кру1'») 1~ыч1 юrнстся по формуле БрэхмаI·утrты
~ = \i(p - п)(JJ - lJ)(p-c)(p - c!) .
а опис:тrrого (а + с= /J + d) - по формуле
S= \i'avcd sin ~.
2
Если же четырёхуголытк n~ н1 сан н оп11саттод-
1ТОI1рсме1 шо. то формула ста1101штся совсем
простой:
S ~ ,'аЬсс/.
Общий метод дня нахождсшш шющадп
нрои:июл ы ю1 ·о 1>1но1 ·о~толы-шка сос1 ·011т в том1
•r TO Cl'O Н~ЩО [ХIЗбИТI> на тpC)" ГOJIPlllll<ll , l\h!ЧllC·
лить 1rx пло 111:~щи 11сложить рс3ультаты . Иног·
да м1 ю r ·оу1·0 ; 1ы шк прt:/1,СТ~tRляю·r· 1<ar< с~·мму 11
р:~эность треуголыткон. Од11:11<0 просюй и
компа ктной формулы дня ОЩ}t'/1слстнtя шю·
щ::щ и пропзnолыюго n - угол.ьника 11ет. Эrо
неудивнтеныю, ведь в пс\1 нензбежно буде-~
слншком м11оrо nеремеплых. Ч тобr,1 задать
п-у1·олышк (его фор1' 1 у 1J ра:змеры ) . нужно ~~i:!
:з:.1т1, 211 - :) ~1·0 алемеr ~та: 11апрпмср, дл ю1Ь1 всех
CТOfIOIJ, кроме одной, и .ВСЛНЧ IЛ-11>1 11-2 обра·
:зtшанных 1 1\1н уиюв.
h
Рис. 9.
РАВНОСОСТАВЛЕННОСТЬ
МНОГОУГОЛЬНИКОВ.
ТЕОРЕМА БОЛЬЯЯ
Г ЕРВИ НА
Не>v1,1ло формул ~• теорем в ге<1-
метрии доказывается t помошью
раiр<'зан ия фигур, а затем nере
кмлывания их частей - вспом-
11нм, например, теорему Пифагор~
!см. статью « Треугольник, про
стейш и 11 и неисчер11,1емый»). Если
лве фигуры можно разрезать н,1
олин.1ковые 11 аборы ч.:~сте~:1 (т. е.
межлу частями 1н таких наборов
мож1ю уст.~новить взаимно ол1ю
знач 1 юе соответствие, при ко 1о
ро"' соuтuетстве нны е части рав
ны/, то :пи фигуры называются
р11вносоставленнь1 ми. Рав1-юсо
rтавле~1н ые фигуры, разумеется,
равновелики - он и имеют равныЕ'
nлошали. для многоугольников
вер11,1 и обратная теорема: любые
АВд равновеликих м 1югоуголь
ника равносоставлены. В 1812 r.
ее доказал ве11герский математик
Фаркаш Больяй (отеu Яно ша
Больяя, одно го из со3лателеr1 н е
евклиловой геометрии) , J голом
nозже, но н~Jависимо от негu, 11е
меu П. Гервин. Ключ к локазатель-
Рис. 1.
1~б
Рис. 2.
Рис. З.
пву - п ерекройка п рямоуголь -
11 ика, показ'11111ая на рис . 1 : раз
резав «шtзкий» nрямоугольн 11 к на
лва rрt!уголь н ика и пятиугольник,
слв 11 нув тр еуголь н 11 ки вдоль н <:1-
клонной ли н ~1и р.вреjа, мы полу
чаем другой, «высо к и й » прямо
угольни к. Этим способом ланный
прямоугольник 11 с трулно превра
тить почти в любой лругои μав 1ю
великий ему- нало тольк о, чтобы
1-ювыи прямоуголь11ик был <<ВЫШС»
исходного, нu 1-te более чем олвое.
Если же <ПIЮШi:'Н ИЕ-' tJЫ< от прямп
угольни ков больше мух (рис. 2,а),
• низкий ~ мож 110 <•сделать повыше»
t помошью п росто го преобразова
ния (рис. 2, б), применённого нуж
ное число ра.3. Теперь любой м1ю
rоуголы1ик мы сумеем перекроить
в прямоуголь н ик какпй-то фикси
рованной высоты /1 _разрежем его
11а треуголы 1 11к и, кажлый треуголь
~1 ик превратим в прямоугольник
\рис. 3), nр~1вед~;;м nо11ученныf:
прямоуrоJ\ыtики к некоторой по
стоянной высоте h и <-остыкуем
вертикаль нhlм и <торон<1ми. [ели
два м1югоугольник.1 равновелики,
то соо rветствуюш~1е ~1м прямо
угольн и ки высоты h равн ы. Таким
обrазом, :эти м н огпугольни к и рав-
1 юсоставле11ы с одной и той же фи
гурой, а uтсюла уже неслож~ю за
ключ1нь, •1 го о ни рс1вносоставле11ы
между собой.
Н амече1 ~ нос .злесь локазатель
сr ео кuнсrруктивно: оно содержит
алгор итм n ерекр()йки олного мно-
Геомt•тр11я нJ 11лос кости
1·оутльника о лрутй. Одн;~_ко воп
рос, как это сделать , использовав
н аиме н ьшее число кусков, в каж
дом конкретном слу ч ае решается
отлель н о. Залач и такого ти nJ
обычно лоеоJ\Ы-IО трудны, но оче1-1 ь
п опулярны в за11и мат~ьной мате
,..,.,,нике. Классический oбp;i:-ieu по
лоnно 11 задачи - преврашс11ие
nрае~1Л Ы юго треуголь~~ика в квад
рат тоt1 же плошали . ЕЕ' рЕ>шсние,
прин<tллежашее и1вест11ому мас
теру этого жанра LLHr ли ч анину
Генри Льюле11и , привеле1ю на
рис. 4. Как видим, дьюле11и ул;:~
лось разрезать фигуры всего на
четыре части.
Интересно, что лля мноrогран
ников утвержден и е, а11алоги 1 1ное
теореме Больяя - Гервин.1, невер
~ю: 11апри...1ер1 куб и nрс1в11ль11ый
тетраэлр равнон> оЬъема не рс11:1но-
1оставле11 ы . П одробнее об этом
расск.1зано u статье • Равновеликие
и равнососта 11ленные фи1·уры».
SlllQ. = VJ
.___
__.....___" J
Рис. 4.
Фигуры
ФОРМУЛА ПИКА
РаLlм<.прим м1·юrоуrолы·1ик, вершины которого
н аходя1ся в умах uелочислс нно й решетки, т. е.
11меют uело•1исленные координаты. Сушествует
формула, позволяюшая 1101йти е го плошаль путем
подсчf'та чиrла содержаш~1хся в нем ус1лов. /\юбои
такси многоугольник легко ра~nить на треугольни
ки с верши11ами в уJлах решё'тки. не солержашие
узлов н и в~1утри, ни ~1а Lторонах. Можно покс.1зJть,
что плошали всех этих треугольников одинаковы и
равны 1/2, а, следовательно, плошаль многоуrоль
ш1ка равна половине их числа Т.
Чтобы найти lTO чи сло, обо1н..~с1им череJ п
число сторон многоуrоль11ика, чере11 - ч~1rло
узлов Вtiутри его и через Ь - число узлов на сто
ронах, включая вершины. Обшая сумма углов всех
треу1 ольников ранна пТ. Теперь найдем 'JTY сумму
другим способом. Сумма углов с вершиной в лю
бом внутреннем узле составляет 2n, т. е. обшая
сумма таких углов рав1м 2iтt; обшая сумма углоtJ
при узлах на сгпронс1х, но не в ВЕ'ршинах равн а
(Ь n)rc, ;:i сумма углов пр11 вершинах многоуголь -
11ика - (п - 2)п:. Таким образом. п:Т = 21n: + (Ь -
-
п)п: + (п - 2) n:, откуда получаем выраже11ие для
П/\ОШал1~ S \1нпгоугольника:
S=~+i-1
2
'
11звсс1 ное как формула Пика Например, на рисун
ке Ь = 9, 1=24, а слелова rельно, 11лошадь много
угольника рl'lвна 27, 'l .
tCJlll м1ю1 ·0~ J'OJll>IШK О l111СШ Oh:OJIO сжруж
НUСТll, его площ;щь можно nырззптr. очень ко
ро гкоfl фо рJ\·1улой. которая слравсд;шна прн
любом чис11с С."1 upuн:
s= 1J7.
1де r- [ХЩJ 1ус окружносп 1. ар - полупср11\1стр
мпого~толыrнка . Чтобы u1>111<:'Ст11 :"!ту формулу,
.чноr ·оу1·011ы111к р:~:1б1111аю·1· 11:1 треу1 ·от .1н11ш от
резl\ам11, соея нт~яющп>,,1п цсптр окружности с
всрrшш~ми (рис. lU).
с
н
Рис.1о. "\RI1>1 = 2.11Я 1·+
1
+_!.ВС r+ +.!.ГЛ r=
2
.:
A/)+(J(+ +fA
'"
2
Н общtl\1 СЛ\"1ае пр~rх.од11тся доnол:ьство
Rат1,ся-формуло~'1. nыражающсй площадь через
координаты (X 1;J'1 ) , (x~~J' ! ),
.. , (х11 ;у11 ) 1юследо-
1~ательных вср ш11н 11-уто.rн,нr1ка:
S = } 1(.'\'1J'J -X2.J'1) + (.'\'2.V ' -X;J't ) +
+ ·- +(.\'"_1'1-. \· , у") 1
Отлнч1пелr.тюй ()С'Qбсrнюстыо 1р111юй фор·
мулы лшш<:'ТСЯ- то, что площадь здесь uыража
<::'ГС.Н не чере з хара1перистпю1 c;iмoro n -)толь
ннка (сторо ш,1, утлы), ;i через коордпнаты его
вершин. Последтше же зависят от расположс-
11 ня 11-~толы 11 ш:а оп юс11телы ю осей координат
А 1ю1 ому данную фор'-'1)11) сч11тают щ: н11олне
«геометр ~ 1ч1 юlr». O;~r r:1 ко она /~ост:1·1 оч1 ю ~/~об·
113 11 11ракт11чс сю1х 3;щачах.
ПАРКЕТЫ - ЗАМОШЕНИЯ
ПЛОСКОСТИ МНОГОУГОЛЬНИКАМИ
У.жt' п11фа1·о рей.ца м бы!lо нзnест110, что име·
етб1 только трп nи[{а праn11лы1ьп; мrюг оуголь·
никоn, которым11 f\IOЖIIO полrюстыо зaмorn1Th
плоскосТh fi~:~ пробелов 11 перекрытш1, - трс·
у1 ·0111~ник. .кн;щрат 11 u1сс·1 · 11у1 ·олы-11 rк (р11с. 1J)
Рис. 11.
В r.;аждом 11з :~·п1х эамо щспиlr тобыс дв:~ i\ll IO·
1·о~тоJ1hнш<: 1 11мсют либо общую сторону, лнбо
TOJJЫ\O общую вср 11111н у. Jl l160 I IO IК'C llC I L\1CIOT
общ11х точек. :3амснщ:1-111я п 1юскостr1 м1ю1·0-
)1'О, 11,1111к:1,111 , уN>RJJС"1·1юряю111нс :·У1 '01ч у трсl10-
1шrн10. 11:н1>111аю·1 1шрксmа.м11
~'()ед~ IThOI Н ТО\.\, ЧТО llJIK:HIOll JЧ'1)'i 'Oll 11p:1-
llHJ\ \1\ ll>ill 1\1\IO\'OYl'OJ\Ы IHK ll:.ip!<CT:l НС' 06р:1~ует .
('(}l!(t~I 11J){)C'TO. 1[ :щес1. нам 1IO! l:Щ(IO! I ТСИ фор
мул :~ суммы )ТJюв :111юго)толы1111\а. Еслп 11 ;1ркст
состаш1е1 1нз 11 -уголыrнков. то n 1<аждо1'r вepm11-
rre п:1р1сста 6у11ст схо;щться k = :i60"/ CJ.11 много
уголы1 1 1ков. IДI.." а,, - ~тол нра11ш 1ы ю1·0 11-у1·0111,
ю1к1.Лtтко наf1ти. •rто о.,= 60", а1 = t)()
0
, о.~ = JU8°,
а,,= 1.Ю" 11 12(Y'< ct"< JFIO " щ11111 ~7 . По:-ному
~61}" / \t!ll\'1'01 \l;\J ~~J IO 11;1 1.1 .11 'l ' Ш Н> КО 11ри 11 = :\: ~\: 6.
Парке~ ы 11 з 111х1в11лы11.1х м11(J1't>)Т<>лы111ков
t':tMll JJpaRIJ!IЫ IЫС li 1'0 .\1 CMl.>ICJlt. ЧТР ()1111 (·()) [11-
ll:tMJIIO }'t:Tpoe нhl » ()'l'H()Cl[TL'Лl>IIO нсех CIIOl l X
11ер 1111111 11 всех сост: 1в.1яющ т1 х г1 :~ркст1,1 кусоч-
1<011 - м 1 юго~то.~ 1 ы 111коti (Эт1 1 1\усочю 1 н:~:~ыва
ются 1 -раня,-.ш :J:.1мощс111ш пт1 просто пл11тка
мt 1.)Др)тн.:1ш СJ ЮJЗам 11 , ддя юобr,1х дnух ljep111ш 1
nраюшъ110 1 '0 п:~ркет::~ мож110 у1оз:пь такое его
са~юсовмсщ~штс. 1 1р11 кuто ром on11:i 11::J всршш1
1 юпа1щ.:т н;J другую. То же:- нсрно для любых
lll!\':\ 11,111пж 11:1ркета.
.11-1 о ж 11 0 11 и1рсбон:п 1" чтобh1 1 1:.1 1жст ()ыл 11p;1-
IШJlьi11,111,1 то11 1,ко ~н\1 нерrп11н~1м » . но 11а :чх.:ш11ть
llCIJU,[ J). Юf\aT1, [': 1 :.1Т1111е lil 11 [1•1 пp:llНIJ1/1Hl1IX MHOП>
~ IO!J11Il l 11\()fi, То1Д; 1 1с ч1t:,1 111.·хiщ1 11 11ч 11аркста~\1
1о();~пя1 Oi с щ ё вскем. 1, . н ~106ражё 1111 ых 11:1
r11c 12.
Рассматриваю·~· и друюt обоще1111е - пэр
!(t"!'ы 113 КОШ1.Й проазвО.'ТЫ!ОJ'О i\!JIOJ'O~fГOI!ЬHlfl\'1,
пращиы 1ые « по гра11я м» (т. с. допуск:1юп_1,ие ca -
\IOCOl)M<.:щc111iя. которые ш::ре 1юдят любую :~<1 -
;{:11шую ш~и· 1 ку в любую .цругую) Чщ:ло так.1'L'\:
1аркстuн - 16, включая 11 ш:рвыс тр11 . М1ю1·0-
\'1 ·0.'rь11111-:и . которые.: мо1-ут бы ть nл 1лъ:а м11 11 .-:1тих
шркс1 ах. 11 а31>1На 1отся 1 utm111?mu1.м11. Я с110, ч·1 о
11л оско<.т1, ~\()ЖНО ул()ЛСJIТI• кош Lя~н 1прои з 1~011ь -
11ого '1'\ll'Y ГOJI Ы·l llK<J. но MCllL:C:: OЧCH l,ЦJi(), ч 1'0
nрш1зво:1ыт1t11'1 чс1ы рёх~1·ол т,н 11к - 1 и1ан11 1 ·01 1
( рис. \.).а). То Жl' nep110 11 /\ЛSI люfio ro шссти
}Толы Шl\:l. 11роп11юпо1южпые сторо1 1ы ко·1·о ро-
l'ис" 12.
I 'O равны 11 пар:ll1m_.лы1ы (р1к l .~. б). Ещё пять
11рим сров 11 оказаны 1r;1 рнс 1-1
13сс рассмотrс11ны<:: ныше 11арКL"1ъ1 ш:"·r 1 ю
N tч11ы , т. l: . к ~'аж.домн :~ 1111х можно кнд1..:J 1а· 1ъ
( 11 даже '"11IОП1 \1Н спосо6ам11) L" ()CT:IНЛCJll IYlO 11.1
ш:с1<QЛЬКl I Л П!JI J'l 'OK o\)JiatT I>. 11;! коп1р1111 11а paJ1-
ll~l bl l l 1l 1\l ll сн11 11г-:1 м11 r юлуч~1 е· 1 ·ся 1~er1, п:1рк<."1.
и 11тсрес учё1 JЬIX 1\'1"<1 К1 rм 1\ОНСТР\'Ю\IТНМ 06·1, ис-
11яе·r'СЯ тем. что пср1юдическпе :laM011{eIIш1.
особс1 шо замощс1111я ттростра11стш1. молслнру
ют 1<рпстаютичесю 1е с.:тр)1\туры. Существуют
Рнс. 1.l.
Фигуры
Рис. 14.
и IJСпери одическнс замоще ния, наnрнмер
оче111. 1qх1слвос сmrральное Jа/\ющсппс rтлос-
1<ости дс1н1т 1 rу1·ш1 1,никам 11 , пр11думанное н
19.16 г. нсмсцк~1~1 ма·1·ематиком Х. Фо.и.србср-
1·0,ч (рис. 15). Впрочем.< )бъещши1:1 :,)ТН 11J 111тки
r ю1 1 арно н 1~е11трзлы ю-симмстр 11чн ыс восьм1. 1-
уголыmю1, можно з:1мосппъ ими mюскость и
IIС{ШО/1,ИЧССК\ 1.
Дол те Rpe 'vfЯ прс,flпол::~гат-1, что 11е суще
е1 ·1~ует 11литсж 11 [(аже наборов из 11есколышх
различных плиток, копни которых могли бы
устилать плоскость топ ько тrепсриод11чес1ш.
Однако в сере[{штс 60 -х гг ХХ о. эта пшотеза
была опровергнута. для чего потт;щобился
набор 113 60J1ec чем 2U ООО rазных. шщuн ПЛll
ток. Ша1· за urar·u м ч11с1ю 111111ток удан<11юсь
умl'ньшнт1" 11, н ::~ко11сц, черсз .цеснть ж."1 · ан 1 ·ли!"t
скому матсм:1тнку Роджеру nенроузу }')\<.1JIOCb
обойт11 сь нсс1·0 дву~tя uчснъ простыми ф 1 1J') р
ками. Но пр11 их ныклады ка 1-11 1н нсобхсщн i\ю
со6mод~пъ некоторые простые п1х1иил:1 соче
тания ф111.)1 рок (вместо :этот•о на крз>tХ фнг~ ро1с
r~е11 аю·1· ci 1ецналы 1ыс :з:~зубр1111ы , 1 1х со 1111адепш:
обеспечивает собтоде11ие пр;~вил). Фор!-1а фи
гпюк может быть различной. но nce они сю1 -
Рис 15.
заны с прак11.11 1,н ым 11si 1 · 11у1 ·шu,ш 1ко,\1 . Одш1 из
rtp11"1l'p011 П()/(О61ю(1 1tары l lJll!TOK - так Н:1ЗЫ
щ1емые ·1 j)C)'l'OЛhIO I IOI r ot1 1Гfll'Ol l <l (тpe) 'J '()JIЫJИ·
ки АВС' и ACD 11а рнс. '> ). Л.ryгori пример
-
роибы с ос·1р1>1м11 )Тлам 1 r 7 2. п )()().Участок 0:1·
rюro 11 з бес1<011еч1юго множества образуемых
нмн паркетов покдзн 11а рис. 1С1. Как н все
друп rе моза1rкп Пепроуза, этт 11аркет квазf1-
пс rшод11чесюtй (от лат. quasi - <-почт1 r·>), т. е.
любая с1 ·0 ко11сч11ая часть повторж.тся в нё.ч
б~:ско 11еч1 ю мнш·о раз. 1lu са \10<.: i11 1тсресное
::.1аключае1·с51 в ~·ом, чтu 1.ккuрс - уже через не
сколько)[(_"[' 1IOCJ!(; uткрыт1 1н IШ:I Э llllCJ11 Ю)\IГЧСС·
кнх з:~чm 1\<.: 111 1й, ш1:1'1:.1л1.: каз~11:1Lш1хся не б()лее
чем 111 ·poi1 ума , - nп1 m1 получсн 1 ,1 вtщt<.."ma с
к11ззипсрr rс>днчtскоИ <..-1·ру1<туро1:.r .
Р11с 1&.
ОКРУЖНОСТЬ И КРУГ
ОПРЕЛЕ/\ЕНИ Е
И ПРОСТЕЙШИЕ СВОЙСТВА
Mrromc 1-штересныс, красиnые, но 11 трудш,1с
тсо rх·м ы с1тзаны с окруж 1r ост 1> ю. Тот. кто
нr llJ}'ЧJIJI сё C!IOЙ<."l'H;J l l ЛH НС: yмet:'I' их прим<.:
нтъ, с11~<.: нt.: :знаС'J ' 1 ·t:o\t <.:"t'p11и . Так что сжруж
ностh М()Ж1ю 1 1::tзн::1·1ъ cRoc 1·0 рода ~колесом
ГCO\ICTPITT I ·>. к тому же ()}(НО нз cнnli C'l'H ко-
11ес:.1 - его ось остаётсн Rсё премя па нен::~ме11-
1юм расстоянии от nonepx1юc1· 11. по котороi1
01 юкатнтся, - в матемап1ческпr~1 фориуллроn
ке nреnра щаетс я u определение 0 1<p~?кr1ocn 1
О1.;ру:;1оюсть - э·го l\111ожество точек шюско
ст11, у7.щлёш 1 ы х от некотороi1 точкп, сё цe111J l}Jt1.
на (};1110 11 ·ro ж<: р<.1сстошше, шш рад11ус
(ОТ //С/111. l":!tl i LJS - <- СШЩа IIO.'IeCa·•, ··ЛУЧ»; р.к t ).
Р;1,.111ус:1м 1 1 на:н,1 наются таюкс отре:зк11. сuсдн
ннющ1 rc центр сточка \1J 1 окμуж..1-1ос1 1 1
Дна CRU(I CTB~t t>Кf1}'Жl IO(. "l ' I 1 111,щсляют t'l' сре
дн ,(\))'1'1 IX Э:.t МКН)'ТЫХ 111IHI 1i'I.I1 J1CЖ/1,l' IKCI'() 011:1
01·r~111н ч1ш:-1ет на1160J 1 пшу10 пло11\:~;~1, 1ю срак
нсн то С() HCei\H I :-1aм ю-ryт1,J\IJI 1-. :p111il1JAH I тоl1 Ж<:
дтшы (Т. е. периметра). ::Это ; 1а к rтазын;зе,·юе
юо11ери.11с>трu чесл-ое (отлат. isos - « раш1ыl1»)
свойство оr<ружност11.
Д:UJcc. окр1?ю-юсть может скалт.зитh 1ю са
мой себt', пр1 1 чс_,1 се nрои:шолы~ая точкd мо
жег сошнсстит ь ся с лrобоl1 дру1·0J'1 Кроме
окруж1 юсти это свойство присущ<.: только од
но11 ли11ш1 - r1рямu1\ нu uна 11с :~ам ю 1у·1 а.
А пота.чу, для т01·0 чтобы кр и ван са61н1 точно
входила 11 1южны, 01-1:1 долж 1 1:.1 быть изо 111 ут::~
ПО OJ\[)YЖJ ЮС'l'И .
Част~, 111юс кост 11 , закл1пчё1111а н ину1 · р1 1
rжр~ж11ост11 (т. е. спстоищан ~1з точек. у;1алt 1 1-
11ых от це 11тра о/\руж 1 юст и 11а р;:1 сстоя11ие,
не большее рад11ус1), на:i ы nастся л:руг0;и . Хор
да - это отрезок, соеди пmощий любые две
rочк11 окрулшости. Хорда, прохо:~;ящ<~я через
астр окружности, пазьmdется дuа.11.1етро..м. Uн
вд1юе д;1 11 н н<.:е ра;...щуса и является на нбuльпшм
fIOJMOЖH hl M p:t C(."l'UH ll Иt'M 1'"1СЖду точк:t ~НI
:)кр~ЖНОСП I (р 11с. 2). Jilon:з>i xopl(fl, :1 З Н 3Чl1Т 11
люfioi"1 отрt.::юк между точками круга. 1~<..;лнком
прю~;:щлеж11 т кругу; друп 1 мн d1оиам 1 1, к руг -
rJы 11~1<л::tя ф111у1х1. П рямая н м<:ст не боле<: пнух
0611 \Ш\ точек с ш<руж1 юс1ъ 10. F.сл н таю 1х то-
Г<:омстр~1я нп П/\О('КО< rи
чеl\ дlie, прямая паз 1,1 1i::tется Cl!h)'1Ц&f1, :1 ecm1
одпа, - 1cacrmzeлыmi1.
Дне 0 1\руж11ост11 11е ~югут 11ме-1 ъ бo:1 t:t: лвух
общrrх точек Ест 1 1 ·:11шх точек /\Ве - 1·<11н 1рят.
что окруж1 юстr111сресе1шются (рнс. 5. а), есл11
же OД ii:l, - ЧТО O II П )~'(lC(llONIC.fl друг 11руга.
Причём r<аснте бывает тюш1111.14 (рнс. 5. б) .
ко 1 ·;_щ окруж1 юст1 1 рас 1 юлuжсны одн ;,~ нrrc /tpy-
1·011 , 11JJ11 вг1;1·m;пт1t11.м (р~ 1 с..\ в), кш·да O/ l ll:J
н:s IН1.Х JJCЖIJ'I' нну·1 р1 1 J(py1·uй. J::CЛIJ у окруж1 IO-
C'\'l:Й нет о6щнх точ.ек, ~ю сст1, общ11 й ц<.:нтр.
ТО ШП1 1 13ЗЫШН()i'СЯ /\'()Hl(& IШl/J11Чl'C101.Al/I,
СИММЕТРИЯ ОКРУЖНОСТИ
Ди аметр /1,елит ОКР)·?ююст 1, шt J"><tRHЫt" ч;:~сл1.
Комментатор «l l ачал» древ11е1·речссю1т1 ф11ло
соф Проt<л (У в.) пр11nпсы вал это открытщ:
Фал<.:су, rюдОJ 1а Ч:IJIЬH 11ку а11т1 1 Ч!ЮЙ фwюсофн 11
Р11с. 1.
P1t<". 2.
Д11fl lfi'llljl
! (1111mf>
о
Рис. З. d
б
8
:)L) 1
Фи1уры
11 11аую1. Уточтш дшнюс утвсржде11не, ,,южно
Ска:.-sать. 1.J Т() Ur<pyЖНUL"l Ь CШvlMCTpHЧI 1:1 OTШ><.:11 -
Tl'JIЫIO любого C IIOCI'() д11аметра (ТОЧТIСС, сuдсμ
ж:1щс101cJ·o11ря.мш\ р 11 с. Ч).
Из с 11 чм.с:тр1111 окруж11ос."1·11 вытекает рщl
r 1 011с.11 1ы х слс:r1стн 11l1 . ПреЖJ(L' нсL·1 ·0,
~ 4 к л1обuй точ1се окруЖ](ОС1'и мож
-ы 110 пос·rроить едmrствспную J<:аса
тельпую . Касател1.пая перпепди-
1сулярпа радиусу, проведёпnому в
точку касаnия.
Дсйстn 11тст.но. llусть
произrю11ьна.н
1 1рщ.1аJ1 , Щ)ОХОftнщая ч<:р<:з то•1ку .4 окружно
ст11 . О 11 уст 11.м 11~1 не<: 1тср11снд11ь.-уляр р r·п 1lt:HT-
p:1( >(р1 rc . ') ). Пртv1ан / ·~:шс; \О.\Ю 1~мс::<:"J' Ш.' f)шн.:t'
/ lHYX о()щн.>с ·1 о че к с окр ужr Шl"t 1,ю, 11 pllчём
l"()ЧК:.1. C: l1MMl"l"Pl1Чlt llЯ motioi1 н:{ Н11Х ( )" 11Юl'IJ
Teл1.110 001 р, тоже леж11т i1 11а лрям оlт, 11 11:1
окр~~п<1югп1 П оэтому А Вуне1 · е; 1и11ствст1rтоli
Рис 4.
обще~'~ TO<JJ\OII в TO.VI 11TOJJЫCO13 ТО;\1 с:rуч;1е. ес.rш
0 1ra попщ·"\ает it:.tp. т <:. коr,1а / 11 ра,ш1ус ИА пер·
l ICil.Д I IК\'ЛЛj)Тl\ 11 .
Д;J.'ll'C ( р11с. 6 ).
,'t:~ отрезки касатсJ1ыrых, nроnедёttных:к
·1,,
окружвоС't' и из одной точки, равны;
цен·гр оI<ружностн. в1тисавноr:t о об·
разованный ими уrол, лежит па его
биссе1сrрисе.
Легко доюзать н так11 с теоремы {р11(. 7):
~· . Диаl\1етр , псрпt:ндикулярпый: хорде,
10..
дедит её пополам; ду1:и окружности,
за кл ючённые 1\tежду днумя парал
лельными хордами, равны; еслн каса·
тсдr.ная параллел ыrа хорде, то точка
касания делит пополам дуrу, е.1·яrнва
емую хордой:.
Рис. 6.
Р111-. 7.
Интсрес111,1 л тс:оrе,...·1 11 :1а,rрч с участпе,,
Оl(Р)"JК\Ю(ТП :1а 'ТЪJСЛLП1 нет р~IЗВ\lТl!Я гсш1етр1111
11акоmтось ~ д11ш tтt:лыю много. Мы ·юлько крат·
!{() oз11a 1<0MIJMOI с LICl~()TOPЫMI 1 I T:1 lll IX. А и каче
стве ор 1 н.:пти рон 13Ыб<:р<:м 11 сс1{олыю 11еслож
н ы х. ~ю 1ю- в;tс1·сн~11н:м~ к11ючевьL\: теорем.
ТЕОРЕМА О КАСАТЕЛЬНЫХ
Кш уже: 6ыm1 с-к:~:з:1 1ю, 01ренп 1 каспс;1ы1ы.х-,
п ронеJ(ё~ 111 1,1 х к сжруж 1 t0c1·11 11 .) <щ1н 1 i1 T()'fюt,
11.меют од 1111 :11-:овую длшrу. Эту ;~т11 1 у 11азьша·
ют л:дсс1111е.1ы1ы.м /XICC:/7lOЯIUl!!. ll от Т()ЧIШ ДО
oкp~IIШOCT I 1
Бс.-:'1 п~орсм ы о касатслъных 11с обх.одmсr
решение 1111 o;~н oi'l :.ццач11о 1ш1 н.:~111 1 ых uкруж.
110с1нх,1шьLr-ш <.'JН)нам 11 , об окр~~жностях, кш·
ЮЩНХСЯ сторон l\1llOl'OYl'OJIЫlllK:I .
Касательные расстолпия n треуrольни1се.
Jlatщ61 ,..t..11 11 1ы 0·1 р~:щоn. на 1.;оторые сторо11 ы
тр<:Уrо.1 1,1111ка ALJ(, ра3611ва ютсн то<1кам11 кa<.:a-
111rn ( IIOHC..1111 IOl'L LI HCI '() ОКр)Жl-ЮСIЪЮ (p!t<.:. ~.а),
11:tr1ptl\ll'p t':H.• l l l',lblIOl' p:tClyl'OЯJJJH; Z, OTTO'U"I 1
;J,001\P\il\IIO(YJ'll С.:юж1 1м t-IOpOl-lhl , , 11 с. а 33ТС\\
llJ ЧМ\11>1 llltlЧ'll'\1 tyl'OpOl-1)' {/ YЧ l lTЫl:\:ltl p:tRCll-
CПIO к:1с11·с111111ых, 11рсн1t",~t:нн1.1л нз u;~нoi1 11tр-
1111111ы 1юл)Чll\t 21 1• 11 т:11<.
11 (IJ+C а)/2 :р - а.
rде. р = (а -r IJ +с)/2 п ону11ср 11метr .1~ншо 1·0
rре> 1 ·0:1ы111 1<а. ,L!,lшны отрезков сторон. Щ)JJ.ТlС
жап~т, 1\ 11ер1111111,1мЬ' 11 G', р~шны COOTЩ.'TCTBCII
!IO/J Ь 11/1- С.
Аналоп 1ч1 ю, ,ц;ш в11t:1~111к:а111 ю1·1 uкруж1 юе1· 11
·1реу1 ·ол 1,ннка . кас:1 ющсl101 ( t·наrуж11 ) cтopo
Hht (/ ( р11с. н. n). кaca•t 'l'JIЬHЫl' /XH.:CTШlltJIЯ от R 11
Gp:tHllhJ С< )() l'l\l''l'C'l'Hl'l 11 J() f J - с 11 jJ - /J, 3 0'1' щ:р-
11111111>1 \
11\)lll~ l'O />
R
б
Рис. 8.
А
:~аме1 ·11м, что з·1 1 1 форму111>1 мож1 ю нспол r.
ю1ш1ъ 11 "" об rат11ую стоrо11)""
•
Jlусть в угол ВАС вписана 01<: руж -
!.f' /
..,~ пость, причём касательное р<1сстоя-
ние от вершины у1·ла до 01'-ружности
равно р или р - ~1, 1·дс р - полупери
мстр трсугольникаАВС, а = ВС. Тогда
окружность касается оря~юйВС (со
ответственно сна ружи или внугри
TpCYJ'OJll•H•1кa) .
В само ,1 :к:н.:. 11~ t 1ъ, 11зnр11 \rer. кзс:не.1ыюе
rасстоя~ 111е раnно р - а. Tor..- ':.t наmз окруж
rюсть кJс.11.:тсн сторон \Тла n тех же са)'\ых
точк:~х, что 11 в1111с<11111зя 01<руж1юстьтрс~то. 1ь-
1111ка rlHG . .1 ;шач 1 п, соnпалает <.:ней. С:н.:доnа
Т(~tыю. 011.1 касается 11μям ой ВС.
ll'l!М('Tf111Я 11;1 flЛOCKO< rи
Фигуrы
Описаl:J'ный че-1ЪJрёхугол1.ннк. ИJ тео рl'мы
о ра1н.· нстRе r<aca 1 ·и1ы-1 ых ср а з) 1юлучdе 1сн
(p11t.:. 9, (1), ЧТL)
Дсж:JЖl'М это /l,JUI Ч<:'JЪJpi..':xy1 ·ш 1L,H I 11<.а, (HЛИ'l
llOI'() от 11:.~р ал111:.rю1рамма . Пус.~1ъ к~KJ1t'-'l'O две
11рот11 1ю 1 tшшжныt' l-юроны чстырt:.ху1·олы 111 к:1.
11~тр11мt:р АВ 11 DC. llJ)(J щю1юлжсн1111 п t:рссе-
!f; ./ есди в чеJЪiрёху:rоль11и1< можно ВШ(-
~J. са,rь ОI<руЖНОСТЬ, ТО суммы его про-
тивополо.жJПdХ сторон равны:
AD+ВС=АВ+CD.
1J
Отмс111м. что ош1сш 1 1ый Чt'Тыреху1олы 111к
обнJатслыю вы11) кль11'1. Верни 11 обрат~ юс·
если четырёхугольник выпуклый и
суммы ero противоподожных сто
роJ1 равны , то n него мож.1-rо nписа·rь
01сружnостъ.
ЛЛИНА ОКРУЖНОСТИ
И Пl\ОШАдЬ l<РУГА
ФормуАы 2nR для лли 11ы окружно
сти радиуса R и пR- ллs~ плошали
ограниче н 11ого ею круга известны
любому стар ш екласс н ику. О н и
пользовам1 сь особым в н има н~1 ем
м;:~тсмати ков и вы ч и слителей 11а
проп1ж~нии rысячеАет ~.-tй. Интер ес
к все более точному определению
постоянно и 1t долгое время п оллер ·
живался 1 1адсждами осуществить
к1:1алра Jypy круга - построить uир
куАем и м1нейкои квалрат, равнп
Аеликии л.:~н н ому кругу (см ст.1тью
«Тр11 знаменитые зала,111 лрев 1-юс
Н1>>), а еще более - стремлением
опроверг нуть Аожные «реше нщ1 .
JТОй задJчи. В дальнейшем уточне-
111<1е .~нач ения Ч \<\(1\а it стал<> пюеrо
рода математичРским спор·~ ом, а в
11awe время - еше и с пособом про
демонстрировать дОlто инства ком
пьюте рных 11р()1·рамм и сам их ком
пьютеров (см. статью «Ч ислотt•/
Собt.-твен но же формулы про
сто выражают тот факт, что лли на
окруж ности проnорuион;мьна её
раы1усу, а nлошаль круга - квад
рату ради уса, п ричем первый 1<0-
:Эффиuиснт nроnорuион альн опи
влвое больше второго. Указа нны е
соойсmа следуют из определении
Рис. 9.
лл ины окружнпrти и ПАошали
круга . Но сами п11 оп релелt' н ия
не CTOl\b nрос1'ы , 1<ак в случае ллины
отрезке) Иl\И Пl\ОШадн M I югоугuль
ника. Ведь здесь н,1м приходится
иметьдеАО с « кривыми " фигурами .
П Аошали кри1юли1 1 L•й 11 ых фи
гур опrелеляют, строя fЗ( (" более
бАизкие к ним по ф'1рме \.1НОГО
у гольн ики (см. ста.тью н длина,
площадь, обь~м » ). Летали опре
делений могут отличатьо1, но в
Аюбом случае их суть своыпся к
tлслуюшем у предложению. Если
пuслелпваiеАь ность многоуголь
ников тм содсржаш11хся в ла н1 юи
фигуре Ф, и nuсАедова'U'Сльность
мноrоугоАьников М," rолержаших
ее (рис. 1), таковы, что р.нность
площадей Мп и m" ст;:э1юви тсs~
А
с коАь угоыю малой l росто\1 п, тu
площади м н огоугольников обеих
nослел<>sа1'ельностеи стрем~пся к
uл1юму и тому же прсдеАыюму
JНс~чению , которое и п ринимается
за площадь Ф.
ЕС'ли Ф - кру1, то LJ ~-.ачестве
Мп и m" ее тественно в~ять правиль
ные описанный 11 вписанны11 п
угольники. О н и полQб11ы друг
другу. Ко:~фф1 1ш1 е1п nолuuня k0
Аегко найт11 , расположив много.
угольt1ики так . чтобы середины
сторш1 первого Lовпали l вt:рши
н,щи второго (рис. 2) :
k0=08:0А=
LO!tLAOB ('Щ 180 °
п
Онюшсни1;> плuшадей пuдоо·
ных фигур равно квалра гу •~ х КО·
эффиuиента полобия. Поrкольк)'
по мере роста п этот коэффнш1·
ент <•ремится к 1, р<11н опь511 -s0
плош:~дей М0 1·1 nlm рав11а~ (k~ - 1)S,,,
стремится к 11улю Таки"' образом,
nлошадь кру1 а рав11d предеАу пло
ШdдеИ е1 о вписанных и ош1санны~
прJВИЛЬНЫ)\ 11 - yГOl\l:.ttИKOB пр11
п~о<>.
Оnишt:>м правильный 11-yroлi..
ник около круrа Рд1111ИЧНОГО ра·
д11 уса и обо.тачим cru пмшаll!~
Геомt-трня н.1 плоскости
кутся ~точке!:.' (рис. 9. б) Вnншем 0 1<руж.1 юсr·ь
в тре\'ГОJ11>111ш ADJ::: Её кас:пслыюс рассто
яние 11. до точки Е nыражае·tсн форм}'Лоf1
ТЕОРЕМА О ВПИСАННОМ УГ/\Е
Теорем~~ о rн..:_1шщшl') 1ла. HJJJ 1саrп-ю1·0 n m\руж
н ость (т. е обра:ю1~ан1-ю1·0 ю~уми xupдa'-'H I с
On ЩJ IM l<()IЩOM) . HKJJH~ I CH КJll<! 1 Jl'KO(I Гlj) l l JICШl'
HШ 1 э:Щ:1'J ofi Ol IHC:1 нной oкpyж110Ct'IJ . в Э'J '( )(!
ТС< >р<:'М.' у·1 нс:ржд:1l"l'СЯ. Ч'lЛ
Но 1[() услuнню суммы прт IНЮПОJ l()ЖНЫХ
сторu н чс· 1· ырt'х-~ 1·от.нг1ка р:~кны, ;1 знач 1 rт,
11D+Ш.'=АВ+СП. нл11 AD=АВ+CD - RG П<щ
ст;.~ющ :::~тп зна че1 111 t: н 111,Jр:~жстrиедл.я 11 • получ r1.'l1
,'fi" вписанный в 11,анпу~() ()I<pyжвoC'rr.
· 1"_,,
уrол изме1')лется половиной уrло
nой вели'-uшы дуги, котору~{) это·1·
уrол стягивает.
11 = ±{(,1Е - Ав)+ (.EIJ- с:п) + вс) =
=~( вн +Ее+ вс) .
:t ЭТО - nолу11ернмстр TpC)'l '()JJЫJIJK;I ВСН. Нз
дока:~ан110 1 ·0 выше услоюш кзс: 11 11m с. 1 елуст, что
на1 11:1 окружность касаст('я ВС
Др\ТН.МИ сло.1:1 амп . Oll р;.~нс11 ПОJ!ОВШ!С цс11 -
·1·р~1лы-ю1·0 угла (т с yl'Jla с нсршш ю 1'r в центр<:
окр~Ж.1 ЮС't'И ), Oll и р:ШНЦ(.'l 'ОСЯ Jt:1 эту / (YI) . ·т:1-
ЧСJ llНI 1(Cl1тр:и1 Ь/-IОГО ) l 'Jt;~ MOl '\ "J 11apt>J1poнa J ,,
от О J(O ,:\(10" (рпс. !()).
Рис. 2.
•1ерез Cn. Правильный n - угольник,
оn1tеа~11 1ы и около круг11 радиуса R,
полобе~1 пе рuому с К(Вффиuиен
том пnдобия R и потому имее1
nлошадь5" =с,,N'. Переходя к пре
делу , получаем , что и плош.:~дь
круга пропорuионdльна Kt.ldдpaтy
его радиуса и 1v1ожет быть :1аписана
в виде cR! . 601 :пот-то коэффи uи
ент 11ропорuиtm<1льнuсrи <. и есrь
та"'енитое чи сло те.
Впрочем, обыч н о числотт оnре
Аел<ilют чере:-1 АЛи ну 01<руж110LТИ.
О1тюдd и обсУ1начениетt- перн<1я
буква гrечеl"оп1 слова « окруж
ность•, - выбр.:~н ное лля 1~с1 u Ле
онардом Эилером. Разобьем uпи
саннь1й правильный n-ytольн11к на
трсугольн~1ки, соели11 ив его uснтр мож н о у·rочнит~. Однако еше луч-
со в<.J:~ми верши11"1'Vlи , и нuидем их
площали . Н<1 рис. 2 плошilдь t)дно
rо ю н их - треу гольникd 08(""
равна
1
1
-ВС 0А=-с1 R
2
211
'
r де а" - l торона мнuгоуrолыi11ка.
Поэl'Ому
S,, = ~ Q,,I<,
rле Q" = па " - периметр описанно
r·о 11 - уrольника. П ло ш адь 5" при
пч"° t1ремил я кl Ri, ,1з11,1чи1, пе
риметр Q" стремито1 к 2r R. По
скольку периметр Р. правильного
вnиciltlttOt о n - уrол ы1и ка равен
Q"/J.." , il k" --+ 1, он сгреми1ся к тому
же nрЕ>лслу . Этот 06Lш1и прелел Пf'
pимerpuu правильных впии1 11ны х и
(!ПИ<.'d Нн1,1х м1111гоугольников для
данной окружноС1·и и прин11мается,
по о пределе н ию, за С!е длин у.
Оuен ить ЧИ( лоп можно 1кходя
непскредственно И"\ определений.
Например, плошадь €'дин11чного
кру1·а меньше плошади егоопис.~н
ноrо квадрата; от~;-юдd те< 4. Ра< -
С"Ма ТрИВЭЯ ВПИ('iiННЫЙ КRадrат ,
~1аходим, что тт > 2. Увсличива~1
чи сло с1оро11 13ПИСt1 ЩI ЫХ и ()ПИ( dН
ных м ногоугольников, :эти оuенки
ше восr ruльзова rvcя не п11ош<1 -
дями, а nt>μимстрами. У любоп>
впи( анно го многоугольника пер11-
мстр мен ьше, чсм у оп 11 са 111юг(J
око,\.О той же окруж11<кт11. Поло
му ллина 2rt окружНО(ТИ радиу
са 1 удовлетворяtJТ нер;:ше нстRам
μ,,<2п<q", где р" 11Чп - 11ср11-
метры ее вn1ка н ногu и onиi;-dн
нoro n-угольн иков. УжР при п = 4
э1 u дJет неплохую оuс11ку снюу;
2тtJ:.р.1= 4 ' 2, т. t::. л;,. L,8.Лрх1·1-
мсд заметил , что , J1 1ая сторону а"
1:1111канно1 u п-уголы1ика, лt•t ко вы
ЧИСЛИТЬ d 111 -
ПOJIOllY ВГ111(JНIЮ
го 2п-угольника. Это t·н.> tложное
оыч~1сле11 ие, о котором 1к гюльзу
етс}J только теорема П11фагор.1, вы
можР'ГР ПГJOдE'll<ITb самостоятельно
и вывесп1 формулу
СJм Архимед, н.1чав с шс>tти
угольника. приме н ил Lвой мt.'тол
удВОfНИЯ Чf'l ЫрРЖдЫ И ( 1IOMOILl bIO
образов,1вшегося 96 - угольник;~
Получил ОU\о:11КИ
10
1
1-< те< 1-
71
7'
которые оставалисu лучшими t'Ше
очень лолгое время.
Фи гуры
l'ис. 10.
(
\
/
---
1юкр~пу Х1юсском~ (\1
"
к./\О11. :-.1.).Аu1·ом,чю
KllllClШ I Ыll ~'l'Oo l , OГ111palOLl \l l iiCЯ H~l J(\ l aMC'Т]J.
прямо1\ :юаm 1 / (ажс и:шшюнянс. С:ч111':1ют. тто
э·1 ·0 утnерж/tетшс NЖJ:зал Фалес
Нз тсщJс.мы о 1шпс:11 ШОi\1 угле можно полу
чшъ nыраже1111я уrла '-1ерсз дуп 1 11 11 с:туч:~е,
когда с1 о нерштща 11е лсж1 п н:~ ОI\р\-ж1юm1.
Тсорt:.щ1оrн~нсз 11 но1v1 :т:1е Кi\1сст~ с 1\сж:па
· 1е11пстпом rrракт11чеrкr1 11 тпм же 111 1, 1е. как 11 11
ССJН[>еме1шътх )Чеб11111<ЭХ. пр111 ююrтсл 11 <-На
ча11 ах» EnrФr11(a . Но она была 1 1звеl1Шl ещё Гнп-
Если вершина уr·ла ~1аход;ится вне
окружности, а обе ("l'Оро ны п ересе·
кают ОЬ.l>УЖНОСТJ" 'L' O этот угол равен
:полуразности уrловых ведиtIИН двух
nмсекае:м ых им 11а окру жности дуг
С1>ис. 11, (1).
Arraлo1·rrчнo.
ЗАЛАЧИ
ИЗ ЯПОНСКИХ ХРАМОВ
С XVll по XIX в., в пери()д правления
сегу1 IUB, я ПUtlИЯ была ПО/\IЮСТЫU
изолирuRана от внt:шнеru мира.
Чтобы обме11иватьсл открытиями,
япu1-н.кие геометры д~::лали кра
сочные чер т ежи 11а деревищ1ых
лошечках и отдавали их в п агоды.
Там их подвешивали под крыша>v111 .
Нсмdло дощечек с задач ами - их
называют сан rdкy- <'охран~1лось
до 11<1wих лнеи. Заддчи с решен ия
ми лuшли до на<.. и в рукопи с ных
списках.
В больши н стве сан гаку раr
см,прив<1ются весьма прихотливые
11 ~няшные ко11сгрукшт с икруж
носrими , вnиганными в юзалрать1,
треугольники ~, более сложные
фигуры , 110 есть и rакие, где пред
ставле н ы '!лли1н ы и t:феры. Вот
несколько примеров.
Задача 1. Есмt в че1ырехуголь
н 11к АВСО (рис. 1) можно в11и<..а1 ь
окружность, то окружнопи, впи
санные в треуголы1ию1 А[Г и CEF.
касаются стороны EF о оыюи и
той же точке. Вернu и обр,пное
утверждение.
З адача .2. Если кр.:кныс окруж
нос ти равны между собой. то и
rи н яя окружность равна им (ри( 2}.
Особенно силы~ое впечатлс -
Рис. 2.
рl:'ма, CHia {)ыла « Обняродована » в
па годе в 1800 г.
З адача З . Провел<?м из вер
шины многоу1 uль н ика, впи<..дн110-
го в окружносrь, В( е диагонали и
впишем окруж~юсти в обр'1зовав
ши еся трсуголы 111 ки (рис. 3). Тогда
сумма радиусов лих окружностей
будет однои и тои же НЕ:'зависим()
от выбора исхол1ю1о1 верш1111ь1.
Все три утвержлен11я локаjыва
ютс_я r П()Мnш ью те()ремы о каrа
тель11ых, причем в первых двух
ние проиJволит слелуюшая тео- зада чах её оыюи и досrаточно.
Пр11 решс11~1и третьей Jада·1 ~1
удобнее лока:~ыв.пь CfM.iY более
сильное с1:11111гrво : сумма рад;1усов
рассматривае...,u~х nкружностеR
ОС! .:ll'TC я П0t:TUЯlll IOf1 дЛЯ люОого
р,вбиР.ния данноrо мно1 uyruль·
н11ка н<1 треугольнf1 ки 11еnересе
каюш11мися димоналями. Пр~
локil :~ательстRе 1кпuль·1уется сле
дую ша я теорем<J Карно:
'-1·"
L·.
Сумма рам1усов вписанном
и описанной окружностеi
треуrоль~1ика рав•1а алгеб
раической сумме расстоя·
ний от uентра оnисанноА
окр ужности ло его сторон,
при•1ём расстоян ие д.о СТО·
роны берётся со зна~оА1
плюс, если ueнrp лежит no
ту же сторону от этоИ сто·
ро~1ь1 , что и сам треуголr
ник, и со 3наком минус,
если по другую сторону.
~, угол, вершина .которо1·0 на..хо,r~;и.тся
~~ :внутри окружности, равен ПОJ[усум
мс угловых величин дут, высека
С ;\fЫХ им и вертикальным уt'ло~1
(рис. 11, б).
Па.rю,-.1 ~ вер1ш 1на y1·J 1:1, р:.1юю1'() 1 10.rюв 1 11 1 е,11)ТИ .
11:1 которую п11 оп11 р<1ется, пrе1да лс,1.:1п 11а
OKp')rif\ I IOL:TИ.
13 :1a,1;:i<1.1x па п остросш 1 е доnолыю часто
11рнход11тся расс,чатр1 шать .'>шожест.1.ю точек f'.
ш которых датrr 1 ы 1'1 отрсзuкАВ «m щс11 по;t ; щн-
1 1ь1ч }ТЛО.'.1» (т. с у1·uлАРВ l lOCTOHIIJ l h ll'I; J.)HC. 12).
Нз теоро1 , 11р 1 шс;1ё 11 ньLх. ны r 1н:, и1сдуст, ЧТ\) .-~то
~нюжс.:спю сос тоит 11:1 !\f~Y-' р:r штых 1J.~'I' окруж
нос-111 с K<JH 11ам 11.t1 11 В, CI J.11,lML"J'PI I Ч I rых OTI !ОС! f-
l't;11.нo AB ;i;1 мс.:·1 1 1м, что сз~111 1юr щы 1l 11П :шю
жест1 1~ ·1·оч1.::к / >1Il' пр r 11 ra;VIcжa·1·
В;~ж11ос следствне ·1·topci'-1 ы о 1шпс11 11юм
~тле - 1 1rаз 1 r;н: 111 шсu 11 ю1·0 <н:тырёху1 ·ол ~.т-111к1:
~- ' Четырёхуrолы-1ик ~10жно вписать в
·J
окру :жность тоrд<1 и только то1'да ,
Jсогд<t сум.~1а с1·0 противоположных
углов равна 180°.
Де~'1 с· 1·в1 1тс11ыю. Cl' _' lJI ЧCTЫ f)ёX~T()JIЫl l JK IШl l
caн н ш:ружность ( рнс. 1:)), ти д)ТН. на rшто
]11>1t: 1т1 1 р:1 ю· го1 11н~ ен) п р0' 1 111101 ЮJюж1 11.1-х ·утл:-~.
<·ос1.111лню1 1 юттую окруж1 юС"1ъ, сё у1·Jюn:1я
RC.'11/ЧI 111;] - 2 .(1()0
,
J :'11 l:JЧ[JT. с-у,\1Vl,I :-УГI 1,\, ~ глоn
rав11а НЮ 0. 11 ()f)рат1ю: ll ~CTЬ сум!\Iа ~'Г!Юf!r l 11 (,'
четырёч 1 ·oлъrm l(a .'ШСD рат 1 а 1~(У. 1lроnс;(ём
<Жруж1юст1, чере:з точ rшА, В r1l.J. Угловая нсm 1 -
б
Р1к. Ll.
Гt·0.\11l' I рия 11 ,1 1 1ло1кос н1
LJИ11a сё!t~ тBAJ)равна .1(10° - 2LВ. Ш = 2( 18()0 -
-
L.131! lJ) = 2L RCO, а u1·сюда. как 6ьvю О'J'Мсч1.·
нu. слс1 1ус1 , что y1·un ГJ('f) 111 11 н·а н н окруж11щ"11,
ТЕОРЕМА ПТОЛ[МЕЯ
Пр11ме1111м · 1 с.:ор(·,чу о 1ш1 1 с:11111ом у1 ·; 1е, ч·1·<н11.1
HЫ11C:lTl l е1н~: t))\IIO c1н>flC''l'HO 1\П1 1 С1 ! 11ЮГО Че'l \ 1l -
рёху1 ·ол ы 111 r<~l. которпе: тоже яплщ·п·н пс;о\>,о
,'\11м ы м 11т1,nl~ 1 ;;t·1·0 . ..тт11. 1 м ~'еле >F11 1 ем в п 1 1 с:н111щт11
Р~кС,\Ютр 1 1.ч <Jen,1pёxy1·oлi.r 1 1tкАВС/ >, uш 1с.1r1
11ый в 0 1\рулшос1ъ (рнс. J-+ ). Uoзr,'vfём такую точ
ку 1! 1ra дн-а го1 rали lJ/J. что L /JAC = L ПAlJ. Трс
у1 ·олы 111 n: 11ADC 11AJilJ НО/\Оi1 1 1ы. так как кро~н:
равных I IO lIOCl'(JOl'HJ llO y l 'JIOH 1 1р 1 1 IK' j)l llllH<.: .4
0 1111 11;vic:ю·1· р11в1 rыс (11п 1 1с:11 11 1ыс) y1 'J11,1 11р11 1кр-
111 1 1нах С 11П. Очс1шюю, что ·1рсу1'олы 11 1ю 1 .-\СП
11 AJJE ТОЖt' 110) \0бllh\. То1 ла ВF.=А/3 ·СП/А С. , ;[
FП =А/)· RC/11(: Н о Hf-
-1 RJ) = RГJ. 1ю.-1то,,1у
AR (J) + ЛП В<.'=11(, B!J. Л,p)TllMllC:IOB:IMJI.
,f.;.r
nроиз.nедение диагоналей 11пис а 11 -
Ъ· ноrо четырёхуголышка равно с~1ме
прои з ведений е1·0 противопол ож
ных стороп .
:._)то ~" l 'lll'pЖJ(l'l-llll' 11р 11 НО,_\11'1 0 1 н J l/:l.\ll'lll l't'f)\I
·1·ру,цс iфCHHC1'f1l''1Cl'KOI'() yчi..'HOJ'() l~ 1 а1щш1 п J'O-
Jll:J\1l'JI (< жш 1 u 90-0h:OJIO J()<J) , . Bem 1кш· .чатс
м а ·1· 11 ч 1..:скоt: нострt )t't111<.: ac."r por юш t1 1 11 15 1..:1111-
1ах" ( ~л11L""1a1 с.:с 1 " ). Tl'1 1ep1, тl'opl'J\t:l нос~ п· LIJ\t:.i
;i(J7
Ф11гуры
I 1·1·о_r1смб1. В11роч<.:м, 011<1 ()ы11а 11 ~111сстт 1 а уже
Apxi ~меду. I 1·1·ш 1 l'"н: l1 11 с 1 юJ11,:.~онзл С'ё 11.ля состав
ЛС/-1/IЯ таблrrцы /(.111111 хоrц /! .13DIIC/l.\10CТI! ОТ
~т:юв~.rх F1eJr11ч1111сп11· 1 ш~н~мьrх1Lч11 ,'1yr (т с" 1ю
с~ щестnу. таб:нщы c1 m ycon). 011:1 бы,1а с~1у
11еобход1 1 ма :ря астро1 юм11чесюrх расчL'тuв
Есrш 11рнме111пъ nр11ведё~пюс вы111с ,\ок:1-
:1ап:льсrnо 1.; 11po11:.Jвu11htJ0~1y че1 ырt::-.у1 о.11,
ш11.:у ABCLJ. nocтpu1111 точку F ~,:;1к нер1111н 1 у
тpt:~TUJIJ.JПrкa ,1 (1'/) , IJO,\()OHOl 'O тр<.:)'1'().'11>11111\)'
АВС (рнс. 1'5), '1'() · 1 ·реу1 (.JJ IЫ!ИКll АС/) 11 1l fШ
снuва буду~· 1101\0611 n1. и~1 11 <.:1ш1~<.:нств:1 ·1·реу1'оm,
н11 ка ВЕ + .En ~ ВП \1Ы 11 ол~'ч1rм ~11e p::tnc1tcт110
r1·r·ш1емси"_АR сп +110 вс~лс RD.1щтorx>t:
D
Рис. l 'i.
Рис. 1&.
обращается в ращ:11спю то.'1ыю н том СЛ\ЧJt:,
ес1111 nсршн11ы .·1. l .J. С 11 D 1 1cтыrtxy1·um.11111\.1
)[ежат на u;o юi1 ОJЧ)\'ЖН< н.~1·н
СТЕПЕН Ь ТОЧКИ
ОТНОСИ ТЕЛЫ 10 ОКРУЖ Н ОСТИ
С111е1и1ш.1nчк11/'о11Юt111т.-~ы ю ,'\:1111ю1'1 01\f)\'Ж
1юсн1 опре1 tе.1нt:тся к::1к ра.нюС1ъ с/ - 1/. 1·дс:
d = PO - pacL-IOНllllC от jJ .J.O центра() 01\Р\'Ж·
1юст11, а N t.:<: !XI, 111 ус. ·r1 а в<.:ш1ч1111а 11\1ес 1· r1po·
cтoi'r rсомсгр11 1 1ссю1l1 смысл. д.-.я npS1\t1.1\, 11po·
L~Cдi.:1 шых через 1~ 11 нcpl:Cl'h:.Jющ11x окруж1 IOL"IЪ
n двух 1·оч1.:ах (060Jнач11м 11х А 11 /З). 11рощ11е·
д<.:н1 1 с /'..-!
· f'N ~нк"1 'm1111ю 11 равно аi1солнmю1'1
llCJllJЧllHC: C'l 'C lll'llll l '()Чl\J I Р. 311:!1( же CTCПCllJI
1юк:пыв:1ет, как раl110.•1ткt·н:1 н1ч1.::-1 оnюсн·
1·с:11,но окружное~ 11· t:rлт 1 сте11е111. nо.1ож11·
п.-;11.11а. то Р ж:ж111 1111е окр~ж1 юстт1. t:c.111 отр11
ц:1п:·лы1::1 - 1
·0 llll)'Тf)I(. :1 есл 11равна11\.IIO m
11:1 ОК[))'Ж1ЮС111
Чтобы у6ед111 1.ся в :-:1тuч. гrровсдё\1 чcptJ
точку Р ;\ве 11рнмыL. 11ср1..тскающ1н: кру1 1ю
хорде .rШ 11 д11а;-.1с:тр} А1Н1 ( р11с 1D. о. ii) 1\J
cuoircтв IНШC<lllllЫX )TJIOll BЫTl'JШC ' I 110/\00 11~
трсугольн~шоn l 1AA 1 11 /ll3 1B (110 y1·11a,\t), а 11J
сравнсн11я 0·1 ·110111<.: 11111'1 11х cotYt ве·1·с1'Нt'Н1J1Н
сторон - l 'JIC/t) )( IЩl'l' (X lllt'I 11..'ТНО:
Р11 l'B=f'.I
l'U ,= lct-R I (tl-R)
С1тпе1 rь точ"11 /'. т:ж:1щс11 1111е окт·,ююсщ
ра11н~1 1<t1;црат') t:f 1,.1спслыю1·0 расстояш1яР.\
, to окр)~f! ю~ 111. по~кш1ы~~. по т~оре,че l J11ф:I·
1·ора. d-- R - 1,0 ()}\ = J>л·- <rшс 16, б)
Отсюда с.r1сд,·с:т тсuро1а r) ющцратt к~1с:tт~:лh·
1юl1: KB:IД JX1T l\.1CITl'!ILI ю1'1 1-'J\
2
рав<.:11 11ро11:1м~
дешпо РА J>JJ сс1.:ущеl! ( 11;1 рве~ 11 Kl' -
/~) 11:1
ct rнн:шнюю ч.1сть (/'Н)
б
Гсометрия на плоскости
ОКРУЖНОСТЬ АПО/\/\ОНИЯ
я1 1но. т. е РЛ/РВ = con::.l ПуС'l 11 :~т() о 1·110111c1111t:
рашю г (!"~ 1) H ::i nр}lмой АВ ес1ъ ,r1.ве точю1
ис1со .чоrо м1южестnа - 1111утр1 1 и вIJe отре:з -
1с1 АВ; обозш.чпм их С 11D (рнс. 17). Пус1 ь Р -
любая 11з осталы rых точек нс1<омого мпожестна
По н :шссптой ·1еорсме . бнсссктрнса утла Р тре
)Толы:1нка rll-'8 дслпт сторшl) АВ в о·п юшстн 1
AP/PJJ = 1· =AC/CR. ;i потому с.ша с.:01шад:~ст с
131-~щ:uощсм} 01 rеомстrу алексат 11'р нйской rr11щ
лы Аnотю ш по Пер1·скому (около 26'5- 170
до 11 э. ) nрш 1адлсж111 з;щаqа. требуется 11ай1·11
:мюжсство шш. 1(:11\ rонориm1 ра11ы11с. rсомет
рнчсскос место точскl,, о·пюшс111 1е рассто.ю 11 1i-1
от кuторых до 1111ух д,1111 1ы х точекА 11 В шк:то-
GCE И!\И НИЧЕГО
Епь лне красивые теорl:"мы об
окружн<н тя х, п охоА<ис по фор
мулироо1<с , 1to различные по су
шспву . ПернукJ ю ни х принят()
наJ1,1вать пори~люм Штеит:ра. Рас
L\Ютрим лее окружности, ()лна •1з
кuтuрых раrnолuжена 011утри дf.>у
Гt1й . В 1 1ишем в обра1ован1-юе ими
(не оf>язателы tо п rавилыюе) коль
uо u 1<μуж 1 юсть, к.каю ш уюся их
обеих, J 1атем пrололжим в п и
сыва ть окружности в кольuо так ,
чтобы кажд.з~1 касалась пrелы11.у
u 1ей (р иr. 1). Образуется uспочка
окружностей. Теорема утвержлаР.т :
Есл11 эта uепочка замкttёт
ся, т. е. её л-я окр)'ЖНОСТЬ
коснётся первой, то, где бы
мь1 ни вписали первую
окружность, такая uепочка
будет замыкаться всегда и
именно nосле п шаrов .
Во второи теореме - аАьтt>р-
11 п11ве По 1ксле - мЕ'жду двумя
01\ружнuстями « ВСТilВАЯЮТС:Я» мно-
гоуrоль11ики. Во1ьмем точку на в11t·
ш11е~1 окружности, проведем иJ нее
1<<1сан:льную к в ну 1ренн ей окруж
ности и п родолжим касатель ную д()
вт ори чного п ереrече 11 ия t внсш11еи
окружностью. И3 пuлучен 1 юй точ
ки пересече н11я снnва пJ.ювелё~1
к<Jrательную к мС'11ьшсй окру>!\ 11ос
ти ( рис 2) и будем nрололж.т, ло
поп роение. Onpa~уется ломJ ная,
вписанная во внешнюю о~-ружноrть
и O ПHUllll l dЯ (JKUЛU 0 11 у1реннеи.
П онятно, ч10 ~ел, леt: во~мож1юс
ти: либо мы 1-ta каком-тn шаге по
п:.\Лём в исходную точку и 11aw~ лo
' vld Haя ым к.н ется, после чего м1;1
отправимся ~1а новый виток по тои
же «Орбите", лиnо в исхолную точ
ку мы 11е В(:рнсмся 11икоrлд. Ока.:1ы
вается1 что r~1улы-;11·, т. е-. то, какая
И3 лвух В()ЗМl1ЖНОСТей осушеп
вится . 11е зависит от исходной точ
ки Более того. ч11rло lненьев лuмJ
ной, если она заv~ кнется, будет
uлним и тем же- лля всех Т()ЧСК. дру
гими СЛО ВdМ И,
либо п-угольников (з амк
нутых п-звенных ломаных ),
вписанных вu внешнюю
окружность и описанных
около внутренней, не сушс
ствует, либо их бесконечно
много, причём з а верши
ну такой лом ано й можно
взять любую точку внешней
окружности (рис . 3).
В этом и соаuит теорема По11ссле.
Обе r1ринеле1111ыt: 3десь н~о
ре,..1ы немеме нтарны. Но первую
и з них довольно легко доказат ь,
("(ЛИ [10\ПОЛЬЗОl:ltlТЬСЯ особым гео
м~ rрич еrк им преnб разовdнием,
так 11азывае.мои и 11 верс 11 €' 1t. Тео
рема П о нп'лс может покJ..:1.пься
ПfJOWt:', IIO на (.dMOM деле IHl!t:Ч 1НЫf>
ее дm<.1~а тельrтва rлож ны и вrлут
к глубuки'Уt обобшr 11 иям.
Рис. 1.
50l)
.1> 1()
РАЛИ КАЛЬ НЛЯ ОСЬ
И РАЛИКАЛЬ НЫ Й UEHTP
В коnрли н ат<~х пеnень тnчки 1'\х; у) отно< иr~льнп
uкружности с ue11 rpuм О(а; Ы и p;iл11 yc.:i R \ЮЖ J ю
;с1 r1 исать т<tк ·
dl-R'=OP-R2=(x- a}2+\y-/))" R2•
1lilйлём множество точек . и"1е1оших ол~1н .зконыс
стеnс•11 и nтн осителы ю л13у;.. окруж н остей . Прирав 11 f1 -
t>м в1,1р,1жения для cп.•nt>1IL' "1 точ ки Р (х; у) ол юситсл ь
~ю ~т и х окруж11 остl:'и П у< ть, лля п ростоты, 111 ~нтр
nлно11 ок ружносr11 - начало коо рди нат, а другой
-
оrли•1ная от НС'ГQ точка (,1; OJ и ил радиусы сnответ
t TBL'lllIO рав11ы r и R. То1·да мы оолус1им урав11с11ис
х1+у2 r=(,\-а)'+у·-N
.
2
, или
,1
1+г'-R'
\ = -----
lcJ
залаю ш ес 1н:>которую пр ш.1 ую. Пl:'fJlll:'Hдикyм1 p 11 y 10
оси Их Таким ofip;:iзoм, точки. И "1С'Юш ие равн ы е сте
пс11и UTllU(И I C/\ЫIO двух uкруж11 остей , СОС ТJВЛ>1ЮТ
11rн1,1ук11 т•рпс11ликулярнук! ли11ии1 соелинякн11<•й
uентры окружноrтей . 'Эта прямая н,1 {bltiaercя рали
"'111ьгюн осью окруж1юС1си В ч..1стности, р,1ы1кал ь11ая
ось т·μс<.екаю шнхс..я окружностей - п рям,1я, про
лоы1 шая чt>рез точку 11 х п ересече 11 ия 1 пос кольку обе
:пи точки нмекн н улевую стс п С' нt, отн оси тель но
лJ.11 11 ых uкружн остсй КоглJ uкруж н ости касtlют<.я,
рi1д11 к,1 л1>нi1Я ось янляется их обш<>\1 касатсль~юй . Если
окруж ности лежат олнJ в не другой, то их раликаль
ну1U ()1ь можнn пuс.. грои J ь к.:н< прямую, проход>1шу ю
череi t t'реди ны отре.~ков и х обшил каспелы1ых, по
тому • 1то пр и таком расположен и и окруж ~юстей сте
пени точек оси р.:~ вны к вадратам отрР ~ков <<ютвет
< гвуюш их каса ГСl\ь11 ых ( рис... 1J.
Втьщ•м три окруж ности и 11опроим их попi1р-
11 ыс р.Jликальн ы е о<. 11 . В обшем слу•1ае, когл,1 цf'н тр ы
окружщн тси не !\ежа1 11а одной пря"1Ой (рис. 2),
рс1лик,~льные оси 11epl:'< екаюп я в ол1 юй точке, rпте-
11и которой относ ительно всех трех окружноrrей nли-
11акооы. )та точ ка наJыоается их ра1111к,1льным иен
тро'VI. ЛейСТВ11 гслы IO, TOЧ KiJ п epel.t' Ч L! l I ия 1\Юбых лвух
И{ рали~..ал1>н ы х щей имееr рав н ы1;1 <пт<.•11 и отно< и
ТСl\Ы ю всех трех окружностей, J з н ачит, лежит 11,1 тре
тьеи 001. Отсюдс:t мож но вывесл1, нап ример, тот
фа к 11 что вые оты треу1 ольника П<:'Рl'<.{'КаютС"я в ол-
1ю11 точке. В с;~мом леле, высrп;~, провелf\ нная к неко
торои сто ро11с , ~н1ли ется об шси хо рдо й окру-А<tюстси,
пс~строенн ых 11а двух других сторu 11ах к.:~к lti.1 дИ<t
метрах \ри(' l). Поэтому ралик<11\ьн ый tJi' HTp окруж -
1юстей, построе 11 н ы х н11 всех трех сторо н ах , и nyлt'T
ТОЧКОЙ пеμе<.ече1IИЯ высот.
Lсм1 Uf'нтры трех окружноСТ!:'И леЖi.I Т HJ ОЛНО~I
п рнмои , то и х раликаль11 ые о<.и ли бо п.:~раллслы 1ы
(тог Л<'! р<tднкалы ю1 о 1Jl:'H rpa п 1 юсго 11с сушестt1уетl,
лиnо с ов п ,1д,~ 101, и в т;~ком случ<1 f' люl><IЯ точка зтоtl
трои1юи оси является р.:~ликаль 111,1 ~1 11ент~юм .
Рнс. 1.
Рнс. 3.
А
Рис. 17.
РС А11а;юп 1ч1 ю, JJD - 61tесtктр1ка с11,1сжнu1·0
с А.РВ у 1·щ1. L111сссктр11сы смежных у 1 ·;юк nсr-
11tнд11кулJJрны: (т1 ·сю;,а LCP/J = С)0 " З11ачнт. со-
1·ласн() тсорtмс а нписанном yrJ1c, точка Р J1е
ж1п 11а uкrуж11осп1 дн<1метр~ со. назы1~аt:,щl1
(1ll/~ l'JJC11r1cmыo гl 11шz.пu1111я для Т()чекА п В. Moж
tJO ,'l,оказйп" что условпс АР/РВ = 1· вып()m 1я
е.·тс}f ;1,ЛЯ любой ТОЧЮI Рдшпюй ОК[)}ЖI IOCHI, т. с.
она 11я1:1ляс.-то1 1кко~11 ,1м м11ожест1:1ам.
ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ
И<.:кусст1ю 1юстrюсш1я 1·еомС'тр11ческнх фнгур
с ll(JJ\1011\hIO ЦН(1К)'Ю1 н лннейю1 быJЮ RЫСОКО
ра:зюпо н Дренней Грсr~ин . Ли11еl1 1юй ттот,:ю
RаJ111с1. ещё 11 Древ11ем Еrиnте. 110 цr 1ркуль, no
01ндетеm1ст1-1у 11ре11 11 ер11мского поэта Ошщнн .
изобрел н именно n Греции. Нозможrю. дn~ эт11х
1шстт мента потому и с1·али оо юв11ым п. что
позволяли 11ачсртпть две простсrшrие: ш1ш111 -
ЩЖ\1ую 11 окруж11uсrъ. ан матсмап1к<: ре111 сннс
'JЩ:IЧJI \,\\•\\-11IМ'.Ш1.НЫМ1'1 ср1:дст1шм 11 t\CC\'}\;1 LЧll
' l ;.~:юс:ь пр11:ш:11-:о ,\1 сuнсрuн.: 1-н.-гк::~
.!l,ля всt.:х, кто 11:зу част l 'L'OJ\1cтp1 1ю, :1а,'\ач 11 на
rюс11)ос1111е 1111когд:111с потеряютсносr'1 пр11нле
ка·1·сл 1.11 ос:т11 . ТаюLх з:1;р ч очс11 1, \11/01 '<1. IТ0:1на
к<щн....1сн с ос 1 юn11ымн меН)/\ам11 11х рсmе111ш.
ПРОСТЕЙШИЕ ЗАЛАЧИ
В зад:~чах 11~1 nocrpoeш1c nесьм;~ в:1'1'1-10 чёткu
сформутrровать « nr:1к11ла 11rрь1» , т. t'. 011ред l.:'
.'11·1·1ъ . каю1е 011срац1111 можно 111,111ш111н ·1ъ с
rюмu ш.ыо щ 1р ку11н 11 т 111с~'1ки . ТТран1111а ::эт11 со
всс:1.1 11роt1· ыс:
!J\ IJ 1с(1ка счнтаL'ТОI ()HHOC'J'()P(>HHCI\ Дt'ЛCHJ J(r
11а неi1 11~1· 11 11:111ос 1пь 1 1х ffCЛ l>:"IH; с с<: 11омощ1,ю
ГС'О\1~Тр1'1Я 11<1 П/\ОСКОСПt
можно 111ю11<:L~п1 прн~1~'1О чере.1 п:ж· ::1:-ц:1111п,1е
rочю1 , 11~-)Т() 1кё:
циркулем по ::~ад;ншот'r точке Он отрt:Н(}'/Ш
разрешается постр01111, окр ужш.>еп , с цс11 -
1уюм О п р~щи~ сом. ра н1r.ы:-.1 АВ:
точкн псрссечс:11ия noc1 росн1 rых ю111 ~{а
Д;.lllllblX JJIIIII!Й СЧ IП:IЮТСЯ IIO<.:TpOL'HllЫM!l,
ра3рt:ш:н.:тся выб11рать nрш·1 з 1юш.ную точ
К} 11а ПJ ЮСК()СТ11, 1-ta 11Л11 нНL' rюстросшюfr прн
мо11 11ли окру,кносrн. (В11рочсм, такие нро11 :\-
1юльньн:: точк11 всегда :vtож1ю пос1ро111 h.)
Нсско111.ко прпстейвшх построе 1 111i1 (/\еле
н11е отрс:1ка пополам , пр<1ведс:н11е 11epr11: 1щ11-
куляра 11 др.) обыч1ю пр11ш1мают за ос1юшrые,
а все более слож 11ы е сво,rщт r< 1тм.
Постrостше ттра11ш1ыюго тре~толышка н;.1
отрезке .11В (рис. 1) 11спользутот для опре:делt.:
шrя серед1111ы отрезка ,-JB: опа ле;кит 11а 11ер<.:<.:с
чеrши отреэка 11 11рЯ .\Юi1, С()('ДПШIЮЩСfi ТОЧЮI
С и. /> псрсссчсш1я окружностей. fl\'>О1-1од11мых
l(p1J э·1·ом 1юс1рuеш111 . ЗJtt:.'l'h 1ю·1 · 1х·бо11:1лоlъ
lljJOH<:C'!'ll тр1 1 HCllOMOl';JTC:.1hHЫ<: .lllllТlllJ - , (НС
о1'руж.ности 11 пря\1\ую. Ме111,1шгм ч11слом л11 1111l1
н Д<JI 11 IOM СJ1уч:1с о(iо(п IН.Ъ l lt.'ll>J>f .
1lo HL'IКO'l'opыc э:1емснт·.ар11ыс :1ад:зч11 1ra по
строе~ 111с:: пороl1 ,,1лж1ю реш1п1, проще, Lieм в
Фигуры
«СТРАННОЕ» ПРЕДЛОЖЕНИЕ
ИЗ (< НАЧАЛ» ЕВКЛИдА
На первых страниuах « Начал» Евклида прноодятся
рlс'шения нvкuтuрых задdЧ на посrрое1tи(.'. Н.щример,
в n релл11жении 1 тpt:>fiye rcl'! 11остроить рdв11uсто1юн
ний треуr nльник rю даннuи СТ()роне. Н Рскол1,ко удив
ляет сегодня предложен11е 2: от данной точки нужно
отложить прямую, р.~вную да1-1нои прям()и \ прямые в
• Н.:~-1алах » конес1ны, г. е. ":>ТО отрезки).
К.Jзалось бы. 3J.лача с.овеем 11<~трудная: установим
ножки uиркуля в конuах ла1111ого отрезка. из"'lс.:рим его,
проведем окружность с uентром в данной точке и ли
нейкой соединим любую точку :>той окружности с
ла111 ю11 Т()чкои . Но нс вс.с тJK nр()ста: [в клил разреша
ет п роводить окруж1юсть только R то", случае, когда
ее р.~диус 1алан к.1к отрезок , 11ровелё 11 11ыи из ш? 1 1Т
ра, -другими Lловами, кuгда заданы uентр и точка на
окружнопи. П ере~ 1 ос ить атрезuк, рав11ы и радиус-у, ю
одной точки в другую можно, поль3уясь спе uиальным
nпстрое нием, которое и излагается в nреможении 2.
учс61-111ка .~... l lапр11мср, 111xme(' Tll через дан11ую
тч1<у 1! 1 1 е р11t:ПJ11П<ую1 р к 11а1пюl1прямой1 ~1ОЖ-
1юс 1юмощъю Л111L1ь , \liy'X вспомог::~те;rыrых лп -
1111(1. а пс трёх. ка1;: в стзпл:.1рт11ых рсп 1 сmшх.
Л:nа случая - коrд::~ точка А лежит tЗПС / и на / -
расс:-.1отрсны на рис. 2. а, б соотвстств<..:111 ю
(lЗ, G - проп3волы 1ыс Т()'-ПШ на г1 рямuй /,а[)
-
вне cf). Ц11фры на рщ:унках указы н:~ ю·t· очсрё; 1-
1щс1ъ ЩЮАt:/\СIНН[ Jl.ШШlJ .
C1·uлh же ()ыстро можно ПOC'J'fKШTh прямую ,
11араJ111слыJую дан1-юr'1 . Ilроводят окруЖiюсть
с ч с: ре.~/\3ННуюточкуА с l~CHTjJ(IM 11 прО11ЗНU.'!Jг
ной точ1<е () (рис. :) ) 11 о кр1?ююст1, d с це11-
1·ром 0 1 в оютой нэ ·тчек ттересечешы с и
д'1111юй прямой / р::щиусом, ра1шыJ\1 расстоя -
11 1 1ю от второй точ"11 перссечепияР до А. Тогда
П[Ш:\1~LЯ ЛВ. 1 ·де В - соответствующая точ1<.1 пе
ресечешrя лвух nостросш 1 ых окруж н остей
(од11:~ из двух). пар:~ллслыш /.
Рщ:. 1.
l'ис. 2.
----~
_ с_-,
'
'·
1
1
1
1
,,Jл;я
].
а
R
с
\
\1
J
.)12
В 1юстроt:.нии правильного 1 рt:.угольн~1кд nf>peнoc
радиуса не нужf:'н. Напротив, само это ПО<lр()е ние
исnоль'lуе тrя в оrтроум11ом решени11 'lалачи ю nред
ложе11ия 2, кот()рое лал [вкм1д.
Н <1учи1:1ш11сь пере1 юсить отрезю1, мы фактически
( IH1MdCM 1\ СЛОдНUС orprlllHЧ("lll t t' и приоGреТ<1(;'М npa -
80 пол1>"'IО R<пьо1 uиркулем так, как привыкм1.
.".",н•"·-"•-•• ·..- •~· ··-·• • -·" · -·•- •-~· - - -
'"'ot·-"
tc:i tli:;"UЩl11;-; t'11m1i fl'q\ CdOl!.1Qtffi~<rЦ11U.,pffl.N!llЩ~li.;1.,;a;,i,\,t Ь.
~.O:f;Ul1'1 !111(.а .а k.t1H:ikfffl\(Jdr..u1i (.Ь (t,{(lC!Qypt!JpOllOJ. ~11Щ. b.lt.
.~Jl).11 .1 .фа•.Ь .k .~ ea.11tt:W.b .s .1 ~.1.L'ittJ.ilk" ~ 9 qil.ltt.•.!it.rП 1a110J: ь,
r.:f\d~ ь.t.rt\nuЬ>i.o.~ tn.a~w.'u;o.!l,tt.t:.dt rт11i 11~Mb:<fit (,i c 1!1
~w f~Nt11n~~!tкi1f!JQ11цc;.1ttQ11'1)1Jb; fl-' t<icu coll0t:o:!Jfttus.
1~1t'pC'lin". 1
!!=''""""•',~ьu""(('""'." ." \Wo:rlb1(( rccrc,pp(tГ1re tqu:im rca·JJn
9'.f.fi.rnntt11ttNtoo~.Ь.C'.f11S(J Ь)1>1'йi~1 rtJn~O.o cu«rrl1
ч.1\'rl5cqnottmtl11c.::.ь с.щ ~5,U~ ~(IM(Qllt1ng•1 :(oki~~ra
р1щщj,11 \1Xl1~!tn\I CQfil'!IШ(lill\:O:.h.f,(Ulrt"i01 "\1!1 "- ,0 .' :
aнta.1~фk1.J tб01Тm\1Шt.t f"CJ"l8ttJ a,r rup4qu~t0111'ti:u.1111:1щ~11bl(t\l.I.
cmJ fm aOOt\'IJ ршsа-щg ~11\i.t.. ,,d.·иn'111J.qtl't'mlA1'1Ш« ~atcQimi;ua
W'n l11щ:ip11J1tl 11 ~.(ir1rнrnn11t1t.f.~rcdtn1dn11•т1C1Jili1o...'f(!tb1fu
ра ipf.im 11r<li.:i fmq1J~Dt1t.s1l i;i~oвol.kbt1«Gllt(ir<lft.t .b.1 l11 rщ1 (1i~~t
. c .: .pa1111uc• 1lfJt'ЛЛOA<l' l·tщ' 2.• Нd•мл ,1 • Е1J к11идJ. ll!:'flHJ~
КШ1Г<1 Иiд,)11 11\' 1482 г.
Тtорию 011т1 1 мальпых 1·ео:чстри<1ссю1х по
строенн11 разработ.ш u XIX столt:т1 ш француз
с1<11й гео метр Эм нль Ле,1уап. Оцеш1н:~я слож
J ЮС'ТЪ построею1i1 , 011 ПО,'1.СЧllТЫВ:ш не '1'(.>ЛЪКО
'Пl<.:ЛО Ilf)OIK"ДtHITЫX mнш.й, Н() 11 ТО. (.'IС0ЛЬ1(0
ра3 пр11ю 1 щ1ы11аето 1 !111н<..:1~1к:1 к ·~· очке ишr
сколыш 1х1з <.~1·ан11·1'01 к точку ножка rщркуля.
011'J'11м~urhн ыс: рсшс11н>1, которые:: Лему:.~н НЗ·
зка11 1 ·сомсч:ю1·раф1 1 чсскr 1 м11 , оаес1 rечнвают
более RhlCoкyю ttO cpaRHCHllIO с 1\PYOIMl'I рсше·
HllЯMH TOЧllOC'J l> 11ocrroe 11 1 11~1 .
КАК РЕШАТЬ ЗАЛАЧИ
НА ПОСТРОЕНИЕ?
Методы рt:шен11я з:~л.ач 11а построс::н11с /\СТ:mь·
1ю р:~зработа11ы . По:таком 1 1м ся с важнсй1Ш1·
ми ll:j 1111Х 11а HCCKQJll,IO I X 11р.1-1мсрах.
6
1
'
lj
/1
А
Рис !.
/1
в, .-
\/!
Lр
(/
Задача 1. Построить трсуrо.1 11,1шкАВС 110 сто
роне с1 = ВС. опущспrюй ш1 тrеё 11ысоте 11" 11
прошволежащему углу а.
llponeдtм отрезок ВС 1щиной а (рис. 4).
Н:~йдём П<)JЮжспис тuчкн А. Первое усJ1ш~ие
1 ·шюрит о тu"ч, что uна расположена па рас
стоннин 11,, от щш~юй R<.... М1южсс·1 ·.1ю точек.
У/(01\ЛС'Тl:ЮрЯ IОЩllХ зтому ус1ю1111ю. - /tBC
ПЩ1:.JJIJlt:JJЫ-lble пrямые, OTC'l'OHЩJlt: от RC на
расстя 111 rl', 1хш1 юс 11, 1
•
Пn второ.'У!у услuнн 1п.
точк::~ А 11р 11 н~щ11ежнт множеству точе1<, 11а
котор1,1х nтр~зок ВС 1i1щсн п1щ у1·1юм ВАС= а,
т. е. паре 11.у 1 ·, с11ммс1 ричных 0·1·1 юс1 1 п:1 1 1.1 ю ВС
(11е1 1·1р () с<ютRетст11)10щеС1 о крулет юсп 1лежит
на ссре;щттом ттер11е11дикут1ре к ВС. r 1 рнчём
)ТОЛ 8()(: paneJJ 1.а). ~3начит, Л - mо6ан ИЭ
ТO'JeIC пеrесечешнr rrapы прямых с napor1 Д\Т.
в сн:1у С!JМ~ IСТрии р1Н.:)1!J<ll,13CC ПОЛ\ЧаЮЩ I !ССЯ
тре-утолы 1ню1 р;1.1шы. а потому рсптс~нн: д~11 r-
1юй :J:ща ЧLI едштст r~еннос ( п 1111 е:го rюuбщt'
Ht' существует).
Метод реш~.:нни . пр11 1штором искомую т1 >Ч
ку стrо нТ К:1К Точку ПСрt:ССЧСНJIЯ MllOЖCCTH
1п:омстр1rчесю1х мест точек). опрсдслJi емнх
1н~кптор ым11 условш1 м 1 1, так 11 11азык1с·1 ·ся -
летт) пересечения .1111m.11cl:'C1nв 1шн лie mm)
гепли!mfmчесл:их .мест.
Задача 2. Постршт. треугот,111 1 к.1ШС п о 2.р
(nср11метру трсу1·олышк:t) , 11" 11 С/.= LBAC.
Эту задачу также мо:жпо peuuп 1, .методом
1н:рсССЧСП1НJ MIIOЖCC'l'l:I. JIO TOJlbKO .ЧIIOЖl'CTB.
состоящнх 11з 11рнмых . Нарнсусм у1·011 а (рщ:. 5)
с вер11 11 11юil 11 точке А. Как 1юстро1лъ 11рнУ1 ую
ВС, чтоfiы ны r1ш 11н1тъ лна /\руr·н х уоюн1 ш :iа/\<1-
ч 11? P:н:Lv1 ·0}11111 e от г1ря.'.НJl1 RC J\O 11ср1111н 1ы 1 111
riep11щ:тр треу1'(Jл1,н1 11<:i должнr.1 61.1 ·1 ·1, ссютАет
t"rве1 11 ю р<1А11ы f1,1 11 2р. Не пы :н.IТ!<1е-1 · сомнет 11 11\
что пер1юс: услотlt: 1\ЫП<J!lll l li\.J() в том 11 'ГОЛЫСО
в том С"Л}'Ч::tе. еслп прямая ВС буд<::т каспель-
11 ой J< окруж 1 юсп1 pa,'111yctl h0 и с цевтром 1:J
1оч1(с А. Moжrro пока:-1ать (см. статью "окруж-
1юсть п кру1·~ ), что 1поро.,tу услшшю УJ\Оl:\.' 1ет
воряст мrюжсство гтрн.чых, J{асающихся н еко
то1юf1 IШIIC:lHHOII R у 1 ·0.11 окружности. ТОЧКl l
кас:1 н11н ,1J 11N э·1·uй ОК[1УЖност1 r со сторо1 1 амr 1
y1·J1:i y11,:J.Jll:H 1, 1 nт с1·0 нсрш1111ы на р::~сстоян11с р
Искомая нрн:v~ан пrи11;:~11лt:ж 1 1т 0()011м се.'>н:- 1·1-
ст11:~м, т. с. н111mс·гся 0611161 (R~ryтpe 1111 ei1 ) 1<:~с1-
те: 11.1ю~1 01<ружностеi1. Остэ<:тся 11:~чсртнт 1 .
окруж1юсп r 11 rюстроптr, 1<асателы1ую к шrм.
ПС\Строе111 Le кас1те; 1 ыюй - от;,\елы1ая ~iздача.
Гео'vlетрия HJ плоскости
Маж1н) и11зче рсш11ть :~~щач) 2. Доп~ст11м.
что HCI<O,\IЫ~1 треуrо.r1ышк А!ЗС построеrL От
ЛОЖlL'v1 на продолжсшшх стороны ВС отре~ю1
ВА1 = ВА IJC:rl2 =СА (рпс. 6). 1Lолуч1 1м 'l'rC)-TO.% -
HllK А1АА ~· \:\ которо1-.1 OClIOR:lK!IC AiA )=2{J. вы
сота прсжння - !111, а ~тол nрп нерш1ше А н:~iпн
1 1<.:трудно. IIOJJb~)'ЯCЬ'l'l'\1. чтотрс}ТШJЫЛ IКl-IА1АВ
и САА 1 р~Аноб<:1чх·1шь1е и cy\t,,1:1 11:-; внс111н11х
~TJ101:1 АВС = р 11АСВ='{11р11 нсршннах В 11 С
р~нта Jr-a: LA 1 AAc=a+(~-1 у) / 2=(тt + сх) / 2 .
11остро нм трt:}толы111к А ,АА > как '.tЫ "·J'l'O с1-\t:
J1алн 1-1 защ1че 1, а затем 11 трсу1'олыmк А ur., чтu
уже 11 рос·ю.
На~ ва1111с тоJ11,ко чтп 11с1ют.:юна111юrо ме
тода Г()fюрнт само за себя - зто .~temrJtJ вc1Zo
Jlt0ccmzшzыюzi фигуры. l3 :щn,аче 1 тэ1ш11 фигу
роfl служит тре)то.rты 111к А 1/\.11 J· Оченr. ч~1сто
рот, l'\("JIOMOГ:tTCЛЫIOl"I 11траст фигура. по
дuбн:tя rrcкu.\юi1. В 1·ако.ч случае l'О l юрнт, что
11 \JИMt'! IЯ(..'ТСН A/('1J1()() 11.odoбt IJI.
Задача 3 . Постро11ть тrcyтt)Л\>Hlll\, t;('Jll\ )~;.\\lbl
TLJJJ CJ 'lJ i!ЫCOTl1J .
Лоскоm'"У про11звt:дt'111 1 я стnрон тре) 1 ·п: 1 1.-
1111к:~ на прn11едl' 1 111ые к 1111м В111сnты 1щ1н1:11ю11ы
(r1 ра11 11ы у71тюе 111юй n;ющаю1 треу1оны111ка).
сторп1 r ы обр:~т1 ю щюппр 1 \1ю11ал ы 1ы соотвст
ст11ующ11.ч высота ·"1: /J : а = 1111 : 111, .
с:а=h11: /1"
P1tc. 4 .
Рис S.
Фигуры
Таю 1'1 обра::ю.v1 . u·1·1·юшсш ш сторо11 11:111L'cT1 1 ы,
:i ·~1 t> :.111а, 11 1·1, ' ITO 1щ.>жно 11остро11ть трсуншь-
1111к. шщоб1 1 ыl1 11ско.\1ому. н:тв за его сторо1-1ы
отрсзю1/, 111,,jh,, и !/111//1, , 1дс 1- 11pn11:11юm,111.1 i1
птреюк. П псле чс:1л останс;тся лтттm. 1 1:Р'1сrп 1тт.
р:1:1мсры ·1рсу1·п11ы1 111.:а т:11<, ч·1·n()ы ero высота.
onym;cr п1ая 11а сторо1 ry /, сгалз раuна 11" (рнс. 7).
Существует 11:шщш,п'r cnoco\J ускорюъ по
строение: соста 1шм треу 1·олы1.ш<. нз высот. ко
торые J\аны n услош11 1 зада'ш, JJронс:.:дём в 11e!l1
нысо·1ы 11 с110ва постронм трс~тш1ы 1 11к 11з по
:1учснн ых вьн.:от. Он-·1·u 11 будет 11одоfJс:н 11ско
чоi\1у, н сш 1 у обр;1·1·1-ю~'1 11 ро 1 юр 1 tr1онал hност11
стnро н 11 нысо·1· 1{ сож:.u1е111110. т;1кu11 способ
пр 1 r\1сн1 1 м нс нсс1·дз.: 11 :i зад:н111ых н1. 1 с<т1 · може1
11 liC: ПОJJУЧ 1пъся тpc~TOJ I f1HH ка.
Любп 1 11.1·1 1 10. что н 1 юс1рое1 1 1 1е треугопыпп<::1
по медианам выпо.1пт.:тоr таютм же способоj,1 .
Постровм отрезок CD, раnпьн'i н параллельный
,- L\J н ;\Ш. где .11
-
середrша АВ (р11с. 8). Как по
каз1,mаст р11су1ток нз отрезков, ранных 11 11а
р~шлслы1ых мсд11апам ттрот·rзволь 1 ю1·0 трс
у1·олы-111к~ 1 ARC, мuж н о сос1·ан11·1·п треу 1 ·олы11 1 к
13.\'J) , 11р11чё.м с1·0 MtJtH:tн ы бv;tуг nа1х111лслr,нr,1
11 ~1ро11пrщ~ю11:111ьны сс коэфф~ 1ц1 1 е1-по,1 .1>/4)
С'10[1ПI [;J ,\ot 11с-:ЛNIОП) трсу1·011ы1 111<а.
А можн<) ли с nомощhю ц1 tркуюJ 11л н11 ей ю 1
гюсгрп11•п, треу 1 ·олг, 1 ш к по 6 1 1сссктрис1.м! В об
щем слу"lае - 1 1ет.
Оrршшое число :~:щач па nocтpocrтrre rеnта
етсн с llОМОЩЫО 11peo6pa:юuaJJJ1(1 ПЛОСJ\ОСТJТ.
Рассмотрнм з~щас1у, u которо li щ:поль:Jуются
сра зу два разных шща преобразuн:11-111й.
:1адача 4 . Ч<:р<:з /tвс точю1 А 11 R. нахпдJ1щиссн
rю (щ1-1у сl'Орону от прн,'-'ЮЙ /, провсст1 1 оrq1уж
ност 1, , к~1са ю11 tуюсн этоfl 1tрн мо11
О 1 ·ран1 1 ч1 1 мt.я 06щ11 .\1. 1 1 :111L1ол<:с 1 1нтср1::сным
случ:н.:м. ко1·J\а 11ря:-.1ая АВ нс n:1ралл1::лы1а 11не.
1 1 ср11е11μ,11к~лнр 1 1а / (р11с 9). Провсдём ссре
дт1 ш1 ыl1 rн:рnснμ11кулнр р к тре:~ку /IВ (це нтр
1 1 скпмоi1 nкружпости ,п:олжсн 11ахnл;11·1ъся на
:-пом перnе1щ 1 1куJJяре) 11 отра:шм от1 юс1пел 1,-
1ю нсrо прттмую /. l lа11ом 1 шм, что окру?ююст1,
CllM.l\1eTpИLlll:l ()ТIЮСИТСЛЫЮ своего днаметра.
Поэтому 11с1ю;v1 :ш окружность с 11олжпа ка
саться I I отражё н но\'1 11рнмоl1 m. Таким обра·
:юм. С 1Ю,\\()ЩЫО UCl- ' f IO(f C/l. ,\LMl- '1 11/JflU ,'l 'lbl СНСШI
Jадачу к 60J1cc н:-1нсlvгной: кп11t.::.1ть н уl'Ол (со
ггоро 1 1а!\m / н 111} окруж:ноt." rъ. 1 1роходящу10
через да нн: ю точку А (та 1\ан окружнщ"п, обя
:1t:1теJ 1 1.1 ю 11ро~'1,Г(ёт 11 ч ерез точку 8). Эту 11с110·
мо1 ·а'1 ·ет,1 1 у10 .1ад:1чу иож1 10 рс111нт1, с помощ1)ю
г(нumи:пшu - прсо6разона 1 шя. 1 1 р11 ко·гором
1<аждая ф11rура псрсхО,Т\ I П n себе подо6 1 1\Ю.
Любал 1тнсаш1:ш в )ТОЛ окружтюстп d r·омоте·
тнчпа I ICT{0;-. 101'1от1 юс~1·1·t:J1ыю нсрш1шы О )Тла
с 1юэфф1щн<.::m·о~1 k = ОА /0..4', t';J.t А' - одн:r из
·1·очеf\ 1н:рессчеш1н ci с прямо(~ ОА . П оэто,1у
ДО('Т:.1точ110 ш11гсап. п }Тол лю()ую окружность,
а IIOT0.\.1 p~I C'l'>lll\" l 'I• (111111 сж;.1· 1 1.) сС' Г\ k ра~.
Можно рс11111· 1ъ зту же ;1адачу 11 с помощью
<·аm ·с:бр:н1 чсског()» метода . Пр< щолж1 1 м /\В до
перtсt:чс:1 1 11я t: / n точке С. П о теоремс- о 1<11:.tд
рате 1<аспел111юi1 (см. статью <·Окружrюст11 и
круг»). 1ш:щрат р:.1сстоян11н от С до ·10чю 1 каса
r 1 ш1 ~ 1 c1<0!vIOII сжружrюспr с npЯ;\IOJ'1 / равен
C I СВ. l 1 оэтому досппоч1ю постронть отре-
:юк д11111ю1'1 , С-1 ·СВ, отложит~, е1·0 11а l 0·1 С,
тем самым получнв точку каса1111я .\ .1, а з:tте\1
11 ронест11 окруж11ость ч<::р<.:з тuчк11А.В 11 ,\1 . От·
Jlt:~IOK можно ОТЛОЖ!IТЬ н днух 11 ~11 1 ранлс1 1 ш1х
Ч'l'О /РСТ ;~ва р<:ГПС:Н'l I Я.
Rот сщё о;~ин прнмер 11r11ме11е1п1я то1 ·0 же
,JЛI е6[Х111ЧССКОГ() 1'v!t:'J'())\;1. Гl ()("J роп:ч 11р;1llllЛЫ-fbl11
ПЯl 11уrот,11ш< (р 1 1с 10, tl). 1-lуЖ!lЫС 11.IOI этого
треэюr т111 углы АЫраз11м формулам11 c1epe;i
:Jaд<.tr 111ыe. а n~,1числсппя no эт11м фор.'\!у.1ам
Щ"JU II:JПCДё M ПJ!ЯМЫМ ШК'TJJOCHllt'M. ()бОЗН:!ЧIП!
с1·орш rу nя · 1·1 1 у1·ольп11ка через а, д11аrо11: 1 J 1ь -
чс::р<:~1 х, нс1 н.н11,:юв,1н 11u:\uбие тpcy!'(JJIЫH нюк
.-ШС 11 ПЕ>А, получ 1 1м АН :'IG =АП: АП =(АС -
-
CJJ) · АВ m111 а/.\' == (.•
-
а).а(1·акк:1кC!J =
= ВС=АВ), ОТКУ/\.1
c1(,'5+l~
.\' =-'-'-----'-
2
flостроенш~ отрезк;1 .У по отрезку а nоказа-
1ю т. pfJC. JU, б.
J]
Рнс. 1Н.
РАЗРСШИМОСТЬ ЗАЛАЧ
НА ПОСТ РОЕНИЕ
В послс71.11ем шктрое1ппr а· 1ре: иш nр11Lшюс.ъ
tю1адывать, /\с1111·1ъ 1101юл:t,\·111 умножать Ll:t "5.
А к:нше nообще аm·ебрапчссюн: опер:щни 11:i11
отрс:::шам11 можно nт,11юшшп. 1щркулем 11 mr
11сl1ко(1? Р:1:зумсстся. СЛОЖС1111С 11 НЫЧ111':lН11С
мс11ы11с1 ·0 11 :{ бш1ы1Jе1·0. Вы 1 1н.· 11ам 1ю·1·рсfiо 1~а-
лос1, nострое1111е \C/IJ, ·1- .
t;. сре;t11его 1'соме
·1гн1чсско1 ·0 отре1коя а 11 /1 . Это лос1рое1 tиl'
OCHOR;Jlf() 11:1 том, что высота ЩНIM<1YJ '()J ll>HПJ 'O
треу1·ш1ы1нк:1 равна сред1-н::1,.о1~ 1 ·еоме"1рнче<.:ко
ыу ;111у х отрс:1ков. 1ru котор1.н: сё ос11011;m1 1 е
делит rиnптепу:-1у (pirc. 11. а). Но па р11с. 11, б
д;~ётся гоr:~здо более 1<0роткое рсше1111е: пpo
BQ,'\ll'l'CЯ всего четыре 1шшш (отре:юк ЛJЗ =а
задан no условшо, а ПyYII\J ир11ые лr111ш1 в c::i -
гсометрия 11<1 f IЛОСКОСН1
.1
п
({
и
АН/ЛП = НЛ/ ВС.:
б
п
.\
'
АН=11D=а;
/:3(7 :=: /J ;
А.____с.=·-____ _ . В
А13 RП
яп=вс =
= ЯЛ=~AR ·RГ.
Рис. ·11 .
2
мом построс111111 11с 1rрю1ы - 0 111 1 rюмо1 ·аrо1
обопюв:лъ рс111с:1111с).
Потрёмдашп,н,, отре:1ю1м cr. IJ 11с11с·1ру,1,1ю
постро11~ъ их "четnёртыi1 пр<юорц11011а.rгы1ыf!"
. \: = a!J/c. 11:нксшо. к;1к это сде.нать с ГЮ.Чt)ЩЫО
Т<.:Uр<.:иы Ф~IJICC::I (рrн.'. J2). COl ') J;\<:IIO 1-:oтupol1
отрt'3КИ, в1,1<.'СКаt'МЫС: 11apaJtЛ('Jlbl-fblMH П]1ЯМЬl ;\.Ш
11:1 щн-юй ("1·оронс ~тл:t, 11ропор 1 11юналы11,1 со-
0·1·вt:'1 еrнующ1 IM O'l'pCЗK;J:'v\ На Jll1)'1'CJlt CTO!'Ol I(',
Пр111\Н:м какоl1-1111()удh итр<.·:зок е 3~1с;\11н 1щу
; 1; 1111 11.1 . Тс>1;1а мы суl\·1еем постр!>11 'п, нс тоm.ко
с~·м:-.1у с1 + /J дпух отре:~ко 11 , 1ro ir 11:-.
11ро1 rзве; Lе
rше alJ - отре:юr<. f\.'11111:1 которо1·0 пр11
r1ыбра111 юм эталоне чпсле111 ю pan11а 11роrr:ще
:1ешно ,1;.rшt 1 t1 11 /J: 0 11будет ра 1~ен отрс:~ку olJ/e
(~1 т~н<ое вv1раже1ш~: сrронть ннрt<улс-~v1 11 Jш-
1t<.:flкo(т мы научил11сь) . Аrrалоп1чтю стrш1тся
Р11с. 12.
:)I5
Фигуры
и mтx::ншa/IJ=ae/IJ r1 ,п =,пе. l lо,1че рю 1 ё>v1 .
uднакu. LП'О <.:CJJJJ ныбрать дру1·ую <.:Дl!IIIЩ\ '
;~; 1 1 1ны е', тu 11 от рс:н: и с.Ф/е'. rю'j/J. , пе' полу
чатся. к< н IL'чно. .~ц 1ут1 1м11. По:-У1'( 1~1у 1·<.тор 1 п1, об
отре:нсе 1J.J1 11111.1 fllJ , a / fJ 1 1л11 \ft, t:Cm 1 t:; 11 п 111 на
11т ir1 1.1 1re :1:i,l\am1 , nроп'о 1 1е 11:-.1еет c ,11,1c;ia.
А/\ГЕБРА В ЗАЛАЧАХ
НА ПОСТРОЕНИЕ
1Jтак,11р1 1 Jaд;I н 1 1tн'1 t'ДllНllЦ<.: ,.:J.J I LJJ IЫ (.'[!()МОЩЬЮ
flllf)K\'JIЯ Н J11 1Т1<.:ЙК1 1 \1UЖН() Rf,ll lOJIHH'IЪ н:1д U'l '-
fX':'{f(:JMI 1 •1стыре ар 1 1фмстн чссю н: 011t'p:1tl11r1,
;i т~rкже 11:111.1н:кат1, н:1 •пrх: з к:1 ктщrап11. 11 ·1 ко
ре ~ 11, В1. 1 р:1же1111н . вю r ючающнt: в ct:t1и ПJJ11.ко
11ер111.1е четыре 011ера1~11и, 11:1:11,1паютсярш~1ю-
11сщы1ыми . а сол.срж<~щис п nятую опс р::щт 1 ю,
т. ё. нэ1.1лt:че1ше кn:щрат1 101·0 rюрrщ, - м1ш)ра
nшч 110 - uррац1ю1щлы1ы.1 ш. ·1ак11м обра:-10,1.
ц11ркулсм 11 лиrrci'rкoi1 мтюю nocтporпr, лю
бое квадратJJLJlJО-нррацшшалыю<:: выражс1111с
uт μ;,~нных ч11ссJ 1 . Uказывастся , НJJLI<::гo др)тu -
1·0 rrос1·ро11п, нсn11зи!
;~с1'ктв11т<.:лы Н>, вн 1 1 .ч:.tТi.'111,н1,1 1'1 анал11J каж-
110 1·0 111~1 1 ~1 в люfiо.-.1 LIO(Tpo<.:11111111tжа :~ы вае:~т: 1 к-ё,
что можно 11остро1п·1, 11,11ркулс.\1 11 ю 1 нс 1'1 коr\
»1шне-1 ·ся .1н60 ра1нюш11 11111ы,\1. л11бо кщ1щх1т11ч -
1ю - 1 1рра 1 ~ 1 юнаm1 111м. 1 вырзже1111ем 0-1· rклод-
111.1 х ;1:.1т1ых ( п аnрнмер, от;1,n 1 111 птрезкон). По
этому nопрос о ра:1рсш1 1 мост11 той 11л1 1 111юlf
зада~111 с 1ю,10щыо ц 1 1ркуля и 111111еi11ш удаётсл
прс.:nр: Lтить n nопрос о р:~зрс 111 ш.юс11 1 некото
рuш уравн~юш в кнадратных р,щ1 шалах J::ош
::~то ку611 ЧССК()(; ура ннсн 11(' с ЦCJJ hJ \1J 1 КО::Jффн-
1lИСI 1' 1 :IJl.111
-
а т:1 к бы НЖ'' I ' ,1 1,()H()JI l1HO чае1'!J, - то
уч1 1· 1 ЫH;J l(}'I' CJICJl,)'IOЩllЙ фак·1
Кубическое уt·щвнен 1-J e с целы1'1п ко
эффициептами, не и меющее 1)ац1ю
налыrых коt>ней, 11ераз реш11мо и в
квадратных радиrсала х.
1le1 PJ·ДIIO до 1~азать . что 1recoкpJ п ~ мая дро61,
р/с;яrшястся корт 1 с.\1 м1ю 1'очлс1 1 :~ с r1,e.'l!.1щ 1 ко
.:>фф1щш.·11т:11\Ш в том и только в то~1 случае,
CC'Jll I н:1 <.:С ЧJ ICJJll'l'CJ!h ДC!ll ITCfl бс3 остатк:1 CI:IO-
Г.o;\Hblt'I член ;-.11101'n член;1, а на ~~на;-.1 снате.1 1 h -
с1·ар 11 1 1 1С1 коэфф111 \1 1 ст 1·1· tсм. статыо <·Уран1·н.:н11я
f\ЫC(JKI IX CTCI IC I1ct'1 ») J lo:'J'l'()MY 11~1.~рсшиMOCI ь
~16
зад;1Lt на 1юстр<х·ш1с: . 1ю1оры<.: сво,r1ятся к кубн
чсскu\1) уравнснню <..: циrыми кuэфф1щис нта ·
~1 11 . 11 ронt'рsн:п: s1 п ро<."1·1 ,1 м 11срсбuром c1 ·u воз
можны:-. ра1~11он:шы1ы,, кор 1 LСЙ
Д.11» r1pr 1J\1tp:1 рассмотр 1 1 ~' ~;щач~ о 1юстрое
н1 11 1 1реу1 <1.r1ы1111<:1 rю трЕ'\1 б 1 1(_'се1<.·'Тр~rсам .Доп~·
l"Г11М. ЧТ() !\Не 11:1 11 11>; patilll 1I . .1 ·1ре-1· 1)» f!Lft'ГRtpo
J\ l t1 1 ьше кхкдоi1 из нпх. Torj\a треугал 1>ш1 1< р;111·
1юi)едре1 1 11ыi1, FI 11еслож1Jо 1 1:1 С1т11, что от1 ю1не
ппе х его боко1юl1 сторо 11 ы L.: основашно \'дов-
11е·1·1юряст уравнсшно l6x ' -t 16.YJ - :)х - 4=U.
Ypaн1 1 cr 11 1L' 11<.: 11мс<.:т рац 1 юнальных, ,1 J1:цщ1т, н
ЗАЛАЧА О ЛСЛЕНИИ КРУГА
'Это ст<1р~1ннм1 {,~лач'1 {<\нима1п в 11гrор11и матема
ти ки н с /\1е 1 1ее почетное место, че.,.1 тр11 зщ1\1еш1-
ТЫ<" 1<1Л.1Ч 11 лрt>ВНО! П 1. К НЕ"Й Тf)€'6уеТСЯ ПО("Трnить
прJвилыrыи м 1югоугол ь1тк с дJ1111ым числuм сто
1ю 11 или, что то жt· t амоt>, р~.1.$дl:'ли ть окружнопь на
равные ч асти.
дрсu11ис у\Н..:ли дсм1ть кру1 на l, З, 4, 5, 6, 8,
1 U, 12 , 1с; чапег1. Roof)Шt', праu11ль н ый lп-уголь-
11ик мож1 ю полу• 1ить и 1 правильного 11 угольн11ка
пун•"1 лелt:ния 1нн10лам луг, нt1 которые вершины
r1-уголы11-1к.:~ (J<IJfiиoaют его описанную о~..руж·
1юсrь. Таки'VI спосооом на основ!" k-угом.ни~-;а лt>Г·
ко постро11ть ВСЕ" !2" kJ-уголы 111ки.
для пострщ: t1ия пят11алuа 1иу голы111ка лuпатuч
но 1'\Пи<·,111> 13 о кружность олноврt'мен но прав11льные
треугоNo11ик ~1 пятиугольн11к с обwеи вершинон. На11·
меньшаи 111 луг, н,1 ко1 оры !:' ~1х вершины разобьют
окруж11ость. и булет p..iв 1 1.:i 360°/15 (2/5 1/3 ::: 1/15
окμуж11щ п 1 ) . Т.:11-- ж~· можно пщ т1ю11 rь 11равильныi1
РС/ угпльник, если в nкру;11.1юст 1 . вп 11са111,1 правиль
ны е μ-у1 uлыrик ~1 ч-уп1л1>11ик. а ч~1t"\а р и ч взаимно
простые ( 1. ( ' 11 1:' ИМl'КП or1wиx Д('ЛИП.'Лt'Й , кrо1о1е 1).
Построить правиль11ые 7- и 9-у1 ·ол~..11ик нельзя -
при ном во~никают Ht'fЫ ~решимы е н квалратных
р.эд1~каАах куби 1 1еские уравнен ия. Однако вопрос,
ка КИ l' CWl' п р,1вилпныf' п -уг ольни~.. и можно (троить
шчжулЕ"м и линеикои, лолгnе время остJвался оr
крытьt'VI. Ответ 1-Ja Hl'ro даl\ Карл Фрнлрих Гаусс на
рубеже XV ll l и XIX ( толет1111. Вел 1 1ки11 м,пр,1~тик
доказал, ч 10 r~ раеилы-Jый 11-yrul\ы1иi-, 1дl:' rr - 1 11.ю·
стое число. может tJыть по< троен с ппмоwью ш1р
куля и АИ11еик11 о том ~, только 13 1ом случuе, когда
r1 11мtч~ г в~1д 2 ' t- 1. Вот первые 11есколько rаких
ч11rел- 1, с;, 17, 217, 6'i ') {7. Сам Гаусс нашелnо
орос 11ие 17-у гольн ика. Кстати ("Казать, ~1ме11ноэто
rпкрытиЕ:' , слf'л;~нное нм в 19 лет, окпнчательно
011 рслслило вt.tбор его профессии.
квцр.1тпч1ю-r1рр:щ 1 ю11алып,о~ кr.>рпеi1, поэта.чу
такой трс) ~·о.rп.шп< гюстрошъ rн:.11,зя. А r1ер:1з
репn1мость задач 1 1 да:;кс в О,J"\1Юм-tд111tстnсшю.м
ч;~ст1 юм случае означает, что у lJCё 1н.т н uбm.c-
1·0 рс 1 ~н::тш Од1 rако н<.:!! ь:~я у·1·нсрж;~ал, , q•1 ·0
д:1нн:1я задача 1111ко1 ·д;1 не рсш;:н.:тся Ecmr, r1анр1 1 -
~1<:11, нс<.: тр1 1 бJ I CC(' KTj)I LCl1I равны . '1 '() (.'(IO'l'HCTC'l'fly' -
IOЩIJJI тpt:)'J'(\JIЫl l lK (XlRHocr·o pnш-111(1 i1 CI'() щ:г-
1\() rюстрп~ 1 т1,
:Эт11м же MC'l'OJ\()M :Vl :-\TC\1tlTl\K\I смо1 ·11~1 устз
11оnнть, что 1тер:J з реттти чы 1'Ht: 11:1 трс:~х :111::1
чешпьL" з::~дзч др<::nrюL~г11 - об удвое1п111 куба
и о тр 1 1сскц1ш yl'Jla (см. статью <·Тр11 з11аме
нп 1ыс задаЧJ1 дрсшюсп1·> ) .
ЭКСПЕРИМЕНТЫ
С ИНСТРУМЕНТАМИ
!} Дреш1с\1 t'рс:.:1~н11 нрсд1юч11та.· 111 11щ~1 рос111111
с rю .чощыо r( 1 1ркуля 11 т111с:l1ю1. О,111ако 11р11-
м~1 1яm111др)1'11е 11р1к 1 шсоблс11ш1 - 11а11р1rмср.
тrней1.:у с 11 :J1 1 с:.:сё11111>1м11 11а 11с:ё 1.~ 1 Iу."1я меткам11
(см. ci·a1'1>10 ·.Тr1 1 :1памсr111тые З<щачн ,'\рt:вrюс
'п1") . 1'а1':ш п11нс\1ка. н чйсr1юст11, rю:щоляе·1
решит~. з;ща чу I l aп11a: пронест11 • н.~ре:1 точК). л:с-
жащую в11утр11 )Т:1а. отре:ю1.: д:1111юi1 дnшrы L
к()нцал111 11а сторо11ах ~ 1·ла. l\'loжJJo nоказать.
что э·r·о IH.' XTJTPOl' пр11сr1ос облсr111с 1/ ОЭНОЛЯl'Т
<·11рат ггы:н со нссм11 3a/ta ча \111. котuрьн: с.тю
д1по1 к рl'шс1111ю ур~1н11с11111"1 нс нышс чствёр
·1·о!'r CTCllC/111 (l<OJJCЧllO , окружнuс1·1, IJ:J'ICj)'ПI'l'I,
m11rt:itкoi·111c,1п:~я. Y(.'J1<H1J1<> сч 11т:11от. ч HJ окр)~IК-
11остп 1н1сr·ри<.:н ~1. си111) к:1:{:1 111 ,r цt:111 р 11 rс1ка>1-
1111())ЛI> t'(. ' ' / оч J<;J.)
t1 1кё же c:i:-. -11,1\'1 n<1лы1юi1 н11тсрес у 1с()~1~т
ро1{ п1>1:111mат1 .1а /1Jч11 , n котор1.rл [Xl:\1IOJ /\О:1НО
.1ешю1·0 11е р:1с11111р>1J11 к1" а ср1.:;1.111сь Гlt'рнос
п :J гсо.чстр1тческr 1х 01·1х11 шчеш1!1 состонло в
·1ом , что р:ктnор нщжутr запреща;юс1, 11з.чс -
1нпъ.1kрсидскн\1 11,1атсмат1 1к f\1ox<i:..~~l:д Лбу-ль
Всфа в Х 13 I1а1111сал трактат на эту тем~'. г;~с:
11р1шi:л IПSIЩJlhl<.: )K'ШCllШI MJIOГIJ'\ :~а;~ач .
В 171.)7 1'. 1п;1J1ьянсu 1\1асксро1111 ш1у6т1ков:и1
ра6оту <-Гс:о мс:1р11и 1~11рк: . 1н ~ В 1-1L'1'r дока:~ын:1-
J1< к~-,. что ;11обос 11остроl:1111с, котороl: ны1 юн1 н1-
с:тся l(l!pK)"JJ(' ,\1 11 . Jl 11 lt'fl коi1. ,\1()Ж110 C1\CJ J;l'JЪ с
J IOMOll\ЫO 0111 IOI'() 1\J l(Ж~ ШI. ( !Jаз~ \Н::стся, 1\1 IJЖ~
Jlt:~J l IClll>.m 11poнt:CTI 1 Пр}! \1~ 1(). llO Э'l'O~f~ ,\(~ 1 скс
роrп 1 CЧIJТ;.tJt П[)И\f)'Ю пocтpoCllllOI\ CC'J tfl 1)()-
сrросны :\ве сё точк11. 1 П озже. \'Же в ХХ н" бы.1.\
обнаружена э:.~быт;~н ю 1нг~1 д~1тс1ю1 ·0 гсо:\1с·1 ра
Фигури
1· ~lop:t, 11ы11JL'/\111ан н 1()7 !. 1 В 1н:i1 учi..'ны\1
:i:p) Пl\1 CllOL(}()().\1 , {OK:! :~J, J ry ЖL' тсорс\1).
F.щt~ о, 11111 к:~ асс З:I рч - ПОСТ(ХК'JIШI ( 110-
\IOЩl.l\I ТО.'1111\() , llllll'llKll 0:01ако пр1 1 Н.1.111'11111
11.1 llJIOCIIOC'TIJ IJeкn1npoi1 IКПО\101 aтt'.ll1llПJI ф11-
I"\ ры 11.шршщ:р, 11.1 р11с. 1-~ \ЮЖllО 1 C1B.i lt'ЧI> 11с
с 1ш;~1.1.;о т.11-. '·' 1юстрос1111i1: ~ .J.JIOt'JJI 1с ()ТJХ'~ка
11 . tl' .l l l 'lllll .: отрезка 11 Qпо.~ал1, сс.1111 ..J,a11:t nJp.1 ..1
1 tL'J11,11.нr L'\1\· пря\1ая, 11 н аоборот. проuедt:шн.:
11p!l\Юit. l l:tp:tJIJ!t:Лl.ltOi l отре.1К\" (.' J:t;J,:\IШOit Ct'-
pc,0111111 '1 .\ 11.1 рш: 1 1пu1<~за11011осчюсш1е l / n
час 111 01рt·н.::1. сс, 111 да11:1 пара!!ж::1ы1.1я см~
11\Hl\t.1>1 Вооf11щ: . L'CЛll 11 а 11.юcкoL"tll :1:11цн 11.1 -
p~1J1Jlt'JIOI р:1 ,, \1 ,· t R(:П, · 1о ·1 очку Р ~ 11астсн 110-
стро 1 rт1, он 11 0 1·1 m 1г1 t'l11шi1 то1 ,ц 11 толг.ко l'Ol'Jla.
ю1 1 ·; 1.1 1~t·кт<1р АР= р~ш+qАо. 1дL' i' 11 ц
p.IЦI 1()1 1 .LЛЫ rые ч l 1CJl:1.
l'иt. 11 .
rнt . 14.
•
. J_.
r-::r-
~l, 1
l lo сс:нr 11:1 11.юcr..:oc:nt п;1рисошл Kf>)T с 01-
'1<.· <1<.1111 1.1\1 l\CllТpO .\I, ТО .'НОООе IIOC'J рое11 11 е.
11ы1111.r11111'loc 1111рку. 1 с~1 11 ;11111сй1юi1. чпж1ю ос.1·
Щl'(."1HIп1, JO. 'lu1'0 .1111 lt"JIKOil. что 6ы. ю ,10K;LШIO
н 1Н~1 '" 111нсiщаро,11м 1·t:o\1t'Tp<)\J }\кобоч Шн:й
11t·po\1 11 .1 рщ: 1'1, а. ,; пок:13;1ны дв.1 nострое-
1111и т:1ко10 ро1 1.1. 11.1 ,цн111>i1TO 'l"11 ...J11ровсде11ы
l\;JC:l I t". l l1 l lltll' к /t:l Jl ll(J\I) "Р)1) 11 ш:р1 ll'll, "tl lh'\ '. шр
,, (. ' IO,\Jl;t\1L'1)1) (Н :пш" llCK TpOC/JllЯX 1\(.'11"1 р кр\1J
IH.: 11~-11\(.:'1\) Дру11\'111 C.IO \ l~\Mll. l'LЛll :{.1 ,'\~1'1~ ;..11.)Ж·
lIO рс111т 1. ( 111 11\IО ЩЫО Ц11j)K)IOI 11 .'Ill llL'i'IIOJ. l\llp·
l\y:1t. дос·1.1точ1 ю 11р11ые1nп1. все 1 ·() о;\1111 раз За·
OДllO ПО.11) 'l.IL ' . \I, что 1\11ркуль с ПO(TШl ll!J11J\I
р:1<""1 норО\1 вп01111t: Jамс1~яст uб1,1•шыi1. Пo:l,t11ee
()(\':J jaJJOCn. 1 1'10 ![ (} 1' окруж 1 IOCi l 1 JtOC"I JT\lЧllO
ll\1l"l 'J , .1 1 юбую с1<0111. у 1 ·0.ц~ю малую ду11 11 цстр
[~то iKl' крt:мн 1юс1 ·1 ю11·1· 1, нентр д:~ш юi 1 ОЩ)\'Ж·
111 К 111 '1"0 '1 h1(0 .1111 IJL'll Ю IJI l ll'Jll>ЗH .
Р11 с. 1'i.
d
6• -4
R XIX стш1е1 · 11и охотно 11зучаm1 построснш1
рхзлнчпыми неr<л :кс 11чесю1:.111 срс,r~,стт1ми. Рас-
01атриu:J.ли съ, n часттюст11 , 11острос11ия с 1ю
мощью дuyxc·гopOIIIICII Л1Пiеliю1 ( ШIЫMll СЛОR;l
.\о!И, разрешалось од11оuрсмстю 1101LЬзош11ъся
дву.\1л сё п;~раллелы1ы;1.ш кр :urм11 ) 11л 11 у1·оль
ннка - прямого yrл;:i. Уголын1к !>IOЖIIO было
распuт.1 1·а·1ъ так. чтuбы <:го 1<μан щюход11л~1
Чl'pt::i / \3НН hlC 'l'О ЧЮ!, а Вt'рши 11:1 11<.Ша,ЦаJiа 11а
,t~11111ую ;111н1нu. Каж.цut: н.t э·1· 11 ,\ 11 с:>: 1 .чыс.'ю-
Гt'OML 'Tpl I Я 11.J ПЛО< КО( 1 И
11:l'Г ЫХ 11 р 11 с 1 юсобле 111тlr JJ('l 'KO За\К'НЯL'Т !(l lPK)'JJI,
11 т 1н е1-1ку, 11 р1 IЧ<:\1 п орой 1ю:mfмщ:т 11 01 1уч11тп
6олt:с прост1,1е реш е1111н . Пс1ю.'1ь:ю калr н.· 1, 1111ря
,\1() -Т:1 Kll '')J<:ЮТТТЧеСКI 1е и 1~с·1румсю ы - н:111 р11-
мср. 11р11 бор для nprшe;\t"I 1 шJ ()11сс<.:ктр11с Но
OIC:1:1:l/IOCI>, что м~шcrr;v1:1J 11>111 11\111 ВСХ\МОЖI IOC"Пl1'vl! I
обл:щас.-г пара) 1 ·олышко n (см. с-га 1ыо <.Тр11 :-1 11:1
~1е1 штые :щ:~,ач1 1 ,11pcm юс111 » ) С нх помощью
у1щ<.:тся рсшшъ люб)1О з:~дач\'. сuо,11ящуюся к
)1)~ш11сш1ю нс выше чстnёртоi1 стеш:ш1.
ТРИ ЗНАМЕНИТЫЕ ЗАЛАЧИ ЛРЕВНОСТИ
С rлу601<011 дрешюст11и:тссn1ы1р11 зад:.~чп п~1
построение. об удвоешш куба. тр11сею.щ1 1 )тла
11 квадратуре крута. U11н сы1·р;;uш особую роль
11 1к·1·оrши .'.1ат<.:матт 1ю r. Н к01щс концов б ыл о
1юка ~{а1-10, что этп задачп 11евозмuж.110 JХ'Шить,
r юю-.зун<ъ ·1 ·uJ 1ыw цщжулсм и л~1 1 н: 1'1коО . Hu уже
ct.\1;1 1шсганокка ::1:1; tач11 - 4/~о ка~ ать 1н: ра ::s
ре11111мос1ъ » - бы11а С 1\\<.:JJым 111:Jгом к11 е рё; ~,.
Вместе r 1 ·с м 11pt:ю1at·ш1 ocn ,,11rожсст1ю рсшс -
11111~1 11р11 1юмощ11 н страд1·щ11 0 1111ы'\ 1-·1н стру
че 11та11. Rсё это 1ч1ннс1ю к Ro3 r1111< 1ю11с:111-110 11
раэвнтшо с0Rе р111е111 ю 1ю111,1 х и.,.-~,еlт 11 1·еож0·т
рш1 11 aJ11·e6 pe. Немало преус 1.1елн о 1rеста11 -
дарт11ых п разюJ'-ШЬL"> прI1 6лпжёт 111ых реше
ШНL'\ любптслп матем:~тикн - срсю1 тщх три
знамс шпые заf\ачи дрешюстн щ:uбетю ттогrу
ш1рны . J;щач11 кажутся 11осту1шьu.ш любому:
кво,r~,мт 11 :J:tбJJуждснш:~ ILX просты<.: фup."1yшr
poRюr. J!.o с1 1 х пор рс/lакцн11 матс:м:..1 ·111чl:ских
журна.1ов нрсV!я от нрсмс1111 получакп 1111сьм:1,
а11тар 1,1 котор 1.1х пытаютсн uпроне рп·1~ть да ю 1u
уст::~ 1 ю1111еr111ые 1кт11ны и подробно 11:ilr:1 га ют
рсmсппе 1<:~коl1-ли60 11 :3 з н аме111пы х :1;щач с
IЮ:VЮЩЫО l\lf[)k.~'JНf 11 ЛHJtet'1I01 .
УЛВОЕНИЕ КУБА
B::r1·0(1задаче требуется постро11ть цнркулсм 11
!11111е1'1коf1 1<уб 1щ1юt бол ьшего объt ,1а . чсм за -
~
11aннhttr Ребро 1rскомоrо 1<уба равно t/\ .! ., 1 -де
а - ребро l IC:XOД HOJ '() куnа. liCJI 11 111)11 НЯТh. что
а= 1, ;т 11сrюм< >t: ребро .\· се1ь 1тре1-11, )·раннс
rгия х - 2 = О У Jla1 1нo1·0 уранне1111н 11 ет р;щ1ю
на;1ьпых. а :-1пачr1т, 11 ю1;1др<1 ·пrчrю - 11рр::щ1ю -
11aJ11->111 .1х корпс!r. С:Г1с7~.ов:..1тел1-.1 ю. уюн >с1п rc ку6;1
НСЛКIЯ осущеС'1'11 1пъ лщжулем ll J ll 11Ie11кolf.
llрнмср1 ю такое расрк.,т1ст111с 61,uю 11р11м ст 1 стю
н 11аL1але XIX n" когд:~ был подготомен 11еобхо
Ю Г!>·1ыi1 для :пого ал гебра 11 Lrссю 1r1 :inr1ap.п.
(:чrrтают, ч ·1·u зад;11-ы uб уд11ое111ш куба по
нн1 шась но 1:1рс!>н:11а 1111фа1 ·ор<.:fщ<.:в, , ЖР!Н >S-10 1'.
/\() н . ::>. во~!\ЮЖLЮ, она HU:!HHK'l:J ll:J зa;t:t 'll I об
y;( IIOC' lll lll KH:l ,._tpaтa , K(J'l 'UP)I{) /Jel'IO) р с1 1111·1ъ.
O Jlll\')'1\.1 (.;I, Н~\ ·1
·c1)pCi\I Y 1\11ф;11 'О\У.1, - 11;що 1 ю
п11011·1 · 1, 1<вад1х1т H<I д11:_~1·ш 1ал1 1 ,•1ан н о 1 ·0 1.:н:1д
р:па . О н'л:к1 ю лerc: r-mc, ж11тсJ 111 Аф1111 , н:1 ко
· 1·ор1 .1' nOПf llllCПOClla.'111 ;:HIH)\l' ,\1 1110 чум111 ,
OTП(XI RHJШ делtта1 \1 ()() к O(JЗl<yJIY 11 :1 ( >Cf'l)()R JJ,e- -
лoc ;ia сонето.\1, как :1алобр11 ·11, !101·ов 11 п:-~ба
питься от мор01ю1·0 nrтетрня. 01 l1t:"1' 61, 1л Т<ШОR:
<-Удво йте жертвсmшк хра.У1а Ллотю11а. 11 ч уыа
прскра т11тся" /Ксртпстн п< вм ел куби<1сскую
форму. Аф111 шнс рсш111111, чтР :1a:i.a 1п1с проl-тс .
111юстршu1и ш >11ы 1~1жt.: р·1·нсн ш1к.r.: 1щ1юс 6uJ1ь
ш11м рl'бро.\1. Он 11а ко чу ма толыш ~т111111J 1 ась
Rтuрич1ю обра ·111л 1къ к uр:11-:улу 11 11РJТ)'Чш111
ответ: •I I олуч111<: llЭ) "Чal1Tl: 1·сu,·к" 1 ·р 1 11u ·> . И с1п
р1 !SJ у\1алч11в:~ет 1) '!( )\\, к:1к у,11: 1 лось у1ч1И111с111-
1111 ·1
·1, n1 IJ 'OR. 1Ю Ч~"\1:1 11 l\\J I Щt: KOI tJ \lН1 Пt )1\11 llYJI:I
r o p CJ/\. Л :Jадач) об у,1вост 1и11 1\у6а c1 ·:iл 1 r 11:1:-1 1.1
ватт, 11слосской :~адачсr'1.
И :incc1~11 a и др:тая лсrс1 r: p Греч<:сюп'1 1юм
.:v~ентатор V l В. i-\0 11. э. СООбЩ:.JС.'Т (/ ПI I C l >M~. rrрС.-,1,
п оложн тсл ыю п:~ш1са111юм царю Птш1сч<:ю 1.
Н 11<.:м говu р11тсн. •.rто царь Mirтroc 1юс1·1юпл па
мu1 · 1111с сы11а 11:1; (1·роб1 rc куб t1чсс ко й фuрм1,1. но
Ol''l' aJIC:H H<.:1J,OHO.'ll'll разл1сра:\1J1 на мят11 111 <:а 11
11р11казаJ 1 у..сtво1пъ l:I о . унt'.1 111ч11н 1:1д1юс pei'irю
куn;1. Ко мм<:11 ·гатор ука:~ьшае 1 · 1tJ. 01111 1 6Ку l l:I рн
М11носа ( 11J1ощ:1,11, 1 юн<.:рл ноп 11 11:1мят~ 11 1к:1
i19
Фигуры
МСЗОЛЯGИЙ
ЭРАТОСФЕ Н А
древнегреческ11и учёныи Эрато
сфен Киренскиr1 не упускал воз
мож ноrrи н аrлял110 n релстав11ть
математи•1еские р!?зультаты и ЯR
ления, а также п реллож1-нь cno-
rofiы получе11ия практических рl:'
usений. Например. он разрабптал
и построил мезоl\ябий (мезоля
б11ю) - прибор лля мсха~1и че
r.кого вы ч и(l\ения лвух срелних
пропорuиональ н ых мсжлу лвумя
л.:111 11 ыми.
Ме.юляб1~й \дб'ld н и.-1 трt:>х оли
наковых прямоуrоl\ь ны х пмк тин о к
(из металл;з, дерева, карто н а и т. п.),
леrкu nuрел1н1r<"1ю ш ихся по лвум
nс11мллельным н с1правм1 юшим; нс\
ка..клои пласти н ке п р ов!:'Аf.'НJ ее
диаго 1-1 аль, как это 0"1л~ю 11i.1 р1ку~1-
к«.: (кажлая плас1 и н ка окрс:1шt:>на в
свой ш~е>т; С'М. ри< унок).
[сл11 залJ ~1 а точка М (на ребре
трстьеи пласп111 ки) 1 то, псрс"1сшая
11 лri< тинки, их у<та н авливают так,
чтобы четыре точки - А, Q, Р и
м - рас.nолОЖИМ1СЬ lld UЛНUЙ пря
мой (точки Р и Q суть точки пере
rе• 1 ения д11 ar0Hdl'\e 11 r краями дру
п1х пласти11ок.). То1да бл<~rол.:~ря
очсвилному гюдобию М<IЛf' Н ЬКИХ
треугольников внутри треуголь -
11 ика AFN получ аются два срелних
п рuпuрuнu11 аль11ых щ~жлу величи
нами Af- и МК:
в ЧJСТIЮСТИ, f.!СлиАГ = 2, i1MK = 1 ,
тоРН={2:
2= AF= АГ (_)С РН (РН)
1
мкCJGРНмк=мк'
что, в свою очерель , позволяет
решить ылачу об улвое1111и куба.
и"~енно nv ·ном способе реше-
11 ия Jнаменитой 1адач и п исал 'Jр;з
rосфсн шрю П rолсмею Эвергсту.
<1 Н JМИ llJIИЛYl\1<J H м·1·кий \ l lOt o(i
реше ни я при помош 11 ~1нструмен
тоо. ПОl'\Ь)уясь им, для двух ЛiJННЫХ
прямых мы можем 11 айти 1 1е тuлько
лве, НО и сколько у1 олно Срt:'дНИХ
п ропорuио н альн ых. П екле этого
мы сможем ооuбшс любu11 зад.:~н
ный (Н р<1ниченный п..~раллелоrрd\.1-
мами объем преврашать в куб, одну
фор..,1у 11 рсобрюовывить в лругу1U,
лелdть п олоб 11ой и уослич 11 вать,
сохраняя 1юло()ие, и жерrнt>нник и ,
11 храмы. Также мерь• жидкостей и
с-ыпуч и х тел ... мы сможем п рсвра
ШсlТЬ в кyfi и 110 с rороне rнклелнеr о
измерять вместимость ра'lличных
cocyлuu. Это изобрсrе1111е будет по-
1\
в
с
F
с
н
лезно и лля желцюших увелич11ТЬ
раз,1еры КJтапулы 11 к.:~м1·1емстов,
гак как для увеличения ллины брос
КJ нужно пропорuио нально увели
чить В\е - и ширину, и вслич1-н1у,
и отверстии, и втулки, и вставляе
мые тяжести, d поrо н ельн1 сделать
без нахожле н ия средних nр()nор
шю11алы1ых ~1 ,
flпокий At ка.лонск1111, 1<ОМ\1ен
тат ор сочинений Архимел;~, в
Oдl-IOM из llИX -
«0 шцре н uи
ЛИНдрС · -
11 оместил пиtьмu Эр.~
тогфена как приложt•ние Т ,1 к оно
1·1 лошло ло 1ыс. В11ли,10, хорошо
.тая, сколь нелuлru13с ч ~1 ы руко
пи<.и и тис.голы (п 11 tьма) - uн
завеловал Алекса 1~лрийской 6116
л1ютеко11, ;)р;посфен поместил
мt' юляfiий в лрамс как лар пu обе
ту, сн<1блив налпиrью - в ней Иl
ложсн ы прцвила р<~боты с np11-
бupuм. И и3uбре 1ение ученого
уuелело лля грялу ш их поколе tщй.
Праролитель 1'\оrарифм11ческо~
м1 Нl'~1ки и нон и уса. мезолябнй так
и не стdл μанноп рdвным 1cuмcтpfl·
ческим 11нструментпм нарялу с MI·
1ю11ко11 н u11 ркулсм. Почему!
D
к
N
11 рL' :~у:н,татс уж·п11чн.rт:.t(Ъ n •н..-тырс, а объf.\1 -
в 1юt:с .чь раз) r1 рассказывает, что то1дJ
1·t'o.мe 1 ·p r,1 1 юпыт:1mкь рсш 1 пъ эту задачу.
1Jo т:1к J 1 11с су,н::н с н сi1 с11раннты.:я с nо
мшцыо 1L11rк>·ля 11 11ш 1t.:Г1ю1, 1реки 1Ю(Jро6онз
J11 111р11ме1111л, /фу1 ·1 1 с 1rнструмсн1ъ1, мL:хан11 ~Jмы
11 ; 1,:1же сщ·1t11:~лыtые кpr 1 вr11t:. Г11ппокр:п Хнск
сю1i1. :11 1 амспитыl1 1't:< 1 ,\1t:тр У в. до 11 з. , c1JёJ1
)'ltIIOCT l lIC куба I< l IOCT[)Oe111110 «f\Byx (РСf\!ШХ
пронорцио11алы1ых» х п у для даш1ых отрез-
ков о 11 Ь. т t:. i -; рсшсн11ю уран11с.:11r1!"1 а .\'=.у у=
=у·fJ (прн /J = 2аНОЛ)•1ае,'.1 х =а~ !. ) Этущею
) /\Jлос1. реал 1rзова1ъ Плато~ ry около .-1-Ю r до в.э.
с по.-.ющыо rre'J радш \IIOJ 11 t ых чертёжных н11ст
ру,1с 1 1тоn - дnух пряыых углов (рис. 1)
,НО
Меr 1 ехм примерно R у;о г. μ,он. э. рсrшл ~а
да чу об у;trюе11ш1 куба, rtCПOJllЛYff KOllllЧCCKflC
ССЧСIПIЯ - Кр}ШЬ!t:, по которым 11.'IOOIOCТIJ ne
ресек:но 1 1<011ус (с"'• · ст::п1 .ю «3а .чсч~tт<:льные
Гсом~трия 11 <1 плоскп<r11
""'с 1.
1'111:. 2 .
j)
С1
'-- - 11 ~-4-~--,ff-~-r-~~~~~~~~~~~-~,--~-
кр11В/1/С», l'ftl" \.ЮЖНО 11айт11 11 дру1·11с решс1 IШI
трёх з11аме111 гп,1х :1ада ч с nомощыо крнвых) .
Сван рете 1 1 щJ дал11 г;нот'е крупнеlтше дреu11с
феческие мзтема1икн Ендо1<с, :;)ратосфс н ,
Аполлош 1 И, Геrо11, Ilanп и др.
Одно из peшc1m(I задачи об удвоении куба
по.каЗ~IIIО на р 11с 2. З:\ссъВС = HIJ ,.tШ =АС= UP,
а прнмая 1=СЕ 11 араллr..~лы 1:1 AD. t lo1ra1 ·asi ВС =а,
АВ =/1/ 2.. Al!. = .~: 11 СР =у, можно на йтн. что .л:
ну- ДВ:l ср~/(ННХ пpoпopt\ИOll:IJll>HЫX Cl 11 h
1/ЛН ЧТО
в час1·1-rост11, ...\·=а ·~· 2 пр11 /J:: la. Rce точк~1 11
II ll!UtlL на этой ф1trype , кроме:.: 11рн мо й AR!•,
строятся цнркулt:м 11m1нсl1ко1\ а прямую мож
но l lJIOHCCTTI, t:СЛН [XlЗptIIH-1'1 '11 метю 1 на т1не1'1-
/\t. Xna·1 нт /\вух меток J::: 11 F; н,-.,: ттуж:но сдt'1rат1,
11а расснJЯI rr1и fJ j 2 ;tр~т п·1 · дру 1 ·:~. То1·да прямую
АП' стро~п . ТТ()местнв ли11еfшу 1'<\К, чтобы её
край нрохо;111л через А, одна метк;~ 11олала 11а /,
а ;1р~тал на пряму10 ВС.
1lикомед и :~ Ллсксапдрш1 (П в. ,ri;o н. э.) ис
пользоnал для решения это /J з:~дачн особ ую
кривую - ко1tхоиду (слово • колхондсс~ в тте
револе С !"J1еЧеСКОГО о:mачаст <•OOДOOt l:lЯ рако
ВИ!\t мн;тии": рис..~) . 1 la рис. 2 сё ош1шtт точка
F, сел и ~1l'чс11ую л1 1 11сйку псре чсщатh т;зк,
чтобы сё кр:1!'1 нсё время проходшт чсрс:~ точку
А (r..:ё 11:~.Jыкнот 1юmut,;u,1i кuнхш111ы) . нто ир<.:мн
как точк:1 Е про6с1·ае'1 нею пряму10 l (ос1ювшtие
конхnщtы). Тl остоя1111ая дл1111а EF на:11.шастся
шт1ерrщло.м. Т<>ч 11 еt, зто бу7\СТ одн~1 нетш, коп
хонды: втор~10 еЕ ветвь опнсыnает то•tка, сим
.\iетрн•шая 1: оп юс 1пелыю П. Нrнюме,1"\ нахО,1\ИJI
ТОЧ!С)' р на рис. 2, чертя конхоиду с П()ЛЮСО;\1 А
и основа ни ем /. Оп даже изобрёл с пециалы1ый
прпбuр для вычсрчнпания этих кривых.
ТРИСЕКUИЯ УГ/\А
Несложно р<!:щелптъ любой ~rroл с помощью
царкуля и лин<:11К1t1 на л,ве, а нек<rгорьк: углы -
и rш трн раnныс ча<.:тп. Последняя ош.:рация
на:.~ьша<.:п:н m/Jl!ceкцzюzi угла. Напр1tмср. мы
11.10.Жl'М 11ПС' 1 р011'1'/, Tj)<.vt•h НГ'JЯ М.01 О Yl'!Ia . 1ЮДСЮ11:3
ПOIIOJ l ;11.\1 YLOJJ llf)<lHl!JIЫIOJ '() тrсу1·011ьн 1 1к:1 . :1
1 1рuнсщ1 б11ссектр 11 су н nб rазонавше мся }ТJН: н
30<', по11 уч1 1 м у1·ол r~t;.11ич111ю!"1 1'1 ° - тре~ъ у 1 ж1
11 ---1'5°. Есп, 11 /1.ру1·ие )'Т'Jti>I. т1л я rщ·1·()рых три
секцrтя иыпо11т1м;1. Наверно<:, nпдо(н11,1<:' гто
стростп 1и 11 nселтт 11 1 талбК!~У отщ1ы·1ъ CП(ICOn
трнсею~тш mобого ~тж~ посрснством цнр1<уля
и шшейки. ~J-ry задачу пытались решнть ещё в
Vн.дон.э.нГреции.
ll ~t рис. 5 АОВ - ::~аданны.й уr·ол. н:.> точюtН
щюнсдс1JJ.1 11р}(мш1 (' = ВС, 1 1ерне11д11куляр11ая
ОА, н н рям~rя /. 11;rралт:лы 1 ая (JA. ~ели тспср 1,
н:о~t1чп·1 п1. 11рямун> а= OPQ так. что6ы <.:ё от
рсаок PQ. .1:1ключёнJ 1ы(1 мtЖд) jJ 11 /, ран11я11-
Оi 1.013, то у1 ·ол Рос· сос1·ан11т тре 1·1. т11 1нп 1 ·0
угл~1. (Этп ~юж 1 ю !1,О 1<а:1а·1 ъ, nnmз:-iyяc1 , т~~r, чтп
р
-т /1-
Рн.... 3.
~21
Фигуры
·греуl'Ольюrкн ОВП н RDQ, l'дt.: D - середиt-1а
PQ, ран1юбедре 11 н~.те, н теоремпй п внешнем
угле тrеутлы-шка . ) Постртгr1 . прямую С/ М()Ж
но с помощью ,.,,1е ченоrl mп rей1<И, т. е. линсй
ю1, на которой наш:сены две метю1 ш1 рассто
шш11 208 друг от дру~·а.
1l пкомсд с той же 1~слыо чертш1 свою ко11-
хо11ду с полюсом О, осно ваниt:м р 11 интерва
JIОМ 20В; 011а псрt.:сскаст f в ш:комой точке Q.
В 1593 г. Фра нсу:~ Виет дuкизал, что любо<.:
кубическое ураRнснне можно свести л1160 к
унвос111110 куба, л1160 к трисскщш уrла. По
скпльку обе зада чи решаются с 1юмо щ1 .ю кон
хонлы . Hыn·1·n11 прелл:lг~л шщючит1. э1у крн
nую r~ чнслп «ста11,п:артш)1 х».
Архимед прпдумал свой способ трисс 1щии .
На рис. 4 данный угол - это угол АОВ между
радиусами окружности. С помощью мече ной
линейки проведём пpя:J'llryю ч.<::рt:з точку А так,
чтобы её отрс:.юкРQ между uкруж1 юе1ъю и 11ро
должением прямой ВО раннялся ра;tиусу окруж
ности . Как и на рис. 3, :щесь образуются ранно
белрснныс треуголы1ики ОАР и OPQ , и легко
доказ;пъ, ч·1·0 утл OQA в'1рое ме111,mе да 1 11 ю1 ·0.
Q
Рис. 4.
l<онеч110, 11 u этом случае, чтобы пайти точ
ку Р, можно нсполиоnать конхонду I-I11кш"1еда
с полюсом А 11 основ;нrисм ОВ, а точнее, сё
нторую , <·внутреннюю" ветвь , вuзник;1ющую
пр 1 1 OTКJЩ[(J,IJi~lllИИ ПОСТUЯННОl'О отрезка uт
ос1 юна1-11 гн к 1ю11 юсу. Дrтн каждш п дан ного у1 ·ж1
АОВ адссь 1 1рнхоf1.л'гся чсрт1 1· 1ъ ноную кo11X()IJ
ltY. Но можно обойi.нсь 11 о;tной кри1юС1 д11н
всех yi·лon. Рассмотрим конхо 1 щу с тем жt.: по
люс о м А., 110 за сё ос 1ЮLiЗ1н 1 е нозьмём 11a 11Jy
<Ж р}rжност1, (рис. S); 1 1наче 1·оноря., эту ко1 1 хо
н,цу 0 1п1шуr• точки Q и Q1 прямой АР, удалё1 11 1ые
0·1
·
Р на р::tсстон1111е, равное ра/l,иусу, ко1·да Р
пробс1·ае·1· окружпост~,. Получающаяся криnая
изnсст11а как улитка Паскаля. названная так в
Рис. 5.
честь Э·1ъс1 ra Паскаля, отца ф~;mософа и мате
матика Блеза 1Jаст<аля. Cpau.ш 1 na>1 рис. ·1 и S.
видим, что сели ~ш рис. 5 1 1 рямая ОВ проведена
под занаштым углом к 0.4 . осн симметрш1 улит·
кн. то L OQA ран<::н е1·0 трети.
Гиппий Эли;tскнй (OK()JIO LJ 20 г. /\О н э.) длв
трнсtкщ111 угла J rcJ юлюnвал крИН}lО, 1шослед
с-1 пни 1 1 азван нуJС > кв:щратр1 ~сой.
Фрапцу:кю·нl математик П. Ra1 нtелъ в 1837 r.
первым строго докаэзл, что 1 1 евозмож110 осу·
ществю·1. тrисею~;ию цщжулем п люrейкой.
Пусть ~ = а./3. По изuестной фоrшуле. cos а=
= 4cos 13 - 3cos13.Тогдадш111ел11ч11ных=
= 2 cos 13 получается ураRнепис х 1- .)х - а= D.
те а = 2 cos а. Гсометрическан за;tач:4 трисек·
ци11fl.'1J11-1.01·0 }TJla о. циркулем и ; шн.ейкой разре·
шима ·1 ·01·да и толькп тш·да, ко1·;р полученное
аr1 1 ·сбраическое уrаю-1 сннс ра:~реuшм о R ю1ад
р::~т11 т.1х радикалах . Rоз 1 .мём , например, а= 60'
Тогда )1):1 1ше11ие примет ни;1 х - 3х
-
1=О
0110 неразре ш имо в квадратных радш(атх, а
потому н трисешщя с rюмо1цыо циркуля и mt·
11еr"ши n данном случае невозможна. Тем более
она невозможна n общем с11учае. Интересно, что
вообще для углов шща 56U0 /п с цслы\1 п 1JШ·
с<.:ю tию удаётся uс:ущсст1шть то1 ·д :~ и толh~О
тогда. ко1·;щ 1z 1н.: делится на 5.
КВАЛРАТУ РА КРУГА
R ~iада qe о ю1а;\рату~->е кру1 ·з требус·1·ся пост~
1т1ъ циркуJ 1ем и липей 1<ой КRат\рат, рав1 ювел1~
кий да111ючу круrу. 1:3ероятно, задач.а бьшаи~
вестпа уже за две тысячи лет до 11. э. в Дреш1СJ
Е1·иnте и Вавнло11е. Но первая r1рямая ссьL~~
на псё отrюс1 пся к V в. до н. э. По свидете.'IЬ·
h
Рис. 6.
стну дpeв нerre<tect<o1·0 исторнка П11у1"арх.а,
фнпософ Ана"Кса1·ор, 1<орота>1 f3rемя '" тюр1.,.ме,
пытался квадрнrюnат 1, щ')уr, т. с. 11rенрат 11ть его
в равновеликий ю~адрзт. Если считать радиус
да11но1·0 круга равным 1. то сторона ис1<омого
ю1а,•1рата 11олж 11 а cocram 11ъ \ л
IТадсжды «КВЩ.r,ратурщнкон~ rюл,01·рсвалнсь
сущест1юва 11иеt'-1 1<ри1юJ1и11t:йнъ~х фиrур, кна:\
раруемых 1\иркулем и т1нсйкой. Ги1mrжрат
Хноссю~й 1 r:шrёл одну нз таю1х фшур, нзнсс.-1·
ную как <·луночкн Гн111юкрJта» (рис. 6). Он
на111ёJr 11 11руrнс Jl}гrючкн. до1 1ус~<аюrц11е квад1х1 -
туру, что. ко11ечно, не 1юмоrло ему рет1 rтr, сал.fу
нсходtJую эадачу. :Заметим, что поnрос о "1ом,
кжне луноч ки кв:щрируемы, оказался сложным
а был nошюстыо решён толыю в ХХ в., совет
сюг..'1 м.атсмаn11сом Н. 1·. Чс бо та рё лы м .
})r,mo нрс;r,.тrожсно множество построений.
В лучше,"1 случ;.~е онн д:~в:.111 11 11рибл11жfююt.:
знэчен11е тr с 11,остатuчно хорошей ·1·uч1 ЮС1ЪЮ
(см__ н;ш рнмер, рис 7 ) . О1~~Jако, 1:1 0·1 ·ю,Lч не 0-1 ·
nрнвс1 1ённ ы л выше ре~ пений ;~вух J\J1yi ·н x :~на
'1.l.'111пыл :3а;рч. эти построения Gыш1 пр11ю~и
ш1алыю 11рибл11жё J1 11ымн. B JJ [>O"lcм, ан-r оры
Геометрия H<I П/10< КОПИ
8
вп "' _\, 141 ~j_~"
"""""'-
Рис. 7.
такf1х построений часю не сомневалис1. fl их
а()солю·1· 1 юй Т()41-ЮСТН \о\ 1 '0\)ЯЧ() ОТСТ<1.нна1111
оюн заблуждення Однн нз самых 1·ромю 1х с1ю
роn rra ЭТ)' тему прт1 ;-юлr ёл в Аш·лин между
дnумя ВЬЩ:1IОЩНМИСЯ учёнымн :хvп в. - фило
софом Томасо-~1 l 'оббсом и матсматrrко,ч ,Цжо
ном Валтком. В пссьма лочтеrп-юм возрасте
Гоббс 011у6юш.онал 0 1щ1ю 11,есати « рсшенr111 ->
3адачи о юзадратуре кру1·а .
.Итак, за)\ача о KH:1l\JX1'1)'1X~ круга оказаJ1;~с1,
наиболее сложной из трёх. Метод, 11сполюо
ва.~ 1 ньrй н ю~ух 11,руп1 х з;ща чах, здес1, 1 1с гю;tо-
111ёл, таr< как числп тт rrмеет сонерше 11нп другую
лр11роду, чем (2 11ли К<Jрни уран11сн11й, к 1ю
торым сподится трисею\ня. Толы<О 11 !RR2 1- .
Фердннанд Ли11де:ма11 доказал, 'ПО число тт
тр:н~сце11де11тно. т. е. нс является 1юрнем 1111-
к:шого мноr·очлена с целыми кuэффнцис11та
м11 Значит, оно и нс кн;.щратичтю -11рр:щпо
нал1>1-ю, rюсколы<у в 11ротин11ом случае было бы
корнем. кпк<Jп>-лнбо мr-югочж:на. Так Лк11дс
ма 11 нако1-1<::1\ лосташш точку к 11роб11сме ра3р<::
шимос1·и nосрсдстком циркуля и л1шейки пo
C71e1~ JJCJ1 из 1·рёх ю1асо1ческих задач щ1сшюl-пr.
Фигуры
ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ
НАЧАЛА СТЕРЕОМЕТРИИ
I3 cuoe~t 1'\еЯТСЛЫIОСТII ЧCJIOHl:K IЮН<.'Юду стал
ютnастся с !Ieoбxoд1L'Vl.OC'l'ЫO 11:5учать форму,
разм<.:ры, в:~аимнuе р:.~с1юлuжешн.~ 11ростран
ствсш1ых ф 1 11ур. l lодоб11ыс 3~1,1рч1.1 рс111~11от 11
:1стрu1-юмы , ltML'IOIJJ,11C лvю с с:1мымн 6шнs
ш11м1 1 масштабам11. 1t физ11 1<1 1 . исслсдующнt'
стр:ткт) ру ~пом он н мплскул. Раздел 1·еометртrи.
111\оторnм 11зучаются такае :~ад~Р-ш, r-rазыnа<::тся
C/IJCfIOO.MelllfJll&й (от греч. «СТереОС» - «ОбъЬ1-
11ы~'i », « npocтpaIICT1Je1111ыi'I»).
Может пок::tзат1,ся пар;щокса:1ьным. но
фа1пическ11 ПОIIЯТНС «ШlOC K<JC'l'h ~ в пла111 1 -
мстр 1 ш - 1 ·еоиетри11 н:.~ п1юскост11
-
Ht' нуж-
110. Ведь еслн ны , н:~1 1 рн.м<::р, 1пнорит<.': • В пm>
скuс·п1 тр<.:у1·011ышка .т1,:1н:1 точка·>, то тем с:1мым
1юдра зущ:в~1 сн.: , Ч'I '\) Cl'Th 11 ТОЧКН Нlle :~T()Jj ШIC.)
CKOC'l 'H . н IJJlaHllML'Tp11H такое l l j)C'/~llOЛOЖCHHt'
1tзли1111-1с: всf ;1,ейств ие 11роисход1 rr в од~юГ1 11
тоi1 же е;\И l I CTBCJПJOЙ ПЛOCI<OC'l'l l . в стсре о
метрни нам приходится име1ъ пело уже с м 1 10-
:-кест1юм плос1юстей. В 1\<tждой из ш1х сохра
няют СИ!!)' нее нзнсстныс из нланимстрпи
определеrшя н теоремы, относящиеся к точкам.
324
1 1 р11мым, р:1L 'lТШ11111им 11 т. д" нu Lвоl1с1·н:1 с:1мнх
l I JIOCl<<JC'l 'CЙ K~I К 'l:J КОНЫХ нужно 0111 I C:ITh З'.11 ЮВО.
Al<CИOMl::>I СТЕРЕОМЕТ РИИ
Ит:1К, в стерсомстршr I< ос1юш 1ы~1 110шm~я~1
ш1а1шметр11п лобавлястс.н ещё одно nло·
сr<ос1ъ. а н;-.н.:сгс с Шh\1 - :tJ\сrюмы. рсгу:нrру·
ющис "в:3а1 L'-'Юопюшt:н 11я ·• nлос1щстсi1 с другп·
.ю1 объектам 11 1·еомt·т1н1 и . Т:uшх ако ю!\1 трн.
Гlсрная - t1лпmма &Ы:\·одt1 в 11/юо11/1tт·
ошю - t1p11,rJ,ai.~т «тс:1тр) 1·t:ощ:·1р11чсск1 1х дсй
стн1111 ·> HOBOL:. 'Г[Х'Тl>С' J\;i'vtt'p<::HllC:
~... Имеется четыре точ1<н, нс лсжащне
'1(,\~ в одной ПЛОСКОС'l 'И. (рис. 1, а).
Таю IM обра:Ю!\1, IIC нее 'l'OЧIOf 11 :1ХО!\ЯТСЯ Е
О,J\ 1ЮЙ ШIOCKOC'l'll. llU Э'l'Ol'O 11сдоста1·о<шо. Н}Ж·
но, чтобы р;~з.1тчны.х шюскостсй было бес.ко·
11е<u-ю мно1 ·0 Это обсс11счнвается н·1·(1ро1'1 ;11ю1·
омо\'1 - m\.01r>.мой 1уюо.,;остu:
.~ Через любые три точки nроходит
"kl, плоскость .
С трст1,ей аксно;-.юit мы стал1швае1>1 ся , к01-д;1
скла,цьшаем ф11гуркн из бумаги: nce з rтают, что
образующш:ся прп этом шш1ш сгиба - пря
~1 ыс. ,.47,·аю.ма 11f!/JeC('Ч(JN/.lJI llJIUCKUC;neй звучит
'] ~]{:
~ Если две плоскости имеют общую
111'
точ::ку, то их пе~>есечение С(."J'Ь nt>лмая
(рис. 1, б).
Отсю,'\а, т<ст::~тт 1 , слел,ует. сели трн тпчю1
не :1ежат ш1 одной прямой, то прохо11.я н~ :нr
через них 11Jюс кост1.> единсп~енная.
Дсi1сгт 1телыю. сели через какш:-то три точ
ю1 JJpuxoщп две разные 111юскосп1. то через эт11
тuчю1 мuжно npuнt:cт11 11рнмую, а 11мt:ннu 11рн
\1)'10, no кото rоi1 плоскости пеrесскаются . 0 1-
\IL"Гil-"l. что IЮСЛСДНСС Cl:IO lll''l'IIO само не редко
.._ __ /_
.
___ ,/
Рис. 1.
ик1 1ю1 1 ;1ето1 к ;ш.с н ом~-.1 . Третья акс1-юж1 н1·р~1ет
nчснь сущсств<."нную 1·1 нс 0 11екндную с 11 ер1ю1·0
11.з1 ·11 яJ(а pom, в <..-Терсо мегр111 ·1 : он~1 11.сласт прп
стра1 ктно в Т()Ч 1юс-1·н ·1рёхмер 1 1111 \J , 1ю·1·ому что
В ПрОСТf)аШ.:Т В<IХ pa~iMC[ШOCTII ЧСТЫ}1С lf ПЫ IП С
п.'юскосп1 .\Ю1 у1· пересекаться по OДIIOii точке.
К трёl\1 ) каза11rrым nр11соедн11яют плани
~1етри ч сскп е аr<сио"rы, пере ос"1ысле11 11ые и
подправленные с учетом того, что теперь i\.п,т
1 1 меем дело не с одн ой. ~1 с ~tно1·и.\ш шюско
стя ,\1 11 . l lапр11 мер, акп10.му прямой - ч срсз J\.RC
раэЛJJЧНЫС точки ;\•ЮЖl/() прпвсеТ IL одну /] 110111, -
f\O одну прямую - 11среносят в стерсо.\1С1тшю
досло нно, но он а расп ростр;~ня ется у-11<с на mn-
1) 1,le дне точю 1 r1рое1·ранстпа.
В качестnе примера nыnедем прямо т1з акс11 -
0~ од но полезное следствие: прямая , имеющая
с плоскостью хотя бы дое общие точки, цели
ком ЛСЖIIТ n ЭТОЙ ПЛОСКОСТИ.
Пусть прямая / проходит чсреэ точ1ш А и В
шюскu(."1 11 а ( рас. l ). Вне ruюскости а. есть хотя
Гео,~етрия в просrранстве
~.с
,
"
,
"
А.
Рис. 2.
бf,1 од на ·1·очк~1 С (rm акс1юме выхо;~,а н про
стр<t нс-1 во). R l'(НJТкстстнт1 с акс1ю ."ю1I гшо
скости через А. В н С можн(> про1к~tт11 п1ю
скость ~- О 11 а от11н чна 0· 1 11жк1«хт11 rx, та..: ~-;ак
со;\ержит С r-1имеет с а дRе оащпе тпчю1 - А 11
8 :111ачнт, ~ пересекается с а по прямоi1. кото
р01\ как 11 /, пр1шадлежат А i1 В. Ilo акс 1 юие
пря:vюf1, лrп1ия пересечения плос1юстсf1 совпа
дает с/. l lo эта JltlHIЩ т. с./, J H:'Жll ' I н tlJtUCKOl'TJI
а.. что и требuва1юс1, ;ю ка 3а т1,.
В д;UJЫJCilllICM II< > MCf)C 1!СО6ХОД 1 IM< JC'l ' l I \'\Ы
будем на 1 юм111-1:-~ть ·п.: акс1юмы 11 тс..:орсмы пла-
1 111мс:три11 , кс.ппрыс нам пон;111обятся. а пока
сформул ируем 1 ·ла 1ты l 1 1"1ы 1 юд:
,'!>. ,
На каждой плоскости выполняются
· tJ nce утnерждени.я планим:етрни.
Впрочем, ссп час rштс рестrсе п оговориn, о 110-
nых п01штнях 11 фактах. которые п оявляются n
гео~1етри11. когда мы "1щхон~1м n 11puL·1 ·paнC'1·вu''·
ПРЯМЫЕ. ПЛОСКОСТИ.
ПАРАМЕЛЬНО СТЬ
Уже т:~коt' осноnпое по1mт11с, ток параллс111,
тюстт, прямых, rrркдается в 1ювом опреде:1ешш.:
11nc прпмыс n простр анстве называются 11ара.л
. 1е.лыtы.ми, с:сл н 01ш лежат n одной nлос~<ост1 1
н не нмеют общих то ч ек Так что нс попадай
тес1, fi 0,1 'II)' н з 11 злюблснны х э.кзамснат()рам 11
ловушек - liC !JЫT:l (ITCCI• «/(OK:l::!ЫB;t'l'I>'', что
чt: рсз дне т1р~·t ллсльныс щ1нмыс мож но 11po-
nccтr1 п 1 юскост1" это Rсрно по оnрсдслсншо
лар~ишеJ 1ы юс 1» 1 пр}1'\1ых! Зна~\1снитую план11-
метр1 rческую аксиому о едщ 1 сп1tн 110ст1 1 11; 1 рал
л сл ы1ой RКЛrочают п в а[(стюмr,т сте реометр1 111 ,
<) с её 1юмощыо до 1<азьш:~ют гл::~впое своi1ство
параллельных: пря~ыых n прострапстnе:
Чере3 то•IКУ, нс лсжащу~о на прямой,
МО)КНО провести одну и 'l'OJJЬKO~од:J
прлпую , параллельную /l,аннои.
325
Фигуры
СQхраняетоr 11 /tругос r:1:1жнuс с 1:юйстно пa
p<tЛ!leJJhllЫX ПJЖMl>IX , назъJRаемпе т.ран.зитив-
1юстью п,ара.п.лелыюсти:
Если две прямые а и Ь параллельны
третьей прл:м:ой с, то они параллель
ны друг другу.
Но доказать это пюйспю в стсрсоЬ'н:тр1ш
с1юж11ее. Н а ГUlоскостн нсшrрзллелы 1ые пря мые
uбяз:зны пересекаться и по1·ому нс могут бытr.
од11овременно 1. 1араJ1лt:льны тре1 · ьей (ин:з•Jе
нарушается аксиома параллел 1111ых). В прп
странсmе существуют не11араллелы1ые и 11ри
том 11епсре секающ иеся прямые - есл11 пни
лежзт в раз ных плоскостях. О та ких прямых
гuворят, что они скрещиваютсн
На рн с. 3 изображён куб; 11рямьrе АВ и ВС
псресекаютс.и,АВ 1·1CD - н:.~ралпещ, ны , а А.В 11
В 1 С1 - с~-;рсщ1-шаютс.и . В μ,альне1:rтщ:: м мы LJacm
будем прибегать к ПО.\1.ОЩИ куба, чтобы 111шюс
трнроват1, пп1 rя 'rня 11 ф:.~кты стсреомtтр 1 rн.
На111 куб склее н 11э шt:стr 1 rра11е!i - квадратов.
ИСХС>/!,Я 113 ЭТОТ(), мы будем D ЫFЮДТ Т1Ъ 11 дp)TJ I C
его свойства. Например, можuо уrве р;.к;tать,
что прямая АВ 11араллелъна G1D 1, потому что
обе они параллельны общей стороне CD со
дсрж;:~щих их квадратов.
В стсреометрю-1 отнumе н 11 е парамслы юс1·и
р :н:сматрн в:~етсн и 11т1 mюскос1 ·е (1 : две пло
скос 1 · 11 ил н прямая и плос кост ь па рат1ельны,
~с1ш он 11 нt: имеют об щи х точек Прям.ую и
плоскос1ъ удобно считать nаралле.r1ы 1ь1м11 н R
с
:)26
то,-.1 случае , 1ш1'да 11рнмая лсжнт в плос1юсп1_
Для llJIOCK<KTCЙ н Г1(1ЯМhJХ 01равед1 111вы ТСО·
ремы о ТJXll IЗИТНВНОСТI 1:
Если две плоскости параллельн ы
третьей плоскости, то 01iн паuал.·
лельны и между собой.
Есди nрямая и плос1<ОС'l'Ъ параллель·
вы :некоторой прямой (иди rиоско
сти), то 01m параллельны друг друrу.
Наиболее 11зж111,1й част11ый случай 1поро1·1
теоремы - rrрпз11а1< 11 араллсл1>1 юст1 r прямоi1 н
ПЛОСТЮСТI 1:
.-.
Прямая параллельна плоскости, если
У.'lг
k она псtралледьна некоторой прямой
В ЭТОЙ JUJOCKOCТИ.
А вот 1rр11знзк 1 1:1раллслы-юст1 1 111юскостсй:
:!L. -
Если две пересекающиеся прямые в
\I одной плоскости соответственно
параллельны двум перссскающи;\fСЯ
прямь1м в другой ru1ос1юсти, то этп
плоскости параллельны.
Ч~кто нсrюльзустся 1 т такая 11рост:н1 теорема:
Прямые, по которым две параллель
ные нлоскос ·1·и пересекаются тре·
тьей, параллельны друг друr·у.
П асмотрнм ещё раз н а н;шт куб (рнс. .)). Из
признака н:lралле-..лы юст1·1 прямоi1 н шюскости
слс/!,ует, 11 :1 при мер, что nrя ,,1::1я А ,В , nарал
лелыта плоскости 11BC!J (так к:~ 1< п11а nзрап ·
лсльна прямо1'1 .1Ш в этой нлоскости), а 11ро1Т1·
воположные грат1 куба. в част 1 юсп1 л 1 в,ср1
и ABCV, пз раю1елы1ы по пр11з11аку пзраттел1"
ноети шюскостсl1: прямые А 18 1и В1С, fl од1101i
1р: 1 ни сои1вс·r·с1·венно 1шр:1ллельны прямы~иш
11 НС и дру1·ой. И '')' l' h менее простой n p11 .~ep.
Плосксх~1ъ, ссщсрж.ащан 11apшu1c111>1-th1e пря~ше
АА 1 и се,. пе::ресt:каст 11араллеЛJ,Нh!С !IЛОСК()("П/
Л1В1С1D1 и ABCD 110 прямым АС и А 1С1• .1нач1rr,
эти прямые пар:тлелhl1ы: ~1н~1 iю 1·ич1ю, пара11-
пель11ы прямые В 1 С 11 A 1D. Он:;~о1шл::лыю. 1111·
раллельпы плос1<ост11 АВ , С н AiDC1, 11ересею!·
ющие куб по трсуrольш шзм.
ИЗОБ РАЖЕНИ Е
ПРОСТРАНСТВЕННЫ Х ФИГУР
Есть 1·акой афор11зм <>Геометрия - это искус
спю пранштъно рассу-Аq(ать нз нсправнлъном
чертеже->. Де 1~1с1·вн'1·елы-ю, еслн вернуться к из
ложенным вшпе расС')'Ж) {е11иям, ·1·0 окаже-1·с.н:
е11инственпая полыа , которую мы изRлеклн ня
сопровождавшего лх рисунка куба, состоит в
том , что 011 сэт<отюмил нам место на об·ьясне-
1ш11 обо:шач.ен11й. С тем же усщ:хо_\1 можно
было изобра:шть е1·0, как теJю на рис. 4, а, хотя,
0'-ll:Rll/(110, ПfJC..:)KTaRЛt: Jl llUC lla J-ICM <·НСУ.ТО»
нс только 11е куб, но и не ·"шогоrраш rик. И всё
жен принсдённом афор11змс заю1ючена ; 11 1шь
чзс1·1, правды . Вещ. прежде, чем <•р:ксужда1·ь» -
нзлагать готоnос 11оказатет1ст1ю. надо егп пр1 1 -
думать. А для этого пу-лою ясrю гrрелст:шлят11
себе зада~ шую фигуру, соотношешш между её
элокптами. Въrработат1, та1юе представление
помогаеr хороший чертеж. Более того, 1<ак мы
ун111111м, в с1·среомстрни уда'JН.ЫЙ ч.ертёж мо
жет стать 1 1 е про<.:Т<) иллюеrрацнсй. а осно rюi1
rеше нш1 :~адач.1 1 .
Художн11к (нсрнс<.:, художн11к-реалнст) на
rисус:т НаШ куб Т<!КИМ, K<lKHM МЫ l'I'() ННДГIМ
(rric. . +. б), .," е. 11 1 1еrс11ект 1 те, 1 1ли ц&uтраль-
1юй lljюe1·1цuu. Прн цетпрал1,ной проею~ин из
точки О (цеш р nрое1щ 1ш) на плоскость а про-
11з1юл1>ная: точка Х 11зображается ТО'LКШ1 Х', в
котороi1 о: псрсссr<астся с прямой ИХ (рис. .:; ).
Uентральшш прщ:1щия сохраняет прямоли
нейное расrюложение ·1·очек, но, как праннло,
лереяоди·1 nаrхuше.11ь11ые прямые в псрссека
ющиссн, нс 1 ·uворя уже о том , что нзменяет
расстою-111я 11 ~тлы. Изучение: ct t:RО11ств при
вело 1< пnя1i,1 1 еш1ю важ1ю1·0 раздсл;.1 rс:омстр 1 1и
(см. статыо «П роекrrншая 1·еаметрш1,~).
Но в гео:11етрттчсских чертежах исполюуетсн
μру!'ая проекция . Мшюю сказать, что 0 1ш полу-
,
,
,
,
,
б
1
1
1
1
1
;-----
Рис. 4.
Геuме1рии н пространстве
\1
1
1
---- -"\-
+---
Р11с. 5.
о
чается 11з 1te11трап1.>1 юl1, ко1да це11тр () у11аляется
н бссконечrюстт1 11 прям1.1 е ОХ ста1ювнто1 11а
раю1елы1ым11.
В ы берем п;юс кость а н пересекающую её
прямую/. Провсдё.ч через точку Х прямую. пз
раллелы1ую 1. Точка Х'. в которой эта пря,1:ш
встрсчастсн с а. 1Jec'1'h 1ш/.Jшu1е.11ьнш111рuел,-цш1
Хна плоскость а н,1юль 11ря.мой L( pJJc. 6). Про
екция фигуры сuсто11 ·т нз проскц1 11I всех сё
· 1·uчск. 13 r·со мстрш 1 1юн н:106ражt1 ше м ф111 уры
11оним;1ют её П<1 ра.11лсльн~·tо 11роскцню.
1
l т---х;;в
"
1
1
1
:
:
1
1
1
-
-
-
-
-
.... в'
Х'
•с'
,
--
-
-
""'D'
l'иt. 6.
Н частности, н:юбражсшrс прямой лшпm -
это пряман шшия шш (н \1СКJ110Ч11ТСЛЫ!ОМ слу
чае, коr;~а ТJ pJ1 ж1я 11а μаллсльна напранлсш но
просrщни ) · ~·очка. l l;i 1 rзображсн 111 1 1 1apam1e11ь
Hhlt' 11рямые так и остаются параллельными,
сохраняетоt здес1, 11 от11оше11ие ллш1 п~1рал
Jн.:лы-п,1х отре:жоR. хот>1 сами ДJ 1 1111ы и 11зме11н
ются. Всё вышесказаrшое можн о уложит~, 11
0/~11)' J<OpO'I 'l --')10 формулировку ОС/lОШЮЮ ШО/l
опва 11арrилмыюir прое1сци11:
327
Фигуры
.-.
.
ЕслиАВ=kCD,аА',В~СиD' -
проек-
W
-
-
k.J ..
дииточекА,В,СиD,тоА'В'=kC'D'.
Черта здео, означает н;шра1:Jж:штые отрс:>ки
(векторы), а р~Шt.:НСТВО - l'OBШ1 ) \Cl llIC нс:.; толь
ко м11 1н, 1 тu и наnранле1 111 й (р11с 6). Т:шим об
разом , ссш r за,Т(ать изображе 1111я точек Ан /З. то
nyl\)'I' Оl\ ! !ОЗНаЧ JЮ ОПJ1СДСЛС IJ Ы 11 1/ЗОnраЖС!IИЯ
l~Ct:X точекХ nрямойАВ, ПOCKOJll>KY Mlf()Жl!TCJJЬ
k в ranc11c1·11e л,у = 1.~АВ 11а пара:1лt:л1>1ю1· 1 про
екции и о рпг 1111 ~tл с он~шакпв. Л.11алоп1чно, по
нзображен~1ям трёх точек, rrc лежащпх 11а o,~
пofl 11рямой, однозначно восстанавm шаются
нзобрюкеr шя всс::х то•Jск проходящс!"1 чсрс~
нпх 111юс1юстн. а ::1адаn 11:ю6ражешrя LlCтыpfx
точек, [[(' 1-IJХОДЯЩНХСЯ ]\ 0/ ~ НОЙ nлocJ<O('"l'l ·J, ;\lЫ
11редоп JX'f\eJJJJt:м 11зоnр<1 же 1 шя нсс:х точек 11 ро
с·1 ·ранст1:Jа .
R 1'0 же: 11pt.::v1и и:юбрзженнс:vt ЩIЮЮЙ тroii
KH ·1оче:: к, ·1'. е. тpt:}TOJIЫ 111ка, может с11ужит1, ·1 рс
~г1 ·ш1ы1и 1< тобой :~:ща11 1 юй фоrмы. В этом ле 1 · 1<0
уf>едитьо1 : проnедём через сторонуАВ дашюrо
трсуrольшша АВС люб-у10 шюс1<ость о:, постро
им 1:J ней трс1то1.1ы-пщ АВС, пужноfl фuрмы н
спроектпруем трсу 1·олы 111кАВС на а 13/\0Jlь пря
мой / = CG'1(рис. 7 ). Взяв н качестRе АВС ра1:1но
бедрснный 1 1рн моугольный треу1 ·01 1ьник п до
строив CJ'U до ющцr:~та АВСП, ующ1 1м, чти н
11арал1 ю1ы ю~1 проскцш-1 кшч1р;п легко rтpcнpa
щaL"l"CJt в лrобо/1 пар<mлело 1 ·рамм. Более ·1·о го,
можно Д <){(а зат 1" что изоfiражсние~1 лю fiой
д<1111юй треугольtIОй пирамr.ты .vюгут б ып, лю
бые •tcrыpe точю1, не леЖ:lщие ш1 о,11ной пря
мой, uместс с соедиrшющп ми 1rx отре:ща ми.
Праnнлыю ш,16рашюе пзображспнс помо
гает ре шат~ , задач1 1 . НаЛi1См, н;1пр1 ·L'l.1ер. отно
ше1111я, н которых трсу1·01.11,нос ссчсн1 1 с:: rl 1B D
Рис. 7.
с
328
11am e 1·0 куба ( рис. 8, а) Jl.елит отрезок, соеди·
H>IIOЩJJЙ cepC,l\Иllbl jJ и Q рёбер AD и l3 1C1. По
смотрим 11а куб со стороны бокового ребра
BJJ, , J точ псс 1·овор}1 . спроектируем куб вдоль
прнмоl! ВП на mюскост1, АА 1 С1 С. l loш1·1·rю, чm
про<.:кц~rсй будет с1м 11рямоутш1ьн11к АА 1 С1 С с
провс.:лённым R 11ём отре:зком. сосдш 1я1ощ11м
ссрсд 1111 ы ос1юк1ю11:1 (точ l<JJ В 11 П сштаду~~
ри с. 8 , 6): рассматриnаемпс сечс111 1 е превrа
тится н <пре:зок ( 1 1а рнс. R, il о п красrюго цвета),
а точк11 Р н Q станут середпнами отрез1.:ов AD
н В 1С1 • Оче1шдпо, что на н::шн:м рисунке
A1.Q = ?>ИJ, ~1 ЗН,!ЧИТ. Pi\.J; _IJQ = 1 ; 5. в салу ОС·
1-юв 1 ю1 ·0 своf1 ства щ1рашн.·л 1,ной nрuекц 111 1.это
ранс::11ст1ю всрнu а в 1 1ростра11tт1:1е. Та же про
с:кц1 ш 1ю:mою1 е:т н:н1тн 0'1·ношс.:н 111..: м~:;.кду чэ
сп1 м11 :110601 ·011ронсдt:11нш·о н кубе отрезка. 1-ш
1<0'1·орые 0 11 рассе1<::1ется гтnскuстыо rJ 1BD. 11
час- 1·tюс1 н , иrрсзо(( f{Q. t'J ~e К - се рещнrа t!B,
шюн 1, дслптся с::ю 1~ от1ю1 11е1ш 1-1 1 : j . :з дш1го-
11альА С1 - ТJ о·люmе1ш11 1 : 1..
t::щё эфф~ктнее решения 11л:нш-.1етр11че
сютх з~щач, 1~оторые получают, « в1> 1 ходя н про
стра11ство ->, т. <.:: 11редс 1 · :шл.н.я данную шюскую
ф111 ·уру fl аиде 11 :юбр:1жен11я н1..:кос1'!) 11ростран
ствсн но1·0 объекта . Вот одна 11з т:1 ю1х задач:
требуется rюстрu11·1· 1, трt:у 1 ·uлы111к с нсрrшrна·
\1И на трёх данныхдучах ОА, ОВ 11 ОС с общим
11ачалом () таr<, что6 1,1 его стороны 11 ро.хо1111ш1
qерез ·1ри [{а1111ыс т1 утри у1 ·ловЛОН,ВОСи СОА
ТОЧТ<ПР,QиR.
Это очень трудная за[{ача. Но если вы дога
даетес1, посмотреть на её чсртёж {рнс. (), а) 1\ак
11а пзобра:же1iис трёхгрзшюго угла с тремя
·1·очкам11 на его 1-р:111ях, то, конечно, 11011мёте,
что и месте ;~ело с: задачей на 1 10строе1111е сече
н 1!Я этого }'IЖl ШЮСКОС1ЪЮ PQN. Pl'lll t:ll i'le за;1~ ·
в
А Р(=К) В(=D) С
б
б
1fll 11pl!ROДl !TtИ НЗ j)llC С), 1); Kt 1.l'Jll CKJJ,1\1" ОН()
ПО»rш1е-1 11 ос но.вно~'1 нр1161 11 острос1 1 11я с~ч l.'·
11лi1. 1lз !!рш r зrю,.-rы юl1 точю1 Е .'Iуча l >С ЩJ, )et-.-
nt[)н.:ч "1:ншы<· r u ч кн Н 11 <} rr;1 11.11оскос1ъ ОАВ
11u11,•ч :11:;\1 TO'u•r1 1<' н Q' П рямая Nf.! 1 1срс>сскаt'· 1 ·
Л,!()Сf{()(.T I, ( JAJJ 1\ ТОЧКt" ,\} 11;1 Пf>НМОЙ f<'Q~ [ l'IO-
CIOJ<."1 1\CKO.\IOГ() tTЧCHI 1Я псрссt.:к.t<.:т п:юсю >Сп.
О 1В по щ1я,1оl1 ,\ff~ ;1.L 1ы1tr'1шet' очет rд11t>.
ПЕРПЕНДИКУЛЯРНОСТЬ.
Уrлы. РАСС ТОЯНИЯ
"1" с11х пор :.11.1 , но с~ ществу, 1111г~е 11с rют,зо
иались та кн мн важны \U\ 1·со:.1<:1 p1 rчl'CIOf\tll rто
tiЯП1ячн. как расс-1 ояння 11 }Таы Дажt' в 11ащеч
1-'\бе 11:1 \I ":щст~п пч 1ю 11ыло 1u;i 1.1<0 тm о. ч m сrл
rp.111 11
-
параллсло1 ра:.Lчы. равенства нсех 1:r.x
сторон 1 1 уrно.в1 1 ~1 са.,юч дс:.1с 11е 1рt-t'<>1:~алось.
Ч 1 >бы 11\tCl1. 1юз:.1ож1 юст1 . 1 1зуч:~ть скоl1ства
K\·1iJ 11"1ру1·пх 11рос-1р;111с-п1с11ныл ф11rур но нccit
ПОЛ!ЮТС, нуж ны ('(JОТТК'ТСТRующш:: (JГ! rсдс:rе
Н!!Я Ilp~ж.;\e вс~ го ра сш11рн)1 1ю1ытне r 1ср11t:н
;щк,-,1 яр11осГJJ. 11зnс-с пюе 11з 1111Jн1~метрн11
Ест1 прииая 11с1х·сск;.11:т 11л1>Сl((}<."1-ь л гочкt.:
Р 11 nсрпеню 1куляrна тобо й npямofl n э1оi1
1 Lюсых. п 1, nроходящ<.'i1 ч ерез 1очку Р. то 1·<Jво
r11т Ч'П> д:11111ые ll/.JfL_Ш/JJ ll JИOCЛ'UCll/b llC!_flll(!lt-
1'11k_l'.r1Я/lllbl.
Напр[/\tер, ИСI Ю, 4ТО реброА.t1 HЗIJ!Cf'O куба
псрщ; 11 , шкУ, 1н рнп оснока111 11<) ABCD. 1l o ic:rк
пронерить, что '}ТО рсбrо ;:iciк·тm 11 ст.но ттср-
11t[ц111>.·у;~ ярно лю6о й лрн \IOI\ , 1сж~1щt:i1 и осно
вашш 11 n poxo;iнщei1 чef)t:J А? Ок~1 3 1.1иас::ти1. до
ст,~то•пю 101·0 , чтuАА 1 сое1·аn... 1яст прямы е yrm,1
<- ;пч \IЯ 10 Шfх
АВ п An пн·:1 ~1с110 щт шсtл)
11еjтендш•у трноспш прн1юй 11 1oor_~m:mu.
ec..n( орюtая 1нерпсндикудяриа дs)?t
r1ересеБа1ощп,1ск прЛС\JЫ:\1 а и lз, то
она nерпЕ'вди:кудярна плоскuсти, со
держащей а 11 /J.
Пр1 tЧl'M 1Дl'( ь пс обя:1:пелпно 11pc:дno,1ar:1 1 ь.
ЧIО 11рнм 1 .н: (/ Jf /J п<.:p('{'lKalO'I /: l"lll'l;ll«Л. ЧIО
ск рt:щr ш;н,1щ11Lсн 11ря:.11>1с riepn e 11;(111-:~.щp 1 1ы
сх Г\IL 1 1c:pщ:н;11 н:y'J}f[)llbl 11:tJ1<lL'ICffi1llhll' 11'1 np.и
;\lbl(.;. 11роходящ11с <tt:p<.:.1 11ро11!щ>"11.н о н.шn·rо
ruч К\ . н часп-юп 11 чt·1х.1·111ч К} rrt:pt"l'l ч1::111 ~н / t
I L IOCKOCTЪJll Так 1'10 ltЛCp 1. \\ 0,\\.НО (K.IJ.l П>. •110
nрм,ч. т . псрJ н:н,ri.11 i,.Y:шpн:UJ IJ_ ' JO("<JC 111 rrt>pt 1с:11-
:~11 "') ·ШР 11а .'llOOOJ 1 I Cfl...tЩNt 11 '')H1l1 11. 'I P('"()CJ'll
npи\1(>J'1. Сnракс;L н ~на так:нr ·н:ореж1:
i1y Чеf'<.'3 дaнJryio точь."У в нро<.транствс
ф~
\tОЖКО проuести одну и 1'0!1ЬКО ОД){)'
u.rrotкocть , n ерnендикудярную дал
ной пpSL'\fOЙ, а также одну н то:1ь){О
од:а[)' 11ря:;\1ую, пернсидикулярн ую
)l.ЗJJHOЙ П.'IOCl<()Cfil.
n~tp:i.'L'IC.iIЫJ:IЯ 11р0С1'.ЦllЯ H,l П.ICIC\(()t-J'Ь 11;1(>,'JЬ
11epm"·11,11-11-.Y:1яp11oi1 сн 11ря:.10!1 11:1J1,нза<:"1ся ир-
11ю?.r111алыюй ('1 ' , е 1 1рящ )уrпль11r~1 1) 11pr1eh'/(f((-' li
н.t "1:шную тюскость. Обычно. ко1 д:.~ 1 ·ивоrят
нросl'() • r1ро~юшя•. 1 1-.1е11>т n tшд~ 11:.tсн1ю ор
то~ 011а11ы 1 ую 11риею ~11ю О11а об;ц1\.1ет нсс'\н r
с.Ющ11щ1 с1ш iктн~)111 лар:ыле,1ыюfr 11pot:кi\1111
Но \' не~ се 1-ь и сnсцнфнчсt.к11t: сно lкти:~. 11х
можно 1 1 с 11 олr,зоиа·1ъ 11р11 μеш1:111111 Jа·(.1ч о
ра<хтои 11ш1' 11 у111:1х н 11ростр.111стnс.
1lз пр1пн.1"а nерпе11,~ш~:щр 1 юст11 нря.\1!11·1 11
плоск<)С'ТU выно.1н·1·ся оч1:111 r1pocт:m 110 в.tжная
тео/х'.iна и трi~У 111!/nu.•нrtllhT mpcL\ ( рщ·. 1О).
Р11(. 10.
1
329
Фигуры
Наклонная а к плоскости перпенди
кулярна пр1rмой l в этой плос.кос't·и
то1·да и тшrько 'J'OJ'дa, коrда её про
екция а ' на плоскость перnендnку
.тшрна 1.
Наклоппой к шюскосп-1 называют любую
пересекающую её, 1ю нс пернендикулярную ей
11рямую. Оба услошrя в этuй 'Теореме р:1нно
сильны TO~I )'. 'ПО ПЛОСК<Х"IЪ, содерж;,tll\<Ш (,/ и
а', пер~ 1ен;\11купнрн:1 11 р>1мой l .
ГJr1 1 меННМ обе теоремы К К)1б)' (рис. l l).
Проею~ш1 11С е1·0 д11а1 ·u1-1аю 1 АС 1 1-1~1 осrюва1 1 иl'
11срnснднкупярна д1 1аго11аJ1и осншш1 1 11я ВГJ: по
тсорt:ме о ·гrёх псрпе1 щ1 1 r<уляр:L-х, 11сэ ма диаr()
нал 1> АС 1 псрnе 11д11куляrна BD. По такой ;ке
прнчш 1 е перпе 1 1л:и1\}'лярны А(,\ rr А 1В. Отсю.п;а
следует, что днаrонал~) щ:рпсндпкулярпа "тμе
у1 ·ол ыюму сс: ч е111по» A 1.l:J1J.
IJ стсрс:омс·1·рии помимо uбыч ны.х 1~лuских
угло.в 11рИХО!\11ТСЯ име1ъ /\СЛО с:щё с тремн IШ
дамн углов. Угил .м&.Ж(~1' Сh1)(Л.l{U&ающzLмися
11р;1.мы.ми. по опрt:деле 1 шю. panc1 1углу между nc-
pcceкaющиl\UJC}I пр>1мым11, К()торыt.: нм 1 1арал
лсльны. Угол ,1-~е.жду 1tря.мой а 11 11JТ00;,остью а
ране1 1 углу между 11р>1мот1 а и её 11роеюr,ией а'
на шюскость (p1rc. 10), а если nрям~т и шю
с1юсть перпе1щ11куляrшы. el'O пртшмают раn
пым <)0°. Это п аи м е11ьш.111~1 пз уrлов между пря
мой а и любuй прямой н r1лоскос"ги а. Усол
"'J·lL'Jl(~J' пери<.:ектощиАшо11иосл·оош1,щ-1 и:зм~ря
<.тся у1·лuм ~1 ежду 11ерпсню11<у! шр<1мн. пронедён-
11ь1ми н ЭТИХ ГlJЮСКОСТЯХ к ЛllНИ11 их пе рсссч<::-
1-J\'IЯ (рис 12). Нес 11:1з13анн ы е утлы п р 11н111v~ают
з11а ч снин 11 промсжугке с >Т () J~o 90".
:S50
Р11 с. 13.
Н~1 irдём, H:111p11Mt'p, )' l 'ОЛ МСЖ,11~ jН1<'11 '0Н:IЛЯМИ
А 1 В 11 В,С 1·r~1 нt' 1'1 11a111eJ'O куба (р11с 13). З:~ме-
11 и.VI прямую В 1 С11а параллtJ 1 1 .11ую ей ди;~1 ·011ал ь
A 1D n[>01 · 111ю1ю1юж 1 юfi rpa1111; тrскомь1н угол
рдве11 углу BA 1D. т. е. (>0" (тpeyl'OJ1Ыll11< BA 1D
раrшосторош-~ий) . ~1гол между .'1иагональю АС1
и оснона~ше~ куба равен углу САС1 ~н::жду nря
.\Шй АС1 11 сё проекцией АС на основа н ие, т. е.
arC[g (С1С/АС) = 3l'CtA (1/ \:2). А )ТОЛ мeждynлo
CKOC' l'HJ\tJ I RПА 1 11В!JС, (р1н.:. 1;\) pa1:1eнyrnyAifl1C1 1
l'Щ' ,11 - середина ВЛ. •1·аи как прямыr:: Jt-! 1 нJЩ
:~ежа 1' н :".ITHX П JЮС КОСТЯХ 11 перле~ Щ11 ку.1ярны их
:111 111 111 пересечения BD (несложное вычнсленне
даёт a1-ccos (1/3)).
Расстоят 1 ием между 1tвумя любыми фпrура
ми называют нанме111,шую длину отрезка.
1<01щы которого nри 11адлсжат данным фнrу
рам. Значит, paccmum-11tf! от т.оч11:r1до1иос11:0·
cmu равно д;!ИНl' псрпс11д 1 Lкуш1ра, опущенно-
1·о и:.1 точки на mюскпсть, - он короче любоJi
H::IIOlOI I HUЙ, та к как Гl1ПU' l 't: Hy3:1 пр»МО)ТОЛЫI(}
1•0 трсугольн11ка корочt: катета . Расстоюше
\1СЖДУ 11ap~uuн.:.ru)11ым11 ПJIOCKOCTЯMll, ()ЧСВIJДНО,
paRTIO paCC'f'()>JJ 11llO ОТ ЛЮtlОЙ ТОЧК11 U ОДIЮЙ 113
11их до друтт1 плоаюсr 11 (рис 1..\, а).
Более ит 1 тересе1 1 вопрос о paccmoяmm.#UX·
~1· дс~1:.мя слрещuаающилшсл 11ряФ1.ы.м11 а 11
fl ровсдём <1ерсз прямую а п1юскостъ <Х, пар:111·
ле1 1 ы-1 ую прямой Ь ( р11с. t4, б). наiщём тoin'
11 t:рt:сесrення А ортоrон::и111 н оi'I проекц1111 Ь'
прямой Ь на а 1t точку В прямоi1 h, которая rrpз·
ектнруеп:н н точку А. Отрt::юкАВ 11ер11енднn·
лярсн тюскоеп1 а и 1ютому янляtтся общи~
lll:'pne1tдu~11J1яpo.м к прямым а и IJ Его дл~11GР
Рис 14.
р;шна расегощ111ю между 1-1а11111м11 скрсщнваю
щ11м11ся 11римым11.
Вмссrо то1·0 чтпбы ныч11слнт1. μасстоянш1 11
уты и пространстве. ч~сто :vюжно наход1лъ
соо·1ж.~тствуш1f\ие величн11ы 11а uр·1·ого11алыюй
11роею.п111 да11 11ой фигуры. H::i рис. 1'5 пока~Jа111>1
.1ве 1111терес11ые ортоrональ11ыс nроекцт1 куба
с ребро,\! длипы а: пrямоуrолышк разм:еf)о~1
,-
ах а, 2 (проекцин па дн~1rон~mы~:.10 тюс1юст1)
1СС 1 А 1 11m 1, что то же:, молъ 11иа1·она1ш BD ос
нова1 н1я) 11 ПJ1<11ЗНJ1ЫП11й ше-сrиуголыrrш со сто-
рuпо1l а'-12/5 (проекция вдоль диаюнали куба
liC1; мь1 nндс;ш, что прямая АС1 перпендику
:1ярна шюскосп1 HDA 1, а пото:-.1у прав1щы1ый
ч1tуп11Н1НltК BL)r1 1 ('() сто роrюй cf..Jl. н такой
проекц1ш не ~rскажаетоr ). С помощью первой
прое1щщ1 можно найти, например, угол между
а
А
B(= D)
Рис. 15.
с
Геометрия о nростра1-1стве
плоскостямиВОrl 1 11 BDr:1 - 011 p:шerr у1 ·лу меж
ду красным.и пря:\-1ы!\1и, 13 1ютор1,1е r~rое1\1·ии
ю·1 01 эти плос1юст11. А р~кстоянис 1· между J (D~"МiJ
скрсщиоающнмасн ,rт,наrо11аля~ш rpaL1e1'i UD н
В 1 С равно расстояпшо на р11с 1'>,а от точю1 В
до нрямuй В1С (В и В1С - изобр~1жсш1я первой
11 втuрой ДH:ll'Oll:tлer1 COO'l'B(.TCTOCHJIO). Jloдy
J\!:IЙ'l't' 1юч е-..1у (Jдссь нажно. что общ11й 11ер11сн
днкуляр диагоналей n::ipa1urt:лc11 1vюскос11111рu-
скц11и.) Л~..:гкu 11al1тr1, что г = а/ ,15. Нетруюю
Bh1ч11сл~ 1·1 ·1, на той же нрuекц1111 tr расстон 1,шс
~н~ж;су 1rрsв.1ь1м11ВО11АС, . Е11(ё 11roщt: наr'пн е 1·0
l' по'<ю1п.ъю рнt: 1') , б. на котором АС 1 11реRr~~
rцается 11 · 1пчк) . расстоян11е сп 1юс1 1ед1-1ей -
не11тра 11l<:>С'ГНу1 l)))hl-НIKa - Д(I вп )ХIШ!О llOiJO-
BllllC стороны 111ест11угольш11.:а, т. с. аj.,'6.
0'1°\1(.:'l'l ·IM llH'I'CPl 'CllOC C'OUT l ·Юшe1-111t:. CBЯ:3hl
~:1ющt.:с 111ющ~1;сьфн1·~ ры . 11J 1ощ:щь е<: 11росю\11н
JI у1·ш1 :vн.~жду 11.1юскос1·нJ\·tИ:
,'fl.,
Площадь sflJ) ор·гогопаJJЫiОЙ 11роек
"1'С ц1ш мноrоуrолыm1<а ра.впа площа
ди S мноrоуrольника, умноже1нюй
на cos <р, где q> - уrол .между его пло
скостью и плоскостью прое1щи:и:
:-это ОЧС!SНДНО /1,JISI тpeyГO!lbHLiK:.1 , U/ lHa 11:.:! cтo
J101J которu1 ·0 сон 11;щ;1ст с m1н11ей псрсссчс111ш
l\flYX Г\JIОСКО('Тей (р1 1с ~6) ~ши 11ap~IJШ<::JlhHa ей.
Л любой мно1·оуго111.нr1к \1Юж110 paci61·1 ·1
·J, на та
ю 1е треуrолы11 щн. Гlрпбл~ 1:ж:н1 кr1шот111tйные
фнгуры м1ю1·оуrолыншамн, nолуч r,1.ч, что фор
мула шющади проекции сnр аnещ1ива н для них.
ДВУГРАННЫЕ
И МНОГОГРАННЫЕ УГЛЫ
Дв1 1г1ю1111ьин угло.м называется фигуrа, со
стоящая нз 11вух полуплос1юстсй с общел
rршш'-11-lой прл."юй ( р11с. 17 ). Полуrшоскости -
с1·0 гртш, а 1 1х общ:щ 1 ·1х1шща - рi!бро. llapa
J 1 учс 11. по которым дву1·ранный угол перссска
t:тся с l l ЛOCKOC'lЪIO, llC[JПCIJ'f\IIK)'JIЯ[)HOЙ t:J'O
ребру, образует л1тейиый угол ;~ пу1-ра1 11 юго
угJ1а . Вес 111 1 нt:й11ые угл ы дuугр:111 1ю rо угла
р:1111 11.1 мс..:жду C()бOfr, JJ IIX вел11читrу Щ)ИШIМ;:\
ют з::~ вtJ111ч111 1 у лвугршпюго )-Т.7а. В отш1чне от
утла меж,1_1,у ПЛОСКОСТЯМ!) сё :!ШIЧ С!IИЯ могут 113-
меt 1яться от () до 1Н(У'
И1ю1·да 1щугрш-шым у1·лом удо61-ю: считать
любую 1 1з дnух ча<.:тсй гrространстна, 11;1 которыt'
c1 ·u р~1 зби ваt:т 11ара полуплоскостей с общt:1'1
1·ра 1 111 щ:й. C<.IO'l 'Bt''J 'CTRCH 1-Ю Л1111cl1 н ым углом тa
l(t)l 'O ~тcJH.:CIIOl'O> днугр;Н-111()1'0 yl'Jta бу;r~е1 У3С'IЪ
плоскост1 t, псрn<:1 1μ11,..;у;rнрнuй ею ребру l f о гра-
1н1чеюю~1 пучам1r, по К()ТQ].)ым ;mуграш 1ы й ~rгол
перссск:~ется с этой плоскостьто. А его велич~;~rта
может 11рнпнмаn, зна чения от О до 36U0
•
Ра ссмотрим ·1·ре-утолы1икАВС и точку S вне
шюскосn1 АВС. Фигура, образованная тре мя
плосю1,\11И углами ASB, BSC а CSA, назыв~1 стся
11!f"~x·гpa1mьL11f у2111.1м ( р1 tc. 18). Са мн 1 11юскис
уr·лы - этu с1'0 гранн, точк:~1 S - нерш ина, лучи
SA, SB и SC - рёбра. Многнмн с1-юимн сnой
стfiамн тrёхграННЫС углы H::llIOMHH<\IOT 06bl '1-
Hh1C.: тpeyJ'OЛ hHHКll . у ·1 · р ёх 1 ·р;1ННО l 'О у1·ла JVIOЖHO
111.щелпть шео·11 осптнтых эле м енто в: nar>ы
рёбер образуют три е1·0 плоскIIх углз. соотnст
ствующ11 е сторонам треуголышка, а пары гра-
11е11 з~щают содержа щие их дl.\уrранттые угды,
котор ым 13 треуrолыrикс отвечают углы 11ри
s
Рис. 17.
Рис. 18.
332
пepu1J111ax. ГL•юс:к 11е yt'Jlhf . КЗI< н t'Торо 11ы обыч-
1-1 ого тре,тол1,1 111ка, у110 влетно ря ют сrюего рода
•·неравенству трt.:уrольш1ка»: кажды й из них
ме11ыпе С}~!МЫ дну~ /(руп 1 х Однако здеС11 же
сеть 11 от.'шчис; "пери.метр-> тр<.:хrраш ю 1 ·0 утла,
т е. <..)'М~1а с1·0 плосюrх у1 :лов, огр:нтчсн - он
BCC' l '/\:I ~\(;'1 IЪЩС ,'i6U". в СU11(Жуп1IOCT I1 указ:тные
нср:1вс1-1стна (а+ ~>у. ~ 1 у> CJ.,
'У+ а>~ 11
а+~ +у< .~(10 ° ) состан лнют 11со6ход11мыс 11
;1остаточ 1 rыt" усттюr су11 1ес1 11онан 1 1н трЕх1ра11 ·
r юrл угла с nлосю1м 1 т угламн а, 1~ и у. Причшы
;i.:HTCKO IIД)'Ще('() СХО,Т(СТВа ме:жду тrёxrp;1111!ЫMII
угла:мн н трсуго.1ышк:~.:--н1 становнтся яснее,
если 11ерсссчь трёхгр=~1mый угол сфероr1 с цен·
тром n по вершине. Тогда свш'1стnа трёхтран·
1 юго ~т; 1 ;1 \ЮЖНО nр~дс 1·анн·1ъ как своlкт1:1а об
р:.1 :.Jую щс1 ocJt в 11срL:ссчсн 1111 <.:t!.н:р11ческого
треугольюrка. а они н оснонно м повторяют -
пусть 1 1н а1ювый лаf\ - снс нlстна обыч1 1 ых тре
угuт,н~rков (см . стат1. ю f(]1111 yp~.1 на сфере•)
Ecm1 li опрс;н:лt:11r11 1 трёлтра1r1ю 1 ·0 уt·щ1 за
менн1ъ треуго11ьтrк п:1 прон:шолыrыт"r n-уrоль-
1 ш1<.t:l1A ! " . А11• то получ нм определе1ше .ююzо
грт того (точнее. п-гратюго) угла (рнс. 19).
ТЗI\ же как LL щ1я трёхгра1шого углз, определя
ются его вершина, рёбра. гранн. плосю·1с н дву
гранные у1 ·л ы. Плоекне у1'.'! ы многогран ного
yma HC<::t'/\:1 МСНЬШС р~звёр11~r 1·01'() yr·;ra (180°),
ti шобоll r1 :3 них меньше суммы ост:~льных.
В яыпуклам м ногurраннп м >Тле (построенном
по въmуююму многоуr()л1>111 1 ку A 1Al ."А") ср1ма
ПJЮСКИХ углов ме11ьше ~(10",
)1.11-утрашщЛ \Тол мrroгorp::t1 11 юm угла есге·
стнешю 11змеря11, «11 зпу1рrl'>. другими словами.
как ~телесный-> дnугратшый угол. содержащпl\
соответствующий в11утренн 1·1rr угол много·
-утольш U<а A 1A J ".А": <:1·0 н<:ш1ч 11 щ1 ).ЮЖС:Т 11ри-
1111.мать любыс :шач~нr ш до .~60°.
Риt.. 19.
ТЕЛА
11:.\lil с11уп-1111< в сrерсомстрнчtх:ко11 акскурснн.
куб. м ы 011 рсде;1 1 1Jш как 1н::кото рую фr11 уру H;j
шt:ст11 К1iащх1тон, т. е . к~11< понсрхнопъ. Пр11со
ед11н11н к ней заю11очё1 111 ые ш1 утрн t:f · 1 очют.
гю;1учнм куб к<~к 1щиш. T t:n ep1, 1ю:~ 1 J ~н<омиr.~ся с
11ескот,ю1м 11 npne1'tйruпм11 вт·щамн тел, а :ia -
t e :\1 Д:JДJ JM Н ()\:) щее 011ределеrше Тела .
Призм:ы и цилиндры. 13о:~ьмём nлоскп й м1ю
rо1толы 1ш< ,\J, который 11еренесём паралле1 1ыiо
ВД()ЛЬ прям.ой, ш.:рсс.:ск,1 ющсй с..то 1 1.1юощсть, в
JIOЖJiКCHI11..' .н ~ ~1 COCДJlHllM все Cl'O точю 1 l' (.'()()'f ' -
RCTCTf\)'IOЩl IMH н м точк:~м11 М'(рис. 2(). о) . Тело,
ннлнющеесн обы.'диш.:1111tм rк:<::х пронсдённых
11ам11 отрс:жпг~ , н :.1 эы 1 1аетсн пр1 1з.м01i (от ?fJl?LL.
<- 1 1 ри:1:v1а• - " 11 ечто отгп ~лспrюе»). Его nовсрх -
1юст 1. состо 1 rт и1 ос1 ювани.й - мIIогоуголr,-
11шюв ,11 11 J\I' и Gоко11ых rpa1 r ей - 11аралле
!Ю1р:1."1мов, построеш 1ых на соuтnстстnсш 11"1х
сторонах ос1тощ1111 1!1. Отрсзюr . сосдшrяющис
соответств:1ощ11с всрш11ны основан 111\- fiоко-
11ые рёбра 11 р11змы . Именуют [Jр 1 1змы 110 <1 н с..:.11у
сторон основ:11-11ш - трсуrот,н~1я , .. ., 11-у1 ·олы 1:1н
Есл11 оснонаннс - 1 1 аrхи~леJю1- рамм , то пр11з-
Н ЕСКОЛЬКО ЗАЛА Ч
НА ПРОСТРАНСТВЕННОЕ
ВООБРАЖЕНИЕ, ИЗОБРАЖЕНИЕ И."
СООБРАЖ ЕНИ Е
1. П о 11р.~вила м чер че11ия прин я то изображать
пункти ром рсб рt1 мнnгогра 11 1-1 ика, рас положе1111ые
н,~ его << обrатной», скр ытой от HdL сторо н е. Н е
который м11огогран 11ик спереди и сверху выглядит
Од"1НJКОВО, как ГIUKiJ.З<lliO Н.1 р~1С 1, а, б. Пункти
ров Нд этих ~1зображениях 1ют - значит, нет н не
в1-1д11м ы х рёбер. П оп р()буйте догадат ься, как он
выглядит сбоку.
2. Может м1 рис. 2 служить юображе1·1ием (11а·
пример, видом сверху} многоrран никд <-тремя че:
тырёхугол 1,ными и лоумя треугол ьным и грд ням и {
3. Н<1 рис. 3 и.юб р.1же11J треугольная пирамида,
11 которой проведены лва отрез ка, сnелиня юшие
точки н а противопплож ны х р~брах . Мnжно ли по
рисунку определить, п ересекаются эп1 отрезки в
п ростра11ствс или 11ет~ А если можнu, тu как?
4. Каждое ребро правильного тетраэдра поле
лили на три равн ые части ~1 через тпчки деления
провели плuскости, пар.млельные гра11ям (рис. 4).
На сколько и каких частей ш1и разрезают тетра::Jдр ?
Геометр и я в п ространстве
б
()
8
Рис. 20.
~1:1 - 11а/тлrц:ле111mе1) ( р11 с. 20, 6), 1ютоr 1 11l1 чн r>
п 1 м похож пз параш1ело1 ·ра .,1i\1: J1анрнмt:р. t rrJ
центр с111•1111етр 1 ш О является ()()щей серед~ 11 ю\1
nccx четырёх дна~ ·он:~леИ. а протиnопо.rтож111,1 е
1·р:1 1 ш параллельны 11 равны . J.2cJ ш боковы<.:
р<.:бр<t 11р 1 1змы ш~рш.:ндикулярны uс.:rюnаншо,
· 1 u 1 ·01юрнт. ч·1·0 она пря.маJJ . Ост;шьныс прпз
л1ы - 11ах:1ш1L11ыf!. Прн м :н1 11 р11J м<1 , в ос.:новашш
с
l'и с. 1.
Рис. 2.
Фигуры
ко·юро~111рямоуюлышк - это 11ря.моугаль11ы1i
паралле.лС'nши1д, куб - его ча<.:тпый случай. Куб
можно рассм ~1 тривать 11 как Р'Jзновид~юсть пра
вш1ын..11~ 1tризл·tы, ·1
·.
с:. 1 1 рямой 11р11змы. uснона-
1tнt.: которой П !ХIRИJIЫIЫЙ MllOl'OYl '()ЛЬIJНK
Заменив в оr1рсделск111·1 11rиз мы многuуголь
ннк .111 -1::1 кру 1 ', мы получим опрt:делениt лрую
впю ц11.1щ1и)jи (от греч. <· Ю·11 1 и11;чюс»; рнс. 20, 11).
Отрезю1, соелнтrяющне соотRстстnс1111ыс точ
т<и на окрулптостях oc110вaiшri 1 называются el'O
обра3ую1цuлш. r:сли 01111 перпе1щи~<улярны ос
пова 1 mю, то n.илнпдр п;тмой. В ::1лсмент;ч)1ЮJ1
геометрии прямой круппюй ц11ли1-щр об.ы ч.но
нмс:нуют 11рос·1 ·0 Ц1·1J 111ндром.
Если в К<NС<.:тве ос1юна1 нrя 111 взять 11ронз
волы 1 ую шюскую фшуру, 1 юлуч 1 1 ."1 обоб1цi!гt-
1-1ы/i цu.11u1u)jJ, част11ы ,\1н случ:-1ями которо 1-о
Яt111>1Ю'1' СН ЦllJl\111,Цp 11 1 1 рнзм;1 .
Пирамида и 1юнус. С.тюnо «ш1ра,,п1да» u 1·ео
метrию ввели ~·реки, которые , как нолагают, за
имсnювали его усгиптm 1, создаnших са мые зна
мс1 штыс пнрамнды на свете. Другая теория
нынод11·1 · этuт термин из !'речсско1·0 СJ1ова ~пи
рОС Р (pUЖI>) - С1 1 11'1':11ОТ, ЧТО ! 'р<.:КН Bblllt.:K:1Jll1
хж:б11ы, имевшие форму 1 1 ирам1щы. 11одобно
1 1 ри~>1\.Н.:, 1шj)(,J.лt111)a - тело , состоящее 11:3 нссх
отрс:зкоп, COC:::J~И I IЮОЩНХ · ~·очки 1UIOCKOL'O M I IOJ'O-
}'l'OJll~l IИKЭ. 1Н - её oclloвamm - сточкойS, не ле
жащеii в плоскости ос1ювашш. - аершшюй
(рис. 21, а) . Отрезки от ·1·очкн S цо вершин м110-
гоу1·ольш1ка "1 11азыnаются бо1швы..ми piiбpa.111u,
а трсуrольпшси, образованные каждой из сто
ро11 ос11ова11ш1 М и бшшным 1 1 рёбрам11, 11 рu
ксt1tнным11 к кон11ы этой стороны, - бштвы
.м" ljJtnl.ЯЛ'/.1,(. ш1рамиды . ll 1 1рам1-ща, ОСНОВ::tНИСМ
которой я влястся н-угольник, называется 1t-
уголыюй. Если оснопанис - праnилы-1ыr'1 мнu
гоу1·от.ник, а боковые::: рёnра рат1ы. то это 1 1н
ра..,,нща 11рщшлы1tт. Тело. nолуча101п.ееся 111
m1rа,,шды, если отсечь её вершшrу плоскос1ъю,
параллелы-1011 ос 1 юванию, называется ycelf{f11-
1юt'1 пирамидт~ (рис. 21, б).
Рис. 21.
отв еты к ЗАЛАЧАМ НА СТРАНИ UЕ 333
2. Нет. П рямы~АО, ВЕ, CF должны пере("екаться
в uлной точке.
l. Можнп. Отрезки пересекаются (т. е "ежат в
одной плоскости) тогда и только тогда, когда либо
точка ПС:!ресС:!чения гиних прямых лежит на прямой
АВ, либо они параллельны.
4. На 15 частей: 11 тетраэдров , етрuе меньших
ланного, и 4 правильных октаэлра.
З<tмtшн1 п опрtдt:Jн::1ши п11рам1Jды мноrо·
у голы 1и1ulf 11а "рут. получ1 1 м 011ре1\еле11ие КР.)!·
гового l\:cmyca (от греч. <· ко1юс» - ~заострё1111ьпi
предм~т»). а 11з IJero - 11 усечi!т юго 1(01~уса
Отрезок от верши11ы кругово1·0 конуса де
от~ружности основа 1тия пазыnают образующе1I.
в ЭЛСМСI ~тарной J'C()Mtтpю·I 110)..( конусом обы'1·
I IO IIOHИM;.!f()l'TIP!IMOЙ крутно11 кuнус,т с кpy
J'OBOll KOllYL' ( .' f1~ 1Н llЫ MI 1 обра:3)' 10ЩИМ I 1; C I'() 1\Ср
ШНН ~J проект11р) ется 11 це нтр основания
(рнс. 2l, 11).
Копус 11 пr 1 rам1ща - :~то ч<1<.:т11ыс t.:л}rча1т
обобщё1t1юго ко11уси. ос 1 юва 1 rнем 1ю'1·про1·0
может быть mобая плоская фигура.
Ша р и сф е ра . Ф11гура. образованная всбш
точка мн про<:тра 1 ктва, у[(алё1п11,~мн от да:шю1i
точ.ки () н~ расстошшс Н, аа:iьшастся cфepoti,
О - сё 1tс11тр, N - р"щиус. Сфера 01·раннчинаст
шар - MllOЖCCTHO ТОЧ<::К. 1 1 аХ<ЩЯЩlfХСЯ ОТ
tttнтpa на расстоян1 1 1 1 11t.: болы н с р~щ11ус1. Ин·
т<::рtт н о, что оба термин:~, несмотря на р:1зJ1и·
ч11е смысла 11 :з11уча1111я, 11po 1 1cxoJl)П ' от грече·
ского слоnа «сфапра» - <· 111 ар», «м>tЧ>}.
Рис. 2l.
б
Рис. 23.
Конечно, вы з аметили, что 011ределспия
сферы и шара повторяют 011рt'делсrшя tжрул<
шк·r1 1 и круга. u с войсгвах эт нх двух паr ф111·ур
тожt ....11 -101·0 uбщt:J'U, Н:щримt:р, рассм:1тр11нан
юа11м 11о е расп оложени е сфе ры 11 111юскост11,
\ЮЖНО об наружнтh три отучан. ECJIИ r~н.:с1ш1ю1е
r/01 плоскости до центrа сферы мснhшс р:щ иу
с:.~. то 11 лоскостъ и сфер :.~ пе ресе1<а ютс н 11п
r
01<ружностн радv1 уса vR 1
-
d 2 ( рис.:. 22, а). fcJJи
G/ = N, '1 '() llJIOCKOl"l ' I, 11 сфер;~ нмсют CДИJJl''l'RCH
H}JO общую 'l'ОЧ ку, Г1 рнчём 1IЛOCKOC'l'h нерпе~ 1-
ДН!-)'ЛН [.JН а p:.t1111ycy, II[IOH<..:/l,ёHH OMy 13 э·1 у точку
(р1к. 2.2, 6). Такая плоскостh 1 1 ~1:.1ынастся 1,:aca-
1m!ЛЫIOil 1\ сфере ( 11 СООТИС'ГС1'11у1ОЩt' М}' r11apy)
Пр1r с/ > R 11 1юскост1, н сфера пе 11ересскаютси.
Пря"'1ая касн:тся сферы, если она нме<.:т со
cфepo ri едннстве1111ую общую точку. Все пря
\11,1с, касаю щиеся сфер1.1 t1 NH1tioi1 точке, лежат
в плоскости, 1<асатслыюй 1< сфс::ре в :этой точке
(р11с. 22. б). Для сферы вср 11а теорема о юса -
1·елып.1х: uce касательl!ыс, проведЕ1шыс к сфе
ре ИJ дашюй точки , точнее, JIX отрезки от этой
точю1 до точек касаштя ( ри с. 23) раrн1ы.
Свойстка фшур н:~ сфере изучаются в с~ 1 е -
1 1щшьном ра:щслс 1·сомстр и11 (см . t.·татhю <·Фи
гуры на сфере»).
Теда вращения. 1~•1111п1rtp м ож1 ю прс~сr-.а ни'11.
как тело, воз ~ 111каюm;ее 11ри вра 1це1 1111.1 прямо -
ГЕ>омt:•трия в простра нстве
а
б
J>ис. 24.
Рис. 2.1 .
уголы111ка нокруг его стороны ( р11с. 2-1, а). Ко
нус - прн uращс шп-1 nрямоуголыю 1 ·0 тrc
yrOJIЫ шка во1<р} 1· 1<атста ( р11с. 2 i. б). а 111 :111 -
полукруr·а вокру1· с 1·0 диам етра . Точю·1 у ка -
3а1 IHhl X 1IJIOCIOIX ф111ур 130 врl":МI нращС!J11}1 (J I llJ-
cын:IIOT окру·ж:ност н с 1 tен·1 ·1х1м 11 , пежащ1 1м11 11:.1
11<::кm·opol1 11рям о il - ос11 пращ<.:н11я, в п1ю
с1<ос п1 х. <::й пср11е 1 щикулнр11ых. f) общем слу
чае любое 06·1,сл.нт 1eJ 111t р<1сnо;южен ных таким
же образом <жруж 1 юс1 ·ет'1 па зын:нот c)Jигypofi
араще1JщJ. Ещё одш 1 r11п ·ереспый 11р11мср фн
гур1.1 враще1шя - тор, т. с. понерхпост1" обра
зующаяся прн н1х1щсш111 окруж1 юст11 вокруг
1rc 11с ресе к:uощсй сё прям ой , лежащей н шю
с1mст~1 ш.<ружпосп1( р11с 2 '5 ). Г::сл н (,запuлн 1 1·1ъ»
тоr, т. с. Rращ;~·1ъ круt', а ш: окружност~., '1'0 1ю-
11vч1 IТСЯ Tl'JН) нращеJ 11 IЯ, нa:{hJB:Jl'M()C fl().!/Г/()Jl1()
/me.м. Имеются r1rюст1,1с 11 крас11ныс фор.'1улы
/\ЛЯ 061.ём:~ 11 1 11ю1ц:щн r юнерх1 1щ·11 1 1·ел 1-~рэ
щснют (см оч<::рк <· Об'1,ём и пл nщ:~;11, 11овсрх -
1 юсп1 тел Г1[Хнце1 шя» ).
Произвольное тело. Тепе р ь можн о nодыто
жнть рассмотрсн11ыс пршvrсры 11 /\ать общее
оnрс;1слсш1с тела. Но пачаТh 11р11дётся пескОJ 1ь
ко нз;tалска .
У любо(~ фигуры в нростра н с•1·вс можно
ВЫJ\t:Л ить 1 ·р:1нн1\у 11 внутрс1111юю обл:к1ъ .
Так, 1·раннц::~ 111 3ра COCTOllT И:J ТОЧl'К соотнст
стнующей сфср1 .1 . а 1 т>а11и11а н111х1м11;11,1 - и э
Фигуры
точ~к её ос1 юваr пш н боконых rp<шcli. Говор}/
более строrо, ~шзонём точку г1ю1шч1юu. если
скол~.. у1:одно близко от неё иож.но указать к:~.к
точю1 , 11рт 1 адлсжащие ф1пурс, так 11 точки,
пс пр1ш:щ1н::жащ11е фигуре . Сама эта точю1
11с обя:щна 11рина11,11с:жатьданно~'1 ф~нуре. Р:~с
смо· 1 рим . 11а1 1 rимер, ф111уру , состоящую нз
всех точек ко1-1уса, кроме с1 о 1крш:ины О. Точ
ка П - 1·ранич 11 ая для этой ф111уры, хnтн 11
нс прrrнадлtж r1· 1 · ef1. Г/ютща ф11гуры
-
это
м 1-тожес~ 1ю её rpam 1ч1 тых тnчск. Ф11гу1х1. котn
р:н.1 со;\сржит с1юю rратщу, 11азьшается зш1п,·-
1~1·тоf1. А потому рас-с мотре1шыii nышс конус
без вершины - ф11гура 11сза~1кл~т~ш. Tu•1101
фшуры. пс являющиеся гратшчвьвш , образу
ют се Вi l~треннюю обласгь: 11.Х так н 11:1 ::1 ы:ва
ют - в1-1утреш·ше то ч к 1 1. Дш1 люnоr1 ннутрс11-
1-1с11 точки ИМССТОI шарик с (\Cli'ГJ10'\1 li :'JTOr'I
точке. который щ~лнком 11р1111а;1;1tж11·1· ф111-у
(1С. Скажtм. ;1,т1 ·ючки 111ар<1 р;щ1 1 ~ са R, yд~urf11-
нui1 0·1· rц:·uтра н:~ 1хкс·1·ою11ц' .У < R, мож1ю
11:ш1·1) 111ар111< радиус" R - х.
МНОГОГРАННИКИ
1\Jнo?o1;ю1шu/\(JJ1f. н:1 з 1,111:н:1·ся тс.:ло. 1ран11ц:1 ко-
1 ·орш·о COCI оит 11:1 MllOl 'OYl'OЛlil-lHKOI! Jtетсю 1(_ "
к~6ию 1. арл1 1тек 1 ур11ыс сооруж:с1 п щ 1rтел11р11ыс
укра!ПСН1 IH - ()\'JIЯIO l'l'CCI) rюr<py 1 ·. 11 нr.1 пайJ1,t:те
"" ю!'о1рt11111ики пощ· юr~у. Вот ку() (рис. 1, а). r.J'O
11011ерхrюс.-гь образ1111ат1а птсстью р;~вными 1ш:.~д
ратам11 - гра1Jл.ми. У к:.~ждоl1 1'ра1111 четыре вер
шш1ы, тю каж:дая IIJ вернптн п ришщлс:->1u 1·1· сра
зу трём граням: 1ксго nсрш1ш у куба восб1ь
Каждая грань нмс<.:т четыре стороны. Сгорщ1ы
гранс::й нменуются рr!бра.1ии куба. Все1'0 11х
днt'Н:t/\11ать, 1,1 каждое ребро нрн11:1д;1сж 1 1т ;сву.\.\
а
б
Рис. 1.
Тело.111 11азы11ак>·1 1шr 1 ечную з;~мкнутую фн-
1 уру, у I<OTOpOil CCTh nнутренние ТОЧКИ, гращща
соnтталаст с гра11нце1'1 в11утрсш1сС1 06лае1 н 11
любые Дl:\С:: .ВH~" I P<.:l!IIIJC ТО'-001 можнu <.:OC/,lllf!Пb
лсжащс1'1 11нутр 1 1 фшуры лuманuй. В вьшуююм
'Гl'JIC МСЖ/\У любымr 1 l\ll)'MЯ TOЧK:lMll МОЖJ-10 про
несг11 лс.:жащ11i1 н t1i.: .'v1 т р<:зок Нструд1ю про
кср11ть, ЧТО raCC.\10TpC111[blC:: IJ l >1Шe ф111 уры -
пр11:зма, копус, шар 11 т. /\ - тела. А nот пр11-
меры фигур, пе л11т1 ющ1 rхот тслам11: шар, "оч11 -
щ1.:1 шый» от сферы; полуnростраr 1стnо: квадра·r,
фшура пз днух касающихся шаров. ДrlЯ каждой
нз штх нарушается 1\акос -то усло 1шс с.111реде
лсшш (уст:.~нон11тс какое) . Гран1 1 11~ ·п:л ;1 11а
зьшаю 1· с1 о 11щюр.'\·1юо11ью.
В:1ж11ыl1 кж1сс ·1·t:л обр:1:iуют мнnгограннв
ю 1- тела, гrа111111а кuтор1.1 х ок"1'<J111 11J м11оrо
~тоJ11,н1·11<он. К m 1 м, в част~юстп. оп10ся·1·ся
пр11 :1 м1,1 11 111 1 раl\1Щ\"1 .
Мrтогогр:.1ш111ю 1о()лал;ают мrюжест1юм нн
тсrсст~ых CJ:JOЙCTB, О Ьl)ТО[IЫХ /Х1СС1Сl3ЬПК!СТСЯ В
дру1·11х с-1 ·аты1х этого раздела.
1раннм . Пож. 1луi1, К)· () (<·ку611к·•) - c1~1111i1 ,xorю
Ll lO :-ша1юм1.1 й пам 11.111р1·{н ·р;~11 1 111к Н п нс са_чш1
11ростоl1 . R ;-пorvt ол юше 11 1111 чс-vtmю1юм шvLЯ·
етсн треуrот... 11ая 1 111рамп;~~1, илн тстрс~~др
(рпс. 1, б). У r1её талыш четыре верrпщщ
а ме11ьше и nзят1, ш::льзн - nсдт, любые ·грн
то<1ю 1 уже лсжа·1· n o,ТJ,тrofJ плос.:кост11 Граней
тоже: че- 1 1,1 рс - это трсу1 ·011hн1 1 кr1 с ве р1111111;1!~ш
в нерr1111нах ·1·етrаэдра. а рсбl'р 11 1 сс1ъ. При 11се11
сноеГ1 11e:i~1"1ыслонатост11 Тl'' 1 ·разщ1 06:1а;щет
м 1 южес·1·1:ю ,-..1 ннтl'р t:с 11 1,1л своltств (<.:м. статью
,.J 'сометрия тетра:щра .> ). Тстrзэдр 11 куб - Щ'КД·
стаrштели двух СС1'-'1сlтсти мтю1·огра1-шиков. ко
торые на 116олсе часто встрсч:нотсн н на п)uках
н школе, и 1юкру1 · нас. Те11Jаэдр - чзстныl1 вид
пиралztды ( рнс. 1. в), :1 куб - 11/шз.мы (рис. 1. ? ).
О11ре;~слс1-пrя этих тел. указыв~1 ющ11с вес точ
ки , 11з которых он1 1 состоят, даны н стать<: « На
чала стерсuметри-1 1 », Но ~110rn1·1х11-n1ики мож-
110 011рсдеJ1ять 11 нпаче - 011ис аn их гр:шп.
Так. п-уrолы1 ая пнрамида - мтюгограшшк,
одна нз граней которого (ос нование) прои~1-
nолы1ый п-уголыпщ. а осталып.1е 17 граней -
трсуп>1rь1п11ш. Можно нс угочншъ, как сё гра1 rи
CUCДJ!l-ШIOTOI дру1· с ДР}' !'О.!11, 1ютому что если
ны начнётс составшпь 11з н11х м.1-юпн·р~н11-tик,
то ср:1зу убедн·1·<.х:ь, 1 1то нсt: треугuлы1ию1 06.11 -
эа11ы 11мt:'тъ общую1~ерш111-1у. а их сгоро11 ы , nро
п1ваполuжныс:.: эт011 нерши1-rс:.:, r~олж 1rы бы ·rъ 11
сторuна ."м1 ос1юваr 1 ня.
Л1 r:tж)1 '11чпо. n-)'ТО11ы rал 11рнзма обра:юва1 L<l
двумя раш rыип п -уrолы шка,vш (ас1 1 0l3a 11 kщми).
11ежащ11ми в пэраллел1.11ьL"С nшхкостях, н п
r~араллелоrраммаf.11 1. Но будьте осторожны.
не пропустите n данном определен~ 1r1 м~ut<::IIL
кyю буковку 11' Н С<1N1ых соли"1ных словарях и
:1ажс 1юро.й в учебниках геоме· 1·р1щ можно про
'1Нт:.1·1ъ 11-р~-16лизн1·елы~о сJ 1 t::;\ующсе: прнзма -
мно 1 ·01ра 1 шик. две rр:111и котор01·0 ра1111ыс м1ю
Юутоm,нrrкн с параллелы-11->1.ми еrп ро11амн, :.i ос
·1ат.ные 1·ра11и - rrар;т1 1елогр;1м ,\1h1. Каза1юсt,
бы, все nepr ю, 0)11 1 ;.~ко 11а самом ;i:eJ1e. как видпо
нзрис. !., это непрз1нmы юе определение. И даже
если оrра 11ичиться толы<0 выпуклыии мноr о
гра1 1111шамн, nраuилы1ым оно 11е станет. Паnро
буflте сами rr rшri;yмaть коптрпример. А заоДiю
nо;~ум: 111тс н над таким нonpucuм: любоi1 ли
м1юt·о1 ·ра1-1н_нк, вес грани кuтороrо к~~адраты ,
является кубом? Оnк:ты - в кuнцс статы 1.
На r11c :) ппк;.13ано сщё НССК()Л!>КО Rl lДOR
мнnгогран1111коn, сnяза 11ны х с nр11змам11 п пt1-
rа~1ида.\11и: усечiJниах нирам.ида. бипира.мur)а
Р11с. 2.
Рис. 3.
Усечё1Jн.ая
1111pa~tt1ut1
Геоме1рия R 11ропранствf-'
(06ъс; щ11с1111е двух пирамн:t, 01ммс::тr11чпых
относитl·лыю 11х общего ос11онания) , тт111-
пр11.з.ма (она t юлуч.астсн И3 правильной 11-уголь
ной призмы , сс1111 1~овсрпуть ei:! основаrmс
нокру1· 1{снтра на усол 180"/п 11 сос1111щ1т1, 1:1ер
вн1 н1>1 оснона11нl1 з1rгза1·nuбра :1ноl! лом:11юГt) .
Ест1 трс}·1·ольную ант1 1 11рнзму • закрут11·п,?
l/O CИJ IЫI CC , 1юлучится .11\IJOГOl '\XHПllll\, ГЮJ<а3:111 -
rтый па рис '"'· Н:1 перЕый fl:1J 'ЛЯfl 011 1111чсм
1rc примечателен. Но у него сс--1ъ о,>що у,1и1ш
тельное, пропшоречащее 1111ту1щ1ш с rюi1стrю:
r<акне бы четыре его исршшп,т мы Ill11Jзяли, оп
РС/\СJmс11,1ый нми п"'Тра:щр н<: бу;tст nомсщ:пъсл
целиком ннутр11 такuй а11 ·1 ·ш1р11змы1 На nло
скост 1 1 гrич'J'О 1 юхожес невоз.\t0жно: 11юбuй
МН( 1гоугольник уд:~ётся р:вбит1, на трсу 1·011ы-~н
ки, 11 е ;~оtlавляя rювых нср1 111 1н. С13язано это п:~
ралоксалыюе сnоИстrю <- перекруче1 ~ной анти-
11ризм ы• с тем, чтn он:t невыrтукпая. (H:.ina~1н11.vt,
что тело, 13 чзст1rос1·11 i\11югогр;1шп1к 1 та з 1 ,1на
~·01 оьпо•клы.м. ест1 uмссте с любыми 7'fJy:-1я
с1юпми точкамп 0110 содержит 11 соедпншощнй
пх отрсзuк; см. статью « 13ыпуклыс фигуры,>. )
Любой впr11уклый м1ю 1 ·огрг1нн1ш, как петрулно
ун1щс ·1 ъ 11а рисун кал . всегда .можнu р~1зрезать
на тстраэдр1.1 , 1'1<.;ршнны к(r1·uрых 1.:овп;щают с
<.тu вср111 ш-r:.~м1г.
Усечё11ная ш1рам11да 11:1 рш: :) п куб об11:1f{з
ют суr_цсе1't1с-11но r:.~з1-11,1мн с1юйе1·11<1!'.н1 - у rrep-
Fюйnce 1-ра1111 раз11ые, у отороJ'О- <1/(11накn11ые,
но -в 011ре11:спё~_ пюм смысле их мож110 отн сст\\
к пд 1юму кткс5" у nбопх м 1 юго1 ·ра~п1111юn пю r-
ш11юFюс число 1p:11Icli (шесть). rке гр::н ш ол1 ю
го пт~ (чстырёхуптr,11ию 1) 1r соедтrены в
од11нактюм порядке (п о три rюкр~т каждой
"ершнны). В ' 1'()1' же класс Rход ит и n;1р;шлс
лсннпсд. l'опорят, что вес 11азванныс· иногu
гр;1н11 нки r1мсют 0,11111-~ ~шов ыlf 1..:ш~б11ниторнъt1i
ml/n. Друr1ши с1юва~ш, ш:рши н~м любLJГО 1 1з
эт11х мнопн·рз11m1ков r.rf 1ж110 так соnnставнт 1 ,
Би1111jтмида
Р11с 4.
Afll1Ull1j>llЗ.Ma
L
Фигуры
1:н::рш1111ы люllor·o другого из НI 1х, что с()m·11е•1 ·
стnие бу[\ет nзаимно од 1 юзLiа ч 11ым , 11 если n
пл,ном м11оrогран11ике к;нше-то вер111и11ы со
единены ребром (или лежат n одной rрани), то
же бу[(tТ верно и для СООТВе'l'СТJ3)10ЩИХ им nер
ШШ I в дру1·ом .-..1ноrоrрапникс. Би п ир:н.шда па
рис 3 и «J1ерекручс 1 шая а пт1-mризмаv (рис. 4)
тuже ~Jмеютодинаконый ти 1 1.Аншю1· 1 1чно мож
но определить и тнп мно1·оугuльннка , но ЗJ~ec h
всё 1 ·ора:здо проще: оче1шдно, что нес много
~'ПJ1 1 ы1и 1<11 с ОДИ liаКОRЫМ Ч11СJЮМ перш1 1 11 11p11-
lta)(J1eжaт т< сщному тиоу. Др~rгое /(ело мrюго
грашшки. Число нх п 11 ю11 при за[(атпю:м ч исле
верши11 lJ растёт очепь быстро. Если в ри lJ = 4
есть толт,ко ОТ\Ш I тип выII)'1(ЛЫХ многограппи
r<аn - треутольная пирамида, а при В = S - два
(четырёху r·ольная пира .мнда и трсу1·0111,наи
би11ирам 1ща), то при В= 6 их 7 (р11с. 5). 11ри
Рис. 5.
В=7их34,приВ=8- у-же2:S7,приН =9 -
2 606, а при В = l О, 11, 12 получаются числа,
превышающие .)0 ООО. 400 OUU ir '5 UUO ООО со
ответственно. Т:жо rо рода оценки и вообще :.-sа
дачи комбннатоrнки много1· μанникоR 11 рнuб
rел11 В наше RpCMS I 11ракт11 ч еСКОе :Ш:IЧеllИС К
cRЯJll с ли11ей111>1.ч 11ро 1'раммиронаннсм - ра~1-
дt1юм 11 рн 1щад1 ю11 м:~тсм ~1 ти ки , п 111.::рпую пче
ред1> математич-сскоil экоrгомн 1н1. 11 1ю·1·()1х),1,1
ра::1рабатьmаются методы пычно 1 е1 11м1 11аиболъ
ППL'< н шiименьmнх :з11ачений ли нейных функ
ций на nыпуклых многограш-r.иках в мно1·0-
~1ср1rых пространствах .
В необъятном 0 1<са11с м11ого 1 -ранных фор,,1
RЫДе.JIЯЮТСЯ своим соnсршснстRОМ llНTh 11ра
НИЛl1НЫХ мио1·огранников, ИJ l l l ПJJaTOHOf\ЫXTCЛ,
гюстроеи 11с котор1,1 х венчает <-l l:Jч~UI:J» Евюн-ща.
:138
П/\АТОНОВЫ И АРХИМЕЛОВЫ ТЕМ
Мтюrоуголышк назынают праn11лып,rм, сели
у него раnны стороны и углы. l1рш•.1срно Т:tкже
определяются и nраютьные м н шоrра н ники.
Вьшуклый многш·р;1нннк назык:н::тся пра
вlfльн.ым.. если e1·u грани - ранные 11р:.~внльнь1е
.\it1iогоу1·ш1ьнию1 и двугр:Jнные у1·лы прr1 Rcex
рёбрах р;.~кны мt:жду собой
Пршшm, 1 11,1х м1 ю 1 ·оу1 ·0111,11ююв бес1<опсчно
м ноrо: при каждо:\11 п ~ :) имеется праниль11ый
п-уrольпик (пр11чём только oд11rr, с точтюс1ъю
до подобня). Лравит, 1 п,1х мтюгофа11щ1Ков
nссго пя1ъ. Попробуем понять поче;\1у.
Сразу заметим, чтu мно1·01·ранныt у1 ·лh1 прн
всех верш 1 1нах правш1ыю 1 ·0 "'11ю1·оr· ра111шка
рав11ы между соGой, поскшrьку равны ILX г1ло
ские и /tRугранныс уrглы . R чзст1 юс1·11, это озва
чает, чтп А каждоir nерш111 1 е сх()д1лп1ад1ю11 то
же ч исло 1·p;11 1ei1. Оfiоз11ачим его(/. Есл11 rр;~ни
рассматриnаемого мно гограштика - правшнr
пыс р-уголыrюси, то е1 ·0 плос 1ше углы равны
rr.(p - 2)/р и нх сумма вокруг каждой верши
пы - rr .q(p - 2)/р . llo сумма I JJIOCIOIX углов
выпуююго м1ю1·01·р:шно 1'0 у1•11а \1С н1,1 11 t 2тт. Сле
дов:пелыю, Ц(/J - 2) < 2р. Это нер~11н:11ст1ю ~юж
но асрсн11с:.1· 1 ·n в ии;tе (q - l)(p - 2) < ~1 Теперь,
учитыван , что р 11 q - целые ч11с1rа, нс MCHl>Шlle
5, нее возможные пары (р, q) легкu 1 1ай'1·н пере
бором. Вот ош1: (3, 3). (4, j), (3, 4), (5. 5) 11 (3, 5).
На рис. 6 tшерлrу для каж[\оrо 11з у1{аза1шых слу
чаев приnе/1,сны «ССТ JШ•>, т. е схемы соединения
рёбер многогранника. Сетка - 11аглндное 11зоб
ражеr111е комб11натор1юго п-mа ~шогограннmа.
Легко провер 1 пъ, что сетка 11раннт,но1·0 м 1 ю
гО1' ранника однозн;~чнu олр<.:деш1ется парой
чисел (р, tJ). Прасто 1 1ар 11 суйте ю1 шюскосТ11
любой р-у1·олъ 1-1ик н нач11нте окружать <.:r·o НО·
н ы ми р-у1·олышкамн. конечно нс обиз~тельно
орани111,ными , но пр11 соблюде111н1 11епре.11ен·
HOI' () услоннн: fl р1 1 K(l)l(JtOC1 1-1ep111111re llX должно
61,пъ С/. По/\ сетками па '!'ом же р11с. () 11зоора·
жены самн _-..11юго1·р~шш 1 ки. .Uce они имеют
ра :шое числ о гра11ей и назва11ия получ11л11 по
этому чнслу: тетраэдр (4 грапи, от гре11. •rет
ра" - «четыре» и <·XeЩ)O li"
-
« 1·р:шь111 ). ге1>:с-аэдр
(6 граней; он HCCKOJ/hKO более flЗllC CTCH как куб~
оюпаэдр (8 гр:111ей), t)m)е1саэдр ( 12 1 ·1ш1сl1}1
икосаэдр (20 1·ранеl1) . Од1-1акР длн матем~n1ка
рисуrюк 11 /РЖ~ трёх."~срная МП/1,СЛh са м 11 1юсебе
ещё нс /\ОК:JЗЫН;IЮТ существо11а 1 111я 06·1,екп
Пр~;(стащ.те себе, 11:111ример, ч ю nы сютсавае~t_
Геометр1~я в пространстве
(.)J)
(..J • •~)
( 3А)
('i .J)
(">.))
~Куб ( гекнt..~0/>)
Oi.-mtt.~af>
f fкr>сюдJ>
Рис. 6.
uз 12 равных правильных пятиугольникоn до
дскаэ,1р, соединяя их по :$ R каждой вершине
Нс ПОЛ} чится ли так, что, rюдкпе и вая очерс11,
ную ~ · рань , RЫ незаметно даже )\ЛЯ себя её
пере1·нете, сrараяст, уместить в обрхюва.вuu,1й ся
3азnр? Кроме того, нужно е щё проверит ~" будут
ш1 иметь мно1·огранники, котnрые пы п осrрш1 -
те, равные диуrра 11 ны е угm,1.
Бу11ем и сходит~. и:~ ·1
·01·0, что куб - пра
вилы1ый м1югограшrпк с (р, q) = (4, )) - су
ществует; это очевидно. На осТi ове куба можно
постро 11ть и остальные четыре nида мпого
гра1-1н1nюn. Недаром И оr~шн Кеплер считал куб
•род11телсм" всех прав11л1.ных те11.
Кuнцы t:крещнвающихсн днаJ ·он :tлеl1 про-
111 1ш 11nложных гране ~! куба я:вляются 11ершина
ми пра1:1н11ы-ю1 ·0 тетр:.1эдра (рис. 7, а). Сосд11-
н11в t\сн·1·р каждой 1·р:l11и 1(уб<~ с цt:гпрам11
шседних граней. лолучпм 12 ра1111ых О'l'rез
кт~ - рёбеr 1 1 ра1шлыюrо октаэдра lрис. 7 , б).
Граrп1 обопх м 1-юr() гранн11ков - правильные
треугольники, а любое ребро каждого 11з Э'l их
тел можно перевести n любое Т\ругое 1101юро
том куба. при котором н ыно1·огрю11rи1< пере
ходит сам n себя. Отсюда следуе-1 равсш:тво
,.1нугранных углов .
1!коса<эдр пострсн 1·1ъ сложнее. 11а каж;tой
гран11 куба 11ара 11 11ел ы ш д11ум сё.' сторона""1
пр( тедем 1ю отрез~-..') пдной 11тоИ же 1v1и ны х с
середнной н 1~ентрс грани так. чтобы отрезк11
11а сосед1 1 нх гrашtх б ыли nерrгепл;п кул яр1 щ
(красные от резки на рис. 7 , в). Соею 11111 м
концы красных отрезков, I<ак nою1за110 на
рисунке (синими лш 1ияыи) . Получится двад
цатигранник типа (3, 5), т. е. все его грани -
треугот,н оки и 11ри каждой вершшrс их пять .
В силу с имм етрич н ости куба, все синне рfбра
11 косаэдр:.1 равны. как и дRу1'ранные у1·nы прн
этнх рёбр::tх. По1\берём х ·~~к. чтобы синие
рёбра были рз1111ы крас11ым. С помощью тео
ремы Пифаго ра nыразим дю111у си него ребра
через х. Тогл;а ( рнс. 7, в)
АВ2 =АС
2
+СВ
1
=Aci + CD.!. +DB.!. =
>
)
,
=(х-+а-+(а-:tY)/4.
1'дt а - 1v~нна ребра к\·ба. Ус11оние АВ.~ = х.! пр11-
вод11т к ура11ш; н1 IIO х~ + а:"; - а.!. = u, ПОЛОЖIПСЛЪ-
1-:JЫЙ корень которого равен .\: = а('11S - 1)/2.1111 -
терес r то, Y'I'() JIOJIYЧИIOLIИ~LCЯ М!-ЮЖИТСЛI> прн а.
т. е. отношение ребрах икосаэдра , 11111ка1111uго
в .к)'б, к ребру куба, - вездесущее золотое се"lе
ние. При данном З Liаче1111и х ясе гранп натпеrо
многограннию1 - правильные треут олы1ики.
Но н адо еще доказ~1ть равенство двуграrшых
yr 'J IOВ. Рассмотрим пять рёбер, выходящих 11з
одщ.>й ве ршнны, н ;трн м ерА; одно из ннх крi.lс
нос, о стальные с шнrе (р 11с. 7, tЗ). Кон 1~ ы всех
п яти рt.:бер р:.~вноудале11ы и от тuчк н А, н от
цt11тра куб::t О. Слсдонателъно, ~т11 пять '101.Je~
11ежа·1 11а 11ересеченш1 сфtр с 1~снтрамJ1 О 11 А.
:)39
Фигуры
Рис. 7.
'J'. (". на
OДHt!JJ oкpyЖtl<>CTlt, Пj)I J Чё\1 CO<.:ЩIHiJ
l(JЩГle их рёбра равны. Впис1 нный в окр}Жtшс..-1·1,
rш·1·иу 1 ·оm.11ик с рая11ыми сторонамн L t рзв11ль
ныl1 . Зпа ч 11'1', 11аши 11я·1ъ точек н точка А - нср
ш11ны праnильтюй пнрами11ы , з её дв)гра1 11r ыt'
углы при вершине равны. т. е. угол при крас11ом
rебрс такой же, как щш с11нем.
ДодскаЭТ\Р :\ЮЖl ю ТЮЛ\'ЧlJТЬ нз шшсюдра Tt;\1
же способо).1, что и <.жтаэ:w пз куба. Сое,(1r1 11 1м
це 1 1тры смежных ~-раней икосаэдра. Мы nндс
ли, что пят1, rранс~г с общей J:1ершшюй обра
зуют нраюи r ьную пятиуголы 1 ую ппрамплу , а
отрсзю г, сос;~иняющие r1х це 1 пры, - пр:шш11 .
ный 11ятиугш11,нпк (рнс. 7, г) . Все1 ·0 тшснх пят11-
у1ллы1н1<01111п:11111кает /'щ:наJ\1 ~;пh. Трёх1р::~ нныс
углы при 11ер111 и11ах 01ра111 1че1 1 1 юго ими нпсн~lk
1tатигра~шm<~"l пмсют ОJ\1 tr 1 аковые 1 1JЮС 1<ие у1 л ы ,
т. е. у ~шх равны и дв~траш rые углы. Слс,тщва
телыю. это ттраштлы-т ый додек:~эдр.
l lтак, для каждоrо пз пяn1 допустнмых зн:~
ч.ений пары UJ , q) построен nраnильныi 1 м1ю
гогр:н-1 ник И любой правильный ~11югограп -
1111к с дш111ы.11шр и ц бу; ~с:т I Ю!\Обсн дру1·ш.~у с
' J'C Mll же jJ [-1 ц. Jl(JCKOJlbK}' ЧllCJ l ;!/J 11ч O/~IJU:maч-
110 опрt:/\СЛЯЮТ форму 1рансl1 11 HCJ I HЧIШ)' днy
l'P::J l ll l J,IX )'l 'JJOIJ пp:lШJJIЫIO l'O МНО l'ОГранн11ка .
Мы !\Ва:жды 1юnь;~оватк1, те~\1, что 1 \1.:11тр1,1
1 ра1Jей п1хшнлыюго м 1 юrо1 ·ран11ш<з ·п 1 па u1, ц)
являются вер ш и11ам 11 пр:шилы-юго много 1 ·ра1 1 -
ню<а типа {Ц, р). Э•1·0 будет верно и в ост:н1ь11ых
случанх. Тзкис дnа многогранника назьшаю1·ся
овоuстнюmыми . У н их одипакоnое число рёбер,
а числз вершин и ~·раней персстаnлспы. Дной
стnенны ; 1 ру1 · дру1у куб н uктаэдр , додекаэдр 11
икосаэдр, а тетраэдр двш'1стнен е1 м себе.
Нажнейтпим с1юйст1юм пранилыlЬLХ м 11 ого-
1·ран1 1 н 1<01.1 ян11>1етс>1 нх симметр 1-1чноl·1ъ. Rhlбc
pcм реброАВ м1ю1'1)1'ра11 1 шка и прнмыкающую
к не-"tУ грань F. То rла существуе-1 · · r-экое e r·o С3-
·"юсо~.11"1е щеr 111е, т. е. д1шжеr-1 ие, п еревоfl,ящее e r·o
3'-Ю
в <.:сб}J , nрн K()'t 'IJf..IOM ребро АВ псrсйлёт 13 /НО
бос з~щ:1нное рсбrю СП. точк:1 .4
-
к любоJ1 нз
/(l~)Л Cl' () КОНЦО}S с HJtJ 1 и. а 1ранh р - к любую
1.1:~ д 1~ух 11rи.\.1ыкающ11х к не,\1 ~ 1ра11 с 1j_ f Iосколь
ку обра3 1 ,1 ре(jря , ен> ко1 щ:.~ 11 он.:жной 1 ·р~uш
од1юзпзчrю :"!:;~дают са.чосовмrще11 1 1е, все1n са
мосовмеще1шй будет 4Р, ГJ\е Р - чиС'JЮ рё()ер,
н ЭТО м ~н<с1 1малыю nOЗMOЖIIOt: ЧТ!С'Л() i ~'l}I ч 1 ю
гогра11шшоn о;оюrо т11п~1. llолошп~а и:~ само
сою.1еще1шй - по пороты (во1<ру1· ocef1, соеди
ннющнх центр многограшнн<а с r~е11тра мн
1раней, серсдн 1 1:.1м11 р<.:бср 11 нершш1ами) на
угпы. крат11ыс 2rr./fJ , n: 11 2n:/(./ СОО'ШСТСТБСIПIО.
l lpyт:Jя 1юJю1:1иr.-1э - сш"1 .\11t.трr-1н относ1пельно
IVJOCKOlTl:Л 11 «~к·рк~UJ nНЫС' 11 о норт IM ( со11ро-
1:1ож.наемыt с11ммстр11cl1 относ ~ tтсды ю плоско
п1 r, пср11е11 1 11 11су1тр 1 101 1 осн 1101юрот::1) Указз.н ·
1юе «CJ.Юi 1cтno M<1I<CHM<1Лbl!Oll с 1 1м~1етр1 IЧIЮСЛ!•
псре~ко пршшм~ют :J:i опрспслс1111е 1 1 раш 1ль-
11оrо м1тогограшшка .
Правил ы 11 ,1с м1101·ограш rшш 11а:~ывают т~к
Жl' 1иатmювыми тела.ми. хотн 11х зналн nпфа
гор<:iщ1.1 за несколько вс:ков до 1lлато11а. l:J дна
;юrс ~тимс(1" Пл:~·1·u1 1 свя3ш1 их с че1ыры!Я
OCHUl:IHЫMll э1 1емt:11т;1 м11 Он CЧll'J'~IJl. Ч'J'(.) h)'б,
·1 ·<..:тrа~.щр, октаэдр 11 1 1 коса :~д р H'>tt'IOT форму
кор1rускул .Jt:,,1m1. 01·ня, rюзлух :~ 11 1:1оды сuответ·
стве11rю. П>1·1 ъ1й же 11-11юп1г1х111нпкон сч11т:v1 мо·
,-~елью nсей Нселеr 11 юr\
С 11Y1e11e:vi дР)ТОrо n~шюго грека. Архш1ед~
связывают так называемые: полущх1нилы1 ые
м 1 юrог1х1m шюf (;~рхrн•~едовы ·1 е.1а). 011 оn11сал
1 1.х J:! несохраннn111с1кя кш11·е (<О ,\IШОrограв·
11I1K<1X». И.мt:"ется 1:J ЩJХИМСl\ОВых ·1·ел, которыt
птr уч;110тсн уссчен11см 11равнльных :.шоrо·
1·1х1нн 1 1ков (p1tc. 8), 11 ещt: две бескuнечныесt>·
рr1 и - пр:ННl!lЪНЫС пр11змы IJ ;.tll'L 1 1ПрИЗ\1Ы J
pa 1-11 11 .1N111 рёара1v.н 1 .
Во1ен :~а nт.~·1·01 юм прс:л;прrтннл ПОГJЫТК\'УIJ~
эат1, строение Bce.r1e1 11 ю~"1 с 11р<11mльными мноJ
гогрш нщкамп Иосаrтн Ке11лср Он расс~ютрс.rr
сферы. COJ~L'pЖaЩHt' орбнты l l°:!RLCTJ!bL\: в CL' U
Rрrмн /Jlt:CTl l П/l:tllt'I' ]'1 суvн:л с 6ОЛ l>ШСl'1 JIJlll
щ:ныш:i1 точностыо ра·1мсст1гл, исжд: сф<:рам 1 1
11нть праш 1лы 1ы х >.:11101·01'р:111нш<0в таю 1 м обр:1-
зом. что ЮIЖ/\Ый был ()111JClll около MCJ11.шсl1
сферы 1 111n11сан 11бстыную.Ою 1ако 11 r еоме 1 р1111
11мя Кеплера псталось n связ~r с c11·1Cr 1,11Nм и 11м
,1n,мя .зщ··:·1r)l{Ылzu 1l{Jar11u1ыщ.1иu тела,нz1. R ссгп их
'!ei ыре (рис. l)); ,J\1-1a .л.рупn\ 11з111ё11 фрапт\рС 1{111'1
чатсмапшЛун Тlyattco в lH<N 1
ФОРМУ/\А ЭЙ/\ЕРА
Сост:ш 11 ~1 ·1·а6лнцу tt 11 ы11нш<:::м 1~ неё ко1111'1t:ст1:3а
иср1шш (В), рёбср (Р) н ~ ·раней (/) /(JJ H нескот,
liНХ Ml IOJ '01 'p:l1-1111JКО11:
Г1:ЧJМРтр1·1я В nрш трс1нrгв<>
,vl нт·о11х1н1rнк
R
!'
г
Долек<lЭ/\Р
2()ю12
Окт: 1::>др
11
1.{J
.Ю
llнрам1111а 11 -у1 ·ит.ная
11+1 21l 11+1
I lрпзма п-уrолън.\Я
2.1!
')11 п+l..
1fc·rpy11r ю 1 11>,1'""'1етт rтr" чтn для ncex .\111n1·0
1·р::1 1 ш111\()Т1 D табл,ще ч1н.:л() nерши11 минус
чнсrю рёбер rurтoc ч1к;ю rр<Шей рав110 2:
В-Р+Г= l.
(")
Ны "'южетс прuвср11т1, с 11 рансдm1вос11, ра-
1к·11сtка (*) tt /~JLН НР)' l 'ИХ рассмотμсш1ыл намн
MHOl 'Olp:IHIJllKOB - /(ЗЖС /IЛЯ любого H l •llly'КJJ(J
J'(} мног·о1р;н111111са гю r1з 111 сму н 1.1бор у. R 1 1српые
это :3аМСЧ3 le.'lЫIOt: COO'lH<J Ш CillLC обн : 1ружш1
Р<:нс: Дс.:карт ощ>.ю 16.Ю 1·. В 1752 r. ту же фop
\1}JI} nсрt:оть:рыл Леон~рд Э1'1! 1t:р. ко~·1щ за 1111 -
д1~~лся ()Пl l C<IHlle\11'1 1110fl 13ЫПVЮIЫХ MLIOl'Ol 'IJ:IH-
HllK()B в 33/lllCИMOCT l l CJT ЧНСJ1а 11.Х uep1111111
Сей•1 :н: её назыt~ают форчу.~юИ :·)11.Jн.:р<\.
Ilщ:ется \11юго док:1затсл t.ст1) соо·1·1юшен11я
Эlvн:ра. В о;о~ом И::! 1111х 11с1юльзус·1·ся форму.1а
для ('У\1 wы уиюn м 11 m·оу1·олышка. Рассмотр11м
это но1сазатt"лuст1:Ю. Боз~.мfм с н аружи мноrо
гран 11ика юч l<Y О пбл н з11 от ю1коi1 .rntбo 1ра1111
Р и сnrоскт 1 1 руt'м осталы1ые 1 ·р~н111 на /<' из
1~сн 1·рз О (рис. l 0). Нх 11роскщ111 uбраJуют
ра:i6не11 н <:: 1·р;1нн F на многоу1·0,1ь111 1к11 (т:t1щ\1
с11особом f!OC.- 1 ро е н ы CCTIO I 11 р:lВ!IЛЬНЫХ чно
rоrр..1ю111ков на rнс. 6). flодсчнтаем J~вумя сnо
собам1 1 сумч~ о упюн ncex 1 ю:1учсн 11 ых мно
rоуго.11,1mков Lt с<1чоl1 1·р;111н J·' . CyмV1;i ) 1 ·лоn
n-y1·ш11>1nuc1 р:11ю::~ тс(п - 2). Слтю 1 ч ::1т11 ч1 ю1а
д.1н нс~х 1p;lllc i"1 (нюпочан и i·pa нr, F). С:) мма
чле1ю11 ш1J1,1 тcJf ранна общему •1 исл> сторон всех
гр:1Неi1. т ~. 2Р - IK"Дt КЮl\/ЮС 11.1 р ребер 11р 11-
над;1еж11т дnум граням. А так к;:~к осс1 ·0 ~- пас Г
сла1·:~ем1,1 х. cr == - л ( lP - l/). Tencp11 11аfщём cp.E\IY
yf'.lтon пр11 1<аж..rю11 11ерш11не pa:!n11emrя 11 с.110Ж11 ,,
э·1·11 сумJ\11>1 . Ес;111 вершина !lcж11t· miy·1p11 гр;~1111
F, то сум!>1 а у1 лон no1~p~ 1· 11её р<1кн.l .? .1t. T::iюrx щ:р-
111 1111 в - k, l'iJC 1г - 'НIС.'Ю ncp1111111 Cl\tOil гр~11111
F, :1 :ш;~<r11т, 11\ uк:1ад 1~ cr ра11ен 1.rr(B k). У'гJ1ы
пр 11 нершл11а' /; с ч 1п а10то1 n су:-.' \\С е1 ,'1 наж:1.ы
(как утлы F 11 кзк у~лы .\11Ю1'о)ТОльн111юв ра :~бн
е111н1); нх нк.1:щ ра.вс11 2.л(k - 2) Т~ншм обrа:юм.
cr == 21t(JJ - k) + .! .n(k -2) = .?.п(В 2). Прн ра11н1шая
дн.1 ре1,·:11,тата 11 <'tЖр:tщ:1 я r1a 27t, 1ю.~-Чаl·:.1 t'p(.:-
nye,юr р:rвеШ."1'/Ю р - 1 = R - 2.
342
Фор,1у;1а Эr'1 щ:ра лоз 1Ю.'IЯL"1· судтъ о с1юi1 -
стн:.tх, 1 1р 11С)'П\11х только r.;;омбr 1натор11ому П111)
м1ю1·пгр:.t1-1 11н1.:он. Допуст11.,1, 11anp1iиep, что
:..1но1·огр<~н 11111\ "f\<.Jмnш•~l'п>rнo 11рзн~t1hныr1•,
т. с. нее е1·0 1·1хн111 - р -у1u.11>1шю1. а 11з каж;ю11
вср1ш111ы ш11ход11т tj рt.:бер. ,l~tжc 1111че1·0 11с шая
о фор"'1е cro гра 11е1\ можно у1·всржд:~ть. что Oll
бу,(ет ю1 ·0 же нrпа, что 1 1 одно11:i mнн 11л:\то·
1roнi.r.\ п:л. В с1:-.юм де:1е, общее ч11сло cro
р(;бср. HhlX:O/(Hll(I tX JIЗ нссх Bt'(/ll ll !11. р:1шю t.j11fi
этой с~ ,\JM(' к:rж:~ос рс::6ро сч f!Т:!l'TCH )\В :IЖ,11,Ы
() нсги два конца). а лт·ому 1" га раина 21'. Под
с<штывая дну."~я с11особам1r общее ч11сю t·10-
puн нссх rpa 11er'J, уста 1юш rм. ч10 21 1 ""рГ. Выра
зн:..1 'll1CJ ta rн В чсре:~ чи с:.10 рёоср 11 подс1';'111ю1
пш1учсн1-1ые выражсш1н 11 ф о 1н1ру Эl1лсрз.
В pe;>ym,1 ·a re nр1 ц<.::.\1 к) p:trшcm1ю
-
--- =- -,- -.
f//!21'
Иэ нет C.1CД)L"I неранснстно
L11
-- t- ->-·
С/р~
которо.чу yдCJBJICTIIOpHIO 'I ТОЛЬ /.\() ГТЯТh :зна
кu,1ых r·mм rт:ip ч1JСе.11р11 (j :"!начс.:шtяl'. Г rr B
в к:JЖДОМ 11.! ПЯТ! J сЛ\.'Ч:\СН МОЖ\10 вычнстrrь
лряJ1t0 нз 11aшJJ.x урав11е1 111 i1.
Фор."1ула ЭfJЛl'pa н~-11н m1 нн.:тсs~. нс тот.ко д.v
Ш•IJJYКllh/X мщнлгр.11111111<01! 11 ,\.IЖС HL' '!'ОЛЬ!(()
;vтя ~11юн1гра111111ь:он. Нар11с~<.::..1 11,1 сфере :oo-
бofr umзrrьn·1 т·раф. ·1 . L'. nо:~ьм61 нсоюлы..;о 10-
ч:ек ( R<.:rnнш) 11 со<..;t 111111.ч час1 ь нх :1н11ия\\11
(рёбр:шн) ·1.LК. ч;о(>ы 11:1 :1юбоl1 Вt'рш11111,1 ~ож-
110 ()ыло гю р<:брам 11срL'Г1·1·11 н .1ю6~ ю ;.1ру1у10.
fl(мcч11т;ii:\1 ч11сю 06р;1~юн:1nrш1хся 1 ·рз11еi1 -
фр:11мс:ннщ11.11.:0 тр... с :111 111 11 1ра:!рс::i:uотсфе·
ру, чнс.10 1·1ы 1 1L'l1Gупс1 св}1:1; 11 ю ,. ч1 1 сж 1 м1 1 nep-
u11111 11 pl:UI:.'\) 1l'J\1 ЖL' COO'l'J f()U f l'l 11 IC\.I. l\t'JlllЧIШ2
В - Р -1 1 . 11азы наем ал .:JfиU!/Юtm1i .Yaprrкmepuc·
т11коi'1. будет раrнта 2 ;1,.1ш всt:х ~111оmгр;1111ш
1'0В, «YL" l '\)OCHl-ll1IX. f\a" сфер:!·;, - 01111 . оuразщ
говори, nр<:нrа ·1·11тс11 11 шар11к, сиш 11.\ c..ie11JJ•
11з ре;щ11ы 11 11<t1~у-1ъ. Т:~к11с ,\1110101·1x11m111i
11мс11уют 11;юстьtм11 Очен11,1но. нес 11ыщ~1~
MIIOl'()l'P<H·IH l l KH nμ<JC'lh!C. //о, [1311р11\1Ср, эNo
рон<I х:~рак-1 ~р11с1·11.,;<1 •·Тр<.:~ 1·0;11,1 ю1·0 6\611J1Ji)I
( р щ·. 11) р~111п:1 нулю. \1ож1ю rюкз·1:пъ, что.'!.'~
.~11ю 1 ·огран11111<а. 11щ~ющt:1·0 р, «с ююз11ых дьrr
он;.1 р:1в11а 2 - 2,ч
T eupc,1a Эйлср:t ст: 1л;1 <щ110\1 1tз пcprшx'l'fO\
fX:M 'J'OI IO.'IOГШI - J1аую 1 О С~М \1\ Х о6щш: ~
с1 в:~х ф1 11ур, которыt> сохра ннютсs1 щщ нещх
rы13НЫХ ЛСфор,\1:!Ц I IHX.
ВОЗВРАШЕНИЕ К ОПРЕДЕЛЕНИЯМ
B;iжнe(пJJJIC теоремы о м1-1ого1р~111111 щ:1х опю
ся·1 ся 1< nы 11 ую11.1м мr1огоrра111111кам. П ока мы
нмеем 11ело с 11ншr, uonpocы nроде «а что ·1 ·а
кое грагrь~» у н::~с, как llpaшrлo. ле возш1кшот,
тюс1Ф11Ьку отоеты н~t ннх просты н ..-:стесТТ1ен-
11ы. 110 1-rевьшукпыс м1101·ограшшю1 слособ11 ы
СОЗЩJl:\:!ТЪ проблt:J\1Ы.
Поставим 11а верхнюю ~ ·рань куба мены1111й
куб (р 1к . 12). ЭлJ 11pucтoJ1, хотя 11 11евыnую1ыl1
\tНОГ1..11'{1аНl!ИК. l [р<1нер11м ДJlH lltTO форму1~:у
Эiiлera. в= 16, р:::: 24,Г= 1 l ;B -Р + Г= 3?! ГТр11 -
ЧН 1 1:1 11t:/~Оразуi\ 1с11ия :-1::1ющ1 чается n том, что
одна из 1· ра11ей нашего м1то1'Ограшшка -
·ra,
что осталас1, от uерхней r р анн большого
куба, - «nлохан->: n вей есть дырка. Из-за этui1
дырю1 рёбра rазбшзаются п:~ дnе нссвязашrыс
rpynnы. Дt"ло можно 11оnрав11ть. ссл'11 проnсс-
111 ДО!ЮЛ J lИТСЛЫ!ЫС рёбра, соеДI IН Ш(JIЦИС ДI3:J
куба . 1!апr нмср. к:.1.к rюказа11u 11 а р11с. 1.) .
С форму11оit ЭйJt(.:ра тсщ:рь нсё в порядке, 110
11р1 IXOДlIТСЯ п р1 l.{l /:J.'JЪ, что 1Н'.: всt: в порядке
с t1аr11им 11 оnре,JJ,с.•1сн11ями , раз м ы nы нужл.е -
Р11 с. 12.
Геометрия в пространстве
н ы объяснять допо;шн·п:лыrо, как счита·1 ь
рёбра н гра~r н .
А вот сщё O,i111 :1 за1':1дка. Пооютрим rн·ювъ на
рис. 9. Почему эп1 тела сч11·1 ают п1х1вш11,нымн
(пус-11 . н :тёзд11ым1 1 )? И х сранr 1 нс ЯRJLНются пра -
1шm,111.1ми мно1·оуrолы 111юtм1 1 , 11верш1111ы у них
устрпе111,1 no-pa~irюмy. Чем 011и ~ 111хшнт .11ее·> тех
же :~rл"ичедовых - тю.чупrавнт.11ыл
-
тел·~
в эпгх I! JIO MllOГllX другн~"{ с1пу;щш1 х О!Сl
зьшастся более сст~::ствсш ~ым представлять
с<::бс м1 ю1·01·рш1ню~ нс как тсJ10. :1 как nu-
вt:рхнос1ъ, сост;1нлс1111ую по Н<:которым 1Lр:1-
внлам 11з м~-югоу1 ·ш1ьшншн. Jlр<нща. ш1ренеж~
нне мно 1 ·01·ранш1ка 11ри этом l~1·аною1тся болй·
СЛОЖНЫМ JГ у НСГО l:CTh ра .:!НЫ<:: вapнa! I Thl. Пгш
недём 1щ1 11 1 1r::i 11 11 х.
Многогрэшп 11~ как ппверхтщсть - это 1<0-
11еч11ы1111абор плос юLх м11огоуголы11шов, рэс
положеrтных н llространствс так, что 1) кажд:ш
сторо11 а .:побt>rо r 1з нпх од1 rовре,"1сш10 слу-...кнт
сторо[[ОЙ ро!3но одного l'pyгoro: 2) J tЮбыс два
н з нпх соед11няю ·1 ·с.н «дорожкоJ'1" и:i "'нюго
у1'олы-111кон 1-t:iбo]Xl . пр11чём н •ЛО)Х)Жкс• по
СJ 1 едонатс;;1ьн ые м 1-1огоу1'011ьнг 1 ю1 1·раш rчат rн}
СТО Г)()НС; 3) Cl'Jlll / \IOJ MllOJ 'P)' l 'OЛ"1-IJJK3 llMCIO"I
общу10 нср1ш1ну, ·1 ·n сnсд11нюощун 1 нх •дортк
ку» м ож но выстроит~. нэ \1КОгоуголr,н111\()В с
тоi1 же нср11лпюf1. 1'·11101·оу1-олышюt 11 аз1i111а
rотся 1·ра1ш.м11. а нх стороны п uершлны -
рёбрамн 1r ве.:ршинами ."4JЮгоrр:нпшt•а.
Услоuнс L обеспечип:~ст .~а.мкиутостъ rю
nерх11осп1 - у неё нет 1<рая; услов 1rе 2 rо1юр11т
о том, ЧТО понt:рХНОС'ГЬ C/3H3JltlЯ - COCTOllT JlЗ
одного куска; условнс "> lICl<!IfOLJ;(t:T 113 Ч! ICJI~/
мноrо1·р;11-1 11 11 кон, н:~11Jтмср, ф111 ·уру 1 1 з дв~'Л
кубон с общеit нcp1шtt-юll, которые 11с 11мсюг
друтнх обЩllХ то<fек. Н~о :1;,iмL"ПtM , ч'rn .:1то оп
рt:,цt:.1н:111 1 с дu11уt:кает само11tресече1 111н по11tрл -
1юсти. ИмеJ 11 10 таковы пратrлы rы е ::~нё:с1:111ые
тела. Наnример , 1·ра1111 rюследнего 11з 1н1х -
правнлъные пятиугол.ышк11: в каждой nерrщшс
о нп обра:Jуют само1 1 сресскаю щ1Jй ся 11аrюдо
бне ПЯTlll<OlleLJJJOЙ знс:щы праЩfЛ],JIЬlЙ ГlЯПl
rрашrьrй у1·ол. А у двух друтх самн rpa11I1 нвт1 -
ютсн :щё~Д НЫМl I ЛНТ11)'1 '0Л1 1НИК<IМН.
Ec11 1L м11111'огр:н1ник-tюнеμхность щ: са:о.нJ
пересекзетс.и , тп о н сшша11ает с поверхнtктью
11t:1<()сго м1юп1гrа1 111и1< а -тела "сuотнетств~1н с
Oll pe;, eлe н11 c,V1, с которо1 о 11ач111-1ается эт:~
С'rаты1 . Однако <Jбратное не11ер1 ю: 1 1<1nр нмер,
вt-1утри: мноrо1·ра1шнка-тела могут б ыт~, 1 юло
сп1, и тогда его х·рашща будет несвязна.
34:)
Ф11гуры
ТЕОРЕМА КОШИ И ИЗГИБАЕМОСТЬ
М Н ОГОГРАН НИК ОВ
В :~аю 1 ючtннс по:таком1rмся с одним п:{ самых
IIOCJ lCJtHИ'X ДОС'l' l lЖбШЙ тсор1111 ~I HOl'Ol'Paшur
KOH. l l o 11:1ч:пъ 11р11 ; tС·1·ся t 1 :щ:шека.
Гfрl'/tст~1н ьте, что у тн.: есть набор картон-
111.1 х MHOf'O)'l 'UЛhHHIOШ 11 и ы XOTl lTL' склеить 11 3
111 1 х м 1 ю1·n1ранннк. Конеч но, зтn 11 е r1cc rдa Fюз
можrrо, тю еСJ1и 1юлуч1 1·1 ·ся, то будет л~1 такой
мно 1·01·ра11ш ш с11и11 с-тnет11 1ы.>-1? Пос1юлъку нам
rrc задан 1юрядок склс1~ши граней, 11етруд110
приmмап. пример, кшда мо гут n олу ,1нть ся
ра:~11ыс мноrогра нннкн - сравтrте много-
1·рuннию·1 на рис. 1 5, п и б. lly :i tCJШ поряло1<
склс:йю 1з:~да 11 ~ И ·1 · u1·.Lp нuлучt: 1 П1 ыJ'r резул ы ·ат,
ROOhЩC говоря, T::IKЖl' 1н: будt."Г СД I 11I CTHCI 11 IЫМ :
рассмотр11тс мно1·01·ра шrики 1-1:.1 рис. 1..), б 11в.
В r юслед11ем лрнмсрс о;tш 1 11 :1 м1югu rраню1-
rюn 1тев ы11 ую1ы й. 11 =~то нс случай1ю. В 1813 г.
фра11цу:кю1И математ 11 к Опостсп Кn111и /\Ш<а
з;u~. 01ТО любыt два выпуклых м1-ю1 ·ограшшка
с од 1п1 ако13ым. наборо м гр:нrей. соеди нё1шые
в однн а1Фвuм порлд1~е. равIIы. Столr, простой
IIO формуш1ровкс и IШТУИТИIШО ОЧ.СRl'ЩНЫЙ
факт имеет весьма хитроум н ое, хотя 11 почти
эж:: мс:11тарнuс ;юкuзат<::л ьст1ю . 01 11 1рающt'еся
на фпрмулу Эйщ~ра.
И:1 тtuрс~1ы Коши. на11рнмtр, и1сдует. Ч'l'( J
нее 11ра1ни1ы-1ы с: много1 ·р а11 11~ 1~.;н зад;.~ нн о 1 ·0
типа (' р, q) с 0)11 гт 1а копой /1,!н 11 ю1I rёfier р:шнr11
между собо й . а таюке что любот1 1<ом61-111<.по р-
110-11 ра uилыu,пr мr югпгра 111 1ик. грани 1<0торо1·о
гrр~1 ш 1т,тr ы е м110 1 ·оу1·олы 1 ию1, яnляется одш 1 м
н;~ платоновых тел. 1Lo сейч~•с нас ш rтс ресует
/\pyr· ut.: следств и е теоремы Кошп : ппк акой
ныr 1 ую1 ы(r Ml:-IOJ 'UГp~ШIПIJ\ IICI IЗl 'нбаем.
l l ояс ш1м на1·1шдно смысл этш·о у1·нерж:ден11.я.
Прс: \стан 1>1 ·с себе, чтu 1ран1-1 м1ю 1·0 1 ·1х111 1 1нка c11t: -
J1<1l LЫ 11:i абсолют но жёсткоJ 'О ~1атернала, но со
снитrе111. 1 11ру1 · с ;~ру~'Ом 1 шрнир1 ю. т. е. е1·0 п о
верх~ юс1ъ М()Ж1 ю с1·1.1Г1:у11, по рёfiрзм. То~ да. tсл и
м~ю1·огрант тк выпую 1 ый, он бу11ст жёстю 1м и в
ЦСJЮ.М. углы межлу е 1·0 l'j)allЯ.МИ И:\ МСШIТJ, (' }1
1 1с см оrу1'. Действительно , будь это не т~u<, то,
чугь-чуть IIЗOГI!Yfl его, мы llOJl)'ЧИЛII бы ,r~:ругой,
но нсё сщё выпуклый многогранник с теми же
1 ·р:111}1м11 , сосдннённымв в том же 11uрядкс, что.
как доказ:u 1 Огюе1 ·сн Коши, не1:юзмож1 ю.
А су 11 ~сстиутот 1111 изгибаемые м1 ю1·01 ·р~11-rнн
к1 t? Ещ~ в 176() L' . Эйле р предположил , что не1 .
1'11С. 13.
Очст1ь лол.го пшотеза Эйлера, 110 краi111сй ~1ере
д.тш простых чт-юr·01·раш1иков, ка:~аласn вполне
праnлопоцо61ю11 Тео рема Kou11 1 её подтвсрж
д;ша, а пuзжс былu дока:iа1ю, что пе толыю
м 1-ю1·u 1р:~1fl1:т , но 11 любая выпуклая эа м ючт:tя
поверхность 11е 11з1·116;н:ма. Однако II 1 97У J'.
и матсмат11 ч сском м 1 Ipl' nро 1 1Зо1ШЮ с1:11са-
1 (ионное cofi1,1 т11l'. :tМL'р11кансц р_ Ко11нслл н
rrостронл пср111.11'1 q>лФccujJ, т. с. 11 зп 1fiэемы(1
(1<01r еч1ю, 11евыГГ}1(лт,1И ) м 1 юг01 ра нн rп<, nра11-
ла 110 1юлы10 замыс_rю 11а· 1·1.1 i1_ F-щ t: 1·0,r( cnycrя
К. lllтсффе11 нашел флексС1р нсе1·0 с девятью
веrш11лами (вероятно, э·rо 11апмет 11.шее 1303-
f\ЮЖНОе число).
Совсс:::м н с/1аннu было док:.1 зано 1п 1терсснос
с1юйство ф11сксорuв. нх объ61 прн из1 ·нбан~ш
не меннетс.н. On ,rго.\1 по;tроб11сс расс1\аэ: 1 но 11:1
с; ll'l(ующей стр ашщс.
От1.rt~·1·ы t ra нoпptX ht, 1щторыс::: быт 1:~а,.1зны в
начале ста 1 ·пн . вы 1шд11тс: ю1 р11с. 14
Рис. 14.
ОТ ФОРМУЛЫ ГЕРОНА
К ОБЪЁМУ МНОГОГРАННИКА
Кажлый старшеклассник "lн;~ет, что формула Герона
выражает площадь треугольника через его стороны:
S=)р(р - a)~J
-
h\(p - с).
То, что нет соответствующей формулы для других
м1ю rоуrоль никоа , вас 11е лолж~ю удивля1 ь. Наличие
подобной формулы, ск.:~жем, для чстырёхуrольннка
означало бы, что его плошаль определяется лишь лл11-
1 1ам11 его сторон . Но ·но 11е так: например, плошадь
ромба со сторо11ами а, в .завио1мости от углоu, мо
же1 быть люfiой между О и а1.
Перейдем к многогрш111икам. Тетр<ндр яолястся
мно1·огран1·1ым а11алогом трсуголь11ика. для нс1·0 так
же имеется формуl\а, выражаюшая его 061,ём чере3
ллины rн:~бер. у тетраэдра шесть ребер; пусть/,, /, , 1,,
/~, 11, 1,, -
квадраты 1-1х дл~-tн (рис. 1), тоглJ
v1=1~4U1l~Ul.+/1 + /4 t /1, -
/1- 1,)+l)"(11+11т
-
11/,/" - 12/l /; - 1,11 1,, - 1. 1"1(,)·
У riOl\!"e с ложных многогранников с треуголы1ыми
гранями объём НЕ' ()Предсляется лишь лли11ами рсбt'р.
За примером ходить далеко не надо. Рассмотр~1м wl'c-
rиrparmик, образованный двумя тетра:здрами Т1 и 7~.
«<рос ·шимися » по грани (рис. 2) . Ofio11i.1Ч"1м этот шеr
т11гр.:~н 11ик через Т1 + Ti. Его обы~м V равен сумме
обьем uв V 1 + V 2 двух тстра::эдров. Возьмем теперь
другш1 много~ р,1нник Т1 - т, (рис. 3), который отлича
етс я от первого лишь тем , что нижни й тетра:>лр
• влавле1-t» в верхнии . Ясно, <1то ре!бра многогранника
Т, - Т2 (и даже его грани) р;~внn1 соответгт11уюшим
ребрам (и граням) многогранника Т1 + Т1 . Но объем V'
втроrо м11огогра11н~1ка будет друrим: снr равен разно
е111 V1 VJ объемов тетраJдров.
Однако имеет место слелуюшая 3амечательная н~о
рема, доказанная R 1g96 г. российгким математ11ко'vl
И . Х . С1битовым. Пусть залJ 11 произвольный м1югu
гра~1~1ик, осе гра1111 которот треугольн ики. Исходя из
этого многогранника (точнее, из ет комбинаторного
типа), можно построить спеuиаль11ый 'v1Ногочле11
F(V) =vп +а У"
1
+ a}t"·i + ... +а",
кшффиuиенты а 1 , ••• , а 0 которого выражаются пр и
nомош11 четырех ар1-1фмстических леистви1-1 через 11а
рамеrры - квадрать~ ллин ребер м1юrогра111-1ика. Если
В\<\есто 11араметров /, подставить квадраты длин рёбер
конкрепюго многогранника, то получим м1юго•1ле11
ГРО\1Е'Тр11Я В ПрОl 1Р•1 1 IС:Т13С
с числоными коэффиuиентами Как 1юкпзал Сабитоо,
обьём дdннuго многогран11икd t<CTb <)ди н 1н кор н !.!й
·ного многочлен;~
Вср11емся теперь к Лl)ум многогрс1нникам 7 1 - Т .
и Т1 + Т1 • КомбиllJТОрно 01-1и у(трос11ы олинакоuо, и
их соот1:1е1 пвснные pi:'бpd pi!iiHЫ. <-огласно н:•ореме
Сабитова, п1-1м лвум многогран11ик<1м отвсчаЕ>т один
и тот ЖЕ' м1 югочлсн. А их объемы пput то раз~ 1ые кор
ни данного м1 югочлеt~а.
Эту пюрt:<му можно прим< • 111нь и к многп1 ра1iн11-
кам, грани которых не обязательно треугольные. Н()
каждую 1-1е треугольную 1рс111ь прежде 11адо р.13(jить
на треуголt.11ики. В кдч~сп:1t:- п<1раметrов, от которых
,ывиrят кп·'>ффиu11енты м ногочлена, наряду< лл11на
м11 ребер исход1юго многогранника слслуt1т рuсrмат
риоать и дли~1ы ~ювых ребер, появившихся в резуль-
1,11 е fМ "-!бИСllИ~.
С другой стороны, как показ,1л f-' . Ко1111елли, rу
шес1 вуют югибасмые м1юrогрJ1111ики (из теоремы
Коши следует, что они мuгут Gыть 1uлько невыпуклы
ми). Каждый и~гибаемый многогранник деформи
руется подоб~ю тому, как леформирую1~я мсх.:1, на
пример, аккордсu1;а. В11утрс1111ий обье\1 мехоа при
леформduии И.{мt:няетс.я, и в э1ом ~•х rуть. Но когда
поrмотrели, как изменяется объём изгибаемых мно
r uгра н11и 1<ов, то оказалось - никак: 1iесмотря на
~<>формаuню, нзп1басмый мноrогранник coxpatt\\!:'T
объем. Была поставлена проблема: доказать или оп
ровергнуть утвержле1111е о постоянстве обьема мно -
1огра1 IНИКОВ при и il иба1iИИ.
Положительное решение этой 11рuблемы <,лелует
из ТЕ'nремы Саf>1-1това: пр11 деформаuии любого из
гибаемо~ о многогранника его обьем 11е менщ~ 1LЯ.
дРйствителыю, при изгиGании сохраннютсн и ком
бинаторный ТИП МНОГОГраННИКа, И ДЛИНЫ С'ГО rебер.
Поэтому как исхол1юму .многогран11ику, , ак и всем
его непрерывным леформ<1uиям сооп:sетrтну<.!т uди11
и тот же мrюгочлсн, ср!"ли корней которого нахо
дятся все возможные ~начени51 объёмов этих много
гранников. Но так как пр~1 ненрерыв1~uй д~формd
u ии оfiъем может меняться только не11рерывно, 10
лля того, чтобы быть корнем конкрf'пюго м ного
чле1 lcl, объем мнС>гогра1111ика пр1-1 изгибани~1 долже11
ULТаватьс~ ПОСТОЯ! 11-11 .>IM.
Р11С. 1.
Рщ. 3.
.ЧS
Фигуры
КАК СЛЕМТЬ ФЛЕ КСОР ШТЕФФЕН А
Выреж t..те ю доrта rоч н() nлоnю й бумаги три летали,
показанные на рисунке. Улобно взять следуюшие
размеры: а= 12, Ь =1О, с = 5, cl = 11, е =17. Склейте
межлу собой сосел11 ие ребра с на двух uли11,1ковы х
деталях так, чтобы в белых круж ках обр<новались впа
дины, а в черных кружкJх - выпуклости. Получатся
д~зе ~1д1;1 1 пи ч н ые фигуры, которы е можно точно совме-
ГЕОМЕТРИЯ ТЕТРАЭЛРА
Кактреуrолышк - нрост~iпнпй l\\\ЮПJ)ТШ1ью1к,
т;;iic 11 ·1·етр..t :7/1.р, И J 111 t· ре)толы1;~я 11 11 рамид::1
(рис. 1). -
нросте:йmтпт м1ю101 р ,ш1 ппс Геомет
рш1 ·1е J ра.эдра 1 1и<1уть нс мcIJ ce бо~·ата, чем
п:омстрш1 е1·0 шюскоrо собрп<~ - треуголь
шrк.а. м1ю1·1·t~ с.1юйства которш·о .1:1 прсображен
но"" шще м ы нaxoд11.i'lil у тс"1·р~1э;\р.1 . Нсм:~ло об
ще 1 ·0 I JMCC'l ' TC'ТfXIЭ/lP 11 с L[ClЪJpёx yП).1 11,Hl!KO~I -
кедь у 0Go11x по че1ъ1р(;' вершнны
Пu;щn 1 ю ·rрt'уrот,ннкам, т~траэ1t ръ1 мож1 НJ
ю1асt:1 1t\лщирона 1ъ 1ю cп:ner11-1 11х с11ммстрич-
1юсти. Рашюбс11.ре 111 ю~1 у треутоJ1ы ш t\у oTRl"fЗ
cт пран11лышя трсутолы 1 ая пирамидз (рис. 2).
П равиm, 11 ан трtуrолы-rая т1рамид::1 nереходнт
сама D себя пр и 1 101юротах вокруг высо~ъr па 120
11 240°, а таюкс прп с и мметрняJс от пос итеныю
шюскостей. nрuхо.цящи.х через ос ь 11 бокоnыt
рё·бра. Об1х1т 11тс В1-шм ан11 е н :~ то, что, Ш) слu
жи вшейсн нс очень лu1·11 чно(1 ·1радJ.-щ111-1, 1·срм11 11
~11рзнильныl1 тс1р::1э;\р·> 06означ.1с t' ч а с1·нh1 l1
случай прав1mьной трсутлы rой пирам1щы -
стить друг с другом. Вложите одну из них в друrу1О 11
склейте их вдоль кр<~ев Ь. Раздв ин ьте Luободные вер·
ш ин ы, пользуясь подвижност ью кон е трукнии, вставь.
те между ними и подклейте влоль краев а третью
деталь. Сборкэ закон чена! Соели11ять детали можно
клей кой лентой или просто полос ками бумаги, смэ
:\а нн ыми кл1:>е....1, при ч ем и~нутри и вдоль всего ребра .
Однакп о• 1е11 ь вероятно, что ваш а модель будет юri1·
баться не 1ак сильно, как вы рассч итывам1.
·1·етр;~:-'щр , у 1<0'1 щ101 о R<.:c рl: бμа ранн ы , ·1 е. &е
гра11н - ра111 юс1 прп111 1 щ.~ ·1·рс) 1 ·om,1111юt Такоn
тетр:!Э/1.Р пn1шдает 11artn()JI l>Ш 1 1.М Ш)З МОЖllЬIМ Ю·
бо ром са,чос онмещешп'~. Имсс1·ся 12 nоnоро
тов, переводящих его в себя, 6 с11мметршl ОТ·
!ЮСИТСЛЫIО llJIO(KOCTC.Й и ещё 6 д ншкеп111i
соч.е-1ающих 1 ю1:1орот с сим:-.1 етрш:-й . Поnробу1)
'1'<:' найт11 вес .:j·1
·11 11μсобра:ю ваrо1н .
П JXlПllJll> ll blЙ тет rаэ,'1,р - l -lt.: Ч Т() r11юе, K;JK
"(Терсомстрическш1 ал 11 ;m ец•.' само 1 ·0 С11ММеТ
рИЧ!Юf() треу1'ОЛЫ!И1(;) - праRИJJ Ы-ТОГ(). 3лес11
нас, однако. ожи~ает сюрпрп3: есть и другой. в
оnрелелёпных опю щеш1ях даже более за1<011-
1 1ый претендент на эту рот,_ l3 11 рпчсм, о пём
мы rю1·01юрнм позже. А пока вслш.ш11.\'1 нско
ТQрыс теоре:vtы из гсомстрю1 ·1 рсутоJ 1hн 1 1к:~ (см.
C'l'ЗThIO «Треу1·олън1 rк, 11poc1·er1 111 1т~'1 11 щ:11счер
пасмый") и Jl()t:.)>HYГ/>11.VI. кш.не нз HJIX 1\.IОЖНО
псрс: 1 1есп1 1 1а тtтраэ1 1р.
ТЕТРАЭЛР И СФЕРЫ
Jlюбой треугольник имеет е,п 1 шстве111 ry10 n ш 1 -
санн~·ю и t'дн нс1 ·ис1-11 ryro опис:н шую окружно
ст11. Тuчнu 'l';JK Ж<: у лю601'(> Тt'Траэдра есть сди н
с'Т11с111 1 ан 111н1с:1 нна.н (юкающаж:н всt.:х 1р<Шt'Й )
JI С/\ННСТl:!СННан OПllCI H llaн (11рохо.цн щая Чt'
pcJ вс<.: вер ш ины) сферы . Доказ;.1тсJ1h<-'1' 1:1а эп 1 х
С!Н)ЙС'l ' В I IOli'l'OpSJIOT C:UOTBt'Tl"l'B~'lOJl\Ile ш1а11 1 1 -
~rетrичсские. центр J:J1 11 1с111 1 ю1::r сферы раn по
удалёr 1 от всех 1 ра11ей н лежит ш1 псрс:ссчсшш
б11ссектор11ых плоскостей дву1·ра1111ых уrлон.
образоn:лпп,rх rра 11ями (т. е. ш есть бнссекrор
вых плоскостей проходят через ortпy точку). :1
цстр 0 1111 саннuй сфе ры 1х1 шюуд<L'ltн O'I нсех
пср1ш111 1J лежнт t1a 11ерессчсн 1111 1 1 ерщ: 1·1,1 1 1ку
:1яrов, 1юсстз.нле1-11-1 ы х к 1ра11ям 11:~ цс1~трон 1 1.х
пш1сан1-11,1х окружност<:tf (т е че1ырс 1н:р1 1 сн
д11куляра т:~К-iКс r 1ересек:.~ютрi 1:1 одно~'r точке).
Но 1чх>,\1е 1 ·ра11ей н кср1ш1 н тстра :щр шtсет
ещё и рё6ра. Во:шнкает 1ю 11 рос: мож1 ю 1111 щю
nеста сферу. касающуюся всех cro шсс11 1 рt;бер
(се ЮЗЫ13:.IЮТ n()Л_)l(ll'lUCa/llIOll; рнс. _1)? " . И НОГ{t::I .
ЗдссL тс:траэ;.ф ведёт себя, как четы рёхуrолып r к.
и ус.:110вис <.:ущсст1юна н пя rтолуnn псапrюй сферы
1ruвтор;1 с·1 11 р 1 1::1нак u n иcu 11 юго чсты рёху1·оль
н 11 ка: такая сфера сущестнует тог~а 11 тuлы<о
·нн'N1. ко1'Да сум м ы /l/1111 1 к:1ж11.uй п ары проп шо
положных p t:oep Т<::Тра:"дра rанн Ы ,\1СЖ/1.У собой.
По су·п1 дела, этn нсё тиr же план1 1 мt.:тричсскнй
пр11з 1 1а1<, 1ю nримсп ёп ныГ1 кпрuстранст11е1-11 1ым
<rетырёхугплъттm<ам - в i\3 11 ном случае ч еты
рёл-уrолы шкам, обра:юнз 11 1 1ым 11вумя n::tрами
прот1 IВОП ОЛQ)Ю \ЫХ рёбе r тетrа:")дра. Тетраэдры.
и~1сющие пш1унписа нную сферу. называются
11.аркасны.1~tu. Всё, что мы п о1<а у:ш:Uiи. по чти
1 юн·1·орсние пл<1ним с-1рии. Но нот дuно11ыю нео
ж1111а 111 1ый фа кт: о казывается, тетраэдр J1и1mстсн
каркасным тuгда н тот.ко ·1·u1·;~:i. ког;1а сум мы
Гсомстрш1 в пространстве
А
Ри~..! .
с1·0 11pU'l 'll IIOП()JIOЖl l ых :-1ву1 pat IНЫ.Х ~ l' . 'IOR ранны !
K:tl\ t;ю.1з;111ы )'l'!JЫ 11сфер;.~? Подумаf1тс.
Но с1 цё 6uл ыm 1с нстк11;щ 111 1;)C'1·1.r об11ар) ж11-
в<1 1отся пр11 1 1сс1едова 1 1 ни 111 1евп1 1са1 111ых сфер
тетра:>,Т(ра, т. с. сфер, касающнхся плооюс1 e-i'r
всех четырёх е1 ·0 ~·1хше11. 110 лежащпх щтс те
траэдра. Как 11зr1естно, у любого трсуголышка
1Lчеется три n11сnп~ тсаш1ыс сжруж1 юсп1 . Пло
стюсти rp~u 1сй тетраэдр'! pa:i61 ша ют 11 рuстра п
стно на 1) uбластсl1 (р1 1 с. -1). Кромt' чt:1 ырех
тp<.:XIlXHlllhlX )TЛtJJ:S. 1 1pHMЫK:!IOЩllX К нcr11111-
ll:lJ\11 ос1 алы1ьн.: l l обл:tстсl! ш·ра~-11 1чс111,1 НСС\Ш
чстырьмн пл1ккосгяl\ш. BII)тpтr тtтра :·щра , а
также Rнутр 1 1 чет ы рt:х «TH>C" t аме 11тn11-> nnлa
cv1·ei1, 11(1J1 Mbll(;Jl()Щ\IX К Гр;1!1S!М, - Ccj)epa, KaCa-
IO l l~;JЯCЯ nccx плоскостей. вс~гд:t ес1ъ. А вт с
шестью облас1я.,,,ш. 11римьшаю1 цимн 1-: рёбрам
11 по форме 1 тапомпrтающ11мп чстырёхскатные
крыпrн илн черд:.11ш. дсло обстоит июж11t.:e.
01\аJьгвается. л3 двух <-ч<.:рдакон" Щ.)11 11ро
т1ню1юложныл рёбр:1 х тоm,ко у 0; ~ 1-нт 1 м о
Ж:l'Т быт1, н1 1 11с: 1 1111: 1 >1 сфt:р~1 Т:.~юJм ofip;.iзoч.
l'ис. 4.
Ч7
Фиrуrы
у npam111ыro1·0 ·1·1:тр:1:.тра - а у нет нее "чсμ
/\:1ю1 » о;111на ковы - «Чt:рд:1 ч11ых » сфер ноо()щс
11<."J', 11 ] tаЧ(;' 011 1t 11pr IL~"l'C"l 'HOB~Н\ 11 6 1,r но нсс.:х «ЧСр
,rрках 1 _ Итак, п.:траэ/\Г Ltмet:т нс мt:ttl't: чс:тырёх
11 1н.: 60J1t<.: сем11 вне 1ши сатr 11 ых сфер, 1rр11чем
1ке проме:;~..~'ТОЧ!JЫС CJ l)'Ч;/lf BOJMOЖIJЫ.
МЕЛИАНЫ ТЕТРАЭЛРА
Всрн ё,-.кя к трсуr·оm,ннку 11 всrюмннм , что <.:J"O
\1Сд11а н ы t r срссскаютсн в 0;11 н)й точке - цс11·1·
рt н rдс - н деш1тсн в ш.:1'1 н от11ошс.:11 1111 2 : !
с \IJ 11-111 \1:.t111>Hbl,\'1J J ll:J\1CJICI IHЯ\1 IJ то же вер но 1J
R ( )'ПI< )U/l' I 11111 Tl"l'P~l :'.l/\pa. MeйtШl-fCtMU н тетр:1:щ
рс называютсн отрс.:зю 1 , сое; 11111якнние е го i~ep-
11111111,1 с 11,е- 1п ро 11;щмл ПJIO't'IШOll('IЛOЖIJГ,J.,'{ Гр3 -
щ;~'i. 3тп четыре отреэка все1·да пересекаются
1.\ 0ДТЮ1~1 точке :11 II ДCJJJl'J'CH й 11ей в О'П!О JЛСТ НШ
1 : 1. сч11'1<tя oтnepwmr (р11с 5). Ч ерез туже точ
ку 11рuходя:т 11 бu.'1ltедиа11ы - отрсэ 1ш. сос:дн
няю щ11 е ссrс,1\1шы прuт 111 ю11олож1-1ых р <.:бср
тстра:-1/lра . !1р11чём 011 11 /\CJIH'l'CЯ ТОЧКОЙ м 11 0-
IIOJ l:l •\I . Ц(mmpour) тст ра ~/lра , к~1к 11 це111·роид
трсуt 'ОJ11,н11к:1 . янляется центром рапных масс
r10 .\1ещfн1 1ы х 11 (ТО 11ер11111111,1, - обстоятет,
стно , которое можно 11 с 1 юm.:>ов: 1т1. N t Я / \OK::t:1a-
тem.cтn;i 11р11nс; 1ё111rых вr.rmc свойств. Ч11сто
геомС' 1 р пчесюr н х мшюю 11окз:1ат1, с по.мощью
слс:дутощей попез1юf1 конструкции .
llpcineдём через 1<аждос ребро тетраэдра
плоскост1" 11зраллеJJ ы rую 1 1рот1 1nоrюложному
.11иi'11ш11а
r•нс. '"
Рис. 7.
рtбру ( рнс. 6 ). Пш1~ •111м тр 11 11 ары п ;1 p:1n" 1{'JlhHhlX
l IJIOCKOl"J'(;'ll , ( н · р;t 1 11 JЧJ 1 H:tlOЩI I;\ 11:1 p:111 . 1c: tl'llJ ll ll'Д,
1r:t:'l Ы на<: мы й (Jl//IL С/ N //fol..11 11прп. 'IЛl:' l/(>711111ei>11.111
·1·страэ; lр;1 . r<:бр;1 нашет тстр: 1 :щра яптrются
д11.а 1 OH~I IOIMI J 1 11э11ей 11ap:L'l!1CJ IC'lll ! ПC/\:I, l'ere -
Дllll bl pf()cp - нх це11трам11 . О 1·с 1<ща следует. что
nce 61rмс; lи аш~1 11poxoдi1·r· сrер1.;з центр О парал
лелепипеда и ~слятся им п ополам. l lет11ущ~о
увнл;сть. что ~1ед11а1 rы тетраэдра лежа·~· rra ,r~.на1·0-
11а11н.." граней парал.1слt'11 11 пс1~.:~ н та1<же прохо
дят чс:рсз точку О. l11rжc чы встрtтныся с др}т11-
ми п рн.\1с: 1 1снию.111 :;этой конструю~.и 11 .
ОРТОUЕНТРИЧЕСКИЙ
И ПРЯМОУГОЛЬНЫЙ ТЕТРАЭДРЫ
Меднапы тетр:~эдра <· ведут себя пр11мерr10о> -
KaIC 1·1 U треу1 ·олhl JИI\e, OllH DССГД:l ТТJlОХОДЯТ
через одну пту ж.с то•tку. Иначе обстоит }1,е:юс
11ькотам11 - гrсрш:11f(1 1 ку.1яра!\ш. ()ГТ) 'Щt:111rым11
rrз всрmин ·1 страэд ра на гrр<л'1шопшюж 11ые
1·ра1-111. Высо·~ы трl')1 1·оль1-11 1к:1 1н.~р1:.тек:нuтся "
01~.н<Jй. · r•oч1<t' - орнщ1.;н·1 pt. TlJ жt' нс.:р110н11ли
l 1t:l<OTOJ-1ЬIX тстр;t:-7/1.[ЮН. IJ чaC'l' l IOl"l ' l -I IJ/ lil нра·
в11лы1ых Тj)t.;~1 'ш1ы r ых 1111р :1м11/l- Но . н :шр11жр.
у тетра:-щр:J .- 18CD, H llll C~IJ lllOГO IJ ку6. /(~1f( Гl()l\:1 -
;~;ню 11а JШС. 7, рёбра АВ н ОС с<1м11 Jшляются
111 .r сота,\1111111с 11ерссскаются.
И uсё же ортоцентр существует у достащ<J-
1ю ur1 тро1,ого ю1асс1 тетраэлроu. 011 11 т:~к 11 т
зываются - ортm~ешщшчесюи, тс'r ·ра~дры.
Любой из н1·L'i. можно n<ыуч11тr,, юнв n t\ачtстве
OCIIOH;J HШI Г[f)OИ:JHOJlblJ l>ll'I тp<.')'l'ШIЫ!llK н СО·
l'ДIIl lllB Cl'<) нсрш1111ы (.' 11106011 'l'OЧK()JI ll:J 1 tер-
1н.: н; ~.11 1<уJ 1яр е 1< t'l 'O l!J!OCKOC'J 'H , 1ю<.·cт;111JJCJl lJ()M
1IЗ eJ '() ( 1рто1 \t:HT[JЭ ( rr ll. К) и oб p<lTl-IO, OC'HOH3-
f f JIH Н('е>. вы сот O[)'f'O l~CТl 'I pнLJCC l\()J·o тетрз
::щра - ортоцс11ч1 ы t.:го [·p:11 1el1. Лр11не1~Ь1 еще
Щ'СК()ЛЫС() кr11терШ:Н ('L'. е. НеобХОДl!МЫХ !! ДО·
статоч1 п,тх ycлomrfr) ортоце11трнч.~юс111: те-~μа
эдр нruш ется ортоцснтр 11чссю 1м тогда в толь -
кu 'IOL'/1.a, 1\0! /Jд его противогrо1юж11htе рёбр~1
ПС[1ПL'НДНК)1ЮТр11Ы ; lr!IJI cercдJIH bl Г!Сt:Х IJlt:CTH
rёfк~р лсж<1т нз одно1v1 сфере; ш1н все рё61х1
ош 1 са111 ю1·n гrараJ1лелет11 н:~дз р:11111111; ю1н сум
~1ы кв:щратnн протr11ю1ю.rюжн1·,1х рёбер равпы.
Нек:торые с1юi1спщ тре)толы11.1ю1, свя~а 11 -
11ые с ортоце1I"г[ЮМ, например теорема о nря
~юй Эйлера 11 об окру;ытости девяти точек в
соотnетстDс11но изме11ё11ном виде, можно най
ти 11 у ортоцс 1пр11<1еско rо тетраэдра. Цt:нтронд
ортощ:нтричсскоr·о тетраэдр:~ лежит н ~1 отрез
ке 'v!CЖJ\Y орто~ 1ен·1·ро," Н 11 цен·1 ·р11.\1 ош 1 е111ной
сс]Х'Р''' Оп /\CJIJП этот отрс:кж 1юп олам, а точка,
котор:н1 раз(i11вж·т rпрс:юк НО н отно 111сшr1·1
1: 2, !U~JIHCTCH 1~ентро.>1 <·Сфср1,1 12 ТОЧС\(» - 11а
11ci111сжат ор·1·оцс 1пры 11 цетрm щы всех сра-
11е1\ ;i также · тч~а1, дел.нщие rнрсзки от Н до
вершнн в отноше1 ша 1 : ~- Дсжаз~телr.стnа этих
теоре~1 (le так уж сложны, хотя и трсб,·ют про
стра11ствсmю 1·0 тюображения.
Об одном nидс ортоцснтрнчt·ских тстр;1<::>д
ров стu1п с:ка~:1ть u'J'/(елыю - ( > тетра.~/фt', в
щ;рш1111t: котор о 1·0 сходнтся тр11 tJ:{а нмн о 11ср
пе 1щ11кулнрн ых pLбp:I (р11с. ()), Очt'11нд1ю, эта
пtрш1111<1 JJ r1 6)/(t:T t:m ор1·0 1 (CI rтром . 'l'aкof1 ·сет
раэдр 11а:зыпаетсн n/1я.A10_yгu/lhNЫ1и. Для 11е1 ·( )
вы1юл11яетсн сRоего рсща «1 еt,ремз Пифа1·ора":
ес.111 S1, S 2 1r .S\ - нлоща,111 е1'0 nрям оvrолы 1ых
1·р~\\\е1\ ( •·1\~тстов" ), ~l S - площадь <-1е-rnёртой
грани ( «гиrютенузьr ·> ), то
r•ис. 9,
s- = Sf+Si+Sf.
В самом деле, г 1р осю(1Г 11 трёх 1·катс·1·оп» н ;1
<·1·н1ште11узу·' р:1:1()11г1ают её 11;1 тр11 ·1
·pey1"om ,-
r1нi~1 . nосколыq np11 прпе1щю1 площадь фттгу
р1.1 ум ножается па 1юс1 111ус угл:.~ между её 1 ~ло
скостыо н плоскостью лрос:1<цrП1, то
s=s, со~<Х1 +s,cos<Х~ +s~ cosа" ('')
ГДС <Х, - ) ГОJ! MC';l\[(Y JJЛOCl<OCПIMII vl'fllIOГl'H}':3Ы·>
11 COO'l'J:K~TCTJ:!}"IO ll (Cl'tl *t<;JTCT:J» , в ТО же времн r.;:1ж
дыi1 и~ <,к;1тсто~~" совп:щаст с проею.1,11cl1 "l'11-
по·л.:11уз ы -> н:~ его плоскос1ъ. гю:-н·ому cos а, =
= S, / S. Ос1·:1i::тс.н 1ю; 1сr:~1нп1, н1.1ражен1 111 кос1111y
con чере з nлощ~щп 11 ур:ш11е11не (*).
РАВНОГРАННЫЙ ТЕТРАЭЛР
Пр11шла пор,1 11с1ю~11111ть о сюрпрн:к'. который
мы нообсщали . н,1ч1111;щ ра:31·онор u Tt:'1·paэдr.J:-.:.
l{ак мы стредt:.11ж.:~t 1Jраю11 1ы 1ы1\ нт1 ра11носто
rю11н нi1 . 'lpC ~' l'OJIЫll!I\~ ECTl'CTHt'IJHt). K::tl< трt'
~ 1'от,тrик. нес о·щюны кОТf>ро 1 ·0 paR111,1 . Л что
т:~кое •· Стороны ·> 1'етраэ!\р<1? F:c1111 сч~1·1а ·1 1 " что
это рё-бра. то а11ал(")1 и"l1 юс с-гереомt:тр11чес~<0е
011JX~f(eJIC/11 re 11 р11 t1е[\ё'1' к 1Юl l}IПJН) пJXI Bl//U1J IOГO
·1·е1р:.tэ/фа. llo. м ожет быть, «c' 1 oporra~111» н:тр,.1-
эдра следует сч~пат1, его гранп ? Тогда мы нрн
хол11м к следующему олрсl(елспшо : тетра эдр,
1кс: 1 ратш которого р<ншы (т. с являю·1·ся равнh1 -
м1J треуru11.Ьнш:ами) . ш13ьшасrсн ри~11U2/ШН11ы"11.
На r1срвы 1'1 K!l 'J LЯ) \ р:1внu1ра11ны11 тетр:1..J/\Р -
ЭТО Пp~IHНJIЬl!Ыl'I 'l 'C'l IXIЭ/\JJ, JI Hlll~IK{)l:I ) \р) l 'UIJ.,
в нe1tC'l'BllTC"Лh!IO C'l'l l 1· paL1\1IU pa111ю1·p~Hl!-(()['(J
теJ'раэдра може1 бып. 11 1обоr1 остроуr 0111.г 11.1 i1
(и 'J'()Лl,I{() OC'T'fJO)'I 'OJТl>J 1ы i1 ) трсу1 <JЛ hНТ 1к llере
Ч НСJIИ!\1 важн еr1r 1нrе своr1 ст t1а рав1 юr~х1 1т11 ых
·1·етра:трст. Перш.1е ,11. 11~ cнoi'1 crna }1<а:~ы11аю·1· и
общнй способ 11х лостроенш1:
1) ол11са1шьп1 пар~и~ж:лепш1ед р:шноrр;нr-
1юго тетраэдра - нрячо11·0.rrы-1ый (р1к. 1О).
2.) развсрл<а тстр:1эдр:1, 1юлу•1с11н:н1 11р11
разрсза!llШ Cl'O no трс::м l'ХОДЯЩ11МСJI н O/(HUJ'j
всрш11н~ рёбраJч, - тр~:упJЛh1-1 11к ( р11с. 1 1. этот
тр~угол1.н11к J\uлжсн бы1ъ остр[)угоЛ1.ным, по
тому что тупоуr ·от.ныi1 1rлr1 прю1оуголы1ыr'1
прн с1 ·и6:.~ш 111 ло средт rм л11111 шм 11е C!I< J1К11тсн
\\ Те'l'\)<JЭДр).
Набор с:1мосо11мещс 1 rнi1 прш1:11юлыrо1 ·0
раnтю1·rашюrо 'J'етраэдра 11 е так 601-ат, 1\:1к у
правнль1 то 1·0 тетра:~,1р~1;
3-. 19
Фигуры
Р"с. 11 .
-~) у 11ei-o 11местся три оси с111\·tметр 1 ш (это
общие перпендикуляры, прон<.:/\ён11ыс к про
·1·111юполож~1ы.>v1 р<:бр<~м, шш же 61-~~СJ\ианы;
р11с 1U). Ою~ако этих снммстр1пl хватает .
чтобы можно было сокмсст11·1ъ любые ; ~не ука
эшшые 1·ран1 1 нтr вершш1ы , 1ю 1 1 е rёбrа.
Пользуясь сrюйстнамн 1- 3 тт пепосре,ц
стве н110 011ределеписм, легко вывестп. что у
раш ю1·ра1 moro тетр;1 эдра
- 1-) все трёХJ'Ранные углы равны;
5) nce медианы (тетраэдра) равны;
6) все пысоты (тетр;ццра) равны;
7) центры впш:анной 11 олrка11110С1 сфер
и 1(ентроид совпадают;
8) раниусы ОПl[са111-1ых окружностей
гране!~ 1хш11ы;
9) периметры граней ран1 1 ы;
1()) тющаю1 1ра1 1e1I ранны.
Некоторые 1 1 з этr 1 х свот·н:·тв настолько оче
вид11ы, ч·1·0 1ra первый юrляд даже не заслу-
ж1 1нают упом111-r:н1ин . Замечате.111>нu (11 вuвсе
Н<.: ОЧ<.:ВИДJЮ) дру1·ос: нп· ЭTll CHOЙL"l'B:J р::~нно
СНJJЬНЫ друr /\J1Y''Y Н К:J.Ж,!~Ое llЗ НИХ В U'1'7J;СЛЬНО·
стн обес1 1еу11 нает равногрш 11 юе.1ъ тетраэ11ра
ПожаJJуй. более исего впечатJJ.яет с1юйство 10.
Вдумайтесь: для равенст1:3а гра11еf1 тетраэдра
лостаточно, чтобы были ра1шы между собойнх
площади!
Подnсдём итог. Все деснтъ псрсчпслсrшых
нами уuювий янля1отся оюювременно н сноА·
стк1м1:1 н пр11зн;,~1<амн равно1ранноru тетря
эдра . Другими словами, любое из н11х можно
1 1 р11 нят1, ~~1 ()Л редслен11с раннuгра 111 юю тетра
:-щра Иноп1а, чтобN вынест11 равногrх1нность
нз какоrо-ни()удh усJl(н11 1 я, надо ныстр()~1т11
целую цепочку промеJiqточ1 1 ых ~rслпвнй, в ко
торой кажлое - прямое t1rе1(ствие прсдыду·
m.ero . Надо 'ГШ1Ы<О пост:-1ратъся 11 найтr1 'rnl<}'IO
r~~почку ". а вот эту задачу ь.п,1 осташшем лю·
боз1 ~ателы п,~м читателям.
Геометрия - значи1 « ~емлt:>м1=:рие1•
ГЕОМЕТРИЯ - ЗНАЧИТ
« ЗЕМЛЕМЕРИЕ»
ДЛИНА, ПЛОШАдЬ, ОБЪЁМ
МИНА
Длнну отрезка 011редс;111ют с 1юмuщыо npuцcc
ca измерения, описанного 1:1t:шrким rсрсищ:rре
'Jесю1м мате м ;пиком Архнмсдом более 2 тыся
челет11й назад Пусты1В - нзмернемый отрезок.
а PQ - единица длины (ею может быть меч),
сант11мстр, дю ~'1 м, аршин, жжот 1, IJЛИ какоii
:tнбо шюй заранее ныбрашп>!i1 отре:юк) . Будем
последоnатет,110 откладыnать па .tlB (от точки
А по направлеIJию к точке В) отрезки. рашп,rе
едшпще измерсн11я: rlL = 1.М = JIJN = .. . =
J
(рис. l ). После щ·1<оторогu (коне'-пюrо') '-шсла
такнх оnсрацн й либо коне~ ~ 1юследнеrо отрсз!О
сокпадёт с 1'0 ЧКО11 д либu получитсн OCT<ITOK,
мerн,m11l1 сд1:шицы измер1::нин (этт хорошо нз
иесl'flый 11з практики факт составляеt' С<mсрж;1-
ние ал;ою.мы Ap.xuмer)ct) f:c1111, н :111ример. ею1-
111ща ~1:iмеренrrя точJю упож11 лась в АВ четыре
раза. то длина ! отре:ша А/3 ра1111а-+ (/ = -1). Если
же после четырех откnадьшаrп1й обра:юnался
остаток КВ, меньший 1, то мы говорим. что L'
ТОУJ10с1ъю ;щ l дпнна отрс з к:1 АВ с недuстuт
ком равна..\ , а<.: 1 1збыт1щм -
"1,11пишс"''..\~l~').
Затем, как 11 прсЖJt<.: , на•11 tнасм опmалыват1,
на остат1\:е КВ десяту10 часть с,щ1111цы 11змерt'
н11я. EcлJJ, отлож11в сё, тшр11мср , дnа ра:1а , 11 0 -
11У'"lим оста·1ок НВ, мс11ьшщ·1 десято~"1 ча стн J,
то 4,2.
-< l <4,3 ,'Т. е. длтпiз отре~1~ А8 с точ
ностыодо 1/10 ( недостапюм panrш 4 ,2, а с rr :l-
бытr<ом - 4,3.
Если 11 т~шая то ч1rос1ъ 11змсре1111я 11Jc
нс ус1рапnаст. тогда будем откл:щьшать на ос
т<1ткс SB со·1ую час·1ъ едшппrы trзме;рсrшя н т д.
OJ 111саннh11'1 (ж:сятнчн.r..u1) 11рс.щес<' н3мерсн11я
А
1
P ---Q
L
Р14с. 1.
,\'
1\.11в
Фигуры
л 11 60 п1юнчится после 11екото 1101·0 чпсла m<.1roв.
и .чы лолуч нм точное :шэчешн; дл1111ь11 отрезка
.t!В в nидс дссятищюi1 дроби (ск:.~жсм. 1= ..J. .27),
111160 шпш1·да не закuпч11тся, и мы сумеем выра
ЗJЛ 'h длш1 у / отрС;jК:.1 АВ J llЩlb 1:1 виж~ бесконеч
но11 J\<Х'Я'J'ИЧ1 ю1\ дробн, н:111рщ...1ср / = "1.27() Lб".
Есл н отрезки 11В11 JJQ cou.>.A1(jlll.м.ы, т. t;. ДJ IШ r: 1
отрt.:З ка r1B ныр;1жастся (при 11 с поm):юванщ-1
сд11111rцh1 111мt'ре1111я PQ) [Хщ1ю11аш) 11ым ч>1с-
110.V1. 1 юслед11ес: может пре;~с·1·а вm1т1, cofioй ко-
11еч11\' Ю 11ш1бес1<онсч11~ro периодическую дсся
т1 1 чную л р обь. 1J:шример, если отрезок АВ
составляет n точ.1юст111./3 сдшнщы 11 з мсретт,
то / = U,U<1bl)." Однако отрсэоr< АН может ока
з;пъся и 11(!сои:и~е/т.мы.i11 с PQ - с1·0 длн11а небу
де~ ны р;1ж:1 т ы_·я 1111 какшч рацио11:и11 . ны1~1 ч~tCJIOM
прr1 t:д11ю1ц<: 11 з м<:рс:11ш1 J1 Q То1 ·да в рс:1ут.татс
1 1змс рсr1IOI но:ш 1ГK:iC'I бСС К<1НСЧ 11ан нс11ерною 1-
чt:ская ДССЯТIГЧН;J}I дро6ь. T~lK, <:C!l l t O'l '[iC:1()1(11B -
ю1а1·011;1111. кн~1драт~. :i t:,'\НТ111щ1 н:1 м ере::1uш PQ -
t:ГО сторо1 ra ( ри с. 2). то, по теорелrс Гf11фаюра.
;~т 111а АВ р::~нт1 ,1 Л сн1с10 ,2 н_rра ц1ю11аJ1ь-
110: нырююн.:тся б1:сконеч1 ю1'1 не11 ~р11u~111ч tcкuf1
,1\еСЯТИЧ11()Й дробhlO ( \ 2 =1, ..J l ..J 2 1.)S.")
Итак, ныбраn какую-н116уд1> t:д1ш111\у щ111 -
11ы - отрс:эuк l, .-.1ы с 110.-.1011\hIO 1rpoцccc:11i:3 1v1c
pe111 rн сшюе1·а1-щя.е:v1 каж;~ому отрс:жу S онрс
/\t:Лёt 11 IOt: ЧI юю - Cl 'O /f.JГl'll-1)' 1 (S) (;1;.1 11 tну от рс.зка
АВ uбыч 1ю 060311 ачаю'1 ' I АВ l 11J11.J 11росто АВ).
дrу1·ш111 C!IOJl:IMl l , z(S) <.:СТ!J ЧИСЛОf\ая ф)1ПЩ!1Я.
:1а,'\а 11нан 11а м1южс:ствс: всех отреэко в. Расс мот
риl'.1 нзж11сI1пше свойс1· оа даrпюй фу11кц11и.
А. Длrша тобо1·0 отрезка (пе сводлщсгося к
од110~1 ·1·о ч1<е) 11 оложите.пьпа: / (S) >О. Это сво 1~1-
ство д1п 1ны 11а 3 ы1;1аегся 11а 1юJ1с11телытстыо.
В. Нели точк:.~ С р:~ з611 в:1ст 0111еюк S =А /3 на
две частн ,-1С 1 1 СВ. то дли 11:1 все 1·0 0·1резка р:1 нна
а
t!
Р"с. З.
р
Рис. 2.
352
cy.-.1I1·1c длин частеi1: 1"Ш1= IAc'J + IС:В 1· Это сnой
стnо дюшы в-азыnаеп.:я аддитивт)(.:тью (от
лпт. adcJ irion - <·Сло жение,, ) ,
С. Ecm-1 два !Yl' pe:;юt S 1 11 S.!. равны, '1' . е OДl lH
1юлуч а стся 1·1 з дру1 ·u 1·0 с по,\tощыu дв 1-1ження
(C' - 't . статью «Днг1же 1t11я "), то 11х 11.11 11ны ранны
1(\1) = ! (Sl). Иначе 1 01юря, щ111н:1 11е 11зменя
l'ТСя пр11 ю111же111нrх. Э· rо с ной ("1 rю JtJ111111>1 нn·
:Jыnэ е·1 ·бr иtuшpumtni/l(JCtnыo (от "ют. i 1ж1ri
;щt - < - 1tензме1-~яю щ1·1 (1ся» ).
D. Длина ОТ{)СЗКа 1 равна СДИllIЩС. / (/): 1
I:>ыбор некоторого отрезка в к:Nсстне сдю11щы
длины 1rа зыnа ется 11орJ1mрои1шй.
Можно 1 юка з:~ть, что Су111сс1·нуст только
одна фу 1 ткrщя. ппредслёню1я 11 а мнuжестве
нссх отрезков 11 обтщающ:1я снойсп1а м 11 А, В
С, D , а 11мс:нно та. ко1 о рая 1юлучастся в рсаут1·
тате пrот ~есса и:1мс:р сr 111н. По:этом у ip11 11i.re
CBOJICTti :l можно пр111 IЯТ!. :ia ::lI<CI юм L•I 11 011рс:
;~ет rп, /VIИПУ ка к фуп кц.r uo ()'rре:1ы1н, удоnлет
воряюrг\УЮ персч11Слt1Пiым СfЮЙС'ш:lМ. ~ ч~сr·
ностн, вес ост;:~лы 1 ые cnoi 1cтnз 7Jf1 1111ы можно
вьшссп1113 аксJюмА,В. С,D.
ПЛО ШАЛЬ
Объ~ч110 гонорят. что Шl1)Щ;l/\l.1 s(F) фr1гуры r
сс1ъ чr 1 сло. п ока.зьтаю щtt.:. н:~ с1<0лью 1х ед11·
ШЩ IUЮЩаТ\И СОСТ;!,ВJl»ется фнгура. 0ДШ11\ОЭ10
11е определение, а тоJ 1ько от1сапие того, qro
т~кое nлоща111•. Ле1 ' 1<(J rrotш·1ъ. ~по прямо уrоль·
ник со сто рош1м 11 :) и 5 см «Соста~_тяется• из
1'5 ю~;:~дратпы х с:~пт11м<-тро13 (его J1 erкo раз
резать 11•1 1 S r<надратuн ('() с1 ·о ро11011 1 см
рн с. 5. а) Hu скш1ько ПО/lО61-1ы.х квадратов
Н}'"'Л<l Ю, LJT()t1bl <•СОСТ:.! НИТЬ? 1<р)-1' р:1л11уса 2 см
( рнс 3, 6). сонсршс11но не.иено.
б
Стрu1·ое м;~тсмат1 1 ческос OJ 1рt:щ:ле111·1е плu
ща1111 мтюю по11 учить с 1юмощыо r~алстки -
лрозр:.~ч1юй пластинки с нанесёпной ш1 нсё
сеткой из р~ншых квадратоn. Предстаrшм . что
такан uалстка лежит на плоскости. Иначе гово
ря , плоскость разбю·а на 1rnадраты со с~юроrюй,
ршшой l . Если фшура Р полностью пом с 1_ц:ктся
1! ф111уре, состаннен 1 юй, например, и:~ R1 кнад
рат<1 щ1; 1стки, 11 содержит фигуру пз 43 кн;1 ; 1-
ратnн (рис. 1), то '°13 <: s(F) ( 81 . )J,Jrн Gольшей
точност11 11:~мер<.:н11я можно каждый кна;1ра·1· nа
летк11 ра :16и·1 11 11а сто к 11адратnв (стороны 1(()-
тоrщх п 1О раз ме11ьше, чем у кnадратоn nервп.й
шшетки, :\ плпщаю, равна 1/100). Ноnая, более
мелкая палетка даст и более тесные rраr111цы, в
которых :;аю11очена пло1цадь фигуры Р, скажем.
'Щ8 7 ~ s(F) ~ 62,.)"1. Еслн каж11ый квадрат вто
ро 1'1 11.алеrки снов:~ разбить на 10() киадратов,
точнuсть и::~мсрсн 1 rя ещё унсл11чится - напри
мер. получатся гrы1 ш цы 60_ 1 .~R 1 (, s(l•' ) (, 60,495 2.
Так, 1·1с1юльзуя набор палеток сп всё более мел
кой ctткoii, мы будем 11риближаться к гrре1 1елу -
площади s(F) фи1уры F.
Но зl',есь есть одна тоштсть. B пaч:l.JLe мы
получпли отрезок [а,, Ь1], rдс а1 = 4). Ь1 =81. n
котором содержится 1rс1<ом()С число s(J.'). За
тем этот отрезок умспъшю 1 и до [а.!i ЬJ, Г/\е
а!= 58,87; Ь 1 =62.:)4 . Потом уменьшили ещё
:10 ltt" b~J, 1ле а ~ = 60,1381; f;~ = 6U.'-1952. и т. д.
Из мате;:м;.1тическо1·0 аншшза известно, что пе
ресеч ение систе.\ILЫ в1юженлых отрез ков
[с11,h1] :J [а~. h~] :J [а,,h;]=> ".
числоной прямой естъ либо одп.-~ ·1·очю1 (n том
случ.-~с , если длины оч)еэков неоrрат1чеш ю
уменьшаются), нибо пекий отрезок В первом
случае, когда имеется только одно tJНCJIO s(F),
принадлежащее nсем рассм.-~трииасмъrм отрез -
/v
~
./
\
Cl1 I
40
,
P1ic. 5 .
~
1
/
Рис. 6.
,.....___
~
\
/
t\
/
"
'./
-
Рис. 4.
11
Геометрия - значит кземлемерие»
кам (рнс. 'i ), фи1уру F 11а:'Jыв:.1ют л:11aдj1t1/~1·e.мoii
(no Жорлапу ), а чнслоs(Р) - 11лощадып фи1)1)ы F.
Второй случай, когда uерессче1 ше всех от
реэков n.редстаnлнет собой отрезок, а не ол11у
точку, на первый uз глнд кажется просто нев()з
можным. Нсдь н~1ш опыт полсказывает. что
нсяк:1я фшур;~ 11меет какую-то шющадь s(F).
Чис;ю s(F) н должно быть С/\1 rнстRенноЛ оfi
щей точкоi1 рассматрияае.мых отрез кu11. Но
нс стоит бс:ю 1 ·01юрочно вt:рнть 011ыту 11 и1пу-
1 1 ц11 1 r. В да111юм c1 tyчat: опн rrac обмз111.1натот 1
С:ледующнй 11римср rюдтnерждает ::~то.
Возьмём 1шадрат Q1 со стороной 1. Выбро
сим ~1З 1-1ern крссгообразпуто фигуру mюuщ11ыо
J / 4. как показано па р11с. 6. Остаётся фпгура Q J
из четырёх ранных кnадратов, nрим.ыкающ1L....:
к sсрш11н:~м Q 1. (Сюрона 1\аждого ~1:з н11.х со-
ставля:<:т v3/4 = (),LJ.:)2".) rенерь в каждом 11з
тщадр:поn фшуры Q~ щюnь построим, а затем
уд::~лим крестообразную фигуру. Её размс::р
опрсделнм из условия, что сумма rшощ~1;1с1'1
четырёх так.11.х ф 1·нур был~ р:т н а 1/R. Получ11м
фшуру Q ,, 11 ~3 16 кв:.щр~l'r·он. И:~ каж,.~.ого нз них
ош1'.tЪ выбросим крестообразную фшуру так,
чтобы сумм;J mющщ\ей всех J6 таких -.крсе1·ов»
была ра1ша J/ 16. Получ1 1 м ф111уруQ4 из 6,1клад
рзтов 11 т. д.
Обозн~1чнм через F пересече1-11·1е всех ф11гур
Q1, Q~. Q,, Q 1, ". Др:тимн слонами .F гюлуч~1ется,
еслн из кнадрат~~ Q 1 выбросить пп очере;tи вес
«кресты ·>. Общаи 11лощадъ фигур, 11ы6расыка-
ll1
1
смыхизQ 1 , ранн<1 4 +8+ 16+ ." =2·Значит, на
,r~.олю множестваР остаfтся nлощ~щь 1 - 1 ./2 =
= l/2. Это 1<ажстся пе~ероят11ым: ясно, что
в фигуре fl нет пи одного, пусть само 1·0
·1·a~ff]ь.!1 ··
1Ь1
1
1
5()
70
RO
qp 0000
Q1
oqoo
-~
DD 0000
0000
;)53
Фигуры
маленького, целого квадратика , и тем пе '"н.:
нсе ож.1.имеет 1 1;ющ~~дь, равную 1/2.
Поп робуем теперь 1 1 з.м<:.:р~гrь ПJющ:щъ фпгу
ры Р по Жорпану (т. <:.: . с nuмощью палеток).
Какую бы мелкую п~1лстку мы н 11 liЗялн, п1ю
ща.11.ь фиrуры, соеrаnж:111-юй из квщ1ратоп па
JJеткн и RJ<JJЮЧЗЮще 11- в сеnн F, бу!(е'I' больше 1/ 2.
Площадь же фигуры. содержащейся в F , равна
1rулю (поскольку в F нет ни од1 юго цсла1·0 квад
рата). Таким образом. каждый из получаю
щихс}! отрезков
Ja1, '111 ;::) 1п~. bJ;::) tt1,, ь,1 ~ ..
(::t rю·юму J 1 пересечение нссх этих отрезков)
содержит отрезок [О, ~]. т. с. нх перссеч:е11ис
пс спстоит из одпой ·~очки. Значит, фшура 1:
11екnадриrусма.
Способ 1 1З.\IC JX1Jюr площадей с помощью па
лсто1< был предложен в XlX n. фра1щузсюrм ма
тсматпком luм 1 шс.м Жорда11ом. Др) 1·ой фр~1н-
1tуз<:кий матсм ~1 тик - Анри Лебс1· пре/1.}южш1
f)ш1се общее опрсдет.·1-ше площади. Постро
енная выше фюур3 Р нскв:щрирусма по Жор
дану, но имеет 11 1ю щадь (ранr 1 у16 1 /2), 1ю опре-
11ет..:н11rо Лебега, или, как творя·~·. измерUJ11с1 по
Лебегу, ЕсJш же фнtуrа. кнздрирусма по Жорда
ну, то она обязательно измерима и по Лебегу (и
ииеет ry же площадь) .
А какне плоские фигуры квадрнрусмы?
Прсж.т..1,е всего многоуюльнш<н, LITO ле 1'КО про
верить непосре;tстне1 1 но по с>nрсделе11ию rvю
щ::~дн. Для дру1·их фи1·ур 11р11меняют слсду
нш1,ую теорему (рис. 7):
•'-
./ Плоская фи1·ура F в том и толr.1<0
- /,:,!. в том случае ~свадрируе~1а, если для
любого положительного числа Е най
дутся два таких мноrоуголыпша Ми
N, что М содержится: в F, а N содер
жит F , ]{ при ЭТО.М:
s(N)- s(M) <Е.
)1,руп1 ми словами, кв::~дрпруе.мы фигуры, ко
торые можно сколь у 1·uд но '!'Очно прибли:зи·1ъ
мног<1у 1 ·ольни1<ами. На 1 1rимср, плuщаf\h круга
находят ка 1< нредел шющали ~зписа111 юго n него
нли аnисаrпюго около пеrо праnилыюго
п-уголы1и1с.1 при 11 -7 оо. Поскольку обе площа
ди имеют общий предел, нх разность ст рс:
мится к пулю, :шачит , круг - ква/1,рирусм;.~н
.354
Рис. 7.
фшура . Вооб1 1 ~с. люб<UJ шюска>1 ны11уклая фи
гуr:з (см. статью •· Вы11у·клыс фигуры~) кв:щри
русма. J{пщ~риrуема и кр1 rno11 ~111еr'1нан ·гrалщня
rюд графиком не11рерышюй фун 1щн11/(х),за
д:.шной па отрезке а ~х ~ IJ (см. стап.ю <· Инте·
грал н лерuообраз11ая фушщню ).
J<ромс привсдёш юго nыще опре,1елсш ш пло
щ:.tди с помощью палеток нi\1 сстся ещё одно;
аксиом;1·1·11чесrюе uпрсдслснис. Прежде чем его
сфuрмул и рона1ъ, рассJlfотрим 1rскоторыс cиofi·
L~J·в::i шющадн (мы будем и мстъ 1:! 1111ду только
ПЛОЩ:.:tДI> ГЮ ЖО)/i\ЗКу).
Обо:ш·,1,шм через Q множссrно нссх кu~дри·
руемых плосю1х фигур, тог.п;а 111ющаN> s(F)
ест1) уислоf!зя фупкцня, опредс::лё111шя пз да11·
ном м1 южестне. Перечи.слим сво йства. KO'rOpъt·
ми ош1 обладает.
А. !iеотрицаm(!ЛЬJЮсmь. Плuщадь щобоЛ
к.в:tдрируе.мой фигуры F веuтрнцат<:льна:
:>(Г) ~О. Мы пс иск.ruuчаем пул е1юt значение
гuющадн, 1юскольку. на1rриме1),любой отрезо~
предстанлн е1 · <:обой кнадрирусмую фНГ}'Р}" ну,
лсной площади
В. Аддитинность. Пуст~. F 1 и F~ - дnе квад
рируем ые фн1у11ы, у 1<0торых нет общих В11)1'·
ренr1нх точек. Обо:~11 ::Рп1м через f' объедш1е·
ш-rе этих фпrур. Тогда фигура 1' квалр11руб1Э и
слраведт1во раnенство s(/') = s(i''1 ) + s(F2) То
же имеет иссто при объсдинсни.и 1 1 с двух, а
большего числа фи 1 ур, гю1rарrю не имеющп~
общих 111 1 утрею-1их точек
С. Ипвариантностъ. Еслл две кв:щрирус·
мые фигуры F 1 н F.!. равны, т. е. одна ПО.'Т)'Чэещ
r1з друго1i с lЮМО ЩЬЮ Дlll l ЖCHllЯ, ТО IJЛOЩMll
таких ф11гур ра1шы: s(F 1) = s(F2). И11аче 10110p?oj
1mощадь пс 11зменяется при юшжеr-1 ю1х.
D . Нор..4-шруе.люсть. При определе111т 111о;
щади фнгуры задаётся 1 1скоторая ед;11нщапло
ща7щ - квадрат К, сторона которо1·0 рав111
едннит~с длины: s(K) = 1 .
()qсщщпо. что п лощад1, s ( f ), олреде;щсмая
с rюмощыо лале;.1ок, деИстт.пслыю удовлетво
ряет сnойствам А и D. Проверить два других
снойства сложнее. Наn рнмер, есш ф11гура F 1
nерсход 11т n F! прн 11оворuте, то эти лве фИJ)'
ры бу11уг nо-раз 1 юму рас1 юлuжены оп юситсm,
но паж."1·01< н до к:.~зат(::льст но р<шt::нt~1·н::1 их nзю
щ;щеii (свойспю С) требует 1tскuторых усилий.
Тем не мс11сс можно утвержда'1Ъ:
~( На множестве Q всех кnадрируе.мых
..с\!. фигур существует одна и только oдJia
функция, которая обладает свойства
JЮ[А,В, C,D.
То есть вtякая фушщш1 11~1 мнuжестне Q,
\'ДUВЛС::Тl:!Оряющ;НI ВС<::М че·1 ыр<:м (.'ВОЙС'l'Н:!М,
со1шад:1ст с s(P).
Ст;що быть, с1юйств::1 А, В, С, D м.ож1-ю пр1 1-
нять :; а аксиомы площади, т. с. опре;1спР п 'Ь
площад1. 1\ак функцню 11 <1 м 1 шжесп1с кв<щр11 -
руемых фигур Q, удош1е'1't10ряющую /\а11нь1м
аксиомам. ~?то н ес1ъ акс1юматическое опре
деление площади. Псе осталь11 ые её сnойства
~южно Rывести из перечисщ~юп,1х :шсио/\-1. l Lа
прнмер, формулы ДJIЯ выч и сле 1 П1я nло щадеf1
~пюго)толышкоn вытсrсают имешю нз аI<сиом
А, В, С, D (см. статью «Р:11н-ювеm1ю1е 11 р:1нно
составленные фн1урьт·}) точ1 ю так же, как фор
чулы пло щали кру1 ·а, эллипса 11 11 ругих ф и гур.
Заметим в заключен.ие, что и в геометрии
ЛоГ1;1чевско1'О 1 1·1 в сферической 1'еомстрин
111ю щ<щь оnрслеляется теми же акс~-юNтами. 0;\-
11'11'\О 11алеткамн 11ользо13ап,ся уже не прихо
ди~ ·ся; за эталон шющ:~д 1 1 пршrпмаrот не квад
рат, а тrую фигуру - квадратов 11а п1юс1<ости
Лобачевского и сфере п росто нет. Ипт~ресно,
что в обеи х гео.мстрнях 1~лоща;\ь ;..шогоуголь
НJ 11<а пропор цио11ал ь на ра~ности м<::Ж/\У сум~
:.юй 1::1·0 у1·1юн }1 суммой. )'Г!\ОВ ПJIOCKOl'O многu
\ТОЛЬНJ I К'а с тем же Ч l·JCJIOM сторо 11 (СМ. CT;ITЫI
•Гсомстрн>t Лобачепскоl'О~. ~·Фшурьт 1 1а сфере.-).
OG определен 11и ПJЮЩ<l/1,И кривоJ1иней11ой 1ю
верх1юсп1 u1,/ сможете 11рочи·1-,пъ в ст~1 т 1)~
•· Площа11.1, rюнерхноспн
ОБЪЁМ
Объем 11рuстр:tнс1вснных тел определяс1·ся
анало 1'1 1чно нлощадн 11Jюсю1х фн1·ур. B\1Clvl'O
П~\ЛСТОК НСIЮJ\ t>Зуют куб11льяжи . т е. ПfЮ<.~1·р:~н -
1еометриs:~ - з1 1ач ит " землемерие»
спю разбиDаIО'г nлоскостями на равные кубы.
Cпa LraJra рассматриnают разби ение на куб ы с
ребром , равным сдшшцс длш 1 ы {рис. 8). Если
тело, сост;.~влсшюс из а 1 та1шх кубов. целиком
ВХОД I IT .А 113МС:рнемое 1'CJIO ,1J, а тело JIЗ /J 1 1'.)'ООВ
содержит тело М, то .ЦJIН об·ьёма и(Л/) TCJ1~1 М
с11ра1.1с1111нны 11ср:ше1 1с1·н<1 а 1~ 1'(1"1) ~ /? 1. З~1тсм
беру~· кубнльнж. в которш1 ребро куб<t ра 1шо
J / 1О, 11 1юл}-ч~1 ют более:: тес н о~ 11ераве11ство
а2 ~ 1·( М) ~ /) 2i1 т. д. В рсзущп~1те воз1шкает по
сле11оnатслыrость 6ЛОЖС1J11ЫХ отrезКОН
Тело назьшастся л::убuруе.мы.м, сс;ш нсресе
чс1 шс nccx ~юлучс:нных отреэкuв с.:uдержит
сJ\и1н.:твсн~юс число, которое н nрнним~1ют :3а
uбъi!..м t•(M) 1 ·ел:.~ /11. Таю1м uбр;~~юм, объём
-
это фу11кц11я t•(Лf), ш1рсдслё11н::ш на мншкесrне
Г. всех hу'б11русмh1х т~J1 . Прямо т1з опрсдf:лсш1я
06'1.~ма слсдус:т. ч1·0 нсяю 1 й '1111 югоrран1111к -
f\)'fiнpye;\'IOC тело. Д.11я 11ругнх ·1 ·сл можно нс-
1юль3оnа·rь слсщ110щую теорему:
Пространственное тело М в то!\-1 и
тодько в том случае 1субируемо, если
для л1<>боrо положительного числа Е
найдутся два таких мноJ'огранни.ка
РиQ,чтоРсодержитсявМ,аQсо
держит М, и при этом
v(Q) - ti(P)<Е.
Крnмс: 11ринсдён110.го 011рспелеш ш 06'1,ёма
(с куб11.11ьяжа:м 11) JI мее-1·сн сщё и ~1кс~ юм.~~тиче
скос определение 061 ,ёма. 0110 базнруе-1·ся на
свойствахА, В, С, D объёма. которые формулп
руются то•шо так же, каr< 11 n случае площадн
Рис. 3.
:И5
Фигуры
(с очев 11д 1юf1 :~аме1юй слов «1mмр 11руе мыi1 » ш1
"к·убируемьп1», «е;~ппичный юшдр:п~ на «Сдн
пичный куб»). Мтюю док::~зать следую щее ут
нерждстп1с :
~".... На множестве С всех кубируемых
~1.r",,.
тел существует одна и 'I'ОЛЬ1'О одна
функция v (М), которая обладает
свойсгвами А, В, С, D.
]11аЧllT, с1ю1·1ства А. в, с, D MOЖllO 11ри1IЯТЬ
за аксиомы и опредеш 1ть объём как фу1 н.;цию
113 множестве С кубнруемых тел, у-доnлетnорн
ющуrо да 1 п 1ы м акс ноi\1ам. Нсе остальные слой
стна объёма можпо вынести ~п нпх: n частно
сти, формулы для 06'1,ёма J\U·югограшшков 11
ш:.~ра. <.jк>rмулы ;~лн вы ч11 с1 1 с н 1н1 объfмов с
ФОРМУЛЬI ОБЪЁМА
Чтобы найти объём, с пзча ла выбирают с/т,111п 1 -
цу 1 1змсрешш. В Дрсш 1 ем JJи ме, например, од
ной иэ единиц 061,ёма служила :-tмфора (около
2') ,5 л). Нефть 1ю nсём мире прюrято сейчас 1в
мерн· 1 ъ н анrло -а мср11канских единицах -
бар релнх , т. с. бочкзх ё мк0Lv1ъю 159 л; впрочем,
~сть разные ба rрсю1 - наимс1 1 ыLшй сuстанлн
ет всего 11 5,6 л . Ан Росоrи распростrа1 1 ё.1 111ая в
быту мера объём а - ведро В гсомс1тт11
за единицу объёма принимают
объём куба с ребром единичной
Д..'IШ-IЫ.
Подчеркнё!'.1. что 06·1,ём куба потюстыо оnре
ж:тн:тся длиной рt:бра - ведь кубы с о;щпа ко
вымн рёбр:.~мн ранны, а, 1ю одном.у из ос11ош1ых
C FIOЙCTR объёма,
~r раю1.ъ1е ·rела имеют равные объём:ы.
~!.
Куб, p efi p o 1<0торого имеет целоч.и слсннуто
длину п, можно разрезал, на п~ ед1 111нчЕ1ых
кубиr<он (рис. 1). Далее,
356
об·ьём объ еди нения нескольких
неnерекрывающихся (т. е. не име
ющих общих внуrреняих точек) тел
равен сумме их объёмов.
Jl()MOЩl..>IO тпсгралщ1 lf т /~ (СМ CT:J'JЪJ() ~Фор·
мулы оf>·1,ём::~ » ).
Есть. 01\ l Ja1ю, одно су1тссстве 111 юе отлrrч11е
тсор11и пл.ощ::щсй м1ю1·о)тоm,1тико11 от·1·еорн и
объемов м11.огогра шшкоn. Оно состоит в том.
1 по. эшш формулу шющаiJ,н rтря~юусолыпrк.а.
можно tюлучитJ, фuрмулы площади ч11ОL"О·
у 1 'OJLЬIП1 К()Н с 1IОМО ЩЫО тот.ко двух аксио~1 -
В 11 С (:-tJ.1J(11т11вносrн н нннарианп-юст11). ~н:~я
ф< 1рм улу t )бъём~1 11 рямr >у1·<1Лhно 1 "<) 11 ~1раллеле
nи педа, JJe удаfтся вынес1н формулы nГ1ъёма
мпогоrра 1 1н 1 11<О1i, полъзуясь лиш 1 , акс1юмdю1
В и С. Нужпа ещё 11 :шс нома А (11еотрнца
тс11ыюсп 1 ), что услож1J.Я е'L теорию оГ1ъёмов
м 1 юrо1·ран tш1юв. Подробr~ее об :опом мож
но прочит<1п, в с1·атьс «1-'ашюnелнкне и равно
соста нл с н ныс фигуры ».
Поэтому объём куба р:1:1J\1ером /1 х 11 х п
р<1не11 11' . Аш~лоптЧ1ю, объём прям о~1·олыюго
п:-tрзллелепипеда. тр1 1 11змере 1 шя кото ро го
целые чнсда а. /; и с. равен 11х проиэве/~ешuо
аh·c.
Можно рассм~1 тр11натh рис. 1 11 I<ar< 1 1зобра·
1
же11 ие l'/\11ни ч1-101 ·о куб;J, ра :3 р<.::з:.t н.ного на 11·
ранных кубиков с ребром 1/n. Сотаснотсr.1 же
C IIOЙC:TR::JM объём;.~, ПOJl\'L[ИM : объём одного та·
кого малс1-1ько1·0 куб~r~а ранс11 l/п1 Знач нт, 11
101 -да , ко1 ·да размеры 11 а раллслсп11педа - ра·
циош1лы11,1е ч исла а = т/п, IJ = k/n 11 с= l/11.
его ОбЪёМ, rавный ПрОИЗВедеIIИТО ЧJ'IOJa 1,убН
КОI3 1Ja объём каждого из них, вычпс.-ляетс~1 по
той же фор.муле: 17 = (тk /) (1/п\) = alJc.
Последняя фор:мул:.~ , конечно. оста.11ется13ер·
ной и в самом. общс:м случае, 1юг1щ а, Ь и с -
Рис. 1.
11рп1 1 з 1юлы1ые числа. Но чтобы это дот<аза·1ъ,
тrсбу<...vrся знать ещё одно свойство объёма:
Если одно тело содер:>1rnт другое , 1·0
объём первого тела не меньше
объёма второго.
Внутр~, пар:ошеж:п1111еда размером ах 11 х с
·"южно помссти·1ъ ггараллеле11ипс1 1 а' х Ь' х с',
11 :_Р4t:рс 11 ия которо1·0 рацтю11а1 1 ы-rые числа,
ГJрибт 1жающ11е а. h п с с недостатком. С:леf(О
nатею.1 ю, объём \/ перnого пзршнtелеп и педа
немею,шс объёма второго:V~V' = а' ·Ь' -с'.
Рассматр~rnая ещё однн параллслешшсд, пзме
рс11ия которого а'', l:J'', с" рацшшал 1 ,ныс числа ,
1tриближ<1ющие а. Ь и с с избытком. пuлучим
11~V" = и" -Ь"
- с".
И·1·ак, \!' < L1 ~ V". Нс> любое
чио ю допускает скuль у1 ·одно точное: прпбт 1-
жс ннt: р;щ1юналы{ым1 1 числами. т. е. 06'1,ёмы
\!' н \! " можt10 \-\ыбрзт1> скою) у1'О7'\Ю близкими
1< al1 c. ТТоэтr>му \f = ahc. т. е. объём 11рямоуl'Оm,
ною 1 1араллсле 1 1нпеда , равен пронзведсrrиrо
el'O t1змсрений.
Четыре перечисленных выше свойtп~а
061,ёма можно принять и з~1 аксио.мы , оn рсл;с
ляющие обr,i{.н. (см. статыо «Дrlиrra, тю щаю"
Об'ЬtМ » ; ()'l'MCTHM, Ч' l'О носле;~нес из IIHX - «MO-
ll()'!'OH1:-J0(~1Ъ \> часто замс:няют на раl{носш 1 пное
с1юйство - «неотрнц ::пельность ») ,
На примt:рс ны1юда формулы объёма пря
чоуголnтю1·0 п::~ралJ1елепнпещ1 xop<>mo tнщно,
1<<11< иснолъзуются ncc четыре пюi'iстна объёмов.
Ана1ю 1 ·нчно вы1юдят формулу площади прямо
~толыrика. Но в планИ~Уiетрни из неё можно по
лучить выражение: для площади любого мпоrо
уголы rи ка , поскольку мноrоуголы-1 1 1к ш:ткu
превратить в прямоугuльн~rк, рюрезая с 1 ·0 11а
чаС'1'11 и скла;~,ьшая нх в другом 1 1 uрядкс. f-k так
в пространстве. Здес1" к сожал<.:н11ю, ~п<.:рс
кра11в:11-1 НС-> одного MIIOl'UГpaннr 11\;1 R дPYl'OJI
того же оnъёма далс:ко не нсе1·да rю1мож1-ю
(см. статыо (• Ранноnелнкис и ранrюсостан
лет 1 ые фигуры•) ). ВыRод фr>рмулы обт,ёма
при:~мы - одип нз тех релтшх прнмеров, кота
такое « перекраИТ1ание » осущестnи.мо.
ПРИЗМА
Перtпиwем формулу объёма nрямоу1·олыю1 ·0
11араллелепипеда в видеV=S ·/-/,l'деS= аЬ -
г1л()щ~щь его осноL1а 11 ия, а Н =с - высота. Рас-
Геоме трия - зн.эчит н земА~мерие »
см о1· рим прнмую треуrол~,11ую приз му
(рис. 2, а) . 12ё лсrк.о <- псрскро1-пь" n прямr>уrолr,
ный паралпелепипед (рис. 2, б) . Объё;\.1 V. пло
щ~щь основан ня S и высота Н п~1 раллелсn~-111сда
буду~· таки мн же, к~1к у призмы . Сле.п,онатслы. ю,
объё,\<1 пrямой тpcyJ '()Jlhl-IOЙ 11р11ЗМЫ НЫЧИСЛЯ
СТСЯ по формуле
V=S 71.
С')
Посколы<у люfiую пряму10 призму можно
ра3резать па треу1·олы rые (рис. 2, в), для неё
спраnсдшша т~t же qюрмулз. Наконец, rюзьмём
11рои:шоль11ую наклонщ·ю призму П. Продол
жим её боков1,1t 1parm 1 111срсссч ё,\111х псрн ен
ди1<ую1рной нм mюскос·1·1,ю 1х . К 1 1 ризм е Г1
!\Об~IКЛЖ.:ТОI СКО<::!\) fХЩа <- КОСО усечёНШISJ П\lИЗ
м :.l -1 К (рис. 2. г). ОчJежtм точно таку10 же 1<0со
уссчё1111ую пр11:1му uт дру1·01 ·0 тор 1 щ вct:rn 1ю
луче111ю1'О тела (рщ:. 2. д) . Осrа 11 етсх прямая
11\)ИЗМ<I П11 TOl'() же об·_ьёма \1, ()чеВИ)ПЮ , ЧТО сё
высота Н paRIШ бокоnому ребру / пр1-r~J\п,1 П. ос
ноnапие как rтрое1щня оснонашш призмы П на
о: и.мест площадь S0 = S cosq>, Г/1.С 5 - площадь
основания при~мы П, а <р - уго>1 между ним и
шюскостью а (см. с1·~тыо <· l1:1чала стерtu
мстр1111» ) . Но нысот;1 Н 11 боконuс ребр о 1
11рнзм ы n соотне·1·е1·вен 1 ю п1;;рпе1щ11ку; 1 ярны
этим шюс кос1·ям 11, знач11т. соС'r·анлшот между
соВой такой же у1·0; 1 <р . СледпнатсJ 1 ы10.
Н=/со:;<р н \l= S0 -/= Sсоя<р · l=SH. Итак, фr>р
мула ('•) llblГIOЛIIЯeTCЯ ДЛЯ ЛТО6Оfi Пpl·I ЭM l1I.
Рнс. 2.
.4
357
Фигуры
ГпиРАМИЛА
()J1нако /\/tЯ ны ч 11слен11я nfiъём:.1 ·1реуголhнuй
лнр:змиды 11риходитсн пр116сгН}"lЪ к ,1.1,01ю;11,-
1ю сrюжной КОl[Струкцнн, нзпсспюй срсдн
358
Рис. J.
ОБЪЁМ КЛИНА
Клином называется многогранн ик, получ<Jюwиися иJ
призмы, если отрезать оди11 ~1 з ее торuов плоскuстыо,
н е параллельной основаниям (рис. 1) . Он огр,1ни ч е н
тремя тра n еuиями и двумя треугольн и ками. Объем
клина А8СА,В,С1 оыражается формулой
V=а+Ь+с5_
(*)
3
'
где а, Ь и с - мины n.:~раллельных рёбер АА 1 , 881 и
СС1 , а 5- - ПЛОШадЬ СГО Оf)ТОГО Н dЛЬНОЙ ПрОеКUИИ на
плоскость, nерпN1дикум1рную боковым рёбрам (Рсли
эту плоскость можно п ровести т.:~к, что 0 11 <1 п ересечёт
все боковые рёбра, го получится плошадь 11ерпе1-~ди
кулярного им сечРния).
Лля доказательства формулы ("') разобьем клин 11а
три тетраэдра : АВСС1 • АВВ,С, ~1 АА 1 8 1 С.; кажлыи ИJ
н их можно ра\с:матр и ват~, как « вырожленный~ клин,
у которого два из трёх параллельны х рёбер п ревра
тились в точки, а 51 та же . Возьмём тетраэлрАВСС1 .
Его обьём не юме 11 итсн , если передвигать t!ер ш и11ы
А и R параллельно ребру се.. (KurлJ мы СМЕ:'Ша~м.
Н'
,\lатематиков ка r< <- qёртова лест1 шца->. 01Ja со
хр:11п-1лао, н учеб.1:ншах Гt'OJv1cтprпt почти в
нсизыс11110м BИfl.C с Енк.;1 1 щовьLх « Начал>. Сч11 -
та<.:тси . что '·метод исчер 1 1ынанш1 " (н<1зваш 1 ыi1
так в XVll н.), с помощью котщ1ш·о 1·рек11 обu
сноныкu1н ~·1 ·0 11 11одпбн~, 1 с ему rапуж;1еш~я,
со:щал Er11i:oкc К 11 1щск 1 1й . П\nже ~~стол \1ьu1
ра :щнт 11 трудах Архимс!l;а.
Поделим высоту пирампды rra /1 р::~в 1 1 1 .1х
частей 11nровс,'\ёМ сечетщ параллелы1ые оспо·
nанпю, через точки дсл<.:шm. На каж,пом сече
ни 11 постро11м две равные L1акло 1 шыс призмы,
как шжазm ю 11:i рис..) . }1,ля о;(но1'1 1 1з НJIX, "в11сш
нс(1 •. это сечение будет 11нж1-1 1 1"'1 uснuванн1.:м,
) 1,ля ;1руrоИ. <- внутренней~. - нсрх 1 111м. Внутрен
н11с прюм ы оnрззуют с r·уттенчатую пирам11ду,
содержаш,уюся ш1уrр11 ла.111 ю~'1 . В11е 11 1 111 1е 11мссr1:
с пр1 1 змоГ1, ностроеш юй таюrм же сттосо60.,111а
ос т юван11r~ . - похо жую пирамн.ду. 1ю ашt вкто
чает в себя лаш1уто. Jамс.1·и.м. •по есл11 уд::tлшь
г1аr~ример, вершиг1у А. о<.1аются nреж1 1 им~1 как npo·
тивоположная гра н ь все,, так и опушенная на неf!
из А высота.) Сдви н ем точки А и 6 так, чтобы гювая
граг1ь А '8 1С стала Пl:!рпендикулярна СС1 ( рис. 2) .
Обьём нового тетр.влр<~ А'В'СГ, р,1вен
1
1 sл·R·• се,,
п ричём п лоша,\ь А'В'С равна ка к р<н У. Итак,
Сложив Т<'lкис [!Ыражсн11я лля всех трёх тетраэл
роо, получим nри1:1едён1iую выше формулу(*).
Величинаr= (а+/)+с)/ -1
-
не что иное. как
расстояние между uентрами масс ос1юоа 1 1ю1 клина.
П ри таком пон 11ма 1-1 ии 1:1ели ч и 11ы г формула V =гsi
будет верна уже для всех тел, обрt1.:Sуюшихся, если
отрезать 1opeu от любой п риз\Лы или 1Jил1111лра
(рис. 3). Следует помнить, что, говоря о uентрах мJСС
О{'1Ю[!а11ия клина , нуж11u представлять их как пла пин
ки nопоянной толшины .
...
'
'
'
Рис. З.
'\
\
'
'\
1
Рнt. 4.
Рис. 5.
нз- ггод 1шt"шНей nнрамнпы перву10 сё ступень
ку, а ос1·::1;1ьные опустить на однн qэтаж'" то 1ю
,rуч11тся 1.1 то•н юс1 ·11 внутrенняя 11нрймида. Та
ю1м обра ;юм, r:~.~-~ность оGъемон ступе 1 1ч ~1 ·rъ1х
П11р'1~НIД p<!B Jl;J ОfiЪёму <-JHllJНJeЙ-> 111IЖI 1 <.:Й CTy-
Пtl-!bl\И. 0 11 становится скоm, у1т>1~1 1 0 ~1 алr.тм с
увет r чет-1ем п. З 1 rзчит, объёмы обе11 х ступеп
чатых пн р амнд стремятся с ростом п к 011 1 юму
11 ТОМ) же з1.1аче11ию - объёму Jl,ашюИ треуrопь
ноfi ппрам 1 щы. к~ш: el'o найти~ 1Iусть S - пло
щад1, ос11оваmш эшрамиды, а 11 - сё высота.
Тогда ссчсннt, нровt"дёююе на расстоншщ х
т нср11 111ны 1111рам1щы , - трсутльн нк, rюдоб
ный оснuва10 1 ю 11 ирам 1.щы с коэфф 1 rr\нснтом
подобия х/11 11 11.rю щадыо (x/fl /s. Длн /г- 1 ·0,
считзн сверл'У. сс•1t1:-1ия х = kll/п. Высот;~ всех
<.'1')111е1-1е1< одинакова 11раtша ff/n. Поэтому объём
1·1
• к:~ждоi1 и:"! / \ В)'"Х сту nе 11е к, n остроеп11ых нз k- м
се•1еr 1 ии, равен
С'..rюжт1 об·1,ём 1,1 С'Г)'11снск на 1ксх сечс:ннях,
11олуч11:-.1 объi::м внешнеfi с1'уn~нч:по1~1 11 нр;1 -
1ш11п1·
-
'fЧ12+21 +...~ ll1
t1
"="•+''!.+
... +l'" - .s
/'J~
Мы видим, что э·rот объёи проп()рцноааnен
оро11зведепшо площади ос rюв:н шя на высоту
nирачщ~.ы, nричём коэффи 1 ~.ис1тт nроrюрцио-
,
,
r
-\
налыюстн с""' ( 1- + 2~ ~ ... + 11')/п пс ~~аnисит
от пирам1IДh!. Значнт, 1Jдля объсма 11 н:~тсй 11с
ход~юn 11ирам11ды верно то же с;11\1ое, ·1
·
с.
V= с · SH (:щесь с - nос·1·ш1н11:1я, т:1кже н с: за
в11сящая от 1111рам 1 щы) . 3ам<::'r11м, что форму11а
V= с · SH вср1 1а ;1,.11н 11юбоi1 (1 1с: обяэ::ас:лы ю трс:
ут:~ы юй) nирами;1,ы, так I<зк каж;-~;ую из них
~южсю разбнт1, шt треугол 1 .н ые пирам 1 щы тoii
rеометриЯ - .1НаЧИТ « Землемерие»
же высоты (р11с 4 ). М11ож11тель с ести предел с11
при n ~ ""· Но. поскольку он Oil,Iщакоn д!lя 1.ксх
1111ра,щщ, достаточrю rrайти его только для ка
ко1·0-н11будь ч al~l'HOl 'U случая. Н ап ример, куб
р:.~зб11н:.1сто1 на шесть р:.1ю 1n1х че'1ъ1рёхугол~-,ны"'
1шр<1 м нд (рнс. 5} Объём куб<• l' р<-'брuм с;1ннt 1 ч-
1юй NН•\НЫ ранt'Н ·1, НЫСОТ;l к:.IЖ}~ОЙ п11pa~1Y\
/tl>I - 1/2. а 1 1лот1\<1i~;1, <JС1юн::н1101
-
l О1 скт:1
l';.= 1 = 6 с 1 ( 1/2).·1·.е.с = 1/3. (1\<"га·1·11.а
смажете лп uы ра:1611т~, куб 1ra тр11 раш 1ыс п н
рамиды ?) Ит~щ объtм любой 1 11.rрам1щы
\/ =lsu
Jf
,.,
-
'
J
ТЕТРАЭЛР
Из формулы ()()·1 ,61а п11рамн,rщ можно выnестн
нескол ы<о 11ыраже 1 шi1 для объёма тетраэнrа
АВСD. На пртrмер:
1
V.1н(}) = 3Sш1 • ALJ ·siп L(rlЯC, Al>) ::::
== ~ .s·.iш Suщ. sin L C"1RC ОВС)
3вс
.
'
.
В этих формулах L(АНС, АП) 11L (АВС, !JJJC) -
углы м<:жду 1 ра11ъю АВС r1 ребром AD. Г[Хl!1Ям11
АВС и DBC соотк1::тс•1·всюю: формуны полу•1а
ютоr нз формулы объём<t п ~1р<1мнлъ1. в кm'Opol!
S = 5 .tBc , : .1 ВЫСОТJ выражена ЧСреЗ / \])УГНt' ЭЛt'
меmы тетраэдра.
Вот ещё одно выражение:
v
1
,
· l .!J(/1 ~ 3'""' .sll\1'111 '
Эта фор,v1ула, н которой .)',
101111 -
1ю11 на.н 110-
верхносп-. тетра::щра , ~1 ~·.11 - р:щнус в1111сан 1 ю-
1·0 н нс 1 ·0 ша 1 х1. ;,~на.rюп:1 чна выр~1жен11ю S = 1-; .J
д; rя 111ющ:зд11 '1·рсу1 ·uт,ю rк:i. 1дt' /J - <:1·0 1юлу
псрнметр, а " -
раднус r1n 1rca111'ro(r окр~-,юrос-
1·11. Лрпчём ;~:-ш 1 1ая форм}? 1з с11р:-1 ведл1 1 щ1 ;r,ля
JJIOбoro (1) м 1 юmrраншша, 1 tмеющеr() впнса11-
1 1ую сферу.
11ожалут1, 11а11бопес шперt:сна формул:\
)
\71щ0 =.::sм 0 ,\лв.cv\.
<*)
.1
В кoтopolr IAB, Cf)j - расстоян 1 Jе между СК[Х'
щ1111ающи~1нся рёбрамн АВ 11 СП, а Sм; m -
п.1101 ца; r,1, сече~ 1ня тстра::1дра шюскос1Nо , про
хо;\>1 Щей через серс;\11ны ос1·ал1>11ых рё\1ср
(рис. 6. а). (Это ссчеш 1е
-
паралле.•юграмм ,
)59
J)
l:J
в
А
Рис. 6.
стороны которого параллельны рёбрам АВ и
СП и ранны 1ю длине их щтошшам .) С;1ви нсм
всрuн шу D на нектар СА (рис. 6, б) liсли uы
числитъ объём получивrпс:п.>ся тетраэдра АВСП
no формуле объёма пирамиды , нри1uш за ос-
1юва11ие гrа11ь ЛВС, ТО ЛtТКО убсДИТЬСН, ЧТО
объёмы rювого У1 исход~ ю 1 ·0 тетраэдров раnнъr.
Пели же юя1ъ за ос rтовапие г р;:~11ь АВЕ, то мы
придём к выражению (*).потому что площадь
АВЕ вдвое бот)ше S~ш сп, как видно из рисунка, а
011ущешшя наАВС высота равна IAB, C.lJ I. З;,~ме
тим, что Sмнп = (l/,l )AB · CL> · sin L (АВ. СП).
С помот;ью формупы (*)удобно ш1хо1111ть р<1с
стш1ние между скрещиваюш.имио1 щжмыми.
UИЛИН ЛРЫ И КОНУСЫ
Впишем в r~илинлр nравилы-Jую п-уrольпую
призму (рис 7) С увеличением п её объём и
площадr, оснонания стре/\1ЯТСя соотвстстnешю
к объ6'1)' V и площади основанш1 S цш1индμа,
а её высота при всех п равна высотс.Н цилинд
ра. Поэтому 11.ля объё м а цнnиндра сr r рзвещншз
та же формула , чтu и юr11 nрнзмы.
Рис. 7.
360
1,~ 1 =SH
\
1\
1
\
1
\
1
'
1
\
.11, \
h
Рис. 8.
н
Точно ·rак же, прнближая кон\'С ш1рам 1 rда
ми, найдём , что
11=~SH
к
3.
ГТлоскос1ь, 1 1аrаJш~ная основанию конус:~
нысоты Н н прохпдящан между оснонаннем и
верl1LИ 1 юй н<1 ра~стоянии Н1 пт вершнны, от
секает от 11ero ме11ьшнй конус , подобный
данному, с коэфф1щиентом k = Н1 /Н = R1/R,
гдеNиN1-
радиусы ос 1 юnани!"! конусов
(рис. 8). Пусть 11=11 - 11 1 - высота образовав
ш<:тося усечё1 шоrо конуса. Найдtм t:ro объем.
П оскольку объём большего кuнуса р:шен
)
-
1
J.
•
(п/3)N-н, а мсныш.:ю- /г (n/3)R''11 (аr11оше.н11е
объёмов подобных тел равно коэфф1щис1i'f"У
подобю1 в третьей степе~ rr. 1). оnъём усtчi::нноrо
кпr 1 уса спсташrнет
7[
\
'
7[
1
,
-
(1-k )R. - J-f =-;-0 - k)H·(J+k +k-)R"=
j
)
что можно за~ 1иса ·1ъ через площзлн оснований
S ],"!
~
L
=п~ н51 =7r1<1 как
('1
По такой же формуле вычисляют объём ус~
чёшюй пир::tмvщы .
Формулы для объёма r~илиндра п конуса
справедливы и д;ш обобщёш1ых 1tнлиндров 11
конусов, т. с. когда n основанш1 лежпт про«з·
1ю111,нан r 1 ;юскан фигура , причё,ч со 1кем иеобя·
зателыю мно1 ·оу1·олыл1к или круг
ОБЪЁМ ШАРА И ИНТЕГРАЛ
Одним И:1 своих r1 а н ВulСШШС достижений лrхн·
мед счит;:~л доказательство того, что объём шарз
в полтор;:~ раза меньше объёма описапноrооко
ло него цилиндра:
4~
V111 = ) rtR,
поскол~~ку объем ~писанного цилиндра ране~
SH = пR- · 2R = 2rtR . Недаром шар, вписанныrlв
цилиндр, был высечен на 1-1адгроби11 Лрхиме..iJ
в Сиракузах. Это док;~затслЪ("-rво. как и nьmщ
формулы объёма пирамиды с помощью •'fёрто-
Геометри~1 - 3начиr «iемлемерие »
вой пестшщы·>, а также вы'-Iи.с.11ение объёмоR
мно1их других тел , ос1-юнаны па 1 1редстаnлени11
тела 1:1 виде ~с·1·011ки » тонких ларзллельных:
слоё в. Объём каждого слоя примерно p;:iRcн
лrоизнеденню r~лощади е1·0 основа11ия на тол
щину (сло\'1 - обобщённый цнт1ндр) , так что.
R СУЩНОСТИ, нужио ВЫЧИСЛИТЬ сумму ШЮЩ:t)\СЙ
11:.~р:иrлслы 1 1.1х сtчсний , то ч нее, 1 1ре:::дслh1-101 ·0
з11ачения п ромзпе11ения ятой суммы 11а тою 11 и
ну слон , 1<01-да последняя стремнтся к 1 1 уню. Ма
тематию 1 11rюшлого 11ролвляли 11емалую 11<1ход
чивость и остроумие 1:1 подобТ1ы х вычисле11иях.
Допустнм, напри.мер, что для некото рого
тела неизвестного объtма удзлось подобратт,
Рис. 9. Мож1ю noк,\JJ lь, ч10 riл<.>UJ<.1д~ любого ct"l('1 1иsi uыра рэвн,1
llJ\Oll lд.i.\H t l:i.ч~IH1S.C HH·i ...ке Пl\cJ( костыо -г~лс.l (L1JOt-ip1.~>кeнu З<:.' Л(\Н l~М
1Шt' rU \<\ ), п o лy•itl{;_l\.\01 u вырt- • (HH11:' + 'vt ," ~ ОПИI c.I Ht-fO f (J Ol<• ~Л<J Ш(\ Рi.1
u11м1н11f)J лuух кt11 1уrов с ol•wt'll вt>ршщ~т1 в ш•11тре t1мр,1 По но"у
11 обь~м ш,tf)il pJвt>1 t оfiь('му зтоrо rел<.1 . т. (',rrR' 21~ - 1 ( 1/1)rrR' R =
= ·lttl~ iJ.
КАК АРХИМЕд
НАХОДИ/\ ОБЪЁМ ШАРА
Рассмотрим прямоугольник разме
ром 2R х 4R, круг, касаюшийся его
минных сторон в их серединах А
и В, и треугольник, вп исанны и в
него, как показано на рис . ·1. Пр и
врашении вокруг оси АВ 'ЭТИ фи
гуры образуют uили ндр, шар и ко
нус. П ересечём их плоскостью,
прохоляшей параллельно ос н ова
ни11м UИ/\И Ндра на расстоя н и и хот
А. Обозt1 ач нм П/\ОШади сеч ений -
булем н азывать их спотвстсmе н
ными - через 5..., 5w и 5•. То гд<~
х·Su"' 2R ·(Sш+5.J .
(*)
действительно Su = 4nR 1; S'" =
=лСЕ1, где СЕ1 = Е01- ОС
1
=R
1
-
-(x- I02=2Rx -х1;5,= nCD1
=rcx
1
,
и равенство (*) проверяется пря
мой rюдстановкой (рис. 11. Ес/\и бы
в его левой части вместо х стоял
11осп.>я 11ны й м н ожитель, т. е. зави
симость между тремя сечен иями
оставалас ь олной и той же для лю
бой 111\ОСкосп'I, то такое же р<1ве1-1-
ство было бы верно и д11я объемов
V,,, Vw и V" Архимед н<Jшёл чрез
вы чайно остроум ны й п уть - обь
елинил равенства ("') при ра"lн ых х
в од1ю соотношени е Лl\Я объёмов.
Он посмотрел на урав нение(•) как
на «правило рычага•: х и 2R он
принял за п леч и, а плоскости се
Ltе11ий - за массы. Его идею иллю
стрирует рис. 2 . На однu плечо
ры ч ажных веС"ов, как на осъ, надет
uилинлр "'к, что точка А совпадает
с точкой опоры ; на другое плечо
на расстоян и и 2R от точки опоры
пuлвешены конус и шар. Спответ
ствен 11 ь1е сечения uили нлра , ко
нуса и шара урав11овешивают друг
друга, а значит, и весы в uелом 11а
холятся в рав новесии . (Сечения
здесь нужно по11 имать как пласт11н
ки из оыюродного мптери ала оди
н аковой и очен ь маленькой 1ол
щи ны.) Ра.еновесие 1 1е нарушится,
если сосредото•t нть всю массу uи
линдра в его uентрЕ' , расположе ~t
ном на расстоян ии R от опоры . Вот
Рис. 1. 2R
мы и избав~1 /\ись от переменной
ллины плеч а! За писываем п равило
рычага для всей системы, учиты
вая, что массы п роп орuио11алы1n1
обьёмам:
RVu =2R(V., + V.).
Сl\едова тельн t),
V=V"-V
w
2•'
откуда легко вывес ти извесп1 ую
формулу объёма шара.
Архимед нашёl\ и лругой спn
соб вычислен и я объёма шара - по
сушеству, очень близк и и к и t1те
rр1~рованию.
Рис. 2.
361
Ф11гу ры
z
Ь,_____~
l'ис. 11!.
1акпс тело 11зRсст1-ю1 '0ибъёма,ч 1·0 ruю щад11 нх
CL'ЧCHHfi любой ПЛОСКОСТhЮ, пар:IЛЛСЛl>НОJI
д:11 111пй, пд1111а1шnы ~на режем» nfia 1 Ь1 а на до
статпчтю тп н кт rе п~1раллслытыс слп н . Tnr11a
объё~1ы ссютветстnешrых слоёв n двух «Сто п
ках». а значит, 11 объёмы сам11х тел равны. Этот
:..fетод был раз1шт учеmшом Галилея - Бона
ве1 11уrюй Кавальери (си статью «Стан овление
,\i\: tTCM:ITI IЧCCKOl 'O aнaJll J;j a» ). На р 1 1.С, 9 I IO K:IЗ:t-
110, как таю 1 ~1 способо м 11~111т11 объём ш:1 ра.
Интсг1хu1ьн ос н счно1сннс. со:щанноt: Нью
тоном и Лсйбн11цем. nptяp~t тнmJ f11>1ч 11спс11111.:
06·1 ,ёмон 1i ct ан1tарт11ую 01 1 ер;·щ 1 1ю. О11з зал 1-1
-
съшается формулой
,,
V = JS(z)ctz,
tl
где ~' - объём тела. раслоложснноп> мс;кду
п1юскu<."1·я1\1н z =а 11 z = /J. а S(z) - шюща;(1, е1 'U
сечен ин 1ШОСКОС ' !ЪЮ, ] 1роходя щer'i ч ерез тпчку
z ос1 t ()z 11српсндику11нрно этой оси ( pt tc. 1U,
см стат1. ю <·ИJJ ге1рал 11 1 1ернообра :-11 1 а» фу11к-
8
б
----"
~,:--------
''
Рис. 11.
362
1 tПН ·•) . ll аnр~ 1м ер.объёN шара радиус:1Rсцев
тром в нач:шс коордштат nычислнют так:
S(z)=rc(N.
1
-z\ -Н~:::~Н:
N
\~"= Jл(Nl.-z.l)clz =
11
ФОРМУЛА СИМ П СО НА
Прпксдём через ссрсди 11у кыст ы )'Сt'Ч<:шюrо
конуса плоскос1ъ, параллельную основ ::ншя м.
R сечеr 1 ин <1i)р::1:1уе-1ся 1\ру1 рад11уса (R+ R1)/ 2.
rл,с R и R 1 - ра;щусы пспонаннй. F.ro площ:~д 1,
1дсS 11 S1- 1rлощад1J оснокан11й. T<Iкже ныр~
жаt:'J'СЯ 11 плurнаНI> «C P~flHC! 'O» СL'Чt' НИЯ любой
усече1 11 ю~'1 1 1 ир tt м1щ1,1 Те11ер1, формул> (")
мож1ю ;iam rcaтr, н nил:е
Это з:1мсчат1::,1 1ьн:ш формула . Она прпмс-
1111м :1 к цшш11д1х11ч . прr1змам , конусам 11 11нра
м11.ц;~м - 11 зто нсуд11R11 тслы-ю , 1 10скольК)' JVJЯ
11их спrа 11сдт 111 а формула (*' ). Л<: t'КО также
O r ~PI н,1 н1111рщ
о 1 м16 11"н1щ ~уба
н,1 1 μ11 р,ш11ыt'
nи ril\<111 Льl .
проверить, что из 1 rсё мтюю получить форму-
11у ('')для тетраэдра, «лост~шлсн1ю 1 ·0 на ребро»
{р11с (), cJ; «оснона ю.Jя» здесь - п ротинополож
ныс рёбрзАВ11C.:D, так чтuS=51= U).Бо;1ес
'IШ'О, 110 (***) MOЖlfO ВЫЧИ0[1 1 ТЬ JI объt.:м шара!
f,1·0 «f)C\IOR::J.1111ЯMl19 надо CЧH'l':l'J ь ,'\Ве J\И:1МСТ
р::~лы-щ 1 1 poтнn01IOJIOЖl l.ЫC ТО Ч КJ Г- П!1ЛЮСЫ. а
cr~f\11 11:-.1 сечсн \[ем - :-ж натор 11 ал~ .1 rvю пло
rтюст1,: (Ш/6) · (0 + 4 · тr.R
1
+ ()) = (4/3) ·JtR~.
Секрет поμобтю ii ~пинерс:шыюсrи н рост. Во
всех этих случаях тющадь S(z) сечения, парал
лелытого осrюuа 1-шлм, uыражастся чсре:~ nысоту
zсечснпя (отсчитт.113асму·ю от нижне го осr ющ1 -
шш IUШ Jrюбой пapaJUICЛЫIOfl ему llJIOCKOCTИ)
\tного"11н.:1-1ом нс в ы ше 11тороl1 стспе11 11 , т. с.
S(z) =Ar +Bz+ С (1rровсμьте!). А д.т1 т:1ю1х функ
щ1f1 справс11лиnа фu}J111:JIJIП Сшшzсо11а:
!>
(
(
.
'
11
'
({+/')
.
JS(z)tlz == Ь S(a) + ~~~ -
2
- ) + .)(fJ)J
"
Геомt:три я - 3нач и т :< землемерие»
1 ·де /1 = h - а: S(a) н 5(1?) - площад11 ()С11оn;э 11 ий
TCJJ :J; s ((./ ; [}) - 1IJtOltЩЦЬ CI 'О <.:рСДНСJ '() сечс-
111JН (•~·очка (П + Ь)/2 -сс.:редпна отрс:шэ !а, bj).
Очевн;.1,1ш, что и ~ш~1роной С-'ЮЙ ''· изображён
ный на рис. I l, t t. 11 час1ъ тстра:цр:1. ;шю1ючё11-
1tая ~-.н::Ж,r\)' дRУ\1Я 11.'ЮСКО(ТНМН. п~ip:'lЛЛCJl\,Hbl 1\\l I
;'\ГIУМ ет рёбрам J-1'3 р11с. 1 1. б, yдoRЛC'1'BOf)Hl<TJ
формуле (***) - llt'l\1• фун 1щнг 1 . 11ы1х1 жающ1 1 е
площад1 1 сече11ий ;')'J'IIX тел. от «уреза.~ 1 1ш» гю
следних тrе мептотся. Фигура на рнс. 11, б. т 1 -
р;~м11да, <UITИHplIЗl\Щ <. IQШll» (рпс. 11, в. г) опю
сятсн к одно11оrу 11 тому же 1шду м11огогра1111юю~з,
н а3ываеиых пр1rзмт1ю11дами: nce всршиIJы этих
,\IJIOJ'O l'pa1111нкoв ннляются H<:'p1111 1H;J,\.JIJ IJX (,()С
нонан11 IJ" - М!Юl'ОУГШIЫIИКОН, , 1ежащ11х Т3 11а
р:.1 л11елпных ГIJIO<.:KOCI'ЯX; <>CHOl\:lH/ICM МОЖ(.'Т'l':JК
же бы·1ъ 0·1·р{:;~ю1< 11ли J\:аже о;\на точ1(а . Объёмы
ncex таких мrюгоr ра. t11 Jико1~ тоже можно ны
чиспять no qюрм~11 1 е Сн м пеона.
РАВНОВЕЛИКИЕ И РАВНОСОСТАВЛЕННЫЕ ФИГУРЫ
Формулы /\JIЯ НЫЧ Н СЛСIJ l/ Я JIJl()Щa,1cl1 ~'>lHOHJ
\'(()Л(.l l l IKOIJ r1 пбъi.:мо н М! IO ГOJ'j)<I Н!-11 LKOH f5 1>1 л 11
и:1вес·п 1ы ещё матем:п11 кз м дрен11рстн. В "На
чалах» ЕвrV1 1 щэ нычисле1ше 1 1лощадеt'i м 1 ю1·0-
у10лышкоn оm~сьmается так. Гuющадъ нр~тмо-
h
Рис. 1.
rнс. 2.
а
2
1
1
1
1
'
1
1
1
1
lt
2
у 1 ·оm,ника р:.шн а лро1 r::1в<:>.деш 110 l'J 'O сторо 1 1. От-
1к·:3;ш от 11 аr~uшt:.:ю1рамма r1рямоуr·ольный трс
уrол1>1 1 ик 11 1 1t:ре~н:стиn с 1 ·0 н Ht)t1oc пож )Жt:нш.:,
МОЖНО П peRJ1;l'l'l l 'J'T> 11:1 paЛJreJJOГ(">aM М А П рн MO-
YГOJll,ПH K с тем же ocнo11a1Lt tt:\t\ 11 то(1 же ныt.:о
той ( рщ-. 1). Гоnорят. ч 1·0 п:-~ра.11 1 1ело 1'р:-1мм н
прямоугольник - ф111уры рав11ососташ1е1111ыр,
·1' . с " rю 011рс1t едсш1ю, пх _,южно ра зр сз зп . н;:~
понарно равные куски. Поэтому площадь па
раллсло 1 'р~1 м ма pau11a площа,111 получс1 1 но 1 ·0
r1ря м оугш 1 hн нка . S == а/1. rJращ1а , ccJ111 взять
OЧClll> нысою 1 1J 11 1-1:1КIJ()f-1 1-JЫJ'I 1 1a p;1JtJJC'ЛO l '(1:lMJI! ,
то столь r1μосто прсоf\1х1:юют1, е 1 ·0 н 11рямоу
rо111, нн1< с теми Жl' ОС 1 101·Н11111<.:М 11 RЫCOTOJI 1-J(:'
у,r~:аё·1·ся (рис. 2, а). Од11а1ю 11 в :·пом случ;~с
р<1ссматр1шаем.Ые фнrуры р:1в1юсос·1·аRнены
(11ало л1 1111 ь сумет1, разf5итr, 11 х 11:1 боm.111е<.:
чнсло часrе11; рнс. 2, б).
Uчсв1щ1ю, •1то любые дв:~ раn~юсоста11леп-
11ых мноrоу1·оm,ню<а нмсют олпу 11 ту же пло
щ:щь. Обра·1·ш1н тс::орt'м:.1 была дока:3а11а
Li XJX ст1Jл<.:т11 11 матсм:.1 ·1·1н~амн Ф. Ьш1ьясм 11
П . Герни~ юм (см ст:1тыu "мнш'Оу1·оль н 11ю1» ).
Площ:.~;1ь треуrош.1-111 l\;J можно J 1 аС1ти · 1 ·оч1 ю
"1'<1IO I M Ж<-' CIJOCOt10!vl: IJ()C[(OJJЪKY тpeyJ'Шfl>H I JK
36.3
L~Рис. 3.
равтюсоставлсн с паралле11u1·рам.Уюм , име
ющнм то же оснuн~н rис и н)l.rюс меньшую высо-
ту (рис. :1), er·o шющадь ранна S = ~а'1. Во1ю1й
11ра1111111.11ый м 1юrоуrолы 1ик равтl()состаrтеп
с пекоторым параллелоrрамм()м (см. р11с. 4
J1.ЛЯ случая чётного ч1101а сторон). J l оэтому
площадь праnилы-юrо мпогоуголышка вычи
сляется по формуле
1
s =2 pl1,
1·,цс:: /J - CJ'O 11ерн.метр , а h - аrюфема (расстоя-
11ие от нентра до стороны).
И точно так же, <.:читая формулу для 1шо1ца
J!Н 11рямоу1'оm.ника и:111ес1·1юй , мы можем nо
J1}'ЧИ'1ъ шюща;(н всех 11руrих мноrоуrолытикоn
метолом «ра1реэаппя и псрекладывашш», т. е.
используя только две аксиомы площади (см.
статью «Дrtина , площад1" объём ·>) - В (адди
тнв1юсти: сумма nлощщей частей равна шю
щади ц<:Лоrо) и С (инвариан.тн.ости: шющади
ранных фигур раш1ы).
С 11ростр::111стве1шымн фи1у1х1м и )1,CJJo пб
стоит несколько иначе. Конечно, и здесь мож
но нахо1~и1ъ объfмы с rюмощыо рап110 -
состапле11 1 юсти . Так, любая 1трямая призма
ра в1 юсоставлена с прямоуrолы1ым параллс
летшс,т~;ом . Однако, например, мя вы<-шсле
ния объёма трс:уголыюй пирамиды изда.в11а
приJ\1еннетс.н с~юсоб, который сnязап с её
разб11с1rием па слои и переходом к пределу
(см. ст~п·ью ~Формулы об·hёма»). И:s-за с;южrю
сти м:.tтсматики прозвал и этот пюсоб ~чёрто
ной щ::ст1 1 ищ:й».
364
J lредельный переход в данном прнмсре, как
и всюду в теории пло1.цадей и объёмов, обо-
сновыв:.Jе1'сн r 1ю ."'ющыо аксиом1.1А (<1 неотр11-
1~атет,1rостн объёма 11л11 площал;н). Из неё
вытекает, что ест~ одна фш111а лежит внутр11
дру1·0!'1, то объём (11л11 шющадь) перuо1! ф111у
ры нс больше, чем второй. Та1< что же, выtшс-
11и '1ъ объем трсуп)Лыюй п11рам11ды qэлемев
тарно <>, нс 11рнмсюш снн:з:~нную с 11μс,11ел<1мн
аксиому А , 11е1:1t>зможн<> 1
:?п1т 1юпrос составлнс1 соцсржан11е тре
тьеi1 пробпl!.!l~ы. Ги.m.берти. Нсм<::1\к11й матс
мапщ Лани/\ Гrтnберт rra Ме:жл}1rарод11о м кон
грессе R Париже в 1<)00 r. сделал f\О1<лад
«Математические проблемы", n которо.'vl сфор
мулировал более двадцати проблем - 11а1160-
лсс нажIIых n соврсмсшюй ему матсм::~тикс. За
nrошсдшсс столетие одна за дμуго 1~1 бьuш
решены почти вес прпблс1"1ы Гильберта . :1 пер
вой 11:3 11нх - в том жс году - третьи щюблсма.
Её решение , полученное нсмсцю1м матсмз
ппюм М . Дt:1ю.1111 , f11.ню дл111шым 11 с1юж~1ым.
Спустя 1 ю1ше 1<а шuейцарец Х. Х;щ1111гер шшёл
другое - короткое и ястюс; правда , отт испол1,
:ювал некоторые тонкие nриёмы современной
математической л:огию1. А сщё через 11ссколъко
лет российс1шй математик В. г_ Болтл11сю1й су
мел l·J;jбшшться п от этих логи ч ес1шх топкоt1'СJ1.
Позн;~комим<.:я с идеей рt:шсния ll. Г. Бол
тннскогu. До11ус1·нм , что м1-югогранн11ки М1 11
М~ рашюсnСТ'~ШJlеНЫ . 1'01·да каждый 113 НИХ МОЖ
НО СЛОЖ11ТЬ l!Э ощюго r1 '1'0 1'0 Жt: 11<1бuра частс(r
МIЮГ()rранннкон . Оf)озн;:~чнм нсt: ;1ву~ ·rаннъ~r
уп1ы нсех э·1· нх .vi1ю1·01-ра1111ико1{, 1i1<.11ючан М1 11
М2, через а1•••"
<х.". Т< числам <Х 1 , ••"
a1t 11обан11м
сщё ttисло а"+ 1 = rr . Рассмотрим произволь
ную фушщшо.f JJа конечном .мrюжсстое ~а1 "",
а". а... + l f. удовлстноряющу10 двум условия~~:
1).f(n) =О; 2) если между числамн а 1 , "" сх1, есть
JlllHCЙHa}I заннСJIМОС'IЪ
Рис. 5.
rдt вс<.: КU;:)ффн1 ~нент ы r, рац 1 ю11аm,н ы (Нt:КС)
юрые 11 :{ н11х М ОГ}'!' быть р;~ю1ь1 н улю). то зна
Чt:J 1lIЯ ф~l-lю ~и и скязан 111 такой же :1;1н 1 1симос 1ыо:
1·1f(a1) + ". + 1·,J(rx,,,) = n.
Пояс11 1 1м эт11 }'СJюнпя нрищ:рпм. Пуст~, т<уб
р;1эnит 11:1 ч:.tсп 1, как rюкзза 11 0 на рис. '5 . Тоща
однп 11з yuюu о.." скажем 0. 1
.-
это двугр;11шый
\'1·ол куба, а 1 = тt/1.. Поскольку 2а 1 - rt = О. длн
юобоi! фу11ю(ш1/; удон.rrеruоряющсй услош u1 м
J Il 2, EЫTTOJlllt'JI() СОО'l'НОШСНИС 2./(а 1 ) - /(1t ) =
""О. Ho.f(1t) =О, 11оэтому н.f(а1) = U. Пусть а~ 1J
IX ~ - 11 рнмьн<;1ющ.ие дру1 · к дру1'у 1 1ну 1 ·раш 1ы е
\1IЛЫ ч :Н."l'СЙ J 11 2 ptJЗfJ~1e1 1 11н. OtlJЩ:t: ребро
кuторых лсж11т ннутр1· 1 1р:1 11н куб а . Тп 1 ·да
а~+((~- 7t =О, а зн:.1ч1гг,/(аJ +/(а,)=О.
Де1tонсю1.м итшристтам м 1 rого грз111 и 1ка .11 1
на:~ыnаетсн uслт 1 ч и 11 а
где1,, "., !" -
ДЛИ!JЫ рёбср 'vП ТOJ'Ol'P~IIIHIYKa i \.1 1, а
~1. .". ~"
-
дву1·раш 1 ыс углы при :,)ТИХ рсбр:lх
(они составляют ч асть 11ct: 1·u набор:~ а 1 . .. , а.м)·
Ан;~ло 1 '1 J11нu олрслслнются дснuвсюrс 11 1 тарн
анты для мно1·01·раш1пка 111~ 11 /~ЛЯ всех частс i1.
uбразующпх рззбне111tя М1 н ,\l2• Дснонскис
ш1иар11анты пбладают замсча·1·елы1ым свой
ст1юм: еслн 11!1= Р 1 u ." v/'111
-
ра:-1611е1 шс мr ю
юграrтника М 1 па ч асти, то
Попять, почему вер но это равенство, нетруд
rю. Сгруппируем nce члены пз ныражсшл1 для
Г(Р1).,((Р~), " .,j(P111 ), отвечающие за uдин н тu·1 ·
же 0·1ре:юк - общее ребро не::скшrьк 11х частей
Р,. Еслн отре:юк лсж1 1 т внугри м1юrогра11 11 ика
ш111его 1·ра1-ш, то f\месте соотнетстнующие сла -
1·ае~·1ы с дадут IТУЛJ>, ка1< в принедё щюм н ы н1е
примере. Еслн же этот отрезок - ребро l, ,\Пю-
1·оrра11т 1 ка нm-1 ч асть ребра, то сумма )'1·лоn CJ.r
входящпх в эти члены, будет рап11а )ТJТ}' ~' при
этом ребре, так что все такие 1 ·ру11тты сла1·аемых
состащп ка.1' раз.f(М 1).
АналогичJ-IОС равенство спра1:1сдтшо 11:лн,11~·
110скnllьку . lfl состоит И3 тех же частей Р 1 , ...,
Р111, что и .11 1 Такнм образом..((1141 ) =/(MJ.), т. е.
~
если два мноrоrра11ни1са равносо
~:1
1:~ ставлены , то осе их де1fовские инва-
рианты равны: .
Геомегрия - 31-1ич и т « ·{емлемсрие»
Pli~. 6.
Друп1м 1 1 CJIOB:l l'v\ll, /\СIЮНСКШ' нннар11з1 1 т1,1
1-Н: ИЗМС I IЯIOTOI 1l[Ш paзre9a t 11·11 -1 много1раННllК:J
и 11CpCKJl:l,l\l 1(Щ.IH J.111 частей ( С.'1011() ~ llHH;;J p11::J НТ->
11оз11 зчаt:' 1 ' "1те1-1з~1е1 11 п,111" ).
Теперь uoJыvrём 11раnилы 11 .1й тс11)а:эдр !11 1 и
куб М2 такого же оGъёма. Tocдaj(,Hi) = О, та 1\
каr< все дnуграrшые )Т.'JЫ куба ра 1шы rr./ 2 )..1,R} -
гранный же vгол <р праrн1лыюго тетра;;iдра
удовлетворяет ураш11.:ш1ю cos <р = l /!> (р 1 1с. 6).
Мuжнu дoкri:.iaтi" что этот >тол 1 1 есш 1 :~мср1 ·1 \1
с 1t, Т. t:. 3:ШflCИMUCTb вил.а 1·, <р + 1·~тr. = о с HCII~ -
JlСВЫМИ paЦIIOil:IЛl>l-fblMJ I коэффиц 1 1сНТ:!i\lll
ос существует. Сж:]1.оватслыю, на tp н<:> 11акла
дьшастся 1111каких ограничсн1111 , и мы можем
nоложн1ъ, 1t апримср, /( ~r) = 1 Л прн та1<0м
выборе фушщ 1111 /деповсю 1 й шmаr11а 11 т nра
RИ!IЫЮГО тетраз~ра paвell Ы/(~) = 6 /*О, ~·де
1 - д;1 ина ребра тетраэдра. Ита1<,./(М,) "#О, а
/(ЛJJ = О. Поэтому
правилhный 'l'етраэдр и k"Уб тоrо же
объёма не равносоставл ены.
Значит. зная фор м улу объёма прнмоуmль
~юго параллелепипед~~. нено:з.можно на1lт 1 1
оf>ЪёМ пр:.IВИJIЫЮl 'О ТетраЭ!lра ПГ' l l ГЮl\ЮЩ11
разбие11ия его 1 1а чаепr. Это и даёт отрr 11 lател1)-
11 ое ре шеш1е -rix·1ъet1 проблемы Гильберта.
Од ншш тем i1 отличается хоро шо п<>стаn
лепная задача . что посвящённыс ей исслt}'!,О
в:шия не зак~шчиnа1Qтся сё решен нем, а порой
только на ч ин аются с него. В 196'5 r. учсшш
Х•щ ню ·сра - >К-П Си;r.лер доказал, что усло-
ние равенства дснонсю tх иннар1 1 а 1 1т1)R двух
MIIOl'O l 'P3 1 JJ I ИKOR при любой ф)·llIO~~ll t _{, удон
Jlе'Г!Юряющеi! указан11ым пышс услон и нм 1 и .2,
явт1ется не тот.ко 1lеоnхuднмым , 1ю 11 до
статоч 11 ы м для р:~вноспстаnлс1т 1 юсп1 7щух
юнпrых м1югогрз 1 11 1 ш<0n.
565
Фигурt>I
ПЛОШАЛЬ ПОВЕРХНОСТИ
Опрсдслсн11с поню11я •дл1111а отрезка" нс RЫ-
31,mat.:т ocnfiыx ·1рудностсf1: мы сра111111uаем
Д:1Jll!ЫIJ ()'!резок с ЭTJЛOi ll IЫM. ()'l'l(JlaДЫfl;JЯ н а
отре:~ке сJТачала сам :"l'l'aлo 1 1, потом его доm 1 ,
папр11~1ер 1/1 U. затем - долп долей r1т. д. Такан
же мысленн~LЯ схем а по:шош1е ·1· определпть
понятщ: площад11 плоской фп rуры, только в
к:Nеств<.: этазюка берут единичный к.в;щрат.
К <:ожаж::нюо, к кривьL"1 ;шнш1.м и nош:рл
ностям такое опр<::де;1сн 11е н<::r1р1-1м с11 11м о.
Мож~-ю, конечно, 11р1.::нстанить, что вдоль кр11-
вой ~rКJ1<1д1.1n:нот 11 екоторую ~ 1 1дсал~,ную рул <::1'
ку·' - 1+r1fiкyю, 111) обязатсл 1,но r1<::рж-1·яжи мую,
с ра:~мсчсшrыr.u1 н<J 11ей эталонами длнпы и
ИJi: ДОЛЯМИ. l lo •rто значит « IIepaCTЯЖlLЧ)'IO ->?
Скажем так при изгибании та 1<ой рулетки
366
«САПО Г ШВАРUА »
В 1890 г. немеuк 11и матем;ник ГермJн Ш варu приду
Мi1Л коt-~струкuию, 11озже 11 азва~ 111 ую «са погом Швар
Шt•. Вы видите еР на рис. l . Высота 11илинлра лелится
плоскосп1ми, пара1\Лельными ос1юва 11иям 1 на п рав-
1-1ых часrек. В образuвавшиеся сечени я (окружности)
епиrываются п равил ьные k-угольники, причем соrел
ни е k-угольники повернуты относительно лруг друга
на угол 1 80"/k. Затем вершины k-угольн и ков соелиня
ются так, что образуется поверх н ость из 2nk тре
уrt)льников; кажлый её «Слой • - анти прюма. Если п ,
k -) оо, то размер ы этих треугольников становятrя
сколь угодн о малыми. С увеличен~1ем k 11а ши k-уголь
ни кн всё плоn1ее прижимаются к их описан ным окруж
~юстям , а вся поверхность - к uили нлру . Можно ожи
дать, что при п, k- .- ,) ""ее плошаль, т. с. сум11.~а плош<:~лей
всех треугольных граней, премится к боковuй поверх
ноrrи uилинлра. Hu это совершенно не так!
Посмотрим н а Шварuев «Са п ог» сверху (риr.2).
Проекция каждой его грани на основание цили 1-1л
ра - :по треугольник, uбра.ю!jанный стороной
k-уrольника и серединой стягиваемой ею луп1 ОКР}'Ж
ности . Его площадь зависит только от 1<; обоз11ачим
ее .)J.. По скольку r1лошаль при проекuии может толь
ко уменьшиться, п олная поверхнос.ть асапо1 «1 » В(п, k)
не меньше 2nk s~ . Теперь лля каЖАоrо k возьмем та
кое11 =п (k), зависяшееотk, •1то n(k) ~J. > 1. При этом
выборе п плошаль В(п, k) > 2k, т. с. 11согра11иче1-1 ~ю
во:iрастает при k _, оо. Поверхность, как на стu яш11й
сапог, собирается частыми складками. Более того,
мож~ю выбрать такую послелователыюсть п(k), чтобы
ДJН 1на лю60 1 ·0 её участ.-а остаётся irc11змe11rюlt
Нn :i/J,cc1. мы ссылае м ся н а пошпие д;шны кр11·
11ой (уч:ктка rуле-пш). То есть, рассуждая по·
доб1 1 ым образом, мы не сумеем построить оп·
ределспис длины кривой.
Пр1-1 измерении площади ШJ1:1<.:рхнuстн ''РУ·
Лt'ТК~•) ~C'L'CL'l'l:l<::HHO з:IJ\1<::HИTh на «М J1ЛЛ 11метро-
11у1u бума1 ·у», rю ко·1·о ро~'1 можно подсчнтать
ч 1J ело кв~щр::~тн ых сант 11"н::тро1~. 1.; в:щrа· 111 1)1х
МИЛЛ\IJ\1С Т[К111 11 т. ;~.• соде рж~ 1щ11 хся п IIORepx-
HOCТl l да111юi1 ф111·уrы . Например, обернуть
1 п 1111 11 щр nрнмоуrолыrым ли стком мrшлиметро·
1юй бумаги. шпрrша кото ро1·0 рат 1а длине
окружности осно rш шя ц11лш rдра 2ттN (rдcR
ero рад 1 rус), а высота - высоте // щ1m1ндра
(рис. 1, а) Говорят, что л1ко !"1 11рямоу1·олы111к
плошали соответствуюших многогрJнных поверх1ю
стей сходились к любому(!) задан ному числу, не мень.
щему боковой п оверхности uилинлрп.
Этот пример демонстрирует те подвохи, которЬl);
нужно избежать, лаоая оп ределение г~лошали поверх.
носп1 ·~ерез приближение многогранникам~• .
Вы можете изготовить модель «Canora Шварuа"
Разли~tу йте прямоугольник ю nлотнои бумаги с Од·
ной с-гuроны на ромбы {по крас ным линиям на рис. J),
а с друго й - на горизонтальн ы е п олосы (по снн~щ
линиям). Прочертите бумагу п о этим 1\Ини ям туnой
сторон ой ножа. А теперь просто све рни те 1\Ист в
трубку, слегка налавливая на 11ентры красных ро.'-l(юе,
•1тобы он лучше складывался по линиям, и склеRrе
противоположн ы е стuро11ы прямоугuлы 1ик а.
Рис. 1.
п
Рис. 3.
1 1 рсдст:н1ю1ст t:oбoi1 ра:звёрmл.7у боконоИ nо
всрх1юст 1 1 цили11дrа. А 1ютому
Точно так же боковую поnсрхность конуса
мож110 развсрнугь n Сt'ктор кр)та, радиус кото
ро 1·0 ранен образующей конуса / (рис J , б).
Дннна дугн ::этот сt:ктор:.~ сост:атяст 2nR. 11tc
н. - р<щ11ус OCJ-ICЖ'1H l·1>! конус~~ . :1 потому ПJЮ
щадь бокшюi! гю1н:рхнос1 1 1 конуса относ ~ rтся
к плош.~щн кry1 ·<J, как 2ттR к 2n l, откуда
S,,= nIO
Н(), 11е говоря о том, ч'Го с1 рогое оттределе
нне разi3ёртюr тоже опирается rra свойст~ю
< !lсрастяжимости», набор п0Rсрх 1 тостсй,
rtrющадь которых удаётся11::~ход1 пьтаким с 1 ю
собом, в прш-щт 1 с, очс: н1, ограннче 11 . Еслн в~1м
довою uюсь занорач1 1 вать ;.i 11cJ1 ьсн н н11 1 1 яблоко
1! буrм:.!Г)', то IЗhl знаL'Тt: , что 11рн этом нен:-~бt:ж -
110 образуются складки, ·1
·. е.
плотно 11рнложи1ъ
г11бкнй, но 1 1 tрастяжим ы й участш< шюскос1 ·11
~<сфере да и к болышшсТRу друг11 х крив ы х по
верхноп·ей просто не1юзможно.
Один из пугсй nрео)\олепия подобньо{ труд
ностей - приблпже нис кр ивых ломаными, а
поверхностей - мноrогранн.ика м 1 r . т~ш, ,шшну
критю й опредслнют как п редl:11 дли н вппс::~н
ных в неё ломаных, когд:~ число знсньсн лома
ной нео гр:н-rичснно растет, а макснмалы-r:~я
дп11 на звен а стремится к нулю, ест ~ , конечно ,
это·r· предел С}rщесгRует (рнс 2). Мnжно дать
ан:то1 ·11чтюе оnределеr rие н длн поверхности.
Толы(() п олучvrтся 0110 з н а •п--пеJiыю более
спож~ 1ы м: для nыражетш площади д;ншой no-
nepxнocrи как предела площадей вписанных в
2 п:R
Рис 1.
а
Геометр и я - з11J'llH «Землемерие•
ПАРАЛО КС МА/\Я РА
Рассмотрим беf конечную с.туп енчатую пластинку
(рис. 1), состояшую из прямоугольн иков: п ервыи из
11 ~1 х - квадрат со стороной 1 см, второй имеет
размеры O,'i х 2 см, а кажды й слслуюший вдвоеуже
и вдвое ллин нее nрелылуш его. Плошаль каждого
прямоугольникi1 равн,1 1 см 1 , J об wая плоu.tаль
nласти нк11 бе\конечна. Разу,~ес•тся, чтuбы rзсю ее
п окр,:юнь, потребуется ГJесконечное (по объёму или
массе) количество кр<1ски. Но прелсrавьтс себе
«сосуд• (рис. 2), nолучаемыи нри врашеtт и nмстин
ки вuкруг се прs~маго бес"онечного края. Со< ул t о
rтоит и> uилинлров. Вщ ота k -1о uилиндра равна
2i ' см, радиус 2 1 (см, а .J11ач11т, его объем р.:~всн
л2'
1
\м3• Таким образом, обье::мь1 ш1ли11дров обра
-~уют убываюшую геометрич~=с кую пμогрессию, ил
сумма кnt1ечна и равна 2л см'. Заполним этnт rхкул
краскои . П огрузим в него пласти нку и оыташим сё;
ко1·1еч 1 ю, она вся булет окрашен i'l с лвух стороt•.
Так все же, можно окрасить nластинку~t
1
22
4
Рис. 1.
РиL. 2.
:)67
368
Фигуры
11её м но1 ·01ран1-111ков нс;\остаточ но 11отрсбо
ват1" чтuбы р~1:iмерп1 11х 1·paнerl 11ешт1а н11че1J-
1ю убыват1, ~1 числ() l'рансй росло.
Мы nриnедём 011ре1\слет1с. ос1-юнаннос на
ор111 ·111 1алыюil 1щес. предл()же1 нюй п~мещ<J 1 м
м;~темаnнюм Гер.vt а1юм М11шюRсю1м . 011~ л.о
статоч11 0 nроста и в то же нремя уrшнер салъ
на - однпм 11 тем же с11 особо)11 определяются
площадь поверхн ости. лтrшt кр.иrюй )(1 анало -
1·11чныс понятня 1:1 простр:.11 тствах большего
чщ:ла 11::1мерснн й. Понсн ить ei..~ можно так.
Прсдст:.~ю,те, что вы pellHUIИ пкрас1 1ть какую-то
11uперх 1-юст1) с обеих сторuн р:11ч-юм<::р1 1ым
ОБЪЁМ И ПЛОШАЛЬ
ПОВЕРХНОСТИ ТЕЛ ВРАШЕНИЯ
При врашении прпмоуrольника размером а х h вокруг
прямой /, nроходяшсй параллельно стороне Ь 11а
расстоянии R от его uентра, образуется тело (на'!овём
его « Шайбой•; рис. 1), которое мож н о предпавить как
раз r юсrь лвух uилинлров вь~соты Ь. Объём этого те11а
равен л(R + a/2}ib - л(R -а/2)JЬ = 2кR · ,1Ь. Если rювер
нуть прямоуголь н ик в его плоскости на 90° вокруг
uентра, то а и 1? просто поменяются месrами и обьРм
останется прежним; можно заткать его в виде
V=2rtR·5,
(")
где 5 - nло шадь прямоуголь ника. Как булто 11 ичеп.J
удивительн ого. Н о, оказывается, фоμмула ("') остаёт
ся верной при повороте прямоуr0Аью1ка вокруг
центра на любой угол! Более того, прямоугольник
можно заменить прои звольной фи гурой плошали 5.
uеликом лежа ш ей по адну сторону от оси 1 и пони
мать R к<~к расстояние от центра масс фигуры (как
плоской пласти~11,j) до прямой/.
Как ЭТО доказать? Пр~t врашении фигуры Ф из
двух прямоугольн и ков (рис. 2) образуется тело, со
стояшее из двух шайб . Мы знаем, что об1,,ём ь1 шайб
можно найти гю формулам
Рис. 1.
сло..: м красю1 толщиноr) h. Какой объi..'м крас
ю-1 11
1, нам 11онадuбится~ Пр11близ11телы ю 2.Sh.
щс: S - площндь 1юиl'rхнuс..-1·1 1 (S/1 ум1-южаем н:1
2 ПOTONI)'. что крае~ IM пuш:рХНОС'IЪ с обеих ("ГО·
гю11). !lр11чём ра11е11с·1·но 1·1
, = 2Sl1 будС't' тем
nолсс точ11ым. че1ч тоныне с1юi1 красю1.
Матема1'ичt:с1<ой м<ще; 1ыо «СЛО}i краски тол
щ1rнот1 /1» служит по11ятие !1-01<рест1 юсти:
lнж.рест11остыо Ф1, фJП)1)Ы Ф 1та:1ьшается м 110-
жсст1ю точек Х п ростра11 стnа, удалёт шых от Ф
на ра сстоя.н н~:. не 6uJ 11 , шcc 11. Дmтпми СJ1овами,
fl.J IH кюкдой н 1 то чек Х 11айдётся ТО'-1ка Р фигуры,
такан , чтоХР ~ h. С11сдо ва'l'(:J1 ыю, h- <.ж рсстность
Значит, оfiъём V, 1юлучаемый при врашении фигуры
Ф, рав<..>н:
V= V1+ V1-= 2n(R,5, + R1Si) =
==2rtR,S, + R,51 (S, +52).
s, +51
(" *)
R,S +R5
Нетруд н о показать, что величина 5
1
5
11
1+l
равна расстоян ию R от / ло точк.и О, которая лел111
отрезок 0 10 1 между uентрами прямоугольн11ков в
о-rноwении 51: 51 (рис. 3), т. е. так, что 52 002 =
= 51 · 001. Но это соатноwЕ>ние
-
не что ~1ное, как
«П равило рычага», определяюшее положен и е uентра
двух масс величи11ой5, и 52, помешённых в точки01 11
0 1 . Т о есть О - uентр масс фигуры Ф, равенство(•")
можно записать в виде V =2nR ·5, где R- rаrстоя·
1111еотuентрамассФло/, аS=S, + 51-ееnлошаАь.
Точно так же доказывается , что есАи фор1.1ула (•\
ВЕ'рн а лля двух частей проювольнои фигуры , то она
верна и для всей фи гуры. На •1 ае (" ол11ого г1рямо
уrольн ика .и образуемой им шайбы, а затем nоrлело
ватеl\ьно Л()баеляя к нему лруrие прямоуr0Аьннк11
с п араллельн ыми сторон.:~ми, можно убели ться, что
PlfC. З.
точю ·l - шарик радиуса 11 с uснтром н этой точ
ке, а /нжрест1юсть 11р о11знолыrой ф111уры Ф -
не что ин ое. к;ш объединснн<:' шарнкон р;:~д11уса
h с 11.сн·1 р:u"1и 1ю все1:1озмuжных ·~оч1<~1х Ф . Ака
Jюп-1чно ш 1 ределяе1п1 о крестность ф111уры н :1
!!ЛОСК()СТ11 (р и с. 3)
Jl.лл н 1 ,1чио1с11ия (110 Mm-ll<()вcr<o мy) 111rо 1 ц;i /\И
S(П) ноnерхност П па .:<Jщя·1 объём её h-окрест-
11осп 1, делят cro на 211 ·1олп~,шrу /нжрес1'1ЮС"1 и
н находят предел <1аст1юго nрн }1 ~ U:
1\(Гl) = 1· \l( П '')
•
1111 2h
11~о
Рнс. 4.
формула выполняется лм1 любой ступенчатои ф~1rуры,
составлен~ Юй ИJ таких прямоу ruльн ~1ков . А проюволь-
11ую ф~1гуру можно с любои точностью прибли~ить пу
nенчатыми фигурt1ми (рис. 4) , чем и 3dl:l~pwi'leтcя дока
з~пельrrво. Ита~<:
1-r Объём тела, образуемого при враwении фи-
IJI;
гуры, лежащей в плоскости uеликом по одну
сторону от оси opaweнlfя, равен произведе
нию плошади фигуры на мину окр ужности,
nробега емой центром масс да нно й фигуры.
Эту Т('uрему обы чнu ~1азывают второй теоремой
Гульдина - Паппа. Первая тепрема говорит о пло
шали поверхности врашения:
Плоwам. поверхн ости, образуемой при вра
wенин линии, лежащей в плоскости uеликом по
олну сторону от оси в ращен ия, равна произ
ведению ми11ы линии на мину окружности,
nробегаемой uентром масс этой линии :
S=2rtrL,
где г - расстояние от llентр а м<IСС линии G ло оси ,
1.
-
дли н а линии (рис. 5) . Исп()льзуя опрелеле11ие
Геоме грин - з н ачит« ~емлемерие»
б
8
Р11с. 3. Окреп 11 осп1 ф11гур " -
кр>1вои б - к11алрата;
в
кn11 1 у1 1, 1 ,А,1др.н.1 ~' Гl jJ(K llklЩIBP,J -- .\>' 'и н а llЛOC Kl>t.IИ
Рис. 6.
плошали П()верхности и лмmы кривои по Мин
кове,кому, формулу ("* ') м ожно вывест и прямо и з
раАе11ства (" ).
Конечно, чтобы П()льзоваться теоремами Гуль
лина - П а пп а, н ужно научиться наход11ть uентры
масс фигур 11 л ин ий. М1ю1 оугuльник- п л<1с-ти н ку
ра'lрезают на треуrольник11 и ~аменяют кажлый И.{
них соответств уюшеи « м.этсриалыю11 точкой 11, т . е.
масс.о й, раонои егu плошад~1 и лежащей в его uе11тр е
масt (точке п ересечения "'1едиан ). Uентр rа ких то
чечных м;:эсс и булет uентром масс многоугольник<~.
Аналогично, вместо лом<11юй лишн1 берут точе•1ные
масс-ы, равt1 ые ллинам ·me 11ьео ломаной и roc рело
точенные в их серелинах. Кривые линии 11 пграни
ченные ими плоские фигуры можно приблизит~..
многоугольниками.
для пр<~ктических uелt:-й коорлинаты Ut! H rров ма< с
вычисляют no уравнениям крнвых с помош~..ю инте
гралов. Но есм1 фигура uен1ральнu-симметри k111<11 ее
uet1тp мае с иrкать не 11ало - 011 находится в щ~нтре
симметр ии. Рr~<.«м(Jтрим, например, тор - п оверх
ность, которая обра з уется при врашен и и окружности
1юк руг 1~е пересекаюш е й её прямой ( рис. 6) Есл и
радиуr окружн ости r, а расстояние от ее uе нтр а ло ос11
R, то объем, ограниченный тпром , раве11 дtR тrr ~
~ lп'Rr-, а площаль пооерх1юсти 4л!Rr.
Фи гуры
н
-,
'
lf
,
'
,
N.\
P1tc. 5 .
Рас:смо·1 р11.м, например, сфсрv р::щиуса R.
О<1енидно, её /т-оr<рсстrюсть. так сrс,13ать
«толстая сфера<>, это раз нuс·1ъ двух ш:о~ рон
r.щиусов R + h иR - 11 ( рнс. 4) Объё\-1 <·'l'ОЛ<."1ой
сфt.:р ы » ранен
41t(CR+h)~ -(R-h/ )=-
3
41t
=3(CR +l1)l+(R +li)(R - h)+(R- h)2) 1./1.
Разделив выражен ие спра ва rra 2h и устреииn fr
r< нvлю , 1 юлу<-шм nе;шчину 47tRl Это и сеть
площаю, сфе ры ра.Г\иуса R.
Теперь 11р\.fмсним 011ре~сл ени е М11 нконс ко
ПJ к бокоrюл аоверхноС'm цил 11 ндр:.1 (рис '1) Её
h-01<рестпость - трубка толщинuй '!.. /1с «'1акр)т
ле1шнм1t1 » (половинкамл тора) на краях Объём
трубки равен разности объёмон д вух цилин -
дров:V =ттН((R +11)~ - (N. -
h)2) = 2тr.Ю1 211
F
l=l
""~
"
1:
lf Н-: r=i:
,_ ,_
1-= ';r± Г-tН-ц__
1•
'
-
1-+
1
-
1
.
н-~
-
1
-!
'
+
j
!н-
-
4
l
+
1
-
1
t
i
1+
t
,_:+1
1
~~
1
~~
j 1~=q=
"
~~
-~·
1
1
Р11с. 6
,о-ЭТО f \a i:T '-!HaKO \.l}'IO ll<l \1 фo pM )'Jl\I
li
-
h~2тrRH,/1-)О
2
А за1(ру1·лепия:\.\'и можно прсхто п ренебречь
эа~о1ючи·r ь 11х п 1·рубоч 1ш fihrcoты /1 О6 11ём эntx
1руnочск будет сгрем 11 п.сн к 11улю r юсле /\еле·
ния H;J 2 h. А 1 l:lJIOl'ИЧHO RЫ!Ю/tИ 1ся формула по
всрхнuс 1и кu н уса
Пp1 mcnt: vi t:'Щё одну пuлсзную фор'!)ЛУ ДЛ!1
площад11 S' сфе/тческоги пояса. ·г е . част11
сфер ы . заключ ё 1 11 ю i1 м еж/1.у l\R) мя 11 араллелъ·
rтым~-1 шюс 1юсгям11 ( рис. 6 ) F.сл11 радиус сферы
R, а рэсстоmтие между ллоскостям 11 1i. то
S11 = 2л.ЮJ.
Обратите вн1 rм аrтис на за ме • 1атслы1)'IО оса.
бснность ·пой фо рму11 hr. РJСсма тр 11 вае.11ая
1-:1:~ 1 Ff- rn
1tt i-
н
"
'
+
-
i
1-
+-
·+
1-+
н-
1· Ц-
Jt
'
i1
1
h
1
-
н--
R=
н-
j:: н: i-t
1
t±а
б
Рнс. 7. п - кa p rJ Jемлн в ран1 ЮОt'ЛНКОй u11ли 1tлрнчt:ской 11рuек 11 ив;11
-
Х - проекния т•1киХ.
370
ПJЮЩа)\Ь :~a1111Cl1'l" l'OJ\11KO LYI' !~ЫСОТЫ IJ 1юж.:а, но
r1e от его 1юложtння на данной сфере - у экв~1-
тора и11и у 1юлюса. Э·1·а ()Собенносп, нспот.зу
етсн картпграфам1..r n т:tк 11азт,ш~1емо11 р;нm0Rс
ли1юй 1\нm,11~дричеоюй 11рое"1щнн (рис. 7, а):
сфера проектируется на or1иc11rrrыi-1 ц11111п1лр,
1<ак nоказ;.пю на рис. 7, б, эатем 1\ш1ш-щр разво
рачнвается n прямоутолышк Прп этом ПJЮ
щадI> любой фигуры на сфере 01<азыr~астся
равной площаrщ сё нроскцни.
Окрсст ност1, ш1н111 1 - как ()ы шл;:шг ра
д11уса 11, 1шутрrr которого проход1п лнния
(р11с. .\ а) . !:го объём прнмерно раnен произве-
Гf'омt->1 р11я - -~н<~чи1 <<.Н'мле>мериf' »
дению шющади его ссченш1, т. е. ттf/, на .ЦJ 1и11у !
.тгишrи. Такнм образом, f\JLИШ! кривой/., по Мин -
17(/,,,)
ковскомv, ран11;,i пределу 0·11юше11ия --
1
.-,- 11р11
•
.
1tfГ
h _,О. Это определение с 11р:~не;"\л11но 1v1н любой
кр111.юt1 к простращтне , напрr1мер ни1-1тоной ли -
111111. F.слн же кр11п:1.я лс/КIJТ 11 плоскости. то её
дт111у можно Е!Ы\ХIЗИТ11 qереэ llЛOЩ<l!~I> её ПJIOC-
S(L)
J\ОЙ /1-окрестrrостн: опа равна 11репелу 2~'
1Ip11 h ~ () (рис. ) , г). I11 ~аче тnоря, <·{(лrша доро-
1·и ранна её ш1тщщи, делё1 нюй на et т11ри11у »]
Фигуры
ГЕОМЕТРИЯ ПЛЮС АЛГЕБРА
СИСТЕМЫ КООРЛИНАТ
1.Jlyч111e од1н1 раз уnндеп,, чем сто раз ус.rLЬJ
шать•, - г;1ас1п и:шесJ 11;щ послоющ~1 Деf1снт
тслыю, умело 11з1·отовлсп1IЬ1е cxc1'.u,r. чертежп п
рисунки способны :Jа/\'lе111пъ ,т~;олги<:: разъл:с11с
н 1 HI. ~щё дрснн lf(~ :{a,\lCHHJlП ;щ~ t::J<.t ' l'l'JIЪCTHa t•l'()-
peм 1·сомt:тр11чt:сю1м чер ·1 ·сжом. со 11рОН<>ж,ц:н1
е1·0 коротю 1м СJювn м: •Смт р11!·' Но э·1·0, в11;1;п
.\!10, тоже край11ость Не .'1учmе лн l·1С1юль:~оRаТ1>
1ice ко:~мож1 нхт~1 с мако 1ма111,ной 111.11 ·01\ой?
Идея r1:юбражат1. ч1 кла R тrде точек, а тпч
кам дa1i~l'l' l1 ЧTfCЛOllhle обо:111а~1е1 IИЯ С}1 1.\еСТВСТ11 ю
продrшнула науку в ·~1 ом 1штраш1е11rн1. Но как
сумели «связат1". ч11сла 11 ·rоч 1шJ Однн~t нз наи
более эффскт111шых способон ст:щи системы
коорди11ат. Простсfшыя нз ппх - чuс.ловст ось.
t:ё нсп<0 получ11ть И3 обыч 1нн'1 прямой .rшшш .
Rсдьмём на нрямой прон:.шолы 1 ую точку 11
на:юнсм её ничапо.м 1соо/1дu7tш11 (сгu rтр11ю1то
обuзнач:~п, буюю~'1 () ). 1ан.:.v1 яыберем сr~11 1 шщ·
11 змсрсн ия. т. е ус1ющ1мо1 , какой отрс3ок сч 1 1 -
тат1. раuным 1. Испо11ьзуя та~ю~: 1 о-rрс:.юк н 1сачс
стnе .~тзло 1та дли111.т, мы сможем 011ре1 1слятъ
расстояшш меЖ,'1)' дnумн 11ю()ыми точками пря -
чot'I и выражать нх ч11сле 111ю. Наконец, 1<:t~'IOЯ
точ1.\е чнсл о uоi1 OCJJ пост:1нпм в соотnетспше
q ~1сл о, pau11oe расстоя1111ю от 11её до 11ачал:~ ко
оrд1шат. tloт так нросто 11 яс1 ю мы ошже.ч меж·
ду C06QiT дейСПН·l'l'СЛЫlЬlt: ч нсла 11 ТОЧЮJ лря~!ОЙ.
В само м JJ.t'ЛC, K:tЖJ\0 1'1 точке ч11 c:10 Roi1 ot1 1
·1L:11cp1, CtIO l 'HL'ТCTHYl"I ' ()j\J-f( ) l!IH)Jllll: tmpc:; Ll'!leH-
HfJt' чниш . Пр:Ш1(а . . \JJ.>J .r1юi100 ~j:J/(J HHOЙ ТОЧЮI
на Ч1 ICJIOROr'I Ol'l 1 \НУЖНО) к;1:1а ·1 ], CI 1~1 \\t"Tp114H}IJO
t'IJ точку. котор:н1 н :.1.хо;t 11101 н:1 1·аком же рас1
стоя rш н от 11 ач:ша коС1р/~111 тат. ч-1 о 111 1срвая. По·
:-Jто~1у АыGсрем на ч11c.rronoi'1 осп одно 11з .~n)~
LЮЗМОЖНЫ.Х нзпраu.гrеш11'т I1 Gудем С<IИ'Г:JТЬ е~
полож11телъттым Нсе,·1 точкзм 11 з оси, rаспо
ложснным ОТ 11~1 ЧЗЛ3 r<0орд1шат 11 ПОЛО/ЮIТедь
rюм напраnлt:шщ. пост:ш11м в соответстuие lj.
расt.тотшя ;1<.1 н;1чал:1 кuuрднн:1т. :1п1чк;ш. ня
XOJl)IЩ l lMCH по другую с1·оро11у от ТОЧК11 о.
то Жt: rасстпяш l t:, 110 сп :такnм \НlнуС Тепr~
соо·1 · 11е-гст11ие меЖд) '1()ЧJ\;lMI111 J\tJI С'ПIИТСЛЬНЫ·
J\'U t чт rслам11стало11J;11 1м1 ю 0;11н> .н1ач11м'1 Ч11с·
JIO, ("()()Л\е' I стnую щt:е ' f ой 1[Jll1 11110i1 ТОЧ)(С, ~rаЗЫ·
nается л:опрдшtаттi. этой точ1<11.
На r1.рактике числовую ось принsп о изоб
ражать щ1 J1истс бумап1 1·оризонт:шьной 11ри
мой, причtм положительное 11:~прапление
чаще псс:го выбирается нгrраво. llоэтом) 11 ерсд
ко 1~~1есто слои «точка с отрнцателы юй 1<оор
!\н 1-штой» rоноrят «'f'OЧI<a, paCllOЛOЖel rrraя СJ[е
ва 0 ·1· начала коор1~:иш1т» или просто «то чка
слева от нуш1», nосколы<у коордrтат~1 самой
точки О есть, консчш>, rrуль.
ПОЛЯРНАЯ СИСТЕМА КООРЛИНАТ
llрнмая л11ния одномерна , ~• пJюскость двумер
на _ Поэтому если точку на nрял·!ОЙ можно за
:1:.1 ·11, одн1 1м-еди 11 ствс1111ым чисюм, то ТОЧК) 11а
тюскости - у...ке двумя ч.1кJ1:~ми. Выбсреr.1 на
11Лос косп1 11роизволънуто точку О и паэовём её
началом координат. Как 011ре1'елитr, место11а
хож,це11ис любой другой то'-lки М? Во-первых,
расстоянием К между ней н началом координат.
Однако такому R соответствует целая окруж
ность. Остзётся «Нh1члсн1rтм на ней единс1·-ве11-
ную тuч.ку.
И:i точк~:t О 11ронедём луч и 11а:ювём его nu-
11яp11uti осью (а сзмо начало коо1щн 11 ~1 ·r 11e rx:-
о
Р11с. 1. По.\ярныt! кооры1наты .
Гсомf!1 рия плюс плгеfiра
11менуем н 11ш1юс) Далее, измернм у1·ол между
этой осью и т·ре~iком ОМ. Поскольку двум точ
к<1.м, симметрнчr 1ы м от1-юситель1rо по;1ярной
оси, соответс·п1ует одна и та же велнчнr1а угла ,
nнед(;~1 з11ак у1"11а. Еслн угол отсчитьтастся от
поляр1ют"1 оси до отрезка ONI пропш часоnой
стрелки, or 1 положитслъный, а если по часовой
стрелке - отрицате.11ь11ыi1 (рис. 1). Та1<ая си
стем;~ координат называется поляр1-tой. Она
прочно укоренилась n математике .
Но совсем необнз;,~телы-ю 011рс;~с:1шть коор
динаты точ1<11 с nuмощыо у1·1юв . Можно вы
бр;пъ H~l l IЛOC l<0<-~1·11 е11(ё 0/(1 IH ГЮJIЮС ll:J. llСКО
тором расстоя н 1111 от псрtюгu и коuрд11н<1та ми
каждой точки считать р<1.сеl'ояния до эт11х по
люсо13. Такая снс1ема коор/\1шат llолучнл:1 на
зн:н1ие бuполя/mой (от лат.\)\ - «дву(х) -»).
ПРЯМОУГОЛЬНАЯ ДЕКАРТОВА
СИСТЕМА КООРЛИНАТ
Н;1ибшrсе удачной оказаJ 1асп прямиугольнttя
пtетема коорл;нна·t . Её также назынают пря
.м.r~1)юлыю1r дексфтовой - в честь францу:J
ского матt:матнка Рене Декарта, окааанше1·0
373
Фигуры
ПрямоугольоiЫt' 1ш11рлина1ы на r1"uпщ гн1
значнтелъrюt' влнянис на стано11ж;н11t ti ра3-
нитие aншummчec.:x:nii 2f!сшетрии - ра3дст1
матема'r'ики , изучающLто Гt'ометричсскис:: объ
екты методами алгебры. 1-l:що сказать. что в
тру1\ах с1мо1·0 Дскаrта нет декартовых кuор
ди11ат в современном смысж:.
Провсдfм 1ш rтос1<0ст11 ,~ ще //ерпспд11куm1р
пые оси 1<оорди11ат, точку их пересечения 060-
зшtч1 rм через О. Одну из 1шх вазоnём осью
абсцисс нли осью Ох, а вторую - осью орд11-
1тт нли осыо (~)'· Как праnило, на лиtте 6у;'11а
ги ось абсцисс расrюлагают горизuн1·<1J1ыю. а
OCh ординат - Rсртнк::~льно. Положнтельными
счrпают направJJен11я otci"r соnтветсгвешю
слсв<.1 направо и снн3у ВЕерх (рис. 2).
Теперь нозьмём любую точку М плоскости
11 сrrрш:ктируем её на обе оси. Коорд1111а·1·ы
проекций па осях (их па:1ы11ают абсцисспй -х
у
)'
.1'
M(::t~ y)
11
r
_
,
х<О,)'>о х>О;)'>()
,'(
:>t:
ох
о
111
l\i
х<О:у<О .\">О:11<о
l)ис. 2.
Pll(:. 3.
н О/}()mштой - у) и бу1tу1· той caмoi'r п:ipoii
чисел , котораи с1~шнто1 в соо·г· нс11·ст1:111е то<Jке
м. Это СО(Уr1:1етст1:111с F1:~анм1 [(")однозначно н обо·
:111а ч::Н~'J'ОJ /1,11}1 П(lOI IЗIIOJl l>IIOЙ точки ;11 Гl!IOCKO·
СТТI чеrк::1 М(х: )'). Таю 1м обр:.~зnм. 1\СЮ()ДJП-JЭТЬJ
)'l<a:-JЫBaJCJ'IПI А ПIOf1I<aX, пrичё,\1 11;- . .
11еЛЬЭЯ Щ·
1шть местами.
Вес точки на оси абсцисс 11метот нулевую
ординап•. а Rcc точки на осп ордrш~1т - нуле
ную абсциссу. Люб:н1 и~J 1щординат или обе
могут оказатhСЯ отрицатеJ1ьным11 . У всех то
чек 11 1 юскости, расположенных нрансе оси
op;t11n:Jт, абсц11сс:1 полож1 rтельна, :1 у н:1ходя
щих01 левее - uтrшц~п е.11ьна. fkt точюt, ;1еж:~
щие ВЫПIС OCJ 1 afJCЦI ICC, JIMtIO'I' l IOJ IOЖИTeJIЬHYIO
ордин:пу . а лежащае 1111же - отрпцзтельную,
Следоnатслыю, каждо1'1 11:1 четырёх частсf1. на
тюторые коордннапrые ос11 разбиnают пло
скоtть. соотnстствует сноё сочстани<: зн:~коn
кuор1\1111ат. Этн ча("1·и нюываются ю.юдрс1нта.
./11и 11л11 четвертями н лрu11умероканы так. как
указ:н-ш на р11с. :\.
КООРЛИНАТЫ В ПРОСТРАНСТВЕ
Напболее 11111роко пр11меш1ются тprr простран
стuенные системы 1<0орютат. Первая 11зних
прямоуr·ольная. rш11 декартова. В 11eir трп по
парно 11ерпспдикулярныс осп: абсцrю: -х. ор.
дннат - у и mm'lикtun
-
z-. Положение пронз·
кuл1,нuй точ1ш М 011рс; tеляетсн коор1111нат:1мп
еёнrоекцнй на нее этн оси - х,у 1-1 z (рис.4).
Вторая , ц1LЛ11ндричесл"'LLЯ сrктема 1шордищт
Т1 редстанляст connй 11ечто crc)(l-fte между пря
моутолr,ной и 1юлярной снстем:1ми. Постро·
им на шюскпсти <1 полярную систему коорли
нат И 11рове11:ём Че[>еЗ ПOJ IIOC (J ЧИСЛОВ}10 ОСЬ
Oz, перпендикулярную nлоскосn1 а. Спроек-
Рис. 4. z
.\'
--------~
,
1
,
1
Г-- -----·{М '
1
1
1,,
Рис. 5.
z
f((J(J['UUN(l//lt1Z
-- ,М
)'
n~ rюв:ш nро11 :"{воль11~ ю точk.·у Jl 11ростра11ст11а
на 11 ;ЮСК()С IЪ. HЗJl}l.t'~1 ' \IK: коuр:.~.111-1аты ()ТОЛ q>
11 расстоя1111t R :-10 110111ос.1 ) .~тоl1 проtю\1 111 в
по:~ярпой сис·тс::мс 1юо1ц1111:1·1 . а третью коор
дшrз·1у (z) noлy•HL\1, С'1 Jj)t)C:I<Tll[X>Ha1з точк~· М 11:1
ось ()z (рис. )).
Gол:с<.: сложr 1а 11.ля 1.юcnpr 1ятия. хотя и вес1 .ма
1юлсзн;J 11рн рсшсшш мтюпrх задач сф<'/m
Чt'Сl\Ш1 с нстсм~ коорщ1111.1т. Она птшжа н·J
l\l l Л llll)(JJllЧ tCK}'IO: н llCIJ та кже Н~1СЮТСЯ llJIO-
Cl\OtTb u с rю11ярноl1 uс ыо 11 доrюлшrтельнан
оа. Oz, nerпeндHk.)')l}JPI 1ая (J, IOCKOC'J 11 а. Одна
ко nо,южсrн 1е то чк11 ,\/ 1 1рос1ранства опрс,це
'!Яется таю 1;-,rн коорд11н:1 r;1м11 · уr·лом <р. как 11 н
Ц11.'1ШIДР11ЧС::Сl<ОЙ r 1I C'l 'tJ\1e, расеJ"ОЯН llC\\ !< от
ючю1 /1/ /\О полюса О (нмс111ю п·1· тuчю1М. а
Jll' UT СС 11рое1щ1ш! ) Л СЩё 0;~1111~1 ) l'JJOM 0 -
L'l'n 06р:1:"{ую1 отрt:юr< ОМ и nоложнтет.1юе11а
п1хнu1с:нис осн Oz (р11с. 6) Сферическан с11
C'l 't 'Mrt КООfЩНН:П 11а116ОЛС:t: 6Ю13Ка 1\. географU
Ч!'СЛ.-Ш( ( rюсмотр 11тс на коuрдин:~тную сс1 ку
.rrюбого rлпбуса), но отл11ч.1t."ТСЯ uт н её тем, что
1РОl\-Ютрия плюс .:~лгебра
1 111л11НЛJ111Ч~( "и" t-OCIJJЛlll!.i 1IA
11а r;ю6усе уго.1 0 отсч 1 1тывается не от в<.:р
TllIOIJТЫIOJI 0('1!. а ()Т 1 ·ор 11 :ю 11та:1 ьной ГLЮСКО
СП I, n J(QTOpOit ЛСЖI 11 ЭJ\.11:tтор КрО\1С IПl'O, н
1·t:оrрафпческо1·1 с1 ~стеме ,1,оба ю1е11 ы rio1rят1 1я
<·C<.:HCpll~I (юж11ая) шнрОТ:l» 11 «IJOCT()ЧIJ;(}I (:1а
r1 :l) \ная) ;1um ·oт;t», чтобы у1<::1затъ 11anp;i11лt.:1111 t
<>тсчt:т:t )'Глов Это п озn о;rнст 06оlп 11сь 6t: 1
OTJll 11 \:ITCJlhH ых :.> н аLJ<.:111 tй
z
'' .., ,н
1<,
0/
/
~"g а
'f::\ .·- " ''
1
,,oif. &"' <р Пр1'А11ия
1110'/h'tl .11
Фигуры
***
Мы рассказали лишь о некоторых системах ко
ординат. Существует и много других. Если про
нодю· оси не под прямыми у1·ла,"1и, то rюJJучаю·1·
косоугольные систt:мы коорr\инат. Искривив
са мн оси, строят К'jщволи1-wйную систему. Мож-
ЗАМЕЧАТЕЛЬНЫЕ КРИВЫЕ
3а~1счатслъ11ыс геометрические объекты
кривые линин привлекают 1311имашrс нс толь
ко lJЗHЩt:CTBOM сnосй формы , 110 и МНОГ\\МИ
У/\НВНТСЛЬl ! ЫМИ с1:юйс·1·наrvш.
КОНИЧЕСКИЕ СЕЧЕНИЯ
Н аряду с окrужностью :1аслужен11ыми ~старо
жнлами" в мате~атике являются конические
сечения - эллипс, парабола и гипербола. Од
пю.-t из первых, кто начал изучать эти кривые ,
был, по-видимому, ученик знаменитого Пла
тона , дренне11Jеческий мате.-,1 атик Менсхм (IV в.
дон. э.) . Решая задачу об удвоении куба, Менехм
задумался: «А что получится, сели раз ре:1ать ко
нус mюс1шс1ъю, 11ерпендикулярной <.:го обра
зующей? Какие крияые предстанут 1 1:н11ему
юору?q. Так, изменяя у1·011 при вершине прямо
го 1<ругового конуса, Ме1 1 ехм гrолучил три вида
376
i
/
\
--
}
!-
""
/ - э.д11t~
Рнс. 1.
,
'
'
/
/
'
v.~ /
;!
(\с;
- v.o.\1c;.
/
'\
1
\
"
110 рассматрш1ать н воображаемые простран
стuа с числом измсрсt rий более тре х, даже
бесконечномtрные пространства. U них также
уд;1ётся RR cc1·11 /\Скартокы коо рди11аты , что
rюзвuляет ра спростран ить на эти пространства
натяд1-1ые геометрич<::скис: гюю1тия.
криnы.Х; эллипс - если угол при нерш11нс кощ
са острый; 11арабuлу - ссл11 yruл прямuй , o,11iy
нетm, гипербuлы - t:cm1 угол тупой (рис 1)
l lазва 111 rя этих криных, ставш11с уже привыч
ными , придумал не Менехм Их 1Jредл()ж1ш
один 11з кру11116iш11х гепметроn /1,ренrюсти
Л11оллп11ий Пергский, посвяпmпшй :Jа меча
тслып;гм 1<рнnым чхштат из восьми книг •К(}
rrические сече11ИЯ». Аnоллоннй показал. что
эллипс. параболу и гиперболу мож110 получить.
проводя ра:im1чныс сечения ощю1·0 и ю1·0 же
кру1 ·ово1 ·0 конус:~ , 11ричём любогu. Пр11 надлс
жищсм накло11е CCK}'IJ\CЙ llJIOCKOCTИ У.'tаётсн 110-
llУЧИТЬ нее тнпы коннческнх сечсн11й Если счи
т;пъ, что конус не заканчикастся в !!сршинс. а
простирается за нес:, тогда у некФ·орых сече
ний образvются дr1е ве-1 ви (рис. 2).
Опнсынзя эллппс, параболу и гr1пербо11~
язьпюм алгебры, математик выберет 1.1 плОСI<О
сти сечения та:кую лрямоу~ ·о;1ы 1ую систему ко-
J'
орд11нат, в 1юторой уравнеrтшr 1<р11uых име1от
наиболее простой в11д. Если направить ось
абсцисс по оси сим:.1етр1ш ко1111•1еского сеt1е-
11ая н помесппь начяло коорюrнат ш1 саму
кривую (рве. :) ), ·1
·0 её уравнение прнмст внд
!
2
'
1
у= рх+лх,
1·11е jJ "' А - 11екоторые гюстоянныс:, прнчём
jJ 1 О Если Л. :::; О, ур<1 пнсние Qп.исыж.J.ет парабо
лу. есни Л. < О - :'!ЛJlипс, tош Л. > О - гнперболу.
Происхождение нз~наний 1<ри11ых объясня
ет рис. 4. Построим fl вер шюrе каждой иэ трёх
кривых любой прямоуrС>лы-шк высотоf! 2р (па
рисунке он коричневого цвета). К нему щри
ставиl'<I>'> ::;слёный квадрат, каснощиi1с.н вер ш11 -
11ой кривой, а стuроной - оси симметрии.
Тогда в параболе nлощад11 квалрата 11 прямоу
юлы111ка раю-1ы , в элл11псе плu1щщь квадрата
мены11с, а в еипсрболс больше, чем прямоу~лль
н111<а. В переводе с rрсческоп) <-параболе~ -
•сопостав; 1 е 11и е~>, «Сраu 11ен ие", «нрикла11ыRа -
1ше» ; «Эллепсис» - «выпаде11ие», «Опущение»:
• юшерболе» - «преувслис1еш1е'>.
эллипс
О с.войсrнах эJ 1липсов 1ю нсех 1юдроб1юстнх
могут р:~ссказ~1ть с11е1\и:.ншсты, и:3уч:аюL1\1 ·11::
движение небесньL-: тел. Согласно з~кону, от
крьпому н нач:але ХVП 1:1. немсцю-~м астроН<)
·"'ом Ип1·;:~ 111 юм Кеш1ером, все 11ю.11 tеты Нflижут
ся Doкpyr Солнца по орбнтам, имеющим форму
эллипса .
У эллиnса ест1. несколы<0 замечательных
свойств, кажд,ое из r<0торых можно прщшть зз
его опредслеr1ис . Начнём с того, что эюшпс -
Геоме:>три$1 плюс aлr~fipa
.\'
Р11с. 4.
это «С1 IЛIОСIТ)'Т:-1 н ->. а точнее, раш юмер1 ю ежатз я
к своему л1 ~а метру окружностr,, Друп1мп сло
nа:-.нr, из окружнос:тн nолуч~к"lтя элл1шс , сслн
вес сё точю1 пр116т1зпть к ш.16рашюму ;~11амст
ру. сократн1:3 расс1·оян1ш в одно 11 то же чrюю
/Хtз (рнс 'i):
fvP N 'P'
, V"P"
,'\!/Р = illf'P' = Лf"Р" .
Иног1~а Х<lчt::"тси украснт1. са!{ l<\XlCнtюlt t\l~С
точ 11ой клумбой. Почему бы н е прнд~~ть er1
необычну~о эллиnтнческую форму? Во61>ём дк1
r<олышка на расстоян11и друг от друга, rщторое
обозначим 2.с, и привяжем к каждому из них
но концу 1н::рёвю1 длиной 2а, причем а > с
(рнс. 6). Пели тспсрh латщй 0· 11·щ1у1ъ 13<:рёвку
н сторuну н провести этuй палкu(1 ;u,u [lllU, то
мы вычсртиi"! дугу эллипса.
И11:.1че говоря, множество нсс:х то 1 1 ек пло
скuст11, сумма расстuяв11!1 от которых до
Р11с. 5.
N
1
Рис 6.
j77
Фигуры
) \aJ:-llll1IX ТОЧt:К F 1 11 р~ IHJC'l'OЯllH:I , CCTIJ :ЫЛl///С
Точ1<11 f" 1 1-1 F2 11азыва1отся t::l'O фокусами.
В спс1·еме 1юорюшат. 1 ; 1е осъ Ох со1щ;щает
с л юшеi~ фокусоn }' 1 Р2, а 11ао..1ало 1>:оор11инат
11а.'\.(>д 1 пся посередине между пами (рнс. 7), это
опрсдспсннс выраж:.н:тсп уравпепнеl\t
1
')
1
/
•
)
J
у(х -с)-+у +у(х+с}-+у- == 2t1,
которое: мож110 1 1р1:1сст11 к 1:1иду
1r1t:1/=а
2
-
с!.
,
'
х· J'
-+-·-= l
(/l /)2
'
Reлнqri1 11,1 а и IJ задают размеры 11олуоссJ·1
элли1 1са (т. с. расстояшш от цс11тра элтшса до
наиболее и наименее удалёшп,1 х его точек) .
Чем блпже друг I< другу ра~мсры 11олуосс 11
эллинса, тем боньше uн похож на окружность
11 11рен ращ:н.:тсн в 1-1сё nри а= Ь. <. Сплюсну
тость'' зютнnса прш1ято также характер11 :ювать
0·1ношс1-ш см Е =с/а. получшнш1м 11 :-tЗRание
.'J1..:cz~c1nnpucu1llem.
Слоно focus n 11еrсво11е с лат1111с~юго озн:~
чзет «Огош»>. <·Очаr». Пропсхождсrше этого
11а:ш:~шш объясняется замечательным оптичс
ским свойством э.rоншса: прямые, с:осдпнню
щие любую его точку с фокусамн, составляют
с касательной к эллm 1 су в это11 точ кс: р<1в11ыс
у1·лы. Есш1 предста1:111ть сс.:бс, Ч'l'О ::111111шс_ гю;106-
но ~cpкaJJy, может ОТ\ХIЖ;J'[Ъ СRСТОНЫ<: лущ1, ll
поместить в ол.нн 11з его фокусом источник
снета, то луч ~ 1. отражаясr, 0· 1
· э11; 1 ипс1 , собеrуrсн
в ;~ру1 'ом cr<>фокусе (рнс 8). Та 1\ же распрост
ра11яюто1 11 акуст11ческпе Н<).1пы, что тrсnоль
зуют архптекторы /\llH со:щащш пора знтел r,-
1 tых звуко uых эффектов : «rовоμя:пц 1 х." бюстов,
<-МНСП / ЧСС1<01"0» шёпота, «ПО'tуегоро нНIIХ'> зну
ков ( р11с. 9).
1lонаблю,1-цсN1за1<0' 1 ·~нком , 11рими с1·1 rнн111 .м
сн на скол ьзящей 1ю стене лсстш11\е (р11с. 1IJ) .
Допустим, '!ТО коте н ок спрыгнет с 11сё не сра
зу. 'ГОl'Д:!, Н:.1ХО/\ЯСl1 tта лестн 1-ще. он ()JНШIСТ в
простр<н 1стне 11у1у эюн111с<1 ( m11 1ду~у 01с руж1 ю -
у
Рис.. 7.
Рис. 8.
378
Р~1 ё. 9" 1.1а..11н l 8 f'HHl..IP f f\Oltf TGrl Jo\J\ ~1Пfit Чf;.' fh.C)Г~t [ (3Uдi-)
Рис. 10.
сн1. еслн будет с11дt'1ъ ронно посередш 1е лест
ницы). Н:1 этuм с но1'1стнс оснuн;~1ю де11сrвие
мсх~1нн зма. npt'fV10жe11нor() Лt:ок;~рло [{:1 Вин
чи длн р 1кuнан 11 я элmшСОR (р11С 1 1).
ПАРАБОЛА
Зафш<снруем 1{а плоскостt1 точку L-' и пртtую/,
которая нс проходит через Р. J\1ножссrво то·
чек плоскости, ко·1 ·орыс расположены 11 а рав·
пом раt'СТОЯН 1ш ОТ точю 1F rJ от Пр>!МОП /,есть
па/шбwш , !'Очка 1-'
-
c..:f фок:ус, а 11ряма.я 1-
(Juper.шj}ftca.
Г-:стr в фtжус ~ ~еркалыrой·> параб()лы rюме·
сnгп, 1 1 сто"Ч111 1 к t:вета. то все нсхоl\ЯlЩ1е нзнеrо '
с вс.-тснJые лучн rюсле тр:~же11ня от неё поlrд)1'
1ю прямы.:v~ , 1шторыс r1ар :илелы lЫ её осн снм
меч)ии. И L1аоборот. все световые П)"Ш, НД)'ЩI!{
парJЛлелыю оси параболы. после отражсrшя
от ~сгс1юк~ кр1шо r1 собсрутсн в 0;1ной тоgке
сё фок~се (рис. J2). Это :замсчателы-юс оnт11-
ческос своГ1 ство m1raбoJiы 11111роко 11р11мсня·
1.:тся н тсхш1ке, на11р11мср в ycтpolrcтRe фар,
r~фЛСКТО))ОВ, а l l'l' el·fH радНОТСJlеСКОПОВ.
!
)'
-
-
-
-
"', :\l(x; у)
р
()F
у'= 2рх
.\'
Чтобы 11~шисат1, ураuнснис парабоJJы, 11а
правпм ось ~}' 11араллст,нu дирсктр псе /, ось
Ох - чсrсз точку F, а ш1ча1ю кuuрдшrат размс
сшм носеред 1·п-н: мсж;~у точкой Р 11 11ря.rvюй /
(рнс 1 .1 ). Ес1111 фокус f' }Лалён от директрисы l
на рассюя11ш:: р. то н тако1'1 с1 ~стеме 01 1 будет
JL"1t1ъ коорди11а·1ъ1 FU1/2; О). :1 люfiая 'ПJЧК<1 11~1
npsiмoli l - o;ory 11 ту же абснпссу -р/2 . Рас
стаю 11 1 е от пронэвольrюl1 то ч ки И(.\:: у) пло
rкосп1 110 ТОЧl(И F(p/2: 0) равно
r-
'
(
.'\ - jJ)- + .,.~
v2
.
'
3 racCTOЯHJIC ДО l!ГЯМ()Й / 0'1' то(t ЖС ТОЧКИ
\J(x: y) рав1 ю .У+ р/2. ТТоскп111,ку парабопе 11р11-
нащ1е--мат тпл ыю те точ кн М(х; у) 1 1а 1 11юс1ю
стн , /\ЛЯ l(()Т0{1ЫХ ЭТJ.1 рЭССТОill!ИЯ ОН1111~КОВЫ.
,--
--
х+Р=
'( .... _EJ·!+ ,,.!
2v.2
.
.
Пuслс .во:~~еr~снил обе1·ос частсй ура.вне11ш1 в
кRадрат 11 11р11всле 1 1ня. нuдобных членов нолу
чнм ранен.ство
)
у· = 2р..\,.
у
F,
~-
.\'
Рис. 15.
)'
ГРЛМ+"l рия плюс ;~лгебра
ото и ес.~л, ураn1~ешн:: параболы. nеrшшт 1 а ко
торой p~ICI юлагастся в нач;uте коорднн:1т.
ГИП ЕР БОЛА
Точкн, ра:11юпъ р:~сстоя11ий от которых до
; (нух д;н шых точек (фol(ycou) одш1 11 та же 110
абсолютной nслиqи11е, распола1'3ются r1J ?U-
пербале. Если лучи света испускаются rл 011 -
ного фокуса (/:'!.) гипсрбоны, то после отраже
нш1 от кр1mой ош 1 и~т так будто nы111m1 11з
друтоrо её фокуса (Р 1 ; рис 14). Выберем с11с
те.му коор;\ин:~т. в которuй. ось Ох проходит
чс:рез фt,1<усы , <1 начало ~-;uо1.щ1·1 нат лежит tю
с<.:ре; (инс ме:ж,ду ннм.11 (р11<: 15) В ::>·1
·0 !1 <:1 1с1·с
мс коорд1111ат ураннс11ис: г1 mсрбш1ы :зап11сы
вастся 1'1 1'\Нде
х2 )'1
---
·
=1
(,/ !
!J!
'
гдеаи/..J
-
uтшrчпыс от 11уля п:1раметры , реrу
ш1ру10 щ1 1с фuрму криnшl. Пμя..мыс. за11:анае.мые
ура1ше11 иям1 r
/J
11=-.х· п
-
Cl
{;
у=--Х,
(/
11a:.Jl1IR<IIOTCЯ c./Cll. i111mOJllClitU ГНПСГ6ОJ111I (ОТ
греч. «аснмnтотос·• -
«I rесовпада ющ1 1J1"). Rет
вп п111ербопы по мере удале1JJ 1я от 11~J<I;:iлa ко
орлит1т всё блшке пршкимаются к асимпто
там, rю тсi\ 1 не менее 1 1 11когда не достпrают их.
Еслн а = /J , то гипербола называется раn
носторо 1 rнсl'1 . В :-:~то.\1 СЛ}'Час, 1юнсрпун с11стс
му коорд~ш:1т отнuс1пс:лы ro tё на~1:1ла на 1-i S".
1 юлучают 1 ювую с1~стt:му коорl\11нат . н ко
торой ураRнс1шс: гнпс:рболы прнобрст-.н...·т ком
ШIК'ГI-1 ы~'! и ХL)рошо з 11 акомыft на ."' вил. .XJ ' = fг,
11л11 у= k/x (рис. J6 ).
у\1·=t
k---~
1
'
х
379
Фигуры
UИССОИдА ЛИОКЛЕСА
Uиссоида Диоклеса (uт греч. «киссоидес» - « r1л10-
шевидный » ) - одна из замечательных кривых, при
думанных для решения 1адачи об удвоею1и куба.
И зобрел её rреческий \11,Пематик Диокле с ео вто
рой половине 11 в. дон . э. На рис. 1 прямая СВ пер
пендикулярна диаметру АВ окружности. Точка М
на луче АС, такая, что АМ = UC, лежит на uиссои
дс. Находящаяся в11утри круга часть кривой вмес
те с дуrой окружности образуt::т фигуру, отдаленнu
11апомин,1юшую лист плюша (рис. 2).
Нарис.3АР11BN,АВ =а,АР :: 2а,точкаМ
лежит на uиссоиде. В этом случае BN =а 1./2 , и,
таким обр азом, BN - не что иное, как искомый
отрезок в 3ад,аче об улвоен11и куба.
с
{)р
А
в
it'f.
~~.i(~
~,:-.v.
Рис. 1.
Рис. 2.
Рис. :J.
ОВАЛЫ КАССИНИ
Французский астроном Джован11и Домеrшко
Кассшш (1625 - 1712) был одним из тех, rсто н
отличие от Кеплера сомнев:uн.:я n том, что 1rла-
11еты движутся вокру1· Солнца по эшшптич.ес
ким орбитам. L<ассинн искал и 1rэн1ёл кривую,
uнр<.:дсннемую как множ<.:с1·но точек, произвt -
11ен11е рзсстоя11ий от котор 1,rхдо J(Ryx задttнt 1ых
точек (фtжусоR) Р 1 и F~ rюстстнно Учё~-1ый об
нарУ'жнл , что 13 заюкнмостн от нсличины ~то1'1
llOCTOЯI (1roC1 форма 1<ри IЮЙ О\ЮЖt:Т при нимат1.
рюличr1 ы е очсртат~я. Есю1поснжпrюе1r[IOИ:1 -
Ref\e111-1c болыnе а
2
, 1'дс а - nолопи11а расстоя
ния между фокусами, то образус:тся крив::~я, uо
юзашrая на рис. 17. а. Еслн постояшrая равна
а2, r<ривая превращается в <-бантик» (рнс. 17, б)
Когда постоянн;u~ ст:Jновится меньше ti, крнн;щ
распадастсн ш1 /\на малснhюrх онал~1 . охк1тын:.1-
ющ1IХ фокусы (рнс. 17, R). Это семсйстяо крt1-
вых тенср1, назынают 0Rси1а.м,и J(щ:r.,ини .
КВАЛРАТРИСА
В V в. ло н. э. лреенегреческий философ Гиппн~ю
Элидь1 nреАЛожил ~в51u.1ный способ реwеt~ия за.дач•IО
трисею.tии угла (см. статью ~ Три знаменитые зшч11
древноС1·и ") Рассуждал он примерно так. Ловолыю
"еrко разлемпь nроизво,\ы1ыii\ отре.юк АВ на ЧJ~
рi1в1-1ые части. Это классическое постrоение оrу111е
ств11яется нJ опюв е теоремы Фалес а, согласн о кqто
рои параллеl\ьные nрнмые , nровеленныс чept!J t<OHIJ.Ьl
равных отре3ков на tмной сторон<.: угла, отсекают
равные отрезки и на другой его стороне (рис. 1), т.~
есм1АМ1=M1Mi = М1М1 и M,N ,HMLN1llM18.то
AN1=N1NJ=N1B.
Если бы ула11ось тем или иным способом увязаn.
между собой nроuедуры деления на р<1ень1е частн ут
и отрезка , то задаLtа о трисекuии угл.:~ был,1 бы решена
Лля lТОй uсли Гиппий изобрё11 чудесную кривую. Зае·
тавим точку М плоскоrн1 олновремРнно уч а ствов~ть
в двух рав11 омернь1х движениях- Пусть раы1ус ОР
( рис. 2) рав~юмер1-ю врашается вокруг uc111 раО ~•ад·
новременно прямая / равн1Jмерно перемешается от
точки А к точке О. Тогда точка Мих перРсечення оnн·
сывает искомую кривую. Поскольку равным углJмrю
ворота радиуса ОР при таком движении отвечаt0т
равные участки пути , преодолеваемые прямой!, ин.~
оборот, то отрезкамN 1N~ = N 1N 1 ::: NjA ~•а рис. 3соот·
ветствуют раш1ые у1-лы LM10M! =LM~OM J =LМДЛ,
гл~ точки М 1 , М2 , М, взяты на кривой Ги1111и11. Тахим
образом, трисекu.ия углаАОМ , произведена.
И:1 т~се:-: опалов KacCJ ши, пожалу1:t. шtнбо.qее
и11тересен «баrп'ш<» Ему уделяJL мнол1е qасы
своих занятий u:шейцарсю.111 матем.~т11к Якоб
Бернулли. Эту крнвую , 11м.с101цую сходство с
бантиком. которым 1:1 Дрсш-Jем Рrще пр11вязы·
налн тшроuый не::1юк к 1 ·ол0Rс: 1юбсднтеля, на·
Зht1-1зютж~t1f.lfcli.·ammi Бе/п1;1 ~l7ЛU (от фl!I/. ~11ем·
нискз·1ус ,~ - "украшенный 11е11тамн ~ )
Лl'мн11ска.та Бернулли 11::1нсст11а 111-rженерам·
желен rо1tорож11111«щ Он:~ служи ·~ · переходной
J1и11ией :.,еж.1у уч.асткз~ш желез1-ю,r\орож1юrо
пшютна rrрямтншейтюй 11 округлоli форм111,
обсспечиваji плз111юс-11, закруглешщ без кото
рой це11тробе:.кная с11ла . l\еИстnующая на пое:щ,
возрастал:~ бы резко , ска'-1ком, доспш.тtяя неудоб
ств< • н пасс :.~жнрам , 11 жсл езнодорожш~кам
ЕСЛИ НЗН'П~ H:l ЛЛОС'КОСТIJ НСКОТОГЮС КОЛllЧС
С'ПЮ t·оч<.:к 1:J, F2 ,
.•. , 1",, 11 з:эс1 аFн1 '1ъ тоqку А!
дш1 1'аться такн.vt образом. чтобы про11звс,цен11с
расстошшй от нсё до каждой 1tЗ взятых точсr
было 110сто~1111ым , то точк:~ М о пишtт крнвую
Кривой Гиппия заинтересова/\ся его у•1еник Ли·
110страт. «Пусть движение радиуса и прямой / будет
таково, - р.ксужлал Динострат, - что в тот мпмент,
когда прямая 1достигнет10•1ки О. радиуL как раз ог~и
шет четверть круга (рис. 4). На каком уда/\ении от
uентра О окажется в этот момент точка М кривойt»
Сразу ответит~.. на "Jтот вnnpoc не так то просто.
Заn11шем уравнение кривой Гиг~nия-Ли110<.трата в
<овременной 1<.Оuрлинатной форме:
ltЛ
y=xctg -,
2а
где а - ллина оrре ·~ка ОА. Ес/\И х fiудет стремиться к
нулю, то второи сом ножитель в пр<шои Ч<1СТИ урJ.в-
11е~1ия - Llg (тсх./2.з) - к бескu11еч11uсти! Тем 11е ме·
нее прuизfj~ение имеt>Т конечный ненулевой предел .
Но какой! Попробуем наити его.
Из теории nр('делов - р,1.~лела совремt"нного ма
тематического а н ализа, в част11ост11, tлелуст, ч10
J'
,
Рис. 3.
л
8
х
Ге()метрия плюс алгебра
t1ем1чи11а дроб~1 (si11 х)/х nри пр~мм:нии х к ну/\ю
стремится к 1. А раз так. то величина
тсх
со~
л.х пх_и2а
xct~la=la . пх 7t
s1n
2а
при убыван1111 х стремится к постоянной 2 а/тr. Л11но
страт замеп1л , что , располагая отрезкuм дли11ы2d/л:,
уже 11 сслож~ю пос 1ршпь отрезок лли11ы п и fJеш~пь
·шаменитую ·~алачу о квадр;пуrе круга.
Леибниu предложил н<1звать кривую Гиппия -
Линостра тJ квалратрисии - кр 11вои, < помощью кu-
1орuй можно решить -~алачу о квадратуре круга. Квал
ратрии1 uтноситси к классу трансuенлен1-ных кри
вых - линий, уравнения которых в nрямоуголь~юй
системе коuрлинат не могут бы 1ь заn11са11ы 'tЩJез
м1 югочлены от кuuрдннат.
.. --
-
-
м,
у
N
~J --~
\'
м
-
-"'\
о N1N2N1A
х
о
А
l'•te. 1.
'А
Рис. :.!.
Рис. 4.
штрую на3ываютл(~-1ишо>rmюf1с11 фи1-сусал111.
в .;ав11с1 IMOCТll ОТ тuru. CKUJll>KU фоку<.:оН 11 K:tK
{)J tll paClJOJIOЖCHЫ Н;! ПJIOCKOCTIJ , Ч<.: .\•tу rашю
прои :111еденпс р4сстояннft от фокусон ло ·1оч-
а
)'
ZJ ....
:.9/
:\:
.,
о
FL
.\'
u~
в Ji.,
еolyа~:\"
о
Ри~ . 17.
Р1н:. 18.
ю1 .\1 , 1юзtтИКJJО'I фигуры <.: с амымн пр11чуд;111 -
вым11 кu11турам11 (рис. 1~). Хотн эт1 1кр1шыс11
сохран11Jш в cвuf,\1 н:~:щан1111 СЛ()IЮ ~т:м1uк
ката·>. банп 1кам11 их 1111.-ак lll' 11азuнсшь!
UИКЛОИдА
Что общсгn ,чеж1~· слrmзм11 «l\ир1< ». « 11;тrrl\y:11,~.
«МОТОЦИКЛ» ?.. ()1<азьшаL'ТСН, 13 IIИX прячется одно
а то же грес1сскос CJIOJ3 () ~,Т<ИЮЮС » -
«l<P)·1 » .
•uкружrюсп"'· Слово •Цикл оид:.~" т:1101--:<.: пр1шад-
11<.:ж11т этому ря,цу. 11 нс случа1!110. Ц111\.тюидо1i
1L\1енуют кр1шую. которую ()1 11 кываст ·1 о чка ок
р~'ЖНОСl'11 . K;JTШЦt"ilCИ ОС:3 СКОJll>Ж<::НИЯ ПО Ht:JIOД
lir! ЖHPЙ 11рнмоi1 (р11с. JС)) . Ha:знcttlll<: 1ч111во11 /t<IJI
Г:ш11т.~о Галале1-1 . пrн::рные об1х1т11нн111ii 11:,i нсё
1шима~r11е. Сrаrт 11 ная nt:c /\11ух мtталлТ1чесю1х
!IШ\СТIЛЮК равной ТШIЩШIЫ, аю1а 11 :-i котор1.1х
была uырсэа11а по циюю1ще. а J'\Г)'l':lя по nкр~r-ж-
1юст11 , гюрож;щющt:й -~ту цшсrю1111у, l'а.rптсй
. 2iRI
Фигуры
обнаружил. что площадь се::гме11та цm<лоиды
н трr1 раза больше шющал:н соотnстствующс-
1·0 I<prт;t .
r1rсдме-1 ом п р11с1 ~шьrю1 ·о пзучешш, а впослед
с1·1ши на ней прuверяmJ<.:ь мuщные ме1 ·01щза
рожю1юще1·uсн M'1' l 'C1\.1:1TI IЧ('('KOl 'O :.IH;J JJIJ ~i:I .
Олыты ГалИJrея далн •1·uлчок с 1 ·μ0 1 ·нw1 \1а 1е
мат1 I ЧС:'СЮ IM l ICClleДOB<!HШIM 1{HКJIOll} \l >I . СН~/Ч:JЛ::!
ст учt:н111< Tuppr 1челш1 . а :1;псм Ро()ерналь, Де-
1<арт 11 Фt:рма 11е гш1ыю ufioc1юпam1 ~авнсн
м< >сть, открытую Г:-1л 1·1J1еем , но н уста~ Ю liHЛII
рнд ;1руп1х с1юйсrн ц1 11{Лсн1ды . ПроС'тота и изн
щеспю определеr111я цшотои,1~.ы привлекалп к
11ей м 1 югих мате.,1атт1ков ХVП -ХУШ вв. Uю за-
1п1м~с1, 1tаскалъ, Ле1'16шщ, l'юi1гспс, Д:шинJ1
Бср11уш1и Прнчtм шrачаш.· циrQю1ща с:~ма бьu1: 1
I J ерl'нсрнем 11,1 1ююн ;1у кыпуююстыо вниз 11
1 11х~л:ста1mм. ч·1л по не (r ск:пываtтся 1ижелзя
часп·1 ца. й:~ какой 6 1,1 точю 1 111 1ююнды 11 1-1 на
ч н 11ала ,r1ni1жeiтнc часпщ;з , 0 1 1а ск;пнтся R1 111з
~э 011.1 ю и то же вреJ\1.Я. Зэиечательнос crюiiaruзQ
и:юхртиюсти пиююнды (от греч. «11зос" -
«рав11ьu1" п «XiX>IIOC" -
« вре,'\.1Я») напело Гюn-
1·енс.:а на мысль 11с1юльзu~а·1 ь сС.: в ч.асонuм м.а
ятн.ик<:. Скатыl!.:1 ющнйся rю щ·1КJю1ща.:н,ному
жi:лuбу шарик сm1111кuм м1ю1·u э 1 н: р1·1ш трап11·
582
КАК ЗАК РУГЛИТЬ
ЖЕЛЕЗ Н УЮ ДОРО ГУ?
Экспресс стрелой несется по же
лезной дороr· е, отбивая ров н ый
ритм п оходной мелоди11 на рель ·
совых стыках . Ero nассажирЬ1 и не
r1редnолагают, •1 то их комфорт
обеспечили не 1·олько проводник и
и машинисты, но 11 м<~-rемат и ки ,
благодаря расче-там которых пово
роты п оезда nлавt1 ы и улоб~1 ы.
Ешё при строительпвЕ:! первых
ж~лез ных дорог nроt-ктиро8шики
столкttулись с неожида н нои п ро
блемой: лви гансь по луге окруж
ност 11 , ва гон поЕ:!зда испытывает
воздейспзие uентробежн ои силы,
которая полнос.тью отсутстоует на
прямолиней н ых п ерегонах. Если
nрямш1 участок желез 1 юдорож1ю
го 11олон1<J сразу переходит о кру
говой , то не только пассажиры в
вагоне, но и все механические
части - гайк и , болты , проклад
ки - получат ре3к и й толчок.
Чтобы и збежать нежелательной
встряски, межлу прямыми и кру-
говыми участками желе3 tюло рож-
диуf соприкгсаюшей1..я окружнос
ти, н•м мен ьше кр и ви .-1на ли11ии
(р1к. 1). Когда криви .та лини11
уме~1ьшается до 1-1уля, ли11ия ст;зно
вится прямuй, а радиус соприкаса
юшейся окружное п~ !! кt.1жлой t:'P
то'!ке у8ели,1ивается до бесконеч-
1юсrи. Мuж 11 0 даже сказать, что
прямая линия - зто луга сжружнu
сти бесконечно большого ралиу<'d.
Лучше всего перехол11ую ли-
11ию железнодорожного пути уст
ра и вать таким обра .юм, чтобы
кр ~1 визна вдоль не>ё и1ме:нялаrь
прuпорuионально лли ~1 е ду1 и . Со
ответствук.нuая математичЕ:!ская
крипая (р и с 2) называется 1-.м1-
фои11оii (от греч. • клофо » -
« Гl рясть») или спиралью Корню -
по имени ф~ника Мари 1\льфрелd
Кор н ю, применившего её в 1874 г
лля оп~1 и111~1 я дифракuии света.
Желез 1 юло r ож 1 1икам к11офоила
больше .шакома как ралиоидаль
ная спира111,,. Uна ог~ исывается
уравне11исм R =k/5, rде R - ра-
1юrо пути ус:тра и 1Зают та к 1~азыва- "-.
Г\/
с,v.ые перехолныt:. /\инии с 11>\авным
""-У'
изменениt•м кри1>изны.
у
Как uпределюот кривизt1 у ли-
нии в какой-либо ее точ ке~ Mepoi1 il
rлужит ралиуr криви зны . т. е. ра -
д11ус окружности, н аиболеЕ> тесно
прилегаю шей к линии в эrой rоч кбl
(такая окружн ость называется со-
при касаюшси ся). Чем больше ра- Р11с. 1.
Р11 с. 2.
диус соприкасаюшсися окружflо
сти в точке кривой, в которой uка
жется пое.'IА, пройдя по ней рас
стоянис 5; k - поrтоян11<1я.
Лля закруглеt1 ий небольшого
радиус d часто ис rюль1уют лемнис·
кату 6ернуми. Радиус кр11Р.изн1>1
лем 11 искаты в поляр~1 ых коорди
натах приближе н но выражается
равенством R = k/μ, rлf' р - по
лярн ый радиус точк~1.
В тех11иL1еских рас•1 ётах в каче
стве перехuл11ои кри 1Зой улобt1а ку
ЬичРrкая парабола у =kx 1 (рис )).
В ()крест~ юсти начала коорли11ат ее
радиус кри ви.:Jt1 ы г1ример 1-ю раве11
R = k/>..
... Машинист ведет поезд ровно,
и о по1:Юротах uы уз11ас г~, лишь
наблюдая последние вагоны соста
вэ и~ ок на пюе го ку11е. НЕ'Ожилан.
но вспl\ывают в памяти рассказы о
сnир;:~ли Корню, лемнискате Бер
нулли и кубиче< кori парс1.бол~. Это
они мягко и плавно наnраВl\ЯЮТ
путь вашего экспресса.
l'и с. 3.
11а тре н~ 1<:, поэтому Гюй1·енс 1 1рt:11,Jюжил 1юд
всс1пъ ш::~рик на ш1·п~ 11 01·р~11-u-1 читh с 1юбо;\у
е1·0 11сре:1-1t: 11 (с11ня ;,ос кп1'~, r<p::ii-1 которой имt:t:т
форму щ.11<1ю1щы (рис. 20). Оказывается, n та
ком случае движе11ие шарика таюкс происхо
днт по цшаrоиде, н, следонателыю, на лep1IOJl
с1·0 колебаний· пе ш1ияст nеш1чина отююпс1 1 ия
шарнка от оертикат1.
В 1696 г. Даниил Бср 11уш1и открhlл дру1 ·u1::
~амсчатс11 t,нос с 1юйство этой кр11ной . По ц111<
JIOJJЛ<: 11ри u·1 ·суf'ст кни тре ния ч:ктнца IЮ1'дей
ств1 1ем силы ·1·ижсс1 и скатынасто1 J1з оююй ~а
да 111юй точки н другу10 за на1·1мстr1,шеt: nремя.
Бра.\71стпхрт11юе ссюйспи:ю 1~и ЮЮИ!\Ы (от греч.
·б рахнС1'0С» - «кра·tча~1ТТL11Й» [[ «XpOIIOC» -
fвремя -> ) до1<азать отнюдь пе r1 росто, оно ста
ло отправной вехой ново1·0 нащхшлення в ма
тсмат11ке - nаршн:щ ошюrо ш.:чнсж::пин .
« ПИРУЭТЫ >> ОКРУЖ НОСТИ
К<1куютр:н.:кторик> 0 1 111п1е1· л1чка <жrр<1rосп1.
"а·1·ящt:r1сн без скольже11ия 1щутри i1P'' l 'OЙ
ш;руж1 юсти ? Как э·1·0 ни уд1m1rтелыю, 110 011а
~южет бытъ." отрезком прямой~ !:::ели радиус
внутренней окружности DдJюс меньше р~щиуса
1111tш11el1, то точка будет 11ерсмr:: щ атьо1 по
диаметру второй окружности (рис. l \ ). Этот
11сож11щ1 нный факт обнаружил н теuретиче
сю1 uбоснuна}l 1lиколай Kont:p1н11c Если же
р;~д11ус КаТЯЩ<.:J1Сн ОКр)'ЖJIОСТИ В тr11 раза MCJ/h-
ШC рад~ 1уса 01 юрной, то точка m 1нсыяаст д<!ль-
11ющ~1·. ил и кривуm Пfт еiшера. Лeplloe 1 1а
зва ш1 е щюнсхО,1\IЛ. от rpeчec1ю lr 6укны д -
•дельта? (рис. 22), а второе дз 1ю н чсс1ъ изу
qавшего кривую шnейцарскоео геометра Якоба
Штейнера.
Умс11ьш:им р~щиус катящейся окруж.1rосt·н до
1/4 рад1,у1.:а вне шней . Тогда нолучаетс}I кра
сивая астроида (от ?/Н!Ч. «астроtн - «::шс3-
да~ ) - кривая , ннеп~нс шш()мш1ающая стнли
зоRанное изображен 1 rс з везд ы (Гис. 23). Хотя
астроида 1 юлучил<! с1юё назна н ис 1~ XJX н " о на
Гсо~летрия nлюс ""гебра
была и:шсс'l'l 1а Лс:f161 шцу а t 7 l ') 1•• 13 начале ста
ты1 мы рассматри нал1 1 11р11мер с ~.:отё~rком, ко
торы1·1. находясь па соскальзьmзющсй со стены
11ест11ицс, ош1сьш~1л дугу этшпса. Промежуточ
ные положеrшя са1vю1'111естн1·щы 01 ·1 rбают дугу
астршщы.
Вес крнш,1<.:, которьl(: нычерч11к::~ет точка на
окруж1юст11, катящс11ся в11утрJ1 ;~ругой окруж
~юсл1 , прин:.щлежат семе 1:1еrву гипт~щi'.лоид ((YI'
грец. (,J'llПO·> - <·IЮД», <·Н1 111:1у? 11 <•Ю fl(}Ю\ЩСС·> -
«Кругоо6ра: н rыi i ~) . Рассматрнn:~я :1rrзлогнч11ыс
« nиrу:пы» окружности, котор:J.я канп·сst по
nr1cш11cf1 с1·орсн re опор~ юго t<pyi·з , мы пtрс11е
сёмся 13 1к· менее разнообр;1:шьп·1 мнр эпицил:
лоид (ОТ lj>t.>11. ··~Ш1?
-
•На•>, «над-•) .
Пuнаfiлюда с.\1 :3а какоi1-н 1 1бу111, точкой
ш<ружн ости . ко1·д:.1 посJ l <:) (НЯ» к:1т1 rтси rю н11е111-
1 1 с й сгnроне l l l'П OДRL lЖH()l'I о кру'ЖJ IOCTH p ::i Rfl( )-
го ра111 1 уса . Тр<н~1<1'орие~1 точки ilудст л:upauom)r1
(Гис 24). По м1те 1 rr 110 матсма·1·111юн, 11ридум ап -
11111х 11а :ша11не крпвсн\ 0 1ra отлалё1ш о т1з1 ю.м11 -
1J:.tет форму сердца (от греч. « карл1 1а,, - ~ сер;l;
цс-> ). Дру 1·ой сrтособ rю строе шш r<ардиоады
состоит в слсду1ощсм Зафнкс ирус:-1'<1 п а опор -
11ой окружност1 ~ точку А llрuведсм J\р}тую 01<-
р;гжност1, с цt.:11тром н Т(.)Ч.Кt :\tJ , в:~ятой 11:1 опор
ной окружности, н ралиусом МА. Пuнтор1 1 н
затем таю 1t' пuе1'р( 1<.:н ня ;v ш J\()статоч 1 tu Ciom,-
шm·o числа точ ек ЛI, рак11омс:р110 распрt.:дt.:
.11ё 1 шых 1 ю onopll(>!I 01<ружнос11 1, ув1rд11м , что
оrнбающая 1кех окру>ю юсте1'1 рад11уса МА вноn~,
является ючщтюидот'1 (р ис. 2-'5).
А п очему, со6стпс 111ю, точку, оп 11сJ..~ш:.tЮЩ)'1О
1q1нвуrо, rtyAaю брат~, на само i1 окружности? Да
nаi!тс 1юэ ьмё м эт\1 точкт 11есколько с:боку. сме
сти в в ту 1щи ипую сторону от центра , н жёстко
свяжем t:i~ с к;.~·1·»щейся окружшктыо (рис. 26).
Мы 1юлучнм кр1 1 вую. н::1зывасмуюулшпкvй Пас
л:аля - Н Чt:CT IJ BllCpBhJC p<ICCMUT[)CBLIJt-' l 'CJ СС
фр:.~н1\у:1ско1·0 матсматика Этьена 1Ън: к<1.юt
( 1')fШ-16')1 ), отц;J :iю1м~::нит()l'О уч ё1 юго Бпеза
Ф1·н уры
r)
\_/
\.\
"
t»н.. 24.
Рис. 25.
... _
--
·'
"
/
Паскаля. Утпк:~ Гlаскаюr 1 1рпмеш1етсн для вы
черч1ш~11 шя пrоф11!1Я ЭJ<CЦCil'l'p11K::L, если трсбу
СТСЯ. чтобы с~:;о.rн,зящнГr по проф 1 тю стержень
conepпrJл гармо1шчссы1с кuлс:ба11ия (р11с. 27).
в OTJ ll!Ч I IC UT ~ксцснтр11юJВ. uчcpЧt"llH ых IJO
снира;ш Арх11м1.ла (см статыu ~с11ираш1?), та
юн: мсх ~11r1 1 змы OTJII!Ч:JIOTOI flJl:lHllПC'J l>IO BOЗl3-
pa·11IO-ПOCT)1l:!l't'JIЫIПl 'O ДВllЖC:JflofЯ с-1 сржюr; l lX,
как правшю. 11 npe,rJ.\ юч11·1·'1ют кон1.~1 рук 1 оры.
Тпчку. кторан nычсрчпвает ·ry 11m1 rшую
1Пl'I epeCLl)"IO КрНП} Ю, МОЖНО орать 1re TOJIЫ<O
МАТЕМАТИЧЕСКИЙ
UВЕТНИК
в11утр11 лсре~\<Пывающслся окруж1rост11, 1 ю 11
с1-iаруж11 <::ё. Все разнообр;:~зпыt ''JJ 1 mыc, оm~
сы васмыс т:1кой точкой, лшrуч11л11 н:t:шанне
IJlj)().).;IJuды (O'I ?/)(!'! ~1 (Ю~ОIЩС('» - «КОЖТО
(>б)ХIЭНЫЙ•) в ~;.JIOl(\IMOC\'11 0'1' 'ЮГО, \')~С псре
К:IТЫ вае-1·<.:н uкруж1 юс·111 - в11утр11 <н~nрнnй
<.жруж1 юс1·11 юн1 t{не c:t: , 1кt:' ·rpox( н 1ю,1 1юдrа:i
J\с11н 101·ся 11а lill)'Tpt:11\НH~ - li(/1()/1/POXOUдbl \\
RI !CII шщ· - . 'UlUllljIO.'\'()ЩJbl ( рпс. 2Н).
Длн тех. r<то за..~очет 1.юспрои:-шестн "ЭТИ 11
шщо6111.~с.: riм фигуры н:.~ гtсрсонадыюм ком
пыuтсрс, 11ршю;щм общие 1_1;~рамстр1Jч<.·ск11е
ур:ш1 1 сш1н кр1шьrх·
.\=(N+mR)('()...ml- hLO~(/+m/),
у=(R+mH)-;iпmf- 11sю(t+mt).
1де N -- ра,111ryc снюрr юr"1 окррю юс1 н: 111 "' 1/N -
()'l'lIOlllCTШC рап11уса /' ПС1ДIШЖНОй ()Круж11ости
к рад 1 1усу R 01юр11от'r; h - расс1·олтше точки,
оnисьша[()щеГr 1<rивую. от центра 11одm1ж1rой
Как-го р<Н итальянский г~ометр
Гв11до Гранди (1671-1742) создал
ро3ь1. Нет, uовсс не те прскр.кныс
растения, которь1е 1носсп1ы всем.
Розы Гвил() Гранли рдлуюr гл<IЗ
правильны....,и и плавными линия
ми, 1ю 11х 0•1ерта11~1я 1-1 е кJnриз
прнролы - они пр~оnрсл~лены
сn('u11ально nодоfiранными мате
матическими завис\liмостями. Се
мейс.тво po;i Гоидо Гра11д11 описы
в.~ется уравнени~м в полярных
коорд~11 1 атах
rде {(q>\ для кажлоru отдельного
расrения прt:>дпавляет 011ределё11-
ную комбинаuию триго н ометри
ческих функuий, Хабеникr путё м
МllОГОЧИI ленных ЭК(Щ'f)ИМСН iОIЗ
11 вырастим ~а....1ечател1..ные :жrпо
наты (рис. 2). В наши д11~• пuдобt1ые
.jKC 11~риме11ты удоб1·10 nроволить.
имея под рукои nер('ональн ы r1
компыотер.
r:a ~in k<f>,
где д и k - некоторые постоянные.
На рис. 1 ю<Jбраже1-1ы эти кривые
при ра.мис111ых :тачениях парd
м~тр.э k.
Очарованныи результатами
Грм1ди, не"1еuкий геометр XIX в .
х.1fiенихт также решил 1аня1ься
математическим «растениевод
ством». Полагая, что <1брис (очер
та 11ие) листа или uоеточ11ого ле
nеrтка в полярн1>1х коnрдинатах
описывается выражением
k=5/3
k =4/3
k::: 1/2
k ::= 1/3
(Б_) CJ
Рис. 1.
r=4('1+cos3q>) - 4>IП~ЗIР
r=411-1 cu~Jq>)t
_,. 4~IПJЗq>
Р11с. 2.
Р11с. 26.
Рис. 27.
Р11с. 28.
окруж11остн (h folt0жei· быт1, как ....1еныне. ·1 ·ак 11
бо11ьше 1·); параметр t :моделнрует времн .
UЕПНАЯ ЛИНИЯ
Какую 1ш11и10 l)бразу1от 11р01знс111ие проно;р ,
тросt.1 . rнршшды? Галилей 11 юшсс "Беседы н
\•tатема r11чесю1е 1~ок азател 1,стпэ.. .• ( l б38 t'. )
прслложил способ nосч.·юег[Н}I nарзбот,1 с
помощью лвух вбитых в стеJiку rвозf(ей и Bl'JC}l-
щcй на 1111.х то1шой цеnочю 1 . Но 011 ошибался.
Спустя полвека после выхода ю1пп1 ['ал нлея.
в J 690 г., J-l коб Бернулт1 доказ:,~п, что форма
СПИРАЛИ
БезобнлваJr rюpom(a, обра:юnан 11 зн nытею
ющей из нашrы водой; св11репыr1 смерч. оnус
тошающий всё па своём пути: вели'-1ествс1111ый
кр~'l'Оt!Орот l'ГП 'аIIТ<.: КО ГО J<()СМПЧССКОI () lШSря.
1~·-~1а1:-1нос:тсЛ 11 r"шrактик - нес он 111 1.меют фор
~1у ст·1рале(I (р 11 с. l )
Одну 11з перных сш 11х1ле1\ онис~н11у.rп Ар
х11мсдом, нам пrодtмонстрнруст светлячок.
()·1пр<.шнм его в пу1'С~Шt:С'ПiJ 1е 1щолh сскунд1-ю ~'1
Р11с. 1.
С1ш р,1льн,1я
галакп1к~
Геометрия плюс <1м·ебра
(5) ",;,Q~J5~
,'r)11111прохоm)ы
сrюбодно nrоннс1ю1щ:·r'1 неnочюr (р11с. 29) 0111 1-
сьшастся урав1 1 е1 шем
е"+е''
_)'=П ----
2
н , слс;\окttт<.:rтыю, пзраб01юll 1·1с sJВ.l\}{C't\'и. Нкоб
Бс:р 1 rуюл 1 сноi: т·r-:рыт11с' :~сржа , 1 к та11не: 1 1уtть
;(pyгirc с;,ел<~ 1т то , что C/(t:Jtaл он . И рон1 ю
чере:1 r·o;( п1х1т1лы тос рса1е1 rне 011убт 1 коваJ 1и
с1·0 1\L'Jадший fipaт Ипг:11п1, а ·1·аюr<е Лей(нrнц н
Гюйгенс. r1ослед11ий и прел.;юЖИJI '1:азва1111е
,].ЛЯ ЭТОЙ крнnой - Цf!lllfШl ЛU111lf/.
стрслю1 ч acun, по.г1 ~11·ан, что п1r будет rrcp<:мt:
пp·rъo1 с 11остою1 1 юi"1 скорnС'lъю, 11с 061х1щ ая
в1шма111ш ш1 рашюмср1юс дn11же1т~1е стрслю1
ч~1сов по кругу. ёсrПt nообра3н rъ бсскт 1еч1 ю
/J,JШI rную стро1ку. то жучок выснетнт 1r:\,ч cnu
/JШlb ApXU"il 'f('()cl (рис. 2)
rасстоян1н: 1", ПJ..IOI·IДCHJ IO<: СВ('Т.1НЧ1~ 0 ~1 rю
cтpt:J1 кt: 0 ·1 точки с:·1 ~IJYl':I, н yro:1 q>, н:1 которьп'1
прr. 1 этом СМССТt [Тl'И стрелка, Гl\X>ГlO[lЦlttH!:l l\hl lbl
Рис. l.
Фигуры
времепн, а :ш~ч1п, и друт другу: 1· = А?<р, где k -
коэффицие1п проnорщю11алыюсти . С]lедова
тслыrо, расстояние d между 11np..нr соссдпимн
витками спир.иш постоя111ю· с/ = /<( q> t- 2тс)
-
-
k<p = 2kтс.
)J,pyl'Oc своi1ст1ю с1111 р~uш Архнмсr1~1 - 11ро-
1юрцион,111 пнпсть щ111р:1щен 11й ра;1.~1 альных
р<~сстонннй и уr·лон На рис. . 3 1юк:1зан::1 с х<:-м.а
1<ущ1 ч ков(Н'о :-1еха 11нзма, 1 1рео6разующе1 ·n ра 11-
1юмерпос вратеппе J(Иcr<a в равномерное тш
же1ше порШiш полеремешю n одну и дру 1у10
сторо 11у. Кот~ец ocenom стержня лорш11я сколь
зит по шайбе, края 1<оторой представляют со
боЛ две: д)т11 с1111рат1 Арх1н.1еда.
Архим.с:л nрсrvтожнл исnс>111,:юв: 11ъ :~то снu1i
сттю rr.ля рсшсння сщ11nС1 И' з11ам.с1ш1ъ1 х задач
1ч1сннпст1 1 - за;~ач11 о тр1 1 сскц1ш ~тла. Четыре
дуr ·11 nкру-ж11nст1 1 , nтсе1<ающне 11 а ра;111усе тр 1 1
рап11 1 .1х атре1ка. n тnчках пересече 1 тш1 со спr r
ралыо Архимеда делят уrол на три равные ча
сти (р11с. LJ) .
Архимет1рс rп пл11оrюлыю труютыс змач 1 1 по
ВЫЧИСЛ<:'НИЮ площади фигуры. Ш'J),IНИЧ.t:ННОЙ
щ.:рв1,1м н11·1·ко:-1 с11ирш 1 н (участок r·шryбur ·o
цн<.:т;.1 11:1 рщ: 5), и rюс1рuс11ию 1<~1с1телыюй 1<
cш1ram1 в тобой её точке И:~ резуJ1ь·1 а'1 он. 1ю
лученных Арх1с'V!едом, следов:ию , в час..:тност11 ,
ЧТО еслн 11роне<."11 ·1 В TOY t<eA . э:.тер11 1 ающей пеГJ
liЫЙ в11то1< спнрал11, касательную и Ji точке О
восставить перпе11д 1 1к)ляр оп 1< 01резку ОА
(В - точка 11ересече11и.я 11epne11дi1К)·m1 pa 11 ка
сатслыюй) , то ;~:липа отрсз1<а ИВ будет раnпа
длине окр}жност11 радиуса ОА Это ::~амсч атсль
нuе сно1~1с· 1 ·но СJ1ират1 1 юзнощ1ет решн ·1ъ т;-~кжс
Рис. З.
в
...". --QS
--
---
~)
-
-
-
-
--
-
-
.
-
-
-
-
-
-
-
-
-
-
=
п знамсmпуто задачу о 1<Вадра1уре ~<руга. на что
обраnш ш шмание сам Лр:л-имсд.
Тс1 1 ер 1, расс..:,10·1рнм е:щ<: одну уд1ш 1 п~.:лы1ую
сш1раль, котпрую 11<1 ccll paJ нариС\' ЮТ трп
светлячка . Пустп иаходяш,нсся f(py1 от др~та на
ранном удалсн 1 т, ·1. t:. в вcp1JJL1н::1x 11рав нлыю
r·о треу1'ОJ11.11нка, жучю r 11, R и С рсш11m 1 позн:~·
ком ит1,ся 11.ру1' с дру1 ·ом. А 11<i 11ра вrmo1 11ря~ш·
комкВ,В-кС,С
-
к А. Путсптсстлуя с
постоmпюfl скоростью, u тобо1'1 ~ю.~,1е11Т uре
мст пr светляч1ш будут располагаться u оер,
ш штах правильного трсуrольшша, подобного
11 сход1 юму. Каж:дьн1 свtтлячок при этом очер
тнт ;\у1у .11oгctp1tф.;11uчl.!C1~mi cnupwtи (рпс 6)
Логар11фм11чсская сп11раJ1ь ош1сынзетс~
ура11 1 1е 1 1ием
,.=а~.
Здес 1, уже не само расстояние '" 1<ак в cпrrpa.1J11
Архимеда. а его лоt·арифм (lo~n ~·) возрасmе;
с~--
Рис. 6.
прнмо rrропорцис)надыю у1·лу 1 ю1юрот~1 !р.
Точка. нокруr которой закручиваюте>1 витки ло-
1-з1111ф:vu1чtс1шй <.:rшр~ши, особая: R её окреп'
ноп·н н~м;п ывается бt;скснн::чнл мно1·n nнткон.
:1·1~t 1·очка на:1ынас."fся гюлюсам.
Впt:рные u Jю1 ·арифм1 1 qеской спирали l'ОJЗО
рлтсн 13 сщном И:l 1~исем фр<uщузскоrо матсм.а
'JИК<t Репе Декарта в 163~ г. Увидеть её можпо.
напршvtер, в 1.штках раковины. Семена в кор:ш
нсподсолнухн также располагаются по кривым,
бпизки"А к д)'Т'<'М ш)1·~1рнфмич.сскuй спирали
Одно 1 1з примечательных сво1"rств ; ю1·ар11ф
,,111чссJ'оl1 CГ111fXIJll ( состоит в том, что ЩJОJ l:З
RО.IЬ НЫЙ луч. ВЫХ()itЯЩJJЙ 1-1:3 её полщса. нсрс
секзст любой оиток спнрали 1юд одннм 11 'J'ем
же углом (рис. 7). Это С11(1йс1·1ю гrри,vтсннется n
режущих ма шипах . Вращающ11еся 1 южп соло
море:lки амеют профит" очсрче1 шыr1 по ло
rар11фм нчес1сой спирали. У1· ол резанпн такого
механизма 11остот1с11 вдоль 1:1cefJ т<ромки 1 юд
в1rnа(ою 11ожа (рис. 8).
Uк;.~:-!ынаето1, трубу.1юд1ю1J,Ящую струю IЮ/(Ы
к .rю1 1 ;~с1·я ,\1 турби1-1rю1 ·u колеса н::~ 1 '11дроэлект
рос.:та н 1 ~111 t, также следуt:·1· з:нюра ч 1 ш;~ть no ло-
1·ар 11фм11ческой с 1 111ралн. То1 ·да потери э1-1<::р-
1и.и ДВIJ)К)'ЩеЙСЯ 1.Ю/(Ы будуr Ml11 1 H,\-1~/Лl>JIЫMl1.
Л.огар11фм1 1 ческая спираль -крипая с «твёр
дым характером". Она не из~1е11яет сное11 при-
ТРИГОНОМЕТРИЯ
Теrмш1 нр 1 11·ономс:трия» 1\Осло11но оэначает
•11змtре11 ис 1'реугол 1 .н11кn11 ·>. Е1·0 нвёл н уrю
тrеnле11 не В ] '595 Г. 11емеЦКПЙ МЗТСJ\.1 З'l'ПК Н
боrпсJюв Ra рфоломей гr нтио<, аnтор учеб1 1 нка
rю триrонометрни и трпrшюметричесюrх таб-
Г еомстрин плюr алгебра
рО/(Ы при м 1 ш1 ·их прсобр:.~.3uвш1инх, к которым
чувств11те11ьны лр) 1· ие крнш,J(;. Сж:пъ ш111 рас
тяt-1~'1Ъ эту спнr:uн, uтноситеш,но ее tюнюса -
то же сзмое, что nпоер 1 1у1ъ сё 11а опре11е.11ё11-
пыiJ угоп Наоборот, сслн пращ;:~п. ст111ра111,
ЫЖ[J)'Т ПOJllOC:l 11 ОДТI)· lfffil др)'Т)lО стор()11у, Т()
.можно наf;людать к:1жущееся растяжение итr
сжатие сп11рал11.
Лрсдnолшютм , что 11з полюс~~ логарифмпчс
Сt<Ой с11ирали выходят лучи света, которые от
ражаютсн от криво\\ , как от обычного зчж:.ща.
Ео11111рос11сди ·1ъ з~1 нсt'ми отражснным11 луча
v~и, то окажется. что он 11 01·11баю·1 некую кр11-
вую, и она 1 1 с ч~то иное, как лоr'зрафм11чсск::~я
с111 f p::urr).
Эт::~ же с11ирt1111 . предстаёт n tзI·Ще о п1бающеl1
1юрм ~1лсИ (перnе1щт,rК\'1 tярn11 к касатслr,11ым).
проведёш1ых n каждой ~оqкс логарпфмическо1~1
с 1 шрат 1. Геометрпческое место oc110nai шй nер
пс1щикуляроn. ощщс 1 шых из лолюса па каса
тельные к Iф1rвой. опя11,-п1к11 нмсст форму ис
ходной с1шрат1.
С 1юйст11<1 .1ю1'ар11фмич1::ской сш1ралн так
1·nубоко 1юраз11ли шне 1'щарско1 ·0 матсмат11ка
Я коба Бср11улJ1 н, что 011 за нсщ::~л ны ссчь сё 11<1
сноём над1'Робном ка~шс::, со 1 1рuнодшз 11зобра
же11ис 11ап1нской фразой <·Eadem 111L1tata rбш
~О» - «Измет 1 ёт111ая. возрождаюсь 11реж11еj1 ».
mщ. Тригшюмстршr - р<t::~дел мзтем<JТШ(lf , ко
торый 11:~учает З:JBИCIJMOCTll мсжду ут'Л3Мll 11
СТОГО l lаМИ "1'(1еугоЛЫНIКОR Н T[Jlll'OHOMCT[>HЧC
Cl<l1e фу1 11<цн1 1 (с11нус. кос111rус , та11гснс , кота11-
ге11с, секанс. косе1~апс). К ко 1 1цу xvr в. 1ючти
Фигуры
все этн функции былп уже, по существу, из
Dестны. Правда , самого понятия триго помст
рпческих фут-шций, как 11 нх обо:тачсtшй,
тогда сщё нс существоRало. Вмссго н11х 1 ·о но
рили о /\ЛИt-1 t1х некоторых хорд, касатслы tых,
ceкyrt\HX в окруж1 юсти опрсдслёНl ю1·0рад11уса.
В три1·онометр11и вы11сляют три вида соот
ношений: 1) между сами.мн триrо1юметрп
ческим 11 фу11кциям11: 2) меж,;n1 элементами
11лоскоrо треу1 ·011 ьшпса (триrономстрпя ш1
плоскости);)) между элементами сферическо
го треуr·олы1ика, т. е. фигуры. высекаемой па
сфере тремя плоскостями, прохсщmцнми через
сё центр (сферическая тр 1 11·онометр11я).
Три 1 ·ономстрия н:.1ч:Jж1 сь нменно с напбо
ж:е слож1 ю!1 , сфсричсскоl1 ч::~ст11. О1 1 а во:1нню 1 :J
~rреждс нсс 1 ·0 н:1 11рактичt.:ск11х 11у·,кд. дrст rие
наблюдал11 за дн11жt.:н11ем небесных свепJЛ.
Учёп1.1 е обrабат1>1папн данные и:-~мерегнтй ,
ч·1 ()nЪI всс..""Ти кале~ щарт. и праnилы ю оnрс/l:елять
время нача;1а ceRa н сбора урожая, даты релн
rиозных праздникои . 1Jo зnёздам ВЫ'IИСЛЯЛ11
Nестонахождение кор:~бля в море т 1лп шшрав
лет1ш.' дважеr-111я каравана в 11усты11с. Наблюде
ния за звёздным небом с незапамятных времён
вели и астрrщо1·и.
Естественно, нес и~~мерення . сnязааныс с
rа сrюлтксн11ем свст1u1 на небuсводс, - изме
рения косвенные. Прямыt: - осущсствлял11с1,
тш1r.1<0 11а п0Rерхносп1 ЗеJ\нrи. Но и Зl\ес1,
да11е1т не nпт; 1:~ удав:uтоп, непосредствеrпю
011ре,Т(елить расстояние между каю1ми-то пун
ктами. И то1·;ц т-юnь прибегали 1с косве1111ыl\1
измерениям. Например. nыЧI1 сляm1 nысоту
дереnа птr разме ры острова в морс, сраюшвая
JVППI)' его тепrf с дл:шюй тс-н~ 1 от како1·0-нибу; 11,
шеста, высота которо1·0 быJJа известна. l l о
добныс зщ~:ачи с~О/~нтсн к :Jнализу тр<:у~ ·оль
ника. в котором OJ\Hll е1 ·0 элеме нты ныраж~1 ют
через друr 1 1с. Этим 11 за ни м:н::тся тритономст
рня. А 1юс1юльк-у з вё:.щы 11 11J1энеты rrрс:;~став-
11яJ 1н с 1> /\рсвним точl\ам11 на 11е6ес 1юй сфере,
то сначала стзла 1х1эвива1· ьо1 н~1еmю сфери
ческая трш·о1юмстрия. t:ё счнт;ти ra:}ДeJI0,\11
<lCTpOJ IО~:ИН.
Первые отрьшочrrые сnсдснш1 1ю тригопо
~rст рин сохранились на КJ111ношн:11ы.х таб
ш1ч.ках Дрещн.то Вак~ uro11a Астрономы [t <1ст
р0Jю1·н Меж,цурсч 1.н н:1учш111сh ттрс1кr«1зынать
1юложеш1я Луны н Солнца, дос.ти~·11ув в этом
nоньш1 rx успехов. Or ю 1 х мы у 1 1асJ1ед()кали си
стt.: му 11змерення утло11 u J'\)Зд)'Сах, м1Л 1 у1·ах 11
l'tr"" dФltrm• tltllNI iJ.tUIUИ.rlкjiJ
Clrp• llt~tt:u•1111z;lиl.,.,fe;..rw
L~
ГltUЛl:'Ml:'Й
АлексJ11;.\ри1осю1и .
Гравюра
1в стар11нно11 j
к11иг~1 Страсбург
секундах, осно Rанную на принятой 11м11111есщ
деснтеричной с11стемс CЧllCJICH l lЯ.
Однако первые по-настоя rцему важные
достпже1-1ия пр1 п rадлежат J\рсннеt'рt:ч~::скнм
учёным. Ro 11 в. 110 11. э. астроном Гшшарх щ
Нпкt.:11 соста1111л табл11цу }l,.lrя опре{\елсння co-
oт110L1 1emrй МСЖ[(у элеме1 !Т:1М11 тре)ТОЛЫШКОВ,
Таю 1е таблицы 11у"ю1ы nотому, что з11аче1ш.11
трнгонометр11ческих фу1 1 кц11И rrельзn выч11с·
лить по 3ргумсптам с nомощыо арифмстпче
сю·1 х операцш1. Tpt 11 ·01-юмстрнчесюн: функцин
пр11ходилось р;ксч1пы1:1~1ть з:1рансе 11 хранпть
н н1щс табю111. Г11ппарх rюдс•111та11 н кр~теза·
данно1·u ра;11 !yc::i дл 111-1 ы xop;l.. отвсч:Jющ11л исе11
углам lYt О до 180°. крат11ьш 7. '5°. По сущtСТS}.
это т~16111 щ:.1 с11нусоu Труды Гип 11 :1рха ;ю llЭC
11е /IOШ Jlll , llO MIIOГI!C сnе;1е1111и 11 3 IН!Х BКJJJO·
чсны н «АЛЫ'vl::\ГССТ» {11 в.) - :шамсшпое COЧJI·
неш 1е R1) ю 1ш':.1х греческог() астртюма и ма·
тематпкз Кr1авд11я nтолемея. ll •Аль~1а гесrе1
;штор щш1.ющtт таблицу щш11 хор,11. окружн!r
CTll рад! 1yc;;i n ()() сдюшц, 1\Ъ{ЧПСЛС1 шых с шаГО!I
05" с ТОЧIЮСТhЮ /{О 1/ 360U ед1 1н1щы , ~1 объяс
няет. как т:~бш.ща с< >ста.11Jшлась. Тру) \ П т:1емеi
нt:сколъко ве ков сл)~жнл нведсннсм Rтptu'01:10-
ML'тp1 l IO /tJ LЯ aCТfIOHOM(J\\
Чтобы ПОН}ПЪ, кз 1\ ) чёныс 11.ренr-юс111 сосш
ЛЯЛ 11 Тр! ГГОI юметрт IЧССК Ие T:lnJt 111 ~1,1, 1103Hali0
.\11Lv1cя с мс·1 ·одом I l тuJ1емся. Метu;( осr-юна11 ш1
теnрt"мс о то,v1, что nро11звед~::ннс д11 агоналсt1
вттнса1 11 IOl'O 11 (Ж\))"ЖНОСТI> -че·1 ·ыrt:Х)'ГОЛ l>I 1нка
ранцо сумме nроизоедеrпrй его 11ротиноrrrJ
лuж11ых сторон (см статью '·М1юrоуrолъ 1t11-
к11·>). Рзссмо·грим nпнса!lный че1ъ1рёхуголъник
А!ЗСD. Пуст~> ЛD - ю1аметr окруж11оспr, а
точка 0-её центр (рис. l). Предположим, ч.то
:..1ы умеем выч11слятr, хорды, стяrиоающис углы
!)ОС= а и D08 = ~. т. с. сторону CD 11 дш11·он;urt>
В/). Тогд а , по теорем.с 1I11фа 1 ·ора, 11з прн~ю
упщы1ых трсуголы-rиков ADB и ADC мож 1 10
нaimrAB нАG, :1 потом, по теореме П1·uле::мс}!, -
НС= (1/С BD - АВ · CD)/AD, т. с. хорду. е1·яп1R;з
ющую у1 ·ол воr: = ~ - а. Не1юторыс хорды . 11а
nр11мер с1лрuпы ю1адr;.па, nра111шы1ых тттести
уголыпn<а 11 носьмлуrолышка, отвечающпс
~тл:.1~1 90. 60, и 4'5 °. лег1<0 о пределить: была так
же изпестна сторона прш:шлыюго 1шти~толь
ни1~а. которая стя п-r:васт 11у1у н 7 2°. Лрщ1ед~н
нос ныше nрапило 11ознол}jет нычислять хорды
для р:.tэно<.·1 ·ей эт11,-.< у1 ·;юн. например для 12° ==
= 72 ° - 60°. Кроме того, нсс.rтоЖJ ю научить ся
н~хощпъ хорды rюпов111111ых уrпо~. Одн:сiкО
всеrо cкa:.J;.iнi-юro 11едост~~точ1 ю. чтобы рассчи
тать. чему раюrа хорда дуrп в 1с. - хотя бы 1ю
ТС>му, сrто нее на~шатпrые у1·лы кратны :) 0
•
Дтш
хпрды 1° Птоле~1ей нашёл оценку. показав, что
она больше 2/1 хорды (3/2)0 11 меньше 4/5
хорды (3/4)0 -днух чисе; 1 , совпадающих с дос
тат<.>чноll для cr·o таблиц точностью.
Если r·реки rю y1 ·Jiaм вычисш1.11и хорды , то
инднйские астрономы в сочинсннях ТV-V вн.
перешли к ПОJ1ухордам двойной душ, т. с. в то ч
ности к линиям с 1 1нус;:1 (рис 2). ()11и поль~ю
пал~1сr. и J1иниями 1<осн11уса - точнее, пе е1·0
само го. а «0б ращённого» синуса. Сейчас эта
фун1<ЦИя, раnпал 1 - cos о., уже не употребляется.
Впоследствии тот же подход привёл к опреде
лешпо триг01rомстрических фу~пщий через от
ношения сторон прямоугольного треу1·uлы пша.
Терм11ны •<:и11ус» и •1коси11ус·> 11риш11и к нам
от нндн й1~ен. Правда, 1re обошлщъ бес-~ любоn ыт-
11оrо недора::1умсния. Лолухорду нн;1ийцы назы
вали ~ардхадж ина~ (н nеревО/\е с C:JНCl<f>ИT~I -
тшю 1:111на тстиuы лука») , а потом сократили это
CllOEIO до "дж1-rв а». Мусульматrскиt астрон омы и
математики, 1толу чивrпие знания no трито
нометрии от индийцев , 1.юсnриrшлн е1·0 как
•джиба", а затем оно превратилось в «джайб»,
что на арабском языке означает <s вьшуклость",
тазуха». Н ако н ец. в ХП н. ~джайб» буквально
Геометри я плюс алгебра
Р1к. 1.
Рис. .!..
нерtнсn11 11а латыш, слоном sinus, которое не
11 мело пика1юr·о отrто1 11 е 11 r!Я к обrJз11:1чаемо.му
им понятию. Са11скр11тское •котиджива,, - си
нус остатJ<а (до 90°), а на латинском - sinus
compli!menti. т. е. c111ryc доrюлпсmш, н Л\' 11 н.
сократн 1юсь до сщта «Косинус·'·
К 1<0нцу Х .u. учен1-,1 е исл:.1м ско1·0 NJtpa уже
01 1 e::pнpo1:1aJ 1 J 1 нарнду с с 11 нусол4 н косJ 1нусом
четыр1,мя дру1··нмt1 функцням11 - т~11 1r ·снсом.
котан 1 ·е11сом, секащ'о м н косе1;:·.н1сом: откры
ли н 11.01с1 залr1 несколько наж111,1х тсоrем плос-
1\О.Й и сфер ~ 1ческот'r тр 11ю1 ю~етр1ш; 1 1 сnолr,:ю
nали ОК{1уж1JОСТЬ С!(IПН!Ч!ЮГО рад11уса (ЧТО
позrюлило толковать тр 11 го 1 юмстr1 1 чесюrе
функции 1~ соврб1енrю.м смысле); придумали
полярный тр еу 1 ·ол ышк сферичсско1 ·0 тре
уr·олъr-н·IКа. Арабские математики составJ1т r нс
кл юч1пел hно точные табтщы, напрпмср таб-
1шцы с инусОР. J\ ТЗНl'СКСОВ с Нl:l\'()M в 1' и
точностью до 1 17оrюооооо. ИJJте ресно . что
о ч ень Rажной приклад1-rог'1 ~{;~дачей была и
такая . науч1·1·1ъсн определять 11а11равлен11е на
Мекку для пяти ежсю1ет rых молит~{, 1де бr.i 11.и
п аход.ился мусульманин.
Особешю большое влияние н:~ ра:1rмтне три-
1·01юметр11и оказал «Трактат о пошюм четырёх
стороншп.:с» астронома 1tасирэщщна ат-Туси
(1201-1274). Это бы1ю пер1юе в мире сочине
ние::, н котором тритном.етрllil траю·он::~ласh как
самосго}jтелh н ая обл;кть м;п~мат11ю1.
Трактат ат-Туси 11роизвёл бот,шос впечат
ление на немецкого астронома н матем<1п1ка
Иоrзнt-1 а .Мюллера ( L436-1476). Сонремtннн
ки бол ьше знали его 1юд именем Региомон
тана (так переnодится па латинсrшй название
его родно 1 ·0 города Кёпиrсберга, 11ьше -
Капининrр ада). Труд Региомоитана "Q тре
угольниках всех родов пять t<HНI'» сыграл в
ЛUlll/JI
389
Фигуры
,u t.Dti,H,J 'tffbl J'H. . . .Н~/1$ riHtCrtт i'3
t(rQ 1"~ 11lwnm 1im b)'fltfЬolt.:oruю ш~ :sn ~("ido ltltttr.t111..1 ,\'tl.
JvJ\11\ de1r1fiffi\r.Jtщu1
-
CAPUT Vll/
• sff Р ~оо1:::~~,~~~~::: ~=i;~·~~~a~
Co.fi."~ ~q!.1111 щi.n Wllilln ~111d qti1nr!~1щ;m mnk.-rid.:11t1Um t:t"
"" · c1м1 Ri tм 1111t-, kd n11m n 1rti• LU&J111hr>• ~'- /t c1;ro~ri
t1.1~1bi.!\. c'J'111111IO ~iNti11 q1i;n.rir;~~ 1n"olvuJ11:1r , f''~~t'
11111
1~~:..~~:!'~t:omi{'\.1~·~:·r~~;'•i;L'" S.1am и;.: 11111 df.:
,
: 1q11r 1iu• l1qUtt Pn1pl\cn.11m hu,J11t Cirt11I• , 1 t11JU1cщ ro
,,"11)1;f,ц, n.;11!.lr o~l\fll ....... pnf!C:. 1~ aa•roJ:lil'~l1(1Cln
;.11mi1 1nн•m ~1 S~t1r~11n•(cт(nna hup.f ~J1:,1h '~.а:-:
J i 1Ч9'4°!Jill}';"9J J}'Sflf)tt<tJ)iJ :~!o"$OJ8s.f 19-1 ~9J9)'J
-
t \~~t1:~-."4,lt+~~ч~111-\6io.o'6"%~1'~:i'nt61Y.~\.;i'.,_ .нн
:1:.~:r~~~1-:~:~rc~:,::~6:г:ii~~~~·::r,~:rJlr:
ci.: CAri-u~1, (1.JjUt R.ild1i:s . =- J • kd -. - nir loi1:;mцfio. Лн:1:"
•"-:- ii•:.JJll.!rl
Pi °'1111111"11!". : Л·cum tiO)tl1 с."'"'' ri111:111n111f"j11ill: t (U-
~I~~=,~·rc:.~ ~:~c"~~~:~}O~~~~v~t:t~~
• 1'1 i"-Jl~n.n• f".) .; mod-1 •Qdi•. -! Jo ,(,,. 4
.t. fo:-u f-"11CN11 ft-- ..е:
C.i6rwrn \'ао hot 11'1(.J~ о( IJ.:., Г'-'U iцir.1111 rf{ ~ lr..1.
t"llГ'1 • lii Лn:vi •8'1", C'!{I j.. c r
-01 t•;.o~=t.&
.fi-. f..- -•, r#f'+ y =o ,f:н .,..=o.цf..-=-J ;
f" +'r"-- t1 иf: " -o•.Jfi' ar -o &н(J.r ::= -J
U1mu a;s<> Sw11• f< c~~u:. 1.rм 1~1»11cs + 1 & - 1 t(ir. •
~•' 1
м~.:,
Ul\:'11
Unрелслt:11ии
1fiH1 (Hl ( )M("" fJ) 11Ч(.'( t.~1X
фун1щи<1 Стран<1uJ
~·1 ~ t{llИI И/\ :':}й;\Рр11
" uведtен11 е в ан<~мн
Ьес ко1 tе•-11 1 ь1х ··1
Изл,1н11е 1748 г
еврппейскоi1 м:ате.\lfатике ·1у же роль. ~по и со
чт 1 11сm 1с ат-Туси n па\1<с мусульманских стран.
Дальнейшее развнтис трнго11uмстрш 1 шлu
по пуrи накопления и си<."1·с матиз: 11\И11 фор
:\1ул, уточнения основ ~ tьrx по11я1 ·r,1 й, еr; 11 юш 1 с
нш1 термино1ю1·и1111 обозначен~ tf1 Мt-юг1,1е е11-
роп с l1 скис ма· 1 ·е:-.1 атнкr 1 р:rбот~1т 1 R области
1·r1 1 1·оно1vн:тр111L Фр<~нсу;э Внет дополн и л и
с 1 1стсматнзировал ~х1з1н1ч1 rые случа11ре111е 11 ня
шюскнх и сферичt:СКНХ тре~ТОЛЫJИIШD, 01-
Щ'1Ы!I "] 1 1юскую» теорему кос1-шусов 11 формулы
,r1.ю1 тр1·11'01юметр(.Jческих функцнй от кратных
yrлon. Исаэк Ныотоп разложил эти фушщш-1 в
ряды и открыл ny""lь для JLX исnоль:юванш1 в
м~1тем;~тичсс 1юм анат 1 зс. Лсонар11. :'1 йлср ннi.'л
и само пошпне функции , и 11rшнятую н 11~шш
д1-111 с и мRолнку. Он также обнар)rжил сFшзп
межлу тpИl'Of-IOM CT PT I Чt:CKHMI! функ~1.иям11 и
ЭКСПО I J('Т I ТОЙ комгше1<с11n1·n :1p1y\•te11 ·1a (С.У!,
статью <-Возвс;1.сннс и п е1 1 е 1 1 1, 11 из1шече1111е
корня H:J комплсксноrо чпсш1»), что по:шоли
ло преnратит т, м 1 юrочислен11ые и зачастро
всс1,ма замысловатые трнrотюмстрнчсстсис
формулы 13 простые слсдст1шя пз пра1311л сло
жеш ш 11 ум110жения комплексных чи сел.
К 1<0пцу XVLlI столетин тр111·uномстμия как
паука уже сложилась Трн 1·0 1rо м стр 11 сrt:скнt:
С}))'НКI\ИИ на1_111r11 r 1рнмснснис в м атсматr 1 ч<:
ском ai 1:1лизе, фи~нке, химии. '1·exi н1 .1<е - L1езде,
1·де 11рихо1 \н· 1 п1 11ме1ъ лело с гтериплическими
прш1,ссс1ми 11 колебаниями - бУ71 1, то а кус
т11к:1 , оптика нл н кач:шие маятника.
390
УГ/\Ы И ИХ ИЗМЕРЕНИЕ
У1 ·ол н элемента ргюl11·сометршr - это два ,'fY'ia
(ДRС CJ'(Jf)(J l lЫ Yl'll<I) , 1\ЫХО)l,Я Щl lС 113 од н ой точ
ки - нсрш1 1 ны yl'lla. У1·ол со с·1 оро11ам~1 ОА 11
ОВ обозн;~чж·тоf L:110B. Yl'liы сравннв:~ют. сю1 а
д1 .шают, нзмеряют. 0 1т р;шны, ccлrr 11 х 'южно
соnместип, f\Виже 11 ием. Есл и луч ОС 11роходнт
внутри угл:~ АОВ (рис. 3), то, по оnрсл;еле111но,
с~ш·1·а~о'1, '"ПО v~·олЛ()С, к~ш и угол СОВ. меньше
углаАОВ п что уголАОВ раве н сумме уrловА()С:
11 СОВ Взн в :{а едшшцу 11·в11е реш ш какой-то
кuн.крстныl! у1·ш1 , онрсд(;JШЮТ нсm 1ЧJ IЩ' любо
r'о y(') J:t , ·1 с. 11ыяс 1 1яют, скu1 1п ко раз ук·1~щыв<1-
стсн к нём такой е;\11 11 и 1 11 1ыl1 у1пл. (Ко11сч1ю.
это чщ·ло может ~1 Н<.; бытп 1\СЛЫМ.) Пр11 1 1:3.че
рt: 1 1 1 111 у 1 Jla 1ICX0/1}1'1 113 двух CIIO(IC'J 'U <.:1-С) пе
Л ПЧНПЫ, знакомых нам по сво1'ктnа~1 f\JrtШЫ
отрез к:~: 1) 13елпчш 1ы рапных углов рав11 ы,
2) ве111 1 ч.и11а суммы двух ~тлов pau11a срr ме их
nсличm1. Еслп яспо. о чём идет речr" вмес1·0
<>ВСЛИЧШiа ]ТЛа·> ГОВ()rят ЩJОСТО <·j'ГОЛ>I
Н аμ1 1 су<.:м окружноС"1ъ 11 расс.мотр11м уг.'lы с
неrшн1 IОЙ в це11тrе этой окrуж1 IO(VГlt, Равные
углы булу1 кысек:1·1ъ 1 1~1 окруж1юст11 р;111 н мс
дуп 1. r1 суммl" углов fiyl\CT отвечат1, сумма ('ТЯ-
1 ·ива<.:м 1,1'\ 1 1 м11 / \]'1 ' (prr<- ' \),А потом) нсл11ч 1 1на
у 1 '!la 11 ро1 юр1 ~ 1 IOJl(lJ Iы1а ДЛI rJ l t:: Bbl(<.:K<lt'MOЙ 1 1~1
дуги 11 сюrншtы пзмерет 1 я углов можно :~э; р
uать, указьшзя. какую чаС'lъ ОЩ)\l)Ю юспr сщ·тав·
JJЯет СООТ8СТСТJ'\\'ЮЩая дуга.
Uбычпо употрсблmот J\RC сюш1щы нзмере-
1 шя УГ-1013: ГJiадус, раШJЫlт дуге В 1/ .~60 АСС!~
окр}жное 1 ·1 1 . 11 рад11а.1-1, т. <.: . цсюральный угол,
1tЫ('с'к:нощн1'1 /~)ту, ран~ 1·ую ра,'1, 1 1усу окружностн
н~1 пр~I KTI IKC чаще всею Гl[JllMCl-lЯIOT l р:1;(у~ы,
обо:л1ачаемые ·1щ1ком ~, 11 нх l / CJO 11 1 /бrJ·'"
= 1/У>ОО; \OJllI - MJ 111~·1 ы 11Ct'K)'I1/(Ы, обu:т:1чае·
мые ' и " Таю 1м nбра:зnм. 1° = ()0' = .)6f)()"
Матема11 1 ю1 предnn'-вrтаю1· 1 юJ 1 1,:ю иа·1ъся
р:щианом. Радиз11 рзl1е11 при:-1ер110 ')7° 17'- l 'i'
()
А
Р1к. 3.
Рис;. 4 .
EJ 'O обознач<.:11 11 <: - рад ч ;1ще всt1'0 просто
011у скают.
Д 1и 11 а f(yl'J1, нысек:1 tмоi1 у 1 ·ло м в и р:-шиан н~
Ш<[>ужностн ра11иуса N. равна aR, :i лля еди1111ч-
1JОй 0 1<руж11ости fVIHIТЭ /J.)'TI1 н nе>л11ч11ш1 угла 11
радианах сотн1:щают. Так как 11лтп1 а единичпоl1
oкpyAUIOC1"1 1 ра1311а 2.п, nерейт11 от Т'р·;щусоn 1<
1хщна1 rам можно по формуле .'\'° = лх/18U рад.
В частностп. 1:к·1шчrш~1 ра звЕрпутого уи1а, сто
роны которо1·0 об разу'То·1 · ЩJЯМ'у10. ранна l8U0
ш111 л. а 1 1рямой у1'Ол сос1·;1ю1Яt''Т 90°11т1 тс/2 .
Yt юмя 1fе >v1 ещё 011ну. блн~кую к 1р :щусу сдн
н нцу 11змере111тя у1 ·л< т - 1·рал. р;111ную 1/ 1()()
11ря.чt)1·0 угт1: ею пот,зую·1·ся р<:;1ко
ТРИГОНОМЕТРИЯ НА ПЛОСКОСТИ
! !роще nccro <.шрсдслнть 1·рш"оrrометричссю1с
фу11кщ111 остр ых упюв . Лuсколысу tзct: 111.шмо
у1·олы 1ые тр<:угольн 11 кн с заю 1нным острым
y1'JI0,\1 ПOl\UOJ 11>1 д руг другу, ()[IJI llM<:IO'I оди н а
КОТ\ ЫС опюше1111я COOTHt'TCTRCl-I HЫX сторо 11.
З1 1:~ч1п, ::rп 1от1 юше1111я зан 11оп· тот, кп п·1• )Тла.
Всего т;~к11 х птпо111е11нi1mест1"11 им отnеч;~тот
шесть тр11rо1 ЮN1етричес 1шх ф~'Т 11щи 11 ( 06оз11а
qс1шя стщю11 11 :тлоn треу1·олытпю 1 101 штт1111
п:I р11с. ') ):
а
IJ
s111А= -
(СИН\'С), со" "1 = - (кос1 н-1) с).
с
'
(
{{
11
1~ А = - (т::1ше11с) CtR А = - (rютат11·енс),
f)
•
11
с
с
~се А= - (сск:шс), соь~с А= (юксl\а 11с)
h
а
Ф}'llКЦНН cet<::t llC II 1сосек:11к 13 1T::t ши ДillI ПОЧТL 1
IJЬfШ!Ш IIЗ упО'I рсбл<:JПТЯ.
Г1 rя _\10 1 1з опрсж:лст t1 rl1 нытскают 11cc1<0JlЬ
l\O p:lBC:l I CTR, снязыв:.11ощ 1 IX трН]'( \H()MCTj)HЧt'C
!\llt' функц1 ш мсж1~у cof5ol1:
щА = s111 A/cosA, ьссА = l/соьА,
co.sec А = 1/si11 А.
Есл 1 1 uспомrп 1ть о сум."'к утлоn треуголы-1111с1.
Т. С Ч'ГО А + 8 "' 90°, ПОЛ\'ЧJIИ
;,11)А=со~В=cos(90°-А),
tgA = ctg (90° -А).
R
Рщ.5.
Г~:-ом~трия плюс алгебра
а
tl
{/
Р1н.:. f>.
1
\б
\
\
\
\
'
а{;; \
2\\
\
----~
а
1
л C:.:CJl l J l'Щl' \'Ч<:С'IЪ 1·1 l'C:.:OpCM\/ 111 1фагор;1
а1 + /J:. = (, 1, то щ;ж110 ныр::~~ нть нсс.11Jес.~1·1, функ
цн [1 ч срс:1 кактю-н1 1U\ 'ДЪ OltHY H :-tПf)ll\1C'p, Cll-
ГI\ с 11 косr111ус CГi}fЭ<IНl>I OCIIOIOIЬL 11 mp11N!llCH/f::'J}/-
puчecюL;H nю.Jt('()ecmrю.111
'
'
siп-11 + сш,-л = 1.
Естт> тш~ькu ;щ;~ 11рямоуrо.11ы1ых ЧХ') 1·0:1_1, -
н11ка, у 1.;отuрых и углы .;хорщштс» (ныражатотся
1~<.:.11ым 1ш11 р:щ1 1011алы 1ым числом 1'р:щусов) , 11
хотя б ы u11но 11 з <Н 1 ю11н:1-111 Г! с1·uрон рацrю11а11п-
1ю Это rх1тюбсд рс1111 ыl1 трсу1·1)Л"1-1JIК (с у1 ·ла
~111 1 1') , /"i , <)0°, ptIC. 6 . а) lf rюлпн111 1 ка ра1шщ·1'0 -
ро11 11 е1'п треу r оm.1111ка (с углам и :\О. 60, 90";
рнс (), n) к~11' раз те 1'\R:J случая. ко1 ·; ~а з11ачс-
111ш тр 1rr ·о н омстр 11 чес ких фу11юпп·1 );tаё-r·ся
nыч.нслнть прл.чо по 0 11ределен11ю. ::.Уп 1 :таче
шш npHUL'ДL'llЫ n т;~блицс IШЖl'. и lfX СТО11Т
ныучнтт" 110то му что соотnстст вующпе у 1·лы
часто нстрсчаютсн в 111ко11ьных а:1J 1ач.1х ;
11
()
1
2
5
1
~0"
.юu ./ ')"' ()\)"
l)()"
l
-
../2 {J;
-;j 11
о
1
1
2
-
2
!..
-
~
cos
l
'12
1
()
-·
-
-
!.
2
!.
,-
\J,
г-
Lg
u
.)
1
"\/ .~
-
:r
,-
~~о
ct~
-
у;,
1
;.,
()с()f>еш ю просто запо1ш н 1 · 1ъ строчку cн
rryc;i: u столбr\е под т~омером 11 с 1·0 :ша чст1е
раn1ю ~ "/2. >' 1юс 111-1уса те Жt' самые J11ачсн1 1я
1щут .в 06μат1-юм порщ1ке.
391
Фигуры
З аннс 11мостLt между сторонаин и yrлa iшt
про11з~юлыю1 ·u трсу1 ·с.тьника.АВС можно 1юлу
ч11т1" разбнн cr·n на примоу 1 ·ольны1.: 1реу~·0111,-
1111 кн ()пус'пtм из нер1111111ы (:высоту Cll= /1 ;
допустим, ЧТ() 011::1 ll<IД <t eт на са:.н» l>C I1 <1В<!П1Н:, <1
пе на его продотке1111е. T Ol'/\<t , обоз 1i ::1чая сто
роныиуглы. какобыч1ю.череза,IJ, спА,В,С
(рис. 7. а), нз '1реуrолышков АС!! 11 ВСН па.хо
дш"1/1=Ьsinг1=аsinВилиa/si11г1=Ь/siпВ.
Т~1кое же ранt ш:тnо, ОЧСШ l/11 Ю, ВС['ШО ДЛЯ любых
; ~вух сторu н треу1·олью1ка. Итак, м1,1 11ри шлu к
rпео;жме с1111усов.
а
/J
с
siлA = o;i11B = si11G'
Однако н ежа 011а доказ::~на на:-.111 то;1ы<0 ;~,ля
остроутолыюго треуrолы 1 и1<а, а сиuус тупого
угла даже не оnределён. Нз причср, ес.'lн )ТОЛ В
'1)11Ой, то 11/а раnно с1шусу его смсж1юrо утла
CBIJ (рнс.:. 7, б) Поэтому определим сш~ус тупо
1·0 у1·1 1 ;1 раиным синусу смсжrюr·о у1 щ1: sin а =
"' s1п ( 1R0° - а), тrяда теорем:.~ синусов бу;\ет
FJ Ы ПОЛНЯТЬС}! ДЮ! 1.1сех ·1·реу1·0J11,никок.
Отнош<::ния . вхо~я11\нс в теорему с инусов.
[-tмеют нростой геомстрпчсс 1<иi1 смысл. Опи
щем около треу1·0;1ы 1ика .tlBC 0 1< руж 1 юст 1)
(р11с. 8). Провс~ём ди аметр BD. Тоrла, по тео
реме о вписанном угле (см. статью «Окруж
ность н круг·>) , LBDC = LA либо. если уJ'ОлА
ту11ой, L80° - LA. В mобом случае а = ВС =
= ВЛ ~U1A =2ЯsinAили
_!!__=2R
siп А
'
где N - раднус о п исанной окруж11остн тре
угольника АВС. :?·1п <усиленнmt» теоре"ма сщ1у
сов. Она и объя с r-~яет, 1 ючему табmщы хnрд
древних бьuш, n o существу, таблицами синуспн.
Рис. 7.
С
а
Рис. 8.
с
с
А
н
вн
392
Верпёмся к р1к. 7. а . I3 трсутшты нtке АВС
сторон::~ ,-IВ = Aff + НВ 1fл11
с= ь cos.4 +({cosв.
(")
Еслн угол R тутю~'1. ·1 ·r > АВ =А 1-1
-
BJ-1, что пuд
с~1зыв;1е·1· 011rс;(t~лсннс косн1-1ус1 ту1 ютугл:~ а
по формуле cos С1. = -cu~ ( JSO" - IX) То1·да фоr
мул:~ (*) ост<tётся вер1 ю й для всс.:х трс~ тm,1н1-
1<ов. Эап11шем ап;:~лоrпчные фпрмулы дпя а п /J:
а=сcosВ+fJcosС.
/J=асо~("+ссо~rl.
Умножщл 1~х сосУп1стстнснно на а 11 /;11 1нычтем
нз 11х суммь~ форму~ tу (*) . умнОЖL'КН) 10 11;1с.
Гfолучнтсн и-+ 1?- - с= 2al? cos С, 1ш11
с~=а.!.+!/- 2al; cos С.
Это раве1 1ст1ю 11азывается 111eпpeмnif 1·1rю111усов.
0 1ю позволяет найтн сторону трс-утолы1111сr по
дnум друпс"1 сторонам и углу ."1ежду 1111~щ а
таюкс уrл ы 110 трём сторонам.
имеется IJ ,\lllOЖ<X'TBO 11руп IX COOTIIOlllCHШJ
между эле::мснтам1-1 треугол~-.1-111ка ТТрнведём
хотя бы rmюpe.J1~1· JJltlHZPlfCOR:
А-Н
а-!1 rg 2
а+Ь
A+R
rg --
2
Другие интересные формулы можно вывес
ти н::~ теорем синусов l'l косшrусоn с помощью
тр и1·онометричесю 1х тождеств.
Ве рнемся к ра ненсп~у (*) Поск01 11-~ку, по те·
оrсмс синусон . стороны треугольника прапор·
ц1юналыn,r синусам 11ро-п1в<mоложных углов,
~тn ра 1~е11ство М()ЖНП переннс:1 ·1r. через }TJlli
siпС=si11Асо:>В+cosАsiпВ.
Чтобы прпдатъ фор1V1уле более 06щи!1 шщ
обозначим нелнч.ины углов А и fJ че::рез а 11 ~
тогдаsiпС= s111(180° - С) =siл(<Х+р),нмы
1!pHXOДliJ\1 к ОЛJ ЮЙ 11 3 днух са мых В<1ЖJIЬL~ три·
1·01-ю метр 11ческих фор мул - формуле сложс·
1-шя ;1ля с11нуса:
::.iл(rt+Р)=si11аcnsР+сш;et.-.iп~.
А сели обозн ачить через а n11ешш1й )'ГО.1
треуголыпrка при вершшrсА, через р - }ТО.1В.
то С будет раnе н разности а и р , отку/\а леп"о
nолуч 11ть формулу си1rуса раз ности:
ФОРМУЛЫ СФЕРИЧЕСКОЙ
ТРИГО Н ОМЕТР И И
Возьмем на сфере три точки А, В и
С и проведем из ее uентра О лучи
в эти точки . /\учи вместе с заклю
ченными между ними плоск и ми
углами оfiразуюттрёхгран н ый угол
ОАВС. Пересекаясь со сферой , он
вырезает из н ее кривол и нейный
треугольн ик АВС, который назы
вается сферическим треугольни
ком (см. рисунок). Его сторо н ы -
луп1 больших кру гов. длина дуги
АВ равна произведению радиуса
сферы tia величи 11 у угла АОВ в
радианах.
дм. прастотъ~ выберем единич
н ую сф~ру, тогда стороны тре
угольника будут числсн 110 рав11ы
nлоtким углам трехгранного угла.
В сферическом треугольнике угол ,
например, при вершине Л с.чиоа
t!Т СЯ равным двугранн{1му углу
>.1ежду гранями АОВ и АОС. По
аналогии с планиметрией стороны
и углы сферического треу голь
ника , т. е. плоские и двугранны е
углы соответствуюwего трехгран
ного угла, будем обозначать а
(=L. BOC), Ь (=LAOC), с (=LAOB)
н А , В , С соответственно. Сооn10-
wе11ия между этими величи11ами и
составляют прелмет сферической
тригонометрии . Приведем важ
нейшие из них; на п омн 11 м, что
радиус сферы мы приняли за 1.
Теорема синусов. Выволят теоре
му п римерно так же, как и обыч
ную 1еорему с~1нусов: приравниеа
ют два выражения для «высоты»
треуголь н ика - расстояния от
тuчки 11а ребре соответствую шего
трехrра 11 ного угла до противопо
ложной грани.
c;inа si11Ь siпс
~iпА=~111В =:.iпС ·
другие формулы тоже выводят
при рассмо 1 рении трехгранных
углов .
Первая теорема косинусов. [ё
выражает дово11ыю громоздкая
формула, мало похожая на LВой
аналог И'\ пла 11 иметрии:
cosа =со~Ь cosс+
+sinЬ~inсcosА.
Но решает 011а ту же задачу - по
зволяет определить rторону тре
угольника ч ерез лве другие rто
роны и угол между ними. Если
11арисовать 11а сф~:ре треугольник
и зафиксировать дл11ны его сторон,
а затем «раздувать )) сферу, устрем
ляя ее раы1ус к бесконечности , то
треугольник Gулет становиться вес
более плоским, 1i формула сфери
ческой теоремы косинусов в конuе
1<01шов превратится в обычную. То
жt> верно и лля теоремы синусов.
Сферическая теорема косину
сов лает возможность, например,
найт11 рас стоян ие между двумя го
родами no их географическим ко
ординатам. В качестве третьеи
верши 1-1 ы треугольника берут один
из полюсов. Тогда углuвые вели
чины сторо н сфери ч еского тре
уrолы~ика, соединяющих полюс с
гоrолами, оп релеляются по долго-
Геометрия плюс алгебра
там городов, а угол между ~тими
сторонами равен разности шир о1
горолов. Лли11а третьей сторо 11 ы и
есrь интересуюшее нас расстоя
ние. Попробуйте таким способом
уз нать расстояние от Москвы (5 6°
сев~рной широ ты, 38° восточной
долготы) до Хабаровr.ка (48° севЕ'р
ной ширОТu1, 135° ВОС1'0ЧНОЙ дО/\ ·
гогы ).
Вторая те ор ема кос ин усов. С
помош~..ю "IТОИ уливительнои тео
ремы н ахолят стороны треуголь
ника, з ная его углы , так же, как
посредством обычнои теоремы
коси~1усов углы выражают через
оороны. Записывается втораи те
орема косину сов так:
cosА=-со~Всш,С+
+!>ltl 8~IПСCOSа.
Здесь проявляется заме,1атслыю е
t.воис~ во геометрии 11а rфере, на
зываемо~ r~ринuиnом лвойственно
сти: n()нятия точки 11 прямой, рас
стояния и у гла взаимозаменяел.1ы .
Привед~нных СООТН ОШСll ИЙ до
статочно для определения всех
элементов сферического треуголь
ника по любым •рем заданным.
<;io(о.-Ю =siaо.C()S~- cosас;111~.
Заме-rим, что перечнсле11ные фор~tулы сrю
жеппя IЮЗВОЛЯЮТ UЫЧIIСЛИ1Ъ сшrусы 11 коси
нусы углон, б6m,щи:х 180° ИЛIJ меш,ших 0° , хотя
сами фушщии для таких углов no1<a uc опреде
лены. Л это бьmо бы нс только удобно для тео
ретических ныкладок, но и IIеобходимо, на11ри
мср , при описании врэщатt.:льного движе11ня .
И н~юборот, рассматривая такое 11в11же ние,
можно понять, кэк следует расrгшрнть опреде
ление тригонометрических функций .
Име111-ю эту формулу в ви11е теоремы, получ.иn
шей его имя, использовал Птолемей при со
ставлении своей таблицы хорд. Далее, выражая
косинус через синус по формуле cos а =
=sm (90<) - а), можно написать формулы коси
нуса суммы и разности:
cos(а±Р)=cosаcosр+siпа~inр.
393
Рнс. 9.
Рис. 11 .
Фигуры
ОБШЕЕ ОПРЕЛЕ/\ЕНИЕ
ТРИГОНОМЕТРИЧЕСКИХ ФУНКUИЙ
Вообра:шм ·10 чку. н1х1щающуюся n o t:J( 11ничнuй
окруж 11ост11 с центром н 1-1а•1але коорл~11 1а'J' И.
Пус-1 ь она J(н11жстся <- сд11 11нч1 юй скоростью
n[ют11н чж·оной с 1ре;1ю1 ( р1. 1 с. 9) в момl'нт t =о
тач 1<J мнr 1уt:т Р" ( 1; () ). За нре'v1я / тnчка 11р()хо
дпт 1'"\Yl'Y 11; 1111rой t п :lатпrмае·1 · ГJ()JIОжетшс Р,, а
значит, угол, r1a 1<оторый nоворач11вается луч.
гrроведё1шьrй в эту точку н:з О, тоже р;шен /.
Таrшм об разом, 1'1IЫ сопоставляе:-1 к:tждо му мо
мс1-пу врс мсн11 , т. е точке / дс 1"rстн11·1·елыюй
11рнмо1\ '('()LIKY JJ, C)11l1 llf'-! H OЙ окружr IOC'l 'll .
ll o;~oбнuL' отображс.: 1111 е 11рнмой 11а оr<ру-ж
нпсть 1шогд:1 н~1 :~ ыв;:~ю·1 •н:.~мо·1·кш1". ТТrс11с.тань
те Дl' J1 СТННТСЛЫ1ую ()C f, В l"IДC neCl\()lleЧf-Юfl
11 ер;1стяж1 1 мой пнпr. Есл и 11рr1лож111ъ точку
t =О к точке Р0 окружrюстп ~1 11~ч ать на1v1аты
вать оба котн~а 1 штн 11а окрулшостт" то кажд1я
точr<:.1 t rюп:щёт как раз в тосшу Р1• При этом
1 ) точки осн, ОТСТОЯЩIIС t''\PYI' ОТ друга па
l\t:JIOt' число 1 \J111н о кружностей. '1 '- L' . на
2тr.k
(k> = ± 1, ± .2, . .), ll01131l<LIOT R одну 11 1у же точку
окруж 1 юст11;
2) l'OЧKll / [1 -/ IIOI Ja/ \aIO'I 1! точки. Сll М1\1СТ
рнчныс OTHOCI 1'1 e.'lbl l(J Ох.
'1
'
1
,
,
1
1
1
1
1
'\
\
'
Рис. 1 U-
'
'
'
о
'--
-t
1- 2л
Рис. 12 .
. 394
.3) при ()~t~1С у1()JI PJ>Pr ОТЛОЖСI1 1! полу
ПJЮСI<ОСП> J'~ о 11ра 11е111 ( ри с \()).
Трп э111х услоnтнт состаnляют фор .vt~1ль1юс
0 11рt'дслс11и с 11ашего отображе1 111я-там()ТЮ1 »
В с11лу усJюшш .3 nрп () ~ / ~ 7t коордш1ан1 точ
ки Р1 равны (cos t, ы11 t). Д<1нное 11аблюде1 111с 11
1юлскз~ыв:1ег 0 1 1 pt'д<:Jic 1111 <:: кос11 н усом псину
сом прu11эколыюго чt1 CJ1a / н:.1 э ынаю·1 ·ся соот
кстс-1ае11110 ~1 бс ц11 сса 11 о рд1 rн<rта точк 11 111 .
Та11ге11с ·тжt: можно 011редt:т пъ чс ре:J 1ю
ордшrаты. Провеi \ё,\1 касатслы 1 }1О r< t)\HI 1 11ч 1-юй
окрvж~-юс1н в 1оч1се (1: О) (р1 к. 11). 0 11:1 1 1а.lы
вается осыо ·1·ангс11соn. Точ1-:а Q, nсрсr<::че1шя
nрнмо11 ОР1 с осью та нгенсов 11меет кооrщ11-
11аты ( l , si111;cus /), и et: ордшrата, no онредс
ж:ш 1ю. равна tg / llo ;~бсолютнuй всm1ч11не это
/ J,Jll IHa ОТ[1СЗК:.l i\ac:1' 1'l:J11,HШI, [] fЮ ll<~/~ё.1 нной п:1 QI
к 01Ср}rж 11ост1 1 , - с~пн1 слонu <·Таю CIK '> н а ;1:1-
ты1 111 0:111 :1ч :r ст <·кас:1н>щ 1-1!1ся ·• Кстат11 . <·се канс•
11ереnодито1 1<<1 1< <·С<::r~1т~ая»: 11:1 р11 с. 11 :-,ее / -
отрезок OQ,, ~тnлтсндт'~ся" npan{\a , 11е- 11cel1 се
кущстr. 110 её ч:.1с1ъю. Н;11<011ец , кота11ге11с мож-
1ю uпрсдст 11 1, ка1\ абсцнссу точ ю1 псресече-
11ш1 И!~ с uсью котапгснсов касателыюЛ к
сд11 ннчн u\1 окружност11 н ·10'-шс (О. 1)· c rgl =
= со'> //sm /
Tc11cpьтp11 1 ·u1-I0\1l"I р11чссю 1L' фун1щшr опре
дL'ж.:1П> l 1\ЛН нссх Чll<.:СЛ 11 MOЖllO 11ерну 1 ъсн к llX
с 1юl!с·1·11а .ч ll CUOTH O ШCJlllHM мсжд~ lllJ.\11
СВОЙСТВА
ТРИГОНОМЕТРИЧЕСКИХ ФУНКUИЙ
И ТРИГОНОМЕТРИЧЕСКИЕ
ТОЖЛЕСТВА
Чё·rность и nерио;~иqность. Фуню(1m кuс1 г
н ус - чt.:тнэя, а сш 1 ус , та1-11·снс 1J кот:11-11·снс
фуню \~ 111 l l l' Ч l~TJ-lble:
Sll) ( - О,)=
-
SIП О.; COS ~- а)= COSCI~
[g(-о:)=- tgа;crg(-сх.) = -
ctg rx.
С ной сп1а чt'тrюст1 1 nытекшот Л:J с1 1 мметрич·
H OCJ'T1 точек р" 11 р " ( [llll'.
11.) 0'11-JOCJff('ЛЬJfO
оси .х. llp11 тако~-1 симмстр1-111 n рдн11 ат:1 точкн
меняет з 11а1< ((.'\:;у ) псреход11т п (.\·: -у))
fke че-1ыре фyHKl(Hlt - 11 ep 1 10/\l lЧ CCКl lC'.CJI·
11 ус и косн11ус И'v1tют пер1ю1 1 2п, а тан 1·енс 11
кота11гепс - л:
siп(а+2k1t)=~111а:cns(rx.+ 2.lгп:)=CORа:
t~(а+krr.) =Lgа;ct~(а.+kтr.)=cr~а.
П<.: r 1 ю1111чнuсть сш ryca 11 кuсннус а слсдуt:т
11:.! TUJ'O. что BCt: тuчки Р.,. ' U •1p ГЛ:t.: /г =О, ±1, ±2, ""
сонпад;~ют, а п ср 1 rо.п;1 1ч ностьт:11 rгснса II кпта 11 -
1·с11с1 - 11:1 того, •1то точю1 Р,,. , kк поочсрёдJ ш
поnа;1;:~ю 1 t1 дпе д 11 аметралыю прот 1шт юлож-
11ыс ·~·очки m<руж1 юсп1, .'рющ н е одну 11 ту жt
тачку ш1 ос11 тат1ге 11con.
Сооnюшепие между тригоноl\'1етрwrесrrn
ми функциями одно1·0 аргум е нта . Осноn
нос тр 1 J l 'OHOM<:."t-p11ч<:cкu<.: 'l'UЖДt'CTIIO
sin
1
et. + coi/cx. = 1
ныр:.LЖает тот факт, ч·1·0 су1\1ма кв:щр: 1 ·пm коор
,111нат тпч 1..:1 1 р:ш 11а кnал:р;пу её р:кстон 1 11 1 :-i 110
щчал:.~ 1<0о рл11 11 ::~т. С учётом ;:,·mro тож.п:ес·1 ·на
cлei'l.] ющне сооттююеш-~я nьrвол:лтся 11рм10 rc1
опрсдсгrе11нй:
'
1
'
1+tg•а=--.- о:scc"а;
СО') - О.
)
1
'
l +crg-r.t =-.
- , - =cosecо::
. sin- а.
Lgо.C't~И.= 1.
Но будт.те nс 1 ·оршю rы, когда 1ip11 рспrен111 1
vp.iв 1 1e1ш..il. nы исполиуете тож,дсстnа с ташт 1 т
с:нш н кота111·е11с1 мп. пх пр;:шые и лсnые 'I:-tcп 1
могут нмстт, р:~зные обл:ктп 011ред<:'лсшш.
Фuрl\'rуль1 приведения. Пu :-:Yl'II.\1 формулам
(см ·r·абл 1·11 \У) зна• 1сн 1 1е тр 1 1 1 ·ономс-1 р1·1ч~скс1r"1
функшпг любого y1·. ta М<)ЖНО 11pt111t:cт1 1 к :.~на
Ч('НI 1ю t<ак той жс, так t l до110лннтСJ1ы toi1 Ф~'нк
ц1111 остро 1'0 уг, 1 ;,~ (поддо 1 ю11111пt:лып,1м11 фу11к-
1
fi11.(-,.- +
z)=+ u r:z
,;
'1'
to[.С+ "+ .t;)= - Jin.z
Jm. ( ,.. +J>)=-jin. t:
(if'. ( ,,,. +:.t.)=-co(t:
fi11.( ; т+z)=-&о/. z
1
cif'.( -;"'+ .:;) = + Jin. z
jin. (а·+z)= +jin.z.
со/. ( 7. ;т+.z ) ::::;; + со/. .i:.
ji1J. ( f-ir- . t.) = + cif.:;
cif,( +... -:r:.) = + ji1; , .z;
}п.("' -
~)=+jin..:;
·
rof. (-...
- <r. )=-cof..!$
fi ~1'
11. ( Z 1r-Z)=-z:of.'!.
со[.(+,.,. _z.) = -
Jin. z
fi~1. ( z..-
-z)-
. .. .. ,_1/1.z:
•oJ.(:. 'll' -. z)= +•if.; ..
ID<111мy~.1>1 npщ1;>дE'Hil\1 ( 1р.1н,,.11а 11'11< н11r" /\ lйi'Rfl~ "- В6едЕ'~111<·
~ана~ю б~lKOllt'ЧH ЫX >. l 13д<11t>I;, 1743 г
Геометр1н1 плкк алгебра
cos(~ + сх) = -sin с1.
:-,in(}+о:)=со~ а
si11 (n: + <XJ= -siп <l
~iп(}- а)= cos а
cos(~ - aj= sin о:
--
Pttc. 13 .
ц11нм11 пог111маюн. >1L· 1 111yc111~cJc11 1 1yc, 1·аш·с 1 1с 11
котапге 1 к) .
ApIJ"1e111' rr
lr+а rr-а тт+о: .11t_o: 51t+о.
~2-а 2
)
2
l'liП~ (_:()~IJ. со~а :-.1па -siп а -<.'О~а. -CO"iCl
С(),1., ~
:=:irнx -~1па -cosa . -со~о:. -:-,iп о" siп и
Г l оэтому n та6т щах ~нтачеr 1ня трг11·01 юмет
р~rчсс 1< 11 х фушщпй ,1аются толы<о ;r,;1я остры\.
у1·:юn, пртrчёи достаточно ОГJ');tпичrrтьса. на
прн мер, с11rтусом и т:-tнгс11сом. Так. ;,~рrу.че11т ~,
расположе1шыfI n третьем кnа,11р;ште, мож110
замс ш rп, на ue1·pыf1 угол о:. 1 юльэулс 1 , форму
ла,\111 длн тт + п 11ли )тс/2 - <х. В т:~бшшс /\аны
т011ыш наиболее )11 rотр1.:611тслы 1 ыt.: форму11ы
принеде 11 т1 /l.JIЯ сннуса 11 кос11н) са Из 1 111х :1с1 -
ко получать формулы длн т~1н1·с11с~1 11 ко
т:1н1·~нса. Но. 11мt:сто тш·о ч 1 ·06ы ны1:юд~ 1 · 1·1, 11
ЗJПОМШJ:!ТЬ ЭТ\1 11 :.1.руrне M I IOl'OЧИCJ1e1 1 1 rые
формулы, мож.110 восrют-,зоваться СJ1е;~ующ11 ,\1
проС'г ым пpani-rJI0,\.1: при rrрнnедешш фуш<ц11и
от аргумента nн.'ta krr/2 ±а. где k - целое
Ч IIСЛО, т~ функции 0'1 ' а (рис 13). 1) 1J<IЗl3aПJ IC
функцю 1 сохраняется, сс1 111 k чёпюе. н меня
ется на «допо; 1н11телы10<.: » . сс~и k 11счё·1· ное:
2) з нак в 1 1 рак0Гr ча<."f'1 1 сu.н 11 ад:11.:т <:о :-н-1;.1ком
припщо1мо1'1 функц1111 н 'Гочкс k>тс/2 ± 1х. ссл~1
} l'OJI а ()СlрЫЙ.
Нэпр 1·1N1Ср, при 1 1р11неде111 н1 c t g (о. - л / 2)
убсж11.аемсн, ЧТ() 1х - л/2 при () < а <rr/2 ле-
жи т в чстнёрн>м кn::щр:1 1-пс, rд<.: J\nтангетк
2тr - 11.
-.S if1 а.
CO'\l 'X
59'5
Фигуры
отр11цателс 11 (знак минус), н. по пр;ншлу 1, ме
няем наз"R~1н11е функцш-1 : c tg (о. - rt/2) = -
rg <х.
Формулы сложения.
sin(<х±В)=siпи.cosВ±cosаsinр;
со~(r:x.±р)= cosаcos13+sinаsinР:
r.i. t~<х±rgр
(g(a±JJ)= -
;
1+tg atg р
ctg actgр +1
Clg(а±Р)=
.
crgа±ctgр
Формулы кратных угло в. Эт11 формулы
НЫЕЮТ\ЯТСЯ прямо н з формуJJ слпжения:
sin2а=2sinаcosо.;
cos 2а =CQs
1
о. - siл~ а= 2cos
1
а- 1=1-2sio
1
а;
') lOC(
2
tg2а= - 1"',
1-rg-a ctga-tga'
) crg1а-1 <.тgа- rgа
crg ~а=
=
~
·
2 crga.
2
'
sin3а=3siпа-4siп"'a;
cos 3о.=4 cos'и. - 3со::>а;
2
_
:) tgа- rg1а.
rg.1а-
2
•
L-:) rg а
2
_
ctg~ a -:ktga
ctg _10.
-
,
3crg- а-1
Отмсти"'1, что фоrмулу дпя cos .)о. исnолnзо
вал Франсуа Вист при рсше 1-1ИJl! кубического
уравненн>i. 011 же впервы~ 11ашёл выражения
для cos па и siп na, которые 11 озже были полу
че 1 1ы более простым пуrём из формут_,, Муапра.
Формуль1 половmurых уrлов. Есл11 в фор
мулах двоf'пюго ар гумента замепитъ а па а/2,
их можпо 11реобразовать в формулы поло
в111 1пых углон:
1
.
а_±
1
11- cos а
. а _+11+cosа.
51112- ~ 2 ;cos2--·~ 2 ;
Ct
, 1- COSCt.
J- cosa
sina
tg2=' ±V1+cosа =
~
siп a
1+cosa
а+/L+cosа 1+cosa
sirнx
crg -
==
=
=
2 -~1-cosа
siла 1- cosа
396
Формулы УJIИверсал:ьной подставовю1.
Иснользуя :::>ти формулы, выражение. включаю
щее разны е трш·онОМL'Т[ШЧескис фу1 11щ1111 ОТ
одного н то1'0 же: ар 1 умента, ,,южно псрсrшсать
Е<;1 к ра ционал ьнос выр:зжсннс ( м но1 ·очлен. по
делё11 11 ый 11 а много член) от пдноl1 функцнн -
Lg (а/ 2), ЧТ() U l •llШ::т ПUЛС:IНО при peшeнrLJ l LICKO-
'l'Op1,1 x урав11е1 ш й, 1-11.1 числе 1 1111 1 11 нтtтра1ю1111 т. д.:
а
1- tgL (J.
2rн
ьiпа.=
)
2
cosa =
.а
,а
1+ц~-
l +tg"-
~2
2
?о:
1,а
~lg -
- tg·-
tgo: =
2 ;<.:Lga=
2
,а
2rg
а
1-щ-
2
•
2
Формулы: преобразованил сумм в произ·
веденил и произведений в CYJ.':11'[ЬI. В до
ко."шыотерную эпоху этп формуJ1ы использо
щvтнс~, шш упрощения вычисленпй. Расчёты
тuгд;~ про11 зною-1л~1 с h с 1 юмощыо логарифми
чес:ю1х таблиц. з п о1же - щ) 1·ар1Jфмичсскuй
1111нейю1. А логарифмы Jl)'Чllll' 1кего nр11<: 11особ
; 1 еL1ы /1,ЛЯ умножсггия ч1кел . Поэтому 11 схщt11 ые
ныраження 11риводилr1 к «вrщу. удобному для
логарr1фмировани>i», ·1'. е. "про11:.1всдснr 1 ям:
.
.
~ 2 . o.+r.i.
а-А
sJnа+ s1n = .sш __JJ cos __JJ ·
2
2'
.
.
р2 а+Р.сх-Р
srna-.s1n = cu::. --s 111 --·
2
2'
cnsа+cos1~=2cosа+рсо~а-~ .
JJ
2
2•
•
•
ri.
>-·
<х+р.а-р
cosa - cosJJ = -- мп --sш
--:
2
2
± 11 sin(a±p)
tga tgJJ =
;
co.s aco.s Р
sJл (а± А)
ctga ± ctgP =
.
.
JJ;
sш as111 р
2 sin а si11 Р=cos (о:-Р) - cos (а+р);
2 cos а cos Р =со~ (а-Р) + cos (а+Р):
2sinаcosР= sin(а-Р)+sin(а+р).
Эти формулы таюке лс:1"ко проверяются по
форм улам сложения.
Формулы понижения степени. Из форМ}'.'1
крат1ю1·0 арrу.мент~1 nыrюдя тся формулы:
Р11С. 14.
б
"/
siп2а= (1 - cos 2а)/2;
cos
1
a= (1+cosl.o.)/2;
si11 \x = ( ..li si11 а. - siп 3а)/+;
cos
1
а= (3 cos а.+ cos 3а)/4.
С их помощью тр11rо11ометрнчсские урав
нс1шя мшюю пршюдитъ 1< ура.~шениям более
ннзких <.тспсней. Имеются и формулы д;ш по
ннжt'н ия более высоких CTt'пe11t'l! сипуса и
косинус;,~ .
АРКФУ НКUИИ
И ТРИГОНОМЕТРИЧЕСКИЕ
УРАВ НЕНИЯ
Еслипензвест1~ый у1·uл входптв урав11ешrе как
:1р1у_,1е1п тригономстрнчссю1х фушщий, то
~ раRнснне называется тр1ион.а.мстричесю1.м.
Таю1е УJХtвнсн 1-rн - одно rrз 1 1юбимых ~бJLЮД·>,
которое еотовят экзаменэторы дш1 а611тур11ен
тоn ннсп1туюв, а 1 ютому методы rеше11ни этих
~раш rtт11 1 й очень подроб1ю11 т11\<1тслыю разра-
6от;11 rы ре11етитор::~м11. С 1юмощ1)ю р:1зли ч1 rых
пр11Ьюв 11 форму)[ триrо1юметриче-с1те урав-
11ения СJЮДЯТ К Н)аВНСl!ИЯМ Blfдaj('x) = а, ГДС.f -
каJ\ая -лнбо из простейших триго1юметрнчс
(КИХ фуIIЮ\ИЙ: CIJHyc, косинус, т~ш1·енс или
котанн:ш:. з~псм 13ыражают арrумспт х этой
фу11кц11и чере::$ её 1:1::$11tттнuе ~начt'ш,1с а.
1lоскольку тр11гономстр11ческ~н,; функцш1
пrр1юдичны, од1юму и тому же а J1:~ uбласr11
3113Чe!IИl'J .f O'J'RCЧaC'I neCK()(Jt'Чl-!O MJ-IOJ"O :шaчt
lll l Й ар1·уме11та, н реmепнп ураю1енш1 нсль:{Я за
nнсать п виде пд11от.'1 фу~1кф1н от а. По:-этому n
ОблаСТII nпре1'еJ 1е 1 ШЯ 1.;аждой ИЗ OCПOlll llJL.'( три-
Геометрия плюс алгебра
в
./
(1
1·стомстричесю1х фушщий nыделяют участок.
на которо.\1 она при1-11 ·н•1ает все сnои значения,
причём каждое только о;~ин раз, 11 11ахо1~ят
фунющю, обр:пную ей нз этом участке. Таю1с
фуню~пи обоз11ачают, пр111шсыван приставку
:нс (дута) к на:ша11ию исходноfl функции, и на
зыnают обра11111ы.ми тригтю.метричео,·11...ии
функциями rtли просто арл:ф111t11цuЯА//l.
Дпя сшrуса 13 ка~1естuе ~и нтервала взаимной
од1юзтrачпости» бl'рётся отрезок 1- л/2, тт/ 21. rra
котором сmтус монотошю noзpaci·::ieт от - 1 до
l. длл коошуса
-
отрс:::.юк 10. n]. /IJ!SI таю·t'11сt н
1<0'r<1 н1 ·снса соотн~1·е1·нснно интервалы (-тт/2,
rt/2) н (О. тт). Таю1м обра:юм, арксшrус - ::~то
функщн1 arcsin с1.. опrеделённ:Jн на отрt:зкс::
[- J . 1 1н ранная 11р11 1<ю1щом а т~1кому эначс
нито et, - п/2 < а < тт./2. что sit1 а= а. Её 0•1е111.>
удо61ю 1 1редстt1влять с помащыо з11аком0Тt 11з .ч
едшш•шой 0 1<руж11ости (рис. 14. а). Обратпте
ШП1Ма1111е: при lal < ] 11а окт')ЮЮСТ/.1 I JMeIOTCЯ
две точкн с ординатой п, снмметрнчные отно
с ~ ITt'JJЫIO оси у. О;1ноt1 ~в IIILX отвечает угол
а= a1-csin а. :1 щ1уrо1"'\ - )'l'OJI тт - о.. С учётом
11ep 1I0/\ 1 1Ч IIOC'l 'IJ с11нус:1 [> e lllCHllC ураннен11н
!iin )(=и затк~-.1к~1ется слсдую 11~1 tм обrз:юм:
х=(- 1/'aгcsi11о+тсn,
l'Де п =О, ± 1, ± 2, ... Так же ре111аются дl1)Т11 е
простейшие тр11r01ю"четр11чсские ура ш 1е1 rия:
cosх=(.{, -l<с1<1: х=±агссоsс1+2тtll,
гдеп=о,±1.±2, ". (рнс. 1~1. б);
lA .\·::::и: .'\" = ::J ITLJ~ ll + rt17,
гдеп=О,±1,±2. ". (р11с l~I. R)~
ctgx ==и: ,,. = :нcctg а + тт1t ,
Г,'\Сп=О,±\,±2.,
...
(rис 14, г).
.~97
Фигуrы
ВЕКТОРЫ И ОПЕРАUИИ НАЛ НИМИ
Всктuр - <>т1юс1 rтел ыю Н< 1шlt мате\1::tт11чсское
по11ятнс. Сам терм~ 1н "нектuр" (сп.пат. \1ecto 1· -
<· нссущ111~1-1) rтерпыс 1Юя11ш1ся н 1R4? r. у 1 1р
м1ндсr<о 1'0 матема· 1·11ъ:а н ао1)снюма Уипънма
Гзм ll!rьтона ( 1Н0'1 - 1 ~()')) n р~1 6отах rю n остро
ешло ч11с;ювых систем, обо6тщ.1ющ1п{ 1\Ом11-
л.екс11~.тс т.п 1сла" l'<1,шльтону nршrадлсжат н тср
мш rы •С I<аляр·>, <•ска!lярнос про 1 1311е1tсн11с ».
<-векторное произнеде11 1 тe». lloч·r•11 од 1·юврсмсн
но с 1111.ч 11сслел.011ан11я в том же 11:1прав;1еr11н1,
1ю с дру1'Оl1 точ~.;и 3rснш1 кёл 11смсцю1l1 мате
м:.1т11к Герман Гр:ксма11 ( J НО()-1877). Л111·1пr
чан1111 У1111 1.ям Ктн.рфор;t (J~4') - J~79) сумел
06·1.едш 1 ит1 . дn:i по;tхода n рамках обшеit 'Гсо
ршт" uю1ючающе1'1 в себн и обычное щ;1сторное
нсчпсление. Л око 11чатслыtый nпд оно пр11rm
ло u тру,тщх американского ф11з1ша 11 матсм:1-
т11ка Джоза i1и У1 шларю1 Гиббса ( LH .~9- 1 <1U3),
который в 19U 1 J'. опу6 J11 1ков :н1 обн1L 1 r11ый
учс61-111к по нскторному ;ш~~лизу.
ЧТО ТАКОЕ ВЕКТОР?
По11ят~-1е ве1пора во:шикает та:v1, где приходнтся
11меть дело с объсr<Там.и, которые характt'ризу
ются Rелнчююi1 11 11~шран.rн.·11исм. С по;1,обны
м11 объектами ;'1ожно нстрсп1т1,01 н с:1мы х
fl:IЗ H Ы.X обл:1 СТЯХ ,\;J;J'l 'Crvl;ITllKIJ И фHЗllIOI. Гl~'С'IЪ
какое-то тело в резул ьтатс 11 ря мо.'111 нс:l11 ю1·0
ПOCT)l l :JTeJIJ,HOГO )~RllЖClll l Я 1 r cpeмecп1JIOCJ1 li:j
01 t1 юго 1 ю1южсн 11н в ,·tругое .;э 1·0 nepeчt:щer111r
аа:t:1ё·1 сн расс·тю1исм, 11:1 которое сдвr 111улосъ
1·ело (расстояrт 11е МСЖ/~У II;lЧЗЛЫ LЬIM 11 J\OIJCЧ-
111.lM положешш"~и любой его ТО'ШП од1шако
во :~;ля всех точек), и rrаправлсписм с,rщп1~1 (все
Л~'ЧIJ , 1щущш: ИЗ началы1ых в IЮНс'ЧНЫС IIOJIO-
Жt:HШI nc<::x точек тела, <:<Jна11ранщ·ны; : 1106011
и;{ ннх 1tу l(а:·1ынаст11:шр:.ш.11е1 он: ;tвнжс11ня) Ф11-
:тческ 1 1с 11011.итин «c1шrt)C'l'Ь·), <·ускоре11 1 1t;~.
"с11щ1" также характеризуются н;111ранл<:н11ем 11
веJ111ч.ю-юй (11р11 выбранпой е;~ 11 шще 11:~мере-
11ия - ЧllСЛОМ). 1lrи:-.repO.'v\ анаЛОl'ИЧIIОГО llOIIЯ
'ItlЯ в м ~1· 1·е:-.1атт111;с служпт 11ap;ume.r1ы1.L1{1 пере
нос ( c~L ~татъю <Дви.же11ПЯ• ).
JJаибо.1ее t1а1-ляюrо вел11чr 11 1у JJ 1 1:шранле11не
одпоnремешю можно задать с 1юмощью 1т-
11раш1(!111 Ю<'О ()117/)(!ЗКа, '1 '. с т· р ез к :: ~ АВ, /!, )1Я K(J' Г()
poi ·o закре 1 и1ён ук;,~з:ш ны1111орн,{ОК с1 ·< 1 концов:
точка А 1-1азыв;.1стся с1·0 11.aчcшQl\f, а тчка B-
h"O'Нt(O.M 06о:н~:.~частсн ,пот 11апр<1R1 1е11ныi1
--?
0·1· рсзш< чсрсз АВ 111111 АН Ис1ю11ьзую·1 · 1r обо-
зна че1111~ 0;~1101'1_бу юю11 со C-IJ?CЛl(O i'i ит r чср
·1ой нанерху: ii. , /J, с,". 11mt ёi,h,c, .". Друl'Ое11:1-
зна1111е /\Юt 11апр<1вJJе111юrо трtзка вr!ю11ор.
Точнее: гонор}!. ~то 01t1 ю 1 1э значе rпл'i тер~шна
<· 11сктор·>. На чер·1·ежах нектор изображаю1 от
резко1'1 со стрстюй у его кош~~. Длшюit (11лн
n6cwzюm1юti ве.ли 11и.1-юfl. Jш11 люr~1ис-щ} вектора
а = АВ п;1зывасrся д;шна uтрезк:1 А/З; 011:1 обо
ю·1а ч аt:тся \ Zi \,а юю1·щ1. просто а. т. е. т()r1 же
буююй, НО fiC:{ ч.(;pTOЧl<l·I . Н~tп(1аКЖ~Нl-Н: ll~Kropa
t:с1ъ на11р~влсн1н: луча, И1'1)'Щс1·0 иэ <.то нзч;~ла
н коне~~ . Рассм~прив~ют 11 нy./le11mi нсктор
О = м, у котороr'О начало 11 1юпс1\ соnпад3ю1·
Нулевой нсктор 1Jc имеет 11а11равлс1шя.
Векторы. жжа 110 1<:: 1-ш nараJ1ж·;1ы 1~.1х щжмых
111111 на о.ц~юй 1 1 μнмuй называют "-(11U1z11-1r!afmы·
.м11 (рщ;_ 1. а); 11улсноl1 нс~.;тор счтп·:~.ется ко;1 -
1•11t. 1.
n1111е араым любому nсктору. L-1.anpaнлcttшt
нtнулсnых h'OJIJIJ 11-:1сар11ых нt:ктuров мо1у1· сuн
:1:цt1ть шн 1 бы·1ъ прот1шо1ют1жн ь1м11; с.:(ют1н::т
ствснно ~-;скторы 1 1;,~ ::s ын:1ютсн сш1~111р:тлсн11 ы
\\11 1 1т111 рот1 1 1юnолож1ю 1 1а11р ;1нлснны.ч1 1 .
Дад1 1 1ч тепер1. важ н t;11шее ft.1я 11ск·1·ор1юl1
а111 ·ебры оnрслеле 1 111е: вею·оры . имеющие О/\1 1 -
т1коnую дшшу н паправнешrе. па1ыв:11отся
ртты.ми (р1 1 с. 1. б) Ест~ раннh!е векторы .11В
11 сп llC Лl'Жат на (ЩllO l'I прямоlt , '('( ) llX КО НЦЫ
об rа :J уют пар ;.~ллс:логр:1 мм ABDC, 11о:~тому
118-= CD Н)П\З 11то,1ько тоmа. 1<01'д:J АС = ВЛ.
П т rятие равенстn'1 вс1поров по :нюю1ет от
влечься от расположешш отрезк:~ па ттоско
ст~ 1 шш 13 простраr1с·1·ве и ВЫl\еJ1.и1ъ длину и
напраnленнс «В чпстом вндс"
В данны х nы ше оnрсJ(еленнях равные
вс~-.торы 1:1ыс.:тупа10т как соверtпсшю р:шпо
нршш ыс 11 н:..1анмо:..1амсшн.:м ьн.:. Это справед;ш
тю 11 ДJШ /tP)'Г ll X ll Ol lЯ'l'J l lJ и ф:~ктuв, OTHUOJ-
ЩJJ XCЯ к векторам . На11р1Jм<.:р , лна в<.:ктора
0,1ш 1 зко 1ю~'1 /J,Лин ы, 1ю проп аюполuжно на
праRJтснны е. 1 1ззыв:1ются протиtю11ало.Jюtы.ми
([ШС 2). Rеюор, Щ1011 1fi()П 0Л0Жf!ЫЙ f\et<TOpy а,
обоз начается <rсрез -а: н част11ост11. - AIJ = Нt1,
но и лю60(1 вектор, раnп ы 11 1ЗА , тоже прот1 шо
ноложен АВ . Ym;1 между 1кктuрами 1J 11 Ь
опrедешrется KJ K вtлнч 11 к;:r Y l '!Ja АОВ между
равнымн нм вскторзм11 ()А = Zi , ОВ = Ь с об
щич нач:uюм о (р11с. 3). JllTKU ВlЩе'lЪ, что ВСJШ-
411Н::I у1·;1а АПВ 1Je ::1аю tснт uт выбора точ ю1 И.
З;tметнм, кстати , что /1.ЛЯ любой /\анной точ
ю 1 Осущест1·1ус:тто ч ка 11'1, и пр1пом толь~о одна,
:\ЛЯ которой ОМ = ёi . ~·де а - 11э 1111ы й вскюр.
Говорят, что точка i\1 получе1 ta откладыва11иен
вектора а ()'1' точки о
L[тоб ы 1юдчtркну1 ъ пеш ную взаимоза мсня
е~юсть p:1Rнh1x век~ о роя R нсктор11 ой аm·ебр<.: п
г(>()МЕ'Тf)ИЯ 111\Ю( aлrt-f>pil
... .
Рис. 2.
Рис. З.
изб<.1.в1 пъсR от 11екото рых лоr'ическпх 1tсу; (обстn
(наприм ер , множсстна нулевых 1к· к·1·о ров
м' вв п 1'. )( ) . DR0)1)1Т IIOIf}ITllC a10rlor)JU)l()
не1,·торо. Сноб е >д• 1J)11:1 Hl'J<Tt >p СО( >'rнстстнус:т
всему юrзссу ранных \1С"'ЖТ\У C'06n(1 11апр:~ н
ле1 111ых отrе::щон (11аэыnасм1.1х 13 :'ЭТ()М CJ1yчat:
.JaflJX!IИi!NJtЫA lll веюпорснш) н поmюс1ъю ха
рактсрнзуется длнной п паттраuлештсм. 1! ш1ьзу
ясъ рас11рщ:тра11ён11ым в математике пр 1 1ёмо и.
с.:воболный вектор ч :1с1u 11 опрt.·;~ет11от кат<
класс р:ш1 1ы х 3акрсnлё~ 111ы х 1к:кт()рuв. IJu Х!ЛЯ
oncpa 1t J1 11 н:щ 1к: кторам11 11л1 1 кuuрднна 1'h1 иск
торз {)прсдс J1ены, t\ сущ1юстн . 11 ме 1111 0 дпя с1ю
Г1оютых вект()рсн\ n() ы ч 11 0 1 1 мснп /\елп с каю1м
тп 0,1\l l И.M ( И Jlll Jl(:'('l\0Лlil\ИM 1 1) 11:! нa11paнлc:fll/ l1IX
отрезков, прс1\СТЗШ IЯIОЩПХ тот 11Л11 11110{1 Cll0-
()();1,IJЪП1 вектпр. Прн этом n о~mят, ч1·0 1rx nccrдa
,\;lQЖIJ O З:l'v!СШПЪ на р;~ю1ые .
U физике 11 матемапше есть :~адач и , 13 кото
рых нажны нс только нст1чиrrа 11 н:~ праnлс11не
13сктора , 110 и точка 1.:1·0 прпложсншL J l апр н
.чср, 11 апрнж(;ннос.:1ъ маrн1пно 1 '0 пuлн :..~:шнснт
от того, 1:1 ка кой ·~·очке 0 11:1 11~11\1<.:рястся. А вuт в
CT3Tl!Kt ТОЧК:t nрнложсн11я С I JЛЫ может СКОЛl>
:11 п1, 11дот . rrpямпi'J. 11араш1ельно\J 11 ~m1х1 ю1сн11ю
силы. Но ест 1сдв инуrь сё 11 сторо 1 ту, то реJу:11,
т11рующее i\Cтl c1·1111 e fiy11cт /tруп 1 м . Мате .\1 ;~·1 ·11-
чес1<о~'! моделью та.кой веr<тпрrю!i велич 11111,1
служит ско..лыящий nсктор. т. с . совокуmюст1,
ncex равных между собой 11апр авлсш 1ых отрс.:::1-
ков с на•1а;юм 11а 11;.1ннш1 прямой.
АЛГЕБРА ВЕКТОРОВ
Лус."IЪ 1i J1 17 - д.ва нсктор:~. Отложнм нсI<тор
а от nронзnолыюй точю1.1l, т с. 11аl1; 1ём таr~10
точку R. что АП =Т1 (рис. 1). Затем 01 точюJ В
от1южн м нсктор h - 1 юстрu 11 r.1 ·1·акую ·1·оч ку С,
Ч1'() вс = ь' Нетрудно IШh':IЗ<t'IЪ, Ч'l'О вектор 1\С J
Фигуры
Рис. 4.
В'
' '"-..
/ '-~ (~'
А'..____
-
11е З31-11 1 С1 1 Т от f\ 1,1 6opa TOЧl(lf А: ес1111 fiЗH"J J,
11р)1)'Ю ИСХО,1\ПУТО точку А' и ОПИСЗ IТПЫМ nыше
способо.м, н;:~чи11ая с А'. построить nсктор .1l'C',
то ()[1 ока;кстсн rав11ым flCl<TOpy АС. Этот
вt:кто р наэ1.111аt:тся ~р11.мо(1 векторов а 11 /J и
обозначается как lJ + fJ . Лруп 1м11 слпн:н.н1, нт1
любых трfх точек t1, В,<: 11:v1et:т место 11/н;mшю
трёх тпчел·:
АВ+ВС ="1с.
И:~nестпоt: 11ер~ше11спю 1·реуголышка на
Dе1порном нзыке uы1·1шщ 1т так
·1.е ;u1яшобыхн11~х нектрон а11/J
lal-li71~la+hl~lal+1ь1.
Ес;111 11е11уле11ые 1 1ек·1 л р1.1 а 11 IJ 11e1mm11111e -
::tp1rы , то нх сумму уТ1оf>1 ю 11 ахо,г11п1, прн помо
щп пртшла nl1рсилелогрш1лtа (рис. ">).Для по
ст роения сум).1ы 11ес1<олькнх ве 1<·1·оро11 а1 ,
а2• ",
а" 11уж110 отлож1 пт, пх ою 11 1 за f{pyrн\·t
Б
п
Рис. 5.
Рис. Ь.
ii
,.
.........
ii -б
() - ---------
·в
/?
Рис 7.
Рис. 8.
1\()()
т:~к. чтобы пачало следующего вс~стора сонпа
ло с кон~ ~о м 11рс:дьщущt:J ·о. Тuща «замыкающиЛ•
вектор - 111су· 1ц1 1Г1 от 11ач~1JГа 11 с::рно 1 ·0 к концу
последне1·0 - и будет суммоi1 {i 1 + а2 + +ti"
(р н с. 6). Замет1ш, что рсзульт;:~т 1 1е -1;шис1-1 ·1 от
J юря/tJ<а, п которuм векторы 0·1·клз1tынаются.
Ilрнне;(ём ос1ю 1'111ые с1ю(1стпа сусю1ы век
тор~ >В:
1) ?i"·т-fJ = /) +Тi;
2) а + (Ь+с):::(а+ь)+ё;
.1) а+u=а:
..j.) (!+(-li)= о.
J:Jектор а - Б = (i + (-Ь) называется рпз110-
сn·1ыо ве1\1·ор«н1 li 11 /J. Чтu()1111юстро11т1. 13сктор
lJ -Ь геометрнчесю 1 , ДОСТ<l 1ОЧI\() O'I JIOЖ llTI>
-
-
векторы 1i 11 h от О/(1 1ш'1 тnчю1 n . с:.:с:~и (i =CJfl,
-
-
-
-
/J = ()В (р11с. '),то р:1 зност ь ё1 -1? = ВА.
Ещi; 01~ H1Ji1 н:~жн< •lt 0 1 н:р:11t 11~(1 >11:1J1нется
ум н ожснJ н: кс1пор:1 на ч11 uю. Эта 0 1rерация со-
1то<." 1 а вл нt"1 нек2·ору 7i r1 дс~'1 стнrпсльнuму
ч11слу 'А ве1<тор fJ=Л.Zi. 011ре1tе.'1яе.ч1.1i1 слсдую-
1щ·1м1 1 )'C!IOHllHMH:
1) дл1 111а вектора h р:шна IЛ.l lal, т. е. IЛ. а/=
=IЛI lal: в частностн, Ь = О. еош ёi =О 11ли Л. =О;
1) ecmr ncrпop h = "J-. Zi ct: (}, то np11 Л >()он
тшс:ет олитr:11юnое 11<mparvte1111e с векторО)\ а,
з пpri /, < о - Пj")ОТJТВОПО!ТОЖJТОС ( р11с. 8).
llрl!НС:J \ённыс Hhl\1 1C ЧCl'h lPL' l'HOJICl'Ha С:t0Ж(.'-
1111Я вс:.:кrорон мож110/lОГн1: 1н11 тr, <: щi:' четырьмя
сноlн.:ткам11 , сня:1ын ;1111щ11м 11'шс rхщ1111 н:1,1 век
тщх1м 11 11 ч11п1:1чr1. :.1т11 с 11оi1ст11~1 с 11ра11с /1,Л нnы
:~лн : 1ю61.1.': 11сю оро11 ct. Б 11 11 ю6ых дсi1спш
тсJ1hш,1х ч11сел Л. 11 р·
'5) Л.U1а);. (1.р)а.
6) /..(ёi+h) =l«ri+Л.Тi ,
7) Л(П + /J)= Ali + Л./J.
R) l · (/"'-1f.
:1а~·1еттl'1, что 11ереч11слеш rые восб1ьсnойств
вес uмсстс сост:шляют ттапболее общее оnре
деле1 ш<: вектора. J1.юбос м1 южсст1ю, лля эле~1ен
тоn ко·1·01.:ю1 о з"1J\;.1ны опер:щ111 1 сложе1111я и
ум1юже1111н 1та число, удоnж:творлющне yкaзJ11 -
rrьtJ•1 сво1kтвам. называется в(!л:торr1ы.м 11fю
стра11ствш~. 13 этом см ыслс 1 шсл<.:J.юкатет:.
нuсти чис<::11 11лн. нанр11!\н:р_ функн1111 .
н<:: прерынн1.1е на отrсзкt , мu 1 -у·1· р:н:см:tтр 11 -
l\:!Тf,СН кзк ":1 бе1·рзктные-> ке::ктnры - ЭJtt'Mt'H 't' Ы
fi(;.КTOpHC)I'() 11 ростра НС'Г:Н;l.
ТРИ ТОЧКИ НА ПРЯМОЙ
В осноnе п ртюжстшй а.rrн:бры векторпn к
рсшепню rсиметр 11 чссю1х зад:1 ч Jtt'жaт следу
ющ11t: ;щ:~ )~шсрждсн11я . _
l) eCJHI IK'K'l'O\)bl п 11 ь K()ЛJll l HCap11ы , 11р 11 -
чём 'й 'F О, то сущсстяуст такое ч1 1 сло Л., что
Б='МJ;
2) точка(. лежит на прямой А В (р11с. 9) ·ю1·щ1
11 только то1·да. ко1')\а сущсст.вуеттакос ч 1КJЮ Л.
что ДЛЯ любоf1 ТОЧЮ I ()
()(,' ::= Л. ОА +(1-J ...) ()В.
В само,\.1 деле::, paнcнet·nu (") мuжно 11р<:обра-
зовап.так: ОС-ИЕ==Л.(ИА - ОВ), или вс~л ВА .
Значнт, соt·ласно утвсржденшо 1, оно раnно
с11льно ТО;\1)', что 11ею·ор 1,1 ВС 11 ВА кош 1и нс
аrнh1; 1'. С. ТОМ)', ЧТО Tj)H ТlJЧКИ А, В JI С лежат H ~I
одной прямой.
Из этого расLумде1шя 1шд110, что сст1 точ
кэ С депит отрезок АВ n от1,-юшс1 шн т /1/.. т. е.
АС/СВ= 117 / JI , ТО в формуле("') А= Ji/(11 + m), а
ЗIJ;JЧ JIT,
ОС=-1-
1
-ОА+ _!!!__ (JВ.
п+т.
п+т
("'*)
В час1ном случае, ест 1 С - ctpt'д 11н э O'l'f)C~
к;iAB.то
-
1--
OC=l(OA+08).
Прнме1 11 L"1 полученные формулы к д01<аза
тел ьству {lЗ~естной теорем ы о мсд11ш1ах. тре
уголы-тка (С1\1\. статью «Треуrольн нк. 11 ростей
ший и нс11счсрrт.исмы11,)).
Рассмотри.ч трtу1·ол1,ник АВС и лроизноm.
ную тС>чку О. Пуст1,А 1 - середина сторон.ы ВС:,
-
1--
rо1 дз ОА 1=2 (OB+ OG'). Точка i\1 дел11т медиану
Геомстrия плюс алгебра
Рнс. 9.
/\А 1 треутолыш1<:11' 0·1 ·1ю1uс11и11 А,\{. ,'\ {А 1 = 2 .
(рис. J 0). 1То формуле("'*).
-
\- )- \- 7('{- -))
ИМ = -ОА+.::о.r1 1 = -04+..::
-
OB+UC .
:>
5
3 .i2
11111\
-1----
0.11 =~(ИА+ОВН)(,')
-'
'fЗ
!)та формула симметр~1ч1 1а относ1-пе11ыю
А,В11С. а потому·1
·<1 же самая форr. 1 ул:1 оерпа
п длн точек. которые делят дnе друтJ1с мс;оr
а1 1 ы н том же от~юшеrнrи 2 · 1. С.11едователы ю.
все три мсди:шы перссст~1ются в одной точке
ll / ~еплтсn R LlCй n ука:{аН! ЮМ OTllOШC!tШl.
КООРЛИ НАТЫ ВЕКТОРА
Пусть "f = ( JA н ) =Г>В - дна не1ют11шеарных
нек1·ор: t на 1 1 Jюс1<0ст11 (р11с. 11 ). Рассмотрнм в
Э'J'C)\r ПЛОСКОСТfI nроизвmtЫ!ЪJIТ всто·ор '[i =ИР .
П уст~, Хн }1
-
такие точ.к11 11а прлмых 01111 013
со<.пntтствснпо. что PXI! 08, а f'Y~ ОА. Пuсколь-
ку 11екторы ИЛ н ОХ , ОН н ОУ rюr1:;1рно ко;1-
ли11с ар11ы, существую·r числах И.J'. l\JIЯ которых
ОХ =.УОА=х7и 01· =уОВ = _J). Отсю;~а
'fl =ОР=ОХ+()}'=хl+Yl·
Ит;щ, если 11а 1шоскост 11 фиксr 1ронат-11.r ;~в;:~
11с1,олли11е(lрпых вект11ра 7 н } , то лrобыl
нектар i' можно пре,~1ста~зюъ 1.1 внде сум.чы
[i :: :xi+yj,
где х н у - лейст.внте.1tы-1ые ЧJrсла. Очсв11;~но,
ЧТО векторы ох 11 ()}~ соотвеТСТНt'! IН О К(JJIЛН
[(еарные ттекrорам 7 11 ] 1[ д~нощне Rсумме i'.
:.i значнт, и чнсла х п у в послс;т.нсм рзнс нстве
oпpt'l~CJfЯIOTCЯ OJtHOЗI rач1 Ю.
Фигуры
•
о
-~~ --'
т 11х
""с. 11.
1'
l 'l.
j
-
P<ic. 12.
у
Числа х 11 у 11азыватотся 11·rюp()uщ.1mcoll!
nею110ра ii отr rос11телыю башса i, ] Зап 11 -
сьш~110т это так: /о (X;_I').
Лнапоп1ч1ю, CCJlJI 7. j rr k - тр11 11скомн
л:111:1рных (т. с. !IL' 11:ipa.rL'lCJU>llЫX ()ДHOll плo
CKOC'l 'll) в<.:i-"'l·opa 1:1 нространсткс. то любо~'1 с1ю-
6сщн h1 lt H<:KT(JP i' \/ЮЖНО СДllllСТIН:нным
стюсобом заш1с:Jт1, н н11;1с сумм1.1 f =i'1 +1·! +fi;.
11ic ве1''!!1р 1.1 Т:1 , i'; 11 i\ колт rнеар111>1 1к:ктор::1м
i . } 11 А' соот11t:тсmС'11110 ( р1 ic. 12). О1·сю;1: 1 слс-
;1уе·1, что любоi1 1к·ктор i' в 11ростра11стRе rщ
тю~11ачно опрс;1еляет тр11 :tеi 1 стш 1тсл~.111,1х
ЧIIСЛа .Y,. J' IIZ, таю1с, •по
i' = хl+у/+zk.
Чии1:1 :\-.у. z н:вы~нот к:иuрди110111ам11 нсктора
/! 1:1ба:шс:t.: l , ] , k.
JILткo 3~1 п11с:1·1ъ н коор;11111ат:~.~олср::щ1о1 нщ1
ИеК'l'Орамн: t.:CЛ JI 1 11::кторы (i Н h Н llJIOCK<>CT11
11.чеют коор1\11н~1·1N (.У 1 ,у 1 ) 11 (х2 ;у.). а/, - дсi1 -
с·пиrгслыюе чн<.:!10, то коордтшаты 11е 1<торо11
а+ fJ r1 Ла рз 1н1ы соотnетствешю (х 1 + ..-
1:
у 1 +yJ и (Лх,; Л.у,). А11~шоп1ч11ы и формуны !\ЛЯ
вектороR n п.ростра11стве.
1lронзволмrан точха И шюскости (начало
1(00 рднн:~т) и 6:1:.шс 7. } обrаэ)'Ю'I ' <.:нсте.чу ко
о р;.1,ш 1ат на этой 1 uюс.кости. Координаты точ
ю1А в Т1,а1 нюй <.:ttстсме, 1ю опрt:rт_еле1 1 ию, р<tвны
..J()2
щ)()рдишпам вercropa ОА н Rы6рашюl\-t б::~з 11се.
:~а.'.1стим, что есл 11 коорд1шаты точки А -
ВЕКТОРЫ И ГЕОМЕТРИЯ ТРЕУГОЛЬНИКА
С помощью век1uрuв мож110 лu~..аза1'ь несколько
интерес~ 1ых соойстR -, рсугольника. Проведем вект0-
rы ю uентра О описанной окружноrти треугольннка
АВС в ега осрш~111ы. Отлnжнм сумму этих векторов
01 точки О (см. рисунок). Пусть Н - точка, полу
чивш ая( я li pt>.~YЛl>l<ITC ОТКЛс1ЛЫ6<1J·JИS1, i. (:'.
011 = ОА +08+ОС.
rlol'..aн.e!IЛ, ч10 Н - IOЧ'r'.<l nсресечения высnт
(nртоuе-нтр) трсуголь11ика. Заме1им, что
АН= ОН - ОА=ОВ+ОС, u
ВС"' ОС - 08.
Поскольку f)dCCТШIH~1 ~1 ОТ ТОЧl\И о дu etex вер
шин треуголь ник а одинаковы (они μаRны радиу
су !< оnисаннnи окружности),
АНВС=(ОС t081 ЮС-081=
=ос-ов
1
=R
1
-
R1 =о,
т. е. отре~ки АН и ВС nерпс::11д~1кулярны и, з11ачщ
Н лt>жит 11а высоте, оr1ущенной и~ вершиныА. Т~к
же ыжа~ываетrя, •по точка/-/ л1?жит 1ы лвух лруг~1х
BblCO'I ах .
В( гюм11им тсnеμь, что <>ели л 1- точка nepere>·
чения Мt'диан треугольн11ка АНС, то
-
1----
ОЛ1.,,. ) ЮА+08i ОС)
(причем лля лю6011 точки(), R том ч1кле &ля ц~шр;~
опнс..1 111 ю~1 окружное~ и) . Сравни!jJЯ эrо равенство
формулuй (~) ЛЛЯ UpTOЩ.'HTf><I, llaX()ДHM:
он = 30М' Иначе 1-оворя, тос1 кd м 11еж11т Na 01·
резке U/-1 и делнт его в отнnшени11ОЛ1 : М/-/ = 1 :2.
OтpeJof\ ОН н.:~зывают nрямои Энлера.
Г<о~ометрия пмо< .мг~бра
(х1, )'1), а точю1 13 - (х1,)'2). то у вектора АВ -
(х~- Х1 .
.J'1 - у,). ПОСК()ЛЫ<у АВ = ов - ОА. Тпч
JЮ ·1~1к же 011рс11слиютоr коор.ц11нзты в щю
с1 ранст1:1t:.
1)Zih=/JZi,
2) 1i-(Л.b):=Л(1i.fi),
.3) а (fi+c) =n Б+а ё:
4)--
'
,
1-1l
а·а=х-+у-=а ,
Особl'нно удоб~ н ()з:шс j , ) на п1юсюхтт 1
(и:rп базнс 7. ] . k li 1 1 р()С'1 ра11L~п1е), кoтop r,n;r
состп11·1 11э еюrт111чпых rюпартrо 11ер11ендп
ктлярных f\СТ<ТОрон. Такой базис п аз 1,m::~стся
nrя-"юуголы1ым . а соот13етствую щ ая система
коорди11а1 - декартовой.
l'/te ёi. h, ё - щ-юи:нюm,11 ые 1ie1<' 1пры, Л - ттро
и.шолъпос л.еl1 стnнтел.ыюе ч исло. (х; у) - пря
моугольные координ аты вектора а. Свойстnа
1-
. l очень 1юхож1 1 на прав11.rrа дейст.1шй с чш:
ла ми; IB это1·0 слсдус· 1 , что 1.1;щ векторным t 1
выражс~-шямн • 1асто '-'Южно осущсс1·вля 1ъ поч
·1
·11 т:нше же гrреобра:ювэ 111 1я, как 11 Юli\ обыч
ным 11 аm'еfiра1 1 чt:скнм1 1 . 11 ::0'1.'-(ё,ч , 11:1пр11 мср,
ск:m5!рн ы~'i кн~щра·1 ра:тост11 лвух ве 1<тор(щ:
СКАЛЯРНОЕ ПРОИЗВЕЛЕНИ Е
С11лТ1ярuын 11ро11.?неде1-шr.>"м нектаров а 1r Б ,
прЯ :\Ю)'Г'ОЛ1 1 llЫС коо рлнш1 ·1 ы K()10f)l>IX p;;tDIIЫ
(х1• у,) r1 (.> .: 2; у2) , 11 а~ьшаетса ,11,ейстfн.пе11ы10е
ЧJ !С!Ю
(а -Б/ =<a-h)·(1i-h) =
=аu-liь-Ба+ББ=(li)2
- 2li· lJ +(b/
1lря.мо 1rз определения .вытскшот слс,~·ю 1 r11 1c:
сноl!С'ша скаляр IIого 11ро 11 :3нс.:1\с1111я 1:1скторо в.
Уч11тыn:щ с1юl1спю 1. отсюда легко кыраз11·1ъ
с1с;шярIIо<: прот~сш<.:;tсн 1 1 е чсре :3 кнu1tраты ;tm 1н
нскторон 11 раз нос п1 нскторо н.
УРАВН СНИЯ ПРЯМОЙ
и плос кости
В ПРЯМ ОУГОЛЬНЫ Х
КОО РДИН АТАХ
И< пользуем скал ярно!;! п рои 'lвеле-
1111е векторов п ри вьнюле коо рди-
11,ннои формулы для расс1 uяния
()Т ТОЧl\И Д() 11 рямой и урсНIН ~Н И\1
прямой.
Пусть 1- п рямJя на плоскости,
Оху - прямоугольная сисп:мJ ко
орлинат. Рассмотрим про1нволь-
ный вектор n, перпендикулярный
прямой / (такс и вектор на3 ываетrя
нормалью к пр11мой) с координата
ми (а; Ь). Зафиксируем какую
нибуль точку А(х11 ; у11) на прям(>й и
возьмём любую точку Р(х; yJ на
плоскости (см . ри сунок). Расстоя
ние гот Р до прямой / раоно дл ине
перпенди куляра , о пушенного 1н Р
на /, или, что то же самое, АЛ11не
проекuи и отрезка АР на прямую,
перпенди кулярную /. Но .на лли на
равна 1АР cos <р 1, гле <р - угол меж-
лу векторами АР и n (знак модум1
jдесь 11уже н н.з слу ч i1и 1упuго
угла <р). По с1щйпву S скалнрноrо
АРn
nрои1веления, АР со<;<~ - - -
.
11
Координаты вскторJ АР равны
(х -л0; у - Y11j, лли11а нормали
п= \/а ~+h ! . Отсюла, nользуs:~сь
кооры1н итны м оп редел стисм ска
м1 рного п ро изведен ия, полу •1а~:=""
форму"у
la(x -х0)+Ь(у- Yo)I
(=
=
\!а1 + ь1
lax+Ьу·~cl
~а2 + 111
где с= - \ах0 + Ьу11). Точка Р лежит
на п1л1мой 1 тuгда и только тогла,
когла расстояние r = О, т. е. когда
справедливо раве11спю ах + Ьу +
+с= О, гле а и Ь однuвреме 11~ю
не об р а шс1ются в (l (поскольку
n*О). Это и есть уравнЕ>ние пря-
мои в npя'Vloy 1 uлы1 ых коорд11 нат.зх
Нс! ПЛОСКОСТИ.
Аналогич но доказывается, что
любая плоскосп, в n р~...,,оуголы1ыл
коорд11н,пах JdAaeТ( я урав 11ен ис:м
вила,rx+/Jy+с2+ri=О,1ле
(.1; /,; r) * (О; О; О) - коорди наты
н ормам1 к плоскостн . И обрат~ ю.
1кякщ· уравне н 11е TdK<)ГU ви да за
дает плоскость. А расrтон ние r от
точки Р(х; у; z ) до :пш1 плоскuсти
fJЫЧ ИСЛЯt:'ТСЯ по формуле
_
lax +Ьу +CL +dl
'=
.
va} -rb' +с!
Фигуры
в
~-Б
О ~_._,_-=-_ _..,А
Рис. 13.
Рис. 14.
и.т;=Ча.! +ь.!-1а-h1l).
2
Отложпм вектор1,.1 Zl н h от одной 'l'()ЧКН О:
а= ОА. Ь = ОВ(р11с. 1:)). В треуrолы1ике ОАВ
стороны ОЛ 11 ОВ р:н1Ны дл~1щ1м а 11 Ь соответ
с1 ·вующ11х векторов , а сторо~-ш ЛВ - дл~111t: их
ра:шости 1а-Б1· fl(J теореме косинусон , ОА.! +
+08
2
-
ЛВ2
= 20А.ив.cos<р,ще<р=LАИВ.
Сраnннвая эту формулу с 1юследш1.v~ выр<JЖС
юrсм для скал51ртю1·0 1~роиз11сдс11ия, получаем
сщё одно его важ~юс с.1юl!ст1ю·
'5) a ·h = ahcos<p, где <р - угоJ1 между nек
тор<н.ш аи ь.
С!юйство 5 показывает. что С!(алярное 11ро
И:j НеJ..1е н ие поmюс1 · 1,ю 011редетrстся «rео
метрней~ некторон, т. е. их ;u1ию1м.и и направ
ления мн , и не закисит от выбора системы
nрямоуГОЛЬНЫХ кооrдИН<IТ , НtТМОТрЯ I Ja '/'О,
чтu мы вFюдили еrп через координаты. ?.~то
с1юr1ство чаС' 1'О припнма ют за определение
rкалярнпго n роизведсния.
Из сно1!с1·ва 5 также tillдr io, что p;i ненст6о
а - Б =О имеет местотогна и то11ы<0тогю1, когда
nекторы а и Ь взанмно перпеr~дикулярны
(вектор 5 считается перпендикулярным любо
му другш.rу). А значит, прнnычпая нам опера
ция сокращеIJия на общий множитель в случае
скалярнш·о ум110же11ин незаконна: из раnенства
li Б =с Ь слеJ1у_sт 1111шь. что вектор а - с пер
пендикулярен Ь , а COIKCf\1 не ТО, ЧТО а= С.
Прияедём сщё ою11-1 прl[мер некrорноrо
f'О 1\азатеm,ета rсометрнческой теоремы. Ле1·
ко пронер1. п11 тождество
сп+ h)2 +(а-Ь)2 = 2са-'- + ь~) .
На гсомстрпчсском языке (рнс 14) 0110 пре
нр:~щ:~ется в так н<Jзынасмос равсвстnо nарап
леJ1ограмма: сумма квадратов диагонзлсй па
раллелограмма равна сумме ква;~ра ·1·он нсех Cl'O
сторон.
Скалярное 11роизведеr 1 ис всктороu в про
стра11с1·не онредсляется ·~ак же, как на плоско
стт1. Если вею·оры а и Ь ~1 мею1 коордиr-1аты
(X1;J11: z 1) н (.У1;у2 ; z 2 ) в прямоуголыюм ба:знсе.
то их скалярное про11зnеде11ие равно
Zf. [? := .\"1.Х1 + .'1'1У2 + Z1Z~
Снойства l - 5, 11р1шедё1шые вьппе, выпол-
1-1яются н для нектаров в 11 ростр:шствс, толь
ко ДJIНII<I tlCК'l'Op:.t li с прнмоуГОJ l hНЫМИ коор
дннатам11 (х; у; z ) ~н,1числяется теr~с:рь по
фоrмул~
Многоликая геометрия
МНОГОЛИКАЯ ГЕОМЕТРИЯ
ДВИЖЕНИЯ
Древ11егречесю1r1 математнк Фалес для доказа
тельства гео.метрическнх теорем 11010;11,:ювал
двюксния (см . статью «Фалее и первые )'{оказа
тельства» ). 1lапрн.м.ер, две половш1КI1 равнобс)'{
ренного треугольника совмещаются с по
\ЮЩhю ис&вой симметрии - псрсгибання
чертеж:~ (по биссектр11сс угла при вершине;
р11с. 1), 3 потому онн ранны. Как <.:ЛС/{СТВИС ПС.)
лучаем , ч1 о углы пр11 uсн.оватш рзnнобед
решюm треугольник:~ р:.1nн 1,1 между coбoll .
R этом рассуждсюш мы nредстанлясм себе,
ч10 одна П()J1()нн11ю1. треугольника передт1га
ется. как твёрдое цел()е, т. е. Rез изме11е11ня
расстоя11ий между точ1(ам11, и совмещается со
второй половинкой. Преобразовашrе фнrур.
лр11 котором сохраняются расстояния между
точкам11, называется двuJ1со1ше.111 (о других
видах преобразонаний см. статью <-Геометрия
11 гру11пы 11реобр<1зUВ<!НИЙ»). Мы l'Онорим, что
;\Ве фи1уры равны. еслп их можно со в м<:<..1·11·1ъ
;~в11же 1 1ием В частност11, симметрнчные отно
аrтельтю пен фюуры равны · не11,ь осевая снм-
11етrшя - O/\И ll 11 :1 l'IНJ \OH дRижсш 1 й.. Налример.
две поло1тнкп кру1·::~, разделfнные диамt·тром,
снм.\1е'1 рич11ы о·гноснтельно д11аме1ра 11 1ютu
му р:шны (1 1 ескот,ко следс11ш1·1 11з ::1·1·u1·u факт;1
~южно найти в ста·1ъе «Окру,кность н кру1"")
Фа;1ес применял r1 f1.ру1 ·ой ннд дR 1 Jжс11ш1 -
повортп Нанример , чтобы 11сжа:за·111 р;шснп щ>
вертш<алы rых углов, 011 nоворач11вал 11зюскостr,
чертежа на 18/J" nокру1 · некоторой точки О.
При: этом 1ю1юротс· (его ещё назьшают 1{(! 11111 -
ралыюП си.111.метрией с центром О) r<аждая
точка А псрсмt:щаетоr в такую точк·у А', что О
Рис 1.
Ч()5
Фигуры
13
1во·
Р11с. 2.
PttC. 3.
янляется серединой отрезка .11А' (рис. 2) . Вся
ю11'r луч. исхом1щий из точка И, персходпт в
противополuжньu1 луч, т. е. луч с те:-.1 же нача
лом О, составляющ11й нмсстс с нс:ходнhlм лу
чом ценую 11рямую.
ФdJle<: r;,iccyжд~UI так nусть () - пбщая нep
JllJIH<I верт11каньных у1 ·ловАОВ 11А'ОВ
1
• Пояер
нt:м ПЛОСКОСТТ1 Чt:fУГС'Ж<I tta НЮ0 нuкру1· ' l 'OLJIOI
О. То1·да ; 1 ~ 0111 1 ерейдёт в щхпшюrюлож111.1й
ему луч ОА', а луч ОВ - в прот11вополтюrый
ему луч ОВ' (рис. )). Эпачит, уrол АОВ перехо
дит в вертикюrьпый угол А'()JЗ'. Итак од1111 из
двух нертикальных углов совмещается в резуль
тате поnорота с другнм. Т:11< как поворот пред
ставляет собой двшке1 шс, кажд;u~ фшур:.111ере
ходит 11ри поворuте в ранную t:i'J фигуру, а
nuтому rн::ртик: 1т,ные утлы равны.
Пр11менял Фал.ее и сщё одно днижс1:шс -
парал.лелtiНьtй пере-нос. При параллельном пере
носе все точкн фтуры смещаются н определё11-
1юм 11апра11ле1 111и 11а одно и то же расстоя 1111е
(р11с. 4). Иметпю с гюмощыо такого ,f"\nижспия
Фалес l\ОТ<азал предложе1ше, которое сейчас в
учебниках называют meopc.лt0t'.f Фалесс1. Оно
состоит о следу1ощем (рис. ') ):
Если на одной стороне угла опю
житъ равuые отрезки и провести
через концы этих о'I'резков парал
лельные пря~rые до пересечения со
второй стороной у~·ла, то ва дру1·ой
стороне угла 1·акже получ атся рав
ные отрезки.
Фалес заметил, что сосед1ше параллельные
прЯ1'1ые высекают из угла трапецию, которую
можно ра:>битъ н а парал:лс.rюrрамм и трсуголь-
1шк. Для дока:щтсльствн теоремы надо бьuю
406
уста1 IOHИ' l I>, ч·1·0 все ·1·акие "f'l1e)'TOЛl>l lllIO1p:ll3HJ1I .
и ОI!И ,J\еЙСТIШТСЛЫЮ равны, поскольку 01\lllJ
треуrолышк получается из другого некоторым
ДFJиже1rием. а именно параллельным перено
сом в паправлешш второй сторош,r yrл:i.
Итак, мы познакомились с тремя вщрм11
/\f~Ижен111~1 - осекой снмметμнсй , 1ю1:Юротом
(на примере це1-1·1ра.rtьной снммt:трш·1) и п:с~рал
лсльны ."'1 переносом . Дальше будет Гiоказано,
как с их помощью можно pt11Ja'1ъ ра:Jнообраз-
11t>1е 1 ·еометричес1<не за1щчи. Есть ещё ощ111 шщ
л.nижепия - так пазьгваемзя с1-;оль:тщая cщi
.J\.tempuя. Это преобразование состопт в том,
что лоследователыю выполш1ются осевая сим
метрия, а затем параллельный перепое 11 на
правлсню1 оси с11ммстрип (р11с 6). А есть ещё
к<1к 11 е-н 11 бу1 ~1, 1ш1щ ;1к11жен 11 й? Может быть.
y; 1ac·1·cj.j 1юлучfl'LЪ что-то 1юное, ес11и скомби-
11 нр()на1ъ несколько 1юноротов с ра111ымf1
нснтрамr1 r1 JП1 поворот с осс1юl1 с1· 1ммt·тр11сJ1i
Ок:.1.j 1,1 ваt:тся , 1н::т' R XIX н. фr;1н11у:к·ю 111 1то
ме-1 р МИ 1Ue,1 1> 111 ат, /\ОКЗ Зал:
Всякое движение плоскости лвля ·
ется либо осевой симметрией, либо
поворотом , либо параллельным
переносом, либо скользящей сим
ме'rрисй.
1Ja11rнмер, ВЬПЮЛI lIO{ ПОСЛС[~l)Н:11'СЛЫ 1О Пl)li()·
рот и перенос , ,\1Ы сно1:1а получr1м ппворот на
тот же )ТОЛ. только с друrнм центром . а пово·
рот 11 скош,зящая с11мметрш1 даду1 · н результа
те с1<оm.:~я111,ую с 1 1мметр11ю с другоГ1 псыо.
13олее тоrо. если нарнсовать на плоскостп про
извольную фигуру, оырезат~.. из б) магн ее
коnшо, ::i з::~тсм положить эту копню ш1 плос
кость совсршсшю случай11ым образом (и лю·
бой стороной кверху), то ВССГД~I MOЖIIO СОВМС·
ст1пь орш·инш1 с кшшеlJ одним нз д~шжеш 1й.
щ:речисленных 11 теорем е Шаля
Рис. 4 . В1,~д1Jиr ,1я ящиk
ГГ()Лсl , мы(}( УШР ПRЛЯ~~,,.,
n.~рамеды11..1r1 п~ренuL.
СU.Л1Мf'111/ШЛ
Рнr. 5.
Рис. Ь.
'
'
'
''
'
,,.,...,
llflliOjJиm У. И
Ф~1щамептзлыrую рот, ДJJ1-1жеш11'1 (11 вооб
ще rеометриче~ю1х преобrазоnаш1й) J3 пони
~1ашш того. что такое t'еометрия, оп<рыл rте
\JСцю 1й .-.1:1 тсматю< XJX n. Фt:лн кс Клейн (см.
ст~тыо «Гсом1.:трия 111'р)'ППЫ 1 1 рсобр:~:.юнаний~).
Hu нсрнёмся к матt:м.~т11ке Древ11t'го м11р;.1.
Ес:1и итtс11 Ф:м<.:с:~ 6;1нз1ш к сонрсмснно му LJО-
11щ·1анию 1 ·епметриr 1 н [(уХС Кле1111а. то Евклитt
в своих «НачаJ 1 ах-> rтридt'ржпвался и 1юй тпчк11
зрешш на J\·1етоны доказательств<t тс()рем 11
решення задач. Подход Епющда был сх:1юn<1п
на раnспстnс треугольников .
Вr 1 рочсм, в самом па<1алс. 11р11 доказатель
стве пр 11знакон р;шсщ:тnа трсу1·ольникон, fвк
, 11.1д nш1ь:юR~urся 1щес 11 дниже 1 JJ tя . J I:..t 11 р11 мер, 1ю
второ.11ч• 1t/J1.1311tдJ'.. ранt.:нстна треуrолы 1 ико11,
ест 1 два трсуголы1ика имсют no одной 1хншо~:-1
стпро 11е- и соптвсrстнснно р:ан11ые угпы , приле
жащие 1< этой стпро11е, ·1·0 1·акие треу 1 ·оm, 11и ки
раnны . Дока:~атслъст1ю F.ню1 ид проволил слет
ЮЩ l lМ образом. Пусть в треу 1 ·олышка_х ЛЕС и
А 1В1С1 рав111.1 стороньи1В и.А1В1 и углы прн вер
шинахА 11А1•В иВ1 (рис. 7,а) Наложим трс
)Тuлы1нкА1В1С1 на трсу1·ольн11кАВСтак, чтобы
сон11али рашrыt.: с..:торuны АН и А 1В 1 . 11р 11 чём
точка/\ 1совмсстнлась с .- 1, точка В 1- с Н, а трс
уl'Олышкн оказалось по одну сторону от
АВ =: /l 1H 1 (р11с. 7 , б). Тоща вс11едст1111е ранснства
}ТЛОR ((ЮТ13СТС1t1e1 11 Ю СОН\НХТЯТСS1 н луч~ 1, С()
:~ержащис лве лруп 1 е стnроны каж/\()Г() 11 з
трсуголышкоu. а потому н обе вершины С и С 1
попадут в точку их 11ересечсния. т. с. треу1·оль
н11ю 1 совместятся вссмн с~>о11м11 вср 111 ю1а;-ош.
Gr1 едо н~1 · 1·с1 1 ьно . эn-1 трсуголпникн равны.
Но н<::дь •11~1Jюж11ть один трсу 1 ·u1 11-~нt-1к на
друr·ой ? о;та L[<ft''t 11 ере .'-'Н:~стить с1·0 поrюбно
т11ёрж1му цсJюму , т. с. примещ1'1ъ нщ1жсн11е~
:Здес ь, кз1< н r1рн дпкааа'r'елt>стве 1 1ру 1 · нх 11риэн:с1-
кон раnепстnа треуrоJ1ы 1и~ю1~. Еnк11ил прн; ,ержи
вался идей Фмеса. Ол;т1ако, 11 оскольку понятие
·наложение" Евклид не опрсл:елял, в рамках его
аксиомапrюr это былн, строго гunоря, 11е дока-
Рис. 7.
М1юголнкJя геомс1рия
~~'',,, __ _
~',~"
Пt1/JСИ7еЛЫ/Ы[/
llC'fl(' lf()L
(~
/
(.'~:(/'11>1}1.ll((IЯ
(/t 11. i/l.!111/Jll>I
затеды.:тва, а ПОЯСJТС I ГИЯ, I JСПО!lЬЗу10ЩИС обраще
Шll' к нашt:му IIOHCCДllCВIIOMy оnыту.
IJ< >как · 1·om,кu прн:шаю1 равснс1·ка треуголь
ников ccjщp:чy.'Jllf)(JH:I HЫ 1·1 ПОЯСJIСНЫ, EHК:llIД в
сншrх <· Начэла,\.·} ктщё'1' 11менно 11х н ос:1юну 1ю
слt'дующ1 I X 1'0K<IЗ<ITCJIЪC"l 8 н C J'(X'\tl IТСЯ пр< )1:10-
ю пъ nce рассуж1tе1111я как можно более t-1 тю1 ·0.
уже ([С ВСПОМИГ l (j}\ () ДIНIЖСIП IЯХ (<·l l ЗJIOЖt' I IНЯХ• ) .
R ка честnе пр11мсра срав 1 11щ рсте11ш1 од
ной и той же задач 11 по Фалесу 1J 110 Ешv111т·.
Зада•Iа 1. В тр.111<::цш1 AlJW углы 11ри 11шютсм
uc но ваш ш А/3 равны. До1'аJать , ч1 о бuкuвыс
сторо 11ы тра11с 1 ~г 11 1 равны.
Фале::<.: рассуждал Gы так. Прuнсдём пt.:рпсн
д11куляр к 111IЖ!н.:му оснонаш 1ю чtрt>з t.то сt.:рt.:
д11ну (рТIС. R. а). Чертёж симме1·р1 1ч е11 от 1 юс11-
те11ыю провсдё111юl1 11ря1110[1 Иначе 1'()1юря,
б
А
А.В
Рис. 8.
407
Фигуры
ссл1r м 1 .1 nереп 1 t:м чертеж no д:11 пюl1 11рямоi1,
' 1о поло111шю 1 r 1и ж.11его псноnаrп тя соnмссппся.
з 11отому (нследстт 1е panc 1 1ства углов нрн 1rнж
нсм ос1юш1111ш) 601<оnые стороны окажутся нз
одном лучt с 11 ач:шом n точке, в которую 11011:1-
~т обе n<.:ршш tы Ан В (рис 8, 6). Ч;н.:ти верх-
11t1·0 OC IJ UB;J.HШl ' l '~ll<ЖC будут H~I XO/ t ИT l>CЯ 11'1
одном луче. ~1 1uчJ 1'1. кшщ1,1 С 11 D нсрх1-1с1'0
()Cl-IOR3111lJ.I ГIOШlflYT н точку псресе чt:ння ЭTl l X
:1yчelr. Таю1м обrа:юм, боко11ыс сто1ю1 rы тр::~ -
1тец1 11 1 соnместя1·ся, т. е. 0 1111 р:нты.
ДСЖЗЗ:lТеЛЪСТВО В лухе Енкmща ПЫГЛНДJП
111шче. Проведём 11е рпещщкуляр к 1ш.жr1сму
ос rюваш110 11В через е1'0 ccpcn:r 1tiy 1iI. Uбu~·ша
чнм через 1-' точку п сресечсння 11српенди-
1')'JШ\)~1 с нерхни м <Jснованисм (р~-к:. 9). r 1rю
.вс.:1 1t:м uтpe:{IO·f t1P 1[ ЛР. тш·да ЛАJ!р = ЛВ.lfР 11()
дl:3)'М сторонам и }'гл у между н нл~11 (er'urю11 1 .1 АМ
11 ВМ [ХIШ 1ы по 11ос1росн11ю, tтop()1 t<1 ,1f? Рбщая,
уты 11МР 11ВМР ра1111ы: онп 1 1рнмыс) . 31 13.Чl !Т, и
осталы 1 1 ,1е ::~леме1 1ты эт 11 х треугольшнюn рав-
1 1 ы - зеJ1ё11ые у1·ны. сш тне углы, стороны АР и
РН. Тепер1, расоютрим ещё O/\I ry аару треуголь
ш~ков: LШР и fJCP. У них равны с10ро111>1 А/} и
PJJ, углы, 11рилсж:rщ11с к НlI M, тоже соuтвст
стн-ешю ракны (t:сл11 от равных }.лежду собu(1
y1"l10I:\ 11 р11 ос нона 1 11111 трапt: 1 ~1н1 от11я1ъ ра 1шы<..:
зснёныс у 1· лы, то u<.:тан 1ш н.:01. рuзuныс утлы
будут также ра в t-1 ы; а 11 ало1· 1 rч 1 ю уста1-1аnлнва
~1'СS\ \)"З.\~~\-\С't\'.\.1 жtrпых '{ПЮ\\). Зн"З.Ч.\П , Н() ""о-
рому при3н аку р:rвt.:нстuа, трсу~·олып1К1 1 AJ.)P11
ВСР ран 1 1ы . Слсдо 11 ателыю, 11 оста11ы1ыс эле
ме11· 1 · 1.1 да11 11ы х трсуголып-11<011 соотnстствеп110
рашIЪ1, В частпосш - боковы е (красные) сто
роны трапсц1 1 и.
Это р~1 ссу:жде н 11е тш1ично ДЛ}{ E1ж.r1иrta: для
установт.::н 1ш к:.1 "0 1 ·u -либо 1'еометр11чt:скоп)
с\х1кта н~tд() рассмо·1· rе1ъодну п~р) трс::у1 ·ш1ы 111-
ко к 11 /(оказ: 1ть. что 011и равны. зате.м J1[)у 1 ·ую
пару трt:у1'олын1кон, t:0111 надо , то и третыо,
11ока нс ()удеr пrтуч.ен требуем 1,1 й peзyJШl':J ' I'.
D
'Р
N
А
в
\>и с. <\.
\>и с. 10.
408
R любом учс61111ке гсометрш 1 вы 1rail1 tётe
много док:~зательстn теорем 11 peшcr111 i 1 зад~ч
с номо щ1. ю 11р11знакоn раuенства трt'уrоль ш1 -
коn - t'ШVТТЩОВСкая тр;,1д11цил J!ЗЛОЖСНИЯ rco-
M<..:TpI 11 1 жнва /(О сих пир. Во тс:: же pcзyJlhTarы
МОЖ.НО llOJIYЧJПh И С \l(IM(.)ЩhIO l 'СО Ме'1'[1ИЧС::С!\НХ
нр<:образонан 1 1й. Р: н.:смотрнм сщё несколько
·:Juлач. которые рt:ш 1 1~1 П<) ФaJJecy.
Задаqа 2. f f;1 боковых сторm1ах AR 11 ВС тrе
уголыш 1<::1 .АВС построены нпе е1 ·0 тшадраты
AШl.JN и BCPQ. Дока3<tть. что отрезки С\1 и QA
равt1ы и перпс 1щнкущ1рrrы (рис. 1 О, П).
Дo<."l '(lTOЧIIO ,цокаЗ<IТI,, Ч'l'() С) щсству<.·т l(()B()-
(JOT на 90°, который 1н: ре во,ц r1 т отре:юк С.:11 в
О'l'р<.::юк QA ~C'Th ' l '()Jl\;KtJ )Щ~\ ПОl~ОрОТ't.1 на Q0°,
F1 резуJ11,т<1.·п: которых ·r·оч к::~ С 1 1 ерехол 1 п 11 тач
ку Q : нокру1 цetl'lp:oi В (i1ротнв часtтой стрtл-
1<11) 11 вокру1 Р (по часово1'1 с-1,рет.;е ) . Оч:е 1нщ1ю,
что 1 1ри поnороте Аокруг В точш1 М гюпадаст в
Л. 1301·, собстнешю, и nсё: указа ~ шыi1 пово рот
nереводнт отрезок Ci\J в отрс:ю1< QA, а значит,
даш1ыс отрсзю 1 рав11h1 (поворот - дт1жt:нне)
и пер11е1-щикут1раы (}Тол uонорота раве н !10°),
llе 11 ос рсдстнснно 1 1з ЭТОl 'И рl:ш<.:шш мuжuо
нзвн<::чь в дру1· нt: заслуж1ш~нощш: L\Юtм:шня
сноl1с.:тва р;:ксматринжма\t фигуры . llапримср.
есл 11 Кн L - ссрсд111 1ы отрезков СМ 1111Q соот
не1·ствс:н1-ю (р11с. 10, 6) тп треу1 ·nлы 1 111< BКL
H\)'1\.V.()~f\'\\ J\Ы\Ъ\\:\ \\ \}'.\."-\\C)Ge\l,\)~\\\\\,\\\ \\'. \ .\(. ~V.
ю ч ка К 1 rерсходт1т11 L nрп ·rом же повороте на
<)Qa 130Крут R),
В след,,1ощем при.мере мы с помощью од·
rю1·0 преобразования докажем сразу три из·
вестных свойства ш1раJ 1.11t'лО 1 'р:tмм;:1,
З адача 3. Доказать. что н 11щ1аmН:·ло1 ·раммt
1) ·1 очка 1 1 ересt.:чении дпагnщ1лс ~-1 де111 1т
1 1х пnполам:
2) п1ют111юполож11ыс стороны равн ы;
3) ГIJХ1ТИIЮ1ЮЛОЖ11Ыt: утлы р:.шrrы.
1~
,\'
Нэм nона;tОВ11то1 следующее лросте сnой
ство цс 1прапт..11о r 1 с 1тмь1стрии:
,~. Если nрЯl\1ые l и т с~1метрищ1ы от
\( носитеды10 не1,оторой точки О, то
они лараллСJJЬНЫ (Н.1111: СОВ1JЗД:1Ю'J').
:-Это снойстRо НЫ'J'екзет нз того, что м11пжес·1 ·н(1
общ нх точек прямых/ и т с11мметричfю сп-
1юс111т1 11)но О, <1 чере:-1 j\fie раз11нч111>1е 'rочю 1
можпо провести только OДII)' прямуто.
Пусть i·enep1, ABCD - параллелограмм.
~lронедём в нём l\Шl rональ 11G' и обозначк""'1
LJt:pt::J О сё ссрсд1шу (рос 1 1, а). При снммст
рuи OTHOCHTCJIЫIO о 11p>1Ma}I 1::::: АВ ш:рt'ХОДИТ
в параллсл1.ную ей прямую т. 11ролtщЯЩ)Ю
•~срез точ"'У С. Ни, п о uщх.:делс1 шю п;~ р:uтс::
ло1·рамма, с1·0 11рот11воп олож1-1ыс егороны nа
раллс:лы 1ы: следонателы ю, т := CD, ·1 · . с. пря
мые АВ и СО симметри чны о·пюси· 1·СJ1 ыю О.
Точ но ·гаt( же прямые AD и ВС симмс:трнч1 1ы
ттюсителыю О. А ~шачит, и nec1, нараллело
rрамм. симметриясн отнvснтеJlьно точкн О. То
естьпетолькоА нС. нои вершнпьrВнJJ сим
ыетрнчны отн щ;итслыrо И. а дщ1гональ ВО
nрuход11т через точку О и дбштся R н.сй 110110-
:r::rм . Снойст1.ю 1 доказано Прн с 11 .чJ"1сJр 1ш от
н ск·1л CJlЫIO О к:1ждан <:торон:J пс1х:хою1т н
nрот11нополuжну 1u сторо ну, и~i че1·0 сщ:дует
сrюйспю 2, а каж1~ы ~'1 у1·011 - 11 проп11ю1юлпж-
11ыlr уrол. чем лока:-з 1-,тается снойс1 гю 5.
П uпупю nалуч<Iем ещё дn:::i утверждеш 1 я.
непосрсдствепно в ытекающие оз с1·1:\1метрич
воспf на раллело1рамм:::~ от1 юснтельrю точ1а r О:
- l) бнссеh-трисы nрот11воп0Jюжных углоr1 nа
раллелогμамм:l пщхщлсльны; 5) любая нрямая,
прuхо;.щщая через точку О, 1 1 сресск:~е1 с 1 ·0 по
отрезку, которы1'i /\С.1t1·1 тся в э·1 ой точке попо
лам (рис. 1 1, б).
М н оr<)Аикая геометр11я
Р11с. 11 .
Л рнме 11е1111е f(о11жс 1 1ш) - од1 11 1 11з С'амых
эффсю'ш1ных :мето;~ов рсшсння :1ад~ч на но
с:трuе 1тис:, н чём .мuж~-ю убсдтъс:я н~1 слс:дую-
11~ ем 11p11 мt'pt'
Задача 4. Постr(11пъ paн1roc·1·oroн1111 i'1 трс:
,_тот, н11к . одна нсрш1111:1 которого лсж 11·1 в з;.~
дэ11 1 юЛ ·~·о ч ке А :1 /\НС друпrс - соот11е·1с·1ве~1 -
1[() !Са /\В]'Х да 1 ll!Ы X: ()Круж1 IO('T}IX.
П ус1' ь АВС - искомый треу1·олы r нк
( ри с. 12. а). Пос1<011ьк~· OJI JXIJJI IOCTOJ10JIJШЙ.
11ри 1101юроте во!'--ру1· точкн А на 60° точr<:а В
п ерсй,rr.ёт n точку С. Но точ 1<а В лолжr1а лежать
11а о;~ной н:J даrшых lжружностс:й (11а нашем
рисунке - 11 1с1 t'()Лубой). 11о~~тому l>бр;.~з В нрн
1 ~оноро·1 ·е, т. <:. точка С, ,1.ЮJ 1 же н <.жа:J<1т 1,сн на
фиг~1ре. я которую rrc:pcй:J.fт 1 'ш1у\1ая ш<руж-
1-юс1ъ; это о кr~ж1юс1·r, 101'0 же рал11ус~1 tна
р11су1-11<е 011а ~~t:лёнзя; ри с. 12, 6). Л rю услони ю,
С пахоюпся 11:1 1л·ороl! 1~JТ1 1 1011 окружности -
кра<.' 1 юй. С::Ле!!.с>пателыю. С есть точка пересе
чения зслёrюй и крае~ юй окружностей. Теnеръ
мы :знаем, как rтостроит1, (.' (ct зтщчнт, аlЗ) До
статоч но провсст 1 1 зслён~'Ю окруж110ст1, (сё
центр 0 1 - обrх1з 1\t:нтра О !'(Шубой окру-.iКно
сти 1 1 р11 рассмотр енно м 1лJ1.юрон.· 11 стрu11тсн
как нерши11;.i равное~ щх 1 1-111с::1 ·0 ·1 ·1x')TOJ11.1il rка
АОО 1 ). TonJ.;.1 С -точка 11еrессчення зелён()й i1
-Ю9
Фигуры
кр::~стюl1 ()Кружнсктсй. Лnе ОJЧ)у?Кrюст1 1 мо1уr
.иметь дuе общнс· точки, од11у нли ни одной;
стоJrыю же решсшн1 д~1ёт указа нное построе
н1 rе. Но при пuдсчЕтс ч11сла рсшс1шй з~щ<1 1 1И
Lrадо учсс·1ъ н то, что мы рассмо· 1 рс:л1 1 ·1
· 011 ько
одно tЮЗNrожное н<1 1тра н11сt 111 с r юнорота ( 1 1ро
т1 1 в часов<>й стрелки). Атрсугол1,1111кА8Сбудст
р:н1нос·1п1)()ннн м н то1·ла, коmа точк;~ С пере
хою1т н В пр11 по2юроте вокрут А 11а 60"' по
часоноСi стрелке. ~ 1 1ачн1', псхолш~н з.tдзча М()
жет rl1\-1еть до четырёх рсшеш1i1 (рнс. 1.! . , в).
ВЫПУКЛЫЕ ФИГУРЫ
Тсор1н1 выпуклых ф 1 1ryp бы11а со:здана н а рубе
же XlX 11 ХХ е1·олс·п11l 1-к:ме1(ю1м м<1тем~пи1юv1
Гt.:рманом м~11 1 1<0нским . J!.m':<l:1:НII1 1 .1 c 11~ изнщ
ные теоремы() снт1ст1:1:1х выпуклых фиt)1) пр11-
нлеклн к себе ш 1нма11пс м1юп1х \13Тематнкоu.
Однако 11сI<оторые иэ них отнеслись к 1ю1юй
теорпн кр11тнчссю 1. Оrш счпталп. что в матс
матнкс главную рол 1, ш· рают 11а1 1 равж.: 1-11 1 я,
nажн 1.1е wщ фн :шк11, т<.:х1-111кн 11 дру1 ·11х «1 1 р11-
юш,r~. 1 1ых" областс:й 11ауки. А т<.:ории ны1 1 уклъ1х
ф1 11·ур нто время казалас1, нм Rtсьма J\а11~ко 1\
от такнх nршюжсний. И 1 1а 1 111н1сь учёные, ко-
1·орьн: ;~а>1 1нm11. что тtория }\.fщшonc1<0ro -
оче 11ъ краснная 11 п ртнще кателы ~ ая . 1ю соnер
шспт ю бесполезнан 1·еоr-1етрическая 1~ гру ш ка.
Прошло столетl!е. н «ш·рушr<:-t -> М 1 r111швского
превратилас1, n мощн ое оμужнс. 11спш 1 ьзус:мое
па персдн с.м крае науки. 01-1~1 c 1·af(a нажн6111шм
ине1 · ру,\н.: 1 tтом тсор<::тн чс.::ской 11 11 рн кладно 1'l
. l l<J:l'J 'CM>J'J 'J JK) 1. Сонремснн:1я м~1тc:v1:iTJJYCl'J{;j}J ЭК()-
1юм 1 1 ка, мате м атнчсск::~н теория у11раш1ст11 '1Я 11
мно1" не дру1· не н~правлеt 11 rя 11аук11 все 1 ~ело
осrтоны1~аютс>1 rra 1юнятш1х , 1 щс:ях 11 rvteтoдax
теор1-1 11 въmуЮiых фи~·ур . [l(};~пакомпмся с э·1·и
мн поrrятнямн и идеsr."1н .
llepnoe п редставлсщrе о выпуклых ф r 1rypax
,'>ЮЖIЮ получ1 rrь, рассм~1трнnая м11огоуголытн -
41()
Расоютрсrшые э:щачн. ка1< 11 J\pyrш~ случан
прнмеllсrпш ;{mtже1тй (01. статью ,,задач11 на
гrострос11ие " ), ш1люс1·р11руют тот факт. что все
прс; 1лож<.:нш1 1·сомс:::трии могу~· бытh 1юк:1Заны
11 <.: помощью 11р1-1 зш1 ко11 ране11ства тμeyruJГh·
1-l l ll<OK, 11 С JЮМОЩЬЮ /~F:llJЖCHИIJ. HTO[IOI\ CIIO·
со(') 1!C p t:/\l<O пrощс:. fioJН:t Тt>ГО , IЩСЯ ('1L.\\MC1'·
р~ 1 и, Т1 1н 1 жt·ния. f\(Ю(} щс:: 11 рео()расю1 1й 11и я стащ1
11е()т1,емлf:мnfl соста1ыяю щей ('()Време1шт1
м~1тематпю1 11 фн:-111ки (см. статыо <·Геометрия
и группы 11реобразона1пrй>}) .
кн . Мно1пупт 1 ,r 1 ик 11<Н1>1па rот нr,тпукm,ш , еслн 011
11,елнком распо.rюжеп 1ro 011r1y стСJротrу от nря·
мой.. содержаще~'r лЮ6)1О его сторон} (рнс 1. а)
В 11евьшуююм многоуголъшшс хотя бы одна
сторона при се 11ро,1олжс1ш11 разрс:;)<1ет '-i!IOГO·
~толы1ик 1ra части (р11с. J, б) Если JJ-}IJ'UJJhHHJ\
вь111ую1ыl1 , то /\liaI'OH:JЛll, l lf)OBC/ \ёHHblt.' нз 0/\llOJJ
всрнrины, разбнкlю'1 с 1 ·0 1 1а 11 - 2. трсу1олhн11ю1
(рис 2). Слс1юв:1тсJ11>1-ю. сум~1а с1·0 1шуrр<:нннх
Yl 'J IOB rав 1 1з (n - 2). 180° Для l ll:BblllYКJIOГO
п-уголы 1ика это тоже нt.'рно . 110 J\ОКJзыв:~ется
1·ора:що C'JIOЖllCC
Общее ттределсште вы1~у·кло.И фш)'j)Ы (nри
год11ое нс толыю длн :мrюrоу~ 'оль11111\ов) фор
мулнруетсн та к ф1 пура /<' 1rазывается аы111 1клоi1,
еслн для пюбы.х её двух точскл 11 В и1·рсзокАВ
цел нком coдep)IOI'l 'CH в фкгурt' f' (рнс 5. rJ). В
н&вы11;1·11лоп ф111урt' F н:111нутся ·1<;Lкш· J(fie точ·
кн, что соед11нюш111 1 й 1rx отрезок не шдер
жнтся цсщж<>м н ф1 11 урс Р (rнс .1, 6). Нетрудно
/\О1<аэат1" чт< 1 нсию11'\ тре~толы11 11\ - ф1rryp3
m.1 гrук.г1зя , T()l'f\::t как четырёхугш 1 ып 1ю 161,mшm
~<а.к 1i1,туютътt:, ·r·а к и 11t::вьшуклыс (р11с. ..J .). Кр}т.
а таюке ссгме11т 1<ру1·а - ф11rуры uыпуклые
(рис '5, а) . Сектор кр~rа (р1к. 5, б) может бьпъ
и нев1 .шук1ьщ (сели с 1·0 1~ентрал1111ый у1'ол
бощ, ш е 180"). Р;н..:сматр11вают 11 нсо1'раничен-
Р11с. 4.
Р11с. 5.
11ые (простнраrощ11есл в бесконечности) ны-
11укт.1е фигуры: острый и развёрнутый уr!1Ы -
6ыnуклыс фнгуры (рнс. 6, с/.), а угол. большш'i
paзnёprry1·oгu (рис 6, б), - 11<.:вьп 1уклая ф11.гура .
Полск:а (ч:кт 1, плоскuст11 между двумн nарал
;rсльным1 1 прямым 1 1 ; р 1 к. с1, в) также 11curp:mн
Llc11нaя выnукпш1 с\лнура.
Вел сщё нримеры: ф11гуры, ограr1J1ченные
эJrm111coм, параболой !1 111пербn1101'1 (рнс. 7}
Любоi1 эллнnс огратrч11nает r11_,1пук.1ту1() фнrу
ру. Парабол;:~ разбивает плоскость па дnе о\Jла
о и, одна и::1 которых выпук.:tая. У rипtрболы
кажд;tя из ветвей огранич r шаст .вы11j101у10 фи
гуру, а обе nмtсте служат границе!"~ нсныnук
по11 шюской обт1ст11.
Расс,..,штрим 11оннт 11я, сннэ<~нныс с располо
жением точек 11 пр.имых относител 1~но вьтук
лой ф1 1Jуры.
Точка ,н Н <t3ыв:н:тся ШLJ'IUjJettНe!I l!IOЧrJ>rl
ф111уры F, есю 1 крут с 1~ентром Ми достаточно
~ta.rrым радиусом цетrко~1 содержится в фи 1 у
ре F (рис. 8). Если же шобой кру1· с центром в
некоторой точкt: В пт<пючает в себя и ТО"П<Н,
принадлежа щ не фтпуре F, н точки ей rre прп
на.цлежащпс, то В называется ?рtmичной точ
кой фи 1 урhl JJ. М1южсстко Rcc:x 1 ·1х1н11чнь1х то
чек 1 1rсдставляет собой грииицу фигуры Р
(Данные определения. примсн11мы к любым,
нс обязателы-ю выпук..r1 ы1111, ф1 11 урам .) О!fифы
тый ~<руг радиуса г (м r южество ксех точсJ<, на
ход>1щнхся т· цt:нтра па расстоянн11, ме1rыш.:м
М1юголик..~н геометрия
1·; р11с С)) - выпуклое м11ожество, в которт.1 11е
содержится пи ощюl1 гравич1юn точ.кн. Прн
сосднлн.в 1< нс.чу nce его граничные точют, ло
лучп.v~ :за.мкнутый кр}т. В далыrсйтем 1•1ы
булем 1 ·01юр11ть тuлы<u о .Jамлнуты,\' (jЬf/{J't>:лы.Y
фигурах, т. с. такнх, которые сuдержnт всt: с1ю11
rра1111чныс Т{)ЧК\1.
Укажем дка доноm,но простых оюirства
IJJJ~тpeш11 1 x f/ 1"pЗ1!1flfl J ЫX ТОЧt:К:
1. Пусп. /1
nf!утр1.:1111ня 11лп r · р;1 1н1ч r 1:1>1
то<1ка выпуклоf1 фнттr>ы f ". : .i В - её n11утре11нлл
точка. Тог[\а н шобая друrая ;очка Ы о1'резка АВ
т~1юкr n11~тре11пяя точr<а фщуры Р (р11с. 1О. а).
2. \13 э·1 ого следует. что если Р JJ Q - дне
гр<~ннчные то чю1 ныпуклой ф1 rrypы Г, то отре
зок PQ ш 1 бо щ:л11кuм ссх"1·он·1 · 11з 1 ·ран1 1 ч11ых
точекфн~rы Р (\.т<.:. tO. б),JН160 сож:рж11т хоти
()1,1 ()JIJ-Г~· нн~~1 рсннюю точk.-у - 111пгда вес тuч
ю 1 о'l'рсзка PQ, кроме коr rцон, я11ляюто1 пнут
рСТ11 Г1Jмн точкамо фНГУ[Н>I Р ( [)IJC. 10, N).
Особенно nажную ртп-, иг 1х1 10·1 опор 11 ые
прнмые nыпуюtых фи1·ур. Прямая т 11а:~ъша<.,"1СЯ
onop11oit дшr выпуклой 1тлос1щi1 фтнурыF. еслн,
nQ-nepnыx, т пмест хотя бы одпу общую точку
с фпгуроi1Р11, во-вторых, вся ф1uура Р цсли
ко.\1 pacrIOJIOЖCHil н одной IIOJIYlJJIOCKUCTll от
носительно пря ,,1.ой т. О1юрную r1ри;-..1ую мож-
1ю провсl-r11 через лю()ую 1 · ра1rнч11уrо точку
ф111 уры . 1lапрнмср, 011орные прямые крут-::1. -
к:.~сатст.ныс (р1 1 с. 1 1, ct). Jfюба>1 11::1 Е 11 1х, ос~еnнд -
1ю, нвлнется сю111ст11с111rоf1 оrюр11оlт 11рямт1
~·~ш
Рис. 6.
...
~
---
---с--
-...
-,
-
--
----- -
-.... ,
........
-
---
411
Фигуры
А·
о·
Р11 с. 10.
f'и с. 9.
в данной точке rr пс пмсет дrJ-тI IX общих то
чек с фшурой. То же справещшво и дlШ пря
мойтпарис.l1,б.НоселиА -угловая
граш1ч11ая точка выпуююй фшурыР (рис. 11. в),
тu через нсё нроход111· бесконе ч но мно1·0
orюp!!1>LX прямых. Точнtс, из А 1н: хоf\SП ю1~1 J1уч·,1
Р1 IJ л ~, 11 азьшаемые nfllJ.}IKacameльnы..11111 фшу
ры F. Образованный нма угол (мень ш нй раз
вёр1rу1 ·0 1 ·0) пю 1 юч<~ет u себя фн1-уру F, ~1 любая
11рн мая т, прпходящан через А н 1re имеющан
/~ругих общих точек с эп 1 м углом, - orюpr raя
прямая фиг;1)ы F. Кро м е того, опор~ 1 ая прямая
nыпу1<Лой фигуры 1; может нметь целый общи11
отрезок с F. lianpимcp, сели F - пы пуклытт мно-
1·о)тольник, а т - прямая, содержащая одну из
<.:ru сторон, тu /\анная стuрона - uбщнr1 uтре
зuкт11J•' (р11с.11.г).
Есл11 F - огра11ич1::1ш:~я выпуклая ф11гура, а
1 - про11звольная прям::1я в сё плоскости, то
имеются две опорные прямые m 1 11 т2 фигу
ры F, кпторые 11 аралпе111.11ы /. Рзсстпя r ше с1
между таким и пряМЫ\1 П 11азыnают шupu1toit
l'11c. 12.
~1 12
в
Q
р
k
т
фшурыF, <.:оотвстствутощсй папранлс111110 пря
мой / (рис. 12, а). Ясно, что е<.:ли }' -
круг, то
его ши 1·н111:.1 О/\11Након:.~ во нссх на11р1шл е ннях -
она ран ~ ta д11 а метру 1<ру1 ·а (рнс. 12. б). А 1ютощ
кру1· - ф11гурс1 поспюя1t110П 11111/mны: el'O шн
рин~1 в люfюм н:шранлснии р:tвн:.J .Ц11аме-,·ру.
А Ct~J'Ь JI 1r дf)Yl'l-lt" ф1 пуры ПОСТОЯ ННОJI ш (rршrы?
Иным11 словам 1 1. может ;111 111 1 1р1ша т.111)-юю11
фт-уры, OTЛИЧI IOII от круга, 6ыт1, OJ~l lllЗKOIIOЙ
1 ю 1кех 11а11раnлениях? На пepnьu"r nзгляд 11е мо·
жет. Но это ш 1ечатле1 ше обманчшю С)щестnу·
ет бес 1<011с• 11 ю много фигур nостоянно1'1 ши
рины! Одну 11з 1111.х в XJX в. опнсал немецкш·1
мсханпк и 1·с:uм<::тр PtJю.
llозьмём рашюстuроr1 1-1111v1 трсу1 ·олhн11к со
сторuноr\ равной cl, 11 11з каждой uср111 1111 ы, ю1к
113 l\<.:1 1 тра. ОПJШ1СМ дугу OI\p)'ЖlIOCTll , соед1 11JЯ·
ющую две друп1е нерш11ны. Получающаяся
фигура - ·1·реу1·олы шк Гелn (р 1 1с 1). а)- нме
ет постоя~1пу10 rпт1р111rу d. R самnм нелt, пз
любых двух парзллельных опnр11ых нрнмых
ni1,1тз проходнт через nершш r ~ треутолыrика .
&
А
cl
С'dcl
U
б
111/fi',
•d
117!
:
о
Рис. 13.
;:i ljтup~н1 к:~н: ается прот1нщположной дуrн
окружности (рис. 1:), б). Пшнпм:у расстояние
между шrми рав110 р:щ11усу дуп r, т t:. с/
Похожу10 фнrуру 1юегояююй rш·1р11111>1 лег-
1<() 1юстр о 11тъ иа nнтиуголы1111(~ с д1- 1 а1'Uн::~лями
одинакоuпй щr1'!ны, еслн и~ 1«1ждо(1 веrннины.
как и:з центра, rrpoRecти дугу оr<руж1юсти ра
диуса с/, соеюнrяющую две противоrюлшютые
нсрmшrы (рис. 1 5, R). Вместо пн·нтутолышl\а
.-.юж110 вэя1ъ м1ю1·оуrольннк с любым 11счет11ым
сrнслом (l.11 + 1) с:горон, у котороr·о 11т ш:1 с/ всех
·больших~ диаго11аJJсй (:за.мыкающих уч:-~сток
его 1'раницы из п сторон) rщна и та же. Су~це
стпую1 11 фи1уры пос·1·ш1н.~юй ширн11ы с гра11и-
1 ~е 11 , 11е COCTOЯ !J\Ci'I 11 3 Д)Т окруж1юс1·е11.
Любая о порная 11рямая ф111)1)ы лос 1·оя111юй
шнр1111ы пмеет с ней толыш одну общую точку
(rюдумайтс почему). Отрезок, сосдш~яющнй
•точка кот1т~11<Та» дuух параллельных опорных
прямых. всегда nl'рпсндикулярс:н этим прямым ,
:1 с 1 ·0 д;1и11::~ равна ш11ршн: фюуры {рис. 1-1).
l\;JЖ/\h11I такоrт отре.юr< н:1зыйаетсн i'>иа.лtетро.м
фигуры.
Фю·уры 110с1·оян 1-Юй шнрины облад:~ют м1ю
жеством интеrссных свойств. 0f(но из них (тt'
()рема Барбье) состою· в том, что Rce крюзъ1е
постонн1юй ширины d нмею·1 · одrшаковый пс
рН,\1етр (длнпу rра11ич1юй крrоюй) . раR11ьп1 тт.d,
как у кpyr;i..
Предста\\ьте tебе несколько цилщщриче
ски.х брёвсн, каждое из 1<0торых 11.мсет поrте
речньн-"1 сечением какую-1н1буд1,фи1·уруnо<..10-
янной ширин ы d . На такнх «к:.пках-> ,.,,1ож110
11<::.редви~ ·2 ть (no ровной местности ,.ши 1ю
репы::ам) любой ва1'О11 илн нной предмет с
l\JIOCKHM ДН()М 1·ТряС1<И-> не будет. ПOCKOJl\,KY
высота люf>оrо бреrн ra p;i 1нrа f./ . С верло с погте
реч11ым сеч.епнем R внде тре~то11ьника Рело
позволяет Rысвершшэ1ъ к11адрат1п,1е отверст ия
(араnда, с закруrлё 1шыми углами; rжс. l '5) .
Одна из с амых 3амечатеm,ньL--.: теорем в тео
ри11 выпуклых. ф1нуμ была открыта австриi1-
скнм м:1тt:матиком Хелли . 01-i доказш1 э·1у теоре
му, ког,гt.а 11аходилс>1 в русском плс:ну. n 11ериuд
ПертюЛ мировой войны . Хелли сообщил сё
формулироику друюму пленному, тоже авст
рюlцу, - Радnну. Rернуuшись н::~ ро11ину рань
ше , чем Хеллн, Ра11оп orryбmл<ou~tл до1<а:1а
теm.ство теоремы (отметив, что авторам её
формупировJ\И ямяетсn ХсJ1лп). А :Jатем и ХсJ1 -
яи, воз.вратившисъ домой. сообщил в печати
собственное дот<азательство - rre такое. кат< у
М1юr11лик.:~я геuметрия
Рис . 14.
Рис. 16.
Радона. Привс,~ём теорему Хеллн для сл\'Чая
нлоских фигур.
ПустьМ1, Ml, ..., Mk - nыпуКIIЫе фигу
ры на плоскости. Если каждые 1'ри
из них имеют общу10 точку, то най.
дётся точка, принадлежаn~ая всем
этим фигурам .
На рис. 16 и::юбраже11ы чет1,fре фигуры
три nря""юу1·ольш1к:.~ и кот,цо. Каж;~ыс тprr 11з
ш 1х ИJv\еют общую точку, однако у всех четырёх
фпrур общей ·1·0"1Ки нет (нх перссечс1111 е пус
то). Ilрощ:ход11т Э1'О потому. что ОД1 1а из фнтур
(кольцо) 11е .нь11 1 ую1ая . Нет~ же 3амеш1ть 1шлL
[Щ кругом , то у 1ксх четырех ф11rур н<1йдётся
общая ТОЧК~I.
Теорема Хеллн ~~мест м1-ю 1 ·uч1·кле11ныс 11r11-
ложен ня . Бот 11ескоm,ко nр11мсров. Tlepвыll н~
аих - теоре .'1/1а, 11зRес-тая сщё RXIX 1~.:
Если каждые три из точекА 1,А:~, ...,А1.:
на плоскости можно покрыть I'PY-
I'Ol\:I радиуса r , то и все точки в~1есте
можно покрыть кругом радиуса r.
н самом деле, 11уст1, о - центр кryra. no-
K[JЫl:IЭJOЩe1·0 ·~·о ч ки л ,, А 2, л~. Тата к~1ждос нз
гасстоян11й А 1 О, А 1 0, А~О не превосхоюrт 1·
(р11с. 17). :1т 1ачит, t'CЛJ 1 юнть круr·н р:щ11уса " с
це11·111ам11 А 1 , А2 , А ~ (зелёпый, жёлтый 11 рпзо
в:ый), то эти три I<руга содержат nбщую точ.к-у О.
Фигуры
Рис. 17.
Расоютр11 м теттср1, круп 1 рал1Iусз 1· с 11с1 пра
~·ш А1,il1, ". ,Al" У каж,ц 1.1х трёх п:~ хшх ест1, общая
точ 1.:а. П() теореме Хелли, кругп с т ~схпра .ч11 А 1.
А •• ...• А.1; 11мсют некоторую общую точку :\1.
Дру1'ими словами, найдётся такан •1·uчка 1'1 . чтu
11 юбос и::~ р:н.:сто н1 п1 й J.lr:I 1, :\/А2. ..•• МА, т: б}дr.:1
l l lJCIIOCXU/ \HTb /' ~ H::tYll 'I', кру1· rадиуса 1· с ЦСНТ
р<щ ,11 покрьш:н:-т сразу нес точю1 А 1 .А2, •. "Ak.
Второl1 r 1 рнм~r> -тсорсма ,, 1сжаз;1 н11 :т рос
снl1 сю1м мaтe .'vl t\THT\l)M М. Kpac1 1oce!Jt,(1'll M. н('-
1(\ 1Ci чуда1<- кn; 1л сr<щ щ11ер 11остроил l{a рт1 пптую
галерею в форме замыслоuато1·0 ~11тоrо}толь
t 1нка п все стены галереи уuещал I<арпшами.
Из точКl't И па рис. 18, 1 Jзоб рзжающем nщш
так01'i галере~~. шщны 1<арт1шыА, В If С. а кар
та.на 1) пе 1шдн;,~ . Тс.-орсма l <p:ic 11 оссльско1·0
\· 1 ·нсрж.п.а ст.
Если для ка:>цых трёх картин в гале
рее найдётся точка, из которой эти
три картины видны , то тогда най
дётся и точ:.ка М, из которой видны
сразу все 1<артины.
Повытайтссь доказатт. сё с помощыо теоремы
Хеллн. А nот сщё прпмср:
~ На плоскости произвольно заданы
1
lc-.,
30 точек. Тогда найдётся ·rакая точка
Q, что по :каждую сторону от любой
проходящей че1>ез Q прямой ле:жит
не менее 10 из данных точек.
Есть м1ю1·0 друrтt х приме11ений теоре,v1ы
Xe.ruш, в том ч~ rслс сущестnен1 1ыхд11.н прrпшад-
11 01-1 матсматпки.
Все рассмотренные вь1шс прим ер ы свя~а ны
с геометрией на п 1юс кости . Однзко теор11.1J
ньш укл ь1 х фигур относится такж<: к 1·ео.метри11
н ·1·rёхмерном и мно1·омсрн ом ттространстпах.
Н :шрим ср. если трёхмсрнос ·1·е.110 М nыпую10е,
414
то чсрс:i каждую ef'() гра1 1нч1 1у10 то~1ку А можно
t1poвecn1 0110р111•ю п1ос1.;.ость CJ. ::1тоt ·о тела. т. е.
TTJIOCKOC'fЪ. ОТIЮС!lТСЛЫЮ котороl:t всё телом
р:~с положенu lJ од11ом 1 юлупросm/ю11стве
(рнс. 19). Теоремы Хет1и, Кр:н:11осельско1·0 11
дру1 ·1 н:· уткержд,СНI IH ' l 'l"Oj)I 1.11 к ып уклы.х фи~'() с
с< ю•1 ·не-1·с•тнующнм11 t1011ранка ."111 с1 1ранt:дл11в ы
ДJJ.» трёх мср11ого (11 п-мср1 ю 1 ·0 ) прост1х111ства.
Как же ·1 ·е()р11я Мтr11 r-:о нского прпме 11яется n
пр<J 1<т1 1 чеrкнх :1ад;1 чах? Российсю 1i1 математпк
Jlto1 r1rд Впт:.t11ьен 11 ч К::шторовнч 11о.r1учrш Нобе
пс:вс1')1О прС\шю :Ja открыт~rя. ст:шш11е сегодня
фунда~кптом .иатематпчсскоl! э~.;оно:.чню1 . Глав-
1-1~1() роль в сто работах сы1·рш1:~ тet)p ttя nьmук
пых фнгур. Оста11овнмся н;1 это м 1н.щробнее.
Прс; ктав11м себе. что 11:1 днух сющ'1,:1х С1 н
С~ llMt:CTCЯ l ICKOC СЫ(11>ё, 113 IIC[1R0\1 СКЛ:ЩС - 8
к01111ч<.:ст11с 2() е11 н11иц, на вторпм - J LI сд11н1щ
CJ,1pьf 11а,цо :~;111е:1т11 на два :~а 1юда З 1 н ~-• пр11чём
rr:i к;:~;1щ1 .1 l1 :>аnод по 12 е;1итпщ (рнс. 2()) , Обо·
э11ач11м чсрс:1 х и у 1юл11чсстnо сыры~ . 1юторое
неоl1хо;щмо отnр::шить со склада С, па первый
11 второй заnоды соответстnсшю. Тогд:~ со вто
рого склада нужно отгру:шть на заrщ~ы 12 - х
11 12-у сд 11н11 1\ <.:ырьн. Пр1,111 i.;м ."У + у~20 (на
t1ep LJuм скла/\t: нмеt:то1 20 е1tн111щ сырья) и
(12- х)+(12- у)<14 (навторомсю1;щехrа
н ин·я 1 1 сд11 ню\ сырья). Разуместсн , з11 ачсн trя
х 11 у нt'o· 1p1Щ<!'l 't:J 1ЬL1ы. llо11уч:1ющш.:<:н ч<:тырс
11<:ра l:lt'I JCTH;I
х+у~2(),х+у>1О.х~(),у>()
онре; \tJ/ЯЮ'\' \ ICl<O'l'OPl')l\' t RЫ 11ую1ыl1 4t:"\ЪТрёх
у 1 олы1 нr< ,iJ па коор1щ 11ат1 юС1 плос1-:оп 1.1
(р11с. 21, ct). То<ши ч.етырёл1тоды m 1<а М 11:юб
ражают вссuо:31''1ОЖ.!1Ые пл ;u 1 ы псре1юзок.
Допустнм , что СТ(.)НМОСТЬ ПС\)t'ВОЗКl l CДllllИ I \1>1
сыры~ со civ1aдa С 1 11а заводы 3 1 11 З1 сост::~шшст
CO(}'J 'llC'J'C 11!CI 1но ") 11 4 )\СНСЖН ,,,е t:,'(11нн1\1>1, а t:'l '(J-
1! \IO("IЪ всрено~~кн с ырья t 'O скл:ща (.l 11 <1 · 1 е Жl:
з:шо,;\Ы - 2 11 .~ елш11щы. Т<п;ц;r оf1ща>1 сто 1 1мос·1ъ
1ю~л 11сре1н1:нж р:jн 11 :.1
°),\'+ -ly +2(12-
.\')+~(l2-J') =60+(3.х+)')
Чтобы 11ы6рать панболсе дет11ёnыi1 вар11ш11
персrюзок, 11 адо найти в Ч<."Т'1.1рёлу1·олыш1<с ,\J
т~н<~ ю точку (х: у), в которщ't значе ние .rн шеi1-
нu!1 фу11к11 1 ш .1х +у на11мс 11 ьшс<:. Ilункп1рньн:
,111111111 на r11c. 21 , И 1 1 :юбр:JЖШ<Л те.: нрнмыl', на
которых фу1 l KЦllЯ ,).\,"+у l lMCt:'f П<JCTO>Oill<J<.: 3 11:1-
Чt:llllt" . J-1:1 pIIC}'llKC J:;JI Д H O, ЧТО 11;1JJMt'lll>Шt'<: : 1нa
Чt:Hlle 11:1 Л/ фу111щт111р11н11 .\1а<:т 11точ 1<е (О; \()) .
Знас111 ·1 , Т1а11бол ее ;1с 1u ё11ы l1 вариант 11t:ре1ю
жж - кщ·да
.\' = О, у = 1О, т. с. на !П'()ро~1 :{~шо;~
нужJJо .1.н~езт 11 10 с:11 1 ш1щ сырья со сю1ада С 1 11
2 едщ 11щы со сю1 ::1да <..:2 (а н а пе рвый заво,1 сле
дует отправить вес l 2 C/\И I JПIL с ыръя со c1illa;1a
С2 ) Та1\.11~1 uбразuм. рt:шсн11l' з:ща ч11 снслось к
нахожж:11 11 ю миним ума л11 н с:йной фуш<ции
f(x,y) = 5"". + .1" рщ:сматр11каt:\ЮЙ на выпукл ом
Ч~IЪtрёх:у1"< >JlЫIИKe ,\f.
Ест 1 нужно оnсс11еч 1 J' l I> Cl>IJ11>to"vl трг-1 .i:шс ),' (:1 ,
т. обо:тачая черt:э х.у 11 zкот 1ч t:стfю с 1.1р1,>1,
з:~возшчого со сю:rа;~а С 1 11а эт11 завrщы, мы гю
луч1 1м :i11aJIOГI1"-щyю 1 ·еоме1·р1тч ес кую :1а11ачу n
трёхмерu ом простр;шсш<.: (ПОС1<олы1.·у имеются
~р11 коорд 1ш аты х, у, z ). Ипачс говоря , надо
бу11.е1 паf1тн !\1шшмум Е1~:которой 1ш11ей1юй
фуню\1 111 11 а вь111уклом м1ю1 ·0.rранш-rк<:. А 11рн
болы u с м чш.:т.: ~ анодов r1 скл:що~; 11рщ~t:тся ·r·y
же :~;щ ачу реш<~ть L~ м1; uгомсрном про стр:111-
ФРАКТАЛЫ
Многие знз1юм ы с прик.тrючеIJИЯJ\1.И девочди
Алисы - 1·срошrи (Юmuебных сr<аз01с англий
:кого матс:::мат11ка и 11исателя Ч.арльза Латуид
ж.а Доджсuна ( 1832- 1Н98) , СОЧИlIЯf\Шt:ГО ПО)l,
Мноп1ликdя reotv1t>1 рия
)'
а
.)'
б
21)
5x+y= IO ,,
20
\\
3х+р=5,\1
'\\
1()
11
10
Jx+1•= О,,
\
1\
\
.'(
'\\\
\\\\
.У
()
10 20
о'1\110 20
\'\."
Р11 с. 21.
(''l'HC'. fl u; 1 o()н hll' :,IЩ\~l Ч11 но:тHK:J IO'l', С'СJШ •1pcбy
L"lOf н~111Gш 1 ес ны 1 ·tщ1 1и рзс кро11тr. м~1тср1 raJJ
111,rбратr . оrтт1 1 чалы 1 ы~'1 рс:жг1м р:-1 боты 11 pe,111pa-
>п11i'i JI Т. / \.
Так LI математ1 1кс слтrшлось . •m11eiuf()C 11ро
грсшм11/ювсшuе - папраn.·1е11не. э<1 1111мя1е>щсt>о1
мr:тод.ащ 1 ре111сннп за{\ач н о ми 1 шмуме ; 1н
rrс 1·шых фушщнi'! н а выпуклых м1ю1·огр:шш 1ках
(н мнu1·омt'рн1,1х нрuстрш-1ствах). Эт11 :1 ад:1чн
11р11хuдн101 рt.: 111 ::пь м атс.\1 атш<ач. работаю щ11J\1
11 ~1 тр:~нспор·11 rr 11x 11pt.:/11 1рш1·1·1 1н х. /(l'j)L'tюu6ра6а
ты11ающ11х ком6нна гах, 11 ~'чрс:ждсн11>1х 1111:11111-
рованю1.
Н:н« 111 ец, утюмнr1ем о теорнн оп·1 11м :u~ы ю1·0
у11ратvн::ш н1 ·1·~хт111ч1.:сюшr11111рп11:11юдстне1111ы~
Mll процесса .ЧИ. no1IЯ'l'llc llЫП YIOIOCТll HГp:i.e·r·
uаж1 l )'IO pOJJb 8 ДОК<!:.-!аТс:лt>С'I'Вс ОД!/\ Jl l 11.! B:JЖI rcr'1 -
1ш1x тсорсУJ этРО тсориJr - пршщтш _нам.:и
.мнма . 1шторый был уста1 10uлсr 1 н сtрсднне
)()-л J't'. совс·1·сю 1.\Ш матс.-.~атиками Л. С IJо1rтря-
1· 11ным. В . С LJшtтннсю1м tt Р. Н 1·a~1кpCJ ШДJC. lla
t 'I '{) OCJr()KC: pal'C Чll 'l'ЫHtll{ITCH Ol l'l'll MaJll.HЫe pe-
ЖllMl>I )'ll():IHJICHllH 'J'cXHllЧt'CКIJ ,\11111/)0IД'(."(.' ~L"lll -
11 олё'тм р;1кет. ра:юr·реrюм ;1::11 ·отонок в ·1·ер,\1Н
ческпх печах, работоl1 дn н1 ·а ·1·е11е~'1 nод1ю;1ныл
ЛОДОI< 11 Т 71, .
С.:егол:r ш теория 11ЫП)'1<!1 ых фшур ( па 1 11t0Сl\О
стн , п трёхмер1юм. м1юrомер!lых п N1Же бес1,<1-
11ечномерных 11роора 1 ктнах) - важный раздел
наую1 , 11м еющ11й большое значе11не к:ш в тсо
ре1·ичL·ско1\ так 11 н нр1 1 клад.1-юй ,-.1Ltтемаn1ке.
литературным псендо1111 мом Лыо1 rc Кэрропл.
13 лоuести « Алиса н Стране чудес>) с деноч 1юl1
происхопит r~елыi1 каскад превр::~ще1111 i'1 . 0 11 (1
то уnслич иваетсн до 11 енсроя тных разi\tерон,
~1 J5
Фигуры
Са'V!()ПОлоЬие
в 1 1рщюде. fkn<«
n.in opo1 ник,1 .
· 1·() умеrrыпастся до пелнчнr~ы 1<рол11ка или
мьuшш. Любопы.т1 ю, что в олних случ~"'< окру
жающие её предметы нс:: претерпевают ника
ких измепспиfl. в других - с1·а 1 ювятся мипиа
тюр11ыми .
Идею с~1 мо1101\обия мало1·0 в бuльшом вы
сказынаm 1 не тш1ько сказочники . Изкестныl1
пе~tе 1 \кий философ и матем<~тик Готфрин Виль
гельм Лс;fiбни ц ( l 6~16 - 17 l 6) рискнул прс11.по
л ожитъ . чти внутр1 1 каш~и вод ы могуг уме
щатъсн цеJ1ые вселенные со сrюим1111ла11етамн,
на 1<оторых предаются 1:1аж11ым размышлени
ям философы, таю 1 е же , т<зк и на пашей Земле .
Валерий Брюсоn в сги:хотворении ,.мир элект
рона» ( 1922 г) облёк эту мысль n поэтпчсскую
форму
Быть.А10J1сет.. эrпи .~леюпро11ы -
Миры, где пять "wатериков,
Исг..усства, З1-Ш7-tья, воiшы, т/ю11ы
11 naмJ/.niь сорока веков!
Ещi!, быть .11ш.ж:ет, кaJfcдьtii. ато.м -
Вселенн.ая. где сто план<!m;
Там нсё, -что зr)есъ. R обьёме сж:ато.м.
Но тах.ж:е тп, чего здl:!сь 1-tem.
Самоподобной 1·ео.метричсской фигурой
н:вывают ф1,нуру, 1<оторуто можно разрез;~ть
на кп1rеч11ое число одинакоfl h1 х фигур , по
/(Qбных ей самой . Самопо,1106 1 IЬu\1И, например,
являются правиJ 1 иный треугольни1< и квадрат
(рис. 1). Од1ш<о существуют и самопсщоб1 11,1е
фиrуры весъма причудливьL~ очерташ,rй. На
рис. 2 пока:1ю 1ы первые 1 1ес~<0лъко стздий по-
416
строения <-.uеточю1• ::>·10 нросте й.шан t:амопо
доб н ая ф 1нура , 11м<:ю1ttан 11еогр:н111ч е 1шое
число э11е::мt:11·1 ·он Она строится с;1 сf\ующ11м
обра з ом. Исхщ\ный <1ТJН~:юк дtнят 11а три
раn11ые ч: ктн. и и з точе1< J\еленшт по!( углом
4 '5 ° 11ртюдят отрезки, составляющпе 1/3 дли-
1 1 ы исхо,r(тюго отре:ша. Затем ry же процед)~)у
повторяю1 по отrюшеншо к тшоnr, nострое11 -
11ым отрезкам и т. 11..
А1 талогичнос свойство самшюдuбнн 061 1 а
ружннаю'1' мно1'нс объекты в r1r~1poдe , стоит
лишь пuю шмателы 1 ее r~рисмотреться к ннм: к
шrниям трсщнн в ~смной кori::, ветвл е ниям
,11срсвьсв, очертаниям l'Op , 06;131<011 н корал
ловых рифон. Рзсоvютрев гор11ый хребст с
рэ:1 1 ю 1 ·п расстояния - и:'! космоса. с борта
самолёта, а затем непосредст11е11110 с rор11ой
uерш ины, каждый раз мы будем обваружиuать
всё новые 11 новые подроб1юстн , пскр11влсш1я
и изломы - р:шьшс они 11рс11станюu 1 11с1. пам
прямыrvш или 111 юсю 1м 1 r11.еталями рельефа. Но
ни;1им мы тем нt: ме1 ree всё те же гоrы. Рельеф
rop 1«11< бы не эанисит от мас штаб~~ - 011 сам()
rrодобсн. Объекты. обладающие тзким с1юJ/
сnюм, совреме1111ыИ змернка 1 1 ски!'i матемап1 к
'\
'\
/
\/
'1
1
1
1
1
------,
1
1
1
1
1
Рис. 1.
l'llc.3 .
Бенуа Манлельброт предложил называть фрак
талам.и (от лат. f1·angere - «ломатr-.·>, «раз
биnать»). В ю1иr·е «Фрат\ТаЛьная 1·епмстрия при
роды~, вьrшелшей в 1982 г., Мандельброт
О'ПЮсит к фракталам объекты, форма которых
может быть описана как зернистая, ветвистая,
морщинистая, запутанная, похожая па мор
ские водоросли.
Внутренние с1:юйства фракталов удобно
оп исывать числовой характеристикой, 11олу
чнвшей название фрактальной раэм ерности .
Проведём несложный эксперимент. Возьмём
1шст чистой ми1111иметровой бумаси 1·1 начер
ти м ш1 1-1ём произвольный пря.молипейнь~й
отрезок (рис. 3). Подсчитаем количество кле
ток с д11.иной: стороны 1 см и количество I<ле
точск с длиной стороны 1 мм, через ~щторые
проходит этот отрезок Во сколько раз одно
число болыuедру1 ·оrо? Ест-1 эксперимент про
водить аккурат~-ю , то nокр.ы~ающих отрезок
щшлиметровых клеток окажстс}I R десять ра з
больше, чем сантиметровых. Резуль1~J·1· пред
сrав.пяется вrюл не естестве~ rнптм: ведь RO скол,,_
к.о раз уменьшили измерителъную к11ет~<у, т-ю
столько раз увел,1.-rчи·t·ся общее число таких кле
ток. Подобную закономерность мы обнаружим,
нсследовав периметры трсуrольннка, паралле
лограм~"Iа или круга. Дру1·ими словами, число
NкRадратиков, покрывающих отрезок, пропор
щюналы-ю величине 1/d, где d - размер сто
роны юш11ратика. Каэалось бы, устаJ-1он.пенное
на~ш свойство должно быть присуще любой
ли11ии 11<1 плоскости. Поразительно, но это
неверно.
13 1890 г. Джузепnе Пеана 1юстроип ли~ rию,
которую мы сегодня без всякого coмrretrия на
зываем фракrалом. Начальные этапы построе
шш кривой Псано показаны на рис. 4 (процесс
дробления tё зuеньев можно продолжать и
дальше). Кривая Пеаио обладает ошеломляю
ЩИ.).1 свойством: как бы мы ни /\рuб11л11 11зм е
рительную сетку - в любом сё мслъчайюем
ква/~ратике окажуrся точ..ки кривой! Получа
ется, что колнчество кнадратиков с р:о~змером
стороны d, rюкрыRающих кривую Пеаво, про
порционалыю не l /d, как !{Ля обычных., ,,бла
гообразных" линий, а l/d2!
Безусловно, кривая Пеана - экзотика, при
чуда, фангазия изобретательного математичс
ско1 ·0 ума. Насколько же были удивлены учёные,
когда обнару.ж.иm1 реальные 06'1>екты, которые,
как и кривая Пеано, не укладывались в [rри:выч-
Многоликая Гf'ометрия
8
l'>IC. 4 .
ные предсrавления 11раю·11че-ско!'·1 1·L·oмei-p1 1и .
Оf\1н1 м J..r з перRых с 11илн1 <'ТОJ1кну11ся ан1·m 111-
ский естествоиспытатель Л. Рнчаr1кон ( 1RЯ1-
1953), исследоваюuий очертания 6ер~1·ивых
лиr-тУ!й. Оказалось, что измеряемая дшш;~ тто6е
режъя L пропорциональна 1 /с/', ~де с/ - длина
стороны квадрата масштабной сетки, а по каза
тель а. характеризует степень нзрс::~анrюстн
берега. Например, для побережья l\сm1кобр11-
тании коэффи1(11ент а состаю~яст J.2 -1; /lIOJ 1ю
берсЖJ>Я Австралии - J , 15 н т ,'\. 11 ;1Ло\1ы 11
шерохоnатосги ли.ю1и бert:1'a, которые нщ(r 11,1
на картах круnноrо мас111таnа. 1юсте 11с111ю 1к
чезают по меrе его умеr ILПICil/f}i. Ест r vщ н:i
мерим длину береrоuой люттш на 1\артах раз
ного масштаба, то увидим, что 011::1 тем бот,шс,
чем крупнее масштаб.
Метод, которым 011рсделяют степень изре
занности или сложности с-1·ру1<"1уры фrакт:1ла,
'ВОСХОДИТ к понятию разм.ерн< н.~1·н , 11 \)l'[l)LOЖt:I L-
1-юму в 1919 г. немецким ма ·1 ·с.,1атнкоч Фt:юrк
сом Хаусдорфом. Пре/1,ст:шим с~б<.: объект
сложной формы, сплошь пuкрыты1'1 кв::щра ·п1-
кам.и, как миллиметровая бумзrа. Число N к.на;1-
ратиков, содержащих точки объекта, :за н1к111· от
формы nослед11еrо и длины стороны квалра·1 -
ной ячейки d. Если N проттор 1~н о 1rалыю 1/ct",
то показатель степени а обышляется rазм~..:р
ностью объекта. На практикс ра:3мерн ость
----
-- ------
-----------
--
-------
417
Фигуры
объекта удобно определят~" 11apнcouan грзфик
::!:щ.и<.:1·1мuеtн фун.кщш 111 N 0·1
-In d. Этот гра
ф111< иэабражасrся 11рн ,\юй 1111 н11ей:1·аю·енс }TJia
наклона которой и бу,це1 разм1::р1 юстъю Ct .
К запутанным, раздробленным юш вствн
С"Гы 'vt сrруr<турам математ11ки nсегда относи
лись несколько ш1етороже111 ю. Кота ti 1860 1·.
извесп1ый немецкий матсJ111атrrк Карл Теодор
Вильгельм Вейер штрасс опубликоnал работу
о чрезвычайно изломанной функции, ~рафю<
которой в меньшем масштаб<.: выглядел точно
т<1к же, к<tк ин более крупном, другой нзвсст
нh1 i't мa'ГCJ\ll<l'l'HК. Шарль Эр.!\ШТ, отреагиров~u1
на это событие весьм:-~ экспа1 1 си11но: ~с омер
зен нем и ужасом я отвор:зч1-1ваюсn 0·1 .. :~по
вредноИ н:з.Rы - непрерывных функций, н1 rr;~c
rre име1ощнх пронзnод11ы.х~ .
Глубочайmес эмоп;иопалытое nозп;еттстnпе
на JUОдей оказьшают творения, возrrиюппе па
самом гребне нау•пю-техничес1ш1·0 про~ ресса
конца ХХ n. Человеку, впервые созерцающему
фантаст11ческис у3оры, пр11ведёш1ые на рис. 7,
трудно rюнсри'1ъ, что иыnол н ила ILX не обла
дающая воображением "бесчувствен ная-> вы
ч11с1 1 11 ·1 ·ел ьн:н1 м:шшна, сл~()IЯ 11еслuж1-юму ма
тсмат1rческому замыслу. Открыл узоры Бенуа
Ма 1 ще.11ьброт. Его ·пюре 1-шл - прскраснст'nп1 1 с
nредста ните111-1 богато 1·0 мира фракталов.
Как же удалось математиr<ам выч 1 юшть кра
соrу? Что з:~ математпческие :~ависимосп1 ле
жат в основе этих шеденрои?
В поисках ответа 13сnомним о комплекс~ ~ых
чис.11ах и о комruн:ксной плоскости. Любое
комплексное число z = ."> .: + iy на данной ruю
скостн 11:юбр:~жается точкой, н её можно най
ти, если задать две координаты х и у - соот
nетстпенно действительную 1·1 мнимую частн
чт 1 сла z Число t (мщ1,\1ая единица) всс 1,ма
необы ч тю: ero t01aдra·1 ранен - 1. В зат 1 си
z = х + Z>1 оно отчасти служит нля то1·0, ч·r обы
отличать дейсrвителы rую часть числа z от мни
мой. Комплексные числа можно складышl1ъ и
умножать, и в результате таюке получится 1юмп
лексное число. При суммирован ии двух комп
лексных чисе1 1 их компоненты складываются
по отдельности, а ум 11 ожение 11ронз1:1однтся
IIO праниJJам умноЖСНJ1Я MHOI ()tUJCHOB. 1l:шри
меr:(2+3i)·(4- 5i)=8 - 1Oi+l2i- lSi.1. =
= 8+2i- 1:,1
2
.
Уч~пьшая, что i2= -1. око11ч<~
телыюполучаем8+2i- lSi~=23+2i.
Отправим точку n пугешестnие по 1сомпле1\с
ной шюскосrn Снабдим её следу1ощим Щ1СJ1ПИ-
·~18
Рис 5
Рис. 6
саш rем. Если точl<а находится в каком-то пунк
те z = .\· + iy (его коорJ1инаты х и у), то следу·
ющий пункт z' она должна выбнратъ по правилу
z'=z
1
+c,
1·де с= с 1 + ic~ - не1шторое фнкс:11рш~а нное
(не меняющееся во нремн оуТ'ешест1шя точю1)
ком l IJ leKCJ юе ч ИСJЮ с ДСЙ.С'ГНИ'l't!I hHOil частью С1
и vrнимой частыо с2. В соm 1Jетс1 ·1ш11 с правw~а
ми ~ыпот1ения операций rтад комллекс11юш
числами это означает, '!ТО новые координаты
(х';у') точки вычисляются по формулам
[:Х'=Xl - у~+С1,
l)'' =2.ху + С1.
На рис 5 и 6 1юкз:{з 1 1ы маршругы П)Теще.
ствия точки с местом стаР' 1 а н на<1алс коорди·
1--1ат , соотnетстnующис разным значсюrя.11 q
на p[IC. 5 с= 0,27+О.О 1 i, а 11а рис. 6 c=0,29i
+ O,Oi i. Н первом случае точI<а не желае:1 ухо·
дитJ, слишком далеко от «домашнего очага~. Во
втором - белшт (•куда глаза глядят»: }даляетсн
всё дальше и дальше. Оказьmается, сущестоует
облаееь ~начсний параметра с, при 1<0торю:
ТОЧ1<И-ПУ'1'~ 111 l'<:'J 'НС Н НИЦЫ, l:!ЫХОДНЩИС ИЗ 113·
ч:~ла координат, п остоянно будут «верте'1ъся~
около мео·а t.."Тарта. Лр11 дryr11x же значеннях
с OHI J устре1\11ЛЯIОТО! на «ЗОВ бссконеч1ЮСТИ».
Гра11и 11а этой обласrn, полу~пшпrан название
множества Мандельброта, устроена весьма
прич:уДJШво. На рпс. 7 поr<аз:шы части границы
~шоже("tва Мандсш,брота. И BQT что ущ,1ни
тепыю - <.:рею~ нрнчуДJ1И1:юl:\ ннзн орнамен
тов. уходящих в бесконечную 1 ·11уби11у, среди
rазнообразия завитков, с1тиралей и <~-ПрО'rубе
ранцев» всякий ра3 11ерсд нами пт1<рывается
картина 11зуми'1·ельной красоты и понвляются
IIO МIТОГО [>аЗ УМСllЫЛеН~IЫС К011УfИ ИЗl1ачаль
IЮГО ;1-нюжесrва Ма1rдет,брота. А в цел()М воз
шшаст бесконечно самовоспроизводя щаяся
красота, т. е. фрактал
ФИГУРЫ НА СФЕРЕ
А 11аше времн любой грамотпъrИ человек з1rае-1',
по есть та 1<:1>1 странная 11ееnютндова геомет
рня - 1·еометрия Лоб:аченского. Она 61.rла со
зда на нашим соотечественником - Никола
ем И13ано1шчем Лобачеоским. Её откр ытие и
рсвотоциоrrш.1я идея и том, что rюзможпы раз
ные и ра1:1нопр;:~вныс 1·сuмстрни, произвели не
ренорот не т0111,ко в математике, но и в пред
С'1-;~ш1еннях людей об окружающt.м м11рс (см.
статью " Геометри.и Лобачевского»). И тем не
менее " пuвсt:Д11еююй жизни. и даже на уроках
rеометри1 1 в ш1<0J1е нам не пр11хо1щ·1·ся с ней
сгаJlкишп1,см, поэтому пе нее представляют себе,
что же на самом rteлe при.Щ'мал Лобачевский.
А между тем одну из неевютидовы:х геометрий
ко времспи открытия Лобачсвско1·0 давно зна
.чи и хорошо изучили. Речь идёт о сферической
rеометрии, в которой рассматриваются фигу
ры нd сфере и соотношения между 1-н·u"1И.
Со 1 ·ш1сно антнчной модели миrозщ1.ння,
звёзды и планеты rасrюла1·аются н:1 нескольких
сферах с общнм центром, в которо.,,.111ахо1\1 rтся
Земля. При этом звёзды нсподnиж11ы, как бы
•прибиты·• 1< своей сфере н F1ращаются нм.есте с
ней вокруг Земли, а планеты на собственных
сферах выписыnают замысловатые ф11гуры -
~сдь само с1ю.во «nшuтета" в переводе с гре
ческого означает «блуждаю щ:ш ·>. С помощью
1~1кой п:оцс1причсской модели дрсm·ше научи-
11жъ достаточно точно uписыв:~тп и предс.ка;jы-
Многоликая геометрия
Рис:. 7 .
nать днижения тшнет Это было пеобхою1мо,
ш111ример, в мореrтанаи1 ш да 11 во ncex облас1 six
« Земноi1~ леятелыюсти 4елове1<а, где надо уч11-
1ыш1ть, что под ногами у JJac шар, а не плосю1й
бJtи.11 па трёх 1ш.т~х. 1lprr изучении закономер
ностей вращения небесных светил 1юзmн<.1и
ра:щuобра:.н-1 ые м:~темат1Jческис з:.~даЧJJ , связан
ные со с1юiктнdми сфеμы и фш·ур. которы<:: об
разуют 11а нс1"i бо.ньш~н: окружности.
1Iоскольку сфеrн наход11тся н uбыч11ом
трёхмерном ев1V11щuво:-1 простр:~нстнс.. тео
ремы сферическоl1 геометрr111 можно пон1-1 -
мат11 как обыююве11 11h1е стереометрнче~кне
Поэтому н сферической геометрии пе видеJJи
(•друтую пла~111..,,1е1·ршо», и опа не пр1mела к 1m-
сnровсржетпо усгоявшнхся взглядов подо6110
гсометри11Лобачевского. Мсждутеi\11, если прн
смотрсrъся к сфере в1 ш.м~1теJТhнее - а мл это~ ·о
1юдойrtё'1' обыкнове нный тuбус, - ле1·ко 06-
н::~руА<.Jпъ немало удинителыюго
:Возьмите нить н натяните сё меж,1у днумя
ггунктамн на r·зюбусс:. Она проllдс::·1 ло кратча1~1-
111ей JJJIНl·Ш J 1 а сфере, сщ·д1111яюш,ей эти 11ункты ,
и укажет, н ...1астностн, 11<нrлучшнl1 мар111ру1 ;u1я
са~юлёта. Если ш.r 11роложите такой маршруг
из Москвы в Ныо-Йорк, находящийся пример
но на одной широте с Баку, то обпаружнтс, что
11утъ лайнера прохщ.1,11т севернее, чем, ~юз.мож
но, вы ожидалн, - черсз Скаuд11навиrо 11 бm1з
кu ш Грtнтн щии. Что же это 3:1 л 11.ння? Ответ
419
Фигуры
е1vJнет нсен, сСJш взять точки на экваторе. То1да
и вся 1111ть нройдёт по эю1атору. Эю1з·1·ор }(ВЮ1 -
етс}( О/J;ной из бсшы11и:х m(,ру:ж:иостей сферы,
т. е. окру-.,ю юс1·ей 11анболыпего радиуса. Они
образуются при nepeceчer rии сферы её диамст
ралы1ыми , проходящи ми через ,,етrтр, пл о
с1юстями. Из друп1х лшшй на глобусе кромt:
экватора бот.шис окружностн образуют так
же меридиаrты (р11с. 1). Им<:нно 6011ы1111м (Жруж
ноl-гя.м и отводитсн рот, прямых в сфериче
ской 1·еомс:трн11. Как правило, через две точкн
на сфере, как и на плоскости. можно пронести
только одну сферич<::сК)-10 прямую. Иск.rночс-
1ше сос1·а нляют д11аметралы-то противоnоло.ж-
11ые точкн: 11апр11м ср, через поюосы 11а глобу
се щюл.0;(11т бесконеч11 0 м11оrо "1ернди:шов.
llo n ОТJП J'-ше от обыч11ой геомстр1ш любые /\Ht.:
сферическне прямые пср есеюнотсн н ; \вух
диаметралыю противоло 1южн1,1х точках - 11:1
сфере отсутст~ует само поr 1я·1·1 rt= 11:.1 pam1em,нo
<.."1·11 . Другое су1щ:стнсн11ос от.111 1ч11 е прямоi1 11а
сфере (YI ' 11 рямпl1 11а ПЛОСКОСТ~I :la КЛ10Ч ае-1 ·01 в
том, что сферичсскан 11rн,,·1ан зам1<1rута: fl.ПИr<1 -
}( Cf) 110 н ей Rсё Rрt:мн в rщ 11 у сторону, ~n,r n кон
це кmщов иср11ёмся в 1rсходн}10 точку, '1'. е.
точка Ne rа.1бияаст сферическую 11рJ1мую на
две части , подобные лучам обычной nрямо11.
Вот сщё «очеnидное неnсроятнос-> сфер11чt'
ской геометрии: треугольник на сфере мuжет
иметь сразу три прямьL\. у1'ла, сслп . 1шпр11меr,
uн ограничен двумя псрпс:: 1 1д11куляr11ы.vш ме
риди::~нам11 11 экR~аоrом (рис. 2) . Дана1·1тl' 110 -
Сеаер11ыi1 1mm11c
Рис. 1.
Южш.11i mищс
Р11 с. 2.
42()
з11акпм11\.1СЯ с понятиям~~ и фактами сфернче·
пюi1 rс:омс::трии. При зтом мы бул,ем постоmшо
сравш1в::1т1, их с фактами обычной геометрии.
ПРЯМЫЕ, ОТРЕЗКИ,
РАССТОЯНИЯ И УГЛЫ НА СФЕРЕ
Ит~1к, прнмыми 11~1 сфе ре считаются большие
окруж1юсr11. Если /\НС точки А и В принадле
жат болы1юй окру-.1Кiюсти. то /1,пи 11а мепьшей
и з сё J\нух 1\у1·, соедю uнощих эти точки. при
шrмаеl'ся за сферическое расстояние междуА
и R. Ca,"f)' меньшую дугу естестf\еmто считать
сферическим отрезком АВ. Диаметрально про
п11ю 1ю;юж1 rые точки сосди 11С1 iы бесконеч
ным числом сферических отре:1 к.он - бпль-
11J11х tюлуокружнuс~·ей.
Сферическое р<1сстuя11исАВ Rыражаст<:я чr
рс~1 1х1ю1а1111ую меру а централы-ют у1·наАО8f1
PN\11yc сферы R (рис. 3): 1ю иэ1~ес1·1 юй фпрмуле
/\ЛЯ ,т1лн1 rы ду1·и, 0110 ратто Ro.. Если принять
радиус сферы за сдшшцу длины, то сфериче
ское раС'стоянис окажется равным уr.rю1Зой nелн
чи нс о. соо111етств}1о щей дуги. Любая то111<а С
сферического отрезка AJ:J разбив:~ет его т двз,
и сумма их сферических длин, как 11 11 ш1з
н11 ....1<:трии , равна дJ/ине нceru отрt:зка, 1ш11
LAOC+LCOB=LАОВ.АдлялюбойточкиDвне
отрезка имсе:."т месго кфсричсскос.; неравtнстоо
трсуголышка~: сумма сферических расеmянн.й
n·r·[)/\ОА и от[)доВбплынеАВ,нJrиLA()Di
+ L.[)OB > LAOB. ~~дес 1 . су11 \естnует noлnoc соот
ветствие между сферичсс1шй и плоской 1·еомсr·
рш1м11. Нсrаnенство треугольника - одно нз
осrювопола1·ающих с1юйстn n геометрии на
сфере. Име111. ю благоларя ему, точ1 ю ·1~1к же l(;)J(
и в шrапимстрии, сферический отрезок короче
любой сферич.ескuй. Jюманой, а :.1н:~ч11т, 11 лю
(iой кривой н:о~ c tj.iepc . соt:'ли няющей cro концы.
Всл<::;t за ппределенисм сфсричсско1·0 рас·
стя 1111}1 на сферу nt:'pe1 госят и 1ючти исе nоня·
·1·ш1 плоской rсометрин. 1ютом у что их можпс
ныра~1ит1, чtf><:::i расс1·()я 11ия lia плоскости. На·
пример, сфери ~tеск.ая пк:руж1юспu, - это мно
жество точек сферы, удалённых 11а оnредс·
лtшюе сферическое расстояние р от заданно11
·1·uчкн Р. Нетрудно пок<1зать, что такое ,\.щоже·
CTIIO J IСЖИТ .в одной шюскости , 11ерnс11дикуляр-
1\()Й ;щаметру сферы РР' (рис. 4), т е. сфер11·
чсс кан окружн осrь как фигура - нс что ИllOC,
к~н< обыч 11ая плоская окр)"'..кность с це11тро~11iЭ
Р'
Рис. 4.
диаметре РР'. А вот сферических цснтрон у 11её
сразу два - Р и Р'; их принято назьшать её по
люса.ми. На глобусе Северный и IОжный по
люсы служат общими «сферическими 1 te 1 1тра
ми » всех параллелей. ЕСJ1 и <-радиус" р равен rr./ 2,
то сферичес кая окруж11ост 1, превращ~н;тся в
сферическую прямую; в этпм случае сё назьша
кrт· полярой каждой из точек Р и Р'
Важ1 1 ейшее понятие t 'еометрии , прямо свя
за111 юе с рассl'Оянием , - ра 1"1е11ст110 фигур: /1кс
фиrуры считаются ра1шыми, если од11у и:~ 1111х
можно отобра~шть на дру1ую rd1<, что при этом
сохранятся расстоm1ия между точками. На пло
скости одну из )1вух равных фигур все ~·да мшю ю
наJ1ожить на другую: 11ибо передвигая фнгуры
по шюскости (рис. 5, а; тоrrщ они на:Jываются
собственно равны.ми.) , либо в ы резан одну из
них из шюскости и 11срсворачивая на дру1ую
:'l'Орону -в таком случае uни .зерка.лыю-fJавны
(рис. 5, б). На сфере собС1·1зешю равные фюуры
всегда совмещаются uращением 01.1,tюй и:.1 ш.о,
~~
бм
Ркс. 5.
М1юголико:1я геометрия
1щl\ру1 · 11е1ютороl1 ос 11 (р11с. 5, r~) Однако >ср
калыю-рав11ые фи1уры, например симмt'трич
ные опюсителыю лнаметралыюй mюскостн
(рис. '5, г), совместить 11еnозмож110, как не1юз
мuжнu сuвмсститL, правую 11 левую перчатки .
О11рсдслим тсrтсрh yl'Jlы на сфере . Рассмот
rим /\НС Сф<:рИЧt'СЮ•Н: ПрНМЫt' tl И Ь ( рис . 6).
Они разб11иают сфсру на чегыrс дву)1гш1ышка
подоб1ютому, как пересекающиеся прямые на
11 1юскостн ра:.1бив:нот её н:l четыре плоских
1тла. Каждому и:1 /~нуу1·оm, 1п11<0n 0·1'вечае-1 од1 111
и::~ дn}ч'Jат нтых уг; юн, образуемых д11аметраm.-
11ыми плос1шстямн , содержащими а и fJ . Нелн
чшюй этого дву 1·ра1шого утла и измеряется.
~ю опрсдслстппо. угол 11р и всрп11111с днуу!'оль
ннка. А у1·ол между сфсрис1ескиJ\IИ прямыми
раве11 мс1-11,11н..: му и:> уr·1ю 11 образусмых имн
нкуу1 ·01Lы1 и1ю1-1 .
Обратите кн11ма11иt: н:а сuо·1·нетLтнис, нuз-
1111к ающе<:: м<::жду llCJllH 'l ' ИHMИ 11 l 'tXJMCTpllИ на
Рис. 6.
сфере и в стереометрии. Каж,1щй точке cфt:p 1.r
сопостаuлнется луч, проведё1111ый в неё из
центра О сферы, а любой фигуре на сфере -
объеди11е11ис ncex 11t:ресскающнх её лучеlf с
общим началом n О. Так, с.:фсричсс1<0~'1 прямой
отвсчает со,цержащ~1я сё диаметральная пло
скос1ъ, сфсричсскому трсзку - 1 uюский }TOJJ,
двуугольн11ку - дuугрзн11ый у1 ·011 , сфериче
ской окр'{'жносп,~ - конич<::ск~"я rюверх1 юст1"
ось которой проход11Т чере:1 1юлюсы окруж-
1 юсти . РаА! 1 ым сферическим фигурам соuтнс·1·
ствуют равны е фи1уры 1 п луче~\ 1~ннже11иям
сферы - движения пространства. леренодя
щис сферу 11 себя. Геометрические величины
тоже нахuдятссбе пары: например, длина сфе
р11ческо1·u отрезка - неJ 111чина с оотnстству
юще1·u щюскu1 ·0 угла .
Рассмотrим мнш ·о 1 ·раш 1 ый yruл с нсрши-
1юй в 11ентре О сферы. Он 11ересекае1· сферу
421
Фигуры
Рис. 7.
110 ф11гуре, н:~зывае.мой сфарическиj11 _.~11юго-
1•галышко.м (рис. 7). Это область н:1 сферt', огра
пнчепная ломзной из сфери1.Jt:сю1х отрезков
д~т. Звенhя ло.м:11-1.ой - стороны сфернчсскоп>
мно1·оуrо11ьник:J. Их ю1и11ы равны не111-1ч1шам
соот кетстнующнх 11 1юс ких ~r1 ·ло к l\HIOI 01'ран
но1·0 угла; у1·ш1 ж~ vt:НОJ'()у1·олhника пр11 11ропз-
1юльноi1 nеrши11еА равеl 1\10 nL':.Jl:Ич ине двугр~п-
11ому ~11·лу мнотrр;шr юго у1·ш1 прп ребре 0.'1.
СФЕРИ Ч ЕСКИЙ ТР ЕУГОЛЬН ИК
Особый пптерес представляет простсйш11й
сфсрпчесю1й ,,1 но1 ·о)то111, ннк - треугол1,нш<
(р11с. 8 ). Первым его 1:1вt11 в 1·сометр 1 1ческ11ГJ
обиход 11 иссле;(онал Мсне11:1r1 н::~ Александршr
(I R.) . Его трун •·Сфеrи1<<~~ стал всртшш()й до
ст11же1111!1 1·реков в сферичсско 1:1 гсометри11.
Мснслаl1 nерснёс 11а сферу е1н<лндову теор~ 1ю
шюсю 1х треу 1 ·олыпню11 и в числе nр()чего тто
:rучнп условие, nр:и котором трн точки ш1 сто
ронах С'фернческого тре)тольника или их ттро
доюкеннях леж:п Ila одной прямой. Интересно,
что соотnетс·гв)110щая 1·еорсма для плоскос11.У
(см. статью «Треуголытк, простейший 11неис
черпаемый») в то нремя была уже 1111rрок() 11з
вест н а, однако u 1-1стоr11ю t'сомстрш,1 01-1<1 rю1ш1а
11ме11но как теорема Мснелая .
Мноп1с св()йс1•ва сферического тpeyr ·omJ
IJикa (а они одновреысю ю нвляются и сн0Ис-1·в;1-
ми трёхгра111 гьгх yrлo L~) почти ДОСЛОIШО повто
ряю1 свойства обычного треугодьшп<а. Среди
них - неравенство 1 реуголыrика. которое на
языке трёхгранпых у1·1юu гласит, что любой
плоский угол трёхгранного угла меньше сум."1ы
двух друп1х. ИJ1и, например, три признака
422
ранепст1~а треу1·011hпи1юп. Пош1·1·но, что все nлз-
1111метричес.кие следствия упомян}-ГЫХ теорем
вместе с их докю:\тел~,ствами остаютсн спр2.вед-
1шnыми ш1 сфере. Так, множсстоо точек, ра~що
уд~щённых от кuнцов отрезка. бу1~ст и нu сффс
псрпенднкулярной к нему nртюй, проходящей
LIC'peз ею ссрею1ну. А uтсюда следует. что сере
ц11нные псрпснднку:шры к сторо11ам сфср11чс
ского трсу1'олы-шка АВС 11меют общую точку,
точ11ее, дnс днамегралы-ю nро·1'ивополож11ые
общие точки Р и Р', явлs~ющиеся нолюсамн его
ею111стnе111 юй оmтсашюй окружности (р11с. 9).
В сrереоме1·рии это означает. что около пюбо-
1·0 трёх1·р~шпоrо уrла можно опнсать конус. Лег
ко перенести па сферу 11 тсорему о том, что
биссектрпсы треутол ьrнша 11срессю1 ются в нсн
· 1 рс е1·0 1:1писанной окружносr11.
Теоремы о персссчс!111и 1:1ысот 11 мсдт~н
то:{{с остаются нер11ым11_ 1; 0 11:- .
обычные док~1-
затtJ11.>сrна н планr1ме'гр11и 1 1 рямо r1J111 кuп1е1 1 -
но 11cnom,::i)'IOT пара.11J1ет.1юст1" которой, как
мы ;~наем, rra сфере нет, и потому проще до
каз;tть ИJ!: :3а~юво, па языке сrерсоме1·р1ш. Ра
суно1< 1О пллюстрирует локазателъство сфе
р11ческой теоремы о меднапах: плос1<осn1,
содсржащас мсднаны сферлчсского треуrолъ·
шrк:~ АНС, пересекают плоскш1 'rрсу1 ·олы 11 1к с
телт же всршинt~,\НI но его 06ы1.J1lh1м !>1сд11а
нам, слсдовател hHO, вес ш1и со;1ержат радиус
("фсры, прuходящиn чсrсз точку лерссече1111я
Рнс. 6.
Р11с. '!.
1
'1
1
1
\
1
\
\
\
\
\
'
',, ',
/
'....',р.,,"
.:: ::. ..;.;: _
тлоских~ мед11а11. Кuнец радиуса и бу,т\ет об
щей точкой трёх ~сферических» медиан.
Можно привести ещё мноrо 11рим<::ров сход
сmа двух геометрий, но различ пн м<::Ж/(У 1-шми
ш~терес11ее. Особенно удивитслы1а формула
для тющади треу1·олы-1ию1 , впервые опублшю
ват1ая голла111~1\ем А. Жирарnм в 1629 r. и 11а
зnаш 1 ая eto именем. Спrлас1ю это(1 формуле,
площ;щь треу1·0J1ы1иr<аАВС па сфере радиуса 1
равна е го угловому избытку, т. е. превышению
суммы <::ГО углов Пад СУММОЙ yГJIOB ПЛОСКОГО
1'реу 1·оньн ика:
S,1131.. = LA+ LB+ L.C-11:.
И 3 формулы видно, что сумма углов t:фсrи
чес 1<огn треугольника все1-да больше 7t. Откуда
бсrётся: сrолъ r1еоЖУ1данная формула? Рассмо·1·
р 1-1м сначала 7lВууголы1ик с угло м а. Прн а =
: 2n / n, 1·де п - I\СЛ ()е число, сферу можно
разрезать ровно на п копий т-.шоrо ;'1Rууrолъника
"
(р.нс. 11 ). А площащ, сферы ра вна 4тсК = 411: ~трн
R = 1, 1юэто м у площадь двууголътжа равна
·1rc/ n = 2(:1.. Эта формула, очевидно, верна и нри
а= 2п т/п. Оr·сюл<t следует, что она верна ;1,ля
flcex а. Есл и теперь продuлж1•nh стороны сфе
р11-ческсн·о трс-утол ы-rика АВС и rюлробпватh ны
ра знть площадт, сферы с1ерсэ площади обра:зу
ющихся при ЭТQМ 11нууго}]Ы rшюn с утлами А, В,
С и его собстве ппую пл о 1щ1д1), ·1 ·0 ;vюж110 прий
ти к nышеприпедёrшой формуле Жнрар:J.
Многоликаи r еометриs~
Уrлама сферического треуголы ш ка од110-
значно задаётся не то11ы<0 <::го площад1., 110 и
он caN1 как фигура : в сферической геометrип
ныпол11нется чет.н<::ртый прн:зн:1к ра1:1енства
трсугольн~rкон - по трём углам . Тзю1м обр::t
эом. на ссрере 11е бывает подобных, но нс рав-
11ых тре~тол1,ников. Более 1 ·сн·о, в сферпчес кой
геометрии птсу1·ствует само ппнятrrе подобия.
потому что не сущест13ует преобrазпваннй.
нзменяющих все расстоя1111я в одинаковое
(нс равн ое J) <-шел.о раз. Эти особепност11 свя
заны с нарушением евклидовой аксиомы о па
раю1еJ1ьных прямых н также 11р нсущн гсо:мст
rин Лоб:.tчевско1·0.
Сферическая тр1.11·оно~1етрня особенно наж
на для ттрактическоео применения (см . С'"атью
'·Трн1 ·01 юмt:трня») . На сфере, каr< н на г1;юско
сти , по трё?.1. да1 rным элементам треу1·оn 111-111ка
1rетрудно 1 1ы4иСJн1т1, осталыrые. И 1<опеч1 ю. со
ответствующие формулы м:шюю рассм::tтrиватъ
как заnисимости между плоскими и дnугранны
мн у1·ш1м11 трёхграююго утла . Сферическая тe
ope:via синусов очень похожа на oбыt.ll-lyю:
siна ~inЬ sinс
'iinА =siпB =siпC'
1·деr1, В. С - углы.аа,Ь,с - сфернчесюrcдл11ны
сторпн треутпы шка АВС. Теорема 1юс1 шусов.
напротив , ~щест, Т1зме11иется до J 1 сузнаnаеJVюс1·и:
cosа=со~hcosс+<;inЬsiлсcosA.
rю тоже связы13ает величшrы трёх сторон и
одноl'О упш. Прн А = 1t / 1.. эта формула превра-
1цаетсн ~ с 1:1оею рода сферическую «теорему
ттнфз 1'() (J:.t ->:
cos а =cos f'J cos с.
На сфер~:: справсдлш:~:.t 11 вторая теорема ко
стr 11 усо.t1. Она с 11я :.i ын::~t:т нсл11чи11ы трёх yl'JIOR ~1
сторону треуго111, 11нк:1:
cosA= -
cosВcosС+sinlJsi11Сcosа.
ДВОЙСТВЕННОСТЬ
Вторую теорему косннусон мож1юполуч11ть11:1
1н::рной с ттомощhю поляр11.ого 11реобра:ювс11шя.
Пyc:rъfl• - ЛOJfIOC сферИЧССКОЙ 11рЯМОЙ ВС, ТОЧ-
11ее, тот из дпух 1юлюсон, н:отор1,1~1 11еж11т по
разные сторп111.1 с точкой А от даппой прямой.
Таким ж:е образом ОЩJе;1ел11м точки в· и с.
Фигуры
Lферичсский треу1·олышкл·в·с (рис. 12) на
:~ьпзается 17/JЛЯjJ1-IЫJ14 по отношению к данному
трсуrольнику АВС. МОЖ!-10 показать, что тре
у 1 ·ольн~11< АЯС' бунет 1юлярнымд11ял·в·с и что
1:1еm1ч11на любuй сто роны одного1реугольн:ика
в сумме с соотнстстную щнм углом другого
р:н~на rt: а +л·:=а·+А н т.д. Спомощыоэтих
формул и щ:р1юl1 ·1еоремы косинусоFJ для тре
утолы 1икал·в·с нетрудно вынести вторую тео
рему косипусоn для треуголыrикаАВС.
Точно так же из признака раоенства тре
уголыннюn rю 1·рсм сторонам нолучае-гся при
:.шак по трём у1·лам, а И:3 признака по двум
стuро1шм и углу между ними - приз1-1ак 110
сторuне 11 J\LiYM пр илежащим )'1'Лам. Вообще,
11з любой теоремы о сферическом треуголь
r-шкс можно выnес.ти другую, как 1·оворят, д1юй
с1•1н::нную ·1 еорему,11 которой прямые .и точки,
расстоя11ин и углы меняются ролями, что
верно 11.е тоm,ко для трсуrолыrи~юв. Например,
11ару двойстnетшых теорем сосrавшнот при
зн:ши описанного и вписан.наго четырёх
угоm,11н коn: ттер13ый требует равенстI~<~ сумм
нроп1во1юлож11 ых сторон ч.етьrрёху1·олын1ка ,
кторой - сумм противоположных углов. (1Iл<1.-
1шме1·р11чt:<..:кая теорема о том, что у впис111-
нn1 ·0 1 1е·1ъ1рёху1'<шь ника сумма противопо
ложных }ТJюв ранна 180° , на сфере ненерн<~ ,
'l'<l к как сумма всех чстырёх утлоr1 за.ведомо
fiom)111e :160" ) Однако принцип двойственно
сти, у 1 ·11ержлающий, что если одна из двух вэа-
ГЕОМЕТРИЯ ЛОБАЧЕВСКОГО
() жизни :i:J rv1ечательного древнегреческого
учё1 ю1 ·u Евю1и/1,::1 известно немного. Одн:ако
оставленны~J им труд « Начала» бесспорно
нвJ1ястсн 1н::личестненным памятником е1·0
деятет.1 roc1 и . Еnюrи/1. собрал f\Оедино всё то,
что с/1,елаш1 его предшесrвеш-пш.и н области
геометрии н <-иювесной алгебры~ (буквсrпrы
ми обо:щаче 11иями и формулами тогда мате
матню1 ещё не мадсли). Но нс только в этом
е1·0 заслу1'а. Он творч.ески н ереработал собран-
1юе, внёс мно 1 ·0 своего, нового, ориРиюUiьно
го. И соз;рл труд нас1·олько за мt:чатсJiьный ,
что, как своего рода математическая «Илиада о>
1111и •Одиссея·>, с1 ·0 " Начала ·~ лроruди через ты
ся.ч.елстия. В ряде сгран Европы вплоть до ХХ в.
им1 ю двойственных теорем верна, то верна 11
другая , в сферич.еской геометрии выполняется
лишь с некоторыми оговорками и огран иче
rrиями Но можно "склеить" диаметрально про
тиво1ю1южные точки сферы и t'ЧИт:пь их за
одну точку Возникающая 1:1 ре:5ультате 1·акой
(,склейки" геометрия, 11азыв:f.емая зл.лuтпиче
ской ю~и 1 ·с::ометрией Рима~ 1а, оказывается зна
читет)н о более стройной. Например, н ней
через любые две точки nроходи1 • единс1·вен-
11ая прямая , люб.ые две nря.мые пересекаются
в одной точке, а принцип двойственности
вы гто1шяется безоговорочно
1'еометрию в школах преподавали по }'Чебнrf
кам, rs которые были в 1<rп0чс ны еАюmдоnы ~ на
чала•), переведённые и литературно обрабо
танные. Именно таков изJ.Jестныri в Россиf1
учебник геометрии А. П. .КИселёва.
Од11а1ю не nсё шшиса1-rnос Е1жлидом удов
летворяло живших после него математ11коs
Конечно, великолепной была его поnыткадать
акс1Иоматическое изложение 1'еомстрии, т е
сформул ироt.s:11ъ небольшое количество прос
тых предложений (аксиом), из которых лоrн
чески JJыводятся все теоремы геометрии Ао
прсдлож<::11ный Ещwидом ст1со1< акс11омсразу
же л О7'nер1 ·ся критике. Например, одна изннх,
уrnерждавшая, что «Все прнмые уrлы равны
между собой", оказал~1 сь ттросто ненуж ной. Её
удалось док<:1 зать как теорему с помощью ос
тал1эньrх е юи1 идовых dксиом.
Но одна из них, ·1 ·::1к называемый пятый по
сгпулап~ ЕRк.лида. nызьrнала особые нарека1 rия
мате м атиков. Именr~о эта аксиома, каl\ nою1 -
зало историчесJ<ое ра звитие пауки, содержала
в себе за р од ыш дру1·ой, нсевклидоnой гео
метрии.
Вот о чём гоnоритсн в пятом r юстул:пе:
Если две прямые а и Ь образуют при
пересечении с третьей прямой внут·
ренние односторонние углы о. и r.,
сумма ве.rrичин которых меньше
двух nряМЬIХуr;1ов (т. с. меньше 180°;
рис. 1), то эти две прямые обязатель
но пересекаются, nричём и:меm-tо с
той стороны от третьей прямой, по
которую расnоложекы уrпы о. и ~
(составляющие вместе менее 180°).
Да нн ое утвержлен ие замет11 0 сложн ее ост::~ль
ных аксиом . Потому-то в соврем енных учсб
tшках его oбnrчrro за м1::няют rта раmюсилы-1ую
аксиому параллшzы-юсти: к да11ной прямой
через да нную nне её то чh.-у м ожно провест 11 пе
более одной параллельно!111рямой. Но дело не
тол ыю в сложности формулировк11 . Очень пе
лсrко убед ить крипrчески r-щстроешrо1·0 чело
века 1:1 том, что это уrверждение дос.-rаточно
обос1юва1-10.
ВообразиJ\1, что мы Езяли две точки: А и В на
расстоянии 1 м друг от друга и прuвеJ rи через
ни.х д ве 11ря..1\1Ьr е а и /J, причём так, что а пбра:lу
ет с прямой АВ утл о.= 90°, а у1·ол между пря
~1ыми h п АВ равен 89"59'59" (рис. 2). Иначе
говоря, сумма двух внуrренних ощюсто ронних
yrпon а и ~ ncero на 1 уrлоnую се кунду меньше
180°. Гlродожим ttрямьн.: а и Ь, пока они не пе-
'
,
Рис. 1.
Рис. 2.
А
-. .,
,'
1
,
'
а
'
'
ь
lм
~
в
Многоликая геометрия
рссс~r1·ся в точк~ G. Н рсзулr,татс лолучнтсн прн
м оуrолы rый треу1 ·олышкАВС, у кu·J·о рол• у1·ол
А прямоf1 . }TOJJ пр1 1 вершине С равен r 11 СОL1·ав
ляет 1 уrловую секунду. К::~тt·тА С эттп трс::уголr,
ника имес::т д1 11-111у c/tg у, r·де с= 1 м. С 1юмо1ць10
калr"куттт9ра rтетруд110 rЮ/'(Сч1па ·1 ·1" что l / rgy ~
"' 2,06 · 1О". С'..ледователы-ю, дли н а ~<:пета А С со
ст~шляет приблизительно 2,06 . 1о"' м = 2()6 км
(на самом деле чутъ больше).
Угол в 1 }ТЛОВ}'!О секу1-щу достаточ но ощу-
11 1 м ( 11 :шр1 1мср, 11р11 ас-грономичесю1х расчl;:
тах). llo нроАерить, что две у к~ ::~а1111ые нышс
прнм1,1с а и /1 псrесск:о~ются на расстон1 111 J 1
206 км о·т nрямо\1 АВ, сонссм. 11~ просто. Ве11ь
из r·отонитъ 11 лоский 1шст бумаги 11 ли неf1ку
длиной более 200 км 1-1 е предстааляется 1юз
м ожпым. Исп ользоnать о опrческие пrиборы?
Но тогда надо добавить ещё однн поС'rулат: свет
распростр аняется по nрямо 11 (а это уже нс
геомс1·р ия. а фнзика) . А сс1ш сумма угло13 Q. п ~
отличается от НЮ0 сrцЕ менее чем H;t 1 у1·ло
ную секунду?! r<ак ющите, пятый 1 юстулат Евк
лида нс так уж 1 1рост 1-J убсд11тtлен.
Сложность формул ~ 1ропкн nятol'U постулата
н его 11 еуGедитет.н ость п ривел11 к тому. чтu
очень м 1 юпr е м:Jтематккп, жr 1в11J1-1~ после Евк-
11 нда , старатк r, 11 сКJ1ю-чип, этот пос1 улат из
списка аIСсном, т. е. лока~ать e r'O как теорему с
помощыо остальных аксио:-.1 Евюшда. Uiлa 11од
т 11 пrая затяжная «BOЙ IG! » математиков с пятым
постулато f\1 . Многие учёныс, жнвшис n разные
века в различных стра нах, 11ришши в ней уч ас
тие. но особенно ll~tлeкo продвлнуЛУiсь в «сра
жениях» Ламберт. С::~ю<сри и Лежа ндр.
Итат,янсц Сакксрн гассматрнвал чстп1рёх
угоm,ник с трем н прям ыми )-ТШ1м11 (р11с . 3).
Четнёрты~"1 угол ( обоэ11ач11м е1'О '-!epe:J (р) мог
оказат1JСЯ 11рямым, 1 упым иmr острым. Сакке
ри устаноннл, что ги11отеза пр~мого уг.< 1 а, т. е.
уruерж,п,ешrе о том, что четвёрn,1i1 угол <Р nсегда
равен 90° , позrюляет доказап, пятый nосту11ат.
Рис. 3.
а
ь
90·
n
90°г
425
Фигуры
1lначе1·овоrя. гипотеза 11р}11'vЮГО угла лре;1став
л яет со60(1 новую ~1ксному, эквиnаж:н111ую пя
тому ГЮСТ)'Jiату.
Гипотезу тутюго утла, доnускающую суще
стnоватше четырёхуrольшrк~1. у которо1·0 чет
вёртый утол <р 1-упой, Саккерн отвер1· при по
мощи строгого рассуж"~епня. Однако доказать,
что п гипотеза острогu угла неверна, ю1 сам
Саккер11 , н~1 его rюс;1е;щватели нс смогли. Не-
11р11ступ1-1:1я ~крепос1ъ <'> пято1 ·0 постулата ост~1 -
лась неrюкорённой.
Очень интересны пl'с;1е11.ованпя француз
ского ~1атем~п ·нка Лдрне11а М:Jрн Леж~нщра. EI'()
ю1111·:-1, rrосвящё1111ая евклнд()IЮЙ rеометрпи,
хороню написана и nыдеrжала пес1<0.'1ЪКО из
даний. Почти в каждом нз них Лежандр при
водил рассуждение, n н:оторо .и. по сго МJ1сшпо ,
доказывался пятый постулат. Но 11е113мешю в
l'ж.·дующсм н:щанш t антор 11р11зна.нал, что н е1·0
рассуждсни~r нсгюлhзов:Jлось некое утвсржде
нпс (нс сформулщюк1шюс 11м явно) - ючс
виднос<>, но в дсйствнтельноl'ТИ ттредстаnляв
шее собо~'1 нnвую аксиnму. ::~кв11в:~ле11т11уrо
пю·ому rюс1у11:пу. Нн од11а 11з nnn1.1т01< Ле
жандра не пр1 rneлa к успеху.
Впт r<раткае оmtСание одной из лаnыток
Лежандра. Пусть а и IJ - две прямые, перпеп
днкулярные одпой н той же третьей прямой и
псрсссюнощис сё в точка,"\': А 11 В. Эти две 11рн
мые а и Ь .1-н:: LLСрес:екаются. До11устим. что
1штый !юстулат Енюrнда нсверс11 11 1 1ерсз А
МОJК1-Ю ПрОВССТН СЩс':: одну nгmмую а', 'l':Oll<ЖC не-
11сресскающую Ь (р1к. 4). Симмстричн::1я ей
(относ~ пслы-юАВ) прямая а" также 1re пересе
к:-~ет nря11-·1ую Ь. РассJ\1 ~.прнвая [(RЭ получаю
щихся острых угла rt..' и а" (симметрич1 IЪL'-' друг
другу), Лежа1щр строго дока::~ьшает, что прямая
а как при продолженнн её вправо. так и лрн
продолжстщ nлсво nсё болсс удаляс.~гся от
прнмой h 1lo прямые а 11 h не могуr вести себн
надобным образом: если они не пересекаются ,
то ;1олжны нахою1ться на огра11ичешю,'v1 р:-1с
стоя11ии 11ру1· от дру1·а на всёt\-1 своём протя-
А ______,-- - - -
а
---------------а'
/ci.'
в
ь
Рис. 4.
Рис. 5.
женн11. Не пра.1-ща ли, уGед11т~льно? Од11ак() на
С!мом дел<:: ::~то просто другая аксиома: он~ сле
;~уе-1 из 11»'1 ·ш ·о 1юс1·у1tа•1·а Е11.кюща , Lt , н с1юю
очерсл:ь, из псё Rытскает спrаnедлтлюсть nя
тоrо пооула-га
8 11aчaJJe XlX в. в •·Сражение'} с пятым пос11•
лато.м встуnил русский матс:\1атш< профессор
К~1занского уннверснтета Ннколай Иванович
Лобачt:Н(.'КI 11"1. Он был 11сключитслhНО т::щант
лr 1в н чре:~выча!"шо 1tаСJ·ойчнк. Пер1ще 1tремя
Лобачсliсю1й ш<:л TC'vf же пу1"ёМ , что 11 его прсд-
111сствснн1тк11. т. е. пы.·г~u1ся рассуждать 01 про
·1 · 1н11 юго. Донусти в, что 11я1ъ111 пос'1'уnат Евю1н
)l;а неnерен. а остапъные аI<сиомы cnpaneмrmы,
мы рано или поздно придём к протнворечию
::>т~1м протиrюречием он и будет доказан.
11так, допусти.1\-:t. что Шiтый постулат неверен:
через тuчху А. нс нрннадш::жащую IJPJL\IOII Ь
(рис. '1 . а) . можно пронест11 более ЧС'l\1 одну JJря
мую, котоrая не пеrесек:~ется с /?. ПусТh пря
мые а' и а" нс: пересекаются с IJ . Прп их распо
ложt:н111t, как на р1кунк<::, будt:м тюнорач1шать
пря.мую а' nn часп1ю~'r стrелке. Тnгщ1 mfщётся
прттмэя с'. которая «n nоследmпu1 рэз » пе пере
секается с 17. 31rач1п, прямые. получающиеся пэ
с' лрн повороте по часо1юfi стрелке (11а сколь
угодно -'1алый угол). будут пересекать прямую
IJ. а прямые. получ~uощпсся из с при малом по
во роте в обратном на11раRленин. не будут лr
μесек<~ть {?. Иначе говuри. сред11 нсех 11рнмwх,
11ruхо;1ищих через тuчку А. 11ри;-.1ан с' <пделяет
11ересека1111ц11с 11 11 р>1м hll' от Hl' пср(:сек::uощнх
еl:. С:1м:1 прямая с' не nерt:l'с:к:н.:т Ь. Так:.~я же
кар·1·1111а 11абл юдается 11 дли п ряJVЮЙ с", симмет
р11чтюi1 с' от~юопелыю nерпепдrrкуляра АР,
опущенного ш.1 (;. Она отделяет пересекающие
!? прю1ые от непересекающшс
Лобачеnскнй называет пряиые с' 11с"11прал
ле.;1ы1ьши прямой Ь, прпч<:м с' параллельна Ь
вJ1раво, а с" параллельна Ь в.лl'во. Остальные
прямые. прохuднщ11t' через точку А 11 неnере
сек~1ющ11е прямуf() IJ (т:.1кне, кзк t/ и и"). 11ме
нуются fJaC:\'OUЯll{lt.J\1UCJi С nrямoii h
б
р
~~ /)
р
Ри<'. 6.
Рис. 7.
/
Дэщ:е. обоз11:.~чнм JV11111y отр~:щз Af> чс:ре1 .\'.
а остры/1 у.1·ол. обрээуемый пр.нмой с' илr1 с"
с пртюй АР. - '-lерез П(х) (рис 5. 6). Ло63че.в
сюri·1 вводит этп определешт и обознJчепиf1,
стремясь, со сnойстветюй ему 11:.~стоt'Jчт1 -
востыо. у-.юатъ, LfТO может получитъся t1~~ ero
Гiр(.:ДПОЛОЖСНИЯ о неверности ШITOJ'U ттосту
Щ!1'(t. 11 быстрt.:е обндруж11ть жt:л;~нноl: протн
вореч11е.
На 11а ш11 '\ ч ертежах л111нш 1·1:1<н·нутм. llo
чнтатслъ должен 1ю няп" ЧТL) Лоi'iачевскнй
r:1сс~~ждае1 1·1MCH I 10 о пр>~л-1ых Л llГll IЯX. Есл11
01резокАР мал. то ocrp1,n"1 yro11 П(х) fiлн:юr< r<
t)()'. Ко гда отрезок АР <"оuсем мал, п;. поо,ют
рев "В MТIKp()C lIOn·> на ТО'Ч1\у р (f>ПС. 6), J\olbl у1ш
д11.м. что прямые с' нс" праю·нчес1<и стшаются,
rюсколы()' у1·ол 11(х) очень близок r< 90°. 13 це
ло~1 же, f! cmry nрсдrю.rтожс:нrrя о неНё'рности
1нrтого пос1улата, 1 1 р11ходится 11зобr:1жаТh ли
f1ш1 нзо1 ну1·ымн . И ссл11 в 1~алы1.сl1шем бу;r.ут
1юяr~11юъсн всё более н более стра нн ые nсщи.
rоэто только хорошо - м~,1 с~юрес наткнемся
на /\ШI гожд:.~ н 1 юс 11 рот 1 ~ворсчиt:.
Ло6;1ч сnскиi1 до 1<:1:л .111ает ( всё 11том же 1rрел
поло:жетш п пеJ.Jер1юст11 nятого постулзта),
что /{Re параллелы1ыс 1 1рямыс неоrратurчсщю
rбш 1.жаютсf! друг с [{руrом в сюро1rу пар::ишс11Ь
носп 1. тю в обратном напраnле1 ши опи r1со1ра-
1шчси110 удаrшются друг uт друга (рис. 7, а). Л
дж: pacxoJ 1,ящ1·1 t'ot r1рнмьн: имеют сд1 1 нстнсн-
Многоликая rеометрия
ныfi пбщнй пеrшеrrд1 11')7Iнр. пс ) обе сторrн 11>1 от
К<)Торого ош 1 неоrр:т11че11110 удv1Я1rнся д[J)т
о·с 11руга (рис. 7. б). Это очеш, похоже па то,
о чём писал Лежа11!{р, по мы уже знаем. •по
эдесь нока сщl' нет rn1какого 11ротнnорсч11я.
3атсм Лобачсnскиit рассматрщшет две па
р~11utсньные;: нрнмыс L1 и с 11 берёт на пркмой. fJ
д 1шжущуюсн точку М, уда.11яrощуюся н сторону,
оt11х1тную nэраллслыюстн (рис. 8). В к:~ждом
nшюжении точки J f 0 11 впсе1·авляет перпенди
куляр р к пря~юй /J f (O L"ГО r 1 срссечен ня с rrpя
:vroli с JI,.riи1 ra rrepnc1~д1 1кулнра непрсрыu11п во~
р:н:тает при дnиже1т1111 точю-1 1\'/, 11, 1<:ота 011а
пон-а.п:ает R 11екоторос nопоже1111е Q, дл1 ща пер
пепДI1к\·;mра стаrrошгrся бесконечной. Точ-
11еl" rоворн, перпе11д11куш1р р, nосст:~влс1111ьп·1
к nрямuй Ь в ТО'П<С _(}, пар:urлелс11 пршvюй с
(рнс. 9. а). Лuс1рш11111рJJМую с1 , с11 мJ\!етр11ч11ую
с от1юс11тсл1,1-10 11errrc11 ;1, 1 rкyюJp:1 р, 1юлуч111\1
1"{1И Лf1ЯМЫL" - /?, С И С 1 , KOTOj)hlC IIOll:!(JHO 11:1-
paJUlCJll>HЫ т~р) 1· Щ1) 1-у (р11с. 9 . й). Во:зн11ка~·t
crюeoб pa;iHhl й <·бес1<0неч~н ый треуа)Лы 11rк·1: ~·
не1'О ю1ж,ц1>1е две сторопы nар:uтщ:лы1ы ;\руг
;~ругу, а вершп11 со.13сем пе-1 ' (0 1т как бы нахо
дятся n аескопечrюстт1: рТ!С. 10). Это уже 1ш
ка1( не со 1·лас,·ется с прrшыч11ыми предст::tnле
нюrl\'\IJ о р:.tсположсшщ пр51мых лп11 нй! Но
Lrротиноречшr н здесь нет.
Тсхда Лоб::~чевск1[J1 преiщрштмает по
п ~-.1ТК)' щ·1 ю; 1ь:ювать "'I01 yщet.'TRO формул Прн
\Н.:ннн t{t1t·;iён 1 r ую ~1М фу11кц11ю 11 (.У), он 1 юJJу
част Э3fHIC l·IMOCTH. ПO:'ШU!l НIO ЩIJ l' по сторонам
Рис. 9.
Рис. 10.
427
,
/
/
/
Фигуры
,
,
,
,
,
,
,
;
,
,
,
,
,
/
"90°
90·
Рис. 11.
Рис. 12.
треуt'ОЛЬН I П<а вычислять его углы. и ОК<1:3ЫНt1-
ется , ч:то в любом треуrолы1икс сумм:а уrлон
меньше 180°. Значит, в qстырёл·угольнике Сак
кери (если его разбить диагональю на два тре
уrолытика; рис. J 1) сумма углоtJ меныне :)60°.
~-=>то означае·r, что мы наход~rмся в условиях
г~-шотезы острого у1·ла - когда в четырёхуrоль
пике Саккери четвёртый yro!l <р < 90°. Kar< будто
.ничего нового нет: Сакксри и его лоследо.ва
теш1 до1 1 rо ломали гшюву над гипотезой ocrpo-
ro у1·ла, но противореч:ю1 так и не нашли.
Однако Лобачевский ок~1зался теперь на
много 601 ·аче: он имел формулы, выражающие
завиоrмости между с1·оронами и у1'ла:м:и любо
го 'Греутолы1ик~t. Пользуясь сrюимн фор,.,,rуламн,
Лобачевский доказал: если известт,1 углы тре
уrолыIИl<а , можно одно:шач1-ю вы<шслить его
стороны . Со.всем странно! Rедь существуют
подобные треугольники, в которых уты соот
ветствеюю ра.впы, а стороны нсодщ1а1<0вы, так
что у1лы трс:уrольн.ика не rюзволяют вычислить
ддины всех его сторон (рис. 12).
qто это - желанное противоречие' Увы,
опя1ъ нет! Наличие подобных, 1-ю неравных
треугольникоидоказывается с помощью акси
омы о 11араллель11ых прямых. А 1101 ·ому с:Jм
факт, что такие треуrоm,1ти1<и существуют, мо
жет рассматриваться т<а1< ещё одна ноnая акси
ома, э1<nивалептная пятому постулату.
И Лобачевского осенила гениальная догад
ка: противоречия никогда не будет! Иначе
,__
428
1·о~:юря, есн11 мы до бавJ1я.см ко всем прочим
сl.КСИОМаМ сщё и пятый ПОС'JУЛ<JТ, TU нолуч:~ется
нспрс;тиворе чив:ая 1'еометрическ<U1 система -
та еrщлидова геоме1рия , к которой мы так при
ныкл:и . Если же ко всем прочим аксиnмам вl'<1е
сто пятnго r1остулата мы добавим отрицанu€
аксиомы параллелыrости, т. е. аксиому о том,
что через точку вне прямой можно npoвecnt
более одной прямой , параллельной данной,
то получим другу'Ю геометрическ}'Ю систему
(Лобачевский на звал её •воображаемой» гео
метрией), которая, О/\11ако, тоже непротиво
речива.
Лобачепсю1й рассмО'I рсл пучок прямых, па
раллелы IЫХ друг 1\РУ'У в 0/\llOM на11р<1RЛСНИИ,
и его ортогональные траекrории., т. е. 11и 11 иtr,
которые псресе1<ают под прямым угло;-.1 все
прямые данного пучка. В евюrnдо1юй геомет
рии тож<; мож1ю рассматр1mат~., ортоrональ
ныt траектории. Например, для пучка ко1щен
трнч~сю 1х окружностей это лучи, исходящие
из центра, :ci для пучкС:1 1 1аралж:льных nря:мы.х -
перпендикулярные им прямые (рис. 13). Но в
геометрии Лобачевского пом1·1мо прямых и
окру-АG юс1·ей п ка чt.:стве ортоrо11альных траек
торий для nуч1<0е этих ли 1 шй поя1тяются но
вые 11ин и и - орицuклы. (юп1 предельные ли
нии; рис. 14).
Дальнейшие события были весьма драма
тичны. Лобачевсю1.й рассмотрел u лространmе
пучо1< параллельных пр11мых и повсрхносщ
ортоrона.111>ные прямым пучка. Такие поеер:шо
сти - ирисферы
-
обладают замеч~1телънымJ1
с войст1:1ами. Через каждые две точки орнсферы
проходит орицнкл , целиком лежащий на этой
rюверх1юстн . А потому .\ЮЖ1ю рассма1риваrь
треугольни.ки, образованные треМ>1 ор11цикла·
ми на орисфере (рис. 1S).
01\азалось, что в геометрии r1a орисфере
сумма упюв любого треугольника равна 180'
Рис. 13.
То есть для орициююв на орисфере справед
лив гrнтый 1юстул:1т - госnодс1'вует 1·сометрин
Евклида.Другими словами, из материала своей
~воображаемой» геомстрrrи Лобачевский сумел
построить модель геометрии Еnклид::~. Какая
злая ирония су11.1,бы! Если бы всё было наобо
рот! Ге11иалыrый учё11ый понимал: создай он
из материала евклидовой геометрии (в непро
тиворечивости которой 11икто не сомневался)
модель собствсrmой "воображас:-.юй» геомет
рии - и законноеrь его геометрической си
стемы устанонлена. Это сделал11 математики
уж<:: следующе1·0 поколения.
Jlобачеr.ский выстуnи11 с докладом об от
крытин неевклидовой геометрии в J824 г., но
поддержки не 11ашёл. Он опубликовал о ней
ряд статей и книr, nричём с её помощью су
мел вычисл!'fть несколы<0 и11теграло13, ранее
неизвестных. llo математики его времени ещё
не были ПОДJ'ОТОDЛСНЫ Т< мысли о возможнос
ти существов<1ния иной, тrеевклидовой геомет
рии. Учёный умер, так и не добившись при
зю1 ния своих идей.
Впрочем, один человек понимал и nодr{ер
жив~ш егп работы. Гениальный Г<tусс, <-ко роль
математиков» (судя по <tрл.':иву, разобранному
\'Же 1юсле его смерти), eJJ {ё я J81') J'., за девять
лет 110 сообщения Лобачеиского, размыtшrял
над а 11ал о гичными и11еями. И хотя Гаусс
не развил 11ееnклидову ~·еометрию т~к глубо
ко и подробIJо, как Лобачевсю·rй, но правомер
ность подоб1-1ых идей оп прнзнавал и I<Ое-что
дuкаJШ J в но.во.й геометрии. И тем не мен<::t: Га
усс, к м н t:нию которогu 11рисл~1пивались нее ,
нс решился ни опубликсшать оюи работы, ни
помсржать Лобачевского. Гаусс поннмал, что
~1атематики не воспримут столь 11 еобычныс
пдеи и даже его м11е11ие будет расце11е110 как
некое «чудачество" гения. Однако Гаусс добюJ
сн того, что Лобачевского избрали иностра 11 -
ным членом-корреспондентом Гётти11ген
ского учётю1·0 об щества. Это единственная
1ючесть, возданнан Лобачевскому как учёному
при жизни.
Кроме Г:.1усса был ешё один челокек. кuто
рый вместе с Лобачсвсю1м деJшт заслугу откры
тия нее.вклидrнюй геометрии . Венгерс кий ма
темати1< Янош Бол~,яй очень ннтересопался
проблемой 11ятого постулата Евклида, о qём
как-то написал в письме т< отцу, математику
Фарюшrу Больяю. Фаркаш ответил сыну, что эта
проблема выше сил чсловечесr<их. Она отни-
Многоликая геометрия
~
1
'
-
Р11с. 14,
Рис. 15.
Рис. 16.
~\ет все свободное время . пиш1п ~окоя 11 здо
роilьн , ею нс стоит заниматься.
Однако Янош не 11ослуша.11 совета отца .
И вскоре достш· yc1Jexa. Он сумел построить
несвклидову 1·сометрJ 110. такую же, как у Лоба
ченского, хоп1 11 мене~ глубокую н 11оследона
тел 11Н)' Ю . В с1юём проиэнедею111 «Appcndix->,
помещёlflЮ ,\·1 н ко 1ще учебника геометри11 ,
Янош Болъяй нзJюжил ноную снс·1·ему. Как 11
ЛобачеnСiштl, от 1 11е добился 11 р1 1 зна rпrя. 01\щt -
1<0 ему сообщали, что за трп года до 11его юш-
1у такого же содерж~шия опубликовал какой-то
русский учё1 rыi'i. Больяй нс поверил, ре1шщ что
его хотят лишить сделанногu и.1vr открыт11я. ()н
спсци;:~лыю изучил русски(~ нзык, чтобы про
честь тру;\ы Лобачевскш·о в nuдm 1н1111ке. l l<:-
пp1 ~знание и огорчt"ние из-за того, чт< 1 его rше
редили, сло.мru1и душевные сш1ы Яноша.
За ме111 м, ч·1 u у Ятюша Больяя быт 1 неко
торые иптерес111.1е построе1111я, которых 11ет
у Лобачевского. Нзпрнмер, он о пределяет орп
циюrы с помощью хорд равпоrо 11ак11011а (а не
как орто гона111... 11ые трасктор1ш, хотя эти д.ва
0 1 1редсления э1шнвалентны; рис. 16).
ма·1 ·ематш<И слег1ующе1'0 пuколення (К.rн.:й11.
КэJ1и, Пуанкаре н др.) сум<:л11 1 юсrрuнть мuдсль
1 ·еоме1 рит1 Лобаче1ккоп> из матери~tпа геомет
рин Евю11щ<t, тс,\t самым устэновив непротшю
речиrюстп 11 ЗaKOIITIO CТI, llOBOif ГСО.\1етр1rи.
И матсматикн 1ю1rяли, что могут бы1ъ раз11ыt:
геометрии н разные пространства .
429
Фигуры
ГЕОМЕТРИЯ И ГРУППЫ ПРЕОБРАЗОВАНИЙ
R зш ебре рассма1ри1~аются ра :шпчные фу11к
ц~нr. На116011ее щюстые 113 ннх - J 1ш-1еr'1нзн 11
ква;lратнчная. K:l.Ж/lOMY ч11слу х нз не1<0тороr·о
м1южеств:,~ (061шстн orrμe;teJ1e11ин) фу11кщ1н /
conocтaR1 1нe-r числоf (х) - ~ша<Jет1не фу1пщ11н
/11 тоt.ше х. Например, футпщня/ (х) = х~ + 1 со
. поста вляет
числу х = 1 чпсло/(2) = J.
1
+1='J.
В геометрии рассматрнваютсл фушщ1111
нного рода, называемые.: гtю.-11етрически.11tи
преобразовт-tия.1ни. В отличие.; 0·1 алrt:бр;1114с
сю1х :.1т11 фунюtни каждш1 точке ст;:нтт ti соuт
нстс1 ш1е точку.
Рассмотr11м, наnр11мер, прос.:ктнрова111rс р
nространстве 1 1110(1 ф11rуры на шюстюс1ъ
(рис 1). Кажд()fr точке r1 ::>то nреобра:юватте
стаnrп n соответспте ·r·очку А,, лежащую в
плоскости nрое1щнй. Мьr гоuорим. что А 1 -
образточкиА при лроект1Iрш1а1nшр, и пишс~1
А~ А 1 Образы всt'х точ.ск про1r:~но11~,ноГ1
ф~н-уры .\1 составляют ф111· уру i\1 1 - образ
фшуры М. На нашем рисунке образом nт1р:~
м 1 1лы М являетоr чстырёх~толын 1к М1 п плоско-
стт1 1~рое1щи 11, т. е. 1\.1 ~ i\11• Лналоп1ч.110
обозна чаются обра:"iы точе1< и ф111ур при 11rо
бых преобразованиях . Если яспо, о 1<аком nре
образованин идёт речт" ero обозначение п;щ
стрелк01'1 опускают: А -7 А 1, М -7 Л1,.
ГсометричссI<ое 1 1реобразование называ
ется дви:ж:енuе.м) сслп R результате е1·0 не из
ме~-шется р:кстоннне ~1<.:ЖJ~У точ.кам 1{, т. <::. сош
lПА -7 А1 и.В -7 В1 CJteдye-J АВ =А ,В,. Так, 17Uf.IO -
в
~
А
'
с
430
~
'1
\
/ют (рнс. 2) - дш 1 ж<::нJ1е. Lюскольку расстоя
ния между точкамн 110CJ1c лш.юрuта не изме
rtяюто1. ЗаJ\.1ет11м, что 11р11 1-сометрическщ1 по-
1111м:н111н дниже11ия обращаrnт нн11м:тие mшJъ
па rraчam.rюe и 1<опеч11ое (образ) 11оложеt1не
дuиЖ)11дейс-я точки, отмекаясь от её промежу
точных положений, скорости 11 т. д. Эnr~1
I't'омстричесюn1 под,ход к движеrшям отлиqа
<::тся ()Т фИЗl IЧ.t'Cl(()J'(),
,[1,~1 ·1же::1111с.; 11:юскuсr11 мuж~·ю прt:Jкт:шить
себе сж:дующнм образом В()обра::шм, что на
плоскоеrп даны какие-10 точю111 фшуры !Jа-
11ож~ 1 м на неё лист кальки 11 обвсдём на нём те
же точки 11 фигуры . Затем ошме::м кальку 11
в<::рпём её обрат~ ю r1а плоскость, 1IO n поrюм
11оложе11и11. llоскольку калька лолуnрозрач11а,
nидны как 1кходные точкп н фигуры на пло
скости, так и их изображс1 шя на смсщённом
J 111сте калы< 1 1 (образы). Кюкдая точка rmocкo
l"l'l J 11ерсходн1 n 1-ювое:: пшюжсние (образ) Это
и t:сть п:оме::трt 1чt'( кос 1rрt>обра:ювание, назы
ваем< >t: Jtl!llЖCHHe::.'> ·1
Дн~ rже1-о 1ем являстсн и нарсии1е.r1ьныii 111'ре.
1юс, когда нее •~·очки шюскосп1 сме ш.аются Б
сщ 1 юм н том же 11;111р<1нле11ин 11а однп и то же
расстстн11е-(рис 3). Векюр, соещ1 1tяющийточ
ку 11 её обrаз при параллельном пере~ юсе. Ol\Тltl
н тот же для всех точек, 13 связи с чем говоrят о
параллельном переносе н<.1 как01'1-то .вс1пор а
Ещt однн прпмср дnнжснпя - осева;1 сщt
.меrприл llycLъ н~ плоскuстн н~tчсрчена пр11-
мая / ( <ХЪ CH"\.IMC'Jp11 11 ), а т·акжс ка кпе-то ф1·1суры
,'1
Рис. 2.
\
1
\
'
Рис. 3.
,- -- ---- - -------- -- --- -
~,~----~-----~ /
1
t
1
1
1
/в.
/,' ~
!,_________
Рис. 4.
Pt1c. 5 .
11 точюJ Наложнм на плоскость J 111ст кальки н
пt:rепсдём на нс1 ·0 прнJv1ую /,а гак.же ф1 .1гуры и
Т()ЧКI! . За·1·ем пеrеаернём калы<у 11 НЗЛОЖl!М её
на nлоскостъ обратr юй сторот-юlr так. ч·1·обь1
каждая точка прямой / сонместилнсь C:ll\1a с
coбoil (рис. 4 ). Тогда всякая точка н всякая
фигура попадут в no1roжc1шt\ снммстрнчное
перво11ачальвому относптеныю прямой 1.
Можно осущестнтъ оссН}'Ю снммстршо 11 11е
ре1·иnая чертёж ло осн !.
J !юбое l\Rнже::нне 11рс1tставлнст собой 1~зан,•1-
нооднозначное прt:о6разон:н1ие шюскостн на
1у;.ке 1rлосr<ос1ъ, ·1. е. двум р<~зличн1,1м НJчю~м А
н В все1 ·да ссютветствуrот различные точки А 1
и 81• Это и пш 1нпю: поскоJ1ы.-у ·~·очки А и В
различны, расстошшс между ними не rarшo
нулю , а та1< I<ar< расстоя~1ия при движении со
храшuотоr, расстояние .ivrcж,цy нх образами А 1
иВ1 тоже не равно нулю, т. с. А1 и81 ра:тичны.
Значит, для к;l)КД01·0 движенин ./можно опрс
дсли1ъ ибрапиюе ему дв 1 rжснис, которое <160-
значастся через r- l: есл11 движе1111е f nepcвu-
.
•
l
д11т точку А в А 1 , то обратное д1шжсние .r-
nереrюднт А 1 u А. 1 ю:3Rращая каж;(ый обраэ на
прежнее место.
Если преобразова~ n re не взаимно одпоз1 rач-
110. то обратное преобразование для пеrо
не определено. Напри.\'1ер, проектпрование
прое1ранства на плос1<0сть не взаимно одно
значно· в Ltаспюсти, у различных тоL1ск В и С
пространства (рис. 1) uбраз.ы на п;юс~<ости
Пf)ОСКЦJ IЙ могут .нс сов11ад;.~1ъ. и потому H('}IC-
\IO, R к:;Н\.')'10 точку про<.vт· 1хшства должен пере
ходи ·rъ этпт общий оnраз прн обратном 11рt'
образовант1.
}1rrя nараллепыю1 ·0 пере 1 юса 11'1 ве\\~1·ор 7i
обратным дв11жеш1е:.1будет11араллельны 11 пе
ренос 11а вектор - ёi (рнс. '5, а) . а для поворота
вокр}'l' точю1 О тrа }·ТОЛ (J.
-
поворот 1юкруг тоf1
же точки О на утол - а (рпс. 5, б). Обратное
дв11жсн11е н оссной симметри11 - т;t же с:им-
1tt"1'рия (ГJ 1с '5. в); з;1есь обратнос д1:11 ~женнс со-
М1юголикая геuметр~1я
а
J:ШЩ\3~Т С 1I СХО)~НЫ М . il CIMU,\1 /\t:JIC, t:' CJI И ГJ р1 J
с 11ммстр11н uтнuс нтелыю прямо 11 /точкаА JJ с
рсходит 1:1 точку А 1• то тu ч:ка А 1 11е::рсходнт об
ратно liA пр11 тш'r же с11мм<::трш1.
Резул1,тат ппс.л.е71,011ател ы юго ны11()J 111сн1-1я
двух движеш rй назьrnается J 1х ;.;о.м;юэuцuеt't .
Нели сначала 1:1ыпол11яется дш1жешrе j. а сле
ном 3:.t пим д1шжение ~, то комnш11щш1 обо
зна t1;Н:"1 ся через/ " !!.·
l1~111р11.мср, <::СЛН /- лар:umельньn"I 11ерсНОС
па вектор а = АА 1 • ;:i g - 11:~раллельпы1'1 пе-
репое шt вектор h = .1 1Al. то их ~..;омпозшtшI
/о м 11редст:.tнлясто>бu(1 г1ар:uurсльны1111.срс1юс
навекторёi+Б ""А.А 1+ А 1А 2 (рис.6).Дсйстнн
тсл ьно . 110 П[XtRИJ1~ сл ожс1111н векторов,
АА~=АА1+А1А2= {i+Ь.
И11ачс rоноря, есJш A~A 1 ~A i . то
.fо к (11реuбр;~зuна1111l'. сразу псре::1.юд.11щсё А у
A l ) есть n;.~рашн.:лы-1ый 11срс:1 юс JJil вt:ю·ор а + h .
Поскольку а+ h = Б + ёi (см. сптыu <"Векторы
11 опсрац11н 11ад 1-!IIMll; р11 с. 7). КОМПОЗ IЩIIЯ пa
paJUJt:'IO>T 1ых пере1юсон 1 1с за1111ст 1т отто1 ·0. в к.1-
ком порядке 01 llf liЬIП()JJJ1mmп1:j'o Д = ,!J о/
0,тщако ;рш друсих ви;(ов днижс1п1i1 перемс
ст.ителы1ый закон не всегда справс..ц.пиn. Рас
смотрим" шшр11мер. квадр11т ABCD с несколь
кимт 1 примыкающимп 1< пе.чу юза,.цратам1r
(р11с. 8). Обоз.начнм LJ<:peз ( по1юрот нtt 9l> 0
Рщ·. 7.
- 1-31
~ Фигуры
в
с
Q
м
D
м
il
!
g
.r
р
Рис. 8.
Рис:. 9.
тюкруг точки С, а чере;~ ,g - n01юрот на 90"
вокруг точки D (повороты nы полшrютсл про
Тl rn часовой стрелки) . Тогда
А~М~С, A~P~Q,
т. е. КОМIЮЗИЦ!1Я (о р, 11epeRO/\ll'I точку А 13 точ
ку С. в то время какμ, o.f переводит А в Q. 31[~1-
чит. .!" g н g o.f - раэные прсобр::~зования.
Так н !\-1 образом , кО.'11\JЮЗнц ня парзлле.111.ных гте
ре1юсов11,rмL1v1ymaпzurma (rюдч~1 1 1яется 11 ереме
стителы-юму эакону):/<> ,q = ~ "j; в то Аремя как
1ю;-1псх1~.щш1 поворотов (воктт ра :щых точек)
11еко.м.iнутшт1в1tа: /о g t: g оf
Прпвсдём сщё д ва прпм ера: 1юмпозицш1
двух центральных сиы.мстрш1 отпоситслыrо
точс:кР н Q (рнс. 9, а) с:сть ш1р;шлельный пере-
нос на век-юр 2PQ. а 1юм11оз1щ1 1 я осе1"1ых с11м
метр 11 И от1юсителыю осет1 / 1 и'" ' составляю
щих утол а ( рис. 9, б), поворот во1<руr точки
пересечен.ил осей на угол 2а.
Однако в любом случае комттозит\ПЯ /\R Иже
ний /и g также есть некоторое движение: по
скольку расстояннн сохраняются 1-1 ттр11f.11 при
μ,,ОНИ НС IIЗMC llЯIOTCЯ II I<О гда пμсобразования
./и к ны1ю1шяются подряд, ·1 · е. пр11J о ,к.
М нuжестно преобразо кан и й r_т назы н:l.ется
г;;:~ •mюй п;нюбразvваниk ссJш l) нля moбor-o
nреобра:юванин / и
1з С существует обратное
ттреобразuван нс/ - , прнкадлсжа1цсс С, и 2)
КОJ\1 по:~ 11ция/о g тобых д нух 11peonpa :ю1\ar 111 l1
111 (,'та ~..же прпп адлежит(;'. И1 сказанно го вьmте
ясно, что множество D всех движени й естъ
группа ореобразова11ий.
Кроме множества всех дю 1 же11и1:1 rvюжпо
указать и другие группы nреобразова 1шА па
пр11мер, множество Т всех nараш1е;1ьны х 11е
реrюсов В са м ом Jl.t' .. 'Ie. если прсобр а зов:нше/
11рннадлсж11т м1Jожеству Т (является парал
лет,ным переносом). то и обратное 11рсобр::~
зова11ие - 1~араллел1111ый пере~ юс Далее, если
б
()
А
2а
/и g - параллельные переносы, то /о ,q тоже
ест1) n epc11 oc.
А вот множество всех осевых сю1мстр11 й
гр-у11n ой преобразований не яВJшется , 1ак IOIK
композш щя 1tвух осевых симм е1 рий не uсевм
01мм.етрия. Аналогнч но, нельзя на з вать груп
пой прсобра:1оRаний и множееrRо Rccx цент
ральных снмметр нй (мы это R1~дели выше).
Од н~1 ко можно доказать, что множество S 1ю::х
1 ~е 11траm .11ЫХ симметрий и параллельных пе
ре1-юсов, uместе взя 1ъ1 х., ]?Ке представляет со
бой группу.
Исходя нз ~·руnпы D всех движений, 11емец
кий геометр Фе1111кс K.11el111 д:LГJ ответ на DOnpoc
~что такое 1··еоме·r· рин? ~ . Более то~ ·о. подход
Клейна по~шш1ил увидст1, внутре 11нсе сднн<-11!0
1 ·еомс:тр и 11 Евкл1ща, 1·еомечши Лобачевского 11
ря,f'\а J~pyrи:x rсомегрнчсских систем. Поз1-1ако·
_,-Iимся с 1ro1txo;\oм J<ле~11 1а на 11римереепкл11до·
вой геом етрии.
Соl'Ласно Кrrейпу. дnс фигпJы равны, eCJni
одна из 11их перенод~пся 13 другую некоторым
дв1 океписм. Ясно. что
.~ каждая фигура равна са!\<ЮЙ себе,
"kI
поскольку то.ж:йесmщ.'1t11оt:' 11/нюбразован11е,
остант1ющсс RCe точки Н "- месте, переводнт
ф 111'Ут>У ca.\lly п себя . Это стюйс•rно равенсгш1
фигур наэынается реф1и?1\С1юностыо
Далее:
Если фигура М равна фигуре N, топ
наоборот - фигура N рав11а фиrуреМ.
В самом лел е. сел и М rтере1юд 1 пся в .V двнже·
ш1емj, то обратгюе /tв11жсн 11еj-1 переводит.У
н М (рис. 1О) . Говорят, ч то равенство фигуроб
л::~дает си..м.метричностыо.
Ещё од 1ю свойс~1.ю равенства ф 11 гур наз~~·
11ается траизитштостыо:
,\/
1
(1
l'нс. 10.
~'•' Если фигура М равна ф1-rrype Nф, а
Ъ. фи1-ура N в свою очередь равна и
гуре Р, то фигура М равна Р.
~~ вюшдда111юt.: сно~'1е1·1ю формул1Jров:.~л 11н ,1-
Ч<:: •Лнс ф111'}'/ lhl , fXIRHhl e '1pl:ThCI\ равны МСЖf~У
собо~'1 -> дL'l1 с1·н нтс; 11,1 ю, так 1<ак фшуrх1 ,1{ ра1111:1
\, сун ~птнует ; ~в~ 1же1111е]. nере1юдящее М в .'V.
Далее. 1 ю<..кол1>1<у N раrн1з. Р. сеть движе11не g.
1
gр
1
щ:реuодящсс.VвР: М~!V~ (рнс. 1 ).
llo тота ком 1 ю::нщня j "g (1·оже дв11жен11 с) nс
рсвuд11т М 1' Р, а з11ач 11т, фштра JJ равн;:~ Р Кзк
в1ц1 1м , вес сво1"tс·1·вJ р~н1е11ств;:~ фнrур вытск::~
Ю'I 11 :l TOI о, •!ТО '-IНОЖССТRО ДBl lЖCHIIЙ D явля
(."ЮI 1рутюl1
Ра 1ш1,1 с .\IСЖД'r' собu (1 фи гуры обладают од1 1 -
нэкот.1м1 1 своl1.сr в;1мн. Например, если ,Н
11pя ."l;I>1, то 11 р::шн:1я еС1 фн 1ура N тоже нрямая
(р11с. 12). F.cm 1М 01< ру-11шост ь раднуса г. 1·0 11
ран11аn c i1 фш·ура N есть окружнос-rь радиуса ,. _
ECJ111 М - 1\оадрат, то и равная ей фшура N нс
премс111 ю юзадрат Еслн ка1<ая -то фигура им<>
:т шющадь S, то и равная ей фигура имеет ту
же 11Jю11щд1" Иначе 1·u.1юря , при переходе от
фшуры к р:11~1юй ей (пр 1 1 ;~в11Же1-111н) , все 1·ео
мс1рt1чсс к~1с снойстна фи~-уры сохраняются,
11л 11 . как тнорнт, о ни uннсфuантпы (неи з
мс111 1ы ). Tcnep1, бу11е·1· понятно клей1ювское
011pcдt:J1e11 11 е: геометрия н:1учает ·J'e свойства
ф111 ур. которые осrаются инвариантными при
1'1к. 11 .
Pt1c. 12 .
Мно1 сJ/\икая 1еометрия
1ксхдо1~жс111 1 s1х. Так. тeopt'~ia 1lнфагора (сп1ма
кващх1то н 1v11111 ка·r·L·ток 1х1нн а ква,r~раl) 1v111ны
ll lllO I C H Y~i hl ) <IТHOCl lJ 'CЯ к свойствам. 1 1:-1~чat:
\1bl~I н н:о мС'1 r1 11 1 1нк·ко.1ьК) :-это сво~-ктно со
лр:1нж'"1 ся r1р11,1в1 1жt:111 1я'<. А то, что точка 11.,1с~
е1 ц; в,111 llHЫ<:' КООр1~1111'1ТЫ, 11е ЯR.\Ис::'\"01 СС
1е< l\ll' 1j)I1Чt'CKlt~ I CllOil(1'1i0;\1
Н о 1юi1дё\\ 1t:L'lы11е. Клсfrн . 1:1ёт более общее
от 1сJ 11н е гсо~1етр rнr . 1lусть G - нскотораs~
гру1ша 11111 1жс11нй 11:юс rюст11. сотшад:нощая с
rp\•111101'1J) 11mr отл 11ч11 :LЯ от 11её. Дnе ф11гуры ,1/
11 /v 11:1зонё.\1 6 /1пт1ьши, t:сли н 1 ·рупnе с, 11af1 -
; ~t:тcs1 т~t KOL' дв 11ж<.'1111 с, которое 11 с рt:вод11т ф11-
1уру t1J н .\'. /~аж:t', Ci' -гl! UAШJJJ/m eй (L11111 .'t-'(1~rem
/m~f'f 1/~) 'IПJ.Ы (;) бу;~с м им<:нова'!'h те сно~ 1 стn: 1
ф111ур. t<oтophll' О/~И1·1:~ко ны у любы,х 1щух <1-ра~-
11ых ф1 rry r. ' J'. ...: . с нойства , J111вариэ11тrrые 11р11
всех 1 11111жс1111н :< грут111 ы С.
Н а пр11м ср. рассмотрим геометршо, которую
0 1 1реде11яст 1т>уnп а 1· всех параллельных пере
н осов. 13от од 11а и з теорем Т-геометр~ш· если
сторо ны АВ 11 Л С трсу1'олышка АВС соотнет
с-1 ненно Т-равr~ы сторонам А1Н1 11 А1С1 тр1:
уголы·111ка А 1В 1С1 (с ~'Чё-ГО.\1 порядка RCpLШ lll ), ТО
:'! 111 1·р<:у 1олы11 1 ю1 Т-(1аRны (р 11с. 1.1) . Н самом
Д(:JН.:. Т-р:шс1-~с1 1ю С1орон АВ и A 1R 1 о3нач~к"Т,
что сст h 11 ар;L1ле.•r1.ныl1 11еренос. 11еревод>11д11\1
АВ 11 А1В1• Тот же 11еренос 11ерсводитА в А1, а
АС 11 Т-ран11ую сторонуА1С1, т. е. и весь пер
вый треугольник во второй. Другим11 слова ми.
в Т· геомстрш1 существует признак равенства
трсуrолы rи1<0n по дRУМ сторонам. Ничс:го по
хожего~ 1 ·сометри и Евклида нет.
Uот с щi.' од rrз необычная (,для с:в.кли11.о.1ю!J
J '<:омс:тр11 н) теuрсм;~ сели R четырёху1 '0ль ник1:
/\В<.: 11рот инmюножные сторон ы Т-р~шны , то
/~<1н ны11 четырёхугольн111< - параллсло1рамl\1
(рис. 111, а). R свкmщо1юИ геnметрии из ра11е 11 -
стпа (D-ra11e11стна) 11.вух nротиво полож11ых сто
рон 11 е сле!lует, •1то четырёл.уголышк яnляется
nараллело1 ·раммом (рис. 14, б).
Теперь рассмотрнм группу преобразований
более шнро 1су10, ЧL'М гру1ша D. Наnомннм, что
N
4:В
Фигуры
~---~ С1
4\;_---!З
(,'
А
Рис. 14 .
Р11с. 1 з.
Рис. ·1s .
подобием 1rазыRается flрсuбразона~-ше плоско
ст1 1. при котором вес расстояни н 11 зменщотся
в k раз, rдс k -- некое положнтеJJыюе число.
назынаемое коэффициентом подобия. Приме
ром по11обия может служить го.мотетия с
це11тrом О н коэффтщие11том k, т. е. преобра
зоnа 1тне, когда каждая точ к<t А пер еходит в
·1зкую НJЧкугl1, что OAt = Jг ·ОА (рис 15).
Ком rюз 1 щия l'Омuтетии /с коэфф1-щиснтом
k и ДIН LЖСНШI /!. тоже ~IRJLЯCTCЯ nодобнем, no-
CKOJl hKY при J·омо·1·ет11н/вt:с р:кстояннн увеш1-
ч11в::~ются в k раз, а прн дваженни ~он и нс ме-
1]}1 Ю'J'СЯ в Ч<lСТНОСТИ, ком позиция гомоте·т и!('
1щэффiщие1 пом k 111 1е 11тром. О и nо1юрота <~ на
y1·nrr а вокруr того же r~ентра О (рнс. 16) пред
ставляет собой поворот11ую гшюпи:тию (с цен
тром в точке О, коэффициеIIтом А> и углом а).
Легко попять, что КОМПОЗJ·ЩНЯДН)'Х подобий
nнон 1, 1 10добие. Jiсли в результате подобия./ нес
расстоя11ия и зм еняются в k 1раз, ан результа те
1юдобням- нk~ ра:\ то пр11 ком1юз1rц1ш/ои
нее р:.1.сстоянт1 ум1-ю~:~ются на k 1 /?2; :3нач 1п,
f o!!,' -
1юно61rt с коэффи1t11ентом k 1 · k~. Лна
·'Ю1'1 rч1 ю, ест t / - 1ю;tаб1н: с коэфф1щис11том
131
l.1
, то оnrатнос прсо6ра:юнз1 1и е - пол,0G11сс1.;о
эфqш1\11е11· 1 ·ам 1/k. ~тп оз11з чэ е·1 , ч1'СJ множ<:
СТIJО Н nccx ттолаб1111 н шrяегся группой 11 реоn
разоu:ший .
Ка.копа же геометрия. mrредслясжш rрушюй
JP Нtдь в результате преобр;~:юва1 111 r"1 подобня
ю111ны отре:~ков ТIС: сохран нются. 11 n ОТО\1}' о
; 1,111-11 Lt отрt:·Jкuн 1 ·uнорить н 1·t:о.мt:тр 111 1 Н нс t1ри
хол11тся. На нt:рвый в:Jr'JIН;~ в п:омстрrш riuдo
()н l r 1ючти нп: п.:орС .'-'IЫ снкл HJ(( нюl1 п:·омстr11г1
тср}11 от 011.1С11 Напр~ rмl'p, теорем() п 1·0 ,,1, что в
раnтюGслрет н том треу 1 ·0111.r~икс1тлы пр11 ос1 ю
в:111ии: раш 1ы. В ран~ ro\ie1tpt1 шо;11треуголы1 1 ·1 1<е
/l,Л llt rы бокоuьLх. стороп 1хшпы. l lo раз у юс 11ет
д1ш 1т, то н ет и раr~нобедре1111ьrх трсуrолы1111<0в.
То же можно <:казать и о теореме llнфагора: в
11 c i'1 11нёт рtч1, о д1 1 ш-1ах сторон 11рн моутuлыю -
1·0 ·1реупшы н1ка. Ош1·1 ·1, д11ннъr! Что же ое1 ·аётся
R l'COMCTp l ПJ I I0)\061 11)~
Однако обе уnо".1я нуть1е ·1·еорем 1.1 в r·со
метрии nп;~аби1-1 су1 1~есп~}'IОТ. Толшо сjюрмуя11-
руются иначе. Л:eJIO н ·1·ом. что хотя нм1ш1
отрезков прн прео6ра:ктэ1 11 шх 1юдо611я щме
пя ются, оnюшение длrш дnух отрезкоо 1шш1-
риан11ю Р;ш1юбе11ре11 1 rый ·1·рсуголыппс можно
определ111ъ как трсуrолы шк. н котором отно-
1щ: н ис длин двух бокоn ых сторон равно 1
(рис. 17, а) . Поскольку велич1 t1 1ы у1 ·1ю8 1шва
риантны np11 пр<::образонан11нх 1 юдоб1щ тео
рема о равнобедренном тре}'1·ол1,н11кс пол-
, ,'N
,
J\1 ,,,,
___
".
I~
'-!
'-
.
Рис. 17.
'
'
Рис. 16.
1юст11ю ~ 1юсс1·а 1 1анп1шаt'ТL'Я н пранах ·•. Л нот
ТС()рема П 11фагор;1 }\ЛЯ 1·еомстрии ЛO/\OnИiJ
(р11с 17, б): в любом nрямоуrолыюм грс:утrшь-
1111кс: амеет место раnстrстно (а/с) 2
+ (Ь/с)
1
=1.
где а/с 11 Ь/с - отшнnе11ил 1'ЛШ 1 ~;атетоu 1\
.11л1ше 1·1тоте11у:3ы.1.300(') 11 1с. нодоб 1 1ьL1v1 образтvt
мож1ю сформулпроn;~ть почто вес тс:орсм ы 11
онрс:дсл СШIЯ IJl КОЛЫ ЮГ() 1<:урса l'COMCTplJI l ,
Пр~·!Н<:ДёМ llj)l!Mt:p: J!ШIИ Н нa :~ ЫJl:tl~l'L.>1 OкpyЖ
HOtThJO. сели сущсс·1· 1 1ус·1· та J\ан ЛNКа О ( це11·1р).
ч10 д;ш люf>ых 11нул тощ;к А 11 /3 ;рн1-ю i1 л11ш111
tл11ошt:ш1с 01-1/ОВ рак1ю 1 (рис. 17, 11)
ПOC\1()'1'j)IJ М, ка l{ с 110:~1 щ1 11'1 ·к,.1t:r1 1-1: 1 МОЖ\10
uн 1101ъ друп 1 е 1·ео:-.·1 с::- 1·р 1л1.
Пр11 J l 1Шжc1111>L'\: расстояния меж,:1у ·1·очr<~1ми
н11в,1рн:111т1 1ы. следоватст.1ю. сохра11яются пря
мотшеfшос расположе1шс точек (прниые 11е
рехощп в прямые) и nелнчипы у1 ·;юв мс.:жду прй
щ,1.чн Из этоr·о f1ытск~1ю· 1 и дру1 ·1 1 <-: сно 1"1с."1 'щ1
~~ш1жсн11й. ) \але<::, в рс:.~ульт:.~тс 11 реобра:юн:1 11 111~1
nо;~о611н отно1 11 с1-1 нн расстпн 111 л'1 межтtу точка
м11 не измсннются. Знач1тг, пр11 по~{)(i 11 нх 11 1-111а
рн;~нтны 11 nрямо1111нст'11 юе рас 1 юложе шн:: то
чек. и lltJП I ЧHllЫ ~TJIOH .
Сущее1·nу1т t"Щё более общне препбра:-~она -
11JIЯ. прr 1 1\Оторых сохра1 rяются 11рямолю1еiн юе
расположение точек и отношение д1ш п любых
цвух параллшты 1 ых отрсзко1.1. Таюrс щх:обра
зова ния r 1 :t:J ыflaютcя аффитtы"11111 (рис. 18).
М11ожс:сттю 1кtх аффи 11 н ы х щх:обр~1зuнаю1й
IVIOCKULTLI тuже Щ1C/l,CTat!JIЯl."I' coбoi'I ГР}nпу п рс
обра:ш11:1 1 1111! ГC0,\1t:'I рня, опрсделя~_:ман этu1'1
r pym юl1. H:IЗЫH:tt:l'CЯ aффu1-t1t0i1 гUUAl(:'/Jl/)lff:'it
Поскольку всякое nщ~об11е я нлнетсн афф1 11 1ным
nptonpaзona111н:м, нее т~оре.vtы аффн111ют1 1 ·еt)
метрнr 1 с н rаnедлиnы 11 11 геометр1 п r ттодо6пй. и
fi 1·еомст р11и Евклида. Однако м1юп1х енкл11 -
доr~ых теорем ( 1<~1к и теорем гс:ометр1 11 1 ~юдо ·
бнй) н :1ффиr-1 1юй геометрии 11ст. В •1асттюст11.
G ней отс утствует те орема l l ифarop:t (утлы н
аффшшой 1 ·сш~стрю1 пси 1-t1:1ариантны. слtдов;1-
1·елыю. нс.:: ll\1l't'T с м1,(с.1 1 : 1 1 ·о кор1·1 т1, о 11рнмо
у1·u.1ы1ых треу1 ·олnНJ 1 ках).
Каюн: жс 11011ят11я 11 теоремы t:l"I ь в афф1 111 -
нoii 1·co ,\1L" I р 1 1 1 1? l l:Jpaллcm.нtx·1 1) 11:1ph111рям1,1 х
(UTC~rПTK[·l e' }' llllX ОnЩСЙ П-,ЧКН) 11{)1 1 aфф111 r
lfl11X прс:оnразо1~:111шrх спхраш1ется, а 110·rому н
аффшшо 11 t"ео;1.1е·1·р 1 1и rvюжпо расс~1атршы1ъ
параллелограммы 11 ' t рапсцш1 . Дrra1 ·он алп [1а
ралш::ло1 рамм3 дслятсн пр11 перссс•1 сrпш 110-
JТOjf:l~I. l la нзыкс афф11111 юй гсометршт ; 1ан11ы~'1
факт заштt· 1,1 н:1 етб1 равс11с1·1.{а,\Н 'J .40/c'I >= 1 11
Мн()rол и ка51 геометр и я
Рис. 18 . Аффинно1· 1 1реобр,нщ1,1 н ие.
130/ !JU = 1, 1 '/\С () - точка т.:рсс~::чсн11н ) \11а1·0-
11:.11 1 с1'1 ш.tр:тлелог:rам~1 а AB<7D. о·п ютс 1 1ш1
;~J1 11 1-1 пара1щс;1ы1ых снрезкон, 1.;ак 11 отрснюн
0;0 10{1 11рнмоС1 (АО/СО. BO/ DO). 1 1мСК)'J ' orыcJ1
1{ афф111 11 юir 1 ·ео мстр11и.
Teope,v1~1 о ТШ•I. что медианы трсуго."1ы1ик~1
nсресекаются J3 0;1ной точке в л:еJJ.ял.:я в 11ell н
оп IOlllC1-i11II 2: 1. также 11рИ11:1/).JIС:ЖПТ афф 1 п 1 HU.ll
г<-:омс.тр 1111 . ЗаJ\1 еп1м, что шобыс дн;1 тре~ го11h-
1111ка '·афф111-11н1 р:1ю1tМ: OД!lll и:3 HIJЛ М()ЖIЮ
11 eptвt:C l'JJ н Jlpy1·0 1'1 с 1 юмоrцыо « П срекосаь
(pllc ! q) r111рсо6р:1зо 11а н1 ~я 11одобня. Поэто~·1 у
·п::орсм у () M CДll <!Н:JX ДОС'Пl'l'ОЧ 11() l\U l\аз:пь ДШ!
ка 1<01·0-1r н il)'дr, од 1 юго,11:н1(юлее удо61 юго трс
угол~, 1 1 11 1«1, 11а11рпмер для рэвносторош-rего .
Лффшптую 1·ео,чстр11ю, как н дру1ую геомет
рическую спстсму - проеютю11ую геанетрию,
:i 11али ещё до работ клей.на. но ему прш1адле
жит 11х осмыслс1111с 1ш ос~юве гр\1ТН1 nрсобра
зuна1шf1 .
3десь мы тол1,ко f{P:JTKO OCT:lll0fll1MCЯ 11 :.1
ос1-юш 1ых п01Jожсн1н1х проектн н ной гсuмс.:т
р111 1 , поскольку ci-1 пuс.:нящсна отдслы1ая ст:лъя.
в этоii J 'Co.'v\CTJ1Иll llЗ)'Ч:lЮТСЯ CIIO!'IC'I ва фнгур,
1111ш1р 11 а 11т11ыс 11 рт1 всех 1z;юал'1m1нны.х нpeпfi
jJct3ona1шяx, - 1-1реобра зпнапт 1 нх , сохра1 1яю
щпх rrpft;1.Юлr111er1 1 юc расппложение ТОЧ'СК Тlо
добшr и вообще все аффинные нреоfiра:юn::ншн
Рис. 19. Пр..,~н·р ,1фф11 1111 010 nр1" 1 )t·1р.нов,1111111 <ПРр<!кщ •
гочю 1 нек<норои n рямсJ11 остаюп я неnолвижным11 ,
. 1 О<"С' сн 1 ._1м.)н~~1v f л1щrп1от4 ~ 1 1 ,1р ._11\ЛРл 1,110 JТОЙ пр"1м с н1
н.~ раrстnяние. nрпп11р ш1он.1"ьное рас ( тоян11 к1
0 1 11J•1к11до111• под0и,.,11011 ll)J~\1 CJИ
4У5
Фигуры
()ола)1ают этим свотkтn()М. Рассмотр11.'Vf сщё
одш1 пример. Спроектируем J1ат1Т1ую шю
скос1ъ а на друrро тюс1юсть ~ из некотороrо
t\снтра. а ~атем снроектнрусм ~ обратно шl а
из дру1'u 1 ·0 11снтра. Можно взять и большее
чисJIО прuмежуточн1,1х центральных проекций.
Одн;нш такая ко,\JЛО~~и1 111н 11рuекц11й будет rк·
нсегд~1 uпрс,г1слсна Н:1 нс~й ш10скост1-1 а. Чтобh1
получит~-, нза11м1ю 0:1.т1 о:зн:1чное отоnраже ш1 е
ПЛОСКОСПI на себн , её l'/OIIOЛIOlIOJ/l - гrрНС()СДН-
1IЯЮТ к каж,~ой прЯJ\.юй дополr 1нтелы1ую, · 1ак на
зываемую бесл;оиеч.по уr)атzёи11ую точку. одну и
ту же для осех параллельных П[нrмых, з к сrню
купrюсти прямых - ещё одну, бес1т1tеч110
yдaлii1tJ1)'IO прямую, образоnанную всеми 1ювы
мн точками.
Поrюлненнан бесконечно удалёшrыми точ
ками плоскость на ~{ьшастся проективной 11.110-
ск.остью. Теперь можно )"l'ОЧ li И'IЪ ЩН 1нос RЫШС
0 11ределе ни<::: отображение проектишюй шю
скости н а себн, 11ри котором любая прямая (n()-
п олнсп ная бесконечно удаленной то"Jкой)
crIOFJ:l переходит в прямую, 1 1аз1.1нается проек
тивным преобразова1 шем. Проектиш rые преоб
разоnа1rия образуют группу (если два преобра
зования переводят прямые в прямые , то же
uерно 11 для их композиции, и Д11Я преобразо
вания, обратно1·0 шобому нз них). Эта группа и
определяет 11роектнвную 1·еометршо .
З:,~мети м , что в nроектиRной 1'еометр ии
Rыраженис «Отношения дли 11 параллельных
отрезков.> теряет смысл - в ней не С)'IIJ.естну<.:т
даже по 1 1ятия параллет,ности: после nопот;е
ния любые две прямые пересекаются! Вместо
отношения д;нш параллельных отрезков рас
сматривается так назьmаемое двййиое ormюute
нue четвёрки точек на прямой. Дrrя точек А. В,
C,D (рис. 20) оно задаётся формулой ~~ : :::З.
Можно показать, что оно сохраняется при
любых проективных преобразонаниях, в част
ности при центральной проекции .
Вообще r·о1юря, окружность 11 результате
проекти в1-ю1 ·0 преобразования переходит н
эллит1с, гиперболу ю 1 и нараnопу. Н <1 существу
ет и бесконечно мноr() проектив1-~ых 1rреобра
зований плоскости, которые переводят данную
О.1<."J)ужность саму в себя. Они составляют группу,
которую мы обозначим через L. Простейшие
примеры преобразований из группы L - пово
роты вокруг Т\ентра окружности и симметрии
436
А' 13'
с'
D' Рис. 20.
опюситеJJыю её ю1:~метров. Гор~1 :що ш1терсс
нее, ЧТ() с 1 /0 ,VIOЩЬJ() llJ10t'KTl1HHUГO нр~обра:зо
ва11ия можно отобразит ~, 01<р}?Кност1, на себя
так, что её центр персf1дёт n mпбую з::щ:11111)1О
внутри окр~ЖI юс·ш то чку.
Рассматривая группу/., 1\л ейн дог:щался. что
с ct.: помuщью можно получить модель 1·еомст
рнн. которую изуч:ш Н. 11 Ло6аче11сю1(1, 11 тем
самым дсжа :зать её не11роти.вuрсч1шость. Ю1е1~ш
рассказал об ~той до 1 ·аю<е сносму учителю,
1~.ыд:нощемуся нс;,11с11ко ,чу математику Карлу
Вейерштрассу. Но тот не поддержал ученик:~ -
счёл его И{\ею ВЗJ\Ор 1 ю~1. Вот как велико nыло
убеждение математиков п том , что с~1дестнует
толыю од11а геометрия - ет<л идов~' Но Клейн
нс послушал совета учителя и заверп 1и11 tIOC' J]JO·
спис модели. Такую же модель 11е:~зnиси.\10 от
него создал а1rглийсr<ий алгеб раист Артуr Кэли.
Вот как выг1rядит.;1юдшzьКэли - Кле1iтю reo·
метри·и Лобаченскш·о (р11с 21 ). Зададим n пло·
скости о кр уж ность К (её называют абсолю
то.м). Условимсн заключа·1 ·h н кавычю1 все
понятия, относящиеся к рзссматриваемой мо·
дели. Нас буд)Тf интересовать только q•1·очю1+,
расположенные ю rутри окр)71А<1-юс-1'11 К, т. е. точ·
к.и её внутренней области (точ.ки самоrо абсо·
люта [{ и с1'0 ннеш11l'i1 uбш1сти и:-~ рассмотрt:
нш1 исключаются). На:ювём <·нрю"юi1" mРбуто
xop,rn' окружности. К без её ко1 -щевых точек.
Очею тно, что через тобые две «точю1» А н В
проходтп одпа н только одна «прямая » . в пол-
1 юм соотnетствии с аксrюмам11 Ештида . Нпут
рст 1 юю область окружности /< назоn61 <-WIO-
ci<ocтыo Лобачсnско1·0", а каждое nроектиm-юе
преобразовшшс, пере1'01щщl'с К в себя , -
"дв11Ж<:нпем->. Подобные ,.диижс11ю1~ 06ра::1уют
rpyнny /,. Н .v1<щ<.:ли Кэли
--
Клеlнtа 11эуч:н.:тс.:н
гсомстrшя . u 11редсш1 е~vшя именно этой 1·руппо11.
U11μeдcmrтh <· расе1-оин~1е » между «точкам11"
• 11.JOL'кoc·1· 11 Jlобаченс1<01'0·, нужно так, 11тобы
шю нс JIЗМСНЯЛОСh пр11 нсе.х <-двтке/ll lЯХ·>. «ДПI 1-
il\C I 11 !Я» Н BJ IЯ I01 'l'Я Пf)()C:K11 IHI ll>IMH пpeof)paЗOH:1-
HIJ>JMl 1, а знач1-П'. l'охра11яrот /tнorl 1 юe 0·1 ·110 111 с-
11щ;. Поэтому •·р::lсстоя1 1и е» в 1vю11елп K:'JJlll -
К,щ:fша ВЫ ражаетсн с1ерсз ,11,ВОlП Юе OT!IOme1111.е.
Точнее, отто 011редсляетсн 11 0 формуле
\
in lлс = .A1JJI,
СВ ПВ
1·:1е С 1r / >- коr 11 \r,1 хор1 1ы . п рохо,'(я rr1ei-1 чсрс:з А
11 В. От.v~ ст1rм. что ,'\эн н ое 11ыражен11с р:щно
ПРОЕКТИВНАЯ ГЕОМЕТРИЯ
ПРОЕКТИВНЫЕ ТЕОРЕМЫ
Пrоскп1в1 r ан гео.чс1р1 ш o<.j)()p\1 ила(.· 1, как са .,ю
с·1 оnтс; 1 ьн~и1 матем:1тнчсскан / \НСц1t11111 ·~на н
1822 1· . ко1 ·да французсю1(1 мат<.:ма·1- 11к н
11нже-
11t:р Жан В11ктор Понсслt:.> onyбm1кm1<u1 .ш:.1м с
н11ты1'1 '·Тр~ктат о проек 1· 11пных сво\1ст1~<1х
ф111 '~'Р"· ();111:1ко мес1 ом рожден1·1>1 '110Ro 1TJ
п.::ометрt 1чсскоГ<11\11>1 111J1е1111л-> слеr1ует сч нтать."
Саратов, г;tе с л.1щт1':1 lHl ~ по ~1юп1) 1Ю4 г. 11а
хо,т1.1~лся ттлсш 1ый лс1'1тена 11т 1f <] nолео1ювскоlf
;1r~11п1 J Jонссле и где 011 11аштсал а.1мстю1. по
слрк1шш 1 1е осrю1юй «Трактата".•> .
Uдн ;шо з:~кончсннан теор 11 н 11с MUl'J !:J. нырас
л1 I1:1 11устом месте. l:i.: корнн уходt 11111 /tалt:ко
н 1 ·лу61, 1-н:тор11 н Перк:.1н фун;1::~мt:н·1·з111,юн1
1·ео1к:ма [lj)()eKПIJ'.\\()l'I ГСU.'-ltетри11 С()Дl'[УЖJ\'1'1..' Я
И ( M<lTt'MЗПl'leCKOM С()браНПН·> (l·laЧaJIO fV 11.),
iHП'Oj)()!\1 KO'ГOj)OI'\) я F!IO!t'TO! /tреnнсrречео<И 11
.11этемат1 11< Паnл Лл~кса11/ Ц)J-rйски 1~1
Многоликая геомстрня
нулю лишь ко 1'/1,Э двойное оi ·1-ю111е11иl' рз1шо l .
т. е. коr:д<~ А = В. «Углы" меж,1\)' 1- nрям ыN11I» тоже
опре11ешнотся с 1юмощыо формул, имеющихсff
в лросктивпой гео~rстр 1111 . Тенерь мо/юЮ
рассматр1U1ать « nерпеr1лпкуюrр11ъ1е » •· rтрямые·>.
<•ДЛИНЫ» сторО!! и <• УГЛЫ» трсуголь JIИК ОВ J3
,.плоскости Лоба чевсн:ого,,
Далее . две « прнмые" в «шюскост11 JJобачt:н
ск<J 1 ·0., условнмl'н на3ьща'1'h <, нар~u111енын,1м1н.
c<.:J 111 общий ко1tl.'1t11 :юбраж:1ющи х 1 rx .хор11 ж:
ж11·1· на окружш н_"1·1 1 К. Д11е <Ч 1р}lм ыс~ ~1.нш11отся
«расходн щим.и с~н, tтЛ11 Н:J<J6ражающиt' 11х
хорды н е 11мсют оnщих точек m1 ннутр~ 1 збсо
лютз /\.. 1111 н:.1 само~~ ;1()солюте Тспср1, ясно .
что через '"Г<1чку» !>, которан 11~ лежит rrэ ~- 11ря
М()Г1" Ь. м()жно проnестн f>ес1юпе'l1Ю м 1 ю 1 ·0
<-прямr.1х», 11сnересекающнх <·nря1щ10» /J.Две из
этих «Прямых" (с' и с" на p1rc. 1. J) «nарал
nелы~ы• « ttрнм.ой ·' l? в дnvx ра:щых в:tпран
лспиях. а остальные « 11рямыс·>, проходящие
Чt' j)СЗ «ТОЧКУ" Г1 кнутр:и д нух :{CJ l l;HЫX нсртн
каJrьны:х )1'JIOH. <- расходятся·> с <- 1ч1я .чой·> fJ _ В по
строен нot'r мо;tслн спракс;~т1вы нее факты
1·со\1стр1111 JJ06ачt'нс ко 1 ·0 . Так с{:1к011 '!1 1лас n
более ч<.:м ; ~ вух· 1 ъ1снчt'л<:тннн б итnз м;1тt'~1ати-
1<он с аяты м 1юс·1у11ато111 Енкл 11/~<l -
С теоремой lJаппа кhr мо 1 ·1 1 и встр<.:'шть
сн. pt'Ш:J H 1•1313t'CTH YJO 1·шю1-юломку: JIOCl/tllTb
Дt'J\Я'l'J, дept'Hb t: H н ДСНН'IЪ j)}Щ()В (f() 'J 'j)I 1 в каж
дом ря11~·- А нт точнан qюрмут1ронк;1 .с1·1uй тt:о-
1х·мы (рис J):
.с Пуст1~ А, С и Е - т1>и ·~·очк~' ка пря-
,а.,.
·:<-С мойр,ав,DиF- триточкина
другой nрямой q; если прлмые АВ,
CD, EF пересекают прямые DБ, FA, ВС
соответственно в точках L , М, N, то
то•1киL, М, N лежат на одной прямой.
Тсоμем:~ Тlа1111а 1tuвол1,но н еобычн;.1 _ Bu-
11 срных . в ct: уо1ин111 1 ничего не 1·oкopll'l'CЯ о вза
имном раслоложе 1н1н r1рнV1ых р и ц 1. 1Т()чек 11.
В, С, П, Е, F 11з ннх. EcJtн по11р~кнт1, rх1зных ;1ю
лсl1 "экс п ер и мt:1rта;11,11О·> пpnнt'pJ п·1. с1 1 p:1RCJ1.J111-
вocтr. ·1'еорсш,1 , то на вер ня ка опи предложат
са:.1ыс р:1з11ые чертежи; на рпс. 1 nредстаuлеrю
437
Фигуры
Рщ:. 1.
два 11 з JЮ:1можп ых. Во - nторых. нет з;1,ест, r11 1
;vппт. 1ш углов, 1111 друпtх сня:~анпых с IПI!\-Ш
лшштrпi - nссго того, что ·\11,111р 11 кh1 ю 1.и 1:1ндеть
н теорсиах из школ ыюr·о учсб1 111 н:а. i lспол юу
ю·1·сн 11111 111, тр 11 11рос гсйшнх т ю1 1 н· 1· 1 1>1 1 ·ео.\1ет
р1н1 - ' l'OЧJC:l. 11ря .ч:1Я н 11 p! ll f::l/l,ЛCЖНOCT l1 ТОЧК11
1 1ря~ю ~'т. Им1.:н н о 1:1к1 1е ·1·ео ремы характt.'рны
11,ля п роектищ-ю\1 гсо~т стрт 1 п.
Ещё CЩ l ll 1 ~амеча·1 ·елы1ыfr пrимер тсорсм 1 ,J
подобного тнnа .11ал в 16:16 1- .
фраr щу:кюrй
1·еометр, архите ктор 11 ш1жс пср Жер ар Деза рr
n малсны<оfi. объёмом 1ктго в l l сграп иц
работе:
Uуст1. npJJмыe АА' , ВВ' , СС', соединя-
1ощи е соответственные верши11ы
треугольникоnАВС иА'В'С', проходят
через одну и ту же точку О. ТОJ'да три
точки попарного пересечепия L, M,N
COOTDCTCTDCHJ-IЫX сторопАВ и А 'В', вс
J[ В'С', СА и С'А', сели та1<:ие точки су
ществую-:r, лежат па одной прямой.
На рис. l, -~· 4 прLШtДt:НЫ лишь IIССКОЛЪКО
нз J\IIIOJ f)YИCЛC J IIIЪIX П ЛОСК11Х 11 11 рост μ ан
СТl:\С11ных ко11фшур:1 ц1,1 й, у;щн11стнорн ю11\нх
ycJJoн1 н1 "'' тсорс,чы Дсзарга. Замl'тьтс: 1Ш/t , . L "l 'CJ -
po1 1 :1м 1-1 -> трс~ l'OJI l>H н ко в ЗДL'СI> 1lOH ll.\1:HO'JC}J
н с t>'l'fJt'ЗK.J1A.8"A'B' н т д., а содt:рж:ШLНt: и х п рн -
До1 1'
1
Р1н.4.
L
А'
/
\ Рис. 3.
-158
а
,L
1'
'
1
мые. Кста·п 1 , этн конфнгур:щ1 п 1 11:1ют рз.1ме
щсппс /\eCHTll дере11 1,ев Н Дt:СЯТН j1ЯД:tХ ПО Tpll
н рнду
С1 1 ра1:1ед;11ню сть ·1сорс:чы Дсзарt'а оч ен11д ю.
кш·:1:1 1 111uс1шс·1· 11 'l '[..X:y 1'c)J1hHlll<OB АВС 11 А'В'С
ра:т 11 чнъ1 (р1 1с. .1). В э·1 ·< щ с.11уч:.1с 'l'C>ЧКJI f.,M, N
пере сеч с t-1ш1 соо·1 ·нетствс ш 1ы х сторон тре·
Yl '<>m, 1 11 1 ...:oв пр~rt-1 а;исж:1 т обеим 1 u 1 щ·костям
/ IBC 11r1'B' C', 1<0'1 Пphlt: пtpt:CtKaIOTOl llU 11rнмоf1.
Есл 11 трсугп1 11 ,1 1 1 1 1< 11 p;:i с 1ю11ожс.- 1 11,1 1~ о;1но~'1
П.'ЮСКОСТl1 ( рнс. 4. ({ ), ;\:IЯ :щк:.t :~;JТ(')! l1(T11:1 1 1адо
просто пре;кт::11-1ип, чер'lёж к теореме 11зfi
и.ю6ражстптс - nроекцшо
-
а11:~логнч1 юl1
1.Jростра 11 ствс 111 юй ко11стру 1щш1 (срашште
р11с. .1, ~1, с1). В нростра11ствс точю11., ,\/и N ле·
жат 11 а u;1 1-ю 1~1 1 1рю.ш(1, 11р11 11рос1щ1 m прлмая
11t: рсход11т в щ1ямую. Знач 1 1т, 11 11а tL'IOL1<0cт1 1
тспрс,1а нср11а
Услuннс тcopeMhl Дcэ:tpl':J - 11 pяl\JJ.1t' А А',
R8'. С( 7' пcptcC t(:l!c Yrcя н 1пчкс () - мож110 ПС·
рсс)ю р ~·'f)J1 11 рп 11з.·1 ъ · 1 ;~к: тпчка О нс 1хсеч1.:ння
АА' 11 ЕВ' ЛСЖТIТ t та n pЯM()J! се 111111 так: пря
м ые il/I' и ВВ'. ЛN и В,Н, Ntl' 11 ,\fR' (стnрn11 ы
трс~толыпшоn AS"I' н В.1113') попарно псресе
каютсн н точ1<ах и. С и С' на од110й 11рямоii.
ТоJ'.ца ~" 1 нсrжде 1 ш ю теоремы пр11д~щим следу
ю1н 1 rй в 1 щ: 11рнмыс АН.А'В' 11 J\',11 псрс<.:с1<аются
J:1 точю:: L. В н ·10 1 ·е ·1 ·сuрсм; 1 Дс:~ар1·а11рещх1п rгся
н C HO IO Жl" 06р: 1т11 уrо '1'<.:Орс "'11~:
f)
р
р
б
i\
о
J>щ. 5.
1- / lё:сл.и точки попарного пересе~1епия
· 10.L соотDетствеппых сторон двух 'l'ре
УJ'Ольпикuв лежат на одной прямой ,
то пря1'1ые , соединяющие соотве·1·
ственные.. вершины этих треу~·олъ
ннков, пtJоходят через ОднУ и ту же
точку.
To!ll~Kt> оnюс11тся обратн:ш тсорб1а к друrим
треугоm,ш1к::~м - АЛА' п H,\11J' (сраnните рнс . ..J ..
а, 6). Но на rшс. ). а соотвстстnеш 1ыс стороны
тре)тольш11<0в"WС пА'В'С' ш:рссскаются в трёх
точ1\а».. нсжащнх на од1 юй щ:шмой , а 11ря~1ыt:
:iA',JJJ:З', CG' нс нмеют общей точкн· uн 1 1 11ар;ш
ле111,ны. В чём же ;(ело~ Просtо мы ::;~1бы1111 о ·1
·0,•1 .
ЧТО 11 TC0f1CMC Дсз:~р 1 ·;1 Пf)CДlJ()JJ;JJ 'ШlOC h суш,t:
С'ПЮН:ШИl: точек L, Ми N, в ка 1·оры-х пt.:рссс 1<а-
1отсн COO'Пlt:Tl"l' Hel IJ ll1lt: cr о ро11ы тpc~TOJ IЫIH J\Of!.
Бе:з Т::t!ЮГО 11рt'дполтке1 IПЯ [(Не СООТПСТС'I не11-
11ьrе сторппы , J[апрпмер АВ и A'R'. м о1уг ока
:~атьп1 паразшслъны ми. U этом случае можно
1щказап" что нм будет г1щх1ллелы1а н nрнмая
. 111\ (рис. ), б) , щш, сстт 11аралщ:льны сщё ,1 щс
стро 11ы (рис. "), в). наrаллl:J1ьнымн uкажут<.:н
11 ·1μ~1ы 1 стuро 1-1ы трс}тольшшон. Попробуйте
с::~м 11 сфориулирuвать прямую н обратную тс
орс.чы Дсзар1 ·а с учёТО\1 во:~х CJJ) чаtп - то1 Д<t
н1>1 лучшt ш~снит~ те nре11мущсс rщ1 . которые
даёт 1 11х>екп 1пr1 ая точка :~ре 1r11н .
ПРОЕКТИВНЫЕ ПРЕОБРАЗО ВАНИЯ
Как 11зuбраж~1 т 1, на плol'KUl'TH трёхмсрпы<::
фшуры? Этот лр:.1кт11L1ескн1'1 нuнрос с дрешю
<:т~r (~J'OЯJJ llC(1CJ~ /'СОМtтрам 1 1_ Реш ался 01[ в ю~ух
нанравлснннх Д,т1 н у-жд :~рх11тсК'1ур1,1 - 11ост
rюсн нн чертежей :Зд:;IННЙ ~ 1 llJl<IHOFI llX расПО -
11( >Жt'Н ин - был разработа п ме·тд орто 1'() 1 [;)ЛJ,-
11о й проетщии Но ху,1();кшrкоn та1те <-плоское»
п:юбr:~жеппе не устраиuало. Они стар:1ю 1с1,
Многоликан г~пмет рии
в
А
пы:шать у зрнтсля ощутnе1 ше рсаm.но стп про
с·1 -ра11стnа. находяп1еr ·uся 1а 11Jюскос.'Тыо кар -
111ны. А11ат1 · ~ ~1 t'Ха 1111 ::1м<1 эрt' 1 [ИЯ 11р1шt:л к 1ю
н>J·п1ям 11с.:р сш::кт11 111>1 , l\С1JТральн о l1 11роскцт111.
" т-.1 кже к вопрос~ об uбщ11х сво\1с1·вах f\l'IYX
11ерснtкт111:1 п. 11 rolr ф111-уры. 11:'1 r<o'mpo ro 1ю:1л
нсс и ра~1внлао, 11роскти1н t;t}! reo~н:" 1pirя .
HaчaJJa тсор1111 t1ерспектнвы за.11о;юш 11р11
проектиrоnании к·утюла соfюра 1ю Флоре~ щии
11талышсюrfI арх11тектор Фшшппо uрупсллес
ю1 (1577- 11 ·16). Uн одшrм 11::J псрnых стал
чтпат1, художн 11 .к:~мл~ю 111и о ril·pc:11cкпшt:. М:.~с
тср;1 Возрожж~ния pa:'l lШJ11-1 этt 1 учснае. ~аме
чап:лы-11,1 й 11рнмс.:μ кар·1 н11 ы. стро 1 ·0 ныстросн
но~'1 rю 11р: 1 н1 1 лал1 J 1 t:рспектн11ы. - ~~н:~ \1CI 111т<1н
«Т::~й н::tя вечерн» Лео11ардо да R 1 1н ч11 .
.\удож111 1кv необходи\1.t
м.1rt·l\м1 "1ка fro 1tc ку<.( rоа Y'-1P1111t•
() ПР[!IПРКТИВР ;тn и nож,пf.111 ,
11 нр~на; ()t.' t 111ч о 1111че1 u xopuWl 'fu
Н Жl1 RO IH1( 11 С (НЛ 11Т I. 1lt'Н< J':SMOA<1.t l0 1>
;\('1111<1/Jдc l , 1,1 Н1111чн
439
<Dигуры
()
i1
б
Рис. f>.
1\llнoro запимался тсорней псрспект1шы не
мецкий художник Альбрсхт Дюрер (1471-
1-528). Особс 1111 0 интсрсс110, чтu 011 рассмат
ривал центральное прuскт11ро11а111·1t: u;~.ной
фщ·уры l l::t две 11 тр 1 т нлоскuст 1 1, 110-ра:шому
р:.~спuложс11ныс t1 нростра1-Iстнс:.
Ч ·1 о же такое rrcpcтreк'ПIRa н гсометрн н?
Пронсдt:м 11з н екоторой ·r·пчю:1 О просгра r l Cтna
(r rз цl:'mnpa 11jюе1щ1ш) прям1.r е чсре:1 псе точт<Н
даш той в nрострапстnе фигуры 1··. Фrлура, 0 6-
ра:юиа.1шая точками ттсресечс::ния этих прямых
с выбранной Yl.llOCKOCrrlЫ(J rфOl!KЦllй 1t, nрС)\
стаnляет собо r1 псрспективrюс 11~юбражс нн<:
фшуры Р, или, /lруп1 м 11 словам11. её цeJLmpa.ль
NJ'IO 11{JOl!KЦLlIO ИЗ тос11<Н () На ПЛОСКОСТЬ 7t
(рис. 6, а). Korreч1 ю, точка ()нс донжн:.t лсжа·Jъ
н 1 1 1юошстн 1t; н остат,ном фнгура, щ:нтр 11
111ю<-кос.:ть 11роt:ю1,н11 мо1ут рас1юла1·ат11си про
rr:-1но11111ю. Выб 11ран разJ11·1ч11ые 11 1ЮСК()СТ11 7t
(1ю с нс1 1 :1менным 1 юл()же11 1 1t:м r tентра 0), мы
П()JJуч:1ем 11 различные иэображений фиrуры.
В Ж1пю1шс11 nлоскость ттрое1щни (нолоттю кар
тш1ы) пбычrю расположена между центром
(глазом) и объскт()м Р, а в фо1·uграф1т центр
(фокs.тс объскт1 1на) лсжrrт мt.:жду п1юс1шстыо п
(фото11лёнкui)) н объектом.
Рис. 7.
Рис. 8.
+-Ю
Це11тралы10е nрnеl\тиро11<1 1 ше ус·1а11:1J1л1ша
ет с.:uотвсптвш: между точ каыи ф• r1уры 1; 11 точ-
1с1ми te и:юбраже11 ни на щюскост11 тт. на31,111аt
м.оl' lll!/)(.'1teкmщщ 111A1 l la рнс (1, (f соо·11з<:."1't'Т1шt·
в~1аи ""но однозначно - каждо~t ·mчкс 1' сuот
нt:тстt1ус·1 pnt11-10 <>ltlf:.t точка на 11зnбр~1жс111п1 , 11
напборот. Вообще, t:'СЛ 11 Р ;1ежr 1т 11 пт >ci-:ocтr1,
rie со;~,ержащсй О (:.i тот,ко тз 1юi1 случа1' 1 ж>J и
будем рассматривать), тп шобая nря,чая , про
вс/tёшrая из О, встречает Р пе более чем в од-
1юl1 точке З11ачнт. вдаrп rом случае каждой ·~оч
ке 11зобр::tжсния отвсчаст ронrю одна тuчк:~
фиеуры. Но ЭТОl'{) t.:111ё НС.:ДСКТ<IТОЧI ю J\Щ\ ю:н IM-
1юй одно:шаЧ!l()(."ТI! COOTHCTCTB llЯ: фнгуrа F МО·
жег содержать точю 1 rшоскости , 11рохощ1щr!1
через П нара;mс111,110 7t (рис. (1_ б) , а таюrм НJ<J
кам 11t соотнетстnуст 11нкакая тпLп<а в 11лос1ю
стп проекцит1 .
Важr 1с11шес cr1< JЙС'nю 1н::нтрvты roit щюскц1111
сс)Стонт в том. что 011;.i сохра1щет прямол1111сй-
1ю<.: рас11 оложе1111с точек. Друrнм11 словамн.
11рuеrщш1 11рямо ii (1к· приходящей чср~з И) -
пр~1мая (рис 7). Вс1юмннм , что 11мс.:111ю это
CBOJK"Гl:IO 11< >:3/IOJ l l'l}IO) 1ам С~С('Тl 1T<.:Opt:,\<IY )\сзар1·а
н:~ 11;юскости 1< боле::е r1ростому с11уч:пu 11 11ро
с1·р~тстt1~. Однако 11:н'1 тн LI :~нако.моiг нам ев"
тщо1ю 11 1 ·еометр1ш 1«1кис-либu друг1 rе пою1т11я
1-1 .1111 сnойстщ1, 1<0т()р1.1е 11с н1ме11»m 1(11 бы прн
1 lt'IГГJXlnы юм 11рое:ктирп11ашш. 1r слепю. Пере
секающиеся прямые становятся nараллелы1ы
мн (рис. б. б), параллельные - псресек:uощ11-
мися, а точrш на прямой. меняют сво i1 порядок
(рве.~. а). Нечего н П) 1юр1пъ о т ом, чтобы
JХI СС'l'ОЯПИЯ 11)11/ yTJIЫ 11:1 проскц rш COXJXIШJ.'lllCЬ.
Даже такая 11рос.:тая ф11 1 ·ура. как трс~то111111нк,
может 11рснраттъся А нечто весьма с111ан11ое -
11ару нерп 1 калы-1ых )ТЛОН, от однш·о 11:1 ко·~орых
б
1t
С'
отрезан трсу1-олы 1:ик (рис. 8. б), или половину
!ЮJЮС'Ы (рис. 6, 6)-
06 изображении ок11ужlюсти надо с~tзать
особо. Прямые, вы.ходящие иэ центра О и пе
ресекающие окружность, образуют конн ч<.:
скую nоверхнос~ъ. Поэтому mобая це1 пт>аш, 1 1аJJ
проекция окружностн есть ссченне 1<01п1•1t
с:кол по1:1срхно<.т11 плоскостью. Получающиесн
т1н1щ (рнс. 9) на з ываютсн л;OJillчeo.:uмu Сt!11е-
1шя.м11 шrн 11.рuными нторо?п rюрядх~С/ ( ~ кuор
:1111 1~1.тах 01н 1 ~щ111ютсн у 1х1"11ещ1ям11 t{'l'Opo1 ·0
порядка; см. статью «'~амсчательные крнные.- ).
Внд т:нщl1 крнной з::~1111с111' uт вза1 JMJf( >1·0 распо
.'ЮЖСIIИЯ ОКГJУЖН()Сm и IJЛ()CJ<OC' l'H. IТIJOXOДIOl(eй
чере:i 1~с 11 тр О ri:lf' <1л; reлы ю 11 1юскост11 11 ро
етщни. Если окrужrюстu IJ l IЛOCJIOC"I ь 1 rc rтерс
сt:каю тся, то проекцией окружности будет
эллилс, сст 1 касаются - rтар;~бола, пересек;~
ются - пшсрбола. Ilpн всей 11спохожссти
f;рнш,1х нтuрuгu nорндка у ни..';. сс1ъ и общнс
сrю1'1стна - как p;i:~ тt::, ко·1·оры"'1 ~удаётсн <.:охrа
ннться" при цt:нтрзлы1ых nроскц1шх. Вuт мы
н ПОДОШЛН к OCIIORHЫM для просктитюй J't:О
метрш r определениям.
П ус1·r, F - фJ11ура н шюскос"п1 rx и мы ор1>
еJ<тируем t:ё 11:1 точю1 О, 11е лежаrцеl1 я а., н:~
1ыоошс 1ъ ~. где абга~~уется петая фигура f'.
3атем м1.1 проектируем фигуру F' издруго1"1 точ.
ю1 ()', нс нриааднсжащсй ~. 11~1 третыо тю
скость у 11 получаем фиrуру Р' Таюrм образо~1 ,
фшура Р" образуется из ф11гуры F по<:л<: двух
rюследо11ате;:ш, ных J tc11•1ральны.х п рuекц111). Эту
цепочку проt:юо1й можно 11 1хщо1 1жи·1 ь. Jkяка}1
K<HfCЧJ ·l:lЯ JlOCJICД()R::JTt:ЛblHK"fЪ llt:Hтpa J ll>HЫ X
щюе ю щ ,~, на;~1,1 на с-то1 прт:!1m·m ш tым преобра
.юат ще"м,
CIIOЙCTll:J фJJ 1·yr. l<OTU()hlt llC >'-'Н:'1 rя
ются np11 11\)()СКГ\\В1\ ЫХ 11рсобра.юн;111Н>IХ, -
11роеl\mив11ы.м.и своuст11а.ми, 3. наука, н:>у"Ч.аю
щая ·1 акне свойстщ1, - пrюе1стишюzi геамет
р11е1'i. (:1аметим, что аналоrн•шым образом, ос
новhтшшсь на 1 rных 1тдах прсобразо1Jанп!r,
~южно t.)llрсдслнть ЩJедмст снкmщовой гсо
~1ет11~н1, 1 ·сомстр1ш Лоб:1чtн<.:кр1 · 0 r1 друг11х
1·ео.чстр11й~ см . статыо <- Гсомстрш1 11 1 ·ру1111ы
пpcofipa~~t >В~ н11i'J;, .)
Гfо сущ<· СТ\!)', так t10Нl\M'1JJ ПpOCKTHHll)'!O
1-есщетрt 1ю и сё сОЗ1\а·1·е111, Понсеж:. Исходи н:~
это li точки зр~ння ш1 изучаемый 11редмt:т, 011
[)t1 З р300Т:lЛ MOlf(l/ЫJf метод ДЛН l!OЛ)'ЧC!llfH
ноnых резулLтатоn. Раэ с~ойстnа, 1юторые r rзc
пнтере<.:уют. сохр::~няются лрн u:ентралыюir
прщ:кцш1 , попробуем спроектироnат1J да.н 1 ~ую
Мt·юrоликая Г<'uм~трия
Р11с. q,
ф11rуру следующим п()р:~.юм: нэ 11рос:кц1111
сnойстnа фщуры должны бы·1ъ есл11 11с;- очс1ш/1-
ными, то лс1·ко;1окаэуе~1ы~ш .
ЛрИМС1!11М МСТО,11, [ l O H CCJtC К ;'1,Оr<а:затсльст11у
тсuрсмы П:тпа . 13 1-1ей утш:рж;рстся. что точки
L, М 11 N , в которых сuот13етст13с111-ю псрсссI<а -
1uти1 пары щжмых А1:3 11 JJE, ПР 11ПG'. AF11 G/J,
лсж::~т 11:1 O/t 1-io1'1 пp}tмul1. Иначе: 1·uноря , 11:1;ю
дока:1а·1 •• , что точка ,\1 л<:ж11 т 11:1 пря.vю1·r U \l.
Пусп> нес Д:Jl!НЫС в 1·еорсмс ТОЧЮ/ fl прямые
(рпс l) распоJ1оже111,1 н 11лос1{осп1 и... Возы"1см
точт<:у о Bll<: IIЛ()C\\OCTll о. 11 llЛOO(()('"JЪ те" 11аrа J l
лельн~10 nлоскос:ти ()/"\{ Снроскт11рус-1\1 пло
скост1 . а. 11з центра О ш1 плоскост1. п:. Лопюлr,..
ку прям.:нr OJ_ nap<1ЛJICJ1ы1~1 п:, нрямме AIJ 11 1JH,
11срссекающ11с.тя п точке L. носле пpoe1<тJ.1po -
1{;LJ щя ста11ут r 1ар;uтсльнымr 1 лрямым11 . ·l 'JJ ' 11
ГJ'F,' (ера вн 1~те с рнс. (>. б). П::~ ршmслыты мн
буду·~ · н п1хн.:кн1ш r1ря\1Ых FJ' 11 НС, 11рохu,ця
щнх чсгк·~~ М. Точк:1 N находится 11'1 rip>IMOЙ }_;\/
' {'(Jl'Ha н толы.:о то1·д:1. 1.;ш·н~1 Н\ЖМ«I}! ON нсжн·1· в
()J~HOIГ llJIOCKQCTll с прЯ1\11>1МН ()/. ll ()ilf, ' 1' <: па
раллелы1з rr. Сле;~ов:~те11 h11О, 11 11poeк1trrr1 щт
мьrх АР н CJJ i!ОЮЮ 1ы быть па р;~;1Лt"ЛЫ 1ы. Итэ к,
на fIJIOcкocп1 проекщ1й п: теорема Паттп~ нре
вращастся н следующее утнер;кдсш rе (рнс. 10):
Еслц две троЙNи точек - А', С', Е' и В',
D',
F' лсжа·r (;Оответствс1п10 иа
лрлмыхр'иq',причё.мА'Н ' 11 D'E'и
E 'F' j(B'C', 1'oA'F' 11 C'D'.
:;это ;ю1<:1з;~т1, уже нетруд1111, поль:iуяо. шщс 1()-
лым11 ·1·реугол~,н11кам11, щх~1п 1 кающ11м11 Н11утрн
угла. обrа~ювэ ш ю1 ·0 р' и с{. ( От;~ет.но 11р11
Фигурь~
Риt. 1 О.
ДOK~IXl'l t"Л11CTHl' 11~rж 1 1(1 [XICl' f\'\01'J1L"ГЪ ~:щё бож.т
простоi r случа 1\ rюг/\а // 11 t/. )
Получ:1 е1 ся r1 а1х111окс /~( 1казатслt.ст1ю ~- 1'11ер
ждешш. ч·1 о тр 11 т1>ч ю1 :н:ж;п 11а 11д11оi1 11гт~юl1.
\1 1,1 с 11с!11 1 к СJl\:чаю. 1юr,ri;~1 1 rп с,1м1 r х точе к ш 1
nрлil-юй r 1~1 чертеже нет! J:!врочем, 111 1жс м1,1 ув11 -
дН.'-'t. что 01ш просто хорошо "3амасю1роn~1тн.: 1",.
ПОПОЛНЕНИЕ ПЛОСКОСТИ
Мы ужt: o'Jмt:ч ат 1, что 11сrк11ек'1·11.ннос соотnLvr
стннс ме:11щу ф 111 урам11, 110061щ: l'Оl-Юря. н е 1~:1а-
1 1 м 1 ю одпозпа·ч 1 ю, Поr,\Ю'1р11 м, 1r:i-:sa чего nро-
11сход11т нарутuеrшс юапм1 юl1OJ\I 10:111ач1 юсти,
Воз1,м ём 11а шюскост н две ттрпм ы ер 11Ji r1 то~1-
ку U, нс пр инадлежащую 1ш од1юl1 11:.J 1 шх
(pllc. 1 L, а). Про 1 r:шолыто11 точ ке А прямой р
.'1'1Ы со 1 1оставю1~м точ ку А ', в котороi1 прямая
<>А 11е rхс~кает 1 1рнмую р'. Но точке Р. /{ЛЯ котu
рu 1-1 11рям:1я OJJ 11:1pa1u1em, н ;1 р', н11чс1·0 1 1 е со-
11оста 1 1J 1 н1..:тос H<i 11 рнм < н·1 // та кже uстаётсн
ро 1Н1 () oдll::t точка Q, которпС1 t rc coo'L'BC'1'Cтnyc·1
н1 гкакзя точка 11:i р, та _Q, ДJIЯ ко·1'оrоГ1 11рнман
OQ nзр:шлслыrар, Сkобе11 1 ю 1 1 еудо6111>1 ,\Н1 ста
тюв>1то1эт и1кюuоче11ия . сс.1 1 1 рассм:лр ннается
цспоч1<а 113 нескольких цсптrат,11ы х 11 роек
цн11 . llусть, папрпмер, гrрн.мая р 11роет<п1рустся
113 цсrпра О на прямуюр', 1юторая. 11 сnою очс
ред!>. 1 1роt:ктируt:тся из того же цс11 тра 11 ;1 пря
rv1ую р" (рт 1с. l 1, б) . l~ рсзультате rюлуч;н:тсн
1 1рuсю \IJJI р HCI юcp~J\<.:THCI JllU 1 1 ар". Пu что Jtp(J-
1ICXOДИT l <• ПЛUX.UJ'I~ ( O'l'l IOL:ИTt'Jlbl [( ) 1н:р нu~-1 rrpo-
CКl\111'1) точкоil Р, т::~кой, что ()Ji ll // / С11:1чала
uпа отпрамяется <· н нш<уд::~~ - 1 -1<.1 п11н мо1! р' ei1
ш1 чеrо пе соответствует, зато 11 рн второй про
е 1щ1ш оп;:~ как бы возв ра щ:~етсн нз «1tио·1·ю1да"
н попадает 1<:.t1< раз r. « ПЛОХ) 'Ю·> точку R прямой
р" (01~ \\ fJ') 1
442
лн~tJ1 01 ·ично, п ри це1rтралыюм nроек·п1ро
в:н u·11 1 111юс кое1·11 а. на шюскостъ 13 (ртrс. 1 1, в)
('()()' 1'1\('Т('ТК 11 t' \IСЖду l1X то•ЖаМ[ I будет ю;н1м
l-J( ) <щ1ю:111 : 1ч 11 ым. t:cл>i толf>К<> y1t:1J11 f'l' I,1 t~ а ir р
'· l"IJIOXIH.: -> 11рямыt'. :t 11 !\ ICHHO 11рячыс. 110 К()
' Юрым о. и r> l ll'(ll'П.:K:JIOTCЯ с (IJl()('KOCTЯM l l , 11 po-
xori;ящrr,'vl l l чере.i О н n;J раллст) 1 1ы ,щ 1 ~ 11 11
соотнетстне111 ю .3 11:1 ч1 гr. 11 злее ~ , "ме 1 н :н:т.- 11а
рш1 J1елыrосп" Так на 11 а 1' 1 тt параллеm,11 ост1>..
устра111 rм вообще,
llрисос;1и1шм 1< 1<юкдоi1 прямо1'1 р одну
/tо1 1 ш1 1 111·1·1:лыч1 ю точr<у l 'I '
-
се на:1ыв:1ют
1/l!COfiCl11Hl'lfff()fi H Jll l бесл:.m / ('1(1 llJ )'U({.il(J·ююli TUlf-
KOfl 11 рн м01! /1, 1 1р11ч61 ко HC'l'M 11ap:tJIJICJ IЫIЫ11!
1\1СЖ/l7 собо/1 щ1яJ\1ым лобан~ 1 м одну н ту же
· 1 -пчку ;")Та опера! (1IH l l f\LCI J\ 't 'TOI J[()//(l 'lHeJll/f!,,11 .
R рсз~11111 ·ате 11ар;u1ш.~лып,1 с nрнм1.1 е 11 1 х:~нраща
ются n nерссек~11()щ 1 1есн - n 10: (J(i1 1\cl1 6еско
псч 1 10 \'далёшюl1 Т()Чl<С. Tc11ep.u пр11 nроск 1·1 1 -
рова111ш н рJ1мойр 11;tp' и:~ щ:т 1тра О (рис. 1 1 , а)
vJ IJJOX:Ш» ТОЧК;.1 JJ ПpJJ.МOi l /J. K:ll\ 11 Щ,.'С «1 IОр.М:tЛЬ-
1-IЫС» 'l'OЧКll. псрtйлёт n точку 1!СJJСССЧСППЯ пo
I J()JJI ICl 11 lbl.X 1 1р.н.мых ()Ji и// . 1' с. н бCCl{()ltCЧ llO
YJt;.tJ1<.:ннyt0 ~очку L/, . а бсско1 rсч1н1 y;taJ 1 C 1 1 1 1aя
точк;~ [~, 11рнмой /1 - в <• 1шохукн тчку U на//.
11 СОО'!'ПС'ГСТНI 1<..: ,\\СЖД~ jJ 11 jl' СТ<! Hl"I K~>:ll1.Mll()
оюю :~ 11:1 ч 1 11. 1м, fiy;tcт н :,~111мrщ ОJ\11О Эн:1 ч1юl1
п J(t:ПтраJ 11,11 ан ll ! IOC.:КJ(J l }I nJIOCIIOC'l l l (У, 1 1 а ~
(рнс, 11, в). fkc <- I JJIOXlle» Т()ЧЮ1 l lJIOl lШCl'~I а
(которым 1ra п.rюст<:ос1· 11 1' 1ш че1·0 пс сост~ет
ствуст) лс;ка't' п nлоскостл. параюн.:лыюй Р и
Щ)()Ходящсй через цеIJтр 11 рщ:кцин И, т, е. 11;1
одно.И щ1ямой а, Э 11~1 чит, прямая t1 проектиру
ется н: 1 м ножt'ст1ю 11ссобстF1снн n1x точек u
LIJl()CIOICTI L ~ . л llOCKOЛhK~ 11pot:Kl \ll }I любой
а
б
• U1"
~
,
N\р
Q_,-'
1
А'
r~.
//,
fJ'
,
р
,
,
1
с,, и,,
--.....
fl
8
().
~-.
Рис. 11 .
'' 110p\1aJJl>fl( )fl-> llj)Я\•1 0(1CC'l' I•11рнчаН . l'СТС'С'['Пl'Н
Н( 111р1 гнятh. что нес 11есо6с1 ·не111 rr.r c ·1пчю 1 са мн
! H)p:l:1YIOT OT[l;elll111}10 lll?CnfiClllt'U?lllf:)'Ю нm 1 бec
h'Olte't!I() y1kиii1111;J'l0 11/m ную.
Итак, по 1юm1с1111е шюс-тюсти окто11т n том.
что к 11et1 добавттются новы е, 6ссконt'ЧIЮ
vдалё1 111ы е точ1<11. н соrюкуп1юсп 1 соста1тяю
щ 11с uд11у ~юную прнмую. llр11 это~1 вес11арал
лсJП,нh1С мсж;1у co6oi1 111жмы<:. т с 11р~мьк 0;1-
1юrо н:111р;111лснr1JJ . 11олуч:1ют сщ 11 у 1r '1'~ ' >.1..:с
б<::с.ко 11 сч 1 ю у;1:1_•1<.:нн) ю точк~. а р:1:{111.1м 11:11 r1xm-
_•1cнi 1я м отв<.:ча 101 раз 11 ыс Gt:t'KOllt'Ч но уд:1л~н
н ь1t: ТОЧКll
О11сра 1~1Jю 11опот1е1 1ш1 ~шж1ю 1 Jр1 1м ~нпт1.
н к r 1ростра11ст1sу. l3o- nepm,,ix, к каж71о l1 1. 1ря
\·ю1' 1 / пр1~соt:дпш1е1·ся <Jдпа ~ юная (11есобстне 11 -
11::1я) то~ш;~ 11 та же точка добавляется т<о вс<..::'11
прямым. параллельным /. Но - nторых. к каждой
1шоо\Qtт11 а. прпсое.диняются вес нС:сQбстн<:н
rп,1с ' l'OЧIOI Ж.'Ж<IЩI J.Х Н Ht'fi пrИ\IЫХ. :·)ТН 'l'U'IIOI
обр.~зуют нt:с< >бспк~1н1ую 11рнмую 11ж1скuст1 t о..
Tt: Жl' с:.1м 1 ,1е rпч ю 1 6y;1yr1· ;1об<tнJ 1 ~11 ы r1 к лtобо1'1
шrоск<х.-1 11 ~, пар::ииrел 1 .нolr о.. 1на ч 11т. после 1t0-
rю.·11 1с::н 1rя шпf\1.1с 11ке 11лискост11 псресек~110101
по 11рнмоr1 . R -трет 1 .1 1 х, пrнпп1мастся, что НС'е
доб:шт:1е.ш,1с т1есо(iстRе11 1 1ыс:: точки о()р:1 :1~1от
()/ ~rr)c 1ювую. ш::.·собствештую плосrюс1ъ.
ПРОЕКТ ИВНАЯ ПЛОСКОСТЬ
1Jр11н 1 ,1кну·tъ к беско н ечно у;щлi.:н11ы1'1 точкам
O'IHIO/ \I' нс CJIOЖ IJO - 1
-J:J / \0 11росто ПO'v\1-lll 'I Ъ, что
каж;1~1}r н:i 1111х 11р<:>дст~ншяе 1 11:1п1х1клс1111с ~сшr
• 1 1ря м~1н ll[ЮХОд11т чер<.::1 обыч11ую тпчку Л 11
Jl(.'C06Cl'llCHl'Г}'IO '!'()ЧК~ u, •>,то~() ()ЗJТаЧ:lет. что
< 11рям:ш 11 рохото 1т чс::рсз точку А R 11 аправле1ши
(n;ip:lJLТICЛl. 1IO) прямоf1 '" 1Т т. д. и МО>ЮЮ бЫJIО
бы от11tст11 сu к попол11е11ию лиш 1, 1.;•ш к у;юб
J Ю\.tу со1·шш1с1шю о тсрм11нах, 1юторос rюзво
.1нет вмещать в OЛJI)' фor!>rymrponкy много слу
Уасn. t:сл11 6 1.1 сущсствонал способ 0· 1·J111чнт 1,
бсско11с"1но уд:шСн1-1~-.1с точю1 от обычны _~ 0111 1-
рансh тш1 Ы<О 1-1~1 п рсн..:К'l'J 1ш 11>1 <.: с1.юl1сп1а. О11на-
1ю т;1когп crrocoб~1 11ст Па11р1Рv1 ср, c 11oriLткo
!1.J 1) •1 ерез любые Д.ВС 'J'ОЧJ\И 11ЛОСI<ОСТИ
r.1.
проходит одна и толъко одна np~.taл
остается вернr;rм для обычных тичекпосле ло
nолн<: rrня 11лос1юсти: 110 оно сттравсдлшк1 и
ccm 1 ро1шо одна из точек I1 есuбсmс1::1н ая (Тю-
М1 ю1 оликая 1t'ометрин
cкoJJ i-. кy через данную 1·очк) нп::1111J()М 1r:тран
ле11н 11 пpn ,\O/ \IIТ 0; ~11а 11 толr,ко <>) (ll;t прям:1я),
н ссл111Jбс точк111rссо\1спзс1111ые (то~л:1 пряi11;1н
· 1·ожс несобстnе1lJ1ая) А1 ~ал оп 1ч 1 10 пронеря
стся. что
2) л1обыс две прямые имеют един
(."J'Ве ннУJН общу:ю ·1·0"rк-у.
J 1 к 60J1t"<.: июж1 1ы х утксржлс11 11н х ,\1ОЖ11<1
ПpHШt'l 'I> к:1кую )TOJ\110ЛрЯ ,\1)1О :1а nCCKOlll'Чllll
удалё1111у10. JIC 11~1. [))111:/Н LIX l lC'l'I lllll OC11 1. ffo С~
щестну, так ,11.1ы 11 1юci:1111J111 Г1)111 1 101с1затетJ
стRе теоремы П;~пnа. 11 ра:шые ч~рто1ш к тео
реме Дезарга (р11с. 2. '5) - вссrо ;шшь ра :шыс.:
спосо6ы 11арпсовзть од 11\ IJ ту же 11роскr111 1 -
11}10 l\OHфliГП);IJ..(111() rra uбыч1юй ПЛOl'KOCTII,
()'j'JJl 1ЧalOЩLICCЯ ТШIЬКО ~ыборО\•\ 6ССJШНСЧ1Ю
у;щлtшю1"'i 11рнмо\1.
l l;r C~l .\10.\1 IO.:JJ~ 11<:pa:m11Чtf\10C'l'h ( 1бЫЧНhl .\. 11
несобст11сн11ых точек ш1шrнl· 1ю1rятна Вс/11• 11рн
щ:нтра.11ы ю11 11росю 11111 ()есконеч 11 0 y;t:1!lё1111ыl'
н оГ1ы LI н ые Н>ч ктr ( 11 11 рямые) могр· 11 ерсхпю1т1,
/~pv1 · 11 друга. а 111ач 11 ·1 . все 11 х прое1\'П rn11 1,1е
с1ю1~1<"пsа со111 1 :щают. По·10му- ·ю u 11рое 1сп 1в1юi1
1·еометрш1 nct.: ·1·очю r 11 ri рямыс по пол 1tc1111< )JI
п1юскост11 со11ер111ешю рав1юправ11ы . Осоз1rан
этот 11 ршщ1 1 1111~1лы1ы1'1 фа1п. дадн.ч tiaжrrы e
01 1рсдсления .
Обычнан нлоскость. по11 ол11снная 11ссоб
стнс1н1ы _,1J.1 точк~1 м11. 11а:1ы 11астсн 17jтел.:11111юm1'1
11.11осл:остып Ан:.1 Jю1·r1 ч1 rо, 11 снюлнсшюс 11ро
стр311с1·1ю наз~-.rвастся 11/юl-"кm11rшы -н 11;щr111jюн
стно.м. Как 111-1а11роt'кт11111ю1'11июс 1<ое1·1 1 ,н 11 ро
t.:10 и11111 >л1 11 \)<>C'tp3 11C'l 'llt' ()'JC)TC'lU)lOT l(.IIOIC бы
то rтн fiьию рз:'l;шчня межд) собствс1111ым11 11
11есо6стне1 11 1ым11 элсме11тзм11("гочкам1 1 , 11рл:-.1ы
ми, ImOCJ<OCTЯMif).
1<онеч110. хо·1·слосu бы пщ:ть та1(ос опрсж:
лс ние просктпmшй плоскостт1, в кuторuм pan
нu11рашнхть вс<.:х тuч.<.:к был:1 бы ::5аложс11а с
caмu 1 ·u 11ача11а . Е1·0 ,vюжно ;~<1'l'h акс1101\1ап 1ч с
скн (см. статhlо ~лкс1 юм 1 ,1") Акс1 ю ,\1а ·11 1 ю1 11ро
t'КТн1:111с 1й плоскоеги проще :~кпюм<1т11ю1 t'KK-
JI П/\ОRОЙ l 't '() .\\C'l 'pl tr 1 R 1161 HCtTO Тр! 1 ОСl· IОТН 1J•IX
н ео1 1 рс;lелнемы:х 1ю11ятнн: · ~·очка. 11рям:ш 11 0·1 -
1юr11 с1 1 ие пр1r11адлеж1 юс·1 ·1 1 , выр:tжаемое cлon:.r
MTI «То ч1<а лежит Тlа Щ)Ям о11 ~. «лрямая прохо
дит 'lерез точку» и т. п. И всё же 1юлныi1 (писок
а 1<оюм стш11<01V1 нст11<, чтоб 1,1 11ршю,111лъ его
ЗДt'СЬ. ()ТМ<:'ГИМ )11 \ШЬ, что н него входят 11 два
в ы <.:ка:3:11fj1 ы х вы lllC )ri'llt' PЖ/tCHJ I>t
Фигуры
ПРИ Н UИП ЛВОЙСТВЕННОСТИ
С 1н.:рво1·0 ю1·тщ~1 на cAoi'rcт1:1a (;1 ксиомы) 1 и 2
11роекгнв1 IOl~I llJIOCt<C>CЛ [ НСС{)М HL'Hll~I l IX <·С:lfМ
метр 1 1ч1 юс1ъ», Она СТ3 1 юви·1·ся особенно ян1юi·1.
если ззv1е1 111тr, разпые тю форме, нп одrrпатю
ные по смыслу ньtражения: <<ТOl.f f(a лежит на пря
мой» и ~ при.мая проходит через точку-> одним:
«точr<а п прямая. 111щL.1дютщы». То1да свойства
l 11 2 будуr формут1роваться соотnетстuешю
так. ~.11юбыс ДВ<.: ТUЧКIГ ННЦИДСIIТIIЫ ОJ(НОЙ (·J
то1 1n1(() одной нрямоll~ н «любые две прямые
инцндс11т1 rы 0; 1 ной и только 0;11 юй точке" Каж
;~ос: 11:.J ,'(нух утв<"рЖJ1еннй 11рt"1:1ращастся А 11r~·тое
Гl!X>CJ'Oll за.vн.:ной СЛСН!а "1'0Ч:К<I" H:J CJJ()IJ() <·11р>1-
мая » , н щюfiорот. Отметим. ч то ш1 обыч1юl1
плоскосn 1 ПО/\Обных « nреRрзще 1 11 1 й» не щ10-
исходит: свойство 1 - одна и:~ аксиом еrншидо
вой геометр ~ ш , ~• сnойство 2. просто пеnерно
(11, консч1rо, опять 11з-:.Jа паrаллслы юсти).
Отмсчсшюс нам11 uбстоятслr,стnu далс:ко
щ.: случайнu. Н нём л 1шн, н а 116uж.:с очсвнднu
11риянлястся замсч:пслышя особенность nro-
CKTllВHOir плоскостн - IJOJJIJ;]Я aJI:IЛUГIIЯ меж
ду точкамн 11 I1р.нмым 1 1. Эту симметр1 110 струк
туры нроек1· шшо~1 111юскост11 формуJ111руют н
яи.11с п;птципс1 дrюйстпештс11ш:
11"
Если в исти11ном: предлож:ении о
1::l точках и прямых на прое1стивпо й
плоскост11, выраженном через 1п1-
цидентно сть, заменить слово +'!"О'-ска ~
словом ~прямая~ и обратно, то снова
получится истинное предложе ние.
Пары днойстне11нi.rx теорем есть н н обыч-
1юй 1·еnмстрн1-1 ( 11а11рнмер, · 1 ·t:орсмы 'Че 1 н.1 11
Мсне.rтая; см сгатыо <-Треу 1 ·от,11нк, 1 1 ростей -
1ш 1 й 11 1Iеисчсрnаемый •}). Но, хотя ош1 были
издавна 11:шест11ы, 1-тикакОJ·о 06ъяс11е11ин я:n
лс11ию J\Нойственrюсти геометры не п:L"COДHJllJ,
IIOKa нс ОСМЫСЛJ:[Jl.И ~го, исходя пз ЛОJIОЖ<.:llИЙ
11роскт1 ш1-rоJ:I гсомстр 1 н1 . Справедлив принц~-m
JJ,IIOЙ.CTKCl-IHOCl'l\ ll 11 црос-1 ·ран.стне , ТОПЪК() здесь
11ереставляютсн слов:-~ <-'1·очка» ~1 •п;юскоL·г 1. ->,
а оrово «1 1 рям:1н» не ~ал,1с 1 LЯL'TCK
Имсют<..:я разн ы е Д<жа:-~атст,стю пrf[IHJ,1 111<1
тю 1k'1 ·1 1е1 1 1юст1-1. Например. мож1ю пострn1п1,
взaII.МIIO 0/(IЮ:11ШЧЛОС соотнеТС'l ' ВНС МСЖl\У
м11ожеспюм точек и множестnом Щ)}l ,'-1ЫХ, со
хр;н rяющее пrщиТ1снт11ость, - так пазыnаемое
полярное прео6разоnш111е. Мы огра11ичи:мсн
Р11 1:.. 12.
./(/
~(/
"-!,_17
./
<ЩllYIM , 1-Ю J\OCl'(.'\'\'OЧl-IO SlfЖllM 11\Jll'll'- . '\)OM: t:фоr
мул 11 руем уrnержде1 11 н: . /Т,нойстве 1 11 Ю<:' ·п.:орс~1е
Пз 11 11а, 11риведё111 юl1 и 11ачалс стэ ·1ы1 .
По аналопш с 06о:зпаче 1 шем АВ для щж
мой. прохо,rvrщей через точки 1l 11 JJ (шщнде11т
ной Л и В), будем обозначать через a/J точт<у
персссче11 ия ЩJямых а н /J ( 111-щ1 щснп ryro а п
/:J) . llослслонатсльно :-~амснял н ·1·euper.н: П;~пш1
<-ТОЧЮI -> «11pЯMhlMll•) 1-1 обратно, 1 1р1щем к T:JKO ·
му утв1::rжл.сш110 : если 11р11мыс а, с, 1! им<..:ют
общую точку J>. а прям ы е fJ , d.(- общую точку
Q, то пrнмые /, /ll, 11 , сое;~1111яющ11с соотвст
с п 1е 1 ню точю 1al111 tle, а/ 11/а , е/11 !к. проходят
чере:1 n1~щ· точку (рис. 12). Прояш111 щ·кnто·
рос тер11е11ис 11аю~11ат11ос1ъ, nы )-1111; ~1 11·<:. чm
дока~1ьm:.1п, здесь нечего
:~·1·0 в ТОЧl юст11 н··
орсма l lаппа lVIЯ соответствующих троек то
чек, например для то•1е1< Р. tlf!. <!/ п Q, ah, hc.
r l uнро6уйтс са~vюстоятслыю :)аш1сать уп~ерж
;~ен11е. дJ-1(Нiе1·11сн1-юс т<.:орсмс: Дс::~ар1 ·а. 11 убс·
ни ·1·tсh. что оно сонпа;щст с тt:opl'мo1'i, обрат·
ной п:·орс,'vн.: Д<..:;.1ар1·а (ко· 1 ·орая , как ч1,1 .таем,
сле;1уст 11:-i 11рнмой) . R ю~ух р<1сс.'41л рt:1111ых
СJ1учаях прп 1 11 (1-111 J (IIOЙC'THC I HIOC'l'J\ lll' }ЩI НО·
вых результатов. Но 1111же 1\\1>1 ~тrнщ11м. какссrп
помощью «бесплатно» получается 11on;m со
держательrrал теорем;.~.
М И СТИЧЕСКАЯ ГЕКСАГ РАММА
Идс11 Де:-1ар1 ·а , с:няза11 1 1ь1с с 1 1 ~1учсн11<.:м 11роек-
1 1 1нныл с11о~-1ств ф11 1тр. увщ:ю111 Rлс:--1:1 J Jаск~ля
R во:.1р:ктс 1(> лет 011 открыл за~1сч:1тс.•11>1r)'Ю
теорему, KOT()Jl:lЯ ;1e1'Jl;.1 11 основу r1p()CK'l'HRHOfl
тсорш1 коничссюrх сече-ш 1 й.
Пас1<алr, 01 1 убпиконал сrюё открытне u фор
ме афиrнн , нзrотоnлснной в I<олнчестRе 50
экземпляров, rюд 11а:шаr~нем "Опыт о кониче
ских сечеш1ях'» И:3 присущ~:й ему скромноеrп
он ука:{ал R ней тuлько собстnенныс нн.1-щиалы .
110 отдал должное снос.\1у уч 11 тслю Дсз:1р1 у
Теорем.а 1Iаскаля формулирус:тсн т::ш (р11с 1.) ) .
Если все вершилы шестffУJ·ольuика
в проектитю й 1щоскос.1'И лежат на
коническом сечении, то ТОЧJ(И по
парного пересечения его противо
положных стороп лежат на одной
прямой (паскалевой прЛJ.'1ОЙ шести
угольника).
1С1к 11 н теореме Дсз:.1р1 ·а , «С."l'орон:зм н " зде<.: 1,
считаются прямы<:: , проходнщис чеrt::з к:1ж-
11ую п:1ру сщ:сдннх и<::ршин 111t:ст11у 1'ш11, ник а.
J щ: отrез к11 , COCJ\ИI 1 яющие псршины. Сам
шестиуrопын-1 к rюr1 и мае-1 ·ся как пронзволь11ая
З<t1'П(J 1угая JJОмапан AВCDEF. котоrая может о г
рани:чноать как выпуклый, так и rtеuьmуклый
шестиугольник или даже самоnерссекаться.
Паск:;1т, с нач ала доказал теорему о «мисти
\!еской 1·екс;1гр~мме" (шестиуголышке) для
окружности (рнс 14). Коннчсскне сеч е ния
он рассматривал как це н.тр ю11"ны е прuекции
tжружностп (рнс. 9), что и 1юзво11н1ю сразу пе
ренестн на ннх дока:.1ан н ую теорему. Ilo ecJJи
нересечь конус ruюскостью, проходящей чере:,:~
вершину, получит ся не крнван, а пара пересе
кающ1 1 хся прямы х, которую Дез:~рг также от
носил к копнч.еским сеченt-шм. (Если мы хотим
бьпъ п оследователыn,1ми, то к пим надо отне
сти и пару nараллелыrьLх прямых, ведь в про
ективной геометрии они тож~ «перссс1<аютс.:я" .)
Замечательно, что и в случае пары прямых
Рис. 13.
\1
\1
\1
1
Многоликая геомеч:~ия
у·1 uсржJ~е1шс теорем1,1 о <- мнст11чес коi1 сскса
rрамме" о стаётсн нерrтым. Более 1·01 ·0 , мы его
уже /Юt<.1. :Jалн - это нс что иное, как ·1 ·еорема
Па1111а! 1\ри т;шом более широком пош1ма11ш1
кон11чео<о1 ·0 се чения вер11:1 и uбр,~т~-rая тсо
рс1•1:~ : когд:1 п рот~ lнопо1южныс стороны mссп1-
у1·ол hH 1 1ка 1юпар1 ю nересекаюто1 н трёх ·1 ·оч1<: 1 х
H:l 01\'1 IOJI 11p}L\>IOl
0
I. С/'О всршr 1н ы 1 1p1rнaJ1,JICЖa'J'
r<о1н1чс:скоv~у сечению. Есл~1 1 1р11 этом н11каю1с
тp rr 11:1 шсст11 11ср1ш111 11 е лежа·~· 1ш 01i110J'r пря
:\ЮЙ. то сечешн: бу1tе1 · 11.мешю крнuо~'! - про
екцней окружности , а не п:ipoi1 пrн1мых .
Отсюда 11ытс1<ает, что 1<0ш1Ческос ceчerr11e К.
точнее, любое число точек на 11ём . .можно п о
стрu1пъ 1 ю пяти :1аданн ым е1·0 точкам нри
110.мош.и Oi(HOJ1 ш1нсJ1ю1 . Пуст~, А, В, С. D. Е
-
ns1тh ~~аNшных точек (рнс 1'5). Пронсдём чсрс::i
точку Е прстзнuлъную прJJмую (J. lluc1·r<mм на
Нt:Й ш естую верu1нну р ВПНС:lПНО l 'О в А" ШtСТ11-
угол hl 11 rка СЛt'/\УЮЩ11М oбr>a::iOM.
Дnе то чю 1 11аск:.теnой ~rрямой нскомо1 ·(1
mестнуrолышка..-JВОJ.ЕР нам изнес111ы: то~IКа Р
пересечения пrя !VlblX АВ н DE 1[ TOLII{a Q nере
сечстшя прямых ВС и fJ(= h'f). Таким образоУ~,
nacкaлen:i. прямая опрt:дслен а. 1lрямая 1= 1;:,- 1
доJJЖН<\ проходить через точку R, где r 1 аск:шсва
пря мая P.Q .нстречает прямую CD. Это опреде
лнет прям ую/, а 11 е ресечс1 1 нс прнмых / н р л:it"'1 ·
нскомую точку Р. То же построен н е может быть
выполне110 и ДJIЯ любой лр;тпй прямой р, rrро
ходящсй чсrез 'l'Очку Е.
Че рез полтора столетия посл~ открытш1
теоремы о « мистической гексаграМ1'1е" Шарлr,
Жюльен Бриапшоп вывел с помощью л:uой
ствещ-юстт·1 теорему о шестиуголы rи ке, т~и
са1-п-юм около коническо го сечспнн (т. е. об
разов'<1нном шестью кас~rельными к данной
кри1юй:; рис. 16).
,_
'
1
Рис. 14.
в
л
'
'
'/
'
'
'
'
'
'
'
... ...
''
445
Фигуры
Рис 15.
РнL. 16.
:р.. Если шсстиу1·ольни1< в проективной
·t"' плоскости олиса.и около коническо
го сечения , то три лрнмыс , соединя
ющие ero противоположные вер-
11111::~п.1, пересека1отся. в одпо.й ТО'-1кс.
Взл1111пая двоi 1 стне111 ЮС"1 ъ теорем Ласкаля и
.Dp 1 1ашuо11а требус1 ()олсс П()дробного обы1с11е
r 1шт . на 1ютором мы останавливатr,ся пе будем.
Как rr rrз теоремы Паскаля, и з теоремы Gрr1 -
аншона можно получrrтт, обрат~ 1 ую теорему rr
11ст ю111,зоють сё щш пос.:тросшт кон 11чес:к01·0
сt.:ч.с1 1. 11н 110 :! Щ~:~н ным 11нт1.1. касатслъ11ым к 11 см у.
ПРОЕКТИВНАЯ ГЕОМЕТРИЯ
ЕСТЬ ВСЯ ГЕОМЕТРИЯ!
1\!Lысль. uьшессrшую n заголонок. высказал n се
редине XLX столетия английский чатемати к
Артур К~т·1 . Пра1111а. 11а такне ра:щившисся п о
:щ1 rt:e <>6ласт11 соnремсн• rш'; rео,у1етр ни. к~н< то -
1ю1ю 1 ·11н и uбщан р.има1юва геометр~ rн , 11рн1ше
ка·1 ·слы 1~н1 и;tсн 1<эт1 уже11с ра слрuеr1х1ннстся.
И 1 ·ем lll" мс11ес про<.:кт1 1кн ан 1 ·cu;v1t.:тp11я -
<·простая·> д 1 1С1~ 11 пm111~1. 11 зучающа}J тш 1 ьюJ те
c11o i"1 c 1ва t\нп~11, котор 1.1с: к:tс111пся ю:шмш нп
ра сПОJIО'Же1111я 10ЧСК npH ,\ 111I X 11 llJIOl'KOLTCII,
де1kтnителы ю нме щ~tt'Т в ссбн \()Дсрж:11 111е ен-
1щндовоJ1 11 1'-'ш огнх r1 ccurv11 щoвыx н:омстрнй.
Как же: это J:\O:>Ы<)Ж I JO. еслв u 1rр оект1ш 1 юf1
п:омстрии пет н 11 1 1 араллслыюст1 1. ш 1перпсн
ю 1кую1 р 1 юсп 1_ 111 1 р:н:стш1н11l1?
Дело в ТО\1, что 11epeч 11('Jl<.:H HhlC IЮIШТ\Ш
\Н)ЖН() HHCCl' I J , CJ\10f(CЛ 1rрон:п ь с ре;1с1·11;1щ 1 11 po-
t:KTllHH< 1J) гсо~1е-1 р1 rи, что ~11>1 11 l lШICllllM llC-
(' J\()Jll,](J 1мтr 11rостым1r.110 11:1ж11ым1111р11мср:1 .\1J1,
l lач11ём с параллс-J 11,1 юс1· 11. H1.1\)tpe,,1на11ro·
t'l\TIШllOJ'r ПJIOCl\OCTJ 1.'IЮбую прямую ( 11:11 IOM I IJll\I,
что нее (ШТ 1раш юnр;щ1 rы) 11 объя ш1l\1 сё 11ecCJ6·
стне1 пюi 1 11р~ш111'1 llазонём ,'\ПС 11рнмые парал
лслы1ы.ми, со111 01-11 1 ш:ресскаются 11 а 11 есоб
е1 нснной npHl\!l)fl. JI,py 1 ·11щ1 словами. выполrп1м
0 11 срац 1 IIO, uбраТt 1ую 11()1 IOJ I llCll шо ПЛОСК()СТll.
Онрсж:щ:нныс: так 1~м 06р а :-1ом 11:1ращ1сльныt:
1 1рямыс обж\Д:JЮТ HCt: \.111 ll ШIOЖCl ll! ЫM ll сно lt
стnамн : ч срс:~ точку мож110 про11сст11 олну 11
·1 ·от,кп од 11у пря мую, п:ip::t:1J1eJ1ы 1yio r~анноr\ 3
лrоuыс Т1.1Зе 11рн,чые, n:Jраллслы1ые треп .еi1 , буд}"Т
параллслы1ы между со60 1'1 (что .rre1 · кo 1 юлуч r11ъ
и з с1юйстr.1 1 н 2. прн веде шrьL-х выше). Te1 1erh
мож но стро нть n::ip:i m 1 c1ю 1 ·p:1ммi,1 , а :шачит,
делитr, поnо;щ,,1 отрсэrш (рнс. 17, а). uьшшшя1ъ
!lар :шлелыrыс r 1 <.:рсн ос:ы (рпс. 17 , 6) н соиоте
т1111 (рис l7, в).
С; 1<.:ла<.:м сл<.:;\ую111,и(1 важныi1 ша1·. пр11бт1-
жающш111а<.: ксв клr1)1.о вой 1 ·со,,11;:тртщ Тс::орс::~ш
П :кк:1.1 1я lllHHOJJ Я ~l' 11rамках11pot:t<TllВllOl'11·eo
Mt:'Tpии опpc11em 1·1ъ ко1 ш ческщ~ <.:l'чсн ш1 Вы·
берем какоt:'- IIИбудъ Ofl,11 0 11 3 ШI Х , l lt: ll MCJOЩCC
общих точек с несобствешюй n1жмо1~1. н 11азо
вём его окруло тост ью. Мы ~шаем, что есл 11 две
кас-J тель11ые к обыч11 ой е шuшдuвой окруж110-
еrн параллелы1ы, то точкп 1<:~с:ш11я - t\01щrx
одного днамС'1 ·ра, т. е. ю..:жа·1 1r::i <m 1ioй rtpямoli
с цснтrом В л ре н.~К'1' ю{но ~'1 1·eu.'-'• L'тp1111 это cool\-
а
б
1
.
\в. //
i-
.
\"А
/
,-~/11
t"П10 11ришrм::~е·1 таку10 форму: есла нз тчск
да11 1ю1! 11рямпй 11ровесr11 1 1 арм 1«катсл1>1J1>1х i,;
ко1н1ческому сечению (рнс 1Н, а), то прямые,
соею11шющис точки касания к~1ждой пары, пс
ресек~тсн н одной точке. Взяв здесь в ю1чссшс
прnмой и коничсс1со1 ·0 ссче1шя nыбрашгую
на.мп нссобстненную лрнмую и <-Окружн.ОСIЪ >,
rнхтронм её «днамстрыь 11 точку и нл т: рссс
ч е 1 шя - ~чентр» нжруж1юст1н. Лр1 1 чём вес
r>бы ч 11 ыс с:войстRа ю-·1а метрсщ, хорд, кзсп·с11ь-
11ых б}'дуr вr1mom 1я·1ъся . Например, есл и хордз
PQ паrа;111е;11,1:1а кacaтell J.J 1ЫМ , п ро1к:дёI11 11>J м Jl
ко11щ1 х дизметrа АВ (рпс 18, б), то её сере
дшrа ЛJ (по нащему 011редслетно) леж 11Т ш~/18.
1:.1 обычrюй 1 ·еометрин такая хорда, юн< 11 ка-
М11оголикая геометрия
с:псЛJ)l\ЫС , 11epnCH/\И1')7ЛHJ11fa Д J ·J:.t,\\(,;' 1р). что
1103воляет ннесги 11011>1тис 11ерnснд11кулнр11 0-
сти . Прпмет 1 яя 1< исхо,11rюГ! окруж1юсп 1 11ар:т
лелы1ые переносы и 1·омоте·1 ии , можпо nолу
У.и 1ъ окружность с любым :1ада1шыJ1.-1 це11тром
I I рад11усом ... llо :J/1,ССЬ мы ОСТ:UЮШJМСЯ. Уr<ажем
.m ш1 1,, ч10 ncl' ·щаrrис сmшидовоii гео~1стр1111
l\HJ:iIOIO шаг з :~ l lЫГOJ\ 1 нысгрОIL'lЬ • IT .3 ЩЮСJ..:
тинных ю1р11ичсй-~.
И3 тп1·0 же ун1 шерсалы ю1·0 матсμ 1 1ала стро
ятся мщ~<.;лн п::омстр111 1 Лuбачснско1о11друп1.х
1с.-оме·1 р1·11·1 И имt;нно на этом 11 ут11 Фt:л11кс
Т<)lей1т 11р11111ёл к фундаментат.1 1rым r111,еям о
rrp11рсщс 1 ·еомстр111 1 , о которых. рJи. казаJ ю н
статье «Геометрия 11 групп1,1tLреоГJра:юв::111111: 1 •.
детерминизм и случайность
ЧТО ТАКОЕ МАТЕМАТИЧЕСКИЙ АНАЛИЗ
Математическпй а11аJ1и:1 - ра;щсл математики,
созданный н ХVП в Важнейшую его час...1ъ со
ставляют днфференциал~,ное н интегральное
исчисзrсния .
Выдаю1цуюся роль в рождени11 математиче
с1<оrо анализа сыграли Исаак Ныт·о 1 1 н Готфрид
Вильrельмllейб11иц. llьюто11 ранънте nрисrупил
к работе над началами анализа, в 1665- 1666 п.
Однако первая публикация, относящаяся к ма
тематическому ;шализу, нринадлежала Лейбни
цу ( 1684 г.).
Именно Лейбниц ввёJJ термины «ди ффе
ренциальное исчислснне~ и «интегральное ис
числение-> . Они с удивителы-юй точностью
определяют суть соответствующих теорий .
Differeпtia 11а латилском лзыке означает ~раз
деление», «расчленение», «раздробление ? . Про
цесс дифференцирован1-нr состоит в замене
функции на малом участке её дифференциа
лом, т. е. кусочком её каса1·ельной. Участку, где
nроизводится замена, Лейбниц дал название
«бесконечно маJJый?. Диффсрс1щирова11ие, ло
Лейбн и 1\у, - это расчл е 1 rение функции на бес
кuнечно м:иrые элементы. Iшeger по-латыни -
«цел ый~; интегрирование - процесс объедн
нения п 1~елое маJJых э11еме нтон, из которых
Исаак Ньютон.
450
сuставJ 1 ены фвгура , телtJ и т. п. (Внач:Jле Леltб·
ниц nреллагал тсрмнн н:умматорное исчи
сление.>.)
У Лейбница cp<i:iy же 1юявили с1 . 1юслеж)f1а
тели , 11аиболее прославились братья Иоганн
и Якоб Бернулли. Термин «анализ~ впервые
встречается в заглавии учебника «Анализ бес
конечно малых величин-> (1696 1·.), шшисаи
тюго учеником Ио1·:шна Бернулли - Гиi'iомом
де Лопиталем
Подход Лейбнищ1 был геометри чссютм · он
стремился да·1 ь общш1 метод определения ка·
сательной к кривым п научиться вь1чи с.1U111
nлощади фиr·уr, 01·раниче1111ых !'рафиками
фу11кций. ПредшестветttJУn<ами Лейбтпща mmя-
11иcL, 1::1e11ю<J·te геометры лревности. Архпмед
nплоттrую П(>Дошёл к интегральному исчисле
нию, определяя площади и объёмы фиrур -
круга, шара, цилиндра, сегмента параболы. Его
идеи развил в ХVП в. ит;uтышец GонавеН1ура
Кав:~льери, который соз.ц;ш метод <.HCJ1t'JlltMЫX•
(но су1·11 дела. бесконечно МШl.ы.х). Касатет.ные
к разю·1 чным кри1~ым изучали в Л"VI T столетшi
Рен е Дек;1рт, Блез Паскаль, Пьер Ферма 11 Хр1·1-
стиан Гюйгенс:. nослtдний оказаJ1 н:~. Лейбн1.ща
особенно силыюе RJ1 1·1я11r1e.
ru rфрид Ви \Ы !.'~Ь\\
Леибн1ш .
l lыOT()f-f Il/)I 1шёJ 1 к ш-1а11113у, IK'XO/tЯ из 11еоб
ходимости оннсыяать rtвижсние теп и эR011ю -
1\ню различных процессов. Он мыслил как
физик, юrнсм атичесю1 : если функц ия .х(!) :1:!-
даёт путъ, 11ройде1нr 1,1.й телом к м ом енту л реме
ни t, 'Л) естестnеr 1но 1ю:нrикает понятие скоро
сти 1·(1) вда1шы1~1 моме11т. Она примерпо равна
отн о шению пуп1, :пройдснноrо телом за очень
~~ал ый отрезок времени лt (т. е. x(t + Л!) - x(t)),
кЛt, а точн о - пределу этого отнощеrшл, когда
11 с1рсм нтся к нулю. С корость тела в момент t
1 fhюто 1 1 обоз113чш1 ;((!) н назвал флюксией (от
лаrп. 1'\L1c tю - ~течь», ~стру11·1ъся"). В совре мt:н
ной матсма·r·ике прню1 ·1 ъ1 те рмин (,про и~Jво.ц-
11ая ~ 1.1 обо:тач ен11 с :r.:'(l) , физики же чаще
ПО.%З)"ТОТС>I СИМЛОЛОМ i.:(t).
Сочш 1е1 111е НhЮТОна «Метод флюксий. н 6сс
копеч11ых рмоn», 11аmкашюе 13 1670- 1671 rr..
было опубшшован о посмертно, в 1736 г. Суть
д11фферснцировання, но Ныотону. - 11ахож
дсние скорости по пути, т е. ."i.:(t) no x (t); и11-
rc1p11p<JR:.1 1шe - обратн;1я операция, а именно
1ю<.:стакш111е11ие 11ути 110 скор<к· ~·и . Инач.е го
норя, интегр 1 1роR:нш е - это реше ни е нроегей
шt.то f\Ифферснцшwы юr'о уравнеt 1 ня
- 1.:(L) = /l(t) .
80 Rсём этом Н1, юто1 t щ1I п1ю1 астафету от РО!\О-
11,1чалы11-1коR соnремепно го естестnо::~нан ня -
Гащшео Галилея и 1101-анна Ке плера .
Созд~н шый l lыото11ом 1>1 а·1·ематнчесюттl ап
п арат 11ривёл его к фундамснт~u~ыю.й ко 1 щеп -
щtи, которую учён ый выразил с начала 13 за
uшфрованном НkЩС :.~на~'Раммой. t:ё су1·1, можно
11cpc/\:JTh словзм 11 : ~м 11р упранляс:тся диффе-
Что такое' математич еский анализ rrм
~··~~--~~-~~-
PHILOSOPHI.tE I
NA TllRЛLI S
PRINCIPIA
МАТНЕМ .\ 'ПСА
-
- ---
-
-
----
t
4\1.; ....i" JS. ~f.iJrJ111to, i•11t . tfJ (," J,\h ~ Mati...r" ~
i'11• .-if"""• ,,,,.., .,,,,. _
,\ ~u..w:•••" fk_g t!I~ ~~bll,
!мТ'lt1млтlllt
сt•i:1РУ"'· ltt;:~ 1'1\.~:.ЕS'.
1~N()J~·1,
1
)\\11. ~\",tt.11J1 ll.iJ:"' .ас T,pr, 7,('f"v N1• ., 01:1. P .o!l.l11t \'. .-,"
f•·1 ~p.'lf s"11 ~iwl1· 1.4 iri•ii~""' f'rin.т•• r1~н,.#1r1('a:m1r•••1('
О r.ш_.~·r·r;ni.muЦ....., ~~\.'...<w1J.иQ ):X~\\t
-
--
Т11Туль ный /\И<'l
к1 1и1 и И Нь11лuн<1
« Мt1ТРм~1тиЧР\k,ИЕ'
l lc!'bl>\d 11,iryp ,t>\ЫIOf!
филnrnфи11 >
t Лондон 1687 1
ре 1щиа J 1 ы1ымн ура11не11иямп » . 13 «Мзтс.ма пr
ческих началах натуралыюli фнлософи11»
(1687 г.) Ньютон описал механическую си сте
му мира, в час1 ·1юсп1 . опнрмсь на закон все
иирно1·0 ·1·sн·отенш1, сформ улирuв:т З;.\КОНЫ
юшжснш1 небес н ых T<.:JI во Вселе нной.
lkcoбщt>c 11p ir :.;н;i1111c 11 rюслелuва~11 1 се З:!
н11м бурное развит11е ю1асс11чL·сl;(ой меха ники
Нью·1·о на укреп1тн п ознц1н·1 l)l!mt:'jJJШ /.'Нt.1з.мct -
фтюсuфского П\lНН\J,НП<!, СОП\З С I 10 которо,,лу
все яrщенин пр11род1. 1 пол 1юст1,ю прt:J \Сказу
е мы, есл 11 1 rмеется11счср11ываrощая t1нфпрм й
ция о состо н1ш11 мнра в к~шо(J - то момент
времени (начальные данн ые) . llрос1 ейш1 1м
прнмером такой предоnредспёшюсш яnruieтcя
возrvюжносп, онисать пуп" x(t) 11скоего тела ,
есл н 11 звс<.:т 11а (ТО скорос1 ъ t'U) на отрезке
ro.Tl Для ::JTO l'O /ЮСТ:lТОЧН() задатъ 1-1ачал ыюе
ц:1н1юс: - коорлrн-r а·1у x(U) 1ю1 юже111 1я тсш1 R
H ~IЧ;JJlhJIЫil M<>MCH'I' нрсмс н11 .
ГJХНi/ \1юзн ы<.: ус11ех11 ест<.:ствознания 11 ма
·1·е::м :Jт1 1 кн 11 1юслеJ ()'1ОЩI !С тр н CTO.llt:THЯ IIO NlНО
ГО,\11 были 0 111-н.~делены всл нким открытием
Ныотопа и Ле1~1бшп \а. В XVIП в. свой ню1ад в
раз nитие математи ческого aII::iлн:1a u1I ec1111
брать я Иоrаш 1 н Якоб Бсрнуллн, Л еон ард
Эйлер, Жоэеф Jlyи Лагранж. 1lъер Снм он Ла -
1шас и дру1·ие учёные. Образrю rouopя, оrш ста
раш1сь захнати·Jъ 1ю::~мож~ю большие ·1 ·сргт
тор н11, 11<: забоТ}J Сh о том , чтобы как м ожно
луч111с:: осно ить уже ИMt::IOЩ l tC<.:Я . Гlpe/\CJ';Jf!JICHIOI
о бесконечно мйлых и 1tx с.уммир ова н11н они
скорее 1юс11р11н:имали интуИ1'ив 1ю, ч ем п од
nер1·алн Jюп1ческому а11ал11зу
1
\
1
1
~51
детермин изм и случай н ость
Тот,ко в XIX в. были [!;а11ы строп 1 е О11репе
ления фу111щпи, неnрерьшности. прои:шодвой.
Современное 1101шт11е фушщнн сформирона
лось в nepвoi'! половине XJX n. благо,rtаря ис
следованиям таких выдающихся .чате~1ат11ков,
как l!.11колай Иванович Лобачевский, Петер
rус1 ·: 1н Лсжён /1,1 rрихл<; н ;1р. Прся~:~Н())\Н :Нl 6 1,IJJ:I
п1 1 рсделе 1 1а как пре11.ел от1~лше 1111я nрнраще11ия
функц1п1 к прнращснию :.~rгумснта (Општен
Кошп); н11тсrр~л - K<JK прt.:дt.:льгюс :п·1ачсннl"
11111 ·е1раJ 1ы1ы х су~ 1м , т. е., 1ю су·1·и деJ1а, r1Jюща
дсй ПО/~ графТ11<0М кусочrЮ- Л()(IОЯТ IНЫХ (ч:ту
П(;J rчатых») фу1 rкций, прибm 1жающих да1 п ry10
(ш1теrр.ируемую) фушщшо (ьернхард J:>иман)
До сих пор математическое образоRапис остю
вьшастся II<t ::-.~тих подходах , хотн в ХХ в. оrш по
луч.или 3н::1чительное развитие. Тu1·.ца ж<:: ношли
н у11uтре6J1сни<:: 1·ерм 1 1ны <'ЭЛ1"'.\1 с нтарн:.~я~ 11
<.высш::~я » матеN1атик;1. ( 1 Iод :..,лсме11тар1юй ма
тсмат!lкой обычно пони:-.1ают ту матсмат11ку.
КОТОраЯ Прt:ДШССТНОВаЛа рОЖДСl-IНЮ MaTбtaTIJ
ЧC:CIO)J'O анали:-~а: высшан 11ач1шае1снс 1 ю1 1я1. иi1
11ре11.ел::1, ттроиз1юдтюй п иптегр~~ла.)
Од1111м 11:-1 t1аж 11 еГrшr1х э;11.юеп~1 111111 м:tтема
тичсского апал11за в XIX в. ст::uю рожне1-111е ·1ео
рш1 а11аюгr11ческш;: фу1нщвй н фушщш1 ком
плекс1юго перемен1ю1·0.
Тl'ория аналитических фупкций во м11оrом
базируется на теории рядов, которая зародr 1 -
ласh uдно.временно с мз·1·<::м;п 11 с1есю1м анал11 -
зом. 1l ервые раз11оже111 ш :=темс1 ~т:1r11ых функ-
1\ш:т R ряды быпн получены к XV ll н. ::Эйлер
научился ра:тагат11 н ряды бол1,11111нст1ю ::~ле
,,1е1п·зр11ых фу111ш, нй. Теор11ю а11<1.111п1 1 ческнх
фу1 п<цт1й nостронл Коштr.
Гсометрня. явтшшаяся сщ1111м 11з краеуголь
ных камней. на которьL'\ з11ждетсн мате.чатн
чсс1сий апализ, n )(\!П l - XIX вв. развиnал;~сь n
:иrаLШТ<:ЛЫ!Ой мере нс:цвисимо от IICГ0. 13 х:х 13.,
уже На HUHUM уроннС, 1tpU11CXUД l lT HCf бОJJЬ Шt:С
ел~ 1 янис ~-со,н.:тр111-1 11 анат 1 :.за. Обл:ктыu пр11-
ложt"1 11 1я а11али~а ст::шовятсн N11ю1·щ1бr:1.шя -
кр11выс 11 повсрхнuст11, расположенные в ~11-Ю·
гом<:>rн~ых простра11ствах, обладJ1ощнх. как
11 ра в1 1 1ю , 1\nrюn 11 1 1те111.1 ю i1 a111 ·efipa11ческоi1
струн:тп1пй ( rруnпот1 11т1жс11m'т r1 т. n.) .
Бескон ечные послеловательности и суммы
БЕСКОНЕЧНЫЕ
ПОСЛЕЛОВАТЕЛЬНОСТИ И СУММЫ
ПОСЛЕЛОВАТЕЛЬНОСТИ
Матсмат1rка постоянно имеет дело с бесконеч
нос1ъю. Особенно это характерно для высшей
м:lтсматики Наnр11мер, матс.:мат11чсский а11али::1
и:~учает беско11ечныс м1 южс:ства чисел, бес r<0-
печ 1 1ые суммы и 11рои~шеде1 1 ия. оттюше 1 rия бес-
1ю11ечпо малых и бесконечно больших Rеличип.
llo уже такое простое понятне, ка1< па1уралы 1ый
рн;~ чисел 1. 2 . 3, 4 , ..., обозначает бесконсчньн1
l>бъс1п. С помощыо натурального ряда ошкы -
11аю·1 11 дру 1'1 1с бесконечные объекты. в часJ ·но
ст11 числовые 1юследов:пеньности.
Допус1нм. указано пр~тило, соп1асно кото
рuму каждому н:Уrуральному числу 1. 2, .3. "" п.. .
пос1·;1 нл<:н 11 сuотнетспщс элеме11' 1 ' а11 не1<01·оро
rо MI ЮЖСС'l \~З (чисел. ТОЧt:К. rеомеч1нчеСКИХ
фнгур 11 т л.). Тпт;~ rоворя1, что ~щт~;;~ 1 1~11юсr1l!ао
rютелыюс1пь элемеrпов а". Её щ1инято обозна
ча·tь с помощью фигурных скобок {а 1, а!,."} и;ш
просто {c1 11 f. Как правило. С/11 - это <JИCJl:l, п та
кие последонатсльностп называют числовыми.
КАК ЗАЛАЮТСЯ ЧИ СЛОВЫЕ
ПОСЛЕЛОВАТЕЛЬНОСТИ
Итзк, м1.1 говорили; «. ..укзз::1110 правило , соглас
но которому... ». Но какука~-~аr-ю. какпм образом?
l<ак у1·одно. лишь бы соответствне было одно
:щачным, т. с. т<аждому п - своё а11•
Одил 1 ·1з спосuбов - описателы-lый. Мы
rrpuc1·0 объяс1-шем. н з каких элсмснтон 11 1~ ка
ком nорядке с.:тронтс>1 110сле;ют~ателыюс1ъ.
Например: ~вес члены 1юслед0Rатсл1>ност 11
равны l », т . е. гюсщ:доватслы юсть 1 1 мест ш1 д
{ 1, 1, 1. ... }. Другой 11р11мср: ~послсдоRат~ль-
1юсп-, состоит н з псех 11ростътх чисел R поря1~
ке возрастания», или {2, 3, '5, 7, 11, ."}.При
оедёш1ые здесь описания rтолне однознаLшы,
хотя во втором с11учае труд~ ю сразу ответить,
L1сму· ранеп, скажем, 1 ООО 000 -й элемент по
следоnа1·~лыюсти.
-1'53
Летермин изм и случа й ность
П ОСЛЕЛО ВАТЕЛЬ Н ОСТИ ,
ОПИСАННЫЕ МГОРИТМИЧЕСКИ
Математи ки вносят утuчнен ие в понятие «Описа
~1ие », заме няя его термином « а11горитм •1 . Алго
ритм - это точное предn и са н ие, о п ределяюшее
проuесс перехода от исход н ых данных к иском ому
результату. Если задано такое точ ное предп иса ние,
которое для любого ч исла n позволяет вы•1ислить
а0, то говорят, что п ос11едuвательностьlа11 1 оп исана
алгори тм~1 чески.
Последовательн ость простых чи<.сл, н апр 1~мер,
описывается алгоритмич ески . Скажем, ес11и из
вестны первые шесть простых чисе11: 2, 3 , 5, 7, 11 ,
13, то очередное простое чис110 наС1дем, перебирая
чис11а, слелуюшие за 1J o.o.tlO Ja другим, и деля их
н а уже 11 айде1111ы с простые чи< лd. 14 дt>11ится 1ш 2 -
оно не простое, 1с; делится на 3 - тоже не про
стое, 16 оюва делится на 2, а 17 не делится ни 11а
одно ИJ t1аших чисел, оно простое и т. д.
Алгоритм ической я влиется и nuслеловат~11ь-
1юсть десятичны х зн аков чием v2:
11,4,1,4,2,1,3,с;,h,2, ...1
(*)
(алгоритм вы•1 и слен и я квадрап1ых корне и из нату
ральных чисел ювестеt1 с нез<1 n амятны х в ремt> н) .
А вот пример н е ал 1 оритмического оп исания п о
следооатслы юсти : а0 = О, ес11и о nослело вnтелыюсп1
(*) есть п гюлрял идуших нум~й, и а11 = 1, ес11и 11ет.
Еще СJ/\1 1н с1 юсоб :J~щ:шня 1юс.не,цонатсл h1-ю
<:тс::1'1 - фо/щ1~11ыtы1i. R этuм с11учас пrшю11ят
фоr.чулу 11л 1J, сслн нс.:обхо;(нмо, 11ескш1ько
формул. nо:{нолнющ1 1х rю за;tа11ному 11 ныч11с
л JЛ 1. С/11· Т::~ к {21t - 1} - ПОСЛС;\ОR:IТСЛ1>1 ioc·1
·r.
11еч ёт11ых чисел, {n1} - к11ад1х1·1·011. (2''-
1} - сте
пснеiт дrюйю 1, {1} - рассмотренн ая m.1mc nо
с.'lсдо вател ы юсть ед1111111 t.
Несьма рас п рострапён релурjю11т11ыi1
метод :~ад:шия пос1tдuuател1.11 0061 . О п
заключаетси н сле,r~.ующсч: первые jJ
чле н о в IIOCJI C,'l,O D!lTCЛЫIOCTll :з:щ аются
н~ню, а ,tV1н нсех uстальных ука з ывж~гся
сtюсuб { на11римс.:р, фор~1ула). как
ПОЛУЧИТЬ Ct11 , :~ ll:IЯ /J 11 рС.:/(ЫJ\) ЩllX
чле1 юн. Таким образоJ1.1, 1ю и:н1ест11ы,,1 р ч11е11ам
мажпо 11айтн UJ+ 1)-й, :~атем по р чле11а~1 со
2-гопо (J> + 1)-11 nю1ючнтелыю - (J> + 2)-й ~1ле11
и т. д. Само название <· рскуррснт1 rый'), т. с. •воз
врат1 1ьu::~ о), 1·01.юрит о C)-T II с1юсu6:1 : чтuбы <щ рt·
дел 11ть ОLJереднuй члс11. надо 1с:~к бы кtрн~~1·ьсн
кр 1Jредt.щущим и llC'I IOЛhЗOH;t'ТЪ llX jH:JЧClllHI.
I lосЛt:л.о rsател ыюс1ъ, содержащая только
t:.Ц11111щы, рекуррснтно описыRастся так: а1 = 1.
11 для Rccx /i ~ 1 а11 , 1= ct11• Л нп·1 1юс11е;tnn::~тс111.-
1юст1, 11ечёт111>1х Ч11СС!1: а1 = I; а1111 =а11+1 1ря
п ). 1. И п ослс11онатслыюстъ ква11рато п ле1·ко
заJtат1. рскуррс11т110: а1= 1, с11111 = а"+ 111 + 1,
11 > 1, не 1·оuоря уже о послсдоnатслыюстн сте
пенейдnойки: а1 = 1. а11_1 =2а11. 11 ~ 1
Мы рассмотрели чш с1юсuба :.J:щан1tл 1ю
с11сдока·1·\.'л1,нос1·с1'1. Пр~1 -:Э'1'ом. пp:tщt:1, 1К'рный
(u1111са·п.:11ы1ы1·1) 11с: нс<:тна можно ощс:1111ь от
/tвул JtP)ПJЛ сщ>с< 11'iок Вt:дъ лю()ан фор1--1~л:1, н
1о м чн слс рl:куррс н тн ~щ - тожt' <1111 1c 1J11lt' Тем
н<: лн:нсt" CJlt'Jtye~r пщ1е, 11 1·1·1, э·1·0·1 с1 юcofi хот» бы
1ю·1 ·т"1у, ч·1 о 111ю1 лэ 11 е у}'"{аётся уъ:з:-~лъ пря~1 у10
:ЗЗFIПСНМОСТЬ а" !J\ I от 11. I ПI от р нредЫД)ЩJJХ
чл сr юв. т~1 ко в а. в часл10011, t1оследо 1.1атель-
1юсть простых чнс<::л .
Л тепе р1, 1 rссле,Т(усм оп:тrу э а~1с чатс.'1Ън\10
послсдоват<:л ы ю<: ть
П ОСЛЕдОВА ТЕЛЬ НОСТ Ь
ФИБОНАЧЧИ
Мrюrи ч гн 11юлс1 1 ш1J11 e11po11ei11~ен Jlec111ap)\O
П1л;11Lс1<и~1 (Ф11nc)lta ч'-t п) 6ыл и:~nсстс11 прсж-
1~е всего юш ;штор «К1шп 1 абака,, ( 1202 с ), по
кото ро fr :з11а.~соМI11шсь с деоп1 1 ч1 ю 1'1 с 1 ктемоi!
СLшсле11ш1. Тепе рь его имя чаще nccro nспо
м и 11а ют n сnязп с ПОСЛСДОВ:IТСЛЫIОС1ЪЮ ЧllССЛ
{1, 1.!. , .1. :;.8 , 1.-1 .2.1, " 1.которую011рассмотрел
np11 рсшt11и11 :шдач11 о разм 1-южс111111 кролн
кон (см стат 1 ,ю ~лс.:0 11 :1р/t<> f l 11 : 1;111 cю 111 11 с1·0
нрсмя ») Здесь 1н.:рные дна ч1 1с.11:J - сд11н1щы. :1
каждое 1юслс1tую1 1 (С.:l' ра вн о сумм<.; ; (вух ПJX:f\Ы -
1~~1 1t11 x. Эта ПОСЛL'ДОН;]'['tJ.IЫ ЮС'JЪ 1:щ:1ётсн C te·
1~~1ощ11.'11 pt"1<yp pc1 1т11 J>J ,\.1 соо·п ю 1 11е 111 1е м:
п,=1.
(/=1,
Cl11c! = U11,1 ~ Cl11 (JI:;,: 1).
LlIJcлa Ф116uн:1LJч11 нстрс.:чаютсн но \1нu1·11х
раз,:.~,слах матt'ма·1·11 ки. 11 кuJ1161 111:1·1·орнкс, 1со-
метрни, теории ч11сел , в :3адачах 11::1 м<1кснмум
и мннимум .
А мож1Iо ли для 1юследоватслы-юст11 Фибo
H:lLJЧll яв1ю, т. с. n nпдс формулы, выразпт.ь зна
ч<::ние а" чс:-рез п? Ныuсдсм эту формулу.
Забудем на время про пача;tьныс:- условия
(и1 = 1, aJ = J) и будем ~ккаr1, пuслсдuватсль
ность 1шдз {L(} , уfl.uнлстнuрюuщу~о рскуррснт-
1юi1 формуле a"+t = а11 н + а11• Почему 11C\1t:1111U
{с('} 7 О111ет дает сuзданнзя Лепнар11ом Э11.l1с ром
ofim,aя теор11 н нозвр;пных пос11 едп11л <:-ль 1 10-
cтeft , обсужде11 1 1е 1<0·1 ·opoit выхою rт :-i::i рамки
задач этого тома.
Подстави."1 q'' nместо а" н формулу а" , 2 =
= а11• 1 + а". 11олучим ур:.1ш 1еrшс
Cf 11
-
J =с;"+1+t/1
•
OтfipocнR рс111е::ннс С/= О, сокр<1т11м об<: чж·1· 1 1
уrх1вн7н11я H:J (/'. ПtJJ1уч1 1 м квадр:.1т11щ· уμ ан1-н:-
1111 е с[= lJ + 1. котороt: имс:ет 11на ненулевых
K()J11 IH:
1
1+\!5
l-v5
Ч1 = --и с7, =---.
l.
-
2
llcpвr .1iI 1i:; 1111х равен знаменитому ч нслу Фадия
Ф (C1\t. ст~1 тыо "Llисла Фидия t1 :юлотос сече 1 11.tе" ).
А 1 юскuльку, по теореме Вне-1'<1. Ц1(/! = - 1, то пто
r<к· ЧИСЛО С:С' IЪ НС Ч:ТО ШЮС, как -1 /Ф = -<р, ГДС
ip- HTOj)()C ЧllCJ IO Фll,/.J,ИЯ.
Итак, ю1fщс~ 1ы /(Ве rюслсдон~1·1·слыюlт 1 1 {ц 1 "}
11 !сч/'}, )7l\ОRлс·1·воrяю щ11 с ураннсншо а11 , 2 =
'"' а" 1+ cf". Болсе:: тш·о, L1рямая 1юдстанонка 110-
ка:~ывает, что l!Юбая 1 1ослслш1атет, 1 юст1, HHJ(;.t
J
11
11}
1C1q1 +( l(;/2
также удоnлстворнет ::этому у1)авпснт1ю. Jначнг,
тс11 ерь можно попытатuся подобратт. т:щие с 1
11 с.!. что первые дв:.~ члена послсдоватслыюстп
()К~IЖ)"l'Ся р~н11-1.ымн 1. И тогда она l'шшадi:'т с
1юсле;\(>Н~1тс:л1,ност1,ю Ф1t6011:1чч11.
Уч1п 1,rная, что а1 = 1 на.!= 1. 11ОЛ) 11:1ем c11-
C1t' .\I)' yp:.tHHl'J-111(1
{
C1t/1+C2Cf2 = 1.
>
'
IJJil l
С1Ч I +C2l{!. = J,
- [1+Jr:,)
· l·1- \1') )
-
]
t1---+(,---
-
'
2
-
2
. [1+\/r:., )
1
.
[1-\'
1
~).! -1
с1 --- +с,
-
-
-
-
.
2
-
!.
Бескон ечн ые послелов.з1 елы-юсти и суммы
сколькими
С П ОСОБАМИ
можно п олняться
ПО 1\ЕСТНИUЕ~
Вспомните, как вы nодн имаетес:ь
по лестниuе: то наступа я на каж
дую ступеньку, то перескакивая
через одну. Сколькими же спо
С()nам и можно в·юf>раться по
лестн11uе~ для лестниuы в од ну
сrупеньку и с п особ еди 11стве11-
н ый , Л/\Я двухступе нч атой их
ма : либо гга новиться на каЖдую
ступе н ьку, либо сразу ш агн уть
11а последнюю.
f ly а сколько «путей» ведут
н ,1 п-ю пупеньку? Обо1на ч им их
число чер ез Ь.,. Очевилно, что
~-юпа сrь 11а 11-ю пуп<>н hку мож
нп.либосделавшагс(п- 1}и,
либо ш агнув Ч(!рез ступеньку с
(п - 2)-й. Количество способов
подннться н а (п - 1)-ю ступе~1 ьку
ест1,, по определению, Ьо-11 на
(п - 2}-Ю
-
ь"_,. Знач и т, Ь,, =
= /J" 1 + Ь" 2• Теперь щ.но: число
ь" равно (п + 1)-му члену после-
ловательноои <Dибоначч и!
Это сист<:ма 11з дRух шшсfшых ур~шш: rш 11 с
лнумя н.е~1звест1 tым11 . которые бс3 труда u11pe-
дcлmO'I ся: с1 = 1/ \.
1
"i п с, = - 1/ \ '5. В рс:1у.'11>т:не
нахо,Т(им, что 11-с число Фнбо 11ачLНJ 13ыражается
через его 1юря;и<оный но.чср слслу71ощсй фор
мулой:
а"=,\[ll+2{5 J' -[1-гп <'1
l l t' уд1ш11·1•t11ы 10 1111: кн:щратныс корн 11 н фuр
мущ;, 3адающей 1IOCJll')(UH:.t'l'tJJЫIOCTЬ JfЗ O/\HllX
только 1 1 атуралhных 1 111сел! Рс;1 ко кто ущ: р
ж11то1 0 ·1
· жс.:.1 1а111 1 я про1н:р11ть « нручную» t:ё
сттравсдJllШОСТI) для HC.:CKOJJЬKHX 11срвых 'Jl.
Выр:.~же1 шс а" череэ /1 /l;1ёт очс.:нь ~1 1 ю1·0. 3а-
ме·п r м. ЧТО (1 - \;S)/2 П!1 aбcoЛJO' l' I LOlJ HC.:Jill-
ЧHLJe меньше 1, поэтому 11р11 nоз вс:11с111r1 ,1 е1·0 п
стспс 11 ь с ростом 1·1будут получатъся 13((· мс11ь-
111не чнсш. Уже 11ри 11 = 1'5 второе сл;.~1·;1емое
г
Летермини.:1м и случайность
в 1шадратных скобках меньше l / I ООО, а 1tри
п= :Ю - меньше l/I ОООООО.Поэтомуможно
смело утве рждать. что члены послсдователr,но
сти Фибон~ччи 11едуr себя 11ра1<тичесю" как
Ф"/~, т. с. каждое последующее слагаемое
больше предыдущего примерно в Ф раз (при
чём чем больше п, тем точнеё).
Лоnробуйтс самостоятсльнu разобраться с
дру~'ой последователы-юс1ъю (а11 }, у которой а 1 =
=О, а 1 = 1, а каждый член, начин::~я с третьего,
раве 11 нс сумме, а полусумме двух предыдущих
Удастся ли nам выразить а11 через п? Вместо на
пуrствия скзжем, что радикалон здt'сь rте будет.
СВО Й СТВА
ПОСЛЕЛО ВАТЕЛЬНОСТЕЙ
Последовательность {а"} называется.л101ютон -
1юЛ, если а,,...1 ~ а11 ИJJИ а,1+1 ~ a11J-VLЯ всех п. В нер
вом случае это .м01-tопюmю неубывающая, во
нтuром - .л·t0н.оmоН?ш невоарастаю1.цая после
доваtпельн.остъ. Если С/11+ 1 > а11 и11 и а"" 1 < а11 д.11я
вс~ п, то гонорят, что nоследоватею,нпс·1ъ {а11}
J!шюпю111ш сюз/х~стающая
~~Ь)~"
.'14тш11щ1 то 11еу()ыRа1011 ~С1>1
&JQ) i:J)Q)ht
Монотонны е nослеловi1 ·1 ель11u<.ти .
456
строго л1л1-ютонна (возрастает н первом спу
чае 11 убывает во втором) .
ТТос;1едов;~телыюсть {а11} 11азывается пгра11и
чешюй, если существуютт•шне ч.исла сн С, Ч1'О
для всех "IЛенов последооателыюсти вьmолня
ются неравенства с ~ а11 ~ С.
Огра1шчеи110Сt свер."к..)' 11азь113а<:гся nослсдо
ватсJJ ьность. д1ш которой сущео·ву<:г такое
число С, что для всех членов 11ослелuвательно
ст11 ныполняется ~-1еравснство а11 ~ С
Огра1-1.иче1аюit снu3у 11азывается последова
тслы юстъ. для J<Оторой· сущесгвует такое ч11сло
с, что для всех членоn 1юслслонателыюсти
ныпоттяе1·ся неравенство а11 ~ с.
Таким образом, если говорят. что nоследо
вателы rость ограничена. это о:щачает, что она
ограничена н сверху. 11 сннзу.
Если сущсстнует такuе на·1уралыюе Т, что,
начиная с некоторого п, l3Ы1юлняется р<Jнен
С'1 'fЮ а//= ali + J' то ПОСJIСДОЩIТt'ЛЬf'ЮСТЬ называ
ется периоди·•tесл:ой, ;1 Т - .тщи~-юй сё периода.
ТТростей 111 ш1 случай - когда Rce чJrе 1 1ы 11осле
допатем.постн 01\i•lllaKOBЫ. nр11.мером CJIYMИT
уже знакомая нам последовательность J.tЗ еди
~.:rи1 ~(здесь Т = 1). Последовательность {(- 1)"},
т. е. {- 1, 1, - 1 . 1, ".},периодична с длютоii пе
риода Т = 2 . А у последовательности, п-й член
которой а" есть остатuк от делешrя 11 на 5
(выглндит она так: {1, 2. 3, 4 , О, l, 2, 3, 4, О,."}),
дJlин~ периода Т= 5.
Обратимсн к рассмотренным ранt:е 1юсле
донатсль.ностям. nослсдонател1,ность, состо
ящая из одних единиц, как уже отмсчало~ь.
перио;~нчна, а также монотоr 11-ю не возрастает
и мо r юто111 ю не убь111ает, да 1< TOJl;I)' же ещё и
огра1 щчена.
П оследоnателыюсп, натуральных ч11сел
строrо моаотошrа (во:3растающая) , ограни
чена с11изу, не ограничен:~ сверлу- и нс пер110·
днч11а. То же от1-юснтся к послсловательносш
11ростых ч11сеJ1 .
П рсд;южt:нн::~я ;~ля самостоятсльно1 ·0 11ссле
до1:1а 11ия посл едоватслыюстъ , у 1<0·1·opol1a 1=0.
а.!= 1. и каждый члt:н , начи11ая с треты.:1·0, равен
nолусум мt: двух 11редьщу1цнх. orpai шчена (так
как нес её 4лены ззве;\ОМО ззю11оqё11ы мtжлу О
и 1).110 11е мо11отош-1а 11 1rt: пер ~ю,цнчна . Одна
ко, <Побы убедитт,ся в этом. Jiaдo выразить а11
через п. Можете проверить свой ответ:
а11=i(1-(-;)"_ 1 ) .
Используя nоня· 1·ия монотонности, ш·рани
ченности и nер 1. юдич1 юсти, мпжr-ю оnиса1ъ
11емало простейших свойств ттоследователы-ю
стей. Вот некоторые из них.
Если п оследовательность {а"} мо1ютон1ю
возрастающая, то последователыюсть { - а"}
мо1ютоrшо убывающая, и ~-rаоборот. Апалогич -
110, если последовате11ы-юстh {а11} монотонно
невозрастающ;.~я, то ПОСЛСДОН~IТСJJЫЮСТЬ {-а,,1
~юното1-rно неубывающая, и 11аоборот.
Монотоr rно возрастаюJJ tая 1юслс,r~ов::~·1·е:.11 ь-
110с1ъ огр::~ничсна с11изу, мснюто11J ю убьшаю
щая - сверху.
Мотю·~ n1пю возрастающая илн мотю·1·ошю
убы1}ающая nоследоuателъ11ость не можС1· бытъ
периодичес~<ой.
Псриодичсскан послсдоватсльностъ nсе:гда
оrраничсr 1а.
***
Итак, н опровержение н:н~сстноl'О изречения
·Неm,зя объять необъятное~. мы не тол 1,ко 11а
rш11ис1~ за11анат1, такие ..- необыrгньте!) 061,сктhJ ,
как бес1<01 1ечн ~.Je числовые последовательно-
Бесконечные последовательности и суммы
сти, н cy."V1em 1 выде.1п1ть некоторые их 1 ·руппы ,
но и ОТТИсалн отдельные снойс['на. Однако 11.:. .t -
стоя щая революция u п ост11жен иr1 11р11роды
бескоIIеч11ости свнзана с поrтятнем предела
(с м. статью « 11 релел последователыюстн:»).
АРИФМЕТИЧЕСКАЯ И ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИИ
АРИФМЕТИ ЧЕСКАЯ ПРОГРЕССИЯ
Рассмо·1·rим послt.>доватеJ 11,нос1ъ {а"}, опrсде
лённую следую щим рекуррентн ым с11осо6ом:
а, з~лаrю, и ;1юr ткех 1'l ~ 1 справе/(Л1 1tю р1не1J
rлю а"+1 =а"+ d, 1·де с1 также 11екоторое ~:1а
,1а111юе чис;ю. Дру1·ими словами , первый член
последоDателыюсти 11звесrе11, а каждый: после
.:tующий бодьшс предыдущего па одну 11 ту же
велнсншу.
Лс1·ко найт11 явп ое (формульное) выраже
н11с et 11 через п. Прr1 псрсхоле к очередному
элемсrrту cro значен11е возрастает н::~ dпо срав
не11111U с предыдущим. Чтобы добраться от пер
вого элемента до 11 ~!'0, нужIIо проделать rt - 1
таких 11ереходов, ткледсгвие че1·0 а11 превыша
Сlа111а(и- 1)d,""е.
Cl/j=CJ1+(11- l)d.
Построенная последоnатеJiыюсть н:tзъшаlтся
арифJ11етич&с1шй прогрессией. а значе пи е а -
pa.mOCJn'blO ;!J1Hфмe'l'.HLJCCK0Й 11porpcCCИi'L
Встретив н оное тто 1-н~тие, хочется узнать u
п ро11схожлен11 н e1·u назв::~н ня. Поч~::му п ро 1 рсс
с11я' Почему ::~рифме~ нческая'
Отнет н::~ первый нопрос почт11 () ч сниден.
ЧJJe1-11,r такой пос.1.tедт1а ·1 ·елыюсп1 всё врсмн
«прираСТ<IЮТ» 0,l{l-IH .'vl н тем же ЧHCJI()M cl, '1' . е.
прогrессируют. либо ПОl\11Имаяо, nсё nыше
(r 1ри d > О), либо опускаяс~. нсё ниже (лри
cl < 0) (Последняя про1·рессJJЯ, правда. больше
похожа аа «регре:ссню», но т~1коl! тер~uш пе ис
пш~ьзую'1 '.) Воз можс1 1 , консчнu, 11 вырожден
ный случа11, кш·~а d ==О. Это будl"'r «з ::~ сто 1lн;нн
ПtJCJI<.:j~Ol33TCЛb!-IOCТI> ИЗ О[(ИН :IКОВЫХ ЧltCt:JТ.
l ly а ар11фмст11•1ескоil nро1р(.:сс11я назnан::~
потому, что н 11 e1I кажды тi член , кроме nер1ю 1 ·0,
раuен среднему ар11фме·111чсскnму 11nyx сосе11 -
ш1х с ш тм - пре;(ыдуще1 п и посJ1е~утощего.
Давайте 13 этом убедимся. Возьмём трп про
п зв6лы 1 ых члена лос11едоu;1те;1ы 10сти, 11,'\у
щих лодряд, 11алрнмср а" 1, а,, 11 t111 " (здесь n
не меньше 2). Согласно пра1шл<1м образоnзн11я
арифмt"1·ическс..н'1 1 1рогрсссин.
детерми1~изм и случай ность
а"= а"_, + d,
откуд::~
а"= а"+1 - Gi
Сложиn пе:р~юе 11 треты:~ р:1вс 1 1ст1З::~, rюлуч::~ см
)
а =а"_ 1+ат1
La" =а"_, ~ ап;11ил11 и.
2
что и тре бо.1:!.Vюсь доказ:пь
Верно и обр:п.ное: сс.;щ l(:J>IЩЫtl член послс
донатс:.лы юсти, кро ме ш.:р1ю 1·0, р:шен средне
му арифмег11чсско.му двух CIIOHX СОССД<::Й, ТО
т:шая nослсдовательность есть арифмет~r
ческ:.~я прогрссс11н . Дпк::~эа1Ъ э' 1 и неСJюжно, 11
удоб11ес всего II СПОЛЬЗОП:.lТ Ь метод ЛОЛl-!011 М:.l
тсм:п11чес1<ой 111 тду rщ и н поп (см . сt·::~тыо ~ме
тод м:~тем:~т11ческой иr1ду1щш1») .
Итак, пусть некоторая ттосле,1\ов::~тепыюст~.,
{а11} облздаст укзз::~нным сuойством. Обоз11зч11м
р:~зностL м ежду сё вто рым и л<:рвым членам 11
черезcl,т.с.а2- а1
= cl,и11иа2=а1+ct.Ипусть
для вс<.:х пот 2дu1г вю1 ючитслы-ю а11 превыш а
ет а11 _ 1 н:~ то же с..::.~мое число c.i; в ч::н:тност~f,
ak= ak-L + cl.
Убедимся , чтп д;1я н = k + 1 это р:~венст13о
т:щж<.: 0 1<ажется верн ым . Посtюлы<у а;, есть
среднее арифметическое между ak-J и ak+L ·
-
а"_,+ а"+,
ai. -
2
'
то
Яняарь
Феnрал1.
Март
Требов:шие инду1щи11 выполиепо, поэтому
опи с~н-п r:ш посл сдов:пелыюсть деtiствителыю
нВJIЯется арифметической проrрессней.
Испо11ьзу.н явное 13ырзже11и с а" через п,
можно без труд~ доказать следующее с1юйстео
арифметической прт ·рессни: ссл11 натураль
ные чис11:~ i,;, k, l такоuы, что 1 + j = k +!,то а,+
+ aJ = ak + а1. Чтобы в это м убедиться, достаточ
но rюдстав11ть i,J, k 11 l пме:с.·то ri u выр:~.же 1шс
а,,= а 1 + (п - J) t l, лр011 эnестн сложс1ше, рас
крыть сr<обю 1 и сl3ср11т1, резут,таты. О 1·сюд:~
следует , что еош рзссмзтриn:.tТL> толысо п ер
вые /1 члепоп арифмстнческой про1·ресс1щ то
cyM1'vlЫ ЧJICH OH , ранн о отстошц их от концов,
будуг ОДИНJКОliЫ :
а1+а"=а2+а"_1=а~+а"_~=... =
= 2а1.., (11 - l)c/.
Послс:д11ее раве1 tстно nо:з воляет вы '111 С'Лить
сумму первых 1l член ов зr 11фм етнчсской про
гре ссии:
s"=а1+а~+ "+а"_,+а".
Го.воrят, 11смс 1 т.rшй ;чзто1:~пщ I<:ipл Фрид
rнх Г::tусс, еще будучи Wl<OJIJ.,llШ<O i\\, су.ч ел з:~
с чнт:ш н ые секу нды найтн су,"~ь1у ucex н:~rу
rаль ных чнсел uт 1 до 100. Он :{:1мет11JJ, что
сум:v1 ы раш-1ооте1·uя1Lщх от концов чнсел р~в
ны:1+100=2+99=j +9R== ." =50+51=JOJ
Все1·0 nолуч:.~ется 50 п:.~р чисел , и сумма кзж
дой парт,~ 1 О 1 , nоэтому общ:u~ сумм:.~ 50 · 10 1=
= 5050. Дейстnите.пыю, nос.тrедо11:Jтельнос-пн~
тур:.~льных чпсел является :.~рпф~1сти ч еской
прогрессией. Эдесь а1= 1 11 d = 1.
Ан рслr,
Вре.ля
Г1' ' 11 ПJ Н >Ш:'НТЬI ( 11~'\.lд,1 < 1 1 11 1.<,Пh ~,))j.,i\Ьll l ~\\'( ЩJ ТП 1-"11111Т,1/\ [!<1\re T 1\ ,1р11ф'1 f'Т11' 11.'( l<П11 Пpr>I per c 1111
Гаусс р:!СС'vlатрнн: иr чётнос кш11 1ч с<т ко c11:,i-
1-:tc'11 r11x, 1юэтпму 011 сум tл ра :{6L 1ть 1 1х на п зры.
У н~1с же ll - тобпе rrатурш 11 .ное ч1tсло. 1fеужс-
ЛI1 np1 щ&lп1 рассматр1 rнат1, o·r;\em.1 ю СЛ)'ча11
чС::·1 rЮГ() 11 11ес1ет11 оrо 11 ~ Нет, С,'"\елае~1 no -дpyf"<>
·"'Y· Но:н,мЬ"1 ещё од1 1у т:.tкую же сумму. 1 ю cJ1 a-
r::te.\1ыe :1;11 ш111 ем fl обр:пном л пряд 1\е:
S11==011+a11 1t ...+a~+o1.
: laJJt't', СЛОЖ!IМ её ПОЧJJСН НО с llCXOДII<>l'I суммо1\
1 1р11чём сл:11·:н.:J11ыс ера:>у 11ш 1:~рно с1ру11111 1rусм.
ПOJ l \ЧllM
1S11 ""(r11+a11)+(02+a111 ) + ". +
+((,/" 1+п,) + ((111 +П1).
В юж.цых скобках закпючепа су,,1м:~ [1, H)'S 1х1ш ю
отстш1 щих от коrщоn чл с1 юн пrю1·рtсс 1н1.
которая. кат< мы :таем. равна .!.а1 + (n - 1)с/. !3сс-
1·0 ;.щ.· таю~х сумм 11 , 110:,)'J'О:М)"
2.S,, = 11е.а1+(IZ- 1)ct)=
.!.1ta 1 + 11( 11 - 1)С/,
.
11(11- l)cl
.s;1 =7Ш1 ·г ]. .
(*)
Таю'"' обр:.tзом сумм::J 11 перn1.1х члt:rю11 ар11ф
~1еп1,1еской ПJ1011хсс 1111 выrажзе·п·я черб п ср
J3Ыi1 ч11е н т 1 р:.tз 1 юсть.
Обрап rтс 1;1 1 1нма11пе: сама а р1 1фмстнчсская
11por pt'CCTISl llOЗ[):I C'l'<ICT Пр0 1 ЮрЦ L ЮШL1ЫЮ ll, tl
С~'\.Щ~I l 1 Срных 11, t'i:: ЧJIC HOB - гор:!ЗДО 6ы (~1·рсе ,
r1ри~1ерно r<ак п-;1. И это не случ:1l1ность, а "д:1-
лёк11й 0·1:звук-> ш1тс 1 р~и1ыю1п н сч 1кле111 1н (см
ст:.tтыо "И11тс 1 ·р:.u1 11 пср ппп6ра:ш :u1 фуню 1,r 111 ·>) .
Тс1 1ер1, 1 1al1.цt:.-..1 ныражt'111 1е:: ,11,лн С)'\1 1\11 ,1 1 1с1 тых
11 чне ~ ю н арнф,,1t:т 11 u.с:с 1<0\1 11р<н pt'cC111 1, еслн
11:тестпы лт11 1 1 1, пероы l1 111юследт1 1'1 чпе111>1. ·1 с:.
с/ 1 и а11• Расс:vютрп:-1 ещё р:1з ~:1нt:~кт110
2.S,1= (а1+ан)+lll.:+а" 1)+." +
+(а11_1+а_)+(a11 +rt1).
<..:ум мы н 1<аждой r rз <.:кобtж р;~нны мt'жJ\у собой ,
3H:!Ч ll'f'.
S =11(al+а,,)
,,
2
.
('"")
l i,IKO IICЦ, Д<!}ЩМ ещ~ более Щ10СТОе B ы paЖC·
llllC д.l н S11
•
пр111'()f\ 1 юс, п р;~вда. 1штш, д.1я 11с•1ёт-
Бс<..кон1 ·ч 1 I ЫЕ--' п щ лr•доВсП('Лi?l IОГГИ и< уммы
111,J'< 11, ·1 · l'. для п = 21..r
-
1 nосколь ку пр1 1 этом.
1+п= 1+(2k- J)=2k =No+k.тоuciu1yра11сс
н:1rщсш·ю1·0 сно1~1с1·на ~1р11фмст11 чсской 1 1 р<>-
1 [JL'C 'Cl 111
1J оэтому
11 (t11 + ti,,) = 11 '.!.п~.
2
2
11 01\':!J H Ч~lТCJIЫIO
("'**)
З11а 11 lit' с1ю lктв а рн ф щ'ти чс:скоfi 11ро1гtх -
С\.1 1 \ П<X\ l~O!lnC'I pi.:: 1111 1' 1 '\, 11eм;1Jl0 р:1:\ЛllЧ11 1>1Л
за~;N. М шк1ю, на 11 rнмt'р. 11af1'J"IJ с~ ММ} nс:р11ых
l / 1!~ \Т\1 \):\ЛЬШ,\,,'\ ЧllCC:.'l )1.ЛЯ npOП:'liIO.:lblIO I'() /! , НОС
пользов:ш ш1 1с 1у 11:1 ныi.1ор формупоГr ("') 111ш ( "* ).
ХОЗ ЯИН И PAbUTHИ I<
Рас смо1ри м 1 а кую iал.~чу. Хоi51Ин нанлл раhотн икJ
н а неделю (с nо11слt'лы1ика по воскрсt.с11 ы"' вклю
чин::l\u1ю), повы ш ая ему кажды й ле 11 1, iарпл<1ту HJ
одн у и Т}' жl:' 1:1с•личи1-1 у. Сколько flcero п олуч11Л
р.:~n<1т11ик, uсли за •1 t>твerr ему з.:~nлатил~1 3 рубля(
В лой Jадач<:: угадывается арифм('тическая про
греп ия, н о каж1:1гся, что не хе;:~т,1е1 д..~н н ы>. . Иi
вестны только 11исло членов 11 "' 7 11 значение
•1етоср1ого •1лс11аJ • = ~- З11аи раз11ость проrрессии
Иl\11 п ер1:1ый Ч Л~ll , мы ЛРI ко опредt:Л11ЛИ бы l;K(' ч ю
rpeuyeтcSJ. А rак".
И rке-т,1ки поп робуем ее решить. Пуст~> а -
nерв ы и Чl\C'f 1 r1porpcco111. J d - раз11ос.т~... Заn1 1 шсм
:iapaGmuк по дн~м в в11дс ~,1бл нuы:
Пн. В1. Ср. Чтв. Пт11. Сб.
Вс.
а a+d ,1+l<I а+Jd ,1+4d J +5d tl+6d
За Нt'ЛСЛКJ pc1Gu1 ~1ик получил 7а + 11J = 7(r1 +
+ Jc/). Hn а + ld - это опл,~та ~" •н:-тверr, т. е.
l рубля. Зна ч 1п, oct?ro 01 1 ~арабо 1Jл 21 рубл1.>.
Л есть и дру1·uй <..nособ. 3арnла 1а за 11сл<>лю -
по t ум,~.,,1с1 нечетного 11 и< л.1 П<:'рвых 1 1ленов а риф
МЕ:·тичесr.ои пр<1rрессии. Замt?тим, чти есл 11 нужно
1-1.:~и ти СУ"''~У 7 "1 1\Сtюв, 10 4 - и чле1 1 как μ;в я~змн:.•1<..я
срсд11им . По.ному мо11<но пр11мL'111нь фор,..,,1улу
S., = nak,
rле 11 = 2.k - 1 . Так что оGшая ·~ар nл,пз ·~а не~слю
р;:~вна 7а.; =7 -{ = 21 рубл~-..
Летерм~1низм и случай~ юсть
Вторан формущ1 и данном случае удобнсе, BC/l h
пеrвое и последн ее сжн·:земые 11звес1"ны (они
p<tHHhJ 1 JI п COOTBt;'ГCTl-ICHH(.)) fl общее чнсло
сл:11'аемых раmю п. Следопате;1ыю,
7
..
_
п(п+1)
1+- +
... +Jl-
.
2
Эта форNtула имеет простое геометрическое
ТОЛ!СОВШU1<.: (р11с. l).
Ну а tо1и требуt:н:н 11ыч 1 1сл1пь сумму пt:р
вмх 11 111.:чстных ТJзтурзлыrых чисел, т. е.
l + .) + ') + .. (всс 1·0 п сж11·:н~мых)? Здесь можно
воспоm,зов~пься формулоr'1 (*) . Искпм:~я сумма
оказывается ран ~ ю~"1
11· 1+n(n-1)·2 = n l.
2
Не правда ли, уди1штельно: сумма первых п
11е'-1ётных <-1.исел в точ ности равна К!3адра1у их
количеств:.~! Такие сов1~адс:ния обы ч но не /tают
1 юкоя. пока для н их не 11~1йдено 1<акое-то на
глядно<:: подтверждеюн.:. В:~J'Jlянитс на рнс. 2:
кв;,~дrат размером п х п сост:lвлсн из п у1 ·олкоп,
назын:lсмы:х п юмо11амн. Пло щади 1~11омо1101i li
ПОГmд~<е IIOЭpaCl'aJ 1ИН 11 редста l~JIH IOT СО6<1Й ГJО
СJJеДОВЭТеЛ Ы·ЮСТЬ нечётных чисел, т. е. 1 + 3 +
+5+."+2rz- 1 =пl.
п
-
1-
l2_J
3
5
7
fJttЧl!CK01"i 11;юг/Jt!Сс1юй , ;1 значение t/ - знtWl!
нamf!лe.1·1 1 ·еометр 11чсской 11ро 1 ресс1. 111 .
ТJJотт11rдс кому ма·rематнку Джану Нt:перу
1 1ри11а;.щежит иле» о том , что от с1юйстн :~риф
метической прогрессии можно перейти к апа
лоrич1rъ1м сnойстnам геометрической прогрес
сии с положи.тельными члена.ми, если сложе11 11е
и вычитание заменить соотвстствешю умноже
нием и дtлtнием , а умножение и дt'лtние - воз
f!Сft<.:н 11 см и стсn<.:н 1 , 11 1 1знлсчсн 11 <.:м кор ня. По
сле такой замены остаются в с1шс нс тол ько
формулировки свойств, но и док:13:псльства1
(Надо сказать, матсм:.1111ю1любятсRолвть1-юиыс
:1адач11 к уже реwённым)
ТТрш1ерттм п ртптт,иm.1 Н епсра 11<1 пратпrrке.
Rсnом1 шм, что каждый чле н арифметической
прогрессии есть среf\пес арифмст1rческос дnух
СОССf\НИХ с rшм членов - гrрсдыдущсrо п по
следующего. Значит, каждый члс11 геометри
ческой 11ро1 · ресс11н должен быть ранен сред
нел·1у 1'сометр11чtскому сноил ~C<)ce1te11 ,) (к том
случ:н:. ко1·да вес чJ1ены 11ро1·рсссин t LОJJО
ж:нтсльны) . Дrн1 1tuказа'Гет,с1'ва r:1<Х1ьмём тр11
1щущнх ГЮiфН/.J. члеш1 Cf1;-1, о" и С/11+1 (11 :> 2). Со·
1"л;:1с1ю11ра ш 111ам обра:юва1 1 ия 1 ·еомегрнчесl(ОЙ
nроrрессин,
откуда
а"= a11 _ 1tf,
ап+ I = a11Cf1
а = и11~1
11
q
Есл11 псрем1-юж 1 пь первое и третье равенств~.
2
11
пшrучим
1
12
.п
Р11С. 2.
ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИЯ
Рассмотр1 1 м те11ср1, 1юслсдоватсл ы юсть !а"} ,
O! lpC/\CJlёl--llJ YIO таю1м nnраэом: а 1 э;ща1ю, 11 /\Шl
1ксх п ~ 1 с11ранс;1,111 ~но ранснстно а".,. 1 = а,н, r11c.:
ц ·1'<J.КЖt неко1·о [юе заданное LJ11C1ro, не р:ш11ое
11 уто. ИJJaч:е гшюря, пер.Rый: 't!reн nоследоRз
телы юсти т1звсстсн, а кюк,.т1ый послсдующт 1 й
больше пре~ьщущего в одно 11то же число раз.
Такая последователь11ость называется геомет-
~160
что 11 требоnалось доказать.
Это ,'юказательстnо n точ1юстт 1 соnпздастс
доказ:пе.11ьст1юм для арифмtтическоl! про-
1·рссс и1 1 , ест1 ар 1 1фм ет11 ч еск11с 011ера11111 1 за
менить н ссю1·11етс 1·ви11 с пр:11шлам 1 1 Нспер~.
То же OTI IOCI ITOI к /\<Ж:J3'1'J 'CJI ьст1~у обр:1т1 Юll
теорем Ы : ССЛI 1 каждый член после11оватсл ьно
СТl'I, нзчи11ая сп второт, есть сред нее геомеr
р1 1 чсскос nрсi1Ыд)щеrо н гюслеm.1ощеrо чле
нов, то такая последотзателыюсть пепремеrшо
ок:~жется 1·еш"1етрнческоii прогресси<.::r'f.
Теперь вспом11и.\1 свойства арифмет1 1ческоl1
прогрrссни 11 nсрсnсдём их с яз ыщ1 сложе1шi1,
Беско1-1ечные посl\едов<:tп~л~,носrи 11 суммы
--1
1 Яашарь
Февраль
Март
(<·~" прпненrы < нклала не с1111м .1ть кажлы11 ""'-'сяu, ro кап11тал ра< 1tc1 R геометри •1t•<ко11 про1 p<>t.0111
вычита 11нй п умноже шrrт на я:1ы1с умножеш1й ,
,1сле 11и11 и nозведспий в cтcncm"
f1 ар нфмсп1чсской nрш рссстги
Cf,1
= а1+(/1- l)(./,
.ш<1ч1 1т, н п:омеrрнческой
IJ- 1
и"=a,tz .
Выrажс1 шю (1 z - 1) ci соnтнетствуст с/1-1. а 11 е
н;.юборот. т. е 1re (JZ - 1)'1
, Это nfi·ы1crшeтo1 тем,
что :-щесь а, мы /1 - 1 раз умrюжае,"1 ш1 q (так
же. как в :tр11фметнс1еской rтр01·рессп11 к а 1 мы
11 - 1 раз nр 1 16анлялп с/). При замене прон:-шс
дсmтл во:щедс1-1.нс-:м в сте 11ень полобньп: тонко
с ш 11<~до 1кегда 11 11.1сть в н~щу.
(, Перевод 1·1м " сJJедующее сRойство ар11 фме-
111чсскоJ'111 рu1 ·рсссш1: если натураJ 1ы-1 ыс ч н сл:J
i.j,k,/T<IКОВЫ, ЧТОi+j=R+/,ТО
а,+ а1 = а1<+ а1•
Д11н п:< 1мстр 1 1 чt<.:кпй 11 роrрссси и анало 1·ичпое
своf1п · 1ю формуш1руется так: ccm1 Шl1)'р~1л1,11ые
чнслз i,j,J..~. /таковы, что i +j = k +!,то
а, а,= а" а1.
Д11я сум мы ар 11 фмсл ГLrсско.й прuгрсссин \1 ы
получшш Ht.:J l bLX тр11 формулы. К~1жлul1 нэ 111 гх
нетрудно 11;:i1\тr 1 ~ 1'еометр11 чесю 1й » з11:iлor, ссш 1
R~н.:СТО суммы S11 рассмотре1ъ nр01 1з 11сдt.: r-11Те l Jn
пtрных 11 ч1н..:нов 1·еомстр1 1 чс-: <.:коll 1tрогrс:сс н и.
Rот что пл11 уч нтся:
11(/} 1)
11
ГI,, = (п101~)~, П" = c1.l ."·
где 11 = 2/г - 1. Uce :-пи формул ы действителыю
нерпы.
А для <.'уммы Ч!J<.:нuн 1·с:uмстрнЧt::(.' кul1 про
L'\Х.:сс н н
S,1
= a1+п1+...+п11 1=а1+a1tf+...+
+ c1,tj' 2
+a1t/'-
1
формуJ1Ы у пас ещё пет. Такая су~ 1ма nре;~СL'<lВ
;шет собой некий 1 · нбрнд сложс1111i1 и во:~веде-
1111й в cтcner11" Попробуем упростrп1. это nы
ражсш1е. Срюу брос:.1стсн н глаз<~. что ~{1 rач.ен11с
а1 vюж1ю вы11ес 1·11 :1::1 скпfiю1:
S"=а1(1+С/+". +с/ .!. +(f11- ').
Тt:псрь 1ю11;1см 11а х1 1тросrъ: 11ерt.:нt'сём и1 в
лену10 часп, (ч1·061,1 нt: мешало) 11 потпм у~1нn
жнм ()6<.: Ч:"\СТИ 1-1:1 1 - q:
(] - q)):
___
. ,_, = (1-{.j)(1+t/+".+ц" 1+(/71 1).
(,/1
Раскроем скобкп в 11раrюй части , снач:т~1 nо
члсн1 ю умножав сд11н.и 1 tY rш вес сл;.11'асмыс втu
pui-1 скобю 1, а ;jат<.:м умнuж 1111 на 1111 х -ц. По
Jl}''Ш М
1/-_;
ll- 1
.!.
IJ- f
/1
i+lf+..+fj +(j - tf-fj-...-С/ -ц
С раμрсtъю уt1ежд~1смо1 , что сред1t ны111ка~ 11 tых
211 слаr·аемых 11рпнсхпд1л мэссоuое взанмrюс
сокращетше чле 11 ов с ofipa1 111 ,1м11 :.ш~шам 11. а
11мешю: (,j исчезает нмс:<.:тс с - q , q
1
nместе с -с7~
нт.д.~ш1ют1,доq" 'н -q"
1
• Что же остаё·1 ся ·t
·161
Ле1ерминизм и случайнuсть
Лпшь Jща слагаемых - первое и последнее, т. с.
1- q"Итак.
(l - q).Sl'I
11
-
-
-- = ]-(j
,
а,
откуда
ПРЕДЕЛ ПОСЛЕЛОВАТЕЛЬНОСТИ
Понят~ IC щх:/1,еЛ: I - этu ТОТ IIOfIOI', ЗJ которым
т-крьшастся дверь 11з элсме11т:1рной матсм:.1 ·111-
ки в высшую. Почтн каждый способ<.:н быстро
восттриrтят 1 . и усвонть интуr 1 т1 1в1 юе 11редстаn
ле111-rе о ттре,1'еле, хотя сч·югое оттределе 1111 е
многим покажется /J.OROЛhlIO СЛШЮJЫМ.
Начнём с прнмера . Рассмотрим последова
тельность ( 1/ 11 f. Её называют га1»101-шческ.mi,
нuскольку каждый сё член, наqиная со 1поро-
1·0, сстъ среднее гармоническое 1"1сжду прсды
дущи м 11 гюс11сдующим членам11 . Н<1 1юмни.м.
что ч11сло с есть срслнес r·армоtшческое чисел
2a!J
11(1IJ
а i1 /J, если С= --, 111111 -
=-
- + - .()бра-
а+ IJ
с2аfJ
т1 rтс: вн11маннс: с ростом п нсl' члены 1"армо
t1иче('1<ой 1юсленов:~1·СJ1ьности убывают н нс
уклотпю rrp1 r бл ижа ютсн к нулю. Jl.e1'1ci·1i1 rтe;rr,1 ш,
t r ::tt.шпaя с Jt = 1000, 1<аждый очерс/\rюй члеtr
462
От.метам Ol\HY то11 кос·1ъ: прп q = 1 формул)
нужно ны1юдить отдельно . Но это совсем rrpo ·
сто.Ведьеслиq= 1,тоа1=а2= ." = а111=а11,11
ПОТОМУ :J~I =а , 11 .
Геометричесю1е пrогрсссни нс1·реч;uотся н
З<Щ~rч зх не рсже, чем арнфмстическ r re. Так, зrrа
менитая 11осле;(она1·ельность Ф 1 1fiоначч11 (см.
L-1·зтыо ~ пос11сдuнательносп1 ?) як.rrяетсн суммой
/ (Rул r·еоме·грнче:сю rx про1·рессиi1 . И тсrrсрь 11аl1-
·п1 C}'JVIM}' ·11 её 11 еr 1:1ых ЧЛСl-Юf\ - f(eJJ() H'XHllKll.
отлич:.~ется от нуля н с более t.1см на 1/ 1OUU, :t
пач11ная с м11ллит1нuгu члсна - 11с бощ.:с 'Jt.\1
ш:r J/ 1000000. И вообще, какuс бы ~ м11кроч11-
сло~ мы ни ныбралн. найдётся тэ.ко!r член по
слс;~овател 1,носr · н , r ra ч ш-1ая с ко·r·СJрого вес
ч11е11ы отл11чатото1 от 11уля менее , чем rra это
«МИКРОЧИС!Ю». 13 T::lKOM случае 11ршшто ГОR()·
f)И1Ъ. что при п, стре,,>Imцсмся к бесконсч110-
сти, данная nос>1е.дователыюсть сходится и
пуль есть сё щюдел. Заnисывается это так
liш1/n=O.
n-·
~3л<:с1, li111 - 1-1:~чалы 1ы е букны JJ<.tTJ rнс К<)l 'О слова
lirлcs - <· 11редеJн. З1-1~1ком 00 11р1111ято 060:311а
чат1, бсrконечrюсrr,
Rозьмём тспер1, .npy1 ую 1юсле;(онателы ЮС'JЪ:
псрный Э.'lемелт ~ё О, второii 1, а каждыir no ·
след}11ощий равен полусумм~ дnух предыдущих.
Можно показ<пъ (см. статью ., последонатель-
1тост11"). что
а =~[1---1--]
/1
-~ (-2.)" 1
•
1
Хотя дробь
1юоче.рёдно П(')111111маетто
(-2)'1-1
nоложителыrые. то отрш~;:~телыrые з1шчеmщ
тем Hl' ме11ес L' ростом п 01 ra тоже стремнтся к
нуто, t 1л:1же r·upa:щo быстрее. • 1 е'1 1/п Поэто
м у вhlраж<:11 1 н: н к ва;\ратных скобJ<ах сr·ремшся
к е;.1.нннце:, а :ш ~1ч<:11ис а11 - к 1/3 О r t; tонатель-
но, неком ый предел lirn t:111 =2 / 5.
Гтюр}J о 111"к:дслах. нeЛ h3fl не у1юмя11у1ъ об
одной э:tмсч~пv~ъно 11 последuватсл ь.r юсти:
Имеет ли она предел?
Каждый член последовательност1 1 получа
ется 11утём во:Jведения n с1·еrн::нь п оснuв~ши r~ ,
p:i 1:1нu1·0 1+ 1/n. С ростом 1·i основ;.~ нщ: стремится
к ед111-11 ще, ~• она 1:1 любой <..vrслею1 сдин~ щей 1J
остаётсн . Поэтому, с одной сторо н ы. пох()жс,
что члены последоnате11ьF-юС'Т'И стрем ятся к 1.
Но, с другой - каrс nы rп-r бы110 велико п, ост-ю
щ11-1ие 1ке1да хоть чуп.-чуть, т ю болъше 1. А по
С'КОльку nока~Jатель стс п еш 1 нео 1'рат1 и чешю
растёт, то и зн аче ние ап доJJ.жно r-1 еограr-в·1<1сн -
110 возрастать. Парадокс?
Нет, лпш ь иллюзия 11ар~1J1окса. ЗТ1.есь мы
СТОЛКНУJIИС I> с двумя ф:~ ктор~LМИ, с двуми ~cи
Л:.tNI и~: е~]Jсмящи мся к Cl\ИJ 111цс основание м н
неогран и ченно поз р аст ;;~ ющим но казателt:м
степ t:нк Каждая из эт11х сил тн11ет в сно ю сто
рону. Какая 1 1 еретя нет?
Отnе-1· быJ1 11ай;1е11 несколько столетий
назад. О ка:1 алось. что щютивоборствующие
снлы приuuш к компроJ.-шссу. rlослспователь-
1юстъ хотя и мотюто m ю во:~растас:т, 1ю п ри
этом I-rмеет предел, равный знамешп'ому чисну
Эйле ра е = 2,718:г8... (см. еrатhю "Чис;ю е").
ОТ ИНТУИТИВНОГО ПОНЯТИЯ
ПРЕЛЕЛА - К СТРОГОМУ
Пусть дана последоnа· 1·елыi0Сlъ {с111 } . rr предел
её равен А. Иптуитит -ю мы понимаем, что это
знач ит: с ростом п члетl ы последов:псJJ ыюсти
всё ближе подходят к числу А. Некоторые мо
rу1· и nообщс совпа сть с А! Естсс'J'l{ешю, эта
бли:юсть на п рямую связа н а с разност1. ю меж
!\)'а,1иА,т.е.а11- А.Или.можетбh1ть,А
-
и11?
Однако заметим, что разности а11 - А н А -а"
()'JJН/Ч;J IO'l'CЯ TQJll,KO з 11 ::~ком, а н л afiCOJll))'f'fl ble
зн ачения равны. Но вед 1, ка к p:i:J Э'Г3 нслнчн11<1
ecn. критер и й f)лизост11 чисел между собой. Так
,~:шайте о перироватт. име 1пю абсолютным зш1 -
чением. Для этого надо всего ;шuп, огра,г~;юъ
нашу разность (любую из дuух) с обеих сторон
з11аком абсолтот1 юй веш 1•1ины: 1а,1 - А 1. И тот
факт, что члены rюслсдоватсл ьности с ростом
Бесконеч ные посl\еловат~/\ьl-Юt ти 11 суммы
11 приб11иж;1 ютсп к А, можно п срt:фQрмуJ1иро
нат1.: с ростом n ныражение 1 а11 - . 41 становится
нсё ближе к нушо.
А как llOllЯTI> СЛОВ::.! «всё бЛ ll ЖС 1< нулю»? Лро
ЩС все1 ·0 таr<: с ростом п 1:1ыраже 11 ис 1(1,1
-
А1
может с'1'<1т1, ме11 ы11е тоnого 1 1алерёJ1 ;1ада11 1 н1-
го положт 1тельно rо <шсла Е, скш1ь бы мало п1 ю
ни бытю. Нап ример, задад11м Е = U,<JUOO 1. Тогда
долж но сущсст.1:Ювать такое N, что для всех
п >N будет спраRедлнnо неравенство 1а11 -А)<
<O,OOU 01. Лровсрнли
-
убедил ись, что это
J\С 1"iстш 1телы ю так. З:щ:щнм 1фу1·ос е, сщё мень
шее, напри м ер (),OOOCIOOOOOOI. Д.rн1 него тоже
;,олж1 ю найти сп соотнстствующее N.
Нз консц, м ожно nо 11ы·1 ·аться 1~оказ:1·1ъ, что
т:-tкос началыюе з на ч ение N н ай;~ётся нnобще
f\Л н про1111юлы ю малого nоло1ю 1 тет .т ю1л Е.
Если это нам удалось, то факп r'-lёСкн нnказа t ю.
что А есть предел rтослеж)вателы юстп {a"f.
lly а теперь 11рнnсдём стро гое опредсленш:
понятия пре дела nuслсдователыюсти :
«
Если существует такое •наело А , что
V.- 0/
1,К для любого (сколь угоди.о мал ото) 1ю-
ложителъноrо числа i: найдt.1·ся такое
uатура.rн)ное N (вообще говоря, з ави
сящееотi:),чтоД!1Явсехп~Nбудет
выпол нено неравеНС'l'DО 1fl" - А 1< Е, то
rовор.ят, что nоследователыюсть {а ,1}
сходится и А - её предел.
Обозн ачается это так:
lima11 =А.
1/.
а В противном с1rучае 11ос11едооа·1·ель
•-"'(
l~ ностъ называется расходящейся.
Опнраяс1, на ~то 011рtДеле11ие, мож1ю, 1 1а
прнмер, жжаэать наличие предела А = О у
гармонической nосле7\01:Jател ыюсп1 { L/n}.
Пусть € - сколь угодно малое п оложительно е
число. Рассмотрим разность
Летерм ин1нм и С/\учай tюсть
la" -AI =l.!. -ol:::.!..
ll
п
Сущесткуст ли такое N , что для нссх tt :Р N
выпол н яется нсравенст1:10 1/17 < Е? Конеч11 0.
существует' Воз 1.мё.м н кз чсствс N J1Юбое 11ату
ра11 ы юе ч нс.тю, превышающее 1Л:. Тогда
н для нссх 17 ;:;.. N
1
-<~
N
]
-
<
<Е.
пN
На это\1 доказатст.стно :!~H1t:rwcнo.
НЕСКОЛЬКО ПОЛЕЗНЫХ ТЕОРЕМ
Доказать наю1•111с предела у тоn или иной по
следоnателыюсти порой б ы вает 11 с такнросто,
ка r< n рассмотренно м пр11меrх~. К счасrъ ю, за
ниматьсн таким и дока~::~тельст.на м1 1 лр 11 хо
;~ится не tKC l'll,a. 1lа11болсс ч асто встрсчаю щ11 -
сся последоватслы-1ост11 хорошо нзучс н ы IJ
пр1нюднтся F1 слраноч 1шках. Кроме того, 11ме
ются теорем ы, 1юз 1 юляю щис сделать uьнюд о
наш 1ч и1 1 предел~~ у даrпюй последоnателъпос
ти (1 1 даже nычисm1ть е1·0), onт-ipaяc r, Шl уже
1 1 эучеrmыс последоuателыюсти. Uот ш~кото
рыс их ::этих теорем.
.fl ."
Если последо:1щ·rедьнос-1ъ им.сет пpe-
lr.l
дел , то ова 01раничеца.
Cдt:/\UH<tTdL Ы IO, <.:ели п < 1сл1.::дона тсл ь ностr,
нс:: 01 ·раннчсна, то предt:ла бы·1 ·п нс можс::·r-. 1-1 :1-
~Сl\И
11С J( Лt'ЛОl:ЫТР/\Ы 1 пrть
не огрJни • 1rна.
ТО Ollii 111.· 6'1M('C J
предел~
п ример, нс и меет предела 1юсл<.:; ~uна1 ·<.:лыюсп,
1Jату р~1льных чисел {n }.
Если последова'rел1нJос1ъ монотон:на
и т11аничеuа , 'ГО она имеет предел .
В качееr1.1е 11p11.v1epa nривсдём всЕ ту же 1 юсле
до1.1ателы·юст1,
{(1+ _!_ )" l.
11J
Оказынаетсн , мож110 доказ~1ть, что. но- щ:рвых,
а". 1 > а" дли 11юfio !'o /1 (т. с. поо гедон:п·е11ыюсть
мо1 юто 1 1 но но~ч1ас·1·ает), а 1ю-Rтарых. что а11
Rcerдa :vre н ы н е .) (т. е. послсдоnателыюс·1 ъ 01·-
ран пчена снерл)'). Оrраниче1111ость с н изу во
обще доI<азьruать н е нриход1rтся. вес члены
заnсломо поло.ж1 пелы1ы н потФ1у бшu,ше U.
1Lоэтuму да нная лосл<.:дошпеJ1Ьнос 1ъ должна
11м<.:1ъ прелС11. Пр:шда, нычиt.:н 1 ~т 1, с::тu тсор<.:ма
11 <: ГJOЗIIOJU!e'l .
•
Если последова'J'ельносr·ь {а"} имеет
~~ предел А, то последоuа·1·елыюстн
{са"}, (а"+ с} и {/а"/} имеют предеды
сА, А + с и 1А1 соответственно (здес1.
с - произвольное число).
~j Если последовательности (а") и {Ь"}
<{\l и:меют пределы, р~шные А и В соот
.ве-.rственно, то посдсдователъность
(ра" + qb") имеет nределрА + qB .
.f~ Еан1 последовательности {а"} и {/111}
·1,J. имеют пределы, рапные А и В сом·
nетственно, то последователъноС'rь
{а"Ь"} имеет nределАВ.
;ft , Ес,,'l н последовательности {а"} и {/111}
-М имеют пределы, равные А и В соот·
ветстве1пrо , и, кро1'1е тох·о, Ь" '# О и
В * О, то последоватеJ1ьност:ь {а" /Ь"1
имеет пре;..1,ел А/В.
ЧАСТИЧНЫЙ ПРЕЛЕ/\
Рассмотри м 11оследонателыюсть HCj череl\уЮ
щих~ся троек 11пятёроr<: {3, 5, ~. '), .. .f . Яс110, что
предела or 1a пс имеет, поскоJ11.>1(у нс существует
того сдш 1стnе1ш01·0 числа, к которому nр11бл11-
жаются члены nоследтзатепыюсти . Н то же
время если nычеркнуг 1, из последовательности
1к:е ч<::тпые члены, то ост-,1нется nод1юсле,Т\О ~а
тсJ1ьност1>, сосr·оя щ;:~я нз одн11х троек, и её пре
дел, очевид но, р:.~нсн ;$ . Если же, н::юборот,
вычеркнуть неч ётныс члены, останетси под
послt:доватсльность, предел котnроi1 раuен 5.
Поэто му трудно отдслат1,ся от мысmт , что
д:тн:~я поСJ1едnпателы юсть имеет сразу дnа
1 rре11ела: 3 и 5.
В cne'J'e сформулировашю1·0 понятия пре
дела подобное утверждение бессмысленно, но
к~l<)'ю-то дополнительную информацию оно
всё же песёт. Поэтому вnе/\ё м новое понятие:
ЧИСЛОВЫЕ РЯДЫ
Можпо ю1 вычислить сумму бесконечно го I<О
m1чества слагаемых? В одно м конкретном слу
чае, а именно когда все сл:1rасмые равны нулю,
ответ напрашиuастся сам собой:
О+О+О+... = U.
С~ОL\И I ГЯ или
ра С)(ОдИТС R 1
Бесконечные nослеловательности и суммы
Если н:еIСоторая подпоследователь
ность данной последовательности
имеет nределА , то значение А назы
вается 11реде.льной то11,КQй или •шс·
ти"~ны.м 1tределам исходной после
довательности.
Такпм образо.1\11, rrоследовател1~1rост1" со
стоящая нз троек и пятёрок, хотя и расходится,
но имеет две предельные точю1: .1 и 5. Понят
но, ':lTO ecm1 у послсдователъностн есть прсде11
А, то она имеет единственную нредельную точ
ку А , rюскопьку Jlюбая её n о; \1 Юспсдо"атедь-
1-юс'1ъ схою,rтся к тu му же пределу.
Ну а как быть в других случ<UJх?
Рассмотрим геометриL1сскую про1 ·рсссию
а" = а 1 q"~ 1 , знаменате11г. которой ц по абсолt<)т
ной величине меньше едюнfцЫ: - l < tf < J.
Вh!числим сумму первых п чле110 А 11ро1·ресси11:
)
111
1- q"
.5,1::;а, +a,q+a,q - + ." +a,r/
=а1--
.
1-Cj
Очевнд1ю, что при J q 1 < 1 с ростом п з11аче-
11ие rj'' стремится к 11уто. То1 ·да S" стремнтся t<
а 1 /( 1 - q), и э'IО число естесТRен 1ю rт:-~ 1вать сум
мой всех членов беско нечной убыn:нощей
геометрической nроrрсссии:
.
•
.
2
1. <-
а1
а1 .-a1q+a1q +." = iп1 L,11 =--.
•н~
L- t/
Точно Т::IК Ж<:: MOЖllO П ОДОЙТТI К любоi! !~py1 ·of1
послеf(Овател ьн ос1·11
ЧТО ПОНИМАЮТ
ПОЛ СУММОЙ РЯЛА
Давайте возы.1ём любую послсдов;.~тслыюсть
/а11 } и фо рмально поставим мс.жду сё членам r 1
знаки сложеш,111 :
~
а1+и2+а1". = Lа".
11~1
(*)
13 n1хшой часп1nр1шс1(е 11а спкращё11н~1 я фс1рм;1
за 11и сн этой fiескrтечтюй суммы . С:ннзу fJ
сверху от 11 ропи с11ой греческой буквы 1:
Ле1ермин~нм и случnй 1юсть
ОПРЕЛЕЛИТЕ
ПЛОШАдЬ ФИГУРЫ
з~1 ан ие геометрических nрогрес
С11Й nомuжет решить олну любо
пьпн ую задачу.
Лан квадрат со сторо ной 1.
Кажлую ю его сторон разделяют
на три равные части и соеди11яют
ближаишие точки смежных сто
рон. П олучен ные треугольники
отрезают (рис. 1). Так же поступа
ют с о ставшимся 8-уr<мьником
/рис. 2), затем - с 16-уrольником
и т. д. до бесконечности. Требу
е1ся найти плошадь фигуры, котu
рая получится в результате.
Почему-то сра3у созлаётся впе
чатле1·1и е. что nосгроенная фи
гура - круг, вписанный в исход
ный квадрат. Сейчас мы убедимся ,
•по :это не так.
Лля улобства вместо nлощали
самои фигуры будем искать сум
марную nлошадь отреза нных тре
уrольникuв. На первом ш.-~ге было
удален() 4 треугольника. Площадь
каждого и з них, как н етрудно nол
считать, рав11а 1/18, а их об w ая
плошаль составляет
l2
4 13=q·
Теперь рассмотрим любой
треугольник АВС, отре1анный на
каком -либо шаге, и треугольник
Vl:A, отре"!анный на слелуюшсм
шаге (рис. 3). Нетруыю :~аметить,
что и основание АО треуголь11ика
DEA, и его высотJ, оnу ше1111ая из
верши ны[, втр()е меньше соответ
ственно основания и высоты тре
угольника АВС. Поэтому площадь
треугольника DEA в 9 pa'I \.\е11ь ше
плошали треу1 ольн ика АВС. Но
самих треугольн и ков «нового по
колениs~ » окажется вдвое больш е,
С/\едовательно , их суммарная пло
шаль составит 2/9 суммзрной пло
ша1н1 «nредков». А это зн а•1ит. что
последователыюсть суммарных
nлошалей la0 ) отсека е мых треу голь
н иков удовлетворяет условию
81 = 2/9,
2
i/11 = '111"1gЛАЯn>1.
Так1-1м обраюм , !,1") - геометри
ческая nрагрессия и сумма площа
дей всех треугольников есть сумма
рял.з
2 (211 ('))1
9+9)+~ +."
Этот р5!л. 1<ак мы зн;зем, сходится.
Сумма е го ровна
2
92
1-2=7.
9
( «С111·ма ») указаны 11.ре)l,слы суммнровашtя: от
п = 1 до беско11е ч1юс'ПL Таtюе въ~rаже1 11 1е па
з ынается чш:ловы.м рядам.
Н акон еu, вычисляем nлuшадь
того, что осталось:
25
1--=-.
77
Таков он1ет. Отсюда слt>лует, что
полученная фигура никак нс мо
ЖЕ'Т быть кругом, вписан ным вис
ходный коалрат (вель плошаль та
кого круr·а ра вна тт/4).
D-0
Рис. 1.
0-0
l'ис. 2.
Рис. 3.
~
L C111=S.
111
Далее, каждому натуральному ч1 1 слу 11 со110-
стан11м сумму нерnых 11 У..11<::ноn послt:,цu натсль
нос111 {а11}:
sll=и,+aJ.+ ...+а".
В 1~рот111ш о м сJ 1учас:: ряд назыRаютрасходя
щи.м ся..
З11:1чен 1 1я s" на :~ьша.кrr· чщ:ти'ЧНЫ.А1.J( g :.мма
j'.Щ рнда ( "). 0 111 1 обраЗ)'101· новуrо гюсл сдо11а
тел ьнос1·1, {S"} - поо1е1~ователы юстъ чаетч
ных сумм .
Еслп последователы-юс~ъ <-1асп1ч11ых сумм
Jl.aннuro f)}fдa имеет предел ), т е. Li111Sn = S , то
1/-*N>
гтюрят, что rяд G"!:одится 11 S - c1 ·u с,ум..мtt . :3а
ш 1сы в::~t.::· 1 сн это так:
466
1'~1к~1 м о() разuм. cy:vtм:.i рН/\~1 - э·1 о, по оr1рс-
1~еJ1 с н11 ю, 11ре1~сл п осл едонатсл п1-юс·111 er·o
частнчн ых су~1 "1.
УСЛОВИЯ СХОДИМОСТИ
Чтоб ы успн-юrs1 1тr., сходится данный ряд илrr
расход11тсн, н с обязател ьно рассматрт~вать по
с1н::дона т<:.1 1ы 10сть <:: t'O •1:1стичн ь1 х суми. Ведь
-
сход11,,1ос·1ь рят1а L_ a11 t1епрсме-нно ;щлжна
б
•1-1
"
ыn, связана с п оведением ca,'vIOH послсдоnа-
тс.'1ыюст11 /t111 }, расположенной лод зна1юм
суммы. В связи с этнм были доказапы ра:~лнq
ныс теоремы, и н перRую очt'редь rrс:обходн-
00
мый прнзш~к схо11имост11 ряда: если РЯl\ I, a11
сходится, то \iща" =IJ.
11 -J
п~-
Т;.~кн м о6раз()М , 11 случае когда nоследоиа-
тет,нос1 ь {а"} 1J ,,1сет лрс:дсJ 1 , отm1чнъгй от О,
шш вообще нс пмс:ет пре;1е.11з, ряд расход11тся
К пр11меrу, ттоследо на·1·елыюст1, {1, - 1, 1, -1 . . .}
пре11.еланеимее-r,поэтомуряд 1- l +1- 1 +...
расходuтся (его частичные суммы образуют
после,т~оватслыrост~., {1, О, 1, О, .. .f).
J\ LОЖdЛению, данный r~ри:шак r~ e Jшюrстся
достаточным: С:СJП J 11 редt:л 1IOLJfCДOBifTCЛ ЫIUCT I 1
\a 11f ра11е11 нулю, то отскща 1-н.: с; ~ с,~уст, что р~щ
.
I, an обsпателыю схо1~нтся. Это можно а()ъяс-
111m сщё и так. нри сложении мъ1, конечно,
прнбавлясм нсё бол<.:е крохот1 rыс слагаемые, J ю
зато 1 1х коm1чествu б<.:0<0нсчно. Что 11t'реж·с1 1т?
Для выяс1 1 ен 1 1я были найдены раз нообра :н1ыс:
достато чные n ризн:~кн сх1щ11мо сти 11ли расхо
;~;ююспt рн/1.ов. Пра1ща, 6u11ыпr 11-н:тво 113 ю r х
от1 юс 1 пся толhКО к рнд:Jм , у которых нее сла1 ·а
емые пuлож 11тс; 1ы 11,1. Гfр1 шедQ.\1 дн~~ 11р1 1:~11 ака.
Признак Д'Аламбера; если сущест11> t'T та
кое 1 ю1н1ж1·1тст)нос с< 1. 1 1тt), н::~чш-1ая с нско
торосо и, 1~ыщ_шня_е1·ся ш:равс11с'lно
то psiд сходится. [ели же, 11зчиш1я с некоторо
го 11. вьmол 1 mстся 11еравспство
а1н1 .;;. 1,
а"
rяд paCXO/~ltTOf Отсн.ща, н чае1 ·носп1, сш::;~уст
сходамос·1· h 1 ·ео метр1 1 чсскu11 пr101 ·рсссю1 при
з11ащ:нателе () <q < 1J1р::~схuднмuс1 ьпр1i q ~ 1.
П р из нак Коши: есл 1 1 существус·1 Т:Jко с
положнтель11ое с < 1, 4то , начина.я с некоторо-
ю 11, выпо;щяется нсраr.енство
1
\ а11 ~ с, :шачит,
PR.-1
схстнтсн. Еслн ж~. начиная с нскоторот
11, вы\юшщется нсравсщ.:т1ю '( а11 ~ t. то ряJ\
~юсходнтся.
Бес ко 11 ечные последователыюс rи и суммы
НЕКОТОРЫЕ ЗАМЕЧАТЕЛЬНЫЕ РЯЛЫ
-
1
1111
' --=1·1--+ -+-+-+. =е =271828.
~п! 112!314!··
'
"
"
(-1)"
1111
1
L -=1--+---+-- ... =-=о,зыs7...
"=0
п!
IJ2!З!4!
с
-
11111
I,-:-+- + -+-+ ... - расходится.
N=lП(2.з4
-
(-1),,_
1
'1
111
I,--= - -
-+--
-+ .. . =ln2 =0,69314...
1<-1
п12з4
"
(- l)"-
1
1111
1t
L..i--
-=---+--
-+...= -
=:0,78539...
"~'2п-11357
4
t ~=~+~+~+~" ·-- =~= 1,64493...
п-1t11·2З4-
б
-
(-l)n-I1111
7t1
2:--l -=-т-1-1-~-2+ ... = -
= 0,82246.. .
,,.1 11
'\2з·4
12
L-11111
n4
-:-+-+-+-+... =-= 108232...
п-1П1 1
4
24 J'
1
4•
90'
467
детерминизм и слус1 <:1иность
Увы, нtмало рядоn 1 1с поддаётся «разоблаче
ш1ю~ с помощью у1<азан11.ых r1 р11з11аков. Такоu,
~l
например. гармонический рнд I n. а также
11= 1
~1
обобщё111ю-rармо11ическ11й рнл L~ , гщ: s -
11=1 1l
некоторое ч11слu. Здесь для а11<1лнза 1 1 рихuдится
пр11ме11ятъ дру1·ие ме1 ·оды, и 0 11 и показывают,
что 0Побщённо-rармоп ичесю.1й ряд сходится
прнs>1ирасходитсяприs.s;l.
Между лроч11м . ещё ЛеоrJард Эйлер об11<1ру
ЖИ1L, что суммы t1еко1·орых обобщён rю-1·армо
пическ~rх рядон при ч ётнъrх s щ;азашrсL, чу)l;СС
ным образом связаны с числом л:
-
17t~~l1t!
Lnl =6'L-;J=90идр.
J/=J
11=)
И11т<.:рссно, что для 11ечётных s /\<> C'ILX 1101=
подобных выраж<.:юtй 1 1 с найде110 .
Далеко 11е нее ряды состо.нт '1·олы<0 1 1з п оло
жителы rых ч.rtе110в. Но и )l;ЛЯ рядоli со смtw:т
ными з11акам11 имеются теоремы. К прнш:ру.
если в сходящемся знакололожителыюм рлд1
лронзrюлы1ьL\1 oбp~13UJ'v1 расставить между чле
на мн знакн 1 щюс н мнпус , то 11олучснньrй ряд
т;~кже схu,г1.1пся.
Особое •"•ссто сред11 р.ндон э:.11-шмают таюtе,
н которых зr rак11 ела гаем ых егросо чсредуютс}I,
а абсолкпные ВСЛНЧНI IЫ члснон рядэ MOl IOTOH-
1IO убы11ают. Оказывается, для ннх 1 1 еобходи
м 1,п'1 признак схот~;имоеп1 рнда яншrется од.110-
врсмеш ю н достаточным, т. е. еслн lim а11 = О.
ll -4"
-~
то ряд I и/1 сходится.
11=1
ФУНКUИИ
ПОНЯТИЕ ФУНКUИИ
Предстани.м себе, что а11то,,юбнлъ едет по пря
\\ЮЛН11ей нQй доро1·с с постоинной скоро
сr t,ю и. Расстоя11ие s, гrройденrюе 1.1м за 1iремя
/,выражается формулой s = ut . Это прямая про
nорпионалъная зависимосп" А nот пример
квадратичной зависимости . тело, падающее
пол действием силы тяже<.:ти, проходит пу1ъ
{2
S=Р,т,
где g - 11с:которан конс:т:шта. Или обратно
11рогюр1 ~1101t<UihJ1ая эаnисимост1.- связь ме>1с;1у
ц:шлеш1ем р и объёмом V 1·аза 11ри nостоя11-
11ой температуре nыражается, согш1с1ю :цко
ну Бойля - Марио·па. формрюй р =с,Л;: Закон
всемирного 1яrотення устанавлипас:т сnязь
между сшюй Р в~~аимодейст1щя дnух тел м:~ссы
.11 и
1п и р:.tсстоянием r между ними:
F =(; Mtn
г2•
rдс G - гра1i~.пационнан. 11остон1-1нан. Здесь мы
11риnеJ1н пр11меръ1 [Jростейшнх фун1щиональ-
Функuии
1
1
1
':х.
ных э:шисимостсй, которые н общем виде мuж-
1ю 11рtдста1ш'Тl> ·r·зк:
у=mY~ 1-hx+с,
с
·1· =-
.
х
и
d
у:= -,.
х-
о ШI<011с пзучают 11 другие функции . ;югз
риф,'>шчеосую у == log" х, показ<псльную у == а ',
трю·онометричссю1е функции у = s111 х,у = cos х,
.J' = CfgХlIТ;~
Функция - 0/~НО 113 OCHOBllЬ1X 06 1ценауч
ных понят111\ оно выр~rж:~ет rп~нrмоснязь меж
ду р::t:11111ч11ым11 обы.:-кт:.~м11 Пош1тие фу11ю\1111
сножипос~, не сразу. В11:~ч<111е 0110 6ыJ10 рас
плыnчат1.1м п 11е имело ско11ько-11ибу,п;ь rнчёт
л1шо1·0 оп11савия Пер11ые попыт1<и очернrтт,
кон гуры этш·о понятия прс::дnринялн n конце
XVIl в. один из родоначальников матсмапrчсс
коrо аналнза Готфрид Нильгельм Лсйбшщ, а
также t•i·u учtники и хюслt>доватl.:'ли - бр~1тья
Иш«1нн и Якоб Бернушти. С::~м тtрм1t1-1 «фу11к
Цl1}!» принадлежи'! Ле йбницу и происхu,п;11т
от латинскО1'О слова fu11ctio, что озн~част ~ ны-
1юлне1 нн~» . ~осущееrвле11ие». Ио1-анн Бернуюrи
469
Лстерми низм и случ айнос1ь
вкладъшаJ1 в это слово ·rакой смысл: фуню_~,ня -
«выраже11не. состанл<:ю-юс какн.м-тп oбraзnl\1
из переме1пюИ пею1 чи11ы н 1 юсто>1111 11.1х ве
личин~.
Эйлер таюке по.гшмал под фрнщией тт
литическое 1JЪtpCV1ce11ue , но D~[есте с те~~1 готuD
был принять и более ши рокое толков:11-ше:
фун.кцня - Э1'0 то, ЧТО можно <'ВЫ Ч<::ртить ка
ращашом на л11сте бума 1'11 ~ (/l.am. -
libcra 1шшu
у
у= J.xJ
Тl
ш
Рнс. 1.
470
dicra). Ему были шшсстны случаи, когда фу11к
ция описывалась словесно илп rеометр11•1ес
ки. Так, фун1щ1 по у= j.'\" 1 (рис l) мо:>1шо опре
делит ~, разны ,\111 сгюсобама, н ;11 1 р 11м ер
~
форму11ой J' = .-Jx~ (анатпнчсс кос nыражс -
т11те) . Ест1, н её геометрическое:: опредеж.:н11е
объед1111е 1ше биссектрис нервоrо и вторnт
квадра1~тоn. Если сказать, что функция у= j:\· j
принимает зш1чс1шс аргумента, ко1·да аргумент
неотрш.1,атеж:н, 11 р:шна «Mтt1 =ryc аргуме нту»,
к01·да ар1тмент отр11щ1тслсrr , то тем самым
будет д:.11 ю сё слонесное описание.
Чт() жt: прt:11почесть? Учёные много спори
ли, было сломано нсм~tло к011нй. Например.
Эйл<..'р счJ1тал. что кжю. фу 11 кц11й, >1вл.нющнхся
«11ро 11 з 1юJ 11>1 ю 1 1ачерчеm 1111м11 к1лш1.1мн~. шире.
чем класс фу 11 ю\1 1 1!, з~щаваем ых анат 1тпчески
ми выражстшяr.ш. Д'Аламfiер .1юзrк1жt1J 1 : 11011)rча
ется одно 11 то же. Дашн1л Бертrулт1 nошёл ещё
далъше: 0 11 заяnнл, что пропзnолыrую 21t-перп
одичсскую фун.кц11ю иожно представить в 1.шде
·1·рш·uно .v1етр1 1 чtтко1·0 рнда
00
L,a!.t coskx+hk si11k..x .
" :tl
Бол 1t11J1·111c· пJy учё11 ых казалось, что это т1шь
петсоторый узrшй класс фу11кцнй: 011 ~·же, чем
аналити ческие выражеш-щ 11 , ра;~умее-1·сн, }же,
чс~ «пропзвольные I<ривые».
В начале XLX n. стало nыкрпсталл11зоnы
ваться понятие функции как соотuетстnая. пра
ви;щ по которому незаиисим;~я переменная х
11 з некоего множества Х 11рt'образуt'то1 в пt
rемс1111ую )' И.З другого МНОжее1·ка У «JJIU6ЬJM
образом » (см . статью «()тuбраж~:ним»). Чтuбы
лучшt> ос1ю1 1п,ся с этт'1 точкn i1 зrсния. рас
смотр 11м 11 ескnлыш г~р11мсрок
1. Каж,л;1.п:f уче1 шк в шкuж: учится в nпреде
лёш юм классе. Если обоз ~ 1ач11т1, через Х м110-
жест rю учеников в данной mкпле, а через У -
мпожесттю ю1ассоn, то мож r ю сказат1" чтn к:~ж
дому элементу м11ожсс1·ва Х (т. е. каждому уче
нику) сопост::1 вJ 1 ен единственный элемент
.множестна У (т. е. тот кл;.~сс , где данный уче
ник учится).
2.. Каждому ученику данного ю1 асса в конце
1 ·ода высташ 1 яетоr 011ре.rtелённая онснка по
м атематнке. EcJ111 обо:щачить чtрtз Х м11оже
сгво учен иков в классе, а '-!ерез У - м11nжеспю
целых чисел от 2 до 5, то можно сказать, что
у
Рис. 2.
Рис 3.
каждому элемсн1у нз Х сопоставлен сд1шс1·вс11-
ный ::>лемснт из }~
31. ЕСЛ1 1 обозт1чш:ъ через х MIIOЖCCTHO ВСс'Х
111:йстн11те11ы1ых чнссJ 1 , а чере:~ У - множество
'
1ю:х неотрн1 tательных ЧJtссл , то фпrмул:з у: .'\.' -
J;tд:1ёт 11 раниJ10, ка·1·ор< >е сопоС'та 1щнет к:1ждо
му чи сду .\' сдиrкп1еmюс число у. рат1ое х в
степенr1 2 (рис. 2 ).
В привелёшrых примерах. несмотря 11а 11х
раэлнчпе, общим юзляется следующ~е; даны два
множества н каждому э11 емснту одпо 1 о нз 1111.Х,
по некоторому t1рав1шу (с пособу, з~ню11у) , со
rюста.вляется единственный элемент 11pyr01·0
множес111а . т~н< мы 11рнхо1t11.м к общему поня
тию функц1т. 11yC't'h Х и У - какне-то мно
жесrна. Если каждому эле менту х 1·rз множества
Х, rro некоторому ттра11ИJТ)' (способу, зэ кону)/,
сп 11оста nляетс>i еди нствен ный элемент у нз
м1южсства }~ Т() говорят. что на мложестне Х
зад:зна (или определена) фунNцuя f со :таче-
11иями в> ~ М1rожсс1во Х назьшается областыо
опреде.ле}{UЛ функци11 (. :t множество У - об
ластыо .значе1щitj. Тот едн11ствеm-1ый элемент
у 11з } ~ кuторый соотнеr·<.~r·1:1ует .х, обознач;нот
f (\'), т. е. у = f (х). и именуют знач<:>ниеJw. функ-
11иu J на элементе х. 06 элементе х 1 :11-ЮГ7'а го
ворят как о н.езшз11снмой перемен.ной или а/J
lумешпе фуш":ции / а об у=f (х) - как о
зааиси.моil переметюй..
В школе изучаю~· числовые фун!{ции, -
фупrщ11и, 011ределёнпые на J\П-южествах дей
ствителып,1х чисел и принимающие значения
т;-~ кже в множестве дсйствнтельных чисел .
П ричём функщюнаш,ная ~авис11мость J' = f (х)
1а;щётсн. как правило, й явном н~.-ще (аналити
ческим 1-1ыраженнсм ). l la11pиrv<PГ): у= х2. у = .х-3,
Функuии
l"ис . 4.
у=~х,у=sinх и т. д. Псрnая. вторая 11чет
вёрт;tя фр-пщии оrrредслеL1ы на множестnе всех
дсйс'1'Витv1ы 1ь1.Х чисел R а третья - па :.11 юже
ст1к· всех 1-1еотрицатеJ1ыfых чисел R +.
11,:шное ш,uле оттределен1н:: фун1щн11 требу
ет, чтобы каждому :х 11з 0611аст ~1 опре;(t:ЛС !-П·нt
фун1щ1-rи отвечало одно -едннстве1~нос значе
ние у. На11р 11мер. rраф1rк, изображён t rый н:t
рис. :$, не 011ре,1езtяе'г ннкакпй фун"ц1111 В дру
·1нх случаях одно ki 'ГО же значеннеу Mt 1ожессва
У соптнетсrвует нес1<0лышм шш rтс спот11~т
ствует ш1 одном у и:~ возможных зш1че11ий
аргументах (рис. .Z). Если футпщия/таксша, что
1<аждос у из множества У сопоставлено одно
му-ед ннеrвсн.ному элементу.\· из М1iОЖ<.~ства Х
(У=/ (Х)), то на ;.u южестве ) ' можно 011рсде
лить функцию .r-
1
• т:.~кую ,
чтох=/-
1
()1). Эта
фу11кцня назыR:.1 е-1 с·н обрат1-ю1/ фуню~1111 /. Л;rя
1
.
.
футщину = :х · . з;ща t 1~:ют1 на мложестrк· R. об-
ра·гноИ будет фун1щ11я х = {у, а для ф) нкц11и
у = \~ на J\1ножс:стве к.. -
функциях=/. По
сколъI<..у аргумент функции всё же принято обо-
эначать череэ .\~ то, например, вместо .\"=;/у
пиurуг у==Vx. Итак, фуr11щш1у =х; и у :::~r.,.
обратные друr другу на R (рис. 4) , а фупю r;нн
у=х2 и у= .Jx обратные лруг Jфyry на R +
(рпс. S).Далее, ест~ фунющюу= si11х рассмат
рнвать лишь на отрезке Х = (- тс/2. п/2], а в ка
честве множества Уозять отрезок [- 1. 1J,то об
ратной ей будет функuия у = arcs in х (рис. 6).
Ан:шоrнч1ю определяются фу:rпщии, обратные
другl'r.И три1·он.ометрическим функциям
-
--- --
-
----- ---
-
-
-
J
471
_,,,
()
а
Летерминизм и случ аи ность
у
7r
у= :ircsi11 х
2
7tх
2
Рис. 5.
Рис. о.
Понятие фу111ш,1111, оn11саннос вы ш t;, бази -
11уе-1·ся 11а кон цепциях теорни м r ruжеств, 11 з
чала которой были заложены Георгом Канто
ром (см статью «!У[ножество и его элемешы»).
:~ти ко1щеnци1-1 произвели большое вnечатле-
11ие на современников. Дави;nт rильберту, од
ному из величайших матсматшсов всех врсмён,
принадлежат слеJ 1уюJ цие cJtoвa u теории мнu-
жест.в: «Я считаю, что она 1 1рсr1ста.нляст собой
высочайшее проявление м:псм;.~тическоео
l'СННЯ и 0/\НО из самых высоких 1'()СТИЖСНИЙ в
духо1111ой ж11 :111и '1ело11ека-> Нужно Д()бэ11111ъ,
ч·1 ·0 1 rрактнчсски rкс соnрсмсшrые математи
ческие работы n тofi пли иrюй степени испот.
ауют ос 1 юв11ые понятия теории ~шожеств и её
СИМВОJШКу.
Но ст r тком смслос применсrше коrщспцш1
теории множест11 r~р11110;1ило 1< 1 1 арадоксам .
М ноп-1е круп11ые ~1~1 т~1v1.:11'11ки ст:ши выска:зы
т1т1,01 :за пrр<1ничt:1111с и<.тrользон:ш1т теорет11-
ко-множt:ствснных понятий. R частнос11r. он11
rюла 1·али, что в 11011ятие фу11ющи 11е()бходи.м()
1\КllЮЧ И'\'1) ч1е6011а111 1 е ОСуЩеСТВИМОСТИ. <• l\OllCT-
py1<Tl IRl-IOCП I ". Это :ш:~чнт, что должны быть
ошканы отчётливые 11равила (11лн, ~<ак теперь
при11ято говорить. алгоритмы), позnоляющие
по задащю.му х отыскивать нужное у. В итоrс
воз никни целые напр;ншснии к математ11ке, uт
рицавш11е нео11ра 1щанно широкое 11р11менен1rе
теоретико-J'.-11 юже<:ткенно 1 ·0 по;(хода.
ФУНКUИИ НЕПРЕРЫВНЫЕ И РАЗРЫВНЫЕ
Срели раэно()бrазных функций Ol\HOif перемен
ной естественно выделить те, график которых
:vюжно нарисоватт, одним росчерко.v1 каран
даша , без отрыва от бума~·и. Такова. например,
фушщняу =.f(x), прсf{СТ:tвлсrшая на рис. 1.
Для фиксирова 1шой TO'llШ х0 (а< х11 < /J)
f{pyryю, бшrзкую к нcir точку nтр<.:зю1 обо:ш:,~
ч1 1 м Xu + дх. Всл11 ч rrна д.х (читается <-дельта
11ко) называется прираще1Juе.м аргу.д,1ента. Эта
величина 1 ю1юж итеm,на, еслн близкая точка
)'
у
(1
:м
1х
о
х
иХохн+дхь
Х11+дх Х<1 h
Риt. 1.
Рис. 2.
472
выбрана правее точки х0, 11 отр1щателы 1а -
ес;ш левее точют х0. Ра:нюегь зпачс1 щй функ
ции у =.f(:x:) в T()LU<ax .х0 + д.'\· 11 х0 11а:;ьшаст<.:я
npufJaU{&NUe.м ф111ис1411и. , <.:UОТВ<::ТСТВ)'IОЩИМ
11р 11 ращ1.:1111ю аргумент:~ д.х, 11uбпзначастсн лу
( ч11тается */\ельт::r 11грск~ ) , т. с.
ду =/(.\:о+ Л.Х) - f(x0 ).
H<i рис. 1 приrаще1н1е фу 11 кци11 рашюrv11111е
nтрезка ВС. Гlр11 стремле11н11 приrащстшя
зрrумента r< () неэаnисимо от того, полож111·е.•1ь
но 0 11 0 илн отрицателыю, прнращенпе ф)'11к
ц11и тоже стремится 1< U: лу ~ U при лх -> О.
il.мссто ,,ду стремится к О» 1·оворят т:нокс. что
предtл нt.1шчины ду равен О 11 ри лх. е1ремн
щемся к U:
Ji111ду=().
,.. ,\'-t (\
Н~ рис. 2 llfX'ДCT<JШtr.:11 J'Рафнк .!J.Р)'! 'ОЙ ф)'IЖ
IJ.IНI у= g(x), <mре1(еJ 1 ён1 юИ н 1<аж,1\Ой тачке от
резт<а la, hj. Оп состоит из дnух непрерывных
фрагментов и в точ 1<е с абсциссой х0 имеет
« ска ч.01<» (з11аче11ие фу11~щии в точ1<е х0 р:нюо
длипе отрсз1<а от точю1 N до точки х0 ) Та.кой
Функuи11
-
/,
Летерми11и~м и глучайносrь
граф11к нельзя нарисонать без отрыnа 1<а
ра1-щаша от бум~1гп . 11 пnтому его естественно
назвать разрhlвным . Каково поведеняс функ
цнн у= g(х) uб111 1 :ш точки •ск~1чка»' Ест~ rrp11-
p<1 те1 Пiе :J ртумf'1 1та tsыбра 1ю 1lOJIOЖИTtJIЫ-IOt:,
то 11рп с.тремленин его 1< () 11рир:нцеt 1 ие функ-
1~и11 таюке стремится к О. Если же прираще1111е
аргумепта лх стремится к О, оставаясь отри
цатt'лыrым , то приращение футщин стре
мтrтс11 к не;1 11ч.ине, ранной длине отрезка MN.
Таю1м обр:1Зоl\1 , ссш1 1 1 риращсниt' :tр1умt:нта
дх стремится к О «люб ым образом", то 11рира-
1 1\с~н1 с функц1шу = . q(x) ужt не с1·рtмится 1-н1 i..:
О, ш1 к jMNI (дунс 1·1мсеr прс;\tла 11р1 1 д.'\~ стре
:..1>шtемся 1< 0).
Пусть фупкцня у =/(х) (юре;1еле11 а 11а (П
рез.ке [а, Ь] , точ1<а Xn принадлежит отрезку и
а< Хо< Ь Функцняj(х) называется иепрерыв-
1юй в тичке х0, если предел приращен1ш фу1ш
ц1 ~н н точке х0 равен О •при mобом стремле
пин» к О 1 1р11р~1щенr-1я ар1умента, т. е.
lhТI Лу = liш (,{(Хо +Л.\')- f(X))= O. (*)
д.V-'IJ
Д,\'-+(1
•
!:ели обоз1-1ач 1 1 т1, х0 -1 - л:л· через х н учесть,
что х -4 х0 11рн лх -4 О, то ранt'нсгво (*) можно
зап нсатъ т~:ш::
Др1тимп слова~ш. функцняj{х) непрерывна
Б точке х0, ест,1 сущс<.:твуст сё предел в точке х0
п есл:и этот нрt'дел равен значсшно ф)1шции в
ТОЧКt" Xr"
Фуню~ия н:вывается штрерыв1-юй 1-щ ин
пщрrзалв (а, Ь), еслr1 она непрерывна н к:JЖ/\Oil
точl\е ннтервала (т. е. u каждой точке х0, такой,
что а< х0 < Ь) . Фу111щ11н 11азыuается непрерыв
тюй иа отрезке [а, h], есл11 она непрерывна в
каждой точке интервала (а, h) . а крпме то1 ·0.
непрерывна "слева" в точке а и пепреръmна
«Справ~ » в точке: Ь. Выражения «Слева» и «Спра
ва» означают, что в точках n и Ь вместо преде
лов иыраженин (*) рассматриваются «часn1 LJ
ные » пределы:
11111 (/(а+ Лх) - /(а)) =О .
~... -. ()
.1.\' "' о
lim (((Ь+Лх) - .f(Ь)) = О .
д.\·~D
6;\'< о
т. е. для левого конца отрезка допускается толь
ко положителыюе приращение аргумента,
а дтrя нраво110 конца - только отрицательное.
474
ОПРЕЛЕ/\ЕНИЕ НЕПРЕРЫВНОСТИ
НАЯЗЫКЕ«Е- о»
f l ср но 11<1Ч<L1 1ню ·"1<1Тt'м:пико.в вnom1c удон.11ет-
1юрюю nрСJlСТа нленис о непрерьrв1юt1 функ-
11ю1 кзк о функцш 1 , 1 ·р:.1фик ко·1·орой мож11u н;~
рнсовать бсэ uтр 1,1на каранд;.~Lш1 от бyмarir -
«с 1юt1од 1 1 1,1 м 1·1J1ече1111ем руки,> (т::~ кос оп ределе
ние в од1юi1 из работ r1 p~шёJJ Лео11ард Эйлер) .
По мере расширения l(Ласса изуч;~ ем ых фу11к
ц 1 1й - а сре;,11 111 1 х н фу111щн11. графню11юто
рых нельзя 11ар11сова1ъ , - тто1штие 11епрсры11-
нuстн 11отребовало уточнения. l la nрочны11
фу11 ; 1амс1-1т 1юю1т11с нспрсрывност 11 встало
JIJ/Шb ТОl'Да, KOJ 'Д:I фp:tHJlY::ICКl l\1 M:J '\'('M~ITllKOM
Огюеге:ном Ко1ш1 было сфорN1у1 tиро1i;1но стро-
1·ое ог1реде.r~с1-1нс пре; (ел::.~ фуню\t1н (около
1820 r. ) . И с 11от,;юн:.111ный нм пtщход ч:1сю 11а
зьmают я:~ 1,п<0м •·r - ()" (ч11таетсн 1.:э пс11л оп -
дельта ·>).
Со гласно Коши, фушщш1j(х), ощ)едслёшшя
на некотuром шпсрв ;L'JС, <.:о,~сржаще;ч точ1<ух(~
н;:~зьшастся 11енрерьш11о iТ n точке X r1, если для
любu1·0 сколь у1·uд110 _,1~и10го полож1пельноrо
числа !;' МОЖ/10 найти T~KUC l/OJIOЖ I I TCJIЫIOe
ч.нсло о, что нсрзвснстно l.f(x,, + д.\') - /(X1.1)I <t
uьшолняется для всех лх, )доuле11юрнющllх
упюn ию jЛ.\·j < о (rис. .:$).
Чтобы пр11м е F1J1т1, это опредtлс 1-шс непре
рывr юСТif, требуется 11 е 1(()торы1'1 опыт. Но :~ато
оно позволяе т исследов:.~ть 11епрер ы 11 1юст1.
каждой кон1<ретной Ф111кцш1.Докаж1::.v1, 1 ~:t1 1ри
мер. что фушщия у= siн х 11е11рерыв11а при
нссх х11. щ1я че1 ·u вос11ол ьзусм:ся од~ 111м своil
ст1юм функч~·111 si п х: jsiнxj ~ lxl для тобоl'О.Х
(см . статью ~ элементарные функц1ш 11 их
сво йства->). Поскольку
)'
28
,_,
1
1
Уо+ е
,
,
У11 ::::::::::•--,- -
---12е
"-1
-г-
-
-
-
-
-
....
•
1
11
11
1
1
1
Хо-0'''Xr1+0
х
Рис. 3.
1( А)
•
J•Л."<(Лх)
5nХо+L\X-~lnXo = - SШ lCO~
Х0 +т
н lcos.:x·I < 1 для дто601 u х, то модуль рпзтюстп
з11ачен11t1 функции u1\сн1шается так·
lsiп(.\'0 + Лх) - si11 x"1~21Лх/21 1 = 1лх1.
Пус1ъ :задано JLюбпе cкum, )TU)\I ю :-.1,uicк rю
лож11телы юе ч1кло f . То1 д<1 мож110 п 1 .16р.пъ
8 =в, 11 очетнщт-ю, ч rо прт 11лхl < о nыполтнтется
11ер::~ве11ство
lsln(.\'0 + Лх) - siп Xol ~ Л.\' < о=€.
с !IОМОЩЫО aнaJJOr'HЧIIЫX р~1ссуждс11ий
дою1зынастся нспрерынность нссх ::1лемсн
тарнЬL'< фуптщи11 f-i311p1L~1cp, функциях~ 11еnr<::
рынна на всей ч 1 1с1юR01~1 прямо\"1. фрrю(ИЯ
log 2 х1-1спрсрыв11::~ при х >О. а фу11кщ1я tg хне
преры 1ю2 11а и1-псрRале (- п./2, + тт./2 ).
СВОЙСТВА
НЕПРЕРЫВНЫХ ФУНКUИЙ
Сумма. разность и пронз.всдснис нснрсрьmнъrх
н одной и тт"i же точкt:: функцш"i обра:зуют так
;ю:: неnр t::ры вныс в Д;JН t юй ·1·uчкс фуl1 ю1ю1 .
А ч~IС'ТН(JС нспрерьшных функц11Л непрерывно
г~рн условии, что знаменатель н рассматр1 1 R~1е
мой точке т·личб1 0 ·1 11уля Су ществуют и
дру1 ие теоремы, которые rюмо1·ают псследо
ваТh 11J непреръгвность ту ит-r ит 1 ую фунюоно .
В особый класс выделшотся фу1пщии, 11епrе
рыв11ые на отрезке. Оrш облапают рядом :.1аме
чателы-1ых свойств. Например, непрерывная па
отрезке функция , пр~шнмающ~ur H<I <:: 1·0 1<01щах
:ш::1че1-11ш с разными ~ш~1к:ам.и, обнз::~телыю обр:t-
у
о
rнс. 4.
Фу11кuии
щается u О в rre1<oтopolf точке: 01рсзка ( рнс. ' 1).
У·гверж,.11е1111е это кажется впол~ re очев~щm,1м и
nрекр::ю ю со1ласуе:тся с юrrунтнтшым прс7'
ставлет шем о r1спреры.1шоri кривой . Пояобная
кривая 1rеи:~бежно rrcpeccчt.11 ос.ъ Ох прн пере
ходе<: одной её стuроны на друтую Напропm,
разрывнt.tя функr (l'IJl. как шщно на р 1 1с 5, т;uшУ~
СIЮЙСТНОМ нс обжщ;н~·1·.
Стро1 пе мате м:.1тн ч tткое дп каз:.1тсльстно
1Jьr 111 еnриве;(ё 1 r1юr1 теоремы о щ_:11рср1.mноr1 нэ
отрезl\е фу11ю\ю1 r11 rер.выс было да1 ю чстпс11им
матемэ·1 иком Г>ср11ардом Г>nлrщз 1ю ( 178 ! -
1848). ()110 uьшвнло то·1 существенный для
далыrе 1~mтсrо [НЗвитня матсмаппп1 факт, что
изучению не11рс рышюст11 фу11кц11й дuлж1ю
прсдшсстнонат1, 1 1зучсr 11 re не1 трерывr юстr 1мно
жесгщ1 , на котором рассматринзстся ф~·11ю (11я.
() l'реюк ЧИСЛОВОЙ 0('11 ЯВJIЯЕ'ГСН к;1 к r;1:~ 1IC'Пrc:
pЫRf-IЫM МIЮЖСС.-ГRОМ (оно нс 111\fCCT «ДЫр•). и
именно это 1 фа1<т лсжн·1 в о<.:новс.: дсжазыв<~с
мого у·1вt'ржле111 ш
С помощью теоремы Ьольцат ю можIIо ре
шить, 11апр1Тмср, такую rrзвссп1ую :3:.11пfма1ель
пую задачу Некий путешсстnешшк n 9 утра 11а
•rал подъ6\1 на гору и pOБIIO n 6 вечера {(ОС'ШI
1:1сршины J:~ночев,ш 11а вершине, на следую
щ11!1день011 ровно в 9 y r·1x1 начал спуск 110 тoir
Ж<:: трuпс 11 рrншо 11 (1 .l:\C.:ЧCf):I /(0С'1'11Г !ICXOf\HOJ·o
пункта у rю11нож11я. Всrно 11и, ч · ю н каком-то
Ml:LTC на ·1 ·ропс гrугешеСТВСННIН\ ll:tX0/\1IЛCЯ в
ою ю 11 то же времн г1ер1ю1 ·0 11 1п оро1·0д11я пу
тетестоия!
Н:эрис)rе м графrпа. 1 rю;~ъёма у =/(х) rт спуска
J' = ,g(x) (rлеу- высот<~. ах
-
время, рнс. 6) п
учтём, что они nредста~ляют собой непрерыв
ные кринь1е, тогда утвердительный ответ o•:re-
1-11 щсн. Ра:11юс1ъ :н-~ачсш 11·1ф) шщпi't/(.\') - g(.\').
оппсh1Вающ11х маршруты путсшсстнснника,
у
Рис. 6.
475
Летерми низм и САуч айность
на KOII Ц<IX отрсЗЮI [а, Ь1 ПрИНИМ<IСТ раЗНЫt: :.н-Ш
КИ И В ('J !ЛУ Н С11реры HHl)("J'll , J Ю Теоrемс БOJI h-
1\~ HU, н нt:кото роl1 точкt: отрезк~1 [а, 11] обра
титсн н О. Значит. rrмен110 н этоii точкt: (в tщшr
11то1 же моме11т време11и суток) фу 1 1кц1 1 и прн -
1\Iут ра11 11 ыt" зн ач.еr rшJ, а 1 1у·1 ·е111естве1 1 щ11<: при
под·r,ёме н c rrycкe буfl.ет па.'{однться в одном и
том же месте.
Подо611ые р:ксужнен11я n озrюляют, напрн
мер, доказать, что rш отрезке 10, l/2J сущестну
ст ~Jсшение уnавнения .'\: - cus тех= О 11л и что кv-
t
J t-'
'
'
•
бическое ур:ншсни е х + а.х- + Ь.?..· +с= О пр11
любых значениях п. /J и с имеет хот>1 fiы одно
решение.
Нспрсры нн 1,1с фуню~ин u\1разуку 1· пс1 юв1 юlt
кщ1сс фу1 1 кцн1"i, иссле,тn1е м ых n мате:\1ап 1ческом
а 1 rалнзе, or r и играют чре:-шыча!пю важную роль
R ттриложеш·IЯХ математики. С шс помощью
оnисьшаются разл:ич r rые изменяющиеся про
цессы и состояния в твердых телах, жидкостях.
газах. Науки, 11::1уч:~ющ1 1 t: ::~ти 1 1роцесс ы , - теu
рия у11руl'Ост11, r11;1рою111а:v111ка , аэрод111 1 ::~м11-
ка - исходят из предположсюrя, что м:н:сr со
uтRетствующс 11 среды распределена без нсяю 1х
просветов в заня•rом ею объеме. Назваш-~ ы е
дисциплины объсдннюо·гС>J общнм 11а:звэ1111см
«.v1еха 11 11ка сmюuн юй среюм.
РАЗРЫВНЫЕ ФУНКUИИ
Разрывные функции 0 1 1исывают ска ч кообраз
ные 11рuцессы н 11рнродс. Н аnр 1 1мер , при удар<:
м1·1-юне1 Lr ю изменнета~ скорость тела; шютноеrъ
1юnы к~~к фу1-tкция тем 11ср;:пуры сю1чком rюэра
егаст н (,точ ке замерэания• н так же 11 адает н
~ точке кнтте11 ш1 •. Графики фушщ111I, отражаю
щ11х 1ю110611ыс процессы, состоят из двух или
песколькш< пепрерьшных фрагментов ш1ний и
t[меют одна ш1и несколько скачко13.
у
'1
у
)'
В н;нталс XIX столетия быm.f 11зобрстс11ы
очень сr·ранные - « tiрезвычайно разрывные»
-
фующи11 . Первой 11з 1-111х стш~а функJ\ИЯ . р:н:
смотреш-1<1я немецким матt: .<v1ат11ком Лежёном
J],прнхлс ( JfIOS-1859):
.
{О. еа111.\' ~1ррат ~1 юrr211ыю
j(x)=
_
1, еслл х р;:щ11оналы ю.
llапр11мер·/ (1 /3) = 1, /(\12)=0. Фу111щ11>1
Д1 1рнх.не определена во 1кех TOtIК:LX, uднако nо
стро 1 1тъ её 1·раф11к ненuзмuжно: на любом
СКОЛ I> )'1 '0/~HU М<IЛОМ 0·1рс:31<е 011а 11рш 1 11ма ст 11
:н-1;1че1111е О, и з11а чеr 1н е 1. Функцr ш /Т,11р11хле
разрывн::~ R кажлой точкt.
Ч ерез 25 лет 1юсле 11 ояRле1111я работ1.1 Д11-
рихле исслс7щnа1шем разрьш r rых фушщ11lr
занялся вы11:ающнйся r тсмецки(i математик
Бернхард Риман. Он шкал. что 11зуче1ше функ
ций, нuдобIJЫХ ф}1нщии Дирихле, тесrю сня
з;~нu с liЬIЯCIICllИCM (.)CIIOllllЫX пр1шц11щ1в м:1 -
ТСМ:IТIIЧ<.х:кuп.1 :11-1ш111за. Оно мажет с11ужить ll/IН
тш·о, чтобы пр11д:.1ть эшм нрш-щип::~м бс:щьшу10
яс1юс1·1, 11 оnределёшюсть.
М1ю1· ис ма·1 см:~.т11кr1, особенно старшс10
ПОКОЛСJ-111>1 . НС CJ'П-IOCJL1JИCЬ ссрьёзно к нсслсдо
ваншо разрынных фушщт1й , (•столь дапёкнх 01·
реапыюrо мира» . Н оnую теорию разрывных
фу1 rкций д1же называтr "тератоло111ей" функ
ций. т. с_ наукоi1 об уродстuах фуr11щий.110 по
сле работ Р11ма11а изучсrrнс разрыв11ых фу11к-
11111'1 уже~ 11с прекращалось Эти 1 1сслсдовшшя
!ЮЛОЖИJШ H:.tЧ:.JJIO НО6ЫМ pa:ЩCJl~IM "vt ;['f 'CM:ITl'l-
IOJ, в кпторы х раJры 1шые функц1111 уже щ: Bhl·
1лндеJ1и чем-тп н еобычным .
В конце XJX в. н р<tбuте молодо1 ·0 француз
ского :-.1ате .v1;rт1тка Pi:-1 т с hЭj)<l nыл:1 1\: 11 1:11'Л:1СС11-
фикацш1 точек разрына. I< разрыв~ 1ым ·1·оч1<ам
11ерно1·0 рода относятся «устrа1 1 нмыс р~1зрьшы•
тrша <-дыры» н 1 ·раф11кс фу11кцш1 11 ко1 Lсч11ы1'r
у=lim-
1
..1
•
1"
п ,."
.,.. ·'
у
2
.~·
х
х
-
1о
и
rис. 7.
Рис. !1.
Рис. 9.
476
у
1
х
)>= --
.
х-1
Рн<.. 10.
P•tc. 11 .
сю1чnк Пре/(С'Тавлет1е п таких тnчках лают
rрафш<и на рис. 7 и 8. Ра:-1рыш1ые точки второ
ю рода - точки. для которых функция: а) с 011-
ной стороны лпбо с обеих сторон стрсмrттся к
бескопсчносn1 (рис. 9 и 1О: в первом случае
функцня слева <:трем1л·сн к конtчному значс-
у
11
1'
'
1
'
Функuии
)'= :)JJ1l
х
тптю); 6) либп слеnа, т16п справа 11е стрем11то1
ш1 к конечному, ш1 1< беско11еч1Ю.1\11у пределу
(рис. 1l).
Заметим, что фуню~ня Дирп:хлс, график ко
торой нсвоз"'южно нарпсовать, в каждой точ
ке имеет разрын ~торо1·u рода.
ЭЛЕМЕНТАРНЫЕ ФУНКUИИ И ИХ СВОЙСТВА
Под .~ле.ме11тар11ы.ми фy111\,ЦUЯl~lll пn11имают
сте 11е1 1111,1е, rюкэ:-~ателы rые, лоrарпфмическис,
триrтюметр 1 rческие. обрат~ 1ые тригонометри
ческие, пшербшшческне, обратные п1пер601ш
ческие. а таюке функпни , получаемые нз rnix с
по:.1ощъю <1етырёх арпфмстпчесю1х операц11й
11 суперпознци11. Здсс h Mhl рассмо·1·р111\11 11 и1111,
нею 1·1 ·оrыс оснонныс :~псме1 1т;ir11ыt' фу 1 rю tин .
ЛИНЕЙНЫЕ ФУНКUИИ
Рассмптрим сначала наиболее простую функ
цию, а имеп110 шшейную: у(х) = kx + /J, где k и
fJ - 11екоторые констаIJты. lJрооедём 11:.1 пло
скосn1 наююшrую прямую, расположс11ную по
от1юшс1шю к коорд11нат11ым оснм так, КШ( по
казано на рнс. J
Прям<tн 1rерс::сскает скъ ор;\11нат н ·1·0 1 rке (О; fi).
Во:~ьмём 11а 11рнмоl1 любые двt: точюJ (х 1 ; у1 ) 11
(х~; у!)· Из понобия трt:угоньн11ков с вершина
ми rз точках (О; /J), (Х1 ;у1). (.х-1; fJ) и (О: h). (х2;У2).
)1- ь )',-/)
(х · IJ) следvет что - ·-
1
--
=-
· --- -. Ес ли 060:1-
!·
.
•
. '\!
х!
нач11т1, 11олучеrнюе 0·1-1ю111ен11е через k (его
часто 11а:-1ываю·1· ~т1юnым 1юэффнщ1е1r·1 ом 11r}i-
мой) , то пля люfю1~1 точки (х; у) на прямой c11ra-
)1-h
ве11,.11111ю раве1к~1·1ю -·
-- = k. 111111 ·1• = k,:>.: + Ь. Зна-
х
.
чит, наша прямая есть график шшt:fmorl
функr\1111 у= k.x + Ь.
У1обр:~т1 ю . 11ус11, :1а~;111а л111 1 t:1"111 :1я фу11к11~1н
у = k:r: + h. Ест1 Jг =О. функцr1я 11р1 rн11мас"1 одно
и то же з 11ач<.:ннс..: /J rю псt:х ТРчк:tх :>.:, т. t:. ci.;
1·рафнк 11редст:нщsн:"1' С()бо1·1 11r»м>' l<l , r1apaл
J 1 eJrы 1ую ос11 абсцисс 11 111юхо;\»Щ)'Ю чере:l · 1 ·оч
ку (0; /J). Если же k Ф О, графтш фу111щ11п пере
секает оси абсцI1сс u точке (- f; / k; 0), а ось
ординат - в точке (О; Ь). Через эп1 две точю1
проходит ед1шстnс1шая прямая Рассуж~ая
у
)'= k:r-+ /;
1(Х1: Ь) :
-
-
-
-
-~-----r(Xl;/J)
1
1
.\
()
Рщ:.1.
•177
Летерми1·1 и~м и cлy•1 at:i1·1ucтi..
ГL·rн:рь ·1очно так же:, кз h 11 ны 111<.; (в <..~Л]'Ч<ll' с по
,11,06111о1м 111peyi0J 1~.r шками) , rюпучасм. что l'CJШ
точr<а (.\:;у) пр11наw 1 ежит /\анной 1 1 рямоl1, 1·0
у = kx + /J, т. с наша nрямая - граф11к ли11е~1-
1ю(r фуш<цш 1. L1т-.нс, rрафнк .rпшсйн()Й ф}шщш r
есть нсвертикальная прдN1ая
В случае 13С JЛНКШ1Ы rой прю.юй ~ело обсто
ит еще проще - она нс "'южст бьпъ графшсом
~шкакой функцл 1 1. В самом дел<:, пусть :-эта
11pJJ .\1aя 11срес1:чёт О<..Ъ ;~бсц11с<. и то ч ке (с; О)
Torд:i од11ому 11 1'01\1у же х = (, бупс1 соотве-1 -
ствnпать м 1 южс:стко рззлич11ых ЗJ ~ачсн111lу (все
дс:fiс·1·111 1тсл ~.т 1ыс LI исп а) .
СТЕПЕННЫЕ ФУНКUИИ
Сте11сш1ш1 фушщш1 j (х) = х" с на~уралыrы;-.1
показателем п опред<::лсн;.1 н:~ всс::й дсйстк1пt'ль
но(1 nрнмuй Прн чЕтнuм 11 с11ран<.:Jщшщ ран<.:н
с11ю /(х) -::./(-.\').Та юн: фу111щ11н 11:.~зык~нотся
чё11111ы.м11 . 11 11х 1тщф11ю 1 с:J1мметр11чш)r отно
с11те; 1 ыю ОС'н Оу (рис 2, а. б) Прн 11t=чё11 юм Jl
ф~111щш1/(х) = .1:'
1
1tеч€iп11шя, т. е./(х) = -/(-
.\:),
d её грзф11к спмметрпче 1 r отпоситспы ю ш1ч~J 1 а
коордитп (рнс. 2, а, г') . Lla рисунках хорошо
1шд1-ю. что две ncтr111 графика устремляютсн
n 6ССJ{ОJ1ечность, прачём чем дальrпе хот на-
у
yl
а
б
11 =х4
)'=.r'
1
х
х
о
()
в
r
у
1' =."<.' '
1'=х5
1
.\'
х
о
P11r. 2 .
..J.78
P1tc. J .
а
Ри с;. 5.
)'
()
у
о
Рис. i>.
J'
о
х
1
11= ~
х-
1·==.х···
:\'
в
l'ис 4.
б
у
1
о
у
2
о
)'
о
у
1
--
.
t1
1
1·--
•~-_yl
х
х
б
.1'= .\']'
чапа коnрд11пат 11лт1 чем болыле 11, тем круче
тто,J\1пrмается (шш онускается) кривая.
При п = 2 r'Рафит< фупrщ~нi j(x) = :х" пред
ставляет собой параболу с фо1<усо:м н точке
/,'((): 1/ 1) 11 днре 1«1рисuй у= -J /-1 (рас. 3; см.
также ста·1ыо «Зам1:ч а·r·слы1ьl(: кривые"). При
11 = -1 ~·рафик функции у= х" = 1/.х - 1·111 н:р
бож1 (рис 4).
По опредеJ 1 еr 111 ю c1·eJ1e11н,х-" - J /:х:". Поэто
му сте11е111 1 ая фупкr ~ия с цc.rrr,1м 0·1р1·1ц;~·1еJJь-
111,1м шжазатеJrем определена rю всех точках
числоrю 11 ттрямо\), 1<рш"1е точки х = О, а чёт-
1юсть илtJ печёт11ость фу1rr<ции устанавлива
ется так же, как и прп положительных 11. Когда
хстрсмится к бес1<онсчности, ~·рафик всё тес
нее нрнжимается к оси абс ~ ~исс. Вблн:Jи начю 1 а
KCIOf)/1,HHaT К[1НRЗЯ устремляется В б<:СКОJ I CЧ
IIOCTb (рнс. 5, а. б).
Стс1 Jснная фу11кц1н1.f(х) =х" с;чюбным 11лн
11ррац1юналытым поrсазателем а с ч11тается
оnре/1,елёпrюй юлыю па положптслыюй по.'lу
осн. Еслл а = О, фупю.цш таюке lle определена в
точке х = О. Графики фушщ 1rй пr11 p::tЗЛ l\\ll IЬIX.
показателях приведены на рве. 6.
МНОГОЧЛЕ НЫ
Ес1сстнt:нны,v1 uбоб1.це11не;;и ш1нёf1ных 11 стt:
ntнных фун1щпir (с на·Jура.11ы1ым ноказ:~телt:м
сте11е1111) яллmuтся многочле11n~, т. е . фу111щ1111
та1'ого nt-щa:
i1
"1
.1' = С!"Х + Cl/I i-'"
+...+а1Х+а".
Многочлены - uснuвные средства вычи:
оштелыюй м:1телн1 ·1 · 11ю1, н ко·1 ·орой данную
функцню llЫ'l '::НОТСЯ зам1;н11·1ъ нан бОJIС(:' 6ЛИ3-
Юl\1 к 11 <:й мно1·очлсном. Г11<1вное достон11с·1·1ю
\lll()['()ЧJte 11 011 COC 'l'OllT н том, что ДJIЯ 11ыч11сщ:
ШJЯ 1rx :т:-1чеrr11й требу10·1п1 J 11ш1ь ·1р11 оснон-
111>1е арнфмс.:тичесюrс операцн 11 - СJН>Жtнне,
вычнта1111е и умноже1 11тс. Область опре/1,еж·1 1ю1
лrоб()го м1101·очле11а - все действптелы-1ые
чн сла. График :vшогочле11а - uшдкая r<ривая:
у 11сё не'l ~1н ра:1рывов, 1ш изломоn.
lkл11 11а11есп1 на коорд11натну10 плоскость
11 1- 1 11p0113130!1hllYIO точку. то ,\ЮЖНО всегда по
добра·1ъ \Л-IOl 'O ЧJICH C'l'CПef-IH не 13blll!C п, r·р:.~фик
KOTOfIOJ 'О J"I f)OJ1/\i:'I ' ч<..:рсз ЭТI 1 T()'I ки. п ро11есс
rю11ска такоJ'О м1ю1·очm::ш1 11а :зr.шаста1 з::щачеi1
1111me/ml).11J1цuu. и её мето;щкя ;~аннu и пол,роб
но разр::~бот~нr~. Далее, 1юличестrю 1щр11ей м1 ю-
/'/ - чет;юе.
а"> О
!'нс 7.
а
у
11 - нt>чёт1те.
ct">()
Рис. 8.
а
~·
•'\
б
Функuии
б
у
у
о
11 - нечетное,
а"<()
гочлспа 11 -й сте11е1111 не преuышаст 11. 3пач11т.
1·ра ф11к многочлена пересекает ось абсr~исс
11е более че1'1 n 11 точ1<ах.
1lоuе,цешн:: мIIoroчлcIIa <- па беско11еч11осп1·,
ПОЛIЮСТЫО 011рсд<:: JШt'ТСЯ сл~11 ·ас:11ым, содсрж~
ЩllМ ар1умс11т в 11 ;111н1,1 с11 1б"i сте11е1-ш, т с a 11:i:".
с ростом хон «11срl'не11шв .1 еТ·> вес остаm,ньн:
СJ1а1·зсмьн.:. Как всдё-1 сL:бя фу11кц11я у= .У" нам
~~А<е l I Зl:!CC'l' I !О. :l ГIOTUJ\f)'"" нс.-тру;1ни C/\t:ЖITI' еле, \Y-
Юllll lt: ВЫ НОДЫ:
еош 11 - чётпое , то пр11 а,,> О м1ю1 ·о чm.:н
1теогра 1шчешю воэрастаст, 1\or11a х ~± со
(правая а лсnшт вствн графш<а уходят нвсрх,
рис. 7. а): при а11 < О - паоборот (р11с. 7. б):
сели 11 - нечётное. то прн п" > () м1югочле11
11еограпичснно нозр :1 стает, когд.~ х ~ +w. и 11с о-
1 ·μан11чснно убынаС'1, 1-:ш ·1щ х -t - оо (рнс. R, с1);
nr11 а11 < О - наоборот (р11с. 8. б). l l::t р 1 r1:унщ.:
в11д1-ш, Ч'J'Оден<1я 11 пран:lя вепш 1тюф11ка ухоюп
в про·пнюположr 1ых 1[:tпrхшл<::ннях.
« НЕРАЗЛУЧНАЯ ПАРА » -
ПОКАЗАТЕЛЬНАЯ
И ЛОГАРИФМИЧЕСКАЯ ФУНl<UИИ
Пел и для стспсн1ю11 фу11ю(н 1 1у=х" ф11кснро
в~111 нскоторы11 1юказзтель степ е ни с1, '' осно
ван11е стеr1е1111 .1,; 11рuбстае1 вссно ~~мож 11ы с
479
Летеrм ~1н1нм и случайность
nоложителы-1ьн~ :шачс ния, то для по1{азателыюй
фу1пщю1 у= t(' н~юборот: основание: стспе1111
ф11ксирnва110, :.i nока :Jатслh мсннстсн. Показа
тет,ная функцин у= tt"' , ~·де а> О, т1редсл1::11а
для всех (1 1 е т011ы<о rю11ожителы1ых) :х.
Чере:~ nошrтие «cтerre11u» 011реде.11яют поня
тие <·до 1·ар11фм». Логариф.м ·•mс.па х 1ю ос1 юна
г 11 1ro а (:шш1сuшается logr, ;;1,.·) сстт., показател,,
степени, в тюторую надо nозuести ос 1 ю.вание а,
чтобы получить 'Пiсло х. Нсnосрсдствсшю 1 1з
определеюш логар11фма следует, LIТO
aJog".\ =.\'.
Таю1м образом. фу11ю.1ии у= tl ,. 11 у = log,
1
х-
обратные !\P)'I ' другу.
ПоказатеJ1ь с1·е11е11н 1"1ожr-ю вьrнос1nъ ;.j<J :31-1ак
_101«..р1 rфма:
log,,х' = сlog"х.
Логарнфм nроизJ1еде 1 шя двух чисел равен
сумме 11х лог<1 рифмuв:
lug" Х)' = logax + log"y.
Для щжаэательствз этих утвержде 1 ш 1'J J (О
е1·аточно нспомннть, что log,, х -та степе1tьр,
в которую надо нозвсстн основание а, чтобы
rюлучп1ъ х, и вос 1 юm)зощп 1,ся рапенстнами
.~:< = (аР)' = а<Р,
ху=аР·alf=аР''1
,
щер=logих и q=log"у.Вотивсё!
По1озателы-1 ;н1 и ло1·ар 11фмичсская функщш
приобретают ряд особых сно~"lств, ко r·д;~ rrx
основание ранно числу е = 2,71828.. О 11 и д:1же
получипи с1юн обозначения и названия: функ-
1~11Я е·1
= ехр х 1 1 ме11уется экспоNюппоu, а функ
ц11я log" :х = 111 х 1щrщральпым логсtриф.мо.м .
)'
.л:
Рис. 9.
Рис. 10.
4tIO
llачнём с экс:понсr1ты. Uбласть определения
с<.', как 1 1 1 1юбой 1кжазателыюlr функции. - все
дейсгвитслы1ыс числа . Экспонента приш1ма
ст тоm.ко п01южJ.1телы rыс :зн;1чснин. С ростом
.х фу1-шц11я е"' но:зрастаст мСJнотон 1 rо, и чем
дальше - тем быстрее. Она непременно 061·0-
нит любvто степе1 111ую с\N11кцию (напрн.мер,
1ooor)(\,
·
у=х
). А если устрс:-.п11ъ х ВJ1е1ю, к - ""',то
экспонента устремится к U (учитываем. что
ех = 1/и-'). Таким образом, прямая .\· = О шw1 -
стся гор 1 rзонтальной асимптотой экспо11е11n,1
прнх~- «>.
Есш1.У=О,то(1' = r/= 1Этоозначает,что
1·р.~фик функции r!y пересск~1ст ocn орJ111нат в
точке (О: 1). По имеющ1 П\КЯ ~ нас свслсн t1я:.1 об
экспоненте, уже мож1 ю пос1ро~r1ъ сё график
(рис. 9).
Дпя вычисления :ш:1чеrппl фушщип f!~ по
лезно псполъзовать её разложе1111с в беско11сч·
ный ряд
,.2 х\
<г°'=l+x+-
··
-
+- +".
2! 3!
Отс1<щ;1 , н частнос1т1. следует. что пр1 r J\1алы.х
х сnранедливо nрнблажённое ранс11ство
е""' 1+х.
На· 1 уралыrый лог;1рнфм, ка!( уже было сказа
но, - фуrнщия, обратная э1<сnопенте: ecmr
у = е ', то х = Ln у. А noтorv1y, •побы получ11111
~·рафик фу1пщии у= l n х, надо всеrо-навсегп на
рис. 1.) r~еренме1-юнать осн: Ux наэвать осью Оу,
п наоборот Тспсrь отраз 1 1м нею картину отно·
снтелпно 611ссектр11сы пср1ю1·0 11 третьею квад
рантоn (рис. 10) и тем самым 1юстроим графнк
фуню-1н11 у = ln х 1Jри об1,1 чнuм расrюложсюш
коордиттат11ых осей. Из этою 1·раф 1 1к;1 мы по·
чtрп нём м1 югие сr-юйстна фу1 11щ1111 11 = 111 х.
Область определе1111я ш1туралыюrо JЮt'а
рнфма - все по1юЖJпелы1ые, а обласn, :щаче·
1 шй - вес 1'Сйстrнrтслы11.1е •111сл:~. ~ростом ,,.
фу11кц11н ln х нl'о1рашrчl'11110 возрастает, :i с
приб1111женисм ,\'к U - нсогр.ш11с11:шю убьша·
ст. 1lоэтому ос 1, uр;t11нат служ1п нс:рт~шалыюf!
'1С11м11тт·о~1 функцнн . С осью :.1бс11 1 1сс 1 раф11к
1 1ерt.:сек;1 стся в точ кс ( 1. О).
Доб~1н11м е 1 нё о1п~о c11olicт110. Из вестно, tпо
эксrюнента нозрасl'ае•1· быстреt:, а ло1 ·:.1рнфм11-
чес1<а н функция медле 1 шее moбof! степе111юИ
фут<ц1111 . Даже если пок:tзатсль nослед 11 е11
равен O.OOOOUO l, она рано нлн позд1ю 11еnре
ме111 ю обгош 1 т лог:J.рпфмпчсскую фу111щ1110.
)'
1·=0'.
1·= и',
п>I
O<.a<I
()
оl
\'
,\'
Рис 12.
tlt:p11C\1l'>1 к 1нн-:а~1:11 ·с..1 1,rюr1 фу ню~1 11 1 у= а'.
R 1«1 1() ю c1·t' 11e1-1 1, cлert.ye· 1 · 110:111t'Cтr1 ч11 ою е.
чтQбы поJ1 уч1 1·п, чпсло а? По 011рею:ж:1шю па-
1 ·ур;иыюго логар1 1фма, этот шжа:1а'ГеJТ1, степе-
1111 есть не что r11то<.: , как 111 а: з11ач1п .
А 1ютому пrи а > 1 функция (/ ' вс:;(Ст ссбн
1·:1к жt:. к:tк 11 экс11ш1с11·1:1, 1·ш1 hr~u 1·р~1ф11к t:<:
<C:Ж:t'I'» 11 0 OCll О.\' 11 lп а [>3З (р 11 с. 11 , О). F.слн Жl'
О<ti < 1, ·1с>lпа=- 111 (1/о).т.с.тр111(~l'Гt'J1cн.
Il p11 таком усл<)r, 11н 11ока ;-1ателhная фу1 1ю(11 я
псп 1 · ра111IЧt'I111() BO~lp::tГГ~l e'I' 1 1 р11 .У~ -
""T I C'l'j)t'
!IНIТСЯк()пр11.\'~ (Х) (р1rc. 11,6).
А11а;ю 1·rrч1 ю .мтю ю р;:~ссуждатr, 11 n случае
ЛOГa(111ф1\ll lЧ C:CIIO i J фylП\\Lllll.J' = [Щ?;" .\ · ([1IIC. 12.).
ТРИГОНОМЕТРИЧЕСКИЕ ФУНКUИИ
Мы :-111ас.-.1, •rто y1·m,1 обыч110 11 :-1.>vн.: рню·1 н 1·1x11ty-
c:1x. Прнмо\"1 }'l'OJI - .:по 90". CJ I L"itoн;1тc.1ыш , <К
трые ) r·лы :1акл юч е1 1111 меж;tу О 11 90°. ·1~111,1<::
-
меж~ <)() 11 180<>. Сущс:1..~г11) е·1· 1tp ~тoi1 спосо() 1~:з
исрсrшя )ТJЮи: :1~1 едшrпну ттр 1·11111 мае ~ ся нст~
· 1 ральrrьп·1 )ТОЛ сжруж1юст11. «Вырс:~ ающ11i1» rr:~
щ:ё 1 () 1 у. равш10 длине ра.:.1и) с1 э·10f1 окрршо-
Функш111
сп1. Tar<0 1I у1 OJ I на.~валrr j)(l(!tю11rн1 fcm 1 ~;ак01'1-
111·1 б~дь ул), 1 111,1 рс:~: 1 с· 1 11:1 окружнuсп 1 \1спыпуто
/lYI'). он Г>у1tст мc111,11 tl:' раю 1а1 1 а, 11 l 'c.r11 1 (i()ль-
111 у10 -
'f '() l10Jl'11Jll'. ПOJlllblll ~ l '()JI (_)()O D) к J>:l;lll :t-
11ax рапсо J.ю/1· = 2тс. ра:н~~рнуr· 1 ,1 i1 ( 1RO") - те.
11 , 1 1 ако1н::1~. пря~1 ой )ТОЛ - тс/2 . С•юно "P:l/(11 a11'·,
1(;11( 11р:1111 uю, OTT)'C'Т\<IIO'I' ll l!Ml'CTO "Cl llГ}C ) l'il:J,
рав1 I()ГО тт p:i;.1,иart » говорит 11гюсн 1 «С ШI) с тт-> .
Расс.ч:пр1пза1от 11 отрнцатслr,т11,1 е yrлur По
сrропм rr:1 кuop,J.111 Iaтr Юil 11.'IОСКОСП 1С,\11111 IЧI l)'IO
сжру:жнопъ с 1tt.·н ·1 ·po.-.·1 н ·1·ос1ю: ( >. >1·лы 6у11см
у
l
Рис. 13.
r~1 c. 14.
()'}'CЧll 'l 'bll:J~П 11 ()'1 IJ( f.l lOЖll' l'CJll,H O I '() 11 :111р.11mс1111н
<н.: 11 < ).\ .· У1 0;1, отложснны1·1 г1рот1111 ч: 1 сшю1'1
C' I pt:.111..:11, 11а;-1 ы11~1ю· 1 l lOJIOЖl lH'J l hlll> l\I , .1 11() Чal '{)
lIOll п pt'm..:e - <УГJ1111 t<l l't', 11)1ll>IМ ( р1 lt. 1 .~) l lp11
отсчётс ут.1 .\ЮЖНО Сl(сл:-1т1, то6ос чпс.'lо 060-
ротоn ноr<р)Т тn<11ш () (р1 rc. 1~ ). :111ачт 1т, 1Je1 111
ч 111 1а )Тла ~южст 6ы-1ъ любы.ч :1сr'1 ст1штелы rым
чпслом. Соотвстствсшю с11 11ус 11 кос11 1 1ус 11р~
нращшотся 11з u 1·1юшсшп'r сторон пrямо~то.ГJ 1, -
1IO I'() l'PCY 1().'JЫ JJJl(;f 11 ч 1IC.' IOHbH.: фyllf<ltll 11 si11 .\' 11
(.' (},. _, .\', 0!1 f1С,\t:..'16ШЫС 11: 1 Ш.:t.: 11 Ч/JCJШHOJI 1lp}I ~IOJ'J
<J•ункция у= C()S .х. R11ок1, 1юс 1 ·ро11м l'/t 111111ч-
11у ю окруж1 юп·1, с 1lt' I1тр< )'-'1 11 11:1с1алс к~ )()рдr 1-
11ат. За/\'1;0 1 м произnот,11ос :1 11 :1чс1шс зр1 ·умс 11 -
·1а .\·0 1 1 оте<1нтасм от оси О.У) гол .\', ,. Этому уг. 1у
на с,'1 11111 1ч1 ю l1 01\ррююст11 ссютвс·1 0 В)'СТ 1 1с1ш
тор:т точка А (р11с 1">.о), :t tt прос1щ11еl111а O(f,
Ux \1yJ\CT точка J1. }lсно , ч·1 0 ;1тша отрезка 0.\1
раш1:1 a6CL)J1J()'J'J-IOJI HCJll JЧHIТC абсцнссы точкп JI.
fi.;.1 111-юму з 11.111с1111 ю ар 1 ·~ .'>Il'нта .\ :11 со 1 юст:шле 1 10
.н 1 ;1 1 1е11 l•IC ф~ 11 юtH11 ]'о = l'OS .\',) к:~" :1fic11,1 l('Cf.1точ
Кl 1/l. Соu1'вl:."1тт1к·н Н1) точ к: 1 В(. \'11 ; _l't,) 11pr111.1/ 1.:1с
ж11т 1-rаф11ку фушщ1111 у= cos х (рис. 1">. 6).
F:CJll l точка "j ll :l.\.O/~ IП 'OI П(Xlllet' lKJ 1 (~)'.то
КОС"1 111 УС будtТ TIOЛOЖll'J't:JJtlt. tCЛll Жt' JJCl!t:t -
отрпп,ателен . Но в .rттобом случае: точк3 А
lt3 l
Летерми н 11зм и случ айность
б
у
в
х
Рис. 15.
не может покинугь от<ружность. Пuэтuму кu
сш-rус лежи-1 в пределах от -1 до 1:
-1 ~со::..х~ L.
Дополнительный поворот 11::1 любой у 1 ·ол ,
кратный 2n:, вuзвращает тuчку Л 1 1а то же \1есто.
Поэтому фун кцня у = cos х 11ериодическая, её
11ерио1t раве 1 1 2п:
cos(х+2n:) = cosх.
Возьмём теперь два зпачення ар1умента,
равпыс по абсолютной nелич11не, но прuп1rю
положн ыс по знаку: х и - х. Найдём 1ra окруж
нос·1· 1 1 соот.ветствую щне точки А_,. н А_.," Как
Rlf/\HO на рис . 15, в, 1 1х проскци~й на o ci, 0.-к.:
является одна и ' J а же точка М. Поэтому
cosс-.\') =соьх,
т. е. !{()СИНУС - фJПl.КЦUЯ чёпшая.
Зна чит, можно исслсдоватr, своПстnа функ
ц1ш у= cos хна отрезке [О, ттj, ~1 :;атем учсеrь её
чётность и пе риодиЧ1 ЮСТI>.
Прн .х = О точка А лежит н:1 ос11 Ох, её абс
цисса рuвна 1,а потому cosО "" 1.Сунеличе11н
ем х точка А п еред н и1·иетсн по окружности
вверх и вл ево, сё r~ росю~ия , сстеств<;ннu, толь
ко влево, и при :>.: = rt/2 1<ос 11 11ус ста1ЮtiНТО1
ранен О. Точю1 А Rэтот момент под1r11 маетсн 11 а
максималы1ую иысоту , з за1·ем продо лжает
двигаться влеnо, 1-ю уже ст~нжаясь. Её абс цисса
всё убывает, п ока нс досттrптет наимсн ыnеrо
значения. равного - 1 при х = 1t. Таким обра
зом, на отрезке 1.0. тс] фушщня )' = cos х моно
тошюубываетот1до- 1(рис 16,а,б).
Вспомнив о чёнюсти косинуса, проанат1-
:шруем е1·0 наведе н ие 11 pt1 отри цательных зна
чениях а р гумент:.~ и получ1-Iм, что на отрезке
r- 1t. 0) функция МОНОТШ!НО воз растае-1 (')Т - \
до L, принимая нулеrюс з нач е ние ттри х = -п/2.
482
)'
у
а
у
б
~пх
о
}' = СО~Х
Рис. 1 Ь.
Если R~нть нескuлькu нериодuв, нолучится вол -
11ообрэ:щая кри ная (рнс. 17).
Итак. функция у= cos х пг1 1 нимае-1 нулевые
з11аче11ю1 н ·1очках ,\' = тr/2 + kл, где k - любоt:
целое число Макснмумы , pa1i 1~ые 1, дост!Н'а
rотсн н точках х = 2kтт.. т. е. с 111 а1·ом 2rt, :1 мини
мумы, paвru,1e - 1, в точках.\'= те + 21..>тс.
Фушщня)1 = s in х. Ещё раз построим ед1шич
ную окру-JКНос·1ъ с цсн·1 ром в начале коордшrат
п отсчитаем uт оси Ох угол х0. 1la ед11нич ной
окру-жности ему бу;1ет соuтRетствовать точка А
(рис t8. а), а сё проекцией 11:1 ос1, (~11 будет точ
ка N. Определим значсн1,1 с: функции у0 = si11 Х11
как орди1 ~ату тuч кн А. Точ 1<<1 В(х0; у0) прн1 tадле
жит графику фу1 11щнну = siп .\ · (рис. 18, б). ЯС110,
ЧТО ф}'JJКЦИЯ у= SiП Х перИr>f\ИЧССКаЯ. ее Период
равен 2тс:
&in (х+2тс) =sinх.
Возьм<-'м тепе рь два значения арrу:мента х 11
-
х. Тlроекцин соответствующих им точек А,
и А " 1 1 а ось (~) ' буду~· раслОJюжены симмет
рично от1юс 1 1телhlю точ"и О. Поэтому
ьiп(-х)= -
!>iп.х,
т е. с н 1 гус - футеt~11я 1111чё11тая (р1 н: 19).
Эа мет~ 1м тепер 1" что если точ 1<у А 1юнеr1 1у~ъ
относи ·1ельно то чки О на угол тс/2 против
часовой стрелки (дру1·ими словами, если }ТОЛ
х vnеличитъ 11а тт/2), то её ордината в новом
Pitc. 17.
положении будет pat1t 1a абс1~иссе н старом
Азнач 11т,
sin(х+~) = cosx.
Иначе 1·01юря, синус - это косинус, ~залоз
давшш1» на rt/2, посколък)' любое значение ко
синус::~ «повторится» в синусе, когда ар 1)1мент
у
б
у
N
Уо
.\·
х
Рис. 1 9.
Рис. 20.
у
х
о
Рис. 21
Функu ии
воз растёт 1 1а тt/2. И чтобы 1юстро11·гь граф~ 1к
синуса, достзточно сдвн11уть rраф11к: косинуса
на тr./2 вправо (рнс. 20).
Чрезв ычайно ~ажпое свойство синуса выра
жается равенством
~iпх 1
lim --=
.
\'-CJ
:Х
Его Уеомстрический смысл легко поня1ъ и:з
рис. 2J.Здесь х - Э'J о пшюнн11адугиАВ, а ::.in :х: -
nозюпи ~rа соотпt:Тствующсir хорды . Очевидно,
что 1ю мере сбл ижеm 1я точек А 11В,lVU1 1 1а хорды
ж:ё точнее прнбю-uкается к длине l\~ти. Из то1·0
же рисунка несложно изnлечь 11ераве11сгnо
lsm xl <lxl,
нсрное пр11 любом х
Формулу (*) математию1 называют за."1еча
телы-rым пр<.;дt:1юм Из нсё , в частностJ1 , следу
ет. что ~iп х"" .'\" rтрн малых х.
Функцииу= tg х,у= ctgх. Дне друп1е три
го r юметрнческне фующ1111 - та111e r1 с rt кота 1 1-
1·е11 с проще ncern опреяелнть каr< o·JIIoшe1111я
уже изnестпых нам сш rуса 11 1<0cлrryc1 ·
sinx
cosx
tgx= --, ctgx= -
.
-
COSX
SIПX
Как сrшус 1J кос1шус. т:ш1 ·енс 11 котанrе11с -
функции пер 11од1rческне , но 1·1 х аср1юдh1 рав
ны п, т. t: 01111 н;щос мены11с:: . чем у синуса 11 кo
crrr-ryca. Пrнчи11а 3тоrо 1юнятна . ест1 сш-rус 11
кпс11нус оба поме11яют знаю1 , то нх отн оше
J 111е 11е 11~ме111л ся.
П оскольку в :'!памеrrателе та11rе 1 rca н::~хо
дится косинус, то тангенс не оnрсделё11 в тех
точках, где косшrус равен О, - r<оц1,а .У = тr./2 +
+ krt . Во всех ОСТ<'\J\Ы\ЫХ точк·ах он монотонно
1юзраста<::т Прямые .У = те/!. + kтr длн тarrrcнca
н ню1ются верт.v11(~льны'lltИ ас1 1 м11тuт:н.1 11. В точ
ках k'тr. танге1 1 с 11 угловоrl коэффнцнснт состав
ляют о н l COOTBCТCГBCIIIIO (рис 22).
Кота 11 генс не опрсдел~11 т:~м , где с11нус
равен О (когда х ~ krc) . В остальных 'J'ОЧ~tл 011
монотшттю убывает, а прямыех = kтr. - его вср
тикалы1ые ас11 м11тоты. В точках .\.·
= rc/2 + kтr.
котапге11с обращзется в О, ;:i уrловоr'1 коэфф11 -
цпент в этих точках равен - 1 (рис. 25).
ОбратиJ.~ е тригонометрические функции .
l/,JIЯ Sin Х, С().') Х, (/~ Х l1 Ctg ."к.' МОЖНО 011рСДС
ЛИТЬ обратн ы е функщ ш. 0 11 11 обоз на ч ;,11отся
483
Л~rермИ I IИ ЗМ И СЛУЧJ lt НО\ТЪ
Рис. 22.
.\'
3rr ;
2•
Р11С. 23.
у
у=t:Lg.\•
.\'
соотвстстnс птю аr<..::-.ю .\' (ч1паетсн "ар 1..:сн 1 rус
х,·). агссо~ :х:. e1rcrgx 11 ~нccrgx. Jlo опрсдслс1111ю.
ап:-;iо х l"cn, такое ч11 сло у. с1то
-. it 1 )'=.У.
А1:-1 ~u101 ·11 ч но рассуж; \:L1от 11 щн1 11ру 1 ·11.х о\'°)
рап11,1 '< ·1р111·01ю .\1етр11чсск11х фунтщн11 . Н \) тэ -
1\Ое 01 1редслс: н11с е1 ·р~щ; 1 ет 11~котоrю11 11 етпч
11ост1 .ю.
Отраз11м siп .\",со~ х. rg .\· 11 ctg .У опюс11тень-
1ю 6 11ссектрнсы первого 11 треть~1 ·0 l(U::Щpa11
тоо 1юор7~шшпюf1 шюсн:ост11. Фушщшr II:J -:Ja
1rx псrшод 1 1ч1юст11 стали тr сuд11о:шачны: одно -
\1~ 11 ПJ\1~ Жl' с 1 111ус~ (tШСНН)С~, l:llll 'L'lll'~ , ко
та1 1 гс 11 су) C!)( ITBCTCTBYL"I ' (')(."CKL>lll'Чll()C K{IJlllЧl"
Cl DO )'01011.
Чтобы 1 вi1 ап пться от нсод 1rо:н1ачrюстн,
вы;J,сm 1м 1 1:11 ·раф1ш::1 каждой т р1 тгоrюмстр11 •1е
с rшй ф)пкц1 111 п о yLJ<KП<) L<pt 11 ю11 ш1rp1t11oi'1 тт.
ки 11м :1·1 с.11 hHO слещr э:1 тс.м. чтобы :v!CilЩ)' ,1pry -
\I<: l l'J 'OM 11 :ша Чt'Шlt.:M фуJ 1КЦJ11 1 соб 1 1 ю;1 aJ1UCb
кза 11мн о О;\Н():{Н;\Ч Н Оl' (.'(Н\ТIH:'l'("I Bll(" llY/\l'\t
111,1ri 11рат 1. у1~1с·1 ю 1 11 0()111 IЖL" к нa ·1 ~1JI) коор:\1 1-
11эт. R чзп·ност11, /\JIH фy11t<1l111 1 siп .\' 11():1м1е~1
)'Ч:l(" l'OJ< 1- -тr.j2 . тr./2]. ДJIЯ С< IS :\" -
(0, л]. /lIOIlg.\· -
(- тr./!.. тr./1). а /l;1a ctg.Y - уч;ктп1.: (О, тr). (k1~11i
пшеся фра1 · \1С11·1· 1·,1 1( р1111ы х c.rтcn;1 11 cnpan:1 от
)'
1'-
.ll't.:t'O~X
тr.
1- ---
-
у
тr.
-1
.\'
1· = .1rcs111 х
rr
2
1
1
1
-
1
'1.У
()1
Р1к. 24.
Рис. 25.
1'
1' = .11'!"1~.У
.У
Рис. 21>.
у
тr.
.J' = .IГLLl!!X
()
Р111.. 27.
\'ча с ~ 1<011 ст рём. 1 lосж· э·1·01о<У1ра :·11 1 м11с1 ·аток
1.;а;1що l1 кр11во1'1 от 1 юс11тслыю G1 ксек1р11 с1.1 .
Тепер1, }Же _-vюж1ю тосню опредvшть обрат-
11ые трнгонометрнчес1<ие фу 1 11щи~J IJa11p.и
Yll'J), пусть :{;~д ан о :·шачешн: аргумента х0, тa
IIOt\ что U ~ .\',, ~ 1. То1·д:1 :т:~чеLшсм фушщ1ш
1'11 = агсsiн х, , будt:т l'ДИHCtl:K' /-11-JOt: :{1-J:ILlб-JИl' .J'Ф
1:1кос,что - Р:/2 ~)\1~ тс/211.У1,= ~iny0
Киротко пt:рсчисл11 \1 ос1-юн1-~ыс: снойстна
п6р;с1 ных тр1 ll'ПHOMl'' l'(J ! IЧ (;:CK I IX фу11кц11 f1 .
arcsin х (р11с. 2-i): облзс1·1, 011рс:де:1е1 111я -
птре:~ш: 1- 1, l j; o\Jл:icтr, :111аче111 rт1 - 1
-
тr/2, тr/ 2];
\Юl ютонтю rю:~ растающая футпщт1:
Функuии
arcco:o; _,. (p11t. 2S): 06.1 1астn 011рс/{t'Ленш1 -
mpe;IOI{ [- 1, 1] ; 0611~1 Стt1 : 111:.1чс11111~1 - (() , 7t}; МО
!ЮТОIПЮ убывающая ф) tt1'1 lttн;
arctg х (рнс. 2(J)· область опрсделетшя
-
вес дсйсгшпслы1ыс чнсла ; областr, з1rачствтй -
111псрnал ( - тr/1. тr/2) : мо rютотrrю nоэрастаю
щая фушщ11я: пpJL\lЫl' у = - тrj.!. 11 у = л/2 -
J'UP• I J()I JТ;1.11ы !ЫС al't l iVll !TUTЫ;
arcctg х (ptlC. 27) : ol)Л:Il"IЪ ОП(J<;Д<.:ЛL:IJИЯ -
нес ~с11стн11п:л~.ныс ч11сла ; область :3r-1aчc-
1111i'1 - 1111тt:р11ал (О . n): мшю·1·0[ 11 1п у61.шающая
фу1 fl(ЦJ !Н: Щ1Я ,\1l>le.J' = о 11 у = тт - 1 ·op11ЗO!f'J ':1JI1,-
11ыe аси~111тот1,1.
КАСАТЕЛЬНАЯ К ГРАФИКУ ФУНКUИИ
l IOШl'J'!!(;' t<:l l'a 't'(;'JI Ы L/Jit - 0 } (1 !О ! 1:~ J\(Jt:IШt:it111 l·IX Н
\l:!П.: .\1:1'1'11 кс. R l'l:Cl\1CTp111 [ к:1 еп СЛЬН) /() к окrуж
][()СП! 01 1 pc.:;~t:!! ЯHJT к:1к tlpfШ)'IO, l ! ~ll'H) lf 1,)10 рон110
r>; ll 1у 'l'()Ч 1.:у J 1ерс:се чс-11 (IH l' :'l 't'Ot't О t<руж11 OCl'I)(()
,"{рсrнптс с гrо;>.rощыо 1\нркуля 11 л~ 11 1бr1.:11 )'мелtt
проrюдпть к:к:.пелы rые к окррююстп (рпс. J ).
,t вn о с:1едсти ни - к 1.;о ш1ческт1м сечешrяи:
эллш1 с;1;>.1. пшерболам 11 гrарабола:-1 .
1111тсрсс к кас:tтсльпым но:3роютлоr n 1Jono c
врем.и. ТоЕ ·да быш1 0·1·крыты кр1шые, которьL"\.
нс :~1-1;ш11 учсн 1)н: ;ц1с ю-ю1.:т1 1 . Harrpirмcp, Гam1 -
nc i'1 1тёл 1(11юю1щу, :i Дск:1рт 11 Ферма rюстро1 1-
,11 1 к 1161 касат<::J 1ьь1у10. В 11e pfюt1 трст11 XVJJ в.
11ач<1.'!!1 l[(JНllM;(Th. что K;1C:!TCJ11>H:НI к кр11rю~:-1
()11ре~емн:-· 1 ·ся 1юведе 11нt'м :-ноl11<р11 1ю 1 1 11n1111з 11
тr>чю 1касш нщ что касзтслытан - пря~1ая. <· r1а11 -
болес TCCJJO прI!J\!ЫКающая» f( Iq)IlПOif Т\ M3ЛOJJ
окреспюсти з::щашюЛ точы1 (хотя ~асзтелы 1·ая
\ЮЖСТ JJMCTЬ Г,'"(С ТО nJ\3ЛII ОТ T01 !IO I 1<аса1н 1я 11
другнс псрсссчсшш с кршют1, рве. 2) . Л егко
нр сдставтъ себе 11 такую снт; ;tцню. ко1·да
н с лr, :ш 110<." 1· ро11·1ъ каса ·r ·слhную к кр 1 1ноi1 н
Д;JlflIOJI '\'01!Kl' ( J11 !С. .~)
ТТо стро<.:1111с касатсJ11,11ых - од~ 1 а 11:{ тех
за1рч _ кот1>р1.1 t: пр1~нет1 к рож;\сн11ю /(t 1ффс
рt:1щ11 :1 111;1101 ·<>11сч.11слсш1я. lkрвый oпy6JlltкO
JШ1 1 rыf1 трут~. от~ юснщ 1 1!1сн 1\ /\t1сjхререш.1,11ат,-
11 о м у псчнслспшо и пршrадт:жащнl1 перу
Jlе!161шца. 11ме; 1 11азваш1е ~ новый метод иак
шмрюв 11 мmшмумоn. а также r<асателт.пых.
;~1я которо го пс служат nрсшпстт 1см ш 1 дроб
ны с 1111 11 рра1(11ш 1 ;u1ы 1ые не; Е11чш1ы , н особь11'1
, !. ' IJI ЭТО\ '() рон llCЧHl'JН..' Hll~I ~ .
llyCTI) Kj)lll\aH l 'l'TI) 1 · paфLIK ф) 'НЮl,1111 /(.\') ,
11.юб1х1ж<.: 1 1ныl1 11:1 р11 с 1. 11 требусто1 111 щ 1к:с
т1 1 к:1с1•гсл 1,1 rун) к :~тоl1 1ч111 но1'1 н точке .\·<··
1l<X"1 'y 1 111~1 с11е;(у1Ощ11.ч 06р. 1:i1>М. Во.1 1,мt:-vт точ
ку .\' = .\'•1 + Лх, \1m 1:it<} ю 1<., ·, 1. 11 11 ро11е;tЬ1 ч ере;1
ТОЧЮI (.\ '! "/(.\ .'
0 ) ) 11 (.\'1, + !\X;J (.'\',1 + t\.\')) 11рНМ}!О
(<.:екущу,о. как шюгда говорят). Ур"ш11с1111с сс-
1<ущей. 1с11.; 1tетруд1 ю 11ро вертъ, I L\·1eeт 1шд
)' = k (.'\' - x,i) +j (.У0),
Р11 с. 1. Г\11< 1 ро1 · 1111и
к.11 а m.\ь1ю11 " ш.руж1ш< r11
IL'p(· J 1оч1< у /-11 IUЧl(J
к.11 ,1н11s1 1\ 1, or но в.1нное н ,1
'°"' ·ч l (J 1f>l'YI OЛL>lll ti- ЛОВ,
t111~1рf11оши~н ~ 11.1 л1мм1·1 р,
прямоуrо\ьн1>11l.
Рис. 3. Кривая, н~: 11мек~шая
k."H. ilП-';\blll)Й И 1o•tKE' /\ .
Риt. 2. kдt,lТt'\bH~я "
1р.1ф11ку фун1о.111111 у= " н
точ~..е ' =~ = 1 n1:р<'<:ек.1t>т
1р,нtнtк <' lllP А олнсн1 TO' JKP .
ffМ
г
Рис. 4.
l'ДС
)'
Летерминизм и слу чайность
}''" + "-'! - /(х;.)
---- ------ ,
-
Xu
Хо+ЛХ
k = /(:х:11 + ЛХ)- /(:х0 ).
д.Х
х
Если су1цесrвует пре,l\ел
r(x" + л:х) - fi(x.1 )
liшk=l1m ·
"
'
= k0,
.J.X~ O
..'. s-11
ДХ
то прямую
7'(х)=k0(.'\" -
Х0) +I (.У0)
11 11аз h111:tю ·1· лдс{,ти1.лыюt1 л. t/Jафил.,1,1 Ф.1 111ю~11и
/ (Х) 1~ тич1се x(I Есл11 ска1а·1ъ 1111.1ч е касатель
ную "10жнс1 ш1ределн1ъ как пря.v1ую, К()торан
я11. 1яе 1 сн пре1~слы1ым rюложен н см секущ11х ,
rюr,ri;a Л .\стремится к О (р1к 5)
Из оп ре11еленин в<::.тп1чтп1ы k 1, пнд110 , ЧТ()
фVIUЩilЯ
Рис. 5.
сrрем нтся к(), ко1 ; ~а лх стремитсн 1< () ТТuслед-
1 1 ее ра uенство озна чае~ что
/ (x(I+ЛХ) =/ (Xn) +!?,, лх+а(Л.х)Лх,
т. е.
/(х)- 7(х)=а(Лх)лх.
ще х =.'\'о+ Л.'\" f(p~'J'~IM I J CЛOR<IMll . чc:vi бл11же х к
х11 ('1' е. чем ме11ы11с дх). тем cJJJir, нcc секущая
~ щтж11мастся ~ к граф 1 1ку функцш1 н 1ом
см ысле. ЧТ() ра.нюсть/ (х) - Г (.л:) стре\111то1 к
нулю е щё б1 11с1 рсс, чем лх Среди нссх пря\1ЫХ,
rr р()ХОJ\ЯЩНХ чере:1 тпчку (х0,/ (Х0)) ;п11м с воil
стrюм обладает л 1 т11. касатслыrая.
Производная и интегра/\
ПРОИЗВОЛНАЯ И ИНТЕГРАЛ
ПРОИЗВОДНАЯ
ТТокяпн.: произ1ю11ко!1 tю3никло R результате
11011ЫНЖ 11pr Щ3'ГЬ l'О ЧН.ЫЙ С МЫСЛ 'Г,I IO I M ПЫ!l~lЖС
llНЯМ, как <· с1<ороС1ъ лnижешrя в да 1п1пri1 \1О
~1е11т времени> и <· К.tсатслы1ая к кривой п
дашюй точке,>. К э1 Иl\1 понятиям пр11вод11т
рассмотрение многих естестветшо- 1 rауч1 1 ых
·iад.tч. Например, движение 11ското роrо тела
11од действием тех нш1 1шых снл обычно оm 1-
с ынают сие1·емо1! ур.1ннс н1Ш, которая н кюкдьн1
\Юi\н;нт временп с 1н~ зынаст меж;1у собо 1'1 коор
дш1::пы ~ела. с 1<0рост11 11х t 1 :iме11е 11ия 11 скоро
сп 1 и с1\1снсния э·1 н х скорос·1 сl1 .
Предст<11111м Lебе , что 1ю дорu1 ·с /~вижстся
а1помоб11m" ()бо:знач1 1 м чepe1S(l) rассюя11не ,
nройлсmюс им к моме111-у нреме 1 111 /. П ус1 1,
Л/ - нею 1й промежуток времени, прvшсmпнй
1юс11е моме11·1·а /. То1 ·,на очеu1щ 1 ю, что раз ность
лs = S (t + Лt) - S (t) сстт~ длина пути, 1<оторый
;нпомобиль преодолел за вре'v!я Лt. Ecm1 Лt до
статочно маJю, то скорос1ъ а1ломобшm за этu1
11р омежутоксу11(ес1 ,нс::нно не i'I J'v1 cннл.t<- ь. А Jн..1-
чт , то, ч·1 о м.ож1 ю 61,uю бы '"131:1а·1ъ скороt·1ъю
двнжсн11я ,1втомп()пля вл~1 кн1>1l1 момеrп време-
ни, пр11ближеш ю раю ю средн е~! скоростr 1 с:1·0
движек1 1 я за nремя д t. т е 1~ел11чи11е
Л<\ S(I+Лl)- S(I)
Л/
Л/
Ч ем д/ меньше, тtм это пр1161шжсш1е луч
ше, н тоr'Да еегествснно онредtлш ь скоро<- 1ь
l ' (L) дш1же 111 IH aH'l'O\i\OбlJJIЯ в IVIOMCHT нремсн11 /
Д(!тt~рми ни ~м и случJиност~,
1\:11< 11редt'JIВс:личтп1ы ЛS/Л! т1р1r стрс:м 1 1 е11 11 1 1 Л/
кО,т.с.
(/) 1
S(L + Лl)-S(t)
/1
=
111) -------
\1- 0
Л/
.
(*)
Е1ю1J1.1 об ра ·ю ,,1 , ссл1 111 звсст11 а фу1 нщня.) (/),
u 1111сы 1:1аю щ ;\}J расстш1111 н: . 11JX>i'1;(c111 юс 11 скu
·rоры "1 Tl:Лl)JI! к MOML'f l ' I ')' нpt.:\1l'Шf /, 1(), по фuр
мулl' ( *), ,\IOЖJ [() н1.1чт JCJll п 1> CKO[XK'l 'h /\IНIЖC IJШ!
:~тогп Tl'JJ:l n каж,п:ыГ1 мnме1 r·1
· uремt: н11 .
R к:lчестnе прнмера тшi1n,ём скпрпст1, crю
(Jnд1 т n 1 ·0 IЩЦC'IIШI J\;lMl lЯ . который /1.С [1Ж(IЛП f\
руке r r~1 рассгоашш 0 ·1 земл ll. а :затем просто
1:1ыпустшп1113 n;L'1ы1св. Соглас1ю закону, откры
l'ОМ] 1 па11ы11 1сюr.'>1 учё11ы~1 l'amiлco l'am.mccJ\1,
пугь S ( t). 11 1ю1\1 \t' ! 1111.1 1'1 ка~·11 1ем Ja 1:1рс.мя /, ны
ражаl" 1 01 ф( >р,1у: ш1"i
с
1,
,)(/)=l!!.1- .
t','[l' ~ - K(llJCT:111т :1 ( t'CJ ll 1 вре.\1Н / 1l.!l\l t'j)I11'1· 11 l't:-
I~) 11; 1ах, а расстояние .~ n мстр:~.х. ю ,g 11 р 11 -
\im 1жL'111юра11110 1) ,R м/с\ Л,ю1 т< >1 ·0 чтоnы вос-
1ю111):1он~1ться фармуJюl 1 ("'), 11уж110 по,ткч 1 1т:лъ
pa::irюc1 ь лs = S(t + Лf) - S(t):
•
J
J
1'
S(I+лt)-
.'.(f)=2RU+Л1)-- -:;i-U- =
1'
1
'
J'
=- 0/ i О/Л/+-"(Л/)---01--
2 ,..,
,,,,
2 ('"/
2 ,..,
1
'
= ,g!Лt +
2 g(Л/)-.
С-:ле;,онатvrы ю,
S(I+л1)- )(/)
1
------= о/+ - "Л/
Лt
,..,
26
llepвoe слага<:мос в пра11о i1 •1асп1 равс11стn:t
11с :>:11111 с1 11 о 1· ~/. а щк·.и,сл 13тор ого. 0 1 11.:1111;-(1 IO,
j):ll:l{:H () 11р11 Л/ ~о. ll OЭ' l()\'I)
1
.
1
{'(/)= 111)(.Ц/;-- <~ ,\/)= .~/
\J ~1)
2
Итак• .,,11,1 11 ;111 1_. 11 1 с1.;:оро<: 1·1, сно1"'>0:1ного 11 :1.'1t· -
1111я н.:-ла , 1J она Ш\<1 ;}~1..1~к1, 11рамо 1 11 ю 1 н1р1(1ю-
11а,1ы ЮЙ нpt'Mt:LШ.
Н гг;~п.с '· l<ас:пелыrан 1< графпк5 ф) т;ц1111 ·•
1101-\а:1атю, что ураш1сш1е к~1 са·1елыюi1 1,: гр;1ф11 -
к~ ф)11КШП1j(.\') в ТОЧl\С .\"" 11мее1 llЩ\ '/'(.\') :
= k<1(x - .Ур) +/(.У, ,) , те угловоiт коэфф1щнентkn
опрсдсля е1п1 1ro фop 1'1 }JJl'
1
1' / (.\'1) + д.\') - /(.\',,)
!<\, =
11n
.
1 1-н
Л.\'
Сра в111111:~я 11ыражl' 1111н ct) 11 С"*), \1Ы вr 1н1 1\1,
ч то 11.ЛН опре:tё' J 1е1111>1 pa 1.'JllЧl 11>1X п о C llOC,\IY
CMlilCllY 11t:Jll [ЧHIJ l iСПОЛI,;1уето1 O/ll1:1 11'1'<1Жl' про
ЦС,11)113: в д:ш1юi1 точке х11 нахонят npe, \eJI от110-
шtнш1 прнращс1111н фу1 11щ1 11 1 д:)' = /(х, ) .J . Л.УJ
- J (х(,) к прнращсmrю арr~ме1па лх = (.\'11 +
+ЛХ) -
. \', , нр 11 услошш. ЧТО пр11ращсш IC ар1у
ме нта стрем 11тси к U. Яcllo, что этот преде:1
.\1ожст бы·1 1, 11:11'1J\l'l 1 11<:з:11111с11 мu от 1..:aкoir -.111 60
l'l'U ф11 з 11чсс1шеr 111111 1 ·со~\1 С'1·р11чсскоt'1 ннтср-
11рста1ti111.
И1: 1к, ДJIЯ нrобо~'1 ф~·111щ1111.fксm1ч1111:1
ll1п .f<x,,+Лx) - .f(x1 ,)
'
1 •(1
t\ ,\"
("'*)
на:~ываегся 11/юи:юоП1ю1/ ф1 •1tю(1111 Гв 11ючл·е х,
11 обозначается ('(.\'11 ) (чита ется ··Эф штрrL'\ от
1шс rтул~,~ ). Из сравнс1шя выражс11111'1 ("'" )11 (** •)
ЯСi:.'11 Гe () ,\lt'I p11Чtl'KllJI CMЫC: J I пp011 :i n o,r11юll
фую,цш1 /к т1>чке .\'0 : ('( .\'0 ) сеть )'l'ЛОВОЙ ко
dфф111t1н.:нт к:н:~1 ·1eJ 11>t1< >l1 1\ 1 ·1 ):tф1 1 ку функц1ш(
у
/1•= ~·(х -х")+j(x0)
/
/(.\'(! + д.'\')
,/
1 ~ /'(Х11)(Х -
.\:1, ) +/{х,1)
х
о
Р11~. 1.
11 ·~·очке ·'"н· Чс'>1 ()()111, 111 с 11рог 1 :то;\ 1 1:~я. тем " 1<ру
Чl"' 1раф11r< фуню\и11 11 л.1111юl1 точке (рве. 1).
Ест1 фуr11<1\1 1Яj в ~ очке х ~ ~мест про11з1юд-
11:10. ' 1. е . сущсстuуе-1 ко11ечвый предс11 ("**) ,
фушщ11я j 11а:н,rnж1·ся дt1ффсре11цztр1 •с.1110[1 в
IJIO'IЛ"(! .У. Есл11 же ф~1 r кц1rя ю тфферспr~т 1 рус.v1а
в каждой 'J оч 1ес нскосr() 11 нтсрна.11: 1 . тu 1·()1юрнт.
чю ф~1 1 кцня r)uффefJl!11ц11n) 1('.t11a 1-1 'J11m11 1 mm1ep-
вcu1l!. Н таком случ~1 с::: мuжно 01 1 рс11.с!111тп 11овую
ф~ 111<1 \ 1 1ю/', 1ш· 1 оран соrн JСТаюшс:·1 каж;\<1[1 ·гоч
К(: .\' 11 .{ i~а11нш ·о t 1 нтсрн:11t<' Чlf<-'JНJ/'(x). Е~ ес1·с:
ст11с11110 1J(!:~ка·1 ~, 11рщц1юд1иН1 фy1110{lltt I 11rt
дttlfll().11 1/1/Jllf!jHJtllU!
F:cmт фу 111щ 1 rя /' в 11екотороlt ючкс _, . са~.1а
11.чсст 11ро11эnсщщ ю. 'ТО ;;~ту 11роr 1 зnод11у10 1 1азы-
1~:~ют второi1 111ю11зво(>1 юй фу 1 11щи 1 r (11 точке.\·
11 обоз11 ~1чают.f"(х). т c.j"(.Y) = (j'(.\"))'. Понят
но. ч.то э1<r>т ттрощ.:сс vюж.но пμо,\011.жнп. rt оп
редел 1 rг1»1ретью 11ро.1пщ1J\ ную. че- 1 в<.:рт~ю1 1 т J\
Пpo11 :ШO!LH hlt' м 1 ю1·11х э11<;.\1снтар11 1,1х фу11к-
111111 (н:111р11J\н.:р.х11, -. i11 .'\', со-., .\' н /\р.) мо1у1· Выть
11аl1дс11ы Hl'IHKpt:дl l' Hl'Hll(J, т. с. с 11Lll()Jll1.1()11a-
IJI IL"vl ·ю.1 1 1,ко опре;1елсн11>1 В ч аст~ юсп 1,
(х")' = /1х11-1.
(~iП.У)' = C<J~ .\ " ,
(cosx)' = - s i11 .\·.
Саму 1 1 μ<.>цС,Т{)'РУ 11ахожд<:1шя r1 рон:шо11ной
на::~ьтают диффе/Jе1-1цuрuш1нuш1"1 Кр<.>м<.: то1·u,
l')ЩCCTll}'IO'I' 11рав11ла ю tффt:pl'HЦI 1рон:1 н1 IЯ C)"Jl.1-
~lhl, про1пш.:!1,с.: 1 шя 11 час1 нш·о днух фу11к11,1111
/ (х) 11R (.У):
(/(х) + ,~ (х))' =/'(.\') + t:'(x).
(./ (.\') М (х))' = ('(.\') .~ (.'\") + ((х) J((.\:) ,
1
(
) (х) 1= j'(X)f!.(X) - J .((x)j'(x) (Ц(Х) ~О)
!{(Х) ,
Д!(Х)
Пr>m1з1юлная и 1111тl'Грс111
ЧТО ТАКОЕ дИФФЕРЕНUИА/\?
Посмотрим на nон>~тиt> прои :.нтл нои с Нt:'СКолы<п
и1 юи точки зрения. Леn<о видет~,, что если nрои1-
вuл11ая 1 '(х,,) сушествует, то 11 р~ел фу 11 кuии
( ) r(x0 +дх)-1(л11) .,(
)
CJ.дХ=
-
tХ
д\
(>
аргуме н та лх рапе~~ О при дх, гrрсмяшемся к О .
Лалее, rюскольку
f(x,, + Лх) = 1 (л 0) + (' (х,1)Лх +о: (Лх)Лх, {*)
пJ при малых лх фу11кuия 1 (х,1 + лх·) аргумента дх
отличаС'тс.я от ли 11еиноi1 функuи и 1 {х0) + i '(х0Jдх
ли ш ь 11а ве11ичи 1 1у щл;.. )Л..\. ПО< лед11 яя <тремипя к
О еше (>Ы( трее, чем лх:
<l\Лх ) 1\х
11111
= ltm 1~(Лл J =О.
~х ~11
д\
\' •!\
Лруг и ми слоuаV1и , 1.ру11кL1и11 1 лифф~рt>1 1 ш1ру
емая в точке х1,, при з н ачениях аргумента , бли{ 1<11х
к х.;, ,.,,южет бып. достато ч но хоро11ю nрибл11же11.:1
( или, KiJI>. ГОВОfJЯГ, <1ППРО/\СИЛ.fllруем.J) MlllCИllOЙ
фую, 11 ией.
~ ф(\рмулс> (•) лин<.?И 11 зя фу11кu11я ('(х")л.х арrу
м~ 11 rд Лх 1-1 а iЫ J3аето1 л11ффереlfиналом фут"и111r i
в точке х" и оfiо~11ачаt:!тся 1/1 (хп) и11~1 про< то rlf. Сле
луя ло гике эп1 х обо~нич ен 1111 1 ли 11ш1ную фу н кuию
лх (которая Lоnос.тавляст Jначению аргум1:>нтадх
с-с1мо Лх) об<нна•1.~ют dx и 11а3ываю 1 л11ффере1ши
алом HI:' 1<1m1( нwon 11ере\1енноо . Т.жим оf)ра.юм,
с/Г =t '(х,,) dx. Отсюл.t nолуч.1С'м другое выр.:1же 11 ис
ЛАЯ l lPOИJ IIOдJ IOИ как 01 11 0Шl::Ш1(.' доух лиффе-
f)(.-)HU\1i1ЛOH:
{'(/\) = Е!....
tlx
такое npt1Д( 1<1UЛеНИ(! 11 pUИJBOд JIOl1 , BUCX()MI Wl't '
к /\еиfiн иuу, ча( то оказывае1ся улсЮным, о< оfн-'н
но красиво Jа n 11с1.,1в,, стс~ дифференциал сложно11
фу11юJии {(х) =~(blx )). TorлJ cH=t?,'d/1.
у
<!l.=/\\)
rl\
{----------- }
: (/. дl\
1.3у
~7
_::-~-_:}dy
()
1
1
·'•)~
Лх=dх.
-J
-8<)
Леrерминизм и случайн()СТЬ
ПРОИЗВОЛНЫЕ НЕКОТОРЫХ ФУНКUИЙ
Конста1па:
Линейная функuия:
Стеленная функuия:
Показательная функuия :
Экс1-ю11е11та:
Логарифм:
Натуральный логарифм:
(а)' = О.
(ах+ Ь)' =а.
(х•)' = ах-1 •
(а•)' :; a' ln а.
(е')' =е•.
1
(log.x)' = --.
xlna
1
(lnx)' =-.
х
Or 1и позволяют находить нроизводныt' мно
г1L-х функций, котuрые являются комби11 ац11ей
нескольких основных функцIIfl. IIапр11мср:
'
)' (siпx) cosxcosx-( -si.nx)sinx
(rgx =
--
=
'
=
cosx
cos- х
cos~ х
cos~ х
Правило дифференцнро1:1ан.ия слuжtюй
фушщии ещt: более р;кш и р11е-1 · кол 1 1чсстно тех
фунюt1 1й . которые r111фферен 1 11·1роват 1-> дост: 1-
то чно щюсто Функц1ш/на~{ЫВ<1 стся ИIO.?IC1Шil,
ссл11 <.:t можно прелстан1п·r, 1s ниде у = .f(х) =
= R(/1(x)). где у= g (f) 11 t = f1(.\) - 11ек11е фу1 11<
ц1ш. Г(тuряттакже, ч·1 ·0 фу11 1<r ( 11н/11rедстэ 1im1 -
ет соб()т1 с.у11ерпо:щцто (или ко.мпо:щцию)
Э КСТРЕМАЛЬНЫЕ ЗАЛАЧИ
l) задачах на максимумы и м.ини м умы мы
\1:.111аС::м в н11<оле. \3()т ол11<1 из 11 нх: требуется
найти наибольшую 1шощадh t1рямоуголы-1r н·о
трсут·оm .т-11-1ю:1 с :.~зданной суммой длю-1 к:лттС)1-1.
Зто :1щ~<1 ч а о .мсщ:с11.ffум&. Ro мноп 1 х случ аях
1111 ~yr _л-1и11им)М1. - щ1име 111 , 111 ее 1 1 1а,1е11ие чеJ·n
лнбо. Обэ r юннтин, ;v1 аr<симум и ми11 и мум,
об1JС!\И1 шютат п:рмипом .сжстре.му.м (от лат.
extreшum - «крайнее»). Зада ч и на отыскание
максимума и MIП 1Иl\1)'1V1 a 11 азыnаются зк.стрс
_л~алы1.ыми 3адачами_ Почти тот же смысл вкла
дьшаетсн в термш-1 ~задачи 01п1 1миз:щ1111».
Ра:.~ныс r 1 р1Р 11 1 11ы 1юбуж;1ают лю11сf1 рс111атn
:3~щ:1ч11 1 1 а :-.кстrсмум. / l.об1 1ться 11:11 шыс 111 сго
-NU
Тригонометрические функuии:
(sinх)' =cosх; (cosх)' =-sinх;
(tgx)' = -
1
-
; (ctgx)' =--
1
-.
cos
2
х
sin
1
х
Обратные тригонометрические функuии:
(arcsin х)' :; ~ ; (arccosх)' = -
_{_l _;
v 1-x
2
•1-х2
(arctgx)' = -
1
-
; (arcctgx)' = --
1-.
1+х2
1+х 2
функций h 11 g. Про 1 1зводную СЛОЖНОII функ
ЦИJ! ВЫЧl l СЛНЮТ по правилу
j'(x) = g'(f1(x)) · f1'(x) ,
r·де 11еrвый сомrюжитель fl пrатюй чэст11 060-
з11ач.ает nро11зnою rую фу11ю\11и ~ fl точке t =
= h(x). Например. фупкци:ю rg :х можно рас
сматриuать к:~к суперпозицию функций t =
= J1(x) =х1 иу = UU) = rg /.Тогда, согласно при
веденному нравнлу.
5х~
(tgx ~ )' =---
cosJ х' ·
E<..:Ju1 1н1е1ъ 11сrед 1·лаза:.111 таfiл1-1цу про11з·
IЮ)ЩЫХ основных ;7лс:Мt'НТ<1.р1-1ых фу11кцнrr. то
1ш й·1·1 1 111ю11 :~ 1ю; 1 ную 11Jl<1.К'1 11 чесю 111 юбш1 фу11т<-
1(1111 бу;(ет совсем 11етруд1 ю: 11en(Jx()J11 ti\нl толь
ко аю<урат1 ю оrе;lонат 1 , сформул 1rротн н1 ым
nыше праnилам диффс:ренцировашrя.
прп :iаданных услшшях реiультата (пrп6ыт 1,
MOЩH OCTll , CKO!JOCTll) 11!1 11 l lO l-l<.:C'l'lf H:l llMCHb-
l llHC JJ0'1·cp11 (l~reмc 1 11 1 . м:пср11;111сщ ;-1 11er1·111 1) -
желан~ IC ШЮЛ!-IС ПОНИТl-IОС ~1 L:с1·сс.~1·вс1-шос:. По·
атому з;·INI Чll ОПТ ll МИЗ31l11Н llL'(l<l.IOT большую
рот , 11 ЭK()llOMlll<C и тех11 (IKC.
Друган 1 1рнчш1а может rю1<а:1<l'1· 1 ,ся 1 1 еожн
l\<U 11 юl1 : 1\31( 1\ЫНСНИJТОСI>. м1юrr 1 е :з:ню1 1 1,1 11р11 ·
роды ос 1 юnа11ы 11а экстремальпьLх пр 1 11 щнnах.
1Iапрнмср, луч спета распростр:щяето1 по са
мому быстрому пут11. Пщрагору приналлсжпт
выска :i ыв:н111е: « Прскрас11сlпш 1 м телом ямя
стсн ш:~р, а 1 1рскрас11сйшс1J iiлucкolJ фнгу·
ГIOlt - кrуг~ 1lочсму "РУГ н 111:1р - «1 1\Х:крас·
нейmие»? Ниr<олай Копертшк в бессмертной
ю 1иге «Об обра щения:х пебесщ,rх сфер» даёт та
кой ответ: <- М ир является шарообразньrм". по
тому, что эта форма обладает наибольшей вме
стнмостъю, что более всего прили<rествуст
тому, что должн о об-ьять всё». Ин;1че говоря,
р~1змышляf1 о строении мира , Коперник пола
гал , что его «архите ктура» гюr~чине на принци
пам экстремал ьн ости и совер111енс1·в:~ .
Зад~~чи на максимумы н мю1нму~1ы Rcer,цa
при мекали внима11ие математико n. Вс1 реча
ются они и в трудах трёх величай ших геомет
ров Дре вней Гре1\и11 - Еt~КЛИ,1\а, Апотю11ия
Пер rскоl'О и Архимеда. 13 « На <1 алах» Евклида
есть такая задача: 13 треугольник !lBC нужно впи
сать nараллел01·рамм CDEF наибоnъlJlей nлоща
ди (рис. 1). Ар11:11мед нашел шаровой сегмент,
nмещающиt1 максим~ш ь ный объем сред и fIO:.:x
ссгментои. имею 111 "1х з:~;~а нную п1ющ~щr. боко
вой rюнеrх 11 uсти (11М ока~аJ I СЯ 1LOJ1y1ш1 р). Алuл
лuний отыскивал кратчайшиt' расстоян ня от
точки до элли п са, гиттсрболы и параболы . Мtю
rне краспные з:~;~;ач 1 1 11 а э кс-фс:-,1 ум геометр1 1 -
ческоr ·о содержа ния 6ылн рещены 11элол.')'13оз
рuжленил.
К 30-м rг. )(VIL в. пояш1лась 11еобход11м ость
отыск:п 1, какие-то общне методы рсшешrл
экстремальных за,11;а ч . Ilcpnr.111 анал11тичсск11й
nриём был пай; 1ен Пьсро,..,1 Ф<.:.рма. Открытие
состшuюсь. tю-в1 щнмому, н Lo29 1·., ~ю н1Lерв ые
автор ДОСТ;JТОЧН() fIOJJHO H ЗJIOЖHJJ с~ю1'1 M e'l 'O/(
тш1ько н 16.-)6 1·. Лриi.:м Ф е рма <:ЕЮ/ ~ ~1 тся к слt:ду
ю1 цсму· ео 111 фуню.~ня у=I (х) л.остн 1 '<К"1· свое1·0
экстре мума R·~·очке .У, то 1 11~:11-1 1 ю1~1 точl\е про 1 1 з -
1юл11а я фу11кцни до11жт 1 а обраттъся IJ нулг"
1". 1 .: . '"стжно >~мет,, место раненстно ./'(Хо) =О.
Намtкн 11а :':!тот нриём 11сч>счаются ·1·:.~юке в :1н:.1-
мешпо11 кнr 1 гс Ио1·ашта Кеплера « Нонан стерео
мстрня в111-1ных бочек» ( 161 5 г.), t'ДС учё11ый
решил множество интересных за,Т\а•1 11:1 м акси -
Р"с. 1.
Производная и интегра"
м:ум и миинмум. Кеплер писал: ~вблн;ш мзкси~
мума измепетшя <функции> бывают печувствн
тельными». На rеометрнческом языке мыслъ
Кеплера и результат Ферма можно выразип, так:
в точке э кстремума касател ьная к ~рафику футп<
ции {!;олжна быть r·оризонталыюй (если каса
тел hн:-ы не 1 ·оризо 11тал ьн;1. то изменения функ
ции ~чувстRитеJrъны»). Ньютон высказ:ш ·ry же
мысл1, п о-друго му: ~ко 1 ·л:1 величнна явля.стся
макси~альной юш мин11ма11ьной, она не тсчёт
11и вперё;1, нп 11азал» (pr-1c. 2) .
Ферма 11ро11плюстр11роваJ1 с1ю 11 метод нз
приf\\ерс той геометрпч еской з:щачи , с кото
рой мы начали расска3. Если через а обоз11а
ч111ъ сумму катетов, а через х - дл11ну одного
из 11их, то площадь nрямоуrолы-юго трсуrоль
н ика пропорциональна х(а - .-~.·). Уран ненпе
S'(x) =О имеет едю 1с1 ·венн1>1й корень ~\:<1 = (1/ 2.
Это 11 t:с 1ъ реш~н11е за;(;.tЧИ : у 11р}.(моу1·олыюго
треу1·ол1>1 1 11ка на11большеf1 площ:щн к:1п.:ты
равны Интересно, что за;tа<1а Евю11ща форма
лизуется тпчтю так же: еслн д.r1 111 ту сторон ы ВС
обоз1 11чпть ~1ере:з а, та площадь ттараллсло
фамма CDF.I' про rторцно11альна S(x) = х(а - .У).
Знач11т. у параJL'ТСЛОI'ра.мма ма1<с11малы юli пло
щади то чка Р - серсщша стортп.1 ВС
Точпыil смысл идея Ферма праобрсла 1 1е
сколько Д<.:СJ!ПIЛСПI Й спус 1·н в 1684 r. I IOЯШl
Jl:ICЬ раnота r ·uтфрн;t~! В11т.1·сльма Лсl16111ща
4 f-Jоный мет011. нахож1lс1-шя 11а11бол1>шнх 11 нal'L·
меныш1х значени~'1...- >, R которо 1:1 : ~шюжены
OCHOHhl .М:l'l'ё'м~l'l'HЧtTKOl'O ан;~л lIЭ::t. Уж<: само
назва1 1 11е труда пок<l :\ываст. каку10 важную ронь
с 1,1 гр :111а :~а ;1ач:-1 о ла,..юж11е1 1и 1 1 экстрс~у м ::t в
стз 1 1 овленнн с0R рем с11 1 юй матем:.~тикн. Бот,
шипство и:щаrае'l.Н»Х Ле 1'1бшщем фак·т()В (шло
к тому времени известно Ныото 1 1у. 1111 рабт·
на эту тему ло 17:)(1 г. ов нс 11ублт11со11ал.
С.:ж:дующ>1 й шаг 13 теории экстрем-у1V1а был
сд<:лан, когда стали нска1ъ крнn~,н.~, 11 аш1 уЧ1Ш 1е
у
И
Хо
Рис. 2.
,.ic) 1
Лt:.> rt:.>рми 11и зм 11 слу ч J 1111 uсп,
с тor't 111111 11110(1 · 1 ·<1 чю1 :чх· 1 -J11}1 . Пt:рк~-10 ~<t1 laчy
тэ1ш1·0 poJ \~t pc11111J1 Нь1ото11. ~-Это тех1111ческз н
3;щзч:.1 t> 1ю11срх 1 [()C'l'tt 11раще 1111 н. 1 кrтытъша
ющtI1 11а11м е 111 .1 11 ее со прот 1шлсшн:: в векоf1
"Ред 1юir» срспс. (Но реш е1ше llьютооа, Г(аrпюс
11~1 n « М:пс:1-1:1 тr1ч~сю 1х нaч:lJlax 11 :пуралыюi1
фtL'l(К:O фr111 ·· ( J 6~7 Г.), T;JT\ ,'1;0 кшща JI IIC поня
JШ вшю·п ДО ccpcf(IIIIЫ хх в., KOJ'ЩI llOSJKl lJIO('J,
но 1 юс 1rапrавлсшн: в теор~ 111 э ..:с1 · 1х·м~ ·м а, 1щ
:ш:.tJ 111 { )(' U1 11171f..1/ a1/bl1Ыlll .) '11/J{/({'lf 'Ji/ ((~\/, - 0/\Н 11 1\'\
11 :i с1 ·0 со:.татс11t:11 был 1хк<.:11 1:1сю 11l ,,~п·с;v1ат 11 к
Лсв Сс:мi.;1 1Ою1ч Пон·1·рн 1·1 1н.)
K;i 1< ре111ат1-> ·1 :щ;1 чн н :1 :~ кстремум? Гlу ст 1.
фу11ю111н/(х) 1>nрсдеж·1 1 а 1 1:11 1е1ю1 лро~1 1111тср
nалс (а. /J), сrщерж;~ще~1 точку .У". Говорят. что
. \'11
-
. :{()}\'tl'lbl /11/ / I .JlllllllL.\1) ~11 (•. HtlЛ"C/l ./l~J:M) фv 1 IJЩIIII
/(.У) . ccmr найдё:101 такой подшпсрnал (a". IJ"),
nр 1 шадJ1ежащ111'1 (a. IJ ) 11 таюкс с:одс ржащ11йх, "
что I (.\) ~ f (X(I) (/(.\') ~ / (.\'1))) д;ш в<.тх .\· 11:.1
:-JTUl'O lfr)ДblltтCpBaЛa (а, 1, lJ 11 } . J1,py1' tl\lll CJЮB :tMJl ,
11 npc/lCJ1ax 1 1U/lh 1н тс:р в:1ла (а1 " /111 ) фуш-:цш1/(х)
н ТОЧК<.' х" fl(Jl" l" Ш ':1t:T CH! )t:)'() MI 11[I J J\.Ja.rt ы101·0
(!\1акс11.\1а111:>ноп1) з1-1а ч t.> 11 11я . На р 1 1 с ;\ то•нс1
." 1"1 - .' 1 0К3ЛhНЫЙ Mfl}JJ11'y\)!.~1 , <J ·1о чк;:1 ""~ ! IOJ\<f}'] ] , -
111'111 м акс11мум. Локал ы11.1i1 м 111111 !\1ум 11лока.;тт,-
11ый м;J кс11 \1y.VI 06ъе111 1 шпотся тt:рми1ю;-.1 ло
л·алыrыi1 . ->1•cmpe.i14J!111.
Тt:орсж1 Фt'рм;1, сформутrроваппая выше,
от1юо1 ·1·сн 11:-к11 1 ю "локалыrому ·->кстрсмуыу.
так как с1:-.ю поняп 1с про и :шоднrн) н точке
характсрнзуст поведсш1с функшш в м:111с11h
ком l ll l'l 'tpHaJIC'. СО} \<. : ржа I Щ:М Л~ll 111)'11) '!'ОЧКу . 0'1'-
MCTI ( ,\1, ЧТО 'l 'CUI X ' \ta Фt:pM;J J1J l lllh нсо6Х(Щ11 \10(.. "
усл(}111н: :-э кс·1 рt:.\1 ума. ·1 С'. ccm 1 н 1 rскотороi1 точ
ке щхщз нолн:rя ра1111а 1 1 у1110, то J l~l 1111;1 }1 ·1·очкэ
11е 0Ияе1:~тс:лы 1<) 1ю 1..:;1J 11.11ы !"1 ;,,кстре-м~'J\.1..ZJ,сйстпr1 -
те:1ыю, 11ро11:11кщ11ан фу11ю (111f./(.\") = .\'' ( р1к..J)
.\'
()
P1t c. З.
Рис4.
-~ 92
р:ш 11.:1 .).\'~-она пбp:tllt;[l.''l'C>I н H)'il!• в ТОЧК(.." .\' = (}
Но ата л 1чка 1ll" J.i вля..:тсн n< n c;v 1 11 1 11>1м :'J1<c1рему
мо:11 ;tа11 1 ю 1·1 фу 1 11\1 l1111 .
И1·3к, соглас по тсорс:ме Ферм;1. ;юк:~лы 1ые
э кстремум.ы / (.\') 1 1 аходятся сре;~11 1\ор1 rc l1 )lХtв-
1 1 сrшя ./ '(\') = О. l<op1JI1 ЭТОГО }11:11\ 1 1С1111Я часто
J rазыв;~ют стс1и,1ю11а;mыщ111 10 ч1\·а ш1 фушщпи
. f(х) Пустъ х,, - стащ ю 11арнан точ ка. Как 11р1)
вср 1 ITh. HКJISH.:TOI JI 11 OH:t J[()l{; f.llы lЫ М :·IKC'IT)l""IY -
чoм? 111 >С1\\( >'1 р11 ~1 сщ<: ра:~ на гн 1с ). В точка.\.
()т 1зкнх к.\·1
. l ,'1l"R:t про11:то;111ан т р1щ;i·1·t'111,1щ
;) C I 1рака 1IOJJ()ЖI ITt'Jll ,J-1:1 н (>К!)t'С'П IOCTI 1 l'ОЧ 1(( 1
. \'2 тtао()<>рt>т: сж:на 1 r ро11 :~1ю;\1 1 :~я 1н >;юж 11 те, 11 . 1 1:1,
а с1 1рэ11:1 n ·1p 111 t::~тс-л1.11:1. Тэю1с усло1шя ,'\О<"
та·1·оч111 .1 для того, чт()6ы ст:~щ10 11:~р1 1:ш точка
61,ща сои1·нетстве ш ro \11ПП1i\1Уi\ЮМ пл11 .чац·11-
мумом. Об ыч но /1()(.:та точ 1 10с уию1шс фор."1у
J111руто т тате: ссл11 х,) - <.: тащ 101 1 арна;.1 точка 11
11ронлюдная. 11сμсхщ.1,11 Чl' f-JC:~ .\ ·" . \1l'ю 1 с1· :.11 1 ;.1к с
-
l!a +, TU.\ '11
-
J IOl,:)ЛЫJЫl'I MIJllll,\.1)'M, :l eCJil l С +
ТJ:t -
.
·г11 .х" - mж:шы 1 ы l1 .111 акс11м у.ч. Есл11 же
11ро1 J3K( !/(l-l:lЯ llC '.1CI JHC'I' 'J J r ак, то .\'р l IC: H!IJIЖ~TOI
ЛОК~UIЫ IJ.IJ\ I :'IKC'1'j)t.Vl)'\'НJM.
PacC •\.IO'J'/)JJM фу 1 шц1 1ю/ (.\") = х; - _-).у_ оnреде
лё1 11 1\·10 11:1 ч1 1 с.rтоrюf1 ттрmюf1 (р11с. '5) . Её про11~
Н()Д11~н /''(.х) = :\х~ - 5 оfф;.1111,астсн 11 l f\"J111J111111ь 11
11nyx точках: - 1 11 1. llpoвepк.J 1 ю1<азы11аст, Ч'ТО
пр н 11ерехож: через - 1 пrон:шод11ая .'1с1 шс·1·
знакс+т~а - . ;i при переходе •1ср<:'3 J - с
-
11а+.
СJ1l',1оватt:л ыю. - J <.'С'IЪ J юка: 1 ы-1 ы11 м:t кс 11 муч, а
1 - лoкaJ IЫIЫJI \1111111 ~1у11 1 .
Ко1·на ~- фу11ю1,111J ./(.\·) t::C'l'h кторан 11р<н13-
в1 щ11~1 н н C'l':JЦl l OH:Jpнo(1 l 'ОЧКС, ДОl" t :ПО ЧllЫ С
устн1 1 rя mжа.11ыю 1 ·0 :~ 1-;с1-рс:му.\1: 1 мож110 сфоr
:-v1ул~1 ровал, \\'()рпче: ест~ .\·11
-
п·:~1\1 1 онарн:ш
TOL\1\:1 ф) 1 11щ1111 / (.\') п/"(.\') > О, то.\'" - локаль-
11ы1·1 1v11 1 11 11мyJ\1 , :J t:cm1/"(x) < О, то .\"11
-
ilO-
1'
у=х ~-5х
.\'
Рис r;_
rсаmл1ы11 маю..:11му\1. В ·голько что р:~ссмот
рснном п р11м<.:рс j "(х) = () х. Слемоватсm, н u .
("(-1)= -6<О.j ''(1)=6 >О,т е.м1.1 1юлуч1u111
11re11• 111111 рсзу.11 ь· 1 ат.
Лn с шl 11ор рt:чь шJ1а о лок~1льных ~ю""1·рс
чума ,\.. А как 11 ахо;11 tть ?.'юnальны 1i .;trlll111"1z11.м
н:111 глиба7ЫtЫft .ма1.-u1..1~нм фу1 rкц1 т . за; 1а111 ю l1 .
11:1 11p11N1c-p , mt 0·1· реэ кс: ? П p<.:Jt110J юж11r-1 . t.тто
фу11к 1 \ШI 11eapepыnrr~1 11<1 этом отре:ще. Тогда
С\'щtттвуют точю 1, 17 1. < .: 011а 11ршшм :.1 ст с нов
M;tKCllo\'l;\ЛЫlOl' И 1'!1 11111 11.\:lЛЫIСН.: Jlf~lЧ t:JllUJ. [<:ЛJ1
;\ОПQnшпt:1ыю прсrо~оложшъ. что фушzнш1
д11ффсре н 1 11 1ру<.»"1:1 нпутр 11 отрезка, то леtыJ
011 11 слъ про 1~t:Л}"РУ1ю11ска хо·1·}1бы1·ло6алы 10-
1·0 M: IKCJ 1 Myч;t фy 11K l\IJl1. И :~ l:l: C'l':IJ~llOl~;tpHЬC\.
ТОЧ <.ъ: ()'1''1 1~ран )'1' TO'J К11. н I ЩЯ ЮЩI l t:CH } J( ж: 1J11.l1hl
MI 1 ~·\ ~tKC I I J\lyмa ,\\J r ( t:СЛ 11 тalCOJ\l,Jl' l'CTh). 1IOCJ l t'
че л1 H l>IЧ I KЛЯIO'J' :~11 :1чt:HlfЯ фу 1 LKl\1111 Г1 ()Т() -
6р<1111 1 ых точкал н 11 а ~.;он 1 1,~1х от ре:l.к~1 . Cr<.:;r\11
nccx пш1учеш1ых :11тачС'1 1нй 11 ахо1\я ·1 м::11<с и
м;vrыюt:. Точка. 1 ·,це это м~н<си111з11ыrое :ш(!че -
Прои шn,/\H.t~ и 1 1 н тегрJл
11ие достпгается. н бул.с1 · пюбалтJ 111 ,1 ~1 маrсп 1-
мумом фушщтш 11а O'J ре:{КС.
J:>с ш11;\1 <.:Jr (t; p:t:i :{а11ачу. t' которой мы 1 1 ~1чалп
ра сск:t::!. i":сл11 обu::! нач11т1, 1 11.:рL'З а c~"Nl:\I\' д11ш1
1<:1·1·<.:тuн 11р нмоу1 ·0J11.нш'l) 1· р1:у1 ·ш 1ы-шк~1. а ч1:рс~~
.'\"
-
l(.'IJIH~ 0)~1 JOl 'O 11 :J HllЛ , '1'0 IJ J IO l.Ц:ць rrp}l .\IO-
~ l 'OJl ы 11 1к:1 ракн;1 S(.\") = .\'(U - х)/2. п ...·рс.чс1111:tн
.\" 11:J :щ:ш1 ето-J tJJ О до с1. т;~ 1, ч 1·0 фу111<ц1110 S(x)
,,,ы p:1 co1aтp111{:1e ,'vl 11 ;1 отре з 1.:е [О. t1J . ДаJ111 : 1 н
(jl)1 11щ 11я 11t:прt:р ы н 1 1а 11 :1 / О. o j 11 ; ~J1ффt:рс111t11 -
руема 11а (О, (/). Урз.1:11 rешн: S' (Х) = О.~ а - х 1ще
е•r· · юнько <щпо реше1111с: .\"0
= ct/ .!. . 1!oci\om ,1,y
S''(.:1.·0 ) = -
l < О, то чках, , = а/ .!. - J1Ок;1т,н1.1t'1
маr•сrщу,,1 фу11 кц1ш S(x) н"1 11~гrсрнз.11е (О , а) .
Ср<:ю1чш·с11 S(! J) =О. '>'(а/2) =а-/ 'd. S(t1 ) = О мак
с 1 1л·1: 111ы 11,1м нкm1L"тсн S(t1/2 ). 11 110:-1· 1·0~1)' н то чке
.\о = (// 2 ф)'llKl\l l H /(()C'l 'lll':tc.:·r ГJI0 6~UIЫIO I '() \1aK-
CllM}'l\l ~t 11а отrх::11{<: [О, о]. .-:'Jто о.т:1ч ;1 t.·т. что 11~1
11\)51 М\ )У\ '( )Jl\,111>11.; ' \ pt:yl'OJI\,\ 111 1<01\ С :\Щ~а 1 11-Н \\\ L' )'M -
MOll J1...' l 111 1 катсто 11 11 ;11 н'iолыщ ю 11J 10щ ~и\1, 11м еет
рашюl)е;1реш 1ы l1 тре\то1 1 ы1111.; .
КАК ПОСТРОИТЬ ГРАФИК ФУНКUИИ
Прt:/\rюложнм . ч1и 111ы хот1 1м построr 1 ·1·1, 1 ·ра
ф1 1 к к:1ко l1 то ко11кре1·1 юй фуню 11111. Xopn1110 .
ест 1 фу11к 1 \ПЯ уже и:~учс:на. а сл е;1n11:1тсльно. 11
с{~ rрэф1 IK, 11 ПО/\рn\'11 Юt" ОПI ГО f 111 е CllO.JILTП :\1ОЖ-
1Ю rrari т 11 LI сн раво<rТrrн<ах. А ест 1 :;,~то не 1~ак?
То гда 1rужтю 1юс11uлr,:юnат1.ся станд:1рт 11 ымн
МСТО/\<1Ч 11 ттостrос11ш1 1 · р:1фl П<ОВ. О 1-:ОТОрЫХ
з:к'Сь II TTOfl)Jё'l' J K' ЧI>.
В 1 1:~шс 1 1рс.ч н соJ.ц:шы прекрасные ко мгr1,ю
н:рн1,1с: 11р<11 ·р:1 1\1,\11,1, 1ю:~1ю11н1ощ1 1с с нысоко1'!
TOЧll() l'' /' 1,1() стро1 1·1 h 1·p:нj'J l lКI! tJ()}J/,ll ll ll l C'l 'K<I
ф~нкц1 1 l1 . Но НС у ксех LJ llt: всtтд:I f)H /(UM eCTh
l<tJMПh\()TC\). к Т<1МУ же l\OJle:'HIO :Л-1:!'1 l). К~1К :'П;О
С1~.ела 1·1, 11 ()с:1 11сг1 ). А 1ют(> \f') вn:'! 1,,..1<:-м 1 1t'скол 1. -
ко ЛПС'Т'О li 6у',\J:1Г11 l\ЛН эсю IЗOn 11 в 1 .1ч1 ICJ1erнn'1,
карющ:.1 111 r1 [<;1лы<улятор . 3ашrшсм 11а 1-11щ1JO:\ot
~Jссте :11ra J 111·11p.1ecкoe nыр:1жеш rе фупю{t111 11
11ач1гём t1ао:.н.· щ:сле11она111 н.:. Его «rе11ер:1лы1ыi1 »
n.'1:111 мы ссС1ч ас 11 п1хлс·1 а1ш.ч. Л /\ЛЯ пр11 мсра
Г); \HOK\Jl'MC:: I 111() будоt L'TfIOil'l 'I, l ' \Xlфttк фу11к1\111 1
\"~-У-)
) ' =/(Х)=· .
-
(")
.
.
2(Х·i2)
1. Ha 1\ri.ё ~1 обла ет~, ш1 1хдt:т.: ннн функ ц, 1111 .
1111()1', (;J :эт:t 06л:~ с1·1, (11,mal'T :iз 1 t:i 1r a . т. <:. 11рн .vю
ука ::~ ыв:J<.:ТСЯ. как 1 н.: ~111а 1 1с11ш 1 \IОЖ(.'Т 11 p111111 -
M:l lh .\' . Ilp11 п1 сутс1н1111 ука :1а 1111(1 on11 :н:TJ.IC)
oпpt:;{t:JI C llll ~I 1 1р111 1 ятn сч1 11 а·11 1 HCt: ~HJ:lЧCH l lЯ
ар 1 учс11т:1 . 11 1\\1тор1.1 х ф~ 11к1111н 1 r .\1L'L'Т см 1.r сл
л fl()'l'()MY Jia/\() l!CIOIHJЧ[I П> те 'l ()ЧIOI, 1·:1с фу11к
l\ИЯ нс (щpeд<::.rit:11~1 . Тсх1 1 оно1 ·11н т;що1 ·0 11po1\t:c
са . в nр1111цш1 е. яс 11.1: ...-с-, 111 :.1 .щаr 11 1 :01 фу111щ 1 ш
Щ)С/\С'l'3ВШН:Т собо i1 01!ЮIПСТ1И е ДН\'Х фyrtl\·
ЦИ(! - З ll:IMCl!:tTCЛЬ пс ДО.11.ЖСIJ р~1Н 1 1Я1:1,(Я О; l'C111
к 11сё ПХО;' ( l 1'1' кupcJIL ЧёТJЮfJ (."l'l'П C f 111 1ю,г11 :0
рс1111uc н1>1р;1 ж<.: 1111 с 11с можl'т б ыть отр 1 11ta1\~ль-
11ы ,,1_ 1·1т.: ~. в :НJ:l\.H.: H:t'l 't'Jll' ф)J l l-:1\1111 ( *) ССГI• co-
MHOЖ\\'l't'JJI, .У + 2 C~ lt'J \Ol~~\Tl'Jlbl 1( 1, l lt.:Oб X O)\l\Mh!M
уи10в11<:м н1щ>iето1 .\· + 2. * О. ·1. t:. х * - 2.
R1.1;(t'lllfM 11::1 :эсю 1:к· «с!аПJХ" 1 ·11ы е " l\tt•t 1·а . f.cm 1
rтскточf1111:rя о()J 1 аст 1 , :1: 111111\1al" I ltt'm.1!1 11н · 1 ·еr -
11ал. n рп1юдят ;~ве 11 ~ 111-:·1·1Lр11ыс 11ерт1 1 1\:1:1ы1 ы с
11рлмыс по е1·0 кр:.1нм: сош же :->то от;1,с-111.r 1:1н
точl\а - то о.'(11у nерп1юшы 1уш 11 у11кт11р11 у10
прнмуrG че реi ;~.атrпую то чку. Висст() п~·1 1кт11р~1
11 (. ' !! 0JJb;))'lU'I ' н ЦBCTIIЬ!t' Лll lllll l. l ':t1\ ll:1 эск1r :;(.'
1р:~ф11ка фу11 1<1 \1 111 С') появ11нс·1·с}1 •·1Jср1шя .' 1a c -
I'( >ЧК;t » - 11у111\TI rpt 1:н1 flj)H 1\1 :Н1 .\ ' = -
.!. (р1IC. 1)
2. Уст:111он11 М . llC' fiy.' (L'T Л I ! 11:1111:1 фун.ю (ШI
ч С:::т1-1с)l1 . 11 еч f.т~1< 1 1'1 111111 ~н~ 1)1-нщ11 чtТ l{<Н'1 . :~т11
"11
11
11:
~t
с:: 1
'S! 1
:s1
Q_1
с:: :
1
-2'
детерминизм и 1.:лу•1айноrть
о
у
В эпюй точке
фу11л.'·ция
не rmреде.11ена
:х
Р1н:. 1.
сведения пригодятся о дальнеnшеи. Нсл11 фую<
ция чётная (рис. 2), обычно ограничиваются
исследовашн::м 11 постро<.:пием тrшь полоnины
графиюt - например, только для нсотр11ца
тt:льных .х, а затем симметрично отражают её
относнтелы-ю осп Оу. Если функц11я нечётн:Jя
(рис 3), т:Jкже досrаточно исследовать и по
строmъ лншь rюлош111у rраф11ка - скажем.
только Д11Я 1rеотр~щатеm.пых х, а з;.пем сш.1мет
р11 ч1 ю траэить её уже относительно начала
кпорд1111ат. В11рочем, фушщ~ш (*) ш1 чёттшя, ни
11ечёт11ая хотя бы потому, что её область 011ре
деленш1 11есимметричн:.t опюс 1 пелыю Иу.
у
Рис 2.
Чс>тнал
фym."41m
Нечетнст
функщт
Рис. З.
у
Если же фу1 1юtия псрнод11ч1.:ская, то е1роят
сё rраф11к только в пределах 0111101·0 периода
(от про.изнолыю1·0 х0 до Хп + Т), а затем <-раз
чножають c 1·r>, С/\1t111«н1 впраnо 11 нлено на рас
стояния, кр:Jтныс Т. О,11.шшо фу111щня С") непе
риодическаsr.
:i. О11ределнм точки пересечения графика
фушщии с осями т<оорди11ат. Праuда, существу
ют 1·рафшш, вообще пе пересе 1<ающне осн Ох
И ~1, 110 I< гр:1ф11ку функции (*) ЭТО IJe ОТ!IОСИТСЯ.
Абсц11сс1 то ч 1<11, н которой 1·рафнк функцш 1
("') лересекается с осыо Оу, раина О. Тогда
о~-о-·) i
Jl=/(0)=
-
=--
.
2(0+2)
2'
т. е 1 ·раф 11к пересекает ось ординат в точке
(О; - 1/2).
Дmr всех точек ос11 абсцисс у= О. Поэтому
попек ТО'-tек пересечсппя с осью Ох сводится к
решению урани~1-шн у(х) =О. Такое ураn11ение
может нметь rаз 1юе число корней Для фу11к-
1\н 1 1 (*)составляем ур:,шненне((х) =О, 11лп
~"~_"._)
-~ _,
-
=о
2(х +2)
Это ране~ 1ство возможно только в том слvчае,
если числитель раnен О, т. е. _\'
2
-
х- 2 =О.Кор
нямп rтосл<.:днегu урав11с1111я яnляются -1 и 2 .
Таким образом, срафик пt:ресека<:т ось Ох n
ТОЧ.К!Х (-1: 0) и (2; 0)-
4 Рассмотр11м повсдс~-ше функц11и нбл11з11
точек rазрьша , если ою1 11м<:ются Может слу
читься так, что по мере nрI16л11жсн11я 1< точке
разрыва фу'Тнщия rтеоrра11иче11тю растёт IIЛJI
уб1.шает, а следоnателыю, кprrnaя 11еудерж11мо
стремится вверх ил11 вш1~1. О11а всЕ теснее 11р11 -
ж11мается 1< верпшалытой прямой, проходящей
через точку разрыва, слошю пытансь слнться с
1 1 ей. Такие нр.нмые , 1< кuторым стремится крн
вая, называют acUA11Unomc.uиu . rtоэтом:у, пахом
·ючю1 разрьша и анализ1 ·1ру>1 1ювt'деш1с фуах·
ц11н нбш1з11 н11х , мы тем с:1мым ою-юврс~1<:нно
0'1ыскин:,~еN1 11 вертr1к;~111,нмс ас 1 н.штпты
У функцит r ('') ест1) 01tна-ею·1 нствt:н ная точка,
где она нс 011pe; teJ1e1ia, -
11 11е11 11 нахо;111тся
р;~зрыt1: э1·0 х =
-
2. Заметим, что числитель
nыраже11ия
х~-х-2
2(х+2)
при х = - 2 раRсн 4. Поэтому предсm,1 слева н
CJJpaнa определяются знаком знаменателя На
прнмср, еош :\: стремнтсн к -2, останансь 1кё
время 111ены11е - 2, то :н·1амс:натсль <."1 рl',"штся к
О, будучи 1:1се 1 да трнцатетtьным. Значнт, ко1·11а
х стремнтся к - 2 слева, фу11кц1 1 н е1рем 1 1тся к
-
"", а еслн спраnа - тп1
. : +оо . СJ1е11оnатt'льно,
прямая х =' -2 является nерт1 1 к:~лы1ой асш1 11-
тотой для ист<омо1·1 кривой как слева от 11ее,
так и справа (рис. 4).
По имеющ1L\1СЯ у пас сnедснштм, уже можно
предполож11·rъ, чтu 11ранее ·rочки х = - 2 кр11вая
снускаетсн с (,:{апблачных высот» , 11сресскаст
псь абсцнсс н то•1кс (-1; О), затем ось ордш~ат
нточке(О,-J/2),агде-томежду.т = - 111х=2
01~ять н::1чи 1 rае·г поrо-п-rм~пъся внерх , 1н:ресская
ось Охв точке (2; U) уме нrа ~злёте». Что будет
дальше - пока неясно, но крнвая опредслённо
не достигнет оси абсцисс , оставаясь где-то
вышесё.Левееточких= -2 и при сбл ижею 1и с
ней кр11ная ус•1реl\lvтяется нниз .
5 Вы ч ислим производную. Прежде всего ,
прир;:ш11ян её к() и решив полученное уравнс-
11ие, опре1'еnим точю,1, где могут бьп ъ локаль
ные экстремумы фунrщии. Найдём значения
функции 1ю псех этих точках, чтобы установить
координаты всроят11ых э1<стремум01з. Вычис
лим таюке значения второй произuодной - так
мы выясним, действительно ли в данных точт<ах
находятся локаJlьныс ::!Кстремумы , а ссш1 да. то
максимум в ю1х ш1и Jvtи1111мум .
Кроме то~·о , отыщем точки, в которых про
нз нсщн:аJJ 11е uпрсдепс 11 а. Вместt" с точками ло
к:шьных экс11·)ему м ов 011и р:цп.еляют пбт1 с1ъ
011редепе11ия на части . R~.~ясним , как велёт себя
функuия 1:1 кюк;юй из таких частей. (()всем
не обнзателъно (хотя и не возбраняется) брать
"для пробы » их nнуr~рештие точки и вычислять
для 1шх значение прш1звод1юй, чтобы опрс
дслить знак Можно 1.юсполь:юваться таким
правило ,\1 · елеи;~ от лuкалыю1·0 макс11мума
функцня 1>.сеrда возраст<~ет, а спраl\а - убы13<1-
ет (д.11я минимума наоборuт). Так нли иначе:,
следует с наименыш-rми :iатр;памн труд;,~ уста
нтшт1,, 1«1 к яеде'r себя функция на мо1ю
то11н1>1х учасп<ах.
()спбпго 111IИJ\·tar-1 ня заслуживают точюr, о
которых фуrnщ1ш определе1 ra н пепрерьнша, а
прои:нюдной пе сущсстнует В таких точках
ВОЗМОЖСII ИЗJJ()М. Обт1ружиn 1ЮДО6ную точку,
у
2
-~ ~/
Точки 11сресечетт
zpaфu-~y,, фу11кцu11
с ися.лщ к.оордzта111
Рис. 4.
Про1нволная и интеграл
надо выяс нить предел про~.-1звод11ой в 11сfт сж:ва
11 справа. В результа те ст~шет понятно, с кэю1-
мн наклонами графш< подхо~тп к 1~:-нuюй точ
ке с обеих сторо11 .
Для фущщии С*) 11ронзво;1ная
r')
xl+4х
(Х=
.
.
2(.У + 2)l
Ilрирав11яв сё к О, получнм кnадратное уравне
т1~ х2
+ .tJx = U . рt:шиn которое найдём два
корня:.\·1=О 11 х2= -
•1. В этих тogicax возм ожны
локальные эк<..:трсмумы. Возьмё.vr в·1 ·орую 11ро -
1131ю;1ную
/''(х) = 4
.
(.х +2)~
Такr<ai</"(- -1-) =- 0 .5<О11/"(О)=О.'5>О.то
n первой нз точек - ло1~лы1ый м:aт<CllJV!)'M, а во
uторой - м 1 rш1мум. tlычнсш 1 м 11 з11ачсшн1
функции н точкс.LХ экстрсмума: ./{-4 ) = - 4 ,5 и
j(O) = -0 5. 3;.~те~ 11 ~1 эсю1эе нане<..:ём э·1·1 1 точю1
и прuнсдём тонки е 1·uр11зu11т:тьные отрезкн -
касательные. Полезно указа·1·1, наюю11 кр11но1'1 н
тuqках её ш.:ресечснюt t' осью абс~ \исс, J1.ля ч~1·0
н:11щём.f'(-1) = - 3/ 2,f'(2) = 3/8 .
Точка, 11 котороi1 11ро~rз rюдн:~я r1e onpeJ1e-
лe11a, все~'() о.т1ла - это х = - 2 . Понедеrrие ф}1Н<
цн11 в окрестностнх датюf1 точ1ш нами уже
было расс мотрено.
13се значения.\" - 4, - 2 н () - раз61mают об
ласть определения фуrнщ111 1 IIa четыре част11,
в nредслах 1<аждой 11::s которых 011:1 мо1юпJ 11 на .
Ор 1·1е11т11руЯ<.:1:> на точки JJOK:u1ы 1ых якстрсму
мuи, вы5н.:ним. где фушщня возрастает. ;1 щс -
убывает (р11с. 5).
6 . Определпм точю1 11срсг11б:~. С 11ачзла
найдём те 11 з онх , н 1<оторых втпрая 11ро11 з
tюлr1ан рав11а (). ()бнаружнв ю1ж; 1ую такую тпч -
1(}, вычислим в ней значс11ие фупющи и наююн
касателыюй, равный значенню производной.
На11есём на эскиз эти точкн , а таюке неболь
шие отре:нш 1сасательпых. Мшю ю, сели есть же
лание, найти трстъю произ1юдн)'10 и уста~ юш1ть
характеr перегиб;~ (какая 1.\ы11 уююс·1ъ '1<;1кую
смеш1ет), но обы•1110 пб ходят<.:н }~Jf{c rrз.нсеп1ы
м11/t~ШJ1ымн: на 11х оснона11и1 r уда ётся. к~1 к 1rр:-1-
н11ло, однозначно устано 1нпъ, 1 ·де функцJ1я
вы11)1<т1 внерх, а те - нн11::~.
Л,лн фун1щ11н (*) мы уже ::~11аем, что/''(.'\") =
= 4/(х + 2) \. С одной сторо 1 ш, ~та функция
Лсг~р....~ини1м и tt\уч<1 Г1ность
1
JloЛ/l lhllhlti
. llrlЛUl ф:11
( --1: -1\'i)
\ :..:. -<- .
1
®'1
о
1
\:
е
\
JllllЩ /111/t.l/l
itlllllt\/) ; 11
( О. O,'i)
Риt. S.
11111·де 1 1е VIOil<e' I' p :1Hll}!'l'I)(}! о. 11()~' 1 '0\·1~' 11 ере1 ·11 -
\)()А её графпк пс нмсст. С 1lP)Tnт'1 сторо пы . ср:~
зуl:ШДlЮ,что.f "(.\') <о11р11 .\' < - 1. 11 /''(Х)>О,
ес.111.\· > - 1.. т. е. ленес TO'IIOt х = - 2 r<р11 тн1 6у11е·1
nсюду выпукла nncpx, а ттращ:с
1ш11:.1 .
7. Остается тсттср1, у:ша1ъ, как нс1tС::т ссGя
фyHKl(llH 11\)11 .\"-У+ оо 11 , \' -У - =. В К:IЖДО М 113
..'> '1 '11\. l'Jl yЧ:t <.:B 1 \0Э\HJЖIJl>I l'Jl<. '/tYIOll(lll' 11~1p11;111 'l' l1I .
1) фу11юtJ1Я стрсм11тсн 1\ к:11ш .чу-·1'(J ОJ 1рСN:'
лl:н11ом у :1 11ачс11111t>:
2) фу111\1t11я 11t'о1р:ш 11ч t'1111<) 110:1раст:1t'т 11:11 1
уn 1.111аст. ·1·. с. стр еJ1.1 11 тся 1.: +м 11m1 -ьс;
i) фушщ11я 1тrr "чему 1 те стрем~ пен.
fслн ф)·1UЩIIЯ стре!\штся 1< ка 1\о му-то опре
;tt:л ё 111 Ю\11У з 11 аче1111ю с 11р11 .У -У +оо (.У~ - оо) .
то он::~ по .мере у,1:L'Те1тшr n пр;шо (nлсrю) от 11::1
чала кuо рдш1ат нсё Tt'CJICC 11 ТССШХ" ПОДХОДИ'!
к 1о р1l j(H 1·1 ·:1111,1-ю 1'1 11р>1 мо1'1_1 · = С. 1 юэтому такая
го р11 ::10 1 1т:1111>11ан прн!\1ая бу;~ст ; 1,т1 фу11к1t1111
:1('11!\l l ITOTOll ( р1 IC. ()).
.\:
()
И1псрссс11 nтopo i1 с.1 rуч:н'1 - ко1-щ1 фушщ1rя
11 ео 1р;~1111чс111 10 1юзра (таст ш111 у6ыnаст. То1'д:~
O l lU может C 'l'j)C.\11 ПЪСSI к HllКJIO I 11 IОЙ :H.' ll ~IПTOTC.
З1 1а ч.ит. 11р11 дост:J·1·оч110 1]ш1ы11 11х 110 а6сш1ют -
1шi1 ис:1 11ч1111с ( flt)J1ож 1 псльнh 1Х 11л11 отр111щ
•1·с:111.111.1х) .\' 011а нс,r1,ёт (Сnн 1Jра1п r111с: сю 1 , 1<:1h
11pS1'\1a}[ у = /..~.\·+ rJ. т. е. m I ЮШl'lllll'./(.Y) j.:l' стано-
111 ITCH 11сё 1iл11жс 1\ OTI IOll lCШ1IO (/;}.\ ' + /J) / x = k +
+ IJ/.\'. с рОСПJ.Ч х IЮСЛt"Д!Iёё nыp:til\CI ПIС стре
~1 11'Г('Я 1.: /...> . CЛ<.'j\O H<I TCJll>IIO. 11 ОТНОШСШfС / (X)j.\ '
должrю стрсмнтъся к k~. Это 11 подсrGtзьшаст 1 ю
рядо к ПOllCK:t l l :IКJIOШ IЫX аО l.\111Т()Т: I Щ'\() 11аlrтп
ттр<.:,'\СЛ н1,1p:tЖ(.'Hl ISI / (Х)/.У 1 1р11х ~+.,., 11 .'\ ' ~
'""
l::с;ш такlJ!"1 11рс;~<:.11 cy1 1LCC' l ' H)'l" I ' 11 р:11к: 11 11<.: [<0' l <J·
ро~1у ч11сл~ /..>, 1·0 на к. 1 0 1111ан ас11\ш · 1·0·1 :1 но:~ \!ОЖ-
110. С) Щt'l~l'l1)'l'T, 11 TOIJ l,;t ci.; ~'1'.'101\()fl ко.-нj1ф1 ЩJI ·
снт сс~1·1, k.
Как 1 п1т'пr1 11. 1-:ог1t:1 !? у;-ке 11::ii1 i'\e1ю? t-:c:11 1
фу11~-::11,1тя /(х) с рщ·то м х стрсм11тс н к 111ж,юl1
у = f.? ..y + fJ , то рассто.шше ~ю uертнкалп ~1<.'Ж;~у
;-)тoli прямой п прям ой у= /..'.\' бу1ГJ,ет ст ре.чl!'lъся
к (J. А 110тоf\1у 1-н:обхощнvю ныч1к;шть предел
nыrх1 женш1 ./(.\") - /.д· 11р 1 1
. \.', с 1 ·рсмнщt~н.:я 1{ t-oo
(11л11 к -е<>) . ~cm 1 т;11.;01·011pc;\cJ1:111c сущсс1'1.!)'СТ.
то~·да 11 :н.:11.лtJ1тс >·1 1,1l ll' су11\l'l'1 вуl: 1
l<ак 1·ол ы<< > ас11м11·1птэ c1n11apyжc:1r:1 , cl: 11:1;to
ll :l lll:' CTll 11;] ЭC IOl ,J 11, [):l:J06pa 111Jll lCI>. l\:IK стрс-
\Нl ' l'OI К 1161 кр1 /li:1Я
снt'рху 11.
1
111 <.: 111 1.Jy, н:1р11-
CO l\:1 1' 1> !\1aJJCI luI01C K)'C()LJl(J 1 ЭTOLI J\j)I IНO il 11 11р:1·
11ni1 u 1eno i1 ) часп1 l·р;:~ф1ша.
f1:1iщё м ас11м1поты для графшсr ф)111щ1111
\'~_,._,
((.\')= ·
'
-
.
.
!.( .\ '+2)
liосколы\у
/(.У) .\' ~ -х-2
1-1 !.
.,.
.\' ~
.\·
2(.г +L\')
) ..j
-+
,\'
1·0 1.;ак 11р11 .\' -> + оо, т;ш 11 11р11 х ->
-
""предел
с~щестнуст 11 p:ineн k = 1/ 2. Те1 1ер1_, 11 аfщём /J:
.\".~-,\'-2
.\'
/(.'\) - !г:>.: = ---
!.(х +2) ..!.
-
1-
2
-
.=)х-2 ·
---- =
__
._
,.
!.(.У+2) !. + ·[
.\'
l lp11 cтre.\.1.'ICll llll .\' 1\ ±ы ЧJI CJJ l l l (.'Jll1 Clpt:·
,ч1пен r: -
. ), з11:1 ме 11 атет, 1< 2, а . сле11n11<1те:111·
11<). llX OТIJOПICITTlt; - 1\ /J= (- :0)/2= - 5/!. ,
Таким образом. имя леnой , и /1/1){ праной пt'ГВи
гр афика асимптотой служит одна и та же
прямая:
~
х3
у=---
)?
Очевидно, что при.~ -7 -оо крн1:1ая подходит к
асимптоте снизу, а 1 1 ри х -7 += - сверл')
8. Если получ:еш 1 ых f(;.~нных Rсё-тdкн Ht.' хва
Т;Jет для nостроснин гр:~фика, то можно Rзя 1 ъ
ещё HCCKOJlbKO ДОIЮ!I Н ИТСЛЫIЫХ значени1I .х,
найт11 для ннх значе11ня функцнн, наклон кри
вой ~1 н<1.нсстr1 спотяе·1 С'1 В)1ощие точю·J вместе
с отрезками КJсателып,rх 11а эс 1ап.
И 1·а к, .шализ фунrщии завершёr 1 . Проводим
плавную криnую ч ерез от,-.1ече1 ш ыс точки,
приrrимая при это,\1 во n11 има11ие касатель ные
11 асимптоты (рис. 7).
***
Надо сказ;,~ 1ъ, что ;~: 1 лско не веста приход11тся
1\ЫПОЛ нять JIC't . ' 8 П~lil\I 011ЭТОl 'О11лана в 1IОЛНОМ
объёмt:. Порой иссле.цощlнне заканчпвае 101
уже 1юст: 11epno1о пункта . Построим, паттр11 -
'
чер. граф 1 1J< фу11кцю1 /(х) = vx + \-Х. Et об-
;1зстъ определспнм З<1Даё1'Ся 11ераRе11ств:~м11 :
.\'#Uи- х~О,откулаодновременнох#О11
Р11 с. 7.
Производная и интеграл
4
3
1 ,,.--2...
J-
,',
-
:)
-~1
-5
у
xz-x -2
у= 2(х1L)
.х ~ О. ПСJлуч.tс:тся . что ofiщ1c1·1. 011рt:;~слс11ия
солержпт е1 (111 1.стnе1111ую точку. х = О. Т<iк I<al\
/(О) = (), l р;\фшюм ">ТОЙ фушщпи ЯDЛЯС1 С'Я на
чало 1соорд 1 ш.tт
ИНТЕГРАЛ И ПЕРВООБРАЗНАЯ ФУНКUИИ
Пре11,стаnим ceGe. что по дороге /tRНЖется авт<, _
'юбил п Стрелка спидометр::~ замерла 11J. отмет
т-:е 100 кv1/ч, J счётчик лройде1111оrо рассто~
шrя" заклсеr~ 11епрозрач1юй бумагой. Можно
,ш сказать хотя б ы что- нибудь о nока:.~апиях
счёт~шка? Коне ч но Яою, например, что в то
бой .чомс111' он пок,1:3~,1н<1ст ронно па 100 км
большее рассн.Jян.ие, чем час 1-1аJа;ц. Постро.и м
\1
l'o
и
Рис. 1.
r рафик заннсимостн скоро<. 1н <л r1реме11и
c(t)= t1
0 = coлst (рис . 1) Если S(t) - пу1ъ, прот·r
де r ш ы й аuтомобилем начиная с каr<оrо -то
1V1оме1 1та nреме11и t 1), то р~\сстшпше, которое
от r покроl'т за промежутоr< npcмcrm от / 11
до L," равно S'(t,J - S(/11 ) == u1,(f,, - t") . Обр::тпс
497
Летермин изм и случай ность
внимание, что эта велиL1 ю1а равна rrлощади
прямоу1'олыtика, т·р:~ниченного снизу осью
абсц1кс, сверху - ~ 'рафико м функции u(t) = z•()•
3 слев::~ и справа - вертик:~льными п рямы,\.tИ
l=t,1иl=lк(рис.2).
А что делать, если скорость 1-1<.."постоянна?
Вьщел 11м n интервале времени от t" до t~ ка
кой - шrбудь промежугок Лt, настолr,ко малый ,
что скоростт, автом обиля не успеет сколько
нибудь замеnю измспиТLся в теч ен ие это 1·0 Л/.
Средют скоросгь на промежутке Лt нсзпачи
тслыто отличается от мгновенной скорости в
любой момент нремени t из ;,анн UJ'О проме
жу·1·ка. А потому ра сстояш1е, пройд~ннос :.1нто
мобилем за время Лt, примерно ранио t'(l)Лt.
Тепер1), если разбит~, отрезок временн от t"
до lк на много маленышх nромежуткон продол
жнтел ыюстью Лt, а зате м сложитu 1-rайден11ые
v
v(t) = Un
1
Uo
:sct.- )
-
S(t"):
1
1
1
1
t
1
о
t"
Рис. 2.
v
о
-.-
Лl
Рис. 3.
у
с
А
в
D
:х:
о
Рис. 4.
498
дпя них расстояния лs = 1 1 (t)Л1, то ~ожнп с
хоротей точностью вычистпь S(t~ ) - S(l11 ) .
При ~том чем уже проме>l\у1·ок Л/ (т. с. чем на
бОЛЬIJIСС ЧИСЛО L1ромежуГКОВ [)ЭЗ61'1Т 01'реЗОК
[L" , l . ] ),тем блаже:: к ДСЙСТВJ IТСЛЬI юму ЗIТ3ЧСН11Ю
S(t,J - S(lн) бу; 1ет найлснная сумм~~. I la рис. .~
ей С()ОТRетствует площадr, заштрихов:ш 1 10й
с~упенчатой фигуры . При стремле1111и Лt к
нуmо фигура стремится к крив()линсйr юй тра
пеции под граф1жом фу111щил (пока з:ша жёл
тым цнстом) , а сё площа,rт,ъ к пло111~щ11 трапе
цин. Эта величвш1 rrазьmастся 011редмёю1ым
zmтегралшt функц11и и(/) н~1 отрс:~кс [t" , t,J и
обознач:~етсJJ
'·
fl '(t)tlt
(чнтается «1-штеграл от ! 11 Л,() t, от 1· 0 ·1
· t dt•).
К вычисле1111ю определёшюго 1111тсrрала
сводится м ножество зал:ач. Рассмотрим treкo
тop1,re нз них.
1. Пусть н~1 коор;1ннатно11 п1юскщ.-п1 з:ща rrа
вы11ую1ая кринолинсйная фю'ура, ш·раничсп
нан 1·раф1 1 камн фу11ю1иЛ.f~х) r1g(.'\') . Требуется
узна'Тъ t"ё rтлощадь.
Прове,цём дnе вертикат,ные кас:пелы 1ысАА 1
и ВВ 1 (рис. 4). Оче1нщ1ю, что иском<1я 11лuщ::щь
равна разности площадет'1 /l.fl}'X кри1ю 111 1 11еl11-1 ЬL\
трапеций: A iL1CBB 1 и A ,ADBB, . П()ЭТОМ~ ест1
абсц11сса точкн А рашrа х1, а точки В - х~. Т()
.\l
\!
S= J/(x)dx - JR(.\')d.\' .
'1
2. Возьмём тоню 1й 1 1 еод1 юроj\ный стержень,
одlfн из концов которог() лр1шс:v1 за 11ача.110 .
Пусты1и11ей11ая плотность матср11ала стержня
H<I расстпm1111 1 х 0'1' J1ач111 а rанна р(х) Нужно
найти массу стерж 11я.
Мыслешю разоб1,ём стерже 1 11, 11а короткне
кусочки лх. Определим массу каждого кусочка
(01-Ia приблиз1rrслыю равна р(х)дх) II слож~ 1м
эти маt'сы. Не правд<~ 1111, мы действуем так же.
как 11 в з:щачс, в которой оnрсдспял1 1 расстоя
ние по скорости? А rюто,"lу и искомая всличхша
равн:J nлощад 11 крюш; 11 1ней1-1011 ·1 ра11ец1 ш 1юд
граф.и ком фуню lHH, т. с. интсгrалу
\'
Jp(.:\')tlx.
,.J
Скорос r ь. r1лотность . мошно сть, плошадь.
;,. Работа, как 11зксс11 ю, р<.1tн1а пршr ·шtJ~снню
сш1 ы на псреме ще111rс. ЕСJш же сила меняется
с расстоянием, тп пр11ходп·1·ся разбт 1в:-~т1, 1:1ес1,
путь на маленькие отрtзкт r л.s, н прсдел;-~х
которых сила F практически не меняется. Тогда
работа на к~ом таком отрезке равна I:лs, а
общая работа - сумме осех «мнкроработ"
'l
JF(s)ds.
,,
ПЕРВООБРАЗНАЯ
З<ща ч.а с днЮhущимся анто.мобнле....1 подсr<а:1ы -
11:~е1 сnособ н:-rхож,~е111-1я определё1111ых инте
гра1юв. В самом деле, ест 1 5(t) - ттуп" ПJЮЙ
дtнный автомобилем за время t, то его скорость
L'(!) - это произnоднан пугн:
и(I) = S'(t).
Таким образом, t:сл11 н~tм известна фу11юt11я
11
(/), то нужно подобрать такую функцшо S(t),
производная которой была бы р:о~нна и(/). На
пример , ссзш и(l) = al (rrpи ранноускоре111 юм
дв 11же11ии) , то н 1<ач.естnе S(t) можно взять
Произволная и интеграл
.ттобую фу~пщ'Ию вида S(t) = а/
2
/2+С,rдеС-
некоторая константа, так как
(
а/2с·)-2at- /
-+
---а.
2
2
Зная S(t) , уже несложно "ВЫЧНСJш'ru 11.н'сеrрал
'•
f11( t)dt = S(t, ) - S(t;, ).
(*)
1"
В частности.
1"
Фуню ~шr Р(:х). п рш1з1юд1 rая которой равна
ла1 11 юii функцr 111 j(x). наз ыщJ~тся сё 1lepuoa6-
jJa.J1юй. Так фуню~11я F(I) = а/ !/2 есrъ первооб
разнап /~ля фу1 t1<uни/(t) ::о пl. Посколы<у произ
воднан ко11станты равна нулю. 11ер1ю образ 1 1ал
определена с ТОЧIIОСТЪЮ ДО ПОСТОЯl-ШОГО сла
r~~.t:мш·о. т . е. сt:ли. Р(х) есть utрвообр~ :шая
функции f(x). то G(x) = Р(Х) + С тоже её пср
вообразнi!я . Длн любой пе рнообразпой Р(х)
функции ((х) слраве11лива фор."1ула Ньютона -
Л ейб н~ща
F(fJ) - F(a) = J/(x)dx.
(/
По сути 7'е:1а. это всё та же формуJ1а (*), к
кото р ой нас прпнела задача о дшrж11демся
а1помобнле. Форму.11а Jlьютона - JLeirбшщa
устана1шиваст с вязь мс:rкду д 11ффсрсr щналь
ны"1 11 111-rтс1·раЛl>Н"1М НС4НСЛСННЯМII, а значит,
между з:щачамн о касателы юl! 11 пло щал ~r.
Ссм:сйстно 1:1ссх 11 ер воо6 ра з 1rых дан1юй
фу11юt1111 называется её 11f!оnределi;1щым. 1tн
тегрилом. и обоз11ачастся
fЛx)ctx.
Если хотят запнсать формулу неопределёп-
1101·0 юпеrрала какой-л1160 футгкцаи , то в ~юн
це формулы облзатслы 1 0 добаnJtnют 1- С,
подчеркивая тсм самым, что это нс как<Jя-1·0
одна ш::рlюобразн :.щ а множесттю всех гн:рно
образных Nlнной функц1111. На11р11мt:р:
Jd
tl.\ 2 с.··
{/.\')(=-2-+
.
499
Летермиг1изм и (..лучай~юсть
КАК НАЙТИ ИНТЕГРМ
Предноложим. чтс мы хотим вычиаr1 1 ть 1 1ло
Щ:1/(1, 1<ри BOJI И 11el11 IOJI Ч);)J 1еции ПОД графп КОМ
параболы у = х
2
па отрезт<е [О, а], где а - 11екп
торое действ ителъпое ч исло (рис. '5). И:~ р11с
смотрен11ы.х выше примеров понятно, что ис
комая площадь раnна интегралу
{/
Jx2dx.
f)
По формуле Ньютон::~ - Лейб ~ шца. д::~1111ый нн
те 1·рш1 есть разност1,
F(a) - F(O}.
где Р(х) - первообразш1я фупкцни / (х) = .\ ·
2
.
Как же найти эту первообразную?
Можно просто посмотреть ~ с11р;,11ю <ши к
(или в приводимую в нашей статье таблицу
нео11редс:лённых ннте1 · μ.t1юJ:1). Но мы шх:тупим
иначе. Вспомним, что если F(.x:) - nсрRооб
раэн<t.я функции /(.х'), то F'(x) =.((х) Дру1·11ми
словами, интегрщювание (т. е. в данном случае
нахожде::ние 1-н::опре11,слённuго пнтсграла) -
защ1ча, обрат11а~ днффере1щиропан11ю По
этому 1\1Ы обратимся 1< табшще 11ронз1юд1 11.r х
( см. статью ~ прои зnодпая» ). 110 В()Спот.зусмся
ею не так, как пол оже110, а наоборот - 11айдЬ1
такую фуmщию, про~пвод1 rая которой «rюхожа»
1 ш фушщию/(х) = .\.'~.Из всего, что r.1 м ссп•. J<ак
будто 1юд.ходит формула
В ее право(~ част11 сто11т (а - J)-я степень х.
Нас 1111· 1 ·ересует m·орая с1·епе1 1 u, :i потому бущ:м
считать, что а = :1>:
Теп~рь, чтобы избавиться от коэффициента :).
Rсnомни~1· rюстоя н ный .иножитель можно
1!ыносн·1ъ за зне1. к произ вод н ой. т. е.
По1юж111:! k = 1/ 3, 110J 1 учым
(.\''J=.).хl = 2
1
,"(
.
:)
~J
'500
J'
о
а
Рис. 5.
И'1·ак. од 1 ю 1~1 из nt:рвоuбразнh1 х функци1
'
'
.((х) = х- бунет F(x) = х / 3, а н<.:t: 1rс:рнообразны1
задаются фориулой
fx~dx=-~'+С.
)
По111·1но J\'tЫ вывели одно вэ пра вил ннте
~·рирования :
Постоянный l\rnожитель можно .вы
носит~. за знак интеграла:
Jkf(.x)dx = k Jf(x)~lx.
Ест1, н другие нрашта. например таr<ае:
ИНТЕГРАЛЫ НЕКОТОРЫХ ФУНКUИЙ
Константа :
Jadx=ах+С.
f
ах2
линейная функuия: (ах~ b)dx =Т +Ьх+С.
XJI~'
Степенная функuия: Jx•dx =-- + С , где а it-1.
а+1
Функuия 1/х:
Экспоне нта:
Н атур альный
логарифм:
J;dx=111lxl+С.
fexdx = ек +С.
Jlnхdx = хlnх-х+С.
Тригон ометрические функuии:
Jsin xdx =- cosx+C; Jcosxdx= sinx+C;
J-
1
-
2- dx=tgx+C; J-.-
1
-
dx = -etgx +C.
cos х
s1rr х
Иuтеграл суммы двух функций равен
C-yNo'fe интегралов этих функций:
J(j'(x) + g(x))d.x =Jf(x)dx + Jg(x)dx.
Одн:эко нернёмся к 11ашеi1 з~ща ч~. На 'V1 ocтa
JIOCh НЫЧJIСJШТЬ значения фу1 I КЦНИ F (.Y) в точ-
1\Шiх=Ои.х =ct,а:затемвычесrьпер1юеиз
второго:
Таким образом, площадь кршюлипсйпой тра
псцш 1ттод граф\п<ом лара60J1ыу = xL на отре3-
ке [О. а] равна t~ л.
За;\ачу о <-К Ва)\ратурс паrаnолы·~ вп ерныс
решил дрсвнс1·реческий учёr1ый Лрхимс;~ Li
IП R. дон. э. (см . стат ью •АрхимеN) R отmfчие
от 11эс он расоютрсл общий случэ11 napa60111,1
СТЕПЕННЫЕ РЯЛЫ
Ранее мы рассмотрели ч11с1ювьн..: р5щ1.1
о0+а1т."+а"+...
А почему бы не сос1.«11ш·1·ь ряд, слагаемые
клтороп.> фуню\ш-1
а,_,(х)+а1(х)+...+ а"(х) +".
Такпе ряды ш1зыватотся фу11кцио11алы1ы.ми.
1lри к:-tждом фикс11ровашюм х нз области
определения фущщп!1 а0(х), а 1 (.У) , "" а,,(х), ".
функцнон;шьный ряд стано внтсн ч11 с1юным 1·1
чожет 1шбu сходиться, J1нf10р:.1сх<щ11тпо1. f\ilно
жестно тс.:х .\', пр11 которых соnтветсткующнii
ЧI !СЛЛ!-ЮЙ IJHД CXQДHTOf, назыr~:н::ТСЯ oбrtaCJ!ZbIO
С.\'О(1и.моспш функцио11ап1. 1 ю1т> рнда
Срtд 1 1 фу11кцпон<1m,пых ря11ов ~~ыделякп
011е1и•шu,/е, н которых а"(х) = с"х
11
•гдес"-
ф1.rкспrован ные ч11сла. 1Lросте.йшим прлмером
степешюго ряда яnляется сумма беско11еч1Jо
\'бынающеЛ 1·еометрнчсской прогрессии со
3 1~амс1 rателсм х, 1.\' 1 < 1:
]
•
i
---
1+х+х-+х -'-
+х''+
(*)
L-x
-
~· ".
"'
."
ОRласть сходпмости степе111ю 1·0 рщр - это
всеrла нскоторh111 интер1:1<1J1 (- R, R), быть мо
жет нк;11оч.;1ющ11r1 одпп ишт оба его ко1ща.
Проюволная и интеграл
А
Рис. 6.
и докаJал, что «проиэnолытый сегме нт, огра
ниченный прямой и параболой, р;шетr 4/3 трс
уrоm~ннка, и.меющего те же основание и вьт
со1у> (рнс. 6). Лр:киJ\·IС~ таюк~ успе шно 1rаходил
11Jющад11 н 06ъёJ1..1ы других фигур, пссмотртт 11<1
то что н ~1атсм:1'1'11кс с 1 ·0 .1:1рс.мсни не бьuю п<.>
ю1т11(1 11нтс1 ·ра11а 11 щ)оизвод1-1ой . Интс.:1р;.~л 1,
rюе исч11сленне да~т общ11й метод рс111еню1
всех 1юдоl1н1>1х :l;:~да ч .
Ино1да он вырождается в точку х = О, шюгда
сон пщ1а <..'Т со iкclr 11рнмой. Llисло R на:~ывастсн
pttol()'CO.м. схш)имости сте11енно 1·0 psщ::i. Iicл11
11нтсрR<1л схо;111мости со1шадает со нcef'I ч11с1 ю
ной прнмой. то говорят, что 1хщнус сход11мо
ст1 1 ране11 бесконеч1-юсп1 . Дли нахож;1сн11я ра
/цrуса сходимостн сте1 1е111 юго pJ:tдa
>
,,
С0+с1.х+с~х-+ ." +с"х-+."
можно полъзоnа1ъся следующими формула.•11 1 :
lc"I
R =lim--,
"_,~ lc11-1I
l
R=liт-,-
"·~"·Jc1
v11
(ест ~ соответстнующие 11редел1>1 сущесп~уют).
Стспсн11ыс ряды иr·рают важную рпт, в
разm1ч11ы.х ра зделах мате::-.1атпю·1 , в ч асттюсп1
в прпближёт 1 ных в.ь1сшслешшх фупы.J,нl1. !::ели
некоторую функцню/(х) удаётся nре/~станпть
в ш 1/1е стс11е нн о1·0 р.нда (1·онорят <· разложтrть n
CTC I 1е 1 11 IO(I JЖ/\»)
~
/(х) == Lс"х11,
п1)
501
Летерминизм и случайность
ТО для приблнжё111 ю1·0 l~ЫУИО!СНИЯ /(~) мож
но воспользоваться лишь конечным чи слом
слагаемых
J(x)~с0+с1х+". +с"х".
Дру 1'и:ми словами, функцию в этом случае за
меняют на мно1'очлен подходящей степени, а
вычислить значение тако1·0 многочлена уже
несложно.
При каких же услоRиях мож1 ю разложить
фуню~и ю п степеш юй ряд? Одно пз зтих усло
вий - оrраниче111rоС1'1> всех проиэводных
в сжрестпости пуля, т. е. существоваrше такой
постош-1ной М, что для всех х из некоторой
01<респюсти нуля 11 всех п = 1, 2, ... выполняется
неравенство
1.r <" >(x)I ~м.
Тnгда фу11к1 ~ия .f(x) разл;~1 'астся н следующий
степенной ряд:
/'(О) ("(О) ,
.f(.x) = .f(O) + -
·
-
1,-х + 2°!.'\:- +
/"'(U)
Р '' 1(0)
+---х;+."+ · х"+."
:S!
n'
Он на:{ывастсярядам Tezl.лopa (шшрядо.м Мак
лорена) д:н-1ной фун.кщ1и .
Таю ·ш uбpa.ЗONt, IJpи вьшоm;е1пн1 услон ия
01·r~ш11чешюсти 1.1ссх nроизнодных в окрест
н ости нуля значе1шя фуню\rtИ R этой окрссr
нос1·и щ.:лнком определяются з11а че11иям11 всех
её 11ро11знодны:х в одной -сдинстnе111юй точке
х =О (сама окрест1юстh может быть и весr,ма
большой - в часттюстн. соnпадать со всей
ЧИСЛОJЮЙ осью).
Для некоторых элеме1сrарн ых функциr'l
р:.~зложспис в ряд Тейлора легко найти. Рас
смотри~, например, функцн ю f (х) = l! ' . П о
скольку любая производная этой функц11н
снова е·\.то/<11\О) = е
0
= 1 . Условие 01·rаничсн
ности пронзв<щных в шобо!'1 окрс:стнuст11 нупя
также нетрудно 11ро.1:1ерить. О1сдоватс:лыю, ряд
Тейлора ,цля фуню ~ии е·' нмест внд
'( ".~ х;-1
"'"
(.!-"
= 1+..:._ +
_
"-+
_
"'_+".+_.-
+".
1! 2! ?>!
11!
причём он сходится дт1 всех х. Отсюда, поло
жив х = 1, получим
1111
е= l+!+-+-+-+--+ ".
2624l20
502
Шс:спj первых чл еrюн :'!'l'ОГО ряда даю1 прнбт1-
жёг11iое з11ачение числа е с пер11hlми тремя вер-
1rыми цифрами: 2,71666".
Определив :.нrачення производных фушщий
~iл .х и cos хн ну.r1е, получим их разложения в
ряд Тейлор;~.
,•
.
х~ х';
IHI ,').' 2" 1
S!ЛХ=.Л:--+-- ". +(- 1)
+". ,
3! 51
(2п - 1)!
х~ х1
,.х~"
cosx=!- -+-- .. . +(-!)' --+".
21 ,11
(2n)!
При 1юстрое11ии лриблr rжё1тных мате~~ати
чс:ских моделей р;~зл11щ1ых процесс()в часто
для малых х полаг:нот
(!\'"' 1+х,
Si.11 Х"' .х·,
х~
COS.:\' = ] --.
1.
Производная или 11нте1-раJ1 от ко11еч1ю~"1
суммы функций есть сумь·1а лро11зnодпых нли
и11тегралоn соотnетствующнх слагаемых . чего
нельзя сказать о «бесконечных» сум.мах. Одна
ко степенные ряды в этом оп-юше111ш усrrо
сны хорошо - .ннутр.и области схuдпмос-r·111 1х
можно почлснно д11фференц11ровать н 11нте
грирu1щть. н~шрнмер, есл11 почленно 11 род~1ф
ференцирокпъ рял (*).то LIOll)"IИTCH рнд, суммэ
у
2
Пр11Ьлиж ен11е
1
фу11кu1111 i' =J--;:
( 1} с nомошыо
СТ(;'Гl(;'НН ОГО ~~Лd
1
y= l +x~x+x +
+х'+Х;\11
При бли жение
функuии у= е'
С ГЮМ()WЫ()
стеnе 11ны х рялов
1 -у=е",
х1
2- у=1+х+
2+
х1 ~·1
-1~ -1-
6 2·1
~-y;l+x+
хl )(j
+т~&;
х1
4- r=lн+
2,
5-)' = 1+х.
которого будет paвJJa нроизводной от суммы
тrсходного ряда:
1
12 ,,
"
1+...
,=
+ ."(+.).'\'- + ...+llX
(1-ху
Теперь переменную х в (*) замещ1J\1 на - t:
1-1
.!
с !)'' 1/
---
-
l+t -
... +
-
t +...
l+f
Если прот1нтtrрнро~ать этот ряд R 11ромежу1 ·
ке 01 ()до.'\· (Jxl < 1), получится степенной рн,ц
.
•
xi х1
"х11+1
111(l+.;\.) =.х - -.-
+-
-
... + (-1) --+
..
2
.)
п+1
А сделав то же самое с рндо.У~
~=J-t
1
+l
1
-
_
+ (-l)n l
2
"+...,
1+1-
найдём р::~з11ожею 1е
х' :xs
xl""'
arctgx = х --+ -- ... +(-1)"--+ ...
35
2п+ 1
Нс только ЧИСЛ О е. 110 и число 1t можно
ориближёшю вычислять с помощыо рядон. По
лож1ш х = 1 13 разложении для arctg х, получим
1t
11
11
1
-
=:Jrctg]=1- -+- -
... +(-1) --+ ...
4
)5
211+ 1
Этот ряд 11аз ынают рядам Лейбница. Сходитсн
он ,цо1ю;1ьно ме,цлешю, и для хороших при
бл ижений приходится брать слишком м1101·0
слагаемых.
Производная и интеграл
Полученные нами раз;южения в степенные
рядыфункцийln(1+ х) и arctgхявляются uто
же время ряд::~ми Тейлора для этих функций.
Вообще, всякий степенной ряд есть рsщ Тей
лора лля своей суммы .
Рассматривают степенные ряды и более об
щего вида:
Со+С1(Х- Хп) +с~(х - Xu)j+... +С11(Х- Хп)" +...
Про пих rоrюрят ~cJ·eneнriOЙ ряд с центром
в точке х0». Аналогично определяется ряд Тей
лора для функции} (х) с центром в точ1<е х0:
!(. . ).f'(Хп)
.
х) = }(:Х:о + --1,-(х - Хо)+
j."(x)
1·<11 )(:\:· )
+
о (х-Хп)l+...+ .
.
о(х-Хоу1+...
2!
11!
Особое знаqсю1с имсютсте11еш1ьн:: ряды для
фу11 1щий ко мплекt:ногu п ерсме111юго. Если за
писать ряд Тейлора M>i фу1 нщии у= е'", а затем
воспользоваться рядамп мя синуса и 1юсн11уса,
то мы лридём к формуле Эйлера (см. статью
«Возведение в степень и извлечение корпя из
комплtкс~ юго ч11сла~) Надо сказать. что комп
лексный анализ существенно отл ич ;1 ется от
ueщel~rneннo1·u. Так, есл и у функц1ш.f(z) ком11-
пексного перемешюrо еl~1ъ непрерывн:111 про
[IЗ1юдн;н1 R окрестносн1 нуJJя , ·1 о у нс:ё t:стъ все
r11щиз1юдныс: нона разлаr:tется в сгене111 юй ряд.
-
1
Прнближен~•е функuии у = , 1 1 ctg х L nомошыо с-теnен111;>1х р~лов·
X'l
XJ Х5
1-у =х, 2-у =х-3, З- у=л 345
х' )!'::; х;
4-у=' -3+5-7•5-у=мщ;-'
503
Летерминизм и случай1-юсть
СЛУЧАЙНЫЕ СОБЫТИЯ
ВСЕ НАЧАЛОСЬ С ИГРЫ В КОСТИ
Случай, случа.И11осп. - с 11ими мы встречаемся
повседневно случайная nстреча. случа11шш rю
ломка, случайная находка, c.rryчai111:ur ошибка
Это·[ ряд ~южно про[(онжать бесконечно Каза
лос1, бы, тут 11ст места ДJIЯ "'атематнки - какие
уж з~1ко нh1 в царе1·Rе Случ.:нr1 Но и здесь наука
обн~1ружила ннтерес11ыс зако11омсрнос1 и -
они позволяют чслонеку увt:рснно чун стнов~п ь
ccfiя пр11 нстр~ч<:: со случайными событиями
Но нрежде. чем рассказа·~ ь о закоrюмер-
1юстях сJ1учай 1 юст11, rюпытаемсн ответить на
Rопрос: что такое азартная игrа? УJЭерепы, сrто
боm,шrшство счнт-ает - это ~trpa на деньги. Не
верно. Ila деньги MOЖIIO играть н в теннис, 11 в
шах,\1аты . Теннио1с1ъJ 11 шахм атисты получа
ют большие 1·онорары за ныигрыши в туr
ш1рах . А но·1· 1<<1рты - аз:tртнан н1 (XI. Почему'
Лu1ому, что в 11ей 1·л;1Rн) ю ro111_, 111 ·р~н:"t ' с.:.11у
•1ай - от нсг·п зав 11с11т. какие н .. .1е-~-1но каrт1.1
окажутся у парт~ 1ёр<>А Пр.н1дэ , 11 fl 1\аr·гёжнш~r
11сре уменнс игрока ~шач111 · много. 1-lo есть
111·ры , в тют()рых ()Т пгроков не ·~μебуется 11и
какого у.меrшя. Например, «Opляrrr<a". монету
504
подбрасьшают, и Dзашrс1 rмос111 от того, какой
сторопо~1 011а упала. вы11rрьmзе-1 первый 11ли
rпорой парт11ёр Ил11 дру1 ·ая 11гра , 1де nластn\
ст сдуч.ай. - игра в коств Uстююш1мся на ней
1юдробнсе. 11ме 11но с нсё матсм;пшс11 н;111аJш
11::~уча1ъ е 1 ·0 велнчеспю Спуча 1I
Игральная кость. 11спрсмсн11ыi1 :.пр11бут
мно1 ·11х настолы1ых итr, - малснью1!r кvб11к,
rран11 которо1·0 помt"чсны ц1-1фрам11 ш111 точ
ка.мн . Раныuе та 1<ие кубню1 ~ел;:~1111 нз кости ,
откуда н пошло нх ш1зва1ше - « 11гралы 11>1е ко
стп». Коща нгральную кость бросают, то 11а её
верхней гра1ш оказывае1(:я какое-1·0 члс1ю -
от 1 до 6. по числу граней
И1·р в косп1 великое .множество. Простей
шая нз ннх такона. двое rю uчсрсд11 бросают
кубнк. Вы111·рынJе1 '1 ·от 11 ;-1 1111.х. ктu •вык1 11-tул"
60JIЫJl<..:C Чl!CJIO BЫI·ll'f1ЫIJI МОЖ<:'1' p:IRHЯTf>OJ llJlll
з ара11ее назначе111-юй су'l-1ме, 11m1 р ~1 ;н-юп11
числа очков, Rыпаш111L'< нз 1<уnнке пр11 броса -
1111юс. Часто бросакп 1rc один, :1 два, тр11 ш111
четhlре кубпка. Естестве1 1 но, всякий ш·рок же
лает, qтобы у псго чащ<:: выпадала шестёрка , по
этому мнопrс игры в кос1·и основаны 11а появ
лсшнr 11.м:сrшо шестёрк11.
Просп~дпм, как выпадает шестёрк;r 11 рн
бросаrп-111 кубик;!. ТТредпо1южим, что кубнк со-
11t:ршенно 11раннльный - 1кt: его 1·1x1J 1н абсо-
11:юпю од1 111 акопы. Ec11r1 11одбр;1сывать куб1rк
десять раз, то чнсла \10 1 ут в1.та;1~~т~.., н~tпример ,
11 1·акu11 очерi.:дгюс·т11: 1, 5, 2, 2, 3. 4, 1, 6, 3, 5 плн
втако~'1:6, '>. 6, 3, 1, 1,4, 2,3,6. В11ерnомслучае
тестёрка в1.111aJra оди11 раз, а FIO 1пором - три
раза. Может случиться, что шестёрка пе nыпа
дет ш 1 разу шш nce деснть раз.
А еслн подбрасьшать кубш< нс деснть, а rtсопъ
тысяч ра:3? Тогда каждая из 1 ·ршн.:r1 будет 1~ыnа
дать примt:рно од 1 1накш;о частu. Чтu это з11а
ч11т? Пус1ъ N1.; - количсстtк> выладеннiТ ~ ·рани с
ц11фрuй k opl! J\' б[юс:111иях кубнка, тогда отно
шение N 1iN кuтирое н:~зывается ч:~стото(1 ныла
де1-111я гра1 111 k, будет пр116J1из11тс.r:rn 1 ю однна1ю
во .ll'Ut 1.ксх rрэ11ей куб11ка . П()сктr~..ку
.'v'1+N2+i'v',, +N1+.V,+N,,=i\',
то uce частоты буду~· бт1зт<11 к 1/6. Сама всm1-
'ШНа J /6 называется пероятпостью выпадения
как шес·1·(:'рюr, так и nятс1жн, чстнt:рки и .," д.
Ес1 ш же: подбрасынатh м сн1<:ту, ·1 ·u 11сrонт1-юсти
JiЫПаденнн н орла. н ре1ню·1 r:1вны 1/2 Чутг.
ппзж<: мы да;tим стр< н ·ое определен не Вt"роят
Fюст11 С< >бытr 1я .
Слоно «событне" в i'iыту 11rнме11яют к знэ
ч11те;11>ным я1·1Лениям. а 11 ,.,,1:пемат11ке - кп nсем
Случайные события
возмож11ым исходам рассм::пр1 111аемоr1 ситуа-
1~и11. Так, А случае бросанин 11rрал1,1юl1 кост11
событие - зто выпаТ1,е11ие той 1шII rпrой грашт_
Собыпшл будеJ'-f обозII~чать бот.шнми латн11-
ски:м11 букnами· напр11мср , появление 6 прн
бросании кости - через А, одного нз •~иссл от
4до6- черезВ.oдiro1·0изч-пселот1до5-
через С. Вt!рояrrиюсть нро11з1ю11ьнu1·0 события
Х бу;~ем обозначать через PjX}.
Впервые нероят1юсти случ<~йных событий
в азарт~ IЫХ и1·рах ВЫЧНСЛИЛJ 1 н хvп к фраю~у:~
скис: ма·1·ематпк11 fi.rтc:з nаскаль 11 TThcp Ферма.
О11н нодсч иты наJ1и '-П1Сл о шанс()н (от (j)jJ.
с11а1ке - «улача», «случай») собыпнт 11з обще-
1·0 1юзмоЖiюго числа равновероятных 11сх о
дов. Проследим за их. расС\'ЖДе1тиями.
Исход како1·0-либо ислытави:я , оттыта 1mн
игры, выражающийся в событни А , назоnём
шансом событш1 А. 1lанример, при бросанин
нr·рал~)ной кос1 ·11 ноэможны шсеrъ равrюнсро
ятных исходовА 1,А2, ." А (, - выпадение 1. 2, ...,
6 очкок. Пусть событие А означ;;~ст вьш:щен11е
ч(;"1·но1·<) •пк·ла 0 1 1кок. т е. 2. 4 11J11 ·J (), В этом
случае Р{А} = 3/<1 = 1/2, т. с:. вц1оятное1ъ Р{А1
ра1ша отно1.1.1енню ч1 1 с_r1э шансов события А к
об щему чнслу pa11110Rcroнтr11,1x 11сходон. Т:~кос
011р<::дсле11 не наз1 .1 нается JС'шсс11чес1аt111 опj>е()е
ле1111е.м сtерпятиост11.
Ит;:~к,
~г" есщ1 при каких-либо условиях и.l\:IC-
1!1!.
ются 1· равновероятных исходов и s
нз них приводят к событию А, то
ве1юятностъ Р{А } события А равна
отношению s/1•.
В прпст1,1х случаях выч11ст1·1·1. веронт1юсr11
11е сос·1 авляет тру11а. Наrтр11мср, rюдброс1111
пnерх монету, мы 111ае.\1, что 1111111;-tДет и л11 орёл,
пли решка. Пусть событие,, о;~11з•1а~т появле
ние орла. Н подобных случаях бу~см .впрс;~1,
писа ть А = 1появлсrше орла 1. l lонятно. что
P{AI = 1/2.
Хорошо перетасусм I\OJIOД) 1r:~ .")6 ~аrт 11 с11у
чайно вынем J 1<арту. Cofi1,1·1·1 1я А = [вынута
к:1рта черLюннm"1 м:1сп1J 11 В = [вынут туз] 11.~
36 1IСХОДОН нмеют COO'J JIC:TCTHCH [J() 9 11 ..j. 111:111 -
(()Н. Поэтому
5())
Летерминизм и случайность
В 1rекоторых случаях вычислять ве роятнос
ти со61)rrий отнюдь 11е просго. Пусть событие
BJ.: оз нач ает, что при бросании двух игральных
костей сумма выпавших на них очков равна k .
Всего имеется 11 подобных событий: В2, В~·
... ,
B 1l, однако веронтности их 1rеодинаконы. Р<tн
ноnсролтным исходам соответствуют п;~ры
чнсел (i, j), rдt: i - число выпавших оч..кон на
J-й коеr·и. j - чн сло выпявllшх очков на 2-й
кост11. Всего таких исходов 36. Шансами соб ы
т11яВ1.> булут rкходы, при котор ых i +j = k . Чис
Jю ша11сrщ кажJ{ого из н1:1х можно подсчнтат1>
с пu.мощыо сле/"(ующей таб; r ицы:
~1
2
3
4
5
6
1
2
3
4
')
6
7
2
_)
4
5
6
7
8
.1
l\
5
6
7
8
9
-\.
5
б
7
8
9
10
56
7
8
9
10
1J
67
8
9
10
1J
12
~
В таблице: каждая строка соответствует
ч11слу очков i на 1 -й кости , каждый столбец -
чнслу OllKOl3J на 2 - й костн, а D юrеткс па пер<:
сеl1е11111т i-й строк11 н/-rо столб ца стш1·1 сумма
i +.! = k . lkc всходы (i,.J) можно считап, раш ю
всроятным 11 - нх 36, а число 1щ1н сов событии
в" равно количеству клсто 1< т:збтщы с ч11слuм
IJ. ГIОЭ'IОМ.)', 110 КЛ:1С С 111 1 ескому опрсдслt:ШIЮ
всршл ности , получаем
Р{В2} = Р{В12} = _
1
1
6,
Р{в~}=P{.R i1}= 2_ =
_I
36 18'
Р{в1} =Р{вю}= 3~ =1
1
2,
P{B-Jl = P{В)Jl =_i_ = ~
'
'
~6 9'
Вс е рассмотрен ны е примеры являются
частным11 случзяivш так называемой урно1юй
схемы Лусть в ящике (урие) лежит г 1ш1rюв .
')О()
Они различаются no цuету или У~етками, 110
не11а ощуш" Обозначим ихu1,uJ, .."и, . Прсд
по1юж11м, что шары u 1, и!, ..., и, белого цвета , а
остальные 1· -
s - чёрпого Еслн из урны слу
чайно Вh11-1 ут ~на р и, с номером i <s, то говорю:
11ро11зошло событие А = rвыl l}"J' белый шар].
В этпм сJ1учас 1гмеt:тt.:н 1· p:-i вновсроятных исхо
дов и1. 11!, .." 111 • Из 1шх событие А 1.1мсt.:'"1 s ша11С()В
u1, и~,
....
и .- По классичt.ткому 01 1реде; 1 е1111ю
nероят1юсп1. Р {А\ = s/ 1·.
Бросание мо11еты можно заменю ь урновой
схемой с дuумя шарами , которые обозначнм
буквами О и Р. Выпадение орла при бросании
монеты 11 вы11ИЬ1а~-ше из урны шара с буююй О
имеют одну и ту же вероятность 1/ 2. Вh1н11ма
нис из KOJIO/~hl кар•t· 1 карты можно замешпь
урно.й с 36 шар:зми, обозн.~чен11ыми n:.Jpoir зна
ков (а, h), 1·де а - буквы 1J, Т, Б, Ч, о:тачающг1е
масти : П - ттию-1, Т
-
трефы, Б - ()y(J111,1 . Ч
-
ЧС[)RЫ, а f; - ДОСТОИНСТIЮ к:ар·1 Ы: !J = 6 -
шестёрка, h = 7 - семёрк:а, ... , Ь = 11 - валет, ..,
IJ = 14 - туз. Собьпи:ю А = tвыпуrа карта l!ер
воr-п-юй масти! соответствуе1 вын11ма1111е из
урны шара, принадлежащего подм 1 южсс:т11у
А= {(Ч, 6), (Ч, 7), ... , (Ч, 14)}. Событию В= 1ныну1
тузJ соответствует nодмножеспю В=((! 1, J4),
(Т, Н), (Б, 14), (Ч, 14)} В общем случ3е в урно
ной схеме предгюлаr:1ется мложестно шаров
U= {и1, и!, "., и,.}; любпму подмножеству А c U
ИГРАЕТ ЛИ ПРИРОЛА
В КОСТИ?
В середине XIX в. г~реподаватель
Высшей реальной школы в городе
Б рюнне (ныне - город Брно в Че
хии) Грегор Иоганн Ме~1дель про
водил свои ставш ие впоследствии
знаменитыми ог~ыты с горохом, в
результате которых были открыты
закон ы н аследстве нности. Мен
дел ь скрестил два сорта гороха с
желтыми и зелёными семен ами,
г~осле чего расте ни я дали только
ж~тые семена (первое поколение
гибридов). После самооnЫ/\ен и я
растений, вырашенных из этих се
мян ( второе г~околение ги бридов),
появился горох и с желтыми , и с
зелен ыми семенами . Ме~1дель п од
сч итал, что отношени е числа рас
тений с желты>.1и семенами к ч ислу
растени и с зелеными семенами
равно 3,01. Учё~1ый скре шивал так
же cop·ra горо ха, различаюшиеся
л нбо по форме 11лод,1, м1бо по
расrю/\ОЖению uветков, либо по
ра3мерам растени й и т. ri. И каж
дый раз в первом поколении
обнаруж ивал ся только один из
противополож~1ых роып ельск их
признаков - его М енлель на з вал
доминантным {отлат. dommatus -
«госnодспю»), л11шь во втором по
коле нии проявлялся и другой -
реuессивный (от лдт. recessus -
«отстуnле1·1Ие))}. В опытах Менделя
отно ше~1ие чис.ла растений с доми
нантным при знак.ом к числу расте
ний с ре u ессивным пр~1знаком
было рав~ю 3,15; 2,95; 2,82; 3,14;
2,84, т. е. во всех случаях ока3ы
валось близким к 3.
Вг~оследствии немеuкий зоолог
Август Вейсман и америка нск и й
бИО/\ОГ Томас Хант Морган объяс
~• или результаты оп ытов ме~1деля.
Используем с той же uелью урно
вую схему. Предположим , что лва
элементарt1ых tюс ителя наслед
ственност и - ь.оми н антный ген А
и реuесс ивный ген а - отвечают
в организме за некий при знак. При
этом дан11ый признак задается па
рой геновАА,Аа, аА илиаа , и осо
би с генами АА, Аа, аА имею~
дом и нантный п ризнак, а особи с
гена ми аа - реuесси вный. П ри
скрешивании ropoxaAA с rорохом
аа гибрид получает от каждого
рол ителя no 1 гену, поэтому все
особи первого п околе 11и я имеют
паругеновАаилиаАиунихоб
наруживается ь.оминантный при
знак: например, семена желтого
uвета. От родителей с п арами ге
нов Аа имf аА мож110 получить
особь АА, Аа, аА ~1 ли ac:J. Все .пи
сочетания одинакоэо возможны,
значит, особь аа с реuессивным
признаком появляется с вероят
ностью 1/4, а особьАА, Аа 11ли аА
с доми на1нн ым признаком - с
вероятностью 3/4. Если во втором
поколе нии было N = N(A) + N(a)
особей, где N(A) - число особей
с доми 11 антным признаком и
N(a) - число особей с реuесс ив
н ым nризннком, то при больш1~хN
N(A} 3
'N:;4'
N(d)
--= -
N4'
а отноше11и е MAJ/N(a) должно быть
близким к 3. Это и уста 1щвил Гре
гор Иоганн Мендель.
Случай ны е соnытия
Меха низм наследован ия так же
случаен, как и исход броса ния мо
~•еты или игральной кости. Поэто
му можно сказать, что пр ирода
иногда .играет в кости» .
В 1953 г. американские учёные
Фрзнсис Крик и ЛЖеймс Уотсон
создаi\и модеi\ь nространстве нной
структуры молекулы ЛНК - носи
теля генет11ческой и нформаuии.
Эта модель объясн яла механ~1зм
случай но го образова ния пар ге
нов. В 1962 г . за своё открытие
Ф. Крик и д. Уотсон стали лауреа
тами Нобелевской премии.
соответс1 нуе-1 собьп исА, сос-гоящее н том, что
1зЫН)'Т 111 ар tt;, г1рн1 -1адлежатпнй tюдмножеству
А Веро>1т1юсть событня А ра1ш<1 отношению
:'!Ом, Rур1 ювоl'f схемt" л 1оnому м 1южеству л <- r;
соотnетстt1ует соб ытнеА = [ныrr ут шар из мно
жества AJ . Собьпие U, соотnетствующее всему
1'11 южествуптаров в ур 1re. 11:~Jьrщ1стсл достовер
ным Ero вероятность равна 1, так как
где/UI= 1·
-
общее чн<::JЮ шаrюв в уrне, IA / -
чис;ю шаров 1~ подм1 южествс А. Таким обрз-
Р{и}; Ju! ; 1.
1И1
'507
Летерминизм и случайность
ЗАЛАЧА КАВАЛЕРА ЛЕ МЕРЕ
Кавалер де Мере, один из французских придеорных,
был азартным игроком. Ленежный выигрыш при игре
в кости обыс11-ю зависит от комб ина uии выпавших
чисел, tta которую делается ставка. Одна их таких
комбинаuий - выпадениl:' хотя бы одной ш естерки
пр~1 •1етырех броса ния х игральной кости. Ле Мере
смог подсчитать число шансов этой комбинаuии.
Обшее число ~•сходов при ч етырёх броса ниях
иrраf\ьной кости равноь • =1296. Число шанс.ов появ
ления хотя бы одной шестерки составляет 6 4 -5~ =671 .
так как шестерка не выпадает ни разу в 5 ~ случаях.
Следовательно, вероятнопь выпадения хотя бы одной
шестерки при четырех бросаниях равна 671/129&~
~ 0,518 > 1/2, поэтому при четырех бросаниях выгод-
11ее делать ставку 11а то, что выпаде1 хотя бы одна
шестёрка, чем на то, что не выпадет ни одной. По
в11димому1 многие опытные игроки знали, что первая
комби11<шия 11оявм1 е1ся чаше, чем вторая, и най1и
партнера на такую игру было трудно.
Более сложные комбинаuии возн и кал и , если
бросали сразу две кости. Ле Мере пып11\ся опреде
лить, сколько раз t1адо бросать пару костей, чтобы
вероятносrъ хотя бы одного появления двух wecreptж
бь~ла больше 1/2. Он подсчитал, что досrаточ но
24 броса11ий. ОлнJко опыт игрока заставил де Мере
сомневаться в г1равильногrи своих вычислений. Тогда
он обратился с этпй задачей к математику Блезу Пас
калю, который предложил прJвильное решение.
Ученый определил, что при 24 бросаниях пары кос
тей две шестерки появляются хотя бы раз с вероят
ностью, ме11ьшей 1/2, а при 25 бросаниях - с веро
ятtюстью1 большей 1/2.
13 с~мом деле, если бросить один раз пару костей,
Лде шестёрки выпадут с вероятностью 1/36, а не выnа
лут - с вероятностью 1 - 1/36 = 35/36. При п бро
са11иях пары косrей число ша1-1сов непоявления пары
Пусюму мнuжеству 0 соо·1 ветствует Hl.!BOЗ
J1IO.J10-юr1 соб ы ти е, еп> нероятгюс·тъ равна О , по-
скольку
Р{0} =~= О
lиl
Ест ~ А с R, ·1 е множество А - под;.111 оже-
ство м н ожества В, то говорят: событие А влечёт
за собой соб ытие В. Это оз11ачает. что еслн про
и:юшло событие А, то пrю11:юшло и собhJТИе В.
Таккаквсегд~10 сАсU,тuО~IAI~IUIнn<:ро
нт1 юсть любо1 ·0 t:uбы·1·1,1н А у;юuпетно ря с-~ нера-
ненстнам
()~ P{ll} ~ 1.
')08
шестерок равно 35", а обшее число исходов соста
вит 36". О6означ11м события
Ап = [хотя бы раз выпадет пара шестерок!.
Ап =[пара шестерок не выпадет ни разу]
Тогла P{An}= З'i "/36", P IA") =1 - З"i"/36", мкуда
следует, что
Р!А141"' 0,491 < 1/2, P!A1,I"' 0,505 > 1/2
Пусть N - ч исло игр, N(Ап!
-
ЧИ('f\О игр, в коПJ
рых хотя бы раз выпадет пара щестерок. По своиству
статистической устойчивости частот, при большихN
N~")"р{л"}иN(A") " PIA"}N.
Поэтому игрок, делаюшии СТ<iвку liil событие А2",
выигрывает примерно в 50,5 % игр, а ИГJЮК, делаю
wий ставку на событиеА !4, - примерно в 49, 1 % игр.
Эта 3адача кавалера де Мере з<~ставила Паскаля
заняться изучением (.лучайных событий. А 1:1 перепис
ке Блеза П <Jскаля и Пьера Ферма впервые стали упо
ми11аться понятия теории вероятностей.
11pou.>вeaeuue.J11.AB событ ю"r А 1113 11азыnаю·1
событ11е. которое про.исходит ·1 01да 11 тш1ько
тогдэ. кuгд;.~ имею·~ мес~ о обз собъrт11я А 11 в_
На11р11мер, событиt: С = lвынут ч ер1ю 1 111ый туз)
}Jlj)!И ется пропзпс}\е 1ше;.1 событ11 й А и В. где
А = lвьшуга карта чер11ошюИ мает~ 1] , а В = lвы
нут туз]
G) •.м.11ю1! А +В событнй А и В н азывают со
быпrс , которое..: 1 11х11r схо1~ 1 п тorJ1a и только
то1·,ца, .коm<1 1~мскл м есто либо собы 1ие....t , 111160
со61 ,1т11 е Н, лнfin об;~ нмссте.
Соnытш1 л 11 В н:~зьт;нотсн н,щ oн.AU!UJШШIU.
если А В = 0 Дют 1rесопмес1 н ых событш1
IA+BI = IA 1+IBI,1юз1лму Р{А +В}= Р{А} + P{R}
Событне А назыв.~ют пjютив<mШюJfснылt
собып1юА, t'c. 111 шю 11роиаоднт все1 ·да , ко1 ·да
Ht' происходит событие А Легко видеть, что
событля А и А .нссонмсстны 11 А +А = U, по-
::Jтому Р{А}+ Р{Л} = 1.
Если собы 1юrмА11 В в ур1 ю1ю{1 схеме сопо
ставляются мпожества А н В, то 11р(НiЗnеде11ию
СКОЛЬКО ВРЕМЕНИ ЖдАТЬ АВТОБУСА?
Вы пришм1 на остановку автобуса. интервал движе
н~1я которого сосrавляет 45 'vlинут . Однако рdLnиса
ния вы не знаете. Сколько времени вам прид~"rся
Ждать автобуса! Ясно, 4ТО ожид;mис nроллится
не более 45 ми~1.
Найдем вероятность того, что автобус прилет
не 1101жt>, чем через 1") мин Воспользуемся лля этого
такои геометрической схемои . Пусть Т - проме
жуток времени межлу двумя появле11иями автобуса .
Момент вашего прихола на осrа~ювку uбо:!начим
точкой С на отрезке АВ ллиной Тв каком-нибуАЬ мас
штабе (например 1 мм с.оответствует 1 мин; рис. 1).
Если точка С находится на раrстоянии 1 от 1\евого
конuа А отрезка, то время ож11дания автобуса булет
равно t.
Момент прихода автобуса ~1а Оlтановку случаен.
Если ра.-~делить отрезок ЛВ точками А, и 8 1 на 1·ри
равные части М1, А18,, В,В (рис. 2}, то можно счи
тать равновероятными nопада~1ия случаинои то•1ки
С в каждую и1 трех ча стей. Вероятн1.кть события
lt ~ 15 минl равна вероятности попадания точки С
в отрезокАА 1 . Отсюда, по класси•1ескому определе
нию, получаем Plll ~ 15миt1J)=1/3.
!-1
-
11--·l
1"5 "1HJJ
f ; Mflli
J:;\1JfН
1
'·
в
Рис. 1.
Рис. 2.
Вообше, можно rчитать, что вероятн()сть rюnа
ла ния точки С n любои отре1ок, сост'1nляющиИ
частu основного отрезка АЛинuи Т, пропорuио
нальна длиt1е отрезка. Поэтому вероятность тогu,
L\TO время ожилания автобуса окажется не боль
шим, чем х, равна х/Т, что записывается так.
Рl!время ожидания автобуса ~хl) =~ ,
еслиО~х~Т
Л вот другой п ример вы•1ислN1ия вероятности с
помошькJ геометрии . Пrелnоложим , что метеорит
упал на территории крупного города, которую мож-
Случаиные события
событнй АВ соотнс:тствуст ш.:рсt'ечен~1<:: мно~
жеl~г1:1 А и В. а су-V1ме событнй А+ В - объедн
не11не мtюжес1 н.А и В.
В более СJ1Ожн1:-,1х случаях не.11ьJя 11редстав1пь
слу чайное собы 1 ие А 1~ ннде ко11ечнu10 мно·
жес п~а та11cOR 11з ко1 1ечн ого ч 11сла ра rн·ю1~t'р< )~
ятпых исхо:~ов На11рпмер, рож,п.епие м.1.'тьчнка
и девочки - 11е раnноnсроятпые случайные
но считать кругом р.алиус;~ R = '18 км. Какова вероя т
ность того что метеор~п оказалп1 в uентре городаt
(Примем цег1 гр города за кру1· радиуса r = 3 км .)
Булем сч итать, что вероятность nuпадания метео
рита в какую-либо 1 1асть города nропорuиональна ее
n11ошалн. По:пому
тrг r
1
32
1
тсR=R2=1131=36
Вероятности , вы•1исленныс подоб11ым образом.
называют геоме1рическими вероятопями В обшем
сщчае "'!ТОТ сrюсоб аычислен~ш состо11т в ('лелуюwем .
Пусть случаи11ая точка С попадает в 11екоторую об
ласть С, последняя может быть отрезком прямои,
частью nлоrК()ПИ ~•ли прост ранства Важно , чтобь1
такая об!\асть имела конечную меру m(G) > О, где
т(С) - м1бо дли11а отрезка, либо плошадь плоской
фигуры либо обьем тела в п ростра н< rве. Тогда при
равномерном pat nрелелении случайной точки(" 1:1 оГ>
лаrти С вероятность того, что С окJ.жется в области
й с С, равна отношению мер
ml.g )
Р{С ей}= m(G)
К оn релсле1-1 ию геuметрических вероятностей
можно свести многие ин тересные задачи .
5()9
Детерминизм и случайность
события. Известно, что на мальчи ков прихо
дится пример~ ю 51 % от обще r·о количества ро
дившихся детей. В этом случ ае за nерояпюстт~
событияА =[рождение маль'-шка) принимается
число PjA}= 0,51.
Мнu1·ие случайные событ11я обладают свой
ством так назьн~асмой статистический ус
тойчивосrпи часттп . П усть пrю1:ю;1ится N
испытаний. R результате каждого нз ю1х мо
жет 1rро1 1 зой·1·и или 11е 11 рои:юй·1•н случ::~й11.ое
событие .4: например, выпадет mестёркз пrп
f>расанни игральной J(()СТИ, ш,mалуг дnа ()рла
при бросании двух мо11ет и т. п. Обо:юа ч им
N(A) число нспытаний, в которых произошJJо
событие А. Если при большом числе испыта
ний N ч<~стота N(A)/N колеблется около неко
торого числ~~ Р {А}, то гонорят: имt:ет место ста
тистическая устолчивостn частот, а чпсло Р {А}
называют в ероятностью события А. Такая
лс:роятность )10/IЖH~I обЛ:'!J\<LТЬ С IЮЙСТВЗМИ, ко
торые совс:тский матема·1 ·ик Л 1 щреl1 Н ик011<1t'
шrч Колмогоров сформулираnал в ВН/1.е трёх
аксиом.
1. Ал:сио.ма иеотрицателыюсти. Люб:~я
uероятность Р {А} есть 11еотр1щателыюе чис1ю:
PjA} ~ U.
2. Аксиам.а нормиμован.нисти. lkроятность
достовс:р 1 юго события r_: ранн<~ l :
P{U}= 1.
3.Аксиuлzа адд11rпит-юсти. lkpuят1 юс1ъ сум
мы f1.11yx 11есо11мест1 1 ых событи!1 А 11 В ран11а
сумме пх вероятностей:
Р{.11 +В} = Р{А} + Р{Вf.
Из этих аксиом легко вывести следующ11е
свойства вероятностей:
а) вероятность невозможr юго события 0
равна нуJ1Ю:
Р{0) = U;
б) если А cJJ. т. е. событие А ш1ечёт за собой
соfiытие В, то
Р{А} <Р{В};
R) вероятность каждого события .4 Уl\Отщет
rюрнет неравенствам
О<P{AI~1;
г) nсроятное1· h со61,1тияА и вероятность про
пшопо1юж1 ю1л событ1 ы А сш1з:1 н ы р:1 нснепюм
Р{li} =1- Р{А};
д) сели событпн /1 1 ,11~, .",А 11 1 юпар1-ю нссов
мсстны, т. е. А,А, = 0 11rи i :t.j, тп
Р{/11 +А~+".+А"} = Р{А1} + Р{А1} + ... + Р{А11}.
Колмогоров показал. что теор11ю uероятно
еrей можно разшmать па осноnе а1(с1ю111 подоб
но обычной м::~тематичсской тсори11, 1<at< это
/1,елается, н:тримср , в 1·со,vtетрни. Правда, тогда
аксиому <щ1111·1·11н н ос1·и нужно расширить 11а
случай бl'сконечного чисж1 сла1·:1 смых:
Р{Л1+А2+...} = Р{/11}+Р{А1}+".
Бла1·одаря системе :Jкс11ом. теорш1 всроит
ностей око 11чате11ыю оформилась в качестве
гюл1юлрашюй .мате~1ап1чсской наую1. О11а ис
rют,зует результаты из других разделов ~1ате
матиюr и в свою очсрСДI. оказывает 11а 11их зна
чителыюс влиm r и:с.
ЗАВИСИМЫЕ И НЕЗАВИСИМЫЕ СОБЫТИЯ
В классе N уче1-шков. Учитель 11ринёс билеты
на очень интересный спе ктакль, но на всех, к
сожалеш но, н.х 1re хnатило. Тогда ребята реrtш
л 11 устроит~, жереб1.ёвку. В 01а11ку пшюж11ли N
свёрнугых бумажек, М из которых отмечены
«крестиком·>. Тшrули жребий 110 очереди . Тот,
кому доставалась бумажка с « Крестиком·>. по
лучал бшн""Г. Спрашивается, в одш1акоnом ли
нолuжении окажутся те ученики , кто тmн:::т
жребий nерным, вторым... последнJ.Jм ?
')10
1lз 1 1 ер 11ый взгляд как будто нет. Более тот,
1.юзникает увере11 11 ос-1ъ, ч ·1·<) пос1е1~1-1ит'1 участ
нr1к находится в Gсобеп 1 ю 11 евыrо; 1 1 юм 1юло
же11и11. У 11его, собстве1шо говоря, 11ет 11111<зко-
1·0 в1,1 6ора: все б}-мажк11, кро.,..,tе одной, уже
вытянули другие учсшrки , таI< что он просто
получит то, чтu осталось. Однако IJac в дашю:-.~
случае интересует нt: во3можность выбора, а
то, зависит вt:роятr-юL~rъ вып1щ11ть бла 1 ·011рв
нтньн'J жребий от ачерёдности 11ли нет. Пр11
решс 11 ин таких задач у;(обн<1 исrrользоватh по-
11ятие «условная вероят1 юсть"
УС/\О ВНАЯ ВЕРОЯТН ОСТЬ
Пусть в рсзульта-rс каких-то испыт:н 1 нй, и;..,1ею
щнх г рав.н:овсроЯ1 ных нсходоn, мuryr произой
п1 случай 11 ые событин А и В. Пусть s (А) - числn
ш;~11сов cofiытиsr А; s (В) - ч н с;ю шан сов собы
тю1 В; s (А.В) - числ<1 шансов события АВ. Тш'μ:J,
но кл::~ссичсс.кому опре,11слению нероятности
(см. статью «Rсё 11ачалоСL1 с н 1'ры в косп t»).
Теперь рассмотриы только те нсттытания, в
которых происходит событие В. 13 этих 1к 11ы
тания..х всего s (В) раш ювсронтн ых исходон.
В них собы'1·ис А имеет s (А В) rна нсов, т. е. оба
событ1,шА н В 1 1роизойду~· н s (АВ) исходах. Оn
редсm1м ус11от 91ю ве/юн1111-шсть собып 1 нА при
услонrш , что п ро 11 ~юшло событ1 1 с В, к:J к от1ю
шен не s(AB)/s(B). ()боз11ачим её P{AIB}. Псрво
нача1 1 ы1}'JО 111:роят1юстr1 Р { /1} можно па:н1а-rъ
nезуслов1юй 11m 1 пш 11 юй RеронТI-rост1.ю собы
ттrА. Таким обр~:юм,
Р{л jв} = s(AB).
s(B)
Разделш.1 чисттте.11ь 11 знаменатель 11а 1·. Тогла
JЮЛ)'ЧИ.М, ЧТО
ll!IИ
P{il1в} = s(AH) .,-
s(B)/t• .
(*)
Сi\учайные события
Это рапс.:нсто МQЖtю сч11тат1, опре1\сле 1 п~
с:\-t услон 1 юИ вероятност11 . Ум1юж~1 я ot)c е 1 ·0
ч асти 11а Р {В}, 1JОлучаем
Р {АВ} = P{B} P{AIB}.
(*")
Раnенстrю (**) часто называют Jnf!.Op(]JJtOLi
J!MHШICl'JШJ/ (·I0/IOJ/.1nJ IO(JIUJfj
Вновь нернемсн к жеребьёнкс н ю 1 ~1ссс :i<1-
мс111 1 в 111 aJJкy урн ой, бум~1 жк~1 с •кrсстиком ~ -
бt:лыми, а пустые бумаж:юr - чЕрны~\111 пr~чх1J1111.
1 юлуч 11 .VL кл::~сс11.чt:скую ~ур1ювуто" схему (см.
статыо ~Всё н;~чалось с ~11·ры в кост11»). Н::1с
буд)'J' ннтересuвать два события:
А = [ l-lr участн111< вынет белый шар] .
В= [2-11 уч<1l·1'1-шк вынет белый ш ар]
По rшассическому опрсдеJJению. лсп<о uы
чнсляютс11 вероятности
Р{А} = м Р{в/л} =:
11
-
l Р{вJ1}==~
N'
N-1'
/
N-1 ·
1·де А - событнt\ проттюпшюж 1 юL: c ofi1>1-
т11ю ,-t (т. е. ,~ ""[1-й уч<iспшк 1tы11е1 чt:рныlr
ш ар]). P{BIA} - усло1н 1ая нероятr юст1. со()мтш1
В при условни , что 11rо1пошл<1 событ11е А ,
Р{В[ Л} - услонная nерояпюсть со~1.п ня В
при ус11uв1-111 , что п ро11зо1шю собыл rc Л 11 (J те
ореме умножении всроя·1·r-юсr«..:~1 (**) ,
Р{АВ} = Л1
·:·1 -l'Р{.-Ш}=N -"\1 -4!-- .
N N-L
N
/v-1
Т;ш каксобыгпеВ мшюю прс,11ст~1i 1 m, ti m1де
суммы В = ВА r Вt1 дnух 11есовмест1Jых собы
тнй, то, по аксиО.\Iе 3ДДПТIШIЮСТИ,
Р{в} =Р{вл}+Р{ВА} =
=N~(.Н-1)+M(N,- J\1)=~ =Р{А}.
/v(N- 1) :V(iv - 1) N
511
Летерми н и~м и случ айность
Следоnатеm"1ю, первый и второr'1 участнюш
жсрсбьёшш имеют одинаковые шзнс1.1 nыта
щить белый шар. ТJ,11}1 f\ЫЯСПС I П1Я Ш:lIICOB на
ус11ех останшихся уч<кv1·никон при;~ётt:я Щ)И
б~::гнуть к болсt: сложным выч 1 н.:л<:1-1ш1м.
Для таких расч ётон у;1обнп поль:юват ьсн
формуло 1'r пол 1 юй веронтностн:
Р{В} = P{A 1}P{BJA 1J + P{A2}P(BJA1I + ... +
+ Р {А;,} Р/В/А(,},
(***)
где.t1 1 ,А2, •••,А;, - попарно несовместные собы
тия, т. t.A,A, = 0 Д.!IЯ J!Юбых i *);сумь1а А1 +А2 +
+ ... + Ak -дu<.:тuнсрное событне;В-любое со
бы'1·11е. Л,ня доказательс1·на формулы (***) н:що
представить событие JJ н l'lидс суммы ВА 1 +
+ В/1 2 + ". + ВА1г, l!OCllOJlbЗOR<!TЫ~'Я CIIOЙCTllOM
&}lДI IТJ 1111 \0C'l 'H верОЯТНОС'l'L:Й
Р{В} = Р{ВА1\ + Р{ВА.!} + ... + P{BAk}
и формулой (*") умтюжеш1я вероятностей
Р{ВА,} = P {A,} P {BjrЦ.
Тенерь рассмотрим в :3адаче о жсребьёв.кс
событ11с
С= [:)-й учасп-11 1к вы 11ет белыn шар].
Дтr вы ч 11слепин Р{С} можно прнмен1п1> фоr
му11у (***),которая n этом случае 1 1 меет вr~д
Р{G} = Р{ Ав} Р{сlлв} + Р{.4в} Р{срiв} +
+ Р{ А в} Р{cj,-ill} +
+ Р{Л:в} Р{ cj.iiв} .
(****)
Вh1чнсЛ11~\1 ~Jеро}lтности
Р{АВ} = М(М - 1),
.
.Y(N- 1)
P{IIв} = Р{лв} == M(N - М>,
N(N- 1)
{- -} ~( N_-_,_ _,11)'-'-(,_V _-1_i1_- ~
1)
РАВ =-
N(N-l)
и условные всрш1 тнuсти
512
Р{СjАН} = .~f - 2
N -2.,
Р{с1лв}= Р{сl~} = ~=~·
pfс1хв} = __:!!___ .
l
N-2
J:::сли nодстаnить ncc эти значения n форму
лу (**""') , то получим
Р{С} = J'v!/N.
Ана1югично можно устаrюп 1 1тt., "ITO вероя·1-
НОLТЬ успеха для любо 1 'u учаеп 1ика жер~бьёuю1
равна M/JV- _
Тат<им обра:юм, вес участники жеребьёвк.и
находятся в равном положении, если, конеч
но, она органпзовапа праnилыю: вес бумажк11
один аковы и тщательно перемешаны . Хотн
психологичс:ски нер.вый и носледний её участ
нню1 чувствуют ссбн ОЧСНI> ПО-р;JЗ!ЮМу. П<.:р
ный ПUНИМ~IСТ, что у 11е1·0 есгь ныбпр: МОЖН()
ощупывать бумажки, персбнра·1ъ их r~ат.цамн
и н:.~консц 111,1та1.1..1.нт1. ту, 1<п· 1 ·орая кажется Rынr
рn~шной. Пт:лс11.ний л:п шёп этой возмтюю·
сrп: 011 пр()СТО -н<tпросто разворачнuает остав
шуюся бума.Ж"-У' и у:шаёт результат. Более того,
н е искшочено, что жереб 1,ёnка закончится
npe1f\J1C, чем он примет в ш.:й учаt:тнс.::, - t:CJШ
вес бумаж к и с крссти1<ам11 11ы11у1 дu щ.:1u.
П р: 1 ма, пuслсд 1 1111! уч:Jстник может надеяться
н ;.~ счастливый жрс611й дольше псрвогu, сели
тому досталась пуст:1Я бумажка.
Н ЕЗАВИСИМОСТЬ СОБЫТИЙ
В теорни вероятностей есть очепь nажпое по
ш1тне - 1ю.зааис11./11юсmь событшi. Событ1 н: А
назыв;.~ется нсзаrшси.мым от события В. если
услов11м всроятноегь Р {А !В} равна бс:зусло1:1tюй
вероятност11 Р{А}. Ес1 1 11 Р{А) = P{A IB}. то с 1 ю·
мощью формул (''') н (**) гюлуч;:~см
{ t-Р{АВ}
-
Р{в}Р{Аlв} - {}
рBIA1- {}
-
{}-рв'
РА
РА
·
т. е. событпе В также будет 11езанисн.'-'1Ым от
события А. ! lоэтому мож1 ю просто rовортъ о
незаписимостп событий А и В. Для неэа.1ш·
симых событпй А н В справедшша формула
умножения вероятностей
Р{АВ} = Р{А}Р{В}.
являющаися слсдстписм фор.v~ улы (**) . Har1p11 ·
мер, пус-1ъ ДJЮе н 1 ·ро1<0в Вросают юзе шраль
r1ы е кости. Оn()значнм событпя
А = [на l-i1 кости вьш:щет шсстёрка] ,
В = [11:1 2-й кост11 вьшадет wecтt:p1<aj ,
СПОРТЛОТО
К;\<:Н:с.и•1ес11;ое определение вероятности nо.\вол'ilет
вычислsнь вероятность выигрыша в лоп•реях . Для
этого удоfi1·ю и сrюльзовать такой вариан т урновой
схемы. Пусть в ур11е имеется N шаров, из которых М
шароn белы~, J остальные N -М черные. Из ур н ы
<лучаино ныr)ирпн)1 п шаров. Выбран~юе мнuЖЕ'ПВtJ
шаров н а .ювём выtюркой объема п. Рассмотрим со
бытия
А,,, = [1:1 выборке солерж ится nr uелыл и 11 - т
чёр11ых щаров1.
Ч11сла N, М, п, т уловлетворяк1r нер..~1:1енствам
O<.M<.N. 0 -'n<.N, О<т~м. О~т~11.
Верт~тноrrь события Ат равна
pJA 1 =с~ с~ -~•.
1. llrf
с~
("' /
На1ю<v1ним. что
1
k(k-1)...(k-i +1)
k!
с,=
=
'
12...j
,, (k- j)!
rле с: - ч и<ло tочетм1ий Иi k "Jле:>ме11тов по; (см.
статью " Со•1 ет.:н1ия » ).
Фор.<v1улu (*) п олучilется слелуюшим образом.
Обще~ чщ.ло рав1юв1;:рuS\1ных щ.холоu (.~ рав110
числу выGщю" оОъема п . Чиt ло Шilнсов <оfiытия А,..
рзвно nро1нведению •1иrл,1 сочетаний С.~; (т. е. числа
rочет.:111и 11 из М белых шаров в урне П() т белых
ш<1ров о выборке) 11а ч исло сочеташ1й С~ '~'1
!т. Е'. чцсло rочt.'таниr:1 11~ N М чер н ых шарт1
в урне по п - т черных шаров в щ,1 боркс). Отно
wеttие с1щ·"а шансuв собьп-ияА01 к об шему чtкr\у ис
ходов и рав110 верояпюп~1 P{A111J.
тоща
.113 = [nыпа/()r1 дпе шесtёрю1/
l lос1<0льку событш1 / \ 1113 11e :1anii ci 1 мы, то
{
111
Р АВ} =Р{11}Р{в} = -
-
=-
.
66.16
Н ескот)ко cofiыт1 1i11:1 1 ,,- 11, ,"1" 1 1 : 1:юнё:v1 11еза
n11с11;1·1ым 1 1, t:ц1 1 1
PJA,ICI =P{A,J. / = 1. .;...., 11.
11.ЛЯ люб ы х собъrпн'1 С: = А;А,.... Afll, J'ДС llllДCKCЫ
/,k,.."т пс равныi.
Случа 11ные соvыти я
Од н ой из самых популярных лотt.'реи долго<>
время было «Спортлото». ЖелJюши11 принsп1> учас
тие в о•юр<:!лном тираже nuкyn<iл кар1u• 1ку, на ко10 ·
рой следовало отr1о1ст111ть 6 номсроtJ ~н 4 9 . Одну часть
карточки игрок о п ускал в яшик ,, сnортлотn ", а
другую ос-r<н1м1л у себя. Во оремs! п1р<.1Жu ю урны с
49 w,1ра"1и , 110мечl!~1~1 Ь1.\\И 11 омерам 11 от 1 ло 49, до(·
тав,~ли 6 любых шар()В. Их номера и оt>ьявлялиrь
выигрышными. Если срел11 11омеров, отмРче1111ых иг
роком. ок1:1зы1ымкь хоп1 бы тр111 вы~1rрышныл. он по·
луч.=tл дснеж11 ыи при.i. Пр11чем ~пJ ра Jl\-tt>p [iыпrо
l!O{p<1< r.1л г уRем1чениеv~ количества угс1ланных нn
меров.
Oбu:J 11ачим череJ р,,, вери~п1 юt ть тoru, что т от
л1t>чt;>нных игроком чис (-'Л ок,нались 1:1ыи1 рь1шными.
для 1:1 1,1 числt'Ния Рт1 где т ==О, 1, ..., 11, 11с пол1.1уеv~
формулу ("' ). Е<.ли rч11тать, •1то шJ.ры с отмес1ен11ым1-1
111 роком номсраl\1~1 белые, д uггмы1ые ч ерные , то
р,,.=РИ,,.J,глеN=49,11=М=6,т =0,1, ..., () Та
ким обр<ном .
С''
l'J, , =-
1
-
1
°" о' 435%,
с:. с;, " IЗOJ
μ' :::
"" l1,4
.. .,
( ·(,
4Ч
С''4'>
Ci с:,=О13238р--с;С~,О бr:
р-
-
"'
'017 ;J,
L-
cf•
'
;~
r t:!,
• ••,
\,
"4
с с~1
сс'
μ,=
"с6 • ~U,OUO<J7' JJ;:; 'с(· " ,,.О,000018,
~
~
С''
р"-= ~ ~ п, (]()()()()(1072 .
С,,,,
Отсюда слелует. ч10 вРроятн(lrть 11роигрышJ
р~ю11J р" + р 1 +р~ :::: 0.98136, вЕ'рояпюсть самого .\IJ.·
ленькоru оы111рыщаμ,::::n.О1765 , а верш1 пюс~ь са
,\.ЮГО кр}1nног11 1:1ы11грыш.:~ р(, н11чтож1ю мала.
)l,.11я тобых 11ез:1 1шс11м1.1х co61.1т1 1i'J .111. гl ~ ,
.. ..
"1 11 нмеют место р:ше1rс 111:t
~i<J(,''"
Р:1ссмотr1ш 1Jp1Jмcp. Псрвыt: ~ш..'ктрш 1 ныс
ГIЫЧllCJllJTC.'JbliЫC: M:.! IIIJ lllbl (3Bi'vf} paG< ITa! IJ 1 на
ЭJ1ектрон н 111 х ла \Шах. ~-;оторыt: Hl' все ~ ·;~;1 6ы1111
шщёжны. Прс;що1 1ожн.'ll1. '-ПО н :7RM r1м<.:лас1,
11 = 1О UOO эле11:тrо 1 шых ламп, r<отор1.1е 11ез~11ш
i..'1вю друг от лру1·а з.1 11сю 1й пер1юд вres1trт1 1 -Г
513
Летермин и зм и случай н ость
MOJ 'J IИ 11ереrорать с nсроят1 юстыо q = О.ООО 1.
Ест 1хотя бы 1 лампа с-1 а11оuилас1, пснсправrш ,
ЭВМ давала неверr 1ые результаты. Какова веро
ю·1 юс1ъ nыхода из строя ЭВМ за крсмя У''
Пусть событие
А,= lвct; время 'J' i-я ламна 11cnpanн ~1].
Tu1·1p событ1·1е
С= [ЭВМ нсп р:н11ю работает nсё nр~мя "/']
мож110 11релста rшть n виде С=А,А2 •. . А,,, веро
ят1 юсть которого
P{G'I = PjA 1fP{AJ} .. Р{А"1 = р",
l'/J.eр = Р{А,} = 1- Р{А,} = 1 - rJ = 0,9999.Веро.11т
r-юсть выхода 11з строн :>)ВМ в этом cJJyчae
Р{с}= i-r{c} = 1-с1-цУ' ""
= 1-(1- 0,000 1)
11
)<11~•-= 1-е 1
"'0,632.
На перных ЭВМ при такой аадёжностн ламп
работатh было очень неудоб но. Прююдшюсь
поеrошшо заменять ставш ие негодными лам
пы. На смену при 111ли ЭUМ, работав ш ие зпачи
телыю стабильнее. В них исноль:.ювал ~rсъ новые
элсктрош r ыс элементы - nuлупrшюдниковыс
тра1r:~ис·1·оры и интсгральныс микросхемы .
СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
В теорни вероятностей: часто рассматривают
случайные события. которые характеризуются
числами: напряжение в сети, ~юк<~зания при
боров в эксперименте 11 др. Таюн.: события на
зыв~uотся случай1-1.ы.ми /jелuчинш1-1и. А pa;j это
с111<.:ла. то 1 1х можно сю1ады13ать, умножать 11а
uбычныс ч11СJ1а 11 т. 11. Д;.1 и дrуr · ие случа11ные
СО6ЫТНЯ ННОГJ1<1 МШКJЮ тrа 1<НН1ат1, IШК ЧllCЛ;l.
Например, выпадению той или и ной гра 1 1 11
11 1 p::inы ЮГ() 1<убика соотnетстnует чиаю на :'Jтой
1 · ра11и. Вытrадеrше орла 11 ри по~брасъшаrшл
монеты можн о обозначить через 1, а nыпаде
ш1е решю ·1 - через О. Тогда сумма з 1 raчer mil
та 1<0й случайной 13еличины при п подбрасыв<1.-
1 rиях монеты рая на числу выпавших орлан.
13ообще, ~слт~ случайная ве.1нrчн1-1а Х может
прннимать значения .х1 , х2• .•• , х,,, то :1начен.ия
р,=Р{Х =х,},
514
Первые
.мектрuнные
ВЫЧ ИСЛНТРЛЬНЬIР
маши1tы ("ЭВМ!
p,1Gu1<1л11 на
~.\Р.Ктронных
л,~м11t\Х
где i = 1, 2 . .. " 11, ш1зьшаютсл рС1сnределrнше1е
вe/Юfm11юum:!1i с.:лучай ной вс.:личнны Х. причём
с11равещ 1 шю ра 111: нство
/7 1 +p~+ ... +j>"= 1.
Во 'VIHOl 'f rx случ~их наж110 энатп « <'ptдHL:t:
значенш:» cлyч;.iii1 юй иеш ~чины. R -reup1 н1 веро
~п·r юс·1 eii ()J ю называется мcиm?J1mmlfчt:xк:ш1
О)и.:щ)ащ,;,е.м. 11 определнетси следующим пбра
зом.
I J ycrъ случайная встrч1ша Х може·r лршш
мат~. зпачспня х 1 , .х-.!., .. , .\:,1 с вероят11остям!f р 1 ,
р2, • . . , fJ" соотвст<:тненно. Тогда часло
М{х}= .)""1 /J, +Х2Р.!. + ···+ .Y11/J"
есть матсмат11чсское ож1щан 1 1с случаl1нпй
13CJШЧl-П l lJI Х.
:?та ф()рмуп::1 очент, похожа н а форм)'лу iVIЯ
rюорлинаты центра масс с 11стемы нз масс m1,
Случайные события ~
1
./
'
\
111,
(;)б~' ··("\-(:;J
1
т,
~
(
~)
.л: \
)
.\, /
.
:r. 7
х!
.\;'
х1>
1
/,
1112, " ., т"' расноложенных в точк~1 х х,, Х2, •.. , х11
на прнмuй . только роль масс з;~есь нг рают
неронтности (см. ст::~тhю «С ре1~нне зт r ачени.~1'>).
М:~тематпчсскос ож~;щан1 1 е сум .\1ы случай
ных ncm 1чин равно с:ум ме их матtмати чесю 1х
UЖ IЩЗН JСЙ :
M{Xr +Xl+...+Х,,}= М{Х1}+М{Х2}+...+М{Х"}.
F.сл11 с - постошшая (т. е. с сеть случайная
велrrч11на, всегда прш-шмаюшая одно и то же
з 11аче1 пrе), то
M(cf=сиМ{сХ}=сMJX}.
Пuнятие ма·1·ематичсского ож~щаннн можно
пр11мс1-ш ·1ъ к ~111аJ111зу азартных 111·р. Игра на
де:: 11ьп1 1-11111 жетоны Н <1 зынается безобщ{ной,
сел и матсмат1 1чсскпе ож11,цанис ныигрыша лля
каждою 11грока ram ю о. в нротнr11 юм случае
о на выгодна П)!\f)· игроку, для которого матсма
т11ческое ожида1111е выигрыша nолож11телыю.
Рассмотрим всем известную игру с подбра
сьшаrпrем ""юпеты. Один нз игрокоu дслае·1 ·
ставк)' на орла, а 1п·орой - rra решку. Монету
подбрасывают. Ест-1 она упадёт ор1 юм, тu i;тo
poJ) пл:пнт 11ер1юму. н::11 1р пмер , рубл h, а e<:J1 11
решкой - 11ервый пш.1т1,r1 · нторому рубль. Так
как нероятt юст11 выпаде11ия и орла, и решк11
равны 0,5, то математпческос ожнщu-~ие вы
нгрыта тоб()ГО l1l'J"Юt<a р:ни ю О:
1.о.5+(-1) о.');:о.
З11~1чит, игра безобидная
Игрок в рулстl\.у, поставиnший 1 жетон. 11а
примср, {Ja лmшю. выш·рываст " жсто1юn с
всро11тност1,ю 6/37 11 про1,11 'Рываст 1 жетон с
неронтносты<> 3 ·1/.)7. ТТuэто.-,,1у мэ ·п.:мапrческое
uж 1 1д::шие с1'0 вынгрыша рав1ю
_
G
31
1
,
-+(-1) -
=--
.
37
)7л
Игра яюю небезобндпая и ш,u-од11а нгор1ю
му дому, 1<0торый с каж1ю1 ·0 постаnлс1 tного
жетона имеет Rыигрыш 1/ .1>7 жетона.
Несколы<0 более сложн:t игра « Пuпытай с:ча
стье», R которую 111·р~ы11 в XIX в. н;~ северо:~ме
р11канском Дальнем Занаде. Бармен прсд;1а1·ал
скуч::ноще.му посетителю постав 1,JТh доллар 11
назнать О/(НО из чнсел: J, 2 , 3, 4. 5, 6. <Тепсрh ты
бросаешь три н~раm,ные кости. - продолжал
он . - Если 1 1~1 одной 11з них выпа11ет ш1:зоа111юе
1·()бой ч1 юю, то забира~"1 свой дoJUiap и ещё 011 и 1 r
моl1 в прндачу. Если это число uыпал:е1 на лuух
костях. то я к твоему доллару доплачу ещё два
А если на ncex трёх, то я ,11аю три дшшара->.
Безобидна ли эта нгра, и еош IJeт, то r<ому
выгuдшt? Вероятность ныпад~н11л нужного
cшcJJa 11ри брuс;н 1 1rи одtюй ко с.:тн р = 1/6. ;1
нероятность нс1:1ып:.t/(С н1~я t/ = 5/6 Расчёты 1ш
I<азынают (см. статью «Б111ю,,111 ~и1ыюс р:1 сп рс
дtж:нне~ ): нсроятное1 ь тоr о, чтu н11 разу Hl ны
падет назнаr1нп е чнсло. равн а
t/ =125.
21 ()
ВероятноС't ь выпаде1шя ну-лшоrо ч11с:л::1 ровн о
11а 1 l<ОСП!
Всрnн·1·11ост1, выпадения это1·0 чи сла ронно н;J
2 KCJC'l'HX
,
L5
~j"Гl] =-.
.
216
515
Лl'Терми1 1 и:1м и случайность
:i rк·ршп1юl~1ъ тро!'11-ю1·0 усш:ха
р' 216'
То1д:~
1)-
7::,
M 1X }=(-l) --- .: :2+1 -+
21<>
2IG
+2 15+)_1_==
_
_ !2_
216. 21() 11()
Значит. посет11тсто иг·ра нс: выгo;J.Ji:t.
Нсл 1 1 матсV1ат11чсскос ож1111.а1111<: }!Rляеп.:л
псрной ч1н:1юно]1 характе::р11ст111mi1 снуч::~i1но~"1
l1eлrrч1 rнrir, то ра:-~бро<:' с:ё .11-rаче111ri1 опrосrrп:'ш.-
1ю мз'1·с:м:п11чепщ1 о ож1ща1 11 тя - второf! Как
ОЩ.'fl!Т'JЪ ра~броС(
Пуст~, т = М {Х} - .матсм:ппчес1<ос ож11щ1-
11пе с.тrучаГrrюЛ nеличш1ы Х. Тогf1.а У= Х - т
<.:с1ъ СJJучаlшая вет1чн11а, ныражающал откло-
11еrшс случаТ-пюi 1 всm·rч11ны Х uт tё \·1л·см.tт11-
Ч<.ткого ож1·щ:11н1н. Пt:рное, что нрахо1t11т н
1·олону. - RЫЧИCJlll'lЪ :11атС.' ,Ч3Т11Чl:СКОе OЖH,ita
IIJ!C M {l1 11 ПрШ-[51'f'Ь ГIOЛ~'ЧCllHbltJ [lL:iym>r·:n з:1
х:1рактс:р11ст11 ку разброса энач.е 111 п·1случз11н(1й
щ~л11чш-1ы Х. Одн:.1кс>. со1·лзс1ю расчёт;l ,'-'f.
М{})=М{.\ -т} =М{Х} -М{тf=т -lll=О,
те. ;.1а· 1ематтrчес1юе:: ожпда1111е отюю11с 1111я с.•1у
чай11ой нелнчш rы от её :-1ате."1атичс:ского ожп
J\ШIНЯ ратнrо 11улю. ficл11 ПО7'у.-.1ать, :щссь нет
н11 1 1сго уд 1 н11пелыю1 ·0. С.11уча!1 ная 1:.1слнчн11а 1·
можс·г пр1 mн.... rать r·r полтк11те11.ы rыс, н отр11-
цатеJJь1-1ые ~н;~•rtния , которыt: н конr1с: конr~ов
ур:шнu11сL111 ш;1 rот др~т дру~ ·а.
А что, CCJI 1Jr:1ссмо·1т1е1·п ю~:Щf)•П O'l'KЛO I rc111 JЯ
'
)
сJ1у"-!аС1ной нс;111чr 1ны у-= (Х - m(' Ro-11ep111,1x,
.'J та
всм1ч11 1 1а rке1 ·7'а 11со·1·р 1 rцатсш".11а. а 1ю
Атnрых. ()11з хар;щтер 1 rзует 11ыеmю абсо.rпот-
11vю llCЛJ!\.JИHY (')ТЮЮ JJ СIШЯ. IJC З:1В1Н.:ЯЩ)'lf) ОТ
') 16
:шuка. То1ла М{(Х - т/} }JHJНtt:тcs1 чатс~1ат11чс
скнм ОЖ 11/р111JС,\1 1\1:1:.1/ЧXJ'!';J OTIOIOl/t:J IШI UJ)11 1:111-
llOЙ ве;11rчи11ы Х 0'1 e::i:: ;,1а· 1·с:ма 1·11чсско1·0 ож11 -
11аr 111 я. О1ю называется ()цсперсии/'1 СЛ\•чаi11юlt
нетrчи 1 rы Х 11 обозначается D {X}.
Итаr.:. если т - ма·1 с:11ат11ческоt ож11л,аш1е
с.пучай11щ'1 nсm1Lпшы Х. то
О\.\'} "'" M j(X - 111/}
сстп1~11с11сrсюr случ:1l1нш1 вL-.111ч11н1.1 \ ' . F.c111X
l/,\1t't"J' расnrс:дслсннс 11ершп 110tч1·t:J1
р1 = Р{Х=i}ттр11i=1 , 2, . . 11
' 1'() <.:ё /~Н<.:пt"рСН>i RЫЧllC'1Яt'TC5I 110 фЩ)\1)'Ле
D{.\f = (.,.,
-
m)~p1 + (:\·~ - m) ·j12 +
+ ". + (.У11 - /l/) ~f>".
Д11с 1 н.:ро1я всс1 ·;т,а нсотр1щатс.J1ы1:1 , т <:
Несмо1 ря н.~ ту RЫ( окую степень ра-1а11т11я, лu ко
торой доведены науки м.пемJ 1ическиС' тrуд.:1м11
вt:ликих геометром трех последних столсти~• , прак
тика яв~ю обнС:1ружив.эет неnuлноту 11х во мноr11х
отношени51х; она предлагает вопросы, rywenвe ~1-
нu новые лля 11<:1уки, и таким образом вызывает на
И'lыскание сuвершен1ю 1 ювыхмстол. - ECJ\11 тео
рия много ~ыигрывает 01 новых приложений па·
рой мt>тОды или пт нпвых развитий f>ё, то она ешi'
более nриобретает открыrием новых метод, 11 в
этом случае наука находит себ~ верного руко
вол~1тем1 в практике.
Пафнутий Лыюв11ч Чебышев
прпчё:-.1 р ::ше11ство D {X } = О в():~мшюю в том
и ТОЛЬ!\() 11 том случае, КОГ,f(а х - ПО(."Т'ОЛfl\ 1ан
( т. е. nсе1·да пμшшмае1· одно 1J то же значе н11с).
Днсперсин су;v1 мы 11сз~1н1-~с11мых СЛ)"-1~11v1 нh1х
всюrчш1 раш~а сумме rr.x 1tн cпcpet rl1:
D{X1+XL+...+Х11}=DjX1} +D{X1}+." +D{X,J
F.c1111 с - 11остот 111ан, ·1
·0
D{cЛl = с
1
D{X}.
Следует отметить, •по дIIсперсня нмеет
размерность, соответствующую квал;рату раэ
мср11остп оппсываемой ею случайной nслн
чипы. Поэтому очсш. •rасто исгтот,зу~от другую
характср11с1·11ку:
а= ~О( Х),
h:O'J 'n py111 rrазыв:нот л.-щ;сд/ю1·пuч11ым mгиu11Jн1:1-
ние.м с:11учай1rой нслич1-111r,r Х. Размсрноеrъ сrта
же,чтоиуХ.
Проr 1лтострируе,,1 1101штпя матем~п1 1чсско
П> ш1шдапия .и дисперсиrr рассказом о «шуле р
скоtr кост11·> - 111·ралыю.й r<ости, в которую
вставлен сни1щ0R~.n:У шщ1ик. Он так располо
жен вну 1 ·ри кости, что нсроят 1 юстr, вь111адсшш
'l'Ой IIЛll ННОЙ l'P<IHИ кубика 11ропорц11ОНШJhl ia
числу очков на этой 1ра1 rи.
J l :з.11/tCM нcpШITl lOCTIJ !ihlП:JДerrmr рд!ШЧ!!ЫХ
1·p~H1l'(11'-убнка. Пусть k - 1<ожрф1щнент пропор
цrюналыюстн, то1·1щ эти 11еронтностJ1 составля
ют: k, 2k, .3k, 4k, Sk и 6k. Их сумма /(ОЛЖJ ra ()ы·rъ
равна1,поэто:муk(1+2+3+4+')+6)=21k""1,
а зrrачнт. k"" 1/21 .
Подсчитаем математичес rюе ожидание
чнсла nыпа,цающих очков:
МjЛ1: l· _!_+2·
2
+"·j_+4·2_+5·2_+
21
21•21
21
21
+6~-
13
-
4 :В.3~
21-.1> -
,. ..•
Теперь ныч11стrм дисгrерст1ю:
" 1( 15)1 2( 1,))
2
)( 13)2
О{Х}=-
1-- +-2-- +-
. J,--
+
21
321
.3
21. 3
1
= --(1()()+98+4Х+4+20+l'50)=
.21 ·9
ЗАКОН БОЛЬШИХ ЧИСЕЛ
М<пем,1 гическое ожидание и диrnерсии свя.ыны с
одним и:~ важнейших ,{акuнов те<J рии вероятно
стей - законом бо11ьших чисел. который состо11т
в Сl\едующем. При больших 11 сред11ее арифмеп1-
ческо е
X,+Xi + ... +Х"
У"=------
11
независимых случайных вели•1и1-1Х1, х_., ... , Х.., име
ющих од1 ю и то же рас.преl\еление с математи
ческим ожиданием т = M lx\, мало отли 1 1ается от
константы m. Более точно, при 1\Юбом Е >О и лос
татос1110 больших п вероят1юсть события
PflY" - mll <€1
("')
близка к 1.
Впервые закон больших чисел установил шве11-
uарский математик Якоб Бернулли дl\Я случаиных
величи11 Х, с зако11uм раtлрсделения
Р(Х,=11=р,
Р(Х,=(')} = 1-р=q.
В XIX в. русский математик Пафнутий Львович
Чебышев в общем случае лока1ал теорему о за "он е
больших чисел, в кото1.юи уточняеrо1 uеличина
вероятнпсти ('")
P{IY"-m[<€}~ 1-a2., ,
("' •)
·
пе-
r·де cr = \/D (X1 1 - квалра т11чное оrклонениt' с.лу
чии~юи величины Х,. Из 11сравен~.:тва (Н) следует,
что при О < cr < 1 с веро~1тноrтью, nрсвосхоляшей
1 - cr, выполняются неравенства
Т,1ким образом, чем ме~1ьшt-> дисперсия, тем
Х,+Х,+ ... +Х"
бl\иже l.реднее арифметическое ------
11
к ма1ематис1ескому ожида~rию т.
=
-120 =2U ""22222.
21·9 9
.
3~1МСТИ:М, Ч'fО ДЛЯ ОбЫЧНОl'О К\'б ика
М{Х} = 3,'), а Dj.Лl "' 2.t .>167. Т~ншм обраЗом, у
«ШуJr ерской KOCTJI " среднее ЧliCJJO ВЫП~Щ<НОЩ11Х
очков ощуr·им о болr,ше. а μаэброс.: мс1-1ьшс, чем
у 06ычнu1'i 1-11·ральной кuсr·и.
'5] 7
Летерми н и'lм и случайность
БИНОМИАЛЬНОЕ РАСПРЕЛЕЛЕНИЕ
ДOBOДJIJIOCl1 Л11 вам tнЩеть, как JIORЯT рыбу
cпr 11 1r 1нr1гом? Забрасывают 1IO/(<Vfhffft:: от бс::реr~1
11 воду блесну - похшкую н::1 м:.1:1 <::111,кую рыбку
мет ::шличсскую прим:.~нк-у с крю ч ком, а затем
быстро сма·1ъ111ают 11;i катун~ ку леску. к которой
она пр11ш1за 1 ra. Чзще nссго блесна возвр;1 щ а
ето1 обратно пустой, 110 шюгда 1 1 а крючке
бьётсл хнщная рыба - 01<упь, судак 11m1 щука ,
прюшвшая приманку за настоящую рыбк).
СкоJ 1 1.1<:0 раз nрпдётся :{абрасыв:1ть бж:сну,
•1тобы l!Оймать 1 рыбку? Это J:.tHJ кит uт нрtме
ш1 1·ода , времс1111 с.:утuк. nor1 щы. Рыболов ,'vю
жс·1 ск<~:.~ать. ч· 1·0 в срtднtм нсобход1 rмо дt'ся·1 1,
:1абрпсо в. То1·д;.~ всроят 11 ск· 1 ъ р 1юr1мать pыfiy
:1а 1·щ111 1 3;,iбpt)C равна (),1 , з 11ероят1ЮС"IЪ вытя -
1rуть пустой крючок q = () ,9. А кзковз ве роят-
1юсть З<l с1·0 забросов пс поймать 1ш од 1 юt'1
рыбы? Илн п01'iм~tть 10 рыб'
Похожая с1 1туацшr возтrш<~н.-т. когда подбра
сывают монету 11 считают, скш 1 ько p:t:> nыnа
дет орёл. Ясно. что всрош11ость ноянлсн11я uрла
11р 1 т К<IЛ(J(О.М бросаннн р =О.'> . как 11 нсро.ит-
1ю<~1ъ вып:1дсн~т pc1111<1r (/= n,s А l{:IKoRa неро
итностh ·1·01·0 , что 11r1 1 ,цес.итJJ бросаr-птх орЕ!!
н1,1п:щt'т. н:шр11мср, пятh ра:1? Ит1 11осем 1 . ра:1?
Та ка.и 11ро1~t:дура 1н1сн·1· 1 1а:зна1111е схе.А1а Бир
'~.J ё'l.Лll - по 1111,.н.·н1 1 ш.1:Selщapr 1щra :11атсматнка
Я1юба J3ерr 1 ущн1, 11ре/1,1юж rшшсrо 11 11эучшз ш е-
1·0 её. Д~nз1~пе nо~m<11<01ю1мся с r16 11юблmке.
ПУст1, производится /1 нeзan иcal\1LL'C. 1 кпы
тш111й 11 в каждом из нпх ул.ача имсt"J' uсро11т
нос1h /J, а нсvдача - нсронт1юс1ъ ц = 1 - /J.
Тог;~а кшrичество ус11сшных 1 rспыта1111/1 Х 11э
общего ЧJКJШ r1спытан1111 11 с:с1ъ и1учаl111~н1
вел11ч11на, которая может ЩJШ 1 11мать /1 + 1 :111а
чt:н11с: О, 1, . , п. К:~ктю cl: распре;~еле1111е~ Дру-
1 ·1 1м11 словам11 , ка коя;~ ncpt m·r 1юсп. Р!Х = k} тоrо.
что в k (1спыт;н 11 151 х 11'1 м аут~ет согrутстnоnать
у~ача, а в ОС"l'<lЛЫIЫХ п - k ТIСТТЫТаIПШХ llOC'J'ИJ "
пeт rtеутщчз?
13ыберсм какие-шrбудь кош<реп 1 ыс k пспы
тапий. Пусть это испытан ия с 110м<.:р:.1м.и i 1,
ij,, " .• iA•· l3ерш1т1 юсть того. что ИCIIЬJT;J.Hll(.' i, :~;t
KUH ч 11тся ; ·спеш1 ю, р;1вна р. А 11:uю1·и • r110 , нсро
нтнос1·1-, TUl 'O, ЧТО l1Clll>IT3 1IHC i2 nудст }'CПC lll HO,
f1<1BH:J /> 11 '1'. Д. С /(pymt'i CTOJ10 Hhl. Hl '(1mll' HOO' l1
то 1'0, чтu .ио 1 ыт:~ннt j ок<.1жетсн 11еу1щч 11 ым,
р:~нн<.1 ц (:щссьj * i1,j i= i2, ""j i= iA,). 311ачпт. нс
роят1юстh TO I '(), ЧТ() и НС! l l)l 'l'Э I 111 е i1. и IKTTЬIТ:l-
518
1111е i 2 , " .. 11 нспытанне ik :занср111атся ~с11схом ,
а нее остальные ис11ы·1-:-11-1юr - H<:.:\~·(aч<:'rt, раины
k n-1:
•
р q , так как нt'рон·1 нос1ъ 11ро11:зве;~е1шя
1 тсз:~n11с11мых соаытиlr р:нта 11ро1 1 з 11е;~е1111ю 11х
вероял юстеl1 .
l lo мы рассмотрелн лишь одш 1 11ар11аю
выбора k усттеш11ых 1к11ыта1 шfl н1 общего
чисJ 1 а пспытаrшй. Всего же таюrл н~1риаю·ш1.
как уч1п ко~1бш1аторика. сущt'е1·вуtт G~~. Пo
Э'J 'oNI) вероят1-юс1ъ ·1 ·01 ·0 . что ус1tt1 1 111ым 1 1 бун)r1
как11с-то k 11спыт<1ш1!1. :i нее ост:utы1ые 11с11ы
"1·:11111я 6у;~)Т 11t'у;.J.ачны. ранна (-;:,' р' cj'' ~.
Та 1<111\.1 о(Jра:юм. вt:роят1юс·1·1, k ~с11е1111н,1л
1кхода111111 с11 ыт:зm1iУ по схем<: Бсрнул.rш мож
r ю выра:~11'11, 01е,1ующеir формулоi1:
Р{Х = A>I = Р"(11) =С,~;/'cJ" ~
(•)
Выраж.ет1е. стоящее n право1-1 ч aLTII ':!Той
t\.юр"1~·лы. нам :шако мu (см. с 1аТ1>[0 ··Бнном
IЗсё, что под Солнuем сушествует или возн~1 кает, -
nрошелшее, 1·1 астояшее имt будущее-само по себе
и объективно вс~гд<t имеет высшую \ТСnень досто
верности"" Случайность главным образnм зависит
от на шего знан ия, поскольку мы не видим никако
го противоречия к 11ебытию события теперь, в силу
Gлижайш(:!й причины, нзм неи.~вегтной, uнu ИN1
uсушествляется с необходимостью, или можетосу
шествиться.
Якоб Бернумr1
1-11,ютона»). Лi;JIC'l 'f\JITeJIЫIU, pa:-iJJOЖИM (/1 + ч>''
по формуле бином~ Нью1·0 1 1а:
(/1+(j)° = //' + 11{J11 1
С/ + с.:; /J11
-
!.{/~+". t
+q'' ·
Слаr;~ем ы е в этом ра:3Ложени и н лвлнютс.н
соот nетстnую щпм11 вероят11остнмн n схе,"1с
Бср11улл 11 . l 1оэтому распрснслстrс nе роят-
1-юстсй ( 0
) нос ит ш1:3нанн<:: бииамиа11ыюе рас-
11/Jr!делГ!нlli!
"(сперь l IOl I р< >fiycм U'l'Be'l'JIТ b 11 а Н()П росы О
."vЮН<::тс
н рыбках. В случае бросашrя монеты
11 = 1O,jJ ~ q ==О,S, k = ') 1.1л11. 8. Соо·1 в~тс1 ве11но
Р-(lИ) = ~ () s~ U,); =-0,246.
'
")!.:;! '
Рн<lО)=~ o.s~ u.51.""U.()44.
8!2!
В :;адаче с р1,tболоном н = 100, J> = 0,1, с;= 0,9.
:1 /J = О 1 ~л11 1U. Н 11ерно:-.1 СЛ} чае
I\( 100J = о,9'щ ~ o,000026u
Есл11 р ы болпв нс 1юймаст 11 1-1 n;1нu11 рыnы.
то <. 01н::р111е11 1 1() ()Ч<.: l !J ЩНО, ЧТ() 011 вср<1ят 1 IОСТЬ
ус11<::ха ([J = 0,1) oцerrнJJ неRерно.
МАТ ЕМАТИ Ч ЕСКОЕ ОЖИ ЛА Н ИЕ
И ЛИСПЕРСИЯ В СХЕМЕ БЕРНУ/\/\И
Пусть слу•1 айная вели ч 11 н <1 Х есть коли•1ество успf'
хов в п И(Пытан иях п о схеме Бернулл11. Подс•1итаем
математи•1еское ожидан ие MIXI.
Мы з нае>v11 чп1 вероя 1ность k успехов 13 п 1<1спы
таниях при ш;роятности успех;;~р, а н еудачи q = 1 -р
выраж<~ется формулой
р() п!
k ·-~
L 11 =k!(П- k)!р(/ '
Поэтому следует сосчитать сумму
О ~po<(+l __п_!-. - р'с1''-' +2 п!
)! л-:+
O!n!
1!\п- IН
2!(11 - 2н' q
1 • •• + П...!!!.. p"q
11
п!О!
.
Как же подсту п1п ься к такои сумме'
Сделать это нетрудно. Вс11ом11им: м.1тематичеLкос
ожидdн и е суммы нескольких слу ч ай н ых величин
равно сумме их математически х ожид,.1 11 ии ЗнаLtит,
можно найти математическое ожидание числа успе
хов при Од~ЮМ ИLПЫТСJ Н И И, а потом ре.'lулыат ум нu-
Случ r1йные <ооытия
АН.TIS CONJECГANDI
PAKS ГК I МЛ,
c;-..,tr/11111
Тr.1cЪ1tt1111 lcTt1genu de R at10c1111is
JJI Lщl o Alco:,
C:1m 4A1111tJ/ttlJrJ111b!.м
JACO!\! Bh1!NOL1LLJ
C HRJS'i 1-lllCENJf
,4
FJIЛNC . ~CILOOTfNIUM
'Prif!шo.
1'm 111 i;dlCJ Y.щ:- c-li =g;111t1tJ:;m ()t\11n 111g,~11 11
l\11 MOflUm(f\!OllJM, фJ 1>1'1 prre m:.111"
lщi nun(' h it1t1, Vtr Cl.i,n1li nн:, 1fi 1111.:r
('(("(,Гil. rr (pt.Jilte: f\:1am, U( \.l lllCL1 (1:-
tt:fUm . q11:Щli11 lГ.t1,J ,1111t1Jtlll 1r11\tш1\\1 1
olt..: 11 .l .is Ч'•"11• l•r t: f'" pr•>tt:ndм ti1v.1111
Л11.tl)'t'""" f<"ltл••1'.. J~('1I( 1nrcJ1 1i;:t> rti.Jltl 1l~;i. pl1mm111H
rzopofitu 1't10 mkrvrre. pntJC, quz d~ AJc::t R:шсн.щщ
А
~Ф''"
13 CJJyчac IJ = 10 получаем
Пrр11.1я ; тр,1ни1.1 .1
~Н11ГИ
Я г,,,рн ум11
• ИСl(УП ТIЮ
r1p1.·лПO/\fJЖ t"'l ll•i1 »
Издан 11ео 171 J г
Р(1()0)=~.(}111
'
О9211
-= ()1~IS7
10
t0!9()1 '
.
.
.
'
Сх<.:ма Rеrнуш111 пр11~1ен11ма как /tJШ /1 по
<."Ледомпелt11ю. та к 11 для 11 0; ~ 11 онр<::м<:11но
жить на п, 4тоfiы получить математическое ож11да
ни е ч исла успехов при п ~1 с111..~тан и ях.
Лля одно10 иtпы1а 11 ия 11ай1 11 мат<:МdТИ Ч t'С Коt!
ожил<1ниt• числа успехов ничего н l:' стоит:
m= 1μ+04=1.1
З11а ч и1,
М\Х\=нт =пр
Пер40•идё'v1 к лис nсрсии. При ол1юм 1кпьпdнии
лиt'nPJX ия чием успехов
с/=μ(1- m)' +q(O т)·.
Уч и ·гы н<Jя, ч гот =fJ, получим
d=p(I-т)'+q(O- m)1
;
d=р(1 p)J+qp
3
= PC/J+l/Pz= pq(q+р) =P'I·
Зл<'( ь мы дважлы во<.110ль.ювались rоот1-юш€ н ием
p+q=l .
При испы гани~1л гю <.хемс 6срнум~1 результат
l<dЖдОГО из /IИХ не 1.шиси1 от рс;1улы •.па Ot,TilAbHЫX,
полому 'vlОЖ но восnользоватьс1-1 фоrмулоИ с-уммы
дисnсрски незJ.оис нмых слу•1аинь1д. в~личин . Т.:~к11м
uбразuм,
D(XI = 11d =npq.
519
Леп'рми11и ~м и случайность
11po1Юj\J IM t.IX llCllЫ 'i ':JHJ ll'·1. 1[анример, Д<:'СНТ1!
крат1 н }t' 11tщfi1 >:кы ваш ll' l мо11 сты 1vюжно :J:.t.Мt'
н 11ть О/\Нuкратным 1ю;\брзсывзг11 1см 10 м.онt:'L'.
Ис1 ют)зуем ЭТ() 06с1·оятtщ,с·гво для рсшснт 1 я
оюто~'i жн зпетпто взжноfi задачи.
Предположим. оы ретпилr 1 полстс1ъ ll<l с1 -
:.юлёте в Саратов и у nac есть nы6ор: летет ь па
;~.nухмотор1юм юш 1ra че-rырёю,юторном само
лi..<тс. Моторы у с;н"юлёто в оди11акоnы, и 1<;D1< -
дый с и<.:роятностыо fJ может отк:~ зать lIO время
1 юлёт<1 . От ~~н ;1комых <tн н:оtторон вы :~наст<.:, что
днухмотор 1 Jы(J с1мш 1ёт С1IOCOfil'll /tOJI C'l'C'JЪ / tO
С1ра·1uна 11 на одн ом моторе, а чс-1 ырёхмотор
ны1:1 - н::~ трt.•х 11 1т дажt на /\RYX мuтl>lXlX. а на
од11ом уже 11 е может. Како~ 1 самоJJёт11алёж 11 ее?
Обо:ша чим через р всроятпостъ выхо}\а
мотора из строн за вреtvш полёта, :.i через q -
вероятность fit.':ютк<1:11 ю 1'1 р;1бrл · 1,1 ;~ н111·;~тl'ля
То 1 ла Н<:[Ю>1тн< к·1ъ катастрофы ;~нух~н 1'1ор 1 101·0
ca.\IOJJt'тa р;ш11а Р!(2) -/,-.
\l чl'тырёхмторно
го- P/-J.) +P.J-0 = р"' +--J.p l/. О11реrtел11м, щ111
i<<JJ<иx :l1 rачешшх р н С/ вероятность разби1ъо1
11 а двv.\моторном самолёте бvдет мс11ьш<:, че~ 1
на чс;,ырёхмотор1 ю~1, т. е. коi·да р2
<р1+4р
1
q.
Очевидно, что() <р < l Сократив па;/- 11 заме
лив С/ 'f l;J 1 - р. 110J1учш·1 . ч·1·u Rеронтность раз-
6Упъся 11 ;1 двухмоторном с:~молётс бyi lt"1 ' ,,1енh-
111 с, CCJIH 3;/ - ~/J 1 1 < о. ~::,то нсраR СНСТВО
с11равс..:1 l111ню пр~~ 1/.-'1 < р < 1 .
Те же.: а11нэ·1 ·ор1,1 п::~м t·ооб щюн1, что :1ля мо
торов, которr.rе уста~ юнле1 11>1 11а таю 1л. само
лё·1·ах. р = 0,()()1 , что, I•онечтю же, ме11~.тне 1/3.
л пот(}му полёт 11а четырёхмоторном с:.~молётс
является более бс:ю пас11ым.
СКОЛЬКО ИЗЮМИНОК В БУЛОЧКЕ?
В тесто для к;1 лорийных булочек доб;шляют
11зюм . А можно л11 оnрt11слитh, сколhко изюми-
1юк<жаже-1·ся \\ 1<;1К()Й- 11н С1уд1, 11:1 НИХ? П() I IOjiMe
на кзжлую бул(}ЧJ\У П(}лагается а 11 зюми1ют<: 11 а
пр11мер, а = 1О. Однако если вы пО 1<)-11аете каж
дый день по булочке, то ровно 1О изюминок
бу~ст содсржз1ъ примерно 1 из 8 булочек По
чему? На этот вопрос п оможет отuс·пгrь теория
вероя1·нос 1·ей.
Пусть ;tля из1 ·0·1·uш 1 tн11}1 очерс; 1н о~'I t1арт1111
булочеJ< 3амешню1tтся ·1·<::сто н коm1чt:стне V кг.
Если на 1 булочку р<~сходуе::тся 1· кг (напр11мср,
1• = 0,J ю ·) теста, то 1rз ()дно~ ·о замес:~ можно
ис11ечь N = \!/11 бу;юч.ек. Поэтому в тесто ~тадо
:1асыnать п = aN изюмиrюк При rазме 111н ва -
11ин ка:ждая п;J l lЗIO MШIOI< С 0IOПI:JIЩBOI1 ВСfЮ
ЯПЮСТЬЮ может попасть в любую 11з N частей
теста, котор::~я ндёт на из готоолеш 1 е 1 булоч
ки. Сnраве;vr.иво н предп оложение. что кажлая
J 1 з изюминок попадает в ту .шш нную часть
теста НСЗ:lRИ СИ М О ОТ друг11х. Тогда число нзю
Мll НQК в бупочке - случай11ая велич и на Х,
11меющая биномиальное рз сп редсление (с.."1.
сг:лъю « БиномиалJ,нле распределt:ниt'·>)
pfХ = п~} =р (п)· =ст ,,mqn-111
l
nt
U/- '
'
(*)
l,,
1·11е/D= -
=-
q=1-f-'Jn=tlN
''
1V V'
'
.
.
520
Т::~к как и:-1 одJ 1011 11арт1111 тес1 ·а делае1ся
несколько C(}Tell 6ул(}чек, то число :~:~сып а
см.ых в ТССТ() И:'\ЮМИП(Ж l l = aN ('(}СТ:ншяет
11 есктrы<0 тысяч. При больших з начепиях
чи сла п3юминоr< п вероятности J>111 (11) вычнс
;шть по формуле(*) очень СJЮ)!ШО.
Жизнь прекрасна благодаря лишь двум вешам - изу
чению математики и преподаванию математики.
Симеон Лени ПуассQн
Случ.::1иные события
РАСПРЕДЕЛЕНИЕ ПУАССОНА
а
"
......
' --1
.,,.. -
"" •,
---
Лстерми н ~вм и rлучdй~юrгь
ТАБЛИUЫ РАСПРЕЛЕЛЕНИЯ ПУАССОНА
Во м ногих ю 1и гах по теори и вероятн остей ~1меются
габли uы распределен ия ПyaLt.uнa. П усть случайная
вели ч ина Х имеет расп релелеt1 ис П уасс<J11а п ри
некотором ::~ начении .1, тогда
Р{Х = m) =Рт(а),
PIX~т}=}Ju(а)+μ,(а)+...+Рт(а).
Вот пример такой таблиuы при а = 1О .
т
PIX=m}
PI X(ml
о 0,00004540
0,00004540
1
0,00045400
0.00049940
2
0,00227000
0,00276940
з 0,00756665
0,01033605
4
0,01 89 1664
0,02925269
5 О,03711JЗ27
0.06706596
6
0,06305546
0,1 3014142
7
0,09007923
0,22022065
8
О, 11259903
0,33281968
<.)
О, 1251 1004
0,45792971
10
О, 1251 1004
0,58303975
11
0, 11373640
0,6967761 5
12
0,09478033
0,791 55648
13
0,07290795
0,864464 42
14
0.05207710
0,9 1654 153
1i;
0,(Н47НЮ7
0,95125960
16
0,02 169879
0,97295839
17
0,0 1276400
0,98572239
18
0,00701)1 11
0,99281350
·1g
0,00"17 '{2 1 6
о, 996"i4"i6&
20
0,00186608
0 ,99841174
Н а рисунке и ;1ображена ли аграмм<1 вероятнос
те~:-1 Р{Х=т) =Рт(d) при d =l О.
o.1s
f1. 12
0.09
0.06
().l)}
0.00
24(j81о1214161820
r.1 с ч ё 1hl сущсствt:шю уnропцются, если
р,1 ссм< >ЧХ"r 1, 11рс; \t'лъ н ы й случаf1 бшюмпальпо
го расr1rеделс1 шя , ко1 ·; ~~1 /1 ~ ""', :1ilfJ =а :~аф11к
с11rопа1ю. Фр:н-щу:iсюrl1 л.1~1тема·11 1 к С11мео11 !lу
ассо 1 т Д()r<аэал. что таю1м 11ре1\еm, 1 1ым с11учае~·1
бyll:CT распре7{сле11 не
а"'
P111(a) =-tJ",
Jll!
1 дt: т = (), l , 2, ".Дашюt: ~твсрждс1 1 ис получ1rло
11а:ша111 н: 11/)(!t)ШLЫ-tU>I JJU.!O/ЩM(I Г(J 1t/CCOllП. :1 CIMO
рас11рс;\еле1-111с /J,,,(a) - /юt 11реашю111ю !~1·ас
со1ш В общем случае в<::ш1ч1111:.1 /Jm(U) сс 1ъ 11сро
ят11ост 1 , рптн-tп т ПOJIOЖllTCJihllЫX lll'XOДOB пр1 1
бшн.mо1'' чис:\е 11е~-;\.t"1сн:-.tых нс11ытан11й. сс.1111
срсдп<;е ЧП("Л() П()Л()ЖIТTeJlf1lll1I х llCXOД()H 11р11
1 к11ыта11иях составляет а.
Воспользуемся распрс;\слt:1111с .ч Пуассона ,
чтобы найти nероятность того. что u 6~7!очке
не бvдt:т 1ш одноl1 изтощшкп. Т lоско:1ьк) О!= l.
r/
1
=·J 11 1:1 нашем случае:а=10.то
Ро( 1О) = l:'-
1
" ,,, OJIOOO-l '5-1.
Итак, нс:rоятность то1·0. ч·1<1 6y}I( 1ч к;t оста
нr::тся б<.:э I ПIOM~I. НllЧ1'0ЖН() \1;!J l~I
Что()ы 11айтиjJ 1 ( l ())-11е1)()ят110С"П1 l'Оrо,что
n булочТ<е \)Of\IIO '\ НЗЮl\11 1 111«1. 11уж1ю llOJ1YLICH -
11oe на1vш чвсло ум.1 южит1, rта 1() 11 1х1.щещ1·гъ
па J. т. е. нросто у1vнюжи·1ь 11а 10. Чтобы выяс
н11ть, к;11щ11а nсроятносп, то1 о, что u б~'JЮЧ l\'У
попа;\ё1 pu111ю211:3юм1111ю1, 11уж1 ю <::щё pJ.1 у~1-
1-южнть IK1J IYЧCHHOC Ч I ICJ IO на 10 11 ра:щеш1ть
11:1 211 ·1.f\.
Всроят1-.юс1 ъ ·1<11 '<>, ч·1·< 1 в буJ1оч кс окажется
10 1 1 :ном 1 1нuк. ранн:.~ 0 , 12'1. 3'10 оз11:Jчаст, что
1ю 1О шюмишж пппалL'т тоm,ко п 12 ,5 <Jr, ()уло
чек. Мож 1 ю так.же т,1ч1 1 ст 1 т1,, чт<1 [Ючт11 все
булочкн (95,7 %) буГ\)'1' содержа·11, от S до 17
11зюм1шок. Меньше 5 11зю.мm ю 1< быв~~С'I так
ред 1ю ( l ~Ч, что ест r покуп;~ть по 1 6улоч1се в
д<.:11ь, то такал булочка '10жет достаться одш 1
ра:.-1 за .)-. :1 месяца
Закон Пyacco IIa действует всякиir раз. когда
НМССТСН MHOl'O H<::J:IHITCllMЫX IJCl1ЫT:tl l l l il 11, а
нсрш1 1·1 юс1ъ /J нскотuро 1 ·о собы·1•1 нr А в юtw-дом
11:J н11х · 1 ак мала. что срцон:с •11rcJНJ с:обh1·1·11йА,
1х11нюt: пр. rrtвслнко. Пшптсю 1с собы·11н1А прн
,'\~НПЮМ 11Cllhl'J'11 11 1ll 00J)IYIIO 1.I:13bll3;\l01' ~rcxo,r~oм.
а общее чпсло событ11(111 np11 п нс 1 1ыта11иях
•шс1юм llCXOДOB _> .;. н T<ll<OM случае МОЖI Ю счи
та1ъ, ~по 1.fi-1c1ю исходов Х н меет расттрс/\СJТе1 ше
l l yaccoпa с а= пр. П рю1ерам11 може1 слулшть
ч11сло лорожно -тра11спор·1 ·ных проис111ест1~н~"r.
I JJJll число пожаро1:1, llJ)ОИЗОШС/\Ш.ИХ. 3а суткн
н 60;1ыно"-1 r ·ородс.
В са мом /(еле, оче11ь .\1:.1ла RС[ЮЯ'J'1 нк~rъ то 1'0.
что :за супси J\<1111-11,11-;i ав· 1·омо611m, 11011;.щёт н
авар1но н , 11-1 что п /(анном :>;1~1 1 1и11 нспых11е·1
1южар. Оюrа1~0 11 - ч1 к1ю маш111 1 1 1т1 :iJt:нr1 11'1
nет1ко, а !IOTOJ\lry х - ЧJICJIO IICПpI1Н'l'llJ1I X 11ро-
11сшест1-111(1 в большо11·1 городе подчшшется
зако11у Пуассп 1та. Это rюзnоляст достаточно
точпо рассчнтьmать число м;1ш1111 ~скорой но
мощи.. иm 1 1южар11ых :v~ап~нн, чтобы. с О/\НUЙ
стороны, 1юнрсмя uкa:{aTJ> лuмощь, а с дру-
1ой - нс /tсржа·1 ъ 11рс:к:р1:1t:111щ11111с машш1ы.
1{01lt''IH(), н таких .\lllIO!'OMl lJIJHIOHHЫX 1·opo;tax,
как Мпскна. 11ро11авс)\сн11е пр ю~я .чслю 1 х ;ю
рож1 ю-тр:1 нспорт11 ы ,, 11po11cmecrв11 it бе:~ ЖС(УГВ
f.IJtJ t 11ыэо11ов маттпm «C1юpoli помоr~rР. 1с1к 11 1х1 -
1ш.'ю, ()Че111, 1:.1елпко. В таком случае зз1ю 1 Ю)~
I l yaccoн:i 1\слесоо бра:шо пол1,зон:пься гтрп
расчётах числс111 юсп1 oepcorraлa 11 , ехш rчс
ской оснащi.:нности служб IН.)i\IOЩIJ н отдел r,-
ных ра11tш:tл 1 ·0 11011а.
/1,J1н тш·о ЧТ()бы нормально работат1. 11 110-
луч :1ть 11р 1 1uынь, с 1 рахuныс клмла111111 110 нсём
м~1ре такж~: 11р116~г~но·1· 1\ ~а1'1н-1у 1\ уас сона.
ПуL"т1,, н~шр11мер, страхuR:зН кпм1r::~н1 1 я :~а L~1·1х1-
хп11ку стр< >е 1 шя п1 1южэра бсрёт г1л:пу, раRную
1. 5 ''., от су1-11"1ы, 11а r<аторую оно аастрэ.х()11а110.
СТАТИСТИКА ЗНАЕТ ВСЁ
•Стат11стr 1 ка знает всё•> - таю1мн слов:~м 11 11а
ч11настс>i nторая час-1 ь pu'vta11a Илы 1 1lл1,фа 11
Епп:1111я Пc'r 'p()Kl «Двснадцзл_, стут .<.:н~. •И:шс-с
т 1 ю, 1..кот,ко кar<ol 1 1111щ11 С1 1е/tает в год сред-
1ш\\ rраж;\<\1rи11 рес11уf>лт 1ки." Изr.ест110. с1ют,
ко 11 стране ОХОТНIПША . балср11r~". CTlllll\013,
со6а1< всех пород, велопптедов, п:1мятm1коu ,
дсnу111ек, мая1<он п швей ны~ мапtиоок.
К:tк M I IOl'O ЖЛЗШ I . ПОЛJЮЙ пыла , страстей и
чыс1111, гляi1 1 1·1 · на жн.: со с1·атш:т11чссн:их таб-
11 1щ! " 0'1' CTa 'J'L IC'I t IKlJ НС cкr)()('llll,CS I НJ1Куда ".»
Сt'\1<ЖН ~H:l Mt:! 1нтоrо гюмак-а \lt: нан Yl'_ консч
нu, научногп oпpCf(CJ l el Ш.» CT~ITI IC1'11KH 0/tl-l ;JKU
113 ЭТ<Jl'О IOM()ГH I C'ГHЧt:CKC)J'(J nп 1 н.:;1 1 1 1 1я МЫ у:~ 11а
ём. Ч 'J'() её Oб'J,CICTOM я llIOI ЮТО! сг: l "П I Гl'JГЧССКI 1 е
11.arr rl hlt' о самьос ра:пюпбр:l .шых m1J1e r1LJЯ .\ жп:1-
1111, со6ран11ьrе n статист11чес ю 1е т<1бтщы.
случdйные ( оnытия
11редполож11 .м, •-п'о компа1 нш застрахова:1а
11 = l UUU хозб.'10 1<011 11а дач 11 ых участках нз
s тыс. рубщ:ll каждый . <..;обрав ДСI IЬП I З;I эту
стра хонку R KOЛ l fЧCC'l'BC 120 т1,rс. рублей. t<OM-
11~\J-lltЯ обн:3;.~1-1а ныпл:~тп· r ъ за каждое с1·ореJ.ш1сс
Rтсче11и<:: 1·0;\:i строе11щ: 8 тыс. рублеr·1. t::c11 1r дня
хозблока вероятность c r ·opcтr, н тсчеш rс год~•
р:111 11 :1 jJ, то при 11еnолы1111х п = njJ сJ1уч:1~11 1 ан
nc.rr11ч1 11 1aX - •л1с·ю с1·орсnш1 1х :1а 1·0,ц :застра
хов:шпых хозбло1..:оn по;1ч11 1 mс:тся расJ1реде
.1сrп 1 ю 11уа<:со11<.1. J<о~ша1шл разор11тся. сс:т
. \ ~ l S, nocкom,1()' n т:Н\01'1 случае Olla долж1 ia
выплаттпъ 1ю1·орельцам 11L' мсшх· 120 тыс. руб
лс 1·1. не 1 ·01юрн уже о дру1·11х :..1н ·1·ратах. JJzн:чi.'т
1нжа:1ы11а~т. что
Р{Х;;. 15f = 0.08.1 щ111;1 =U,O1.
Р(Х ;;, l S} = O.U17 11р11 /1 = o.ou~.
Р{Х ) 1'5} = 0,()IJ(J 11р11 р = ЩI07.
Исходи п:.~ эт1 1 х вершrт1~остеl1 комл::11 1 ш1.
ШIДJ I MO, Н<::ВЫJОДНО рабо·1·ать пр11 р = 0,01 11
HI Ю!Шt' ДОJ JYL" l 'l I \Н.) 11pll jJ;:::: 0,[JLJ~ 11 /) = (),()()7.
Пuдоб11ы\111 но бодсс сложн ht\111 расчётамн
:~<1 1-нrмаетсн ст/т.х:овст, 11m1 . как с::.С' ещi.: 1rаэ1.1 на
ют. ою1~\'П/>ш1я. ма·1·1.:~.,~:.1т11ка . Ro щ:ё м 1'111\Х: вы
'од1п 11есю>т,ко ю1уч11ых актуар11ых журн:1mщ
Jtрnнолято1 11:1уч111,1 е кш1фере 1 ш,1r11 на ма·1·с\tt1 -
п1чесю1е темы, спн:з;1 1 111ыt· со страховаю rем.
l lu Jaчс,ч нужны так11с 1':16111 щы, как 11:х сu
став.ш1·1ъ 11 о6рабзтынать, каю tt: выводы .чож1 ю
дt.:л:1·1ъ 11:..1 J111x? Отн<.:ты 11:1 эп1 lюпросы 11 .цаёт
сг:п11с1'11ка (отит. stalo - <· r ·<кy;J.apc1110" , ..7(/IJ/.
:o.t;1tш; - ~состш1111 1l' <>).
ИзвеСJЛО, ч ·1п у'lк<:: в щ11.: 111 1 11х 1 ·осу;~арст11<1х
ne.mт учёт 11аселе1пщ с11осо61ют-о пла ппь 11:.1
лоп1 . С рззв11п1ем естестве1111ых 11ayr< 11 уСJюж-
11е1 ше:м 1101:31 ш общест11а потребоnал11с1, 11а
учпыс методы обработки 11 а11;1i1и:1а самых
разнообразных снсдс1шf1 . В част1юсп1. в XI Х 11.
\ \Ш\Н\ tJt:кь 61 ЮЛ()\ ' \ lЧCCJ.aSI CT~l'l'l ICTI\IQ, КО' \ орая
н работах ан1 ·л нйск 11 х интпрон fi1,1лa 11:1 :та 11;1
Г11юмет11ико 1I . ()на а 11 :1 ; 11 1з1 1 руст статнеп1• 1 t:
скr·1 е ла1111 ые, свяаа1· 111ы<:: с ч 11с11ен11 ы~111 харак
тер 1 1сп 1кзм 11 t<<ll( O'J'Дt:Jlhl l l1l X 611ш10ПIЧt:t'l(llX
осnбе!1, · r·al\ 11 1 1 х 1ю11у.гн1 1 ~1 11~1. R ; 1 t>мо1·р~нj)11 1 1
524
Лt>термин1нм и случайноt ть
большую рот. lfграст дсмu1раф11qес1сш1стат~ 1 -
ст11ка , 113учающая чн<.:J 1 t:нное1ъ настлеюш, его
нозрасп-ю1! , соци;~лы1ый, пр(>фt:союн;1111,нh10
состан , 11еrсд1шж1:111ш насслснш1 н 1 1рt",цс11ах
стра 11 ы 11 т. п. :.=)коно,"н1 чес1<ая ст~~п ктик<1 ра:зра
батt .1 нает Mt'TU/J.Ы про1·1 юзнро11аш 1 я роста 11ли
о 1;~да 11r()И:1щщстnа 11роf(У'lщ 1 н1; l 1 зме 11 е111ш цt'11.
сnросз п предложещш н;~ товары . Можпо на
звать ещё песr<олr,ко леснпшн различн ых ста
т 1 кт1щ: 11:шр11мер, м:ед1щшккую, фн1 rансовую.
страховую и т. д.
Методы обработки стат~ 1сп-1 чссю1х данных
но нссх н:!званных видах статнсr1 1 юr имеют
много общеr·о 11 Оl'нон;,~ны на зна111111 т~ор11и
нсроятностсй В ХХ 11. 1щ:J111 1 ют~1 нuн:н1 наука
-
J\1атсматнчсскан стап1ст 1 11<а. Во·1· 11ескол~,ко
при~еров её ис 1 юл 1"1оnашш.
В 1111юлыюм курсе физики ж1учаrот фи:~и
чсс1ше :1аконы, оnределшощие сnяэн мсжлу
чr1 сле1. 111ыми характеристиками физ~1ческих
явлений. Так, закон 13ш-шя - Мар1ютrа ш,rража
е1ся формулой
plr= coлst,
означающе~-1. что при постоянно!1 тсмпераrу
ре t про 1 1знt:до-шс д::111ле 1 шяр 1·аза на за1-шмас
Л·tьrй IIM ОnЪ\::М \ICCTI> AeЛl l Чll Jl :l I ЮСТОЯ!11!:1Я.
R Л"VТI n. а 111 ·11нчашш Робсrт Бойт, 11 фра11 -
цр Эдп Мартютт открыли этот з.шон экспери
ментальным nутём. Опп налиnаш1 ~лу1ъ в стек
лн r111ую трубку, загтаяшrуто с одного ко 1 щл,
11змсрял11 объём, занимасмьн1 BOЗf\YXOJ\I, и пе
рсмнож;ши ВСЛИЧИJ lЬl Об'hёма 11 Д;J.1:\Лt'lПШ воз
/tуха. н 1 .1р:1жснно1·0 дш1 1 ю(1 l'Толб1 1 ка р·1ути.
р
'/' = l'Шl~I
1,н, он ь"йм1
Мар110тта
-}i..( n er~tMt'll 1.1 1\Ы-ttol(
точ~ и и r11111•роола
р\1: ' оr1ч
Окаэллось. что та.кое 11рои;~не;1е1111е 11ракп1'fе
ск11 постот 11ю, естr пс ~"Чнт1,11 1:1·1ъ 011111601< FI
11змсрениях. которые JЗ подобнт.1 экс~ 1ер11мсн
те доволыю :нтзчнтелт, 1 н.1.
С.: разн1:1·1 ·11см фи~ичсскоr1 теоршr стало очс
Rид110, lПО :ia ко1 1 ьо~"1ля - МарпотL.t следует
утuчнтъ. В 1R7 .)1'. 111 -111t:рт11-1;\скнй ф11з1ш йо
ханн<.::с Дидср 1 1к Ba11-;tcp-B:t3ЛhC 11рсдJюж1111
формулу, наз~анную н11осле;\стш 111 ет 11менем
(./
(р+ -)(11- IJ) = coпsr.
~/~
Здесь ан /J - нс 1юторые 1юлш1штель11ые ко11-
ста 1 пъL Чтобы rтайтп этн :константы н С Аесrи I<
минимуму оши6ю1 пр11 11х 011ределс111 1 11 , 11уж
нu былu ис1юль:ювать 11с ТОЛЫ(О усоuерше11-
ствою1 шую а ПJ ~ар:пуру для экспсримс1 1 тоu, но
11 разш 1тыс к тому нрс.:ме1 11 1 \1\lТUДЫ матсм;1111-
ческо(1 статисn1кн.
В 11аш11 д1111 стат11ст11чсску10 тсортпо обра
()опш 0 1лиnок 1 1р11мс11яют Г1р11 особо точных
и:~мсрсrптях. Сам1,1 й щюстоr1 rтр1тмср - повы
шение точ1юстт1 оттрелеле111н1 ка1юi1-т1бn не
лпчины с помощью нс:стш;rъких nоnтор11ых нз
меренп.й.
ГТрсшю;южим. LПО пр11 п нзмере1 шях полу
чс.:ны зна<1снш1 .'\' 1 "У!. " .. :1:11 • Оuн r бко1'1 11змере11ия
х, на.ю1:1Ем paJ1 Ю<."IЪ :х1 - а. ~де а
-
точпос. но
HC l iЗBCCTH()C нам 31 1 ачс1 ll•IC нскомull ВСЛП'-1 111/Ы .
F.ст1 а()солю'п1~1я вt:>личнна CJl\'Чa1~rнol1 ош 11бк11
lx, - с11 каждого н:iмсрсння ·н<: 11рс1юсход11 т
11екотороrо чно1~1 ь > О, ·10 среднсt: арнфмt:"гн
ческое :\- = (х1 + х~ + ." + х11)/11, к:.~к 11раu11ло. бу!(еТ
имеп, ош11бку 1."ё - а 1< '6/ \ ' 11 . что ус1 ·анав;1 11-
nаt:"тся с- 1юмощ1.ю т1::оrнш 1к:рш1тностс1"1. Таю1м
образом, при n = 9 мож1 ro уз11;пъ искомое з1-1 а
чс11ие измеряемо!~ nс1rичш1ы n тр11 раза точнее,
чс~ при оююкрапюм 11змерст111и.
Rот дру1·ой [\PI l .ч<.:р - 113 ; \смо 1 раф1ш Ещt· R
XVIJI н. на болыпом ст;;~т11стнчсс1<ом матер11з
ле nr.mo уст" ~ ювле~ю , что 11 общем числе н.ово-
poждl:IllIЫX / \OJ IJ{ M 3Jl\,Ч I JK<Ш вы 111 е. 'i.eM Дt:J\ОЧСК.
Н ко11це ХVШ в. фра1 щ~ :;с1шf1 матсмат1гк П1,ер
С11;1ю11 Лаплас обп3ррютл, что в разных рзй -
0 11ах Фраr щюr доля родшшшхсн м:шьчш<ов
р:ишял,кь 22/4.3, а в J l арнже, I< сго у;н тнлеш1ю.
нсс1 u :1 11ш ь 2'i/ 19 . За 1 тнтр и1 онашrы Гr та1ш:.·1
ра~111 1 ч11см, Ла1шас нашt:л /1,ю1 неl'О ра3ум1юс
0Сiънс11е ш 1<.:: в общ<.:с ч 1~ело 11 ово рс ~ж;1ённых н
П ар11жс Rl\JL1oчa111 1 ct, 1 ·:1кжс П О/\К1Щ ы1t111 , ~1 11:i cc-
Jlt1111c н::1 11р1 ll '()P(l/lUK ш щ()рJ<- 1111\;uю к ()CJ 1( >Н
IТОМ /\еВо ч ек 11 CKJIJOЧ1 1 н IТСЩКИ/\1>1 111 6 1 11 :1 \ )\)Щс
го чпс:т::.~ млал.е1ще" 1 1, Ла плас nолуч 11л 11ол 10
родlШLШIХСЯ M;JЛl,ЧT ll<OB, блнзкую 1( 21/-Н.
::)т3 нсторш1 ПО)'ЧИТСЛЬll(\ в дnух ОТlЮПIС
ШIЯХ Но псрю,1х, очеuщлю, что ,1остонер11ые
ны1юды м01ут быт1, с:~еланы Н))lЬJЩ n том слу
ча<.:. t:сл 11 uбраба·1ыuасм ыс с1·:~т11ст ич<.:с к11<.: да11 -
ны<.: r1().'J}'ЧCllЫ llU .l:IOЗ 1\ilUЖllUC'l ll в 0/\ 1111 :11\ОНЫХ
yc.JO IШIO( 11 11<: IКК;JЖ<.:НЫ по каю 1м -1 111 ()у;\I> 11р11-
ч1111ам нрfЩt: тolr. о которо1·1 рассказа но 1~ы1ш: .
САМАЯ НЕОБ ХОДИМАЯ БУКВА
В А/\ФАВИТЕ
В 1111 шушей машинке tJyкRы О,[. И, А, Н, Т, С, Р 11,)хо
лятся D uентралыюй •1 .:кти клавиатуры . Он 11 н.н1бu
лее частu исполь1уюн я 1ю вре\1Я печатс1ш1}1 П-'К( т<1.
Релкие fiуквы Ф, 1, Ш , U, Ю, Ш помешйютr:я ближе к
её краям. Пр 11 таком расп оложен и и бу к~~ машиш1стк;~
может бы<. 1 рее печатать и у 11её ме н ьш е уLГают μую1,
поскольку палы 1ы рабо га ют в щ ~н 1Rном fl Lt«-'н rpt-1 кла-
1:111 <.пуры . Ппдсчитано, как111е буквы в русском ТЕ'ксте
встречаются Ltaш<! все~ о.
да шtы е гюдсчётов острсчасмuсти буко 1н~3ам1~-
11 имы при ле ш111фrо вке тсксга, t'сли пр и его состав
лен ии поль·ювалиСL. wифpo.'vt замены.
Попробу111тс;: r1рuчи тать следуюшии 1а шифрован-
11ый Тt•ц!:
Т ЭВЧО РКХЬЬ ТЫЬЪК Т ОЬРЫЬОЗПЬЧНРУ Нhl
:ЗЕОРФ /,/ ВUЗЗ 3Ч [РЛШБШСО ЧК [Р::жозк J ЫL>Б
ШдШОВОИ 1,ЭРФJЙ ЫП G/\Ьдl-'Т ЬВ0Ь1ВОJНЗ :
ВЛФЬАЫИ , ОЬРЬ\33 П ЗЧЬЛ, ОЬРЫЗ З ТЬЫРКО
ЭРЧОЬУ, ОЬРЫЗЗ LJдРГЭРЧОЗ ВдФР l>13ОЪ rТ 3
ТИП ЗЧдЬЭЗУ 3 UBH /\Вд Ьl> . [РЮО l'ЪШ МК
ЧРТЫЬЬЬЭЭРФ Р НЫЗЕОРФ ЫВUВ [ЬIЬГЛЬ ТЧЬФР
Т ВГЭВ ЙРЫРМВК ЪВОЬЪВОЗ ПЬЧНВК ЕРl\Ф-
1'< )f> гнв .
В прив~:>ленном текпе кJждuй буквЕ' соо1 вt:•тс тву
ет другая Ьукв.~ . Это ~1 ес.:ть ключ ш ифра 3ная ключ,
11етруд1ю проLt ИТ <пь текст. 1lo ис 1 ~uльJуя р,1311ую
естречаl'МОСТЬ букв и И)\ LUЧ СТс11tИЙ н 113ЫК~, можн о
Случаиные событи>1
Rо- ннJрых. 1юзн11к;1 с-·111<11 1 рос1юЧt:J\1 у 11р1 1 бОJ 1h
тст·1 i \ OJlt' рож;\сн п1'1 \1а 11 1 .•ш ков J \СМt11 · раф11 -
t1е:ская CГdTI IC' l ' l 1K<1CВl\Дt:'J'CЛЪ('l ' li)t' 1 . ч 1'() ЖCllЩI IJ 1
60.111, ш е::. че::м ;\tркqнт ~? I lр нчшымп 1 1J\111 1одасмо
го янлсшш наэьш,шп. как г1~х1щ1:ю. вой1 rы 11 11е
:щороnый обрd3 Жll:H П I. l<Ol'OpЫIJ с1а щс f!C1'1,~ 1
мужч1 шы, чем ;ке1 1щ1 111ы. 1lо 11<.: rкё 1·ак лросто.
Дсiк·т ннтсльно , 11 rюlrпы, 11 1 1t':щоровыfт образ
ж11:~111 1 ока:.1ыка101· н1шя1н11: на μа:щость мсжлу
Ч! l t'JIOM Жt:llЩl lJI 11 \·1ужч11н. 0;11 1.11<0. СУ/\Н 110
;\е:v10 1 ·раф11чссю 1 м таб1 111ц;1ч . ~-n<c срсдн дсп~Гr в
rю:~p;JC'I с 1 1-12 . JICT м:JJ111Ч 1Jk:()H ~l el-l hUJe. 'ICM
.'J,CR()ЧCK f[O ,~:l llfl'111\1 r1cpe111101 19')() 1· , H;.t llt:p-
BOIЧ году ж11:311 и С\1 ер·11 fl)CTЬ \1:1Л11ЧJ 11\()11 11а 0.7 ""
преnыш:1ет смерттюст1 , деuочек Пенн 1,rt1 t м\Jм).
пр11чшты этпrо фе1ю.чс11а носнт тр:13д() более
1·л )'О() 1( и 11 ( 61 IOJJO пIЧССЮ 11"1) ха μ:u~'J с р.
л. тt·1 1 срь обfх1·1 1 11'кя к <."1 ·а· 1 ~к·1· 1tю..: н:j 1,1ка 1Lа
пр1 IMt:p, ПОЧ<.:'-'IУ J/11'1 сры l' б} KHIJJ1 о н:ш:шпша
ЮТОI R IJJ/Пl)'l! l,ll X \\:tllllll!l{aX 6ыс 1 ' р<.:с ; \p}TllX-'
п ро•r ит.:~ть текст 11 без ключ,1. (.олр ,1 11С'11ие промс>жу т
коt:J М(.;!ЖдУ СЛО l.!dМИ 11 iHdKOU Пpl'ПИ lfcll l ИЯ ill<lЧИl(>Лb
HO ofiлerч<teт дело . -rdКШ' чтенне { 1t>~ ~,.л1очd н на шв,1-
етrя лС'11 1 11фрооа1 t11C"1 .
1ада•1 .:~ услuж11яется 1 с·сл~1 1:1 1 к•р1ю11,1чалыюм гск
< тс 13 nром~·жутки Мt'А<ЛУ (ЛOIHI MH ('ГdtHIГb ве{Лf'
дополни тельную Ьукву, 11аnримеr L. ЛалеЕ' весь рус
скии ,1лфа[IИТ и латИtККJЯ бу1<вJ z ЗJмеttЯЮТСЯ 11 со
ОТВ(.;!ТСТВИИ ( каким-нибуль ключом: llclП fJИMt'iJ, l:!Mt'C -
1о /\ павяr z. вместо Z Ж и т д. И получаРтrя
сплошное, чш11фроо.:~ н11t.1 и Т('КСТ б<.'3 промежутков
между слоu.:~ми. Его также мож1ю 1ыскμыть бс..s клю•1а.
для ~того п-1 ,1ч алс1 оп редем1кн , KdKdЯ буквd ·-1а ш11ф
rов<~нного текста озн ачает nромежупж МРЖЛУ rле>
в;~ми. Буква, Зi1"1CJ 1 яюш.:~я промежуток, дО!\ЖНJ остре
чаться 11ам1 юга чаше друп1х букв Когда 11рuме11\у1ки
1\о1~жлу словами уст;:~новлены, -1алс1 ча уnрп ш аетrя.
НижР приводится ч;:1стот<1 Rстре•t,\Е'\ЛОсти буко в
русском я1ык(;' (%):
А-6.2
1\- 3,5
U- 0.<1
Б -1,4
М-2 ,б
Ч-0,4
В- ~,В
Н-1,1
Ш-0,6
Г-1 ,J
()- 9,0
ш О,!
Л-2.5
п- 2.3
Ы-1,6
Е,Е-7,2
Р-4,0
Ь, Ь-1,4
Ж-0,7
C -4,'l
э О,1
3 1,6
Т-'l,J
1О - (),(,
И -6,2
У-2,1
я 1,8
Й-1,0
Ф-0 ,2
Пробел - 17,5
К-2,Н
х о,t)
Летерми н изм и случайность
526
Отвt:т прост: буква U встрt:ч:1с..:тсs1 н любом
Hl' и111шком коротком ру(.'ском тексте чаще всех
1 1роч11х бую~. Интсрt:с к чктотt' ра~111 1 чных букt1
в языке сrтсем 1 1 е случас1r. 13 тнrю1 р<1ф11ях nрп
руч1юм наборе текста всегда 11мелн опрстtелё 11-
11ы1·1 запас ра:~лтrчных литер Их колпчестnо с11а
чалj уста11::шшшзл 1 1 nссъма пр11 6J111знтелыrо.
Вьщспяли папболее чкто встрсч~пощпеся бук
вы - J-\ рус.:ско.ч языке это 1·,1аснh1С А. Е. И, О и
соглас.:н ые В, К, Л, Н. С. Р. Т. Длн рс1~к11х букu Э,
10. Щ. Ц, Ч трс6о н:тся м:im.1Ji запас ;штер Ос
т;1111,нп1с буквы 1 юянш1Л1Кh н тс..:кстс со средней
частотой.
Со:~щп ·елt, гс..:1н.:1гафа С~мю;,; 11 , Мор:к: прн
состаnлспю1 своей азбуки чаще nccro) потреб
лне ,,1ые n аш·лийском яэы1~е 6~1шы Е 11 Т обо·
:1пачил макс11мал 1;но кратко - оц1ю1I точко1'111
одн И-'-'1 тирс. Рсд1шс буквы u 11 и:юб р~:тл дли11-
11ым11 сочt'та11иям11: например, Х -
"-"-», ::t .1 -
«-
-
-
9. Uбо:шачсшш д.rш букн Мор:.к: 1юд611 -
рал 1:ш, чтобы телtтраф 1 ~ые сообщс 111 1я бhlЛН
как можно короче.: Говорят, что 1 1:юбрст;~тел 1,
ОЛрtДt:JШЛ IKTpCЧaCMOL-IЪ nукв lJ :1 Tll'Jl11IICKOM
1/#//
,,*"
•s(/
языке очень просто: 3аmёл в б;rижайШ)10 ти
поr·рафию 11 нодсчи •1·<111 число 1111·1·ер н на
борных кассэх. Этот довольно 1рубыr"1 полсчёт
привё11 к не1·очностям и 11е позволил сделать
11ередачу по теле1' рафу м<1ксима11 1,1ю эко-
1юм 1 юй. Например, буква О, ззннмающая в
анrл11йском языке 4-е место по встречаемос
ти (7,94 %), в азбуке Мор;~с IJзображается тремя
тире 1·- -
-» , а бую~а l'vl (16-е .место; 2,25 %) -
дВ)'J\!!Я тире «-
-
».
Более точная статистика ж:тречаемост1 r
букн 1ютребОRаJ1ась в lill'tфpoвaю,нuм /(CJIC. Её
nриходшюсь уч 1пыщ1ть, чтобы r::~скрыть про
СТСЙIПНЙ нтнфр , известный сщё со нремён
Юлня Цt::::~аря, - шифр з;.~мены . В н(;м по неко
торому :1;шону (ключу 1_uнфра) вмеСТ() одннх
б}1<в исnот-.зоnалисr. тr.ругне Например, Fl."1eC-
Сl\учайные события
тобуквыЛ- Я.вместобуквыI> - 10ит.тr..
Так11м шифром по11ьзов~шисJ, на проптжешш
м 1 ю1 · их 1кков, пuка н~: догад;uшс1" что шпфр
замены легко раскрыть бс::{ ю1юча. Лс1 ·ко 11ото
му, УТ() на116ШН::'е часто HCТ[X:' Ч:JIPЩllCCH fi}'Kl!bl
н ~ашифронанним тс::кстt: <:<ю·1·нt"1·ствуют 11~111-
более часто yлcYl'pefiJ1я10щ1 rмс>1 букн:1м в нзы к<:: .
Установив такое соответС"t ю1е. дdJtc:c 11с1 юл1,зу
ют частые сочеташш из ;щух 111111 трёх бу1ш.
н:шртrмер с..;т, ПРО 1r 1 ·.
n. Для окот 1 чзтелыюй
/\ешифровки обращаютсн к та1< 11а:iыnаемой
читас ..,.юстп текста, т. с. нсдостающнс буквы
впсст:1н;,ш1111вают , nuкa не пш:rучастсн uсмыслсп
ныn текеr'. Э·ют мето,ц р;1скμыпш шйt.рра 11ро
стой замены хорошо 01111с1ш 1 н сно11х racc:кa
:'Jax :::Эю'ар По ( <·Зшюто1~1 жук") 1-1 Ар·1ур Кон:111
Дойл (<·Пш1шущ1rс- чсжтечки» ).
Фундамент математики
МНОЖЕСТВА И ОПЕРАUИИ
МНОЖЕСТВО И ЕГО ЭЛЕМЕНТЫ
-
Ссрёжа, поо.·ютри . какая кош1екцш1 пти ц за
окном! - малыш тсрсб11л за рукав с1юе 1 ·0 брат;~
школьника.
-
l k колл екция, а стая. Бывает коллсю ~ин
рисунков, коллскцня 11рагпцснных кам1 1ей .
А 11тиц ы л ета ют стаями, рыбы пл авают r<0ся
ка.'Vlи ."
А почему по-раз~ 10.,1 у т1азыв<~ют? Вещ,
ОДТю нТО же...
j'vf~1лыru прав. ДсйсТ13ителыю, в этпх поня
т иях заюночсн о нечто общее. В матсматнкс н
подобных случаях чащ<.: nccro используют у11н
всрс альное слово м1юJ1с(!с11ию, а тс rip e;tмc- 1 ы,
ко1о рые СО/\срж атся в ра ссматривае м ом мно
жесr·ве, 11;.~ зы ваю·1 его ЭJtf!Atщtmaлt11 . Если а -
эщ:ме11т множества ['vl, то пншуr а Е Лf; сели же
Ь нс ннлястся элеме 1 ~ том множества Jf, то пи
шут h е .Н. Пуст1" 11априм ер, Р - мпожсство
всех арабских цнфр. Тота 2 е F. О е f', 12 o:z; Р,
-
'1~F.
530
Когда в м:пе.матикс говорят 1.,чножсство», то
лод разумснают, что есть Dозмож1юсть выш.:
н11ть, пришщл ежнт любой из данных ~1ре11м е-
тов рассуш·1·р1rнасмому м1-южсству 1и1н нет Jlo
1оворя «Cel'h RОЗМОЖI IOC'I ь BЫЯCHllT I>", Mhl со
всем J 1е имеем Ji виду, что это С;\сю1ть проею.
На[Jрнмср, обттачнм через М множсст~щ, t:о
стоящсе нз цнфр l , 2, :1. ЧерсJ а обо:111:~.чю1
цифр у, находящуюся на стотысячном месте
после з:ш ятой .в десяп1ч 1 юй запис11 ч11сла
л: .:::; 3,141 '59". llр111щншrалыrо ( 11 апример, с
nомощыо 1юмпыотсра) можно 0 11ределпть.
верна ли запись а е Al. 1Jo но-r · так· сразу ска
зать, юшос и:1 соот1-ю11н.:1-111й а е М, а е: М нмеет
место, нСJ1ьз н
Ино~ ·;~ :J кажется, что дан1-юе м1 южс:: стtю ЮСJ
но и четко 01 1рсдслсно, хотя r 1 а са М()М /\СЛс это
не T::IK H~lllp! IMCp, ГЮПЫТ'JСМСЯ О llрСДСШГГI> МНО
ЖССТНО JI слсдующ1 IM обр::~ зом: оно COCl'Oll 1 1iЗ
ncex 11 а·1 уралыrых чисел, 1<аждо е 11з t<оторых
удзётся о прсдел11ть 11 р1 1 п омощп пе более
двадцат11 CJ10B русского языка Множество ко·
неч110 (поскольку имеетсн ;~ишт. копсч1юt
число слов русского язы~<а). JJ.onycт 11м. что 111,
111, . . • n1: - все :.·темент ы м 1 1о жес11ЗаА. Вu:.Jьмём
числот=IJ1+11;:+ +п",·1 е.тестьсумма
всех натуральных ~1иceJJ , которые можно
определить с помощ1.ю не более двадцати
русских слов. То 1 ·д:.1m;\олж 1 ю11r 1 1r 1 а;\лсжат1,
м1 южсству fl. 1юскольку оно ош1са1.-ю фразой
(ныдt:лсна жr 1 rни1м 111 р11фтом), содержащеi1
нс болсс.: /\Н:.lд1\:JTI1 руссю 1х 01011 . Зш1 ч ит, т сов-
11~щ~1::т с u,r\1ш.м 11з чисел н 1 , 11 2, "., нk. Но t1ед1,
111=111+п2+." +nf.!,т.е.бол1.шt'каждогоиз
спкел п1 , 111, . ". nl>. Отсю[l;а следуе·1·, что м1 юже
ство А 11е определено коррею1ю.
Сраnнительно просты Л,О1юц1-1ые Jl/HO.>fC<!cm -
вa. Смысл Тt'рмнпа }KCII: это мгюжсстт~а. состо
ящпе из консч1 ю 1 ·0 ч1~сла элеме н тов. О;1нако 11
\.ШT<.:M:t'l ' l IKt' р:1сСматр 1 Ш;.tЮТбl 11 fiССКО I Н.:чные
.\.1нuжсстна. т с. такне, 1-1 которых бсскон1::чно
\11 шго эле~1ентов. nсскот.:чны :vн rожеспщ всех
1.-1aтyp:iлrJнr, 1 x чн<.:е1 1 ..V1rюжес1 · rю 11сех р;:~цио -
11:1лы1ых ч нсе1 1 . -..птожество всех леlктш1тель-
11"'х чнсеJ 1 , :v1 11ожестщ1 ксех ;\111 югочле 1 юв, м1ю
жсп·1ю всех окружrюсrс1't 11а плоскосrи н др.
Ест~ множеспю 1\011е:чтю 11 nprtтoм содеr
ж~1т нсбольшщ~ ч11сло элсмснто:н, то с 1 ·0 удоб
но 01 1 редl"ЛИТh, nе:рсч 1 1сю111 всt: элсме11ты. Дня
:JTOJ 'O ~I C!IOJJl>ЗYIOT ф1 11ур11ые скобки. :1a/\~ЩJ J .~I
таю1м спосо6ом рассмотренное кы ш с лнюжс
ст1ю F:
F={О,1,2.:), ..\,">,(),7,Я.9}.
М1южесrnо МРЖСТ С()С'IОЯ'П> 1( IIЭ ОДJ юrо ;")J1е
мсн 1·а, т<:ш, нзпр11мер, м1южсст1ю {О} Мпоже
стnо {О} IТельзя пут::~ть с el'O элемс11том О 11 с
11uюжсслю.'lll j(O}I. т. е. м11ожестuо ."1. ед1111стuеI1 -
1n,1 м элсме1Пl)~·1 которо1·0 яnляется м1южt.ттно,
ЭЛСМС!J'J'ОМ KO'l'OfIOI'() является О.
0 Е {()!, {(}! Е {{О}}. 11() {Of >!' {Of 11()17.: {{01}.
и HOl '}\a J IJ1 11.\0/lf IТСЯ paCC\ll:Y1p1н~aTh l~l 'Cll IOI!
Аrно.ж ·еипво. т. L. 'l';tKOt:. н 1\ОТОрШУI Ht:'I .1 I И О/\НО
го эле.мt:нта Ero обо3начзют с11мко1ю11 1 е>
Rоз 1 .мём м1южее1·1ю Т нсr:х прн 111оуrот,н1>1х ·1ре
~то11ы1шю11 , у которых 1\JI ШIЫ строт1 - цст.1 е
числа, ::i псрнметр nыражается простым <шс.'10~1.
Ср;:цу понял, труl(по, что собой 11рt::.J.СТ~1ВJшет
мпожсстnо Т, по если 11ем11оrо порассуж.гщть,
.чож1ю убсд1 1ты.:я. что .vпюжсство Тнс сuдtрж11т
1111 одн<)l'О ~-)лt.:мt.:пта, т. с Т= 0 Заметн.~v1 , что
м 1 южсс1·во 0 со;~ерж 1 rт О э11емс.;нто11, а 'Vl 11 ожс
t·пю {0} - один элt::мснт. а име111ю
0Е{0}.
Бывае·1 гак. ч· 1·0 сщ1 ю м ~тожество 11хсщн·1· в
другое .множество: наттр 1 1мер, м1южсС11Ю {1, 2,
:)f - '-l:кv1ъ м1 южсств:1 F. Nlатсмат111ш, говоря о
м1южсстuJх, nместо слоuа <- 1 1асп," \'Потребля
ют термш1~собствешюt.:1ю,r~.м1южссn10» .
Нооб щс. м1 южсствu А называют 11од.;111ю"JКС!
ствш1 .rvнюжt::с1·ва В. с<.:11н ю1Ж,1\ы)1 ::JJll: ,'vfCHT мно
жества .А 0/\ HO:Кpl'\tl'Ш ю ;:)Лl'Ml'H 1' ,\11 ЮЖССJЩl в
Это 11ыр~1 ж:~ют за1 11 1сыо А с Н С:1мо м1-южt:с 1 ·но
IJ также ЯHJ I J-!l.:1'CЯ свuнм J I0/(~11-IOЖt.:l'l'H( !!\1: в с в
Вснкоt: Жl' 11ry1·oe ЛОДМJ-ЮЖС'СТНО А MI I OЖCC'l' l !:t в
('1. е. такое, что в 8 1 1l!1Щётся хотя бы <щ111 1 зле
мспт, 11 с при11адлежащн!1 А) 11мt::11уетсн cn6-
cmAeи/iЫM noдNfЮ.JJCl:!ClntШм м.1южества R. Итак,
есл 11А есть ПО[(МI южество м 1южt:ст11<1 В. то ш160
А r1/J совпадают, либо А - собстве 1111 ое полм1ю
жtст1ю (т. с. часть) /3, Dот 11есколько пр11мсров:
ЛсF,(1,1, .)1с:Р,1юРCJ..~1,2,:Н.
С ч ит;:~ется. что гrустое множество янлнстс.11 mщ
множс:.:ством 11ю60.1 ·0 множестн:з .11: 0 с М.
Пред~ юлож t1 м '1·с11ер 1) , что м1-южс:.:t~1· на А 11 13
сос-1·nнт 11;з ра3;1нч11ых "1J 1 емс11топ. Можно 1111 н.х
срав111 пъ;.~ Р:зссмотр 11 м такОJ:1 прнмср.
Фунламент ма1ема1 ики
Учсrшю1 одного ю1 асса гrрнсхали копать
огород. Как у~н;лъ, f\ОСr:1точrю 1ш ) них ло
пат? Конечно, мuжно nt'ресчита·1ъ ученнков и
u'1 'J(<:J 1ын > 11ересч итать 1101 tаты. l lo можно 110-
t:ту1 1 ить 11 н:-1 чс: пусть учени КJ·J по оче::рс:д11 под
ходят к ящнку 11 1~аждый nсрё1· Of( lt)' ;1сн1ат)
Еслн ок<1же'го1, что каж;1,01\1у μост::июсь 1ю 1ю
пате 1111р1пом вссJю п :пы разобратrы,тонбе:1
11ересчёта ясно: }'Чеm11щн и лопат оказа1rосr,
одинаковое 1<оличсство. Мы устаrrовнли юа
t1J111ю oдNoз11aL/l(Oe соответствие между r.ню
жестnом учсш·1ков и множестnом лопат, т. е.
каждому элеме::н·1у nepnoro множе::ст.ва (уче н и
ку) постани1 1 "r R соответст1шс 01t1 1н ~л<:мс:rrт
в·1·оро 1 ·0 м н ожества (ту ;юr~ату, которую он
в~1ял; р1 r<.:. 1). Есл 11 ()ы on1 rаружнлся нскотпры й
11збh1'1·ок нт1 r1едост:.:пuк лопат, тu нэа11м1ю од-
1ю;~ начно1·0 сrютнстстння не 1юлучшюс1~' f1 1,1
(r11c. 2, 3). Устэ 1 юю1снис ю:-1нм1юQд1ю:~rrа чно
rо соо· 1 ·11етстn11я между ~J1еме11тэм1r l\ВУХ м1ю
жест~1 означает, что н э· 1 ·их мпожестnах «оди -
11 аксщо мrю1 ·0" элементов.
Часть мeнI.>ure целого, шасит 011ин иэ 11рн11 -
1 \пгrов, сформулиро.ванньLх nсликим дрс1н~е-
1·речесюн"·1 мыслнтеле.м Лристотеле::м, созда
телем ло1·ики. Иначе гоuор>1 , есл и уюн~тся
)'CT:lliUBll'JЪ B:J:111M110 ОДJ-IОЗН<JЧНОС COOTBCT-
CTHllC l\·tC)tЩ)' всемв элсмснтамн м1южсстваА 11
БЕСКОНЕЧНЫЕ МНОЖЕСТВА
1.) одном тсатрt' с бесконсчrrым множеством
мест вес они бьиш перенумерованы натураль
ными чtн.:JJамн . .место Nv 1, мсстu Nи 2, ".место
N<111, ".На прсмы~rу все билеты р~1скуш1лr1 , 11 н
театр 11 plНIJJI() бcCKOllt'ЧI 1() м HOl' O 3р1 ITeJLt'JI:
гrсрвый (т. t:. uбла,r1ате11ь бнпста fra местn N° L) .
нторой, "" п-!1, .. Шёл дож;\1'>, 11 нее :~ р11тел11 яв1-1-
111к1. с эо1 1·1·11ками , котор1.1е и 1юn еси.rш в Г<lр
неробе (R порядке самообслуживашш) ш1 сn-
0· 1встств)''1Ощне крючю 1: перuый - 1ra I<рючок
N• 1. ;пopor'i
-
11:.t крючок N° 2 н т. д. llocлe
спектакля псрвыл з ритель впопыхах юнл зоп
пн< с 1<рючка No 2. второr1
-
с крючка No" 3, ".,
п - й зрнтсль нзнл ЗOllTИI< с крНJЧЮI Nv 11 -1 1, ."
(р ~к:. l). В резуJ 1ьта'JI.:' нес з pJJ'l'e.JШ ушлн с :ю11-
тик~м11 , lIO (к у1~пв.11с 1 11110 ;щ,v111нr1стра1 ~11и ::>'rп1·0
5:32
А
в
А
в
А
в
t-J t-i i-~
t-1t-J t J
tlt"-??-t
Всем
JIO JrOl.La'I'C" .
l'н с. 1.
А моя
допа'l'а 11.1.с?
/'нс. 2.
Это чмr
лоuа1-а?
•1астыо элсмснтон множества В. то в .tl мс:11ь
шс эл<:мсtпон , чем n В. Од нако нрr11-щ11n
Лристот<.:ля хuропт только ·1·u r ·щ1, когда
рассматрив:нотся 1ю11счныс \1НОЖt'С1 ва.15t:скu
нсчныс J\!IIOЖCCTHa в ::~тuм OT IIOШClilll l ведут
се::бя 1-1спр1 IRЫЧНП.
бесконечно 6011ы 1 юго теа·~ра) на 1<рюч1<е N° 1
OC'l ':tJICjJ •IO ILlllJllJr· • ЗO H T l l K
Так11м обра:-юм. с.:с111 1 .\1Ы обозначг1~1 зр11 1·е-
11сй с11мнuлам1r и1 , 11~. "., ~i :~онп1ю1 - с11щюл:~-
s,S2S;s~s,
~~~~~
///!~/
/'
л
j
J
и,и~ll1и,Us
Рнс. 1.
М~юж<>ств;~ и о прраL1и и
SJ
S•
'i
•
\-
vf1fi... fji~ ~··
,'9
///../'/
F
---
_
о
_
_
S1
s, ~~
S1
Ss
S1
\~S, s1 S<; S,
(~
f"v"vq i ... :
1
~~·vvt;.n il
j\~~~".,. ,_.,'---._
/ ~~/----\\\ 1
~~~ ~ ~1··· i /ft~~f.··· ~ .
-
--
Фу~1дамент математики
м11 s 1, s! , ""то с 11ту:щию мoЖirtJ оп11сать слсду
ющ11 ."1 обр<1зом. Кажлы1·1 зрнтель 11р 1 1111ёл cu
своим ЗOll'ПJKOM, 'Т. С. IIML:ЛOCI> вз:111мно од11u
з11ачное соответспнrе мсжду м1юж~ством
f! = {и1, и2, ".} всех зрнтелеif п мrюжеспюм
S = {s 1• s~ . . .. j всех :юнтптюв. Однако после спек
такля установилось /Ч)уrое соответспте, 1 1р11
котором nзаимно одно:1пачно соотnетствоnа
т--1другдругум110жсстnоU = {и1,ul, ... }всех зрн
тслс:й и подмножество {s2, s5, ."1 множества всех
зонтиков. Выхол.нт, что час1ъ {s2 , s\, ."} .м110-
жее1 ·ва S всех зонтиков содержит ~столько же·~
элементов, сколько и всё множестно S.
Из рассмотрснН(.>1 ·0 примера следует, что
принцпп «Час1ъ меньше целоt'О» 1 1 еправомерен
дли бесконечных м1 южесгв. Вообще, r1 любом
бесконеч 1-юм множестве М можно выбр;пъ та
кое его собственное подмножест.1ю 1И 1 , что су
щестоует взаимно однозш1чное соответствие
между iltl и М 1, т. е. между множсстrю.м и его
частью . Это - характерное отлнчнс беско
нечных МllOЖtC1' 1{ от K()IICЧПLIX.
Чтобы лучше прсжтаRнть себе спсциф11ку
беско 1 1еч1-11>rх множеств, оп11шем события, ко
торые пронсходили в уже уnомш-1 ав ш емся бtс
кон.счно Ol'[IOMHOM театре во вреt.1Я дPYl' lL-..;
слектаклей.
Как-то <.:нова была дожл,лнвая ло 1 ·ода , и все
зрители пришли в театр с зонтиками. Пока
после спекта1<ля первый зритель беседовал с
режиссёром , осталы 1ые ynmи. Второй зрителт,
взял зонтик Nv 1, третий зритель nзял зонтик
No 2 и т. д. (рис. 2). В рсзул~.татс пе рвый зри
тель остался без :юнтика!
В один нз дней (т-dкже 1щждливый) первый
зритель после спсктаюrя взял зонтик N!2 2, втu
ройВЗЯЛЗОНТИКNo4, .. , n-Й ВЗЯЛ ЗОНТИК No2IZ, ."
(рис. 3). В нтоl'е все уmлн с зонтикамl t, но в
гардеробе осталос1) бесконечно много зонn,1-
ков (но только зонтиков с нечётнъ1ми 1юмер::~-
Рис. 2.
534
мн) . На следующий ;~ень нее пр1ш 1J111 без 3011 ·
т11кьн по слуlJаю солнечной 1 1ш·оды. Но rюк.~
шёл спскт::~кль, rюпща нс1юртнлась н хлынул
11.ожщ,. Од11акu алм1,111нс-1ра1 ~ия уС"rюкоr111а зри
телей, сказан , что n гарL1еробе r1мсется беско
нечно м 1ю 1 '0 11е востреnон:~ 1111 r.1x вчера зонти
ков. Значит, натуральный рял как бы содержн·r·
вдвое больше элементов, чем в 1 1ём. имеется".
СЧЁТНЫЕ МНОЖЕСТВА
Введt:м некоторые 011ределения , сня3~11-1нь1с с
бесконеч11ыми м1-южестнамн. Дна М.llОЖсствз
11азываются эквивален.тным11, есл11 между
пимr 1 можно уста~ ю1нлъ нз;шмно однозначное
соотоетстпие. Однако это вовсе не пз11ачает.
чтп любая попытка со1юсташ1ть :::~лементам
первого множества элеме 1 1ты второго м1ю
жесгиа позволит уста~ ювить между МJ южествз
ми вза11м110 однозначное соответстоие, в чём
:-1ы н убедилисr., 1-ш примере с зоптнками. llo
ест~ удастся хотя бы одю 1 м способом устаJ10-
ви1ъ взаимно однозначное соотвстстние мсж
i~У элементам.и множеств А. и В , то эт1 -~ мно
жества эквивалентны.
Каждое множество , эк1н-1валентное нату
ра; 1 ыюмуряду N = {1 , 2, ". }, назыв;~стся счi!птш1.
Иначе го1юря, множество М счётно. когда его
можпо запт-1 с;1'1Ъ в .виде
М= Jm1, m2, m1, ...},
(можно 11.еренумероnать все элементы r-.-шо
жестн::t М натуральными 'IИслами). Ию1 LI(aжe~
по-дру 1 ·ому: множество М счётнu. ссл~1 оно со
держит бtсконе,ню л-п юго эJ1еJ1.1ентон и 11р11том
11х нсе можно расположитn в в 1 ще посл едона
теm,ности, пере~ 1ум~ронанной н;1туралы-1ыми
чисJ1ами : первый элемент, второй, · 1·ре1·ий."
С одной стороны, 1н11<акое конечпое м 1 то
жество не является счётпым. С другой - лю
бое бесконечное под.множество счётного мно
жеспза само счётно. В 't.:rастrюсти, 1<акос бы мы
mr nзяли бсско11еч 11ос подмножt'с1·1ю нату
ральных ч.иссл, оно буде~· эквивалентно мно
жс:сгву всех натуршrьных чисел. 1-lo 11 ::1тu с::щё
не всё.
Множество всех целых ч11сел (содержащее
натурзльныс числа, нут. 11 о·t•ри ц ателы 1 ые
целые числа) яшmетс}! счёпu,rм, поскольку его
элеме1 1'1'ы мож 1 ю rтрелста nитъ 11ослс11оnатель-
1тостыо:
О, 1, -1, 2, -2,:), -3, ...
Несколько неожид:нп-ю на первый ю1·шщ
)'Гвержденис, что счётно м1-1ш1:<<::стнu нссх 1~ело
ч11сле н н ы х точек коuрf1,1111атJюй плоскости
(точеl<. у которых обе координаты - целые
чнсла). Но на рис. 4 rток:~з:шо, как р:1сттшюж 1лъ
элементы дa1-11-1uro м 1 южеств:э li виде rюследо
вательпост, д tтr·ансь вдоль спиралевидной
ломаной ли rrии.
Множество всех рациональных чисел
(чисел вида p;q, где р н q - целые числа,
прнчём q > 0) также счtтно, хотя это и 1<;,1жется
невероятным: если целые числа разме щаются
на qисловой прямой дискретно, то р:.1 1 (ионал ь
ные числа - п лотно, 11 н~1 шоnом отрезке, как
бы мал он ни был, имеются рацион~vтьные точ
ки. Расположим р:н.~ион;~m,ные ч нст1 в виде
последо.Rателы·юсти сле.п:ующи м обра:ю м. Ci 1а
'lала :~аоишем чиоrа с суммой мо[(улей ч исли
теля и зна,\1енателя, равной 1, т. е. единствен
ное число 0/1 =О . Затем возъмём числа, у
которых та же сумма равна 2: 0/2, 1/1, -1/1;
первое из ню" пуль, и оно уже было, :l следую
щие - 1 1,1 - 1 . Потом следуют ч11сл<.t с сум."1ой
модулей числителя и зн<~ мснателя, 1х1ш юй }
2/I , - 2/1, 1/ 2, - L/2 (неучитьшая ранее юятого
:г~:
-----LrPl--1--~--
.
!.":".....
.
....._ _... ..,.__
'
~_......._.
.
.
"
Рис. 4,
Множества и операuии
О/~ = 0) и т. д. Ясно, что любое рац1юнаJ1ы-юе
число p/q ра 1 ю нлн по:щтю пстrетится н такт:r
ттоследова'Т'елънос-rи.
Вот сщё примеры. Множество всех много
членов с рациональными коэффициентам11
счётно. Множество ncex рацнональных точек
на плоскости (точс1<, у которых обе 1юорди
наты рзцион;.~льны) счёп-ю. Tu же СЩ)~LВсд..rш -
1ю лля точек н прuстра н стне. Счёт1-ю и мнuжс
стuп всех алгебр:111ческих ч11ссл, - 1 111ссл.
ю1ж11,ое нз которых янтrется кор 1 rем некоторо
го м1ЮГ()Чле 1 1а с целыми коэффицие 1 1там11 .
НЕСЧЁТНЫЕ МНОЖЕСТВА
Всякое ли бесконечное множес.:т.1ю счётно? От
рн цателы-iый uтвет на этот конрос был дан
Георгом Кантором, сu:щат<::лс:м т<::ор1-111 бсс
конеч I1 ых .множестн Согласно теореме Кан
тора, м11ожество R всех дсйС'rвите11ьных чисел
песчётно. Вот е п > пес1,мз ;элеrа11·п юе до1<аэ<1 -
тельстно, известтюе как J<апторовскrrй л11аrо
налъr1ый nрсщесс.
(;11 ачала рассмотрим не вес дсйстнитслыrыс
числа, а лишь те, которые расположены .v~ежду
О и 1. Докажем, что данное множество весчёт-
1 ю. Дока~ательство будем вести от противно
го. Предnолож~1м, что он:о счетно, и перенуме
руем все входящие н нет числа:
а,. а2, ••.,а,,, ...
(*)
Каждое действительное ч и ело можно запи
сать u виле беско11ечтюй лесятичноil дроби.
Если десятичная дробь конечна - значит, с
некотuрого места nce цифры десятичной за
ниси равны нулю: например, 0,4 = 0,40UOO ...
Зашшr ем ч11сла (*) в виде дссятичнъL"\: дробсх"1;
пусть, .например ,
at = О,:!83751 .. "
а2 = U,41951.2 .. . ,
а~= O,Oi.8.179... .
а.,= U,576209...
В нри.ведёш-юй за 1 111с11 подчёркнуты щ1фры.
стонщие no диагонали. Сосrавнм теперь бес
конс:::ч ную десятичную дробь Ь. руководст.13уясь
следующим пр:сшиJJО М : с:сди у числа а" H<t д1 ш1 ·u
нзm,ном ('r. е. 12-м) месте после эаnятой сто 1л·
цифра 7. то у числа !? на п-м месте напишем
'>35
Фундамент матем атики
« ПАРАЛОКС»
РАВНЫХ ОТРЕЗКОВ
Возьмем два отрезка АВ ~' СО,
не равные межлу собои, ~' pa rno·
ложим их nарамельно друг дру гу.
Прямые АС и 80 пересекаются в
некоторой точке О . Теперь лля лю·
бо й точки Х отрезка АВ провелём
nрямую ОХ, которая пе ресечет
второй отрезо к в 11екоторой точке
У. Точку У мы и поставим в rо(.)т
ветствие точке Х ~1а А8- Тем самым
уста11овлено взаимно однозна чн ое
соответствие между отре,камиА/З
и СО, т. е. данные отрезки содер·
жат оди11аковое количество точек.
Значит, они имеют оди11аковую
длину.
Разрешить этот 1< Парцлокс J>
несложно . Лействительно, оба от
резка содЕ:'ржат «оы1нdковое ко
личество точек», следовательно,
011и имеют оди11аковую мошность.
Ол11ако мо ш1 юсть и лли11а - это
поня11н1 разные, и и3 спвnадения
мошностей м н ожеств не вып?
кает равенство длин.
А ,,_______Х-+- _
__..., В
цифrу 3; вп нсс::х скталы tl>L'< случа я х у ч1 tcл:t Ь
11а n-м месте будет стоят1-. цифра 7. Так, u
nриведёшюй nыtue заnисн тш1ы<О у '-П rсла а~
[1.Шtrо1-1~шьная (nодчёркнутая) r\нф ра 7. а у
чисел а 1 • а ,, a..i диагональные цифры отличны
от 7. Поэтому в ч11слс:: Ь вторая 1\11фра 5. а ос
та11ы-1ы<: 1 \ифры (~1 з 11<.: р!\ы х '-lCТЬ!f)tX) 7:
h = 0,7.)77...
Итак, 1-1~1 11ер1~ом месте у числа h стu11т
цифrа . ()'f'JIИЧHaH ()Т nt:p!IOЙ цифр ы ЧI JCJl;J а , ;
на втпром ме<.тt: у чнс1 1 ::1 IJ стонт 1tифр а, О'l'
л и чная от втпрпi1 цнфры числа а2, и т. fl.. Вооб
ще, н а 11-м месте у числа Ь стонт цнфра, от
личная от п-й цнфры числа а11• И получается,
что ч щ:ло Ь не со!3падает с а 1- nepnыe цифры
у ннх различны Ч11с1ю h ш: соттадает и с а~ -
вторьн.: rtифры у 1 1их р:tзлнчны . Оно нс сов па
/\<I СТ НИ С ОДННМ Чl!СЛОМ а11, П ОСКОЛЬКУ I J:J 11-М
месте у чисJ1з an rt у "Числа 1-J стоят раз1шч11ые
цнфrы. Так11м оара:щм , чи сла h нет среди
'm сел (*). О; 1нако :::JTO прптнноречнт утнсрждс-
1 11-tЮ, что сред и чнссл (*) 11ме1с)ТСЯ все [(еik·1 ·ни
тель11ые числа, заю11очёш11,1 е '1е11.щу () н l.
Мы оиди.J'.11, чтп предположет 11 1е о счёт1юст 1 1
множества пршюдит к проти1юрсчшо. Следо
nатспыю, наш е предположс11и.е 1юж110 : мтюже
стnо А несчётrю. А т ююму множество f{ nccx
ДC(I CJ 'BI п е11 hНЫХ ч 1н.:сл l'CM болсt' 11<.:счётно.
Нt:тюсрс[(<.."Т'нснно из тс:uрсмы 1·eopr·:.i Кuн
торз cnt:J~C'г су 11( есттюва нн с тра11сцсн1~сн·111ых
чисел. - чнссл. не >1шtяющихс>1 а; r 1 ·с:браи чt.:
С 1(НМИ. R самом дсле, если б ы 1кt' ,r1.сйст1тп::л1,-
11ы е числа Gътлн :т гебр аичес1<им11, то м11оже
стrю ncex де йст11ителы 1ых чисел было 6 1,1
с~1 ётны м , что не верно.
536
МОШНОСТЬ МНОЖЕСТВА
()6 ЗКНИ В:!ЛС llТll ЫХ M Jl ()ЖCCTHax 1 '()1Юрят, ЧТ()
01 rи обла~ают однrr а 1ю rюi1 .л1тц1 юоnыо Такпм
образом, мощность m1ля стся обоб щеr те:v~ по
нятия «ч.исл<> элементов ·>. име ю ще го смысл
J 111 шь для конечных мтюжс<.:Т13.1"tощпость счёт
ноI 'О множ<::ства <>бо:тачаетоr через к (I (буква
к. « алеф" - nернш1 в дрсннее13рсйском алфа·
13итс), а мошнпсть множес1·на нссхдсйствнтель·
ных чисел - бук13ш1 с (от лап-z. co11ti11uur11 -
<, r1еnrсрын11ый »). Посколы(}' J\1н ожt'стно всех
l\CЙC'l'lll l 'Гt'Лbl fbl X чнсел Нt:СЧёТI !О, то с > N o
Мощность Kn - 1 1з1·1меш,mая бесконеч 11ая
.мощrюс1ъ. Это означает, что из 11ю6ою бескп
нсч1юго множества можно выбратr, счётнос
подмножество. 13 самом деле , гrусть М - беско·
неч1юс множество. Возьмём 11роизволы1 ый его
элемент , rшторы~:-1 обо:л 1 ;1ч11 м а 1 Поскопьку
м1 южсl'тно l\!J ()есконечно , то кршv1е а , н 11е ~·1
11меются и /\русие ~лсмснты. llyt~1'h t l ! - од11н из
них. Kpn1\tt: а1 и а2 в мтюж:ествс М 11111еюто1 сщё
зле мснты - М беско н ечно; обо:1нач11м через а 1
катшй-ли()п из rr11x и '1'. ;~. В 1<оrще кш-щоа. д-u,1
пострпн м счётr юс множестnо М1 = {а 1, tt!. • а ;, ...}.
входящее ft множество М. :~нач.ит, бсощ11ечное
множество ,\1 со,1'\ер>юrт 11с мс1tь ш е :·теме11тов.
чем счё·1·1 юе множество М 1 .
Любо11 0·1ре:юк. юн< 11 любая лт.1а 11 ан mш1~я.
любан окруж 11о с1 ъ, любL1 >1 /\у1 ·а. 11мест 1у же
мо11\1tос'1ъ, что 11 1 1рн .\1t.1н. т. с. с. Ржтмотрнм n·1
-
резок. EcJ111е 1·011:юrну 1 ъ в 1н1лс по11уокружнос
·1
11с 1tентро.м 11 TOYKL: О {р1 1с. 5), то. 11росктируя
·r·акую л ()Jтуокруж 1н кть1 1з 1~е11тра ()на 11 рямую,
парал1 1 еJ 1 ы 1yro диаметру PQ nолуо1<ружн ости ,
мы устаноы1м взаимно 0;11ю:тачrюе соотвсr-
стnне меж1'"(}'·1·очк;1мr1 пср11011ас1ал1,1ю1·n о·r рсзка
н в\емн точка1vш щ~я.мой. Пrав,11а. конц1.1 от
ре:зка (нли ~юнцы PQ лолуокруж1юста) не nо
стаrщспы в соотАtтстннс 1шкаю1м 1·очкам 11ря
мой. L3 рсзулnтатс отрезок содержит <·ь1 а две
точкн болъш<:>. чем прнман. J l o добавJН::1шс к
бtCKOl-I CЧ 1юму 'vl ножсстну КОНСЧНОJ '() ЧJH.:Jla тu
<{СК не HЗM<::l LЯC'I' Cl"O ,\IJ()Щl fOC'l'JI,
Оnр;пr-1мся ·1 ·c::rrep1} к т1оск11м фигурам. Ка
жется очеттидrrым, что КJ~алrат сrщсржнт 60111.-
ше ·1·очек, чем отрезок (па11ример, сторопl'!
~азаJ1рат3) . Ощ1аr<0 :'>то ненер 11 0. Подоб1ю ·1·0.му
ка1< р::щ11оналъ11ътх точе1< 11а nлоскпстп сrолыю
же, ско11 ько н рационалънмх точек на nрямой
(оба мrюжества счё.'тны). так н ncex точек на
ПЛОСКОСТI 1 CTOJIЫ<O же, CKOJI Ы<О 1( точек на при
мой. Иным 11 словамн , :vющность множ<::ства
Rcex точек п1юскоt~1 ·1 1 (ит1 трёхмсрного, нтr
м но1 ·омерно1 ·о. 1mи щ1жс бсско 1iечно:-1с:р1 ю1·<1
простра11с·1·на) сонпадаст с мощнос-1но м1щ
жес1·Rа nccx то•1ек nрямпl1 .
Приведём канторпвскос J\Оказ:1теm,с·1·в()
то1·0 факта, что в кnадрате «столько же» точек,
сколысо и n его стороне. Рассмотрим па коор
д~шатrюй плосrюстr1 кnадр:п с nершинами (U:
0). (1; О). (1; 1), (О; 1) (рнс. 6). Ю1жд:ш точк:1111
1шадрата 11мест щн.: координаты (х; у) , причём
юобзя нз 1111 х гхрсдставтrет со601т дelrc·1 •1m·1·em, -
1юc: чнсло, 11р 1шщ~лежащеt: отре:шу (О, 11 , т. е.
()~х~ 1и О~у~ J.З11ач11т, •1исл~1 ,'\· иу могут
быть зап11саны в ии,r~,е бссконеч-ных десят114-
11ых лробсй:
х=О,а,а1а~.",у::О,IJ1/J2b1".
(3аме1·1 1 м. •по всегда можно с:чнтать rieлyro
часть раиной Liулю: сели х = 1, то 1 1r~1 вомер110
Множества и оnср3ции
(0; 1)-----~ ( 1, 1)
)'
------·
.11 ',
(О: О)
(1: О)
наnнсап. ,\· = (),9999") <- Псремсm:~см» ; \t:CЯ'J'J rч-
1 1ыс: 1\11фры '-i!1CCJ I хну. Hl1IПl lCЫR<HI 11Х ПО()"J{"
рёд1ю. и рассмотр11м YIJCJIO
z = О, a 1h1a2Ь~а,IJ, ..
KO' l 'UJX>t:: и пuста1шм н COOTBC'J 'CTRlfC НЗЯТ(}JJ точ
КС:' t1J квадрата ( С коорн~rна·1·ам11 х: у). Пuлуча
стся HЗ~Нl.VlllO ОДГЮЗJJ ;lЧIЮС C()O'IНC'l'CTllllC ~IСЖ
ду tксм11 Тt>'-1камн кt;,адрата 11 тuчкамн отре1ка
[О, 1] . Сле7\ОпатеJ1 ы-ю, к11адр:11 11 отrс:юк 11 м<.>ют
(),rl,11) l·I '1)1 же МОЩ I ЮС'IЪ - MQIЦIIOC'1'1> KOll' I \IН)'
ума.
Нс слстrет. одт~аJю , думат1., ЧТО ' -
<·1 Г~IИ
большан » из бесконечных мопuюстеii. Обо6 -
щ~1 я приuсдёшrое nъшrе дсжаз~пелr,стnо тео
ремы Кантора, .\ЮЖНО устаrютrть, что ecmr
М - пrо11~Н()ЛЬНОС беСК<JllСЧ!Юе MIIOЖCCTIЗO, ТО
М НОЖ<.;СТНU f3CCX C l 'O по;.1,множеств нмсст 1VlOЩ
I ЮС'JЪ большую , чем иоrцнос-!'ь множсе 1 ·на 111
Мощ11ос:ть вс<:::<: [Юдм1южест1~ 1\lf обоз1-1ачзсто1
через 2111
, J 'Д< -' т - .'l:IOЩI юсг1) м1 южестн;:~ А./. T:J-
l<HM образом 2/)/ > т. в ч:ктностн. MllOЖt:CTBO
ncex 11одмпожестн ч11сло1юй 11рямо1! нмt:ст
мощ1юс-п, i > с. Эта мощ1юсn, 2с 11а:1ы13:~стся
гшюрк011т111~1:Jщам.
ОПЕРАUИИ НАЛ МНОЖЕСТВАМИ
С} 1 11с::с1ъу~1· очс111. )д<>611ыr:i 11р11ё~1 напш;с1101·0
11.юбр;.1же1r1 1 Jо1 н:Jаt1моопrо 1 11L'11нй чежду м1юже
(т11ами -
·1'ar< назы1i:1сrv11 .1с ()1югра1zмм .71iлира -
В01111а. l la rrиx множt'ства rrp<:;1cтa1шtrr1>1 пло
сю1м11 фюурамн, ч::~ще .всег() J<P}T~J\НJ.
l la рнс. 1, а л.ва множсстnаА в В пзо6ражс11ы
круr;-~м11 , пр 1 1чём nндно, чтu -"ПЮжсстnо 1:З со
дсrжнтся н МНОЖССТRС А, т. с л с: А, (1 /3 - соб
СТ'ВСJ\J-ЮС 110/ \Mt ЮЖСС'1 ' Р.О Ml-IOЖCCTl'>~\A 11 \-\С СО\~
ЛЩ \аСТ С н11м ./J;1н MIIOЖCC'J'R l l 11B, ПOK~l ~i:lt-U I ЫX
на f)lfC. 1 , б. Т:JКЖС с 11ранс;~ш1110 B"11IOЧL' l-I JI(.'
В с А. но прн :-+т()м множ<::с1 на r1 11 R сонп ;щают.
·1·;11<1 rм обр:1 :юм , зш 11 rc1, R с "1 о:'! нач:к··1 . что т16()
В нnл.иетсн собственным rю;~м11ожест11ом 'v!JГО
жсства Л. Л1f6ОА = В. На ри с. 1, n п11е1tст;:шле11ы
;ща множестАа, ни олrю нэ кот о рых нс Яllл~
стся под.'-111ожестnом друl'Ого .
Пус1ъ, щшрнмср, !·· есть множество ncex 11 а
тур:.~льных ЧILCCJI , IIC llj)CP.0<.:XOДЯЩll:X \(), ," 1 -
МНОЖССТRО f\CC'X 11счётных на -1ураЛJ,J rых Чlf C t:Л .
Фундамент математики
Рис. 1.
не 11ре1юсходящн:х 10, ;i Pl - м1юж~:с1·1ю нсех
прос-гых ~.пке:л, r1e 1 1рt:1юсходн1цнх 1(). Иначе
1'01 1()рЯ,
1:={1,2, .1,4.5,6,7,8,9,LO},
F1= {1..~.5,7,9},
FL=(2, :), 5,7}.
Диаграмма Эйлер~~ - Ве:н на на рис. 2 1-1:11·ля!(
но изображает юаимсютношсння мсждуэтим 11
множествами. Каждое нз множеств F 1 и Fl есть
ПОДМНОЖССГIЮ M I IOЖtCTB3 F, Т. с. F1 с F, F2 с F,
причём F 1 и F 2 - С<1fkтнс нн ые nодмножестuа
м1 южестnа F. Чт() же касается NUЮжесп~ F 1 и F2 ,
то ни ()ДIJO из 11ш< не является П()дмнткеством
11pyroro: каждая из фигур, представлшощих
множества Р1 и Р2 , nыхо11ит за пределы другой..
·8
.4F
.6
Рис. 2.
П ЕРЕСЕЧЕНИЕ МНОЖЕСТВ
ПустьА иВ - днамнтксства. Все те элемеrrты,
которые принадлсж:п · к<1к м 11ожеству А, так и
множестн}' В, 13месте Rзятыс, составляют некое
м1 южество, 1 1азы ваемое ne/Jeudчe1-1.ue.м м 110-
жестпАиВ,илиАпВ(рис.3,а).Еслим1rо
жества А и В не имеют общих элеме нтов, т. е.
А n В = 0, то JVшожествз А и В называются нсте
рсс(!кающи.мuся (рис.:), б). Например, для мтю
жсств F 1 11 F!. (рис. 2) спраnедли nо соотноше
шrе F1n F !. * 0 ,дру1·ими словами, пересечение
этих множес1·н 11 е пусто:
F1nP:. = {3,5,7}.
538
ооРис.З.
Из 1 1JКom,нoro курса rсоме1111111 можно пр11-
uест11 м1ю1 ·011римероА пересечения мтюжестR .
В частности, полосу - часть шюскости между
двумя параю1ельными прнмыми - легко пред
ставить как нересечепне дnух полуплоскостсli
(рис. 4, а), а любой параллелограмм - как пе
ресечение двух полос (р11с. 4, б). У1 ·uл мсныне
ра:шёрнуюrо Т;.tК'А<е есть nсрссече1111с /\вух по
луплщ:костсй , а тrсугольннк - пересечен11е
трёх полуплоскостей (р11с. 1! , в'). Вообще любой
выпуклый многоуголы-11 1к я1.11u~ется 11ересече-
1-шем rюлуruюск<1стей .
Рзссмотрпм такую :{а[l,ачу. На плоскост11
[1,атn,1 три Т()ЧКИ А. В и С, не лежащие па одной
пря.мой . Требуется ттостро 1 пь окрулшость, 1 1ро
ходящую через эти три точки.
Чтобы решить зад'1 чу, ра:юбьЕм е:е требuва
ш,н: п а две часrи: 1) нскuман окрУ',кность ;юлж
на 11роход1.1ть ч ерс::з Т()ЧКН А l l В; 2) HCKOM<UJ
окружнщ:ть должна 1 1 роход1пh через тпчки А
11 С Окружность, улош1с:тпоря 1ощан 1<ак усJю
вию 1, так и условию 2, 11 есть ре 1 ненне :lа[(ЗЧ11.
Если окружнос1ъ удою 1 ет 1юряст условию 1.
то её 1 ~ентр О нахrщится от точек А и В 11а оди·
наковом расстошши, равном радиусу. Следоnа
телыю, точка О располагается па ссрсдшшом
перттепдикуляре Р,1, н точскА и В. Dсрно и обрат-
б
Рис. 4.
нuе: ecJll·J точк:~ О 11еж1п на то,v1 жс с1::рею 1нн ом
11ерпс нд1шуляре, '!'() окr~'ЖНОL~Lъ с Цt.:НТ[ЮМ О,
проходящая чt:pt.::s ·ючху А, 11 ройдёт н чсре:з точ-
1<) В. Ин,1чt: го1юря,~.111 ест1, -.н-южес1·1ю 1кехт~е11 -
rрт1 окруж.1-r0стей, }'довлетворяrощих усло
IНIЮ 1. Лнало1нч~ю. середнн11ый перпеIIдикуляр
Р 1 с то,rек А и С ес1ъ множСС1"(Ю всех центров
охружностей, отвеча101цнх услоuшо 2. llo ис
комая окружностъ должна удовлетворять 060-
н.ч услов11ям. Следовательно, её центр должен
принадлежать ю~жд01.1у нз множеств Р. 1 LI н Р.1• ("
т. е. О Е /~~ 11 nР 1• (. ]ак как пересечение двух
нря ~1 ых 1~4. и п Р,, ( состоит ТОЛЫ(() из ОДllОЙ
точки, то эта точ ка 11 IO!JIЯCTOl llcнтpoм uкруж-
1юсти U)ИС. 5). Помсстив в нсrо и1·олку циркулii
11 11ровсдя окруж 1юсп, чере:1 точку А, мы решпм
задачу, поскоJJьку 01<руж1юсть пройдёт также
чере:3 ТОЧЮI в и с
А вот пример из ~1лrебры. Пусть требуется
графическим способои решить си~.:те i'1)' урав
нений
{х~-2...У -у -4 =О,
)\6
х-+у-=L.
Рис. 5"
MHOЖt:'CI ва и Ont'PJUИИ
Л.ру1 · 11ми CJ10B:tм 11 , нужно на1lт11 т:нте nap1,1
ч tн:е1 1 х и у, которые удо1тс·1·1:iоrню·1 оnо11м
уrаннеr r11нl\1.
1kрвое урав11е1 шс ~1()Ж 1 ю 11 ереnис:1·1· 1. в т 1; 1е
)'= (.\'-
1)2- '>.
J\1ножсство ncex. точе1' координатной плоско
стн, удоnлетворяющих данному ураr111с11ию,
представляет собой 1tараболу. вершина кото
рой (т е. н 1 1ж.няя сё Т()чк:~) 11~1сет коорюп1:1ты
( L; -">)."Второе ур:шнснис :Jадаt-т окру.1ююlтn с
це нтром в 11:1чале координат 11 pa[\r1yco"1. р:1в
ны.м 4. Пары чисел х иу, у;10 1щс.:т1юрюощие обо-
11м урав11е11и.ям, - не ч·1 о шiое, как )(Оордт 1ат1,1
точек пересечет 1ня парзболы н окружности
(рис. 6). Т:ших точст< всего четыре. 31 ~ачпт, рас
смзтриваемзя система имеет четырt: реше 1 rия:
1)х::::-1,917'у "'3. ')/();
2)х=О,у = -4;
3) х:::: l, 3 J9, у""-.\ l 59;
<!)х::::~.597,у,., l , 7...J8.
ОБЬЕЛИНЕНИЕ МНОЖЕСТВ
Все элсме1пы м1южестuз А 11 все элеi'1е11ты
множестnа В, вместе в:3ятые. состзвлюот 1ювое
множество, называемое обоедине11ие.м м110-
жссrвА и .Н. Это заnисьmается к;шА uB. Диаг
рамма Эйлера - Венна, прннедё11ная на рис. 7,
пок:.~.зы.васт nзаи.\юотношсния между м1 южс
ства.l\lu1 А и В, J-fX 11ере1:еч.ение н о6ъединенне.
Двойной 1u·1рнхонкой обu:шачс110 перссече
t-lие множеств А и В, а во1 заштрнховэнная
фнтур::~ (хотя бы 01\1J1 11 аrно.Й штрнх()r11шй) -
и.х об1)е,1.щнеr1и е
Ч·тбы гюлуч1 1 т11 обиедн rrc1шe А v В. мож1 10
nзя:1ъ 1ке злеме11ты м1южестш1 J\ 11 до6:,~мt1ъ к
ним те элементы мпожестnа В, которые Т1 А
не нходят. Или наоборот: взять ве<.: элеме1 пы
множесгоа В и добавить 1< ним Tt' эле;vн.:11ты
множестваА, КО'1·uрые в В нс входят. Из сю1з:11-1-
нш·о ясно, что nересечен11с множсстнА н В со-
7'ержится 13 их объедин~:::1-11U1:
AnB c AuB.
Длн любого элемента множества А v В нмt
ется 1·ри nозможности: либо 011 прштаJVIежит
А, по 11е пршrадлежитВ (точ-каХна рис. 7);либо
принадлежит В, во пе 11ринадлежи1 А (точка )')"
либо принадлежит каждому из множеств А и Н.
т. е. принадлежит И1>': псресс..:чсншо (точка Z).
_\
539
Фунламснт матL·мати ки
11
х
Рис. 7.
Р11с 8.
1 lс<.:олн-1е нн о. прСJ\СТанленt н.: об объt1tнrrе
н111 1 днух нсnересекаю щнхся множеста ( r1знр 11-
'1ер , соенн11ен11с 1\1-IYX отдепы1 ы х куче1< nрсд
\1f" 1 ·он 1{ О,Г\НУ nбщvю к~rчу) прсд ш сстuоu:~ло
nо:цтю 1 сн1е1 11 1ю nт 1ятия о сумм е f\HYX чисел .
Если )\Ва 1юнсчпых м11ожесrва А и В щ: псрссе
кают<"я (пе имеют общих элементов), пр н чtм
ПCpllOC 113 llHX СО!\СрЖИТ а :·mt'Mt/ITOll, а llTO-
poe - ь ЭЛСМСI rтов, то MlЮЖССТfЮ А u н ('( щеr
ЖI 1т а f- IJ эдсм<.:нтuв. Поскольку /JJIЯ ~смс ш нна-
1 шя в uдну кучу» бс:чх1злично, в каком гюрндке
беру~ · ~кучки~ А 11В, то
5.1()
АuВ=В1..)А.
МОШНОСТЬ О БЪЕДИН ЕН ИЯ
ДВУХ МНОЖЕСТВ
Мощность м ножества А п ри нято обозгtач ать сим во
лом IA1. Если конечные множеств<~ А и В не имеют
обш~1х элеме нто в, то спраоелли во равенство
IAuBI = IAI + IBI.
Когла пересес1е н иеА f'\ В не пусто, это соотно ш е
ние заменяете » следуюш и м:
IAu/31 =IAI + IBI - IAr"IBI.
и ~1ыми словами, есл и множ:ествп А содержит а
)лсменп1в, м1 южество В содержит Ь элеме1-~тов, а их
11ересечение А f'\ В содерж итμ элементов, то число
элементовм1южестваАu Вравноа +Ь - р. Всамом
деле, пересч итав все элементы м 1 южестваА, а затем
вес эл~>мен 1·ы множества В, полу•~ и м а+ Ь элеме~tтов.
П ри этом кажлыи из р элементов, вхоляших в 11 ~рt>
сеч енщ' А n В, засчи таем дважды, тогла как в мно
жестве А u В кажл~.1 й из r 1их следуеr зисчитыва ть 1\ИШь
один раз .
Если хотя бы олно из множ~ств - А или В - бес.
конеч 1·ю, ro формула булет другая. Пусть мtюже
стоо л бесконечно и его мощtюсть не ме11ьше мош-
СJтстt<.111:~телы ш. су-.,1 ,ча ч 1 tп:л нс зан11с11т от rю
Р»/tт<:а сла1 ·асмых:
а+/; = 1? +а.
Р;,~;~умеется. э·1·0 11е доказа.телнтпо, а ттп,
пот::не1ше переместнтелы юго заъ:она сложе -
1шя 1 lеремесп1теJты юс сrюйспю сложс 1 шя (•·От
11срсстаношш слаг~1 емых сумм.1 не меннс1п1 ~) .
подмеченное наш111\н1 11ре;tк:.1 ми пр11 <.:1'-Н:шива-
1-111 11 « К)'ЧСК ~ 1 1 :~ нсбшrы1 ю1·u ЧllCЛ:J прсл~·I СТОВ,
nЫJIO KfIOCJLCДCТRI IH cфorмymtjIOll;l 11() Юl J{ .JCll(,011
C.JIOJIO.!lll/Я. н;~туrалhНЫХ ЧТIC'C'JI
n р 1 1 :-.н:р 1,1 объе1tи 1 н."J11 н~ м 1южестн лсгтю 1 1а1'1-
ти в 1·t'oмe"1 ' r1-1 11 К<н: мы :нтзсм, угол ме1 1ъше
разnёрнутого можпо 11зобразить u виде пересе
чсrпш двух 1юлуллос1<остей. Угол болынс раз
вёрнутого представить в т.~ком виде нt: уJ~аётся.
Однако 01 1 яв;шсто1 06ъt:дш-1t.:нш.;,ч двух полу
mюскостеll (р 1 1с 8).
Всяк11й чстырс~.толышк m.:гко р:~з611ть по
ftl l :IГOH:1ЛII 11:1 Дl:!а ТJJC) l 'ОЛЬНJ!К:!, П(ШЧСМ ЭТО
верно нс только длн ны г1 ую11 .J.'( чет1.1 рёл1п1лъ-
1 гиков, I\() 11 для 1 1е 111 м1 уклых. Вообще любой 11-
утолы 1111\ мож 1 ю ра:1бн'Тъ ;т,н аго 1 r;.1ля;-.,11 1 11а 11 - 2
тpey1 '()J(l>1 II11{a. в случае в ы путтогп MI ЮГО~ТОЛЬ·
ннк:~ ,r~пст.аточ но провести нее ,циа1·011ал11.
нuсти множ~стваВ, т. е. IAI ~ l вl, тогда справеЛl\И·
во равенство
IAuBI = IAI,
причём независимо от того, и меют или нетА и В об·
шие ::>лементы. Аналогично, если В бесконечно 11
IBI ~ IAI, ТО
IAuBl=IBI.
В общем случае если хоп1 бы одно из VlножествА
или 8 бескш1ечно1 то мощность их обьеди11е11ия рав11а
максимальной и3мошнопей IAI и 11:31:
IA v BI =rnax( IAl, IBI).
В частности . объсд~1 ~1с11ие счётногu и коне•1ноrо
м ножеств также 1101\яется счетн ым множеством. На·
пример , еtли
А =!а,, а,, 0 3, ".},Я= l/J1, Ь !, 11!1,
то, « Перем е шав » ~лементы дан ны х множеств, мы за
пишем их оGьединенис в виде
Сl\еловат<:льно, элементы А u 8 мож но перенумеро
вать г1атуральным и с1нслам и , 1. с. оно c•teтi ю .
Р11с 9.
AhlXllДЯЩIJ{? 11:3 O/ЩOLI (.'1'0 LIL'p!ШIHЫ ((111(.', (). П) .
Для нсвы11уЮЮП) - нс ВСНК<!}! /\H;.JJ'OHG!Лb прrr-
1 ·од11а, олн<~ко 11 11 :=JTo.r. , 1 случае ула~тся 1юдо
брат1, диа1·011али, которые делят е1·0 1t<i /1 - 2
тре)ТОЛЫП!К<I (р11с. 9, б).
Рассмотрим теперь пример нз ::tm'<:~бры.
11 леrюй частп уравнения
(х{-5х2 +-1х-12)(х
1
-с:;х-16)=0
нахсщ1 l'l'Ol 1 1 ро11 iKt")\Clll lC / I И)'Х M I IOГOЧJICHOI:!
/(:,i)=х{ - :Sx~ +.:.\х- 12,
>
,
Д(Х)=Х - ),\'+6.
Очевнд1 ю. LJIO кажл~.rl1 корt11ь пер 1ю1·п j\ПЮ
гочлепа (т. е. такое чнслп. 11рн подстаt IOJJI<t
которого вмеего х этот м1юго"пrс 1 1 обращается
в О) бу;\~т ~1 корнем урагшенш1. поскuлы(у при
~ !\шожешщ любш о чнсла н;,~ О получастсн И.
А11:11ю 1 ·11ч1ю. корнем ура.~ше 11 1 1 н б\цст любой
кор<.:1 rn м1 щ1·очm:·на К(\'). Есл11 же чною х llC
ЯВJНIС l'CH корнем f-1 1L./(.Y), 11 1·1~(.У), ТО 011() 1Н:.' бу;1ст
11 r..:npr 1<.:м )'раш н:11 !IЯ, таr< как 11 po11 :3пe/\Cf-lt te /IH}'X
отл~1ч111.1х от О ч11се.r1 11е равно О. V111аче гоноря .
.\1т-южес1 ·1ю нсех 1юр11е1I дашюго ур~tннсш 1 я
предстаnлне-1· собой объелн11еп11е F v (,', J'ДeF -
\Jножество кор11ей м11оrочле11аj(.\') . а(/ - .'-'ШО
жсст1ю 1<ор11t'й м 1 тогочлена д(х).
ЛРУГИЕ ОПЕРАUИИ
Обычtю всякое множество расо·1ат r1rв:1ют как
часr1. f-ICKCY!'O(XJl 'O ()r)JIJ"llJCJ'() M I l()ЖL:CTR~J. ] la11p1 · -
мер, ·1реуп).l[ЫП1Ю1 , окру--жности, r<надр:1·1·1 .1 У!ОЖ-
110 считат1, rюдм1южсства .\1f! плостшст1 1 ~ целые
числа - ПО/\МIЮЖеСТАОМ [(е.ЙС'l'ВИТСЛЫ-!ЫХ чл
ссл и т. д. Такое объединяющее множество 1tа
зывастся }'' шверсалы 1.ы.111 лиЮ?tсествам. Д:111ьше
н т<:'ксгс слоnо «м 1 южсстnо» нсегда будет озна-
М1 южсства и 011~раL1ии
чат1, 1 t0дм1южест1ю некоторn1 ·0 у1111нсрсал1,но-
1·0 мтюжесrва rJ. Tt11cp1. 1111tдt:м сщс сщну 011с
ра1 ~1110 nn/l(lП/leJ-t//('. Для лю(~t.) 1uJ\1 1 10.IКL L -1· 11 ,1 А
чсрс:3 сА Об():~начнм HOIIOJIHCHl!t: ~1\IOЖCCIHar\.
т. е. м1южсство всех тех элеме 1 1·1·011 11з U, 1<0то
rыс 11е прш1аютl"жа·1 А.
Н:~пр11мер. ccm1 А tфyr. тn crl - то. Ч '1'<>
осташ:тся на 11лоско(т11. ест~ п~1 11сё uыре1<1ть
этот крут (рпс. 1U). ucmr рассм~приnать реше
нш1 л')авнсн1tй нли нt.:ра1к·1к гn. то н ю1ql'с.:твс
y1111НC::[1t'ШIЫIOI '() \1H(JЖCl"I t!~I r.r l \l'Jlt'COo()p : 1 :н-ю
сА
Р11с. 10.
Рис. 11.
11р1111я·1ъ мно:жсстно R 1ксл иt:ш.Lттнс:нных ч11-
ссл В 1 ·аком случ:~е, в:знв. н:111р11мер. в к:1чс<."1 кс
'Vlf-IOЖCCП\<1111 Mf-l()Жt'C'l'll() f)l'll LCШ lII 11t:р,111снства
,\'~+.У - ();;, () _ получ11м 11 ({;IЧ<::CI l:\t.: M l lOЖCC'I 1\;\
см м' южестнn решеIП1Й 11JХП11 НUЛЛJЮЖ I l()J'O
11сра11е11стuа: х-' + х - 6 <О, которое прсдст<~1i
ш1ет сuбой и11терва11 ( -
_1 . 2) . Напом1111м. ЧТ()
концевые тuчю1 интt'рвала е~1у 11е прннад;1е
жат - они входят JJ M I IOЖl:CTB0 1H.
Яс1ю, ч' 1 'u дunолнсн1н.:.м 11устого м1-южсств~1
0 11вш1<::тс.н всё униве:rсалыюе !\>.1ножест1ю U, а
.Ц<>П()JIHCHllC:M 1: бущ:т пустпе MIIOЖt'CTlIO.
Ин-1 ·ерtс1 ra снязь опера~ 11 rн J\O ПI иrнсн1 н1 с
; 1р)тнмп rтер:н11 rямr1. Так, 1щполнс 1-111е 110 0Gъ
е;1ннснш1 ;111ух :.11южс('Т11 ю1лястп1п ересече н~1-
ем 1 1 х долот1е111 1 /1, что за11ном1;н:то1 сле;1уrо
щпм nбразом.
с(ЛuВ)=с1\fiсВ
А допоJ1нсю1е псрсссчt:юш двух множеств ссп,
оfiъсдт1н<.:н11с 11х 1юnu1 1н<::н11й (р11с. 1 l , 1L) :
с (,..J nB) =сА u св.
В всдём сщё 011ну 011<.:рац1110 - ;ю.з1шс111h
.Jшюж·есmR. Пуст ~, ~~ar\~l 111>1 ;1н:1 \111ожс:-с111:1 - А
11 В. Рассм()трнм :\Н1Ожсст1ю <., состоящее 11 з
всех ·1·ех элеме11тон ,,1пожсстн<1 А, которr.1е 11е
принадлежат множеству В (рис. 1)). Мrюже
стuо С пазовём ра:пюстыо !\>uюжестu А н В н
обоз~ t:iчIIм та1<: G =А \В.
Фунламенг м<11ем;ники
Необходимо отмеппь, что разнuсть м1ю
ж<:ств лс1'КО нолучи ·1ъ н:с1 у?Кl' н~Кl'Стных 011L'pa-
1\1 ! й. ДсйС'ГНI l ' J'('JI hHO. м 1южестко с ('()('ТОИ'!'! I Э 'J 'l 'X
ЭJJ~Ml' ! f'J'OK м HOЖl'CTBJ .4 , J<O'l'Opыc пр 1 11 rщvicжa·1·
iIOll OJ JH<:JJllIO м1южес1'Ва R. Зт1ч11т, rаз1 юст11 (.
t:ст1, гн,;рt:сече1 шс м 1южеств А п с13. ·1
-. t:.
r1\B =1l ncВ.
Ест 1 1:1 стер<щи.нх объсJ(н11е11ня ir п ересе
чеш~я о()а м1 южестnа уч аств11от ра нr-юпраn~ JO
(матсм;пнки ronopm'. что т;1ю1с шrcp:i11 1 11 1 КО1\1-
\J~-гап 1 вны ). то отr<:рация раJностн мнoЖl'L'IR
уж<: Н(' коммут;1 т11вна:А\R ~В\А. 1-r11ч с1т1 У/ (J1 Н11-
тет,но1·0 здссn н с-1 - Rt.:J(l'> 11 :~рнфметнчсская
рJзно<..-1 ·1, чи сеJ 1 тоже нс комм}т:.п11нна. 0)1нако
н теорш1 л11южсст11 рап:матринается сщt~ од1Iа
rн 1ерац 1 1я рз .з 1 юстн, 11азш1аемая си1иютричес-
1.-о/1 ра:щостьт, ко1'орая уж:е комJ\rутаттша. Для
мтюжес-п~А н В нх снммстрнческой разтюстью
называется '<нюжестrю 13сех тех нх. эпсмсптоL1,
которые при 1 1ад.11ежат только од 110;-.1у 11 з м1 то
жt:стн А 11 В. :)та разность :~а1 111 сыuас rся так:
А л R. Из р11с. 14 слс:дуст. чтu
АД/3=(Аu В)\(АпВ)=(ВuЛ)\(ВnЛ)=ВЛА.
Друп 1J\111 сnоnамн, снмметр11ческая рэ:111ос1ъ
м 1южtс1·в А и Н еоъ раз~ 1осrь меж,цу объсдит 1е
п11ем 11 11 е р~сс'fс11ием дап11ых множеств.
;1
в
P1tc. 12.
Рис. Н.
А
в
Рис. 14.
J?ассм отр 11м ·1 ·е ш:р1, :1:сщачу, 1\ш1 рсшс1-1ш1
котuрой 1ю·11Jсб~ ютсн рассмотрс 1 11 1ы с 01 1 сра
цш1.
М111шс1трст1ю посm1Jю 11t>f\JIH11зm 11 (ссн 1111-
с1 1 t::.ктор3 ; 1,т1 проnеркн, как в 11ём nел:ётся пре-
1 ю.ц:щаrше н11остра1111ых языкоu. Сотр)д1111к
мш 11rсп:рстн;1 н отчёте зап 1 кз.11, что н ющес
учjтсsт 1UO детет·1. Каждый 11зучаст по кrай11еi1
мере О/(ИТ Т 1 1 з трех языков: фр;шцузсю1ir. ш:
мсцю 111 нлп пс11а нсюri 1 . llр11чём вес трп я:3 1,1 ка
11:с1ус1;,~10т 5 челпве..:; нс:;-.к:ц101\ 1 11 не11:1щ·к11l1 10,
фр:~нцу:-1сю·1li 11 rrc1131-н:юc1J'1 R; нt:мl' r \к11l111 фр~111-
1(узсю 1112();11c11aHCIШLI 30. HCMCЦJ<HJI 2.\фран-
1 \УЗСЮI1~1 '>О. и 11 спсктор, 11 pt:ll,CT;J f\И 1111111 JI O'J'ЧtT,
б ыл у1ю11t1 r. Поч:ему '
Начrтём , 1<<1К щ:сг11.а. с о(')о:таченпlr. На:юnём
Ф множество учащихся. нзу•Iающ11х фраrщуз
скиff язык, 11 - м11oжecrnu учащихся. 11зучаю
щ11х 11смсцю1f1 языт<, 11 - тех, кто изучает 1к
папски.й. 13 uтчtтt: сказа н о . что [<аждый н~ 1OU
тщсистон 1r:3уч;1с:т х.оп1 бы uд1111 11 ::.i трt:х н:1ы
ков. Прпнс:р11м , соотвс:тстнуст лн эп1 уrнсрж
дt:1111 t ос1·;v1ь111мv1 )1ан 1-1ым отчёта . Vfx можно :1а-
1шсат11·1ак.!ФI= ')0,IHI =23,IИI=~ЩФ n HI=20,
IФnИI= н. 1н n И:i= 10. IФ п н r1Jllj=<) По
сколы<у м llOЖCCTIIO 1-\Lt:X т 'Цt'l ·ICTOI\ ес 1 1. oGъe
/\ll JJ eпиc ~1 1южеств Ф, Н и И, мощпост1, кото
рог<1 РсШНа НЮ. Т<1 \О() = IФ\+\H\+llЧ
-
(jФr'I1-11+IФnИI+IIJn И/)+[Фп11n ЩПо;t·
ставим соотnетствуrощие :шачсннн и получJL\1:
SU+25+.~О-2()-8
-
Ш + '5 = 70. Прот1шuрt:
чис: HJU * 70 Лонробусм из отчё"l",1 ннсш::ю·ор<1
ПОЮJ 'IЪ. скол ько )'ЧCHllKOH нзуч:нот то : 1 1,ко
11 <::мсцк 1 н1 я:-1ык. Как слелуст 11:{ р11с 15, мощ
НОС'J'I> дdнно1·0 м1 гожсс·1 · 11:1 равна IHI -IH п ФI
-
\Н n И \+ IHn И n Ф\. \lQJ \CT:\\Шfl СО()'J' Il<'Т
стнующ 11 е :ша чс11 ня н по сле; (11 Юто формулу,
110J1учим 23 - 20
-
J()+'\ = - 2. Ошп1,а()сурд!
Въню..ц очсшще11 - проверка 61>111:i лроnсдеr1;"1
шюхо \'fJ\\t сонссм не npOIIOД\1.'l<\Cb. Не НСI\JТЮ
чено, ~по ш rст к·ктор nзял про 1 rзnолы 1ыс •11 r сла
[ / ()Зl-l:.IKOMHMCJJ С L' Щё 0)\1-JOfJ ТС::< l[X" l' l JK()· 1'1НO
ЖC'CTHClfl-IOЙ 0 11 t:paц11c 1't - щт.~1ым 11/Юfl.Шl!де
/-11/(~,Н. \ lуст1, А 11 Н - N':J прш1J1юлы1ых J\-ШU·
жсс1 ·на. Р:н.:сrvю 1 ·р 1 1,,, у11оря;(оче111-1ую 11 :1р) (х,у),
1'ДС. \' П /)1 IН3ДЛСЖI IT М J-IOЖl:CГR)' А , :1 .J' -
\1 НОЖ<:
СТП}' в. С:овокуТ11ЮС'l'l1 11ССХ 1ю;10G111.1 х 11эр 11 JТ:!·
знп:~стся nря,..uлм nро 11:1вt;\с1тем l\Шожеств.4
и В; пбо:шачэется она ; t х В.
Н сс."ютря т1з столь пышгюе и IТе11р111шчтюе
н<1:шаш 1 е, эта опсрац11я нам давrrо зн;шо.ча.
Воз1,мём в рую1 желсэт тодuрож.1п,~й бвлст. В нtм
а
б
)'=~У!- -х+2
\.
.
()
()
\'l<азано, куда 11 кшла отп ранляется 1юсз;1, н:н ·uн
и ме;:сто, с1п1 1 мuе1ъ бнлета 11 сщё 1-н:скол ько уже
Ht' нужных нам с11е[\сний: 1юмср бнт::та н т. д.
А Г)\С жt :щссь прямые лроизведе1111я·! Bm· 01111!
Во -щ:рных, 1щх1 чпсел. п11ределхющая месю
11~ссаж11ра в П()Сз;~е, - номер ванта и номер
места . Если в пое.1де 2.2 вагона. а в щ1ждом 11з
н11х 36 мест, то мrюжеспю А - м1южеспю
t!I1CCЛ 1, 2. "" 22, 3 МlЮЖССПЮ В - ~IHOЖCCTJIO
ч1ксл l,2, .",
.
16. Во-нторых, мu,-.,1ент l>'1 ' 11рэвле
ш~я. напрнмср, 13.-1R. 1:3 качестве мнr>же с·1· 1 1:111
ныступаю1 ч11сл:.1 О , 1. ".. 23, а н рошr ,\1ножс.'
ств~1 В - _"нюжсст1{0 щ.:лых ч11 Сt'Л от ОД() ')9. А
ещt? Есть 11 с111ё. меся1111 1-од 11111:1 номер 6 1 rле-
1·а - сl\~жем , К 211S6S4. Сн 1Увз пзрз , в кr.Уюрой
перв ы й элемент 11р11щ1л1 1 ежнт мr южестnу ()укв
(!Лфавита, а второй - множеству целых чисел
от OUOOO 1 ~о 9<)t)()<)<).
llрямос nроизЕсдс11ис множеств можт~о
встретить ни билете u юшо. Там указаны ряl( 11
често , а значит. nрнмuс прuнзвсдt: 1 111с мнu
жсстн:.1 рндов в к~11-ютс::1трс на м1южсстtю мt:с-1· R
ряду. Или н загшсн шахм:.~т110(1 n::ipт1111 . Каждая
ОТНОШЕНИЯ
К'.tЖJ\ЫЙ чс1юнск рuжл~н:тся нну1·р1.::ннс сщ )60)\-
ным. К сожа11е1111ю, н сJ 1 ь3.н то же ска~~атп об
oбщt:el'Hl', 1~ кпr·оr()е с )Н 11 рн хо;11 1т 11 котоrюе
011 11:.:1мснне·1· сво11м ппявле1111ем, - fiyдi, тп
с.:смы1, 11 ~щия. 1·осударс1·1щ 1шбо нсt чсловече
спю. Кэж.11ое из 1 1 11 х обла11.ает системой о'Г1 ю
mе11иi1 между своимн сочленами, 1<0торая ~т
рсдсляет нх ПОJIОЖСПИС о обществе. А лотом у
сын рабыни, к~ш nр:ншло, был рабом , сы11 i<o-
pcmя мог стать коро11<:м. Можно ш1 матсм~1-
т11 чссю1 ошrсать слож ные и разнообrазныс
с11ст<::мы 0·1·1ю1 11 <.:ний ' ОказыR:1 <::тси , что до
М1 южссто.:1 и оnсраuии
Pt1 L. 18.
Рис. 1 Ь.
Рис. 17.
ЮI CTJ<:.I Ul:IЛ ,\laПIOi"I /ЮС Ю1 ОТ~1СЧСI 1а 11;ipoil nу1-:
на - число.
llo самс>е п:~жнос 11р11;v~енс11ие прнмпе 11po -
нзrsc;ie1 1 ие i юлу чюю с nон пленпсм с1 1 сге;-.1ы 1ю
ордиш1т т 1 а rиюсrюсти. Дс!iст111 п·елы ro, 1<аждой
точке ГIJIOCI<OCTH СТ3ВlfТСЯ u CO()Tf'ICTC 'l 'BlfC пара
чисел (.\';у) . Тем самым пл оскос1ъ IJрсдстаn
ляе тся n 1нщс прямш ·о пptH1Jвcдcн1tsJ днух
nрямыхR х N. Что co6u 11щх·дставляет, 11;111ри
мер, 1·rаф11к фу11к~t11н) 1 =х! -х+ 2? :;:;J1 ·0 1ю;t
м11ожествu прщмн·о пrон1не;1сн11..и N х R, как
и 1\.11южс.:ст110 рс111с11нй 11сраве11ства у - х
1
+
+х-2) 0(j)HC.1(1).
Что 11 ол~'Ч~ 11·ся. если в:тть прЯ .\Юс.' прш1:1нс
де11ис прям()й н сжруж1 юс1·11~ t-kтr>ymю пош1т1"
что обраауется бепюJ 1 ечпый 1tилш щр (р1 к. 17),
точнее сю1 :i ат1" цилин11рическая nо11ерх1юс1ъ.
Л если nзят11 нрямос 11рш1эвсдсю1с f{nyx <Жруж-
1юстсй? Опн.:ппь 11а ::~тел волрuс тру/( 11<.:е, 1ю,
ПO/l)'Mal:! , .\ЮЖНО ДОГЩЩ'l'ЬСЯ, ЧТО IJOJJ~'ЧllTOI 110-
l:ICJJXllUC'IЪ, Jl~IЛU\1\ IH:lIOllЩJI 1юн1:рх1 ЮС1Ъ oбык
l IOBCHJ IOI ' () nубл11ка. M::tTl:M;JTllKI! lla;~ЫH:ll< )'[' <:l;
CJIOIIOM eror» (р11С. 18')
llCKlY\ 'Oj)OЙ t:Tl'Пl'llH ' П)Ч\ IO L~l'\1 :~то 11 1\ ОЛI ll' с \l' ) ' -
Щ<::С'l 'ВИМО.
Р::~ссмотр 1 1м конс't.!1t0е множее1 ·но ,Н = {и 1 .
о:! ,"., rtп} 11 его 11 рнмос: 11po11:mc/(e1111<:: на t'<::Gн
М х1Н, т. е. м 1южсст1ю всех ) 1юрядоче1111ых nэ~)
(а1, а1): ясно, что чпсл о нсех таю1х ш1р рав110 п -.
В дапно м случае прямое про11:шслс11]1(.' мож11 0
изобра:шт1. графнчсск1111 nпдс юшжсс1 ·на всех
цслых точек R квадр~1 1·е разм<:ра /1 х /1 (на р1 rc 1
11 = ~1). f{ажд::~я чС:.;рная точка 11:1 рщ:ункс сuuт
нстс- 1 нуе1 нск< т >ро1! 11 аре (а,, а1) , состаRле1 11 101·1
113 :-щс,\ентон HCXOJ\lIOl' O мн.ож<.::(.Тl~з.JJ . Пр11чём
(/1
•
({
•
(/,
•
({1
tt1
ФунлJмент математики
t11
(а,, и1) ((/!• fl;) (fl~·(/1) (tl,, tl.1)
С/\
ta 1,ri,) (а!. п,) (а,, а,) (/'l1,llJ
({~
(fl/• il .) (а,, tlJ (а,.а,} (tl_., tt,)
а,
<а,.а'} (и~.п1) (а,.а,J (а,.а1)
и,
а~
({1
о.,
Рис. 1.
представ:1с11ы вооб ще все nозм ож11 ые 11::~ры
п:J 1\1. :J 1 1;:~ч11т, .чuжно ш 1 ш.:ьшать любое парное
HЗ: ll li\100TГIOШ~l IJ н.: М/::Ж/\У :-Jllt'MCI rта м J·t м н о
Жt'С'l'IЩ М.
1l;inp11мcp, пустп tt1 - /\1rрсктоr, а~ IL п1 -
два t'l 'O замt:с1 нтеля, а 1 - рн110 1 юr'i сотрудник.
ТТuстут 1 м та~<: если а, 11аход1 пся н 1 юдч11111:1111 1 1
у а,, 1·0 точку, соопк·тствующую паре (а" а,), с;1е
лаем краспого цпет;:~ (рис. 2) . Н итоге получJ1м
11еюУгорпе <-крас1юс» полм 1 тожество нря.J\.10 1 ·0
11ро11зведt: 1 rия М х J\1, которое полтюст~.rо 01111-
сывJе·r uсю систему В:{аимоподчтrспиir этнх
четырех человек.
Да1шыl1 11р1 1 мер 1 1 щ(СК<J::5ынаст и общее::
опрt:делс1 11 !С: lla/J1-tЫM НJ ll I бt./I Ш/JllblM ONllШШl'
NU('. .11 1. 11:1 M I ЮЖС'СТ IК' 1\1 Н:J :>ывастся любое 1Ю/~
м ножест1ю Н 1 1рнмо1 ·0 пr011:шс/1,сн 1 1я ,1/х 1vf. Так
как R - nоl(мтюжесттю NJ х ,н, 'l'O1< ·1·ожс: сuстт 1т
н:1 у1ю ря;1очеш1ых пар (а,.а;). И ecJ111 (а,. а1 ) е Я,
то 1 ·0 110рнт - элемент а, 1 1 ::~ходптся п оттютпе -
1ши R к а1 (в пашем п римере а, •·rлав 11ее" а1) .
•по 111 ю 1 ·д:1 заrшсьш;!!ОТ та1<: п1 R с1" А есл~1
(а,, с11) 11' N. ·1 ·0 П1 1шут а, Na.1 Ilосколъку i\Ш nпра -
••
tl1
Д11ре1;:rор
С/\
/!) ~
(/i
З.IMCC!llTC!!I> ~ :3,1\.\('CT lll' CJ\ \,
а,I
~ /Q;)
U1 а~ t.1,
с11 груд1111к
тк: нh1бр:п 1, mrнioe 1юдм1 южсстно R с 11/ х ,\J, то
11(1 11 110МОЩИ ()JllТ<lp1101 '() ()'ПIOШt ll llЯ l\!OЖJICI
пре11с 1·авить ,-1юС'iую с пстсму 11 ар 1 11.1 х в:1а11-
моопюшс1 пп· 1 _\1ежду ЭJJ C1111e::1 гп1м1 r м1 южсст111. \/.
r l:i р.ис :) 11ре::дст~шл:епо пщ~.множес·1·но R.
кото rюс мuжно <·11рочит:1 ть·" папрпм~р. сж:ду
ющ11м о6раJом :
п 1 «rл:.шпсс" себя. а:. 11 а ,:
(/1 <• IЛаШIСС ;) себя и(/, ;
а , и r1 1«l 'Jraш1c::т" ЛJШLЬ самнх себя.
Fktюмшrзtтся бытоnашппй в СрсJ1 1 1екек:оа11е
прн 1 щнп: * Bacc~JJ .''1Ое1·0 nасс<1п<1 - FI C мой
на ссал·' Исходя нз этого пр111 щина .чожпо
прстктащ 1'JЪ, ч·1·0 а1- король. а2 н а, - ma его
ра н нопран11ых 11accL'1: 1, ; 1 с1 1 - насс.:: 111 а2 . Тогд<~
1ЮJ ЮЖСНИС ~К<IЖДЫlJ 1лав11се са м<)] '( ) ССбН·' озна
чае1 , Ч'l'О НСНЮIЙ KШICl l J-1:1/ ( CIM l l'vl cono1"1. ( lрн
меча l'CJ\ 11110. что ПОСЛСJ\ НL'С >'CЛO tll I C H~I l l :JШCM
р 1~сунке 1 1:юбражает поm 1 <1 я диа1·011а111. {(о, , а,) },
i= 1, 2, ... Те бинарные от1ю 1 11е 1 1 11 н N, 1ю·1'(1rыс
IЖЛЮЧ:.t[()Т 13 себя 1ю.rшую Д/I:IГО113ЛЬ {(а" a,)J,
i с R , назыnаются рсфлексzтиылш. Следовэ
телыю. в рсфлскс 1 111 1 юм 6н11::~р1юм олюшепт1и
uсе1да с/ R а, 1. с вссгд;~ «а rл;шнес а·).
Korr1.a в сисгеNIС в:~а11моотrюшеr 11 rf1 выrюл
rurстся пе «В: 1<:са111,ны 1'н•, а обратный пршщrm,
на 11 р1шер «Др~т мо<.:1'() друr: 1 - мо~'1 /\РУ' ">, тu
C()()TBt:'J'C'l'Hyк.>11 \(X.: 61 1нарнсх· ОТНОШ<:: l 11Н.: 1 1:1:1ы
к1 ется трпнзmm1&1-1ы.лt. В нём. c.:cm1.Y Ny 11у N z.
uбяза.тслыю х N z. Само же ~нассалhНСК'» 1 1ра
т1;ю n тсрмшrах 61 111 ар11ых 0·1·1юtш.::11иl1 назы
ваю'~· штштрt11131tmщ!_!mопью : ест1xRy1J
уRz, то нспремен110 хRz.
Рассмотрим в кач<.:стnс примера б;шз1.;ое
11сем OТIIO W CIIIf<: ЗII~l l\OMCTПa мо1щу JUOДb.МI I .
•
~
•
••
~
•
({\ al (/" (1\
i
Риt.. 2.
Рис. 3.
0110 l-l t06>1Зa1'eJJЫ-IO тra11ЗJl'ПJRH(J ИJlll <IJЛТП -
!1<1HЗИTl-1 Jil Ю, 11.0 , 1<0 1 IС Ч1 I0 ;кt:, рефЛtКСI IНJ Ю: Ве'Дh
кажлы11з1 1ает себя. Оп rошенис зн ак().мстна об
ладает ещё ОДI шм лрИ~V1ечателыrым свойством:
~ели а знаком с Ь, то 1r Ь знаком с а. Та1<0е свой
ство бинарного отнотuениSI R назы.ваетсн си.м
~иетрич1t0стью. Сн!\>Lv~етричнос бшrарпое от
ноwсниеН Rcerдa с11м.метрично относительно
rл:шноГ~ диаt'онали {(а" а1)} н uбратно (рис. 4).
Ан·r11симме·1·рич 1 юстью 1 ~снуется обратное
с1юйстrю:еслиаRЬ,тоhR et.
Еслн д:н 11 юе 0·1·ноше 1-1ие од1ювремс1 1 но реф
лекс~m1 rо, транзититню, симметрично, то оно
11аз111 вается orm-1oiueu11e.м э11:нuвалеит1-юсти .
Дпл такого отношения справедливы nравила:
1) а эюшвален тно а;
2) если а эквивалентно Ь 11 Ь эквиuалснтпо
с, то а экви.в:иrею·1 ю с;
5) ~ели а эю1 1 шалентно h , то lJ эквивалент
но а.
Отношсниt: экйивалентности разби в ает
миожество 111 на не11ересtк::11ощиеся подмно
жества экнивален·1·:ни1х между собой элемен
тов - л·лассы эквивалет тюсти. Пример от
ношения э квивален тности - MJ южество пар
целых чисел , которые имеют одинаковые ос
татки при 1'\СJJении на од1-Ю и то же число т.
Если каждый класс эквивалент1юсти содер
жит в точности один элемент, то отношение
называетсiJ un 11юш.eнueJJ·l то.ж'десm(:Jа или ра
вшц:тва .
Хорошо знаком ~-.rй ч:~стный сдуч:Jей бинар
ного 01·ношt:н11я - функция де 1'1сrвитсльного
nереме11тю 1 ·0 - ec1·r, по сути дела подмноже
с1·во прямого 1 1ронзвс;~епия чт1с.rювоС1 прЯМ()Й
на себя. котоrое изображаЮ'J' графmтм. Здео>
требуется лишт} одно оrра~т ченне: если хR у
их R z, то у= z. Попробуйте сформулировать
е1'0 словесно.
Таким образом, еслн ,\11 - множество всех
11ейс.."гви·1·ельных чисел, то отношс1-1ие R сМ хМ
можно понимать к::~ к мно1пзн:~чную функцию.
Например, футrкrщн у=±'\'Х дну:н1эч11а (рис.
1). так как кажд<1му х> О соответстнуют два эна
чснияу, удовлетворяющие раnенству J'=± Jx.
11э приnедёrшых прнмерон и иллюстр:щий
с.rr<:дует, что существуют разные способы зада
rrия бинарного 01110111ешщ unрочем, как и лю-
601·0 м1-южества. всдъ R - подыrюжсст1.ю М х 1Н.
Су ществует и специфический сносuб задаr111я R
дпя кон еч ных М: в н 1ще мач)нцы из 1~улей и е/щ-
МНОЖССТВ<\ И 01 l efJдUИИ
/.
.
•
Рис. 4.
Рис. 5.
ниц. Способ 0•1ень 11рост. а в резут,тате нс
бш11->ша>1 матриц<l ~аменяет громозюшй рису-
1rок. При составленни м<1.тр1щы пользуются пра
вилом: ед11t11111у нужно стави 'rъ тогда 11 толъко
то1·да . когда н;.1 соотнетсп~ующем м есте стоит
элеJ111ент из бижарного от11ошения R (рис. 6).
(
() -101 )
1о1о
l1оо
1ооо
l'ис. ь. М,1три11J OТIIOШPllИSI,
nр!'лгrавлf> ННОГ(') l\ругим (ПrJrl)бnм
н,1 рис J.
ЗАГАЛОЧ Н ЫЕ ОТ Н ОШЕНИЯ
Сын моего отuа мне не брат - кто ')10!
***
два отuа и АВЭ сына n оделил11 между собой три
апельси н<~ , и каждому досталось no ш>лому апель
сину. Как они :это сделали?
***
На одном спиритическом сеансе в Петербурге rю
бесnокоил~-1 дух Пушкина вопросом: «Како1;1u ваше
отношение к Анне Керн ?» Блюдечко ответило:
Я вновь клянусь тебе, мой друг,
Что без тебя мне жизни нет,
И в жизни л1не олна печаль,
Минута в жизни тяжела.
5Ч5
Фундамент математики
ОТОБРАЖЕНИЯ
Одним из основных понятий в совремешюй
математике является понятие функции. Функ
ции встречаются букналыю повсюду. Напрп
мер , если натяну1ую над костром проволоку
счита'rъ частью число.вой осн, то функцией
будет температура проиолокн в каждой из её
точек. Температура 01<ружающего воздуха -
фу11кцю1 уже пе от одной, а от трёх 11ере
ме11пых: Т(Вух географических коорд1111ат и
высоты над п1ош-rем "юря. А если /\Обавить
время - то от четырёх.
Общее в привсдёш1ых примерах - то, что
и аргументом (или аргументами) фу111щ1ш, и
ее значен~rсм nыс1уш110т числа. Однако нr~что
не мешает в качестве аргументов и возможных
з11ач~ю 111 функции рассматр1 шать объекты лю
бой природы . Так мы пр11ход11м к обобщенпю
по1-штия функции - к понятию отобz1а_ж:ения.
Простой пример - отображение, которое каж
домv жителю планеты ставит в соответствие
знак Зодиака, под которым тот родился.
Мы говорим. что задано отображе1 rие /мно
жества А в м1 южество В, если указано правило,
со1 ·ласно которому каждому элементу х Е А
соотистствуетодпн нпоm-1е определённый эле
:'11 е11т множества В, на:3ы1:щемый образам эле
мент;1х1·1 обознач:аемый через/(?;'). Отображе
ние(м1южестваА R м1южество В обозначается
зап1:1сыо/:А~8 или А~В (а нно1;л.а про
сто А ~В, если из теr<ста nrщят1 ю. о каком ото
бражепни идё1· речь). При этом множество А
называется областью определения отображе
ния I На рис. 1 схематичес1ш показано неко
торое отображение множества А в множество
В: от каж;ю 1'0 элемента изА проведена стрелка
к е1·0 uбразу
Заметим, что один и тот же элемент мно
жества В может быть образом несколью 1х эле
ментоn riзА.Так, па рис. 1элементрЕ В- об-
А
в
А
546
раз каждого из элементов Ь и с, т. с./(Ь) = р и
/(с)= р. Может оказаться, что н<::который ЭJ 1е
мент .\11-IОЖСС,'Т.ва в не Я.ВJIЯСТСЯ обра:.юм HJI од
ного эле.мента из А. Например, н.~ рис. 1 вА нет
элемента, образ которого сонпадал бы с q е В.
Но для шобого отображения А -7В непремен
н() должно nыть вы по1111е1 ю ус;юн11е: каждаму
. 71.· е А соотнетстнует только один элемент мно
жестна В в качестве ero образа . Соответствпе,
показашюе на рис. 2, отображением сч11тать
нельзя, посколы<у у элемента с е А нет образа
n мложествсВ. К тому же от ~лемента а е А идуl'
стрелки к двум элементам множества В, а не к
одному.
Простые примеры отображений, которые не
являются функциями, встречаются в 1·еомС'гр1ш.
Все геометрические преобразования, играю
щие nажлую роль н даrпюй области математи
ки, суть отображения. Например, центральная
симметрия отноопслыю точки О есть отобра
жение: каждой точке А соответствует такая
точка В, что отрезок А.В имеет точ~<у И своей
серединой. На рис. .1 обр<~з точки А нри цент
рuльной. симметрии относител1>но ·1 ·оч:ки О -
точка В, обраэ точки В - точка А. образ точю1
С - точка D, образ точки D - точка С.
Поворот 1· плоскости Р 1 1 а у1·ол п/2 rют<руr
цен '11Jа О тоже прел.с1·аR11яе1· собой вект·орое
отображе11ие t·: Р ~ Р данной ттлост<остп. Точку
А, отличную от(), отображение r:P~P пере
водит в такую TO'- Il<y В = 1'(А), что Ан В лежат на
одной окружности с центром О н угол LAOB,
отсчитываемый .в положительном направле
нии (т. с. против часовой стре.11ки) , ранен тt/2
(Рис. 4). Вообще. любое 1'еомстрическос пре
образонаниеf плоскости Р (осевая симметр1щ
лараю1ельный перенос, поворот н т. д.) nред
стаRля ет собой некпторое отображепне
/:Р~ Р, другими словами, как бы «геометриче-
о
Рнс. 4.
скую фушщию». Последняя в отличие от чис
ловой функции имеет сноей областыо опреде
лешш не некоторое множество чисел, а множе
стно Р, состоящее из точек, и обра::~а.ми нвЛЛJОтся
не чи.сла, а ·~·очки.. Знач11т, д1utюобой точки а е Р
её образ Ь =.f(a) таюке есть точк::1 плоскости Р.
НЕКОТОРЫЕ ВИЛЫ ОТОБРАЖЕНИЙ
Пустъf:А-+ В - какое-то отображение. Возьмём
элемент Ь е В и рассмотрим в А подмножество,
состоящее нз всех >rex элементов, образом
которых является Ь. Это подмножество назы
uается п1хюбразо.л.~ элемента Ь и ОбQзначается
/-1 (Ь). Так, для отображении, показанного на
рис. J , прообразэлементар е Всосrоитиздвух
элементов: /-
1
(JJ) ==' {Ь, с}. В прообраз каждоrо
нз элементов r и s входит ли1ш, оди 11 элеме~-rr :
Г1(1·) =а;/ -
1
(s)=d. ЧтожекасаетоrqеВ,то
его прообраз не содержит элеме1 rтов:/-1 (q) = 0 .
Теперь рассмотрим на плоскост11 круr А и
прямую В, а qepeзg :А~В обозначим ортого
налыюе проектирование круга па э1у прямую
(рис. 5). В данном случае прооб ра з каждой из
точ.ек р и q содержит лишь один элемент:
g-
1
(JJ)::: а, g-\q) = /1. Далее, для любой точки
1·е (р, q) её прообраз~-1 (1·) есть отрезок. Если
-
1
же s ЕВ\ [р, q], та прообраз g- (s) - nyC'l'Oe
MllOЖeCTl:IO.
Вндьт отображений различают прежде нсеl'О
110 тому, сколыю объектов содержат прооб
разы различных элементов м1 южества В. Если
в прообраз каждого элемента множества В
входит не более одно го элемента множества
А (т. е. прообраз либо содержит один. элемент,
лнбо пуст), то отображение называется вло.же
нием или 1.tн'Оекти.вны.м отображ·ение.м. Та
ким образом, если .f:A 4В - вложение, то,
отождестнлня каждый элемент с е 1 ·0 образом,
мы как бы нкладьшаем множество А п множе
сnю В в ка'Честве его rюдмтюжестна (рис. 6).
Отсюда и происхОl\ИТ термнн (, tшожение».
Еслиf:А~В - вложепи:е, то в множестRе В
могут быть «ЛИШI-ше·> элементы, не являющие
ся образами каких-либо элемеатов из А. Ины
м.и словами, моженис /:А~ В устанавливает
нзаимно од нозначное соответствие между
множеством А и некоторым nо1tмножеством
м1 южества В.
Если для любо1'О Ь е В прообраз / -
1
(h) не
пуст, то.f: А ......:, В 1rазыnают или .,.~tJю.?кenиeJtt, н1~и
Множестоа и оnераuии
А
а
ь
р
t•
qs
Рис. 5.
Рис. 6.
А
Рис. 7.
сюр-ьектuв1lы.м отображением, или отображс-
1-шем на множество В (рис. 7). Друrими слова
ми, отображеНУ1 е .f: А ...._,,В пр«::Дставляст собой
наложение, ест 1 в В нет ~лишн"LХ» элементов
(каждый элемент множеств:J В - образ хотя бы
одного элемента из А) .
ТТус~ъ f:A-+B - прои:шольное отображе
ние. Обозначим чере3/(А) образ .множестваА ,
1шач:е говоря, множество нсех элементов из В,
являющихся образами эле.ментов из А Если/(А)
совпадает с множеством В, то f - наложение;
сели же в В есть ~лншние~ элементы, т. e.j'(A) -
собственное подмножество множества В, то .f
изложением назвать нельзя.
Наконец, отображение, которое одно.вре
менно является и вложен11см , н наложени е."'1 ,
назьшаетсн вза11J11н.о однозначн.ы.м или бие~
пmв11ым.. Такое. отображснне/:А ~в устанзв-
111шает взаимно одноз11ач:1-1ое соответствие
между множествами А и В. Ясно, что nэаимно
однозначное отображение множества А 11а
множество В существует только в том случае,
ec.rrn эти множества имеют одинаковую мощ
ность. Можно сказать 11 иначе: отображение
.f:A~B в том и только в том случ ае взаимно
однозначно, если уравнениеf(х)::: Ь нмеет для
любого Ь Е В единственное решение х Е: А.
547
Фундамент математики
ОБРАТНОЕ ОТОБРАЖЕНИЕ
13 случае кu гда отображе ни е /:А -4 В вз;.шюю
од1юз~ачно. сущесL·вуL.т обратное omuб/Xf.J1ce
Т1uej : В -4 А . Оста 1-юв 1 1мся подробнее 1ta этом
ПОНЯ'Т' Иll.
Если.f:А-4В - юанмно ощ-юз н ачное ото
браженне, ·r·о1·да для ~LЖДого эле мен.та у Е В е1'0
npoonpaз.f-t(J 1) содержит ропно один ~лемснт
.х м1южеста А. Знэчи'1', имеется толnко од ш1
элемент х е А, !VIЯ кС>тnрого j ('\:) = у. На р11с. 8
()Т элсме11та :х; к ;:,лементу у nедёт стрелка . П о
ставив в соответст вие злементу у этот эл емент
х = f - 1()1), получае~1 некоторое отображение
множества В на множество А. Его удоб но пред
ставить схс:vrати ч ссю ·1, есл и направленне всех
стрелок, ведущи х от эле!v1е1-1тоR множсстR::~ А к
множестну В, изменить 11а проти вогюложное.
Получ:Jемое отображсш·rе В-4А обозна<r:Jется
через/ -1 и называется отображением, обрат
ным отображению .f Ин аче говоря. обратное
отображенне можrю опредслИ'lъ так:
/-
1
()•) = х, еслн/(х) = у.
Рнс. 8.
Допустим. юаимно 011;1юз11ачн ое отображе
ние.{: А --t В uыражается соотн ошен rшми
/(а) = q,j(l:J) = m,j(c) = pJ(d) = nJ(e) = 1·.
Тогда обратное отображение/ 1 имеет1шд
/-
1
(q) = aJ-
1
(m) = h.f-
1
(p)=с,
/-
1
(п) = d../
1
(!•) = е.
Отображение/ ~ нереrюдип ::~лемент а е: .А в
ЭJJемент q Е В, а обр:зтное отuf)ражсн1·1е.f 1 как
б ы <.< нозвращаL'Т» е1 ·0 на прежн ее месю:
/(а)= q,J-
1
(cJ) :о а.
КОМПОЗ ИUИ Я ОТОБ РАЖЕНИЙ
Пусть даны три множества А, В. С, а также не
кuтuры <: отображешш j : А->JВ u g: В-)С. Их
можно за11исать в 1:11щс « цenOLlIO I »
S48
А~8~С.
У кvrщoro элемента а е А сvществУсr его об
раз Ь = . f(a), приш1межащi1й м11ожестnу В.
В свою очередь. кажлый элемент Ь Е В имеет
свой образ с= R(b), <:одержащнйся н м.ноже
стнс с (рис. 9). П оставим R CUOTlle'l 'CTBl'IC элс
м е11ту а сразу элемсн·1· с, .мннуя 11рuмежутuч-
1 юе множе ство В (пункп1р н ая стрелка на
J)ис. 9). ТеС1·1 еt1мым пmrучнм 11екптороео·г<)uр:~
жение .мно.жества..4 в .м1 южество С (рис. 9). Оно
на зьrnэется л:о./1mоэици.ей отображений} и g и
обозначается черезд a.f . При этом первое ото
б ражение (т. е. /) всегда rтишетсн справа , а nто
рое отображенпс (т. е. g) - сле ва . Та1<ая фuрма
записи 11рименяется rю следующим соображе
ния м Элемент с, который в рсаультате ком t ю
аи 1~ии ста витс я в соответств11е элсме1-1ту а,
имеет нид с = g(h), где 1? - обр~1з элемент::~ а
11ри гн::рuом отображе нии , т. е. h =.f(a). Таким
обра;юм,
с = g(b) = g(/(a)).
в записнgU(а)) второе отображеш1е ею на
ходится слева, что и у~шт1,mаtтtя прн обозна
чении ко.мr1озиции:.f- справа. к - слева . Итак,
по 011ре;~елснню.
(g o./)(Ci) =p,l((a))
11.Jtя любш·о а Е ;-J.
Нэnримс:р. если/- 1~eJ1 · 11)алы-tая сим м етр 11я
llJIOCKOCTИ р OTHOC IПeJJЫ-10 точки о. а g - це1r
тральная с1 1мметрия той же тюскости о'г1ю
сителы-ю точки О' (рис 10, а), тогда ком nо
:зицш1доI отображе1-шйI Р--tР н д.Р~Р
ттредставняет собой параллельный перенос на
вектор, вдвое 60J1..ЫJ1ий, чем вектор 00' (см.
статhю "Геометрия и 1 · ру1111ы преuбра зов~
ний ~). В самом деле, отображение~ <>/пере.1ю
/\11т тоЧ"Ку А н точку С. В треуrоJJышке АВС от
rе:~<..ж 00' НреДL'"'J'<1tlЛЯСТ СО61)Й СредНЮЮЛllLШЮ,
L'JТ~/\Онательно, АС = 200'.
l:щё 01щ r 1 11рнмер. Во:~1.мём R качест1~е/осе
Rуто симметрию плоскостп Р отно сительно
прнм ой К а в 1<ачестве g - occny10 симметрию
той же плоскости uт~юсип.:лыю прш.юй L,
причёl'111 К и '~ щ:ресскаются в некоторой точ
к~ И. l l:J рис 1О, б.. на кuторо!v! отмечены раR1 1ые
у.1·J 1ы , сл1::луст, чти то • 1 каА е Р nt:рснщ\ится ко~1-
nоз1 щисй ~ о.f н такую точку С. чтu угол LAOC
Множt>< 1в<1 ~" оnераuии
А
в
в =.f (!1)
J_ак
а
.гl ,,__________. С= !{(В)
В =j(A)
C=g(B)
l'ис. 9.
Рис. 10.
вдвое больше угла Ct между rт рf{мым и К и L,
11ричёмА и С находятся на оди11:ошовом рассто
янии от ТОЧК11 о. И наче говоря , КО!IШОЗИЦИЯ,!\' о/
предст~шлнет собой поворот плоскости в01<ру1 ·
ТОЧJ<И о Н3 уrол 2о..
Припсдё1111ыс 11римеры ~~оказывают , ч то
компози1~.ия отображсн_ий играет важную ролт,
прн аналнзе геометрических лреобра:юва н111:1
Пусть тепер1, f - nзаимпо rщ1юз 1 1ач1юе ОТ()
брwкение. Рассмотрим 01едующу10 щепочку»
отображе1 шй :
A_L_ _,,B 1 1
.А.
Если/(а) == h, то, ~ю определению обраттто1·0
отоб ражения,.{ 1 (Ь ) =а. Поэтому (/ -
1
0.()(а) =а.
ГРУППЫ
Представьте, что вы находитесь на гrлацу. где
солдат обучают въшоJшению строевых ко
манд. Вот прапорщик комаrщуст солдату.
• Нале -1ю, шtлра-во, н;шр~1 -во, r<py-roм , штра
во, ошрно, кру1 ·ом!-?, а тот старнте;1ыю нспол
няет е 1'0 приказ~1 ния. Дан;1йте 1 10думаем . нет JJИ
3дссь математики .
Bhl можете 1ю~Jра~~ить: ~какая .'.-татем;1тика мо
жет бытr, R солдатс1юй муш1·ре!>) - н Пудстс:
непраны. Вот солдат стонт лицом 1' праТlорщи
~-у. Следуют ком~11 щы ,, 11але-тю, кру- 1 ·ом». R ре
зультате он оказывается n том же положешш,
что и 11осле едш1ствснной кома 1 щы «11алра-во•),
Если обозначить командr,1 буквами : Л - «пале
но», [1 - «наr1раво», К
-
<> 1<ру1·ом». С - <.смир
но»- 1
·1 сосдн JJ ить команды, отд:.~нные одна за
др)'J'()Й, знаком +, то это наблюдение запишется
простенькой формулой Л +К= П Сост:шим
1'аnтщу <-сложения • кома• щ.
И это спраnедшшо длл любого элемента а м 1 10-
жества А.
Точно так же в ~цепочке» отображений
В-"-1-'._,,Л__i_ _,, В
(/о/- 1 )(Ь)::; h для любого элемент::~ Ь мно
жсст1З<t В
Таким оt1разом, спобrаже 11и с /-J of : А ~А
став нт в соответс.'Тние каждому э11еме 1 пу .м110-
жесruа А с::~м это·!' элемент, а 13 результате ото-
J
•
бражснил f о Г : В-') В то же самое происходит
с эле.ментами множества В. Подобн ые отобра
жения, несмотря па их элеме1 rтар 1 rость, таюке
приходится рассматр11nат1" Их называют 1tюJ1с
дественпым11 отображениями.
Кома111{а
с
л
к
п
с
с
)1
к
п
л
л
к
п
с
к
к
п
с
л
п
п
~
л
к
Выч 11слите С :3МИ ~сумму 11 семи ком~1нд, с
1ютоrf,1х мы начали П1)Jl)'"ЧllTC>1 ком~шда 1<1<ру
rом -} (К). По ходу ныч1-1сле1111н час1ъ команд вза
имно уrптчтожнтся. А 11р1rбаиле11н е команлы С
к любой другой никак nосле,Т{нюю не меняет:
по комапде «Смнрrю" солдат остаётся в преж
нем п0Jюжс1-ши. Не правда ли, это похоже 1ш
роль нуля при обычном сложени11?
И вообще, сложение команд оче11 1, напоми
нает сложение чнссл · сумм.а l\HYX ч 1ксл - снона
чнс1ш, сумма /{нух ком анд - снова ком::tнда .
'>49
Фундамент математики
LНо при сложении tJисел для всякого числа а
есть противоположное ему число Ь, такое, что
(t + Ь =О. Вынолняется ли это в ктроевой~ си
стеме? Да! Дпя С такая кш11анда - С, лля П
-
Л,
дляЛ- П,адляК
-
вновь К. Мы знаем, что
при перемене мест слагаемых их сумма не ме
няется . Нетрудно nровери1ъ, что и такое спой
стtю выполняется в «строевой» системе.
Внимательно посмотрев вокруг себя, вы
пайдёте немало «с истем кома~щ», в которых
используется сложение того или иного рода.
Например, если па выключателе n комнате две
ююттки, отвечающие за ра3пые лампы, то с
ними с.1.шзаны следующие команды: «наж<пъ
(переключить) ле 1~ую кнопкр (Л), «Наж<пъ пра
вую кнопку~ (ТТ), «нажать сразу две кнопки-> (Д),
«останить как есть» (О). Ясно, что последова
тельное выполнение:: mобых двух из указа 1шых
четырёх команд приtlодит к тому же результа
ту, что и какая-то одна из 1-шх. Составим таб
лицу cлoжemrn таких команд.
Команда
о
л
п
д
о
о
л
п
д
л
л
о
д
11
п
п
д
о
л
д
д
п
л
о
Здесь роль 1-1уля играет r<оман11.а О - юста
вить как есть». Может быть, «кнопочная» си
стема т:шаяже. как и ~crpoenaя,)? Нет! Вдашюм
слуqае каждая команда, повторённая дважды,
приводит к команде «оставить как есть», а в
«строевой» это не так. Однако 1 1рн этом лрави
ло ют nеременъr мест слагаемых сумма не ме
Н.Я е'l'СЯ Р вновь выполняется.
550
И ещё одш r пр11мер «Кnма1щ1юго» сложе ния.
На nnm<e стоят трп разт,1е ктп·m. 1: пертз;:~я слеuа,
затем вторая и третья. Испотrим первое при
казание: « Перnую ю1ш) остаnить на месте, а
вторую и третью пuменять местами ~. Запишем
перее1·анонку следующнм образоМ:
(
1 23)·
132
З11.ес 1, i ~ифра R rsерхней CТJIOJ<e у~<азывает, ка
кое место занимала книга до перестановки, а
цифра под ней - на каком месте она оказа
лась. Второе приказание: «Книгу, стшrщую пер
вой, поставить на nторое место, ~аrигу, стоящую
на втором месте, поставить на трс.'Тье, а с трс
·rъего места кннгу пере(.'1·а1шть на пер1юе* - за
пишется так:
(
1 23}
2:)1
А •по получится, если nыпоmшть сначала
первое, а потом второе пр1n<азаюrе? Книгу, за
нимавшую nepnoe место, сначала пс трогаем, а
потом помещаем на второе место, поэтому под
1 будет 2 Книга, стоявшая на втором .месте,
сначаJ1а переходи т на тре-1ъе место , а 0·1·1у;щ н:~
первое, ·1. е. под 2 будет J Кн111·а с ·1рс-1 ьего
мecr.:i сначала псрс.\IJещастся н<1 второе, а за
тем нозвращается на прбк.нее NICC'I'O. Получаем
следую щую за 1111сt,
(
123J
21:)
Вновь <:С'IЬ возможность «Сю1адьшать" рас
сматрннаеJV1ые uбъекты. Правда, н случае 11ере
становок обычно гонорят .не об и:х сложенш 1,
а об умножении Соотнетственно п ерестанов
ка , умножение на которую не меняет любую
да111Jую перес1атю11ку, назынается 11е нулевой,
а единичной. Это тождесmве7-mая псреста-
1ювк~1
(12 3J''
123
ко1·дз все книги остаются ШJ местах. После
любой нереста ноuки можно вер1 1у1ъ книги 1ta
места, которые они занимали до неё; соответ
ствующая перестановка пазr,mается oбpamnofi
дашюй. Чтобы получить её з~mись, нулаю про
сто поменять местами верхнюю и ттжюою
строки в заппсн данной перес1·:~новки и рас
ста.1:111ть е1·олбuы 1ю 1 юрядк.у номеров в Rерх
ней строке. с~т;,~бшща умножения'> оерестано
RОК нс при~юдится из-за её 1·ромоэдкосп1 .)
Яс1 ю, что мож1 ю рассматриват1) переста
новю,т не толы<О трёх, 1ю н любого числа эле
ментов, и nри-rом пе обяззтелыю юти 1'. Пер
nым, кто это сделал, был О1'ИН из самых ярких
математиков в истории науки Эnарист Галуа,
жившш1 в XIX 13. Он изучил 11ереста1ювк"1 кор
ней мноп.><mсна и на основании их сFюйстн
доказ:1J1, что в общем Rнде корни мно1·очле11а
сrепсни больше 4-й нельзя выразить через его
коэффициенты с помощью радикалоn (см.
статью «Уравнения высоких степенсi1 »). Он же
первым ввёл в математику понятие, ч<~стtТhrми
случаями которого являются рассмотренные
нами и многие более «Серъёзные» и важные
примеры.
Пусть на некотором множестве задана опс
рания , которая любы:м 11вуr-1 элементам а и Ь
этого множества сопост:.~вляет неv"ий энемент
с= а • h тоr·о же множсстR~I. Если выполнены
следуrощие условия :
J) дш1 любых трёх элементов а , h. с из
рассматрнвасмого м ножсстnа
(а·Ь)•с =а·(Ь •с);
2) для любого элемента а данного мно
жестnа существует элемент eJ назьmаемый 11ей
трtиzьиы.1и, для которого
а·е=ld •а.==а;
3) для любо1·0 элемента а существует эле
.че11т, называемый обрапп-1ь1.tw к а и обычно
обозначаемый а-1• та1<ой, что
а· а-1
= а-1·а==е,
то это множество вместе с операцией • назы
вается группой.
Множеств.:1 и операuии
<..:амый зпатсомый нам пример группы
м1 южсстnо всех дсйствителытых чисел с опе
рацией сложенин. Первое свойство такой груп
пы - ассоцитпивн.остъ, т. с.:. нсем известный
сочетательный закон сложения. 1-rейтраль 11 ь11I
элемент из нторого с1юйств:~ - число нущ"
(Вообще, если операция над элементами име
нуется сложением - а это мо1уr бьгл-, числ;~,
векторы и другIIе :матем:l'l'I-rческие об'ьекты , -
то её нейтр3ЛЬньп1 элемент называют нулём;
ест1 же операция над элементами именуется
умножением или произведсн11см - то едини
цей:ведь1·а=а ·1 =адлялюбогочш:л<.1а.)
Обратным для чвс;щ а при сложении СЛ)""А\.ИТ
противоположное ему чнсло -а. .Множестно
всех ненулевых чисел с операцне1l умножения
'Г'<НОКе Группа (F1 1'31\ОМ случае Оfiра'ГНЫМ ДЛЯ
ч.иОJа а ;t О яi1.11яется число 1/а).
Существуют и другие числоF1 1 ,1е 1 ·рупп ы с
теми же операциями. Например, rруплу по сло
жению образуют нее цельте или только все
ч~тные числа. Часть ~лсментов дашюй r-руппы
с той же 011ер::щисй называю'Г её 11vдгрутюй.
Самая маленькая подгруппа r·руппы ч.иссл с one-
paц11cil сложе1-шя сос'Го 1 п всего из одного эле
мента - нуля (проRерьтс, что все три услов11я
для 11 её выполт~яются). Под111уппы с операцией
умножения образуrт·ся всем~ 1 П()}ЮЖJ rтслы IЬThU r
числаМ11, 11е11улевыми ра ц11011альным 11 числами,
числом 1. а также парпй чисел 1 и - 1.
Сложепие и у~шожеш1е чисел rюдчи11яются
закону «ОТ перемены мест слагаемых сумма
не меняется •), ин:~чс ronopн, данные операции
к.о.м.л~1·тапи.1в1tы. Hu это свойство выполняется.
не дш1 каж;ю11 группы. Д;1J1 «стrюеноl1 • 11 <- ю-ю
почнойt) групп - да, а вот для груплы пеrеt~га
но~юк Кl-IИГ - 11ет .
Действитслыю. как мы 1тделн, сделав пере
становку
(
12~)
231
вслед за перестановкой
(
123)
132,
получим rrерестатюnку
(123)·
213
551
Фундамент математики
Поменян пuрJщuк lL'{ ныпшшсния, получим
псрсстшювку
(
J2-))
:)21
Группы,вкоторыха•Ь =h •адшJнсехэле
ментов а и h, назьmзются л-nлif.JV~)1mшnurmь1Ми.
Рассмотрим группу, состоящую из четырёх
элементов - остатков от деления целых чисел
на 4, т. е. из чисел О, l, 2., :). Будем сктщыватr,
ост;~тки. как обычные числа. но если сумма
превысит :1. за.мен 1 rм её остатком от её деле
нщ1 на 4. Эта оперщш1 рассматри~,s~tтся в ста
тье ;;Арифмет11ка остатков и теорин сранне
н11fi ,>; ot1a гtазъшае'l·ся «с1южt11 11ем по модуто
4». Сос~·авим таблицу данной опер<щиt 1 .
Остаток
о
1
2
:)
о
о
1
2
3
1
l
2
.)
о
2
2
3
о
l
3
3
о
l
2
Мож1 io проnерить, что нее три своГ1 ства
груnлы з1~ес1, 111.1110111rяются. Hu проще сраянить
:-:1ту т<1блицу с таблицей «строеной-.> 1·ру1тпы.
Снязь между двумя группами сразу же обнару
живается. Если в «строеrюi1» группе заменит~, С
наU,Лtra1,Кна2т1Лн::~:),тополучитсятаб
лица сложения ост;пков по модулю 41 Дпя ма
темати1<и т::~кне группы одинаковы. Их назы
нают и:тмирфн:ы.ми. Сформуларуем rюш1тие
11зоморфизма более стросо.
llycт1, имеются 11.нс грутты; оп ерацию в од
ной 11~~ них обоэначим •. а в дР}'Го11 о. Гру11пы
называются изоморфными, есл11 суп.1,сствуст
вэаимно однознач н ое соо·1· L~етсrвие между r-rx
э; 1 еме11тами, переводящее ОТ\ПУ операц1· 1ю 11
,т1,rут~rто, т. е. если ,,лроизведепшо» а• Ь тобых
двух элементов первой rругпты отвечает во ~по
рой группе «nроизвсдсrшс» а" ~ элементов а и
р , СООТRетстиующих а и ь.
Понятие изоморфизм<1 - одно из важней
ших в ·1·еор11и 1'рупп, поскольку 11:! множсстн:1
всех изоморфных ,'\pyr др)ту 1·рупп 11остаточ
но изучи ·1• 1, J 1иш1> одпу - осталr.ныс будут об
ладать точно такнми же с 1юйс1·13ами.
552
Изоморфные группы могут быть очень
11е r юхож.ими на первый в3гляд. Возьмём, rrа
примt'р, rpynny действительных чш:ел с опе-
рацией сложстшя lf гру 1 шу ПОЛОЖИТСЛЫIЫХ
ДСЙС1'НJIТСJlЬНЫХ ч:нссл с операцоеt1 у.\1.IЮЖе
ния. Вз:п1мнu однuзначнос соответствие .меж
ду ним11 мож1ю уст:1110вить , со1юстав1-ш каждо
му дейстщ 1·1•елы-юму числу х (элементу ncp13oil
группы) 1 юлож11тельнос числоу= 2:'. Есл11 чис
лам х1 и Х;, сnrюстанленыу1 11J'z, то, в c1,rny тож
дества 2·'
1
' ·'·,
=2'
1
• 2\ C)'J'-t.мe х1 + х2 будет сопо
сташ1ено произведение у 1 • у1 - СJ1оже11ие
персхолит н у;\пюже 1 ше.
Дру1·ой пример. Рассмотрим упомяну·1·110
вьппе г·рупну из д.нух чисел - 1 и 1 с операцией
ум11оженш1 и 1 ·руш1у симметрий (или самосов
мещеннй) рав1-юбе1\ренно1·0 треу1·ольш1Ка -
дннжений, r1 срс1юдящих треу1-оль1-111к сам в
себя. (Harl0)\.1llHM , что ДАИЖСНИЯМ l l НЗС\h!Нают
nрt:образоnания шюскости, r<оторые не меня
ю·~· расстояния между точкамн.) Онерац11еП rю
-яторой группе CJrY?KИT l\70MflOЗltU,UЯ. - гюследu
ватеm,1юе выnОJшение дш1же11ий; её або:з11ача
ют зн~rчком о. Ясно, что эта группа тоже содер
жит только два ::>лемснта - тождсстнен1юе
nреобразона11и~..:Е, т. с. 11рсобразова1rис, остав
ш1ющее EJce точки на сво11х местах, и осевую
сим.мстр 1лG S относителыю высоты трсу1·оль-
11и:ка. И элементы, и оrrер::щии в 11знных 1·руп-
1шх совсем rазны~, но очевидно, что 1 ·ру1шы
изоморфны: числу - 1 соотнстствует S. с.ше
лу1- Е. Элементы 1иЕ- 11ейтралы1ыс,а
раненстоу (- 1) (-1)=1 отвечает S оS = Е, Во
обще, легко убедитьсн, что ncc груnпы из
дnух элсмептоn изоморфны. Их табтща умно
жения l!ЫГЛЯДIIТ т:щ.
Элеме 11т
('
а
е
е
а
а
а
е
1·.'\ ожrю показат1,. ч:f'О нее 1·рупш,1 к1 трёх элс
ментоn также изоморфпы. Две из 1 1нх - 1руш1а
сложения остатков по модулю 3 и группа пово
ро1·ов nравильноготреуголы1иш1. состоящая из
Е (mo1:1opo1~,t.; П~\ 0 °) и потюротов треуl'Ольника
nокру1· ею центра на 120 и 240°. В обоих слу
чаях, 060:3щ1чнв ней'1· р~иьные элементы (О или
Е) через Е!, а два др~пrх элемент~~ - как а и Ь.
,\>JЫ уииднм, что nерны равенства
а•а =h,Ь •/?=а,а •Ь =Ь •а=е.
А вот из четыrёх элеме11тов мож1 н1 сост·а
нит1 . уже две 11е11зоморфные группы - мы 1ю-
зпакомилнсь с 1шми в начале статън. llо тобая
другая групnа из че:гырёх элементов обязатель
но будет и:юморфна одной нз эп1х двух. :Н;,1-
пример, 1·руппа симмстриi:j прямоугольник::~ .
состоящая иэ осевых симмстриrt относитель
но его сре;~нюс шn-~ий, поворота на 180° вокруг
центра и Е, 11Зоморфна «ЮсЮпоч1-юй·> группе.
Между прочим, ясно, что «строе1ч-1.0~ группу
тоже мож1 ю предст<шить геометрически - ка1<
группу поноротов квадрата. т. е. поrюротов
вокруг одной то<1ки на углы, кратные 90°.
В связи со сказанным возникает вопрос: неr
ли какого -то универсального способа пред
ставления груш~? ДruI конечных 1·рупп такой
способ есть. Любая группа из п элементов изо
морф11а нод1·руnпс группы перестановок п эле
ментов: эту теорему доказал в XIX столетин
а11глюkкий математнк Артур Кэли.
Тс:перь rюзнакомимся ещё с одним видом
rрупп с1 1 мметрий - симметрюrми Тiеrнодт1чс
ских у:юрnв на ПЛОСКОСТJ 1.
Заrлm1е~1 в пчешшыИ улей (рис. 1). Отме
тим однн из составляющ11х соты шсстнуголь
ников. Теперь зададим себе нопрос: какими
лв11женияи11 uтмеL[енньп1 пrсстиу1·олышк мож
но пере1юднть н /~руп1е urестиупты-шки?
Сое;t1·1н1t.М центр О этою шестиутольник.:1 с
r ~ентрами 0 1 и 0 2 двух сосе; 1н11х шест11уго111,н11-
lIOB (r11c. 2). Чтобы перевести 11аш 111естиу1 ·оль
гrтrк 1~ rтервый или второй из них, достаточно
параллеJ1ы10 перенести е1 ·0 соотве-1 ·стве111ш на
--
--
вектор а= 001 или вектор li = 002 . Тенерь
уже пстру;\1Ю заметить, что для переноса 11ер
вого шестауrолыпща в произвольный шестl'l
угuльшrк достаточно совершить щ1раллельньrй
перенос на вектор па+ тБ , где п и 1п - соот
ветствую1.цие целые числа. 11:1 рис. 3 кrюме пер
но11а чальноrо шес1иут·ошэн ика розового цвета
отмечены ещё зелё11ы11 и l'Олубой шестиуголь
ники. Дrrя зедёного шестиуголыцша п = 2, т = :),
адляголубогоп= .3.т=2.
Множество параллел~,11 ьLх переносов 11а
секторы вила nn+mli, гле ·п и т - т\елые
числа, образует коммутативную группу. В част
ности. её нейтральный элемент - тождествен
~ юс: 11реобразо11ание можно представить r<~1к
nererюc на нектар о "" о. а+ о· Б.
Обр::~тит<.: внима11ис, что вес эJiсУ~енты дан
ной гру1шы nопучаются КОМ110ЗИЦИЯМИ ИЗ l(H)'X
переносов - нз ёi и Б и обра ·111ых 11м. В таком
случае пторят. что 1·рупш1 порождена этими
Множества 11 операш1и
Артур Кэли .
элемснтамп, а сnми они называются её uбраау
ющи..ми . В нашеfi ~стрuевоfн группе можнu
выдсю1т~.-. одну образующую, напр11мt.:р Л ( ~ на
лево·>):К=Л+Л,11=Л+Л+Jf,аС =Л+Л +Л+Л:
l3Mec1 ·0 л можно ВЗН'!Ъ 11, тю не с. в ~ ЮJОПОЧ
IIОЙ~ rpy1me образующих две: Л и П.
Но вернёмся к «Сотам» . Любой шсспrутоль
ник можно перенес111 в соседний IJe только
пзраллелыrым переносом , но и, 11апр11мер.
симметрией отпосите11ыю их общей с·гороны.
Рис. 1.
Рис._. 2.
Фундамент математики
Рис. З.
или поворотом 11а 120° вокрут их общей FJер
шины, или поворотом на 60° вокруг пентра
шестиугольника, rр:шичащего с ними обоими.
Назваппые преобразов~шия переводят саму в
себя 11 всю бесконечную шестиугольную моза
ику, т. е. .входят в группу ее симметрий. Отме
тим важные оюйств::1 этой группы: 1) она со
стоит из д1шжен.ий шюскости; 2) в 11е1"1 есть два
переноса на неколли11еарные векторы (а и Б );
~) среди вектпров всех nход>Jщих в неё пере
носов ссп> ненулевой вектор наименьшей
ЩllLIIЪI (например, а или Б ). Группы, облада
ющие такими свойствами, именуются крtк
таллографичес!(,UМU, так как возника~от прп
11ссж.:дова11ии симме1 рий кристалличесю1х
струк-1 ур. Первым полное он11с1нис кр11сталло
графических груnн на плоскосп1ин11ростран
стве дал русский кристаллограф Евграф Сте
панович Фё~оров (см. статью «Матемэтика и
кристаллография~). В частности, он показал,
что имее-гся ровно 17 различных плоских кри-
сталло графичес.ких групп . Все этп группы
можно найти на литографиях н грапюрах rол
ла1 rдс1юго Л)'дож1-пша М. Эшера, который соз
дал десятю 1 причудливых орнаментов из птиц,
нсаднико.в, рыб.
Группой симметрий фш~уры щ1зывается
группа преобразований (11.в 1 1жений) , сол-раня
ющих данную фигуру, т. е. пере~юднщих ее R
саму себя. Вообще. множество всех преобра
::юванпй, кпторые что-тп сохраняют, как не
трудно понять, ncerдa будет группой, чем бы
ни было это «что-то». К таким группам от1-ю
сятся: группа всех движений rvюскости - они
сох раняют расстояния между точк;:~ми; rрутша
преобразований подобия - они сохраняют
отношения расстояний; rрунпа т;.~к наз.ыв<1-
емых аффинных преобразованш1 , сохра.1-JЯЮ
щих прямые. н др. Груш1ы ш~рают в геометрии
юночепую роль. Мож1 ю даже определить евк
лил:ову геометрию ка!\ теор1110, изучающую
свойства фигур , не изменяющиеся. под дей
ствием элементов группы движе1шй. С той же
точки зрения можно рассматривать и другие,
неевклидовы геометрии, которъJм соотnетству
ют нные грртпы преобразов<uшй. Подробнее
о таком нодходе к геометрни, предложенном
немеJ(Ким математиком Феликсом Клейном
( 1849-1925), рассказывается в статье ~rеомет
рня и rруплы преобразтзат1ий •),
Феликс Клейн поместил 1101 r.ятне груттпы R
фунламент 1·еометрии. Но 0110 тубоко проник
ло и в такие области математики, как анализ и
I<омбинаторю<а, не гоuоря уже об алгебре. На
ос1юnс этого понятия был3 построена тополо-
1·ш1 . Группы стwи рабuч11м 1шструмептом и в
приложениях ма1·емат1ткн - теории кодиро
в~1ния , кр11стшuюграфии. А некоторых разде
лов сонременной теоретической физикп, 11а
пример теории элементарных часп-~ц, просто
не существовало бы без теории групп.
Математические рассужления
МАТЕМАТИЧЕСКИЕ РАССУЖЛЕНИЯ
ЛОКАЗАТЕЛЬСТВА 8 МАТЕМАТИКЕ
Что отличает книгу по математике от книr11 по
какому-то другому предме1у? Обилие формул?
Но онн есть 11 в книr·ах по физике, асгро:но
м 1111 нли мостостроению . Наличие доказа
телъстu - вот что прежде всего отличает мате
:-.1атику от друr:их областей знания.
Первую попытку представать в одном труде
всю ма'Т'ематику предnринял древнегреческий
учёный Евклид в Ш в. до в . э. В результате по
Яl!ишrсь е1·0 знаменитые «Ha'IaЛ<t<> (см. статью
•"Начала" Евклила"). А в'Т'оран попы·1·ка состон
лась только в ХТХ в" во Франции, коrда некто
Никола Бурбакir 11ри с-1уп:ил к изданию мно1'()
томно.го трактата <.Элементы ма·1·ематики». На
самом деле ма·rематиf(а Никола Бурбаки 11е су
щестrювало. Это коллективный псевдоним
группы учёных. Вот какой фразой открьшает
Бурбаки свой труд: «Со времён греков говорить
"математика " - значит говорить "доказатель
ство'·.,_ Таким образом, слова «математика~ и
•/\ОI<азательство» - почти синонимы.
Доказательства встречаются и в других
сфер ах человеческой деятельности, например
в юриспруденции. Однако матсма1· нчссюrе
доказательства убедительнее тех, которые мож
но услышать в суде. Математпческие доказ:!-
1·ельстuа пр11зшнотсн этало1юм бесспортюсти.
Что же такое доказательство в математике?
Доказательство - рассуждение. которое убеж
дает нас настолько. что мы готовы убеждать
других. нсаолъзу.я то же рассуждение.
Позвольте, скажут некоторые ч11т::~т..:ш1,
доказател1,ство - важное мате,1атнческое
гюнятие, а чёткоrо определения не им~ет llри
ведём два возражения. Во-псрных. даже н м~пе
матике нереально опрсдет:rть всё. Одни поюr
тия объясняются черс::з друrие, этн друп·1е -
через третьи, третьк - через четвёртые... И так
до бесконечности? Нет, где-то приходится ос
тановиться. Во-вторых, доказательство не есть
математическое по1rятие, подобное, например,
понятию ~дейстнительное ч:ис.'Ю·> или ~много
угольник». По отношению к математике она
не внуrреннее, а внешнее и nри~-щцлежит r~си
х:оло1'ИН, а отчасти - лингвистике. Однако без
него нелюя пrедстави'rъ себе математику.
-
---
-
-
--
-
-
-
-
---
-
---
-
555
Фунламеt п математики
Можно л1·1 11редлuжш.ъ кл~к:сифик:.~цию /~u
ка:1ательстн, ·1· . с:. убеди·1·елhных рассу..кдений!
Вряд ли. Тем более что док:~.зател1,сгво, как пр<t
вшю, состо ит н:з 11ескuлъких, иr югда м1-ю 1 ·их
э·1·апоn, п 11а каждом из ~ 1 их прим еняется сnой
с п особ убежления. И всё же несколы<о ос1юв
тп,1х, часто повторяющихся схем доказательств
nыделить удаётся .
ле вую часть. Это дол:азате.льство .методи.м
перебора.
Можно постуnитh иначе Вс1юмним: если
тrро11:н~е~ет 1 ие раш-ю rrулю, то 1rелрt:мс 11н о
равен пулю хотя- бы од ин из сомножителей.
А потому корнями нашего уравнения яnляются
числа 1997, \ 216 и '548, из этих четырёх чисел
толы<о 3 и 216 одноБрс менно неотрицательны
и меныпе, чем 420, а значит, только они удuв
летворяют услов 1110 зад;lЧИ
ПРИМЕРЫ ДОКАЗАТЕЛЬСТВ
Конечно, второе доказательство короче.
Пример 1. Требуется доказать. чт о средн
целых неотрнца·rельных •шсел, меньших 420,
нет дpyl'lIX кортrеИ уравнетп1я
Однако с логической точки зрения и первое
доказательство абсолютно убедительно, а сле
доuательно. безупреqно. Пусть 0 1ro длиннее,110
зато 11роще: не r1 yAGIO и сттользоnат1, у1<азанное
выше свойство произведе1птя, которое те тому
же кто-то .rvюг и забытъ.
(х+l997)(x- 3)(х- 2lб)(х- ">48)=О,
кроме чисе.'J 3 и 2 L6. Подставляя одно за другим
числа О. 1, 2, 4, '5. 6, 7, .". 213. 214, 2JS. 217. 218,
219..", LI 17, 418, 419 в уравнение. убеждас:мся,
что 1-ш uдно нз ннх не обращ:сtет в нут, е 1·0
Пример 2 . Требуется доказать, что среди
трёх:>начtn,1х ч11сtл нет числа. которое можно
ра зделить на 7. 1 1 и 13 Шкодьннк: мла.цших
ОПРЕЛЕ/\ЕНИЕ
Пu11sпье всякое "меет
СвоГ. tмысл, 1<оrорым ~• полно ,
Но от '1НОГU мыс11ь немееr,
Котоrш• 6"'3uано оно,
Тdю1е есть срел11 nuня1 ин,
Ч<'й tмысл ПОСТ114Ь 11ам не д3НСJ,
Их оос тюf(енье - С\\ЫСЛ занятии ,
А зто ~ смысл открыт давно .
Как-то Платон сказал: "Человек -
эго двуногое животное бе.з пе
рьев». Лиоген в ответ nринёс."
ошиnанноrо 11етуха со С.1\Овами:
«Вот человек Платона ». Платон
попытался найти выход из поло
жения: «Человек - это двуногое
животное без перьео с широкими
ногтями». Что на этот раз nринёс
бы л~юген?
О чем спорили два великих
мужа, отчего, н есмотря 11а муд
рость свою, ошибались? Почему
так важно ппрелеление? Зач ем
тратить силы на объяснен1.1е, каза
лось бы, очевидного?
На сей счёт весьма емко выска
зался М . В. Ломоносов: «С самого
11 ачала надо uстерегаться ошибок
в самых ОLновных положениях,
иначе, блуждая по всему физи
ч ескому учению, мы неизбежно
уклонимся далеко в сторону».
В математике определение
строится по тем же nриtши пам, чrо
и в классической логике . /\оrиче
ское определение есть словесное
(образное) описание некоторого
понятия с L1елью вскрытия его 1-1аи
более сушественных свойств
допускаются раз11ые опреде
ления uдно го понятия: простое
чи сло можно определить как це
лое неотр11цательное , имеюше е
своими делителями лишь себя и
единиuу (прич~м само чи с..ло от
лично от единицы). Можно его
определить и как число, не пред
ставимое суммой одинаковых ела-
гаемых.
В математике «словесное опи
са1~ие•. конеч но, допускает и при
мен еttис формул. Так, если мы пи
шем, что, по определению, у(х)::: х1,
то тем самым задаём , т. е. опреде
ляем, П<1раболу.
Встречаются трудноопрелеляе
м1:.1е либо совсем неопределяемые
понятия. Тогда в качестве опреде
ления и спользуют описание их
н аиболее важных, неnремен1-1ых
(атрибутивных) свойств. Напри
мер, [вклил писал: «Точка - это
то, что не имеет частей; л11ния -
:по то, что не имеет шириttЫ».
Поэтому, чтобы латh исчерпы
ваюшее определение какому-либо
п о нятию, нужно уметь выделять его
наиболее сушественные свойства.
Не менее важно в ч!:!реле многих
понятий, логических и математи
ч еских конструкuий суметь уви
леть и определить принuипиально
новое понятие.
классов. знакомый mш1ь с делешrем, способеп
справиться с задачб\ лерсбр::н-1 и испробовав
все l)UO трtхзпачпыJ( чисел. Но старшекласс
Ю!J< зщ1.ет, ч.то 7 , 11 1-\ tj суеь нростые ч.исла и
что число, делящееся H:l каждое НЗ I IHX, / \СЛJ IТСЯ
11 на ~1х произведение, т. с. на 1001. А это ;1;ля
тrёх-"шачноrо числа не~ю~можно
Пример 3. Необходимо дока:1а·1ъ, что уранuе
~гиех4 +у4 = z
2
11е нмеС'r· решения среди целъп::
положнтелы1ых чисел , не nревосходл:щих
числа 100.
Для доказательства можно перебрать все
десятъ тысяч n2p (х,у) - таких, что 1 < х < 100,
1 < у< 100, подставить их в уравненнс и в
резулътате убtдиться: сумма в его леfюй части
нс является лолным квадратом. Можно по
пытаться. как-·ю инач.е доказать, что урав tLение
неразрешимо. Второй способ труден. пср
льнi - скучен, а по·1 ·ому кто-~-шбудь вьттюл11ит
расчёты 11:i компыотере . Однако если nместо
нерхней rраницы НЮ uэять дpyryIO, неизмери
мо болыuу10, то и компьютеру перебор будет
нс под силу. Принедё:м пример перебор:.~, с ко
торым не R состон1-ши спраuиты:я самые мощ
ные совреме нны е ком11ьютеры .
Пример 4. В 1742 1' .
м::~тtматик Христиан
Гольдбах сфо рмулирон;.~л п-~nотезу· лсякое на
тур~шьное число п, 60;1ыаее илн равное 6. ест~"
сумма трёх nросгых чисел. Для 11еболь111их ri
1·rmотсзу Г()лънбаха 11етрудно пронерить мето
дом перебора: налриJv1ер, 96 = 2 + 4 7 + 47.
Для оче11ь болы пих п гип отеза таюке спра
ведлива. Как доказал в 1937 1' . совстсI01й мате
матик Ив:нr Матвеевич: Вн1101·р ;-щов, гипотез<~
Гольдбаха верна для ftcex п, болhших некото
рого rромад1ю 1·0 1z0• По результ:этам, 11олучr::н
ньu\1 Вин.0rра;~овым и er·o rюследоRателя.ми, н\)
~10
не прсвпсходит 3 . Достаточно проверить все
ИЗ Б ИОГРАФИИ КО/\МОГОРОВА
В биографии замеч ательного росс~1 йского мате
матика Андрея Николаевича Колмогорова есть
любопып1 ый эпи зод. Когда Колмогорову было сем
надuать с половиной лет, он реш ил и1учать исто
рию Нuв1 ородской земм1 XV в. Н.эчинаюший ис
тор и к закончил исследова ни е, когда ему ешё
не исполнилось девят11адuати, и u своеи работе
доложил на заня тиях университетского семи нара.
И сторик В./\. Янин всnuминал: «KorдJ работJ была
доложе н а им в семинаре, руководитель сем инара
профессор С. В. Бахрущин, одобри в результаты,
заметил, однако, что выводы молодого исследова
теля не могут претендовать на окончательность,
так как ,,в и сторичеrкой н ауке каждый вывод
должен быть обоснован несколькими доказатель
ствами"».
Рассказывая об этом впоследствии , Андреи Ни
колаевич добавлял: «И я решил уйти 1:1 науку, в ко-
1о рой лля окончате....ьного вывода л.оста1·очно одно
го лока3ательства ». История потt!ряла гениального
исследовс~теля - математика навсегда его приоб
рела. Рукоп иси Колмогорова no истории л.uлrое
врем я считались уте р янными, 1-1u впоследствии
были на йдены и опубликованы, уже после rмерти
автора. Ero кн и га « Новrородское земi\евлаление
XV В.» получила высокую оuенку спеuиалистов.
~,,,
-
числа от 6 до 3 - н r1тотеза оудс1 лиfiо
дuка ~~а н а. J1ибо опршк:рr н:·1':J. Но с1·0111> обlШ1р
ная rip oнtrжa rюка не;(остуn11а д~1же вы•1исл11 -
тельной техлике. Есrь основания 11олагз.'1Ъ, что
ПО!l.Обный перебор вообще неосуществим.
Остаётся надеяться> что удастся 11айти др}тое,
меньшее зна ченне. для п0.
УБЕЛИТЕЛЬНОСТЬ ЛОКАЗАТЕЛЬСТВА
Выдающн!"rся фра11цу1L:кн~'r матемап11< А1 1pJJ
ПyaJU<ape писал н 1908 r.: « Если мы чптасм кни
гу, папи с:uшую nятъдесят лет назад, то pac-
cyждer 1wi, которые мы u IJeй щL'Ходнм, ка:жутся
пам болъшс:й частью лншёнными 1ю1 ·1·~чсской
С1роr ·остн».
ДJ1я илшострации прине,f\ёМ странные, 1ю
н.ынешним меркам . утнерЖ,Г\СНllЯ 11з кн1 1 г~1
Эйл<.:р:э ~вв~денис в анали з бсско11еч11ых»:
<·е·\ = ( 1 + x / i)'. Гl\t i uзl!~i'..J:leт " бескане'-1110
557
Фунда м ент математики
6om.11JOe чи сло·'... так ка1< дуга 2kn/ i бесконеч
но мала, то
2k
2k1
)
COS- те =1- --тс-
i
;1.
член .У1/i1 может быть опущен без опасения ,
потому что даже nосле умножения на i он оста
нется бесконечно малым->.
В наши дю·1, ес;ш бы студе1 1'1· прнnё.1 1 11одоб-
11ы е утверждtння на э1<замене, 0 11 получал бы
двойку. Однако автор ю rиrи - великий мате
матик, а процитированные фрагменты тек
ста - часть доказательства одной из ero зна
мепитьrх формул, а именно формулы для
разложения синуса в бесконе чное 11 рои зне,r..1,е
н11е. Это и поныне одна из жемчужин мате м.а
н1ческо1·0 ащlЛиза.
Таким об р азо м, понимани е того, что ЯRЛЯ
ется, а что не ямяется доказательст1юм. меня
ется со в реме~-1 ем. Если вдуматься. нпчеrо уд и
внтел ыюrо 11 это м 11ет. Убедительность довода
нстор11чес ки обусло влена. Дrrя средневековых
судо n, напри мер, доказателъства nинов1юс111 и
невшrовности были очспъ своеоб ра:шы, с на
шей точю1 ::.~рения: сели '-1Сло 1:1ек мо1· удсрж:пь
в рукс рас калённuе же; 1 езо, то он признав ался
невин овным; есл и брошенная н воду связанная
женщина не тонула , её объявляли вед1,мо11 Убе
д 11теJJьн ост1> м атематическо го доказательстuа
имеет те же психо1ю г'И"Чес кне осJ-юnы , чт() и
доказательства юрнд11чесrю1~0, а rютому та~; же
зависит от исторических обстоятел ьстn.
L
558
ТЕОРЕМА, О ПР ЕДЕЛЕН ИЕ,
АКСИОМА, ЛЕММА
Теорема (от греч. «Теорео» -
« р ассматрива ю», «исследую » , а
также "теорема 11 - 1< nредстав/\е
ние», «Зрелише») - это математи
ческое предлож ение, истинность
котороrо устанав/\и вается с по
мошью доказательства. Такое на
звани е закре11 илось за н им, пото
му что в древности тео!Jемы часто
доказы вали публично, на nлоша
лях. Случалось, доказательства но
сили характер яростного с; пора,
доходи вшего ино гда до рукопри
кладства.
Каждое доказател ьство стро
~1 тся на других высказываниях,
пр11 нятых ранее, а в конечном ито
ге - ни оп ределениях и аксиомах.
Опрелеление - это такое предло
жение, в котором у к азываются
ос новны е свойства математиче
ского объекта, которые выделя ют
его среди других объектов. Акси
ома (от греч. « аксиома » - « уваже
ние•, «авторитет » ) - некоторое
зара нее выбра н ное высказыва ни е.
В сре.rт.невековой Индии , напрп мер. rео
метричес кие утвсрждс r щя до к азывал и так:
Аксиомы полаrаются и стин н ыми
без доказательства Следователь
но, истинными считаются и тео
ремы. Подчерю-1ём, что лаже дока
занные теоремы ~•е могут считаться
абСО/\Ю"НЫМИ истинами, ПОСКО/\ЬКУ
всякое их доказательство базиру
ется на при нятых аксиомах.
Локазате/\ьство конкретной те
оремы совсем не обязательно на
чинается от аксиом и определе11ий,
оно может оп~1 раться 11 а ран ее
доказан н ые прелложения - тео
ремы и леммы . /\еммой (от греч.
« лемма * - « взятка)) , «П рибыль»,
«доход » ) назы вают всп омогатель
н ое n релложение, используемое
для доказательств а од н ой ~• ли
нескольких теорем.
Всякую теорему можно раз
делить 11а две части: условие и
заключение, хотя в конкретной
формули ровке они могут явно и
не выделяться. Например, хорошо
извест1-1 ую теорему Виета обыч 110
формулируют так:
Сумма ~<орней квадрап~оrо урав
нения равна коэффиuненту при х,
взятом у с противоположным зt1а·
ком и лелённому на коэффнuиент
nри х2; произвеь.енце коркеИ рав
но свободному члену, делённому
на коэффиuиент при х2•
Услови е теоремы состои т в
том, что nрелпо"агается суше ство
вание кор ней урав нения. Такое
п редположен ~1е легко ускол~.зает
от внимания, а это может п ривес
ти к ошибке при решении той или
иной залачи . А потому теоремы
оч ень часто формулируют в виде
условных nре лложе1-1ий: «если...
то...•. Часть тако го прелложения ,
Сl'.едуюшая после « если » , - усло
вие теоремы , а другая часть, посл~
• ТО •, -ее заключен ие. Всякую тео
рему, н апример ту же теорему
Виета, можно сформулировать в
таком виде :
Если квадратное уравнение ах2 +
+Ьх+с = О имееткорних1их2,то
сnравелливь1 соотношения
ь
с
х,+х2=-- х,·х2=-.
а'
а
Математич еские рассуждения
-
-
-
-
-
-
-
---
--
-
- ----- -
-
-
---
-
-
------------
СОФИЗМЫ
В Лревней Греuии развитие искусства ведения дис
куссий нередко приводило к изобретению хитро
умных «доказательств» 11еверных утверЖАений. Такие
« доказательства» называются софизмами, посколь
ку 1-1х часто использовали софисты - учителя фило
соф ю1 и красноречия в древней Эллале. Анализ
различныJС софизмов в конечном итоге способств о
вал развитию логики. В частности, одна из книг
д.ревнегреческоrо философа Аристотеля так и назы
вается «0 софисти ческих опровержениях». Вот
несколько примеров софюмов:
((Если равны половины, то равны и uелые. Полу
пустой стакан равен пощполному; следовательно, пу
стой стакан равен полному».
с~ Это твой шенок? - Ла, он сын моей собаки.
-
Значит, он твой, и он сын, то есть он твой сы н» .
1t Всё, что ты не потерял, ть1 имеешь. Ты 11е поте
рял рогов. Следовательно, ты их имеешь».
Многие софюмы основаны на подмене значений
гюнятий. Например, в последнем софизме с11ачала
рассматриваются предм еты, принамеж ашие данно
му человеку, а затем - все предметы вообше. На эту
тему есть любопытный анеклот:
Учитель:
-
Надеюсь, Иванов, что я не увижу, как ты спи-
сываешь.
Иванов;
-
Я тоже на это надеюсь.
Геометрию часто называют искусствьм правильно
рассуждать на неверных чертежах. Это определение
имееi право на сушествование, поскольку абсолютно
точных чертежей не бывает. Так, нельзя на плоскости
изобразить точку и прямую: вместо них рисуют ма
ленький кружочек и полоску небольшой ширины. Тем
не менее геометрические софизмы часто опювыва
ются именно на неправильно построенных чертежа х.
Вот два таких рассуждения.
П ример 1. Рассмотрим произвольный треугольник
АВС. Проведём биссектрису угла В и серединный
перпендикуляр к отрезку АС. Точку их пересечения
обозначим через М (рис. 1, а).
Так как МО - одновременно и высота и медиана
в треугольнике АМС, то этот треугол~:.ник равно
бедрен11ый и АМ =МС. Теперь опустим из точки М
nерnендикуляры МЕ и MF на стороны АВ и ВС соот
ветственно. По свойrгву биссектрисы,МЕ:: MF, сле
довательно, прямоугольные треугольники АМЕ и CMF
равны: у них рав1-1ы гипотенузы (АМ и МС) и кате1ы
(МЕ и MF). Отсюла у них равны и вторые катеты АЕ
11 CF. По тому же свойстоу биссектрисы, равны nря
моугольш.~е треугольникиМfВ и MFB , а значит, равны
вторые их катеты ВЕ и BF. Из сказанного \,ледует, что
АВ=ВС,посколькуАВ =АЕ+ЕВ,аВС=BF +FC.
Возник парадокс: все треуfольники равнобедрен
ные. Более того, взяв в качестве основания треуголь
ника не АС, аАВ, мы таким же способом получим, что
JJC =АС. Значит, все треугольники равносторонние!
Этого софизма не сушестоовало бы , если бы
не было ошибки в чертеже. Середи~rный перпенди
куляр, проведённый к оrнованию, и биrсектриса про
тивоп оложно го основанию угла не могут п ересе
каться внутри треугольника. Тоцка их пересечения
лежит t1a окружности, vписанной вокруг треуголь
ника АВС, и делит лугу АС пополам, в чём нетрудно
убедиться {рис. 1, 6). Если мы проделаем те же по
строения на пра61-1лы1ом чертеже , то вновь увидим.
что АМ=МС, МЕ=MF, а потомуАЕ =CF. И далее,
ВЕ::::BF,ноАВ =ВЕ+АЕ,аВС=BF -FC.
П ример 2 . На рис. 2 на клетчатой бумаге изобра
жены nрямоуголью1ки. Один из них имеет размеры
5 х 13 клеток, всего 65 клеток, а второй - квадрат
В х В клеток - 64 клетки. А теперь обратите внима
ние на то, Чl'О оба прямоугольника разрезаны на no-
r1apнo равнь.1е ча сти. Значит, их плошали равны, т. е.
65 =64.
Ошибка заключается в том, что точкиА, В, С и О
(рис. 2, а} не лежат на одной прямой: точка В нахо
дится чуть выше, а точка С - чуть ниже прямой АО,
поэтому ABCD - nарамелограмм, он н е покрыва
ется частями, на которые раlрезан квадрат на
р1-1с. 2, б. Плошаль nараллелоrрамм а в точности равна
nлошади одной клетк11.
Приведённые примеры показывают, что неточный
рисунок может ввесrи в заблуждение, и довод « Как
видно из р1-1сунка }) не всегда служит доказательством.
P1tc. 1.
а
Ркс. 2.
б
559
Фундамент матема1 ики
11ре; vш1·:т11 чертеж, по;~ котоrым стоя1 ю все~ о
одно CJIOfIO 1·С.мотр11!·'. На рнсунке нос11роизве
;сено н нд1 1 йское дпказател L.ство фuрмул ы тю
ш,адн круrа: эта окружrюстъ рав11а rиющади
nрямоуголыrика, высотой которого служит его
радиус , а основанием - отрезок, равный длю re
полуокру?Кiюсти круга.
В древних еI·инетских текстах встречаются
вычислсr 1 ия простейших шющадей, ош:рации
с ;шиюютнымп дробями (см . статью <Лренний
Iirппt1")). Р<~счL~ы приводятся без какого бы то
н1 1 было обос 1 юuания. По-видимому, в то
время не сущеспюuало психологической
неuбходимости 13 подобном обосновании -
снособ ы решения исхсщит-1 от ::шторитет1 ю
го лтrца , например жреца , и записывались.
Большего и нс требовалось. (Нс так ли и мы
сейчас отнuсимо1 к медl'щинским рецептам?)
Первые доказательств;,~ в их современном по
нил·шн.vш приnисьш;:нот J~ревнеrреческнм мыс
литtлям Фалесу и Пифагору Считаt·1·ся, чтu
именно н Дрtт-1t:й Грtцщ1 в VТJ-VI вв. дu н. э.
возник новый обы чай: со11ро1юждат1) матс:ма
тический факт ето обосновани:ем. Очев11д110,
11оя1111лась потребность нс просто сообща1ъ
;щнный сjх1кт, 11<1 н ;~оказынать е 1 ·0 истншюсть,
т. с. убеж;~ать елу ша геля.
Дре и11егрt:ч tскиt: доказательств<~ быт 11ючт11
бt:зупречны. Попожение вещtй начало ме
нятьсн с ХVП в., когда в матем:атику нрщнл:н nс
р емеr-п1ые величины и стало сю1а,ц.nша'lъся
предстаJЗлснис о nредельrIО.'>1 перехоле. Б011ее
чем триста лt.-т спустя эти предсrаnления о пе
ременнuй н uμеделс нс выглядят достаточно
чfткими , а nuтому и /tuказатсльства того време
ни кажутся нсс.трог11ми (испо:мним 1 t11тату из
ю 1и1·и Эйлера) . Замечательно, од11ако, что столь
нестро1 ·ие доказатепьс.тва приводили к стрuгим
результатам , прочно вошедшим в арсенал ма
тема·1·ики. :Н 20-е rг. ХТХ n 11шшиm1сь работы
фра1тцузско1'0 математиt<а Оrтосте11а Кош1\
(1789-1857). В его трудах п01-штие предела 11
опирающиеся на неrо понятия впервые нача.'!11
приобрет:лъ современную логическую форму.
Иници:пика Когни бhlла ра3вита 3атем м11оrи-
1У1И матем::~ти_ками, преж;tе Rce1.·o, уже во второй
пuлоннне XIX в" нсмсцкн.м .матем;-~т11кuм К<1р
лом Всйер11лрассом. Но нuвые прс11стаw1ения
о необходимом нюш-1е с1ро1·ос-1 ·1-1 Бход нли в ма
тема •п1ку в тсчеrте дпт·о1·0 1iременн.
ДОКАЗАТЕЛЬСТВА МЕТОЛОМ ОТ ПРОТИВНОГО
Доказательство м етодом от прот1шнш ·о заю1ю
часто1 в следую щем. ] lре;1rюла 1'ают, ч·1·0 Rерно
утверж·де1 1 и<: В, «противное>), т. е. противопо
ложное, тnму ут1:1ержде11ню А. котQрuс требу
ется доказать. Далее, опираясь на это В, 11рн хп
дя т к противоречию и тоrТ(а заключают, что
есю 1 В неверно, то верно А
Пример 1. Пусть даны треуголыrик и f{na его
неравных yrл<i. Требу<::тся доказать угвержде
нне А: прnт1ш болы11е1·0 угл<t лежит боньшая
сторона .
С;tсщ1см противополож1 юе 11редположе
н11е В: сторона, лежащая в нашем треугольни
ке прот1rв больше1·0 )' l 'JJa, ме11ыле или раuна
сюро11е, лежащей против меньшего угла. n ред
положспне В вступает в противоречие с ранее
доказантюй теоремой о ТШ•t. что в любом тре
угольнике пр(пив равных сторон лежат равные
1тлы, а ест• стороны неравны. то против боль
шей сторо11ы лсж 11т болыuиt"1 угол. Зн:~чит,
'560
предположение В неверно, а правильно утвер
ждение А. И1 пере<.:но, что 11ря.\Юе (т. е не «ОТ
протиRного~) доказательство утвержден ш1 А
намного сложнее.
Чаще всего метод от нроти111-юго использу
ется для доказатет,ства то1·0, что объею·а с :~а
да 1 111ыми свойствами не существует. В самом
деле. ecJHI требуется дока:'!ать существотза1111 е
такого объекта, то можLJо просто предъявить
его. А 1<ак доказать, что какого-то объекта нет?
Хорошо, е<.:.11и е 1'0 нужно некать среди конеч
ного количестRа элементов - тогда .можно
попробовать ме-гоr1 перебора. А еслн средн бсс
консч ного' Приведём три пример<~ ~11ок'1з:.t
тельст1:1 несу~цествuвания», в которых исrюль
зуется .rv1етод от проти1шо1·0.
Пример 2. Требуется доказ~1ть, что диагональ
юзадрат<t и его сторона несоизмеримы.
llаnомним, что отрезок а называетсн ~1ерой
oтpc."lr<a Ь. ecJ111 а укшщывается в /J целое число
(ели тр()бу<.;тd'. дока>il rь
lYШl'CТ!JUBJHИ ~ uыжт.1 . можнu
прост() nредьяв11ть е"о.
раз. То1·щ1 общая мер<~ двух 0·1рсзкоn - отре
:юк, ННJIНЮЩИЙСЯ мерой для каждuго IIЗ них.
Есщ1 обща51 мера ;~вух отрезков существует. то
·,r1·н отрезки 11а зьшз ются cou3.M!фUM'htЛIU. ~ про
·гпвном c11y~tae - н.есои.з.мери.мыми .
Ме·го/l персбор<.1 rvп1 f\Оr<азателt>С'l'н<1 ;111ес1)
11епр~1ме.ним: певозможно перебрат1, нее от
резки и притом убедиться. q1 о каждый нз tf1'1X
не общая мера стороны и диагонали юзадратз.
13се известные доказательства дашюrо факта
веду1·ся _"Уfетодо."1 от пропшпш·о. Одно нз 1rих
чы и 11ршзед{;м.
Гlрt:дrюложнм. что отрезок и - общая мер;1
,щз1·он:.\ли и С1оронн К\:'.:о~драта Q. гtостропм
друl'ой , мс1 1ы1ш й квадрат Q' -
т;~кой , что
Rсяк~1н общая мера диатн::~ли н сторо11ы Q ста -
11ет 0611.1.ей мерой диаrон:ши н стороны Q'. На
днагт1:1лн вс ИCXO/J,IIOГO кп:щрата Q ОТJIОЖИМ
оrрезокВО, равный стороне тш::щрата (р11с. 1).
Из D 1юсстаrшм .пеrnендr.шуляр к ВС ;т.о пере
сечения с АС u точке Е. Прямоугольный тре
)Тольник CED - р:ш11обедрёнr1ый: лосколы<r
)'1'L>Л ECD р~ше11 4:;
0
,
то и другой острый угол
ра1~ен 4'5 °; значит, L EC:lJ =: LCED; следователь
но. CD = ED. Поэтому треугоflьник CED можно
1юrюлнп1ъ до квадр::~та EDCF, который и возь
мём в к:.1 чссrве Q'.
Квадрат Q' меньше кнадрата Q: так как
ВС<1JВ+АС==2ВD,аВС-АВ<АС,то11CD<АС,
т. е. сторона кnадрата Q' мс..:ньшс стороны кnад
рата Q. Пр11чём, ка1(ова бы ни была общая мера
стороны i1 диаrонал11 юзадр~1та Q. она служн·1
общей мерой стор<жы 11 ,цнагон:ши кн;щрата 5.J'.
в самом j~CJLC. прЯ~'vЮ~!t'(ЩЬНЫt треуеоJIЫIИ!<11
ВЕЛ и EBD равны по днум сторонам, следо1:><1-
тельно,АЕ:::::: ED. Если CD =ED. то АЕ = СП. Пуст•>
тerrer1, некО'l'Орая общая ."1ера е1'<Jр01-1Ы II ДИЗJУJ-
1rаJСИ к.н::~лрат:J Q укJJаμывастс};t в его с1·uронср
раз, а в 7\ИаJ 'ОШIЛИ - r] r:1з. Тогда она )'l(J!<lДЬШа
етсяq-рразвотрезкеCDнстолькожеpa:'Iв
равном ему отрезкеАЕ. Значит, в отрезке ЕС она
укладьшаС1ся р - (tJ - р) раз. Ита1.: , :эта мера
укл:щывается цсзюе число раз а -в стороне CD.
и R днаt'онани ЕС кнадрата .Q', т. е. srnняето1 нх
общей мерой.
АН::!ЛОL'И Ч НО ПOC'Г)IПl-lfl OTHOC IJTCJJЬIIO Q'. 11()-
Л}1ЧНМ кRадрат .Q" , Мt'НЬШИЙ Q', гакой , ЧТ ()
F
Рнс. 1.
1
'1
1
\
_I
561
Фунламент математики
УТВЕРЖЛЕНИЕ И ОТРИUАНИЕ
Каждый из вас безусловно сталки вался и с вер ны
ми, и с неве р н ыми утверждениями. Интересно
сравн ить, какие р ас.:сужле ния следует провести дЛЯ
то rо, •побы доказать утвержде н ие, и для того,
чтобы е го опровергнуть.
Начн ем с простого примера. Предположим, что
вы услышали такое высказывание: «Выражение
(х + 1)l положительно» . С п раведЛиво оно или нет?
Проверим. Подставим х = 1. Получим (1 + 1)2
=
=(2)2 =4 >О. Подставимх =2,х =3 ит.д. Всякий
раз будет получаться положительное ч исло. Мож
но считать при ведённ ое рассуЖАе н ие доказа тель
ством{ Конеч но, нет. Чтобы доказать утвержлеt1 ие,
нам п отребуется подстав ить все возможные з на
чен иях. А их беско~1ечно много.
Что нужно сделать, чтобы опровергнуть то же
высказывание? Пусть х =-1. Получим (-1 + 1)1 =
=01 =О. Ч исло О н е является положительным, чем
и доказано, что высказывание • Выражение(х + 1Р
положительно» неверно. Чтобы опроверrt1уть
высказывание, оказалось достаточ но привесrи хотя
б~..1 один пример, когда оно неверно . Вспоминается
известная п оговорка ~ ломать - не строить ~.
Эл1м обстоятельством ч асто пользуются. Лопу
стим, требуется доказать ут вержден ие : «В этом
томе имеется по крайней мере лве страниuы , на
юJrоры х напечатано оди11аковое число слов•. Ко
нечно, желаюший может посчитать, сколько слов
содержится на кажлой стран и це тома , и сделать
вывол, верно высказывание или нет. Но можно по
ступить п о-другому. По п ытаемся опровергнуть
выс казыван ие « В этом томе на любы х двух стра
н иuах ч исло сло"' различно• . Известно, что на стра
н иuе такого формата помешается не более 600
слов. А сколько стра н иu в этом томе~ П риведённое
сравне н ие доказывает, что две иском ы е страни uы
обязательtю су шествуют. Утвержден ие доказано, а
мы даже представлен ия не имеем, ~t a каких име~1-
но страниuах число слов совпадает.
нсикая общая r.1epa диаr·онали и стороны Q'
послужит общей мерой д11а1 ·оющ11 11 стороны
Q". Подобпым же образом для к:вщ~.рата Q" по
строим квадрат Q"' и т д. Возю-1кнст беско
нечная последовательность RСё уменьшающнх
ся кв:щратов Q, Q', Q".Q'",
.. , причём всяюtя
общая мера щ1а1·()11али и стороны квадрата .Q
будет в то же время и общей мерой диагонали
11 стороны квадрата Q', общей мерой диагош1-
ли н стороны квадрата Q", общей мерой диаго
нали и стороны Ю3адрата Q"' 11 т. д.
562
Те11ерь 11реююложим. что отрезок а, т. с.
общая мера диагонали 11 стороны квадрата Q,
укладывается в стороне кflадрата Q п раз, n сто
роне кnадрата Q' - п' ра3, в стороне квадрата
Q"-
п" раз и т. д. Поскольку эти квадра·1·ы
уменьшаютсн, топ> п' > п" > п"' > ... В резулt>
тате 1ю11учается бесконечная последователь
ность убывающих натуральных чисел, что,
конечно. невоз можно. Значит, исходное пред
положе11ие о 11а11нч11й у стороны и дпагопал~1
кнадрата Q общей меры неверно.
Использоваrшый здесь вариант доказатель
ства методом от противного, прн ко·1·ором ноз
никающее протинорсчис состоит в появлеюш
бесконсчrюй последова·1·ель н.остн убывающих
натуральных ч.исел , называется .меmт)о.м бес
конеч:ного (11лн бе:згранuчного) сиуска.
М атематические рассуждения
---- -
-
-
-
-
-
-
-
--
-
-
--
-
Н ЕОБХОЛИ МОЕ
И ДОСТАТОЧН ОЕ
УСЛО ВИЕ
8 матем атическ и х текстах часто
можно встретить слова « необходи
мо ~ и «достаточно». Повсеы1 ев
ный смысл этих слов, конечно, по
няте н каждому, но математики
вкладывают в н их более точ ное со
держа н ие.
Необхолимое условие лля ка
кого-либо утверЖАен11я - это лю
бое утверждение, без выполнения
которого данное утвержден и е
заведомо н еверно. Лостаточное
условие - это утвержден ие, из ко
торого следует данное утвержд е
ние . Лостаточное услов ие может
не быть необходимым, и наоборот,
необходимое усло в ие не обяза
тельно является лостато ч 11ым.
Привелём п ример условия
необходимого, но 11е достато ч но
го. Лля того чтобы четырёхуrоль
ник был прямоугольником , необ
ходимо , но не достаточно , чтобы
ero диагонали были рав н ы. дей
ствительно , диагонали равt1ы и у
равнобокой тра nеu1-1и.
А. вот приме р усl\овия доста
точного, но не необхолимо10 . Лля
,-ого чтобы четырёхуrоl\ьник б1>1л
nараллелограммом, достаточ но ,
но не необходимо , чтобы его сто
ро11 ы были равн ы. В самом деле,
четырёхуrольник, все сторог1ы ко
торого равны, - это ромб, а па
раллелограмм может и не быть
ромбом.
Ино гда указыва ют не одно, а
несколько разли ч ных достаточн ых
(или необходимых) усло вий. На
пример, ЛАЯ того чтобы четырёх
угольник был параллелограммом,
дос таточно вы полнен ия одного из
следуюwих услов и й :
1) две противополож ные сто
роны четырёхуголь ника равны и
п араллель н ы;
2) точка пересечени я диаго на
лей делит их 11оnолам;
З) четырёхугольник имеет uентр
01мметрии .
Особенн о важны условия, я в
ляюшиеся одновремег1 но и необ
ходимыми и достаточн ыми . Необ
ходимое и доста точное ус1ювие -
это любое утвержлег1ие, из кото
рого следует дан ное утвержление.
А п ервое утверждение само следу
ет из второго.
Необходимь1ми и достаточны
ми уСl\ОВ И ЯМИ S\BЛRIOTOI, напр и
мер, хорошо из.вестные признаки
делимосrи натуральнЬJХ ч1.1сеl\. Так,
чтобы чисl\о делилось на 3, необ
холимо и достаточно, чтобы сумма
ero uифр дел и лась на 3. Немало
подобных утвержле1тй имеется и
в геометрии: для тоги что б ы в
выпуклый четырёхугольник можно
было вписать окружность, необхо
димо и достаточ1-1 0, чтобы суммы
дли н его проти воположны х сторон
были рав ны.
Выражение « Необхолимо и до
ста точно11 в формул и ровка х часто
заменяют словами « В том и только
в том случае, когда» , « Те и только
re", .если и только если», атоrда и
толь ко тоrда, коrда ». Нап ример,
можно сказать:
1) тело является ш аром тогда и
только тогда, когда любое его се
чение плоско стью есrь круг;
2) треугольн ик со сторонами а,
Ь, с является прямоуrольным в том
и только в том случае, когда выпол
tiяется соотношениеа~ + IJl := с 2•
Теорему, выражаюшую необ
ход11 мое и достаточное условие,
называют критерием. Вот, на при
мер , кри терий арифмети ч еской
прогр ессии: числовая последо
вателыюсть являете~ арифмети
ческой прогрессией тоrдd и 1оль
ко тогда , когда каЖАый её член ,
начиная со второго , nрелста6/\я
ет собой средне е ар11фметиче
ское nрелшествуюше r<1 и nщ:ле.ду
юшего членов.
Пример 3. В статье <>Доказател ьства в матема
гикс~. говорилос~, о том, чтu уравнение х'1 +у' ' =
'
v
""Z- ir c нмес'l' решении среди целых ч исел.
Обыч1 ю этот факт доказывают методо м от nро
тию-юrо: предттола гаю т. что Су1.Ц естnуют 1·ри
целых числа а, Ь н с, которые являются реще
нием уравнения, т. с. а4 + Ь4 = с
2
, n<>сле чего при
меняют метод безграничного спуска: находят
ещё три целых Ltисла а', 1:/ и с', которые также
01ужат решением ура1щения, причём \ с'\ < \cl. За
тем берут трн числа а", Ь" и с", являющиеся
рrшением уравн ения, такие, что lc"I <lc'I, и т. д.
В резу11ьтатс 1юзтщает убывающая посJiедова
rелыюсгь натурэлы 1ых чисел: lcl > /c'I ::> /с"! >
>jc"'I>..., что невозможно. Значит, наше пред
положение неверно и уравнение х4 + у'= z1
нс И~\fеет решений среди целых чисел.
Пример 4 . Докаже м , что MIIOЖC..:CTIIO Hl"t.X
д во ичных n ослt::д ов;1тел ы-1 остей н ссчёт н о.
(Числовая посJ1едовател1)ность 1 rазы ва~тся
дRон ч1 юй, ес.11 11 каж,цы й её чле1 1 ране~1 нулю нли
еднннце. О счё111ых и 11есчё11 1ых множеств::~х
см. статью «Бесконечные мr южеств<н.)
Предположим:" что .множесТБо М всех дво rr<r
ных лоследователъностей счётно. Лересчита
ем множестRо л11 и обо:щачнм его n - i\ элемент
через а.,,. Этот эле-ме нт есть дноичная. ~юследо
ватет,н ость 1).11
.
1, а,1. !, ci.11
.,, ••• Таким oбp:.t:\i>M , а",;.,
е<..~rъ k-й член п-й IIOCЛCAOlia'J'eJ!ЫIOCTH.
Terr ep 1) нозъмём двоичную последовате1н,-
1юсть Ь, хотор::~.я отли с1ается от а1 с1юнм 1 -м
членом, от а2 - своим 2 -.м членом. от а.; - сво
им 3-м членом и т. д. Ясно, что nоследователь-
1юс1ъЬпесовладаетписа,,ниса,"ниса.>
l11
\
1
1
1
563
Фундамент математики
и т. д., т. е. ни с одной из последоnателыюстей
а11• llОСЛеДОВаТеЛЬIIОСТЬ h - ЭТО ПОСЛеДОВа
ТеЛЪНОСТЪ ~1 , ~2, ~~. "., где ~111 = l - ат.т· Значит.
предположение , что мы нерссчита.~ш вес rю
слс.:доRатс::лъности м1-южестщ1 М, неверно. О1е
довате1-.пно, множество М 11есчётно
Есл 1 r к:~ждой из последовательностей а 1, а ~'
а,, ... отвести строку, ci строю ~ размсс1•нт1, друг
под дру 1 '0м. Г() получнтся :~а п"н.ъ , н котороl1
члены <Хщ,,,буду1· рас1ю1 1а 1 ·а·1ъсн 1 ю дна 1 ·ана"rп1.
Потому и сам мсто.п. ,'\ОКазател~,ства 11а:~вал11
диагоNr./ЛЫ·LЫ...М . Он нередко используется в
до 1<ззательствах от противного. Диаrоrталr,-
11ы!I метод изобрёл в XlX столетни нсме 1 \
кий ма1 с::мат11к Гсuр1· Кантор. разработавIШLЙ
основы тс.:uр1111 множс.:стн.
ЛОКАЗдТЕЛЬСТВО СУШЕСТВОВАНИЯ
l
В математш<е большое значение имеютта1< на
зываемые док:азаmf!льстиа существовсщш1.
Самый просюй снособ доказа· 1 ъ сущестнова
ннс объ<:кта с з;Иl,:mными снойсгнами - ~-1то
указать (;"!'() 11, (1:13)1МС:е'ГСН , уб<:ДИТЬСЯ, ЧТО ОН
дt:йстнителыю обл~щает нужнымJ 1свойстR~м11.
Например, чтобы доказать, что ура вн<:нне име
ет rc::шeJ I Иt:, ) \OLl':;J'f'OЧI Ю ll ()ИL1eCJ'l1 каr<ое-·1 О е1·0
решение. Доказательства существова1 шя т<1ко
го рода называются 11pл"мыviiu или К.ОJtструк
тишtы.ми. Прямым, в частности, яшIЯетсн
доказательство сущеспюнанин несоизмери
мых отрезков: 13е11ь пара 11иаrопаль п сторона
квадрата прямо указана (см. статью «Доказа
•1 ·ельстна МС']'Одом от npoт~rnнo 1'0»).
Но бывают 11 косвет1ые ;~ою1зательстна су
ществования , когда обоснование факта, что
искомый объект сущестнует, происходит бе:1
npi:rмoгo указания на с:1м объе1<Т. Рассмотрим
11ecкoJJ ыю nрн меров.
При...'lер 1. t3 ш ах.м.аттюй партии чёрныс сд:.1-
лись после 15 -го хода белых. Требуется дока
затт" что хотя бы одпа из чёрпых фи1ур 1-111 разу
нс покидала своего поля (к ф111урам отнесём
11 лешк и).
f:сли 1ш1 хм:.1·1 ный мщ не рокировка , то nе
редвигас."Гся 1 фигур;~ , в случзе рокироuкн - 2 .
Чёрные усnел11 сдела·1ь l<.\ ходон, и no правн
лам игры лишь o,L1иr 1 из них мог быть рокиров
J(ОЙ. Поэтому самое большое количество
qёрпых фигур, сделавших ходы, - 15 . Всего же
чёр11ых фнгур 16. Значит по н:райнtй мере
какая -то из них 11с сделала ни одн01·0 хода.
Пример 2. В самолёте нетнт 380 пассажиров.
Докdжем, что rю крайней мере двое r·1 з них
родшшсь в один и тот же деш, года.
'564
Всего n Ю,rr)- .36"> или :$66 ,1\Пей. а пассажи
ров в с~молёте :)80 - значит, их д1 ш рожде
ния Hl' моrуг приходиться только на ра31шч -
11ые Jtаты Вообще. если нассажиров больше,
чем .~66. то хотя бы у Д1ЮИХ ДHll рОЖ,Цl'Нl!Я co-
Rll3/1.aIOT. А 1ютсс1 1и пасс.tжирон 366. не 11сю1ю
чt1 ю, чтu все он н род1·1л 11ch в раз ~ 1ьн:: дш1 1·о,1а,
НО ЭТО Малонсрuятно. (Ояласно теоr1111 вt·ро
япюстей , н случай ~ ю выбра 1 11 юй 1·т.11пе чнс
лешюстыо свыmе 22 человет< совпадет те днеr'i
рождения у некоторых тrз нпх более ве роят
но, нежели то. что у всех дпи рождения при
ходятся ш1 разные дни года.)
Ло1·ичесю1й прнём, использоnатпп,111 ~з прп
ведённом доказательстве, назьша<:тся 17J>11нци
иам ДиfJU.\..Ле - no нмснн Пстс::р.1 Г'уст:~в~1 Д11-
рихлс ( 18())-18'5<:>). немс r~ кого матсма п n<а ,
автор:~ оm 1санного мtтода . Нuт общан фuрму
шrро11ка 11р111-щ1ша Д11рихлс.':
Если имеется 1i я-щи~<оn, в кото1)1JХ
находится n общей сложности
нс J\<1ен:ее ·п + 1 предмета, то непре
меJmо есть ящик, в котором лежат
по крайней мере 2 предмета.
Пр101ер 3. Требуется доказать, что существует
хотя бы одпо нрр:щноналыюс числu - такоt:
ДСЙСТНilТСЛ:ЪПОС YllCЛU, которое НСJ1Ь3Я 11редста-
1шгъ н Rн,це 0· 1·1-юшения m/11 двул н а ·1')'Г'алы1ыл
чисе11 \см. статы<1 <·Ирр ацнонаньные чv1сла»).
Такое чнсдо - это \ 2 . В само:м дt:J1c, по те
ореме 1!нфагор~• . \ 2 сеть дн<~го наJ 1ь к1'щ1ч1ата
со сторо ной 1. F.сли бы оно выражалось отно
шен ием 11 :1·1уральных У!l сел т и п., то отрезок
длино11 1/п уклздьгвался б ы п pa:i н cтopoJJ e
с71и1111ч ного квадрат:~ 11 т раз него диагонал 11 ,
а знач 1 1т, был fiы их onщeil мерпi1 , что невоз
можно (см, с 1 ·атью "Дока:затедьстnа методом от
ПрОТl·ШПОГО») .
Мuжно пр1.:длож11ть 11 косвенное доказатель
ство. Поскольку множест1ю всех рацr ю11алы-1ъrх
чисел счетно, а м нuжес1· 110 всех дtйств11тель-
Мдтt:>матическиf' рассуждения
JН,L\: чиссJ 1 нtсчётно (с.м. с1·:1тью •Бсскuнечны с
м1южсст11а~). тu должны сущ~:спюкзтп дl:Лсгш1-
·1 ·~лы 1 ые ЧllCJl:.J, н е }lliJfHIOЩll CCH рацно11 ~1JТЬ НЫ
МIГ, т. с. числа 11ррац1ю11:J,11,ныl' .
При:ь~ер 4 . J)J,llj'1JOT случ.ан. r<о 1·да косвешюе
доказате;rьствп 1 ·ораз,\о проще г.рям оrо. На
пример, докажем, 'IТ() существуют траrrс цен
дсп111 ые числа. НапомшL\11, что действителыюе
число называется :1лrебра11"1сск11м, есл н оно
ЯНЛIJС'l'СЯ корнс.>1 Mll()J'OЧЛCH:I с целыми ко.-.1ф
Ф•·l l (l l(:: нтам11; к 11ро·1'ннном с1 1 учае это чнслu
тр:~r1сцснде11тнuс (см. статыо «Транс1(сндент
ные ч11с13-> ).
Прямое доказатсльстrю сущеепюt1аннн
тра 11 с г~енле11т11ых чисел заr<.точ;~ется ri щ1е;\ъ
>J 1тент111 011раз 1 (С'IН таких чнсел. Оказыnается,
/\не зпамешпы1.: константы с (осrrованис нату
рального логарифма) и n (отношенне ,rvтин ы
окружности к её диаметру) суrь трапсце 1 r.дснт
ные чнсл:1 Для того 'IТобы избежать доволыrо
СllОЖНОГО дuкaзaTt'J lbCTBa , сран111-1 м МJЮЖССТIЮ
всех Дt:l!CTИ llTCJIЫIЫX чнсел 11 МНОЖL'СТНО всех
:щгсбран•1ссю1х чисел. Первое нз r-шх, как мы
уже знаем, нссqёпю. Счё'1 r юсть второго с11еду
е1· из того. что каждое аJ11'ебранческое чнсло
мож1ю «Наз1:1а1ъ» - пр11 своить ему 11мя. Н ка
честве имен и 11rощс nсего взять выраже1n1с,
56')
Фундамент математики
состоящее из двух частей: 1) из записи соот
ветсТАующего многочлена 11 2) 1 юрядкового
номера рассматриваемого числа среди корней
этого многочлена (корни беруrся в порядке
возрастания). Такие имена уже нетрудно пс-
ресчитатъ. Если множество всех действи
тельных 1..rисел несчётпо, а множестuо нсех
алгебраических чисел счёпю, то существуют
числа, пе принадлежащие к ашебраическим,
т. е. трансцендентные числа.
МЕТОЛ МАТЕМАТИЧЕСКОЙ ИНЛУКUИИ
Метод индукции Rсамом общем смыа 1е состо
ит R перехо{(е от частных формуJ1ирово1< к
формулировке ушшерс::ит:ыюй. Метод матема
тической индукции приме~ rяется, когда хотят
доказать, что некоторое у-тверждение справед
ливо для всех н атуральных чисел .
Пример 1. Докажем, что всегда
1?1
n(n+l)
('")
+-+. + ...+ tl= 2
.
С этой целью установим два фаr<та. Во- пер
nьтх, для п = 1 утверждение (*) nерно. Действи
тельно,
1 = 1 ·(J+l)_
2
Во-вторых, предположим, что у1·вер.жденне
(*) верно JV1Я п = k , н убедимся, что тогда оно
верноидляп=k+l:
l+2+3+ .. . + (k+ 1) = (1+2+:)+ ... +k)+(k+l) =
= k(k+1)+(k+l)=(k+l)(k+2).
2
2
Значит, утверждение (*) верно для ncex зна
чений n: для п = 1 (первый факт), а в силу вто
рого факта - для п =2,откуда, в силу тою же
факта,- дляп =3ит.д.
Пример 2. Те м же способом легко убедиТ1'СЯ u
исr·ин~-юсrи сле~)'1ощ11х равенств ~три всех п :
2
?2 ~z
2 _ n(n+l)(2n+1)
1+_ +:)+...+п-
6
,
1-1+2!>+3·
1
+." +п~=(1+2+3+...+п/.
Таким обра:юм, изложеннън'I метод расс.уж
дения требует устаноnлешш двух фактов:
1) ,п:анное утверждение верно для l ;
566
2) если юттер есующее нас утвержд ение
верно для какого-то числа k, то оно верно и для
следующего за нпм числа k + 1. Когда оба факrа
установлены, тогда, переходя от 1 к 2. от 2 к 3
и т. д., убеждаемся в том, что рассматриваемое
утверждение верно для всех на1уральньLх чисе11.
Первый факт называется бази.со.м ин.ду11.1,(иu,
второй - zmдукцион.н:ы.м 11ерех.одам нли шагам
индук.чии. Индукционный переход u 1<mочает в
себя rюсы.тсу (или предпалож:е1ше) шtдук:ции
(утnерждение верно при п = k) и .заJСЛючение
(утверждение верно при 11 = k + 1). Другими
словами, шаг индукции состоит в перех оде or
посылки к заключению, т. е. в uьшоде , что зак
лючение верно, если верна посылка. В целом
весь логический nриём, 1 юзвш1JuОщий заю1ю
чить, что рассм<tтрн н<~емое угнержденне верно
для всех натуральных чисел, коль скоро спр а
ведливы и базис, и переход. назьшается npu11-
14uno.;. .i J11.ате.м.атич.еской индукции. На 11ём и
основан N.етод мате"мати:чес1соu uндул.,.,,щи.
Этот метод может быть успешно пр1rLченё11
в том случае, когда имеется некоторое утверж
дение А, зависящее от nар<1метра , прш111маю
щего натуральные значения, и требуется дока
зать, что А справедливо при нсяком ~значении
пара:мстра. В примере 1 у1 · вержден11е А имело
следующий вид:
)2
_
11(1l+l)
1+-+~>+...+п-
.
2
Сам параметр п пазыnается парш.и:mрQ;н
и11ду1Сu,ии. Говорят таюке, что происходит ин
Д)'lщия по данному параметру.
Утверждение А при значении параметра,
равном 1, принято обозна чать черезА(l ), прн
значении пар аметра, р;.~вном 2 , -
через А(2) 11
т. д. В примере 1 утверждение А( 1О) есть
1+2+3+...+ 10 = 10(10+1).
2
Утверждения Л(1), А(2), А(3), ". называют
цаспты.мu фор~~rулировка,~и, а утвержденнс
•ДГIЯ вСяl<ого п имеет мсстоА(11)» - уNиверса.ль
ной фор.i11)иировкой. Если ВhJразиться иначе, то
бази с 11нлук~~ни есть 11е что ин ое, как частная
формуJ1ировка A(l); шаг индукции - утверж
дение <.каково nы ни было п, из истинности
частной фор....1улиро1жи /1(11) 1Jытекает нети~ 1-
нос1·1, час1'1 юй формулирою<и А (п +1)».
Если мы до1<азали и базис, и шаг, то истин-
1юсть униnерсалыюй формулировки ос110 -
вана на следующем стандартном рассуждении :
•Утверждение A(l) истинно, поскольку оно
есть базис индукции. Применян к нему индук
ционный нереход, получаем , что исти н но и
угве рждс ние А (2). Применяя к нему индукци
онн ый переход, получа ем, чт о истинно и
утвержде 11иеА (3). Применяя: к нему ш-щу~щи-
0111 1ый переход, получаем, что истюп-ю и уr-
11е рждениеА(4). Этим способом мы можем ис
пытать каждое значение п и убедиться, •по
A(n) нстинно. Сле.поn ательпо, для всякого 11
имеет местоА(11)~.
Таким образом, nринJ~иn м ат<::матич еской
11ндукцин заключается, по сущес·mу, в разре
шен.1.н1 не 11011ьзонаться стандартн ым рассуж
де 11ием в каждой конкретной ситуации, т. е. он
позволяет сделать заключение об истин ности
у1 шверсал ы юй формуm1ропки сразу, как толъ
кп установлена истюп-юсть ба:шса инду1щии и
индукционного перех ода.
Пример 3. Докаже м с помощью принципа
математической индукции справедливость
нераненстна
(1+0:)11 ~ 1 + па,
гдеа.*О.а~-L.
Базнс индукции пыпш111еп , п оскольку при
п = 1 леван и нраная части нераnенстnа оди
нако вы . Формулировать шаг индукции начи
наем с предположения , что данное утверж
дение ве рно при п = k ; тогда посылка шага
индутщии есть (1 + a)k > 1 + ka. Умножая дан
ное н е рав енс тво на неотрицательное число
1 + а, 11олучаем
(1 +a)'(l+J~(1 +ka)(I +а).
Последнее неравенс~·во преобраэуем так:
(1+ a)k+t> 1+(k+ l)a+ka~.
В то же время
Математические рассужления
1+(k+1)о.+ka2~l+(k+1)а.,
откуда
(1+a)k~i~1+(k+l)a.
А это и есrъ заклю ч <::нпе шаг~1 и~-щукциr1. Мы
установили нст1шность и базиса, п ш ап1 . Дока
зате.1 1ы::лю методом 1·1ндукции зafj epmeнo.
Иногда nриходится дока зьшатъ утRсржде
ние не для псех 11атур:ты 1п1х чисел, а толъко
начиная с некоторого числа.
Пример 4 . До1<ажем, что сумма углов uьшук
лоrо н-угольш1ю1 panп::i п(п - 2) , где п - раз
вё рнугы й угол. Ясно, что привсдёш-юс утверж
дение спранедтню лиш 1, ттри п ~ .3 .
Чтобы мы могли при менить метод ма·гема
тической индукци11, слегка изменим фор!\1ули
ровку: сумма углов выnуктю 1 ·0 (п + 2)-уголъника
раш1а тт.п. Такое утверждение )7"'А<е имеет смысл
при всех натуралыrых п Базис !l:Оказываетс~ с
пом ощью тeope.illrы о сумме углов треугольника.
Теперь вынеде.м заюпоченне ипдукционного nе
рехсщз «сумма углов многоу1 ·ол ьника с сшслом
сторон (k + 1) + 2 равна тт(k + 1)~из его посылки
«сум м а углов многоугольника с число м е1·орон
(k + 2) р<~вна ттk ~. Н мнотугольннке с числом
сторо11 (k + L) + 2 возьмём две нершины,
ближайшие к какой-либо сщr-юй вер
unше, и соедю 1им нх диа гощ1лы(),
которая ра:юбьёт исхо,r{пый мно
гоуголы-1ИJ( на две части: на тре
угольник и (k + 2)-угольник.
Сум му уr·;юв исходного мноrо
у r'ольн ю<з можно получить,
сложив сумму углон треуголь
ника (она равна n) и сумму
у 1'лов (k + 2) -уголъника , nо
СJ 1 ед 11 ян (11 осылка 11ерехо1~а!)
составляет лk. Сю1адыная эти сум
мы, получаем n(k + 1) - то, что
нам и требоиа1юсь дока;3:а·1 ь.
567
568
Фунлам t' нт ма -rем атики
ПАР.А.ЛОКС ИЗОБР ЕТАТ ЕЛЯ
Попробуем доказать методом математическои иНАук
ш1 и неравен ство
13...(2п-1) f
<-,
-
.
.
2·4
...
2л v11
Баэис инлук uи и п роверяется без трула:
111
-<-=- ·
21~1
По предположению и 11дукuии ,
1·3 ·... (2k-1)(2k+I)
2·4
...
2k·(2k+2)
1З...(2k-1) 2k+1 1 2k·rl
-
-
--
--
-
<-- -·
24...2k 2k+2 .fk2k+2
и нам остаётся доказать, •1то
1 2k+1
·1
---~~·
Jk 2k+2 ~k+ 1
Возводя обе ч аt.ти нера венства в квадрат и и~бав
ляясь от з н аменателей , п ри ходим к эквивале нтному
неравенству
(k+1)(2k+1)2~k(2k+2)2
(**)
и далее, раскрывая скобки, - к неравенству
4kJ+8k1+Sk+1~4k1+8k1+4k.
Стоп - это неравенство н евер но! Слелователь
но, невер11 ы и неравенства ( **) и("). Можно считать,
что неверно и исход11ое неравенство~
Нет, нельзя. Наша неудача говорит лишь о -ruм,
что не rолится конкретн ы й метол лок.:~ зательства -
и 11дукuия.
Попрuбуем теперь доказать не::равенство
13...(2п-1)
1
<-= ·
24 ... ln ~п+1
Неравенство ( ***) с ильнее нащего исходно го
неравенства, и, казалось бы, доказывать его тем же
метолом - инлукuией - дело безналёжное. Все же
поп робуем.
Базис и нлукuии опять лаётся легко:
11
1
-
<-
= --·
2 fi ~1+1
По nрел11оt1ожению инлукuии , мы имеем
13 ... (2k- 1)(2k+1)
2 4 ... 2k (2k+2)
1·з ." (2k-1) 2k+')
1
2k+ 1
-
--
-
-
-
-
<--
·-
-
,
24 ... 2k 2k+2 ~k+l 2k+2
и нам fiaAO локаз.а rь, что
1
2k+ l
1
~--(~.
lk+1 2k+2 lk +2
v
\
Снова воз 1юля обе части неравенства в квадрат,
избавля ясь от з наменателей и р.:н:кр ывая скоб1<и , мы
п риход им к эквивал е11тному неравен ству
4k3+12k'+9k+2~4k3+12k2+12k+4.
О чудо! - это неравенство верно ! Слеловате11ь110,
мы док<1зали (метолом индукuии ! ) неравенство (**~),
из которого н емелленно выволим наше первоначаль
н ое неравенство.
Как же так получ и11uсь? дело в том, что хот51 во
втором случа е r-raм и пришлось доказывать более
сильное заключе н ие, но мы могли пользоваться и
более сильным предположени ем инлукuии. Подобная
ситуаuи я получила назва н ие ndралокс изобретателя .
Ило1да уrnержд~1ш t: не содсржлт параметр
в явном nиде, и требуется нзnестная сообрази
тель11ость, чтобы его вnестн.
Пример 5 . да1ю I<анеч ное м1южс:сгно прнмых
нз 1 11юскост11. Требуется /\Оказать, что части,
н~1 которые плос1шс1ъ разбит::~ нрямым--~-1, мож
но «п rавит)НО » раскраснть дву мя красками -
т. с. в резулътатt: никакие две части. имеющие
общую граи ицу, 11е будут одипаковог() цнета.
и~1енпо таr< раскрашивают rсо1·рафичес юrс
ка рты . И в нашем случае плоскость, разбитую
на части, тоже на:ювём 1<:.1ртой.
В nысI<аза rшом упзерждении о т.1·1урат)ных
У.11сщ1х ничего не CIGtзaнo, по~тому сформули
руем его и11<1чс: 1кs~кую к: 1р·1у, uбр;.~:;,01~:1нную п
r1рямым11, можно праRнльно раскрасить в дв;.~
цнета. оазис справедлив: rтрн /1 = 1 пряман ро в-
110 ьдн::~ , и д11е части, на которь1е он<1 делит rпю
с1<0С"1 ъ, мы лрост() 1<р :.JС нм различными цветами.
Пос1>111кэ 1-111ду1щион 1 юго шаrа состоит в преJJ.-
11оложени11, что правнлытую раскр~ску можно
всета осуществить н случае k лрнмых. 1 l ереход
от посылю1 к заюно чению (11равилыrую ра с-
1<раску »Сет·щ1 можно осущсствип, для k + 1
прю1ых) 1юка з~1 н на рнс. 1.
а
Рис. 1.
Пример 6. Выпукт,r й м нuгu~1 ·uлънш< 1~tликом
шжрыт дру1·им кыпуклым MI-t<Jl'OY l'OJIJ,HHKOM .
Тр~бустсн ) \оказать. что r1сриметр КН)Т!)сннс
го м110гоу1'ольн r1ка не 11ренuсходнт пер11метра
ннешнс:1 ·о много угол 1,н1 11<::1.
Назо11ём скободной f\CЯl,yIO стоrону внут
рt:нпего м11огоуго1 1ьпика, которая пе лежит 1ш
на од11ой из сторон внешнего. За параметр
индукцин примем количеспю свободных сто
рол плюс сднпнца (nосI<олы<у свободных сто
рон может и не бытh, а ш1раметр индукции -
натурш1ьное чш;ло). Уто~ним формузшроl'.КУ
11сход1 юt'О утnержле1шя: каконо бы нн б ыло на
тур<н1ыюс ЧИСJЮ 11, 8 П<tрс ВЛОЖСН ll ЫХ ОДШ-1
вдру1·ш1 многоуН)J[ЬНИКUВ сп - 1 свобО)\llЫМИ
Математичес"ие рассуЖд1:> ния
сторо1 1 а1\'1И nери::-.tетр nнугреш 1его м1ю1'О}ТОJJЬ
mша не превосходит перпмстра 1:mewнero
многоуголынrка.
F.сли снобо.цных стuрон 1-1 е1· совсем (в этом
заклю ч :tетсн 6:13 1IC ннлую {1 111 '), СП(ХIВ<.:ЛШ1ВОСТЬ
утверждения очевидна. П усть утверждс11нс
верно NlЯ нссх случаt"н, l{OJ'дa н 1шрс юю
жt:11ных м1ru1·оуГ(}JТ1>11J11\он 11меется k свобод
ны х сторо 11. Докаже .>v1 е 1 ·0 для всех случа~n.
ко1·да в паре вложен11ых 1'ШОгоуrо.r1ын 1 ков
ш"1сетсн /;.1 + 1 с.1юбодrrых сторон. Итак лусть
R - внутренни й мпоrоуrольни.к Т - 1.шеtш1ий
п коm1чсст1ю сгюбод~щх сторон k. + 1. Tpeбy
t:'l'бl доказать, что p(J() <, p('l).r;tep(l<) 1i fJГf) -
пернм~:-1ры мнш ·оу1·олы1 11кон П 11 1: 1Iролод
ж11м одну пз оюбо;\ных сторо1-1 (АВ) 11 обои:<
11а11р :н.1лсниях до псрссечс:11ий со с1·оро1-1амr1
мно1·оу1·ол1>1нша Т. Обrазуется nршvtежуточ-
1iЫЙ мно1'0у1·олып-11\ S, ·1·ак что R н.rюжс11 в S. а
S-в
·1: Чере:з р(,)) обозначим 11ериметр л-пт-
1 ·оуголы 1ика S. На рис. 2 r.шдно, что p(S) <р(Т),
rюс~<0J1ьку отрезок, стягнвающнй концы ;ю~-1<1-
ной, короче ca.• .io1'1 ломаной. НСJш тt'пс:рь рас-
01отреть лару вложенных мноr·оугольнш<овN
И S, ТО 11етрудJЮ З'1 МС'1'11"1Ъ - Н ::ПОЙ наrс КОJ\11-
ЧССТНО сноfiод11ых сторон Jia 1 мe11hwc: колн
чсстна снобо,~rrых сторон н ш~рс: R и '/. 01ю
ран1ю k. Деl1ствите;1ыю, сF1общ1,1 юi1 111::рсстала
б ыть та cтopur1:t (11а рис 2 егоро 11 аАН) м1ю1·0 -
:толы1ика R, с которой 1v1ы начали ло11011-
ш~тел 1.11ое построе1111с. З11ачпт, по предноло
жсниrо шщу~щин ,р(R) ~ p(S). СоедJ1.11яя да1 шое
1rераuепстrю с 11ер::11ю1стnом p(S) <p(J). полу
чсш1ым ранее, приходим к требуе:-юму 11сра
нс1 rс1·ву f.J(R) ~ jl(T).
N
l'и с. 2.
l
Фундамент математики
ПРИНUИП НАИМЕНЬШЕГО ЧИСЛА
Сущсстnует ещё один принцип доказательстnа,
тесно связанный с методом математичсс1<ой
11ндукции , - пртщип наи.лtен.ьщего числа. Он
гласит: н кажлом неnустом множестве нату
рзльных чисел существует наимен-ьшее ч11сло.
Этот принц1-ш может бы'!ъ использован для no-
CJ роения новою нарнанта «Ста ндартного рас
сужл,ет-тия» , тюторое обоснует нстю1ность у11н
версалыюй фОр/\1улировки. Если прежде при её
обосновании мы делали последователыlli1е пе
реходы от A(l) к А(2), от А(2) к А(3) и Т. д.. то
теперь будем рассуждать от протйв1юrо.
Вернёмся к примеру 5. Предположи~1, что
есrъ нек:~я карта , которую неJLьзя правильно
раскрасить. Образована она п пря.\l{ыми. Назо
nём :по ч:исло 1z *Плохим» . Если <·плохие» числа
сущестr~уют, то множество всех такнх чисел
11еnусто. Согласно принципу 11а11ме11nше 1·0
числа, в мпшкестве «ПЛ()ХИХ» чисел есть наи
меньшее «плохое» число а. В силу базиса ин
ду1щии,а:;t 1.Значит, а=k+1, гдеk - нату
ральное число. Поскольку а - н~шменьшее из
« Плохих» чIIсел, k не яюшется «плох~1м» Сле
доватtльно, вснкую кар1у, образованную /е пря
мыми , можно прзnrmьно раскрасить. Но то1·д;,1
н соотнстствии с 11ндуктивным пшrом удаётся
пра13ильно раскрасить всяl\ую карту, образо
uа~шую а = k + 1 прямыми. Мы 11олучил.и 1.1ы1.юд,
противоречащий исходному предположеr 1 иrо.
Следовательно, карту. образованную 11 прямы
·"'ш. ~южно раскрасить правильно .
ПОЛНАЯ И НЕПОЛНАЯ ИНдУКUИЯ
Говоря об 1 rндукции вообще (т. е. не только в
матсматr1ке), различают палную и неп олную
индукцию. Применяя полную индукщ rю , мы
J 1н1щ, то1·щ1 сч11таем себя впра1:1е объявитn об
истинности универсалъной формулировки,
когда убедшrись в её истинности для каждого
без исюпочения значения п. Метод неполной
и1 rду~щии состоит в переходе к универсальной
формулировке после проверки истшпюсти
ЧЗСТ НhlХ формулировок дл я ОТДСJIЬНЫХ, но
не всех значени!'1 1z.
В повседневной жизни JVLЫ постоянно поль
зуемся методом нелолной индукции. Так, желая
ку11и·1ъ ябл оки, 1 1робуем одно. Если оно нра
нится, покупаем, например, 2 кг, рассудив так:
570
~Если одно яблоко хорошее, то и все хоропше>) .
Это и ссп, метод неполной индукции в дей
ствни. Одн~ко IIC ИСКШОЧСIIО, что все куплен
!IЪIС яблuкн окажутся шюх11ми. кроме того
однОГ'О. которое 1vtы попробовали. Другой при
м.ер. Маrазин :'iа~rупает пар-п1ю }{блок, и тов:~
ровед проверяет не одно яблоко, а по несколь
ку ПJl()JЩJ:J н:~ 1<аждоrо ящ11ка. Rслн пыбранныс
яблоки спелые, то ма1·азпн: прнмет решение
<· все яблоки спелые». т. е. поспаm,зуется мето
дом пепоmюй ипдукцни, и закупит все ящшш.
Даже универсальные законы природы форму
лируются на основе отдельных наблюдений.
А потому н наши новседневные решения (ска
жем. о качестве яблок) , и научные ны1ю~ы (на
пример, о законах природы), есш1 они выска
заны н виде у 11иверсал ы1ы:х формулнровок,
верны не абсолютно, в лучпrем случае лиш1) с
t1ысокой степеныо прав1щподобия.
Иное дело математика, истины которой при
зпа ются незыблемыми. Метод неnошюй шrдук
ции, используемый n естестве1111ых 11ау1<ах, в
мзтематпке н е имеет лр:1ва на существов;шие.
Нере;1ко случ;:~ется , что частная фор.мулировюt
А(11) верна для ОТ/\е_r1ы1ых значений п, и вместе
с тем не удаётся найт11 таки х з11ачен111'1, для
которых она нсвсrна. Tor/\a c<..~rh оеt-юАа 1111е
предположить. что универсалъная формули
ровка истинна , - по всего т1111ь предположить,
поскольку то, что пе удалось rtайти сегодня,
будет, возможно. откrыто завтра. Вот три при
мера , говорящие о то.\1, что метод неполной
инду~щии в математике не работает.
Числа Ферма. Знамсн11тый матем~п11к XVII в.
ТТr,ep Ферма изучал числа вида 2/' + 1. Их та.к 11
назв<ШИ - чнсла Ферма . Учёный 1юш11·а.r1. что
ncc эти числа су1· 1, числа простые. И у него на
то, ка:'iалось бы , имелись nс1юва! 11 1я· /tейстн11-
тельно, чнсла Rида 2!." + 1 являютоJ. простыми
прип=(),1,2,3,4 Однако11ХVША.Леонард
,,
nйлер обнаружил, что число 2- + 1 ес.ть про-
извел,енне двух простых <-шсел 641 и 6 7UU 417.
Более того, ш:извеспю, с.уществуют ли простые
числа Ферма помимо пят11 вышеуказшшьrх.
Трёхчлен Эйлера. Зна чения , принимземыс
трёхчленом х2
+ х + ...J .1 (указ:~н Леонардом Эй
лером), smлятотся простыми числами прих= О,
l , 2, ..., 39. Одна"о при х = ...J .O его :шачепием
будет число составное. а имешю 41 2
•
Матемап1чесю1е рассуждения
ОПТОВАЯЛРОДJIЖА ФРУКrоВЪ
•
\.~р - nростоеЧlf
~-"
=-----~ <4-о
Двучлен х" - 1 . Еслм разлагать двучлен х" - 1
на множители при различ:ньеr з.начен 11J1Х п. то
окажется, что у .каждо1·0 из многочленов-со
м ножителей коэффици-ен1ъ1 равны либо J. ,
либо -1 . Нап~имер, х
6
-
J=(х -1)(х+1)х
х (х2
+ х + 1)(х - :х + 1). Была впrсказана гнnо
теза, что это сnранедливо для тобого п. Одна -
АКСИОМЫ
Крупнейший древ11егрсчес~-..-,,1й мыслитель
Арисготель (JV в. до r1. э.) создал основы логи
ю1. К тому времени: Фалес уже 1щёл 13 матема
тику рассуждения н доказательства (см . статыо
«Фалес и первые .п;о1<азател~.,с~а»). Аристо1ель
учил, что изложен.не теории должно начинать
с первоначальных предложений - аксиом,
из которых выводятся д<!льнейшие факты
(тео ремы).
Первое аксиоматическое построение гео
метрии предложил Евклид (см. статью ~"нача
ла" Евклида~). Исследуя доказател ьства теорем,
Епюn-t.Д выделил те самые простые, «Очевидные·>
положе~ rия, с помощью которых .п;ока зынаютс.н
все теоремы . Так он получил cucrneJJ~/' ал,сиам
ко доказать гипотезуучёным почему-то нс уда
валuсь. А 1:1 19,11 г. выяснилось, что указа11 -
нан особенность разлuже 11ия н нучлена х" - 1
н::~ множители существует 11рн всех п до LO..+
включительнu, а в случае 11 := 10'1 rюянля<::т-
01 м11ог<Jчлен, отдельные коэффициенты ко
торого равны -2.
(или, как ттюрят, аксноматику) 1·еометрю1. Нот
две аксиомы , сформулированные Евклнлом :
«че рез две точки можно пров1:тп1 прямую?; «nо
рознt1 рапны е третъему равны меж,1~,у соб<Jй>).
Современный подход к аксноматr1ческому
построению некоторой теор ин состоит в сrrеду
ющем. Во-первых, указываются перuоначаль
ныс (11еоnредепнемые) пошrтня. 13 геометр.ин
к 1шм относятся: точr<а, прямая, р:~сnоложсш 1с
точки на 11рям ой, равенство qшryp 11 /\Р Даль
не1-1ш ие понятия нводятся с помощью опреде
лений. Пранда. Енкли11 rюпыталсн опрсд<::лить
все понЯ'П'fЯ. включая и псрвоначалъныс. На
пример: <·точка сстъ то, что не имеет ч:1стей».
т. е. Щ\еализированная , геометрическая точка
57J
Фу1-1ламснт матt:матнки
лн 1 11 е1:-1а р;,с~мерок. Но, конечно, это н<:: точ1 Ш<:
математ 1,гчсскnе оп рс:дслс 1 rие, а на 1'лядн< к: оп 11-
сtt н нс точки, как че1 «>-'1·0 1 1 редельно малого.
C1·011i, неясным определе нием точю1 ЕnкJJид
пигf(е не поm,зуетсн.
Во-вторых, после перечнслепия первона
чальных (11еопредсля:емых) поняп1й формулн
руются ~ш:сиоN11>1 - псрrюнач<111ыrr.rе п оложс
шrя, ук:tзывающне на с1шз1. между понятнями .
Вопрос об «Очев1щноспн ;1 КСИ()\1 не r:н:смат
рнвается (к тому же нечто. оченидноt одному
человеку, может показаться 11ругому со нсе м
нс оче1тдным). Далы-1ейшие фак~ъ1 - теоrt:мы
дока:-~пrRаются на оо r1та1 п1н аксном н \'Же дrжа
заJ нJь1Х теорем. Это означает, чтп, J:1~третъих,
должны бытъ чётко сформ ули рованы правила
пьшода - те лоrнчсскне срсдстnа, которые; ис
пользуются прн докаэательствах.
Разумеется, ат<сио.мы (;i таюке понят1,1я) -
шюд многовековоru ш1ьп«1 чело1к·чt:стна. IТ0'1 ·0-
му-то абстр:.~ктно сформулиров;ншыс акс1юмы
11 11ыводI1мые нз 11и х тсорt:,чы тесно сnязан ы с
жнзныо. ()днэко прн ч 11сто акснома1·нчес1<0м
1юL·троепин теорил rюпрос о nр()11схС>ж11,е111-111
аксиом, об их пра1сrпческоi1 зпа чи.vюс1·и пс рас
сматри13аетсн .
Ешишд пе пш1ностью осуществил :шсиома
Т11 '1еское постросн11е геомстрин. Оп часто
обращался к 11аJ·шrд1юстн чертежа. что при
<111сто :1ксиомат 11ч<::ском построении тсорни
не доnускаетоL llanp11мер, 1 ·оноря о сно1·1ства"'I:
г1р11моуголы-ю1·0 трt::~'l'ОЛьНJ1.Ка, J:::ккJ11щ сч11тал
понs1тным (ссылаясь на чеm·ёж), что 11срне11-
д11k.)'Ляр, опу1цt:н111>11! п:{ нсршr111ы пр.н ....101 ·0 углз
на пнюте11у·~у. ll[ЮХощп · ннуrр11 ·1ре:угот>11111{а,
т. е. основанне перпс1щr1куляра лежнr меж!()'
котща11ш гппоте11узы (а пе вне треугольника;
рис. 1). Но что :~начит «между·>~ Ясно, что речь
llДёТ о сщё одном llOII0,\11 ПОПЯТllИ геомстрш1,
11, следов:-tтсльно, нужны аксиомы. описываю
щие его с.войств<1 . Ведь слова «смотри!» и ~оче-
с
А
А
О
в
Рис. 3.
P1t c. 1.
572
н11днu~ н качестс 1юдтнерж;\еню1 каl\01·0-тn nu-
ложе1-111я для стро1·ой <1ксиома·1·11чесl\ой 1't;Op1 rи
11еvмсст11п1 .
Поэ·гому, 11есмотря 113 то что "начма » Евк
лида была великолепно написаны и служили
основным у•чебrшхом гео.метрни в теченне
более дJЗух тысячелс.-тиi1, многие математ11ю1
пьггались дополптъ евкmщову спстему акси
ом 11 доnt:сти её до совершенстка.
Н XIX н н с мецкнl1 м:1тематнк Мор1щ !Ъш1
сфоrмулнrонал нескuлr,ко акпюм n рас11uло
жен11н точек н прямых. Н::шр11мср: 11:3 ·1рёх
разт гчных точ1:к на 1rрямо1I o) t11a 11 · голhКО од н;~
находи·1~ся между двумя другим11 (р1к. 2). Эт:~ 11
друrне аксиомы, ~<асающ11еси сво11ств понятия
«меЖД)';>, лозволmот определить отре:ю1<: ест1
А и В - две различные точки, то отрсзоr\ с ко11-
цам11 А 11 В сод<:рж11'1· все точк11 нрямой АВ, лс
жащи<.: м<.:ж.цу А и В, а также с;1м11 точкн А и В
(кuнцы ()тrезка). Из опре:дt'ленин 11 аксно~1
можно лоп 1чссю 1нынссл 1рн/\ сно1\стн uтрсзка.
н Ч3СТНОСП I , такое: t::CJllI с 11 j) - [\ВС TOЧJ\rl ()Т
резка ЛВ, 1 о вс-сь m ре:юк r.л 1\ел111<0м со,11;ер
ж11тс» н отрс:ше АВ ( рнс. 3).
Следующая ;11<сном::~ П;iwa гоnорнто распо
ложснин прямых 1ra плопю сти: если 11рямая.
нежащая n 11лоскост11 треугольника 11 не про
ХО/~я1щ~я rш через одrгуиз е!'О всршнн, пересе
кает одпу нз с.тора~ 1 треуголън11ка. то 011а обя
затt:льно 11<.:peCt'LLfT ОJ~ ну И:.i 1\Вух .цру1 '.ю:: ег·о
сторо н (рнс. L1) ИJ1аче ~·онщ1и, RХодя к тре
у1·олы111к Чt'ре:~ OJ tH)' сторону, Пj)}!J\1:1.и нс: может
ост:пье>1 ннутрн его, ~ выхо/\IП из тμt.·у1 оль-
11r1ка, пересекая к~ti<) ю -лнбо нз /\fl)'. X д[))'l'J 1 х е1· 0
стор()11
Еm.ё одна акснт1а была добавлена (вскоре
после тш·о, 1~ак Евкпид наmкад с1ю11 (• Начала->)
вели ким матеl\·1аnпюм дрешюсп1 Ар:хпмедом:
• присоединяя дР)·Т к дР}ту о·rрсзки одной и той
же длины, .'-·1ы рано шш поздно прсnзоlщtм
любой 0111сзок» Акс1- ю,V1<1 Apюfi\1c;1a н1 ·рает наж-
в
спв
Р11с. 5.
H}lO роль пр11 иэмсрснии отрсэкпн (см. сгатыо
•дmш<t. rиющад~,, объё;\t»). За.четим также, "!ТО
;~кстюма Лрхамс.:11<1 исноль::~ует<:я и в математи
ческом ar 1ащще прп аксиомап1ческом описа
нни mюжестuа действительных чтrсел (т. е чис
ло1юй прямой). I311роч<:~. за последнее .время
пробуl1.1 шся интерес к неархимсдовой гсоме1·
р 11 и. неарх 1 1ме;101Jу (нест~щцарл-10:-.1у) ана111 1 ~у
11друп1м тt:ориям. в кuтпрых аксиомаАрхпмсда
:!:1ме11яется с:ё отrи1 tа н нс м .
А.ко1оматнэац~1я t: 11 клнлоноf1 1·еомстр ~н1
бьиа :.1анерше11а на рубеже XIX 11Л'Х с~·олетий.
ПоJ\ы1·ткнR вес пrед1,щущ11е нсследоnа1нщ ве
чецю 1 й математш<Дапид Гильберт в юшrе ~·Ос
нования геометрии» ( HN9 г.) пред.'тожш 1 пол
ный списокаксаом евклидовой 1·еом<.:трии. 011
содержит двадцать ~\ксиом, которые а 1пор
р~tзделил н а ~ш1ъ групп.
П<:рвоначальные ш<с1юмы F.кклид;.1 Rходят н
первую 1руппу - нх называют сисси1.1м,ами со
rйин.еюtЯ. I< нпм отнооп·ся llксипмы о том, ч·ю
чере:.~ каждые две тoчJ( t J проход1·п пр}1 мая, и
прт·ом толы<о одна; что 11а каждое~ прямой
ш1сется не менее д1:1ух точек (~того 11остаточ-
110, чтобы потом доказать бесконечность мно
жества точ ек на прямой): что сущсств~1от трп
точки, не лежащие на одно:й прямой. и др.
Вторая грунпа объедш1щ:т ахсиоАtЫ 1ю
рядка, которые 01шсын:1 ют <..'войстно тоt1кн н1е
ж11ть между·> ;щумя друrим н точкамн на прямой.
Сюд;,~ отн осятся так.,,кс аксиома Морнцз П:uаа
о лерс<..'ече1 rии прямой с трсугол ы 1 иком н дру
п 1 е аксиомы.
Третья гpym1<i - aкci1nJ11t'ЬI 1шн2руэнт1юсти
(т.е. геометрического равенства) Сред11 J-111X -
первый и nторой приз~ ~аки равенства треуrоль
шшоп (рис. 5). Они у Гильберта аксио.мы, а
ие теоремы. Дело в том, что Евклид на<mнает
сво11 доюэательства с1юва м н: (,НаJюж.им один
грсугольник на другой ПJК, чтобы ... <> . И н аqе
t'ОВоря , Евклид применяет ютжения, хотя
р<1нъше об rr:x свойст11<1х речи не вёл. Значит,
строт творя, Rвклид прнэ 1 rа ки равенства тре-
Математ~1Ческие рас< ужл~ния
Рис. Ь.
уго111,ников 1re доказынает, ~1 тол 1 .1<0 пояс11яе1.
Потому-то Гпльберт и объяu~и этн nр11знакr 1
не теоремам11. а акс1юмамп. Другие зкс1юмы
дашюй группы хорошо з 11а1юм1.1: u нш.; утuер
жл.аетсн . что равенство фнг~11 есть отношение
эквив:итентности (см. ста1ъи <·Опюшения ·> и
« Геометрия 11 1 ·μуппы преобра:юва1 11 11'1 »)
В четнёртую 1·ругшу нхсцнт только одн:.~
:аксиома - иксио.ма параплелыюсти (см. еrа
ты1 <>,,H:J ч :lJJa"' Евклида" ~ 1 ~гсол.1етр1нr Лоба чен
скт'()»).
Нако1н:r\, пятая r·rp1пa объединяет ил·с1юА1ы
1 1 е11рерывност11 . Например, нз этой группы
аксиом вытекает. •по сели точ ки А и 1J распо-
1южень~ на плоскости 1ю разные сюроны от 11с
которой прнмой /, то 11рямая АВ имеет общую
точ.ку с прниой f ( рУ!с. 6 ).
ЧТО ТАКОЕ Н ЕП РОТИВОРЕЧИВОСТЬ
АКСИОМАТИ КИ
Гпльберт не тn11ы<0 1гtал 1ю1111ую спстему акси
ом евклидовой геомечхш, 1 ю и до1<азал её от-
1тоситетшую 11епротшюре•ш1юсть. Пшr<:тп1м,
что это зна•шт на простом прнмсре с тремя
акс1юмамн (а нс с двумJJ дссятт<ам11 аксиом , к:.1 к
в аксиоматике Гильберта).
Уч еникн хотели ор 1 ·ан11~-юв:пъ ш;.~х,\1атныl1
тур111 1р . Чтоfiы улож11тъся н болt:t короткнс
сроки, они решш~и пршзест11 спJ no упрощ~н
ной схеме:· 1<;1ждый н 1 ·rает por~• ro трп п:1р·1 ин
(по зара11ее состамепному pacnrrcar 1ню), а бе
;1ымн 11 JIJ1 черными - П() жреf)шо, Н о расп11са-
1 ше составить никак не улаnзлось, и де-тн об
рат~-шись к учителю. 1la его вол рос, чётно ли
число участников. уче11ики. посмотрев сm1сок,
ответшш , что число участнит.юн нечётно. Тотj\<1
учитель предложил ГJ(Щ<>йп1 к вопросу акс1ю
матичесю1.
Он рассуждал так. Имеются трJ[ первона
чалnных понятия: «ИГ[ЮК•>, Нl а{lТИЯ». «учаС:П·I С
нгрока R партии » - и СJ I С/\ующне <1ксиомы·
573
Фундамент математики
~ис;ю игроков нечётно; 2) I<аждый игрок
1
;~з:".нует н трёх пэртиs1х; 3) в каждой партии
учзствуютдR;.~ игрока. С rюмощью этих аксиом
можно доказьшать теоремы . для чего введём
1ю1юе понятие: еслн g - r<акая-то napт1t>J н А
-
один из 11грсжоn, которыJ1 н ней участвует, ·1
·0
пару (g, А) 11азовём выстуnлеt111ем нrрока. За
тем: уч1--rrел1, доказал теорему: чнсло всех вы
стуnленшvr иrроков нечётно. В самом деле, каж
дьв1 игрок участвует ровно в трё.х партиях
(аксиома 2), а п отому число всех выстуш1ен11й
игроков равно 3n, где 11 - число участников
1урн11ра. Так как п IJечётно (аксиома 1), то 11
312 нсчёпю.
Но од11н 11з школьников возразил, что он
мож~т доr<аза1Ъ чё'пюсть числа выстуnJJений
игрокоn. Действительно, сслr1 в партии g уча
ствуют игроки А и В (аксиома 3), то выступле
ний игроков Д13а (.q, А) и (g, В). Значит, число
всех выступлений игроков ~1ётно, лоскольку
оно вдвое больш<: числа всех партий.
Итак, из трёх п срвоначш1ьных ~1ксиuм пuлу
чнлн две теорсмh1, противоμечащне ;1ру1 · другу,
поскольку одно и то же число не можt."Т' быть
одноврсм.снно и чётным и нечётным. Иначе
го1юря, взятан аксиоматика 11ротиворечнщ1 , а
слелпватеJ 1ы ю, трсбова1Jня, сфuрмулиrова 11 -
ные школnпикаыи, 11есовмесп1м1.1 . Теперь по
нятно, почему детн не смогm1 составит~, распи
саrrие, - его просто не существует
Тогщ1 учитель пр~::дложил оргаю 1зuвать rур
ннр иначе: каждый участник 11.олжеи сыграть
не три., а четыре п311тю1 с кем-либо нз остаJJь
ных уч::~стюrков, т. с. оста1ш1ъ <lксиомы 1 и :)
без изменения, а аксиому 2 замен1-пъ на аксио
му 2': r<аждый игрок участвует R четырёх п:-1р
тиях. Причём учителr, заверил uнюлы-Jикоn, ч то
теперь никако1 ·0 противоречия 11е получится.
Вот как учитель убедил их в ЭТ()М.
Рассмотрим праnилы-1ы11 девятиуrолышк
(рис. 7) или мrю1·оуголыш1< с mобым ш::чётпым
числом сторон, б6m)Шl·ш трёх. Провсдём в н<::м
все /tиагонали, соединнющие верпп1ны через
онну. Верш11ны девятиуrолhника будем сч1тта:rh
и 1'рокзми , стороны 11 диагоналн - партинми,
а концы отрезка - игроками , участвующпми в
,1\а1 rrюй партии. В резутi1"ат~ мы построили мо
дель интересующего пас тур~ 1ира, поскольку
аксиомы 1, 2', 3 здесь выполняются. К тому же
модель построена из «Матерпала» гсометрип -
пауки, в неnропшоречивости которой никто
не сомневается. Если бы, исходя из аксиом 1,
<574
Рнс. 7.
2', 3, мы получюш две противоречащие друг
другу теоремы , то доказатеш,ства послс::дних
можно было бы повторить 11 в полученной
модели. и~1ы~ш словами, рассуждая о прав11ль-
11пм девятиуrолы 1ике, мы приmт r бы к двум
про·1 · ююречаmпм л.ру1· другу теоремам, а зна
Ч11Т, и к выводу, что геометрия - паука про1·н-
13оречивая. чего 1ш один нз нас не допуст<ает.
Очсв11дно, что па основа1111и акс rюм 1, 2' и 3
нельзя 1:шве с·1 ·11 две противоречащие друг другу
теореl'-'lЫ.
В общем cJJyчae пусть рассматриваются две
тео рюr А 11 Х nрнчём теор~н1 Х зал.аётсн аксио
матически (и в сё непро·rнворсчивости мы ~<tpa
нi::e не увере11ы). ТеuрияА 1-1 ам хорошо 11знеt.1'11<1,
и в её 11епротиворечи1юсти мы 11е сом 11 еваемся.
Есш1 из материала теорин А удастся п()строить
мо;~ель. в которой выполняются псе ат<с1юмы
теории Х, то этим устапаnливается непrютюю
рсч илость теорип Х.
В с..'Тат 1,е <-Геометр1Iя Лобачевского» расска
зывается, как J J11 колай Инанович Лобаченсюн\
пользуясr) матернал ом СRОСй <>воображаемu11 •
1·еометрн11 , смог построить J"юдель 1'еометрш1
Евюшда 1ra поверхности, ко11·орую наз1:1:ш uри
сферо 1~r. Одпа1ю ЛобачсRско1·0 прежде все1·0
·интересовал противоположный реау11ьтат:
если мы не сомневаемся R непротиворечиnос
ти геом.етрпи l::m<лrщa, то 11спротиворечива и
« nоображаемая» геометрJ.ш. То есть надо было
из матершша евюшдоnой п:омс.."Грни постро
ить мо;~е;1 ь 1 ·со метрин Лобачt'вского Но он
такую модель созмtть не смог. Пе 1юстронт1
(уже после смерт11 1'eri 11 .im,нoгo матсмат11ка)
Фс1шкс Клей11 и /1.ругие учё11ые. И тем с:~мы,\1
установили, что обе п:омстрии - 11 Евклида, 11
Лобачевского - одш1аково непротивореч11вы
Если непротиворечива од11::1 , то же вер1 ю t-1для
др~той, и наоборот.
Однако как же док<~зать не 11 роти воречи-
1юс·1ъ евкд!'щовой 1·еометрии:? Оrедуст tюстро-
1тгь её мoдell J>, u которой ВЫПОЛШIЮТСЯ все
аксиомы Гильберта. Но материалом для 1 1 её
должна послужить каf(ая -то теория А. в непро
тиворечивости которой никrо бы не сомне
вался. Гильберт оnнсал таку'10 модель.
В качестве теории А, непротиворечивость
которой несомненна, он взял теорию действи
тельных ч 1 1се.11. Идеи nостросния модели соего
яла в рассмотренни системы координ<~т на
шюскости . В такой системе каждой точке А1 на
mюскости соответствуют дв~1 дей ств11тельных
ч1 1сла х и у - её координа1ът (рис 8). Чтобы
попять суть ттостроет r ия модели , забуде~1 о
11;юскости и об имеющейся тта 11ей ксюrдинат
ной системе; условимся назьшать «точками->
упорядочсш1ыс пары действительных 'ПiССЛ
(х,у),т.е.пары (х,у) и ()', х) с различными х и
у будем считать различными.
Ит:Jк, «точки~ у нас уже есть. Что же такоt'
4Прямая->? Вспомним, что кажлая прямая опи
сывается В f\()()rДИH:lTaX ЛJIНеЙНЫМ yp:ШHt'HII
CMах+Ьу+с=О,щехотябыодиниз1<оэф
ф1 щиептnn а и tJ отличен 0·1 нуля Например,
ур<1в11е1111е прямой, не параю1елыюй осн ОР1'f1 -
нат, имеет виду = kx + !, илтr, что то же самое,
ах+Ьу+с=О,гдеа=k,Ь = - 1,с=1(рис.9.а).
Если же пplli\1:1Я параллельна оси ординат, то
Рис. 8.
у
у ---- -,
х
о
х
Рис. 9.
у
а
у
б
1
1
1
~·11 1
:-.: :
1
1
1
1
х
о
Р'1
о/
,
,t
Математ и ческие рассужлен ия
ей соответствует уравнение х = р (т. е. уравне
ниеах+Ьу+с=О,гдеа=1,Ь=О,с=-р,
рис. 9, б) . При этом если 1:1се коэффициенты
уравнения ах+ hy + с = О у.11-шожить на ())\НО и
то же число k:;: О, то полученное новое ура нне
пие н1 юuь огшсывает ту же 11рямую. Теперь за
бу,rtем о геометрии и бу11см называть «прямой»
в рассматрпваемой модели mобое лш 1ей11ое
уравнеrше ах+hy+с=О, вкотором хотя бы
один из коэффициентов а и: Ь отличен от нуля.
П ричё.м коэффициенты рассматриваются с
точностью до ненулевого множителя лроnор
цшша;1ьност11 (при k *О уравнения a:x· - i
/Jy +
+ с= О и (ak)."J..· + (bk))' + ck =О считаются одной
и той же '·прямой»).
Далее, «'l'()чка» (.х 1 ;у 1 ) nеж1 1 "1' на ~ прямоr1 '·
ах+ l'J)J +с= О, если чисJ1а х1 иу1 удовлетворя
ют у1<азанному уравнению Как видим, 1!)1Я оn
ределепия <• прямых ·>, «точеt<» и расположения
точки па «прямой » не надо знать ничего, кро
ме действитслыr:ых чисел. Леп<о проверить, что
в рассматриваемой мuдслп выполннются. ш1 -
nр11мср , такне аксиом1,1 .
через две различные <'Точки+ прохо
дит «прямая»;
на "прямой» имеется не менее двух
~точе1с" .
Легко определить, в каком случае одна нз
трёх «Точек» на <'ПРЯМОЙ* находится « между"
л:вумн дру1·нми. Когда А(х1: у1), B(xJ.; у.!) и
С(х ,; у,) - три <~-ТОЧУ.и», н еж:ш.1.ие н:1 одной
«прямой», ~точк~н В счнт::tется р~спшюжс:;н1-ю1!
« между» А 11 С пр~~ условн11 , что числох2 эаклю
чепо междуxJ11 х, (если х1=л:2=х" то)'~ за
юпочено между у, rry1) . Tor11.a яс110 , ч · 1·0
из трёх «Точек·>, лежащих на одной
•прямой", одна и только одна распо
дожена между дву~ш другими .
Выполняются и дpyr!fe аксномы 1юряд1<а
(в qастности , прнведё нная выш е ~ а ксиома
Паша») . Заметим, что мы специально не ил
люстрируем содержание а1<с 1 юм чt:ртсжам11 ,
поскольку при чисто акоюматиче\1<ом 1-1:1.110-
жепии не слелует нсп011ьзовать привычные
геометрические nре11.стаnле11ия.
Будем го.ворить, что две «прямые» а 1 х + h ,у +
+ с1 =Оиа~х+bly +с2=() «параллслыпм.если
575
L
Фу 1 1дамент математики
коэqJфищ1е11ты а1 , Ь 1 и U2 , ь,! 11ропорцио11алы-IJ>I .
Это мож110 Щ)ат1ю зап11са·1ъ равенством a 1b z -
-
а/> 1 = О. Нетрудно 11рш1ернтъ, что)l,не «nарал
лелы1ые» «Прямъ1е» лнбо не имеют ш.1 одной
об щей «ТОЧIШ», либо соnпадают (n обычной
геометрии тоже часто пр1пнrмюот , что прямая
параллельна самой себе). Более тон),
через любую t-точку• А 1 (х1 ;у 1) nрохо
дит одна и только одна «прям ая~,
парадл елъная д а нной ~п рямой ~
Ах +Ву+ С= О.
И11аче гоноря, в дан11ой модели выполняется
ai-:c1ю!\-ta щ1раллелыюств .
Мож1 ю :щесь rо1юрить и о длинах отрезков.
и о nелпчинах -утлов. Например, <- расстоянием->
между двумя <(J'ОЧК:IМИ»А1(.У1 ;У 1 ) И/12 (X2;J'J 11а
эывастся чнсло
1-. -
-
-
.
--
-
-
)
А1А2=v(·\·2 - Х1)~+(У2 -у,)-·
Дапес, в 11рнкычной с11клндоnоr1 гсол.1етр11н
с 11раве,rv 11 гва теорема коеннусо 11 (.РНС. 10):
ABJ""ACl +ВС - 2АС ВС cosС.
13 нa111eiI модел11. оснпnаш-юй только на рас
СNЮТI-:~сн 1 ш rtейст1штелы1ых чнсел, за пис:н шос
.выше р:щенстnо исполь:{уl'ТСЯ для определения
велич 1 1ны уrла :
'
АС~ +вс.! - АВ~
eos(.. =
2АС·НС
( вСJ111ч11н:~ угла С paвr r a арккос1шусу правоr1
част11 равс:нс1·па) ,vJ ожно возразить, что трнго
rюметрические фупJ<ции (и в частост11, кос 11 -
нус) rшре~еляются геоl"1етрически и обойтио,
без привычной еrsющцовой геометрии вдашюм
случае как будто нельзя. Однако это неверно.
В матем:1 п 1 •1сском анализе Д(Жазывается, что
функцин cosx задаётся бесконечлым рядом
х2хчхо
спsх =1- -+ -
-
-+ ...
1!4!6!
'
в
с Рис. 10.
'576
котоrыli СХО/ \ l !ТСЯ ДЛЯ ЛIОООГ'О !{CЙCl'Rl!TeЛl,J-J0-
1'0 .71'. Таким обраяо.м , в рассматриваемой мor1e
m 1 допуст11мо 1·отюрн·п, 11 о 1х1сстояннях, н о
uелпчинах углов.
Terrcpь мшюю проверитr,, '-ПО n ne11 13ьrпо11-
11mотся аксиомы конгруэnпюстп (в част11ос
п1, первый и второй признаю 1 раве 1 icтna трс
) l 'Олы н 1коn). В нтш·с псе гильбертовы аксвомы
(прt:дстанляющие со601~1 ра:ш 1пис н )rl'очнсmте
аксиом Енктr 1ща) к рассм<.t1' р11н~н.:мо 11 мо1~сm1
Вl>IГIШJ!fЯЮТСЯ. ?)то TI О:jН::Jч;н.т , что CllCTt'Ma
аксиом евклидоко!t rсомечтн ус1 rовно 1тепро
·гитюрсчива. Дf))'l'HMJ 1слnвамн. она 1 1 еnrот1 1 во
рсчнва при усло1нш. что 11е 1 1рот1шоре ч ш1а тео
р11я ~ейстщ1телы~ых чисел.
ПОЛНОТА АКСИОМАТИКИ
Крuме 1 1 е 1 1ротнноrечююст11 ест1, ещё од11а наж
н а>1 х<~рактернст11ка системы акс1юм - т:.~1< на
зываемая Jt0лнтпи. Поясним её сначал::~ 11а
rrрнмере коммутатнт-rых rpvmт (с-м . ст<пъю
<· ГруП1 1 Ы») . Теория !Ю."1МУТатнв~n,1.,х Гp)' llГJ ВЮIЮ
qает всего четыре а1<сиом111 (трн :~кс1юмы
группы и а 1<с~-юму коммуrапштюсти: а+ Ь =
~ Ь +а дЛЯ любых элеме11тоrs а и Ь) Дле моде
л и коммутатиnтюй l'руппы называются изо
морфиы.ми, <:слн существует юа11м1ю uдно
з11ачнос:: отображс::~ rнt: щ(нш1 мuдсл11 на дру1ую.
сuхран.юu щее 011ерацшо (.н данном случае та
кое . что <.:умма д.вух ЭJ1ем~нтои uсре.х.од 1 1т в
<.:ум....1у их uбраз1ш) . Наnрнме:р, тождественное
отображе1ше Е плоскпстr1 11симметрия1 отно
ситетмп зада111юfl ·гочки n оаrазуют, имеете
nзл1ъте. коммугаn шпую rрупну и;~ дпух зпеме11 -
тов П() комтю:)иn,~ш. Си1'шоль1 Ч и Н (чёт - не
чет) - это таюке коммутатнвная группа п:з двух
элементов отпосителыrо оnерацш1 , олределя
СJ\Юй правилом чё111юсти суммы: Ч + Ч = Н +
+Н=Ч, '-1+Н=Н+Ч=Н.Э'п1днегру11пы11зо
морфнht Вuобщt, любые ;1не i11y1111ы. в ко·юрых.
по дна э11с:мен1~1 , и зомuрфны дrу1 · дру1у. к:lк и
любые дне коммут;{пшн1:>гс 11)упr1 ы из сем11 эле
ме1ао1:1 . Л нп1· коммутативных групт~ 11з 1юс 1,~ш
элеNrtнтоu нмеется ·гrн rа злr1ч 1 1ых , попарно
1 1 еи;~оморф1 1ых F11 iдa.
Непротиворечивая снстема аксном щ1::~ ыuа
еrся полной, если любые две модели, удовлет
воряющие дашюli системе. изоморфны . Грубо
говоря, полная система акеном опреле.r~яст,
с точностью до и з оморф11зм:1 , то1 1ько одну
н·\)р11ю. На11рнмt:р, тюбаннв к чстырём :н<сно
мам кпммуrат11щюй груп11ы ещё оюту - 11
rpy111 1e н,"'1еется ронно семL. элементов, - м1.1
получаем полную систему аксиом (таI< как
любые две группы нз с:.тми элемс.:: втов изо
морфпы). А добавив к аксномам КО,\1М)г1·ати11-
нu1J группы дру1ую аксиому - в груrше и..мс
ются ровно вuс<.:мь элемс н тон, - мы получаем
нспонную систему аксиом (.nоскольку суще
ствуют II не11:юморфr1ыс дру1· другу коммутз
т1111нn1с r'руппы, каждан из котuрЬiх соде рж11т
rюсемь элсметттоt1). Так чтn сис1·ема al\c1 юм
1юмм)"1 ·ат1m1юй rру11пы тем более 11eпomra.
Оказалось, что гил ьбертова аксиомапша
яnляется поmюй. Иначе rоrюря, она определя
ет (с точностью до изоморфизма) единстnсн
ную теорию - евюmдону 1·еоме11)ню.
В кач<.:стне сщё ол. н оt'О прнм<::ра рассмот
р11м ·1 ·ак называемую абсототную 1'сометрию,
т. е. снстt.:мутсорем, к:отор ы е нытекают из всех
аксиом евклидшюй 1·еоме1тти, кроме аксиомы
11<1раллслыюсти. Очс:вп11но, ч'1'0 снстема ~11<с11-
ом абсолютной 1 ·еометрии 11епою1а . Добавив
к её аксIJомам аксиому нараллсзrыюсти, мы
получаем одну теорпrо - евюшдоnу rеомет-
Аксиоматический метол поипине был и остаётся
ПОАХодяшим и неоuе1н1мым инструментом, в наи
большей мере отвечающим духу каждого точного
исследования, в какой бы области оно ни про
водилось.
Лавид Гильберт
Математич~сю1е рассужлеt 1ия
рию. Включнн в с1ктему т<::х же акс r юм uтр 1 1-
11а1111 е аксио ·мы нараллелы юстн, при хоJТ,И.'11 1<
друтоr\ 1L еизоморф1юй пеrной теор нн -
геометрии Jlобачевскоrо.
НЕЗАВИСИМОСТЬ АКСИОМАТИКИ
Любая ок~rсма аксиuм J\ОЛЖНЗ uбн;цр·п" свой
СТRОМ 1tе:швисимости (хотя оно м1;;1 1 сс сущl'
стве1 1110. чем 1re11ротшю речи1юс1•1, н пот юта)
Сисrема аксиом тrа:~ьтаегся 11 e:ia1111c11 мот\ ecm 1
rrи O[l, t ry из аксиом 11ено:~мож1 ю дока:-~ат1. 1<ак
тeo re,viy т 1сходя и;~ остальных акс 1юм. На
пример, :шсиома параллслыюсти rrезаnисима
от остальных аксиом 1·еомстрпи (1юсколы<у
нс только с н стема аксиом, н которой ;1аш 1 ая
:lKCHOM<t НЫПОЛННl:'ГСН, нcпpO'l'l ,IВOpt:Lll-IJ:l:J, JJ(J 11
снстема аксиом, в которой. ны1 ю11юн:тся отр 11-
11:.tнн е зксиом1,1 11зр:uшеm.нос1·1 ·1, также 1-н:t1110-
'пнюрсчнв;'! ). Rообш.с. ч·1п\'i1.1 /'(оказа·1ъ 11t>: 1;1AI1-
с~ 1,"1ост1, ЮiКОй -11 11 60 акспомы от оста111.11ых .
надо построить дnс модели, в 0;(110й 11:i ко
торых nыnол11яютоr все аксномы, nк1ючая
11 оыбрашrуто, а 1! другой модели nы1ю:шя
ются все акспомы, 1\ромс nыбра1шо11 - 011:.1
НС ВЫПОЛI JН('ТСЯ.
ДРУГИЕ СИСТЕМЫ
АКСИОМ ГЕОМЕТРИИ
Спус1'}J десять ле-1· rюслс появления п 1Л1)6ерто
вой акоюматиюr Фp11дr1L'i: Шур, сJ 1едуя ттеям
ФaJJeca и Клс~'ша, предлож11л другу10 систему
аксиом rеомстрrти - осноn;нттrуrо 11:.1 рассмот
рсI111и тщжений. l:3 снсте.мс Шура ес11, трн ;нсси
омы, утвсржд:11ощ11с. ЧТО ДJ:ШЖCillIЯ (ПJIOCI<OCTIТ
11т 1 простра 11стн;.t, в заnнси мостн от того, какая
1 ·сомстрия - плоскан 1v 111 простра1-1<.:тв<.:1111ан -
им<.:стся в шщу) образуют группу прсuбра зон~1-
1111й (см. ста·1ъю ·Г~омстри.>:t и гру1111ы 11реоб1х1-
зова11ий» ). Перпоначалъным11 1101 штннмн (в пла
ш1мегр11и) ЯВЛЯЮ'J'С}I у 1Пура (<'J'ОЧКИ», <Прнмые».
"движеш1}!'> и понятие <>МСжду». а ко11груэ11т -
1 юсть фпгур олр<::деляется с помощью ДВ[ l
жсниn (а нс приз11акоо 1<опгруэ11·пюсп1 тре
у1·ольнш<ов).
Ещё дссн·11111ст11t> спус·1·н нсмсцкн11 :-.1ате
м;1тнк Герм:.111 ВсйJ1ь со:щзл нскторну10 ~~кою
матику rеuметрии У Вейля пернон~1ч11J 11>ные по-
11ятнн - ночка» 11 <- нектор», а прям:нt 11 uтрt':юк
Фундамент математики
определяются с их ттомощыо. Имеются аксиомы
сложения nскторов (означающие, что векторы
обра3у10т коммутативную группу) , аксиомы
умножснин в~:=кторu на дсйсrвителъное LШCJIO,
аксиомы отклздыван11н векторов (n ч:.1ст~юс.-т11,
аксио м а ·1реуrолы1ика: АВ + ВС = АС), аксиомы
с1<алярного произведения векторов и акоюма
размерности (для rmа11име-грии н ней уп"lерж
дастся: сели даны три ненулевых векrора а, Ь
и с, то какой-нибудь нз них nыраж<1стся в виде
комбинации ,~вух других: с= ха+ уЬ). При за
да1111ых то чке А и ненулевом векторе а прямая
(А , ёi) 011ределнется как множество нсех точек
М, для которьLх вектор A.1\lf пропорт~о11ален а,
т. е. найдётся такое действительное число t, что
АМ = /.а (рис 1 1). Далее опредепяютсн отрез
ки, у1·11 ы , мноr·оуголынши , окружность и дру1'11е
фитуры . 11:.~прим ер, расстояние между А и В -
как к~адратный корень н:.; скалнрного кщщр~tт<t
вектора АВ, т. с. АВ = JАв. АВ. Теорема 11ифа-
Рис. 11.
гора легко доказывается с помощыо скалярно-
1·0 11рnнзnеде11ия, а аксиома пар аллел ыюсти -
с помощью векторного о пределения прямой и
аксиомы размерности .
В заключение отметим , что гильбертова
аксиоматика геометрии полностью угочпила
не впот-1е совер ше нную систему аксиом, со-
3данную Е Rкли;1ом более /\нух тысич лет тому
на зад. Аксиомзт11ка Фридр~-Lха Шура и аксио
матика Гсрм:ша Вейля связали евклидову гео
метрию с пон ятиями 1·руп11ы ттреобразrтат1й
и 1~ектор 1 юсо 11ростра1ктва, 1<оторые играю~
важнейптуrо роль R() многих ра:щелах совре
менной математшrn, физики, экономики, хи
мин, биолоп rи и /\ругах областей зна1шя.
\
)
1
Математическая 1\ОГИt<а
МАТЕМАТИЧЕСКАЯ ЛОГИКА
РАССУЖЛЕНИЯ, ПРЕДЛОЖЕНИЯ , ВЫСКАЗЫВАНИЯ
Л01 · 11ка - это учение о с11особах рассуждсниi!
11 доказатслhС' гв безотноси+1·е111,но к тому, где н
,7'ЛЯ чего они испоnьзую·r·ся : 1~ споре, научном
11сследовапии или в зале cyr\a.
Матемаrпическая логика нсслс[(ует сnо
собы рассуждений, применя емые в математи
к-:. Впрочем, есть и другой взгляд, сог;1аспо ко
торому математическая 1юп1ка изучает любые
рассуждения, но t.: 1. 10.мощыо методов матсм~1-
·1 ики. 1lакон.е1 ,, еслн математич.еские методы
применяются для изучения матем.атических же
рассу-А<Дений, то r·о1юрят O J11emt1.,wcmze..мam1nce,
1~ли гпеории д9ка1ателы:rпв.
Э11еме1 1 1 ы математнчес 1<0й поrию-1 можно
найти уже n рабо1 ах древ11е1'rеческпх филосо
фов. В XVII в. Г. В. Лейбниц высказал идею а
том , что рассуж.дснил могут быть сведены т<
механическому вьшот 1 снню определёш тых
M<t'J см;~п1чсскю1 л о пни есrъ J101 · ик:L 111> 11редм ету.
м,1тематика 1ю ме-1оду.
n1шт.он Cej>2l 11.>imtt П()р е1.ршu .
рос апiский .мат е..,mтш.
деl1с·1 ·ний 1ю уст<11iонлс:нным пр;ншл;tм . Одн;~
ко как самостоятсль11ьrй раздел мате м.атию1.
м:пематическая ло1·ик~1 начал:! формирuнатьо1
только с середины XlX и.
'В ХХ L'. в рамках. м::tтематич~ской 1ю1·икн
1юзни1< ноный раз;tел - теория ал1 ·оритм ов . 1'де
изучаются пе способы рассуждать. а сrюсобы
вычислять в самом шнроком смысле этого
слова.
Paзn1:'rrиc матем.атичtской логики ознаме
пuналос 1, дос~гижсниями в двух протн1юпшюж
ных направJJениях. С uд1юй сторu 11 ы, форма
nиэация матс::матики достигла такQй степени,
что сс 1~час почти нее теоремы дейсrвнте)(ы-rо
мrнуr бьп1 . вымедены по определt1-111ым чёт
кнм r1равилам , и , rз прю-щиле, ~1U можеr сде
лать даже ко м пьютер. С друтой стороны , была
установлена неизбежная огра11нче 11 ность
579
Фунд.:~мент матсм<Jтики
...Можно
придумать ~1екии алфавит человеческих
мыслей и с помошью комбинаuии букв этого .~лфа
аита и ан;;~ лиза слов, из них составлен ны х, всё мо
жет быть и открыто, и разрешено.
•**
Эта письмен ность... должн01 стать чем-то ероде все
об ше И алгебры и дать возможность рассуждать
посредством вычислений; таки м образом, вместо
того, чтоб ы спорить, можно будет сказать: подсчи
таем ! 111 тогда ста11ет ясно, что ошибки в рассуЖАе
ниях суть не что и1·юе, как ошибки, свя за1 ты е с
вычислениями, и их можно булет обнаружить nутём
проверки, как в ар ифметике .
Г. 8. 1'ейбi1Иu
любой <-механической~ снстемы нолуч<:.:ния
м.атсм:пичt.:ских результатов. Таю1м образом,
'V1счта Лсйб11ица частично осущсст1:1ил: 1 сь, :·1
ЧЗСТl! ЧН О OK3:.!:JJtaCI, I ICRЫ l l()JlHHl\1011.
Основное co;terжa11ие д:.1111 юй 1·лаRы 1 юсRя-
11 \е но Т[1Зf\11ц1ю11110й, ·1·зк 1-1аз1.тнзе~vюй л:!l.accu
чf!CJcoit .11u1me./vtcm1uчecл·m't логz111:е. Немно1 ·()
уз11ат1, о Щ'))'Т 1,1 х ло1·нках вы можете 11 з ноппл
111 r·1·елъщ, 1 х очерков <· Кто прав , кто ви новат",
«Хлеба пли з рслнщ·>, «Моды ссэона».
**"
Дтr Т()ГО чтобы р~tссуЖJ(ать. чсловtк дш rжен
испоJ11,3оват1, какой-·1·u }{:iык - русскшl, Ш-Ll '
лш!скнй". Не )'J(ИВI 1·1·е::лыю, 1 1Т<> м;1тсма ·1·1-1чtх:кан
ло 1'ика нач111-1 ш 1ась с анализа того. к~~ к .\·tы 1 •01ю
рим и пишем н а CCTCCl' HCHIJl,[X HЗl>!K~lX, а Ct
ра:iви т ~-rс шло rro пуп-r пострпеrrня 1ккусст
вt:1-1 11ых qюpм:lJLЫTЪIX ЯЗЫКОR.
Знакомство с математнчсской ло1·пкой мы
щ1qт1ём стого, что рассмотрим повествователь-
11ъrс н редложеlJИЯ. Это JJ~имсньшие языковые
коrrструкции. которые могут быть 1 ктинtн,rми
ИЛ11 ЛОЖПЬL'vJИ.
Читатс11ь, по-1-111димому, без кОJ 1 ебан ий со
гл:аситсJ1, что 11 ри1:1едt:11ны е 11и жс упiерждею 1я
Rерны:
Два в квадршпе ратю четырё.м.
3е-.1н.ля является тре-тьей от Сол1ща плсте
той GQ/lJ{(]Ц}-{,()zl Cl/Onf'.MЬl.
И ни у кого, очевидно, не вызовет сомиспю1
о шнбuчrюсть таю1х прелложешu1:
580
Три в квадртпе рав1 ш во'-'1,,,.ми.
Св11шщ т.· нющJm а aouc.
Даже если вы затрудпитесъ сраэу сказать,
вер rrы JШ <:ледуrо щн е уrnерж,rt;ения. то сможе
те это ВhIЯс1шть. загля:нув в rrодходящий спра
nочн1п<;
'J&.мnepcm~)fH.l 11.Jlt:l({T/&f-lШl .M(!JJ1tLЛJl.C/ fJCЬ.MUй
бшlее 3000 "С.
1(/"'6 1)/
Число 2- -- - 1 является npocmыJvt.
Впт ещё ряд 1 1pc,rt;1южc1111i1:
1la /vlap ce быrш 1к11зm,_
G)•щ<!cm(~)юm бесло1ючно .1mюго простых
ч11сел 1ш<lа 2" - 1.
Дино:Jавры были 11щ1щuл:,;ювным11 жu
вотньLМ.ll.
1 .март.а 1 гщ)u 1t0нщ( эры 1tt1 nnppumopuu
сопре.ме111юй Москпы 11/юшi!л до;1сд1"
Уз 1rатт,_ кarc(.IC нз ннх верны, сегоднн 11 ел1,:ш 1 щ
нз о;~:ноИ э нциклопетнш . Но от 1 ~ос1пелыю
перnых трёх ес1ъ надежда. что когда-нибудь это
nсё же станет н:шестно. 11 хотя .'vt:lJюncpoяпю.
ЧТО 11l''l И 111 \ОСТЬ ИJI И ЛОЖI JOC'l'I> ПО<:JIСДШ:ЛJ
у~1 ·нсрж;~с.::11ш1 кu1-д;н 1 ибо будет ус·1~ 1нuнлсна. 1 1 ет
l'ОМНСН11Й, что оно JJJJ6U 11 сr11нн1J . л 1160 JIOЖ ll<J.
Но бывают\[ r~руп к пrt:)l,.ll()Жl'llШI . Возьмё
ТССI> 1111 RЫ yтRtpЖf\::tTь. что слс1 1у1ощ1 lt' фра:jы
«ХОЧУ ВСЁ ЗНАТЬ11
Интересно, каковы будут мненин чит а гелей no по
воду приведенных ниже nрелл<>жени11 . Какие из них
истинны, а какие ложны?
Маяковский написал «ВОйNу и м11р».
Самая высокая ropa в мире //dЭЫвается С.1rар
матхэ.
Иrолки хвой11ых 4еревьев - эrо FJиАоюмен11в
шиеся листья.
Треть!:' rысячелетие нпвой эры 11ачнiпся 7 ян
варя 2000 rола.
Отчество пушкинской rероинн Татьяны Лари
ной - Ллттриевна.
ЛЯАЮ Евгения Онеп 1на .шали Андреем Петра-
вичем.
С11он с11'1.ьнее кита.
Математиче< кая Аоrика
КАЗНИТЬ ИЛИ ПОМИЛОВАТЬ?
... И
первь1,\Л ле/\ом явиАся к 11ему /Санею Пансе l
один приезжии, которыи в присутствии мажор
дома и прочей челяли заявил слелуюшее:
-
Се1-1ьор, по влалениям олного вельможи
протекает многовод1-1 ая река , разлеляюшая их на
две части... Так вот, через ?ту реку п е реброшен
мост, и около него стоит висел11uа и нечто вроде
судила1ша, в котором обык н овенно 1аселают
четыре судьи, н аблюдая за выполнен~1ем закона,
изданнn го владе11ьuем рек11, мое-та и поместья и
глася шего следуюшее: « Кажлыи , перехоляший по
мосту с одного берега на лругои, обязан пол при
сягой заяв~1ть, куда он илёт и с какой целью; и,
если он скажет правду, его п poпyet<iHQT дальше,
если же солжет, то его без всякого снисхожле -
11ия лиwаlОт жизни, взлёр11ув на стояшую рядом
виселицу» . С тех пор как суровые услоаия этого
закона стаАИ всем известны, много людей пере
ходило через мост, и как только выяснялось, что
он и говорили правду, суды1 позволяАИ им сво
бодно с11едовать дальше. Н о однажды случ иАось,
что некий человек, привелё нный к присяге, по
клялся и заявил, полтвержлая слова свои клят
вой, что он пришел сюда лля того, чтобы его по
весили на это й виселиu е. Клятва эта смутила
судей, и они сказали : «Если мы позвом1м этому
чеl\Овеку свобо дно прО Сl\едовать дольше , то
выйдет, ЧТО он ПОКАЯЛСЯ ложно, и в таком слу
чае, согласно закону, должен умереть; если же
мы его повесим, то ведь 011 поклялся, что яв1~лся
сюда лля того, чтобы его повес11"и, - следова
тельно, клятва его правдива, и , соглас но тому
же закону, он должен быт~, отпущен на свобо
ду». И вот я вас сг1р а ши ваю, ваша ~м1лость, се
ньор губернатор, что дt!лать с.ульям с этим чело
веком, потому что они и по сей лень пребывают
в смушен~iИ и н ерешительно сти.
Сервантес. «Лон Кихот~
***
Спешим успокоить тех, кто еwё Ht! читал рома~•
Сервантеса: губернатор Санчо Панса веле11 су
лы1м отпустить того прохожеrо. Ведь, как сове
товаА ему Ло11 Кихот , если судеб110е деАо вну
шает сом н ение, всегда слелует склоняться на
сторону милосеры1я. А выражаяrь юридическим
языком, Санчо вы11сс реwе11ие н;:~ основан ии
презумпuи~1 11 еви нов11ости.
581
582
Фу нламент математик и
fi ТИХОМ oMy'f'i-
'-ICf ТИ fJOДJJ7'C/f
ПАРАЛОКС БРАЛОБРЕЯ
AtliJJ~
Говорят, что в некой деревне был всего один
брадобре й . 0~1 брил всех тех и только тех мужч ин ,
которые не брились сами. Брил ли 7ТОТ б радобрей
самого себя ?
можно разумш,rм образом разделить на псти11 -
н ы<:: и ложные:
В mU.'\'O.i- .t o.мymf! черти fюдятся.
С 17-ОМОЩЬЮ фшюсофсл:.ого Ktl..M71Я .i°'IOJКIIO
превратить сви11ец в :зплото.
Утверждш ше,
заключённое в
CU1tIOIO /JCL-11.К')! на
этой странице,
лuжгю.
Утвер:нсдша 1е,
заключi!нное в
красную ра.м/\.'}' на
этой стра1ш~~е,
UCfltul-t/-U).
Что i<acaeтc}j утRерж,~е11ий в рамках, то :щес~,
непонятно даже, с какого начать выяснение
иегинности. Разберём дnа возможных случая.
1. Утверждение в синей рамке истиmю. ::.>то
uзнача ст, что утвержде н ие в красной рамке
тоже истинно . А и:~ эт01·0, в свою очередь. с1 1е
дуст, что утнсржде11 11 е в сн 11 е::й рамке ложн о
Таким об разом, предположение об истин1юст1 1
уrвержде н ня в синей рамке приводит к про'1'11-
FЮре ч ию.
2. Утllержде1111е н сине.И рамке ложн о. .111а
чи1·, уrпержде11ие R кpacrюrr рам1<е тоже лшк
но, из ч его вытекает, что утnерждсrrие в синей
ра.мке истшшо. ПредпОJюже11 ие о 1юж1 юстн
утж:рж:11сния в синей рамке таJ<жс п рнвод11т к
протиnорсчию.
Мы видим , L\TO естественный нзык допускает
гра ммати ч ески правильные конструю tин, кuто
рые 1~ы 1·11нл,нт как осмыслен ные утнерждс н ия, но
о которых тс::м не м енее нет, :т в 1 1 р111-1ци11t
реши ть, исти 1 111ы 0 11 11 или 1юж11 ы А застрахо
ваны лн мы 0·1
· 1юдо6 11ых утверждений - триз ра
ков» 13 матема'fичес1шх доказательствах? Оказы
вается, нет. На рубеже XIX-XX столетий в
одном из фундаментальных разделов матема
тики, теории множеств, были обнаружены тра
доксьr - противо речня , возникаю щ 1 1е в резуль
тате, казалось б n1 , сонсрt11 е н но корректных
рассуж;\ений сна пример. та к 11а:3ывасм ый ~пзра
докс бrздобрея») . llроти норечис, к которому
1 1 ас привели угвсрЖf\сния н рамках , восходят
к гораздо бn; 1 ее дреш ~ему паралоксу - паралок
су Еnnулида (N н. до н. э.).
Как же избежать парадоксов' Один L1З пред
ложеrшых путей - построение искусствешю
го формалыюго язъl!(а, лиmёшюго «волыrос
Т<.:й'> я:iыков естественных.
БУЛЕВЫ ФУНКUИИ
Пусть нмсется некото рый набор нысказ ыв:н1ий ,
о которых можно опрсд~::лённо J'ОRОрить, что
он н истю1ны тrи ложн ы . Для обозш1ченн я этих
высказJ->mаний булем исnолюо13ат1, латинские
буквыА,В,G'ит.д.
Если у нас ееrъ два nростьrх прсдложе~шя,
ТО НЗ IJJIX можно образоJЗать !IOJ30C, СЛОЖJЮСО
чинёюrое предложе ни е с помощью союзов
«ИJIИ,, либо ЧI». В математичсс1<ой логю<с для
аналогич:ной цели используют слецнальны е
сн.мвол. ы: знаJ< дизъю11:;сции v; знак к.онъю1f.х:z,~ии
& (иногд::~ прим еняют тзкже символ л).
т~1ким образом , И~\ утвержде11ий А , в с по
МОП\hIО Зl l ЗК013 ДИЗЪЮН1<1\11И \.\ IЮН 'ЫОllКЦИИ
получим ноnые уrве рждев ия:
А v в (читается "А ИJШ в~),
А & В (читается «IL и В»).
Утверждение А v В счнтастся мстит 1ым тогда
"' TOJ JЪK() тогда, когда ИСТ! IHHO хотя бы одно из
1кход11ых утверждсниil ; утLJерждениеА & В -
КОГД;I ИСТl!НRЫ оба уrверЖf1ения.
Ди зъюнкцию н конъюн1щ11ю можно рас
сма 'rрнватъ как особы е операции, определё1 1-
ные не на числах, а на логических .зн.ач1С1-1.uях
ИСТИНА и ЛОЖЬ.Д.Г~я этих операций сущесrву
ют табли цы , подобные таблщ1е умножения.
ИСТИНА v ИСТИНА = ИСГИНА,
ИСТИНА v ЛОЖЬ = ИСТИНА,
ЛОЖЬ v И СТИНА,,,. ИСТИНА,
ЛОЖЬ v ЛОЖ /) =ЛОЖЬ,
ИСТИ НА & :ИСГИНА = ИСГИНА,
ИСТИНА & ЛОЖЬ = ЛОЖЬ,
ЛОЖЬ & ИСТИНА = ЛОЖЬ,
ложь & ложь = ложь.
fioлee традицно1 шой для таких 1паблuц истип
щ;сти являстоr следующая форма запис н:
А
в
AvB
ИСТИНА ИСТИ НА ИСТИНА
ИСГИ.НА ложь ИСТИНА
ложь ИСГИНА И СТИНА
ЛОЖ !)
ложь
ложь
А
в
А&В
ИС.."ГИНЛ ИС1ТIНА ИСТИНА
ИСТИНА ложь
ложь
ложь ИСТИНА ложь
ложь
ложь
ложь
Математи ческа51 логика
Лог11ческне :311:lч ен1:rя ИСТИНА 1-1 JIO)Kb н<t
зьш:нот также булевы.лш :таченuя.ми - в честь
:шгл11йско1 ·0 м:.~тем атнка Джо рдж::1 Буля, кото
рый u /(JX в. заложил основы современной ма
·1·сма'mческой J1Оrики. Функцrrи , ар1умеJ1тамн
н эначе1·1иf1ми которых являются ИСТИНА и
Л ОЖЬ, называются булевы.ми футщиями. Опе
рации КО!I'.ЫОШЩИИ и дизъюнкции - это два
примера булс.вых функuий от двух арrумсп топ.
Сколько все1·0 .имеется булевых функций от
;~вух артум ен·юн? Н етрудно 1 юдсч:ит~1ть, что их
шестнадцать. ДейстRителъно, з~1полняя тзблицу
А
в
ИСТИНА. ИСТИНА
?
HCTИJIA ложь
?
ложь ИСТИНА
?
ложь
ложь
?
мы мож<::м на месте каждого 11 3 вопрос11тt:.1 1ьных
з наков напис;.~ть .как значение ИСТИНА , так и
:таченисЛОЖЬ,чтодаёт2х2х2х2=16
в~1риантов .
ДJJя всех булtных фуню1ий от двух ар 1 ум ен
тов имеются: соотне~·сп1 ующие кт1струкц1 1.и в
русском языке. Рассмо·гр111\1 в качестве примера
операцию, задаваемую таблиней
А
в
л~в
И СТИНА ИСТИНА ИСТИНА
И СГИНА ложь
ложь
ложь И<.:ТИНА ИСТИНА
ложь
ложь ИСТИНА
Эта опсrация t1азынается логическ.UJН сл.едо
r:юнщ!.м или и.м 1 vtикацией. Фут-1к~~иrо А=> В
можно ныразить словами «НЗ А следует В» или
«если А, то в," Наряду со знаком ~ использу
ется зн:u< :::> .
Обратите вннма1те , что имплиющинА ~В
явлнется ложной, только если А истинно, а В -
нет. Если А ложно, то о В ничего нс угвсржда
стся, и потому в д3Н1Юм случае имплнка н ия
считается нсп1нной вне :~анисимос11 1 от зна
ч ения В.
в отличие o·r КОIJЪЮrlК ЦИИ IJ ДИЗЪЮJIКЦИИ в
имллиI<ац ит,1 арrуме 1 rты 1rет .з~т поменятъ ме
стами. С.дела-в это. мы получ11м уже друrую
булеl'У оnерацню - обратную и.м1иикацшо.
583
Фундамент матем.пики
БУЛЕВЫ ОПЕРАUИИ
В ПРОГРАММИРОВАНИИ
Операuии ко нъюн кш1и и дизъюнкu и11 являются
неотъемлемыми :элемен1 ами всех языков программи
рования. На клавиатурах компьютеров нет символа
v, и для обозначения лизъюню.1ии часто используют
а~1глийское слово OR (« или•). Соответстве1-1но конь
юнкuия пр~1 этом обоз11ачается AND («и»).
Употребление слов вместо символов часто при
водит к ошибкам начинающих про граммистов. Они
наивно полагают, что в языке программирования OR
и AND можно использовать точно так же, как в обыч
ном языке. В результате новички получают сообше
ние об ошибке , написав
IFХ>УANDZTHEN".
(«если х больше у и z, то".»}
вместо правиль~юго
IFХ>УANDХ>ZTHEN".
(«если х больше у их больше z, то".») .
***
Султан возврашался домой с nоб1.мной
войны По тр;миuии , в стол11u1~ армию
доl\Жны были еrтр ечать артимер ийrким
салютом , Н() гор()дСl<иР nушки мп11чал11.
Султан nриЗ1;1с1Л к себе r11авнОГ() вюиря и
потребовал обьясненн1·1.
-
Повелитель, - начал глав ный ви
зирь, - на то было лвеналuать причин .
Во-r1ервы)(, у нас кончился порох...
-Дооольно!- сказал султан и велел
01 руби ~ ь визирю го"ову.
В математике всё равно - сказать «А и В• или ска
зать « В и Л », подобнu тому как при перемf:'не мест
слагаемых сумма не меняется . В программировании
Её rvюжпо ттерепат1, слона ми « из В следуе-1· л').
Вот соответствующая таблипа:
А
в
А-.=В
ИСТИ llА ИСТJ11 1А ИСТИНА
ИСГИ ILА JЮЖЬ И СТИI lЛ
ложь .И СТИllА ложь
ложь
ложь И СТИIJ Л
Операция ~ . которую задаёт с11сдую щ~1я
таблица. 11а:1ыв:1стся .~-х:Ruва..пе1tт1юсrпьт.
л
в
!l ~B
ИСП111А ИСТИНА И СТИНА
ИСТИ11Л ложь
ложь
ложь И С1И1-1Л ложь
ложь ложь ИСТИНА
5Н4
же замена А AND В на В AND А может сушественно
изменить повеление программы. Например, во всех
языках про грамм 1~рования последует соuбшение об
ошибке: "деление на н уль», если перед выполнени
ем оп ера гора
IFУ/Х>ZANDХ>ОTHEN".
значение переменной Х равно О. В то же время ника
кой аварийной оста~ювк~t може1 не проюойти, еслн
написать
IFХ>ОANDУ/Х>ZTH[N...
Лелu в том , что, согласно семантике некоторых
языков про граммирова ния, компьютер может дей
ствовать n олобно упомянутому выше султа ну: сна
чала вычисляется значение первого члена конъюнк
uии, и если оно /\ОЖЬ, то второй чле11 просто
игнорируется. Аналогично, игнорируется второй член
лизъюнкuии , если 1начение первого ИСТИНА.
А <=> В соответствует фразе «А тоща и тоm)ка
·1 ·0 1 ·да, когда В». Наряду со :шакоi\-1 <=>/\ЛЯ оrю
;п-1 аче1-1и~1 эКD11нале 11т11 ости использу1uтся зна
ки= и=.
Оnерацш1, з;щанасмая табшщсr'1
А
R
ИСГИIIА ИСТИllА ЛОЖl>
И СТИНА ложь ИСТИIIА
ложь ИСТИ LIА ИСТИНА
ложь
ложь
ложь
-
на:~ыnается искпючающсй ouз7510111щueli. C.: .11oua-
J1-rn её можно nы р;:~ зпть к;щ «либо А. 111 160 В·>.
в ОТ!lИ ЧНС от ДН:.:!ЪЮНКЦИН А v 13 псключающая
ДИЗЪIОIJI<Ц11И НШIНеТСИ ЛОЖН{)JI, CC'Jll l 1 1А,11 R l lC-
т111111ы У этой 011ер;щни нет общепр111-1ято1·0
06оз11аче 1111.н , можно 11с1ю111>зовать, 11а11ример,
симnол $.
Посмотрите n~шмателыю па эч· табтщу:
А
в
ИСТИНА ИСТИНА ложь
ИСТИНА ложь
ложь
ЛОЖh ИСТИНА ИСТИНА
ложь ложь ИСТИНА
ФормаJ1 i- .1 ю э1~сс 1, за ла~ 1 а 11 екоторая булева
фу11кция от нвух арrументон. Од11 а ко лег1<0 убе
дюъо1, что :шаtrе1ше фун1щии 11е 1ависнт ст1'
второго ap1yмe11rJ и nсе 1·д а протююnо1тож1ю
значсшnо перrю1·0 аргумента . Поэтому вместо
нее рап:матр1ш:~ют оrтерацшо l с одн 11м <1ргу
ме 1 1том.
А
lA
ИСТИНА ложь
ложь ИСТИНА
Оnерац 1Jя 1 пазьшается логичесл:и.м отрица
иие.м.
Для передачи отрицания в русс1<ом язмке
1н.:1ю11Ьзуется част1щ:.1 <-Не». Она может стояп.
псрсл. ра:Jным 11 члt: н аt-·111 11редложс111н1 , н от
этого завис1 1т смысл нысказыв:~ н ю1. Напр 11м ср:
Петя JU! KJ'lllL7L .моро.женое.
J Je J lетя лу1щл Аm/ю.ж:еное.
Петя купил 11е люроJ1<хmое.
Лоп1чсскоl' отр1 ·1ц,ш:ис соотнстеrnуст «11е»,
стоящtму 11срсд сказуем ым , 1-\al\ н псрном прс11-
1южсн 1111 . Другой с1 юсоб ныр:~з11ть ло1·ическое
0·1 р111рппе - ;щf1ап~1т~-. к 11ыс1<а:3ын:11-111ю-~1р1 у
.мепту слова <•псnер 1 ю, что» . С:рз.н 11ите псрнос
предложение со следую1цt 1м:
l lевер1ю. •-тю l Jе111я /\)'/'JlL'I моjЮ)1tе1юе.
Н заннсн.Nюс111 от типографских uозмож
н остеi1 з11 а1< отрнца1шя может вы1ля,11.ст1. по
раз1 юму: 1 или -. , н1ю1·да 11 с 110 ; 11,Jую·1· таюкс
снмнол -. Ещl' сщ1 1н способ 06оз1 1 ;~чt.:н1 ш отри
' ~а н ю1 - 1 ·ор11:Jо1-1т~шьнан черта, С'J'(JНЩан н:щ
ар1умснтом: А
А11;шоп1щю тому r<ак мы поткч1 1тат1 кшш
чество булевых фуню1:нй 0'1 днух :~ргуме1 1то11.
легко найти, что ,11олж1 ю быть 2 х 2 = - + булсnы
фушщ11и от ОДНОГО з.рrумента. с OДtIOIJ ИЗ
них - отр 1 щаш1см
-
мы уже познаком1шись.
Три друп.1е з~ща ютсн табшща""и
А
А
ИСТИНА ltСТИНА Иt;ТИНЛ ИСТИНА
ложь ложь
ложь истинл
А
ИСТИllА ложь
ложь
ложь
Пt:рная 113 эт11 х функщШ 11мест значt'1ш с. сон
nа/1:аю щсс со з 11 ачсн11см ар 1 1·.\1с 1-п а, 11 шшаких
спец11;u1ьных языкстых конструю (Hi'J /J,JШ t'i.:
Rыр:~же1тя 1 1с требуется (ссл 11 хот11тс, можстс:
ПЕТЯ IНfE КУПИJ/
МОРОЖЕНОЕ
ti=4 fE ЛЕТЯ КУПИJl
МОРОЖЕНОЕ
ЛЕТЯ КУЛИJI.
~fE МОРО)КЕНОВ
Фундамент математики
с1<азать <1Вер110, что А» ). Остальные дFle 1юобще
не завнсят от сnоего аргумента, это просто уже
известные нам булевы 1<онстанты ИСТИНА и
ложь.
Возвращаясh к буден ым функцюu.1 от двух
ар1ументов, nтметим, что сре11.и них есть ещё
нес:1<оллко таких , значении кото ры х з:11~и
ся·1 не 0 ·1 исех аргуv1е нтон . Им соответствуют
таблицы
А
в
11
ИСТИНА ИС:ТИНА ИСГИ! {А
ИСГИНА ложь ИСТИНА
ложь ИСТИНА ложь
ложь
ложь
ложь
А
в
в
ИСТИНА ИСТИНА ИСТИНА
ИСГИНА ложь
JlO)ICb
ложь ИСГИНА ИСТИI L.\
ложь
ложь
ложь
А
в
lв
И(:ТИНА ИСТИНА ложь
ИСТИНА ложь ИСТИНА
лож1, ИСТИНА ложь
ложь
ложь ис:тинл
А
в
ИСТИНА
ИСТИНА И СТИНА ИСТИНА
ИСГИНА ложь ИСТИНА
ложь И СГИН А ИСТИllА
ложь
ложь ИСТИ!!А
А
в
ложь
ИСТИIIА И СГИН А ложь
ИСТИНА л ожь
ложь
ложь И СТИНА ложь
ложь
л ожь
ложь
Опеrацню 1• 11азыт:~емую штрихом Шеф
ферtt, задаёт т~блица
А
в
А\В
ИСl'ИНА ИСТИНА ложь
И СТИНА ложь ИСТИНА
ложь ИСТИ НА ИСТИНА
ложь
ложь ИСТИНА
А IB М()ЖНО ттереr1а·1ъ слонами •неверно, что А ,
или неверн о, что В».
Следующая таблиЩJ предс.-тавляет оперз ц11ю
.J, , именуемую стрел.кой llupca:
А
в
AiB
ИСТ Иl L~ ИСТИНА ложь
И(,'ТИllЛ ложь
ложь
ложь ИС..1И11\ ложь
ЛОЖL"> ложь ис:тинл
A.J,B мшюю прочесп, к::ш: « 11евер 1 ю . чтоЛ , и не
верно, qто В» .
Остал11сь сщё две булевы фушщии, которые
не имеют общепринятых названий и обозна
ч1.:ннй:
11
в
ИСГИНА И<..'ТИНА ложь
исгинл ложь И<:ТИНА
ложь ИСТИНА ложь
ложь ложь ложь
А
в
ИСТИНА ИСТИНА ложь
ИСТИНА ложь
ложь
ложь ИСI ИН.А И СТИIIА
ложь ложь ложь
01-111 могут быть выражены сuответствсю ю
сло11а;\>111 « нсв<.:рно , что и з А слел.ует В» н ~ нс
вер1 ю. что w.i В следует А».
ПРОПОЗИUИОНАЛЬНЫЕ ФОРМУЛЫ
Имея в своём распоряжении зна ки матема
тических оп ераций - сложении, вычита нии ,
ум1южения и т. д., - мы строим с их помощью
ал1 ·еб ра и ческне выраж~ ния пз чисел и пере
менных. ПО/"\Обным же образом можно строи'fъ
логические выражения, наз ываемые также ~uze-
586
ВЫ.МИ 1IЛ И 1/.f-I01IOЗU'L(ll01ia.JlЫtbl.MU фOfJA~)!Лa.fftU.
(flослед11се 11 ~1 з в;.111и е происходит от лтп.
propositio - «11редложе 1 rие •>.) Крuмс знакон
булевых фуню ~и й для эт01 о требуются булеВ'Ы
(.иJJ и нропо:шционалъньи:') иере.мен.ные, т t:. пе
ременные, nр111 1 имаю щиt з 11ачения ИСТИНА
или ЛОЯ<:Ь. В качсегнс т:нrnх перемс1111ых 11ри
нято использовать загш1Rные л:..пинские букны .
Дздим оnрсделе11ие nропозиционалпн()Й
формулы.
1. Каждая прапозиционаm,ная переме1111ая
является пропо:нщионалыюй формулой.
2. Если Ф
-
проnозицио11алъная формула ,
то выражение (l Ф) также является пропози
ционалыюй формулой.
). Если Ф 1 и Ф ! - 11ролозиционалън ыс фор
мулы, то выражения (Ф1& Ф~). (Ф1v ФJ,
(Ф1 ~Ф2),(Ф1 ~Ф2),(Ф1=Ф!),(Ф1 ]ЕФJ,(Ф11Ф1).
(Ф 1 i Ф2) также ню1яются проло:шционалы-1ыми
формуJJами .
4. Никакие другпе объекты не яR.rтяrотся ттр()
позиционалъными формулам11, кроме тех, ко
торые ими являются со 1 ·ласно предыдущим
пунктам этого определения.
Мы описали исходные простейшие фор
мулы (пункт J ) , а затtм правила ГЮС'I росшн1
новых формуJJ из уже nостроен11ых (11ункты 2
11 3). Такой способ определе ния назын:Jстоr
шtдул:тию-1.ым или коиструк:тиниы..м. В на
учных публ нкацнях гrу11кт 4 всеrда 11rщразуме-
11ается, rю обы ч но mню 11 е 01·овариnается, по
с1щ;1ъку не содержит никакой инф()рмации о
ПОС1'роении формул.
Скобr<и n пропозициональн ых формулах иг
рают 1у же роль, что и в алгебре: определяют
порядок выполлсния оuераций. Так же ка ~< в
алгебре, некоторые скобки можно опускать,
ccлIJ даговори:rься о ~старшинстве» операций .
Традиционно логическое отрю~а1-111е счит;:~ется
более сильной операцнсй (т. е. выполняется
раньше) , чем любая дuухмест 1 1ая операция ,
l(() J l'ЬIОНКЦИЯ - более сит11юй, чем ~JЗЪЮНКЦНЯ,
каторая, в свою очеред1" силы;ее импликации .
Это означает, что в формуле А & lв ~ Cv D ону
щенпые скобки доmкны быть восстановлены
так ((А&(lB))=>(Сv D)).
По;1обн.о тому ка к в алгебре можно вычис-
1111ть значение много•тен::~ , зная з11:Jче1-111я всех
RХОJ tЯЩИХ н него переменных , MOЖllO Нl1lЧИС
лить логическое :зна ч ение (ИСТИНА или
ЛОЖЬ) пропоз ициональной формулы при
данных 1ю1 ·нческих С1наqе11иях вхою1щнх в неё
переменных. Тем самым каждая та1<ая формула
задаёт 1у или ипую булеву функцию от оДiюrо
или нескольких аргументов. Более тш~о, ока
зьшается, что любую булеву функцию можно
задать с номощью формулы, со;1ержащсй толь
ко знаки l , & и v . Bor1· некоторые 11римсры .
Математическая логик;~
А~В=lAvR,
А=В=(А&В)v(lA&lВ),
А~l:З=(Л&lB)v ClA&l:З),
А1В=lAvlВ,
АlВ=lA&lB.
В свою очередь, од r rого штрп:<еа Шеффера
или одной стрсm<И Пирса достаточтю для за
д;~ния люfiой булевой функции.
КТО П РАВ, КТО ВИ Н ОВАТ?
Если изАследуt:тW,товерноли, что изА & Втак
же следует W? Конечно, это так, скаж ет матема
тик , ведь формула
(А=>W)==>(А&В=>W),
истинна при любых значениях переменных
Представьте себе, однако, та кую ситуаuию. Рас
смотрев вешественные док азател ьства и свидетель
ские пока3<1ния А 1, А2, ".,Ат, суд присяжных засе
дателей единодушно приш ёл к выводу W о том, что
подсудимый виновен:
А1&А2&...&Ат=> W.
Апелл~шю н ныи с уд принял во внимаt1и е также но
вые вешественны е доказателы.тва и свидетельские
показания 81, 81, "., В" и н а основе всех материа
лов при шёл к п ротивоположному выводу о неви
нов11ост и :
А1&Al&...&Am&8,&82&...&Вп~lW.
Для формального о п исания подоб ных ситуаuий
б ыли п р~1дума11ы немонотонные лm ики.
587
<Dy11ммс11т математики
Ro \\\( ))\\114к·1'11 ныrажа·1 11(ЩI111 бупепы ()П<::ра-
1,1111 черt"З НР) 1 ·11с rю:шо.rrщ.-г прн пострпе т1 1 1
npono:H tl 'I IOll;l!l\11 111/ Л фОрМ\'Л ИСЛО.'IЪЗОnаТ11
не LIC't о 1чnол ы опсрацs rт 1 , а ;н пuь 11есколък о
OCllOBJIЫX. 13 1'Щ.1blfCJПUl'\1 М Ы 01'р:t 1 ШЧJI}.1СЯ Зt!a
K:Jt-111 1 . &, v 11 ==>, т. с. бунсм сч111а·1ь, что в пунк
те: ~ ()1Jрl'дt:щ: 1111 я Пp0 11 03 111tl lOH:tЛhHUЙ фop
\l)'Jlbl Ol t';t llJ/C.:llЫ l'UJIЬKO ( Ф1 & Ф~). (Ф1 v Ф2) 11
(Ф 1 => Ф2 ) <>1 \ll'Tll\1, кс1~1т11, что фор.\1у11а Ф 1 нa
:{ l>llial"l'CH Jюuч. •1ло(1 11мп1111кааин Ф 1 => Ф ! · а
форч~ ; 1 ;1 Ф2 - l'l: 3ак1юце11uе.,11 .
ТОЖЛЕСТВЕ НН О- ИСТИННЫЕ
ФОРМУЛЫ
С., рсд 11 1 1ро11о:нщ1ю1 1 ;urы 1 ыл формул особую
ролп 111·р:11от ·1·с:, которые пр11 любых :шачс11ш1х
11t·pt·.\tl't111 ы х 1 1р 1 11 11 1м~11uт з на чсннс I1CTИIIA_
Так~1с фo/)'l}'JIЫ 11 : 1 з ы11~1 10· 1ся то.нсд ествпt -
1ю-uс11ш1шыми 1111 11 тtтmа1щгuЯJ1.ш. 1301 · 1 1t:ко
торые 11р11мер111 та11·ю1ю пrf1:
А=> (Я =А),
(,4 =(Я-> С))=> ((11 =>В)=> (А=> С)).
(А & /З) =>11,
(А&В)~В,
А=>(/З==>(.1&В)).
,-1 =>(А v В),
JJ=> (:1v В),
(А..;;.>(~);:;;:) ((/1;:;;:) С:)~ ((.tl v В)=> С)).
(А;:;;:)/З);:;;:)((А~lВ)=> lА),
llA~ A.
(*)
l la уμою1х русского к11,1 ка уча·1 , что тавто
лu1·11t'1 ( 11р:11ща , н дру 1 ·о м с мь1 сле) 11аж> 11збlтать.
м~пt:ма 1 · 11ко11 же 111tTl'JJL'C )'IOT н,,1е111 ю ·1 а1.1·t0ло-
1·111 1, lft)l KOJll•' -) ' Ot-11 1 ЯНJIЯIОТСЯ 11с.~п-шнъrмн н сш 1 у
оюеi1 форм1.1. По; 1с 1·а\-\НВ в:.1есто 1 1 р01юз1щ1ю -
11ат.11111.\ 11 t' p t."1 t1 111ыx прпп :толыr ые СКi\11,1-
сле 1111ыс nыска:11 11н :11 11 tн. uсегд:~ получ и.\r вер11пе
\Т»ерж,щ:ш н.:.
Воз1111кает uonpoc: кзк для пропзволыю l1
nрuпоз1 щ1ю 11алы ю~'i формулы узн:IТь, являс.-гся
. 11 1 он. t ·1.1 втuло1·11сt'r ' Он1111 спосuб очев11дсн ·
1.:с:111 н фuрму.1<.: 1 1 м сстсн 11 11еrе.\\енных, надо
1 1с рсбра 1ъ нес 2" воз м ожных комб11н~ш.11!1 бу
. ll'НЫ \ ·$ н.1чс 1 t1 11't ~т11" переменны х 11 ;1,.: ш каж-
1 tо11 l\()\1\Jllll:ll,1111 RhlЧllCJlll I)) :Jll:tЧCillIC фоr-
НЕКОТОРЫЕ ЗАКОНЫ
ЛОГИКИ ВЫСКАЗЫВАНИЙ
Поскольку тавтология есть формула исчисления
выскаJыudни11, ~1ст111111ая в силу одной своей фор
мы, 1<1flH>лorи11 можно было бы наз вать формаль
ными 'аконамн лоп1 ~..и высказыван 11 й. Вот некото
рые TJl\иe законы:
Закок nроти1щречия . Выска>ывание А не может
быть OЛHORpe'vlE'llltO ИСТИJl l lЫМ и ложным.
l(A&lAJ.
Закон исклю•1ённоrо третьего . /\ибо вср110, что А,
либо 11свср110. что А, трстьеrо t1 e дано:
АvlA.
Закон двоЯноrо отриш1ния. 1.::сли 11свер110, что 1-1е
оер110 А, то Л исти 11 tю:
llA=А.
Закон троИ11ого отриuания . Если неверно, ч10 1 1 е
верно, что неверно А, то А ло,._но:
lllA=lA.
Закон контраnоз иuни . Есм1 ю А следует 8 11 не
вср 1 ю, что 8, то неверно, что А:
(А=81 =(18 ::::)1А).
Закон прив едения к абсурду. Если и3А следует, что
вср 110 В и что нt>верно 8, то Л ложно:
(А~81--? ((А ~181::::)lА).
му.11ы . \.1\ сож~1;~ е1 111ю , l' poct't) \1 ll llpoцccc ст~ню -
" <::
11
J (~I
н1 1 то1 1кт 1)0JICl' 1р~ 1 1ос,1 ю r '1. a11p1t\1Cp. уже_
ком()1111а1~11l1 1111к:1коt"1 C{ 1t\f1C11.1cн нh111 кu,111ью
·1ер 1 1ере6ра 11. 11с \Н1жс1
Друго1' 1 CJIO('()\) llr.tДt.') 11111 > T:t llTO.'IOПlll сщ·m·
н1 13 п острос111111 cncн11aJ11>1101·0 11счиСJи!1111я
аыо.:азывт шi1. Основная ндся ~дссь тз же. что
11\' 1111m,-1m нпюго оnреде:1ешш: некоторое ко
HCЧllO<..' J111ЮЖССТIЮ форчул обыш.rr яется IfCXOД
ны\1 11 даю·101 11 раш1ла, которые п озuолшот н:t
ос11онt· OJ(ll11\ ·1,1н 1 ·шю 1 ·11 i't с.-гровть др~тв с
ИСЧИСЛЕНИЕ ВЫСКАЗЫВАНИЙ
!Jьmo nредложено м11ого различш.1х 11ари~11 по11
11сч11слсtп1я 11ысказьшашп-1. Рассмотрим тшл,
ОДИН из ШIХ. 13 к~чсстnе ИСХО[\НЫХ формул
нuзьмём нс~ формулы("'). Правил юн1 носr·роt.:
н1ш 1ю11 ы х формул будет ) \На . Пt'рнос нз них .
rю cyщcLvrнy, нам уже и знестliо 1 rз шкш1ьноп>
курс:~ ал1·сfJ ры . 'Г:1к. сс1 11 1 локаэ::u ю rож11ествu
(а+ /;)
2
=а
2
-1- 2а}-; +1/,
то можно подставrrть нместо пере.меттпой а
любое :1лrtбра11 ческое выражение. Скаже м.
'
~
ЮЯВ t/ = .\" ]'+ у. ГЮJ!У'lИМ
)
~
i
'
{'
J
~
'
(Х)'+J' +Ь)- =< (.t~)' +J')-+ 2(.YJ'+у )IJ+о·.
То же 11равнло дс..: l~стнуt:т н н нсчнl'J1с н 1ш
высказына11ш~1.
Правш10 1 (llfJurшлo 11одопшюнк.u). Ест~
АЫl:lеде 11а ПDOll(ДJ·ЩI I01-13J llJllЗ>1 формула, ТО И ;'!
11 еЕ можrю получтъ 11 онуто, 1юдсташ111 1J:11есто
всех пхn>1\,.1\е1111 й юшо l1 -л нбо 11 ереУiешю l1 дру
гу10 nропо:ш1 tно 1 ~алыrую фориулу. I l аnрнмс р,
из тавтолопш
А=> (13 ~А)
выведем
ХЛЕБА И ЛИ ЗРЕЛИ Ш
Булем считать, что билет в кино стоит 1 рубль и что
пирожок также стоит 1 рубль. То гда
А= В:Есм1уПетиесть 1рубль, тоонможетпо
смотреть фильм.
А = С: f(:ли у Пети есть 1 рубль, то 011 может
съесть пирожок.
Формула
((А=В)&(А=С))=(А=(8&С))
яв"яеп я, как легко проверить, тавтологией . Можем
ли мы на основе ~того заключить , что
А=(В& С):ЕслиуПетиесть 7рубль, тоонмо
жет посмотреть фильм и съесть пирожок?
Нет, мы скажем «... посмотреть фильм или съесть
т1рожок ». В ч ем же тут дело?
Оf>ьяс11С'ние связано не с ко11ъюнкuией и ли ::1ьюнк
uией, а<' "1мnликаuией. Если математик дока3ал неко
торую теорему А, то лотом он может использовать её
1~еограничен 1 юе количество раз лля доказательств.:~
других теорем, например вывuдя по правилу модус
Математическая логика
(llС=С)=(В=(llС=С)). (**)
Правило 2. Есл и вьшс,'1,е11ы rrcr<aн фоrму
ла вила (Ф1 =ФJ и формула Ф1, то из этих
;1нух формул ,\/ЮЖНU нынсхти формуflу Ф~. Н:.t
лримrр, 113 фирмул (*") и l l С~ С 11uлуч11м
формулу
В=<llС=С).
ТТrавило 2, 11а зьmаемое .АЮ( ~1 1с IIOllt!IU:. как
прави.11t,ный: способ умозш.u1юче11ня 1шсрnые
nыделил уче 1111 к Лристотеля Теофраст. жтrв
тий 1J JV- 111 l.Jl\ . ДО TI. э. KOIIC 'il 10, 1шту11т1ш110
люди гюльзовались этим ттр:~вилом задолто д<'
Тt-офраста .
11рuпо:ш1 (н uн:и 1 ы raf1 фщн1ущ1 Ф сч 1 1та<:"1·сн
НЬl8()()U.мой R f·JCЧИCJICHIJlf llЫCK33ЫH;'!J IJl ll , CCJl l l
су-щсствуе1 · список ф<1μмул <I\. Ф L· "., Ф". Ф , Т(!
кой , что каждая формул~~ R 11ём 1u111 й1u1н~1п1
1tсход1юй , нлн 1 юлучаетсн н:з сто>J ще!r ра11ес её
формулы по праши1у полста1юnю1. ил11 1 ю11у
чае-1 ся ИЭ ДВУХ СТОЯЩIIХ (>;'tlICe формул llO npa-
!3T:UJY модус по11евс Такой сrшсок на:~ыnаетсн
вьиюдо.м формулы Ф.
OшrcaR 1к:ходrrы.l' формуды и пра~нuщ nы
тюr1а, МЫ 3;,iR<:рШИJШ фuрм~ЛЫ-10~ O !!pCl\l:ЛCHVll:
HC'IHl'JJCHHЯ ныск:~ :iЫRаНJ 11'1.
nоненсизА=В,А=С,А~О, ". следстn~1я В, С, О ...
Такое использоваt1ие теоремы А никак ~ё 11е « Портит».
В нашем пrимере с Петей грамматическая конст
рукuия «если..., то ... » такая же, как 1• у математичес
кой импликаuии, но связь между nосылко11 и з.:~клю
че 11 ием и н ая, так как предполагает ислользuва11ие
некоторого расхuлуемого ресурса -денег. В других
задачах подобным ресурсом может бы1ъ энергия,
nлошаль или объём, занимаемые обьектами, величю1:~
памяти ЭВМ и г. п. Лля правильного планирования
ле11ств 11 й в подобных ситуаuиях используется ли
нейная логика, лридума1111ая фр<1 1 шузским матема
тиком Жирарuм.
589
59(J
Фундамент матема тики
МОЛЫ СЕЗО Н А
В субботу вечером Петя решает с.ъездить на слелу
юш1>1 й день к бабушке в деревню.
А ~ С: Если в воскресенье весь день будет
жаркая солнечная погода, то Петя знает, как ему
одеrься завтра утром .
В~ С: Если в воскресенье весь лень будет идти
проливной ложль, то Петя знает, как ему одеться
зав тра утром.
Петя включает радио и слу ш ает прогноз погоды
на слелуюш и й ден ь:
А v 8: В воскресенье весь лень булет жаркая
сол нечная погода или весь день будет идти пролив
ной МJЖАЬ.
Формальн о из этого можно вывести такоеслел
ствие:
С: Петя знает, как ему одеться завтра утром.
Вы н е согласн ы? rле же ошибка?
Тут п роизошла замен а модальности . до сих пор
мы имели дело только с модальtюстями ИСТИ НА ~1
ЛОЖЬ, здесь же воз ни кла новая модальность П ЕТЯ
З НАЕТ, отлич н ая от них. Лействнтельно, есл и лаже
некоторое утвержление нсти11 но, 10 Петя про это
может и не знать .
Наш пример «ИЗ жизни», в математике же кро
ме И СТИ НЫ и ЛЖ И важной модальностью является
ЛОКАЗ УЕМО ( в какой -то формально й с и стеме).
Утвержление можеr быть и стинны м, но не доказуе
мым средствами данной системы. Лругие модально
сти, важные на п рактике, таковы: Н ЕОБХОЛИ МО,
ПРА ВЛОП ОЛО БН О, ВОЗМОЖ Н О. В молальных
лоrи ках мя обозначе ния молальностей исrюл ьзуют
сп еuиал ьные символы и залают свойства модальн о
стей с помошью nоАХодя шего набора аксиом.
П риведен ный выше прогноз пuгоды в виде дизъ-
1онкuии является мало п олез ны м. Мы не можем дей
ствовать на его основе, так как не знаем, какой
имеt1но члеt1 лизъю11 кuи и истинен. Иrтолкование
смысла лизью нк uи и в математике также породило
бурн ую лискусrию. В частн ости, сомнению был под
вергнут закон исключ енного третьего : А v 1А. П ра
вомерво ли считать эту лизъюнкuию истинной, если
мы не можем установить, которое из двух утверж
деt~ий, А или 1А, истинно? В результате были пред
ложен ы логичес к ие системы без закона 11скл ю
чен 11ого третьего - интуииионистская логика (в
н ачале ХХ в.) и конструктивная математическая ло
гика (в середине ХХ в., с раэвитием теор1>1и алгорит
мов) и на их основе построены математическ~1е тео
ри и , сушестве н но отличаю ши еся от класси ч еских.
Итак, пu форме 11счислсние высказы1:1а11ий
оче1 1 u похоже H<I 01тределе11 нt: проnозицно
нал ы-юй формулы. Имеется, ою1ако, и суще
ствеrшое отm-~ чие. О1 1 ределяя какое-либо 1IOROe
понятие, напри.мер в нашем случае логическую
формулу, мы ничем не связаны и можем это
делать как утодrю (другой вопрос - будет ли
r-ютюе по.нят11е ::1аслу)юшающнм изучен и я). А
строя исчисление выска3ыва 111 1й , мы nрсследu
вали опрсделёнпую цель - указать способ об
разова r rия обы:ктов (п1в10110 1•11й), которые
нами уже f1ыл11 определены. В сnязи с :'!Тим нуЛ<
по /1.ОТ<азат1, два факта.
Теор ема о корректности. Каж;"\ая фор
мула, выводимая в исчислении uысказьmаттий,
является тавтоло1·ией.
Теорема о nолноте. l<ажцая тантология вы-
1юдима н 11СЧИСJJСНИИ ВЫСК:1ЗЫВ:11-1 1 1Й.
Теорема о корректнuсти не шшнетс.н чем
то удивительным и неоЖУщанн ым, ведь правила
выrюда спец~·Lально ныбир:l;rис.:ъ таюrм обра
:юм, чтобы иэ та1пшюпп1 мтюю В ыло пuлу
чить ТОЛЬКО Taf\TOJIOl'ИИ.
Теорема о потюте 11счисле11ия высказы
ваний - это горазло более глубокий н не
ОЖ1'1J1ан 1 1ый факт Действительно, сущесгвует
бссконсчпос множество тавтологий, а мы в ка
честве нс.ходных ВЗЯЛИ Jll111Jh KOl-lt' Ч J-IOC, и со
всем 11еболыrюе, их количсство. J~алсс, имеется
много спосо6ов делатh умоз:.~юr ючения, а мы
Ot"p::tIO-I YIOJИCb l:!Cel'O /\В)7МЯ 11rавилам11 . ДОСТОЙ·
r ю удивления то обстоятсл 1 .ст1ю, что этот
Recыvia а1ра 1 шченный набор средстн оказ~uтся
достаточным fl.ITЯ порождения всех таJП()Л()t'и_й
Итак, теперь у 1тас естт, дnа метода, позволя
ющие установить, что некоторая формула
является тзnтолоrией: перебрать ncc nозмож
ные значения nходящих в нсё псрсмсrшых ил11
най'1·и вывод формулы в исчислении высю.1зы-
1:1аний. Хотя процесс 1юиска ВЫlЮ/\а может быть
весr,ма трудоёмr-шм , 11 е исключено, что er'O
резут,тат - с::~м ныnод
-
Оf\ажется дос1·~почно
коротким И с эп 1 м связ<~но rrреи,"rущество вто
рого методз. Действителыто, если мы ус1·ано
вили тавтоло1· ич1юсrъ 11екоторот1 форм}JJЫ
первым методом и кто -то хо•rет проверить
результат, то он должен. по существу, поnто
рить ~юлностыо нашу ра61лу 110 перебору всех
:з 1 шчен11й. А t!ри втором ,\11ето;1е е::му нет необ
ходимости путём нроб и ошиб<ж 1юv.торs1ть
про 1 \есс rю11ска вьшоJ\а - достаточно nрuвс
р11·1ъ уже н:н1ленный выкrщ.
ВЫПОЛНИМЫЕ ФОРМУЛЫ
Помимо таnтолоrий важную рол ь, особеп н о
ДЛЯ решения ·L'еХНИЧеСКI·IХ:.-1<.tД::tЧ, Иl'{1::tIOT ВЫLЮЛ
НН:МЫе формул ы . Ло гическая формула Ф назы
нается вьтолии.мой, если она при~ 1им ает зн а
чение ИСТИНА хотя бы при одн ом выборе
значений nхо~ящнх в неё nepeмe1n-tъ1x.
Очеnид1 ю, что каждая тавтоло1· ия является
вы п оmВJJ\.!ОЙ формулой. Кроме того, имеется
дf>}'Т'ая, бодее rлубОJ<ая связь тавтологичности
и вьmолнимост1 r, а именно:
формуда Ф является выполflимой
·rогда u только тогда, когда её отри
цание 1Ф не явдяетсн тавтологией;
формула Ф является тавтологией
тогда и только тогда, когда её отри
цание 1Ф пе являете.я въmоJI11ИМой
формулой.
Таким образом , изуче~-mе тавтологий и изуче
ние Rыпот-шмых. форм.ул rю сутн дена од11а н
та же проб;1ема.
Многие за/\ачи естественнее фоrмулиро
вать в терминах в ьшол ннмости. R качс::стuе пер
вого 11ример<1 рассмотрим задачу о том , ю1к
состан и ть т колы-юс расписан ~ re.
..,
1
Ма rематическ.~я лоr ика
Им еется м1южество ютассовК1 , К1., ".,~, м1ю
жсство nрсподав~пелс!1 Р1, PJ, .... Р,,,, каждый н~
которых 11реподаё1 опрелелённый 11редм ет, н
множестно урокuв И1 , U!, ... ,и,, (есл1:1 н ка.Nщы~:1
из 6 учебных дней недели проходит 6 урокон,
то11= 36).
М1,1 можем рассмтретъ булены 1rерсме1 1 н ые
BIJk•гдеi==1,2, ...,l;j=1,2,.... m;k=1,2, ...
1ll,и
считать, что B1i1.: = И СГИНА тогда и только тог~<I ,
когда k-й урок педел11 в i-м классе провод11 ·1 j-й
преnодаRатсль по соответствующему пр едме
·1у. И с11ользуя B,1k, ле гко записать в нидс логи
ческнх форму.fl требо\\ания к р:кписанию, н~t
пример
-
КаЖJ\ЫЙ преПО[{ЗВ3ТСJIЬ ВСj\ёТ урок только
Н ОДf. ЮМ KJl<lCCC:
BIJ" => l В"1,.
(i * i');
-
каждыfr урок н данном 1<лассс Dедёт тош,
ко однн преподаnатслъ:
и~л;
-
кл<~сс ш1когщ1 не остзётат без 11р~ 1 юд~ша
теля:
Далее надо залисатъ 1ребонания. чтобы да 1111 ыЛ
класс имtл . напримёр, 2 урrжа ф 11 зкул 1>туры в
неделю, 11ричём эт 1 1 УJХЖИ не проходнлн в
один день (ил и, наоборот, в один дсrrь и п.од
ряд ), 4 уrюка математики и т. д. Состаnнть
расписаrше - з начит найти такне значения
нерс1>iенннх. при которы х. конъюнхция всt:х
п одобн ых фор,vtул истинна .
Вот щ1уrая зад:~ча. Вн~шне она щшска от
1югики , но 1га са м uм 11елс её лс1·ко предстапнть
13 виде з:ща чн о н ы потн1м ос1·н некоторuй булt'
впй формулы .
Дано 1-1атуральrюе числоN. Требуется ~знап"
простое оно или составное .
ЧислоN ЯDЛЯСТСЯ составным в ТОМ и ТОЛЫ<О
в том случае , если оно предстаnнмо в виде uро
нзвсдения днух чш:сл Р и Q, каждое из которых
60J1ьu 1e 1, но меньше N. ПредстаШ'L"-1 числа N , Р
11 Q в двоичной системе: счпсленш1:
т
т
т
N= I.п_..2"', Р= L Pk2k,Q=,Lc1~.i1,
,:, ,n
1.:~о
k~o
1·дс 1{<1)JЩОе из чисел ll1.:, Р1< 11 qk раnт ю либо О,
либо 1. Мы не знаем, как именrю nыглнд1 1 т
двоичная ;1аrrись чи сел Р и Q, но можем рас
смотреть буле13 ы псрсменпыс Р0, Р1 , ••. , P m;
'191
Фунламент ма тема1 ики
Q(,, Q 1, .." Q 111 • считая:. что РА- = ИСТИНА тоrда 11
только тогда. кшда Pk== L ( соотнетствснно _Q,, =
=ИСТИНА тшда 11 толькu тоща. ко1·Jщ ц" = l ) .
НС'1 ·руднu сост:нштъ л01·11ческне формулы
Ф,» Ф1. ".• Ф111 с псрсм<..:нным11 Рп, Р1, .", Р111; Q0.
Q 1, ""Q,,,, т~1кие, что Ф,, и'Vtеет :СJ11аче111·1е ИСТИНА
TOl 'fЩ i .1TOJJI>[(() 'l'()l'Щl , 1\01'Д3 k-я 1tllфpa R лвоич-
1 ЮЙ :1а1шс1 1 прои:1вслсппя PQ раnпа 1. Вот для
примера две начальные формулы:
Фu= Pu&Qo.
Ф1=(Pu&Q,) 'f(Р,&Q0).
YL'J IOш1e , что чисш1J111 Q болпше 1, запнспн~а
стся как
Р1vР~v...vр11"
Q,vQ2v.vQ/11
Tenep1..> можно запис1ть формулу, которая
будет RЫПОЛ11IIМО:Й в том и только н том слу
чае. когда N - состанное 1 1иСJю. Зта формула
ннт1стся КОНЪ1011КЦ11ей / \IJy'X 1ЮСЛСДl-JИХ )\ИЗЪ-
1()11Ю \Иl\ формуJ1 Фk /\ЛЯ тех знач.сний k. /ЩЯ
которьLх nk = 1, и формул l Фk /1.ЛЯ тех Зl1~1ч е
ниl1 k . /l,JIЯ которых пk =О.
3;~дач11 о школыюм р::~с11иса11и11 11 о co-
e1 ·: .i нн 1.1х qу1слах имеют од1 iy общую черту: когда
01 tи рtшены , нронерить ответ нетрудно (n<..:ре
множ11т1, ч11сж1 Р r·1Q и срав1-111т1, рс:~у1 1.nтат с i\'
или убедиться. чтu вес трсбов<1н11 я к p<icr1 11ca-
нrrю тн,111ш1нL'ны). Выянж: н огромныi1класс1ю
доб11ых :Jад;~ч (1 rtскот,ко ·1·1.1сяч) с лё1·1ш~1 11ро
веркой ответа. Было дока1а1ю, что все 011н
сnодятся к задаче распо:шава~rия вьшот шмости
булевых формуJ1. llo вот шtйти способ быстро
го её решения мат<::матнкам 1-шкак не удастся
Возможно, 11 нет дру1·01·u []у1 ·и . кроме 11еребор:1
1 10чтн всех нозможн1,1х з начсн111'1 б ул е вых
НСИЗНtСТllЫХ , в таком CJ IY't:"IC' IIOЗlШK:.Jl"l' друг:~я
це.111> - доказать, что нс су1щ;стнуег мt:тода . по
зволяющс1··0 быстrо наход11т1, 111:1ч t:нии 11ере
ме1111ых , 11ри которых да11ш1н 6улсnа формула
принимает значение ИСТИН.А. Помнмо теоре
тического интереса такое доказательство нме
Jю бы uаж11ое праrпичсс1<ос зп;1чснис. Дело n
·1 ·01\1 , что мrюгнс соврсмсrшыс с11стсмы крипто-
1·рафни (ш11фронки), на 1 1римср ·1·с. к1х1 ·орьн:: 11с
полк1у1ото1 при осущес1·1.111<.:11ни банконских
расчё':'l'ОВ 1юл11 НИЯ м Сl.\ЯЗН, OCHOH:JH hl ВС<..:ГО лишь
11а llPC/J,!IOJIOЖCHИJI , чтu нснозможсн быстрый
с1 юсоб рdспознаван 11я выпоm 1нмых формул.
ЯЗЫК ИСЧИСЛЕНИЯ ПРЕЛИКАТОВ
Если в:щть любую тa.1:пOJIOl'IJIO 11 ;j:!менн·1·•· к не~"1
нее булены 11сремснныс н;,~ м<1т<.:.:-1атнческие
выск:.~ :-1пrnання, то П(Jлучитсн истинное у 1 ·11tрж
дсниl' - теорl'ма. Например, из форму11ь.1 (А=>
=> В) => ( l В => l A) можJ ю нывес111такое11ер1 юе
утnержденне :
Если иа того, что 119 - просто11 число, сле-
1~11ет, чпю <.)и1.1иаyvzoв врштостор01те.м тре
уго.лышл:,е равна UIO", то из того, что (VJ11Jll/a
уг.лов в рашюсгпорои71ши. треуголы-rих;е 1-ю рав -
1tа 180", слl!дуС'rп, что 119 не являепи""Я 11ро
сты.м '<tl/(:/1.0.М..
ПО/\Обные "теоремы» , олнако, 11е представ
ляют 'J 1:.Jуч1-ю1'0 ннтсрсса. Bc/ \h кысказываннн,
которые мы подставляем вместо 11ереме1111ых,
мену~ · быт1, соаерще111 ю нс связаны друт с
лругом по смыслу, как в прнведёшюм выше
примере. Эти поные уmерждения нерны бла
годаря одной сuоей форме, а пе содержашпо.
СформуJIИроnатъ (<настоящнс» м:псматическне
592
теоремы М())ЮЮ с по.мощью 60J1ee развитого
формальЮ)l 'О ЯЗЫК<! - языr..·а UCЧllC..l/('1-1/JЯ lфl!·
дmcamoR.
ПРЕЛМЕТЫ И ИМЕНА
Вспомним, что к исч.ислс11ию 11ыс1са:1ьша1шl! мы
приm11и, обоз11ачая булевыми ттеремет11,1щ1
цс11 ыс прсщюжепия . Нас интересовала нс 11х
сгруК"1ура , а только то, что они мо1уJ быть 11с
тиш1ь1ми шш Jюжным11. Теперь дслаr:м следую
щий 1JJa1· и обнаружинаем, что в любом ныска
зыва11ии можно выделить оди11 ил11 11есколько
объе 1<тов, о которых в нём и у~·нсrждк·тсн чтu
либо. Эти 061,екты могут б 1,1т1, окружающим11
нас нещамн или жиnымп сущестnамн. реальны
ми предметами или ::1бстрактным11 сущ11остям11,
в прсдложе1ши они мОI)'Т называться ншю либо
только подразумсnа1ъся, но n любом случае om1
есть. 1:3 математнчесю1х уrяерждепнях ()оъект::t
ми явлнются числа, фmуры, фуню_(rш и т. /1..
Вопрос о 1'ОМ, в ка1<ом смысле н ~1·де» сущс
стр,ую·1· математические объск·1ъ1, давно 1щл110-
н::т м.атем:.tтнкон и вызын:u 1 сноры . Мы, од1-1:.~ко,
осгавюvr эту философскую пробт:-,rу R стороне
11булем11росто считатh, что име<.;тся нскотор;:rя
1'ljJед.мет11ая пбласпu, - мr южество 1\·rатемати
ческих 06·1,ектnв, о ктпрых н бу11ут что-л и бп
утnержт1:1т 1, ЩJС/АЛОжепия нового языка.
В тобом языке - естес-rDеш 1 ом шш иr
кусствешюм - для обоз11ачення предметоl\
служат имена . Некоторые из них назьш•нот
1юнкреп-1ыс обы:ю·ы. Например. в математике
1·рсческая бутена тt траднцнонно обо:ш:.1 ч:.1 t"1'
отношение дm 1н ы окружности к её 111щм <.:'1 ру.
Десятичную з<Jm1сь ю:1·1ур:иты tьtx чисел также
"южно р:~ссматрн.нать 1:1 качестве нн1t11виm.
алы-1ых нмён.
Важ~n,1м 0·1·лнсщем математнческоrо лзыка
является наличие переменных. Переменные
tIOЗIIOJIЯIOT говорить н думат1, об отJ(ельных
объектах прсдмС'JПОй области, пс 1щнкре11"13и
руя э·п~ объсt..~гы. В ру<.:ско.м языке есть средства ,
которы<.; в какой -то мере позволяют дещ1ть то
же с::~ мое, к 11римеру мес1·01,IМеннс <'некоторан».
Можrю ска :з:-11 ъ «рассмuтрнм 11скоторую тuч~')'».
Труднr>сп-1 Iю:=tнн ю гут, когда чере;-s какое-то
uремн т ющ" 11ал.о будет 1·онортъ о Т()Й же точ-
1\е. Нель:'\я сказать «11rюведём через не1<оторую
Т()ЧКУ ттрямуLО·>, есnн имеете.я 13 11н:т1,у · 1·а точ1<а.
которая уже рассматриnаласъ ранее. Теперь
следует r кnопьзоJЗать другое местонмение -
~эта». Но Ttu< можно 1юGvrу11ать, J<огда речь JJДt'т
об одном-rщух, но Вб•ком <.:лучас о нсбольшом
кuлочестве объектов. Есл11 же их м1ю1·0, то
Курт Гелель.
Математич€ска~ логика
r()pa:i;щ y;\ofi1-1t'e пвестн, п:срсмс11ные. кот< )рьн.:.
па существу , CJ l)l)Kaт nремс11нь1м11 11менэмн .
Переменные, допустимыми з11:1че1111ям11
которых. яшшются. объекты предметной обла
сти, называются 11р(!д.ме1пнъ1J1tи. В качестf\е
таких лерсмеrн-1ых прпнято использовать
стрnчлыс латннсю1е букны , чтобы отличнть их
от булсньL'; переменных. Просrе11шн.й в~1риант
нс~11rслс11ш1 прс;111катов. с которым мы 110зна
ком1 rмся, 11азы 1:1аетсн исчис:пl!'nиеvи пред~псатов
пероого порядка 11 с:п7'ерж1н тоз 11>1<0 nре,1мет-
11ые nереме1шые; в и:счисле1 шлх nре.ци1\~поn
более высоких nоря;\ко11 исполь~уют<"и nepe-
MCLII 1ые и других типов.
ПРЕЛИКАТЫ
Элементы 11ре;~мст1 юй обтtсти обла/\<LЮТ раз-
1-1n1м11 сuойспзами: скажем. натуральные ч11с; 1::1
бынают чё'1·11ымн, 11ечётным11, пrостыми и т. rt.
На свойс113а можпо смотреть как на фу[1ю~ин,
аргумент которых - :')Лемент предметной об
ласп r, а ~~ю1 чс11п·е - лоп1•1еская КОJJстанта
ИСТИ11А или ЛОЖЬ. Для обозначения свооств
возы,1 ем соот1ктствующие русс1шс слоn:1 н
бу;\ем нс1юль:юн;1ть нх как 11мсш1 футrкц11й,
н:шримеr ЧЁТНОЕ (х) , J1POCTOE (У).
Помимо CRoйcrrи - фушщий с rщннм прел
метным ар1·ументом - можно рассматривать
фуt11<ци11, :-н-1ачення которых - ИСТИНА или
ЛОЖЬ, а пред.мет11ых аргументов уже /lHa и
более. Такие фушщии задают om1ю1.UC'1LUЯ меж
ду элементами предметной обт1сти. Д~:Iя пр11-
мсра возьмёJ1.1 отпощсние <-мепыш:~• между чнс
лами. Тр:щицнонно оно записывается как
х <у, но для едиrюобра:тя мы будем т1сат~,
МЕНЬШЕ (х.у) .
Свойства н u11101uc1-1ш1 объедивиют nод об
щнм !-tазнаннсм - 1t/Jel)икam.
В математике наряду с переменными, 1<011-
ста 1 l'fЗJ\lfИ, стюйстнамн и OTI ЮШ<.;IJИ.ЯМИ ИСПОЛl•
зуются т~ноке oпepaL~нr--r и фу11кцн11. :~1-1а ч еr111н
которых - элеме11n,1 предметной оnластн. Дпя
унрощения изложения рассмотрим вариант
исчислсш1Я прсдпкатон без фунJ<ций. Это
01·рю1иче1-1не 1-1~1 с~1мо.м. )1t11e не ум~::нъшает вы
ра:iитез1ьных нозмож11остей я:~ыка. Нап.римср,
нмL'сто операни:и сложенюt /~остаточ.но 1к-
1юльэон<J·1ъ трёхмt=ст 1 гый прt:f(икат СУММА
(х,у, z'), счит;:~я, что 011 ие'1ннен тата 1-1 толыш
то1·да, ко1·11а .х +у= z .
_I
593
Фундамент математики
ФОРМУ/\Ы ЯЗЫКА
ИСЧИ СЛЕ НИЯ ПРЕЛИКАТО В
РасnоJ1агаи 11мс11ами прсю,1юппв, именами кон
кретных uбъсктов предмет11ой 06J1асти r1 пред
"1ет11ым 11 переменными, мы можем строи ть так
11аэьшасмы<:: атолтриые (nрост<::йшие) фор
мулы. Например, БОЛЬШЕ (х, 2) ,ДFЛИТСЯ (х,у),
ПРОИЗВЕДЕНИЕ (р, q, 1").
Используя атомарные формулы nмссто n ро
nо:шцион:шы 1ъrх переменных. с помощью зн:l
ков ОТр111\аI1ИЯ , КОНЪЮНЮJ.ИИ , ДlПЪЮНКЦИН И
нмпmшации можно постронтъ 60J1ec сложные
логические формулы, скажем ·1·аю1е:
МЕНЬШЕ (3. 4) & МЕНЬШЕ (4, 6). (*)
МЕНЬШЕ(:). х) & МIШЬШЕ (х.у). (**)
В 11ерnой формуле нет предмстII ых пере
менных, и потому, оычпстш значения входя
щих в неё атомарных формул, мы найдём и
значение всей формул1.1 (*) . Очевидно, что она
IJCTИПita.
Логическое значе 1 1ие формулы(**) не опре
делено, сслн uc указаны значения входящих в
неё 11рt:дметных rтсрсмен1 1ых хну. Тем н<:: ме-
11се. не 11рнданая ко111сретных зна ч.еr 11 1й этим
пере:менным , можно спрашивать, 1тапример:
-
1iep110 ли, что прл всех значениях х и у
ко11ъю111щия (**) истишrа;
-
верно ли, что существуют такие значения
:\: и у, при которых кш-1ъюнкцня (**) истинна?
-
верно ли, что длн каждогu знач.ения х су
ществует знач<..:ние у, при котором конъюнк
ция (**) ИСТИI 1на;
-
не рио л 1 1, что существует з1-1 ачсниеу, при
котором для всех значений х конъюнкция С*)
ист11н1-1а?
В ма' 1·ематп чсской лш·ике вместо слов «Су
щест11ует» и «ДЛЯ всех" используются специал ь
пые символы, называемые JСНантора;ш1: кван
тор существования 3 и квантор вссобщ 11ости
V. (Эти символы - перевёрнутые первые буквы
апглийсю-Lх слов cxis ts - «существует~ и all -
<- все».) С их помо щhю предыдущие фр::~зы за
писываJотся как
594
(Vx (V:.Y МЕНЬШЕ (3, .х) & МЕ НЬШ~ (x,_v))),
(3.х (3у МЕНЬШЕ (3, х) & МЕНЬШЕ (х,у))) ,
(V.x · (3у МШ I ЬШЕ (3, х) & МЕНЬШЕ (х,у))),
(~)' (''rfx МЕНЬШ Е (3, х) & МЕНЬШЕ (х,у))).
Кванторы тесно связаны между собой и
выражаются один ч.ерез Jtpyl'Oй. К примеру ,
вместо <-длн всех х нсрно А(.х) » можно сказать
«нснсрно, что существует х, т<.1кое, что 11eF1ep-
110, чтоА(х)~ , а вместо «Существует х, для котп
ро1'О верно /\(х)» - «неверно, что для ucex х
неверно, что А(х)».
Подоб1 ю определ<::1 шю проnозициопалы1ых
формул. мы можем дать и1 щу1<Тиштос опреде
ле1 rие формулы исчислсшш прtд11катоn:
1. К:.tЖJщя ато:марнан формул<• ншн~ется фuр
мулой исчислеюш 1 1ред111<атон.
2. Если Ф
-
фор.мула нсчнслсння прt:дню1-
тов, то ныражt:1111 е (l Ф) также янляется <.рорму
лой исчнслення прt.:д11кэто 1~.
3. Если Ф1 и Ф~ - формулы псчнслещ1н 11ре
д11катов, то nыраже11ия (Ф 1 & Ф,) , (Ф 1 v Ф 2),
(Ф1 ~ Ф2), (Ф1 = Ф1) также являются формула-
ми исчисления предикатов.
4. Если Ф
-
формула исчисленю1 предика
тов, ах - предметная псрс ."1енн;1я, тu выраже
ния (Vx Ф) 11 (Зх Ф) т<~кже являются формула
ми исчисления прсднкатов.
S. Ннкакнедруп1сuбъt.кты 11е ЯN1яются фор
мулами нсчислснин пrе.rtш<атов , кроме тех,
кпторые ими шзляются сотас1ю предыдущrv'1
r1 ун 1<'Т'Эм этuг·о 01 1 редеJ 1епия .
Как уже го 1юрююсь, предметные пс:ремеп
ныс - временные имена объектов. Скобки в
пуш<те <1 определения формулы 11счисле11ия
п рсдш<атов оr 1х1нич 1mаrот :юну, в которой пе
ременная :х· «сохраняет своё ли1ю». !lзнример.
хuтя никакuе число нс является одновремt:н-
1-ю чётным и нечётным, фор.мула
(Зх (ЧЁТНОЕ (х) & БUЮ)ШЕ (.У, 2))) &
& (ЗХ (IIEЧEП-IOE (х) & МЕНЬШЕ (х. 5))) (*••)
истшша. В формуле использована nесго одна
предметная переменная, однако здесь уrnерж
лается существование двух чисел: 11epuoc -
чётно<: - больше 2, а второе - нечётнос:
-
мен~,mе 5. По ан:1..1юrичной причине мь1 н е ,\10-
жt:м спрашивать, ист111ш:1 ли формул:&
(З.х (Чf:TI-IOE (х) & БОЛЬШЕ (х, l2))) &
& J-ШЧ.ЁТI-108 (х) ,
(****)
поскольку то х, которое является аргументом у
преднката НЕЧtТНОЕ, не имеет пи:как01·0 от-
1юше1шя к х, стоящему после квантора сущс
ствован11я. Принято говорить, ч··r·о в качсстне
ар1умет rта у предиката 1LЕЧЁТI LOE переме11 1 1ая
х Rхrщит в э1у формулу свобоr)ио, а n качес111е
<1ргументов у прсдюс1тоu ЧТТl !ОЕ и !30ЛЬ
ШЕ - связащ ю.
Формула.
.1:1 которой ncc вхождс::пия пред
метных псрсм<::шrы х свя заны (1«1к в примере
(***)), н <1зыв~н.:тся .з a.л-iю-iymoit.. Есни формула
!!С замкну1·а , ТО l'OHOpИTh о её ИС'П I ШЮСТИ 111111
1юж1юстн можно , только указав :-~нач.ения всех
перем енных, которые входят н форм)'JIУ сво
бодно. Так, фо рмула (****) nерна прн .\' = .3 н
ненершt ПJШ х = 4.
Но что сможет сказать об этих фо рмулах
lrеловеъ:, который не знает смысла слоR «чёт
rюе», « rтечётнос», «больше», «мень ше~? Для rrero
вrrз'-1алс на1tо будс1· описать .иодмь, которую
мы ~1меем в uиду, :.i именно сказать, что ны
бр:.~ нная нами предмстн::~я обл~~стh - натурал ь
ные ч11сла, <1 ЧЁПIОЕ, I JЕЧЁП-JОЕ, БОЛЬШЕ 11
iv1EHbillE - COO'L'BCTC' l 'HYfOЩИC С IЩЙС'ГВ:l ЧHCCJI
11 отношения меж;~у числами .
ОБШЕЗНАЧИМЫЕ ФОРМУЛЫ
Итак, для при:шання формулы (''**) истюшой
1'ребуетск знание см ысла нходищих в псё снов.
И это обстоятельство с 1:шдете11ьст вует о том,
что мь1 сщё11едостити 1юлной формали ~шции .
Подобн[)Й 11роб немы не воз11икзет nри
l!KCИO.'vt/ITИЧCCKOJ\1 11<хтрое 11ни той или иной
матtматичес 1юй теории. Задаётся 1 1екоторое
кол 11чtствс) :1ам1<1 1утых форму11 А,, Лl, ." , А,,, ,
называемых аксиомами. И те перь вместо во
проса, истинна форм ула или нет. стаnим
вопрос, сле дус:т ли она нз 1'анных аксиом.
ОТ ЕВК/\ИЛА К ГИЛЬБЕРТУ
Истори чески акс иоматический метод построения мате
матики начался с геометри и . В классической работе а На
чала» Ееклил предпринял попытку дать rюлн ый список
требуемых аксиом. В послелуюш ие столетия было обн а
ружено, что этих аксиом не хватает, т. е. где-то в доказа
тельствах происходит апелляuия к зрительным образам.
Эi()ГО недостатка смог избежэть Д. Гильберт, прелло
ж.ивший в ко1ще Х!Х в . свою аксиоматику элементарН()й
rеuмстрии. Широко известной стала фраза Гильберта :
•Слелует добиться того, чтобы с равным успехом можно
бш.о говорить вместо точек, п рямых и nt-.оскостей о
столах, стульях и пивных кружках».
Матем1:1тическая лоrик11
Л именно: ~амкнутая формула Ф считаетсялп
гuчес/(,U./11 с.ледспшuе.м. аксипм А,, А 2, ••" А111, если
она иститша на любой модели, па которой ис
тн1шы uce фор.мую.1 А1 , Лz., .. " Ат· Таких моде
лей может быт1" ноо б ще говоря, много.
Дlm примера но:~ьмё м сленующую аксиома
ти"-у:
Л 1 • "ifx V:)' (СУММА (х, 1 ,у) =>(ПАРНОЕ (х) =
=lПАРНОЕ (11))),
А2. "ifx \fy (СУММА (х, 2, у) =
=Зz(СУММА(х,l,z) &СУММА(z, l ,J'))).
В качестве первой м одели, на кото рой вер
ны обе :1кс.:номы , рас с м отрим натур:1 ль.11ыс
чисJ1а с тр:щшtио1:-н-1ым пшгнманием от1ruшс-
1П1Я СУММА, а под CJiOЙCTl:IOM ПАРНОЕ буде м
подразумевать ЧЁТНОЕ. В этоИ модели ::1кс 1 1-
ома Л 1 оз 11ачаt.:т, что t.:СJ 111 11атураль ное чиLJюх
ч tтrю , то х + 1 нечётно, 1-1 rт<!оборот. Аr<с ипма
A l соответствует эл е ~1ентар11 ому тож,11еству
х+2=(х+1)+1.
Вторая модель отличается от первой тем, что
под свойством ПАРНОЕ понимается НЕЧЕТНОЕ.
Несмотря на то что в этих двух моделя:.,...._ стюй
ст 1ю L1APHOE толкуется в противопоножно м
смысле, аксиомы А 1 н А.! остаются 13ер11ыми.
Примеро м сл с::дствия а:ксиО'-'1 А 1 и А1 служит
формула Ф:
Vx V:J1 (СУММА (:\·, 2 J') =>
=>(ПАРНОЕ (х) =llAPHOE (у))).
tl 11срnой модели она иrrтернр етнрустсл та~<:
сели натуральrrое число х LJёn юе, то х + 2 также
Фyндd'lllt'H r -.л,1 1~мд1 ики
ч<."nюе. 11 11аоборот. IJз того. что обе акс 1 ю,1ы
верны 11:1 обеих ржтмо·1рснных кыте 'Юдслях.
НЫТСКJеГ, что 11.1HllX нерн:~ 11фоr.чула Ф, О/IЯ l'h -
1':11{/J нсс,1отря 11:1 11ро·1 1 1ноnо1тожноl' пон11 .,1:1-
н11с (.'1\Ой(' 1H:t ПАРНОF
Rщ·е1'<> '/'()('()чтобы R опrе;1еле1 11111 следстп11я
1-пнор1111" ч·1·с > фпр,1у, 1з Ф 11ст11ннз на все.х \1()-
,1слях, Н.1 К<Уl'()ры:-. веr11ы аксиомы А , . А;• ... , Лт.
\Н>Жr ю ci.;a:-ia 1ь. что фор~rула
Л1&Л2&". &А,,.=>Ф
вср11а на любоrr модслн. Де11 спнпелы ю. с<.·1ш
н:1 1<а1<ой -то модсJш одна 11з а ксн()М нс верна,
'1'0 llC щ:рна I J нсн КОНЪ ЮНК'!(llЯ , стоя щэн в 110-
ChlЛKC ll MllJ l ~ I K;tl\ 111 1. а :iH:IЧ ll T, HMПJllJK:Щll H 11 с
т1 111 11 а . С 11ру1 ·ой стороны. t.:c m s для 1 те1сотпроl1
ма1~<.:т1 с 11 ра 1 н:11111111 ы в('е аксномы, то 11:-i 1111x 11
фор"1~·лыЛ1& А,& ". & А111=> Ф получзем нс
тm 11 Ю{"П, Ф 11() r1parиiлy модус понеrrс.
А 11а 111 f'м nр11мере ис11 1 шюi1 на всех моделях
штяется фор11н1л;~
(V'x'v)• (l.Y~l .vLt\ (х. 1 . у) =>
~ (llЛPIIO!i (Х);; l l lAPI IOE (}•)))) &
&('lfx'li')• (СУМ.МА(:\', 2. )') =
=3z (C'Yv['vfA (х. \ , Z) & \.У~1~1А (Z. \,)')))) ~
:> (V'.\' V)' (('V,\1f\.1A (.\', 2 .J') ~
=> (llbl'llO[ (.\')=ПАРНОЕ()•) ) ) )
/\авая 11раn11л:.1 посrроешт формул псч нс
ле11т1 11ре,1н1<атов, мы для облегчения ПС)1ш:-.1~1 -
1111н 11сnст1,зова.111uкачестве11мён пр<:днкатон
Р\'СС'кне C.' IOH:t. uолсе тр:1ДIЩ I ЮП11ЫМ ( н IП1ТСР
нац 1 ю1 1 ;VI1>11L1 1У1) шvure1·cл 11 сrюльзон::~1 нк· б) кн
J1атю 1с1щ 1 ·0 алфак 1 rта. В т: 1ю >й, бопее ~Тбl-1· рак1-
11 01"1 з:t 11 1101 1юсл<.'i\11ня формула '1nжC'r' вы r·лн
/ \C'l'h t·лс:;~у 10 11 111м образом :
(V'xV'y (S(.'\:, Cl,J') ;;:;) (f'(x) =l P(I•)))) &
& (V'xv)• (S(x, Ь,у) = 3z (S(x, а, z) &
& S(z, а, у)))) => (V'x'v)• (S(.'\:, Ь.у) ~ (Р('\') =P(J')))).
Jlo cyi11 :-нu \Ж<: Hl' матс:.1;п1rчсская , а ч1к-1u
Jl(J! llЧCCK:JH 1<.:оро1а . 1\3 н<.:е можно l/()J l) Чl/Тh
p.1J. 111ч11ыt• ман:ча 111чссю 1<: ·1·сu гх:.чы , ныfi11rая
р;нныс 11pt',\\1<:11 11>11:: 06лаt -1·11 11 1.1авая pa:mыt'
1р:1кн) 11ю1 11ре1t11кат11ы:-.1сrошо.та.'1Р11 S. ;i TJK·
A<t' с11 .\11ю, 1а~1 t111 /J. о(ххщачающн.\t ко11крет11ые
01)ъе1uъ1
Свойс-11.ю 1а.\1ю1~тоi1 формулы быть испш-
1юi1 11а .1юбоi1 модели 11аэьшзется обtи,€!з1ючи
.~юс:ть10. Общс:тач11мh1С фор:-.tулы псч11слс111щ
11рсд1 IK<l'l'Ull н llJISl/()'1'01 :111а11ш·ам 11 тожде<.-r'ВС I IHO
11ст1111111>1х фор,1у: 1 ( 1·авт0Jю1·11 1-r) нсчнсле11ш1
11 1 .1ска:1ы11а111 1 l1. Пр 1 1 аксrrом:1тнческом 1 щстро
с 11 1111·1 ·1>1'<J111111111-10 1 ·0 ра.тела математ111<н нока
:i:rтсл 11ст11с) ма 11::мат1 1 чес 1<а1'1 тсорсм 1,1Т сrю;~11тсн
'' 1101<а:1а ·1 ·t"J 11,ству обще:шач~11\1ОС' 1 1 1 1 1 м11л11ющm1
Л1&Л~&". &А"~Т,
1·де л,, Л , , "" л" (.'()()ТlJlТСТВующне ;JKCИ()Mbl.
Как же ус·1·;111шш·1ъ. что 1'<!1шая замюrvгая
формула 11с1 11 1 1на на любой :..юдслн~ В оi ·т1-
ч11<.: uт т:11ножн ·11i1 :щссь Нt'ЛhЗН rн:рсбрать вес
li!>:i,\\Oif\l lblt: с, 1~ чан. Пп.э1 ОМ) одш 1м 11з главн1,1х
, (ОС l llЖt'llllJI r.1 атем::п11ческо/1 ЛOГllKII \10ЖН О
сч 11'1':1'1'11 l/Ol Т(X>t:ll llt: llCЧ l ICJICHIIЯ пред11 катов
По,; \061-10 11 сч11с.11::1111ю 111,1 ска.Jына1111~'l. 1кчис:1е-
1111е 11pt:1\lll(:l'IOll за,1'Ж."ГСЯ llt'KOTOpЫ ,\111 ll('X0 , '\-
1lltlMll 01)щсJ11ач11мыми фор~1улами и rтравш1а
м11 ПO<..TPOt'llll>I 1ЮllЫЛ форМ)Л (Э111 правнла ((('
11р1шодятся Jлссь, поскольку они дово!tыю
слшю 1ы ) . Uб 11сч.11слt'ШШ преднкатов д<ж:.1:д11ы
дnс тсорсмы, .111:uю1 ·11чньн:: теоремам об ш:.:ч11с
лсшш BЬICKaJ l•IK;tH/111.
1'СQр<.:ма о корректности . Вес фор.нр1ы
HhlHOJ(ll\1bll' н llCЧllC/11::111111 1Jрl'д1 1 катон, Яf!ЛЯ
}( )'1'01 0Сi щс::11 l:I ЧI JМ lolMI 1
Теорема о 1 юл11оте. Rснк~ш 06 111е:111:1ч1 ш rtн
форму11:1 ш .111о;1 1 1ма н 1 rс ч 1клt.:1 1 н11 преJ \1 1 1.:атон.
Teopc"1:i о nпл 1юте доказз 11а Ку1тюм Гё11слс~1
п 19 :Ю r. 11.лл 11с•шсJ 1 еш1я прсю 1катов перво1·0
пор1щ1<:t. Щrя 11сч1 клс1 шй более высоюrх nоряд·
ков аmlЛоп1ч1юl1 теоремы о полноте нет.
ДОСТИЖЕНИЯ МАТЕМАТИЧЕСКОЙ ЛОГИКИ
Ес1111 lll' KOTO(XIЯ замкнуrая форму.'13 яв..тяетсн
оfiщС~i11:1ч11мо1\ 1·0 n это,1 можно убе;-щтhся за
К()НСЧНО\: Чl l СЛО 111~11 '()/1 с П()\10ЩЫО IfCЧIICJ1e11m1
nр<.:н11к;11011. А ч т /\с,1ат1., если формула 1 1е al> -
596
щсэ11ач11м а? 1нес1, ~-;01тчаl"гся а11алап1я с про
1юJ 111ою11:IЛыrым1r формулами. 11е-1·автолопrч-
1юст1, которых, no 1<раl111ей мере в прннщше.
устанаол11ваетсн 11ерсбором конечного коли
<<ЛОГИЧЕСКАЯ МАШИНА»
СВИФТА
П рофессор объясг1 ил мне, что он
работает над изготовлением осо
бых механических приборов,
предназ 11 аче11 11 ых для открып1 я
отвлеченных исти н ... Б лагодаря
ero изобретен и ю самый невеже
ственный и бездарный человек при
11ебольшои затрате срелсrо и фи
зических усилий может п исать
книги по философии, поэзии, по
мпике, праву, матема-rике и бого
словию. Тут он подвел меш1 к раме,
по бокам которой стояли все его
ученики. Рама эта имела двадu<~ть
квадратнt~х футов и noмeuiaл<icь
nuсреди 1~е ком наты. П ове рх1юстъ
ее состояла из множества дере
вянных дошечек, каждая величи
ной с игральную кость - одни по
больше, другие nоме11ьше. Все они
были сuеnлены между собой тон
кими проволоками. до щечки были
обклее11 ы кусочкам и бумаги, и на
эти х бумажках были нап иса н ы BLe
слова языка Бальнибарби в раз
м1чных наклоне1·1иях, временах и
11 алежах, но без всякого 11орядка.
Профессор 11опрос ил вн и маниs~ ,
так как соби рался пустить в ход
сGою маши ну. По его команле уче
ники взялис ь за железные рукоят
ки, вставленн ые по краям рамы, и
быстро повернули их. Все лошеч
ки 11еревер н улись, и рdсположение
слов совершен но И':Sме11и лось. То-
Матt>мdтичРская лоп1ка
гда профессор при казал трилuати
шесп1 уче н икам мелленно ч итать
образовавшиеся строки в том по
рядке , в ка ком он11 размеп11лись в
раме. Есм1 случалось, что три или
четыре слова составляли •1 асть ос
мыслен 11ой фразы, ее диктовали
осталь н ым Чf.'тырем уч ен икам, ис
rюлнявшим роль писuов. Это уп
ражнение ()ыло повторено три или
четыре раза. Мащи tiа была устро
ена таким обр,ном, •1то после каж
дого оборота лошечки поворачи
ваl\ись ~, nеред611rаl\ись . и слова
размешались по-новому.
Лжона таN Свифт.
• Путешествия Гуллиоера »
Чl:CTli:-1 но:.sможных :JНаЧ<::НИЙ пt: ремс: 11 11 ых
0/~НО Jf З H:.IЖHC:Й llJI rx /~ОlТИЖС:НI 1(1 матt;мат1 I ЧС
С'К()Й }1() /~ 1[J<t1 COC'l'Of1T LI '!'ОМ , ЧТО f>ыло доказаJ Ю:
Прн акс11оматичt:'Сt<uм щ>счюен и11 какш·о
лнбо /Х13/~ел;-~ м<~тсм;пн~-: 11 к выбору :1 кс н о м А 1 .
А~ ,- ·· А 11 прсдъявлястсн, гю су1щ:ству, 11 11ш ь u;~н о
требован~ 1 е - нenjюJJmfюjJeчшmcmь, т. t:. /~OJ1ж11:.1
cyщc.:CTIIOf!3TI> ХОТ>! бы 0/l! 1 а модст,, H~I K()'l'opoli
все аксномы 11 сп1 1111ы. R nр () тнвr ю м СJ 1 ~'чае
любш1 формула окажется лоеичсским слеl\с'Пш
см акоюм. в Ч:1СТI ЮСТ11, I•aJIOB:! бы Ill J былJ :З:U\1-
кнутая формула Т, в н счис.11сrши ттредик::~тов из
А,,А2•..., А " можнu будет RЫHl'CTll 11 Т, IIl'<.' отри ·
tt:tнл e lт. Понятно, что такан м :пем;tтичсская
теория, f! которсн"1 нсl- 1 1сг1 111но 1'1 нсt~ ложно ,
1-шк:.~кой ценносrн не представ11яет
1'" Не сузцествует универсального
l!J.
!\'1етода , J'<ОТОJ>Ый позволлл бы ло
nроизволыюй замкнутой формуле
исчисления предикатов узнавать ,
цвля<:;'rСЯ л и эта формула общ~та
чи~ой.
Для то 1 ·п чтоt11,1 док;~ззть это·r· факт, потрс
!10 1~алос 1, со:ща·1'ь 1ющ.1 й рз :Щl;Л матсма·гнче
ской ло1·икн - теорию алгориr11..!~:юв. 0 1ta з а
шrмает ся НЭУ'"Jе 11ием LfC то1·0, ч·ю мож 1 ю н что
нельзя доказатт,, а того, что молпю и что псш,эл
вычислить.
Другое желателыюе , но HL' обя:~атt:льнос
свойс 11ю arccиo/\fa·1 r 1 кт1 - 1:ё тинпта. Э·1·0 о:ща
ч ае 1 следу1ощее: есл н мы во:~1,мём 1 1 ро11 :~нот,
ную замкнутую фор~·1улу Т, такую, что все
597
Фунламе нт мат~ма1 ики
входящие в неё снмrюлы прсдик;пов нстреча
ютсн в а1<сиомах, то лнбо сама форм ула Т, либо
её о·гри ц;шие l Т ло1·ически сле;'(ует из аксиом.
Оказалось , для любой 11е сm 1ш ком п rюстой
а ксиомат ич есК()Й тсори11 , н;шрим ер у-,ке для
аrшфм етики на"1уральных ч11сеп, 11епрпт11воре
чиrюсть и полнота ако-юмати ки - сш1йстна
11есонмес ·1 · 11 мые , как утве рж~а ет :~ наме1штая
первст тпепре.л.~а Гё1)еля о 1и:полиот.е. Нё мож-
110 сформ;тирова ть .u усю 1еr1 1юй фор ме следу
ющим образом:
Для любой непротиворечивой си
стемы аксиом А1, Az, ..., А,, можно ука
зать мноrочлен М от мноrих пере
мев-ных с цельrь1и коэффициеитами ,
такой, ч·rо уравнение
Jlll(x1, х2, ••• , х,,,) = О
пе иl\'1еет решений в целых числах,
но это нельзя вывести И:i А1 , А2, .",А".
S98
ВОТ В ЧЁМ СО/\Ь
Формальн ое лока.~ательство, прелназначе1-111ое для
проверки машиной , а не человеком, может иметь
очень нестанларп1 ую форму, и с :~тим свяо~аны пора
зител ьные результаты последних лет.
Тралиuионное математическое локазательство,
как и вывод в исчислении высказываний или в исчиr ·
лении преликатов, подобно грузу, висяшему на uепи.
Кажлое звено должно быть крепким : если олно звено
рвётся , то груз палает. Проверsн:1 традиuионное лока
зательство, математик илн компьютер обяза11 убе
литься в правильности каждого шаг.:~. А н ельзя ли
« Провер ить» локазательство, 11е читая его полностью?
На первь1й взглял илея кажется абсурлно й. Но
да8айте рассмотрим слелую шую аналогию.
У нас 1~меется ба н ка с сахар11 ым песком (доказа
тельство) , но есть подозрение, что тула попала кру·
пинкn соли (ошибоч1 юе звено в доказательстве) . Мож
но, конеч~ю . перебрать всё солержимое банки,
пробуя каждук.> кру11инку на вкус (тралиuионный
метол проверки}. Но можно поступ ить и ина ч е. Ра
створ им всё солержимос банки в воле и провелём
химиче<-кий а нализ ол1юй капли. Если 0 11 обнаружит
соль, то .доказательство было ошиGочным » . Если же
во взятой на пробу капле волы молекул соли не r>б
наружится, то ешё нет гарантии, что крупинки соли
вообше не fiыло - влруг в момент взятия капли вrе
м<>лекулы соли переместились в другую чаrть ба нки.
Од1-1а ко сра внение коли•1ества крупинок в банке с ко-
Таким обра:юм, од.ин 11з вrщоn деятельнос
ти м~rп;матнкuн - ныработ~ систем аксном
-
HHKOl'Д:I Ht: бу/1.L~ 1 · IKЧL:p П ~JI! . Казалось б ы. это
нt:Gюжr lая р~16ота (н отш1ч11 с от ;1оказатс..r1ьства
тcopt.:vt), но Rдейст11 и ·1·е1 1ы юел 1соблюстн тре
бование 11 епрп·1·t 1 воречиности аксноматшш
оч ен 1, 11 е 11 росто. R самомдс;н::, какдо1«1:1ап" что
да нный набор ~шсиом 11епрпт1нюреqтш? Само
доказательство непротиnоре<rивости некото
рого набора аксиом л1, А~, .", А" можно было
бы попытатьсн 11 ров<.:ст1 1 1щ ос 1 юнс 11t' которu-
1·0 дру 1 ·ого мн ожсстnа аксиом А'1 , А~,"., л;11 • К со
жат:.: н и ю, новая а 1<с1юматик;~ долж н а быт1,
н <:: сл:1бее той. нсn рот11Rор<:ч иность которой
хотелось б ы /1.ОКаз~пь. ~то следует И3 вmoj.юil
тrюремы Гёделя п 1lе1юл1юте:
Непротиворечивость н1псакой не·
тривиалыюй аксиоматической си·
стемы пе может быть доказана сред·
ствами: ca.l\tOй этой системы.
личеством мплекул в крупинке пока зывает, что зто
крайне малов ероятно.
Лля формализованных математических лока
зательств удалось придумать подобный «распю
ритель ». А именно: произволь н ое традиuионное
доказательство Л можно преобразовать в нетради ·
uионное локазательство Н (н: волой », и гютому
более лли н ное). Проверка всего доказательства Н
гарантирует правильность теоремы. В то же время
если теорема 11еверна, то почти любая Ч dсть доказа
тельства Н окажется неправильной («<:олnноватой ») .
Так, если наугад выбрать фрагмент Н, имеюшии не
которую ллину /, то о шибочность Н будет обнару
жена по ла t 1ному фра1 менту с некоторой вероят
ностью р , зависяшей от /, но не от ллины Н. Пусть
лаже р невелико, скажем, р = 1/2. Если п раз повто
рить проверку, в сеr да выбира я новый фрагме нт
наугал, то вероятность не обнаружить ошибку (если
она на самом леле имеется) составит не более 2 ".
Уже при п = 100 эта всроят1 юсть, 2 ~нп, горазло мень
ше вероятности аппаратн ого сбоя компьютера и тем
более много меньше вероятности ошибки, лопушен-
1юй челове ком .
Лля п одобных с некоторой вероятностыо п рове·
ряемых дuказательств было пре<\ЛОЖено н есколькu
названий, олно и·~ них - m11оrрафические. Полобtю
том у как даже маленьк ии фрагм ент голограммы со
лсржит и11формаuию обо всей •< Картинке », нсбольшuй
« кусочек » ош ибо чного голографиче ского доказа
тельства 11 очти наверняка сам солсржит ошибку.
В нашиrtнн математика nо 1 юm-н1ется новы
ми зксиомами довольно редко. Это на само.м
деле и не очень существе111-10 для её дапьней
шс1·0 разRития. Давно и:..~всст1 ю, что в основе
болыпеl1 част1 1 совреме 1 uюй ма·rематикн ле
жит ·сеория MfIOЖCCTll, :1 ДЮI пеё y,l"(:lJIOCЪ 110-
строить конечную аксиоматпку, пр11чём в
языке 11счисления ттредиrотоо пер rю1·0 порядка.
Сущестnуют разные варианты такой аксиома
тики, 1:-шиболес извесп.tыми 1шлmотся. аксиомы
Цер.мс;Jю - Френкеля. Почти вес математиче
ские теоремы нnнюдятсн из них: 110 правилам
нсч11сления прсд1tк~1 тов. н больш111-1егво матс
мат 1 rкоn Ht' выходят зd эт11 рамюt
КОМ ПЬЮТЕР ДОКАЗЫВАЕТ ТЕОРЕМЫ
Возмо)ююсть формалиэов:1ть математаку сред
сп3ами аксиома111ки теории множеств 11 исчис
ления преднкато11 делает работу матема тикон
rюхожей на р<1эьнрын:.~tп 1 е LШL\':мат1юй пар'1· 1,ш:
есть стрm·ис пр:.шила и надо просто сле)~онат1>
ам. И, т::~ким r>бразом, немеднепно 01·кры11<1стсн
гтуtъ к маши~ 11 юму дока:~атсю,с1·ву теорем.
С:равт1ител~,1ю 11еслтюю написать про1рам
му N•я ЭВМ, которая f>удет 1 tровеrтть r1рав1 111ь
ностт, выво~а формулы в исч 11.Слст1ии предика
тов - это примерно то же самое. что nроnерять
11равп11ыюсть шахматr 1 ых хuдов. А /ЩЯ того,
чтобы находить доказательства 1ювых теорем,
можно 1~рименитъ метод, полvчинший шут-
Маrематическая логи ка
мшое название «алгоритм ста тысяч обсзьm r» .
Вообразите: сто тысяч обсзы1н 06уче11ы «бара
б:н-11-:пь» no клаnиатур;~.У! компъютерон, а комп~,
ютсры проверяют, является ли то, что обезьяны
«r-rабили », дсжазате11ьс_т1юм. !::ели процесс r1р()
/\ОJ1жа"П> дост::поч 1ю дою·о, то с ненулевой нсро
нт 1 юс1ыо обез 1>нны ~щжажут • любую тсоrему.
Понятно, что вместо обезьян мож1 ю 11с1юлюо
вать механические или электронJiыс rеr1ер:1 -
торы случайrп,rх текстов либо, t 1аоборот, систе
матически леребирап, вес мыслимые тексты.
заставляя компыотс:р отссиваl'ь всё, что пе явля
етсн доказатет.стRом. По суrи, имснно ·r·акой
мсто~ слеrю1·0 п~rебор ;.1 был рс;~лизонан в
пtрвых мзшинных програм,"12х, н:{писанных
для доказатсл 1,ства теорем в ко1щс 50-х r1" ХХ н_
Естсстuентю, маломощ 11ые машпт11,1 то 1 ·да смо 1 ·
лн доказать лишъ очет, простые теоремы.
В дальнейшем развитие методов мапrшшо
rо доказате.1 1ьства теорем шло 110 пуш зэме11ы
случайности или слсп01·0 перебора 11а более
эффекл 11~ные 11μиёмы . Пр11 этом ок~1залось. что
традиJ(НО! 1 ное 11сч11с11сш1с 11рею 1ю1тс >11. ра:~ра
fiота111юсд.11я фор'1алыюп111зложсн 1 m матема
т11чссюо< доказател ьств, не очень по;~хо;~1. 1т ;1,.11н
их rю11ска . Были 11 ре11ложсны /(руп 11.: фор;ч :ut11-
ные снстемы, ор 11е 1 1тиропан11ыс 11мснн о на
110пс1с н на ·1
·0 , что его осущест нт1ст не чело
век, а машина. n .ма шш н юм f(оказательстве тео
ре!11 удалось достигнугъ определёrшого про
rр<::сса, 1ю далеко 1к такого впечатляющего, юн<
n шахматных прш·раммах.
Математика за работой
ИСКУССТВО ВЫЧИСЛЯТЬ
ПРИБЛИЖЁННЫЕ ВЫЧИСЛЕНИЯ
Известно, что математика - точная ш1ука. Но
при решении праюических задач часто прихо
r~;ится делать приближён11ые оычисJ1е11ия . На
пример, выч:исли:м пугь тела, броmепrюrо nер
·1 ·1J кально вн 1 1з со скорос-1ъю u0 = 32, Jм/с. за 4,2 с:
1
(.
'
s= 't+gt- =32142 9•81·4
,z-
t,,
2.
'
'+
2
= 221,3442 (м).
Однако :щесъ ветr•п~ш~ д"'" 9,81 м/с2
-
rраnи
тациоштая постоннная - юнта округлённо. На
чалыrуто скорость тела и nремя его полёта так
же нельзя определить абсоmотпо точно. это
з~t ниснт от нозможностсй измеритслыrЬL'< при
боров Нозник.ает вопрос: наскот:..ко точно по
лученное зн::1ченнс 221,3442? Сколько вер1rых
1~ифр в этом числе? В какпх пределах заклю
ч еЕЮ то ч11ое е1·() 1 11ачен11е?
Ответt.t 11а Э't и uо11росы даё'1· теория 110-
греzшюстей, которая формулпрует праnила
дейсший с прибл11жёш 1ым11 веJiичиш1м11.
602
ПРИБЛИЖЁННЫЕ ЧИСЛА
И ПОГРЕШНОСТИ
В древност11 лю)\И н е р~1Jлич~11 1 11 точных JI
11рибпижённых чисеJt . Так. в вакплонскJJх кш1-
1юпис11ы.х таблпчках сообщнлос1" что квалрат
ный кореш. нз днух paueJ1 7/'1 или что о н р:.tнсн
17j'l 2. В Бибю1и [tри ошrсаrши: храма Соломона
rо1юрится о металлической ча1 11 е, у 1<0'l'Opol1 в
диаметrе 1О локтей, а в окружности 30 Jl()l(Tefl,
т. е. отношение /\Лины окр"жности: к диаметру
считалось равным (не при бл юкёrшо) .1. ]:) те
времена особо точные выч11сле rшя нс были
У гужны (нанрн."!ер, нри земпемерных или стро
ителы1ых работах).
По1-1л ·1·не 11рибл1 1.жё11.но1·0 з1 1ач:с 11ия появr-1-
лось MI юr·о 110~.IЖС, ГIОСЛС ТОГО как IТI ttjXll'Opct'iцhl
открыли 11ррацио11алы 1 ы е ч1 ~ ела Дрсв1-н.:1рс
чсскr1с учёныс чётко разттчали попятня <·р:ш-
110» н «приближёшю равн о». Эпт пош1тш1 за
nосле1~11ие дuе тысячи лет пе претерпели су
щсстnешrых изменс11иi 1 .
Иску< С1·вu вычиtлять
Jlр11бли:ж:ё1111ы.м .з11а<иmие.14 числа А 11азына
ется чною а, 1-1ез 1-тачитс11ыrо отю1011яющесся
от точного ЧИСЛ:! А 11 за.меняю щее пuследf!ее
в нычислен11ях . Еслн а < А, то а нн:~hlваю·1·
пrиближённым знач<;ннсм А пu нежктатк~·. а
tсш 1 а > А - пр11блнжён11ым ::S11аче11нем А по
J r эбытку . Напри .чер, 7t "" ) , 14 - приближение по
Пед()статку. а 1t "" 3 .14 16 - 1ю изfiытку.
Ошибка, ит r ппг/){!ш1щсть, ч11с11а а: ла = ,4 -
-
а - это 1х1~1юсть между точным 11 пр~16ди
жёш1ым :щачениями . t:слн число А вычи сле
но точ110, то Ла = () . Например, 11оrрс1шюсть
приближения 55/1] 1 "" 1/2 соста1:1ЛЯст "'5)/111 -
-
l/2= - 1/222.
Абсолютной п.огjнm 1н остью лрабJJнжё11-
но1·0 за:.1чсння а н азьш:~ют д = IЛпl = IA - al
Так, абсолютная 1югрешносл, щ111бn11ж<;н11н
55/111 "' 1 /2соста 1~ттет l-1 /222 1 = 1/ 222.
Однако чаще всегп чнслоА 11 ам 1Lенз1~естнп .
н поэтомv по r·реш 1 10сп, егп Щ)ИfiJ 1 иже11пя
nычисmп" нет,.зк 13 таком случае ! Лаl мож1ю
оценить св<::рху некоторым числом ; это qисло
л" > IЛal = IA - al назын<tется nрf!дмыюй. абсо
люпиюл пс.ыреш'l-юопыо. }!сн о, что о - л,, <
<А<а+Ла.
Предслън:t$1 <16сощотная 1нJl'рсшнос1ъ опрс
/\слsн::тся НСОДl-IОЗ\-1<\ЧНО', <;:СЛИ И3Вестно UДJ:IO
::~ 11аченас Лm то любоt болы 1J ее ч11сло тоже
будtт предслг,rюй абсолютной 1югрсш1юстью
Естестnеmю, прп расчётах 11а/\{> стара 1ъся.
чтобы Л11 было 1'ак :-.южно мены1J е.
11 1101 да абс()лЮ1"11у10 nогрешнпсть з амешнот
предслыюй абсолю·r11011 логреншостыо для
удобства ВЫЧl!СЛСШIЙ в ДС:СН'ШЧJlЫХ числах. На -
11р11.мср, поскольку L/ 22.2 = U, OUЧSO-l'i(JЧ.50·1'50 ."
пределы юi1 абсототной 1ю1 рс ш1 юс~ъю 11 р11-
бл нжсн ня 55/ 111 <>< 1/ 2 можно взять чrrC.'IO
(),005, юнr 0,0046, ишr 0,004S04504'51 - н зав11-
симос1 ·и т то1·0. н.аскш1 ько ТQЧНО трсfiуето1
решнт1, ::~;щачу.
Сама П() себе пре;(еm,н::ш а()с олют11::н1 rю
грешность не Аnо1ше характери::~ует то чr юсrъ
nычнсления. Так, л" = 1 м - очень малеrrъкая
п оrрсплюст1" если мы измеряем расстояние
между центрами Зсмли 11 Jlуны, .и та же веюrчи
на Л11 = 1 м станонится очс111. бол1шо1) nогреш -
1-1остыо, ссл н 11змеряют ,тvш11у жилоir к<.>мн:-tтьr.
Отношение Б = Л/IAI 11аэынают ит1юси
·1л елыюй rюzрешн.ос тыи прибдuJ1сепия и , з
Б(, == Л;,/ '111 - предел1:/Ноit относителыюй по
греитостыо nfJlfб.пu_ж·ellиЯ а. Еслн Л.~ << [o l
И, CJreдonaTeЛl> I JO, Оп<< 1 (:нтак << ОЗllЗЧаСТ
60.)
МатематикJ за работой
«M I JOl'O MCHblllC~) , ТО M()ЖllO l'Чll'l'a'l'Ь 5" ;:< .~<1 / lal,
Лп:::: lиlot,.
Понятне 1югрешности 0·1 · 1-юснтt::J1 1, 1-1 0 чоло
/tО - оно поя 1:1нлос 1 , щ11ш, 11 ХУ н. В 1tре111юст11.
если чr1с110 11е могли nычис11н ·1 1> ·rоч но, !f()
важно было :н-tа1'ь ошибку при расчhах, мате
матики определяли точ11ые гратщы, в кото
рых лежит это ч1 rсло. 1lаn ример, Архимед вы
числю ~ довольно точпыс границы для числа л:
10
1
1> - <ТТ<~-
-
71
.
7.
1
1
//
/ /' _,./
/
604
Uu.шбк:1 11р~1но1·0 н дсвого 11риближ<.:ш1й мень-
111с 1/71.
1lрнблнжё1111ые чш.:ла чаще 1:1се1 '0за11 1 1сы1:1а
ю 1 н десятнч1-юl1 сиСl сме счнслснпя. Псрвыt: 11
1tJJфp (7'ССЯТНЧ li ых :н-1акоR) ч f!Clla сч Иi':J ЮТС}/
11ер111>1ми, еслн ошибка не пре rюсхпд1п· поло-
1шпы едшшцы разряна , выражаемого п - й 1 tt1ф
рой Например, в прнблнженин 1,00"' 0,997 nce
цифры всрrrые. Зная предслытую абсолюn~утп
пorpeJIJ H UC'J'b \UIИ nрс~еш,ную UTIIOCIIТCЛЫryIO
1 ю1·рсu11юст1, ч 1 1сл:1 , 1 1редст:~юн.:ннu 1 ·0 в деся~
т11чнuй .iJll l JC I I. MUЖl !U u11pcдCЛIITh ЧНСJ Ю tl'O
нср11ых ц11фр.
КАК ОКРУГ/\ЯЮТ
ЛЕСЯТИ ЧН ЫЕ ЧИСЛА?
llpи р;tботс с !(Сся111ч11ьuv111 числами часто пр11 -
хо~итсн ноль:юв:пься nри6лиже1шямн, в ко·1·0-
рых ч:кть u11фр в конце заr1 1 1с11 ч11сла отбра
сынастс>1 l Ianp11мcp , изучая 1·со 1 ·раф11ю . мы
ГOROpllM, ЧТО д11:1метр :kмJllJ сос1а1:1ю1t·т UKOJIU
(1400 км, отбр:н.: ыная точное зна ч е1-шс дсс>1ткон
11 сдш-1111 l в этом числе. :-1дес1, нам южно :ш:~·11,
11е точное чис;ю, а tто поряйол - 11:1мl'рясто1
1111 01 ю n лссятк: 1 х, сотr1ях плп ·1·ыо1с1ах ю1ло
метров.
Соблюдают такне правнла окру1-1н:1 1 ш1 .
l. 1.:СJШ первая слева нз отброшст шых цнфр
меньше 5, то остаnшиесн десятичные знака
НС ИЗ.МСЮI ЮТСЯ
2. Еслн nср1~::ш слсЕа нз отброшенных
ц11фр fiольшс 5, то к 1 юслс;tнс~"r щ:т:1111 1 1сйся
1111фrс 1 1рибаrтя~nт 1.
3. Если перв;:~я слепа нз отброше 1 rr 11,rx цr~фр
рат1а ')и сред~ 1осталы1ых отброше11 1 rых r(r1фp
11меюп:я непуленые. то к nослет~:11ей и:~ ncraR-
ппrxcя цифр прибавляют 1.
4. Если перш.ш cлen:.i аз отброшенных цифр
ра1ша 5 11 вес осталън ые отброшсш щ е цифры
равны нулю, то послсдlТЯЯ оставшаяся щтфра
сохра11 ястся , еслн ош1чёт11ан , 1 t увелнчнв:~стся
на 1 , сели он;~ нечётная (правило чётной
ц11фры).
При выполн<.'1-11111 этих условий сум ,\1арнан
ошибка окруте11ий в ср<.:;(1 r ем будет бли з ка к О
Исно. что вместо <· 11рJ1111ла чёт1юй цифр1,1•
мож1 ю было бы тrспользовать п «п11аnило 11ечtт
ной цифры·>, 110 выбоr нз этих двух прат11 rл y--t1<e
сделан до нас, и мы окрутл.srем в сторону бли
жайшей чёт1 юй цифры.
Вот правильные окру~ле1нтн чнсла тt =
=_
;i,, l<-11592653.": л "" 7>, 1·1159265, 1( "' 5, 1415927,
7t"'5.l•l l593, п ==3,14159, л:::3,14 J 6, it "':1,H2.
f("" 3, lc.I.
П О ГРЕШНО СТИ РЕЗ УЛЬТАТОВ
АРИФМЕТИЧ ЕСКИХ ЛЕЙСТВИЙ
Какие правила с:облюд~ют при арифNетичс
сКJ..L'< /(СЙ(.'ТВНЯХ Н:<IД приближённыии '-П'I CJI:JMII ?
Как ()Пределит1, лре/(елы1ую аб<.:олю·1 · ну~о и
предельную относ~ ~тель н ую па1·решностн ре
зул ьтатов нычисленнй?
При сложенн1-1 пли нычнтаннн пр11бт 1 жён-
11ых ч11сел их 11ределъные абсолют11r.1с гю1'реш-
1юсти складьшаются . Например, 11рн сложен ни
nриfiлижённых величш-1х = 121 .:) и у= 128,7,
предельные абсолютные погрешности кото
рых составляют ЛА = U,U6 и л1 = O,OUOO1, nре
дельнал абсолютная ногрешность нх суммы
.х +у= 1ll,3 +128,7 = 250 составнт
Л~+1 == Лх +Л1,= 0,06 +(),00001 = 0,06001 ""0,U6
Прсдеm,ная относительная п01 ·решн()СТЬ это~'1
суrv1МЫ сuстанит
0,-н = Л_\ +д 1 =О,06+О,О<ЮОJ == О,()ОО24
.
-
х+у
250
При uыч11та11ин близких прнблнжёш 1 ых
величин nредслы1ая относительная пu rреш
ностъ сильнu во:sраст:1t.·т. Т;1к, ттредслъная 0·1 · -
1-ю<.:ите.; 1 ьню1 IIOJ'PCWJ:IOC'l'Ь pa З IIOC'l ' I! тсх Ж<.:
прнближённых вс1н1ч 11н _у = 121,5 11 у== 128 .7 с
1 1 рсдеш,ным 1 1 ::tбсол ютными по1'рсш11ск·гнмн
Л 1 = 0,0(1 и д, = 0.00001 будет ра1:111:~
0,. i·=д1+Л1 = О,Об+О,<JOO<J1
-
Jx- yJ
7,4
При делении ини умножении нриближtн
ных чнссл .их прс11елы1ые отн uс итслытые по
rре 111 но с•1·и сКJщцыв;~ются. LL::111рнмер , псрс
~1нож<Jн 11р1t6лнжённые нелr 1 чины .х = 1Q() 11
у= 250 с nределы 1 ым11 абсолютными JЮ l'рсш
ностямн л_,"" o,os 11 д" = 0,01 н пpCДeJJЬHЫJ'vlH uт
.1юсител 1 .г1 ыми 1югреш 1-тос·1·ям11 о,= 0,0'1/100 =
= 0,000') ri о,, = O,U 1/250 = 0,0000..J., rюлуч 11 м
для пр о11зведепия х у= 25 ООО 11редельную
Искусство ВЬIЧИСЛRТЬ
605
Математика за работой
O'l'l\OCHTCЛbllYIO nоrреш1юсп, о, 1 = о.,+ 0 1· =
= 0,0005 + 0,00004 = 0,000'54. Те11ерь мы можем
оценить абсолютную по1 решностъ этого 11ро
нзведения: л"- ) =о... ,. х · у=О,00054 25000 = 13,5.
~слн приближёшюе число возводят в сте
пспъ, то ero 11редель11ая относительная ло1·реш
ность ум1южастся на ноказатель этой степени
При и знлсчении корня из прнбднжёrшого
числа его предельная О'l 1-юснтелы-~ая 1югрещ
ность деJ 1 ится на показатель сте11ени .корня .
R змаче о г1у1·н тела, брошенно1 о нертнкал 1,-
110 ~н1иэ со скорост1.ю и0 = 32,l м/с, за 4,2 с,
считая, что все цифры данных нер11ые, мы мо
жем взять такие предельные абсолютные по
rреш 1 юсти :
606
Л,11 =0,05, Л1= 0,05, дg= 0,00'5.
Следоватслы ю, пре;~ельные относительпыс nо-
1ре 111 ности составят:
о = O,O'i =О 001-'576'
1"
:)2,1
,
')
:'>,
0 = (),OS = () 01 J<)()Lf7
1
-t, 2
'
'
б =О, OOS =() 000509684 .
}.!.
9,81 '
01 .1 = 01" +01 = U,01)46233,
o.~r· = 8..: + 201 + ёJ =О, 024j19084
2
(поrреnпюсть точ11or·o числа нсег;1а рапн:~
О: 01 = 0). Далее,
лtqr = L't1 ·t о,~, = J,815,
fJl2
.
л'=-
о . =2,]042,
RT
2дr
l
I'. с. при нашнх прн бл ижё шш х данных пр с
/\ел ьная отно с итель н:,~.н лпгр ешп ость
01 =(),()177063 <2"·f.,
;1 вел11чина S заключ t:на в пределах
217,425 < s < 225 ,2634.
Результат н аших вычислений имееr две вер
ные цнфры: поrрешностт, S z 221 составляет
_\1енее 5%.
Ит юl'Да решают и rораэдо более СлФю1ую
обратную защ1чу: зн:ш предельную догrустимую
ошибку результата, 0 11реде.11 sна1 , с ка ко й точ
ностыu необходимо вычислять (1пмерять) иt
ходные f(анш,tс. Впервые нычислсю1я с з::ipa-
11 et ~~аданной 1'0Чl-ЮСТЪЮ ycпcLl!IIO R/->l l IOЛHИJ\
срец невеrювыИ аrабоязьrчпый ма тема·1 нк и
Искуrстоо вычи слять
астроном ибн Масуд зль-Кш 1 и. работавший в
обсерватории Улуrбека, внука Тимура, nрави
тст1 Самарканда в XV в. Уnерснньul в TOJVt, ч·ю
небес ный с нод имеет диаметр, равный 600 UЩ)
диам етрам :1смл 1·1 , аль-Ка шн задалсн цслыо
В ЫЧНСJ!ИТh ,цлину е 1 () окружн остн l: 'J'ОЧНОС'IЪЮ
ме11сс толщины ншюса 11 з 1 ·р1шы коня (около
0,06 мм). С11ачал:1 учё н.ый ныш.:н1111 , что n1х1 -
аилы-1ы.й 80'5 306 368-у1 ·ольн 111<, в пи са11н ый 13
окружrюсгь стол1> боJtьшоrо диаметра, 11мсет
периметр, от;шчный от её ЩJ 1 1ны мс 1 1ее чем шt
ПОJЮНПНу волоса. Затем 0 11 ОЧС l! Ь TOЧILO оnре
дслнл сторо ну н 11ср11метр 80'5 306 568-уголь
ника. вычисл1ш, таким образом, 17 np,ш1tлЫ:IЬL"'I:
Jtесятнчных з наков числа тt.
Аль-К:.1 11 111 0 11 ср11rо нал •н 1 <.'!1 ами , з~11111санны
ми н lR ра зря1\ахшестндесятерн чнш:1 спстс мы.
и каждую 011ер:.щию пртк:рш1 дв:оt -тр11 раза .
Э·1 от ве~1икнй щ,1чнслнтеп1, f\r)11ютн·1н rю11с
'Гине тита 1 J~1ческу10 работу.
КАК ОПРЕДЕЛИТЬ ЗНАЧЕНИЕ КВАЛРдтноrо КОРНЯ
Да же nри ре ш ен 1л1 матема·п'lчсскнх з адач
далеко нс Rce1 ·д~J б ывает нужно з нать абсол ют
но точ 1-1ый отнст, ;щстаточно 11айт11 е 1-о 11рн
бт 1жсн 1 юе зн;1 чение с прнемлсмпй точ 1 юстью.
Более то1 о, часто указ<1ть ТО'lНЫЙ результ~1 т n
в1ще ч11с11а вопбще нево:з мпж 1 ю. Например ,
решив юзалратное уравнение x z + х - 1 = О. от
ве-1 обычно заnисыnают в шщс::
-
1± J~
х=---
"
2.
О;tнакu с практич еской точки зрения это лншь
полуотвст. Ч.тоб ы получ:ить 'tИ<.:ловой рсзупь
тат, следует за 1 дя нут ь в таблицы квадратных
кор11ей и.гr1 1 nооружиться калn1<ут:1 ·юром . Ну
а если в пужньп1 ·1vюмен1 их не окажется nсщ
рукой, nрндё1·сл рассчитывать только на свои
собственные с11Лы.
Существуе-1 мноrо с пособов nриблнжённо
го нычислеrmн корней. 06 одном из них, ло
зволйю щем находить наи11учшне рационал.ь
ные nрнf>лижсния квадратных корней нз целых
n олож нтел ы-1ы х чисел, рассказано в статье
~ Цtпны е дроби». Рассмотрим е щё нескопько
пr н ёмоВ, ГIOJICЗlfЫX В 11f)Зк1' ИКС ВЫЧllСЛеlШЙ .
11ус.'1ъ требуется найти 11р116J1ижённос зн11чс
ние -v1998 Самы й 11 еJ:.1т<..:r1лн111>1(1 с1юсо() - это
uодбиратъ числа, 'Кl\адрат которμ~х nриближался
бы к 199S. Испытаtм число 44 442 = 19.)6 -
нсдосrаток. Л сели взять -15 ? ~1 ')~ = 2025 - избы
ток. Зн:зч11т, искомое ч11сло - дrобнос н 11а хu
д1 1тся Г/(С-ТО между rJ4 11 -15 Д:IЛЫ1ейШIIС /tСй
СТШ IЯ 1юзnолню1· суэ ить ш1тсрн<1л, содtржащ11й
· ." r'- ...4
~4'с(,:"~~ ~·. D
·~··<· r;..~~
. ......
k •;4
·-·~ ••
607
Математика :;а работои
истш11юс зн~1чение кор1-ш, до предс:лон +1,6 -
44,7 . Конечно. Э'l'U"I' проце::сс MUЖJ ю 11родоJ1жа·1 ь.
Но чем ·1·01шеt: з начс::нис, тем 60J1ee громоз11кн
ми ста~ ювятся промежуточ11ыс :ныкладкн. н
нычислеttия идуг всё мемеш1се.
Другой нзвестпый метод гораздо быс1·рее
недёт к цели. Uп осноnан на классическом
неравенстве между тремя срсдннмп значения
ми двух пронэволъных поло:житеЛ1>11ых чис.:сл
а и Ь - средним гармо1шческнм. срс,Т(ним
1·еомстрнческн.м н сре;1нн.м арнфметнческим
\см. статью 1.Сrед11ис знзчснин·)):
2аЬ
~ а+Ь
-- <.vab~--
а+Ь
2.
<.;реднее гармошrческое !.с1Ь/(а-;- /J) и сред
нее арифметнчсс1юе (а + Ь)/2 пр:имсчателы1ы
тс;-..1, что если Д1UI них, в свою очередь, найти
новые среднее гармон 1 ·1ч<хкоt: и среднее арнф
мстичсскuс, то они ок:окутся расположс1111ы-
r
ми к ...,аь ближе:, чем нрсдылущис срt:дн 1н::,
есл н только а '1' Ь. В этом и состоит идея метола
пр11блшкё1-111оrо 1'Ыч~1слсн11>1 ..., А.
Предстзш1м 11ан11ос ч11с;ю/1 в uиде r1ро11:.1ве
пс11и>1 двух произuолытых сом11ожителей:
А = a1,IJ0, таких. что а0 < Ь0. Это будет началы-юе
пр11бл11жение к v'л, rтри,1ём а0 прнбл11.жает ·./А
с недостатком, а Ь1} - с 11збытком.
Оrе;\ующее (nср1юе) nри61пrжеюн: Rычислн
ем 1ю форл,1улам
60S
2aJJ,J h - Cln + /},1
а,~-..........,'-
llo +J:>o' l-
2
З;псм ·1очно т:lк же 1юлуч :о~ем второе п рибю 1-
же11не , треть<::, четвt:ртое и т. д" nocтcnc1-1110
сужая «1.юрота», n которые должен 1ю11зС'1ь v г1
llр11меним этот способ для вычисле111fЯ
, 1998. Ч 11сло 1<J<)H можно разлож1-1·1 ь rrз /(А:1
ПОЛОЖНТСЛЫll)/Х COMIIOЖIITeJlЯ 6есчнсле111111Р!
количеством способов: 1998 = ';Q 39,9(> =
= 100 19,98 и т. д. Разумеется , чем более «1·ес
ную» пару мы выбере.'V!. тем быстрее пайдём
хuроше<:: прибпижс11и:с. Ilоложп;ч, например.
а0 = · Ю, Ь11 = ' 19,95. IJuследоватслы-ю получим
Номер Срсдш::е
Среднее Разностr,
Ulal'П 17 тзрмотш- арифмсп 1 - f)11 - а11
чсское ап ческос hп
о4U
49,9')
9,95
1
44А2-1 68 ·'11.97')
0.5'5032
2
44,698146 44,6~{)84 0,00 J694
-~ 44,698993 44,69906') 0,00007l.
С ростпм 11 1штернал (аф 17") стрс::ми1 ел ы-ю
С)l"'No:Зется, поэтому грашщы 111-1терв~ша - чиоtа
а11 нл~1 h11 - выстуnаю1 всё болt:с то~шым11 rirm
блшке1111ямн к з11аче11и10 \''1998.
Следующий с1юсоб 11рибл11жённоrо 1·1звлс
че1111я кналратно1 ·0 корня имеет;\анн1то 11сто
rню . Им ГIOJJb:JO R;JЛCЯ t:щё лрсвне1·рсчесю1i1
мзтсм;п' llf( и ас1тюном 11 Li. Клавдий n·тлt:мсЛ
гrри сост~rще11ии асr·роrюмических тa11nell\ .
Cпocofi ос1тонаJ1 нз хоропю 11звест1юй форму
ле юза;1р::tта суммы:
1
'
,
(а+l])~=а-+2.сФ+ь-.
Прс111юло)ю1м , путём грубой пр1шидю1 Ml>l
установит~ цифру /~ССЯ'l'КОН 11СКОМО!"О ,;'19<)8 -
4, н теперь ш.ш1:а задача - найти цифру единиц
х. Посколы<у (40 + х)
1
= 16UU+80х+.У
2
• uе.тr11-
чи11а НОх + .У
2
= х (80 + х) rютк11а ма110 от11и
чаться от 1t)9~ - 1бUО = 598 То есть следует
подобр3ть такую цифру х, чтобы рсз ульта 1·
умножения
8х
хх
~??
был близок к ч 11слу ,:;<)8. Ясно, что для "lтого нуж-
110 в:нпь :х =~k 8-4 4::: 5:16. И1·ак, , 1998 ,,., 4Ч.
Если, окр1,utё1-1ныс успехом. мы продолжнм
L'HOH ЧИСЛОflЫС н:~ыСК:JI НIЯ , .1о, естесгвснr ю, 1-f:l
следую щем шаге захотим уточJ-1ит1, цнфру
11еся·1ъ1ху в деогruч 1юй дро61 1 11с1<0мого кор11я.
Прнм:ешrм y·N<e нсnыта1шу10 схему. Зпачсшrе
выраженнл
(.~.:.1-+L).! ~ 191>6 + 2 Ф~L+L
JO
-
LO lOO
дшtжно мало u'1'JJ1·1•щ't ьсн от 1998. а для: .;r1 ·01·u
)'(
}'}
неоnходимо, чтобы tO 88 + 1
-
0 было блнзко
к чнслу I 998 - 1<J:)CJ = 6!. = 62.00 (доб~шл.яем
дна ну11я после запятой, rюсколь:ку у - цифра
,.LССЯТЫХ . " Щ'С!П'ЫС пр11 во:3веден1111 н КН~!др~l 'Г
11ереходнт а р~1зр~щ сотых).
Пр 11 каком у rтроизвсденпе
8Н, 11
x___l,
??.??
б; 1ижс R<.:e r() к числу 62,001 l(онсч1ю же , прн
J' ~ 6. ПОСКОЛЬК}' 88,6 · 0 ,6""' 1:1, 16. Зн~ЧIЛ,
"1998 ,,, -+4,6.
!3ычнслешш МО)[аю продолжJ.1ъ, nосnедоnа
rелыю определял цифры сотых, тыо1•шых
11 т. д. Всломогатею,11ые выкладки удо(>но nро-
11.щодп1ъ nрнмер1ю так, как это дел;1ется nри
Искусство вычислять
Дt'ЛСнн11 ч11сла «угош.;ом» Отю r чш: в том , что
з;1есъ на каж;1ом 1u:11т щл1ВJ1с::кается (о-юситсн)
нс:: 0,1'\Ш! JJOB:rЯ ц11фр:~ СЛСДУJО ll\СГО р~1з ря;t:J. а
пара цифр двух м11адших разрядоR. Для ::этого
вJJачалс все ц11фры nодкорс1111оl'О ч11 сла удоб-
1ю ра:16J.-пъ rt::i пары : снрава щ1лс::1ю н це1юй
'i:ic111 ~1 слева 11апра130 в 11rос111ой (1<рзi111яя
леnан ц1 rфра может оказаТhСЯ 11 без пары) .
Приnедём нес1<олы<0 первых шаrо11 извлс
<Iё1шя квадраnюrо корня 11::1 ч.нсл;.~ 1998:
\; 191)8 ::: ...{'-\, (JС)н ."
16
х841 ~9Н4 3.)6
886 61.00
:><
х
6 5:1>16
~9 2<) 88400
У 8U.J61
89388 80.1900
х н 71508~1
888'1600
Однн тrтерсс1 rыir способ прибт iжerrr ю1 ·0
и:шлечения. КRадратпых корней: ос1щван на
сле~ующе:v1 простом факте. Если вырI01<е1ше
, А - а nо.зnсст11 н 1raтн)~U!ЫJ)'lO степе~ п, n по
формуле 6111юм:.1 1lыотона . а з:.~тсм 11 :~6ан.11ты:н
от кuрней пр11 ч ётных стелегIЯх, ·ю rюлуч1пп1
выtх1же1-1ие пида М,1А + N , 1·д1: 11! 11 N - 1tелыс
'НI<..:ш1 . Напр11мср:
{)1998 - 44)! == 39:)4 - R8~ tt)98,
(,t99S - - 1 4)' ""7Rn6...,IC)l)S-;114s920,
(\1998- -14)1
:::: 30948868-692.'184 \ -1
-998 IIТ.JТ..
Заметим, что если юять 11риближен11е а ющц-
рат1ЮГО K0}1H5I нз А, T<IК()е,_ЧТО 1\,.1 - aj< 1, '\'О,
вознодя :iатем разност1. .J А - а в квадрат. r~б,
четt1ёртую creneн1, н т. д., мы будем 11олуч.ат1,
609
Матеман1ка 1<1 ра6отой
:л1ачсшш, но.: более 6Jщзюн: к нушu. Лоэтuму,
пошн ·зя 1 1 х пр116л11жённu ракны .,1и 1 1 улю, пос
лсдоватслыю получим
i
3934
~
v 1998 ,:: "88,:: 44 ,7U4)"-15 .
1
1998 "".:)
48920
"' 44 69894()
v.
7НО6
'
,
'
11993 = :IOl)<-J8SьS ~ 44 698991
\.
()92.)84
•
.
.
В пuслслнем случзе нее шесть :ша ков гюслс за
пято11 ·1 ·оч111,1 е.
r\ те 1 1ерh оста 1 юnпмся 11а ~1лгорнтме, К(Уt'О
рому <· Обучены» практичесю1 нес соnрсмстп,1с
вычислитеJ 1 ы 11,1е мa1m1rrы. :..Jтому способу две
тысяч 1-r лет. О 11ём рассказал древ11е1·ре<:rеский
учё1 IЬп1 Герон АJ1скс-1ндр~1trский, ч1,и ,\1атсм<t
тичесю1е р<lбот 1,1 - своеобразн:.ш :~нциклопt'
д11я а11т11ч 1 юй прию1а)\но 11 мате м атнки .
П rе1~1юлож11м , 11зnе(~l'Но щ~котurюс нр 11бю 1-
жснис Clo кв::~11rат 1-ЮI'() кор1 IЯ 113 ПОJЮЖIIТСЛЫ-Ю
го чнсщ1 л с 11е,цос 1 ·ат1юм. Tot')\a nс1 1 1 1 чнну А/а11
можно считат 1> приближением к , А с 11зб 1,1т-
г:
1<ом. Истишюе значсни<: vА нахо,цнтся между
uим11, ll 1< нему мож но е щё прибли:шп"ся, если
юятъ среднее арпфмстическое а 1 двух ч11 се11
а11 иА/ао:
(Bct ска:~аннос СП()анещ1ино l f TOl'NL, ког;~а l lC-
X OД I Юt' Щ)1t6J 1 11же1111е а() нзято НС с JICДO<.'Т:-lT-
КО\/\ , а с избытком . В этuм с.пуча<.: зн:~ч<.:1111<.:А/аr,
окажется п рнбп 1~же 1 11 1 е""1 к '-1 А с 11t'дос1·ат1щм )
1\ n11онь нолучешюму :зн::1 чсн11ю и 1 мож1-ю 11ри
мсн 1 пъ прот1ссс д:tлы-rеlпut'гО уточr 1 ет 1 ня 11 т д
'
Н:шримср. юяn для корня \'1()98 пачалыюе
прпбm1же1ше a t' = 4 4, последонателыю получим
ll oмep
Значсшrс
прнбл11же1 111я
11р11бт ~жешш
о
44,00lIOOUOUOOOUU
1
44,70-i '>4'>4'>4 '54))
2
44,(>9Н99 :$()220 :\(>6
3
4-1,698993277 2540
·1
4Ч,698993.277 2ЧО
Как видно нз таблнцы, 1ю1 ·решное1ъ 11p116J11 1-
жен11я с каж;~ым 111а 1 ·u м быстро убыв~1ст -
ч етвертое по сч:ёту з11ач:с1 ше ш шо·1ъ до 1.1-1·0
знака 1юсле запнтой сонп:.щаег с тр<.:1ъ11м.
***
Герон рома 1 1::1 Жют1 Вер11а «ТаинсТАеmтый ост
роа» волею су1~еб попали на 1шочок суши, затс
ршшый n просторах Тихого океана. У 1111х не
6 1,,1JIO 11 ик:но 1 х счётных приспособленш1, 11 те~!
пс менее благодаря изобретатсльнос·1·и и смt'
калке инженс:ра Callp<::ca Смнт:.~ 11м ую11ю<:1.
довольно точно оцсн11т 1, коор11ина·1ъ1 111япuтив
u1 е1'0 11х острова. l1 1-1жс:1 н:: р смо1· это С/ \t.:л:н ъ
тшrько 1ютому , ч·1·0 НJ1~щсл мс:тщрмн прнбл11-
жённ1,1:х АЫЧJJСЛtl-ШЙ, п Ч:lC'l'l-IOCTI 10)\l111J\J 11 З CI ю
собон изш 1 ече 1 111я ю-1з,11рапюго r·юр11я.
ВЫЧИСЛИТЕЛЬНЫЕ МАШИНЫ - ЧТО ЭТО ТАКОЕ?
На вunpoc, что такое машина, са:r..п,1й простой
ответ, пожалуй, слсдую щ иir: ма ш ищ1 - :-:JTO
устро 11стrю, которое может вьшu;шять какую
то работу без уч::~стия чело1:1ск~1 . На работу, 1<;,~к
\1Ы знаем и~-~ ш коm,ного курса ф 1 1з н ю 1, затра
чиваетсн ф1 1 ~1 rчес1<ая знсргия: механическая.
э11е 1сrри ческая , тепловая. Часто для вы non 11е
ния та11:их работ приходится 11реоfiра:юны ватh
оюш вид э11ер1·ии в друrой: электрическую
энер1·ию в тепловую - чтобы нагреть элек·г-
610
роrшиту, тешю1:1ую н ,-..tех~1 нич~скую - что(')ы
11ривеt'ТJ1 в ,'.\KllЖCl-IИC антомоб11л 1, llJIH ' J '(.'ГI J I O
KOЗ 11 т. н. Hu щ1ж.:ко нс всякая работа 0 1 1ре
леля.ется только расхот1ом энер 1 ·1 111. Можно л11
no КОЛН'1С't'ТПУ З~Тр;.! Ч СНПЫХ фиэ нчес1<11х усн
лнl1 оце11иватt. pafioтy ча1.:оnrr1н1щ кассира n
ма1'азит 1 е или ТТПсолытика, решающего трудную
за[{ачу?
Работа - это процесс, в ходе которого
вы11011нню1·ся ра зличные действия. Од1111 из
,),ал<о>1<n Hf' 11ся1-.оя pafinта oпp<0дe11яerrl'I только рап:олом эн~ рги11
Hl•LX трс:буlUТ :J:lM<.:THЫX затрат энс:рпш - ТТОf(-
11ят1, Jpy:J. u·1·нс:р11у1ъ 1·:-i l1кy. р;1скшю·1ъ пuлсно.
Э'J'О ;~ейстнш1 э11<.:r1 ·ет1 1 чt:скис , или ф1ннчес.:ю rc
ДруП·I С f\ci'ICTHИЯ l !C З:1В1101Т н~т рямую от
прнnожсния фнзичссю1х с11л . Т;1коны , напр11-
мер, устные 1н,1чнснсш 1 я или гюнск нужного
с.лона А сжшаrе Эта panm·:1 стпа11:1 11с с энер-
1'Ией, а с 111 тформагщс 11 Что можно лела1ъ с
1шформ;щ 11еИ? Её можно иск;1 1ъ (слона о сло
варе, тсж:фоны н снравочш-ще, кrшrи в библи
отечном катало ге) . :3ююми11ат.ь (в уме, :;апнсы
в:~т1, JJa бумаге ил11 n элсктрош ю й t~ амяти).
At:J"~O•· 1 мж~) 1 ие "но11h.и - ~, 1.:~м1и f1ольшой
JНергет11чеlкии эффект '
Искусе~ вu оычиlлят~.,
··-~
M•1ШllllЬI \Юryr /JF' S У'МСПIЯ 1.1.;,щв<:Кtl Bl,/fl U/\ll>ffu
послt>11nВ.П("/\~НОrти ОПР\').11,JИИ
11срслаnат1, (n шкъментюй т111 yc-rirofr форме,
rю тс:лефur 1у 1 1ли тсдсграфу) , 11рсобразоnьт:t тh
( 113 UДl ll LX 'll!CCJJ nу"lём м:а ICM:t'Г J !Чt:CK!IX 0 11 cpa-
1111n лолуч:пь дpyr1 Je, J/l'Pt'J:Юf(IJTb 1'СКСIЪ1 с од-
1 \ОГО Я3ЫК:1 на другой)
Н аконец, бьш:зют дсйеш 1 1я , LtcJtь ко-1орых -
1/ОRЛИЯТЬ на дру1·11с· ДСЙСТНllЯ l!ЛН СОС/J.ТIШПЪ
ОД /f() леl1стrше с ЛР}'!'l!М: Ч ТО-Т() ВЮПОЧI 111> ИJ/IJ
иыкmлчнт1" у11е111rч111ъ 1рол·11<ост11 '1·em.:в 1 r:iopa ,
перед;пь другому рабаТТ ШК)' указа1111я, что ему
делать д:u11,шс. Таю1с дейстnr rя п:~зт.~nаю·1ся
уnр~1nляющн м и . Их результат пе завнснт от
кол11чества 3атраче[!НОii энергии . Неважно, с
какuй силой нажим.~·rъ кнопку - л~1rп1> бы 11а
ж:пъ. Это лёгкос 11а.жат1 re ....южст DhlJJ{:l'ТЪ боль
шой энер1 ·стич~скн й эфс/:><~ кт: вю1юч11 ·1 ·0J мu
·юр. в:юрвётся мост 11л r1 гюлн: 11 метсн л шj.Jт. А с
11руп>й стороны. может 11 рuиJu йт11 дсГн..:·1 н 1 1l'.
01ысл 1<оторuго в 11 t'реда ч ~ r шформ~11 ~1т : 3;;~
.ше111 1· г J111<0JJ11HNЙ :1Н0Н()1\ (<-Н:tч lIH :JC1 01 УРОК •>),
~;;~гудт сирепэ (<»1 рево1·э·1), з.~жжё1тя 11ам11очк::1
ааддuс.:рыо f(абr шет:а nрача («можно вoi'rпt» )
Дош·ое uремя машшr•l умела nылол 1 rя·1·11
ли тuь одно или нескош,ко механнчсскнх дсС1-
ст.ви~1 , напри.мер под 1 111~1 ать IiJП.t олус1«1 ть 1руз.
СоеД1 ш1 rт1, одно дейстnие с ;фуr·п.м мог TOJILKO
че;юнск, улр<1 в1tЯ н r11нй этоi1 маш111юй. В~1 :жным
<.:обытнсм ст~ю ИЗ()бре-1 е 1-ше м;1111нн , которыl'
'Vl.orл 1 1 без участия ·~е.пu~ск.1 вы1юння·1ъ uп1х:
;1,<.:11ён ную ПOCJIC,ТJ,OB<lTCJJhJ IOCJ'Ь оr1 ср:щ1 JЙ, 1<ак,
11<intx1 мep , ТК:.11 1кн11 станок ,\ нтом ;1т1 1:{;1ц11н в
том vr эаюлочаетсн , ч'1'06ы co:1/(:J11a·1
·h маш11кы
или Т<ОМШIС:КСЫ машн н. crюcofi 1 Jblt' 1!1 . ПIOJ IIOIТI>
611
Математика за работuй
слож 1 ~ыс 1юслсдuнател1,нuсп 1 р:I :·н юобра:~н ых
()11с раци й.
Та ю 1 м оRра :юм. 1:1ыч 11сл_111тс;11,н ан ма111ищ1 -
этп мз н11111 а. которая автомати:11 Lруе- 1 · 1 1роцесс
nычи сле 1т й; 1111форма1~ня - это то. с че,,·1
работ~нот вы-~и сл r пелытътс машины; упраш1е-
1ше нозnоляет отдслы1ые простые 011ерацт1 с
11нформац11ей соедшшть 13 сложные вы4нсл11-
тслыr ыс процессы.
АЛ ГОРИТМ
Длн а1ппмэт11 эаци11 той или ~11-юl'r р а(')оты её
llY'A<IIO предстантъ н юще ПN 1 ю 011ре11елётпюf1
nосле1(оватсm, 1-юсп 1 11rюстых л,ействий , rде
рабочие деt~стnня соедипшотсн между собой с
1ю~ющыо управляю щих у1<аза 1 rиi'r: что д<;л:пь
,Т(альшс Ра бота, которую [(олжт1а вы11ш1шпь
ВЫLШСJШ ТеJJы 1 ая машина , - ВЫЧIКJ11 1ТСЛ 1>14ЫЙ
11роцесс. 11 ростьн: дейс1·вю1 зтоru 11 pu1 LL'CCI -
разл 11 ч ны с 11рuсты с ont:pa1 ~ш1 с 1'-'1а·1·с,"1зп1чс
сю1м11 п6'1.ектам н : с1шжс1111сдвух 1 11 1фр. подста -
1-ювка 11 фСJр.'1улу ч1 1 сла нмссто переме 111 юй 11
др У11ранш1 ющис указанин содержатся, напри
мер. н рэсо:~нонке скобоl( в qюp.-..r~mc (сш1чала
па;~;о nычпс11ят1. ш 1yrpe 1 п11 1 е ско(}ки) , n правилах.
о письш аю щ1,1х n оследователыюс1Ь деЛст~шИ
при дслснrrн. 11ахожден11и паимсньшсго обще
го кратного и т. д. Для про цс<.:са вычнслен1н1 .
пр сдставл сшюrо в щщс 1 юсJ1 сдоватс J 1ь r-юстт 1
Вь~"-11-t Сл~нельная маш 11н а :) 10 '1с1Ши1tа, котnр .н:•
автомаТ11 '1ирус r проuес с вь1ч 11с.лЕ'нин.
612
прост ых /(t:Й<."1'н1 1Г1 , в м;.~тtматню:: cyщcl"'I нуt:т
с11с 1 ~иалы 1 ос 11 ~1 :{1:1эг111 е - апLо/11т1.;11. П оэтому,
уточ 11нн 11ашс nt:pRuнaч<1Л1>11oc опрс1tеле1 111е.
можно скаэ ~пъ. что 11ь1чис.~ 111тет.11ая, 1 1т 1 иате
....1:п11<1есюя.
маmнш1 - устройство, способное
ныпотштr1 алгоритмы . Конечно, 1ю11ят~rе а!11·0-
ритма возн11ю10 в мате...,1атm<с пс n сnя:11 1 с
выщrслителыn,11\ш :v~аш1ша~\Ш, а ~·ора:що раньше .
Но 11мснно orro лежит 1:1 оснuнс нсс(r наую 1 о
комлыотерах.
Со:щ<11-111 е всякш·о ЗJ1 1 ·ор 11тм<1 11рпход11т 1р 11
ст:щин. Ct1 ауаж1 :1!1! 'Uр11 п·1 11р11ду~1ына1nт. ~;:пе~1
1\)'ЖI ю Т(О1(33;п 1,, что он } \eJIC'l'AИTt'Л l1I ю «pafio·1·a
ст•), т. с. решает rюст:н1.1е1111\'Ю залаЧ)'. Н аконец,
матемапщ N)J 1 жен описать сво!t алгортпм так.
чтобы его мог вы полнить .11106011 человек, даже
11с обладаю щиi"r боm,шпмн ~ш;uшя.\НJ нлн талан
там и . Оп 11 са11ис :ш1·ор 11тма ~юд41 1нжтс11 впол
не.: uпpt:) \CJii.:JШЬL\1 тpc60.1:1aн11JJJ\.I H(;~;lВllCIШO 1)'1
тпго, к к:~ко1'1 uбласт11 матсмат11кн /\а 1 шыl1 ал1·0-
р11тм относ11тся . К:1ковы же ~н1 трс6онаю 1 я?
1. К:~ждпt дt:йстн~ 1с алгор1 П' \t:t долж 1 ю n ыт1,
элемсrттар11 1.1м, т. t: 1<:11\ мож1 ю бплсс nросты.\1,
:.:Элементарные дейст111 1 я nfi1,1•1пo 11а3ыn<!ЮТ ша-
1 ·ами а.'п·оrитма Так. сложст111е ~ух од1ю:шач-
11ых ч1ке.•1 можтю счrrrать .~.'1е:v1е11т~1р11ым (КУ.!Р
уж проще!). а с:южетше дu~х многоз 11 ач11ых
чисел <-столби 1<0м » - это vл:е целый :uп·орит,ч,
кuтuрuму обучают в nе:-рвом класс<::. Чщ:ла н. 1~\О
: 1;1 rt l1 Cl'IЪ /\PYI ' 1юд дру 1'U 1\\ ( μ:.tJ\.ЖJl ( IOJL ра;~рндu~1)
и 1юсле1~онатсJ1ьнu справа fHI J l t'lЩ сюr:щынать 1L\.
11нфрf11. Если пoлy•1at't'OJ дну:~ н:1чнос ч1кл о, то
t:Jt1н1нцы е1 ·0 ст~1р шс1 ·0 ра~рн,: (<1 пр116аплнют к
сумме сле11ующ11 х Jl.ПYX t(1 1 фр.
2.. Порядо1( ша1 он 110J1же11 быт1, тосшо опре
делён. То есть R СJ писашш нужно укзза1ъ. с к~1 -
1<оrо шаг~1 r-1ач1111зт1,, кal\oli шзс вьшолшпъ пос
ле 1<аждоrо о ч еред1ю1·0 шага н како й будет
з~1ключптелы1ым. llапр и ~'1Ср. при сложснш1
чнсс.r1 2.1 (1 41 последш 1 м ша1·ом буде-1 аюжс
ние с1·арших разрндов: 1 + ·1 = ь . При с1юже~1 1 111
23 и 49 на 1юслс;111ем ша1·е щн 16авлясм к сум.'>н::
старшнх разрядов ''П<.:рснос л - с/\1tннr1у, котп
ру:ю :1аnомш 11ш н~111ред ыдущс м шаге (3 + С)= 12.
"д11а 11н111ем, 1щ1-1н н уме·>) . Пр11 с11оже 11111-1 8?> и
.. ic; последний tшн · - 11риткат1. к рс:Jульт:.~ту
слева еди11и 1 1у старшего разряда. получе11ную
при СЛОЖСIШИ 8 и 4.
Заме1ъ·l'е, что уже n нашем простом при:-.1с
ре для трёх разных пар слагае:-мьL'Х: последние
111 а1·11 оказалнсь р:~зли<шы~uс Но нед 1. ~и 11 ·ор11тм
должен 1·од11тhСн /\Л Я тuбых сл :.1 r~1смых! И обсс-
11еч11ть это, т. е. 01шсать алгоритм «Н общси
BIIТ\C». - задача того. iao его нрндумал. В :~лго
ритмс сложения столб1шом для определения
JЮСЛ<.:ДIIСГО ша1·а нужно BRCCTH провt>рку усло
ннн: сt~1ъ ли перенос 1юсш:: су~L\нтронан11я стар
ншх р:1зрн;юв l::слн н ет - 11:t это,v1 1 1с(' закан
ч1rнаетсн Еслн сеть, то эначсннс переноса
(едиюн~у) делаем стар1ннм ра:>rидом суrv1мы.
()дним из 11 а~ 1 бuлt:е распрос1 · ран~нных
ин11011 общt: 1 ·0 опнса1-1ия алгоритмо1i ннлякУr·ся
алтебранческие выраже11ия. В пыражет-н~ ти11з
(а+ fJ)(2c + d) nоследоватст,тюсть действий
не занис11т от того, какие <-шсла буJ(ут подстав
лены вместо букв. Эта последовательность
определяется расстановкой скобок и прави
лом, требующим 11рн отсуп:твии скобок умпо
жс 1ш с 11деJJение13ылuлнтъ ра11Ъ 111 е сложения
11 ВЫЧИТ:JНИН .
3. Нужно точно определить дан н ые,
·1· е
06ъе1пы, с котпрым11 работает аm·орнтм н
целом 11 е1·0 от11елытые шaJ ' tJ . Напрнмер, n
геомстрнческнх ~зтрчах участйуст несколыт
nидоn объектrш: фигуры и их ЭJiементы (утлы ,
nысоты, диагонали), числа (велич1111ы углов,
дл1шы отрезков 11 т, д. ). Каждое дейстnис при
.111еtшмо только к опредслёшюму виду объск
тон. Фшуры можно 11еремещать ~1 1юнорачи
н~1·1ъ. Вслнч111-1ы можно сю1;:~дыват1, н умножать,
11<1 11 то 11е в любом CJJyЧ<Je - бсССl\•tЫСЛСННО
склалын~1ть нет1ч11ну у1·лэ с /1,J1111юй отрезка.
Искусство еы,1нсля rь
Для раз11ы.х видоn чнсел одна и та же п1ю
uедура. (скажем, сложе1 шс) Пу1~ет ор 1 ·аюiзО1iа11:1
nо-разно.му Сколько будет 1 1 1 + 1 1? Вы скаже
те - 122' Да, если это 'ПКJЩ предстаn.пе1шые в
деся·1 ·11чнuй системе сч11слспия. I Io они могут
6ыт1. и двоичными. А то1·да 111+11 == 1010.
Другой 11р11мер: еслн складываютсн целые
чнсла, то щ1г1 з:нrнсн стuлбиком с;да1·:н::мые
uыраnн11ваются 1ю правому т<раю (1ю млалше
му ра~риду) Дt.·сят11ч 11 1>1е дроб11 р::~спощн·:ноп:я
110-др-утому: ~1 х ti1.1раnниRают по э:.~пятпй (11лн
точке), от11еляющей целую чап·1 , от дроб 1 то(r.
Л простые дроби вообще нелъ:нr с1щадьшал.
<.:толбиком. Дrш .их сложения пrпменлют сов
Сб1 другой алгоритм - с пр1шедеш1см к об
щсму знамt:нитслю .
Как внд11м, 11р11 рабtУ1с с ч11ишми 11собхо
;~11мо ук::~з::~ть форму нх прснс-1·ав.rн::нш1 (СИl~гс
му счисления) . целые:: они 11ш1 дробные, и сслн
это дроб11 - то дсопнчные шш простые.
4. ЛJ1гор11тм прсдnола1·ае-1 нзл11чис 11 а ,v1ит11
-
места, Г{l.С з::11111сываются исходные да11111>1е ,
рсзуJ11,таты промежуточных вычнсленнй 11
окончателы1ый резулътат. Уже в простом алго
ритме <.:ложения столбиком 1юзнш<а10т проме
ж~r1·оq11ыс результаты. которые надо заnисы
nать (~дна пишс:\1") или запоми11ать (•Один n
уме->) . R щJкссдневных 11ыч11сле11шrх мы 11но1 ·щ1
обхtщимся снос11 11амятыо. В ней хранятсн ал1·0-
рнтмы , нскотurые нанныс дш1 них (например .
·1·аfi11нца умнuжсни.н), (!при устном счете - н
Нуж1ю точно опрелf'лнтn мнные. т. е, об1,;,1;1ы ,
l KtПC>fJЫ"llf p.Jt)()J ,Jl•1 dl\1-upнт"
613
Математика 1<1 работой
Память - меrп>, rлt- ldn1~<:ы1ыюп я 1к·лолные донные.
fJt:.'-\}'ЛbT1lTЫ промР.ж утu'1 1 1Ьlд ljUt '-8ИLЛt.'llИi1
И ОКОНЧd f!,'ЛЬНЫЙ ре,ультат
llCt" nромеж1r1·очныс рt:{ульт;пъ1. Hu Ч:JLVJ'O н.1-
мм·1·11 ~ 11е хват<1t:т>.>, н тuгна J11ы ною; 1ь:1уем бума
гу: у:r.п южат 1, 11 лет 1·1 ·1> ,,11 ю1·о:зrr~1чш,rе ч11сJ1а бе:s
бумаги уже тру,11тю.
В с;ю;.ю1ых вычпслспютх с большим коm1 -
чсством lfCXOДIJЬL'i: 11 ЩХ>МСJ!>.уrочных даШIЬL'С
(таюIХ, 1,ак денежные расчёты 1та nrк·rtпрнятшL'<:
11 н м ~11 ·азшшх, расчёты 11р11 11ропюзс погоды,
1rр()(.: кт11роF%1н1 1 11 самолi:'тов) 11а П<1ми·1ъ нола
rзтhся нельзя Гlрнхо;~итсн нс 11росто racxoтщ
li:lTh 011юм1-юе количество брtа 1 ·н μ,ля з~1 п11<:11
11аt-1ных , но 11ощ1с11слёш1ым обра:юм эт1 1 :'{а111 1 -
си 01х:1ни :ювынать - 1·ру1111нров:~т1 . нх R таб
лит~ы. р3СКГIЭДЫl~Э ' IЪ В пrону'v!ерова 1 II r 1,1 е 113!1КИ,
заводтпъ картотею 1, что6 1 ,1 1~нчсго не проnап:а
ло п необходимые дашrыс можно было быст
ро отыскать.
Чтобы алгоритм был предсльпо тоtr11ым,
при его описапи и пужпо ук~\3Ышlть мпоrо
разных мелких деталей, нс позволяющиJ( ую10 -
1111ться в сторону, случайно сдtл:.1ть что -то не
то, ошибнться. И3-з;.1 это1·0 ~настоящий» 1111·0-
рИ'rм. удовлстворя~о 111 11й всtм требован11ям
TOЧIIOCTll и О/tl-IОЗНачности, всегла ВЫГЛЯДИ '!
) l,Jll•ШliЬIM . 1·ро11·ЮЗДКИМ 11 «МеЛОЧJIЫМ·>.
В алгоритмах, которые излагаются tl ма
·1·ематиL1 есюrх книгах. многие деталп , кзк пра
вало, опускаются. Считастсsт. что какие-то
.вычпслспия читатель сможет продслап, н без
подробных объясне111-1й. В т:u<их оппсаниях
мu 1 у1 встретиться фразы т11 11 а "д;~лее надо
rе1ш IТЬ 'l':tKOC-'tO ура.внеIIИС Ч<.:ТнёрТОЙ t"l'CLIC-
614
НИ" 1IJll1 "те ~ 1tp1• . \~ I J\'JЧa СНО) \1\ \ 'С Я \\ 11()11СК) r;paт
чa1'·11L1tl 'O гrут11 н та1<ом-·1·0 1·рафс •. Яс110, что '1 ·от.
f\'1 '0 1 1 е .~ l!aCT , Ка!С re111a ·11, ур:1 Bllt'HllЯ ~l - (1 ('1 с'JН::
IП!, тrт 1 11е умеет нскатs, 1<ратч:1(тше пут11 н
r1х1фе, 11t' с~южст rюсгrользоuатьсн ,1:&1 п1ым 01111-
с:нтпсм - н . :шач11т, это, строп> пшоря, не <·11а
t'тоящ11f1·> аm ·uр1пм.
В школьных уч~.:бн11ках 11ри (ЩIIC<ti11111 ащ·о
р11тмu.в (налождс1111я общСJ'О :-шам е нат~.:ю1,
BЫЧИCЛt'l-JIH'i ПО фOfH1)'J1:1 .\1 . )'(l'ЛCHJIH ~TOJll((!M )
также 1-1е все 1 юдроб11осr11 указьшзются Прс11-
11олагас:-гся. что уче 1 111 к nом 111п табmщу у\11 ю
же11 11я, умеет СКЛЭ/\ l1l1i;:!Т11 CTOJIO\ IKCJM. ГIOJ111:IO
naТI1CH Jю1·ар11фмrrческпм11 табт щами, з нает,
что в выр<1же11ш1 с+ 1с/ Мt'Ж.11)' 2 11 с/ 1ющх1:~у
мев;:~ется :шак ум11оже111н1: с+ 2 с/ ( прнчём ум
ножсшrс З/t<.:Сь надо про11 :шсщнтт. ра11ьшс сло
жсн1ш) н т.;1.
Ну а et:JIН ш1 нt:<.~ i ·u ::i·1 ·oi·o нс :ща<:т? Сможет
ли 011 работать с аm·орн ·1 мамн' Да. есл 1-1 нее
«J1[1СJЩОЛ:11 '(Н:'МЫС •) знанш1 HКJJJ()Чll'IЪ kOIJJ1CUiJll'
: 1 л 1 лрн·1 ·м;1. CJtt'Ji<JR его nрt.:/1.СЛЫ-ю 1ю,r~робным .
Скуч[l()t А пастшrщ11 й а111·ор 1 1 ·гм н д01оке11 быт1)
скучным.{:) нём нет MCCT<I фз11таэ1 1 1r. ОIТ ПС ТJ1С
()уст (пне нмеет прав::~ трсб0Rат1>) ю1ких-лпбо
:·шапий пmr тала~ пов. Дел<1ir. что сказано. - 11
1шкакJ.LХ волы юстеir. Работа!~ внимательно 11
-"1сха1Jичесю·1, как падёжпая ма111ш1а .
Вот rJ ск;1э:11 ю кажно<:: для пас ою1~u - .м:1-
1111 IH ~I . С..:уты1юб()J '() aЛJ'()PI 1·1м:1 к том 11 C'()CTO I f'I ,
чтu ОН 1 1ш1жен быть 0111 IC:IH 1-f::ICTOJLbKO '1'04110 11
шщробно 11 сш~1 ·шпь 1·1:1 тзю1х простых шатв ,
ЧТ()бht е1·0 MOl' . fl:J ПhlllOЛHllTЬ ,\1:11111111:1.
• Наrтоя111и>1 • ,1лr()р111м 8Ct>r11<1 вы rм1мн лл111111 ым, rро-..nз .~"ич
l·t « Мl''\()ЧНЬ1"1• 1
Искусство вычислять
ОТ ПЕРВЫХ ВЫЧИСЛИТЕЛЬНЫХ МАШИН
К ПЕРСОНАЛЬНОМУ КОМПЬЮТЕРУ
ВЫЧИСЛИТЕЛЬНЫЕ МАШИНЫ
ЛО ЭЛЕКТРОННОЙ ЭРЫ
М1-юп1с, н <шер1ше, думают, что ма·1·с:м:п11кн
.rнобят счнтать. На сам()м деле ма·1ематrпш дока
:1ывзют 1·еоремы, вы 1 юдят формулы, изучают
свойства чнсе11, фигур и друг11х объектов.
А д1шнные расчёты с коакрет11ымп чнслами
им. как правило, не шпересны. В nыч11слеш 1JL'С
легко оurибиться. 01rн опшмают м1ю 1·0 вре1-н:
нн, а нu rюс математ11ческut: зн:~н 1 1с: nршюсят
неч~1 сто. l3 тu же uрсмн слож1 1 ыс: 11точные рас
чёты ок~ваJ1исr, нс:обходнмы в друг11х нау ках,
11с110льзующих матсм:п11ку, - сначала в астр()
ном1 1 1 1 , а затем в фиэ11кс. Поэтому матем:~тнкп
11 за;1умал11сь, как обl!е 1·ч1 1н, в ычт 1сле1п ш с
n()мощып маш1r1 1 .
Перuую мсха1111ческую счётную маu11rну
сконструировал в 1642 1'. ф р ан цу зс юп1 уч ёпый
Блсз Л;1 сюшь_ Она 1Jредстамял;1 собой спс1·е
му юаи1vюдействующих колtсшсов, каж,цuе 11::1
кuтор ых соотвстс:rвовалu одному разрялу /\есн
тичщ)1'0 ЧИСШ! И СО)\(::рЖ:JЛU ц11фры ОТ 0 ЛU 9.
К01·д~1 кuл<::сико сонер ш ало пол н ый оборот,
слс1\у1ощее C/1.l:IJ·1raлocь н а одну ц и фру (:::i·l 'O 1 ю
хоже на 11рш-1ц~ 1 п ручных счётои) Ма111и 11 '1
Гlаск;:u 1 н умела толы\о сю1адывз·1· 1-, и r11,1чтпать.
Много в 11 1 1 ма 11 ин проблеме механ иззцни
выч11слени(1 уТ(С.'1ЯЛ немецкий математпк l 'от
фртщ Вильгельм Лейбн и ц. Со:щаш ~ ан и м н
1694 г. счётная ма1ш ша облалала гораздо боль
шими В()ЗМОЖНОСТЯМIТ - ВЫПО!ШЯJtа вес ар11ф
.ме'l'J1ЧССЮ·IС опсрац1ш . Однако она была (.')lи 111 -
ком 1 ·rомоздко:й, а работаJ1;т '"1е;1,ле111 ю.
Значителr, 11ый вклаТ( н ра:шитис нычнсли
телы той техн ики ннёс н XIX 11. ат11 ·11ийс 1<ий ма
темати1< и н:юбрстатс:т) Чарлз Бэ()бндж Более
4() ЛСТ ОН габотал 11 ад 11р()еТ<Т()J\1 nрограмм_и
руеУIОЙ 11ыч ислнтелыюй машиш)r, кот()рую на
звilл аналитической. Бэбб1щжу врш 1адлежала
сама идея про 1 рi1ммирот~ання вычислепи:й. а
также сп особ сё рсализuции: ввод программ в
маш и н у с помощью перфокарт. Он впервые
нвёJ t 1 1амять ДJШ нромежуточных вь11 111слений,
0 11 же 11ре; 1лож и л исrюль:~онать н машине
двоичную систему счисления .
Мащи11а Бэб611,пжа была чисто механическun
и ·1 рt'бовала ПЗГОТОВЛСJJИЯ бОJJЬШОJ'{) KOJJJ1ЧC(~1 ·вa
высокоточных деталей. Прос кт ост~u1ся не:.sа вер
шён н ым . Уже 1 юс11с смсрт11 Бэfiб1щжа н~кото
рыt с:го Hl\t:Yt бы1111 11с1ют,:юнаны 11pt1 со:з;1а11ни
1rept1ыx элсктрrнн.~ханн ч ес1<1 1х счёл 1ы х маппп-1.
До серслнн~.r ХХ н. на та 1<нх маu11.11тах делали
сложные бух 1 -алтерсю1е р;кчёты и обрабатыва
ли стат~ 1стн ч ес 1ше ,Т(знные.
ПЕРВЫ Е ЭЛЕКТР О ННЫЕ
ВЫЧИ СЛИТЕЛЬНЫЕ МАШИНЫ (Э ВМ)
К концу 30-х r1'. ХХ столстш1 11отребность в
антом:пиза1 \1111 сложных BhlЧI I СЛСНИЙ CИ!IJ1H()
во:Jросла. Ведь ш-rи ок:1эат-1с1, нужr11~1 и при
nроекrирт~анин самолётов, и в атомrтой фи
:~шсе, а с н ачалом Rторой мировой войны -
дтr м1ю 1·1 1х военных целей: расч ётов при ар
тнллерийски:х с.1рельбах, расшифрою<и кодоn
разnсдки п р опшшща, разработки атомной
бомбы и т. д. Разумеется. работы дпн ноен ных
11уж;1 fiьин строго засекречены. 1ю зато к 11HJ1·t
11р 1 1нлекаm1Сh луч111 1 н: спс.:циалисты, ;р и с фи
на1-1сиронu н1 rем Ht.: IIOЗllИK~lЛO 11[106JIC ,\1. (А RC{\I>
имс1 п ю 1 1 з-за нехв:~тю 1 дснс 1· Чарлз Бэббидж
не смог закончить спой проею'.)
615
Математика за работой
ЛЖОН ФОН НЕйМАН
Лжш1 фон Н ейма1-1 (1903-1957) родился в Б уда пеш
те в сем ье состоятельного ве н герского ба н кира. Ро
дители 11 азвали его Яношем , в годы учёбы и работы в
Швейuарии и Герма нии он имен овал себя Иога1-1 ном,
а после переезда в США (в 1930 г. ) - Лжоном .
В 1933 r. в Принстоне (США) начал работу Ин
ститут персп ективных исследований . Сотрудник и и11-
ститута, исключ ительно про фессора, н ~• перед кем
не отчитывал и сь и разрабатывал •~ и нтересую wи е нх
проблемы, а институт фин а н сировал их исследова
ния. Фон Нейман был принят е институт в 1933 г.,
вслед за Альбертом Эйн штей~юм.
Во в ремя Второй мирово й войны американские
учёныс стали выполнять Аоенные заказы_ Фон Ней
мана пр ивлекли к участию в наиболее секретном и
крупном проекте «Манхэттен» - по созданию атом
ной бомбы.
Олноеременно 0~1 познакомился с другим военным
проектом - электронно-вычислительной машиной
«ЭНИ АК11. Проа н ализи ровав конструкuию «ЭНИЛК » ,
фон Нейма н пришел к идее нового типа логической
В 1944 '" 1юд руководством прuфессор~1 Гар
нард<:кого университет<~ (США) Говарда Ы1ксна
разработэ t 1 э последняя электромех:н-111 чсская
машина <.J\•Iapк I»_ Она Выла L5 м ;щн 1 юй и 1 1с
ремножала дна 2)-разрядных чнсла :{а 4 се
кущ-1ы - 1'ораздо быстрее всех сноих 11rс.::дпrе
стве 111 1.иц.
Уже 11 l 94) г. fl США колле~<тив, руководи
мый Джоном Моучли а Джоном Эккертом, соз
дал первую электронную вычислитель ную ма
шину «ЭlIИАК» По размерам он а бьmа 13/\НОс
больше .:Марка l» СЮ м в д;11111у) и считала в
т 1,1с;ячу раз быстрее: прuнзводила :юо умножс
Н l fй в сску!l/\У- Пыч11сле1111я в ы J юm 1 яли схемы
из эт~ 1<'1ронных 1 1 ~1 мп. А нот нрuграмму н ма
шнну пrшходююсь вводить непосреде1·не111-10
11ерс.::д сё в 1,11 юлне н ием. Делалuсь это нrп.~кер
пым методом: бnо1<и :..1ашины соединяли н 1-~уж-
1 юй ттосll едоватсл ь11ости, Rты кая штекеры в
соответствующие разъёмы.
Ilовую струюуру 13ычис1штелы-юй 1'1.а ш ш1ы,
которая н uc1 ювных Чt'ртах сохр~шшr:н.:ь 110 снх
пор, прt'ДJЮЖJ 1л 13 1946 r. оди1:1 Н:1 кру11нейшнх
матем:п 11 ков ХХ 13. ДЖ\)Н фон llейма н . Он
роднлся н Rснгrин, нскоторuс.:: нpcl'vtя rабuтал
11 Германии, а fioJIЫLf)'IO часть жизнн nровёл н
США. Фт 1 Не:: 1;tману принадлежа1· работы в
самых paзrn,1 x областях мa·1·e.'v1::t1mcr1: математи -
616
ор1 анизаuии ЭВМ. С тех пор принuип хранимой про
граммы (т. е. такой, котораs~ хранится в запоминаю
шем устройстве в ч исловой фuрме) остае;ся осново
полагаюш и м и, оероятно, 1 1икогда не Г>удст пос тавлен
пол сомнение_ Одна из ЭВМ - «ЛЖО Н ИАК • (1954 г.),
в проектирова нии которой фон Нейма11 п рин имал t1е
п осредственнuе уч асти е (011а и H<IJf3atta так в его
честь), - сыгр<1ла решаюшую роль в обработке инфор
мации при со3ла ни и волоролнои бомбы.
Кру11 ней ш им научt1ым достижением фон Неимана
в послевоен н ы й пер и од стало построе 11и е теории
автоматов. В 1952 г. в р аботе « Вероятнос.тная логика
и си нтез надежных ор ганизмов из нен адёжных эле
ме1iТОВ » 01-1 пuкаJал путь создаt1 ня 11адёж 11ых ЭВМ и
других автоматпв.
В 1954 г_ фон Неймана назначили членом Комис
сии по атомной энергии США, и весtюи 1955 г он пе
реехал из Приt1сто 1 1а в Вашингтон . Череа несколько
месяuев врачи обнаружили у него костную форму
рака 8 февраля 1957 г. Лжщ1 фон Нейман бе:1вре
менно з;звер ш ил свой жизненныи путь. ПоследtiЯЯ
кн ига, нал которой работал фон Нейман, - « Вычисли
тельная маш и 1~а и мозг• - осталась н1:чако нчен1юй.
ческой физике, матема·1·ической экономш<с,он
соз/(:.tл нuвую науку - тсор1 -1ю ш·р . акт~шно :;а
нимался математичсс1<lн'1 1ю1·нкоi1 и тcup11ef1
алторитмuк Фuн HeiJ ,\l\aн сч11т:::~етсн сш1дател<::м
сонрс:м<::нноl1 теореп1ческой ннформат11ю1.
Одной и:1 глав11ых и~ей el'O nрое 1<та RЫ
чнслителы юй маттrи 1 1ы яnляется 11ртщ1т хра-
1tuмой програ.111мы, т. е. прогрЭМl\.1Ы, которая
хра1111тся n памят 11 м::шпшы наряду с да11ным11
и промежу~·оLшыми рсзут.татзмп . 13nагодаря
этому в машине од понремс 11 110 содержится
CI<OЛl>KO yп.>J\1 IO 11 ро1·р~1 мм (JШШ Ь бы l! :tМЯ'ГИ
Х11атило!) и любую нз них мuжно 11ем<:дленно
запустить н ра601у Перн~u1 м:.1111ин:~ с хр:11111мuй
11рограммой была ~юс-троен::~ н lkлнкобр 11та
н11н в 19491·. под руководством
М. У1шкса.
Перt1ая советская ЭВМ - « М:-эсм., (малая
энектроннаи счётпая машина) была создана в
1<)') 1 1·. пол руководс1· вом ающем11ка Сергея
АrrсксеевичаЛебедева.До c1Lx пор nce машшrь1
изготовлялись n од1 юм эюемнлярс, а в SO-e rr .
r-rачалось серийное производство Э IJM и 1Jx
триумфа; 1ьШ>t' 111ест13не пu '"111РУ.
За r1ро111сдшнс лолнt:ка ныч11сл1 1 тельные
м;штны с11m,но rпменплись с;1м11 r·1 сщё бот,
ше HЗM<:Hltлll общеспю. Их ВОЗМОЖНОt."ТТI вы
ШJIН дv~1:ко ээ 1ч11:дслы мс.::чт:н-шй со:{,'1,атслсй
первых :;эвм. Соврс:меп11ые компыотер.ы
пе тот,ко вычислmот, но и управляют, собrrра
ют информацию. rюмоrают нздаnатr, книгн,
с1шма1ъ филъмы и даже рювлскают.
Так чтu же r юявшюсь 1-юнuго н что осталось
11енз,..,1енным в ком11ыотерах 33 эти годы?
АРХИТЕКТУРА ЭВМ
Ос1юrн11я rтpy1<· 1wa, 11л11. как nри1што ГС>ВС>
r1пr,, ap:'i:'lone1.:n~1фa. эвм (т. е. набор функц110-
нзлы1ых блокон н cuязei:i между нами) за '50 лет
практическп пе из.менпл:ась. (;овременныс
компьютеры <.:охрш-шют -,фо1 1-псйм:н-юнс:кую
арх11теюуру» , которая включает
-
ap11фMC'J'II KO-JIO J ' HЧCCKOt устройство
tAJIY), нли бжж ныполне1111я элемс11т.ч1ных опс
р;~цнй (м;uшrнных команд);
-
блок унра 1те111 щ котur 1,111 указы вае· 1 1ю
rщи.01< IНЗl 'Ofl. Т. е. уr1ратщяет ПрОТ1еСС'ОМ JЗЫЧIIC
llCHl 11\
-ус~ройства rтода данных If ньлюда резуль
татоJЗ:
-
память .
Через устройстно ввода 1~аш-1ыс 11 nроr·рам
ма внодятся в rrа.мнт 1, и '1·ам храннтсн . Пр о-
1рамм·а сос1·о~л· н:о~ ма1111111ных команд. Каждая
ком>1нд~t , в свою о черед ь, содержит код опера
ции, которую надо вылолю1т1,, аргуме1rты,1uн1
тzераиды. это1'! оnерац11и (f(()нкрет11ые числа
ниб{) адрес~ иqеек памятн, rде 01111 нежат) и,
Искусство вычислять
наконец, адрес ячейки памятн, n котору10 сле
{(уст <'ПОЛОЖИТЬ» результат. Для UЬIПОЛНСНI/Я
каждой выч11слнтслыюй кома11ды программь1
блок у 11р:1нт.: 1-1ш1 осуществюн:т сл<.:дующую
nuсл<.:довательность лсйств11й:
l) определяет адрес (место в nамят11) очс
редно(t к<1ма1щы;
2) считы нает ком:11-ту 11:з rтамятн 11 расш 1rф
ровы вает сё;
:'>) nы:~ьmает нз nамнти её операнды и пере
сылает их n 1V1Y;
~~)настраивает АЛУ на вьшо;шсние iry1юю1I
операц11и:
5) вересына<.'т rюлучснш~1й результ~1т по
адресу. ук:.13а1 1 ном}' 1~ команде.
Гlt>MILМO BЬIЧJJCJlllTCJlhJIЫX блок упр:нтення
н1->тшн1не-1 · 11 ;\руг11е кома111\ы · 11~:-ресы1 11<11 111-1 -
формац1111 rrз о;~нr1х меlт 11а мя1·н н лр~т1 1 е, ;\
такжt' 111щна о 11ын()да ю1фоrмаци11 .
Пам:ят 1, н комn1,ютере opra 11rrз0Ram1 та1<:
каждая нчейка имеет l'UOй намер (адрес), эти
адреса в n11де дnончных кодов у~~азьша10тс}1 .u
качес'Гl!<.: оnерапдоu мащи1-шых ком.нщ, а спе
циалы1ая аппаратура (дсшифр:пор), п ол)"Ш13
на rixo;tc кuд адреса , открывает ка11ал дuстуш1
1< СО0'1'13С''l'СТВутощсй HЧCllK<:.' . 1-J:~JllJ ЧHC адрt'СНСJ
го досту11а к памят11 - сущее1·нен.г1:н1 сост: 11шя
ющю1 фо~1-не11мансшской арх1 1тсктурьL
У11нвtрсаль11аи ма шина. претендующая 11 а
выпо11ненне любых :.u11·оритмов, должн~~ н метr,
бесконечную пам~пъ, О/'\на1ю '- I HCJIO а;\ресо"
617
BCtl'/\:1 KOllt' ЧI IO. ПocK<JJlhKY дос ту11 п о адресу
рс;.111 11 :~устсн а 1111 аратурой, то кол 11ч е<.~1·вn адре
суемых ( нмскн 11и .х :tдрсс) ячеек Щ)JIЖ Н () ()ыт1,
.1::1фнксирп11а1ю прJ1 проет<тироrк1нин маш1111ы.
0 1ю одю 1 акоnо д11н 1кех м::шпш ,ца 11 rюrn т1ш::t
11 11 е может .че 1 t >1 ться в процессе работы "-Iа
пппты. Как же \-i1.1тL?
Вьошд напши т::шоl1: n:~мять раздепилн н;t
ш1угрет11ою и внешнюю. Вп)rгре1 11 1яя память,
щ1зьшж·м~ш 011ера1т1тюй, ш1л.нстся адрссусмuй
11, сm:дuнат<.:лы ю, и мееr ф1ткс1 1 рова н н ы1'r объём.
Об'пём от:rхпш:~ной n;1 ,,1яти - о;~н~l их наж1-1сf1-
1ннх характср1tет11клю601т) компью·1·с:ра Внс111-
ш1я 1 1амят 1, - это магн11·1 ·ныс днсю1 11 лс 1 1·11,1 ,
ч1 1 СJ1С) которых может мет1яты-я. Маш 1 111а раnо
тает 1·nлыю с д:т111.1ми , со11сржащ1 1ми сй n опс
рапrrнюй !llMЯTll. Пrежде чем DОСПОЛЬ:ЮJЗа'!'ьСн
r шформац11ей и~ внешней памяти, её нужпо
переписатr, n о пе ратнвпуто. А чтобы о пер а
тивная п;1мять l re rrс рсполпялась, приходится
проводить онер;щии по cf оч исп<с: информа
цию, ш: исnоль:~уе."1ую дм1 текущи х ныч1~слt::-
1-1н 1~ , n<: pt::llHCЫHaть no RHt::ГllHIO lO П<!МЯТh, :1
1 н":11ужную (уст:1 рt:в шн с щ1нН1.1 е 1-1 програм м1,1 ,
результаты промежуточных пыч1-1слсю нl 11 т д.)
llJ10l"ГO унаш1 ·1ъ. в СНЯ3 И с ЗН1М IIO:JIНI Kaeт ещё
щщ11 111-1;1 :-.·1а1111 11111ы х кома 1 щ - cmera 1 tт111 об
J\1е 11 а 1 шформ:щней между шrеш 1 тей и шr)трен
ней п:~мятыо.
Другой воnрос. с13лз;1шrый с адрссш;пс11, -
каю rм ;\Олжен бытr, разм t::р адреl")'СМОй ячейкн ~
Мн11имально 11 сд и1-шцей 11амят 11 n.ш1нетс»
бит - яче~-11<~{, н которой может хр:11 шт hо1
J111бu О, л н бо 1 О11а ссютвст<."1·11ует О!\Ному
б!Н
ра:Зj)Я/ \У /\IЮl.fЧТЮГО ЧJ ICJ 1;1, l ln ЛОЛЖСТJ 1111 кaж
J(bll016r1т нмсть cnoi1 щ1;рес? Это пеудо611011 про
rраммнстам, а проскпrровщrша~1 маnнпт. Про
грамм нстам для запис и 1 1ли LПCimя одr ю 1·0
ч1 1с11а придfтсн обр;1титьсn. к 1шJ\нJТ1 1 столько
раз, сколько лно11 1 1ньL'С ра::~рндон (нулсfl 11 t::ди
шщ) н этом числе. Проt:кт11rо 1 1щ1·1 ка."1. ч:пJбы
uбt:Cllt:ЧJ ITh /tuступ к каждому 61 1 ту, пон адо
t111то1 cm r111ком ."11101·0 а11пагатуr1,1.
])oлtt' кру 1111 ая с11 11 нина памю·1 1 11 хра 1н1 моl1
11 11 el1 111 тформ~щ1111 - бс1/т1, rpynn~I 11:3 8 nп
СJ1е11оn~пслы1ых 611тоn. О11.1ш б::tiiт может со
лсржать ЛI060fi ПЭ i 1, = 2 ')6 ДПОИЧI 1hlX l\OДOJ3,
IJOC'J<OJJЫ<y общее KOJJJ JУестrю C II;\\IIOЛOJ.1 IOJ:ШJJ:l
тypы (латп 1 кю 1 л 11 руссюrх букв. включая
строчнЬJе 11 11рош1сныс. 1 t11фр. з11:1 коn прс1111-
нання 11 1tpy1·1 1x зн:1чкон) :1-1снп 111 l' i'ITOJ'O ч1н:ла.
' l '(J 1\ ОДLШМ байте можно paЗMl'CT И 'l 'h лю()о!t
с 11 мнш1 обыч н о1·0 текtта (т<1 1<n 1 ·0, в котором
н с нс11олt1:зуется мно1·0 раз111.1х 111рпфто н 11 ра:\
н1)J (Re-1 ·11 ы х букn). ~?то де11ает байт удоn1 юЛ едн-
1111 цеi1 11~мере11ия н е толысо машш1Jю1\ 1ю н
тскстово1'1 ннфор.1\шцш1 вообrт\с LUICJIO сим
волон u обычном печатном тске1·с 11римерно
раш ю числу бай тов Rе го машинном п редстаn
лс пи11. Kui·д;l же 1 rу;юю с:-.J1ш 11uм 1 ~т 1, место в
памяти ЩJИ записн боль uJ11х объемов 1tнфор
~1аци 11 , 1~сnользуют ра::1юJ11 1 1ыс nр11ёмы сё бо
лсс ком11:жтноi1 дnо1 1ч ни~-1 ко1\11ро11ю1 (nш 1 на
зьш:~ются упакаmсой).
О11нако в современных кпм 111. ютеrах 11 бar1·r
ока:3ЫВае'1'01 ll CДOCTaTOЧIIO Kf1YTT1ЮiI t[\ 11111 11~e it
дл н адрсса 11,1 m . Вед~. u 11 его мож11 0 :1а1111от1. тплъ
rю nпсьмир.1зряд1 юс двои <11 юе число. т. е. целое
число 11 1ш дробь, содержащие ш.: более трс:х
деСЯТIIЧILЪL'\: цифр, да и ТО не НС<:'. ДJtи работы с
i)()льm11мп ~J11с.11~1мн или для ш,1<нклс::rтшl, трс:
буrощ11х uысо1<011 точ1юст11, т. е. болыного К(1ЛJ1-
честnа :та кон в дроби после :-~ашrтой. этого явт ю
недостаточно. Нот IIOЧ<: ...,ry CCГUДII>I OCHOBJ-IOII
~щреl'уемой t:J\ШIИцей tЛfACJIТ маt11н111-юе с.11ово.
со;1ерж;1Щt:t' .~2 дно 1 1чных ра:~рнд:1 ('-1 fial1т:1).
ПОКОЛЕНИЯ ЭВМ
С 1~а чала ')0-х п -. был налажен rrром.ьшrленныf1
выпуск выч110111тет,1rых машнн. Torд::i же нача
:1ас1, 1 ктор.шr т;: бур r то1 ·0 раэnнтня 11 совt:рwtrr
ствования. Н хотя 1 1 х осноrшые фу1-11щнола;1ь
ныс: блоки n обо щх ч~:ртах ост~1л 11CL 11рсжнп~ш.
II03MUЖHOCTl l :;:>НМ очень 113 .\JCHllJl!llЪ с точкн
.\рС!-iНЯ 1ш11nзов~1те11н, псрuыс Ш>1ЧНС)IИТСЛЫ1h1С
\f3Jllllllbl 11 CUHГJCMel!HЫe KOMIJЬIO'l'Cf)l•I H<mfiщe
11(' llMCIOT HJIЧCI'() oflщtтo
ЭRМ '50-х 1т. :1<1 1111м зла бот) 11юi 1 зал, е(' oB-
CJl)'ЖHn:iлз целан команда ю1а.rшфтщ11fIOt1:J1111ыx
uнженсрон. программистоu н оператороu .
lloлъ:юв:JTeJI IJ в ЭТОТ з:~л не }'(ОЛ~'Сl{;IЛТJСЬ. ()шт
табивзлrr-> сnон nрогрзммы т1::t nерфок:~рты
(са"ш шш с поиощыо спец11алыюй слу-.жбы
11ерфор:щ1111) , 11ереданшш нх оператору 11
1 1cpt:~ несконько Ч<LСов ! ю11yLt~1J11t ре-1у111,тат,
раслсчат~11-1ны~'r 11<1 fiолы1111х л11с' 1 «rх б~маr·н.
Ес11и в программе былн uшибю 1 (а наш1спь
бuлыную про1рамму cprmy без о шибок практи
чесю1 m.:1ю:1можrю). вес1, ц11ю1 р:.1бот1.1 с м:нпи
rrоli повторялс.>1 - 11~lч11rта.н с персбиnю1 11енра
вm1ы rы х кзрт. На 07111ой ма111шrе работало
м1юrо поль:юв:\-rелей. Им приходилось ;~ел1пь
машп111 юс время н ,\'1awш111)FJ:O 11амя.'1ъ. А счи
тал и ЭН.М тех лет. rю пынсшшr.м l\1t'ГJr<aм. до
l1скусстоо вычислят[.,
смсrшюt·о медле111rо: всего rтсскшrько тысяч
операцm:f в секунду.
Соnрс.меtпн.rй персо11а!1ы1ый КОС\tпьютер -
компактный нас1·от.ны(r прr 16(1р. И "'1 поль зу
t"Те>1. ка~-: Hp;IВllJJ(), ОЮ IН ЧCJJOИtK с lЮМОЩ1'10
экрана он кuнтрот rpyc1 l:ш<.щ ;~:11 ш1,1х." t'p:.1Jy 11<)
OKOllЧa lГ l·l IJ вы чнст: н1111 HIJД I П' 1 1.Х pt.>:J)'JlhT:п.
6 1.1 сТ[>О FНIOCL IT 1кправ.пс1111>1 JI pacш":чa·1'f>ff\(ICT
1ол1,ко то. ч1·0 c,v1y нужно. Н1щако1л 11оснтr1 -
1 ю1·0 06спужиnзшн1 1юрм-алыю ра(кнающему
комrтыотеру не требуется
К:11< л за с1ёт 11ero прш 1 зошт1 сто;д, р;щн
калы-1ые пзмс11епин? 1lрсждс всего о т1 свя
з~шы с колоссалытымн усттех~1м11 электронн -
1ш. U основе элсктрошюl1 а 1 шаратуры ЭIJ.'\1
JICЖI rт э.11e..JH('NnlН{/Н (J(./30, 1' . с. ЭЛ(;Кtро1 t .l IЫC ЭJl('-
1'1! .:l-tTl•I , 11:1 которых стршrн.:я ос1101·шые б>tоки
м:11111111ы. Быстро;~с l1стн1н: (чr1сло oлtp::i1~1111 н
секунду) ;'=)ВМ :>а11 1 к 11 т 0·1
·
скоrюст1 1 работ1.1
.~·п1х элеме11то1-1 - числ:~ 11х перею1ючеr1~н'r п
секу~ ~д) . Н ра:1л.те[>ы м:Jп1шrы ш 1рс11еллютс>1 в
KO l!C ЧllO~! с•1ёл. размерзм11 сё ЭЛCMC: llTOll.
;)тапы coвcpUICl IСТВО13Ш111Я ЭJICN!eIITIIOЙ базы IТ
соот1:1стствующт 1 х хзраю·ср11стнк Эl3Nl nршш
то IIаЗЫJЗ<lТЬ J /OЛ.-OЛf!Jl/fJLMlf
В rr<::pnш1 nоко;1сш111 Э ВN! (конец .+U -x
-
се
рс11ш1а '50-х. 1'1 ' . ) ЭJICr.l<."H'J'HOCl ба~юй <.:Jl'fJКl IJLI \
обы чны е элс ктро11r-ю-накуум11ыс: 1 1:1мпы, н:.t
ко'1'орых ещё до 11е; 1:шне1"О нрсJ11с1111 раfютат1
телевизоры. В одrюй ЭВМ ис 1 юлr,:юналось
нeCJ.\OJIЬJ(() JJ,CбlTKO!i Тl>.IСЯЧ щ1м11. COt"/1,ИllёHllЫX
1 1рово11:ами. Лампы ч;~сто ны.хо:~lf.'111 11:з строя
(в месяц nрпход11лосh ааi\н.~11нть 110 1О 'Л, т1мп) 11
потрсбш1m1 большое t<олпче<тво энерпп1. Вот
П()Чему отдслыюй проблсмо1'1 была защит;~
блсжо1:1 .:.1ашнны от перегрева. Бысгродейстnис
llЗNIC(JЯЛO(.'b IICCK()JlhIOJJ\11I1 лссятк: 1м1 1 тысяч 0 1 1е
ра 1\1 U~l R секунду. Ma·r·eivla'П1J<-11JXH'j)<1MМ1 ICI' l JCI 10•
среж:тRС!-11-10 :~;.( l!YJ\h'l 'OM м:ШLllH!>I coc 1·:1ш11t J I
пrn1 ·r;:r м му: нылr tC:hl вuл К< щы команд , ~тк,1 эпш; 1н
пrнмые :щрес~1 нчсек пэмя·1 ·11 , >'ч~ктпу1ощ1 1х li ко
мандах. Работа чре-:знычай1ю тртоёмкая. rr ci.;
11~ша1< 11е1111зя быпо l<n1-пpom rрон:~ть.
эвм в1 ·ороrо IIOKO.IICJIHЯ (ссредIПl.:1 )0-х -
середтrа 60-х rг.) рзботал11 11а Gазе полупро
rюд11иковых элеме11-1·ов - трзп зисторо-в и
диодо~. По разчср:~м 01 т заметно мс111,ше ламп
11 потребляют ме111,шс э.нерп-111. Элементы со
сд1111нm1сь посрсдс1·но:--·1 !1счатньL-х плат. 1lла
т:~ - :")ТО 11ластнна с 1 ·1 1 ё:11щм11 , н кuторые нст:1н
пяютс11эJ1смс11т1,r, 1 1 меташ111ческ11J\11И по1юсам r1 .
соею1 11н ю11~ 1r м 11 1·11ёз:1а (вместо IJ[l{HI0/ \011) .
6 1t)
Математика за работой
Платы 0 1 ужю111 ос нонн ым и ко11структ1шным11
<:; 1н111щ::~ ми, 11з которых и соб нрал11 машш 1ы
(ч'10 1 ·ора :ц10 проще ручно1 ·0 монтаж:.1 < лдс:;ль
ных элсмt' 11тт1) . Проиэводстпо Э ВМ нз1'>ШОl'О
у1~ешеви1юсъ, поuысиласt. их падёiююсть. Упро
стился и рс}.'ЮН"г: в СJ(учае пеи справ 11 остн за
м еrшлл пл:пу, а не отдеJtьный элемент. Быс1 -
родеnсл1не выросло до сотен ты сяч операций
в секу1 1.r1у.
l! ачюшя с третьего поколения (середина
60 -х - ccpcr11111 a 7 0 -х 1т.) э11 смеm·н:~я ба~а ЭВ М
c'l'a.'Ja м11 кроэ11ектронншl В её осно ве ; 1 c:;ж:.t'J'
11нте1·ральныс схс:;мы - схем1>1. рс;uти~о1:1а нны е
11:.1 nдном крнстзлле крсмння . l/L-x рззмt:ры -
1-н.:скол r,ко кнэдратных 11н1mн1метроn, так чтn
( >тде11ы1ыт1 элемс1-1 1 11 е1юоружёнпым 1·ла::юм
уже 11е m1ДIIO- Вр)'ЧI rую такую схему нэrотовить
11еваз}.'юж110. Для их вы11уска пс обходн.м ы
полная антомат азация и высокая куль·1ура про
нз1ю,11ства (шшример. особе нно нысuки трсбо
ванпя к чистuтс производ<."1·вtнных по.м<:ще
rшй) . И<:rюльзо вщше таю1х схе м н м;~шш-~ах
тpt:Tl>C I'() IIOKOЛC l-ll'!Я ПО~ЩОJШЛО в 1о - 20 раз
ущ:ли•!llТЬ бьJ(.Тр0!1,СйСТВIIС , ПОНЫС IПЪ 1-1адёж-
1юсть, уме нышrть сто 11мость .к:~ждо1·п эле.мента
н размс::ры схем .
R д:злы1ейтттс м эле ментная ба~-~а сnнерше 1 1
с1 новалась за счёт поnыmстпш сте::пе11и пптег
р:~ц1ш, т. е. уnеличсш ш количества элементов
n од н ом кристалле . Пер вые ивте1· ралы-1ыс
схемы содсрж;,11ш несколько десятков элемен
тов. Затем nшшились больши<:.: интсrр~mьные
СХСМЫ (13ИС) - до 10 тыс. ЭЛ<.:МСll'l'С)Н и с1:1срх
бш 11, 11 111 е ннтегралt>ныс схемы (CБJilC) -
нссколыш дt'ОJТК<ш тысяч элементон. Это зш1 -
620
Чl iТ, Ч'l'О В (J/ \J-IOЙ Cl:) l.JC 1 1р11мер н о C'l'OJll>KO ЖС
.ЭЛС'МСIП'О В. СКШIЬКО но вссr'1 м;1ш1111t: 11ep t:IOJ'O
покn11е1нн1. В нач;~лс 70-х 1·1 ·. бытr со:та1-1 1,1
СБИС, которые 11мещаю1 н бтж }'ПJХ1t1ле111 щ 11
ЛЛУ. С 1'ех пор этп f\H:l централы 1ых бло1<а ком
пыоте ра объед шшются общ 11м п ;~:ша1111б1 -
проциссор, а СБИС 11 х содержащая , называется
.l/IШJ\jJOJl/XЩ(!CCVpaм.
До того J<ак пояншшсь СБ И С. уменьшение
разм<:ров элеме нтов 11 е clll ш1ком в; 1ш1 1ю 11 ;1 об
щи е разм<..'ры ;:;)ВМ Хон1 отд<:ль11ы с схемы ста
нониm r<ъ :3аметно мс...:нnшс , но колr~чсстtю <lm1а
ратуры росло. н м а1ш 1111,1 третhеt'О поколе1111н
1 ю- 11режнс:му ;"1а 1111м али болыrI11 е 1юмещет1я .
Усложпялас1 . архитектура ЭВМ , расrпнрялись
их возможтюсти · упет 1чнnалас 1, о п ерапшr r ан 11
ВНСППIЯЯ па.чять. .чобаМЯЛJIСЬ .IJODЫe ком;шды
Машины од1-юnрсмс шю р ешали псскоJlЬКU
~iадач разных поль:ювателеfl , и псобход 11Nu
былu uрга1шзо1:1а·1ъ рзботут<lк, чтобы Lщин про-
1 \ссс 11с м<:ш:u1 ;~,ругому.
С ПО>J11Лс 1 111 ~м СБИС сllту:щия резко 11змt.>
ю 1 л ась Выч1rсл11тtлы1ан ·1ею1 11ка чеп1Ерто1·п
1 юколен11я, основа1111ая 11а СБИС, стзла разт1-
ваться Rт-1ссколы<их различных 11а 11ра1111е1 rт1 я х.
Трал1щио1 1 11а я лип пя ра.>ви·1·ия - разработка
,1'орог11х 11ы со rш прои :шод ител ы 11,1 х ма ш 1111 -
сохранялась. Чтобы повысить быстродействпе.
rпr чали создавать мrюгопроцессорпън.: ЭВМ.
В т:.~кнх ма щиш.1х возможны параллсл ьны с ны
числе н ия. т. с. о,д нонрсме ннh1С расчёты разных
Ч(tСТСй uдной и тuй же :Jа/~а чи (нз11рнмер, с11 -
стем ы уравнt:1-1 11й) на раэных 1 1 рuцессорах,
рабт·::tющ t1х с общей памятыо. !.>ти м а1111 1н ы об
СJJ}'ЖJ 1Ва1от отраснн, 1 :цс 1 1 с оnойт11 с r, 61:-;1 с; юж-
ных BЫЧ//('JICllHJI· R/tерную ф11;-111ку, IIOCMOC,
rешюrпр;внещ;у 1r др.
С друпн'1 сторонh1 , но:~мож1юс1·1, раднкат.
но умены111п1, раэмеры f(омm.ютеrа открыла
. 1,ЛЯ BЫЧ!ICJJllTeJIЫIOЙ 'l 'eJQIИIOl COJ3CflШCllIIO 110-
f\Ые 06Л:1CTlt Прl l~tetreHИЯ.
Во-первых, тюя:вились 11астольпыс: (псрсо-·
налы-~ые) 1<оr.mыотеры Ло быстродейст1шю 11
объёму 1tамя:ш OHl-'t ш: уступают 60Jrьш1 ~ и ма
m11н::~м трет1,его поколенля, но щ111 этом 1·ор;~з
: 10 )(C:ШCf\J!C и не 'l'Рсбуют СЛt..'ЦН;JЛ ЬН ОJ'О обLJl >'
живанш1. Поль:3оt1атею, может с~1м осгоятсл1,но
Ht..'lv l 1'1 Cf\Ot 11po1'j)aMMHOt' XO~iMICTIIO 11 не зав11-
сст1, от лру11rx Имefll ю персоrrа.111,1rый1<0м1 rью
тер стало R1_,1год1ю и.с1юлкюnать "качсс·1·вс opr-
тexr 11 rкн - /_(./IЯ 1ю11.готовю t и печатаrпш текстов
п доку~с1поu. У него orpoi\urыe nретrмущесп.1з
псрtд 061.1чнымн пншущнмн. машш1каj\ш: мож
но быстро nноснть нспраnпсшщ 1.1ст~1влять, 11е
ренос11ть н уд;urнть любые куски текс.-г·а, мс::нять
шр11фты, хр:11-111ть нсё, что было сu:щано HJ111
нне:1е1-ю ранее, 11ечатать нужное <rrrcлu коrтнй
11 т. д. l<аждая 11с:больш:;~я фирма те11t:рь имеt:т
сстрсменную вычисли' 1't:лыгую техннку. Более
тоrо, компыотер может к~гn11·1ъ ;1юбой человек
кзкдля рабо·rъ1 1rа ; 1ому, таки д.тrя лич11ых пужд.
Во-вторых, вычнслнтелытая тел'lШК<l стала
широко применяться А различных отраслях
промышленности. Микролроцессоrы ссй«rас
11спользуются в самых разньос приборах: CT<IH-
Искусство вычислять
ю1х, 11~;1 г,тах у1 rравлетщ устройстnах сня~11
11 т. л. Rся а 11то~1а1 ика , котор:1я р:~пее 1х1бпт:~лз
11:1 т~де11ы1hL'\ эле1<тро.меs~111ичесю 1х 11 элек
тротrых схемах, rюстсnен110 rrcpeuma 11а
_'\нtкролроцсссоры . llрое1<тиро1.1апис, монтаж
11 [!ЗJJ:l.ДКЭ КОJПЧ)СТtIЫХ CXCJ\t заменяются р<IЗ
работкой и отладкой 11ро 1 ·р;~.чм упра1.1J 1 ен11н.
вложе нных н м11крО1<О11,1111,ю·1·t:р 111. Тру;1 н11-
жt:нер1н1~:·тсктрикон 1:3 значt 1'1'сJJы-юй с1·t11с-
11и нытссняе1 ·ся трущщ 11нжснсртн1rо1 р:1м-
11,111стоя.
И 1·1а м)11сц, треп)е 11зпр:ш11ен1н:.: ра:щн·1·ия .
кпторое осоf!сн1 ю э кт11tш:шропалос1, в послед
нее 11есятиле'll rе. - C0:1Д:JIHJC RЫЧJ!СЛИТСJlЬТТЫХ
сетей. Выч.ислптелы 1ая сеть nрсдст~:шляст со
бот'1 соrюкушюсrь комльюrероn, соедю1е1 11 1ых
общеir сшrзыо. Такая связь, щ; нарушая само
стоятелы-юстн н <·персоналыюсти» отдслып.1х
ком1 1ьютс1.юв, 1юзно11 н ег 11м обме 11и1:1::~ ться 1111-
форма1 (Иclr Это 1rу-.,юю ; 1ля 'J'u1·0 , •побы 11с1 н>ль
:ювать общую ннформ;щию 11 коорниш1ровать
совмесп 1ую 1х1 боту - к:~к н 11ре;1слах оДJюго
11рсдпр11нтня, так 11 мсж,i\)' ра3ными прt'f(11рш1 -
тнями н ор1·а11 1 1э:щ11ям11 {11апр11м~р, вхtщнщи
м11 в одну корнорацшо). Кромt: тm·о, во:тикла
н бурно развивается rлобалы1ая сеть Интернет.
Она исrюльзустся и для пер есылки сообщешrй
по кош<ретным адресам (элст,1ронная rючта).
и юrя поиска разнообра:шой юrформ:щни. и
для различных коммсрческнх нелtй.
()21
J<tllll'ЧllO , L IOJll1 (" 1f)t'"IJI н::ll1ITl1ltl Г1pt>1'[)l'CC
111.1.1 :\< >L 11111rrr11с тплы:а :ia счёт сстерше11( ·1·щ >-
1~а11ш1 '>J1<::чс11т1ю ir 6J:1ы. 0~1ronpe\le111ю ра:1
1ш1ы.111с1, 11 ;i.py1·11e еюр оны вычпс1 птслыюi1
1ех11шш. llрсждс вссrо это ...:асается пз.юпн.
В т1.101ч11 ра з н ырос;111 объt.чы опсрат1mной па
щп 11 11 скорое:~ h uбщсн 1ш <.: нclL Р~щик а"-~ы ю 11з
мс1111;1ас1> 11 1i111.:11111 ян 11а.чн·1 1•. Ещt н трс:ты:.ч
1HIKOJJClllll1 ~А\1 , \. IH 11сё llCПOJll>3U11:1ЛlllЪ 1·pu-
мo:;,'(IOI(.' \1: 11 '1111111111{~ /'1.11СКI! , KO'IOpЫt' pa:iм<::щa
,lllLЪ 11:1 0·1
·1 i .e .11 .111 .1" стоi1ках в \1а 111 11нно:о.1 з~1лс
Псрс:о 11:1 лr.11ы iт I<()мnыnтер стэл 1IO.Jl\10ж111 .1 \1
1<1т.1ш 1юсл~ со:щ;.~ш rя соnреме птюrо ~в~ 111 чес
·1ср11()1·0" , i.11 c1<:1 болы11ой ёмкос п т н мал ы х
р:1:1мсро11. 1юторыlf 11омещается 13 корпус ком -
11ыотt:ра, а таю1<с rнбкнх 11 1 к 1ю1.:1 (дискет).
Уже 11 'l'!K'Tl1l',\1 1IOKUJll'HIШ ПОЯВllЛИСЬ )'доб
l lЫС "жра 1111 1>1 (.' Cj)l'i\t"l 'll;t <·ll НТСрф<:: йс:а " (uбщс-
1111>1 (.' KU,\11 1hl()'l 'L'P01\I) - /О IC1 Ult:l I; н: 11ср1> нх •1ащс
11:1 Jhl к:1 ю1· i\I< 1н 11тор:1 \111 Он 11 1ю31юлюо·1·1юл1,:10-
к:1 '1 L·mo of'i11i:11·r,cя 11.: 1 жс с C\oлhшoft чаш 11110\1
l ll'I н к 1к·: 1{-1'11t'111 ю, м1111) >i 0111::ратоrюв, 1iво, 111 1ъ 11
11(11р:11111н11, nporpJil-1.чы 11 ;щ1111ые. с:1ен11 1 11 :J;i
ло, \о\1 111.11ют1е1111я проrрам~1 и п плуч:п1. 11:1
жrа1 rc рс зу.111 > 1 :1·1ы. С 1юнв.1е1111е~1 мошпо rюn
у1л; 1,1 в npom.1oc подготовка д::ншых 11а ntpфo
...:arт.tx l l cpco11aлыrыr1 же 1<о~шьютер вообще
11сщ.1с11111'1 б<.:;$ 'юн11·1·uра.
« Ж[Л[30» И «БУМАГА »
д< 1с11:-.. 111Jp рt'ч1. 111л:1 о() 1ктор1111 :т11:1рату{'ы -
. ~J1<::К'1·1ю11110iт п :-.1сха 1mчес 1ю~-1. Од11 :1ко :'!То -
толr, 1.;() ч:1с·п, coupt.мc111 юго компыоте ра . Оф11
цr 1 ат11ю or1a 11азыnастсн шnшpanlllы.м обис
m!ч~•1111е11. а на жарrо11с профессио11а;юв
«жс11е:юм" 11m1 a111·mrr1 cю rм слогюм « хардвер»
(l1 a1·d\.v:t 1·c) 1la 1 11 ютнжс1 11111 всей нсторш 1 nы
ЧIIСЛllТСЛЫ ll>IX м:11111111 всё бOJlhШCe 3ШIЧС 11Иl' 13
11л работс 11p110nrcт: 1 1 1a ,()ума1 ·а" - npuгf.JФ1tм
l/(J(' обеоtl:'Че1111е, <-софтвср» ( sol't \\'ап:). ~дсс.ъ
lli\ICIO'I 01 111111/l.~ 1IC 11ро1раммы /1,ЛЯ KOHKJ1L"L'llЫX
llЫЧll(.)1L'lllli 1 ( 11р11ю1:щ111.1е 11p01·1x1M 1'lll1 1I ), KtYJ'O-
p1.1c ~ l\,o",,r\oro поль:юнателн сно11. а щ10 1 ·1х1м~1ы
общс.;10 11.1 ·311.1чс111ш. Оrт11 ~11равтrю1 ра60·1·()11
C:IMOII мапr1111ы 11 OC'\'ЩeCTUJIЯJOT связь мtжд~·
1е,1. что 110:1ь:юв,1п:.1ь 11абнраст на клавна1) ре.
IT а1111ара !~ p u1'1 KOMllbIOTl'JXI .
Ы2
Uo nрс:чсн. 1 11срно1 ·0 1юколt'ния ЭВ.\11 т~ю 1х
общ11х про1 ·рамм 11с 61>1J1u 11 11uль:юв а1·сJ tь-[Jро-
1 ·раr.1\11К"1 ' 11 ML'J1 J~CJ I <> нсrюсрсдсти<:нно с а 111 1:1-
рлуро\1 011 11 1н. ал tно11 11рш·ра;.1мh1 н ча
1111111Hhl' 1\( )/\;\ .\ ' 11 K:I Ч L'LTRC ко маt-1,~ы (t'K~IЖ C: M.
C!I< •Жl"111 IЯ) ) 1\'1111111'1.'1 ei:' !'(>,\, .l<ITC'\1 ащх:с1 и Ч l'l'h,
н кпторых .1с;кат опсрапл ы этпi 1 ко ман, rы 11
:ЩрСС flЧCi1IOI, tq;.t .a C.'teдye·t ПОЛОi1'.'Н'П1 rезу.1ы~П
jj() Bl OpO~I 11 Тр<."IЪСМ ПОIЮ.lеlШЯХ ПfЮГрЗ/\11\1111
стJ . 111 1111 с а 1 ь на я::~ьшах проrра~вщровJшrя.
·1с1((:1 ы 11pu 1 ·p:1~1'1 уже нс бьшн пос.1сдоn:пе.11г
JIOCTHMl·1 М:.IШНННЫХ ко1юв. :J ()()JlbW(.' I ШХОДШНI
на о\)ыч111.11.: матемэ·1· 11чссю1с тскс1ъ1, хотн н на-
1111с11111Ыf' 1ю !J.О1юлпfю жt:стким 1 1 ран1· 11131\1 ::~п1х
язьшо11. Для кaжll.n1 ·0 языка созд:~па с1teт t11ат,1 1 ая
ЩJОJ'р::tмма - тр:.~нсшпор . которая <1ВТО1'1Нтп
чески nере1юд 1 п текст, 11е содержащJ1i1 ошибок,
в послсдова·~·елытость машн 1 шых ко/~ов. Если
же в текс1·е сеть ошибки, то тра.нс:лятор пх ука
зывает }Jсно, что та1<01'1трансляторнужt"н1ксм,
К'\'() !IНШСТ 11;\ :'}ТОМ }13ЫКС , И ОН ДОЛЖС:l-1 i\OCl'U -
ЯIJHO хран11·1ъсн н 11амнтн \1;ш11 1ны Кроме то 1 п,
ПOCTCl l ClllIO 11:JK~lllJ\l l B:IЛ11c1. 611fi11иот1..:кн про-
1р::~мм длн ра :т11чных ст~нщарт11ых 111,1ч1 1 слt:
г1 ий: тр11го1ю.\lстричесю1х фу1 1rщш'~, ло1·ариф-
1'1ОВ 11 1· д. Ло:~тому по 1 1dдо61 1л1кh служебш.1е
програ:-.1мы - «опбшютск:~ри» . I<отор ые 11од
держ1шают 11орЯ,'\ОК в общстl бибшютске н 1.1
част11ых бпблиотсюtх разных 110.т,зuватслсй,
автоматп Чt'Ски размещают их 11 11амт 11 и по
i\ЮГ::tют быстро 1щrп·11 нужную Ilри1·р~1м \1У
Начнна}I с трt'тьс1·0 1юколс.нин. оfiычным
дt·лом l-1·ала од11онремс 1-11 1~1я обр'16отка 1:1 м:tш н-
1 1с l l~l'KOJll>KllX 1 1 ро 1 ·рамм. :1т11м ! \OCl' Hl':tt:TOI
более 1юлт1;~н за 1 ·руэка блоков м:~ш11111,1 · од1 1 :1
программ.а вычпслнето1 ll JJOЦt'CCOJIOM. /\руган
псч::~таст своп ре::~ут,таты, треты1 обмещ1наt'тот
шrформ:щией с 1.шешш.:й намя'ТЪЮ. Д.rш ()рга
низаци 1 1 та1ю1 ·0 режима рабо·1·ы 61.unr созда11ы
слс1 щальньн: программы - опер;щиошrые си
сте мы. В н: 11 1ы1с:йшем 011срац11онньн.: с11стс."1ы
()OЪt:)\llHll.flll н себе все ОС I ЮННЫС фун кщш уг1-
ранлснш1 RЫЧl\l'J I ИTCJIЫIЫM llj)lЩt::Cl'OM. обслу
ЖI IH:.IJ-11 (}1 бнблнотск пrограмм. OP J'(l 1-Ш:i;tl tJll I
BЗЭ.J I MOДt:J'·il-l 'Bl1}J IIOJll o:'IORaH::ля с КО,\ШЫО'l'С[)ОМ ,
а т~~ кже с11я:з11 1 1 ро1·рамм (и 11po1tt'cce 11х panoтr,1)
с внеuл111ми устр()frстuам 1 1 (J11ккамн, ::жра~юм.
nри11теро\1 11 11р.).
Без опс рацио1111ых систем р;1бота на с0Rре
мс111юм комньютсрt: бьJJia бы пр:tктическн
Hl'U()::IMOЖl-la. Ко1 да ПОJIЬЗОЩП(.']JЬ ны:н.н1аст ме1 по
сн(х:1'1 011срац11онной сисп:мhl. одн1 1 м нажати
ем кнопю 1ны611 р:к-1 · 1-1уж111.1(1 ф:11'u1, содсржащ1 1 й
при!'рамму ш111 текст. 11 l'Щё: 01 1 н11м наж: 1 1·1 1см
запускает прсн рамму н работу 11п 1 1 начr1на~т
11ечата·1 ъ текст, ·1•0 кажд1.1r'1 ра:1 н~-.11юnняются ты-
01ч11 (бе1 преувсm 1 чс:,1 1 11я!) с11ужс611ых 1тма1 11\,
которые: от 11ero "спрятаr11 .1·•" ()1111 осущсс-1 ш1я
ются. 0 1 1еrационн011 системой.
! ! о и сам пользоl3:.1Те; 1ь :·)13.М зн·ач~пельно
изменился. Ссi1 ч ас nрогра_у1щ1с-1·ы прн р~1зра
nот.кс сво11х про1рамм полъзу10то1 разнообраз-
1IЫМИ HCIIOMOl'<J 'J 'CJlbHЫM 11 ( « И H CTj)}'l\•\CIJ'l':IЛЬII hl-
Иrкус слю нычиr мнь
ми») программами. 6116тютекамп rотоnых
нро1 ·рам м. срсдстnамн о·rладкн и ктпроля
щю1 рамл1. Болынюrство же соврt'мс1п1ых ПОJIЬ
:юнатt:лсй вообще никuJ'Да нс быш1 про 1 'р<.1~1-
,'ll11кт:~мн 1·1 нl' ~н;1ют. чтu 'l'aKOl' щю1р: 1 ммнр()-
11а1111е. За последшн: 20 лет 11аμнду с рынком
KOMllliIOTepuв l lOЯHJ fЛOI f)ЫHOJ< П>ТОВЫХ 11рt) -
1рамм ( «rrpo1·paiv1 мн ыл продуктов») : для н:.11111 -
сания н щ\юрмнен1штексто н (т1..:1<стовыl." редак
торы). нзготовлс11ш1 рисушшн 11 чертеже~\
бул-талтерскнх р::~сч:<..~ов, обработю 1 с1 :зт11сти
ческих дапr1ьL'\, соз1~:ншя ба:~ даш1ых 11 т. д.
Поль:юnатс:лю остаётся толт,ко вводить сво11
да~ п1ые и у11раnлю 1, х.одом работы программы,
f"J I JЩЯ на ЭК(ХШ 11 HaJiGl ,v1:1Я IJYЖilblt' КПОТIКП. Р;1:~
р~1боткой же нuных 1rро 1 ра,1м ~~а1-111м ;1I01'01 бот.-
11 1 нс f\OJIJ I L'1 'l'I J/ibl l lj)!JфL:lt'l I Ol l:IJJJ,f IЫХ 11рсн·рам
м11ет11, работаЮ11 l 11х 11 011::ц1 1~u1ыJ1>1х ф 1 1рм:.1х
Итак, рш 11, прогr;.1 ,чмнu1 ·0 оf1<:'Спечс1111;J 11р11
ИC ll OЛl>.~OH~~ 11 Ю1 f<O .' V\ 11 hlO'J'epOll lll'i: ttpl'IVIH IIO:{j°};JC-
T:JC"J'. Ссf1 ч:к 11е-,фста'J'<)Ч1юrrpocтo 1<у1 111·1ъ х11ро
шш'1 1юмnыоп.:р Нс 11мс:я t\OMЛJJCI<Ta 11~ж1г1.1х
nро1 ·ра."1м, rraLш1r:.ш с or 1 ep;щ110 1 rrroi'1 с11стс,-...11,~.
вы просто щ: сможет<.: ira нём ра6отатr,. Сто-
1 1мость прu1·ра;.н1. 11сп0.1u,зусмых для ссры.:з1юi·1
профссс1юналыю(1 р:1боты , как правнло, t·ор;1 :>
до выше стоJ 1мuе1 ·11 а1ш:~ратуры кu11.шыuтс:ра.
ГТ0 1 нп 1 10, что 1col\11 11 .roтep с1111 1,110 06пе1 ·ч;н:'·1
р::tботу !\\:1'1'tM:1TllKЗ 11011rём, что сняз:ню ( JIЫLH\l"
ЛCill шм11. Но :.:,то т.пт11, O,l{rrэ сторонз дu1;J. Ма · 1 L'
~·1ат и1ш впервые UЫ/J,J\ltтryли илею ан·1 ом ат11 -
э~1цш1 вычислениrf.11 1 1х ролъ в компьютерных
Математика за работой
нелах не тоm,ко пе закоr 1чнлас1, t ia этом. а 11ро
доmкала В<>:Jр:н:тать Разрабuтка ап п арат ного и
upш·pa.rvlМ.НOI'o обt:с11еч.<.:ния ком11ьютеров по
ста 1111 ла сuнсрш<.: нн о новы<:: матем ати ч ес к~ it:
ЧАРЛЗ БЭББИЛЖ
Ч:~рлз Бэббидж родился 26 декабря 1791 r . на
ю1·0-1.юс1·оке Аш·11и11, в ;101щонс1<0J\'11l риго роде
Уолворт. Ero отец, совлащ:лст~ ба11 ю-1рс 1<0й
фирм ы « llрэд, Макворт и Бэбб1щж". посл<:
смертн оставIJл сыну бuль ш uе состояш~t. До
l I лет Чарлза уч 1 1J1а "1а·1ъ. nuтuм он обучалси 11
частных J1LКШ 1ах. С детстна у Ч ар11::1<1 было Дt:>:J
унлечt: н11н - V1атсмат 11 ка 11 во..:н1Ю\1uжныс; ме
хаю 1змы.
R IC) лет 0 11 пос1ут11-1л н Трr 11111·1 1.нюл11 елж
(1юллеюк CRятoii Тр<1ИТ\Ы) Кембрнl\жскпrо упп
nс::рситета. Тогда о6наружплось, что Бэббидж
знает .математику луч ш е сноих све рстннrюn.
В 1812 г. Llарлз 11 е го ближ;,tйrrшс друзья Джон
Гершель и Джордж 1Lикок вместе с другими
молодыми :v~атсмат 1 1к~1ми ос1-юш1m1 «А.нал11тн
с1ескuе общество». EJ'O ор1·:11-нr зацтr стала l:ШЖ
НЬJМ событием н раз витнн ма.тсм:1тню r н !k1111-
кобр1 rтан HI 1.
В 1R J.) 1·. в «Записках Лналнтичtтко1 ·0 об
щестuа·• Бэ661щж ()1 1ублнкоuаJ1 Cfl()IO п ер ную
научнуrо стзтыо «О \>eci<rн-reч1 rых 11рои:щеде-
111UL- .. :: » и nскоре получил степе11 1, \1акалаnра.
Втора.а е1·0 работа «О черк фушщ1юн;:~лы10го
псч1 rслеrтия» посnящеrта ПЗ}" 1er пrro ф}11нщ1 ю
rrалыrых ур:шш:r шй общего внда. Она бьиrа за-
624
задасш, которые пр 1шст1 к вu:щнюювспито
1ronыx uбл:кте 1~1 математ11ю1, на3ывасмых в со
вокушнктн ШtфojJ.Mtf111lf.Л'OU ( ГIU-:IHl'JIJ1 1lcКl l
Cu111 pL1tc:1· Scicпcc).
ч11-гаш1 на зас<:даш·ш Лондо 11ского королсnско
го общtства (ак;щtмии 11~1ук) . 11 Б.:)бб rщжа из
брали с1·0 чж: ном .
в 18 17-IRlO П' он напечат:u1 с щё Н ССКОJ!Ь
ко .\1U'J'CMa'J11Ч(;:СКI L'\ JlU.OOT, Прt111'-'l}'ЩССТНеННО Н
обJt астн функц1,юнат.ногn ~•н~1т1 за А в 6()-е 1т
ХХ кн Брита 1 1С1<ом .v1узее fi 1>1J ю 11 ailдe1юJ 1еопуб
лнкован11ое сочнне1111е Rэббн; \жа «Ф 11J1Ософ11>1
анализ;l-> . паписашюе в 1R2 I г. Оно СОJ\ержит
м 1 ,1с; 1н. очень 6лн~ю1е нде.ни Дж. Пнкака. кQто
рые тnт изложил 1i «Трак·тате Jю мтебре» - пер
вой серьtз 1 ют1 п оп~,ттт<с развития в алгебре
аксноматн чсскнх прш-щ1шо11 .
Послt: 182 1 1'. Бэбб 1 щж мсныuе заю 1мадся
математикой 11, к~11< 11р:н111;ю. <.:1'0 рабuты бьuш
связаны с прню1а/\1 1ы ,,1и :1::~начамн. Н екоторh1 е
труды посвящены те< )р111 i верщп1 юстеfт. Осо
бе~ 1но 11 нтсрссно -~~амсч ан1 1 с об аргументе I0.\1a
OTHOO!'l 'eJll>l IO Ч)дес» ( 1837 1'. ). l'Дt: вt:рОЯ1' flОСТ!1
экстраордин~1рнr.rх соб ытий полсчитывается 11а
основе свидетельских пока:~аний - с учётом
ч1 1 а1а очевидцев и степени доnертш к нr1 м.
Б~ббпл;ж начал 1ю 11стру11ровал, uычисш1 -
тель1Iыс машш1ы . н это стало глаnrтым пслом
его жнзни . В 1 Н2.21·. он постршur действуrощ-у10
модель механической в1>11111сл11телы-1u1! ~·1а
ШI ШЫ - так 11азыв ~1 емую ра з ностную ма 11111ну.
llo в нолном объёмс замысел реаJ111 зонать
нс у; 1;uюсъ. В то врс11.н1 проста нс было обору
дов~н 1ия, чтобы l!ЗГОТОВl!ТЬ IJCOбXOДllMЫC /1,ЛЯ
такой м а ши ны детзл 11 ( 11 :111р11мер. Бэб611дж
11р ое1<·mровал вычислешrя с точп остъю до
18-1 ·0 десятичного зна ка).
Работая над разrюспюй маши1юй, Бэбб 1щж
n осто ящю вносил из м ене rтия n чертеж11, пере
делывал уже: 1·отоные у3лы. И во·r' в 183·1 г. у него
воз11ию1а мысль созда 1 ъ универсальную вычис
лительную машину , которую он назвал аналr1-
т11чес1<оr1. В этом проекте Бэббпдж впеrвые
П\)ИШёЛ К llДСЯМ ПрО!ТJаММНОГО упр~IВЛСНТIЯ
ныч11с1tителы1ым прощ:ссnм. Дпя u вuда п ~ll-
11шну чисел н кома1111 от 1 и спол 1):ювал 11 еrфп-
Кd[ПЫ, :J J 'JiaRlIO~, ([Pl·L'v\t.:HИJf КОМ<IНДЫ условно1 ·0
перехода. м~1111и1-1а формиронал ~с 1. из четырёх
ocrron1 1111x блоrюn: арифме·1·нческо1·0 («мепь-
11ит~;.~» ), :~аломипающего («Сю1ад->), управляюще
го н nuода-вывода. Бэббиюк работал над пей
до носледпи:х д11сfт жнзшr. Тем нс менее про
ект остался пезавершёш r ым.
Проект ;шали·r·ичсской машины 11а столе
т11с 011ерс1111л с1юё время Только в 30-40-с п.
ХХ в. I<онр<IД Цу::к в Гсрм<ll 11111, Гuвар;\ Айкен и
Jlжпрдж Стн()нц н CllJA, иоюлюу}t элекrроме
ханичссюк: рс:лс , смо1·ли построить ком11ью
тер ы, СОПОС'ГаRимые по JЮЗМШЮЮСТЯМ с М~IШИ
н оl! 6эбби;1;ю1.
В ·rеqение nсей жи::ши Б~бб и,11ж живо инте
рt'сов·алсн самымн разными научп1J1ми щюбле
мами. В 18:)2 r'. он опубликовал книгу «Экот ю
мнка ~1аruин и произ1юдст1:Ш», Эта моrю1·р~Щ.шя
была 1 1 ерrюй р<tбо·юй, 11uс:ннще н11ой ор1·;шнз<~
цт1 nрои:нюдстна нd научнuй uс1юве К11н1·а
11мt·л:~ 601LЬ1UОй усщ.:х, не rаз 11 е рензд:.ша113Сh.
Её на11еч:п::uн 1 к США, 11ерскеш 1 11:1 щ.:мет (IOJJ1,
фр:н-щу:к 1<r11\ 11т:т ьннс-~-ан1 и 11сп:.11-1Сю·н·1 язы кн.
ГТосле :1э·1·ме11ш1 Со111н1а в ISSI 1. Б~Е16ндж
~11.rтёкся 11;!уче11 нем сол нечно.й кпгю11 ы и rrpo-
1yf'>cpa ш lt'B. Кроме тогп. он 11anнcaJJ р::~6оту
" ЛРсNЮЛОЖСНИЯ по ПОВО..'-\У фн:тческого co-
CTOШ lfНI поверх1юстн Лупы» (поэтому в ХХ в.
11.чснем Бэббидж<1 назnали о,.циТJ из лунных
кратеров).
Бэббндж ны;\нннул ряд идей в гсосризнкс 11
rео_·юл 1 н. Он кысь:азал г1111оте~у образо кант1
пе/\ 1IHKOB, 11()(;'/\ПОЛОЖf IЛ, что 8 /\3Лёком гrро11uюм
Искусство 1:1ыч~к мпь
1-1:1 Земле был .ЦJ1]'ГОй ю1има·1 ·_ Чтоб1,1 гюдт1к·р;l11'1ъ
С!IШО до1·;.щку. 01-1 ИС.'СЛtДОi\а.'J и ср:11'1НИВ;Ш пщич
н 1 ,н:: 1юльца 11::t ;~ерен hях ещё пст~нш111хсн дрен-
11их лесов. (Этот .метn;\ был за ново открыт в
нач:.1ле ХХ в. в США)
Бэ661щж всета стремился прУL\fс1шп, JЗ ис
следоnанинх числеr-шыс методы. Например ,
11роанал 1,1зировав, с кшшй частотой встреча
ются те иш1 иIJые букны IJ нх сочетаннн 1-1
p~1:JJIHЧHЫX н:-~ык:~х , он p:.iзp~•бOT;JJI MCTO/\llKY
шифровки н дс11шфроню1 текстов.
В 1855 г. Бэбб tщж опубли ков~.Jll с..-1·атью с чср
тежам11 и оnиса1шсм пощюд1юго cy/lll:.t , кото
рое ~олж1 ю было нспоm,зопаться r1ри 11оt.:1111ых
дсйстn1тх. В rrём четыре челоnекэ могт 1 нэхо
J\ит,,ся под rюдой в течение двул д11с11.
оЭ66НДЖ Г.~ '601Ю 13Срt!Л Т! МОТ)'ЩССТFЮ JJayюr.
Он с<штал, что всс1\r гrропс.ходящим в мпрс
можно у11раnш1тъ с пш-ющы о матс.\1ап1чссю1х
MC'f'UЛOB. Вера в HOЗMUЖlIOCTl I человеческого
р:lзум а ро;tннт 1--;эбб11джа к:_~ к с э1 юхой Иозрож
/(с1111я. так 11 с щ:ком Проснсщс1iш1.
01.1 был -~Н;:\КО1\' со MHOПIMl·I 3::\МС'Ч;JТСЛJ>НЫ
\.'IН со1-1рсменн11кзмн. Оn1,1чно 110 суббптам Б~б
f>ндж устраивал вечера, на котор1.1t пр 1 тходн
nо от 2()0 /\О 3()0 J'ОСТей. CpCJ\11 CI'() 11py:icii 11
знакомых были Пьер Симон Л.ат1ас. Жа11 Фу~<о,
Александр Гумбольдт. ЧарлзДарвпн, Чарл:1Дш:
кетrс. У11лъям Теккеrсй , 1'енр11 Лонгфелло.
герп.01· Велшн-1rто11 и многие дру1 ·ие.
Э нергию и жиrюстп ума учёный сохр;н111л до
глуfюкой стаrюс1·н. 01--1 ск01 1чr1лся t 8 октября
18 7 1 1' , Н(" ДОЖИR ксе1 ·0 днух MCCHI(CJ:{ J(O 80-JIC'l 'l IН.
Математика за работой
1
•
'
о
..,_,'~
' ...~/
/
/)." _/ /
\'
/. /~ :;'
__ \ ,,;'#!
v
ВЕ ЗЛЕСУШАЯ МАТЕМАТИКА
МАТЕМАТИКА И ФИ З ИКА
Одна из важнейши:х сфер, где м ате.матика
демонстрирует себя во всей своей силе, - это
описание законов, т. с. завис нмостей меЖ;11у
разли~rньrми физическими l'lеличин;~ми, и11аче
roRopн , функций. Тому можно 11ривести бес
числе m11>1е примеры . Р<~ сс мотрнм тш11, два.
РАС ПАЛ РАЛИЯ ,
ИЛИ ЛИФФЕРЕНUИАЛЬНЫЕ
УРАВНЕНИЯ ПЕРВОГО ПОРЯЛКА
Как из вест1ю, атомы некоторых хими ч еских
элеме нтов способны с течением нремсни са
мо11роизвольно распадатьси. Это яш1ение н:,~зы
вается радиоакт и в ностью. У;(иm 1тслъная осо
бе111rостъ радиоактиu 1 ю1 ·0 раеtщца состонт н
том, что. хотя и невозможrrо предугадать . коrда
ржпадётся каждый отдельно взятый атом -
•1ерез секунду или через тысячу лет, для боль
ших количеств р:щиоактив1юrо вещества доля
:.t T OMUB, распад<IЮЩИХСЯ в единицу вptMCНl·t, от-
626
JJИЧ<tется пopa ЗИTeJ ll>HhlM ПОСТОЯ I IC'J'BOJ\.1 . Напри
мер, если из каж;щ1·0 кюю1'рамма ради оакти.в
но 1'0 всщесrва з а час распадается один грамм ,
то так будет прои сходит~, нсс 1-да, не~~анисимо
от температуры , r1:.шле11ия , 11реме11и 1'О/ \а."
Попробуем выяспить, 1<а1< меняется со вrе·
мепем количество N атомов радиоактивного
вещества , если в началыIЬп1 момент в реме11и
! = о 11Х бьuю N" (СЧИТ::IЯ, что }\/о - ОЧС IIЬ боль
шое число). I lor<a мы можем с 1~1 з:~ть только
одно: N(t) - мопотошю убывшощая функция ,
ведь атомы раснадаются 1юс1·оя111ю.J~<.>11 уст11м,
что за час из ю1лограмма нсщссп:1э ра спадается
од11111рал.1м . Соответственно 1 1зднух ю1Лоrр;1 м
мон распадается лва грамма 11 т. 11.
Возьм~м м:&лый промtжуток нреме 1 ш от
мш.1е11та t до моме11та t + Ы. Так как N - п е1ш
торая фупкния от L. число атомов 113мешп-ся
заэтовремяотN доN - ЛN,гдедl'/
-
количе
ст.1ю атомов. которые ра спались за время Л/
Ско рость ра спада - это предел отношения
числа ра спавшихся атомов к промежу1·ку нμе
мени, в течсн11е кuторо1·0 01-111 расrшл 1 к 1" ·1 с
ЛN
liш -
= -N'(t).
лно Лt
Поскольку доля атомов, которые р::1с 11а
наются за О/(инаковые промежу.,-ки иремени,
rюсrо}(нна, то скорость распада -N'(I) пропор-
1(1-юн;mы-1::1 величине N(!) с 11екоторым коэф
фицне11том lf >О:
- N'(t) = ~N(!), ИJll I
/\/'(/) = -k N(t)
(*)
Мы получили уращ-1сш 1с, сnязывающсе количе
ство «поюt ещё ж1-1 1:1ых~ атомов радноактивного
вещества в момс11'1 нременн t со скоростt>ю их
убывании. В отличие от ;.tлл.:браическ.и.'С уран-
11сн11(1, 1·дс 11знест11ые н неизвестн1"1е всл11-
ч11ны - чrкла, з;(ес~, в качестве неизвестных
высту11зют функц1ш .V(t) 11 её прснrзвод11ая.
Такие ура н11е11ия назыuаются диффере1щиаль-
1tЬl./J.1ll у/юrтеииЯtни nep1101·0 порядка. Слоnа
«Первого порядка» означают. что в ураюrепrш
встреч:~етсн;ш шь п срnая производ r rая искомой
фун1щи 1 1.
Существуют р~1 зные методы рtшепия днф
ферс1щ11a1tыtьLX ур:н1неш1й , 1ю мы нс будем н:~
ннх оста11авmrв;пъся . l3 ;щ1-шоы случае нам 1ю
можС'1· nросн>с н :1блюденне: как 1:1 1-щ1 ю нз уран-
Вездесущая математика
11ения (*), nроизвоютая фующни N(f) отлнча- \
ется от самлй фу11кцш1 лпшь на rюстоянный
множитель -k . Именно так ведёт себя покаэа
тельная функция (см. сгатыо ·Лроl'r:щодная»),
а потому будем некать ретение уравнения (•)
в виде
N(/.) = А 1/11,
где А и В - некоторые константы. Найдя про
извод н ую этой фу11 ю\шf и подставив её в уран
' rе1ше (*). получим, что
АВ е81
= - kАе81
для любого t. Отсюда находим В = - k и, следо
n:пельно,
Вuт и п олучена зависнмость числа атомов
N u·1 · вpc.iv1eНJ1 t. Осталось только и збалиться от
11роиз1юльной ко11сганты А. Дr1я этого 11еобхо
дпмо учесть так на з1,шаемые 1tt1-чcutыtыe уою-
11ия. О~-п1 состоят в том, что в моме 1 ~т времен~ 1
1 = U число атомов должно равняться N0 . Под
ста.виn эти значения в выражение (**), получа
емN0 =Ае
0
, откуда А= N0 и, на1<0нец (рис. 1),
N(I) = N,.&-1:1.
.l lo ч то такое k? Мы опреж:лнли его 1111шь
как не котор ый коэффш(иснт nропорциональ
н ос~·и. Фактически же зна ч ение k пр11х.однтся
уста 1-1авлива·1 ·1, из опыта , поскольку о но зави
сит от C IIOЙCTR l(()J 1 крстноrо радиоаКТИRНОГО
11ещестRа. Чем быстрее распадается вещество,
тем больше k. l la практике часто иснольэуют
uсличину 1', 11а зыnаемую пер11одом полурж
пада. Это промежуток nреме11и, в течение 1<0-
торо го колоч<::с.:тво nещества уме н ьшается
n;,ное. Найти связь мсждУ k и 'Г очень просто:
N
о
Рис. 1.
6'27
Математ~~кс:~ за работой
по определе1 ппо, N(T) = N 0 / 2. По,п,сташ1 н ('IO,H<l
выраженае щш i'l/(t), получим
()' l 'K)'J(:I
/\/ -/;:/ - \1 /)
i,(,e
-
1 (•, ....,
k=ln2
т·
ЛИФФЕРЕНUИАЛЬНЫЕ УРАВНЕНИЯ
ВТОРОГО ПОРЯЛКА
О1111саr111я ра зличных процессов n механнке,
физике, электротехнике часто нриводлт к ,~иф
ферс1-11 \1 1 алы-1ым ур;шп<-:ння м нторu1 ·u 11орядк~1.
К 11р11 .\н:: ру, 11 мсхан11кс •~асто трсбу<-"1·сн найти
~j:.lKOH /~НИЖС.1-11 I Н 11<.:КОТО/)01 '0 тела 1Ю/\ ДСЙСТIШ
ем · 1 ·1::х 111ш ннъгх с.:111 1. Сю1а, со 1 ласно ю opo:v1)·
з:11<011~· 1Iыотuн:1 , г1ря\1О 11ро1юрцио11альна
ускорению, а ус1шре111fе - это вторан нрощ
водная ггутн по време1 ш_
В кач.естuе илmостр;щи11 рассмотрим двп
жспис малтт1ит<а. Пусть это будет шарпк массы
т , 1юдut'шсш rt.n1 на нсрастяжнмой шпп JIJТI 1ны
/. ДJн1 нростоты nреJ1полож11м . что ,\1асса ш rтп
ранн :.1 нуп К), а ра:~.меры 111ар 1 гка столь малы, что
МОЖI 1О ('ЧНТ<!ТI> (:J 'O ТОЧКОЙ
Отклони '"' 111 ар111< в мuмснт нреме.1-111t=О11а
11екоторый угол 0.11 0·1 · нер·1·ик~uн1 н отпуст11м,
rюзкот 11:1 eJ\·fY спобо;1но 1<ача·1 1 .01 . Ш:чл1к н:Jчнёт
оnуС'кат1 .с>1 1с~11н з, по, ра:юп1ав1 1 1 1 к1" 11росю >ч1л
rпDю1ее П(J1юже1 11 1е, 11осле чего, замс11,пю1с1" с1·а-
11ет поднпмат1..ся, поr<а не откл.сшитс.:я 11а татю1~1
же угол а0, но в противоположную CJ орону. За
тем он т~ш: же nернёто1 обратно и т. д. Н ас ин
тересует закон движст1ш1 шарика.
1lон.нтно , что трас.кторнсй шар11ка бущ:т
ду1 ·а окружности р;щиуса !, гюэпJ.\tу 1 1р1 щfтся
6д3
/
s
Рис. 2.
IЩ~СТИ кr1111у10 ЧIJCJIOR) Ю ()('1 , Н/1,ОЛl> Э'l'<Jl't ; 1,у1 ·11 .
Ja нулевую тпчку э·!'оr'1 оси 11рнмем 1 п1 ;ю-1сс
nоложе r rне шарик;1, а за щ)ложт1тел111юt 11 ~1 -
nравлс1ше - 11аттравле1111е 1< rтерnопачэлы ЮМ)'
по11оженшо шар~ша (рпс. 2). Кажлому гтоложе·
1 rию11 1 ар11 ка 0·1веч.н:т на кри.1юй оси некоторая
кrюрд и 11 ;1 т:.1 s ( 1ю; юж 1-1·1·е11 ы-1 ан нш1 отрпца
тсл 11нан ), котороl'I ~южно 1юст:ш 1·1·1· 1, н сuuтвст,
l·пщс цснтрал ьньu1 ~тол а (то1·0 же :~11:1к;1).
Каю 1 е силы дсйствунт1 1r;_i шарик. ко1 ·д;1 с.:1·0
rщордппата pt1111 1:-i s? Их всего лне· сн11;1 ·п1 жсст11
тР, 11 с11ла 11атнжс1:11 lJ-t 11r1тr1 N (рнс. .1) . IJu IJ.JllJ
нас важны пс са мн эт11 силы, а нх nрое 1<щ 1и нз
касательную к Щ)11Jюi1оси13 точке s, т-Jк как мы
р:.tссматрнваем двнжспие 1щоль оси , а 11е
rюпс:пёк. С:нла У , таю1м образом, «nы11;iдa<."I '• -
её 11росю щ11 р :1 нн;.~ нуто, 1юскш1 ьку опа nер
Пl:'Нд11кул.н р1-1а чис.1 ювой оси. А 1ют 1~рос:кцпя
<..:J игы тя:--,кесп 1, K;tK Н\ЩНП 11 3 р1 1 ~· 5. ч l ICJICHHO
pa111 L<1 rrщ ::.in а. Спедо11<1тt:т,но, 1111шь э· 1 :1 сю1а
сп:1f(аёт 1що11ь трасктор111 1 двнжсн 1 1я ускорен~ 1 с
веmтLппюй д si11 о"Д;~лсс, оfiратнм 11111 rман1 rc на
направлеоие упшре1н1я flpи положитеJJыюм
s ускоре1111е .11аправл стrо против чнс10в о l1oci1 .
а np11 отрицателыю.\11 - по осн. П оэтому n про
с1щ11и на числовую oci, ус коре11и е шарнка в
11юбо11 мо.\'1с11т време1111 р<ш110 - g si11 а. llaкo-
11c1 ~, у 1 1тСм , что ус1шрс11щ: сстh нтор:.~я про11з
нrщ1-1ая пут11 (в fl,a11110\ol случ::~с - кuuрд11н:1ты
s) по ApCMl'\-111 , Т. <.: . s"(().
ИТ<11\, мы 11Ml'l'M ; 1,1 -1<1 р:t~лнч111,1х вп1rаже 1111я
,'\ЛЯ ускоре1111я . Пt:riюt: С()/ 1,ерж1 1 т пелrrч11н) }ТЛ а
а, а второе - смещени<:: s. Хороt1ю nы 11.1(J а
ш1т1.01 либо от а, либо от s. К сч;ктью. :по сж:
ш1ть лспщ, ПСТ\1> а н s свя:~ашл мсж;\у собой о ч е
lнrдным соотrюшеш1t'м s = /а. rI о сколы<у
ГIOCTШIH.1-JЬJI°J м~южнтелr, l\1 0ЖII O Вl>ПЮС I ТТI, З:l
:ша1< 11ро из.1юд1юй, :>апrк1, 1 Rасм рав<..:11сто о
Рис_. 3.
/и"(/) =-R o. ,in а.(1)
~11,1 1юл~ ч 11, 111 1~11t/>Ф<-тх:1 щнал ЫiОс нх11тс1111с
11тпrюrо порн:{tц ~:.·ст1. 11 11зча.·u,11ы<:: условня. Но
перuых. MJ,J OTl<.'IOllHJIJ I .Ч :lЯТIП!К rra )TC>. 'l о~) 11
01 пустнлн , слсдоuателыю, а(О) = сх.,1• Во-нтпрых.
в м о.ч с11т upcмt:'rн1 t ~ О шарик еще нс успел
набrать скорщ; ь, з rrач11т. а'(U) = о.
О\1ыч11 0 . tJ1-1П J1Нтули колсбаннl1 м:щпшка
:.1:ща 1н> с ран111·1111ю с с1 о .'\.!111\Jой . т. с. CL.0 бm1з1•0
1, ll)'J\I\) в ~~· Jt}\\ CJI~ час МОЖl\О L'ЧНТат1•. ч 1'0
siп <Х ~ <t ( }1с1О/~а 11ш1учасм 1101юс уракнс11щ:.
a''(f) = - ·j a(t).
(*"*)
Тепер1. llCП0,\111 1 f .' \IJ, что тр1 IГO I юмс.-тр r 1сrссю !С
фушщ1111 <;ir1 1ircost06л;tд~1ют похожим сnой
стnом: 11 х вторая про11эною1ая раnна нм са~111 1'1.
1ю с 11р1Уп1во полож11ым з1r::t1<0J1. Поэтому будем
11скать рсr11с1нн.: >р:11нн:1111я (""*), н;шрн.чср. в
ШJ, ((.'
11(1) "" .-1 со~ (Н/ +L),
1 де11. R н С - н~:J.:оторыс ко11ста11ты .
а."(!) ;; A!J- cos (JJI 1 (,) :; - j ,-\ cos (JJt +С)
1[3 1JO:l\''ICI II !О!"() ) JXIHllClllHI ЮIХО;Щ.\1
:.)ту 1к·.11 1 1•1111 1у 11а :н,111ают 1\11юл1чсскоl1 часто
п1i1 кt>J 1t:i):11111i1 11 0()1):i11:1чают 1 ·рс,1сской Gук-
1ю1'1 ll\ (<·OMt"l':I'> ) , (. уч\.:'\'( >М ЧС\"()
().( /) -= 11("()~ ((1)/ + (')
Сkтал ос 1, 11 сrю111..:1пв:п1. н:~ чалы п.rс усл от rн:
ц(О> - ,..1со~с = 0:,1.
,/(0) - -Ам~i1) (~ = ().
О 1·оод:1 11:1.: - 0 , 111 \1 . что ('=О 11 А = сх.,,. CJl(:;1ona
J't:.1 1IJI l t \
11(/) = <t 1 СО'> w/,
l l tщoб11nr11 рода 1юле6а11ш1 н:t змваю·101
. !Cl/J. 1101111 11<'L "li"ll1111 .
,
1
1
1
1
1
1
1
1
1
1
t
1
1
\
Ы9
Математика за работой
КОМПЛЕКСНЫЕ ЧИСЛА И ЭЛЕКТРОТЕХНИКА
Одна 11з пр11м ст наuн: 1 ·0 времен11 - по1:1ссмес1·
нос нс1юлиован11с эпектро прибор с.щ 6ОЛ1>
шинст1ю н:3 которых работжт н;.1 переменном
токе. Элею·ри четкий ток, 0'1·1:1стстнен ны lr за 1те
редачу 11:юбр:lжепи>1 r1зну"э во uсево:iможноi'i
ауюю- и нидео:шпар;пурс, т;ноке переме11ный:
он услmmается и ос11абевает, пульс~ ~руст в такт
заrюдпым ритмам шлягеров илн мельк::шшо
кадр()в 11а экране телеnи:юра.
Среди бе<жонечно разнообразных нзм.енс-
1111 r~ сигнала во времени особое з наqс1ше име
ют m1авные сннус01.щалы-1ые, 111111 гсфлш1шче
ск11е кплебситя (рнс. 1). Отш оп 1-н.:ьшзются
формулой
lJ(t) = fТ0COS((J)f + <i>u)·
(*)
3/(ect, (J(t) - вели'-lн1rа nсременн<>1·0 сигнала,
например ЭJJекгри ческоrо 11аnрш1<ения, u мо
ме11т време11и /; U0 - <Lvt1iли1yдa колсба11.и1\ ro -
t\ИКJ111чсс.:кая частота колсб;:нrпй; <р0 - 11ачаль
ная фаза. Циклич:сс1<ая <шс·rог.:1 OJ ратша 2rr;t; где
j - uбычнан qастот;.~, измсряемаs1 в герцах, т. е.
кnл 11чеством колеnа1-ш й н секунну.
Пuче.ч} · мы ньщеляем 11мешю 1 ·армо11нчс
скнс кож:ба1111я? Во-11срвых, это nростсй11111й
1шд 1юлеба1111й. Име1-1110 так колебтотся э11скт
рическое напряжение н сети, к:1 ,\1ертон, идешь
ный мзятн11к Во-ю·орых, любые лериоj\иче
ские 1rзменеr1ия ка!<оi1-то велнчш 1ы можно с
про11:шолытой точностью предстанн1ъ в ю~де
сум.,.vtы rармо1тчсск11х колебаниil.
и
С(!) = l!,,co~(<ol + ср0)
Рнс. 1.
U(t)
N
Рис. 2.
630
Лрсдnоложим. qто имее::тся источ11ик nсре
мснr IOI«J электрического наrсряжсннл. нз,..,1еня
кнце1·осн по закону ("), и к 11ему IНJДКJ1ючнлп
актиююе сопротивление!<. например эщ:.:ктро
ламгючк}' (рис. l). K;J1( булст мешпъо1 u1 >нремс-
11н CJIJJa тока!, rlpOXO/LЯЩCI'() ч:срез Jl3Ml!OЧK)''
Па за 1ю11 у Ома, f = l '/N. Г1аэтому
с
1(/)=~COS(())/+<j)0 ) •
N
Мы rпщ111ч, что ::~ако11 и:~ме11е1111я остался тот
Жl', ·1·оль1<u н дан1-ю:.1 случае ампmtтуда с11 J1ы
тока ранна ам11 1 111·1'удt' н:111ряжс1-11-щ дслё1-11ю\1
на сопротинле1шс:
j-{j(I
r,-
R.
в щ l<ОЛЫ Юм курсе фнзпю 1 i<pOJYH:= а 1\П IRHO-
ro распштр1ща10ттакжс реакпrв1юе соnрот1rв
лс11ие. Отто хотя п в;uuJcт на uслич.1111) снлы
тока, но пс потребляет элеr\"гроэнсрr·r1и. Про
ст<::йш 1п1 пример - элскгр11чесюrй r<o1щe1rca
тop:f\Bc МС"l'<1лл11qесюrс пласпшы. расположен
ные 11;i некотором расстоншш дру1· O'l д/J}Та
(рнс. ?>) Кон;\снсатор х:,~рактер11зустся элект
рt1ческо{1 fмкосrъю
C=!l('.
1·де q - заряд конде11сатора.
К;щ 011ределюъ силу то1(а. про1·ск:11ощего
через ко1 щснсатор. которыi1 11одключё11 1( 11с
точн11"''У перемс1шо1 ·0 т1апряжешш? Перепишем
выражен~1с Jl)JЯ ёмк0<.:тн кuнf\епсатора в шщс
CJ=Ct/
и гтрод11фс(1t:rенц11ру<:м ел) по i:spcмe111·1 , уч11-
ты вая, что q'(t) = f(L):
/(/) = (,'{f(t).
Остал<Jс1, лнurъ nоспот.~юва ·п,ся форму;юli (*)
и ·1·ем, что cos' / = -sin t.
1(/) = CC'(t) = -шG'Ц 1 sin (со/+ q>0 )
С 11омо щью формулы приведения -sin. а=
= c os (а+ л./2) окончатслыю находим
1(1)= roCUn cos (rot +q>" +l).
(•*)
l,
"#fllll:
~
!~
J_
те
Рис. 3.
l'ис. 4.
Таким обра::юм, в этом случае t!мплитуда
СИЛЫ ТОЮ!
/0 = wC['0
занис11т от час·1·оты. Но э'J'О сщё не 11сё. В отл н
ч.нс от а~п1ш 1 ю1·сJ сопротинле11ин. колебания
сш1ы -rока, идущею черt:з 1ю1-ще11сатор. 11ттерс
жают колебаuия 11апряжепия по фазе на л/2.
А1 шлоп1:чпо ве;\ёТ себя к:.~.тушка нндуктнвно
ст11 - кусш< мед пого или сереб ря 1юго проnода.
н~1 ~ютаr1ный на металлический сердечник
(рис. -1 ). Толыш колсб:шнн <.:илы тока здесь уже
не опережают, а отстают от колебаний 11анря
жt:н1 rя на те/2:
(/( lt)
1(L)=:J.,cos wt+<р11-l ,
где L - m щукr-ив1 юст1, ка'Iу1 uкrr.
Итак для о r~исания процессов в элеюр1тче
ско й цепн переменного тока, содержаще(r реак
пшн ыс ::~лсменты (ко1щс1-1Саторы и ка·1·ушки
индукт1-ш 1 юст11). 1-1с/1остаточ110 одного зако 11~1
Ома И = l /N. И скнза1 ю это с и::~менсннем фазы
колебан11i1 эJ1сктрнчсско1·0 тока относ1пеJ1ьно
фазы колсб~11rий 1-1:~пряжен11я. Естественно, nоз
ш1кает вопрос- а нс111,:_1я JJJI какой-то ою-юй нсли
ч111 ю(1 охарактер и зовать 11 амплитуду, и фазу 11е
ремеш ю1·0 си1 · нзла? Оказывается, можно.
МЕТОЛ КОМПЛЕКСНЫХ АМПЛИТУЛ
Добавим к нр~вой ч;.1сти формуны (") мнимое
01:.11 ·аемое i Ц 1 sin (ci>I + <р0) и полученную вели
чину назовём комrщексным напрнжением :
U(t) = U,>cos(rot + <р1>) + i Uнsin(rot + <р0) =
=U0(cos(rot +<р0) +isin(rot + <р0)).
Вездесушая математика
Согласно этой формуле, обычное на11ряже
ние естъ нс что иное, какдейсТRителъная часаъ
комплексного наnряжеuия. Если восполr,зо
ватьсн фuрмулой Эйлера 1/'. = co s х + i si11 х н пе
рейти от трш·о1юметрической формы записи
F<r>мплсксного числа U(t) к :'!кспон.е1-щ1rальной,
пплучнм
l/(l) == U"l:!l( <nl+Ч>o \ ::= U r//Ч>·+ (Jl<fli.
Ko:vt11лскс1 юе чнсло U11 e
1
' P" сож: рж1~тн~1форм::~
u.ию как об амnлатуl\е, та1< и о фа~е псреr.-1с11 -
пого с11п1ала U(t) и называется его тюмллекс-
1юй амплитудой.
Точно так же преобразуем формулу (**):
/( f) = u>(,'Uoe'1"• +10" +• / ~! = о)(,'{10 eml 2e1<"• +41,,J .
Tcп ert> замстt1м , что
п
е'2 ::::cos~+isin~=i
2
2.
Поэто.му окоr 1чатепыю 1юлучаем
1(1) =iwCU0eщ" ''I' •
1 = ;щ:U(l).
Выхолнт , т<омплексш1я сш1а тока rав11а
комллексному11:шряжс1rню , пом1юже1пюму 11а
не.ш1ч111-1у io>C, так что можно го~:юрить о неко
тором аналu1 ·с :~акон<I О:м;1 для комплексных
налряженнй 11 'J'ОК2. l(OMllJlt"KCHOl' Чl!CJI(.)
)'
-
1-
i
х-- ---
.'
i<OC о\(.'
естестве 11н о будет на :=н1:1т~, комплскс11ым со
протнвлен нем 1<01-r .n:e1 rсат()ра С. НеСJюж1 ю на ( 1-
пr и комллекс1Jое сопротинлеш 1 е 1сатушки ин
дуктиr11-rос-1 ·11:
х., = iro.L .
Таким образом , 11сnоль:1ун комt1лсксиые со-
11ротн.влення, можно сущеС'п-1енно ут~ростить
р::~счёт электр пч сскнх 1~е11сй переменного
тока . Рассмотрим в качt:ствс 11p1L'vlcpa 1юс;1сдо
пателыюе <.:ое;1~111енис конденсатора н кату111-
ки 1111дуктитюсти (рнс. 5) . Сн:.~ч.~ла 11ах одим
сумма рное r<омnлетсс1юс сопрол11111е1-1 11 е Х:
х=х, +х( =i·((JJ/. -
w~ ).
Из это1i формулы .видно, что на некоторой
часто те
б:Н
Математика за работой
cl
( f(t)
L
1'
U(l) I(-l с 1. 11,
1
Рис. 5.
Рис. 6.
11.меет м естп р<..:зонанс - сумм ар н ое соп ротин
; 1 с.:нис.: 1хшно нуJ 1 ю.
Ещё более У/1.ИВ ите::льныс факты пткрына
ются пр 1 1 пар:mJJелыюм сое11.н 1-к·ни 1 1 ко1 1де 1 1 -
сатора и катушки ин11.уктнвrюсл1 (ри с. 6). Сум
мар11мй ток 1~щ<::сь ране~1сумме токов lr н!1 в
ветnях цепи. Ilоскот.ку чеrез конденса'Гор
протекает ток
1
{J ·, _,"
r = -= 1w-.,U
х(
а через 1111 / \YKT I 1HHOCl"h - ток
f,=~:=- .~r(/'
ЛJ
IШ~
то сумм:1rн 1ы ~:! ·1·пк ранен
1(+11 ==(iшС--
1
-
·
)U.
ш!.
H::i частоте резо11аш:а u>0 суммарныif ток n цсш 1
отсутстnуст, в то вpt:}..-Ul как в nствя:х цсш1 тою 1
имеются. Эти токи раnны п о всличинс 11 11ро
п шш юлож1-1 1.1 по 1 1а пранш:нию.
КОМПЛЕКСНЫЕ ЧИ СЛА
И ТР ЁХФАЗ НОЕ НАПРЯЖЕНИЕ
Мощ11ая ;:,лектр11ческэя маттпrпа, именуемая
трёхфаз11ы:-1 1·е11ераторпм. nыр<16~пываст п с
одно. а целых тр11 сш 1усо идальпых щшрнжt'
ния. которые 11:..tз ывают фаз 11ым11 и обоэнача
ют U 1. UN 11 U< (р11с. 7). Jlo абеототной нслнч11-
11с вес они равны между сuбо.й, но 1 ю ф:1эt' li8
0·1·с..:таё·1 от и_4 11а 2тr./.) ( L..Ш
0
), а С( нз стшLЬко же
l)Ш.:f)t'Жаст и,. :1 н <J Ч11Т, t'Ull I КЛМJ IЛC::KCH::Ul :.tJ\1111111-
туд~ фа~-Jно1·0 1 1а11ряжсн11я И" равна Ио(.11~", ·m
для фаз 11ы х 1 tа11ряжt'н11й U8 и l/c этп соотnст
стве111 ю
632
и
Рис. 7.
Потр еб итсл 11 электрической э нср пт . как
11р~1нило. подключаю·10:1 к 11улю 11 к од1 юй 11.з
трёх фаз. <·нитаяс ь" фазным напряже1 1 11ем . Нп
ко 1 ·11а 0 6opy; 10 11a 111rc требует для р аботы поnы-
1uе111ю1 ·0 напряжеппя , ·1 ·0 ero подсосдшtшот не
к фаэе и нулю, а 1.: двум ф;~:~ам (11а11ример, 1с-1
н С). Ком п лсr-сспая амплитуда этого напряже-
11ия (его называ ют .'1ннеГ1 н ы м)
Выч 1 tеm1м :з11а чс1 п1с выраже11ня н скобках,
11ое1 юлr,зоRашuисu формулоt1 ::Э11 лера:
1 !.х
2rr,.
21t
е 1-1=со~-+1s111 - - L=
~
:1i
'
1 .\1:1i 1 ) ·~'-!>
=-- +1--
= --+1-
.
21.
22
Учитын:I}!, ч 10
1
\·~
)тт1.')тт
-- =COS - l·t
-
2 :::: sн1 -6.
2
(1
11 месм
1
(1
]
.) .\'.~
v:'i
.1
-
-
+1-=\11 --+!-
=
2l
.
22
= \':)СО.::.- +1SlП-
= 'J.)
·('
1
'
•
(
:;тr. . . ')тт) 1
' '>n
()
()
Поэтому ком плекс 1 1 : 1н :~мпл 11тул:1 111 111 ei' 111 () 1·n
f-f:Нf['>XЖellH H [ ~1( r aBJ1<1
.J 3 floe'('P11'~. 1 1ч.
Похожие выраже ния п олучаютс я 11 л:ля
ос·1·ал ы1ых липс1~пLых на11ряже 1 п111.
11 ~11~ряжснне н бытовых :::>;1ск·1·μо{'~Тих со
стантн:т 220 нuльт (01то так назыв;,~смос /\С11-
<..~1 ·ную 1цt:l' значе 1-111с 11 ~11 1рнже 1111 н) . Оно ф:внuс.
:н1ач.1п, Jшнсйнсн~ на н рнжснш: состаRннет
220· ,
13 "' ,38() rюлr.т.
Сле~е-1· отме1·ить. ч·t·о. ко1·д:~ ком1mекС1i.Ы~
чи:сл;,~ щюнию111 в электротехJJику, бу1-:ва i в пей
была уже 3~11 ш·rа Она обозначала м.гновешюс
з11аqс11ие силы тока n пwшый момент 1:>рс~1с1ш.
И во и эбсжаю1с nу1·:1ницы мннмую с:,r\11 н1щу в
э;н:к~ротсхннке ofio:.iнaLJaют буквой j. Прнн ц 11-
ш laJ I bH{)I~[ pз:il 1н цы ш.:т, но Э'l 'U нужно ЗН3'1Ъ.
ТЕОРИЯ ИНФОРМАUИИ
I3 любом об ществе л1011и персl\ают, хранят н
пеrераб;~тыnают инфор.мацию. Сообщсн11е по
радио , зrюноl\ н<1 урок, крае~ 1 ый свет cuc'ru-
фopa - всi:: это передача 1rнформац1111 . З:ши
сt 1 влневш1кс,древ11ие 1 1а 1ш русы, бибшютски,
;~рх11вы, спр:1ноч нь1 е с и стемы - это хра шши
ш,а ннформа1\11и . П ри ныt~ислсннях, пnискс
нужной справкн, 11аписа1111н 1tayчf-ю(t t.-r·аты1
п ре.те ходит 11 ерсработка и 11формэ ц1111 . Ра~1 1-ю
обrа:т ы е дсlктвня с и11форма ц11еfi и пх кпм
fн,п 1 ацпп 11азьшаются информациошtым11 nро
цсссам11.
С 11аш111х nop .mод11 эаду.\1ывались пад тем,
1<ак с помощыо те.хш'fЧеских средстn ''llfЮсппъ
и ускорит~, работу с ипqюрмап11ей. И :юбрсп:
Нllt' Кlllll'OГIC 1 1 ;J..l'<l!-IIOI IIO:;HUJIHЛO nыс.-1·ро КО11Н
f10ВаТЬ 11нфпрмац11ю и 06ле1·ч 11 .гю t:ё хра 11 е н11С.
В XIX н. :заметно увслич11лись 1·с...,,11 1ы псрсд:1чн
ннформацнн: сначала пароходы 11 нарuво:-1 1 ,1
стал 11 11срсRО З1 1ть 1ючту, :-~атсм 1IO>i BИJIC>i тсле -
1раф.а11ко1ще11е 1<а - тtлефm1. R ХХ н. ш1фор
м:.1тt1rя nревратш1ась в гло6алы 1ую - её можJ ю
персдаватъ за сча-rа1шыс мшrугы н любую точ
ку зеМ I ЮГ() 1ш1ра, nрнс1ём не TOJIIЖO ТеJ<СТЫ, но
1 111зображе1шя. Информация х.рапнтся теперь
в эагтисях на бу)!(а 1 ·е, магюпных лентах, ком-
11ак.·т-днск~х . н KOMllЫO 'l't:rнoй П<IМ}IТИ.
в хх 11. 1/( )НШ IJI llCh Т{,:Х ни ЧССl<Не ус1·ро1kтна 1·1
11рнб<1ры для псреrаботю 1и нформацн 1r. Любое
а АТОМ <ITI 1Чt:(' кос устрой C'l 'l\(J л epepaбaTl>I АЗ е·1·
11нформа1~11ю: 1t<1<:::11\, 11ажимая на 01 1ri;:rt.e11ёiшый
учаею" рельса, перс;рёт с111·11ал, nю1ючающий
кра с ный о~ет све·1·офора; нрибоμы автоматиче-
Ве>.лссушая математика
***
Как-нибудь, rr\ёJJк:m включателем 1 1ли нты кая
11пе11ссль 1:1 розетку, ны , может 6 1,пъ , нспом11 11-
тс: 11р11 раJрабо'гкс 1.1 и~н·о·1·оr1лсt-11ш все1·0_ что
снн з:ню с :ыск'1·р ичеством. 11е обошлнс 1) без
нспользова ш-rя комттекс11ых чисел. Вс::1де, 1 ·де
речь 11дёт о 1шш::баниях, 1-1 теоретияесю1х рас
чётах у1юб1ю ЛОJlЬЗ()flа·1ъся J(0МПЛСКС1IЫМ11 чис
лам 11 . Сслн бы учё пыс XV!I - X\'lll вв. :шала,
Н<ККОЛЬКО бyJ\HИ'-11ILIM буде· ~· 11рнменсп11я :;)TIIX
• 1-н;1-юзмuжных,> объеJ<'1 ·uв. н .математике, 1i~рu
я:тн о, не пшr.вшюсь бы ·1 ·акогu стран н о1 ·0 тер
миL1:t - "м1 шмыс ч 1 r сл:н.
ской телсфонно1! спm щи (АТС) преобразуют
номер телефона, наб1 1раемый памп, в соедн11е-
1 ше с нужным абонен то м . Вершн1ю1I тсхн1-1че
сютх достижений н обл : 1сти р:.1боты с информ;~
цпей Яl:IJIS! CTCH l<OMПЬIO'l'Cp.
ЧеловсчестАо нссгд::~ поль:ю налось 11нфор
маJ \11 ей, но только н серед~ rнс ХХ н. и нформа
L\! Ю 1-1 н.ые прсщt:ссы стат~ t 1рс1~мстом 1--шучнh1Х
1 1CCJlt'/\o вa 1111l1. Сонокут 11 rосп, 11 аук об 11нфор
.матою1 111 ых 11ропесс<Lх пазьшают u1tфopмamll-
11oft. О)"\11а из них
-
наук~ об 11~\мереш111 и пе
редаче тшформаци11 - пазыuастся murфueil
ш 1фop.;11at{ltu.
КАК ПРОИСХОЛИТ
ПЕРЕЛАЧА ИНФОРМАUИИ
JI 1060111 1 р<ЩlХ'С 1н: ре/tЭ ЧI 1ш rформ:11 \1111 М! >Ж I [()
11редс1з 11 11 ·п, несложноi1 с:хс м оi1 . ка 1< 11;1 р11с. 1.
Каж.аая пз '1 ·рЕх ч:~стеf1 11 11рт111е;.tё r11юl1 схе.,1е
11,чсет оп ре1tеЛё1111ые сво 1:1сп3з (к::~к 11р1111яп1
1·овп рrrт1, - лара,"1етры). От этих спо 11стп заJш
сит качсстuо передачи.
К01·.да nы 11ишете з~ш 11 с 1<у 11отдаётс её в рую1
:.~дрс:сату. то nы ш·раетс роль 11 персда·1ч111\а, 11
Переда1'Ч'11 к
пнформа1~ии
Pt-tt: . 1.
'"'
Прпёмяю'
янформад.JJ И
-,
Математи ка за работой
Каuал СВЯ:JИ
fiOJl(CXa
Шлt;rr с. IТHUMDM OJIO. rонца,
Чтоs оsрадобdТЬ orrцa. ...
-
'i..J
r<<1 1 1.1л;.1связ 1 1 . 13нд ннформац11и лр 11 псрслачс n
д~1 нном случ.н: не мснястси н;ншсанньп1 тею_--т
f\TOM же 1:1.ИДС' 11 сред::t~'l'СЯ и 1rp1·IH l lM:Je'l'OJ н нуж
IШt врб·tЯ 11 f>e1 1-1скажсю 1 й. Ест 1 же вы посы
лаете :~а11иску чере ~1:-1 1 1:]комо 1 ·u, то к;~н;ш сня зн
станою1тся самсктоятелыюС1 с1ас1ъю lXC' -1 h l 11
в нём .'>югут произоrlтн 1re заш 1 сящ11t 0·1 ваt
событmr. На пример, :з-::т иска потеря.етсн ш111
nппалет под дождь. В таких обстоятсл иствах
говорят: в 1<а11але связи nозни 1<Лн помехи . Или
передача задержится, если :такомьн1 нс сразу
11айдёт ад ресата . Jначит, унеш1чится в ремя
передачи. Или з н акомы й зашкку прочитает 11
сообщит адресату её Соfl.ержание н <1 сло нах.
13 рt:зулh'J 'атс и:1мснится ( 11реобразуется) ви11
информации - из писъ мt:нной о н <~ ттрев ра
тится в устную. П р1-r э1·ом 11е 11СI01ючено, что
содержание шrформации исказнтся - «ка нал
св>tзи·> скажет либо не всё, либо не то. И 11ако
нец, вас, ве роят но, огорчит, что запи ску ттро
читал не только ваш адресат. т. е. произошёл
634
А tr'l(~ЧИ}lt\ (, "Of:>/J./й1)<.Dft,
С аrлrьей Gt:нivй 6ar;apwлon
n9еня r~ гони.а бtляr...
11есшкц1юнироваш1ый (пс разрешённый пе
редатчиJ<ом) дост) п к информации.
И:з этогu пр11мсра в~щно, каюrс шtрJмстры
может l lMCTЬ ПfЮЦССС нcpCJ(:JЧ ll 1111форr"1:.щш1
н какие пр()бЛе'-'tЫ , связан н ые с ними. прихо
д1лтя рсша·1ъ. Нас интересуют надежность н
врем я пере;\ачи, 1 1рео()разоп<J.ю1я и ~{ащ 1 па 11н
форм:.щн и. Сами ч:Jст н схемы перед:.~чн могут
быт1, оче 1 LЬ сложны. Напр~ rмср, 1<а11a!I п:;~ефо1 1 -
11ой связи - это ве только проnода, но 11 уст
ройства на АТС, сосди~rяю щ1 1с абонентов; при
бор ы . усиливающие с 11 г11ал прн передаче 1ш
дальние расстш11-1ия, 11 т д.
Разли ч ные технические средства обсспс
ч н нают необходимое в каж;\ом кон кретном
случаt: к;;iqtcтrю передач и. Их ра:ч1абатываю'1
специалисты по тех11ике свя :ш. От~нако боль
шую ролъ в теории ннформацин играют и м::1-
тематичес 1<ие методы . В и х основе леж=-tт 11р11н
циnы измерения информации, с т крытия
которых и началась теория информации.
Везлесушая математика
-1
Ка.над связи
ПрrtЬfНИК
ивфор1'1ации
ДonьJJHCA rонц~ поя-r
((~к ус.лыш1н цо.р~ -оrец,
Что }.Рнёс ему rонец "
11 ts суму ао nytтyw
Сую-r r;м.J.OT!J другую. "
ИЗМЕРЕНИЕ ИНФОР МАUИИ -
БИТ Ы И БАЙТЫ
По нятно . что 11нформации бывает ~1-101·0 нш1
\\:1JIO. Но ДJIЯ прас1« 111ропання CHCTCMl>f rте rсд:l
ЧН ипформ:lци11 необходимо :-1нз11, более ·~ оч
но, скол 1. ко ннфпрмацип н ~а катюе flремн m1<1
"-Южс·1 передать. Даже <1бычная почтовая связ 1,
нс способна чётко фу11кц.ио1-111ровать, не имея
сведений о тои, какой 1ранспорт понадобится
1'1)Ш перевозок, сколько потребуется почтовых
отд~яений и 11очталь01юв. Поэтому ннформа
ц1гю нужно уметь 11змеrя·1ъ.
Пuчтd 11р11 расчётах количества информа-
1\И ll может обойт11сь традиционны ми физи
qескими мерами - 1}есом и объёмо м нисем и
посылок Но для соnрt мешfЫХ систем таких
«грубых~ :мер недостаточно. При 01 11равке те
ле1 ·рамм мы платим за каждое слово. Чем длин
нее телеrрамма, тем она дороже - не толыю
нам, по 1t тепеграф 1 юй с11ужбе: дтuшы1'1 те1<С1'
доm, шс 1<одируется в передатчике (т с. rтрс.:nра
щаетсн к энектр11ческщ: сигн:lllы) , доныне 1 ~ско
д11руется 1:1 прнёмнике, долы 11 с нсред:1ется по
канзлу свнз 1 t. Ита~-;, прн псредаLiе сообщеюш
nажна cr о дпина . 1fo тоr ·да точнее нэмс ртъ c.: L'
11е ч11слом ою 11 , а ч.нслом буtш н цифр, короче
rовпря - '-НI CJIOM символов (з 1-rакон) . Одн;~ко 1t
:щес 1, не ксё так 1ч)(кто .
Представим себе , что мы передаём числа.
То\'Да '-U'1сло l'S rюсле превращения~ энет(трн
чсскнс сигналы будет выражено тштыо :шака
ми вдвои41юйсистсме: 11001 11обои.хслуч~шх
соде ржание информа1\ 1 ш од110 н то же. 110
ДJtи н а зашксl1 разлнчн~1. Она зав11сит от числа
использус::мых эн акон, илн . как пр 1 1нято 1·ово
рить, uт мо111,1 юсти исnол ьзусмого алфаRита.
В десятнчtiОЙ системе мощность алфавит~~ рав
на 10 (десять цифр). пл;воичной - 2 . Ч ем боль
ше мощ1юст1, алфавита , тем 1<ороче за nнс~" Са
мый бедный анфавнт - двонч1 1ый : он сос~-оит
635
1
1
\
1
Ма 1емати ка .за работnй
IJЗ двух CHMIIOJIOK, 1-1еважно K:JKHX. и у бою,шо
го, [J у М:JЛСНЬКОГО алфа1ш 1r<1 есть свон l lЛIOChl 11
м11нусы. Дс>етоннст1 1а больпrо1·1> а 1 1факнта -
1<оротю н.: за1 ~иен, но 011 ~рсбует более сложных
устrойств для 1<0днrоR;:11-11 1 я. Чем болыпе ра:1-
~1ых CИ~1f\OJIOB, тем СЛ())Ю 1 ее IIX paЗJlHt.faт1" <1
значит, и труднее передаnать 6<:::1 нск:,1жепит1.
Нс;цро1"1 n о,гщом нз первых телеграфных
кодо-в - азбуке Морзе
-
исполъзо~алось толь
ко три зн:1ю1 (точка, тнрс, пауза), а во Rсей ком -
1tьютерноl1 технике пrннята д1ю 1 1чнаs-1 Сllстема.
К::~кой алф~1 nит кп1бр:1тт, - реш:нот нроект1 r-
ровщ11ки конкретной си:стемы псрс/1,ачи. J lo
;1,ля 11 :iмсре11ин инфnрмз 1 (11ижелатслыю иметь
ею11 1 н 1~ы, которые не заm 1сс.111 1 бы от злфан 1 па.
В качеС1 не такой едmнл (Ы выбрали 61т1 - е.::д1 r-
ш-щу мшrнмалыюй по '-ПIСЛу СИМIЮЛО!i ДВОИЧ
пой системы кодирования. (Сло110 «бит» полу
чилос 1, в резуm,тате сокрзщепия а11гт-rйско1·0
выражения Ьinагу digit - ,.двоичная цифра».)
Бит - один симrюл днои:ч1-юй системы. Дllя
сообщею щ :>а п нсан 11oro н двои ч ной. октtме,
количее1 ·tю ннформа1(НИ1:1 нём - просто число
дво1rчных сr1мв01ю11. Число 25. Rыр:..~ж<.:ннос н
дnо1rчной. системе как 1100!. содсrж11т 5 сим
волов 11. слеJ\()U:.1телы ю, 5 бнтон 11нформа1,1,т.
Праnда, в той же снсrеме е.::1·0 можно :.~~тисан
11по-дру1·()му:00 11 ()01. Такое сообще11и:е бу; tе-1
сонержать 7 битов 1тформ~щш1. ОднIIм битом
можно nеред:1·п~ TOJlbKO ОДНО ИЗ двух сообще
нш1 - U н ;ш 1. Эти короткие сооб ще11ня rro -
poll н~:сут большую с..1111ысловую наrру:шу -
мо1у1· 0311~1 чать ответ ''да~ ил11 ,, нет ~. с11тнал
HKЛJOЧCl-IH>J нлн O'l'КJI IOYCllHH эm.:ктро::~иер 1 ·и 11 .
f-J() длн 11ерt:дач~J 01-:111 Пf>C/~CJ I ЬJ I () lljIOCIЪI. /J,нух
битов достатпч1 ю /(ЛН 11 ереr\ачн чt:тырёх СО<)б
щс 11 riй: 00, О 1, l О. 1 1. Сп1 ·.rгасно 01хнп1лам r<ом
бинатоrпки, зап нсыо 11;3 11тюич 11 ы.х сн мnrJ; 1 oп
~южно nеред:~ть rJд 1 ю и:i 211 пюfiще1 1ий.
UОЛСС К\))-l!НОЙ С/ЦШИ.ЦСЙ ИllфОрМаЦНИ ЯR
!JЯ<.:ТСЯ байт - з;~писr.. 11з вос1,.мн битоn. 06-
Ш.t't' I<OЛJIЧCCTBO Cfu\1130ЛOB , /"IСЛОЛ 1,зуе.мых f!
об1,1чных т<.:к<.:тах, больше чем 27
= 128. но
мс 1 1ы11е ч<::м 2к = 2S6. (На клаrт::~тур<: 1(()м11ью
тсра мuж1ю ш1сч 11тат1> около 150 :Jнаков.) По
:'lтому OJ\llOl'П байта как p:i:1 ;~остзточно, что
бы ~1~\1\О/\иро н~1ъ R J\1Ю11чной системе любой
симnол о(:iычrю 1 ·n текста. Дпя с1южных мате
матическ11х снм 1 юлов (квадраттю1·0 кор 1 1н.
11/lTerpaл;:i 11 др.), буКН rj:ШИЧ IIЫХ 111рнфтnn И
алфашпон (папрнме.р, ~·реческого) од 1 юrо
байта 1 1е.до<.."r<1то1.1110.
636
А t\ак нзмсрнть котrчество и~ 1фоrмации в
сuобщс11ии, если оно :~апиб11-ю пс n д1юнч1101'1
снсгс:ме? И J<tчем 11:3 мсрять т;нюе сообщешrе в
битах н ();н1тах? Это нужно /(Лн '1·u1·0 . чтобы
:и 1 ат~" с1<0лuко снмволок бутt<.:т в с1юnщенин ,
если t.:го зающ 1 1рова ·п, с помощпю дно11чно1·u
алфа1:11-п·а. КrJ 1 1еч 1 ю, и t1 днонч ной cr1l"1емс:. к::~ к
м ы nrтели, О[J.НЛ нто же ч11сло ~юж н о за1юдн
роиать по- разному. Одпа1ш для ка.Ж)\ОГО \(Юfi
щсfшн сущестnу~:т :мшшмалыюе rюлпчество
611тов Ю.1к сп> определить?
Рассмотрим з~ннсь ДССНТНЧIIЫХ с111ссл в
двоич н ой систем.с. Псркьн:: 2/l чнсел. - от() до
211
-
J - мож1-ю за11нс11ъ 11 бита;\111 . llапричср,
11.ля :3::umc1 1 чисел uт О до 7 хк1тит трL;х бнтов,
nтО11.031- 11ятиит./(.ЕслиN- стс11ень
числа2(N= 2''),тол,ляе1л :Jan11c11 11уж1юп+1
бит. Так, 32 = 2~ = l 00 ООО (6 бrrтов). Дrтя /1.Р:-тнх
чнсел коли1.1ество битов pзni ю показ:~·1 ·е.r1 ю 1 1аи
болъшей степешr дnойюr, не п ревыш:нощеf1
"*тпго ч11CJ 1 :.t. птос 1. На11р11мс::р, л,ля чr ктt 57
эта степеш, рагнrа '>: '>7 больше :)2, ею 1>v1.е11 ы 11с
64. По::этому lVIЯ :1аnисн ')7 rryж110 пс '"reпь ur e
'5 + 1 == 6 бнтоn. Чтобы ш1йти м;1ксю1Jальную
стспс11 .ь числа 2 ~ля любого ,У, необходн.мо
вы~шслнть loglN и в:щтъ от нсr ·о целую ч;~.сть;
сё обозн:.~ч;iют кнадра·1 ным н скобк;1.м н: [Jog21vi.
/'J'J ': JK, Mlllll ·l .IV!aJ I ЫIOC ЧИСЛО 6 1 1'('(.)Н Дllll :JafllJCH
любuJ ·о дссf{тич 11 01·0 ч11сл:.1 N p:iнrrn (log1 Nl + 1.
Пrн ;jап11с 11 uf1 1,1чных текстов каж;1 ыl1 с11м
rн>11, как 11р~н1нпл, к1>/\1·1рустся од 11 t 1 м баr1·('()м.
О r <.>,ц<>вателыю, ч.ислп бай'f'<)I\ пр11мер 1 ю р::нню
чщ:лу оrм:волпu; но бзйтоо J'vlOЖCT бьп·1, бплъ
ше за счёт пробело в в тексте.
И:1 мере11не ннфоrм;,~щш, основанное на
подсчётс числа снмnолов u сообщсн.ии. r rсоб
ходимо для того. •побы OЦCHJIТI> l:ЮЗМОЖIЮ<.:ТИ
т~:ю-11 1 чссю1х устрuГтстн, рL!бuтаюгцих с нс::\'1 .
Кол11 чс.:стн( > 1 1 1-1формац 1 н 1, ус1·а1-:1uнлен 1юс т:~
ю 1м сrюсuбuм, 1;;1з ы1:1ают обоёмам ш 1.фирма
ции. Для запом11 н :нощ11х устройств - опсра
тн ю юr'1 памяти к<Jмnыо·1·ер;,~, дrrcr<UD. дискет
11 т. /1,.
-
аn1.ём н11формацин, 1юторая можс·r· R
11нх храшаъся (061,ём п ~1мнти). п:змериС'1·ся в
11"://J/Oбalima.Y (тыоrчах байтоn) 11 .мегабайтах
(м иллтюнал байтов) . Чем боль ше объём памя
ти l<OMIIЬIOTepa, тем шнре С!'() JЗOЭMOЖIIOC'J'II.
Время IТt'ре,~ачи сооб щ ения по ка н алу связи
Заl:\ИСИ '/' 11<.: толькu ()' l ' fVПHП>I текС'ПJ, IIU н U'l'TOJ'U ,
какой объём 11 нформацни :J<t tднн r щу време-
111 1 можно пtрсд:Уr ъ ч ерс::~! К;Jна;1 , 11лr1 uт про-
11ускно!1 способн ост11. Эта 1~t:11и ч нна 11~{м<.:ря
lтсн обr.JЧН(> в ю rтюб;tйтах н секунду.
Но 11нфоrмацию м ожно н:1мерят11 tf инач е.
И НФОРМАUИЯ
И НЕОПРЕЛЕЛЁННОСТЬ:
ПОНЯТИЕ ЭНТРОПИИ
~\1-101·:1;,i 11рихо;1нтс}! сл ышать: «Ты соuf>щнл :-н-tс
то, что я. и так л~аю» . Однако 11,.ая 11,ру1 ·01·0 нолу
чатсля :по Жt' сообщс:11иt" может сонерж;~ть 1-1уж-
11ые с вс) t,с:ню1 - ес;1и он их 1-1с знал. R данном
случае v.аж1 ю у-Жt' не число сим tЮJЮН. Сообще-
11ие 1111фоrмати.:шю, сели 0110 уnеличнnает :ша
н11е. Иначе говоря. сшо умсш,ruает нсзнаш1с -
нео пределё1~нос т1.> относительно то1·0. про
нзо шли и1111 нет 1(акие-то событин, 1:1срr 1 ы 111щ
1·1ст r<акис -то ф:tкты. Поэтому хотелос r. бы 1r:~
~н:рнтl'> не объём сообщсш rя, а с.:1·0 ннl\:юрм;,~тнк-
Всздесуш.:~я матемап11<а
r юст1,, т. t:. \fe{ly ум~.:11ы11е11ня 1 1 сппрс;~слtш юt-1' 11
JVIЯ пплучан:J tЯ.
Самое простое тшфпрматнrнюс <.:oof.iщt:
шre - это 01 1л1ъ-·1·;1ки О J .UI11 1, т. с. 1 бнт. Такое
сообщепнс псредаt.'т ответ нз nопросы, rюто
рыс допус1<шот д1юичпыi:~ отnет: «да » (1) 1 1;н1
<' НСТ» (О). И снова бит оказына<."r·сн мню1м ыль -
11ой ~ДJ 1 н11цt:С1 1<0.'11 1 чсстна 1Jнфо рма1щ11 . Hu
ДHOИЧl-lhllJ отнст MOЖl-f(J 1 1Сf1 ед: r ть 1t н ()U J,JЧH(} .\I
l'CJ\(."J 'OHOM кнде: « Rе рно • Н/IИ « НС.:J:Н::р но ·>, " МОЖ
/1()'' нлr,1 «11e.11r,:m ·> . I Toдo61 11,Jc тс.: 1<с1· 1,1 нм сю'r·
ра :н 1у10 ;1/I IН I) '. 1ro содеrжа' r· одну и ·ry же т111 -
форм~щпю, liЗМеряем ую од r 1 нм битом.
J3 более общем случа е получателъ пнформа
лип ожнда ет сообщеrrис о ·1·о м, что щюrr:юш
JЮ <.:обытнс из м r юже<.:тва С== /с 1 , ". , с \1· Есл11
множссrвu С содержнт всс 1·0 дна элс.:.\1енп1
(N = 2) , то ищfюрмiЩНЮ u конкрстrюм собы·
тнJJ удастся пс.:р<.:д:rть сJд1111м б 1 1том (U - пср
нщ; событие: , 1 - второ е событ 1 1с ). Есл11 же
N > 2, то одн11м б~rтом не 0601! ·1ис 1" Зд1::<.ъ nрн
ход111· на помощ 1, такан 1щсн .
Оди)( бнт - это атnет 11а од и11 двоrrчт.1 11 во
прас. Однако любую т111формацI1ю можно r ю
лучнть, :за,1'аnая ДТJОТiчные rюпросъr. Пппробу
ем ш1мерять шtфоrмацпю, солерж:1щуюся в
сообщени1 1 , кот1чест1юм д1юнчrrых вопросов,
н:~ отнетuв на кuтор.ые мы получ11 .•..~ тt: же снс.:
дс н11н , что 11 rrз 1(;1н1 юго соuбщснлн. Расс~vют
рим 11рнмер.
1Iрсде1·аtш1 ·с сс:бс . что к нам :{axu; o1 'J' лрн
нтел l'>. fюm,шo!r люб1п1:11ь p:1з 11nix J:111 :.111 ск . 11
rовогнп: <·Пр r ~вет! 5Т с ф)•1·6от1 . И1·рал 1 1 "Спар
·r·ак·' 11 "Динамо"». <·Ну, 11 к::~кой счЕ·r?~ - с11ра
п 1 иnаете въ1. «Так н тебе и СI<:~зал! Скажу 1'<m ъ ко.
что болъще трёх .мячей 1шкто 1 1с заnшr. Хоче1L1ъ
у:1нать счёт, зада8ай IIОПрС1СЫ, а я буду от1к·ч.;,11ъ
"да" ~vп1 "нет". Но 011~счу толы<0 на четыре во
проса. Так что nодумаf!, что будешь сnраuщ
вать" . Вот nы н заду:мал11сь. Всего nо:3 мuжных
варнанто)i счfт:1 м:1тq;.1 - 16:
о:()
():1
0:2
():,)
] :()
1:1
l:2
1: ,)
2:0
2:1
~:2 2:.3
3:0 3:1
3:2
.1: ~
Есз1и сr1рашнв;~ть о кош<рст1 ~ом с·чётс \ «С1мра
пи ОtШ 1 : Р·> ), то , l\0~{),южно, прндё'1·б1 за,n;ать
l ') 1:1опросов , пока угадаешь <l (>-й :1адаnать
ос обяза'Гелыю - нпю , что пр:шип ы1ым булет
носледний счёт) . А сели спросить: <' 1lнчые» .
rrpи <.>'1·пете «да~ , uстанетсл тольк() ' 1 1:1аμи :.шта:
Математика за работой
О·О,1:],2 :2,3:3.Здесьужеможноипросчёт
спрашивать - 3 вопросов как раз хватит. А с:сли
<-нет»? То1·да остаётся 12 Rapиa 1 11'0fl на ?> 1ю
проса - мно1·онато. il общем случае каждый
вопрос разбивает множество вариантов па дn;:i
подмножества : одно соответствует ответу «да",
а другое - ответу тет». Если получен ответ «да•),
то варианты из множества «IIeт» рассматривать
уже нс rl)l)IOJO. Почему не стоит спрашивать о
конкр<.::тном счёте~ Дело в том, 1.по этот вuпрос
разбивает множество на две оче 1-1ь неравные
части: одна содержит 1 вариант, дру1·3Я - 15.
Нс }Тадал счёт - м 1 южество остаnшихся вари
<Н-JТОu уменьшилоо. всего ш r шь на ед и ницу.
Друюй вопрос (п ро ничью) также де.пи·~· мно
жество нариатrтов на нерашп,те частм (4 и 12).
Значит, вопросы надо задавать так, чтобы мно
жество вариа 1·П'ОВ дслшюо, пополам юш почти
пополам (если 'IИCJIO вариантов нс:чётно). Итак,
сч итаем вопросы.
1. •Забил ли "Спартак" больше одного
мяч<t?» - «да~,
-
1 ·01юрит принтель. Отлично,
остаt...'тся 8 вариантов:
2'о
2:1
3:о 3:1
2.2
3:2
2:.:)
.:):3
(Н о если бы он ответил «нен, оставпrихся
в<lриаIJтов было бы тоже 8 - вот что В<l)юю!)
2. «Забил ли "Спартак" 3 мяча?» - «Нет»,
-
го1юри·r приятель. Остаётся 4 вар на нта (и
вновь - при дру1·ом ответе их осталось бы
столько же)·
2·О,2:1,2:2и2:3.
3. •Лроnустил ли он больше одно1·0
м.ячtl?•) - «Да». Осталось 2 варианта: 2 : 2 н 2 : ).
4 . « Пропустил ли он тр1 1 мяча?»
-
~нет». -
<·Значит, 2 : 2».
«Ну что ж, молодец, - говорит nрJ1UУтель.
-
А теперь скажи, почему я решил, что 11уж110
задать 4 1.юпроса? Может быть, 11 ~ вопросов
хватило бы?->
Ясно, что зад~1ч<J вашего " рю1тt.:ля - и том,
скuт,ко llC06XOf\11MO задх 1ъ /\ВОИЧНЫХ но 1 1ро
сон, чтобы узнать о конкретном событии нз
м1-южсства, содсрж:ндс1·0 N событ11й.. 1[осмот
рим, а чё ."1 состоял метод tё реrпения ,т1;;01
случая. когда N = 16. Каждый раз чт1сло элемен
тов останантпе гося ,1\11-южестnа делилосъ па 2.
ПоскоЛЫ\'}' делить лриumось четыре раза, в 1-по
ге мы ра:щелилиN па 21
• т. е. на16.Вmобом
случае мы проходим к множеству, содержащс -
638
му 1 элемент, что 11 явтtетсн искомым ответом .
Число :~ада1111ых двоич11ых воnрос()н ран110
числу деJJе11нй. Еслн, l(aK в напrе~1 случае, N -
сте11е111> числа 2, ·1
·0 ч11сло noпpoc()R равно её
nо1<азателю, т. e. log2 2-
1
= 4.ПоэтомудляN= 16
трёх вопросов мvю. Uсли жсN не является стс
лс:ныо числа 2 , скажем N = 20, то нужно в:зять
следующую стещ;нь числ;~ 2, т. е. 5. Знач.~п, об
щее реш<..:н11е выг1шд1п так сели /\7- степень
числа 2, то достаточно ззлать Jog~ N двоичных
вопросов. сели нет, то - (!og2 Л.j + l.
Это реwенне nочти совпадает с ·1·ем, кото
рое мы по11уч1rл11 , когда выяс11ял11, сколько
би1·01111еобходимо длн дnончтюrо 1.:одировапия
десятичных чисел. (Небольmан ра:шнца сш1-
зана с тем . 1.по среди ч 11сел мы т<0днруем и О.
т. е. ч:нсло 16 - семнадцатое, а нс шсстн;щца
тuс по счёту.) Лочсмутак 1 1 роt 1 сходит? И какое
отношение 1,1:v1etт у~·адынание элементов мно
жества к кuт~ированию сообщен11й?
Оказывается, самое 11рямос. Четыре вопрос.~
о рс:зультатах ма·r·ча можно сформул11рова·1 1,
так, что 011и бутw.r при1·одны ,rvui любо1 ·0 счёта
и каждому счёту будет соответствоRать опреде
лё1 11J ая последователы-юсть двоичн ых ответов.
Посмотрим, как вопросы разбивают исходный
ква/\рат вариантоn (рис. 2). I l ервые два вопроса
разбивают его горизонталъпы.м:и чертами (сна
чала па пары строк, потом пару - на две:: стро
ки), ~1 два 1юслелних разбивают ныбран11}1Jn
строку вертикальными чертами Лри 01·нете <'да ~
выбирается нижнее (д1~я первых двух нопросоf\)
1rли прэuое (для вторых двух Rоттросов) мн.ожt"
ство. Напри.мер, счёту 2 : 2 СО()Тветствует 1ю
следователыюсть 1()1 () (!Щ тrет, /~а, нет). счёту
:):1- 11О1,асчё·1у1:2 - последонатсльность
0110. Подобнан очерё,71тюсть вопросов юvност
рирует правило коднрования сообщений о
рсэультатах матча. Если получатеJ1ь сообщс 1 шй
l-й
вопрос
Риr;. 2.
0:0
1:о
2:0
3:0
О:1
]:1
2:1
,;;:1
5-zi
<ю11рос
0:2 0:3
l;l
1: :)
2.2 ~:.)
5:2
.):j
2-li
(Юlip(I(
1ч-11
tюпрос
знает это правило, то результат ему можно со
общить ч.етыръмя двоичными символами.
Рассмотрим теперь сJiуч.ай, коrда н~о регу
лярно передавать сообщения о том, какое со
бытие из множ~:ства С = {с1 , .... c.v} проиэощло.
При 011исанном методе кодирования длJJ и.х
передачи каждый раз понадобится Jog 2 N или
flog 2 /\/] + l бит. F:сли сообщения переданы, ска
жем, 200 раз, то н f)нтов будет за1]1ачено в 200
раз болыrrе. Однако, l(ак оказалось, общее ко
J1 ичест1ю перелаnаемых б~пов можно умень
шить, если события имеют разную вероятность
(т. с. разную Ч:.tCTO'I}' 110flНJICHИS1).
Пусть , ~шпример , множество С содержнт
четыре события с 1 , ".,с~, которые происходят с
вероятностямир,= l/2.р2= 1/4,Р~ =р1= 1/Н
(сумма нсех че1ъ1рёх вероятностей должна
рэвняться 1). Тогд;.1 для у1·щ-1ыв:~ния события во
просы лучше задавать 11u-другому. Сначала сто
ит спрос111ъ, не 11рuи:ю11Uю ли событие с1 -
ведь оно происходит в ло1юви1 1 е всех случаев,
и , зпачит, мrro/rcec1·no ncex возможностей (но
пе множество (с1 , ... , с 1 }!) делится пополам. При
отnете «нет» спросим о с~ (множество Ос'Га.вших
ся возможностей опять разделится пополам) и
в случае t-Lсущ1.чи- о с~. По)!учим следующее ко
дирование:с1 ~ l,cl~Оl,с~ 4 001,с44 ООО.Ка
:3алось бы, этот метод коднрован~-1J1 хуже 11рс
дыдуще 1·0: некоторыt: коды оказ~шисh дли.ннее ,
чем log2 4-= 2. Од11ако посмотрим, ч'rо 11олучит
сн , сели передавать сообще11ия часго, например
200 р<~з. За 200 р;.~з с 1 п оявится nример110 100
раз.с2- 50раз,с1ис4- по25раз.Дляrrрежне
т (равномерн ого) кодирования сrастота 1юнв
ления событий rre имеет значения: любое сооб
щение состоит из 2 битов, а всего лридётся
затратить 400 битоn. Прн новом кодироnани0
чаще будуг передаваться короткие коды. Вс.:его
будет затрачено примерно 100 · 1 + 50 · 2 +
+25·3+25·3=.)50бю·он,ансреднемнао;цю
сообщение - 350/ 200 = 1,7'5 бита кместо 2.
Такая экш-юмия 11ро:изоuта сУг1·01·0, что при
выборе коднрrтан1н1 уч.итывvt:иl'Ъ F:1ероsп11ос
ти пояяле1111я событий. Этот яероят1-10с·1·1iы й
110дход и принят .в теории 111-1 форма11ин nрн
измерении количества информации. А имен
но: nводится понятие меры неоттрсделённости
множества событий С = /с,,"., cs}. Она называ
ется энтропией, обо:щачается Il(C) и nычис
ляется по следующей формуле:
Вездесушая математика
1/.д~ ftflf cЛllfeft%1(1e fot)«llll,
621.111;ali &lfJle 011ttf0&1/(.. '
rле р, - вероя·1·носп1 собы·гий. Энтро nlfЯ всс1'/\Э
отрицателы~а. 11nС' 1<0Jт1.>ку не1111чtн-rы JtOД этщ:~
мн лоrарифмон меньше ещнrнцы. По смыслу
она противоположна ипформэцин. та!{ 1<а1<
информация снимает неоnрелелёттост1,. По
этому сред1 rec количество информации в юrо
жестве С, т. е. ко11ичест~зо информации:, при
хо;,J!щсеся в среднем на одно сообш,сни:е о
сuб1,1тнн из С, R1~1ч11сдне-1сs1 1ю формуне
!(С)= -If(C). Зне1чит, ко1 1.ичест1ю информ<щю1
ДJ1>1 наш его при.мера равно:
(
1
11
1l
1
!(С)= -
-
Jog , -+-loo,-+-/оа , -+
2L24t'>-'-\Rь_Н
+- [OQ. ,
-
::-+ -+-+.::.= ]7').
J
1)113~
-
8 ..., _8
2.2я8.
т. с. совладает с полученной ранее средней ..wп·1 -
ной сообщен11я iЗ битах .
639
Математик<1 ·1<1 рабо1ой
Ну а как же в пp1 1.tvtcpc с фуrболы1ы.м мат
ч<.:м ' Рассматрив::н~ Cl'O , мы фактичс<.'ю1 11рсд
ПtJлагали. •/TlJ нес 16 сuбыт111'1 раннuR1.:роятны:
каждое 11мt:ст всрuятнuетъ 1/ 16. Дш1 щ:пJ
J(C)= - Hi(_!_log, _!_)= - 1(1 _!_ ( -4)=4
16
1(1
16
'
т. с. 11 :щесь мы 11олучш111 тот же резут>rат, что
11раньше. 13 теорн lf ннqюрматцпт дока::~ывается,
что величина l(C) .:v1аксималы1а и равна 1о~2 N
( или (log.t N] + J ). ко1.·да вес события равно
вероятны.
ПO/tllt:/tё .\1 И1't)Г и 11формац11ю J\ЮЖНО ИЗМ('
rятn /tЛИllОЙ сообщсн1ш в 611тах. Taкoii сно
соб 1 шчt:J 'О нс говорит об 1-1нфuрмат1ш1-юстн
сообще::ння (0110 может быть маJ1оинс\:юрм<1-
1 · ивr1ым 1 1 11и 11аже бсссмысш::пным), 110 :1:~то
х:~рактсри:1у<--т объём рзВот 1 ,1 систе.v1ы СRЯ:1Н
прн пеrел;а<1е. Если же 11ео()холимо ~{Н(!ТЬ, на
<.КОЛЬКО ЭКОНОМ! ю !Ю,Г(ируются сообще1 IИЯ, то
СJ1едует пользоnаться энтроп и йным 1юдходОJ'v1
1< 11з.:-.·1ерс11юо информацнн. 1Iрн этом нужно
угочн1л·1,, о каком множестве событшl будет
сообщаты.: я , 1с11«Jны 11х неронтнuст 1 1 , 11ослс:
Чt;I'() ВЫЧl l СЛИТh /(С).
КОЛИРОВАНИЕ ИНФОРМАUИИ
Уточпим смысл оюuос-пчет::тия «тюлпрс)Rа1rис
информации» . 1:3 теории информа11ии под ко
дироuание ,\11 по1пrматот :1апись информации по
опрслслё1шым правилам. А 11::ишчие 11раn11л, по
которым сост:штrют те 1<сты нли 1тзображс1пт
и:.~ м 1-южсст11:1 эт: ~·tС1 tтарных единиц (алфа
t1и·1·;,~) , х;.1рактсрно ДШJ каж1ю1·u н::~ыка. В од1 11 1х
CJJ~Ч:HIX - ЭТО CCTCCTBClllТЫC ЮЫКИ , Н дp)' t'l l X
-
сстсс1·нс н ныс я:..1ыки с каю1м11-то огр:1 ничснин
ми (напри.мер, те.11е1 ·рзммы пишут на обычно.\1
нэыкt:, 1 ю11ри это."1 опускают прсд11оги. а вмес
то точки и Jапятой n ш1ry1· их с0t<рзщё11 1 t.ые 1 1а
:;ш11 JШJ : «'IЧК» J1 «ЗIЛ'» ) . ~CT I> и форм~~льпые Я:1ЬП(И
со своими 11равилами: языю1 двоичн ого коди
рования , ~пыки программирования и '1'. д.
lJыбор язьша код11рова 1 шя заниснт от кон1<
рt'тных цсJ1с й . О н определяется Tl'МJJ пара
мстр;.1 мн (хара ктери<.:т11к~1 .vш) 11 нформ:11 ~ и и,
которые нужно улучши·1ъ. J lp11 1 1 с::редз'tс:: н11-
фор:'.t ~щ1111 важны её оnъё м, нрем>1 нсрсдач11,
г1адё~'lюст1, (:-1:нц 11 та <п помех) , тсхничссК11L'
)лобстн;1 11ере11ач-н, :1ащнтз от r-1t:сю-1 кцнот 1 иrо
вз11 1 юrо 11:оступа, например 1юдсл}1 п11 ша11ия.
llовысить кач<:"ст.1ю 1.к:сх 1шрамС'1 ров оДiювре
мсн н u НСЛ l>JЯ: улучшсНИl' U/l.H()J' () l\З llИX, как
nр~1 ш 1лu, ухудш:.~с::·1 д[)У1'ОЙ Выхtщ нз по1юже11ия
нашл н н том , ч·10 нз раз1-1ых этапал 11срс,11ач1-1
11нформацни соверше 1 1с1 · вую·1· ра~111.1е 1 1 ::~рз
ме1ры , т е в 11роцессе перед<1чи 1111фор.мациrо
1 1 есl(олыю раз псрско,11,пруют, тrричём с ра:1тn11-
ми целями. Например, текст телегра.\11~1ы. 11ани
са1шый на обычном языке , преобразуют в один
из тс11еграф11ых I<одов. который тсх 1 шчссю1
удобнсс 11с::редавать, а 11р1 1 11 рнёмс снова прс
нращают н обычный тскеr'. Но 1шо1 ·ла ныбира
ют на116ол<:е в:1ж11ый r1<!р<1ме1р и улучшают li
r 1 еркую очередь el'O. При кодиронан11н ннфоr
мац111-1 часто ст<~лкнн<~ются l' про' r' 1•11юрtч11ем
мсжлу i :IKOl IOM 1ЮС'IЪЮ 11 11а;~еж 1 l\)(''\'hlO 11 ередэ
ч и. Рассr<хке;ч об этом rтсм1юrо подробпес
При дnонЧiюм коднровашш, как нравило,
и11тересу1отся только одним 1 1араметром - эr<о
ном1юстыо заниси. в сообщсrrиях 11с /\<>ЛЖЩ)
бы1'1. m1rurп1x символов. 110 имсшю это н дсла
ст передачу ннфuрм ~щ1 1 1 1 н е нан<.:жноl1 . сс1 1 11
11pu11 a;(:t<;''I' IUIJI l1JM(;'Jl.Я(''L'CЯ ХО'\'Я fiьt 0/ \J.111 CIШ
IIO.!I , часть 1 1 11формац1ш утрачивается либо 11с
к::~ж:.~стсн . lla 1юм о щ1; прнходят матсм<~тичсскис
методы коднронант1.они ТJ(>:толнютобt1аrуж11-
н::~т11 11 11 спранля'1ъ 0111r16кr 1 , 110:1 н 1 1к:1 1ощ11t:: нр11
псре;1аче. Такое кодн1ю11а1111е 11::111.1н::~ют ппмехо
)'стоirчивым.
Пр11 11:uшсIУш 11омех 11р1111лть сообтце111 re без
ошибок LЮМО!'ает 11режде Dcero его нзбыточ
ность. Нели сообщение псизбыточrю, 11Jбыточ
тrост 1 , ННО,1\ЯТ СПСЦИ<VIЫIО: повторяют одно 11 ТО
же несколько раз шш нсредают. как, на11р1 1 мср.
фам нлию , ~ 1то буквам·> (Гр~11 тт: 1 ·p1tгop11i1 - ~'о
м~111 - Анна
-
Н11на - Таня).
Самый прuстй 11экuнuмнr.111 с.11t)С'об борt,61.11
с ошибками н / {1юичной и1.1qюр ....1ации
-
ко1 ~т
рот) чё'J.'1 ЮС'l'И , ко1·да lIOCJLeДOHЗTeJIЫ IOCTI>11улей
и единиц раз6 1 1R:э.ют на группы с одr 1 ш11<0вы~1
ЧИСЛОМ символоu. 13 каждой фуппе IJОДСЧ!J'IЪl
вают <-1.иою едшшц. t:сли оно чётнос. то спр;ша
добавляют О; сслн нечётrюс, - доб~1 вляют 1.
В любом слус-rае число сюпшцдолжrю быть ч<..'т
пым Добаnосшый CI-Ll\ШUJI 11е несfт информа
ции, ::sато 1юзною1<.:· 1 · обн:1ружит1, 011 1 11fiкy. Еt,:лн
l lf)И Пе f)едаче 110Э I ШКаеТ OWIJ6Ka . ТО () ll ЗМеНН
СТ<.:Я на 1 ил11 1 - на О 11. следователы 10, ч11 с110
С/111\-1 1-Щ CT<IJ IОПИТСЯ 1 1 t:чет1 \ЫМ . Прн 11 рием t: со-
06ще1 1 иl! с 1 1011а н каждой 1 ·р~1111е сим1ю1юн тто11-
с читы 1-1ают ч1 1 сло е11и11 1 щ . Если nтю чёт11ое,
01пибок нет. Котrсчно, таrюй вывод .верен толь-
тю тогда. J(О1да заранее нзntст rю. что ларные
ОtШtбкн n ОДIШЙ L'PYLШC практLLЧССК\[ нс1ю:i
.\ЮЖШ1!. Поэтому количество символов н 1ру1 1 -
11ах 1 юдбнрают в ::!авнсимостн uттu1 ·0, насколь
ко часто 11ш1nляютсн 01ш16ю1. Чем реже он11
случаются, тем щшннсt: мтуr бытr. 1руппr.~. Лрн
этом уменьшается ч11сло сам 11 х 1l)y1m 11 лоба
вочных сим1ю1ю1~. а э11ач нт, 11 и:~fi 1,1точ 1 юс·1ъ.
:Эн>т мсто,1 штrроко прнме r1 щ"r·ся о 1шм11ыо
тср;1х, 1де 1-1сроят1юс1ъ 01 11ибок 11еве1шю1.
Есть коды, которьн.: ос: только обнаружива
ют. по н исттр:~юшют о шнбю1. Один 11:.1 пер.uых
таких ~tетодоl~ кодировання прн!-1сня~тся до
сих нор. U нём также донус:к:н.:тся. что во:.1-
11юж1-1:.1 ·r ·uлы\u ою ~1ю•111ая оw116к:.1, 1--1 1н.·11оль~iУ
е· 1·ся бож:с с1южнаJ1 <.:хсм~1 контрош1 ч~·1'н<кт11.
Понсн1rм эпл мстщ1 на nр11мерс (см. рисунок).
ТJ111)юрмац1110 raJбillJ~IIO'I' 11:1 1·ру11п 1 .1 по qe-
·1 ыре ДtKHI ЧI LЫХ. l'HMlIO!I~ Cl. ь. с. d . к каждой
1т>у11пе лобаnтr ют трн прсшерочпыл с 1 ~пю.1а
e,j, g. Vlx вы6прают так. чтобы былп чётными
сум.v1ы с1+/')+1.: + (! (пepna5J стrою) , (.{ + /J +с/ +.f
(втоrан стрсжа) , а+ с+ с/+ д (трсты1 строка).
ПрпL'м1111к ныч11с.rп1ет н :.~налнзнруст эт11 трн
СУЧ.\!ЬI. ~CЛll вес OHll Чi:.>П l hJ(', то OW ll OКll нет;
С::СШ J одна 1(:{ /-IJJX нeчi:.>'J'H<OJ, '\ '() OШJJбK;I н Щ)UJ:l('
рочном с1 1мнолс. Ест ~ юн.: С\'111:v1ы нечётные, то
оr11и6ка н том <.: r шnот.::, 1штор1.rl1 дJ1я н11х о()
щ1rt'1 _но 1rc: нх< щнт н трс·1·1,ю сумму. Есл1 r неетрr r
сумм1,1 нечёт11ыс, ·1 ·0 01т1бк~ н симnоле а.
Соnрс::ме1mые мt::тn11ы колирован~ 1н. испр:ш
тtющсrо оr1.111бю1, используют высшую алгеб-
Ве~десушаs1 математика
ИпфорJ>1ац1ю1111ыс
биn,1
Проvсрочны е
биты
@
®Ф®
ру, теорию сшсел 11 т. д. С 111vшолы уже 11е ,цс:-ллтся
на ннфор!v1~щионныс 11 прощ::рочны<::-. код ан.~1 -
.111внру1.:1·ся н дско)щр~·стсs1 как слшюе uслос.
Ч ;rсто 11 р11 х:о;\11·1тн 1K'LI r: 1 ·rъ обратную :Ja)t:t-
чy - yмc11h!U<t'1ъ t'L·1-t:<..:тненную 11~6ппоL11-ю<..:1ъ
текстон. Та1~ая t1poцt:nyra 11азыв;11::то1 сж:1 l'llC:ч
11лн уп:11<пвt<01'1 J1нформ:.1Ф 11 1. ЕЕ пр11л1tнню1· 11
тех с11 учаях, коr11,а храшлъ ннфщтмац11ю щш
ход11тси ,r~олп\ 1ю рз6отатъ с пе(r - редкп. а
·1·акжt прн ш.·редаче дл шmых текстов.
Защнто!°J 1111фоrмацни от 11ес:нпщ1юш1ро
на111 юго доступа стат 1 ш 1·1·сресоl:!атм:я задол
го до IIOЗIJllIOIOBCHIIЯ тсuр 1 111 г 1 нформац111 1 .
UJвфровка 111-rфuр~1:щ1111 нсс1 ·;.щ была 11уж11 а
раз.в<.:J\чJ 1 кам, д1 111 1юч:1там , р:~ :тнчнЪJ ,\! г1р:н-111-
·1·СJ111е1'Нсш1ым служб~I;\~. Л,0:11·пе нре111я методы
шнфровю1 .1ав11селr1 от нс1'усспз:1 11 н:щ()рст:t
телы юсr 11 1 1х <:n:щ(!телеi1 11 бr,IJ 111 стот. же сск
rе- 1 i\ЫMJ1,1~\К и сама Н11r\Х'1рм ;.щия . Е нз сто>~щее
время ·r·copeIЯ :1~111.1,1.п 1.1 и 11сj'юр~1~щои (лртшю
графия) стала точ1 юй матем:~тпческой 11:1}'1Юй.
МАТЕМАТИКА И КРИСТАЛЛОГРАФИЯ
С: 1онп ~ кр11e1·:.uuн к~ )' дрс..:нн 1rx 1'рс 1,;01~ оз11ач а
ло <·Лl'/\». Гомс..:р, 0 1111с.ъш;н1 ос:;щу Тро11 грек:1м11,
го11ор11т, что в 11t'рвую моро:11 rую 1юч.1.~ 1ц1.1ты
1тросв 11окрыт1сь <•Кр1кталJЮС» - ЛL,1Юм. Поэ
же. 1-\ОГ/\а в J'OJ1:1X н атлмr мт1ера11, ГIЭll OMIП l :J.13-
ПllfЙ лё11, его r r:1зв:v 11 1 rорпый хруст;v 1ь - гор
пыll лёд.
С XVIII IЗ. кр11стаплаии стали ИМt'JЮ]}ать тела,
111"1сющпе ivuю1·01·ранную фtJрму. 01111 щ:трl''-1<1-
ютсн н прнро;\С, 1111\'t 1 1х нскусстнеLiн.ым ну1·ём
nол уч:.r ют н J 1 afSopaт< >р1. 11 1.
Мноt·ис 11 в наши ;~ни считаtот, что крнс
т:.1.rrnы в лриrо;1с .встречаются ре;що. Одн~шо
:л·о 11е так: кр1 1 е1·:011mы 6ую1:.1лы10 окрУ',каrот 1r::ic .
rи1 11 НЭН'IЪ JllOricJt'I nt.TфOpMCllllЫ(r nyJ111IЖHfll<( 11
p~!CC.\.1Ulpe1ъ C..: f 'l) чсрl'З ~'llCJJllЧll'l't:JIЫH>t' C'l't 'l.VIO.
ТО МОЖНО З::J,"1l'Tl lTl1, ЧП! 011 COCTOllT 11:1 0 1'-
Дt:Лbl[blX очс111_. i\J:lЛC l !f)f(IJX. ClIOl'IJП I Xt'Я .\-IСЖ/1.У
собо~'1 кр r rс1·алл 111<00.
ЗАКО Н ПОСТОЯН СТВА УГ/\ОВ
01 1 11са н 11е"'1 с1юйстн кр 11ст:и1 .rю11 :Ja 1:111масн:я
н:iyr<a кpHC'l':JJLIIOJpaф1 IH JiC рождсНН<.: (.'Шf~{ЫН:l
Ю1' С l)ТКрЫТ11С~1 з::НЮНЭ ПОС'l'ОЯI ICTЩI у 1 JIOH. nhlJIO
, , \:1 нно 11 :ш1..т ·1 ·но, Ч'I (1 l\P IK'ТaJIJIЫ МОЖ/10 н1>1p:1-
Щllli:tTIJ в раствора х. :.Это llCTPY/\I J (} 11p0Bl'p1 ITb,
6·11
Математика за работой
наблюдая, как обра:1уютс}j мале111.кие кристал
лики на дне сосуда С" п еренасыщенным раство
ром соли. В далёком прошлом думали, t1то кри
сталлы питаются и растут nодобно животным
шш ржтениям, /(а/( бы изнутри.
(3 XVll н. датчанин Ilюrьc Стснсен (Стена,
16.)8- 1686), рабuтан11111 1I но Флоrе 1 щии , ис
слс!(овал мно1 ·очнсленные формы крнсталлон
КВ<tрца. ()нн OTJ ll JЧ tVIHC n Дj)~'Г ОТ !tруга ЧНСЖJМ
гране~\ формой и размерами. Стенсе 1 J :заметю1 ,
что грани ра~1.rrнч11ых кристаллов ю~арца мож
но сопоставн '1 1, так, что углы между соответ
с1вующ11ми гранями у разных форм будут
равны (рис. 1) .
Закон Сте11се11а о постояпст13е углов в крис
таллах 1 ·о~юрит о том, что у крист;uuюв одного
и того же вещества число и форма гр:шсй. как
и их размеры, мuryr быть разиыми, но углы
между соответственными гранями постоянны .
Замети'l'L> ПОСТОЯНСI'ВО углов между 1·pai IЯМИ
крисrаллт1 бьmо непросто, нотому что rте всег
да какой-то 1·р;,ш11 о одтюм кристалле соответ
ствует грань R ,'\руrом кристалле того же ве
щества. Объясним закон Стенссна на та 1<0м
примере. Что общего у различных м1 югоугол ь-
а
·о оп
Рис. 1.
642
Рнс. 2.
никон 11а рис. 1? Несмотря н<1 их ра:~нооnра
зие, можно зам ет11ть, что у л 106оl'о мноrоу1 ·оль
ника кажд::~я сторона паралл ельн;~ одной н:i
сторо1 1 п ранит,ногu 1юсьм 1f)ТОл1>11 и ка. Поэ·1·0-
му угол между днумя сторт1ами м1 югоугоm,
ника будет равен углу между соответствующи
ми сторонами в праnилыюм восьмнуголытке.
H;,t рис. 2 показано несколько крист~UJлоп
кальцита (исландского шпата). Соотв<:тстве11-
ные rран 1 1 у ра:юых кристшuюв выделены оди
наковым цнетом _ Углы между такими граr-1ям11
одинаковы .
Стенсе1 1 объяпrил, в чём пр11чина paвerrcтua
у1·1 юв. Вещество послойно откладывается rra
поnерхпости кристаJ1J1 а, nлаrо~аря чему он
растёт, а шюсrюсти граней в процессе роста
остаются параллельными самим себе, и, слсдо
вателыю. углы между ними не :изменяются.
По утам между гранями можно опредешпь,
из ю1ксн·о Dсщсстш1 состоит кристшш. Это -
один из ос1Iовных вопросов минtралогии. Для
рас11озна1:1ания м1·1нералон н старых у•1сбниха.'<:
минсрало1' ии 11редлаг~111;;~сь класснфик~щия,
котnрая учитыв~V1а 23 внеш1111х пр1 1 з 11а1<а. Сре
ди них - цвет, внешний пид, блес1<, 1 1розrач
ность, :1Rо 1 1кост11 , запах, вкус 11 даже хладность,
а таюке прили11а1 1 ие 1< языку Нетрудно пред
ставить спор двух исследователей, одному из
rюторых минерал на BI<yc 1<ажется горью 1 м , а
другому-1шсловатым . После о·rкрытнн з<1кона
rю<.-1·оннстна углов ст~uю проще 011реде.11н·1ъ , и з
како 1 ·0 вещест ва состоит мннерал .
В 11ai.w,r дн11 у1·лы между гранями измеряrт
с помощью прибора , К()ТО[>1,1й на~;ывастся
ro1гиометром. Ре::~ ул hТаты и:1мерен 11~, Cf)a 1111н
вают с лаш1ыми 11 ми11ералоп1ч еских таблицах
во:~можных з11аче11ий уг;юв у раэличных ве
ществ (атл.ас состаnлен русским кристаллогра
фом н ми11ералогом Н. И. К(жшаровым).
ОТ КРИСТАЛЛОВ К РЕШ ЁТКАМ
Аббат Рене Жюст Аю11 (1743-1822), француз
ский крисrd1шо1'раф, получил в кругу знакомьLх
про:звище Кристаллодроби1·е;11" Однаж;t.1>1 , бу-
дучп в гостях у коллекцноIJсра мине р а;юu 11
рас:сматриван друзу nр~пматн чссюrх крнстал
лон кальцита, .Аюн уронил сё на nuл. Дру:3а -
нсскuлыю крнстаююн, 11apucJJJиx на общее uс
нuва11ис. - rассытталась 11:i множество мелки х
осколкон, 11мсвш1 LX форму ромбоэдра. Сре1\и
осколков кальцита nыли и параю1 СJ1ештсды с
)Тлами, как у ромбоэдра. 1ю с рt:брам11 ра~н-ю1I
,i.Iдl 11 rы (Ромбоэдром 1ru:Jьmaeтcя п:~рат1елеп н
пед. rш·r·opы rl получается 1в куба » результа·r·е
р:.tстнжеrшя нлн сжатия последнего вдолъ нро
странствстшой д11агон~tл11. lkc ero rранн -
однна1<оныс ромбы. Отсюда и пазван11е: оно
о бозначает .многQ1·р~тн1ш, у котороr·о все
L'ран1-1 - ромбr.t; рнс. 3.)
Вер н уш ш 1ch д< >мой, аббат про;щлжал кшють
КJlИLт:.u1лы кш11,ц1 1 та. теперь vжс .и:j собс:тFJен
ной кол11екции. И ош1тh nнJJ' rх1ссыщiлис1, на
·1 ·акпе же мале 1-н,кне па раллелепипеды. 1<0тo
pnJe, в свою очередь, распаf(апись 1 1 а ещё меН1,
шие м1ю1·огранники Т()ГО же вида. Аюи поду
мал, что яз эт1-iХ мменькнх параллспепипедов,
как из ю1рпичш<0n, можно сложить кристалл
любой ВСJШЧИНЫ (рис. 4).
Аббат-крнсташю1раф с.цещ1л :нерный вывод:
криста;ш - это соедине 11 Re равных м ельчай
ших 11аралле.11еn~-тедон. Т<~кн м образом, на
чи11ая с первой 1юло1н1 ны Х1Х в . кристалл
стзли рассм;..~трннат ~-. как твёрдос тело, цен -
Рис. J.
Рис. 4.
Рнс. 5.
Rездесушая математика
-п1
/J-и
!.h и+!./> !.а+.!.!)
!1ll + l.J
.
.
.
-IJ а-IJ1.а-Ь 5а
-
IJ
Рис./,.
б
тры атпмов которОl'О обра:--1уют прострап
ственную решётку (рис. ';_) .
Что такое реmётка? Откроем тетрадь в КJlет
_11.у. Выделим точки. н которых r·ор11зонтаm,пые
люшн пересекаются с вертиканьными. Сово
ку 1J нос1ъ всех этих точе1< - 11 р1 1 мср плоской
рt"шётки. А опрсделнть общую шюскую ре11 1 ет
ку можно так: 1юзьмём дн;1 семейства прямых.
в каждом нз ко·1·орыл 11рямые nар <l ллелr,ны
между собаr1: и равноотсrоят друг 01· друл1 .
Мпожеспю уз;юв пересечения пrям 1 .LХ OДl-IOJ'<J
семейства с прямым1 1 дру 1'Ого и естъ prh.ttifmкд.
Решёт1<а - простое, но важное понятие,
nричём н о кристаллографии, и 13 математйке.
Её можно задать при помощи вектоrо11 .
n роведём из одной точки два нсктора а 1'f ь '
нс лежащие на одной прямой. Р~смотриN всс-
1юзможные суммы вида mli + 11/J, 1 ·;~е т 1-r п -
н роизволы 1 ые цел ы е числа (рис 6, а) Концы
таких векторов н состанят плоскую ре111ётку
(рис. 6, 6).
Прос-1ра11C'r'Re1 шая рсшётка пnределяется
соnерше 1r но а 1 rалоп1 ~1ю . Для этпrо 11уж1ю
взять три вектора а, Ь , с, не JJежащие n ОТ( -
1юй плоскости, 11ОТJЮЖИ1'Ь ОТ одной точки nc-e -
D03MOЖl IЫe и~ суммы с целыми коэффициен
тами: mZi +nl? + рё . Коr щы всех такнх сумм и
образуют пространстве:1шую рсruётку.
СИММЕТРИИ РЕШЁТО К
Выбе::ре."1 в решL:.Тке любые дut: точки А ~' В. Ра с
смотрим 1·1 аrаллет,ныi1 ш:ре::нос Lla нс1-;.1·ор АВ .
Точка А прн этом переносе перемещается 13 точ
ку Н. В с1ю10 очередь, точr<а В перt:дви1·астся в
точку В', которш! 11рнн:тлежнт той же решёткс.
И. 1юобще. любая точка решё'гки r~еремещастсн
при параллельном переносе обяэ:пеш,но и
некоторую точку рt.:шёткн. Итак, 11ара1 1лсл ьный
пере н ос 1 1а любой щ::ктор решi..:,·кн совмещает
_
_J
64)
м.пематика {а работои
решётку саму с собоИ, ~1ли. другиl\111 слова:-.1и,
яnлястся спмметр1н:1'1 рсшёткн . Под сл01юм
•CII;\L\-ICTp!Ш7 ЗДСС h TIOll\IM:tCTCH 11 юf5осдн11жеr-111с,
т1сре во1\.51щсс рс1нl'тк1 с.1му в ссб.н. - нс обяза
·1тлыrо 1r.с1 1 1· р:.~л 1,11ая 1 ш 11 осснан с11:\1мстрш1.
В част110ст1 1 , рассмО'I рснная сн.ч,\1С'1рня- 1 1ере
нос 1rа:11,~настся тра1тС11я 1 ti ю111 юй (тра1 1 сю11 tlIЯ -
др~тос 11~1з1J<11111е п~1r>aJU1e.rrыюro 11ереноса). llо
'1Т1мо тра1 LСЛЯЦIЮШ IЫХ CIIJ\.JMC'I рий у решётю 1
11меются и цеIIтральные с1 1 ммстрш1 относ11-
телъ110 любой се точкн. Такие си.:.1мстрш1 пр11-
сутствуют в любо~-1 рсшс.'ткс
BO~bl1<ICM тer1ept. гк:шетку, пщ:троенну10 1~1
1:\3:111\ПI() Пt'р1JСНJ111К)'дЯрНЫХ llCKTOp;t., _ а Н fJ .
13 такnй рс 111 i;тк~ но11влшотся кроме уже су
щестнующ1-1х 11опот нп eJ1 пнне: :'lлt'мснты снм
'-1СI pr111. :Это СИl\1МСТГ1П 1 ()'l'llOCHTt:Л l>IIO лвух
семе11ств юанмно пер11е11д1псулярных ()Сей
(p1fc. 7,и)
Нзме1 н ri\.f /(лш1ЬI :R3апм1ю нcpncrщнi-')'.'lЯp
rrыx векюров li п h (р11с . 7. б). Ilолуч1пся
новая решё'п<а . ЯcIIQ, что характер СJL\1метр111 1
1ю1юй рсшtткlI ос1·;:шстс:я тем же n t'pyr1rry сё
с11ммстриf1 будут гю~прсжнему входотт, n:1p:u1-
11err1,11ыc пе:-реf-ЮСЫ, с11м ,\'JСтр1111 отн< ките11 1,но
точек 1х·111L:тки, с11мм с.:тр1111 относнте.1LЬно в:за-
11мн о 11српе1щ11кулнр11ъrх 11ря~11.1х.
Рсш~тк~1 с пох()ж11м11 1111и, I<:ш с11~ё 1·01юрнт.
11:ю1V1орф 1 1ым1 1 1'руп11:11чн с11ммстри~'1 061,сдн-
11}1 ются п n;~нr 1класс, 1 1:~зыnасмыi1 11 1<р11ста.11ло
граф1ш типом Gpaue. R ХТХ в. фра111~;у:-юшi1 ~<р1т
сталлоrраф Опост Браве покаэал, •по ncc
11ростра11стве1 rт1ыс решётю т можно расщк·дс
.m IТЬ П() 1.+ тпл ам.
Все rтлоскнс р<.:шётю1. 1юс1 роен.н~,1<.: 1 1 ~1 двух
ю:111м110 ш.:: р11с11;\и1<у 1 1ярt 1 ых . но ра:.н1ых tlL>
J1111шс нс.кторах, 11р1 1 н:1,11лсжат 0;1нuму т~tп}- Бра
нt: Еслн у прямоуrолышii рстётюr д1 1111-1ы п~.::к-
а
б
ii
п
Р11с. 7.
6-1 1
Рнс. 8.
торов li 11 IJ од1111а 1ш11ы . т. с 011а квадr. 1 111:Jн
(рлс. 8) , у 1 1её llОЯВЛЯЮТС'Я 1 \ ()ТТО.'IШ1тел~.тrыс
с1. 1 ммстрщ1 1ю сраш1е1111ю С' прлмоvголыюtr.
А лото~1у эта новая решётка попа;.'.\ает в Щ">\'J'Oi1
тнп I>p;mc.
Кяадратн;ш рстпётк1 с11~1мстр11чш:с прямо
)-Тоm,1юl1: у IIcё.' 6ол h111 с ·~лсмснтон с11мчстр 1 111 .
Срс;(11 ни:х - rюнороты на у1·ол l rc j 1 Лсп:о
1rocтrn11Tb Н pc111f.Tl\l I, у которых CC'l'I> CJ1~1.\IСТ
р!ННЮ!ЮрОТ на ~тол 2тс/_~ ю 1 1 1 2.n/<l. Но 1к·1руk
110 1 1ока:3:пъ, что нет рс111ёток с с11 .rv1ме-r·рннм11-
11nноротамн 1-1<1 ~тол lтс/5 11m r 11:1 у1 ·;1 hl 2п/11.
l'Дtll>6.
Нз 1-1 Т111юв Браве I1a11м етнх с11.ч.метрrrч11ыf1
объсдш.rяет ncc II:шбo.'Iec общие реш<:тю1. С1L\1-
мстри11 1ю1oruLX - толr.ко п~1раю1еm.11ые 11ере -
11осы 11 СJIМ!11етр1ш OTllOCIITCJIЬI то ТО'Iек
11очсму тате nажно 11::1~ 1 1ат1, с11м:-.н.~· 1·р1110 крн
стаю111чссr.шй рс111f·1·ю 1' Но -т:рны .,. 011а 1:10 мно-
1 ·uм onpt=/ \t'.llЩ~' I IНIL'ШHIOIO фор~1у кp1icтa. LJ l :t.
cr о 0 1 ·ранку . Во-1.п< >рых. <Л с11м,\н; тр1111 :~:ш11снт
ф1 IЗI LЧССКl lt' ('lIOJllTB:t К[111ст;u1ла.
Как с1111ьно може" 1 и: 111ять 1 ·еометр1 1чсское
lтр1) е 11 1 1 е крнстаJJт1ческо1'<> вещества. 11 1 ·с щ
чи сле и с1·0 с11 м мtтрш1. 11:1 ф11:mч<.::сю 1с c вoii
cтna IфllC"l ':J.ЛЛa, хорошо онюю 1 1 а прн:ж.:рс .1л
маза и графита. l Ia псрвыл нзгля11 мсжд;у 1 пт'ш
нет шrчсго общего. Ллма1 - самый твi.:рдыi1 .\,ш-
11срал . l k случа(шо этот pcl(1<11 й .цра 1·or 1с11 11ыl1
1(амснь нспользуt:тся 11 каLrестве абраз1ш:1 ДJ 1 н
cнi.'·pJ1 , фрез н ;1ру1·11х t1Ню1щ11х, рt.:ж~ щ 1 1х. с н<.: р-
11ящ1tх шк·трумс:нтов . Графнт наст()1 11.1ш .чяпж.
что 1 1 з 11er·o дt:лают 1<:~р:н-щаш11ые с·1 •t:рж1 1 н .
Коне~ 1 1 ·рафнт1 t<11 ·0 стержня 11р11 л~rком со11рн
l(ОС' 1 ЮRеr1ни с (ryмaro lт ра:1ру1 11 ается, щта1111>1я 11:1
11elf след. Ллма:~ - про;1 рач е11, граф11т
-
п~.::т.
Ллмаз - дтrэ.rн.:ктр1н<. графит
-
11 роnодш пс
l'щ:. 10.
Г1 •u"'' 1р>1•1е rк.111
пруктурJ
1рпф"г.1
Р11 с. 9. Гl'ОмРтrиче1 кая
структура a(lмa ·ia
Везлеrуш.:~я м;псмuтика
Тем не ме11сс, с ~ о чки зрениs~ х11м 1-rка. алм~1:1
н графнг - блнжа~'rшнс ~юде1 ·не нннюL И тот
и другой ~шляются чистым у1·11сродuм . Более
то1'0, 06~1 вещества - криста.~Jm,1 , т. е. ус·грое11ы,
к::ш гшюрят кристаллографы, по Jакону решет
ки. Откуда же такое песходстrю в .их физ11чс
ст;:их свойствах? Оно выз11ано rазличнсм их
геомстр11чсских с.:трукrур (рис. 9 11 10).
Еош посмотреть на расположение атuмuв
углерода в алмазе и в ~·раф 1 1те, то Лlтко уви
деть трансляционную ст 1 м 1\1стr 11 ю Rобо 1 1х кри
сrалл ах. Однако их 3'1 омы составляю·~ vжс
не рсшё:п\у, :\ боле~ сложную сч~укгуру.
ПРАВИЛЬНЫ Е С ИСТ ЕМЫ ТОЧЕК
J3о::н.юж1-юсть определят~. структуру крнсг;.uнюв
1 10.НВl!ЛЗСЪ ЛИlШ1 ]:! начале хх СТОЖ.'ТИЯ /Zщё в
r<о нцt: XL'< А. крнстэ11;юг1х1 фы могл н лн шь 1101 ·а
дынаться по различн1,1м косненным прнз11акаi\1.
•по крист;.1лJtЫ нмеют 6011се:: сложное, чем rrpo-
CT() рсшётка, ст rюе11 нс. Перпы м ВЫС'К~IЗ~\J\ та l\YIO
до 1 ·адку н 1879 1·. пемсцкнii кр1 1 с1·аллuграф
Л. Зонкс:. 011 прсдттоложнл . что а•гомы и кр11с
та.плах образуют nра1:1иJ11.нутп систем}.
Пол 11a:s:i матемаn rческ:ш теор ~ in пра 1шлы 1ых
снстем - фундамент С()времtшrого прс1ктав
лс11ня о геометрии 1<ристзлли...1еского nещсства.
Эту теорню созю~л русск11.й кр1 1 сталло1 ·раф
Ев1·раф Степанович Федоров ( 1851-1919). Ра:~
вптне кр1.кташюrраф11и в Х:Х в подтвср/\И!Ю
теорию Фе;\орон:1 .
Прсr1с· 1 ·ан11,ч ссбс ~•том и ВJl/1.C шарш<~1 како-
1·0-то раднус:1 1- .
То 1'да c1py1<1yra тпбого кр~rс
талла будет п ыr ·лнrr.еть "111-южеспюм таю 1х тnа
р1 п<011, которые пс Rходят друr в 1\ру1·и. Но
11р иро1 1а нс тер11ит пустоты. п можно предтто -
1южип. с;1едующее:
1) рассrоюшс ~eil<дy цcr 1 'фtl;\-UI двух ~ шар11 -
коn» не ме11ыле 2.1~
2) любоО ~ттустu1't шар11к» (нс с.:одсрж:.1щJuv1
центров <'(!ТОМОВ») ИMl:C'I' ра.ц~1ус, Melll>ll l\I Й
11ско·1·оро1·u значении R.
М11ожес11:ю тuчск, u'1·всчаю 1111 ~х 11аJванны .ч
услшшям, /IМt.:Нуют (г,R)-МНОЖССТJЮМ llJll.I М!Ю
Жt:С'ПЮМ Де;ю1 1 с - в че;спэ советс 1ю 1 ·0 JVШ'Гема
тнка Бориса Николает1ч;1 ДсJю11е. 011 llJ)'Чaл
с1:1о йстnа этих м 1южестR и в11ёс больш ой нк.11ад
в N1ате ма т1 1Lrескую крнсrаллографшо.
Как вн1сно нз определсн11я. множество Де
лоне весьма проиJволыюе множество. В нёf\1
МатЕ>матика 33 работо11
11е-1 · 1111 чересчур пло111ых скпr1пе1 1нl1 атомов .
1111 стrпт1<ом больших пустот. Квадрат11ую
решётку, nостроен11ую с едиш1чным шагом
(рис. 11 ), можно рассматр11в::пъ к.1к (г.R)-м1ю-
жество с 11~1раметраr.п1 1· =
l/2 11 К= ~·2./!..
Рассмотрнм те11ер1, сн~ё О/\НО усло1шс
услuв1 1 с nран11ль1-юст11:
3) · r·o•1кc.t правилъного множестн:J rжryжe11;:i
всеми осгалы.rыми точкамтr этого множестна
точно так же. как любзя дру гая его точка.
М 1 южесmо. удовлетворяю щее 1:1сем трём
условиям, называют правилыюй систе.;w.ой.
Простейший прим.ер 11ранилыюй с1rсгемы -
энакомая нам рсшётка. Все её точки имеют
одно и то же окружение. Но кроме решёток
существуют 1111нh1е111х1в1tлы1ые с11стемы . Еслп
бы кто-то, ок::~ :~ЗВШНЙС51 и такой CИC l 'Cl\1C, з:кнул,
угомJJён ны й однооnраз11е.\1 этш·о м11 ра. :t :~а те м
проснуJrся н другой его точке, то не до 1 'ЩJ,ащ:я
бы () не~юлы юм путешее1·вин: картнны вокр) г
бьшп бы т<::l\ш же. что и прежле.
Попробуем объяснить, rючe .VI~' т:сн: ес· 1 ·е
стве 111 ю условие правильности стростrя 1<р11-
сталла. Прелставим, что Iq)1 1сталл образу<:.'ТСЯ н1
раств()ра, в котором «плавают» какие-то ()ДИ
на1<овые атомы. Пристраиваясь дру1· к дру~~'·
они рано шш поздно тrахо,11ят положе~ те, от
вечающее 11аимсн1,шей 1ютенц11алъной эпср
ти . То 1 да ccm1 впкруг олно1'0 атома собралась
группа 1юдоб ных атомов. то Roкpyr любого
друго1'0 атома группа атомов должпз быть та
ко~'"1 же - ве1~1, ~ПОМl11 UДГ IН~IКОВЫ .
То, что 13 11р авш 1ы юй системе вес точКJr
имеют одно п то же окруже1 ше, н так до бес ко
т 1 еч~-юсти, означает, что каждую то•шу А дзш ют1
системы можно передвинуть в любую другую
её точку В лри помощи движения - спммет
р1111 сис-гемьr. Вспом1шм, что решётка облада-
Рис. 11.
ст ::1т11м cкol1 c1110 .V1. Пр11ч61 в (..') Jучас рс111['·1·ю 1
характсрноiт с1 1мм е·1риt'1\ псрс: .чсщающе~"1 Ан
R, н 1 mяt"101 параллслы 1ыi1 11с-рс: 1 юс на Rсктар
r1R . 0/\Н:.11<0 C'CЛll праТ!IГ.'IЬН~О I CllCTCM:I ()'l'JIJl 'l<l-
L'TCЯ от р~111ётr<11 , то с11,1мстрш1 , 11ерtнодя1ца11
одну ci.; зада1111ую ·~ ·очку n д[l)'1')1О, - нt' 06я ~{:l
·1
·eJ11.1 ю пс:рt:1 юс. Это ; 1н 11 же1 11 1е можс:т бппп 110-
норатом , С'И.Чi\оlетриt:й ОТПО(! гreJJl>l IO llJIOCKOCTI 1
1 L1п пх комбнr1ацней.
М 1 1ожсс1·1ю нсt:х с11м ."1стр11й 11р:.1ш1ль11<>й с11-
С''гt:мы сскvrаnлн ет 1·ру1шу. которая называется
11puo1ш.rvzo1paфuчeCJ1:0Li . В ч:кт1 шст11, 1·ру11 -
па 11 араш1елыrых перс11осо1i - с11ммt:трнli
рстётю1 - о,цш1 из кр 1ктаттограф11чt:сю 1 х
r·р}ТIП. Но сс1ъ 1-1/\Р}Тие1<р11сташюграфпчесю1е
rруnпы.1:3 н11х входят т:1 юке понорот1.1. с11ммет
рии OTJ IO(. 'HTCJJ l,HO 11 рЯ.'VIЫХ . плоскостей . их
р:tзт1ч11 ыс ком6нна 1 1~ 11 1. Чтобы описать nсе
нозможн ые с 11мметрr·11 r прос1·ранС.'тне11 ных
11 rан1 и 1 ьных сис1·см . нужно ()ьuю сна чала 011 ре
деш rть вес ''рист:н1лограф 11чссю-1е 1·руп пы н
пространст1iе.
!)' 1 у ·1рудную матем::пнческую задачу решил
F.. С. Фёдоров. Сначала учё11ыl1 олределш1 пес
крткталло1·рафнчес кне гру11тты, су11 (ествующие
н:.~ плоскост11 . Их оказалось 17. Плоские 111у1111ы
11звестны .\f!юro веков. Н XlV в" в эпол'у1 1 ш1выr
шеrо расцвета орнаментального 1 1скусства u
Исnашш, на манр11танских орнаментах встрс
с~ались все 17 nлuскнх 1'ру1111. Поэтому будет
11равнльнес ска~ать.. что Фё;юроR доказ:1Л пол
ноту Cl lll CК: I IUIOCI01X 1·rynrr.
В 18<) 11· . Федоров 011pc;1eлru1 l3Ce 11ростран
стнсннп1 с 1 ·ру 1111 ы. И х ок:1:J<1Jюс1. 2.:Ю. 0) 1новрс
ме1 11 ю с Фёдороnым кр 1 кта11ло1·р:1ф11чtскr 1 е
груп11ы открыл немецютfl математнк Артур
Шёт 1флис ( 18';,:.S - 1<J2H). ТакТiм обра:юм. ФёN>
роn и Шёr1фл11с дала полное ош 1саrп rе nrе 1юз
мож11ых ВIЩОВ Cll:'ollMCTpий кр11СТ:lЛJЮВ.
Теория кристашшческого nещестnа, осно
ва нная па по1-1н ·11111 крнсталл01·раф11чсской
l·ру1шы, не 1 нм1.::1 ш е1· сущсс:l'нuвания траш;ля
ц1юнной симметр 1 rи. Важнс(1 шсе свойство
любой пространствен 1щй крнс·1 ·uл1ю1·раф11че
ской i·pynnы заключается и том, '11'0 н 11elr
ucc 1'~a ест1, параJ1лелп11ы<: персrюсы в трёх на-
11ра1те1ш>Jд, 11е 11ар<1; 111t:J 11111ыл 01~1 юr'1 1111оско
стr 1. Rn epnыe это свойство предска~ал Фёf(орон
n 1 Ш3'> г., но строго доказал Шёнфлис в 1891 t' .
Таю1.\1 образом, по теоре.м.е Шёнф.1нса, пра
шtл ы rая с11стем;.1 точек cocтo1rr пз решё·юк, 1ю
нс 11з од1 юй , а пз неоюльких, р~внъIХ дру1· другу
11 паралщ;ды-ю распuложенных.
Носх1uцаст то. что Фi:дuрон 11остро11л ::пу
п~ор1110 в то время, ког1щ е1 11ё не yмl'лrt экспl'
римс11тапьно определять структуру кр11ст:~ллов
Однако Фёдщюuу выпало счастьс.: увидеть тор
жестпо сrюнх и.п;ей. В 19 12 r. 11смецкнй фнзнк
Mal(c фо11 Лау?~ п11е~ 1юлож11л : если кр 1 ктат1
деl~стnитеm.11 0 имеет решётчатос строение, то
11,Олжна происходнть дифракц11я пропущен
ных через него ренn·еrювски:х лучсi~. Его до
гадка бllсстяще rюю·всрдилась. А уже через не
сколько мссяцен ш11 ·лнl!ские ф11:шки Уильям
Гснрн орэ1т 11 Уипьи.м Лоренс Брэ1· 1· (отец н
СЫН) lll!C'pHЫC С /J()МОIЦЫО [)CHTJ't'IIOBCКI 1Х лучей
расо:шфровалн структуру несколью1х крнега;r
лов. Рсзут.та·1·ы со1:1пат1 с 11редсказаю 1 ым11
ФёJ\оровым . То 1ла же русский кристалrюrр:.tф
Ю. В. Вр11,ф (186:' - 1<)2'5) вывел формулу (11:{ -
весmую теперь как формула Вульфа - Ьрэгга),
которая лежит в оснопе всего рентrеп острук -
1ур1101·0 анан11за крпстаююв.
Ра сшифронаТh структуру крщ;1·ал1rа - слож
н:~н эксп ериментальная защ1ча. Тем не менее к
H:lt.~1'( JЯ ЩСМ}' Rreмe1 В! }"А<е СОЗД;!Н~I «Гa.1 1Cf1CSJ ГЮf1-
треТОВ» 1\-1ногих тысяч крнст:;шлов. Иссле;\ов:з
юrя С'l'[lуктуры крнста1шичсских вещестн ПО/"(
тнерднли прсдска ~{ания Фёдоро Rа· 11х е1 рпенне
псе1да соuтветствуеr ол1юй 11з найлент"1х им
2 :ю кристаллографичес1<их т·ру1 1п .
Итак, с одной стороны, определение крис
т~лла юн< правильной системы позволило при
олсчь к изучению его струюуры математичс
с1шl1 ап11ар:1т теор1ш групп. С другой стороны.
как сж:дует 1-tз опрс1~еленнн r 1р:.1н илыюй си
стемы , необхо;~имо, чтобы все атомы былн
окруже ны другими совершенно одинактю
11.0 бесконечности. Но почему тогда n прсщсс
се крн(.'та1111и.зацни атомы выстраю~аются R
нрапильную систему, хопт нзаи.мо;,ействуют
между собой на срашппелыю 1Теболыпом
расстоянии, соотf!етствующем длине химиче
ских свюей? Всцъ из тако1·0 характера вз::шмо
действия слсдуе!" идсrпич1-.юстъ окружения
ато,\.ЮВ другими I1e до бес1<онечности, а л~1шъ
н некоторой ш<рсспюсти. Н 1976 г. nод руко-
1юдст1юм Е. Н. Делоне е1·0 ученики Р. 13 Га1111-
улнн, Н. П Долбил ин и М. И. Штогрин доказа
ли такую Тt;орему: если в (г, R)-системс Rce
точ1<и имеют оди11ако11ые пкрУ',кения 1:1 11рс
деJ1ах сферы раJ\иуса 8R, то снстема является
правнлыю(1. Наппмним , <по R - радиус наи -
Ве-,,десушая математика
Е11 rрд ф Стl"n,1 нови ч
Фелоро н
ndm,rш:тo пустоr·о ш:1r<1 R н ашел системе то
чек. З11ач1л, ,f1,<1J 11-.ний 111::риодичес1<иi1 поридок
в кристаллах в1>1Rо/~11то1 н:J 1-1де1 пнчrюсти J1О
l(алы 1ьrх окруже11нй атомон.
Если потребовать идентич1юстт 1 01<руже-
1П1й точек в слишком м<~ленькой окрестлоС't'и.,
то система точек может бытъ весьма nро.и з
волыюй. В ~том случае 1111 о каком щ1лы1СJ\1 по
рндкс 1<ак будто и говорить 11 е лри"'l:одится. Од-
11 ако .в 19'В г :11-1l'Ш'I йский физ111< Ро;\жер
Пенроу~ открыл моз;шю-1 , н котпрых ят-ю 11р11-
сутствуст далы1нй п орядок. 110 совсршс JJно
другого характера, чем на бтодаем ый R крис
тз;1я-ах (см. CT:l'l'ЪIO «M1юroyГOJlbHllKH<>). в М ()
з~н1ках Пенроуза , 11анрим ер, встреч;.1101·сн
екаю, уrодпо болыnие фра 1·мент1>1, имеrо1цие
оси '5-ro поряДI<а. 11011ый вид симметрии ка
зался лишь нгроil ума. не имеющеiт mнса1юго
отrюшснюL к структуре рс:.иrьных nещсств На
стоя щей сснсацней стало от1<рыт11с, сде.шншос
в 1984 J'. н:~раиль с ю..~м физиком Ш ехтмаrюм 11
его сотруJ~1111к~1ми. Они п о11 вер1'л н рсн'1те1юн
скому ан:ншзу быстро ОХЛ<lЖJ\ённый сnнав
алюми1 1 ия 1:1 м:.1п1ш1 . На диф 1х1кци он 1юй кар
ТИJiС учёные 1юл у чнJJи чёт1<0 ныраженну10".
S-1<ратную симметрию. Еспн бы сnтш пред
стаnлRл собо й ::~морфное 11е11.1,ество, то ero
«nортрет~ был бы совершенно размыт. Но и
кристаллом его с<1итатт, нельзя, так к;:~к ось 5-
ro nорядк;:~ в кристаллах невозможна . ПО- 1311/\И
мому, струюура ::iтocu снлав~1 обнадает но~ым
щ.-що,\1 с11мметр11и
Открытие н природе струюур с некр 1 1ст;.~л-
1юг1хtс):тческнм дальним порядком сооб щюю
мо11\,ш,1'1 имnульс ноному научному наnр~1ю1t"-
11ию - юsаз11кристатюrрафи-и .
647
Математика :-ia работой
МАТЕМАТИКА НА ШАХМАТНОЙ ЛОСКЕ
У ша..'\:мат и математики м11ого родстnсптюго.
Выдающ11~"\сн м~1тсмат11к Гuдфри Хароньд Хар-
11. 11 :~:JМ1:1'1 1 Л 0)\J l :IЖ/lhl, ЧТО pl::lUl:llИC 11pU6JICM
шахмат1-юi1 ИJ 'РЫ с:сть н<:: что нно<::. как матt::ма
т11чL:скос упражнсн1 ·1t:. а с<1ма 111'Ра - наск11-
стыв :11ше матема1·нчес1тх мелоднгl. Форм111
мы111J1е1111я математик::~ и шахматиста до 1юJ11,
тю блпзкп, п пс случайно математпки часто
бывают способными шахматистами.
Шах:.чаты ПОСТОЯl!IТО используются для ИJl
!IlОСТрацшт разлпчпых матсматичес1<нх nоня
тпй н идей. Шахм~tтныс пр11мсры п тсрмш rы
.чожно BC'J рсппь в литературе по кибсрнстп
ке, ·1·сор1111 и 1 ·р. теории 1р:Jсjюв, 1шмбю 1 а·три
кс н т. ;~. Важное место занимают шахматы и в
«КОМПЬЮТсрной 1-1аукt:->.
ШАХМАТН ЫЕ ГО/\080/\ОМКИ
Шахматная матсмат1ша - один из самых по
пулярных жанров эанимателыюй математики,
логических ш·р и развлсчею1й. Впрочем, неко
торые шах ма·1 ·но-м атсматнчсские 1·01юво;юмки
т:rк слож11ы. что ви;~ныс м<~тt:матики разраба
тывал11 для них специальный математический
аm1ар:п.
Прежде uce1 ·0 uсtюмш1м стариш1ую не1·ен
/1.У о пронсхож,1\епин тахмат, спяза11J1ую с о,r~
нпм 1rсожид~шным арифметическпм расчётом.
Награда за игру в шахматы. Когл;;~ индий
ский щ1рь впервые нознакомился с шахматами,
он восхитшю1 нх своеобразием и 061шием кра
сивых комбнн:.щнй. У::~нан, что ::~амсчате;1ьную
ю·ру нзобрёл его nод;\а1111ый, царь 11р11звал 1<
себе мудрена , жс.rтая лично н~11·р:щить за
нt~щумку. В11зстет.111 обе1щ~л пыполнпт1, любую
его ЩЮСI)бу н 61.rл У/1.ИВЛёН, J<ОГДЭ Т()Т nожелап
получить в награду всего лить ТJекоторое ко
л:нчество пшеничных зёрсн. Н а п ервое поле
досю1 он попросил положить одно зерно, на
второе - два и так далее. па каждое послеJW
ющсс поле нужно было класть вдвое больше
зёрен. чем на прс11ыдущсе. Царь рапюрнднлсн
1юбыстрес вьщать изобретателю его ничтож
ную на1 ·ра;1у. Одн:JJ<() 1-1а следующий де11ь при
д11ор11ые матсм<пики сообщили своему 1юве1Lи
тетСJ, что щ1я nы1ют 1 е11ия его пr11юJ ~lй 11 е хnатит
648
пшстщы , храняще11ся нс только в амбарах
все 1 ·0 царС'гна. 1ю 11 но всех амб:.tрах м11ра. Муд
рец скромно потребон~1л 1 + 2 + 2.! + ". + 2''~ =
=i'1
-
1 :з<.:рно. Это число зш111сыuзстсн дная
цатыо цифрам11 ~r фш-1·1·астнчсски нсл11ко.
А тспер1, nринеJ1ём д 11а 11р11 ,\1ера, пока:.1ы
пающие, как шахматная досю1 может () 1,1т1,
1 1 с-пот,:ю1.1а1 ia д.~ш решения иате.матичсскпх
задач.
До1сазате.тJ ьство теоремы Пифагора. Шах
матный rшролh 1 ·россмсйстер 1\tlихаил Таль од
нажды пр11зналсн. <J 'J'O в детстве был потрясён
ДОК~l:~~ПеЛЬСТIЮМ ТСО[lС:МЫ , КОТорую НСра / \ИНЫС
школьн111ш nрои:1 1 юся·1"' 1 ·ак: «П1·tфа1·оrопы шта
ны но -нее стороны paR11 1 м
Нарисуем на IШL'i:матrюй доске ква,11рат, каr<
показ<ню 11а рис. 1. Доска разбита здесь па пяти
частей - са:м кщщрат и четыре одИI1<:1коuы:х пря
моуrольаых треугольника А теперь сделаем
рис. 2. Перед намн те же <1етырс треу1'0JIЬ1шка .
а вместо одногu кн;щрата уже д1щ но меньшеl'О
ра3мера. Треугольнню.1 11 06011х случаях О/\НН 11
те же, а значит, имеют равную гиющщ(ь. Слс110-
вательно, равную тюn\адь занимают н остан-
1ш1есн части доски. : 11<1 щ:рном рису111<с один
кпа11р;~т, на втором - l(Ba. nостсолы<у болыuой
квадр:rт· построен па гипотенузе прямоуrоJ 1ыю
го треу1·ольш1Ка, а маленькие - 11а его катетах ,
nрихо!(нм 1< выrюду, что квадрат гипотенузы
равен C)-~L'-fC юзадратоn катетов.
Головоломка с домино. Ущ1еt·ся л~1 111 ютно
11окры·гь KOCTЯMIJ 1\0.МИНО р:.1:1.мерол·t 2 х 1 11.UC:K)'
8 х 8 кна;1рэтон, нз которой выреза1 1 ы протнво
nшюжные у1·лс)Выt:: кнадр:~ты (рис. ;))?
Можнn бы;ю бы :за1 1 я·1·1)ся ат ·е<lрзнчесюrми
rассужденнями, 110 шахматное ре111е1111е и 111х>-
1це, и t~знщнее. Окрасим уреза 1 111ый квадрат
чёртrым и белым цветами, превратнu его в шах
маnrую .n:ocr<y без угловых полей а1 и Ы3 (рис. 4).
При искомом покрЫ1'ИИ ДОСКИ каж,цая KOCTL, до
мино за1-1 ш·"1аст одно белое 11 одно чi:~р1юс поле.
и, значит. весь набор костей (.~ 1 111тук:1) 1юкры
наст одинаковое число белых и чёрных 11олсf1.
l lo 11а урезан11ой доске чёрных полей на два
ме11ьше, че~1 6t::J11>1x (выреэанные поля чёрные) ,
и, CJICДOB~JTeJ11>1IO, 11еобходНМ()J "О !ЮКГJЫ 'l' ИЯ
доскн 11е су1цсствуст!
Рис. 1.
Рис. 2.
llт:1к, раскр:JСка /{Осю 1 11е тоm.ко помоr:1ст
щах ,\/(:l'l 'I rc.- ry OpllCI l'! 'И J'Oll;'!TЪO! на щ:1'1 no вpC.VIH
11гры. 110 н позnоляст решать пеобыч11ыс м~1т~:-
матпчесю1е голо1.1олом1ш. •Красиnо, IIIl'-1tгo
нс скажешь!,> - nосюптюrул чемпион мира 1ю
шах.м~1та1v1 Гарри Каснароu, ко1да позш11<ом1mся
с решением 3адач.и.
С точки ::1рен11.н матсматика. н:111601н:е интс
рсснос CBOitCTIIO Ш ~IХМ~IНЮЙ доскн З:.IКJlIO'l:l
CTCH в том. что расстшш1 r с на ней rrc сuнс~м
оnыч11u. кратчаiiший путь меж,.\у двумя то ч
к ~н.н1 (nолям11) 11е обязатtльно п змер>1 ется
по прямой лн1шн.
Ни~rья. Рассмотри.ч з11амс11итый этюд Рети
( 192 1 г.). 1·дс это снойство досю1 проявляется
особенно эффективно. 011 показан ш1 р.ис. 5.
Трсбустся, чтобы 6eJTh1e свели пар ·1 ·ию к ннчьей.
К:J.Жстся нсверuят11h1м, что белый r-.:орщ 1ь в со
стш1 нии догнат1. чёрную 11ешку. Одн;.~ко он 1:1с-
премеrл-ю 11астн1 ·rrст её, ccmr от11раRито1н11угь
f re ПО ••()tlh!ЧI JОЙ~ l liJЯ M0 171 118 - 11! , а ПО ~J(OfJOJlt:B
CI\O ~J" Лlll l ИИ (ее :~ fll'Э;IГ IJ<Ж:J1<1H на рисунке).
Рнс. 4.
Ве ~лесушаи м;~ 1ем;~ти ка
Рис. 1.
1. KpR7! 114 2. КрГб ! Kph6 После 2..11 .'> .). Крс7
112 4. с7 КрЬ7 '). Крс1 7 п:сшю г с1·:1новятся фср:зя
МL 1 01щоnремс:111ю. Такан у1ро:1а 11с могла бы
nо:111ию 1 ут1" ecm1 бы 6eлr,n'1 корот, д1111г:u1ся з;.~
неnриятельскоl! neш"oi1 ттрнмо111111еС11 ю, 1ю
шшин 11.
:~ .KpeS! Кр:с6. IJrroщ, ~".115 4. KpdC:> 112 '5. с-;
КрЫ 6 . Крс.17 приnод1п к ПОЯRЛСНl!!О lla ДОСl\е
сразу двух ферзей.
· 1. к:рИ 11:) 5. Крн.111L 6 . Kp:l12. Король ДОШ;.L'l
пешку на поро1 ·с её 11ревр:~щсння. Ннчья! Нс
вероят1 юс стало uчсннrtным.
1Toн>tTJ ю, что с ~точ 1ш эрення» бсJН.>1 ·0 ко
роля, сумм::.~ 11;;п~пт 11рямо)тш1ыюго •1рсуголь
пик:а, изображёпного на р1-к. S, рюша 1 ·н1 ютс
пуСJе! :-этюд Ретн Rсноё RJХ:мя ны:~нал на стuнщую
сенсац11ю н mзхматном мrrpc. I lo чнсто·r·е фор
мы и лако1шч1тос111 материала 11реRЗойт11 этот
гсо мстрнчесr<ий шедсnр псnозыожно.
Задэ.ча о коне А·rrилы. 1ld дuскс нахuднтся
дне фнгуры - белыl1 конь н чер11ый корою"
Некоторые полн 06ъяв11н1uтся •·l'Uр>1щнмrн .
РнL. 5.
g
Математика за раnотой
Рис. 6.
Рис. 7.
Kot 1ьдолжеr 1 ,гщИп1 до нс r 1рнятсльскut'() корш1н,
понсрrнутт, ег() 11 11ер11у·1ъсн 11 нсход1 юt: поло
же11 ие. fму запрещено :~ан и мат1, каr< ~ 1·о rя 1дие»
поля, так 11 поля, уже про11дештыс им одrrажf\ы.
+Трава IJ e растёт там , где ступ ил моr~
конь!» - похвалялся nождт. rушюu Атт11ла,
т-:огд;~ хо1 ·сл сказt11ъ, что его полчища v~rн ч то
жают вес ж11вое н.~ сnоём 11уп 1. Il:1 рис~ 6 ко11ь
л·1·1 нлы μаспо;юж~н Jra g4, ;l 11с 11 р1rнте;1ьсю 11~1
1.:оро111, - нз Ь). Горн щ11е 1юля выдслс1 1ы.
C<Jt:f\llНЯЯ отрезками вес пары досту п н ы х
коню 110.11ei1. между которым11 возможен е1·0
хо;(. пол~-чаем граф ко11н для данной эалз ч и
(tюлям досюI соответствуют нерш ш rы гра
фа) - рнс. 7 (см. статью «Граф ы») В результа
те дело стюдитсл 1< нах.ож.цению в графс такого
щ•ш, котйрый пс содсрж11т 1-пr одной вершипы
более однш·о раза и. кроме того, проход1 1 т
через обе: ныr(еJ 1 t:нньн:~ (на рисунке 0 1ш обве
дены кружкам11).
Мето;tы рсшсю rя псщобных :зада•~, называ
t:мых ш1бирш 1тами. хоро ш о известны ~ теорин
1·р;~фов. Впро ч ем. для коня Аттr r лы искомыl1
Рис. 9.
650
Рис. 8.
11у1 ·1, 1ft'' I PY/tHO ll;JЙ'l ' l 1 11 11(.' ПОСре;tстtк·нно ()11
ссщсрж 11 ·1 · IR ХОДОВ: Kg,~-t"6-cR-g7 -c6- f'8-
g6-c7-c()- a5:h;) cl2 - h l -a3-IJ5-< .:16-f7-
116 - g4. Д.rrя Т(остиже11ш1 цели 1<01 110 ттр11шrюсь
побывать Шl lH ПОJШХ ИЗ 35, 11е COЖЖtl lllblX в
rтачалс ср;~жешш.
В KJIIIгax по :за1111мзтс:лыюй м:.:тем:.~тпке
встрсчае-1 сн ~·rножсство ЗJда•1 о марш ругах
ш ахмат11ых ф111 ·ур - не только I(O IIЯ, 110 и
слона , тщьи. короли, феμзя. Н:шрн мср. дока
з;.~ но, что фсrзь мuжст обойт1 1 всю доску за
l ') хо;~ов (р 11с. 8). Есш1 11р11 этuм разрешить
ферзю 1 1робегать мнмо н екоторых полей дваж
ды, то ОДИ!I ХО/ 1МОЖ.11() CЭl<UH\JMJ.ГГb. Итак. крат
чайший маршрут фе рзя па шзхма'1 ·1юl1 ;ще ке
C'OC "l 'OHT из 14 ходов (рпс. 9).
Задача о ферзях-часовых.. Около каждоf1
тюремной К~\11:еры можно поставит~.. часового.
Находясь у UJtнu r1 1tз н11х. часовой видит. что
прuисходнт ин ,11руг1 1х к:1мсрах , от которых к
дан н uй нсдут коридоры Ю.11ш 1ю наименьшее
ч исло часовых, нсобход11мое rvn1 наблюдент1
за всемн 1<амерамт 1 ?
Есл11 шал'Матпую J 1оску р:1ссматр1 шать как
тюры••У (пусть простят riaм 1J1ахма·1·1 1 с1ъ1 это
срав нение), причём её 1101ш счита1ъ 1самерамн,
а вертик;~ли. горизонтали и диагонали - r<o
ридорамн. тп часовымн сстсствстшее всс 1"О t1J-
зна•1 юъ ферзей. способных веС111 наблюдсrше
во всех н :11 1 ранлс ниях. Тогда задача о часовых
формулируется так какое наимсныuсс число
фе р:-~ей можно рассt-:шить 1-ш ш:1хм: 1 тноi'11щскс,
чтобы 011и держ<Jли ГI О/\ обстрелом все ее сво
боr1н h1с 1ю;1я?
Ока:.1 ывается. 5 ферзе11 111юлн1:: справляются
со всей шахмJТIЮЙ «Тюр r.,мой » (р и с. 1О) Кро-
8
7
Рнс. 10.
мс ТОГ(). ДОК:.1 :1с11 ю, ЧТ() н лз11ей, JLГIH 8 СЛОНОR,
или 9 r<npoлefI. 11m1 11 копей также способны
ко11тро:1иро1>атъ 1кс сrю6одные поля доски.
Интересно. что 11:.i 11.осках прш1зволышго
размера п х п рсшсн11с найдено 11алекu не но
всtх случ;шх.
Рассмотрим теперь :{3д: 1ч11 о 11epet" 1·: .i1 rон
ках ф111ур на ) \оске. которые носят ю101шс ма
тсм~1т11чссю 11~1 ларактср.
Стар11:1rная головоло~н<а. Эту зада чу при -
1\}'Ма11 птальш1ец Гуаршн1 ещё 13 XVI в. О11а
rrерсдко нстречается в 1<1п11·ах по затrнматtль
нотт :v~атематнке. В углах доски ра3меро,\1 3 х 3
стоят два белых и дuа чёрньпс коня (рис. l 1, t 1).
Требуется помсняn, '"'lClvf'~tMtJ белых и чёрных
коней за наименьшее LJHcлo хщщв.
Нанболеt 11зящно за11.<1чз ре111аетС>f 11 рн 1ю
мощи +метщ(а 11yt'OBИ I( {•L НИ'['СЙ • , открыт<.1ru
11 :шсстным м~1е1 ·ером матем:.~тичсских rо1юво
ломок Г. Д 1,1<тени . H<t каждае поле малеrты.;ой
дос1<11. "роме 1~е 11траныюго (11~1 него кони
поrrастп rre мтут) , nоместнм 110 пугов~.щс
(ria р11с. 11, б их з<.1ме11яют кружки). Если меж
ду двумя nош1мн возможен ход коня, то со
отвстстt1у1ощ1 1 с луготщы свяжем 11атью (на
рнсупке rштн - это отрезки прямой) П олу
qсвный ~<Лубок пу1·ониц и нитей JУJС1~утае:.1 т~1к ,
а
Р11 с. 11.
®Ф®
4ф
QJ®®
б
Вездесуwзя математика
чтобы Rce П) 1 ·011иц1. 1 ра<Тrп11ож1 u 111 сь гю кругу
(рНС. 1\,R).
Tene p1, :~адача рtшается nочтн автомат~ fLJ C-
cки. Выбрав одно нз IIa1 1 рG1Влснпi1дш1жешrя по
кругу, будем переставлять копей до тех нор,
пока O!IH не ПО.МС! IЯЮТСЯ МССТаJ\Ш . Чтобы пс
реМСС'П IТЬ конl'й на доске, нужно замсш 11 ъ 11)1-
1'он 1 1цы со<л 1ктст1:1ующ11.м11 1 1 ш 1 нм1 1 . 1l t"грудно
yбel{l-l 'I ЪCJI , Ч'J'() ре111с1 н1е l'OCTl) IJT 113 J 6 rн.·reм<:
Щ(.'H l-IJf конс1'r (KOCf1,\'IJ 16C'J I ЬIX11 IIOCЪMll чёрных) .
11р11чём к()1111 11 rот11вополож1-ю 1 ·0 цвет;.~ М()Г)Т
ход11тrj 1ю очсре(l.н [слн щтою111тс:;11>1ю 1ютре
боват1" чтоб ы 1ю11 1 1 ра~1101·0 цвета прп 1щткс
rпщ 11е угрож::~л 1 r ,Т\Р!Т дру1у (очерё11.1юстL> хо
дов в этом случаr:: тюзnолЛ"етсн нарушал,). то
pe111eIIпe тоже 1шiщём 11а рнс. 11, в. J l собхо;щ
мu 1ол ько слсднть з:1 тем, •1то бы бел1>1с 11 чёр
ны~ KOl-Ul НС ОК~\ЗШIИ('Ь COCCJl)lMII в клубке 'Если
кру1·овпс /( 11riжc1111c ( 11рот11в •1:1<.:01ю1'1 с1·рс; 1 ки )
11<11 111наст б<:льв'1 кпн ь ~11 , тu рсш<:н11е бу; \~·1 та
кое: K.i \ - \)), К:1.~-с2. Кс)-Ы -~1.), Kc l-~12-L':),
КЬ.)-с!-а2 , Kc2 -a l-1):), K<1.3-c2-;,1 f . Кс .3-
Ы -а). Ка2 -с.). Кl):) -cl.
t-.'1е·1·од f12.Т()Ш щ 11 !1l1ТСЙ пе11\О ()6ЪЯС1 Ш'Тl• 'В
·1срмпнах теорнн rр~1фов . Деiктвптелыю, за11а
•1е о перестановке ко11с11 можно соrюстшшт1,
rраф. nерuп шы которого соотвстстRуют nою1м
доски (пугов11щ1м ). а рёбра - возе.южным
хода.\1 кош1 между 1 1ш1ям 1 1 ( н11тяы). тш ·д:~ ра с
r1утыванн<: кл~1бка 11 у1·оющ IJ н1JтcfJ есть не ч1u
11нuе. к~ш более Н~J1щ~нuе 1x1 crюJIOЖl'H l·ll' графа
J-f~I 1IЛOCKUC'J 1!.
Р~1:~умеетсн. мстод п~тошщ 11 н11т61 может
6ы·1·t, нс110:1~..зо11а1 1 д..r1н реше 1 шн 11е 'tолы<n . 1а
,1\ачн Гуар1ш11. 1ю 11 це;юго кщ1сса переста~ю -
1:ючных задач 11 гош)1юломок (нсобяз~lТеJ1ыю
Ш~ХМi.11.' \IЫ Х).
В ~1:шлточе11ис приведём ещё од1 1\' з:щачу
о пересrановке фпгур, nрищ-~'1~ШIГ)'•<> rросс
\\>tейстером З'JНJLчатСJ1ыю:й матсматию 1 Сэмом
Лойлом.
Переход через Дунай. Н~ рис. 12. трсбуL"101
за [ l;tимснъшсе ч1 к1ю хо;1ов псрестанl!'lъ •1е1ъ1 -
рёх белых IIOI J tЙ с ферЗt:НОГО флзн 1'~) на ко
р0ЛС13СЮ·I Й (с 1~ерти1<алеi1 э , \'),с, d 11 :1 е. t·, g и 11),
а трёх чёр11ых - с королеве- кого на ферзевый
(с вертикалей f~ g, h шt а, Ь и с). Короче говоря,
кош~ должны поменяться фла11 1·ами - "бсре-
1·ами реrш Ду11аИ~- СоблrодатJJ очсрс:д 11и сть
ходов не щжпо, 1 то коням з~рсщс 110 отстут1а·п,
(бслым - 1нtс1ю , ч ё рным
-
ю1μанu), Кр оме
Математика ы работой
,,
1> <.
rJ
Рис 12.
Р11с. 13.
тою, на каждоf1 Gертпкали rкcrr1::i может нr1хо
д11ться только однн конь.
Эту голо1юломку Ло(1Л сч 11 тал o;1нui'1 1t ~{
самых тру;1ных и вес1,м:J 1·ор;11 1 л с.и тем. что
мало KO ,\ol) 1.1:{ е1·0 друз~~/ уд:ша1юсh 11 еребро
с1 1ть ко н сli «через Л:унз11·~ (Rсрти-к~urь с). Цслъ
/ \остн гастся :1~1 19 ходов, лрнч~м rгри пере t:ЮДL
1 1а }JЗJllr< ·1 ·еор 1 1и 1·рафон :1а /р11ие становится
совсем простым.
:~адача может быть решена н прн помощн
~метода П)Тuшщ и 1ш·1·ей". Llоскольку безраз
лично . на ка1'.)'Ю половину доски. nерхптоrо илн
1-п1жнrою. попадают кони , n рсшсшш досгаточ -
1ю указать ·1ш 1 ько 1:1ертн к: 1J 1н 1щсю1. Итак, кон 11
отnраню1ютt'.и 11 11ла1~а11не: de, f( i. ~Г. eg. се, hc.
JIJ, Гtl_ 11Г, ~l1, eg, се. ас, Ьа, Li!), Гd, el , се, Llc. Река
Ду1-1а 11 гнжорсна'
КОМПЬЮТЕР РЕШАЕТ
ШАХМАТНЫЕ ГОЛОВОЛОМКИ
13 решен 1 ш математ 1 тчсских головоломок па
u1axмanюii доске, глс требуется огромный щ:
рсбоr вариантов. чсш.)нtк даннu усту1 1 ае1 КШ-1~-
1 1hю·1 ·сру.
l l :.iч 11i.:м со :шаменнтпй задачн о 1.юсьм1 1
ферзш:: требуется 1юдсч1 ~тать число различ
ных расстановок н а нrах ,.,,tат н ой ;1оскс 1юс 1. ми
фcp:1cli . 11 с у 1рожаю1цнх дру1·дру1 -у, т. е 11 е ст
н щ11х 1 1а од 1 юi1 верти1с::~m1, 1·ор 11 :ю11таm 1 11
днагонал11 (цnет фигур пе имеет з начения). Го
ловолом1юй о 1юст,м11 ферзях интересовался
Карл Фри,1\рих Гаусс. во и 011 пе сумел 11айт11
всех во:~можных решений. Позднее дока:-~али ,
что общt'е число расс1·ановок 8 tj:н:рзей раRнО
92 (о; ,11а из 11их 1юказа 11 а 11а р 11 с. 1:)).
/,-)
v)-
8
7
б
5
,,
P1tc. 14 .
Когла-то подсчитап, чнсло ретпстrиir это!l
зад;1 чн бьL•ю всс.hма тμуднu. В н аш11 дн11 ПОJLНЫй
1-1:1бор р;1сст;11-1011ок. прн 11вс/\<:1-1ии н ко:-.11 rыотер
соответстuующсй 11ро 1 ·1х1ммы. можно 11а11·1 ·и з:~
сч1пан 1 1ые сскун; \nl . lft: СJ 1 уч:~й 1 ю 1·01ю1ю1юмк;~
о фср:шх ястрсч:н.:тся как полсз нос уп 1х1жнс нис
110 м 1 ю 1·и х пuсоб~tях 1 ю про 1 ·1х1мм1чхша11~1ю.
А нот О/l.Па r 1 еобычпая шра. которая 11м ее'1
прямое отношение к тoi'r же задаче. Двое 11гро
ков по очеред11 ставят ферзей на uсрт11кат 1а.
Ь, с и т. д" нр11чём ферзи 11 е должны нап<1дать
npyr па l\pyra. П ропrрыnает тот. кrо 11е и состо
яш111 сд(;лать очсрсд1 юй ход - щ1 доске уж<.:
C:'l 'C JllT 8 фepзtl"I ил н Hl:Jl 1> :3fl 1юста HJITb H(.)IIOI'()
ферз.и tk3 1 J~tр)Ш<.::1шя указашrо 1 ·u уош11ш1 .
IJ:i р11с 14 ()елые Вh11 11 ·р:злн · нее 1 ю1 1я верти
кал 11 r ПОД 1\ОНТJ10ЛеМ ферзей , Н у ЧёJ1НЬI,\ He' l
хода. А в 11оложсюн1 на рнс. l '; побсдd на ею
рон~ чёр111,Jх · 11а 11ер·1· 1 1ка1111 е 11 с:т 1111 од1ю1л
доступного поля для белого фе рэя .
Есть и другой вар11ант тoli же ш·ры· то1, кто
делает rюследш 1.й ход, выш·рывает стш1ы<0
очков, сr<олысо ещё осталос 1. на лос1-\е с 1ю
бод 11ых всртикал~сй . Тогда n перnо,"1 пр1 1 мсре
белые i3ьuн ·ралн Tp ll uчка. а 1ю втором чi.;р
ные - ч<::тыре очка .
К:~ков же 11то1· такr 1 х 111 · р 1 1р11 н~шлучш11х
f(С!1ств11ях обс11.х сторон? Что61~1 отнст1 1ть н:1
это· ~ 11сн 1 рос, нуж1ю 11 срсбрать нес но:з можные
11арт1111 (l lX I H::C t<Ш lbl(O'l'ЫCЯЧ ), что. C() l 'Jl:IOIТCXЪ ,
;101юnы ю С1<уч1 ю. Рабоr1 у 1 юруч11111 1 1<0м111,юте
РУ- Вот к r<а1ш.м выводам 01 1 11р1 1ш~л.
В первом варианте игры 11обеж;рют чёр1 1 ые,
а во второ.ч - ш1rт1ш .-~аканчивастс.:я вничыо.
Хотн послсдютй ход прпн~щлсжнт •1ёр11ъrм. 11х
1;;ыи 1 ·рыш coc.~1·aJ:Ы}.IC'J' нуJ1ь uc1 кOL{! Одна 11з н11-
ч tГ111ыл партю'1пре; кта1ш е11а11а р11 с. 1.1 .
Везлесушая математика
8.561512.32'17f()
714i!J.'5516Jl3411
,,53•1348~:i•918
-
~ 22')54.503'i
~-k-
43952-19264~•198
124 540'il
~-Н38522
14.2~42.г
~
"
(
,,
l'ис. 15.
l»1c. 16.
Другая нопу;1 ирная г0Jюнолом1~а. сnюа1111::н1
с путс111естnпем кош1 ло шахматной досr<с, 11a -
3I,J[~:tcтcя Jадачей о ходе I<OIIЯ. 1l ужпо, чтобы
КОШ> uбошёл вес tюля 111ахматной лосю~, не с."Та
новяс1. нн 11;J од11u 11J 1111х днажды.
11 этu!'1 t 'OJIORCЫOMKOLt Зatltl~t aJШ<.'t~ ~tIO l'ttC
11зкt:сп-1ы t: матсма 1 ·нки. ~1 кслr 1 ю1i1 Эl1лср даже
11осю1 ·1·1 .1л ei'1 бu,н.ш ое 11ссл едонаrн1с. О61цсс
ЧLJC!IO ~1;1рrпm'гuв кошт огромrю ВпрС1'JС\1. ко,v1-
т,rо·п:р 1111<::с р·оч 11е1 шя 1:1 .метод по 11ска об
ход11ы х м::~ршрутов ко1m.
Етцё с середТllIЫ xrx n. l IЗBCCTIIO правило
Варнсл.орфа: чтuбы 1юн1, обошёл доску. при
KмKi\OJ\1 XOJ\l: его слс;r~ует ст<.11-ш ·rь i1a поле . с ко
торо 1 ·0 OI I МОЖС"I ' C).l.t'Jl:l 'IЪ II:fl ·( \1Сf11>ШСС ЧllСЛО
<· пμ1.1жкul\·1 11:1 е щё не 11μul'rд <:нные 11м 11шш.
Ecml та1<11Х llOJIC:r'I FICCKOJlbl<U , ТО вы n~rр;нот ЛЮ
()ое r1з н11х.
Roнe.t' 1')() 11~1 пракнло R~~рнс;~орфа счл1·з.
.1ос1, С:н:·:-iукор11 111е1r 1 1ы м. Одн:;~ ко ма1ш rr 111 ый
эм·11ер11ме11т. проnслёшrый ~~же 11 11 аrпе время.
показа1 1: прон.шолыrое пр11.менсrше в·t·opm'i
части 11раrш11а rтr ю1·д<.1 з:шо:1111 коня n туmrк
Посдсдоват<:.rrыю пуJ\1еруя поля, гrосещ~1смыс
конём ( rп с. 16), ыы тшДI1м, что. 1Jача в марш
р~r1 · ('ПОЮ! 117, он CДCЖIJJ 55 .XO,' LUB, / LОбрался ДО
Ь8, а д:т сс двнн}"IЪСЯ не может. Со 1 ·ласно пра
в~ lЛ)' Ва р11с; (орфа , кон п вы 11у-.,к;1сн был 11< н1ТL!
с (17 H:t l)R (номер 56), ПОСКОJLЬКУ llMCllHO на
Ь8 0 11 обл:щ;н::т н;111мен1.11111м11 1{03 "южностя м11
/ЦН! 11еремсще1111lт: 11х чи слu ра111 ю О. R рсз ую,
татс •1аст1, нолей - а8, Ьб, с7. u~. cR. t'4,t6, 11'~ -
осrал3сь 11сnро(1,r~;ешюй.
Конечно, комnыотср в дашrом случ:~е
НС OlipOnepi' праUИЛО В~!рПСДОрфt.1, :1 Лl!llib уrо ч
НIШ с 1·0. Лрuсто t.>К~валось, что второй ч;tстыо
нранш1а 11 ужно 1 юль:зоватм: н ак кура тнее.
562-4420
4:i46-20
6 21zsГ4s
1
1gh
Рис. 17.
С потt Ь4 щ)11Ь ;-ою1· по1-iт 11 на а(, 11 ct'1. 110 т;1коf1
же nыбор был у него 1111а полr= Ц - па cl') п 11'1.
1lоследнш·1 ход 11 надо было 11рс1щочсс.1ъ. То1·,'1,;1
конь ле 1·ко заuсршзл 1 1с1юмыi1 м.~ршрут: сна
ч:v1а посещал нее ранее: нс пrо~"щсш 1h1 с поля:
IO".::\- l1') -f6 -~8-c7-:t8 - [)()- (15. а з:т.:м полн
52 - 56 11рсж11 с1·0 .\1:1р шру1 ·:1: Kc.l')- l1· 1- a6-bl~
cl7- c'). В JJT01·t' 1-1:1 доске нс ос1 :шшюс1, 1111О/\-
1-ю1·0 nпля . н :.~ которОJ1·1 fiы нс 1юбы11:и1 11:01 п"
лрпчём ровно 110 о;\1 юму р:J:ту.
Л IIOT Cll\~ 0/Lll:I :1:.t ll>! 'l'IOIЯ t 'O .IIOBOJIOMKa, < .HH -
:1:H1IJaЯ С IOHIЖCl/llcM КОПЯ IIO ll l <lX~Чa'1110i1
доске. Еслн к~1жды11 cr·o ХО/\ 11эо6ра:шт1, на 1\(>ске
отрt.::11\ОМ прJlМОЙ , СОСДИI Щ\ОJЦ11М не11тры СО<П -
11стствующ1rх полсl1. то 1юлу~1еш1ыi1 графm<
ж1ршру1·:1 н конце концов с .1 моперс:схчётся. !3оэ
н11кает вопрос .какон са.~шй дл11нны11. т. с. cu-
/tcμжш1t1rll11:111бш11 .ш~:=е ч111.~ш 1 хu:~(щ нсс1\·юпс
rссск;нощнйсн 11УТЬ KOl-\H 1\~\ 111~1~.М~ l'l\O~I ДОСКС?
fl<: у к::~ж;щго хн:1·11 п · ·1 ·t'ptr-l"HШJ ни.-1 1 ггы:н с
:'Jтo rl 1 ·оло1юло~ 1 1щi1. Л.ру 1 ·ое дt.:JIO - \1;111пr1-1:1.
И м еш ю она 11 п:нш1:~ ре1<0р1~11ы11 11)"1·1" cot '1'Ш1 -
щ1 u·1 111 у; xnдon. Изш 1 .•111стыl1 ,\1< 1p111pyr 1<<111н
и:юбражён на р11с. 17. Любо!1 с:1едующ1 п'1 х1>.1.
ведёт к сам о11ерссечст 110 rр;:rфнк;:r.
l lanoм нп:м, что 1~ ucJJoвc компьrо·1·ер 1 ю1·0
исследонання 111 ах:м:.~ т11ы:х oкorrчa!Iи i 1 .'1с;ю 1 т
рстроанаJ 11 1:.i - перебор 1ы р 11 аrпон щti..1,1. нс rнн:
р<::д, к:1 к в 11~1рт1111 , а ll:JЗa,'J,, от Vl:lTORl,L ';: [JOJJШKC:-
1111 (1 к 11сходтrому. Мстnд рстр(х11-r:111нз,1 , 11р1щу
.v1~111111 ,11~r доктором фт1 з r r ко - 'v1: 1т<.:мат11 ч ссюrх
11~1ук Л. Бpy,ri.1 ю, nnерные f>1,1;1опро6011анl1a пр11 -
мсре. лежащем 113 грат1 межл;у ш::.~хм::tтrтп1'1 н
м:1темаn1ческni1 rоловоломка:м11.
Задача о Irеnрикоспове1п1ом 1юроле. Бс
J Lьн·1 король c1·0L r.т на с6 1.L нс 1t мсс1 пrана
Математика ~а раnотnй
двиrатьсй . На .11,0ске ШlXOl\Я'l'CH также бе11ый
ферзь 11 черный король (рис 1Н) . Всегда ли
белые мшуг ОбЪЯlШТJ> M:l.'1' чёр1юму КОfЮЛЮ(
Хотн стщ111m13н 1 ·01юволомка о королсн ~~а
ниматсльн;:~ по форме, она требует ссры:::щого
~111ализа. Некоторые гроссмс1"iс1 ~rы 1юла1 ·:u 111 ,
Ч'IО 11ри указ ;11111 ых усJJОНИЯХ ма't'О13ая ПО:111ЦllН
созлаё'1 сн г rс nсе1·да . Тогл;а Бруr~но ре1J111л убе-
1~ит1,ся 1}этом пр 1 1 1 юмощи ма1 11111 1 ы. Резуm.таты
были неожиданные.
На компьютере 11сслсдо!3:1Лпсь партии пр и
rазm1чпых исходных 11оложе11шrх белого ко
рОJш. И 01<аз:шось, что 1'-'1ат неизбежен только
тu 1 ·..ца , ко1да 1-н.: 11рнкосно 1к:ннь111 король белых
:1а1111мает од 1 ю нз четырёх с и мметр11•1ных пo-
11crl: с~ . сб. Г3 . f6. l!:оти он стоит на друп·1 х rюJ 1 ях
3-й JIJIH 6-й l 'OjJИЗOH'laЛll. ПCpT11K<1Jll! С ИЛИ f. '\'()
мат ' 1ОЖ(; F\0:1Можен , lfO 11 JН:IOТIO'I J rтел ЫIЫХ
случ::~ях. 11ри nоз1щии бел()1 ·1>коrоля 1 1 атобо:-.1
;фуrом nOJ1e доски м ат объшшть нельзя-.
Таким образом, n наше:\'! случж при белом
короле на с6 мат чёrшому королю неизбежсп.
Компьютер доказал, что, где бы тогда ни н<~
ходнл ся чёрный корuнь, 011 11011участ мат
пс пuзднее 2.) -1·0 хода . П ривсдё11ная позиция
как раз и Яl\JUfeтcя ре1юрю-юй rю 1~и· 1 ·елыю(.'
тн игры.
1. Фhfi+ Kpg2 2. Фh4 Krgl 3 Фh3 Kpf2 4 Фg4
Kpfl S. Фg3 Кре2 6. ФГ4Кре1 7. ФГ3 Kpd2 8 . Фе4
Kpdl 9. Фе3 Крс2 1О. Фсt4 Крс 1 11. Фd3 Kpl12
1 2. Фс4 Кра 1 1:). Ф1?4 Кра2 14 Ф<.14! Kpl? 1 1'>.
Фе) Кра2 L6. Фсl Kpt):) L7 Фd2 Крс4 18. Фе:-\
КрЬ419. Фd:) Кра4 20. ФЬ'5+ Kra:J 21 . Фl?l Кра4
22. ФЫ Кра5 2:). Фа:)х.
К;,~к _1щдите, бt'лому фер:.ио приаuюсь про
я1шт1, нt:м:uю и:.юбрст:пельности, чтобы одо
леть чёр1-ю1·0 корuш1 . ;;1тот пp11:viep заме ч ап.:-
6
6
7
7
б
5
4
j
2
1>с
Рнс. 18.
Р11с. 19.
654
tl
лен тем , что щ1ервыс н в исторнн шахмат, и в
истории компьютеров машин:~ рсш11ла ~щ.1'ачу
раньше, чем ч<::лоnек. Правда, 1Iадо nризна·r1,,
что CCJIИ кв:1m1фнц1УрО!iашюму шахматноу
соuбш,ают, ч1'0 м:~т есть (например, пр 1,1 белом
корш 1 с 11а сб) , он е1·0 R KOH l \C кuнцон н;L~OДJIT.
Голо1юломка о нелрнкос1юr1с1-~ном короле
доnо111,1-10 заба1i 1 ra , но, с точ ки зре1111я шахма
тиста, имеет оли111tе;1ос1 -~1ток: R 06 1.1чноir 111 ·ре
королю не запрет111111, дсла1ъ холы, 11. стало
быть, да нную з :.щачу нельзя отт rссн 1 1< ч 1кто
шахматным. Orrr с~шо профессор матсмаnп<11 нз
Австрии И. Халумбнре1< придумал необычную
ко1 1 с_·1 Р}'Кцпю, н 1<0торой ндсн о нсприкосно
ве111 юм корол е реализу<.:тсн ~же nри соблюде
н11и Ш :JХМ:J ' r·нш·о КОJ\екеа
Гру11па фшуr н;.~ р11с. 19 эафикс11rюк: 1 11(.1 , а
вот беJrому фер:"lю и чёрнпму корол ю разрс
t11асто1 1 1ахu,n.1 ·п~,сн т~~м, 1·дс::: им за6ла1 ·орассу
; \итсл. Но хотя гrредподнтето белых фигур
п икта не запрещает /\ВШ"Зться (формалы11,rх
оrрапичепий нет), 011 сам не мС1жет себе поз
во;шть такую роскошь после КрсЦе2) сН Ф
чёрныс фигуры вырываются на свободу.
В течение I 5 лет. с 19,17 по 1<;62 г" Халум
бнрек 0 1 1убликш1аJ1более 10 зад~111 с μазлпчт 1 1..1м
11 оложением Г>е1 ю 1 ·0 ферзя 11 чёр1-ю1 ·0 королн .
Олна их эп r х задач заноеваJ1а 11 рнз на 1щ1хмат
ном K(}l-fКYJlCe.
Мат в 17 ходов (рнс. 20). l<aк 11вп всех po;t-
C't L>etшыx задачах , здес1, ферзь з:н-оняе- 1 непр11 -
ятсльского короля ~та rюпс h 2, после че г·о сле
дует Ф l14х.
1. Ф<:7! Kpl18 2. Фg'5 Kμh7 5. Фе5 1 Kpg84. Фt6
Kpl17 '5. Ф18 Kpg6 6 Фс7 Kpf'5 7. Фс16 Крс~ 8 _
ф(.'') Kptl) 9. ФIYI Крс~ 1() Фс4 Krf.1 11 . ф(l 1
6
ё
(1
~
4
j
.2
....
-
-
~
е
L1
tl
е
l'ис. 20.
Kpg3 l 2 Фе4 Kpl1.3 13. Фс6+! Kpg~ 14. Фf5 Кр114
1') . Фg6 Kph3 L() . Фg'1 Kpbl L7. Фh4х.
Очет1дrто, '50 лет н:вад кратчайший rryrь r<
матоnой rюзит ~ и.и 11скалrr без помощи ЭВМ. Но
nосле того, как бьи придуман комныотер11ыИ
ретро;:шализ, и3учснис схемы Халумбирсю1 по
ручнлн тю.~шыотеру. 11 в результате, с одной сго
роны, убсдш1ио. в 1cuppeI<тr-юcr·и нсех тrрс;vю
женнмх ранее ·~;щач, а с r~pyroй - нашпи рнп
нuвых интересных ГЮЛОЖСНИll, н ТОМ ЧllСЛС и
рекорднnt: по р,литсm .ности иrры: решение ок:t
залось почти н два раза длиннее 11.риведён 1 тою
выше - мат был объяв.пен па 32-м ходу (рис. 2 1).
Во·г ка1< при наилучшей игре обенх сторон
ферзь ззмапинает чёрноrо короля па поле h2:
1. Фа8+ Kμl13 2. Фа l Kp l14 3. Фа2 КрЬ') LI. Фа3
КрЬб S. Фа4 КрЫ 6. Фа'5 КрЬ8 7. Фаб Крс7 8.
ФЬ'5 Крс8 9. ФЬ6 Kpd7 LO. Фс5 Крс18 l l. Фс6 Кре7
ВездесущJя математика
Рис. 21.
12. Фd'> Кре8 13. ФdG Kpt7 14. Фе5 КрfН 15. Фе6
Kpg7 16 . Фf'1 Kpl18 17 Ф~'5 Kpll7. н на доске nо
зиtщя, nозниюшш n осле r~нух ходов предыдущс-
1·0 решен~ ~я. Складыншт, 11ш1учаем: 17 t 1'5 = .Н
Математика за работой
t\'-1'1\J,,.
"l "J
t
.. .. .. !'\!
~
"~
." ~"
.;.
\1) /\
··/-;..
\(\ l-.
"(
'\\·"
--r· ~\, '\;
1
1
\~
'
\
'1•
1'
'
;'1
,,---
МАТЕМАТИЧЕСКИЙ МИР
13 1ч9.:; 1 u немецко.ч 1о роде Ахене сое10ш1 ась
1<0 1 1фере1щт1под 1 1азnа11 1 1ем " 1 2UОлетеnроnсй
ской ц11ш1.'lн::1ацшr п паукн" За то ч1<у отсч<.:та
6h1JI 11р11ннт ]L)') 1·" ко 1 ·11а Карл Всm1ю11°1 1юнелсл
прt·:11 Ш"I< ш:лъ н cнne i1 с юю щс Ахе11с школ) Там
11 ~~учат 111 м~нс.ч :111Jк~ . С1,чът.ч 3 НЗ'.·IСНJ 1·1ым прс-
1шд:1н:пслсм б111 л у1южснс 1 \ Брит:~ю111 A.'1Fiy11н
0 11 1 1 ~1m 1с 1 л nepRyro п чх·д11снско 1юй F.11p1mc
ю1111-у ;1,т1 11 11,:0111111 111<011 - «З,111ач 11 , 1,.1 1н 11 1о щре
тrия ума юrrо ш сй·> (Мноr пс 1 г1 iадач Алкут1а
l'IЗRCC l lli.t всем l la11p11мcp, Зi1/\,1Ч3 () BOJll<C', J<ОЗС
и кащс'!е , которых t t a,цo переве:ни н а др)тоlr
берег о JlОдке.) В ахе 1 rcкoi1 школе было едвJ ;ш
бt)JJЪШС ДL'СЯТК:.t учет шков, а ССГ()Ю tя ( ОС\ ЮАа
М 11 \;J;tH.:мa ·1 ll IO I '1H.1KO\JHTC.IJ ШKOJlbHJLКll во HCL'X
с1·р:11 rax 11 рофссс1 н н1 алы ю же .J:11111ма1ото1 tv1 ,1-
тсмат11коl11-1сс1шлько c n·r тысяч человек н м 11р с
Он1 1 1 юлучаю·1 чэ·1сwа ·111чсскоL' 06р;1 · юна1шс,
llC/\YT 1IL СJТС/\О l~атсm,скую pafiO' I') . 1I CЧ:J 1 ·,1 k)'I
с~ю1 1 1РУ1 \111 11 ж~ р11ал:1х, ~э 11\ 11щ:шн ;\llС'сертэ-
1~1 1 11, о6щштсн с 1шллсга.,,111 Rсё :.:по вмсс1 е 11
сос 1 авю1е1 м•11е"'1 а111чесю 1i1 ~шр.
МАТЕМАТИЧЕСКОЕ ОБРАЗОВАНИЕ
И ПРОФЕССИОНАЛЬНЫЙ РОСТ
МАТЕМАТИКА В ШКОЛ Е
Первое зп~щомство с матсматпкой происходит
н раш1ем детстве. когда роди1 t<ли, дедушки 11
бабушк11, старш1 rе сёс·1 ры н братья учат нас
сч~rта•rь. скr1алыка1ъ, у,"11-южа ·1ъ, кыч н 1·а·1ъ, J\С
ш п ь 11 11peдJJ.Jt ';(J()' \ 11p oC'l't'IШlllt' :~.1.Ц.1'1 11 110 -
6'56
том - школ:.~., гимт1зия, л11 1\ей. где nреnоюнот
арнфмети1<у. аш ебру, геометрию 1t н ачала ан;~
лиза. Остюnы .\lатсматию 1 ны11с ,·спаивают ncc.
~U l'Я ОДI ШМ ЭТ()Т ШКОЛЫIЫЙ предмет даётся
легко. а друтпм пр1о-п::одт 1тся приЮiадывать з11 а
чн·1·сm,ныс у<.'11J1ия. В России ·1p am щни ма·tс
м:1тнч еско1 о о6ра юнания складынаш 1сь прсж-
д<.: все1·0 1юд 1юздейст»ием немс1щих 1 1~да1·0-
1··ичсск~Lх ндеi1, котпрыс:: нel'JIИ н::i l'eбt' от111:~ча
ток 1щю11111я нелнко1 ·0 Гзусс:о1. ()6р~1:~ова111.uо н
r1ервую ()черс11ь с1 ·ре ,чю111с1, 11рнл:Jть пракгн
чсскую па11ра 1Jле111 ЮСТl>. И потому, быть может,
сотни ·1ъ1 сяч гим11а71истоn, а :затем мию1но11ы
сове тских школы1нк ов :>убри л-и трпrоно
мстрнчсские фopд'fYJJЬI и приnодили 'J1)Иго1ю
метричсскис выраженпя к uи,'{у, «удобному для
:1Оrарифм.иро13<Н-11!Ш ~ (~ся эт::~ премудрость
применяласr, Гауссuм Rегu п.:о.цезичсск~tх ис
следован 1rн х).
1lроблсмы срСJ,нсИ ш1ю11ы жнно of>C)'Mдa-
1u1c h научным сооt1 щестrщм сщ~ ti Л'JХ н. Им
удtля1юсt) болы11ое n11имaнrtt 11 а эасед:т иях
мате~1атнчt'стшй ссю.tи11 nсероссийсю1х с1,е:>
дов естеспюисnыта·1·елс~1 11 враче.И. 11 числе
прочпх там подшrмзлнсь н nопросы о 1Н\J11О
чени11 n ш.колы rуIО проrр:-~мму элеме11тов ма
теJ\1ат11чсс1шго ;шалн:iа, аналитической ~то
мстрнн 11 д:~же теорш-1 всрuятнс>Стеr'L J l аряду с
кру1 11 н::йt11 1 L"1Н матем~1·1·11 юнv1и в эт11х :~ассдан11ях
~ частвовал11. ;1елтел11 средней школы, н ч:~сгно
с1·11 Аt-щрсй. Пе·1-ро1шч Кнсеnёв, по У'Н:~бннку
котороrо уч11лис1, а;1111н де,r1у1лт<и 11 баб~1J1К11.
IJЗПЫ 11 ма.\1Ьl.
В i<o1 ще ХГХ столетия rpynna математшюn
п пс~агоrов во главе с немецю1м у•1ё1Jым Фе
mщсом Клеiтт-юм начала р~16оту по под-готовке
реформы 1111юлпно1·0 матсsщтическuго образо
вания. Uспью реформы было пр 1 1611t1:3нть нpr:
Ш)Jlaвu НJ re матсма·1·н1<н 1< уро1:1ню науки ·1
· 01·0
временн. В 1908 1' . КJ1~йн орг~н:и:.юв<Jл между
н:~рсщну10комиссиюш1реор1--::111и~ацин нрсш.>-
11аван11я 111~пс-маптк 1 1. 1:1 сосган ко·горuй во 11 1л1-1
11 русею 1с учё11ые. Ком и ссщr 11 рnдслала !lот,
тпую работу, rю 11ро1iест1-1 реформу 11 ж11:-111ь
памеша111:1: гаэразю~шанся вскоре Перван ),,шро
вая война, а затем rrосле1юен11ая разруха, гит
леровская дик·rатур:~ н ещё более раэрушн
те11ы1ая Вторая миров~1я но-Ина.
Uд11ако носле ес заRер11 1 е11ня уч<::ные 1:1rt0в.h
нернут1с 1, к обсужден ию рефорJ\.1ьт. lJа этuт раз
р01~ь лидеров BЗ}JЛIJ 11;i себя французскнс У1:1тс
матнкн, н прсжr~с всего t'рупшt. выступав111ая 1rод
кши1с.t<тивнh1м 11l'с1що11имом Никола Бурбакп.
Н:1чзлось у11лече 1iиС форма;1нс1·н 1шй в щколь
пом обра:юнаи11и, ко1·да на noapoc, ско;1Ы<()
будет 2 + :\,надо было отвечать, что 2 +) panrю
. 1 + 2. ибо сложс: 11 11е коммутативно. От форма
.'Iи:стики в кон ечном итоге отт<азались. по 1'0 с11х
нор сщё не nыработапа 1:13nешешшя ко1щспция
Ма гемJтическии мир
<>57
Математика за работой
препоf(авания математики в школе. В чём целъ
школьно го образования - научить при.менять
математику на практике или давать пищу для
~изощрения ума» юношей 1rдевушек - предсто
ит разобраться будущим rюколе н 1тм .
УНИВЕРСИТЕТЫ
После Шiшлы, как nрани110, определяются ин
тересы молод11JХ лю/1,ей. 0f(ни выбирают rума
нитарI-rуrо профессию и больше не занимаются
математикой, друп1е связывают свою жизш, с
естественными пауками: технююI1, медициной,
эко1юмю<ой - и тогда их м атематическое об
разов~шие в том ш1и ином объёме 11 родолжа
ето1 н ныс111их учс:бных ~iа11еде11иях. Те же, кто
ныбрал с 1юей профессией математику, посту
пают в университеты.
Университеты - это не то11ько учеб11ые за
ведения , 110 и круп ные научные 1 ~е1пры. Работа
там организована в форме научных семинаров.
На н их обсуждают статьи, опубликованные в
математических журналах, и докл адываю т но
вые резул ьтаты, получе нные участн икаr.ш се
мш1а ра или его !·остями .
В университетах России научные сем и на ръr
вознию1и в начал е ХХ в" тогда они наз ы вались
«семинариями~. Такой ксминарий" орган изо
вал в 1914 1'. в Моско1кком: ун :иnеrситете про
фессор Дмитрий Фёдорон и ч Егоров. В следу
ющем году научный семинар начал Rести и его
ученик Н икол а й Николаевич Лузин. Сред и
участников п ервых семина ров были будущие
знаменитые математики П . С. Алскса r щров ,
д. Е. Меньшов, М. Я. Суслин и А. Я. Хинчин. В
30 -е 1т. в Московском ун и:верс:и тете сложилас~-.
уникальная система 11ауч.:ных семинаров, мно
гие и з которых задава;Lи тон в исследованиях
в том или ином научном направлении.
Кстати, 11 а 11ауч.11ых семинарах обы ч но н
11роннJ1яются математическиеталапты. Бывают
случан, когда о результате, полученном студен
том, рассказывается в сошщ1юм математиче
ском журнале. Так, летом 1916 г. студент Мос
коnского университета М и хаил Яковлевич
Суслин открьm новый класс множеС'1:в - так
назынасмыс: А-мнuжества. О сноём открытиlf
он н;~писал статью для журн:т:.~ ~доклады
Французской академии наук» . и это принесло
ему славу выдающе сося м.атема·гика. (В 19 19 г.
L· Я. Сусли~1 ско11чался: от сытюrо тифа .)
658
А Владимир Игореннч Арнольд, сщё будуч_11 сту
дентом третье1 · 0 кур са. решил знаменитую
1:'но проблему Гит"берта .
КАРЬЕРА МАТЕМАТИКА
n o оконча н ни у1-1 ~1 Аерси1·ета в ы пускник может
nрегюд~шатh матем:.~тику в шкuле нли работа·1ъ
li од 1-1шvт из на}'ЧН0 -исследовател 1,ских ннсти
тугов. Н аиболс::с: одарёт 1ые гrрсщолж:нот учёбу
в аспирантуре . (В XlX в. твор11ли, что студе11т
оставлен nри у1 шверситете /1,ЛЯ подгот овки "
профессорскому званию.) За время трёхлет
него обуче11ин аспирант сдаёт экзамены (так
н азыRаем h! й I<аtrдидатский минимум) 11готовит
11аучное исследонанне , содержащее 11оные ре
зультаты . Это и сслс/(Ованис 0 11 з: 1 щ 111ц;1ет как
;щссер·rа1 ~ию 11::J учё 1 юм совете, состоял ~см 1rэ
квалифищ1рованных математиков, и в случае
успешной защиты получаt'т свою первую науч
ную степень - ка1щидата физико-математи:че
ских наук (до революции 1917 г. она 1rазыnа
лась иначе - магистр чистой или при кладной
математ и ки) .
После защиты молодой учёпый может пре
подавать n выс ш ей школе и претендовать на
звание доцента или стать сотрудником научно
исследовательского иt·н:титу1·~1 Один 11э ннх -
Математич:есю·1й инстИ'IуТ' т1мсн1 1 В. А. Стсклова
РоссийскпйАкадсмни наук, имеющий фшrиалы
в Москве и Санкт-Петербурп::.
Для то1·0 ч·1·обы 1 юпучнть :т::н-1 ие 11 рофес
сора, нужJ-ю написать и :~ащитить ещё одну
диссерт;щию - на степень дою·ора физико
iv~атем атичсских наук
Далы1е~:-ппес восхождение на математиче
сю·тй Олимп - выборы в чле11ы-коррссnон
дснты 11 ;,сr1 стnителы-1 ые члены Росс 1111скuй
Академии наук или :~арубежных академий , по-
11уче11ие той 1 1ли иной научной премии - за
висит от науч 1 1ых досгиже1111й учс:1ю1·0 э·1 · 1 1
достиженнн обычно 11одтнерждаются нублика
цпями в м:пемат11чесю. 1 х журш1Лах и ю1111·ах.
Самые известные тrз тактrх журналоn в нашей
стра не - матем::1т11чесю1е серии «Доюrадов·} 11
~и:3вt'стий1> Российской ЛI\адсмпи rrayI< , <· Мате
матический сборник~, J!х)'Рнал «Успехи матема
тич.сских наук" . Антuр 1 пет этих журнал о в и
з н ачимость публ11куемых в 1111х м<1тср11<1 1ю11
с1·олl1 LIЫCOI01 , ЧТО уже МНОl 'Ие l 'ОДЫ (JJ-/J 1 псре
rюдятся па английсю-~й нзык.
Математический мир
ЖИЗНЬ МИРОВОГО МАТЕМАТИЧЕСКОГО СООБШЕСТВА
В XV11-XVJll вв. ведущими научны.ми учрсжде
н11ямн были акадсм11и Имtнно 1н.н<ру1· tiиx
яырастаJ 1 ::~ нова>1 t.:вроn<.:йская наук<~ . В
ХVШ столетии особое место з::~ним:1л~1 Петер
бургская Акадtмия наук. С реди её членов был
крутшейший математик тогd t~ремени, ле1·ендаr-
11ый: Леонард Эйлер. Наряду с Петербур1 п<ай
важнейшими академиями бьши Ло1-щонс1ше ко
ролевское общестnо, IЪtрижская и 13ерлшккая
:~капемии наук
Академии выnускал11 науч11ые журналъr, ~·де
лечатал11.сь р<~боты по различным областям зна
ний - t)' I' истории J\O ~атем~1тню1 и мс;\ици1-1 h1 .
Та1юны, Jla11p1 1 мc:;p, <·КОмментар 1 111 Летербур1·
ской Акапемни наук•. том:-1 которых сс t·сщня
~1ожт-ю найти но 1-кех крупнейших бнбт-ютеках
мира . Чнсто матема·пfческ.ие журналы гюяflи
лисп tl XIX в.
Оп11.н из перJ'\Ых математических жур11а
ло1З - <-Анш~лr,1 чистой п прикладной матема
тики» - выходил во Фр~н-щии R начале Х!Х в.
Ло имени издателя его назык1Лн просто «Ан
налы Жt:р 1·оню1 ->. Он нздавался л.о 18 .~ 1 r . H;i
смену ему прщuёJI <-Жур нал чистой и nрнклад
ной математ11ки», выпускавшийся изнестным
французскпм математиком Жозефом Лиув1т
лсм. Он сущест13ует 1ю11ынс. Матсм ;пики. ссте
сrве11110, сжрестнлп его «Журналом Лиун1иrля».
Точ 1 ю так же nых(щящий 11в наши- д1111 11емсп
кш1 fЖурпал чистой и прикладrюl1 матема
тики<> сташ1 име11оват1> «Журшшом Крелле».
С 1868 г. n Германю-r 11убтжустся одно из веду
щих .ма ·1·ематиqеских и:ща 1п1й - "математиче
ские а 11н алы». ГlерRый 11з ны н е существующих
μоссн!1ск~1х. ма·1 ·ема'1 ·ичсс1.<1а журналов - « Ма
·1 ·смат1 rчес юJй сбор1 шко) полнился в 1866 t' . Е 1'0
н;.tчало выпускать Москонскос математическое
об1 1(ееrтю.
П()Сl\Оm,ку число кrтых матсматичес rшх
н:ща1-r1-1й 61,1СТ})О ГЮС'JЮ и СJ1едит 1·. за 11им11 ст2 -
rюuилось всё тру;~нее, пршплось соз.п:а·1ъ рефс
ратишrые журпалы. Это спеrr.налъныс изда 1 1шr,
в которых печатаются рефераты, - кароткие
обзоrы работ, опубликованных в р<1зн:ых стра
нах. !311ерныс такое 11зданне - ~ книга успехов
математики з :1 l'OJ\i> - в1,шустн.л11 не,'1ецr<не
м~tтематнкл я ! 871 г
\.('t'Одня существует несколько ведущих ми
ровых рефсратнR11ых матем:1тических журна-
ло.в. Зто прежде всего амери1<анское «Матема
тическоt: обозрение.::", немецкая «Цептралыrая
1 ·азета» 11 росснйсю 1й «Реферативный жур11ал
математика •. Их можно н<1йти н любой матема
тической бибтютеке мир:.~.
Знакомспю с научными журн~U!:!МН не заме
няет лиq11ых контактв мате м атиков, живых
л.искусснй. В XIX п. тако го рода нстречи стал и
нормой с нач:ала н пределах од ноI1 стр~шы .
Математические классы ака1J;емий, математи
ческие кафедры ведущих университетов, ма
тсматичссrще общества взяли ш1 себн труд
орrаниз<щии националы:tых математических
сооб ществ и .между1-1~1 род1-ю1·0 сотру;~ничеств~1 .
Одно и.~~ старейtш 1х матсматнчсск11х об
ществ л.н 1р з - Москонское мат~::матнческос
обш.ество. Оно уч[)<::ждеr-rо при Московском
у1-щяерс 11те1е в 1R64 1·. Лон до1 1ск ое ;v( атс м<~ ти
ческое общество бьJJю ос1 юна1 ю в 1865 1·" в
1872 r. -
Французское, о 1884 г. - Математи
ческий кружок в 1Iалермо (Ит:~лия), в J Н88 г. -
Нъ10-йоркское, 1} i89U г. - Геrманское объеди
нсни~:: математиков.
К началу ХХ n. математика достигла на
стот,ко :iначительных уснсхов, что возн..има
6'59
Математикс1 ,~а работои
потрсбнtХТI> 11 о р1 ·:~ 11и.1 а 1щ11 мt:жлу11арщ~ных
лш ·1·t:ма·пtч ескпх копгрессо11. П е р11ы(1 "1·:~1щй
коr 11·ресс состоялся в Цюрихе в 1897 1·" ~по
рой - в Пар11же 1:1 1900 г. На пём выступил
,1.1,авнд Гнльбсрт - r~ р уттнеИший мзт<::матик
мира. В сnо<.:м доктще он сформую-1ровзл ттро
блс:мы. которые, 1ю е1·0 мнt:нию. должны опрс
деюл •ь ра:~ннтне м:1тематик11 н ХХ стоJ1етии (см.
CT:l' l 'hIO \•ХХ FICK» ).
До Пt:рвой м 1-1ро 1ю~-1 1юй 11 ы 1<oi11pet·cы нро
вод11ли<.ъ каждыt:: ч етырt:: гощ1. r::iзp<1a 1 нш1~ШС}J к
1914 1. пойпа 1та1юлrо прерн:ша 1 юр м алы-юс
·1·ече11иt:: 11ауч11ой жи ·щн. Что()ы её 11алад11 ть,
110·1реfiсщались годы и 1rем:l!!ыс успл ня. R 1919 '"
был оснопан Международный математич1.:сю1~r
сою:1. Н о о п объениrтf!.r~ лишь ма те11.-1апшо в
стран-нобсднтсл ышц. lla Мсждуна рот1ы i'i ма
тсматичсскт 11·1 кон1рссс f\ СтрасбурJ·с, созва11-
ны11 союзом в 1920 1·" 1rс .чсцк 1 1с у чё11ы<:: даже
не 6111лн 11рнглашены.
С11сную11(иl1 Мсж11.унарuдны1'1 м.::~те м.атr1че
скн~'1 кою'ресс собрало~ в 192...1 1". п канадском
городе Торонто. И сам выб()р ора1 LЫ, д::tлёю)Й
от соб ылrй прошедшей nой11ы. и прrrглатттенпе
на коrтrресс математиков ncex стран. 11 ус илпя
п ре:дседатсля о рп<шштета ДжоLJа Фшщса спо
собствовали тому, что этот кош· р есс стал
n::i.жrюt1 нехuй в исторш1 ,'Ушров ого математи
ческого соо61 1(<.:с1 ж1 . 3а· 1 ·см кою рессы прохо-
ПРЕМИИ МАТЕМАТИКАМ
Науч1-юе открытие С~'1О по себе - пелнчайmее
счасть е . Открыв законы движения планет,
Иоганп Кеплер писал: « Я предаюсь радост11 и
11е стесняюсь 11ох:в~шиты..-я пер ед смертными : я
пох11пт зuлотые сосуды сг1 штm1. чтобы со
здать н:-1 1н1х храм моему божtству вдали от
r1рс; ц::лов Епшта". Пр очтётся 111 1 ::~т;1 кнн1 ·~1
MO(IMir сопремс нн11ками , нли по·1 п.\1с 1 ·но ,\1 -
нс стонь уж важ 110 , - она н а!щё:т CJ:IO C I ·о ч11т;1-
тсля . Ра:ше Гос~ юд11 Бог н~.; жд;_~л шt::сть т ы сяч
лL"т с< >3српзтешr Своего тно ре н:ияi".
Труд у<-rё1юго пршюсит Rел ичайшее удо11-
леrворс1-111с, но в то же время челове1<. ищущий
пстину. нуждается в моральпой, а ч.асто и в
мате риальн ой 1юддеrжкс. Пuхnала и прпзна-
11нс uкр ылн ют. дают новые силы ,тщя работы, а
1ЮТО-"1У и госу[(:1рстненные стμуктуры, и отдсль -
660
д11л11 в Болонье ( l92R 1' .}, Цюрихе (1952 r .) .
Осло(193(> 1·) .
0,Т{Нако прот111юстшп111с Первой м11ро1ю~-1
B()Itlll1J Щ)ОДОЛЖ~IЛО c1<aЗI1lli:.l'l'l>CЯ 11 а )1(1 131-111 м11-
ро1юго мате м апrческого сообщес1 ·на. Поэтшvtу
кош'РеС<.' н Цюрихе прш15L'1 реш~rшс и т1юш -
1 1аци11 Между·на рuл:rюго м:'!темап1•rt:ского со
ю:{а Была обр:1::1она 11 а ком1rсс1ш по созданию
н овой меж1tу 11ар u!1,но 1~1 0 1яанн:.Jацни мате;ча
·111 к<-ш. lfo к кшrгрсс.:<')' н OCJIO ::~та коянссия
ш.: CMOL'JJ:-1 ныработатп r 1pllt:'l.IJH:ЛU1J X IJJX'IOIOЖC
Hlli'I . Me/IЩV тем 1 1:щnнгаmкh · г ра 1 · 11Уl' ск 11с 1.·о
(lыт 11я: НЭ/t F:пporюl1 11:11'\НСЖI тень фaШIJ CTCKO JI
с11ас 1·н кн. впсрсю r 1)ыла RтopaJ1 м 1 1р(mая В( >йнз.
Очередно1 о ма·rсм:птrчео<01 п ко 11тресс1
приmлосr, жла ть до 1ty;o г И внош, он cofip:111cя
111Je Еnропы - в ClilЛ, А f'арнарде. Тогд,1 же
возобJJОRИЛ CROIO ДСЯТt"Л ЫLО СТЬ и Мсждун;~ро;J,
ный мап:l\r:1т11чt:ск~ 1С1 союз. С тех пор конгрессы
собнраются рс.тулярно - раз н ч етыре 1·ода.
l la кон1"рссс:Jх вс;tущJ1е учё11ыс т~елают об
зор1-1ь1 е )t()ю1;,щы по н.;1ибш1сс 1шж11ым н:1пран
J 1 сн 1 rям conpe'\1e1 11 юi1 ~~:1л:м;1т1 rю1, соос1ща1от о
резуm1 1 ·а тах, получ сш1ых з;~ 1юслt::д1 шt: 1 ·011ы.
пбсуж./1:1 ют проблемы п прое 1\'Jъ1 . 11ш1 11 ующ1 1е
матемзт1 1 ческое сообщество. Там же r1ро11сло
,rtит вруч с1 1 ис 1т а J1 6олее почён1ых матсма111че
сю1х премнй и самоi1 1tpecпDююlr и: ~ ш1х -
прсмт 1 и медали ,1.1,ж Ф1-тдса .
11п1 е JtJO/(И помогают учё111,1 м Ою1а 11:1 фuрм
такой 1юддержки - мt::дали 11 премш 1 :ia 111,1 -
дающпеся 11а)"ШЫе результаты.
Кто 11 ког,rщ в первые стал 11~грщт<1щ1ъ учё1 1111х.
0·1ве1ить111удпо. I lo n XIX u. uру,1:11ш уж<.: доста
тuч1ю мно 1 ·0 .чедал<::й 11 пpe~>vtнfl, 11 с.~мн фаюы
'l'<IКl lX пr11су·,кд1.: 1 Jl IЙ CT;J HUlc\ll J!lТCЬ ПрСДМСТО,> L
на 111 юналъно.i1 1·opNX'T11. <J; 1н о1°1 .из са .чых боль -
111 н х rю чс.х.'тс l1 , которы.\ )'i\Осто1 1 л11сь p)CLKLtl'
M :J'l't:мaт1 IIOI R \.'ТХ CTOJLCТI Jll. была llPl' ,\Hl}I Бор
де нз Парнжс1{(){1 ак:щсм1rн наук В 1RRH t '.
сё
нручню 1 Софы: R:к11т,еп11е Кон;u1снскоl1 .
R настоящее время Росснйска}! Лl\алtмнн
наук присуждает трн tv1 едал11 и д<::nять прс.ч11~'1
по ыатсмаптке: ме;~али 6ыт1 учреждспы н
честь Jl . Эйт.:ра. f'I. JI. Чебышева 11 J\'1. 15. Кел
лыпrа: пр~.:мш1 - 11ме1tи 1'1. М. Ви11оградова,
Софы~ Вао1 \1,евна
КОЩIЛ<'!!(IЦ:,1.
С В. Коваж:вскоil. А f 1. l{олмогuрuва, М. А. Лан
рснт 1,ен;1 , fl И. Лобачснсt<uго, А. М. Лнnу н ова.
Л. И. Малы~сва , А. А. Ма.rжона (старше1•0) и
И. Г. ТТетровскnl'О.
Н 1 пеrсс11а пс10р 1 1я премиr 1 Лобачепско1·0.
Ka :i:i 1 1ское ф1 1з1ню-матем;:~тrrческое общество
пост:шнло себе целью сосщатъ каттнтал для
13ручепт1 мсждунаrоююй пре .:vrпи нмеют Jlо
бачс1К1Сого 11 ;1 пригт1шс11нс 06 11 ,естnа стать
IЮЧёТНЫМf l сuн.:намн КОИLПСТа ПО О\JГ'1tlНЗаЦt1И
HIO-JJ<:"l'нt1·0 юбюrся со юн1 рож,.'\енил нст 11<0-
L·о руссю.)L'О ['сомегр::~ uтКJ111кнуткь ~штсмати-
1'11 Г~лыv11'0J1ьц, ::Эрм 11т, Чебыш<.:н, С1шьщ;стр.
Кэнн, Пу~1111<аре, Бс111,'!·раN111, Клсй11. Дщ16у. Ли...
Remrчal111rт 1 e ~'Чё 1 н,1е TOI"'() нре .чснн! 13 пожеrт
ноnа11ннх н cnope l\e11e1· прнш1т 1 участие н
Л01 1ло11скос- королевское о()п~;естn(), п члс 111 , 1
Фrанцуао<о1·а ф.н<ультета 1 шук, и срс~~rше
уч<.:611ыс завс1~<.:шн1 уездных горо[(О13 Росс1111,
11 11еrк' uн~1л ьпы<:: пожсртвователи . Собрали
907 1 рубт, Н6 ксшсск. На эти средства у<.трон
:Jн юбиле\1ш,1с торж1:<."1 1:1:1, 1юстав1ши памятни1<:
Лl)6;!ченскп\1у н Каз::ш 11 , ;.i 6000 рублей бы !щ
о(-)ъявнt:н ы нс1·1 рнкос11онс1 1 ны"' 1\:ш ит:~лом
~1еж;1у11:~ро,1~, 11 ой 1 1 рсм1-111 нме1111 Н. И. Ло6ачсн
с 1юrо. B<YI' стртщ 11~1 <Лшюже11ня о 11ремии~:
<•Uc1юurюi1 1<arшnm премни остаёня 11t:1 1 рJ1 -
кос11овеш tым на всчлые npe~1e1 1 a... ". Имt:т ю
так - па uсчныс uрсмена!
Пср~юс пр11L")1ЖДС I IИе СОСТО>IЛОС1> в 18()7 1·.
Пpt.\'UllO (1ю uтзh1ву ФелJJкса Кпсi 1 1-1а) получил
Соф-,. с Л11. Он.:;\ующ;.1я нрсмня ( 19001'.) J l\)llC)'"'A<-
1\t:Ha В. К11лш 1 нгу. В l 9U.~ 1. 1 1 1х·мии удостоен
Д~11~1щ Г11m,61.:рт. От:3ЫВ на с1·0 р:1f)оту tlllC1J\
Л11р11 T l ya11ю1pt:. В 1906 1. 11рсм 1 1н 11р}11 1ен:1
Б. Лет 1. а в 1С)()() .1·
-
Л . 1Плt::~11111'сру. В 191 2 г.
лаурса· 1 ·0,\11 с1 ·ал Ф. ТПур... 11 <·вечные времена ·> :J~1~
К()] r ч плисъ - рззразt~лаСJ, llерная миро11;~11
uо!н щ а следом революцш1 I 9 17 г. 11 Poccr111.
Jlo с:~.мое удпвителытое, что премия нозоб
ношт:~с·1,. J3 ]927 1". её ЛOJl}"ЧHJI f. l3CilJJ Ь, :1 В
19~7 '" -
Э . Карт:ш н совстсю r й геоr.1стр
В В Rа1·нср. И cнuua н:1чалас1, вuйна. LJ снощ1
персрыв. В J9'IO 1'. t~рслшю 11 . И. Ло6:1 чс1ккuJ ·о
учрt:юш;.~ .Л.к~1;(смш1 наук СССР. Её у1юс1·011mн:r,
Л. Д Ллс1<с::~11,r~рон. Л. 13. Погорсжщ Л. С Гl()НТ
ряпт, Х Хо11ф, П. С. АJ1скс11rдрон. Б. Н. Лслонс,
С. П. Ноников, Г. Бузема 1 1, А. 11. Кш1мо1·щюв,
Ф. Хнрцсбрух, В И. Арноль1\ 11 Г. Л. М~~ргул11с. Как
хочется nсритт•. что этот список 11е прернётся п
6y1te"J· продолжен сто11ъ же сл~ш11ымн 1шс11а-
~111 ) ICЙC1'HIITCJIЫIO на llCЧI JЪl(:' nрсмсна!
МЕЛАЛЬ дЖОНА ФИЛЛСА
Пожалуr1 , саман 1 1:шестная 11.1 мсждунарсщ 1 11,1х
11рсмю\ которым 11 п:праждаются ~ 1 ::~темат11 -
ки. - это премия Фшщса. Её учредителъЛжо11
Ч арлз Филrк родшкн н 186) l'. в Канаде, ок он
чил ~'ппверситст в Торо 1 по . 1ютом доJJго iюm
в Европе, но nepпyяcsi н Торо1 tто 1t рабuтаJ1 там
до конца жиз11н. Его пауснrые работы связ:шы
с тсuрн сй ш1L·еnраt1чссю 1х функ1 lL·tй 1t алl'с6-
ро 1'1 . Од11;1ко 6олыrrс нсс1·0 Ф11лдс 61,llJ нзнсс
т<.::н как t!611\еt'тке1111ый щ~итсш" Им~111ю 611a -
1·0 ; 1;ip}I L'l 'O ~H"'Tl l HlJ<KT l l Н l 92LJ Г. COCTOНJICH
Между11арод11ыИ ма· 1 ·~.;м:1·1·нческий ко111-рссс к
Торонто. На ~TO.'vl 1<0111·peccL оnсуждатнъ l'JJ\d!
Фнлдса - учредить ме">l<д) 1 1 ;\pOJ\II~ ю npt"MИJO
и мед~1т, пu математике. Фи.rrдс П11сал: ·Я осо
бо nодчёркиnзю, что ме/1,аль должна <1ыт1, 1111 -
тсрп~1ц11011алы1а 11 061,ектншrа, п:1скоJIЬ1<t> это
ВО:!.МОЖIЮ. ...Она Ш1 1107\ каЮ ·\i\•1 f\lЩOM нс Д()JIЖ
на 11кл1очать ~'1юiv1llJ1.i ю :rс о ка кой-лп6о ci·pa-
11c, I ПIC'l'ИTYTe HJ\11 Jll·IЧH()("f\\ ?.
Мt"~аль Л.кон.1 Фнллt ,1
661
М.зтематика ЗJ. рt:tбото11
Впервт.rс эта на1рада была нручсна 11а Меж
f(ународ 1 юм ко11 1 ·рессс 11 Осло R 1()36 1·. С тех
лор 11 а каждом между11ар0Аном 1<0111'рессе её
rrрисуждают са.\'fым 11ыf(ающнмся математикам.
На медали выrраuи рова11ы только фамилия лау
реата и год 11рпсужде11ия прсмш 1 . Т:~м нет ни
ка 1<ого упоми н:шия о Филдс(;. И тем нс ме11ее и
гrрсмшо , •'С медаль назьшают его именем.
Фт1;~с сч11таJ1, что Щ1<::мня ;~олж~1а Ht" толь
ко (УГМеч:ать )ПКС .' \OCTL 1l 't -ry• l' bl(.' ус11 е.х1 . 1 , но 11 l:Тil
мут 1рова'ГЪ тrюрчсскую 11еятСJrьноС1ъ л::~уреат:~.
Сонрс~н;11 1 rr1ю r Фнлдс:~ 1ктолкопаш 1 :-:rry фразу
как ук::1запис на то, что 1 ш 1·рюкl1,ат1, СJ1едует uт
носнтслыю мОJЮf\ЫХ учf11ых. Чу~ъ по~жс уст:1-
1юшт.1~1сь uозрастная 1·рапица: лауреат долже11
быть не старше -4U лет.
МАТЕМАТИЧЕСКИЕ ОЛИМПИАЛЫ ШКОЛЬНИКОВ
М:.пе,V1атичес1<ие 011.1-tм11на,r~;ы 1 1 1коJ 1 ьн11ков -
россиi1ское 11~юбрете1 rис. Это cei<i •1 ас 011 11 про
nодя.тся почти 1ю нсех стран;~х м11ра, а бьию
время. когда."
Середина 50-х 1т. ХХ в. R СССР по-1ё'гом 11
<:JiaвolJ окружены J1fтчию1 н геопш· 1 1. строитс-
1111 и мсташ1ур1 ·11 ". А уч<:'нn 1 <::, например матt:ма
тики? У всех 11а устах 1'1.Wt ака11смика 0 1·1
·0 I Оль
еннча Iilмндта, 110 м:то ю·о знал, что он -
nыд:.Jю1111 1 йся а111 ·еб р:н1ст. Рукоподитс111, гю
llяrных экспещщп й~ Да. Но мат<::матик? Пrо
фессия учё1 юго, тем более ., та 1<ой 0'1·1 1ю;11.
11е рома11·1·11 ч~с1<ой области, t<ак ма'I'ематика,
была малопрнвлскателыюй. На математш<о -
1>-~ех;ншческнй фа 1<упьтст Jlешшградского
(ньше Снпп-Пстербургскоrо) и мсханико-ма-
1см:пич<::сюrй ф:1культст Московско1·0 упинер
с11тето11 поданали ;1;ншлсния лишь 20-30 аби
·1урнс11тон в ГО}\, а f\l>IПYCKHИKH IШlИ работ: 1ть н
ШКОJ 11>1.
к-1·0 же бунет прс1юда11ат1, мате:vtатнк~· бу11у
щнм ш1жt11ерам. ге011езис-там, штурм:нrам ,
учнтслям' Кто продолжит слаnу nсемирно
J!~FICCTIIЫ.X петербургской и MOCK013CKOif мате
матических школ? Эти проблемы вол1ювали
математиков страны. Псрnый шаг к их реше
нию <.:Дt:n<LТI члсн-корр<:спон;1спт Акаж:мии наук
Борис НИJ<олаевич Делоне. В 1t):H1· . он пр и 1· л ;~
<.:ил 11~нинтрадски.х школыiнков на матсмат11 -
ческую олимпиаду - соренноие11-11-н~ l:I ре1п1::111ш
нестант\артно сформул 1 1ров<1 1-111ых з;щ:~ч повы
шенной с1южнос1·и. Так уд~1Jюсь выяl:!итъ ма'1·е
мат11чески одарё1111ых IЛKOЛl> ll HKOFI, КО'l'ОРЫХ
;~ате!'-1 пр11rласили учиться в университете.
На следую щ1:1Й rсщ rшицнативу Бориса Ни
t«таевич<t поддержали московские математи
ки. Причём пом имо соревнований читалпсь
воскрес н ые лекции по матсматикt\ р:1бота;~
661
матемапrчt'сю1l1кр:r>А<Ок11р11 Москоко~ом у1111-
всрспте't'е. Его не.11и стущ; 11ты , аст 1pJ11ты 11 мо-
1юдыс преподавател11.
l lacrconы<0 большой п плодот1юрrrо1'1 был а
эт~1 дею елыюсть, можно суДJпъ по десяткам
брошюр серин "1 [опу·.т1рные лекuни по мате
ма·1 ·11кс >} I I днум ДСl'ЯТ.К;J ,\1 ЮIШ l'Cp\111 «БI16J 11 ю-
1 ·ека м.~1'J'(:м:.1т11ческо1·0 кружка•, 11;т11с11111ым 1ю
м<tтерш.1ш1м лекцнl1 11 :1ашпнй кружк:.1111131щ1t-
1-11,1м в р;~зное t\[JCMЯ ИЗД<!Tt'J lhCTIIOM +I:.iyкa->.
IlocJ1c окончан~rи Великоi1 0'1'l'У<:с1·в<::н110!1
1ю~1 ны эта работа 1ю~юб110111 щ;1с~, с сщё nоm,-
111н м р~1змахом . М3тем3т11чесю1t ш111мп11;щы
шко11ыrикоu с1·алп nроно,1'\ 1 11ъся в Т611лнсн. K11-
enc, Смоленске и друrш~ l'Opo;~ax. Пом11м о ма
тсма'J'ИчссrulХ олш.шнад устр;нщ:щ 1 к 1 , фнз11 -
чссю1с, ХИМllЧССЮН.: , J IНIJГШН.:Тичесюн.: 11 др.
0/(Нако участвовать к ОJП1мш .1адах мопш тот,
ко Ll ll\OJJnн11ки болы1111х l 'Ородов А всд1, <.:ели
бы у;(аJюсп 1 1 р11 06щ 11тh к 11:1укс учащихп1 1ю
все ~\ стр~н 1 е, о;ррt:н11:~и м01ю;(ёж1. по111л:~ !11,1 в
11узы - 11е 1ол1.ко в сам1.1е 11:шест111.1е. 1ю 11 1ю
\. '1"1
•
"
.
f:.
1шовъ СО:-J/(ающнеся. таю1е, как Н овос11б 1 1рскт·1
ушшерситет.
И сноТJа ~ёные обратюшсь J{ олим 1 ша,даJ\·1.
Во:3rл~шил это дnнжение щ,щ:нощийся матема
·л~к, а.кадемик Израш 1 ь Монсесrщч Гсльфан.ц.
Чтuбы пр1-шле ч ь к:.tк можно бuльше шк<.т1,нн
ков , ор 1 ·:.1низош,щ:!J1нсь заочные 0Jшм11нан1 .t.
ЗадачJ1 эт1 ~,--;: ол~rмп 1 1~щ 11ублнко1шлись на стра
н11цах <· IOJ,'v!CrJMt)ЛJ,cкnй прав,r(Ы" и «Уч 11тсль
с1юй !'азеты». Устрашзал11сь райо1111ыс ~1 обJ1:1-
стш,1е математические ол11мпr 1 ады, ;i с 196'> г.
11ачала проводиться Всеросс.и йская пщгм1 1 наJ 1 э.
011:-1 состояла из 11ес 1<ольких тyron: школъные,
рш·юнные, областные олиNmнадъr и :~аюrючи
тсл ыrы й тур. L3 к;~ж}l.ом последующем туре
уч:1епюналн 1юбС1\ 11тсли предыдущего.
С тсче11rrсм времени рс1 ·л:н11с нт ш1нмпиаrtы
1\1енялся. С 1970 по 199 1 г. ш 1 :.~ был:1 Всесоюз-
1101'1. Кол11чест1ю участншсон ;{а этот псрпо,71
уме11ыт 11 1 1 юС •> с 80() 1\rJ 1 :;о. Вссроссийскзя мз
·1 ·с::матнческа>1 олим 111-rа}1.::1 ороводитсн в 11нт1 .
этапов: 1) школы1ые олим 11 Шll\ hl; 2) райо 11 11ы е
и городс~шс олимпиа}l.Ъr; .3) областные (крае
nыс, респубднк;шские); 4) зо11алы1ые (в ыделе
ны четыре :юш,1: Ссоеро -Запад н~ш; Цсптраль
нш1; 1Оr·u-За1 1адш1>1; Сибирь и Дальний Восток)
11 5) з;1ю1ючнт<::л ьны lr этан.
Математи ч ескии мир
Пп результа ·1·ам за.клю чител.ьн ог() эта11а
формируется команда на Между н:.1родную м а
тем ати ческую олимпи:.1ду. Пало ск:-1.за'Тъ. чтu не
1ке буД)'ЩИt круn 11 ыt мд1·tм:пики ноказывали
на олим.rшадах 6J1естящие рt::iулhтаты . Ведь 1-ra
таком r<0 11ку рсе n первую а 'rередь требуе1·ся
способность решать большое колнчестно зана ч
за короткое время. В лрофсссио налыю.й же
деятель н остн матем:атию1 часто и м еют дело со
сuерхсложными з;ща ч :.t.ми и :5а ·1· рачи нают на r1x
р<.:111е11ис ,71есятю1, а то и CO'l'HH часон.
Междун;~родная матем:~т1 1ч.есr<:tя ол 1 1м11иад::~
(ММО) стала про1:1одиться с 1C)')R 1' . 1 1 0 ю·нщиа
тиве Ру"11>1 1 ши. Пcpm,Jc ;~есять лет к ней 11рнни
малп участие то1Lько с1ра11 ы Востч1 юй Etipom,J
и Монголия, 11 ричё.1\i[ СССР nocлaJ1 свою коман
.'(у л п ш ь на пятую ол 1н4.rтиаду. 1lo со uрсменем
ММО nы:шала 1 11персс в в зал::1;~1юе:nро11с1kю1х
странах . Сейчас колпчестnо стра11 -уч;1ст 1 шц
11 рнб1шжаетс}! к ст<~ .
ПРИ МЕРЫ ЗАдАЧ
С МАТЕМАТИЧЕСКИ Х ОЛ ИМПИ АЛ
1• Скольк им и с п особами мож110 представ и ть
число п в виде суммы трёх uелых полож ительных
слагаем ы х~
2. В пруд nусrи ли 30 шук, которые ПО( 'Теnf:'нно
поедают друг друга. Щука СL1итается сытой, если
uна съест трёх шук kытых или голодных). Какое
н<J и большее LJИСЛО щук может насытиться? \•Тур
нир городов», 1 qн 3 г.)
3. Н<1 r лавноi't диагонали шашеL1но~1 доск1t1 1Ох 1О
стоит десять ш ашек (все в ра1ных клетк,1хJ. За один
ход разрешается выбрать любую пuру шашек ~ пе
редви нуть каждую из них на одну кле1·ку вни~. Мож
но ли за несколько таких ходов постав1-1rь все w ,1шк~1
на нижнюю rоризон-т аль доски / \20-я lkepocr 11й c -к;:iя
олимпиэда, обласнюf.1 тур, 9 - й класс.)
Ответы и р(~шени я .
1.Числоспособовравно(п - 2)+(п- 3)+ ... +1.
Лейrтвительнu, если х +у + z = п, то \' может быть
рав11ым1,2,3, "., п -2;у+z=п х11прификс~t·
рован ном х у 1~ас есть п - х - 1 возможностей для
значе11ий у и z.
2. Чтобы была nд11а сытая шука, нужнu не мень- Q}--t r
we четырёх шук. Число30=7 4+2.т.е.сытых
шук 1·1е больше сем и .
3. Чтобы поста вить шашки на нижнюю гори
зонталь,нужноО+1+2+J+". +8+9=4')оы1-
11очных ходов. Но число 45 - нечёнюе, поэтому
указанным и в зада че хоD.ами этu rо сделать нелын.
66..J
М,11t>мс1 гикd за работu1l
1rродолжитсm,гюст L МсждупарОДIIОЙ олим
пиады - два д1щ в каждый 113 которых кою,) р
сантам 11рсдла1·аю·1· 1ю:) задач11. На нх рс:111сю1с
отR07~11тся .+.S ч~1са BaжJJo 11t: только само со
реннованис. но и общсн 1 гс членов кuманл ir r1x
рукшюдн·1·слt>й, обм t11 заrр ч ами, 011ытоN1 щю 11е
де 11 ия ко 111<урсон, з 11 ~Н<омс 1·1ю со стра 1 юl1. nр11 -
1111мающей олимmr3,Г()'. Трюмы Мсжлупаро,тщая
матемап rчсская олиNmш1да проводилась n Мос
кве. Команды Росси11, к:ж в своё время 11 1<0 -
мa r t,l '\i.t СССР, на ММО щ:сгда з:ши.мают почётное
.'>·1ссто в п<;рвой пятёрке прнэёров.
и Те.' же задача решают комлщы Роспш. США,
Кнт:.~я и , скажем, комаIIды республик Цент
рал ыюr1 Амсриют тr остроn11 ых rосударсто Т11-
хо1·0 nкealia . llоэтому сейчас проводятся нс
скот,ко рLт11ональн1,tх олим1 111а/ \: Ба1 1 ю1 н скш1
( l.рецю1 , КJ111р, 001 11 ·аrю1, I О1·оt:ла1111н) . Иберо
Лмер111<а1 tскш1 (Испанин , Порту1·ал11>J 11страны
А.Nrсрики, гоrюрящне на и спанском шнr по р
ту1·зльском нзыке) , Т11х()океа1 1 ска>1 11 рял
друг их .
l1еобы ч11 а ош1мш1ада «Турнир t'Ородов» .
нобедитt1щм11 в котороit, 1.;;нс с11едует нэ 11азuа
н1н1, ст:1новятся го рода. У•1астrшкн ко111ч1х·:.~
pt:Ш::tIOT :~:.~дачи 0,1.ЩOilpCMt'IШO, 110 каждый .н
своём 1·о[юдс. А 11р11 011редслею1н 11 uбсд11 ·1·1:1 1 еl1
учитываю·~ • ЧIJCJ]() Жl lTeJlL'Й l'OPOД::t: 'l{:M 0 1l ML'J lb-
rнe, тем rra бол ьп11 rfl коэффт \11<.:нт у~1ножж-тся
Главным недостапщм в 11ронс;\сн1111 Мс:ж-
1~унаро1t н о\1 математ11ч1.:сК<)Й олим 1 1н:оtды яш1я
етс.я :.1 11 ач нте.11ы 1 : ш ра з шш,а в математнческо\1
подrптовке школhн1. 1 кон разных стран. Уча
ст воват1, в MJ'vtO 11рес1.·нж1 ю, о,щ1 а1<0 здес1, ON п 1
«МАТЕМАТИЧЕСКИЙ
КЕ НГУРУ »
Любuпыл-1а щ1импиада « Матема
тический кенгуру ». Из названия
ясно, что родилас.ь 0~1а в Лвс1 ра
ли11. В Е вропе ее пропагандирует
Фраtшия. Несколько раз она про
водилась в Москве.
Что этu эа олимпи,1да~ В о
пе рвы х, в ней участвуют только
школьники 5-8-х классов, в то
время как остальные олимп иады
рассчитаны на учашихся 9- 1 1 -х
классов. Во-вторы х, в ней участву
ю 1 кома~1ды отдел ьны х школ,
прис1ем ч1<1сло шкnл-уча стни u и ко
личесr1ю школьников не огра н и-
чены. Результаты подводятся как
командti ЫС (школы) , так и ли-1 н ые.
В-третьих , конкурсные зала1 1и
носS1т тестовый характер , 1. е . лля
каждого вопро са -.:1 алс1 ч и при во
дится несколько вариаюов ответ а,
из которых нужно выбрать пра
вильныи. Вот дlК' Jадачи: r1t·puaя
предложена на олимп 11але « Мате
матический кенгуру» в 1997 r . (5 ·-
7 классы), вт()рая - в 199R г. (7 -
8 классы).
1. У Мэри ест1, 5 каранлашей, у
Тома их меньш1.•, чем у М?ри, а у
Ника карандашей столько, сколь
ко у М эри и Тома вместе. Какое 1-t .i
ука~анных ниже чисел может оз
начать количество кар андашей у
всех тро их вместе?
а)8;б)11;в)1З;г)14;д)20.
2. Коля и Ва<'я живут в ол ном
доме, на кажлой лестничной клет
ке которо1·0 4 к1.-1ар1иры. Коля жи
вёт на 5-м этаже в квартире номер
83, ,1 B.ir·я на 1-м пажР в ква ртире
номер 169. Сколько лажей в ломе~
а!1'i;б)10;в)8;r)9;л)нельзя
определить.
Ответы и реше ния.
1. За метим, что обшее число
карандашей - че·1 но; 8 кара нлашt:-й
был, нс может, nС>скольку у М"!ри и
Ника вместе нР меньше 1О ка ран-
1начпк ол•1мn~1::1 лы <11v1ате'А ,1тич еrt\,1и
KClll YfJY •·
лашей. 20 кара 11даше й также быть
не может, так как у Мэри с Томом
вмспи 11 1! боль ше 9 кара11лашей ,
значит, и у Ника их не больше tJ, а
вместе 11 е больше 18 кара11лашей.
2. UЬозначим Ч ИС<\О этаже 11 в
дuме череJ х. тuгда 4 х - ком1че
ство квартнр в одном подъезде.
Если п - 1юмер пол~,езда, в кuто
ром живет Коля, а т - номер
подъезда, в котором жиuёт Васи ,
то4х(п-1)+4 4+у=В:!и
4х(т- 1)+2·4+~=169.Здесьу
11z- числа1,2,3или4,nозтому
у=3,Jz=1.Получаем4х(11 - 1}t
+44=80и4х(т-1)+2 4=
= 168илих(п- 1)=16их(т- 1)=
= 40. Таким (>бразом,х ест ь обший
делитель чисел 16 11 40, т. е. или 1,
или 2, или 4, или 1'\. Но мы знаем,
что число этажей не меныrJе 5, по
этомух=8.
.... .
.." .
...... ."
срс;.1ш:с 1юmrчссшо о•шоn, 11абра 1шых чле11:1
м11 команды нз да 1111 ого горо1ц Ишщнатпр:t
~111 ЩK>Bl'ДL'Jll IН l'aJ.\01 'U 1vрн11ра быт 1 Ч ОСI(ОГ\
2
4
Мс1rt•мJ11 1чсск и11 мир
1 - <Н .14К11
ВсFJ11)1 с шн ~'"
олим п11ал
.!
-
HI JЧKH
\t t!;<\Л У 11·1 /Ю,\11Ы ~
ОМtМ1111 ~1Л
·нltlЧIOI
n~"1~.М\И~J\ р'?<. {'у6ли"'
l({ f'
~ll,11 t0.k.
Вс < ·с.оюз1ю11
t1 ..-,~l\.1 Пt.. t I ЛЫ
('IOJ(.' Malt:i\1J1JJKIJ ffx l llllll(ll :ПllR~ ГIO;l,l~CpЖ:UIJI
Бол1 ·зр1rя 11 Л.в< тр.1лш1 Tt'ncp1. 11 rтр1111рс \'Ч.1
CTJJ) ют 1 оро.'\'1 ш:< rсо.1ыт х дсся 11шn < 1р.ш
Список основных обол1ачений
СПИСОК ОСНОВНЫХ ОБОЗНАЧЕНИЙ
Некоторые ма1·е1'1атt1ческие кокС'1'аН1"Ы
~· = 2.71~28.l." UCl!OJJ<lШH: H;JT)'P<IJ IЫ lbL'( JЮ1'<1р11фм ов
л = :\J4J593".
uт1~uщеш1с д.;ш1u.,1 окружн осrи
1<дш1м етrу
с:= 0;)7i2 16 ... nостон~111:н1 Эйлер:~
-
Маскерон11
Г
"•(v'> - 1)/ 1=
0,6 1 80.Ч".
:1оло1'(><:: се ч<.:ни t'
Об1цеl\rатем:ати •1есr<.t1е с~mолт.r
lct l
:Jбс:оmот1 Н)(' ЗIНI ЧСI Н1С (чnдут.) ЧllCП:I /1
lrtj, [r1j цсл:~л час1ъ чиста а
>
<..
г
у
2:
11
[):IRl lO
11t· p a r-1110
l'OЖДC:(;'l' l\C llf IO ра~шо
приб.•111жё 1н ю р::~в1ю
6олыш:-
болы не 11.m1 p'w110
.\1Clfbl!IC
МСТl"IПС IIЛIJ j):JHI IO
кор<.:нh кн:щрап1ыt'1
1Юр<.:11Ь /'l-Й <. ,1 'C11C:lll!
;н 1:1 кс1'."1МЫ
:J I l<I K lJj)OH:.JHe;tt;: I rпя
•следоватслы10 •
•р:1шюсп111 .11О• . .,·1·0 171:1 11 ·1·0Jrы.:o тог11а. когда"
: \lt:1K CLICTCMhl (Y\"Kl lllll.:IH·ti1 , нcpaRCHCTtl}
Э~l:IK { '01\Оl<УГПIО<.."111 (ур:~нне~111 й , IK'l"XLIK' llП"li)
Кul\1бнш1торнка
11!
11 фа l\T\Jри:и
Р,,
ч11СJ Ю 111::реста 1-ю1ю1\ нз 11 э.1смt:tп ·о11
А ;;•
чпсло раз~1.ещс111·1 l1 11:111по111
('щ
"
чнсло сочет.ш111'1 r-тз 11 tю 11i
Множества
{а,. Gll, ". {/111 Щ·JOЖCl"I ко 11:1 :IЛl:Mt:HTOH (/\, {/ !, ". а"
.J
11 )«.:тоt: м 11ожеепю
~
z
Q
R
1 н1тyp:1Jtli!1.ЬlС '11 LCJЩ
цCJlhlt: числа
(XIГ\l lO l l~IЛl•H hlC Ч11 СЛ;t
1tсйс•1·1штс;1r.111.н.: чrкла
ГРЕЧЕСКИЙ АЛФАВИТ
л(1
альфа
1111
вр
б<:та
(-1 {)
Гу
1;tмма
lL
Л()
f\СЛьта
Кк
Er
ЭПС.: ИЛОLI
лл
Zt
лзета
Мμ
:;па
тета
iю1•а
к;1nпа
щtмбна
МЮ
[а, l1J
(а, l:J)
аЕА
({ tl .t!
лев
/1 r/..B
АufJ
.·111в
,-1 __ .!_ _,, 13
j1
,!!.•/
отрезок
ннтерн;т
а 11р1 шаш11::ж11т множсс:тву А
и 11е пр11tщ:vн.:жнт множее 1·нуrJ
А еоъ 1юдм1 южестtю В
А 11е ec-n. TIOДМJIUЖt:LTLIO в
oi'i'hcд1111e 1111e мrюжестн г1 11 J3
tl<' r<.:cc •t clllfC М l·ЮЖСС'П\А 11 в
O'l'(JO(Xtжcгшcj м 1южесrnа rJ 1~ ~щожс<т1ю В
обратное отобр:tжс1111с
ко:-.11 юзtщ 11я u·юfipaжeннi1j 1t ,!{
Комп;н~1<с1п.1е чнсда
м1111мая ед1пr 1111 ;1
Rcz
дсl1 сттпст.11ая •1:1с1ъ К()мплексноrо ч 11с:л:1 z
lin ::
z
l.z l
:н·f\ .2
мн 11 ~·1 ан ч:1стh ко~·mлскс1 ю1·п • 111 с11: 1 z
KOMllJIC'KCl!(lt: Чll CJIO , (.'(>Г1ряжё1пюс к z
модут. ко.1.1плекс1юго ч 11 СJ 1 а z
<1ргу~1с1п 1щм11лс::кс1юr·о •шс.• 1<1 z
Геометрпл
LA
VГOll r1
л.-JJJC
трсу1·от. 111 IK rШС
tf 1111
1l (x:y)
а,iШ
Jaj ,а
П n;ip:UIJICJl bHO fJ
;·оч юt.1! с коор;\11 ~1:~'l':1м11 . '1: 11 у
вектор
J1Л!П1:1 Нl'К'1 ·ора а
Последовательности и фуню~11и
ltt"f
11111 а"
,, "~
1J( IСЛ<::i\ОЩПелы \Ol"IЪ
11 редсд пo<:Jle)\U li<l 'l'<::J!Ы 10l:'I'J1
lim f(x) 11ре1~сл фушщш 1/ в точке х"
.\-.\,1
ЛJ
t{/
/'{х)
('(х)
11р 11 р<1щс11ш: фушщ1111}
д 11ффtре1щ11ш1 фу11ю11111}
н ронэuод11<1я t\J)1trщ1111.J в ·1oчl\l' .\
вгорая r1 ро11зuою 1:ш фу11кц1 111 / u ·~·очке х
J/(x)clx 11с::о пр<::де11ё1111ыl 1 1ш·1·t:гр:111 с!N111<щш.J
"
Jf(x)rl.\' опредслё 111 1ыi1 ю rn:тp:tл ф} шщ11 11 )оти110 /1
Nv
111()
Тт
1·ау
~~
KC l'I
у"
111 IC ll!IOll
Ou
омикро11
Фq
ф11
ll 1t
Гlll
Хх
XlI
Рμ
pu
4'ф
llCJJ
L<';
сигм:~
~~ l•t
nме 1·а
УКАЗАТЕЛЬ ИМЕН
Абель Нил1,с Хt'нрш< ( 1802 - 1829).
1-юрвсжский мате.vtап1к: дuка.J:~л,
что а.r11·сбра11 чсские »Р<Шнешш сте-
11е1ш выше 4 -11 11 обще.~1 случае 11е
разреш11мы В rai\ ll J<aJl;JX; И:JfЧ;1JI
нн п:граnы uт :1111· ебр:)ичес101х
фун 1щ 1 1ii ( абелевы 11 кте1·r.1лы ):
пдин нз co:1л:iтcJ1<:l1 т1::01н111 :-шю111-
т11ческих фу1-1ю\11l1 \Ol, !..;,;,
Абу KaittИJJ (около H<iO - <ЖШIО
9;Ю). :.1p: 16tю1l1\tан:,,1а·111к1:1ыхож·ц
11:~ f.1 ·1 шт;~; ра:~к1 Ut 1·ео р1 но ю1;щрат
!-lЬIХ ~PШJllCH 1111 шzь-.'ll:opt:!.H!U ' ~--11..:
Hl!t:.Дll()фll!lllШ u 11е011pt:дt:.•1t:11111лx
)1)~ш1е111 шх: au·1~op тр:11с 1 ~i; а 11<.1 aJ1-
1·eopc <- КН111'01 ut1 аль-джаор 11 аль
.чукаба11 .1" ( ко11сц 1Х - 1 1a<taлu Х в.)
8S
Абу-л:ь-Вефа Мохамме/1 иб11 Мо
х;1.\lмt:д ( 9· 10 -99 Н), 11epc1·1,r1cкнli ас
тр<mом н м:~тсм:~тик, 1\0~ 1 мс111 :поr
"Ар1rфл1 ст11 юr-> Дtюфанта; nодр<1f>
но рассмотрел тtор1110 J1робе1\ ис
с1едова,1 оп1овн1>1с 1·сометр 11ч с
ск11t' 11ос·1 · рщ:~н ют 11р11 1 юмощ11
Ц11f11<У!IЯ 11 /lllllL'ЙКIJ j 17
Адам.ар Ж;1к ( I H<l'i-10(1.)), фра11-
щ~~сю I Й M:!Tt;M:ITШ<; ~1:1ряд у l" Jla
На ие Ц1 1си•11(JА/ uбос1 юu;~л з::~кш1
[Х1С'ЩJt:дс.11е1шя Щ)Ое1ых чш.:сл; ав
тор 1pYдt)n 1ю диффсрt11 1 щ-.1;u..НЫ1'1
~1хш11с1шя:.1. 1·topr111 фу111щн~1, rсо
рнн '111ссл. ;1.1сха 111шс 1lU, J 51
Аяекса.ндров П~ше1l Серrес1щч
( JH9u 1'Ж2 ), совстск11n J\.1:1тем:1-
тих . OC I IOB:ITCJll, н:~уч1 !ОЙ ltll\ (}JIЪI
тся1шю1 ·и11: [1:tбот~т также в пбшн:
тr1 тсоrн~1 МН()ЖССТВ 11 ТСnрии
фу111щ11f1 112, 661
Аnолловиii ll e p1·cкuй (око1rо
260 - OKO! IO 170 J\() 11 , э.) , дрсв1-1с-
1·рt: ЧС("Кf 1(1 м:псм:л ИК 11 :.llvl р01 toi\I,
дал ПОЛl-Юt: и:moЖt llll t; Тt:ор 11и КО·
HI 1чеСЮ·IЛ l:CЧCI 11 1!1 в тру;~е «Кониче
ские сечс1ш.я->: ~шюр тсор1ш, ofi·1»JC
няющей HИДll MOl" ДBJ IЖt l Шt: 11/Jallt:'I
+i-
..+6. 309, .i21, 576. 491
Ариабхата (uкuлo-t7'5 -'), 1щций
скнй .1етро 1 юм и матеы~1пп{; :штор
.lс-rро1юмическоrо трактата «Ар11-
,1бхз·1 11ам,~ 59. 60, 6 1. 62
Аристотель ( ;~ 8<\-j22 до н э.),
древнсrрсчесю1 i1 фил()соф, труды
которого охваты к;11от 1ючп1 вес
mpaCllп :ша11ия то 1 ·0 нреме~1и. в ча-
стrюсти ш.:pliOe сисrематическос
исслсдошш11~.: 110 1iu 1 ·rн<e 6. 40, 49,
72. 532. 559, ')71
Арло;rъд l3JJ<1/\ 11 ~шp Игоревич
(родился в l 9.'17 r.J, росо11'кюп'r ма
тсматпк~ ~нтоr трудоn 110 днффс
ренц1 "~л 1,н ы ч урав11сн1 тм, функ-
1~иuналы ю:-1 у анат r:;y и п.:ор1111
фy11K l\ll Й Д\:'ЙСТНl lТ\:'ЛhНО\ "() IH•.:pl~
·"ICHllOl'O; 13 ]9')7 1'" буJ\}ЧИ СЩё C'l'}'-
)tt:HT0:-1, i11 .:uu1 11 1 :i-к111rобж.:."1) Ги11ь
б~.:р·1.1 117, (l')~, ()() 1
Архимед (около 2Н7- 212 ;\о 11. э.),
Д(JCBI Н..Tj)t:ЧCCK~I й ~tан:матнк 11 фи
ЗIШ; раэв11л МС."ПJДЬ! Bbl Чl 1t:Jie11ш1
пло 11tадсй. гюнерхнос·1·ей 11 uбъё
мов разл нч11 1,L'( ф~11ур 11 ·1ел. а
т:~юке МСТСJДЫ К:IC'aTt:Jl bllblX н :жс
тремумон. прё/tвосхнптш нс 1111-
тсrrаны·юс 11 диффс:рею tll.l!lbH()C
ИСЧ I l('Jlt.'HИЯ; ШI гр<ЖО 11ри~1с1 1 }1!1 M:l-
'l'CM:tПtЧlX."KllC Мl"юды к ссте стно
:~на111111 11 ·1 СХНИК(' Ф-1 , ') 1-5'). 126.
12Н, 167 , 175. l 9n- 197, .~05. ЧО.
3'> 1, 5SH, 5ЫJ, .161 , 58">- .~Н(;, "1'iO ,
4':) l, '501, 'i7l.-
' )7_1
А.юн (Гаю11) l'снс Жюс1 ( 1745-
182.2) . фp:.tlЩ)'.JCКl lЙ l'ШIJt:jXUIOГ 11
криlТ<!)! .'JОГр:.tф : UTl<J1 Ыll OДlJJ 1 н:1
OCIIOBl ll>! X .JШ<О I Ю!З кр1-1ст;uu101ра
фи.1--~ 642- 6 -k)
Jiappoy Hct'.IK (16)0- 1677). ;tш
т-rйсю111 М:IТС1\1:!ТИК, фJUIOJIOI ', fЮ!"О
слов. 11рофсссор Кс"1fiриджс1<0rп
)-НllВерс11тета. OДllH 113 11 re.ТJ.lllCCT
liCI 1н111шв /./ыотона 11 Лei16mщn в
J>:.t:1pafioткc 11сч11сле1-шя беек( 11-1сч1 ю
мат,1х L),_l - 9 ">
fit;/J,a Достоночте1:1ный (67l иm1
67;) - ОКОЛО 7 .~) ). ;tHl 'J I0("'3 KCOHt:Кl·!Й
Jle"l 1Шf IC't"Ц, МОН;!Х: В T[>:.tKT<lTC <{) СЧЁ
Тt:. вpcMt:llll», llCJCBЯЩt'HIJOM р:~счi.::ту
1\Llt:.й Лзсхи. д;u1 011иС<J ш1t о н ·гсN1ы
счета lra 11:t.r1ьца"" 7 L
Белътрамн Эу;tженио ( НЗ.1 '5 -
1<)00), италынккий математшс; по
.казал, ч1'О геоме· 1 рrm Лобачевско1·0
рс:11111 зуето1 на поверхност11, на
зв~1н1 ю1'1 nссвдuсфсрой 105. 661
Бернулли Л:1111шл (J700- 17R2),
11шеiщарсю1й учёныt1, сдсщшший
вкжщ во вес обл :1ст и сстеспю
знанш1 своеr·о нремсн11 , сы11 И. БеjJ-
Ука.1<:1тель имён
ll)CL'I//; :ш·1оr 31i;.\!Чt'lH1'1'Ul"O тpy,u;t
<· Г1 щрод~111а.ч111<:1" ( t 7.i8 1'.): 1<;1к .ма
тематик работал в облает~~ тс.-ор1111
рндив. тсорю 1 llepoятi юcтeii: стоял
у 1ICTOl<OR ."1aTC~l:\ ТIJЧCC'K01·1 физикrr
98..'18.:J , <\70
Бернулли Иога1-111 (1bl)' -
17·1H) ,
1 11вс1·11~а р ск11й матt'м:1т111< , бр а ·1·
я. пеzту,1ии, 11дш1 11;~ со:щ~11·с.:ж:i1
;111ффср~.:J 11t~1:шы101·0 11 111 1тс 1 р:1л1>
нон > llCЧllCJН;IJKI\ OCl101!01IOJl\)Ж.Н ll('(
!\:tрн;ЩI IOH!iO l '~I Ht"ЧHC.:Jll.."1-\1 lit: <:,;te!l:tН
C~'l l \t'LTU<.:11111.IJ) вю1:1д в t\!t'X;Jl JllKY,
11 р11.чс:111щ u 11t: l1 мс-1 0111,1 матсма ·гн
чсскurо :11 1ат 1за 97, •)8, 18<;, -~50, -IS 1.
469 17()
Бе рнулд11 Якоб ( 1(1'5.:J - 170'>),
tlil.ICЙl\apcкнif мате1щ1 ·11 1щ ра:Jш 111 ме
тоды 11сч1к11с1щя бсско11еч 1 ю \Ы
лых всm1ч 11 1-1 Леr'1611111(а; залож 11л
фунл:1мс1-1т1'<.:opr 111 нсрояп-11 ><тt:fJ, н
1штороl1 док:1·1:111 11poc·1·t: i11ш 111 слу
чай :~ако11:1 болы1111х ч11ссл: 0/(1111 11:1
(.'():щ~11·еж·й в: 1 р1 l:lftllOlillOI'() llCЧHC
JICl lltЯ r.:л, lJH, 1] '> . 199. 1Н'), .'SIO , •1'>0 .
1'51 , l<1l), '>17. ' i lK
Бертран Жо: н:ф )Jy11 Фр:.~щ·у:1
( 1822- 1tIOO). фра111~~Jсю1 11 ж1тем:~-
1·1 1к: JjJ,ICKa:l<!!I l 'IJШП езу u pac11pt:дc:=
JIC Шlll 11рос-rых ЧI !CCJI ( JIO C'l')'J1 : 1т
ьертра 11;1)'. ;штор тру)1ои 1ю мат1.:м<1 -
п1 ч tсr<ом у :ш:v111 зу ~f теорJ111 груrш
L'iO
Болтяксюni Владш.111р Гр~11 ·о ры~
внч (рnд1 шея R l <>2=. 1·. ) , рuсс111'кю 11'1
м~1ТС\·1:.1тик.1tобнло1 сущсст11снны"
реJу1ш1';1тов в с >fiл: tстн тоrюлоп [fl 11
ГОПО.'ЮГИЧСС'КLIХ MCTO/\Ofl, 1<0111611
11аторной геомt:"1рнr1, / tl 1ффсрt·н111-1-
:1111,ных ~ р: 1 внс111 1~1 5C• I. 41::;
БОJIЬЦЗltО [)срнар;t (1-:'Hl - I H· -IH),
ЧC l llt'IO 11"1 ~Pl' l'C,\1:JТll 1\ 11 ф1 IJIOCOф; Н
1шчш1с XJX в. наря;~у LКоиш дал 011-
рещ:.'1<01 ше щх:,це:щ ;111ффсре1 щш1-
J1а r1 11 1пе 1 ·р:та. а т:~к-же щх::vюж1 t •1
строгое матсма·1·11 чсское 1ю1<а:1з
l'ель ство теорс.\lы о 11с11 реры1111uй
на отре:жс фyi11<1t1·111 : бш 1 1 1ре,1\111е
c-1 ·ueшrviкo.ч Ка111пора в 11сс11сдоn.1 -
нни бс:ско 11ечных множсст11 -Р5
Болълй (Gой:~и) Фа рка111 ( 1775
1Н'><1), вс 11 гсрск 11й мат ем. 1т111< ;
!} H~jl г. докаа:ш, 'ITO любы\:' Дl'I<'
равноБе.llШ<И:Х \IHOП)YJ"OJlbl-ШК::I pt11:!-
HOC'OC'"l';ll3JICl-lbl 297..16.:S
_
I
667
Ука"lател1> имён
Боды1 й (linйa11) Я11uш ( 1802
l ~(J0), 1к· 111 ·с::рсю1i1 м;l'l'Смаnш" сын
Ф. Б(Нl.ЯЯ. 11е\авш.:11мо от Л<к'iачен
сл·ш'о 11 ft~J 'C'C({ O'l ' "PL>UJ HCCHKlll'ГДOBY
ГСОщтр1110 /(Н, Ч2<)
Бо~1белл и 1':1фф:1эт: (окопо
J ')26- 1::,72), 11т:1лыrнск~1lr м :1тсм:1-
т1 1 к 11 111-1жс1-1ср: автор TJ)}'i \:I «Am·e -
\lp ;I• (l =; 7 2 1'. ), н 1ю·юr<щ вr1ерв1,rс
ннi.'л 11 м :tT('i\l;t 'IJff{\! Kt)MllJICf<CllhfC
ч11сJ1а 83 -~Н !)7, ~)1. 2~0
Борель ::>м1 шь ( 1Ю1 -19)(>), фрш 1-
цр~.:ю1?t м;~тсмапн(; ат ор трудов 110
чал::ма·п 1 чсt 1<0.,1у ,111анизу, 1·еорш1
ф\·11кшii1, матсi\1:Jп1 ческой фи з111'<::
и 1·сu1.нш в~:рон t 1юстt:·И LLO , l 12.
ни
Боэций А 1 11 11 щ!1 Ма11.nю'1 Се11ер1111
Торкнат (околn · !НО '12·~) . фш10-
С(')ф-1 1со 1 1J 1атон1 1 к 11 р11.\1СКI н'i госу
;~:1рстRL'Н НЫЙ дснтсль, 11ерс:вt'л н:1
х1т11н~.:ю1f1 Н :'IЫК «ЛрпфМt:'ТI IK}'» l lи
IIO~·•ax:1 11lll'PRЬI(' 1р11 ю 1111·11 « 1 laч~U I "
r. к1v1н;р . J1<>HIЧL~(·ю1e соч 111-1 t,н1 1н
11jпи.mшпеля 11 ПopфJJ]JJIЯ 6 7 - bl·j
Браве 0 1 ГОl' l' ( 18 J l-186-\). Ф1хш
црс ю1!1 l\РНС'Л!ЮШ l'Р:-1 ф; UCIHШO
ll OЛOЖJ Jl ll( 1COMt"l'\)IIЧt: Cl(O ~t ·1·еорни
11pu<.-гp:ШC!'JSCI 11 ll.I X рсшё l'Ot< l\pr 1-
C'I :1.' IJIUIJ (1+J
Бра,1.1,nардип То!'>1 :к (UКРЛО 1290-
1:)." J.<) ) ••111 1 ·1111 ~'1сю 1!1 .чагt·м:~·п1к и 60-
1 т1сло11: 1-1:1нl">от .1111 н'1 1штсrсс 1 1 1х·;1 -
ст:1 вт111 его труJ1 •-Тсорс11тчсск;1я
1·соv1("Гр11я» . где <111 р:ксматрнв:.~л
·3вё:щч:п1,1t• \\1-IOТ'O)'l'OJI ЪI НЩ\ 1, !ЮПГХ )
l'l ·Т 1Т:юпср 1Рv1 С"1 1·н111, 1шср н1,1с у11от
рсб111 1 тсрмнн •1 1рр:1111юн:ты-1ы~:н• 11
.ч :1 ·1·<.:'ма· 11 IЧl 'CKOM l ' l\lbll'Jl(:' 7 5, 71\
Б]Jахм·агуuта ( Нр:1м: 11 у1·:.~: около
){)li-(1(1/J). IЩ.tlllKКl l i'l 1vl<l 'ICMaTJIK 11
.ICTГJO llP .ч: автор t<JЧ lll l l:JlltH <- Yco-
1Jtp111c:11c1·11uua1 шос 'чс 1 1иt.: Брах
ч w ·> . :ш:1 ч1 1'J '(:;1 1.11<1я Чаl'Л> 1\(/'I U!)OI'()
1юотщс11а ~1р 11фм е·1 11 ю~ 11 ашсnр<;:
~(). 60, 15:, 197
Бриа 1.1шо11 Шарш . /Кюлr.с:-11
(1 ""8'; - JkC- . ·I), фр:11щу:;ск111'1 '1:1·1 с
м:~·пщ: ра()от:ш 11l1бл:н:т11 Пl)ОСК'I 1·ш
но1'1 1·cu., к·тr 111 r. 1лс 11 знест1-1а тсор с
м;~ l:>p11 :1r111ю11 a ( IH0 6 1· ) t..J -1
Hpoyн-кt: JJ ~ 11лы1м ( Н1.2О 1<>Н·-1),
:11-1 1 л 11й с1,1 li·I м:~тсм:1т1 1к" <>11 н1-1. 11:J ос
н< )K<J'l L' .! 1cl1 11 11t·pн1,rf1 11рс:1Н/ (t·11 т Лон
J(онско1 ·0 корож· 1ккоrо оt1щсств:1 :
11 l66H 1'. 011уб1ш юш;111 11 р11<::м р::t:t110-
же1111я :щ1·щJ11ф ,,щ ра 1t •ю1 1~11u,1 ю1 ·(1
ЧНСЛ:l в Ol'Cl<UI-ftЧJJL>lil РНJ\, flOJIOЖlШ
1'(;.\1 C:l MJ>li\! ( 1 1арнду с )11!/Жt111Ю/ЮМ ~1
668
Ныо11ю//1:.н1) ш1 ча.rю 1 1 рс;ктав.1Jс 1 1111u
фушщ11i1 с 11ш.-ющью бccr<tJ1ttч111,i ,'\
р~щов 'Н
Брэ1-1· У11лы1м Гс 11р11 ( L8bl - I <)·12).
:~нглийсю1й фн:нrк; пл:r1r 111з сх.1-rОR()-
1юложюш()н [Х'НТl'('НОСТГ)'l<'l)'РНОГ()
а11:штr:1:1: ЮЛ:'СТС с Cl>ll-f()M , j . л. 1-ijн?
<Шt. 1~ 19 J3 r. р:к11111фровал :~тсщ
нун >("1 '\ >yК'l")l1Y !)}1)(:1 K\)J ll'TШUJOB ()..j7
БрЭJт У1 1лы1 м Лоренс ( 1kt>0-197 J},
ан1 ~111 1:1сю11:1 ф1r:н1к: l'hll-I J ·: 1: LJ[н1гс1:
OДl JJI lf.l l)l'l 1 01\0llOЛOЖI IH l<OI\ рс 1 пте-
111ктрукт\р1101 ·0 а r 1а:ш:1а 6 i 7
БуJ1ь Д>кL>рдж t 1 Sl'5 - l8(н ). :~111 ·
л1111с1<и r'1 матсмаnш: 0111111 11;3 соэда
тспеit М<Hl'M'.l\'tt'lCCl<OH l\01 Ш'11 'JR~
Gурбаюi Н111ют - coб11pa·rem,
r1ыi'1 l[Ct'BДOШ\f\t 1ру1111ы фр:l111\)1З ·
скнх ~-~:~· 1·с мат1 1 ков , ВЫС"• )1111н~m1х в
1\) :N 1. с ll)lCCЙ 110<.трои1ъ RCICI м:пх:
\•lаТ!1К\' н:1 ;1кс 11< >~1ат1 l'fl' CKШ'r ()('1 (( IKC
11.->. -=;s'),(1')7
Бхаскара Лч;1р1,н ( 11 1 1~-11H"i).
llH, \ИJICIO IJl \l~!'l't·м~ITИK 11 Ж"l'f)OH<)J\1:
:штор труда « Ве1 1е1 tучснr1>1 •, 111юто
ро,ч lO,!..tt'pЖ:J'l'CSI p<::ШC llШJ p:t .3ШJ'l
lllAX алrtt1р:111чсских :1адач "i9 . 60.
bl, Jbl,2H9
Бэббидж L{арлз ( 1791 - 187 1), а 11 1 ·
ли itею1 i 1 1чате~1атик: скu11<..т руиро
ВiИI пери~ ю [jJ,IЧИC!!l11'eJ11, 1 1 yiu .M<IШll-
11\' (1] ') , б24 -<12)
БЭр Рс11с Лун ( 1Н7-1 - 1<):)2). фр::н 1-
ц~~кю rй \•1 ;1·1 ·см:tтп~.:; 1пуч:~л р:1:1 rыв-
1 1ыс фу111щr111 ; д:и 1 кл:ксификац1110
' l '()'ICK р;1: 3рЬ11'1:1 \ 12 , -\7(-,
Валлис Джо11 ( 161()- 1 70.~), :~1-11·
л11йский .\1 :1темат11к: с1·0 1·pyl\
«Лрифмст11к а rkcкo11t.:<J1-H НX>» ( 1<)'>)
f ) {;ЬlГр:111 l.!~IЖl-f\'IO рот, и l о.-1д;1111111
lf( ЧIJlЛCIIJ l>J 11<.:CKOl!C'Jll() м:и1 1 ,1:'\ llt-
)lllЧl l ll 92. L);\, ]')7. 196. I L)7, "I0'.:).2:)
8ан-дер-Вардс11 I>::~ртел Л:u 1;.1ср1
( IL)() _
') - 1<)96). м;1тб1:1п 11<.1ю н:щи
<)1 1аJ11.1 IOCТIJ ГОЛJI .11 1/\t:'Ц, pa\1(J 1·;щ 11
J·сr м:н 11111: а1Зтор тру;,он по злгсll рс.
щ1rс6ра 11чt< с1шf1 1-ео ~1 етр1ш, 1н·то
р1111 \1:1TCv!;1TJIIOl :\2. 1 15
8а1щслъ ( В:1 1 1т~,сль) Пi-.t·p Лор:1н
(IHl 1 - НЦН).ф[)Шll\~~!СКl l Й M:l'fX .: ,\1.1-
' l'llK: нrн.:р11ыс ;1ока:1:1J1 , что ос~11~сс· 1-
1мт1, ·1р 11секц1 110у1·ла 11\'/tHOl' 1 1 1 1t' 1,1.
ба (' ll ()МОЩЫО ц11рку:1н 11 Л1 IJ JCllКI 1
1Jt:BOJMOЖ110 172, 321.
Бе б t:р J'с1 1 рн х (18-1-2-IЧL)).
r1сv1ецкиl! м~п сма·1нк ;штор ·1ру
доо 11lJ 't't:• Jpш1 а111 \;бра 11 чес1шх
ЧJIC(;JI. а,1гсбр:ШЧt:l"t-.:I 1.Х фу11•щ1 11\
.1ш·tб ра 11чсl!ШЙ J 'C()!\ol(' l'JJШI 11 .\1:1'1 '( '-
(о.Щ'\ 11qecкol1 ф11 J1t1<;<::: l\ \Xt)!:\ 1' . t:фо р
J.Ч 1111p t ша.1 .1KCJ1UM:J ' lI1 'lt:CJ(\!l" 011ре
дс,1е1111с гру 1 11щ 1О :1-
Вейер11.1трасс Т<:1рл Tc"/ l<>p Rтt.ri1 .
rcJ1r " , 1 ( 1HJ"i-1H97), llCMCli\\l!Й ~ 1 <1 -
TCM:JTl l l<, ;JRT0[1 тр~лов по М;JТС~1 111Н
ЧССКОМ)' а11: 111 11:1у, теор• 111 фун1щ1-11\
11арп:щноr 11 rому 11с.числс 1111 1О, ,'111ф
Фч)(:111t 1r: 111ыю 1"1 1·сомt:·11н11 1 11 mr-
1 1clrнo1·1 :L 11·са1х·: ра:чхн'iо·1 ·:111 l'Хсч ,·
.' IOl llЧl'CIIOГO (}\)()\ ' f lOIJ:JJТll>I \1а IT-
,\la Tl·IЧ ("Cf((Jl 'O :ш:1.1111 э: 1 6. 1~:1 . 19..J,
...\18,)()()
Веfшь Герман ( LR81 lt)"i"i), 111 .: -
мсц1шir ч ;1 тс~1:1·111к с ICJ-1) 1'. р:1 бс•
тал 11 СН IЛ: ;штор 1р~лоn по 1·cop11 1r
фу11 кщ1r1 , ·1сор ни чнссл. теор1111
гр!r111. pa:3 p:i noт~1;1 Rсктор1~10 :1ко1 -
ом.1т11к~ гt'OML"1p1111 8 .111 . 11 0,:;-7,
')7Н, (1()1
DесссльК.:ю1ар(17·1'1-1Н18).дат
<·ю1й учfны1'1: lilf CPBЫC д:IJ I l'CO\,lCT-
j)I JЧ<..:CK( ){:: ll j)('ДCl':JВ.11e1-111c 1'0ЛlllJl<'l{C
llЫ X Чlk't'Л 2()7
Виет Фра11суа ( 1с,,10-1 (1\J)), фр:11-1-
11у:~ск 11 И м;пс:м:1·1 ·1 1к: ра:ч):1бот:111
пt•Ч 111 1\СЮ ,Щt.Ч<:IJT:lp l-1\10 '1.' 11 с()р~.
1Jffi::JJ u .ин сбр' б)· юJс1 11 1 1,н: uбu:н 1аче-
111 щи 11опрu11л 11cp[joC: t-iy1щ<..:1111ot
llC<JI l l.IJL'l ПJt:; ДО IJCl°tJ li М.1Тем:п11ке
щ: было lfюрч)'Л 7'i. ~ - к-1. 87- 88.
1%. 1СУ'. 2 1(\ 22). 2 '>!. ).! .2 . 5<)0. '%
Пинер l loriicpт ( 181)4 - 1<J<)...j ). а.,1t:
рш.:з1 1 сю1й учё111 .1i1 : <\IП()j1 труд:1
"1{11fit•p1 1l·п1к.1 •, в 1ютор<ш сфпрчу
Л11ровал <X'llOH Hhll' П()J10ЖС f 11 IЯ :~то1'1
11аую r: 11 :1r)j >T:1J1·1
·:1 IOKl' в <>f1Jrac1·11 ~1 :1-
Тl",1;1т1 1ч<::скш ·1 > a1-1 am 1:1:i 11 1·<;11р11 11
всршr·1·1-юс1 ·с~-1 1 1 1. 1J()
Вн ноградоо Н1~~111 ,\ ·l:i 1·11tтн11 ч
( IHL)J- I ЧH ..i .), C()f\("l 'CК-Иil M;J'IL" \1:1 -
T llK: :штuр t/J\"I J/ \:l Щ'НТ:l i!ЫIЫХ 1py-
i\U6 (j o6Jl:1Cl'l I a 11:11u 11 l lЧCCKt •il 'ft:O-
p11 и ч1ю:л 117. 'i'17
Dулъф IU p1111 U11к1ор111111ч ( Геор1 ')
( 186.\ 1 <)2'>) , руссю 1 (1 1\рнст:1лло-
1·раф.1к:-~,\1\11Сltм11 L)'\ '!>:.П. 13/HNtl }L-
т:1110т IJТ н 1t) l 5 1·. )'СЛ ()ВI IC Дl 1фр;щ-
11111 1 рс1 ГГ!'Cl-lllHClOfX ;1 учсi1 (J г
Га..11 1-J) I СЙ 1':1 "111.' l l'O 1l'i(1l-l<)l2),
l f'l ':l.IJl,HllCl\ll(I ф11 il lli, \lt" X:IHllК. ас
тро11О,\\ 1r м:1· 1 t'\1~1·1 ·111;, ою 111 11 :1 o t'110 -
u:iп·: 1 c i1 точ11<11 о ('t "l't·спю:1нан 1 1 ii
IЗЫIJCJI :J:JIIOll IJ~'111 ll() cкoptJC11 1. 11 р11-
мс1 нш. 110 ~уги. ~1сто11 111 11·<::Jр~ыь-
rюгu Hl 'il1C; I CIJИ>J ; 13 e1'(J ТР) д,L'{
11стрсчаютс.:я ::l!lcмe1 1'1 '!.! теорин 11е
рuят1 юс1·с1'1 7, -JC1. 7). 79. С) 1
. 5RJ
582, 585. -151. - J H'), </~Н
Галуа ~)ваr1н:т (lMl 1 - lH.\2).
Фrа 1 щузt'КI 11'1 матt'.\<1:1'1'1 IК, ('1'() тrулы
1ю:L11·с.:Rr~аичсск1 1."1 уравне н 11J.щ по
;юж1 1m1 н:.1ча1rо соврс.чен ноi1 алп.:
брс ; С JЩl:HMH Г~l 1l}'a СВН:1а11 1>1 'l';JКl l C
каж11сй1 11н<: 1 ю11ятш1 а~н·сf.ры , K'JK
1·руш1 :.1. 11tJ. 11.: 11 '1. ; t. 102- 10:\ , L.~3.
2iii, ') '51
Га!\1иль·rо11 ~ 11лы1."1 Puya 11 ( HIOS -
18(•) ). 11рла1щсю1й .ч,11·с:-1а1ш;; д.1,1
llOl!!IOC ~пложсш н..: тепрнн ко"u•
ле1(СНЫ.\ • шcc.:Jt: f1Jбu1·ш1 в об)Jас1тr
тсор1 ш 1 раqхш l<J:, 59R
Гаусс Kap:r Фри;1р11х {1777 - 18') ')) .
11емс1(ю 1i1 ~1 :1те~·1:1п 1 к: егL • труды
ока:~:uш п1рп\11 1Ос в.1111лн11с н:1 [Х1:1-
1нm 1с :.ин·сбры теор111 1 • пrссл. л;1 1 ф
фсре1 1 цт 1: и11,1 юй 1 ·<..:о.\1С'1·рн 11. м~1тем:1-
1· 1 1ч1:ткоi1 ф11з1 1 к1 1 . 1· с.:одс.:з 11 11,
а<..·1(ЮН(Щ I 111 5 1. Нс! , 1() 1- 102. 1!Ц.
1()(), 1ОН. J"i(J- J ') 1, l '5'5, JC>L. 1 7Ч,
.!06. 207
• 2:Р.516..+"N. -J')~
Гелъфоuд Л..кю.:а11/\Р Оп 111ош 1 ч
\ 1f)()() 1968\ . сuие·1·ск1 1i1 м:пема
Нtк: 1 1 е:з:ш11с11"чu ur 1lf11дйдl!ра 1х·
rнш1 7-ю 11put.'iлe,,1y Г 1.1лr,берта
( 19.1- -1 г.): :mтup тр~д(ш itu теории
'ШСL'.'1 II '1'\.'Uрш 1 ф)·111ЩJI.il 1О<)
Герберт нз Op1 1i1 :.t кa (oкonu 940--
НЮ.), с 999 г. П;i.-ia Римский Ош.u
вссч1 11 ) , фра r 1 щ~кю1i1 математ и к;
:.~втор тра"-r:п:1 <( ) правил:~х абак а ,
70-72, 1 .Ч
Герон Але:ксанщнrйсю-rй (окот>
1 к.). /(l)CHJK'I рс.:чс.:скт'i 1'1;J 1<.;M:t'I HK Т1
1щ· ха111 IK: j\<IЛ (' /.l(" f't'M:t'J' l I ЧtXF'O(' 11:.i -
.'1\)Жt'l 1111.: t)L:Щ >ННЫХ /\( )Cl'i!Жt:Ш 1i 1 ан
П JЧ 1 11.)(.:Тl 1 н ма1·1::"'1а·111 кt' 11 щ:хан 11
ке 29. -!<), 8">. 17'5, :,2 1, (11 О
Гёдсдь К)'['Л ( 1 90<> - 197Н), шк·1·
р11iю<нй м:~ l't::M a'l'(.I К, l 19-Ю J'. ЖlL' I 1~
1.;u~ '1 1н·ор 1·руцов 1 ютсuрш1 ~шо
жсств. ~1ате!\1.1 1·~р1ескu(r 1101·1щс н
тсор1 111 OTI IOCl!TCJ!hJIOCTH 11 6. J 17.
. ::;<) ~. 596
Гильберт Даn1щ ( 18t12 - 194 ,) ),
нс~tt:цю 1 й м:.1·1 ·сма1 11 к; с:гп 'Ll3f. 1рчест
во ока:1;11ю 01 rом1юс.: в..'1 11т 1и с 11;1
ра:н111т~ те :\J;1тб1;~т11кr 1 11ХХ н.: :~втор
1р\71ок 110 ·1i·or11 11 11 11 ни р1 1: 1 J-Гmк. гео
р111-1 а~ 1 гсбр:111 чсскr 1 х •11к·<.:11, оснона
н11нм "1: 1'1 ема1·1 1ю 1, н~1 р11 :щ1 1 онно \1 \'
1 1t·ч 1 1 L:н.:н1 но, м,1· 1·t:,\1;1 ·1 ·нчсt·ко1-1 !1<>1 '11-
ке, "1ат<.;~1ап.1 чес к( н'1 ф1 1:т кс. тсо
рш 1 ч.иt:L'" 1 11 др" щ1 11 Меж;\унщ11)J\ -
JI0."1
MLl' l 't:M;l'l 't l '!c Cl<U"" I KUIIl'j)t:Ct:<::
( l 90U 1· ) сфuр1ч ут1ронал 2i щ)(lбле
м1>!. С' l 'ОЯЩI !С П С !JtД '1:1те~1:1пшоt'1
(),8.109.110,llI. 113,114. ll(,
l Р, lt)7, 19;\-t()'J, ,)U4.
-
172, )::\
57"> . )77. с:,95, ('160. 661
Гиппас 11 з Мс ·1 :шонта (VI 1{
до 11 . : -,>. ) , щх·m 1cгpcчt:cr.: 11i1 матсм:~ -
1 1tк- 1111tjх11·оrес ц . 1 1~ш построс1111е
11 1ара, 011\ K~IHHO\'O f\(Нф)Т )\ОДС!{:lЭ,'\
р:.t, ра:iработ:1J1 ученне о cpq[J1см
l 'Щ)~IOH11'Н:'t'KOЛ I 1НО
Г11nпократ XHUCCKJIЙ ( \• 11.
, (U 11. а.), дJ ><:::f1 1Jt: I j)(;Чt:СК Н Й J'C( IMt: l'J1;
auтup r11.:pno r·o о r1..- 1·с:м~т н че<: кurо
соч111iе 1 1 11 я 11u rt:oмt:тp1111. НашЕл
кв:щра '1 )'j)ы 1-рёх лy1 J0'1t:1< (1 ~l!\ 11:1 з 1J1-
нае;о.1ыс п 1111 юкратов ы л~·1ючю 1 )
-1ц .ЮС>, .110. :)2.. -\
Гольд.бах Xpиrl'l!.1 H ( 161')0 176-1),
.
\ J,ITC'M<l ' l 'JIK. 11<) 11 pOтtCXOЖ/\t'i ll1 IO
IJl'MCЦ, pa\XY l ~IЛ R Росс 1111: ;tRП1p тrу
;,он 1 101 ·cor1111 ч11сел 1 1 ~1 :~тсмат~·1че
<:J<.ому а 11ат1э) 1 17. 'i ')7
Гранди l 'н1 що ( 107 1-1742). 11тащ,
ю1ск 11!1 1 ·срчстр; рае< .~1атр1~н:т т:r к
н а:1ы шн.::мыс де11с<·тюmы<.; кри ныс.
1 1alll>M l llШ ll>ll \l! C 1\1\СТ!\11 _)f{, \
Гpt:l"OJШ ДЖt:ЙМ< ( 165:1 - 167-1) ,
ШOTJl, IJ IДLКll il .чатс~t;/'J 11 1< 11 :l(" l 'PO-
llO;\\; 11а1111 с111 работу о ыщдр;~т)'(lt:
1,руг::~ 11 п111 србuпы. Г/tl' 1 1cc1 1 eдoli;JJ1
Gссконсчrrыс схо;\н щш;:сн рл;\111 ()2,
()~
rуго Сен - Внкторс1п1й (О IЩЛО
1096- 11-11 ). ф11Jюсоф схоласг, rж1-
11а ~"СГl-8111\TU(lCl<Ofl 1111\ОЛЫ; ;щтор
тра кт.1·1 ов no 11р::~ю· 11 •1сской 1·сu111е
тр111 1 69. 70
Гурвиц А.11011 1,ф ( IH.::;l)- l lJ l 9),
Ht:Ml'HIO 1i1 ~·1атсмаТИ1<: ост IOBllЫC ра·
()u11>1 <)'1·1шо1·101 1< \·1аТС\1:·1·1·11чсском ~
а 1 1:uп1:Jy, теор ~ 11 1 фу~ 1кц111'11 1тс.:ор1 111
ЧНСl'.11 J R .~
Гюй1·енс .'\ р1 кт1 1:1н ( l<129- J6t1';),
ш111~::рна 1·щ,с1<:1,1 i1 :.1~п·~::~1ат11к, ф11:шк.
мех.а 1111к и :ктрutюм; 11Juбрёл мшп -
1 1 111юn 1,1t часы, со:зд:~л их тcop r t ю,
усr:111ош1л закон ы кuлеба 1i1Н1 ф11:1 11 -
чсскоrо :-.1а.~1т 1111 ка. сuз~ал uош юву1v
теорию сnета l97. :i,82- 38:), :)8'5.
..j.')()
ДАла~~бер Жан Лсрон (17l7-
178.i ). фра1 1 1 ~у:к·ю·н~ ~1 :tтсмат1 rк, мс
ха111 1 к 11 ф1 mocoф -11pocвc·1 1f'l'CJ11,,
сфор му1111ро в;Jл 11 р аг.1 11 1а соtта в
. 1 с 11ш1 Дllффl'J1C Hl \11':1ЛIJ\-l bl X )11;\Н -
YKJ.iilTE:i\b ИМ~ l 1
11(..'H JJl'I /\Bll Ж(..'HHH ,\1:t'J't•p1 1 a.lll>t-I ЫX
снс1 t:!\1 ; авто р 1рущ.1к 110 жJ 1·ем~1т1 1-
ч ескому а1 J;L·ш ay. н·ор111 1 11 11ффс·
j1t:IЩЩl.'IUlll1!Л \(XIШJC.:lllUJ. 'Jl'(Jp1111
рщ1u 1 1, ,u11·c6p c .В7
ДедеJ(ИJIД Ют1ус В11лъrсл1.м Р11-
хард ( 1 н:,1 19 16 ). 11с.,1ецю 1i1,\!<Нt:
м а 11rк; дa.ri обос 1 юnа 1111 с: ·1eup1111
дс\1С'1 н1 1rc;rы1ых: ч 1 1ct:Jr: :~11тор 1py-
l\OR 1\0 тсор1ш ,щгсбр,111 чссю1х чи
п:лN.1
. 7-1. 1Н5
Дсаар r· Жерар ( L5Y5- J(16l 11лп
1')9 J - 1()(1 1), францрсю 1!1 мат1.:: ,,1а
·1·11к :1рхи·1·ск1ор. 11нжс1-1ср, ол111 1 11:1
<KI ЩIJ() t !(llIOЖtHll<t\H 11 \ll)(' KT ! IK \-! (\il
п:о .\·1 етр1 11 1 ..J. :\H. ·-~-(')
Дс1{арт Pt:fle ( l ')()(i-1 (l'JO). фра н-
1 \~'JC IO111 ф11жкоф 1 1 .чи1·ематн1(, ф11-
зш< 11 ф11:.IHOJJU I : ЩJIШКШ I оr.:11 uвы
а 1 1аш 1тпческui.1rсо:-. 1етр 1 11L,1\a11 по1 ш
т1 ш псремс:111 ю1'1 Jiе:шч1ш.ы 1.1 Ф> 11к
ц1111 , ВJ-1('л \ 11 юп1с· а,'П'с6р;ш чссю 1с
06оз1~~1ЧС' 1 1!1Л 15. 79, tШ. Н9. С)(} 91.
l)_~-<> '/ , l...J I, 1 U, 1S.) , 216. 2:)7, .!.69 .
.~ 12. :iH2, 5К7. -1 )О, -JH'i
Дt:лоне llupнc 11rU\< ыаёт 1 ч ( 1INO-
l 9HO). p yccl\111'1 матсщ1т111-;, '1r:r1·o r
тр);11 J11 11t 11·сомс.:ч111 11. тl'1)р1 1 11 ч1н.·l'л.
M:l'l't'\l:l l 'l I ЧC.:<'K< l f l к1)JIC l':UIJl(11'(la<1>111 1
,,,.1:; , (>-Ji, (;(~ 1, (1(1J
Ден MJl\C ( J Н7Н- JL)')l). HC.: "l t:l! КI 111
~ 1 атс:матик. ре1 111111 5-НJ 11р(1G11см~
l"1 1,1ь6ерт:.t о p;ш1Ю llt'! Ш KlL~ MltUl ' O -
гpa111 r ш<ах ~64
Диофа1 1 ·1· АJ1е1<са 11,цр~1ос1с11.й
(111 u.) . дpcщrerpcчecro1iJ .чап: мJтrш.
автор •·Лр 1 1ф1'К"J 11 юr» в 1:\ юш 1 ·:1.х
(cuxp;11 щлосг. 6 по -дрет 1 ~:грсчес:rш
11 1 н :1r:11.)(..'1\Ом пt: рс 1 юде); 1 11н:р 11ы е
BB~I 6уквс11ныс '160::111.IЧCI Г1 1 ~1 /\ЛЯ
11L'I ПВСС 1'1-10П> 11 его CTCJ rl:Ht'il: ocнo
f\:l' l 'CJllJ \ IJCJlllSI () 11co 11pCJ[l'Лi.:Hш .1x.
(щ 1оф:111товых) уrавнс111 шх "N, :iO .
17- IН. ')<;-.::; 7, Н .\ Н'1 . 157. 1-10,
J6'i - 1<16. 1oli, 2 1:;
Дирихле 111..:те р [\1 с·1·ан Jli:ж\: 11
(!НО') - l H')t)). неш.:1tк 111"1 ~ 1 :m.:l\1:1 -
11 ш:: :11r1up ·1ру,цоu 1 юш 1:11шт1 1чс.:с 1нн·1
' l'l:IJJ)IJll Чl i (.CJ!, l't:Op1111 фу11 1'.Цfltl.
щt·1 сма·1·1 1ч1;;с1<оf1 ф11;ш ке 1'57. 1Х..!,
- \ '52 . 47(,, ')()-\ - ')()')
Евдо1<с 1{пидс101й (1..11..:олu 40Н -
около 555 до 11 э.). :1рсR1 1сгрсчс:
L' 1<1 1i1м: 1т~·,·1;~пш 1 1 :1стро1юч; обос
1I OB<IЛ • M~'l't:\t:l'I И ЧCCl\l ·l ll <JI 1:11111 3 "
J \ре::внr 1 х - со:щал оi"нцу 10 тсоршо
(J'l но111с н 11й (эюшнащ:-н1· учсн нн о
669
Указа·гель им i:'н
деikтвител 1.11ых числ:~х) 11 метод
11c чcpri ывания (элеме нты тсори 11
trредслов) -Ю-42, 48, 49, 'i.3 . 196,
:?21 . .:\S8
Евюшд (конец rv - 111 н. ;ю н . ,j,),
дрсн 11сrрсчсский матсм::~тик; шпор
тrу11а ~ 1 1 ача11а» н 13 кнш-:~х. u котu
rом И:i.ГН>ЖСНJ 1! OC llOU Ы Гtометрнн.
тtup1 rи чисел, метод 011рtщ:;1с11ин
lUJUЩ~IJ\t.:й н объёмuв, включ ающ11 i1
"1J 1сме 1 пы теории 11ределов: оказал
огром ное:: lJJ IИнt 111с 11а развитие м:t
те~1а·1·11ю1 37, :\8- 19,43 44,48- 51.
146. I SU, 190, 191. 280, 289, 295 • .)06.
51~, -Ю7, -1-91, 571- 572. 575, 574.
57Н, S'J5
Eropon Дм итриn Фtдорuннч
( IH6') - 19:J L), русский м:.пематик:
ант()р трудоR r ю 1111ф1J~ренциа11 1,
н1 >11 1 х:uме1ри1 1 , ию·егrх1л 1,ным урав
нсr1~tя~·1 , ·1-еори ~1 ф}1нкц11й 1 11 . 658
Ж.11рар Ал1,беr С 1'195 - 1632), ни
щ:ржu щс 1снй м;tтс.:м:л~-1 1\; ш 1ерные
выс1\азал uс1юн11ую теорему алгеб
ры о 1 1 аличии корня у ал1·ебра11чс
ско1 ·0 уравнения с одним нсиз11сст-
111,1м 14.2, 178, 423
Жордан Mapr~ u 11 мо11 I<:~миль
( I H38- 1922), фраrнn1С1ский м:~тема
ТИК; ав1·ор трудов по ~urгебре , тео
рии фун кций, TOIIOJIOJ 'ИJ-1 и кри
ст:1ллогrх1фии 10.), 292, 354
Зенон ИJ :>ж~и (около 190 - око-
1ю 4.:ю до н. ~.), ;1рев 11с1т>еческий
фшнJсоф ; и:шсстссr :ншме 1rи ·1-ы.ч1 r
нар;J.J(сжсами (:шориям и) - <-Дихо
ТО/\tl lЯ ». «AXИJIJJCC и череп аха» .
<-Стрt:ла» 11 др" 1ю·1·орые обосr-ювы
вал п 1-1 е1юзмож1 rость движения ,
Mll()ЖCCJ BC I11 Юсти вещен -1-0 . -1-l
Зо110тарёв Егор Иванов ич ( 181\7 -
1878), pyccю-rt1 математ111<; р;~зр:~i1о
тал арифметику ;m1·ебра11чсскш;:
ч1 ~ сел 1 1 сзависимо от Дl!ileкю1rla н
l(fJШ Шh"r!/Ja 17 ~1
Ибн аль-Ванна ( J 2')6- 1_2>2 I ), м:t
rокка~ ICКI I JI )'Чt.:Hhlil: (/{t.:Jt;;UI 1JCM:-IJIO
сам0t""1'< mтслы-rых открьпий в мате
м:~ ти кс, 1! част11ос1-и в •1рш'О1 юмс-1-
рш1; 061шружш1 11ару дружсстве11 -
11ы-х чнсел 17 296 н 18 -11 6 . автор
юпm1 '· Кμ;пкое 113!южс11ие арифме-
1 Тlf'{сскн.к дс~ктв_ии
_·_"_1_5_3_____
670
Ибн J<yppa (Саб и т 11 б 1-1 l<yppa ;
856-901 ). :1рабс ю11I ма·1·ем;1·1 ·11 1< н
астроном; 11еренёlr на :1pancкr-111
н:1ы к • l-I aчaJ1:1» J!.HJ<.111 ·1/J,:i , COЧl IHCH!ft:
Лрх1-1мс.;щ1 4() 1 11щх· и цнли1 щре->.
<· Кш-шч сс кис сечения» Аполлuннн;
u соос.:й . кн11ге об н:iмt:рении кuни
чсс1ю 1·() сеч еllия, 11аэuа1-11-101'0 1 1 ара
бош-1чесю 1м» нриuёл рс111е1 ше зада
чи о ющцратурс щ1раболического
се1·мс 1 н-.1 11рн помощи шrтerpam.
m,1x сум.\1 44. 45. 66, 152
J<аваяьери J)он а вснтура ('1 SЧН -
1647 ), итальянски i1 математик; t:о
;щ:111 мсrод о НСДСЛl\МЫХ·, - /J,J l>I tlbl-
Ч Jl('Jl("HШI ГfЛ(J\ЩlДСЙ н объi:1щш
ф111ур; Мt.:ТОД Cl l lJCOбerвol!:JЛ фор
~ш рованиl() ин·1·сгралыюго исчис
лешш 92, 362, Ч50
Каи1•01) Гсор 1 · ( 1845 - 19 18), немец
юrИ мате~-1<.1тш<; творец тсорш1 мно
жеств: дал обоою ва1111с теории
дейстщ пелы 1ы х чисел L11 , 1 13,
11 7, 1 Н~, 47.2, 535, 564
Канторович Лсо111щ В11талъев 11 ч
(19 12- 1986). (У)В("l'("l(ИЙ М:JТСМ~IШ:К
и экономист. лаурс;~т Нобелевской
ПpCMl·IH ( 1975 !' ); anтor тrудов ПО
функц1 юнальному анали:1у 11 вы
ч 11<.:лительной м~1темат и кс, l 1ОJ1О
жт1 нач:lЛu ли 1-1с1lгюму про 1·рам
ми рова 1ш ю, один 11;1 соз;штелс 11
теории оnти м ~шьно 1·0 11л :н11 1р01~а
шm 11 унравлс.:ния н<1ро1~11ым хо:1яй
ством. Те0[1 И1•1 Ol lTИMaJ!bl·LOГO ИС
ПОЛu30 НЯН 1·1Я СЫ[JЬеt:J ЫХ рt:сурсон
-1-14
Караджи (ал 1,-Карадж11) (? -
10 16) Абу Г>акр Мух~1ммед иб11 а11 1 .
Хаса1 1 , иранский м~1теJ1-1 апш: автор
<ДОС'!';J 'ГОЧНОЙ КНИГ!{ о н:tyi;;e ари ф
ЧСТllКС ->, книги ПО алгебре ,,А.1Jh
Фахрп~ 64
I<ардано Джсрол:~мо ( 1501-1576).
1 1·r.111 ы111скнй м:~тем:~тнк, ф11лос<х \) 1-1
Арач; с его H\I CHCM CRЯЗl>l t:J;Jl()T фор
мулу реш<::1-1ш1 кубичсско\'О ~раннс
н1н1 :\О, 77, Rl - HZ . .20:1. l:Щ
I<ас с ини Джов:шнн Доменико
(Н).2') - J71l ),францу:кю1й <1e1·po-
tiu,ч; tT() HM\. ' Ht "M 11:1 :ша11:J llJIOCK<l>I
аm·сбра1rчtсю1я Iфшшн 4-гu норн;~
К.'1 (овал Кассш1 1-1 ), кu'l'Орую 0 11 рас
сматриuал 11р и ноп1>m<ах опреде
mш_, орбнту Зсмю-1 _i~O
KaтaJiьp,n П1,е 1·ро Антон 110
( 1552-1626), lпалwшсю 1 И матсма -
т11к в *1.'paJcraтe о кратчайшем п10-
со()(: н;;~х:ожде11ш1 1ша11ра·1 ·1 ю1'0 кор
нн 11.1 чr1CCJI ·> rшсрRЫ (' /ЦЛ ('11(1('()()
изuле ч с 1111я к1;1адратных корне!'~ с
nомощыu нс11рсрынных /~poбcil:
за 1111.м ался теор11 ей нщхuшс:11> ных
149, 15j
Каши (ал.u -Кащи) Джем1шщ иб 11
.Мас:уд (? Ol<UJIO 14:)6 1 1л.и 1437).
сред~ к·азlf:t'l"сю-н1 мате:-.'L111п< н астро-
1юм; :~нт()р трудов •Ключ :tрифме-111 -
ки•. •Тракт;1т об окруж1 юс-1·1 , ., _~Тр:~
ктат о хор;1с и синусt:<>-, 1шt'л в
у1 ю·1·pt'nJ 1cнi lC f\Corт1" 11-1ыс дроn11 ,
l IЗJIOЖI IJl 11 (11Jt'M Ы l IЗ1Vlt: Чt'l-ll1H KOp-
H<:: l'I 607
1\ е плер ИOJ·;i1111 ( 1 5 7 1-1(-) .)0).
1lCMt;ЦKllil :lCl'POHOM и м;псм:JТI 1к:
открыл 3(1 1\() НЫ /ЩИЖСl 11 [}! llJl<IШ:~'J': 11
работе •Новая сt·t:рtомстрш1 в1lJ 1-
11ых (ючек-> ( 1615 1·.) 11ред.rюжJm 1ш
терсс~1ый с1 юсоб опрсд<.::.1н': 1 1 ю1 uбъ
i.' мов тел
враще 1нш, n 1624 г,
o n y6m11<0113J1 таблицы логарифмов
!\С1. 91- 92, .В9. :~40-1·-Н ..177, ' l'i1,
491' 660
Кт1ейн Фt"Ли1<с ( I R49-1925), нl'
v~е1(ки й M:l'J'C M:ITllK; ;Jf\T()P тру,'\СЖ по
гсомt:'1р1111 , оказавm нх значитсm,
ное нлияние н::~ сё разв1rт11с, 1 ю :1л-
1-сбрс 11 1·шри11 фуню111~:1 106, 11 0.
<\3.2, ·1:\5, ·135. ·~ .~6-437. 'i'i·I. 6'17.
661
Ковалевская Соф 11н В::~о1л1>евш1
( 18')0- J 8С) 1) , J1YCCКI l Й ,\1:1ТСМЗТИК 11
Jll!Tepaтup; 11срная ЖClJЩllШI ЧЛС[l
кuррес 1 ю1 t/tt:H 'I П етерб,·р1·ско 11 ака
демии 1Ja)'1<: :штu р ·1 рудоu 110 мате
матпческом) ' а11алнз1 ·. .чеханнкс 11
:1сrро11ом и и 660
Колмогоров Андрей 11111<олзсв11ч
( \ 9().~ -19Ю ). COBC'L'C l<Иi1 матсм:t
'11·rк; ос110Rатель н:-tуч 1-1ых школ по
тспр11 11 в<:роят 11 осrс~1 11 ТС()ри11
функцт1й ; :Jl\1'0['> фу1Щ:1 •\I СНт:~l\ЫIЬГХ
·1рудо11 1/() ' l'С()рт-rи ф)'HIO(l lJI. маТ<:\Ш
·1 11че скоl1 , юr11кс . тшюло11111. 111 н)1-
фсрс н11 1ш1 ы1ым ураннсн1шм. ф~н к
ц1-t0на,11,11ому ан ~о111:~у. т сор1-111
11сроя ·11-1щ-1·сй 11 тсор 11 11 11н t)шрщ1-
1~1111 ll.2, 11:'>. 1\(), ') щ ">'17. 6(11, 66:1
Коши Оп• >с " 1't.:н ЛyJI ( 1789- 1857 ).
Фf"11 ~ц) зс к 1111 м:.1тt"м:1п11<: ;щтор
кла ссичес ких K\ 'pcou •"• атсм::tт11 -
ческоrо ariam1зa, ос1 юнз1шьLх на
систем:tт 11чсс1ю)·I примеrн::шш по
нлтня 11pC/(~JI~/ ; OДll ll HJ OCIIOIIOJЮ
J IOЖltl11<0R тео рlПI ,111атпических
футтк:r:tпй. ;штор трудон 1ю тсор111 1
днфф<.:ренциа11ы-1ы.х урзвнений, м11-
темат11чс::ской фи:-~икс, тсоrии чи
сел, 1-еометrии 172, 206, )44 . 452,
474,';60
Кро1-1екер Лсоrю1п.д ( 182~- 1891),
немецк11й ~tатема1пк; ав·тр тр)'-
1~ов по алгебре и теории ч иссл
174
Ку~1мер Эрнст Эдуард (1810-
189)). r1емец1шй матема·гик; труды
гю теор1т ;1лrсбра11чсских чнссл,
геометрии , матсмат11 чс:скпму ана
:н1 :~у . теорет11чс.:ско(r меха1-н,1ке
172- 17 .)
Rуратовский Каэнмсж (HN6-
19HO), 11()/fJ,CKИ l:t v1 ::~тема·1·1н<; (HIT()P
тpv11on по ТОIЮJЮГИИ 11 ТСЩJ11Г1
фун:~щнi1 2б9
Кэлн Артур ( 1821 - J 895), ;нн·лий
ский ма·гемати1t антор трулоv no
теории 1 ·ру11п. математичес~<ому
ar r:~лиэу. проект 1 ш1 юй геометрин
105. 272. Лб -437, .J.+6, 55.3. 661
Ла Валл е Пуссе н Шарл~, Жан
( 1866-1962), беnы·ийсю1й матема
ти-к; н:1ря1()' с ~дамс1/ЮЛ1. оfiоснш1;т
закон распрсде11снюr 11ростых чи
сел ; ивтор трунов 1ю тсорнн чисеJf,
теоrии функн и А, м:~тематнческой
фщике 151
Лаrраttж ЖФефЛуи (1736- 1813),
фр•11щузскиИ матема1-и1( н механ111с;
раэработаJJ ооюш-1ы<:: norJJn'liH 11 ме
тоды вариа1_що 1 1но1·0 исчисления;
amop трудов по математнчео<0м~·
анализу. теории чнсел, атu·ебре, д11ф
ферс1 щ11алы-!ЫМ урав 11 ен11ям 60,
]02. 185, -1-51
Ламберт Иоrанн Гснрнх ( \ 72i{-
1..,77 ), немецкий математик , астро
ном . фll :ЗИК; в .мa'l'CM:JTIO<t: сгро 1·0
до~1ззл иррацнонш11,ностъ ч11сла л
( 1766 г.); ~11з-1·пр тру; юв tIO ;uн·ебре.
1·1:< >м етр1111 , сфер~ 1чсско 11 три 1 ·01 ю
метрн~1~ 1~ астро1-юмии нсслсдон:v1
upfi1tты комС'!·, с1роt:11и<.: Всещ: н-
110И; ~ш·1 ·ор и;rен ушшеr с1лы:ю1 ·0
нзыка знакон НЮ. 149, 11)8
Ламе Г;~бр11ел1, ( 179)- 1870),
фралцузсю1й матем;1пш и инже
нер: а в1·ор ·1 ·рунов по ~1а·1 ·ема·1·ичс
с;юl1 физике, теории уnругос1·и ;
разр:1!1ота11 теор11ю 1<ривп11инсй
ных КСЮ[ЩИН:l'I' 17 .2
Лаплас Пьер С11мон ( 1749-1 Н27).
фраш\узсю1й аегртюм , ма·гсма·п1к ,
фн:111к; :.1нтоr классических ·1 рудан
1ю теор1-1н кс11оя·1·н()С'l'ей и t-1ебес
ной меха11ике , сочнr1сннй "лнали
тнчесЕ<ая ·1сор 1 1я вероятностей.
( 1812 1' .) и •Tpiti<:l'<П о 1к:6ес11ой мс
ха1rнке» (Н 5 томах: 1798- 1825 г1-.).
мl IOT'O'IНCЛCI u-IЪIX 1рудон по д11ффс
ре1-rц 1 tаJТL,~IЫМ ур<1ВL 1еню~м. иатема
тической ф11 зш<С и т. 11. 1 15.
-151,
52';
Лебег Анри t 1875- 19,11 ). фр;~ 1 1 -
п;узсюtй ,ЩIТ('М;] 'l'ИК; (}Д lll-1 НЗ СО~Jда
телсй теnрин фуню (Ий 11ейстш1-
телп1 ю1·0 11 еремен1ю 1·0; н:~ о< ·ноне
теоrи11 меры д:щ иес1,ма ofiщec
опредс11сн11е интеграла 1 J О, 1 12,
"\S4
Ле:ои-Чию·rта Тулл110 (1Н 7,-)-
1941 ). ИT:IJlbl\НCKHЙ м:r1·е~1:J.ТИJ{ 11
мехаrн11<; 11 анбuJ11,шсе з 1-1а<1 е11 11 е
Ш•1ею·1· его работы по диффс:ре1 щи
:1111 ,ной rеометрии ~шo1·oмtp1lL1 X
проl'транстn 11 0, 114
Лежандр Адрне11 Мар:и ( J 7'52 -
Ш3.)) , фра1-щу:ккнй ~1:пематю;о. ан
тор трудон по тсори11 чнсt:11. элл~rn
п-rческим 11нтс1ралам и 1'. д . 426
Лейбниц Готфр 11 д 13илы·еnьм
( 16./6- 1716), немецю 1('1 фю1< к:оф,
матемап1х, ф11:з11к: ОJ(ИН из со:ща1·е
лей ;1.иффере 1 ЩИ<UIЬНОГО 11 ИJ:-1ТС
гр:.111ьно1'(> ИСЧИС!JСНИf'I 44. б2, 95,
96-97, 197 , 3Нl, 383. -~85, 450. 451,
.. J69, 48), 491, )79, )80, 6 15
ЛеоJrардо Пизаnсrwй (ФuбоJ:Iач
чи) ( l НЮ- 1 240) , итальлнскнй ма
·1·ем:атик; u своём rп;tв1-1ом труде
<·Книга аба 1<а• ( 12 02 г.) в 11ерные си
стемати'1ес1<и 11 вес 1,мэ ори111.11а.т11,
нn изложил дост11Жсншт арабской
мзтсма1нки ; внёл й р;rссмотреннс
1lCJ1P.) 'IO BtX~RpaT l-1)10 ПОСЛСJ,ОВ:1ТСЛ!,
J-ЮС1Ъ - так нззыв::н:·мыИ рид Фибо
наччr1 :Щ 31, 70. 7">-77. 122, 124,
142, 14Н. 45<1
Jlилио Лу11{1ж11 ( 1520-1 '1 7 6) .
11·1~m,янсквй ирач н м;пс:матик: со
:щатсль прос::1<."1'а к:~лс~щзrп, кото
rы й OЫJI ЩJИТIЯ'Г Н pCЭ~'/IJ,T~l'l'C: р<:
фОрМЫ Пш1ы Г'11м с1щ1·0 Гр11гuрия
ХШ ( l 582 r . ) И НОСИТ ltMH ПOCJlC::/L
HcГO ( 1 ригоршщск111'1 ка;1с1 1,дарь)
187
Ли.ядеман К:~рл Фep 1 t 11 I 1 a11 rt
( 1R'12 - l939). немецю1й матсма
тю<; /{ 18Н2 Г'. П(JК:ЗЗ:UI, Ч'ГО число 1f
тр:1НС'ЦС11Д("llП-Ю 1 9·~ , 1')8, 52:)
Л нувилл ъ Жозеф ( 1ROl) - 1НН2).
француккш·~ M:JТCM :l'll'fl': :lВTUf) TJ)y·
/ \OR 1ю тсор1111 фу~ 11щн 1:\. дисjхрсrс н-
Указатем, имё11
ц~1аны11->1м уrанн ениям 11 м1.::-:а 1 1нкс
] 72, J94, ()')l)
Лобачсвскн:й Нш<0ла1i Ива1ювич
( t 7<-)2 - 1H'16). ру< ·ский мат<:матш<;
соз,дан:.:ль 11 ееuклидо1:1ой гс:оме·1·
ри 1J, автор 1рудон по :1лr-ебрс. ~1:~те
матич<::екому анаш·rзу, теuршt неро
ят1юстеiJ, мех ;111икс. фпз икс и
астрономии 10-i- - l 0'5 , 106, 10/-
109, 426- 42<) , ,152 . 57,,
Лоrrит:1лъ Г11йом Фpriн cy:i AН-l)"'JJ 1
де ( 1661-170-1), фратщу:-ккиО ма
·r·с.м:J '1·11к: :tB'l'O[) llC(1R()t "O llCЧЭTHOl 'O
учсбн~1к" по /1,l'lфферсгщналыюму
нсчн1.:ж:нию ( 1696 1- .) 96. ':Л. ' \')t>
Лу:~ин 1111ко11 :1 О I-1нкщ1а с н11ч
(J HR~- l 9'i0), rуссю 1й соrк:тсю 1J'1
математик ; ос •ю»атели 11:1у'-1по й
шкuлы nu теории фршднй J J n.
1J1, 112, (J')8
Л10 Хуэй (Ш н.), катаJ1скнй м~1т<:ма
·1 ик; an1·op <Трактата о морском
острове~ , со;1ержащего :задач11 11;:i
определение р~1('стшн111й до нед()
(у1у111-rых nр~дметон 19, .)0
Лнпуков Алсксан:ч> Михайлович
( L8')7- \ 91R). русский ма•1·е м~111п<;
соэд::~те..1 1, ноной науки - теор111 t
усrо i1 ч 111юс1'и лR1 ~же 1-11н1 11 U, 1 16
Маrщельброт }:)ен~а (Jюд11лся в
J 9 24 1'.) . америка 1J ский матс::мати.к,
родился ~ Варшаве: со:~;\атст, фра
кталыюй rеометрю1 4 17 . -Н8
Мар1<0в А11дрей Аliдреевнч ( 1856-
1922), русскнй математик; работы
в обл:~С1 и 1еораи вершп110стей .
теории чисел 11 мате м::~тического
а11:1ли:1а 110, 114, 1Jб
M~тi-iяceВJ~'l Юrий Вл:~;\ихн1ро
в11ч (_J)(Щl JЛСЯ в 1 ~),~7 г.), росс11 i1 скн{1
математнк: основн1,1с тру/\t-.1 110 ма
тсм:1тИЧ(:{"1<Ой ло1·11ке . U 1970 r-.
ус
т~11;uнил :v1гор1л·м 11чсскую 111:'()а:Jрс
ш11м ост1, 10-1111роб; 1см 1,1 Г11JП,б срт;~
117. 167
М с::зириак К.110; 1 Г;ю 1 ар Ва111(· /\е
( l'iHJ - l () :)H). фре1нщ1:кю 1(1 М:Пl'
матик н 11uэ·1~ lЦ[(<t:t ...:бuр11щ; « Прн
ят11ыс: и за1 1 имэ·1·с::ль11ы<:: .Jaд<lcrн "
( L612 r .) . ;1 также "Арифмет111~'"Дu
oqxrmna на 1р:чес~ом 11 ла1 ш1 -
с1ФМ 11::11.11\:JX с cofiCTT!CШil.Н\111 ком
ментарнl!}.11 1 ( 16 2) г. ):дал рбuе т1е
lll't)IJPCJtl'Лё l lllЫX ур:ш11 е 111 1 (1 пср
В()(I СТt:ПСНП 1 22, 2(J.~
М ене.лай Александрийский (1-
11 вв.) , щ)с1111сгрс ч есю rir мат см:.1т11к
671
Ука.:~ап:ль имён
11 асгrоноч, автор ·1 ру/\а «Сфсрика»
(н 5 ю 1111 ·:1-<) - 11 0 сф<.:r 11чсскоii гео
ме1р11 11 11 1р11r·ономс·1ри11 "11 , (16.
1.U
Менехм ( IV в. J(O 11 . :~.). щк·нщ·1рt·
чсс ю1й м;,пемап1к; 1пуч1 1:1 основ-
111.>1с Cfl()J/CTB;( KOllllЧ.<::<.IOI~ п;чсн11i1 .
IШTO\)UIC:: ш.:1ю.11 1.:юна111\,. HJ pc!UCIJllЯ
.~адач 11 uб у:шuсшш куба -t'> , :\20.
576
Меркатор (Кауф:-1а11) Н11кола ус
(UKOJl<J 1620 16R7), llC.\JCЦIO!fl
матсм;п 11к , ам·rотюм. 1nrжевер, ра
бо·1·:u1 н Кnr1с1-1г::нтне, Лондоне и
llарнжс : н <.:воt й кнr r1 ·е •.Jl Or':ip1rф
"ю·1·ex1шкa ~ ( lbl1H 1·) в11срвы с 1ч1 и
R~1 p:l:JJIOЖl'l 11 K' фу~1 кц1 пт ln( 1-~ .i')
1\ ()lTKOl l!.'Ч fll>IJI C"J'(:;l lt.'111IOJJ ряд '):\
Мерсенн M:ircн ( 1 ')НН - l6c~ H).
фр:.Шl(\~\ОШЙ ~'ЧEl lЫfl, :-нн-1 ;1 х: OJl l~·l-
1111 :юuа.11 в llаршке 11a yч.J1111i1 кру-люк
К\ПОрыl1 ш1.1вш1 Парижi.· кu(1 aк:.чtt:-
11шti1: 6.11а 1 ·одар>1 свосl1 обш 11р1 юй
11срсгтискс п nyreшc::crnин~1 со:щ;t11
цепую сеть. по кuтopoii учё11ыс все
го мпра обмс 11и11:1л11с1, сообщешш
м11 l 'iO, 151, l');)-l5'i
М!nщи:нг Фсr,п;ш-1:11-1;1 1'< •1'либовт1ч
(1K06- IHH5). росс11i1ск~ 1й чатс м::~
тнк: 11:1уч:1л 11онсрхнос·1 ·1. 1юстпт1-
ноi1 отрr,11 щтст,но1'1 щ111н11:шы -
11ссвJщсферу: 11;11116 1( IH 10 r) три-
1 ·0 ~1ом <.·гр1 1 Чt:('l\l H.'
COO'l 'l IO!llt'l 11 IH н
т рt:\' 1 \IJI l 1HI 1К{;. обр:1:ю1:1а1 IH0." 1
H:t
11<.'l' IЩ(Н'фС ре: 1·со:1е:::111ч(:'('KI1м11
( кратча itШI IMJI) llИIUШMH; 11~1(:!\ тру
ды по 1·еомt:трии 11 ма·1·с::м;пичсско
му :ш;и111зу 10 5
М:1ннсовский Гер ма 11 ( L8u4 -
LQ09). немецкий матеча · 1~111< 11 фи
:шк; автор 1·рудо1 1 1ю геометр 1111 ,
reu:-1t" 1p1rчсс ю1.\1 ~1сто.гщм в теор1ш
•ш ссл, м:~·1·смат11чсск<•fr ф11з11ке.
1 ·111~рО/\111гам111<е: дш1 rео ме 1·р11•1с
ску1() 1 1нтерпрет:щ111u юшс~1ат11ю1
CГICl\JiaJJЫ-IOll 'JCO[! l lJI OТIIOCJJTCЛЬ
llOC"JI [ (1!p(>l"l1)<1Hl"П:HJ Mtrl-IKOHCKO I'())
1(1(1. 1 1О. 36Н. 11 О
Мо11 ертюи П1.ер Jly11 Моро , \с
( 169Н- 17')9) фра1щу:кю-11) учi."н~-.rй:
в 175<> 17 ;,,7 rт. руковою rл r~1к н:1-
.J 1 1ш:1 смой Л~U1Jl:tl-IД<.:IШЙ :i1'l'IH:ДИl(ll
(;Й дш11·1 хщуо1ы х 11змерс 11ий : 111.::р
вы,ч сформул ирnвал прн11ц1111
Н<LllJ\!CIJl>Шel·u ДС-ЙСШИЯ ( 1 71Ю 1.) 99
Myanp Абра:ха.м де ( 1(>67 - 1754),
,111гт1й ский м:~·1 ·см:~т 11к; по пропс
ХОЖJ11.: 11ню фраrЩ)'З: rнtuёл пра в11 -
1ю Н03RС,1'СНПЯ в стспент, IIOMllЛl:l<C-
672
11nrn чпсла (форчул:1 Муавра): p:i-
fioт:tл в оfiласт 11 ·1·со ри11 11ср( 1нт 1 ю
tте1I 211
Нейма11 (фо11 Hel1~1<1 11 ) ,J.жо 11
(}11 ющ 1905- J9"i7), амернюuн:ю. 11'1
магс::м;rгш<. [Х)ДJ L'rcн 11 Буда11с::ш1 ~ р~1
бо1·Jл u раз111.1х uб;~:к1 щ( матсмат1J
кн: p<ilTMU' l 'j)C.il а1<С1 IUf.1'\'I ику теорн~ 1
Мl!ОЖССТIЗ 11 ГИJJЬuерТОВУ Тt:Opl!IO
ДOК:.IЗ<J.1(.>JIJ,C/1!: t'IYJ Кf1111 ~1 <·Ма'1'См :1·1·r1-
Чс?СЮ IC OCI IOBl>I KR:ll JТ()BOЙ MCX:1HI r-
I01·> оказала зн;~ ч ~гrс_rн,нос вmrш-пн:
11:.1 rазвитис этой н:1ую1 11 ei." ч:1тс-
11.1:1тrrчсско1·0 :н111 :1р:па , н 11о сл41~1111е
годы ж1 1:1 11и p;160'1 ': .tJ1 н оf)ж1с1· 11 · 1 ·ео
р1111 111р, 'l'l'Op11 11 BЫЧlf t'J lll'l'('Лl 1Hl>lX
~1:ш1нн. тсор1111ан то.ч:.t 1 он (1Н1
Непер Джо н {1'5 'Ю - Lbl7). шuт·
жшдсю1l1математrш:11:юбрет;.~ L't:Jll•
ло1 ·арш.jJ,,ю13 <) 1. 20 1. 460
Нё'1·ер Лма.·111 Э.,·1 ,>v111 ( 1882- JtH')) ,
1101C .Lttшi1 м:~тематик: се труды по
алгебре способспюnали созд:шию
1ю11ого 1rа11равл е1 r ин т;J 1< 1 1 :вына
смоt'1 общс 1'i, шпт : tбcrrarпнor'-r. aл-
1·ci1 pi.r (оf!п1.~1я теорrн1 колец, гто.;тей ,
11/\С;.JЛОВ) 110. 1 1.)
Нико лай Кузансюпi ( l 10 l -
H -6 . . .J ). тсо.1101· и м:11е~1:1т1 1к. к:rр;1 1 1-
11:и1 : автор ;111атt: ....1а·1 ·нчl:'ск~ 1 х тр:1ю :1-
·1·он, 0;(11 н 11:1 11 pL·, (1Г1t:ст вt: 1111111с<Нi
ко<.'."101101·ии Ко11сршша 41 , / 4. - :;
Нико~1ед Але1iсапдрийский
( 111 11 вu. /\о 11. э. ) . др<::ш1е1речесюu·1
1 ·сом етр; и:шtе1·с::и как 11 ~юбpe·1·:1 -
Tt Jlli Щ)lШOl't, UIIOCJle/\Cl ' IНBI 1t;JЗli<ll1 -
I IOll l<O!IXO l·l/LOJI )21
Нилаканта ( 1-1-Н - 01ю:ю 1'5 01 ) .
шщ111кю1И матсма·1н1с; :~нтор •Науч-
1ю1·0 сбор11111с.1 • 1·1 коммснт:tрпсв к
•Лр11;1бх:~·1·щ1 "1" - тр:11<'Г;J '~'- наm1-
с:11111ому Ари11бхатоi1 59. 62.
Ньютон Исаак ( 1645-1 7 27). а111 -
л11irскиi1 м:1тем:пнк, мсхаш 1к. :rc-
·1po1 !0"'1 11 ф11:~11к: а1т >р фун;щмен
т:u11,нm ·о ·~·руда • 1\·Jатсм:1·111чссю 1<:
н:~чал;t н:1туралы юi1 фш1осщ\ши "
( 16Н7 1.); 1к:1;11111с 11"1(J CYI ' Jlt:>1/611111(ct
ра~1ра\ютал диффере::1щ1~алы10<:: 11
1111'1СГ11<ULЫЮС 11сч1к11е1 шя. Bt:Ji::Л lТ•::-
11 е1н1ые ряды н Clll'J 'CM,1 '1'H LJ CC1CI 1
IIOJIJ>ЗOB~IЛCЯ ИМ11 для предст:ШJJеrшя
функций: работы J 1.ыотuна н paз
m1ч11r.,rx обл::tстях сстсс 11 юз1 1 :1111н1
наМJЮГО 011срс7(1ГЛl l CROi:' Rрсмл ·I '),
46. 62. 95 -9Ь. 197, Ч.!.. ·1'50. ' 1">1.
- 191.
- 192
Омар Хайлм (о коло 1 0-1Н - нос
JIC 1 122). Нt'[Х'1 1;1сю rlr 11o::r1'. м :t1·см :1 -
т 11 к 11 ф11 ;1ософ: 1-1 м:1Т<.:'м:1·1 · 11кt' л:~л
f)CJ!ll:IJ\1t.' \ ' Р ~IВН ~н11 1'1 /\О 5- й Cl \: 11c нr1
lll<J ILllЧll ll'JIЫH! С L LО~ Ю ЩЫО IJ.C(X'< .:C·
ч.ешш КОШIЧ.ССЮLХ ce•1eLшii 6"i , 66,
18'7. 2(10
OpeJ\i Н1 1 кuл;1 (u1<0110 1 ~.25 1 1~2),
фра1щу:1сш1f1 ~tатt'матик фи. пне н
::JKO I\0 .\111CT; ввi:.'л дробllЫ(:' П<.Жа.Jа l 'c-
!111 сте11е1 111; с с1·0 l IMCIIC'M ('llH31>Ш:J
roт r1с рвыс по пытю1 rюстросшrн
с1к-r·е111ы 11рнl\юл11нсi111ых rшорю1 -
11:1т: :11поr ·Тракт:~та о сфере " 7 .~-
71
ОстрОl')JадСЮ-tЙ м 11ха• 1 !1 в~к •C'Jl>C-
1:111 Y (IHOl- I H61), р~ сскн (1 "1ате-
1ц:1·1·11к 11 ~1сха1111к; :.111тор ·1ру;щв 1ю
M:tTtM<l'J ll ЧtCKOMY а1 lttJl.JJ:3y, M:t'l'C \1~1-
'П1Чt'CKUJI ф11 31 ll(C. ;11 1 ::U111Т~IЧС СКОЙ 11
1 1ебес 1 ю i1 ~1CX:IJIШ\C 105, 108
Папп Александр •-JЙС1'-ПЙ (нто рня
ГIOJIOHI 111:1 llJ Н.), /\(°1СН1 ICl'f1CLf('ClШil
м:i тc!l.1:J11oc в тру71с «М:1тсма11rчсское
<.:06р:-1н1 rC • ( 11 Н ю 1111 ·ал) и :тожпл
1-t :HlhlЩСС CYll\Cel'l\L'l IHl,JC fK" !Y:!h'l ':lThf
болl'L' ра111111х нре1311с1ро.:чс.:ск11х ав
·1 •орон IH. 1 ·1') , ."i l7. .HI, 157
Паска;сь b!lc:1 ( 1t12 .'\- J6bl), фран-
1() :!<. KI 11~1 \·1:1l'l'M:l'l 'HK , ф11 .\ 1 IК, фl·IJIO
COф 11 шка·1сль: автор тру ,:.юв 11 0
арафмtтикt. ;11п ·ебрt. 1·сuр~1 и ч 1ке~1.
тещши вероялюс 1·ей: 1IOJ!}'Ч llJ1 од
ну нз uc1ru111 11.1 x ·1сорем 11рое1<"т1ш
щ)i1 1·соме1·р1н1: в H1-J.1 шп1 l (i.-12 r-.
скопструиров:.~л су:-.·11vшр~1ОЩ)·10 l'ta -
ш1111y 92. 115. l .~(), 258. :i22. Н'-1 -
-11:;. ·1'50 . :;1>'1. :;он. ci 1:;
Паскаль :->ты: н ( 1'SHH- 1651)
фр:1нц~"1t·кшl ,\1атсм:.1· 1 ик. oтcrt
Jj_J /acк:al/JI: r:1 ссмотрсл :1а.~1счатет.
ну10 крш1ую l-1 ·0 1юrя1tка , в 1 ю'-'llС7\
с1·внr1 IJ;l '!H:tlf l1) to е1 ·с) 11\.ll 'IH 'M ()'JTTIT-
к:t l lккаю1) :\Н:\
П:i•IOJJИ Лука (01<0!10 1 -~ '5 - 0 1\0-
JIO 1 ) 14 ), 11·галы шсю11'1 .ча·1·t.ча·1· 11 к:
н:щоЖ.IL'J ЩХLШIЖI apllфMt"l 'LtЧC'CЫJ~
J\t f~. твий, ptillt lJl-UI l LC::J(()'I O\H1L\. a. ' l -
1·1::бpa11чelIOL\. урав 111;;1 1 111\ ·1 0.:uршо
1 ·1::uме 1 р11чссю1.х. Ltро1юрц11r1 : ,штор
учсб 11111а1 ,,сумма зu:uш.11 1ю ар н ф
_щ:"п ше. Г<.:OMC'l'Plll'I , O'l 'IIOJНC llllЯIV[ 11
11р()11орц11О11:1ЛЬНОСТll• 79. Н7, 1 .Ю,
l_~J. 1/7, l.Ш
Паш Мор1щ ( J H·l 5- 19:\0}, Ht'Mt'l\-
KИl'r матсмат111<; Ol\f'IH 11:i 11срн ы х.
l ICC!ll'ДO l\aJl ;tl(\. ' l IOM:!TJ 1ЧССКIК' ОС -
1ювы геомсrрии: ра:1работал груп
пу :uююм порядка; .в 1822 1'. сфор
~1улирuв:u1 :11\CIIOM}', ВI IO CJ I C ДC " l ' IШ ll
11:вва 1-111 ую его 11менем 572, 573
Ileaпo Джузеппе ( 1858- 19.)2) ,
11талья11сю1й матсма·r·ик; трущ..1 110
ocr юв:н11 1ям 'Vlатсм:пнки, матсмати
чес1юму :шш11пу; создал :~кс 1 юмати
ку н~1туралъно1·0 rяда чисел Ч J7
Пифагор (Vl в. дон. :i. ) , дрс::внс::гре
ч<::ски1"1 философ и мат<::мат~1к, ос
нонателъ 1гифа1·оr<.:йской 111кш1ы ;
прсобразuна:1 математику и:~ с<Юра-
11ия фор.rо,,1ул 11 pt:HCl lТ().В t! :iBCТJXlКl'
II}'lO дt:/!УТ<'ПШНУЮ 11ауку; б!У пршш
сывают 1пуче111 1е свшkтв целых
чисел и 11 рu1юрщ11\ доказан::.111,с 1·
во теоре:-.1ы о соотношении сторон
пря.моугuлыюrо тре)1'0лы 1ика )6-
,)8, 151 , 152. 175. 180, 288, 560
Платон (428 или •12'7 - 34Н иm1
.:Н7 до н. :i.) , дрсвнсrrечсский
философ; основ:u1 в Афинах собст
ве11ную школу - Академию, 1JнёJ1
м:~тем:1тику R ч11сJ10 rсредме-юR 11.rx::-
1юд: 1ваню1; 011ин н:1 осно1;1а ·1 ·с11ей
,1ю1·ичсско1·0 метода р'1ссуж,це ния от
11ротиш ю1·0; уделял болыное ш rи
ма11ие геометрическим :JaЩJ"l<IJ"I ш1
построе 1 rне с 1юмощию циркуля и
Л111iСЙКИ 6, 57. 4 l, 175, :)40
Ilонселе Жа11 Виктор ( 1788-
1867), фр<нщузосий математ111< и
механ 111<; заложил ос1 ю.вы прое1<
т11ш юй 1·сомстрии 106, 4 .37 , 441
Понтрягип Лев С.:с мёнович
( 190H- l9RR) , р<ксийский матсм~1-
тик, UCHOIIOJIOJIOЖHИK 1\ШIОЙ IШ)'
К11 - теор1111 011тималь ного у11раJ:1-
ления 11'), 4 1'5, ·~92, 6б 1
Пто.тrемей Кландий (около 90 -
около 160), дрсвнс1·рсчсский ас
троном и математик; разработал
,\1атематич.tскую теорию движе
ния 1ща11е1· вокру1• 11е11одвижпой
Земли; в его главном тру;\е «Алима
гест~, в котором были обобщены
асrрономичесю1е знания древних,
приводятся r.:ноке сведения по пря
мол 1111 ей1 юй и сферической триго
нометрии 17,47,66, 197,307, 388-
589, 393
Ilyaaxape Жю1 1 ь Анри (1854-
1912), фр<1нцу.:1ский матем;~ти к. фи
зик и филосnф; автор трудов 110 ма
темати ческому анализу, то1101югии,
математической физике, небесной
механике; в 1881- 1883 1т. д;и1 свою
11 1-1тер11рета ци ю 1·еометр.ии Лоба-
че.вского 8, 17, НЮ, 106. 110, 111 ,
113. 114, 217, '5')7, 661
Пуа.нсо Луи ( 1777 - 18'59), фрщ
цу:ккн i t ~~атс1-1ати1(, :.1exai LHI{ и фи
зик разработал геометричесю1е
методы нсследо.взния меха11иче
сю 1 х c 1KTC\J, 1юстро11л 1·сометриче
скую стат11 ку на основе теории
П:![J СИЛ; ВЫВt:Л теорему О В[J;Ш~Сн И И
твёр/'\ОГ() тела в отсутегви r1 сил
l61, .1Ч 1
Пуассон Симеон Денн ( 1781-
t 840), фра1щ)~1ский математи к, м<.:
ха1 LИК и фи:зи к 120, 122
Рм1ануджан Срн111шаса (l887 -
192U), 1шдийсю1i1 матема111к; сов
ыеспю с Хсфди получил первые
прибтrжё11 11ы с форму;11,1 чист~
всех рззб11сни 11 числ:~ п 200. 25'-1
Рассел Бсrтр :1н Артур Уильям
(1Н72-1У70). uю·лийский матема
т11к. JIOl'llK , фИJЮСОф; антО[> труЯОll
1ю матt:мати ческой логике н О('НО
юн иям M<ITC.\i\<ITИ!{K сформуш1рu
нал однн 11:1 11 арадоксон теоrши
M I IOЖCCl'B (11ара/~ОКС' Рассела) t 10
Ризе Адам { 1489- 1'>59),11<.:мсцкий
~1атематнк 11 нt:даrог; в с.воих учеб
нш<ах 1шёл современный с1юсоб
ум 1 южс1шя, 11ользовалсн з11акаь111 +
11-86
Роман Бернхард ( 1826- 1866).
1r.смецкий математи1<: положил н а
ч:зло геометрическому 1r::~11ран.11 е
нюо в теории фуню 1и й комnлекс
но1 ·0 lICJ>CMCHHШ'O; расС ,';l;!Трюшл
1·еомс·1ри ю как yчt:~u1e о 1-ie 11pe-
ph!8HhlX совоку1нюстях шобых
07\Норот~н ы 7'> объектов; изучал раз
рынныс функции; внёл fi математи
ку так называемые ри мановы 11 ро
СI'[Х111ства 11 разработал их тео рию
(рим;.то.ву ~-·еомсrр ию); работ:т в
области теор11 и диффере1щиаль
ных уравне ний , триrовометриче
с1шх рядов, интегрального исч11с
ления 105-106, 151 , 452, 476
Робервал ь Жиль (1602 - 1 675),
французский математик; од ин из
создателей метода 4 НСделим ь~х~;
нашёл квадратуру циК11оиды 94,
3R.2
Ром:ен (ван Рамен) Адриен (1561 -
1615), нидt:рJ1андский математик;
работал в области 1 ·еометрии и
трию11омстрии; определил 17 дсся
ти чных з1:-1аков числа л: 88
Указатель имён
Руффиrш ll::юло ( 17<15-1 HL2) ,
rп:1лия 1 ~сю1й мате~1~п11к; ;щл 1 1срвос
(110 11едuсг;,~точ 110 обос1юваш юс)
доказате.~1ьст 1ю 1-1ераJрt:пrнмuсти 11
радr11«111ах общего алгебраического
ураnнеш~я 5-i1сте пе 1111 .23j
Сак кери Джованни Jtжсроламо
( 1667-1733), ИТ::tЛЬЯНСКИЙ М::tТС
.маТИК и 1ю1111<; uди11 из тех матсм:1-
·n1к<щ KO'lOph!e l lOДl '01'(!t\ИJIИ Сf\()И
ми ИLCJ!(;/\OR~I HИ}jMll открытие
нсснкm11tщю 1·1 l'С<>метрнн ; 11ыта лси
;юказа1ъ пятый пос.·rулат Евкл1 1д:э (о
Шlр:V1Лt:ЛЫ I ЫХ прЯ."1ЫХ) от пр1пиn-
1101·0 -12 5- -126, 428
Стев1п[ Симо11 ( 1548- 1620),
нидерландский матемапrк и шDКe
IICp: 1313ёJI в употреблtтше Д(:'('ЯПfЧ
ныс дроб и (в Европе) 11 отр1ща
тс.тrъные корни уран11сн11й 87, 1 '10,
141, 17Н
Стенссн Нилъс (Стсн6 Николаус;
1()3Н-16Н<1), датский ec1 ·ee1ж1 иc
llh1тaтe.r 1 t>. монах -матем:1т11к; устано
нил ОД11Н llЭ :J:IKOHШI кr11("l'3JIJI01p: 1 -
фш1 ( 1669 1'. ), 11э:1нанный его
ИMCl lCM 642
СтирJDш1· Джеймс (1692- 1770),
шuтла1щс1шй матtма·rнк; получ ил
1 1р11бт 1жё1111ую форму1 1 у ДJ111 вы
числения факторналос, 11азваШI)10
uпоследстшш ero именем 2') 1
Суиь-цзы (Ш в.), китайский мате
матик автор •Математического
·1тх1ю~п:н: Т1а.п 11p:tюma ар11ф.\11е'11iЧе
ских дсйствш'1 на счс'тноti /(оскс .
11 :щожил слособ [')сшсния в целых
числах ураннений 11ерной сте11ешt
29. 31
Сусдин М и.ха1111 Яковленнч (1894 -
Jl) 19), f>)'Сски й математик, уче ни к
f~}'.Зtиш; н t У16 1·., бу;\уч и сrудснтом
Мос1ю.вско 1·0 }'1-ш верснтета, открыл
1ЮВЫЙ IС!ШСС MI южеств - 1 ':11\ 1 1а:1ы .
вае:-.1ые А-м ножесr·ва 112. 658
Тарталья Никколо (около 1499-
1 557), итальянский учёный; нашёл
способ ре111е1 rия куб ических уран
нений 80, 81-83, 260
Теэтет Афиr-1ский (около 410-369
до н. э.), древ~ 1еrреческю1 м~1тематик,
уч<::ник Феодора Киренск.ого и Пла
тона; псх·1ро иJ1 теорию иррацио
на.rп>носгсй, открыл додекаэдр , ико
саэдр и октаэдр 37, 38, 48. 49. 181
673
Ук~з.:1теАь имён
TopJJlf<Ieд л 11 Эванджс:::л11ст а
( luO~ - H1-J.7) . ll'lа.·1ьянсю1 i1 фнзш< н
ч:~ 1 е::>.1:1п 11<, ус• нзершс: 1 1ствов.1 л и
ншро1со 11р 1 tмс:вял MC'I O;t 11едет1 -
ч1.1х 11р11 рещс- 1 1 1111 :~:щ;1ч о 1<аспсл1,-
11ых: о<'ю1"1щ1 m пр:1в1ит кв:1/1rа~ры
lli1(Xl()(1Лbl 11 \.1 ~ 1 1:1<:' p:tЦllO l !:lЛhHOГO
r1СЖа:1. 1·1 ·с:;· 111 r1с:1авпt.1 що <)Т Робi'/НШ-
• ?Я LH lj)l',(t:.111 1
. 11 KB~/\P:t'I )'И ЦllK'Юll,llbl,
нс:;1:m11с1 1 м1) 0·1 /ll'1 . '(1jJ111t1 н~1шё.:.111v1 и-
11~ ,l()Tll .IIOJ';Jj> f.llj).\1И'll:< 'IOJiJ t'JНl /XL'11'1
Чl. 9· 1, 292. :)~L
Уай.i1с Э1цр10 (J>U111 1.н.:я н J952 1.).
ш1111 1 1iicю1i1 щ11с:1' 1 :п ш..:: D L')95 1·. д:-tл:
11(,);1Н\1е ДOl\JJ:l'I С:ЛЫ.ТВО ijCЛHl<\)J'J
1·еuрем:ы Ф<·рм,1 17j. 1·ч
Фалсс МJшетский (около 625 -
ОКОЛО 'i:.J";' ДО 1-1
. 4.), ,\(>CP.HtT(X.:Чt.:
lKПII \l l1l('JlllTc.rt1" OCHOll:t'll:Jl l> UH-
' 1 1 1'11l0i'I фи11u<:uф11и 11 на ук~~ .5.~-56.
2.НО. 2Н 1, :IOC1, -105-4()(>, ')(){)
Фаньяно дс:::11 Тосю 1 Дж;тфра11че ·
<.ко О11ор1 ю ( 17 1'i· 1797). 1п<и1ы111-
t ю 1й ,\1a 1·e.ч ~t'L'IJK; в 17'5'.i 1 011yб.1111-
l(()D:LЛ :111:1. 'l l! Tl! 'IC:CKUC:: рс:ШС'JJИС
!<!да'IН. t.:oтopyiu CI ал11 11<1ЭIJllJ3TI>
c::1·u 11.чсне:ч 290. 201
Фейербах 1\арл Вш11.1-сJ1ыt ( 1800
18?>-t). 1 1смсцю1Тr \1:1те'1атнк /\OK:J-
:iaл ·1 copcJ.1y об 01(p:?Кr10C11t, 11 ровё
д<: 111 юй через OCHOB:lllJ.IЯ kh!COT
трс~ТОЛЬНI ~ка (IIЫHt: Тt.:Орсма HOLIП
(ТО Г!.'vlЯ) 2.Ч')
Феодор l<иренскю·1 (V-IV в11,
до Н, :~.). J\Pl:Hl~Cl'PC.:Чl:<.' I01Й м:1тсм<1-
1·11к-1111фа1·щн.:t:l ( j IШёl OOJll>lllOЙ
НК'ШJ\ в paЭIЗl'ITllC: тсорш1 И(1 (ХЩl lО
н:vш-1ых чш.:СJ1 _)7, .?8 . lH 1
Ферма Пьер ( 1601 - 166'5). фрш1-
11у:1скиl! математик, uд1.111 и:1 K)J)·ll -
11c::l1wиx 1чатематшщв Л"VП lj,: за 1111 -
м;111ся теорней ч11сел, л::ul\1стрнеi 1,
;UП еброй, M<l'fб\,f;j]JIЧ('('l(/1 _\,j ;ш;uшЗО\1
(метод 1, li\ХОЖДсТIИЯ M:JKC111'Ij.J\1.0H 11
МИI шмумоn). Тt::орнсi1 RС{'ЮЛ'ПЮСТС1'.t:
вJ.1.естс сДекартаtt был (J<.110ва·rслс,\1
а 11 али111чс<:1<оi 1 геометр~ 111; в тс::о
ри и чисt:л ocofiyю и:~нсстнос1ъ 110-
Л)'Чl 1. ' 11 1 двt: t.:1·0 ·1·со рсм1,1 - н<:'лнк:т
и м;u1 ая l't:орсм ы Фсрм:1 •15. 57, 61).
75, Н9-90, 1)2, 9.J, 1l 'i, 1 ')3, 1')'i, lбб,
167, 16Н-172, 29 1, .)Н 2, 4'>0, 4Н5, -19 1,
. +92, '505, '50Н. 570
Феррари ЛуJ\Ш1юю ( 1')2.2 - 1'5б5).
ита:11.1юкю 1i1 ман:.чатте: 1шшi::.~ 1 сно-
п•б рсшс1шя ал:1 'ебраич1::аш.х yp:lil-
11c1 111!1 4-11 Lтс1н:1 11 1 Hl -8:). 1 .31
Ферро (Д;~.111, Фс:рр()) Сl\ 11111 ю11
( 1-ttJS 152(>) . 11талынкю1ir м:t'Н:'
ма·1 ·ик; OThlJJ>tл 11р;1ш гпо решс 1111 и в
ра,'tИI~.ш:1х о;щого тш щ ,,уfнrчс~-кнх
ур;~ннсн111i НО. Hl, Н2
Фёд нров ЕR1·р:1ф Степ:~ н он 11 ч
( 1H'55 - l 9 l Ч), русскнi1 кр11ст:u1J10-
1·раф: 1Щl1 н 11~1 ос11< нюrюлож 1111 ков
J\/)llt"1:J.'J"ю1-p;1ф11Н. Н J />{\)() 1' . Н /XIU0-
1<. '
"Clh\!Mt"J р11н 11p:U111J ll,HЫ,\ ClK-
l't':l-1 фi!L'H1" LНlt'IJBIJLC::: H ЫB t:; I 21,()
1р~1ш t:llMMC'lf>llll KJJl!CT:IJIJHJD: ашор
гру1\u11 110 геvмс::1р11 11 11 др ')'5 -J. ,
u-1 'i. <>-f(> (,4~
Фибонач•111 <..11. Леонар,цu П~1:~.111-
сю 1Тr
Фредголt.м Э р111\ J l в;tp [ 1НС)()-
1927), lJIHCJKIOlil м:l'l'l:M:lTllK, п:IЛО
ЖИ!! о<:ноm 1ыс своiктн:~ rr тсорсм1,1
Tt'0(11'111 l lLГП.:11>.l; l l>l l l>IX )11aBHt'lllti'I ,
разработ:и~ оt1щ11с .четод1,1 рс1111::1 1 1 щ
llCIO)'l'OJ>ЫX llЛ В!ЦОН 11 О. 1 j 1
Хадвш'ер Х) L'<J (родш1п1 u 1')()Н1.J ,
швс:::lщщкю 11~1м .1те/\1а111к: автор tру
дш~ 1ю комбина1uр1 юй гt:O.\ll'l'JJt 111
3u-I
Харди Гuдфр11 XapuJщ ( UP7
1947), .1111 ·1111!кю п'r м;1·1 с..:мапш: t'OJ\-
мec·1 110 с f>CL">1Clll\'й.)/Cl7/IO\/ IHJ.'l\1ЧILТJ
нсрныс пр11бm1;1<:ё'1 1 ные фор.~улы
чrкла всех ра:{n11 сний ч111.:л :1 11 :
:tRтop '1'(1YJ10B 110 тсор1 t11 ЧllCCJI н
Tt'oprш ф~ HKI(f{if J 10, 25L1, (1,4Н
Ха.у<:.дорф Фt.:m1кс ( I H6H- l'Чl).
1кмс1~КJ11'1 ~1 а·1•смJти к: ;11пор ·1Р\'
дон 110 1-еор н11 м ножес1·н, \·1ан м~п11-
чсскому a н aJJи~N, т01юло1·1 ш 1 J О,
! !2. ~17
Хорезl\111 (аю, - Хорс::::1~111 ) Мрi.а"'1-
мед бе 11 Мус:1 (787 01ю1ю 8'50),
сре; t11саз11атсю1l1 ус1ё111.1 й; :нпuр ра
бот по ар11фмС'Пп<е, :uн ·ебрс, астро
номни, 1·согр:н).н111 19. 29, 62 6-t .
85, 129, 215- 21(!
Цейлс11 ( 1i:tH Цсi1ле11) Лудолыр
( L540-16H!), н1 щt.:f)J 1:111дt'кrп~1 ма1(:
м;н11к; н J61 5 1' 0 11 y6JIHKOllJJI JХН'Чi.'
ты числu л с 52. )\С:<.:н 11 1ч11ыми зна
к:tм11 197
Чеб.ышеn ( 11ruнз1ю<..:11ти1 1 kби1 -
шёu) Паф11у1·иИ Л ьв<шич ( J82J
J.'~'Ч). PYl'L' Kl1i°I !-1~l'IC:::\l:t 1·11;;; l)l'll!JH;t-
тt:,111 11c 1 ·t·p6yp1·cкuC1 lt:t\ 111101! ш1щ
.т1ы, со:щ<~л ·1t:up11 111 11<111л) ч:ш{· 1 ·0
11р11uлшк<::111ш ф~111щ1111: 11 п.:ор1111
всро1 1 1 ·11ост<::f1 до1:азал в общt:1' 1
форчс :uюJ11 6ол1,111r1х стссл, н
' 1'('!)(11111 'lШ..:с-л
<ICI 1,v1ПТО1'!1ЧСС!\11i1
·~:~ю1н рас11рс,'1,с.1сн1 1 11 11рr1с1ъ1" ч11 -
ссл 11 ·1. / \.: nро1ю7111л р:1С11 юобр:~.11-11.1с
11р11 к,1;щ ныс 1н·c:1l'l\<1t1:11-11ш н 1<:0-
1т11 MCX;J/-1/l:!,\.f()J!, ( 'J'() тру;11,1 JН)!'/()-
11\11!111 11:.!Ч:t.'1() ,\1111 >1 IЩ L·l()lil>IM о\1.11а
(. IН..~1 м:~н·r-.1:1 l HKll 1 1(1, 1 '50. 1~1 ,
:; ](), ') 17' (1()\)
Шалъ J\1 11ш u 1 1, ( 17!);) 1880). фрш1-
Н):Jсю1\1:o.1;1'1't~l.LТIJJ\1111(\~JIЛLК м;11'1;
\1:1Т11Юi. ;штор ю111пt "1 1 стор11чt:
сr.: 11й обзор 11р о11сх11i1:.1сн 1111 u
р;1·1ю Г11ВI 1'('( •МСТ[11 l'll:C'IOIX М(vrо;юв»
( 1Н5 7 1' . ); его c1>l1L·11~с1111ыt· Гl'Оче·1·
р1 гч1хю rc i 1l'CJ l l'J loн; 11-п тя с1 юсоnст
вона.111 ра:1раf1откt 11рос"·п1н110.i1
l'C(),Щ"l'[>I 111 l)(), !()(,
Шё нф11ис Арт\р ( IH'1:\ - l'JlKJ.
11t:1.1tЦКJ1i1 м;1н·мат11t-<. ll\;.1:ш11t:1щ<1
от Фi!с!О[>щш в lH'J0-1НЧ1 1'1 ' . o\!t: 1·0-
дамн п:ор1111 1 рУ!Ш 1х · 11111.1 :ыдач:У о
кл<1Сl.11фш.:ац1111 нее:.. кр11t.-1 ;L•1"11t чс·
сю 1:\. щ юс1ра~ 1ствс11111,ix рсшснж
(J...(()
lПuайдср Tt:t.1/l•IP ( pцJ, 11 .1L'H н
J <) 1 1 Г ), Jll ~1(.'1 \1'1 li1 :'-1;J'L'C'1:1TllI\,
1Н."J:IНI IL' llM< ! U'I ((~·1t.фш11>1t 11 [ 9.Ч 1.
рсшш1 7 - ю про6лсму Т'1111ы1срт;1
jt)')
ш ·1·ейне р Я кofi ( l '7l)f1- I Н<).~ ),
1111:\i..'Й 1~:чхю111 матс::,1:1·111к : од1 1 н rrз
('0.Щ<i'l'CJICfl 1lj)O\;K"П111 1 Юfl 1\'0 .Щ"l'f> I 111
LЖJ, 2<)J, :\ I H, -)8:)
Штифст. fl·l1r лc:m, ( 1 /Н7-1 ~6~).
Llt:~ltЦIO 11'1 ,\1:1 l'CM:l' ll ll< 11 CJ р;а1tс1·ну
шщ11i1 11ршю1Зt:μ1шк : ~111·1 ор ю 11 11 ·11
•Лu:111,ы :i рифмс·1 '1t1Ф·" 1'1 rt tt! 1ю -
1шш ВС(' 11:}мс1 1 е 111 ш u uбuз11ачеш1
ях .1р11фм\"1 JJ LJ(.'CIШX 011ср;щш) и
не11ЗНССТТIЪIХ ВМСС'1'С с IIX сте11е 1 !Я
ма, 1юторые нро1 1зornm 1 I\ ·1 ом~
нpC:'<I Cll\-1: uвёл СНМRОЛ для обоз11а
чсн11я кnа;1ратноrо корня. 11родол
ж11л ар11фмст11чсск11с 111х1111ссс 11 н н
OnJl<IC'l 'I·. tУгр 1 1 ц:~-1·с:.1 11,ных ЧllCt:! I , а в
l'tUM(;'l lJИ Ч(;CIOIX ll( IOI'(JCCCШIX 1 \ВёJJ
отр1 щат<.~11,н 1,1 с 11m<а :1атt.:л11 СТ(~11с1ш
Нб. ~)1
Шур Фр1щр и х ( l 8'>6-1931) .
11смсцю 11\ мате.чат1 11<: ос11шшыс
Ч'Уд1.1 110 1·с-uмс::тр1111, r·ру1ша"1 11 ре-
оnра;юJШ 1111\ антоr ra\10·1 · 110 j)ИMa
HOl!CКJ·IM 11pocтp:llIC1'fl~U·I !IОСТОЯН·
Н\/й кр11н11:н1ы ')7' . S7R
Шюш: Н111юла ('- 1500). фр<111-
цу:кю111 :-.1а·1с::мат11к: перв1,1м иc
fН.JJIЪJoвa: 1 noк;1з:i.·1eJ111 Nш 06uзщ1-
чсн1н1 с1·спс11еi1 11енз 1н::ст11ого:
ав·J'ор 1(11111и «Нэуюt (J •нrслахв rpt'x
ч:1стлх• (l--18.~ г) 70. Я7. 127
Эйлер Jlcoн:1p;\ ( ! 707- \ 7Н.~), ' - 1:1-
те,\1:1т111{, \1ех:~н11к. фJJ'{JJE< 11 апро-
1ю.v1 , J[(J llj)OIJCXOЖДl' HIJI< ) IllRCi1ц;1-
1x·ц: работал в l'occ1111 11 l'cpмaJIJ rн:
.нпор сны1щ; яоо panm 1н > м:1·1 е.ч:1-
тнчспшму анат-r:1у, тсор1111 ч1·кел.
диффС[Jt:I Щl•l <JЛЫ J( 11) l 'i .;OMc.: 'I [>1111, Щj
тeмaTllЧt:CKOIJ ф11:щы:. нс6есноf1
~lt:X~lllНKC l\ др.; OKit:l<!JJ Зt1ач1п·~.11..>-
1юе ll!lIOШIIC Ш1 раЗШП[Jе 11ауки
~1. ;:,7, (>0, 9-; - 11)1, 117. 1'> .\. 1'>'5,
J ~8. 168. J70- 17~. !94. 196. 198.
ЮО, 20'5 , 21 l, 237, 264. 2М, l.(>Q,
184, .·Ю'5. Ч2. } l-! . ~90, 451. 452.
-16Н, -1""0, 557, '1 7 0
:>-)йнштейн Лльбсрт ( lH...,9 - \<.) ')C.) .
фl~ИК-'Т'С'ОрС'ПIК CO:Щ;ITC!lb OOЩCl'I П
CI ICЦI 1:итьной 1'<:'( Jj)ИH OTJ IOCJ rтел 1.-
1ro<.·11·1. . :.штор осгюво1 юл:J r ·ающ11 х
ПРЕЛМЕТНЫЙ УКАЗАТЕЛЬ
Абак ~о 71, 12R-1:ю
Аб~ж:в:~ 1·pyn11a sc, l
Аi'>сплют 1иrпскостн Лоб:~че'ВСl{ОГО
jj(1
А6со11 ю·1 ·1 1:1я 1·сомстр11я )77
'\ДДll'l'llRHOCTh _:S'>2. :)"i. .j, 556
Лке110 .,1:1 49, 'i7l
Ap.XllM(:'/l:I 55 l . 572-">75
Jl:.Jj):t!JJIC!ll>liOCTll "10-" >1. 10·1 ,
~.2s. S7 :\. '576
Акс но"ч;1пша
гсо.четри11 4'), '57 2
теор 1111 uерст·1·1юС'1еi1 '510
Лкс1.-юм.1.11
1<011груэ 11пюстн '571
непрсрыт юr..~ги ')..,}
r~прядк:~ 'i7,)
сосдн ненпя 57 5
Аl\·туарная м;.~тсм:пнка '123
А.11гсб1х11J11сскос ~1хшненне 195
А;11·сf!ра11ч.сское число 193
Алгор1 пм 4'1~1. 61.2 -614
E1iIOll щ~ 1~)!- J t)O
AlJHKDO'J 'H<l>I J Цlo\11, 2,2, 176
Лльтср1 1 ат1 ша 1l о11ссле ,:)09
.\11алит11ч.еская 1·еом\:Тр11я R9- 9 l
лщ~лит11ческое »ыражснпс функ
ции 47U, 471
AJп1 1npнJ:v1a ?>!17
А1п11сим метрич1IOC'J 'f .> 545
Антнтр:шз11т1шность 544
Anop1-rn Зе1 ЮН() 40. 41
ApryJ\1e1-1т К()Мnлексноrо чнсла 209
Арrу\.lент фуню(ни ·171
Арифмеrичссr<ая 11 рш·ресс1 ш 457-
-160
A['JX!IMl'ДOKhl 'l'l'Л:I -'140-341
Асшнтто·1·а 379. -1 .80, -196. 497
\СС01\И'1Т11ВПОСТЬ ~~.1
Лстро11/1а 38.1
Аффннн;~я J'Сомстрнн 455
Афф11ннск· преобр:1:юна11нс •135
Байт 125.6JН.6.)6
11<.:СК< )H{'<j Н<) удалё11 Hhl C 'l'О Ч ю 1 11
пря~1ыс- 141--4 -'13
l)Ht:l<'l 'lШI 1ое (J'ЮбражеШ!(' '5 32. ')!Г,
'5-18
J:5111шаμра r·нщ: }1l::ш11ениt: 227
Б1-!М.t:ДИ',\Ш) 348
Бн11ар1юе о·п10ше1111е .:;44
v1шом Ньютона 257
Gн110:"щ;щы-юс раснределение '> 19,
522
fiино~1и:\ru"ные ко;.1ффю.1,щ;11ты 258
fJ 1-1ПИ[XIM l fj'(:J :$37
l.-)11CCCIПJ'!l1C:I 27R
Б11т J2.) , 6 JН, 636
Булева функция 5HJ
В~КТ<)р )9В-399
Некгорное 11рпr1ранс/'fю 401
Всл11кая теоре~1а Ферма 16Н-17•1
Вероят1 юеп" 50'5, 'I07, 510
Взаи ,mю 0111 юз11аЧJ юе соотнетстuщ;
u1. Бисктшщое отображеине
!Зложен не S47
В11свписаш1ая окружпосn, 28"~
Внсн гни~! \'ТОЛ 282
В1 1утреншm точка ф11rуры 3J6, <111
Нnзвратная послсл.ов:~телыюсть
"11•1
ПреАМетнь1l1 y"a'laтt>l\ь
трудок 110 KB.lllTOIIOЙ Т<'Ор1111 CRC'l ': I
1()(), ] 1:\-1 1·1
Эратосфен Кир~Jiскнй (01<оло
27(J-19·1 /f,O Н. :-J.), 1 \Pt'KIJ t'ipCЧ t:CIO!(I
м:~тем:1тик 11 а.сч>t нюм: ~а!ЮЖJ.\.' 1 (к:
LJ< ШЫ .\J:J'l'~M~IПJЧ{' CKOJ'I l 't'Ol'I 1аф111 lj
ш1ср1.11,1е 11 :j!\1l'p1111 д)Т) мсрщо1:111:1;
аю ор ·1рудов 1ю :.1.1:1тем:1·1·111<с::. ас1ро·
110.,11111. ф1L'Юl'оф1111. ~1уэ1.u(е 1-1 6, 520
Эрl\tиТ Ш:~рт. ( l~ 22 - l.•)(J l). фр;:ш
11у:кквй ,\l[l'f't'M'8TIЛ{; в 187 ~ 1' HI 1ep-
R1.1c ?\О1<:1з~ш. что ч~11:.10 е тра11с-
1\ен1tе нт1т: :i втпр тру;tов п о
математ11чсско?.1у . 1нал11з~-. тсоr11н
ч11 сt:л, aлrct'1rc l l)9, 200, 11 Н. 6(1 1
B ш кaIJJ 1:.tя. окружности 285
J3ынуюtыс фш)111,1 41 О
Rысота 279
Г;JM1 L'1ЪT(.J! !()К ЦJ1 l{Л 26/i
1·:1 p"-IOJ н·тчсск:ш rюслс:юfl.:~те;1ы10сть
- 162
Гармон11чсскпf1 рл,r1 -1<17 . 4(1Н
ГсксаэitР .'>У>. :>.·Щ j)(1
Геоме1р 1чесl'ая 1:1<::ронтнос1ъ 509
Гt~о.щтр11 чt'o.::.1J1 11р< 11 ·ресс1 Ll-1
--\(1(J-
.:J62
Гео~1етр11ЧССКО1.' Пr>ttIOJY.t:J~)ill1! 11lt:..\3\J
Геомс::тrшя
Лобачt:1JС1-:оm 103 - 10), 107 -
109. - 119
Римана 1()5. - 124
Гвльбертоrю простра~1с1·00 11 l
Г11пербола .1 ., 77 , ~79
Г1шоте1-1 уза 279
Г111 ютрохо11да 3НЧ
l'11no1~rпuтo1111;:i ;SH5
ГOM(IТC'l J JЯ ;) 1ч. [5·1
Грr~дус .)90
Гj)'JHlll\~I фиrуры :В6
Граrшчная точка ф111·урh1 556
Граф 166
l11'РЫ 270
Гр1·11па 1О .\ ?"> 1
Гм.уа 2:)4
CJ.f~\.IИC1 рНЙ )'54
Движею 1 е 34. 4<J5 410. "t:IO. 431
Двоич11ая система сч1.1слешщ 121 -
125
67)
Прелмеп-1ый указатель
Дне )й<:rненн< >C'l'h
в сферич<::ской геометрии 42:$-
. .. \2...J
в проективной геометрии 444
J1<1но1·огра1шиков 3-Ю
дu>1ра1 r11ый у1·011 532
Двууrолышк 421
Действ1пелы юе число 18 3
Дельтонд 293
Дельтонда 38~
Десю11чна>1 с1 1с1·е ,-..1а СЧ'ИСJ1е11ия 18-
19, .$0, 59, 120-121
Дп~1rрамм<1. ;;-)ИлС [ХJ - Вснна 5;$7-
5.)Н
Дil;j'bIOI 1КЦИЯ 58 j
Днректрнс1 378
Дискриминант 22'i
Дисперсия случайной величины
516, ')17, '519
Дифференциал 489
Диффере11ш1а11ьнос ур авнение
626-629
Дифференцирование 4 50, 4 51, -+ 89
Диффере1щируемая функция 489
Дтша :~51-.152
До/l;скаэпр 3·10
Дополнение множества 54 1
Достаточ ное условие 563
Досювсрное событие 507
Дру-..ксстве~1ныс чииtа 152-15;)
За.п:ача
Фан1,яно 290
Ф<::рма 291, 292
Закон рас11ределе1-1 ия 11рос1ъ1 х чи
сел 150- 151
Зам:кнуrая фи гура 336, 411
Зсёздные правильные тела 341, 343
Зеркально-равные фигуры 421
Зеркалы 1 ый поворот 340
Знаменатель геометрической про
грессии 460
Золотое сечение 19l, 539
Изобrажение 327
Изо1'он111 ьные точки 285
Изuморфи~{М
r·рафов 268
групп 552
моделей 576
Икосаэдр 339, 340
Импликация 583, 588
Инвариант Дена 365
Инварианпюсть 4 :В
ИНj\)''Ю\ИЯ 566
Интеграл 362, 452, 500
Интегрирование 450, 451, 5ЬО
676
Информ~щия 6.B-64l
Игtъектив 1 юс отображение cilf. Rло
женис::
Ирра 1 ~~юнат.ное ч щ'JЮ 179
Исключающая f\ИЗЪrо н кция 584
Исчисле~ ц-1е выо«1~1ьша11и 1'1 5Н8-589
К.аLJтороuский 11щн·о1-1а;1ы-1ый про
цесс 535- 5?16, 564
I<ардиоида 383
Касательная .)0 1, 485
Кас:~тслъная 11лоскость :\ .) 5
Кпет 279
Квщратично -иррационалънuс 1:1ы
раже11 н е .)lfi
Квадратное ураннсJiи С 225
Квадrатрис1 380- . :JH 1
Кlщцратур:,~ КГJУГЗ 322-32.)
Квадрирvемая фигура 313, 35-+
Ква~гrор 594
Клофо11да 382
Кол.;шнеарность 398
Комбинаторно-правильные м но-
1·01·раш1ики 544
Комму-rатив11ая rpyiшa см. Лбелева
группа
Комплексное чнсло 205
I<оrvпu~ексно-сопряжённыс <nн":ла 206
Ко~1 поэи ция
ДВИЖС!IИЙ 4}11, 4)2
комбинаторная 254
отображений 548
Кони чсск11е сечения 45-46, :)76-
377. 441, 4-t5
Конус 334, 360
Ко~-~хоида 32 1, 322
Концс1-1тр ические окруж1-юС'1'1 1 301
Конъiон~щия 583
Коорд инатные оси 373, 374, 576
Корень уравнения 219
КосвегпiОС доказатеm,ство 564, 565
Косоvrолы 1ая система координат
376 .
Кривая
l"и 11 11ю1 см К6адр:1трнс1
Штейнера см. Дедьтоида
Т<ри1:1олинейнан Otl"1·e м ;1 коорди
нат 576
Кристаллографическая Г'Р}'ППа 554,
646
Kpyr 30 J, 304
Куб см. Гексаэдр
Кубируемое тело 355
Кубическое уравнение 228
Лемма 558
Лсмн искат'.1 380
111·1t1сй1шя функция 477 --17Я
Линей1-1ос 11рограммиrованис
·~ 1')
Линейный угоJ1 ;1ву1 ·ранно1·0 у1 ·ла
332
Логарифм 91, 200, -t7<J - 4Hl
Ло1 ·ар ифмическая сrшраш" 386-
387
Логическая фушщшr с~1. Булева
ф~111щил
Логrrчсское отр1щаr111е 585
Логическое слс11онан11с см. Имплн
к~щия
JIOJ'ИЧ<.:CKOC СЛСДСТВllС 'i95
Ломаная 292
Макси.ч ум фушщин -+90, -i92. 495
Мала>J 1·tорема Ф<::р~1а 1G8
Математическая шщv1щня ')66-
567, 568-571
.
Математическая лог11ка 579
Матем:tтическая статистика 524
Математич еское ожидание 514-
517. 519
М<.:дю1 на 27Н, 34Н
Метод
бесконс:•1ного спуска J 70. 562
Гаусса решения сие.тем 1шней-
1-1ь~х уравliений 2.39
~fHT<.:[)BaJIOB 2 11)
11счер11иша111~я Евдокс~t -11
математической 111щукци1 1
см. Математическа>1 и~ щую 1ия
tiеонредепёш 1ых ко:~ффици<::11 -
·гов 235
Феррари реше11ин урав11е11111i
4-й степенн 231
Минимум фу1 rюtиif 490, 492. 493
Мнимая е11.иниrtа 2()5
Мнимое число 8.~, 2()4
Многогранники 3.36
комбинатuрноru типа .33 7
мн:отrраннт.1 й угол )52
MHU l 'U)'ГOJlbH.ИKИ 292-293
MIIOl 'OЧJICH 479
М1южесшо ';.)0-532
J\'lа•те;11,бrюта 4 19
Модель К.··ти - Клейнз 436
Модуль комш1екс1 101·0 числа 206
Модус по1 1енс 589
Мо1юто1 111ая последователыюсть
456
Мощность множества 556
На ибо)lьший общий делитель 1Н9-
190
Наложение 547
Неоо:1\1ожно(,; coG1>1111с 'ЮН
Нсзаш ICH."ICX.~1 ь <IKCl1\)M ')7""'
Нс:заu1101мwс; соuыт1 1я ::; 12 ') J. \
Нt:обхо;111мос \'С.ю1111е ')6~
Hennpe;.1eлc1111ое урав11е1 ше 163
Неопрс.Jелс1111ыi1 1111теrрал 499
Не11ол11ая и11л.укц11я SiO
llеnреrынная дро61,, 184, 188
llenpcpыA11:lЯ фу111щ11 я 174- 476
llenpon1Rnpeч11мcт1.> а1<с1 юм '573-
"1 7(1
1lеравсщтн1> 2·1.~
1/ера11с:нt·1·110 трс.:у1·олh11111G1
Д.1111 'fТX'X I p:tHHhlX ) l 'JJOH .~.32
11~ llJIO(' KO('l 'I 1 2t)0
l lесшiмс.:с1·ныt: со6ыт1 1н '508
Норма КС)~1 1 1J 1 <.:к<..· 1 ю1 ·0 чнс.11:1 206
Норма111, 40~
Об;тасп, ;31 1ачс1 111l1 фу111щн н 471
Обласrъ 011ре.~сле1 1 ш1 фу~ 1ю~ии 4 7 1.
41)~
Облает~, t'X()f\111-юc-111 рнда 501
опr:1з s 16
Обра·1 нют 11 \111Л11к:щ11я ">Н.3- ''>84
Обра1 н.111 1·р111"0110"1с:·1 рнчс:ская
ф}НЮ\llЯ IH.~-· I H5
Обр;m1:1я Ф>'111щ11я 171
06рннос тобр:rжен1 tc 'ЦН
ОбЫ:l\ИНСШК' '<\IIOЖCCl1i '539-'540
06ьt:J\1 :)'5')
.- \'56
011Ja11 11 че1 Щ;t}! lIUCJle/tt)UaтcльШК'J'h
4)6
Окр~ж11uС'11, 101
AЛUJIJ!Ol IIOl :Ю9, ~ 11
девяпs щ•н.:1< 2~'5 286
Ою·аэдр ~.~9. 340
Оннеt1111м1 <жруж1юс1ъ 282
С >rюрн:.~л 1 1лпс1юс1ъ ' 11·1
Оnnрнан 11 рлм:~я ·11 1
OnpL')tt:.11c111 1 с 556. 558
011p<:;tc11t:н111,1 t1 1111тсrрал • 1 9Н
О11т1 1мш1ыюс упраялс 1 11 1 с 1115
Орrраф 2.71
Орисф<'р:t ...JLH
О1111Ц1\К!I 428
Ор1·01 Oll:JJIЫJ:l>i Jlf>OCKЦllЯ .~29
Or1"0·1·r<:~ 1·олы 1ик 1R-1
Ор r'Oцerr 1р 28 \ -\48
Орюцс111р11чес!'11i1 тетраэдр Ч8 -
.1 49
Осеван <:11N\l<..'ТJ)t1я 40'5.
- 130
Ocr юв11ая тrnреж1
aJtГ('tipЫ l. _\;
::J р11ф\\t."П1Ю1 1 ')()
О1но111сн11с 5·13
~KRI lllaJ1CllTHOCl11 515
() iol>p<!Жt:llJ н.: 5.16
Парабола ,; 77, .ПН- ,П9
Пара1u1СJ1с111111сд 353, 5.$- -1, 356. 3')7
Пщх1ллело1рамм .293
Параллельная щ:х>екщ1я j!.7 - 529
Пар.иледь11опъ
u стереu.щ1рш1 3.2'5 - 52(1
на плоскости Лобач.1::1.1tкu10 426
Паралщ~ЛЬ1iыl1 nе~нос 406, 4:Ю
Первообраз11ая ф)'шщ1111 499
Перемесrнте11ьны1 1 зако1 1 130. 217
Перссе•1е11 1tе :-1110;.ксстn 538 , 53<)
Псрестановк11 .И9
С ПOATOJX lll lЯMИ 250
Пнрз ~ида J34. 35Н- 359
Пнф:н·оро~ы 1·рш~ 11 чи<·сл 2К . lб-1
Пла ни1 ·оны 299
Платоно1:Н1J тс:ла .ЧО
Плоскость Лобачснс1ю 1 о В7
ПЛОЩа/\1' 35.2 -35')
llЛOCIIOЙ фи~уры 296- 298, :)')~
1ювер хшх.-1·н 3(J6- 371
сфер.иче('К()ГО тpe)'l'OJIЫJ Нl<:I 4.В
Поверхность 3:%
Покор01· ·Ю5, .i 30
Повороп1ал гомотетнн 4 .i . ./
Погрешность 60.i - 601
Подгррша 551
Подмножесnю S.il
Подобие .282, ..J 3..J
Подходящая дрuбь 187
Позиционная сн<-тt'-13 сщ1с1ения
124
Покззатсль н ;1я фун 1щ11н Ч79- IHI
Поле 178, 1Н3
Полвm-а СНСТС"IЫ :JКСИОМ 176- '57 7
Лолукаса·1•ет,ная 41 2
Полупраuильнr,11; MHUГO l 'J):JJ 11 11I KH
С41 АрХI1..чсдuuы ·1·ет1
Полюс 387, 421
Полнра 387. 421
Полярная ось 37:)
Полярная система 1<оордю 1:п 37 .1
ТТОП()Л11ение ПЛОСКОС1'11 436. 442
44.)
Поризм Штсtп 1ера .5U9
Последонательносп, Ф11бон:~чч 1 1
75 • ..\5..\, 456
Посту11а·1 &Jnp:Jнa 150
Правило 1юдега ~ювю1 21Н. 1Н9
n ранн.11.н ые м н01·01·р:1н111r к11
см. Плато1ю11ы тел:~
Правильные многоу1uльн11к~ 1 ~t) . J
П равильный i-eтpaэ:.tr i46
Предел 11ос..1едuвателы10<..'п 1 462
463
П редел функц1111 474
Предельная теоре~ха П уассона )22
Пределr,ная rочка 464
1l редикат 593
Предметный ук<натель
J lр11зм:1 .В.,. 5.Ч. 357
f fpIO~l:JTOHД ~65
1lр11:1нак
:rлл:1мосра сход11мое111 μяд.а · 167
Ко1ш1 <."«ЩТ1~1uс111 ряда Ч67
f lр11 :щаю1 , \СЛ11МОС'111 154-137
Пр1шц1111
Д11рнхлс '>(н
максимр1:1 4 15
11а11:-.1 е11ьше1·0 ч11сла "i70
Прираще1111е 472
Лроею11в11ая гео."lетрня 439. 44 1
Проек1 н1111ая 11J1ос 1юсть 436, 443
npocю1mr юе 11рео6разов:шие 4:'>'5,
4.39- 4-Н
Гlрос1\111вное nростра 11стRо ..ц.1
l lpoCIO\l l Я 527-3.3U
Про 11 :lнод11 ая 4'52, ЧЮ-489. Ч90
r lpoofipaз ')117
П ро110:11 1111 ю11;V1ь~1ая фuрму11:1 <i8б-
187
flpocтoe число 146- 147, 149
l lptYl'lil\OIIOJIOЖllЫC события '){)9
Прямш~ '57'>
Ган;са 294
Э1.:шСрJ 284- 28'5. 349
Прямое доказательство 564, '>6"i
nrямос пронзве.1енпс множеств
5-Н 545
Пrямоуr()111.11:тя декартова снсте>~а
1<00\), ' \ ll H:IT j75-.P4
11рямо~1'0ЛЪН I 11{ 29:)
l ly< ·r ·ш· \IHOЖCCJ"BO 5.11
1lяты il 11ос1ул:~т llвктщ:~ c.1t. Акс11-
О\1а 11ара, u1 ст.носгн
Р:ш1 ю11СТ111к::и~ цш111н,дрнческ:т Щ)( >-
t:1щ11я ~71
Рао1юut:л н ю1с фш-у11ы 363
Рав1ю1ра 1111 ыi1 ·1·етраэдр .349, 3'Ю
Рз 01ю.мощ 1 юсr1, множеств 5 .14
Р:шrюс1 1лы 1ые 11 рt:обра::юuан11я 1J
алп~брс 22 1, 241, 24'>
Р:1R1Юсоснnлсшrые фиrурьr 163
Ра:11·r;н r :190, 48 1
PR,tиyc .)(11
РХ\11)-С CXOi\11 МОС1'11 pЯJl:I 50 \
Ра :1б11стrе (КО\lбннаторнос) 2"i4
Р:1:1мсщс1111я ..'152
С JIORl '0(1CHl\Яi\ПI 1'52
Р:1:1но<.·11. множс:егв '5--11
/>;1.Jpt·11111 .чoe1 ь
:Jад:~ч на 1юстрое1111с 31S-31(>
\11'111Не\\1\Й \~ [ЩIИ.КЗЛЗ.Х 13.), 23..\
Р;~зрыш rая ф~ нющя 176-4.. .,7
Раснрt:дt:лен11е
ВCJIOЯ11JOC1'CJI ) 14. 518
Пуассона S2.2
1
677
Прелмст11 ыИ указатель
Р:кпредеюп·сJ 1 h ны1~1 эако 11 1 .'Ю, .2 LS
Р:~сходнщ1 1 ~ю1 ря;, 4G6
Рацно1 1а11 1.111 ><:: чнслu 177
Рскуррептн;ш пос1н::дователы юс1 ·1,
р1. Во:.шрат1-ця 1юслсдош1тслыюсть
Рефлекс ~ ш1 гость ..f 3 2
Решето uр:носфепа Цб- 148
Рс111ётка (~5 -М5
Po:v16 2l) 3
l>яд ·16'5 -466
Tei1лupa 502
Лсi1бница '-J7, 503
Сня:JНыi1 t'p:tф 2()6
Секущ:lЯ 30 1
Спмедщша 2Н5
Снм.'1.!етрн ческа я ра:шость ,'>11ю
жес1 ·u :;42
Спмметри•uюс1ъ 29.3. ЧО, 4 .32, 545
Система коор;\и11~п :~72
С11с-1ем:~ уравнений 2.)9
Ск;~ш1 rнос произведение [1скторов
51)8. 403-404
Сколь:шшщ1 с11м~1стрня 106
Скрсщ1та10щ иеся прямы <: 3.26 . .))О
О1у чэйн ая величнна 5 111
Собt'r·нен но р:шныс фн1·уры 421
Событ11с '>05
Сuвчщ1с шюе ч~~сJю ·151-152
Сово кушюС' 1 1> уранненr1й 2.'>9
Со 11р икас,1ющисся ок р : ж1юст11
382
Cvc1ашюе ч.1-н.:лu 146
Сочетания 25'i
с повторе ю1ями 256
Сочетател ы11;111 з:н.;011 L30. 2 17
Спираш.
ApXИMCi'\:l 54, 185
Корн ю с.м. Кгюф01щ:~
Сравне ни е 1 ю м одулю 16l-H1.:S
Cpi:/\l·K :C
ар11фмl"l'НЧССКОС 14 .3 . l+I
K~BCIJICHHOC 145
1·армu т1ч еское 1-13, 1+ 1
1·сомстрнчсскос 14.\ 144
квадратич н щ: 14.:S, 115
Средняя линии ЛН
Степеuн::~я фу1-1кция ..J.7R - 4 79
С1·е11ешю1'1 ряд SU L- 'i03
С1·е 11с1 1 1, ~ ·очки tп110сите.г1инu uк
руж1 ЮСПf 308
Стрелка Пнрса '58(,
Сумма рнr(а 466
Суnсрnоа1щ 1 ш фу11 кцнil 490
Сфер:~ 3.54. 5. - 15
в тетра::э/(рс .Ч7, .:НН
Сфс рич<:ская rсо\fстр11я 4 19
С:фер 11 ч<::ск:JЯ п рямм 42 1
678
Сфсрачссюш система 1<uорд11н;п
.П'5
Сфернчсс 1,ан 1р11го 11омсrр ия )88,
39'>
Сферический м 1 юго:"·ол ~.r 11ш ~1 .2 1
Сфер ~1чесrш 1'i трсутолыrнк L122-
423
Сфсрпчсс1шс расстояю·rе ·12U
Сходящ:шся 1 юсл<.:дов:п<..:лыюст 1,
-l bl -+6.J
<..:хuднщш1сн ряд 466
Счётное множество 53,1, 5.)5
Сюръ<.:К'П'111нос отображение lhl. l l а
!Южсн 1 1с
Тавто.1ш·ш1 '>88
Te!l<'I 55:), :BS -336
вращешш 3.15
Теорема 558
ЛбслJI - Руффюш 2.:\3
Gсзу 2.JLI
Болъяя - l'срвина 297
1.:iр1шншона + 15
В11ста 225, 558
Г\1J 1ьдсн :1 - П;1 1111а .~69
Дс:з~р~·а -158-439
косину('ов 288, 392
l<uш и о м1ю1 ·01рш11 111ках 34LI
Kp<1c rюсельскоrо ..f 1-1
Мепелая 286- 287
Морлея 287
о беско н счност11 м1-южестщj
простых чисел 146- 14 7
о впис:~ююм иле :)05-
.-\07
о кюtтелы-rы~ 502 - ,\07
о трёх пер 11е 1 1111шулярах .329
Па1111:~ •1.)7. + 11
Паск;JЛя .:J :l5. 446
l lнф;1 юр:t 187-290
П толсмеи 307
е1111усuв 392
ум1 южсг1 11J1 нершпност<.:й '> 11 -
'> 12
Ф:-Ul t'C<j -Ю6
Ферм:.~ см. Вешшая тtoμe,\ta Фt:р-
ма
Хешш 4 1j
Чевы 286
Шаю1406
ТсС1 Люка - Лемера 1'54
Тетраэдр 336, 3 :П, 5'.Ю. .)46, 359, .360
Тождест1~е111 юс ото6рnжс ние 549
Тождественное nреобра:юыа 1111с
-132
Тождсствсннu 1кти1 1 1 1 ая фuрму.rы
G!v/ . T~Ш'l'OJ IOl ' ll}f
Тождсст1ю 2 17, 222
Т0110лоп1я 11l - 112.
Тор 13')
Точка '>7'>
Жергшша 286
На1·с:т1 286
Торри челли 2<) 1
Ферма 2t)l
Трашит11 в11ость .1>2.6 . -1-.Н, 5..\4
Тра11с11с1 щс11·11юе ч1tело 19.J
Трсутольник 1lаскаля 25Н-260
'l'J1ИTOH( >МСТ[11 IЧС:СК:Н! фуню \ИЯ )Н9-
-~90, .~91-596, ·1t! l - ·
18'5
Трисекция у1·.11:1 521-522, 586
Tpoxo1 1/ \J jН<I
Удвоеrше кvба '1 19 - 121
) ·ЛIГШ<I П,к i<а.:ш :)8)
У11ив1::рсаль 11 оt.: м 1 южес1uо '541
Ур:ш11с1 шt.: 2 1<)
Пелля 167
Уо101111ая всронт1 юсть 5 l 1-5 12
Фактор11 :u1 249. 26-1
Ф11ry1J:i rюe1·oнt1 t101I 11111р11н ы -11 .2 ,
-1 15
Флексор 5..\ 'i , 346
Фокус ..57Н
1111 tсрбол ы 379
JfCMШICK<'l1ЪJ 380 - 381
ш.1 11абол ы -)78
ЭJIЛШIC:t 378
Фuрм~ла
Валлнса <)2
Вr1 ет:1 225 - 22(1
l'ероп,1 288, 5. .\ 5
Ж11рар;~ .ц5
Кар11~11 ю 229
Му:1 вра 1.J 1
l lыотою - Jlсйбн1 11 \:t -IY9-500
П11ка 298
С им~ rcuнa :'162
Э i1Jtcpa
/1,ЛЯ КОМ llЛСКС НЫХ Чlll'C'J I .21 l
Д!IН MHOl'tll p<il111llKOIS 341,
~42. 34 .)
Фор:-1улы
11p.t11.!C,:.\C ШlfJ 395
сокра щс111101·0 умножения 2 18
Фу1 1к1 1ио11алы 1 ый ат1;JЛ 11з 111
Ф}·11кц1ющ1льньп1 рsщ 501
Фушщия +5 2. 471
Хорда 30 1
Ц<::11'1'p:tJ ll>rl :LИ 11\ )0t:KЦllИ 1.3'), 1·\О
Центральная с н ~1 ме 1·р11я -Ю">
1~t'lПpШI /\ 284, :\49
Ц1.:ш1ая 11 111111я .18'1
Llc 1111 <ш .щюби t:·it. Ht1 1 ре.-р ы наая
дро61,
Ц11кло1ща ~80-58 1 . .)8:)
Ц1J.' 1 11НДр :\;) ,~ . 360
Ц1 f.'Н11 1Др 1 l'ICCl<afl CllCTC."la l(OOP/\11-
11-IT ,'i7 1
[ 111t\ТШ/\;l :\НО
Ч аеп·1чr 11.1 l1 11рсдсп с11. Прсж:m,н;н~
~очка
Ч11с1:1
Кат:1:1а11а L6.:i
Ме.-рсс 1111а J 'i3 - 15'1
Фtp1v1 ,1 15')
Ф н бонач•ш с.м. Послсдоватеш··
ност 1, Фпб011:~ч.•ш
Ч11слов:н1 1юследов ате.-лыюсти 4 с;5
ЧHCJJO (! 198 200
Чнсло тт 2.:1. l -1, l 9'i
Нl ;1р :\:\·1. .- >5'i , 560-:162
Штрих Шсффср<t ')R()
Предметны~~ указатель
Э1'1.11 t'ро11а ,\арак~ t: p11ст11к:1 5112
.:ЭЛ~tt'j.)OD 1~11 IVI 2(1()
Экш 11зале.-1 1т1 юс1ъ (Jю 1 1 1 ч1::ска> 1 ) 'i8-I
Эк.в1U1;V1t' 1 гr·1юсп. м.tЮЖ(.;lТВ 1.:и. Рав ·
l lOo\IOЩTIOCT I, MIIOЖCCt"D
3кc-l'pet-tyм. функц11н 490, 492.. 49l
Э1.:сцс 11трно 1·1 ·ст :\78
~).1емснтар11ан фу1 пщш1 1.., . .,
Э11111-111 с :)77 -:17Н
~)нтроnия 6 :~9
'•)nнтрохо11д~ )Н,./
~·)1 1111\ll IOIOl lД.I 5Н:\
"~•)pЛ:.t Hl 'C H Cl\~IJ! 11po1p:1 "1M:t• 106
СОЛЕРЖАНИЕ
К читателю (Влади.мир Тихам.иров) .. ...... . ..... ......... . . . ....................... . .. ...... 5
ИСТОРИЯ МАТЕМАТИКИ
Старинные системы записи чисел (!111ексапдр Жуков)............ ... .... . . .. .............. .. 12
дополн ительные очерки
О чём могут рассказать ч ислительные (Александр Жуков) - 15. И з истории uифр (Анатолий Савин) - 18.
МАТЕМАТИКА ДРЕВНЕГО ВОСfОКА.
Древний Египет (Галина С.мuр1tова) . ................................. ... ................... 20
Междуречье (Галина Сиuрно1т).......... ...... .. .. . .. ..................................... 25
Древний Китай (Александр Валодсфсr;:ий) ..... . ... ...................... ... ................. 29
доп олни тельные очерки
О формуле плошали четы рёхугольни ка (Влалимир Болтянский)- 24. Как могло появиться первое приближен ие чис
ла л (Галина Смирнова) - 24. Как возн и кла шестилесятеричная система счисле 11 ия (Влалимир Болтя11ский) - 25.
Как вавилоня не реш али квадратные уравнения (Галина Смирнова) - 27. Задач и на теорему Пифс.~гора (Александр
ВололарскийJ - 3 ·1•
АНТИЧНАЯ МАТЕМАТИКА
Фалес и первые доказательсrnа (Влад~llиир Балтщ1с1сий, Сергей Смирнов) . . ... .............. 33
Пиф:tгориего1111юла(ИзабеллаБашмакова,Га.;1u1шСмujт.ова)... ...... ............... .36
Геометрическая алгебра и понятие бесконечности (Иаабе.лла Бащм.акова,
Галина C-.iujJнoвa) ............ . .... . . ... ............. . . . ........... . . ... . . ................. :38
Э1юх<1 эллинизма и закат античноеl'и (И..забе.лла Баu""'шкова, Галина Сиирн.ова) ........ . . . 42
«Н:-~чала" Евклида (Владимир Бо.11rпянский) .. ... .. ..... .... .................... . . .. ... . . .... 48
Архимед (Владшшр Балтян.ский) . . . . . . . . . . . . . ......... . . . . .... . .......................... 5 1.
«Арифметик;н Д.иофанта (Изабелла Bau1./rta'Kot:JCt, Галина. САшрнова) . . .. , .. . .. .. . . . .. . . . . . ... 55
дополнительные очерки
Теэтет (Владимир Болтянский) - 38. Апории Зенона (Изабема Башмакова, Галина Смирнова)- 4 ·1. Геометрия римских
землемеров (Евrе11ий Зайuев)- 47. Содержа ние • Начал» Евклида (Изабелла Башмакова, Галина Смирнова) - 49.
СРFДНИЕ ВЕКА И ВОЗРОЖДЕНИЕ
Ср<:дневековая Индия (Алексщ1др JЗQ!юдсфск:ий) .... . ....... . . ...... .......... . ...... . ...... 5В
Стран.ы арабского Востока (Евгений Зайцев) ..... . . ... ...................... . ...... ... ..... 62
Средпевековая Европа (Евгений Зай~~ев) . ... ....................... . . ... ... . . . , . . . . .. . . . . . . . 66
Леонардо Пи3анский и его время (Изабелла Бащ.макова) . ......... . . ...... ... ...... . ...... . 7'5
Эпоха Возрождения : славные открытия (Галина Смирнова)............. ........ . . ... ...... . 77
Рождение буквенной символики (Гапи11~ Сwирнова) ...... . ... . ... . . ........... . . . . . . ... .. . 84
Лополнительные очерки
Аль-Хорезми (Ярослав Головагюв)- 63. Омар Хайям (AлeKCilrfAP Вололарский)- 65. Срелневековые схоласты против
античных философов (Евrений Зайuев) - 73. Живопись и геометрия (Евrений Зайиев) - 78. Лука Пачоли (Галина
Смирнова) - 79. Никколо Тарталья (Галина Смирнова)- 80. джероламо Карла но (Галина Смирнова)- 82. Фра нсуа
Виет (Галина Смирнова) - 84. Научн ы й вызов ван Ромена (Галина Смирнова) - 88.
680
НОВОЕ ВРЕМЯ
Становле1rиематематическогоанализа(ВладимирКирсанов)............... ............. .89
Идеаль11 ый математик - Леопард Эйлер (Сергей Слщрнов) . . .. . . .. .. ... . . . . . . ............. . 97
XIX ве к освоег1ие а бсrра кткоrо (Алла Дорофеева) ..... ....... . .......... ........ ... .... ... 10 1
Нико;1ай И ва 11ов 11ч Лоба <Iевскнй (Николай Дол.билш-t) ... ............................. ... \ 07
ХХ ве к (Владимир Тихамиров)
..
.
....
. .................................. 109
ЧИСЛА
АЗБУКА СЧЁТА
ПоЗ1'ЩИ(Жные сис1·е мы счислепня (Ал.ексстдр Ж:уков) . . . . .... . . . ........ . ................ 120
Назва ния больших ч исел (Аr~ександр )Куков) . .
.. . ...... . ... _. . ... ...............
_ 125
Четьr ре действия арифметики (А1-tаmалий Савин). ..................• . ... .. .. .. .. ... .. .. .. 128
Делится или н е дел ится? (Ап.ександр Жуков) . . .
. ...................................... 134
Отрицательны<:: •1и cJJ a (А11аталий Савшt) . . . . . . . . . . . . . ................................ 137
Проценты(ANamaлuйСавин) . . .. . .. . .
.
........................... 139
Во:;~всдение в сrеnень и и звлечен ие корня (Александр JКуков) ............................. 140
Средние значения (Татьяна Пuz(vtKинt.i) .. ........................................... \ 43
дополнительные очерки
Задача о разновесах (Алексанлр Жуков) - 122 . Почем 1(11ло баитов? (Алексанлр Жуков) - 123. (4ёт люжи~1ами (Алек
сандр Жуков) - 123. Игра «UЗЯньшиuзы» и чием Фибоначчи (Александр Жуков) - 124 . Сколько песчинок во Все
лен1юиl (Алексанлр Жуков) - 126. Числа-« великаны» (Александр Жуков) - 127 . Как появился значок корня (Алек
сандр Жуков) - 142. Как построить срелние значения (Татьяна Пиголкина) - 145.
ЦFЛЫЕЧИСЛА
Простые чи сла (Александр )Куков) . . .
.
.
...
.
.
.
..................
. 1-16
Совершеш1ые и дружестве нные чнсла (Александр :я91ков) . .
.............
. 151
Числа Мерсенна: заблуждения и рекорды (Борис Стечкин, Ил ья Шар100в) ............... 15 3
Основная теорема арифметики (Александр )!(укав) .... . . . . .
. ...•......•... 155
Арифметика осrаткоnитеориясравнений (Алекса11дрЖул·ов) . ........................ .159
Нео 11ределённъrе уравнения {Ал&л:сандр Жуков) ............... ... . .... .. ...... . .. . .. . 163
Вел икая теоре ма Ферма (Изабелла Ба~им.ак.ова) . . . ....................................... 1uB
дополнительные очерки
Близнеuы (Алексанлр Жуков)- 147. Шестьсот ш естьлесят шесть (Борис Стечкин) - 152. Числа Ферма (Борис Стеч
кин) - 155. Формула веч~юr·о календаря (Александр Жуков) - 159. Как составить расписание турнира? (Александр
Жуков) - 163 . Фигуры с uелочисленными ллинами элементов (Алексанлр Жуков) - 166. Малая теорема Ферма (Иза
бема Башмакова) - 168. Идея доказательства великой теоремы Ферма для п =3 (Изабема Башмакова) - 171 .
« Последний штурм» великой теоремы Ферм а (Лмитрий Абраров) - 173.
ДЕЙСТВИТFЛЬНЫЕ ЧИСЛА
Рацион ал ы 1ы t числа (Александр Жуков) . . ......... "
.....• " ... ...•.....•.... "
......
. 175
Ирраци он альные числа (А.ле?Сса11др Жуков) . . . ............................................ 1 . 79
Цепю,~ с дроби (А11е11:сандр ){{уков) " . .
"
........ ""
.."
.."
.•.. "
.."
... "
.
1~
.АлrорнтмЕвклида(АлександрЖуков). .. ...... ... .. . ...... .................... .189
Чиа1 а Филия и золотое сече ние (Алекса1tдр Жуков, Л11атолий Савин) . ..................... 190
Tpar1сцеН,'\е11тные чнсла (АлексаNдрЖуков) . . . . . . . . . . . . .
.."
......... ". ""
. 193
Ч ис1то n ( 7атья1-ш Пиголкина) . .
. ................................................ 195
Число е (Татыша Пuгал'К:Ина) .....................................• .. ....•. .... .• ... .• .
. 198
дополнительные очерки
По слелам открытия r1ифагорейuев (Алексанлр Жуков) - 180. Раuиuналы·ю или ирраuионально? {Анатолий Са
вин) - 181 . Uепные лроби и календарь (Алексанлр Жуков) - 187. Как запомнить первые uифры числа 7t (Алек
санлр Жуков) - 1<15 . Формул чуАНых совершенство. . . (Александр Жуков)
-
196. Простые и п (Юрий Матиясе
вич)- 198. Задача о рuстовшике (Александр Жуков)- 199. Локазательсrво ирраuио1rальности числа е (ВлаАимир
Тихомиров) - 200. Прекрасный союз (Алекса нлр Жуков) - 200.
681
КОМ[ШЕКСН ЫЕ ЧИСЛА
Jачс ,1 н уж н ы н о ныс чпсла? (Виктор Антонов)
Свойсr:ва КU \1ш1е кс ны х чисел ( Игорь А9wич) . .
Гсо .мtтр1m комrтексных сшсел {/.1/горь А 19иич)
Возвсдснис: в стеш::нь и извлечение корня из комnлексноrо числа (Нгорь Ак:1~лич) .
Лополнительны е очерки
2()2
2 ()')
.Щ7
.211
Кое-что о квадратн ом уравне нии (Виктор Аюшюв) - 204. Формула Муавра и три 1·онометрия (Игорь Акулич) - 2 12 .
К;ж получ ить формулу Эйлера (Виктор А~1тонов) - 212.
УРАВНЕНИЯ И НЕРАВЕНСТВА
U ·1 J риф.\1еп 1ки к ал геб ре (AlleкcaJfдjJ Жуков)
•..•••. .••••• 21..J.
Нес колько сове1ов начижtюЩИ1\1 воmпсбттит<а м , или Как ре шать уравнсю~я
{Алсксаидр)Куков,Влади.~шрДубровский)............. ... ..
............
Квадратные уравнения (Ал.лаДорофеева) . .. . . .. ... . .. . .. .................... ..
Куб11чесю1е урав11е11ия (Влад~.1.мир Д11бровосий) . . . . . . . . .
.
....
..
. ...•.......
Уравнсн11я четвёрто~I сте11 е11 и (Зтюида Ку:шчева, Геш tадий ГТJ 1Nшtсл.·ий)
...•......•.
Ураt11"1енпя высоких степещ:й (Влаr1и.мирДубровсюtй,!'ещщдuit Пущл.1tсh'Uй) ...• . . .. .•• .
С:исте,v~ы ур ав нений (Леонид Кузь.1иu1t, 8.ltади.лшр Д116роrюсий) .
. .. . ........ .
Ре ш еt-~ие 11 е ране r rств (Лео rиtд Ку:л"ми1-t, Влади.,нир .Дубровский) ................. • ... .. . .
219
223
. 228
231
23~
238
243
Лополнительные очерки
Задача о стае обезьян (Алла ,Дорофеева ) - 224. Залача из вавилонской таблич ки (Алла Лорпфеева) - 225. Как ого
родить наибольший участок земли? (Алла Лорофеева) - 226. Экзаме1·1аuионная jадач а (Алла Лорофеева) - 226.
Уравнения , сводимые к квадратн ым (Анатолии Савин)- 227. Алгебра ич еские уравнения и группы Галуа (Вера Пу~
нинская, Гет-rалий Пунинский) - 234.
ПЕРЕБОР ВАРИАНТОВ
«Осо(Jаяп1Jиме1·а"кол.16инаторныхза;1аq(ИгDрьА11,Jиич). ............................... .ИН
nсрсстан овкн (Игорь А·к:улич)
..
.
.
.
........
...............
21 19
Разм е щения (Игuрь Аh._")!Лuч) ...................................... . . . . . .
.....
..
25 2.
Сочет~11-1 н~ ( Игорь Ал.._1иич)
..
...............
...............
......
........
255
Бш 1uv1 llьютона (Игорь А'л).. 'ЛU't) .. _.. ... .
_.,.............................
...
..•
.
257
Задачипокомбинаторr-щс(ИгорьАл;иuч). ...................... • . . . . .
......
.
261
Грщры (Aнcmu.vruif. Савu11) . . . . . .
......................•.....................
266
Лополнитель ные очерк и
Композ и uии и разб иения (Борис Стечют) - 254 . Треу гольное решето (Юрии Матиясевич) - 260. Меланхолия и
магия в квадрате (Борис Стечкин) - 263 . Грибы и знакомства (Борис Стечкин) - 265. «Требуются. . требуются ...
требуются ".» (Анатолии Савт1) - 27 1. Зада ч а о четырех красках (Анатолий Са вин) - 2 72 .
ФИГУРЫ
ГЕОМЕТРИЯ НА rшоскости
Треугольшu<, 11росте йпшй и неисчерп ае мый (R'laдu/'rtufJ Д)16poвcкuif)
........
278
Многоуголышю1 {.Влади.мuр Д,убровский) . . . . . .
. ... ... .... .... ... ... 2<.)2.
Окружность 1 т r<pyr (Влади.мир Д11бровсл:ий) ................ <
•
••
•••••••••••• •
•
••••••••••••
_
·IO I
Геометричесю1еностроения(ВладUJиuрД11бронсл:ий)..... . ............................ 51l
Три :ш:Jмеrштые задачн дреш юсти (Влщ)uмир Дубрпrю,:ий) ......................... . ...... ~ 19
Лоп олнителы~ ые очерк и
Метрические Сtютношения в треугольнике (Владимир Лубровский) - 288. Ч етыре дока.3 ательсrва теорем ы П ифа
гора (Владимир Лубровский) - 2 89 . Из геометрии четырёху гольника (Владимир Лубровскии) - 294. Равнососта в
ленность многоугольнико в. Теорема Больяя - Гервин а (Влалимир Лубровски R)
-
297. Формула П и ка (Владимир
Лубровский) - 298. Ллина окруж~юсrи и плошадь круга (Владнмир Лубровскии) - 304 Задач и из японских хра
мов (Влал имир Лубровский) - 306, Всё 11л и н ичего (Влалимир Лубровский) - J09 . Радикаль ная ось и радикальный
uентр (Влалимир Лубровский) - 3 1О. « Странное» предложени е из « Н ачал » Евклида (Влалимир Лубровский)- 3 12.
Задача о делен и и круга (Влалимир Лубровскии) - 316. Мезоляби и Эратосфена (Борис Стечкин) - 3 20 .
ГЕОМЕТРИЯ 8 ПPO CTPAJ:ICTBE
!J ас1ала ст1...реометрин (В!1.адn1пфД)1бfJовский)
Многогранники (Влади.мирдубровсл.1лl) .
Геомстр 1 1я тетр,tэдра (Влади.мuр ДубровсJ.'ий)
Лоnолнитель н ые очерки
.1 24
.~~6
:Чб
Нес колько задач на nросгранстве~1ное воображе 1 1ие. изображение и... соображение (Влалимир Луброиский) - 33 3 .
Ответы к задачам на страниuе J ЗЗ (Владимир Лубровскиtl) - 334 От формулы Геfона к объему многогранника
(Николай Лолбилин) - 345. Как сделать флексор Штеффена (Вла.лимир Лубровский
-
346.
ГЕОМЕТРИЯ - ЗНАЧИТ < ЗЕМЛЕМЕРИЕ"
fl.; 1 ин а. площад11. uбъём (Владимир Билrпя11сл·ий) . . . . ......... .
Ф ор\1улы абъё ма ( Влади.мир J(J 16JюRc1й11/) .
Р:.шн оветrю~с и r~шносоставл с::нные ф r 11 уры (13ладU/•ШfJ БшmlЯHG1Щtf)
П1ющ<t/\h 1юверхностн ( B11aдzLMltjJ /(J~бровскu.й) . . . .
ЛопоN1ительные очерки
.~5 l
)56
563
. 366
Обьём клин а (Влалимир Лубровский) -3 58 Как Архимед 11 ахолил об~;.ём шара (ВладИм11р Лубропскии) - 361 «Са
пог Шварuа » (ВлалимирЛубровский) - 3 66. Парадокс маляра (Влалимир Лубровский) -167. Объём и площадь по
верхtюсти тел врашения (Владимир Лубровский) - 368.
ГЕОМЕТРИЯ ПЛЮС АЛI'ЕБРА
Системы координат (ИгорьАh)ЛUЧ)... . ... " . .. ..... ..............• . ...... . ... .... . " ...
:'>Тl.
Замечатслы-1&1екривые(Ллексаидр)!(_уh:ов)...................• . . . . . . . . . . . .• .• . . . . .••• . . . :'>76
Спирал11 (.ЛлексаllдрЖуков) . .................................. " ........... " ............. 385
Тrигонометрия(Влади.мир,Ц}1бровСh:uй)............•....•.. .....•.....••......•. ....
:)Ю
Векторыr-1операциипм1-1ими(ВалерийВавилов) ..".......".... . . . . . . . . . . . . . . . . . . . . . . :)98
Лоnолнительные очерки
Uи ссоила ЛиоКJ1еса (Александр Жуков)- 380 Квадра1риса (Алексанлр Жуков) - 180 Как закру глить железную до
рогу~ (АлекQmлр Жуков) - 382. Математическии uветник (Алексанлр Жуков) - 384. Формулы сферическои три
гонометрии (Влалимир Лубровский) - 39.1 . Векторы и геометрия треугольника (Влалимир Лубров ский) - 402 . Урав-
11ения r1 рямой и плоскости в прямоугольt1ых координатах (Владимир Лубровский) - 403 .
МНОГОЛИКАЯ ГЕОМЕТРИЯ
Дuи же11ня (R1tадимир Болтянск.uй) . .
... . ............. ... ............. " . . . . . . . . .
юс;
В1,mуклыефитуры(В11.ади.мирБа11тянск:ий) ... .................. •• . . . . . . . . . . . .
.....
Ч10
Фра кт:ты (Александр ~укав) . .
. .... . .........
. .... ....... ....... .......
415
Ф11гуры н~ сфере (Владимир Д 1 •nрова~щi) .
.
....... "". . . . ...
.
.
.
..
419
Геометрия Лоб аче вс ко го (Владимир Балтянск:и~':t) .
........
................
4 2-1
Гео м е-1 рня 11 rру111 1ы нрс::обр;:tзОJэаний (Влади.мир Балrпянсх:ий) . .
. .................
"'130
Гlрuективн:т rеометрнн (Вал~рий. Вс1вuлов, !3Jtадим.ир/7,убровскui't) . . . . . . . . . . . . . . . • . . . . . .
} :)7
ЛЕТЕРМИНИЗМ и елУЧАЙНОСТЬ
Что такое ма тсм атнческий ан::uшз ( Влад~JJиuр Тихомиров)
150
БЕСJСОНЕЧНЬffi ПОСЛЕДОВАТЕЛЬНОСГИ И сУММЪJ
Гl OC.'I<:'ДUBa'T'Cl l bHOCТI I (ИгopьA'l\.l'JlUЧ) .
.
...•..............
-15.li
Ар ифметич еская и геометричсск:.tя прогрессии (Игорь Акули ч) . ......................
· 157
Предел последовател.hн ости (Игopь AhJVlUЧ)
................ . . "....
162
Llи сло вые ряды (ИгорьАк;улич). . .
...
......................
....".............
. 46'5
Доп олнительные очерки
Последовательtюсти . описа11ные ал1·оритмис1ески (Владимир Тихомиров) - 454 Сколькими способами можно под
няться no лестниuе? (Игорь Акул11ч) - 455. Хозяин и работник (Игорь Акулич) - 45 9 " Оnрелелите n11.ошаль фигу
ры (Игорь Акулич) - 466.
6Н3
ФУНI\ЦИИ
Понятие фуню(ин (Георгий Магарил-Илъя.ев) . .. .. ..... . . . . . . .. .. . .. ..... ... .... ...... . . . . . 469
Фуrпщин непрерывные и разрЫБные (Татъяиа ЛuгQЛкuн.а) .. .. .. ... ........... ..... ...472
Элементарныефункциииихсвойства(ИгорьЛл.)IJlU<l}...... ..............................:.177
Касательная к гр~{фику функции (Георгий Магарwt-11лuяев, Влади.мир Тихалшров) . . . . . .. . . 485
ПРОИЗВОДНАЯ И ИНТЕГРАЛ
Прои~водная (Георгий.Магарил-Ильяев)...................................................487
Экстремальные задачи (Влади.мир Ти.хо.мирrщ Георгий. Магарил -Ильяев) . . . . . .... . . . . . .. . . . 490
Какпостrюить графикфу1·н<ции (ИгорьАкулич)...........................................493
Интегралипервообраз11аяфункции(ИгорьAК)Ulll:ч).................. • . . . . . . . .. . . . . . . . .. . . 497
Степенныеряды(K01tcmaнmu1-tОсипен.ко)......,.........................................501
дополнительный очерк
Что такое дифференuиал? (Влалимир Тихомиров) - 489.
СЛУЧАЙНЫЕ СОБЫТИЯ
Всёначалосьсигрывкосr·и(БорисСевастьлн.ов)......................................... '504
Зависимые и нс::зависимые события (Бори.с Севастьянов). .. . . . . . .. .. ... . ..... . . . . .. .. ..... 510
Случайныевеличины(БорисСевастыпюв)................................................514
Биномиадьнос р:~спрсдсленис (Норис Севастытов) . . . . . ..... ... . ..... . .. .. . . .... . . . . . . .. . 5 18
Сколькоизюминок.вбулоч1<с?(БорисСевастьшюв).......................................520
Статистиказнаетвсё(БорисСевастьянов)................................................523
дополн ительные очерки
Играет ли природа в кости? (Борис Севастьяпов) - 507. Залача кавалера де Мере (Борис Севастьянов) - 508. Сколь
ко времени Ждать автобуса~ (Борис Севастьянов) - 509 . Спортлото (Борис Севастьянов) - 51 3. Закон больших ч и
сел (Борис Севастьянов)- 517. Математич еское ожидание и дисп ерсия в схеме Бернулли (Анатолий Савин) - 519.
Самая необходимая буква в алфавите (Борис Севастьянов) - 525.
ФУНЛАМ ЕНТ МАТЕМАТИКИ
МНОЖЕСf8А И ОПЕРАЦИИ
Множr::ствоиегоэлементы(ВладимирБалтf/.1tасий)......................................530
Бесконечныемножества(Влади.мирВолтянс1·сий).........................................532
Олеращш над множествами (Влади.1rt~ф Бал.тянский) .. .... .. ..... . . . . . .. .. ... . . . .. . . . . .. . 537
Отношения(БорисСтечкин).............................................................543
Отображения(Владu.мирБалтянс"'ий)........,..........................
................546
Группы(А11атолийСавин)........................................... ....................549
дополн ительные очерки
« Парадокс» равных отрезков (Влалимир Болтянский)- 536 . Мошност ь объединения двух множеств (811алимир Бол
тянский) - 540. За гадочные опюшения (Борис Стечкин) - 545 .
МАТЕМАТИЧ ЕСiili Е РАССУЖДЕНИЯ
Доказательствав.математrпсс(Владид1ирУспе1tский).......................................5S5
Доказ ательства методом от противного (Владu.,н.ир YcneNcкuil) .. . . .. . .. ... ..... .. . .. . . . ... 560
Доказательство сущесrвования (Влади.мир Успе1юс.ий) . ... . ..... . . .. . . . . ... . . .... .. ..... . . . 564
Метnд математической m1;n.rr<1т;vп-i (ВлСlдuмир Успенский) . . . ..... . .... .. . . . . ... . . . .•. . . . . . . 566
Л~<сиомы(Влайи./11:ирВощпя1tс1сий).................................. • . . . . . . . . . . . . . . . . . . . . 571
дополнительны е очерки
Определение (Борис Стечкин) - 5 56. И з биографии Колмогорова (Влалимир Успенский) - 557. Теорема, опре
деление, а ксиома, лемма (Анлрей Якушев) - 55 8 . Софизмы (Анатолий Савин) - 559. УтверЖде ние и отр нuа н ие
(Анлрееt Якушев) - 562 . Необход имое и достаточное условие (Андрей Якушев) - 5 63 . Парадокс изоб ретателя (Юрий
Влалимиров) - 568.
684
МАТЕМАТИЧЕСКАЯ ЛОГИКА
Рассуждения, 11 редложения, высказывання (Юpuii ВладUJ1шров) .......... . .. . .............. 77<)
Бупевы функции (Юрий Влади.миров) . .. .. .. ...... . ........................... . .. . ........ 58~
Пролозrщионал:ьные формулы (К)рий Влади.lУtиров) . ............. . .... . . . .. . . .... . . . ...... <;8(,
Яэы:к исчисления предикэтоu (Юрий Владимиров) ........ . ... . .............. . .......... . . 592
Достижения математической логики (Юрий Владимиров) .. ..... ... .. ... . .. ... . . ... . .. .. .. 59(,
дополнительные очерки
« Хочу всё знать• (Юрий Влалимиров) - 580. Булевы операuии в программировании (Юрий ВлалимировJ - 584 .
Кто прав, кто виноват~ (Юрий Влас.имиров) - 587. Хлеба или зрелиw (Юрий Владимиров) -:-- 589. Моды сезона (Юрий
Владимиров) - 590. От Евклида к Г11льберrу (Юрий Влалимиров~ - 595. Вот в чём соль (Юрий Влалимиров)- 59 8.
МАТЕМАТИКА ЗА РАБОТОЙ
ИС КУССТВО ВЫЧИСЛЯТЬ
Приближённые вычисления (Галина Зверк:ина) . ... . ........ . . .. . . ... . .. . ..... .... ..... ... ~02
К~1к определить значение квадратного корня (Алекса11.др Жук,ов) . ... . . . .. . .... . ........ . ... 607
Вычислительные машины - что это такое? (Olleг Е<;уанецов)
......
.... . ..... . .... .. ....... 610
От нерuых вычислительных машн н к персональному компьютеру (Qizeг Кузнецов) . ... .. . . . 615
Чарлз Бэббидж(ИгорьАпокин) ...........................................................624
дополнительный очерк
джон фо11 Нейман (Игорь Апокин) - 616.
ВЕЗДЕСУЩАЯ МАТЕМАТИКА
Математика и ф изика (Игоръ А71?1иич) ... . ....... . ........... . . .. . . . .. . . ...... ... ... .. . . ... 626
Ко"Nmлексные числа и электротехника (ИгорьАкулztч) .......... . ..... . .... . .......... . .... 630
Теория информации (Олег Куаиецов) ...... .. . . ..... . ................ . .... . . . . ........... . 633
Ма·rематика и кристаллография (НщmлайДол.билин) .. ... . • ...... . ...... . ... .. . . ... • . .. .. . 641
Математика на шахматl:iОЙ доске (Евге1tuй Гик) . .. . ....... . ..... . ...... . ........ . ....... . .. 648
МАТЕМАТИЧЕСКИЙ МИР
Вве!(ение (Влади.мир 1'ихо.ми{юв, Серге~7.Демидов) . ...... . ...... ... ............. . ...... . ... 656
Математическое образование и профессиональный рост (Влади.мир Tuxaw.upoв,
G'epгeuДeлiz.fдoe)..........................................................................656
Жизнь мирового математического сuuбщества (Влади.мир Тихам.иров, СергейДемидов) .... 659
Премии матем:1т...Jка м (Влади.мир Тихам.иров, Сергl?йЛе.мидов)
...............
.............660
Математические олимпиады школьнико в (Ан,ато.лий Савин) ... . . . ... .. ... .... . . . .... . . .. . 662
Лополнительные очерки
Примеры задач с математических олимпиад (Анатолий Савин) - 663. « Математический кенгуру ~ (Ана толий
Савин) - 664.
С!~исок основных обозначений .. .... .... .. . .... . ................... . . . .... .. . .... .. . ... .. 666
Греческий алtравит .............. . ..... . ...... . . . ....... . ..... ... .. . ... . .. . . . .... . ........ 666
Указатель имён...........................................................................667
Предметный указател ь . . ........ . ....... . .. . . . ... . ....... .. . . .... . .... . ..... . ............. 675
ЭНЦИКЛОПЕДИЯ ДЛ Я ДЕТЕЙ
Т. 11. МАТЕМАТИI<А
Генеральный д иректор
r. Хра 'юн
Главный редактор
!\1 . Л1.;сё 1 юв;,1
Главный
~'"УДОЖНИI<
Е. ЛуксJ1ы.:кан
Методологический
и отвстстrн::нный
редактор том а
В. !1ожщ11 н
Отвстствснньui:
peдaicrop тома
л. u;щ)Oua
Научные реда1сто1Jы
разделов тома
1 А. С:ш1111 I
11, U'1Ш .'v1al<OU:l
В. IJо:ггянский
11. Дш1()1~л1 11 1
R. Дубронскиi1
13. Тнх~1ш 1 ров
Редактирование
и корр е ктура
С. С\1ставова -
нача111,н11к ОТJ (Сла
о. Ept>MlTB;J -
ста р 111и(1 ре;1акюр
М. Аброси мова - реда1\' 1·ор
Н. Cnt:тлoua - коррс:ктор
!:. Кондратьева
-
редактор 1 1 ронерки
Художественный
редактор
М. t::фремет 11<()
Ассистенты
Х)'ДОЖС(~Твенной
реда1щии
Л. Пущн11:.1
м. Раю11 1;1
Изгото влепне
оригинал- макета
К 1l ванон
л X:ipЧl' fl KO
11. l ll'Tj101iCIO 1(1
Р. С~т>11н
Л. Воло.1'~1rк1п 11'1
Помощниt< ОТDСТ(.':ТВСЮi:'ЬfХ
реда1сrоров
О. Торпакова
Набор и считка
М. Кудрявцена -
пачалышк отдела
10. Лm.\'1ар 1ша
10 АI1тшюва
11. Гольд.\Iан
О. ДСМИ)\ОВ:!
11. Самсо1 юва
Ф. Тахиrова
П. Хохлова
Н . Шt:тк:р11 11нскэя
О. llkпчt 1 1кu
Коордипатор
О. Гор1 ·ун
Директор
по производству
И. Кошелев
Технолог nроизводстnа
Т. ЛЮf>Т~()RЭ
Художники
Н. Доброхото нэ
Т. /(оnр() х о·1·n 1i~1 - Майкпна
А Е1:1,!.ЩКИ!\1ОВ
Е. Пн;(uювюва
11. Краснока
10 JlL:H 11JIOllCIO l lJ
F. Нсн:~стиж1
Е. С~т11 ~кона
А. \\\еч1~1 т
IO. Юron
Фотографы
IU Любцов
Н. l l11cкaμi.;н
Фотоl\1атериалы
предоставлены
I NTERFOTO. PRf:SSF:RllЛ
ЛC~F.NT1 'R BllJ)ЛRCНI\'.
ЛКС p llnt(), Reг l iп:
ы,·эес'\1 юш1·11 Pocci 1t"1cкol1
1 ·осу;(арстuе111юi 1 6н6Л1ютсю1;
фотоаrсптством "сипа Сел»:
10. Nlаз)1ювыч
Суперобл ожка
А. ЕВ/\ПКI t М< )К
Шмуцтитулы
Е Д~1\СЛ1 >('1\t!Я
".\.ванта+» благодарат
з;1 1ю1'ющь в подготовке
l!ЗД:tНШI f{Q ,'vll IJll:Kl'J-JЫЙ отдел
111 1 тср:1турh 1 по HCK)'CC 'l ' t1y
Веер( кт иr'tc ю)1'1
тсул:<1 tхтнснно1! 6 1 1бл1ютсю1
н1 юстранно(1 литературы
llM. м. И. Р\ЛОМ111Ю.
«Л11а 1 1та+» бла1 ·0/(ЩJJIТ Тнt:рское
отдс:.11сппс СбсrегатеJ1ы ют
ба111<а 1·opo;i:i МОС'КАЫ
з;.t фн11:~1 1 совую лоддерж~~·.
оказаIПf)'ТО nрн 11здашш юu,1 г
серин -.этщнюю11едия
ДЛЯ ДСТСЙ ·>.
Особую благодарность
выражж~м Г. Мона,.,.,т11нuй,
Л. Гос1 11-ю!t . В. Доброхотовой
В СЕРИИ «Э НUИКЛОП ЕЛИЯ ЛЛЯ ЛЕТЕЙ » ВЫШЛИ В СВЕТ ТОМА :
• Rсt>мирная щтория » , 1 Б1юло 1 и11 •, • Геология • ,
• Чсловсчеtrоо XXI век •
• История Pototи»
(части 1, l, 1)
• Иtкусст8О »
(чапн 1, l, 3)
• Всемирная литература •
(чапи 1, l)
• Руttка.я литераl)'ра •
(части 1, 2)
•Я •ыкознание. Рус~кии 11-~ык•, " l'оссия: физичt'ская и эко номи•1('('кая
география», «<:т раны Нароль1. Uив11лиэаuии •, • У11иuсрс.\Аы1ыи
11мюстрированв1.1и энuикло11сдическии и.оварь•, «Тех1111ка •, •Гсоrрафия •
«<l>ИJИKil»
(час~ и 1, :.!)
« Pt'Лl1ГltH Mt4pa»
(•1аtт11 1, 2)
•Математика •
•Челооt:I\ »
(частм 1, 2)
сЭколоп1я•, •Сtюр1•, •Обшссrво• (чаt'ТЬ 1), • Х11ми11•,
• Птиuы и Jоерн•, «Информатика•
• Росс11йски(' столищ.1 . Моtква и Санкт- П етербург•,
сr Истор1111 ХХ оска. Зарубежные страt1ы • ,
•Личная безо пасносrь•
УВАЖАЕМЫЙ ЧИТАТЕJIЫ
Adaluii4~ осущсс-1 нляст доставку почто~'~ <;;11-щиююr1сю111 1и1я детей» по Росси11 . Вп1 можстt.: ~i:-tк:1за·rъ нее
nыmедтие в свет тома. Запросы об условиях доставки кннr почтой п:-.tправляliтс по адрес\•: 123022. Москвtt,
'Jjи 7 3, ~центр достаJ3ки '/ldaltffla • Мы также будем блаl'Uдарны 3а любые nожслаi-п-ш и заме'-1:11mя
ОНЮСН"l'еды1 0 t1аши..х. ЮН11'.
Ada-ltffla. -1 - теп ерь в Интернете. За 1'лян1-~те на с<1йт www.a v anta. rn
Фирменные ма1'азины Adaltйi.a.---7-:
• Moc1<t1a, ул. 190') нща, J\. 8;
• Ореховый бульвар , /\. 1'5, «Галерея Во,11олей», 2-й этаж (ст. м. «Домодедовская ·));
• ул. Пятницкая, д. 73. магазин ~ хоротсе настроение~ (ст. м. «Добръщипск:~я->).
Все маr-а:~1 1 1 11 ,1 rаботаrпгс10°0 ло 2()(Х> Ge:i ПЫХО/\llЫХ.
Напоминаем , что кпубная карта A da.ltffla.-+ ,'(аст В~1:-.1 возможнrкть получать нее книги излатст,ства и другие
товары 11 ll:llПИX фирмt:l 111ЫХ M<IГ::tЗИlf:JX по ЛЬl"()'П I ЫМ l' \elfaM .
Телефоны
в Мnсквс; (095) 259-2~05, 259-54 l 2 (/1/I Я с11ра11ок) ,
(095) 259- 7627, 259-6052 (оптовая продажа);
(09'5) 259-6U44, 259-41 7 1 (бесIUiатная доставка по ую1:-~а111 юму адресу 11 Москве
от 5 КIIИТ серии «Э1щиююпедия для детей~):
(RJ 2) 567 -2746, 567- . )67 1 (оптовая 11 родажа , 1ю;1пис1-101"1 пункт).
в Санкт-Гlетсрбурп:.
В серии •Энциклопедия длл детей~ DbllIL'IИ в свет тома:
~ всемирна>~ история·>, «Биолоп-ш», «География», «Геология»,
<1.Исгорил России-> (час1'11 1, 2 11 3), "Рсли1·ии мира-> (ч ас1·и 1 и 2),
«Искуссшо» (части l, 2 н ~). 6Ас1р0110м.ш1 ~. «Русо<ая
литература » (части 1 и 2). • Я3ы~<ознание. Русский лзF-~rк», ~ матt:матика",
"Россия физическая н эко1-юми ч сская география»,
«С~раны. ПарО/\Ы. Цивилиза1 \ИИ», <.Техниr<.'l»,
«Вссмир11ая Jtитсра·1·ура• (ч:.~сти 1 и 2) , «Физика• (части 1 и 2). •Химия •>,
«Че;юве1<-> (час1·и 1 и 2), <.Э 1<0Jю1w1». "Снорт-., •Общест1:ю» (час·1ъ 1),
«Инфор\1атика·>, ~Унивсрсалънъrй иллюстрироRанный
э1щиююгrедический слопарь", ~Российские столицы .
Мос1<Ва и Сашсr-llстсрбург·>, «Личная бсзопаснос."rм,
<-l!fcтupшr ХХ века. Зарубежные страны», ~ птицын звери»,
«Человечесrво. XXJ век~.
Планируется въптуск
TOJ\>108:
«Общесt·1ю» (час1ъ 2),
~чслонск·> (ч:ктп ;'i), • l:>щ1нсс -> ,
"Космо1 ~антика• ,
~ выбор гrрофсссю-1->.
В серии •Современная энциклопедия Ada-ltffla/'>
BЬПJIJПI в свет :книги:
«Мода и стиль», «Музьn<а наших дней~ ,
•Кул1-11-1ар1-1ыс тrщцн11,1-ш мира •, • Мир вещей•
В серии +Самые красивые и знаменитые• вышли
в свет книrи:
<·Бабочки мира<>, «К:111мLи 1\оtира>.>, «Цве:ты мира·>,
<•Жители моря·>, «Замки . Дворцы» , «Парусные корабли-.,
«Зшюто ми1х1», «Хrамы. Монастыри·>.
Планн1>уется выпуск книг:
"кую1ы", «Автомо611ли>.>, ~сады. Парю1»,
•Дре1:111ости мира».
Изда1·едъское объединеJ:Iие Ada-ltffl.a
- 1- 1-арантирует nысокий 11ауч1LЬLЙ и художестве1шый
уровень своих книг.
Эн1 \ иклопелил J1.ЛЯ 11етей. Том 11. Матем атик~~ .
Кн и га издаё'гся в супероблож l\е.
Изд. лиц. No 053:$0 от 09.07.2001. Подписано в печ ать 21.04.2003. Формат 84 х10Н/16.
Бума~"а офсетная. Г<~рнитура «Гарамон.>. Печап, офсе-п 1 ая. Усл. печ. л. 72,24.
Тираж 12 000 экз. Заказ No 481/16.
ЗАО Детское изд:пелпстно *А.ванта+*. 125047, Москва, Оружейный пер" д. l 5, стр . 1
(помещение ТАРП ЦАО г. Москвы).
От1 1 ечата110 с 1·отовых диапозитивов в СП ЗЛО •Конта.кт РЛ~.
L15054, Москва, yJI. Валовая, д. 30/73, стр. 4.
/>(11\Ц11l'l/()(/Н(/1/(1 .\ '11/m8.fl('IJl/l'. M uбtlif!IO ЦNднеги vбfJCIЗ()(JaJIUЯ
ll111111c111epcmtш общего 11 професаюm1. 11ыюю обрС1Jош11111л
/>()сси!"ккщi Фt:дr.:рсщиu. (Писмю N ' 1192/ 1-/ .-1 О
от JUJГ.98.)
Ре1-.(1щ•11д1юа1ю Jl<!Жд)'11арод11ьн1 це11тра.., 06_1••шющих
с.иит..:.. 11(МТ(ПС)11 . 1tl!W.(~J'НajXXnюй 1шфед/юli-сетыо
/( )//N,"/<"( )/, \JЦОС н h'ff'll!Cmвe )''l(!О/ШЮ }/()UJV/(JI
(ll11cn~ю ,....,,, 95 от 080491).)
11/ю..itшt Пре 11и)111тщ /lrкotй(Kmi Фе1)11/тц1ш
u ()б.'Ш< 11111 образования .ю 1001 с
(У1-.·r1з.\ 1• 1 1 J..f от O·U 002J
3HUИKROПEOИJI
OllJI ОЕТЕЙ
1
•
'
///
//
----
/
-----
/
---
/
-----
-----~"":.--------------
1
(1
"·
"
.· ;..·
·~:.-." . ·.
.. ." ...
..
·
.....
..".
-~· ·~:-- .. .
~··" ... : ..
...
..
.::
.·
·- :·:; .·····. .. ....•. ·.
. ....
.~
...
... :.~ :...
... .
·:. . .. . .·.~·.. ··
......" ... . ····· ··
.. .. ....:
j
" ... "_,.."" .. ..... •.
•'"'"''' ~·"
..
...
Аои
.... ,"~
.. ............. ,.
.-~"··~·-~~," , .
·~~-~-,.. .."
.
...." .. ' "" "..
·." ...
" ....
.•
.·
.··
·.. ..
... ·
.·
.
1
..
."
... ""
. ....~-
!\
.·
'• ::
...
· ·..
-~--·
....
. ·.· .."
.-
"...,~,,,..
...
. .,.
.·
" ,,,.1.11"#"~- . ... .
.'
.... ~