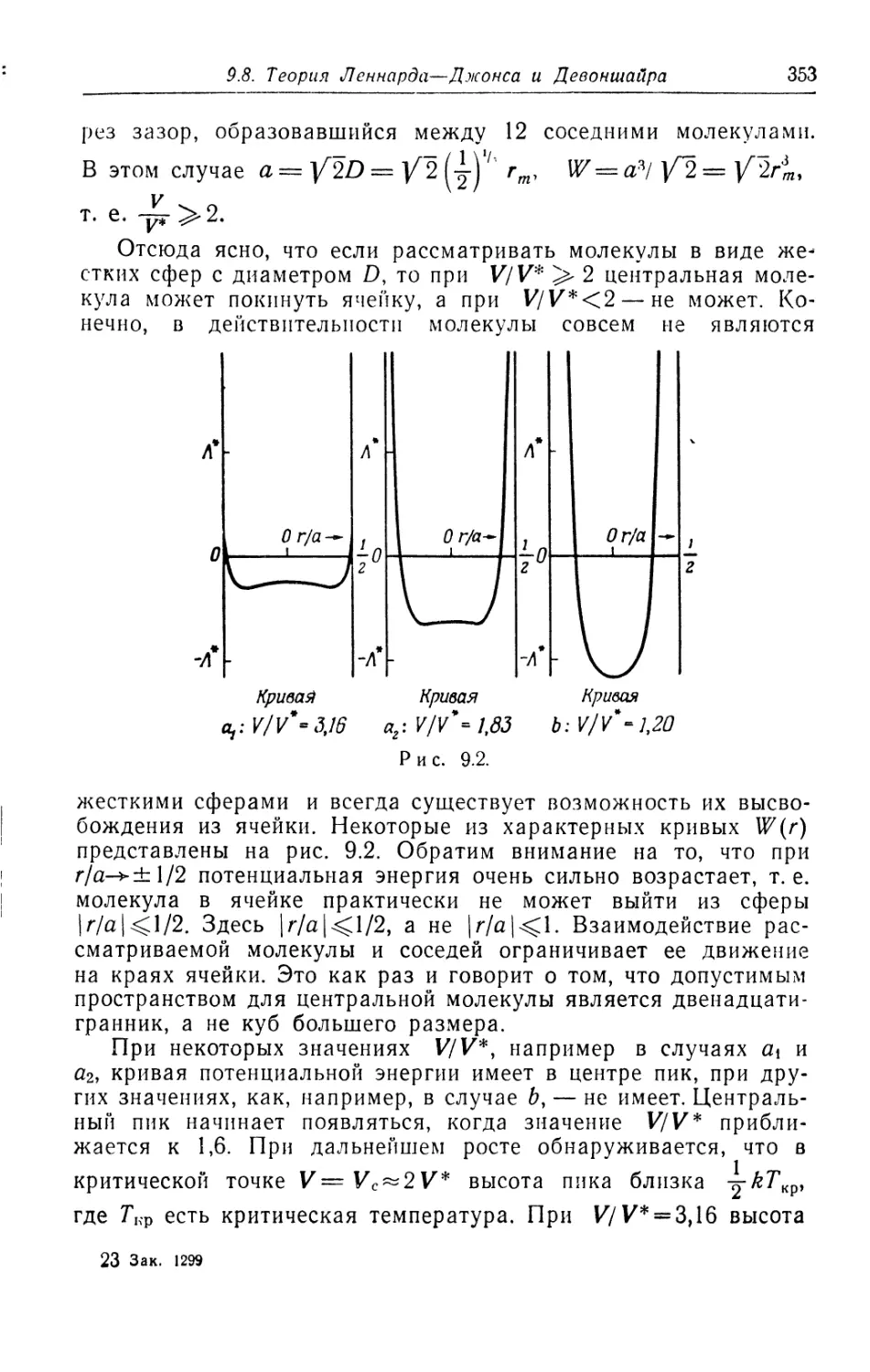
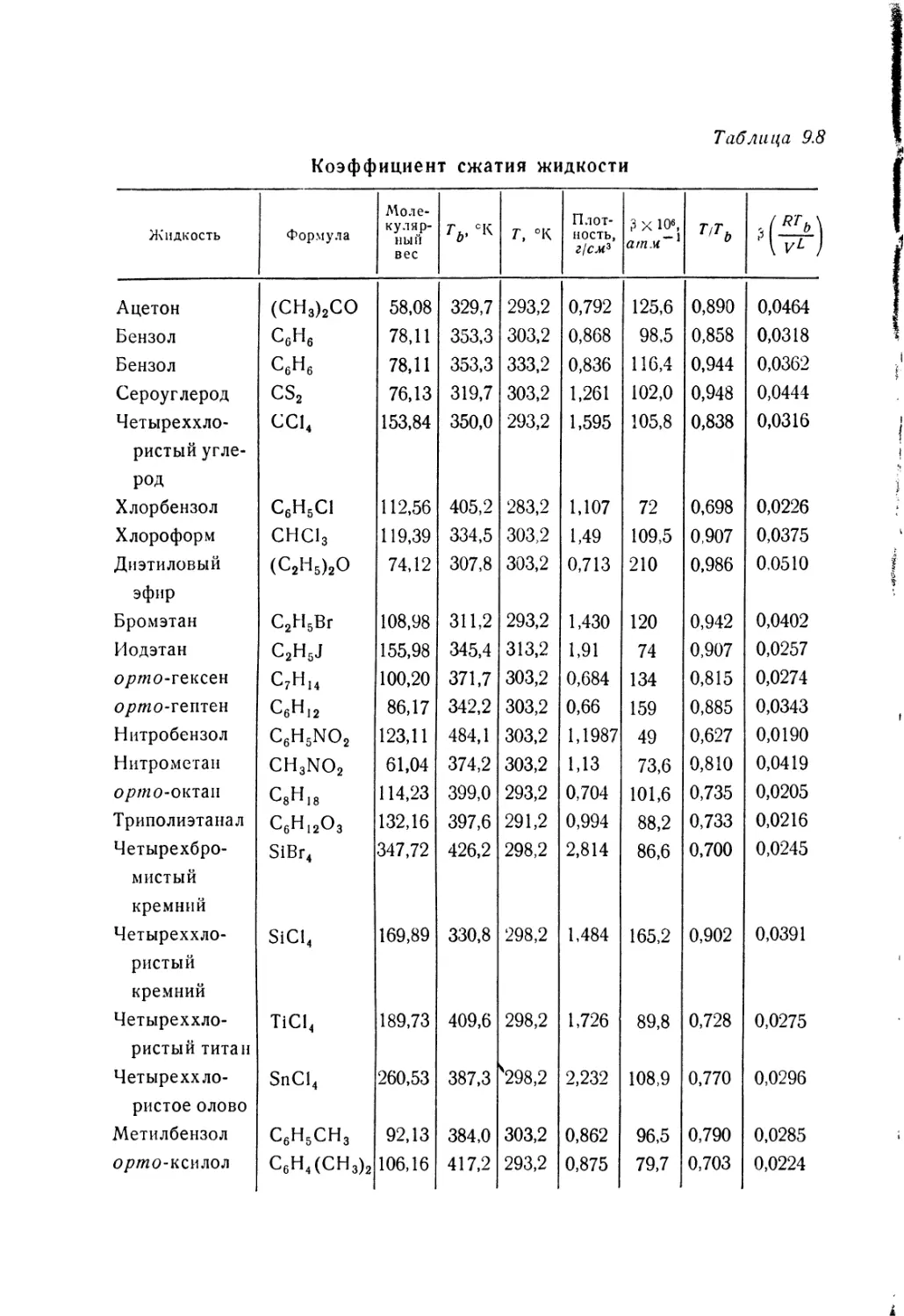
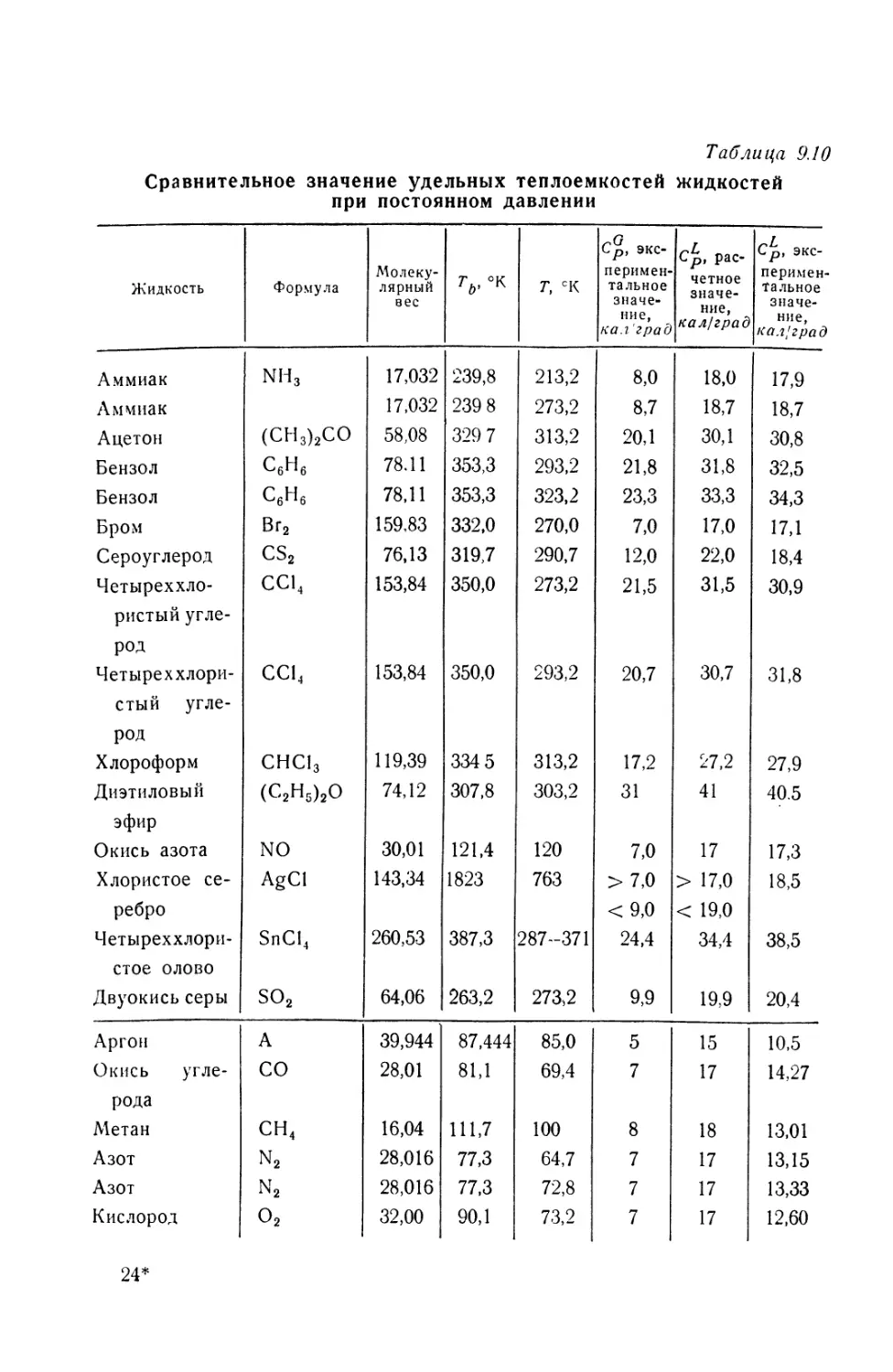
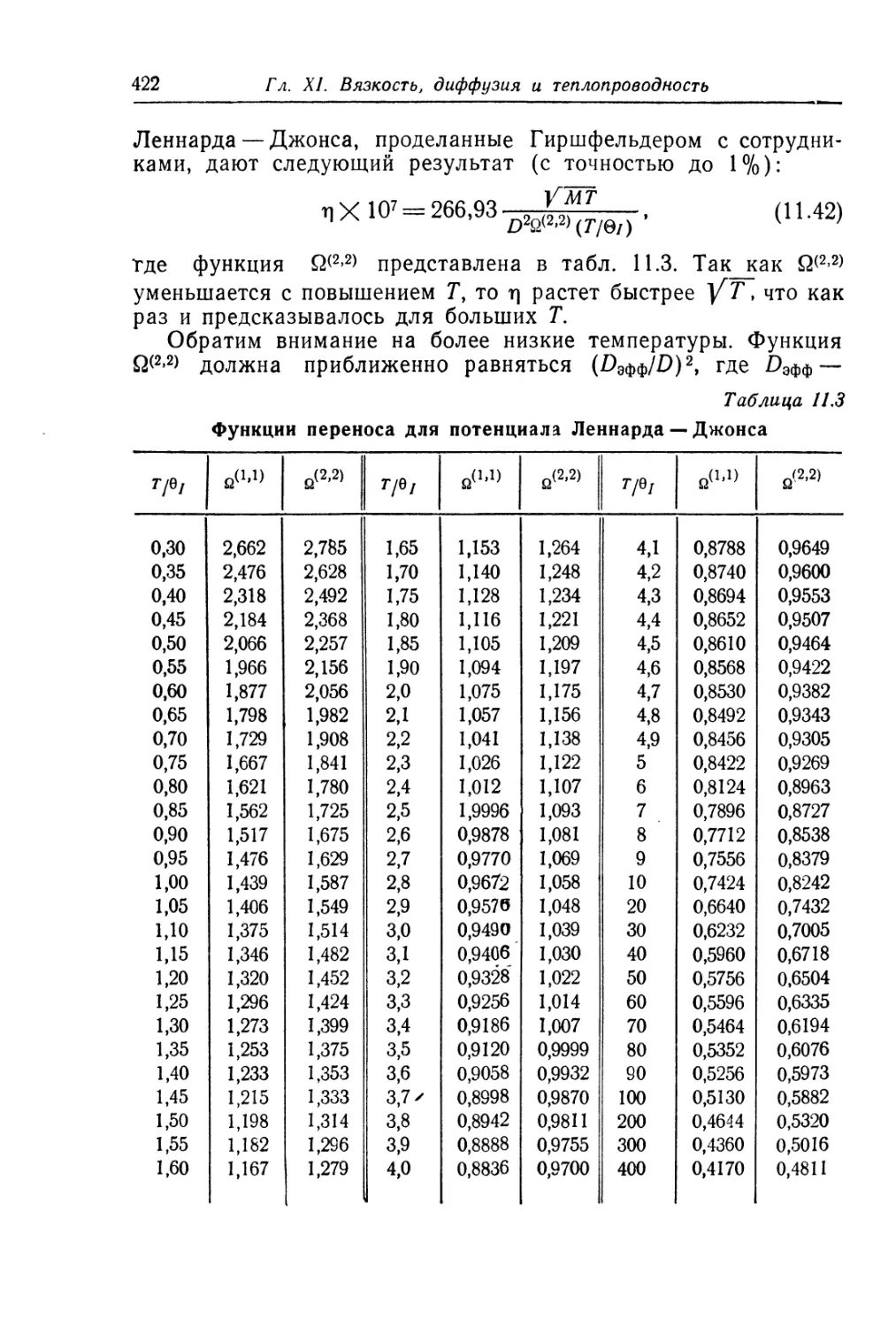
Автор: Цао Сюэ-цинь
Теги: механика газов аэродинамика физика плазмы физика механика физическая механика
Год: 1965
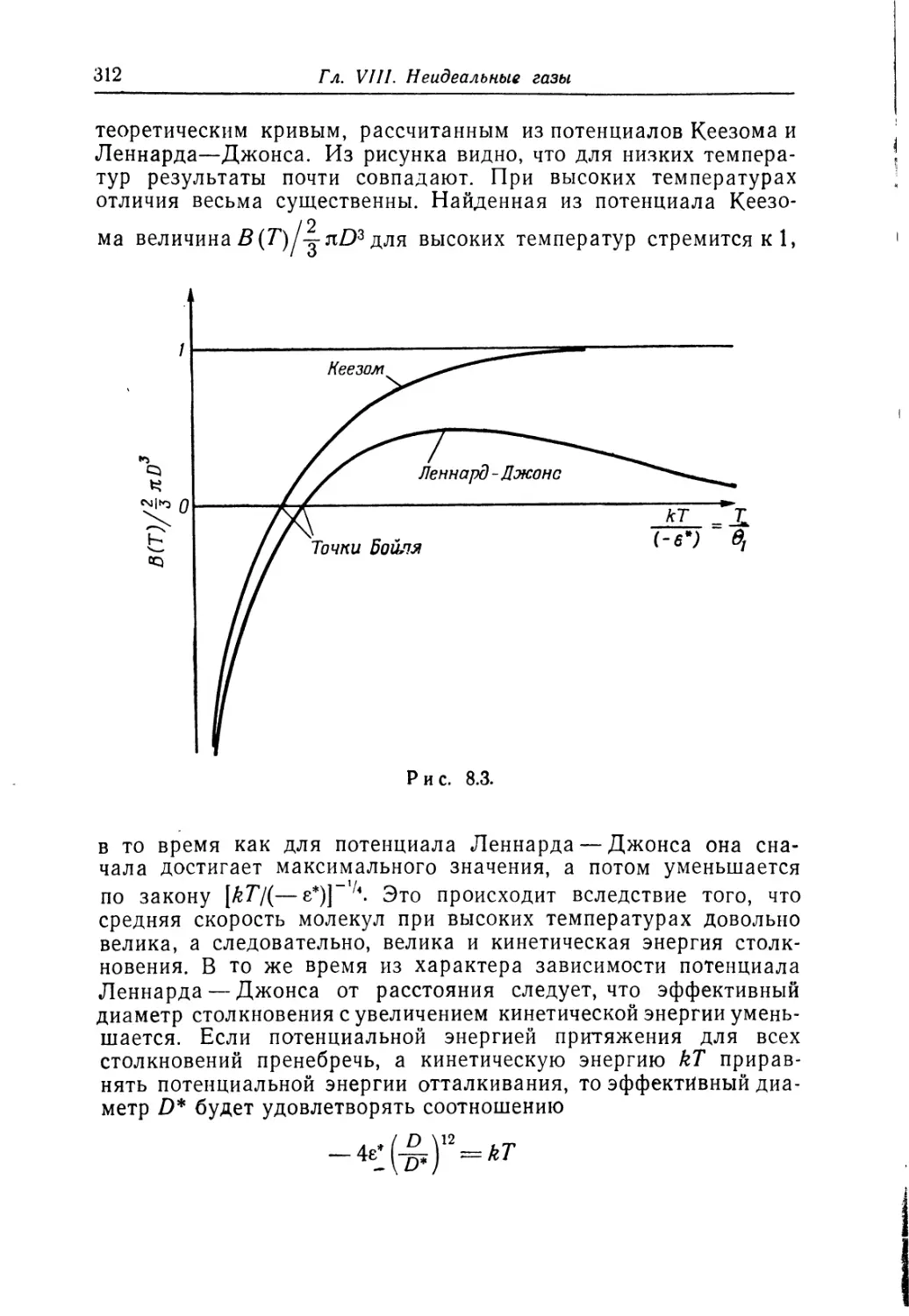
Текст
I Цянь Сгоэ-сень
ИЗИЧЕСШ
МЕХИНИМ
ИЗДАТЕЛЬСТВО
«МИР»
W S Jj z
ЦЯНЬ СЮЭ-СЕНЬ
'ИЗИЧЕСКАЯ
МЕХАНИКА
ПЕРЕВОД С КИТАЙСКОГО
Р. Г. БАРАНЦЕВА, Н. А. СПЕШНЕВА,
Б. В. ФИЛИППОВА
ПОД РЕДАКЦИЕЙ
С. В. ВАЛЛАНДЕРА
ИЗДАТЕЛЬСТВО <МИР>
Москва 1965
УДК 533
Один из крупнейших механиков современности, китайский
ученый Цянь Сюэ-сень знаком советскому читателю по переводу
его монографии «Техническая кибернетика» (ИЛ, 1956)) и много-
численных статей, публиковавшихся в различных сборниках.
В этой книге собран и систематически изложен с единой точки
зрения материал, на котором формируется новая область науки —
физическая механика, объединяющая общие проблемы исполь-
зования физики микропроцессов для объяснения и предсказания
макросвойств изучаемых сред и использования макроэксперимен-
тов для уточнения наших сведений о микроструктуре веществ.
Ценность книги определяется не только ее фактическим содер-
жанием, но и позицией автора и общей направленностью идей.
Книга написана как учебное пособие и благодаря этому
сравнительно легко воспринимается. Она будет интересна ши-
рокому кругу читателей (специалистам и студентам, инженерам
и теоретикам), работающих в самых различных областях меха-
ники.
Редакция литературы по математическим наукам.
ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
Если речь идет о том или ином разделе естествознания, то
представляется совершенно ясным, что используемые в нем
научные средства находятся в зависимости от того круга явле-
ний, который рассматривается в этом разделе естествознания
в данный конкретный период его развития. Представляется
также совершенно ясным, что расширение круга рассматривае-
мых явлений влечет за собой и расширение научных средств,
необходимых для их трактовки.
Практические потребности заставили (в последние 15—
20 лет) давно возникшую и в общем сложившуюся механику
сплошных сред существенно расширить круг физических явле-
ний, с которыми она вынуждена иметь дело. В связи с этим ме-
ханика сплошных сред обогатила свое содержание, ускорила
темпы своего развития и, можно сказать, обрела вторую моло-
дость.
Расширение круга вопросов, рассматриваемых механикой
сплошных сред, естественно, связано с общим прогрессом есте-
ствознания, но прежде всего обусловлено развитием новой тех-
ники, для которой потребовалось решение задач о движении
сплошных сред с большими скоростями, при высоких темпера-
турах и нагрузках, в условиях высокого вакуума и с учетом
физико-химических превращений, сопровождающих движение
в таких условиях. В связи с этим существенным образом изме-
нилось и само содержание механики сплошных сред.
Еще совсем недавно механики имели возможность тракто-
вать большинство практически важных вопросов, основываясь
на сравнительно простых предположениях относительно свойств
сред, движение которых они рассматривали. В большинстве
случаев было достаточно средств классической механики и не-
скольких простых и устоявшихся схем вроде схемы идеально
упругого тела, идеальной сжимаемой жидкости неизменного хи-
мического состава, вязкой жидкости неизменного химического
состава с простыми представлениями коэффициентов переноса
и т. п.
6
Предисловие редактора перевода
Расширение круга рассматриваемых явлений сразу же вы-
явило недостаточность устоявшихся схем движения газообраз-
ных, жидких и твердых сред. В связи с этим начался (и далеко
еще не закончился) период обогащения в известной степени
формальной механики сплошных сред физическим содержанием.
В орбиту механики сплошных сред сразу же попали целые
области знания, ранее развивавшиеся в значительной мере не-
зависимо от нее. В частности, сюда относятся квантовая меха-
ника, статистическая физика, кинетика химических реакций,
электродинамика, теория излучения, физика твердого телаит. д.
Механика сплошных сред качественно изменила свой характер
и начала превращаться из механики, в значительной мере фор-
мальной, в механику, которую можно назвать физической ме-
ханикой.
Быстрое изменение содержания предмета механики сплош-
ных сред создало известные трудности как для механиков, так
и для физиков и выдвинуло перед теми и другими много важ-
ных и интересных проблем. На первом этапе «офизичивания»
механики основная трудность для механиков состояла в том,
чтобы в короткий срок овладеть содержанием ряда разделов
физики, осмыслить их и применить результаты (когда это было
возможно) к решению вопросов механики сплошных сред. Для
физиков основная трудность состояла и состоит в том, что до-
стигнутые ими результаты в подавляющем большинстве случаев
недостаточны для целей механики сплошных сред с существен-
но усложненными физико-химическими,свойствами.
Из сказанного в общем ясно, что физическая механика воз-
никла из практических потребностей, развивается и будет раз-
виваться и еще не одно поколение механиков и физиков будет
совместно работать в этой области.
Работа в этой области нужна, полезна и проводится в до-
вольно широких масштабах. Однако она тормозится отсутствием
соответствующих руководств, ибо из-за молодости нового раз-
дела механики сведения физического характера, необходимые
для его развития, разбросаны по многим специальным руковод-
ствам и сотням журнальных статей.
Учитывая это обстоятельство, известный китайский ученый
Цянь Сюэ-сень взял на себя большой труд по сбору, осмысли-
ванию и обработке весьма значительного количества сведений,
которые необходимы механику для того, чтобы он мог овладеть
физической механикой и включиться в ее разработку. Этот труд
Цянь Сюэ-сеня привел к созданию книги «Физическая меха-
ника», перевод которой и предлагается вниманию советского
читателя.
Предисловие редактора перевода
7
Предмет, которому посвящена эта книга, слишком широк,
чтобы его можно было исчерпывающим образом осветить
в одной книге, принадлежащей одному автору. Поэтому в книге
не нашли отражения некоторые сведения физического и химиче-
ского характера, которые нужны для физической механики, по-
нимаемой в широком смысле. Этот недостаток книги естествен
при современном состоянии физической механики, ясно осо-
знается ее автором и может быть преодолен только в будущем,
после дальнейшей научной разработки соответствующих разде-
лов знаний.
Однако нам представляется, что и в ее настоящем виде
книга Цянь Сюэ-сеня, несомненно, окажется полезной совет-
скому читателю и будет способствовать развитию физической
механики.
При подготовке русского издания работа между перевод-
чиками была распределена следующим образом. Подстрочник
всей книги был выполнен Н. А. Спешневым. Первая глава пе-
реведена совместно Р. Г. Баранцевым, Н. А. Спешневым и
Б. В. Филипповым. Главы 2, 5, 10, 11, 12 и 13 переведены
Р. Г. Баранцевым и Н. А. Спешневым. Перевод глав 3, 4, 6, 7 и
9 выполнен Б. В. Филипповым и Н. А. Спешневым.
Редактор перевода и переводчики считают своим приятным
долгом поблагодарить автора книги, любезно приславшего уточ-
нения и исправления, которые были учтены при подготовке рус-
ского издания.
С. В. Валландер
ИЗ ПРЕДИСЛОВИЯ АВТОРА
Основной целью физической механики является разработка
методов определения динамических свойств сред и материалов,
используемых в технике. Содержание предмета, его основы и ме-
тодика подробно освещаются в введении. В целом физическая
механика исходит из микростроения вещества, используя дости-
жения современной физики, физической химии, квантовой хи-
мии и других наук для того, чтобы облегчить труд конструкто-
ров при исследовании сред и материалов. Таким образом, эта
наука служит инженерной практике.
Книга была задумана как учебное пособие для преподава-
ния данного предмета, и поэтому автор стремился по возмож-
ности сжато и четко формулировать основные понятия и поло-
жения. Кроме того, методика изложения менялась применитель-
но к характеру рассматриваемых вопросов.
Во-первых, в конкретных вычислениях, когда возможно по-
лучить численные значения при сравнительно малом количестве
математических операций, применялись наиболее эффективные
математические методы.
Во-вторых, при решении более сложных вопросов примене-
ние строгих математических методов для получения численных
значений привело бы к длинным и сложным выкладкам, в ре-
зультате которых читатель потерял бы четкость представления
о сущности теоретических проблем. В этих случаях автор не
стремился к точным вычислениям, а использовал предельно
упрощенные модели, сохраняя лишь основные положения. После
упрощения взаимосвязей различных параметров точно форму-
лировались результаты, так что читатель может, минуя сложные
вычисления, усвоить математические решения.
В-третьих, в тех случаях, когда основные понятия ясны, но
еще нет возможности проанализировать явление количественно,
для выяснения сущности явления используются сами понятия,
а количественные закономерности определяются непосредствен-
но из эксперимента.
Физическая механика как наука находится пока еще в про-
цессе зарождения. Об этом свидетельствует третий круг вопросов,
10
Из предисловия автора
о которых речь шла выше. В действительности существует
еще и четвертый круг вопросов, таких, в которых даже основ-
ные понятия еще недостаточно ясны. Например, проблема пла-
стической деформации и прочности твердых тел — проблема, где
до сих пор пока еще нет более или менее общей микротеории и
нет твердо установленных результатов, которые можно было бы
использовать в практике. Поэтому данная проблема, несмотря
на ее исключительную важность, не освещена в настоящей
книге, и это, безусловно, большой пробел.
С другой стороны, недостаточная зрелость физической ме-
ханики как науки проявляется в книге следующим образом:
сравнительно большая часть материала является продолжением
и развитием положений более старых наук, и если даже и встре-
чаются специфические трактовки в свете данного предмета, то
они не всегда совершенны. Так, основные положения второй,
третьей и четвертой глав настоящей книги являются общефизи-
ческими и не относятся к собственно физической механике.
Здесь автор еще не имел возможности изложить специфические
требования этой науки и поэтому ограничился лишь общим
описанием вопроса, в частности третья и четвертая главы в из-
вестной мере повторяют первые две главы книги Фаулера и
Гуггенгейма «Статистическая термодинамика».
Мы решили издать данное пособие, несмотря на то, что оно
имеет ряд недостатков. Автор надеется, что их можно испра-
вить. Недостатки и ошибки непременно выявятся при непосред-
ственном использовании книги и тогда после доработки сле-
дующее издание, несомненно, будет более совершенным. С этой
целью автор убедительно просит читателей направлять ему свои
критические замечания.
Цянь Сюэ-сень
Глава I
ВВЕДЕНИЕ
1.1. Предмет физической механики
Физическая механика — это новая область механики, а сам
термин предложен всего лишь несколько лет назад. Ее цель со-
стоит в том, чтобы посредством микроанализа веществ обоб-
щить и упорядочить результаты макроэкспериментов и в даль-
нейшем с их помощью предсказывать макросвойства других
веществ. В особенности это относится к материалам, находя-
щим применение в технике, например рабочая среда в маши-
нах, металлы и металлоиды в конструкциях и т. д. Таким обра-
зом, это техническая наука, которая служит инженерной
практике.
Естественно, что при определении новых границ какой-либо
технической науки мы не можем исходить только из субъектив-
ных соображений. Важнее выяснить, есть ли в ней необходи-
мость с точки зрения техники. До настоящего времени инже-
неры для решения вопросов, связанных со свойствами
материалов, широко использовали экспериментальные методы.
Так, термодинамические свойства пара определяются экспери-
ментальным путем, прочность и упругость стальных конструк-
ций тоже определяется на испытательном стенде. Происходит
это потому, что, во-первых, вопрос о выборе материала инже-
неру решить совсем несложно, да и экспериментальный метод
тоже весьма прост. Во-вторых, до тех пор пока не выяснена
микроструктура вещества, нет возможности построить теорию
применительно к макросвойствам вещества.
Однако сейчас перед инженерами встают вопросы, связан-
ные с поведением материалов в условиях высоких и сверхвысо-
ких температур и давлений. Столь же необходимо решить
вопрос относительно свойств материалов, подвергающихся
облучению. И если полностью полагаться на эксперимент, то
для этого потребуется громоздкое оборудование и большое ко-
личество времени. Все это представляет некоторые трудности.
С другой стороны, в результате достижений современной фи-
зики и химии проблема микроструктуры вещества, за исключе-
нием атомного ядра, не вызывает каких-либо сомнений, поэто-
му появились предпосылки для формирования такой области
12
Гл. 1. Введение
технической науки, как физическая механика, которая давала
бы инженерам методы расчета свойств материалов. Другими
словами, конечная цель физической механики сводится к следую-
щему: по техническим условиям, предлагаемым инженерами,
создавать такие среды и материалы, которые бы полностью
удовлетворяли этим требованиям.
Конечно, любая новая область науки имеет определенную
преемственность и обязательно содержит в своей основе уже
сформировавшиеся науки. Физическая механика наиболее тесно
связана со статистической механикой и теорией молекулярного
движения (область статистической физики). Столь же близки
к физической механике квантовая и физическая химия. Все эти
науки исходят из атомного и молекулярного строения вещества:
сначала выясняются свойства отдельных атомов и молекул, за-
тем с помощью статистических методов вычисляются свойства
сотен миллионов атомов и молекул вещества.
В этом и заключается путь физической механики — от мик-
роструктур к макроструктурам. Легко понять теснейшую связь
перечисленных наук с физической механикой.
Обратим внимание на следующее: в прошлом у физиков и
химиков при исследовании макроскопических свойств вещества
была иная цель, чем теперь. Тогда вопрос о микроскопической
структуре веществ еще не имел положительного ответа, а тео-
рия атомов и молекул, на первый взгляд, была всего лишь
вполне логичной гипотезой. А если учесть еще и реакционные
атаки идеалистов типа Маха и Оствальда, то становится понят-
ным, что многие относились с некоторым недоверием к атомам
и молекулам. Для уточнения понятий микроструктуры физики и
химики исследовали способы выведения из предполагаемой
микроструктуры уже известных макроскопических свойств.
Если ответ совпадал с результатами непосредственного измере-
ния, то и предполагаемая микроструктура становилась более
достоверной. Поэтому можно сказать, что в прошлом физики и
химики использовали макроскопические свойства веществ для
определения их микроструктуры.
Ныне положение стало обратным. Для нас уже очевидно,
что молекулы состоят из атомов, а атомы — из очень плотного
атомного ядра и весьма разреженного электронного облака. Эта
модель стала нашей надежной точкой отправления. Известно,
что благодаря статистическим методам мы можем определять
макроскопические свойства. Здесь в роли неизвестного высту-
пают макросвойства. Поэтому если сравнивать прежнее поло-
жение с настоящим, то соотношение между известным и неиз-
вестным в микроструктуре и макросвойствах стало противопо-
ложным.
1.1. Предмет физической механики
13
Несмотря на то что физическая механика включает много
теоретических положений физики и химии, ее нельзя целиком
относить к разделу статистической физики или физической хи-
мии, так как фундаментальная наука (чисто теоретическая) не
в состоянии полностью разрешить вопросы, выдвинутые инже-
нерной практикой. Например, мы можем в принципе использо-
вать методы квантовой механики для расчета структуры атома
кислорода и таким путем рассчитать свойства молекулы
кислорода (ее величину, силу взаимодействия и т. д.). Однако
такое вычисление сопряжено с чрезмерными трудностями. Даже
для определения свойства, которое легко рассчитать, мы все же
опираемся на эксперимент. Например, измеряя вязкость кисло-
рода, мы вычисляем размер его молекул и силу их взаимодей-
ствия; или, например, мы измеряем уровни колебательной
энергии при помощи спектра, а затем теоретически вычисляем
термодинамические функции кислорода, его коэффициент теп-
лопроводности и другие макроскопические свойства, не требую-
щие дополнительных экспериментов.
Вопросы, относящиеся к физической механике, зачастую не
так просты, как приведенный пример с кислородом, поэтому
в таких случаях тем более нельзя пользоваться упрощенной ме-
тодикой. Здесь необходим гибкий синтетический эксперименталь-
ный метод. Несомненно то, что основы физической механики
еще включают в себя все данные эксперимента и практики, ко-
торые можно использовать (например, имеющиеся в справочни-
ках по физике и химии данные о свойствах веществ и металлов,
накопленные за длительный период в металлургии, а также
о свойствах сред и строительных материалов и т. д.). Все это
говорит о том, что взаимодействие теории и эксперимента
должно быть основным методом физической механики. Есте-
ственно, что, будучи технической наукой, физическая механика
оказывается промежуточным звеном между фундаментальными
науками и техникой, в которой, с одной стороны, используются
закономерности и методы фундаментальных наук, с другой —
опыт и закономерности техники (к примеру, опыт химической
промышленности или основные положения, полученные в про-
цессе испытания материалов на прочность). Лишь слияние этих
двух сторон дает необходимый эффект. Методы исследования
физической механики совпадают с методами исследования дру-
гих технических наук. В своих общих принципах они мало чем
отличаются от методов всех естественных наук, тем не менее
следует обратить внимание на следующие две особенности.
Во-первых, в методах физической механики уделяется особое
внимание анализу самого существенного, выяснению главных
особенностей явлений, т. е. их самых важных факторов. Затем
14
Гл. 1. Введение
в физической механике для данного явления строится простая
модель, учитывающая наиболее существенное. Только на таком
пути можно надеяться довести аналитические вычисления до
конца. Естественно, что одно и то же вещество в различных
условиях может проявлять различные свойства, поэтому одно
и то же вещество в разных случаях может иметь различные
модели. Например, при изучении вязкости газа молекулы рас-
сматриваются в виде изотропных взаимодействующих мате-
риальных точек. Но при расчете термодинамических функций
газа такого представления недостаточно и необходимо учиты-
вать внутреннюю структуру молекул. При более глубоком ана-
лизе часто обнаруживается, что под руками нет достаточного
количества сведений. Тогда приходится ставить новые экспе-
рименты. Поэтому при развитии физической механики необхо-
димо сочетать теорию с экспериментом, не отдавая предпочте-
ние чему-либо одному.
Во-вторых, в физической механике обращается внимание на
методику вычислений, т. е. на применение эффективных матема-
тических средств, с тем чтобы инженеры могли использовать
достижения физической механики и, кроме принципиального
решения вопроса, имели бы еще и количественные результаты.
Причем вычисления должны быть обязательно доведены до
конца. Эти вычисления сложны, и естественно, что без примене-
ния высокоэффективных методов расчета трудно завершить
поставленную задачу.
Проблемы физической механики можно разделить на две
большие группы. К первой группе относятся равновесные явле-
ния: уравнение состояния, удельная теплоемкость, химическое
равновесие и др.; ко второй — неравновесные явления: диффу-
зия вещества, теплопроводность, вязкость, химические реакции
и др. Для исследования явлений первой группы мы используем
методы статистической механики. Задачи второго типа мето-
дами статистической механики полностью решить невозможно.
Для этого необходимы методы кинетической теории. Положи-
тельной стороной методов статистической механики является их
общность. Полученные в результате анализа закономерности не
зависят от особенностей каждого вещества. И сталь, и кисло-
род подчиняются общим законам термодинамики. Лишь при
конкретном вычислении термодинамических функций требуется
введение характеристик вещества. Именно вследствие общности
методов статистической механики нельзя рассматривать с их
помощью более сложные неравновесные явления. Как правило,
последние можно рассчитать только в том случае, если с самого
начала ввести конкретные модели, вплоть до того, что почти
каждое явление необходимо рассчитывать отдельно. В этом
1.2. Структура вещества
15
одна из трудностей исследования неравновесных явлений.
Именно по этой причине в настоящей книге будут рассмотрены
сначала равновесные явления и лишь затем — неравновесные.
1.2. Структура вещества
При обычных условиях вещество может находиться в трех
агрегатных состояниях: газообразном, жидком и твердом. Эти
три состояния имеют ярко выраженные отличия и свои спе-
цифические свойства. Характерным свойством газообразного
состояния является отсутствие упорядоченности в расположе-
нии молекул. Фактически молекулы газа, исключая моменты
их столкновения, движутся почти независимо. Поступательное
и вращательное движение молекул, а также колебательное дви-
жение атомов внутри молекул можно считать независимыми от
действия одновременно существующих других молекул. Поэтому
при исследовании газообразных состояний наибольший интерес
представляет поведение отдельных молекул.
Твердое состояние является примером другой крайности.
Молекулы расположены очень плотно и упорядоченно, образуя
кристаллы. Естественно, что роль взаимодействия молекул ста-
новится основной. Жидкое состояние является промежуточным,
однако в обычных условиях оно ближе к твердому состоянию.
Таким образом, точнее будет говорить о бесструктурном или
расплавленном твердом теле, чем об организованном или кон-
денсированном газе. Предельное состояние обычно более про-
стое, и для него легче подобрать модели. Жидкость обладает
свойством как газа, так и твердого тела. Поэтому проблема
жидкого состояния более сложна и требует более детального
анализа. Это станет ясным из дальнейшего.
Взаимодействие между молекулами твердого тела настолько
сильное, что образуется совершенно упорядоченная структура —
16
Гл. I. Введение
кристаллическая решетка. Например, щелочные металлы Li,
Na, К, Rb и Cs имеют одинаковые объемноцентрированные
кубические решетки, как это показано на рис. 1.1. Атомы располо-
жены в центре и в вершинах гексаэдра. Если ребро гексаэдра
равно а, то расстояние между ближайшими атомами составляет
В табл. 1.1 приведены значения а и d, выраженные в ангстре-
мах А, для перечисленных выше металлов. Один ангстрем равен
10"8 см. Длины в мире атомов и молекул всегда заключены в
интервале от нескольких до десятков ангстрем. Если естествен-
ной мерой длины в наших жизненных условиях обычно яв-
ляется метр, то ангстрем — это естественная мера длины в
мире атомов и молекул. Одновалентные благородные металлы
Таблица 1.1 Щелочные металлы; объемноцентри- рованная кубическая решетка, А Таблица 1.2 Одновалентные благородные металлы; гранецентрированная кубическая решетка, А
а d
Li 3,46 3,0 а d
Na 4,24 3,67
К 5,25 4,54 Си 3,609 2,55
Rb 5,62 4,87 Ag 4,078 2,88
Cs 6,05 5,24 Аи 4,070 2,87
Си, Ag, Аи имеют, как это показано на рис. 1.2, гранецентриро-
ванную кубическую решетку. Кроме вершин, атомы занимают
и центр каждой грани гексаэдра. Если длина ребра равна а, то
минимальное расстояние между соседними атомами равно
1/* 2
-у-а. Величины а и d для этих металлов приведены в табл. 1.2.
Объемноцентрированная и гранецентрированная решетки
имеют наибольшее число осей и плоскостей симметрии. Другие
металлы, такие, как Mg, Zn, имеют так называемую гексаго-
нальную кристаллическую решетку, как это показано на рис. 1.3.
Кристаллическую решетку здесь характеризует параметр а и с,
а — это длина стороны шестиугольника, с — его высота.
В табл. 1.3 представлены величины а, с и d структур подобного
типа. Естественно, что существуют еще более сложные кристал-
лические решетки. Например, структуру кристалла хлористого
1.3. Радиусы атомов и структура молекул
17
Таблица 1.3
Металлы с гексагональной структурой,А
a c d
Be 2,28 3,59 a
Mg 3,20 5,20 a
р-Са 3,98 6,52 a
Zn 2,65 4,930 a
Cd 2,97 5,61 a
Ti 2,953 4,73 2,892
натрия можно представить в виде упорядоченно расположенных
ионов натрия и хлора (рис. 1.4). Ее можно принять за систему,
образованную взаимосочетанием гранецентрированных кубиче-
ских решеток ионов натрия и хлора. В настоящее время основ-
ным признаком твердого тела считают любое его кристалличе-
ское строение. Стекло не имеет кристаллической структуры и
поэтому считается жидкостью.
1.3. Радиусы атомов и структура молекул
При изменении температуры кристаллическая структура ве-
щества не обязательно сохраняется неизменной. В действитель-
ности многие вещества имеют так называемые аллотропические
модификации. Например, железо при низкой температуре имеет
вид а — Fe, что соответствует объемноцентрированной кубиче-
ской решетке, для которой а = 2,86 А и d = 2,58 А. При высо-
2 Зак. 1299
18
Гл. I. Введение
кой температуре происходит преобразование в вид у — Fe и
возникает гранецентрированная кубическая решетка, для кото-
рой а = 3,56 А и d = 2,57 А. Аналогично этому кобальт при низ-
кой температуре имеет вид а — Со и представляет собой гекса-
гональную структуру, для которой а = 2,51 А, с = 4,11 А и
d = 2,51 А. При высокой температуре он превращается в вид
Рис. 1.5.
При аллотропических преобразованиях наблюдается один
интересный факт: даже тогда, когда изменяется кристалличе-
ская решетка, расстояние между атомами d остается неизмен-
ным. Постоянство расстояния *между атомами в решетке, по-
видимому, является их специфическим свойством. Поэтому
можно предположить, что атомы в кристаллах ведут себя как
соприкасающиеся сферы. Радиус сферы и есть радиус атома,
который в этом случае равняется V2 d. Поэтому радиус атома
металла Fe составляет 1,29 А, а радиус атома металла Со со-
ставляет 1,6 А. На рис. 1.5 изображены кривые зависимости ра-
диуса атомов металлов от их порядкового номера. Здесь перио-
дические изменения очень наглядны, к тому же они подобны
тем, что существуют в периодических изменениях химических
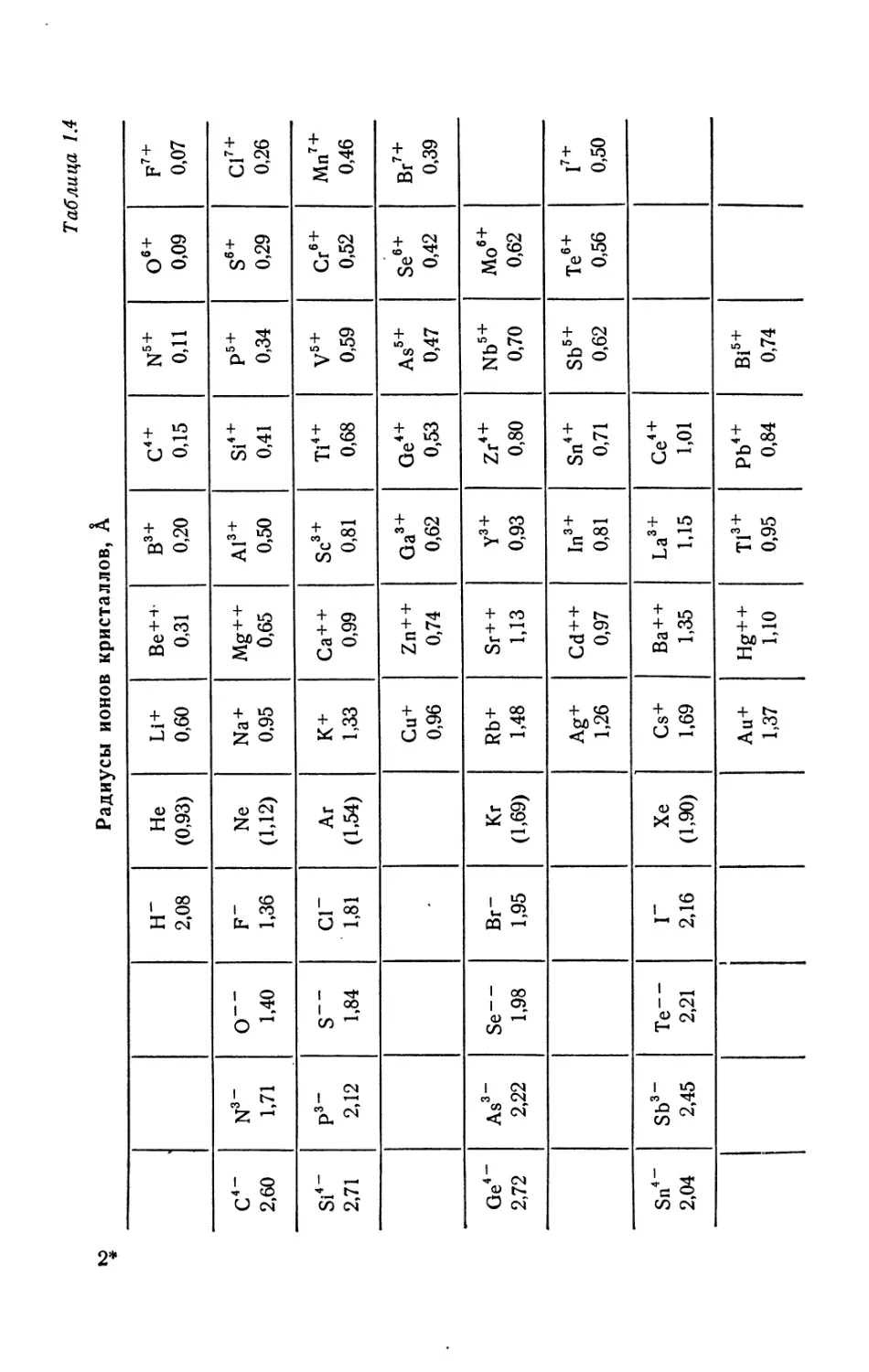
Таблица 1,4
Радиусы ионов кристаллов, А
Н“ 2,08 Не (0,93) Li+ 0,60 Be4*4, 0,31 B3+ 0,20 C4+ 0,15 n5+ 0,11 O6+ 0,09 f7+ 0,07
с4- 2,60 N3- 1,71 О-- 1,40 F" 1,36 Ne (1>12) Na4* 0,95 Mg+ + 0,65 Al3+ 0,50 Si4+ 0,41 p5 + 0,34 s6+ 0,29 Cl7+ 0,26
Si4' 2,71 рз- 2,12 S““ 1,84 СП 1,81 Аг (1.54) К+ 1,33 Ca4*4* 0,99 Sc3+ 0,81 Ti4+ 0,68 V5+ 0,59 Cr6+ 0,52 Mn’+ 0,46
Cu+ 0,96 Zn+ + 0,74 Ga3+ 0,62 Oe4+ 0,53 As5+ 0,47 Se6+ 0,42 Br7+ 0,39
Ое4- 2,72 As3- 2,22 Se-- 1,98 Вг- 1,95 Кг (1,69) Rb+ 1,48 Sr+ + 1,13 y3 + 0,93 Zr4+ 0,80 Nbs+ 0,70 Mo6+ 0,62
Ag+ 1,26 Cd4*4* 0,97 In3+ 0,81 Sn4+ 0,71 Sb5+ 0,62 Tee+ 0,56 I7+ 0,50
Sn4“ 2,04 Sb3- 2,45 Те-~ 2,21 Г 2,16 Хе (1,90) Cs+ 1,69 Ba4* + 1,35 La3+ 1,15 Ce4+ 1,01
Au4* 1,37 Hg++ 1,10 Ti3+ 0,95 Pb4+ 0,84 Bi6+ 0,74
20
Гл. I. Введение
свойств. Самыми большими являются радиусы атомов щелоч-
ных металлов, затем следуют щелочноземельные металлы.
У переходных металлов радиус сравнительно мал.
Вышесказанное можно распространить и на кристаллы
ионов с той лишь разницей, что узлы кристаллов теперь заняты
ионами (не атомами). Табл. 1.4 дает величины радиусов ионов
кристаллов; вычисления выполнены Паулингом1). Из таблицы
видно, что металлические ионы намного меньше соответствую-
щих им атомов. Это, разумеется, можно было предвидеть, так
как при образовании ионов атом теряет валентный электрон. На
основании тех же соображений можно предвидеть, что положи-
тельный ион намного меньше отрицательного иона того же эле-
мента. Табл. 1.4 подтверждает этот вывод. Согласно таблице,
расстояние между атомами в кристалле NaCl составляет
0,95 А + 1,81 А = 2,76 А. Это лишь немногим отличается от вы-
численной в соответствии с рис. 1.4 величины 2,81 А. Причины
небольшого расхождения можно будет выяснить лишь после
более тщательного исследования геометрии кристаллов.
Рис. 1.1, 1.2, 1.3 и 1.4 не соответствуют тем понятиям о ра-
диусах атомов и ионов, о которых говорилось выше. Атомы и
:юны должны быть изображены значительно большими.
Объемноцентрированную и гранецентрированную кубические
решетки следовало бы изобразить так, как это сделано на
рис. 1.6 и 1.7. На этих рисунках атомы соприкасаются, а радиус
составляет половину расстояния между атомами. Такое пред-
J) Pauling L., Nature of chemical bounds, Cornell University Press,
1940,
1.3. Радиусы атомов и структура молекул
21
ставление о стандартном или среднем межатомном расстоянии
можно распространить и на молекулярные структуры. Конечно,
при этом необходимо учитывать, что расстояние между атомами
зависит от типа взаимодействия или связи между самими ато-
мами. Мы уже видели, что вследствие различия между метал-
лической и ионной связями получились две группы радиусов.
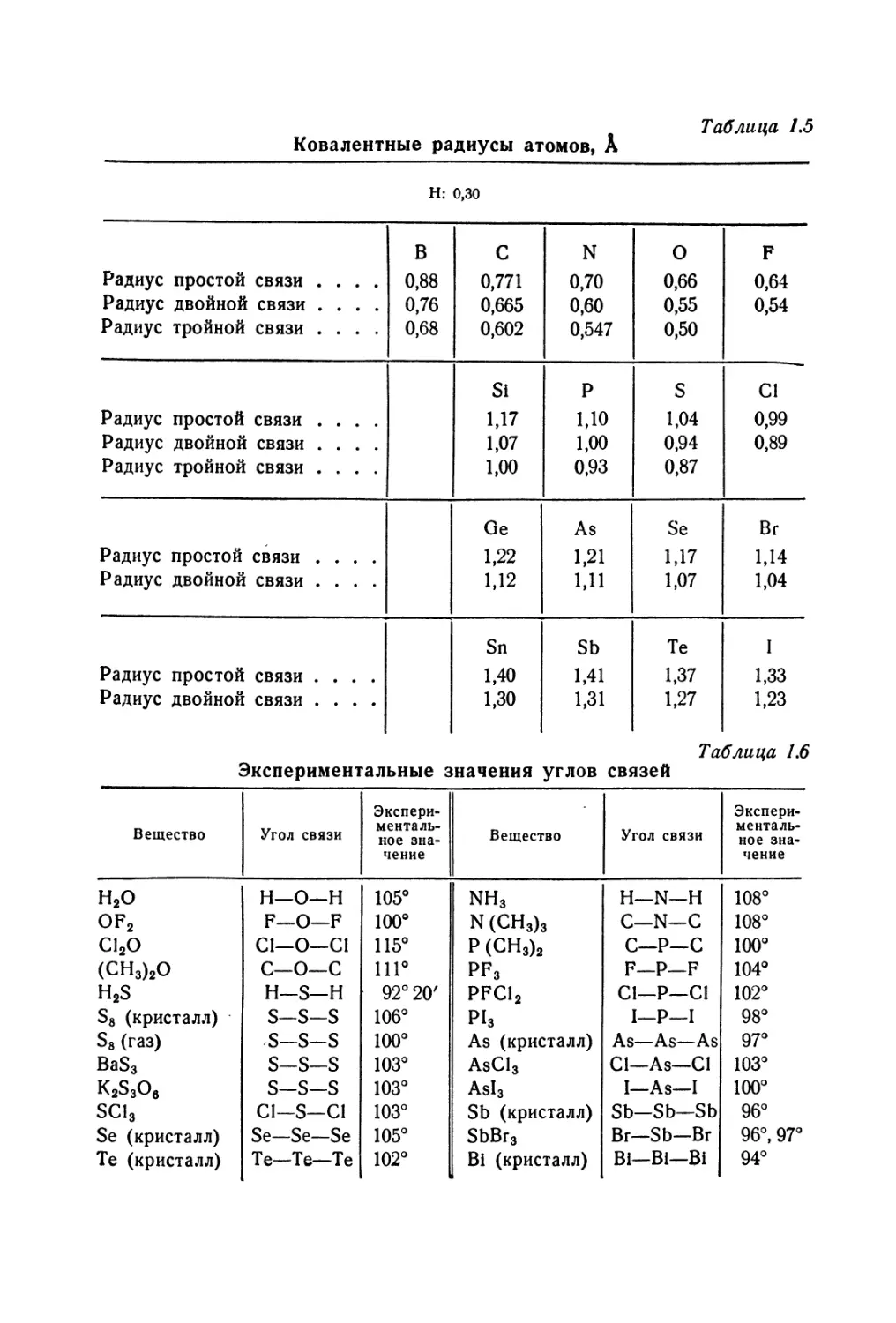
Для большинства молекул характерна ковалентная связь. Она
имеет свою группу радиусов. В табл. 1.5, составленной Паулин-
гом, приведены ковалентные радиусы атомов. Расстояние
между атомами в этом случае представляет собой сумму кова-
лентных радиусов атомов, образующих связь. Например, рас-
стояние между атомами С и I в иодометане представляет собой
сумму ковалентных радиусов простой связи между атомами
углерода и иода, или 0,77 А+ 1,33 А = 2,10 А. Вычисленные
данные составляют 2,10 А ± 0,03 А. Расстояние между атомами
С и Н в аналогичном химическом соединении равно 0,77 А +
+ 0,30 А = 1,07 А. Вычисленные данные составляют 1,09 А.
Используя ковалентные радиусы из таблицы 1.5 и зная на-
правление связи, т. е. угол связи, очень легко построить про-
странственный каркас молекулы. Если взять, например, молеку-
лу иодометана, то вся задача сводится к нахождению свойств
атома С. Теоретические и экспериментальные данные показы-*
вают, что у атома углерода, связанного с другими атомами че-
тырьмя простыми связями, направления связей приближен-
но образуют четыре угла правильного тетраэдра, а сам атом
расположен в середине. Угол, заключенный между двумя свя-
Таблица 1.5
Ковалентные радиусы атомов, А
Н: о,зо
В С N о F
Радиус простой связи .... 0,88 0,771 0,70 0,66 0,64
Радиус двойной связи .... 0,76 0,665 0,60 0,55 0,54
Радиус тройной связи .... 0,68 0,602 0,547 0,50
Si P s Cl
Радиус простой связи .... 1,17 1,10 1,04 0,99
Радиус двойной связи .... 1,07 1,00 0,94 0,89
Радиус тройной связи .... 1,00 0,93 0,87
Ge As Se Br
Радиус простой связи .... 1,22 1,21 1,17 1,14
Радиус двойной связи .... 1,12 1,11 1,07 1,04
Sn Sb Те I
Радиус простой связи .... 1,40 1,41 1,37 1,33
Радиус двойной связи .... 1,30 1,31 1,27 1,23
Таблица 1.6
Экспериментальные значения углов связей
Вещество Угол связи Экспери- менталь- ное зна- чение Вещество Угол связи Экспери- менталь- ное зна- чение
H2O н—о—н 105° NH3 H—N—Н 108°
of2 F—О—F 100° N(CH3)3 с—N—С 108°
C12O С1—О—С1 115° Р (СН3)2 С—Р—с 100°
(CH3)2O С—О—С 111° PFs F—Р—F 104°
H2S Н—S—Н 92° 20' PFC12 С1—Р—С1 102°
S8 (кристалл) S-S-S 106° Pis I—Р—I 98°
S8 (газ) S-S-S 100° As (кристалл) As—As—As 97°
BaS3 S-S—S 103° AsCl3 Cl—As—Cl 103°
K2S3Oe S-S-S 103° Asl3 I—As—I 100°
SC13 Cl—S—С1 103° Sb (кристалл) Sb—Sb—Sb 96°
Se (кристалл) Se—Se—Se 105° SbBr3 Br—Sb—Br 96°, 97°
Те (кристалл) Те—Те—Те 102° Bi (кристалл) Bi—Bi—Bi 94°
1.3. Радиуса атомов и структура молекул
23
зями, близок к 109°28' (центральный угол тетраэдра). Кристалл
алмаза имеет такой же угол связи. Углы связей других атомов
представлены в табл. 1.6, также составленной Паулингом. Крем-
ний тоже имеет углы связей правильного тетраэдра.
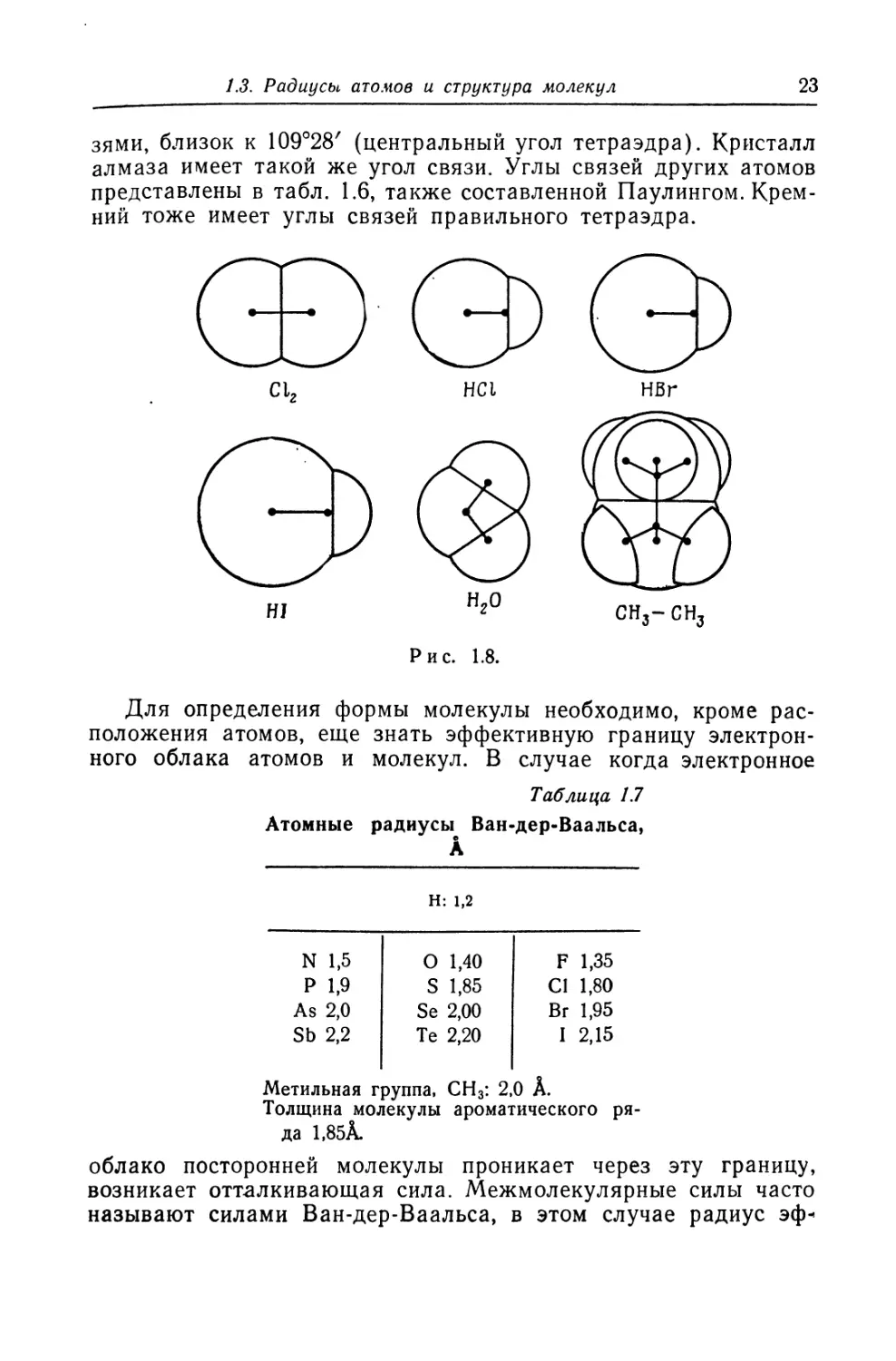
Рис. 1.8.
Для определения формы молекулы необходимо, кроме рас-
положения атомов, еще знать эффективную границу электрон-
ного облака атомов и молекул. В случае когда электронное
Таблица 17
Атомные радиусы Ван-дер-Ваальса,
А
Н: 1,2
N 1,5 Р 1,9 0 1,40 S 1,85 F 1,35 Cl 1,80
As 2,0 Se 2,00 Br 1,95
Sb 2,2 Те 2,20 I 2,15
Метильная группа, СН3: 2,0 А.
Толщина молекулы ароматического ря-
да 1.85А.
облако посторонней молекулы проникает через эту границу,
возникает отталкивающая сила. Межмолекулярные силы часто
называют силами Ван-дер-Ваальса, в этом случае радиус эф*
24
Гл. I. Введение
фективной границы называют радиусом Ван-дер-Ваальса. Если
построить сферы, центры которых совпадают с центрами ато-
мов, а радиусы — с радиусами Ван-дер-Ваальса, то можно по-
лучить модель молекулы. На рис. 1.8 показано несколько про-
стых молекул, нарисованных таким образом. В табл. 1.7 при-
ведены примеры радиусов Ван-дер-Ваальса для некоторых
атомов, которые также найдены Паулингом.
1.4. Использование представлений о структуре вещества
В предыдущих пунктах мы сделали попытку ввести конкрет-
ное изображение для молекул и атомов. Наша цель состояла
в том, чтобы подготовить основу для рассмотрения макроско-
пических свойств, так как молекулы и атомы являются состав-
ными частями любых веществ. Представление о том, что
каждый отдельный атом и молекула имеют определенную вели-
чину и форму, само по себе часто дает полезный толчок для
решения важных инженерных проблем.
В качестве нового примера можно привести закон для раз-
меров атомов, которым руководствуются при образовании за-
мещений. Этот закон сформулировали Хьюм-Роузери и др. За-
мещение— это сплав двух видов металлов, в котором некоторые
ячейки кристаллической решетки основного элемента заняты
атомами другого элемента. Очевидно, исходя из чисто геометри-
ческого анализа, можно сделать вывод, что размеры двух типов
атомов не могут разниться очень сильно. Иначе может серьезно
исказиться структура кристаллической решетки в процессе за-
мещения, и тогда произойдет лишь частичное сплавление. Фак-
тически эти авторы обнаружили, что при различии в размерах
атомов свыше 15% невозможно образование твердого раствора
с какими бы то ни было компонентами. Под радиусами здесь
подразумеваются те радиусы металлов, которые приведены
в табл. 1.1, 1.2 и 1.3. В табл. 1.8 приводятся радиусы атомов и
растворимости различных металлов в Си и растворимость Си
в этих металлах.
Согласно указанному закону, система Ag— Au должна
являться лучшей иллюстрацией высокой растворимости, так как
оба компонента представляют собой гранецентрированные куби-
ческие решетки, имеют одинаковую валентность, а их атомные
радиусы отличаются лишь на 2%. Такой вывод вполне оправ-
дан, так как система Ag— Au образует гомогенное замещение
всех компонентов.
Другим примером является существование некоторых специ-
фических молекулярных соединений. Соединения включе*
1.4. Использование представлений о структуре вещества
25
Таблица 1.8
Начальная растворимость некоторых типов медных сплавов
(растворимость рассчитывается по процентному содержанию атомов
растворяемого вещества)
Компоненты Соответствие радиусов Растворимость в меди Растворимость меди
Си—Be Соответствует 16,5 Be 2,0 Си
Си—Mg Не соответствует 6,5 Mg 0,01 Си
Си—Zn Соответствует 38,4 Zn 2,3 Си
Си—Cd Не соответствует 1,7 Cd 0,12 Си
Си—Оа Соответствует 20,3 Ga Очень мала
Си—Т1 Не соответствует Мала Мала
Си—Ge Соответствует 12,0 Ge Мала
ниях) —это такой тип соединений, в которых большие молекулы
включают в клеточную структуру сравнительно малые моле-
кулы или атомы. Этот термин часто употребляется применитель-
но к химическим соединениям типа гидрохинона [р—СбН4(ОН)2].
Канальные соединения представляют собой аналогичное явле-
ние. Это продолговатые, изогнутые кристаллы цилиндриче-
ской формы, образованные молекулами мочевины. В этих хими-
ческих соединениях между молекулами, образующими внешнюю
оболочку, и внутренними молекулами не образуется химической
связи; просто один тип молекул оказывается захваченным
внутрь решеткой молекулы другого типа. Прочная связь, суще-
ствующая между тремя крупными молекулами гидрохинона,
приводит к тому, что соединения устойчивы. Конечно, лишь
кристаллизованные молекулы могут образовать устойчивую
клетку. И такие соединения могут образовываться лишь тогда,
когда эта клетка достаточно велика по отношению к содержи-
мому. Если внутренние молекулы очень малы, то они могут
проскальзывать сквозь щели кристаллической решетки. Напри-
мер, можно образовать соединение типа гидрохинона с А, Кг,
Хе, SO2, НС1, С2Н2. Для этого нужно, чтобы гидрохинон, поме-
щенный в сосуд с этими газами, превратился под давлением
в кристаллы. При повторном нагревании газы смогут высвобо-
Крамер Ф., Соединения включения, ИЛ, М., 1963.
26
Гл. 1. Введение
диться. Это явление представляет большой интерес для инже-
нерной практики. Мы можем «хранить» инертные газы при
постоянном давлении и постоянной температуре. Кроме того,
можно использовать этот метод для разделения и очищения
инертных газов.
Канальные соединения из мочевины и серомочевины имеют
еще большее значение для техники. Молекулы мочевины не
образуют такой шарообразной оболочки, как молекулы гид-
рохинона, а представляют собой кристаллические изогнутые
цилиндрики, состоящие из трех связанных цепочкой спиральных
тел. Они имеют трубчатую полость, в которой могут быть поме-
щены продолговатые молекулы. Внутренняя полость мочевинных
соединений несколько меньше и может с успехом хранить в себе
линейные молекулы. Сечение же трубочек, образованных моле-
кулами серомочевины, больше. Линейным молекулам в них бу-
дет слишком свободно, поэтому они могут хранить в себе моле-
кулы с боковыми ответвлениями.
Очевидно, что в структурах подобного типа отношение ингре-
диентов зависит только от длины внутренних молекул. Поэтому
можно допустить, что большая часть соединений подобного типа
не имеет стехиометрических молекулярных отношений, так как
возможность их появления зависит только от пространственных
характеристик. В инженерной практике такие процессы можно
использовать для разделения двух типов соединений, у которых
близки точки кипения, но различны формы, так как один тип
молекул может быть помещен в трубку, а другой — нет из-за
несоответствия размеров. Те молекулы, которые могут быть по-
мещены, образуют канальные соединения и кристаллизуются, и,
таким образом, их можно отделить от тех, которые невместимы.
Например, С11Н24 имеет точку кипения 195,8° С, а СюН18 193,3° С.
Бензол имеет точку кипения 80,1° С, а циклогекнафтены 80,8° С.
В молекулах, образованных таким способом, можно освобо-
диться от мочевины при помощи воды.
Аналогично ведут себя и молекулярные фильтры. Искус-
ственный цеолит обладает всеми свойствами естественного цео-
лита, но если исключить из искусственного цеолита молекулы
соли и воды, то в кристаллах искусственного цеолита на месте
бывших молекул появятся ячейки. Эти ячейки имеют опреде-
ленную величину. Поэтому молекулы, у которых подходит раз-
мер, очень легко могут быть захвачены кристаллами, а непод-
ходящие по размеру молекулы очень легко просеиваются и
«отфильтровываются». Применяя различные кристаллы и ме-
тоды подготовки, можно получить «фильтровые отверстия»
разной величины. Это эффективный метод разделения газов.
1.4. Использование представлений о структуре вещества 27
В заключение мы также можем упомянуть, что до сих пор
еще не получены M+FO3 или M+FO4, в то время как уже полу-
чены хлорат, перхлорат, бромат, пербромат, иодноватокислая
соль, иоднокислая соль. Вопрос здесь не только в химической
связи, которую обычно рассматривают в литературе, но и в са-
мой структуре. Образуется положительный ион семивалентного
фтора, который слишком мал (см. табл. 1.4); его радиус со-
ставляет всего лишь 0,07 А, а соответствующие радиусы для
иона хлора — 0,26 А, для иона бария — 0,39 А, для иона иода—
0,50 А. С другой стороны, радиус отрицательного иона двухва-
лентного кислорода равен 1,4 А. Поэтому, хотя ионы кислорода
во фтористой и перфтористой кислотах уже прижаты вплотную
друг к другу, ионы фтора, расположенные в центре, настолько
малы, что не могут соприкасаться с ионами кислорода и не мо-
гут образовать химическую связь. Это еще один пример значе-
ния размеров в структуре молекул.
Глава II
КВАНТОВАЯ МЕХАНИКА
Если объектом нашего исследования являются атомы и мо-
лекулы и если мы ограничиваемся выяснением их поведения
в различных условиях и средах как одного целого, то для этих
целей вполне достаточно, знания законов и формул обычной
квантовой механики. Лишь при исследовании атомного ядра
и составляющих его элементарных частиц возникает необходи-
мость в более новых квантовых трактовках явлений. Поэтому
применительно к нашим целям, к целям физической механики,
теоретической основой служит лишь классическая часть кван-
товой механики.
В настоящей главе кратко рассматриваются некоторые по-
нятия именно этой части квантовой механики, которые помо-
гут нам при дальнейших исследованиях. Здесь особенно необхо-
димо ввести понятия энергетических состояний динамических
систем и дать некоторые методы расчета простейших систем.
Мы не ставим своей целью дать полное описание квантовой
теории. По этому вопросу существует ряд прекрасных учебни-
ков, к которым и может обратиться читатель.
2.1. Волновое уравнение Шредингера
Динамические системы Шредингера по целям и способу опи-
сания отличаются от динамических систем Ньютона, Лагран-
жа и Гамильтона. Уравнения Ньютона дают нам возможность
рассчитать точное значение координаты и скорости частиц в си-
стемах с заданным начальным состоянием. Шредингер пред-
ложил иной способ: рассчитать для системы некоторую функ-
цию координат и времени (не количество движения или ско-
рость). В интерпретации Борна эта функция применима для
определения координат системы и нахождения других возмож-
ных динамических величин. Позднее стало известно, что, при-
меняя динамическое уравнение такого типа, нельзя более на-
деяться на точное описание классического поведения систем.
Другими словами, степень точности, которая может быть до-
стигнута в описании поведения системы методами квантовой
2.1. Волновое уравнение Шредингера 29
механики, ограничена принципом неопределенности Гейзен-
берга.
Применяя волновое уравнение Шредингера и некоторые до-
полнительные гипотезы, можно определить функцию Т коор-
динат и времени, называемую волновой функцией, функцией
Шредингера или функцией амплитуды вероятности. Квадрат
модуля волновой функции интерпретируется как плотность рас-
пределения вероятностей координат заданной системы. Уравне-
ние называется волновым потому, что оно представляет собой
дифференциальное уравнение второго порядка, имеющее неко-
торое сходство с волновым уравнением классической механики.
Но это сходство имеет лишь формальное значение и поэтому в
дальнейшем нами рассматриваться не будет.
Кроме волновой функции Ч1*, уравнение Шредингера еще
дает метод вычисления значений энергии стационарных состоя-
ний, существование которых давно уже подтверждено дискрет-
ностью атомных и молекулярных спектров.
В наших дальнейших рассуждениях в качестве основного
предположения будем использовать уравнение Шредингера, а
также дополнительные ограничения для волновой функции Ч7
и ее физический смысл. Точно так же обстоит дело в меха-
нике тяжелых масс, где роль основного предположения играют
законы Ньютона. Эти предположения могут быть подтверждены
лишь совпадением результатов расчетов с результатами экс-
перимента. Если законы квантовой механики вызывают у нас
недоумение и к тому же чуть ли не противоречат нашему по-
вседневному опыту, то это только потому, что мы не привыкли
к ним. Кроме того, наш повседневный опыт (макроскопического
характера) не может распространяться в область атомов и мо-
лекул. По мере того как мы узнаем, что все большее и большее
количество теоретических вычислений соответствует действи-
тельности, квантовая механика становится для нас все более
близкой. Мы будем так же хорошо ее знать, как и законы Нью-
тона. Она будет так же естественна, и можно будет удостове-
риться в том, что квантовая механика также выражает законо-
мерности природы. В действительности квантовая механика
включает в себя механику Ньютона как особый (предельный)
случай: когда масса имеет такую величину, как в макроскопи-
ческих явлениях, квантовая механика вновь становится механи-
кой Ньютона.
Рассмотрим сначала ньютоновскую систему, имеющую одну
степень свободы: частица с массой m движется по фиксирован-
ной прямой. Примем прямую за ось х и предположим, что си-
стема определяется одной потенциальной функцией У(х)
(—оо <х< + оо). При этом гипотетическое волновое уравнение
30
Гл. II. Квантовая механика
Шредингера имеет следующий вид:
8л2т дх2 । \ / \ ’ / 2m dt v 7
где функция Ч^х, t) называется временной волновой функцией
Шредингера или функцией амплитуды вероятности; h — по-
стоянная Планка, равная (6,6252 ± 0,0005) X10-27 эрг-сек. За-
служивает внимания тот факт, что это уравнение формально
имеет некоторое сходство с волновыми уравнениями в других
областях механики.
Временное уравнение Шредингера и уравнение классической
ньютоновской механики
H(px,x)=T(px)+V(x) = E (2.2)
между собой тесно связаны. Уравнение (2.2) указывает на то,
что общее количество энергии равно сумме кинетической энер-
гии Т и потенциальной энергии V, а также равно функции Га-
мильтона Н(рх,х). Раскрывая зависимость кинетической энер-
гии Т от импульса рх, имеем
x) = A-^+V(x) = £. (2.3)
Если теперь рх заменим дифференциальным оператором
величину Е заменим на—введем функцию Т(х, Z), на
которую действуют операторы, то уравнение принимает вид
<2Л>
полностью совпадающий с (2.1). Часто волновое уравнение пи-
шут так:
H4 = EW, (2.5)
„ h д h д
где в Н и Е нужно ввести операторы ’2ni~dx и —
Следует учитывать, что взаимосвязь между волновым ура-
внением и классическим уравнением энергии лишь дает способ
удобного описания системы, позволяет нам использовать бога-
тую терминологию, разработанную в течение длительного вре-
мени исследователями классической механики, для описания и
составления волнового уравнения. Чуть ли не ко всем атомным
и молекулярным системам можно применить метод описания,
принятый в классической теории, и вывести надлежащее вол-
новое уравнение, а затем при помощи вышеописанного метода
перевести их на язык квантовой механики. По крайней мере по-
2.2. Уравнение амплитуды колебания
31
добные формальные связи очень удобны. Так, в дальнейших
рассуждениях вместо слов «волновое уравнение для системы с
шестью координатами и одной функцией е2/Г12» будем говорить
«двухчастичная система с силой притяжения, обратно пропор-
циональной квадрату расстояния».
2.2. Уравнение амплитуды колебания
Для решения уравнения (2.1) используем метод разделения
переменных, т. е. введем
W(x, /) = ф(х)ф(/) (2.6)
в уравнение (2.1) и разделим затем на ф(х)ф(/). Тогда полу-
чаем
-.Л ... I__1_ у (х) ib (х) 1 —_______-____- (2 7)
ШИ 8л2/п dx2 2ш ф(0 dt ’
Справа в уравнении — функция времени t, слева — только функ-
ция координаты х. Поэтому величины, стоящие в правой и ле-
вой частях уравнения, должны равняться некоторому числу, не
зависящему ни от х, ни от t, другими словами, постоянной вели-
чине. Назовем ее Е. Теперь уравнение (2.7) можно написать в
виде двух уравнений, а именно
=2л££ф(/) (28)
И
- Д • d2&X) + V(X) t (х) = (X .
Второе уравнение принято писать в виде
- V (х)) t (X) = 0. (2.9)
Уравнение (2.9) часто называют волновым уравнением Шредин-
гера, а иногда — уравнением амплитуды колебания, так как
ф(х) определяет амплитуду колебания функции Т(х, t). Это
уравнение имеет различные решения, соответствующие различ-
ным численным значениям постоянной Е. Для обозначения раз-
личных значений величин Е будем использовать индекс п. Ана-
логично функции амплитуды колебаний, соответствующие Еп,
обозначим через фп(х). Уравнение для <р(/) можно сразу про-
интегрировать
<ря(/) = <Г2л^Л. (2.10)
32
Гл. II. Квантовая механика
Уравнение (2.1) является линейным. Его общее решение пред-
ставляет собой суперпозицию всех частных решений с произ-
вольными коэффициентами. Поэтому волновая функция систе-
мы обычно имеет вид
Еп
44%, (2.11)
п п
где ап — постоянные. Знак 2 выражает суммирование по дис-
п
кретным значениям Еп или интегрирование по непрерывному
интервалу Е. Этот знак может также одновременно содержать
случаи двух типов и его точный смысл определяется в зависи-
мости от конкретных условий.
Далее мы еще будем говорить об обычных предположениях
относительно физического смысла волновой функции и нахо-
дить значения энергии системы в различных стационарных со-
стояниях, обозначаемые через Еп. Эти значения называют ха-
рактеристическими или собственными значениями волнового
уравнения. Поскольку мы будем рассматривать квадрат мо-
дуля волновой функции как плотность распределения вероят-
ностей, то в целях более ясного изложения необходимо
установить некоторые ограничения для волновой функции, напри-
мер однозначность и др. В действительности для получения над-
лежащей волновой функции необходимо, чтобы решение волно-
вого уравнения Шредингера обязательно было непрерывным,
однозначным и ограниченным во всем конфигурационном про-
странстве системы (т. е. в отношении всех возможных коорди-
нат х системы).
В заданной системе характеристические значения Еп мо-
гут представлять собой совокупность дискретных величин или
ряд непрерывных интервалов, а могут быть и тем и другим.
Аналогично и в спектре. Поэтому говорят, что энергия обра-
зует или дискретный спектр, или непрерывный спектр, или их
сочетание. Характеристические значения системы, изображен-
ные на рис. 2.1, принято обозначать так: Ео — самое низкое
положение, — следующее и т. д. Эти значения энергии соот-
ветствуют волновым функциям фо(*), ф1(*)> фг(*) и т. д. Вели-
чины Еп и индексы п (целые числа) у фп(*) называются кван-
товыми числами. Для рассматриваемой одномерной системы
число п равно числу всех узловых точек фп. Если Е больше
одной из величин V(—оо) или V( + oo), то результат анализа
показывает, что величина Е является непрерывной. Поэтому,
если при —оо или х->оо величина V(х) стремится к конеч-
ной величине, то совокупность характеристических значений мо-
2.3. Физический смысл волновой функции
33
жет одновременно иметь непрерывный и дискретный спектры
(рис. 2.1).
При физическом толковании волнового уравнения и его ре-
шения сопряженная комплексная величина Т*(х, t) равно-
сильна W(x, t). Волновое уравнение, которому удовлетворяет
Рис. 2.1.
Т*, является комплексно сопряженным уравнению (2.1), а
именно
-8Хг + 0 = °’ <2Л2)
Решение такого сопряженного уравнения имеет вид
¥* (х, 0 = 2 (х, /) = 2 «ж " " • (2-13)
ZZ п
Следует обратить внимание на то, что временной член в экс-
поненте неодинаков в Т*(х, t) и W(x, t). При образовании
Т*(х, t) во временной экспоненте Чг(х, t) изменяется знак.
С другой стороны, функция амплитуды фп(х) часто является
вещественной. В этих случаях ф* (х) = фя (х).
2.3. Физический смысл волновой функции
Рассмотрим теперь какое-либо заданное решение Т(х, t)
волнового уравнения. При данном значении t функция W и про-
изведение комплексно сопряженных величин Чт*(х, /)Т(х, t)
определены при всех х в интервале от —оо до -Ноо (т. е. во
всем конфигурационном пространстве одномерной системы).
3 Зак. 1299
34
Гл. II. Квантовая механика
Для выяснения физического смысла сделаем следующее пред-
положение.
Величина Ч7* (х, t) Ч^х, t)dx представляет собой вероятность
того, что физическое состояние системы находится в момент t
в промежутке от х до x + dx и определяется волновой функ-
цией ЧДх, /). Местоположение характеризуется точкой в конфи-
гурационном пространстве. Другими словами, Ч1** (х, /)Чг(х, t)
является плотностью распределения вероятности точки распо-
ложения системы. В простейшем примере, о котором говори-
лось выше, Чг*(х, /)Чг(х, t)dx представляет собой вероятность
нахождения частицы в момент t в промежутке от х до x + dx.
Для того чтобы это предположение было справедливым, не-
обходимо функцию Чг(х, t) нормировать. Так как вероятность
нахождения частицы во всем пространстве равна 1, для этого
требуется выбрать в выражении (2.11) постоянные ап так,
чтобы
f Т*(х, /)Т(х, t)dx — \. (2.14)
— оо
Каждую функцию амплитуды колебания фп(х) также можно
нормировать, т. е.
оо
f (2.15)
— оо
Одновременно можно доказать, что независимые решения ура-
внения амплитуды колебания всегда могут быть построены
так, чтобы удовлетворять интегральному соотношению
оо
J (х) фл (х) rfx = О, т^п. (2.16)
— оо
В таких случаях говорят, что функции взаимно ортогональ-
ны. Такая совокупность фп, которая удовлетворяет (2.15) и
(2.16), называется совокупностью ортонормированных функций.
Используя эти соотношения, можно обнаружить, что если ко-
эффициенты ап удовлетворяют соотношению
2<«й=1, (2.17)
п
то функция Т(х, /) = 2алЧ'л (х, 0 нормирована.
п
Рассмотрим функцию распределения вероятностей ЧГ*ЧГ
состояний какой-либо системы. Эта система находится
2.3. Физический смысл волновой функции
35
в состоянии, представленном волновой функцией Ч^х, /) =
= (х) ехр |— 2л/-~-/| и ее комплексно сопряженной
п
величиной Т*(х, /) = • 1|:*( (х) ехр/2л/. Перемножаем
т
эти два ряда, и тогда ЧГ*ЧГ принимает следующий вид:
чг< (х, о т (х, t) = 2 +)+
п
Е„-Е„
ЖЧ ' * Л / / 2л/ — , t,
+ 12 атап^т(х)^п(х)е л
т п
где S' обозначает суммирование лишь по т ф п.
Вообще говоря, поскольку в двойной сумме имеется множи-
тель, зависящий от времени, то функция распределения ве-
роятностей связана со временем, а свойства системы также
изменяются в зависимости от времени. Лишь в тех случаях,
когда, кроме коэффициента ап, соответствующего какому-либо
значению Еп, все другие коэффициенты равны нулю, величина
Ч^Т не зависит от /. В этом случае волновая функция имеет
только один не равный нулю член фл(х)ехр<—2л/-~п,а
функция амплитуды колебания фп(х) представляет собой част-
ное решение уравнения амплитуды колебания. При этом свой-
ства системы, определяемые функцией распределения вероят-
ностей, также не связаны со временем, и такое состояние на-
зывают стационарным.
Если спросить, каким получится средний результат измере-
ния в момент t координаты х системы в физическом состоянии,
представленном волновой функцией Т, то приведенная интер-
претация величины Ч^Ч7 дает следующий ответ:
х = J Ч'’* (х, f) Ч7 (х, /) х dx,
— оо
т. е. величина х усредняется по всем местоположениям с весо-
вой функцией ЧГ*ЧГ. Аналогично этому среднее значение произ-
вольной функции F(x) имеет вид
F — J Ч1** (х, /) Чг (х, t) F (х) dx.
—оо
(2.18)
3’
36
Г л. 11. Квантовая механика
Для того чтобы получить среднее значение еще более об-
щей механической величины G(px, х), содержащей импульс рх
и координату х, сделаем более общее предположение.
Для системы в физическом состоянии, представленном вол-
новой функцией ЧДх,/), среднее значение механической вели-
чины дается следующим интегралом:
оо
Q= f^(x, х)Т(х, t)dx, (2.19)
— 00
где оператор G воздействует на Чт(х,/), а в G(px, х) величина
h д .J
рх заменяется на -у-г-т-т. Интегрирование распространяется на
и Л
все конфигурационное пространство.
Обычно результаты измерения величины G совсем не опре-
деляются величиной G. В действительности G имеет смысл
среднего арифметического, вычисляемого по результатам одно-
временного измерения для одинаковых систем (состояние пред-
ставлено Т), или же среднего арифметического, вычисляемого
по результатам повторных измерений для одной и той же си-
стемы, возвращаемой перед каждым измерением к одному и
тому же состоянию. Например, если величина х меняется в не-*
котором интервале (рис. 2.2), то измеренное значение х может
быть любым числом в этом интервале. Вероятность появления
некоторого значения х составляет Т*ЧГ. Лишь в случае, когда
х = а, величина Ч'*1?’ равна нулю при всех х, кроме х = а, какэто
показано на рис. 2.2. Вероятность появления величины х = а при
измерении х составляет единицу. В этом случае вероятность по-
лучения аг при измерении хг также составляет единицу. По-
этому для такой функции распределения вероятностей имеет
2.4. Осциллятор
37
место равенство хг=(х)г. Это условие (при всех г) является
и достаточным для сосредоточенности распределения1).
Даже в тех случаях, когда система находится в стационар-
ном состоянии, представленном волновой функцией t) =
= Фл(л:)ехр{— 2л/для произвольной механической ве-
личины можно вычислить лишь среднее арифметическое. Однако
количество энергии системы в стационарном состоянии, соответ-
ствующее функции Гамильтона Н(рх,х), все же имеет опреде-
ленную величину и равно собственному значению Еп, получен-
ному при решении волнового уравнения. Поэтому, когда система
находится в стационарном состоянии, количество энергии можно
вычислить точно. Для доказательства подсчитаем Нг и (Я)г.
В интеграле
оо
множитель, содержащий время, сводится к единице. Используя
уравнение (2.9), получаем
оо
#= / ^(x)En^x)dx,
— оо
оо
или, так как Еп — постоянная величина, a J Ф* (х) фл (х) dx — 1,
Н=Еп. (2.20)
Подобным же способом можно получить Нг = Егп. Таким обра-
зом, НГ=(НУ и энергия систем имеет вполне определенное
значение Еп-
2.4. Осциллятор
В качестве первого примера решения механической системы
с помощью уравнения Шредингера рассмотрим одномерный ос-
циллятор. Выбор пал на эту систему не только потому, что на
ней можно хорошо продемонстрировать метод применения вол-
нового уравнения, но и потому, что эта система в дальнейшем
найдет важное применение.
В классической механике при коэффициенте упругости k
пружины в некоторой точке х ее потенциальная энергия состав-
ляет V2fex2. Пусть m — масса, v — частота колебаний, тогда
9 Такое распределение называют также 0-образным распределе-
нием.. — Прим, ред.
38
Гл. П. Квантовая механика
k = 4n2tnv2. Поэтому можно написать V(x) =2ji2mv2x2, показы-
вая, что мы рассматриваем осциллятор, имеющий классическую
частоту v. Введем эту потенциальную энергию в волновое урав-
нение одномерной системы. Тогда
^ + ^(£-2nWx2)i|; = 0. (2.21)
Для удобства обозначим
% = Q^mE/Zi2,
а — ^mx'lh. (2.22)
Тогда
-g- + (%-a2x2)4>==0. (2.23)
Будем искать функцию ф(х), которая при всех х в интер-*
вале —оо<х< + оо удовлетворяет этому уравнению, а также
требованиям непрерывности, однозначности и ограниченности.
Если ввести
1 = ]/ах, (2.24)
то уравнение (2.23) примет вид
-^+(|-ф=0- (2-25)
Рассмотрим функцию
где С — нормировочный множитель. Для того чтобы выяснить,
может ли она удовлетворить уравнению (2.25), сначала нахо-
дим производную
d2yi> _ г JL J ^2/2 dn I —
dtf ~ dl2 г dln k J )
= Ce*12 U2 + 1) + 2| Л— (г-V) + (e-v} =
I “S J
t2/O ( (Г1 + l + l )
= CeE(t,!+ 1)(«-Л + 2s ^rr(«-E’) - 2 .
I J
последний член в скобках раскрывается по формуле
- 1 -^ТГ <&-*’) = - 2ь Е’> - 2 (» + 1 (<!-').
Таким образом, уравнение (2.25) дает
Й = = Ш2+1)~ 2(«+ 1)} =(2«+ W
a (Zg
2.4. Осциллятор
39
Поэтому собственное значение
/ 1 \
X = (2/г 4- 1) а — (п yj 2а.
Следовательно, согласно (2.22),
Ел = (п 4-у)/tv, /г = 0, 1, 2, 3........... (2.26)
Отсюда видно, что периодическое энергетическое состояние
имеет равномерные интервалы. Число п определяет порядковый
номер квантового энергетического уровня и обычно называется
главным квантовым числом.
В формуле (2.26) содержится один результат, заслуживаю-
щий внимания, а именно самое низкое энергетическое состояние
не является нулем, а равно VsAv. Это и есть так называемая ну-
левая энергия. Она указывает на то, что даже в самом низком
энергетическом состоянии материальная точка продолжает свое
движение. Этот факт тесно связан с положением о невозмож-
ности точного измерения. Он означает, что в действительности
материальная точка никогда не прекращает колебания. Для
макроскопических масс v всегда невелико, а так как h — вели-
чина чрезвычайно малая, то hv по величине тоже очень мало.
Таким образом, нулевой энергией можно пренебречь.
Следующий энергетический уровень отстоит от предыду-
щего на величину hv, поэтому интервал также очень мал. От-
сюда следует, что для макроскопической массы энергия яв-
ляется почти что непрерывной, поэтому в отношении макроско-
пических масс квантовым эффектом можно пренебречь. Лишь
в отношении микроструктур квантовый эффект является важ-
ным. Величина энергии на низком энергетическом уровне од-
ного порядка с произведением /zv. Таковы характерные резуль-
таты квантовой механики и в дальнейших рассуждениях мы
будем часто обращаться к ним.
Найденное решение волнового уравнения можно написать
в более распространенном нормированном виде
^ = {(Й'А (2.27)
где Нп(£) —полином Эрмита степени п, вычисляемый по фор-
муле
= (2.28)
40
Гл. II. Квантовая механика
Для самого низкого энергетического состояния (/г = 0) и для
следующего (п=\) имеем
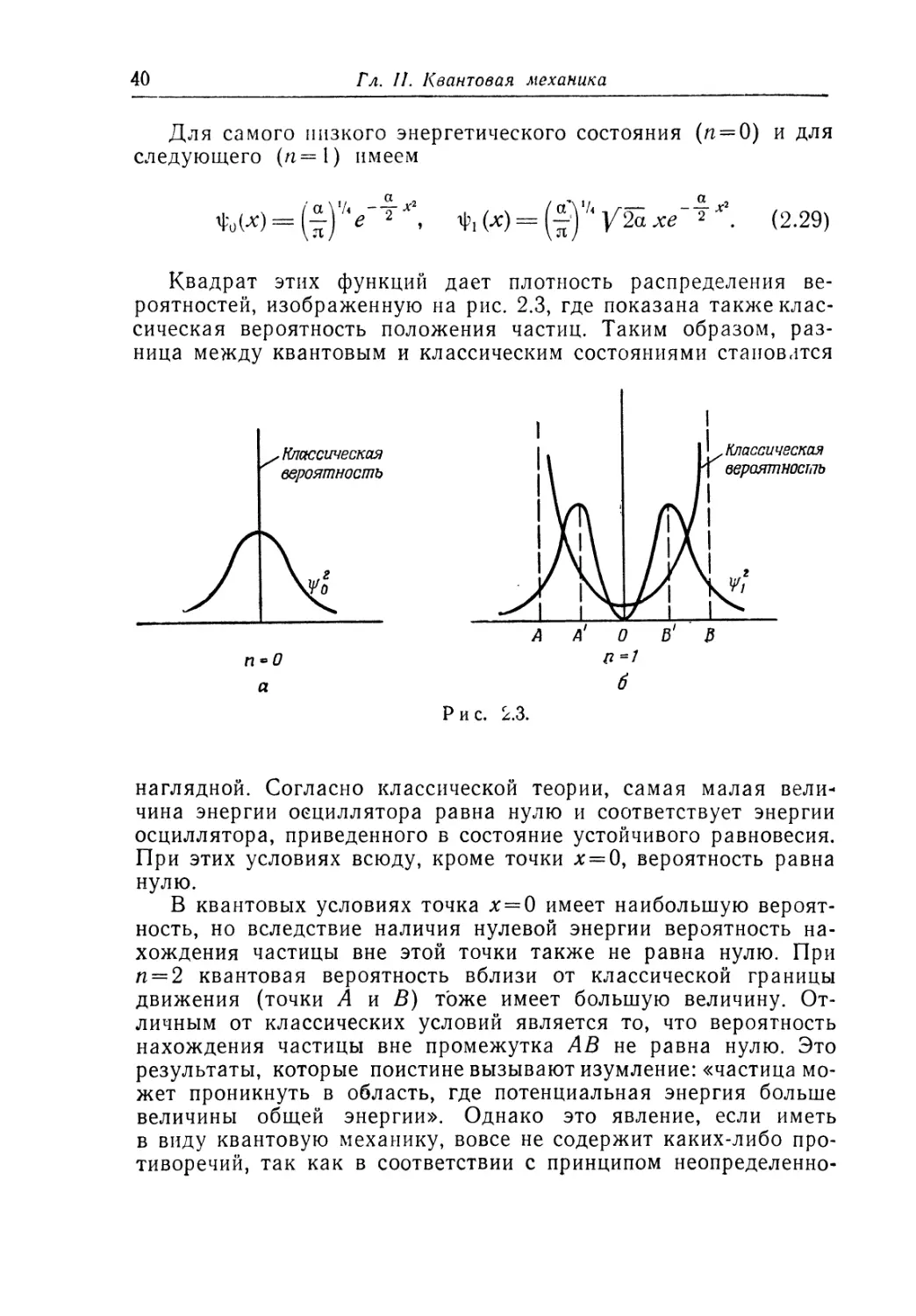
W) = 2-r- ^1 (x) = ^lty2axe 2 х\ (2.29)
Квадрат этих функций дает плотность распределения ве-
роятностей, изображенную на рис. 2.3, где показана также клас-
сическая вероятность положения частиц. Таким образом, раз-
ница между квантовым и классическим состояниями становится
Рис. 2.3.
наглядной. Согласно классической теории, самая малая вели-
чина энергии осциллятора равна нулю и соответствует энергии
осциллятора, приведенного в состояние устойчивого равновесия.
При этих условиях всюду, кроме точки х = 0, вероятность равна
нулю.
В квантовых условиях точка х = 0 имеет наибольшую вероят-
ность, но вследствие наличия нулевой энергии вероятность на-
хождения частицы вне этой точки также не равна нулю. При
и = 2 квантовая вероятность вблизи от классической границы
движения (точки Л и В) тоже имеет большую величину. От-
личным от классических условий является то, что вероятность
нахождения частицы вне промежутка АВ не равна нулю. Это
результаты, которые поистине вызывают изумление: «частица мо-
жет проникнуть в область, где потенциальная энергия больше
величины общей энергии». Однако это явление, если иметь
в виду квантовую механику, вовсе не содержит каких-либо про-
тиворечий, так как в соответствии с принципом неопределенно-
24. Осциллятор
41
сти координата частиц и их скорость не являются величинами,
которые можно точно измерить одновременно.
Поэтому количества общей и потенциальной энергий также
не являются величинами, которые возможно точно измерить
одновременно.
В более высоких энергетических состояниях (п>0) имеет
п нулевых точек, поэтому функция распределения вероятностей
тоже имеет п нулевых точек. Это также является
Рис. 2.4.
интересным результатом квантовой механики. Но если мы не
будем обращать внимания на существование нулевых точек, то
общий вид функции распределения вероятностей при п-+оо все
более приближается к классической функции распределения ве-
роятностей для осциллятора. На рис. 2.4 показан случай, когда
п=10. Этот результат можно было предугадать, так как если
говорить о макромассе, то лишь большая величина п имеет
реальный смысл, и в этом случае результаты квантовой ме-
ханики приближаются к результатам классической меха-
ники.
42
Гл. II. Квантовая механика
2.5. Системы точечных частиц
Система, состоящая из N частиц, взаимодействующих в
трехмерном пространстве, чрезвычайно сходна с простейшей
системой с одной степенью свободы, рассмотренной в предыду-
щих пунктах. Временное уравнение Шредингера в этом случае
является дифференциальным уравнением в частных производ-
ных с ЗЛ^4-1 независимыми переменными (ЗМ декартовых ко-
ординат для N частиц и время). Волновая функция является
функцией этих 3W+1 переменных. Как и в простейшей системе,
можно расчленить временное уравнение на уравнение, содер-
жащее только время, и уравнение амплитуды колебания, содер-
жащее ЗМ координат. Первое уравнение оказывается таким же,
как в случае простейшей системы, поэтому в системе точечных
частиц связь между волновой функцией стационарного состоя-
ния и временной функцией сходна с одномерной системой. Од-
нако уравнение амплитуды колебания является уже не обыкно-
венным дифференциальным уравнением с одной независимой
переменной, а дифференциальным в частных производных с
ЗМ независимыми переменными. В целях удобства будем гово-
рить, что это уравнение написано в конфигурационном про-
странстве ЗМ измерений. Наша цель заключается в том, чтобы
найти решение этого уравнения при всех значениях (от —оо до
+ оо) ЗМ декартовских координат Xi, ..., zN. Такое решение
является функцией амплитуды колебания от 3W координат,
иными словами, функцией в конфигурационном пространстве. Со-
вокупности координат %1, ..., zN соответствует точка в конфи-
гурационном пространстве, поэтому определить положение ча-
стицы в таком пространстве — значит определить местоположе-
ние системы в целом. Дополнительные требования к волновой
функции и ее физический смысл такие же, как в системе
с одной степенью свободы. Единственным отличием являет-
ся увеличение размерности конфигурационного простран-
ства.
Рассмотрим систему, содержащую N точечных частиц. Мас-
сы этих N частиц, m2, ..., tnN, находятся под влиянием си-
лового поля, описываемого потенциалом V(%i, t/i, ..., гд<, /),
и движутся в трехмерном пространстве. Здесь хь ..., zN — де-
картовы координаты W частиц. Взаимодействие частиц между
собой и с внешним силовым полем может выражать только
функция ЗМ координат или функция ЗМ координат и времени.
В первом случае V=V(xi, ..., zN), поэтому наша система кон-
сервативная. Основной интерес концентрируется на системах
такого типа, поэтому цаши рассуждения ограничиваются этими
системами. Волновым уравнением Шредингера такой системы
2.5. Системы точечных частиц
43
является уравнение
N
___Л2 у 1 /jW . . jW \ . inr —___h dw
8л2 “ mi у дх\ dyj dz^ / 2ni dt
(2.30)
Это уравнение часто пишут в виде
уХ^т+^= ‘ «1,
8л2 пц 2.ZU dt
i — l
где V? —оператор Лапласа для Z-й частицы, т. е.
^i=JL^JL + JL
1 дх] dy] dz]
Можно обратить внимание на то, что формально временное
уравнение Шредингера взаимосвязано с классическим уравне-
нием энергии. Их связь такая же, как в системе с одной сте-
пенью свободы, описанной в предыдущем пункте. Существует
уравнение энергии и для ньютоновской системы точечных ча-
стиц
•••’ PzN, Х1..ZN' 9 =
= 7'(Аг1’ •••» PZn) + •••» 2jv> ty = E. (2.31)
Выразив кинетическую энергию через импульсы, получим
H(PXi.....PzN' XV •••> ZN' 0==
N
= + + .....0 = £- (2.32)
Z=1
_ h d h d
Заменим теперь рх>, ....^операторами ............
a E— оператором—и введем функцию T(xi, ... ,zNi /),
на которую воздействовал бы оператор. Уравнение примет вид
f-fl h h & х ? i\ Ф—
Л^2л/ dxx ’ 2л/ dzN ’ Xi’ ’ * ’’ т —
— - у -1— v24; I IZT = ——
8л2 mi 1 ' 2л/ dt ’
/=1
совпадающий с (2.30), как и в одномерном случае. Волновое
уравнение можно формально написать в сокращенном виде
= (2.33)
44
Гл. II. Квантовая механика
Сосредоточим теперь внимание на консервативных систе-
мах. В этом случае V является лишь функцией ЗА/ координат.
Решая волновое уравнение в таком случае, мы можем, дей-
ствуя как в п. 2.1, решить ряд простых вопросов. А именно,
введем в уравнение (2.30)
...» zN, = •••. *х)ф(0- (2-34)
Тогда получим два уравнения для ф и <р:
= (2.35)
И
( = 1
последнее уравнение часто пишут так:
S v^+-ж <2-36)
Это есть уравнение амплитуды колебания Шредингера для
консервативных систем точечных частиц. Для возможности фи-
зической интерпретации волновой функции нужно, чтобы ре-
шение уравнения удовлетворяло дополнительным условиям,
данным в п. 2.2. Эти условия должны выполняться во всем кон-
фигурационном пространстве, т. е. от —оо до +оо по каждой
из 3N координат. Так же, как и в одномерном случае, подхо-
дящее решение существует лишь при некоторых значениях энер-
гии Е. Эти значения могут быть дискретными, непрерывными
или теми и другими.
Обычно при помощи ЗМ целых чисел можно обозначить ка-
ждое характеристическое значение энергии и соответствующую
функцию амплитуды колебания. Они представляют собой кван-
товые числа ni, ..., n3jv, связанные с ЗМ координатами. Фор-
мулу связи мы разъясним в дальнейшем на примере. А сейчас
буквой п обозначим всю совокупность квантовых чисел
Hi, ..., n3N и заменим и хЦ на Еп и фп.
Интегрируя уравнение (2.35), получаем
-2л/ t /г.
Ф(0 = * А , (2.37)
2.5. Системы точечных частиц
45
что полностью совпадает с одномерным случаем. Различные
частные решения волнового уравнения имеют вид
_2Л( £" t
zN, 0 = i|>„(*i» ..zN)e " (2.38)
и соответствуют всем стационарным состояниям системы. Об-
щее решение волнового уравнения есть
4r(Xj, .... zN, t) = ^anxVn{xx, ..., zN, t) =
n
En
= 2аЛ(*1> •••. (2.39)
n
где an — постоянные. Знак S выражает суммирование по всем
п
дискретным значениям Еп и интегрирование по непрерывным
значениям Еп.
Волновая функция Ч7*^, zN, t) является решением со-
пряженного волнового уравнения
................г- z>+
i=l
+ Г(х„ ..., zN, ..., zN, 0=2^^. (2.40)
Для консервативной системы общее решение этого уравне-
ния имеет вид
.... zN, /) = 2аХ(хР .... zN, ,) =
п '
Е
V?! Ф Ф Z V 2Я/ —--1 .
= 2 «Л (Хр •. •, zN) е й . (2.41)
п
Рассуждения относительно физического смысла волновой
функции такой системы чрезвычайно сходны с рассуждениями
в п. 2.3 о системе с одной степенью свободы. Поэтому величина
, zN, t) • Т(Х1, ..., zN, t)dxi ... dzN есть вероятность
нахождения системы в физическом состоянии, представленном
волновой функцией Ч7 (хь ..., zN, t), в момент t в элементе объ-
ема dXi ... dzN конфигурационного пространства. Величина
Ч7*Ч7 играет роль плотности распределения вероятностей ме-
стоположения системы. Функция гР(Х1, ..., zN> t) должна быть
нормирована, т. е. должно выполняться соотношение
f T*(Xi, .... zN, .... zN< t)dx=\, (2.42)
46
Гл. II. Квантовая механика
где знак dx обозначает элемент объема dx^ ... dzN в конфигу-
рационном пространстве, а интегрирование распространяется
на все пространство. Полагая
.... Z^n(xx, .... zN)dx = \, (2.43)
имеем нормированные функции амплитуды колебания
фп(хь ..., zN).
Далее можно считать, что
/С(х1> •••• •••’ zN)dx = Q, m*n, (2.44)
чтобы волновые функции были взаимно ортогональны. Если ис-
пользовать эти ортонормированные волновые функции и взять
Ч7 и W* в виде (2.39) и (2.41), то условие нормировки
Т примет вид
2«Х = 1. (2-45)
Рассуждая, как в п. 2.3, приходим к выводу, что функция
распределения вероятностей, полученная из'РДХр ..., zN, t)~
= фЛ(хр ...» z^expj—2ш-у-Н, не зависит от времени и
поэтому соответствует стационарному состоянию.
Как и в п. 2.3, можно указать для волновой функции более об-
щее физическое толкование. Если О (^рх > -Pz , • • •» zNit )
есть некоторая динамическая величина_системы, то ее среднее
арифметическое, обозначаемое через G, имеет вид
G = f .... zN, OX
x G (ъй ~dx[' • 2йг 1^7 • xp ‘ * Zn' • • • •
(2.46)
где оператор G получен путем замены в G (рх , ..., рг^> хх, ...
.... zN, t) выражений рх, .... рг„ на ....
Интегрирование распространяется на все конфигурационное
пространство.
2.6. Атом водорода
47
2.6. Атом водорода
Проведем теперь квантовомеханический расчет атома водо-
рода. Известно, что атом водорода состоит из двух частиц:элек-
трона и протона (ядра). Исходя из этого, мы сможем очень
точно рассчитать стационарные состояния и другие важные
свойства атома водорода. Взаимодействие между протоном и
электроном может быть вызвано силой тяготения или электро-
статической силой. Однако электростатическая (кулоновская)
энергия намного больше энергии тяготения, поэтому последней
можно пренебречь. Имея в виду более широкую цель, будем
считать, что электрический заряд ядра равен + Ze (для протона
Z=l), а электрический заряд электрона равен —е. Тогда по-
тенциальная энергия системы равна —Ze2lr. Здесь г — расстоя-
ние между ядром и электроном. Если декартовы координаты
ядра и электрона обозначить через и х2, #2, z2, а их мас-
сы через mi и т2, то волновое уравнение примет вид
1 / д2^т д2^т
тх дх% ду\
д2А>т \ 1 /д2$г
dz\ J m2 \ ^х2
= (2.47)
где
К(*1 — хг)2 + (У1 — У*)2 + — ^г)2 ’
(2.48)
Нижние индексы у Е и ф указывают на то, что это физиче-
ские величины всей системы, содержащей 6 координат. Из вол-
нового уравнения (2.47) разделением переменных можно легко
получить два уравнения. Одно будет описывать поступательное
движение атома как целого, другое — относительное движение
двух частиц. Когда потенциальная энергия представляет собой,
как в (2.48), функцию относительных координат двух частиц,
т. е. V=V(Xi—х2, — У2, Zi— z2), тогда для разделения ура-
внения не требуется знать конкретной формы V. Например, если
атом водорода находится в электрическом поле с направлением
z, то возникшая от напряженности поля Е потенциальная энер-
гия составляет eEz2— eEz^—eE(zi — z2) и условие раздели-
мости также выполнено.
Для удобства разделения введем новые переменные: х, у,
z — декартовы координаты центра масс системы, и г, 0, — сфе-
рические координаты второй частицы относительно первой.
48
Гл. II. Квантовая механика
Зависимость этих переменных от декартовых координат двух
частиц следующая:
т{хх 4- т2х2
т\ + т2 ’
У = • (2.49)
z_ mizl-\-m2z2 .
^1 + ^2 ’
г sin 0 cos ф = х2 — хр
г sin 0 sin ф = у2 — yv (2.50)
г cos 0 = z2 — zx.
Уравнение (2.47) преобразуется к виду
^{ET-V(r, 0, <p)}ipr = O, (2.51)
где
^1^2 1 1 I 1 /П гп\
и = —I-2— или — =--------------------. (2.52)
r Wj-f-^2 М- т2 v ’
Здесь р представляет собой приведенную массу системы.
В тех случаях, когда и т2 сильно отличаются друг от
друга, р приближается к массе более легкой частицы. Видно,
что в первых скобках уравнения (2.51) находится оператор Ла^
пласа фт в декартовых координатах х, у, z, а во вторых скоб^
ках — оператор Лапласа фт в сферических координатах г, 0,ф.
Поэтому попытаемся разделить это уравнение, представляя
функцию фт в виде
фг(х, у, z\ г, 0, ф) = /7(х, у, г)ф(г, 0, ф). (2.53)
Подставив выражение (2.53) в уравнение (2.51), получим
д2Г I I д2^ I 8л2 (тп\ т2) р р_______~ /п сд\
dy2 "Г- dz2 "i" h2 CtrF —V, (2.0^
_L A (гч 4________5___-^1 4_____J___- (sin 0 +
r2 dr \ dr / ’ r2 sin2 9 dtp2 r2 sin 9 d9 \ d9 / ’
+ {£_V(r)H_0) (2.55)
где
Etr + E = ET. (2.56)
2.6. Атом водорода
49
Эта система уравнений имеет простой физический смысл. Ура-
внение (2.54), очевидно, является волновым уравнением для
частицы с массой mi + m2 и пространственными координатами
центра масс mi и т2: Потенциальная энергия здесь равна нулю,
поэтому уравнение в действительности описывает движение сво-
бодной частицы с кинетической энергией Etr. Уравнение (2.55)
есть волновое уравнение с потенциальной энергией V для ча-
стицы приведенной массы ц. Оно описывает внутреннее движе-
ние системы. Здесь Е — внутренняя энергия системы.
Так как потенциальная энергия V является функцией только
г, то уравнение (2.55) методом разделения переменных также
можно свести к двум уравнениям. Имеем
ф (Г, 0, ф) = /? (г) 0 (0) Ф (ф), (2.57)
после подстановки в уравнение (2.55) и деления на /?0Ф полу-
чаем
1 d ( dR\ . 1 | 1 Л2Ф } . 1 f 1 d ( \ 0 дЮ \}
r2R dr \ dr / ’ г2 sin2 0 ( Ф dq2 j ' г2 sin 0 ( 0 d§ \ 1П dQ ) J ’
+ ^H-{f-V(r)}=0. (2.58)
После умножения на r2sin20 оставшаяся часть -фвторого
члена может быть лишь функцией независимой переменной ф,
но с точки зрения уравнения в целом она может быть равна
только некоторой величине, не зависящей от ф. Поэтому этот
член должен быть равен постоянной величине. Обозначим это
постоянное число через —т2:
т
(2.59)
Теперь уравнение, содержащее 0 и г, можно написать в виде
1 d ( 2 dR\ т2 , 1 f 1 d / . dQ \,
R dr \r dr / sin2 e "I sin e I e dQ \Sln ° '
+ ^L[E-V(r)]=Q.
Второй и третий члены этого уравнения не зависят от г, а
оставшаяся часть не зависит от 0, поэтому каждая из этих двух
частей равна постоянной величине. Пусть часть, содержащая 0,
равна постоянной —р, а часть, содержащая г, равна +0. Полу-
чаем два уравнения:
^^гЬ95-)-даге+|'9=0 <2-«>
И
w W (г2 4г) - к R+ т-R=°- <2-61)
4 Зак. 1299
50
Г л. IL Квантовая механика
Для определения допустимой величины энергии теперь можно
решать уравнения (2.59), (2.60) и (2.61). Этапы решения сле-
дующие: сначала находим подходящие решения уравнения
(2.59) и соответствующие численные значения параметра т.
Вводя эти значения т в уравнение (2.60), можно обнаружить,
что лишь при некоторых численных значениях 0 уравнение
(2.60) имеет подходящее решение. Наконец, все эти резуль-
таты вводятся в уравнение (2.61) и находятся энергетические
уровни Е.
2.7. Свободная частица
Перед тем как начать подробный расчет внутренней дина-
мики атома водорода, исследуем сначала движение атома в це-
лом, описываемое уравнением (2.54). Обозначим общую массу
mi + m2 ансамбля через М. Волновая функция свободного дви-
жения частицы удовлетворяет следующему уравнению:
a2/7 I d2L . д2Г 8л2Л4 F
дх2 ду2 dz2 ‘ h2
(2.62)
Рассмотрим решение
F (х, у, г) = X (х) Y (у) Z (z). (2.63)
Уравнение (2.62) дает
1 d2X . 1 d2Y . 1 d2Z , 8л2М F __
X dxi+Y dy2 "Г" Z dz2 h2 ~
Здесь каждый член должен
так что
быть постоянной* величиной,
d2X . 8л2Л4
dx2 ' h2
d2Y ! dy2 ! 8л2Л4 1 h2 EUY =0, (2.64)
d2Z _ dz2 ! 8л2Л4 1 h2 EzZ =0,
ГДе
Ех-\- Еу Ez — Etf
(2.65)
2.7. Свободная частица
Решения уравнений (2.64) имеют вид
X = Nx si n { -у- У2МЁ~Х (x — x0) |,
r = ^sin{-^ V2ME~y(y-yQ)\, (2.66)
Z = NX 5!п{^/2Ж(^-г0)}.
Теперь надо выяснить, какими могут быть F и Е1г=Ех+]
+ Ey + Ez, чтобы были выполнены требования к волновой функ-
ции, указанные в п. 2.5.
Так как синусоидальная функция непрерывна, однозначна и
ограничена при всех вещественных значениях аргумента, един-
ственным ограничением для Е является требование, чтобы Ех,
Еу, Ez были положительными числами. Поэтому Etr может быть
только положительной величиной. Таким образом, возможные
значения энергии свободной частицы являются непрерывными.
Переходя к обсуждению физического смысла волновой функ-
ции этой системы, выясним сначала, каково физическое состоя-
ние, представляемое волновой функцией при Ex—Etri Еу, Ez,
равных нулю. Функция
Etr
V (х, у. z, /) = W sin {У 2MEtr (х— х0)|г h 1
представляет собой волну, в которой ось х перпендикулярна
фронту. Длина волны определяется формулой
В классической механике свободная частица с массой М и ско-
ростью движения v имеет энергию Е(г = -^ Ми2. Записывая ее
в виде Тх= 2^- р2х, находим среднее значение
г — — f (—V
х ~ 2М J \
дх2
= 1ЯГ ( 2St)! (т f 'Г‘Ч'dx = Е"-
Аналогично можно найти Tx = Ertr = (Tx)r. Согласно рассу-
ждениям п. 2.3, этот факт говорит о том, что кинетическая энер-
гия движения вдоль оси х имеет вполне определенную величину
Etr. Ее функция распределения вероятностей во всех точках,
4*
52
Гл. II. Квантовая механика
кроме этой, равна нулю. Отсюда имеем 2MEtr = р2х = Mv2.
Уравнение (2.67) можно написать в виде
h
Mv
(2.68)
Это есть длина волны Де Бройля, зависящая от массы М и ско-
рости v движущейся частицы.
Рассматривая функцию монохроматической плоской волны
N sinУ%МЕ1г (х~х0)|ехр| —
можно обнаружить, что среднее арифметическое рх от рх рав-
но нулю. Это нельзя объяснять тем, что направление движения
частицы вдоль оси иногда положительно, иногда отрицательно.
Частица движется по одному из направлений, но вероятность
движения по обоим направлениям одинакова. Чтобы получить
волновую функцию Ч7 для частицы, движущейся в любом на-
правлении, можно использовать наложение основных решений.
Мы не будем здесь делать этого, отошлем читателя к литера*
туре по квантовой механике.
2.8. Внутренняя динамика атома водорода
Обратимся теперь к вопросу о внутренней динамике атома
водорода. Прежде всего заметим, что решением уравнения
(2.59) является функция
Фяг(ф) = р1=-^ф. (2.69)
Для удовлетворения условия однозначности параметр m дол-
жен быть целым числом. Поэтому т = 0, ±1, ±2, ±3 .... Ве-
личина 1/)/2л—нормировочный множитель, т. е.
2л
J Фт (<р) Ф,г1 (ф) dtp = 1. (2.70)
о
Для нахождения функции 0(0) введем
z = cos 0. (2.71)
Уравнение (2.60) принимает вид
4- [(1 - г2) 4^1 + [р ~УУ 0 = 0- (2-72)
dz Lv dz J 1 L 1 — г2 J 4 '
2.8. Внутренняя динамика атома водорода
63
Решение этого дифференциального уравнения является хо->
рошо известным присоединенным полиномом Лежандра Р™ (г),
определяемым по формуле
P«(z) - (- If (1 • (2.73)
где Pn(z)—полином Лежандра степени п. Отсюда сразу же
делаем два вывода. Во-первых, величина m обязательно дол-
жна быть положительной; лишь тогда при z= ± 1 (0 = 0, л) ре-
шение не обратится в бесконечность. Поэтому в действительно-
сти это решение нужно писать в виде
е = (—l)|m| (1 — z2)|ml/2 • (2.74)
Кроме того, степень I полинома Л (г) должна быть положитель-
ным целым числом, равным или большим \т\. Только тогда
решение не будет равно нулю. Подставляя это решение в ура-
внение (2.72), находим
p = Z(Z+l), l=\m\, |m| + l, |т|+2, .... (2.75)
Более подробное исследование показывает, что определен-
ное таким образом решение является единственной приемлемой
волновой функцией 0(0). В физической терминологии т на-
зывают магнитным квантовым числом, a Z азимутальным кван-
товым числом. Необходимо подчеркнуть, что полученные функ-
ции Ф(<р) и 0(0) никак не связаны с функцией потенциальной
энергии V(r), они подходят к любым V(r); в дальнейшем мы
воспользуемся этим фактом. Эффект V(r) проявляется лишь
по отношению к волновой функции R(r), что мы сейчас и по-
кажем.
В силу (2.75) уравнение (2.61) можно написать в виде
<2-76)
При кулоновском притяжении V(r)=—Ze2/rt где Z— электри-
ческий заряд ядра или порядковый номер атома. Отрицатель-
ная величина Е означает, что общее количество энергии недо-
статочно для того, чтобы произошла ионизация атома. Введем
2 8л2ц£
“ — Л5"
И
a 4ji2|1Z^2
Л = --------
(2.77)
54
Гл. 11. Квантовая механика
а также новую независимую переменную
р = 2аг. (2.78)
Уравнение (2.76) примет вид
+ + 0<р«х,.(2.79)
Делая теперь замену зависимой переменной
_ р
7?=pze 2£(р), (2.80)
получаем
p-^-+{2(z+l)-p}^4-(x-z-l)£=0. (2-81)
Решением этого уравнения является присоединенный полином
Лагерра L2n‘+i (р), где
К — п, га—целое число, (2.82)
(Р) = W R W (Р^“ ₽)} ’ (2,83)
Из (2.83) видим, что величина в скобках — полином степени г.
Для того чтобы присоединенный полином Лагерра не равнялся
нулю, необходимо, чтобы
ra = Z+l, Z4-2, .... (2.84)
га называют главным квантовым числом.
Используя уже известные свойства полиномов Лежандра и
Лагерра, можно найти нормировочные множители для 0(0) и
R(г). В результате имеем
(0) = ]'Л m l(cos 0)’ (2,85)
п /г\___ [7 2Z\3 (л I 1)! "I1/? -р/2 I Г 2Z + 1 / ч /О О£\
2n{(zi+7)TFJ е ?Ln+l(^ <2’86)
где
<287>
Так как все эти полиномы взаимно ортогональны, то волно’
вые функции фп/т(г, 9, <p) =Z?n;(r)0/m(O)O,n(<p) тоже взаимно
2.9. Энергетические уровни водородоподобных атомов
55
ортогональны, т. е.
со л 2л
fff €im (Г> 0> Ф) %'Z'm' (г> 0- Ф) г2 S5n 0 ^Ф d<ddr = 0
ООО
при п ф п', I I', m ¥= m'. При п — п', 1=Г, m — m' интеграл ра-
вен 1.
Сделаем краткий числовой расчет для состояния на самом
низком энергетическом уровне п=1, /=т = 0. Тогда
Среднее расстояние г между электроном и ядром равно
со оо
7=f Crw2 dr=4 (^-)3 f е~Рг3 dr-
о о
Используя (2.78), имеем
1 1 / Z \з 7 з / Z \з
r==T7FU) J pe’₽dP = -2^U) •
о
Согласно (2.77), получим
Аналогично
(2.89)
Основываясь на понятии эффективного объема, можно считать,
что эта величина есть радиус атома в основном состоянии. Для
атома водорода Z=l,
ао = О,529А; г = 0,794 А; (73)'/з= 1,046 А.
Последняя величина близка к вандерваальсовскому радиусу
1,3 А, приведенному в табл. 1.7. Это показывает, что наша тео-
рия соответствует действительности.
2.9. Энергетические уровни водородоподобных атомов
Вводя в (2.77) выражение для X и разрешая это равенство
относительно £*, находим
р _ 2^Z^ _ RhcZ2 _ z* п
— w — п2 — п2
56
Г л. II. Квантовая механика
Я = EH = Rhc.
Отсюда видно, что, когда водородоподобный атом находит-
ся в состоянии, представленном квантовыми числами и, / и т,
количество энергии не связано с I и т, а зависит только от
главного квантового числа п. Поскольку m может быть нулем,
равенства (2.75) и (2.84) указывают на то, что п может быть
равно 1, 2, 3, ... . Кроме случая п=1» каждый энергетический
уровень является вырожденным и может иметь несколько не-
зависимых волновых функций. Волновые функции, соответ-
ствующие различным совокупностям и, Z, т, являются незави-
симыми. Допустимые значения этих квантовых чисел
zn = 0, ±1, ±2,
Z=|m|, \т\ +1, |т|4~2,
n = / + l, Z4-2, /43, ....
Можно записать это и по-другому:
главные квантовые числа
п=1, 2, 3 ... ;
азимутальные квантовые числа
Z=0, 1, 2, ..., и—1;
магнитные квантовые числа
Z, —Z + 1, ..., -1,0, +1, ..., +(Z—1), +Z.
Таким образом, при заданных п и Z имеется 2Z+1 независи-
мых волновых функций; при заданном п имеется п2 независи-
мых волновых функций, т. е. каждому значению энергии соот-
ветствует п2 независимых волновых функций. Число 2Z+1 вол-
новых функций, имеющих одинаковые п и Z, образует полную
подгруппу, а п2 волновых функций, имеющих одно и то же зна-
чение п, образует полную группу.
Проводя аналогичное исследование волнового уравнения для
положительных £, получаем, что при всех положительных Е
имеются подходящие решения. Поэтому их энергетический
спектр является непрерывным, при отрицательных же Е энер-
гетический спектр дискретный. Этот факт можно было предви-
деть на основе общих рассуждений п. 2.2. Мы не останавли-
ваемся здесь на волновых функциях для положительных Е, так
как в дальнейшем они нам не пригодятся.
2.10. Спин электрона
57
2.10. Спин электрона
В предыдущих пунктах рассмотрен водородоподобный атом
и дано полное описание энергетических уровней. Выясним те-
перь, каким образом ведет себя электрон в многоэлектронном
атоме. Известно, что существуют некоторые условия, ограни-
чивающие число возможных состояний электрона. До сих пор
мы рассматривали лишь три квантовых числа п, I и т, но этого
еще недостаточно для полного описания поведения электрона.
Кроме этих чисел, электрон еще имеет орбитальное число
]/$(1 +$) • Л/2л, с которым связаны магнитный и механический
моменты; последний обычно называют спином электрона. Эту
гипотезу предложили Гаудсмит и Уленбек для объяснения яв-
лений кратного расщепления спектральных линий атома. Па-
раметр s в вышеприведенном выражении называют спиновым
квантовым числом. Оно может принимать значения ±!/2.
Недостатком этого толкования является то, что из уравне-
ния Шредингера невозможно получить спин электрона. Реляти-
вистская квантовая механика и уравнения Дирака хотя и нахо-
дятся пока на такой стадии развития, когда их можно исполь-
зовать лишь для описания отдельной частицы, однако они
позволяют все же сделать вывод, что состояние частицы описы-
вается четырьмя квантовыми числами, среди которых одним яв-
ляется спиновое квантовое число. Два значения спина можно
рассматривать как две возможные ориентации спинового мо-
мента относительно орбитального. Считается, что два электрона
в атоме, имеющих одинаковые спины, имеют параллельные мо-
менты спинов. Если же спины двух электронов неодинаковы,
т. е. $ — —|—*2" и s = — у, то спиновые моменты антипарал-
лельны.
Уяснив необходимость четырех квантовых чисел и, /, m и s
для описания состояния электрона, возвратимся к вопросу о
возможном состоянии электрона в многоэлектронном атоме.
Принцип запрета Паули гласит: в одном и том же атоме не
бывает двух электронов, которые имеют полностью одинаковые
четыре квантовых числа. Если два электрона атома имеют оди-
наковые значения /г, /, т, то их спиновые моменты обязательно
антипараллельны. Используя это положение, можно описать
поведение электронов многоэлектронного атома в различ-
ных состояниях. Мы не будем давать здесь подробного изло-
жения, которое можно найти в учебниках по физике и
химии.
58
Гл. II. Квантовая механика
2.11. Классификация энергетических уровней молекул
Масса атомного ядра много больше массы электрона. Эта
простая особенность является основой приближенного метода
анализа молекул различного типа. Благодаря ей энергия, свя-
занная с движением ядра, много меньше, чем энергия обраще-
ния электрона вокруг ядра, а период вращения атомного ядра
в молекуле больше, чем период электрона. Отсюда при расчете
движения электронов ядро можно считать неподвижным. Та-
ким образом, электроны имеют свое определенное движение,
соответствующее положению ядра.
Атомные ядра в молекуле требуют устойчивого равновесного
положения между почти полностью размазанной и полностью
концентрированной структурами. Полностью размазанная
структура неустойчива и вообще не может образовать моле-
кулы; полностью концентрированная структура тоже неустой-
чива, так как заряд атомных ядер положительный и на корот-
ком расстоянии они будут взаимно отталкиваться. Движение
атомных ядер можно разделить на поступательные перемеще-
ния, жесткие вращения, а также колебания каждого атомного
ядра вблизи равновесного положения, т. е. внутренние колеба-
ния молекул. Поступательное движение, как и в случае свобод-
ной частицы, не имеет неклассических особенностей движения.
Таким образом, энергетические уровни молекулы можно раз-
делить на три типа: энергетические уровни электронов, энерге-
тические уровни колебания и вращения. Нетрудно подсчитать
соответствующие относительные величины энергетических уров-
ней. Пусть линейный масштаб молекулы есть а. Энергия, свя-
занная с движением валентного электрона (при своем движении
он проходит почти через весь объем молекулы, а не нахо-
дится в ближних к ядру слоях), имеет тот же порядок вели-
чины, что и энергия электрона с массой т, движущегося по
круговой орбите с радиусом а. Другими словами,
h*2 / h\
Е~-Ь- (4* = к)- (2.91)
В том случае, когда а равно нескольким ангстремам, это коли-
чество энергии соответствует частоте в видимой и ультрафио-
летовой областях спектра.
Для того чтобы подсчитать колебательную энергию, рассмо-
трим каждый тип простого колебания как гармонический осцил-
лятор с массой М и- коэффициентом упругости Ко. Масса М
имеет одинаковый порядок величины с классической ядерной
2.11. Классификация энергетических уровней молекул
массой. Коэффициент До можно вычислить следующим спосо-
бом. Если в направлении колебания сделать перемещение па
расстояние а, то обязательно возникнет изменение энергии по-
рядка Ее, так как такое большое перемещение вызовет иска-
жение движения электронов. Поэтому мы допустим, что До~
~Ее1а2. Тогда энергия, связанная с низким колебательным
уровнем, имеет порядок
Если М — масса пяти протонов, то Л4/т~104 и Ev примерно в
сто раз меньше Ее, что соответствует частоте, близкой к ин-
фракрасной области.
Энергию вращения Ег можно подсчитать, используя момент
инерции молекулы J(~Ma2). Она имеет порядок й*2//, т. е.
Л*2 ш р
(2.93)
что примерно в сто раз меньше Ev.
На основании (2.92) и (2.93) энергетические уровни элек-
тронов, энергетические уровни колебания и вращения можно
рассматривать как последовательные члены разложения по ма-
лому параметру (m/М) (обычно порядка 10-3— 10~4). Фактиче-
ски в этом состоит метод Борна — Оппенгеймера1). В качестве
параметра разложения они использовали отношение классиче-
ской амплитуды колебаний ядра к межъядерному расстоянию
(порядка а). Величина колебательного перемещения с количе-
ством энергии Ev и коэффициентом упругости Ко имеет поря-
док
\ Kq / \ /
Поэтому параметр разложения равен
Согласно такой терминологии, энергетический уровень электро-
на есть нулевой член разложения, энергетический уровень ко-
лебания — член второго порядка, а энергетический уровень
9 Born, Oppenheimer, Ann d. Physik, 84 (1927), 457.
60
Гл. II. Квантовая механика
вращения — член четвертого порядка. Движения, соответствую-
щего количеству энергии первого и третьего порядков, не суще-
ствует, поэтому и членов разложения первого и третьего поряд-
ков нет.
2.12. Волновое уравнение молекулы
Согласно п. 2.5, можно сразу написать волновое уравнение
молекулы, не содержащее время
/ 2 п n \
(2-95)
\ 4 = 1 7=1 /
где п — число электронов, Af—число атомных ядер, V — сумма
потенциальных энергий, Mj — масса /-го ядра, Е — общее коли-
чество энергии. Если взять за эталон величину, приведенную в
(2.94), то очевидно, что в уравнении (2.95) перед всеми чле-
нами, связанными с движением ядра, имеется малый множитель
четвертого порядка. Если их отбросить, то ядерные координаты
Rj в волновой функции ф будут просто параметрами, а уравне-
ние (2.95) с координатами ц будет волновым уравнением, опи-
сывающим движение электронов. Ядро атома характеризуется
координатами в Rj. В этих условиях волновая функция элек-
трона ^Яу(Гг) соответствует энергии U(Rj). Рассматривая
U(Rj) как потенциальную функцию, можно получить уравне-
ние движения ядра и с его помощью — волновой коэффициент
® (по-
напишем i|) в следующем виде:
Ф(Г/, /?;•) = uRj (ri) w (Rj), (2.96)
где и удовлетворяет уравнению
(—+и % w=и%(М7)
V 4 = 1 /
Для каждого типа ядер U(Rj) находится как собственное зна-
чение уравнения (2.97). Обычно имеется несколько решений, со-
ответствующих неодинаковым электронным состояниям моле-
кулы. Необходимо обращать внимание на то, чтобы гаранти-
ровать последовательное изменение и и U вслед за Rj, особенно
при вырождении системы.
2.13. Двухатомные молекулы
61
Умножим уравнение (2.97) на Тогда вследствие того,
что оператор V/ не воздействует на w(Rt), получим
i = l /
Вычитая это уравнение из (2.95), имеем
что можно переписать как
N 2
Мг/) + w(Rj) =
- 7 = 1 J -1
N
VI h*2
= W) (O + 2’;” ra v A; W]-
(2.98)
Однако мы уже показывали, что амплитуда колебания у
электронов значительно больше, чем у атомного ядра, другими
словами, параметр (2.94) очень мал. В этих условиях сфера
движения электронов, включает в себя целиком атомные ядра
и не чувствительна к их движению, т. е. волновая функция
электрона uR. (rz) не может существенно зависеть от /?;, по-
этому — величина малая. Отсюда вся правая часть
уравнения (2.98) также величина малая, и ею можно прене-
бречь. Поэтому
(2.99)
Это — приближенное волновое уравнение движения атомного
ядра.
2.13. Двухатомные молекулы
Рассмотрим теперь самые простые молекулы, для чего ис-
следуем сначала волновую функцию атомных ядер двухатомной
молекулы и соответствующие энергетические уровни. Пусть
энергия Un для п электронов является известной функцией
межъядерного расстояния г. Волновое уравнение колебательно-
62
Гл. 11. Квантовая механика
вращательного движения двухатомной молекулы имеет вид
4г V + 4г V + V - (г)] V„, v = О, (2.100)
где v v (xi, у\у Zi, х2, Уъ £2)—волновая функция движе-
ния ядер, а Л11 и М2— их массы. Но
v‘=^+i+i' ;=1'2' <2-101>
где Xi, z/i, Zi есть декартовы координаты f-ro ядра относительно
оси, фиксированной в пространстве. Уравнение (2.100) по виду
совпадает с волновым уравнением атома водорода, хотя здесь
частицами являются атомные ядра, а не протон и электрон. По-
этому при решении этого уравнения можно воспользоваться со-
ображениями, использованными при решении уравнения для
атома водорода, о котором речь шла ранее (см. п. 2.6 и п. 2.8).
Весь путь решения до введения уравнения по координате г
остается прежним. Поэтому уравнение внутреннего движения
молекулы превращается в следующее:
+ 7^ГГ + ^<£-С/(г>>* = 0’ <2'102’
где ц— приведенная масса
ц = 4- Л12), (2.103)
а г, 0, ф — сферические координаты второго ядра в системе с
центром на месте 1-го ядра. Если написать
ф(г, 0, ф) = /?(г)0(0)Ф(ф), (2.104)
то, как и в случае водородоподобных атомов, имеем
<I^(<p)=-pi=-^<₽ (2.105)
И
(°)={(2жКГ Г р'к"1 (cos 6)> (2-106)
где /^’(cosO) — присоединенная функция Лежандра. Соглас-
но традиции молекулярной спектроскопии, К называется орби-
тальным числом, а М — магнитным квантовым числом. Вели-
чины К и М должны быть целыми числами:
/< = 0, 1, 2, ...;
— /<41, .0, К— 1, К. (2.107)
2.14. Свойства функции U(r)
63
Так же, как у атома водорода, квантовые числа М и К связаны
с угловыми моментами.
Уравнение для /?(г) имеет вид
4 (г2 4) + [- —У~ + {£• - О (г)}] R = 0. (2.108)
Делая замену
Я(г) = 2£1, (2.109)
находим
^+j-_^±l)_aL{£_Z7(r))ls = o. (2.110)
2.14. Свойства функции U(г)
Теоретическое вычисление функции t/(r) требует решения
волнового уравнения движения электронов. Это очень трудный
Рис. 2.5.
вопрос. Удовлетворительный ответ можно дать лишь в случае
такой простейшей молекулы, как молекула водорода. Поэтому
обычно определяют [/(г) опытным путем. Берется некоторый
вид функции [/(г), содержащей параметры. Эти параметры в
конечном итоге определяются сравнением наблюдаемых энер-
гетических уровней с вычисляемыми.
Результаты расчетов и экспериментов над простейшими мо-
лекулами типа молекулы водорода показывают, что функция
[/(г) для устойчивой двухатомной молекулы при равновесном
расстоянии принимает наименьшее значение. При г<ге кривая
64
Гл II. Квантовая механика
резко поднимается вверх, а при г>ге меняется плавно, как это
показано на рис. 2.5. Когда молекула находится в низшем ко-
лебательном состоянии, ядро расположено вблизи от равновес-
ного положения. Для этих энергетических состояний лишь уча-
сток Щг), близкий к ге, является важным. Для высоких
энергетических состояний амплитуда колебаний велика и необхо-
димо рассматривать всю кривую U(r). При увеличении г ве-
личина U приближается к постоянному значению. Это свойство
имеет особое значение для высоких энергетических уровней и
отражает следующий факт: при передаче молекуле достаточ-
ного количества энергии она может разделиться на два атома,
т. е. диссоциировать.
2.15. Простейший вид линейного ротатора
Самым простым предположением, которое можно сделать
относительно межатомной силы двухатомной молекулы, яв-
ляется следующее: сила прямо пропорциональна разности
межъядерного расстояния г и его равновесного значения ге. Так
как U в ге имеет минимум, то вблизи от ге
('~О2 + •••• (2.111)
Здесь величина U при г = ге принимается равной нулю, иными
словами, энергия отсчитывается от величины [7(ге).
Пусть
(2Л12)
е
И
р = г-ге. (2.113)
Из уравнения (2.110) получаем
^-+Л|£-1У-—*w+1)k=-o.
tfp2 /г*2 | 2 2ц (r^ + p)2 J
Так как это приближение применимо лишь при малых р, то
последний член здесь следует разложить в ряд
2.15. Простейший вид линейного ротатора
65
С точностью до членов порядка р2 уравнение можно написать
в виде
d2S
dp2
где
п \ ге
— 1)4 + 1 a1p2U = 0, (2.114)
ге J J
А*2 _ h*2
2gr2 2Ie ’
(2.115)
Ie — равновесное значение момента инерции молекулы.
Используя
Р = Ь Ч---(2.П6)
3K(K+l)'+±kr2
можно преобразовать (2.114) в такое же колебательное урав-
нение, как (2.25),
d2S . 2ц
+ Л»2
Е — /С(/С-Ь1)оЧ--{/<(К+1)«у---
3K(K+D<y + ±kr2e
— ’ljfc + 3K(K+l)41 £2U = 0. (2.177)
Ге J J
Граничные условия: при r=0 и r=oo S равно нулю. Эти усло-
вия несколько отличаются от граничных условий осциллятора,
для которого S равно нулю при £=±оо. Но так как S за пре-
делами классически допустимой области быстро уменьшается,
можно рассматривать эти два условия как равносильные.
В действительности большой ошибки от такого упрощения не
будет, поэтому волновую функцию осциллятора можно считать
приближением функции S. Тогда энергетические уровни та-
ковы:
Ev< к = К (К+1) о--------+ >..?]----------Ь к + у) Av; (2.118)
3K(K + l)o + -Lkr2e v
(t) = o, 1, 2, ...; K=0, 1, 2, ...),
где
1 рг2 + бК(К4-1)<И'/а__ 1 pV4i 1
e 2л I J 2л \ц/ I kr2 I
(2.119)
5 Зак. 1298
66
Гл. II. Квантовая механика
Если ввести частоту колебания вблизи равновесного состояния
’.“•й/тр <2-120’
то получим конечную приближенную формулу
/ I 1\ Л , I Л*2 /<2(К +1)2Л*4 /О1П1Ч
EV) К 2/ 8j12v2/3 ’ (2-121)
Очевидно, что первый член представляет собой колебатель-
ную энергию осциллятора; второй — энергию вращения моле-
кулы как твердого тела. Появление третьего члена связано с
тем, что вследствие вращения возникает удлинение молекул,
после чего угловая инерция опять претерпевает изменение. Чле-
ны более высокой степени не очень надежны, потому что пред-
полагаемая потенциальная функция недостаточно точна. Опыт-
ные данные большинства молекул очень хорошо согласуются
с формулой (2.121). Для еще более точной работы нужны сле-
дующие члены разложения, а также более точная потенциаль-
ная функция, чем в (2.111).
Выше уже говорилось, что квантовое число К связано с вра-
щательным движением молекулы. Полученная теперь энергия
Л*2
вращения составляет К ^+1)^у-. Если ре—момент коли-
чества движения, то, как и в линейном случае, энергия враще-
ния равна "2/” Ре- Поэтому для каждого К момент количества
движения равен
рв=У^+1)Г = №+1)|, /С=0, 1,2, .... (2.122)
Так как, согласно (2.107), энергия, допускающая 2^+1 значе-
ний ЛГ, соответствует ряду различных волновых функций, а так-
же различным направлениям оси вращения, то вращательное
состояние (2К-Т 1)-кратно вырождено. В действительности одна
из проекций момента количества движения имеет вполне опре-
деленное значение. Например, проекция на ось молекулы
(ось z) равна
Л А'. (2.123)
Этот результат имеет место для любого жесткого линейного
ротатора с моментом инерции 1е- Следует указать, что, согласно
(2.115), не атомная масса определяет /е, а расстояние между
равновесными ядрами и приведенная масса ядер.
2.16. Потенциал Морзе
67
2.16. Потенциал Морзе
Приведенные только что простейшие расчеты не вполне со-
ответствуют опытным данным. В предыдущем пункте получены
энергетические уровни, имеющие равные интервалы, а наблю-
дения показывают, что эти интервалы могут увеличиваться или
уменьшаться в зависимости от квантового числа v. Для того
чтобы получить такую особенность, необходимо иметь потен-
циальную функцию £7(г), которая была бы ближе к реальной,
чем описанная в предыдущем пункте. Особо следует обратить
внимание на поведение потенциальной функции при больших
значениях г.
Морзе предложил потенциал следующего вида:
U (г) = D {1 - ехр [- а (г — /J] }2. (2.124)
При г=ге величина U принимает наименьшее значение, равное
нулю, при больших значениях г величина стремится к некото-
рой конечной величине D. При г=0 реальная потенциальная
функция должна иметь бесконечно большое значение. Потен-
циал Морзе имеет в нуле конечное значение. Однако величина
его здесь очень велика, поэтому этот недостаток оказывается
не существенным. Подставляя выражение (2.124) в (2.110),
имеем
d2S . ( /<(/<+1) . [£ д Pe~2a(r~r^ -U
dr2 ( г2 Л*2 L
+ 2De~a(r~r^] }S = 0. (2.125)
Сделав замену
„ = = л= (2.126)
’ dr ” ly '
получим
d2S 1 dS , 2ц f E — D 2D Ar2\ „ ~ ______„
1 1--4- 1 D e-]S = 0. (2.127)
dy2--------------------------------------у dy a2h*2 \ у2-у-y2r2 /
Последний член связан с эффектом взаимодействия вращатель-
ного и колебательного движений, поэтому в низких энергети-
ческих состояниях он очень мал. При г=ге имеем у=\. Разло-
5*
68
Гл. II. Квантовая механика
жим (ге/г)2 в ряд по степеням (у— 1)
1пуГ2_J1 _ ‘"[I +(»/-О] Г2
аге
(relr)2
( а/р
(у-1) . 1 (у—1)*
аге , 2
— (у -1)4
аге
ЪГе J
1 2 2
ОГе а ге
-2
Сохраняя в уравнении (2.127) лишь написанные три члена раз-
ложения, имеем
у
d2S , 1 dS . 2ц [E—D — Cq ! 2D — С,
dy2 У dy a2h*2 \ у2
где
о
С
С2
1-------+
4 6
2 2
аге а ге
—!_ + _
аге с
5 = 0, (2.128)
(2.129)
Преобразуем теперь уравнение (2.128) к виду, рассмотренному
выше в связи с атомом водорода, делая следующие замены:
S(y) — e~*l2zbi2F(z), z = 2dy, <Z-(D+C^ b2=-^E-D~c°>- (2.130)
получаем d*F p + 1 iHF ! P F —0 dz2 z J dz z? U’ (2.131)
где V =- -V (2£ — ct) — (b +1). a2ft*2dv v 2V ' (2.132)
Это уравнение сходно с уравнением для радиальной волновой
функции и может быть решено с использованием полиномов
Лагерра, Собственные значения v составляют 0, 1, 2 ... . При
2.16. Потенциал Морзе
69
помощи (2.130) и (2.132) находим Е
Ек, v — D Со
(Р-С,/2)*
(£> + С2)
2ah*(D-Cl/2) / J_\
“Г /2И(D + С2) I '2)
a2h*2 [ . 1 \2 00
—(’+?) (2ЛЗЗ>
Так как А очень мало, то следует разложить приведенное вы-
ражение по степеням CJD и С2/Р. Тогда
/ J \ / J \2
Де V- = (Ц'Р + у)— хеае + У) —
- DeK? (К +1 )2 - ае (-V +1) /<(/<+ 1), (2.134)
причем
и=_£_1/2£, xe = J^c_ в
‘ 2пс V Ц 4D ’ 4 8л2/ес ’
D =_______*_____=_____hl_____
е 128л6ц3со2с3г® 128л6/3®2с3 ’
ЗЛ2<ое / 1_____1_\
е \^IeD \ аге а2/*2 ) ’
(4=^
(2.135)
где с — скорость света в вакууме.
Эти выражения могут давать чрезвычайно точные числен-
ные значения энергетических уровней для всех двухатомных
молекул. Нет необходимости разъяснять, что все расчеты отно-
сятся к более низким энергетическим уровням, чем у электрона.
Опытные значения констант в (2.134) были предложены Герц-
бергом1).
Очевидно, что для взятой потенциальной функции U(r) ве-
личина £, вычисленная по (2.134), имеет смысл лишь при
E<D. А при E>D, согласно общим рассуждениям из п. 2.2,
энергия должна быть непрерывной. Поэтому дискретные энер-
гетические уровни ограничены. При использовании (2.134) этот
факт необходимо помнить. Энергия основного состояния (и = 0,
К = 0) равна
1 1
А), о
he
(2.136)
!) Herzberg G., Molecular Spectra and Molecular Structures, Vol. I,
Diatomic Molecules (Prentice-Hall), 1939, 121 (русский перевод: Герцберг,
Спектры и строение двухатомных молекул, ИЛ, 1949. — Прим. ред.).
70
Гл. 11. Квантовая механика
Разность EKtV и Е0>0 составляет
—+ 1)В0 —
— tf2(K+l)2D0-^(tf+l)ae, (2.137)
где
©*==®е(1 — 2хе), х*©* = хе<ое, Во = Вг4--у , DQ = De. (2.138)
Энергия диссоциации равна D — Е0<0, т. е.
fдиссоц = D -1 (1 - j he. (2.139)
Величину D можно вычислить через сое и хе из (2.135), поэтому
энергию диссоциации тоже можно найти по данным спектра.
Но формулы (2.135) получены с помощью различного рода при-
ближений. Поэтому нельзя надеяться, что вычисленные таким
способом значения энергии диссоциации являются точными.
В действительности они часто не совпадают со значениями, ко-
торые определяются более прямым способом. Приведем в ка-
честве примера расчет £дИСсоц для молекул (НС1)
ое = 2988,95 мм'1,
= 51,65 Л£Л£-1,
23^=10,5909 мм'1.
£^ = 0,0004 мм'1.
ае = 0,3019 мм'1.
£диссоц _ D ае , хе<*е _ &е , хе&е _
he he 2 -т" 4 4хг®е 2 4
__ (©£ — хе®е)2 (2988,95 — 51,65)2
4хеое 4 • 51,65 ’
—£диссо“, =6,02472 • 1023 • 6,6252 • 10~27 • 2,997929 • 1О,оХ
гр. мол. НС1 ’
X • 2,3889 • 10""*^^- =
/х 4-51,65 ’ моль
_ 6,02472 • 6,6252 - 2,997929 • 29,3732 • 0,23889 ккал _ j 19 2 кксьл
4-51,65 моль ’ моль
Экспериментальное значение этой величины равно
102,1 ккал/моль. Ошибка составляет примерно 17%. Но этого
вполне достаточно для представления о том, что по данным
спектра можно вычислять энергию диссоциации молекул.
2.17. Многоатомные молекулы
71
2.17. Многоатомные молекулы
Из предыдущего пункта видно, что, хотя в принципе строе-
ние молекул и энергетические состояния можно рассчитать с
помощью квантовой механики, практически решены лишь са-
мые простые вопросы; с такой точностью рассчитать можно
лишь водородоподобные атомы. Даже относительно простые
двухатомные молекулы нуждаются в введении межъядерного
потенциала. Поэтому теоретический расчет многоатомных мо-
лекул почти невозможен. К счастью, для дальнейшего нам до-
статочно грубого приближения. Поскольку объем ядер различ-
ных атомов мал, часто можно рассматривать ядро как мате-
риальную точку.
Тогда относительное движение ядер в многоатомных моле-
кулах складывается из различных типов колебаний. В грубом
приближении мы считаем, что каждый тип колебания предста-
вляет собой гармонический осциллятор. Однажды найденные
основные частоты, как, например, в п. 2.4, позволяют очень
легко вычислять распределение энергетических уровней. Мы
пренебрегаем также взаимодействием между вращательным и
колебательным движением, т. е. рассматриваем вращательное
движение как вращение твердого тела.
Для линейной молекулы вращательные состояния уже об-
суждались в п. 2.15. Если же молекула является нелинейной,
но существуют такие оси симметрии, относительно одной из ко-
торых момент инерции равен С, а относительно двух других
(взаимно перпендикулярных) равен Л, то молекула представ-
ляет собой симметричный волчок. Для такого симметричного
волчка уровни энергии вращения вычислены (см. литературу по
квантовой механике) и равны
= (2.140)
г Kh
J — главное вращательное квантовое число, ------компо-
нента углового момента вдоль оси симметрии волчка. Кроме
этих квантовых чисел, существует еще одно квантовое число М;
величина 4^ дает компоненту вдоль любой фиксированной в
пространстве оси. Эти квантовые числа могут принимать значе-
ния
J=0, 1, 2,
ЛГ=О, ±1, ±2, ..., ±7; (2.141)
Л4 = 0, ±1, ±2, ..., ±7.
72
Гл. Л. Квантовая механика
Когда К = 0, выражение (2.140) превращается в выражение Е
для линейного ротатора. Отсюда следует, что количество энер-
гии не связано с М и не зависит от знака К. Поэтому кратность
вырождения энергетического уровня при данном J составляет
27+1 или 47 + 2 в зависимости от того, является ли К равным
нулю или нет. Когда структура молекулы известна, величины А
и С могут быть вычислены по массам атомных ядер.
Частоты колебаний многоатомной молекулы можно опреде-
лить из инфракрасного спектра. Если п — число атомов в мо-
лекуле, а каждый атом имеет три степени свободы, то в сумме
имеем Зп степеней свободы. Поступательное движение моле-
кулы в целом имеет три степени свободы. Линейная молекула
имеет две вращательные степени свободы, нелинейная — три.
Поэтому у линейной молекулы Зп — 5 колебательных частот,
у нелинейной Зп — 6. Однако в молекуле часто имеется неко-
торая симметрия и не обязательно все частоты различны. С по-
мощью теоретико-групповых принципов волновой механики и
математики можно найти число этих различных частот, а так-
же кратность каждого типа колебания. Мы не будем вдаваться
здесь в подробный анализ, так как для многих молекул эти
данные уже собраны в работах Герцберга1). В отношении тер-
модинамических расчетов, вообще говоря, достаточно еще бо-
лее грубое приближение для колебаний многоатомных молекул,
о котором пойдет речь в пятой главе. Этот приближенный метод
не нуждается в вычислении точных частот колебания молекул.
!) Herzberg G., Molecular Spectra and Molecular Structures, Vol. II,
«Infrared and Raman Spectra of Polyatomic Molecules» (D. Van Nostrand),
1945 (русский перевод: Герцберг, Колебательные и вращательные спектры
многоатомных молекул, ИЛ, 1949. — Прим. ред.).
Глава III
ОСНОВЫ СТАТИСТИЧЕСКОЙ МЕХАНИКИ
Предметом статистической механики является отыскание
макроскопических свойств веществ, исходя из их микроскопи-
ческой атомной структуры и из законов взаимодействия микро-
элементов, составляющих эти вещества. Макроскопические
свойства, выявленные с помощью даже самых чувствительных
приборов, все еще представляют собой свойства большого со-
брания атомов. Поэтому мы собираемся здесь рассматривать
лишь результаты суммарного поведения большого количества
атомов или молекул, а не поведение отдельных атомов или
молекул.
Отыскание свойств отдельных атомов и законов их взаимо-
действия не является задачей собственно статистической меха-
ники. Как было сказано в предыдущей главе, это задача кван-
товой теории. Исходя из свойств атомов и молекул, найденных
с помощью квантовой механики, или из более общих физиче-
ских соображений и экспериментов, статистическая механика
предлагает способ вычисления термодинамических свойств ве-
щества. Цель этой и последующей глав заключается в том, что-
бы разъяснить основные положения статистической механики и
в дальнейшем использовать их для решения конкретных задач.
Кроме того, как и в предыдущих главах, мы не будем пытаться
применять строгие, но чрезвычайно громоздкие методы для по-
строения основ статистической механики. Мы лишь по мере воз-
можности будем стараться четко описать результаты. Для изу-
чения основ статистической механики мы отсылаем читателя
к специальной литературе.
3.1. Ансамбли систем
Рассмотрим некоторую однородную часть вещества, в каче-
стве которого может быть газ, жидкость, твердое тело или по-
верхностная пленка. В случае газа мы имеем дело с собранием
более или менее независимых атомов и молекул. Эти атомы
и молекулы лишь случайно взаимодействуют друг с другом.
Напротив, в твердом теле нельзя сказать, что атомы или
74
Гл III. Основы статистической механики
молекулы близки к независимым. Однако часто движения атомов
можно рассматривать как почти независимые нормальные коле-
бания. Естественно, что в других случаях такого рода рассмо-
трение некоторых слабо связанных систем либо менее полно,
либо в настоящее время практически невозможно. Это создает
значительные трудности в развитии и применении методов ста-
тистической механики. В действительности для измерения вели-
чин, характеризующих изменения системы, обычно можно ис-
пользовать разложение состояния и движения сложной мате-
риальной системы на состояния и движения почти независимых
систем. По этой причине возникла методика трактовки сложных
систем, состоящая в том, что исследуемая сложная система
рассматривается как ансамбль систем. Этими системами могут
быть атомы или системы движений, совершаемые атомами при
нормальных колебаниях. Однако независимо от того, чем они
являются, их свойства определяются квантовой механикой.
К тому же с точки зрения статистической механики эти свой-
ства считаются известными. Такие ансамбли включают в себя
большое число систем. Первоочередной задачей статистиче-
ской механики является определение равновесных свойств
наблюдаемых ансамблей в заданных макроскопических усло-
виях.
В некоторых случаях различение ансамбля и образующих
его систем подчас невозможно или неудобно. Тогда можно до-
пустить, что ансамбль содержит всего лишь одну систему, но
сама система является сложной и обладает очень большим чис-
лом возможных состояний. Разница в энергии у одного состоя-
ния и другого весьма мала, т. е. распределение по энергии очень
плотное. Анализ показывает, что применяемые в этих случаях
методы не подвергаются какому-либо изменению. Хотя описа-
ние вещества с помощью ансамбля, состоящего из большого
числа систем, является необязательным, однако во многих слу-
чаях это удобно, поэтому в дальнейшем мы будем применять
такой метод описания, характерный для статистической меха-
ники.
Как мы уже говорили, поведение отдельной системы в ан-
самбле, например поведение атома гелия в литре этого газа,
при нормальных температуре и давлении не является объектом
нашего исследования. В самом деле, поведение отдельного ато-
ма становится невероятно сложным из-за бесчисленных взаимо-
действий со стенками сосуда и другими атомами газа. Иссле-
дование в равной степени невозможно, пытаемся ли мы для
определения поведения отдельного атома использовать законы
квантовой механики или в более простом предельном случае
использовать законы классической механики.
3.2. Предварительные сведения о микросвойствах
75
Квантовое описание отдельного атома действительно отли-
чается от его классического описания и совсем не представ-
ляется определенной траекторией. Однако это приводит чуть ли
не к еще более запутанному положению. На первый взгляд мо-
жет показаться странным, что, хотя отыскание поведения ин-
дивидуальной системы ансамбля далеко от наших возможно-
стей, мы все же можем успешно отыскивать общие свойства
ансамбля в целом или свойства грамм-молекулы вещества. Од-
нако при более внимательном подходе станет ясно, что сомне-
ния напрасны. Можно обнаружить также, что такое положение
очень похоже на то, с чем человек хорошо знаком в повседнев-
ной жизни. Это связано прежде всего с тем, что при отыскании
свойств грамм-молекулы вещества мы производим описание ан-
самбля и притом не полное описание. Такое описание намного
проще описания траектории отдельного атома. А подробное опи-
сание ансамбля в действительности включает в себя подроб-
ное указание траекторий всех атомов. Во-вторых, такой путь
отыскания свойств грамм-молекулы (как это мы вскоре уви-
дим) связан с описанием среднего, или наиболее вероятного, по-
ведения большого числа систем. Относительно понятия среднего
мы также имеем представление из повседневной жизни. Напри-
мер, мы совсем не можем сказать, может ли живущий сейчас
явно здоровый мужчина тридцати лет в течение этого года уме-
реть внезапно, но мы совершенно точно можем указать среднее
количество таких людей в каком-либо государстве, которые так
умрут. Другими словами, мы можем знать вероятность смерт-
ности в этом году каждого человека в обществе, в котором он
живет.
3.2. Предварительные сведения о микросвойствах
Во второй главе мы уже сделали предположение, что мо-
лекулы и атомы состоят из материальных точек. Этими
материальными точками являются атомные ядра и электроны.
Если Z — атомный номер, а е — заряд электрона, то тогда атом-
ное ядро имеет заряд + Z|e|, а электрон обладает зарядом —е.
Однако мы теперь знаем, что атомное ядро не является простой
частицей, а обладает структурой и состоит из Z протонов и
А—Z нейтронов, где А — массовое число.
В настоящее время остается открытым вопрос о том, яв-
ляются ли протон и нейтрон простейшими частицами и не явля-
ется ли невероятным предположение, что они также могут иметь
тонкую структуру. Поэтому представление относительно атом-
ного ядра элементов, о котором мы говорили в самом на-
чале, действительно является чрезмерно упрощенным. Кроме
76
Гл. III. Основы статистической механики
энергетических уровней атомов и электронов, энергетических
уровней колебания и вращения, мы знаем по крайней мере о су-
ществовании энергетических уровней атомного ядра или энерге-
тических уровней нейтронов и протонов. С этой точки зрения мо-
жет показаться, что если мы попытаемся с самого начала про-
изводить статистические расчеты, исходя из моделей простых
атомов и молекул, то мы будем стоять не на прочной основе.
Однако после более тщательного анализа можно увидеть,
что такого рода опасения совершенно напрасны. Интервал ме-
жду энергетическими уровнями ядер велик даже в сравнении
с интервалом между энергетическими уровнями электронов, так
как ядерные силы обычно в 106 раз больше межатомных сил.
Для легких элементов интервал между энергетическими уров-
нями ядра измеряется мегаэлектроновольтами. Возможные
энергетические уровни ядер нейтронов и протонов должны
иметь еще большие интервалы. Из дальнейшего анализа будет
видно, что вероятность энергетического уровня энергии е в ос-
новном прямо пропорциональна e~zlhT, где k — постоянная
Больцмана, равная (8,6164±0,0004) • 10-6 эв/°К, и Т является
абсолютной температурой этого вещества.
Поэтому для газов, содержащих легкие атомы, при темпера-
турах, меньших 1010 град, вероятность нахождения атомного
ядра на энергетическом уровне выше основного крайне мала.
Другими словами, можно сказать, что вплоть до температур в
несколько миллиардов градусов энергетический уровень основ-
ного состояния атомного ядра является занятым, а существо-
вание других энергетических уровней никак не сказывается.
Это говорит о том, что для газов, содержащих легкие атомы,
нам достаточно лишь удерживать температуру ниже 1010 град,
и, даже зная, что модели атомов и молекул несовершенны, мы
можем все же верить результатам наших вычислений. Для тя-
желых атомов вследствие большей плотности энергетических
уровней ядра предел температуры, о котором говорилось выше,
должен упасть до нескольких миллионов градусов. В астрофи-
зике температуры могут быть выше 109 град; при этом воз-
можно появится необходимость рассмотрения энергетических
уровней ядра.
Однако существует еще один момент, который нам необхо-
димо добавить к нашей простой модели атомов и молекул.
Это — спин ядра. Вследствие наличия спина у ядер мы должны
допустить возможность существования у них различных ориен-
таций. К счастью, кроме вычислений статистического веса, нам
нигде не потребуется совершать более глубоких исследований,
связанных с существованием спина. В противном случае поло-
жение было бы хуже и из-за отсутствия полной и совершенной
3.3. Общая природа состояний ансамбля 77
теории тонкой структуры ядра применение статистической меха-
ники стало бы невозможным, даже если бы ее применяли к
условиям более низких температур.
3.3. Общая природа состояний ансамбля
Ансамбли, состоящие из электронов и атомных ядер, яв-
ляются частью всей материи. Влияние остальной материи во
вселенной можно с достаточной степенью точности представить
себе в виде полей и стенок. Эти поля можно считать более
или менее консервативными. При наличии таких силовых по-
лей ансамбли обладают некоторыми важными свойствами, ко-
торые желательно найти. Для ансамбля, находящегося в таких
условиях, можно построить уравнение Шредингера, которое в
принципе можно решить.
Если ансамбль заключен в объем, ограниченный стенками,
то, как известно из соответствующих рассуждений во второй
главе, уравнение Шредингера имеет ряд дискретных собствен-
ных величин для энергии Ео, Еь Е2, каждому из которых соот-
ветствует одно или несколько различных решений волнового
уравнения. Эти решения называют собственными функциями.
Знание их не является основной целью статистической меха-
ники. Здесь самым важным является следующий факт: эти
решения существуют и представляют возможные состояния дви-
жения ансамбля. Их обычно называют стационарными состоя-
ниями или сокращенно состояниями. Когда мы говорим о со-
стоянии в этом смысле, мы всегда подразумеваем такое
состояние движения, которое соответствует некоторому стацио-
нарному решению уравнения Шредингера для такого ансамбля—
каждому состоянию соответствует одно решение. Справедливо
и обратное. Для большого ансамбля, состоящего из почти неза-
висимых систем, может существовать большое число собствен-
ных функций, поэтому существует также большое число состоя-
ний, соответствующих любому возможному значению энергии
ансамбля.
Во всяком случае, у большого ансамбля энергетическому ин-
тервалу £, E + dE соответствует очень большое число состоя-
ний. Рассматривать же малый интервал энергии более есте-
ственно, чем ее точное значение, так как не существует реаль-
ного ансамбля, который в действительности находился бы под
воздействием истинно консервативного поля сил. Даже в равно-
весном состоянии в результате столкновений атомов реальный
ансамбль непрерывно обменивается малыми порциями энер-
гии с окружающей средой.
78
Г л. III. Основы статистической механики
Поэтому сначала рассмотрим ансамбль, имеющий данную
энергию или энергию из заданного интервала. Этим энергиям
соответствует очень большое число возможных состояний. Да-
лее, исходя из законов квантовой механики, мы должны найти
поведение ансамбля.
Если мы предположим, что уравнение Шредингера для опи-
сания целого ансамбля является верным, а также допустим, что
оно действительно включает в себя все взаимодействия между
системами ансамбля, между ансамблем, стенками и внешними
телами, то в принципе можно найти решения этого уравнения,
причем каждое собственное значение и собственная функция
принадлежат реальному стационарному состоянию, в котором
изолированный ансамбль может находиться неограниченное
время. Свойства такого ансамбля соответствуют свойствам от-
дельного стационарного состояния.
Такая ситуация даже в самом грубом приближении никогда
не сможет в действительности реализоваться. Причина этого
состоит хотя бы в том, что при написании уравнения Шредин-
гера мы уже пренебрегли излучением и процессом излучения, а
также предположили, что все взаимодействия ансамбля с внеш-
ним миром можно представить через консервативные силы.
В принципе представлять взаимодействие излучения через лю-
бое консервативное поле сил, не зависящее от времени, невоз-
можно. Действие реальных стенок и внешних систем также
нельзя представлять в виде членов в потенциальной энергии, не
связанных со временем. По этим причинам невозможно по-
строить строгое консервативное уравнение Шредингера.
Таким образом, хотя стационарные состояния, описываемые
точными решениями, в принципе вроде бы возможны, но в дей-
ствительности весьма абсурдны и соответствуют лишь прибли-
женной трактовке явления. В самом идеальном случае теоре-
тически можно найти решение приближенного уравнения Шре-
дингера, которое зависит от помех, связанных со временем.
Эти помехи в специальной терминологии называются возму-
щениями. При наличии возмущений ансамбль может совершать
переходы из одного так называемого стационарного состояния
в другое стационарное состояние. Таким образом, в принципе
мы всегда имеем дело со свойствами не отдельного стационар-
ного состояния, а со средней величиной каких-то свойств боль-
шого числа стационарных состояний или со свойствами наибо-
лее характерных из них. Все эти состояния могут либо обла-
дать одинаковой энергией, либо оказаться распределенными в
очень малом энергетическом интервале.
Таким образом, мы вынуждены признать, что любой ан-
самбль нельзя рассматривать как неизменно находящийся в
3.3. Общая природа состояний ансамбля
79
определенном стационарном состоянии. Как бы точно мы ни
строили и не решали уравнение Шредингера, необходимо по-
мнить, что в действительности при построении и решении его
никогда нельзя достичь абсолютной точности. Пытаясь прак-
тически построить и решить уравнение Шредингера для какого-
либо ансамбля, мы надеемся построить достаточно точное ура-
внение. Оно действительно может быть полностью и точно
решено, но так как само уравнение не является абсолютно точ-
ным, его собственные значения и стационарные состояния яв-
ляются всего лишь приближенными, а все взаимодействия с
внешними системами опущены, хотя они реально и существуют.
Поэтому между двумя состояниями обязательно происходит пе-
реход.
В нашем рассмотрении включены также взаимодействия
(более или менее слабые и не постоянные) между системами
ансамбля. Полученные таким образом приближенные состояния
почти не изменяются, кроме случая перехода. Однако свойства
ансамбля можно найти, производя усреднение по приближен-
ным состояниям ансамбля, описываемым формулами, найден-
ными из приближенных уравнений.
В этом случае приходим к следующему. Мы построили и ре-
шили приближенное уравнение Шредингера для рассматривае-
мого ансамбля. Погрешности уравнения выражаются через воз-
мущающие члены, которые вызывают переходы между стацио-
нарными состояниями приближенного уравнения Шредингера.
Эти стационарные состояния находятся в более или менее стро-
го определенной области энергий. Мы можем признать, что та-
кой способ решения проблемы является верным, так как в прин-
ципе нет ничего, что мешало бы нам построить идеально точное
выражение, состоящее из возмущающих членов. Возмущения
могут зависеть от времени, но они не должны входить в точное
уравнение, из которого находятся собственные значения и соб-
ственные функции стационарных состояний.
Ансамбль, находящийся при неизменных внешних условиях,
может теоретически обладать характерными свойствами, вос-
принимаемыми нами и прибором как неизменные. Эти харак-
терные свойства мы можем назвать наблюдаемыми равновес-
ными свойствами ансамбля. Так как они действительно наблю-
даются, то в дальнейшем, несмотря на отсутствие строгого до-
казательства, мы будем по мере необходимости считать, что
такие характерные неизмененные свойства ансамбля, несомненно,
существуют и их можно найти. Единственное, что остается, это
вывести реально наблюдаемые свойства ансамбля из наших
предполагаемых сведений относительно свойств состояний ан-
самбля.
80
Гл. III. Основы статистической механики
Основная трудность, с которой мы сталкиваемся, заклю-
чается в необходимости правильно выбрать стационарные со*
стояния. Свойства этих стационарных состояний должны опре-
делять наблюдаемые свойства ансамбля с достаточной сте-
пенью точности. В частности, мы должны решить, стремится ли
ансамбль к тому, чтобы находиться в каком-либо стационарном
состоянии из ограниченной группы состояний, ибо существует
и другая возможность: ансамбль не выявляет таких стационар-
ных состояний или групп стационарных состояний, которые за-
нимали бы особое место среди всевозможных стационарных со-
стояний, допускаемых общими условиями задачи. В последнем
случае равновесные свойства ансамбля могут быть лишь свой-
ствами большого числа стационарных состояний. Таким обра-
зом, расчет равновесных свойств можно осуществить только с
помощью усреднения либо по всем стационарным состояниям,
либо по группе наиболее часто встречающихся стационарных
состояний. Можно применить и некоторые другие методы, но
о них мы будем говорить в дальнейшем.
3.4. Правило для усреднения
Из предыдущего пункта видно, что мы должны провести вы-
бор состояний. Однако до сих пор этого нельзя еще сделать од-
нозначно на совершенно строгой, теоретически доказуемой ос-
нове.
Возможны многие способы выбора состояний. К счастью,
в применении к большим ансамблям все они приводят к оди-
наковым физическим результатам.
Мы не намереваемся здесь описывать все многообразие ме-
тодов выбора и теоретические положения, которые делают их
вполне правдоподобными. Мы лишь сформулируем необходи-
мые основные предположения, которыми мы будем пользо-
ваться в рассуждениях по другим вопросам. Оправданием лю-
бого толкования основного предположения служит то, насколько
оно надежно в употреблении. Поэтому из нескольких взаимоза-
меняемых предположений мы выбираем следующее.
Найдем все различные состояния ансамбля, соответствую-
щие определенной энергии или интервалу энергии и каким-либо
другим заданным условиям. Значение Q какого-нибудь свой-
ства Q ансамбля, которое будет характеризовать его равновесное
состояние, подчиненное указанным условиям, может быть полу-
чено усреднением по всем этим состояниям путем приписыва-
ния каждому состоянию одинакового статистического веса (рае-
3.5. Описание классического ансамбля
81
ного единице). Формально мы можем написать
Q= Sq / 21 • (3.1)
по всем по всем
состояниям состояниям
Такое утверждение пока несколько неопределенно и должно
быть в дальнейшем уточнено. Для проведения усреднения мы
уже выбрали состояния с данной энергией. Это кажется очень
естественным и не нуждается в дальнейшем анализе, так как
ансамбли, которые мы имеем в виду, по предположению обла-
дают постоянной или приближенно постоянной энергией. В этом
случае трудно обнаружить систему в состоянии, соответствую-
щем другому значению энергии. Но может возникнуть вопрос:
не существует ли других, одинаково важных функций атомных
переменных ансамбля? Может ли их неизменяемость являться
частью прочих общих условий, которые уже упоминались в вы-
шеприведенном толковании правила для усреднения? Исследо-
вание подобных функций приводит нас к вопросу о появлении
тех или иных состояний, т. е. к вопросу о допустимости состоя-
ния. Прежде чем давать ясное определение правила для усред-
нения, необходимо уточнить это понятие, что и будет сделано
ниже.
3.5. Описание классического ансамбля
До сих пор мы не пользовались положениями классической
механики и положениями, имеющими к ней отношение, так как
мы знаем, что классическая механика в принципе не может
быть применима к атомным ансамблям и дает правильные ре-
зультаты лишь в соответствующих предельных случаях. Здесь
же описание классического ансамбля и исследование условий
применимости классической механики является удобным, так
как такое описание и исследование очень естественно приводят
к некоторым еще более тонким условиям, применяемым в кван-
товой теории.
Ансамбль, подчиняющийся законам классической механики,
описывается полностью, если его энергия задана как функция
N' обобщенных координат и соответствующих им N' обобщен-
ных импульсов. Если внешнее поле, в котором находится ан-
самбль, является консервативным, то энергию ансамбля можно
написать в виде функции Гамильтона Н(х,рх), х — сокра-
щенное написание N' координат Х2, ..., xN,f а рх — соответ-
ствующие им импульсы рх^ Рх2> • ••, PxN,-
В этом случае функция И не содержит никаких других пере-
менных величин. Если ансамбль находится в неконсервативном
6 Зак. 1299
82
Гл. III. Основы статистической механики
поле, например если поверхность и другие тела вне ансамбля
заданы координатами х в функции Гамильтона Н и сами эти
координаты являются функциями времени, то временную часть
можно извлечь из Н и впоследствии ввести в качестве возмуще-
ния. Мы пока пренебрежем силами, связанными с временем,
однако надо помнить, что в принципе они никогда не могут
быть опущены из любого реального ансамбля.
Для идеализированного ансамбля в консервативном поле
классические уравнения движения Гамильтона имеют вид
dx дН dpx дН
= -аГ=—дГ- <3-2)
Всего их насчитывается 2N' уравнений. Координатами х может
быть любая группа величин, которая полностью описывает гео-
метрическую конфигурацию ансамбля в любой момент времени.
Например, для групп W бесструктурных частиц с массой m
естественными координатами являются ЗМ декартовых коорди-
нат
Уа> za (а=1. 2, .... N).
Поэтому соответствующими импульсами (обычно они назы-
ваются сопряженными импульсами) являются следующие 3W
переменных:
mxa, туа, mza (а= 1, 2, ..., /V).
Из уравнения (3.2) мы можем вывести соотношение
Оно означает, что энергия не изменяется со временем. Уравне-
ние (3.3) можно написать в проинтегрированном виде
Я(х, Рх) = Е^ (3.4)
где Е— Постоянная.
Вообще, когда однозначная функция всех 2N' переменных
х, рх или их части при движении всего ансамбля остается по-
стоянной, тогда она называется однородным интегралом урав-
нений движения. Поэтому уравнение (3.3) означает, что энер-
гия является однородным интегралом уравнений движения. Ко-
гда все координаты х и импульсы рх известны как функции
времени, тогда все поведение классического ансамбля стано-
вится заданным. Таким образом возможно получить геометри-
ческое изображение состояний классического ансамбля, которое
полезно при любых общих рассуждениях.
3.5. Описание классического ансамбля
83
Когда известны все х и рх как функции времени, то пол-
ностью известно состояние ансамбля в любой момент времени.
Мы будем изображать состояние ансамбля точкой в гиперпро-
странстве 2Af'( = 6Af) измерений, условившись, что х и рх пони-
маются как ее декартовы координаты в этом пространстве. Та-
кое пространство называется фазовым пространством ансамбля,
а путь, который проходит в нем точка, — ее фазовой траекторией.
Фазовая траектория подчиняется уравнениям движения (3.2)
и для консервативного ансамбля полностью определена этими
уравнениями и начальным положением ансамбля как точкой
в фазовом пространстве. Две траектории консервативного ан-
самбля никогда не могут пересекаться, так как в противном
случае, если в качестве начального положения взять точку пе-
ресечения, то решение неоднозначно, а это противоречит изве-
стным результатам.
Любая траектория в фазовом пространстве расположена на
гиперповерхности, определенной уравнением (3.4). При нали-
чии неконсервативных возмущений соответствующий дополни-
тельный член должен быть в составе этого уравнения, поэтому
возмущенная траектория естественно становится намного слож-
нее. Можно предположить, что после более или менее продол-
жительного времени траектория может приблизиться к одному
или другому семейству невозмущенных траекторий. Можно
представить это так: фазовое пространство, заключенное между
двумя поверхностями энергии с не слишком широким энергети-
ческим интервалом dE, является фазовой областью возмущен-
ного движения. Под действием возмущений фазовая траек-
тория ансамбля может подходить ко всем точкам из этой об-
ласти и при этом время от времени медленно переходить от
траектории одного семейства к траектории другого семейства.
Траектории семейства можно определить как точные траекто-
рии консервативного ансамбля, приближенно представляющего
реальный возмущенный ансамбль.
Для нас ценность рассмотрения классических ансамблей за-
ключается в принципе соответствия, согласно которому класси-
ческий ансамбль всегда можно считать предельной формой со-
ответствующего квантового ансамбля. Для того чтобы иметь
возможность использовать классические теоремы для объясне-
ния соответствующих реальных квантовых явлений, необходимо
знать, каким образом можно сравнивать дискретные собствен-
ные состояния квантовой системы с непрерывным рядом состоя-
ний, соответствующих точкам в классическом фазовом про-
странстве. К счастью, на этот вопрос, давно уже дан исчерпы-
вающий ответ: состояния ансамбля с N' степенями свободы, со-
ответствующие каждой собственной функции, удовлетворяющей
6*
84
Гл. III. Основы статистической механики
граничным условиям и уравнению Шредингера, занимают об-
ласть классического фазового пространства, равную hN'. Такого
рода соответствие сразу же заставляет вспомнить, что оно со-
ставляет часть теории соответствия Бора и является некоторой
общей теоремой, справедливой для больших квантовых чисел.
В следующей главе в подтверждение этого будут приведены
численные примеры. А пока мы принимаем как факт наличие
соответствия между каждым квантовым состоянием и областью
фазового пространства с объемом hN'.
3.6. Пределы применимости (главным образом классическая
часть)
В классических ансамблях такого типа, который мы только
что описали, кроме интеграла энергии, при определенных ус-
ловиях могут существовать и другие однородные интегралы.
Компоненты импульса и момента импульса ансамбля не под-
вергаются влиянию взаимодействия систем и при отсутствии
влияния извне сохраняются. Поэтому они тоже являются одно-
родными интегралами. Можно предположить, что существуют,
может быть, еще и другие однородные интегралы такого типа.
Любой новый однородный интеграл оказывает сильное влияние
на траекторию изображающей точки в фазовом пространстве.
Как мы уже объясняли, каждый однородный интеграл выра-
жается соотношением
F (х, рх) = const. (3.5)
Например, в ансамбле, образованном из элементарных ча-
стиц с массой /и, постоянство х-компоненты импульса выра*
жается соотношением
У рх = const, (3.6)
г г
а постоянство z-компоненты момента импульса — уравнением
2 (УгРхг — XrPyr) = const. (3.7)
Рассматриваемая функция F является однозначной (однород-
ной) функцией положения в фазовом пространстве. Существо-
вание этой однородной функции ограничивает траекторию ка-
кой-либо определенной поверхностью в фазовом пространстве,
или если условия допускают постоянной изменяться в некото-
ром малом интервале, то этот объем заключен между двумя
соседними поверхностями; здесь ситуация точно такая же, как
та, когда интеграл энергии ограничивает траектории поверх-
3.6. Пределы применимости
85
ностью равной энергии или областью, ограниченной такими по-
верхностями.
Возможность существования других аддитивных однородных
интегралов, кроме интеграла энергии, показывает, что необхо-
димо быть очень внимательным при выборе области усредне-
ния, о которой уже говорилось в п. 3.4. Когда существуют такие
однородные интегралы, они должны быть точно учтены как
часть общих условий, указанных выше. В этом случае мы дол-
жны производить усреднение лишь по состояниям и областям
фазового пространства, удовлетворяющим дополнительным тре-
бованиям. Такие области и состояния мы называем допусти-
мыми областями фазового пространства или допустимыми
состояниями.
Необходимо обратить особое внимание на то, что все требо-
вания относительно допустимости должны определяться пол-
ностью из реально существующих условий. Например, возмож-
ность существования однородных интегралов для компонент
импульса и момента импульса обычно не учитывается, хотя
справедливость этого не очевидна.
Разъясним это подробнее. Любой реальный ансамбль обыч-
но считается заключенным в некоторую оболочку. Представле-
ние о том, что сама оболочка не является частью ансамбля,
является в какой-то мере идеализированным. Оболочку обычно
рассматривают как стенки с упругим отражением. Системы ан-
самбля совершенно не обмениваются энергией с этими отра-
жающими стенками. Следующим шагом по пути упрощения яв-
ляется предположение, что отражение является зеркальным, по-
добным отражению света.
Компоненты импульса такого ансамбля не сохраняются, так
как любые компоненты импульса системы, перпендикулярные к
стенке, в процессе отражения изменяют направление на проти-
воположное. Таким образом, из уравнения движения ансамбля
следует, что ни одна из компонент импульса не может стать
однородным интегралом. Если эта идеализированная оболочка
является шарообразной, то компоненты момента импульса не
будут изменяться под влиянием столкновений с оболочкой, по-
этому, рассматривая ансамбль в целом, можно сказать, что эти
компоненты сохраняются неизменными. Конечно, реальные обо-
лочки не обладают такими идеализированными свойствами, по-
тому что их поверхности всегда имеют шероховатость атомного
масштаба. Поэтому между системами и оболочкой происходит
обмен энергией, импульсом и моментом импульса. Если обо-
лочку включить в ансамбль, то для полного ансамбля будут
существовать однородные интегралы энергии и импульса. При
этом, как мы обнаружим в будущем, условием равного обмена
86
Гл. 111. Основы статистической механики
энергией между оболочкой и другими частями ансамбля яв-
ляется равенство температур. Отсюда вытекают все положения
термодинамики.
Однако условие равного обмена импульсом является непол-
ным, так как при этом еще требуется, чтобы различные части
ансамбля обязательно образовывали систему, движущуюся как
твердое тело. Но это условие, по существу, не дает ничего
нового, так как мы всегда можем не рассматривать групповое
движение различных частей ансамбля, а учитывать лишь его
внутренние свойства, соответствующие его движению относи-
тельно центра инерции. Эти свойства не связаны с движением
системы как целого. Поэтому во всех выводах термодинамики
можно не учитывать существование однородных интегралов им-
пульса и момента импульса. Если считать, что они не суще-
ствуют, то можно рассматривать ансамбль как заключенный в
неподвижную неотражающую оболочку, а тогда все части ан-
самбля должны находиться в состоянии покоя. Если считать,
что эти однородные интегралы существуют, тогда оболочку
можно включить в ансамбль.
Такой целый ансамбль должен совершать движение как
твердое тело. Если он вращается, различные его части вместе
с оболочкой могут соответственно двигаться, но это нисколько
не отразится на проводимых по отношению к ним термодинами-
ческих исследованиях. Если эти системы образуют газ, а обо-
лочка вращается, тогда центробежная сила будет влиять на
распределение плотности газа, однако действие такой силы не
отличается от действия обычных внешних сил. Поэтому в даль-
нейшем мы не будем учитывать однородные интегралы им-
пульса и момента импульса.
Коснемся попутно одного любопытного примера. В тер-
модинамической теории Ферми1) процессов множественного об-
разования л мезонов при столкновении ядер высоких энергий
вопрос относительно сохранения импульса и момента импульса
ансамбля нельзя решать так же, как это было сделано выше.
Это объясняется тем, что отсутствует сосуд. Поэтому при по-
строении теории таких процессов мы должны обращать особое
внимание на сохраняемость импульса и момента импульса.
Для классического ансамбля возможно существование и
других однородных интегралов. Однако вплоть до настоящего
времени не было найдено ни одного другого однородного ин-
теграла. Поэтому можно сделать следующий вывод: если гово-
рить о классическом ансамбле, то вся область фазового про-
*) См. Fermi Е., Prog. Theo. Physics, 5, (1950), 570; Phys. Rev., 81
(1951), 683.
3.6. Пределы применимости
87
странства, соответствующая постоянной энергии, вообще го-
воря, является допустимой, поэтому в процессе усреднения не-
обходимо обращать внимание на каждую точку этой части фа-
зового пространства.
Однако с таким выводом мы в какой-то степени поспешили.
Например, мы не учли возможность существования временных
и метастабильных равновесий, которые имеют большое значе-
ние. Поэтому их следует подвергнуть более тщательному ана-
лизу. В действительности мы уже сделали предположение, что
между состояниями из допустимой области фазового простран-
ства имеется эффективный свободный обмен за время порядка
времени наблюдения или проведения эксперимента. Слово «эф-
фективный» в данном случае весьма существенно. Легко пред-
ставить себе такие условия, при которых в течение времени на-
блюдения изображающая точка не успевает покрыть полностью
допустимую область фазового пространства, а пробегает лишь
ее часть. Однако за достаточно большой промежуток времени
изображающая точка в действительности может покрыть все
допустимое фазовое пространство.
Другими словами, за время порядка времени эксперимента
положение изображающей точки в действительности ограни-
чено особыми областями фазового пространства. Лишь эти об-
ласти фазового пространства следует считать допустимыми;
изображающая точка полностью покрывает эти ограниченные
области. Мы можем привести простой пример: при комнатной
температуре смесь кислорода и водорода находится в метаста-
бильном равновесии; истинное состояние равновесия наступает
тогда, когда смесь почти полностью переходит в водяной пар
или воду.
Однако при комнатной температуре процессы, ведущие к
превращению молекул водорода й кислорода в молекулы воды,
происходят крайне редко и начальные числа молекул водорода
и кислорода при обычном времени эксперимента не изменяются.
Практически все эти начальные числа являются эффективными
однородными интегралами всех уравнений движения ансамбля,
а допустимое фазовое пространство ограничивается теми обла-
стями, в которых эти числа сохраняют свои начальные значения.
Хотя при метастабильном равновесии и происходит образование
воды, его все же можно отнести к обычному равновесию и, сле-
довательно, для расчета свойств можно применить методы тер-
модинамики и статистической механики.
Этот факт хорошо известен, но обычно недостаточно под-
черкивается его значение. Важно понять, что даже для класси-
ческих ансамблей может возникнуть любая степень метаста-
бильности. В примере, использованном выше, ограничения для
88
Гл. 111. Основы статистической механики
допустимой области фазового пространства* практически спра-
ведливы и в более продолжительный промежуток времени.
В других примерах ограничения могут иметь место только при
ограниченном времени и поэтому являются неполными ограни-
чениями. В этих случаях термодинамика и статистическая
механика применимы лишь приближенно. При строгом их при-
менении всегда необходимо точно • определить, какие области
фазового пространства полностью допустимы, а какие области
совсем недопустимы.
Практически всегда можно сказать, что толкование приме-
нимости меняется вслед за конкретными условиями. Необхо-
димо уметь разделять все процессы на два класса: одни — на-
столько медленные, что эффектом изменения за время экспери-
мента можно пренебречь; другие — настолько быстрые, что
изображающая точка ансамбля практически покрывает все фа-
зовое пространство. К процессам, протекающим с промежуточ-
ной скоростью, термодинамика и статистическая механика не
применимы. Все эти выводы легко перевести с языка классиче-
ского фазового пространства на язык квантовых состояний, но
мы не будем на это тратить время.
Мы сделали эти замечания о применимости потому, что их
правильное понимание позволяет более естественным образом
уяснить смысл новых условий допустимости, вводимых кван-
товой теорией. Более тщательные исследования в квантовой ме-
ханике показывают, что не все состояния ансамбля, состоящего
из одинаковых систем, являются допустимыми. Используя свой-
ства симметрии, можно разделить их на несколько групп, не
связанных друг с другом. Тип симметрии какого-либо опре-
деленного состояния является абсолютной постоянной движе-
ния, что в классической терминологии равносильно некоторому
интегралу движения. В соответствии с тем, что было сказано в
п. 3.4, ряд допустимых состояний, по которым происходит ус-
реднение, представляет собой группы, имеющие требуемые свой-
ства симметрии.
3.7. Допустимые состояния для ансамбля одинаковых систем.
Симметричные и антисимметричные группы состояний
В следующей главе мы подробно обсудим всевозможные и
допустимые состояния ансамбля, состоящего из множества оди-
наковых систем, а также выведем основную формулу равновес-
ного состояния. Здесь же ограничимся рассмотрением- только
общих принципов и исследованием вопроса о том, какие огра-
ничения накладывают требования симметрии на допустимые
состояния.
3.7. Допустимые состояния для ансамбля одинаковых систем
89
Начнем с ансамбля, который содержит группу полностью
одинаковых систем (электроны, молекулы водорода, атомы ге-
лия...). Рассмотрим прежде всего ансамбль, содержащий одну
такую систему. Функция Гамильтона для нее Н(х,рх) является
одновременно и энергией системы, а уравнение Шредингера
имеет вид
["(* <3-8’
где е — энергия системы в отличие от £ — энергии ансамбля.
Возможное состояние системы соответствует возможному
решению этого уравнения, при этом необходимо, чтобы функ-
ция ф удовлетворяла граничным условиям и была ограниченной
и однозначной функцией от х. Для ограниченной системы допу-
стимые значения е являются дискретными, однако при большом
размере оболочки их часто можно рассматривать распределен-
ными непрерывно, как и в классическом случае. Эти допусти-
мые значения (собственные значения уравнения) можно прону-
меровать натуральным рядом чисел 0, 1, 2, ..., причем таким
образом, чтобы не было двух одинаковых значений с разными
индексами. Каждому собственному значению еа соответствует
одна или несколько собственных функций уравнения (3.8).
Число таких собственных функций обозначается через соа и на-
зывается весом состояния. Иногда для удобства можно пред-
ставить себе, что вырожденная система (соа #= 1) превратилась
в невырожденную включением подходящего консервативного
ПОЛЯ ((0а=1).
Предположим теперь, что ансамбль построен из двух таких
одинаковых систем 1 и 2, между которыми существует очень
слабая связь; в первом приближении гамильтониан этой пары
систем можно рассматривать как сумму гамильтонианов
каждой из двух систем. Полное уравнение Шредингера для дан-
ного ансамбля будет иметь вид
[»(*•• + <3-9>
Это уравнение можно разделить на две части, причем допусти-
мое значение Е равно еа4~ет. Соответствующим ему решением
является функция
ЧГаг=^(Х1)^(Л2> (3.10)
где еа и ет — некоторые собственные значения е уравнения
(3.8), а фа, — соответствующие собственные функции. Са-
мым важным здесь является то, что даже для невырожденных
90
Гл. III. Основы статистической механики
систем ансамбль, по существу, вырожден, кроме случая, когда
о=т. Это объясняется тем, что при о =# т существуют по край-
ней мере две собственные функции Чгат = фа (*1)фт (х2), Чгта =
= фт (Х1)г|)а (%2), которые можно получить перестановкой коор-
динат систем. Обе они соответствуют одному и тому же соб-
ственному значению Е = еа + ет. Такая перестановка систем яв-
ляется необходимой, так как состояние системы выражается
лишь через собственную функцию ф. Так как ф определено на
всей оси х, то при любом конкретном значении х система может
быть в состоянии 1 или 2. У нас нет способа различать их. Если
отдельные системы вырождены (<oQ> =# 0» то общее число
различных собственных функций, соответствующих E, = eff + er>
будет равно
2о)а(от (а =# т) или (о = т).
Этот вывод является чрезвычайно общим. Если ансамбль
состоит из Af слабо взаимодействующих систем, то для него
уравнение Шредингера имеет вид
+«('« <3-1»
Его собственное значение равно
Е — £(j + ет + • • • + есй> (3.12)
где нет ни одной пары индексов о, т, ..., со, которые были бы
одинаковы. Этому собственному значению соответствует ряд
из М собственных функций, которые могут быть получены пере-
становкой систем 1, 2, ... по нижним индексам собственных
значений о, т, ..., со. Простейшая собственная функция имеет
вид
(3.13)
Для вырожденных систем общее число собственных функ-
ций, соответствующих собственному значению (3.12), равно
ЛЧ(о0сот ... (Оо). (3.14)
Наконец, рассмотрим самое общее собственное значение
Е = ••• “Ь (3.15)
3.7. Допустимые состояния для ансамбля одинаковых систем
91
когда Па, Пт, и© образуют группы собственных состояний,
в которых собственные значения равны между собой. Если
Tig ••• "4“ = N, (3.16)
то мы имеем
ЛИ
I • • • п^\
(3-17)
(3.19)
групп различных собственных функций, которые можно полу-
чить путем перестановки. Например, одна из них имеет вид
= . ^(хЯа)я|ч(хЯо+1) • • • ^(-’Ч+'ч) • • • гМ*л'). (3.18)
При наличии вырождения в каждой системе общее число раз-
личных собственных функций равно
...оЛ(д
а т со •- - -
Ла!пт! ••• лсо!
Более подробные выкладки можно найти в следующей главе.
Любые линейные комбинации собственных функций, соот-
ветствующие одному собственному значению Е, могут быть ис-
пользованы вместо первоначальных собственных функций.
Если к ансамблю мы добавим группу одинаковых между
собой систем, отличающихся от первоначальных, то для них
получим группу собственных функций, аналогичную (3.18).
Умножив каждую из них на собственные функции типа (3.18),
получим линейно независимые собственные функции всего ан-
самбля. Мы, конечно, не можем сделать перестановку пары раз-
личимых систем, так как таким путем мы не получим решения
уравнения Шредингера для ансамбля. Поэтому для двух раз-
личных групп одинаковых систем А и В собственному значению
Е = + nr£r + • • • + «X- + • • • + «у (3-20)
соответствует число комплексий
N. to"0 ... ®я“ to”?' ...
А (5 СО В (5 О
ла» ... 7Z0! ПОЛ ... п^Л
(3.21)
Штрихи относятся к системам В.
Если между системами ансамбля или между ансамблем и
внешним миром ввести слабые взаимодействия, то это позво-
лит ансамблю из состояния, описываемого одной из собствен-
ных функций, переходить к любому другому. Допустимые со-
стояния, по которым производится усреднение, можно вычис-
лить или по формулам (3.19), (3.21) или по их аналогичным
обобщениям. В действительности это не так просто.
92
Гл. III. Основы статистической механики
Мы уже указывали, что собственные функции уравнения
(3.18), описывающие группы одинаковых систем, после объеди^
нения их в подходящие линейные комбинации можно разделить
на некоторое число групп Д, В, ..., S, исходя из их свойств
симметрии. Эти группы включают в себя собственные функции,
соответствующие всевозможным собственным значениям, и об-
ладают чрезвычайно важными свойствами, а именно: любое
сколь угодно сильное взаимодействие, симметричное относи-
тельно координат одинаковых систем, никогда не переводит
собственную функцию ансамбля одной группы А в какую-либо
собственную функцию другой группы В. Таким образом, если
ансамбль первоначально описывался собственной функцией
группы Л, то он всегда будет ограничен собственными функ-
циями группы А. Лишь те состояния, которые представлены соб-
ственными функциями группы Л, являются допустимыми.
Среди различных некомбинирующих групп есть две, кото-
рые выделяются простотой своих свойств и простотой их мате-
матического описания. Одна из них представляет собой группу
собственных функций, симметричных относительно перестановки
всех систем. Такую группу мы будем называть симметричной
группой или сокращенно — группой S. Любая собственная
функция группы S не изменяется при перестановке координат
любых двух систем ансамбля. Другая группа включает функ-
ции, которые антисимметричны относительно перестановки всех
систем. Такую группу назовем антисимметричной группой или
сокращенно — группой А. При перестановке координат двух
систем из группы А собственная функция меняет знак. Для не-
вырожденных систем, у которых каждому собственному зна-
чению £’=S8a соответствует одна собственная функция,
реально существуют только эти две группы. Собственные функ-
ции группы S всегда строятся однозначно.
Для группы А это имеет место только в том случае, если все
о различны, т. е. все п равны либо 0, либо 1.
Легко проверить, что следующий определитель порядка N
представляет антисимметричную собственную функцию
МО МО"-ММ
МО мо - -мм
(3.22)
МО МО • • • мм
Симметричная собственная функция будет представлена похо-
жим выражением; для этого необходимо только все члены в
3.8. Типы симметрий собственных функций реальных ансамблей
93
развернутом выражении взять со знаком плюс. Из (3.22) вид-
но, что, если среди индексов функции ф есть два одинаковых,
то две строчки в определителе будут одинаковы, а тогда и опре-
делитель будет равен нулю, следовательно, и собственная функ-
ция не существует.
Аналогичные построения можно обобщить на ансамбли из
вырожденных систем. Например, если соа > 1, а другие со, как и
раньше, равны 1, то из соа различных фа можно составить Т.
Отсюда видно, что выполнение неравенства п0<^хоа достаточно
для существования
na'(®a-na)!
собственных функций из группы А, в противном случае их бу-
дет нуль.
Число собственных функций в группе S при всех значениях
па равно
(й>а+Л~1)! . (3.24)
и0!(Ща-1)!
Однако нет никакой необходимости строить или использовать
эти общие формулы, так как в дальнейшем мы увидим, что
очень легко перейти от невырожденных систем к вырожденным.
Поэтому займемся сначала невырожденными системами.
3.8. Типы симметрий собственных функций реальных ансамблей
До сих пор еще не создано законченной теории, которая объ-
ясняла бы причину того, что физически конкретный ансамбль
всегда характеризуется вполне определенной группой симме-
трии. Поэтому для отыскания группы, к которой принадлежит
реальная система, мы должны прибегать к помощи эксперимен-
та. Мы не сомневаемся, что ансамбли всех веществ можно раз-
ложить на ансамбли, состоящие из электронов, протонов и ней-
тронов. По крайней мере это соответствует обычным требова-
ниям термодинамики. Для таких систем собственные группы
всегда являются антисимметричными. Для электронов это сле-
дует из принципа запрета Паули, согласно которому два элек-
трона в любом атоме никогда не могут иметь одни и те же
четыре квантовых числа, или, иными словами, никогда не
могут иметь одинаковые собственные функции, учитывающие
спин.
94
Гл. Ill. Основы статистической механики
Вообще пара систем из ансамбля группы А не может нахо-
диться в одинаковых состояниях, характеризуемых одинаковы-
ми собственными функциями. В действительности только груп-
па А обладает этим свойством. Причиной того, что собственные
функции электронов в любом атоме принадлежат к группе Л,
по-видимому, являются внутренние свойства самих электронов.
Для протонов исходных данных меньше, но из интерпретации
линейчатых спектров водорода и на основании теории его вра-
щательной теплоемкости при низких температурах можно сде-
лать аналогичные четкие выводы. Для нейтронов данные яв-
ляются в некоторой степени косвенными, но все же достаточно
надежными. Они получены главным образом из изучения
свойств дейтерия и его вращательной теплоемкости. При даль-
нейшем изложении мы будем учитывать эти требования симме-
трии. Их статистическое обоснование будет изложено в даль-
нейшем.
Так как все ансамбли можно разложить на электроны, про-
тоны и нейтроны, то можно точно вычислить число различных
состояний (собственные функции этих состояний являются со-
ответственно симметричными по отношению к электронам, про-
тонам и нейтронам). Каждое такое состояние будем называть
комплексией. Нам не известно, какие абсолютные ограничения
еще существуют, имея в виду допустимость, но с точки зрения
успехов, достигнутых от уже введенных ограничений, дополни-
тельные ограничения не являются необходимыми.
Однако в особых случаях можно столкнуться с частичными
ограничениями, которые играют такую же роль как в отноше-
нии поведения во времени, так и абсолютных ограничений. При-
мером такого рода является метастабильное равновесие газо-
вой смеси водорода с кислородом. Этот пример мы уже рас-
сматривали выше. Другие примеры можно встретить при ис-
следовании теплоемкости обычных газов (таких, как кислород
и азот). Каждое колебательное состояние настолько медленно
обменивается энергией с состояниями поступательного и вра-
щательного движений, что при быстрых адиабатических сжа-
тиях в звуковой волне каждое такое состояние ведет себя так,
как если бы его энергетическое состояние было бы постоянной
движения. Поэтому молекулы с заданными колебательными
квантовыми числами в газовой смеси ведут себя как отдельные
газовые компоненты.
Мы можем рассмотреть и другие примеры, но самый приме-
чательный из них встречается при исследовании свойств веще-
ства при низких температурах. Вследствие очень слабого вза-
имодействия обмен между молекулами с нулевым результирую-
щим ядерным спином и молекулами с ядерным спином, равным
3.9. Кратчайший путь вычисления допустимых состояний
95
единице, в этом случае очень медленный. И в обычных экспе-
риментах газ ведет себя как смесь двух совершенно различных
газов с различными вращательными теплоемкостями. Лишь
после соответствующей катализации обмена ситуация меняется.
Таким образом, общие условия проанализированы нами до-
статочно точно. Они могут ограничивать или не ограничивать
допустимые квантовые состояния (или области фазового про-
странства). Основываясь на приведенном подробном анализе,
можно более точно сформулировать правило усреднения, опи-
санное в п. 3.4.
Если принять во внимание время, необходимое для устано-
вления равновесия, то можно вычислить все различные допу-
стимые состояния или комплексии ансамбля. Каждое из них
характеризуется одной линейной независимой собственной функ-
цией, соответствующей некоторому значению энергии или ее ин-
тервалу. Значение Q некоторого свойства Q ансамбля можно
использовать для характеристики его равновесного состояния
при заданных условиях. Оно может быть получено усреднением
по всем допустимым состояниям с весом, равным единице. Та-
ким образом,
Q= 2Q / 21 • (3.25)
по всем допусти- по всем допусти-
мым состояниям мым состояниям
3.9. Кратчайший путь вычисления допустимых состояний
обыкновенного ансамбля
Теоретически требования симметрии дают возможность пра-
вильно определить допустимые состояния любого ансамбля. Но
практически, когда системы ансамбля почти полностью неиз-
менны (например, ансамбли атомов гелия и молекул водорода),
не совсем удобно рассматривать ансамбли как собрание мно-
жества электронов, протонов и нейтронов. К тому же таким
путем мы не сможем получить реальных результатов. Более
удобно рассматривать эти сложные частицы (например, атомы
гелия или молекулы кислорода) как основные системы, на ко-
торые распространяются все требования симметрии, полученные
из первоначальных.
Рассмотрим сложную систему, содержащую I электронов,
р протонов, п нейтронов. Тогда перестановка пары таких си-
стем означает перестановку Z+p + n электронов, протонов и ней-
тронов. По отношению к каждой паре этих частиц собственная
функция ансамбля является антисимметричной. Поэтому если
в сложной системе число l+p + п четное, то собственная функ-
ция ансамбля будет симметричной; если l+p + п число нечетное,
96
Гл. III. Основы статистической механики
то — антисимметричной. Это только что полученное необходи-
мое правило симметрии строго доказано как всеобщее пра-
вило.
Теперь мы можем избежать трудностей и недостатков, о ко-
торых говорилось выше. Если, исходя из свойств некоторых си-
стем второго порядка (атомное ядро, атом, молекула, кри-
сталл), можно заранее определить, какие из них можно в ка-
ком-либо классе задач считать неизменными, то мы будем
пользоваться следующей теоремой: при подсчете числа комп-
лексий (допустимых состояний), или, говоря точнее, собствен-
ных функций ансамбля, достаточно формально построить и
подсчитать все те линейно независимые собственные функции,
которые обладают соответствующими свойствами симметрии от-
носительно «неизменных» систем (как целых), из которых со-
стоит рассматриваемый ансамбль. Собственные функции любой
«неизменной» системы должны отвечать соответствующим свой-
ствам симметрии относительно электронов, протонов, нейтро-
нов, из которых состоит такая система. Однако нет необходи-
мости разлагать весь ансамбль на электроны, протоны и ней-
троны, так как число комплексий не изменится при более де-
тальном разложении.
В соответствии с этим принципом в большинстве проблем
статистической физики атомные ядра можно рассматривать как
неизменные сложные образования. Для них правило симметрии
является более универсальным. В настоящее время его при-
нято формулировать в следующем виде: собственные функции
всех одинаковых ядер, имеющих нечетное массовое число, дол-
жны быть антисимметричными; собственные функции ядер с
четным массовым числом должны быть симметричными. Мас*
совое число равно суммарному числу протонов и нейтронов в
атомном ядре.
Предыдущая теорема сформулирована относительно разло-
жения «неизменяемой» сложной системы на электроны, протоны
и нейтроны. Однако в этом ограничении нет необходимости.
Она в равной степени может быть применима и для разложения
«неизменяемой» сложной системы на какие-либо «неизменяе-
мые» вторичные системы. Например, в ансамбле атомов хлора
35С1 собственные функции ансамбля относительно ядер 35С1
должны быть антисимметричны. Но такой ансамбль обычно
полностью состоит из «неизменных» молекул 35С12. Поэтому,
если считать собственную функцию каждой молекулы антисим-
метричной относительно ядер, а собственные функции ансамбля
симметричными по отношению к молекулам, то требования сим-
метрии для ансамбля будут удовлетворены и подсчет собствен-
ных функций произведен правильно.
3.10. Вычисление комплексий для локализованных систем
97
Этот принцип можно распространить и на ансамбль, состоя-
щий из кристалла и равновесного с ним пара. Кристалл пред-
ставляет собой лишь особую молекулу, рассматриваемую как
систему. Требования симметрии для ансамбля в целом будут
выполнены, если удовлетворить лишь требованиям симметрии
для свободных молекул в газообразном состоянии. Естествен-
но, что при этом кристалл мы рассматриваем как «неизменяе-
мую» систему, состоящую из такого числа молекул, которого
требуют конкретные условия задачи. Этого достаточно, чтобы
правильно рассчитать состояние кристалла.
3.10. Вычисление комплексий для локализованных систем
Практические соображения в предыдущем пункте относи-
лись главным образом к ансамблям газов или к таким ансам-
блям или частям ансамбля, одинаковые системы которых рас-
сматриваются на совершенно равных основаниях, т. е. их со-
стояния выражаются через собственные функции, получаемые
по общим правилам. Примером могут служить атомы и моле-
кулы в одном и том же сосуде, электроны в отдельном атоме
или куске металла. Первоначальные правила для электронов,
протонов и нейтронов, естественно, без всякого исключения мо-
гут быть применимы ко всем веществам и ансамблям. В опи-
санных в предыдущем пункте случаях они сводятся к практи-
чески удобным вторичным правилам. Конечно, применение этих
вторичных правил должно быть ограничено сферой, определен-
ной в предыдущих пунктах. Если у нас нет необходимости счи-
тать, что все собственные функции имеют один общий источник
и что их можно различить, то в этом случае вторичное правило
можно еще более упростить.
Эти еще большие ограничения можно понять из следующих
примеров. Рассмотрим ансамбль, содержащий два различных
сосуда, в каждом из которых находится множество электронов.
Предположим, что электроны могут проникать из одного со-
суда в другой, но с некоторыми затруднениями. При равновесии
электроны в сосудах будут распределены в определенной про-
порции, вычисление которой составляет часть нашей задачи. Од-
нако в том случае, когда мы можем приближенно фиксировать
принадлежность электронов к одному или другому сосуду, не-
обходимо считать, что сосуды различны.
Пусть состояния электронов, относящихся к одному сосуду,
описываются собственными функциями фг, а соответствующие
энергии равны ег; состояниям электронов, относящимся к дру-
гому сосуду, соответствуют функции и энергии ег. Пусть ан-
самбль содержит пять электронов. Рассмотрим распределение,
7 Зак. 1299
98
Гл. Ш. Основы статистической механики
при котором три электрона находятся в одном сосуде и зани-
мают состояния, соответственно обозначенные через ф1, гр2, фз,
а два электрона находятся во втором сосуде и соответственно
занимают состояния фр ф^. Конечно, осуществляется лишь одно
допустимое состояние ансамбля. Оно удовлетворяет требова-
нию, при котором собственная функция всех электронов яв-
ляется антисимметричной. Это состояние выражается собствен-
ной функцией, которая дается следующим определителем:
4b (ха) 4’1 (хь) 4’1 (хс) 4’1 (xd) 44 (xe)
42 (ха) 4’> (-*/>) 4-2 (хс) 4’2(*d) 4'2 (xe)
4>з(*а) 4?з(*&) 4ъ (•*<?) 4’3(*d) 4’3 (xe) . (3.26)
44 (ха) 44(*г>) 4>4 (хе) 4’4Ud) 44 (xe)
4?5Ua) 4’5(^) 4’5Ut) 4>5 (xd) 44 (xe)
где индексы a, b, с, d, е у координаты х относятся к электронам.
Теперь удовлетворим нашему добавочному условию, а имен-
но: электроны а. Ь, с должны относиться к первому сосуду, а
электроны d, е — ко второму. Если мы построим собственную
функцию для такого ансамбля в виде двух сомножителей, то
она будет удовлетворять следующему условию: каждый сомно-
житель описывает электроны в отдельном сосуде и будет анти-
симметричен по отношению к электронам этого сосуда. Этим
условиям удовлетворяет одна собственная функция
tl (ха)
Ъ(Ха)
4’з(*а)
(Хь)
4’2 (ХЬ)
(хс)
(Хс)
4’з (хс)
4’1 (*</)
4Ж)
(3.27)
которой, как мы уже выяснили, соответствует лишь одно допу-
стимое состояние.
Можно доказать (в действительности это почти очевидно),
что эта эквивалентность является чрезвычайно общей. Если ан-
самбль имеет несколько частей, которые можно различать, и
каждая из них содержит определенное число одинаковых си-
стем, то при подсчете допустимых состояний ансамбля доста-
точно того, чтобы его собственные функции по отношению к оди-
наковым системам в различных частях ансамбля при переста-
новках удовлетворяли требованиям симметрии. Это и может
гарантировать правильность подсчета допустимых состояний
ансамбля. При таком подсчете нет необходимости рассматри-
вать какие-либо обмены системами между различными частями
или сосудами.
3.10. Вычисление комплексий для локализованных систем
99
Требование симметрии мы можем еще более упростить.
В некоторых ансамблях число различных частей и сосудов
можно вполне обоснованно увеличить настолько, что каждая
система будет иметь свой сосуд или место. Примером могут
служить атомы в кристаллической решетке, так как в этом слу-
чае за время одного наблюдения или эксперимента атомы не
могут обменяться местами. Каждая часть ансамбля теперь
имеет свою собственную систему, и если мы хотим применить
вышеописанное правило, то достаточно каждую систему закре-
пить за ее собственным местом, но не налагать на нее других
требований симметрии. Это дает возможность точно подсчитать
число допустимых состояний ансамбля. Если подсчет произво-
дится таким путем и больше никаких ограничений на симме-
трию не накладывается, то такой ансамбль или часть ансамбля
называется ансамблем локализованных систем.
Важным следствием отсутствия требований симметрии для
этих ансамблей является то, что квантовый метод подсчета до-
пустимых состояний полностью совпадает с давно нам извест-
ным классическим. Действительно, допустим, что системы та-
кого ансамбля имеют состояния с энергиями е0, еь ... . Они не-
вырождены и каждому из них соответствует одна собственная
функция. Закон распределения для такого ансамбля должен
отвечать на вопрос: сколько систем (общее количество V) об-
наруживается в среднем в каждом состоянии? Об этом мы смо-
жем узнать в гл. IV. Здесь же нам требуется знать, сколько
допустимых состояний имеет ансамбль, соответствующий ка-
кому-либо типу состояний, при котором По систем имеют энер-
гию е0, ni систем имеют энергию ei и т. д. Это число допустимых
состояний, очевидно, равно числу способов, с помощью кото-
рых N систем можно распределить на группы, каждая из ко-
торых содержит По, Hi, ... членов соответственно. При этом
должно быть выполнено соотношение n0 + fli+ .. • + nt = N. Если
вычислить это число, то получим
__м__
... nt\ ’
(3.28)
что и представляет собой искомое число допустимых состояний
с данным распределением энергии.
Классический способ вычисления числа допустимых состоя-
ний для локализованных систем приводит к тому же резуль-
тату (3.28). Это число не совпадает с числом допустимых со-
стояний ансамбля одинаковых систем, находящегося в одном
сосуде и удовлетворяющего требованиям симметрии. Принци-
пиально физическое различие между ними можно объяснить
следующим образом.
7*
100
Гл. III. Основы статистической механики
В случае одинаковых систем, заключенных в некоторой обо-
лочке, нет смысла говорить о том, что некоторая система имеет
такую-то энергию и находится здесь, а другая система с другой
энергией находится там. Это не имеет никакого физического
смысла с точки зрения собственных функций описываемого со-
стояния. Однако в локализованных системах «здесь» и «там»
по-прежнему имеют физический смысл. Система ансамбля, об-
разованного из локализованных систем, находящаяся «здесь»
в г-м состоянии, физически отличается от системы, находя-
щейся «там» в г-м состоянии. Отсюда следует, что они нахо-
дятся в различных состояниях.
На языке собственных функций такие особые локальные
свойства можно сформулировать следующим образом: различ-
ные собственные функции в этом случае оказываются непере-
крывающимися, другими словами, в некотором месте может
появляться лишь некоторый тип систем, а системы других ти-
пов появляться не могут. В примере с двумя сосудами с пятью
электронами волновые функции Ф1(хе)» ^2(xe)
4(0’ 4(0- 4(0’ 4(0- 4(0 4(0- 4(4) и 4(0
в действительности равны нулю. Поэтому собственные функции
(3.26) и (3.27) равносильны.
Глава IV
ОБЩИЕ ТЕОРЕМЫ ДЛЯ АНСАМБЛЕЙ
СТАЦИОНАРНЫХ СИСТЕМ
Системы, у которых отсутствуют химические реакции и из-
менения фаз, называются стационарными. В этой главе речь
будет идти относительно ансамблей, состоящих из почти неза-
висящих друг от друга стационарных систем. Наша цель —
установить для этих ансамблей основные теоремы статистиче-
ской механики. Такие ансамбли легче всего поддаются точному
рассмотрению, поэтому они больше всего изучены. Выводы на-
стоящей главы можно непосредственно применить к идеальным
газам, однако методы могут быть распространены и на кри-
сталлы.
Расшифруем теперь термин почти независимые системы.
Если с достаточной точностью можно предположить, что энер-
гия ансамбля равна сумме энергий отдельных систем и что
энергия каждой системы зависит только от ее координат, то си-
стемы такого ансамбля называются почти независимыми. Так
как в дальнейшем мы часто будем пользоваться этим поня-
тием, то естественно разобрать этот вопрос более подробно.
Необходимо обратить внимание на то, что ансамбль из почти
независимых систем является предельным случаем реального
ансамбля. Последний лишь приближенно можно рассматривать
как состоящий из почти независимых систем.
Понятие реального ансамбля включает в себя следующее
содержание: ансамбль представляет собой динамическую си-
стему, связанную одним интегралом энергии, а не суммой не-
связанных друг с другом частей. Если бы энергия ансамбля
действительно не зависела от смешанных членов, представляю-
щих взаимодействие между системами, то системы никогда бы
не взаимодействовали друг с другом, а ансамбль не мог бы
стать связанным целым. Поэтому мы обязаны учитывать взаи-
модействие, реально существующее между системами. В пре-
дельном случае очень слабого взаимодействия систем можно
пренебречь той долей энергии, которую взаимодействие вносит
в общую энергию. Так как взаимодействие между системами
всегда имеет место, то в действительности существует только
один интеграл энергии. В этом случае следовало бы рассмо-
102 Гл. IV. Общие теоремы для ансамблей стационарных систем
треть и структуру взаимодействия, однако для изучения общих
законов равновесия она оказывается несущественной. Это и
будет основным предположением всей теории.
4.1. Статистический вес
В третьей главе было дано определение допустимых состоя-
ний (комплексий) ансамбля как состояний, которым соответ-
ствуют линейно независимые собственные функции. Было так-
же указано, что при определении равновесного состояния мето-
дом усреднения каждому допустимому состоянию (комплексий)
приписывается единичный статистический вес. Это означает, что
среднее значение Q любой величины Q должно быть вычислено
так:
Q=SaQa/C (4.1)
где Qa — значение Q, соответствующее определенной комплек-
сии о, — суммирование для всех комплексий, а С обозначает
общее число комплексий
С=Ео1. (4-2)
Формулы (4.1) и (4.2) часто можно преобразовать к дру-
гому виду. Прежде всего очень часто некоторое число Qa раз-
личных комплексий может по многим причинам обладать свой-
ствами, не отличимыми друг от друга, например одинаковыми
значениями величины Q. В этом случае можно сначала под
знаком суммирования в формулах (4.1) и (4.2) сложить ком-
плексна имеющие одинаковые значения Q, и, таким образом,
образовать группы комплексий. Формулы (4.1) и (4.2) можно
тогда переписать в виде
Q=2aQ0Qa/C, (4.3)
С= (4.4)
где суммирование ведется по всем группам комплексий. Так
как свойства отдельных комплексий, взятых из группы комп-
лексий, неразличимы друг от друга, да к тому же нам и не
нужно их различать, то для удобства часто рассматривают эту
группу комплексий как одно отдельное состояние ансамбля со
статистическим весом Qa.
Рассмотрим теперь статистический вес Qa. Так как ансамб-
ли, о которых будет идти речь, можно рассматривать как со-
стоящие из почти независимых систем, т. е. пренебрегать вза-
имодействием между ними, то уравнение Шредингера, опреде-
4.1. Статистический вес
103
ляющее собственную функцию и энергетическое состояние ан-
самбля, распадается на уравнения Шредингера для отдельных
систем. Собственная функция ансамбля Т может быть пред-
ставлена в виде произведения собственных функций ф отдель-
ных систем.
Известно, что энергетическому состоянию системы может
соответствовать сог различных собственных функций. В этих
случаях мы по-прежнему рассматриваем их как одно отдель-
ное состояние системы со статистическим весом сог. Для удоб-
ства состояние с cor> 1 называется вырожденным, а с cor= 1 —
невырожденным. Рассмотрим следующие состояния ансамбля
из Af почти независимых систем. Пусть каждое из состояний
системы имеет статистический вес со о, он, ..., а число систем со-
ставляет соответственно По, П1, ... . Тогда все состояния си-
стемы являются вполне определенными. Если нет особых огра-
ничений на их допустимость, то число комплексий, соответст-
вующее состоянию ансамбля, т. е. статистический вес этого
состояния равен
Ч = ПЛ"'- (4-5)
Формула (4.5) получается следующим образом: известно,
что каждая система ансамбля может находиться в состоянии,
описываемом любой возможной собственной функцией, незави-
симо от того, в каком состоянии находятся другие системы. Для
первой системы имеется соо способов выбора собственной функ-
ции состояния со статистическим весом соо, для другой систе-
мы — то же самое, следовательно, для обоих систем их будет
(Оо, а для по систем — соо0 и т. д. Аналогично для состояний со
статистическим весом coi всего имеется со"1 способов выбора
и т. д. Поэтому число возможных независимых собственных
функций, соответствующих состояниям ансамбля, равно Пг^г-
В предыдущих рассуждениях мы в действительности использо-
вали еще одно предположение, что эти системы физически раз-
личимы по каким-то признакам, поэтому собственная функция
ф(1)ф'(2) отличается от ф'(1)ф(2), т. е. каждая из них соответ-
ствует различным комплексиям.
Формула (4.5) получена для случая, когда число систем в
различных состояниях является фиксированным. Число комп-
лексий, соответствующее такому способу распределения состоя-
ний, дается формулой (4.5). Если число систем в каждом со-
стоянии не является фиксированным, а может быть произволь-
ным из N систем, то число комплексий, соответствующих такому
104 Гл. IV. Общие теоремы для ансамблей стационарных систем
способу распределения состояний, будет больше, чем дает фор-
мула (4.5). Число их равно
Q = —j—--------г . а"', (4.6)
О HolnJ ... пт\ 0 1 г ' ' '
где сомножитель
n0!nj! ... пг\
представляет собой число способов, с помощью которых из N
систем можно построить ансамбли, содержащие п0, п\.........пг
систем в различных состояниях. Естественно, что в приведенном
вычислении нет никаких дополнительных ограничений на допу-
стимость состояний.
4.2. Статистический вес состояний некоторых простых систем
В п. 2.4 уже указывалось, что энергетическое состояние гар-
монического осциллятора с частотой v равно
ev = ^-|_-L^v (х> = 0, 1, 2,...). (4.8)
Любая возможная траектория в классическом фазовом про-
странстве для исследуемого случая описывается уравнением
1 1
j + у (2nv)2 mx2 = е’ (4.9)
которое представляет собой эллипс с полуосями (2me)'/1 и
(2e/m)'/72nv, и площадью
л (2me)'/’ (2e//n),/’/2nv = . (4.10)
В классической теории все траектории, удовлетворяющие
уравнению (4.9), являются возможными. В квантовой теории
e/v может принимать лишь значения 4-А, где о — или
нуль, или положительное целое число. Площадь между сосед-
ними траекториями равна h. Поэтому, когда квантовое число v
велико, возможные траектории почти сливаются, но по-преж-
нему разделяются площадью h. В этом случае каждый элемент
фазового пространства с площадью h соответствует отдельному
квантовому состоянию. Это и есть принцип соответствия для
осциллятора (который описывался в п, 3.5).
4.2. Статистический вес состояний некоторых простых систем 105
Рассмотрим теперь двумерный изотропный осциллятор, у
которого классическое уравнение энергии имеет вид
4 (^2+р2у)/т+4 (2jxv)2 т +у2)=е- и-11)
Соответствующее уравнение Шредингера можно записать сле-
дующим образом:
^ + -^ + -^[e-4(2^)2/n(x2 + f/2)]^ = °. (4.12)
Разобьем это уравнение на два с переменными х и у. В этом
случае полная собственная функция может быть записана
в виде
= (4.13)
где (х) и фУу (у) — собственные функции осциллятора, со-
ответствующие квантовым числам vx и vy. Собственные значе-
ния энергии для полной волновой функции ф имеют вид
e = (^ + 4) Av + (^+4)Av==(^ + ^ + 1)Av
(т>ж = 0, 1, 2, ...; ^ = 0,1,2,...). (4.14)
Пусть vx + vy = v, тогда различным v соответствуют различ-
ные значения энергии. Однако каждому значению v соответ-
ствует (^+1) различных комбинаций значений vx и vy. Поэто-
му одному значению энергии e=(t>4-l)/iv соответствует v+1
различных собственных функций. Следовательно, статистиче-
ский вес энергетического уровня е= (v+\)hv равен и4-1. Для
проверки справедливости принципа соответствия достаточно
лишь указать, что объем классического фазового простран-
ства, связанного с одним квантовым уровнем энергии, для
больших v отличается от (t>4-l)/z2 незначительно. В фазовом
пространстве (х, у, рх, ру) объем, ограниченный поверхностью
равной энергии е, имеет вид
J dx f dy J dpx J dpy, (4.15)
где область интегрирования задается выражением
4 (2nv)2 т (х2 + у2) + у (р2 ч- р2)//п < е. (4.16)
Произведя замену
АГ = (1 т}112nvx, Y = (д 112ту,
Z = (2m)-'1’ рх, W=(2m)~'/2 ру, (4-17)
106 Гл. IV. Общие теоремы для ансамблей стационарных систем
вместо (4.15) получим
2m
- fdXfdYfdZfdW,
(4-18)
при этом область интегрирования преобразуется в простран-
ство, ограниченное четырехмерной гиперсферой с радиусом
]Ле, т. е.
(4.19)
Общая формула для объема Л^-мерной гиперсферы с радиу-
сом г имеет вид
лЛ72
rN, если Л/ —четное число, (4.20)
\2/
ЛЧ
/Л если N — нечетное число.
(4.21)
Для нашего случая воспользуемся (4.20), где ;V = 4, г=]Ле.
Тогда (4.18) после интегрирования примет вид
Я2 9 1 £2
-----------------------
2 ji2v2 2v2 ‘
(4.22)
Объем фазового пространства, заключенный между поверх-
Ti-h-gj/Tv и е = + у) и соответствующий
квантовому состоянию с собственной энергией е= (^4-l)/zv,
равен
у Л2 [(^ + 4 )2 - (к + 4)2] = А2 (* + 1), (4.23)
что находится в согласии с принципом соответствия.
Аналогично решается задача для трехмерного изотропного
осциллятора. В этом случае число собственных функций, соот-
ветствующих энергии
e==^ + |)Av,
равно числу способов, которыми можно составить vx + vy + vz =
= v из целых положительных или равных нулю квантовых чи-
сел vx, vy, vz. Подсчитаем это число. Пусть vx имеет значение
ш, тогда число значений, которые может принять vy, равно
4.2. Статистический вес состояний некоторых простых систем
107
(27-Ь 1) —ш. Отсюда искомое число собственных функций равно
V V
2 1) —/и] = (г)-|- 1)2_ 2/п = (^ + 1)2--^±Д =
m=0 m=1
=4 (^+1)^ + 2). (4.24)
Объем поверхности равной энергии е в классическом фазо-
вом пространстве равен
J .. . Jdxdydzdpxdpydpz, (4.25)
где область интегрирования задается выражением
у (2nv)2 (Х2+У1 + *2) + 4г (Рж+Р2у + < е- (4.26)
С помощью замены, аналогичной (4.17), можно доказать, что
интеграл (4.25) равен
Объем фазового пространства, заключенного между
е = (^ -]- 2) Av и е — (р + 1) Av
и соответствующего квантовому энергетическому уровню е =
/ . 3 \ .
= 1т; +'2'1 Av, равен
-g- й3 [(-и + 2)3 — (v + 1 )3] = Л3 4 4 + 3v + у). (4.28)
При больших значениях квантового числа v он мало отли-
чается от А3—(т>4~ 1)(^ + 2). Это и есть принцип соответствия.
В качестве последнего примера мы рассмотрим жесткий ро-
татор, имеющий ось симметрии, но не имеющий собственного
вращения относительно оси. Пусть А — поперечный момент
инерции, 0 и ср — полярные координаты. Сопряженные им им-
пульсы равны
р0 = А0, — A sin2 0ф. (4.29)
Классическое уравнение энергии имеет вид
(й + дат К) = («0)
108 Гл. IV. Общие теоремы для ансамблей стационарных систем
Из п. 2.15 нам известно, что возможные значения энергии е
для квантового ротатора равны
Й2
-8^г/(/+1) (/ = 0,1,2,...). (4.31)
Число собственных функций, соответствующих /-му состоянию,
равно 2/4-1. Поэтому его статистический вес равен 2/4-1.
Объем фазового пространства, заключенного внутри поверх-
ности постоянной энергии е, равен
л 2л
f ае f d<pff dp&dpv (4.32)
о о
где область интегрирования для р0, задается выражением
2Я (^е'+
(4.33)
sin2 9 6
Двойной интеграл по р0, рф дает площадь эллипса с полуосями
(2Ае)1/2 и (2Ае),/2 sin 0, которая равна 2nAesin0. Поэтому ин-
теграл (4.32) превращается в следующий:
л 2л
sinOdOj dcp = 8x2Ae. (4-34)
о о
2лДе j
Объем фазового пространства, заключенного между поверхно-
стями
е=(j+4) (/ + 4) л2/8л2^ и е=(/ 4- 4) [j—4) л2/8л2^
и соответствующего квантовому состоянию с энергией
е = /(/4-1)Л2/8л2Д,
равен
л2 [('+4) (•/+4) - (у -1) (>+4)]=h" 1)’ <4-35>
т. е. принцип соответствия имеет место.
4.3. Нахождение допустимых состояний (комплексий)
Рассмотрим более детально, каким образом по состояниям
различных систем ансамбля вычислить комплексий ансамбля.
Здесь могут возникнуть существенные отличия в результатах
классического способа расчета и квантового. Напомним о разли-
чии между локализованными и нелокализованными системами.
4.3. Нахождение допустимых состояний (комплексий) 109
о которых говорилось в третьей главе. Нам известно, что число
допустимых состояний (комплексий) у ансамблей, состоящих из
локализованных и нелокализованных систем, различно. Приве-
дем для этих двух случаев простые примеры. Для простоты
предположим, что системы невырожденные.
Тип I. Ансамбль локализованных систем.
Рассмотрим ансамбль, состоящий из N одинаковых линейных
осцилляторов (не обязательно гармонических), которые имеют
устойчивое местоположение в ансамбле. Например, электроны,
надлежащим образом связанные в атомах твердого тела. Ка-
ждый осциллятор имеет группу дискретных стационарных со-
стояний, которые характеризуются квантовым числом г, при-
нимающим значения 0, 1, 2, ... . Собственная функция элек-
трона а, связанного с атомом а, находящимся в r-м квантовом
состоянии, может быть записана в виде где ха — коор-
дината электрона а.
Пусть число осцилляторов, находящихся в состояниях с
квантовыми числами 0, 1, 2 . .., соответственно равно п0,
Hi, ..., nt. Существует много состояний ансамбля с таким рас-
пределением. Все их мы рассматриваем как одно состояние со
статистическим весом, равным числу состояний ансамбля в та-
кой группе. Из формулы (4.6) следует, что число собственных
функций этой группы равно
Приведем одну из них
< К) • • • ^0 (**) Ф? К) • • • Ю’ (4-37)
где число сомножителей равно п0, число сомножителей ф1
равно /11 и т. д. — всего N сомножителей. Если переставить ме-
жду собой энергетические уровни электронов а и е, то получим
другую собственную функцию из той же группы состояний ан-
самбля
ШО ••• ВДВД ••• ЧЖ) ••• <4-38)
Число различных сомножителей здесь не изменилось. Пере-
ставляя энергетические уровни электронов, можно получить
столько собственных функций, сколько указано в (4.36). Сле-
дует отметить, что здесь мы воспользовались еще одним пред-
положением, состоящим в том, что каждый электрон принадле-
жит одному атому и собственные функции ансамбля не яв-
ляются антисимметричными по отношению к перестановке
электронов. В действительности каждый электрон может нахо-
диться около различных атомов, следовательно, собственные
ПО Гл. IV. Общие теоремы для ансамблей стационарных систем
функции должны быть антисимметричными. Однако, как об
этом говорилось в п. 3.9 и п. 3.10, из каждой собственной функ-
ции, аналогичной (4.37), перестановкой N электронов между N
атомами можно образовать собственную функцию, антисимме-
тричную по отношению к электронам, притом только одну. По-
этому формула (4.36) является правильной, хотя при ее вы-
воде полные требования симметрии совсем не учитывались и ка-
ждый электрон считался прикрепленным к одному атому. f
Тип II. Ансамбли нелокализованных си- I
ст ем. Рассмотрим ансамбль из N электронов (или других ана- j
логичных систем), которые могут свободно перемещаться в за-
данном замкнутом объеме. Для них собственные функции не j
будут иметь индексов а, ..., х, ..., обозначающих местополо- i
жение систем. Пусть п0, Пь . • ., П/, как и раньше, обозначают ;
число электронов в состояниях, определенных квантовым чис* >
лом г. Число собственных функций, не подчиненных требова-
ниям симметрии, будет по-прежнему определяться формулой :
(4.36). Однако нам необходимо построить собственные функции
ансамбля, антисимметричные относительно всех электронов, а
это возможно только при /г, равном 0 или 1. Для ансамбля, соб-
ственные функции которого симметричны относительно пере-
становки систем, такое построение, как показано в п. 3.6, тоже
проводится однозначно.
Таким образом, мы владеем основными сведениями, необхо-
димыми для вычисления средних величин, характеризующих ।
свойства двух типов ансамблей. Рассмотрим прежде всего ан-
самбли локализованных систем.
4.4. Ансамбли, состоящие из двух групп локализованных систем
Рассмотрим для простоты частный случай, на котором мож-
но усмотреть особенности задачи и методы ее решения. Пусть
имеется ансамбль, состоящий из двух больших групп локализо-
ванных линейных осцилляторов. Обозначим их число через NЛ
и AfB. Каждый осциллятор группы А имеет ряд стационарных
состояний с единичными статистическими весами и энергиями
80, 61, ..., ег, ... ; аналогично осцилляторы группы В имеют
ряд стационарных состояний с единичными статистическими ве-
сами и энергиями т]о, T]i,...» ....
Еще раз подчеркнем, что стационарные состояния и энер-
гию ансамбля мы представляем здесь через стационарные со-
стояния и энергии систем. В действительности это соответ-
ствует предположению, что системы являются почти независи-
мыми, т. е. большую часть времени в своем движении они не
подвергаются воздействию со стороны других систем. Это пред-
4.4 Ансамбли, состоящие из двух групп локализованных систем 111
положение является очень важным при рассмотрении ансамб-
лей, состоящих из большого числа почти (но не полностью) не-
зависимых систем, так как такое представление состояний ан-
самбля через состояния отдельных систем сильно сокращает
вычисления.
Одновременно с этим необходимо предполагать, что между
осцилляторами обязательно происходит достаточно интенсив-
ный обмен энергией. В противном случае такие системы не смо-
гут образовать ансамбля и для них не сможет установиться
равновесное распределение. Можно представить себе, что в рас-
сматриваемом случае обмен энергией происходит с помощью
небольшого числа свободных атомов, находящихся в замкнутом
сосуде, содержащем осцилляторы. Однако число свободных ато-
мов должно быть настолько малым, чтобы их энергией по сра-
внению с энергией осцилляторов можно было пренебречь.
Наша задача состоит в отыскании законов распределения в
ансамбле, т. е. нахождение равновесного или среднего распре-
деления осцилляторов по различным возможным состояниям.
Каждую реализацию распределения, будь она равновесной или
неравновесной, можно принять за статистическое состояние ан-
самбля. Отсюда видно, что нас интересует только макроскопи-
ческое, а не микроскопическое состояние ансамбля.
Если имеется группа положительных целых чисел (включая
нуль) nr, n's. которые удовлетворяют условиям
^rnr = NA, (4.39)
(4-40)
(4.41)
где Е — энергия ансамбля, то эта группа чисел nr, n's дает воз-
можность определить допустимое статистическое состояние ан-
самбля. Об ограничениях на допустимость уже говорилось в
третьей главе, однако там энергия всего ансамбля ограничива-
лась малым интервалом Е, E + dE, а не точной величиной Е,
как это задано в (4.41). Поэтому логичней было бы использо-
вать не (4.41), а неравенство
+ + (4.41а)
Позже мы сможем доказать, что замена выражения (4.41) не-
равенством (4.41а) чрезвычайно мало влияет на конечный ре-
зультат. Поэтому для краткости и удобства воспользуемся
(4.41).
112 Гл. IV. Общие теоремы для ансамблей стационарных систем
Условия (4.39), (4.40) и (4.41) выражают несколько фактов,
а именно что общее число систем А равно общее число си-
стем В равно NBi а общая энергия равна Е. В (4.41) нулевые
значения энергии sr системы А и энергии тр, системы В могут
быть выбраны произвольно; а нулевое значение Е получается
из нулевых значений гт и т]8. При данных NA, NB и Е любая
группа положительных целых чисел (включая нуль), которая
удовлетворяет (4.39), (4.40) и (4.41), представляет статисти-
ческое состояние ансамбля.
Так как ансамбль относится к первому типу и к тому же
статистические веса всех систем равны 1, то число комплексий
данного статистического состояния равно
W i N ’
А______________В________
п0! пх\ ... пг\ .. . nQ\ п[\ ... ns\ ...
(4.42)
что представляет собой лишь обобщение формулы (4.36). Об-
щее число комплексий С равно
VI VI -/V Л! N !
С = S S . - .--г-*—,-----------Г,-7, в ....... (4.43)
n0! nJ ... пг\ ... n0! пх I ... ns\ ...
где суммирование ведется по всем п и п', удовлетворяющим
условиям (4.39), (4.40) и (4.41). Равновесное распределение
для ансамбля получается путем усреднения по всем комплек-
сиям. Таким образом, мы можем прямо получить среднее зна-
чение nt для nt или любой другой аналогичной величины. Для
nt из (4.3) имеем
— VI VI n JV л! N ’
С«, = У У ----------------------......-В.--- (4.44)
п0! пх! ... пг\ ... nQl nJ ... ns! ...
Одной из самых важных средних величин является ЕА —
средняя энергия систем группы А. Для Ел имеем
VI VI (У " £ W ’. jV ’
СЕА=У У г г) ^А_ ..В -----. (4.45)
А no!nj ... пг\ ... n'lnj! ... ns\ ... v 7
Суммирование в (4.44) и (4.45) производится по всем пт, nrs,
удовлетворяющим (4.39), (4.40), (4.41). Как будет показано
ниже, правая часть выражений типа (4.43), (4.44) и (4.45)
представляет собой коэффициент некоторого простого степен-
ного ряда.
Если все er, T)s являются целыми кратными некоторой еди-
ничной энергии и не содержат общих множителей, то вычисле-
ния значительно упрощаются. Обычно это условие точно не удо-
влетворяется, однако, выбирая для энергии достаточно малую
4.4. Ансамбли, состоящие из двух групп локализованных систем 113
единицу измерения, ему можно удовлетворять с высокой сте-
пенью точности. Будем считать, что такая единица выбрана.
Впрочем, можно доказать, что если ег, точно и не удовле-
творяют этому условию, то результат мало изменится.
Прежде всего построим функцию fA (2), которую будем на-
зывать функцией состояний систем 4:
f а (*) = г6» + ze> + ... = 2, z\ (4.46)
Рассмотрим произведение
Используя теорему о возведении многочленов в степень, разло-
жим его в ряд по степеням z. Общий член ряда имеет вид
—i——j— nrer пГ = Na).
nQl nx! ... nr\ ... T AJ
Аналогичным образом построим функцию состояний fB(z)
для систем В
fB (z) = z11» + z1’- + • • • = IL . (4.47)
Разложим {fB (z)]nb в ряд по степеням z; общий член ряда
имеет вид
Перемножим эти два ряда, тогда коэффициент при члене с zE
в выражении
{fA(z)}NA{fBWNB (4.48)
будет равен
у у NA-________________NB-
/70! nJ , . . пг\ . . . Ид! п\\ ... ns\ ... ’
где суммирование производится по всем положительным це-
лым числам (включая нуль) /г, п', удовлетворяющим (4.39),
(4.40) и (4.41). Из сравнения с (4.43) видно, что этот коэффи-
циент и есть число комплексий С. _
Точно таким же способом получим СЁА. Только что было
показано, что
I/А \ И по! nJ ... пг\ . . .
8 Зак. 1299
114 Гл. IV. Общие теоремы для ансамблей стационарных систем
Если продифференцировать обе части равенства по z, а затем
умножить на z, то получим
Умножим обе части равенства на {/в(г)}Лв, тогда получим
{^[1а (z)]NA}{fBWNB =
= у у , /в! , (4.49)
п0| ... цг\ ... Ид! П|! ... ns\ ...
Суммирование производится по всем положительным целым
числам п и //, удовлетворяющим (4.39) и (4.40). Рассмотрим
коэффициент при zE в правой части (4.49) и вспомним выраже-
ние (4.45). Из сравнения видно, что коэффициент при zE и
есть СЁ а.
Для Cnt можно получить аналогичную формулу. Из (4.42)
имеем
= Л,Л5У£ -----—, (4.50)
А МпМп' Ло!П|! ... пг1 ... ... ... v
где 2.7 2д> отличаются от У первых суммирование
производится по всем положительным числам (включая нуль)
п, п', удовлетворяющим следующим условиям:
2>г = ЛГл-1, (4.51)
= (4-52)
+ = £ —ег (4.53)
Если функцию
Na Wb(z)\Nb
разложить в ряд по степеням z, то можно обнаружить, что ко-
эффициент при zE'^ как раз и есть выражение (4.50), а огра-
ничения на суммирование, как и раньше, выражены соотноше-
ниями (4.51), (4.52) и (4.53). Поэтому Cnt равно коэффициен-
ту при zE выражения
NAz4fA(z)VA~' {fB(z)VB- (4-54)
4.5. Краткое изложение метода перевала
115
Теперь мы видим, что общее число комплексий С, средние
значения СЕа, Cnt и другие аналогичные величины можно вы-
разить через коэффициенты некоторых степенных рядов. Сле-
дующая наша задача состоит в вычислении этих коэффициен-
тов. Самым эффективным и быстрым методом является сведе-
ние их к контурным интегралам с последующим вычислением
их асимптотических значений методом перевала. В следующем
пункте будет дано краткое описание этого метода без подроб-
ного доказательства1).
4.5. Краткое изложение метода перевала
Из предыдущего пункта нам известно, что интересующие нас
величины являются коэффициентами в некоторых степенных
рядах. С помощью теоремы Коши можно выразить их в виде
контурных интегралов по комплексным переменным
С = f (4.55)
zjiz J z
Y
= (4-56)
Y
Cnt = ы f If a {fB (4.57)
Y
Здесь у — произвольный контур, лежащий в круге сходимости
степенных рядов (в действительности его радиус равен 1) и об-
ходящий точку z=0 один раз против часовой стрелки.
Эти интегралы являются точными выражениями и имеют
место для любых значений NNb, Е. Однако они имеют фи-
зический смысл лишь при очень больших значениях NА, NB и Е,
так как ансамбли, доступные нашему наблюдению, все со-
стоят из большого числа систем. Поэтому будем сначала искать
асимптотические значения интегралов при NA, Мв и Е, стремя-
щихся к бесконечности, но при сохранении некоторых фиксиро-
ванных отношений между ними. Физически это соответствует
тому, что мы ищем предельные свойства ансамбля, когда его
размеры стремятся к бесконечности, а локальные (интенсив-
ные) свойства остаются неизменными (локальными называются
свойства, не связанные с размерами ансамбля). Можно пока-
зать, что свойства конечного ансамбля, как правило, можно
найти только из его предельных свойств. Асимптотические
9 См. Смирнов В. И., Курс высшей математики, т. Ill, часть вторая,
раздел 78.
8*
116 Гл. IV. Общие теоремы для ансамблей стационарных систем
значения интегралов как в исследуемых нами сейчас, так и в бо-
лее простых случаях можно совершенно строго найти с по-
мощью метода перевала.
Рассмотрим множитель при dz/z в подынтегральной функ-
ции выражения (4.55). На вещественной оси при г->0 и z-И
множитель стремится к бесконечности. В некоторой точке z=0
из интервала (0,1) он имеет единственный минимум. Пусть
у — окружность с центром в начале координат и радиусом 0.
Тогда z = Qeia. Когда значения Na. Nb и Е очень велики, мо-
дуль этого множителя принимает в точке 2=0, а = 0 макси-
мальные значения. Производная от подынтегрального выраже-
ния в точке z=0 равна нулю. Поэтому значение интеграла поч-
ти полностью определяется значениями подынтегрального выра-
жения в окрестности этой точки.
Если под интегралом в (4.56) появляются добавочные мно-
жители типа
д 1 , z df (z)
' А
то указанные свойства остаются справедливыми. Свойства не
сохраняются, если дополнительный множитель содержит сте-
пени, сравнимые с Е и N. Результат мало изменится, если в до-
полнительных множителях заменить z на 0 и вынести за знак
интеграла. Точка на действительной оси 2 = 0, в которой подын-
тегральная функция имеет минимум, является действительным
корнем уравнения
д
дг I гЕ
на интервале (0, 1). Или, что то же самое, 0 удовлетворяет ура-
внению
^А0 = Е- <4’58)
Используя (4.58), перепишем (4.56) в виде
СЕл = Wa9-"*^18) f If л 1Л. (2)ГБ
V
Сравнивая с (4.55), получаем
д1п/л (0)
д0
(4.59)
4.5. Краткое изложение метода перевала
117
И аналогично
= д'У (4.60)
Сравнивая (4.58), (4.59) и (4.60), мы видим, что всегда выпол-
няется необходимое условие
ёа+ёв=е.
Три последних соотношения определяют распределение энергии
в двух группах гармонических осцилляторов в большом ан-
самбле.
Аналогичным образом сравнивая (4.55) и (4.57), получим
«, = ^0^(0). (4.61)
Из определения /а(0) следует, что nt удовлетворяет необходим
мому условию
2г«г = Л/д.
Теперь следует выяснить, как изменится результат, если вме-
сто условия (4.41) пользоваться (4.41а). В этом случае энергия
задается в малом интервале. Ниже мы покажем, что добавки
в формулах оказываются малыми и ими можно пренебречь.
В предыдущем пункте мы выяснили, что значение С равно
коэффициенту при zE в разложении по степеням z функции
[М<Л1Ь(<В-
С помощью тех же аргументов можно показать, что при за-
мене (4.41) на (4.41а) значение С равно сумме коэффициентов
при всех тех z в том же выражении, показатели степеней кото-
рых содержатся между zE и zE+dE. Аналогично СЕа равно сум-
ме коэффициентов при z, показатели степеней которых лежат
между zE и zE+dE в выражении
{г^1Ь(<фв (*)]"*«
a Cnt равно сумме таких же коэффициентов в выражении
Применим для вычислений разработанный выше метод.
Тогда (4.55), (4.56), (4.57) заменяются контурными интегра-
118 Гл. IV. Общие теоремы для ансамблей стационарных систем
лами
f ••• + (4.62)
Z I Z Z I
Y
СЁл = 7- f j > + 7 + • + тк П * ~ If л (<>' 1 Ш"'
(4.63)
c"< “i"-5 /7^! 1 + 7 +'" +7S > 2'‘
(4.64)
Полученные интегралы отличаются от предыдущих только до-
полнительным множителем в подынтегральных выражениях
1+1+ ...
2
1 (l/z)d£+1 — 1
2dE ~ (1/2) — 1
(4.65)
Легко видеть, что формулы для средних значений, особенно
для Еа и nt, формально совсем не меняются, так как дополни-
тельный множитель сокращается. Изменению подвергается
только формула, определяющая положение минимума подын-
тегральной функции на действительной оси. Она принимает вид
, N N
д2 I 2Е
1 Ml л
1 + ) =0’
Поэтому (4.58) следует изменить на
dlnf-(0) ainfR(0)
ДГл0-----+ 7V Л:-----------=
А дЪ в дв
dE+l
F-|____Z___
1
1—0 ’
По сравнению с (4.58) здесь справа появилось два добавочных
слагаемых
dE+l_____1
1—0^+1 1 — 0*
Легко доказать, что значение дополнительного выражения
для всех 0 между 0 и 1 лежит в интервале 0, dE. Поэтому фор-
мулу, определяющую 0, можно переписать в следующем виде:
(«б.
Обычно всегда предполагается, что dE^E. Поэтому разница
между (4.58) и (4.66) пренебрежимо мала.
4.6. Средние значения и статистическая шкала температуры 119
Таким образом доказано, что усреднения, основанные на
(4.41) и (4.41а), практически не отличаются. Поэтому в даль-
нейшем нет необходимости пользоваться этим сравнительно
распространенным определением средних величин. Все форму-
лы для средних величин с точным значением энергии могут
быть применены в тех случаях, когда энергия задана в малом
интервале.
4.6. Средние значения и статистическая шкала температуры
Обсудим теперь основные результаты, полученные чисто ма-
тематически в предыдущем пункте, и те предположения из
и. 4.4, которые при этом использовались. Предварительно обоб-
щим выводы на ансамбли, состоящие больше чем из двух ти-
пов систем.
Рассмотрим ансамбль, состоящий из NA систем типа Д, из
систем типа В, из Nc систем типа С и т. д., где NA, Nb,
Nc, • • • очень велики. Пусть возможные состояния 0, 1, 2, ... си-
стемы являются невырожденными и их энергии равны 80, 81,
82, ... соответственно. Как следует из результатов предыдущего
пункта, среднее число пг систем А в состоянии г равно
~пг = = Af л9е7/л (б), (4.67)
и смысл параметра 0 будет выяснен ниже. Среднее число ii's
систем В, находящихся в состоянии с энергией t]s, равно
\ (6)- (4-68)
Для других типов систем формулы аналогичны. Из (4.67) и
(4.68) видно, что следующие необходимые условия:
ЗЛ = ЛГД, (4.69)
^sn's = NB (4.70)
выполняются автоматически. Распределение средней энергии
среди различных типов систем находится следующим образом.
Средняя энергия всех систем А равна
dlnf.(O) 'Xе/’’
= (4.71)
при этом
2ЛА = ^л- (4-72)
Для величин Ев, Ес и т. д. имеют место аналогичные формулы.
120 Гл. IV. Общие теоремы для ансамблей стационарных систем
Наконец, для суммарной энергии выполняется необходимое
условие
ЁА + ЁВ+ЁС+ ...-Е. (4.73)
Если Е задано, то 0 будет определено. Наоборот, если задано 0,
то будет определено Е.
Осталось рассмотреть смысл параметра 0. Очевидно, что по
отношению к математическому аппарату 0 является основным
параметром, описывающим состояние ансамбля, и, следова-
тельно, он должен быть связан с некоторыми физическими свой-
ствами ансамбля. Наиболее характерной особенностью пара-
метра 0 является то, что средние свойства всех систем опреде-
ляются через один параметр 0. Из этого следует, что 0 является
параметром, определяющим состояние ансамбля и имеющим
одинаковое значение для всех групп систем ансамбля. Именно
такими свойствами обладает температура. Поэтому мы с необ-
ходимостью приходим к заключению, что 0 играет роль темпе-
ратуры. Конечно, это не температура, измеряемая по обычной
температурной шкале, поэтому 0 называют статистической тем-
пературой или температурой, измеряемой по статистической
шкале. В дальнейшем будет установлена связь между темпера-
турной шкалой 0 и обычно употребляемой термодинамической
шкалой Т. Забегая вперед, укажем, что эта связь имеет сле-
дующий вид:
0^^-W, (4.74)
где Т — абсолютная температурная шкала (шкала Кельвина),
a k — универсальная постоянная.
4.7. Системы с большим числом степеней свободы
и вырожденные системы
До сих пор мы рассматривали средние свойства ансамбля
локализованных линейных осцилляторов. При этом предполага-
лось, что дискретный ряд состояний осцилляторов определяется
одним квантовым числом и что состояния невырождены. Боль-
ше никаких предположений не делалось. Полученные резуль-
таты относятся, вообще говоря, ко всем системам, имеющим одну
степень свободы, однако наиболее важными остаются линейные
осцилляторы. На практике мы обычно имеем дело с системами,
обладающими большим числом степеней свободы. В предыду-
щих рассуждениях относительно осцилляторов совсем не ис-
пользовалось условие, что они обладают одной степенью сво-
боды. Поэтому полученные формулы будут годиться и для си-
стем с большим числом степеней свободы. Для этого достаточно
4.7. Системы с большим числом степеней свободы
121
потребовать, чтобы состояния системы с р степенями свободы,
характеризуемые квантовыми числами rlt г2, . .., гр, были не-
вырождены, т. е. энергии sr для гь г2,..., гР состояний были
различны.
Теперь необходимо освободиться от предположения, что нет
двух состояний с одинаковой энергией, и обобщить наши фор-
мулы на вырожденные системы. Предположим, что сог состоя-
ний имеет одинаковую энергию гг. Объединим их в одну группу
и назовем ее вырожденным состоянием с кратностью выро-
ждения (Dr или состоянием с весом сог. При изменении должным
образом внешних условий, в которых находится система, на-
пример при малом изменении (возмущении) внешнего поля,
энергетические уровни состояний разделяются и система стано-
вится невырожденной. После этого все предыдущие формулы
можно применять непосредственно, а каждый из сог разделен-
ных энергетических уровней соответствует в функции состояния
члену 2г 6 т- Если устремить возмущение к нулю, то придем к
первоначальному положению, сог состояний вновь будут иметь
одинаковую энергию sr. Теперь функция состояний 2г 0 г со-
держит (Dr одинаковых слагаемых, поэтому ее можно перепи-
сать в виде 2r ^ге?г у где при суммировании каждое вырожден-
ное состояние или каждый энергетический уровень учитывается
только один раз.
Проведем эти рассуждения в более общем виде. Причем по-
лученные результаты будут справедливы и для вырожденных
систем. Пусть ансамбль содержит МА систем A, NB систем В
и т. д. Предположим еще, что система А обладает рядом со-
стояний с энергиями so, 81, ..., 8г, ... и с весами (d0, (di, ...,
..., (Dn ... . Тогда функция состояний системы А имеет вид
/:А(г) = (0оге° + 0)12е1+ ••• +<ofze'’-4- .... (4.75)
Распространим (4.67) на вырожденные системы, тогда сред-
нее число йг систем А в энергетическом состоянии sr можно не*
посредственно написать в виде
nr = ^r9e7f4(0). (4.76)
Из (4.67) можно найти среднюю энергию системы А этого вы-
рожденного состояния. Она равна
122 Г л. IV. Общие теоремы для ансамблей стационарных систем
Суммируя приведенное выражение по всем г, получаем сред-
нюю энергию Еа системы А
Ёа = НА 087/л (0) = NaQ —"Ц<е> . (4.77)
Для других типов систем справедливы совершенно анало-
гичные формулы, причем величина 0 везде одинакова. Наконец,
имеет место необходимое условие
ЁА + ЁВ +
Если задано Е, то можно найти статистическую температуру.
Наоборот, если задана температура 0, то можно определить Е.
Для локализованных систем функция состояний /(0) най-
дена. Следует обратить внимание на то, что движение систем
с большим числом степеней свободы часто может разделиться
на два или множество независимых друг от друга видов. В этих
особых случаях функция состояний может распасться на мно-
жители, которые соответствуют функциям состояний отдельных
видов движения. Разделение движения системы на несколько
несвязанных друг с другом видов соответствует пренебрежению
в гамильтониане уравнения Шредингера членами, содержащими
произведения координат. Поэтому собственные значения энер-
гии, определяемые различными квантовыми числами, соответ-
ствуют различным степеням свободы.
Таким образом, из определения функции состояний можно
непосредственно вывести, что она может быть разложена на не-
сколько множителей. Например, для двухатомной молекулы,
если можно пренебречь связью между ее колебательным и вра-
щательным движением, колебание и вращение разделяются и
функция состояний распадается на две — функцию состояний
вращения и функцию состояний колебания. У свободной моле-
кулы поступательное движение всегда не зависит от внутрен-
него. Однако только в газах можно считать, что молекулы сво-
бодны. Комплексий таких ансамблей подсчитываются так же,
как для ансамблей второго типа.
4.8. Линейный гармонический осциллятор
Рассмотрим теперь некоторые конкретные примеры построе-
ния функции состояний.
Ранее мы уже рассматривали линейный гармонический ос-
циллятор; в частности, было найдено, что его собственная
функция характеризуется одним квантовым числом v, кото-
рое может принимать следующие значения:
^ = 0, 1, 2, ...,
4 9. Двумерные и трехмерные гармонические осцилляторы
123
соответствующая им энергия равна
ev = + у) Av
Здесь за нуль выбрана энергия в положении равновесия. По-
этому функция состояний для осциллятора равна
/ (в) = У е<’+^ *’ = (1 - 1. (4.78)
Из (4.78) и (4.77) получим среднюю энергию ЁА для NA ли-
нейных гармонических осцилляторов, выраженную через стати-
стическую температуру 0:
ёa=n ло—in{ ei" Av(i — eAv)~1}=л/л (-avh—£—
Средняя энергия отдельного осциллятора равна
£. 1 Av
-JL = _ ь Ч-----т----. (4.79)
N. 2 e“/,v— 1 v 7
А
Если энергию самого низкого квантового состояния у hv при-
нять за нуль, то
4.9. Двумерные и трехмерные гармонические осцилляторы
Рассмотрим сначала анизотропный двумерный гармониче-
ский осциллятор, т. е. осциллятор, у которого естественные ча-
стоты для двух взаимно перпендикулярных колебаний различ-
ны. За начало отсчета примем положение с минимальной по-
тенциальной энергией, а основные оси обозначим через х и у.
Тогда классическое выражение для энергии имеет вид
т (р!+p$lm+у (2jiv<)2 тх2+J (2jrvJ2 ту2 =е>
где рх, ру — импульсы вдоль осей х и у, a vx, — частоты, за-
висящие от коэффициентов упругости вдоль двух главных осей;
е — энергия, которая в начале координат равна нулю. Соответ-
ствующее уравнение Шредингера имеет вид
[е ~ i (2™Л2 тх2—т <2nvy >2 ту2] =°-
124 Гл. IV. Общие теоремы для ансамблей стационарных систем
Это уравнение с разделяющимися переменными по х и у. Оба
этих уравнения, получающиеся после разделения переменных,
являются уравнениями линейного гармонического осциллятора,
обладающего частотами vx и vy. А тогда энергетические уровни
рассматриваемого осциллятора имеют вид
еVy ~ + ?) hVx + + 1) hVy
{vx = Q, 1, 2, vy = Q, 1, 2, ...)• (4.80)
Функция состояний равна
+(v+4W
(4-81)
Средняя энергия Еа, распределенная по NA таких систем, равна
— э Г 1 1 hvn )
= в 47 +-V-T+7 Г
{ Z U Л — 1 2 U * — 1 J
(4.82)
Рассмотрим теперь двумерный изотропный гармонический
осциллятор. В п. 4.2 мы уже указывали, что его энергетические
состояния равны (v+ l)/iv, t> = 0, 1, 2, ..., а вес равен v+1. По-
этому функция состояний равна
f(e) = 9',v + 202/jv+303Av + ..
Энергия, распределенная по Na системам, равна
ЁА = naQ 41П И0) = 2АЦ |
(4.84)
Все эти формулы можно получить из (4.81) и (4.82), если по-
ложить vx = vy = v.
Аналогично этому для трехмерного изотропного гармониче-
ского осциллятора можно доказать, что уровни энергии равны
(^ + 4)Av’ ^ = 0, 1, 2, ... , а вес составляет ^-(^ + 1) (чу-]-2).
Поэтому функция состояний имеет вид
00 / 3\ .
f(9)= 2|(^+1)(г’ + 2)0 V==
v«0
i-eAv
(4.85)
4.10. Жесткий ротатор без аксиального вращения
125
Средняя энергия ЁА для Na систем равна
ЕА = NAb 4 ln f (0) = ЗНА [1 hv + . (4.86)
Как и следовало ожидать, она как раз равна утроенному зна-
чению средней энергии линейного гармонического осциллятора.
4.10. Жесткий ротатор без аксиального вращения
В п. 4.2 и во второй главе было показано, что энергетиче-
ские уровни жесткого ротатора без аксиального вращения
равны
еу = у(у+1)й2/8л2Л, / = 0, 1, 2, ...»
где А — продольный момент инерции. Вес состояния / равен
(2/+1). Поэтому функция состояний имеет вид
оо
f (0) = 2 (2/+1) еу (У+ ” л’/8л’л. (4.87)
/ = 0
Произведем замену
А2 1
' = иг'«т Н-88)
тогда
Д0)= £ (2/+1 )£-><>+^. (4.89)
7=о
Произведем сначала приближенное вычисление для случая
(такая ситуация часто встречается в действительности).
Так как при т<^1 показатель степени очень медленно изме-
няется с изменением /, то суммирование можно заменить инте-
грированием. Используя подстановку
/(/+1)т = ^ (2ЛН)т4/=^,
получаем
оо оо
f (в) „ f (2/+ I) ««> <dj = 1 fe-1= 1 = . (4.90)
0 0
Более точные вычисления можно произвести с помощью метода
Эйлера — Мэльголлэнда, суть которого состоит в следующем:
если F(x) является аналитической для всех значений к в
126 Гл. IV. Общие теоремы для ансамблей стационарных систем
диапазоне то1)
J F(x)dx — &^F(а) + F(а + со) +-Z7(« + 2©)4- ...
а
+ -^(« + ™)} + ‘>гут-.[Г~->(а+гМ)-
т-1
-F^-^a)}^^- [ <р2я (J /7(2") (а + тб) + ©/)
О ( /72 = 0
dt, (4.91)
где Вт — многочлен Бернулли степени т, ф2п(0—многочлен
Бернулли степени 2и; а
Г7(Ц) / \
F w=^'
Применим это разложение для (4.89). В этом конкретном
случае
F(x) = (2x+1)£~х(х+1)т, со=1 и г—>оо.
Пусть п->оо, тогда
f(0) = ^(2/+1)^Я>+1)г«
/=1
« f(2x + 1) е~х ^+»* dx +1 +
о
, у1 (— р^Дт. I ^2'” г?2Л _1_ 1) g-x(jr+l)Tl I
+ 2^ (2т)! L •
772 = 1 ’
Известно, что
— б- ’ 52 = зо - 5з = 42 ’ ^4 = 30 ’ ^5 — 66 • • • >
поэтому
f<e)^| + |--i-(2-T) + 1T±w(-12T+ ...)+ ...^
“И,+Тт + 1Тт!+ ] (4-92’
9 См. Смирнов В. И., Курс высшей математики, т. Ш, часть вторая,
раздел 76, формула (175).
4.11. Жесткие ротаторы с аксиальным спином
127
Этот результат сначала был получен Мэльголлэндом после
очень сложного анализа; им были проведены вычисления и по-
лучено приближенное выражение для разложения. Наши же вы-
числения просты, но не очень доказательны. В пятой главе по-
лученная здесь формула будет применена к случаю двухатом-
ных молекул.
4.11. Жесткие ротаторы с аксиальным спином (симметричные
волчки)
Предположим, что А — поперечный момент инерции, а С —
продольный момент инерции. Возможные значения энергии уже
приводились в п. 2.17. Они равны
Р ЯУ+1) । 12 /1 __ 1П
К m — 8л2 I А А Н ’
где
-/4-1, ...» -1, 0, 1, 1,/,
J~ ’ ' ’ ’ l/n = — j, — / + 1, ..— 1, О, 1, ..j — 1, j.
Так как система имеет три степени свободы, то имеется три
квантовых числа /, X, т, но вследствие пространственного вы-
рождения в действительности для полного определения значе-
ния энергии требуется только два квантовых числа / и К. По-
этому можно пренебречь последним индексом m в ej, х, а
2/4-1 состояний, обладающих различными значениями т, счи-
тать вырожденными состояниями с весом, равным 2/4-1. Сле-
довательно, функция состояний равна
оо j
f(0)=2 2 (4.93)
У=0Х=-у
где
А2 . 1 , А2 / 1 1 \ . 1
Т— 8л2 Л П 0 ’ Т — 8л2 (с а) П 0 ‘ (4’94)
Без приближенных методов дальнейшие упрощения (4.93)
невозможны. Но в действительности для конкретных случаев
часто справедливы неравенства т<^С1, т'<^С1. Тогда заменой зна-
ка суммы интегралом и перестановкой порядка интегрирования
можно получить приближенное выражение
оо J
f(0)« f (2/+l)e-/<>+1’T4Z/ f e~wdk =
0 -j
0
Так как т и т' очень малы, то основное значение интеграла
определяется областью очень больших значений Z. Таким
128 Г л. IV. Общие теоремы для ансамблей стационарных систем
образом, в той области, где подинтегральная функция сравни-
тельно велика, Х(Х+1) может быть заменено на V. Поэтому
можно приближенно записать
г J Т (f -f- т )'2
о 2 I 2лЛ ) ( 2лС 1’А
~8л 1 Л2 In (1/0) Н Л2 In (1/0) | • (4-95)
Для полностью симметричного вращающегося тела С = Л,
поэтому т' равно нулю. В этом случае энергия не только не за-
висит от т, но и не зависит от Z, поэтому степень вырождения
увеличилась. В этом случае
ДО) =1(2/+ 1)2г-я/+1)г.
; = 0
При тС1 суммирование можно заменить интегрированием
и получить следующую приближенную формулу:
f(0)« f 4j2e-i2xdj =
О о
т8/2 1 Л21п(1/0) J
(4.96)
4.12. Ансамбль, состоящий из двух групп нелокализованных
систем
Расчет равновесного состояния ансамбля второго типа, ком-
плексии которого подсчитываются по правилам, описанным в
п. 4.3, требует применения новых методов. Пусть для простоты
ансамбль содержит две группы нелокализованных систем А и В,
число которых равно соответственно Na и Nb> Пусть, кроме
того, состояния систем А и В являются невырожденными; их
энергии равны
е0, еь ..., 8Г, ... и т)о, Пь •••> П*, • ••
и выражаются целыми числами через единичную энергию. Как
и раньше, число систем, находящихся в этих состояниях, обозна-
чим через /io, , ..., пг, . .. и Пд, n'v ..n's, ... . Этот ряд чи-
сел полностью определяет статистическое состояние ансамбля.
Случаи, когда собственная функция ансамбля симметрична или
антисимметрична относительно всех систем группы, требуют
различного подхода.
4 12. Ансамбль, состоящий из двух групп нелокализованных систем 129
1. Собственная функция ансамбля симме-
трична по отношению к системе данной группы.
В этом случае говорят, что ансамбли, образованные из таких
систем, подчиняются статистике Бозе — Эйнштейна. Из п. 4.3
следует, что для каждой группы положительных (или равных
нулю) значений чисел nr, ns имеется лишь одна соответствую-
щая собственная функция. Поэтому общее число комплексий С
равно числу групп положительных целых (или равных нулю)
значений nr, ns, удовлетворяющих необходимым условиям
^гПг — Na, = '£ге.гПг+ 'ЯцЪп'^Е.
Покажем, что при разложении в ряд двойного произведения
1L 0 +Л;Л + + • • •) И, 0 + i/z’1 + + )=
= 11,(1 -угЧ' (4.97)
N М Е
по степеням х, у, z коэффициент при члене х Ау Bz равен С.
Рассмотрим множитель, соответствующий r-му состоянию си-
стемы А. Для этого при вычислении произведения возьмем член
типа x^z’^r. Общий член суммы, получающейся при развер-
тывании произведения Ц г имеет вид x^rz^r”^', где Пг может
принимать любые положительные целые значения (или нуль).
Общий член суммы, получающейся при развертывании другого
Ле ЕЛЛс '
s имеет вид у 5 sz s s \ где ns может прини-
мать любые положительные целые значения (или нуль).
Тогда общий член суммы от обоих произведений имеет сле-
дующий вид:
xZr"ry^sn'Sz^r"rer + ^sn\i
где nr, n's могут независимо принимать положительные целые
значения (или нуль). Если в развернутом выражении взять
член х Ау Bz , то пт, ns как раз удовлетворяет необходи-
мым условиям. Поэтому коэффициент этого члена равен С.
Легко заметить, что переменные х и у играют ту же роль,
что и г. Переменная х выделяет те члены, которые удовлетво-
ряют ограничительному условию для комплексий группы 4,
контролирующему неизменность NA; переменная у выделяет
те члены, которые удовлетворяют условию для группы 5, кон-
тролирующему неизменность NB. Для локализованных систем
эти условия выполнялись автоматически. Переменная г, как и
9 Зак. 1299
130 Гл. IV. Общие теоремы для ансамблей стационарных систем
в случае локализованных систем, выделяет те члены, которые
удовлетворяют заданному точному значению Е.
Таким образом, самым интересным для нас членогл в урав-
нении (4.97) является Сх Ау Bz . Он представляет собой
/V N Е
сумму С равных членов х Ау Bz , каждому из которых соот-
ветствует комплексия. Рассмотрим одну из них. Если в этой
комплексий имеется nt систем А с энергией то в члене
/V N Е
х Ау Bz , который соответствует этой комплексий, содержится
множитель х lz t Г К тому же множитель с таким индексом t
в этом слагаемом только один. Если заменить множитель
xntznt^- на ntxntzntZt и сделать такие же замены для других
N Nn Е
комплексий, то коэффициент при х Ау Bz из 21 превратится в
где суммирование распространяется по С комплексиям.
Согласно (4.1), такое изменение равнозначно тому, что мы из-
N N Е
менили коэффициент С при х Ау Bz на Cnt. Так как
О • 1 + 1 • xz‘ + 2 • x2z2e< + 3 • х3г3е< xz*‘ (1 — xz"')”2,
то, заменив в (4.97) SП(хп*гп?* на '2intntx"tzn‘\ что эквива-
лентно замене всех хп‘гп‘г‘ на ntxntznt\ получим
хге< (1 — хг8<) 2II (1 — хггг) 1 Ц (1 — yz^d \
Z^=-t S
ИЛИ
xzzt (1 — хге0-111г (1 — хЗГ' IL (1 — (4.98)
Из всего сказанного следует, что Cnt как раз является коэф-
N X Е
фициентом при х Ау Bz в развернутом выражении (4.98).
2. Собственные функции ансамбля являются
антисимметричными относительно систем
данной группы. В этом случае говорят, что ансамбль, со-
ставленный из таких систем, подчиняется статистике Ферми —
Дирака.
Для такого ансамбля каждой группе возможных значений
пГу it's по-прежнему соответствует только одна собственная функ-
ция, но nr, n's могут принимать значения 0 или 1, так как по
принципу Паули они не могут быть больше 1. Поэтому число
комплексий С равно числу систем значений nrs, которые удо-
влетворяют (4.39), (4.40), (4.41) и могут быть только 0 или 1.
Аналогично тому как было проведено для статистики Бозе —
4.12. Ансамбль, состоящий из двух групп нелокализованных систем 131
Эйнштейна, можно доказать, что число комплексий С равно ко-
t N. N~ Е
эффициенту при х Ау az в выражении двойного произведения
Пг (1 + xzr} IL (1 4- (4-99)
Как и в (4.99), заменим член xntzn‘ei на ntxntznt\ тогда ко-
N N Е
эффициентом при х Ау Bz является Cnt. Однако теперь nt мо-
жет быть лишь 0 или 1. Поэтому множитель (l-|-xze') с ниж-
ним индексом t в (4.99) следует заменить на хгеС Это равно-
сильно умножению (4.99) на
xze'(1 + xze') \
N N Е
Отсюда видно, что коэффициент при х Ау Bz в выражении
xzRt (1 + лге<)-1 Пг (1 + ^r) Hi (1 + (4.100)
и есть Cnt.
Заметим, что формулы (4.97), (4.98) для статистики Бозе —
Эйнштейна и формулы (4.99), (4.100) для статистики Ферми —
Дирака отличаются лишь знаком. Поэтому их можно объеди-
нить в одну формулу, предусмотрев тем самым, что две группы
систем ансамбля одновременно могут подчиняться различным
статистикам. Таким образом, мы получаем результат, имеющий
широкое применение, а именно число комплексий С равно ко-
эффициенту при х Ау az в выражении
Пг(1 ±J/2^)±1. (4.101)
Здесь в первом произведении нужно взять знак «4-» или знак
«—» в зависимости от того, подчиняются ли системы А стати-
стике Бозе — Эйнштейна или статистике Ферми — Дирака. Ана-
логично этому во втором произведении выбор знака опреде-
ляется в зависимости от свойств систем В. Другой результат
заключается в том, что если среднее число систем А, находя-
щихся в состоянии /, равно nt, то Cnt равно коэффициенту при
иА nr е
х Ау Bz в выражении
х/'(1 ±xze') 1 Цг(1 ± xz8')*1 JJ5(1 ± (4.102)
В следующем пункте эти коэффициенты вычисляются непо-
средственно.
9*
132 Г п. lV. Общие теоремы для ансамблей стационарных систем
4.13. Математические выкладки
Таким образом, нам известно, что С — коэффициент при
члене х Ау Bz в выражении (4.101). Применяя теорему Коши
для каждой из трех переменных, получим
Г— 1 Г Г Г dx dy dz
С- (2ш)3 J J J ^л + 1^в + 1/+1 X
X (1 ± xz'rf' (1 ± (4.103)
Аналогично из (4.102) получим
- _ 1 Г С Г dx dy dz
J J J /д + 1у^ + 1/ + 1 X
Х{хге*(1 ± xz?t) 1} Цг(1 ± x^£f)±1 (1 - • (4.104)
Подинтегральная функция в (4.104) отличается от подинте-
гральной функции в (4.103) только на один множитель
xz*t = 1
1 ± XZ^ (xz*t) ± 1
Можно доказать, что множитель при dxdydzlxyz в (4.103)
IL(1 ± ± yz4 /x%V
является основным и определяет все поведение подинтеграль-
ной функции в (4.103) и (4.104). В интегралах с дополнитель-
ными множителями типа {(хг£/) ± 1} поведение подинтеграль-
ной функции также определяется этим множителем. Когда пе-
ременные х, у, z принимают конкретные числовые значения, то
основной множитель имеет единственный минимум в точке Ха,
Хв, 0. Выберем контуры интегрирования так, чтобы они прохо-
дили через эту точку, тогда на этом контуре в этой точке под-
интегральная функция будет иметь единственный максимум,
играющий главную роль. Значение подинтегральной- функции в
окрестности этой точки дает главный вклад в значение инте-
грала. Такая точка носит название седлообразной точки. Если
вместо %, у, z в (4.105) или в других аналогичных дополни-
тельных множителях подставить Хд, Хв, 0, то его можно выне-
сти за знак интеграла. После этого разделим (4.103) на (4.104).
Тогда получим
ХЛ9е/ 1
Л —------4----—-------------,
' 1±хЛее/
А
4.14. Некоторые результаты
133
По определению точка Лд, Хв, 9 есть точка минимума глав-
ного множителя подинтегральной функции, поэтому частные
производные от этого множителя по х, у, z в точке Хд, Хв, 0
должны быть равны нулю. Отсюда мы получим уравнения для
определения Хд, Хв, 9
А
1 ±
А
М115
1 ±
у
1 ±
А
1 ±
(4.107)
(4.108)
(4.109)
Из (4.106) — (4.109) видно, что следующие необходимые ра-
венства удовлетворяются автоматически:
2 Л =
2 rTlfir -1“ 2 == Е •
4.14. Некоторые результаты
Подведем некоторый итог результатам, вывод которых крат-
ко изложен в предыдущем пункте. Одновременно с этим снимем
ограничение на число групп систем ансамбля. Пусть ансамбль
состоит из Na систем группы А, из NB систем группы В и т. д.
Среднее число пг систем А, находящихся в невырожденных со-
стояниях г с энергией ег, равно
- _ _ 1
Пг — ~ *
1 ± г г ± 1
А
(4.110)
Эту формулу можно переписать в виде
= (4.111)
А
где знак « + » или «—» нужно выбирать в зависимости от того,
являются ли собственные функции ансамбля симметричными
или антисимметричными относительно систем группы А. Ка-
ждая из групп систем А, В, . . . характеризуется, вообще говоря,
своими параметрами Хд, ZB, .... Однако параметр Лд входит в
134 Гл. IV. Общие теоремы для ансамблей стационарных систем
формулы, аналогичные (4.110) для всех различных состояний г
систем группы А. Значения Хд, Хв, ... определяются необходим
ными условиями, например Хд определяется из условия
VT ХЛ0 r VI —
2 А е—S "r=NA. (4.112)
1 ± л,ле г
А
Средняя энергия Ёа для NА систем А равна
Е
£n = S «А = 2 -^^=«42 1п(|±М,')±'. (4.113)
1 ± А,„е г ™
А
Наконец, легко заметить, что параметр 0 имеет одинаковое
значение не только для всех состояний г какой-либо одной груп-
пы систем, но и для всех групп систем Д, В, ... . Если задано
значение Е, то из необходимого условия
Е— ЁА-\-Ёв-\- ... (4.114)
всегда можно найти 0 и, наоборот, при заданном 0 всегда мож-
но определить Е. На основании изложенных в п. 4.6 соображе-
ний 0 можно рассматривать как температуру, измеряемую
статистической шкалой. В дальнейшем мы приведем краткое
доказательство того, что статистическая температура 0 и темпера-
тура Г, измеряемая по шкале Кельвина, связаны соотношением
0 = £-w;
где k — универсальная постоянная.
4.15. Вырожденные системы
Мы уже видели, что равновесные свойства ансамбля нелока-
/ е \ ± 1
лизованных систем зависят от функций In (1 ± ХА0 г) , каждая
из которых соответствует одной из групп систем. Очень легко
распространить полученные выше результаты на вырожденные
системы. Для этого достаточно разрешить сог состояниям иметь
одинаковую энергию. Предположим теперь, что состояния си-
стем А могут быть вырожденными, допустимые уровни энергии
заданы рядом е0, 81,..., ег, ..., а их веса равны соо, coi,...
..., (Dr, ... . Тогда среднее число систем Д, находящихся в вы-
рожденном состоянии г, равно
А = 4-1„ (1 ± • (4.115)
4.16. Классическая статистическая механика
135
Средняя энергия систем А в состоянии г равна
5ахл-^-1п(1 ± 1/)*'=®,04in(1 ± х/О*1. (4.116)
C//V - U V
А
Средняя энергия всех систем А равна
= S, Sa = 7 27"(1 ± аХ')1 ' = 2, .
кХде Г) ± 1
(4.П7)
Значения Хд и 0 определяются следующими необходимыми ус-
ловиями:
Е = ЕА + ЕВ + .... (4.118)
4.16. Классическая статистическая механика
Нелокализованные системы могут свободно перемещаться,
если они находятся в одном сосуде. Их среднее распределение
по возможным состояниям определяется (4.115). Если для всех
ег выполнено следующее условие:
__р
г, (4.119)
то логарифмическую функцию в (4.115) можно разложить в
ряд. Оставляя первый член разложения, получаем
In (1 ± xXr)±1 «Хд9®г.
Этот результат одинаков как для статистики Ферми — Дирака,
так и для статистики Бозе — Эйнштейна. Формула (4.115) с
учетом (4.119) упрощается и приводится к виду
пг = Хдсо/Л.
Необходимое условие по-прежнему имеет место
На = 2г пг=^а 2, = Ч (9). (4-120)
где f(9) —функция состояний, определенная в п. 4.4. Исключив
Ха из двух приведенных уравнений, получим
nr = NA&rQ '/Ъ,, <о,9 ' = NAco,9 7/(9).
136 Гл. IV. Общие теоремы для ансамблей стационарных систем
что совпадает с (4.76) для распределения локализованных си-
стем.
Таким образом, мы получили очень важный результат, а
именно: если неравенство (4.119) выполнено, то статистика
Ферми — Дирака, статистика Бозе — Эйнштейна и статистика
локализованных систем приводят к одинаковым законам рас-
пределения. Для этих условий больше нет необходимости раз-
личать три типа статистик, и мы будем говорить, что ансамбль
подчиняется классической статистике.
На данной стадии изложения еще невозможно указать пол-
ностью условия, при которых неравенство (4.119) будет вы-
полнено. Однако для обычного газового ансамбля из атомов и
молекул после установления связи между 0 и Г мы найдем, что
неравенство имеет место для всех температур, исключая очень
низкие (Г<С1°). Этот вывод не распространяется на «свобод-
ные» электроны в металле. Поэтому в целях упрощения мы
везде, кроме случая свободных электронов в металле, будем
применять классическую статистику. Однако предварительно
будет показано, что все три статистики приводят к одинаковым
термодинамическим соотношениям.
Кратко и не слишком строго рассмотрим теперь условия,
при которых неравенство (4.119) выполнено. Нам известно, что
в статистике Бозе — Эйнштейна существуют комплексий, у ко-
торых в одном состоянии может быть несколько систем. Однако
если полное число систем А много меньше числа возможных
состояний с не слишком большой энергией (содержание терми-
на «не слишком большой» мы подробно объясним позднее), то
число таких комплексий будет намного меньше тех, у которых
в каждом состоянии находится не больше одной системы. А так
как различие между статистикой Ферми — Дирака и статисти-
кой Бозе — Эйнштейна состоит лишь в том, что первая допу-
скает присутствие в заданном состоянии не больше одной си-
стемы, а вторая таких ограничений не содержит, то приведен-
ного выше условия оказывается достаточно, чтобы разница
между ними стала несущественной. Поэтому справедливость
условия (4.119) в основном зависит от того, действительно ли
общее число систем намного меньше числа состояний с не очень
большой энергией. Ниже еще более убедительно будет показа-
на правильность такого заключения.
4.17 Движение бесструктурных частиц в ящике
В п. 2.7 уже рассматривалось свободное движение бесструк-
турных частиц; их собственные функции находились из (2.65)
и (2.66). Допустим теперь, что движение частиц ограничено
4.17 Движение бесструктурных частиц в ящике
137
прямоугольным ящиком, каждая из взаимно перпендикулярных
сторон которого параллельна осям х, у, z\ длина каждой из сто-
рон равна а, Ь и с, а одна из вершин находится в точке х0, //о, z0.
В этом случае волновые функции X, У, Z обязательно должны
удовлетворять граничным условиям, т. е. при х = х0, у = у^ z = z0
их— х0 = а, у — Уп = Ь, z— z0 = c они должны равняться нулю.
Вводя граничные условия в (2.66), получаем
•у- /2МЕха = /л,
У 2МЕУЬ = пл,
У'2МЕгс = пл,
h * z
где Z, /и, п — квантовые числа, они могут независимо прини-
мать любые положительные целые значения (кроме нуля),
М — масса частицы. Энергия состояний с любыми заданными
/, т, п равна
= + + = + + <)• (4.121)
Все состояния являются невырожденными. Предположим те-
перь, что для всех ег условие
Х<С0~6г
выполнено. Тогда можно применить классическую статистику.
Для этого необходимо вычислить функцию состояний
оо со JO h2 / /2 т2 п2 \
Ц0)=£ 2 2 (4.122)
I = 1 т = 1 п = 1
Предположим опять, что
A2 In (1/0)/8/Иа2 <С 1,
А21п(1/0)/8Ж2<<1,
A2 In (1/0)/8Ж2 <С 1. (4.123)
Это эквивалентно тому, что энергетический интервал любой па-
ры состояний мал по сравнению с 1/1п(1/0) (а если учесть
связь 0 с Г, то мал по сравнению с АТ). Из (4.123) следует, что
суммирование в (4.122) в действительности можно заменить
138 Гл. IV. Общие теоремы для ансамблей стационарных систем
интегрированием. Тогда получим
оо оо оо
f (0) « f 0OTW dl f елгт2,8Л,Ь2 dm f 6Aln2/8MC2 dn =
0 0 0
co oo oo
— J* e-[Л’1п (l/0)/8Af<z2] P(Ц J £-[Л’1п(1/0)/8Л«’1 m2dm J e-[IP In (1/9)/8Mc2|h2 dtl =
0 0 0
__( 8Ma2 л VA ( 8Mb2 л )'A ( 8Mc2 л VA
— A2 In (1/0) 1 ) I ft2 In (1/0) T f ( Л2 In (1/0) T |
__f 2лМ VA , j 2лМ VA т »
— ( A2 In (1/9) J at)C ~ 1 /г2 In (1/9) ) Vi
где V — объем ящика. После учета связи 0 с Т находим
Ц0) = (2nMkT)4’V h3 (4.124)
и, учитывая (4.120),
/(9) _ N h* ~ V (2nMkT)4^ ’ (4.125)
Теперь необходимо проверить справедливость (4.119) и
(4.123). Подставим 0 = е“ ,kT в левую часть (4.123) и заменим по-
стоянные их численными значениями й=1,38Х10~16 эрг!град,
Л = 6,63X10-27 эрг • сек, М в расчете на атом водорода равно
Л4= 1,67Х 10~24 г. Тогда получим
й2 In (1/0)/8Л4а2 = h2/8Ma2kT = 2,36 X МГи/а2Т.
При температуре 0,001° К для атомов водорода, заключенных
в ящик с длиной ребер 10-3 см,
й2 In (1 /&)/8Ма2 = 2,36 X Ю"5,
т. е. условие (4.123) выполнено. Тем более оно выполнено для
частиц с большей массой при больших размерах сосуда и более
высоких температурах. Даже для легких частиц, например
электронов, в обычных ситуациях условие (4.123) также может
иметь место.
Проверим (4.119) или
k<^eRr/kT (для всех ег).
Так как kT и все ег положительны, то приведенное неравенство
эквивалентно следующему:
4.18. Внешние реакции ансамбля
139
что, согласно (4.125), эквивалентно неравенству
2V Л3 1
V (2nMkT)^
Заменим постоянные k, Л, М их значениями, считая М массой
атома водорода. Тогда условие, которое необходимо проверить,
принимает вид
5,2 X 10~21 — -V<C1-
’ у т I2
Плотность молекул в обычном газе при нормальном атмосфер-
ном давлении и температуре равна
= 2,7 х 10’19 см3.
Если при 71 = 9°К сохраняется такая же концентрация, то вы-
ражение в левой части равно 0,005 и условие (4.119) выпол-
няется.
Для более тяжелых частиц при больших температурах и
меньших концентрациях X будет еще меньше. Поэтому для
реального газа можно считать, что К очень мало, и, следова-
тельно, можно пользоваться классической статистикой.
В наших последующих исследованиях единственным исклю-
чением являются ансамбли с довольно большой концентрацией,
или, например, свободные электроны в металле (концентрация
составляет около одного электрона на атом). Так как масса
электрона слишком мала, то даже при температурах в 2000° К
Х^>1. Поэтому к данному случаю формулы настоящего пункта
не применимы.
В пятой главе мы еще вернемся к ансамблям, которые здесь
обсуждались. Причем мы будем исходить из еще более знако-
мой нам точки зрения.
4.18. Внешние реакции ансамбля
Кроме формул для законов распределения, о которых гово-
рилось выше, нам необходимо еще рассмотреть формулу, опре-
деляющую среднее значение сил, действующих со стороны ан-
самбля или группы систем ансамбля на внешние тела, харак-
теризуемые геометрическими переменными. Самой важной из
них является формула для давления газа.
Допустим, что уравнение Шредингера решено, состояния си-
стем найдены и потенциальная энергия из этого уравнения со-
держит параметры Xi, х2, ... , характеризующие внешние тела.
Поэтому энергия возможного состояния ансамбля ег обязательно
140 Гл. IV. Общие теоремы для ансамблей стационарных систем
является функцией ... . Но вес состояния сог не зави-
сит от них, так как он представляет число независимых реше-
ний уравнения с заданными значениями энергии и внешних па-
раметров Xi, х2, .... Только в исключительных случаях при из-
менении х может произойти скачкообразное изменение если
же потенциальная энергия является непрерывной функцией х,
то такого изменения вообще быть не может.
Необходимо заметить, что здесь мы хотим единый объект ис-
следования разделить на две части, одна из которых представ-
ляет ансамбль, непосредственно интересующий нас, другая
часть — внешние тела. В вопросе о внешних реакциях выделе-
ние последних очень существенно. Конечно, какую часть счи-
тать ансамблем, зависит от конкретных условий.
Ансамбль и какое-либо тело, производящее внешнее сило-
вое поле, тоже могут образовать квантовую систему и, если нет
возмущений, то для нее имеет место закон сохранения энергии.
Возьмем параметр х, определяющий местоположение этого те-
ла, и изменим его на величину dx так, чтобы система ансамбля
продолжала оставаться в первоначальном состоянии г. В этом
случае энергия полной квантовой системы (ансамбль + внешнее
тело) останется неизменной, а энергия ансамбля увеличится на
d&r, т. е. система ансамбля по отношению к внешнему телу про-
изведет работу — der.
Иными словами, со стороны системы на внешнее тело дей-
ствует компонента обобщений силы Хг, которая при любом
бесконечно малом смещении, не выводящем систему ансамбля
из первоначального состояния г (обратимое смещение), произ-
водит работу, равную Xrdx, где
Хг = — дег/дх. (4.126)
Поэтому в любом состоянии ансамбля суммарная обобщен-
ная сила, действующая со стороны одной из групп систем,
равна
* = <4-127»
Здесь направление X совпадает с положительным направлением
х. Для других групп состояний и других параметров справед-
ливы аналогичные формулы. Среднее значение силы в равно-
весном состоянии ансамбля равно
<4Л28>
4.19. Связь между статистической механикой и термодинамикой 141
Подставим сюда пг из (4.115), тогда
(4.129)
4.19. Связь между статистической механикой и термодинамикой
Мы уже получили все законы распределения равновесного
(т. е. среднего) состояния для ансамблей почти независимых
систем. В дальнейшем эти законы мы обобщим на ансамбли,
у которых существует взаимодействие между системами. Рас-
смотрим сначала связь между уже полученными законами ста-
тистической механики и классической термодинамикой. При по-
лучении всех законов распределения мы совсем не обращались
к каким-либо термодинамическим представлениям, за исключе-
нием указания на то, что между 0 и абсолютной температурой
обязательно имеется связь. Понятия термодинамики и основы
статистической механики совершенно различны, последние в ос-
новном носят динамический характер. Обычный путь установ-
ления связи между ними сводится к тому, чтобы дать описание
свойств ансамбля в терминах, аналогичных термодинамиче-
ским, а затем доказать справедливость термодинамических за-
конов для ансамблей статистической механики. В последующих
пунктах будет приведено такое доказательство. И тогда мы
увидим, что вывод законов термодинамики не представляет ни-
каких затруднений.
4.20. Законы термодинамики
Так как основные законы термодинамики можно сформули-
ровать различными способами, то для наших целей установле-
ния связи со статистической механикой необходимо выбрать
наиболее подходящий из них. Поэтому естественно описать
именно то толкование законов,’которое будет изложено ниже.
Среди многих толкований некоторые очень логичны, но слиш-
ком абстрактны; мы выберем классическое толкование, которое
не слишком абстрактно. Однако установление связи между ним
и законами статистической механики является трудной задачей.
Поэтому придадим ему такую форму, которая непосредственно
выводится из классической, но является более удобной для на-
ших целей.
Для краткости опустим определение таких понятий, как
«термодинамическое состояние», «тепловая изоляция», «тепло-
вой контакт», «адиабатический процесс», «тепловое равновесие»,
142 Гл. IV. Общие теоремы для ансамблей стационарных систем
но все же подчеркнем, что их определение не содержит ссылки
на температуру.
Введем сначала понятие температуры. Для этого прежде
всего введем постулат, полученный в результате обобщения
опыта. Если два ансамбля находятся в тепловом равновесии с
третьим ансамблем, то они находятся в тепловом равновесии и
друг с другом. Отсюда следует, что условие взаимного теплово-
го равновесия между ансамблями состоит в равенстве некоторой
определенной однозначной функции термодинамических состоя-
ний ансамблей. Такая однозначная функция называется темпе-
ратурой t. Из такого определения температуры t следует, что
в качестве «термометра» можно выбрать любой ансамбль. Та-
кой же произвол имеется в выборе закона определения число-
вого значения температуры (шкалы).
Температура /, определенная таким способом, называется
эмпирической температурой в отличие от абсолютной темпера-
туры. Определение последней будет дано ниже. Например, эм-
пирическая температура t может быть определена посредством
измерения при постоянном давлении объема некоторого постоян-
ного количества произвольно выбранного вещества. Постулат
«температура является однозначной функцией термодинамиче-
ского состояния» можно назвать нулевым законом термодина-
мики.
Сформулируем теперь первый закон термодинамики. Если
теплоизолированный ансамбль различными путями может быть
переведен из некоторого состояния I в другое состояние II, то
работа w, произведенная таким ансамблем, будет иметь одно и
то же значение для каждого из этих (адиабатических) путей.
Отсюда следует, что существует такая однозначная функция Е
состояния ансамбля, которую мы называем полной энергией и
увеличение которой в любом адиабатическом процессе равно
работе, совершенной над ансамблем внешними телами. Таким
образом,
\Е = т&) (адиабатический процесс). (4.130)
Для теплоизолированных и механически изолированных ан-
самблей их полная энергия обязательно сохраняется постоян-
ной, т. е.
ДЕ = 0 (изолированный ансамбль). (4.131)
Отсюда следует, что результатом взаимодействия двух частей
изолированного ансамбля может быть только такой процесс,
при котором увеличение энергии в одной части равно уменьше-
нию ее в другой. Для того чтобы полная энергия Е имела ука-
занный смысл, необходимо и достаточно потребовать, чтобы
4.20. Законы термодинамики
143
имелась возможность с помощью адиабатического процесса пе-
реводить ансамбль из состояния I в состояние II или из состоя-
ния II в состояние I.
Определим теперь теплоту q, поглощаемую ансамблем, как
разность между полной энергией ансамбля и произведенной над
ансамблем работой внешних тел, т. е.
q = KE— w (любой процесс). (4.132)
Сформулируем второй закон термодинамики: существуют
две однозначные функции состояния, одна из них Т называется
абсолютной температурой, а другая S — энтропией, такие, что
1) Т является функцией только t;
2) энтропия ансамбля равна сумме энтропий всех частей
ансамбля;
3) для любого бесконечно малого изменения в совершенно
однородном ансамбле имеет место соотношение
q^TdS, (4.133)
где знак равенства соответствует квазистатическим процессам,
а знак неравенства соответствует естественным процессам (не-
обратимым процессам). Если ансамбль не полностью одноро-
ден, то соотношение (4.133) необходимо использовать для каж-
дой однородной части.
Приведенные три постулата являются основой термодина-
мики. Из них можно вывести все формулы термодинамики. На-
пример, из этих постулатов непосредственно можно вывести
формулу цикла Карно для коэффициента полезного действия
обратимого цикла. В действительности в термодинамике сравни-
тельно более употребительной является та часть, которая дает
условия полного равновесия ансамбля. Ниже мы кратко опи-
шем, каким образом из этих постулатов вывести условия тер-
модинамического равновесия. Если ансамбль находится в равно-
весии, то каждое мыслимое бесконечно малое изменение его яв-
ляется квазистатическим.
Из приведенного соображения и (4.133) следует, что при
полном равновесии для каждого процесса с бесконечно малым
изменением должно иметь место соотношение
q=T dS (равновесие). (4.134)
Учитывая (4.132), приведем (4.134) к виду
Т dS = dE — w (равновесие). (4.135)
Некоторые специальные формы этого выражения являются осо-
бенно важными. Приведем две из них.
144 Гл. IV. Общие теоремы для ансамблей стационарных систем
Для механически изолированных и теплоизолированных ан-
самблей
w = 0, dS = 0, dE—-Q (равновесие). (4.136)
Для механически изолированных ансамблей, находящихся в
термостате,
w = 0, dT— О, d(E—TS) — 0 (равновесие). (4.137)
Величина (Е — TS) называется свободной энергией и обозна-
чается через F. Она сыграет важную роль в последующих раз-
новидностях формулировок законов термодинамики, а также в
выводе законов термодинамики из законов статической меха-
ники.
До сих пор мы говорили о классических формулировках за-
конов термодинамической функции. Ниже разговор будет идти
об их применении. Предположим, что любой не вполне однофаз-
ный ансамбль можно разделить на несколько однородных ча-
стей, называемых фазами. Каждая фаза имеет свою энергию,
энтропию и температуру, а энергия или энтропия целого ан-
самбля равна сумме энергий и энтропий каждой из фаз. Для
того чтобы произвести полное описание состояний всего ансамб-
ля, необходимо произвести полное описание каждой из фаз. Для
этого необходимо сначала определить состав каждой из них,
т. е. числа NA, NB, . .. содержащихся в ней систем различного
типа, а также необходимо установить значение всех геометриче-
ских параметров х (в практических вопросах объем обычно яв-
ляется единственным часто употребляющимся параметром).
Но, кроме этого, фаза еще имеет одну степень свободы, по-
этому для полного описания фазы необходимо ввести еще одну
величину. В классической формулировке такой величиной яв-
ляется энтропия. В этом случае заданную фазу характеризуют
следующие независимые переменные: S, х2, ... , Na, NBi . . . ,
или, короче, S, х, N. Любые другие свойства фазы, например
общую энергию, можно считать функциями независимых пере-
менных S, х, N. Поэтому для всех изменений в фазе имеет мес-
то соотношение
dE=^dS + ^^dx^-^dN. (4.138)
Если изменения происходят при сохранении геометрического
параметра и химического состава, то (4.138) упрощается
dE = -гё-
\ X,
(4.139)
dS (х, N — постоянные).
4.20. Законы термодинамики
145
В этом случае Е является однозначной функцией S. Единствен-
ным процессом, который может происходить при постоянной
конфигурации и химическом составе, является поглощение или
отдача тепла, так как при сохранении конфигурации работа не
совершается. В этом случае (4.132) преобразуется к виду
q = dE.
Подставляя эту зависимость в (4.139), получаем
q = (~ds\r,NdS-
Если процесс поглощения квазистатический, то из (4.133) имеем
q~TdS.
Сравнивая два вышеприведенных соотношения, получаем
= r (4-140’
Так как при заданных х, W энергия Е является однозначной
функцией S, то соотношение (4.140) не должно зависеть от про-
цесса, который использовался при его выводе. Поэтому для лю-
бого процесса (4.138) можно написать в виде
dE=TdS + ^^dx + ^^dN. (4.141)
Если фаза находится в механическом равновесии с окружаю-
щей средой, то —dEjdx есть обобщенная механическая сила,
действующая со стороны фазы. Она имеет знак х и обозначает-
ся через X, Коэффициент dE/dN в (4.141) ввел Гиббс, он обоз-
начается через ц и называется химическим потенциалом. После
ввода этих обозначений (4.141) можно переписать в виде
dE=TdS — 2 Xdx+ £ ndN. (4.142)
Эта формула показывает зависимость Е от переменных S,
х, М Величина Е как функция этих переменных называется
термодинамическим потенциалом для переменных S, х, АЛ Фор-
мула (4.142) называется основной формулой термодинамики для
этой группы независимых переменных. Она справедлива для
каждой фазы ансамбля. При определении равновесных свойств
ансамбля, как правило, исходят из этих формул. Именно в та-
ком виде метод был первоначально применен Гиббсом.
Для каждой фазы ансамбля справедлива формула вида
(4.142). Из этих формул мы можем получить следующие вы-
воды:
10 Зак. 1299
146 Гл. IV. Общие теоремы для ансамблей стационарных систем
а) Теплота всегда переходит от фазы с более высокой тем-
пературой к фазам с более низкой температурой.
б) Любое перемещение геометрической границы между
двумя фазами происходит в сторону меньшего давления.
в) Химические реакции всегда происходят в таком направ-
лении, что определенная линейная комбинация химических по-
тенциалов уменьшается.
Из а) следует, что тепловое равновесие двух фаз имеет ме-
сто только при равенстве их температур. Этот факт уже изве-
стен нам из нулевого закона термодинамики. Так как для нас
основной интерес представляют равновесные свойства ансамбля,
нам нет необходимости рассматривать все следствия из пункта
а), достаточен вывод относительно ансамбля с одинаковой тем-
пературой.
В связи с этим второй закон термодинамики можно сфор-
мулировать в более простой и удобной, но менее общей форме.
Температуру ансамбля можно взять в качестве независимой
переменной вместо энтропии. Это и упрощает формулировку
второго закона. С помощью следующего равенства введем
функцию F и назовем ее свободной энергией
F — E—TS. (4.143)
Продифференцируем (4.143) и учтем (4.142). Тогда получим
dF = — SdT— 2 Xdx± 2 (4.144)
Формула (4.144) представляет собой основную формулу тер-
модинамики, в которой независимыми переменными являются
Т, х, N. Функция F по отношению к ним является термодинами-
ческим потенциалом. Формулу (4.144) можно по желанию счи-
тать одной из возможных формулировок второго закона термо-
динамики. С точки зрения статистики использование Г, х, N в
качестве независимых переменных более соответствует реаль-
ным экспериментам, чем переменных S, х, 2V. Однако пойдем
дальше и произведем еще одно преобразование—исключим
энтропию S.
На основании (4.144) имеем
# = (4.145)
Из (4.143) и (4.145) следует, что
d(F/T) _ 1 dF _F__ TS-\-F E
у J* 2 ^2 ’
4.20. Законы термодинамики
147
С помощью (4.146) исключаем S из (4.144). Окончательно по-
лучим
d^^-^dT-^^Xdx + ^iidN. (4.147)
Эта формула является основой другой возможной формули-
ровки второго закона термодинамики. Ниже мы приведем за-
коны термодинамики в том окончательном виде, который наибо-
лее удобен для наших целей. Нулевой закон, первый закон и
определение теплоты сохраняют первоначальную форму. Фор-
мулировка второго закона отличается от классической и имеет
следующий вид:
Второй закон: существуют две однозначные функции состоя-
ния, одна — Т, называемая абсолютной температурой; дру-
гая — F, называемая свободной энергией, такие, что:
1) Т есть функция только t;
2) свободная энергия ансамбля равна сумме свободных
энергий его частей;
3) если внешние тела производят над ансамблем работу в
изотермическом процессе, то всегда выполнено соотношение
dF^w (d,T = G). (4.148)
Знак равенства имеет место при квазистатических процессах,
а знак неравенства — при реальных (естественных) процессах;
4) если F рассматривается как функция от Т, х, N, то ее за-
висимость от температуры Т характеризуется соотношением
— <4.149)
Теперь посмотрим, как в новых условиях вывести законы
равновесия, аналогичные тем, которые получены при классиче-
ской формулировке законов термодинамики. Возьмем Т, х, N в
качестве независимых переменных. Тогда имеем
<<) = <4-15°)
Коэффициент при dT определяется из (4.149). Если воспользо-
ваться формулой (4.148) для условий квазистатического изме-
нения геометрических параметров ансамбля и при сохранении
химического состава, то получим— [dFldx}NT=X. Это выра-
жение может служить определением обобщенной силы.
Наконец, химический потенциал определим соотношением
/ dF \
\dNi /т, х,
(4.151)
10*
148 Гл. IV. Общие теоремы для ансамблей стационарных систем
И, следовательно,
d(£) = — ~dT — ±^Xdx + y 2 vdN
ИЛИ
Td (4-) = — ^dT — dx+S^dN. (4.152)
Эта формула совпадает с формулой (4.147), выведенной из
классической формулировки.
Квазистатичность всякого изменения состояния является обя-
зательным условием полного равновесия ансамбля. Согласно
(4.148), его можно записать в виде
сГГ — 0, dF = ,w (равновесие). (4.153)
Для химических изменений при сохранении геометрических пе-
ременных оно принимает следующую частную форму:
dT = 0, rfx = 0, dF = 0 (равновесие). (4.154)
Формула (4.154) является общей формой условий химического
равновесия.
Кроме ранее определенных функций Е, F, Г, ц, других термо-
динамических функций можно не вводить. Однако для полноты
можно определить и энтропию
S = (E — F)/T. (4.155)
Из (4.149) и (4.155) имеем
^ = г^)+л==_| + ^ = _5 (4156)
Можно определить энтропию при помощи (4.156), а (4.155) вы-
вести.
Функции Е, Г, Е, S являются единственными и не связаны
с выбором единиц измерения и выбором начала отсчета для
Е и S. Произвольная постоянная а в S появляется в виде аТ
в Е. Этот член совсем не влияет на свойства Е, а поэтому не
имеет и физического смысла.
4.21. Вывод термодинамики из статистической механики
В статистической механике нам уже известен закон, соответ-
ствующий нулевому закону термодинамики, а именно: ранее го-
ворилось, что параметр 0 обладает всеми свойствами темпера-
туры. Первый закон термодинамики тоже можно получить
непосредственно. Для этого достаточно отождествить полную
4.21. Вывод термодинамики из статистической механики
149
термодинамическую энергию с выражением
Е = Ё = ЁА = з, «А- (4.157)
Для того чтобы вывести второй закон в требуемой форме,
необходимо определить две подходящие функции в качестве Т
и F. Мы подчеркиваем, что это сделать можно. Так как 0 мож-
но рассматривать как эмпирическую температуру, то можно по-
пытаться использовать следующее выражение как определение
температуры Т;
= (4.158)
где k—произвольная постоянная, которая определяет величину
градуса температуры Т. Затем определяем F как
Е = ^аЕа, (4.159)
Fa In 0 = - In (1 ±X#')±1 -^1пХл. (4.160)
Далее необходимо показать, что F и Г, определенные таким
образом, обладают свойствами свободной энергии и абсолютной
температуры именно в той форме, на которой мы остановились
при формулировке второго закона. Аддитивность свободной
энергии непосредственно следует из определения F по (4.159).
Для того чтобы получить другие необходимые для F свойст-
ва, необходимо считать F функцией 0 (или Т), х и 2V. Тогда
Лд будет функцией 0, х, Nа 8Г только функцией х. Поэтому
полный дифференциал от FA In 0 равен
д(Рл 1п0) де дР.
“л9>“9 + 1"9S, Лс+|"dN*+
dF. ( д\„ дХ„ дКл )
+ 1п9тЛ(-Tr4-dln0 + -^-dx + -^.flW, . (4.161)
1 д^А j д 1 п 0 1 дх 1 cjNa а J v '
Найдем значение dFAld'kA и подставим в (4.161). Из (4.160),
используя (4.115), получаем
Хл1п0^- = 2 -----= S „Г_дгл = о. (4.162)
А Г 0 Г ± 1 Т
Отсюда следует, что все члены в (4.161), содержащие множи-
тель dFA/dKA, можно исключить и считать ХА постоянной. Тогда
(4.161) упрощается и приводится к виду
д(/7Л1п0) VI дР. де дР л
d V*°) = -г,,-, d8 +9 S, 157 si л +1"9 да; dN*-
(4.163)
150 Гл. IV. Общие теоремы для ансамблей стационарных систем
Дифференцирование здесь производится при постоянном Ха. Из
(4.160) и (4.117) получим
/4FAln9h = ^[F4lneh =
\ dln0 /х, Na \ <?InO Jx,na,ka
= 0^Sr®Jn(1 (4-164)
Аналогично этому из (4.160) и (4.129) получим
Из (4.160) следует
— g
ЮЛ9Г дЕг=_х. (4.165)
1±л.еЕг дх
А
Подставим (4.164), (4.165) и (4.166) в (4.163) и произведем
суммирование по всем группам систем. Используя (4.159), полу-
чаем
d (F In 0) = Ed In 9 — In 0 2 Xdx — 2a In ^A dN A. (4.167)
Подставив вместо 0 его выражение через Т (4.158), получим
d (-£-) = — ^dT — ^Xdx+k^\nlAdNA. (4.168)
Формула (4.168) получена на основании определения функ-
ций Т и F с помощью формул (4.158), (4.159) и (4.160) и фор-
мул статистической механики. Из сравнения (4.167) с термоди-
намической формулой (4.147) видим, что если считать Е и Ё, X
и X одинаковыми величинами, то зависимость F от Т и х в обо-
их формулах одинакова. Этим мы частично доказали, что Г,
определяемое в (4.158), и F, определяемое в (4.159), представ-
ляют собой термодинамическую абсолютную температуру и тер-
модинамическую свободную энергию. Для доказательства их
полной тождественности необходимо доказать, что члены с
в (4.168) и (4.147) эквивалентны. Если они эквивалентны,
то между X и химическим потенциалом ц существует следующая
связь:
цл = &Г1пХл или ХЛ = ^Л^Г. (4.169)
Если теперь доказать справедливость (4.169), то тем самым
будет доказана эквивалентность членов с dN А и, следовательно,
доказана тождественность функции F, определяемой соотноше-
4.21. Вывод термодинамики из статистической механики
151
ниями (4.159), (4.160), с термодинамической свободной энер-
гией.
Критерием правильности соотношения (4.169) является то-
ждественность условий полного равновесия, получаемых стати-
стическим и термодинамическим методами. К настоящему мо-
менту полного доказательства такой тождественности при об-
щих условиях мы дать еще не можем. Однако для частного
вида равновесия такое доказательство может быть проведено.
Все равновесия можно разделить на два типа: фазовое, или фи-
зическое равновесие — равновесие каких-либо систем, распре-
деленных между несколькими частями (фазами) ансамбля, и
химическое равновесие — равновесие между взаимопревращае-
мыми системами в ансамбле. А так как в настоящей главе мы
имеем дело только с ансамблями, состоящими из неизменных
систем, то докажем (4.169) для случая фазового равновесия.
Исследуем сначала статистические условия равновесия ан-
самбля из двух фаз. Как правило, значками А, В, ... мы обо-
значали группы тождественных систем, т. е. систем, которые в
каждой группе имеют одинаковые допустимые состояния. Дру-
гими словами, все системы А не только должны иметь одина-
ковый химический состав, но и должны находиться в одном и
том же сосуде. Если имеются две группы систем с различными
химическими свойствами, причем системы каждой группы
имеют одинаковые химические свойства, но помещены в разные
сосуды, находящиеся в тепловом контакте, то все полученные
результаты могут быть применены и к этому случаю. Для этого
достаточно обозначить две группы химически одинаковых си-
стем, находящихся в разных оболочках, различными символами
А, А', В, В'. Здесь одинаковые буквы обозначают тождествен-
ность химического состава, а штрих наверху — различные со-
суды.
Температура (0 или Т) этих двух частей ансамбля одина-
кова, но значения Ха для различных сосудов, вообще говоря,
могут быть различными. Обозначим их через Ха, Хв в одном
сосуде, Ха, Хв—в другом. Теперь устраним барьер между
двумя фазами и заменим его на полубарьер, проницаемый толь-
ко для систем А (конечно, включая и А'). В этом случае А и
А' перераспределяются в двух сосудах вплоть до установления
равновесия. Такого изменения не произойдет лишь в том слу-
чае, если и до устранения барьера эти сосуды уже находились
в равновесии.
Однако из статистической теории известно, что если для си-
стем группы А (включая А') все состояния со штрихом наверхх
и без него являются допустимыми, то все состояния группы А
(включая А') вне зависимости от того, в каком сосуде они
152 Гл. IV. Общие теоремы для ансамблей стационарных систем
находятся, будут иметь одинаковое значение Ха- Следовательно,
если при удалении барьера никаких изменений не происходит,
то величина Ха должна иметь одинаковое значение в обоих со-
судах, именно то, какое она имела до удаления барьера. Таким
образом, для систем группы А условие равновесия между двумя |
сосудами имеет вид ’
Х;=ХЛ. (4.170)
Для остальных видов систем В, С, ... с другим химическим {
составом имеют место аналогичные условия равновесия. 1
Покажем теперь, что статистические условия равновесия
(4.170) и термодинамические условия равновесия двух фаз ।
эквивалентны. В п. 4.20 было показано, что термодинамическое
условие полного равновесия выражалось формулой (4.154). Рас-
сматриваемый нами процесс представляет собой перенос систем
с некоторым вполне определенным химическим составом из
одной фазы в другую при постоянной температуре и постоянной
геометрической конфигурации. Для такого простого процесса
условие (4.154) записывается в виде
Ид dN А + Ид dN'A = О,
где dN А и dNA удовлетворяют соотношению
dNA-\-dNA = 0. ,
Здесь верхний индекс обозначает вторую фазу. Исключив из
этих двух уравнений dNA и dNд, получим термодинамические
условия равновесия двух фаз
Нд=^. (4.171)
Если X и ц связаны выражением (4.169), то очевидно, что
(4.170) и (4.171) являются эквивалентными. Поэтому условия
равновесия двух фаз (4.170), полученных из законов статисти-
ческой механики, одинаковы с условиями равновесия (4.171)
двух фаз, полученных из термодинамических законов путем на-
хождения минимума функции F при заданных Т и х. I
Полученные здесь условия фазового равновесия в действи-
тельности верны и для химического равновесия. Это тоже может
быть доказано, но мы не будем приводить здесь подробного
доказательства. Общий вид равновесия может быть получен по-
средством суперпозиции этих двух типов равновесия. Таким об- I
разом, полностью доказано, что F, определяемое (4.159) и 1’
(4.160). обладает всеми важными свойствами свободной энер- I
4.21. Вывод термодинамики из статистической механики
153
гии в термодинамике. Одновременно из сравнения (4.125) с
(4.168) можно найти, что предполагаемая раньше связь между
статистической температурой и термодинамической температу-
рой (4.158) тоже является правильной.
В настоящем пункте термодинамические законы были полу-
чены из статистической механики и при этом нигде не была
использована гипотеза Больцмана относительно связи энтропии
с вероятностью состояния в статистической механике. При та-
ком построении гипотеза Больцмана стала теоремой, которая
может быть выведена. Хотя гипотеза Больцмана появилась
сравнительно давно и к тому же достаточно обоснована, но ме-
тод, который здесь выбран, с точки зрения логики, более строг
и более четок.
Таким образом, законы термодинамики теперь выведены на-
ми из законов статистической механики ансамблей постоянных
систем. Вызывает удовлетворение тот факт, что, хотя термоди-
намика была построена, опираясь на опытные данные, до обна-
ружения квантовых эффектов, последние никак не отразились
на ее общих законах. С точки зрения излагаемой физической
механики еще большего внимания требует тот факт, что даже
при неизвестных априори закономерностях термодинамики мож-
но вывести их с помощью строгих статистических методов, опи-
раясь только на микроскопические свойства систем ансамблей,
описываемых квантовой механикой.
Значение такой возможности особенно четко проявляется в
следующей задаче: требуется получить термодинамические за-
кономерности газа при сверхвысокой температуре в несколько
тысяч миллиардов градусов. Это связано с тем, что, с одной
стороны, не известно, как осуществить эксперимент при таких
высоких температурах в лабораторных условиях, поэтому не-
возможно получить экспериментальные данные, а с другой сто-
роны, известно, что при такой высокой температуре относитель-
ная скорость частиц, образующих газ, близка к скорости света,
и их движение нельзя рассматривать при помощи классической
механики или классической квантовой механики, описание ко-
торой было дано во второй главе, а необходимо применить ме-
ханику теории относительности.
Однако теперь мы уже владеем аппаратом теории относи-
тельности, к тому же на основе большого экспериментального
материала знаем о характере различных процессов между
элементарными частицами, составляющими вещества, при энер-
гиях движения в миллиарды электрон-вольт, т. е. ясно себе пред-
ставляем микроскопические закономерности, соответствующие
нескольким тысячам миллиардов градусов. Поэтому, если по-
явится необходимость, мы можем на основе микроскопических
154 Гл. IV. Общие теоремы для ансамблей стационарных систем
закономерностей, имеющих экспериментальную основу, пол-*
ностью вывести макроскопические закономерности термодина-
мики для температур в несколько тысяч миллиардов градусов.
Для этого уже нет необходимости действительно проводить ма-
кроскопический эксперимент при сверхвысоких температурах.
Все это говорит о глубине и силе научных теорий.
4.22. Соотношение между величинами термодинамики
и статистической механики
В предыдущих пунктах было показано, что законы равно-
весия, вытекающие из статистической механики и термодина-
мики, эквивалентны. Поэтому можно по мере надобности обра-
щаться и к формулам термодинамики. Это вполне допустимо,
лишь бы было для нас удобно. Напомним еще раз о тех связях,
которые существуют между различными величинами статисти-
ческой механики и термодинамическими функциями. В будущем
это нам пригодится. Прежде всего выполнено следующее соот-
ношение между шкалами статистической и термодинамической
температур
о = иди <4.!72)
Полная термодинамическая энергия Е равна средней стати-
стической энергии Е. Одновременно из (4.129) и (4.168) сле-
дует, что свободную энергию можно рассматривать как потен-
циал для среднего значения силы при изотермических измене-
ниях. Таким образом, мы имеем следующие крайне простые со-
отношения:
Е = Ё, (4.173)
Подставив (4.172) в (4.160), получим
FA = — ±\Ае~*'1кТГ'+ NAkT\nKA, (4.175)
в то время как
F^aFa- (4-176)
Аналогично подставив (4.172) и (4.173) в (4.117), получим
£ —____Т2 - ^А^.1 — V (4 J 77)
Е = ^аЕа. (4.178)
4.22. Связь термодинамики и статистической механики
155
Соотношение между статистическим параметром Ха и химиче-
ским потенциалом цд имеет вид
цд = АПпХл. (4.179)
Параметр Ха называется абсолютной активностью систем Л,
а имеющаяся в термодинамике относительная активность аА
определяется соотношением
Ид = ^(Л + ^1п аА, (4.180)
где ц^(Г)— произвольная однозначная функция Т. Из соотно-
шения для Ха и ца можно найти, что условием равновесия си-
стем Л, составляющих две части (I и II) ансамбля, можно вы-
разить в одной из эквивалентных формул
= = (4.181)
Из приведенных соотношений между статистическими и тер-
модинамическими величинами можно вывести термодинамиче-
скую формулу
dfy) = -^dT-^XAdx + ±itAdNA (4.182)
или, производя суммирование по всем видам систем,
</(£) = — JpdT—±^Xdx + ±^vdN. (4.183)
Как описано в п. 4.20, энтропия S определяется следующими
двумя выражениями:*
5 = (4.184)
SA = (EA-FAYI\ (4.185)
откуда следует, что
=-s* (4-186)
Подставив (4.175) и (4.177) в (4.185), получим статистическую
формулу для энтропии систем Л:
= k ln (1 ± ЕгД6г *л-
V Т '^А'± 1
(4.187)
156 Гл. IV. Общие теоремы для ансамблей стационарных, систем
4.23. Термодинамические формулы классической статистики
Ранее было показано, что законы термодинамики, получен-
ные из статистик Ферми — Дирака и Бозе — Эйнштейна, оди-
наковы. Кроме того, известно, что статистические формулы ан-
самбля локализованных систем можно рассматривать как пре-
дельные при для статистической формулы Ферми — Ди-
рака или Бозе — Эйнштейна и, следовательно, статистика лока-
лизованных систем приводит к тем же самым законам термоди-
намики. Мы уже упоминали, что условие выполняется
почти для всех ансамблей. В этом случае все три типа статисти-
ки имеют один и тот же вид, т. е. вид классической статистики.
При мы с достаточной точностью имеем
In {\±\Ае-гг1кТ^=\Ае^г1кТ.
Поэтому (4.175) упрощается и приводится к виду
FA = -kT\AjA{T)^NAkT\nKA.
Подставляем (4.120)
^a = naHAT)
и получаем
Fa = - KAkT {In fA (T) - In Na 4- 1}. (4.188)
Продифференцируем (4.188) no NA и воспользуемся определе-
нием (4.151). Тогда получим
(4.189)
С другой стороны, (4.189) можно получить подстановкой
(4.120) в (4.179).
В дальнейшем нам постоянно будут нужны выражения
(4.188) и (4.189). Основной задачей дальнейшего изложения
будет вычисление функции состояний fA(T) для различных ти-
пов ансамблей. Если функция состояний известна, то из (4.188)
получим свободную энергию ансамбля. Применяя затем обыч-
ные законы термодинамики, можно вывести любые необходи-
мые нам равновесные свойства. Например, из (4.188) можно по-
лучить энергию Еа
д(РЛ/Т\ dinfA (Г)
= -W) = ~ от (4.190)
и обобщенную силу ХА, соответствующую обобщенной коорди-
нате х,
d/7 л д In/. (Г)
= = (4.191)
4.24. Постоянная Больцмана и газовая постоянная
157
Вклад теплоемкости &а систем А в теплоемкость всего ан-
самбля при постоянном значении геометрического параметра
равен
сл' = -^. (4.192)
После подстановки (4.190) получим
C{f^NAk-^^
d'*fAW\ „ J'\2d^A^
дТ I д(\/Ту
(4.193)
4.24. Постоянная Больцмана и газовая постоянная
В соотношение, характеризующее связь статистической 9 и
термодинамической Т шкалы температур, входит постоянная fe,
которая определяет лишь величину температуры на шкале Т и
ее знак. Рассмотрим сначала вопрос о знаке. Если выражение,
определяющее подставить в (4.193), а затем продиффе-
ренцировать его, то получим
C%}lNAk = (Р In ^е~Ег/кт) =
1
Л272
1
2A2r2
-ег/^
е*/кТ
«Xе
1 £Г<М^-Ф~(С^Г
2^7-2 (2r Zre~er/ky
Принято считать, что Е увеличивается при увеличении абсолют-
ной температуры Т, т. е. Сдх) всегда является положительной.
В таком случае постоянная k тоже положительна.
Значение k выбирается таким образом, чтобы интервал тем-
ператур между точками замерзания и кипения воды при атмо-
сферном давлении был равен 100°. Определяемая таким обра-
зом шкала температуры называется шкалой Кельвина Г, а
численное значение k равно (1,38042±0,00010) X Ю-16 эрг/град,
постоянная k является универсальной и обычно называется по-
стоянной Больцмана.
Среднее значение любой экстенсивной величины, рассчи-
танной на 1 грамм-молекулу, равно ее среднему значению,
158 Гл. IV. Общие теоремы для ансамблей стационарных систем
приходящемуся на одну молекулу, умноженному на постоянное
число Авогадро N,
[N = (6,02472 ± 0,00063) X Ю23 грамм-молекул].
Если энергии 8Г отнесены к одной грамм-молекуле, то k сле-
дует заменить на R
R = Nk. (4.194)
R называется газовой постоянной и имеет значение (8,31662±
±0,00038) X 107 эрг)г • моль • град, или 1,986 кал/г • моль • град.
*
4.25. Выражение законов распределения через температуру
Кельвина
Поскольку мы уже установили между 0 и Т соотношение
(4.172), будет удобнее выразить закон распределения через
температуру Т. Подставим (4.172) в (4.115) и получим
пг = И---------->
Лд
где определяется из необходимого условия
Для классической статистики (%а<С1) соотношение
упрощается
- « ~ _Лг е^кГ д7 в>ге
пг NА „ ~ -tJkT Мд f (Т)
<t>re г' 'л' '
Формула (4.197) была получена подстановкой (4.172) в (4.176).
(4.195)
(4.196)
(4.195)
(4.197)
Глава V
ИДЕАЛЬНЫЕ ГАЗЫ
Идеальный газ определим как ансамбль систем, энергией
взаимодействия которых можно пренебречь. Общая энергия
ансамбля представляет собой сумму энергий поступательного
движения различных систем, а также вращательной, колеба-
тельной и электронной энергий, отнесенных к осям, проходя-
щим через центр инерции каждой системы. Для удобства
назовем сумму вращательной, колебательной и электронной
энергий внутренней энергией. После этого разложим функцию
состояний f(T) на два множителя, один из которых, /(Г), отно-
сится к энергии поступательного движения, другой, ЦТ),— к
внутренней энергии. Если вращательное и колебательное дви-
жения можно рассматривать независимо, то /(Г) в свою оче-
редь распадается на множители r(T), g(T) и е(Г), соответст-
вующие вращательной, колебательной и электронной энергиям.
Вначале мы не будем учитывать структуру ядра, т. е. будем
рассматривать ядро как материальную точку, затем сделаем
необходимые поправки к полученным результатам.
Начнем с поступательного движения молекул идеальных
газов. Так как одноатомные молекулы обычно не имеют изме-
нений внутренней энергии, то многие их свойства полностью
определяются функцией состояний ЦТ) поступательного движе-
ния. В дальнейшем рассмотрим вращательное и колебательное
движения, для того чтобы вывести свойства газов, состоящих иэ
двухатомных и многоатомных молекул.
В четвертой главе свободная энергия F и общая энергия Е
были выражены в виде суммы величин FA, FBi ... и ЕА, Ев,...,
относящихся к каждой из систем Л, В, ... . Условием того, что
F и Е могут быть выражены в этой форме, является отсутствие
заметного взаимодействия между системами А и В. Это усло-
вие выполняется, когда системы Л, В, ... помещены в различ-
ные оболочки или когда ансамбль представляет собой идеаль-
ный газ. Если Вв, ... и Еа, Ев, ... — вклады однородных
фаз, то имеет место первый случай. Ансамбли, рассматриваемые
в этой главе, соответствуют второму случаю.
160
Г л. V. Идеальные газы
5.1. Квантование поступательного движения
В четвертой главе была выведена формула для поступа-
тельного движения ансамбля частиц, заключенных в оболочке.
Нас интересует здесь случай, когда применима классическая
статистическая механика. Пусть масса молекулы типа А рав-
на тА\ тогда, согласно (4.124), функция состояний /Л(Г) посту-
пательного движения молекул равна
lA (Т) = (2лтАк Г)’/г V7A3. (5.1)
Отсюда по (4.188) получим свободную энергию
F=-kTyiNA{\nlA(T)JA(T)-lnNA + \} =
А
I (2лт AkT\ l2V I
= ---V-------ln^+1 \~kT^NA\njA(T)==
A A
mV I (2л 7П 1 (
= -kT^NA (in*-------------1п^л + 1 (5.2)
A
где —вклад внутренних степеней свободы (включая враща-
тельную). По их природе можно считать, что ]'а(Т) и FW не
зависят от V. Если V принять за параметр или обобщенную
координату, то соответствующей обобщенной силой будет да-
вление Р, которое может быть выражено в виде
Р = — dF/dV = NAkT!V. (5.3)
А
Это хорошо известное уравнение состояния смеси идеальных га-
зов. Оно включает законы Бойля, Шарля, Авогадро и Дальтона.
Для ансамбля, состоящего из молекул одного типа, уравнение
(5.3) приводится к простой форме
P = NkT/V. (5.4)
Следует, однако, сказать несколько слов относительно об-
ласти применимости этого уравнения. Поскольку все реальные
газы не являются идеальными, то, строго говоря, свойства
идеальных газов нельзя наблюдать. Однако соответствие между
наблюдаемыми свойствами реальных газов и свойствами
идеальных газов становится тем лучше, чем меньшей становит-
ся плотность реальных газов. Таким образом, идеальный газ
представляет собой экстраполяцию реального газа к нулевой
плотности. В этой главе будем считать, что такая экстраполяция
уже сделана. Уточненные формулы будут приведены в восьмой
5.1. Квантование поступательного движения 161
главе. Кроме случая систем при температуре, близкой к абсо-
лютному нулю, когда используется статистика Ферми — Дирака
или Бозе — Эйнштейна, уравнение (5.3) обычно является точ-
ным пределом для уравнения состояния недиссоциирующихся
газов и газовых смесей при различных температурах. При
давлении в одну атмосферу уравнение состояния большинства
простейших газов очень близко к своей предельной форме даже
при очень низкой температуре.
Нам потребуются следующие две формы уравнения (5.3):
1) Если парциальное давление рА системы А в газе (иде-
альном или неидеальном) определить формулой
Рл=^-Р> %Ра=Р> (5.5)
% А
то, согласно (5.3), для идеального газа имеем
pA = KAkT/V. (5.6)
2) Для любой фазы парциальный молекулярный объем Va
системы А в термодинамике определяется как
VA = (dV/dNA)TP. (5.7)
Для идеального газа из (5.3) находим
VA = kT/P. (5.8)
Из (5.2) можно получить общую энергию газа
Е = - р = £(Л (5.9)
А
где — энергия внутренних степеней свободы (вращательных
и колебательных), не зависящая от V (или Р).
Молекулярная энергия Ел системы А в любой фазе термоди-
намически определяется выражением
EA = (dE/dNA)T,P. (5.10)
Следовательно, для любого ансамбля
E = ^NAEA. (5.11)
А
Согласно (5.9), для идеального газа получим
EA=3.kT + E(J), (5.12)
где Е^ не зависит от V (или Р).
Н Зак. 1299
162
Гл. V. Идеальные газы
В идеальных газах, когда Е не зависит от V (или Р), имеем
любопытный результат
(dE/dN^, v = Ea = (dE/dNA)T< Р. (5.13)
Однако необходимо помнить, что (5.13) верно только для
идеальных газов, а соотношения (5.10) и (5.11) имеют место
для всех однородных фаз. Далее мы увидим, что для свобод-
ных электронов в металле (5.11) применимо, а (5.13) нет.
Предположим, что газ помещен в прямоугольный ящик. Со-
гласно рассуждениям в п. 4.17, поступательное движение можно
разложить на движения, параллельные трем сторонам ящика.
При этом функция состояний I (Т) распадается на множители
1Х(Т), 1У(Т), lz(T), соответствующие направлениям этих трех
движений. Энергии являются аддитивными. Согласно (4.121),
уровни энергии движения вдоль оси х равны
где а — длина ящика в направлении %, а квантовое число г мо-
жет принимать любые положительные целые значения. При
движении в этом направлении состояние полностью описывается
квантовым числом г, поэтому вес каждого состояния равен 1.
Функция состояний для движения в направлении оси х равна
/ /'ГХ V ( r2h2 1 ( r2h2 ) ,
— lexP 8rn.a2kT -J ехр|— 8m,a2kT —
Г 4 A J 0 k A J
= (2nmAkT)'12-^-. (5.15)
Заменяя сумму интегралом, необходимо предположить, что
h2/(8mAa2)<^kT. (5.16)
В п. 4.17 мы уже убедились, что это условие удовлетворяется
для обычных газов. Число молекул, находящихся в состоянии
г, равно
NAh ( — r2h2 )
яг = Л/лехр {— zrlkT}llx (Г) = „ exp . (5.17)
Квантовое число г имеет простой физический смысл. Квадрат
импульса для состояния г в направлении х равен
|Л|2 = ^2/4^2,
ИЛИ
г = 2а | рх \jh.
(5.18)
5.2. Классический вывод закона Максвелла
163
Поэтому с достаточной точностью можно сказать, что число
уровней энергии для поступательного движения в направлении
х, при которых абсолютная величина импульса находится меж-
ду I Рх | и | рх | + d | рх |, равно 2d | рх | . В то же время энергия
ег может быть выражена в виде
= уI Рх \2/тл- (5.19)
Среднее число молекул, имеющих абсолютные величины им-
пульсов между |рх| и | рх | -\-d | рх |, равно
_________ ^{Px?lnlAkT\&alh'>d\Px\
n[d\px\) = -^-----1—2 1------—. (5.20)
J* exp | — J I px \2imAkT | (2Л/Й) d. | px |
0
Пределы интегрирования в знаменателе обусловлены тем, что
| | может быть только положительным. После вычисления ин-
теграла в (5.20) находим соотношение
________ ЛС г 1 I
п (d I Рх I) = .T^t exp — - | px \2/mAkT 2c? | px |, (5.21)
которое представляет собой закон Максвелла, выведенный из
квантовой статистики. Перед d | рх | имеется множитель 2, по-
тому что в классической механике каждому интервалу от рх до
px + dpx соответствует интервал от —рх до —(рх + ^Рх), а в
квантовой механике мы можем описать только движение моле-
кулы в обоих направлениях с постоянным значением величины
импульса | рх |, но с переменным знаком.
5.2. Классический вывод закона Максвелла
Формула (5.21), строго выведенная из квантовой механики,
аналогична закону распределения Максвелла. Однако только
такой способ вывода этого хорошо известного закона вряд ли
удовлетворит кого-либо. Уже указывалось, что ограничения,
налагаемые на допустимые состояния квантовой механикой,
обычно играют небольшую роль для систем, находящихся в га-
зовой фазе; к тому же интервал между значениями энергий по
сравнению с величиной kT очень мал даже при понижении тем-
пературы до 1° К. Поэтому при выводе закона распределения
Максвелла и аналогичных классических теорем естественнее на-
чинать с классических методов. Такой подход ценен еще тем,
Ц*
164
Гл. V. Идеальные газы
что он позволяет лучше видеть физический смысл результатов.
Переходим к его изложению.
Для простоты предположим, что ансамбль содержит N ча-
стиц одинаковой массы т, которые свободно движутся в объеме
V. Его энергия представляет собой лишь энергию поступатель-
ного движения. Рассуждения будут применимы также и к ан-
самблям, содержащим совокупность таких систем (смесям).
Внутренние степени свободы молекул (вращательные и колеба-
тельные) могут быть учтены через отдельные функции распре-
деления.
Фазовое пространство свободного атома характеризуется
шестью координатами х, у, z, рх, ру, pz. Разделим его на малые
ячейки с объемом
d®r = (dxdydzdpxdpy dp^r. (5.22)
Согласно положениям п. 3.5 и 4.2, соответствующий вес равен
br = darl№. (5.23)
Чтобы учесть тот факт, что системы ограничены объемом V,
предположим вначале, что они находятся во внешнем силовом
поле с потенциальной энергией и, а затем преобразуем это поле
так, чтобы оно выполняло граничную роль стенок сосуда. Энер-
гия, связанная с r-й ячейкой, равна
',=®гИ+^+/’Э + “' <5-24>
где и — функция х, у, z, не зависящая от рх, ру, pz. Все точки,
находящиеся в элементе фазового пространства day, соответ-
ствуют одному вырожденному состоянию системы с энергией
ег и весом (5.23).
Функция состояний /(Т) в таком случае равна
ЦЛ = ехр {—er/kT}, (5.25)
или после интегрирования
оо оо со сю оо оо
/(0 = -^- f dx f аУ f dz f dPx fdPyfdPzX
— oo —co —co — oo —co —co
xexp{-[i(^+^+^)+«]A7'}- <5-26)
Для ансамбля, ограниченного объемом V, граничные условия
можно представить так:
^ = 0, х, у, z внутри V\
U = оо^ х, у, z вне V. (5.27)
5.2. Классический вывод закона Максвелла
165
Поскольку
dV = dxdydz, (5.28)
то
= рР,рР.ехр{-(',’+2^+,,а}. (5.29)
где интегрирование по V распространяется на объем, о котором
говорилось выше. Вычислив остальные интегралы, получим
l(T) = (2nmkT^ V/h\
что совпадает с (5.1). Среднее число молекул, состояние кото-
рых изображается точками, находящимися в элементе объема
фазового пространства da = dx dy dz dpxdpydpz, равно
«(rfo) = y-(2л/и^7')"’/2 exp| —x
Xdxdy dzdpxdpydpz. (5.30)
Это и есть закон Максвелла.
Интегрируя по рх, ру, pz, получаем физически четкий и яс-
ный результат: среднее число молекул в элементе объема dV
равно
= (5.31)
Это означает, что в объеме с однородным полем потенциала
молекулы распределяются однородно. Аналогично, интегрируя
по х, у, z в (5.30), получаем среднее число частиц с импульсами,
лежащими в интервалах рх, Px + dpx; Ру, Py + dpy; pz, pz + dpZi
n(dpx, dpy. dpz} =
— N (2nmkT)~'h exp {— j + ptynikT| dpx dpy dpz. (5.32)
Соотношение (5.32) можно записать и в другой форме. Среднее
число молекул, обладающих компонентами скорости в интер-
валах и, u+du; v, v + dv; w, w + dw, равно
n(du, dv, dw) =
= N (ml'lnkT)*1' exp| — (a2 + + w^/kT }dudvdw. (5.33)
Это и есть закон Максвелла для распределения скоростей мо-
лекул.
166
Гл. V. Идеальные газы
5.3. Классическая статистика и классическая механика
В п. 4.16 рассматривались три вида статистик: статистика
локализованных ансамблей, статистика Ферми — Дирака, при
которой собственные функции антисимметричны относительно
всех одинаковых систем, и статистика Бозе — Эйнштейна, при
которой собственные функции симметричны относительно всех
одинаковых систем. Вместо этого часто можно использовать
одну и ту же статистику для всех ансамблей. Такое универсаль-
ное описание всех трех видов ансамблей получило название
классической статистики. Условие для ее применения, грубо
говоря, заключается в том, что число состояний с не слишком
большой энергией должно быть значительно большим, чем
число систем в ансамбле. Обычно, за исключением свобод-
ных электронов в металле, все ансамбли удовлетворяют этому
условию.
Формулы классической статистики с динамической точки
зрения представляют собой формулы квантовой механики, по-
скольку они относятся к квантовым состояниям системы. С дру-
гой стороны, классическая механика описывает энергии,
импульсы и другие величины без какой-либо связи с квантова-
нием. Вообще говоря, можно считать, что классическая меха-
ника является приемлемым приближением до тех пор, пока ин-
тервалы между квантовыми уровнями энергии намного меньше
всех энергий, встречающихся в рассматриваемой задаче. В ста-
тистической механике самой важной и часто единственной
величиной, связанной с энергией, является kT, поэтому в каче-
стве общего правила можно не пользоваться квантовой теорией
тогда, когда интервалы между уровнями энергии меньше kT.
Именно такое явление наблюдалось при изучении поступатель-
ного движения газовых молекул. Выражение классическая сте-
пень свободы будем использовать для обозначения любой сте-
пени свободы, к которой с достаточной точностью применима
классическая механика.
5.4. Классические и невозбужденные степени свободы
Для любой классической степени свободы функция состоя-
ний получается предельным переходом от суммы к интегралу.
Поэтому для одной классической степени свободы
f(T) = ±fe~^dxdpx. (5.34)
Условием того, чтобы некоторая степень свободы была класси-
ческой, является малость по сравнению с kT интервалов между
5.5. Электронные степени свободы
• 167
соседними уровнями энергий. Наоборот, в противоположном
случае
ei — ео k (5.35)
где ео, ei обозначают энергии наинизшего и следующего за ним
уровней энергии. В этом случае от функции состояний остается
лишь первый член
f(T) = ®Qe-^kT. (5.36)
Такую степень свободы называют невозбужденной. Обычно са-
мое низкое энергетическое состояние каждой степени свободы
удобно брать за нуль, так что ео = О, а (5.36) упрощается
/(Л = ®о (ео = О). (5.37)
5.5. Электронные степени свободы
В функции состояний j(T) для внутренней энергии есть мно-
житель, который является вкладом энергии электрона. Каждый
электрон имеет четыре степени свободы: три степени свободы
поступательного движения и одна — спина. При обычных усло-
виях интервал между наинизшим и следующим энергетиче-
скими уровнями электрона для большинства, но не для всех
молекул, намного больше kT. Поэтому электронные степени
свободы обычно являются невозбужденными. Функция состоя-
ний е(Т) электрона имеет тогда только один член иоехр (—EQ/kT),
где иг — вес r-го энергетического уровня электрона. Если энер-
гию отсчитывать от основного уровня молекулы, то е(Т) будет
просто равна ио. Поэтому нужно лишь ввести множитель и0 в
функцию состояний, чтобы исключить из рассмотрения элек-
тронные степени свободы. В отдельных случаях, например у
газа NO, нельзя пренебрегать вторым электронным уровнем, и
тогда вместо ио следует поставить и0 + щехр (—&\/kT).
5.6. Теплоемкость идеальных газов
Согласно (5.12), энергия одной молекулы идеального газа
равна
E = ^kT + £(У>. (5.38)
где не зависит от V (или Р).
По определению молекулярной темплоемкости Cv при по-
стоянном объеме
с,= (^)и (5.39)
168
Г л. V. Идеальные газы
из (5.38) имеем
г _ 3 , , dE^
Ч' —jy-.
(5.40)
Аналогично молекулярная темплоемкость СР при постоянном
давлении равна
Так как энергия идеального газа не зависит от Р или V, то на
основании (5.8)
CP = CV + P(^\ =^k+^+k. (5.42)
Сравнивая (5.40) и (5.42), получаем
Ср- Cv = k. (5.43)
Как известно, соотношение (5.43) выполняется в газах доста-
точно точно, так что когда найдена одна из величин СР, Cv или
их отношение у = СР1Су, то легко определить и другую или ка-
ждую по отдельности.
Для более глубокого анализа нужно знать форму Е^\ что
в свою очередь требует изучения внутренних степеней свободы.
Для этой цели удобно рассматривать отдельно газы с одно-
атомными, двухатомными и многоатомными молекулами.
5.7. Одноатомные молекулы
Если электронные степени свободы являются невозбуждеи-
ными, то одноатомная молекула не имеет внутренних степеней
свободы (за исключением ядерного спина). При этом функция
состояний ЦТ) внутреннего движения сводится к и0, если энер-
гию отсчитывать от нижнего энергетического уровня электрона.
Для поступательного движения функция состояний дается фор-
мулой (5.1). Следовательно, функция состояний одноатомной
молекулы имеет вид
= ---hT—«о- (5.44)
Согласно (4.188), свободная энергия ансамбля из N молекул
F = — Д^Пп {(2nmkTJ/2-Xyo |_|_NkT(In N — 1) =
= NkT{ In £ - 1} -1NkT In Г — ^Пп { ®ят£'1гp° j. (5.45)
5.7. Одноатомные молекулы
169
Для энергии Е и давления Р имеем
Е = -Т*Ш^\ (5.46)
\ дТ /V. N 2 v ’
п (dF\ NkT
p==~\-dv)T,N = -v~- <5-47)
Химический потенциал равен
ц = = kTln£ — %kTlnT—kTln( u° ], (5Д8)
\ ON /т, V V 2
или no (5.6)
H = ^rinp — — }• (5.49)
Согласно (5.46), молекулярная энергия одноатомного газа
(при нулевой энергии низшего состояния) равна
E = ^kT. (5.50)
Таким образом, по формулам п. 5.6 имеем
cv = ±k,
cp=^k,
С„ 5
? = < = ?• (5.51)
Из трех величин Су, СР, у наиболее трудной для измерения
является Cv. Обычно определяют либо СР методом истечения,
либо у методом измерения скорости звука. В табл. 5.1 приве-
дены экспериментальные данные, экстраполированные к нуле-
вому давлению. Видно, что совпадение с теорией хорошее.
Электронные степени свободы мы считали невозбужден-
ными. Легко убедиться в законности этого предположения. Для
атомов, которые при обычных условиях могут существовать в
свободном состоянии, энергия, необходимая для перехода из
основного в первое возбужденное состояние, равна 4—20 эв, а
&Т=8,60-10‘5 Т эв. Поэтому в функции состояний электронов
отношениями первого и всех последующих возбужденных чле-
нов к основному можно пренебрегать, пока Т не превышает
10 000° К.
170
Гл. V. Идеальные газы
Таблица 5.1
Значения Ср и у для одноатомных молекул.
Ср
Теоретические значения: Cp[k — 2,5; у = =— =1,667
с V
Вещество Измеренные значения Измеренные значения
темпера- тура, °К ср k темпера тура, °К Y
Не 291 2,51
Ne — — 292 1,64
А 288 2,54 284 1,66
Кг — — 292 1,69
Хе — — 292 1,67
Na — — 750—920 1,68
К — — 660—1000 1,64
Hg — — 548—629 1,666
5.8. Двухатомные газы при средних температурах
Двухатомные молекулы по сравнению с одноатомными об-
ладают дополнительными степенями свободы. Атомные ядра
могут вращаться вокруг центра масс. В первом приближении
такую молекулу можно рассматривать как жесткий ротатор.
Кроме того, ядра могут колебаться .вдоль линии, соединяющей
их. В первом приближении это движение можно представить
как колебание гармонического осциллятора. Если молекула
почти жесткая, так что частота колебаний очень высока, то
вращение и колебание почти не зависят друг от друга. При
очень низкой температуре колебания ядер не возбуждаются, и
все дополнительное движение сводится к вращению. В действи-
тельности неколеблющиеся молекулы под воздействием центро-
бежных сил могут удлиняться, но для жестких молекул с очень
высокой частотой колебаний при умеренном вращении, т е. при
низких температурах, этот эффект очень мал.
Как и в одноатомном газе, электронное движение обычно
является полностью невозбужденным и соответствующая функ-
ция состояний сводится к первому члену иоехр(—е0/6Т) или
к ио при отсчете энергии от основного состояния. Однако могут
быть и другие электронные состояния, достаточно низкие, кото-
рые существенно влияют на функцию состояний. В этом случае
и0 необходимо заменить на и0 + щехр(—zJkT). Таким образом,
для расчета свойств двухатомного газа следует подробно рас-
5.9 Классическая трактовка вращения двухатомных молекул
171
смотреть главным образом функцию состояний вращательного
движения.
Двухатомная молекула не имеет момента количества движе-
ния относительно оси, проходящей через ядра двух атомов. Та-
ким образом, точной моделью для описания ее вращательного
движения является жесткий ротатор без осевого вращения, рас-
смотренный в п. 4.10. Функция состояний для него имеет вид
Г (Г) = s (2/+ 1)ехр {-/(/ + 1)0,/ Л. (5.52)
где
h2
®r~'WAk И —момент инерции). (5.53)
При обычных температурах для всех двухатомных молекул
(а для молекул, не содержащих атомов водорода, даже и при
низких температурах) всегда 0г<СТ и можно воспользоваться
приближенной формулой (4.92)
Т ( 1 0Г 10* / 0* \ ]
+ + \“П / J ’ (5.54)
Отсюда по (5.2) получим вклад вращательной степени свободы
в свободную энергию
( 0_ 10г 10* / 0* \ 1
FBp = — ^Г1пг(Г) = ^Г|1п-у — у у2— 90 \7^/ г
(5.55)
а вклад вращательной степени свободы в общую энергию'равен
dF^/T
£ВР
I 1 ©Г 1 ( ®г \ I
У-Г-45 7^+ °Wr (5‘56)
Наконец, вклад вращательной степени свободы в молекулярную
теплоемкость найдем путем дифференцирования (5.56) по Т и
последующего деления на N
„ I . 1 0Г хл ( ©г \ 1
СВР=Ф+ 457^ + ° Wb
(5.57)
5.9. Классическая трактовка вращения двухатомных молекул
Мы уже видели, что при обычных температурах 0, <^Т, по
меньшей мере для молекул, не содержащих атомов водорода.
Это значит, что вращательные степени свободы являются клас-
сическими и можно воспользоваться принципом предельного
172
Гл. V. Идеальные газы
+ 8)1 8л2Л*Г _ Т '
2AkT J— h2 ~ вг ’
соответствия для заучены функции состояний фазовым интегра-
лом. Классические формулы динамики жесткого ротатора без
осевого вращения были даны в п. 4.1. Используя их, получим
фазовый интеграл, дающий предельную форму функции со-
стояний г(Т) в виде
2л Л оо оо
-1-J / dQ fdpe f dp^exp
О 0 —оо —оо
что совпадает с первым членом (5.54).
5.10. Симметрия ядер
При вычислении интеграла в предыдущем пункте мы не об-
ращали внимания на симметрию относительно ядер. В молеку-
лах с различными ядрами (гетероядерные молекулы) в этом
необходимости нет. Если же молекула имеет два одинаковых
ядра (гомоядерные молекулы), каждые полоборота приводят
ее к положению, не отличимому от первоначального. При ин-
тегрировании в пределах, указанных в формуле предыдущего
пункта, каждая физически неразличимая ориентация будет под-
считана дважды. Возникает вопрос — нужно ли с целью по-
правки делить результат на 2? Опыт показывает, что такая по-
правка необходима. В таком случае, согласно принципу пре-
дельного соответствия, можно заранее сказать, что в строгой
квантовой теории должна появиться аналогичная поправка.
Рассмотрим теперь, каким образом она возникает. Покажем,
что эта поправка связана с необходимостью различать между
собой симметричные и антисимметричные собственные функ-
ции ядер.
До сих пор предполагалось, что движение молекулы можно
разложить на поступательное движение ее центра масс, вра-
щение, колебание и движение электронов. Собственная функция
распадалась на соответствующие множители. При этом игнори-
ровалась возможная структура ядра. Строго говоря, следовало
бы ввести этот ядерный множитель. Однако при обычной тем-
пературе единственным существенным фактором оказывается
спин ядра в основном состоянии. В остальных состояниях энер-
гия больше нормальной на величины, значительно превышаю-
щие kT. Благодаря ядерному спину при наличии внешнего маг-
нитного поля имеет место пространственное квантование,
причем каждой ориентации будет соответствовать своя собствен-
ная функция. Когда внешнего поля нет, эти состояния ориента-
ции становятся неразличимыми, но их число р остается тем же.
5.10 Симметрия ядер
173
При этом ядро можно рассматривать как бы в вырожденном
состоянии со статистическим весом р.
Рассмотрим сначала гетероядерную двухатомную молекулу,
состоящую из ядра а с ра собственными функциями фь ф2, ...
... ,фр и ядра-6 с рь собственными функциями ф', ф^, •••»
Молекула имеет собственные ядерные функции вида фг(а)ф^ (6)
Таким образом, если учитывать ориентации ядра, то в функцию
состояний молекулы следует ввести дополнительный весовой
множитель рарь. Рассмотрим теперь гомоядерную двухатомную
молекулу, состоящую из двух одинаковых ядер а и 6, каждое
из которых имеет р возможных ориентаций с соответствующими
собственными функциями фь ф2, ..., фр. Когда два таких ядра
образуют часть системы, например двухатомной молекулы, соб-
ственные функции ядерного спина этой системы можно полу-
чить, комбинируя собственные функции каждого из ядер. Су-
ществует -gP(p—1) комбинаций вида фг(а)ф5(6)—фз(я)фг(6),
антисимметричных относительно ядер; -^рСр—1) симметрич-
ных комбинаций вида фг(я)фз(6) +фз(я)фг(6) и р симметрич-
ных комбинаций вида фг(я)фг(6). Молекула в целом имеет
~р(р—1) антисимметричных и yP^ + l) симметричных соб-
ственных функций ядерного спина. Заметим, что общее число
антисимметричных и симметричных функций равно р2, что сов-
падает с числом собственных функций гетероядерной молекулы,
содержащей два ядра с одинаковыми значениями р.
Перейдем к исследованию свойств симметрии относительно
ядер собственных функций перемещения, вращения и колеба-
ния молекул. Поступательное движение центра масс не зависит
от относительного расположения ядер; его собственные функ-
ции не содержат ядерных координат, поэтому относительно пе-
рестановки ядер они симметричны. Собственные функции вра-
щения являются сферическими функциями. При /=0, 2, 4, 6, ...
они симметричны, при /=1, 3, 5, ... антисимметричны. Анало-
гично собственные функции колебательного движения при V —
= 0, 2, 4, ... симметричны, при v= 1, 3, 5, ... антисимметричны.
Для любого данного типа ядер допустимыми являются лишь
те состояния, которые либо антисимметричны, либо симметрич-
ны относительно перестановки ядер. Известно, что у атомных
ядер с нечетными массовыми числами осуществляются анти-
симметричные состояния. Наоборот, у атомных ядер с четными
массовыми числами состояния симметричны. Если считать,
что атомные ядра содержат лишь протоны и нейтроны, то
174
Гл. V. Идеальные газы
соблюдается следующее правило: собственная функция каждого
допустимого состояния является антисимметричной относитель-
но перестановки электронов, протонов и нейтронов.
Рассмотрим теперь, каким образом можно применить эти
соображения к двухатомным молекулам. Если молекула яв-
ляется гетероядерной, то, как мы уже видели при исследовании
ядерного спина, нужно просто ввести дополнительный весовой
множитель рар&. С гомоядерными молекулами положение слож-
нее. Если ядра имеют нечетное массовое число, то для получе-
ния собственной функции, антисимметричной относительно пе-
рестановки ядра, нужно четные собственные функции враща-
тельного движения (/ = 0, 2, 4, . . .), симметричные по отношению
к перестановке ядер, комбинировать с одной из турф—1) ан-
тисимметричных ядерных функций, а нечетные (/=1, 3, 5, ...) —
с одной из 2"Р(р4~ 1) симметричных ядерных функций. Таким
образом, четные вращательные состояния имеют дополнитель-
ный весовой множитель -^-рф— 1), а нечетные—|-р(р—Н 1)-
Наоборот, если массовое число является четным, то, для того
чтобы результирующая собственная функция была симметрич-
ной относительно перестановки ядер, собственные функции вра-
щения и ядерные собственные функции должны быть скомбини-
рованы в обратном порядке. В результате четные вращательные
состояния будут иметь дополнительный весовой множитель
ур(р+1), а нечетные —ур(р—1). Окончательно для враща-
тельного движения с учетом ориентации ядер получим следую-
щие функции состояний:
гетероядерные молекулы
сю
Гп (T) = 9(fib s (2/4- 1)ехр {-/(/+ 1) ©,/П; (5.58)
;=о
гомоядерные молекулы с нечетными массовыми числами
сю
r„(T) = yp(p-l) V (2/4-1)ехр{—д/4-1)0г/Л4-
/ = 0, 2, ...
сю
+ jp(p+l) S (2/4-1) exp {-/(/4-1) ©/7’); (5.59)
J = 1, 3, ...
5.10. Симметрия ядер
175
гомоядериые молекулы с четными массовыми числами
оо
гя(Л=4р(р+1) S (2/+1)ехр {-/(/+WH +
J=o, 2, ...
со
+ |р(р-1) S (2/+ 1)ехр {-/(/+1)0,/Т\. (5.60)
/ = 1, з,...
В простейшем случае, когда нет ядерного спина, р=1, и, как
мы видим, требования ядерной симметрии приводят к полному
исчезновению чередующихся вращательных состояний гомо-
ядерной молекулы. Это ранее подтверждалось спектром О26’
так как ядро атома О16 не имеет спина.
Численные значения выражений (5.58), (5.59) и (5.60) при
различных значениях параметра 0Г/Г представлены в табл. 5.2,
Таблица 5.2
Энергетические функции вращения гетероядерных
двухатомных молекул
оо
Л2 VI
0Г=8Л4Г' r= L (2>+l)exp{-;(/+l)0f/7’}
/ = 0, 1, 2, ...
8г Т Г 1п г „ d , т ат пг гЛ^тЧ\ ег Г г 1п г т d 1 тИт |пг Тт^тЧ
0,02 50,3347 3,9187 0,9933 1,0000 1,00 1,4184 0,3496 0,6252 1,0733
0,04 25,3360 3,2322 0,9866 1,0000 1,1 1,3392 0,2921 0,5797 1,0879
0,06 17,0041 2,8334 0,9799 1,0001 1,2 1,2759 0,2436 0,5330 1,0968
0,08 12,8387 2,5525 0,9732 1,0002 1,3 1,2249 0,2028 0,4860 1,0955
0,10 10,3401 2,3360 0,9664 1,0002 1,4 1,1855 0,1702 0,4388 1,0787
0,15 7,0103 1,9475 0,9495 1,0006 1,5 1,1500 0,1397 0,3945 1,0568
0,20 5,3472 1,6766 0,9324 1,0010 1,6 1,1226 0,1134 0,3515 1,0197
0,25 4,3508 1,4704 0,9151 1,0016 1,7 1,1003 0,0956 0,3111 0,9727
0,30 3,6883 1,3052 0,8976 1,0025 1,8 1,0821 0,0789 0,2737 0,9178
0,35 3,2155 1,1680 0,8802 1,0034 1,9 1,0672 0,0650 0,2396 0,8575
0,40 2,8623 1,0516 0,8624 1,0047 2,0 1,0549 0,0535 0,2087 0,7940
0,45 2,5885 0,9511 0,8445 1,0061 2,2 1,0368 0,0301 0,1564 0,6651
0,50 2,3703 0,8630 0,8263 1,0084 2,4 1,0247 0,0244 0,1157 0,5424
0,60 2,0455 0,7156 0,7892 1,014 2,6 1,0165 0,0165 0,0847 0,4332
0,70 1,8164 0,5968 0,7702 1,024 2,8 1,0111 0,0111 0,0614 0,3404
0,80 1,6473 0,4992 0,7110 1,036 3,0 1,0074 0,0074 0,0443 0,2638
0,90 1,5186 0,4178 0,6691 1,055
176
Гл. V. Идеальные газы
Таблица 5.3
Энергетические функции вращения
гомоядерных двухатомных молекул
0 = V
оо r WAk '
Q> = 2 (2^+1)exP(-y^+1)er/n
; = 0, 2, 4, ...
ег т Qi In Qi d , л n 131 W ln Q1)
0,08 6,2636 1,8593 0,9732 —
0,10 5,0254 1,6429 0,9664 —
0,15 3,3716 1,2543 0,9495 —
0,20 2,6739 0,9835 0,9318 —
0,25 2,1766 0,7778 0,9098 1,040
0,30 1,8492 0,6148 0,8772 1,117
0,35 1,6205 0,4827 0,8290 1,287
0,40 1,4566 0,3761 0,7639 1,3428
0,45 1,3371 0,2904 0,6859 1,4287
0,50 1,2493 0,2218 0,6010 1,4648
0,60 1,1367 0,1281 0,4332 1,3770
0,70 1,0750 0,0723 0,3254 1,1458
0,80 1,0411 0,0403 0,1897 0,8748
0,90 1,0226 0,0223 0,1193 0,6298
1,00 1,0124 0,0123 0,0734 0,4353
1,10 1,0068 0,0068 0,0446 0,2923
1,20 1,0037 0,0037 0,0268 0,1921
1,30 1,0020 0,0020 0,0159 0,1241
1,40 1,0011 0,0011 0,0094 0,0791
1,50 1,0006 0,0006 0,0055 0,0499
5.3 и 5.4. При обычных температурах для всех двухатомных
молекул (а для тех, которые не содержат атомов водорода, и
при очень низких температурах) @Г<^Т и с весьма большой точ-
ностью
оо
2 (2/+1) ехр {-/(/+1)©,/Л =
/ = 0, 2, ...
оо
= 2 (2/+1) ехр (->(/+ W) =
; = i, з,...
оо
= | 2 (2/+1) ехр {-/(/+1)0,/Л- (5-61)
/ = о, 1,
5.10. Симметрия ядер
177
С?2 Таблица 5,4 Энергетические функции вращения гомоядерных двухатомных молекул
оо - 2 / = 1, 3, 5, (27+ 1 Л2 )ехр {-/(/+ 1)&Г/Т].
d d / d \
1П Q2 T-dT^ ~dT {T2~dT In ^2)
0,08 6,2636 1,8593 0,9732 —
0,10 5,0254 1,6429 0,9664 —
0,15 3,3716 1,2543 0,9494 —
0,20 2,6737 0,9835 0,9332 0,998
0,25 2,1742 0,7766 0,9204 0,963
0,30 1,8390 0,6092 0,9182 0,8869
0,35 1,5950 0,4469 0,9322 0,7705
0,40 1,4057 0,3405 0,9645 0,6347
0,45 1,2513 0,2242 1,0138 0,5247
0,50 1,1210 0,1142 1,0774 0,3816
0,60 0,9088 —0,0956 1,2345 0,2059
0,70 0,7414 —0,2993 1,4149 0,1038
0,80 0,6062 —0,5006 1,6063 0,0500
0,90 0,4960 —0,7011 1,8026 0,0233
1,00 0,4061 —0,9012 2,0010 0,0106
При этом функции состояний гп(Т) для вращения с учетом
ядерных спинов примут следующий вид:
гетероядерные молекулы
гя(Г) = г(Т)рор6, (5.62)
гомоядерные молекулы
/л(Л = тг(Г)р2, (5.63)
где г(Т) определяется рядом
г(Л = 5. (2/+1) ехр {—/(/+1)0/Г). (5.64)
1^0, 1, ...
Проведенный анализ требует уточнения классификации со-
стояний вращающейся гомоядерной молекулы. До сих пор
мы рассматривали атомные ядра как бесструктурные точечные
12 Зак. 129Q
178
Гл. V. Идеальные газы
частицы. Такой метод оказался несостоятельным. Когда ядро
имеет р возможных ориентаций, необходимо приписать ему ста-
тистический вес, в р раз больший, чем для бесструктурной то-
чечной массы. Двухатомные молекулы из-за ориентации ядра
имеют статистический вес рар&. Дополнительный множитель р2
гомоядерной молекулы, исходя из требований симметрии ядра,
приводится либо к -^-р(р — 1), либо к у р(р+1) и может быть
заменен на ур2, исключая случай очень низких температур. Пе-
реход от р2 к~р2 представляет собой квантовый аналог введе-
ния числа симметрии о в классической статистике.
Положим сг = 2 для гомоядерной молекулы и о=1 для гете-
роядерной молекулы. Тогда формулы (5.62) и (5.63) можно
объединить в одну
rn(T) = r(T)papb/<j, (5.65)
где г(Т) по-прежнему определяется формулой (5.64). Исполь-
зуя формулу (5.54) для г(Т), имеем
т I 1 0r 1 0? _ / 0? \ ] РЛР„
^(^=0?|1+з-г + 15^ + ОЫН п <5-66>
Здесь следует указать, что при выводе формул (5.59) и
(5.60) допускалась возможность свободных переходов между
всеми различными состояниями. Однако в действительности не
всегда бывает так. Например, в обычном газообразном водо-
роде (р = 2) имеются два типа молекул. Пара-водород, у кото-
рого собственные спины ядер направлены противоположно, при-
нимает вращательные состояния лишь с четными номерами.
Орто-водород, у которого собственные спины ядер направлены
одинаково, принимает вращательные состояния лишь с нечет-
ными номерами. Взаимные переходы между пара-водородом и
орто-водородом происходят очень медленно. При обычных экс-
периментах переходы между ними совершаться не успевают и
их можно рассматривать как два различных газа.
Статистический вес ядра пара-водорода равен-^рф—1) = 1,
функция его вращательных состояний (см. табл. 5.3) имеет вид
S (2/ + 1)ехр {-/(/+ l)0f/r} = lQ1 (-^).
У = о} 2, ...
5.11. Уточненные формулы для одноатомных молекул
179
Статистический вес ядра орто-водорода равен ypfp-f- 1) = 3, а
функция состояний (см. табл. 5.4) имеет вид
оо
г0(Т) = 3 2 (2/+1)ехр(-Д/ +Ж/Л ==3Q2(-^).
; = i, з,...
По статистическим весам видно, что водород представляет со-
бой смесь V4 пара-водорода с 3/4 орто-водорода, поэтому при
низкой температуре для теплоемкости имеем
3 1 д ! dlnQA 3 д /^d\n3Q2\
k 2 4 дТ \ дТ 4 дТ \ дТ '
что полностью соответствует экспериментальным данным.
HD — гетероядерные молекулы, и с ними затруднений не
возникает. Дейтерий (D2), как и водород, распадается на пара-
дейтерий и орто-дейтерий, и к ним можно применить аналогич-
ные методы, только р для D равно 3.
5.11. Уточненные формулы для одноатомных молекул
Чтобы привести формулы п. 5.7 для одноатомных молекул
к виду, аналогичному формулам для двухатомных молекул, до-
статочно ввести возможное число р собственных функций ядра.
Тогда полная функция состояний одноатомной молекулы при-
мет вид
f(T) = +---------иор. (5.67)
Свободная энергия газа, состоящего из одноатомных молекул,
равна
F = /VAT |1п у- — 1} — | NkT In Т — NkT In j (2я^) Л vopj, (5.68)
химический потенциал выражается формулой
1 гр,, N 3 «гр,, гр, р /р,, ( (2зттиА?)
р = Л71п -у -^kTini — ki In j -- Лз - r>op ? =
= kT\np — у AT In T — kT\n j Uop j , (5.69)
абсолютная активность равна
12*
180
Гл. V. Идеальные газы
5.12. Формулы для расчета термодинамических функций двух-
атомных газов при средних температурах
С учетом спина ядра и симметрии полная функция состоя-
ний двухатомной молекулы принимает вид
/(Г)= (2Я^р2т.Гд(Г)Го>
где гп(Т) дается одной из формул (5.58) —(5.60). При ©гС?
можно воспользоваться (5.66), тогда
/(Г) = (2л^Л/а£ r(?) Uo =
{InmkT)^ V Т J1 ( 1 0Г ( 10?
{-О (5.71)
Далее, исключая молекулы с очень малым моментом инерции,
можно ограничиться первым членом разложения г (Г), так что
г /Т’х %n2AkT Pafib /с ynx
I К* 1 ) —-дз------дг-4) • (°-'
Согласно (4.188), свободная энергия равна
F — NkT {ln-£_ 1|—g-MfeTln T —
— NkT In { У™1*''*1' u0 Ml| , (5 73)
энергия равна
£=_pdy) =^NkT, (5.74)
химический потенциал равен
ц = =kTln^ — ^kT\nT —
\dN ]TtV V 2
, т. ( (2я/яй),/2 8я2Лй рар6 ) _
— hl in |--------Д2~ го -у- | —
= kT\np — ^kT\n T-kT\n | (5.75)
абсолютная активность равна
(5J6)
5.12. Формулы для расчета термодинамич. функций двухатомных газов 181
Наконец, для молекулярных теплоемкостей при постоянном
объеме и постоянном давлении имеем
Cv = ~k, (5.77)
CP = ^k. (5.78)
При Г>0Г эти классические формулы являются весьма точ-
ными. Когда нельзя пренебречь отношением 0Г/Т к единице,
нужно заменить функцию (5.72) на (5.71). При этом в выраже-
нии свободной энергии (5.73) появляются дополнительные
члены
{10 1 0^ / 0^ \ ]
1 + Т ~Т +15 + 0 (/ ) =
{1 10 / 0^ \ 1
3+-90-Г + 0(-7МГ (5<79)
Энергия и теплоемкость будут равны
Е
77
Г2 d(F/T)
77 дт
5 ( 1
-^kT — kQr I -g-
1
45 T
1 дЕ 15
У = 77" ~дТ = k I *2
1 ©2
45 Г2
(5.80)
(5.81)
Видно, что Су приближается, и очень быстро, к своему классиче-
скому значению ~^k сверху. Необходимо отметить, что форму-
лами (5.80), (5.81) можно пользоваться лишь при 0ГСТ. Фак-
тически они являются достаточно точными при 0r < Т.
При очень низких температурах, когда Т<С0г, функция со-
стояний вращательного движения сводится к первому члену
суммы. Вклад Свр молекулярной теплоемкости падает до нуля,
а Су принимает значение у k. При промежуточных температу-
рах нельзя написать простую формулу для Свр.
При температурах, когда вращательные степени свободы яв-
ляются классическими, а колебательные степени свободы не-
возбужденными, величины Су и СР определяются (5.77) и
(5.78). Их отношение равно
С 7
Т=С7=3=1,4. (5.82)
182
Гл. V. Идеальные газы
Табл. 5.5 указывает на то, что эти значения совпадают с экс-
периментальными данными для многих двухатомных молекул в
весьма широкой области температур.
Таблица 5.5
Значения Ср и у для двухатомных газов.
Теоретические значения: Ср/# = 3,5; у = 1,40
Вещество 0f, град %/103, град Темпера- тура, °К Расчетные значения Ср/Й Расчетные значения У
Н2 85,4 6,10 289 3,45
N2 2,86 3,34 293 3,51 —
92 3,38 —
О2 2,07 2,23 293 3,51 —
197 3,43 —
92 3,47 —
со 2,77 3,07 291 3,52 —
93 3,40 —
NO 2,42 2,69 288 3,64 —
НС1 15,2 4,14 290—373 — 1,39
НВг 12,1 3,7 284—373 — 1,43
HJ 9,0 3,2 293—373 — 1,40
Формулы (5.59) и (5.60) не могут непосредственно исполь-
зоваться для молекул водорода и дейтерия при низких темпе-
ратурах. Причина указывалась ранее. Переходы от пара-водо-
рода и пара-дейтерия, содержащих антисимметричные спино-
вые собственные функции, к орто-водороду и орто-дейтерию,
содержащим симметричные спиновые собственные функции,
крайне медленны и за время эксперимента не происходят. Эти
две формы водорода и дейтерия следует рассматривать как раз-
личные газы.
5.13. Колебательные степени свободы
При высоких температурах колебательные степени свободы
двухатомной молекулы не являются невозбужденными. В каче-
стве грубого приближения предположим, что колебания и вра-
щения независимы друг от друга- Чем жестче молекула и выше
частота колебаний, тем лучше это приближение. Допустим так-
же, что колебания гармонические с частотой v. Однако посколь-
ку при некоторой энергии % молекулы диссоциируют, то число
гармонических колебательных состояний не может превышать
какое-то конечное значение р. В действительности интервалы
5.13. Колебательные степени свободы
183
между колебательными уровнями не являются одинаковыми, а
чем ближе к пределу х» тем плотнее (см. п. 2.16). Тем не менее
в первом приближении это предположение является все же до-
статочным. Принимая энергию низшего колебательного состоя-
ния за нуль, для функции состояний колебательного движения
имеем
Л-1
7(Г) = У expj ^exp(~^g. (5.83)
kT } 1 — ехр(—hv/kT) v 7
г/ = 0
Если % или phv намного больше Av, то имеется сравнительно
большая область температур Т, где величиной ехр(—phvjkT)
можно пренебречь. Для таких температур q(T) сводится к пол-
ной функции состояний гармонического осциллятора
?(Г) = [1 — ехр(— hv/kT)]~l. (5.84)
В этой области температур формула (5.84) является хорошим
приближением для функции состояний колебательного движе-
ния. При такой функции состояний колебательного движения
вклад колебательного движения в энергию W молекул равен
/7кол — NJbT2 & — N_______—______ ос\
В предельных случаях
Екол = 0 (kT<^hv),
Екол = NkT — /V-^ + О (4-) (kT^>hv). (5.86)
Если за нуль принять не энергию низшего квантового со-
стояния, а ее величину в положении равновесия, где потен-
циальная энергия имеет минимум, то функция состояний коле-
бательного движения примет вид
<7(0 =
(5.87)
Теперь вклад колебательного движения в энергию составляет
Екол — NkT
2 din q (Т) _
дТ ~~
(5.88]
184
Гл. V. Идеальные газы
в предельных случаях
E^NkT+O^]
(kT^hv),
(kT^>kv).
(5.89)
Формула (5.89) говорит о том, что при абсолютном нуле
колебательная энергия (нулевая энергия) равна колебательной
энергии самого низкого энергетического уровня. Ее можно на-
звать также остаточной энергией осциллятора. Сравнение
(5.86) и (5.89) показывает, что классическое значение NkT
энергии колебательного движения оказывается более точным
при втором способе выбора начала отсчета.
5.14. Двухатомные газы при высоких температурах
При высоких температурах можно улучшить ранее приве-
денную формулу для двухатомной молекулы, если ввести функ-
цию состояний колебательного движения. При температурах
ниже 10 000° К, кроме поступательного, вращательного и коле-
бательного движений, никакие другие степени свободы обычно
не возбуждаются. Используя аппроксимацию (5.84) для q(T),
получаем полную функцию состояний в виде
кт (2nmkT^V ^AkT Г _exp/^Vr\r1Uo (5 90)
Энергия отсчитывается здесь от низшего квантового уровня
колебательного спектра молекулы.
Свободная энергия и химический потенциал равны соответ-
ственно
F = NkT (in — 1) — 4 NkT In Т + [1 — ехр (- —
— ЛГЛПп (5.91)
и = r = Win 4 - | W In т+ kT In [1 - ехр (- £)] -
J (2лт*)’/2 8л2ЛА рарй |_
— ДУ Ш | и0 —— j —
= kT\n р — ^-kTln T-j-kTln р — ехр (— —
— kT In { u0 -Psp. j . (5.92)
5.14. Двухатомные газы при высоких температурах
185
Для полной энергии и молекулярной теплоемкости имеем
Е = — Г2 - (^Г) = W
ехр
/zv
/zv \ 1
~kT) 1
(5.93)
{ kT^
(5.94)
Часто удобно вводить температуру О, связанную с энергией со-
отношением 0=е/&. Такой температурой0Г мы уже пользовались
при рассмотрении вращения. В случае гармонических колеба-
ний 0V определяется равенством
k&v = hv, (5.95)
где 0D можно назвать характеристической температурой осцил-
лятора. Значения 0Г, полученные из спектральных данных, при-
Таблица 5.6
Функция Эйнштейна
П ©И I2
, I \ т )
Й1)1
S 0г/Г S S %/т
0,001 1,0000 0,80 0,9484 1,70 0,7903 3,40 0,4128
0,005 1,0000 0,85 0,9420 1,75 0,7796 3,60 0,3743
0,010 1,0000 0,90 0,9353 1,80 0,7688 3,80 0,3381
0,050 0,9998 0,95 0,9282 1,85 0,7578 4,00 0,3041
0,10 0,9992 1,00 0,9207 1,90 0,7467 4,20 0,2726
0,15 0,9981 1,05 0,9130 1,95 0,7354 4,40 0,2437
0,20 0,9967 1,10 0,9050 2,00 0,7241 4,60 0,2169
0,25 0,9948 1,15 0,8967 2,10 0,7013 4,80 0,1927
0,30 0,9925 1,20 0,8882 2,20 0,6783 5,00 0,1707
0,35 0,9898 1,25 0,8795 2,30 0,6553 5,20 0,1507
0,40 0,9868 1,30 0,8706 2,40 0,6320 5,40 0,1328
0,45 0,9832 1,35 0,8613 2,50 0,6089 5,60 0,1168
0,50 0,9794 1,40 0,8516 2,60 0,5859 5,80 0,1024
0,55 0,9752 1,45 0,8417 2,70 0,5630 6,00 0,0898
0,60 0,9705 1,50 0,8318 2,80 0,5404 6,60 0,0636
0,65 0,9655 1,55 0,8218 2,90 0,5182 7,00 0,0446
0,70 0,9602 1,60 0,8115 3,00 0,4963 7,50 0,0310
0,75 0,9544 1,65 0,8010 3,20 0,4536
186
Гл. V. Идеальные газы
ведены в табл. 5.5. Введя можно написать (5.94) в виде
(5.96)
(0 \
-у- — функция Эйнштейна. Ее значения приведены в
табл. 5.6. Обозначая через Скол вклад колебательной степени
свободы в молекулярную теплоемкость, в предельных случаях
имеем
<»кол
Скол ।
(Г :>©,).
(5.97)
Таким образом, приближенный метод, использованный в дан-
ном разделе, приводит к учету зависимости теплоемкости двух-
атомной молекулы от при высоких температурах, причем
формула (5.96) справедлива почти для всех двухатомных мо-
лекул.
5.15. Поправки на ангармоничность и взаимодействие
Формулы предыдущего пункта являются приближенными,
так как мы пренебрегали ангармоничностью колебательного
движения молекул и взаимодействием колебания и вращения.
В п. 2.16 проводился более точный расчет энергетических уров-
ней двухатомной молекулы и получено выражение (2.137) для
энергетического состояния er>J-, характеризуемого квантовыми
числами v и /. При отсчете энергии от низшего квантового со-
стояния это выражение имеет вид
£
(5.98)
где постоянные со*, х*, Во, DQ и ае расшифрованы в (2.135) и
(2.138). Предыдущий приближенный расчет соответствует слу-
чаю, когда х*, Dq и ае равны нулю. В действительности они не
равны нулю, но довольно малы. Поэтому к предыдущей фор-
муле (5.98) следует сделать поправку, тогда получим
= {v — x*v(о —1)) + -^/(/4-1) (1 — 4y7(/4- 1) —to}>
(5.99)
5.15. Поправки на ангармоничность и взаимодействие
187
где ©V — характеристическая температура колебания, ©г— ха-
рактеристическая температура вращения, у и б — безразмерные
параметры. Они определяются формулами
Ф ___ hv __ h®*c ~ _____ Behc _ BJic Л ае \
v ~ Т ~ Т~ ’ г “ Т" ~ V — J ’
дЛ,2_ D0 _ ~ х _ ag ag
Y “ Во — Во ~ Ве ’ ° — Во - Ве •
(5.100)
(5.101)
Отсюда видно, что зависимость характеристической темпера-
туры колебаний 0Г от энергии та же, что и была раньше, но
если исходить из характеристической температуры вращения
0Г в (5.53) для вычисления 4, то это А не будет являться мо-
ментом инерции 1е равновесного вращения. Три безразмерных
параметра х*, у2 и б много меньше 1.
Колебательно-вращательное состояние с квантовыми чис-
лами v, j имеет статистический вес 2/4-1, поэтому функция со-
стояний j(T) внутренних степеней свободы (без электронных)
равна
2(2>+1)ехр{-^т4}' <5-102)
V J
где суммирование ведется по всевозможным значениям v, / всех
8Г) j, меньших энергии диссоциации. Из (5.99) видно, что v и j
не могут стремиться к бесконечности. Однако даже при высо-
кой температуре состояние с большой энергией занимает очень
мало молекул, так что рассматриваемое приближение в целом
оказывается достаточным. Для низких квантовых чисел, поль-
зуясь малостью х*, у2, 6, имеем
ехр ( — -^41 = ехр {— [-^ v+j'(jr+1)] 1X
X ехр (v — 1) 4-14Y2/2(/+1)24-bvj(/4-1)}
= ехр { - [-^ v 4- JU+1)]} [1 + (v -1) +
+ {4y2/2(;+ 1)2+^/(/+1)} 4"] •
Используя это приближенное выражение в (5.102) при всех
значениях v, j, получаем без большой погрешности /(Т) в виде
/(Г) = 2 ехр (-4И 2<2'+ 1) [1 + - 1)-^ +
V = 0 j = о
+ {4у2/2(/+ 1)24-6г>/(/4- 1)} 41] ехр{—^/(/+ !)}• (5-ЮЗ)
188
Гл. V. Идеальные газы
Суммирование по j можно выполнить по формуле Эйлера —
Мэльголлэнда (4.91)
у; (2/+1) [1+-1)+
/=о
+ {4у2/2 U + 1)2+&Ц/(/ + 1)} -^] ехр{ -/(/+ 1) =
J [^1 1)4? + {4y2z2+du?} 4?]ехр(— z~jdz +
о
+т ~ 4=i; f t1 + x*v ~1 > +{4y2 i;112+6wi}]e '11 dX[+
r 0 T
+1 = <57 [1 + - 1) T + 8v! + «”] +1
В результате имеем
oo
И так как
оо оо
г/=0 t>=0
ОО оо
& ехр (—V = д ^v/T)2 S ехР (~ v -/) =
г/=0 »=0
__ ехр(~0р/Т) 2 ехр (—20Р/Т)
— [1—ехр(—0^/Г)]2 [1 - ехр (- 0р/Т)]з ’
то окончательно получим
j(T) —______________Г.-?2^. -р 1
1 — ехр(—0р/Г) [ 0r Т
!______________I____2х*0р/Т 1
ехр^/Г) — 1 [exp^/n-ipj-
Когда ангармоничность и взаимодействие не существенны,
результат (5.104) и вышеприведенная приближенная формула
совпадают. Обозначая через jo(T) внутреннюю функцию со-
5.16. Влияние электронов
189
стояний без ангармоничности и взаимодействия, можно запи-
сать
= (5.105)
где jc(T) — поправочный множитель. Согласно (5.104),
Jc(T)— [-0^- + 1 + exp(е^/т1)—1 + [exp(©„/D—ip J ’ (5-1 о6)
откуда
In je (T) «4----------—Г + 7—112 • (5Л07)
Jc v 7 0r 1 exp (0^/7) — 1 1 [exp(0v/T)— I]2 v '
С помощью этой формулы можно вычислить поправки к любой
термодинамической функции, возникающие в результате ангар-
моничности и взаимодействия колебания с вращением. Напри-
мер, для энергии имеем
ДЕ = NkT2-^- In jc(T) = NkT Г-^ + б I®*7 ffle/n(ep/i? +
дТ jc\ / L ©г [exp (@v/T)— I]2 1
I 9 J (©t//^)2 eXP (©7?/^)______©p/T_____/С 1 f)Q\
1 [exp (0v/n - l]3 [exp (ev/T) -I]2 fj •
Численные значения параметров Qv, @r, у, d и x* можно най-
ти в работах по молекулярной спектроскопии1)- После введе-
ния такой поправки даже при высоких температурах теория
совпадает с экспериментом, до тех пор пока не возбуждена
электронная степень свободы.
5.16. Влияние электронов
Как уже упоминалось в п. 5.5, возбужденные энергетические
уровни электронов могут давать заметный вклад в функцию со-
стояний. Это происходит тогда, когда основное состояние яв-
ляется одним из нескольких состояний мультиплета. Рассмо-
трим случай дублета. Обобщение на триплеты и мультиплеты
будет очевидно. Энергию основного состояния примем за нуль,
энергию второго обозначим через Тогда электронная функ-
ция состояний имеет вид
^(Т') = ио +vi ехр , (5.109)
где ио и Di — статистические веса двух состояний дублета. В ре-
зультате свободная энергия равна
F3X = — NkT In (v0 + ще~е'/кТУ (5.110)
9 Например, Herzberg G., Molecular Spectra and Molecular Structures
(Prentice-Hall), 1939, p. 121 (см. русский перевод: Герцберг, Спектры и
строение двухатомных молекул ИЛ, 1949. — Прим. ред.).
190
Гл. V. Идеальные газы
а энергия и молекулярная теплоемкость будут содержать до-
полнительные члены
Т2д(Г™/Т) ______________________
дТ “ 1+ (1)0/1)!) ехр (£1/ЛГ)-
Гэл_ 1 №л (^/ьту
~ N дТ к {1 Ч-(г0/и1)ехр(Е1/^П} {1 + (г)1/1)0)ехр(-£1МЛ} *
(5.112)
Примеры для Сэл показаны на рис. 5.1. Из (5.112) следует, что,
когда kTI&i очень велико или очень мало, Сэл обращается в
нуль лишь при kT порядка еь величина Сэл отлична от нуля.
Рис. 5.1.
Когда верхним состоянием дублета можно прене-
бречь. Когда /г7^Э>Е1, состояния становятся неразличимыми и
такой слившийся мультиплет можно рассматривать как одно
состояние с весом и0 + щ-
Применим эти формулы к молекуле NO. Ее нормальное со-
стояние 2Пi/2 принадлежит дублету 2IL/2, з/2, каждая компонента
которого имеет вес, равный 2. Тогда (5.112) дает
‘ ch2 (tJZkT) '
Максимальное значение достигается при 8i/£T=2,4. Для NO
имеем 81/^=178° К. Поэтому максимальное значение теплоемко-
сти Сэл находится вблизи 74° К. При подходе к этой темпера-
туре вращательные степени свободы уже полностью возбужде-
5.17. Вращательные степени свободы твердых тел
191
ны, а колебательные еще заморожены, поэтому изменение мо-
лекулярной теплоемкости происходит лишь за счет Сэл. При
увеличении температуры выше 74° К можно ожидать, что мо-
лекулярная теплоемкость NO будет понижаться. Это подтвер-
ждено экспериментами (рис. 5.2).
Основным состоянием молекулы кислорода является триплет
3S. Однако лишь при температуре ниже 4° К становится замет-
ным разделение между этими тремя состояниями, поэтому об-
наружить их с помощью термодинамических методов не удает-
ся. При обычных температурах можно считать, что молекулы
кислорода находятся в вырожденном состоянии с весом, рав-
ным 3, и влияние мультиплетности на электронную теплоем-
кость отсутствует. Она обнаруживается лишь при очень высо-
ких температурах вследствие наличия у молекулы кислорода
*Д состояния. Статистический вес состояния 32 равен 3, а со-
стояния !Д равен 2, поэтому электронная функция состояний
имеет вид
е (Т) = 3 + 2 ехр (— zJkT), (5.113)
где si — разность энергий !Д и 3S уровней. Экспериментальное
значение 81 равно 0,97 эв, так что sjk = 1,13 • 104 град. Формула
(5.112) показывает, что лишь при температуре в несколько ты-
сяч градусов может стать заметной электронная теплоемкость
кислорода. Это наблюдается и в опыте.
5.17. Вращательные степени свободы твердых тел
Многоатомные молекулы можно разделить на два типа: ли-
нейные и нелинейные молекулы, в зависимости от того, нахо-
дятся ли равновесные положения их ядер на одной прямой или
192
Гл. V. Идеальные газы
нет. Для обоих типов вращательные степени свободы факти-
чески являются классическими. Линейные молекулы имеют
только две классические вращательные степени свободы, а вра-
щательно-ядерная функция состояний имеет ту же классиче-
скую формулу, что и у двухатомной молекулы, с числом сим-
метрии о в знаменателе. Когда молекула имеет центр симме-
трии, о = 2, в противном случае о=1. Таким образом,
/^т\ Ир 8л2Л/г7 Пр /г- -I 1
гя(Л=='-Ц)-/ = —Д2---------(5.114)
где Пр — произведение спиновых весов отдельных ядер моле-
кулы.
Нелинейные молекулы имеют три классические вращатель-
ные степени свободы, и мы должны заново рассмотреть их
функции состояний. Будем рассматривать только классическую
форму. Известно, что вращение твердого тела с главными мо-
ментами инерции Д, В, С можно описать с помощью трех эйле-
ровых углов1) 0, ср, ф и соответствующих импульсов р^.
Согласно определению эйлеровых углов, кинетическая энергия
вращения 8 выражается через три главных момента инерции и
три угловые скорости 0, (р, ф в виде
е = у {А (ср sin 0 cos ф — 0 sin ф)2 + В (<р sin 0 sin ф + 0 cos ф)2 Д-
+ C(cpcos О +Ф)2}-
Напишем также формулы для импульсов
* *
ре = —— = А (<р sin 0 cos гр — 0 sin гр) (— sin гр) +
4- В (ф sin 0 sin гр + 0 cos гр) cos гр,
* *
p — —r = A 4<sin 0 cos гр — 0 sin гр) sin 0 cos гр +
ф dtp
-|-5(ф sin 0 sin гр 4~ 0 cos гр) sin 0 sin гр С(ф cos 0 4-гр) cos 0,
p =-^- = C(<pcos0+ гр).
ф дф
Выражая входящие в е комбинации 0, (р, ф через импульсы р0,
рф» Др, представим энергию в форме гамильтониана
е = {(Ар ~ cos °)cos — Р0 sin 0 sin гр)2 +
+ 2Д sin^O {(^<Р — РфСО5 0)81пгр + р0 sin 0 COS гр}2 + -Др2. (5.115) 9
9 См., например, Л а н д а у Л» Д.2 Л иф шиц Е, М., Механика, М., 1962.
5.18. Колебательные степени свободы многоатомных молекул 193
При отсутствии симметрии вращательная функция состояний
имеет вид
Л 2л 2Л оо оо оо
r(T) = ±- f def d(p f dy f dpe f dplf f dp^exp(^f-).
0 0 0 —oo —oo —oo
(5.116)
Представляя энергию в форме, удобной для интегрирования,
__ 1 / sin2 ф , cos2 ф \
6 ~ Т А~ "1 В~j
„ _|_И_________1 ) sin ф cos ф
"б ’ \ В А ) . А / sin2 ф . cos2 ib \
1
^(/’ф РфС08®) H"2HBsin20 Sin24> , COS21|)(^<P ^ФCos ^У+гС^Ф
А + В
и выполняя в (5.116) интегрирование по р6, рф, рф, получим
,. 1/ л 2л 2л
Г (Г) = j ^sln в = jjWlW
ООО
(5.117)
Если молекулы обладают симметрией, то в знаменатель вра-
щательно-ядерной функции состояний следует ввести число сим-
метрии а, равное числу неразличимых ориентаций молекулы.
Таким образом,
8л2(2лАТ)9Ь(АВС)^ Пп _ л
гп(Т) = —-------(5.118)
где Пр — произведение спиновых весов всех ядер. Число сим-
метрии, например, для Н2О равно 2 (равнобедренный треуголь-
ник), для NH3 — 3 (трехгранная пирамида), для С2Н4 — 4
(прямоугольник), для СН4—12 (правильный тетраэдр) и для
С6Н6— 12 (правильный шестиугольник). Если моменты инерции
В и С относительно двух осей одинаковы, то формулы, приве-
денные здесь, совпадают с формулами в п. 4.11.
5.18. Колебательные степени свободы многоатомных молекул
Многоатомные молекулы могут иметь несколько нормаль-
ных колебаний. Их число зависит от структуры молекул. Ли-
нейная молекула, состоящая из а атомов, имеет (За — 5) нор-
мальных колебаний, а нелинейная молекула с тем же количе-
ством атомов имеет (За — 6) колебаний. Каждому колебанию
13 Зак. 1299
194
Гл. V. Идеальные газы
частоты vv можно сопоставить характеристическую температуру
©и по формуле
k% = hvv. (5.119)
Если рассматривать такие колебания, как гармонические, то
функция состояний для них будет равна
gJT) = [l-exp(--^)]'1. (5.120)
При этом каждое колебание влияет на свободную энергию,
энергию и теплоемкость формально так же, как колебание двух-
атомной молекулы с соответствующей характеристической тем-
пературой. Если молекула обладает симметрией, то два или три
типа колебаний имеют одинаковые частоты. Такие колебания
рассматриваются как вырожденные с весом 2 или 3. Их вклад
в каждую термодинамическую функцию в два или в три раза
больше, чем у невырожденного колебания той же частоты.
5.19. Общие формулы для термодинамических функций много-
атомных молекул
Объединяя найденные выше разновидности функции состоя-
ний, получим окончательное выражение для функции состояний
многоатомных молекул:
линейные молекулы
нелинейные молекулы
f г (2amkT)'l'V ^{2nkT)4^ABC)'l‘ п Г. / ©„Х"1 ПР
IV1 ) — дэ дз [1 ~ ехР т5") Г0 “5“ •
(5.122)
В этих формулах число симметрии а равно числу всех неразли-
чимых конфигураций вращения молекулы как твердого тела;
произведение Щ взято по всем нормальным колебаниям; и0~
статистический вес низшего электронного уровня; Пр—произ-
ведение спиновых весов всех ядер в молекуле.
Если, помимо низшего уровня, существенны другие элек-
тронные уровни при тех же значениях моментов инерции и
других молекулярных констант, то ио нужно заменить на
е(7) = «0+2»г ехр (— trlkT), где ег — энергия r-го электрон-
т
ного состояния. Когда молекулярные константы этих электрон-
ных энергетических уровней различны, то функцию состояний
е(Т) нельзя выразить простой формулой указанного типа. Од-
5.19. Общие формулы для термодинамических функций
195
нако предыдущие формулы можно применять к каждому энер-
гетическому уровню электрона в отдельности, заменяя ио на
Vj ехр > р2 ехР и т- Д- Найдем теперь термодинами-
ческие функции:
1) Свободная энергия:
линейные молекулы
F=NkT[\n-y— 1} — |^Пп7' + ^г21п[1 — ехр(—У1)]-
V
кти'гх J (2лти£)8/2 8л2Л£ Пр J
— /Р2---a J’ <5Л23)
нелинейные молекулы
F = NkT^n~ — 1 (-ЗЛ^ПпГ+МЬГ^кф — ехр —
V
-NkTin{i2"f' П,| (5)24)
2) Энергия:
линейные молекулы
£ = + (5.125)
V
нелинейные молекулы
E = -r^P- = 3mT + NkT^ (5.126)
V
3) Химический потенциал:
линейные молекулы
'*=(-®-)r.v=‘7'lnv-447'i"7'+4ri1"[1-4-^F
— АГ In 8"^t »a-b.|=trinp — imn Т +
। «.'rV’i Г, / ®t>\l iTi ( (2лт),/!А6/! 8л2ЛА Пр )
+ kT2Jn[l — ехр(--^)j —ЛГ1П^—---------Л5“ио a J’
V
(5.127)
13*
196
Г л. V. Идеальные газы
нелинейные молекулы
g = kT In — 3kT In Г+ kT 2 In [1 - exp (- ^)] -
V
J (2лтк)’1г 8л2(2n£)’/j(ABC)'11 „ np |
1П I Лз Лз Vo a J
= kTlnp — 4&7'ln7'-|-&7'^ln[l —exp (— -^-)] —
V
— fe? in ! 8“г „„ 4 }. (5.128)
(4) Молекулярная теплоемкость:
линейные молекулы
л.
<5-129>
v Stl \2Т)
нелинейные молекулы
/6с,\2
С.. 1 [дЕ\ ХИ 2У
UL=3+2^>y (5J ’
В вышеприведенных формулах для многоатомных молекул
считается, что внутренние степени свободы обусловлены глав-
ным образом колебаниями и вращением молекулы как целого.
Однако в некоторых молекулах существует еще относительное
вращение между группами атомов. Например, две метильные
группы этана могут вращаться относительно друг друга. Такое
внутреннее вращение не является свободным. Потенциальная
энергия, зависящая от угла поворота <р, приближенно может
быть представлена в виде
= — СОБО(/)ф) = UQ Sin2 (дО(/)ф),
где минимальное значение потенциальной энергии принято рав-
ным нулю, а максимальное равно и0, —число внутренней
симметрии, равное числу всех неразличимых относительных кон-
фигураций двух частей молекулы. Для этана c»(i) равно 3. Пит-
цер !) вычислил энергетические уровни такого движения и соот-
ветствующую функцию состояний для различных числовых зна- 9
9 Pitzer,/. Chem. Phys., 5 (1937), 469.
5.20. Приближенный расчет колебательного движения
197
чений u^kT. Основная трудность расчета связана с отсутствием
хорошего способа определения и0. Спектроскопические измере-
ния не дают нужных результатов, так как внутреннее относи-
тельное вращение не создает фундаментальных частот в инфра-
красном спектре или в спектре Рамана. Таким образом, можно
оценивать и0 лишь апостериори, проверяя, какие значения при-
водят к совпадению с опытом (например, по теплоемкости).
Если в функцию состояний ввести члены, связанные с относи-
тельным внутренним вращением, то они заменят одну или не-
сколько колебательных функций. В формулах (5.121) —(5.130)
не учитываются эффекты ангармоничности и взаимодействия
колебания с вращением. При необходимости можно ввести по-
правки, действуя таким же образом, как и в п. 5.15 для двух-
атомных молекул. Подобные расчеты проводили Пеннингтон и
Кобе !).
5.20. Приближенный расчет колебательного движения
Общие формулы для термодинамических функций много-
атомных молекул, приведенные в предыдущем пункте, требуют
знания характеристических температур 0г; различных типов ко-
лебаний. Иными словами, нужно знать частоты vv отдельных
колебаний (5.119). Эти частоты vv или более употребительные
волновые числа mv = vv/c можно получить из спектральных дан-
ных. Они известны для очень многих молекул и для этих мо*
лекул можно проводить расчет термодинамических функций.
Однако даже когда спектральные данные не полны или отсут-
ствуют, то и тогда приближенные расчеты возможны, если ис-
пользовать следующие факты. Характеристическая частота ко-
лебаний между двумя атомами обычно не сильно зависит от
других атомов. Поэтому влияние остальных частей молекулы
можно приближенно учесть, считая, что есть два различных по
своей основе типа движения: колебания растяжения и колеба-
ния изгиба. При таком предположении каждая химическая
связь имеет характеристическую температуру колебания растя-
жения и характеристическую температуру колебания изги-
ба ©12). Обозначая через п число химических связей в молекуле,
имеем 2 п колебаний и 2п соответствующих характеристических
температур.
Если число атомов в молекуле равно а, то общее число коле-
баний для линейной молекулы равно (За—5), для нелинейной
равно (За—6). Для многоатомных молекул это число обычно
больше 2п. Естественно считать, что эта разница представляет
!) Р е n n i n g t о п, К о b е, J. Chem. Phys., 22 (1954), 1442.
198
Гл. V. Идеальные газы
собой колебания сравнительно большой части молекулы, имею-
щей много атомов. Приведем опытное правило для учета этой
разницы, предложенное Беневицем и Рознером1): средний
вклад каждого недостающего колебания можно заменить сред-
ним вкладом колебаний изгиба химических связей. Например,
молекулярную теплоемкость Cv можно вычислить следующим
образом:
линейные молекулы
нелинейные молекулы
Таблица 5.7
Характеристические температуры химических связей
Связь е(о2)(°К) Связь е^гк) 0^2)(°К)
С—С (алифати- 1307 935 Н—0 5030 1940
ческий ряд)
С—С (аромати- 2154 862 Н—S 3694 1235
ческий ряд)
С=С 1724 1307 s=o 1797 748
с=с 2990 539 S-C 992 402
С—н 4315 1510 N—N в N2O 3190 848
1 Z со Z ю р 1402 719
С—О 1480 1610 N—N 1437 1290
с=о 2500 1120 N—Н 4740 1724
С—N 1437 647 N—О 1823 949
Ce=N 3190 345 N=O 2112 935
С—Cl 935 374 Si—н 3132 1335
С—F 1510 1724 Si—0 1510 575
С—Вг 877 1365 в—н 3668 1654
С—I 762 1264 В—F 1280 992
Экспериментальные значения для связи В—N: 0^ = 1940° К, 0^2) = 719° к
9 Bennewitz, Rossner, Zeit. Phys. Chem., 39B (1938), 126.
5.20. Приближенный расчет колебательного движения
199
Численные значения и 0»2) различных типов связей предста-
влены в табл. 5.7. Вторая строчка таблицы дает связь каждых
двух соседних атомов углерода в ароматической группе,
существенно отличающуюся как от простой связи углерода
(С—С) в углеводородных соединениях, так и от двойной связи
(С = С) в тех же соединениях. При расчете соединений, содержа-
щих ароматическую группу, эту связь нельзя не учитывать. Таб-
лица первоначально была составлена Беневицем и Рознером, а
позднее расширена Мегреблианом !), который провел сравнение
приближенных значений Су с более точными по формулам (5.129),
Таблица 5.8
Молярная теплоемкость, рассчитанная
приближенным методом
Молекула Температура (°C) Удельная молярная теплоемкость при постоянном давлении,
точные значения приближен- ные значения эксперимен- тальные значения
СН3ОН 137 — 12,9 11,8
N2O4 27 15,86 15,63 —
NH3 0 — 8,4 8,7
300 — 11,06 10,27
500 — 12,51 11,31
700 — 13,74 12,92
850 — 14,52 13,22
1000 — 15,15 14,65
сбнб 20 19,1 20,4 21,8
100 24,5 25,7 25,8
350 38,35 39,45 38,9
ch3nh2 10 11,72 11,85 11,72
25 — 12,29 12,41
78 12,62 13,04 13,79
с2нб 64,5 13,6 14,1 13,4
n2o 20 10,24 10,14 9,24
(СНз) NH 10 — 15,8 16,8
50 — 18 18,66
СНС12Вг 27 16,2 16,9 —
42,7 21,48 21,72 —
c2h3cn 25 15,24 15,04 —
32,7 23,11 23,7 —
*) М е g h г е b 1 i а п, /. Am. Rocket Soc., Sept. (1951).
200
Гл. V. Идеальные газы
(5.130), а также с экспериментальными величинами. Из табли-
цы 5.8 можно видеть, что приближенные значения достаточно
близки к точным.
5.21. Константы химического равновесия
В предыдущих пунктах приведены различные формулы для
свободной энергии и функции состояний. Объединив эти резуль-
таты с законами термодинамики, можно точно определить кон-
станты химического равновесия. Таким образом, достаточно
при помощи спектра найти энергетические уровни молекулы,
чтобы получить возможность вычислить эти важные параметры.
Однако здесь мы не будем приводить подробного анализа. Чи-
татель может обратиться к другим учебникам.
5.22. Равномерное распределение энергии
Мы не рассматривали еще самый важный из классических
законов распределения — теорему равномерного распределения
энергии. Эта теорема формулируется обычно следующим обра-
зом: если в ансамбле имеется совокупность N классических си-
стем, каждая из которых имеет s степеней свободы и энергию (в
форме Гамильтона), состоящую из суммы s + t квадратичных
слагаемых, то при равновесии среднее значение энергии этих
систем равно N (s + kT, т. е. равно ^kT на каждый ква-
дратичный член в выражении для энергии. С помощью изложен-
ных методов можно дать простое доказательство этой теоремы
и указать область ее применимости.
Рассмотрим ансамбль из N систем Л, такой, что энергию е
каждого состояния можно разделить на два члена
е = еклас + еквант, (5.133)
где первый член еклас — энергия, соответствующая классиче-
ским степеням свободы, а второй член еквант — энергия, соответ-
ствующая остальным степеням свободы. Таким образом, функ-
ция состояний системы распадается на два множителя:
/клас(7)—для классических степеней свободы и/квант(Т)—для
остальных. Средняя энергия EAN систем А также соответствен-
но разделяется на два члена
Ёа = ЁТс + ЕТ™. (5.134)
Теорема равномерного распределения, которую мы хотим дока-
гтклас квант ,, /-квант
зать, использует ЬА и не зависит от е и , если, ко-
5.22. Равномерное распределение энергии
201
нечно, две группы степеней свободы действительно являются
разделимыми, как это предполагалось в (5.133).
Пусть число классических степеней свободы равно s и пред-
положим, что потенциальная энергия этих классических степеней
свободы есть сумма t квадратов координат pb q2, , qt с
коэффициентами, которые являются либо постоянными, либо
функциями остальных s — t координат qt+r 4t+2' 4S- Для
удобства эти координаты мы отметили значком *, чтобы разли-
чать два типа координат q и q*. Кинетическую энергию всегда
можно представить в виде суммы квадратов импульсов рь
р2, ... , Pt, р*+Р Р*+2, •.., р* с коэффициентами, которые пред-
полагаем либо постоянными, либо зависящими от q*+v q*M' * • •
..., р*, но не от q^ q2i ... , qt. Полная энергия классических
степеней свободы еклас тогда имеет следующую форму:
е“" = |м? + 4“!?г + + +
+W- (5-135)
где <Х1, а2, .. • , а/, Pi, р2, ... , Рз — постоянные числа или функ-
ции только q*+v q*t+2, ..., q*s<
Так как рассматриваемые степени свободы являются клас-
сическими, то функция состояний /клас(Г) эквивалентна класси-
ческому статистическому интегралу, т. е.
/клас(Г) - h~s f ... f dq, ... dq}dp1 ... dp} exp (-
(5.136)
где еклас определяется по (5.135). Интегрирование по коорди-
натам q и импульсам р, р* ведется от —оо до +оо, а пределы
интегрирования по q* определяются геометрическими свойст-
вами системы. Локальные граничные поля, например стенки со-
суда (см. п. 4.2), можно рассматривать как геометрические пе-
ременные, определяющие пределы интегрирования по р*.
Используя 8клас в виде (5.135), легко выполнить $ + / инте-
грирований по р, р, р* в (5.136). Получаем
ГС(Г) = h-s^kT^{S+t) f ... f dq}+1 ... dq}(aia2. . .аД ... Р5р.
(5.137)
Подинтегральная функция в (5.137) есть лишь функция р*,
поэтому интеграл равен постоянному числу, не зависящему от Т.
В результате средняя энергия классических степеней свободы
202
Г л. V. Идеальные газы
Na систем равна
Ir^NkT2 + (5.138)
т. е. равна ^kT на каждый квадратичный член в (5.135). Это
утверждение представляет собой точную формулировку теоремы
о равномерном распределении энергии (по степеням свободы).
Средняя энергия поступательного движения молекулы (три
степени свободы) равна ^kT. Средняя энергия классического
ротора без осевого вращения равна kT. Классический волчок
(симметричный и несимметричный) имеет среднюю энергию
^kT. Гамильтониан гармонического осциллятора имеет два
квадратичных члена, и классическая внутренняя энергия его
равна kT, что совпадает с (5.89) при hvfkT->0.
Задачи к главе 5
5.1. Доказать равенство (5.61).
5.2. Найти функцию состояний, свободную энергию и моле-
кулярную теплоемкость с поправками на ангармоничность и
взаимодействие. При 3500° К вычислить поправочный член
&Cvlk = NCPlk для НО и найти при той же температуре моле-
кулярные теплоемкости Cv и Ср.
Глава VI
ТЕРМОДИНАМИЧЕСКИЕ СВОЙСТВА ТВЕРДОГО
ТЕЛА
Как уже говорилось в первой главе, реальное твердое тело
представляет собой либо один кристалл, либо совокупность
кристаллов. Поэтому, прежде чем исследовать термодинамиче-
ские свойства твердого тела, необходимо сначала исследовать
термодинамические свойства кристалла.
Для того чтобы применить методы статистической механики
к расчету кристалла, мы рассмотрим его как единую механи-
ческую систему. В рамках классической механики движение та-
кой системы в первом приближении можно рассматривать как
совокупность малых колебаний около положения равновесия,
которые в свою очередь можно расчленить на нормальные коле-
бания. В рассматриваемом приближении каждое колебание
является независимым гармоническим колебанием. Такая кар-
тина правильно отражает реальное состояние кристалла до тех
пор, пока амплитуды колебаний достаточно малы, т. е. темпера-
тура кристалла не очень высока; при сравнительно больших ам-
плитудах колебаний в выражении для потенциальной энергии
необходимо учитывать члены более высокой степени, чем ква-
драт смещений. Но здесь мы не будем рассматривать этот слу-
чай. При переходе от классической теории к квантовой необхо-
димо только сопоставить квантовые состояния гармонического
осциллятора с каждым из нормальных колебаний.
Для отыскания функции состояний в рассматриваемом при-
ближении достаточно рассчитать частоты нормальных колеба-
ний кристалла с заданным числом молекул. Причем, чем точ-
нее вычислена частота, тем правильнее будет результат. По-
строение точных методов для вычисления частот представляет
пока большие трудности. В настоящее время существует
несколько приближенных методов, которые существенно опи-
раются на более или менее правдоподобные предположения.
Первое решение задачи дал Эйнштейн, который предполо-
жил, что для кристалла, состоящего из N атомов, достаточно
точным является выбор ЗМ равных частот. Этот метод является
грубым приближением, однако он не потерял своего значения
вплоть до настоящего времени. Дебай в качестве развития этого
204
Гл. VI. Термодинамические свойства твердого тела
метода предложил за 3^ частоты выбирать самые низкие соб-
ственные частоты некоторого континуума, имеющего одинако-
вые с реальным кристаллом коэффициенты упругости. Все ре-
зультаты теории кристаллов подтверждают, что эта интерпрета-
ция имеет огромное значение. Поэтому остановимся на теории
Дебая, приведя ее, однако, к той более общей форме, которая
предложена Борном.
Теория Дебая настолько успешно объясняла наблюдаемые
факты, что позднее многие абсолютизировали ее и стали оши-
бочно применять вне пределов самой теории. Причем тогда,
когда факты не соответствовали теории, считалось, что это —
аномальное явление, и без всяких оснований требовали спе-
циальных решений. В работе Блэкмана было показано, что
предположение Дебая относительно распределения частот нор-
мальных колебаний, даже после поправок Борна, является не
таким уж точным, хуже чем это предполагалось ранее. Поэтому
расхождение между фактами и теорией Дебая, как правило,
можно объяснить только неточностью определения частот нор-
мальных колебаний.
6.1. Нормальные колебания непрерывной упругой среды
Для того чтобы построить функцию состояний упругого кон-
тинуума, необходимо найти собственные частоты, соответствую-
щие его степеням свободы. Предположим, что любое устойчивое
внутреннее движение среды можно описать посредством супер-
позиции гармонических стационарных волн. Каждая волна ха-
рактеризуется направлением колебания, частотой и амплитудой.
В упругом теле для волны, распространяющейся в заданном
направлении, существует три возможных независимых направ-
ления колебаний: одно продольное и два поперечных. Если из-
вестны возможные частоты волны, то для вычисления среднего
значения ее энергии (это равносильно вычислению среднего
значения амплитуды) можно воспользоваться функцией состоя-
ний гармонического осциллятора.
Таким образом, вопрос в целом сводится к отысканию воз-
можных значений частот. Найти возможные значения длины
волны очень легко. Предположим, что среда помещена в пря-
моугольный ящик, определяемый следующими неравенствами:
0<x<a, (6.1)
Тогда для волны, распространяющейся параллельно направле-
нию оси х, сторона а должна быть целым кратным половины
длины волны (целым кратным !/2 Z). Другими словами,
2 I
(/ — целое число). (6.2)
6.1. Нормальные колебания непрерывной упругой среды
205
Для волн, распространяющихся параллельно осям «/иг, спра-
ведливы аналогичные условия. Для волны, распространяющейся
в произвольном направлении, по граничным условиям можно
получить общие ограничения на ее длину
(Z, т, п — целые числа). (6.3)
Таким образом, для заданного типа колебаний, например про-
дольных колебаний, число возможных длин волн, больших Хо,
равно числу положительных целых чисел /, т, п, удовлетворяю-
щих условию
(6-4)
т. е. равно числу целых точек внутри эллипсоида
(6-5)
координаты которых g, т], £ есть положительные целые числа.
И следовательно, оно равно одной восьмой объема эллипсоида
1 4л abc 4л V
(6-6)
где V — объем ящика.
Можно также показать, что если длина волны Хо достаточно
мала по сравнению с линейными размерами ящика, который
к тому же вмещает достаточно много вещества, то число волн
будет зависеть лишь от объема ящика V и не зависеть от его
формы. В этом случае скорость продольных и других типов
волн в непрерывной среде не зависит от их длины и в частном
случае изотропных сред не зависит от направления. Обозначим
значение этой скорости через cL. Тогда связь между частотой
v и длиной волны Л имеет вид
Xv = rz, (6.7)
Поэтому для продольных
стот, меньших vo, равно
волн, например, число возможных ча-
4nvo v
Зе?
(6-8)
Аналогично если скорость всех поперечных колебаний равна ct.
то, учитывая существование двух независимых поперечных коле-
206
Гл. VI. Термодинамические свойства твердого тела
баний, получаем, что полное число частот, меньших vo, равно
2^4^ (6.9)
3 с*
а общее число независимых поперечных и продольных волн с
частотой, меньшей vo, равно
(6.10)
Наконец, дифференцируя (6.10), получаем число независимых
волн с частотами в пределах от v до v + dv, равное
4nV(-V + -^-\v2<*v- (б-11)
\ ci ct /
Такой классический аналитический метод разложения дви-
жения на простые типы колебаний легко перенести в квантовую
теорию. В рассматриваемом приближении уравнение Шредин-
гера для кристалла может быть преобразовано таким образом,
что оно распадается на ряд уравнений для гармонических ос-
цилляторов. Каждому нормальному колебанию соответствует
одно уравнение гармонического осциллятора. Так как распре-
деление частот гармонического осциллятора выражается фор-
мулой (6.11), то очень легко найти его функцию состояний.
6.2. Функция состояний для сплошной среды
Для определения средней скорости поперечных и продоль-
ных волн удобно использовать следующее соотношение:
4=-5г+4- (6-12)
Тогда число простых колебаний с частотами между v и v + dv
равно
Рассмотрим каждое такое колебание как колебание гармо-
нического осциллятора, за нуль энергии которого принимается
энергия наинизшего квантового состояния. Тогда его функция
состояний имеет вид [см. формулу (5.84)]
(1 — (6.14)
Полная функция состояний f(T) представляет собой произведе-
ние величин, аналогичных (6.14), показатели степеней которых
6.3. Тепловое излучение
207
определяются из (6.13). Логарифмируя, получаем
lnf(7') = —Jv2ln(l — e-h^kT)dv. (6.15)
о
6.3. Тепловое излучение
Поле теплового излучения можно считать некоторой сплош-
ной средой. Для расчета теплового излучения в сосуде с вакуу-
мом методами статистической механики можно непосредственно
использовать все результаты предыдущего пункта, за ис-
ключением одного места, где необходимо внести изменение. Так
как излучение в вакууме представляет собой электромагнитные
колебания, которые могут быть только поперечными, но не про-
дольными, то в (6.11) необходимо оставить только второе сла-
гаемое, и если функцию состояний умножить на 2/з, то получим
функцию состояний /?(Т) поля теплового излучения
1П/?(Г)=—8^- Jv2ln(l — e-^kT)dv =
о
= f l2ln(l-e-4dl, (6.16)
о
где с—скорость света. Разлагая логарифм в степенной ряд и
производя почленное интегрирование, получаем
оо оо оо
- f yin(l-^)dl = f ^^-e-^dl =
0 0 л = 1
= = = (6.17)
0 л=1
Подставляя (6.17) в (6.16), находим
<6Л8>
Энергия поля равновесного излучения равна
Гзл=А7’2-^-1п/?(Г) = -^ЛК (6.19)
Это и есть закон Стефана — Больцмана, в котором теоретиче-
ское значение постоянной Стефана равно
208
Гл. VI. Термодинамические свойства твердого тела
Для того чтобы получить энергию волн с частотами из оп-
ределенного интервала, разобьем R(T) на два множителя, один
из которых Ri(T) для частот из интервала (v, v + dv), другой —
/?2(Л для остальных частот. Тогда, согласно (6.16), имеем
1П (Г) = — V2 In (1 — e~^kT) dv. (6.20)
Из предыдущего выражения получим энергию E^dv волн с ча-
стотами из требуемого интервала, т. е.
= = (6.21)
Это и есть распределение Планка, из которого берет свое на-
чало квантовая теория.
После того как в п. 6.8 будут рассмотрены термодинамиче-
ские функции кристаллов, можно будет найти, что свободная
энергия F поля излучения равна
/?изл = — kT\nR(T) = — Si T*V. (6.22)
Тогда давление излучения Ризл равно
Р"зл = — = (6.23)
dV №с3№ v 7
Это полностью совпадает с электродинамическим соотношением
Ризл = |£из7К (6.24)
6.4. Кристаллы, состоящие из атомов без внутренней
структуры
Вернемся к основной теме этой главы. Для простоты рас-
смотрим сначала кристаллы, состоящие из бесструктурных оди-
наковых атомов. Позднее мы рассмотрим кристаллы, состоящие
из многих видов атомов, обладающих внутренней структурой.
Непрерывная среда имеет бесконечное множество частот
простых колебаний, в то время как рассматриваемый здесь
реальный кристалл, образованный из N материальных точек,
чему соответствует ЗМ степеней свободы, может иметь только
3jV частот колебаний. Точное распределение частот этих колеба-
ний нам неизвестно- Допустим, что в интервале частот v, v + dv
имеется Ng(y)dv колебаний. Таким образом, заменив в (6.15)
член, имеющий место только для континуума, на соответствую-
щее выражение для реального кристалла, мы получим функцию
6.4. Кристаллы, состоящие из атомов без внутренней структуры 209
состояний 7((Т) кристалла
In Л'(Т) = — W fg (v) In (1 — e~kvlkT) dv. (6.25)
0
Так как всего имеется 3V частот колебаний, то должно быть
выполнено соотношение
Jg(v)dv = 3. (6.26)
о
Блэкман провел тщательное исследование функций распре-
деления g(v). Развивая работы Борна и Кармана, он показал,
что можно дать общее описание функции g(v), однако нет ни
одного случая, для которого было бы найдено простое аналити-
ческое выражение. Как бы то ни было, всегда справедливы сле-
дующие утверждения:
I) существует максимальная частота vmax, такая, что при
v>Vmax имеем g(v) =0. Поэтому в (6.25) и (6.26) верхний пре-
дел интеграла можно заменить на vmax.
II) Для низких частот, т. е. для длинных волн, распределение
частот нормальных колебаний кристалла совпадает с распреде-
лением для континуума с таким же коэффициентом упругости,
т. е.
g(y) — av2 (v->0, a— константа). (6.27)
III) Если v возрастает от очень малых значений, то в боль-
шинстве случаев, хотя и не всегда, g(y) сначала увеличивается
быстрее, чем av2, и имеет вид
g(v)~av24-pv4 (Р>0). (6.28)
IV) На конце интервала функция g(v) имеет два или несколько
максимумов. Из некоторых проведенных ранее исследований
известно, что один из максимумов весьма близок к vmax, а после
него g(v) очень быстро падает до нуля.
На рис. 6.1 изображено поведение функции g(v) для про-
стого кубического кристалла, причем отношение постоянной
квазиупругой силы, действующей на данный атом со стороны
ближайшего соседа, к постоянной квазиупругой силе, дейст-
вующей со стороны атома, ближайшего к соседнему, равно
20:1. Силами взаимодействия между атомами, расположен-
ными на больших расстояниях, при вычислении пренебрегали.
Вследствие большой сложности формы функции g(v) функ-
цию состояний нельзя выразить простой формулой. Поэтому
14 Зак. 1299
210
Гл. VI. Термодинамические свойства твердого тела
для вычислений по-прежнему есть необходимость в использо-
вании некоторых упрощенных представлений для g(v). Такие
упрощенные представления часто использовались физиками в
тех случаях, когда истинная функция распределения оставалась
Рис. 6.1.
в значительной степени неясной. Поэтому при сравнении ре-
зультатов вычислений с опытом необходимо помнить о неточ-
ности самой функции g(v)>
Одно из приближенных представлений было предложено
Эйнштейном и состояло в том, что, за исключением бесконечно
малой области вблизи Ve, g(v)=0, т. е. частота всех колебаний
одинакова, а условие (6.26), конечно, будет выполнено. В этом
случае функцию состояний /<(Г) можно написать в виде
1П К(Т) = — 3N In (1 —e-hvE/kT) = — 3AZ In (1 — e-W), (6.29)
где
QE — hvE!k. (6.30)
На первый взгляд кажется, что это приближение как будто
очень грубое, но так как обычно g(y) в окрестности vmax имеет
весьма острый пик, то при высокой или обычной температуре,
т. е. при приближение Эйнштейна сравнительно не-
плохо выражает самую важную часть g(y). Учитывая к тому
же его простоту, им по-прежнему удобно пользоваться при гру-
6.4. Кристаллы, состоящие из атомов без внутренней структуры 211
бых оценках. Однако при низкой температуре оно всегда очень
неточно, так как в этом случае роль низкочастотных колебаний
в функции состояний сравнительно велика, чего приближение
Эйнштейна совсем не учитывает.
В приближении Дебая предполагается, что колебания с ча-
стотой, меньшей vD, распределяются согласно (6.27), а колеба-
ния с частотами, большими vD, не существуют. Выбор частоты
vd производится таким образом, чтобы общее число колебаний
равнялось ЗЛГ, т. е.
3 = f av2tZv==~ av^.
о
(6.31)
Таким образом, функцию g(v) в приближении Дебая можно на-
писать в виде
g(v) = 9v2/v^
g(v) = 0
(v<vd)>
(v > vD).
(6.32)
В теории Дебая постоянная vd (или а) является вполне оп-
ределенной. В действительности, как будет видно из дальней-
шего, ее можно выбрать различными способами. Однако ввиду
того что длина волны у длинных волн соответствует нескольким
тысячам кристаллических ячеек, то по отношению к ним кри-
сталл можно рассматривать как континуум, микроструктура
которого не оказывает никакого влияния. Таким образом, со-
гласно (6.13), имеем
(6-33)
Из (6.25) получаем
VD
\пК(Т) = — -^- f v2ln(l — e-Av/*r)dv =
vd о
VD
= — J V2 In (1 — e~hvikT) dv, (6.34)
0
где c—средняя скорость звуковых волн низкой частоты. Опре-
деляется она соотношением (6.12) и может быть вычислена по
коэффициенту упругости.
По аналогии с QE температуру можно определить с по-
мощью соотношения
hvn he I 3N Л’
А —____2. —___I____
k ~ k ’
(6.35)
14*
212
Гл. VI. Термодинамические свойства твердого тела
Выразим (6.34) через 0D, тогда можно написать
1пЛГ(7') = — 9N f Vln(l— (6.36)
®D 0J
Интегрируя по частям, получаем
з ®D/r
ln/C(T) = _ 3Wln(l — e^DlT)^-3N~ f (6.37)
Если T^>®D, to второе слагаемое много меньше первого, кото-
рое совпадает с приближением Эйнштейна (6.29). Таким обра-
зом, при 7^>0D приближение Эйнштейна мало отличается от
приближения Дебая.
6.5. Влияние электронов и атомных ядер на функцию состояний
В предыдущем пункте была найдена функция состояний для
кристалла, образованного из одинаковых бесструктурных си-
стем. Попытаемся теперь в дополнение к этому простому ана-
лизу учесть электронную структуру реальных атомов. Мы по-
прежнему ограничимся довольно грубым приближением. Одна-
ко полученные выводы почти для всех приложений являются
достаточно точными и полностью подтверждаются при более
глубоком анализе влияния электронов.
Пусть электроны либо сильно связаны с атомными ядрами,
либо связаны чрезвычайно слабо. Сильно связанные электроны
можно считать локализованными около определенных атомных
ядер, образуя внутренние оболочки атома. Внутренние оболоч-
ки атома являются локализованными системами и в общей
функции состояний каждая из них характеризуется одним мно-
жителем е(Т). Их вклад в полную функцию состояний равен
(е(Т)]ЛГ, где е(Т)—функция состояний электрона внутренней
оболочки. Обычно лишь самый низкий электронный энергетиче-
ский уровень оказывает существенное влияние на функции
е(7), и, таким образом, последняя сводится к одному первому
члену. Поэтому если мы, как обычно, примем энергию этого
электронного состояния за нуль, то е(Т) сведется к статистиче-
скому весу и0 самого низкого электронного энергетического
уровня.
Если имеются электроны из другого класса (слабая связь),
то их обычно рассматривают как свободные электроны, т. е.
6.5. Влияние электронов и атомных ядер на функцию состояний 213
предполагают, что они свободно перемещаются в периодическом
потенциальном поле. Для наших целей периодическое поле мож-
но приближенно заменить усредненным, а движение электронов
принять за свободное движение в однородном поле. Таким об-
разом, они будут подчиняться статистическим законам для ан-
самбля частиц в однородной потенциальной яме.
Так как масса электронов очень мала, а их концентрация в
рассматриваемом случае очень велика, то эти законы совсем не
являются знакомыми нам законами идеального газа. Выра-
жаясь простым физическим языком, это означает, что не число
состояний с низкой энергией намного превышает число электро-
нов, а как раз наоборот, имеется недостаток состояний с низ-
кой энергией. Состояние электронного ансамбля полностью
определяется следующими условиями: все самые низкие состоя-
ния поступательного движения заполнены, причем каждое со-
стояние занято двумя электронами с противоположными спи-
нами, в то время как остальные состояния являются пустыми.
Другими словами, имеется только одно состояние группы
свободных электронов, которое влияет на средние свойства ан-
самбля.
Окончательно мы получаем чрезвычайно простой резуль-
тат, а именно вклад, вносимый всеми свободными электронами
в функцию состояний кристалла, представлен множителем,
который равен 1. Естественно, что наши рассуждения были
преднамеренно упрощены; в некоторых случаях свободные элек-
троны играют существенную роль для теплоемкости. Но мы сей-
час не будем рассматривать этого случая, отложив его до
п. 6.17.
В заключение введем множитель р, являющийся статистиче-
ским весом ориентации ядерного спина атома. Таким образом,
введя добавочный множитель и0 для связанных электронов, мно-
житель 1 для свободных электронов и множитель р для ядер-
ного спина атома, мы вместо (6.25) получим полную функцию
состояний для кристалла
оо
1п/С(Г) = -М Jg(v)ln(l — e-Av^r)fifv + Nlnvop. (6.38)
О
Следует помнить, что при получении функции состояний за
начало отсчета энергии было принято самое низкое энергетиче-
ское состояние кристалла, но этот самый низкий энергетический
уровень в каждом простом колебании включает остаточную
энергию 1/2k(v). Теперь сделаем поправку на эту остаточную
энергию.
214
Г л. VI. Термодинамические свойства твердого тела
6.6. Равновесные свойства кристаллов
До сих пор мы рассматривали кристалл как совокупность
3 N локализованных гармонических осцилляторов. Во многих
случаях нет необходимости в таком строгом подходе, а доста-
точно предположить, что имеется 3?V локализованных осцилля-
тора, которые не обязательно являются гармоническими, и для
каждого осциллятора имеет место функция состояний более об-
щего вида
fx(T) = ^re-Er/kT, (6.39)
где индекс т относится к т-му осциллятору. Если при вычисле-
нии вклада электронов и ядер оставаться в рамках того же
приближения, что и раньше, то функция состояний К(Т) кри-
сталла будет иметь вид
37V
ln/<(7') = SlnfT(7’) + Wlnv0p. (6.40)
В качестве классифицирующего параметра удобно использо-
вать собственные частоты осциллятора. Это позволяет нам груп-
пировать очень близкие по свойствам Ng(v)dv осциллятора и
рассматривать их как классические ансамбли из одинаковых
локализованных систем. Выбор именно частоты в качестве клас-
сифицирующего параметра не имеет существенного значения.
В более общем случае для классификации можно выбрать лю-
бой параметр т, лишь бы он давал возможность выбрать груп-
пы осцилляторов в количестве Nx = Ng(x)dx, имеющих в дей-
ствительности одинаковые состояния и функции состояний. Та-
ким образом, запишем (6.40) в следующем виде:
\пК(Т) = К f + (6.41)
причем число пг в r-ом состоянии т-й группы осцилляторов со-
ставляет
e'er/kT
(6.42)
Выше приведенное выражение может быть написано только
в том случае, если Л\ достаточно велико, а это может быть
всегда гарантировано при достаточно большом АЛ Другие вели-
чины, характеризующие свойства кристалла, например энергия
и внешняя сила, всегда могут быть вычислены с использова-
нием пт из (6.42). Отношение nr!Nx всегда меньше 1.
6.6. Равновесные свойства кристаллов
215
Если формально допустить, что Л\ = 1, то nr!Nx уже нельзя
рассматривать как относительное среднее число осцилляторов
т-й группы в r-ом состоянии из Nx осцилляторов, а можно — как
функцию относительного времени нахождения системы т-го типа
в r-ом состоянии. Это и есть гипотеза Гиббса. Ниже мы уви-
дим, что предварительная классификация осцилляторов не яв-
ляется необходимой. Продемонстрируем это на примере вычис-
ления средней величины Е. Прежде всего, используя (6.39),
найдем среднюю энергию осцилляторов т-го типа
Ет = 2; «Л = Nx (Т) = NxkT* in (Г). (6.43)
Полагая Nx = Ng(x)dr и суммируя по всем т, получаем
E^xEx = Nfdzg(x)kT^\nfx(T) =
= g(x)\nfx(T)dx = kTi-^\nK(T), (6.44)
где К(Т) находится из (6.41).
Если не применять метод классификации и допустить, что
М = 1, то будем иметь
Ex = kT^\nfx(T).
(6.45)
Суммируя по всем осцилляторам и используя вместо /((Г) вы-
ражение (6.40), получаем тот же результат, что и раньше,
£ = 2г 4 2г 1П 4 1п (6‘46)
Поэтому в дальнейшем к вопросу о классификации мы не бу-
дем больше возвращаться.
Если энергетический уровень гг осциллятора зависит от па-
раметра х, то среднее значение обобщенной силы, с которой
осциллятор т действует на внешние тела, равно
*=I, (- тг)=- 2, iT iмп
(6-47)
Выражение для силы, с которой весь кристалл действует на
внешние тела, аналогично выражению для силы, действующей
со стороны ансамбля нелокализованных систем (газ).
216
Гл. VI. Термодинамические свойства твердого тела
6.7. Термодинамические функции кристалла. Поправка
к энергии
Перепишем полученные статистические формулы для сред-
них (равновесных) свойств кристалла в термодинамической
форме. Проще всего это сделать, если, исходя из формулы
F = — kTlnK(T), (6.48)
определить функцию F и показать, что F имеет свойства сво-
бодной энергии Гельмгольца. Для этого необходимо более тща-
тельно рассмотреть зависимость К(7) от объема. До сих пор за
нулевую энергию мы всегда принимали энергию ансамбля, на-
ходящегося в самом низком квантовом состоянии. Однако нам
известно, что объем кристалла меняется с изменением темпера-
туры, а следовательно, и состояние с нулевой энергией также
смещается.
Таким образом, за нулевую энергию необходимо принять
энергию действительно фиксированного состояния, не завися-
щего от температуры. Возьмем за начало отсчета энергию та-
кого состояния, когда атомы кристалла удалены друг от друга
на бесконечно большое расстояние. При этом каждый атом на-
ходится в некотором заданном основном состоянии. Энергию
кристалла, который находится в состоянии с наименьшей воз-
можной энергией, обозначим через —Aty, где % — положитель-
ная величина.
Очевидно, что энергия правильного макроскопического кри-
сталла прямо пропорциональна числу атомов до тех пор, пока
он подвергается равномерному сжатию (растяжению). В этом
случае % определяется только объемом V/N, приходящимся на
один атом. Величина —содержит остаточную энергию нор-
мальных колебаний с наинизшей энергией. Эта остаточная энер-
гия для колебания с частотой v равна V2/1V.
Используя выбранную таким образом нулевую энергию,
вместо (6.41) получаем следующее выражение для К(Т);
со
lnW(7') = ^- —W Jg(v)ln(l—г-**/*7’)dv +Winиор. (6.49)
О
Функция распределения g(v) будет сильно зависеть от N и V,
но для заданных значений V/N, или, говоря в более общем
плане, для заданных значений размера и формы базисной ячей-
ки кристалла, можно доказать, что при очень большом W она
стремится к некоторой предельной форме. Поэтому естественно
ввести объем V, приходящийся на один атом, определяя его как
V = NV, (6.50)
6.7. Термодинамические функции кристалла. Поправка к энергии 217
и функцию х, которая имеет вид
К(Т, N, У) = [х(Г, (6.51)
Удобно рассматривать х(Г, К) как функцию состояний каж-
дого атома в кристалле. Таким образом, мы имеем
1пх(Г, V) = ^ —Jg(v)ln(l —6rftW)dv + lnvop, (6.52)
О
a F, определяемая формулой (6.48), будет иметь вид
F = — MfePlnx (Г, И) = —Л^Ппх(Г, V/N). (6.53)
Покажем теперь, что F имеет свойства свободной энергии, т. е.
является термодинамическим потенциалом для независимых
переменных Г, V, N. Будем рассматривать FIT как функцию от
Г, V, N. Дифференцируя это отношение, получаем
d(^}= — Nk dT — Nk(^-\ dV —
\т I \ дТ )VtN \ dV }T,N
~k[in%+N(^r)T,N]dN- <6-54)
С другой стороны, согласно (6.44) и (6.51), имеем
<6-55)
Так как единственной геометрической координатой х является
объем V, а соответствующей обобщенной силой является давле-
ние Р, то, согласно (6.47) и (6.51), получим
Р = ®г(4^)гаг. (6.56)
Сравнивая (6.54) с (6.55) и (6.56), находим
d^ = — ^dT — -^-dV — + }dN. (6.57)
Если отождествить среднюю энергию Ё кристалла с внут-
ренней термодинамической энергией Е, то с точки зрения зави-
симости F от Т первая должна быть отождествлена со сво-
бодной энергией. Зависимость свободной энергии, определяе’
мой выражением (6.57), от объема также является верной.
Если к тому же предположить, что химический потенциал ц
218
Гл. VI. Термодинамические свойства твердого тела
определяется соотношением
ц = =-£7jlnx + W к (6.58)
\ON/Т,у ( \ ON /т,у) v '
то легко видеть, что F обладает всеми свойствами термодина-
мической свободной энергии. Но так как х зависит от N только
через V/N= V, то, используя (6.56), мы имеем
— =PV. (6.59)
\ oN )t,v \ dV n v '
Подставляя (6.59) в (6.58), получаем
+ (6.60)
Доля F каждого атома в свободной энергии равна
F = p—PV= — kT[n^ (6.61)
что совпадает е (6.53).
Таким образом, мы видим, что если функцию F, определяе-
мую выражением (6.53), принять за свободную энергию кри-
сталла, то зависимость F от V и Т является верной. Зависи-
мость F от У, приводящая к (6.60), в действительности тоже
верна, но для доказательства этого обязательно необходимо
рассмотреть процессы с изменяющимися например испаре-
ние. Здесь мы не будем рассматривать этого вопроса, а ограни-
чимся случаем, когда N не меняется. Ниже мы будем пользо-
ваться формулой (6.53) как определением свободной энергии
кристалла.
6.8. Термодинамические функции в приближении Дебая
Вернемся теперь к приближению Дебая и выпишем термо-
динамические формулы предыдущего пункта в этом приближе-
нии. Ограничимся рассмотрением правильного кристалла, под-
вергнутого равномерному сжатию. В приближении Дебая часто-
ты нормальных колебаний распределятся согласно (6.32), при
этом vD или 0d зависит от V = V/N, а вклад остаточной энергии
в —х равен
/ hvdv== = (6.62)
о D
6.8. Термодинамические функции в приближении Дебая
219
Подставляя (6.32) в (6.49), получаем
1Пх(Г, V) = —----— J V2 In (1 —g-Av/ftT) Jv_|_ln Uop =
Vd 0
s ®D/r
= l2ln(l-^)^ + lnvoP- (6.63)
eD j
Окончательно для свободной энергии кристалла, отнесенной к
одному атому, имеем
4 вр/Г
Г==Л = -Х + 9А-^- f £21п(1-е-^-£Лпи0р =
N во {
= - х+ 3kT In (1 - e~^T) - f dl-kT In rop. (6.64)
o n j e* — 1
D 0
Что касается полной энергии, то при ее вычислении следует
обратить внимание на то, что % и ©d являются лишь функциями
Т и V = V/N. Учитывая это, имеем
Е_ T2\d(F/T)i _ ьГ2р1пх\ _
№ TV [ дТ \ дТ ]v~
eD/T
=-х+9* { (-^)3ln(1 J-ЭЛ / 3|2 In (1 -е~^=
9d/t
= -x + 9*-S-f (6-65)
0 e ~ 1
Если T/@D очень велико или очень мало, то для приведенных
величин легко получить простые приближенные выражения.
При высокой температуре T^>&D, а ©d/Т очень мало; разло-
жим £3/(е*— 1) в степенной ряд по | и проинтегрируем почлен-
но, a In (1 —e~eD/T) разложим в степенной ряд по ©d/Т. Таким
образом, при Т^>©р получим
F ( 1 3 0^ 1 /0^\2 /ОгЛ4)
дГ== —Х + З£7|1п^ з”-“8 Т" + 4б(т“/ )
-A7’lnvop = (-x-4^0o) + 3^7’ + +
/е„\41
+ <9(“г) ) —АПпгоР (6.66)
220
Гл. VI. Термодинамические свойства твердого тела
И
4 = (- X -1*%) + 3kT {1 + -50 + 0 Icr) } • <6-67)
Заметим, что член, содержащий 0D, как раз вычитается из чле-
на, содержащего остаточную энергию в — %, а член (0р/Г)3
совсем отсутствует.
^d/t
При низкой температуре интеграл J заменим на раз-
о
со оо
ность J — J. Первый интеграл вычислим так же, как это сде-
о ©р/г
лано в (6.17), а второй проинтегрируем по частям. Тогда при
T<^®d получим
£=^- = — х — £7' In т>ор —
— 3^7 ---з^1г-во/г_]_о (2Le-<W\] (6.68)
| 1503d 6d \ &2d П
И
£= —= —х + 3£Г}^ —ЗгГ0о/г + О /—е-0о/гИ. (6.69)
N 1 50d \ ez> / J
Продифференцируем (6.55) по температуре при постоянных
V, N. Так как % и 0р являются функциями только V, то они
остаются постоянными. Таким образом, мы получим атомную
теплоемкость Cv кристалла при постоянном объеме
k дТ
/ Т \ *DJT ^е^ \
= 9( —) f rr^2dt = 3^ ’ <6-70)
\0D/ 0 \ Т /
где 3& y-y-j— так называемая функция Дебая, численные зна-
чения которой приведены в табл. 6.1.
При высокой и низкой температурах из приведенных выше
приближенных значений для Е можно непосредственно полу-
чить значения Cv. При высокой температуре
( 1 ©л / ©л \41
сг=3^(1 - 20-7^ + О(^) j. (6.71)
Таблица 6,1
Функция Дебая ^(OD/T)
/ Т \3
(&D/T) & 77,92729/-g— ) при T/@D < 1
0,0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0
0,0 1,0000 0,9995 0,9980 0,9955 0,9920 0,9876 0,9822 0,9759 0,9687 0,9606 0,9517
1,0 0,9517 0,9420 0,9315 0,9203 0,9085 0,8960 0,8828 0,8692 0,8550 0,8404 0,8254
2,0 0,8254 0,8100 0,7943 0,7784 0,7622 0,7459 0,7294 0,7128 0,6961 0,6794 0,6628
3,0 0,6628 0,6461 0,6296 0,6131 0,5968 0,5807 0,5647 0,5490 0,5334 0,5181 0,5031
4,0 0,5031 0,4883 0,4738 0,4595 0,4456 0,4320 0,4187 0,4057 0,3930 0,3807 0,3686
5,0 0,3686 0,3569 0,3455 0,3345 0,3237 0,3133 0,3031 0,2933 0,2838 0,2745 0,2656
6,0 0,2656 0,2569 0,2486 0,2405 0,2326 0,2251 0,2177 0,2107 0,2038 0,1972 0,1909
7,0 0,1909 0,1847 0,1788 0,1730 0,1675 0,1622 0,1570 0,1521 0,1473 0,1426 0,1382
8,0 0,1382 0,1339 0,1297 0,1257 0,1219 0,1182 0,1146 0,1111 0,1078 0,1046 0,1015
9,0 0,1015 0,09847 0,09558 0,09280 0,09011 0,08751 0,08500 0,08259 0,08025 0,07800 0,07582
10,0 0,07582 0,07372 0,07169 0,06973 0,06783 0,06000 0,06424 0,06253 0,06087 0,05928 0,05773
11,0 0,05773 0,05624 0,05479 0,05339 0,05204 0,05073 0,04946 0,04823 0,04705 0,04590 0,04478
12,0 0,04478 0,04370 0,04265 0,04164 0,04066 0,03970 0,03878 0,03788 0,03701 0,03617 0,03585
13,0 0,03585 0,03455 0,03378 0,03303 0,03230 0,03160 0,03091 0,03024 0,02959 0,02896 0,02835
14,0 0,02835 0,02776 0,02718 0,02661 0,02607 0,02553 0,02501 0,02451 0,02402 0,02354 0,02307
15,0 0,02307 0,02262 0,02218 0,02174 0,02132 0,02092 0,02052 0,02013 0,01975 0,01938 0,01902
222
Гл. VI. Термодинамические свойства твердого тела
при НИЗКОЙ
Cv = 3k[~^+o№-e-»t>/T\\. (6.72)
6.9. Сравнение приближения Дебая с экспериментом
При высоких температурах значение Cv по теории Дебая
равно ЗА. Пока Г>36р, это значение является достаточно точ-
ным с ошибкой, не превышающей 0,5%. В действительности это
есть пример на применение теоремы о равномерном распреде-
лении. Полученный результат на самом деле справедлив при
более широких условиях, чем теория Дебая. Он остается вер-
ным даже тогда, когда разница между g(v) и av2 очень вели-
ка, лишь бы только выполнялось неравенство T>3Avmax/A. Ра-
венство Cv — ЗА соответствует теплоемкости грамм-атома в
6 кал)град. Это и есть уточненная формулировка старого зако-
на Дюлонга и Пти.
Следует указать, что удельная теплоемкость в этом законе
есть теплоемкость при постоянном давлении Ср. Оба типа теп-
лоемкости для любого вещества связаны между собой следую-
щим термодинамическим соотношением:
-Ж =-ГШ7Ш=!^, (6.73)
г v \иТ Jр \оТ )у \оТ)р/ \оР/т р v
где а — коэффициент объемного теплового расширения, £ —
коэффициент изотермической сжимаемости. Разность между
NCp и NCV равна в среднем 0,4 кал/град • грамм-атом. По-
этому при высокой температуре закон Дюлонга — Пти и тео-
рия Дебая примерно совпадают.
При использовании поправочной формулы (6.73) для чистых
твердых тел и соединений можно обнаружить, что теоретиче-
ское значение NCV, равное 3/?, применимо лишь при высокой,
но не очень высокой температуре, так как в этом случае при-
ближение нормальных колебаний становится слишком грубым.
Теплоемкость некоторых металлов, особенно металлов переход-
ных групп, сравнительно сильно отличается от того значения,
которое предсказывает теория Дебая. Это происходит потому,
что у них значительный вклад в удельную теплоемкость дают
электроны, влияние которых мы исключили.
При низких температурах Cv должно, согласно приближе-
нию Дебая, изменяться как Г3. При T<0D/1O отклонение от
этого закона составляет не более 2%. Такая температурная
зависимость подтверждена уже для многих веществ, однако для
некоторых веществ отношение Cv /Т3 отнюдь не является кон-
6.9. Сравнение приближения Дебая с экспериментом
223
стантой; объясняется это тем, что температура еще не настоль-
ко низка, чтобы главные нормальные колебания распределялись
согласно предполагаемому закону av2. Как показывают иссле-
дования Блэкмана, закон Г3 строго может быть выполнен лишь
при крайне низкой температуре.
Многие имеющиеся области справедливости закона Т3 яв-
ляются до некоторой степени случайными, так как Су при про-
должении понижения температуры вновь начинает отклоняться
от этого закона и лишь при еще более низкой температуре на-
чинает строго подчиняться ему. Вообще для реального металла
очень трудно ожидать существования такой области. Еще до
того, как эти условия будут достигнуты, главной становится
удельная теплоемкость свободных электронов, которая изме-
няется с изменением Т линейно. Для того чтобы теория по-
прежнему соответствовала эксперименту в этой области, необ-
ходимо очень сильно понизить значение 0D.
В промежуточном интервале температур значение Cv/k по
Дебаю является универсальной функцией ©р/Г, которая задана
выражением (6.70), а численные значения приведены в табли-
це 6.1. Пусть экспериментальные данные в некотором интер-
вале температур согласуются с теоретическими значениями.
Тогда можно найти 0D. Определенные таким образом значения
0d приведены в табл. 6.2 (для Na, Си, Fe, FeS2 при температуре
выше предельного значения, указанного в таблице, эксперимен-
тальные величины будут больше теоретических).
Таблица 6.2
Характеристическая температура Дебая
Вещество Интервал температур, °К ер. °к Вещество Интервал температур, ер, °к
РЬ 14—573 88 КС1 23-550 230
Т1 23—301 96 Zn 33—673 235
Hg 31—232 97 NaCI 25—664 281
J 22—298 106 Си 14—773 315
Cd 50—380 168 Al 19—773 398
Na 50—240 172 Fe 32—95 453
КВг 79—417 177 CaF2 (флюорит) 17—328 474
Ag 35-873 215 FeS2 22-57 645
Са 22—62 226 С (алмаз) 30-1169 1860
Для окончательной проверки теории воспользуемся экспери-
ментальной кривой Cv — Т для некоторого вещества. Найдем
224
Г л. VI. Термодинамические свойства твердого тела
соответствующую ему величину и сравним со значением,
вычисленным из коэффициента упругости. Изотропное твердое
тело имеет два коэффицента упругости, коэффициент сжимае-
мости р и постоянную Пуассона о. Скорости звука ct и ct выра-
жаются через р и о следующим образом:
2_ 3(1—а) 2_ 3(1—2а)
ci— (1+а)₽р’ С'“2(1+о)₽р’
(6-74)
где р — плотность. Подставляя (6.74) в равенство, являющееся
следствием (6.12) и (6.35),
1____4лУ Л3 /_1_ . _2_\
e3D~~ 9N h3 \ с3 "с3 )’
(6.75)
получаем как функцию р, о и р. В табл. 6.3 приведено срав-
нение для четырех веществ.
Таблица 6.3
Вещество р, г[см2 0x10“ см2!дин и 0£) из тепло- емкости из коэф- фициента упругости
А1 2,71 1,36 0,337 398 402
Си 8,96 0,74 0,334 315 332
Ag 10,53 0,92 0,379 215 214
Pb 11,32 2,0 0,446 88 73
6.10. Кристаллы, образованные молекулами
Формулы теории Дебая могут быть непосредственно приме-
нимы лишь к кристаллам, состоящим из атомов одного вида.
Рассмотрим теперь случай, когда кристаллы содержат один или
несколько видов элементов, в которых атомы уже образуют
молекулы. Допустим, что кристалл содержит N молекул, ка-
ждая из которых состоит из s атомов. Очевидно, что состояние
кристалла можно приближенно охарактеризовать 3N колеба-
ниями с частотами, распределенными согласно теории Дебая,
а оставшиеся 3Af(s— 1) колебаний относить к внутренним сте-
пеням свободы молекул. Это возможно потому, что в первом
приближении внутреннее движение в молекулах и относитель-
ное движение молекул в кристаллической решетке обычно счи-
тают независимыми.
6.10. Кристаллы, образованные- молекулами 225
Таким образом, функция состояний К(Т) кристалла, образо-
ванного из молекул, может быть записана в виде
^D/r
\nK(T) = ^-9N f ^1п(1-г-Ч^ + ЛИп/(Л.
D о
где /(Г)—функция состояний для внутренних степеней свобо-
ды молекул, включая электронное движение и ядерный спин
атома. Обычно, кроме движения электронов, 3(s—1) внутрен-
них степеней свободы каждой молекулы в кристалле можно
приближенно рассматривать как простые гармонические коле-
бания с одинаковой частотой. Таким образом, их вклад в термо-
динамические функции часто пишется в форме Эйнштейна. Если
эти частоты обозначить через kQJh,..., kQJh,..., k@3slh или в
общем случае через kQilh, то функция состояний кристалла бу-
дет иметь следующий вид:
D о
- N 2 ln (1 ~ e~ei/T) + /V In и0Пр, (6.76)
/ = 4
где Пр — произведение статистических весов спинов атомных
ядер каждой молекулы. Свободная и внутренняя энергии равны
соответственно
^d/t
+ ^in(l-e-4^+
N ®D S
+ £Г21п(1-<Ге</г)-£7'1пи0Пр, (6.77)
i = 4
И
®D/T 3s
<678>
D 0 /=4 1
Дифференцируя (6.78) по T, получим теплоемкость
3s а /т
Cv = 3k3) + k 2 • <6-79)
15 Зак. 1299
226
Гл. VI. Термодинамические свойства твердого тела
Иногда встречаются такие случаи, когда поведение одной,
двух или трех внутренних степеней свободы молекулы в кри-
сталле значительно лучше моделируется вращательным, а не
колебательным движением. На эту возможность впервые ука-
зал Симон и исследовал Паулинг, который к тому же рассма-
тривал процесс перехода из почти чистого вращательного дви-
жения в колебательное при понижении температуры, когда
потенциальная энергия ориентации значительно больше kT. В не-
котором узком интервале температур имеются резкие переходы
от одного случая к другому. Выбор различных приближенных
моделей в этом случае необходим, так как истинные колебания
совсем не обязательно гармонические. Вполне возможно, что на
низких энергетических уровнях они больше похожи на гармо-
нический осциллятор, а на высоких энергетических уровнях на
«свободный» ротатор. В тех случаях, когда более удобно ис-
пользовать приближение свободного вращения, чем гармониче-
ского колебания, то один, два или три члена Эйнштейна долж-
ны быть заменены функцией состояний одно-, дву- или трехмер-
ного ротатора.
6.11. Кристаллы с ионными или комплексными решетками
Если в кристалле все атомы различны или одинаковы, но
различным образом расположены в решетке, то они образуют
несколько кристаллических ячеек, каждая из которых содержит
5 атомов. Все ячейки представляют собой точные копии друг
друга. Кристалл из N кристаллических ячеек, содержащий sN
атомов, обладает 3s группами различных нормальных колебаний
и частот. Если точкой в трехмерном пространстве обозначить
нормальное колебание, то величина вектора от нулевой точки
до обозначенной есть ее сферическая координата, а направление
совпадает с направлением распространения волны. Длина век-
тора равна волновому числу (величина, обратная длине волны),
причем волновые числа каждой группы распределены равно-
мерно в трехмерном пространстве. Этот результат Борна яв-
ляется вполне строгим, но им нельзя пользоваться для вычис-
ления функции состояний до тех пор, пока не установлена связь
между частотой и волновым числом.
Прежде чем установить эту связь, исследуем движение одно-
мерной цепочки равноотстоящих атомов. Рассмотрим случай,
когда все атомы одного типа. Перенумеруем их от начала коор-
динат числами от 1 до N. Пусть хп — смещение n-го атома от
его положения равновесия. Кроме этого, предположим, что ка-
ждый атом взаимодействует только со своим соседом. При та-
ких упрощениях уравнение движения n-го атома записывается
6.11. Кристаллы с ионными или комплексными решетками
в виде
m = — И — Хя-1) — — Х«)1’ <6-80)
где ц— коэффициент упругости силы, действующей между
двумя атомами, a m — масса атома.
Уравнения движения крайних атомов, очевидно, отличаются
от уравнений движения внутренних атомов, так как у них один
сосед отсутствует. Этот факт осложняет процесс решения (6.80);
для преодоления этой трудности можно использовать метод
Борна и Кармана. Предположим, что к краям атомной цепочки
добавлены атомы для того, чтобы уравнения движения крайних
атомов стали такими же, как уравнения движения внутренних
атомов. Если число атомов достаточно большое, то это никак не
повлияет на распределение частот. Кроме этого, предположим
еще, что фаза Xi одинакова с предполагаемой фазой (М+1)-го
атома. Тем самым мы как бы выбираем цепочку в N атомов из
бесконечного ряда. Пусть длина волны есть делитель длины
цепочки из N атомов. В такой постановке можно найти число
степеней свободы выбранной цепочки.
Будем искать решение в виде
х.(1. v) = Aen‘^^-'l (6.81)
где А — постоянная, I — целое число, удовлетворяющее гранич-
ным условиям. Подставляя в (6.80), имеем
— 4n;2mv2 — — ц2 ^1 — cos = — 4ц sin2 . (6.82)
Соотношение (6.81), являющееся решением уравнения (6.80),
в действительности описывает бегущую волну с длиной, равной
k —Nafl, где а — расстояние между атомами при равновесии,
число волн (5=llNa, их частота равна v. Извлекая корень ква-
дратный из обеих частей (6.82), получаем
v=I sin I=i /£ ।sin । • <6-83)
1 -J- N '
Максимально возможное число волн соответствует 1 = ± -у,
знак « + » соответствует прямой волне, а знак «—» обратной.
Поэтому о изменяется в интервале от —до 4--^-. Если
значение N очень велико, то (6.83) можно рассматривать как
непрерывную функцию, которую можно изобразить графиче-
ски. При очень малых значениях а справедливо, как мы и
15* <
228
Гл. VI. Термодинамические свойства твердого тела
думали раньше, соотношение
(6.84)
При больших о, как видно это из рис. 6.2, частота v увеличи-
вается сравнительно медленно.
Поместим теперь атомы с массой М в средние точки между
атомами с массой m так, чтобы расстояние между соседними
атомами стало а/2. Перенумеруем все атомы последовательно
положительными целыми числами от 1 до 2N, Тогда нечетные
числа будут соответствовать атомам с массой т, а четные —
атомам с массой М. Уравнения движения имеют вид
m d2x2n+Jdt2 = — jx [(х2л+1 — х2п) — (х2л+2 — х2л+1)],
М d2x2llldt2 — jx |(х2л x2n_j) (х2л+1 х2л)],
где ц — коэффициент упругости силы, действующей между со-
седними атомами различных типов. Как и раньше, здесь учиты-
вается взаимодействие только между соседними атомами. Ре-
шение системы (6.85) можно записать в виде
х2п+1 = А ехр j 2л/ (z — vzj I,
( 2гг <6*86)
х2п = В ехр < 2л/ (Z — vt \ >,
где I — положительное целое число. В рассматриваемом слу-
чае число волн о равно IjNa. Подставляя (6.86) в (6.85), полу-
6.11. Кристаллы с ионными или комплексными решетками
229
чаем
(4ji2mv2 — 2ц) А + 2ц cos (лаа) 5 = 0,
2ц cos (лоа) А + (4л2ЛЬ2 — 2ц) В = 0. (6.87)
Решение будет отлично от нуля, если выполнено соотношение
(4л2Лк2 — 2ц) (4л2/т>2 — 2ц) — 4ц2 cos2 (лаа) = 0. (6.88)
Решая (6.88) относительно v2, получаем
v2 = [M-j-m ± ]Л/И2 + пг2 + 2Mm cos 2лоа]. (6.89)
Отношение амплитуд A/В равно
А 2М cos лоа
-- =------------ . (о.УО)
В М — т + У Л42 -j- т2 + 2 Мт cos 2лоа
Область значений о по-прежнему находится между —7га и
+ 720. Но теперь для каждой волны определенной длины
имеются две соответствующие им возможные частоты, которые
соответствуют различным знакам в (6.89). Одна частота не-
сколько выше другой так, как изображено на рис. 6.3. При
М'^>т обе частоты сильно отличаются друг от друга. Для ко-
лебаний, частота которых сравнительно низка, связь между
230
Гл. VI. Термодинамические свойства твердого тела
частотой и числом волн приближенно имеет характер прямой
пропорциональной зависимости. Для колебаний, частота которых
сравнительно высока, частота почти не зависит от числа волн
и остается постоянной. Из (6.90) видно, что для сравнительно
низких частот (нижний знак) отношение A/В является положи-
тельным. Поэтому фазы легких и тяжелых частиц почти оди-
наковы, как это показано на рис. 6.4. Для сравнительно высо-
ких частот (верхний знак) отношение A/В отрицательно и фазы
легких и тяжелых частиц почти противоположны, как это по-
казано на рис. 6.5.
При построении приближенного метода расчета функции со-
стояний ионного кристалла или комплексной решетки Борн ис-
пользовал ту особенность, что два типа колебаний кристалла
чрезвычайно сильно отличаются по своим свойствам. Он пред-*
ложил разделить все колебания на два класса, которые назы-
ваются акустическими и оптическими (инфракрасными).
Акустические колебания при малом числе волн имеют ча-
стоту, прямо пропорциональную числу волн. Поэтому скорость
распространения са равна
ra==v/o.
Скорость са в действительности связана с о, но Борн упразднил
эту зависимость, что эквивалентно приближению Дебая. Для
оптических колебаний Борн считал частоты постоянными, не за-
висящими от длины волны. В кристалле, образованном из N
элементарных ячеек, каждый ряд таких колебаний включает
в себя Af тождественных частот. Это и есть приближение Эйн-
штейна. Таким образом, в этом грубом приближении каждая
группа акустических колебаний дает в функции состояний и
термодинамических функциях член приближения Дебая, а ка-
ждая группа, состоящая из W оптических колебаний, — член
приближения Эйнштейна.
6.11. Кристаллы с ионными или комплексными решетками
231
Остается рассмотреть, сколько групп акустических и сколько
групп оптических в- 3s группах колебаний являются, или грубо
говоря, даются приближениями Дебая или Эйнштейна. Ответ
на вопрос зависит от конкретной структуры кристалла. В п. 6.10
мы уже видели, что если каждую кристаллическую ячейку
можно рассматривать как отдельную молекулу, то естественно
считать 3 группы колебаний акустическими (содержащих в сум-
ме 3W частот) и 3(s—1) группы колебаний — оптическими (в
каждой группе имеется W равных оптических частот).
Для простой ионной решетки, состоящей из двух типов ато-
мов с почти равной массой, например КС1, очевидно, было бы
естественным предположить, что существует 6 акустических
групп, каждая из которых состоит из N акустических частот.
Это является достаточно хорошим приближением. Для кристал-
лов, у которых массы атомов различаются сильно, такое при-
ближение ухудшается. Примером может служить СаСО3. Так
как кальций намного тяжелее углерода и кислорода, а атомные
веса углерода и кислорода разнятся незначительно, то мы дол-
жны предвидеть, что в его пятнадцати группах колебаний де-
вять обязательно оптические с довольно высокой частотой, а
три группы обязательно акустические; остальные три группы
с ними не совпадают и являются промежуточными по свой-
ствам. Их частоты очень малы и сильно меняются в зависи-
мости от числа волн.
При всех этих рассуждениях необходимо помнить, что если
акустические колебания происходят с низкой частотой, то они
обязательно подчиняются закону g(v)~av2, а при высоких ча-
стотах возможны отклонения от него.
Таким образом, функцию состояний любого кристалла, кото-
рый может быть составлен из молекул, т. е. функцию состоя-
ний, учитывающую свободное вращение радикалов, всегда
можно грубо выразить через произведение 3s функций состоя-
ния, среди которых по крайней мере три относятся к типу Де-
бая, а остальные — к типу Эйнштейна. При высокой темпера*
туре, когда T^©D, теплоемкость, которую каждый тип вносит
в отдельные базисные кристаллические ячейки, равна k, а при
крайне низких температурах когда Т стремится к нулю,
каждый тип дает член, который тоже стремится к нулю.
Поэтому только в области, где температуры Т и 0D близки
друг к другу или Т по крайней мере ненамного меньше 0D, раз-
ница между этими двумя типами является существенной. В дей-
ствительности из опыта известно, что теплоемкость кристаллов
многих простых соединений достаточно хорошо описывается
простой формулой Дебая, где каждому атому соответствуют
три члена и лишь одно значение 0р.
232
Г л. VI. Термодинамические свойства твердого тела
Значения 0D представлены в табл. 6.2. Для кристаллов бен-
зола Лорд, Алберг и Андраус использовали шесть членов
приближения Дебая, три из которых относятся к межмолекуляр-
ным колебаниям, а три — к связанным крутильным колеба-
ниям. Остальные тридцать внутренних молекулярных колеба-
ний относятся к оптическому типу с частотой, равной частоте
колебаний, наблюдаемых для свободных молекул бензола. Так
как частота внутренних молекулярных колебаний довольно вы-
сока, а при 60° К членом приближения Эйнштейна можно пре-
небречь, то при температуре ниже этой необходимо рассматри-
вать лишь шесть членов приближения Дебая. При 0D=15O°
сумма равна 6&^(0D/T), этот результат очень хорошо соответ-
ствует экспериментальным данным.
6.12. Металлы и диэлектрики
В предыдущих пунктах мы не касались разделения кристал-
лов на проводники и диэлектрики, так как не рассматривали
движения электронов. Если учитывать влияние электронов на
термодинамические свойства твердого тела, то мы обязательно
должны разделить кристаллы на два больших класса—метал-
лы и диэлектрики. В металлах электроны, как правило, свобод-
но движутся в трехмерном периодическом поле, создаваемом
атомными ядрами с положительными зарядами, расположен-
ными в виде правильной кристаллической решетки. Очень важ-
но знать поведение теплоемкости движущихся электронов при
низких и высоких температурах. Однако прежде чем вычислять
вклад электронов, предварительно приведем простое качествен-
ное разъяснение различия между проводниками и диэлектри-
ками.
Движение электрона в трехмерном периодическом силовом
поле логично исследовать двумя приближенными методами.
Приведем их оба. Начнем сначала со случая, когда атомы в
кристалле расположены в обычном порядке, но на большом
расстоянии друг от друга. Будем считать собственную функ-
цию атомов первым приближением электронного состояния, а
затем попытаемся определить изменение атомных состояний
при сокращении расстояний между атомами до нормальных.
С другой стороны, можно начать со свободного движения
электронов в равномерном потенциальном поле и исследовать
влияние, которое оказывают на электронные состояния малые
изменения потенциального поля с периодом, равным периоду
кристаллической решетки. Оба метода приводят к одинаковым
общим результатам, но в различных конкретных случаях один
из них может давать более убедительную физическую картину.
6.12. Металлы и диэлектрики
233
Для относительно слабо связанных состояний лучше начинать
с изолированных атомов; для сильно связанных состояний, на-
оборот, лучше исходить из равномерного потенциального поля.
Для того чтобы описать общие свойства электронов и их
распределение в кристалле, лучше начинать с изолированных
атомов. Рассмотрим сначала систему Af одинаковых атомов, рас-
положенных так же, как в обычном кристалле, но с увеличен-
ными расстояниями между ними. Для каждой группы значений
трех квантовых чисел (без спина) каждому из двух направле-
ний спина электрона соответствует одно состояние атома, по-
этому N атомов имеют 2М состояний. При больших расстоя-
ниях между атомами они имеют совершенно одинаковую энер-
гию и поэтому образуют некоторое 2/V вырожденное состояние.
Если теперь уменьшить расстояние между атомами, то вслед-
ствие взаимодействия между ними это 2М-кратное вырожден-
ное состояние распадается на группу состояний, энергии кото-
рых распределятся в некоторой энергетической полосе. Ширина
полосы увеличивается по мере уменьшения расстояния между
атомами, но она не зависит от N, по крайней мере при очень
большом N.
Вообще говоря, энергетическая полоса содержит W различ-
ных энергетических уровней, в каждом из которых электроны
могут иметь одно из двух направлений спина. Таким образом,
такая полоса может вместить самое большее 2М электронов.
Если энергия каждого состояния в энергетической полосе до-
бавляется к энергии электрона, то из-за изменения заряда энер-
гия тоже несколько изменяется, но эти поправки не могут из-
менить числа состояний и их специфических свойств. Так как
ширина энергетической полосы В не зависит от /V, то разность
между энергиями соседних состояний будет порядка В/N и при
очень большом N становится очень малой.
Для реальных кристаллов отдельные состояния в энергети-
ческой полосе в действительности распределены непрерывно.
Можно показать, что каждое состояние атома, соответствую-
щее определенной собственной функции с фиксированной элек-
тронной энергией, вследствие взаимодействия атомов в кри-
сталле преобразуется в полосу из N состояний, в каждое из
которых можно поместить два электрона с противоположными
спинами. Энергетические полосы, относящиеся к собственным
функциям различных атомов, могут перекрываться, хотя и не
обязательно. Однако такое различие очень существенно, и имен-
но оно приводит к различию в электрических свойствах кри-
сталлов.
При абсолютном нуле электроны в кристаллической решетке
занимают только те состояния, которые соответствуют самым
234
Гл. VI. Термодинамические свойства твердого тела
низким уровням энергии. Это остается приблизительно верным
даже при высоких температурах. Если энергетическая полоса
вся заполнена электронами, то они называются связанными
электронами. Если самая высокая энергетическая полоса не
полностью заполнена электронами, то такие электроны назы-
ваются свободными электронами. Свободные электроны запол-
няют сравнительно высокие состояния, которые отстоят неда-
леко от энергетической полосы, заполненной связанными элек-
тронами (строго говоря, это совершенно верно при абсолютном
нуле, а при более высокой температуре выполняется лишь при-
ближенно).
Состояния со свободными электронами могут быть располо-
жены в одной энергетической полосе, как, например, у щелоч-
ных металлов; в двух перекрывающихся полосах, как, напри-
мер, у металлов переходной группы. Эти случаи будут рассмо-
трены в следующем пункте. Электрические свойства кристаллов
зависят от того, является ли самый верхний энергетический
пояс при абсолютном нуле частично или полностью заполнен-
ным электронами, т. е. имеются или нет свободные электроны.
Сначала опишем различные свойства хороших и плохих про-
водников. При этом будет видно, что разделение твердых тел на
хорошие и плохие проводники является не формальным, а имеет
свой глубокий смысл. Известно, что хорошие проводники обла-
дают следующими свойствами: электрическое сопротивление
возрастает при повышении температуры и увеличении содержа-
ния примесей. Что касается плохих проводников, то их элек-
трическое сопротивление с повышением температуры вплоть до
некоторой определенной величины уменьшается, и, как правило,
оно уменьшается также с увеличением содержания примесей.
Плохие проводники, обладающие этими свойствами, называют-
ся полупроводниками, а те из них, у которых электропровод-
ность совсем низка, называются диэлектриками. Между полу-
проводниками и диэлектриками нет такого резкого различия,
как между полупроводниками и металлами.
Квантовая теория электронов в периодическом поле дает
основу для такой классификации. Если при низкой темпера-
туре самая высокая энергетическая полоса, содержащая элек-
троны, лишь частично заполнена, то при любой температуре
электроны на верхних энергетических уровнях могут очень лег-
ко переместиться в соседнее не занятое состояние. Такими свой-
ствами обладают хорошие проводники, т. е. металлы. Наоборот,
если самая высокая энергетическая полоса, содержащая элек-
троны, при низкой температуре полностью заполнена и отделе-
на от следующей более высокой энергетической полосы запре-
щенной областью, то при низкой температуре электроны не
6.12. Металлы и диэлектрики
235
могут сами перемещаться в соседние состояния и такие веще-
ства называются диэлектриками.
При повышении температуры имеется возможность того,
что малая часть электронов за счет теплового возбуждения пе-
рейдет в более высокую пустую энергетическую полосу. Как
правило, при повышении температуры в прежде, казалось бы,
пустых энергетических полосах появляются электроны, а в ра-
нее полностью заполненных образуются незаполненные состоя-
ния— «дырки», которые играют такую же роль, какую могли
бы играть в почти заполненных полосах свободные «положитель-
ные электроны»: и те и другие могут перемещаться в сосед-
ние состояния. Поэтому проводимость таких веществ с повыше-
нием температуры возрастает. Таким образом, мы делим твер-
дые тела на металлы и диэлектрики. Такое деление можно
обосновать строго теоретически, однако вышеприведенное крат-
кое разъяснение уже является достаточно ясным.
В настоящее время еще не во всех случаях можно успешно
провести теоретические вычисления, которые давали бы ответ
на вопрос, является ли кристаллическая решетка, образованная
данной группой W атомов (или молекул), определенного типа
металлом или диэлектриком. Коротко опишем лишь некоторые
конкретные случаи: атомы щелочных металлов имеют один ва-
лентный электрон в состоянии $, их энергия очень четко отде-
ляется от состояния электронов других оболочек. В кристалле
из N атомов имеется пояс $, способный вместить 2А электронов,
а пока он заполнен лишь W электронами. Поэтому твердое тело,
образованное из атомов щелочных металлов, само является
металлом.
Можно рассмотреть другие случаи и попытаться показать,
что атомы с любой нечетной валентностью (или молекулы,
имеющие нечетную остаточную валентность, например NO или
TiN) в твердом состоянии также обязательно образуют металл.
Однако это далеко не всегда является правильным. Для того
чтобы в этом разобраться, достаточно рассмотреть элементы
галогенов. Атомы галогенов имеют неполную внешнюю обо-
лочку, содержащую не восемь, а семь валентных электронов.
Если атомы способны образовать кристаллическую решетку, то
собственная функция четырех атомов внешней оболочки может
образовать один или несколько поясов, образованных состоя-
ниями, могущими вместить 8А электронов.
Так как имеется всего 7А электронов, то должен был бы по-
лучиться металл, в действительности, однако, совсем не так.
Это объясняется тем, что с энергетической точки зрения атомы
галогенов сначала образуют двухатомные молекулы, а не кри-
сталлическую решетку, которая образуется уже из этих
236
Г л. VI. Термодинамические свойства твердого тела
молекул, а не из атомов. Каждое электронное состояние моле-
кул заполнено двумя электронами, а энергетические полосы
кристаллов, которые могут быть образованы, заполнены пол-
ностью (или совершенно пустые). Поэтому такое твердое тело
является диэлектриком.
По тем же причинам TiN образует проводник, а NO — нет.
По-видимому, молекулы NO сначала соединяются и образуют
молекулы N2O2, в которых все электронные состояния целиком
заполнены. Поэтому в образующейся кристаллической решетке
энергетическая полоса оказывается заполненной. Могут встре-
титься и обратные случаи: твердые тела, образованные из ато-
мов с заполненными энергетическими уровнями основного со-
стояния, не обязательно являются диэлектриками, так как если
энергия других атомных состояний отстоит не очень далеко от
энергии основного состояния, то соответствующие полосы будут
налагаться и кристаллическая решетка будет обладать свой-
ствами металла.
Примером могут быть щелочноземельные металлы. Их сво-
бодные атомы имеют два s электрона и заполняют последнюю
$ оболочку. Однако в кристаллах энергетические полосы s и р
перекрываются, и поэтому кристалл является металлом. Таким
образом, по-прежнему об электрических свойствах каждого
твердого тела кристаллического состояния можно судить, толь-
ко основываясь на свойствах и расположении электронных энер-
гетических полос. Теория отводит свое место для каждого из
двух типов веществ.
Здесь необходимо особенно подчеркнуть, что свойства веще-
ства зависят от концентрации атомов или атомных ядер. При-
мером может служить появление электронной энергетической
полосы, о которой говорилось выше. Отсюда легко понять, что
если вещество находится при очень сильном давлении, то сте-
пень концентрации атомов или атомных ядер сильно повышает-
ся, распределение энергетического потенциала электронов силь-
но меняется, а следовательно, сильно изменяются свойства ве-
щества.
Например, водород при обычном давлении представляет
собой газ, состоящий из двухатомных молекул. При высоком
давлении и низкой температуре он сначала превращается в мо-
лекулярный кристалл, еще не проводящий электричества. Одна-
ко было подсчитано, что при давлении в 800 000 атм водород-
ный кристалл переходит в металлоподобное состояние, анало-
гичное щелочным металлам. Увеличивается сжимаемость, и он
так же, как и щелочные металлы, становится хорошим провод-
ником электричества. Этот факт был использован при изучении
внутренней структуры Юпитера, Сатурна и других больших пла-
6.12. Металлы и диэлектрики
237
нет, а именно для объяснения того, почему эти состоящие в
основном из водорода планеты имеют такую большую плот-
ность, как это получалось по наблюдениям.
С другой стороны, известно также, что вследствие изменения
энергетического потенциала электронов внешней оболочки ато-
ма при высоком давлении химические свойства атомов могут
изменяться настолько сильно, что при давлении в несколько
миллионов атмосфер увеличение концентрации приводит к тому,
что энергетические полосы электронов полностью перекрывают-
ся и вещество утрачивает обычные химические свойства, элек-
троны внешней оболочки полностью становятся свободными, а
вещество — хорошим проводником. Это и есть новое состояние
вещества, т. е. состояние при сверхвысоком давлении, которое
можно также назвать пятым состоянием (четвертым состоянием
является состояние вещества при высокой температуре и пол-
ной ионизации).
Вследствие появления свободных электронов вещества в
пятом состоянии имеют не только высокую плотность, но могут
также проводить электричество. На этой основе можно еще
раз проанализировать старую гипотезу относительно того, что
внутренняя часть земного шара образована из сплава железа
и никеля, и оценить ее справедливость.
Некоторые считают, что в земном шаре не может быть скон-
центрировано такое большое количество железа и никеля.
В земле действительно имеется сплав железа и никеля с кон-
центрацией, соответствующей обычному давлению, кроме того,
существует магнитное поле земли, из чего можно предполо-
жить, что вещества внутри земли являются проводниками элек-
тричества; однако эти люди утверждают, что вещество внутри
земли содержит элементы в тех же пропорциях, что и горные
породы внешней оболочки земли. Но находясь при высоком
давлении, эти элементы изменили свойства настолько, что пере-
шли в пятое состояние и не только сильно увеличили свою кон-
центрацию, но и стали проводить электричество.
Эта новая гипотеза очень перспективна. В предельных со-
стояниях вещество, например, белого карлика из неподвижных
звезд, аналогично звезде van Maanen, имеет концентрацию при-
мерно 500 кг/см\ т. е. плотность в 500 тысяч раз больше плот-
ности обыкновенной воды. Здесь не только электроны внешней
оболочки, а все электроны становятся свободными. Эти при-
меры полностью разъясняют относительность деления веществ
на проводники и диэлектрики. В пятом состоянии при высоком
давлении и концентрации все вещества становятся проводни-
ками.
238
Гл. VI. Термодинамические свойства твердого тела
Простая модель металлов при нормальном давлении была
построена Друде, Лоренцем и Зоммерфельдом. Их теория под-
черкивает важность рассмотрения свободных электронов, т. е.
относится к так называемой теории свободных электронов в
металлах. В этой модели свойства металлов определяются тем-
пературой, объемом, числом W свободных электронов и их по-
тенциальной энергией — %о. За нуль принимается потенциальная
энергия электрона в свободном пространстве вне металла.
Сразу же возникает вопрос, какое количество электронов мож-
но считать свободным. Для щелочных металлов, согласно пре-
дыдущим рассуждениям, естественно считать, что каждому
атому соответствует один свободный электрон. Для других ме-
таллов это число должно определяться из сравнения с экспери-
ментальными данными для веществ с различными электриче-
скими свойствами.
В теории Зоммерфельда предполагается, что равномерное
потенциальное поле — %0 в металлах не зависит от температуры-
Мы не будем пока исследовать основания для такого предпо-
ложения. Единственным доказательством, на которое можно со-
слаться, является то, что определяемое теоретически значение
по форме одинаково с экспериментально наблюдаемым. В сле-
дующем пункте мы непосредственно займемся теорией Зоммер-
фельда, которая является наилучшим примером использования
статистики Ферми — Дирака.
6.13. Статистика электронного газа
Известно, что электроны подчиняются статистике Ферми —
Дирака, согласно которой число электронов пг в состоянии г
с энергией ег и статистическим весом сог при условии, что всего
имеется N электронов, дается формулой
п' =-----тЧ/^’ (6-91>
где X определяется из условия
^nr = N. (6.92)
Г
Если X удовлетворяет неравенству , то статистика
Ферми — Дирака переходит в классическую статистику. Но для
свободных электронов в металлах, даже при температурах по-
рядка 2000° К, это условие не выполнено, В действительности
6.13. Статистика электронного газа
239
справедливо как раз обратное
1 е*°1кТ.
(6.93)
Таким образом, свободные электроны в металлах необходимо
рассматривать как ансамбли, подчиняющиеся статистике Фер-
ми — Дирака.
Укажем здесь, что в паре, находящемся в равновесии с ме-
таллом, плотность электронов очень мала. Поэтому, несмотря
на малость массы электронов, условие перехода к классической
статистике для парообразных электронов выполнено. Если за
нуль принять энергию свободного электрона, покоящегося в га-
зовой фазе, то для последней будем иметь обычную формулу
для идеального газа
х==
V 2(2nmekT)^ ’
(6.94)
где те — масса электрона, множитель 2 в знаменателе — весо-
вой множитель, связанный с двумя возможными направлениями
спина электрона.
При определении X для свободных электронов в металле мы
должны исходить из того, что оно одновременно удовлетворяет
двум соотношениям (6.91) и (6.92). Другими словами, для на-
хождения X необходимо решить следующее уравнение:
"=2—<6-95)
т 1+те
Здесь более удобно за начало отсчета принять энергию элек-
трона, покоящегося в металле. В дальнейшем можно будет
легко заменить это начало отсчета другим.
Первый шаг состоит в вычислении значения энергии. Из
п. 4.17 известно, что квантовое состояние материальной точки,
движущейся в прямоугольном ящике с длинами ребер а, Ь, с,
характеризуется квантовыми числами Z, /и, и, принимающими
всевозможные положительные целые значения, не равные нулю.
Энергии этих состояний равны
_ А2 / Z2 . т2 . и2 \
m, п — 8те [а2 Ь2 с2)'
Для материальной точки все эти состояния являются невыро-
жденными, но для электронов вследствие наличия спина каждое
состояние имеет вес coz, т, п=2.
Здесь удобно объединить все состояния с одинаковой
энергией. Значения квантовых чисел /, т, п, всех состояний,
240
Гл. VI. Термодинамические свойства твердого тела
имеющих одинаковое значение энергии ег, находятся на поверх-
ности положительного октанта эллипсоида
/2 . т2 - п2 8теег
~а? ’ ’~~с2' " h2
(6.96)
Кроме того, все состояния, у которых энергия меньше или рав-
на 8Г, находятся в положительном октанте этого эллипсоида. Но
число точек с целыми координатами в одной восьмой эллипсои-
да равно ее объему
л / вадЛ-Ь ь = л v (6.97)
6 \ h2 ) 6 Л3 '
где V — объем сосуда. Ранее было доказано, что (6.97) не за-
висит от формы сосуда.
Вследствие наличия у электронов спина число электронных
состояний с энергией, меньшей или равной 8Г, будет как раз в
два раза больше, т. е. равно
2 л (8т^г)*/» v (6.98)
6 fl3 ' '
Для того чтобы получить число электронных состояний с энер-
гией в интервале от 8Г до 8r+d8r, продифференцируем (6.98).
Тогда получим
(б 99)
Если все эти состояния принять за одно вырожденное со-
стояние с энергией 8Г, то выражение (6.99) превращается в со-
ответствующий вес (Dr. Подставляя это значение сог в (6.95) и
заменяя суммирование интегрированием, получаем
N = ^- .£8-™//г. V f——=24 (8w^Г)ЗЛ V F x'\dx (6.100)
Л Л
Для краткости введем характеристическую энергию 8*, ко-
торая определяется тем, что число состояний с энергией, не пре-
вышающей 8*, как раз равно общему числу N свободных элек-
тронов. Из (6.98) видно, что 8* можно найти из соотношения
У___о л (Зтег*)^2
V~~Z *6 h3
или (6.101)
* _ h2 / ЗУ \7»
8 8те \ лУ )
Обратим внимание на то, что 8* определяется концентрацией
электронов N/V, к тому же для заданных N/V она не зависит
6.14. Разложение при очень малых и очень больших X
241
от температуры. Подставляя (6.101) в (6.100), получаем
1
(6.102)
Для того чтобы получить выражение для средней кинетической
энергии £кин электронов, необходимо к интегралу в (6.100) до-
бавить множитель 8. Тогда получим
27кин____2 — |
Z 4 Л3 v J
о
л (9,mekT)^kT
4 Л3
es/2 de ____________
(6.103)
Г х’/з dx
i
Используя определение 8*, это выражение можно переписать
в виде
00 8/
£КИН С x^dx 1плч
— = W 2kTJ 1 Г <6-104>
о
Если можно вычислить интегралы (6.102) и (6.104) *), то мы
можем получить связь между 8* и X и между EKIIH/W, е* и X.
Если, кроме того, сможем исключить X, то получим, что E™n/N
является функцией е*, т. е. N/V.
6.14. Разложение при очень малых и очень больших X
Необходимо теперь вычислить два интеграла
(6.Ю5)
° > + Р
J(X)= f x%fx . (6.106)
о ’ +
’) См. McDougall, Stoner, Phil. Trans. Roy. Sac., 237 (1938), 67.
16 Зак. 1299
242
Гл. VI. Термодинамические свойства твердого тела
Рассмотрим сначала случай, когда температура очень вы-
сока, т. е. В этом случае можно написать
оо оо оо
Z(X) = % J v f =
о оо
оо Г (.— оо
(блог.
Аналогично
СП Г* °° 4-1
<6ЛО8>
Поэтому (6.102) и (6.104) приводятся к виду
£КИИ _ (kT\Чг 9 /Й V / 1 \П Я.Л + 1
AT “U*/ 8 Zt' (л + 1)'/»'
Оставляя только два члена из (6.109), имеем
£кин _ ( kT^, 9/я Д Xs ,
...I * I tc 1 I А/ >/ I
N \ е ) 8 \ 211
(6.109)
(6.110)
(6.111)
Исключая 1 из (6.110) и (6.111). получим
4 / е* у/1 Г 2_ 1 / £ки" \ _ 11 _ 1 ~ 1 / 4 \г / е* \з ’
Sfiiltr/ [ЗЛТ’^/ J 2’/’ 2МЗ/л/ U?7 ‘
Для очень высоких температур приближенно получим
£КИН
^~N~
(6.112)
Соответствующая теплоемкость, приходящаяся на один элек-
трон, равна
cV = |s[i-
1 / е* VA
б/2я \ЛГ/
(6.113)
6.14 Разложение при очень малых и очень больших X
243
Таким образом, и в этом случае свободные электроны при вы-
соких температурах обладают классической теплоемкостью k.
Выражение (6.113) получено Моттом1).
При больших значениях X получить разложение для /(Z) и
J (X) довольно трудно. Одним из прямых методов является
использование контурного интеграла Барна вместо разложений
(6.107) и (6.108). В этом случае
7(1)
._ a+ico
__ у л / 1 \ С л Xs ds
2 \ 2л1 / J sin ns (s+l)’/2>
a-Zoo ' '
___ G + i<x>
Зу л / 1 \ С л Xs ds
4 \ 2ш/ J sinjis (s-4-l)8/2’
а-Zoo 4 *
(6.114)
где —1<о<0. Пока мы не будем использовать этот метод, так
как нам достаточно найти только первые два члена разложе-
ния. Для их вычисления значительно проще воспользоваться
методом Фаулера и Гугенгейма. Произведем преобразование
интеграла, выполняя интегрирование по частям,
оо оо
Z(*)=4 f = l f (6.115)
0 ' x o'
где p = InX.
Разделим область интегрирования точкой х = Тогда по-
лучим
Р оо
27(X) = f Д1П(Ц-АХ)+/ ^|1п(1 + ^) =
Р Р оо
о ' о г р '
= —х)+ f ln(l+g-g)+ f “<=== In (1
') Mott, Proc.. Camb. Phil, Soc.t 32 (1936), 108.
16*
244
Гл. VI. Термодинамические свойства твердого тела
Разложим логарифмическую функцию в двух последних инте-
гралах в ряд. Тогда
Р 00 . 0
W) = f + f e-^(^_y)-^dy +
у X S J
0 r 5=1 0
oo co
+ S (-1/~ f e~sy ft + yT'hdy.
5=1 0
До сих пор все выкладки были строгими. Теперь перейдем к
приближенным вычислениям. При больших р квадратный ко-
рень в двух последних интегралах может быть заменен на р,/2 и
даст главный член. Предел интегрирования первого ряда (не
делая существенной ошибки) можно расширить до бесконеч-
ности. Таким образом, имеем
(3 оо оо
f + fe-^dy^^^ +
л* J \f Y О J U
0 r 5=1 0
oo
5=1
= |(ln%)s/l + -g(lnZ)-’\ (6.116)
Порядок величины погрешности равен O(lnX)~5/2.
Подставляя (6.116) в (6.102), получаем
(^yMinv/2+4(in^r,/2. (6.Н7)
Решаем уравнения относительно In X
lnl = 1 -4 (47Г }• (6.118)
Применяя для вычисления J(X) аналогичный метод, получаем
оо оо оо
J&) = f = i f V^ln(l+Ax)cfx«4 f Yx(fi-x)dx+
0 + 0 0
oo oo
+ 3₽'/2 2 f e'sv dy « 4 + 4 P,/2 •
5=1 0
Подставляя его в (6.104), получаем среднюю кинетическую
энергию
£КНН / \ 3/2 3 5, j 5Я2 2) /с 1 1Л\
— 5 ^Г(1пЛ)/2| 1+-8-(1пЛ) (6.119)
6.15. Термодинамические функции электронного газа
245
Если (6.118) подставить в (6.119), то получим
£кин _ 3 5 л2 (kT\z\ ( .,5л2 lkT\v\
N ~ 5 £ ( 1 2 12 I, е* J (( 1 + 8 е* )
5л2 МП2!
12 \ е* ) Г
(6.120)
6.15. Термодинамические функции электронного газа
Согласно (4.179), химический потенциал связан с абсолют-
ной активностью соотношением
и==£Г1пХ. (6.121)
До сих пор за начало отсчета бралась энергия покоящегося
электрона в металле. Если ограничиваться только явлениями
внутри кристалла, то такой выбор начала отсчета энергии яв-
ляется несущественным. Однако если необходимо, например,
рассмотреть равновесие металла и. газовой фазы, то начало от-
счета должно быть общим для обеих фаз. В этом случае за
нуль лучше всего принять энергию покоящегося электрона в
паре. Если произвести такой сдвиг начала отсчета, то (6.118)
принимает вид
Химический потенциал электрона будет равен
тг2 £2Т2
Не = - Хо + е* - , kT С е*. (6.122)
Если воспользоваться первым приближением, то
Не^-Xo + e*, kT^e. (6.123)
Отсюда видно, что химический потенциал электрона равен
разности энергий почти заполненных и почти пустых состояний.
Для получения полной свободной энергии Fe ансамбля элек-
тронов воспользуемся термодинамической формулой
w
Fe — J \iedN (Г, V—константы). (6.124)
о
Подставляя (6.122) в (6.124), получаем
N
Fe — f [— Хо + е*— ^—константы). (6.125)
о
Так как, согласно (6.101),
8* (6.126)
246 Г л. VI. Термодинамические свойства твердого тела
то, интегрируя (6.125) и считая, что %0 не зависит от N/V, по-
лучаем
^-==-Хо + |е*-4-?1 (АГ« (6.127)
Для внутренней энергии Ее электронов имеем
Ее _ . r?(d[fe/T]\ _
N - t дТ )N,V-
3 «2 Ь2Т2
= -Хо+у e* + 4^F- (6.128)
что полностью соответствует (6.120).
Можно также получить выражение для давления электро-
нов Ре. Из (6.127), используя (6.126), получаем
р _ _ 2 ** k2Ti I
dV 3 V dt* ~ V 1 5 6 ~1*~ j •
Сравнивая (6.129) с уравнением энергии (6.128), имеем
/>вУ = -|(^ + ^Хо) = |^ин. (6.130)
где через Е*™ обозначена кинетическая часть энергии Ее.
В п. 5.1 уже подчеркивалось, что связь между энергией Е
ансамбля и энергией Е отдельной системы всегда имеет вид
Е=(Х=т <б-131>
Отличие от случая классического идеального газа состоит в том,
что здесь
Mwh- (6Л32>
Согласно (6.128), Ре определяется через Т, V и в*, а е* через
V. Поэтому (6.130) можно заменить соотношением
£= О),...- <6-133)
Используя (6.128) и считая хо постоянной (так как V или с*
сохраняют постоянное значение), сразу же получаем Е = E/N.
С другой стороны, используя (6.126), имеем
I дЕ \ । , я2 £2Г2 Е
UaJt, v~ Zo + e + 12 е* ЛГ ’
Термодинамические функции электронного газа, рассмотрен-
ные в данном пункте, могут быть непосредственно применены
к электронной составляющей ионизированных газов. Но в этих
случаях необходимо сделать две поправки, Во-первых, так как
6.16. Поправка к формуле, применяемой для металлов
247
ионизированные газы не имеют суммарного заряда, то Хо=О.
Во-вторых, между электронами и положительно заряженными
ионами имеется, согласно закону Кулона, сила взаимодействия,
вследствие чего термодинамические функции изменяются. При-
ближенный расчет поправки от этого эффекта можно произ-
вести с теорией электролитов Дебая — Хюккеля. Более подроб-
но читатель сможет ознакомиться с этим в первоисточнике1).
6.16. Поправка к формуле, применяемой для металлов
В предыдущем пункте был получен ряд термодинамических
формул для электронного газа в сосуде с равномерной потен-
циальной энергией хо, не зависящей от Т и N/V. При переносе
этой модели на свободные электроны металла необходимо обра-
тить внимание на пределы ее применимости, вне которых ис-
пользовать модель не следует. При подстановке численных зна-
чений давление электронов в металле, например, оказывается
равным при нормальной температуре нескольким сотням мил-
лионов атмосфер. Это говорит о том, что Ре нельзя рассматри-
вать как вклад электронов в реальное давление Р. Этот невер-
ный результат возник вследствие нашего предположения, что
Хо не зависит от V. В действительности вклад Ре в Р является
только вкладом от движения электронов. Он как раз компенси-
руется почти таким же членом V") jv, который мы до сих
пор полагали равным нулю. Таким образом, очевидно, что для
решения любой задачи, связанной с изменением давления и
объема, наша модель совершенно непригодна.
Однако к формулам предыдущего пункта можно ввести по-
правку, учитывающую эти явления. Можно получить совершен-
но идентичные формулы даже при учете зависимости хо от У
и V/N. В самом деле, сохраним для свободной энергии прежнее
соотношение (6.127). В любых условиях с помощью хо можно
только грубо выразить среднюю потенциальную энергию сво-
бодных электронов, так как она получена через усреднение
поля ионизированных атомов. Формулу (6.127) можно рассма-
тривать как определение хо при заданных Т и V, Примем те-
перь самое главное предположение в том, что хо зависит только
от V и изменение хо при изменении Т происходит только че-
рез V. Перепишем (6.127) в более точном виде
Fe = N { - Хо (Ю + j е* (V) - (Ю }. (6.134)
9 См. Цянь Сюэ-сень, J. Am. Rocket Soc., Jan — Feb. (1953), 16.
248
Гл. VI. Термодинамические свойства твердого тела
Отсюда с помощью только методов термодинамики можно
вывести все равновесные свойства. В частности, получим
F _ _ Т2 (д<Ре/Т)\ _
е~ к дТ )N>V-
= К { - Хо (Ю + 4 е* (К) +1 ЖГ/е' (К)}, (6.135)
что по форме совпадает с (6.128). Для давления Ре получим
выражение, отличное от (6.129),
р 17 >7 ^Хо I 2 л2 k2T2 1 Q£\
PeV~ ^>+56 +-§- — • <6Л36)
Здесь Ре, действительно, есть давление свободных электро-
нов, являющееся частью общего давления, действующего на
металл или со стороны металла. Величина Ре равна разности
общего давления в ансамбле, содержащем свободные электро-
ны, и в ансамбле, не содержащем таковых, при прочих равных
условиях. Можно с уверенностью сказать, что Ре по величине
может иметь самое большее одинаковый порядок с реальным
давлением Р. При обычном малом давлении можно воспользо-
ваться приближенным выражением
<6-137)
Из (6.134) получим химический потенциал электрона
И _( ____
“ k dN )v “ к dN )v N2 к dV )N~
= -Хо+И-^-+е*-^-^. (6.138)
Непосредственным расчетом можно убедиться, что формулы
(6.134), (6.136) и (6.138) не противоречат общему термодина-
мическому равенству
PeV+Fe = N^
При нормальном давлении и &Т<Се* имеем
3 ТГ2 72
Не ~ - Хо + f е* - . (6.139)
Эта формула несколько отличается от (6.122) для электронного
газа. Другими словами, если %0 становится функцией И, то фор-
мула (6.121) перестает быть верной, так как при ее получении
в п. 4.21 было сделано предположение о том, что энергия е не
зависит от N. Здесь же, ввиду того что V -=V IN, е становится
функцией N, указанное предположение становится несостоя-
тельным.
6.17. Теплоемкость электронов в металле
249
6.17. Теплоемкость электронов в металле
Согласно (6.113), (6.135), вклад каждого электрона в тепло-
емкость при постоянном объеме равен
; г 1 л (6.140)
где
(6.141)
е 8mek \ л V) ' 7
Здесь 0е — характеристическая температура свободных элек-
тронов в металле. Обычно предполагают, что на каждый атом
приходится один свободный электрон. В этом случае N/V равно
числу атомов в единице объема, которое можно вычислить по
плотности и атомному весу металла.
Таблица 6.4
Характеристическая
температура свободных электронов
Металлы L1 Na к Си Ag Аи
0еХ1О~3(оК) 55 36,5 24 82 64 64
Соотношение (6.140) одновременно дает и теплоемкость
отдельных атомов, если они имеют по одному электрону.
Результаты вычислений @е, проведенные при сделанном выше
предположении, представлены в табл. 6.4. Отсюда видно, что
даже при обычной высокой температуре теплоемкость элек-
тронов линейно растет с увеличением температуры. Однако при
более низкой температуре теплоемкостью электронов в метал-
лах по сравнению с теплоемкостью кристаллических решеток,
о которой говорилось в первых разделах настоящей главы,
можно полностью пренебречь. Они могут стать сравнимы лишь
при очень низких температурах. Это происходит вследствие
того, что теплоемкость кристаллической решетки изменяется
пропорционально Г3. Теоретические выводы для (Ag) и (Zn)
очень хорошо согласуются с экспериментальными результатами.
Однако по тем же причинам, о которых говорилось в
п. 6.12, приближение свободных электронов в действительности
250
Г л. VI. Термодинамические свойства твердого тела
применимо только к щелочным и щелочноземельным металлам.
В твердом теле структура реальной энергетической полосы элек-
тронных состояний описывается при помощи функции распре-
деления g(e), причем
Vg-(e)de (6.142)
есть число состояний в энергетическом интервале 8 и е + б/е и
в объеме V.
Два различных спина учитываются как два состояния; обыч-
но это число сильно отличается от того, что дает функция рас-
пределения свободных электронов (6.99). Мотт и Джонс пока-
зали1), что при произвольной g(e) и очень низкой температуре
теплоемкость, приходящаяся на один электрон, выражается в
виде
и
<6-143)
где V—объем, приходящийся на один атом, g*— численное
значение функции распределения g(e) при абсолютном нуле для
энергии е высшего занятого состояния.
Если функция распределения выражается формулой (6.99),
то 0е преобразуется к виду (6.141). Для переходных металлов
значение g* намного больше его значения, соответствующего
формуле (6.141), записанной в виде (6.143). Поэтому для пере-
ходных металлов значение 0е будет намного меньше. Для ни-
келя расчетное значение 0е составляет 3470° К, для палладия
оно понижается до 1750° К. Это объясняет, почему при обычной
высокой температуре переходные металлы обладают значитель-
ной электронной теплоемкостью. Конечно, последнюю нельзя вы-
числить столь же точно, как в случае полностью свободных
электронов, но в первом приближении ее можно рассчитывать
по эффективному числу свободных электронов и0, приходящихся
на каждый атом (для никеля оно равно 0,6, для палладия 0,55).
Таким образом, вклад электронов в теплоемкость атомов можно
написать в виде
_ л2 Г
' k ~П<> 2 Qe ’
« - п, Г1 -
2 0 L
(6.144)
6 \ Т I J ’
9 Mott, Jones, Properties of Metals and Alloys, Oxford, 1936, p. 176—
179.
6.17. Теплоемкость электронов в металле
251
Расчетное значение теплоемкости атомов палладия с учетом
вклада электронов по (6.144) при определенном объеме равно
(3+ 1,5х0,55)& = 3,83&. Экспериментальное значение несколько
ниже, при 1500° С оно равно 3,64£.
Задачи к главе 6
6.1. Уточнить Су до члена (е*/£Т)9/2.
6.2. Найти термодинамическую функцию электронного газа
при высокой температуре и kT^>Q*.
Глава VII
УРАВНЕНИЕ СОСТОЯНИЯ ТВЕРДОГО ТЕЛА
В этой главе мы продолжим обсуждение термодинамических
свойств твердого тела, в особенности его уравнения состояния.
Для этого необходимо более подробно проанализировать по-
тенциальную энергию %, введенную в п. 6.7. В соответствии с
макроскопической теорией упругости / есть энергия деформа-
ции твердого тела. Однако энергию деформации твердого тела
можно рассматривать как функцию шести компонент деформа-
ции: трех компонент деформации растяжения—сжатия и трех—
деформации сдвига. Поэтому первоначальное предположение
о том, что % является функцией только V, очевидно, является
приближенным, так как V может характеризовать только де-
формацию от равномерного давления, которая не разлагается
на три компоненты деформации сжатия и совсем не характе-
ризует деформацию сдвига.
Таким образом, при более точном написании термодинами-
ческих соотношений и уравнения состояния твердого тела в об-
щем случае необходимо в качестве переменных величин исполь-
зовать не давление Р, а шесть компонент напряжения. Точно
так же объем, приходящийся на один атом, следует заменить
шестью компонентами деформации. Тогда шесть компонент на-
пряжения и шесть компонент деформации соответствуют обоб-
щенным силам и обобщенным координатам. Именно такие пред-
ставления были использованы Гиббсом.
Однако столь точное и полное описание термодинамического
состояния твердого тела наталкивается на большие трудности.
Более того, вследствие введения в теорию дальнейших упроще-
ний оно становится не совсем достоверным. Поэтому мы все же
вернемся к сравнительно более элементарному описанию энер-
гии деформации % только как функции V. Тогда единственным
напряжением, которое поддается рассмотрению, будет давле-
ние Р, а единственным имеющимся коэффициентом упругости —
модуль объемной упругости х, или коэффициент объемного сжа-
тия р. Второй коэффициент упругости — коэффициент Пуас-
сона о нигде в расчетах так и не появляется. Несмотря на это,
теория вносит существенный вклад в решение задачи об оты-
7.1. Уравнение состояния
253
скании зависимости между упругостью и термоупругостью в ши-
роком диапазоне температур. Основы ее были заложены Грю-
найзеном1), и развивается она в течение почти 40 лет. Изложе-
ние этой теории является основной целью настоящей главы.
Особое внимание будет сосредоточено на расчете динамических
свойств твердого тела при низких и высоких температурах.
7.1. Уравнение состояния
Расчет функции состояний кристаллического твердого тела
с одним членом приближения Дебая и несколькими членами
приближения Эйнштейна был уже проведен ранее. Для нее по-
лучено выражение (6.76). В соответствии с (6.56) давление Р
можно найти дифференцированием функции состояний по V.
Однако из предыдущей главы было видно, что для большинства
твердых тел членов приближения Эйнштейна либо совсем не
появляется, либо если они и появляются, то их характеристиче-
ская температура близка к характеристической температуре
члена приближения Дебая. Поэтому можно получить удовлет-
ворительные результаты при наличии в функции состояний
только одного члена приближения Дебая. В этом случае давле-
ние Р определяется из соотношения
/д\пК\ ду де [
p=kT\dvrlT,N = N~ ^kTN~dv дё~/лЧпЦ— e T jdx\ =
u 0
„ d@n / ’I3 T d1]
аьт___О- I ___-_____-
dV J e^D/T^_1 ~
qd/t .
' r 44 r l3dl
J
0
Здесь совершенно явно использовано предположение о том, что
X и ©d являются функциями только К. Соотношение (7.1) пред-
ставляет собой уравнение состояния твердого тела. Пусть
qd/t .
74 г В3 dZ
4—
©3DJ ^-1
dV
^Х
dV
(7.1)
D
(7.2)
Тогда, согласно (6.55), величина £* представляет собой ту часть
энергии, приходящейся на один атом, которая зависит
9 Grfineisen, Handbuch der Physik, 10 (1926), 1—52.
254
Г л. VII. Уравнение состояния твердого тела
от температуры. Перепишем уравнение (7.1) в так называемой
форме Грюнайзена
py-yd* d'neD £*
dV din И C •
(7-3)
Независимо от того, какое из двух уравнений (7.1) или (7.3)
мы будем рассматривать, основная задача состоит в отыскании
функций x(V) и 0n(V). Ранее указывалось, что в х входит
заданная соотношением (6.62) нулевая энергия —Од-
нако ее отличие от нулевой энергии осциллятора, как правило,
очень мало и им можно пренебречь. Прежде чем вычислить
d\n@D/d\nV в приближении Грюнайзена, попытаемся полу-*
чить его из соотношений (6.74) и (6.75). Действительно,
1
©О
9 \Л/ Ц
1+°
3(1-а)
₽р},/2+2
( 2(1+а)
( 3(1 — 2а)
Если ц — масса атома, р = ц/V, р = —то
1 _ 4л / д\3 Г ( 14-а Р/s . 2 ( 2 (1 —|—<У) ]’/г 1 1 / dv_\"/г
e3D — 9 \Л/ L ( 3(1—а) ) + ( 3(1—а)) J И Г2\ дР)Г ’
или
- 3 In 0 - In (AV „’/г Г f 1 + п )•/« , 2 J 2(1 +а) НЯ \ _
dlnuo m 9 и 4-2|з(1_2а)| jj
-21пГ+А|П(-^)г. (7.5)
Поэтому если х(Ю Уже известно, а коэффициент Пуассона яв-
ляется константой, то, подставляя (7.4) или (7.5) в (7.1), сразу
получим дифференциальное уравнение второго порядка для
V и Р. И если какие-либо два состояния при некоторых темпе-
ратурах известны, то в принципе уравнение состояния стано-
вится полностью определенным. Однако этот способ сложен, а
из-за приближенного характера теории Дебая нецелесообразен
и вряд ли приведет к правильным результатам.
7.2. Взаимодействие между атомами
Ми в своих основных работах по динамической теории твер-
дых тел представлял взаимодействие атомов в виде суммы двух
составляющих: притяжения и отталкивания; обе они принима-
лись пропорциональными отрицательной степени расстояния
между атомами. Если ф — потенциальная энергия, р — расстоя-
7.2. Взаимодействие между атомами
255
ние между двумя атомами, то в соответствии с представлением
Ми
Ф = -4г + ^. (7-6)
Г г
где а, b — положительные постоянные и п>т. Потенциальная
энергия каждого из атомов пары равна !/2ф.
При расчете полной потенциальной энергии кристалла необ-
ходимо произвести суммирование по всем атомам, составляю-
щим пару с данным, и результат умножить на N. Тогда полная
потенциальная энергия кристалла равна
Введем характерную длину г с помощью соотношения
r3=r=w-- (7-8)
Тогда уравнение (7.7) можно переписать в виде
Ф = + (7.9)
где
Суммирование проводится по всевозможным парам атомов,
включающим данный. Особое внимание здесь следует обратить
на то, что Gm и оп полностью определяются кристаллической
структурой, т. е. зависят только от типа кристалла и индексов
т или и, и совсем не зависят от V.
В этих рассуждениях нигде не фигурировали специфические
особенности поверхностных атомов. Однако при достаточно
большом V их влиянием можно пренебречь. Перепишем (7.9)
в виде
Ф =-----+ А = аот, В = Ьоп. (7.11)
Если абсолютная температура и внешнее давление равны
нулю (7 = 0, 7 = 0), то атомы должны находиться в положении
устойчивого равновесия. Поэтому объем Ко, приходящийся на
один атом при 7=0, 7 = 0, должен удовлетворять уравнению
(дФ/дУ)у0 =0 или
кт/3 ун/3 *
256
Г л. VII. У равнение состояния твердого тела
Если потенциальная энергия равна Фо, то из (7.12) получим
(7.13)
° V™/3 п V 7
Числа тип подчиняются единственному ограничению п>т,
их конкретные числовые значения должны быть определены из
эксперимента. Попыток теоретического определения т и п на
основании изложенных представлений, по-видимому, делать не
следует, так как модель взаимодействия Ми является только
удобным приближением, в действительности же взаимодействие
может и не быть изотропным.
Если пренебречь нулевой энергией, то Ф/N, очевидно, равно
—%. В этом случае Фо есть теплота возгонки при Т = 0 и Р = 0,
так как при абсолютном нуле тепловых колебаний не сущест-
вует. Согласно (7.3), при Т=0 можно получить
9 г^+3
Следовательно, коэффициент сжимаемости Ро при абсолютном
нуле равен
1 _ yr I dP \ __ А т(п — т) _ А т (п — т) /у \д\
°\dv)v^W^ И0га/3 ~~9 г™+3
Здесь мы воспользовались соотношением (7.12). Теплота воз-
гонки —Фо равна
_ф
0 тп ро
(7-15)
где Vo — объем, приходящийся на один атом при абсолютном
нуле (Р = 0, Т=0). Это полезное соотношение называется пер-
вым, законом Грюнайзена.
7.3. Характеристическая частота как функция деформации
Исходя из формулы (7.6) для потенциала взаимодействия
между атомами, вычислим частоту колебания атома с малой
амплитудой. Пусть £— смещение атома Р по отношению к паре
7.3. Характеристическая частота как функция деформации 257
фиксированных атомов А и В, расположенных симметрично от-
носительно его равновесного положения, а 6 — угол между £ и
р. Тогда при малых £
р' р -]- £ cos 0, р" р — £ cos 0.
Сила f(p), действующая со стороны двух атомов на атом Р,
равна производной по р от его потенциальной энергии, заданной
выражением (7.6),
f(P) = -^r + ^T. (7.16)
Положительный знак f(p) соответствует силе отталкивания.
Компонента силы вдоль направления £ равна
Ир') cos0 — Ир") c°s0-
Компонента силы, перпендикулярная направлению £, уравнове-
шивается аналогичной компонентой от другой пары атомов,
представляющих собой зеркальное отражение А и В относи-
тельно £. Поэтому если NP — число атомов, симметрично рас-
положенных по отношению к Р, и если 0р— угол, заключенный
между рР и £, то «упругую» силу можно найти из следующего
соотношения:
— DZ = У 2 {f (Рр + Z cos 0р) — / (Pp — р cos Op)} cos Op • NpK
p
(pp) Np cos2 Op.
p
Здесь f'— производная от f(p) по Р» 3HaK 2] обозначает сумми-
рование по всевозможным атомам во всем пространстве. «Ко-
17 Зак. 1299
258
Гл. VII. Уравнение состояния твердого тела
эффиционт упругости» D определяется из следующей формулы:
о = — 2 f' (рр) Np cos2 6р = —
р
(7.17)
Здесь r3= V, а
SZ г \ п + 2
Ш 2Vpcos2ep. (7.18)
„ \ >Р /
Величины sm, sn зависят только от tn, п и структуры кристалла
и не зависят от V.
При вычислении коэффициента упругости D предположим,
что все остальные атомы, кроме рассматриваемого, находятся
в положении равновесия. В действительности колеблется вся
кристаллическая решетка, т. е. все остальные атомы также сме-
щены относительно положения равновесия, причем смещение
имеет вполне определенную фазу относительно атома Р. Таким
образом, все построение производится на основе понятия «сред-
него» положения, что дает возможность не рассматривать пере-
мещения атомов, кроме выбранного.-Если р, — масса атома, то
частота простых гармонических колебаний равна
Используя (7.17), получаем
v2 —. 1 1 I ”(”+1) /п (ш 4-1)
~ 4л2 р I rn+2 п rm+2
Подставляя о^, о/2 из (7.10), имеем
m
Здесь
fin+2 }
v2_ 1 \ tl(n+l) \
4л2 р ( гп+2 Ь^п\от)
-ф =
1ш От
(7.19)
Но на основании (7.11) и (7.12)
nb0n/maom = r^rn.
Таким образом, окончательно
v2 = i {(« + - (т + 1Ж} •
(7.20)
7.3. Характеристическая частота как функция деформации 259
Вводя коэффициент сжимаемости (7.14) при абсолютном ну-
ле, получаем
Qr ( /, \Л+* 2 /г \™ + 2)
{('+1)4’.^ -И+Иф }.<7.21)
Если еще воспользоваться соотношениями для объемов V и Уо,
приходящихся на один атом, то
{//4-2 m+2 А
(я+отф) ’ ).
(7.22)
Предположим теперь, что v прямо пропорционально харак-
теристической частоте Дебая vo. Тогда
2 In ©о=С\ +
{п + 2 m + 2 'j
(«+1)Фл(+)~ - (7.23)
где Ci — константа.
Дифференцируя, получаем
rfin еп
п + 2 т+2
= i-----------^++2----------------- - (7-24)
(л + 1)ФЯ(-£-) 3 -(«4-1) Фет 3
где фт, фп — числовые множители, зависящие от структуры
кристалла и чисел т, п в законе взаимодействия, но никак
не связанные с V. При очень большом п суммы в числителе
и знаменателе (7.19) могут быть заменены первыми членами.
Тогда фп фактически не зависит от п. Что касается фт, то здесь
суммирование в числителе и знаменателе необходимо проводить
по всем соседним атомам. Однако при малых т имеем sw<Co?n,
это объясняется тем, что степень г/р в числителе много больше,
чем в знаменателе. Поэтому фт<Сфп. В этом случае (7.24) силь-
но упрощается и принимает вид
dln0n п + 2
din V = Y — “б-
С другой стороны, если
п + 2 т + 2
+++=++)-
17*
260
Гл. VII. Уравнение состояния твердого тела
ТО
^1п0л п-]-т-\-3
din V —Y = g
(7.26)
Безразмерная величина у называется постоянной Грюнайзена.
7.4. Уравнение состояния Грюнайзена
Если не принимать во внимание вклад в % от нулевой энер-
гии гармонического осциллятора, то
у (V) — — Ф(У) ——--------—. (7 27)
N yml3 уп/3
Отсюда, используя приближение (7.25), можно получить уравне-
ние состояния Грюнайзена для твердых тел, являющееся част-
ным случаем уравнения (7.3),
PV+G(V) = yE\
р __________ mA п В
1 3 vm^ ~з vniz 1 (7.28)
п + 2
Величина Е* в соответствии с (7.2) равна тепловой энергии ка-
ждого атома. Она зависит от параметра 0П. Но так как ранее
было предположено, что прямо пропорционально v, что было
использовано при получении (7.23), то его можно вычислить
при всех V, если задано значение 0р при V, равном, например,
Vo. Кроме Е*, в (7.28) есть еще четыре постоянные Л, В, m и
п. Однако из (7.12) ясно, что Л, В связаны через величину объ-
ема, приходящегося на один атом при абсолютном нуле. Теп-
лота возгонки при P = T=Q находится из (7.13), а (7.14) дает
коэффициент сжимаемости р0. Поэтому величины Vo, и
могут быть использованы для написания трех условий, которым
должны удовлетворять четыре постоянные Л, В, п и т. Четвер-
тое дополнительное условие можно написать, если воспользо-
ваться коэффициентом теплового расширения, который мы
вскоре будем рассматривать. При наличии этих данных уравне-
ние состояния Грюнайзена становится полностью определенным.
7.5. Процессы при постоянном объеме
Если продифференцировать уравнение состояния (7.28) по
температуре Т, то будем иметь
<7-29)
7.5. Процессы при постоянном объеме
261
Это соотношение можно переписать в более знакомой форме,
если V считать функцией Р и Т. При V= const, т. е. для про-
цессов с постоянным объемом, имеем
или
ЙРХ _ <аг/аг)р_а
дТ /._ ^VjdP)T ~ ’ I'.'j’J;
где а — коэффициент теплового расширения, а р — коэффи-
циент сжимаемости. В этом случае соотношение (7.29) имеет
вид
Это и есть четвертое условие, необходимое для написания уравне-
ния состояния Грюнайзена. Все четыре условия для атомного
объема, коэффициента теплового расширения, коэффициента
сжимаемости и теплоемкости называются вторым законом
Грюнайзена.
Здесь мы имеем возможность проследить, как изменяется
величина п, определяемая соотношением (7.31) при изменении
типа кристалла, и выявить имеющиеся закономерности. К про-
стейшему типу относятся одноатомные правильные кристаллы,
образуемые некоторыми химическими элементами. Числовые
значения, имеющие к этому отношение, представлены в
табл. 7.1 (Т=20°С). Марганец необходимо выделить особо,
что объясняется трудностями определения его кристаллической
структуры по экспериментальным данным. Последнее вызвано
тем, что марганец имеет три модификации: две сложной куби-
ческой структуры и одну четырехугольной кристаллической
структуры. В последнем столбце таблицы приведены значения
п — 6у — 2. Так как, кроме допущения о том, что m меньше п,
никаких ограничений мы не устанавливаем, то силами притяже-
ния могут быть как силы взаимодействия нейтральных атомов,
так и кулоновское притяжение заряженных ионов.
Из таблицы видно, что область значений п весьма мала. Это
тем более привлекает внимание, что максимальное отклонение
коэффициента сжимаемости достигает отношения 400:1. Если
сгруппировать элементы, имеющие одинаковое кристаллическое
строение, то наличие закономерности в поведении п становится
еще более очевидным. Из табл. 7.2, которая иллюстрирует этот
факт, видно, что значение п для объемноцентрированной ре-
шетки ниже, чем для гранецентрированной. В то же время при
262
Гл. VII. Уравнение состояния твердого тела
Таблица 7Л
Группы перио- дической си- стемы элемен- тов Атомный вес, М Плотность Объем грамм- атома, V 4(й -108 V \oTJp —L (.Ю12 V\dP)T cv< Су-10-7 V п
Li I 6,94 0,546 12,7 180 8,9 22,0 1,17 5,0
Na 23,00 0,971 23,7 216 15,8 26,0 1,25 5,5
К 39,10 0,862 45,5 250 33 25,8 1,34 6,0
Rb 85,5 1,53 56,0 270 40 25,6 1,48 6,9
Cs 132,8 1,87 71,0 290 61 26,2 1,29 5,7
Си 63,57 8,92 7,1 49,2 0,75 23,7 1,96 9,8
Ag 107,88 10,49 10,3 57 1,01 24,2 2,40 12,4
Au 197,2 19,2 10,3 43,2 0,59 24,9 3,03 16,2
Al III 26,97 2,70 10,0 67,8 1,37 22,8 2,17 п,о
С (ромби- IV 12,00 3,51 3,42 2,91 0,16 5,66 1,Ю 4,6
ческая струк- тура) Pb 207,2 11,35 18,2 86,4 2,30 25,0 2,73 14,4
P (белый V 31,04 1,83 17,0 370 20,5 24 1,28 5,7
фосфор) Та 181,5 16,7 10,9 19,2 0,49 24,4 1,75 8,5
Mo VI 96,0 10,2 9,5 15,0 0,36 25,2 1,57 7,4
W 184,0 19,2 9,6 13,0 0,30 25,8 1,62 7,7
Mn VIII 54,93 7,37 7,7 63 0,84 23,8 2,42 12,5
Fe VIII 55.84 7,85 7,1 33,6 0,60 24,8 1,60 7,6
Co 58,97 8,8 6,7 37,2 0,55 24,2 1,87 9,2
Ni 58,68 8,7 6,7 38,1 0,54 25,2 1,88 9,3
Pd 106,7 12,0 8,9 34,5 0,54 25,6 2,23 Н,4
Pt 195,2 21,3 9,2 26,7 0,38 25,5 2,54 13,2
одинаковом кристаллическом строении п почти не меняется для
целой группы элементов. При увеличении порядкового номера
элементов п имеет тенденцию к увеличению.
В табл. 7.3 приведены числовые данные для ряда ионных
кристаллов, в которых, по-видимому, нет малых молекулярных
групп, состоящих из атомов. В этом случае правильно будет
вычислять тепловую энергию с помощью только члена прибли-
жения Дебая. Причем слагаемое, характеризующее притяже-
ние в законе взаимодействия, определяется главным образом
кулоновскими силами, и так как т~1, то приближенное выра-
жение (7.25) должно выполняться точнее, чем для элементов
7.5. Процессы при постоянном объеме
263
Таблица 7.2
Объемноцентрированная кубическая решетка Гранецентрированная решётка кубическая
Y n Y n
Li 1,17 5,0 Al 2,17 11,0
Na 1,25 5,5 Co 1,87 9,2
К 1,34 6,0 Ni 1,88 9,3
Rb 1,48 6,9 Cu 1,96 9,8
Cs 1,29 5,7 Pd 2,23 11,4
Fe 1,60 7,6 Ag 2,40 12,4
Mo 1,57 7,4 Pt 2,54 13,2
Ta 1,75 8,5 Au 3,03 16,2
W 1,62 7,7 Pb 2,73 14,2
Таблица 7.3
Молекуляр- ный вес, M Плотность Объем грамм- молекулы, V .10» _ 1 ) -1012 V\дР)г Cjz-io-7 Y п
NaCl 58,46 2,16 27,1 121 4,2 47,6 1,63 7,8 (8,0)*
NaBr 102,9 3,20 32,1 (120) 5,1 48,4 (1,56) (7,4) (8,5) *
KC1 74,6 1,99 37,5 114 5,6 47,7 1,60 7,6 (9,0)*
KBr 119,0 2,75 43,3 126 6,7 48,4 1,68 8,1 (9,5)*
KJ 166,0 3,12 53,2 128 8,6 48,7 1,63 7,8 (10,5)*
RbBr 165,4 3,35 49,4 (107) 7,9 48,9 (1,37) (6,2) (10,0) *
RbJ 212,4 3,55 59,8 (102) 9,6 49,5 (1,41) (6,5) (11,0)*
AgCl 143,3 5,55 25,8 99 2,4 50,2 2,12 10,7
AgBr 187,8 6,32 29,7 104 2,7 50,1 2,28 Н,7
CaF2 (флюо- рит) 78,1 3,18 24,6 56,4 1,24 65,8 1,70 8,2
FeS2 120,0 4,98 24,1 26,2 0,71 59,9 1,47 6,8
PbS * Числ 239,3 ювые 31 7,55 лачен 31,7 :ия по 60 > Паулингу. 1,96 50 1,94 9,6
из табл. 7.1. Хорошо видно, что п ведет себя весьма закономер-
но и хорошо согласуется со значениями Паулинга, полученными
Таблица 7А
Группы периодической системы и структуры Атомный или молеку- лярный вес, Л4 Плот- ность Объем грамм- молекулы, V -1А .10«’ V\др)т си-ю"7
Mg 24,32 1,69 14,4 75 3,0 23,8 1,51
Zn II Гексагональная 65,37 7,13 9,2 90 1,72 24,0 2,01
Cd 112,4 8,65 13,0 93 2,25 24,5 2,19
Т1 1 I 111 204,0 11,8 17,3 90 2,3 24,8 2,73
Sn ’ 1 iv Тетрагональная 118,7 7,30 16,3 64 1,91 25,5 2,14
As 74,96 5,7 13,2 16 4,5 24,3 0,19
Sb V Триклинная 120,2 6,68 18,0 33 2,7 24,1 0,92
Bi 209,0 9,80 21,3 40 2,97 25,2 1,14
s 1 32,07 2,07 15,5 180 12,9 21,6 1,00
Те j VI Ромбическая 127,5 6,2 20,6 52,8 5,18 25,2 0,83
J VII Ромбическая 126,9 4,9 25,9 250 13,0 24,1 2,07
SiO2 (кварц) Триклинная 60,3 2,649 22,8 36,2 2,67 43,1 0,71
TiO2 (рутил) Тетрагональная 80,1 4,250 18,9 23,7 0,58 59 1,30
SiO2 • ZrO2 (циркон) Тетрагональная 182,9 4,6 39,8 9,1 0,85 100 0,43
Be3Al2 (SiO3)6 (берилл) Гексагональная 539,3 2,703 199 1,2 0,57 447 0,09
CaCO3 (кальцит) Триклинная 1 1 ЛЛ Л7 2,71 37,0 15,4 1,34 80,5 0,51
CaCO3 (арагонит) Ромбическая ? 1ии,и/ 2,932 34,2 61,9 1,53 81,5 1,68
Все значения в таблице получены при комнатной температуре.
7.6. Отношение двух типов удельной теплоемкости
265
им при приближенном теоретическом рассмотрении взаимодей-
ствия электронов замкнутых оболочек1).
В табл. 7.4 приведены данные для относительно сложных
кристаллов. Для тех из них, атомы которых не образуют моле-
кулярных групп, например Mg, Zn, Cd, Tl, Sn, J(?), значения у
и п аналогичны прежним. Для других кристаллов значитель-
ный вклад в Cv дают члены приближения Эйнштейна. По-
этому тепловая энергия в (7.28) должна быть намного меньше
значений, представленных в табл. 7.4. Это объясняет тот факт,
почему значения для кристаллов, приведенных в табл. 7.4, мень-
ше обычных. По-видимому, используемая зависимость характе-
ристической частоты от V для членов приближения Эйнштейна
является неверной. Поэтому если считать Е* в (7.28) только
той частью тепловой энергии, которая соответствует члену Де-
бая, то приближение будет достаточно хорошим.
7.6. Отношение двух типов удельной теплоемкости
Из соотношения (6.73) предыдущей главы с помощью (7.31)
можно получить отношение удельных теплоемкости при по-
стоянном давлении и постоянном объеме
Сп а2ГК Т [dV\
С7 = 1 + = 1 +YCt7 = 1 'V\дт}p^ (7.32)
Если воспользоваться определением числа Грюнайзена [(7.25)
или (7.26)], то получим
Считая у постоянной и учитывая известный экспериментальный
факт о том, что отношение -y(dV/dT)p к СР, как правило, не
зависит от температуры, из (7.32) получаем
cp/cv = 1 + аТСр «(1 — аТСрУ1,
Ср — Cv = аТСр. (7.34)
Здесь а — постоянное число.
В табл. 7.5 представлены значения отношения двух удель-
ных теплоемкостей для твердых тел. Из таблицы видно, что
разница между СР и Cv действительно весьма мала.
J) Pauling L., Proc. Roy. Soq. (A), 114 (1927), 181; Journ. Am. Chem.
Soc., 49 (1927), 765; Z. Krist., 67 (1928), 377.
266
Гл. VII. Уравнение состояния твердого тела
7.7. Адиабатические процессы
Энтропия S определяется соотношением
нр Р
Таблица 7.5
Отношение двух типов теплоемкостей при 20° С и низком давлении
Элемент Ср/Су Элемент Ср/Су 1 Элемент CpjCy Элемент CpjCy
Li 1,056 Та 1,010 Си 1,028 Со 1,020
Na 1,079 Мо 1,007 Ag 1,040 Ni 1,021
К 1,10 W 1,006 Аи 1,038 Pd 1,022
Rb 1Д1 Мп 1,044 . А1 1,043 Pt 1,020
Cs 1,11 Fe 1,016 РЬ 1,067
Согласи о (6.57) предыдущей гл авы,
£ = _ _ р jL . Р □ — — — д (F
дТ\Т' а т dV \Т
Поэтому
dS = — ±d[r2 д д f7
дТ \ Т Л dV \1
= — р diF riT дТ2 0/1 dV ( дТ ’
а тогда S = —( дР\ dT)v- (7.35)
Однако на основании (6.64) предыдущей главы
1
F —— х + 9^Т 'п21п(1—expf—-у- — kT\n о0р.
о
С помощью соотношения (7.35) для энтропии можно получить
следующее равенство:
1 / \ 0 / 3 ,
5 = k In о0Р— 9k у т|2 In \1 — е т /с1ц-\-9к-^- J —g-—-— =
о о т ч
е 1 — 1
0D/T Ор/г
= Л1по0р-9б(-^-)3f ^1п(1-е-^ + 9л(^-)3у'
(7.36»
7.7. Адиабатические процессы
267
Таким образом, энтропия кристалла является функцией только
Qd/T. Поэтому дифференцирование при постоянной энтропии
эквивалентно дифференцированию при постоянной ®D/T. Со-
гласно (7.2),
Поэтому изменение температуры при адиабатическом процессе
можно вычислять следующим образом:
1 i от \ 1 /деп\ 1 fdV\
'r('dp)s=='e^(~dp’ls==~Y й(др)5- (7-38)
Продифференцируем уравнение состояния при постоянных S и
Используя дополнительно (7.37), мы получаем
v+P(-)s+v =
= |Pr+O(V)][-v4(^)J.
или, решая относительно —(д V/dP)s, находим
(dV\ V
\dP)s~~ P^+\)+G'(V) + yG(V)/V ’
При абсолютном нуле Р = 0, О(У0) = 0. Тогда
_ Ио
\дР )р=о, г=о — O'(V0) •
Поэтому коэффициент сжатия 0О равен
(7.39)
^-+i
ft_____LL_ _ i ____ 9^>
Po Va \ dP)p=o,T=o G'(Va) m(n — m)aam
При произвольной температуре и сравнительно малом давле-
нии первым членом в знаменателе (7.39) можно пренебречь.
В этом случае адиабатический коэффициент сжатия равен
д 1 !<>V\ V/Vo _ft (У/Г0)О'(И0)
Ps“ r.W.- g.w+v ™ O.w+V og)
(740)
268
Гл. VII. Уравнение состояния твердого тела
Заменяя G(V) из (7.28) и используя (7.12), получаем
п m
/ V \2____________3'~~3~____________
('£._vW±».V/3_
U v) \ з Щ v )
pr1+(i+|±i_
v-v01
Vo J
(7.41)
В следующем пункте будет найдена зависимость между изме-
нением объема и теплоемкостью (см. (7.64)), которая имеет
вид v~ v° ~ (7 42)
Здесь • (7-43) \ V \ дТ ) / т’-о \ дР / i-q
Используя эти добавочные соотношения, перепишем (7.41) в
следующем виде:
Ps = ₽o[I+(i+j+^)|:]. (7.44)
Отсюда следует, что адиабатический коэффициент сжатия пря-
мо пропорционален тепловой энергии кристалла и возрастает
с увеличением температуры.
Дифференцируя логарифм от (7.41), получаем
1 /м + п4-б \ 1 dv
ps дТ ~\ 3 V V дТ •
(7.45)
Отсюда видно, что относительная скорость изменения ps с тем-
пературой и коэффициент объемного теплового расширения по
величине одинакового порядка. С другой стороны, дифференци-
руя логарифм от (7.39) по Р при постоянной энтропии, полу-
чаем
_1_/2₽Л J1 + Y) + [б- (Ю - G (Ю + G' (V)] )5
p(i+Y)_j_G'(K)+^G(K)
1 (дУ\
у \дР}$’
7.8. Изотермические процессы
269
Используя еще раз (7.39), перепишем это соотношение для слу-
чая низкой температуры, когда
Up )s ~
VG"(V)-±G(V) + yG'(V)
С'(Ю+у G(V)
<2+v> m
' m -|- n 4-9\ 1 / dV \ _
3 J И0М$“ \ 3 P*-
(7.46)
Отсюда следует, что относительная скорость изменения коэф-
фициента адиабатического сжатия в зависимости от давления
по величине того же порядка, что и сам коэффициент сжатия.
Для твердых тел, меньше сопротивляющихся сжатию, скорость
изменения несколько больше.
Значения величин, найденные в этом пункте, с трудом под-
даются экспериментальной проверке, так как эксперименты
обычно ставятся для изотермических, а не адиабатических про-
цессов. Однако, используя (7.31) и термодинамическое соотно-
шение
Cv(dV/dP)r = Cp(dV/dP)s,
получаем
аУ
у~ hcp
Если величина у постоянная и коэффициент в (7.45) мал, то
6S медленно меняется с температурой. А тогда из предыдущей
формулы следует, что также медленно меняется с изме*
нением температуры.
7.8. Изотермические процессы
В этом пункте мы вычислим коэффициент изотермического
сжатия твердого тела. В п. 7.11 будет показана тесная связь
между коэффициентом изотермического сжатия и модулем
Юнга для твердого тела. Модуль Юнга является одним из са-
мых важных динамических параметров твердых материалов. По
зависимости коэффициента изотермического сжатия от темпе^
ратуры можно найти такую же зависимость для модуля Юнга.
Последняя, действительно, характеризует реальные низкотемпе*
ратурные динамические свойства материалов.
Согласно определению частных производных, имеем
270
Гл. VII. Уравнение состояния твердого тела
тогда
1 1двр\
дР ls— eD \ дР JT^ qd\ дТ )p\dP]s’
Используя (7.38), получаем
_Lldeo\ _Ji Т 1двр\ I 1 (двр\
@D\ дР &D 1, дТ )р j eD к дР Is-
Поэтому можно, используя (7.33), получить
1 (д%\ Sl
&D дР ]т- @D дР Is cv -
Воспользуемся общим термодинамическим соотношением
1 (дТ\ _ 1 I dV \
Т [dP)s— Ср \дТ)р-
Предварительно упростим его. На основании (7.49) и
имеем
1 (д®о\ _ 1 (dv\
ё^\~дР~1т — ~С^\~дТ1Р*
(7.49)
(7.50)
(7.38)
(7.51)
Так как для твердых тел Cv есть функция только от QD/T, т. е.
Cv при постоянной S является константой, то (dCv/dP)s = 0.
А тогда (7.48) дает
\дР/т~ ~ e^VdP~)s УдТ/р-
Аналогично
/д£*\ 1 1д@п\ Г„/дЕ*\
\~дР1т = — \dP~ls Iт \~дТ/Р ~ Е'
(7.52)
(7.53)
Из всех этих соотношений следует, что скорость изменения 0D
в зависимости от давления при постоянной температуре больше,
чем при постоянной энтропии. Их отношение для обоих случаев
равно СР: Cv. Величины Cv и Е* с ростом давления при
постоянной температуре уменьшаются. Значения величины
(дЕ*/дТ)Р находятся между Ср и Су, поэтому выражение в
квадратной скобке в (7.53) положительно.
Для расчета коэффициента изотермического сжатия рт вос-
пользуемся общим термодинамическим соотношением
с да -с да
p\dPls'
7.8. Изотермические процессы
271
тогда
CD Т !dV\
Mbs = = 1 + Y V\дТ]Р •
Используя (7.41), получаем
₽г — ₽о[1+( з YJ Уа l-YT(‘dr)p+• • •]• <7,54)
Однако из (7.38), (7.41) и (7.50) следует, что
^Са[1+(^+з_7)Х=А+...].
Поэтому (4т’*')р>0’ а всегда больше разности V— Vo.
Таким образом, из (7.45) получим
1 д₽г « + « + 6 1 dv 1 <?₽5
₽Г"^'> 3 ~уй'дТ> ~^"дГ-
(7.55)
Из соотношения (7.45) следует, что ps/ V сохраняет почти
постоянное значение. К тому же, так как у является константой,
1/И (дУ\
то из (7.47) следует, что и -g— (+тг1 сохраняет почти постоян-
ное значение. Из (7.42) и (7.43) получаем следующее прибли-
женное выражение:
1 / _ Ср V— Ко ~ £*
V \.дТ)р~ Qo И Ио ~ Qo ’
а тогда можно приближенно записать в виде
Рт Ро [1 + m +j " #• + j- (ТСр - £*)]. (7.56)
L ° VO Vo J
Здесь необходимо обратить внимание на то, что в области низ-
ких температур чрезвычайно важным является третий член, так
как в этом случае Е*~ТА. Даже при T~@D третий член по-
прежнему дает существенный вклад и составляет примерно30%
от второго. С помощью этой формулы можно вычислять измене-
ния коэффициента изотермического сжатия твердого тела в за-
висимости от температуры, особенно при низких температурах.
Это очень важная для инженерной практики формула.
При высоком давлении и низкой температуре основной
вклад дает потенциальная энергия. В этом случае разница между
272 Гл. VII. Уравнение состояния твердого тела
Р- (7.57)
относительной скоростью изменения коэффициента изотерми-
ческого сжатия и относительной скоростью изменения коэф-
фициента адиабатического сжатия с изменением давления весь-
ма мала и ею можно пренебречь. А тогда р в (7.46) можно пи-
сать без нижнего индекса
1 др _
3
Отсюда видно, что относительная скорость изменения коэф-
фициента сжатия с давлением прямо пропорциональна самому
коэффициенту сжатия. Однако относительная скорость измене-
ния коэффициента сжатия с температурой прямо пропорцио-
нальна коэффициенту расширения. При m = 3, n = 9 (m + n +
+9)/3 = 7; при m=l, n = 9 (m + n + 9)/3 = 6,3. Это и есть значе-
ния коэффициента пропорциональности.
Полученные результаты можно непосредственно сравнить с
экспериментальными данными. Грюнайзеном была предпринята
попытка использовать для расчета коэффициентов сжатия меди,
платины и железа формулы (7.54) и (7.56). Из табл. 7.6 видно,
что экспериментальные данные очень хорошо согласуются с
Таблица 7.6
р«1012, см^дин - 273 с С -190° с -17° С + 131° с + 165° С
« Эксперимент т+ +б Си ——о = 7.4 — 0,718 0,773 0,815 0,828
(Расчет 6 0,710 0,717 0,776 0,815 0,825
р( ( Эксперимент от + „ + 6 = § q — 0,374 0,392 0,401 0,404
(Расчет 6 0,371 0,374 0,391 0,401 0,404
(Эксперимент R Fe -m + ” + 6 =65 — 0,606 0,633 0,664 0,675
(Расчет 0,600 0,603 0,638 0,663 0,672
теоретическими при тех значениях (m + n + 6)/3, которые приве-
дены в таблице. Эти значения получаются в том случае, если
для m взять значение, немного превышающее ранее принятое
т = 3, а п взять из табл. 7.1 (для Си, Pt, Fe они составляют
6,3; 7,4; 5,5). Это, возможно, объясняется тем, что изложенная
теория является в принципе приближенной. Грюнайзеном были
произведены также сравнения средних значений -^-{др/дТ) и а.
Ро
Их отношение должно равняться (m + n + 6)/3. Для алюминия и
7.8. Изотермические процессы
273
серебра при температуре в пределах от 190 до 18° С значение
отношения равно соответственно 9,1 и 7,3, что тоже является
очень точным.
Потенциал взаимодействия между ионами кристалла яв-
ляется, как правило, кулоновским. В этом случае т=1, а = е2,
где е — электрический заряд электрона, а (7.14) переходит в со-
отношение
9г4
₽о = т---гг—2- (7-58)
(и—l)cr/7+ v 7
К тому же при непосредственном вычислении при 7 = 0
1 д₽0 _ 11 „ п+10 (7 ,
₽о дР “ ₽о т=о“ 3 Ро-
Поэтому при определении п из р0 можно, кроме (7.31), исполь-
зовать еще (7.58) и (7.59).
Для правильных металлических кристаллов, состоящих из
двухатомных щелочных галогенидов, такую работу уже про-
делал Слэтер. Результаты, полученные различными способами,
представлены в табл. 7.7. Экспериментальные измерения отно-
сительной скорости изменения коэффициента сжатия с темпера-
турой (от 30 до 75° С) и давлением (вплоть до 12 000 кг/см2)
выполнили Слэтер, а коэффициента расширения — Файзин, Бэк-
стер, Уоллис. На первый взгляд кажется, что значения п для
солей лития, вычисленные из (7.59), особенно велики. Однако
порядок величины, как правило, является правильным.
Таблица 7.7
р. 10’2(30° С), Р = 0, см2!дин 1 d? 3 dT _12L/₽ ₽ dPl it из (7.59) n. из (7.58) n из табл. 7.1 n по Паулингу
1 V dT
L1F 1,53 — 7,6 14,3 5,9 6,0
LiCl 3,41 — 5,8 11,9 8,0 — 7,о
LiBr 4,31 — 5,7 12,8 8,7 — 7,5
NaCl 4,20 5,6 5,2 9,8 9,1 7,8 8,0
NaBr 5,08 6,2 5,0 9,5 9,5 (7,4) 8,5
KF 3,31 — 6,1 8,9 7,9 — 8,0
KC1 5,63 4,2 4,7 6,5 9,7 7,6 9,0
KBr 6,70 4,8 4,7 7,1 10,0 8,1 9,5
KJ 8,54 4,7 4,6 6,8 10,5 7,8 10,5
RbBr 7,94 — 4,4 6,2 10,0 (6,2) 10,0
RbJ 9,58 6,7 4,5 6,8 n,o (6,5) и,о
18 Зак. 1299
274
Г л. VII. Уравнение состояния твердого тела
7.9. Изобарические процессы
В этом пункте мы рассмотрим другой параметр, имеющий
большое значение для инженерной практики, а именно коэффи-
циент теплового расширения при изобарическом процессе. Ана-
лиз, проведенный в предыдущих пунктах, дает нам возмож-
ность из уравнения состояния твердого тела находить зависи-
мость между коэффициентом теплового расширения твердого
тела и температурой, т. е. по значению коэффициента теплового
расширения при определенной температуре находить его значе-
ния во всем диапазоне температур от низких до высоких.
В соответствии с правилами вычисления частных производ-
ных имеем
Однако
и, следовательно,
(7.60)
(7.61)
Сравнивая с (7.33), мы видим, что при постоянном давлении
скорость изменения тепловой энергии с температурой колеблет-
ся между СР и Cv.
ч
з г
П3 ./ — 1
о
TCv-E* = -3kQD^
Следовательно, при Т -> оо имеем TCV — Е* = — QD.
Из (7.31), т. е. из второго закона Грюнайзена, имеем
(7.62)
Если для Cv взять его численное значение при полном возбу-
ждении, а р0 за рг, то оказывается возможным приближенно
7.9. Изобарические процессы
275
рассчитать коэффициент расширения а при постоянной темпе-
ратуре. Например, для NaCl Cv~§k (удельная теплоемкость
грамм-молекулы), ги=1, п = 9. И, следовательно, используя
(7.58), при ош = 2,202, г=3,55Х10~8 для NaCl получаем а =
= 120хЮ~6. Экспериментальное значение равно 121Х10"6. Для
PbS, кристаллическая структура которого аналогична структуре
CsCl, при ст — 4X2,0354 = 8,142 имеем г=3,74Х10-8, а = 34Х10“6.
Экспериментальное значение равно 60хЮ“6. Для флюорита
CaF2 при от = 7,33 имеем r=3,44X40~8, Cv = 9&, т=1, п = 9,
а = 52хЮ-6. Экспериментальное значение равно 56Х10-6.
Так как рг с изменением температуры меняется медленно,
то коэффициент объемного расширения а приближенно пропор-
ционален Cv, и, следовательно, для очень низких температур
а должно изменяться по закону Г3.
Из уравнения состояния (7.28) можно вывести другие фор-
мулы для коэффициента объемного расширения. При низком
давлении можно положить Р = 0. Тогда получим
G(V) = \E*.
Разложим G(V) при абсолютном нуле в ряд Тейлора по сте-
пеням Д= V— Уо.
G(V) = 0(V0)4-AG4Vo) + A2^G''(y0)-f- ... .
Из (7.12) и (7.40) следует, что
О(П) = 0, О'(У0) = А-
и
п" tv \___4~ ” 4~3 1
О (Vo)— з роКо-
Тогда
c(K) = £[1_z^+|+11* + ...] = vE..
Решая это соотношение приближенно относительно А, получаем
А =__________vPpg*________
1 m + » + 3 уро с, ,
6 v0 +
Но из (7.47) следует, что
vn / с_ \
(7-63)
\ V дТ JT=Q
18*
276
Гл. VII. Уравнение состояния твердого тела
Таким образом, при низком давлении имеем
д
Е*_____________
m -]- п + 3 Е* "I
6
(7.64)
Так как Q0^>E*, то относительное увеличение объема при
возрастании температуры от Т=0 до Т приближенно пропор-
ционально Е*, причем этот закон более строго выполняется при
низких температурах и малых значениях Е*. При высоких тем-»
пературах отношение A/Vo растет быстрее, чем Е*, так как
множитель (m + n + 3)/6 положителен.
Тепловое расширение определяется значениями трех кон-
стант 0D, Qo и (m + n + 3)/6. Причем для расчета теплового рас-
ширения твердых тел, не содержащих оптических колебаний,
этого оказывается достаточно. При отыскании значения &D не-
обходимо помнить, что оно должно совпадать с тем значением
©г, которое используется при вычислении Су. Теоретически
значение (m + n + 3)/6 колеблется между 2 и 3. Однако если с
его помощью получить кривую теплового расширения, то полу-
ченные значения далеко не полностью согласуются с теоретиче-
скими. Причина этого состоит в том, что на самом деле 0D яв-
ляется не константой, а функцией температуры при постоянном
давлении. Если через 0ро обозначить значение 0D при Р=7,=0,
то, разлагая Е* в ряд, получим
£-=™-M^U,+ - =
Здесь Ео есть значение Е*, вычисленное через 0оо. Таким обра-
зом, (7.64) можно переписать в виде
Здесь можно считать, что изменение 0d играет роль поправоч-
ного члена для Д/Уо. Таким образом, если в (7.64) 0D принять
постоянной, то необходимо предвидеть, что значение постоянной
(т + /г + 3)/6 может отклоняться от теоретического.
7.9. Изобарические процессы
277
Дифференцируя (7.64) по Т, получим
(дЕ*\
1 _ UtJp=o _ CV
^\дТ)Р=0 w + n+3 £*12 ~ ,и + п + 3£*-|2-
L 6 Qq J L 6 Qo J
(7.66)
Замена (дЕ*1дТ)Р=ь на Cv допустима, так как на основании
(7.61) их разность очень мала. Соотношение (7.66) является
искомым уравнением для коэффициента объемного расширения.
Коэффициент линейного расширения составляет от него 7з- При
изменении температуры в интервале от 7\ до Т2 он равен
1 _ 1 А2 /у /'ух
/о дТ — 3 (Г2 — Т{) Vo 9
где Л/Vo берется из (7.64). Соотношения (7.66) и (7.67) можно
проверить экспериментально.
Алмаз представляет собой наиболее простой случай. Для
него &d равно 1860. Это значение настолько велико, что в (7.64)
можно вообще пренебречь поправочным членом. Таким обра^
зом, необходимы только две константы 0D и Qo. Результаты
приведены в табл. 7.8. Из нее видно, что соответствие между
расчетными и экспериментальными значениями весьма хорошее.
Для металлов, представленных в табл. 7.9, значение постоян-
ной (m + n + 3)/6 для платины и иридия больше теоретического,
для меди и золота они очень близки к величинам (Сп = 2,7,
Аи = 3,7), соответствующим т = 3 и п из табл. 7.1. Это доказы-
вает, что изложенная теория действительно может быть приме-
нима для расчета коэффициента теплового расширения твердых
материалов в широком диапазоне температур. И так как этот
Таблица 7 8
Коэффициент теплового расширения алмаза
LT, °К 1, дТХШ Отклонение
расчет эксперимент
Алмаз: 84,8/194,1 0,16 0,18 —0,02
0D= I860 194,1/273,2 0,61 0,58 +0,03
Qo = 457 ккал 273,2/296,2 0,97 0,97 ±
296,2/328,0 1,17 1,17 ±
328,0/351,1 1,37 1,45 —0,08
Таблица 7.9
Коэффициенты теплового расширения некоторых металлов
Т, °к -I /о дТ Откло- нение АГ, °К Откло- нение
1 ,ЛЯ 1ц дТ
расчет экспе- римент расчет экспе- римент
Платина: 0р = 230 Qo = 231 ккал т p,+3 _ 4 g 6 96,2 139,2 190,9 217,2 225,9 247,1 267,2 283,6 6,62 7,64 8,24 8,42 8,48 8,60 8,70 8,76 6,66 7,57 8,16 8,28 8,42 8,57 8,74 8,85 —0,04 289/329 329/373 289/523 523/773 773/1023 1023/1273 8,85 9,02 9,18 9,87 10,60 11,38 8,95 9,11 9,23 9,84 10 52 11,1—11,4 —0,10 —0,09 —0,05 —0,03 4-0,08
1-0,07 -0,08 -0,14 -0,06 -0,03
—U,U+ —0,09
Иридий: ео = 283 Qo — 307 ккал w+n+3_ = 65 6 98,0 132,3 209,2 229,0 266,5 283,0 1445 1695 1924 4,44 5,27 6,09 6,22 6,40 6,46 9,35 10,1 10,9 4,43 5,22 5,85 6,19 6,38 6,72 9,2 10,1 10,8 н d 1-0,01 -0,05 -0,24 -0,03 -0,02 -0,26 1-0,15 t ho,i 90/290 290/373 295/2003 5,77 6,62 8,66 5,71 6,58 8,75 4-0,06 4-0,04 —0,09
Медь: 0D = 325 Qo = 120 ккал /п-{-и-^-3 г) о 6 103 123 143 163 183 203 223 243 263 283 10,6 12,1 13,1 13,9 14,5 15,0 15,4 15,8 16,0 16,3 10,4 12,1 13,1 14,4 14,7 15,0 15,9 16,1 16,1 16,3 4-0,2 ± ± —0,5 —0,2 ± —0,5 —0,3 —0,1 ± 20,4/80,5 82/289 289/523 523/648 648/773 4,0 14,0 17,4 18,7 19,5 3,8 14,2 17,2 18,6 19,6 +0,2 —0,2 К? —0,1
Золото: 0р = 190 Qo = 145 ккал m-j-n-j-З __ з q 6 103 123 143 163 183 203 223 243 263 283 323 11,7 12,4 12,8 13,1 13,4 13,6 13,75 13,9 14,0 14,1 И,4 11,8 12,3 12,7 13,05 13,3 13,7 14,15 14,2 14,3 14,4 14,5 —0,1 4-0,1 4-од —0,05 4-0,1 —0,1 —0,4 —0,3 —0,3 —0,3 —0,1 83/290 290/373 323 373 573 773 13,2 14,4 14,4 14,6 15,5 16,4 13,2 14,3 14,4 14,6 15,5 16,3 ± 4-од ± ± ± +0,1
7.9. Изобарические процессы
279
Таблица 7.10
т ±2L.io. z0 от Отклонение
расчет эксперимент
Флюорит (CaF2): 94,4 7,10 7,17 —0,07
0D = 474 124,9 10,42 10,26 +0,16
Qo — 309 ккал 157,3 13,09 13,02 +0,07
m-\-n-\-3 __ § § 6 186,9 14,83 14,65 +0,18
209,8 15,93 16,04 —0,11
231,4 16,80 16,78 +0,02
255,6 17,62 17,58 +0,04
278,6 18,30 18,53 —0,23
313,0 19,22 19,12 +о,ю
Пирит (FeS2): 108,0 2,88 2,95 —0,07
@D = 645 129,7 4,00 3,95 +0,08
Qo = 556 ккал 155,0 5,15 5,16 —0,01
w + " + 3 = 4,65 0 214,8 7,22 7,09 +0,13
237,4 7,77 7,73 +0,04
269,7 8,41 8,43 —0,02
313,0 9,10 9,08 +0,02
коэффициент является важным параметром в инженерной прак-
тике и тесно связан с тепловым напряжением материалов, то
полученные нами результаты также обладают большой прак-
тической ценностью.
Изложенную теорию можно распространить на ионные кри-
сталлы, которые характеризуются только температурой Дебая,
как, например, кристаллы CaF2 и FeS2. Из табл. 7.10 видно, что
вычисленные значения соответствуют экспериментальным. Од-
нако, как правило, для T<O,30D экспериментальные значения
существенно отклоняются от (7.64). При этих температурах экс-
периментально измеренное значение Д/Уо намного превышает
вычисленное из (7.64). Байл и Палэн1) полагают, что причиной
отклонения является возрастание у с уменьшением темпера-
туры. Они приводят следующие доводы: так как при одинако-
вой длине частоты продольных волн ниже частот поперечных
волн, то при низкой температуре продольные волны возбужде-
ны сильнее, что и может вызвать увеличение у. Конечно, этот
!) В i j 1 D„ Р u 11 a n Н., Phil. Mag. (7), 45 (1954), 290.
280
Гл. VII. Уравнение состояния твердого тела
факт (кроме коэффициента теплового расширения, о котором
мы только что говорили) оказывает влияние и на остальное.
7.10. Амплитуда колебаний и точка плавления
Средняя энергия гармонического осциллятора с частотой у и
массой р зависит от амплитуды колебания е и равна
у (2л\^)2 ц.
Пусть она равна средней энергии гармонического осциллятора
с основной частотой у
hv
e^kT-\ ‘
При kT"^>hy можно получить следующую зависимость:
1/ kT 1
V 2л2р, v
(7.68)
Частота колебаний в твердом теле имеет вполне определенное
распределение. Допустим, что оно имеет форму (6.32). Найдем
среднее значение е в соответствии с таким распределением:
е =
/kT 9N
2л2ц Vp
j* у dy/3N =
6
/kT 3 1
2л2ц 2 yD
После возведения в квадрат получим
9 kT
е2 =----2"2— •
8 л VpH
При высокой температуре E^ — ZkT. Из (7.69) имеем
Е* = ji2v2 е2ц.
о Ь'
(7.69)
(7.70)
Если пренебречь изменением объема
кристалла, то из
(7.22)
следует, что
Уа
Ро •
На основании (7.63) Vo/Po ~ Qo, а на основании (7.64), как и
ранее, считаем, что E*/Qo<Sl. Учитывая это, из (7.70) получаем
— — 1/4 — « —Щ —.
г0 V Vo 2/2 У Vo
(7.71)
Отсюда видно, что относительное приращение средней ампли-
туды изменяется с температурой так же, как и квадратный ко-
7.10. Амплитуда колебаний и точка плавления
281
рень из относительного приращения объема. Если считать их
отношение некоторой характерной константой, то для того, что-
бы она была одинаковой для различных тел, достаточно равен-
ства приращения их относительных объемов.
Из эксперимента известно, что относительное приращение
объема в точке плавления Тт достигает 8% 9, т. е.
Vo 'T = Tm
0,08.
(7-72)
Отсюда, используя (7.71), получим
т = тт
^0,105,
(7.73)
т. е. в точке плавления отношение средней амплитуды колеба-
ний и атомного размера достигает почти 11%. Если эти факты
связать с (7.70), то немедленно получим связь в точке плавле-
ния между собственными частотами vD,m. Если считать, что в
точке плавления Е* равно 3kT7n, то
V2 = 3* Тт <3RN^ Тт
D’m 8л2(0,105)2 8л2(0,105)2 MV%> '
Поэтому если Тт выразить в °К, а за Уо взять объем грамм-
молекулы в кубических сантиметрах, то получим
или
в- = 119/зЙ
(7-74)
Соотношение (7.74) представляет собой так называемый закон
Линдемана. На основании (7.60) скорость изменения &D с тем-
пературой в интервале от Т=0 до Т=Тт в у раз превышает
скорость изменения относительного объема в том же темпера-
турном интервале. Если для у принять значение у~2, то при
вычислении Cv характеристическую температуру 0D необходи-
мо брать на 15% больше &Dj т, т. е.
в'’“137
(7.75)
0 Bonfiglioli G., Montalenti G., J. Appl. Phys., 22 (1952), 1089.
Эти авторы считают, что это значение должно быть функцией кристалличе-
ской структуры и будет меньше для не очень симметричных кристаллов.
282
Г л. VII. Уравнение состояния твердого тела
Полученное таким образом QD можно проверить путем сравне-
ния с 0п, полученным из кривой С+, и тем самым проверить
правильность формулы (7.75). Результаты такого сравнения
представлены в табл. 7.11. Из таблицы видно, что, хотя при
вычислениях вместо Vq при абсолютном нуле было использо-
вано значение V при обычной температуре, совпадение весьма
хорошее.
Используя формулы (6.74) и (6.75), можно найти связь
между точкой плавления, модулем Юнга и коэффициентом
Таблица 7.11
Значения 0D, найденные по точке плавления
Веще- ство Л1 V T °K m, 0D (из Су) Откло- нение
РЬ 207,21 18,26 600,6 89 88 +1
Hg 200,61 14,85 234,3 60 97 —37
J 127 25,7 386 81 106 —25
Cd 112,41 13,01 594,1 134 168 -34
Na 22,997 23,70 370,7 191 172 +19
Ag 107,88 10,26 1234 213 215 2
Са 40,08 26,82 1118 241 226 +15
KC1 37,2 18,9 1051 273 230 +43
Zn 65,38 9,17 692,7 214 235 —21
NaCl 29,2 13,5 1083 350 281 +69
Cu 63,54 7,12 1356 330 315 +15
Al 26,97 9,98 932,9 375 398 -23
Fe 55,85 7,11 1808 405 453 —48
C 12 3,4 3600 (?) 1940 1860 +80
Пуассона. Однако в этом случае влияние кристаллической
структуры и закона взаимодействия атомов для твердого тела
является существенным. Поэтому полученная таким способом
формула может быть использована только для грубого расчета.
Таким образом, хотя полуэмпирическая теория Грюнайзена
крайне важна для кристаллов с произвольной дебаевской ха-
рактеристической частотой, однако при отыскании взаимосвязей
между различными твердыми телами она недостаточно точна.
Конечно, можно еще проводить аналогичное исследование твер-
дых тел с учетом нескольких членов приближений Дебая и
Эйнштейна в выражении для тепловой энергии и более слож-
ными законами взаимодействия между атомами. Подобная ра-
7.11. Коэффициент Пуассона и модуль Юнга , 283
бота для щелочных металлов была выполнена Бэрдиным1).
Однако, несмотря на усложнение вычислений, точность резуль-
татов повысилась незначительно. Это говорит о том, что, по-
видимому, такие усложнения метода нецелесообразны.
7.11. Коэффициент Пуассона и модуль Юнга
В начале этой главы отмечалось, что в теории Грюнайзена
X является функцией только V, что позволяет исследовать изме-
нение формы твердого тела только под действием равномерного
давления. Поэтому результаты нескольких предыдущих пунктов
могут быть выражены через коэффициенты объемного тепло-
вого расширения а и объемного сжатия Коэффициент линей-
ного теплового расширения вычисляется очень легко, так как
он составляет !/3 от коэффициента объемного теплового рас-
ширения.
Отыскание модуля Юнга Е представляет большую трудность,
так как излагаемая теория не рассматривает деформации сдви-
га. Однако из теории упругости известно, что если о есть коэф-
фициент Пуассона, то модуль объемной упругости х равен
» = ?; = т>(Т^эд- <7-76>
По 0т и о можно вычислить модуль Юнга
3(1-2а)
(7.77)
Таким образом, если о уже известно, то проводившийся в
п. 7.8 расчет зависимости от температуры Т также может
быть использован для определения зависимости модуля Юнга
от температуры. Эксперименты показывают, что коэффициент
Пуассона для каждой группы твердых тел является почти по-
стоянным. Для ионных кристаллов о~0,25; для металлов
о—Уз*, для резины о~0,5. Поэтому для ионных кристаллов Е^
для металлов 1/рт; для резины Е<^ 1/рт. Для каждо-
го материала о остается постоянным в широком диапазоне тем-
ператур. Следовательно, при различных температурах (1) и
(2) отношение модулей Юнга Е2/Е^ равно
_ (P?)i
Е1 (М2 ’
(7.78)
Это сразу же позволяет использовать расчет изменения коэф-
фициента сжатия для определения изменения модуля Юнга.
1) В а г d е е n J., Journal of Chemical Physics, 6 (1938), 367.
Глава VIII
НЕИДЕАЛЬНЫЕ ГАЗЫ
Известно, что физические свойства достаточно плотных га-
зов невозможно полностью объяснить, исходя только из законов
идеальных газов, и поэтому теория, изложенная в гл. 5, не
может быть непосредственно использована; в этом случае не-
обходимо дополнительное исследование. Различие между иде-
альными и неидеальными газами, по существу, состоит в том,
что энергия ансамбля неидеального газа является функцией
координат всех систем ансамбля.
Допустим, например, что мы имеем две системы (молекулы)
аир, находящиеся на большом расстоянии друг от друга и
обладающие энергиями 8а и ер. Можно заранее предсказать,
что при сближении они перестанут быть независимыми и их
энергия будет равна еа + Ер + еа|з, а не еа+е?, где 8а?—малая
поправка, зависящая от координат двух молекул, и, строго го-
воря, от их скоростей. Если молекулы аир сближаются доста-
точно медленно, то все изменения происходят квазистатически
и поэтому зависят только от координат молекул. В этом случае
8а? является потенциальной энергией, зависящей только от
координат двух молекул, а производные от 8а? по относитель-
ным координатам дают компоненты сил взаимодействия между
аир. Как правило, относительные скорости сталкивающихся
молекул много меньше скоростей электронов в молекуле. По-
этому и столкновение их можно считать квазистатическим.
В общем случае функция 8а3 обязательно зависит от кван-
товых чисел молекул аир. Поэтому для разных электронных
состояний атомов и молекул 8а? будет различным. Однако при
обычных температурах подавляющее большинство молекул на-
ходится в основном электронном состоянии и в этом случае
влиянием последних на 8а? можно пренебречь. Кроме этого,
часто допускают, что 8ар не зависит от вращательных и коле-
бательных состояний молекул, что при обычных условиях яв-
ляется достаточно хорошим приближением. Если же в действи-
тельности это не выполняется, то все молекулы с различными
8.1. Функция состояний неидеального газа
285
вращательными или колебательными состояниями необходимо
рассматривать как молекулы различных типов.
В настоящей главе мы везде будем пользоваться классиче-
ской статистикой, предполагая вместе с тем, что ошибками при
классическом рассмотрении потенциальной и кинетической энер-
гий поступательного движения можно пренебречь.
8.1. Функция состояний неидеального газа
Так как энергия ансамбля неидеального газа содержит сла-
гаемое, являющееся функцией координат всех молекул, то есте-
ственно считать весь ансамбль, как это было сделано при рас-
смотрении кристаллов в гл. 6, одной большой системой. Энер-
гию неидеального газа можно разделить на две части: одна из
них — суммарная энергия внутреннего движения молекул, дру-
гая — кинетическая энергия поступательного движения молекул
и потенциальная энергия взаимодействия их между собой. В со-
ответствии с этим функция состояний распадается на функцию
состояний внутренних степеней свободы и функцию состояний
поступательных степеней свободы. Вследствие предположения
о том, что потенциальная энергия межмолекулярного взаимо-
действия зависит только от координат центров инерции моле-
кул, т. е. от поступательных степеней свободы, функцию состоя-
ний для внутренних степеней свободы можно находить точно
так же, как это было сделано для идеальных газов.
Рассмотрим ансамбль из смеси неидеальных газов, состоя-
щей из молекул типа Л, В, С,..., причем, NNB, Nc,. • • есть
число молекул каждого сорта, их массы равны mA, mBf
Предположим также, что химические реакции отсутствуют.
Функции состояний, соответствующие внутреннему движению
каждой системы, будут тогда функция
состояний для внутренних степеней свободы всего ансамбля
равна Пл {Ja(T)]Na • Найдем функцию состояний для поступа-
тельных степеней свободы. Пусть хА, yAi zA, иА, vA, wA — коор-
динаты и соответствующие им компоненты скоростей молекул
типа А. Тогда элементарный объем фазового пространства всего
ансамбля равен
Лгл КВ
(mAAfnBB )3 П (dxA • • • ^л)г П №хв • • dwB)s ... (8.1)
Г=1 5=1
и соответственно вес
h3 (N -j- N 4- • • •) ТТ JJ №хв • • • • • • • (8-2)
' А В Г = 1
286
Гл. VIII. Неидеальные газы
В этом случае классическая функция состояний Л(Г) для по-
ступательных степеней свободы равна
L{T}-h\NA + NB+ ...)
Г^Л
21^4 (4 + ^ + ^),+
/VB
5 = 1
х e~W‘kT П ^dxA • • • dwA)r И (dxB ... dwB)s
Г=1 5=1
(8-3)
где W— потенциальная энергия всего ансамбля. Если внешние
силовые поля отсутствуют, то W есть суммарная энергия меж-
молекулярного взаимодействия и является функцией только
координат центров инерции молекул. Состояния с конфигура-
циями, отличающимися лишь перестановкой двух или более
молекул, мы считали различными. Поэтому, для того чтобы
исключить повторения одинаковых состояний, выражение (8.3)
необходимо разделить на NAl . После интегрирования по
скоростям получим
, Лл
х
na nb
X JJ (dxA dyA dzA\ JJ (dxB dyB dzB)s .... (8.4)
r=l 5=1
Это выражение можно переписать в виде
Д(Г) = ПЛ|(2"У } ХП(7-), (8.5)
где
а<.т>=т^в,... (dxAdyA dzA)rX
X Ц (dxB dyB dzB)s .... (8.6)
- 5=1
8.1. Функция состояний неидеального газа
287
Функцию Q(T) удобно называть функцией состояний для по-
тенциальной энергии конфигураций. Умножая ЦТ) на функцию
состояний для внутренних степеней свободы Дд {Ja(T)}Na, по-
лучим функцию состояний ЦТ) для всего ансамбля
тт I ftnm.kTX^ Нл ~
Кг)==ПлГ—xfi<r)=
= Пл №а(Т)]*аХЩТ), (8.7)
где
(2лт ,kT\ -
= -(8.8)
Если положить W = 0, то в результате получим функцию со-
стояний для ансамбля идеального газа в отсутствие внешних
силовых полей (по форме она аналогична функции состояний,
при нахождении которой в гл. 5 каждая молекула принима-
лась за отдельную систему)
1 (2nmAkT\*l'V 1
= Л5 7(7)/ • <8-9)
В (8.6) интегрирование производится по всему пространству
ансамбля. При этом предполагается, что между материальными
точками возможно существование сил отталкивания, причем
таких, что при их сближении W может бесконечно возрастать
или по крайней мере стремиться к очень большому положитель-
ному числу, и не может быть случая, когда W-^—oo. Справед-
ливость такого предположения можно обосновать с помощью
квантовой теории взаимодействия двух молекул.
Из (8.7) видно, что функцию состояний для классической
кинетической и потенциальной энергий неидеального газа мож-
но разделить на две. Функция состояний для кинетической энер-
гии Пд {<Рд (T)}NA имеет точно такой же вид, как и для случая
идеального газа, и отличается от последней только тем, что в
ней отсутствует множитель VNa+Nb+ “7Пд^д вместо кото-
рого теперь входит Q(T).
Формулы (8.6), (8.7) и (8.8) являются общими. Для их
справедливости достаточно лишь, чтобы каждая молекула ан-
самбля независимо от степени неидеальности газа, протяжен-
ности межмолекулярных сил и наличия или отсутствия внешних
силовых полей могла бы рассматриваться как молекула с от-
личимым индивидуальным движением. Допустим, что внешнее
силовое поле отсутствует, тогда W является потенциальной
288
Гл. VIII. Неидеальные газы
энергией взаимодействия молекул. Если степень неидеальности
газа невелика, то W можно приближенно считать равной сумме
потенциальных энергий парных взаимодействий молекул (т. е.
сумме таких членов, как 8ар). Однако нужно иметь в виду, что
при достаточно высокой степени неидеальности газа такое до-
пущение совершенно неприемлемо.
Если внешнее силовое поле отсутствует, то W является функ-
цией только относительных координат молекул (влияние гранич-
ного поля от стенок сосуда здесь не учитывается, для этого до-
статочно только, чтобы весь объем сосуда был намного больше
той части объема, на которую распространяется влияние гра-
ничного поля).
Из функции состояний (8.7) так же, как это делалось для
кристаллов в гл. 6, можно получить все равновесные свойства
газа. Для свободной энергии F имеем
F = — ^ANAkT\nqA(T) — kT\n£l(T). (8.10)
Если считать, что 11^=0, то Q(T’) = _|Дд"]уТ
(8.10) и используя теорему Стирлинга, получаем
Подставляя
F = - 1 п Фл (Т) - kT ^aNa {In (V/Na + 1)], (8.11)
т. e. свободную энергию для идеального газа. Сравнивая (8.10)
и (8.11), находим вклад ЕвнУтр взаимодействия молекул в F
FBH^ = — kT\nQ(T) = kT^ANA {In (V/NJ + 1}. (8.12)
Вклад Евнутр в полную энергию равен
£внутр = _Т2 д(Р^Р/Т) = kT2 . (8.13)
Введем теперь сокращенные обозначения. Вместо
"а "в
(dxAdyAdzA)r будем писать (d(dA)r, а вместо
Г=1 5=1
... будем писать —ЦдО^д)^- Перепишем теперь Й(Т’)
в виде
(8.14)
8.2. Законы распределения молекул
289
Пусть некоторая величина Q является функцией координат
всех молекул. Тогда среднее значение Q будет равно
у... j Пл
(8.15)
Например, среднее значение W энергии взаимодействия
кул W равно
моле-
(8.16)
f ...fV' ’“][>/' <НлО(Г)
Из сравнения (8.16) и (8.13) видно, что EBH^ = W. Справедли-
вость результата очевидна и физически.
Если потенциальная энергия W зависит от некоторого внеш-
него параметра %, который не влияет _на внутренние степени
свободы молекул, то среднее значение X обобщенной силы, со*
ответствующей этому параметру, равно
= kT‘ aing(r) (817)
Сравнивая (8.17) и (8.10), получаем известное термодинамиче-
ское соотношение
*=~№!т- <8Л8)
Если х — объем V, а X — давление Р, то (8.17) преобразует-
ся к виду
P = kT д^у(Т) • (8.19)
В дальнейшем мы будем рассматривать в основном этот случай.
8.2. Законы распределения молекул
Рассмотрим теперь законы распределения молекул неидеаль-
ного газа в пространстве для случая, когда внешнее силовое
поле отсутствует, а межмолекулярные силы короткодействую-
щие. Мы увидим, что закон распределения молекул неидеаль-
ного газа точно такой же, как и идеального — распределение в
пространстве равномерное.
19 Зак. 1299
290
Гл. V1H. Неидеальные газы
Что касается так называемых сил дальнодействия, то под
ними мы подразумеваем здесь силы, действие которых значи-
тельно на расстояниях порядка размеров ансамбля, например
кулоновское взаимодействие статических зарядов. Для того
чтобы функция состояний Q(T) для потенциальной энергии
была правильной, мы разделили ее на несколько факториалов
с тем, чтобы устранить повторения состояний с переставлен-
ными одинаковыми молекулами. Полученную таким способом
функцию состояний мы приняли за квазиклассическое прибли-
жение. Однако такое деление никак не влияет на относительные
вклады различных интегральных множителей в функцию со-
стояний. Этот факт можно рассмотреть чисто классически, не
касаясь требований симметрии. Та часть множителя, которая
соответствует положению молекулы а в данном пространствен-
ном элементе объема 6V, равна
fd^f.../е-JJ' {d^NA, (8.20)
(6V) (И)
где интегрирование по всем переменным, кроме од, производит-
ся по всему объему V. Если долю этой части в Q(T) обозначить
через 6Q(T), то вероятность появления молекулы а в 6V, или,
другими словами, отношение общего времени пребывания моле-
кулы а в 6V ко всему времени рассмотрения, если оно доста-
точно велико, равна
J f - f
«г (О _ 1Ю ,о „.
(V) (Ю
Если внешние силовые поля отсутствуют, т. е. W зависит
только от относительных координат молекул, и межмолекуляр-
ные силы короткодействующие, то выражение
(Ю
для данной температуры — почти постоянная величина, не за-
висящая от положения молекулы а в 6V или от положения &V
в V. В этом случае (8.21) можно переписать в виде
bti(T)/Q(T) = bV/V. (8.22)
Для каждой из молекул типа А можно получить аналогичные
результаты. Поэтому среднее число молекул типа А в 6V равно
МдбУ/К как и для идеального газа. При более точном кванто-
8.2. Законы распределения молекул
291
вом исследовании детали изложенного должны быть изменены,
однако результаты будут аналогичными тем, которые получены
классическим методом.
С помощью тех же рассуждений найдем вероятность одно-
временного появления пары молекул а и р в элементах объ-
емов dcoa и Лор. Она равна
f...
(Ю
где интеграл в числителе не содержит Лоа и Лор, оставшиеся
переменные интегрируются по всему объему V.
Если взаимодействие между молекулами невелико, то инте-
грал в числителе (8.23) будет только функцией относительных
координат элементарных объемов data и Лор. В этом случае его
можно переписать в форме
Qe~Wa^r.
Функцию Wa? определяем таким образом, чтобы IFap ->0 при
бесконечном увеличении расстояния между dcoa и Лор, а вели-
чину Q считаем константой. Таким образом, И^а₽, кроме того, что
является функцией положения dcoa и dcop, также может быть
функцией среднего положения остальных молекул, поэтому Wa?
зависит только от Т. Если Wa? с увеличением расстояния между
Лоа и Лор быстро стремится к нулю, то
f ...fQe~ Wa^kTdaa da>? « QV2, (8.24)
что в действительности всегда имеет место. Вероятность паре
молекул оказаться в избранных элементах объема в этом слу-
чае упрощается и записывается в виде
e~wrt/krduad<>)?/V\ (8.25)
После интегрирования по Лоа найдем, что вероятность появ-
ления какой-либо из молекул типа р вблизи заданной моле-
кулы а в элементе Лор, расположенном произвольно в ан-
самбле, равна
e-w^/kTd<>)?/V, (8.26)
причем сама молекула а тоже может находиться в любой части
ансамбля.
Формулы (8.25) и (8.26) представляют закон распределения
Больцмана. Теперь необходимо получить более точное значение
19*
292
Гл. VI IL Неидеальные газы
для в законе распределения. Используя определение
UZa?, из числителя (8.23) получаем
(8.27)
Пусть — одна из координат молекулы р, расположенной в
rf(Dp. Продифференцируем обе части (8.27) по хр, и так как
Q — постоянная, не зависящая от хр, то получим
р (Ю
=J(8'28)
(Ю i
откуда |
dW „ dW I
= <8-29) j
где через обозначена сила, действующая на молекулу р !
при заданном положении ее вблизи молекулы а, причем напра-
вление совпадает с направлением оси х, а знак усреднения
означает усреднение по положениям вех остальных молекул.
Иными словами, Wai есть потенциальная энергия, градиент ко-
торой равен средней силе, действующей между молекулами
аир.
Величину Wa? можно назвать также взаимной свободной
энергией молекул аир, когда их относительное положение за-
дано. Однако следует заметить, что такое определение не яв-
ляется полностью строгим; в некоторых случаях Wa? не обяза-
тельно должна равняться вар, и только в тех случаях, когда
силы взаимодействия между молекулами являются короткодей-
ствующими, в первом приближении теории возмущений спра-
ведливо равенство Wa$ = &a$.
8.3. Первое приближение для неидеальных газов. Силы,
действующие на коротких расстояниях
Для удобства рассмотрим сначала мономолекулярный не-
идеальный газ. Результаты легко распространить на случай
смеси неидеальных газов. Предположим, что около а или р
существуют ограниченные по размеру области, в пределах ко-
торых 8а!з не мало. Пусть — размер той области около а, при
попадании в которую молекулы р величина еа{3 будет отлична
8.3. Первое приближение для неидеальных газов
293
от нуля. Точно таким же можно считать объем около 0, при
попадании в который молекулы а величина еар ¥= 0. Сначала мы
не будем учитывать внешние поля. Допустим, что W предста-
вима в виде суммы некоторого количества членов еа₽ и что
взаимодействие между молекулами можно разложить на пар-
ные, т. е. при сильном взаимодействии трех и более молекул
их можно рассматривать попарно. Кроме того, будем считать,
что с»ар много меньше V/Ny и, следовательно, членами более
высокого порядка малости по сравнению с Nva^/V в расчетах
можно пренебречь. Что касается других членов, которыми мы
будем пренебрегать при последующих вычислениях, то их не-
обходимо рассматривать более тщательно.
Независимо от того, как велико Nva^Vt всегда можем на-
писать Q(T) в следующем виде:
Q <Г) = Л f • • f Ц е~еа?/кГ <8-3°)
(Ю
где число сомножителей равно числу комбинаций образования
пар из W молекул, т. е. —1). Здесь делением на ЛП
устраняем повторный учет состояний, отличающихся только пе-
рестановкой двух или более молекул. Определим величину т]ар
с помощью уравнения
v = e-ea₽/^_L (8.31)
Тогда (8.30) можно переписать в виде
В<Г> = 77Г f ''' J IT О + V) W" <8-32>
(Ю
Разложим подинтегральную функцию по степеням т]аР и обо-
значим индексами а, 0,... молекулы разного типа. Тогда по-
лучим
Q = Ж / • • • Л 1 + IX + S Vav +
(Ю
+ 2 VA+ 2 Vv6 + • • <8-33)
Каждый член 2лаз соответствует таким конфигурациям,
при которых имеется только пара взаимодействующих молекул,
члены в 2лазЛау соответствуют конфигурациям, при которых
каждые две пары взаимодействующих молекул имеют одну
общую; конфигурации, соответствующие каждому члену в
294
Гл. VIII. Неидеальные газы
2 содержат три взаимодействующие друг с другом
молекулы; конфигурации, соответствующие членам в 2ларЛуб»
имеют только две различные пары взаимодействующих молекул,
и т. д.
Предположим теперь, что одновременным взаимодействием
молекулы более чем с одной другой можно пренебречь. Пред-
положение является очень важным, и все нижеследующие фор-
мулы будут на него существенно опираться. Конечно, в дей-
ствительности оно может выполняться лишь приближенно.
Можно заметить, что если принять его, то велична Q(T) вычис-
ляется точно до членов первого порядка относительно Nva^/V,
а следовательно, и эффективно оно лишь при очень малых
или, другими словами, оно может быть использовано
только при рассмотрении слабо неидеальных газов. Если вос-
пользоваться этим приближением в (8.33), то всеми членами
типа Лар'Пау’ которые соответствуют одновременному взаимо-
действую молекулы с двумя другими, можно пренебречь. Тогда
получим
(V)
+ 2 Wk + • • •} <8-34)
Подсчитаем число членов под каждым знаком суммиро-
вания. Число пар молекул типа ар равно N (N—1) =
= ~-N!/^ — 2)!, число действительно различных комбинаций
ар и уб равно * "(дП^4)Т2Г ’ Число всех комбинации по
г пар из 2г молекул, взятых из W молекул, равно
(т) — 2г)! г!}. Используя это из (8.34), получаем
N
= WT r!(/V —2r)!2Vrl 2" W J • (8.35)
г = 0 I (Ю J
Так как rja3 зависит только от относительных координат мо-
лекул а и р, то можно проинтегрировать по координатам одной
из них. Поэтому
J / 4,3 <4 d^ = V { % d<i> = V f _ 1) rfu>. (8.36)
(Ю
8.3. Первое приближение для неидеальных газов
295
В двух последних интегралах в (8.36) областью интегрирова-
ния, строго говоря, должно быть V, однако эффективной обла-
стью интегрирования является v^. Для простоты введем вели-
чину g, равную
1 = 44/f ^^«^3 = 44- f (8.37)
(Ю
Здесь опущены индексы оф у еа3, так как в них уже нет необ*
ходимости. Подставляя (8.37) в (8.35), получаем
Д/v
й (Т) = "тТГ rl(N — 2r)lN' (8>38)
7 = 0
Отсюда видно, что по крайней мере для нескольких первых
членов (8.38) величину можно приближенно написать в
форме
у V _ И‘у(1 + ё)" (8 39)
ЛЧ Zu r\(N — г)I s — М! ‘
7 = 0
Это наводит нас на мысль, что Й(Г) можно написать в виде
Q (Г) = VN {1 +1 + О (g2)}"/N! (8.40)
Строгое доказательство (8.40) было дано еще Урселом1). Так
как оно сравнительно сложно, то мы не будем приводить его
здесь. Иногда при выводе (8.40) оставляют в (8.38) только два
первых члена и считают, что второй меньше первого, как это
должно быть при почленном сравнении. Однако такая точка
зрения недостаточно обоснована, так как отношение двух пер-
вых членов равно (М— l)g. Мы же лишь допускаем, что g очень
мало, но является ли оно достаточно малым — этого мы еще
утверждать не можем.
В соответствии с результатами Урсела предположим, что
(8.40) справедливо. Тогда, пренебрегая членами более высо-
кого порядка малости по сравнению с g и используя теорему
Стирлинга, получаем
1пЙ(Г) = ДИп [V+1)] — N\n N + N =
= Л/{1п^ + 1 } + 2Vln [1 +44 f =
=N{in4+i }+44J’^-e/sr-1)flf(d- <8-41>
l) Ursell, Proceedings of Cambridge Philosophical Societyt 23 (1927),
685.
296
Гл. VIII. Неидеальные газы
Формула (8.41) строго выполняется только с точностью до
Nv^V. Так КЭК
(Ю м
только при условии, если в (8.40) мы пренебрежем степенями
выше первой, то полученные результаты верны лишь с точ-
ностью до Nva$/V.
Можно заметить также, что вообще в том случае, когда не
рассматривается одновременное взаимодействие данной моле-
кулы более чем с одной другой, точность (8.40) не может пре-
вышать членов первого порядка относительно Nva$/V. Это объ-
ясняется тем, что относительный вклад в (8.40) от конфигура-
ций, при которых молекула взаимодействует более чем с одной
другой, имеет более высокий порядок малости по сравнению
с g, что служит дополнительным указанием на необходимость
при получении (8.41) из (8.40) оставлять члены только первого
порядка малости по отношению к g. Для смеси неидеальных га-
зов с помощью аналогичных рассуждений получим
1п£2(7')^2л^{1п4;+1} + 2л^1п{1+42в'^><
X J(e-e/*r_ 1)^}==2л^Л(1п^-+1} +
+ 2лв^-/(е’8ЛВ/ЙГ-1)^, (8.42)
где gab — обычное число симметрий. Для двух одинаковых
молекул оно равно 2, для двух различных—1. При получении
формулы (8.42) были оставлены члены порядка и
опущены все члены более высокого порядка малости.
Обычно предполагают, что потенциальная энергия межмоле-
кулярного взаимодействия в является функцией только относи-
тельного расстояния между ними и не зависит от взаимной
ориентации. В этом случае в полярных координатах е будет
функцией только г. Если записать для такого случая (8.42) в
полярных координатах, то
in Q (7) = %Na jln^- + 1 j + - 1) W dr.
(8.43)
До сих пор мы всегда предполагали, что область, в которой
е не равна нулю, является ограниченной и объем ее равен
8.4. Термодинамические свойства неидеальных газов
297
т- е- 0ГРаничена и область действия сил межмолекулярного
взаимодействия. На практике более удобным является зада-
ние энергии взаимодействия, обратно пропорциональной т-й
степени расстояния между молекулами. При т>3 интегралы
в (8.43) и (8.37) по всему пространству будут сходящимися.
Если они сходятся достаточно быстро, то результат интегриро-
вания по всему пространству практически не отличается от ре-
зультата интегрирования по области порядка величины одной
молекулы. Поэтому (8.37) и все аналогичные интегралы можно
заменить интегралами по всему пространству, т. е.
1пй(7')=2л41п^+11+
А I A J
+ (^AB'kT ~ О dr. (8.44)
8.4. Термодинамические свойства неидеальных газов
Подставляя полученное приближенное выражение для Q(T)
в формулы п. 8.1, мы можем получить все термодинамические
функции слабо неидеальных газов. Для удобства введем функ-
цию Вав(Г)
оо
в АВ | f (1 - е~ем/*Г) 4лг2 dr. (8.45)
О
Тогда (8.44) можно переписать в виде
1п й (Л = 2 А 1п—+1 - 2j д в <8-46)
А I A J Аа АВ
Подставляя (8.46) в (8.10), получаем выражение для свободной
энергии
АГ =2Д^{1П_^Г
nanb wab^\
\ав V оАВ
(8-47)
С помощью свободной энергии мы можем, используя общие
термодинамические формулы, вывести все остальные равновес-
ные свойства. Например, Для давления получим
Ул Na Na No 2Вло(Г)
= + <8-48»
298
Гл. VIII. Неидеальные газы
Химический потенциал ца каждой молекулы А равен
(dF \ N N
ЯГ =‘ri"A + t7'S,-iA2^m. (8.49)
А / Г» V ТД а
Введем объем, приходящийся на одну молекулу сорта Д,
v=^~- (8-50)
Тогда (8.48) и (8.49) можно упростить
Py=kT{\+^P-}', (8.51)
(8.52)
Другой важной термодинамической величиной для неидеаль-
ных газов является коэффициент Джоуля — Томсона, который
определяется как скорость изменения температуры при измене-
нии давления в процессе с постоянным теплосодержанием
(E + PV). Используя термодинамические формулы, получаем
(8.53)
С
\' E+PV
Рассмотрим (8.53) при сравнительно низких давлениях. Счи-
тая в этом случае уравнение (8.51) приближенным и записы-
вая его с точностью до членов порядка В (Г)/ V, получаем
PV=kT-±-PB(T). (8.54)
Из (8.54) имеем
kT ( TdB(T)
Р ‘ 7 dT
(8.55)
Подставляя (8.55) в (8.53), получаем коэффициент Джоуля —
Томсона для области низких давлений
R(T. । т
(дт\ -вау+т-^-
Т2 d\T
Сп dT
(8.56)
'dP'E+PV СР
Из (8.56) следует, что при Р->0 коэффициент Джоуля — Том-
сона стремится к конечному пределу, знак которого опреде-
ляется сортом газа и величиной температуры. Из (8.56) видно,
что лишь при
<ЦВ/Т) — о
dT ~
(8.57)
8.5. Несколько простых моделей
299
коэффициент Джоуля — Томсона равен нулю. Температура,
удовлетворяющая (8.57), называется температурой инверсии
Джоуля — Томсона.
Из формул этого пункта видно, что все равновесные свой-
ства слабо неидеального газа будут известны, как только ста-
нет известной В (Г). Для определения В(Т) необходимо в пер-
вую очередь найти г — энергию взаимодействия молекул.
Вплоть до настоящего времени мы еще не можем теоретически
рассчитывать функцию 8, поэтому при проведении вычислений
естественно заменять реальные молекулы простыми моделями.
8.5. Несколько простых моделей
Простейшей моделью молекулы является твердая сфера
диаметром D. При этом предполагаем, что силы притяжения
между молекулами отсутствуют. Модель определяется следую-
щими соотношениями:
8= оо
8 = 0
(r<D),
(r>D).
(8.58)
Подставляя (8.58) в формулу для В(Т), получаем
ОО
В(Т) = ± f (1 — <?-*/«’) 4яг2 dr = 1 £>з. (8.59)
* J Z о
о
Тогда уравнение состояния (8.51) можно переписать в виде
PV=kT\\ -|-2л£>з/у1
(о )
(8.60)
Несколько более точными моделями являются твердые сферы
диаметром D, обладающие силой притяжения, которая убывает
обратно пропорционально некоторой степени расстояния. Эта
модель определяется соотношениями
е = 4~ оо
8 = 8* (Dlr)m
(r<D),
(г > D).
(8.61)
Здесь tn — безразмерная положительная постоянная, которую
часто полагают равной целому числу; е* энергия взаимодей-
300
Гл. VIII. Неидеальные газы
ствия двух соприкасающихся молекул, ее значение—отрица-
тельное. Потенциальная энергия взаимодействия молекул, опре-
деляемая соотношениями (8.61), называется энергией Кеезома.
Подставляя (8.61) в выражение для В(Т) при /п>3, получаем
B(T) = -Lf (1 — е-^г) 4лг2 dr ==
о
оо
= |л£з_|_2л J (1—<?-е’°т/'т*г)'-2^ =
D
rmkT J йГ~
= 1-2
3
s! (sm — 3) \ kT )
(8.62)
5 = 1
Эту формулу, выведенную Кеезомом, для расчета В(Т) целе-
сообразно применять при сравнительно высоких температурах.
Формулу (8.62) можно записать через гипергеометрические
функции
8.6. Эмпирические и полу эмпирические уравнения состояния
301
При асимптотическом представлении 9 функции iFi для низких
температур получаем
в (Г) ~
9 ~~
4 л£>3 Г
2Г0(1; 1-^-; kT
е*
1
гШ
(8.64)
8.6. Эмпирические и полуэмпирические уравнения состояния
Самым распространенным уравнением состояния реальных
газов является уравнение Ван-дер-Ваальса, которое имеет вид
(Р + aN2/ V2) (V — Nb) = NkT. (8.65)
или
(Р + a/V2) (V — b) = kT. (8.66)
Переписывая (8.66) с точностью до членов порядка b/V. полу-
чаем
PV = kT-\-^^-. (8.67)
Допустим, что а = 0, тогда предыдущая формула преобразуется
к виду
(8.68)
. Г (р) V Г(а + п) 1 „
) 1 1 (а, р; z) — г г (р_|_ Л) Л| г ~
п = 0
Г(р) ег „ / . 1\ Г(р)<?г
Г(а) zp~a г/ Г (а) Г (р —а) Г (1 —а)ер-а
vV Г(р —а + «)Г(1 —а4-п)
XZl ’ a
п=0
(а; р; г) — решение уравнения
d2w , z . dw л
z 4- (р — z) —2-------aw = 0.
dz2 1 ' dz
Поэтому асимптотическое разложение можно найти из функции Уиттекера
(см. Смирнов В. И., Курс высшей математики, М., т. Ill, ч. 3, стр. 123).
302
Гл. VIII. Неидеальные газы
что по форме совпадает с уравнением состояния для твердых
сфер. С точки зрения этой модели для Ь необходимо положить
b = ^nD\ (8.69)
т. е. b равно учетверенному объему -^-л£)3 одной молекулы.
При аналогичном сравнении более общей формулы (8.67) с
(8.63) получаем
“ = т2тт<^=3)Ш- <8-70>
5 = 1
Таким образом, при объяснении b с точки зрения модели твер-
дых сфер и сравнения с результатами Кеезома оказывается, что
а должна зависеть от температуры Т, в то время как в уравне-
нии Ван-дер-Ваальса а и b — постоянные величины.
Из этого примера видно, что попытка принудительного срав-
нения эмпирического уравнения состояния с теоретическим для
неидеальных газов приводит к неестественным результатам. Бо^
лее правильный путь состоит в отыскании уравнения состояния
с помощью теории неидеальных газов и последующего сравне-
ния непосредственно с экспериментальными данными. Теоретик
ческое уравнение состояния имеет вид
PV=Ar{l+4 + -^+-^-+ (8.71)
где В, С, D,... называются вириальными коэффициентами, В —
второй вириальный коэффициент, С — третий, D — четвертый
и т. д. Все они являются функциями температуры. В настоя-
щее время самое большее, что дает теория неидеальных газов
в первом приближении, это второй вириальный коэффициент
В (Г). В такой форме ее использовали Камерлинг Оннес, Кее-
зом и другие, причем Кеезом впервые применил ее для изучен
ния силы взаимодействия между молекулами.
Если энергия взаимодействия между молекулами известна,
то теоретически мы можем рассчитать Q(T) с любой степенью
точности и, таким образом, найти точное уравнение состояния.
Однако практически это очень трудная задача. Вплоть до на-
стоящего времени число расчетов вириальных коэффициентов
выше второго, за исключением модели твердых сфер, очень не-
многочисленно. Однако если необходимо вычислить свойства
газа вблизи критической точки или свойства газа при большой
плотности, то расчет вириальных коэффициентов высоких по-
рядков становится очень важным. Майером в 1937 г. были най-
дены выражения для всех вириальных коэффициентов, и вопрос
8.7. Взаимодействие молекул
303
был в принципе решен. С помощью своей теории он рассмотрел
явления конденсации газа. Мы не будем здесь больше останав-
ливаться на теории Майера.
8.7. Взаимодействие молекул
В нескольких предыдущих пунктах мы считали, что энергия
взаимодействия молекул нам известна. На самом деле, кроме
простейших случаев атомов и молекул водорода и атомов ге-
лия, нам относительно нее ничего неизвестно и вычислять ее мы
еще не умеем. Теоретически задача представления энергии
взаимодействия через электронную структуру атомов или моле-
кул принципиально возможна, однако практическое осуществле-
ние встречает огромные трудности. Во всяком случае, осуще-
ствление таких вычислений с помощью ручных способов счета
невозможно. Поэтому в настоящее время данные об энергии
взаимодействия молекул могут быть получены только с по-
мощью косвенных методов. Развитие электронных счетно-вычис-
лительных машин в дальнейшем полностью решит проблему
вычислений, и положение теории будет в корне изменено.
Наличие конденсации газа при низкой температуре доказы-
вает, что между молекулами обязательно существуют силы
сцепления. С другой стороны, при малых расстояниях между
ними существуют и силы отталкивания, в противном случае не-
возможно было бы образование веществ с определенным объе-
мом. Таким образом, взаимодействия между молекулами всегда
должны удовлетворять этому принципу, т. е. быть силами при-
тяжения на далеких расстояниях и силами отталкивания —
на близких. В уже проделанных вычислениях этот принцип вы-
полнялся. Самой простой моделью, удовлетворяющей этому
принципу, является твердая сфера с полем притяжения, так
называемая модель Ван-дер-Ваальса. Формула Кеезома была
получена с помощью именно этой модели.
В общем случае взаимодействие молекул зависит не только
от расстояния между ними, но и от их взаимной ориентации.
Можно заранее предвидеть, что учет ориентации молекул при
вычислении физических свойств веществ внесет значительные
математические трудности. Поэтому сейчас мы ограничимся
рассмотрением только сферически симметричных молекул, на-
пример инертных газов или молекул, не имеющих определен-
ного дипольного момента и приближенно считающихся сфери-
чески симметричными, таких, как Н2, N2, СН4. В дальнейшем
мы увидим, что при рассмотрении второго вириального коэф-
фициента или свойств переноса сильно несимметричные моле-
кулы или молекулы с отличным от нуля дипольным моментом
304
Гл. VIII. Неидеальные газы
можно приближенно считать сферически симметричными,
результаты же получаются хорошие. Этот вопрос мы еще
рассмотрим в п. 8.13.
Необходимо заметить, что выбор модели зависит от рас-
сматриваемого вопроса. Например, использование модели твер-
дых сфер для молекул газа приводит к разумным результатам,
в то время как для жидкого или твердого состояний ее приме-
нять нельзя. В противном случае мы вынуждены были высчитать
жидкость и твердое тело конгломератными средами, а сле-
довательно, не смогли бы объяснить многие их физические свой-
ства, как, например, сжимаемость и др. Еще один пример: при
рассмотрении свойств газа часто молекулы можно приближен-
но считать сферически симметричными, полученные результаты
при этом весьма удовлетворительны. Однако попытка использо-
вать такую модель при исследовании жидкостей сразу же при-
водит к затруднениям. Объясняется это тем, что свойства моле-
кул на сравнительно близких расстояниях проявляются очень
отчетливо; молекулы же газа подавляющую часть времени
движутся независимо, и, следовательно, их физические свойства
проявляются очень слабо. Поэтому предположение о сфериче-
ской симметрии газовых молекул не может быть непосредствен-
но использовано при рассмотрении его конденсированного со-
стояния.
Модель Ван-дер-Ваальса является простейшей; модель твер-
дых сфер без поля притяжения еще проще, она полностью опре-
деляется только одним параметром — диаметром. Вследствие
достаточной простоты и сравнительно неплохих результатов для
газовых состояний эта модель употребляется довольно часто.
Однако в настоящее время из результатов квантовой теории
известно, что модель Ван-дер-Ваальса далека от действительно-
сти, и особенно модель твердых сфер. Допустим, что энергию
взаимодействия молекул можно разделить на две части и пред-
ставить в виде суммы двух слагаемых: одно из них соответ-
ствует притяжению, другое — отталкиванию. Слагаемое, соответ-
ствующее притяжению, можно назвать дисперсионной энергией,
второе, соответствующее отталкиванию, — обменной энергией.
В следующих двух пунктах мы кратко рассмотрим их смысл
и формы выражения е точки зрения квантовой теории.
8.8. Формы дисперсионной энергии
Природа сил взаимного притяжения двух молекул, обладаю-
щих собственным электрическим моментом, была впервые
рассмотрена в 1930 г. Лондоном с помощью квантовой теории.
В действительности эта сила притяжения возникает всегда
8.9. Формы энергии обменного взаимодействия
305
вследствие взаимной поляризации молекул. Молекулы, не
имеющие постоянного электрического момента и являющиеся
по своим средним свойствам полностью симметричными, на са-
мом деле обладают остаточным движением электронов, кото-
рое можно представить в виде некоторых внутримолекулярных
колебаний. Колебания электронов внутри каждой молекулы вы-
зывают колебания электронов другой молекулы, а так как ме-
жду этими взаимно возбуждаемыми колебаниями сохраняется
фазовая зависимость, то возникает сила притяжения. Механизм
возникновения этой силы притяжения — взаимная поляризация
молекул — тот же, что и механизм рассеяния веществом элек-
тромагнитных волн, поэтому Лондон и назвал эту силу притя-
жения дисперсионной силой, а соответствующую энергию дис-
персионной энергией.
При отыскании выражения для дисперсионной энергии Лон-
дон выполнил простой полуквантовый расчет. Он предположил,
что все электроны внутри любых двух молекул совершают сво-
бодные гармонические колебания по трем взаимно перпендику-
лярнььм направлениям. Тогда по его расчету главным членом
в дисперсионной энергии является
3/rv01 е |4 1
3k F ’
(8.72)
где vo — частота колебаний, —|е|—заряд электрона, k — по-
стоянная квазиупругих сил, г—расстояние между молекулами.
Конкретный вид коэффициента при г-6 зависит от принятой мо-
дели, для других моделей коэффициенты отличны от получен-
ного. В общем случае главный член энергии взаимной поляри-
зации всегда представляется в виде —цг-6, где р—положитель-
ная постоянная, значение которой определяется видом молекул.
Принятая Кеезомом приближенная эмпирическая форма для
энергии притяжения в модели твердых сфер —pr~m аналогична
результатам квантовой теории. В дальнейшем мы сохраним эту
формулу и для полного соответствия с главным членом диспер-
сионной энергии примем, что т = 6.
8.9. Формы энергии обменного взаимодействия
Название энергии обменного взаимодействия обязано тому
факту, что она оказывается существенной только при наложе-
нии электронных орбит двух молекул (или орбит эффектив-
ных электронов). Природа такого взаимодействия впервые была
разъяснена Гайтлером и Лондоном с помощью квантовой тео-
рии. В общем случае обменное взаимодействие на малых рас-
стояниях может привести к появлению как сил отталкивания,
*
20 Зак. 1299
306
Гл. VIII. Неидеальные газы
так и притяжения. Возникновение тех или других сил опреде-
ляется электронной структурой атомов и молекул. Во многих
случаях благодаря действию принципа запрета Паули обмен
электронами невозможен, а следовательно, невозможно и появ-
ление сил притяжения; с другой стороны, если обмен электро-
нами возможен, то возникает сильное притяжение, которое
приводит к образованию химического соединения. Например,
атомы водорода подпадают под второй случай и способны обра-
зовать молекулы, чего нельзя сказать об атомах гелия. Допустим,
что все возможные химические связи молекул, рассматриваемые
в данной главе, уже такие, что обменное взаимодействие при-
водит к отталкиванию. В квантовой теории показывается, что
обменная энергия при сравнительно больших взаимных рас-
стояниях между молекулами представляется в виде /?(г)£“г/р,
где /?(г)—многочлен, содержащий положительные и отрица-
тельные степени cap — постоянная. Это выражение можно по-
лучить в квантовой теории с помощью метода возмущений.
Для некоторых случаев, как это было показано, например,
в расчетах Слэтера для гелия и Блейка и Майера для неона,
функцию /?(г) можно заменить постоянной. Аналогичный факт
был обнаружен Борном, Майером и Хаггинсом при исследова-
нии свойств ионных кристаллов. Они показали, что если энер-
гию отталкивания ионов с заполненными электронными оболоч-
ками выразить в форме Ре~т1& (гд$Р— постоянная), то удается
весьма успешно объяснить упругие свойства ионных кристал-
лов. Таким образом, очевидно, что по крайней мере в неболь-
шой области изменения г функцию /?(г) можно приближенно
считать постоянной величиной.
8.10. Общее выражение для энергии взаимодействия молекул
Из вышеприведенных рассуждений видно, что энергия взаи-
модействия молекул должна быть записана в форме
е = Рг-'/р —А-. (8.73)
Введем параметр rm, который равен расстоянию между молеку-
лами при минимальном значении 8 = е*. Тогда (8.73) можно
переписать в виде
е = —(8.74)
а
Это и есть потенциал Букингема. Характер изменения потен-
циальной энергии в зависимости от расстояния представлен на
8.10. Общее выражение для энергии взаимодействия
307
рис. 8.1. Видно, что при r=rmax потенциальная энергия макси-
мальна, при г = 0, наоборот, стремится к —оо. Такое поведение
не соответствует действительности и объясняется принятым
приближением для члена отталкивания. (Используемый здесь
член отталкивания является приближением к действительному
только при сравнительно большом г.) Для исправления этого
несоответствия будем считать, что
е = -{-со при г<гтах. (8.75)
В совокупности обе формулы (8.74) и (8.75) можно назвать
модифицированным потенциалом Букингема. В последнее время
Рейс и Гиршфельдер использовали его для расчета второго ви-
риального коэффициента. Однако вследствие сложного вида
этого потенциала ими был проделан численный расчет.
Хотя потенциал Букингема является приближением, соответ-
ствующим результатам квантовой теории, однако вследствие
сложности применять его неудобно. В 1924 г. Леннард и Джонс
предложили другой вид для потенциальной энергии, в котором
оба слагаемые пропорциональны отрицательной степени рас-
20*
308
Гл. VIII. Неидеальные газы
стояния, а именно
ц , V
е = —-^- + 73-. п>т.
(8.76)
Пусть при r=rw потенциальная энергия минимальна и равна 8*.
Тогда (8.76) можно переписать в виде
где характер изменения потенциальной энергии 8 в зависимости
от г такой же, какой изображен на рис. 8.2. Если две молекулы
с малой начальной кинетической энергией сближаются из бес-
конечно удаленных точек, то кинетическая энергия —8* при
г=гт достигает максимального значения, после чего при даль-
нейшем сближении до расстояния, равного О, кинетическая
энергия становится равной нулю. Поэтому D можно считать
эффективным диаметром медленных молекул. Расстояние D
находится из следующего соотношения:
1
D __[ т \ п~т
гт~\п )
(8.78)
8.11. Выражения для второго вириального коэффициента
309
8.11. Выражения для второго вириального коэффициента,
полученного из потенциала Леннарда —Джонса
Согласно (8.45), второй вириальный коэффициент В(Т) ра*
вен
= (1 — e-^kT) 4лг2 dr = [г3 (1 — -
о
- К - f £ <8-та>
о о
Последнее упрощающее условие, которое было принято при вы-
воде (8.79), есть tn>3- Возьмем из потенциала Леннарда — Джон-
са т = 6 (в соответствии с формой дисперсионной энергии),
и=12 и введем в качестве параметра величину D из (8.78),
тогда
= = (-4s-)[(v)‘!-(^)T (8-80)
Поэтому
0£ = (-4Е-)[-12(ДГ + О’].
Подставляя в (8.79), получаем
оо
г(П=-р1(5-Ш12(ду"_б(ду}х
о
оо (—48*) / D \12 оо
х/W {12(ду°-в (Ду}2 Дддд (Д)%(£).
О s=0
Введем новую переменную интегрирования
(_4е*) /Р\12
kT \ г ) ’
тогда
><)”<)=-КГ=
=-Ю"К>=-
310
Гл. VIII. Неидеальные газы
_6(4р^)=244)’=2(^)-\(гЧ=
1 / —4е*\-*/«
=тНН z dz-
Поэтому
о 5=о
оо сю 3
1 /_4е*\’/< f V 1 / —4e*VZ i/2-T ,
2 kT ) j e 21 s! ( kT ) Z dz
0 f=0
Нам известна следующая формула для функции Г:
Г (/) = J e-^z^dz.
о
Поэтому
1 / —4е*у/«у 1 /4е*\^гр , 1\
2 \ kT J si [kT) 1 \2 4/
5 = 0
Если воспользоваться 'свойствами функции Г, то В (Т) в конце
концов примет вид
В(Г) = -^(=Н''2-^
5 = 0
(8.81)
Формула (8.81) лучше всего соответствует сравнительно высо-
ким температурам. В этом случае, взяв несколько первых чле=>
нов ряда, можно найти В (Т) с необходимой точностью.
При сравнительно низких температурах для (8.81) необхо-
димо найти еще асимптотическое разложение. Для этого пере-
пишем сначала ряд (8,81) через обобщенные гипергеометриче-
8.11. Выражения для второго вириального коэффициента
311
ские функции:
Гг 4/ / —4е*\* ,
4(2s)l kT ) “г"
Используя асимптотическое разложение для iff, получаем
Из формул (8.81) и (8.82) непосредственно видно, что при
высоких температурах В(Т) положительна, при низких темпе-
ратурах— отрицательна и при крайне низких температурах
абсолютное значение В(Т) соответствует все более возрастаю-
щим степеням Т. При некоторой температуре В = 0 это значе-
ние температуры называется точкой Бойля, так как зависимость
между давлением неидеальных газов и их объемом при этой
температуре точно удовлетворяет закону Бойля (конкретные
числа представлены в табл. 8.1).
На рис. 8.3 представлена зависимость В от kT/(—е*).
Здесь каждая из двух изображенных кривых соответствует
312
Гл. VIII. Неидеальные газы
теоретическим кривым, рассчитанным из потенциалов Кеезома и
Леннарда—Джонса. Из рисунка видно, что для низких темпера-
тур результаты почти совпадают. При высоких температурах
отличия весьма существенны. Найденная из потенциала Кеезо-
ма величина В (Т)/-|-л£)3 для высоких температур стремится к 1,
в то время как для потенциала Леннарда — Джонса она сна-
чала достигает максимального значения, а потом уменьшается
по закону [kT/(—Это происходит вследствие того, что
средняя скорость молекул при высоких температурах довольно
велика, а следовательно, велика и кинетическая энергия столк-
новения. В то же время из характера зависимости потенциала
Леннарда — Джонса от расстояния следует, что эффективный
диаметр столкновения с увеличением кинетической энергии умень-
шается. Если потенциальной энергией притяжения для всех
столкновений пренебречь, а кинетическую энергию kT прирав-
нять потенциальной энергии отталкивания, то эффективный диа-
метр D* будет удовлетворять соотношению
Таблица 8.1
Второй видаальный коэффициент B(T/GZ), рассчитанный
по потенциалу Леннарда — Джонса
Г/0; В (770/) *0 T(d,dT)B(TieI) Т2(д!дТ2) В (Tlhj) Г/07 В (Т/0/) Ьо (д/дТ)у х в (т/е,) Т2 х В (Т/е,)
bo bo
0,30 —27,8806 76,6073 —356,8768 2,7 —0,2236 1,1000 —2,5242
0,35 -18,7549 45,2477 —189,4654 2,8 —0,1845 1,0495 —2,4062
0,40 —13,7988 30,2671 — 116,3660 2,9 —0,1485 1,0030 —2,2983
0,45 —10,7550 21,9895 —78,8780 3,0 -0,1152 0,9600 —2,1992
0,50 —8,7202 16,9237 —57,3395 3,1 —0,0844 0,9202 —2,1079
0,55 —7,2741 13,5822 —43,8825 3,2 —0,0558 0,8833 —2,0234
0,60 —6,1979 11,2488 —34,9187 3,3 —0,0291 0,8489 —1,9451
0,65 —5,3682 9,5455 —28,6405 3,4 —0,0043 0,8168 —1,8723
0,70 —4,7100 8,2571 -24,0627 3,5 4-0,0190 0,7867 —1,8045
0,75 —4,1759 7,2540 —20,6131 3,6 4-0,0407 . 0,7585 —1,7411
0,80 —3,7342 6,4541 -17,9419 3,7 4-0,0611 0,7321 — 1,6817
0,85 —3,3631 5,8034 -15,8255 3,8 4-0,0803 0,7072 —1,6261
0,90 —3,0471 5,2649 —14,1156 3,9 4-0,0984 0,6837 —1,5737
0,95 —2,7749 4,8128 —12,7108 4,0 4-0,1154 0,6615 —1,5244
1,00 —2,5381 4,4283 —11,5399 4,1 0,1315 0,6405 —1,4779
1,05 —2,3302 4,0977 —10,5513 4,2 0,1467 0,6206 —1,4339
1,10 —2,1464 3,8106 —9,7074 4,3 0,1611 0,6017 —1,3923
1,15 -1,9826 3,5593 —8,9799 4,4 0,1747 0,5838 —1,3529
1,20 —1,8359 3,3375 —8,3470 4,5 0,1876 0,5668 —1,3155
1,25 —1,7038 3,1404 —7,7922 4,6 0,1999 0,5505 —1,2799
1,30 —1,5841 2,9642 —7,3023 4,7 0,2116 0,5350 —1,2461
1,35 —1,4753 2,8058 -6,8669 4,8 0,2227 0,5202 —1,2138
1,40 —1,3758 2,6626 -6,4778 4,9 0,2333 0,5061 -1,1831
1,45 —1,2847 2,5326 —6,1281 5,0 0,2433 0,4926 -1,1537
1,50 — 1,2009 2,4141 —5,8123 6,0 0,3229 0,3840 -0,9194
1,55 —1,1235 2,3057 —5,5258 7,о 0,3761 0,3083 —0,7577
1,60 —1,0519 2,2060 —5,2649 80 0,4134 0,2525 —0,6399
1,65 —0,9855 2,1142 —5,0263 90 0,4406 0,2097 —0,5498
1,70 —0,9236 2,0293 —4,8074 ю’о 0,4609 0,1759 —0,4788
1,75 —0,8659 1,9505 —4,6059 20’ 0,5254 0,0287 —0,1704
1,80 —0,8120 1,8773 —4,4198 30 0,5269 -0,0175 —0,0720
1,85 —0,7615 1,8091 —4,2475 40 0,5186 —0,0393 _0,0241
1,90 —0,7141 1,7454 —4,0875 50 0,5084 —0,0516 4-0,0039
1,95 —0,6696 1,6857 -3,9386 60 0,4982 —0,0594 0,0221
2,00 —0,6276 1,6297 -3,7997 70 0,4887 —0,06-15 0,0348
314
Гл. VIII. Неидеалъные газы
Продолжение таблицы 8.1
Г/07 в (T/ej) ь0 Т(д/дТ)В (T/fy) Г2(д/дГ2)В (T/0Z) Г/0; в (TIQ,) Ьа -yJd/dDx (Г/ву) та (д!дГ)Х X В (Г/fy)
Ьь ьа
2,1 —0,5506 1,5275 —3,5481 80 0,4798 —0,0681 0,0441
2,2 —0,4817 1,4366 —3,3265 90 0,4716 —0,0706 0,0510
2,3 —0,4197 1,3552 —3,1297 100 0,4641 -0,0725 0,0564
2,4 —0,3636 1,2819 —2,9540 200 0,4114 —0,0775 0,0773
2,5 —0,3126 1,2155 —2,7961 300 0,3801 —0,0765 0,0814
2,6 —0,2661 1,1552 —2,6536 400 0,3584 —0,0748 0,0821
или
Так как В(Т) прямо пропорционально Z)*3, то
при высокой температуре прямо пропорционально (—
Это почти соответствует нашим точным вычислениям. Поэтому
считают, что результаты, полученные из потенциала Кеезома
и Леннарда — Джонса, отличаются вследствие того, что потен-
циал Леннарда — Джонса допускает упругость молекул, в то
время как в потенциале Кеезома молекулы — недеформируе-
мые твердые сферы.
8.12. Сравнение с экспериментальными данными
Хотя потенциал Леннарда—Джонса получен не из квантовой
теории, однако второй вириальный коэффициент, вычисленный
с его помощью, хорошо согласуется с экспериментальным.
В потенциале Леннарда—Джонса всего четыре параметра т, п,
ц, v; в соответствии с формой для дисперсионной энергии для чле-
на притяжения примем т = 6; практика показывает, что каждое
из значений п между 9 и 14 может дать результаты, соответ-
ствующие экспериментальным; для удобства вычислений возь-
мем /г= 12. Теперь в потенциале Леннарда — Джонса осталось
только два произвольных параметра, а именно ц и v; вместо
них можно в соответствии с (8.77) и (8.80) выбрать е*, г* или
8*, D. На самом деле, вместо 8* можно взять другой параметр
0j, определяемый соотношением
= (8.83)
8.13. Вращательное движение молекул и внутрен. потенциалы*. энергия315
Величина 0/ называется характеристической температурой
взаимодействия. Таким образом, второй вириальный коэффи-
циент (8.81), полученный из потенциала Леннарда — Джонса,
можно написать в виде
В(Г)/4лПз = /(^. (8.84)
Сравнивая экспериментальные данные с теоретической функ-
цией f можно найти D и 0/. После этого можно сразу по-
лучить результаты, соответствующие практически наблюдае-
мым в широком диапазоне температур. Значения D и 0/, опре-
деленные с помощью изложенного метода, хорошо согласуются
со значениями, найденными через коэффициент Джоуля — Том-
сона. В действительности существует еще один метод определе-
ния D и 0/. Из формулы для потенциальной энергии можно вы-
числить коэффициент вязкости. Сравнивая теоретическое зна-
чение коэффициента вязкости с экспериментальными данными,
можно определить те же параметры. В табл. 8.2 приведены об-
работанные результаты Берда, Гиршфельдера, Кертисса, где в
каждой строчке представлены различные экспериментальные
данные для одинаковых газов. В третьем столбце приведены
значения эффективного молекулярного объема в расчете на
одну грамм-молекулу Д^-АО3, где N— число Авогадро
[ (6,02472 ± 0,00063) X 1023]. Из таблицы видно, что значения, най-
денные различными методами, все без исключения согласуются.
8.13. Вращательное движение молекул и внутренняя потенци-
альная энергия
Из табл. 8.2 становится ясно, что потенциальная энергия
взаимодействия для сферически симметричных молекул приво-
дит к реальным результатам. Очевидно, что для инертных га-
зов потенциал взаимодействия должен быть сферически сим-
метричным. Однако из той же табл. 8.2 видно, что и для несфе-
рических молекул, таких, как Н2, N2, О2, а также для молекул
с такой же удлиненной формой, как у бензола, можно восполь-
зоваться сферически симметричным потенциалом, что на пер-
вый взгляд кажется немного странным. Для молекул с удли-
ненной формой, приведенных в конце табл. 8.2, таких, как орто-
С6Н14 и С2Н5ОН, оказывается возможным применять такие же
модели, хотя этому и трудно верить. Решение этого вопроса
зависит от того, насколько сильно возбуждаются вращатель-
ные степени свободы молекул при обычных температурах.
Таблица 8.2
Из второго вириального коэффициента По коэффициенту вязкости
0/, °к D, А 9 У см^моль в/, °К г>, А
Не 6,03 2,63 23,00 10,22 2,576
н, 29,2 2,87 29 76 33,3; 38,0 2,968; 2,915
d2 31,1 2,87 29,77 39,3 2,948
Ne 35,60; 34,9 2,749; 2,78 26,21; 27,10 35,7; 27,0 2,789; 2,858
А 119,8; 122 3,405; 3,40 49,80; 49,58 124; 116 3,418; 3,465
Кг 171; 158 3,60; 3,597 58,86 190 3,61
58,7
Хе 221; 217 4,100; 3,963 86,94; 78,5 229 4,055
Воздух 99,2; 102 3,522; 3,62 55,11; 60,34 97,0; 84,0 3,617; 3,689
n2 95,05; 95,9 3,698; 3,71 63,78; 64,42 91,5; 79,5 3,681; 3,769
О2 117,5; 118 3,58; 3,46 57,75; 52,26 113; 88,0 3,433; 3,541
со 100,2 3,763 67,22 ПО; 88,0 3,990; 3,706
со2 189; 205 4,486; 4,07 113,9; 85,05 190; 213 3,996; 3,897
NO 131 3,17 40 119; 91,0 3,470; 3,599
N2O 189 4,59 122 220; 237 3,879; 3,816
СН4 148,2 3,817 70,16 137; 144 3,882; 3,796
CF4 152,5 4,70 131,0 — —
СС14 — — — 327 5,881
so2 — — — 252 4,290
SF6 200,9 5,51 211,1 — —
f2 — — — 112 3,653
Cl2 — — — 357; 257 4,115; 4,400
Вг2 — — — 520 4,268
J2 — — — 550 4,982
НС1 — — — 360 3,305
HJ — — — 324 4,125
AsH3 — — — 281 4,06
HgJ2 — — — 698 5,625
HgBr2 — — — 530 5,414
SnBr4 — — — 465 6,666
SnCl4 — — — 1550 4,540
Hg — — — 851 2,898
С2Н2 С2Н4 199,2 4,523 116,7 185 205 4,221 4,232
с2нв 243 3,954 78 230 4,418
СзН, 242 5,637 226 254 5,061
8.13. Вращательное движение молекул и внутрен. потенциалы*. энергия 317
Продолжение таблицы 8,2
Из второго вириального коэффициента По коэффициенту вязкости
в/, °К D, А у см^/моль в/, °к D, А
о/>/ио-С4Н10 297 4,971 155 410 4,997
wao-C4H10 — — — 313 5,341
op/no-C5Hi2 — — — 345 5,769
opmo-C6H14 — — — 413 5,909
о/>то-С7Н1б 282 8,88 884 — —
о/>то-С8Н18 — — — 320 7,451
opmo-C9H20 — — — 240 8,448
цикло-СбН12 — — — 324 6,093
сбнб — — — 440 5,270
CH3OH — — — 507 3,585
C2H5OH — — — 391 4,455
СН3С1 — — — 855 3,375
СН2С12 — — — 406 4,759
СНС13 — — — 327 5,430
c2n2 — — — 339 4,38
cos — — — 335 4,13
cs2 — — — 488 4,438
Если характерное время вращения много меньше характер-
ного времени столкновения молекул, то за время столкновения
молекулы успеют сделать много оборотов. Поэтому даже если
молекула не имеет сферической формы, однако по отношению
к другой подлетающей молекуле она ведет себя как сфериче-
ская. Что же такое характерное время вращения? Предполо-
жим, что мы рассматриваем линейную молекулу, имеющую
только поперечный момент инерции. Если со — угловая скорость
вращения, то, так как средняя энергия вращательного движения
при обычной температуре равна среднюю угловую ско-
рость можно определить из следующего соотношения:
Если 0Г— характеристическая температура вращательного
движения, так что
Д = Л2/(8л2ег£),
318
Гл. VIII. Неидеальные газы
то характерное время вращения, или время, необходимое для
оборота на 2л радиан, будет равно
2л h 1 1
— =-----г-— ~ о X Ю _.
Для кислорода, если 0Г~2°К, то при Г=100°К характерное
время вращения равно 2,5Х10"12 сек. Известно, что время ме-
жду двумя столкновениями молекул кислорода, находящегося
под давлением около 100 атм, приблизительно равно 10~9 сек.
Поэтому в течение времени одного столкновения молекулы сде-
лают несколько тысяч оборотов. Таким образом, именно бла-
годаря тому, что одна молекула при сближении с другой ведет
себя как сферически симметричная, можно приближенно счи-
тать сферически несимметричные молекулы сферически сим-
метричными.
Эффективный радиус молекулы, вращающейся с большой
скоростью, равен расстоянию от центра инерции молекулы до
самого отдаленного атома. Его можно определить, если извест-
ны структура молекулы, углы и длины химических связей, ван-
дерваальсовские диаметры атомов и их атомные веса. С по-
мощью этих данных Хэман и Пирс1) определили эффективные
диаметры г* для некоторых молекул. Полученные ими резуль-
таты приведены в табл. 8.3. В этой же таблице представлены
эффективные диаметры, найденные из вириальных коэффициен-
тов для газа. Они характеризуют положение минимальной точки
в потенциале Леннарда — Джонса. Из таблицы видно, что наша
точка зрения правильна — значения г* и I для большинства
молекул совпадают. В таблице помещены данные и для более
удлиненных молекул, таких, как, например, гептан. Для них
значения г* и I действительно несколько не совпадают. Это
вполне возможно, так как для очень длинных молекул момент
инерции велик, а скорость вращения сравнительно мала. Счи-
тать молекулы сферически симметричными, очевидно, нецеле-
сообразно.
В табл. 8.2 представлены данные для некоторых молекул
с соответственными дипольными моментами, таких, как, напри-
мер, НС1. Что касается взаимодействия молекул, обладающих
собственным дипольным моментом, то Штокмайер2) предло-
жил для потенциальной энергии смешанную форму, промежу-
точную между потенциалом Леннарда — Джонса и потенциалом
!) Hamann S. D., Journal of Chemical Physics, 19 (1951), 655; Ha-
mann S. D., Pearse J. F., Transactions of the Faraday Society, 48 (2)
(1952), 101.
2) StockmayerW. H.7 Journal of Chemical Physics, 9 (1941), 398.
8.13. Вращательное движение молекул и внутрен. потенциальн. энергия 319
взаимодействия двух дипольных моментов,
Е = — е* [(у-)12 — 2 (-у)6] — тг I2 cos cos 02 — sin 01 sin 02 cos <р],
(8.85)
где 01, 02 и ф — углы, характеризующие взаимную ориентацию
двух дипольных моментов (см. рис. 8.4). Подставляя (8.85) в
выражение для второго вириального коэффициента при сфери-
чески несимметричном потенциале (потенциале, не являющемся
сферически симметричным), получим
оо Л Л 2л
5(7) = A J г1 dr sin 0j t/0j J" sin 02б/02 J" [1 — e-ZIkT\dsp. (8.86)
0 0 о о
Отсюда можно найти В(Т). Гиршфельдер, Хэман и Пирс по
результатам сравнения теории и эксперимента нашли числовые
значения параметра г*. Однако именно эти результаты не мо-
гут быть удовлетворительными. Например, «размер» г* молекул
пара и аммиака почти равен вандерваальсовскому диаметру
единичных атомов кислорода и азота, как будто атомы водо-
рода в этих молекулах не занимают никакого объема. Мы счи-
таем, что причина появления таких результатов заключается в
том, что не принималась во внимание большая скорость вра-
щательного движения молекул при обычной температуре.
При вращении молекул между двумя собственными диполь-
ными моментами возникают силы притяжения и отталкивания,
320
Гл. VIII. Неидеальные газы
Таблица 8.3
г*, А /, А г*, А г, А
Ne 3,08 3,20 цикло-С3Н6 6,56 5,78
А 3,83 3,83 с2н6 5,10 5,54
Н2 3,28 3,14 с3н8 6,33 6,59
n2 4,10 4,09 «зо-С4Н10 6,90 6,94
О2 4,02 4,00 С (СН3)4 7,79 7,08
со 4,10 4,10 С3нб 6,09 6,60
NO 4,29; 3,56 4,04 изо-С4Н8 6,98 6,98
N2O 5,15 5,21 opmo-C4Hj 0 7,03 7,88
СО2 5,13 5,13 ор/ио-С5Н12 8,23 9,04
сн4 4,28 4,16 ор/ио-С7Н1б 9,98 11,56
с2н4 5,54 5,33 азо-С5Н8 6,96 7,76
а при большой скорости изменения ориентации они в среднем
исчезают. Именно поэтому при достаточно сильном возбужде-
нии вращательных степеней свободы молекул практически бо-
лее разумно не рассматривать взаимодействия собственных ди-
польных моментов полярных молекул. Если экспериментальные
значения для второго вириального коэффициента пара и ам-
миака сравнивать с результатами вычислений, полученными на
основании потенциала Леннарда — Джонса, то тогда можно
ожидать для них приемлемых значений величины г*. Приводимые
здесь рассуждения, хотя и кажутся точными, однако они еще
не являются строгой теорией. Последняя должна рассматри-
вать собственное вращение и взаимодействие молекул одновре-
менно, что значительно сложнее изложенных здесь вычислений
и ждет дальнейших исследований.
8.14. Уравнение состояния при большом давлении и вириальные
коэффициенты с большими номерами
Ранее уже было получено выражение для второго вириаль-
ного коэффициента
В ~ — 2V J J (8.87)
где т|12 определялось из (8.31), dcoi — элемент пространствен-
ного объема молекулы 1, d^2 — элемент пространственного
объема молекулы 2. Рассматривая одновременное взаимодей-
ствие многих молекул и используя тот же метод, можно найти
8.14. Уравнение состояния при большом давлении
321
выражения для следующих вириальных коэффициентов:
с (Т) = — ~ f J J (8-88)
и
D(T) = — 87 / f f f [ЗП12П2зТмП41 + бП12^М1з1-|-
+ П12-П23т1з4т141 П13П24] «Ч «4 rfc°4- (8 -89)
Однако, кроме простейшей модели твердых сфер, практиче-
ский расчет этих вириальных коэффициентов с большими номе-
рами очень сложен. Гиршфельдер и его сотрудники, используя
потенциал Леннарда — Джонса, рассчитали третий вириальный
коэффициент (конкретные цифровые данные приведены в
табл. 8.4), однако четвертый вириальный коэффициент еще не
вычислен.
На рис. 8.5 представлен характер изменения этих вириаль-
ных коэффициентов в зависимости от температуры. Из рисунка
видно, что при температурах, в несколько раз превышающих 01,
вириальные коэффициенты с большими номерами очень незна-
чительно меняются с температурой и стремятся к положитель-
2?т
ным числам, равным некоторой степени от &0 —Напри-
мер, С(Т) стремится к bl, D (Т) стремится к bl- Исходя из этого,
Гиршфельдер и Роузвир предложили для расчета третьего и
21 Зак. 1299
Таблица 8.4
Третий вириальный коэффициент C(T/GZ), рассчитанный
по потенциалу Леннарда—Джонса,
, 2 л о — £*
b0 = ~ D3, 0/ = ——
о к
T&J [Т(д1дТ)С]Ц>1 [г2 (й/ЭГ2)с]/*2 Г/07 с/ь2 [Г (д/дТ) X X C\lbl [г2(д/дг2)х X С1/02
0,70 —3,3766 28,68 —220 3,1 0,3484 —0,1148 0,400
0,75 — 1,7920 18,05 -140 3,2 0,3449 —0,1060 0,369
0,80 —0,8495 11,60 —92,1 3,3 0,3418 —0,0983 0,340
0,85 —0,2766 7,561 -62,1 3,4 0,3389 —0,0913 0,313
0,90 4-0,0765 4,953 -42,7 3,5 0,3364 —0,0851 0,288
0,95 0,2951 3,234 —29,8 3,6 0,3341 —0,0796 0,266
1,00 0,4300 2,078 -21,0 3,7 0,3320 —0,0746 0,246
1,05 0,5108 1,292 -14,9 3,8 0,3300 —0,0702 0,227
1,10 0,5576 0,7507 —10,6 3,9 0,3283 —0,0663 0,210
1,15 0,5822 0,3760 —7,52 4,0 0,3266 —0,0629 0,194
1,20 0,5924 +0,1159 —5,29 4,1 0,3251 —0,0599 0,183
1,25 0,5933 —0,0646 —3,66 4,2 0,3237 —0,0571 0,169
1,30 0,5882 —0,1889 —2,46 4,3 0,3224 —0,0546 0,156
1,35 0,5793 —0,2731 -1,57 4,4 0,3212 -0,0524 0,145
1,40 0,5683 —0,3288 -0,910 4,5 0,3200 —0,0504 0,134
1,45 0,5561 —0,3641 —0,420 4,6 0,3189 —0,0487 0,125
1,50 0,5434 —0,3845 —0,050 4,7 0,3179 —0,0471 0,116
1,55 0,5306 —0,3943 +0,224 4,8 0,3169 —0,0458 0,108
1,60 0,5180 —0,3963 0,427 4,9 0,3160 —0,0446 0,100
1,65 0,5059 —0,3929 0,572 5 0,3151 —0,0436 0,0934
1,70 0,4943 —0,3858 0,680 6 0,3077 —0,0389 0,0449
1,75 0,4832 —0,3759 0,755 7 0,3017 —0,0399 0,0258
1,80 0,4728 —0,3643 0,806 8 0,2962 —0,0423 0,0192
1,85 0,4630 —0,3516 0,837 9 0,2910 -0,0453 0,0183
1,90 0,4538 —0,3382 0,854 Ю 0,2861 —0,0483 0,0199
1,95 0,4452 —0,3245 0,859 20 0,2464 —0,0644 0,0502
2,00 0,4371 —0,3109 0,856 30 0,2195 —0,0675 0,0654
2,1 0,4226 —0,2840 0,830 40 0,2001 —0,0671 0,0717
2,2 0,4100 -0,2588 0,794 50 0,1853 —0,0657 0,0742 .
2,3 0,3990 —0,2355 0,749 60 0,1735 —0,0639 0,0750
2,4 0,3894 —0,2142 0,700 70 0,1638 —0,0620 0,0748
2,5 0,3811 —0,1950 0,651 80 0,1556 -0,0603 0,0741
2,6 0,3738 —0,1777 0,602 90 0,1486 —0,0586 0,0732
2,7 0,3674 -0,1621 0,557 100 0,1425 -0,0570 0,0722
2,8 0,3617 —0,1482 0,514 200 0,1068 —0,0460 0,0619
2,9 0,3568 —0,1358 0,473 300 0,0894 —0,0397 0,0547
3,9 0,3523 —0,1247 0,439 400 0,0786 —0,0355 0,0496
8.14. Уравнение состояния при большом давлении
323
четвертого вириальных коэффициентов и отыскания приближен-
ного уравнения состояния использовать модель твердых сфер.
При этом сложность вычислений уменьшилась, а значения коэф-
фициентов, за исключением сравнительно низких температур,
по порядку величины почти совпадают с вычисленными по бо«
лее точным моделям. С помощью модели твердых сфер для С
и D получены следующие значения:
с (Т) = 4^0, £>(?) = 0.2869^.
Одновременно с этим были рассчитаны значения для пятого
вириального коэффициента, причем предполагалось, что моле-
кулы газа при высоком давлении можно моделировать твер-
дыми сферами. Численное значение для пятого вириального
коэффициента получилось равным 0,1928^0- Следует, однако, за-
метить, что возможность замены молекул при большом давле-
нии твердыми сферами физически не очевидна. Уравнение со-
стояния в этом приближении имеет вид
pV=kT[\ + ^Д + 0,625 + 0,2869 (^3 + 0,1929 (ф)4].
(8.90)
Гиршфельдер и Роузвир воспользовались полученным ими
уравнением (8.90) для определения коэффициента Джоуля —
Томсона и сравнили полученные результаты с эксперименталь-
ными для случая аргона. Они нашли, что если положить
6оА^ = 4О см3/моль (в табл. 8.2 bQN = 50 см3/моль), то при давле-
нии в 200 атм и температуре в пределах от 0 до 300° С теоре-
тические и экспериментальные данные полностью совпадают.
Это свидетельствует о том, что уравнение состояния (8.90) яв-
ляется хорошим приближением для высоких давлений. Следует,
однако, заметить, что при низких температурах оно ведет себя
неудовлетворительно.
Рассмотренная нами в п. 8.1 функция состояний Q(T) для
газовых ансамблей в действительности имеет смысл не только
для газообразного состояния. По крайней мере в принципе мы
можем, учитывая одновременное взаимодействие все большего
числа молекул, вычислить вириальные коэффициенты с боль-
шими номерами и получить уравнение состояния, справедли-
вое для трех агрегатных состояний. Теоретически этот вопрос
был решен Майером в 1937 г. Однако при практическом приме-
нении его метода к расчету свойств веществ в трех агрегатных
состояниях возникают значительные трудности. Вместо него
обычно применяется метод построения моделей, когда вначале
выбирается упрощенная модель плотной фазы, а затем по ней
21*
324
Гл. VIII. Неидеальные газы
рассчитывается функция состояний. Например, в шестой главе
мы прибегали к этому способу, когда рассматривали термоди-
намические свойства твердых тел. В следующей главе мы также
будем использовать этот метод для рассмотрения свойств плот-
ных газов и жидкостей.
8.15. Термодинамические функции неидеальных газов, выражен-
ные через вириальные коэффициенты
В настоящем разделе будут получены выражения для термо-
динамических функций неидеальных газов. Согласно общим
термодинамическим соотношениям, для внутренней энергии Е
справедлива зависимость
(#)Г=Г(Т7)„-Р- <8-9D
Используя уравнение состояния (8.71), получаем
/ дЕ\ bT2 ( 1 dB । 1 dC . 1 dD . )
\ дv)T ~~I V2 dT ' V3 dT V4 dT ' ” ’ J '
Предположим, что E^ — внутренняя энергия газа при беско-
нечно большом объеме (она же является внутренней энергией
идеального газа). Тогда
со
(E-E„)r = - /
V
____ ъ Г 1 Т2 _|__L Т2 I_____L Т2 d& I 1 (Я Q0\
— L V dT ' 2V2 J dT ‘ 3V3 dT ’J ’ '
Поэтому
(CK - CVm)T = ± (E - EJt = - 44- 4 (P 4) +
+ 2v*~dT (7'2'7г)“*~зрз’‘гт {Т2~ат)^~ • • •]• (8-93)
Теплосодержание H находится из следующего соотношения:
-^-щг="[(г-7'4г) + т(с-т#) +
+ tHD~t4t-)+ (8'94)
8.15. Термодинамические функции неидеальных газов
325
Вычислим теперь теплоемкость при постоянном давлении. Со-
гласно общей термодинамической зависимости,
Дифференцируя (8.71) по Т, получаем
/дУ\ ?Г 1 . 2В . ЗС 4D . I
\ дТ /р 7 L V2 и3 И4 у5 ' * ’ * J
ИЛИ
41+v^<rs,+i^<rc)+-^4<™>+ •••] ,
4+^+£+4S-+-]
Дифференцируя (8.71) по Р, получаем
’dV\ ,ГГ 1 i_2B.3C.4D
дР)т к! L V2 F3 * V4 ' V5 ’ ’ "
Поэтому
г(4г)’ . [>+v<^)+тг4<™>+ - Г
-m/ [>+^+£+^+-j
или
l-1L[27-^-2D + 2(7'^-B)(7-4£.-2c)-
-2В(т£-В)г]+ ...}.
326
Гл. VIII. Неидеальные газы
Тогда
/р р —h J _________ — -I_________ Г7 _(J___* Т2 d2C I
(Up — Upoo'p ну у л?! -г у2 и ат 2 1 dT2 ‘
+(^~4]+тМ4г^-“Ч7'!4£+
+2(7'4т'_'в)(7'4г~2С)—25(7'-5f_j8)2]+ •••}• (8-98)
Скорость звука с. являющуюся очень важной ’’величиной
в гидромеханике, можно найти из соотношения
где р — плотность, 0 =-----~{dV!dP)T— изотермическая сжи-
маемость. Используя (8.97) и известное соотношение
ОО V ОО (YoO 1 оо’
где
получаем
1 I СР~~СРоо
с<1^ У^Т Fl I 2£ I ЗС , 4D_ 1 Ф Уоо k
м L v v2 v3 • • ’J c.7~cD
l + (Yoo-l)-V.b PCO
где М—молекулярный вес газа, R — газовая постоянная. Под-
ставляя сюда (8.93) и (8.98), получаем
с2 - {1+1 [2 д+2 -1) # +(vco~1 )г ]. }.
(8.99)
Если вириальные коэффициенты газа известны, то с помощью
приведенных формул можно вычислить термодинамические ве-
личины.
Глава IX
ЖИДКОСТИ И ПЛОТНЫЕ ГАЗЫ
С давних пор все жидкости принято делить на нормальные
и ассоциированные, хотя такое деление и не может быть вполне
строгим. Вначале оно носило чисто эмпирический характер и
основывалось на том, что у большинства жидкостей, особенно
органических, был обнаружен ряд физических свойств, таких,
как давление пара, поверхностное натяжение, вязкость и пр.,
подчиняющихся общим эмпирическим закономерностям (среди
них можно указать, например, на закон Трутона). Такие жид-
кости были названы нормальными. Было обнаружено, однако,
что свойства многих других жидкостей отклоняются от этих
эмпирических законов. Они были названы ассоциированными.
Обычно считают, что отклонения вызваны тем, что молекулы
пара могут при конденсации ассоциироваться в более крупные
молекулы. Примечательно, что большинство жидких веществ,
содержащих гидроксил и аминогруппу, являются ассоцииро-
ванными жидкостями. В дальнейшем по мере накопления дан-
ных мы сможем по химической структуре молекул предсказы-
вать, к какому типу относится данная жидкость.
В последние годы благодаря исследованию оптических и
электрических свойств жидкостей, а также применению для их
анализа рентгеновских лучей в наших знаниях о структуре жид-
костей произошли значительные сдвиги. В ' настоящее время
можно уже дать вполне удовлетворительное определение нор-
мальной жидкости, исходя из ее молекулярной структуры. Если
внутренние степени свободы каждой молекулы в жидкости не
подвергаются возмущению со стороны ближайших соседних мо-
лекул, то такая жидкость называется нормальной. Ее можно
рассматривать как ансамбли, функция состояний которых пред-
ставляет собой произведение функции состояний поступатель-
ного движения молекул и функции состояний внутренних сте-
пеней свободы каждой отдельной молекулы, причем последняя
очень похожа на аналогичную функцию состояний для молекул
газа. С другой стороны, в ассоциированных жидкостях моле-
кулы настолько сильно взаимодействуют друг с другом, что
это оказывает значительное влияние на их вращательные или
328
Г л. IX. Жидкости и плотные газы
некоторые колебательные степени свободы. Некоторые враща-
тельные движения могут быть «заморожены». Существует даже
такое сильное взаимодействие между атомами различных моле-
кул, когда можно говорить об образовании новой химической
связи.
Современный взгляд на структуру нормальных жидкостей
остается таким же, как и раньше, когда впервые был применен
термин «нормальная». Что касается ассоциированных жидко-
стей, то здесь положение изменилось. Ранее считали, что в них
образуются группы в две или три газовые молекулы, которые
ведут себя как отдельные молекулы нормальной жидкости. Од-
нако такое представление является чрезмерно упрощенным.
В настоящее время существует несколько способов, с помощью
которых различаются нормальные и ассоциированные жидко-
сти. Причем способность двух или более газовых молекул ассо-
циироваться в более крупные при переходе в жидкое состояние
является среди них далеко не самым главным. Все эти раз-
личные способы были подробно рассмотрены Берналом. Ко-
ротко опишем здесь его выводы.
С чисто геометрической точки зрения образование ассоции-
рованных жидкостей происходит вследствие непрерывного во
времени силового воздействия на молекулы со стороны соседей,
что приводит к образованию тесно связанных групп. При этом
силы имеют определенную ориентацию и локализацию в про-
странстве. При существовании только неориентированных и не-
локализованных вандерьаальсовских или металлических сил
образование ассоциированных жидкостей невозможно. Различ-
ные степени ассоциированности зависят от числа эффективных
связей, которые может образовать каждая молекула. При нали-
чии только одной связи образуется простейший тип ассоцииро-
ванной жидкости, состоящей из двух молекулярных групп.
В большинстве случаев это оксиспирты.
Если имеются две эффективные связи, то возможно образо-
вание как замкнутых колец, например фтористоводородная кис-
лота, так и открытых цепей. Эти два вида жидкостей сильно
отличаются по своим свойствам: жидкость с кольцеобразными
группами ведет себя как нормальная с большим молекулярным
весом; жидкость с группами из открытых цепей обладает боль-
шой вязкостью. Возможно, что это сложный синтез жидкости
и кристаллов. При повышении температуры кольцо может пре-
вращаться в цепь. Примером может послужить жидкая сера,
вязкость которой увеличивается с увеличением температуры.
Все жидкости, молекулы которых образуют три или более
эффективных связей, являются ассоциированными. (Самым
классическим примером^жидкости такого вида может служить
Гл. IX. Жидкости и плотные газы
329
вода.) Здесь не существует промежуточных групп между от-
дельными молекулами и всей массой жидкости. Все они имеют
аномальное тепловое расширение, большую вязкость и низкое
поверхностное натяжение, легко переохлаждаются и быстро об-
разуют стекловидную форму. Большинство так называемых ас-
социированных жидкостей относится к этому виду. Индиви-
дуальные особенности жидкостей определяются количеством
эффективных, а не количеством возможных связей. Тепловое
движение может понизить количество эффективных связей и,
следовательно, понизить и степень ассоциированности. К ана-
логичным результатам может привести и давление. При при-
ближении к критической температуре все жидкости перестают
быть ассоциированными. Это говорит о том, что обычные ассо-
циированные жидкости проявляют свойства аномальной тепло-
емкости и теплового расширения.
Постепенно становится ясным характер связей в ассоцииро-
ванных жидкостях. Если говорить о жидкостях при обычных
температурах, то преобладающими в них являются водород-
ные связи. В веществах с высокой температурой плавления
образуются в основном ковалентные связи. Примером может слу-
жить связь S—S в жидкой сере или Si—О—Si в расплавлен-
ной соли кремниевой кислоты. Дипольные моменты, за
исключением водородных, как правило, не могут вызвать ассо-
циированности, так как они не имеют определенной ориентации
в молекуле.
На примере воды были проведены подробные исследования
роли водорода в ассоциированных жидкостях. Для кислот и
спиртов исследований было значительно меньше. Количество
эффективных гидроксильных связей в воде можно найти с по-
мощью дифракции рентгеновских лучей и лаймановских спект-
ров. Результаты говорят о том, что максимально возможное
число, равное 4, наблюдается только у льда. При повышении
воды от 0 до 100° С это число с 3 понижается до 2. Спектраль-
ный анализ подтверждает, что все спирты и некоторые кислоты
обладают гидроксильными или водородными связями.
Пока лишь положено начало в изучении ассоциированных
жидкостей, и общую картину мы можем составить только по
отношению небольшого количества ассоциированных жидко-
стей, исследованных современными методами. До сих пор нет
еще общей теории ассоциированных жидкостей. Количественные
или по крайней мере полуколичественные методы статистиче-
ской механики мы умеем применять только для нормальных
(неассоциированных) жидкостей. Таким образом, в настоящей
главе речь будет идти почти целиком о нормальных жидко-
стях.
330
Г л. IX. Жидкости и плотные газы
Даже при исключении ассоциированных жидкостей приме-
нение статистической механики к жидкостям сталкивается с
большими трудностями, чем для разреженных газов или кри-
сталлов. Для разреженных газов характерна почти полная бес-
порядочность конфигураций, для кристаллов, наоборот, — почти
полная упорядоченность. Расположение молекул в жидкостях
не похоже ни на один из двух вышеописанных случаев, и это
сильно затрудняет отыскание подходящей модели. Лишь в са-
мое последнее время здесь были достигнуты некоторые успехи.
Еще совсем недавно все попытки рассмотрения структуры
жидкости основывались на теории Ван-дер-Ваальса, согласно
которой она ведет себя как плотно сжатый газ. Формально это
верно, и нет причин считать, что между ними нет никакой связи.
Однако имеется и существенное различие, о котором следует
сказать. Вспомним, что по теории Ван-дер-Ваальса неидеаль-
ного газа одной из двух поправок, вводимых в уравнение
идеального газа, является замена полного объема V на эффек-
тивный свободный объем V — Nb. Любая теория неидеального
газа, претендующая на успех, обязательно содержит предположе-
ние, что Nb<^iV. Это означает, что свободный объем несильно
отличается от полного объема и газ лишь слегка неидеальный.
В жидкостях справедливо условие V — Nb<^V; даже при кри-
тической температуре V — Nb^^ V.
Поэтому для жидкости самой простой и удобной моделью
является не слишком плотное и не слишком свободное скопле-
ние шариков. По крайней мере для жидкостей с сферически
симметричными молекулами этот факт подтверждается рентге-
ноструктурным анализом. Отсюда следует, что если говорить о
сходстве, то лучше о сходстве жидкости с кристаллом, а не
с газом. Для выбора наиболее подходящей структуры жидкости
удобнее рассматривать ее как точный кристалл. Известно, что
в кристалле около каждой молекулы есть определенное неиз-
менное число ближайших соседей (координационное число),
которое для жидкостей не является определенным. Однако при
температурах значительно ниже критической координационное
число для жидкости все же имеет довольно определенное сред-
нее значение с небольшим отклонением в ту или другую сто-
рону.
Можно сказать, что в среднем геометрические связи между
каждой молекулой и ее ближайшими соседями аналогичны свя-
зям в кристаллах. Точнее, эти отклонения не сильно влияют на
закономерность геометрических связей с соседними молеку-
лами. Конечно, в некоторых внутренних точках жидкости такие
отклонения оказываются значительными, но их количество
9.1. Свободная энергия газов и жидкостей
331
сравнительно невелико, и они не могут изменять свойства всего
тела. Однако появление отклонений в расположении ближай-
ших соседей или внезапное нарушение закономерностей обычно
достаточно для полного разрушения определенного характера
геометрических связей между отдельными молекулами. Есть и
исключения. Например, необычайно длинные молекулы обра-
зуют анизотропные жидкости (их тогда называют жидкими
кристаллами).
9.1. Свободная энергия газов и жидкостей
В предыдущей главе было показано, что свободная энергия
ансамбля, состоящего из N молекул с массой m и ограничен-
ного объемом V, равна
F = — NkT In — NkTIn J(T) — kT\nQ(T), (9.1)
где j(T)—функция состояний всех внутренних степеней сво-
боды (включая вращение, колебание, электронный и ядерный
спины), a Q(T) определяется как
ЩТ) = ±( ... (9.2)
где W есть потенциальная энергия (исключая внутреннюю энер-
гию молекул) ансамбля, значение которой будем считать рав-
ным нулю при бесконечном удалении молекул друг от друга;
(d($)N — произведение W элементарных объемов, в которых рас-
положены молекулы; кратное интегрирование производится по
всему допустимому для молекул конфигурационному простран-
ству. Деление на М необходимо здесь для исключения повтор-
ного учета физически неотличимых конфигураций.
Для идеального газа, когда все N молекул находятся внутри
определенного допустимого объема V, мы имели условие:
Ц7=0 для всех внутренних точек сосуда и W=oo для внешних.
В этом случае формула (9.2) преобразуется к виду, описываю-
щему идеальный газ,
(9.3)
В предыдущей главе мы уже видели, как вычислить Q(T) при
малых значениях N/V. В этом случае разложение в степенной
ряд естественно приводило к уравнению состояния, выражен-
ному через вириальные коэффициенты. При увеличении плот-
ности требуется знание все большего числа членов степенного
ряда. Таким образом, хотя метод и верен, однако он очень
332
Гл. IX. Жидкости и плотные газы
Трудоемок и вряд ли эффективен в настоящее время для опи-
сания плотных газов или жидкостей.
Есть другой, совершенно отличный от него приближенный
метод вычисления Q(Г), который успешно развивался Леннардом,
Джонсом и Девоншайром. В настоящей главе будет дано по-
дробное описание этого метода. Перед этим необходимо рас-
смотреть условия применимости (9.1), которые не имеют ника-
кого отношения к способам приближенного вычисления Й(Г).
Первым условием эффективности (9.1) является возмож-
ность разделения движения ансамбля на внутреннее движение,
характеризуемое j(T), и движение молекул относительно друг
друга. Согласно второму условию, поступательные степени сво-
боды молекул должны быть классическими. Именно при этом
условии энергия может быть разделена на кинетическую и по-
тенциальную и из правой части (9.1) может быть выделен член
—fe71lnQ(T). Третье условие состоит в том, что весь объем V
является допустимым для каждой молекулы ансамбля, за ис-
ключением, конечно, случая, когда содержащаяся в W энергия
обмена станет настолько большой, что может исключить воз-
можность перестановки двух молекул. Обычно все эти условия,
по крайней мере приближенно, выполняются для плотных газов
и даже нормальных жидкостей. Водород и гелий представляют
собой исключение, так как их поступательные степени свободы
при низких температурах нельзя трактовать классически. Мож-
но считать, что формула (9.1), как правило, справедлива для
нормальных жидкостей (кроме водорода и гелия) и газов.
С этой точки зрения различие между нормальной жидкостью,
плотным и разреженным газами целиком определяется разли-
чием в Q(T). Это станет более понятным, когда мы рассмот-
рим приближенный метод вычисления Й(Г) для плотных газов и
жидкостей, предложенный Леннардом, Джонсом и Девоншайром.
9.2. Некоторые грубые модели жидкости
Прежде чем предпринимать попытки более успешного коли-
чественного определения Q(T), полезно сначала рассмотреть
несколько простых моделей. Несмотря на их сравнительную
грубость, они могут дать полезные качественные и даже полу-
количественные результаты относительно свойств жидкостей и
плотных газов.
В предыдущей главе разбиралась модель молекул из твер-
дых сфер диаметра D при отсутствии сил притяжения между
ними. Для слабо неидеальных газов с ее помощью была полу-
чена следующая формула:
i Nb\N
9.2. Некоторые грубые модели жидкости
333
где b = т. е. равно учетверенному молекулярному
объему твердой сферы. Вместо (9.4) можно записать следую-
щую равноценную ей формулу:
Q(T) = e"(V—b)N, (9.5)
где V — V/N — объем, приходящийся на одну молекулу. Мож-
но грубо считать, что (И — Ь) — объем отдельной молекулы.
При принятых значениях b формулы (9.4) и (9.5) могут быть
получены только при малых отклонениях от идеальности. Од-
нако для модели твердых сфер без сил притяжения (9.5)
остается формально верной при любых степенях сжатия. Для
этого достаточно лишь считать, что b не является более по-
стоянной, а зависит от V. Поэтому для рассматриваемой мо-
дели при любых степенях сжатия имеем
Q(T)==eN {v(V)}N, (9.6)
где и ( V) — свободный объем каждой молекулы.
Рассмотренная модель имеет весьма малое практическое
значение, так как она не учитывает сил притяжения между мо-
лекулами. Гуггенгейм предложил грубое, но тем не менее по-
лезное приближение: заменил величину W из (9.2) на ее сред-
нее значение для всех допустимых конфигураций. Так как для
жидкости с заданным физическим состоянием это значение,
очевидно, прямо пропорционально числу молекул и отрицатель-
но, то мы обозначим его через—N%. В этом приближении пред-
полагается, что каждая молекула свободно перемещается в рав-
номерном потенциальном поле —%, которое при непрерывном
изменении относительных конфигураций заданных молекул ме-
няется непрерывно. Если предположить, что сила притяжения
имеет малый радиус действия, то лишь самые близкие соседи
существенно влияют на —%. В этом случае х можно определить
через среднее число ближайших соседей заданной молекулы.
Другими словами, оно определяется главным образом числом
молекул в единице объема или его обратной величиной V)N=V.
Таким образом, приближенно можно считать, что х> так же как
и и, является функцией только V. Эта модель приводит к сле-
дующей формуле:
Q (Г) = eN {v (K)^^x(mr = еиv)/kT}N' (9J)
Для удобства назовем ее моделью усредненного потенциала.
К недостаткам модели следует отнести то, что она не учиты-
вает изменение энергии взаимодействия молекулы при ее сме-
щении относительно среднего положения. С помощью кристал-
334
Г л. IX. Жидкости и плотные газы
лической модели жидкости можно провести существенные улуч-
шения модели усредненного потенциала. Предположим, что в
жидком кристалле имеется N положений с минимальной потен-
циальной энергией —хо(Ю и каждая из молекул движется
в некотором поле около положения с минимальной потенциаль-
ной энергией. Это поле соответствует трехмерному изотропному
гармоническому осциллятору с частотой v. Можно считать, что
величины хо и v определяются значениями V. Если г есть рас-
стояние от молекулы до положения с минимальной потенциаль-
ной энергией, то в этой точке ее потенциальная энергия равна
— Хо + 771 (2rcv)2 г2. Это дает возможность получить для Q(T)
еще более хорошее приближение, которое имеет вид
0(0 = eN(K+*T)llfT Г fе 2 m(2ltv,’r2/*7’4я/.2Дг
_0
__fef у/2 |
2nmv2 J J
о
kT \42\N
2n.mv2 ) J
" N
— eN^kT)!kT 4Л {
Модели типа рассмотренной выше были предложены в основ-
ном Ми. Назовем их кратко моделями гармонического осцилля-
тора.
Теперь можно поставить (9.7) или (9.8) в (9.1) и полу-
чить выражение для свободной энергии. Используя (9.7), для
модели усредненного потенциала получаем
-£ = — х (V) — &Пп —kT — kT In j(T) (9.9)
и с помощью (9.8) для модели гармонического осциллятора —
^^-UV)-^kT\ni^-kT-kT\nj(T). (9.10)
Формулы (9.9) и (9.10) соответствуют различным моделям и
представляют собой довольно грубое приближение. Приведен-
ные две модели нельзя смешивать. Пусть для любых заданных
значений Т и V х равно хо, а значение и определяется соотно-
шением
— J kT Г/2
Г ( 2л/иу2 J *
(9.И)
Тогда обе формулы становятся одинаковыми. Однако если
предполагать, что и и v являются функциями только V, то при
9.3. Связь жидкости с газом и жидкости с твердым телом
335
температурах из некоторого интервала они не могут быть пол-
ностью одинаковы. Действительно, при использовании модели
гармонического осциллятора с помощью формулы (9.11) мож-
но найти эффективный свободный объем. Наоборот, при ис-
пользовании модели усредненного потенциала можно опреде-
лить эффективную частоту
/ kT у/, ,п.
V=\2nm’) ” • <9Л2)
Это v можно рассматривать как частоту хаотичного движения
молекулы между двумя противоположными гранями кубиче-
ского объема и, а тогда соответствующая такому движению ки-
нетическая энергия равна m (2kTInni) = kTln. Рассмотрим
теперь некоторые свойства жидкостей, описываемых форму-
лами (9.9) и (9.10).
9.3. Связь жидкости с газом и жидкости с твердым телом
Хотя рассмотренные в предыдущем пункте модели и яв-
ляются грубыми, с их помощью все же можно исследовать
связь между жидкостью и газом, а также между жидкостью и
твердым телом. Связь с газом лучше всего наблюдать на мо-
дели усредненного потенциала: при увеличении разреженности
Х(У) уменьшается, a v(V) увеличивается. При возрастании
V в пределе мы имеем х(^)->0 и v(V)-> V, так что фор-
мула (9.9) совпадает с формулой для идеального газа. Это ясно
указывает на характер преемственности между газовыми и
жидкими состояниями.
При сравнении жидкого и кристаллического состояний удоб-
нее всего воспользоваться формулой (9.10) для модели гармо-
нического осциллятора. С этой целью рассмотрим кристалл в
том же грубом приближении, которое соответствует модели
жидкости. Воспользуемся приближением Эйнштейна, согласно
которому все простые колебания имеют одинаковую частоту v.
Это означает, что в кристалле колебания каждой молекулы от-
носительно положения равновесия не зависят от колебаний дру-
гих молекул. Это приближение как раз соответствует модели
гармонического осциллятора для жидкости. В соответствии
с выбранным приближением свободная энергия твердого тела
равна
^ = _Хо + ЗЛГ1п(1-^/*Г)-ЛПп/(Л- (9.13)
336
Гл. IX. Жидкости и плотные газы
При достаточно высокой температуре (kT^hv) колебания мо-
гут быть классическими и (9.13) будет иметь следующую пре-
дельную форму:
р ЬТ
^ = -Хо-3^1п^--^1п/(Л- (9.14)
При сравнении ее с весьма похожей формулой (9.10) для жид-
кости обратим внимание на то, что, кроме разных значений
Хо и v для жидкости и твердого тела, в свободной энергии для
жидкости появилось добавочное слагаемое kT. Ему в значении
энтропии, приходящейся на одну молекулу, соответствует доба-
вочный член k. Это означает, что при заданных хо и v упорядо-
ченность в жидкостях несколько слабее, чем в кристалле.
Этот факт совершенно понятен с физической точки зрения
и характеризует одно из важных отличий жидкостей от кри-
сталлов. При замене модели гармонического осциллятора на
модель усредненного потенциала подмеченное различие сохра-
няется. Для доказательства рассмотрим всю жидкость как еди-
ную систему. В этом случае полная функция состояний жидко-
сти равна {f(T)}N!N\, где f(T)—функция состояний отдельной
молекулы. Деление на ЛИ производится для исключения повтор-
ного учета физически неразличимых состояний. Каждая из мо-
лекул может находиться в любой точке жидкости, лишь бы она
не налагалась на другую молекулу. Поэтому существует эффек-
тивный свободный объем (V — Nb) или No.
Таким образом, функция состояний для всей жидкости со-
держит множитель (Nv)N/N\ или (ev)N. С другой стороны, каж-
дая из молекул кристалла имеет свое собственное равновесное
положение и представляет собой локализованную систему. По-
этому функция состояний всего кристалла упрощенно предста-
вима в виде {f(T)}N, где f(T)—функция состояний отдельной
молекулы, в которой теперь содержится только один объемный
множитель и. Это объясняется тем, что молекула вынуждена
оставаться вблизи от фиксированного равновесного положения.
Таким образом, функция состояний всего кристалла содержит
множитель vN, а в жидкости (eo)N. Это приводит к тому, что
в энтропии жидкости появляется дополнительное слагаемое
k\ne = k, что согласуется с числовыми значениями, получен-
ными выше.
9.4. Вывод термодинамических функций для грубой модели
На основании формул (9.9) и (9.10) для свободной энергии
мы можем вывести все остальные термодинамические функции
для жидкости, соответствующие предполагаемым моделям. Вос-
9.4. Вывод термодинамических функций для грубой модели 337
пользуемся сначала моделью усредненного потенциала. Для
давления Р в этом случае получим
Р= — Ж = — (9Л5)
\dV}T,K N kdV/r, W dV ' dv v '
Формально это соотношение верно всегда. Однако, когда зави-
симость % и и от V не известна, оно не может быть использо-
вано для количественных расчетов. Для нормальных давлений
и температур, когда они далеки от критического значения, свой-
ства жидкости, например объем, слабо реагируют на изменения
давления. Поэтому во многих случаях давление можно полагать
равным нулю. Таким образом, мы имеем связь между -|^и
дХ । ьт*
~dV ~1V~
(9.16)
Свободная энергия F, приходящаяся на одну молекулу,
равна
F = £ = — х - kT In _ kT - kT In j(T).
Химический потенциал p равен
или
g = —х— &Г1П (2nmkTfl2v^ _kT-kT\nj(T) + PV. (9.17)
Энергия E, приходящаяся на одну молекулу, равна
е=~ л N= ~ *+т kT+£внутр)
(9.18)
где Евнутр характеризует вклад от внутренних степеней сво-
боды молекулы. Теплосодержание Н равно
H = E+PV=—t + ikT-YER"^-YPV. (9 19)
4
22 Зак. 1299
338
Гл. IX. Жидкости и плотные газы
Аналогичные формулы можно получить для модели гармо<
нического осциллятора
p=^-3kT^~0, (9.20)
F =— fa-SkTln^ — kTkT\n J(T), (9.21)
g = — Хо — ЫТ In — kT — kT In j(T) + PV, (9.22)
£ — — XoЗ^У-|~ £BHyT₽, (9.23)
—Хо + 3^7’ + £знутр + РК (9.24)
При постоянном давлении членом Р V во всех формулах мож-
но пренебречь.
Так как используемые здесь при выводе формул две модели
являются очень грубыми, то нельзя надеяться, что они приведут
к результатам высокой точности. Однако сравнение с полуколи-
чественными экспериментами говорит о том, что они обе по-
лезны, причем в особых случаях возможно упрощение вычис-
лений за счет выбора одной из них. Обычно при рассмотрении
свойств, общих для жидкостей и некоторых газов, удобнее поль-
зоваться моделью усредненного потенциала, а при рассмотре-
нии свойств, общих для жидкостей и твердых тел, удобнее
пользоваться моделью гармонического осциллятора.
9.5. Основы термодинамической теории плавления
Если воспользоваться моделью гармонического осциллятора,
то, согласно (9.22), химический потенциал при постоянном дав-
лении равен
— ЗА Лп -ГГ - kT — kT In J (Г) + PVL, (9.25)
u hv
где значком L обозначена жидкая фаза. Согласно приближе-
нию Эйнштейна, аналогичной формулой для кристаллов яв-
ляется
= — — ЗАЛп-^- — kT\nJ(T)-}-PVK, (9.26)
где значком К обозначена кристаллическая фаза. Можно пред-
положить, что ансамбль с упорядоченными конфигурациями,
соответствующими твердому телу, будет иметь сравнительно
меньшую потенциальную энергию, чем с неупорядоченными
конфигурациями, соответствующими жидкости. Причем вслед-
9:5. Основы термодинамической теории плавления
339
ствие упорядоченности и большей жесткости связей все воз-
можные частоты больше vL. Отсюда, так как Хо < Xq\
< vK, при малых значениях Т справедливо неравенство
рЛ<рА Для достаточно больших значений Т jiL>pK. Поэтому
при некоторых температурах имеем рь = цк, что и определяет
точку плавления. Если предположить, что функция состояний,
соответствующая внутренним степеням свободы, в точке плав-
ления всегда непрерывна, т. е. jL(T) и пренебречь очень
малым членом P(VL— VK)/kTm, то для температуры плавления
Тт получим соотношение
7*_V к
-^-Л=31п— +1. (9.27)
kTm V
Для определения теплосодержания, приходящегося на одну
жидкую молекулу, воспользуемся формулой (9.24) и соответ-
ствующей формулой для кристалла. Из предположения о том,
что функция состояний (энергия), соответствующая внутренним
степеням свободы, всегда непрерывна, для теплоты плавления
Aw получим равенство
Лт = ^-^ = хок-Хо£. (9-28)
Подставляя (9.28) в (9.27), получаем энтропию плавления,
равную
^- = ЗМп 4- + k. (9.29)
Так как vK больше vL, но обычно мало от него отличается, то
из (9.29) можно заключить, что энтропия плавления молекулы
будет больше k, но ненамного.
В табл. 9.1 представлены экспериментальные данные для
различных металлов. Согласно теории, \mlkTm должно быть
немногим больше 1. В четвертой колонке таблицы приведены
соответствующие экспериментальные значения. Одно из пред-
положений, которое обычно используется при выводе формул,
состоит в том, что колебания являются классическими, т. е. тем-
пература точки плавления Тт больше характеристической тем-
пературы @D=hvD/k. Значения отношения Tm/®D Для известных
кристаллических фаз приводятся в последней колонке. Можно
заметить, что для Li и Na очень трудно удовлетворить условию
Tm/®D^> 1, a Sb, Bi в твердой и жидкой фазах имеют сильно
различающиеся молекулярные или электронные структуры.
Кроме этих четырех особых случаев, у восьми из оставшихся
тринадцати элементов значения Km!kTm находятся в пределах
22*
340
Гл. IX. Жидкости и плотные газы
Таблица 9.1
Теплота плавления и энтропия плавления
различных металлов
Металлы m кал!г-моль T . nv °K kTm T m
Li 830 459 0,90 0,9
Na 630 370 0,85 1,85
К 570 335 0,85 2,65
Rb 520 311 0,85 3,65
Cs 500 299 1,7 4,4
Си 2750 1356 1,0 8,9
Ag 2630 1233 1,1 5,7
Au 3180 1336 1,2 7,7
Zn 1700 692 1,2 2,9
Cd 1500 594 1,25 3,5
Hg 560 234 1,2 2,4
Al 1910 933 1,0 2,3
Ga 1320 303 2,2 —
T1 1470 580 1,3 6,0
Pb 1120 590 0,95 6,6
Sb 4660 903 2,6 —
Bi 2600 544 2,4 —
от 0,85 до 2,0. Для такой грубой модели подобное согласие с
теорией можно считать удовлетворительным.
Мотт и Гурней указывали, что введение в {Q(T)}1/JV постоян-
ного множителя е, как это было сделано нами по примеру
Эйринга, является грубым приближением. В действительности
этот множитель не сохраняет постоянного значения. При пони-
жении температуры жидкости он становится меньше е, причем
при приближении к точке затвердевания (данное значение вы-
брано только с целью сравнения) его значение ближе к 1,
чем к е. Поэтому слагаемое в (9.29), значение которого ранее
мы принимали равным k, в действительности будет меньше и
член, зависящий от vKlxL, становится существенным. Ранее
Мотт1), основываясь на (9.29), провел интересное исследова-
ние. При приближении температуры металлов к точке затвер-
девания он отбросил член k и в соответствии с общепринятой
теорией.проводимости электронов в металлах связал изменения
электропроводности при плавлении с vKlvL. Такая связь позво-
ляет найти vK/vL из некоторого наблюдаемого значения элек-
’) Mott, Proc. Роу. Soc. (А), 146 (1934), 465.
9.6. Основная термодинамическая теория точки кипения
341
тропроводности. Таким образом, он выразил Лт через коэффи-
циент электропроводности и сравнил ее с непосредственно на-
блюдаемой теплотой плавления. Введение такой связи проводи-
мости с теплотой плавления оказалось крайне полезным для
вычислений.
9.6. Основная термодинамическая теория точки кипения — закон
Трутона
Условие равновесия между газом и жидкостью записывается
в виде
= рЛ, (9.30)
где значки G, L обозначают соответственно газовую и жидкую
фазы. Для pG мы имеем
уА = кТ\пр — — kT\nja(T), (9.31)
где р — парциальное давление пара. Значение pL находится
из (9.17). Подставим (9.17), (9.31) в (9.30). Тогда в предполо-
жении, что функция состояний для внутренних степеней сво-
боды в обеих фазах одинакова, получим
i„p = _JL+i„AL + ^,
или
р = e-(i+bT)ikTePvLikT' (9 32)
Согласно (9.19), теплосодержание, приходящееся на одну мо-
лекулу в жидкости, равно
HL = — x + 4^7'+£BHyTp+PVL. (9.33)
Для газа
Яо = —] = 5 £Г + £внУтР> (9 34)
\ V/ / р А
Если предположить, что вклады Евнутр от внутренних степеней
свободы молекул в двух фазах одинаковы, то для теплоты па-
рообразования Ле получим равенство
Xe = HQ — HL = z-\-kT — PVL. (9.35)
Используя (9.35), можно переписать (9.32) в виде
е~^кТ. (9.36)
342
Гл. IX. Жидкости и плотные газы
При постоянном давлении отношением PVL к kT можно пре-
небречь. От этого точность не ухудшится. Однако в некоторых
случаях такое пренебрежение при дифференцировании может
привести к противоречиям. Поэтому надежнее сохранять эти
малые члены вплоть до конечных результатов.
Давление пара почти для всех жидкостей в широком диа-
пазоне температур (включая и точку кипения) с хорошей точ-
ностью описывается следующей эмпирической формулой:
р = ае-^ту (9.37)
где а — почти постоянное число, причем для многих жидкостей
с неполярными молекулами оно различается незначительно.
Для них используется среднее значение а. В этом случае эм-
пирическая формула имеет вид
р ж 2 X 107£“л^г мм pm. cm. ж 2,7 X 104£~ А*/А!Г атм. (9.38)
Как правило, она остается верной при изменении множителя
в интервале от 0,5 до 2. Согласно (9.38), при атмосферном да-
влении температура кипения Ть удовлетворяет соотношению
-щ- « 1п (2,7 X Ю4) ~ 10, (9.39)
которое может быть также записано в виде NAe/Tb=lQNk =
= 10/? = 20 кал!град • моль. Эта эмпирическая зависимость и
есть известный закон Трутона. Его точность можно проверить
по числовым данным в табл. 9.2. Водород и гелий при этом не-
обходимо исключить, так как такие легкие молекулы нельзя
рассматривать при помощи классических методов. Кроме того,
следует исключать образования, содержащие гидроксил и
аминогруппу, так как они могут иметь ассоциированную форму.
Закон Трутона можно применять только для нормальных жид-
костей. Однако и для них существуют систематические откло-
нения от закона Трутона. В общем случае XelkTb с возраста-
нием Ле растет. В настоящее время еще нет достоверного тео-
ретического объяснения отклонений от этого закона. Даже при
наличии систематических отклонений закон Трутона все же
представляет собой полезное грубое приближение.
Если сравнить теперь эмпирическую формулу (9.38) в точке
кипения с теоретической формулой (9.36), то мы получим
—____NkT> =___________
2,7 X WamM 2,7 X
(9.40)
Для того чтобы определить порядок величины и, положим Ть =
= 334 (это температура кипения хлороформа). При этой темпе-
ратуре /?7\ = 2,7х 104 атм • см3/г-моль. Подставляя это значение
9.6. Основная термодинамическая теория точки кипения 343
Таблица 9.2
Теплота и энтропия парообразования жидкости
при нормальной точке кипения
Вещество гй. «К NXe ккал]г-моль N\lTb кал/г-.чоль
Неон 27,2 0,415 15,3
Азот 77,5 1,36 17,6
Аргон 87,5 1,50 17,2
Кислород 90,6 1,66 18,3
Диэтиловый эфир 307 6,47 21,1
Сероуглерод 319 6,49 20,4
Хлороформ 334 6,97 20,8
Четыреххлористый углерод 350 7,14 20,4
Бензол 353 7,35 20,8
Салициловый метиловый эфир 491 11,00 22,2
Органические соединения (не — — 20—23
ассоциированные)
Гелий 4,29 0,022 5,1
Водород 20,4 0,214 10,5
Метиловый спирт 337,7 8,38 24,8
Муравьиная кислота 373,6 5,54 14,8
в (9.40), получаем Nv~l см3. Плотность хлороформа (СНС13)
равна 1,49, молекулярный вес—119,39. Отсюда объем грамм-
молекулы жидкости равен 80,1 см3. С другой стороны, равно-
весное ’расстояние г* между молекулами хлороформа на осно-
вании табл. 8.1 равно ]Л2 X 5,430Л. Поэтому если считать, что
мы имеем дело с соприкасающимися друг с другом шарами,
то объем, который они займут, будет равен N — г*3 = 71,3 см3.
Это говорит о том, что порядок величины свободного объема,
приходящегося на одну молекулу, равен разности между объ-
емом, который приходится на каждую молекулу, и объемом,
который занимает сама молекула.
Таким образом, свободное движение молекул жидкости в
основном ограничивается движением среди своих ближайших
соседей — молекулы жидкости как бы изолированы среди своих
соседей. Конечно, следует помнить, что в действительности жид-
кости не могут сохранять все время такую структуру, соседи
344
Гл. IX. Жидкости и плотные газы
молекул в жидкости постоянно меняются. В твердых же телах
соседи фиксированные. В этом и заключается существенное
различие между жидкостью и твердым телом.
9.7. Потенциальная энергия взаимодействия между молекулами
и приведенное уравнение состояния
Одна из двух рассматривавшихся ранее моделей жидкости
определялась параметрами %, и, другая — %0, v. Значения их
можно выбирать произвольно. Упомянутые две модели являют-
ся упрощенными вариантами другой еще более распространен-
ной модели, в которой каждая молекула может перемещаться
во всем доступном объеме под действием определенного сило-
вого поля. Последнее определяется энергией взаимодействия
молекул со своими соседями. Работа Леннарда — Джонса и Де-
воншайра1) является очень важным шагом в этом направле-
нии. Они, исходя из экспериментального выражения для энер-
гии взаимодействия молекул, найденного из свойств слабо не-
идельных газов, использовали аналогичную модель для
вычисления равновесных свойств жидкостей и плотных газов.
При этом энергия взаимодействия е(г) может быть выбрана та-
ким образом, что, с одной стороны, можно получить довольно
точную зависимость вириального коэффициента В от темпера-
туры для слабо неидеальных газов, с другой — правильные чис-
ленные значения для критической температуры, температуры
кипения и теплоты парообразования. Ниже будет дано подроб-
ное описание метода, использованного Леннардом, Джонсом и
Девоншайром.
Прежде чем начать подробное изложение теории, мы попы-
таемся получить некоторые общие выводы из предполагаемого
потенциала взаимодействия Леннарда — Джонса. Сам потен-
циал имеет вид
« М = 4е* [(^‘ - (i)“] = [2 « - . (9.41)
В (9.41) величины 8*, D или rm соответственно имеют размер-
ность энергии и длины. Поэтому можно ввести безразмерный
объем V* отдельной молекулы с помощью соотношения
у* = у/Д3 = v/MD\ (9.42)
Безразмерная температура, очевидно, равна
T*^kTK— (9.43)
*) Leonard —Jones, Devonshire, Proc. Roy. Soc. (4), 163 (1937),
53; 165 (1938), 1.
9.7. Потенциальная энергия взаимодействия между молекулами 345
а безразмерное давление —
P* = PD*l(—z*). (9.44)
Если нет необходимости учитывать квантовые эффекты, то все
величины, характеризующие равновесное состояние вещества,
уже введены. В этом случае уравнение состояния для трех со-
стояний вещества имеет вид
Р* = Р*(У*, Г). (9.45)
При учете квантовых эффектов необходимо ввести новый пара-
метр Л*, содержащий массу молекулы /и,
Уравнение состояния в этом случае принимает вид
Р* = Р*(Г, Т\ Л*). (9.47)
Для многих веществ ввиду относительно большого значения
т, Л* очень мало. Поэтому при всех температурах, кроме очень
низких, приближающихся к абсолютному нулю, квантовым эф-
фектом можно пренебречь и пользоваться (9.45).
Выражение (9.45) есть приведенное уравнение состояния,
которое показывает, что когда термодинамические переменные
выражены в надлежащих единицах, то функциональная форма
их взаимосвязи является всеобщей и совершенно не зависит
от индивидуальных свойств веществ. В действительности эти
надлежащие единицы могут быть любой группой значений да-
вления, объема, температуры. Для этого достаточно лишь, что-
бы при переходе к «молекулярным единицам» с помощью урав-
нений (9.42) — (9.44) они стали бы группой постоянных чисел.
Например, давление, объем и температура в критической точке
образуют именно такую группу. Единственное, что мы можем
сделать, это считать закон приведенных состояний эмпириче-
ским законом и выписать для него формулу. Никаких основа-
ний для дальнейших шагов мы не имеем. Поэтому будем рас-
сматривать его как следствие закона взаимодействия' между
молекулами, что и представляет собой физическое толкование
эмпирического закона.
Согласно нашей точке зрения, применение (9.45) приводит
к успеху только при использовании (9.41). Закон взаимодей-
ствия в форме Леннарда — Джонса, как об этом говорилось в пре-
дыдущей главе, есть только полезное приближение. Лучше
всего он выполняется для инертных газов. Однако для гелия
и неона при низкой температуре вследствие их очень малого
346
Гл. IX. Жидкости и плотные газы
атомного веса квантовыми эффектами пренебрегать нельзя.
В табл. 9.3 приведены значения величин, соответствующие кри-
Таблица 9.3
Тройная и критическая точки инертных газов
Вещество смъ[г-моль —TVe* кал)г-моль ~е*/й 0/, °K -е*/£>3, а тм г* 1 tr ♦ Q Ptr Xiod <r * Гкр У* 1 KP
Ne 12,51 70,74 35,60 233,6 0,690 1,882 1,292 1,247 0,1150 3,333
A 23,79 238,0 119,8 413,2 0,699 1,646 1,182 1,258 0,1162 3,164
Kr 29,35 330,1 166,1 464,4 0,698 1,556 1,161 (1,26) 0,1167 3,163
Xe 36,74 456,6 229,8 513,2 0,702 1,570 1,162 (1,26) 0,1134 3,095
Среднее значение 0,70 1,56 1.16 1,26 0,117 3,16
тической и тройной точкам. Из таблицы видно, что для приве-
денных газов полностью справедлива формула (9.45). Согласно
Гуггенгейму ]), все вещества можно грубо разделить на не-
сколько типов. Причем последовательность их такова, что, как
правило, для любого из них приведенное уравнение состояния
выполняется хуже, чем для предыдущего, и лучше, чем для
последующего:
1) Тяжелые инертные элементы Аг, Кг, Хе.
2) Легкие инертные элементы Ne, Не.
3) Неполярные или почти неполярные двухатомные молекулы,
например N2, О2, СО.
4) Более легкие неполярные двухатомные молекулы, напри-
мер Н2.
5) Неполярные с высокой симметрией и слабо поляризуемые
молекулы, например СН4.
6) Менее симметричные, полярные и слабо поляризуемые мо-
лекулы, например СО2.
7) С высоким фактором симметрии, неполярные, но поляри-
зуемые молекулы, например СС14.
8) Сравнительно асимметричные, неполярные, но поляризуе-
мые молекулы, например CS2.
9) Слабо полярные сравнительно небольшие молекулы, напри-
мер COS, СНС13.
10) Молекулы с более сильной полярностью, например слож-
ные эфиры, кетон.
’) Guggenheim, Thermodynamics, North-Holland Publishing Co.,
Amsterdam, 1950. p. 139.
9.7. Потенциальная энергия взаимодействия между молекулами 347
11) Сильно полярные молекулы, например азотистые соедине-
ния.
12) Молекулы, образующие водородные связи, например Н2О.
13) Химически активные молекулы, например NO2.
Степень пригодности потенциала Леннарда — Джонса к этим
молекулам также соответствует их положению в приведенной
системе. Будем считать теперь, что взаимодействие между плот-
но расположенными молекулами одинаково с взаимодействием
в разреженном газе, описанным в предыдущей главе. Однако
теперь форма и дипольный момент молекулы сказываются
намного сильнее, чем в разреженном газе. Именно поэтому чем
дальше расположены молекулы в приведенной системе, тем
труднее применять потенциал Леннарда — Джонса для описания
взаимодействия между ними.
Конечно, для каждой группы эффективный потенциал ме-
жду молекулами можно выразить через длину и энергию, при-
чем он не обязательно имеет форму потенциала Леннарда —
Джонса. Поэтому в этой группе молекул закон приведенного со-
стояния по-прежнему остается верным. Однако теперь уравнение
состояния, такое, как (9.45), отличается от приведенного урав-
нения состояния для тяжелых инертных газов. Это отражено
в табл. 9.4. В таблице рассматривается группа сложных орга-
нических и некоторых неорганических молекул, значение kTjPV
для которых в критической точке приближается к 3,8. Это
Таблица 9.4
Вещество Формула т . °к кр’ х Ркр( атм NV . кр’ см* W/PVXcp
Диэтиловый эфир с4н10о 467,0 35,6 281,9 3,814
Бензол с6н6 561,7 47,89 256,2 3,755
Бромбензол С6Н5Вг 670,2 44,64 323,4 3,813
Хлорбензол С6Н6С1 632,4 44,62 307,9 3,776
Этиловый эфир муравьиной С3НбО2 508,5 46,76 229,0 3,895
кислоты
Этиловый эфир уксусной С4Н8О2 523,3 38,00 286,0 3,885
кислоты
орто-Пентан С5Н12 470,4 33,04 310,9 3,762
изо-Пентан С5Н12 461,0 32,92 307,3 3,734
Октан ^8^18 569,4 24,65 490,9 3,864
Гептан С7Н1б 539,4 26,88 537,8 3,945
Гексан С6Н14 507,4 29,62 366,9 3,830
Четыреххлористый углерод СС14 556,3 44,98 275,9 3,677
Четыреххлористое олово SnCl4 591,9 36,95 351,2 3,755
348
Г л. IX. Жидкости и плотные газы
говорит о том, что уравнения состояния для них могут быть
одинаковыми. В то же время приведенное значение, очевидно,
больше соответствующего значения для тяжелых инертных га-
зов (где оно равно 3,4).
Таким образом, закон приведенного состояния является
важным понятием, имеющим широкое применение. Результаты
табл. 9.3 можно использовать и для других выводов: если изве-
стны критическая температура Ткр и критический объем N/VKp,
то можно вычислить характеристическую температуру 0/ и
диаметр D
^тк7^0’7947^ (9.48)
И
£>3=зЛбКк₽; D = °-682 W7’- <9-49)
Определив таким образом критическое состояние вещества, мож-
но вычислить величину потенциальной энергии взаимодействия
между молекулами, вириальный коэффициент и свойства пере-
носа неидеальных газов.
Вследствие того что многие ученые1) составили таблицы
термодинамических свойств и коэффициентов сжатия жидкостей
и газов, область применимости закона приведенного состояния
увеличилась. Эти таблицы составлены в предположении, что
различные термодинамические величины при различной приве-
денной температуре 77Ткр являются функциями приведенного
давления Р/Р^. Они составлены на основе средних значений
численных данных для Н2, N2, СО2, NH3, СН4, С3Н8 и C5Hi2. Так
как эти молекулы принадлежат различным типам, то нельзя
надеяться, что полученная группа кривых сможет вновь точно
выявить представленные в таблице свойства любого газа. Одна-
ко эти таблицы чрезвычайно полезны при приближенных вычис-
лениях. Более полное описание таблиц читатель сможет найти
в первоисточниках2). При проведении реальных вычислений
можно использовать расширенные таблицы3).
9.8. Теория Леннарда — Джонса и Девоншайра
Ранее мы всегда предполагали, что потенциальная энергия
молекул жидкости во всем доступном для них объеме постоян-
!) Например, Hougen, Watson, Chemical Process Principles, Pt. II,
Chap. XII, John Wiley and Sons, 1947.
2) Например, Hougen, Watson, Chemical Process Principles, Pt. II,
Chap. XII, John Wiley and Sons, 1947.
3) Например, Hougen, Watson, Chemical Process Principles Charts,
Democrat Printing Co. Madison, Wisconsin^l946.
9.8. Теория Леннарда—Джонса и Девоншайра
349
на и соответствует потенциальной энергии изотропного гармо-
нического осциллятора. Рассмотрим теперь более подробно за-
висимость потенциальной энергии молекулы, определяемой бли-
жайшими соседями, от ее местоположения. Эта энергия яв-
ляется одновременно и функцией доступного объема. Допустим,
что местоположение молекулы ограничено одной занимаемой
ею ячейкой. Очевидно, что чем выше плотность, тем справедли-
вей будет это приближение. Если в разреженном газе суще-
ственны только бинарные столкновения, а один атом может
быстро перемещаться из одной части ансамбля в другую, то
в плотных газах и жидкостях движение одного атома ограничи-
вается ближайшими соседями, и чем больше плотность, тем
меньше возможность побега из той области, которая ограничи-
вает его местоположение. Мы будем пренебрегать этими редко
осуществляющимися перемещениями.
Только при сравнении свободной энергии жидкостей или
плотных газов со свободной энергией кристаллов необходимо
учитывать возможность перемещения и дополнительный член
kT. Смысл этого члена уже разъяснялся в п. 9.3. При передви-
жении каждой молекулы в своей ячейке силовое поле, дей-
ствующее на нее со стороны других молекул, меняется во вре-
мени. Приближенно заменим это колеблющееся поле некоторым
средним. Используемое нами простое предположение сводится
к следующему: движение любой из молекул происходит в усред-
ненном поле, образованном молекулами из ближайшего окру-
жения, причем каждая из них находится в равновесном поло-
жении, т. е. в центре своей ячейки. Рассмотрим этот случай в
качестве подходящего первого приближения.
Так как молекулярное поле быстро ослабевает с расстоя-
нием, то будем учитывать только ближайших соседей. Таким
образом, будет рассмотрена следующая задача: перемещение ча-
стицы в поле частиц, расположенных симметричными рядами
на сферических поверхностях. Если ближайшие соседи располо-
жены очень тесно, то поле ячейки имеет высокую степень
симметрии. Для наших целей достаточно заменить реальное
поле сферически симметричным относительно центра ячейки и
выбрать для его характеристики подходящие средние значения.
Пусть молекулы находятся на сферической поверхности, цент-
ром которой является центр ячейки; средние значения потен-
циальной энергии в каждой точке поверхности представляют
значения поля на ней, т. е. последнее эквивалентно средней по-
тенциальной энергии ячейки при условии, что ближайшие соседи
распределены на сферической поверхности равновероятно.
Пусть а — среднее расстояние между ближайшими соседями,
а е(а)—потенциальная энергия взаимодействия при заданном
350
Гл. IX. Жидкости и плотные газы
расстоянии а. Предположим, что положение одной из молекул
остается фиксированным, в то время как другая движется по
сфере с радиусом г. Центр сферы находится на расстоянии а
от фиксированной молекулы. Тогда средняя энергия е(г) взаи-
модействия двух частиц равна
е (г) = f d<p f е {(r2 + а2 — 2аг cos 0)^} sin 0 dQ —
о о
= ~^f е {(r2+a2 —2arcos0)^} sin0rf0. (9.50)
о
Если z есть число ближайших соседей для данной молекулы,
то ее среднюю потенциальную энергию в ячейке №(г) при г<а
можно написать в виде
W(г) = гг(г)== уz J*е {(г2-1-а2— 2arcos 0)^} sin 0^0. (9.51)
о
Воспользуемся теперь для потенциальной энергии формулой
Леннарда— Джонса (9.41). Тогда получим
W(r)—z £*^ f J___________________________|-
w\r> — 2 (г2-]-я2 —- 2ar cos О)3 ’
о
I Z (—e*) Г f
.j___________________} sin 0 dQ = —_____- I i___________-________k
(r24-a2 —2arcos0)6 J 2 (r2 + a2 —2ars)3
— I
r12 1
.J________—_______
(r*-\-a* — 2arsy J us'
В результате очень простого интегрирования получим
При г->0 имеем
Эту формулу можно получить непосредственно путем умноже-
ния потенциальной энергии (9.41 )^на координационное число z,
9.8. Теория Леннарда—Джонса и Девоншайра
351
когда расстояние между двумя молекулами равно а. Используя
(9.53), можно переписать (9.52) следующим образом:
Г (г) - W) = z(- О { (-J) - 2 (ffin (-J) }, (9.54)
где /(у), т(у)—функции, определенные следующими соотно-
шениями:
/(у) = (1 + 12t/ + 25,2t/2+12у3 + у4)(1 — у)"10—1,
m(t/)==(l + «/)(! —УГ4 — 1- (9.55)
Для удобства введем положительную энергию Л*, которая
равна
Л* = —ге*, (9.56)
и объем V*, равный
у г3 е
у* = —гз (9.57)
ал т у v '
где V, как обычно, — объем, приходящийся на одну молекулу,
а у определяется как
а3 = уК (9.58)
Величина у есть постоянная, определяемая геометрической рас-
становкой молекул. Вводя новые постоянные Л* и V*, можно
переписать (9.54) в виде
W(r) - 1Г(0) = Л* { (^1 (Д.) - 2 (4)2m (£) }. (9.59)
Можно переписать также (9.53), которое будет иметь вид
Н7(0) = Л* { - 2 (-£)2 + (-£)41. (9.60)
Формула J.59) и дает закон изменения потенциальной энергии
при перемещении молекулы в ячейке. Вместе с тем (9.60) дает
значение потенциальной энергии в центре ячейки. Как обычно,
за нуль принимается значение энергии .при бесконечном удале-
нии молекулы. Правая часть (9.60) является функцией только
Л* и V*/V; правая часть (9.59) тоже зависит от этих двух ве-
личин и, кроме того, через а зависит от геометрической постоян-
ной у.
Рассмотрим теперь, каким образом определить геометриче-
ские параметры. Прежде всего необходимо выбрать локальную
структуру нормальной жидкости и плотного газа. На основании
общих данных будем считать, что имеет место гранецентриро-
ванная кубическая структура. Из рис. 9.1 видно, что если за
352
Гл. IX. Жидкости и плотные газы
центр гранецентрированной кубической структуры принять ин-
тересующую нас молекулу, то симметрично к ней на одинако-
вом расстоянии а будут находиться 12 соседних молекул. В этом
случае наш параметр z равен 12. Длина одной грани куба соста-
вляет У2а, а объем куба, следовательно, равен 2]/2а3. Одна-
ко этот объем не равен объему V, так как не весь куб являет-
ся доступной областью для центральной молекулы. Для ее
Рис. 9.1.
нахождения необходимо соединить линиями центральную мо-
лекулу с каждой из 12 соседних с ней и провести к ним перпен-
дикулярные плоскости, из которых в свою очередь образуется
двенадцатигранник, являющийся искомой доступной областью
для центральной молекулы.
Нетрудно видеть, что объем двенадцатигранника составляет
лишь четвертую часты от объема куба, т. е. V=-^2 У2а3 =
= а3У2 или у — ]/2. Как из рассмотрения расположения моле-
кул, так и из рис. 1.7 следует, что самый большой зазор обра-
зуется на грани куба. Как только а )Л2 = 2£), где D — диаметр
молекулы, то центральная молекула может покинуть ячейку че-
9.8. Теория Леннарда—Джонса и Девоншайра
353
рез зазор, образовавшийся между 12 соседними молекулами.
В этом случае а = y*2D = У 2 Л rm, W = а?/ У~2 = У2гУ
т. е. -рг>2.
Отсюда ясно, что если рассматривать молекулы в виде же-
стких сфер с диаметром D, то при V/V* > 2 центральная моле-
кула может покинуть ячейку, а при V/V*<2— не может. Ко-
нечно, в действительности молекулы совсем не являются
жесткими сферами и всегда существует возможность их высво-
бождения из ячейки. Некоторые из характерных кривых W(r)
представлены на рис. 9.2. Обратим внимание на то, что при
г)а-+±\12 потенциальная энергия очень сильно возрастает, т. е.
молекула в ячейке практически не может выйти из сферы
|г/а|<1/2. Здесь |г/а|<1/2, а не Взаимодействие рас-
сматриваемой молекулы и соседей ограничивает ее движение
на краях ячейки. Это как раз и говорит о том, что допустимым
пространством для центральной молекулы является двенадцати-
гранник, а не куб большего размера.
При некоторых значениях V/V*, например в случаях а\ и
а2, кривая потенциальной энергии имеет в центре пик, при дру-
гих значениях, как, например, в случае Ь, — не имеет. Централь-
ный пик начинает появляться, когда значение V/V* прибли-
жается к 1,6. При дальнейшем росте обнаруживается, что в
критической точке V = VC~2V* высота пика близка
где Ткр есть критическая температура. При К/У* = 3,16 высота
23 Зак. 1299
354
Гл. IX. Жидкости и плотные газы
пика становится нереально большой, она равна 0,9 kTc. Таким
образом, как форма этих кривых, так и случай возможного вы-
свобождения молекул из ячейки, о котором говорилось выше,
объясняют, почему модель движения молекулы внутри ячейки
пригодна только при V, меньших 2V*, т. е. неприемлема для
разреженных газов.
Если потенциальную энергию частицы в центре ячейки при-
нять за нуль и воспользоваться для нее формулой (9.59), то
функция состояний для молекулы, движущейся в данной ячейке,
будет иметь вид
а'2
VamkT)1 г W(r)- W(0)}/kT dr =
h3 J
о
= «2 2mlS exp [£ {- (£)• Z (s) + 2 (-£)’»(.,)} ]
0
(9.61)
Верхний предел интегрирования, очевидно, не может быть со-
вершенно определенным. Однако Леннард — Джонс и Девон-
шайр считают, что это не столь существенно, так как основной
вклад в интеграл вносят значения г, меньшие а/2. Поэтому до-
статочно положить его равным а/2.
Обозначим через —N%q энергию ансамбля, когда каждая
молекула расположена в центре своей ячейки, а энергию бес-
конечно удаленных друг от друга молекул примем равной нулю.
При таком выборе нулевого значения функция состояний, соот-
ветствующая движению молекулы в заданной ячейке, равна
Д./2ехр_(Гуz(у) + 2(Гу/п(у)
о
Но так как каждая из молекул может находиться в любой из
W ячеек, то функция состояний каждой молекулы в ансамбле
равна
•^2—еъ:кт 2nNa3 J уу2 ехр [ \4 z
о
+ 2(-^У m(y)]]dy. (9.62)
Опустим множитель (2nmkTyiyh\ а оставшееся выражение воз-
ведем в степень /V, чтобы учесть наличие N молекул. Разделив
затем все выражение на М, для того чтобы исключить повтор-
9.8. Теория Леннарда—Джонса и Девоншайра
355
ный учет состояний с переставленными молекулами, получим
полную функцию состояний Q(T’).
In Q (Г) = N + N^/kT + N In (2na3) +
+ 7Vln
(9.63)
Подставляя (9.63) в (9.1), имеем
F=^ = -kT[n^^--kT\nj(T)-kT-Ъ-
— kTIn 2лл3 J y'h exp |
0
A‘; / K* \4 ,, 4 . o A*
kT \ V ) Z(^) + 2 kT
(9.64)
Энергия хо, очевидно, непосредственно связана с ^(0). Эту за-
висимость, по крайней мере приближенно, можно записать в
виде
-Хо-4 W) = Л*{-(-£)’ + 1 . (9.65)
Множитель 7г необходим для того, чтобы избежать дву-
кратного вычисления энергии вазимодействия между парой со-
седей. В приведенной формуле учитывается энергия взаимодей-
ствия только между ближайшими соседями. Если ввести до-
полнительное слагаемое, учитывающее взаимодействие между
неближайшими соседями, то формула изменится. Ранее указы-
валось, что для гранецентрированной кубической структуры
взаимодействие между этими молекулами может увеличить
член, соответствующий притяжению, примерно на 20%, а вкла-
дом в энергию отталкивания можно пренебречь. Учитывая этот
факт, мы вместо (9.65) будем иметь
- Хо - Л* { - 1,2 (V7K)2 + 0,5 (Г/К)4| •' (9.66)
В итоге после подстановки значения /о в (9.64) для свобод-
ной энергии получим следующую формулу:
F = -^— — kT\n (-2лт^!г —kTlnj(7) — kT~
— Л* { 1,2 (-у-)2 — 0,5 (-£7 } - kT In (2лу^Ю- (9-67)
где
g = j f/,/2exp{ — (-pr-j4 /(г/) + 2 m(y)^dy (9.68)
О
23*
356
Гл. IX. Жидкости и плотные газы
и является, таким образом, функцией только от A*/kT и V*/V,
причем у определяется из (9.58).
Если сравнивать полученные результаты с результатами для
модели усредненного потенциала, то из (9.67) и (9.9) видно,
что при х, равном хо, и свободном объеме
'u = 2nygVr, (9.69)
по форме они могут быть одинаковыми. Однако такое совпаде-
ние является чисто формальным, так как здесь g является
функцией не только V, но зависит также и от Т. Однако при
У->оо величина g стремится к постоянному числу, а хо->О, т. е.
свободная энергия (9.67) превращается в свободную энергию
для идеального газа.
Такой вывод несколько отличается от выводов некоторых
авторов, рассматривавших теорию жидкого состояния Лен-
нарда—Джонса и Девоншайра. Они считали, что вблизи границы
ячейки потенциальная энергия W (г) имеет бесконечно большое
значение. Это соответствует тому, что молекулы полностью изо-
лированы в потенциальных ячейках и не имеют возможности
покидать их, т. е. каждая молекула может находиться только
в какой-то определенной ячейке. Поэтому эти авторы исклю-
nn
чали из (9.62) множитель Af, а из Й(Т) множитель -дгр- В этом
случае в (9.64) и (9.67) пропадал член —kT, а энтропия не-
сколько уменьшалась. Поэтому в противоположность преды-
дущим результатам выражение для свободной энергии не
могло при V->оо переходить в свободную энергию идеального
газа.
Наша точка зрения совпадает здесь с точкой зрения Лен-
нарда—Джонса и Девоншайра, которые считали, что наличие
бесконечно высокого барьера на границах ячеек вызвано несовер-
шенством моделей и их нельзя принимать за истинные. На са-
мом деле молекулы иногда могут выскакивать из ячеек, хотя
это и происходит очень редко, возможно даже один раз на ка-
ждую тысячу колебаний. Однако эти случайные блуждания
вполне достаточны для того, чтобы за макроскопический про-
межуток времени возмутить ансамбль и дать дополнительный
вклад в энтропию для жидкости. Эта ситуация сильно отли-
чается от наблюдаемой в твердых телах, где молекулы часто
остаются в определенных узлах решетки, т. е. в действитель-
ности за время обычного эксперимента почти не имеют возмож-
ности покинуть свой узел решетки.
9.9. Уравнения состояния
357
9.9. Уравнение состояния и значения параметров
при критических условиях
На основе ранее полученной формулы (9.67) для свободной
энергии с помощью обычных термодинамических формул мож-
но вычислить любые другие термодинамические функции. Для
давления имеем
где gi и gm, как и g, являются лишь функциями Л*/kT и V*/V.
Определяются они следующими соотношениями:
gj = ехр{ — 1(у)+ 2-^ m(y}^dy, (9.71)
о
1/4 » * 4 2
y',2m (У) ехР {— Тт (т-)4 z (у) + 2 тг (иг)2 m аУ- (9-72)
О
Энергия, приходящаяся на одну молекулу, равна
Е = -Т*^Р- =уЛГ-Л*{1,2 (-у-)2-0,5 (-£)4} +
+ Л* (-£-)4 - 2Л* (-£)2 + Езнутр. (9.73)
Химический потенциал ц и теплосодержание И, приходящееся
на одну молекулу, можно получить из термодинамических фор-
мул
И = (9.74)
H = E-\-PV (9.75)
подстановкой известных соотношений.
Таким образом, основной задачей при применении теории
жидкого состояния Леннарда — Джонса и Девоншайра является
получение функций g, gm, gi. Некоторая работа в этом напра-
влении была проделана автором и И. Пригожиным, но основ-
ная заслуга в составлении функциональных таблиц принадле-
жит Венторфу, Бюлеру, Гиршфельдеру и Кертиссу !). Мы не будем
давать здесь подробного изложения этих вычислений. Однако
обратим внимание на то, что при сравнении данных для крити-
ческого состояния, найденных Леннардом—Джонсом, с данными
!) Wen tor f R. Н., Buehler R. J., Hirsch (elder J. O., Cur-
tis s C. F., J. Chem. Physics, 18 (1950), 1484.
358
Гл. IX. Жидкости и плотные газы
из табл. 9.3 картина, очевидно, получается не очень хорошая,
о чем свидетельствует табл. 9.5. Объем и давление сильно
Таблица 9.5
* т кр * VKP * Ркр * , * * р V IT кр кр' кр
Деннард — Джонс и Девоншайр Экспериментальные значения для инертных газов 1,30 1,26 1,77 3,16 0,434 0,117 0,591 0,294
отличаются от экспериментальных данных. Да это и неудиви-
тельно. Ранее уже говорилось о том, что для случая У/У*>1,5
излагаемая теория недостаточно точна. Отсюда можно сделать
вывод, что данная модель оказывается слишком грубой
при больших значениях К, которые включают и критическое
состояние.
Таким образом, модель нуждается в усовершенствовании.
Ранее такие попытки предпринимались многими исследовате-
лями. Их работы были подвергнуты критике со стороны Рау-
линсона и Кертисса1). Наиболее важное из высказанных пред-
ложений заключалось в том, что в теории Леннарда — Джонса и
Девоншайра необходимо допустить возможность существова-
ния у гранецентрированной кубической решетки свободных
ячеек, не занятых молекулами. Это позволяет для сравнительно
больших значений объема еще более приблизиться к реальным
условиям, т. е. приблизить структуру жидкости к структуре га-
зов. Описание здесь этой расширенной модели и расчет по ней
представляют слишком сложную задачу. Обратим лишь вни-
мание на то, что жидкость при постоянном давлении и темпе-
ратуре, а также газы при высокой температуре и давлении
имеют малый объем, поэтому теория Леннарда — Джонса и Де-
воншайра должна быть довольно точной.
9.10. Асимптотическое разложение при малом объеме и низкой
температуре — жидкостная теория
В жидкостях при постоянной температуре отношение N*lkT
по порядку величины равно 20, а У/У* близко к 1. Таким об-
разом, функцию g можно разложить по степеням kTI\*. Пусть
s = 7r (~Я • <9-76>
!) Rowlinson J. S., Curtiss С. F., J. Chem. Physics, 19 (1951),
1519. См. также De Boer J., Proc. Roy. Soc. (Д), 215 (1952), 4.
9.10. Асимптотическое разложение при малом объеме
359
Введехм новую переменную т] с помощью соотношения
sn = 1 (у) - 2 ± (-£)’ ш (у) (9.77)
П = —(9.78)
где 1(у) и определяются из (9.55). Разложим 1(у) и т(у)
в ряд по степеням у. Тогда получим
л == [22 — 10 (-^)2 ] у + [200,2 - 28 (-^)2 ] у2 +
+ [1144 -60(-К.)2]г/з+ ....
Обращая этот ряд, найдем
У = Л1П + «2112 + «з113+ • • • . (9.79)
где
200,2 —28(К/Г*)2 zQo0x
2 [22 —10 (И/V*)2]3 ’
2 [200,2 — 28 (V/V*)2] — [1144 — 60 (V/Г)2] [22 — 10 (V/V*)2]
аз~ [22 — 10 (V/V*)2]5
Нижний предел у интеграла g (9.68) равен г/==0, поэтому соот-
ветствующее значение т] = 0. Верхний предел У = -^, поэтому
соответствующее значение т|=/(-^— 2(V/V*)2m . Но на
основании (9.55) Z 90, т 3. Причем $ имеет большое
значение. Поэтому можно верхний предел интеграла по т] поло-
жить равным оо. Тогда
оо
g = р-- [п’- + | Л 1’ + ; | (Л)*] 4- ... ] Л,.
о
--- Ул /_£iV 2 j 1 j 3 • 5 а2 1 . 3 • 5 • 7 Г а3 . 1 / а2 \2-| 1 ._)
___________________________________________________________________2“ ( 1 * 2 • 2 "^7 s ’ 2 • 2 • 2 [ * 4 J s2 ' ' ‘ Г
(9.81)
360
Г л. IX. Жидкости и плотные газы
Подставим $ и fli из (9.76) и (9.80). Окончательно для Ing по*
лучим следующее выражение: __
. , /л . 3. \ V*) 3-5 / V у kT
lng~ln 2 + 2 1П [22_10(_12)2] 2-2 (р) Л* Х
200.2 —28 (-рг) .3-5-7 / V\4kT\*
Х [22— 10(V/Р)2]2 2-2-2 \ Р/ Х
12 [200,2 — 28 (У/Р)2]2 — 7 [ 1144 —60 (У/У*]2 [22 — 10 (У/У*)2] .
Х 7 [22 — 10 (У/У*)2]4 +---.
(9.82)
Подставляя (9.82) в (9.67), найдем вырая епие для свободной
энергии F, приходящейся на одну молекулу,
F = -£• « — kT\n_ kT In j(T) — kT —
Отсюда энергия, приходящаяся на одну молекулу, равна
£ = - Г iiffl « £-">’- — Л- { 1,2 (-£У — 0.5 ( £)' } +
( 5 / у \4 kT 28 (~р* / у \ в / \2
+ з^{1 ЛГр—^L27+“(^J («) х
12^200,2 — 28 (-рт)2]2 —7[1144 — 60(У/Р)2] [22— 10(У/Р)2]
X 7 [22— 10(У/Р)2]4 1“ • • • •
(9.84)
9.10. Асимптотическое разложение при малом объеме 3G1
Дифференцированием (9.84) по Т найдем удельную теплоем-
кость Су, приходящуюся на одну молекулу, при постоянном
объеме. Если через Ср обозначить удельную теплоемкость при
постоянном давлении, приходящуюся на одну молекулу и сов-
падающую с аналогичной теплоемкостью в идеальном газе, то
= (9.85)
Тогда можно написать
Как мы увидим в дальнейшем, для температур, близких к нор-
мальной точке кипения, Тогда из (9.86) видно,
что третий и второй члены в скобках одного порядка. Однако
из общей теории асимптотических разложений известно, что
когда порядок величины двух соседних членов одинаковый, то
последним можно пренебречь. Поэтому в дальнейших вычисле-
ниях третий член в скобках будет опускаться.
Дифференцируя свободную энергию по И, получаем уравне-
ние состояния. При этом обнаружим, что в первом приближении
можно пренебречь членом, содержащим квадрат Т, и прибли-
женное уравнение состояния для жидкости примет вид
Р = [2 (Я’ - 2.4
У* \ 2"1
т) J
kT
(9.87)
Для низких давлений можно положить Р— О и найти зависи-
мость между объемом и температурой. Для упрощения вычис-
лений воспользуемся близостью V/К* для жидкости к 1. Пусть
(V/V*)2 = 1 -Ь А.
(9.88)
362
Гл. IX. Жидкости и плотные газы
Подставляя (9.88) в (9.87) и полагая Р=0 с точностью до А,
получаем следующее уравнение для А:
(1,6 - 3,672 А = 9,14 - 0,4.
Таким образом, при низких давлениях имеем
Z „ х, 1.2+ 5,468 4т
kT
9,14 44- —0.4
ьт
1,6 — 3,672 44
ИЛИ
Д =-------Д-----(9.89)
1,6 —3.672 44
В последующих вычислениях
это приближенное выражение.
мы будем использовать именно
9.11. Равновесие жидкости и пара
Химический потенциал pG газовой фазы, имеющей парциаль-
ное давление р, определяется формулой (9.31), а химический
потенциал жидкой фазы, как правило, — формулой (9.74).
Используя равенство этих двух потенциалов, имеем следующие
условия равновесия:
1 t kT 3 .
Ъ 1Г1 А * о 1П
2 А* 2
/ V \2
3-5 kT / V \4 28
14т—+•••• (9-90)
Если приближенное соотношение (9.89) для объема подставить
в (9.90), то левая часть (9.90) будет функцией только &Г/А*.
Поэтому в действительности (9.90) дает давление пара над
жидкостью в виде функции от температуры. Правая часть
(9.90) в интервале температур от точки плавления до точки ки-
пения меняется почти линейно, и график ее близок к прямой.
Это как раз согласуется с эмпирической закономерностью, вы-
раженной формулой (9.37).
Нормальная температура кипения жидкости Тъ может быть
определена из (9.90). По заданному значению р, равному, на-
пример, одной атмосфере, находим соответствующую темпера-
туру. Ясно, что так как V*/A* иди —8*/П3 не являются постоян-
9.12. Коэффициенты, теплового расширения и изотермического сжатияЗЪЗ
ними, то значение отношения нормальной температуры кипения
к ©j не фиксировано. Однако для многих газов разброс значе-
ний —в*/£)3 не очень велик, как это видно, например, из
табл. 9.3 для инертных газов. К тому же в формуле присут-
ствует только логарифм от Л*/И*, поэтому значение отношения
Тъ/®1 почти постоянно, что и показано в табл. 9.6. Вычисления
Таблица 9.6
0/, СК ТЬ’ СК ТЬ./в1
расчетное значение наблюдаемое значение расчетное значение наблюдаемое значение
н2 30,7 26,4 20,3 0,827 0,661
Ne 35,4 29,6 27,2 0,837 0,768
n2 96,0 79,0 77,2 0,823 0,805
А 120 94,3 87,4 0,785 0,729
были проделаны Леннардом — Джонсом и Девоншайром с по-
мощью метода, несколько отличного от вышеописанного. Поэтому
в очень грубом приближении для 0/ можно написать соотно-
шение
07^ 1,25Гд. (9.91)
Отсюда, согласно (9.56), при z=12 имеем
15. (9.92)
9.12. Коэффициенты теплового расширения
и изотермического сжатия
Коэффициент теплового расширения а и коэффициент изо-
термического сжатия р теперь можно вычислить из приближен-
ного уравнения состояния (9.87). Коэффициент а определяется
соотношением
(9.93)
Дифференцируя уравнение (9.87) по Г, имеем
364
Г л. IX. Жидкости и плотные газы
Теперь, так так Р~0, для
пользоваться (9.87). В этом
упрощения уравнения можно вос-
случае имеем
(аТь)
НЯ-4-8 О
Т.г . / IZ* \2 / V* \41
__ М 9 4 I и I _ 9 I к I
Т L ’ \ V ) \ V ) J
или, используя (9.88) и сохраняя только члены, содержащие А
в первой степени, получаем
пТ _ Л ____________________(0,4+1,6 А)_______________
т I 360 kT \ 360X 17 kT \
3,2--ъг -ГТ — л п'2 Ч----------£------л*"
\ 72 Л* / \ 1 73 Л* /
0,4-^-
360 kT
72 л*
360X 11 kT
73 ’ Л*
о п 360 kT
Используя приближенную зависимость (9,89) для Д и прибли-
женную зависимость (9.92) для 1гТъ/А*, получаем
«Л
0,4 Ц-
3,2 — 0,490
т гл
34 — 0,77 0,609 -4-0,4
________1 ь______1 ь___
3,2 — 0,490-Т- 1,6 — 0,2446
I b 1 b J
(9.94)
Результаты представлены на рис. 9.3, где для сравнения приве-
дены данные из табл. 9.7. Хотя (9.94) отражает характерные
свойства поведения коэффициента теплового расширения с уве-
личением температуры, но теоретические результаты оказы-
ваются заниженными. По-видимому, это объясняется не воз-
можной ошибкой в расчетах Леннарда — Джонса и Девоншайра,
а недостаточной точностью приближенного уравнения состояния
(9.87), из которого мы исходим, и последующих приближенных
вычислений. Если в выражении для свободной энергии (9.83)
сохранить большее число членов и точнее вычислить V/V*, то
результаты, возможно, получатся лучше. При дальнейшем
анализе будут использоваться экспериментальные кривые из
рис. 9.2. ч
Дифференцируя уравнение состояния (9.87) по давлению Р,
найдем коэффициент сжатия
₽=--ИЧ+ (9'951
9.12. Коэффициенты теплового расширения и изотермического сжатияЗбЗ
равный
Р и с. 9.3.
Вновь используя условие Р~0, получаем
V __ Л*
krb
[8
Подставляя в (9.89) и сохраняя, как и раньше, члены, содержа-
щие Д в первой степени, находим
1
360X 17 kT л
’ 73 Л* Л
360 kT
72 д* J
Л* | 360 kT 1
kTb[^ 72 А*1
Таблица 9.7
Коэффициент теплового расширения жидкости
Жидкость Формула Tb’ °K T, °K ax 10 s, OK“* T>Tb aTb
Ацетон (СН3)2СО 329,7 293,2 1,071 0,890 0,353
Анилин c6h6nh2 457,6 293,2 0,855 0,641 0,382
Треххлористый AsC13 403,4 293,2 1,029 0,728 0,415
мышьяк
Бензол С6н6 353,2 293,2 1,237 0,830 0,437
Бром Вг2 332,0 293,2 1,132 0,883 0,376
Сероуглерод CS2 319,5 293,2 1,218 0,918 0,390
Четыреххлори- СС14 350,0 293,2 1,236 0,838 0,433
стый углерод Хлороформ СНС13 334,5 293,2 1,273 0,877 0,426
Диэтиловый (С2Н5)2О 307,8 293,2 1,656 0,953 0,510
эфир Йодистый этан C2H5J 345,4 293,2 1,179 0,848 0,407
Триметилэтан С5Н12 301,2 293,2 1,598 0,973 0,481
Трехброми- РВг3 446,1 293,2 0,868 0,657 0,387
стый фосфор Треххлористый РС13 348,7 293,2 1,154 0,841 0,402
фосфор 1,211 0,422
Треххлористая РОС13 378,5 293,2 1,116 0,775 0,423
окись фос- фора (хло- рокись)
Пентан С5Н12 309,4 293,2 1,608 0,948 0,498
изо-хлорпро- С3Н7С1 308,6 293,2 1,591 0,950 0,491
пан
изо-амилен С5Н8 307,2 293,2 1,567 0,955 0,481
Четырехбро- SiBr4 426,2 293,2 0,987 0,688 0,419
мистый кремний
Четыреххло- SiCl4 330,8 293,2 1,430 0,886 0,473
ристый кремний 0,456
Четыреххло- SnCl4 387,3 293,2 1,178 0,757
ристое олово
Четыреххлори- TiCl4 409,6 293,2 0,998 0,715 0,409
стый титан
орто-метил- c7h7nh2 473,0 293,2 0,847 0,620 0,401
анилин
9.12. Коэффициенты теплового расширения и изотермического сжатия 367
Зависимость Д от температуры выражена в (9.89), а выражение
A*/kTb дано в (9.92). Отсюда
/ 11,2+ 1,190 4-V 0,609 ~ — 0,4
j | _____________1 b j _______1 ь______
, ч \ 3,2 — 0,490-Т- /\ 1,6 — 0,2446 ~
ь_\ ___ х7 4_________________________________1 ь
' ' 15(3,2 — 0,490^
\ 1 ь/
(9.96)
Сравним теперь эти результаты с экспериментальными данными
на рис. 9.4. Числовые значения представлены в табл. 9.8. Из
Рис. 9.4.
таблицы видно, что соответствие между теорией и эксперимен-
том удовлетворительное. Более точное уравнение состояния
улучшит этот результат. Эмпирическое уравнение, полученное
обработкой экспериментальных данных, имеет вид
1
101,6 —82,4 4-
\1 ь
(9.97)
Естественно, что использование вместо (9.92) более точной
зависимости (9.48) внесет в теорию коэффициента теплового
расширения и коэффициента изотермического сжатия поправки.
Однако после этого она будет соответствовать критической тем-
пературе, а не нормальной точке кипения. Но нормальную тем-
пературу кипения гораздо легче измерить, чем критическую, по-
этому используемый нами метод в применении к конкретным
Таблица 9.8
Коэффициент сжатия жидкости
Жидкость Формула Моле- куляр- ный вес Tb’ °K T, °K Плот- ность, г!см* 3 X 106, атм~} T'Tb 0 \ vL )
Ацетон (СН3)2СО 58,08 329,7 293,2 0,792 125,6 0,890 0,0464
Бензол С0Н6 78,11 353,3 303,2 0,868 98,5 0,858 0,0318
Бензол С6нв 78,11 353,3 333,2 0,836 116,4 0,944 0,0362
Сероуглерод cs2 76,13 319,7 303,2 1,261 102,0 0,948 0,0444
Четыреххло- СС14 153,84 350,0 293,2 1,595 105,8 0,838 0,0316
ристый угле- род Хлорбензол С6Н5С1 112,56 405,2 283,2 1,107 72 0,698 0,0226
Хлороформ СНС13 119,39 334,5 303,2 1,49 109,5 0,907 0,0375
Диэтиловый (^2^5)2^ 74,12 307,8 303,2 0,713 210 0,986 0,0510
эфир Бромэтан С2Н5Вг 108,98 311,2 293,2 1,430 120 0,942 0,0402
Иодэтан C2H6J 155,98 345,4 313,2 1,91 74 0,907 0,0257
о/;/я о-гексен C7HU 100,20 371,7 303,2 0,684 134 0,815 0,0274
ор/ио-гептен C6HI2 86,17 342,2 303,2 0,66 159 0,885 0,0343
Нитробензол C6H5NO2 123,11 484,1 303,2 1,1987 49 0,627 0,0190
Нитрометан ch3no2 61,04 374,2 303,2 1,13 73,6 0,810 0,0419
о/?/ио-октан CgHie 114,23 399,0 293,2 0,704 101,6 0,735 0,0205
Триполиэтанал C6HI2O3 132,16 397,6 291,2 0,994 88,2 0,733 0,0216
Четырехбро- SiBr4 347,72 426,2 298,2 2,814 86,6 0,700 0,0245
мистый кремний Четыреххло- SiCl4 169,89 330,8 298,2 1,484 165,2 0,902 0,0391
ристый кремний Четыреххло- TiCl4 189,73 409,6 298,2 1,726 89,8 0,728 0,0275
ристый титан Четыреххло- SnCl4 260,53 387,3 x298,2 2,232 108,9 0,770 0,0296
ристое олово Метилбензол C6H5CH3 92,13 384,0 303,2 0,862 96,5 0,790 0,0285
орто-клд\ лол C6H4(CH3)2 106,16 417,2 293,2 0,875 79,7 0,703 0,0224
9.13. Удельная теплоемкость при постоянном давлении
369
вопросам имеет свои преимущества. К тому же систематическая
обработка экспериментальных данных, проведенная Карапеть-
япцем и Чэн Гуан-юе1), позволяет рассчитывать температуру
кипения многих веществ непосредственно по молекулярным
данным, не прибегая к экспериментальным измерениям.
9.13. Удельная теплоемкость при постоянном давлении
Для многих инженерных расчетов нужна не удельная тепло-
емкость при постоянном объеме Су, а удельная теплоемкость
при постоянном давлении Ср. На основании общих законов
термодинамики разность между Ср и Су равна
CLp— & = J-VT, (9.98)
где а и р — коэффициенты теплового расширения и сжатия.
Здесь Су уже определена формулой (9.86). Третьим членом в
скобках можно пренебречь и для простоты принять
Таким образом, из (9.98) имеем
Cp—Cp = k
0,5 —0,4 —4
1 ь
т
Ть
(9.99)
Используя эмпирические зависимости для коэффициентов теп-
лового расширения а и изотермического сжатия р, правую часть
(9.99) при вычислениях можно считать функцией Т/Ть. Резуль-
таты такого расчета приведены в табл. 9.9. Из таблицы видно,
Таблица 9.9
Разность удельных теплоемкостей
жидкостей и газов
г/г, аГЬ 3—/ Уь (аТь)2 т т 0,5— 0,4 -г~ 1 b р — е р
з(^) Ть \ vL)
К
0,6 0,392 0,0192 4,80 0,26 5,06
0,7 0,398 0,0232 4,78 0,22 5,00
0,8 0,410 0,0280 4,80 0,18 4,98
0,9 0,445 0,0365 4,88 0,14 5,02
1,0 0,525 0,0520 5,30 0,10 5,40
’) Карапетьянц М. X., Чэн Гуан-юе, Температура кипения и
давление насыщенного пара углеводородов, М., Гостоптехиздат, 1961.
2-1 Зак. 1299
370
Гл. IX. Жидкости и плотные газы
что, за исключением температур, близких к температуре кипе-
ния, удельная теплоемкость грамм-молекулы жидкости и удель-
ная теплоемкость грамм-молекулы газа при постоянном давле-
нии отличаются друг от друга примерно на 5/?, т. е.
Ср — Cp~\Q кал!град. (9.100)
Это действительно чрезвычайно простой результат.
Значения удельной теплоемкости жидкости, найденные экс-
периментально и вычисленные при помощи (9.100), приведены
для сравнения в табл. 9.10. Так как теория годится только для
нормальных жидкостей, то следует исключить те из них, моле-
кулы которых содержат гидроксил и аминогруппы как слишком
длинные. Для жидкостей, состоящих из двухатомных молекул,
значение Ср при низких давлениях равно 7. При температурах,
когда колебательные степени свободы полностью возбуждены,
это числовое значение равно 9. Первая половина таблицы ука-
зывает на хорошее совпадение расчетных величин удельной
теплоемкости грамм-молекулы жидкости при постоянном объ-
еме с экспериментальными. Отклонение находится в пределах
допустимой ошибки. Более того, для NO и хлористого серебра
единство теории и эксперимента проявляется в очень широком
диапазоне температур — от 120 до 763° К. Единственным исклю-
чением является CS2.
Отклонения расчетных значений удельной теплоемкости,
представленных во второй половине табл. 9.10, от эксперимен-
тальных более существенны и достигают 4 кал/град, что на-
много превышает допустимую ошибку. Характер отклонений
аналогичен отклонениям в законе Трутона для тех же самых
жидкостей (см. табл. 9.2). Хотя рассматриваемые температуры
низки, но все же недостаточно малы для того, чтобы возникла
необходимость учета квантовых эффектов1). Появление откло-
нений нельзя объяснить какими-то особыми силами взаимодей-
ствия между молекулами. Когда плотность невелика, расстоя-
ние между молекулами сравнительно большое. Поэтому изме-
нение характера действующих сил еще не может привести к
сколь-нибудь существенным отклонениям. Свойства переноса
при этом остаются обычными. Истинная причина этих отклоне-
ний до сих пор еще не выяснена.
Из предыдущих рассуждений ^сно, что формула (9.100)
может оказаться пригодной для нормальных жидкостей даже
при комнатной температуре и высоком давлении. В настоящее
9 Hamann S. D., Transactions of the Faraday Society, 48 (2) (1952),
303-307.
Таблица 9.10
Сравнительное значение удельных теплоемкостей жидкостей
при постоянном давлении
Жидкость Формула Молеку- лярный вес ть> °к т, ск Ср, экс- перимен- тальное значе- ние, кал град Ср, рас- четное значе- ние, кал/град Ср, экс- перимен- тальное значе- ние, кал', град
Аммиак NH3 17,032 239,8 213,2 8,0 18,0 17,9
Аммиак 17,032 239 8 273,2 8,7 18,7 18,7
Ацетон (СН3)2СО 58,08 329 7 313,2 20,1 30,1 30,8
Бензол с6н6 78.11 353,3 293,2 21,8 31,8 32,5
Бензол с6нб 78,11 353,3 323,2 23,3 33,3 34,3
Бром Вг2 159,83 332,0 270,0 7,0 17,0 17,1
Сероуглерод cs2 76,13 319,7 290,7 12,0 22,0 18,4
Четыреххло- СС14 153,84 350,0 273,2 21,5 31,5 30,9
ристый угле-
род
Четыреххлори- СС14 153,84 350,0 293,2 20,7 30,7 31,8
стый угле-
род
Хлороформ СНС13 119,39 334 5 313,2 17,2 27,2 27,9
Диэтиловый (С2Н5)2О 74,12 307,8 303,2 31 41 40.5
эфир
Окись азота NO 30,01 121,4 120 7,0 17 17,3
Хлористое се- AgCl 143,34 1823 763 > 7,0 > 17,0 18,5
ребро < 9,0 < 19,0
Четыреххлори- SnCl4 260,53 387,3 287-371 24,4 34,4 38,5
стое олово
Двуокись серы SO2 64,06 263,2 273,2 9,9 19,9 20,4
Аргон А 39,944 87,444 85,0 5 15 10,5
Окись угле- СО 28,01 81,1 69,4 7 17 14,27
рода
Метан СН4 16,04 111,7 100 8 18 13,01
Азот n2 28,016 77,3 64,7 7 17 13,15
Азот n2 28,016 77,3 72,8 7 17 13,33
Кислород 02 32,00 90,1 73,2 7 17 12,60
24*
372
Г.i. /X. Жидкости и плотные газы
время точность этого метода намного превысила точность экс-
перимента. Для газа тоже нет никакой необходимости исходить
из эксперимента при определении удельной теплоемкости Ср
при постоянном давлении. Для этого можно использовать лю-
бой из методов, изложенных в пятой главе. При расчете некото-
рых вновь полученных молекул иногда бывает полезно исполь-
зовать первоначальные расчеты удельной теплоемкости с уче-
том средних характеристических частот их химических связей.
(9.101)
9.14. Скорость звука в нормальной жидкости
Формула, согласно которой обычно вычисляется скорость
звука с, имеет вид
\(VdP\
С ~ р \ dV Д’
где р — плотность жидкости, а дифференцирование производит-
ся вдоль изоэнтропической линии. Если частота звуковой волны
достаточно низка или если характерное время малых возмуще-
ний велико и достигает периода релаксационных колебаний
около термодинамического равновесия, то очень легко получить
соотношение
(9.102)
(9.104)
=
Р₽ CLV '
где р — коэффициент изотермического сжатия, определяемый
из соотношения (9.95), которое для нормальных жидкостей
имеет вид (9.97). Разность (Ср—Cy)/R можно найти в четвер-
том столбце табл. 9.9. Поэтому
Ср — Су ^9,6 кал)град. (9.103)
Пусть М — молекулярный вес. Тогда окончательно получим
101.6- 82,4
М \ Ть/ Ср —9,6
Сравнение расчетных значений скорости звука с наблюдае-
мыми приведено в табл. 9.11. Из таблицы видно, что, за исклю-
чением CS2, разница между значениями скорости звука, вычис-
ленными по (9.104), и экспериментальными не превышает 1%.
Такую степень точности можно ожидать, так как (9.104) выве-
дено на основании эмпирических формул для Ср и р. Однако
это соответствие демонстрирует также внутреннюю стройность
нашей теории. Случай с CS2 можно частично объяснить весьма
заниженным экспериментальным значением Ср, Из табл. 9.10
следует, что теоретическое значение Ср для CS2 довольно вы-
9.15. Свойства газа при высокой температуре и давлении
373
сокое. Если принять такое предположение, то расчетное значе-
ние скорости звука для CS2 уменьшится и согласие с экспери-
ментальными данными улучшится. Поэтому можно утверждать,
что (9.104) является удобной и точной формулой для вычисле-
ния скорости звука в нормальной жидкости. Так как Ср с ро-
стом температуры увеличивается, то скорость звука в соответ-
ствии с (9.104) будет уменьшаться. Такое поведение скорости
звука в нормальной жидкости противоположно его поведению
в газе, где скорость звука с увеличением температуры возра-
стает.
9.15. Свойства газа при высокой температуре и давлении
Рассмотрим теперь теорию Леннарда—Джонса и Девоншайра
в применении к газам при высоком давлении. Прежде всего
под газом при высоком давлении мы будем иметь в виду газ,
плотность которого приблизительно равна плотности жидкой
или твердой фазы, т. е. когда параметр К/И* близок к 1.
В п. 9.8 и 9.9 указывалось, что теория Леннарда—Джонса и Де-
воншайра пригодна лишь для случая, когда К/К* близко к 1.
Если И/И* приближается к 2, то в расположении молекул по-
являются чрезвычайно важные пустоты, которые делают тео-
ретический расчет непригодным. Однако даже в рассматривае-
мых условиях, когда теория справедлива, конкретное вычисле-
ние все же встречает некоторые трудности: температура газа, у
которого параметр V/V* близок к 1, может достигать несколь-
ких тысяч градусов, а числовое значение параметра А*/6Г при-
ближаться к 1. В этом случае значения переменной s =
= А*/йТ( )4, использовавшейся в п. 9.10, не очень велики,
а колеблются около 1. Следовательно, и вычисление основных
термодинамических функций с помощью асимптотического раз-
ложения g, gmy gi и др. непригодно.
С другой стороны, значения s и не малы. Поэтому нельзя
применить метод разложения в ряд по положительным степе-
ням. Точные численные значения можно определить только не-
посредственным вычислением с помощью таблиц Венторфа
и др., о которых речь шла выше. Однако применение числовых
таблиц в конечном итоге дела не упрощает. В настоящем пункте
будет предложена упрощенная формула, составленная на осно-
ве этих числовых значений.
Прежде чем предлагать упрощенную формулу, проанализи-
руем сначала возможный окончательный вид уравнения состоя-
ния газов при высокой температуре и давлении. При чрезвы-
чайно высоких температурах, т. е. при Т->оо, скорость молеку-
лярного движения необычайно велика. Следовательно, и скорость
374
Гл. IX. Жидкости и плотные газы
взаимных столкновений молекул, а с ней и энергия столкнове-
ний растут до бесконечности. Независимо от того, описывается
ли взаимодействие потенциалом Леннарда—Джонса или общей
теорией взаимодействия молекул (см. гл. VIII, п. 8.7), изве-
стно, что чем сильнее столкновения, тем меньше минимальное
расстояние между молекулами в процессе столкновений, т. е.
проявляется «упругость» молекул. Поэтому при Т->оо «эффек-
тивный» диаметр молекул стремится к нулю. Другими словами,
при Т-+ОО газы еще раз становятся идеальными, a PV/kT->\.
На этом основании уравнение состояния газа при высокой тем-
пературе и давлении можно записать в виде
(9Л05)
где 0/ — характеристическая температура взаимодействия мо-
лекул (см. формулу (9.43)), a K* = D3, причем D — диаметр мо-
лекулы в потенциале взаимодействия Леннарда—Джонса. При
7707->оо f->0.
Анализируя численное решение по теории Леннарда — Джонса
и Девоншайра, найденное Венторфом и др., обнаружим, что
зависимость (9.105) при V/V*, близком к 1, и большом T/Qn
т. е. при высоких давлении и температуре, можно еще более
упростить. Две переменные Т/02 и У/У* можно объединить в
одну £ с помощью соотношения
C = (W/e-^- (9-106)
В этом случае формула (9.105) примет вид
±L=i+_______1____
kT 1 0,278^ — 0,177 ‘
(9.107)
Точность этой формулы не слишком низка; при значениях К/У*
из интервала 0,8—2,8 и 770/ из интервала 10—400 отклонение
от численных значений Венторфа и др. не превышает 10%. При
очень больших значениях V/V* формула (9.107) еще более
упрощается и принимает вид
4г=1 + w=1+3-594 (* (Я' ’ • (9-108)
Исходя из теории второго вириального коэффициента, изложен-
ной в восьмой главе, при больших V/V* для него можно полу-
9.15. Свойства газа при высокой температуре и давлении
375
чить только первый член разложения (см. формулу (8.82)). По-
этому
= l + 3,63o(^p(^f.... (9.109)
Сравнивая формулы (9.108) и (9.109), видим, что приближен-
ная формула даже в случае большого объема совпадает по
форме с точной формулой и отличается от нее только показате-
лем степени у (770/). Поэтому естественно считать, что, хотя
упрощенная формула (9.107) пригодна в основном для высоких
температур и давлений, она все же применима при высоких
температурах и низких давлениях.
Используя вывод о том, что ошибка при низких давлениях
не очень велика, можно с помощью (9.107) вычислить различ-
ные свойства газов при высоком давлении и температуре. Так
как при таких вычислениях будет встречаться интегрирование
по V/V* и верхний предел может расти до V/V *->ОО, то ДЛЯ
того, чтобы получить удовлетворительные результаты, необхо-
димо, чтобы формула (9.107) при V/V*-+oo не давала слиш-
ком больших ошибок. Выпишем сначала общее термодинами-
ческое соотношение
= -р.
\ 3V / р \ дТ /у
Подставляя сюда формулу (9.107), получаем
1дЕ\ kT 0,278g
V (0,278g —0,177) *
Если Еоо есть средняя энергия каждой молекулы при
V/V*-* оо, т. е. средняя энергия молекул идеального газа, то,
интегрируя предыдущее выражение, получаем
Е(1ЛГ)--Е.т = -4Рож;-<>.|77-
Результаты вычислений, проведенных с помощью этой формулы,
сравнивались с табличными данными Вепторфа и др. Было до-
казано, что при высокой температуре и давлении ошибка не
превышает 10% •
Теплосодержание Н можно вычислить аналогичным методом
dH=dE + d(PV\
т. е.
d\H(V, Т) —Н „(T)\-=d\E(V, T)-E^T)\-Md(PV-kT).
376
Гл. IX. Жидкости и плотные газы
Используя предыдущую формулу, получаем
H{V, T)-HJT) = E(V, л-^(П + ^таД0Л77 =
~ kT 0,278g__0,177 ^(Dl- (9.111)
Если (9.110) продифференцировать по температуре Г, то полу*
чим удельную теплоемкость при постоянном объеме Су
Cy(V. (9.112)
Для определения удельной теплоемкости при постоянном давле-
нии Ср воспользуемся следующей формулой:
_ (дН\ (дИ'\ (dPldT)v
Lp~\dT -'к ' \ 0V )т дТ lT~\ dT lv \ 0V JT ' (^P/dV)T ’
С помощью формул (9.107) и (9.111) получим
Г' (\7 Т\ С (7'\ 7k 0,2317g 0,177 /q
Ср(К, Г)-Ср.Д/) = -Г1те-=(П77р-. (9.113)
В заключение выпишем формулу для энтропии
S(K Т)—(V, 7) = -q о,278g —0,177 —0Д77 ,П ( 0,278g —0,177") ‘ 1
Точность формул (9.112), (9.113) и (9.114), возможно, хуже
точности (9.110) и (9.111). Ошибка могла увеличиться из-за
того, что мы дифференцировали приближенное выражение.
Однако полученные формулы очень удобны в применении и ме-
жду ними существует внутренняя согласованность.
9.16. Более точная теория жидкости и плотных газов
Вычисление термодинамических свойств жидкостей и плот-
ных газов по известным свойствам молекул сводится к вычис-
лению конфигурационной функции состояний Q(T), зависящей
от потенциальной энергии и определенной выражением (9.2).
При этом реальная картина обычно заменяется различными
моделями, описывающими некоторые особые типы состояния
ансамбля. Нельзя ожидать, что за пределами области, для ко-
торой введены эти специфические модели, они по-прежнему
останутся верными. Это видно хотя бы из того, например, что
теория Леннарда — Джонса и Девоншайра при приближении к
критическому состоянию становится неверной. Для газов срав-
нительно малой плотности она действительно является неудо-
влетворительной, так как применяемые модели хорошо описы-
9.16. Более точная теория жидкости и плотных газов
377
вают упорядоченные и малоподвижные состояния молекул и
плохо — их беспорядочное движение в газе. Основная цель бо-
лее точной теории жидкостей и плотных газов состоит в охвате
всей области физических состояний ансамбля. В ее развитии
принимали участие Кирквуд1), Борн и Грин2), Майер3) и
Айвен4). Так как эти исследования еще окончательно не офор-
мились, то мы не будем рассматривать подробно эти трудные
теории, а приведем лишь их крайне упрощенное описание.
В этих теориях притяжение и отталкивание между молеку-
лами считаются сферически симметричными. Затем вводят
функцию g(r) и определяют ее следующим образом. Вероят-
ность нахождения любой пары молекул на расстояниях из ин-
тервала г и r + dr равна
4лг2£ (г) dr.
где g’(r) определяется из экспериментов по рассеянию рентге-
новских лучей. В действительности оно представляет собой не-
которое преобразование Фурье. Если, как и раньше, е(г) есть
потенциальная энергия взаимодействия между молекулами, то
в соответствии с этими теориями уравнение состояния имеет вид
~NkT~~\ 3VkT J Г ~drS(Odr> (9.H5)
0
а энергия E равна
/?_£внутР 3 , 2nW f", . ,n11„
—NkT—=- ^+vkT J r'e(r^(r)dr, (9.116)
6
где Еппутр— внутренняя энергия молекул (энергия вращений и
колебаний).
Таким образом, центральный вопрос теории сводится к опре-
делению g(r) через закон взаимодействия между молекулами.
Здесь были проведены некоторые упрощения, преследовавшие
цель избежать сведения вопроса к решению бесконечной после-
довательности интегральных и дифференциальных уравнений.
В теории Кирквуда использовано приближение, отличающееся
от теории Борна, Грина и Айвена, однако разница в числовых
значениях невелика. Во всех случаях, кроме модели твердых
сфер5), конкретные вычисления очень сложны. Для твердых
’) Kirkwood,/. Chem. Phys., 3 (1935), 300.
2) Born, Green, Proc. Roy. Soc. (A), 188 (1946), 10.
3) Mayer, J. Chem. Phys., 15 (1947), 187.
4) Y von, Actualites scientifiques et industrielles, Hermann et cie, Paris,
1935, p. 203.
5) Kirkwood, Maun, Alder, /. Chem. Phys., 18 (1950)4 1040,
378
Гл. IX. Жидкости и плотные газы
Таблица 9.11
Скорость звука в нормальных жидкостях
Жидкость Формула Молеку- лярный вес ть> °* т, °к кал/град С рас- четное х X Ю"5, см/сек С экс- перим. х X 10“ 5. см/сек
Бензол СбН6 78,11 353,3 290,2 39,8 1,176 1,166
Сероуглерод cs2 76,13 319,7 288,2 18,2 1,350 1,161
Хлороформ СНС13 119,39 334,5 288,2 27,9 0,967 0,983
Диэтиловый эфир (С2н5)2о 74,12 307,8 288,2 39,8 1,022 1,032
сфер уравнение состояния имеет вид
PV
NkT
, , 2л /2 / V \ .
(9.117)
где V0 = 2Va3/]/2 —объем плотно расположенных твердых
сфер, « — диаметр молекулы. Функция gi(X) зависит лишь от
(V/Vo), как это показано в табл. 9.12. Независимость PVfNkT
Таблица 9.12
Твердые сферические молекулы
Л gi (М и(г0 (Кирквуд) VyQ (Борн, Грин, Айвен)
5 1,45 4,74 5,15
10 1,80 2,83 3,20
20 2,36 1,78 2,10
27,4 2,66 1,45 1,73
33 2,85 1,29 1,53
34,8 2,90 1,24 1,48
от температуры объяснялась Цванцигом ’) тем, что в реальных
условиях приведенное уравнение состояния соответствует пре-
дельно высоким температурам. Однако такое объяснение не
всегда имеет обоснование, так как в действительности моле-
кулы являются не твердыми сферами, а упругими. При высоких
температурах эффективный размер молекулы может стремиться
к нулю, а газ стать идеальным. Так или иначе р V/NkT все же
должно стремиться к 1, о чем и говорилось в предыдущем
пункте.
9 Z w a n z i g, J. Chem. Phys., 22 (1954), 1420»
Глава X
ОБЩАЯ ТЕОРИЯ ПРОЦЕССОВ ПЕРЕНОСА
В предыдущих главах рассматривались макросвойства ве-
ществ при термодинамическом равновесии. Среди характерных
свойств такого равновесия выделяется прежде всего наличие
однородной температуры. Однако в природе равновесие являет-
ся, конечно, исключительным состоянием, чаще встречаются не-
равновесные состояния. Когда температура тела неоднородна,
вещество уже не находится в равновесном состоянии. Согласно
экспериментам, тепловой поток из части вещества с высокой
температурой устремляется в область с низкой температурой.
Иными словами, между отдельными частями вещества наблю-
дается перенос энергии. Экспериментально установлено также,
что количественно перенос энергии в неравновесном состоянии
характеризуется коэффициентом переноса энергии и градиентом
температуры, причем коэффициент переноса одинаков для всего
вещества, и, следовательно, существует единый процесс пере-
носа энергии. На практике в макромире наблюдаются лишь
необратимые процессы переноса.
Эти закономерности распространяются на любые отклонения
от однородного состояния термодинамического равновесия. На-
пример, если в веществе имеет место градиент плотности моле-
кул какого-либо типа, то существует коэффициент переноса
этих молекул (коэффициент диффузии). Кроме того, могут воз-
никать и перекрестные эффекты подобно переносу энергии,
вызванному градиентом плотности, или диффузии, вызванной
неоднородностью температуры. Цель этой и последующей глав
состоит в том, чтобы рассмотреть такого рода процессы пере-
носа в веществе.
До сих пор основой нашего исследования макросвойств ве-
щества в равновесном состоянии была статистическая механика.
Принципы статистической механики применимы не только к
состоянию термодинамического равновесия. Однако для изуче-
ния свойств в неравновесном состоянии еще нет метода сравни-
тельно широкого использования статистической механики, так как
в самом применении содержатся некоторые трудности. Другой
путь, основанный на непосредственном изучении молекулярного
380
Гл. X. Общая теория процессов переноса
движения, оказывается более полезным, так как он дает
возможность связать коэффициенты переноса с микросвойства-
ми вещества. Хотя в основном мы будем использовать такой
подход, в этой главе для начала познакомимся с общей теорией
процессов переноса, построенной на положениях статистиче-
ской механики, а именно с так называемой термодинамикой
необратимых процессов1).
10.1. Малые отклонения от термодинамического равновесия
В настоящее время термодинамика необратимых процессов
ограничивается случаем, когда состояние ансамбля мало откло-
няется от термодинамического равновесия. Далее мы увидим,
каким образом проявляется критерий малости отклонений, опи-
сываемых этой теорией. Начнем с объяснения того, как следует
понимать эти так называемые малые отклонения от термодина-
мического равновесия. Очевидно, что при последовательном де-
лении куска вещества, находящегося в неравновесном состоя-
нии, на все более и более малые части отклонения от однород-
ности в каждом из них будут постепенно уменьшаться. Таким
образом, этот процесс превращает систему, находящуюся в не-
равновесном состоянии, в большое число почти однородных
подсистем.
Но деление системы на все более и более малые части нельзя
продолжать без ограничений. Дело в том, что в каждой части
число молекул должно остаться достаточно большим, чтобы
был возможен статистический подход. Поэтому градиент темпе-
ратуры в веществе, вообще говоря, всегда не нулевой. Однако,
например, в объеме газа, содержащем, скажем, миллион моле-
кул, отклонение температуры от средней обычно настолько не-
значительно, что им можно пренебречь. Линейные размеры та-
кого объема имеют порядок средней длины свободного пробега
между двумя последовательными столкновениями молекул. Та-
ким образом, сравнительно малую неоднородность или незначи-
тельное отклонение от термодинамического равновесия для
большого объема газа можно понимать так: на расстоянии по-
рядка длины свободного пробега относительные изменения тер-
модинамических величин пренебрежимо малы.
Следовательно, малость отклонений от термодинамического
равновесия означает, что возможно условное дробление веще-
ства на части, в каждой из которых состояние неотличимо от
равновесного. Тем самым оправдывается использование термо-
!) См. Де Гроот, Термодинамика необратимых процессов, ГИТТЛ,
1956.
10.2. Соотношения взаимности Онзагера
381
динамических методов для локального описания вещества.
Это-—основное положение термодинамики необратимых про-
цессов, которым мы неоднократно будем пользоваться.
10.2. Соотношения взаимности Онзагера
Важную роль в термодинамике необратимых процессов
играют соотношения взаимности Онзагера. Основная идея Он-
загера *) состояла в том, чтобы, пользуясь статистической меха-
никой флуктуаций системы, близкой к равновесному состоянию,
найти связи между макро- и микросвойствами, не зависящие от
динамической модели. Рассмотрим три основания соотношений
взаимности Онзагера. Первые два (теория флуктуаций и микро-
скопическая обратимость) связаны с общей статистической ме-
ханикой. Третье основание (затухание флуктуаций) состоит в
том, что отклонения от термодинамического равновесия должны
быть малыми.
Главная опора соотношений Онзагера — теория флуктуаций.
Рассмотрим адиабатически изолированную систему. Для опи-
сания ее термодинамического состояния введем ряд параметров,
характеризующих отклонения ее от термодинамического равно-
весия,
а„ а2, а3, ..ап. (10.1)
Эти параметры могут быть, в частности, температурой, давле-
нием, плотностью и т. д. Их число, до некоторой степени произ-
вольное, может быть бесконечным и даже несчетным. Исполь-
зуемые здесь параметры состояния а$ рассматриваются как от-
клонения от равновесных значений, поэтому при термодинами-
ческом равновесии они равны нулю. Энтропия в состоянии рав-
новесия максимальна, так что отклонение ее от равновесного
значения можно представить в виде
и
= —4 2 Sikaiak^ (10.2)
I, k=l
где gik=gki, а квадратичная форма ^gikatak положительно
определенна. По определению Больцмана (см. п. 4.21), эн-
тропия есть произведение постоянной Больцмана k на лога-
рифм вероятности появления состояния. Тогда в рассматривае-
мой нами системе вероятность появления состояний, характери-
зуемых значениями параметров между oci и ai + rfai, аг и аг +
J) Ons a ger, Phys. Rev., 37 (1931), 405; 38 (1931), 2265.
382
Гл. X. Общая теория процессов переноса
+ da2, .. ., должна быть пропорциональна экспоненте отклоне-
ния энтропии AS, деленного на k, т. е.
PduA.. — (&S[k)dax... б/а/г /| f ... f ехр (AS/Л) dv^. . .da/z|.
(10.3)
Знаменатель в правой части обеспечивает нормировку Р во
всем конфигурационном пространстве. Для удобства вычисле-
ний введем линейную комбинацию параметров
п
(Z = l-2, (10.4)
£=1
Разрешая эту систему относительно а/, получаем
п
о°-5)
£=1
где g'ik —матрица, обратная gik.
Используя выражение (10.3) для вероятности каждого со-
стояния, можно вычислить среднее значение любой функции
переменных а, в частности
atXj — J ... J aLXjP dax . . . dan. (10.6)
В силу (10.3) и (10.4) это выражение можно записать так:
aLXj = kT f ... J at^-y-Pda! ... da„ =
= kT f ... f dax ... daj_x dah x ... da„ f daj.
Интегрируя по частям, имеем
f az -yr- j = [azP] — f P-^-da:.
J L daj J 1 L J J daj J
Проинтегрированный член обращается в нуль, так как AS отри-
цательно, и при подходе параметра а;- к предельным значениям
величина Р стремится к нулю. Кроме того,
дщ _ . / 0, z =# у,
daj ~ iJ~[ 1. i = j-
В таком случае 1
a4Xj = — kT f . . . f da. . . . du.j_x daJ+1 . . . dan J Pb^daj —
— — kTbLj J ... J PdaY . . . daa.
10.2. Соотношения взаимности Онзагера
383
И так как величина Р нормирована, то
^=-1^. (10 7)
На основании эргодической гипотезы такое среднее значение
можно рассматривать или как среднее по ансамблю систем,
или как среднее по времени для одной системы.
Формула (10.7) будет нужна нам в дальнейшем. Другие по-
лезные формулы легко получаются из (10.7) с помощью (10.4),
(10.5)
Щ = - Т t = kT*gi}, (10.8)
tl
= - T S = kg7j- • (’°-9)
k = \
Введем теперь понятие микроскопической обратимости, не-
обходимое для вывода соотношений Онзагера. Свойство микро-
скопической обратимости может быть выражено с помощью
корреляционной функции в следующем виде:
at- (/) aj (t + т) = az (t) aj (t — t). (10.10)
Оно означает, что в среднем (по времени или по ансамблю) со-
отношение между значением аг- в момент t и значением а,
спустя промежуток времени т такое же, как соотношение между
аД/) и значением aj на промежуток времени т раньше момен-
та t. Эта зависимость основана на том, что в микромире обра-
щение направления времени в консервативной системе не ощу-
щается. Если изобразить изменение at и aj во времени графически,
то частота отклонений состояния консервативной системы в
ту и другую сторону от равновесия получится одинаковой и не
зависящей от изменения направления времени. Подставляя
в правую часть (10.10) t' = t — т, получаем другую форму этого
равенства
az (/) dj (/ т) = az (/' + т) (Л) = az (/ Д- т) ay- (/). (10.11)
В (10.11) можно применить другой способ усреднения, т. е.
сначала, фиксируя значение параметров в момент t, усреднить
величину, рассматриваемую в момент / + т, а затем произвести
усреднение фиксированных параметров. Результат выражается
следующей формулой:
(0 Ь (z + T)}ai(/)...%(0 = «у (0 + (0...0л(/) • (10.12)
384
Гл. X. Общая теория процессов переноса
Верхняя черта означает среднее по времени или среднее по
ансамблю, другая черта — среднее при фиксированных значе-
ниях параметров, указанных в индексах (включая ccjz) или
аД/)). Если исходить из среднего по ансамблю, то это есть
среднее по части фазового пространства, соответствующей фик-
сированным значениям параметров ai (/)>.••, an(/). А если ис-
ходить из среднего по времени, например в левой части (10.12),
то нужно брать те моменты /, при которых величины
ai(Z),..., an(0 принимают заданные значения, и находить
среднее значение параметра aj в соответствующие моменты вре-
мени / + т. Вычитая из обеих частей равенства (10.12) одинако-
вые величины, имеем
МО (a7(/ + T)-ay(/)}ai(/) %(/) =
= ay (/) {<(/ + т) - at- (/) % (Л. (10.13)
При наличии магнитного поля полученные выражения несколь-
ко усложняются в связи с появлением лоренцевой силы
F = eVXB, (10.14)
где е — электрический заряд, V — скорость частицы, В — век-
тор напряженности магнитного поля. По отношению к микро-
скопической обратимости эта сила находится в особом положе-
нии. Для того чтобы при изменении направления скорости сила
F не менялась, нужно изменить и направление магнитного поля.
Равенство (10.13) в таком случае следует заменить другим, в
котором aj слева будет функцией В, а справа — функцией —В.
При наличии кориолисовой силы ситуация аналогична, так как
эта сила также линейно зависит от направления скорости.
Два рассмотренных основания теории Онзагера не выходят
за пределы общих методов статистической механики. В третьем
пункте своего доказательства, как указал Казимир1), Онзагер
использует новую гипотезу. А именно, он предполагает, что в
среднем затухание флуктуаций подчиняется обычным феноме-
нологическим макроскопическим законам. Это предположение,
кажущееся на первый взгляд несколько необычным, можно объ-
яснить следующим образом. Когда отклонение какого-либо
параметра аг увеличивается, вероятность Р, вычисленная по
(10.3), стремится к нулю, но существует такая комбинация а,
для которой убывание Р будет наиболее медленным. Иными
словами, флуктуации вблизи равновесного состояния имеют тен-
денцию концентрироваться на особом пути. И если допустить,
0 С а s i m i г Н. В. G., Rev. Mod. Phys., 17 (1945), 343.
10.2. Соотношения взаимности Онзагера
385
что в процессе переноса отклонения от локального термодина-
мического равновесия невелики, то распределение вероятностей
не будет заметно отличаться от равновесного распределения,
получаемого из (10.3). Поэтому путь, проходимый системой в
пространстве а, можно также считать и путем процесса пере-
носа. Конечно, в процессе переноса осуществляется только путь
приближения к термодинамическому равновесию, однако раз-
ницы между флуктуациями приближения и отклонения нет, и
феноменологический закон для необратимого процесса пере-
носа аналогичен закону флуктуаций в области термодинамиче-
ского равновесия. Тогда пишем
J, = a( = V LihXh 2, ..., п), (10.15)
Л = 1
где производная по времени, обозначенная точкой, строго го-
воря, должна рассматриваться как отношение конечных разно-
стей, так что (10.15) лучше писать в виде
_____________ п
а‘ (<+т)-а^ (о = з? Lihxh. (юле)
А = 1
Интервал времени т ограничивается неравенствами
то<Ст<Стг» (10.17)
где то — характерное время порядка среднего времени свобод-
ного пробега молекул. Для отождествления феноменологиче-
ских величин со статистическими средними нужно, чтобы вы-
полнялось левое неравенство (10.17). С другой стороны,
гипотеза Онзагера требует, чтобы т было мало по сравнению
с временем затухания флуктуаций тг. Подставляя (10.16) в
(10.13), получаем
а/ (0 S L}hXh = a, (t) £ LlltX„. (10.18)
ft=1 h=1
Ho Ljh и Lih — феноменологические постоянные, не зависящие
от флуктуаций, а поэтому, пользуясь (10.7), имеем
или
А=1 А=1
1^ = 1^ (i, j=l, ..., п). (10.19)
Это и есть соотношения взаимности Онзагера. Они означают,
что матрица, связывающая обобщенные силы Xh и потоки Л,
симметрична.
25 Зак. 1299
386
Гл. X Общая теория процессов переноса
При наличии внешнего магнитного поля В равенство (10.13),
как было указано выше, несколько усложнится и вместо (10.19)
нужно записать
Zy/(B) = £/7(-B). (10.20)
Т. е. левая часть как функция В равна правой как функции —В.
При /=/ соотношения (10.20) не становятся тривиальными, как
(10-19), а выражают четность диагональных элементов Ьц от-
носительно напряженности магнитного поля.
10.3. Термодинамика необратимых процессов
Производная по времени от приращения энтропии AS, выра-
жаемого формулой (10.2), имеет вид
п п
AS = —2 ^gik^iak> (10.21)
1 = 1 Й=1
или, согласно (10.4),
Г AS := 2 а, (Ю.22)
4 = 1
Заменяя оы на Л и обозначая через g скорость возникновения
энтропии в неравновесном процессе, с учетом (10.15) получаем
п п п
L^X*. (10.23)
4 = 1 Z=1 Л=1
Таким образом, если каким-либо путем без использования прин-
ципов статистической механики вычислена скорость возникно-
вения энтропии, то можно подбирать соответствующие потоки
/г- и обобщенные силы «Поток» Ji и «обобщенная сила» Xi
с одинаковыми индексами называются сопряженными парамет-
рами. При выборе потоков и обобщенных сил имеет место неко-
торый произвол, так как выражение для g может быть расчле-
нено на сумму сопряженных Ji и Xi различными способами.
Однако во всех случаях соотношения Онзагера (10.19) и (10.20)
остаются в силе. Такая зависимость между коэффициентами
переноса имеет большую практическую ценность.
В итоге термодинамика необратимых процессов сводится к
использованию термодинамических функций для вычисления
скорости возникновения энтропии. Конечно, у нас уже есть
уравнения, описывающие физические процессы с помощью тем-
пературы, давления, плотности, концентрации и т. п. Вопрос за-
ключается в том, как ввести энтропию S и, используя соответ-
ствующее макроскопическое уравнение, определить скорость ее
10.3. Термодинамика необратимых процессов
387
возникновения. Поэтому необходимо уяснить связь между S и
прочими макроскопическими величинами. Основное предполо-
жение термодинамики необратимых процессов относительно та-
ких связей состоит в том, что обычное термодинамическое соот-
ношение
TdS = dE + PdV— ShcW (10.24)
распространяется на неравновесные состояния. Если s, е и v—
удельные энтропия, энергия и объем, а ц* и ck — химический
потенциал и концентрация k-и компоненты, то
Т ds = de + Р dv — S ц* dck. (10.25)
k
Следует более обстоятельно разъяснить это предположение.
Оно очень важно, ибо затрагивает вопрос определения термо-
динамических параметров системы, находящейся в неравновес-
ном состоянии. Как уже указывалось некоторыми авторами,
для возможности введения в теорию понятий удельной энтро-
пии и температуры функция распределения ансамбля систем
должна быть разложима в быстро сходящийся ряд
f = + fd) 4- f(2) + ..., (10.26)
где f(°>— равновесное распределение, a и т. д. — следующие
приближения. Это требует выполнения ряда условий: например,
средний свободный пробег молекул должен быть значительно
меньше размеров сосуда; на расстоянии средней длины сво-
бодного пробега изменения температуры, скорости, состава
и т. д. должны быть очень малыми.
Это общие условия малости отклонений от термодинамиче-
ского равновесия. Но остается количественный вопрос: так как
при изучении процессов переноса на основе функции f разло-
жение (10.26) обрывается на то соответствует ли f = f<P> + f(r>
формулам (10.24) и (10.25)? Пригожин1) проделал значитель-
ную работу по выяснению этого вопроса и получил количествен-
ные оценки. Он сравнил результаты термодинамической теории,
основанной на (10.24) и (10.25), с результатами кинетической
теории газов, полученными методом Энскога — Чэпмена. Ра-
венство (10.25) означает, что и в неравновесном состоянии s
явно зависит только от переменных е, v и а не от градиен-
тов, которые имеются в каждой точке системы. Эти градиенты
могут входить в термодинамическую теорию лишь неявным
образом.
0 Р г i g о g i n e I., Etude thermodynamique des phenomenes irrfcversibles
(Thesis), Dunod, Paris and Desoer, Liege, 1947.
25*
388
Гл. X. Общая теория процессов переноса
Пригожин сделал подробный расчет по методу Энскога —-
Чэпмена, включая третье приближение в (10.26). При этом
оказалось, что результаты кинетической теории, основанной на
^=^(0)4-^!), совпадают с термодинамическими, а при включении
удельная энтропия становится явно зависящей от градиентов.
Поэтому область применения термодинамики необратимых про-
цессов имеет здесь определенные пределы, и лишь в этих пре-
делах она верна. Требования, определяющие такие пределы, со-
стоят в том, что явления переноса можно описывать функцией
распределения f=p>+p\ а химические реакции протекают на-
столько медленно, что не нарушают этого вида функции рас-
пределения для каждой из компонент системы. Этим условиям
удовлетворяет довольно большая группа явлений. Следователь-
но, при изучении таких явлений можно употреблять термоди-
намику необратимых процессов. В то же время видно, что эф-
фекты, требующие для своего описания р) или членов более
высокого порядка, например течения сильно разреженных га-
зов, не могут быть рассмотрены на основе излагаемой здесь
теории.
10.4. Теплопроводность в твердом теле
В качестве простого примера применения термодинамики не-
обратимых процессов к процессам переноса рассмотрим вопрос
о теплопроводности в анизотропном твердом теле (например, в
монокристалле). Если р — плотность твердого тела, q — вектор
потока тепла, то хорошим приближением уравнения энергии
будет
р^+7-ч=0- (Ю-27)
В таком простом случае зависимость между термодинамиче-
скими функциями Е и S имеет вид
dS = ^-. (10.28)
Подставляя (10.28) в (10.27), имеем
0°-29)
Поскольку
V.(q/T) = ±V.q + q.V»-l. = ^V.q-^-.vr,
то, исключая -^-V-q из (10.29), получаем
g=р £ + 7 • (т) = - £ • (i о.зо)
10.4. Теплопроводность в твердом теле
389
Так как q — вектор теплового потока, то q/Г— вектор потока
энтропии, т. е. энтропия, проходящая через единичную площад-
ку в единицу времени, a A* (q/Г) —поток энтропии через гра-
ницу единичного объема в единицу времени. Первое же слагае-
0S
мое р-^- есть скорость увеличения энтропии внутри единич-
ного объема. Поэтому сумма двух членов дает общий прирост
энтропии единичного объема в единицу времени, т. е.
Tg = ^iJiXl = -^-.VT = ^- v(ln4)- <10-31)
i
В полученном выражении для скорости возникновения энтропии
легко связать потоки Л с обобщенными силами Хг*. Потоками Л
здесь являются компоненты q^ q2, q$ по осям хь х2, х3, а обоб-
д Л 1 \ д Л 1 \ д Л 1 \
щенными силами — компоненты -ч— In , -з— In , -ч— In -~-
ох^ \ Г / 0x2 \ * / ох3 \ Т /
градиента температуры. Так как поток направлен всегда про-
тивоположно градиенту температуры, то общее условие поло-
жительности удовлетворяется.
Теперь можно ввести линейный закон процесса переноса
тепла
3 3
<10-32’
/=1 /=1 7
где Lij — феноменологические коэффициенты Онзагера, a kij —
обычные коэффициенты теплопроводности. Они связаны зави-
симостью
~ipLij = kij, (10.33)
Эти коэффициенты могут быть функциями термодинамических
параметров, здесь же единственным термодинамическим пара-
метром является температура Г, поэтому и кц, вообще го-
воря,— функции Т. Теорема Онзагера (10.19) указывает, что
= (10.34)
Смысл этого соотношения состоит в том, что для обычных
анизотропных материалов поток тепла в направлении хг-, вызы-
ваемый градиентом температуры с направлением Xj, равен теп-
ловому потоку в направлении xj, вызываемому градиентом тем-
пературы с направлением хг*. Этот закон подтверждается в экс-
периментах с монокристаллами. В изотропных материалах при
вращении и зеркальном отражении координатных осей не
390
Гл. X. Общая теория процессов переноса
меняются и, следовательно, для изотропных тел
кИ = кЪИ. (10.35)
При этом (10.34) удовлетворяется автоматически.
10.5. Общие процессы переноса в изотропной среде
Макроскопические свойства веществ в жидком или газооб-
разном состояниях, а также ненаправленных поликристаллов
должны быть изотропными. Для изотропных веществ связи ме-
жду «потоками» и «обобщенными силами» в значительной мере
упрощаются, подобно (10.35) для коэффициента теплопровод-
ности твердых тел. В данном пункте мы будем рассматривать
процессы переноса в изотропной жидкой (или газообразной)
среде. Макроскопические переменные, описывающие такую си-
стему, — это численная плотность i-й компоненты иг-, средняя
массовая скорость V и температура Т. Эти переменные опреде-
лены в каждой точке пространства и в каждый момент времени,
т. е. они являются функциями радиуса-вектора г и времени t.
Следовательно, уравнение неразрывности для f-й компоненты
имеет вид
+V • •v - 7 •W*+<10-36)
где Vi — скорость диффузии r-й компоненты, а Кг— скорость
образования r-и компоненты в единице объема; — «субстан-
циальная производная», характеризующая скорость изменения
в элементе жидкости, перемещающемся со скоростью V. Общее
уравнение неразрывности получается из (10.36) умножением на
Шг и суммированием по i
^ = -| + v-Vp = -pV-v (10.37)
F(p — плотность среды). Уравнение движения имеет вид
-S- = t + V'vv = -}('-’' + |S'1^ <10-38)
I
где л — тензор напряжений, Хг— вектор внешних сил, дейст-
вующих на z-ю компоненту. Если U — энергия единицы массы,
то уравнение энергии имеет'вид
DU, — — + V • VZ7 =
Dt di и
= - 7 V • (q + дя) -1 я : VV+12 ntVt • Х/( (10.39)
10.5. Общие процессы переноса в изотропной среде
391
где q — вектор потока тепла, вызываемого молекулярным дви-
жением, a qH — вектор потока лучистой энергии. Две точки
означают тензорное произведение, так что если компоненты
тензоров А и В суть Ац и где I, /=1, 2, 3, то
3 3
A:B=S
/ = 1 у = 1
Рассмотрим физический смысл написанных уравнений. Уравне-
ние (10.36) показывает, что изменение плотности i-й компонен-
ты вызывается тремя причинами. Первый член справа свиде-
тельствует об изменении мг- в результате расширения жидкости;
изменение, представленное вторым членом, вызывается процес-
сом диффузии; изменение, выраженное третьим членом, проис-
ходит благодаря химическим реакциям, которые приводят к
появлению молекул Лй компоненты.
Согласно (10.37), изменение общей плотности происходит
только благодаря расширению жидкости. Уравнение (10.38) по-
казывает, что изменение скорости жидкости вызывается гра-
диентом тензора напряжений и действием внешних сил на моле-
кулы каждой компоненты смеси. Тензор напряжений л можно
разложить на сумму двух членов
я = Ри + р, (10.40)
где Р — статическое давление жидкости, р — тензор вязких на-
пряжений, а и — единичный тензор,
/1 ° 0\
и= 010.
\0 0 1/
(10.41)
По (10.39) изменение внутренней энергии вызывается следую-
щими причинами: первый член в правой части выражает изме-
нение U за счет потока энергии, включая эффект излучения;
изменение, выраженное вторым членом, вызвано работой тен-
зора напряжений; изменение же, описываемое третьим членом,
происходит благодаря работе, совершаемой в процессе диффу-
зии под действием внешних сил.
Исходя из макроскопических уравнений (10.36) — (10.39), вы-
числим скорость возникновения энтропии g. Для этого введем
энтропию единицы массы S и вектор потока энтропии о. Тогда
P-75T = p4f + pV-+ (10.42)
392
Г л. X. Общая теория процессов переноса
Соотношение (10.25) теперь можно написать так:
TdS = dU-\-Pd (|) - 2 v^d (-^), (10.43)
где — потенциальная энергия грамм-молекулы /-й компонен-
ты, т. е. химический потенциал. Перепишем это равенство в
виде
у _____ DU I р & О/Р) _X1 и & /1 п 4д\
1 Dt ~ Dt к Dt Dt *
i
Исключая с помощью уравнений (10.36) — (10.39) производные
по времени в правой части (10.44), найдем для о и р следую-
щие выражения:
» = т Г(Ч + Чя) - 2 Vzl. (10.45)
L /
£== - i((q+Чя) • - I IP : VV]-
-• {v“г}]-(10-46>
i i
Преобразуем эти выражения к более удобной форме.
Вектор а представляет собой обратимый1) поток энтропии.
Это легко увидеть из следующих соображений. Общий поток
энергии q + Яд можно записать в виде суммы двух членов
Ч + ЧЛ = е + 2«да, ’ (10.47)
i
где Hi — парциальная молярная энтальпия. Второй член дает
поток энергии, связанный с процессом диффузии, тогда как ве-
личина в (определяемая этим уравнением) есть поток тепловой
энергии. Из (10.45) и (10.47) следует
’ = т + (ю.48)
I
где Si — парциальная молярная энтропия. Из этого выражения
видно, что о — сумма двух членов, первый из которых есть по-
ток энтропии, вызываемый тепловым потоком, а второй член
обусловлен процессом диффузии. Скорость возникновения эн-
тропии g можно выразить теперь через скорости образования
молекул различного типа Кг- Химические процессы, протекаю-
!) Термин «обратимый» здесь имеет тот смысл, что 1-й член в правой
части (10.42) в отличие от 2-го может быть знакопеременным. — Прим, перев.
10.5. Общие процессы переноса в изотропной среде
393
щие в реагирующей смеси, описываются уравнениями реакции,
которые имеют следующий символический вид:
МЧ + М21+ + ••• • (10.49)
Здесь и т].ц—целые числа, а [/]— концентрация z-й компо-
ненты. Пусть ky, — постоянная скорости для ц-й прямой реак-
ции, a k [л—постоянная скорости для ц-й обратной реакции.
Тогда скорость прямой реакции равна
(10.50)
где fi — текущая концентрация z-й компоненты. Аналогичное
выражение можно написать и для обратной реакции. Общая
скорость образования z-x молекул в результате всех химиче-
ских реакций равна
^ = 2(ч,и-₽,„)[у>г?" ... -*»/>...]• (Ю.51)
ц
Химическое сродство и скорость ц-й реакции определим
выражениями
= (10.52)
гц = • • • -• • •)• <10'53)
Согласно (10.46), скорость возникновения энтропии за счет
химических реакций равна
--г2'*л=т2'-л- <1054>
z ц
Подставляя это выражение, а также выражение для потока
энергии (10.47) в (10.46), получаем
+ О0-55)
< 1 И
где ji = nimiVi — поток массы z-й компоненты (nti — масса мо-
лекулы z-ro сорта), а
Az = — + vr — —. (10.56)
1 ГП[ 1 mi mi v 7
Химический потенциал цг- зависит от состояния системы и, в ча-
стности, может рассматриваться как функция Г, Р и zif. Част-
ные производные по Т и Р исключаются с помощью термодина-
394
Гл. X. Общая теория процессов переноса
мических соотношений
здесь Vi — парциальный молярный объем. Поэтому
Л, = —
^-VP----
mi mi L
(10.57)
Из (10.55) видно, что скорость возникновения энтропии необра-
тимых процессов является суммой четырех членов: первый
член — следствие диффузии, второй член — следствие переноса
импульса, третий член — следствие переноса энергии, четвер-
тый — следствие химических реакций. Форма этого уравнения
позволяет непосредственно применить принципы термодинамики
необратимых процессов для анализа процессов переноса, что
мы и сделаем в следующем пункте.
10.6. Феноменологические законы процессов переноса
в жидкости
На основании (10.55) можно выбрать в соответствии с
(10.23) потоки Ji и обобщенные силы Х{. Эти потоки и обоб-
щенные силы представлены в табл. 10.1, где поток импульса р
Таблица 10.1
Потоки и обобщенные силы
Потоки Обобщенные силы
название выражение название выражение
Поток диф- фузии Z-й компоненты У/ «Градиент концентра- ции» -Az (формула (10.57)}
Тензор напряжений (давлений) р = л — Ра Градиент скорости — v V
Поток тепла — ZniMiVi 1 Градиент температуры —
Скорость |1-й реакции (10.53) гч Химическое сродство Уц (формула (10.52))
10.6. Феноменологические законы процессов переноса
395
есть тензор напряжений л без гидростатического члена Ри, а
поток энергии е отличается от суммы векторов переноса тепла
q и излучения qR диффузионным членом —
i
Согласно общему закону переноса, если состояние системы
мало отличается от равновесного, то каждая компонента пото-
ков может быть представлена как линейная комбинация всех
обобщенных сил. В табл. 10.1 jz, Az, ez, VP — векторы
(тензоры 1-го ранга), — скалярные величины (тензоры ну-
левого ранга), р и VV — тензоры 2-го ранга. Для изотропной
среды можно показать, что некоторые связи будут отсутство-
вать. Действительно, пусть, например, векторный поток А свя-
зан линейно со скалярной обобщенной силой В. В проекциях
на координатные оси х, у, z имеем
Ах = схВ.
Ау = с2В, (10.58)
Аг — с3В,
причем эти законы должны иметь место в любой системе ко-
ординат. Так как физические явления в изотропных средах не
могут зависеть от выбора системы координат, то и с2, с$ не
должны зависеть от системы координат. Обозначим через х'
направление, противоположное оси х. В новых координатах
компонента Ах меняется на —АХ'. Тогда, согласно (10.58),
— АХ' = с\В. (10.59)
Но в соответствии с требованиями изотропности
АХ=С\В. (10.60)
Сравнивая (10.59) и (10.60), имеем ^ = 0. Аналогично с2 = Сз=0.
Следовательно, векторный поток в изотропной среде не может
зависеть от скалярной обобщенной силы. И обратно, скалярный
поток не может зависеть от векторной обобщенной силы. При-
меняя аналогичные рассуждения, можно показать, что в изо-
тропной среде связи тензоров, ранги которых отличаются на не-
четное число, будут отсутствовать. Связь тензоров одного ранга,
конечно, возможна. Однако более интересен тот факт, что воз-
можна связь между тензорами, ранги которых отличаются на
четное число. Например, поскольку единичный тензор и не ме-
няется при любых ортонормальных преобразованиях координат,
то скалярное произведение и* и тензора второго ранга есть ска-
лярная величина, которая также не меняется при этих преобра-
зованиях. Более того, сам тензор и, умноженный на константу,
396
Г л. X. Общая теория процессов переноса
может служить коэффициентом связи допускаемой условием
изотропности. Таким образом, скалярный поток А может быть
пропорционален тензорной обобщенной силе 2-го ранга *В
А = си\ В, (10.61)
а тензорный поток 2-го ранга А может быть пропорционален
скалярной обобщенной силе В
А = сиВ. (10.62)
Учитывая результаты предыдущего пункта, мы теперь можем
сказать, что потоки массы и энергии е будут связаны только
с —Лг и------^-V7\ поток импульса р — с — VV и Уг-, а скоро-
сти реакций — с—VV и Уг-. Таким образом, пишем
(10.63)
(10.64)
(10.65)
(10.66)
Здесь латинские индексы i и j означают номер компоненты сме-
си и могут принимать значения 1,2.... Индекс 0 указывает на
градиент температуры и поток тепла; т] и % — коэффициенты
сдвиговой и объемной вязкости. Постоянная является ко-
эффициентом связи потока импульса с химическим сродством
ц-й реакции и вследствие соотношений Онзагера также коэф-
фициентом связи скорости ji-й реакции с градиентом массовой
скорости. Соотношения взаимности Онзагера далее дают
Ll} = Ln, (10.67)
Ll0 = L0i, (10.68)
= (10.69)
10.7. Эффекты Соре и Дюфура
397
Все эти величины являются функциями макроскопических пе-
ременных Т, Р и tii.
Законы переноса (10.63) — (10.69), установленные для дви-
жения жидкости с химическими реакциями, являются полными
и общими, насколько это возможно. Конечно, здесь мы ограни-
чиваем систему состоянием, близким к термодинамическому ра-
вновесию. Поэтому если рассматривать химическую реакцию, то
вещества, участвующие в ней, обязательно должны находиться
вблизи состояния равновесия. В следующем пункте рассмотрим
подробнее значение полученных результатов.
Отметим еще, что не все обобщенные силы являются гради-
ентами в обычном смысле этого слова. Например, не яв-
ляется градиентом. Однако это обобщенная сила, вызывающая
поток. В действительности любые «реакции» от состояния, близ-
кого к термодинамическому равновесию, до равновесного со-
стояния, например аллотропические превращения в металлах и
сплавах или малые пластические деформации металлов и спла-
вов, — все они являются процессами переноса, подчиняющи-
мися законам термодинамики необратимых процессов.
10.7. Эффекты Соре и Дюфура
В (10.63) коэффициенты L;j и LiQ не являются совершенно
независимыми, так как должно удовлетворяться условие
2j/ = 0, (10.70)
I
вытекающее из определения скорости диффузии Уг-. Подстав-
ляя (10.63) в (10.70), имеем
- 2 А/ (2 - т2 £‘-о=°-
j \ ‘ / <
Так как это равенство выполняется при любых значениях
Ау и у VT, то
2Ло = О, (10.71)
i
££,7 = 0, (10.72)
и по (10.67) и (10.68)
2^ = 0, (10.73)
= (10-74)
398
Гл. X. Общая теория процессов переноса
Выражения для потоков ]*г и е можно записать в другой форме,
более удобной, например при сравнении с результатами кине-
тической теории. Для этого введем функцию
= + (10.75)
Исключая А, с помощью (10.56), получаем
ч.=? 2 я ~ Т) ’<1п
-^7 х< — S «ухЛ • <‘оге)
где Vi — парциальный молярный объем. Используя свойства
парциальных молярных величин и применяя соотношение Гибб-
са— Дюгема, можно увидеть, что d/ = 0. Принимая во вни-
i
мание (10.75) и (10.71) — (10.74), получаем следующие выраже-
ния для потоков: ____
(10.77)
j
(10.78)
Коэффициент Loo, следовательно, равен произведению коэффи-
циента теплопроводности и температуры Г, а выражаются
через коэффициенты самодиффузии (при /=/) или взаимной
диффузии (при i =# /).
Особый интерес представляют коэффициенты перекрестных
эффектов Лг0 и LQi. Коэффициент Li0, очевидно, связан с терми-
ческой диффузией, т. е. диффузией, вызываемой градиентом
температуры. Этот эффект был открыт Соре1). Согласно
(10.77), при наличии градиента температуры состояние равно-
весия (/г = 0) достигается лишь компенсацией термической диф-
фузии обычной диффузией. Так как существование обычной
диффузии означает существование неравномерной концентра-
ции, то, создавая градиент температуры, можно установить и
поддерживать градиент концентрации. Этот факт использовался
для разделения изотопов, причем градиент температуры под-
держивался разностью температур стенок сосуда, содержащего
газ.
*) Soret С., Arch. Sc. Phys. Nat. (Geneve), 29 (1893), 4; 32 (1894), 12.
10.7. Эффекты Соре и Дюфура
399
Коэффициент Лог связан с потоком тепла, вызываемым не-
равномерной концентрацией. На существование этого эффекта
впервые указали Дюфур1) и независимо Клаузиус и Вальд-
ман2). Возьмем вертикальную трубку, которая разделена на
две части непроницаемой диафрагмой. Если одна часть трубки
заполнена сравнительно тяжелым газом, а другая — легким,
причем температура и давление поддерживаются одинаковыми,
то при снятии диафрагмы получится физическая смесь, которая
со временем вследствие диффузии станет однородной, и темпе-
ратура, как и вначале, будет всюду одинаковой. Однако в про-
цессе диффузии условия меняются. Сразу после снятия диа-
фрагмы в двух частях трубки температура остается одинаковой,
следовательно, потока тепла, вызываемого градиентом темпера-
туры, не возникнет. Но на границе двух газов существует гра-
диент концентрации. Поэтому, согласно (10.78), между газами
возникает поток тепла; один газ подвергнется нагреванию, дру-
гой — охлаждению. В процессе диффузии градиент концентра-
ции уменьшается, вместе с ним уменьшается и поток тепла, вы-
зываемый градиентом концентрации. Градиент температуры,
установленный первоначальным потоком тепла, не может долго
сохраняться, так как обычная теплопроводность вызывает об-
ратный поток тепла. Поэтому тепло возвращается, и во всей
трубке устанавливается равномерная температура. Таким обра-
зом, температура газа, принимающего первоначальный поток
тепла, становится выше исходной, а температура газа, из ко-
торого возникает тепловой поток, понижается. Результаты экс-
периментов Клаузиуса и Вальдмана, показанные в табл. 10.2,
Таблица 10.2
Эффект Дюфура по измерениям Клаузиуса и Вальдмана
Газы Максимальная и минимальная температуры, полученные при измерениях
H2 CO2 в Н2 4-0,15° С в СО2 — 0,63° С
H2 n2 в Н2 4-0,17° С в N2 — 0,65° С
n2 CO2 в N2 4- 0,029° С в СО2 — 0,063° С
n2 o2 в N2 4-0,017° С в О2 —0,019° С
Светильный газ воздух в светильном газе 4~ 0,1 Г С в воздухе — 0,29° С
свидетельствуют, что хотя эти эффекты и незначительны, од-
нако возможность их измерения существует.
!) Dufour L., Arch. Sc. Phys. Nat. (Geneve), 45 (1872), 9; Ann. Phys.
(5), 28 (1873), 490.
2) Clausius K., W a 1 d m a n n L., Naturw., 30 (1942) ,711.
400
Г л. X. Общая теория процессов переноса
10.8. Процессы переноса, сопровождающиеся химическими
реакциями
Подчеркнем еще раз, что при малых отклонениях изотроп-
ных жидкостей от термодинамического равновесия химические
реакции не связаны с образованием потоков массы и энергии.
Поэтому рассуждения предыдущего пункта об эффектах Соре
и Дюфура сохраняют силу и при наличии химических реакций.
В выражениях (10.65) для тензора вязких напряжений р и
(10.66) для скорости Гц отдельной реакции р довольно обыч-
ными являются первые слагаемые. Напряжения вязкости опре-
деляются прежде всего скоростями деформаций и коэффициен-
тами вязкости г) и х. В изотропной среде существуют лишь два
коэффициента вязкости, т] и х, и оба они являются функциями
макроскопических термодинамических переменных Г, р и щ-.
Если молекулы газа не имеют внутренних степеней свободы или
внутренние степени свободы «заморожены», т. е. не могут воз-
буждаться при столкновениях молекул, то значение х равно
нулю. Однако для многоатомных молекул х того же порядка,
что и т), а для жидкостей х может быть намного больше т|.
Первая сумма в выражении для скорости химической реак-
ции (10.66) содержит коэффициенты Lgv, удовлетворяющие со-
отношениям взаимности (10.69). Здесь мы встречаемся с прин-
ципом детального равновесия. Согласно этому принципу, если
система находится в состоянии равновесия, то каждая отдель-
ная химическая реакция также находится в равновесном со-
стоянии. Этот принцип вместе с химической кинетикой газов
дает соотношения взаимности (10.69) 9- Однако обратное не-
верно, так как соотношения Онзагера вовсе не должны вклю-
чать детальное равновесие. Можно иметь соотношения взаим-
ности, ничего не зная о химической кинетике. Конечно, в таких
случаях невозможно провести преобразования, аналогичные
(10.49), (10.54), однако можно получить соотношения взаимно-
сти рг- и Кг- Таким образом, соотношения Онзагера являются бо-
лее общими по сравнению с принципом детального равновесия.
Особого внимания в (10.65), (10.66) заслуживает влияние
химических реакций на диагональные компоненты тензора на-
пряжений, а также влияние объемного расширения на скорости
химических реакций. Эти эффекты вплоть до сегодняшнего дня
не исследованы сколько-нибудь подробно. Они очень важны для
описания фронта волны детонации, где взаимосвязаны высокие
скорости химических реакций и быстрые сжатия и расширения.
1) См. Де Гроот, Термодинамика необратимых процессов, ГИТТЛ,
1956.
10.9. Приложения термодинамики необратимых процессов
401
Разумеется, мы не можем здесь проводить анализа на основе
термодинамики необратимых процессов, а должны опираться
на микроскопические молекулярные свойства, т. е. на кинетиче-
скую теорию движения неоднородных газов с химическими реак-
циями.
10.9. Приложения термодинамики необратимых процессов
В предыдущих пунктах мы ограничились рассмотрением
термодинамических, химических и динамических величин и не
касались величин электромагнитных. Связывая тепловые и элек-
трические эффекты, можно с помощью термодинамики необра-
тимых процессов построить феноменологическую теорию термо-
электричества !). Все эти примеры описаны в упомянутой книге
Де Гроота. В настоящее время областью, еще не исследован-
ной с точки зрения термодинамики необратимых процессов,
является магнитная гидродинамика. В этой области гидромеха-
ники, кроме уравнений п. 10.5, используются еще уравнения
Максвелла. Ясно, что здесь мы имеем дело с новыми и более
сложными процессами переноса.
Судя по этой главе, прикладное значение термодинамики
необратимых процессов фактически заключается в том, что с ее
помощью можно дать общее описание некоторых ситуаций, ука-
зать общую структуру феноменологических законов, выявить
все возможные эффекты взаимодействия процессов переноса.
Численные значения коэффициентов переноса остаются неопре-
деленными, но благодаря соотношениям взаимности Онзагера
только половина коэффициентов переноса для перекрестных эф-
фектов подлежит теоретическому или экспериментальному опре-
делению. Освобождение от другой половины — хорошая эконо-
мия сил. Поэтому в любых исследованиях процессов переноса
применение термодинамики необратимых процессов всегда дол-
жно быть первым шагом — первым шагом на пути к сложным
расчетам кинетической теории.
Задачи к главе 10
10.1. Доказать (10.35) для любой изотропной среды.
0 Связывая эффекты количества движения и электричества, можно
создать теорию электроосмоса.
26 Зак. 1299
Глава XI
ВЯЗКОСТЬ,
ДИФФУЗИЯ и ТЕПЛОПРОВОДНОСТЬ
В данной главе мы продолжим рассмотрение свойств пере-
носа неравновесных ансамблей. Для более тщательного иссле-
дования этого вопроса используем понятия кинетики. Централь-
ным понятием в кинетике является функция распределения
вероятностей f для описания состояний ансамбля. РЗсли рассма-
триваемый ансамбль представляет собой разреженный газ,
состоящий из одинаковых молекул, то ввести функцию распре-
деления вероятностей очень легко. Состояние отдельной моле-
кулы описывается положением и скоростью центра инерции, а
также другими координатами и импульсами, относящимися к
внутренним степеням свободы.
Поэтому если пренебрегать возбужденными электронными
состояниями, то многоатомная молекула из s атомов обладает
3s степенями свободы и 6s координатами и импульсами. Обо-
значим координаты молекулы (х, у, z), скорости (u, v, w), а вну-
тренние степени свободы <71, 72, ...» <7з«-з; Рь Р2, . .., Рзз-з. Тогда
вероятность нахождения молекулы в элементе фазового про-
странства dxdy dzdudv dw dq{dq2 ... dq3S_3dpidp2 ... dpZs_z в
момент времени t равна
/(%, у, z; и, v, w, qv q2, ..., ^_3; px, p2, .... p3i_3; t)dx ... dpis_3.
где f — плотность распределения вероятностей, или сокращен-
но функция распределения. Приведенное определение функции
распределения применимо лишь к разреженным газам, моле-
кулы которых взаимодействуют очень слабо. Найдя Д можно
вычислить макроскопические величины, такие, как напряжения
и т. п. Для плотных газов и жидкостей необходимо знать би-
нарные функции распределения и функции распределения бо-
лее высокого порядка, характеризующие одновременно более
двух молекул. х
Таким образом, нахождение функции распределения является
главным вопросом кинетики. Однако математический анализ
реальных проблем весьма сложен даже в сравнительно простых
случаях, таких, например, как разреженные газы с фиксирован-
ным набором молекул. Затруднения математически выражают-
11.1. Число столкновений в газе
403
ся в нелинейности уравнения для Д Это свойство можно понять
из следующего факта: так как изменение f вызывается «столк-
новением» двух молекул, то оно связано, следовательно, с про-
изведением двух значений /, и уравнение для f будет нелиней-
ным. Ввиду этих сложностей познакомимся вначале с так на-
зываемой «элементарной теорией явлений переноса»1). Такая
теория является приближенной, но, кроме того, что она более
проста, она еще и более ясна с точки зрения физического смыс-
ла. Изучив свойства переноса с помощью элементарной теории,
рассмотрим затем более точные соотношения на основе кине-
тики.
11.1. Число столкновений в газе
В элементарной теории явлений переноса в газах сущест-
вует величина, имеющая первостепенное значение. Это средняя
длина свободного пробега молекулы, т. е. среднее расстояние,
проходимое молекулой газа между двумя ее «столкновениями»
при термодинамическом равновесии. В дальнейших расчетах
придется часто пользоваться этой величиной. Наиболее удоб-
ным способом определения средней длины свободного пробега
является нахождение числа столкновений молекулы в единицу
времени. Очевидно, что внутренние степени свободы в этой за-
даче не сказываются и достаточно знать лишь функцию рас-
пределения по поступательным степеням свободы.
Кроме того, газ, находящийся в термодинамическом равно-
весии, является однородным в пространстве х, у, z. Поэтому
функция распределения зависит лишь от скоростей и, v, w и не
зависит от координат. В п. 5.1, 5.2 такая функция распределе-
ния f(u, v, w) уже была найдена. Если через п обозначить чис-
ленную плотность одноатомного газа, находящегося в равно-
весии, то число молекул со скоростями, заключенными между
и, v, w и u+du, v + dv, w-\-dw, равно
v, 'w)dudevd<wi
где
f(u, v, = !exp{ — -2^-(м2 + г>2 + ®»2)}, (11.1)
Для расчета столкновений нужно знать закон взаимодей-
ствия молекул. Если молекулы сферически симметричны, то за-
кон взаимодействия можно выразить с помощью радиальной
функции типа потенциала Леннарда—Джонса (8.78). Но, как мы
!) См., например, Jeans J.. An Introduction to the Kinetic Theory of
Gases, Cambridge, 1940.
26*
4Э4
Г л. XI. Вязкость, диффузия и теплопроводность
уже видели в восьмой главе, наиболее просто взаимодействуют
твердые упругие сферы. Для простоты, а также в связи с тем,
что элементарная теория является лишь первым приближением,
будем считать молекулы гладкими твердыми сферами диаметра
D. При этом столкновение будет упругим, и так как сферы
гладкие, то передача внутренней вращательной энергии проис-
ходить не будет.
Рассмотрим сначала простейший случай столкновения. Пусть
две молекулы до столкновения движутся по одной линии со ско-
ростями и и и'. Эту линию можно принять за ось х. Общий им-
пульс вдоль оси х, m(t/ + uz), при столкновении сохраняется, а
относительная скорость и' — и меняет знак, поскольку столк-
новение упругое. Отсюда получаем, что молекулы обменивают-
ся своими скоростями. Если до столкновения скорости равны и
и и', то после него они будут соответственно и' и и.
Компоненты скорости вдоль осей у и z при столкновении не
изменяются, так как нет сил, действующих в этих направле-
ниях. Таким образом, если до столкновения молекулы обладают
скоростями
w и uz, uz, w',
то после столкновения их скорости будут соответственно
uz, у, w и и v', w'.
Рассматривая множество столкновений со скоростями в интер-
валах
(u, u+du), (и, v + dv), (w,w + dw)
и
(и', u' + du')y (v\ v' + dv'), (w'f w'+dw'),
после столкновений получаем скорости в интервалах
(uz, u' + du'), (у, v + dv), (w, w + dw)
и
(ut u+du), (1/, v' + dv'), (w^w' + dw').
11.1. Число столкновений в газе
405
Обратим внимание на произведение шести дифференциалов
du dv dw du' dv' dw'. Видно, что этот элементарный объем про-
странства скоростей до столкновения du dv dw du' dv' dw' и после
столкновения du' dv dw du dv' dw' одинаков.
В рассмотренном случае предполагалось, что столкновение
происходит вдоль оси х. При этом, накладывая относительную
скорость вдоль оси (с надлежащим знаком) на скорость до
столкновения, получаем скорость после столкновения. Этот вы-
вод остается в силе, если не выделять в качестве специальной
ориентации (ось х) линию столкновений. От выбора осей не за-
висит и другой вывод — элементарный объем пространства ско-
ростей до столкновений du dv dw du' dv' dw' равен соответствую-
щему объему после столкновений.
Снимем теперь ограничение, что столкновение происходит
вдоль оси х, и рассмотрим более общий случай (столкновение
типа а), определяя его тремя условиями:
а) одна из двух сталкивающихся молекул относится к мо-
лекулам типа Л, скорости которых находятся в интервалах
(и, u + du), (v,v + dv), (w, w+dw);
b) вторая молекула относится к типу В — со скоростями в
интервалах
(и', u'+du'), (1/, v' +dv'), (w', w'+dw')\
с) линия столкновений имеет направляющие косинусы /, m,
п и находится в телесном угле dco.
Если молекулы имеют одинаковые диаметры Z), то столкно-
вение происходит всякий раз, когда расстояние между центра-
ми любых двух молекул равно D. Построим мысленно вокруг
каждой молекулы типа А сферу радиуса D. На ее поверхности
телесный угол dco, упоминавшийся в условии с), вырезает пло-
щадку D2da. Очевидно, что столкновение типа а происходит
всякий раз, когда центр молекулы типа В попадает на эту пло-
щадку D2da.
Пусть до столкновения относительная скорость двух моле-
кул равна V. Вторая молекула, двигаясь относительно первой,
за время dt проходит путь Vdt в направлении V. Таким обра-
зом, в течение времени dt перед столкновением центр второй
молекулы находился в области D2dmVdt cos 0, получаемой в ре-
зультате перемещения площадки £>2dco в направлении, противо-
положном V, где 0 — угол между направлением (/, /и, и) и век-
тором— V. Поэтому если столкновение происходит в какой-то
момент времени в интервале dt, то центр второй молекулы на-
ходится в цилиндре, образуемом указанным перемещением эле-
мента D2d& (см. рис. 11.2).
406
Гл. XL Вязкость, диффузия и теплопроводность
Основание этого цилиндра равно D2dco, высота равна
УЛ cos 0, а объем, следовательно, VD2 cos 0 Ло dt. Число молекул
типа В, находящихся в таком цилиндре, согласно (11.1), равно
nf(u', v', w')du' dv' dw' VZ)2cos0d(od/. (11.2)
Это есть также вероятность столкновения типа а для одной мо-
лекулы типа А за время dt. В единице объема газа содержится
nf(u, v, w)dudvdw молекул типа А. Умножая выражение (11.2)
на количество этих молекул, получаем общее количество столк-
новений типа а, происходящих в единице объема газа за вре-
мя dt,
n2f(u, v, w)f(u', v', w') VD2ws§dudvdwdu'dv'dw'd&dt. (11.3)
Этот результат подтверждает высказанное ранее утверждение
о нелинейности уравнения для /. Если заменить f(u,v,w) и
f(u',v',w') выражением (11.1), соответствующим термодинами-
ческому равновесию, то число столкновений в единицу времени
будет равно
«2 ( 2^т}3 еХ₽ { — + w2 + “/2 + Х
X VD2 cos 0 du dv dw du' dv' dw' da), (11.4)
где V — относительная скорость, определяемая выражением
I/2 = (и — и')2 -|- (v — v')2 -|- (w — w')2. (11.5)
11.1. Число столкновений в газе
407
Проведем интегрирование по различным переменным, содержа-
щимся в (11.4).
Рассмотрим прежде всего выражение D2 cos 0dco. Очевидно,
что D2da) есть элемент площади на сфере радиуса D (Р на
рис. 11.3), a D2 cos — проекция Q на плоскость АВ, перпен-
дикулярную V. Если скорости молекул и, v, w\ и', v', w' фикси-
рованы, то и V фиксирована, а Р может находиться в любой
точке полусферы радиуса D. Интеграл от D2 cos 0dco дает пло-
щадь сечения АВ или л/)2. Таким образом, число столкновений
со всевозможными ориентациями линии центров равно
л£>2«2 ехР { — 217+ «'2 + "а'2 + ^/2)} X
X — #')2+ — v')2 + — w')2 du dv dw du' dv' dw'. (11.6)
Это есть число столкновений молекул типа А с молекулами ти-
па В в единице объема за единицу времени.
Для удобства интегрирования по скоростям сделаем замену
1
^/ = 7Т(и+а/);
n = —X), т1/ = р=г(^+'у');
(11-7)
г 1 .
(«'+«'')•
408
Гл. XL Вязкость, диффузия и теплопроводность
Тогда (11.6) примет вид
* w (iSt)3 ехР | - w +^+^2+*'2++^2)} х
X /2 (^2 + п2 4-С2) dl Л] dl dt,' d^' dZ'.
Интегрируя по т/, получаем
xDW ( 2^7 )3 ехР { - -^Т | /S^ + T' + C2) dt, dr] dZ.
Это выражение равно не числу столкновений (со скоростями g,
т], g из dg, dv\, а удвоенной величине, так как каждое столк-
новение подсчитывалось дважды (один раз — молекулы типа А
с молекулой типа В, другой раз — молекулы типа В с моле-
кулой типа Д). Таким образом, истинное число столкновений
со скоростями g, rj, g из элементарного объема dg, dv[,d£ равно
4 (W Г “Р {—w &+n!+О} X
X /2(g2 + n2 + C2) d\ di\ dt (11.8)
Пусть теперь
V2 = 2 (g2 Д-Л2 + С2)»
а
g =-7=^ cos ф sin ft,
K2
T) = p==- sin ф sin ft,
Тогда (11.8) после интегрирования по ф и 0 примет вид
l/-L)3nD2n2 /_2?_y%xp(----V2 J V4ndV =
2\f2l \2nkTl 4 4kT )
= 2/л ^£>2 ехр | V2| V3 dV^ (1! ,9)
Это есть общее число столкновений с относительной скоростью
в промежутке между 1/хи I/4-dV. Если, наконец, выполнить ин-
тегрирование по V от 0 до оо, то получим общее число всевоз-
можных столкновений
П2Д2 1 /
г пг
(11.10)
11.2. Средняя длина свободного пробега
409
Согласно (11.1), вероятность того, что молекула имеет ве-
личину скорости между с и c + dc, равна
exP(~ J ехр(—
' о
Таким образом, средняя величина скорости молекул газа, нахо-
дящегося в термодинамическом равновесии, равна
fехр ("2^7"с2)c3dc ____
= __________________— 1/ ..г —2 |/ ?kT (11 11)
6 00 V m Г(3/2)~2и nm ' V11-11)
f ехр [-2^CT2dC
о
Отсюда общее число столкновений в единице объема за еди-
ницу времени (11.10) можно написать в виде
(11.12)
где п — численная плотность газа, a D — диаметр молекулы.
11.2. Средняя длина свободного пробега
Рассмотрим свободный пробег как расстояние, проходимое
молекулой между двумя последовательными столкновениями.
Это так называемая средняя длина свободного пробега Макс-
велла. Так как при каждом столкновении заканчиваются два
свободных пробега, то общее число свободных пробегов вдвое
больше числа столкновений (11.12). Таким образом, число сво-
бодных пробегов в единице объема за единицу времени равно
/2 nn?D*c.
Общая длина всех этих свободных пробегов естественно есть
общее расстояние, пройденное п молекулами в единицу вре-
мени, т. е. пс. Поэтому после деления получим среднюю длину
свободного пробега
Фактически длина свободного пробега зависит от величины
скорости молекулы. Рассмотрим молекулу, движущуюся со ско-
ростью с. Вероятность ее столкновения в единицу времени с мо-
лекулой, обладающей скоростью с', равна числу молекул
410 Гл. XI. Вязкость, диффузия и теплопроводность
в цилиндре с основанием л£>2 и высотой V, где V — относительная
скорость. Пусть 0, ср — углы, определяющие ориентацию век-
тора относительной скорости, причем 0 — угол между направ-
лениями скоростей с’’ и с. Число молекул второго типа в еди-
нице объема (со скоростями из элемента с'2 sin QdQdqdc') равно
п I ) ехР( — ~2kr~c )с sm 6 dftdqdc .
Интегрирование по ф дает 2л. Умножая на объем цилиндра
л£>2У, имеем
2nD2 j/"л (“2^Г’)3,п3 ехР (-Wrc^c'" sin 0 ^0 de'. (11.14)
Когда с, с' фиксированы, V изменяется только за счет 0.
V2 = с2 + с,2 — 2сс' cos 0.
Дифференцируя, получаем
VdV=cc' sin 0 б/0.
Следовательно, (11.14) можно заменить выражением
2raD21/л (^Гехр (— с'2') de’ V2 dV. (11.15)
у у ZfK 1 j у Z/v/ j c
Интегрируя V2dV в пределах от \c — c'| до с + с', находим
J V2</I/ =
с(с2 + 3с'2) при с'
с' (с/2 + Зе2) при с'
с,
с.
Таким образом, после интегрирования (11.15) по V имеем
4 nD2 \ f п ехр (~9ту- £/2) с' (с2 + Зс'2) de' при с' > с.
О г \ 1 / \ /
4 nD2 \f л ехр с'2} (с'2 + 3<?2) de' при с' < с.
О Г \ / \/£К1 / v
(11.16)
Это есть вероятность столкновения за единицу времени ме-
жду данной молекулой, движущейся со скоростью с, и молеку-
лой, имеющей скорость с'. Интегрируя по с' от 0 до оо, полу-
11.2. Средняя длина свободного пробега
411
чаем
/ехР(-2^?
О
c'2)^(c/2+3c2)rfc' . (11.17)
Выражение в квадратных скобках равно
С V 2kT ехР ( 2kT с2) +
«1/-2-
V 2kT
+ (^7rt?2+1) J ехР(— y^dy
(11.18)
Второй член выражается через функцию ошибок. Однако более
удобно ввести функцию
Ф(х) = х<?-*’+(2х-Ь1)/е~«3(1у. (11.19)
О
Тогда (11.18) примет вид
Если величину (11.17) обозначить через 0, то
e = О1-20’
\2kT ]
Средняя длина свободного пробега /с молекулы с величиной
скорости с равна
= (И-21)
Пользуясь (11.11) и (11.13), получаем
(11.22)
412
Гл. XI. Вязкость, диффузия и теплопроводность
Численные значения 1с/1 как функции отношения с/с представ-
лены в табл. 11.1.
Таблица 11.1
Зависимость свободного пробега
от величины скорости
С/С 1 / с de 'с/; ,!1с
0 0 оэ 1,772 1,2572 0,7954
0,25 0,3445 2,9112 2 1,2878 0,7765
0,5 ' 0,6411 1,5604 3 1,3551 0,7380
0,627 0,7647 1,3111 4 1,3803 0,7244
0,886 0,9611 1,0407 5 1,3923 0,7182
1,0 1,0257 0,9749 6 1,3989 0,7149
1,253 1,1340 0,8819 оо 1,4142 0,7071
1,535 1,2127 0,8247
11.3. Сохраняемость скорости после столкновения
Исследуем теперь средние эффекты, связанные с изменением
скорости при столкновении. Столкновение не обязательно ме-
няет направление движения на противоположное или обращает
скорость в нуль. Имеется тенденция к сохранению первоначаль-
ного направления скорости. Проследим степень сохраняемости
скорости при столкновении.
Моделируя молекулу^упругой сферой, рассмотрим столкно-
вение двух молекул с одинаковыми массами и скоростями с и
с'. Пусть ОР и OQ на рис. 11.4 обозначают эти скорости, a R—
середина PQ. Тогда можно разделить рассматриваемое движе-
ние на два:
а) движение центра инерции двух молекул со скоростью OR-t
11.3. Сохраняемость скорости после столкновения
413
б) движение относительно центра инерции со скоростями
RP и RQ, равными по величине, но противоположными по на-
правлению.
Проведем через R плоскость RTS, параллельную общей ка-
сательной плоскости к сферам при столкновении. Пусть Р', Q'—
зеркальные отображения Р, Q относительно этой плоскости.
Тогда ясно, что RP' и RQ' — скорости после столкновения по
отношению к центру инерции, а ОР' и OQ'— реальные скорости
в пространстве.
Рис. 11.5.
Так как взаимное расположение сталкивающихся в про-
странстве молекул не является упорядоченным и все ориента-
ции плоскости RTS допустимы в одинаковой мере, то все на-
правления скоростей RP'y RQ' после столкновения равновероят-
ны. Поэтому тенденция изменения направления скорости моле-
кулы при столкновении определяется вектором OR. Найдем те-
перь среднее значение всех возможных направлений скорости
второй молекулы при фиксированной ее величине. Пусть на
рис. 11.5 ОР и OQy как и раньше, обозначают скорости двух
сталкивающихся молекул, a R — середина PQ, т. е. скорость
центра инерции двух молекул. Будем искать среднее значение
скорости OR при условии, что Q находится на сфере с центром
О. Легко увидеть, что средняя компонента скорости OR, перпен-
дикулярная направлению ОР, равна нулю. Поэтому можно
искать только компоненту в направлении ОР, т. е. ON. Мы не
можем предполагать, что вероятность по каждому направле-
нию OQ одинакова, ибо, как указано в п. 11.1, вероятность
столкновения молекул, обладающих произвольными скоростя-
ми, прямо пропорциональна относительной скорости. Поэтому
вероятность направления OQ между 0 и 0Н-б/0 пропорцио-
414
Гл. XI. Вязкость, диффузия и теплопроводность
нальна не sin 0d0, a PQ sin 0d0, где PQ — относительная ско-
рость, Среднее значение компоненты ON, следовательно, равно
Л
J ONPQ sin ем
ON = ^—^-------------. (11.23)
У PQ sin 0 de
о
Напишем теперь
ОР = с, OQ = c', PQ = V,
так что
V2 = c2-i~c'2 — 2cc'cos0. (11.24)
Отсюда
ON = 1 (OP + ОМ) = 1 (с + с' cos 0) = ± (Зс2 4- С2 — V2).
(11.25)
Дифференцируя (11.24), получаем
V dV = cc' sin 0 dQ.
Теперь (11.23) примет вид
____ f (3c* + c'2-V>)V2dV , fv<dv
ON = —---------------------= ------~r------• О1-26)
4с I V2 dV 4с I V2 dV
После интегрирования (в пределах от |с'— до с' + с) найдем
при с > с'
ON= 15f + c,4 2. . (11.27)
Юс (Зс2 4 с'2) v ’
при с < с'
ON = с(5с/243с2) (11.28)
5 (Зс'2 4 с2) ' ’
Так как при всех значениях с и с' эти выражения являются
положительными, то независимо от скоростей двух сталкиваю-
щихся молекул математическое ожидание скорости первой мо-
лекулы после столкновения действительно находится в том же
направлении, что и скорость до столкновения. Конечно, это
справедливо и для второй молекулы. Если обозначить CW через
а, где ON— математическое ожидание скорости первой моле-
кулы в направлении ОР после столкновения, то отношение а/с
можно назвать коэффициентом сохраняемости скорости первой
11.4. Элементарная теория вязкости газа
415
молекулы. Выражения (11.27), (11.28) дают значение а, а сле-
довательно, и коэффициент сохраняемости а/с. Можно заме-
тить, что величина а/с зависит только от отношения c/c't а не
от каждой из с и с' по отдельности. Если обозначить с/с' через
х, то коэффициент сохраняемости будет равен
с 1 а
при X = -F-> I т
15х4 + 1
10х2 (Зх2 + 1) ’
с . ч а
при х = — < 1 -
Зх2Ц-5
5 (х2 + 3) •
(11.29)
(11.30)
Численные значения, найденные по этим формулам, помещены
в табл. 11.2. Видно, что коэффициент сохраняемости представ-
Таблица 11,2
Коэффициент сохраняемости скоростей молекул
после столкновения
с/с' со 4 2 4 1 2 3 1 2 1 4 0
а/с 0,50 0,492 0,473 0,441 0,400 0,368 0,354 0,339 0,333
с'/с 0 1 4 1 2 2 3 1 >4 2 4 оо
ляет собой дробь, которая может меняться между 7з и !/2. Сле-
довательно, если в первом приближении допустить, что коэф-
фициент сохраняемости равен 40%, то можно получить доволь-
но хорошие результаты.
11.4. Элементарная теория вязкости газа
Используем результаты, полученные для газов при термоди-
намическом равновесии, чтобы рассчитать вязкость газа. Так
как эффект вязкости появляется лишь тогда, когда в газе
имеются неодинаковые макроскопические скорости, то приме-
нение теории равновесных явлений к неравновесному процессу
переноса оправдывается лишь при условии, что отклонение от
равновесного состояния мало. Смысл этого условия уже разъ-
яснялся в предыдущей главе. Коротко говоря, когда отклонение
от равновесия очень мало, при описании его можно пользо-
ваться функцией равновесного распределения, поскольку ошиб-
ка будет представлять собой лишь величину более высокого по-
рядка малости.
416
Гл. XL Вязкость, диффузия и теплопроводность
Рассмотрим течение газа в направлении оси х с макроско-
пической скоростью и0, зависящей от z (рис. 11.6)._Пусть ц =
= tnu — импульс молекулы в направлении оси_х, a ц— среднее
значение импульса в любой точке газа. Тогда ц равно muQ и яв-
ляется лишь функцией от z. Для определенности предположим,
что ц увеличивается вместе с z. Молекулы проходят через лю-
бую плоскость z=z0 в обе стороны с некоторыми импульсами ц.
Величина ц, которая переносится при прохождении любой
молекулы сквозь эту плоскость, конечно, различна для разных
молекул. Для начала допустим, что она зависит только от по-
следнего столкновения молекулы, т. е. предположим, что моле-
кула несет величину р,, соответствующую месту последнего
столкновения.
Рассмотрим теперь молекулу, которая сталкивается при про-
хождении через плоскость z = zQ в точке Р. Предыдущее столк-
новение было в точке Q. Пусть компоненты скорости этой моле-
кулы равны u, v, w. Разложим вектор скорости и на две состав-
ляющие:
1) 110, с компонентами и0, 0, 0, — макроскопическая ско-
рость газа в точке Р;
2) с, с компонентами и — uQiv,w — относительная скорость
молекулы в точке Р.
Пусть QP на рис. 11.6 обозначает путь молекулы после послед-
него столкновения, a RP — расстояние, пройденное газом в се-
чении Zq за то же время с макроскопической скоростью О,
О, Тогда QR обозначаем путь молекулы относительно макроско-
пического движения окружающего газа. Пусть /г — длина QR,
а 0 — угол, образуемый QR с осью z.
Так как все направления скорости молекул можно считать
равновероятными, то вероятность направления между 0 и
11.4. Элементарная теория вязкости газа
417
0 + d0 пропорциональна sin 0 dQ. Поэтому число молекул в еди-
нице объема, для которых 0 и относительная скорость с нахо-
дятся в элементарных интервалах d0, de, равно
^nf (г) sin 0 dQ de,
где f(c) —функция равновесного распределения величины ско-
рости молекул с, получаемая из (11.1),
= ( 4лс2ехр( 2*7"с"2) ’ (П-31)
Очевидно, что J* f(c)dc— 1. Число молекул, скорости которых
о
удовлетворяют этим условиям и которые в течение времени dt
проходят сквозь единичную площадку плоскости z=z0, равно
числу молекул, содержащихся в цилиндре с основанием еди-
ничной площади на плоскости z = z0 и высотой с cos 0 dt, т. е.
nef (г) cos 0 sin 0 dQ de dt. (11.32)
Величина импульса ц в направлении оси х, которую несут эти
молекулы, соответствует точке Q, а не Р.
Координата точки Q по оси z равна
г0 — lr cos 0.
Среднее значение ц в точке Q меньше, чем в точке Р, на ве-
личину
/rC0Se(-^).
Таким образом, вообще говоря, группа молекул, о которых идет
речь, имеет значение ц, которое отличается от соответствующего
значения в точке Р на величину
-Zccos0(-g-), (11.33)
где /с — средняя длина свободного пробега молекулы, движу-
щейся со скоростью с. Общая величина ц, которую несут все
эти молекулы, проходя сквозь плоскость z—Zq, равна произве-
дению (11.32) на (11.33), т. е.
— ~ lc cos 0 j nef (c) cos 0 sin 0 dQ dt.
Интегрируя это выражение по 0, получаем импульс, перено-
симый молекулами через плоскость z=z0 при всевозможных
27 Зак. 1299
418
Гл. XI. Вязкость, диффузия и теплопроводность
направлениях движения со скоростями между с и c + dc. Угол О
меняется в пределах от 0 до л; значения 0 от 0 до у относятся
к молекулам, проходящим через плоскость z=z0 снизу вверх,
а значения 0 от у до л относятся к молекулам, проходящим че-
рез эту плоскость сверху вниз. Результат интегрирования ра-
вен
— ±ncf(e)lc[^dcdt.
Знак минус показывает, что перенос происходит сверху вниз.
Далее, интегрируя по с от 0 до оо, получаем импульс, который
несут с собой все молекулы, проходящие через единичную пло-
щадку упомянутой плоскости в единицу времени
_ оо
О
Общий закон макроскопического переноса (10.65) свидетель-
ствует о том, что в рассматриваемых условиях газ, находя-
щийся под плоскостью z=z0, оказывает силовое воздействие на
газ, расположенный над этой плоскостью. На единичную пло-
щадку приходится сила, равная —Приравнивая эти два
разных по форме усилия вязкости, получаем коэффициент вяз-
кости
оо
т] = у/ш J cf(c)lcdc. (11.34)
о
Это и есть общее выражение коэффициента вязкости газа, ко-
торое дает элементарная теория.
11.5. Вязкость газа, состоящего из упругих сферических
молекул
Если молекулы представляют собой упругие сферы с диа-
метром D, то свободный пробег /с получается из (11.13) и
(11.22). Используя также выражение для /(с) из (11.31), полу-
чаем коэффициент вязкости в виде
т] = у nm J
о
. / m \ъ1ч , ( — m \
4 ( ) С ехР ( 2fer с ) dC
nnD^(c
- - ОО , 2
2тс Г х°е~х dx
3/й>2 J 4>(х)
(11.35)
11.5. Вязкость газа
419
где функция ф(х) определена в (11.19). Численное значение ин-
теграла в (11.35) равно 1,051/2 )/2тс.
Однако такого рода вычисления обладают сравнительно
большой погрешностью, так как в них пренебрегается влия-
нием сохраняемости скорости, которая рассматривалась в
п. 11.3. Пусть молекула после прохождения пути, имеющего
проекцию £ на ось г, пришла в точку Р со скоростью, компо-
нента которой на ось z равна w (рис. 11.6). При ее движении
в прошлом математическое ожидание скорости, параллельной
оси г, равно 9w, где 0 — коэффициент сохраняемости скорости.
Математическое ожидание пути вдоль оси z, таким образом,
можно принять за 0£. Аналогично математическое ожидание
предыдущего пробега вдоль оси z можно принять за 02£ и т. д.
Таким образом, следует предположить, что эта молекула при-
шла не из точки, расположенной на расстоянии £ вдоль оси г,
а из точки, находящейся на расстоянии
£+0С+П+ ... =1=0- (П-36)
Однако, вообще говоря, нельзя считать, что молекула обла-
дает импульсом ц, соответствующим сечению z=z0+£/(l—0).
Так как описываемая молекула проходит расстояние £/(1 —0),
подвергаясь возмущениям, то ее избыточный импульс частично
передается молекулам, с которыми она сталкивается. Проще
всего предположить, что при каждом столкновении одна поло-
вина избыточного импульса передается, а другая сохраняется.
Тогда математическое ожидание оставшегося импульса соответ-
ствует це (11.36), а расстоянию
:+|{ес+|[02:+|(0^+ •••)]}=—V- о1-37)
i-ye
Поэтому в подинтегральную функцию (11.35) нужно внести
множитель 1Д1 —^ля ПРОСТОТЫ предположим, что с'=с.
Из табл. 11.2 можно взять 0 = -у. В результате после вычис-
ления получим
П = 0,461 -™с . (11.38)
/2 лДг ' ’
Эта формула, выведенная для упругих сферических молекул,
показывает, что ц не зависит от плотности газа. Ясно, что не-
зависимо от модели молекулы средняя длина свободного про-
420
Гл. XL Вязкость, диффузия и теплопроводность
бега в первом приближении обратно пропорциональна численной
плотности газа. Поэтому естественно, что из (11.34) полу-
чается значение т], не зависящее от п. При увеличении плотно-
сти увеличивается число носителей в заданном объеме, но эф-
фективность их понижается. Так как при увеличении вдвое чис-
ла молекул в единице объема свободный пробег уменьшается
наполовину, то и переносимые импульсы также уменьшаются в
два раза. Таким образом, мы получили закон Максвелла: коэф-
фициент вязкости газа не зависит от его плотности.
Очевидно, что этот закон имеет место только для разрежен-
ных газов, так как лишь для них законно проведенное рассу-
ждение. Первоначально он был выведен Максвеллом чисто тео-
ретически и лишь потом подтвержден экспериментально. Это
было одним из блистательных достижений кинетической теории.
11.6. Вязкость реального газа
Из предыдущего анализа видно, что результат (11.38)
нельзя считать точным, так как использованные упрощения
несколько уменьшают эффект сохраняемости скорости молекул
после столкновений. Основным недостатком любой элементар-
ной теории как раз и является отсутствие точности. Для вос-
полнения этого пробела нужно воспользоваться кинетической
теорией неоднородных газов, развитой Максвеллом и Больцма-
ном и изложенной в книге Чэпмена и Каулинга1), где полу-
чены точные результаты. Однако такой сугубо теоретический
подход оказался бы слишком сложным и излагать его здесь
не представляется возможным. Поэтому ограничимся описа-
нием некоторых результатов, полученных по этой точной тео-
рии, и рассмотрим ряд вопросов, связанных с ее применением
к реальным газам. Прежде всего эта точная теория в формуле
для коэффициента вязкости газа из гладких упругих сфер дает
иное значение постоянной. Выражение (11.38) после уточнения
принимает вид
(11.39)
Следовательно, погрешность результатов, полученных по эле-
ментарной теории, составляет 10%. Для удобства практических
вычислений перепишем (11.39) в виде
nX to7 = 271,4-^^-, (11.40)
4 = 0,499
1 /2лР2
9 Чэпмен С., Каулинг Т., Математическая теория неоднородных
газов, ИЛ, М., 1960.
11.6. Вязкость реального газа
421
где [л] = ... ; М — молекулярный вес газа; Т — абсолют-
0^41 * Lu/v
ная температура, °К; О —диаметр молекулы, А. Таким образом,
коэффициент вязкости упругих сферических молекул пропор-
ционален квадратному корню из абсолютной температуры.
Даже после уточнения результат (11.40) все же не может
быть применен к реальным газам, так как упругая сфера не
является достаточно точной моделью реальной молекулы. Вза-
имодействие реальных молекул не похоже на взаимодействие
упругих сфер. Закон их взаимодействия лучше описывается по-
тенциалом Леннарда — Джонса (8.81). Вид этого потенциала по-
казан на рис. 8.2. В выражении для потенциала Леннарда—Джон-
са D есть диаметр эффективного взаимодействия при столкно-
вении молекул с низкой (нулевой) энергией. Когда энергия
сталкивающихся молекул сравнительно высока, то молекулы
могут сближаться на расстояние, меньшее D. Это происходит
в газах с высокой температурой, так как при большой темпе-
ратуре средняя энергия молекул выше. Таким образом, можно
предвидеть, что с увеличением температуры уменьшается «эф-
фективный» диаметр молекул. Отсюда, используя тот факт, что
диаметр D в (11.39) и (11.40) при увеличении температуры дол-
жен несколько уменьшаться, можно сделать грубую поправку
на «мягкость» молекул, в результате чего коэффициент вязко-
сти будет расти с температурой быстрее, чем УТ. Можно по-
лучить этот вывод и количественно, для чего достаточно поло-
жить в (8.81) г=ДЭфф, а потенциал взаимодействия е прирав-
нять средней кинетической энергии kT При высокой темпе-
ратуре членом притяжения можно пренебречь, и расчет упро-
щается. В результате имеем
или
(U.4!)
где 0/ — характеристическая температура взаимодействия моле-
кул, определенная в (8.84). Таким образом,используя потенциал
Леннарда — Джонса, мы можем сказать, что при высокой тем-
пературе коэффициент вязкости растет, как Т2/\
Для получения более точных результатов необходимо обра-
титься к полной кинетической теории, использующей не модель
упругой сферы, а более реальный потенциал взаимодействия
между молекулами. Расчеты подобного рода для потенциала
422
Гл. XI. Вязкость, диффузия и теплопроводность
Леннарда — Джонса, проделанные Гиршфельдером с сотрудни-
ками, дают следующий результат (с точностью до 1%):
nX Ю’ = 266.93 piX”8„- 01-42)
где функция Q<2’2) представлена в табл. 11.3. Так как Q<2’2>
уменьшается с повышением Г, то т] растет быстрее УТ, что как
раз и предсказывалось для больших Т.
Обратим внимание на более низкие температуры. Функция
Q(2»2) должна приближенно равняться (£>Эфф/£>)2, где Ьэфф —
Таблица 11.3
Функции переноса для потенциала Леннарда — Джонса
T/0; й(1,1) й<2'2> г/е. а(2,2) T/0;
0,30 2,662 2,785 1,65 1,153 1,264 4,1 0,8788 0,9649
0,35 2,476 2,628 1,70 1,140 1,248 4,2 0,8740 0,9600
0,40 2,318 2,492 1,75 1,128 1,234 4,3 0,8694 0,9553
0,45 2,184 2,368 1,80 1,116 1,221 4,4 0,8652 0,9507
0,50 2,066 2,257 1,85 1,105 1,209 4,5 0,8610 0,9464
0,55 1,966 2,156 1,90 1,094 1,197 4,6 0,8568 0,9422
0,60 1,877 2,056 2,0 1,075 1,175 4,7 0,8530 0,9382
0,65 1,798 1,982 2,1 1,057 1,156 4,8 0,8492 0,9343
0,70 1,729 1,908 2,2 1,041 1,138 4,9 0,8456 0,9305
0,75 1,667 1,841 2,3 1,026 1,122 5 0,8422 0,9269
0,80 1,621 1,780 2,4 1,012 1,107 6 0,8124 0,8963
0,85 1,562 1,725 2,5 1,9996 1,093 7 0,7896 0,8727
0,90 1,517 1,675 2,6 0,9878 1,081 8 0,7712 0,8538
0,95 1,476 1,629 2,7 0,9770 1,069 9 0,7556 0,8379
1,00 1,439 1,587 2,8 0,9672 1,058 10 0,7424 0,8242
1,05 1,406 1,549 2,9 0,9576 1,048 20 0,6640 0,7432
1,10 1,375 1,514 3,0 0,9490 1,039 30 0,6232 0,7005
1,15 1,346 1,482 3,1 0,9406 1,030 40 0,5960 0,6718
1,20 1,320 1,452 3,2 0,9328 1,022 50 0,5756 0,6504
1,25 1,296 1,424 з,з 0,9256 1,014 60 0,5596 0,6335
1,30 1,273 1,399 3,4 0,9186 1,007 70 0,5464 0,6194
1,35 1,253 1,375 3,5 0,9120 0,9999 80 0,5352 0,6076
1,40 1,233 1,353 3,6 0,9058 0,9932 90 0,5256 0,5973
1,45 1,215 1,333 3,7 z 0,8998 0,9870 100 0,5130 0,5882
1,50 1,198 1,314 3,8 0,8942 0,9811 200 0,4644 0,5320
1,55 1,182 1,296 3,9 0,8888 0,9755 300 0,4360 0,5016
1,60 1,167 1,279 4,0 0,8836 0,9700 400 0,4170 0,4811
11.6. Вязкость реального газа
423
эффективный диаметр молекул. При высокой температуре эф-
фективный диаметр для потенциала Леннарда—Джонса связан
с температурой по формуле (11.41), так что мы должны иметь
2(2’2> (7» ~ const, Т/Q, >> 1. (11.43)
Используя табл. 11.3, можно вычислить значения (77©/) ,/6Q(2’2)
для больших 770/. Как видно из табл. 11.4, выражение (11.43)
при изменении T/Qj от 10 до 400 остается постоянным с точ-
ностью до 10%. Если учесть
член притяжения в потен-
циале взаимодействия, то
получается еще более хоро-
ший результат.
Определяя эксперимен-
тально коэффициент вязко-
сти, можно по формуле
(11.42) найти две постоян-
ные D и 0/. Адекватность
формулы (11.42) можно
проверять различными пу-
тями. Прежде всего, если
результаты экспериментов в
большом диапазоне темпе-
Таблаца 11.4
Экспериментальное подтверждение
соотношения (11.43)
Г/0/ (T/Qj) 6 & ' Г/0/ (Г/0/),/дО(2’2)
10 1,210 80 1,260
20 1,222 90 1,263
30 1,234 100 1,266
40 1,243 200 1,286
50 1,248 300 1,295
60 1,251 400 1,306
70 1,255
ратур могут точно согласо-
вываться с теоретической кривой, то теория верна. Факты
показывают, что это так и есть1).
Далее, если значения постоянных D и 0Ь полученные из оп-
ределения вязкости, совпадают с соответствующими значения-
ми, полученными другими путями (например, из второго вири-
ального коэффициента неидеальных газов), то теория также под-
тверждается. Судя по табл. 8.2, это тоже справедливо. Поэтому
мы будем считать правильной теоретическую формулу (11.42).
С ее помощью можно вычислять коэффициент вязкости, если
известны или предугаданы постоянные D и 01, характеризую-
щие молекулу. В п. 8.13 уже рассматривалось влияние молеку-
лярного вращения на закон взаимодействия. Все, что сказано
там, можно с успехом применить к явлению вязкости. Иными
словами, дополнительными эффектами взаимодействия между
несимметричными молекулами, например эффектом взаимодей-
ствия диполей, можно пренебречь. Тогда, за исключением слиш-
ком длинных молекул, формула (11.42) должна быть справед-
лива для всех газов.
’) См. Г ирш фельдер Дж, Кертисс Ч., Берд Р., Молекулярная
теория газов и жидкостей, ИЛ, М., 1961.
424
Гл XI. Вязкость, диффузия и теплопроводность
Конечно, эта формула тоже имеет определенные границы
применимости. При очень низких температурах появляется
квантовый эффект, особенно заметный для легких молекул. Па-
раметр Л*, характеризующий квантовый эффект, дан в (9.47).
Однако, к счастью, для большинства молекул Л* достаточно
мал, вплоть до того что квантовым эффектом можно полностью
пренебречь. Даже у Не и Н2 квантовая поправка коэффициента
вязкости при комнатной температуре меньше чем 0,5%. Поэто-
му мы не будем рассматривать здесь подобные расчеты1).
На другом конце температурной шкалы, т. е. при очень вы-
соких температурах, вследствие большой средней кинетической
энергии расстояние между молекулами при столкновении мо-
жет быть очень малым. Известно, что потенциал Леннарда —
Джонса не является точным, прежде всего потому, что потен-
циал отталкивания должен быть скорее показательной, чем сте-
пенной функцией. Если взять потенциал в виде (8.74) и при
очень высокой температуре пренебречь членом притяжения, то,
рассуждая, как выше, получаем следующий эффективный диа-
метр:
kT = Р ехр (— £>эфф/р),
ИЛИ
^эфф ' ' | >
к 2^7
где Р и р — постоянные. Отсюда при очень высокой темпера-
туре коэффициент вязкости ц должен быть равен
Л------f~Tp х > -/-^1- (И-44)
11,2/№—| ^>kT
Эта формула дает более медленный рост ц, чем закон Т2/з, по-
лученный из минус двенадцатой степени потенциала Леннарда—
Джонса.
Если газ представляет собой смесь нескольких видов моле-
кул, то кинетические расчеты еще более усложняются. Происхо-
дит это потому, что следует рассматривать не только взаимо-
действие молекул одного типа, но также и взаимодействие
различных молекул. Результаты этой теории чрезвычайно
сложны. Кроме того, дох сих пор мы знаем очень мало относи-
тельно взаимодействия различных молекул и приходится вво-
дить многочисленные упрощающие предположения. Поэтому
9 См. прим, на предыд. стр., гл. 10.
11.7. Теплопроводность в газах
425
здесь не будет исследоваться вязкость смеси газов. Читатель, ко-
торый заинтересуется этим вопросом глубже, может обратиться
к литературе по газовой кинетике.
Мы дадим только сравнительно простую приближенную фор-
мулу. Согласно опытным результатам, погрешность этой фор-
мулы не превышает 4%. Пусть в смеси газов содержится v ти-
пов молекул, Xi — доля z-й компоненты, щ — коэффициент вяз-
кости z-ro газа, тг- — молекулярный вес z-й компоненты. Тогда
коэффициент вязкости т] газовой смеси равен
v
V
П
(11.45)
где
Эта формула полезна для практических расчетов.
11.7. Теплопроводность в газах
Молекула, имеющая скорость с и энергию Е, проходя без
столкновений расстояние Z, переносит энергию Е. Рассмотрев,
движение различных молекул по двум противоположным на-
правлениям, видим, что перенос энергии происходит из обла-
сти с большей энергией в область с меньшей энергией, т. е. из
области с высокой температурой в область с низкой темпера-
турой. Допустим, что температура газа одинакова на каждой
плоскости, параллельной х, у. Тогда средняя энергия Е яв-
ляется функцией только от z. Рассмотрим молекулы, проходя-
щие через единичную площадку плоскости г = г0. Те из них,
которые идут в направлении, составляющем с осью z угол 0,
последнее столкновение испытали в плоскости
z = z§ — Zcos0.
Будем приближенно считать, что средняя энергия таких моле-
кул соответствует как раз этой плоскости. Ее можно записать
в виде
Е — Zcos 0-^-,
dz
где Е — средняя энергия в плоскости г = г0.
Число молекул, проходящих через единичную площадку в
единицу времени в направлениях, образующих с осью z углы
между 0 и 0 + rf0, равно у яс cos 0 sin 0^0 (см. (11.32)). Если
предположить, что каждая молекула обладает средним значением.
426
Гл. XI. Вязкость, диффузия и теплопроводность
энергии, указанным выше, то общий поток энергии через еди-
ничную площадку этой плоскости равен
f (е — I cos 0 —i пс cos 0 sin 0 dQ = —- ncl . (11.46)
J \ OZ J £ о UZ
О
Если Ё не зависит от z, то этот поток энергии должен быть ра-
вен нулю, так как энергия, проносимая через плоскость z=z0
в обоих направлениях, одинакова. Если же Ё увеличивается вме-
сте с z, то молекула, проходящая через плоскость z=z0 в на-
правлении уменьшения z, несет больше энергии, чем молекула,
которая проходит через эту плоскость в противоположном на-
правлении. Поэтому существует некомпенсируемый поток энер-
гии в отрицательном направлении оси z.
Пусть X— коэффициент теплопроводности. Тепловой поток,
проходящий через единичную площадку плоскости z=z0 в на-
\ дТ
правлении оси z, равен —Приравнивая это выражение
к (11.46), имеем
Л дТ_ _ - dE дТ
Л дг — 3 па dT dz ’
откуда _
. 1 dE
Е — ncl —pr •
3 di
тт dE
Но есть молекулярная теплоемкость cv при заданном
объеме. В результате получим
K = ~nclcv. (11-47)
Если рассмотреть перенос импульса, порождающий напряжение
вязкости, то аналогичное рассуждение дает соответствующее
приближенное выражение для коэффициента вязкости
т\ = ^пс1пг. (11.48)
Сравнивая (11.47) с (11.48), имеем
’=’1^ = 4-^. (11.49)
где Су — молярная теплоемкость, а М — молекулярный вес.
Формула (11.49), полученная по элементарной теории, не
точна. Рассмотрим возможные уточнения. Для молекул,
не имеющих внутренних степеней свободы, например молекул
инертных газов, надо учитывать только энергию поступатель-
11.7. Теплопроводность в газах
427
ного движения. Нетрудно понять, что энергия, переносимая че-
рез плоскость z=z0, должна быть больше той, которая дана в
(11.46), так как вместо с правильнее было бы взять среднюю
скорость, вычисленную по функции распределения с весом с2.
Таким образом, для одноатомного газа следует считать, что X
ЗУ?
больше, чем 'П 2лГ* Точный кинетический расчет подтверждает
этот вывод. Истинный результат для одноатомного газа дается
формулой
Х = (11.50)
Для многоатомных молекул полный кинетический расчет до
сих пор не производился из-за недостатка знаний о передаче
энергии между поступательными и внутренними степенями сво-
боды. По этой причине пока еще нет точной теории теплопро-
водности в многоатомных газах. Кроме того, поскольку коэф-
фициент объемной вязкости также связан с передачей энергии
между поступательными и внутренними степенями свободы, то
нет и точного метода теоретического расчета коэффициента
объемной вязкости. Для теплопроводности Эйкен предложил ис-
пользовать формулу (11.49) для внутренних степеней свободы,
а формулу (11.50)—для поступательного движения. Это пра-
вило означает, что внутренняя энергия молекул переносится так
же, как импульс, а перенос энергии поступательного движения
совершается, как в одноатомном газе. Таким образом, общий
коэффициент переноса энергии дается выражением
Cv~^R 15 R 15 R /4 Cv , 3\ , „„
= n м 1"Т Т Ч~лг(т51г + !>)’ (11-51)
Если ввести отношение удельных теплоемкостей у-Ср/Су, то
(11.51) можно переписать в виде
Х = -^- [пт + тСУ— 1)1 • (11.52)
4 1 уЛГ L 15 1 5 'г 7 J v '
По этой формуле коэффициент теплопроводности X вычисляет-
ся через термодинамические данные и коэффициент вязкости т].
В гидромеханике практически важной величиной является чис-
л
ло Прандтля Pr==_jf'Y‘ И3 (И.52) имеем
Рг
Y
1 +|(Y-О
(11.53)
~ М X
428
Гл. XI. Вязкость, диффузия и теплопроводность
В основе предложения Эйкена, ведущего к формулам
(11.51), (11.52) и (11.53), заложено предположение, что обмен
энергией между поступательными и внутренними степенями сво-
боды происходит достаточно быстро. Для вращательных степе-
ней Свободы это предположение оправдывается. Однако для ко-
лебательных степеней свободы оно неверно, так как известно,
что возбуждение колебаний молекул проходит довольно мед-
ленно. Поэтому если в удельной теплоемкости газа имеется зна-
чительный вклад колебательного движения, то необходимо
подвергнуть формулы (11.51), (11.52) и (11.53) критической
проверке. Экспериментальные результаты полностью согласуют-
ся с этим заключением. В п. 11.9 будет рассмотрен вопрос о ре-
лаксации колебаний.
11.8. Диффузия бинарной смеси
Трудности, которые возникают при исследовании диффузии,
в сущности, те же, что и при изучении вязкости и теплопровод-
ности. Как и в предыдущих пунктах, сначала рассмотрим эле-
ментарную теорию, а затем укажем более точные результаты
кинетической теории.
Предположим, что два газа взаимно диффундируют в на-
правлениях, параллельных оси z. Движение в каждой точке
плоскости, перпендикулярной оси z, является одинаковым. По-
этому газ расположен однородными слоями, параллельными
оси z. Если молекулы двух газов одинаковы по массе и вели-
чине, то это самый простой случай. В других случаях вслед-
ствие различия массы и величины молекул имеется тенденция
к образованию разности давления. Макроскопическое движение
происходит, конечно, вдоль оси z. Обозначим через w0 макро-
скопическую скорость в направлении оси z и предположим, что
плотности газов равны соответственно гц и п2. Тогда пь п2 и
являются лишь функциями z. При рассмотрении этого вопроса
можно считать, что макроскопическая скорость газа мала по
сравнению с молекулярной. Кроме того, предполагаем, что от-
ношение плотностей не меняется значительным образом на рас-
стоянии среднего свободного пробега молекулы, иными слова-
ми, состояние газа близко к равновесному. Поэтому можно в
каждой точке использовать распределение Максвелла с локаль-
ной температурой, одинаковой для обеих компонент смеси.
Число молекул первого типа, которые в единицу времени
проходят через единичную площадку плоскости z=z0 в напра-
влении оси z, равно z
{ П!ехр {—5т1«2 + 'а2 + (®' —dvdw,
(11.54)
11.8. Диффузия бинарной смеси
429
где интегрирование по и и v распространяется от —оо до 4-оо,
а по w — от 0 до оо. Поступая, как и раньше, значение бу-
дем вычислять в точке последнего столкновения. Молекулы, ко-
торые движутся в направлении, образующем с осью г угол О,
можно считать выходящими из точки с координатой z=z0—
— I cos 0. Значение /г± в этой точке равно
«i = («iU^-/cos0
(11.55)
После подстановки этого выражения в (11.54) интеграл разби-
вается на два. Первый отличается от (11.54) тем, что вместо
появляется за интегралом. Если wQ мала, то, огра-
ничиваясь линейным приближением, имеем
4(«1)г=го(тс1 + ®о).
(11.56)
где ci — средняя скорость молекул первого типа, вычисляемая,
как в (11.11). Второй интеграл равен
+ (w — w0)2] > w cos 0 du dv dw.
(11.57)
Благодаря множителю / выражение (11.57) уже представ-
ляет собой малую величину, и при вычислении интеграла мож-
но допустить, что ^о = О, a cos 0 заменить на wjc. Тогда получим
где интегрирование распространяется на все значения u, v и по-
ложительные значения w. Этот интеграл легко вычисляется,
если обратить внимание на то, что он равен
интеграла по всему пространству скоростей,
половине такого же
1 1
т. е. равен I l-gj
умноженной на среднее значение w2/c для всех молекул газа
при отсутствии макроскопического движения. Это среднее зна-
чение равно среднему от ^(и2 -\-v2 -^w2)/с = с. Поэтому вы-
ражение (11.57) равно
430
Гл. XI. Вязкость, диффузия и теплопроводность
Объединяя это выражение с (11.56), получаем общее значение
(11.54) в виде
+ (И-58)
где все величины вычислены на плоскости z = z0.
Выражение (11.58) представляет собой общий молекуляр-
ный поток через единичную площадку плоскости z=z0 в напра-
влении оси z. В противоположном направлении соответствую-
щий поток молекул равен
— wo)+4Z(4r)^- (И-59)
Разность этих двух выражений дает приращение числа моле-
кул первого типа (в единицу времени через единичную пло-
щадку) на верхней стороне плоскости z=zQ
= (11.60)
Аналогично приращение числа молекул второго типа равно
r2 = ^0-|/2(^')F2. (11.61)
Если плотность газа является постоянной, то общий моле-
кулярный поток через любую плоскость должен быть равен
нулю. Это требует, чтобы
Г1 + Г2 = 0. (11.62)
Так как давление в газе также должно быть постоянным, то
4- п2 = const, (11.63)
или после дифференцирования
5L+-fr = °- (11.64)
Исключая Wo, получаем
__ р _ р _ 1 ^1^2С2 + п2^1С1 дП[ /gг\
1 2 3 П1_|_л2 ()2 • ' ’ /
Известно, что закон Фика -в макроскопической теории диффу-
зии дает
(11-66)
где pi — плотность газа первого типа, /1 — масса, проходящая
через единичную площадку плоскости z = zQ в единицу времени
11.8. Диффузия бинарной смеси
431
в направлении оси z. Поэтому можно написать
р^т^, (11.67)
где mi — масса молекул первого типа. Из (11.66) получается
= (П-68)
откуда после сравнения с (11.65) имеем следующее выражение
для коэффициента диффузии:
67V __ 1 П1/2С2 + Н21\СХ 1
^12 —"з • (И.ЬУ)
Задача теперь сводится к тому, чтобы каким-то образом
связать длины свободных пробегов /1 и /2 со свойствами моле-
кул. Стефан и Максвелл, обобщая (11.13), предложили исполь-
зовать следующие выражения для свободных пробегов упругих
сфер:
1
i/'O+£) я”2£>*2
/2 —
(11.70)
т2 \ гч2
—- яп^/Хп
тх 1 12
где D — среднее арифметическое диаметров двух типов моле-
кул. Используя эти формулы, можно написать (11.69) в виде
12 Зя (Hj + n2) D22 У(тх + т^
= 2 /"2kT / 1 i 1
Зя (пх 4- л2) ^12 И Я \ т\ т2
Согласно (5.3), (nx-]-n2)kT = PV, и исключая п2, имеем
__ 4 , /-^ Г г3 (Af! + М2)/2МХМ2
12 Зя8/’ У PD212
или _________________
3) = 0,002960 /гз (Л41 + (11J2)
12 PD22 сек
(И.71)
где Т — абсолютная температура, °К; Л4] и М2 — молекулярные
веса соответственно первого и второго газов, Р — давление, атм,
a D — средний диаметр молекулярных столкновений, А.
Полученный результат для коэффициента диффузии, конеч-
но, не может быть очень точным, так как на разных этапах
было сделано множество различных приближений. Используя бо-
лее совершенную кинетическую теорию, а также потенциал Лен-
нарда— Джонса (8.81) для взаимодействия между молекулами
432
Гл. XL Вязкость, диффузия и теплопроводность
первого п второго типов, Гиршфельдер и его коллеги провели
более точные расчеты и получили следующий результат:
5>12 = 0,0026280 — Г-(> 1 , (11.73)
где Z>i2 — расстояние между молекулами А, на котором потен-
циал взаимодействия равен нулю, Q*1’1) — функция отношения
температур 770/12, а 0/12—характеристическая температура
взаимодействия молекул различного типа. Когда нет точных
значений этих параметров, используют опытный закон: в каче-
стве £>12 берут среднее арифметическое значений D для моле-
кул первого и второго типов, а в качестве 0/12 — среднее геоме-
трическое для молекул первого и второго типов. Численные зна-
чения функции ДО»1) даны в табл. 11.3. Она уменьшается по
мере увеличения температуры. Это объясняется тем, что
при увеличении температуры диаметр столкновений уменьшает-
ся вследствие увеличения кинетической энергии столкновений.
Другими словами, зависимость Q0’1) от температуры очень на-
поминает зависимость Q<2’2> от Т. Для грубых расчетов можно
пользоваться простым представлением о мягкости молекул, ко-
торое уже встречалось выше.
Формулы (11.72) и (11.73) показывают, что в рассмотренном
приближении коэффициент диффузии £>i2 не зависит от моляр-
ных долей компонент смеси. Более точная формула говорит о
том, что некоторая зависимость все же имеется. В многоком-
понентной смеси общая теория диффузии изложена в упомяну-
той книге Гиршфельдера с соавторами. Формулы в этом случае
очень сложны и неудобны для приложений, и говорить о них
здесь мы не будем. Читатель сможет обратиться к указанной
книге.
11.9. Время колебательной релаксации и коэффициент
объемной вязкости
Мы уже касались того факта, что равнораспределение энер-
гии между вращательными и поступательными степенями сво-
боды достигается довольно быстро, а передача энергии на ко-
лебательные степени свободы^ как правило, сильно запаздывает.
Такое отставание любой степени свободы I можно приближенно
описать с помощью релаксационного уравнения
^(Л==Й’-Л (ИЛ)
где е® — энергия /-й степени свободы молекулы, ее равно-
весное значение, %i — время релаксации. Из (11.74) видно, что
11.9. Время колебательной релаксации
433
приближение к равновесию описывается показательной функ-
цией, причем за время т/ отклонение от равновесия уменьшается
в е раз.
Для поступательных степеней свободы еще Максвеллом бы-
ла предложена следующая формула:
тПост = ^- (11.75)
Например, коэффициент вязкости воздуха при 0°С равен
0,000172 пуаз. Отсюда при атмосферном давлении тПост=Ч7Х
X Ю-1и сек, что может быть сравнимо со временем, необходи-
мым для прохождения молекулой средней длины свободного
пробега, и согласуется с нашими предположениями. Энергия
поступательного движения достигает равновесного значения в
течение времени, которое нужно молекуле для прохождения
нескольких средних длин свободного пробега. Эксперименталь-
ных данных относительно времени вращательной релаксации
сравнительно мало, но можно заметить, что оно немного больше
времени поступательной релаксации, хотя порядок их величин
одинаков.
Для подтверждения этого можно воспользоваться формулой
Эйкена для двухатомного газа при температуре, когда энергия
колебаний пренебрежимо мала. Что касается времени колеба-
тельной релаксации, то эксперимент показывает, что оно зна-
чительно больше времени поступательной релаксации. При
обычной температуре значение времени колебательной релакса-
ции находится в промежутке от 10~6 до 10~5 сек. Недавно
Шварц, Славский и Герцфельд1) предложили метод теоретиче-
ского расчета времени колебательной релаксации. Из много-
атомных газов больше всего исследован СО2. При обычной тем-
пературе время колебательной релаксации для него равно
10~5 сек. Однако при небольшом добавлении водяного пара это
значение может понизиться до 2Х10-6 сек. Здесь примеси ока-
зывают каталитическое действие, способствующее передаче
энергии колебательными степенями свободы.
С кинетической точки зрения вязкость газа связана с вре-
менем релаксации процесса достижения равновесного распре-
деления энергии, соответствующего локальным условиям. Для
поступательных степеней свободы это совершенно очевидно.
Мы уже говорили, что объемная вязкость х есть результат
f) Schwartz, Slawsky, Herzfeld, J. Chem. Phys., 20 (1952)t
1951; 22 (1954), 1768 (см. сб. «Газодинамика и теплообмен при наличии хими-
ческих реакций», ИЛ, М., 1962, стр. 399—477. — Прим, ред.),
28 Зач. 1299
434
Гл. XI. Вязкость, диффузия и теплопроводность
релаксации внутренних степеней свободы. Фактически связь
объемной вязкости с временем релаксации дается следующей
формулой *):
nk2T v 1
и— 2 ^£07» (П.76)
СУ I
где — вклад /-й внутренней степени свободы в удельную мо-
лекулярную теплоемкость. Однако за исключением таких про-
стых примеров, как распространение звуковых волн, нельзя
объяснить вязкостью явления с очень большим временем ре-
лаксации. Большое время релаксации говорит об эффекте, ко-
торый почти не меняется за время свободного пробега. Поэтому
мы не должны пытаться упрощенно при помощи объемной вяз-
кости объяснить релаксацию колебательного движения. С дру-
гой стороны, релаксацию вращательного движения, сравнимую
с релаксацией поступательного движения, можно связать с объ-
емной вязкостью. Если время вращательной релаксации при-
равнять ко времени поступательной релаксации (П.75), то для
линейной молекулы [cv = cty = k} получим
nk2T , ч 4 Z1 _ ч
х — / 5 \2 "р “ 25 Т1, 1
2*
(3 \
cy = 3k> cty = -^k\ имеем
х
_ nk2T 3 , n _ 1
— (3£)2 2 * P 6
(11.78)
В действительности время вращательной релаксации, как пра-
вило, немного больше времени поступательной релаксации,
поэтому х должно быть больше значений, указанных в приве-
денных выражениях. Для молекул, колебательной энергией
которых можно пренебречь, экспериментальные данные по коэф-
фициенту объемной вязкости согласуются с этими теоретиче-
скими результатами.
НЛО. Процессы переноса в плотных газах
Свойства процессов переноса, о которых шла речь в преды-
дущих пунктах, были определены применительно к разрежен-
ным, т. е. идеальным газам. Даже для такого простого случая
расчет вязкости, диффузии и теплопроводности оказался слож-
9 Wang-Chang С. S., Uhlenbeck G. Е., University of Michigan,
Engineering Research Institute, Report No. CM-681, 1951.
11.10. Процессы переноса в плотных газах
435
ним. Для плотных же газов, где уже не сохраняется независи-
мость молекул идеального газа, можно предвидеть, что теоре-
тический расчет будет исключительно сложным. И это действи-
тельно так. До сих пор численные методы теории переноса
плотных газов еще не развиты (хотя формальная теория уже
существует). Однако можно воспользоваться методом, который
употреблялся при рассмотрении уравнения состояния плотных
газов. Применяя принцип соответственных состояний, можно
составить безразмерные диаграммы на основании эксперимен-
тельных данных.
Из п. 9.7 известно, что состояние газа определяется двумя
безразмерными параметрами 7701 и PD3/(—е*) (если потен-
циал взаимодействия молекул содержит две постоянные, как,
например, потенциал Леннарда — Джонса). С другой стороны,
свойства переноса ранее уже были определены. Единственный
недостаток их заключался в использовании лишь одного из
двух параметров Т/©/ так как давление PD3/(—8*) считалось
пренебрежимо малым. Однако эти результаты легко расширить.
Например, обобщенная формула вязкости получается из (11.42)
в виде
ПХ.0^ 266,93^,,,,^^^^, (11.79)
где единственная сложность состоит в том, что Q<2>2) предста-
вляет собой функцию двух переменных и пока нет возможности
определить ее теоретически. Однако эта функция может быть
определена путем сравнений с экспериментальными данными.
В этом и заключается метод соответственных состояний, пред-
ложенный и использованный Камерлингом Оннесом (1881).
В самом деле, пусть безразмерными параметрами закона
соответственных состояний являются приведенная температура
Тг=Т/Тщ) и приведенное давление РГ = Р/Р^ где ТКр, —
критические температура и давление. Тогда если т|Кр — коэффи-
циент вязкости критического состояния (в критическом состоя-
нии 777\ф=1, Р//>Кр= 1)» то отношение т)/т)кР (приведенный ко-
эффициент вязкости) можно представить следующим образом:
= Л)- (11.80)
Функция т]г находится экспериментальным путем. Диаграм-
ма 11.7 представляет собой грубые контуры более крупной диа-
граммы, составленной Хоугеном и Ватсоном1)- Интересен тот
факт, что если в газовом состоянии давление сравнительно
’) Hougen, Watson, Chemical Process Principles, John Wiley, 1947.
28*
= Ju
Рис. 11.7.
11.10. Процессы переноса в плотных газах
437
велико, то коэффициент вязкости будет увеличиваться. Ранее го-
ворилось, что т] не зависит от Р, что справедливо лишь при не
очень большом Р. Приближаясь к критическому состоянию, ко-
эффициент вязкости увеличивается с понижением температуры,
что также представляет собой любопытный факт. Такое поведе-
ние полностью противоположно свойствам разреженных газов
и соответствует скорее жидкому состоянию. Конечно, для опре-
деления коэффициента вязкости т| необходимо знать значение
т]Кр, которое можно найти из сопоставления диаграммы с
(11.42). Для грубой оценки т|1ф можно пользоваться формулой
ПкрХ 107 = 616—^, (11.81)
Икр
гДе [ЛкР] — > М— молекулярный вес, Гкр измеряется в
°К, а Укр — критический объем, измеряемый в см3.
Полностью аналогичные выражения могут быть получены
для коэффициента теплопроводности и диффузии. В каждом
случае приведенные коэффициенты представляют собой функции
от Тг и Рг, но в настоящее время еще нет достаточных данных,
для того чтобы составить диаграммы для этих приведенных
коэффициентов. Однако это не означает, что у нас нет выхода
из создавшегося положения. Можно применить метод Эн-
скога, заключающийся в использовании кинетической теории
газа из твердых сфер. Так как взаимодействие в нем сравни-
тельно простое, то можно рассчитать свойства переноса в таком
плотном газе с помощью точной молекулярно-кинетической тео-
рии, а затем полученный результат перенести на обычные плот-
2 л
ные газы. Обозначая через D диаметр сферы, b = -^-D\ V —
удельный объем, y=(PV/RT) — 1, по этой теории Энскога по-
лучаем для плотного газа из твердых сфер следующие отноше-
ния коэффициентов сдвиговой вязкости, объемной вязкости,
теплопроводности и диффузии к соответствующим значениям
в разреженном газе:
^ = ^7-(1+0,81/+ 0,761 у2), (11.82)
-+ = ^-1,002//, (11.83)
А = _^(1 + 1,2у + 0,755г/2), (11.84)
й = (11.85)
438
Гл. XI. Вязкость, диффузия и теплопроводность
Для применения этих результатов к обычным газам Энског
предлагает вычислить у по формуле
у = ‘Л7г[7'(д7г)и]~1- (11.86)
Величину, заключенную в квадратных скобках, иногда назы-
вают «тепловым давлением». Как видно из формул (11.82) —
(11.85), для того чтобы при V->oo, т. е. при разрежении газа,
а параметры плотного газа приближались к соответствую-
щим параметрам разреженного газа, необходимо, чтобы b~yV.
Тогда с помощью формулы (11.86) и вириального разложения
уравнения состояния (8.72) можно получить формулу для вы-
числения 6, а именно
Ь = В(Т)+Т-^р-. (11.87)
Из (11.87) видно, что для обычных газов b не является по-
стоянной, а зависит от температуры. Если взаимодействие ме-
жду молекулами описывается потенциалом Леннарда — Джонса,
то Ь легко вычислить по табл. 8.1. Фактически с увеличением
температуры b уменьшается, т. е. уменьшается эффективный
диаметр молекулы, что вполне естественно. Этот метод был при-
менен к вычислению коэффициентов вязкости азота и окиси
углерода. Сопоставление результатов расчета с результатами
эксперимента показало, что в пределах нескольких сот атмо-
сфер такой метод расчета вполне надежен.
При расчете коэффициента теплопроводности следует обра-
тить внимание на то, что формула (11.84) отражает только
передачу поступательной энергии, но не внутренней. Здесь так-
же можно использовать предложение Эйкена и разделить ко-
эффициент теплопроводности на две части. Одну часть, соот-
ветствующую энергии поступательного движения, вычислять по
формуле (11.84) с [см. (11.50)]. Другая часть —
CV~^R
т]--, где Cv — удельная молярная теплоемкость при
постоянном объеме, которая^отражает передачу энергии вну-
треннего движения молекул. Общий коэффициент теплопровод-
ности представляет собой сумму этих двух частей. По той же
причине объемная вязкость х, определяемая формулой (11.83),
также относится только к поступательному движению, и к ней
нужно добавить объемную вязкость внутреннего движения мо-
лекул, вычисляемую по формуле (11.76).
11.11. Коэффициент вязкости жидкости
439
11.11. Коэффициент вязкости жидкости
Метод соответственных состояний в принципе можно распро-
странить и на жидкости. Что касается механизма вязкости в
жидкости, то можно предположить простую и наглядную мо-
дель, связанную с теорией абсолютных скоростей реакции и
позволяющую вычислять коэффициенты переноса.
Основным уравнением этой теории является уравнение Эй-
ринга для удельной скорости реакции &'1),
k'o = $(kT/h) ехр (—*!) = ₽ (kT/h) ехр . (11.88)
где AG, АН и AS — свободная энергия Гиббса, теплосодержа-
ние и энтропия активации соответственно. Активация означает,
что система находится в состоянии с сравнительно высокой
энергией и, так сказать, готова к появлению событий; k — по-
стоянная Больцмана, Т — абсолютная температура, h — посто-
янная Планка, R — обычная газовая постоянная. Множитель р
является безразмерным и носит название коэффициента прохо-
ждения. При нахождении системы в активированном состоянии
он представляет собой вероятность того, что процесс действи-
тельно происходит. Для большинства процессов р меняется в
пределах от !/2 до 1. В дальнейших рассуждениях предполагает-
ся, что 0=1.
Очевидно, что для применения этой теории к изучению диф-
фузии, вязкости и теплопроводности необходимо предположить
наличие определенного типа механизма, который вызывает по-
ток молекул и в котором имеется медленная стадия — так на-
зываемое «активированное состояние». Нужно также знать
число молекул, участвующих в основном процессе потока, но в
точном определении самого механизма нет необходимости. Од-
нако априори невозможно установить, сколько молекул уча-
ствуют в основном процессе потока — одна, две или много.
Эйринг предположил, что в поток вовлекается обычно только
одна молекула, так что процесс является одномолекулярным.
Результаты расчетов хорошо согласуются с экспериментом.
Кроме того, получающиеся значения энергии и энтропии акти-
вации могут быть объяснены на основе простой одномолекуляр-
ной модели.
Для описания процесса вязкого течения рассмотрим модель
жидкости, изображенную на рис. 11.8. Пусть в каждой единице
объема содержится п молекул. Так же, как и в девятой главе,
можно предположить, что жидкость имеет решетчатую струк-
’) Glasstone, Laidler, Eyring, Theory of Rate Processes.
McGraw-Hill, 1941.
440
Гл. XL Вязкость, диффузия и теплопроводность
туру, причем молекулы ограничены соседями и находятся ка-
ждая в своей ячейке. Расстояние между узлами решетки обо-
значим через а, а расстояние между соседними плоскостями
через б. Рассматриваемый нами основной процесс представляет
собой движение молекулы к соседней свободной ячейке. Чтобы
пройти сквозь «коридор», образованный ближайшими соседями,
блуждающая молекула должна пройти, как показано на
рис. 11.8, через область с высокой потенциальной энергией, или
потенциальный барьер.
Если в системе нет внешних сил, то потенциальный барьер
«коридора» симметричен. Если же на единичную площадку дей-
ствует внешняя сила F, стремящаяся сместить один слой моле-
кул относительно другого, то потенциальный барьер подвер-
гается искажению, так что молекула, двигающаяся в напра-
влении силы, спускается «под гору», а молекула, двигающаяся
в обратном направлении, поднимается «в гору». Движение мо-
лекулы в полость по направлению действующей силы назовем
прямым процессом, а такое же движение молекулы в направле-
нии, противоположном действующей силе, — обратным процес-
сом. Пусть k'f и kr — частоты этих двух процессов. Тогда об-
щая скорость потока жидкости относительно узлов решетки в
направлении приложенной силы равна
VQ — a{k'f — k'r).
Частоты k'f и k'r определяются из (11.88), однако свободная
энергия активации для этих двух процессов не одинакова, так
11.11. Коэффициент вязкости жидкости
441
как прямой процесс осуществляется легче, чем обратный. Сила,
действующая на отдельную молекулу и вызывающая ее движе-
ние, представляет собой силу F, умноженную на площадь
занимаемую одной молекулой. Величина п по-прежнему яв-
ляется числом молекул в каждой единице объема жидкости.
_ F
Сила уменьшает свободную энергию активации молекулы,
двигающейся в прямом направлении, и увеличивает свободную
энергию активации молекулы, двигающейся в обратном напра-
влении. Если активированное состояние находится посредине
между двумя узлами решетки, то работа, производимая внеш-
ней силой при перемещении молекулы на расстояние а/2 в акти-
1 aF ъ к
вированное состояние, равна ^та работа представляет
собой то количество энергии, на которое изменяется свободная
энергия активации в двух направлениях. Таким образом, часто-
ты kf и kr можно записать в виде
, ' / aF \ ' ' [ aF \
kf = k^^\^kr)' (11.89)
где k'o—значение k'/ и k'r при отсутствии внешней силы F.
Отсюда общая скорость потока одного слоя по отношению к
соседнему равна
= а (k'f — k'r) = 2ako sh (J). (11.90)
\ £ VUK 1 j
Отношение касательного напряжения к скорости сдвига и есть
коэффициент вязкости, поэтому из (11.90) имеем
л = —=-------,-—--------. (11.91)
vQ/6 2akQ sh (aF/^ bnkT)
Когда напряжение очень мало, гиперболический синус можно
заменить на aFI2bnkT. Тогда
Обычно для простоты предполагают, что расстояние между
слоями молекул б равно расстоянию между двумя узловыми
точками, т. е. множитель (S/а)2 равен 1.
В (11.92) вязкость выражается через свободную энергию
активации AG, которую можно получить из эксперимента. Для
образования полости цепь молекул должна быть разорвана.
Преодолеваемые при этом связи те же, что и в процессе испа-
рения. Отсюда можно сделать вывод, что энергия, необходимая
442
Гл. XI. Вязкость, диффузия и теплопроводность
для образования полости (размером порядка объема молеку-
лы), равна энергии испарения ДЕИСП. Следовательно, свободная
энергия активации пропорциональна энергии испарения. Эн-
тальпия испарения Д/Лтс^ЛЕисп + ^Т1 более привычная вели-
чина, чем ДЕисп. Эмпирически найдено, что
= (11.93)
Эта формула показывает, что процесс вязкого потока начи-
нается еще до того, как энергия активации достигает уровня,
Рис. 11.9.
необходимого для образования полости величиной с одну моле-
кулу. Размер образуемой полости будет только частью моле-
кулярного объема.
На рис. 11.9 показан возможный механизм вязкого потока,
согласующийся с этим результатом. Здесь две молекулы под-
жимаются и после поворота на 90° снова разделяются. Необхо-
димый дополнительный объема равен примерно V3 молекуляр-
ного объема. Формулу (11.92) можно написать в виде
Т] = 0,003990 ехр / А£исп (11.94)
1 1.2,45/?7 j VL v 7
где h] == Z — > VL— объем одной грамм-молекулы жидко-
сти, см3. Очевидно, что вязкость жидкости уменьшается с повы-
11.12. Теплопроводность в жидкости
443
шением температуры, тогда как в разреженных газах она воз-
растает. Если жидкость является нормальной, то энергию испа-
рения можно оценить по закону Трутона
Д£ИСП^9,4/?Л,
где Ть — температура кипения при атмосферном давлении. От-
сюда для нормальной жидкости имеем
0,00399 -j^exp (з,83-^Л. (11.95)
Эта формула удобна для грубых оценок.
Теория диффузии в жидкостях легко получается из теории
вязкости, коротко описанной выше. Однако теоретические ре-
зультаты не согласуются с экспериментальными. Поэтому мы
не будем здесь рассматривать эту простую, но неприемлемую
теорию.
11.12. Теплопроводность в жидкости
Согласно (11.47), коэффициент теплопроводности, получен-
ный по элементарной теории теплопроводности в разреженном
газе, равен где ncv—теплоемкость единицы объема.
В одноатомном разреженном газе носителями энергии являются
сами молекулы, а энергия содержится лишь в поступательном
движении молекул. В жидкостях, как и в твердых телах, энер-
гия содержится в поперечных и продольных волнах упругих ко-
лебаний, т. е. в звуковых волнах. Следовательно, носителями
энергии являются эти звуковые волны. Поэтому для теплопро-
водности жидкости в грубом приближении можно использовать
ту же формулу, что и для газа, только с нужно рассматривать
как скорость распространения звуковых волн.
Если не различать продольные и поперечные волны, то по-
лучим-
1
Г —
/рр
(11.96)
где р — плотность жидкости, а р — коэффициент изотермического
сжатия. Величина / должна представлять собой средний сво-
бодный пробег этих упругих волн. Вследствие отсутствия упо-
рядоченности «кристаллической структуры» жидкости волны
подвергаются рассеиванию и дифракции. Упорядоченная струк-
тура в жидкости сохраняется лишь на расстоянии порядка раз-
мера молекулы. Поэтому если V есть объем, приходящийся на
444
Гл. XI. Вязкость, диффузия и теплопроводность
одну молекулу, то
Z~0\
(11.97)
так что I имеет величину порядка нескольких ангстрем.
При Z ~ 10~7 см и с ~ 105 см/сек период волны имеет поря-
док 10~12 сек. Как видно из п. 11.9, время релаксации, связанное
с внутренними степенями свободы, намного больше. Поэтому
энергия в жидкости переносится только упругими волнами, и
внутренние степени свободы не участвуют в теплопроводности.
Для степеней свободы поступательного движения теплоемкость
каждой грамм-молекулы жидкости близка к 3/?. Согласно (9.85),
ncv — ^' (11-98)
где VL — объем грамм-молекулы жидкости.
Объединяя (11.96), (11.97) и (11.98), получаем
_L. у'/з
ГЙ VL
где остается неопределенным коэффициент пропорциональности.
Сопоставление с экспериментальными данными показывает, что
этот множитель равен как раз 1. Максимальная ошибка при
этом составляет всего лишь 20%. Так как сам эксперимент не
легок, то отклонение от теоретической формулы в большинстве
случаев свидетельствует о ненадежности экспериментального
значения Z.
Точное численное значение коэффициента теплопроводности
воды известно и отличается от приближенного теоретического
всего лишь на 1,3%. Таким образом, достаточно точная формула
для коэффициента теплопроводности жидкости имеет вид
__ 1 I М у/з ЗЯр
— Кр₽ \ Wp / М ’
(11.99)
где дг — число Авогадро, а М — молекулярный вес. Сравнивая
это выражение с ycln^, видим, что средний свободный про-
бег нормальной волны примерно в 3 раза больше расстояния
между молекулами. Локальйую структуру жидкости можно
описать с помощью кубической кристаллической решетки, имею-
щей 12 соседей по отношению к центральной молекуле. Так
называемый свободный пробег нормальных волн в три раза
превосходит расстояние между молекулами. Это согласуется
с понятием жидкого состояния, использованным в девятой
главе.
И.13. Теплопроводность в твердом теле
445
Достаточно знать молекулярный вес, плотность и коэффи-
циент сжатия, чтобы из (11.99) получить коэффициент тепло-
проводности. Для нормальных жидкостей выражение (9.98) для
Р найдено, так что
1 = /101,6 — 82,4— Н/2(—Г’’ (11-100)
N ’ I М ( Ть ] J (м / ' '
где Ть — температура кипения при атмосферном давлении. Та-
ким образом, чтобы вычислить коэффициент теплопроводности
нормальной жидкости, достаточно знать молекулярный вес,
плотность и температуру кипения. Так как плотность умень-
шается с увеличением температуры, то, как видно из (11.100),
коэффициент теплопроводности нормальной жидкости тоже
уменьшается с увеличением температуры. Однако это пониже-
ние не такое быстрое, как у вязкости (см. (11.95)). Поэтому
число Прандтля в жидкости срх\/Мк, как правило, уменьшается
с увеличением температуры.
11.13. Теплопроводность в твердом теле
При рассмотрении теплопроводности в твердом теле необхо-
димо обратить внимание на различие между проводниками
(металлы) и диэлектриками (ионные кристаллы). Дело в том,
что у проводника перенос тепла осуществляется в основном
свободными электронами в металле. Даже в не очень хоро-
ших проводниках, как, например, в никеле, вклад свободных
электронов в теплопроводность при комнатной температуре
достигает 90%. В хороших проводниках, таких, как медь,
важность свободных электронов становится еще более оче-
видной. Конечно, это столь же справедливо и для жидких
металлов.
Что касается диэлектриков, то передача тепла в них осуще-
ствляется звуковыми волнами — так называемыми фононами.
Если с заменить скоростью звука с, a Су— удельной теплоемко-
стью Дебая, то можно воспользоваться формулой (11.47). Од-
нако для различных частот нужно брать различные длины сво-
бодного пробега I. Это необходимо потому, что в твердом теле
фононы рассеиваются на различных дефектах кристаллической
решетки. Малые дефекты приводят к рассеянию только корот-
ких волн. Поэтому для различных длин волн величина I не оди-
накова. В заданном твердом теле I может быть также функцией
температуры тела, так как от температуры зависит совершен-
ство решетки. Для простоты будем считать I функцией только
446
Гл. XL Вязкость, диффузия и теплопроводность
частоты v и температуры Г. Согласно (6.70), имеем
(jT, Т) dj
(11.101)
где &=hvlkT\ (11.101)—общая формула для коэффициента
теплопроводности кристаллической решетки, данная Макинсо-
ном ’).
Трудность расчета коэффициента теплопроводности твердого
тела заключена в определении Z(£7\ Т) или Z(v, Т). Вследствие
границ кристалла, примесей, дислокаций и других причин
Z(gT, Т) связана с процессом рассеяния. Даже когда распреде-
ление и свойства этих дефектов структуры известны, найти Z
довольно сложно.
Но еще хуже то, что число и распределение этих дефектов
легко изменяется под влиянием механических воздействий. Ка-
чественно можно предсказать, что в твердом теле, образованном
достаточно большими кристаллами, значение I будет увеличи-
ваться при понижении температуры. Поэтому для температур
выше 0р, когда cv близко к 3£, такое изменение I приводит к
тому, что коэффициент теплопроводности также увеличивается
с понижением температуры. При высокой температуре величи-
на Z равна нескольким периодам кристаллической решетки. Зна-
чение Z растет с понижением температуры до тех пор, пока не
становится равным размеру^ зерен кристалла. Величина I огра-
ничена размерами зерен кристалла, и если температура пони-
жается дальше, Z должна сохранять это значение. Отсюда при
очень низкой температуре % пропорциональна с у и, следова-
тельно, меняется как Т3. При температуре немного выше, т. е.
близкой к ©о, величина X достигает максимального значения.
!) Maki ns on, Proc, Cambridge Phil. Soc., 33 (1937), 371,
11.14. Теплопроводность в металлах
447
Поэтому обычное поведение коэффициента теплопроводности
твердого тела в поликристаллическом состоянии должно быть
таким, как показано на рис. 11.10. При низкой температуре чем
больше зерна кристалла, тем лучше теплопроводность. С другой
стороны, если зерна кристалла настолько малы, что прибли-
жаются к размерам ячеек кристаллической решетки, например
в некристаллической замороженной жидкости (стекле), то вели-
чина I всегда ограничена величиной порядка нескольких интер-
валов решетки и является постоянным числом. Для таких
аморфных веществ величина X пропорциональна cv и при уве-
личении температуры постепенно повышается, как показано
пунктиром на рис. 11.10.
В действительности тугоплавкие материалы обычно не яв-
ляются чистыми кристаллами, а представляют собой смеси кри-
сталлов с аморфными веществами в различных пропорциях. Их
теплопроводность определяется теплопроводностью этих двух
компонент, а зависимость X от температуры Т находится между
двумя крайними случаями, показанными на рис. 11.10. Если
данное соединение содержит больше кристаллического веще-
ства, чем аморфного, то при средних температурах коэффициент
теплопроводности уменьшается с повышением температуры.
В обратном случае X увеличивается. При некоторой пропорции
коэффициент теплопроводности может быть постоянным в до-
вольно большой области температур. Таким образом, хотя наша
теория и верна в принципе, но применительно к обычным ма-
териалам можно сказать, что надежд на отыскание точной за-
висимости теплопроводности от температуры пока немного.
11.14. Теплопроводность в металлах
Если с3*— удельная теплоемкость электрона, пэл — число
электронов в единице объема, / — средний свободный пробег
электрона в металле, a v — средняя скорость, то, пользуясь эле-
ментарной формулой (11.47), можно получить выражение для
коэффициента теплопроводности, вызываемой свободными элек-
тронами в металле, в виде
х = 1 n3*c™vl. (11.102)
Удельная теплоемкость вычисляется по формулам (6.140),
(6.141) и (6.143). При температурах до 1000° К величина с3?
пропорциональна абсолютной температуре. Среднее значение
скорости электронов зависит от их кинетической энергии. На
448
Гл. XI. Вязкость, диффузия и теплопроводность
основании формулы (6.135) кинетическая энергия электрона
равна
* ( 3 . 1 9 ( kT\2]
6 }•
Но отношение kTIz* при температурах ниже средней чрезвы-
чайно мало, поэтому кинетическая энергия электрона почти
постоянна. Другими словами, величина v почти постоянна. Од-
нако численное значение v очень велико, поэтому теплопровод-
ность, вызываемая свободными электронами в металле, соста-
вляет главную часть теплопроводности.
Величина среднего свободного пробега электронов I опреде-
ляется процессами рассеяния электронов в металле. Если кри-
сталлическая решетка является цельной, то создаваемый ею по-
тенциал полностью периодичен. При этом электроны движутся
беспрепятственно, а величина I является бесконечной. Однако
в действительности периодичность в кристаллической решетке
не полная. Нарушение периодичности вызывают следующие
причины:
а) смещения, возникающие в результате отхода атомов от
равновесных положений в узлах решетки из-за собственного
теплового движения;
б) примеси, нарушающие цельность кристаллической ре-
шетки;
в) разрывы кристаллической решетки, вызванные смеще-
нием положений, границами кристалла и т. д.
При средних температурах первая причина является глав-
ной. Можно показать, что средний свободный пробег обратно
пропорционален среднему квадратичному смещению атома при
тепловом движении. Однако среднее квадратичное смещение
пропорционально кинетической энергии гармонического осцил-
лятора и потому пропорционально кинетической энергии коле-
баний кристаллической решетки. При средних температурах это
соответствует пропорциональности Т. Таким образом, при та-
ких температурах I обратно пропорционально Т. Отсюда и из
формулы (11.102) находим, что при средних температурах ко-
эффициент теплопроводности Z не зависит от температуры; это
подтверждено и практикой.
При очень высоких температурах характеристическая тем-
пература электронов 0е, определенная в (6.141), (6.143), для
некоторых металлов может оказаться достаточно низкой, что-
бы их состояние стало невырожденным. Тогда кинетическая
энергия электронов становится пропорциональной Г, -Величи-
на сул постоянна, а величина v пропорциональна ]/~Т. При
этом коэффициент теплопроводности электронов изменяется с
11.14 Теплопроводность в металлах
449
температурой как 1/УТ.т. е. величина X может уменьшаться
при очень высокой температуре.
При очень низких температурах рассеяние электронов также
не определяется тепловыми колебаниями кристаллической ре-
шетки, так как они очень малы и не оказывают заметного влия-
ния. Главной становится 3-я причина. Дефекты кристалличе-
ской структуры для любых кристаллов оказываются примерно
одинаковыми. Поэтому при очень низких температурах I по-
стоянна. Таким образом, v и I не зависят от температуры, а
с3/ пропорциональна Т. Следовательно, при очень низких тем-
пературах коэффициент электронной теплопроводности являет-
ся линейной функцией температуры.
С точки зрения температурной зависимости в целом пове-
дение коэффициента электронной теплопроводности должно
быть таким, как показано на рис. 11.11. При очень низкой
температуре вклад электронов в теплопроводность довольно
мал. Согласно результатам предыдущего пункта, вклад кристал-
лической решетки в теплопроводность при низких температурах,
наоборот, довольно велик. Коэффициент общей теплопровод-
ности Л показан пунктиром на рис. 11.11, где видна важная
роль фононной проводимости при низкой температуре. Таким
образом, при низких температурах отличие между диэлектри-
ком и проводником не так велико, как при средних и высоких
температурах ]).
Свободные электроны в металлах являются носителями и
электричества. Среднее время между двумя столкновениями
электрона равно l/v. За это время электрическое поле X при-
дает электронам некоторую дополнительную скорость еХ1те,
где е — электрический заряд электрона, тР — его масса. До-
1) Экспериментальные данные см. в статье Estermann, Zimmer-
mann, /. Appl. Phys., 25 (1952), 578,
29 Зак. 1299
450
Г л. XI. Вязкость, диффузия и теплопроводность
полнительная скорость приводит к тому, что скорость в конце
свободного пробега становится равной а средняя ско-
еХ1 ~
рость zz = 2v « Эта скорость накладывается вдоль направле-
ния электрического поля на беспорядочное тепловое движение.
При втором столкновении дополнительная скорость разбивает-
ся по разным направлениям и превращается в тепловую. Если
в единице объема содержится пэл электронов, то плотность
тока равна ] = пэлеи, а по закону Ома удельное сопротивление
равно
X 2mev
V = -=WT- (11Л03>
Так как I изменяется как 1/Т, величина v почти постоянна, то
р должно изменяться как Т. Этот факт подтвержден экспери-
ментом. Таким образом, для средних температур удельное со-
противление зависит от температуры линейно.
Согласно (6.140) и (6.141),
Если пренебречь слабым при обычных температурах воздей**
ствием фононов на теплопроводность, то (11.102) дает
(11.104)
Умножив (11,103) на (11.104), получим
Но mev2 — удвоенная кинетическая энергия электрона; кроме
того, согласно (6.135), приближенно 2^ = -^k@e. Таким обра-
зом,
^ = ^^ = 2’94Х10“8^—. (11.106)
Это закон Видемана — Франца. Для большинства металлов,
как видно из табл. 11.5, экспериментальные значения постоян-
ной очень близки к теоретическим. Этот закон показывает, что
в металлах с хорошей теплопроводностью, например в серебре
или меди, где X велико, значение р должно быть малым, а когда
удельное сопротивление мало, то и электропроводность хоро-
шая. Такой вывод полностью согласуется с тем, что мы обычно
11.14. Теплопроводность в металлах
451
Таблица 11.5
Постоянная Видемана — Франца (10“8 вольт2 °К""2)
Металлы Си Ag Аи Zn Cd Pb Fe
Т = 291°К 2,28 2,36 2,43 2,31 2,42 2,45 2,88
Т = 373 °К 2,32 2,37 2,45 2,33 2ДЗ 2,51 3,00
наблюдаем. Приведенные расчеты дают этим опытным резуль-
татам теоретическое обоснование и показывают, что факторы,
определяющие теплопроводность и электропроводность, одина-
ковы— движение электронов в металле. Причем чем меньше
помех для движения электронов, тем лучше проводимость.
29*
Глава XI1
ДИФФУЗИЯ И ЗАМЕДЛЕНИЕ НЕЙТРОНОВ
В введении к предыдущей главе говорилось, что применение
кинетической теории к изучению процессов переноса матема-
тически осложняется тем, что уравнение, которому удовлетво-
ряет функция распределения, является нелинейным. Однако не
во всех случаях это уравнение нелинейно. Если рассматривае-
мая среда содержит два типа частиц Л и В и число частиц типа
В значительно превышает число частиц типа А, а задача физи-
чески заключается лишь в исследовании отклонений частиц
типа А от термодинамического равновесия, то состояние частиц
типа В в основном определяется взаимодействием этих частиц
между собой, а их функция распределения почти не зависит от
распределения частиц типа А. При изучении функции распре-
деления частиц типа А достаточно рассмотреть столкновения
частиц типа А с частицами типа В. Число столкновений между
частицами типа А должно быть значительно меньше числа
столкновений между частицами А и В; следовательно, это эф-
фект второго порядка и им можно пренебречь. Таким образом,
если говорить о функции распределения частиц типа А, то эф-
фект столкновения является линейным. В таких случаях кине-
тическое уравнение линейно, и в математическом отношении за-
дача значительно упрощается.
Примером такого рода является теория Лоренца для сво-
бодных электронов в металлах. В этой теории частицы типа А —
электроны, частицы типа В — атомы. Вследствие слишком гру-
бых допущений, заложенных в основе этой теории, ее резуль-
таты даже при безупречном выполнении кинетических расчетов
оказываются недостаточно точными. Поэтому мы не будем рас-
сматривать этого примера — читатели могут ознакомиться с
ним по соответствующим учебникам1).
Другой пример — диффузия и замедление нейтронов в ядер-
ном реакторе. Здесь частицы А являются нейтронами, части-
цы В — атомными ядрами других атомов в материале реактора.
!) См. Чэпмен С. и К а у л и н г Т., Математическая теория неоднород-
ных газов, ИЛ, М., 1960, гл. 18.
12.1. Диффузия нейтронов в поглощающей среде
453
Предположим, что реактор работает не с очень большой интен-
сивностью. Тогда плотность нейтронов будет значительно мень-
ше плотности атомных ядер. Поэтому если говорить о реакторе
со сравнительно низким или средним к. п. д., то диффузия и за-
медление нейтронов — линейная задача кинетики. В данной
главе мы рассмотрим эту задачу и дадим простые примеры точ-
ного кинетического анализа процесса переноса. Используемый
здесь материал взят из работ Маршака, Брукса и Гурвица1).
12.1. Диффузия нейтронов в поглощающей среде
Приступая к изучению «физики нейтронов», сначала не бу-
дем рассматривать замедления нейтронов при столкновениях.
Будем считать, что столкновения полностью упругие и энергия
нейтронов в результате столкновений не меняется. В элементе
пространственного объема dr=dx dy dz в момент времени / число
нейтронов с направлениями скорости между £2 и £2 + d£2 равно
N(r, £2, t)drdQ, (12.1)
где Л/(г, £2, /) — скалярная функция, являющаяся плотностью
распределения. Пусть V — величина скорости нейтронов (посто-
янная). Скорость изменения числа нейтронов N можно запи-
сать в виде
DN = dN(r.Q, t) . vw (r Q (1 2.2)
Dt ot v v '
Первый член в правой части выражает локальное изменение,
второй — изменение в результате собственного движения ней-
тронов. Эти изменения функции распределения происходят по
трем причинам. Во-первых, рассеяние и захват при столкнове-
ниях приводят к уменьшению Л/(г, £2 /). Захват полностью уни-
чтожает нейтрон; при рассеянии изменяется направление дви-
жения, т. е. £2. Во-вторых, воздействие рассеяния на нейтроны
заключается не только в том, что они покидают область rf£2, но
также и в том, что нейтроны, находящиеся вне d£2, в результате
столкновения могут попасть в эту область, т. е. скорости их бу-
дут направлены в телесный угол d£2. Третья причина — образо-
вание нейтронов (со скоростью V) из независимых источников.
Для аналитического выражения этих величин введем поня-
тие сечения столкновения. Когда нейтрон попадает в мишень
(атом), происходит столкновение, вероятность которого пропор-
циональна размерам мишени. Поэтому вероятность столкнове-
*) Marshak, Brooks, Hurwitz, Nucleonics, 4, May; 5, July
(1949).
454
Гл. XII. Диффузия и замедление нейтронов
ния можно связать непосредственно с величиной мишени и на-
звать ее сечением столкновения. Величина сечения зависит от
рассматриваемых нами процессов: рассеяния или поглощения.
Общая величина мишени в единичном объеме равна произве-
дению одного сечения на число мишеней (атомов) в этом
объеме. Пусть о — общее сечение рассеяния и поглощения в
единичном объеме. Тогда вероятность столкновения в единич-
ном объеме в единицу времени равна Vo. Каждое столкновение
выводит нейтрон за пределы области dQ. Поэтому скорость из-
менения функции распределения, происходящего по этой при-
чине, равна — W(r, О, t) Vo.
Далее пусть os— общее сечение рассеяния в единичном
объеме. Тогда число нейтронов с направлениями О' из dO', рас-
сеянных в единицу времени, равно N(r,Q',t)VosdQ'. Но не
все нейтроны в результате рассеяния изменяют первоначальное
направление О' на направление О. Поэтому необходимо ввести
функцию F, определяющую долю нейтронов, изменивших на-
правление О' на О. Очевидно, что F зависит от величины угла
между О и О'.
Можно сказать, что F является функцией косинуса угла ме-
жду О и О', т. е. F — функция О-O'. Таким образом, среди
нейтронов из dO' число нейтронов, изменивших при рассеянии
направление О' на О, равно Af (г, О', Z) VosF(O • O')dO'. Инте-
грируя по О', получаем общее число нейтронов, рассеянных по
направлению О
J N (г, Й', /) VosF (Й • Й') d й'.
Поскольку упругое рассеяние изменяет лишь направление ней-
тронов и не может изменить их число, то
fF(Q-Q')dQ' = ]>(Й.Й')^Й = 1. (12.3)
Остается учесть нейтроны, порождаемые источником в еди-
ничном объеме с направлением О. Пусть их число в области
dO выражается функцией S(r, О, f)dO. В итоге проведенных
рассуждений получаем интегродифференциал ьное уравнение
для функции распределения
f N (г, Й', Й, t). (12.4)
Это уравнение эквивалентно уравнению Больцмана для функ-
ции распределения молекул неоднородных газов. Все уравнения
этого типа называются уравнениями Больцмана. Однако, как
12.1. Диффузия нейтронов в поглощающей среде
455
уже отмечалось выше, уравнение (12.4) для неизвестной функ-
ции N является линейным.
Рассмотрим установившийся процесс при наличии плоской
симметрии, т. е. одномерный стационарный случай. Уравнение
(12.4) при этом упрощается. Источник S будет зависеть от z
и 9. Если, кроме того, рассматриваемый источник изотропен, то
S — функция только z. Поэтому N является функцией z и ц, где
ц— косинус угла между направлениями Q и z. В сферических
координатах (рис. 12.1) pi = cos0. Таким образом, имеем
5 (г, Q, /) = ЭД (12.5)
и
2V(r, Q, /)rf9 = 2V(z, и)^И^Ф- (12.6)
Тогда уравнение Больцмана преобразуется к виду
= —Wo + fw(z, р') (Iio) dll'dq>'-ь S (z), (12.7)
где цо — косинус угла 0О между начальной и конечной скоростя-
ми. Используя тригонометрическую формулу
cos 0О = cos 0 cos 0' + sin 0 sin 0' cos (ср — q/)>
можно написать зависимость между тремя величинами ц0,
И и ц', _____ _________
ц0 = |1ц'-Е ]Л1 — ц2 • — ц'2 cos (ср — q/). (12.8)
Число нейтронов в единичном объеме с любыми значениями
ц и ф равно
NQ(z)~2n f N (г, ц) (12.9)
456
Гл. XI1. Диффузия и замедление нейтронов
12.2. Связь между плоским и точечным источниками
Приведение уравнения Больцмана к одномерному нена-
много уменьшает его общность. Это объясняется тем, что реше-
ние задачи с точечным источником можно выразить с помощью
производной решения задачи с плоским источником (так назы-
ваемый плоский источник — это распределение источников с
некоторой интенсивностью в плоскости, перпендикулярной
оси г). Действительно, пусть g(r)—плотность нейтронов при
наличии точечного источника, т. е. решение уравнения Больц-
мана при наличии в точке г=0 источника единичной интенсив-
ности. Тогда для однородного источника с произвольным рас-
пределением So(r) соответствующая плотность нейтронов опре-
деляется интегралом
N0(r) = f dr'S0(r')g(|r'-r|). (12.10)
Суперпозиция решений является решением, так как наше урав-
нение Больцмана линейно.
Рассмотрим особый случай S(r)=6(z), где б (г) определяет-
ся соотношениями
+& +е
f d(z)dz = l, е->0, f d(z)f(z)dz=f(0). (12.11)
-е -е
Этот источник распределен по плоскости г=0 с единичной ин-
тенсивностью на единичной площадке, так что
I Г' — Г I = ]/(Z — Z')2 + Р2,
где р — радиальное расстояние от оси z. Таким образом, для
источника, распределенного в плоскости z=0, выражение
(12.10) упрощается
2л оо оо
^о(г) = f dtp fp dp f dz'b (z') g (/(z — z'}2 + P2) =
0 0 —oo
2л oo z oo
p dpg (У z2-j-p2) — 2л f pdpg(yz2 + p2) —
0 0 0
oo
= 2л f RodRog(Ro) (/Й = ? + р2).
IzI
12.3. Теория диффузионного приближения
457
Поэтому если х(2)—решение для плоского источника с рас-
пределением единичной интенсивности, то
Х(г)=2л fRodRog(RoY (12.12)
Ml
Дифференцируя, получаем
^-13)
Таким образом, решение задачи с точечным источником можно
выразить через производную решения упрощенной задачи с
плоским источником. Имея решение задачи для точечного источ-
ника, можно методом суперпозиции найти решение задачи с лю-
бым распределением в пространстве.
12.3. Теория диффузионного приближения
Для решения основного уравнения (12.7) разложим функ-
цию столкновений /?(р,0) в ряд по сферическим гармоникам
оо
(12.14)
/=0
где Pi — полиномы Лежандра, а Л — коэффициенты разложе-
ния, выражаемые через F(po) в виде
F^fF^P^dQ. (12.15)
Точно так же можно разложить и функцию распределения
оо
Л^(г, ц) = 2^-М(г)Л(ц), (12.16)
»=о
где
(г) = fN(z, ц) Рг (н) dQ. (12.17)
Если процесс диффузии нейтронов не очень интенсивен, то
нейтроны находятся в состоянии, близком к локальному равно-
весию с атомами, и функция распределения мало отличается
от локально равновесной. Следовательно, коэффициент No(z)
должен быть много больше ?Л(г), а Afi(z) в свою очередь
больше других. Такое положение свойственно любому слабому
процессу переноса (например, вязкость в газах). Принимая
сейчас это предположение, мы в дальнейшем уточним область
458
Г л. XII. Диффузия и замедление нейтронов
его применения. Так как Р0(ц) = 1, Р1(ц) =ц, то наше прибли-
жение можно записать в виде
N(z, + (12.18)
В силу (12.17) и Р0(р) = 1 физический смысл Mq(z) становится
очевидным — это ранее определенная плотность нейтронов. По-
ток нейтронов J равен
JN(z, ц) ViidQ = VNX (z). (12.19)
Таким образом, Afi(z) = 7/V, и наше условие Ni<^Nq просто озна-
чает, что диффузия сравнительно небольшая. Для удобства вы-
берем единицы измерения так, чтобы V=1 и о= 1, и обозначим
1о2-20)
Уравнение Больцмана (12.7) примет вид
= + W- ц')/7(Но)dll' + S(г). (12.21)
Подставляя в выражение под интегралом разложения (12.14) и
(12.16), имеем
f N(z, jx')F(|r0)dfi' =
оо
= f S J^M1(2)PZl(H')^±1^/’/2(Ho)rf2'. (12.22)
Zb Z2 = 0
Раскрывая Pz2(Ho)» гДе Но имеет вид (12.8), применим теорему
сложения сферических функций
^,(По) = Л,(н)/\(н') +
+ 2 (-If g;~g,1 Л»ЛТ(И cos zn (ф -ф'). (12.23)
m = 1
Интегрировать в (12.22) нужно по всем значениям ф'. Но, как
видно из (12.23), ф' входит в подинтегральную функцию толь-
ко через cos m (ср — q/), так что все слагаемые в (12.23), кроме
первого, при интегрировании обратятся в нуль. Поэтому
f N(z, ^)F{^d9.! =
оо
= 2 /2^M,(z)Pz1(p)^!-Fz2Pz,(h)Pz?(h')^'. (12.24)
h, W
12.3. Теория диффузионного приближения
459
Применяя соотношение ортогональности для полиномов Ле-
жандра, получаем
оо
= (12.25)
/2=0
А уравнение Больцмана теперь можно написать в виде
оо
1* U - 2 Nt F^T pt М + 5 <*)• (12-26)
/=о
Обозначая через S0(z) число нейтронов, образующихся в еди-
ничном объеме в единицу времени, имеем
S0(z) = 4jtS(z). (12.27)
Интегрируя (12.26) по ц от —1 до +1 и возвращаясь к перво-
начальным единицам, содержащим V и о, получаем
^. = _0ЛГо + а(1_/)ЛГо + 4.5о(г). (12.28)
При этом использовано соотношение, вытекающее из (12.3),
F0 = J>(n0)<Z2=l. (12.29)
Второе уравнение можно получить из (12.26), умножая его
на ц. Учитывая, что
= | + (12.30)
после интегрирования по ц от —1 до +1 и отбрасывания M(z),
Z^>2, в исходных единицах получаем
I = - aNi + ° О - (12-31)
Уравнения (12.28) и (12.31)—два уравнения для двух не-
известных функций No и Ni из (12.18). Этих уравнений уже до-
статочно для решения задачи о диффузии слабого потока ней-
тронов. Уравнение (12.28) фактически есть уравнение неразрыв-
ности. Градиент в нем уравновешивается разностью
S0(z) — fNo между образовавшимися и рассеянными нейтрона-
ми. Из этого уравнения также следует, что мало по сравне-
нию с No тогда, когда источник S0(z) является слабым, т. е. доста-
точно удаленным, а коэффициент f небольшой, т. е. рассеяние
является главным, а поглощение второстепенным. Это и есть
460
Гл. Х/1. Диффузия и замедление нейтронов
условия применимости рассматриваемого приближения, о ко-
торых говорилось выше.
Поток нейтронов, согласно (12.31), можно выразить через
градиент концентрации нейтронов; их связь имеет форму фено-
менологического закона диффузии. Так как f и Ni— малые ве-
личины, то fNi — малая второго порядка. Поэтому в (12.31)
членом fNi можно пренебречь.
Исключая Ni из (12.28) и (12.31), получаем
- зо-Ь?;-)" + г 5о (г). (12.32)
Это и есть так называемое уравнение диффузии нейтронов.
Обычно его пишут в векторной форме
VW0—^^+4-5о = О,
где (12.33)
£2 ______1____ £) _______К___
3o2f (1 — Fl)’ За(1—f,)
Выясним смысл коэффициентов уравнения (12.33). Величина о
есть общее сечение столкновения в единичном объеме, а 1/о=/—
средняя длина свободного пробега между столкновениями ней-
тронов и атомов. Аналогично средний свободный пробег относи-
тельно рассеяния определяется соотношением
'. = £• (12.34)
Связывая множитель 1/(1—Fi) с эффектом сохраняемости ско-
рости (11.3), можно ввести средний свободный пробег переноса
'«=7(Г^)- (12.35)
Таким образом,
D = jltrV. (12.36)
Величина /о есть сечение захвата в единичном объеме. Следо-
вательно, средний свободный пробег относительно захвата равен
(12.37)
Таким образом,
£2=у/Л- (12-38)
Интересно, что следствия из линейного уравнения Больц-
мана, получаемые в этой главе, совпадают с результатами эле-
ментарной теории переноса из предыдущей главы. Это связа-
12.3. Теория диффузионного приближения
461
но с соответствующими упрощениями при физической постанов-
ке задачи, позволяющими получить точные результаты, не при-
бегая к приближенным приемам предыдущей главы. Совпаде-
ние с элементарной теорией отнюдь не означает, что результаты
этой главы, в частности (12.33), следует считать неточными и
требующими дополнительной корректировки численных множи-
телей.
Приступим теперь к решению задачи о плоском источнике,
считая, что распределение на плоскости z=0 имеет единичную
интенсивность. Так как вне этой плоскости интенсивность источ-
ника равна нулю, то уравнение (12.33) принимает простую
форму
-^--^ = 0. (12.39)
0 —lim fj
e->0 J ’
-e
в
dz*
Поэтому в бесконечной среде концентрация нейтронов вдали
от источника выражается в виде
Г Ae-Z>L, z > 0,
N° = ( Ae*'L, z < 0.
При удалении от плоскости z=0 концентрация нейтронов стре-
мится к нулю. Для точного определения постоянной А необхо-
димо использовать уравнение (12.33), включающее источник.
Так как интенсивность источника равна 1, то S0(z)=6(z). Инте-
грируя уравнение (12.33) от z=—e до z=e и полагая е->0,
имеем
1 аг । б(г) ) ,
£2 -|- р | dZ -
__ p/A^o j рлго1 . _1____2Л _1_
L dz ]г=+0 L dz D “ L D ‘
л__ L
2D '
В результате концентрация нейтронов выражается формулой
M)(z) = -2pxp(— \z\/L). (12.40)
Отсюда
Имёя решение задачи с плоским источником единичной ин-
тенсивности в бесконечной среде, мы можем, применяя метод
суперпозиции, сравнительно легко находить решения более
сложных задач. Рассмотрим, например, плоский источник при
z=zr в полубесконечной среде, граничащей с вакуумом (Мо = О)
462
Гл. Х/1. Диффузия и замедление нейтронов
при 2=0. Эта задача решается методом изображений. Решение
для плоского источника при z = z7 накладываем на решение для
плоского стока (отрицательного источника нейтронов) с той
же интенсивностью при z = —z'. Вследствие симметрии посре-
дине между источниками, т. е. при 2=0, интенсивность обра-
щается в нуль. Решение задачи имеет вид
N0(z) = -^- А —^-|г+г’|/£}> (12.41)
где второй член принадлежит образу.
12.4. Точное решение уравнения Больцмана
Если допустить, что рассеяние изотропно, то Го=1, Л = 0,
I + 0. Тогда в случае плоского источника с единичной интен-
сивностью при 2=0 уравнение (12.26) записывается в виде
= H)+(1 <12-42)
Можно получить точное решение этого уравнения Больцмана
без дополнительного предположения о слабости потока нейтро-
нов. Сравнение такого решения с результатами предыдущего
пункта покажет уровень точности диффузионного приближения.
В кинетике неоднородных газов аналогичное сравнение не-
возможно, так как уравнение Больцмана там является нелиней-
ным и вплоть до настоящего времени не найдено его точного
решения. К счастью, в случае неоднородных газов нет настоя-
тельной необходимости в такой проверке теории первого при-
ближения, поскольку основное предположение этой теории
(средняя длина свободного пробега много меньше характерной
макродлины) хорошо выполняется при обычных условиях1).
В случае же диффузии нейтронов средняя длина свободного
пробега измеряется, как правило, сантиметрами и, следова-
тельно, не настолько мала по сравнению с макроразмерами,
чтобы теория первого приближения могла быть достаточно на-
дежной. Поэтому при средних и больших длинах свободного
пробега требуются уточнения, которые и рассмотрим в этом и
в следующих пунктах.
Будем решать уравнение (12.42) методом Фурье. Введем
преобразование '
со
М(у, ц)= fN(z, ц)е{уг dz. (12.43)
’) Это утверждение, к сожалению, теряет силу по мере того, как начи-
нают выполняться условия, при которых число Кнудсена сравнимо с едини-
цей. — Прим, перев.
12.4. Точное решение уравнения Больцмана
463
Умножая уравнение (12.42) на и интегрируя по z от —оо
до +оо, в левой части получаем
оо оо
J^p.-^-rfz==[li(V(z, —н/у fel^H(z, p)dz.
— OO — oo
Для плоского источника в бесконечной среде при z=±oo имеем
М=0. Следовательно, первый член в правой части этого ра-
венства равен нулю. Интеграл во втором члене равен как раз
М(у, ц). Таким образом, преобразованное уравнение имеет вид
(_/№ + 1)Л1(у. и) = 1=1лШ + _1-, (12.44)
где М0(у)— преобразование Фурье N0(z), т. е.
М^у) = J* eiyz N{i(z)dz. (12.45)
Разрешая (12.44) относительно М(у, ц), имеем
м (и 1____|__L
/п0 (у, Н) — 4п 1 _ ,-уц. -Г 4я
1
1— W
Если это равенство проинтегрировать по Q, то после переста-
новки порядков интегрирования по ц и z слева получим МЛу}-
Так что
2л 1 2л 1
М0(у)= (1-Ь мо(У), Г Г -------------1_ 1 ? d f
4л J v J 1—W 4л J T J 1—typ,
o-i o-i
Ho
Поэтому
1
/d[i —lil — iy 2 .
---£---— -T— In -j—= — arctg u.
1 — l ур ly 1 + ly у
— 1
arctg у
•
1 -(!—/) arclgj/
теперь формулу обращения преобразования
Применяя
получаем
= f e~l^M0(y)dy =
f___________e-^du
J y-(l-f)arctgye аУ-
(12.46)
Фурье,
(12.47)
464
Гл. XII. Диффузия и замедление нейтронов
Подинтегральная функция многозначна, точки ее ветвления
у — ±i и у= ±оо. Кроме того, подинтегральная функция имеет
два простых полюса в точках z/=±zv, где v — решение урав-
нения
arctg v 1
(12.48)
На плоскости у (рис. 12.2) сделаем два разреза, от +i до
+ ioo и от —i до —zoo. При обходе точки ветвления по часовой
стрелке значение arctgу увеличивается на л. При положитель-
ных значениях z можно сдвинуть контур интегрирования Ci в
нижнюю полуплоскость, оставляя подинтегральную функцию
ограниченной. При этом контур Ci преобразуется, как показано
на рис. 12.2, в два контура с2 и с3. Интеграл по с3 равен —z,
умноженному на вычет в точке —zv, т. е.
1 f
2л j
zArthvg_V3
у
°У L У Jу-
Arth v
------е
v
1 Arthv
v(l—v2) v
В силу (12.48) это выражение'упрощается
1 уд-^2) с.
2л J (l_f)(V2-f) е
г.
Для вычисления интеграла по с? сделаем замену переменной
у — — На правой стороне разреза arctgу больше, чем на левой,
12.5. Сравнение точного решения с приближенным
465
на л. Кроме того,
. Л 4. 1
arctg у = — arctg у,
— i Ar th л = v “ ‘'Arth Jr •
Z T]
Поэтому на правой части контура Сг берем
arctg у = — г Ar th 1-J- -у,
*1 *
а на левой
arctg у = — i Ar th 1 — .
Таким образом, имеем
В результате для концентрации нейтронов получим выражение
дг _ —v(l_—_у2) г .
lNo\z> -r
со />-’Пг
4-1 f______________П___________
Hi-1=1 Arth ir+pLOzdm
I \ n n/ L 2т] J|
(12.49)
В следующем пункте выясним значение точного решения
уравнения Больцмана.
12.5. Сравнение точного решения
приближением
с диффузионным
Интеграл в (12.49) убывает с увеличением z как е”2, факти-
чески даже несколько быстрее, так как на нижнем пределе
т) = 1, знаменатель подинтегральной функции обращается в бес-
конечность. С другой стороны, первый член в (12.49) убывает
несколько медленнее, чем е~2, ибо, как видно из (12.48), даде§
3Q Зак. ед
466
Гл. XII. Диффузия и замедление нейтронов
при очень интенсивном захвате, т. е. при f~l, величина v не
превосходит 1. Таким образом, на некотором расстоянии от
источника, достаточно большом по сравнению со средним сво-
бодным пробегом, вторым членом в (12.49) можно пренебречь.
В действительности если захват незначителен, то даже на
расстоянии порядка среднего свободного пробега первый член
(12.49) является хорошим приближением. В случае слабого
захвата уравнение (12.48) можно решить путем разложения
Arth v в степенной ряд. При этом получим
Возвращаясь к первоначальным единицам измерения, т. е. вновь
вводя о и V и учитывая, что при изотропном рассеянии Fi= О,
имеем
(12.50)
Таким образом, при /С1 приближенное решение имеет вид
ехр~!Жехр
В исходных единицах измерения получим
что совпадает с результатом (12.40), полученным ранее по тео-
рии диффузионного приближения.
Значение точного решения состоит е том, что благодаря ему
мы имеем возможность уточнения диффузионного приближения.
Действительно, вдали от источника интегральным членом мож-
но пренебречь, а первое слагаемое имеет ту же форму, что и
диффузионное решение, если за L взять величину, обратную
точному решению уравнения (12.48), а интенсивность источни-
ка модифицировать так, чтобы получить тот же коэффициент,
что и в (12.49).
Далее, согласно (12.13), решение для точечного источника
в изотропно рассеивающей среде при больших г имеет вид
лг / \ а v2 —^2) £Г/£ Т — 1 /in
No(r)— v (1_— f) 2лг ’ w‘ (12.51)
Здесь мы уже ввели общее сечение о и скорость V. Путем су-
перпозиции решений (12.51) можно получить асимптотическое
решение для плотности нейтронов при произвольном распре-
делении источников. Если ввести функцию No, которая удовле-
12.5. Сравнение точного решения с приближенным
467
творяет дифференциальному уравнению
-L\V^Nl+VOcN^X-^-^S^r), (12.52)
то вдали от источников концентрация нейтронов Nq будет асим-
птотически равна Nq. Это действительно так, потому что реше-
ние уравнения (12.52) в случае, когда S0(r) есть б-функция,
совпадает с асимптотическим решением (12.51) уравнения
Больцмана для точечного источника.
Уравнение (12.52) дает еще один способ уточнения диффу-
зионной теории, когда ос/о не является бесконечно малым. Этот
способ заключается в замене источника So эффективным источ-
ником
й = (12.53)
При этом для потока нейтронов J нужно использовать выражение
J = — L\VVN*o. (12.54)
В терминах J и S' уравнение (12.52) примет вид
VJ + ocI/No = So. (12.55)
При малом ос/о значение S' приближенно равно S и
что также совпадает с результатом диффузионной теории.
Приведенные рассуждения оправдывают уравнение (12.52)
только для бесконечной среды. В случае ограниченной среды
это уравнение можно применять в точках, не близких к границе.
В общем случае решение для плотности нейтронов состоит не
только из членов вида (12.51), но также из однородных членов,
являющихся решениями уравнения (12.52) при S = 0. В области,
далекой от границ и не содержащей источников, эти члены удо-
влетворяют точному уравнению Больцмана. Таким образом, если
дополнить (12.52) соответствующими граничными условиями, то
указанный ранее рецепт будет применим и для ограниченных
сред. Когда границы достаточно далеки от источников, гранич-
ную задачу можно рассмотреть самостоятельно и, как мы скоро
увидим, граничные условия могут быть сформулированы про*
стым способом. Таким образом, уравнение (12.52) дает возмож-
ность разделения задач об источниках и границах.
Как уже подчеркивалось, решение уравнения (12.52) не опи-
сывает концентрации нейтронов вблизи источников. Природу
отклонений можно обнаружить путем исследования строгого
30*
468
Г л. XII. Диффузия и замедление нейтронов
решения (12.49). При достаточно малых z (меньше среднего сво-
бодного пробега) наступает момент, когда интеграл в (12.49)
будет играть главную роль. Действительно, если положить в
интеграле zx\ = t, то пределы интегрирования преобразуются в
t—z и /=оо. При очень малых z благодаря тому, что знамена-
тель под интегралом в большей части области интегрирования
близок к 1, имеем
г<1. (12.56)
Z
Вблизи 2=0 этот интеграл логарифмически расходится, что
резко отличается от диффузионного решения, в котором кон-
центрация нейтронов остается ограниченной. Бесконечная плот-
ность в точном решении создается частицами, выпущенными ис-
точником и еще не испытавшими столкновений; причем главный
вклад вносят частицы, испускаемые почти параллельно плоско-
сти источников. Эта бесконечная плотность не противоречит ко-
нечному потоку как раз потому, что распределение по скоростям
сосредоточено в направлениях, почти параллельных указанной
плоскости.
Применяя (12.13), из (12.56) можно получить концентрацию
нейтронов вблизи точечного источника
'«ь
или в исходных единицах
or <С 1-
(12.57)
Это есть как раз распределение частиц, еще не испытавших
столкновений после выхода из источника. Этот факт говорит
о том, что можно усовершенствовать диффузионную теорию, за-
меняя б-источник так называемым источником первого столкно-
вения, имеющим форму o3e~ar/4n(or)2. Такой вариант исполь-
зуется в следующем пункте.
12.6. Поправки к диффузионной теории вблизи границ
✓
Мы уже рассмотрели поправки, обусловленные сильным по-
глощением и близостью к источникам. Рассмотрим теперь по-
правки, вызываемые близостью к границам.
Пусть нейтроны диффундируют в полубесконечной среде
2^>0, граничащей с вакуумом. Допустим, что поглощение от-
сутствует, и будем пользоваться единицами измерения, в кото-
12.6. Поправки к диффузионной теории вблизи границ
469
рых о и V равны 1. При больших положительных z верна диф-
фузионная теория, которая в данном случае (/=0, L = oo,S0=0)
дает
^0 А
dz* “ ’
т. е.
^ = а(г + г0). (12.58)
Поток нейтронов равен
<12-59)
Найдем величину 20. Вблизи границы важно рассматривать
плотность нейтронов как функцию р. Обратимся сначала к при-
ближенным рассуждениям п. 12.3. Согласно (12.18), N(z, р)
приближенно описывается двумя коэффициентами N§(z) и
N^z). Поток нейтронов J по (12.19) связан с Afi(z). В наших
единицах
= (12.60)
При z=0 должно выполняться следующее условие: ни один ней-
трон не возвращается из вакуума в среду. Это значит, что при
ц>0 функция распределения на границе равна нулю, т. е.
дг(О, и) = 0 (р>0). (12.61)
Но так как в разложении Af(2, р) по сферическим гармоникаАм
мы оставили только первые два члена, то условие (12.61) не мо-
жет быть удовлетворено точно. Поэтому мы потребуем обра-
щения в нуль при z=0 только суммарного потока частиц с
р>0, т. е.
1
2л f nN (0, ц) dy. = 0 (ц > 0), (12.62)
о
используя (12.17), (12.58) и (12.60), имеем
1
/г 1 11
ц [а20 — ар] dy. = a — -g-1 = 0,
о
или
2
2q = . (1 2.63;
Следовательно, на границе вакуума (2=0) концентрация ней-
тронов не равна нулю. Величина No равна нулю лишь при
2 2 1
2 =—-g*, или в первоначальных единицах при 2 =—у—.
470
Г л. XII. Диффузия и замедление нейтронов
Плоскость z=—Zq расположена за физической границей и по-
тому называется экстраполированной границей. Иначе условие
на границе вакуума можно записать в виде
«"=4? (S’ (12-64>
где п — нормаль к границе, направленная внутрь среды. По-
правочный эффект в (12.64) имеет порядок среднего свободного
пробега. Так как то при малых ltr на границе AZo~O.
Рис. 12.3.
Если вместо (12.62) потребовать, чтобы при z=0 обращался
в нуль интеграл от произведения N на некоторую другую функ-
цию от р, то получаем другое значение z0. Так что найденное
значение z0 содержит некоторый произвол. К счастью, задача
распределения нейтронов вблизи плоской границы может быть
решена точно. Путь реше-
Таблица 12.1 Ния следующий: сначала за-
Экстраполированная граница
/ 0 0,5 0,9 1
z0O-f) 0,7104 0,7204 0,85 1,000
при / = 0. При малых z истинное
дача сводится к интеграль-
ному уравнению, которое
затем решается методом Ви-
нера — Хопфа. Результаты
такого анализа показывают,
что плотность нейтронов
асимптотически приближает-
ся к (12.58) с г0 = —0,7104
значение No ниже асимпто-
тического, как показано на рис. 12.3. В точке z=0 имеем NQ —
*=а/]/~3 = 0,577 а, в то время как асимптотическое решение дает
здесь 0,7104 а.
При наличии поглощения экстраполированная граница г0 в
известной мере зависит от f. Как видно из табл. 12.1, величина
Zq увеличивается почти пропорционально 1/(1 —/). Поэтому при
12.7. Некоторые простейшие примеры диффузии нейтронов
471
малых f можно взять zo = O,71/(1 —/). В дальнейшем вместо
(12.64) мы будем пользоваться уточненным граничным усло-
вием
\Т — 071 (dNo\ — °»71 ( ^0 \
° а (1 — f) \ dn ) as [ dn / ’
(12.65)
где учтено соотношение (12.20). Использование диффузионной
теории с такими граничными условиями позволяет получить до-
статочно точные решения многих практически важных задач,
связанных с проектированием ядерных реакторов.
12.7. Некоторые простейшие примеры диффузии нейтронов
Для иллюстрации полезности экстраполированной границы,
связанной с (12.62), решим задачу с плоским источником в по-
лубесконечной среде z>0. Пусть плоский источник расположен
при z=Zi. Будем считать, что 24 настолько велико, что между
источником и границей имеется область, достаточно далекая
как от источника, так и от границы. Если источник испускает
в единицу времени с единичной площадки один нейтрон, то об-
щее решение уравнения (12.52) равно
11___v2 of i Г 1. 1
L +А> ‘J’ <4 * * * * * * * 12-66)
где А — произвольная постоянная, определяемая по условию на
границе. Из (12.65) имеем
4- А — у — л),
(Jy L
откуда
0.71
. 1 -4 ( I 1,42\ /.1
0,71 в еХР{ Os
+ osL
В результате
Wo(z)—2 (1—f) (v2 — f) ocVL [exp{ L f
-ехр^-^ + ^+^Д}]. (12.67)
Нужно помнить, что это решение, как и все решения, получен-
ные методом экстраполяции границы, не верно вблизи границы.
В частности, не следует делать из него каких-либо выводов от-
носительно плотности нейтронов при z<0,
472
Г л. XII. Диффузия и замедление нейтронов
В качестве второго примера рассмотрим плотность нейтро-
нов в непоглощающей изотропно рассеивающей сфере с единич-
ным источником в центре. Вне источника S = 0, и уравнение
(12.52) с учетом того, что ос = 0, упрощается к виду
VWo = O.
Отсюда, используя условие равенства нулю плотности нейтро-
нов при r = /? + 0,71/crs, получаем
(г) = 4д7 — R„s _|_ 071) • (12.68)
Этот результат можно несколько улучшить, пользуясь ис-
точником первого столкновения. По (12.57) распределение ней-
тронов, еще не испытавших столкновений, равно
п
°’ ехр(-а5г)
ov/ 4лУ (а4г)2 •
После однократного или многократного столкновения плотность
нейтронов No (г) удовлетворяет уравнению, которое выводится
из (12.52),
V 1 d ( „ dN'n \ о2, е~1
3 d\ \s dg / to? ’ 5 5
Так как в источнике g=0 поток нейтронов целиком представлен
то при £->-0 поток, образуемый N$, должен быть ну-
лем, т. е.
Поэтому решение No можно написать в виде
, За^ /1 е~^ \
^°(У —4л7[ У + J 1“*"^
\ 5 /
где с — постоянная, которую нужно определить. Общая концен-
трация нейтронов есть сумма Nq и No. Следовательно,
Г е
(У — Ь 3
— +с.
12.8. Замедление нейтронов, вызываемое упругим рассеянием 473
Постоянная с определяется из условия, что NQ(£)=0 на экстра-
полированной границе r = /?crs4-0,71. В итоге
I- £ + J s'
ЯОу+0,71
. (12.69)
v 3
Jras
Без граничной поправки диффузионная теория дает
в2 Г 1 1 1
(г) j •
Сравнение трех вариантов решения (12.68), (12.69) и (12.70)
представлено на рис. 12.4, где дана зависимость
(12.70)
4nVr2No(r) от
ros при Ros = 3. Радиус сферы здесь лишь втрое больше сред-
него свободного пробега. Поэтому эффект среднего свободного
пробега на этих кривых, несомненно, сказывается. Видно также,
что в данном случае простая теория диффузии является плохим
приближением.
12.8. Замедление нейтронов, вызываемое упругим рассеянием
В предыдущих пунктах предполагалось, что все нейтроны
имеют одинаковую энергию. Это, вообще говоря, неверно, так
как даже при упругом рассеянии, когда внутренние степени
474
Г л. XII. Диффузия и замедление нейтронов
свободы ядер не возбуждаются, нейтроны могут передавать
ядрам кинетическую энергию поступательного движения, теряя
в результате довольно ощутимую часть своей энергии. Рассмо-
трим здесь решение уравнения Больцмана с учетом такой по-
тери энергии.
Замедление нейтронов зависит от сечения рассеяния, кото-
рое в свою очередь является функцией энергии. Обычно сечение
рассеяния уменьшается с увеличением энергии. Водород пред-
ставляет собой крайний случай; его сечение рассеяния состав-
ляет 20 мишеней (1 мишень=10-24 см2) при эпитепловых энер-
гиях (порядка 1 эв); при 0,5 Мэв оно уменьшается в два раза,
а при 5—10 Мэв доходит до 1 мишени. Для углерода сечение
рассеяния при эпитепловых энергиях равно 4,8 мишени, а при
высоких энергиях оно уменьшается до 1 мишени.
Напишем уравнение Больцмана для функции распределения
нейтронов, замедляющихся при упругих столкновениях с атом-
ными ядрами, при следующих трех предположениях.
а) Неупругим рассеянием можно пренебречь. Такое рассея-
ние имеет место, когда ядра находятся в невозбужденном со-
стоянии, а кинетическая энергия столкновений, измеренная в си-
стеме координат, связанной с центром инерции, не превышает
энергии возбуждения первого уровня ядра. Для многих замед-
лителей, особенно в случае легких ядер, пренебрежение не-
упругим рассеянием является хорошим приближением. Напри-
мер, у углерода первый возбужденный уровень выше основного
на 4,7 Мэв, и число нейтронов с энергией, превышающей эту
величину, будет пренебрежимо мало. С другой стороны, для
алюминия энергия возбуждения первого уровня близка к 1 Мэв,
и вклад деления в замедление будет значительным. У тяжелых
элементов, таких, как свинец и уран, первый возбужденный
уровень еще ниже и пренебрегать неупругим рассеянием в слу-
чае этих элементов не следует.
б) Можно пренебречь эффектом химической связи. Для
этого энергия нейтронов должна быть много больше энергии ко-
лебательного кванта, равной k0v, где 0V — характеристическая
температура колебаний. Так как 0^—1000°К, то #0^0,1 эв.
Следовательно, для нейтронов с энергиями больше 1 эв тре-
буемое условие выполняется.
в) В системе координат^ связанной с центром инерции,
упругое рассеяние является изотропным. Это утверждение бу-
дет правильным, если длина волны нейтрона велика по срав-
нению с размерами рассеивающего ядра, что соответствует
условию
Мзв,
12.8. Замедление нейтронов, вызываемое упругим рассеянием
475
где А — атомный вес ядра, Е— энергия нейтрона. Это неравен-
ство согласуется с условием отсутствия неупругого рассеяния.
При очень низких энергиях изотропное рассеяние может нару-
шаться резонансным эффектом, однако это случается редко и,
кроме того, влияние его не очень велико.
Чтобы написать в рассматриваемом случае уравнение
Больцмана, необходимо ввести в качестве независимой пере-
менной скорость нейтронов v или кинетическую энергию Е. Тог-
да функция распределения N определяется так: число нейтро-
нов в элементарном объеме dr со скоростями в телесном угле
da и логарифмической энергией и[и = Inгде Ео — некоторая
начальная энергия в интервале du, равно
ЛГ(г, 2, и, t) dr du da.
Причина выбора логарифма энергии в качестве аргумента вы-
ясняется позднее. Скорость изменения плотности нейтронов в
движущемся элементарном объеме теперь запишется в виде
-^ = ^+v.W(r,2,B,0- (12.71)
Пусть о/(а)—полное сечение столкновения, т. е. сумма сече-
ний рассеяния os(a) и захвата ос(г>) в единичном объеме, ка-
ждое из которых является функцией модуля скорости нейтро-
нов v. Захват и рассеяние приводят к тому, что нейтроны ухо-
дят из dii и du с частотой Nvat(v). Функция S(r, и, /) (источник
нейтронов) выражает интенсивность появления нейтронов в мо-
мент t в точке г с энергией, соответствующей и.
Вычислим теперь скорость появления нейтронов в da, du в
результате рассеяния. Число нейтронов с энергиями из du' и
скоростями в da', подвергающихся рассеянию в единичном объ-
еме в единицу времени, равно
N(r, 2', и', t)v'vs(v')du' da'.
Вероятность попадания в da, du зависит от косинуса угла
цо между й и Й' и от отношения энергий и — и'. Обозначим ее
через /(цо, и— и'). Тогда скорость увеличения N за счет рас-
сеяния равна произведению числа рассеяний на f, проинтегри-
рованному по всевозможным значениям и' и 2Х. Так как столк-
новение нейтронов с неподвижными атомными ядрами всегда
приводит к замедлению нейтронов, то столкновение может
только увеличить значение но не уменьшить. По-
этому интегрирование по и' нужно провести в пределах от О
476
Г л. XII. Диффузия и замедление нейтронов
до и. В результате скорость изменения /V запишется в виде
W = — Ww((ti) + S(r, и, t) +
+ J du' J dQ'N(r, Й', u', t)v'os(v')f(ii0, u — u'). (12.72)
0
Это и есть уравнение Больцмана для нашей задачи.
Прежде чем идти дальше, необходимо найти функцию столк-
новений /(цо, w), где и — логарифм отношения энергий до и
после столкновения. Для решения этой задачи перейдем к си-
стеме координат, в которой центр инерции двух частиц, ней-
трона и ядра, покоится. В этой системе координат общий им-
пульс, очевидно, равен нулю; следовательно, индивидуальные
импульсы должны быть равны по величине и противоположны
по направлению как до, так и после столкновения. Далее,
так как энергия при столкновении сохраняется, то в этой си-
стеме координат величина скорости нейтрона до и после столк-
новения одинакова.
Пусть М — отношение массы атомного ядра к массе нейтро-
на, причем в лабораторной, системе координат атомное ядро
покоится, а начальная скорость нейтрона равна v'. Тогда в си-
стеме, связанной с центром инерции, скорость нейтрона равна
[Л4/(Л4+1)]у', в то же время скорость самого центра инерции
будет [1/(Л1+1)]у'. Ситуация изображена на рис. 12.5, где 0 —
угол рассеяния в системе центра инерции. Скорость после рас-
сеяния v в лабораторной системе координат получается вектор-
12.8. Замедление нейтронов, вызываемое упругим рассеянием
477
ным сложением скорости центра инерции и конечной скорости
нейтрона относительно этого центра. Как видно из рисунка,
или
о_ I М Д2 / 1 \2 2Mv/2 Q
v v ) +U+i v ) + (лГ+Трcos0>
£ _ 14-уИ2 + 2Л4 COS0
Е' (М + 1)2
где Е' и Е — начальная и конечная энергии в лабораторной си-
стеме. Полагая Е/Е' = ехр[—(и — и')], отсюда имеем
cos е = - 11+^. +1 (М + (12.73)
Угол рассеяния 0 в лабораторной системе координат, как видно
из рисунка, определяется соотношением
cos 0 = cos 0 + лгр
или
0(и—иг)/2 ( Л4 п । 1 )
= е {м + 1 cos 0 + м +11 *
Используя (12.73), получаем
cos 0 = но = (М + 1) е-<“-“'>/2 — ± (М — 1) (12.74)
Благодаря предположению об изотропности рассеяния диф-
ференциальное сечение рассеяния на угол 0 в системе центра
инерции равно
do = ~ os sin 0 dQ = — — osd (cos 0),
или, согласно (12.73),
= fdu = du. (12.75)
Отсюда видно, что вследствие зависимости между величиной
угла и энергией двойной интеграл в уравнении Больцмана фак-
тически является простым интегралом. Сохраняя двойной инте-
грал, введем на основе (12.74) 6-функцию, указывающую, что
при интегрировании по нужно брать величину p0, соответ-
ствующую значению и.
478
Гл. XII. Диффузия и замедление нейтронов
Так как dQQ = <2nd\i^ то имеем
/к «-«')=-^г-(“-в,)х
Хб[ц0—"2-(Л1+1’)г!_<“~“,)/2 + 4(УИ— (12.76)
Это и есть требуемая функция столкновений.
12.9. Вывод возрастного уравнения
В большинстве практических случаев основной интерес вы-
зывает вопрос о способах нахождения стационарного распреде-
ления нейтронов. Поэтому мы опустим в уравнении Больцмана
член dN/dt. Кроме того, за исключением случаев, оговаривае-
мых особо, всюду предполагаем, что захвата нет, т. е. сг^ = сг5 = а.
Далее преобразуем уравнение, вводя новую функцию
Т(г, 2, и) = ЛДг, 2, (12.77)
которую можно назвать плотностью столкновений нейтронов,
так как это есть число столкновений нейтронов с ядрами в еди-
ничном объеме в единицу времени. Подставляя (12.77) в
(12.72), имеем
1q.VT + T = fdu'fdQ'W(r, 2', U')f(no, u-u') + S(r, a).
0
(12.78)
Найти решение этого уравнения в общем случае трудно, осо-
бенно при произвольной зависимости сечения о от энергии. По-
этому желательно получить приближенное уравнение, решение
которого находится легче и имеет асимптотический характер.
Рассмотрим, каким образом можно получить это асимптотиче-
ское уравнение.
Для простоты предположим, что влияние местоположения в
пространстве сказывается лишь по направлению z. Это позво-
ляет нам заменить в вышеприведенном уравнении г на z. Если
это так, то функция распределения будет зависеть не от й, а
только от ц— косинуса угла между 2 и z. Аналогично простой
диффузионной теории п. 12.3 допустим, что градиент концен-
трации и поток нейтронов^ очень малы, так что функция
^(z, ц, и') почти изотропна и достаточно рассмотреть только два
первых члена в разложении ее по сферическим гармоникам,
В результате сделанных предположений имеем
¥(г, 2, «) = Т(г, ь [%)(*. и) + 3^ (z, «)]. (12.79)
*** и л
12.9. Вывод возрастного уравнения
479
где То и Ti — функции только z и и, связанные с Т следую-
щим образом:
1
Tq (г, и) = f (z, у, и) Ро (у) dQ = 2л J Т (z, у, м) dp,
_11 (12.80)
Чг1(г, и) — f Т (г, у, и) Рх (у) dQ — 2л J* уТ (г, у,, и) dp.
— 1
Подставляя (12.79) в (12.78), имеем
14^+31*^-] + Ч'»+з|1ч-1 =
и 1
= 2nJ du' § dp' [То (z, «') +
о -1
+ Зу'Тj (г, «')]/(у0» и— u')-[-4xS(z, и). (12.81)
Если умножить уравнение (12.81) на некоторую функцию от
у, и проинтегрировать по всем й, то получается уравнение для
То и Ть Интегрируя сначала само уравнение (12.81), имеем
и 1
7^ + ЧГо = 7 fdQf du' f dp'[W0(z, «') +
о -i
-^Зу'Т^г, w')]f(y0, и — w') + 4л5(г,«). (12.82)
480
Г л XII. Диффузия и замедление нейтронов
Сменим порядок интегрирования в (12.82), передвигая на пер-
вое место интеграл по О. Напомним, что ро— косинус угла ме-
жду й и й'. При фиксированных прочих параметрах 6-функция
в (12.76) выделяет лишь одно определенное значение ц0, при
котором f(jio> и — и') не обращается в нуль (рис. 12.6). Приме-
няя (12.76), находим
/ « — «') =
[Ио _1(М+ +
+|(Л1-1)Л“ ] >.
Наименьшее значение ц0 равно —1, поэтому нижний предел ин-
тегрирования по и' должен быть корнем уравнения
_ I = (М 4-1) е'~ —i- (М -1) е~,
откуда
, , /М+1\2
и = и — е,
где
« = (12.83)
Эта величина соответствует наибольшей потере энергии,
имеющей место при лобовом столкновении. В результате инте-
грал в (12.82) принимает вид
и 1
(1+лГ)г «9 + 3И'Ч\Сг, «')]•
и—е —1
После интегрирования по у/ остается
и
J ^(«-«')чго(г, и')du',
и-е,
Наконец, после подстановки
W = и — и'
(12.84)
12.9, Вывод возрастного уравнения
481
из (12.82) получим
1 . ш _
о дх * 0
е
- - uf)2 p-“X(z, a-w)^ + S0(2, и), (12.85)
О
где
50(г, ^) = 4л5(г, и). (12.86)
Если в 8-интервале То меняется не слишком сильно, то
(12.85) можно еще более упростить, ограничиваясь лишь двумя
членами разложения То в ряд Тейлора в окрестности и' = и,
^(г, « —w)«4f0(2', «) — w-—ц).
Учитывая (12.83), имеем
е
(12.87)
О
е
02.88)
О
Результат (12.87) вместе с (12.75) показывает, что вероят-
ность рассеяния нейтронов в различных направлениях одина-
кова. Соотношение (12.88) определяет новый параметр g, фи-
зический смысл которого — среднее значение меры уменьшения
энергии нейтронов w при различных углах рассеяния. Следует
подчеркнуть, что g не зависит от энергии нейтронов и для дан-
ного атомного ядра является постоянной. В окончательном
итоге уравнение (12.85) принимает вид
= “)• (12.89)
Умножая теперь уравнение (12.81) на ц и интегрируя по О,
получаем второе уравнение для Чт0 и Ti,
и 1
JrfQ J du' J d\i' [рЛ^г, ^z) + 3pp,4f1(z, u')\ f (p0, u — u').
о -1
(12.90)
Первое слагаемое в квадратных скобках является нечетной
функцией от ц и при интегрировании даст нуль. Далее,
31 Зак. 1299
482
Гл. XII. Диффузия и замедление нейтронов
благодаря d-фупкции в (12.76) цо принимает значение cos© из
(12.74), т. е.
Po = cos0=y(M+l)^-^ — ±(М- 1)Л (12.91)
Тогда (рис. 12.6) при фиксированном р/ имеем
J d(.if(n0, и — и') И = 2ncos0p/ •
Таким образом, с помощью (12.76) интеграл в (12.90) приво-
дится к виду
1 е
|- J Н/2 J e~w4r1 (z, и — w} cos Qdw —
-i о
— Jи — w)cos©dw.
о
Поэтому уравнение (12.90) теперь можно записать так:
е
+ «-^)cose^- (12.92) ‘
о
Уравнения (12.92) и (12.85)—система двух уравнений для
двух неизвестных функций То и Ть
Если в 8-интервале Ti изменяется очень мало, то в (12.92)
можно положить Ti~Ti(z, и) и вынести из-под знака интегра-
ла. Оставшийся интеграл дает среднее значение cos©; обозна-
чая его через [соз©]ср, согласно (12.75), имеем
£
° (12.93)
Уравнение (12.92) тогда принимает вид
^ = 37ТГ=7Ж?ы TZ- <12-94)
Уравнения (12.94) и (12.89)—упрощенные уравнения для То
и Ti в случае, когда изменения То и Ti малы в 8-интервале и.
Решая эти уравнения, нужно помнить, что наибольшая вели-
чина энергии нейтронов равна начальному значению Ео, поэто-
му и всегда больше нуля. Другими словами, если м<0, то для
всех z
То^Т^О.
(12.95)
12.9. Вывод возрастного уравнения
483
По аналогии с (12.34) и (12.35) можно ввести длины свободного пробега ls и /<г, т. е. средние
/ - 1 tr - о {1 — [cos 0]ср) • (12.96)
Вместо (12.89) и (12.94) тогда можно написать
. d'Fl д'Го е / \ дг । ди ~S^Z' (12.97)
И hr дЧо _ иг 3 dz р (12.98)
Уравнение (12.97) есть уравнение неразрывности для плотно-
сти нейтронов, а (12.98)—уравнение для потока. Исключая
Ti, имеем
3g Wo 3 с /_ х n2qq)
Это уравнение легко распространяется на случай трехмерного
пространства
<12'100>
Введем вместо и переменную
x = fl^-du'. (12.101)
о
Для чистых элементов, согласно (12.88), величина g не зависит
от энергии и выносится из-под интеграла, но в смесях £ может
быть функцией от и. Величины ls и lfr зависят от и через о. Ве-
личина т называется возрастом и имеет смысл квадрата дли-
ны замедления. Если ввести новую функцию источника
S (г, т) = - hhs 5о(Г’ И) (12.102)
и новую плотность У (г, Т)= ^о(г. «). (12.103)
то (12.100) принимает форму v дх S(r, т). (12.104)
Это уравнение называется возрастным уравнением Ферми.
Функция q — так называемая «плотность замедления» — выра-
жает число нейтронов в единичном объеме, с которыми еже-
секундно происходит понижение энергии Е, соответствующее
31*
484
Гл. XII. Диффузия и замедление нейтронов
возрасту т. Формулу (12.103) можно понимать так: согласно
определению, данному в (12.88), величина g есть среднее пони-
жение энергии на одно столкновение, измеряемое по шкале и.
Если и изменяется в интервале du, то для каждого нейтрона та-
кое изменение происходит под влиянием du/% столкновений, а
всего в единичном объеме в единицу времени подвергается та-
кому изменению q нейтронов, так что интенсивность столкно-
вений равна q dufe, а это и есть xVndu. Отсюда получается соот-
ношение (12.103).
В ходе вывода возрастного уравнения были введены много-
численные упрощения; все они являются ограничениями теории
Ферми. Прежде чем исследовать область применимости этой
теории, рассмотрим простой пример решения возрастного ура-
внения.
12.10. Замедление моноэнергетических нейтронов
от плоского источника
Для источника с фиксированной энергией Ео имеем
S(r, т) —Q(r)d(x). (12.105)
В задаче с плоским источником единичной интенсивности в бес-
конечной среде возрастное уравнение имеет вид
(12.106)
Для решения этой задачи можно воспользоваться преобразова-
нием Лапласа. Введем
оо
<p(z, s) — j e~sxq(z, x)dx. o (12.107)
Начальным условием, согласно (12.95), будет q (г, 0) = 0. Тогда из (12.106) получим (12.108)
д2<р . , ч д]г *<Р= 6 Сн- если обозначить (12.109)
то придем к задаче, уже решенной в п. 12.3. Поэтому ана-
логично (12.40) имеем
Ф(г, = (12.110)
12.11. Область применимости возрастного уравнения
485
Обращение преобразования Лапласа дает
1 -X
T) = Vr=^ 4т-
У 4лт
(12.111)
Уравнение (12.111) показывает, что при фиксированном z плот-
ность замедления нейтронов как функция т сначала увеличи-
вается вместе с т, а затем, достигнув максимума, уменьшается.
На расстоянии, близком к источнику, вершина очень высока,
и при увеличении z она смещается вправо и понижается
(рис. 12.7).
12.11. Область применимости возрастного уравнения
При выводе возрастного уравнения, помимо условий, ис-
пользуемых в диффузионной теории (п. 12.5), фактически до-
бавлены следующие:
1) Средняя длина свободного пробега не меняется замет-
ным образом в 8-интервале логарифмической энергии.
2) Число столкновений, испытанных нейтроном после выхо-
да из источника, велико.
3) Расстояние от источника не очень велико.
Согласно предположениям диффузионной теории, можно
ожидать, что возрастная теория нарушается вблизи источника.
Однако по мере того как энергия нейтронов в результате много-
кратных столкновений достаточно понижается, возрастная тео-
рия становится верной даже на расстояниях от источника, мень-
ших среднего свободного пробега. Дело в том, что нарушение
диффузионной теории, как мы видели, фактически происходит
за счет нейтронов, которые не успели столкнуться после вы-
хода из источника, но именно эти аномальные нейтроны и
486
Гл. XII. Диффузия и замедление нейтронов
исключаются, когда мы ограничиваем внимание частицами с
погасшей энергией. Кроме того, исследование поведения вблизи
плоской границы показывает, что надлежащая «экстраполиро-
ванная граница» определяется средним свободным пробегом,
соответствующим наиболее медленным нейтронам. Наконец,
условие относительно захвата не появляется, так как мы уже
предположили, что захват отсутствует.
Чтобы увидеть, где и как сказались сформулированные ус-
ловия при выводе возрастного уравнения, рассмотрим более по-
дробно аппроксимации, введенные при решении уравнения
Больцмана. Для этой цели используем решение (12.111) воз-
растного уравнения с плоским источником. Прежде всего если
применять разложение (12.79), то необходимо, чтобы было
Но Vi связано с То по формуле (12.98). При исполь-
зовании (12.111) отсюда имеем условие
т. е. должно быть
1 hr2 w и/
3“ ~2т 0<^Т1’
бт /_ г \
hr hr s) ’
(12.112)
где
(12.113)
— так называемая длина замедления; это — расстояние, при
прохождении которого энергия нейтронов уменьшается на вели-
чину, соответствующую т; уравнение (12.112)—это третье из
условий, сформулированных в начале пункта. Укажем порядок
величины т. Например, от расщепления (Ео = 2 Мэв) до тепло-
вых энергий (£ = 0,025 эв) возраст нейтронов равен в бериллии
т = 98 см2, в угле т = 350 см2.
Далее, оставляя только два члена разложения То(г, и — w)
в (12.85), мы предполагали, что
Но из (12.87) и (12.88) нам известно, что средним значением
w является g. Используя (42.111), имеем
dT0 _ <PF0 dx 11 / *2 । 1 \ ш
du dx du~ 6 ь™\ 2т2 x) °*
Таким образом, должно быть
_I______г2 6
X 2х2 !s!tr ’
12.12 Применение возрастного уравнения
487
откуда
(12.114)
Это второе из упомянутых условий.
Наконец, мы предполагали, что xFi(z, и — w) можно заме-
нить на ТДг, ц), т. е.
Но = -у- -j—. Поэтому если условие (12.114) считать уже
выполненным, то
_ dltr 1 ч,
ди du ltr 1
и
Уравнение (12.115) показывает, что относительное изменение
среднего свободного пробега в е-интервале энергии много мень-
ше 1, а это и есть первое из рассматриваемых условий. Для
тяжелых элементов е сравнительно мало, а о слабо зависит от
энергии, так что все условия удовлетворяются.
Таким образом, мы видим, что условия 1) и 2) связаны с
приближенным интегрированием в (12.85) и (12.92). Если, не
пользуясь этими приближениями, оставлять в указанных фор-
мулах интегралы, то имеем лишь третье условие. Такую тео-
рию можно применить и к рассеянию на легких атомных ядрах,
например водороде и дейтерии.
12.12. Применение возрастного уравнения
Для источника с фиксированной энергией Ео возрастное
уравнение имеет вид
V2? = #-S(r)6(4 (12.116)
Плотность замедления q зависит от плотности нейтронов
Л70(г, и), т. е. от числа нейтронов в единичном интервале лога-
рифма энергии и в единичном объеме. По (12.77) и (12.103) эта
зависимость такова:
q (г, t) = £N0(f, u)v(u)o(u). (12.117)
Величина Nq(v, u)v(u)ci(u)du — это число нейтронов, испытав-
ших столкновения в энергетическом интервале du в единичном
объеме за единицу времени. Так как среднее изменение и при
488
Г л. XII, Диффузия и замедление нейтронов
одном столкновении равно g, то в области применения возраст-
ной теории (г, т), очевидно, можно считать плотностью потока
нейтронов в пространстве щ тем самым <?(г, т) выражает ско-
рость изменения числа нейтронов в единице объема, энергия
которых упала на величину, соответствующую т. Так как мы
предположили, что поглощения нет, т. е. число нейтронов по-
стоянно, то общая скорость образования нейтронов, равная ин-
тегралу от ^(г, т) по всему пространству, не зависит от т. Это
условие фактически содержится в (12.116); его можно получить,
интегрируя (12.116) по всему пространству. Интеграл от V2<?
есть нуль, следовательно,
4 f q(r, x)dV = b(x) fS(r)dV.
Отсюда
ГО, т < О,
f a(r x}dV = г - (12.118)
J q ( ’ ’ f S(r)dV, т > 0.
Это имеет место лишь в случае приближенной возрастной тео-
рии замедления.
Для плоского моноэнергетического источника плотность за-
медления q находится по формуле (12.111). Для нахождения
плотности замедления q в случае точечного источника можно
воспользоваться связью (12.13) между решениями задач для
точечного и плоского источников. Если г — расстояние от то-
чечного источника, то для него
р-г2/4л
• <12Л,9>
При фиксированном т формулы (12.111) и (12.119) дают рас-
пределение нейтронов с данной энергией в пространстве. В обо-
их случаях можно вычислить средние значения г2 или г2 соот-
ветственно при фиксированном т. В результате получим для
плоского источника
z2 = 2т,
для точечного источника
С2 = 6т. (12.120)
Так как уТ имеет смысл длины замедления Ls, то из (12.120)
находим __ __
£2=4 = 4. (12.121)
Отсюда видно, что расстояние нейтронов с заданной энергией
от точечного источника несколько больше, чем от плоского.
12.13. О поведении решения вблизи границы
489
Коснемся еще одной задачи, вызывающей большой интерес,
которую также можно решить с помощью возрастной теории.
А именно рассмотрим замедление нейтронов в двух различных
смежных областях. Пусть атомы в обеих областях одинаковы, а
плотности различны. Тогда
М£) _ li (Е) _ р2
о, (£) ТАё) р, •
Для некоторых значений энергии нейтронов имеем
j!
Т2 Р1 ‘
(12.122)
(12.123)
Если источник находится в 1-й области, то возрастные уравне-
ния имеют вид
(12.124)
Для удобства можно рассматривать <72 как функцию Ti, что поз-
волит для нейтронов с одинаковой энергией проводить одно рас-
суждение для обеих областей. Согласно (12.123), имеем
На границе областей N0(r, и) и МДг, и) должны быть равны.
По (12.117) сначала находим
затем
^ = 77^’ (12.126)
^2 _ /£2_\2 <fyi _ I Р2_\2 ддх
дп \ dj / дп \ Pi / дп
(12.127)
где и — нормаль к поверхности раздела. Уравнения (12.124) и
(12.125) вместе с граничными условиями (12.126) и (12.127)
описывают замедление нейтронов в двух смежных областях.
12.13. О поведении решения вблизи границы
По диффузионной теории, как мы уже видели, плотность ней-
тронов на границе рассеивающей среды и вакуума не равна
нулю. В задаче о замедлении мы ограничиваемся случаем
моноэнергетического источника, обобщение которого особых
490
Г л. XII. Диффузия и замедление нейтронов
затруднений не вносит. Но для нейтронов, обладающих одина-
ковой энергией, вблизи границы применимо рассуждение, при-
веденное в п. 12.6. Следовательно, аналогично (12.64) имеем
(12.128)
где п — нормаль к границе, направленная внутрь среды, а 11г
зависит от т. Начальное условие (12.108) и граничное условие
(12.128) вместе дают те полные сведения, которые однозначно
определяют решение возрастного уравнения.
Так как ltr — функция т, то математически задача является
сложной. Для упрощения можно положить
Если А — малая величина, т. е. о зависит от энергии слабо, то
решение задачи с переменной ltr можно считать возмущением
решения при постоянной /<г, что упрощает математический ана-
лиз.
Задачи к главе 12
12.1. Рассмотреть диффузию нейтронов в U238 (плотность
равна 18,68 г!см\ атомный вес равен 238,07). В U238 сечение за-
хвата тепловых нейтронов равно 2,8 мишени на атом (1 ми-
шень=10~24 см2), а сечение рассеяния равно 8,2 мишени. Рас-
считать о и Д а также ls и 1С.
12.2. Используя решение задачи 12.1, найти по (12.48) со-
ответствующее значение v.
12.3. Исходя из (12.85) и (12.92), найти соответствующие
уравнения для преобразований Лапласа от То и ЧЛ по и.
Глава XIII
ТЕПЛОВОЕ ИЗЛУЧЕНИЕ
При выводе общих формул теории переноса в десятой главе
были введены два вектора потока энергии q и qR. Вектор q —
вектор потока тепла, рассмотренный ранее. Предметом ис-
следования данной главы является вектор qR—поток энергии,
передаваемой посредством переноса излучения, т. е. путем рас-
пространения электромагнитных волн. Почему этот вопрос рас-
сматривается именно здесь? Во-первых, потому, что тепловое
излучение оказывается существенным только при очень высо-
ких температурах порядка нескольких тысяч градусов, и для
большинства вопросов, связанных с инженерной практикой, до-
статочно ограничиться обычной теплопроводностью. Во-вторых,
с точки зрения методики перенос излучения весьма сходен с
диффузией нейтронов, поэтому удобно рассматривать его на
основе предыдущей главы.
Во многих учебниках для инженеров имеется раздел по
передаче энергии излучения, однако в них вопрос обычно ак-
центируется на передаче излучения между поверхностями
твердого тела, причем пространство считается абсолютно про-
водящим. Таким образом, среда не оказывает влияния на излу-
чение, и вопрос сводится к излучению и поглощению на поверх-
ностях, а задача распространения относится к геометрической
оптике. Анализ производится просто, и мы не будем здесь на
нем останавливаться, отсылая читателя к соответствующей ли-
тературе.
В данной главе речь пойдет об излучении и его поглощении
в непрозрачной среде в пространстве. Перенос излучения про-
исходит скачками (от испускания до поглощения), среднее зна-
чение которых называется «средним свободным пробегом излу-
чения». Это говорит о том, что передача излучения в непрозрач-
ной среде очень похожа на процесс диффузии. Именно такова
природа поведения излучения железа в плавильной печи. Дру-
гим примером может служить излучение в горячих газах вну-
три камеры сгорания. Если рассматривать перенос излучения
как движение фотонов, то это будет еще более похоже на
492
Г л. XIII. Тепловое излучение
диффузию нейтронов. Только нейтроны заменяются фотонами,
а скорость движения повышается до скорости света с. На этой
основе мы и будем развивать теорию переноса излучения.
13.1. Поле излучения
При изучении переноса лучистой энергии в излучающей и
поглощающей средах понятия геометрической оптики недоста-
точны, поэтому используются другие методы. На рис. 13.1 Р —
фиксированная точка,! — линия, проходящая через P,da— эле-
Рис. 13.1.
ментарная площадка с нормалью М, 0 — угол между Ми!.
Проведем из каждой точки Р' площадки da в направлении, па-
раллельном !, элементарный конус с телесным углом dw. Вся
фигура в целом будет представлять собой полубесконечный усе-
ченный конус с основанием da.
Излучение передается через площадку da. Пусть dEv —
энергия, которая переносится за время dt через площадку da
в усеченный конус с частотами в пределах от v до v + dv. Мож-
но обнаружить, что отношение
dEv
cos 0 da da) dv dt
при уменьшении dt, day, da, dv имеет конечный предел. Этот пре-
дел положителен, является функцией от Р и ! и не зависит от
угла 0. Обозначим его через /v и назовем удельной интенсив-
ностью излучения в точке Р в направлении !, или просто интен-
сивностью в точке Р вдоль !.
Количество энергии, проходящей в течение dt через da в на-
правлении, которое образует -е нормалью к da угол 0, внутри
конуса с телесным углом dw и с частотами в пределах от v до
v + dv, выражается через /у в виде
dEv = /у cos 0 dadadvdt. (13.1)
Если интенсивность в данной точке не зависит от направле-
ния, то поле излучения в этой точке изотропно. Если же интен-
13.2 Взаимодействие излучения с веществом
493
сивность одинакова во всех точках и по всем направлениям, то
поле излучения является однородным и изотропным.
Поясним появление cos 0 в предыдущем определении. Когда
направление L отклоняется от нормали к da, энергия, проходя-
щая через площадку da, при прочих равных условиях умень-
шается. Поскольку перенос излучения фактически представляет
собой распространение электромагнитных волн, то поток излу-
чения в направлении L означает, что фронт волны перпендику-
лярен L. Из рис. 13.1 видно, что характерной площадкой дол-
жна быть не da, а ее проекция daf — dacosQ на плоскость фрон-
та волны. Поэтому lv можно также определить как энергию,
протекающую в единицу времени в единичный телесный угол
в направлении L в единичном интервале частот через единич-
ную площадку, перпендикулярную L, в точке Р.
Энергия каждого фотона равна hv, а скорость — с (скорость
света); деля Iv на hvc, получаем плотность потока фотонов с
частотой v в направлении L. Так как направление L выра-
жается единичным вектором Й, то Iv является функцией век-
торов г, Й и скалярной величины v, т. е.
Л = А(г, Й, V). (13.2)
13.2. Взаимодействие излучения с веществом
При столкновении фотона с молекулой или атомом он мо-
жет быть рассеян или захвачен. Захват означает поглощение
фотона, а рассеяние вынуждает фотон изменить направление и
войти в другой пучок. В отличие от диффузии нейтронов рассея-
ние излучения в однородной непрозрачной среде много меньше
поглощения. Поэтому в дальнейших рассуждениях мы им пре-
небрегаем, рассматривая только поглощение. Поглощение из-
лучения часто описывают через коэффициент поглощения на
единицу массы kv, который определяется как относительная по-
теря интенсивности Iv при прохождении через слой единичной
толщины и массы. Пусть р — плотность среды. Тогда уменьше-
ние интенсивности излучения в единицу времени равно kv pclv.
Размерность pkv обратна длине, так что l/p£v— величина по-
рядка среднего свободного пробега излучения с частотой v.
Под воздействием внешнего поля сама среда может излу-
чать энергию. Количество излучаемой энергии с частотой v в
точке г в направлении й характеризуется коэффициентом излу-
чения /(г, й, v), так что увеличение интенсивности за счет такого
источника излучения в единицу времени равно pcj. Допустим
аналогично диффузии нейтронов, что поле излучения находится
494
Гл. XIII. Тепловое излучение
в состоянии локального равновесия. Тогда
сП. V/v = — kxpclv + pry,
или после деления на pt?
Ia.vzv=-Vv+/. (13.3)
Г
Уравнение (13.3) —основное уравнение переноса лучистой энер-
гии. Необходимо помнить, что поглощение является следствием
того, что у молекул или атомов среды возникают скачки энер-
гетических уровней, поэтому оно связано с энергетическим со-
стоянием молекул и атомов. В заданной среде коэффициент по-
глощения kv зависит от термодинамических переменных Тир,
т. е. для любой частоты
kv = kv(J\ р). (13.4)
Молекулы и атомы вследствие химических реакций могут по-
падать в метастабильные возбужденные состояния и излучать
энергию. Это явление называется хемилюминесценцией и опре-
деляется кинетикой фотохимических реакций, причем каждый
специфический случай требует особого рассмотрения. Мы не бу-
дем рассматривать излучение подобного типа, а ограничимся
лишь тепловым излучением, т. е. излучением, обусловливаемым
тепловым движением среды. Будем считать, что вещество и поле
излучения находятся в термодинамическом равновесии. При этом
большую роль играет закон Кирхгофа1)
j = kvBv(T\ (13.5)
где BV(T) —стандартная функция Т и v, не зависящая от й.
Следовательно, излучение является изотропным. Фактически
BV(T) есть излучение абсолютно черного тела. Согласно (6.21),
энергия равновесного излучения, возникающая в единице
объема в единичном интервале частот, равна
______8лЛу3____
с3 [ехр (hv/kT)— 1]
После деления на hv получим число фотонов в единице объема
8лу2
с3 [ехр (hx/kT) — 1]
*) См. R и а г k А. Е., U г е у Н. С., Atoms, Molecules and Quanta, McGraw-
Hill, 1930, 60.
13.3. Поток энергии теплового излучения
495
Деля на 4л и умножая на hvc, имеем плотность энергии излу-
чения, т. е.
я-(Л = ^е,р(4Г)„,. (13.6)
Подставляя (13.5) в (13.3), получаем следующее основное
уравнение теплового излучения:
2 • V/v = -pMv + pMv(D’ (13.7)
В случае одномерной задачи имеем лишь одну пространствен-
ную координату г, и все величины не зависят от х и у. Если
0 — угол между вектором Q и осью г, причем
cos 0 = |.i, (13.8)
то для любой частоты Iv будет функцией только от z и ц. Тогда
(13.7) преобразуется к виду
h) + p^5v(7). (13.9)
Уравнение (13.9) является основой теории переноса излучения
в астрофизике1). Эта теория изучает перенос лучистой энергии
в атмосфере Солнца и других звезд. В ее задачу входит, напри-
мер, объяснение зависимости /v от v и ц, наблюдаемой на по-
верхности Солнца. Анализ этой теории очень сложен и требует
для описания длинных рассуждений. Поток излучения, рассма-
триваемый нами, значительно проще, так как нас интересует
лишь энергия, переносимая при всех v и ц, а не точные измене-
ния, связанные с отдельными v и ц.
13.3. Поток энергии теплового излучения
При фиксированной частоте p£v является лишь функцией от
z, и уравнение (13.9) можно переписать в виде
Iх (^),
где
£= J p^-dz', d^ = pkvdz. (13.10)
о
Форма его решения такова:
£
Д>(£, = f±Bv(T)(13.11)
0 Чандрасекар С., Перенос лучистой энергии, ИЛ, 1953. К о и г g а-
noff V., Basic methods in transfer problems, Oxford, 1952,
496
Г л. XIII. Тепловое излучение
Нижний предел интегрирования определяется граничными усло-
виями. Напомним, что kv зависит не только от v, но и от Г и р.
Поэтому BV(T) в правой части (13.11) есть функция от t/ и
должна находиться под знаком интеграла.
При ц>0 направления излучения выходят из нижнего по-
лупространства. Предположим, что поле излучения является
бесконечно большим и при —оо /v = 0, т. е. на бесконечности
нет притока энергии. Тогда
Л& ц) = f I Bv (Г) (%', И > 0.
J и
(13.12)
Аналогично при ц<0 направления излучения выходят из верх-
него полупространства. Если при £->+оо нет притока энергии,
то
г 1 ——
М£,ц) = f±-Bv(T)e и dt,', H<0.
J р-
(13.13)
Поток энергии теплового излучения q^v с частотой v есть
энергия, протекающая в единицу времени через единичную пло-
щадку, перпендикулярную оси z, при всех й, т. е.
q/?,v = J* Лр J ц/у4/ц = 2л J ц/у^ц. (13.14)
о -1 -1
Подставляя выражения (13.12) и (13.13) в (13.14), имеем
qz?v==2njrfH J 8v(T)e » dt/— J Bv(T)e * dt/ . (13.15)
Для упрощения предположим, что термодинамические вели-
чины на среднем свободном пробеге излучения l/p£v меняются
мало, и разложим By (Т) в степенной ряд около £
|BV (Г)]£, = |BV (Г)] + (£' - 0 ч-
2!
г -L . .
Ц* -г • • • •
3!
13.3. Поток энергии теплового излучения
497
Подставляя это разложение в (13.15), получаем
dBv(T) I ,
4r,v = — 4л ! — j dV J
0 0 , 1 d3B (Т) / f „ + 3! f f r]3e-^dt]+ ... L 0 0
Интегралы по q легко вычисляются. В результате имеем
1 dB.AT) 1 d3B(T) 1 з i ;£з +•••}. изд?)
Пусть L — характерная макродлина, a lR— средний свободный
пробег излучения для всех частот, т. е.
/
R IPMcp’
Тогда отношение второго и первого членов разложения (13.17)
имеет порядок величины (lRIL)2. Поэтому, когда размеры поля
намного превышают средний свободный пробег излучения, вто-
рым членом в (13.17) можно пренебречь. Возвращаясь к про-
странственным координатам х, г/, z, напишем
ч»..=~ж7в”(7')’ (13'18)
распространяя тем самым найденную зависимость на трехмер-
ный случай. Общий вектор потока излучения qR является инте-
гралом от v по всем частотам, т. е.
4tf = -i/^v|4^v(r)Jdv. (13.19)
о v
Но BV(T) зависит лишь от частоты и температуры, поэтому
V[4n5v(r)] = -^H4nBv(r)]Vr,
и формула (13.19) переписывается в виде
(13.20)
О
Это выражение можно еще более упростить. Для этого опре-
делим средний свободный пробег излучения lR формулой
32 Зак. 1299
498
Гл. XIII. Тепловое излучение
Росселанда
оо
1 — о
где интеграл в знаменателе есть плотность энергии излучения
черного тела. Согласно (6.19),
Т ^пВ.АТ) 8л5&4
/ »7' (13.22)
О
Здесь а — постоянная Стефана — Больцмана (7,569хЮ~15 эрг-
• см~3 • град~4). Вместо (13.20) теперь имеем
clD d (аТ*)
q₽ = —(13.23)
Формула (13.23) имеет простой физический смысл. В ней
с — скорость света, a d(aT*)ldT — удельная теплоемкость фото-
нов в единице объема. Согласно (11.47), коэффициент перед
градиентом температуры в (13.23) является коэффициентом
теплопроводности, связанной только с фотонами При этом теп-
ловой поток излучения пропорционален VT, что согласуется с
общей теорией переноса [см. (10.64)].
Приведем интересный пример расчета теплового потока из-
лучения в твердом теле. Пусть /д=10’3 см, Т = 4000°К. Так как
с«ЗХ1010 см/сек, то
~~d(aT4)/dT —
О
= 4 X 7,569 X Ю'15 X 40003 X 3 X Ю10 X Ю~3 X Ю~7 X ttU =
О т*, 1оЭ
= 0,00047 кал • см~{ • сек~{ • град~\
Это численное значение обычно намного меньше проводимо-
сти электронов в металле и-по порядку величины сравнимо с
решеточной проводимостью в диэлектрике. Другое дело, если
речь идет о газе, находящемся под давлением и при крайне
высокой температуре, например внутри звездных сфер. ТахМ
тепловой поток излучения qR намного больше q, так как зави-
симость проводимости излучения от температуры намного силь-
нее молекулярной проводимости (Г3), да и lR также больше
численного значения для твердого тела, приведенного выше.
13.5. Излучательная способность
499
Фактически при расчете потока тепла внутри звездной сферы
часто пренебрегают молекулярной проводимостью и рассматри-
вают только проводимость излучения.
13.4. Граничные условия
Когда среда ограничена, то для полного решения задачи
распределения температуры, кроме уравнения теплопроводно-
сти (13.23), необходимы еще граничные условия. Если прово-
дящая среда граничит с вакуумом, то нормальная компонента
потока тепла q на границе существует только благодаря излу-
чению в вакуум, ибо вакуум не может получать энергию по-
средством теплопроводности. В этом случае поток тепла через
границу обычно задается и граничное условие имеет вид
П _ Г, I ClR dT
4w— [ ' з dT J dn ’
(13.24)
где X — коэффициент молекулярной теплопроводности, an —
внешняя нормаль к границе.
Если среда граничит с твердым телом, то обычно задается
температура и граничное условие имеет вид
T=TW (на стенке). (13.25)
Поток тепла через границу считается суммой потока излуче-
ния (13.23) и молекулярного потока тепла.
13.5. Излучательная способность
Рассмотрим слой излучающей среды между плоскостями
z = 0 и z=b. Пусть при р>0 интенсивность излучения на пло-
скости z = b равна /v, а на плоскости z=0 имеем /v = 0, т. е. че-
рез эту границу излучение не входит. Тогда, согласно (13.11)
и (13.14), поток излучения на плоскости z=b равен
00 1 (£о-£)
qff = 2nf dvfdn f Bv(T)e и (13.26)
ООО
b
где Co = J* pkydz. Если зависимость плотности p, коэффициента
о
поглощения kv и температуры Т от z установлена, то по этой
формуле вычисляется qR. Однако общий случай является до-
вольно сложным, и мы проведем анализ для простого случая
однородного слоя.
32*
500
Гл. XIII. Тепловое излучение
Если температура не зависит от £, то интегрирование по С
дает
f Bv(T)e м ^ = цВу(7)[1-е-М*]. (13.27)
о
Интегрируя далее по ц, получаем
f dp. f Bv(T)e d£ = Bv(T) j — f fie~^dp
0 0 L 0
Последний интеграл сводится к интегральной показательной
функции. Пусть so/P = тогда
fne-^dn=$f ^3-^ = 4 e-^-^+^of ^-dS, .
о io L u -
Поскольку pkv не зависит от z, то ^ = p^v6. В результате
qJ} = nf Bv (Т) {1 — + pM*"pM _ (pkvb)2 Ei (— pM)} dv,
0
(13.28)
где
00
Ei(—x) = f -^-d£,. (13.29)
Согласно (13.22), величина
л f Bv(T)dv = ±aT* (13.30)
0
есть излучение абсолютно черного тела при температуре Т.
Если отношение qR к излучению черного тела назвать излуча-
тельной способностью е, то для слоя толщины b с температу-
рой Т и плотностью р имеем
оо _
e = ^frf ^Bv(B)[l — e~p*vb + pfivbe~p*vP — (p6vb)2Ei4—pkvb)]dv.
О
(13.31)
Проведенные рассуждения показывают, что излучательная
. способность связана с величиной и геометрической формой из-
лучающего объекта. Попытаемся расчленить оптические и гео-
13.5. Излучательная способность
501
метрические эффекты. Для этого введем понятия пути луча и
длины пути. В предыдущем примере длина пути z/p — это рас-
стояние, проходимое лучом в слое толщины z с ориентацией р.
Как и в случае (13.27), удельную интенсивность луча длины L,
проходящего через однородное поле излучения, найдем из
(13.11) в виде
Bv (Т) [1 — exp (— pjfevZ)].
Интегрируя по всем частотам, получаем выражение
J 5V(7")[1 — ехр(— p£v£)]^v,
о
которое дает плотность излучения на отрезке длины L. Для луча
эмиссионную способность 8(Г, рЛ) можно определить формулой
оо
е(Л pZ) = f ^Bv(T)[l-exp(-ptvL)ldv, (13.32)
о
по которой и рассчитывается обычно излучательная способ-
ность. Рассмотрим излучающую среду, ограниченную произ-
вольной гладкой поверхностью (рис. 13.2). Вычислим излуча-
тельную способность в точке Р. Через р обозначим косинус угла
между направлением луча и граничной нормалью и, <р — соот-
ветствующий азимутальный угол. Длина пути L есть функция
от р и ср. Излучательная способность г в точке Р получается
следующим интегрированием:
2л 1
е = ^- j" d<pf ре[Т, рЦц, <р)]г/ц. (13.33)
о о
Для слоя толщины b имеем L = bl\i, и результаты (13.31) и
(13.33), как нетрудно показать, совпадают. Формулы (13.32) и
502
Г л. XIII. Тепловое излучение
(13.33), таким образом, осуществляют разделение геометриче-
ского и оптического эффектов. Излучательная способность рас-
считывается по формуле (13.32). Когда функция е(Г, pL) из-
вестна, любую конфигурацию можно рассчитать по формуле
вида (13.33).
13.6. Коэффициент поглощения
Предыдущие рассуждения показывают, что основной вели-
чиной при расчете потока теплового излучения является коэф-
фициент поглощения единицы массы kv. Его роль в вопросе из-
лучения по своей важности напоминает роль межмолекулярного
потенциала в расчетах свойств вещества. Так как мы предпо-
лагаем, что вещество и излучение близки к термодинамическому
равновесию, то процесс переноса вызывается слабой неравно-
весностью и эффект поглощения можно считать результатом
взаимодействия излучения с атомами и молекулами, находя-
щимися в равновесном состоянии. При термодинамическом рав-
новесии распределение атомов и молекул по различным энер-
гетическим уровням определяется законами статистической
механики, рассмотренными в предыдущих главах. Когда атомы
и молекулы подвергаются воздействию со стороны электромаг-
нитного поля излучения, может происходить поглощение энер-
гии, сопровождаемое скачкообразным изменением энергетиче-
ского состояния. Термодинамическое состояние вещества опре-
деляется двумя переменными, например температурой Т и
плотностью р. Поэтому для каждой частоты излучения v, как
это уже принято в (13.4), kv есть функция от Т и р.
Молекулы газа почти независимы. В качестве первого при-
ближения можно считать, что взаимодействие излучения с га-
зом представляет собой сумму взаимодействий излучения с ка-
ждой молекулой в отдельности, происходящих независимо, т. е.
не подвергающихся влиянию со стороны других молекул. Тогда
задача сводится к подсчету вероятности перехода отдельной мо-
лекулы от одного энергетического уровня к другому. Определив
с помощью статистической механики число молекул на каждом
энергетическом уровне и просуммировав по всем состояниям,
получим общую вероятность перехода. Переходу сопутствует
поглощение энергии. Таким путем, опираясь на свойства моле-
кул и атомов, можно рассчитать коэффициент поглощения kv.
Однако если пренебрегать взаимодействием между молеку-
лами, то энергетические уровни будут дискретными и переходы
возможны не на все частоты. Излучательная способность выра-
жается интегралом по всем частотам, но подинтегральная функ-
ция будет отличаться от нуля лишь в дискретных точках. Так
13.7. Временное возмущение уравнения Шредингера
503
как математическая точка не имеет ширины, то излучательная
способность почти всюду равна нулю. Однако такое описание
недостаточно реально. В действительности различные возмуще-
ния приводят к уширению частот перехода (спектральных ли-
ний). Поэтому спектральные линии, кроме положения, имеют
еще толщину, так что вероятность перехода распределяется в
определенных интервалах частот. Хотя интегральная вероят-
ность такая же, как при отсутствии взаимодействия, уширение
спектральных линий дает излучательную способность с ненуле-
вым значением.
Следует обратить внимание на то, что электромагнитные
волны могут взаимодействовать лишь с внутренним электриче-
ским полем атомов и молекул. Поэтому излучение действует
только на внутренние степени свободы, но не на поступатель-
ные. Это подтверждает сделанное нами в прошлом предположе-
ние, что спектральные линии являются дискретными, а не не-
прерывными. Непрерывный спектр бывает лишь тогда, когда
эффект уширения вызывает наложение линий.
Таким образом, теория коэффициента поглощения состоит в
следующем. Сначала рассчитываются вероятности переходов от-
дельных молекул и атомов в изолированных состояниях вну-
треннего движения. Затем эти результаты объединяются с дан-
ными по числу молекул в различных энергетических состояниях
при термодинамическом равновесии. Получается общая интен-
сивность линий поглощения. В заключение учитываются эффек-
ты возмущения взаимодействия, вызывающие уширение линий,
и определяется коэффициент поглощения. Наконец, с помощью
коэффициента поглощения рассчитывается излучательная спо-
собность газа.
13.7. Временное возмущение уравнения Шредингера
Для того чтобы вычислить вероятности перехода, нужно ре-
шить задачу взаимодействия между электрическим полем, соз-
даваемым электромагнитными волнами, и внутренним движе-
нием молекул. К счастью, интенсивность электрического поля,
создаваемого излучением, в сравнении с интенсивностью поля
в молекулах или атомах намного слабее, и мы можем рассма-
тривать электромагнитные волны как возмущение. Так как со-
стояния молекул или атомов изменяются вследствие такого
взаимодействия, само возмущение должно быть связано со вре-
менем. Поэтому сначала опишем теорию временного возмуще-
ния уравнения Шредингера.
504
Г л. XIII. Тепловое излучение
Пусть волновое уравнение невозмущенной системы имеет
вид
<13-34)
Нормировка осуществляется обычно так:
W°=San41 (13.35)
// = 0
где ап — постоянная, причем а — собственные
п
функции стационарных состояний, соответствующих значениям
энергии е°, Ер ..., .... Предположим теперь, что гамиль-
тониан реальной системы, кроме HQ (не зависящего от време-
ни), содержит еще член возмущения //', который является од-*
повременно и функцией времени, и функцией координат систе-
мы. Запишем общее уравнение Шредингера в виде
(№ + //') 4' = -^-^-. (13.36)
Волновая функция, удовлетворяющая этому уравнению, зави-
сит от времени и координат системы. Для заданного значения /,
например /', функция Чг(//) является лишь функцией координат.
Разложим Чг(//) по уже известным собственным функциям
невозмущенного гамильтониана
Т (Хр ..., zN, t') = s апЧ°п (Х„ ..., zN, t'). (13.37)
п
Временные множители у ..., гдг, tf) вычисляются также
в момент величины ап — постоянные. Для любого значения/
можно написать аналогичное разложение, но постоянные ап
при этом будут иметь различные числовые значения. Общее ре*
шение уравнения (13.36), таким образом, имеет вид
Т(х1( ..., zN, /) = 2ая(/)Т?((хь ..., zN, t), (13.38)
п
где an(t) зависят лишь от Д
Подставляя (13.38) в волновое уравнение (13.36), получаем
2 ап (/) Н°Ч°п 4- dn (t) =
а п
==~ 2лГ W“ 2^Г ^~дГ’
п п
13.7. Временное возмущение уравнения Шредингера
505
где dn(J)—производная от an(t). На основании (13.34) и
(13.35) отсюда имеем
- 4а 2 ««W ч'°« = 2 & н'^
П п.
Умножая это уравнение на и интегрируя по конфигураци-
онному пространству в силу ортогональности функций Ч'О, по-
лучаем
оо
f^H'^dr. т = 0, 1, 2, ... . (13.39)
/2 = 0
Это есть система дифференциальных уравнений для функций
В каждой конкретной задаче из нее определяются коэф-
фициенты разложения (13.38).
В качестве простого примера использования (13.39) рассмо-
трим систему, которая при /<0 находилась в стационарном со-
стоянии с фиксированной энергией. Волновая функция, предста-
вляющая систему, равна где I — собственное значение.
Предположим, что при0<7<7'на систему действует возмущение
Н', причем в этом промежутке Н' не зависит от времени. Пре-
небрегая всеми членами в правой части (13.39), кроме п — Ц т. е.
предполагая, что в правой части уравнения остается лишь az(Z),
можно решить (13.39). Сначала рассмотрим уравнение для са-
мого ai. Оно имеет вид
_ 2ni ( }Н,
dt h
где H'u = J* H'^ dt. Это уравнение легко интегрируется
и дает
az(f) = exp(--^-tf«/), 0 </</', (13.40)
если принять, что az=l при Z=0.
Формула (13.40) дает форму изменения коэффициента в
процессе возмущения. В этом процессе волновая функция (пре-
небрегаем членами с m =# Z) равна
аДО*? = ехр +//„)/].
Рассмотрим теперь остальные уравнения (13.39), определяю-
щие поведение коэффициентов aw(Z) при т =# /• В правой
части (13.39) заменяем сц на начальное значение az(0) = l, пре-
небрегаем всеми остальными коэффициентами ап и получаем
506
Гл. XI11. Тепловое излучение
приближенную систему уравнений
^(0 = 2£» J
ИЛИ
</аот(/) = —^-Я,п/ехр[—-^-(ez —ет)^Л, т±1,
где
Hml = f dr- (13.41)
причем H,ni не зависит от t. Волновые функции ЧС и Ч^ мы
заменим на амплитуды колебаний и Ф2’ выделив показа-
тельные временные множители. Эти уравнения непосредственно
интегрируются. Учитывая, что ат(0)=0 при т I, имеем
, 1—ехр Г—-^(em—ez)/|
am(t) — Hml-------n c-----------1, m + I. (13.42)
Следует помнить, что индекс I относится к начальному состоя-
нию, а т—к другим состояниям. При t', меньших Л/(е™~е/),
экспоненту в (13.42) можно разложить, тогда
am(t') = -^-H'mtt, т*1. (13.43)
В момент tf волновая функция системы (при /=0 она была
равна Т?) приближенно равна
Т (f) = at (t') 2' ат (П (13.44)
т
Знак суммирования 2 обозначает члены, не содержащие
т
т = 1. В (13.44) а/~1, а все ат очень малы. Если система остает-
ся изолированной, то волновая функция (13.44) в момент t' по-
прежнему представляет эту систему. Вероятность нахождения
ее в m-м стационарном состоянии равна а*пат. Согласно
(13.43), при малом f вероятность перехода из начального со-
стояния I в стационарное состояние т равна
а*тат (13.45)
Таким образом, имеет место пропорциональность f2, а не как
это первоначально предполагалось. Однако в большинстве слу-
чаев природа системы такова, что экспериментально наблю-
дается не вероятность перехода к отдельному состоянию, а со-
вокупность вероятностей перехода к группе соседних состояний,
которая, как увидим ниже, пропорциональна t'.
13.8. Вероятности перехода Эйнштейна
507
13.8. Вероятности перехода Эйнштейна
Рассмотрим два невырожденных стационарных состояния пг
и п системы с энергиями соответственно ет и 8n (em>en). Со-
гласно принципу частот Бора, переход из одного состояния в
другое сопровождается излучением или поглощением энергии.
При этом частота определяется следующим выражением:
= (ет — ел)/Л- (13.46)
Допустим, что при нахождении системы в сравнительно низком
состоянии п она подвергается воздействию излучения с плот-
ностью энергии p(vmn) [для излучения с частотой от v до v + dv
энергия излучения в единице объема равна p(v)dv]. Вероят-
ность того, что в единицу времени она поглотит один квант
энергии поля излучения и перейдет в более высокое состояние,
равна
Вп-+тР (Утп))
где Вп^т — так называемый коэффициент поглощения Эйн-
штейна. Здесь мы предположим, что вероятность поглощения
пропорциональна плотности энергии поля. Предположим далее,
что вероятность излучения есть сумма двух частей, одна из ко-
торых не связана с полем, а другая пропорциональна плотно-
сти энергии поля. Иными словами, считаем, что вероятность пе-
рехода системы из состояния m в более низкое состояние и, со-
провождаемого излучением энергии, равна
Ащ -> п Вт _> пр (v /пл)»
где — коэффициент Эйнштейна для спонтанного излуче-
ния, а Вт-+п — коэффициент Эйнштейна для вынужденного из-
лучения.
Рассмотрим теперь большое количество однотипных систем,
находящихся в равновесном состоянии с температурой Т в поле
излучения. Согласно закону Планка, плотность энергии излуче-
ния равна
. ч 8n;hv3 1 /1О
с3 exp (/zv/^T) — 1 ‘ (13.47)
Пусть в состоянии m находится систем, а в состоянии п —
Пп систем. Тогда число систем, переходящих в единицу времени
из состояния п в состояние пг, равно
N аВп-^тр (утп).
А число систем, переходящих в обратном направлении, равно
Nт {Ат->п ~И Btn-^np (V /пл)} •
508
Гл. XIII. Тепловое излучение
При равновесии эти два числа одинаковы, так что
N п Вт-+пР (У тп)
Nfn Вп-+тР (Утп)
(13.48)
Согласно формуле статистической механики (4.197), при
равновесии
2i = exp{—Ь^} = ехрр§4 (13.49)
Из (13.48) и (13.49) получается следующая формула для плот-
ности энергии излучения:
о (V \ =_________Лт->”___________
ryVmnJ— / hv \
о PYn I nvmn I О
/2->тСЛ"1 I Dm-*n
(13.50)
Для того чтобы она совпадала с законом Планка (13.47), не-
обходимо связать три коэффициента Эйнштейна следующими
соотношениями:
Вп^>т z==: Вп (13.51)
и
8л7п£,
Ат-^п ==) Вт_>п. (13.52)
Таким образом, коэффициенты поглощения и вынужденного
излучения равны, а коэффициент спонтанного излучения отли-
чается от них только множителем
13.9. Вычисление вероятностей переходов
Согласно классической электродинамике, в пространстве с
единичной диэлектрической постоянной и магнитной проницае-
мостью плотность энергии излучения с частотой v выражается
формулой
p(v) = ^W, (13.53)
где E2(v) —среднее значение квадрата интенсивности электри-
ческого поля, соответствующее этому излучению. Если поле из-
лучения является изотропным, то
±F(7)=4(7)=4w=47:j, (13.54)
о
где Ех(у)—компонента электрического поля в направлении х
и т. д. Электрическое поле зависит от времени следующим об-
13.9. Вычисление вероятностей переходов
509
разом:
Ех (v) == 2£° (v) cos 2.™/ = Ех (v) (е2яМ 4- е>-2яЩ. (13.55)
Форма с комплексным показателем более удобна для расчетов.
Так как среднее значение cos2 2nvt равно V2, то
рМ = 4^7) = 4й« = 4£?М. (13.56)
Рассмотрим теперь два стационарных состояния m и п не-
возмущенной системы с волновыми функциями и Ч'я, при-
чем ew>en. Предположим, что при / = 0 система находится в со-
стоянии п и подвергается возмущению со стороны излучения с
целым рядом частот, близких к vmn. Интенсивность электриче-
ского поля для каждой частоты выражается формулой (13.55).
Используя метод, изложенный в п. 13.7, считаем вероятность
перехода в состояние m результатом этого возмущения. Элек-
трическое поле, относящееся к электромагнитным волнам, изме-
няется не только со временем, но и в пространстве. Строго го-
воря, величина Е* является также функцией от х. Однако да-
же при 10 000° К соответствующая длина волны примерно в
100 раз больше величины атомов и молекул. Для таких длин
волн пространственными изменениями £°(v) можно полностью
пренебречь, считая электрическое поле в масштабах атомной
системы функцией только времени. Отсюда в электрическом
поле Ех, параллельном оси х, энергия возмущения системы из
заряженных частиц равна
Н' = Ех%е}хр (13.57)
J
где ej — электрический заряд, Xj — координата /-й частицы. Вы-
ражение ^CjXj (суммирование по всем частицам системы) яв-
j
ляется компонентой дипольного момента системы вдоль оси х
и обозначается через рх.
Рассмотрим сначала случай, когда возмущение вызывается
одной частотой v. Полагаем в правой части (13.39) ят(0)=0,
an(0) = 1. Тогда
ат (0 = - f Л =
=~т / ехР е^)W (е2лМ+е~2лМ'> х
X ejxj^n ехР (— е^) dx-
J
510
Гл. XIII. Тепловое излучение
Если обозначить
^тп = J С 2 eJxM dx = f (13.58)
J
то получим уравнение
= _ 2=£ (v)| exp [2^(em - ея + hv) /] +
После интегрирования имеем
am(t) = ^xmnE°x(v)
сл ~Г
сл п v
(13.59)
В двух членах правой части (13.59) только один является
существенным и лишь тогда, когда частоты v и vmn == | (еш — ея)/Л|
близки друг к другу. В каждом дробном выражении абсолют-
ная величина числителя может изменяться лишь в пределах от
О до 2, причем поскольку имеется только одна частота, то
\kXmnEQx(y) очень мало. Следовательно, если знаменатель не мал,
то значение выражения в целом очень мало. Другими словами,
существование так называемого резонансного знаменателя
ет— — hv вызывает сильное влияние возмущения (система
из состояния п переходит в состояние т), когда частота света
близка к частоте Бора. В случае поглощения важен второй
член; для вынужденного излучения (е™— еп<0) аналогичную
роль играет первый член.
Рассматривая случай поглощения, можно пренебречь пер-
вым членом в (13.59). После небольших преобразований полу-
чим выражение для (/)
sin2 ——Av)4
< т <>„. w=
(если является комплексным числом, то берется квадрат
его модуля). Это выражение написано для случая, когда в поле
возмущения имеется лишь одна частота. Реально приходится
рассматривать ряд частот. В этих случаях эффекты различных
частот можно сложить, т. е. достаточно проинтегрировать пре-
дыдущее выражение по области частот. Подинтегральная функ-
13.9. Вычисление вероятностей переходов
511
ция дает существенный вклад только в области, близкой к vrnn,
поэтому можно заменить на Ех(ут;1) и вынести из-под ин-
теграла. В результате имеем
“ sin2^(em — е„ — Av)А
— СО
со
Так как J* ^^-dx — я, то в конечном итоге получим
< (0 “т (0=t. (13.60)
Можно видеть, что после интегрирования по v вероятность пе-
рехода в состояние т за время t стала пропорциональной /, что
является обычной закономерностью для вероятности перехода.
Пользуясь (13.56), введем теперь плотность энергии p(vmn).
В результате получим вероятность перехода из состояния п в
состояние т в единицу времени под влиянием поляризованного
излучения в направлении х
8л3 9 / \
Выражения для у и z аналогичны. Таким образом, коэффициент
Эйнштейна для поглощения равен
= ). (13.61)
1 тп Jmn тп}
Полагая а7?(0)=0, ат(0) = 1, аналогичным путем получаем
коэффициент Эйнштейна для вынужденного излучения
= ). (13.62)
1 тп итп тп1
Результат совпадает с требованием (13.51). Однако в этих рас-
четах не использовалось условие равновесия, которое служит
основой для расчетов в п. 13.8. Поэтому зависимость (13.51) яв-
ляется более общей и имеет место даже тогда, когда нет тер-
модинамического равновесия. Вследствие этого мы имеем право
предположить, что соотношение (13.52) для спонтанного излуче-
ния также является общим. Тогда коэффициент Эйнштейна для
спонтанного излучения равен
Л 64л4v^
= +g2 Ч-н’ }. (13.63)
ОЛС I лтп Утп £ГПП*
512
Г л. XI IL Тепловое излучение
11а основании вышеизложенного становится ясным, что для
расчета интенсивности спектральных линий и выделения разре-
шенных переходов необходимо прежде всего изучить интеграл
дипольного момента, определенный в (13.58). В следующих
пунктах рассмотрим важнейшие конкретные случаи.
13.10. Правило отбора и интенсивность излучения
гармонического осциллятора
Когда частица с зарядом е и массой т совершает гармони-
ческие колебания вдоль оси х (в начальной точке имеется элек-
трический заряд —е), компонентой дипольного момента вдоль
оси х является ех, а компоненты вдоль осей у и z равны нулю.
Единственным интегралом дипольного момента, не равным
нулю, является — ехтю гДе
Хтп = f f dX-
Величины и есть функции амплитуды колебаний гармони-
ческого осциллятора, данные в (2.27). Имеем
1
[an2" + mm!n!]'/s
За исключением случаев, когда т и п различаются на единицу,
интеграл обращается в нуль. Остаются лишь
у 2a ’
j/”»
4л2/иу0
h
(13.64)
Таким образом, вследствие ограничения со стороны теории
возмущений система может переходить из каждого состояния
только в два смежных. При переходе система либо испускает,
либо поглощает энергию. Другими словами, правило отбора
для гармонического осциллятора формулируется просто в виде
Дп=±1, а частота v0 излучения или поглощения также являет-
ся однозначно определенной. Естественно, что мы получили та-
кой результат, потому что в расчетах возмущения в преды-
дущем пункте пренебрегли некоторыми членами более высокого
порядка. По сравнению с оставшимися членами они очень малы,
13.11. Правило отбора и интенсивность излучения
513
но нельзя сказать, что они равны нулю. Поэтому, строго говоря,
имеется возможность переходов, не содержащихся в указанном
правиле отбора, однако вероятность этих «запрещенных пере-
ходов» намного меньше разрешенных. Для обычных целей
можно пренебречь всеми переходами за пределами правила от-
бора.
Объединяя (13.64) с (13.61) или (13.62), получаем коэффи-
циенты Эйнштейна для поглощения и вынужденного излучения
Вп^п = Вп^ = ^-£. (13.65)
Коэффициент равен Эйнштейна для спонтанного излучения (13.63) л 64лЧ^2 п ,13«)
13.11. Правило отбора и интенсивность излучения
центрально-симметричной системы
В п. 2.8 указывалось, что при центральном потенциале V(r)
система из двух взаимодействующих частиц имеет волновые
функции следующего вида:
где 0/т(0), Фт(ф)—сферические гармонические функции, не
зависящие от У(г). Поэтому можно одним разом получить пра-
вило отбора и интенсивность частот I и tn для всех центрально-
симметричных систем.
Компоненты дипольного момента равны
рх —р(г) sin 0 cos ф,
fiy = р (г) sin 0 sin ф,
рг = р (г) cos 0,
где р(г) есть лишь функция от г. Для двух частиц с зарядами
+ е и —е, находящихся на расстоянии г, она равна ег. Каждый
интеграл дипольного момента, например
= f f f И 81П 9 C°S Ф Х
X Rn t- (г) (9) Фт- (ф) г2 sin 0 d<f dO dr,
33 Зак 1299
514
Гл. Х111. Тепловое излучение
можно записать в виде произведения трех интегралов: по г, по
0 и по ф
х nlmn' V т' х1тГ т’£хтт’'
У nltnn' I' т’ nln' г!у 1ml’ Утт'1 (13.67)
^znlmn'r mf 21тГ т'^тт'1
где
оо
Рд/я7' = / (Г) и (И (Г) r2
о
( sin 9
=/0*m(0)
Hi 0
I z 'Iml'm'
sin 9
cos 9
cos <p
sin <p
1
0/'m' (9) Sin0d?0,
(фИф.
(13.68)
(13.69)
(13.70)
Из (13.69) видно, что должно быть равно fyiml, ,•
Рассмотрим сначала поляризованное излучение, соответ*
ствующее дипольному моменту ц2, т. е. поляризующееся вдоль
оси z. Вследствие ортонормированности
g = 0, т' + т\ g =1.
zmm *тт
Используя свойства сферических гармоник, легко показать, что,
кроме равных /4-1 или I—1, все равны нулю. Про-
водя аналогичное решение для интегралов по х и у, получаем,
что вдоль этих осей энергия излучается лишь с изменением
т и / на 4-1 и —1. Таким образом, правило отбора таково:
Дт = 0, ±1 и Д/=±1. Произведение двух множителей fug
может принимать следующие значения:
- 7 — 1 ! (Z + I"*I)(Z+I"*|-1) ГА
lm,_1 — 2 1 (2Z 4-1) (2Z — 1) J
— ,1 f (Z — I m| )(Z —| m I 4- 1) ГЛ
— i 4g)y — 2 j (2/4-1) (2/ — 1) /
_ I Y/2
— ( (2Z+1)(2Z —1) f
(fg\
(13.71)
(fe).
и аналогично для /->/-j- 1.
13.12. Правило отбора и излучение двухатомной молекулы
515
13.12. Правило отбора и интенсивность излучения двухатомной
молекулы
Основываясь на приближенной теории п. 2.15, можно дать
простой метод расчета поглощения и излучения двухатомной
молекулы. Для сложной системы, образованной из двух ядер
и множества электронов, дипольный момент ц(г) можно разло-
жить в степенной ряд по г — г0
п(г) = Но+Ш (г-Го)+ .... (13.72)
V - Го
где Го — равновесное расстояние между ядрами, (dp,ldr^—по-
стоянная. Дипольный момент ц0 является величиной, которая
часто используется в теории диэлектрической постоянной по-
лярных молекул, и его численное значение для многих веществ
можно получить из диэлектрической постоянной.
Подставим в (13.68) это разложение. В качестве первого
приближения используем волновую функцию гармонического
осциллятора. При этом п может изменяться на нуль или ±1.
В первом случае излучение и поглощение вызывается постоян-
ным членом цо, во втором случае — членом 8 (г — г0). Интегри-
рование дает
где
а=4лЧМ( (1374)
ц— приведенная масса молекулы. Правило отбора и коэффи-
циенты интенсивности для I и m даны в предыдущем пункте.
Это правило отбора подтверждено экспериментом. Однако в
эксперименте наблюдаются также колебательно-вращательные
полосы для Дп = 2, 3,...; это вызвано тем, что функция потен-
циальной энергии не строго пропорциональна квадрату расстоя-
ния между ядрами.
В предыдущих рассуждениях предполагалось, что электрон-
ные состояния молекул не изменяются при переходах. Когда
имеются изменения электронных состояний, то правило отбора
и интенсивности для п становятся иными. Согласно принципу
Франка — Кондона, это определяется главным образом свой-
ствами потенциалов электронных состояний. Как мы видели
в п. 2.12, между электронным и ядерным движением молекулы
существует небольшое взаимодействие, и при электронных
33*
516
Гл. XIII. Тепловое излучение
переходах расстояние между ядрами и движение ядер несколь-
ко изменяются.
Рассмотрим два электронных состояния А и 5, потенциалы
для которых изображены на рис. 13.3, где показаны также энер-
гетические уровни колебаний. Если основной энергетический
Рис. 13.3.
уровень молекулы, находящейся в верхнем состоянии, равен
п' = 0, то функция распределения велика лишь при г~геА-
Можно предугадать, что вследствие малой кинетической энер-
гии ядра переход в состояние В заставляет молекулы оставать-
ся вблизи точки Рх на потенциальной кривой. Это условие соот-
1312. Правило отбора и излучение двухатомной молекулы
517
ветствует энергетическому уровню п" = 7 или 8 более низкого
состояния.
Эта простая точка зрения подтверждается квантовомехани-
ческими расчетами. Обозначим волновые функции верхнего со-
стояния через фа,, где — волновые функции ядерного
колебания с квантовыми числами /г', а фа, — остальная часть
волновой функции (электроны и вращение ядер). Знак о' вклю-
чает все остальные квантовые числа. Аналогично волновая
функция нижнего электронного состояния равна Инте-
гралы электрического диполя и ^zG'n'
имеют следующую форму:
= f dx- (13.75)
Предположим, что в случае, когда электронное состояние изме-
няется, дипольный момент ц по-прежнему слабо зависит от
межъядерного расстояния г, которое определяется координа-
тами электрона. Пренебрегая зависимостью р, от г и интегрируя
по всем координатам, кроме г, получаем
= (13-76)
Интеграл по г, определяющий относительную интенсивность
перехода для различных пх, /г", имеет форму ортогонального
интеграла. Если две функции потенциальной энергии Va и Vb
с точностью до сдвига одинаковы, то для п' ¥= п" интеграл ста-
новится нулем, а правило отбора для п есть Дп = 0. В случае,
показанном на рис. 13.3, волновая функция при п'=0 вели-
ка лишь вблизи г = ГеА- Волновая функция при п"=7 или
8 должна иметь большое значение в этой области, поэтому пе-
реход п' = Q->n" = 7 или 8 является интенсивным. Для меньших
или больших значений п" интенсивность перехода ослабляется.
Для сравнительно малых значений п” волновая функция
экспоненциально убывает (соответственно тому, что классиче-
ское движение ядра не распространяется на эту область); а для
больших значений п" функция быстро колеблется между
положительными и отрицательными значениями, что вызывает
уменьшение интеграла от положительной функции ф/2, при
п' = 0 (колебания функции r|> между положительными и отри-
цательными значениями соответствуют сравнительно высокой
скорости классического движения атомных ядер).
Аналогично при переходе, начинающемся с энергетического
уровня п'=5? волновая функция имеет максимальное значение
518
Гл. ХИГ Тепловое излучение
вблизи точек Р2 и Р3, что соответствует энергетическим уровням
п" = 2 или 3 и тг" = \Л или 12. Точное проведение квантовомеха-
нических расчетов возможно для водорода и водородоподобных
атомов. Их невозмущенные волновые функции, как показано в
п. 2.8, определяются точно. Вследствие особых свойств волно-
вой функции правило отбора для главного квантового числа п
отсутствует, и разрешены любые переходы Дп. Такой случай
несколько отличается от рассмотренного. Однако мы не будем
обсуждать этот случай, так как он имеет отношение лишь к
атому водорода и другим высокоионизированным атомам и ва-
жен только при крайне высоких температурах. Интерес к нему
проявляют в основном астрофизики.
13.13. Дипольный момент и эффективный электрический заряд
двухатомной молекулы
Как было показано в предыдущем пункте, при расчете
свойств двухатомных молекул имеются две важные величины:
постоянный дипольный момент ц0 и скорость изменения диполь-
ного момента . Величина ц0 определяется диэлектрической
постоянной молекулы, поэтому ее очень легко рассчитать. По-
стоянная (d\kldr\^ имеет размерность электрического заряда и
иногда называется эффективным электрическим зарядом в. Его
измерить труднее, и обычно он рассчитывается при помощи ин-
тенсивности поглощения Дп=1. Для вычисления излучательной
способности двухатомных молекул лучше всего иметь некоторые
зависимости между (dvldr)rQ и другими легко измеряемыми ве-
личинами. Эти зависимости могут быть только опытными, так
как у нас нет общей точной теории для двухатомных молекул.
Эрости1) получил недавно зависимость между е и Е/г^ для
четырех типов молекул НС1, HBr, NO, СО в виде
р
е^0,072 4-(г), (13.77)
го
где Е— энергия диссоциации (эв), г0 — равновесное межъядер-
ное расстояние, А.
Однако этой зависимостью нельзя пользоваться без огра-
ничений. Прежде всего она неприменима к двухатомным моле-
кулам с одинаковыми ядрами, так как на основании свойств
симметрии 8 равно нулю. Далее, последние работы по молеку-
лам типа JC1 говорят о том, что (13.77) не имеет широкого при-
*) Aroeste Н., /. Chem. Phys., 22 (1954), 1273,
13.14. Расчет суммарного поглощения двухатомного газа
519
менения. Наконец, в отношении двухатомных молекул с ион-
ной связью, например LiF, можно считать, что как положитель-
ные, так и отрицательные ионы имеют единицу электрического
заряда. Тогда 8=1е. Бенсон и Гофф1) после тщательных рас-
четов определили, что значение е для LiF равно 1,08е. Таким
образом, хотя мы и можем изложить некоторые сведения отно-
сительно эффективного электрического заряда двухатомных мо-
лекул, метод вычисления, который реально мог бы быть приме-
ним, пока еще ждет более глубокого исследования.
13.14. Расчет суммарного поглощения двухатомного газа
Перейдем теперь к расчету коэффициента поглощения двух-
атомных молекул. Мы не будем рассматривать чисто враща-
тельных переходов, так как длина волны, которую они дают,
находится далеко в инфракрасной области, что не очень важно
для температурной области, где имеется ярко выраженная лу-
чистая теплопроводность. Мы рассмотрим лишь колебательно-
вращательные переходы. Первый шаг заключается в том, чтобы
рассчитать общую вероятность перехода для всех возможных
квантовых чисел т, так как энергетические уровни не зависят
от этого квантового числа. Легче всего это сделать с функцией
|/п|,/-Ы'п|ИЗ (13.71), для которой сумма по всем m имеет
вид
У/Гпл2 _ ^у 1 (Z + |/n|)(Z--|m|)
|m|, /-1, |т|~~ (2Z~h 1)(2Z —1) —
m m = -l+l
! m^"1 Z2(2Z —1) —-g-(Z —1)/(2Z—1) (
~ (2Z-f-l)(2Z —1) (I2 —m2)= (2Z-|-1)(2Z —1) ~ 3"•
m = -/+l
Сумму по всем m для (fg)x можно разделить на четыре части:
две для Дт=4-1 и две для Дт =— 1,
m = l-l m = -\
m m = l m=—l
m = l m = — l
*4“ 2 | m|, Z—1, |ml-l~^ ^g^l, |m|-l, /-1, |m |
m = l m = -/ + l
_ 9m’y 1 (Z-|W|)(Z-| w|+l) , о ”y G + |m|)(Z + |m|-l) _ £
4(2Z+ 1)(2Z — 1) z 4 (2Z 4-1) (2Z — 1) — 3 '
m-1 m = \
!) В en s on, H o f f, /. Chem. Phys., 22 (1954), 469.
520
Г л. XIII. Тепловое излучение
Сумма по т для (/g)^ та же самая. В результате, как и пред-
полагалось, по всем трем направлениям поляризации х, у и г
общая вероятность перехода одинакова. Сумма по всем напра-
влениям равна /. Если обозначить через j вращательное кван-
товое число двухатомной молекулы, то общая вероятность пере-
хода равна /. С этого места мы будем рассматривать группу
состояний с одинаковыми п и /, но с разными т, как отдельное
состояние с единичным статистическим весом.
Объединяя полученный результат с (13.74), имеем, соглас-
но (13.61), коэффициент поглощения Эйнштейна
rj 8л п h . ле^ п . Q '-7о\
J — зд2-е д 8лЧй" J = ~5hv^ (13.78)
Если N— общее число молекул в единице объема, а все воз-
можные состояния т приняты за одно состояние, то среднее
число молекул, находящихся в состояниях п — 1 и / — 1 в еди-
нице объема, дается, согласно (4.197), формулой
= H exp {—e^i.y-i/AT'l/XT'),
где /(Т)—функция состояний колебательного и вращательного
движений. Аналогично число молекул, находящихся в состоя-
ниях п и j в единице объема, равно
— N exp {— ея, jlk^ljiT}.
Отсюда в поле излучения с плотностью энергии p(v) число пере-
ходов п — 1->п, / — 1->/, обусловленных поглощением и вы-
нужденным излучением, равно
" Ж? 7 7ТЙ11 - ехр I- <'” I - х
X ехр [- ея_ь р (13.79)
По правилу частот Бора имеем
\ j - е„_1> (13.80)
Энергия, поглощения каждой единицей объема, составляет
от величины (13.79). Умножение P(V;Z}5;) на с дает
удельную интенсивность hn-\^n- Таким образом, энергия, по-
глощаемая на единицу длины, равна
ЛЕ2/? / \
N W(D \-J^)Hi~exPl-hcaK^j/kT]} X
X exp [- гп_х j^/kT]
13.14. Расчет суммарного поглощения двухатомного газа
521
где coo=vo/c, т. е. числу волн колебаний основной частоты моле-
кулы. Сравнивая это с выражением pkv/v, получаем
2
ле п
ЗцсУ (Г)
X
X /{1 — ехр [— hc^z^kT]} ехр [— en_, ^kT]. (13.81)
Мы не можем приравнять pkv правой части (13.81), так как
еще не введена ширина спектральных линий, создаваемая раз-
личными эффектами. Выражение (13.81) есть общее поглоще-
ние линий п—1->п и /—1->/. Обычно для удобства вводится
условное волновое число со*, соответствующее запрещенному
переходу п = 0->п=1, / = 0->/=0, т. е.
heed == 8^ q—£q, о* (13.82)
где со* есть та же величина, что и в выражении (5.98). При-
ближенно со* = (0о, так что
о
П
X
Х/{1 — ехр[— ехр [— гп_х^/ЬТ]. (13.83)
Для переходов п— 1->п, j-+j — 1 аналогичный расчет дает сле-
дующее выражение для общего поглощения на единицу длины:
2
ЛЕ Л?
ЗцсУ(Т’)
X 7 (1 — ехр [— hc<y^+ykT]} ехр [— еп_х JkT]. (13.84)
Формулы (13.83) и (13.84) описывают общее поглощение вра-
щательно-колебательной полосы. Выражение (13.84) часто упо-
требляется для расчета поглощения атомов и молекул, а также
излучательной способности двухатомных молекул при темпера-
туре в несколько тысяч градусов (°К).
Теперь можно, применяя полученные результаты, вывести за-
кон Кирхгофа (13.5). Согласно (13.63) и предыдущим расчетам,
число спонтанных переходов п-+п—1, /’->/—1 в единицу вре-
мени равно
3hc3 ь " 8лЧн
_ 8л2
3c3v0ii
&nj.
J
Число состояний пи/ (включая квантовые состояния с различ-
ными /и) есть
N
7(7) ехр (— tnJkT).
522
Гл. XIII. Тепловое излучение
Таким образом, энергия, излучаемая единицей объема в еди-
ницу времени, равна
n^nh ( a)nf Jzt7/ \ 8л exp (—Jk
'v Зрс/(Т) V \ (D0 /7 c* 2
(13.85)
Деля (13.83) на (13.81), получаем как раз закон Кирхгофа.
13.15. Коэффициент поглощения двухатомного газа
При выводе выражения для общего поглощения в предыду-
щем пункте предполагалось, что колебания молекулы можно
заменить простым гармоническим колебанием и что оно не
взаимосвязано с вращением молекулы. Как было показано во
второй и пятой главах, реальная двухатомная молекула лишь
приближенно описывается простым гармоническим осциллято-
ром. Более точный межъядерный потенциал, например потен-
циал Морзе, позволяет учесть ангармоничность и взаимодей-
ствие с вращением. Оппенгеймер1), Крауфорд и Динсмор2) при
расчете вероятностей переходов ввели такую поправку. Оказы-
вается, приближенные расчеты в основном верны, нужно
только, чтобы при вычислении энергии 8 и частот перехода при-
менялась точная формула, включающая ангармоничность и
взаимодействие. Единственным местом, нуждающимся в по-
правке, является фактически расчет и Согласно
(5.98), имеем
®"Z}+" = — 2 (га — 1) X*®* 4- 2/50 — 4j3D0 — / (2га + / — 1) ае.
Если остановиться на члене с то
= со* — 2 (п — 1) х*со* + 2/В0- (13.86)
Аналогично
= (д* _ 2 (п — 1) х*(о* — 2/В0. (13.87)
Цель ввода параметра ангармоничности х* заключается в том,
чтобы избежать наложения спектральных линий, принадлежа-
щих частотам с одинаковыми значениями / и разными значе-
ниями п. Линии поглощения для различных значений п в дей-
ствительности являются разделенными, что одинаково важно как
для влияния на коэффициент поглощения, так и для расшире-
ния спектральных линий поглощения. Поэтому их надо рассчи-
’) Oppenheimer J. R., Proc. Camb. Phil. Soc., 23 (1926), 327.
2) Crawford B, L., Dinsmore H. L., J. Chem. Phys., 18 (1950),
983, 1682.
13.15. Коэффициент поглощения двухатомного газа 523
тать. Для всех других величин ангармоничность не суще-
ственна.
Функция состояний вращательно-колебательного движения
приближенно равна
xpi-e./?-)' <13-88»
где 0Г и 0Г есть характеристические температуры вращения и
колебания, определенные в (5.100). Для энергии приближенно
имеем
& й <13-89)
Далее пусть Л7р равно 1/т, р — плотность газа, ш — масса мо-
лекулы. Если mi и т2 — массы атомов в двухатомной молекуле,
то приведенная масса равна т^г/+ или т^т^пг. Ис-
пользуя эти выражения и вводя соответствующие упрощения,
можно переписать (13.83) и (13.84) следующим образом:
при волновом числе со*[1—2(п—1)х* + 2(0г/0Д/] имеем
7 = 3^77 (т) t1 - “Р W X
X [1 -2(»~ 1)л> + 2 -f^/exp [- (»- 1)^-JU- 1)-^-];
(13.90)
при волновом числе со*|1—2 (я—1)х* — 2(0r/0j,)/] имеем
(т) О - «р (-е„/П1! х
х[1-2(»-1)-2^-/]/ехр[-(»-1)^-/(/+1)Ь]. (13.91)
Расширение спектральных линий является результатом влия-
ния различных возмущений, возникающих при столкновениях и
при беспорядочном тепловом движении молекул. При высокой
температуре и низкой плотности основной причиной является
эффект Допплера, т. е. смещение частот колебаний, вызываемое
движением молекул. Однако при температурах в несколько ты-
сяч градусов и средних плотностях эффект Допплера перекры-
вается эффектами столкновения и так называемого естествен-
ного расширения. Можно считать, что в этом случае есть только
столкновение и естественное расширение. Если b — половина
ширины спектральных линий (слг1), S — общее поглощение
спектральных линий с волновым числом соо, a — коэффициент
524
Гл. XIII. Тепловое излучение
поглощения единицы массы, соответствующий области волно-
вых чисел от со до co + dco, то
+ (13.92)
Интегрируя по волновому числу, вновь получаем общее погло-
щение S. У нас нет еще хорошей теории для определения 6; на
практике обычно для всех спектральных линий используют одно
и то же значение Ь. Это означает, что вклад каждой линии из
(13.90) и (13.91) в коэффициент поглощения определяется
(13.92). Поэтому общий коэффициент поглощения на единицу
интервала волнового числа равен
Соотношения (13.86), (13.87), (13.90), (13.91) и (13.93)
дают конечное выражение для коэффициента поглощения еди-
ницы массы двухатомного газа. Вычисление коэффициента по-
глощения по молекулярным данным очень сложно и требует
дальнейших упрощений. Приведенные формулы также являют-
ся приближенными, так как не учитывались так называемые
обертоны, т. е. переходы с Дп = 2, 3,.... Эти переходы связаны
с ангармоничностью колебаний. Естественно, мы можем пред-
сказывать, что вероятности переходов для этих обертонов очень
малы. Действительно, отношение эффективных зарядов первой
гармоники 8о и основного тона е в грубом приближении Розен-
таля1) равно
( £° У ~ (1 §хе) /1 о пд\
(1—Зхе)2 ’ (13.94)
где хе — параметр ангармоничности из (2.135). Так как пара-
метр хе очень мал, то вероятности перехода для обертонов тоже
очень малы. Однако длина волны обертонов короче, чем у
основного тона, и дает поглощение в области длин волн, кото-
рые основной тон не поглощает. При высокой температуре
энергия излучения концентрируется на коротких волнах.
В этом случае эффект обертонов становится заметно важнее.
13.16. Расчет излучательной способности двухатомного газа
Когда давление газа очень высоко, что встречается, напри-
мер, в камере сгорания ракеты и во многих других инженерных
вопросах, расчет коэффициента поглощения можно упростить
9 R с s е n t h а 1 J. Е., Proc. Nat. Acad. Set., 21 (1935), 281.
13.16. Расчет излучательной способности двухатомного газа 525
еще больше. В этих условиях, когда частота столкновений ме-
жду молекулами велика, полуширина настолько увеличивается,
что спектральные линии вращательно-колебательного спектра
полностью перекрываются и полоса становится сплошной. Рас-
пределение ^о) принимает вид, показанный на рис. 13.4. При
этом в первом приближении можно в полосе спектра заменить
Рис. 13.4.
kv средним значением &v, считая, что вне полосы fev=O. Такой
метод был предложен и развит Пеннером1).
Приняв эту точку зрения, прежде всего видим, что так как
х* обычно имеет тот же порядок величины, что и отношение
6г/©«, а значение j может достигать 100, то для небольших зна-
чений п (при средних температурах) член (п—1)х* в (13.90)
и (13.91) не существен и при определении полосы частот им
можно пренебречь. Тогда для всех значений п частотный интер-
вал Av спектральной полосы одинаков. Однако как же опреде-
лить Av? В выражениях (13.90) и (13.91) ширина спектральной
полосы фактически определяется множителем /ехр(—/20Г/Т).
Эта функция как раз и изображает линию общего поглощения
на рис. 13.4. Если обрезать спектральную полосу на некотором
значении /, выбранном так, чтобы множитель j exp (—j2&r/T) для
него был достаточно мал, например 10~3, от максимального зна-
чения, то можно определить эффективную ширину спектральной
полосы. Так как при больших значениях j этот множитель убы-
вает чрезвычайно быстро, то /щах и эффективная ширина спек-
!) Реп пег S. S., Л Appl. Phys., 21 (1950), 685; J. Appl. Meeh. (ASME).
18 (1951), 53.
526
Гл. XI11. Тепловое излучение
тральной полосы не очень чувствительны к условию обрезания.
Видно, что /max пропорционально УТ/$Г* Практически имеем
Утах = 2,97 (13.95)
Начальная частота спектральной полосы равна
V, = VO [1 - 2 |чтах] = v0 [1 - 5,94 , (13.96)
а последняя
v2 = v0 [1 + 2 -fj- утах] = v0 [ 1 + 5,94 . (13.97)
Ширина спектральной полосы Av равна
Av = v2 — v1==11, v0. (13.98)
Этот результат говорит о том, что ширина спектральной полосы
растет как квадратный корень из температуры Т. В работе Пен-
нера вычислена эффективная ширина спектральной полосы
(в волновых числах) для молекул СО, НС1, НВг и др. при тем-
пературах от 300 до 3000° К. Для получения частотного интер-
вала достаточно умножить на скорость света с. Результаты со-
браны в табл. 13.1.
Теперь можно рассчитать общее поглощение, создаваемое
всеми частотами спектральной полосы, по-прежнему пренебре-
гая параметром ангармоничности х*. Воспользуемся разложе-
ниями
ехр [— У (У — 1) -у1] ~ ехР (— У2 -7-) (1+У-7 + • • •) •
ехр [— У (У 4-1)-у-] «ехр(—У2-у1)(1 —У'Т'4
Отсюда S/p для общего поглощения равно
1 е____К?' Х'1 f 1 1 । 1 <»«-1 1 ___
п = 1 j - 1
^4Hi-e*P(-tvr)Px
оо оо
х s S2п^ ехр [- («- п-7 -г 4Н •
л = 1 / = 1
Таблица 13.1
Ширина спектрэльной полосы (в волновых числдх)
з w ® А Э св СХ Основной тон Обертон
ч ье ф sTcL £ S св ф Н ” н св Ф Е vmax/c» vmlnA» &vn->n + l/c, vmax_A- vmln_A-
о £ X <у s ч ье СТ) ф о S Но см~1 см~1 см~1 см 1 см 1 см 1
1 2 3 4 5 6 7 8 9
300 2235 2021 214 4337 4124 213
500 2256 1982 274 4349 4078 271
СО 0,812? 1) 1000 2287 1908 379 4357 3981 376
1500 2306 1841 465 4357 3890 467
2000 2317 1782 535 4357 3808 549
2500 2322 1732 590 4357 3737 620
3000 2325 1694 630 4357 3682 675
500 4305 3343 962 7938 6995 943
1000 4359 3110 1249 7938 6676 1262
1500 4374 2866 1508 7938 6320 1618
2000 4374 2678 1696 7938 6032 1906
HF 2500 4374 2423 1951 7938 5621 2317
3000 4374 2295 2079 7938 5405. 2533
3500 4374 2165 2207 7938 5183 2755
4000 4374 2040 2334 7938 4955 2983
4500 4374 1851 2523 7938 4603 3335
5000 4374 1661 2708 7938 4241 3697
300 3088 2553 535 5831 5304 527
500 3129 2438 691 5835 5152 683
1000 3166 2221 945 5835 4851 984
НС1 0,086? 1500 3168 1990 1178 5835 4500 1335
2000 3168 1854 1314 5835 4282 1553
2500 3168 1784 1384 5835 4168 1667
3000 3168 1503 1665 5835 3685 2150
300 2755 2261 494 5172 4685 487
500 2785 2167 618 5173 4559 614
1000 2813 1964 849 5173 4270 903
НВг 0,075? 1500 2814 1801 1013 5173 4024 1149
2000 2814 1575 1239 5173 3658 1515
2500 2814 1517 1297 5173 3561 1612
3000 2814 1400 1414 5173 3359 1814
300 2387 1988 399 4513 4119 394
500 2420 1880 540 4514 3974 540
1000 2439 1703 736 4514 3720 794
HJ 0,033г 1500 2439 1577 862 4514 3528 986
2000 2439 1379 1060 4514 3208 1306
2500 2439 1311 1128 4514 3093 1421
3000 2439 1196 1243 4514 2894 1620
е —электрический заряд электрона = (4,80288 ± 0,00021) х 10 10 ед.
528
Г л XIII. Тепловое излучение
Сумму по j можно заменить интегралом
V 2/ехр(—/2©г/7') » J ехр(— фг/Т) dx\ =
j = l о г
Далее,
п ехр [— (га — 1 )-£?] = exp (&V/T) п exp (— nQjT) =
П = 1 /7 = 0
= exp (— Gv/T) д(^--/Т) 2 ехР (— nQv/T') =
л = 0
= -ехр(0г,/7')^775[1 - ехр (-©№=41 -exp(-©№-
Таким образом, получаем довольно простой результат
Средний коэффициент поглощения спектральной полосы равен
. ле2 Л , V, < V < v2, (13.100)
V 7 3cWim2Av 1 2 '
где Av вычисляется по (13.98). Так как Av зависит от Т, то kx
тоже зависит от Т. Вне спектральной полосы kv равно нулю.
Расчет излучательной способности двухатомного газа стано-
вится теперь весьма простым делом. Используя kv, определен-
ное в (13.100), из (13.32) получаем
п_ехр(—рМЛ] V2/n 4лВЛ,(Г)
е(Л р£)=-!------f ----------------r^dv. (13.101)
vt(T)
Здесь интегрируется излучение абсолютно черного тела в ча-
стотной области вращательно-колебательной полосы. Можно
ввести так называемую предельную излучательную способность
е'(П
v2(D
1 р 4лВ (Т)
е'(Г) = е(Т, 00) = ^- f -----^-dv. (13.102)
van
Это есть излучательная способность для бесконечного оптиче-
ского пути, зависящая только от температуры. Для конечного
пути из (13.101) и (13.102) имеем
ЦГ, рА) = (I — ехр(— pAv£)]e'(r). (13.103)
13.16. Расчет излучательной способности двухатомного газа 529
До сих пор мы рассматривали только основной тон. Пеннер
использовал этот метод также для расчета первого обертона.
Ширина спектральной полосы этого обертона близка к ширине
спектральной полосы основного тона. Поэтому для первого
обертона средний коэффициент поглощения пропорционален
квадрату эффективного электрического заряда е0 обертона. Со-
гласно (13.94),
7(1~5У. (13.104)
V1 оле)
Предельная излучательная способность обертона е'(Г) прибли-
женно равна
Va+Vo л _ _
ео(7’) = ^ч / (13.105)
Vj + Vo
где vo — основная частота колебаний двухатомной молекулы.
Поглощение обертона возникает в области частот, больших vo.
Когда имеются основной тон и первый обертон, общая излуча-
тельная способность равна
е(Г, pZ) = [l — ехр(—p££v)]e'(T)-h[l — ехр(—рЙ>°)Ы(7').
(13.106)
Пеннер указывает, что излучательная способность, вычис-
ленная этим методом, согласуется с экспериментальными дан-
ными по СО. Можно надеяться, что предлагаемый здесь метод
для остальных двухатомных газов также дает сравнительно хо-
рошие результаты. Другое преимущество этого метода заклю-
чается в том, что расчеты различных геометрических конфигу-
раций очень просты, так как множитель [1—ехр(—p^vL)]
здесь не зависит от частоты. Как правило, согласно (13.33), из-
лучательная способность равна
2л 1
J*|j.[l —ехр(— pZ([i)Av)]dp.-|-
о о
г (ТУ 2л 1
+ °я J* d(f J р.[1 — ехр(—р£(р) &”)] d\i. (13.107)
о о
Для слоя толщины b из (13.31) получим
е = е' (7) [1 — ехр (— p6£v) + pbkv ехр (— pbkv) —
— (pbkvf Ei (— рЖ)] 4- ei (T) [1 — exp (— p££°) 4-
4-pbk°v exp (— pbkty — (pbkty2Ei (— pftFv)]. (13.108)
34 Зак. 1299
530
Гл. XIIL Тепловое излучение
Когда имеется смесь различных излучающих молекул, по-
прежнему можно использовать понятие среднего коэффициента
поглощения, достаточно только сложить коэффициенты погло-
щения pAjv и основных тонов и обертонов различных
молекул. Для наглядности можно поступить так, как по-
казано на рис. 13.5. После того как найдено общее p£v, интегри-
рование (13.32) дает излучательную способность газовой смеси.
р—*
Рис. 13.5.
С помощью среднего коэффициента поглощения Пеннер1)
рассчитывал также излучательную способность простых много-
атомных молекул типа СО2. Но даже для таких довольно про-
стых многоатомных молекул вследствие очень большого числа
их колебательно-вращательных полос и недостатка знаний об
интенсивности или эффективном электрическом заряде каждой
спектральной полосы расчет излучательной способности стано-
вится сложным и имеет лишь ориентировочный характер. Это
очень печальный факт, так как СО2 и молекулы воды при не-
скольких тысячах градусов являются интенсивными излучателя-
ми, играющими важную роль во многих инженерных проблемах.
В рассуждениях данной главь^ подчеркивалось, что расчет ко-
эффициента поглощения и эмиссионной способности по моле-
кулярным данным более сложен, чем расчет термодинамических
функций. Причина кроется в том, что анализ энергетических
уровней должен быть более детальным, а знания в области
энергетических уровней молекул требуют подтверждения пра-
вила отбора и величин интенсивности. Второе особенно трудно
PennerS. S„ J. Appl. Phys., 25 (1954), 660.
13.16. Расчет излучательной способности двухатомного газа
531
получить теоретически, а экспериментальные данные в настоя-
щее время еще недостаточно полны.
Если плотность газов низка и ширина спектральных линий
настолько мала, что их можно считать полностью разделенны-
ми, то также возможно произвести приближенный расчет излу-
чательной способности1). При этом поглощение на любой ча-
стоте будет представлять собой ординарную линию — случай
неперекрывания. Эмиссионная способность будет зависеть от
ширины спектральной линии Ь. Получается, что для обычной
длины оптического пути L излучательная способность пропор-
циональна L1/a. Естественно, что для очень малой длины оптиче-
ского пути L излучательная способность должна быть пропор-
циональна L. Для большой длины оптического пути L нельзя
пренебрегать эффектом наложения. Но когда оптический путь
очень велик, применим приближенный метод расчета, основан-
ный на среднем коэффициенте поглощения. В настоящее время
пока не ясно, каким способом рассчитывать промежуточный
режим. Эта область требует большой работы и еще ждет своих
исследователей.
Задачи к главе 13
13.1. Вывести формулу (13.84).
9 Penner S. S., Ostrander М. Н., Tsien Н., J._ Applt Phys.t 23
(1952), 256.
34*
Таблица физических констант
Название константы Число Авогадро Скорость света Нормальный объем идеального газа Газовая постоянная на моль Постоянная Больц- мана Заряд электрона Отношение заряда к массе для элек- трона Постоянная Планка Масса покоя нейтрон протон электрон Отношение массы про- тона к массе элек- трона Соотношения между единицами энергии Числовое значение W = (6,02472±0,00063) X 1023 моль~' С = (2,997929±0,000008) X 10"» см • сек~' 22420,7±0,6 см*-моль~' = (8,31662 ±0,00038) X Ю7 эрг (моль • град)~* R = (1,38042 ±0,00010) X Ю-16 эрг град~х = = (8,6164± 0,0004) X Ю-5 эе град~г е = (4,80288± 0,00021) X Ю-10 ед. СГСЭ = = (1,60207 ±0,000007) X Ю-20 ед. СГСМ = (5,27299 ± 0,00016) X Ю17 ед. СГСЭ/Г = = (1,75888 ± 0,00005) X Ю7 ед. СГСМ/Г Л = (6,6252 ± 0,0005) X Ю27 эрг • сек 1,008982 ± 0,000003 а. е. м. = = (1,6747± 0,00010) X Ю-24 г 1,007593 ±0,00003 а. е. м.= = (1,67243± 0,00010) X Ю“24 г (5,48760 ± 0,00013) X Ю-4 а. е. м. = = (9,1085 ± 0,0006) X Ю~28 г 1836,13 ±0,04 1 эв = ( 1,60207 ± 0,00007) X Ю~12 эрг 1 а. е. м. соответствует 931,162 ±0,024 Мэв Масса электрона соответствует 0,510984 ±0,000016 Мэв
•ИМЕННОЙ УКАЗАТЕЛЬ
Айвен 377 Алберг 232 Андраде 232 Дальтон 160 Дебай 203 Девоншайр 332, 345 Де Гроот 380, 400 Джонс 250, 307, 344
Байл 279 Беневиц 198, 199 Бенсон 519 Берд 315, 423 Блэкман 204, 209 Бозе 129 Бойль 160, 311 Больцман 381, 420 Борн 28, 204, 226, 227, 377 Брукс 453 Букингем 307 Бэкстер 273 Бэрдин 283 Бюлер 357 Динемор 522 Допплер 523 Друде 238 Дюфур 397, 399 Зоммерфельд 238 Казимир 384 Карапетьянц М. X. 369 Карман 227 Карно 143 Каулинг 420, 452 Кирквуд 377 Кеезом 300, 302, 305, 312 Кертисс 315, 357, 358, 423
Валландер С. В. 7 Вальдман 399 Ван-дер-Ваальс 23 Ватсон 435 Венторф 357 Видеман 450, 451 Кирхгоф 494 Клаузиус 399 Клемм 25 Кобе 197 Кондон 515 Крауфорд 522 Лагранж 28
Гайтлер 305 Гамильтон 28, 82 Гейзенберг 29 Герцберг 69, 72 Герцфельд 433 Гиббс 145, 252 Ландау Л. Д. 192 Леннард 307, 344 Лифшиц Е. М. 192 Лондон 304, 305 Лорд 232 Лоренц 238, 452
Гиршфельдер 315, 323 Гофф 519 Грин 377 Грюнайзен 253 Гуггенгейм 10, 243 Гурвиц 453 Гурней 340 Майер 302, 377 Макинсон 446 Максвелл 420 Маршак 453 Мегреблиан 199
534
ИМЕННОЙ УКАЗАТЕЛЬ
Ми 334 Трутон 370
Морзе 67 Мотт 243, 250, 340 Уоллис 273 Урсел 295
Ньютон 28 Файзин 273 Фаулер 10, 243
Онзагер 381 Оннес 302 Оппенгеймер 522 Ферми 86 Франц 450, 451, 515 Хоуген 435
Палэн 279 Паули 57 Паулинг 20, 21, 23, 263 Пеннер 525, 530 Пеннингтон 197 Пирс 318 Питцер 196 Пригожин 357, 387, 388 Хьюм-Роузери 24 Хэман 318 Хюккель 247 Цванциг 378 Цянь Сюэ-сень 10, 247 Чандрасекар 495 Чэн Гуан-юе 369
Раман 197 Раумлисон 358 Розенталь 524 Рознер 198, 199 Роузвир 321 Чэпмен 387, 388, 420, 452 Шарль 160 Шварц 433 Шредингер 28, 29 Штокмайер 318
Славский 433 Слэттер 273 Смирнов В. И. 115, 126, 301 Соре 397, 398 Стирлинг 288 Эйнштейн 129, 203, 210 Эйринг 439 Энског 387, 388 Эрости 518
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Активность систем абсолютная 155
----- относительная 155
Ансамбли систем 73
-----локализованных 99, 109,
-----нелокализованных НО
Атом водорода 47
Атомов радиусы 17
----- вандерваальсовские 23
----- ковалентные 22
Вероятности перехода Эйнштейна 507
Вес состояния 89
Взаимодействие между атомами 254
----- молекулами 254
Вириальные коэффициенты 302
-----с большими номерами 320
Вириальный коэффициент второй 313
-----пятый 323
----- третий 321
-----четвертый 321
Возрастное уравнение Ферми 478,483
-------область применимости 485
------- применение 487
Волновое уравнение молекулы 60
Временное возмущение уравнения
Шредингера 503
Вычисление вероятностей перехода
508
Вязкость 402
— реального газа 420
Газы идеальные 159
-----двухатомные 170
— неидеальные 284
Гипотеза Гиббса 215
Граница экстраполированная 470
Группа антисимметричная 92
— симметричная 93
Движение бесструктурных частиц 136
Диффузия 402
Диффузия бинарной смеси 428
— и замедление нейтронов 452
Диэлектрики 232
Длина замедления 486
— свободного пробега 409
Закон Авогадро 160
— Бойля 160
— Видемана — Франца 450
— Грюнайзена второй 261
----первый 256
— Дальтона 160
— Кирхгофа 494
— Максвелла 163
— Планка 507
— распределения Больцмана 291
----молекул 289
— Стефана — Больцмана 207
— термодинамики второй 143, 147
---- первый 142
— Трутона 327, 341
— Шарля 160
Замещение 24
Жидкости ассоциированные 327
— и плотные газы 327
— нормальные 327
Излучательная способность 499, 500
----- предельная 528
Излучения поле 492
Ионов радиусы 19
Квантование поступательного движе-
ния 160
Квантовая механика 28
Квантовое число азимутальное 53
-----главное 39, 54
-----магнитное 53, 62
----- орбитальное 57, 6?
536
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Квантовое число спиновое 57
Комплексий 94
Константы химического равнове-
сия 200
Коэффициент вязкости жидкости 439
---- объемной 432
— Джоуля — Томсона 298
— изотермического сжатия 368
— поглощения 502
---- двухатомного газа 522
----Эйнштейна 507
— прохождения 439
— Пуассона 283
— теплового расширения 278, 363,
366
— Эйнштейна для излучения выну-
жденного 507
— -------- спонтанного 507
Кристаллы 225
Критическая точка 346
Металлы 232
Метод Борна — Оппенгеймера 59
— Гиббса 145
— перевала 115
Модель Юнга 269
Молекулы двухатомные 61
----гетероядерные 173
----гомоядерные 176
— многоатомные 71
— одноатомные 168
Общая теория процессов переноса 379
Обобщенная механическая сила 145
Осциллятор 37
— гармонический двумерный 123
----линейный 122
----трехмерный 123
Отношение теплоемкостей 265
Полупроводники 234
Постоянная Больцмана 157
— Видемана — Франца 451
— газовая 157
— Грюнайзена 260
Потенциал Букингема 306
----модифицированный 307
— Леннарда — Джонса 309
— Морзе 67
— термодинамический 145
— химический 145
Правило отбора для гармонического
осциллятора 512
Принцип детального равновесия 400
Принцип запрета Паули 57
— неопределенности Гейзенберга 29
— соответствия 83
— Франка — Кондона 515
— частот Бора 507
Процессы адиабатические 142, 266
— изобарические 274
— изотермические 269
Равновесие фазовое 151
— физическое 151
— химическое 151
Равновесные свойства кристаллов
214
Равномерное распределение энергии
200
Растворимость медных сплавов 24
Релаксация колебательная 432
Ротатор жесткий 125
— линейный 64
Свободный пробег относительно за-
хвата 460
------ рассеяния 460
------ переноса 460
Связь жидкости, газа и твердого те-
ла 335
Седлообразная точка 132
Сечение столкновения 305
Сила дисперсионная 305
Симметричные волчки 127
Симметрия ядер 172
Системы вырожденные 134
— точечных частиц 42
Скорость звука в нормальной жидко-
сти 372
Соединения включения канального
типа 25
------ клеточного типа 25
Соотношения взаимности Онзагера
381, 385
Состояние вещества пятое 237
---- четвертое 237
Состояния допустимые 85
Спин электрона 57
— ядра 76
Статистика Бозе — Эйнштейна 129,
135
— классическая 166
— Ферми — Дирака 135
— электронного газа 238
Статистическая механика 73, 135, 141
Статистический вес 102
Стационарное состояние системы 35
Структура вещества 15, 17
— гексагональная 16
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
537
Структура гранецентрированная 16
— объемноцентрированная 16
Степени свободы вращательные 191
----- классические 166
-----колебательные 182, 193
-----невозбужденные 166
-----электронные
Уравнение состояния твердого тела
252, 253
— Шредингера 28
— Эйринга 439
Уравнения Больцмана 454
— движения Гамильтона 82
— состояния полуэмпирические 301
---эмпирические 301
Таблица физических констант 531
Температура инверсии Джоуля —
Томсона 239
— статистическая 120
— характеристическая Дебая 223
Теория вязкости газа 415
— Дебая — Хюккеля 247
— Леннарда — Джонса и Девон-
шайра 348, 355, 357
— Лоренца 452
— плавления 338
Тепловое излучение 207, 491
Теплоемкость идеальных газов 167
— электронов в металле 249
Теплопроводность 402
— в газах 427
----жидкости 443
---- металлах 447
----твердом теле 388, 445
Теплота парообразования 343
Термодинамика необратимых процес-
сов 386
---------приложения 401
Термодинамические свойства неиде-
альных газов 297
----твердого тела 203
— функции двухатомных газов 180
---- кристалла 216, 218
---- электронного газа 245
Термоэлектричество 401
Точка Бойля 311
— плавления 280, 339
— тройная 346
Точное решение уравнения Больцма-
на 462
Угол связи 23
Уравнение амплитуды колебания 31
— Ван-дер-Ваальса 301
-- диффузии нейтронов 460
— состояния Грюнайзена 260
---- приведенное 260
---- при критических условиях 357
---- смеси идеальных газов 160
Фазовая траектория 83
Фазовое пространство ансамбля 83
Физический смысл волновой функции
33
Физической механики смысл 11
Функция амплитуды вероятности 29
— Дебая 220, 221
— распределения вероятностей 402
— состояний для сплошной сре-
ды 206
----- неидеального газа 285
----- систем 113
— Шредингера 29
— Эйнштейна 185
Характеристическая температура вза-
имодействия 315
— частота Дебая 259
Цикл Карно 143
Число Кнудсена 462
— столкновений в газе 403
Ширина спектральной полосы 527
Электроосмос 401
Электроны свободные 234
—- связанные 234
Энергетические уровни молекул 69
Энергия внутренняя 159
— дисперсионная 304, 305
— обменная 304
— свободная 159
-----газов и жидкостей 331
Энтропия парообразования 343
Эффект Допплера 523
Эффективный электрический заряд
518
Эффекты Соре и Дюфура 397
ОГЛАВЛЕНИЕ
Предисловие редактора перевода .................................... 5
Из предисловия автора ............................................. 9
Глава I. Введение ...................................................И
1.1. Предмет физической механики........................П
1.2. Структура вещества ...........................15
1.3. Радиусы атомов и структура молекул................17
1.4. Использование представлений о структуре вещества 24
Глава II. Квантовая механика........................................28
2.1. Волновое уравнение Шредингера ....................28
2.2. Уравнение амплитуды колебания.....................31
2.3. Физический смысл волновой функции.................33
2.4. Осциллятор .......................................37
2.5. Системы точечных частиц...........................42
2.6. Атом водорода ....................................47
2.7. Свободная частица ................................50
2.8. Внутренняя динамика атома водорода................52
2.9. Энергетические уровни водородоподобных атомов . . 55
2.10. Спин электрона ..................................57
2.11. Классификация энергетических уровней молекул ... 58
2.12. Волновое уравнение молекулы......................60
2.13. Двухатомные молекулы ............................61
2.14. Свойства функции U(r)............................63
2.15. Простейший вид линейного ротатора................64
2.16. Потенциал Морзе .................................67
2.17. Многоатомные молекулы............................71
Глава III. Основы статистической механики . ........................73
3.1. Ансамбли систем ..................................73
3.2. Предварительные сведения о микросвойствах .... 75
3.3. Общая природа состояний ансамбля..................77
3.4. Правило для усреднения ...........................80
3.5. Описание классического ансамбля...................81
3.6. Пределы применимости (главным образом классиче-
ская часть) ............................................84
Оглавление 539
3.7. Допустимые состояния для ансамбля одинаковых си-
стем. Симметричные и антисимметричные группы
состояний ..............................................88
3.8. Типы симметрий собственных функций реальных ан-
самблей ................................................93
3.9. . Кратчайший путь вычисления допустимых состояний
. . обыкновенного ансамбля .............................95
3.10. Вычисление комплексий для локализованных систем 97
Глава IV. Общие теоремы для ансамблей стационарных систем ... 101
4.1. Статистический вес ...............................102
4.2. СтатйсТичеОкйй вес состояний некоторых простых
систем.................................................104
4.3. Нахождение допустимых состояний (комплексий) . . . 108
4.4. Ансамбли, состоящие из двух групп локализованных
J * систем.............................................НО
4.5. Краткое изложение метода перевала.................115
4.6. Средние значения и статистическая шкала темпера-
туры ..................................................119
4.7. Системы с большим числом степеней свободы и вы-
рожденные системы .....................................120
4.8. Линейный гармонический осиллятор..................122
4.9. Двумерные и трехмерные гармонические осцилляторы 123
4.10. Жесткий ротатор без аксиального вращения .... 125
4:11. Жесткие ротаторы с аксиальным спином (симметрич-
ные волчки)........................................127
4.12. Ансамбль, состоящий из двух групп нелокализован-
ных систем ............................................128
4.13. Математические выкладки..........................132
4.14. Некоторые результаты.............................133
4.15. Вырожденные системы..............................134
4.16. Классическая статистическая механика.............135
4.17. Движение бесструктурных частиц в ящике...........136
4.18. Внешние реакции ансамбля ........................139
4.19. Связь между статистической механикой и термоди-
намикой ...............................................141
4.20. Законы термодинамики.............................141
4.21. Вывод термодинамики из статистической механики . . 148
4.22. Соотношение между величинами термодинамики и
статистической механики ...............................154
4.23. Термодинамические формулы классической статистики 156
4.24. Постоянная Больцмана и газовая постоянная .... 157
4.25. Выражение законов распределения через температуру
Кельвина . , 158
540
Оглавление
Глава V. Идеальные газы................................................159
5.1. Квантование поступательного движения............160
5.2. Классический вывод закона Максвелла.............163
5.3. Классическая статистика и классическая механика 166
5.4. Классические и невозбужденные степени свободы . . . 166
5.5. Электронные степени свободы.....................167
5.6. Теплоемкость идеальных газов....................167
5.7. Одноатомные молекулы ..............................168
5.8. Двухатомные газы при средних температурах .... 170
5.9. Классическая трактовка вращения двухатомных мо-
лекул ....................................................171
5.10. Симметрия ядер......................................172
5.11. Уточненные Еормулы для одноатомных молекул . . 179
5.12. Формулы для расчета термодинамических функций
двухатомных газов при средних температурах .... 180
5.13. Колебательные степени свободы.......................182
5.14. Двухатомные газы при высоких температурах .... 184
5.15. Поправки на ангармоничность и взаимодействие . . . 186
5.16. Влияние электронов..................................189
5.17. Вращательные степени свободы твердых тел........191
5.18. Колебательные степени свободы многоатомных молекул 193
5.19. Общие формулы для термодинамических функций мно-
гоатомных молекул ....................................... 194
5.20. Приближенный расчет колебательного движения . . . 197
5.21. Константы химического равновесия....................200
5.22. Равномерное распределение энергии...................200
Задачи к главе 5..........................................202
Глава VI. Термодинамические свойства твердого тела.....................203
6.1. Нормальные колебания непрерывной упругой среды. .203
6.2. Функция состояний для сплошной среды...............206
6.3. Тепловое излучение..................................207
6.4. Кристаллы, состоящие из атомов без внутренней струк-
туры .....................................................208
6.5. Влияние электронов и атомных ядер на функцию со-
стояний ..................................................212
6.6. Равновесные свойства кристаллов......................214
6.7. Термодинамические функции кристалла. Поправка
к энергии ............................................... 216
6.8. Термодинамические функции в приближении Дебая . . 218
6.9. Сравнение приближения Дебая с экспериментом . . . 222
6.10. Кристаллы, образованные молекулами..................224
6.11. Кристаллы с ионными или комплексными решетками 226
6.12. Металлы и диэлектрики...............................232
6.13. Статистика электронного газа........................238
Оглавление
541
6.14. Разложение при очень малых и очень больших X. . .241
6.15. Термодинамические функции электронного газа. . . .245
6.16. Поправка к формуле, применяемой для металлов . . .247
6.17. Теплоемкость электронов в металле..............249
Задачи к главе 6.....................................251
Глава VII, Уравнение состояния твердого тела......................252
7.1. Уравнение состояния ............................253
7.2. Взаимодействие между атомами....................254
7.3. Характеристическая частота как функция деформации 256
7.4. Уравнение состояния Грюнайзена..................260
7.5. Процессы при постоянном объеме..................260
7.6. Отношение двух типов удельной теплоемкости .... 265
7.7. Адиабатические процессы.........................266
7.8. Изотермические процессы ........................269
7.9. Изобарические процессы..........................274
7.10. Амплитуда колебаний и точка плавления..........280
7.11. Коэффициент Пуассона и модуль Юнга.............283
Глава VIII. Неидеальные газы......................................284
8.1. Функция состояний неидеального газа.............285
8.2. Законы распределения молекул....................289
8.3. Первое приближение для неидеальных газов. Силы,
действующие на коротких расстояниях..................292
8.4. Термодинамические свойства неидеальных газов . . . 297
8.5. Несколько простых моделей.......................299
8.6. Эмпирические и полуэмпирические уравнения со-
стояния ..............................................301
8.7. Взаимодействие молекул.........................303
8.8. Формы дисперсионной энергии....................304
8.9. Формы энергии обменного взаимодействия.........305
8.10. Общее выражение для энергии взаимодействия мо-
лекул ..........................................306
8.11- Выражения для второго вириального коэффициента,
полученного из потенциала Леннарда—Джонса . . .309
8.12. Сравнение с экспериментальными данными.........314
8.13. Вращательное движение молекул и внутренняя по-
тенциальная энергия ................................. 315
8.14. Уравнение состояния при большом давлении и ви-
риальные коэффициенты с большими номерами .... 320
8.15. Термодинамические функции неидеальных газов, вы-
раженные через вириальные коэффициенты................324
Глава IX. Жидкости и плотные газы.................................327
9.1. Свободная энергия газов и жидкостей.............331
9.2. Некоторые грубые модели жидкости................332
542
Оглавление
9.3. Связь жидкости с газом и жидкости с твердым те-
> . лом ............................................335
9.4. Вывод термодинамических функций для грубой мо-
дели .................................................336
9.5. Основы термодинамической теории плавления .... 338
9.6. Основная термодинамическая теория точки кипения —
закон Трутона........................................ 341
9.7. Потенциальная энергия взаимодействия между моле-
кулами и приведенное уравнение состояния ........... 344
9.8. Теория Леннарда — Джонса и Девоншайра ..... 348
9.9. Уравнение состояния и значения параметров при кри-
тических условиях ................................... 357
9.10. Асимптотическое разложение при малом объеме и
низкой температуре — жидкостная теория..........358
9.11. Равновесие жидкости и пара.....................362
9.12. Коэффициенты теплового расширения и изотермиче-
ского сжатия .........................................363
9.13. Удельная теплоемкость при постоянном давлении . .369
9.14. Скорость звука в нормальной жидкости...........372
9.15. Свойства газа при высокой температуре и давлении 373
9.16. Более точная теория жидкости и плотных газов . . .376
Глава X. Общая теория процессов переноса..........................379
10.1. Малые отклонения от термодинамического равновесия 380
10.2. Соотношения взаимности Онзагера ...............381
10.3. Термодинамика необратимых процессов............386
10.4. Теплопроводность в твердом теле................388
10.5. Общие процессы переноса в изотропной среде . . . .390
10.6. Феноменологические законы процессов переноса в
жидкости..............................................394
10.7. Эффекты Соре и Дюфура..........................397
10.8. Процессы переноса, сопровождающиеся химическими
реакциями.............................................400
10.9. Приложения термодинамики необратимых процессов 401
Задачи к главе 10....................................401
Глава XI. Вязкость, диффузия и теплопроводность...................402
11.1 Число столкновений в газе.......................403
11.2. Средняя длина свободного пробега ...409
11.3. Сохраняемость скорости после столкновения .... 412
11.4. Элементарная теория вязкости газа ....415
11.5. Вязкость газа, состоящего из упругих сферических
молекул.............................................. 418
11,6. Вязкость реального газа .420
Оглавление
543
11.7. Теплопроводность в газах........................425
11.8. Диффузия бинарной смеси.........................428
11.9. Время колебательной релаксации и коэффициент объ-
емной вязкости ..................................... 432
11.10. Процессы переноса в плотных газах..............434
11.11. Коэффициент вязкости жидкости..................439
11.12. Теплопроводность в жидкости....................443
11.13. Теплопроводность в твердом теле................445
11.14. Теплопроводность в металлах .......................447
Глава XII. Диффузия и замедление нейтронов..............................452
12.1. Диффузия нейтронов в поглощающей среде..........453
12.2. Связь между плоским и точечным источниками .... 456
12.3. Теория диффузионного приближения................-457
12.4. Точечное решение уравнения Больцмана............462
12.5. Сравнение точечного решения с диффузионным при-
ближением .................................................465
12.6. Поправки к диффузионной теории вблизи границ . . . 468
12.7. Некоторые простейшие примеры диффузии нейтронов 471
12.8. Замедление нейтронов, вызываемое упругим рассея-
нием ......................................................473
12.9. Вывод возрастного уравнения.........................478
12.10. Замедление моноэнергетических нейтронов от пло-
ского источника .................................... 484
12.11. Область применимости возрастного уравнения . . .485
12.12. Применение возрастного уравнения...................487
12.13. 0 поведении решения вблизи границы.................489
Задачи к главе 12.........................................490
Глава XIII. Тепловое излучение................................. . .491
13.1. Поле излучения .....................................492
13.2. Взаимодействие излучения с веществом................493
13.3. Поток энергии теплового излучения ..................495
13.4. Граничные условия...................................499
13.5. Излучательная способность...........................499
13.6. Коэффициент поглощения..............................502
13.7. Временное возмущение уравнения Шредингера . . . 503
13.8. Вероятности перехода Эйнштейна......................507
13.9. Вычисление вероятностей переходов...................508
13.10. Правило отбора и интенсивность излучения гармони-
ческого осциллятора ................................. 512
13.11. Правило отбора и интенсивность излучения централь-
но-симметричной системы...............................513
544
Оглавление
13.12. Правило отбора и интенсивность излучения двух-
атомной молекулы ......................................515
13.13. Дипольный момент и эффективный электрический за-
ряд двухатомной молекулы ........................ 518
13.14. Расчет суммарного поглощения двухатомного газа 519
13.15. Коэффициент поглощения двухатомного газа . . . .522
13.16. Расчет излучательной способности двухатомного газа 524
Задачи к главе 13......................................531
Таблица физических констант ......................... 532
Именной указатель ................................... 533
Предметный указатель . ............................. 555
НЯНЬ СЮЗ-СЕНЬ
Физическая механика
Редактор А. С. ПОПОВ Художник А. Смеляков
Технический редактор В. Сизова Корректор Л. В. Соломатина
Сдано в производство 9/Ш 1965 г. Подписано к печати 11/VIII 1965 г. Бумага 60х90*/1б=
17,0 бум. л. 34,0 печ. л. Уч. изд. л. 29,25. Изд. № 1/2256 Цена 2 р. 20 коп. Зак. 1299
~ ИЗДАТЕЛЬСТВО «МИР»
Москва, 1-й Рижский пер., 2
Ленинградская типография № 2 имени Евгении Соколовой Главполиграфпрома
Государственного комитета Совета Министров СССР по печати. Измайловский проспект, 29.