Автор: Резник А.Д.
Теги: математика статистика математический анализ издательство санкт-петербург
ISBN: 5-9268-0727-1
Год: 2008
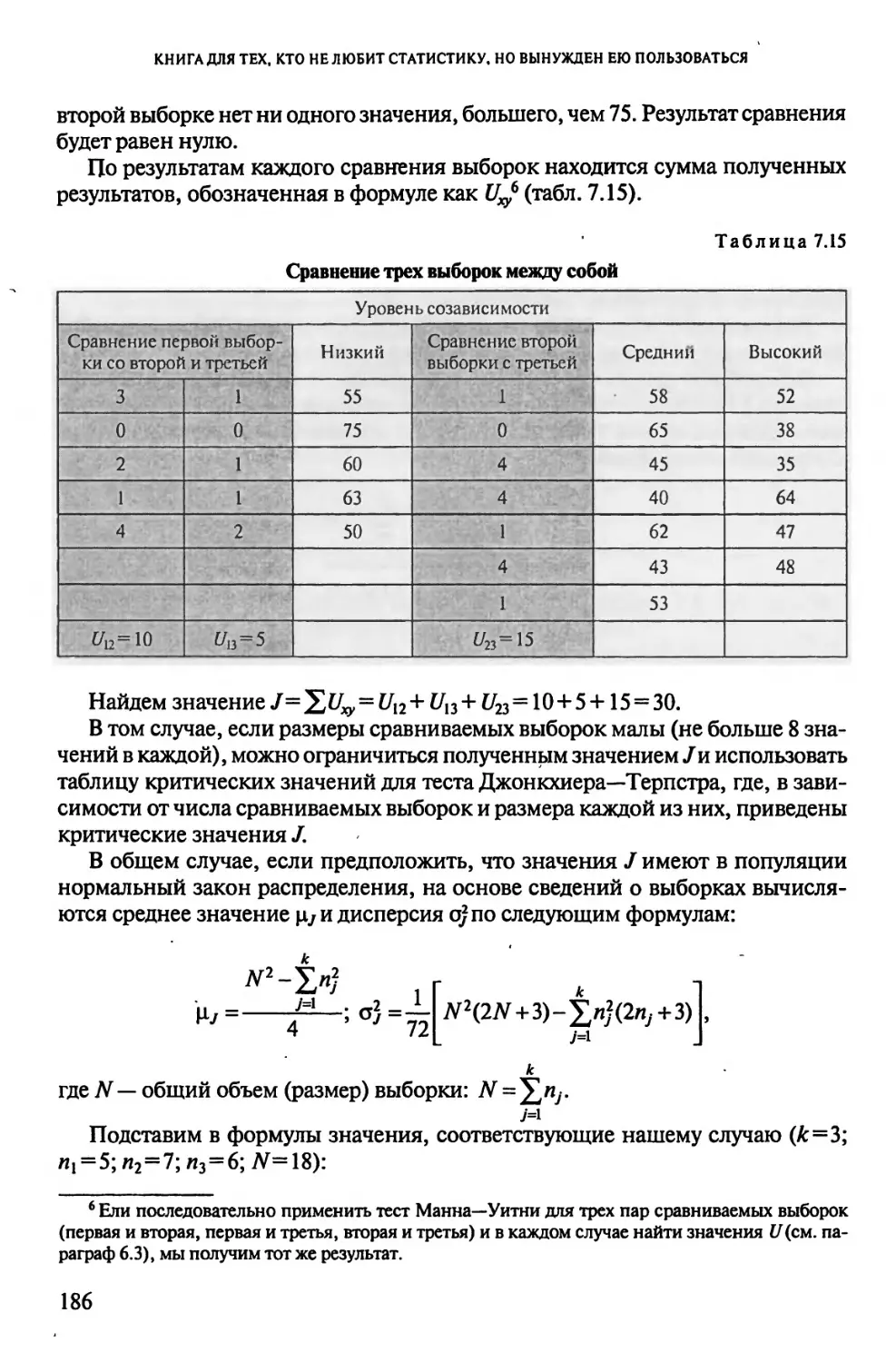
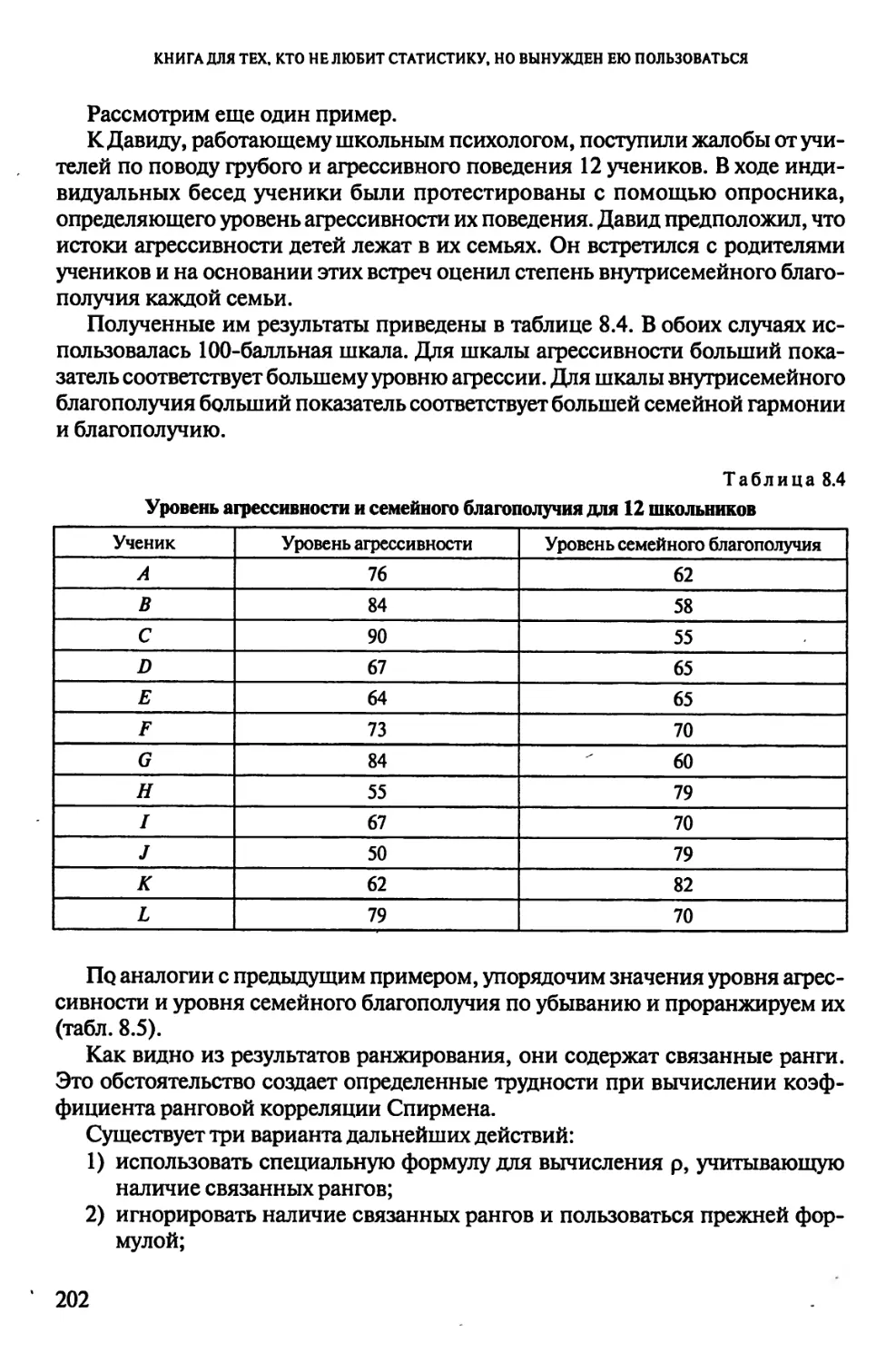
Текст
А. Д. РЕЗНИК
КНИГА ДЛЯ ТЕХ,
КТО НЕ ЛЮБИТ СТАТИСТИКУ
НО ВЫНУЖДЕН
ЕЮ ПОЛЬЗОВАТЬСЯ
непараметрическая статистика
в примерах, упражнениях
и рисунках
*
РЕЧЬ
Санкт-Петербург
2008
ББК88.4
Р34
Резник А. Д.
Р34 Книга для тех, кто не любит статистику, но вынужден ею- пользовать-
ся. Непараметрическая статистика в примерах, упражнениях и рисун-
ках. — СПб.: Речь, 2008. — 265 с.: илл.
ISBN 5-9268-0727-1
Данная книга посвящена описанию наиболее популярных непараметрических
методов статистики. Одна из центральных особенностей таких методов — возможность
получения обоснованных статистических выводов при наличии небольшого числа
испытуемых, что превращает непараметрическую статистику в незаменимый инструмент
там, где сложно говорить о больших выборках, массовых опросах или обследованиях.
Для использования некоторых из вошедших в книгу методов достаточно выборки в
6-8 человек. Другой привлекательной стороной непараметрических методов является
простота процесса математической обработки результатов. В ряде случаев необходимые
вычисления можно сделать в уме, не прибегая к калькулятору или компьютеру.
Книга представляет собой пособие для пользователей, не имеющих серьезной
математико-статистической подготовки, но желающих (или вынужденных) исполь-
зовать статистические методы в своей деятельности. Написанная доступным для
языком, она не требует для своего чтения специальных знаний в области математики
или статистики. Описание всех приводимых в ней методов производится на конкрет-
ных примерах, взятых из результатов различных исследований, опыта деятельности
специалистов гуманитарного профиля (психологи, социальные работники, консуль-
танты и др.) или обыденной жизни. Отличительной особенностью данной книги
является то, что все рассмотренные в ней примеры сопровождаются описанием со-
ответствующих процедур для программы SPSS, что делает ее полезной для начинаю-
щих пользователей этой программы.
Книга будет полезна специалистам, студентам и преподавателям социального и
гуманитарного профиля, а также всем желающим получить в свои руки достаточно
простой и качественный инструмент статистического анализа данных.
ББК88.4
Главный редактор И. Авидон
Зав. редакцией О. Гончукова
Художественный редактор П. Борозенец
Технический редактор О. Колесниченко
Корректор Я. Борисенкова
Ответственный секретарь М, Фомичева
Генеральный директор Л. Янковский
© А. Д. Резник, 2008
© Издательство «Речь», 2008
ISBN 5-9268-0727-1 © П. В. Борозенец, оформление, иллюстрации, 2008
Подписано в печать 23.07.2008. Формат 70х 1001/16- Печ. л. 16,5. Тираж 3000 экз. Заказ № 3384
ООО Издательство «Речь». 199178, Санкт-Петербург, а/я 96, «Издательство „Речь"»
тел. (812) 323—76—70,323-90-63; sales@rech.spb.ru
Интернет-магазин: www.rech.spb.ru
Представительство в Москве: тел.: (495) 502-67-07, rech@online.ru
За пределами России вы можете заказать наши книги
в интернет-магазине www.intematura.ni
Отпечатано с готовых диапозитивов в ГУП «Типография “Наука”»,
199034, Санкт- Петербург, В. О., 9-я линия, д. 12
ОГЛАВЛЕНИЕ
Предисловие.....................................................7
Глава 1
ВСЕ, ЧТО ВЫ ХОТЕЛИ ЗНАТЬ О СТАТИСТИКЕ, НО БОЯЛИСЬ
СПРОСИТЬ (глава почти без формул, но с пояснениями)............10
1.1. Бросить курить никогда не поздно, или Немного об описательной
статистике.....................................................10
1.2. Для любителей живописи: гистограммы, полигоны, распределения
и немного математики...........................................17
1.3. Передается ли интеллект по наследству, или Немного о корреляции
и регрессии....................................................25
1.4. Кто более компанейский, или Несколько слов о дисперсионном ана-
лизе ..........................................................32
1.5. Что сказал Господь Моисею в Синайской пустыне, или Кое-что о вы-
борках и популяциях............................................37
1.6. Полнеют ли от счастья, или О зависимых и независимых выборках... 38
1.7. Покупка обуви как точная наука, или О нулевой и альтернативной
гипотезах .....................................................39
1.8. Любит — не любит, придет — не придет, или Об ошибках первого
и второго родов ...............................................41
1.9. Можно ли одновременно сидеть на двух стульях, или Все о проверке
статистических гипотез.........................................44
1.10. Молодежь и наркотики, или Как проверяют статистические гипо-
тезы ..........................................................47
1.11. Дороги, которые мы выбираем: статистика параметрическая и непа-
раметрическая..................................................53
Глава 2
КАК ИЗМЕРИТЬ НЕИЗМЕРИМОЕ:
НЕМНОГО ОБ ИЗМЕРЕНИЯХ И ШКАЛАХ.................................57
2.1. От качеств к количествам и обратно........;...............57
3
КНИГА ДЛЯ ТЕХ, КТО НЕ ЛЮБИТ СТАТИСТИКУ, НО ВЫНУЖДЕН ЕЮ ПОЛЬЗОВАТЬСЯ
2.2. «И нарек человек имена всем», или Шкала наименований..58
2.3. В чем измеряются землетрясения, или О шкале порядка...60
2.4. «45 Г по Фаренгейту», или Как получить шкалу интервалов.65
2.5. Во сколько раз лилипуты меньше Гулливера, или Шкала отношений... 67
Глава 3
МОЖНО ЛИ САМОГО СЕБЯ ВЫТАЩИТЬ ЗА ВОЛОСЫ ИЗ БОЛОТА,
ИЛИ НЕПАРАМЕТРИЧЕСКАЯ СТАТИСТИКА ДЛЯ СЛУЧАЯ
ЕДИНСТВЕННОЙ ВЫБОРКИ........................................ 69
3.1. Где лучше провести вечер, или Биномиальный тест..'......70
3.2. «Форд», «Фиат», «Тойота», или Тест х2 для единственной выборки .... 76
3.3. Красота любимой в глазах любящего, или Тест Колмогорова-
Смирнова для единственной выборки .........................80
3.4. «Точность — вежливость королей», или Немного об анализе последо-
вательностей ............................................. 86
Глава 4
«ЧТО БЫЛО, ТО И ТЕПЕРЬ ЕСТЬ, И ЧТО БУДЕТ, ТО УЖЕ БЫЛО»,
ИЛИ СЛУЧАЙ ДВУХ ЗАВИСИМЫХ ВЫБОРОК............................91
4.1. Роды без проблем, или Тест МакНемара..................91
4.2. Как стать отличником, или Тест знаков.................97
4.3. Помогают ли диеты, или Тест Вилкоксона.................103
Глава 5
«ЧТО ДВИЖЕТ СОЛНЦЕ И СВЕТИЛА», ИЛИ СЛУЧАЙ
НЕСКОЛЬКИХ ЗАВИСИМЫХ ВЫБОРОК................................110
5.1. Эффективны ли телефонные опросы, или Тест Кохрана.....110
5.2. Студенты голосуют ногами, или Тест Фридмана............115
Глава 6
ОТДЕЛЕНИЕ СВЕТА ОТ ТЬМЫ, ИЛИ СЛУЧАЙ ДВУХ
НЕЗАВИСИМЫХ ВЫБОРОК.........................................123
6.1. «Некоторые любят погорячее», или Снова тест х2.........123
6.2. Секрет семейного счастья, или Точный тест Фишера.......131
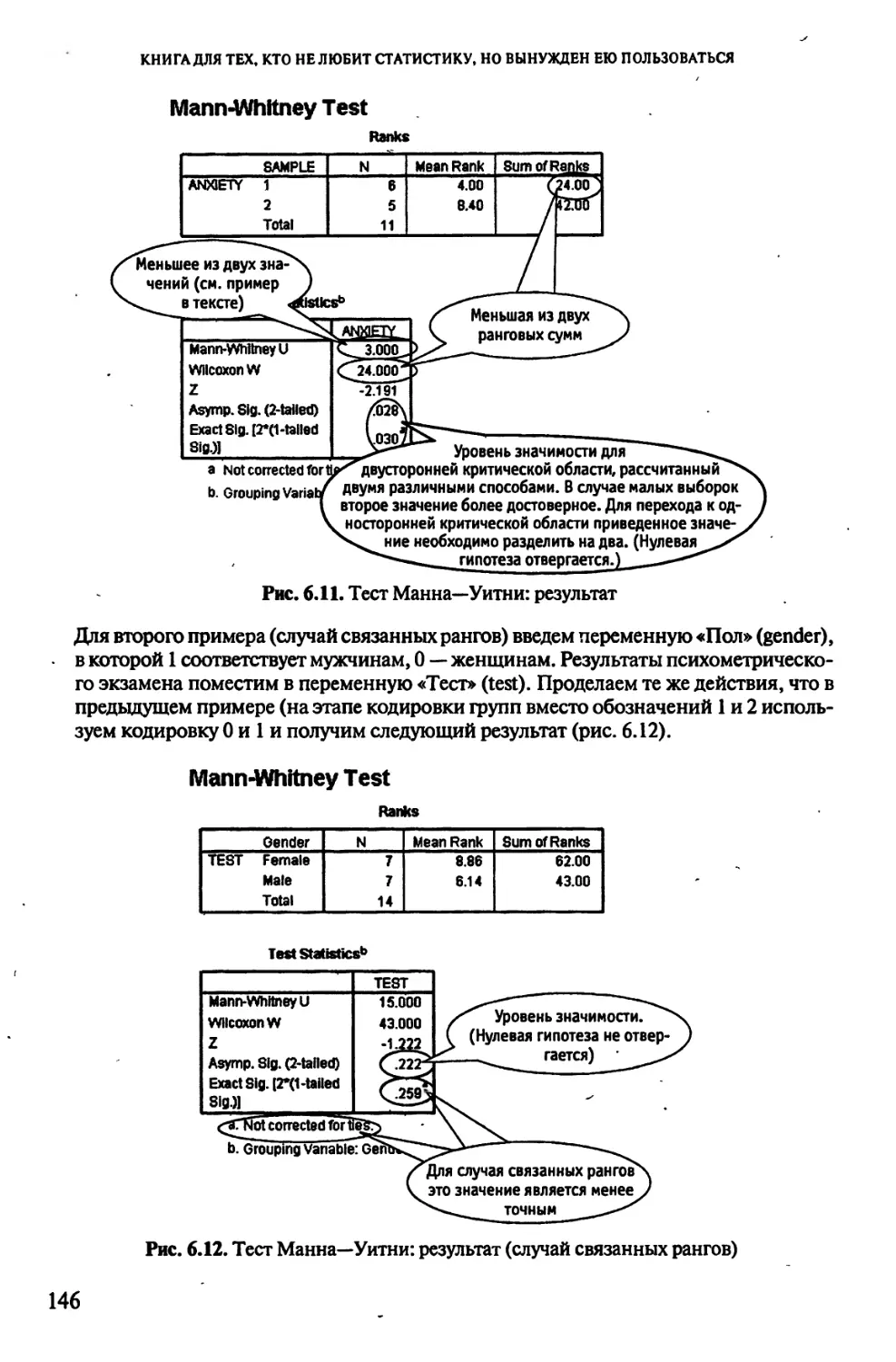
6.3. Кто менее тревожен во время беременности, или Тест Манна—Уитни
........................................................ 138
6.4. Сигарета как символ материнства, или Снова тест Колмогорова—Смир-
нова......................................................147
6.5. Пророк Даниил как первый диетолог, или Тест Вальда—Волфовица ... 153
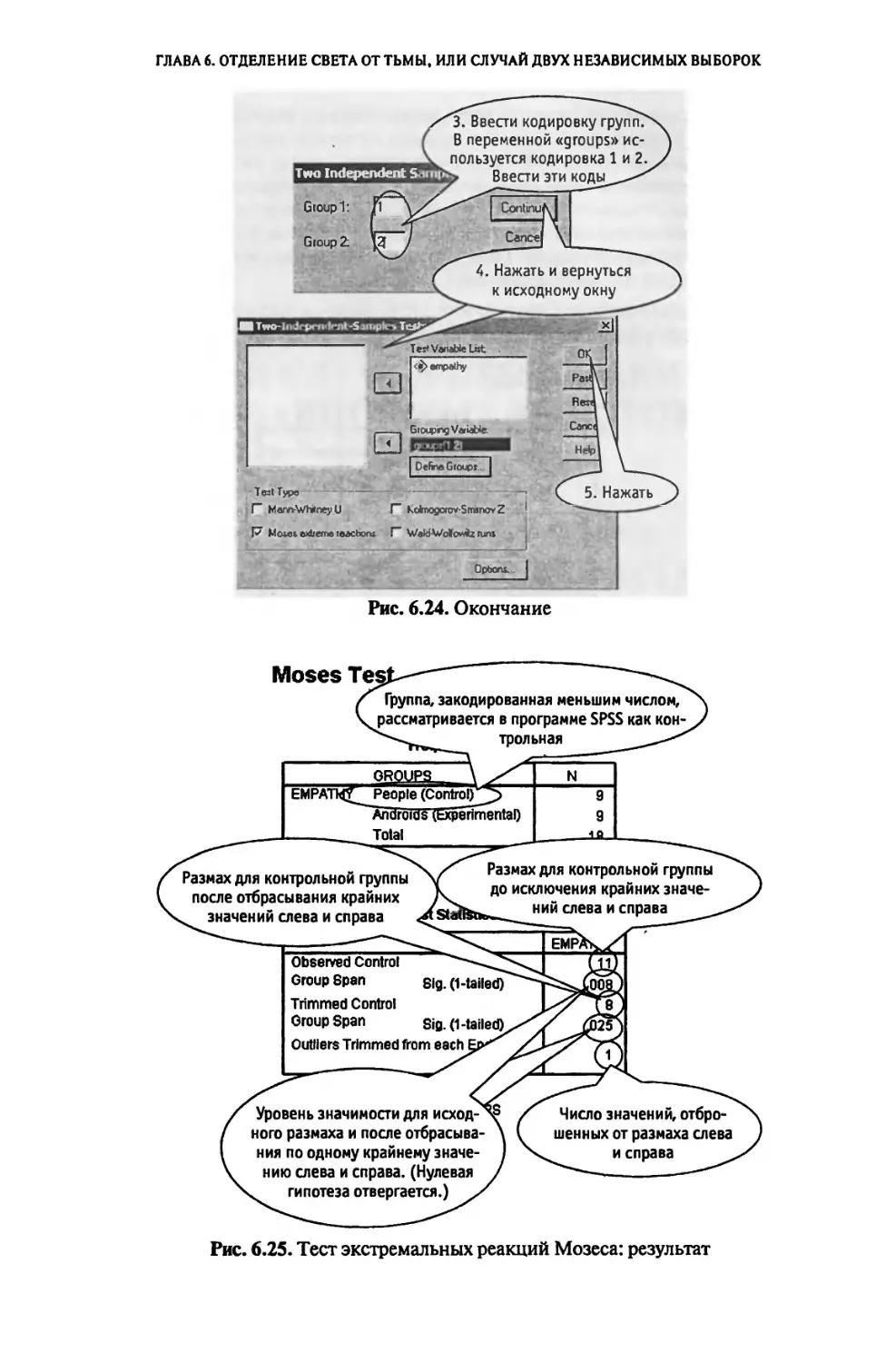
6.6 «Мечтают ли андроиды об электроовцах», или Тест экстремальных
реакций Мозеса.........................:..................159
4
ОГЛАВЛЕНИЕ
Глава?
«ВАВИЛОНСКОЕ СТОЛПОТВОРЕНИЕ», ИЛИ СЛУЧАЙ
НЕСКОЛЬКИХ НЕЗАВИСИМЫХ ВЫБОРОК............................169
7.1. Из жизни наркоманов, или Снова вездесущий тест х2....169
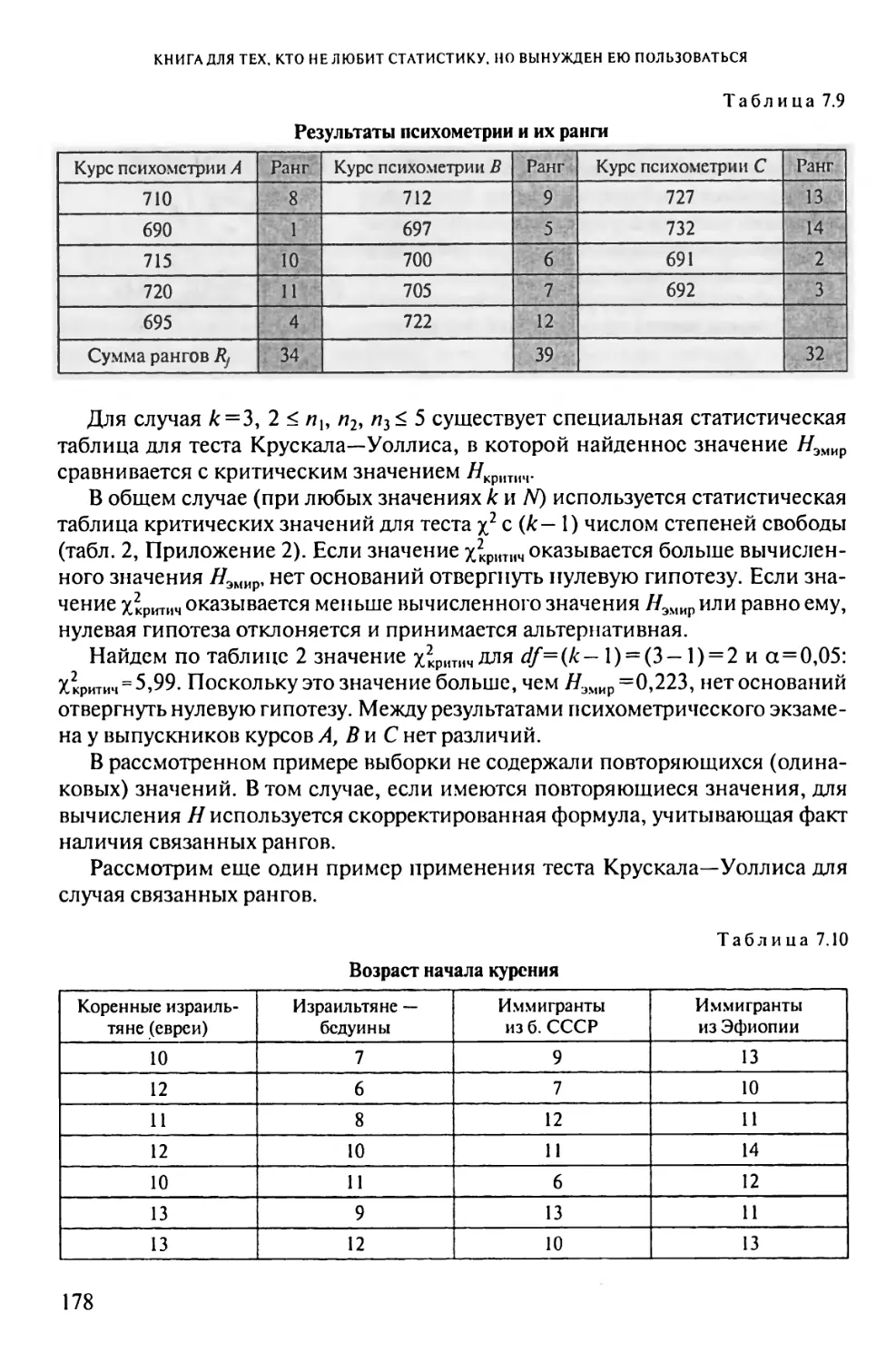
7.2. Какой курс психометрии лучше, или Тест Крускала—Уоллиса..176
7.3. Легко ли быть женой алкоголика, или Тест Джонкхиера—Терпстра .. 183
7.4. Часто ли родители бывают в школе, или Медианный тест для несколь-
ких независимых выборок ..................................193
Пгава8
КОРРЕЛИРОВАТЬ ВСЕ, ЧТО КОРРЕЛИРУЕТСЯ......................198
8.1. Красота на все времена, или Коэффициент ранговой корреляции
Спирмена..................................................198
8.2. Еще раз о женской привлекательности, или Коэффициент ранговой
корреляции Кендалла.......................................207
8.3. Почему подростки начинают употреблять наркотики, или Коэффици-
. ент конкордации Кендалла...........................:....216
ПРИЛОЖЕНИЯ................................................221
Приложение 1. Непараметрическая статистика в лицах........221
Приложение 2. Статистические таблицы......................226
Приложение 3. Все непараметрические методы в одном месте..238
1. Тест х2 для единственной выборки....................238
2. Тест Колмогорова—Смирнова для одной выборки ............239
3. Тест последовательностей......................... 239
4. Биномиальный тест...................................240
5. Тест МакНемара для двух зависимых выборок...............241
6. Тест знаков для двух зависимых выборок..............242
7. Тест Вилкоксона для двух зависимых выборок..............242
8. Тест Кохрана для нескольких зависимых выборок.’.....243
9. Тест Фридмана для нескольких зависимых выборок..........244
10. Тест х2 для двух независимых выборок...................245
11. Точный тест Фишера для двух независимых выборок........246
12. Тест Манна—Уитни для двух независимых выборок..........247
13. Тест Колмогорова—Смирнова для двух независимых выборок ... .248
14. Тест Вальда—Волфовица для двух независимых выборок.....248
15. Тест экстремальных реакций Мозеса для двух независимых
выборок................................................249
16. Тест х2 для нескольких независимых выборок.............250
17. Тест Крускала—Уоллиса для нескольких независимых выборок... 251
18. Тест Джонкхиера—Терпстра для упорядоченных альтернатив.252
5
КНИГА ДЛЯ ТЕХ. КТО НЕ ЛЮБИТ СТАТИСТИКУ, НО ВЫНУЖДЕН ЕЮ ПОЛЬЗОВАТЬСЯ
19. Расширенный медианный тест для нескольких независимых выбо-
рок........................................................252
Приложение 4. В жизни всегда есть место статистике (Вместо домашнего
задания).................................................. 254
Библиография..................................................258
Указатели.....................................................260
, Предметный указатель......................................260
Именной указатель......................................... 263
ПРЕДИСЛОВИЕ
В свое время я был весьма обескуражен тем, с каким упорством студенты-
гуманитарии избегали всего, что было связано с математической статистикой.
К сожалению, к моменту окончания университета от курса статистики в памя-
ти многих студентов остаются лишь разрозненные сведения и уверенность в
том, что лучше с нею не связываться.
Я не собираюсь в этом никого разубеждать. В самом деле, те статистические
методы, которые знакомы большинству из нас, требуют для своего корректно-
го применения десятков (а лучше сотен) испытуемых, громоздких многоэтаж-
ных вычислений, и, что самое главное, они не дают каких-либо гарантий в
получении желаемого результата. Как следствие, использование статистики
становится для многих студентов и специалистов непозволительной роскошью:
потратить несколько месяцев на сбор, обработку и анализ данных, чтобы в
результате не получить ожидаемых результатов.
Это тем более обидно, поскольку вот уже не один десяток лет существуют и
широко используются специалистами методы так называемой непараметриче-
ской статистики, позволяющие получать обоснованные статистические выво-
ды при наличии крайне небольшого числа испытуемых. Зачастую для исполь-
зования некоторых из этих методов достаточно выборки в 7—8 человек, что
превращает непараметрическую статистику в незаменимый инструмент там,
где сложно говорить о больших выборках, массовых опросах или обследовани-
ях и т. п.
Другой привлекательной стороной непараметрических методов статистики
является простота процесса математической обработки результатов. В ряде
случаев необходимые вычисления можно сделать в уме, не прибегая ни к каль-
кулятору, ни тем более к помощи компьютера.
Описанию и показу возможностей таких методов посвящена данная книга.
Ее основная задача — познакомить тех, кто «не дружит со статистикой», с эти-
ми методами и пробудить у них желание их использовать в своей повседневной
деятельности. Содержание книги в первую очередь ориентировано на специа-
листов и студентов социального и гуманитарного профиля (психологи, соци-
альные работники, консультанты, педагоги, журналисты и др.).
7
КНИГА ДЛЯ ТЕХ, КТО НЕ ЛЮБИТ СТАТИСТИКУ, НО ВЫНУЖДЕН ЕЮ ПОЛЬЗОВАТЬСЯ
Книга вряд ли может использоваться в качестве серьезного учебника по
непараметрической статистике. Она скорее представляет собой пособие для
пользователя, не имеющего серьезной математико-статистической подготовки,
но желающего (или вынужденного в силу обстоятельств) использовать стати-
стические методы в своей деятельности. Несмотря на то что описание приво-
димых в книге методов дано по возможности подробно и корректно, при воз-
никновении противоречий между научностью и доступностью изложения
выбор делался в пользу доступности (и, возможно, в ущерб научности).
Чтение книги не требует специальных знаний из области математики или
статистики. В первой главе приведены минимальные сведения из математической
статистики, необходимые для понимания того, о чем пойдет речь дальше.
В ряде случаев желающих использовать непараметрическую статистику
отпугивает обилие здесь непривычных статистических таблиц. Однако на прак-
тике выясняется, что при решении многих задач достаточно всего двух хорошо
известных таблиц: таблицы z-распределения и таблицы критических значений
для распределения %2. Эти и другие статистические таблицы, необходимые для
рассмотрения описанных в книге методов, приведены в приложении.
При описании непараметрических методов статистики в книге использует-
ся типичный в англоязычной литературе термин «тест» вместо более привыч-
ного для русскоязычного читателя термина «критерий».
Приводимые в книге примеры частично базируются на результатах иссле-
дований, проводимых исследовательским центром RADAR (Regional Alcohol
and Drug Abuse Recourse Center) Университета Бен Гурион в Негеве, частично
взяты из опыта реальной деятельности психологов, консультантов и социаль-
ных работников и частично носят гипотетический характер. Одно из назначе-
ний приводимых в книге примеров — показать, что необязательно быть,
допустим, психологом-исследователем, чтобы испытывать потребность в ста-
тистических методах. Им может найтись место не только в деятельности мно-
гих специалистов, но и в обыденной жизни.
Отличительной особенностью данной книги является то, что все рассмот-
ренные в ней примеры сопровождаются описанием соответствующих процедур
для программы SPSS.
Программу SPSS использует в своей деятельности все большее число спе-
циалистов различного профиля. Однако опыт консультирования по вопросам
статистики показал, что знание этой программы не избавляет от проблем.
Овладение данной программой зачастую происходит по принципу «Нажми на
кнопку — получишь результат». Формально правильное выполнение всех опе-
раций в программе SPSS часто сопровождается трудностями в понимании и
интерпретации получаемых результатов. Поэтому каждый из приводимых в
книге примеров рассматривается дважды: первый раз д ля вычислений вручную
и второй раз для программы SPSS с необходимыми пояснениями. Это особен-
но важно, поскольку программа SPSS выявила «подводные камни» ряда непа-
раметрических методов, которые до этого применялись исключительно вручную:
использование упрощенных алгоритмов вычислений, игнорирование ряда
8
ПРЕДИСЛОВИЕ
особенностей в экспериментальных данных (например, наличие в них совпа-
дающих или повторяющихся результатов), ограниченные возможности стати-
стических таблиц и др. Как следствие, результаты, получаемые при вычисле-
ниях вручную, могут не совпадать с результатами, выдаваемыми программой
SPSS. В книге рассматриваются подобные случаи с описанием тех более стро-
гих статистических алгоритмов, которые используются в программе SPSS при
работе с непараметрическими методами.
Разумеется, все, связанное с SPSS, не может служить заменой более серьез-
ным пособиям по использованию данной программы. Тем более что даже для
рассматриваемых примеров за рамками книги осталось описание многих ее
возможностей.
Книгу можно читать как «слева направо», так и «справа налево». В первом
случае речь идет о тех, кто испытывает потребность в статистике и собирается
в дальнейшем перейти к программе SPSS. Во втором случае — о тех, кто освоил
программу на уровне «кнопочного интерфейса», но не представляет, что про-
исходит в ее «недрах» и что стоит за выдаваемыми программой результатами.
Я надеюсь, что книга привлечет внимание специалистов, студентов и пре-
подавателей социального и гуманитарного профиля. Надеюсь, что она также
будет полезна всем, желающим получить в свои руки достаточно простой и
качественный инструмент статистического анализа данных.
Желающие самостоятельно попрактиковаться в использовании программы
SPSS могут получить файл, содержащий все рассмотренные в книге примеры,
обратившись по адресу reznikal@bgu.ac.il. Буду рад получить по этому же ад-
ресу ваши предложения, замечания и отзывы.
Доктор (PhD) Александр Резник,
Университет Бен-Гурион в Негеве, Израиль
Глава 1
ВСЕ, ЧТО ВЫ ХОТЕЛИ ЗНАТЬ
О СТАТИСТИКЕ, НО БОЯЛИСЬ СПРОСИТЬ
(глава почти без формул, но с пояснениями)
1.1. БРОСИТЬ КУРИТЬ НИКОГДА НЕ ПОЗДНО,
ИЛИ НЕМНОГО ОБ ОПИСАТЕЛЬНОЙ СТАТИСТИКЕ
Если вы курите, то в каком возрасте закурили в первый раз? Именно об этом
спрашивали израильских подростков в ходе одного из исследований, прове-
денных центром RADAR.
В таблице 1.1 приведен фрагмент полученных сведений о поле респондентов
и возрасте начала курения для 35 подростков.
Таблица 1.1
Возраст начала курения
Респон- дент Пол Возраст начала курения Респон- дент Пол Возраст начала ку- рения Респон- дент Пол Возраст начала курения
1 М 11 11 Ж 12 21 М 10
2 М 8 12 М 9 22 М 8
3 М 12 13 Ж 12 23 Ж 11
4 М 6 14 Ж 10 24 М 12
5 Ж 13 15 Ж 12 25 Ж 13
6 М 12 16 М 12 26 Ж и
7 Ж 11 17 Ж 14 27 м 13
8 Ж 10 18 м 7 28 м 7
9 М 12 19 м 10 29 м 10
10 М 15 20 м 14 30 ж 6
10
ГЛАВА 1. ВСЕ, ЧТО ВЫ ХОТЕЛИ ЗНАТЬ О СТАТИСТИКЕ, НО БОЯЛИСЬ СПРОСИТЬ
Окончание табл. 1.1
Респон- дент Пол Возраст начала курения Респон- дент Пол Возраст начала ку- рения Респон- дент Пол Возраст начала курения
31 М 12 33 М 13 35 М 10
32 М 11 34 Ж 12
В статистике для описания подобных данных обычно используют:
□ меры центральной тенденции (мода, медиана, среднее);
□ меры изменчивости (дисперсия и стандартное отклонение).
Модой (Мо) называется наиболее часто встречающееся значение среди
имеющихся. Для того чтобы разобраться с модой, построим дополнительную
таблицу. Поместим в нее значения возраста от минимального (6 лет) до мак-
симального (15 лет), и укажем, сколько раз встречается то или иное значение
возраста (табл. 1.2).
Таблица 1.2
Упорядоченные данные о возрасте начала курения
Возраст начала курения Частота
6 2
7 2
8 2
9 1
10 6
11 5
12 10
13 4
14 2
15 1
Всего 35
Как видно из таблицы, чаще всего подростки начинают курить в 12 лет (это
значение возраста встречается чаще всего — 10 раз). Поэтому мода возраста
начала курения — 12 лет.
Новая таблица содержит ту же самую информацию, что и предыдущая, но
она заметно короче, данные в ней упорядочены по возрастанию, и с ней удоб-
ней работать.
Медиана (Me) представляет собой значение, которое делит упорядоченные
данные пополам таким образом, что одна половина данных оказывается мень-
ше медианы, а другая — больше.
11
КНИГА ДЛЯ ТЕХ, КТО НЕ ЛЮБИТ СТАТИСТИКУ, НО ВЫНУЖДЕН ЕЮ ПОЛЬЗОВАТЬСЯ
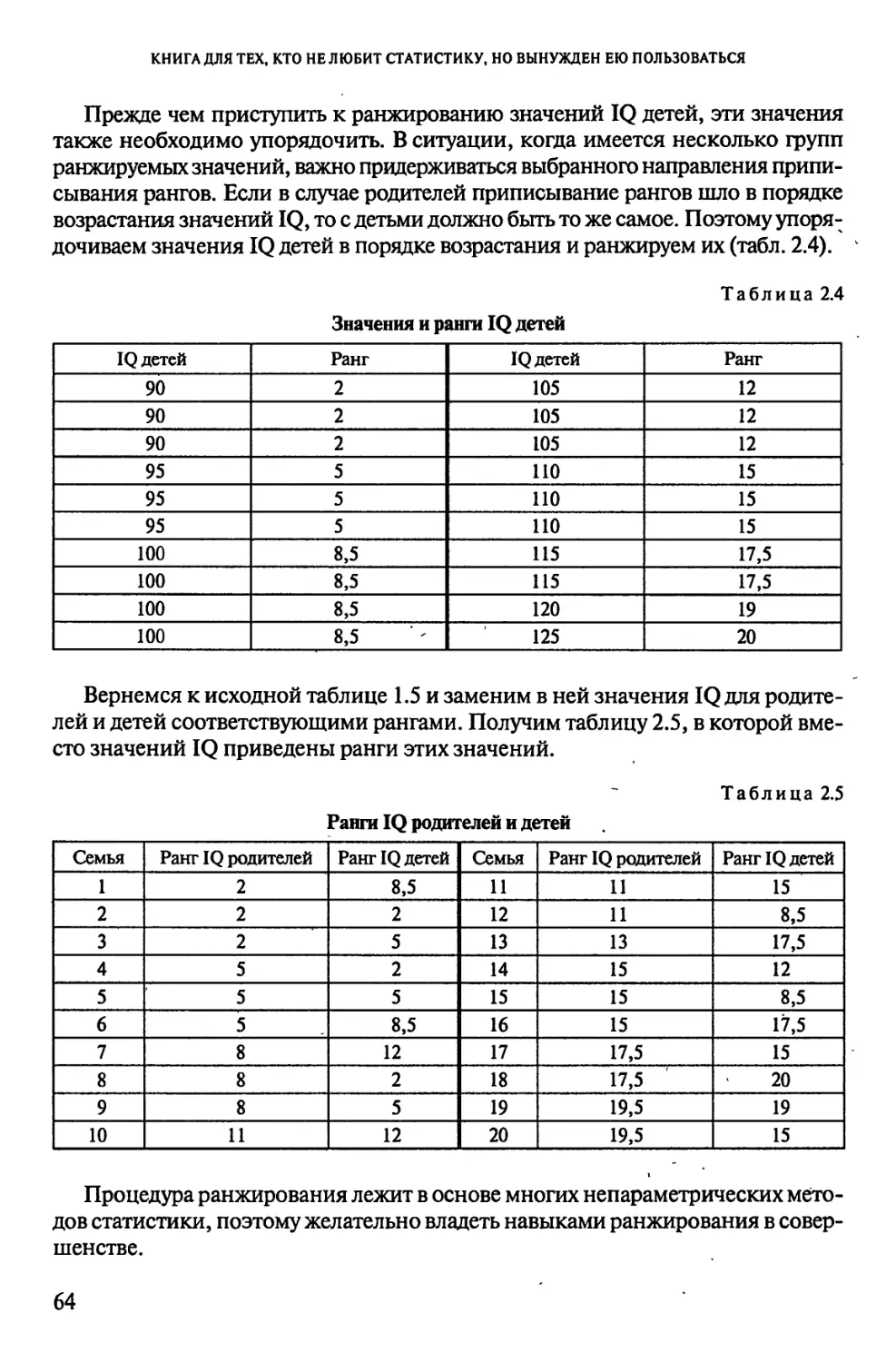
Нахождение медианы не носит столь наглядного характера, как нахождение
моды. Для определения медианы приходится прибегать к дополнительным
преобразованиям и вычислениям. Во-первых, дополним таблицу 1.2 еще двумя
столбцами (графами) и получим таблицу 1.3.
В первом из дополнительных столбцов запишем значения так называемых
«накопленных» (или кумулятивных) частот. Представьте, что мы обходим строй
из 35 подростков, которые стоят в шеренгах в зависимости от возраста начала
курения. В первой шеренге (6 лет) два человека. Во второй (7 лет) тоже два и т. д.
Наша задача — подсчитать, сколько подростков при таком «обходе войск»
осталось за нашей спиной. После первой шеренги за нашей спиной два чело-
века. После второй — уже четыре (два в первой шеренге и два во второй) и т. д.
Это и будут накопленные частоты. Очевидно, после конца «обхода» за нашей
спиной будет 35 человек.
Во-вторых, запишем в следующую графу, какой процент от 35 подростков
составляет каждое значение накопленных частот.
Таблица 1.3
Вычисление медианы
Возраст начала курения Частота Накопленная частота %
6 2 2 5,7
7 2 4 Н,4
8 2 6 17,1
9 1 7 20,0
10 6 13 37,1
11 5 18 51,4
12 10 28 80,0
13 4 32 91,4
14 2 34 97,1
15 1 35 100
Всего 35
Попытаемся понять смысл полученного в последней графе результата.
При переходе от шеренги «10 лет» кшеренге «11 лет» за плечами остается 37,1%
всех результатов. А при переходе от шеренги «11 лет» к шеренге «12 лет» за
плечами уже 51,4%. Медиана — это та точка, которая делит все данные в отно-
шении 50:50. Очевидно, требуемая точка где-то внутри шеренги «11 лет». То
есть Me=11.
На этом можно остановиться, хотя обычно для вычисления медианы ис-
пользуются более сложные вычисления.
Наиболее популярной мерой центральной тенденции является среднее (Т).
Для нахождения среднего используется простая формула, смысл которой в
том, чтобы сложить все значения (в нашем случае значения возраста начала
12
ГЛАВА 1. ВСЕ, ЧТО ВЫ ХОТЕЛИ ЗНАТЬ О СТАТИСТИКЕ, НО БОЯЛИСЬ СПРОСИТЬ
курения) и разделить полученный результат на число значений (в нашем слу-
чае 35).
Дальше можно идти двумя путями.
Во-первых, начать непосредственно складывать все 35 значений возраста
из первой таблицы.
Во-вторых, догадаться, что если некоторые значения возраста встречаются
несколько раз, то можно воспользоваться данными из таблицы 1.2 и перейти
от сложения повторяющихся значений к умножению этих значений на число
повторов (например, возраст 13 лет встречается в первой таблице четыре раза,
то вместо 13 + 13 + 13 + 13 записать 13 х 4). Тогда:
j = Х(возраст)(частота) = (6)(2Н(7)(2>(8)(2)+(9)(1Н(10)(6)+(11)(5) +
число значений 35
+(12)(10>(13)(4)i-(14)(2)i-(15)(l) _ 1Q 89
35
Меры центральной тенденции показывают, вокруг каких значений группи-
руется большинство экспериментальных данных. Обычно в качестве «центра»
такого группирования рассматривается среднее (X).
Меры изменчивости говорят о том, в какой степени полученные результаты
отклоняются от «центра группирования», что чаше всего приводит к опреде-
лению меры отклонения экспериментальных данных от среднего.
В принципе, в качестве меры изменчивости можно было бы использовать
среднее значение отклонений текущих значений от среднего. Для этого необ-
ходимо определить, насколько каждое значение возраста отклоняется в большую
или меньшую сторону от Х= 10,89, затем сложить все результаты и разделить
на число значений. К сожалению, этот путь невозможен, поскольку, как пра-
вило, отклонения от среднего в большую сторону (со знаком «+») и в меньшую
сторону (со знаком «—») компенсируют друг друга и в сумме дают ноль.
Для решения этой проблемы лучше использовать не отклонение от средне-
го, а квадрат этого отклонения, потому что такая процедура позволяет изба-
13
КНИГА ДЛЯ ТЕХ, КТО НЕ ЛЮБИТ СТАТИСТИКУ, НО ВЫНУЖДЕН ЕЮ ПОЛЬЗОВАТЬСЯ
виться от влияния знака. Вначале делается та же операция — определяется,
насколько каждое значение возраста отклоняется в большую или меньшую
сторону от Х= 10,89. Затем каждый из полученных результатов возводится в
квадрат, все складывается и делится на число значений. Получаемая таким
образом мера изменчивости называется дисперсией.
Еще раз вернемся к таблице 1.2 и дополним ее двумя графами, необходи-
мыми для вычисления дисперсии. Получим таблицу 1.4.
Таблица 1.4
Вычисление дисперсии
Возраст начала курения Частота (Возраст — Среднее) (Возраст — Среднее)2 (Частота) х (Возраст — Среднее)2
6 2 -4,89 23,91 47,82
7 2 -3,89 15,13 30,26
8 2 -2,89 8,35 16,70
9 1 -1,89 3,57 3,57
10 6 -0,89 0,79 4,74
11 5 0,11 0,01 0,05
12 10 1,П 1,23 12,30
13 4 2,11 4,45 17,80
14 2 3,11 9,67 19,34
15 1 4,11 16,89 16,89
Всего 35 Е=169,47
Дисперсия - ^^03Раст ~ Среднее)2(Частота)
Число значений
На практике по ряду причин теоретического характера, которые мы здесь
не обсуждаем, для вычисления дисперсии используется другая формула, не-
значительно отличающаяся от предыдущей:
Дисперсия - ^^3Раст~^'Ре^нее^г^астота^
(Число значений -1)
Подставим в эту формулу необходимые значения из таблицы 1.4:
Дисперсия - ^АВозРаст ~ Среднее')2 (Частота) _ (~4,89)2(2)+(-3,89)2(2)
(Число значений -1) (35-1)
(-2,89)2(2)+(-1,89)2(1)+(-О,89)2(6)+(О,11)2(5)+(1,11)2(1О)+(2,11)2(4) !
(35-1)
। (3,11)2(2)+(4,11)2(1) 169,47 .
(35-1) 34
14
ГЛАВА 1. ВСЕ, ЧТО ВЫ ХОТЕЛИ ЗНАТЬ О СТАТИСТИКЕ. НО БОЯЛИСЬ СПРОСИТЬ
К сожалению, дисперсия оказывается не очень удобным показателем меры
изменчивости. Наличие в формуле квадрата меняет размерность входящих в 1
нее величин. Например, если мы хотим определить меру изменчивости роста
для группы людей, то в формуле для дисперсии будет использоваться значение
(Рост — Среднее)2. Размерность этого значения см2. Но см2 — это уже размер-
ность площади, а не длины. То есть среднее значение роста будет измерено в
единицах длины, а отклонение от среднего — в единицах площади.
Для решения возникшей проблемы вместо значения дисперсии использу-
ется квадратный корень из нее. Полученное таким образом новое значение
называется стандартным отклонением и является наиболее популярной мерой
изменчивости. Стандартное отклонение часто обозначается как о (сигма):
Стандартное отклонение (о) = ^Дисперсия.
Для нашего случая:
Стандартное отклонение (о)=-^Дисперсия = 74,98=2,23.
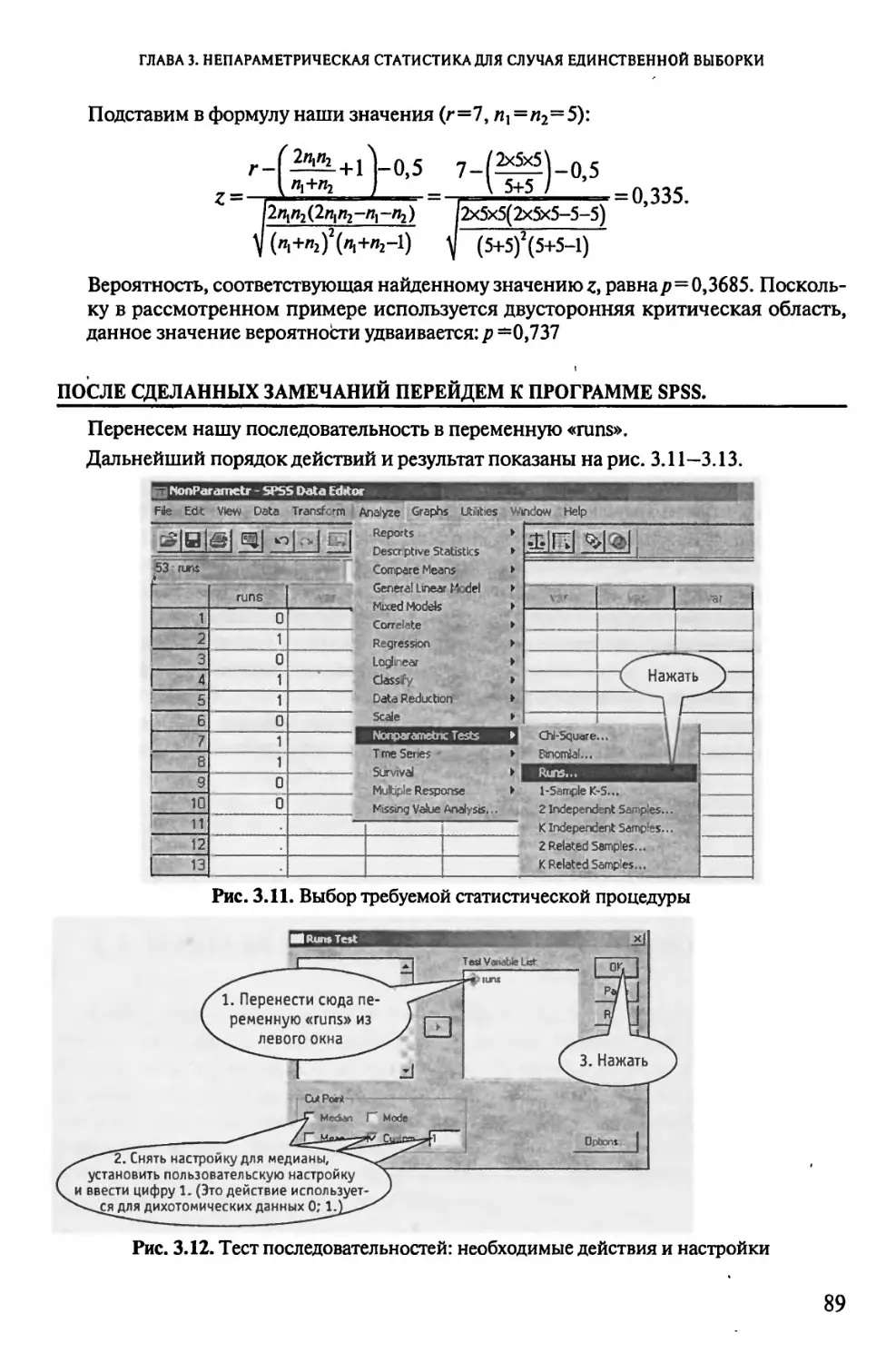
ВКЛЮЧАЕМ КОМПЬЮТЕР И ЗАПУСКАЕМ ПРОГРАММУ SPSS'
После ввода данных о поле респондентов (переменная «Sex» с обозначением «1» для
мальчиков и «2» для девочек) и возрасте начала курения (переменная «age») присту-
паем к их обработке. Очередность действий и конечный результат показаны на
рис. 1.1-1.3.
cor
Fie Edit View Data Transform I Analyze Graphs Utilities Window Help
pf * gender
2
3
4
5
6
7
8
9
10
11
12
13
14
gender
2
2
2
Reports
Descnpbve Statistics
2
Г
2
2
17
9
12
10
Compare Means
General Linear Model
Mixed Models
Correlate
Regression
Logbnear
Classify
Data Reduction
Scale
Nonparametric Tests
Time Senes
Survival
Multiple Response
Missing Value Analys s...
Frequencies...
Нажать
Descriptives...
Explore...
Crosstabs.
Ratto...
Рис. 1.1. Выбор требуемой статистической процедуры
1 Мы предполагаем, что читатель имеет определенный опыт работы с этой программой. Поэтому
операции по вводу данных, их кодировке и др. не рассматриваются.
15
КНИГА ДЛЯ ТЕХ. КТО НЕ ЛЮБИТ СТАТИСТИКУ, НО ВЫНУЖДЕН ЕЮ ПОЛЬЗОВАТЬСЯ
Рис. 1.2. Необходимые для обработки данных действия и настройки
ГЛАВА 1. ВСЕ, ЧТО ВЫ ХОТЕЛИ ЗНАТЬ О СТАТИСТИКЕ, НО БОЯЛИСЬ СПРОСИТЬ
Statistics
AGE
N Valid 35
Missing 0
Mean 10.89
Median 11.00
Mode 12
Std. Deviation 2.233
AGE
Frequency Percent Valid Percent Cumulative Percent
Valid 6 2 5.7 5.7 5.7
7 2 5.7 57 11.4
8 2 5.7 5.7 17.1
9 1 2.9 2.9 20.0
10 6 17.1 17.1 37.1
11 5 14.3 14.3 51.4
12 10 28.6 28.6 80 0
13 4 11.4 11.4 91.4
14 2 5.7 5.7 97.1
15 1 2.9 2.9 1000
Total 35 100.0 100.0
Рис. 1.3. Результат обработки
1.2. ДЛЯ ЛЮБИТЕЛЕЙ ЖИВОПИСИ:
ГИСТОГРАММЫ, ПОЛИГОНЫ, РАСПРЕДЕЛЕНИЯ
И НЕМНОГО МАТЕМАТИКИ
Во многих случаях для анализа имеющихся результатов используется их
графическое представление.
Так, на основе таблицы 1.2 можно построить график распределения частот.
Если по горизонтали (ось X) отложить значения возраста, а по вертикали
(ось Y) — частоту каждого значения (сколько раз оно встречается), то можно
получить либо гистограмму распределения частот, либо полигон распределения
•частот.
В первом случае распределение частот изображается в виде набора столби-
ков, середина основания каждого из которых совпадает со значением возраста,
а высота равна значению частоты для этого возраста (рис. 1.4).
Рис. 1.4. Столбиковая диаграмма (гистограмма)
17
КНИГАДЛЯ ТЕХ, КТО НЕ ЛЮБИТ СТАТИСТИКУ. НО ВЫНУЖДЕН ЕЮ ПОЛЬЗОВАТЬСЯ
Рис. 1.5. Полигон распределения частот
Во втором случае значения частот изображаются точками, расположенными
на соответствующей высоте над значениями возраста. Затем эти точки соеди-
няют друг с другом отрезками прямых линий. Получившаяся «горная гряда»
называется полигоном распределения частот (рис. 1.5).
Если вернуться к уже рассмотренным нами мерам центральной тенденции
и мерам изменчивости, то моде будет соответствовать самое «высокое» значе-
ние возраста (можно видеть, что это 12 лет). Медиана—это то значение, которое
делит площадь геометрической фигуры, образованной, например, гистограм-
мой, пополам. А среднее — это то значение, сумма отклонений от которого
влево и вправо будет равна нулю (рис. 1.6).
Ill
J Me Mo
Рис. 1.6. Мода, медиана и среднее
Если экспериментальных данных очень много, то в подавляющем числе
случаев распределение частот начинает приближаться к виду симметричной
кривой, похожей на колокол. На рис. 1.7 приведено распределение возраста
18
ГЛАВА 1. ВСЕ, ЧТО ВЫ ХОТЕЛИ ЗНАТЬ О СТАТИСТИКЕ. НО БОЯЛИСЬ СПРОСИТЬ
участников одного из всеизраильских исследований на тему «Молодежь и
наркотики», проведенного в начале 2000-х тт. центром RADAR. В исследовании
приняло участие 1235 человек в возрасте от 12 до 21 года.
40° -| |----
350- ----
зоо-
250-
200- -----
150-
100 -
12 13 14 15 16 17 18 19 20 21
Рис. 1.7. Распределение возраста участников исследования
В математической статистике доказывается, что по мере увеличения числа
данных (в идеале — до бесконечности) такого рода распределения приближа-
ются к виду, который называется кривой нормального распределения, или
кривой Гаусса (по имени немецкого математика Карла Гаусса (1777—1855),
который в начале XIX в. исследовал свойства такого распределения). Вид кри-
вой нормального распределения показан на рис. 1.8. Оно получено на основе
данных того исследования, о котором шла речь (число участников 1235).
В рис. 1.8 использованы значения относительных частот, получаемых делени-
ем каждой частоты на общее количество значений.
19
КНИГА ДЛЯ ТЕХ, КТО ЛЕ ЛЮБИТ СТАТИСТИКУ, НО ВЫНУЖДЕН ЕЮ ПОЛЬЗОВАТЬСЯ
Нормальное распределение обладает рядом свойств.
Во-первых, для него все три меры центральной тенденции: мода, медиана
и среднее — совпадают друг с другом: Мо =Ме =Х. Из этого факта следует сим-
метричный характер кривой нормального распределения. Поэтому в большин-
стве статистических таблиц для этого распределения приводятся сведения,
относящиеся только к одной из его частей (чаще всего правой).
Во-вторых, несмотря на то что теоретически нормальное распределение
простирается вдоль оси А'от минус бесконечности (—°°) до плюс бесконечности
(+ °°), на практике ограничиваются диапазоном (Х± За), где а — стандартное
отклонение. В этих пределах лежит 99,74% площади под кривой нормального
распределения2, что вполне достаточно для решения большинства задач3.
Например, для нормального распределения, изображенного на рис. 1.5,
Х= 16,5 лет, а=1,5. Рассмотрим какое-либо значение возраста (обозначим его
как Л,), не равное среднему. Например, Х(= 18 лет. Введем в рассмотрение ве-
личину z, которая будет вычисляться по следующей формуле:
Xt-X
z=—------.
О
Для нашего случая
Xt-X 18-16,5 ,
z=——=----------—=1.
о 1,5
Для Xt= 13,5 получим
Xi-X 13,5-16,5 _
=’2-
Нетрудно видеть, что значение z показывает, насколько далеко от среднего
(слева или справа от него) расположено какое-либо конкретное значение воз-
раста. Если возраст меньше среднего (отклонение влево), z отрицательно. Если
возраст больше среднего (отклонение вправо), z положительно. Если возраст
равен среднему, z равно нулю.
Как мы уже знаем, 99,74% площади под кривой нормального распределения
лежит в пределах (Х± За). Поэтому когда речь заходит о максимальном откло-
нении от среднего, то на практике обычно ограничиваются значением, равным
±3а. Иначе говоря, если участники исследования «Молодежь и наркотики»
имели среднее значение возрастав 16,5 и стандартное отклонение а= 1,5, то
можно сказать, что 99,74% всех участников имели возраст не меньше чем
(16,5—Зх 1,5)=12 лет, и не больше чем (16,5 + 3 х 1,5)=21 год.
2 «Хвосты» нормального распределения, в которых расположено 0,26% площади (по 0,13% с
каждой стороны), играют важную роль при проверке статистических гипотез.
3 Выбор диапазона ± Зо не носит принципиального характера и сделан из практических сооб-
ражений. В ряде случаев рассматривается диапазон ±4о, в пределах которого лежит 99,997%
площади под кривой нормального распределения.
20
ГЛАВА 1. ВСЕ, ЧТО ВЫ ХОТЕЛИ ЗНАТЬ О СТАТИСТИКЕ. НО БОЯЛИСЬ СПРОСИТЬ
Найдем значение z для этих значений.
_ 12-16,5 _ _ 21-16,5
£min ~ — Л ^тах । 5
Если мы возьмем любое другое нормальное распределение с известными Т
и о (например, распределение значений уровня интеллекта IQ), то получим
аналогичный результат. Используемые на практике максимальные отклонения
от среднего значения IQ влево и вправо от него, выраженные через значение z,
также будут лежать в пределах от zmin=—3 до Zmax=+3.
Это очень важный вывод, поскольку он позволяет не учитывать природу
тех конкретных данных, на основе которых было получено нормальное рас-
пределение. Вместо конкретных значений, например, возраста, IQ, заработ-
ной платы, тревожности и др., откладываемых по шкале X, можно перейти к
единицам г-шкалы, имеющей диапазон значений от —3 до + 3 (реже от —4 до
+4) для любого нормального распределения. Тем самым все нормальные
распределения как бы приводятся к «общему знаменателю», в роли которого
выступает z-шкала, и появляется возможность сравнивать различные распре-
деления между собой, независимо от того, на основе каких значений они были
получены.
Кроме этого, любое нормальное распределение всегда можно преобразовать
к виду, называемому единичным нормальным распределением, при котором
среднее Х=0 и стандартное отклонение о= 1 (рис. 1.9).
Рис. 1.9. Единичное нормальное распределение (Y=0 и о= 1)
Это преобразование позволяет заменить большинство вычислений, связан-
ных с использованием нормального распределения, работой со специальными
21
КНИГА ДЛЯ ТЕХ, КТО НЕ ЛЮБИТ СТАТИСТИКУ. НО ВЫНУЖДЕН ЕЮ ПОЛЬЗОВАТЬСЯ
статистическими таблицами, где приведены все относящиеся к такому распре-
делению значения и результаты. Чаще всего используется таблица стандартно-
го нормального z-распределения (для случая Х=0 и о= 1).
В-третьих, долю площади под кривой нормального распределения, ограни-
ченную одним или двумя значениями z, можно понимать как вероятность того,
что нормально распределенные результаты будут лежать в определенном диа-
пазоне своих значений.
Чтобы понять, о чем идет речь, рассмотрим пример.
Лена—очень умная девушка. Она изучает психологию, пользуется популяр-
ностью у молодых людей, но имеет высокие требования к интеллектуальному
уровню тех парней, которые не прочь завести с ней дружбу. Она считает, что
IQ ее избранника должен быть не ниже 130. В окружении Лены постоянно кру-
тятся 10 парней. Есть ли у нее шанс встретить среди них человека с IQ> 130?
Как будущий психолог, Лена должна знать, что значения IQ распределены
по нормальному закону таким образом, что среднее значение Т= 100, а стан-
дартное отклонение о= 15 (рис. 1.10).
-3-2-10 1 2 3
Рис. 1.10. Кривая нормального распределения для значений IQ (.¥=100, о= 15)
Для нахождения вероятности встретить парня с IQ> 130 необходимо опре-
делить, какую долю площади под кривой нормального распределения отсека-
ет это значение.
Данная задача решается в два этапа. Во-первых, перейдем от шкалы IQ к
Z-шкале. Для этого по уже известной формуле определим значение z для Xt= 130,
^=100 и о=15 (рис. 1.10).
22
ГЛАВА 1. ВСЕ, ЧТО ВЫ ХОТЕЛИ ЗНАТЬ О СТАТИСТИКЕ, НО БОЯЛИСЬ СПРОСИТЬ
Xt-X 130-100 оп
G 15
Во-вторых, в таблице z-распределе-
ния (Приложение 2, таблица 1) для каж-
дого значения z в диапазоне от 0 до +4
приведено значение соответствующей
площади под кривой нормального рас-
пределения, лежащей правее данного
значения z4.
Эта площадь понимается как вероят-
ность встретить в нормальном распреде-
лении результат больший или меньший
какого-либо определенного значения.
Находим из таблицы, что значению
Z=2,0 соответствует вероятностьр =0,0228. Это означает, что от площади под
кривой нормального распределения отсекается 2,28%, лежащих правее z=2,0
(рис. 1.7). Но это же означает, что вероятность встретить парня с IQ> 130 рав-
на 0,0228.
При наличии десяти парней вероятность, что хотя бы у одного из них будет
уровень интеллекта не ниже требуемого, возрастает до 0,228, что явно недо-
статочно. Лена может пойти двумя путями. Во-первых, расширить круг обще-
ния с молодыми людьми и довести его до (40-45) человек, но это может повре-
дить ее репутации. Во-вторых, снизить планку предъявляемых требований.
Если остановиться на IQ> 120, то получим z=l,33 и вероятность/>=0,0918.
В этом случае вполне возможно, что среди десятерых парней найдется один с
требуемым уровнем IQ.
ВКЛЮЧАЕМ КОМПЬЮТЕР...
Для построения гистограммы используем введенную выше переменную «Возраст»
(age). Дальнейшая последовательность действий и получаемый результат показаны
на рис. 1.11-1.13.
Полученная гистограмма несколько отличается от гистограммы, приведенной на
рис. 1.4, поскольку есть отличия в масштабе по горизонтали. Одновременно с гис-
тограммой приводятся среднее значение и стандартное отклонение для тех данных,
на основе которых она была получена.
4 В таблице приведены значения только для z>0. При работе с отрицательными значениями
Z используется тот факт, что кривая нормального распределения симметрична относительно z=0.
Этим значением площадь под кривой нормального распределения, равная 1 (или 100%), делится
на две равные части. При работе с таблицей необходимо ясное понимание того, с какой областью
кривой нормального распределения мы имеем дело: лежащей левее z, правее z или между двумя
значениями zi и z2- Существует несколько модификаций подобной таблицы. В большинстве
случаев в ней приводятся сведения для значений z от 0 до 4 или от 0 до 3.
23
КНИГА ДЛЯ ТЕХ, КТО НЕ ЛЮБИТ СТАТИСТИКУ, НО ВЫНУЖДЕН ЕЮ ПОЛЬЗОВАТЬСЯ
QNonParametr - SPSS Data Etfitor
Pda Edit View Data Transform Analyze Graphs Duties Window Help
GS|H|<S| E3| 4^1 r-l МИ Gallery Interactive > Map ► $|R|
36: gender
gender age Bar... line... Area... Pie... High-Low.., Pareto... Control...
1 1 11
2 1 8
3| 1 12
4 1 6
5 2 if
6 1 12
7 2 11 Boxplot... Error Bar... Scatter...
6 2 10
9 £ 12
10 1 15
11 2 12 P-P... N Q-Q... Sequence... ROC Curve,.. Time Senes ►
12 1 9
13 2 12
14 2 10 ( Нажать
15 2 12
Рис. 1.11. Выбор требуемой статистической процедуры
Рис. 1.12. Необходимые для построения гистограммы действия и настройки
Рис. 1.13. Гистограмма: результат
ГЛАВА 1. ВСЕ, ЧТО ВЫ ХОТЕЛИ ЗНАТЬ О СТАТИСТИКЕ, НО БОЯЛИСЬ СПРОСИТЬ
1.3. ПЕРЕДАЕТСЯ ЛИ ИНТЕЛЛЕКТ ПО НАСЛЕДСТВУ,
ИЛИ НЕМНОГО О КОРРЕЛЯЦИИ И РЕГРЕССИИ
Если у вас есть дети или вы только задумываетесь об этом, возможно, вас
уже посещала мысль о том, в кого: маму или папу — пойдет ребенок. Будет ли
он умный, как папа, и красивый, как мама, или наоборот — умный, как мама,
и красивый как... ну, допустим, Байрон?
Поскольку красота — вещь непостоянная (и субъективная), многие роди-
тели охотнее согласились бы с тем, чтобы их дети переняли от них лучшие
интеллектуальные качества. В таблице 1.5 приведены сведения о значении IQ
у родителей (усредненные данные для супружеской пары) и их детей (усред-
ненные значения) для 20 семей.
Таблица 1.5
Уровень интеллекта родителей и их детей
Семья IQ родителей IQ детей
1 90 100
2 90 90
3 90 95
4 95 90
5 95 95
6 95 100
7 100 105
8 100 90
9 100 95
10 105 105
11 * 105 110
12 105 100
13 110 115
14 115 105
15 115 100
16 115 115
17 120 ПО
18 120 125
19 125 120
20 125 НО
25
КНИГА ДЛЯ ТЕХ, КТО НЕ ЛЮБИТ СТАТИСТИКУ, НО ВЫНУЖДЕН ЕЮ ПОЛЬЗОВАТЬСЯ
Можно ли на основании приведенных данных говорить о наличии связи
между IQ родителей и IQ детей?
Поиском ответов на подобные вопросы в статистике занимается корреля-
ционный5 анализ, в рамках которого вычисляется мера связи между двумя
рядами значений — коэффициент корреляции. Существует несколько видов
коэффициентов корреляции; выбор одного из них зависит от того, с какими
данными приходится иметь дело. В том случае, если взаимосвязь устанавлива-
ется для данных, имеющих нормальный закон распределения, чаще всего ис-
пользуется коэффициент корреляции Пирсона (г Пирсона).
Независимо оттого, какой коэффициент корреляции применяется, все они
обладают общим свойством: коэффициент корреляции никогда не может быть
больше чем 1 и меньше чем—1:
—1 £ Коэффициент корреляции < 1.
Для того чтобы ответить на вопрос о существовании или отсутствии корре-
ляционной связи между какими-либо данными, необязательно прибегать к
вычислению соответствующего коэффициента (тем более что в ряде случаев
для этого используются довольно сложные формулы). Во многих случаях мож-
но ограничиться графическим представлением полученных результатов в виде
так называемой «диаграммы рассеяния».
Для ее построения рассмотрим пары значений «IQ родителей — IQ детей»
из таблицы 1.5 и для каждой пары отложим значение IQ родителей по оси X,
а значение IQ детей по оси Y. В результате получим совокупность точек опре-
деленной конфигурации: диаграмму рассеяния (рис. 1.14). Ее форма и ориен-
тация относительно осей Хи У позволяют сделать определенные выводы отно-
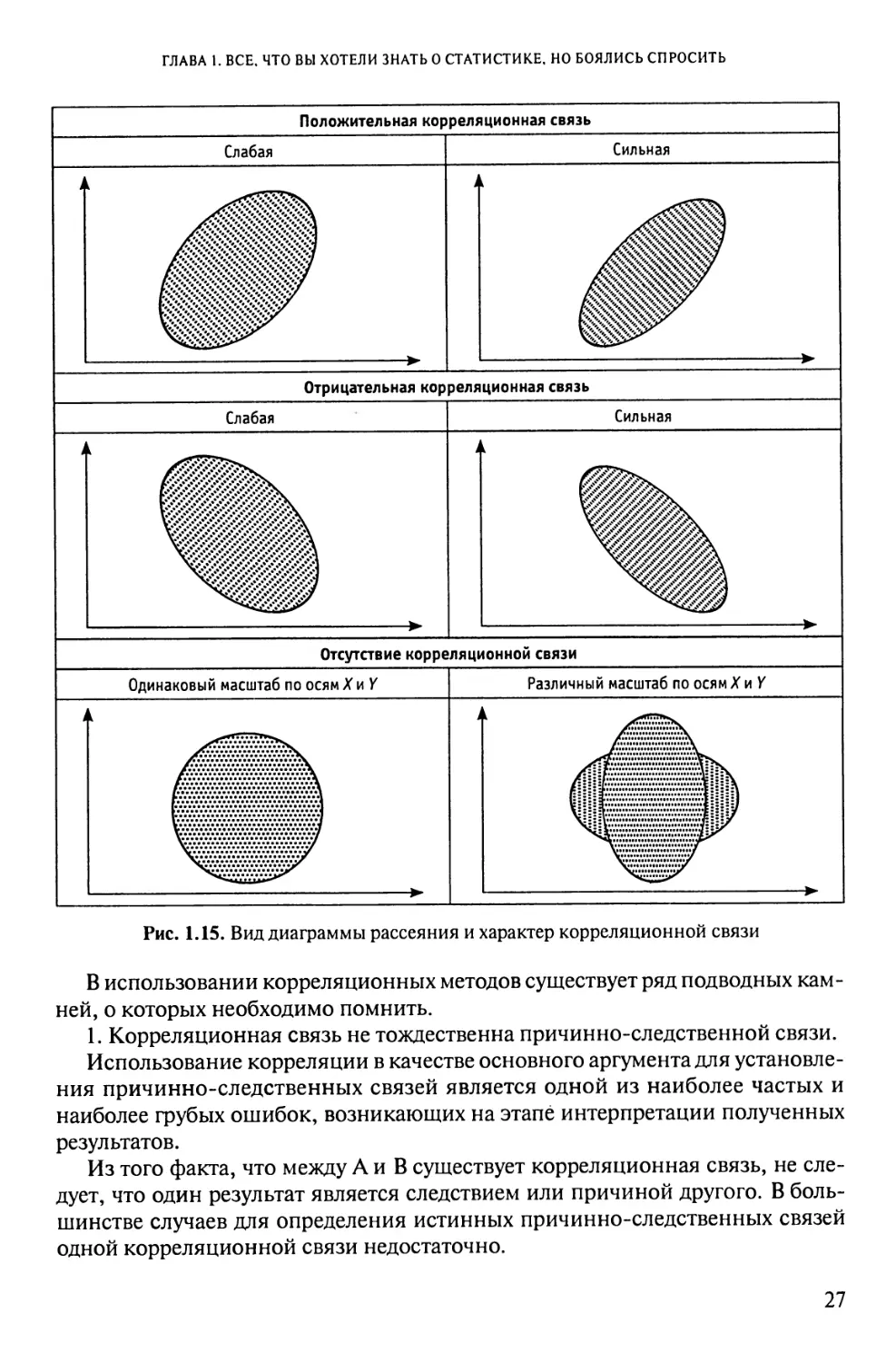
сительно характера корреляционной связи (рис. 1.15).
130 т------------------------------------------------------
о
120- о
о о
110- Q а а
а а а
100- о а а а
а а а
ф 90- а а d
2
JC
О
О 80 ________
80 90 100 110 120 130
IQ Parents
Рис. 1.14. Диаграмма рассеяния
5 От л л/и. correlatio — взаимосвязь.
26
ГЛАВА 1. ВСЕ, ЧТО ВЫ ХОТЕЛИ ЗНАТЬ О СТАТИСТИКЕ, НО БОЯЛИСЬ СПРОСИТЬ
Положительная корреляционная связь
Отрицательная корреляционная связь
Отсутствие корреляционной связи
Одинаковый масштаб по осям X и Y Различный масштаб по осям X и Y
Рис. 1.15. Вид диаграммы рассеяния и характер корреляционной связи
В использовании корреляционных методов существует ряд подводных кам-
ней, о которых необходимо помнить.
1. Корреляционная связь не тождественна причинно-следственной связи.
Использование корреляции в качестве основного аргумента для установле-
ния причинно-следственных связей является одной из наиболее частых и
наиболее грубых ошибок, возникающих на этапе интерпретации полученных
результатов.
Из того факта, что между А и В существует корреляционная связь, не сле-
дует, что один результат является следствием или причиной другого. В боль-
шинстве случаев для определения истинных причинно-следственных связей
одной корреляционной связи недостаточно.
27
КНИГА ДЛЯ ТЕХ. КТО НЕ ЛЮБИТ СТАТИСТИКУ. НО ВЫНУЖДЕН ЕЮ ПОЛЬЗОВАТЬСЯ
Существует много примеров неверных выводов, сделанных вследствие ото-
ждествления корреляции с причинностью. Например, в США в свое время
была установлена сильная положительная связь между загрязненностью тех
или иных городских районов выбросами промышленных предприятий (сажа)
и заболеваемостью туберкулезом в этих районах. На основании полученных
данных была развернута борьба с вредными выбросами, как основной причи-
ной туберкулеза. Однако давно известно, что туберкулез — это в первую очередь
социальная болезнь и она чаще встречается у представителей социально слабых
слоев населения. Поскольку загрязненность городских районов выбросами
приводила к тому, что в этих районах никто не хотел жить, то цены на жилье
здесь были очень низкими. В результате основными квартиросъемщиками в
этих районах была городская беднота, среди которой уровень заболеваемости
туберкулезом изначально был выше, чем у более благополучных жителей го-
рода [Ackoff, 1978].
2. Равенство нулю коэффициента корреляции не всегда означает отсутствие
корреляционной связи.
Во-первых, формулы, используемые для вычисления коэффициента кор-
реляции, предполагают наличие корреляционной связи, близкой к линейной.
Например, если рассмотреть взаимосвязь между ростом и весом, то увеличение
роста, как правило, сопровождается соответствующим увеличением веса и
наоборот.
В ряде случаев характер корреляционной связи не является линейным.
Поэтому перед началом вычисления коэффициента корреляции имеет смысл
получить диаграмму рассеяния и по ее виду определить, каков характер свя-
зи — линейный или нелинейный. Например, на рис. 1.16 приведена диаграмма
рассеяния, показывающая связь между числом иммигрантов, въехавших в
Израиль с 1978 г., и данными о правонарушениях в области наркотиков (упо-
требление и торговля).
28
ГЛАВА 1. ВСЕ, ЧТО ВЫ ХОТЕЛИ ЗНАТЬ О СТАТИСТИКЕ, НО БОЯЛИСЬ СПРОСИТЬ
Using and trading drugs
(Police files)
16000
14000
12000
10000
8000
6000
4000
2000
1600 1800 2000 2200 2400 2600 2800 3000
Immigration, cumulative data (thousands)
Рис. 1.16. Пример нелинейной корреляционной связи
Если связь нелинейная, механическое вычисление коэффициента корреля-
ции может ничего не дать. Нелинейная связь требует использования более
сложных методов вычисления.
Во-вторых, негомогенные (неоднородные) выборки6 зачастую могут создавать
видимость отсутствия связей. Например, в выборке, состоящей из мужчин и
женщин, может отсутствовать связь между длительностью курения (в годах) и
количеством ежедневно выкуриваемых сигарет. Но эта связь может быть обна-
ружена для мужской и женской частей выборки по отдельности (рис. 1.17).
Отсутствие корреляционной связи между
длительностью курения и количеством
выкуриваемых ежедневно сигарет
Та же ситуация отдельно
для мужской и женской частей выборки
Рис. 1.17. Диаграммы рассеяния для негомогенной выборки:
видимость отсутствия корреляции
3. Наличие отличного от нуля коэффициента корреляции не всегда означа-
ет наличие корреляционной связи.
6 Подробнее об этом понятии см. ниже.
29
КНИГА ДЛЯ ТЕХ, КТО НЕ ЛЮБИТ СТАТИСТИКУ, НО ВЫНУЖДЕН ЕЮ ПОЛЬЗОВАТЬСЯ
В негомогенных выборках могут быть обнаружены ложные корреляции.
Например, можно обнаружить связь между длительностью поиска работы и
показателем уверенности в себе — чем дольше ищется работа, тем меньше
уверенность в себе. Однако если рассмотреть отдельно мужскую и женскую
части выборки, то выявленную ранее связь можно не обнаружить (рис. 1.18):
Отрицательная корреляционная связь между
длительностью поиска работы и уверенно-
стью в себе
Та же ситуация отдельно для мужской и жен-
ской частей выборки
Рис. 1.18. Диаграммы рассеяния для негомогенной выборки:
видимость наличия корреляции
Вернемся к вопросу о связи между интеллектом родителей и интеллектом
детей. Если эта связь установлена, то можно попытаться решить другую зада-
чу — предсказать, каким может быть интеллект будущего ребенка, если извест-
но значение IQ его родителей:
Решением задач предсказания и оценивания в статистике занимается ре-
грессионный анализ. У его истоков стоял Френсис Гальтон, английский уче-
ный-энциклопедист XIX в., который считал, что антропометрические и интел-
лектуальные характеристики людей в последующем поколении возвращаются
(регрессируют) к средним для популяции показателям. Иначе говоря, если рост
родителей значительно выше среднего, то, скорее всего, рост их детей будет
также выше среднего, но ниже роста родителей. Таким образом через несколь-
ко поколений произойдет регрессия: значение роста вернется к среднему для
популяции значению. По мысли Гальтона, те же правила действуют и в отно-
шении интеллекта — у гениальных родителей рождаются дети с высоким ин-
теллектом, но его уровень ниже, чем уровень интеллекта родителей. Несмотря
на то что современные методы регрессионного анализа далеко отошли от идей
Гальтона, само название метода сохранилось.
В результате регрессионного анализа выводится формула, в которую можно
подставлять значения, например, IQ родителей и получать предполагаемые
значения IQ детей. Существуют способы минимизации ошибок подобного
оценивания и повышения его надежности и достоверности.
Для нашего примера эта формула будет иметь вид:
/едет=0,667х72род+32,188.
30
ГЛАВА I. ВСЕ, ЧТО ВЫ ХОТЕЛИ ЗНАТЬ О СТАТИСТИКЕ, НО БОЯЛИСЬ СПРОСИТЬ
Если IQ родителей, например, 115, то, подставляя это значение в формулу,
можно предсказать возможное значение IQ (будущего) ребенка:
/бдет=0.677 X115 + 32,188 « 110.
ВКЛЮЧАЕМ КОМПЬЮТЕР...
Для получения диаграммы рассеяния поместим данные о IQ родителей в переменную
«Родители» (parents), а данные о IQ ребенка — в переменную «Ребенок» (child).
Дальнейшая последовательность действий и конечный результат показаны на
рис. 1.19-1.21.
й NonParametr - SPSS Data Editor I
He Edit View Data Transform Analyze | Graphs Utilities Window He'p
^|яЩ| ej| ^|c.| ь|.с?| Gallery Interactive ► •±.|E| 4
1 Map ►
parents child W' Bar... Line... Area... Pie... High-Low... var
1 90 100
2 90 90
3 90 95
4 90 90
S 95 95 Pareto... Control...
6 95 100 i ]
7 100 105 Boxplot... Error Bar...
8 100 90
9 100 95 Scatter...
10 105 105
11 105 110 P-P... । Q-Q... I Sequence... ROC Curve...
~12 105 100
13 110 115
14 115 105
15 115 100 Time Series _ r Нажать
16 115 115
17 120 110
18 120 125
19 125 120
20 125 110
Рис. 1.19. Выбор требуемой статистической процедуры
Рис. 1.20. Необходимые для получения диаграммы рассеяния действия и настройки
31
КНИГА ДЛЯ TEX, КТО НЕ ЛЮБИТ СТАТИСТИКУ. НО ВЫНУЖДЕН ЕЮ ПОЛЬЗОВАТЬСЯ
Рис. 1.20. Окончание
130
120 -
110 .
100 .
90.
9
О 80,
80 90 100 110 120 130
PARENTS
Рис. 1.21. Диаграмма рассеяния: результат
1.4. КТО БОЛЕЕ КОМПАНЕЙСКИЙ,
ИЛИ НЕСКОЛЬКО СЛОВ
О ДИСПЕРСИОННОМ АНАЛИЗЕ
Если вы стали замечать, что среди ваших друзей-приятелей становится все
больше и больше семейных людей, то как это обстоятельство может отразить-
ся на ваших с ними контактах? Нет ли у вас ощущения, что семейные люди
становятся менее компанейскими, предпочитая большую часть своего свобод-
ного времени проводить в кругу семьи? Именно это обстоятельство стало
32
ГЛАВА 1. ВСЕ. ЧТО ВЫ ХОТЕЛИ ЗНАТЬ О СТАТИСТИКЕ. НО БОЯЛИСЬ СПРОСИТЬ
предметом повышенного внимания Марка и Стаса, двух закоренелых холостя-
ков, компания которых заметно поредела за последние годы. Для поиска отве-
та они обзвонили своих друзей и знакомых, часть из которых не была жената,
часть была, а часть, увы, уже успела развестись. Вопрос был один: сколько
часов из своего свободного времени эти люди проводят вне дома.
Ответы трех групп отпрошенных приведены в таблице 1.6.
Таблица 1.6
Семейное положение и свободное время, проводимое вне дома
№ Свободное время (в часах), проводимое вне дома
Холостые Женатые Разведенные
1 5 4 6
2 7 5 8
3 4 3 5
4 6 8 4
5 8 6 7
6 7 7 7
7 9 6 9
8 . 5 4 6
Остается сравнить между собой результаты в каждой из колонок и ответить,
значимо ли они различаются между собой.
Решением подобных задач в статистике занимается дисперсионный анализ,
обозначаемый сокращениями ANOVA и MANOVA. Эти магические слова в
состоянии ввести в транс людей, далеких от статистики, усиливая желание
держаться от нее подальше. ANOVA и MANOVA для непосвященного уха зву-
чит почти как Гога и Магога.
На самом деле за этими сокращениями (ANOVA — Analysis of Variance и
MANOVA — Multivariate Analysis of Variance) скрывается система методов,
позволяющих проверить и оценить влияние различных факторов на получен-
ные результаты.
В нашем примере есть единственный фактор (семейное положение), влия-
ние которого на интересующий нас показатель (свободное время, проводимое
вне дома) мы хотим проверить. Если говорить языком экспериментальных
исследований, существует независимая переменная, контролируемая исследо-
вателем и имеющая несколько уровней. В нашем примере независимая пере-
менная — семейное положение. Она имеет три уровня: холостой, семейный,
разведенный. Кроме этого, существует зависимая переменная (свободное вре-
мя, проводимое вне дома), находящаяся, по предположению исследователя,
под воздействием независимой.
Во многих случаях дело не ограничивается наличием единственного факто-
ра. Например, логично предположить, что на приведенные в таблице 1.6 ре-
2 Зак. 3384
33
КНИГА ДЛЯ ТЕХ, КТО НЕ ЛЮБИТ СТАТИСТИКУ, НО ВЫНУЖДЕН ЕЮ ПОЛЬЗОВАТЬСЯ
зультаты влияет не только семейное положение, но и пол участников опроса.
В этом случае таблица результатов могла бы выглядеть следующим образом
(табл. 1.7; предположим, что в каждой группе четверо мужчин и четыре жен-
щины):
Таблица 1.7
Свободное время, проводимое вне дома,
в зависимости от семейного положения и пола
Пол № Свободное время, проведенное вне дома
Холостые Женатые Разведенные
Мужчины 1 8 4 9
2 7 7 7
3 9 6 5
4 6 8 4
Женщины 1 5 6 7
2 7 5 8
3 4 3 6
4 5 4 6
Здесь возникает более сложная задача — проверить не только влияние ка-
ждого фактора (семейное положение и пол) по отдельности, но и взаимодей-
ствие этих факторов. Задача может еще более усложниться, если ввести в рас-
смотрение третий фактор. Например, проживание в крупном городе, где нет
проблем развлечься вне дома, или в небольшом населенном пункте. Кроме
этого, необязательно ограничивать себя только одной зависимой переменной.
Возможно, более интересные результаты могут быть получены, если проверить,
например, сколько денег представители каждой из выделенных групп ежеме-
сячно тратят на развлечения вне дома.
По сути дела, ANOVA — это система методов, позволяющая решать подоб-
ные задачи в случае наличия нескольких независимых переменных (факторов)
и одной зависимой. MANOVA (многомерный дисперсионный анализ) позво-
ляет делать то же самое, но для большего числа зависимых переменных.
Математический аппарат, используемый в ANOVA и MANOVA, несложен
(вычисление средних и дисперсий), но громоздок, поэтому эти методы полу-
чили свое повсеместное распространение с началом эры ЭВМ.
Вернемся к первому примеру. В очень упрощенном виде основная логика
однофакторного дисперсионного анализа выглядит следующим образом.
1. Если объединить три подгруппы (холостые, женатые, разведенные), то
для объединенной выборки (24 человека) можно вычислить среднее и диспер-
' сию (общегрупповая дисперсия).
2. Аналогичным образом вычисляется среднее и дисперсия для каждой из
подгрупп (внутригрупповая дисперсия).
34
ГЛАВА 1. ВСЕ, ЧТО ВЫ ХОТЕЛИ ЗНАТЬ О СТАТИСТИКЕ, НО БОЯЛИСЬ СПРОСИТЬ
3. Кроме этого, вычисляется дисперсия средних значений при переходе от
подгруппы к подгруппе (межгрупповая дисперсия).
В соответствии со свойствами дисперсии, общегрупповая дисперсия будет
равна сумме внутригрупповой дисперсии и межгрупповой дисперсии.
Основой для принятия решений служит сравнение внутригрупповой и меж-
групповой дисперсии.
Высокие значения внутригрупповой дисперсии (по сравнению с межгруп-
повой) означают, что внутригрупповые различия «перекрывают» межгрупповые
различия. В этом случае нельзя утверждать, что фактор оказывает существенное
влияние на полученные результаты.
Если же межгрупповая дисперсия преобладает над внутригрупповой, меж-
групповые различия «перекрывают» внутригрупповые и можно говорить о
наличии существенных различий между имеющимися подгруппами результа-
тов. Фактор оказывает существенное влияние на полученные результаты.
В случае введения еще одного фактора (например, пола участников опроса)
появляется еще одно слагаемое дисперсии, обусловленное взаимодействием
факторов (например, семейным положением и полом). В принципе, при ис-
пользовании специальных компьютерных программ для ANOVA и MANOVA
количество вовлеченных в дисперсионный анализ факторов и зависимых пе-
ременных может быть довольно большим. Но уже при наличии трех факторов
(семейное положение, пол, местожительства) основные сложности возникают
при интерпретации результатов дисперсионного анализа.
ВКЛЮЧАЕМ КОМПЬЮТЕР...
Создадим две переменные: «семейный статус» (status) и «свободное время, прово-
димое вне дома» (time). Для первой переменной используем следующие обозначения:
1 — Одиночка; 2 — Женат/Замужем; 3 — Разведен/Разведена. На рис. 1.22—1.24
показаны последовательность действий для решения задачи однофакгорного дис-
персионного анализа (One-Way ANOVA) и полученный результат.
NonPar metr SPSS Data Editor
File Edit View Data Transform Analyze Graphs Utilities Window Help
Reports
Descriptive Statistics
Compare Means
General Linear Model
Mixed Models
Correlate
Regression
Loglinear
Classify
Data Reduction
Scale
Nonparametrlc Tests
Time Series
Survival
Multiple Response
Missing Value Analysis...
Means...
Рис. 1.22. Выбор требуемой статистической процедуры
35
КНИГА ДЛЯ ТЕХ, КТО НЕЛЮБИТ СТАТИСТИКУ, НО ВЫНУЖДЕН ЕЮ ПОЛЬЗОВАТЬСЯ
Рис. 1.23. Необходимые для однофакторного дисперсионного анализа действия
и настройки7
тот
Рис. 1.24. Результат однофакторного дисперсионного анализа
Показатель межгруп-
повои изменчивости
Среднее этих
показателей:
6,083/2-3,042
6.083
57.750
57,750/21-2,750
Проверяемое значение
F-3,042/2,750-1,106
TIME
Between Groups
Within Groups
Total
Показатель внутри-
групповой изменчи-
вости
2
21
23
2.750
Итоговый (общегруппо-
вой) показатель
6,083+57,750-63,833
Результат проверки, говорящий
о том, что фактор семейного положе-
ния не оказывает значимого влияния
на свободное время, проводимое вне
дома
7 Программа SPSS предоставляет большое число возможностей для дисперсионного анализа,
рассматривать которые у нас нет возможности.
ГЛАВА 1. ВСЕ. ЧТО ВЫ ХОТЕЛИ ЗНАТЬ О СТАТИСТИКЕ. НО БОЯЛИСЬ СПРОСИТЬ
1.5. ЧТО СКАЗАЛ ГОСПОДЬ МОИСЕЮ
В СИНАЙСКОЙ ПУСТЫНЕ, ИЛИ КОЕ-ЧТО
О ВЫБОРКАХ И ПОПУЛЯЦИЯХ
603 550 человек — именно столько сынов Израилевых старше 12 лет насчи-
тал Моисей по указанию Господа в Синайской пустыне. Но только 12 из них,
по одному от каждого колена Израилева, пригласил он в свой шатер...
Вряд ли Моисей или помогающий ему считать Аарон думали в те времена о
статистике, но то, что они сделали, вполне соответствует современным стати-
стическим представлениям о популяции и выборке.
Популяция — эта общая совокупность людей, которые теоретически могут
быть исследованы, опрошены, проверены и др. Поскольку в большинстве
случаев осуществить это невозможно, реальное исследование проводится на
незначительной части популяции — выборке.
Главное требование, предъявляемое к выборке, — ее представительность
(репрезентативность). Поскольку выборка является частью популяции, репре-
зентативность предполагает, что на основании изучения выборки можно со-
ставить представление о популяции в целом.
Важное правило, реализация которого позволяет выборке считаться репре-
зентативной, это правило случайного отбора: каждый член популяции имеет
равные с другими шансы войти в выборку* 8.
Если популяция неоднородна, например, по полу, социальному статусу,
образованию и др., то эта неоднородность должна быть пропорционально от-
ражена в выборке. Так, например, если среди молодых людей в возрасте от 17
до 22 лет только 30% учатся в вузах, то будет неправильным формирование
выборки, состоящей исключительно из студентов.
Если вернуться к результатам «переписи» сынов Израилевых, проведенной
Моисеем и Аароном, то, например, сынов колена Иуды было 74600 человек, а
сынов колена Манассии 32 200. Но в «выборку» вошло по одному человеку как
от колена Иуды, так и от колена Манассии.
Невозможность достоверно знать характеристики популяции порождает
одну из центральных задач математической статистики — задачу проверки
статистических гипотез. Смысл ее в принятии наиболее обоснованного сужде-
ния относительно свойств и характеристик популяции с опорой на результаты
изучения выборки.
8 К.сожалению, по ряду причин это правило не всегда выполняется. Например, если психолог
изучает мотивы суицидального поведения подростков, то популяция здесь — все подростки,
совершившие попытку самоубийства. Очевидно, у них нет равных шансов войти в выборку.
В выборку могут войти только те из них, кого удалось спасти. Отклонение от правила случайно-
го отбора при формировании выборки порождает при проведении исследований ряд проблем,
обсуждение которых выходит за рамки данной книги.
37
КНИГА ДЛЯ ТЕХ, КТО НЕ ЛЮБИТ СТАТИСТИКУ, НО ВЫНУЖДЕН ЕЮ ПОЛЬЗОВАТЬСЯ
В статистике существует детально разработанная методология проверки
статистических гипотез, основные положения которой мы рассмотрим ниже.
1.6. ПОЛНЕЮТ ЛИ ОТ СЧАСТЬЯ,
ИЛИ О ЗАВИСИМЫХ И НЕЗАВИСИМЫХ ВЫБОРКАХ
Ученые и специалисты по борьбе с лишним весом в течение многих лет
пытаются понять, какие факторы влияют на развитие склонности к излишне-
му весу и ожирению. Группа американских ученых, работающая в этой облас-
ти, на протяжении пяти лет наблюдала почти за 8000 молодых людей в возрас-
те от 12 до 28 лет, среди которых были 1200 семейных пар (краткое описание
исследования см. USA Today, 22.10.2007).
Изучение того, как семейная жизнь влияет на вес супругов (исключая си-
туацию с беременностью), шло по нескольким направлениям. Во-первых,
проверялось, что происходит с весом одного из супругов после свадьбы. Во-
вторых, проверялось изменение веса в супружеских парах. В-третьих, вес се-
мейных людей сравнивался с весом их холостых сверстников.
В первом случае значение веса регулярно измерялось у представителей одной
и той же выборки с интервалом в несколько месяцев. Во втором случае выбор-
ка была образована из супружеских пар, в которых соблюдалось взаимное
соответствие измеряемых показателей: вес мужа сравнивался с весом его соб-
ственной жены, а не с весом жены друга. В третьем случае имелись две авто-
номные выборки (холостые — женатые), относительно которых не выдвигалось
требования взаимного соответствия измеряемых показателей.
Описанные три случая показывают различия между так называемыми зави-
симыми и независимыми выборками.
Выборки будет называться зависимыми, если есть возможность каждому
значению из одной выборки поставить в соответствие единственное значение
из другой выборки. Например, росту или весу мужа поставить в соответствие
рост или вес жены, интеллекту одного из близнецов поставить в соответствие
интеллект другого из близнецов и т. д.9
Очень часто зависимые выборки образуются тогда, когда измерения каких-
либо показателей в выборке происходят по принципу «до и после» — вес до
свадьбы и после, самооценка до групповой психотерапии и после, артериальное
давление до сеанса аутогенной тренировки и после и т. д.
В том случае, когда условие взаимного соответствия значений между пред-
ставителями одной и другой выборок не выполняется, выборки называются
’ Первый пример подобной «выборки» описан в Торе («Ветхом Завете»). «Население» Ноева
ковчега было образовано именно по такому принципу: от всех живых существ было взято по паре
мужского и женского полов.
38
ГЛАВА 1. ВСЕ, ЧТО ВЫ ХОТЕЛИ ЗНАТЬ О СТАТИСТИКЕ. НО БОЯЛИСЬ СПРОСИТЬ
независимыми. Например, формируется выборка курящих мужчин и выборка
курящих женщин с целью проверки, кто больше за день выкуривает сигарет.
Во-первых, эти выборки могут не совпадать по размерам (например, 70 мужчин
и 50 женщин). Во-вторых, между одной и другой выборкой невозможно уста-
новить взаимное соответствие значений.
Понятие зависимых и независимых выборок играет важную роль при про-
верке статистических гипотез. Выбор того или иного способа проверки зависит
оттого, с какими выборками — зависимыми или независимыми — приходится
иметь дело. Например, если мы сравниваем количество сигарет, выкуриваемых
ежедневно мужчинами и женщинами, то можно использовать /-тест Стьюдента10
для независимых выборок. Но если в исследовании принимали участие только
курящие семейные пары и сравнивалось количество сигарет, выкуриваемых
ежедневно мужем и женой, то здесь необходимо использовать тест Стьюдента
для зависимых выборок.
1.7. ПОКУПКА ОБУВИ КАК ТОЧНАЯ НАУКА,
ИЛИ О НУЛЕВОЙ И АЛЬТЕРНАТИВНОЙ ГИПОТЕЗАХ
Покупку обуви по своей значимости можно, пожалуй, сравнить только с
женитьбой. Мучения от неверно подобранной обуви способны отравить жизнь
самому отъявленному оптимисту.
Одна из проблем, возникающих при покупке обуви, обычно связана с тем,
что на одной ноге обувь сидит как влитая — нигде не жмет и не давит, а вот со
второй ногой вечные проблемы: башмак то мал, то с ноги слетает. Не остает-
ся ничего другого, как примерять одну пару за другой в надежде найти подхо-
дящую.
Посмотрим на эту ситуацию с точки зрения математической статистики.
Тот факт, что для одной ноги (например, правой) проблем при примерке не
возникает, но левая нога вечно создает проблемы, позволяет выдвинуть, как
минимум, два предположения, или, как говорят в статистике, две статистиче-
ские гипотезы, по поводу происходящего.
В соответствии с первой гипотезой, можно предположить, что трудности с
подбором обуви носят случайный характер. Достаточно примерить еще не-
сколько пар, и обязательно будет найдена та, которая устраивает.
Вторая гипотеза утверждает обратное: вся партия примеряемой обуви бра-
кована, и продолжение примерок не имеет смысла.
Первая гипотеза получила название нулевой гипотезы (Яо). Ее особенность
в том, что независимо от того, какими фактами мы располагаем, она всегда
10 Псевдоним английского статистика Вильяма Госсета (1876—1937).
39
КНИГА ДЛЯ ТЕХ, КТО НЕ ЛЮБИТ СТАТИСТИКУ, НО ВЫНУЖДЕН ЕЮ ПОЛЬЗОВАТЬСЯ
будет утверждать случайный характер всех имеющихся результатов, отличий,
связей и т. п. Даже если мы станем сравнивать число мужчин и женщин в жен-
ском монастыре, нулевая гипотеза все равно будет настаивать на том, что здесь
существует полное равенство, а то, что мы видим своими глазами, — не более
чем дело случая.
Иначе говоря, все результаты, полученные при изучении выборки, в рамках
нулевой гипотезы объявляются случайными и не имеющими никакого отно-
шения к популяции.
Вторая гипотеза получила название альтернативной гипотезы (Н\). Если
нулевая гипотеза утверждает случайный характер всех имеющихся результатов,
то альтернативная гипотеза, как следует из ее названия, утверждает диамет-
рально противоположное: все имеющиеся в наших руках результаты носят
неслучайный характер и отражают свойства популяции.
Основанием для выдвижения нулевой гипотезы служит простое обстоятель-
ство: для того чтобы утверждать о неслучайном характере каких-либо резуль-
татов, необходимо обладать всей полнотой информации на уровне популяции
в целом. В подавляющем большинстве случае этого не происходит. Следовательно,
те результаты, которые мы имеем, вполне могут быть делом случая.
Например, популяция — это все израильские подростки, которые курят.
А выборка — это всего лишь 35 человек из них, вошедших в табл. 1.1. Поэтому
если из таблицы следует, что мальчики начинают курить раньше девочек, то
всегда есть сомнения: данный вывод справедлив для всех подростков (для всей
популяции) или только для 35 человек? Нулевая гипотеза будет утверждать, что
для всей популяции этот вывод несправедлив. Альтернативная гипотеза будет
говорить обратное: несмотря на то что данные получены только для 35 человек,
они справедливы на уровне всей популяции.
Аналогичная ситуация с обувью. «Популяция» здесь — это вся обувь из той
злополучной партии, которая, как мы предполагаем, бракованная. А выборка —
это то реальное количество пар обуви, которое мы примерили.
С точки зрения нулевой гипотезы те несколько пар обуви, которые мы при-
мерили (выборка) и которые нам не подошли, — еще не аргумент объявлять
всю партию (популяция) бракованной.
40
ГЛАВА 1. ВСЕ, ЧТО ВЫ ХОТЕЛИ ЗНАТЬ О СТАТИСТИКЕ. НО БОЯЛИСЬ СПРОСИТЬ
1.8. ЛЮБИТ - НЕ ЛЮБИТ, ПРИДЕТ - НЕ ПРИДЕТ,
ИЛИ ОБ ОШИБКАХ ПЕРВОГО И ВТОРОГО РОДОВ
Многим молодым людям, пришедшим на свидание с девушкой, знакома
ситуация тревожного ожидания. Уже прошло десять минут, пятнадцать, два-
дцать, а ее все нет и нет. В те далекие времена, когда люди обходились без
мобильных телефонов, оставалось одно: ждать и верить в чудо. Один из моих
друзей в свое время ждал свою девушку на морозе пять часов, не в силах пове-
рить, что она не придет.
На принятие решения «ждать дальше или уйти» в первую очередь влияют
наши предположения о причинах опоздания. Если мы твердо уверены, что
опоздание носит случайный характер и девушка обязательно придет, то мы
готовы ждать хоть всю ночь. Но если мы считаем, что опоздание неслучайно и
это признак разрыва отношений, то и пяти минут ждать не будем.
Застрахованы ли мы от ошибок в принятии решения? Конечно нет. Ведь
наше решение опирается только на наши предположения о причинах опозда-
ния. Мы ничего не знаем о том, что произошло на самом деле. Можно продол-
жать ждать, когда девушка приняла решение не приходить, а можно уйти за
минуту до ее прихода.
Если от свиданий пойти дальше, то можно сказать, что все события, которые
происходят с нами или вокруг нас, носят либо случайный, либо неслучайный
характер. Если утром ваш автобус не пришел вовремя, то это может быть делом
случая. Но если вовремя не пришел следующий автобус, а за ним еще один,
имеет смысл поинтересоваться, нет ли сегодня забастовки на общественном
транспорте.
Кроме событий, которые происходят, есть наша интерпретация этих собы-
тий. Возможно, кто-либо склонен многое из происходящего в его собственной
жизни считать не более чем делом случая. А другой не верит в случайность и
считает, что все в жизни предопределено и у всего есть свои причины.
Если совместить то, каким на самом деле было какое-либо событие — слу-
чайным или неслучайным, и то, что мы думаем по поводу данного события,
можно получить следующую таблицу (табл. 1.8).
Из таблицы видно, что возможны четыре варианта развития событий, из
которых два являются ошибочными.
В статистике ошибку, допускаемую в случае объявления случайного события
неслучайным, называют ошибкой первого рода.
Ошибку, допускаемую в случае объявления неслучайного события случай-
ным, называют ошибкой второго рода.
Ошибки первого и второго родов отличаются друг от друга не только по
смыслу, но и по «цене» своих последствий. В подавляющем числе случаев «цена»
ошибки первого рода намного тяжелее «цены» ошибки второго рода.
41
КНИГАДЛЯ ТЕХ, КТО НЕ ЛЮБИТ СТАТИСТИКУ, НО ВЫНУЖДЕН ЕЮ ПОЛЬЗОВАТЬСЯ
Таблица 1.8
События и наши предположения о них
Событие: Девушка опаздывает на свидание. Истинная причина события
Случайная Неслучайная
Интерпрета- ция события. Ее опоздание Неслучай- ное Интерпретация не совпадает с реальностью. Случайное событие истолковано как не- случайное. Принимается оши- бочное решение «уйти» ' (Ошибка первого рода) Интерпретация совпадает с реальностью. Принимается правильное решение «уйти»
Случайное Интерпретация совпадает с реальностью. Принимается правильное решение «ждать» Интерпретация не совпадает с реальностью. Неслучайное событие истолковано как слу- чайное. Принимается оши- бочное решение «ждать» (Ошибка второго рода)
Например, у педагогов есть сомнения в отношении уровня интеллектуаль-
ного развития одного из учеников, и решается вопрос о переводе его в специа-
лизированную школу. С тестовым заданием, которое должно было определить
его судьбу, ученик справился плохо.
Ошибка первого рода будет заключаться в том, что плохие результаты тес-
тового задания, вызванные случайными причинами (ученик был рассеян, ему
было неинтересно, он плохо выспался и др.), объявят неслучайными и нор-
мального ребенка переведут в специализированную школу.
Ошибка второго рода будет заключаться в том, что неслучайные низкие
показатели по тесту объявят случайными (дескать, ученик был рассеян, ему
было неинтересно, он плохо выспался и др.) и все оставят без изменений.
«Цена» ошибки первого рода — ярлык интеллектуальной неполноценности,
который будет «наклеен» на здорового ребенка со всеми вытекающими послед-
ствиями, возможно, на всю оставшуюся жизнь.
«Цена» ошибки второго рода — ребенок, нуждающийся в особом подходе,
будет признан нормальным и продолжит учебу в обычной школе.
Возможные последствия ошибок первого рода приводят к тому, что основные
усилия направляются на то, чтобы такие ошибки случались как можно реже.
К сожалению, полностью от них избавиться не удается и приходится признавать
право таких ошибок на существование в виде крайне редких случаев.
В статистике такие ошибки считаются допустимыми, если они имеют место
не чаще чем в одном случае из 1000, одном случае из 100 или в пяти случаях из
100. В этом случае говорят о том, что вероятность ошибки первого родар < 0,001
(то есть не более чем одна ошибка на 1000 случаев), р < 0,01 (то есть не более
чем одна ошибка на 100 случаев) и р < 0,05 (то есть не более чем 5 ошибок на
100 случаев).
42
ГЛАВА 1. ВСЕ, ЧТО ВЫ ХОТЕЛИ ЗНАТЬ О СТАТИСТИКЕ. НО БОЯЛИСЬ СПРОСИТЬ
Часто, когда говорят об ошибках первого рода, используют понятие «уро-
вень значимости» (обозначается как а). Численные значения аир совпадают
друг с другом. Уровень значимости можно понимать как некую «красную
линию», пересечение которой позволит говорить о данном событии как о
неслучайном.
Теоретически с каждым событием можно связать вероятность его случай-
ного наступления. Например, вероятность того, что автобус городского мар-
шрута опоздает, довольно велика. Поэтому, если автобус опаздывает, никто не
бьет тревогу по этому поводу, понимая, что есть масса причин (пробки на до-
рогах, много пассажиров на остановках и др.), по которым он может опоздать.
В то же время есть события, вероятность случайного наступления которых очень
низка. Теоретически таких событий не должно быть вообще (например, кру-
шений самолетов). Если такое событие, увы, случается, то первое, что прове-
ряется, — наличие неслучайных факторов (теракт, ошибка пилотов, ошибка
диспетчеров и др.). Поэтому, если событие, вероятность случайного наступле-
ния которого ничтожно мала, все же произошло, всегда есть основания утвер-
ждать, что это было неслучайно.
Уровень значимости а задает то малое значение вероятности, с которым
связано случайное наступление подобных событий. Для а=0,05 это означает,
что определенное событие случайным образом может иметь место в 5 случаях
из 100. Например, из 100 косметических операций по «омоложению» 5 могут
оказаться неудачными вследствие действия случайных факторов. Если подоб-
ная операция завершилась неудачно и клиент настаивает на том, что это было
неслучайно, а была допущена врачебная ошибка, то в 95 случаях из 100 он бу-
дет прав. Но в 5 случаях из 100 его претензии будут отвергнуты. Таким образом,
значение а определяет вероятность ошибки при объявлении случайного собы-
тия неслучайным. Если произошло событие, для которого уровень значимости
а=0,05, то, объявляя данное событие неслучайным, мы ошибемся в 5 случаях
их 100 (ошибка первого рода).
Возникающая здесь проблема связана с тем, где должна пролегать граница
между нашим отношением к событию как к случайному или неслучайному.
Однозначного ответа на данный вопрос нет. Решение в каждом конкретном
случае принимает исследователь.
Если в примере с учеником, которого предполагают перевести в специали-
зированную школу, использовать тесты, обеспечивающие принятие правиль-
ных решений на уровне значимости а=0,05, то это означает, что в пяти случа-
ях из ста может быть принято неправильное решение. Видимо, в этом случае
а=0,05 является неприемлемым уровнем значимости, поскольку риск приня-
тия ошибочного решения довольно велик (в пяти случаях из ста нормальный
ребенок может быть отправлен в школу для умственно отсталых).
Но если предположить, что в школе работают специалисты, которые тести-
руют учеников и на основе результатов тестирования дают рекомендации ро-
дителям и учителям по поводу профессиональных склонностей детей, то уровень
значимости а=0,05 можно признать вполне допустимым. Даже если кому-либо
43
КНИГА ДЛЯ ТЕХ, КТО НЕ ЛЮБИТ СТАТИСТИКУ, НО ВЫНУЖДЕН ЕЮ ПОЛЬЗОВАТЬСЯ
ошибочно порекомендуют вместо математики изучать химию, то особой тра-
гедии от этой ошибки не будет. В конце концов, это не более чем рекомендация,
с которой можно не согласиться.
Если в каком-либо научном отчете или публикации сделанные выводы
сопровождаются указанием значенийр или а, то чем меньше эти значения, тем
больше доверия к представленным результатам.
1.9. МОЖНО ЛИ ОДНОВРЕМЕННО
СИДЕТЬ НА ДВУХ СТУЛЬЯХ, ИЛИ ВСЕ О ПРОВЕРКЕ
СТАТИСТИЧЕСКИХ ГИПОТЕЗ
Вернемся к нулевой и альтернативной гипотезам. Поскольку они не могут
существовать одновременно (одно и то же событие не может быть одновремен-
но случайным и неслучайным), то после их выдвижения начинается увлека-
тельный и не лишенный риска процесс их проверки. Цель проверки — найти
аргументы в пользу только одной из них, что автоматически определит судьбу
другой.
Творчество начинается уже на этапе формулирования гипотез. Их неудачная
формулировка в состоянии либо свести на нет усилия по их проверке, либо
привести к неверным выводам по итогам этой проверки.
Вообще в статистике принято проверять только нулевую гипотезу. По ре-
зультатам проверки она либо принимается, либо отвергается. В том случае,
если нулевая гипотеза отвергается, на ее место приходит альтернативная гипо-
теза. Но при ближайшем рассмотрении все оказывается не так просто.
Допустим, два сторонника здорового образа жизни, увлекающиеся стати-
стикой, затеяли спор по поводу того, эффективны ли диеты. Один из них
утверждает, что диеты неэффективны и не влияют на вес (нулевая гипотеза),
другой — что диеты в состоянии эффективно влиять на вес (альтернативная
гипотеза).
После статистической проверки оказалось, что нет оснований принять ну-
левую гипотезу. Она отвергается и принимается альтернативная: диеты в со-
стоянии эффективно влиять на вес. Казалось бы, сторонники диет могут тор-
жествовать. Но на самом деле полученный результат всего лишь означает
влияние диет на вес, которое может быть двояким. С одинаковой вероятностью
диета может привести как к снижению, так и к увеличению веса. Вряд ли сто-
ронники диет хотели получить такой результат.
Как видно, альтернативная гипотеза, не соответствующая характеру решае-
мой задачи, может привести к ошибочным выводам (диеты снижают вес) из
статистически корректных результатов.
44
ГЛАВА I. ВСЕ, ЧТО ВЫ ХОТЕЛИ ЗНАТЬ О СТАТИСТИКЕ. НО БОЯЛИСЬ СПРОСИТЬ
Если еще раз вернуться к злополучному покупателю обуви, то нулевую ги-
потезу можно сформулировать следующим образом:
Hq.X=Y(обувь на правую ногу Xравна обуви на левую ногу У).
По отношению к данной нулевой гипотезе можно сформулировать три
альтернативные гипотезы:
Н\а: X > Y (обувь на правую ногу больше обуви на левую ногу).
Н{Ь'. X<Y (обувь на правую ногу меньше обуви на левую ногу).
Я1С: X*Y(обувь на правую ногу не равна обуви на левую ногу).
В результате мы получим три отличающиеся друг от друга пары гипотез,
результаты проверки которых могут не совпасть друг с другом. Например, по
результатам проверки для Яо и НХа мы можем получить основания для отказа
от нулевой гипотезы, но по результатам проверки Но и Hic этих оснований
может не быть.
Что касается риска при проверке гипотез, то он присутствует всегда и связан
с тем, что принимать решения приходится в условиях неопределенности. У нас
нет возможности примерить всю обувь из вызывающей подозрение партии или
опросить всех подростков по поводу возраста начала курения. Мы уже говори-
ли о том, что решение относительно популяции приходится принимать на
основе изучения ее незначительной части (выборка). Здесь неизбежны риски
и ошибки, а сам процесс проверки статистических гипотез становится процес-
сом вероятностным, поскольку все решения приходится принимать с опреде-
ленной долей вероятности.
В статистике решение о том, отвергнуть нулевую гипотезу или нет, всегда
сопровождается указанием меры риска, роль которой И1рает значение вероят-
ности возможной ошибки.
Таблица 1.9 поможет понять, какие ошибки возможны при проверке гипотез.
Таблица 1.9
Возможные ошибки при проверке статистических гипотез
На самом деле
HQ верна Нх верна
Принятое решение HG неверна (при- нимается Отклоняется верная нулевая гипотеза, и принимается не- верная альтернативная гипо- теза (ошибка первого рода) Принимается верная альтернативная гипоте- за
Нх неверна (при- нимается Яо) Принимается верная нуле- вая гипотеза Отклоняется верная альтернативная гипоте- за, и принимается не- верная нулевая гипотеза (ошибка второго рода)
Мы вновь вернулись к тому, о чем говорили раньше. Поскольку нулевая
гипотеза говорит о случайном характере проверяемых результатов, то отвергнуть
45
КНИГА ДЛЯ ТЕХ, КТО НЕ ЛЮБИТ СТАТИСТИКУ, НО ВЫНУЖДЕН ЕЮ ПОЛЬЗОВАТЬСЯ
верную нулевую гипотезу и принять неверную альтернативную гипотезу озна-
чает ошибочно объявить случайное событие неслучайным. Такую ошибку мы
выше называли ошибкой первого рода.
Отклонение верной альтернативной гипотезы (она говорит о неслучайном
характере наших результатов) и принятие неверной нулевой гипотезы означа-
ет ошибочно объявить неслучайное событие случайным. Такая ошибка была
выше названа ошибкой второго рода.
Вероятность ошибки первого рода (вероятность отклонить верную нуле-
вую гипотезу) была названа уровнем значимости (а). Именно значение уров-
ня значимости определяет меру риска при проверке гипотез. Поскольку це-
на ошибки первого рода, как правило, значительно выше цены ошибки
второгорода (принятие неверной нулевой гипотезы), то значение уровня
значимости стремятся выбирать как можно меньшим (обычно от а= 0,001 до
а=0,05).
Вероятность ошибки второго рода обычно обозначается как р. Между а
(вероятность ошибки первого рода, или уровень значимости) и р (вероятность
ошибки второго рода) существуют сложные взаимоотношения. К сожалению,
стремление уменьшить значение а приводит к росту значения р. Это еще раз
подтверждает мысль о том, что при проверке статистических гипотез всегда
есть риск принятия неверного решения. Если исследователь бросает все силы
на устранение ошибок первого рода, возрастает риск ошибок второго рода
(неслучайные события будут объявляться случайными). Например, стремление
уменьшить число ошибочных направлений нормальных детей в школу для
умственно отсталых может обернуться возрастанием числа случаев, когда дети,
нуждающиеся в такой школе, будут продолжать обучение в школе для нормаль-
ных детей.
46
ГЛАВА 1. ВСЕ, ЧТО ВЫ ХОТЕЛИ ЗНАТЬ О СТАТИСТИКЕ, НО БОЯЛИСЬ СПРОСИТЬ
1.10. МОЛОДЕЖЬ И НАРКОТИКИ,
ИЛИ КАК ПРОВЕРЯЮТ СТАТИСТИЧЕСКИЕ ГИПОТЕЗЫ
Итак, для проверки статистических гипотез нам необходимо:
1. Сформулировать нулевую и альтернативную гипотезу.
2. Выбрать значение уровня значимости а.
3. Выбрать тот способ проверки, который будет использоваться.
Чтобы понять, что происходит дальше, рассмотрим пример.
Мы уже имели дело с нормальным распределением, полученным на основе
исследования «Молодежь и наркотики». Для этого распределения среднее
возраста равно 16,5 лет, стандартное отклонение — 1,5 года.
Предположим, что для проверки ситуации с употреблением наркотиков
среди девушек из участников исследования случайным образом была сформи-
рована выборка объемом в 100 девушек. После проверки оказалось, что их
средний возраст — 16,0 лет. Можно ли утверждать, что среднее значение воз-
раста принявших участие в исследовании девушек (16,0 лет), меньше обще-
группового показателя (16,5 лет)?
Сформулируем нулевую и альтернативную гипотезы: .
Но: Средний возраст девушек, принимавших участие в исследовании, не
отличается от среднего возраста для всей совокупности испытуемых.
Я(: Средний возраст девушек, принимавших участие в исследовании, мень-
ше среднего возраста для всей совокупности испытуемых.
Выберем уровень значимости а=0,05.
Приступим к проверке.
Предположим, что верна нулевая гипотеза и на самом деле средний возраст
девушек не отличается от значения 16,5 лет.
Данное предположение означает:
Если из участников исследования раз за разом случайным образом форми-
ровать состоящую из девушек выборку численностью 100 человек и раз за разом
определять среднее значение их возраста, то получаемые каждый раз значения
будут отличаться друг от друга (например, в одном случае среднее значение
возраста будет равно 16,0 лет, вдругом — 15,9 лет, в третьем — 16,3 летит, д.).
В математической статистике доказывается, что:
□ после многократного повторения этой процедуры все средние будут иметь
нормальный закон распределения;
□ среднее всех средних будет равно общегрупповому значению (то есть
16,5 лет); '
□ стандартное отклонение для этого среднего будет равно о/>/Я , где о —
стандартное отклонение для всех результатов (в нашем случае и= 1,5),
N — объем извлекаемой выборки (у нас N= 100).
47
КНИГА ДЛЯ ТЕХ. КТО НЕ ЛЮБИТ СТАТИСТИКУ, НО ВЫНУЖДЕН ЕЮ ПОЛЬЗОВАТЬСЯ
Для нового нормального распределения с У= 16,5 и о=-1’^- = 0,15 опреде-
лим значение z для ^=16,0: чУЮ
Xt-X 16,0-16,5
с 0,15
По таблице 1 (Приложение 2) найдем вероятность того, что z сможет принять
значение z < —3,33 (или, что то же самое, площадь, отсекаемую от площади под
кривой нормального распределения левее значения z=—3,33)* *: р =0,0005.
Вернемся к нулевой гипотезе, которую мы проверяли. Мы предположили,
что значение среднего возраста (16,0 лет), которое было получено для девушек,
носит случайный характер и на самом деле их средний возраст не отличается
от значения 16,5 лет. Однако вероятность случайного получения такого резуль-
тата ничтожно мала (р=0,0005).
Поскольку столь маловероятное событие все же произошло, есть все осно-
вания посчитать его неслучайным и тем самым отвергнуть нулевую гипотезу.
Если мы это сделаем и примем альтернативную гипотезу, говорящую о неслу-
чайном характере полученного результата, то такое решение будет ошибочным
в 5 случаях из 10 000 (р=0,0005). Это гораздо меньше того числа ошибок, кото-
рые мы были готовы себе позволить (а=0,05, или 5 случаев из 100). Мы имеем
полное право отвергнуть нулевую гипотезу и принять альтернативную.
Рассмотрим иную ситуацию.
Исследователь, воодушевленный полученным выше результатом, решил
облегчить себе жизнь и для очередного изучения ситуации среди девушек
сформировал выборку в 20 человек. Для этой выборки он вновь получил сред-
нее значение возраста 16 лет. Может ли он сейчас сделать тот же самый вывод
о том, что средний возраст девушек, принимавших участие в исследовании,
меньше среднего возраста для всей совокупности испытуемых?
Повторим прежнюю последовательность действий и вычислим значение z
для N=20 (помним, что о=-==4^ = 0,33):
\[N л/20
^-^16,0-16,5 152
Z а 0,33
Из таблицы 1 (Приложение 2) найдем вероятность, соответствующую по-
лученному значению z: р =0,0643.
Если мы вновь отвергнем нулевую гипотезу, то это решение будет ошибоч-
ным в более чем шести случаях из ста. Но максимальное число ошибок, кото-
рые мы можем себе позволить, это 5 случаев из 100. Следовательно, у нас нет
оснований отвергнуть нулевую гипотезу. Мы должны признать, что в данном
11 На самом деле из таблицы мы находим площадь, лежащую правее значения z=3,33, но,
поскольку кривая нормального распределения симметрична, это то же самое, что найти площадь
левее г =—3,33.
48
ГЛАВА 1. ВСЕ. ЧТО ВЫ ХОТЕЛИ ЗНАТЬ О СТАТИСТИКЕ. НО БОЯЛИСЬ СПРОСИТЬ
случае средний возраст принимавших уча-
стие в исследовании девушек не отличается
от значения среднего возраста для всей со-
вокупности испытуемых.
Из приведенных примеров следует один
очень важный вывод: результат проверки
статистических гипотез в значительной сте-
пени зависит от размера выборки. Если ис-
следователь изучает какую-либо ситуацию,
то чем с большей по размеру выборкой он
будет иметь дело, тем более достоверные ре-
зультаты получит12.
Как правило, проверка статистических гипотез связана с четким алгоритмом
действий.
Вначале, в зависимости от характера решаемой задачи (что конкретно мы
проверяем или сравниваем — средние значения, дисперсии, корреляции и др.),
определяется способ проверки, формулируются нулевая и альтернативная
гипотезы и выбирается значение уровня значимости а.
Затем, на основе имеющихся данных, вычисляется определенное эмпири-
ческое значение Аэьтир (процедура вычисления Кзмпкр определяется характером
решаемой задачи и выбранным способом проверки).
Дальнейшие действия могут идти двумя путями.
Первый путь связан с определением вероятности р получения эмпириче-
ского значения ЛГэмпир. Если эта вероятность окажется меньше или равна вы-
бранному значению уровня значимости а, нулевая гипотеза отвергается и
принимается альтернативная. Если вероятность;? оказывается больше выбран-
ного значения уровня значимости а, у нас нет оснований, чтобы отвергнуть
нулевую гипотезу.
Во втором случае решается другая задача. Определяются значения Хкритич
для фиксированных вероятностей ошибки первого рода, используемых при
проверке статистических гипотез (в большинстве случаев это р=0,05, р =0,01,
р=0,001). Значение А'критич служит границей междутой областью, где нулевая
гипотеза принимается, и той областью, где нулевая гипотеза отвергается.
Область, где нулевая гипотеза отвергается, в статистике называется критической
областью. При использовании этого понятия необходимо учитывать ряд под-
водных камней, с ним связанных.
Вернемся к примеру с покупкой обуви. Мы рассматривали три варианта
альтернативной гипотезы (обувь на правую ногу больше обуви на левую ногу;
12 В этом одна из проблем проверки статистических гипотез на основе свойств нормального
распределения. Во многих случаях нет возможности получить большую по объему выборку.
Психолог, работающий с аутичными детьми, социальный работник, исследующий случаи суи-
цидов среди подростков, врач, изучающий очень редкое генетическое заболевание, — во всех этих
случаях вряд ли можно рассчитывать на выборки численностью в сотни человек. Данное обстоя-
тельство стало одним из толчков к развитию непараметрических методов статистики.
49
КНИГАДЛЯТЕХ, КТО НЕ ЛЮБИТСТАТИСТИКУ, НО ВЫНУЖДЕН ЕЮ ПОЛЬЗОВАТЬСЯ
обувь на правую ногу меньше обуви на левую ногу; обувь на правую ногу не
равна обуви на левую ногу).
На языке статистики это означает необходимость использования правосто-
ронней критической области, левосторонней критической области и двусто-
ронней критической области. В качестве критических областей выступают
«хвосты» нормального распределения, соответствующие вероятностямр =0,05,
/>=0,01 и />=0,00113 и расположенные слева или справа от медианы. Если ве-
роятность, соответствующая значению А"ЭМПИр, попадает вовнутрь критической
области, то нулевая гипотеза отвергается.
При использовании двусторонней критической области применяются оба
«хвоста» нормального распределения. Происходит объединение двух предыду-
щих вариантов альтернативной гипотезы: вначале проверяется предположение,
что обувь на правую ногу больше обуви на левую ногу, а затем предположение,
что обувь на правую ногу меньше обуви на левую ногу.
Что при этом происходит с вероятностью ошибки первого родар (или уров-
нем значимости а)? Эта вероятность удваивается (суммируется площадь двух
«хвостов») и может выйти за пределы допустимых рамок. Например, если пер-
вые две гипотезы проверялись для уровня значимости а=0,05, то третья будет
проверена для уровня значимости а=0,05 + 0,05 = 0,1. Но это значение прак-
тически не применяется в математической статистике при проверке гипотез.
Чтобы уровень значимости а при использовании двусторонней критической
области14 не выходил, например, за рамки а=0,05, необходимо, чтобы провер-
ка гипотез для односторонней критической области происходила на уровне не
большем чем а/2=0,025.
Иными словами, если, например, на уровне значимости а=0,05 проверя-
ется гипотеза Но: Х= Y при альтернативной гипотезе X* Y, то это означает
объединение двух односторонних критических областей (правосторонней и
левосторонней), соответствующих уровням значимости а/2=0,025. Поэтому
проверка гипотез при применении двусторонней критической области носит
более строгий характер. Если по результатам такой проверки нулевая гипотеза
отвергается, то она тем более отвергается при использовании односторонней
критической области (право- или левосторонней).
При проверке гипотез иногда бывают ситуации, когда при применении
двусторонней критической области нет оснований отвергнуть нулевую гипо-
тезу, а при использовании односторонней — есть. Например, при использо-
вании двусторонней критической области выяснилось, что граница, отделяю-
щая область принятия нулевой гипотезы от области, где она отвергается
(критическая область), соответствует/?=0,08. Это превышает верхний предел
уровня значимости а=0,05, и нулевая гипотеза не отвергается. Но значение
р =0,08 образовалось путем сложения площадей двух «хвостов» слева и справа,
13 Легко показать (см. табл. 1, Приложение 2), что этим вероятностям соответствуют значения
z=±l,64, z=±2,32 иг=±3,08.
14 Ее признаком обычно является знак неравенства в записи альтернативной гипотезы: X* Y.
50
ГЛАВА 1. ВСЕ. ЧТО ВЫ ХОТЕЛИ ЗНАТЬ О СТАТИСТИКЕ, НО БОЯЛИСЬ СПРОСИТЬ
по 0,04 каждая. Поэтому если мы соответствующим образом сформулируем
альтернативную гипотезу и перейдем к использованию односторонней кри-
тической области, то будем иметь дело с площадью (вероятностью) только
одного «хвоста», равной/>=0,04. Это меньше чем а=0,05, и нулевая гипотеза
будет отвергнута.
Во многих статистических таблицах, используемых при проверке статисти-
ческих гипотез, указывается, какой критической области (односторонней или
двусторонней) соответствуют приводимые в ней значения. Важно ясно пред-
ставлять, для какой из них (односторонней или двусторонней) производится
проверка15. От этого зависят значение и, как следствие, результат про-
верки.
Во многих случаях значение вычисленное для определенной веро-
ятности ошибки первого рода р, зависит также от другого статистического
показателя, называемого числом степеней свободы (обозначается как df—
degrees of freedom).
Число степеней свободы df является важным показателем, определяющим
наши возможности в варьировании экспериментальных данных без изменения
полученных результатов.
Например, известно, что среднее арифметическое трех чисел а, Ь, с равно 4:
(a+Z>+c)/3=4.
Очевидно, можно найти много чисел а, Ь, с, которые удовлетворяют этому
условию (например, 7, 3, 2 или 15, —8, 5). Но обратите внимание на то, что
фактически мы свободны в выборе только двух чисел из трех. Третье число
предопределено выбором двух предыдущих. Если мы выбрали 6 и 5, то для
получения среднего арифметического, равного 4, в качестве третьего числа мы
можем использовать только число 1. Другой возможности нет. Таким образом,
для трех чисел мы имеем две степени свободы.
Аналогично, если вы складываете мозаику из 100 элементов, то только 99
из них «обладают свободой». Последний элемент должен встать на единствен-
ное определенное ему место, не имея «свободы выбора».
В ряде случаев (но не всегда!) число степеней свободы определяется как
(N— 1), где У — размер (объем) выборки. Например, для выборки N=35 (чис-
ло подростков, опрошенных о возрасте начала курения) при проверке ряда
гипотез число степеней свободы будет (35 —1)=34.
Для большинства случаев проверки статистических гипотез данные о АГкритич,
соответствующих значениях вероятности ошибки первого родар, и числе сте-
пеней свободы df приводятся в специальных статистических таблицах. Это
15 Во многих случаях можно перейти от результата проверки для односторонней критической
области к результату проверки для двусторонней критической области путем умножения значения
а на два. Например, если нулевая гипотеза для односторонней критической области была отверг-
нута для значения а=0,01, то это означает, что она будет также отвергнута и для двусторонней
критической области на уровне а=0,02. Аналогичным образом в ряде случаев можно переходить
от результата проверки для двусторонней критической области к результату проверки для одно-
сторонней критической области путем деления значения а на два.
51
КНИГА ДЛЯ ТЕХ, КТО НЕ ЛЮБИТ СТАТИСТИКУ, НО ВЫНУЖДЕН ЕЮ ПОЛЬЗОВАТЬСЯ
избавляет от необходимости дополнительных вычислений, поскольку про-
цедура проверки превращается в выбор значения уровня значимости а и срав-
нение вычисленного значения /Гэмпир со значением Ккртт, которое берется из
соответствующей статистической таблицы для случая а=р16.
В большинстве случаях (но не всегда!) здесь используется следующее пра-
вило (рис. 1.25):
1. Если Лзмпир < /Гкритич, нет оснований отвергнуть нулевую гипотезу.
2. Если Аэмлир > Британ, нулевая гипотеза отвергается и принимается альтер-
нативная.
(нулевая гипотеза принимается) (нулевая гипотеза отвергается)
Рис. 1.25. Правило принятия решений при проверке статистических гипотез
(случай односторонней критической области)
Используемые способы проверки гипотез (тесты) в большинстве случаев
носят имена своих создателей — тех исследователей (статистиков, математиков,
экономистов, инженеров), которые впервые предложили тот или иной тест и
рассчитали для него соответствующие статистические таблицы. В Приложении 1
приведены краткие сведения о тех людях, чьи имена носят популярные стати-
стические тесты, рассмотренные в этой книге.
16 Как можно видеть, судьба нулевой гипотезы начинает зависеть от значения а. У исследова-
теля появляется определенная возможность для маневра, связанная с варьированием этим зна-
чением. Например, для выбранного значения а=0,01 может оказаться, что Кэмпир < Тритии-
Оснований отвергнуть нулевую гипотезу нет. Но если выбрать а=0,05, то ему будет соответство-
вать другое значение -АГкрихич и вполне возможно, что сейчас АэМПИр > Ккритич и нулевая гипотеза
будет отвергнута.
52
ГЛАВА 1. ВСЕ, ЧТО ВЫ ХОТЕЛИ ЗНАТЬ О СТАТИСТИКЕ, НО БОЯЛИСЬ СПРОСИТЬ
1.11. ДОРОГИ, КОТОРЫЕ МЫ ВЫБИРАЕМ:
СТАТИСТИКА ПАРАМЕТРИЧЕСКАЯ
И НЕПАРАМЕТРИЧЕСКАЯ
Статистические методы, объединенные понятием «непараметрическая ста-
тистика», стали набирать популярность к концу 1940-х гг.
Существует несколько теоретических и практических предпосылок, обусло-
вивших развитие непараметрического направления в статистике.
1. Большинство наших рассуждений и рассмотренных выше примеров явно
или неявно отталкивались от предположения о нормальном распределении
экспериментальных данных. Во многих случаях это предположение оправдано,
однако встречаются ситуации, когда либо о характере распределения мало что
известно, либо оно явно отличается от нормального. Например, на рис. 1.26
приведены сведения о числе госпитализаций в течение жизни, полученные при
опросе 763 человек, употребляющих наркотики:
Как видно из рисунка, характер распределения даже отдаленно не напоми-
нает нормальное.
В том случае, когда экспериментальные данные имеют неизвестный или
отличный от нормального закон распределения, нельзя использовать методы
проверки статистических гипотез, базирующиеся на свойствах и параметрах
нормального распределения.
Это обстоятельство стало одной из основных предпосылок для создания
методов проверки статистических гипотез, в которых свойства нормального
распределения не применяются. Тем самым стало формироваться направление,
получившее название «непараметрическая статистика» (в отличие от «парамет-
53
КНИГА ДЛЯ ТЕХ, КТО НЕЛЮБИТ СТАТИСТИКУ, НО ВЫНУЖДЕН ЕЮ ПОЛЬЗОВАТЬСЯ
рической статистики», использующей параметры нормального распределения
или других распределений, полученных на основе нормального)17.
2. Важным фактором, обеспечивающим надежную проверку статистических
гипотез, является размер (объем) выборки. Мы уже приводили пример, показы-
вающий, как, в зависимости от объема выборки, меняется результат проверки.
К сожалению, в поведенческих науках (психология, педагогика, социальная
работа и др.) далеко не всегда есть возможность получать значительные по
объему выборки (содержащие, например, не менее 100 значений). Во многих
исследованиях приходится ограничиваться выборками, содержащими не более
двух-трех десятков значений. Но на столь малых выборках обычные (парамет-
рические) методы проверки статистических гипотез не работают. Это обстоя-
тельство стало еще одним толчком к разработке непараметрических методов,
пригодных к работе с малыми выборками.
3. Развитие экспериментальных методов в психологии, педагогике, соци-
альной работе и др. привело к формированию нового подхода к пониманию
измерения. Классическая теория измерений (невозможная без опоры на ма-
тематическую статистику) имела дело исключительно с физическими измере-
ниями, производимыми в шкале отношений18. Однако измерительные про-
цедуры, например, в психологии связаны с более частым использованием
других измерительных шкал.
Науки о человеке оказались в наибольшей степени заинтересованными в
развитии измерительных и статистических методов, не привязанных к мето-
дологии физических измерений и нормальному распределению.
17 Сказанное не означает, что эти методы нельзя использовать для нормально распределенных
результатов. Речь идет о том, что эти методы можно применять, вообще не думая о характере
распределения. Поэтому в ряде случаев непараметрические методы статистики называют мето-
дами, свободными от характера распределения.
18 Подробнее об измерениях и шкалах в следующей главе.
54
ГЛАВА 1. ВСЕ, ЧТО ВЫ ХОТЕЛИ ЗНАТЬ О СТАТИСТИКЕ, НО БОЯЛИСЬ СПРОСИТЬ
Непараметрические методы статистики целесообразней всего применять
при сочетании трех факторов:
□ малая выборка;
□ неизвестный (или отличный от нормального) закон распределения;
□ нефизическая природа изучаемых явлений (качества, психологические
характеристики, мнения, установки и др.).
В этом случае непараметрическая статистика обладает явными преимуще-
ствами по сравнению с параметрической.
Как правило, основным критерием при выборе непараметрической или
параметрической статистики является объем выборки. Чем выборка меньше,
тем более оправдано применение непараметрической статистики. Отражением
этого обстоятельства стало то, что многие статистические таблицы для непа-
раметрических методов ограничены объемом выборки в 30—40 значений.
При выходе выборки за эти пределы приходится прибегать к дополнительным
вычислениям и, как правило, переходить к статистическим таблицам для
нормального распределения или распределения %2. Если же приходится иметь
дело с еще большими по размеру выборками, то в этом случае применение
непараметрических методов возможно, но нецелесообразно, поскольку в боль-
шинстве случаев уже можно пользоваться обычной параметрической стати-
стикой19.
В принципе, как параметрические, так и непараметрические методы стати-
стики применяются для решения одного и того же круга задач: сравнение за-
висимых и независимых выборок, вычисление мер связи (корреляций) и др.
В зависимости от конкретных обстоятельств, одна и та же задача может быть
решена как параметрическими, так и непараметрическими методами. Например,
при сравнении двух независимых выборок часто используется /-тест Стьюдента
(сравнение средних). В непараметрической статистике та же самая задача будет
решаться с использованием теста Манна—Уитни, который является непара-
метрическим аналогом теста Стьюдента.
Таблица 1.10 является путеводителем по методам непараметрической ста-
тистики, которые будут рассмотрены ниже.
19 При условии, что характер анализируемых данных позволяет сделать это.
55
Таблица LIO
Основные непараметрические методы статистики20
Уровень изме- рения Случай одной вы- борки Случай двух выборок Случай нескольких выборок Непарамстриче- скис меры корре- ляции
Связанные (зави- симые) выборки Независимые выборки Связанные (зависимые) выборки Независимые выборки
Номинальный Биномиальный тест Тест х2 для одной выборки Тест МакНсмара Точный тест Фи- шера Тест х2 для двух не- зависимых выборок 0тест Ко- храна Тест х2 для не- скольких неза- висимых выбо- рок
Порядковый20 21 Тест Колмого- рова-Смирнова для одной выборки Тест последова- тельностей Тест знаков Тест Вилкоксона (/тест Манна—Уит- ни Тест Колмогорова- Смирнова для двух независимых выбо- рок Тест последователь- ностей Вальда— Волфовица Тест экстремальных реакций Мозеса Тест Фрид- мана Расширенный медианный тест Тест Крускала- Уоллиса ТсстДжонкхи- сра—Терпстра для упорядочен- ных альтернатив Коэффициент ранговой корре- ляции Спирмена Коэффициент ранговой корре- ляции Кендалла Коэффициент конкордации Кендалла
20 Перечень нспараметрических методов статистики не исчерпывается теми, которые вошли в таблицу 1.10. В частности, за рамками нашего
рассмотрения остались немногие методы для шкалы интервалов, меры связанности для дихотомических данных (например, коэффициент Крамера),
частная ранговая корреляция и др. Подробнее об этих и других методах см. Conover [Conover, 1999], Siegel [Siegel, 1956], Siegel and Castellan [Siegel
and Castellan, 1988].
21 Разумеется, непараметрические методы могут применяться для данных, представленных в шкале интервалов или отношений. Но в этом слу-
чае анализируемые данные рассматриваются как порядковые.
Глава 2
КАК ИЗМЕРИТЬ НЕИЗМЕРИМОЕ:
НЕМНОГО ОБ ИЗМЕРЕНИЯХ И ШКАЛАХ
2.1. ОТ КАЧЕСТВ К КОЛИЧЕСТВАМ И ОБРАТНО
Использование любых статистических методов будет невозможным до тех
пор, пока не будут получены числовые данные, являющиеся предметом стати-
стического анализа. Во многих случаях, когда речь идет, например, о возрасте
человека, числе детей, уровне доходов и др., получение соответствующих чисел
не связано с большими проблемами. Однако зачастую приходится иметь дело
с характеристиками, качественными по своей природе. Например, удовлетво-
ренность трудом, состояние здоровья, статус, удовлетворенность браком, мно-
гие психологические характеристики и др.
Качественные показатели невозможно измерять привычным образом.
Данное обстоятельство в течение многих лет тормозило использование мате-
матических и статистических методов в психологии, социальной работе, пе-
дагогике и других науках, оперирующих качественными характеристиками
изучаемых явлений.
Преодоление разрыва между качествами («какой») и количествами («сколь-
ко») связано с именем американского психолога С. Стивенса [Stevens, 1951],
который в 1940-х гг. предложил новый подход к проблеме измерений. По Сти-
венсу, измерение понимается как процесс приписывания чисел объектам или
событиям в соответствии с определенными правилами. Каждое из этих правил
определяет тип шкалы, в которой производится измерение (или шкалирование)1.
Стивенс предложил четыре типа измерительных шкал, позволяющих перебро-
сить мостик между миром качеств и миром количеств:
1 Пред ложенный Стивенсом подход позволяет говорить об измерении, не употребляя поня-
тие «измеряемая величина». Нечто подобное произошло в психологии, когда из фундамента
одной из психологических теорий (бихевиоризм) было убрано понятие психики. В целом созда-
ние «шкального» направления в теории измерений привело к возникновению в ней кризиса,
который не'преодолен до сих пор [Берка, 1987].
57
КНИГА ДЛЯ ТЕХ. КТО НЕ ЛЮБИТ СТАТИСТИКУ, НО ВЫНУЖДЕН ЕЮ ПОЛЬЗОВАТЬСЯ
1) шкала наименований;
2) шкала порядка;
3) шкала интервалов;
4) шкала отношений;
Четыре типа шкал образуют иерархию, в которой каждая последующая
шкала включает в себя свойства нижележащих шкал (табл. 2.1).
Таблица 2.1
Измерительные шкалы и их свойства
Тип шкалы Действия в шкале Пример
Отношений Определение отношений между свойствами (качест- вами) объектов Кофе вдщхраза дороже, чем моро- женое
Интервалов Определение интервала ме- жду свойствами (качества- ми) объектами Кофе дороже, чем мороженое на 5 шекелей
Порядка Установление отношений между свойствами или каче- ствами объектов Кофе мороженое
Наименований Наделение объектов имена- ми Это' ^0^ Это к°Фе г мороженое
С каждой из шкал связан определенный диапазон допустимых математико-
статистических преобразований. Выход за пределы этого диапазона приводит
к тому, что получаемые результаты оказываются лишенными смысла. Об этом
необходимо помнить на этапе планирования работы по сбору данных. Например,
к данным, представленным в шкале наименований, нельзя применять методы
анализа, допустимые для шкал порядка или интервалов.
Рассмотрим свойства каждой из шкал более подробно.
2.2. «И НАРЕК ЧЕЛОВЕК ИМЕНА ВСЕМ»2,
ИЛИ ШКАЛА НАИМЕНОВАНИЙ
Использование шкалы наименований позволяет наделять объекты или их
свойства (признаки) именами. Телефонные и автомобильные номера, различ-
ные цветные фигурки на шкафчиках в детском саду и т. п. — это примеры имен,
2 Быт. 2,20.
58
ГЛАВА 2. КАК ИЗМЕРИТЬ НЕИЗМЕРИМОЕ: НЕМНОГО ОБ ИЗМЕРЕНИЯХ И ШКАЛАХ
которыми мы наделяем различные объекты.
При этом неважно, что будет использовать-
ся в качестве имени — цифры, буквенные
сочетания, условные обозначения и т. п.
Основное требование здесь — не присваи-
вать одно и то же имя двум разным объектам
(или объектам с различными свойствами).
В то же время если мы имеем дело с одина-
ковыми объектами или объектами, обладаю-
щими совпадающими свойствами, то они
должны в шкале наименований получать
одинаковые имена. Например, если выбор-
ка состоит из мужчин и женщин, то можно
всем мужчинам присвоить «имя» 1, а всем
женщинам — «имя» 2 (или любое другое, не совпадающее с первым). Если нас
интересует семейное положение, то можно всем женатым присвоить «имя» 1,
холостым — «имя» 2, разведенным — «имя» 3. Количество используемых имен
должно быть не меньше числа типов объектов или их свойств. Например, трех
«имен» для обозначения семейного положения может оказаться недостаточно
в случае наличия в выборке вдов/вдовцов. Для их обозначения потребуется
дополнительное «имя».
Несмотря на то что шкала наименований образует «низший» уровень изме-
рения, ее использование является необходимым этапом при использовании
статистических методов. Переход к шкалам более высокого порядка зачастую
оказывается невозможен, если не решен вопрос о том, к каким объектам будут
относиться получаемые данные: чтобы они были данными о чем-то, объекты
должны иметь имена.
Выше отмечалось, что с каждой из шкал связан определенный набор допус-
тимых математико-статистических операций. Поскольку в шкале наименова-
ний числа — не более чем ярлыки, «наклеиваемые» на объекты, с этими чис-
лами нельзя производить никаких действий. Их нельзя складывать или
вычитать, делить или умножать. Возможен подсчет числа объектов с одинако-
выми именами (например, число мужчин и женщин в выборке) или с одина-
ковыми свойствами (например, уроженцы Израиля и иммигранты).
Таблица 2.2
Сведения о поле и семейном положении
Семейное положение Итого
Холост(ая) Женат/Замужем Разведен(а)
Пол Мужчины 35 27 10 72
Женщины 47 32 13 92
Итого 82 59 23 164
59
КНИГАДЛЯТЕХ, КТО НЕ ЛЮБИТ СТАТИСТИКУ. НО ВЫНУЖДЕН ЕЮ ПОЛЬЗОВАТЬСЯ
Статистическая обработка данных, представленных в шкале наименований,
чаще всего начинается с построения таблицы сопряженности, показывающей
распределение «имен» в соответствии с числом типов объектов и/или их
свойств.
Если в такой таблице к столбцов и г строк, будем говорить о таблице разме-
ром (к х г). Выше приведен пример такой таблицы для пола и семейного по-
ложения членов выборки (табл. 2.2). В ней &=3 и г=2.
Наиболее популярным статистическим тестом, используемым для таблиц
сопряженности, является тест %2.
2.3. В ЧЕМ ИЗМЕРЯЮТСЯ ЗЕМЛЕТРЯСЕНИЯ,
ИЛИ О ШКАЛЕ ПОРЯДКА
Наделение объектов именами позволяет приступить к выявлению сходств
и различий между ними. Например, можно обнаружить, что одни студенты
более успешны, чем другие, автомобили одних марок быстрее автомобилей
других марок, одни блюда вкуснее других и т. д.
В том случае, когда между объектами возможно установление отношений
типа «быстрее», «успешнее», «вкуснее», «ярче», «громче», «тверже», «популяр-
нее» и др., появляется возможность расположить объекты в порядке возраста-
ния или убывания определенного признака. После этого остается наделить
упорядоченную последовательность числами таким образом, чтобы, например,
большее число соответствовало большей степени выраженности признака.
В результате получим шкалу порядка, в которой отношения между числами
будут соответствовать отношениям между объектами. Такие шкалы широко
используются в повседневной жизни.
Одна из наиболее распространенных шкал порядка — шкала школьной или
университетской успеваемости. Чем более успешен студент, тем большее чис-
ло в этой шкале ему соответствует. Существуют и другие, столь же широко
применяемые шкалы порядка, например шкала твердости минералов Мооса,
шкала Бофорта для силы ветра, сейсмические шкалы для оценки силы земле-
трясений и др.
В то же время расположение объектов в порядке возрастания определенно-
го свойства (например, минералов по твердости) еще не дает ответа на вопрос:
на сколько больше? Шкала порядка не позволяет определить «расстояние»
между объектами. Об этом особенно необходимо помнить в тех случаях, когда
из соображений удобства шкальные значения отделяют друг от друга равные
интервалы. Например, четыре студента получили на экзамене оценки 75, 85,
90 и 100 баллов. Оценка второго студента отличается от оценки первого так же,
как оценка четвертого студента отличается от оценки третьего, — на 10 баллов.
60
ГЛАВА 2. КАК ИЗМЕРИТЬ НЕИЗМЕРИМОЕ: НЕМНОГО ОБ ИЗМЕРЕНИЯХ И ШКАЛАХ
Но из этого не следует, что знания вто-
рого студента больше знаний первого
на столько же, на сколько знания чет-
вертого больше знаний третьего.
Шкала Мооса содержит значения от
1 до 10, но из этого не следует, что гипс
(вторая позиция в шкале) тверже таль-
ка (первая позиция) на столько, на
сколько алмаз (десятая позиция) твер-
же корунда (девятая позиция).
Таким образом, выбор чисел, ис-
пользуемых в шкале порядка, в извест-
ных пределах произволен. Числа могут
быть любыми, но они должны подчи-
няться основному требованию: объекту с большей выраженностью определен-
ного признака должно быть приписано большее число. Так, наши суждения о
студентах по результатам экзамена не изменились бы при переходе, например,
к шкале оценок от 0 до 50. В любом случае более успевающий студент получил
бы более высокую оценку.
Особенности шкалы порядка позволяют определить для нее группу допус-
тимых математико-статистических преобразований. Результаты, представлен-
ные в шкале порядка, нельзя использовать для пропорций (знания, оцененные
на 100, не являются вдвое большими знаний, оцененных на 50). Эти резуль-
таты нельзя складывать (знания получившего на экзамене 100 баллов не рав-
ны сумме знаний получивших 40 и 60 баллов). Если говорить о мерах цен-
тральной тенденции, то из них можно применять только моду и медиану.
Вычисление среднего (например, средней успеваемости) является недопус-
тимой операцией для шкалы порядка (к сожалению, это требование повсеме-
стно нарушается).
Шкалы порядка широко используются в психологии, социальной работе,
педагогике и др. Многие непараметрические методы статистики были специ-
ально разработаны для шкал порядка. С этими шкалами связана одна из наи-
более популярных в непараметрической статистике процедур — процедура
ранжирования.
Если какие-либо результаты расположены в порядке возрастания или убы-
вания, то можно определить, какое место занимает каждый из них. Ранжи-
рование — это процедура определения места, которое должен занять данный
результат в упорядоченной последовательности всех результатов.
Часто ранжирование идет по направлению убывания каких-либо значений
(например, оценок на экзамене). Тогда первый, наивысший ранг получает об-
ладатель наибольшего значения (например, обладатель наивысшей оценки).
Допустим, 11 студентов получили на экзамене следующие оценки3:
3 В Израиле используется 100-балльная шкала академической успеваемости.
61
КНИГА ДЛЯ ТЕХ, КТО НЕ ЛЮБИТ СТАТИСТИКУ, НО ВЫНУЖДЕН ЕЮ ПОЛЬЗОВАТЬСЯ
Оценка 80 88 94 96 83 95 90 85 100 93 86
Необходимо проранжировать полученные оценки и определить, какое место
(ранг) каждая из них занимает. Вначале упорядочим результаты в порядке
убывания:
Оценка 100 96 95 94 93 90 88 86 85 83 80
Сейчас определим, какое место (ранг) занимает каждая из них:
Оценка 100 96 95 94 93 90 88 86 85 83 80
Ранг 1 2 3 4 5 6 7 8 9 10 11
Обратите внимание, что «расстояние» между рангами не соответствует «рас-
стоянию» между оценками: ранги отстоят друг от друга с постоянным интер-
валом 1, а интервал между оценками колеблется от 1 до 4. В этом проявляется
та особенность шкалы порядка, о которой мы говорили: в данной шкале мож-
но определить порядок следования результатов (этот порядок задается рангами),
но нельзя определить, насколько один результат отличается от другого.
Трудности, возникающие в процессе ранжирования, связаны с ситуацией,
когда среди значений встречаются повторяющиеся. Это приводит к возникно-
вению так называемых связанных рангов.
Например, 11 студентов получили на экзамене следующие оценки:
Оценка 88 94 96 90 92 88 100 88 86 92 98
Как и прежде, необходимо проранжировать полученные оценки и определить
ранг каждой из них. Упорядочим результаты в порядке убывания:
Оценка 100 98 96 94 92 92 90 88 88 88 86
Как видно из результатов, оценка 92 повторяется дважды, а оценка 88 — три-
жды. При ранжировании ранги совпадающих значений не должны отличаться
друг от друга4.
В том случае, если среди ранжируемых результатов встречаются группы
одинаковых значений, ранг внутри каждой из таких групп определяется как
среднее арифметическое тех рангов, которые имели бы результаты, будь они
отличными друг от друга.
Предположим, что совпадающие результаты немного отличаются друг от
друга:
4 Здесь как в спорте. Если два бегуна показали одинаковый результат, наилучший среди ре-
зультатов остальных бегунов, то они делят между собой первое и второе место. Фактически ранг
каждого из них равен 1,5.
62
ГЛАВА 2. КАК ИЗМЕРИТЬ НЕИЗМЕРИМОЕ: НЕМНОГО ОБ ИЗМЕРЕНИЯХ И ШКАЛАХ
Оценка 100 98 96 94 92,1 92,2 90 88,1 88,2 88,3 86
В этом случае проблема ранжирования решается просто:
Оценка 100 98 96 94 92,1 92,2 90 88,1 88,2 88,3 86
Ранг 1 2 3 4 5 6 7 8 9 10 11
Найдем среднее арифметическое рангов для искусственно измененных
значений:
(5+6) (8+9+10)
Вернемся к исходным данным и припишем повторяющимся значениям
одинаковые (связанные) ранги:
Оценка 100 98 96 94 92 92 90 88 88 88 86
Ранг 1 2 3 4 5,5 5,5 7 9 9 9 11
Рассмотрим еще пример.
В таблице 1.5 были приведены значения IQ родителей и их детей.
Проранжируем эти значения и создадим новую таблицу, где вместо значений
IQ будут стоять соответствующие ранги.
Поскольку значения IQ родителей уже упорядочены по возрастанию, мож-
но сразу приступить к процедуре ранжирования (так как значения IQ упоря-
дочены по возрастанию, первый ранг будет приписан наименьшему значению
IQ). Среди значений IQ много повторяющихся, поэтому при ранжировании
получим много связанных рангов (табл. 2.3).
Таблица 2.3
Значения и ранги IQ родителей
IQ родителей Ранг 1 1 IQ родителей Ранг
90 2 1 105 11
90 2 105 11
90 2 110 13
95 5 115 15
95 5 115 15
95 5 1 1 115 15
100 8 120 17,5
100 8 120 17,5
100 .. 8. .. 125 19,5
105 н | 1 125 19,5
63
КНИГА ДЛЯ ТЕХ, КТО НЕ ЛЮБИТ СТАТИСТИКУ, НО ВЫНУЖДЕН ЕЮ ПОЛЬЗОВАТЬСЯ
Прежде чем приступить к ранжированию значений IQ детей, эти значения
также необходимо упорядочить. В ситуации, когда имеется несколько групп
ранжируемых значений, важно придерживаться выбранного направления припи-
сывания рангов. Если в случае родителей приписывание рангов шло в порядке
возрастания значений IQ, то с детьми должно быть то же самое. Поэтому упоря-
дочиваем значения IQ детей в порядке возрастания и ранжируем их (табл. 2.4).
Таблица 2.4
Значения и ранги IQ детей
IQ детей Ранг IQ детей Ранг
90 2 105 12
90 2 105 12
90 2 105 12
95 5 НО 15
95 5 НО 15
95 5 110 15
100 8,5 115 17,5
100 8,5 115 17,5
100 8,5 120 19
100 8,5 125 20
Вернемся к исходной таблице 1.5 и заменим в ней значения IQ для родите-
лей и детей соответствующими рангами. Получим таблицу 2.5, в которой вме-
сто значений IQ приведены ранги этих значений.
Таблица 2.5
Ранги IQ родителей и детей
Семья Ранг IQ родителей Ранг IQ детей Семья Ранг IQ родителей Ранг IQ детей
1 2 8,5 И 11 15
2 2 2 12 11 8,5
3 2 5 13 13 17,5
4 5 2 14 15 12
5 5 5 15 15 8,5
6 5 8,5 16 15 17,5
7 8 12 17 17,5 15
8 8 2 18 17,5 20
9 8 5 19 19,5 19
10 11 12 20 19,5 15
Процедура ранжирования лежит в основе многих непараметрических мето-
дов статистики, поэтому желательно владеть навыками ранжирования в совер-
шенстве.
64
ГЛАВА 2. КАК ИЗМЕРИТЬ НЕИЗМЕРИМОЕ: НЕМНОГО ОБ ИЗМЕРЕНИЯХ И ШКАЛАХ
Многие из непараметрических методов чувствительны к наличию связанных
рангов. Связанные ранги могут существенно повлиять на получаемые резуль-
таты статистического анализа. Для их учета во многие расчетные формулы
приходится вносить различные корректирующие поправки5.
2.4. «451° ПО ФАРЕНГЕЙТУ»6,
ИЛИ КАК ПОЛУЧИТЬ ШКАЛУ ИНТЕРВАЛОВ
В ряде случаев (но далеко не всегда!) удается упорядочить объекты или их
свойства таким образом, что возможно определить «расстояние» между ними.
Чаще всего эта задача решается путем договоренностей о том, по каким при-
знакам можно судить об одинаковости «расстояния», отделяющего друг от
друга различные объекты. Если такая договоренность достигнута, то одинако-
вым отличиям между объектами будут соответствовать равные числовые зна-
чения.
Например, можно договориться, что ум студента будет измеряться в коли-
честве книг по специальности, которые он прочел в течение семестра. Тогда
тот студент, который прочитал 10 книг, будет на 4 единицы «умнее» того, ко-
торый прочитал 6 книг. И «ум» будет равен нулю, если не прочитано ни одной
книги.
В качестве примера рассмотрим, как решалась проблема определения «рас-
стояния» между телами разной температуры. В этом случае использовалось
явление теплового расширения тел (жидкостей). За меру «расстояния» между
телами разной температуры принималась высота подъема или перемещения
столбика жидкости (ртути или спирта). Если д ля двух разных тел высота подъ-
ема столбика жидкости оказывалась одинаковой, то этот означало, что тела
имеют одинаковую температуру. Оставалось договориться о «длине линейки»,
точке начала отсчета и единице шкалы. Для этого использовался тот факт, что
существуют физические (или физиологические) процессы, всегда протекающие
при одной и той же температуре (высота подъема столбика жидкости всегда
оставалась одной и той же).
Цельсий и Реомюр в качестве таких процессов применяли таяние льда и
кипение воды. Реомюр в своей шкале высоту подъема столбика жидкости при
таянии льда обозначил как О’, а высоту при кипении воды как 80’. Цельсий
5 К сожалению, авторы многих учебных пособий по статистике и математическим методам в
психологии обходят стороной вопрос связанных рангов. О существовании данной проблемы либо
не упоминается, либо наличие связанных рангов в приводимых примерах игнорируется и вычис-
ления проводятся по нескорректированным формулам.
6 «Fahrenheit 451°» — известный фантастический роман Р. Брэдбери. Температура 451°F — это
температура горенйя бумаги.
3 Зак 3384
65
КНИГА ДЛЯ ТЕХ. КТО НЕ ЛЮБИТ СТАТИСТИКУ, НО ВЫНУЖДЕН ЕЮ ПОЛЬЗОВАТЬСЯ
обозначил точку таяния льда как 100°, а точку
кипения воды как 0° (направление шкалы
Цельсия было изменено позже другими физи-
ками). Соответственно разность высот подъема
столбика жидкости делилась на 80 (Реомюр) или
100 (Цельсий) равных интервалов. Фаренгейт
же решил создать шкалу, ведя отсчет высоты
подъема столбика жидкости от уровня, соответ-
ствующего температуре смеси воды, льда и на-
шатыря, обозначив ее как 0°. Для выбора второй
точки он использовал тот факт, что температура
тела здорового человека всегда остается неиз-
менной. Этой температуре, измеренной под
мышкой или во рту, он приписал значение 96°.
Из описания того, как возникли хорошо из-
вестные температурные шкалы, можно сделать выводы об отличительных
особенностях шкал интервалов. Во-первых, для такой шкалы существует три
произвольно задаваемые операции:
□ выбор нуля шкалы (точки отсчета);
□ выбор единицы измерения (величины интервала);
□ выбор направления отсчета (в первоначальном варианте шкалы Цельсия
за 0° была выбрана точка кипения воды, а за 100° — точка таяния льда).
Во-вторых, в шкале интервалов отсутствует возможность сравнивать отно-
шения измеряемых признаков с целью получения ответа на вопрос, во сколько
раз больше (увеличение температуры с 10°до 20° не означает, что стало вдвое
теплее).
В-третьих, многие шкалы интервалов содержат отрицательные значения
(отрицательная температура).
Другая популярная шкала интервалов — календарное летоисчисление. Как
известно, христианское (европейское) летоисчисление берет начало от произ-
вольно выбранной точки отсчета («рождение Христа»), величина интервала
(день, месяц, год) «привязана» к видимому движению Солнца, а выражение
«до нашей эры» означает, по сути, что в этой точке летосчисление меняет свой
знак7.
Многие из используемых в психологии шкал интервалов получаются искус-
ственным путем из шкал порядка за счет математико-статистических преобра-
зований и введения ряда допущений. Обычно первичные результаты тести-
7 Мусульманское летосчисление ведет начало от даты Хиджра (Hijra, арабок. — переселе-
ние) — переселения пророка Мухаммада и его приверженцев из Мекки в Медину, которое совер-
шилось 16 июля 622 г. по юлианскому календарю. При халифе Омаре I (634—644) этот год объяв-
лен началом мусульманской эры. Исходной датой для него принято 16 июля 622 г. По сравнению
с христианской и мусульманской традицией, летосчисление, принятое в иудаизме, носит «абсо-
лютный» характер, поскольку берет начало от сотворения мира.
66
ГЛАВА 2. КАК ИЗМЕРИТЬ НЕИЗМЕРИМОЕ: НЕМНОГО ОБ ИЗМЕРЕНИЯХ И ШКАЛАХ
рования, представленные в шкале порядка («сырые баллы»), с помощью
специальных таблиц переводятся в стандартизированные психометрические
шкалы, являющиеся шкалами интервалов (например, шкала IQ, Т-шкала и
др.). Перевод «сырых баллов» из шкалы порядка в шкалу интервалов опирает-
ся на предположение о том, что в популяции результаты распределены по
нормальному закону.
Шкала интервалов позволяет применять большинство математико-стати-
стических методов для обработки и анализа данных, полученных с ее помощью.
Можно использовать все меры центральной тенденции и рассеяния, коэффи-
циент корреляции Пирсона и др. Имеющиеся здесь ограничения в первую
очередь связаны с исключением пропорций. Отвечая на вопрос «На сколько
больше?», шкала интервалов не дает ответа на вопрос «Во сколько больше?».
Например, нельзя утверждать, что человек с IQ= 140 в два раза более интел-
лектуально развит, чем тот, у кого IQ=70.
Следует помнить, что ответ на вопрос «на сколько больше» также не уни-
версален. Он зависит от выбора точки отсчета и единицы измерения. Например,
в шкале Цельсия температура выросла с 20 °C до 30 °C, то есть на 10 °C. Однако
если перевести эти результаты в шкалу Фаренгейта, то температура вырастет с
68 °F до 86 °F, то есть на 18 °F.
2.5. ВО СКОЛЬКО РАЗ ЛИЛИПУТЫ МЕНЬШЕ ГУЛЛИВЕРА,
ИЛИ ШКАЛА ОТНОШЕНИЙ
Если свойства объектов таковы, что становится возможной операция их
объединения, то математическим аналогом объединения является операция
суммирования. Это справедливо для многих объектов физической природы.
Например, суммируются массы объединенных тел; при объединении двух
проводников с током суммируются их сопротивления или проводимости
ИТ. д.
Если операции объединения всякий раз можно поставить в соответ-
ствие операцию суммирования, то мы получим еще одну шкалу — шкалу от-
ношений.
Если мы объединяем одинаковые объекты, то операция суммирования за-
меняется операцией умножения. Например, объект В образуется, если объе-
динить вместе пять объектов Л. На языке шкалы отношений это можно записать
либо как В=(А +А +А +А +А), либо как В=5*А. Иными словами, в шкале
отношений появляется возможность сказать, сколько раз необходимо взять
объект А для получения объекта В или, что то же самое, во сколько раз объект
В больше объекта А.
67
КНИГА ДЛЯ ТЕХ, КТО НЕ ЛЮБИТ СТАТИСТИКУ, НО ВЫНУЖДЕН ЕЮ ПОЛЬЗОВАТЬСЯ
В случае объединения объектов или их свойств результат объединения,
выраженный в шкале отношений, не должен зависеть ни от точки начала от-
счета, ни от единиц измерения. Например, если масса одного тела в два раза
больше массы другого тела, то данное отношение не должно зависеть от того,
в каких единицах измеряется масса — в килограммах, фунтах или драхмах.
Такое возможно только в том случае, если у шкалы отношений существует
«абсолютное» начало отсчета, характеризующееся отсутствием измеряемого
признака или свойства. В шкале интервалов это условие не соблюдается.
Температура, равная О °C, не означает отсутствие температуры как таковой.
Для шкалы отношений 0 означает абсолютное отсутствие измеряемого свой-
ства. В такой шкале нет отрицательных значений (нет тел отрицательной дли-
ны или массы). Как известно, температура О °К в температурной шкале Кельвина8
означает, что молекулы тела как бы застыли и прекратили свое тепловое дви-
жение, мерой которого является температура. В этой точке понятие темпера-
туры теряет свой смысл.
Шкалы отношений наиболее широко используются при проведении физи-
ческих измерений. Их применение в психологии, социальной работе, педаго-
гике и др. ограничено двумя существенными и взаимосвязанными обстоятель-
ствами. Во-первых, объекты и их свойства в этих науках нельзя объединять.
Можно объединить два тела и сложить их массы, но объединить двух людей со
средним IQ с целью получения IQ гения нельзя. Во-вторых, для объектов из-
мерений в этих науках практически невозможно указать «естественное» нача-
ло отсчета, «абсолютный» нуль.
Математико-статистические методы, используемые для обработки и.
анализа данных в шкале отношений, можно применять без каких-либо огра-
ничений.
Термодинамическая температурная шкала, названная в честь английского физика Уильяма
Томсона (лорда Кельвина [1824—1907]).
Глава 3
МОЖНО ЛИ САМОГО СЕБЯ ВЫТАЩИТЬ
ЗА ВОЛОСЫ ИЗ БОЛОТА,
ИЛИ
НЕПАРАМЕТРИЧЕСКАЯ СТАТИСТИКА
ДЛЯ СЛУЧАЯ ЕДИНСТВЕННОЙ ВЫБОРКИ
В ряде случаев в основе исследования лежит изучение единственной выбор-
ки без проведения в ней повторных измерений или без сравнения с результа-
тами, полученными в другой выборке.
Например, семейный консультант хочет проверить, кто чаще — жены или
мужья — обращается к нему за помощью. Или дорожная полиция хочет знать,
подчиняется ли число дорожных аварий каким-либо сезонным колебаниям.
Непараметрические методы статистики предлагают несколько возможностей,
позволяющих анализировать единственную выборку и проверять соответст-
вующие статистические гипотезы.
Основная задача, решаемая в случае единственной выборки, — проверка
соответствия эмпирического распределения какому-либо теоретическому.
Ниже описаны три наиболее популярных непараметрйческих теста, исполь-
зуемых в случае единственной выборки. Это:
□ биномиальный тест;
□ тест %2;
□ тест Колмогорова—Смирнова.
69
КНИГА ДЛЯ ТЕХ, КТО НЕ ЛЮБИТ СТАТИСТИКУ, НО ВЫНУЖДЕН ЕЮ ПОЛЬЗОВАТЬСЯ
3.1. ГДЕ ЛУЧШЕ ПРОВЕСТИ ВЕЧЕР, ИЛИ
БИНОМИАЛЬНЫЙ ТЕСТ
Вначале две ситуации.
1. Алекс и Том, два друга-студента, любители пива, предпочитают проводить
свободное от учебы время за кружкой пива в одном из пабов. Но каждый раз
они спорят друг с другом, какой паб предпочесть — «Пивная корова» или
«Безумный Макс»? Один из них утверждает, что наиболее популярной у сту-
дентов является «Пивная корова», в то время как второй верен «Безумному
Максу». С целью положить конец спорам было решено опросить других сту-
дентов: какой из пабов они предпочитают. Друзьям удалось опросить 25 чело-
век, из которых 15 предпочли «Пивную корову», а 10 — «Безумного Макса».
Можно ли на основании полученных результатов утверждать, что один из пабов
популярнее другого?
2. Володя и Алексей, два любителя игры в нарды, решили устроить сорев-
нование, чтобы выяснить, кто из них лучший игрок. Они сыграли 24 партии.
Володя победил в 17 партиях и объявил себя чемпионом. Алексей не согласил-
ся и заявил, что победа Володи носит случайный характер. Кто из них более
прав?
Что объединяет оба примера?
Во-первых, в обоих случаях в нашем распоряжении всего одна выборка.
Во-вторых, в обоих случаях результаты представлены в дихотомической
шкале наименований типа «да — нет», «согласен — не согласен» или «выиг-
рал — проиграл».
В-третьих, в обоих случаях требуется проверить, соответствует ли распре-
деление результатов в выборке известному (или предполагаемому) распреде-
лению результатов в популяции.
Для решения подобных задач чаще всего используется биномиальный тест.
Основу теста составляет формула Бернулли, определяющая вероятность
того, что в N независимых испытаниях, в каждом из которых вероятность по-
явления события равнар, событие наступит не более к раз:
х (дг \ (n\ лп
/>(х^А:) = Х . АЛГ-/. где^=(1-р); . = ‘
J V J i'.(JV-i)!
Если вернуться к первому примеру, то можно сказать, что было проделано
25 независимых испытаний (опрошено 25 студентов). Вероятность выбора в
пользу первого паба примем равной вероятности выбора в пользу второго паба:
p=q=0,5l. 1
1 Зачастую условие р=д=0,5 не выполняется. Например, педагоги, проводящие встречи с
родителями учеников, знают, что на них чаще приходят матери учеников, чем отцы. В подобных
случаях также возможно применение биномиального теста.
70
ГЛАВА 3. НЕПАРАМЕТРИЧЕСКАЯ СТАТИСТИКА ДЛЯ СЛУЧАЯ ЕДИНСТВЕННОЙ ВЫБОРКИ
С помощью формулы Бернулли вычисляется вероятность того, что в пользу
первого паба будет сделано не более 15 выборов из 25 (или вероятность того,
что в пользу второго паба будет сделано не более 10 выборов)2.
Как известно, если вероятность случайного наступления какого-либо со-
бытия ничтожно мала, но событие тем не менее имело место, то можно говорить
о нем как о неслучайном. Мы уже говорили, что в качестве границы между
нашим отношением к событию как случайному или как к неслучайному вы-
ступает значение уровня значимости а.
Таким образом, если событие имеет место (определенное число выборов в
пользу одного из пабов), а теоретическая вероятность случайного наступления
такого события ничтожна мала (меньше значения а), то это будет говорить о
неслучайности полученного результата.
После этих рассуждений приступим к проверке.
Выберем уровень значимости а=0,053 и сформулируем нулевую и альтер-
нативную гипотезы.
Но: Оба паба пользуются одинаковой популярностью.
Н[. Первый паб пользуется большей популярностью по сравнению со вторым.
В данном случае при проверке гипотезы используется односторонняя кри-
тическая область. Если бы нас интересовало не то, какой из пабов более попу-
лярен, а одинаковы ли они по популярности, альтернативная гипотеза выгля-
дела бы следующим образом:
Яр Популярность пабов различна.
В этом случае необходимо было бы использовать двустороннюю критическую
область.
На основании имеющихся данных можно приступать к вычислениям с ис-
пользованием приведенной формулы. Подставим в нее все необходимые для
вычислений значения: к=104,р =#=0,5, N=25.
7
2 Это аналогично ситуации, когда после 25 подбрасываний монеты «орел» выпал 15 раз и
требуется определить, мог ли быть такой результат получен случайно, или мы имели дело с фаль-
шивой монетой.
3 В этом и последующих примерах проверка статистических гипотез осуществляется для а=0,05.
Этот выбор сделан из соображений удобства и не носит принципиального характера.
4 При наличии несовпадающего числа выборов в пользу каждой из альтернатив в формуле
Бернулли используется меньшее из них.
71
КНИГА ДЛЯ ТЕХ, КТО НЕ ЛЮБИТ СТАТИСТИКУ, НО ВЫНУЖДЕН ЕЮ ПОЛЬЗОВАТЬСЯ
В случае использования статистической
таблицы для биномиального теста необхо-
димость в самостоятельных вычислени-
ях отпадает. В таблице 3 (Приложение 2)
для соответствующих значений N и к ука-
зывается вероятность того, что при нали-
чии двух равновероятных альтернатив
(p=q=0,5) сделанное число выборов в
пользу одной из них может считаться слу-
чайным. Приводимые в таблице 3 значения
соответствуют односторонней критической
области.
Если найденное по таблице значение
вероятности больше значения выбранного
уровня значимости а, у нас нет оснований
отвергнуть нулевую гипотезу.
Если найденное из таблицы значение
вероятности меньше или равно значению
уровня значимости а, нулевая гипотеза от-
вергается и принимается альтернативная.
Поскольку на практике число выборов в пользу той или другой альтернати-
вы редко бывает одинаковым (в нашем случае в пользу первого паба высказалось
15 студентов, а в пользу второго — 10), в таблице используется меньшее из двух
чисел, обозначенное какх (то есть х=10).
Находим в таблице 3, что для N=25 и х=10 вероятность р =0,212 (что, ра-
зумеется, совпадает со значением, полученным путем самостоятельных вычис-
лений). Поскольку р=0,212 больше значения а=0,05, у нас нет оснований
отвергнуть нулевую гипотезу. Оба паба пользуются одинаковой популярностью
у студентов, а различия в выборах в пользу одного и другого объясняются дей-
ствием случайных факторов.
Вернемся к игрокам в нарды и разберемся в их ситуации.
Выберем уровень значимости а=0,05 и сформулируем нулевую и альтерна-
тивную гипотезы.
Но: Уровень мастерства игры в нарды Володи не отличается от уровня мас-
терства Алексея.
Нх\ Уровень мастерства игры в нарды Володи отличается от уровня мастер-
ства Алексея (двусторонняя критическая область5).
Нам известно, что А=24 и число побед у Алексея равно семи (выбираем
меньшее из двух чисел). Вновь обратимся к таблице 3 и найдем, что для А=24
их=7 вероятность^ =0,032. Это меньше значения уровня значимости а=0,05,
поэтому нулевую гипотезу можно отвергнуть и принять альтернативную.
’Альтернативная гипотеза не утверждает, что Володя играет лучше Алексея. Она лишь утвер-
ждает, что они имеют различный уровень мастерства.
72
ГЛАВА 3. НЕПАРАМЕТРИЧЕСКАЯ СТАТИСТИКА ДЛЯ СЛУЧАЯ ЕДИНСТВЕННОЙ ВЫБОРКИ
Однако сделанный вывод неверен. Приведенные в таблице 3 значения со-
ответствуют односторонней критической области. Мы же, в соответствии с
альтернативной гипотезой, должны использовать двустороннюю критическую
область. Вопрос о том, как от результата проверки для односторонней крити-
ческой области перейти к результату для двусторонней критической области,
рассматривался нами выше. Здесь действуют те же правила: для того чтобы
получить результат, соответствующий двусторонней критической области,
найденное значение вероятности необходимо удвоить. Получим значение
/3=2x0,032=0,064.
Новое значение вероятности (0,062) оказывается больше значения уровня
значимости (0,05), поэтому нет оснований для того, чтобы отвергнуть нулевую
гипотезу. Между Володей и Алексеем нет различий в уровне мастерства игры
в нарды6.
Если вернуться к таблице 3, то видно, что она ограничена значением
N=25. В том случае, если объем выборки N> 25, для проверки гипотез обыч-
но используется формула, с помощью которой вначале вычисляется значение
Z, а затем, с использованием таблицы ^-распределения (табл. 1, Приложение
2), определяется соответствующая найденному значению z вероятность (пло-
щадь под кривой нормального распределения, лежащая правее или левее z).
Если полученное значение вероятности больше выбранного уровня значи-
мости а, нет оснований, чтобы отвергнуть нулевую гипотезу. Если это зна-
чение меньше или равно а, нулевая гипотеза отвергается и принимается
альтернативная.
Значение z вычисляется по следующей формуле7:
__(x+0,5)-Np
^Npq
(х+0,5) используется в том случае, когда х < Np;
(х—0,5) используется в том случае, когда х > Np.
Подставим в эту формулу данные для первого примера (У=25, х = 10,
Р=?=0,5):
_(х±О,5)-Ар (1О+О,5)-25хО,5_ „
jNpq >/25x0,5x0,5
6 Если бы мы сформулировали альтернативную гипотезу для односторонней критической
области («Володя играет в нарды лучше, чем Алексей»), мы бы могли этот вывод принять (по-
скольку 0,032 < 0,05). Однако гипотеза «Уровень мастерства игры в нарды Володи отличается от
уровня мастерства Алексея» означает двойную проверку: «Володя играет в нарды лучше, чем
Алексей» и «Володя играет в нарды хуже, чем Алексей». Двойной проверки альтернативная ги-
потеза не выдержала.
7 Данной формулой можно пользоваться при любых значениях N, однако по сравнению с
формулой Бернулли она дает менее точные результаты, особенно если //мало. Различия между
результатами двух формул уменьшаются по мере роста N.
73
КНИГА ДЛЯ ТЕХ, КТО НЕ ЛЮБИТ СТАТИСТИКУ, НО ВЫНУЖДЕН ЕЮ ПОЛЬЗОВАТЬСЯ
В таблице для ^-распределения (табл. 1, Приложение 2) находим, что зна-
чению z=-0,8 соответствует вероятностьр =0,2119=0,212, что совпадает с
ранее полученным результатом. Поскольку это значение больше выбранного
уровня значимости а=0,05, у нас нет оснований, чтобы отвергнуть нулевую
гипотезу.
ВКЛЮЧАЕМ КОМПЬЮТЕР И ЗАПУСКАЕМ ПРОГРАММУ SPSS8
Для ответа на вопрос, в самом ли деле один из пивных баров более популярен, чем
другой, создадим переменную «Пиво» (beer) и закодируем выбор в пользу первого
паба («Безумный Макс») как 1, а выбор в пользу второго паба («Пивная корова»),
как 2. Дальнейшая последовательность действий и конечный результат показаны
на рисунках 3.1 —3.4.
Рис. 3.1. Выбор требуемой статистической процедуры
’Общее замечание к использованию программы SPSS для приводимых в книге примеров:
1. Программой SPSS рассчитывается либо значение Z, с последующим определением соответ-
ствующей вероятности р, либо реальное значение вероятности ошибки первого рода (в отличие
от априори выбираемого значения уровня значимости а, обычно равного 0,5; 0,01 или 0,001).
В большинстве случаев получаемые в SPSS результаты, говорящие о значимости различий, соот-
ветствуют двусторонней критической области.
2. Если выбранное исследователем значение а больше (или равно) тех значений, которые
были рассчитаны программой SPSS, нулевая гипотеза отвергается. Если выбранное исследова-
телем а меньше этих значений, нет оснований, чтобы отвергнуть нулевую гипотезу.
74
ГЛАВА 3. НЕПАРАМЕТРИЧЕСКАЯ СТАТИСТИКА ДЛЯ СЛУЧАЯ ЕДИНСТВЕННОЙ ВЫБОРКИ
Рис. 3.2. Биномиальный тест: необходимые действия и настройки
Количество выборов
в пользу одного
и другого пабов
Mad Мах
Beer Cow
BEER Group 1
Group 2
Total
Пропорции сделанных
выборов
15/25-0,6
10/25-0,4
rved
TestP
Проверяемая
пропорция
(2-tailed)
.424
40
1.
Уровень значимости для двусторонней критической области.
В примере альтернативная гипотеза сформулирована для односторонней
критической области. В этом случае приведенное значение необходимо
разделить на 2:0,424/2-0,212. Получили тот же результат, что был получен
ранее при использовании ручных вычислений или статистических таблиц.
(Нулевая гипотеза не отвергается.)
Рис. 3.3. Биномиальный тест: результат
Binomial Test
Category N Observed Prop.
GAME Group 1 1 17 .71
Group 2 2 7 .29
Total 24 1.00
Уровень значимости для двусторонней кри-
тической области. Получен тот же резуль-
тат, что в рассмотренном выше примере для
игроков в нарды. (Нулевая гипотеза не
отвергается.)
Рис. 3.4. Биномиальный тест: результат (пример игроков в нарды)
КНИГАДЛЯ ТЕХ. КТО НЕ ЛЮБИТ СТАТИСТИКУ, НО ВЫНУЖДЕН ЕЮ ПОЛЬЗОВАТЬСЯ
3.2. «ФОРД», «ФИАТ», «ТОЙОТА»,
ИЛИ ТЕСТ X2 ДЛЯ ЕДИНСТВЕННОЙ ВЫБОРКИ
Покупка машины — важный этап в жизни каждой семьи. По улицам изра-
ильских городов бегает несколько десятков марок автомобилей на любой вкус,
но если присмотреться, то создается впечатление, что некоторые марки встре-
чаются чаще других. Для проверки этого предположения Анна и Даниил, со-
бравшиеся обзавестись автомобилем, решили проверить, какие машины чаще
всего встречаются на улицах их города. При этом они договорились фиксиро-
вать не конкретные марки машин, а то, откуда машина «родом», — Америка
(США), Европа, Юго-Восточная Азия (Япония и Южная Корея) или другое
(Россия, Индия, Китай и др.). Случайным образом было проверено 80 машин,
которые распределились в зависимости от места производства следующим
образом (табл. 3.1).
Таблица 3.1
Распределение автомобилей по странам-производителям
Место выпуска Америка Европа Азия Другое Итого
Количество 17 23 32 8 80
Можно ли на основании полученных данных сказать, что все машины поль-
зуются одинаковой популярностью?
Основное отличие данной задачи от предыдущей в том, что сейчас резуль-
таты распределены по более чем двум категориям (в данном случае по четырем
категориям). Остальные условия те же самые: одна выборка и необходимость
проверить, соответствует ли распределение результатов в выборке известному
(или предполагаемому) распределению результатов в популяции.
Для решения подобных задач применяется один из наиболее популярных
непараметрических тестов — тест х2. На страницах этой книги он будет встре-
чаться не один раз.
Существует два основных типа задач, решаемых с помощью этого теста.
Во-первых, сравнение эмпирического распределения качественных признаков
ас теоретическим. Во-вторых, сравнение между со-
бой двух и более эмпирических распределений ка-
чественных признаков. При наличии достаточно
большой выборки тестом х2 можно пользоваться
вместо биномиального теста.
Что касается вида теоретического распределе-
ния, то в нашем случае используется равномерное
распределение. Смысл его в том, что все результа-
ты считаются равновероятными. При наличии
76
ГЛАВА 3. НЕПАРАМЕТРИЧЕСКАЯ СТАТИСТИКА ДЛЯ СЛУЧАЯ ЕДИНСТВЕННОЙ ВЫБОРКИ
четырех стран-производителей автомобилей вероятность встретить машину,
произведенную в какой-либо из них, должна быть одна и та же и равна 1/4=0,25.
Иными словами, если бы эмпирическое распределение результатов полностью
совпало с теоретическим, то в каждую ячейку таблицы попало бы одинаковое
число машин, равное 80:4=20.
С учетом данного обстоятельства запишем окончательный вариант расчет-
ной таблицы для нашего примера (табл. 3.2).
Таблица 3.2
Теоретическое и эмпирическое распределение автомобилей
по странам-производителям
Место выпуска Америка Европа Азия Другое Итого
Теоретическое количество 20 20 20 20 80
Эмпирическое количество 17 23 32 8 80
Дальнейший алгоритм действий прост.
Формулируем нулевую и альтернативную гипотезы и задаем уровень значи-
мости а=0,05.
Но: Все страны-производители машин представлены одинаковым образом
(вероятность встретить на дороге машину, произведенную, например, в США,
равна вероятности встретить машину, произведенную в Европе или в Юго-
Восточной Азии, и т. д.).
Яр Различные страны-производители машин представлены неодинаковым
образом (вероятность встретить машину, произведенную в США, не равна
вероятности встретить машину, произведенную в Европе, в Юго-Восточной
Азии и т. д.).
Затем вычисляется сумма отклонений между наблюдаемыми и теоретиче-
скими значениями по формуле:
7=1 LJ
где Oj — наблюдаемые (observed), или эмпирические, значения (частоты) для
каждой из категорий таблицы 3.2; Ej — ожидаемые (expected), или теоретиче-
ские, значения (частоты) для каждой из категорий таблицы 3.2; к — количест-
во категорий в таблице 3.2.
С учетом введенных обозначений перейдем от таблицы 3.2 к таблице 3.3.
Подставим соответствующие значения Oj и Е} в расчетную формулу:
2_у (Pj-Ej? _(17-20)2 (23-20)2 (32-20)2 (8-20)2 _
Х £ Е} 20 + 20 + 20 + 20 "
=0,45+0,45+7,2+7,2=15,3.
7 7 7 7 7 х
77
КНИГА ДЛЯ ТЕХ, КТО НЕ ЛЮБИТ СТАТИСТИКУ, НО ВЫНУЖДЕН ЕЮ ПОЛЬЗОВАТЬСЯ
Таблица 3.3
Распределение теоретических и эмпирических частот
Категории
1 2 3 4 Итого
Ожидаемые (теоретические) (£) и эмпирические (О) частоты РМ II II ю м о £2 = 20 О2=23 II II NJ О Е4=20 О4=8 80
Полученное значение х!мпиР сравнивается со значением Хкритич, которое бе-
рется из таблицы критических значений для теста %2 (табл. 2, Приложение 2)
в зависимости от выбранного уровня значимости а и числа степеней свободы
df. В свою очередь, число степеней свободы для теста %2 зависит от размера
расчетной таблицы и равно df=(k— 1). В нашем случае df=(k— 1)=(4—1)=3.
Если х1мпир меньше Хкритич, то нет оснований отвергнуть нулевую гипотезу
(нет значимых различий между эмпирическим и теоретическим распределени-
ем: автомобили всех стран-производителей одинаково представлены на город-
ских улицах).
Если Хэмпир больше или равно х1Ритич, то нулевая гипотеза отклоняется и
принимается альтернативная (эмпирическое распределение значимо отлича-
ется от теоретического: автомобили одних стран-производителей встречаются
на городских улицах чаще или реже, чем автомобили других).
Из таблицы 2 находим, что для df=3 и а=0,05 Хкритич =7,82.
Поскольку Хэмпир = 15,3 больше, чем х1ритич=7,82, то нулевая гипотеза от-
клоняется и принимается альтернативная. Автомобили одних стран-произво-
дителей встречаются на городских улицах чаще или реже, чем автомобили
других.
Сделаем несколько замечаний относительно теста х2.
1. Для его корректного применения необходима достаточно большая вы-
борка (не менее 30 значений).
2. Если df= 1 (или к =2), все ожидаемые частоты должны быть больше 5.
3. Если df> 1 (или к > 2), часть ожидаемых частот (не более 20%)могут быть
менее 5. При этом не должно быть ожидаемых частот меньших 1.
4. В том случае, если предыдущее условие не выполняется, требуется укруп-
нение категорий (объединение нескольких категорий в одну) с целью
избавления от ожидаемых (теоретических) частот меньших 5 или 1.
Например, в рассмотренном примере вместо четырех возможно исполь-
зование трех категорий «Америка», «Европа», «Азия и другое». Это при-
ведет к росту значения теоретических (ожидаемых) частот (80 значений
будут распределены по трем категориям, по 26,67 значений в каждой
категории).
5. Тест х2 позволяет выявлять отличие эмпирического распределения от
теоретического или отличия между несколькими эмпирическими распре-
делениями, но не выявляет направление этих отличий9.
’ Из этого следует, что здесь неприменимо понятие односторонней критической области (за
одним исключением, которое рассмотрено ниже).
78
ГЛАВА 3. НЕПАРАМЕТРИЧЕСКАЯ СТАТИСТИКА ДЛЯ СЛУЧАЯ ЕДИНСТВЕННОЙ ВЫБОРКИ
ВКЛЮЧАЕМ КОМПЬЮТЕР...
Создадим переменную «Автомобили» (cars) с использованием следующих обозна-
чений: 1 — США, 2— Европа, 3 — Азия, 4 — другие страны. Представим в этой пе-
ременной данные о странах-производителях для 80 автомобилей. Дальнейшая оче-
редность действий и конечный результат показаны на рисунках 3.5-3.7.
Рис. 3.5. Выбор требуемой статистической процедуры
Рис. 3.6. Тест х2 для единственной выборки: необходимые действия и настройки
79
КНИГА ДЛЯ ТЕХ, КТО НЕ ЛЮБИТ СТАТИСТИКУ. НО ВЫНУЖДЕН ЕЮ ПОЛЬЗОВАТЬСЯ
Chi-Square Test
Frequencies
Наблюдаемое (эмпири-
ческое) распределение
частот
uSA”
Europe
Asia
Orher
Ожидаемое (теоретиче-
ское) распределение
. частот
Эмпирическое значение
для теста %2
CARS
ExpecteA^TResiduat
ЗЮ
Разность между эмпирически-
ми и теоретическими частотами
Chi-Square*
df
Asymp. Sip.
а. о cells (.0%) h
5. The minim
ected frequencies less than
ected cell frequency is 20.0.
Рис. 3.7. Тест x2 для единственной выборки: результат
Уровень значимости.
(Нулевая гипотеза отвер-
гается.)
3.3. КРАСОТА ЛЮБИМОЙ В ГЛАЗАХ ЛЮБЯЩЕГО,
ИЛИ ТЕСТ КОЛМОГОРОВА-СМИРНОВА
ДЛЯ ЕДИНСТВЕННОЙ ВЫБОРКИ
По мнению ряда психологов, размер глаз является одним из факторов,
определяющим степень привлекательности лица противоположного пола.
Для проверки этой гипотезы группе молодых мужчин из 12 человек предъяв-
лялись 5 фотографий одной и той же молодой женщины, снятой в различных
ракурсах. Различия между фотографиями заключались в том, что после ком-
пьютерной обработки на каждой из них у женщины был различный размер глаз
(испытуемые не знали об этом). От мужчин требовалось выбрать наиболее
привлекательную, с их точки зрения, фотографию из пяти предложенных.
Результаты их выборов приведены в таблице 3.4.
80
ГЛАВА 3. НЕПАРАМЕТРИЧЕСКАЯ СТАТИСТИКА ДЛЯ СЛУЧАЯ ЕДИНСТВЕННОЙ ВЫБОРКИ
Таблица 3.4
Количество выборов фотографии в зависимости от размера глаз
Размер глаз на фотографии в порядке возрастания 1 2 3 4 5 Итого
Количество выборов (частота) 0 1 5 4 2 12
Можно ли утверждать, что выдвинутая гипотеза о влиянии размера глаз на
привлекательность верна?
На первый взгляд данная задача мало чем отличается от предыдущей.
На самом же деле между ними есть одно принципиальное различие. До сих пор
мы использовали результаты, представленные в шкале наименований. В этой
шкале не важно, в какой последовательности расположены те категории, на
которые разбиты полученные результаты. Результат, полученный в предыдущем
примере, не изменится, если мы расположим страны-производители автомо-
билей в другой последовательности.
В данном случае результаты представлены в шкале порядка и расположены
по мере возрастания определенного признака (размер глаз на фотографии). Мы
уже не можем произвольно поменять эти категории местами.
В остальном решается та же задача: необходимо сравнить эмпирическое
распределение результатов с теоретическим. В качестве теоретического рас-
пределения может быть выбрано, например, нормальное распределение. Однако
в данном случае выберем в качестве теоретического распределения уже встре-
чавшееся выше равномерное распределение. Если размер глаз не влияет на
степень привлекательности лица на фотографии, то можно ожидать одинако-
вой частоты выборов для каждой из них. Она будет равна 12:5=2,4 (дробное
значение не должно смущать, поскольку мы имеем дело с теоретическими
значениями). В этом случае таблица приобретет следующий вид (табл. 3.5).
Таблица 3.5
Распределение теоретических и эмпирических частот
Размер глаз на фотографии в порядке возрастания 1 2 3 4 5 Итого
Теоретическая частота 2,4 2,4 2,4 2,4 2,4 12
Эмпирическая частота 0 1 5 4 2 12
Для подобных задач часто применяется тест Колмогорова—Смирнова10
для единственной выборки. Он позволяет сравнивать эмпирическое распреде-
10 Оба автора работали независимо друг от друга и решали разный круг задач. Колмогоров
решал задачу сравнения эмпирического распределения с теоретическим, Смирнов — задачу
сравнения двух эмпирических распределений. Поэтому в ряде случаев, когда речь идет об анали-
зе одной выборки, говорят о тесте Колмогорова; когда анализируются две независимые выбор-
ки — о тесте Смирнова (Conover, 1999].
81
КНИГА ДЛЯ ТЕХ, КТО НЕ ЛЮБИТ СТАТИСТИКУ, НО ВЫНУЖДЕН ЕЮ ПОЛЬЗОВАТЬСЯ
ление с теоретическим для результатов,
измеренных в шкалах не ниже, чем шкала
порядка.
Выберем уровень значимости а=0,05
и сформулируем нулевую и альтернативную
гипотезы,
Но: Эмпирическое распределение ре-
зультатов выбора фотографии не отличает-
ся от равномерного.
Яр Эмпирическое распределение ре-
зультатов выбора фотографии отличается
от равномерного.
Как и в случае теста %2, вычисляется величина расхождений между теоре-
тическим и эмпирическим распределением результатов. Но если для теста х2
рассогласование между теоретическими и эмпирическими значениями вы-
числялось отдельно для каждой ячейки расчетной таблицы, то в тесте
Колмогорова—Смирнова для единственной выборки последовательно срав-
ниваются накопленные к данному разряду таблицы эмпирические и теорети-
ческие относительные частоты. Затем определяется значение:
Р = тах|^(Х)-5;.(%)|.
В этом выражении F/Af) — накопленные к данному разряду значения отно-
сительных теоретических частот; S^X) — накопленные к данному разряду
значения относительных эмпирических частот; D — максимальное значение
разницы (по модулю) между Ft(X) и 5|(X) из всех имеющихся.
В статистической таблице для теста Колмогорова—Смирнова (случай един-
ственной выборки) (см. табл. 4, Приложение 2) приведены критические зна-
чения D и соответствующие им значения вероятностей в зависимости от объ-
ема выборки N. Если приведенная в таблице вероятность, соответствующая
найденному значению Яэмпир, больше выбранного уровня значимости а, нет
оснований отвергнуть нулевую гипотезу. Если приведенная в таблице вероят-
ность меньше или равна выбранному уровню значимости а, нулевая гипотеза
отклоняется и принимается альтернативная.
Создадим новую таблицу и проведем все необходимые вычисления. Учтем,
что выражение для D не содержит данных о размере выборки. Поэтому в данном
тесте используются значения относительных частот. Чтобы перейти к ним,
необходимо каждое значение в таблице разделить на размер выборки (в нашем
случае в выборке 12 человек). Также предусмотрим в таблице возможность для
вычисления накопленных относительных частот F^X), S^X) и разности между
ними. Таблица примет такой вид (табл. 3.6).
Выбираем в последней строчке максимальное значение D=3,8:12=0,317.
В таблице 4 (Приложение 2) в строке, соответствующей N=12, ищем зна-
чение £>; равное 0,317. Это значение находится между двумя табличными зна-
82
ГЛАВА 3. НЕПАРАМЕТРИЧЕСКАЯ СТАТИСТИКА ДЛЯ СЛУЧАЯ ЕДИНСТВЕННОЙ ВЫБОРКИ
Таблица 3.6
Итоговая таблица для теста Колмогорова—Смирнова
Размер глаз на фотографии в порядке возрастания 1 2 3 4 5
Относительная теоретическая частота 2,4/12 2,4/12 2,4/12 2,4/12 2,4/12
F^X) — накопленная относи- тельная теоретическая частота 2.4/12 4,8/12 7,2/12 9,6/12 12/12
Относительная эмпирическая частота 0/12 1/12 5/12 4/12 2/12
St(X) — накопленная относи- тельная эмпирическая частота 0/12 1/12 6/12 10/12 12/12
2,4/12 3,8/12 1,2/12 0,4/12 0
чениями D =0,296 (р =0,2) и £>=0,338 (р =0,1). Можно сказать, что вероятность,
соответствующая значению £>эмпир=0,317, расположена между значениями
jp=0,2 и р =0,1, или 0,1 < р < 0,2. В любом случае это больше, чем выбранное
значение уровня значимости а=0,05. Следовательно, у нас нет оснований,
чтобы отвергнуть нулевую гипотезу. Эмпирическое распределение результатов
выбора фотографии не отличается от равномерного. Изменение размера глаз
на фотографиях не оказало значимого влияния на результаты их выбора.
ВКЛЮЧАЕМ КОМПЬЮТЕР...
К сожалению, компьютерный вариант теста Колмогорова—Смирнова для единст-
венной выборки заметным образом отличается от рассмотренного выше. Данный
тест был адаптирован для осуществления вычислений вручную, что не лучшим
образом сказалось на его качестве. Упрощенный алгоритм вычислений сделал дан-
ный тест более удобным для использования, но менее точным, что приводит к
ошибкам при проверке гипотез.
В программе SPSS этот тест реализован в своем первозданном виде. Применяемый
алгоритм вычислений [SPSS Statistical Algorithms, 1986; Sheskin, 2004] отличается от
того, который использовался нами в рассмотренном выше примере. Покажем, как
работает неадаптированный алгоритм вычислений, а затем перейдем к программе
SPSS.
Запишем результаты эксперимента в нёсгруппированном виде и выполним все
необходимые для теста Колмогорова—Смирнова для единственной выборки вы-
числения (табл. 3.7).
В первой колонке расположены испытуемые, во второй — сделанные ими выборы
той или иной фотографии. Испытуемые упорядочены в соответствии с номером
выбранной ими фотографии.
Относительная эмпирическая частота выбора той или иной фотографии у всех ис-
пытуемых одинакова и равна !/12. В третьей колонке расположены значения нако-
пленных (кумулятивных) частот, которые меняются от Уп до 1 (эмпирическая ку-
мулятивная функция распределения).
83
КНИГА ДЛЯ ТЕХ, КТО НЕ ЛЮБИТ СТАТИСТИКУ, НО ВЫНУЖДЕН ЕЮ ПОЛЬЗОВАТЬСЯ
Таблица 3.7
Тест Колмогорова—Смирнова для единственной выборки:
Неадаптированный алгоритм действий
№ Номер выбранной фотографии (х,) х‘ . Xjnax -X-min Дх,)-Г0(х/) (А) (Д)
1 2 1/12 0 0,083 0
2 3 2/12 1/3 -0,167 -0,250
3 3 3/12 1/3 -0,083 -0,167
4 3 4/12 1/3 0 -0,083
5 3 5/12 1/3 0,083 ' 0
6 3 6/12 1/3 0,167 0,083
7 4 7/12 2/3 -0,083 -0,167
8 4 8/12 2/3 0 -0,083
9 4 9/12 2/3 0,083 0
10 4 ‘ 10/12 2/3 0,167 0,083
11 5 11/12 3/3 -0,083 -0,167
12 5 12/12 3/3 0 -0,083
В четвертой колонке расположены значения теоретической кумулятивной функции
распределения. При использовании равномерного распределения вычисление зна-
чений теоретической кумулятивной функции распределения производится по сле-
дующей формуле:
^max ^min
где Fo(Xi) — кумулятивная частота, соответствующая значению х,; xmin— минималь-
ное экспериментальное значение. В нашем случае это фотография номер 2 (посколь-
ку фотография номер 1 не получила ни одного выбора, она исключается из анализа);
хтах — максимальное экспериментальное значение. В нашем примере это фотогра-
фия номер 5.
В пятой колонке записана разность между значениями накопленных (кумулятивных)
эмпирических и теоретических относительных частот для каждого из 12 испытуемых.
В шестой колонке записана разность между предыдущим значением эмпирической
кумулятивной частоты и текущим значением теоретической кумулятивной частоты.
Например, для второго испытуемого значение —0,250 получается, если из предыду-
щего (то есть первого) значения эмпирической кумулятивной частоты, равного 7i2,
вычесть текущее (то есть второе) значение теоретической кумулятивной частоты,
равное 1/з:
1/12-1/3 = -0,250.
Выбираем в пятой колонке наибольшее положительное значение. Это Д=0,167.
Выбираем в шестой колонке наименьшее отрицательное значение. Это Л/=—0,250.
84
ГЛАВА 3. НЕПАРАМЕТРИЧЕСКАЯ СТАТИСТИКА ДЛЯ СЛУЧАЯ ЕДИНСТВЕННОЙ ВЫБОРКИ
Сравниваем их абсолютные значения и выбираем среди них наибольшее. Очевидно,
что это 0,250.
После этого находим значение параметра Z, который используется в тесте Колмо-
горова-Смирнова для единственной выборки:
Z = тах(|Д I, |Д \)4n = 0,250V12 = 0,866.
Сейчас переходим к программе SPSS.
Представим в переменной «Глаза» (eyes) сделанные испытуемыми выборы (цифры
означают, какую фотографию выбрал испытуемый). Все дальнейшие действия и
получаемый результат для теста Колмогорова—Смирнова для единственной выбор-
ки показаны на рис. 3.8—3.10.
® NonPar ametr - SPSS Data Edftor
Hie Edit View Data Transform [ Analyze Graphs Utilities
Reports
Descriptive Statutes
Compare Means
General Linear Model
M*xed Models
Correlate
Regression
Logbnear
Classfy
Data Reduction
Scale
12. eyes
2
3
4
5
6
7
8
9
10
11
12
13
eyes
______2j
______3j_
______3!
з|
___3'
3"
4
4
______4
4T
______5l_
51
NonparameWc Tests
Window Help
Time Series
Survival
Multpie Response
Missing Value Analysis...
Chi-Square.
Bruxrual...
Runs...
1 -Sample K-5...
Нажать
r
2 Independent Samples.
К Independent Samples.
2 Related Sampes...
К Related Samples...
Рис. 3.8. Выбор требуемой статистической процедуры
Рис. 3.9. Тест Колмогорова—Смирнова для единственной выборки:
необходимые действия и настройки
85
КНИГА ДЛЯ ТЕХ, КТО НЕ ЛЮБИТ СТАТИСТИКУ, НО ВЫНУЖДЕН ЕЮ ПОЛЬЗОВАТЬСЯ
N
Uniform Parameters
Most Extreme
Differences
Смысл всех значений
рассмотрен выше
Test
EYES
Minimum
Maximum
Absolute
Positive
Negative
.441
Kolmogorov-Smirnov Z
Asymp Sig (2-tailed)
a. Testdistributlonjs-L^---
b. CalculateF^yp0BeHb значимости.
( (Нулевая гипотеза не
X. отвергается.)
5
.250
.167
.250
6
Рис. 3.10. Тест Колмогорова—Смирнова для единственной выборки: результат
3.4. «ТОЧНОСТЬ - ВЕЖЛИВОСТЬ КОРОЛЕЙ»,
ИЛИ НЕМНОГО ОБ АНАЛИЗЕ
ПОСЛЕДОВАТЕЛЬНОСТЕЙ
Как известно, в процессе индивидуальной или групповой терапии многие
формы поведения клиентов представляют собой явные или неявные послания
в адрес терапевта или других клиентов. «Расшифровка» таких посланий может
дать ценную дополнительную информацию о ходе индивидуального или груп-
пового терапевтического процесса. Например, в роли одного из подобных
посланий могут выступать различного рода опоздания клиента, переносы или
отмены им встреч с терапевтом и др.
В ходе длительной индивидуальной терапии терапевт решил сделать случаи
опозданий своего клиента предметом обсуждения с ним. Предварительно, на
протяжении последних 10 встреч, он фиксировал случаи своевременного (1) и
несвоевременного (0) прихода клиента на сеанс терапии. В результате была
получена такая последовательность:
0,1,0,1,1,0,1,1,0,0.
Можно ли на основе полученных результатов утверждать, что опоздания
клиента носят неслучайный характер?
С подобного рода задачами часто приходится иметь дело при наличии по-
следовательности дихотомических значений какой-либо переменной (напри-
86
ГЛАВА 3. НЕПАРАМЕТРИЧЕСКАЯ СТАТИСТИКА ДЛЯ СЛУЧАЯ ЕДИНСТВЕННОЙ ВЫБОРКИ
мер, чередование мужчин и женщин в очереди, чередование черного и крас-
ного цвета при игре в рулетку, чередование выигрышей и проигрышей
спортивной команды и др.). Основной возникающий здесь вопрос — подчи-
няется ли чередование результатов какой-либо закономерности (извечная
мечта любителей рулетки — вывести «формулу успеха») или носит случайный
характер.
Для ответа на данный вопрос чаще всего используется тест последователь-
ностей (или серий).
Как обычно, выберем уровень значимости а=0,05 и сформулируем нулевую
и альтернативную гипотезы.
Но: Чередование случаев прихода клиента вовремя и с опозданием носит
случайный характер.
Нх-. Чередование случаев прихода клиента вовремя и с опозданием носит
неслучайный характер.
Для приведенного примера определим число случаев своевременного при-
хода клиента («| =5) и число случаев его прихода с опозданием (п2=5). Затем
определим, из скольких серий повторяющихся значений 0 или 1 состоит при-
веденная последовательность, и подчеркнем их (одиночное значение нуля или
единицы также образует серию):
Как видно, последовательность состоит из 7 серий: три серии из одного нуля,
одна серия из одной единицы, две серии из двух единиц и одна серия из двух
нулей.
Полученное значение (обозначим его г) сравнивается с двумя критическими
значениями, которые находятся в специальной таблице, используемой для
проверки последовательностей при известных значениях пь п2 и а (см. табл. 6,
Приложение 2).
Если полученное значение числа серий г меньше первого критического
значения или равно ему, или же больше второго критического значения
или равно ему, нет оснований принять нулевую гипотезу. Она отвергается
на заданном уровне а. Последовательность в этом случае признается неслу-
чайной11.
11В любой последовательности можно найти определенное число серий. Предположения о
неслучайном характере последовательности возникают тогда, когда серий или слишком мало,
или слишком много. Поэтому вначале проверяется предположение о том, не слишком ли мало в
87
КНИГА ДЛЯ ТЕХ. КТО НЕ ЛЮБИТ СТАТИСТИКУ, НО ВЫНУЖДЕН ЕЮ ПОЛЬЗОВАТЬСЯ
В нашем примере г=7, ~п2=5 и уровень значимости а=0,05. В таблице 5
находим, что первое критическое значение гкриТич|=2, второе критическое зна-
чение Гкритач2= 10. Поскольку ни одно из условий для отклонения нулевой ги-
потезы не выполняется, она принимается. Опоздания клиента носят случайный
характер.
В ряде случаев длина последовательности может быть больше возможностей
статистических таблиц, рассчитанных для выборки ограниченных размеров.
Например, «помешанные» на игре в рулетку могут часами наблюдать за игрой
и фиксировать результаты («красное» — «черное») в надежде получить «фор-
мулу успеха». Для больших выборок (больше 50 значений) используется иной
подход к анализу последовательностей, основанный на свойствах нормально-
го распределения и реализованный в программе SPSS.
ВКЛЮЧАЕМ КОМПЬЮТЕР...
Здесь мы вновь сталкиваемся с ситуацией, знакомой по тесту Колмогорова—Смир-
нова для единственной выборки. В программе SPSS используется алгоритм вычис-
лений для теста последовательностей [SPSS Statistical Algorithms, 1986; Sheskin, 2004J,
отличающийся от рассмотренного выше и предназначенного для случая малой
выборки и вычислений вручную.
В программе SPSS рассчитывается значение z по следующей общей формуле (ис-
пользуются введенные выше обозначения):
r_f
f2nln2(2ntn2-nl-n2) ‘
У (^+«г)2(«|+Л2-1)
В случае маленькой выборки (менее 50 значений), в эту формулу вводится по-
последовательности серий, чтобы она могла считаться случайной. Затем предположение о том,
не слишком ли много в последовательности серий, чтобы она могла считаться случайной. Из этого,
кстати, следует, что здесь используется двусторонняя критическая область.
88
ГЛАВА 3. НЕПАРАМЕТРИЧЕСКАЯ СТАТИСТИКА ДЛЯ СЛУЧАЯ ЕДИНСТВЕННОЙ ВЫБОРКИ
Подставим в формулу наши значения (г=7, п}=л2=5):
r-f’Si+l'Lo.S 7-(^-0,5
(”i+”2 J \ 5+5 /
12x5x5(2x5x5-5-5)
V (и1+л2)2(Я|+Я2-1) ]j (5+5)2(5+5-1)
Вероятность, соответствующая найденному значению г, равна р=0,3685. Посколь-
ку в рассмотренном примере используется двусторонняя критическая область,
данное значение вероятности удваивается: р ==0,737
ПОСЛЕ СДЕЛАННЫХ ЗАМЕЧАНИЙ ПЕРЕЙДЕМ К ПРОГРАММЕ SPSS.
Перенесем нашу последовательность в переменную «runs».
Дальнейший порядок действий и результат показаны на рис. 3.11—3.13.
NonParametr - SPSS Data Editor
Fite Edt View Data Transform Analyze Graphs Unities Window Help
cslHlel ^1 «|.-Чк| Rep0"‘
.1 - J~J £XJ J Descrptive Statistics »
53 runs Compare Means ►
Рис. 3.11. Выбор требуемой статистической процедуры
Рис. 3.12. Тест последовательностей: необходимые действия и настройки
89
КНИГА ДЛЯ ТЕХ, КТО НЕ ЛЮБИТ СТАТИСТИКУ. НО ВЫНУЖДЕН ЕЮ ПОЛЬЗОВАТЬСЯ
Длина последовательности
RUNS
Рис. 3.13. Тест последовательностей: результат
Test Value*
Total Cases
Number of Runs
. Z
Asymp.Sig. (2-tailed)
----------—^Usi
Уровень значимости
(нулевая гипотеза не
отвергается)
Проверяемое значение
(в соответствии с пользо-
вательской настройкой)
Число серий в последо-
вательности
Этим примером мы завершаем рассмотрение случая одной выборки. Как
можно видеть из приведенных примеров, анализ одной выборки в первую
очередь связан с поиском ответа на вопрос, отличается ли эмпирическое рас-
пределение результатов от теоретического, которому подчиняется популяция.
В качестве теоретического распределения в приведенных примерах использо-
валось равномерное распределение. Разумеется, это не единственно возможный
вид распределения, хотя, возможно, один из наиболее популярных для круга
тех задач, которые были рассмотрены.
Следующий шаг — рассмотреть ситуацию с двумя и более выборками, ко-
торые, как известно, могут быть независимыми и зависимыми.
Глава 4
«ЧТО БЫЛО, ТО И ТЕПЕРЬ ЕСТЬ,
И ЧТО БУДЕТ, ТО УЖЕ БЫЛО»',
ИЛИ СЛУЧАЙ ДВУХ
ЗАВИСИМЫХ ВЫБОРОК
При проведении различных исследований с одной и той же выборкой за-
частую приходится иметь дело несколько раз. Например, при изучении эффек-
тивности групповой терапии какой-либо показатель (например, уровень тре-
вожности участников группы) измеряется, как минимум, дважды — до начала
работы группы и после ее окончания.
В подобных случаях мы имеем дело с зависимыми или связанными выбор-
ками. Многие непараметрические методы статистики предназначены для ра-
боты с такими выборками с целью выявления происходящих изменений по
принципу «до и после».
Ниже рассмотрены три наиболее популярных непараметрических теста,
предназначенных для работы с двумя связанными (зависимыми) выборками.
4.1. РОДЫ БЕЗ ПРОБЛЕМ, ИЛИ ТЕСТ МАКНЕМАРА
Катя — будущая мама, через несколько месяцев ей предстоят первые в ее
жизни роды. Она очень тревожится по поводу протекания беременности и
будущих родов. Психолог в Центре матери и ребенка, к которому она обратилась
за помощью, предложил ей начать посещать группу поддержки для беременных
женщин. Катя склонна принять предложение, но она не уверена, сможет ли
участие в группе снизить уровень ее тревожности. Она решила пообщаться с
женщинами, у которых был опыт участия в подобных группах. Расспросив
35 женщин, Катя получила следующие результаты:
1 Еккл. 3,15.
91
КНИГА ДЛЯ ТЕХ, КТО НЕ ЛЮБИТ СТАТИСТИКУ, НО ВЫНУЖДЕН ЕЮ ПОЛЬЗОВАТЬСЯ
1. Из 20 женщин, которые до начала участия в группе имели повышенный
уровень тревожности, 6 человек сказали, что группа им не помогла, 14 человек
сказали, что их тревожность значительно понизилась.
2. Из 15 женщин, которые не имели проблем с тревожностью, 4 человека
признались, что после участия в работе группы их тревожность повысилась,
11 человек не заметили каких-либо изменений в уровне своей тревожности.
Можно ли на основании полученных данных утверждать, что участие в ра-
боте группы влияет на уровень предродовой тревожности?
Приведенный пример является одним из типичных для зависимых выборок
типа «до и после».
В том случае, если результаты «до и после» выражены в дихотомической
шкале (в нашем случае рассматриваются два уровня тревожности — повышен-
ная и пониженная/нормальная тревожность), чаще всего применяется тест
МакНемара. С его помощью можно определить, есть ли значимые различия
между результатами первого («до») и второго («после») измерения, выражен-
ными в дихотомической шкале.
Представим результаты «до и после» в виде таблицы 2x2 следующего вида
(табл. 4.1).
Таблица 4.1
Предродовая тревожность до и после участия в работе группы
После
— +
До + А В
— С D .
В нашем случае «+». означает высокий уровень тревожности, а «—» низкий
или нормальный.
Несложно видеть, что индикатором изменений по принципу «до и после»
являются значения А и D. Значения В и С говорят об отсутствии изменений.
Ситуация «до и после», представленная таблицей 4.1, близка к ситуации,
рассмотренной нами в параграфе 3.1, где был описан биномиальный тест.
Имеются две альтернативы для возможных изменений: высокая тревожность
после участия в работе группы понизится, низкая тревожность после участия
в работе труппы повысится. Обе альтернативы равновероятны (то естьр =q=0,5),
в пользу одной из них получено А результатов, в пользу другой — D результатов.
Необходимо определить вероятность получения такого результата.
Так же как в биномиальном тесте, искомая вероятность (для односторонней
критической области) вычисляется по формуле Бернулли:
р(х <к) =
i[A'D
/=0у 1
(0,5)<л+-°>,
где k=min(A, D).
92
ГЛАВА 4. СЛУЧАЙ ДВУХ ЗАВИСИМЫХ ВЫБОРОК
Проделаем необходимые вычисления.
Выберем уровень значимости а=0,05 и сформулируем соответствующие
гипотезы. Поскольку именно значения А и D говорят об изменениях «до и
после», зачастую нулевую гипотезу формулируют по отношению к этим зна-
чениям. По сути дела, проверяется, существуют ли между А и D значимые
различия.
Но: Участие в работе группы не влияет на уровень предродовой тревожности.
Яр Участие в работе группы влияет на уровень предродовой тревожности
(двусторонняя критическая область).
Построим таблицу для полученных Катей данных (табл. 4.2).
Таблица 4.2
Значения предродовой тревожности до и после участия в работе группы
Тревожность «после»
Низкая Высокая
Тревожность «до» Высокая 14 6
Низкая 11 4
Л = 14; В =6; C=ll; Z)=4; k=min(A, Z))=min(14,4)=4.
Подставим в формулу Бернулли необходимые значения.
р(х^к)=5\ Р+2)1(0,5)<л+р> =|-^-1(0,5)18 +f—\о,5)18 +|-^-)(0,5)18 +
/ J' ’ ^0!18! J ^1!17! J 7 ^2116! J
+f——1(0,5)18+f-^-1(0,5)18 = 0,01544.
^3!15! J (4!14! J
Если значение (A +D) не выходит за рамки возможностей таблицы для би-
номиального теста (таблица 3, Приложение 2), то потребность в проделанных
выше вычислениях отпадает. Находим в этой таблице для N= (4 + Z)) = 18 и х=4
вероятность р =0,015 (для односторонней критической области, что, разуме-
ется, совпадает со значением, полученным выше).
С учетом того, что альтернативная гипотеза была сформулирована для дву-
сторонней критической области, удваиваем полученное значение вероятности:
р =0,031.
Поскольку полученное значение вероятности (р =0,031) меньше выбранно-
го значения уровня значимости а=0,05, нулевая гипотеза отвергается и при-
нимается альтернативная. На уровне значимости а.=0,05 можно считать, что
участие в группе поддержки для беременных женщин влияет на уровень пред-
родовой тревожности.
На этом можно было бы остановиться, если бы не одно существенное об-
стоятельство. По сути дела, мы получили подтверждение предположения, что
93
КНИГА ДЛЯ ТЕХ. КТО НЕ ЛЮБИТ СТАТИСТИКУ, НО ВЫНУЖДЕН ЕЮ ПОЛЬЗОВАТЬСЯ
предродовая тревожность после участия в работе группы отличается от анало-
гичной тревожности до прихода в группу. Но мы не получили ответа на вопрос:
в какую сторону отличается? Тревожность уменьшилась или увеличилась?
Очевидно, результаты теряют смысл, если тревожность участников группы
возрастает. Для Кати важно снижение тревожности, поэтому в данном приме-
ре была неудачно сформулирована альтернативная гипотеза.
Другая формулировка альтернативной гипотезы будет выглядеть следующим
образом:
Hi: Участие в работе группы снижает уровень повышенной предродовой
тревожности (односторонняя критическая область).
Нам необходимо вновь вернуться к результату, полученному по формуле
Бернулли, и использовать его (без удвоения): р =0,0154. Это значение разуме-
ется, меньше чем а=0,05, поэтому нулевая гипотеза вновь отвергается и при-
нимается альтернативная. Участие в группе поддержки для беременных женщин
снижает у них повышенный уровень предродовой тревожности.
В том случае, когда (A +D) > 10, можно пользоваться менее точной, но более
удобной расчетной формулой, по которой вычисляется эмпирический показа-
тель, близкий по смыслу к рассмотренному выше показателю %2 и имеющий то
же обозначение:
(-4 + 0)'
Полученное по этой формуле значение Хэмпир сравнивается с Хкритич, которое
берется из таблицы критических значений для теста х2 при выбранном уровне
значимости а и числе степеней свободы df=(r—1)(£— 1), где г—число строк в
таблице, к — число столбцов. Поскольку в тесте МакНемара всегда использу-
ется таблица размером 2x2 для дихотомических переменных, г=к=2 и значе-
ние df всегда будет равно (2 -1 )(2 — 1) = 1 х 1 = 1.
Если эмпирическое значение Хэмпир будет меньше Хкритич, нет оснований для
того, чтобы отвергнуть нулевую гипотезу. Если же значение х2эмпир будет боль-
ше или равно Хкритич, нулевая гипотеза отвергается и принимается альтерна-
тивная.
Подставим в расчетную формулу для х2 необходимые значения:
Х2 =
(Л-D)2 _(14-4)2 _Ю0
(Л + Л) (14+4) 18
В таблице 2 (Приложение 2) для теста х2 находим Хкритич Для df= 1 и уровня
значимости а=0,05: Хкритич = 3,84.
Поскольку Хэмпир(5,56) >Хкритич (3,84), нулевая гипотеза отвергается и при-
нимается альтернативная.
При использовании теста МакНемара рекомендуется вводить так называе-
мую поправку на непрерывность, смысл которой в том, что теоретическое
94
ГЛАВА 4. СЛУЧАЙ ДВУХ ЗАВИСИМЫХ ВЫБОРОК
распределение %2 носит непрерывный характер, но применяется к дискретным
данным. Исправленная формула для вычисления у2 выглядит следующим об-
разом:
(4+л)
Вычислим новое значение х2 с учетом поправки на непрерывность:
(|Л-О|-1); (|14-4|-1)\.В1
* (Л + Д) (14+4) 18 ’
Поскольку новое значение Хэмпир по-прежнему больше Х^ритич“3,84, то все
сделанные ранее выводы остаются в силе2.
ВКЛЮЧАЕМ КОМПЬЮТЕР...
Перенесем сведения о тревожности (0 — низкая; 1 — высокая) до и после участия в
группе в переменные «До» (before) и «После» (after).
Остальная последовательность действий и получаемый результат показаны на
рис. 4.1-4.3.
Q NonParametr * SPSS Data Editor
File Edit View Data Transform Analyze Graphs Utilities Window Help
|2|я|£| ЁЦ| уф.I Ej|
52: runs
before after
Reports
Descriptive Statistics
Compare Means
General Linear Model
Mixed Models
з__________
4 II
5 1_
6 __________|
7 __________1_
8 _____II
9 __________II
10 ___________II
11 1
Correlate
Regression
loglinear
Classify
Data Reduction
Scale
Nonparametnc Tests
Time Senes
Survival
Multiple Response
Missing Vakje Analysis...
12 _________|
13 1
1 1
2 1
Рис. 4.1. Выбор требуемой статистической процедуры
2 Мы уже говорили о том, что проверка на уровне значимости а для двусторонней критической
области фактически означает проверку на уровне значимости а/2 для двух односторонних кри-
тических областей (правосторонней и левосторонней). Поэтому, если на уровне значимости
а=0,05 принимается альтернативная гипотеза о том, что участие в работе группы влияет на уро-
вень предродовой тревожности, то это одновременно означает, что на уровне значимости а=0,025
принимается гипотеза о том, что после участия в работе группы повышенная предродовая тре-
вожность снижается.
95
КНИГА ДЛЯ ТЕХ, КТО НЕ ЛЮБИТ СТАТИСТИКУ, НО ВЫНУЖДЕН ЕЮ ПОЛЬЗОВАТЬСЯ
Рис. 4.2. Тест МакНемара: необходимые действия и настройки
Рис. 4.3. Тест МакНемара: результат
ГЛАВА 4. СЛУЧАЙ ДВУХ ЗАВИСИМЫХ ВЫБОРОК
Test Statistics^
N
ExactSig (2-tailed)
a. Binomial distribution
Anxiety before
& Anxiety alter
35
<03Г
Рис. 4.3. Окончание
Уровень значимости для двусторонней критической
области. Для перехода к односторонней критической
области это значение необходимо разделить на 2.
(Нулевая гипотеза отвергается.)
4.2. КАК СТАТЬ ОТЛИЧНИКОМ,
ИЛИ ТЕСТ ЗНАКОВ
/
Не секрет, что пропуски занятий не такое уж редкое явление среди студен-
тов. Часть преподавателей смирилась с этим фактом, часть ищет способы по-
влиять на студентов. Один из преподавателей на каждом занятии проводил
проверку посещаемости и в конце семестра составил список студентов с ука-
занием того, сколько занятий в течение семестра каждый из них пропустил.
В начале следующего семестра он объявил, что те студенты, которые пропустят
меньше всего занятий, получат до пяти дополнительных баллов на экзамене3.
В конце семестра он вновь составил список студентов с указанием числа про-
пусков. Оба списка приведены в таблице 4.3.
Можно ли на основании приведенных данных сказать, что во втором семе-
стре пропусков занятий стало меньше?
В приведенном примере мы очередной раз встречаемся с ситуацией «до и
после». В принципе, в подобной ситуации ничто не мешает использовать по-
пулярный параметрический тест Стьюдента, позволяющий сравнивать средние
значения в зависимых и независимых выборках. Однако, во-первых, примене-
ние этого теста становится некорректным при работе с малыми выборками.
В случае малой выборки нет уверенности в том, что результаты подчиняются
нормальному закону распределения. Во-вторых, тест Стьюдента связан с ис-
пользованием шкал интервалов или отношений, в то время как часто прихо-
дится иметь дело с результатами, выраженными в шкале порядка. В-третьих,
тест Стьюдента может оказаться нечувствительным к незначительным разли-
3 Еще раз напомним, что в Израиле используется 100-балльная шкала академической успе-
ваемости.
41ак 3384
97
КНИГА ДЛЯ ТЕХ. КТО НЕ ЛЮБИТ СТАТИСТИКУ. НО ВЫНУЖДЕН ЕЮ ПОЛЬЗОВАТЬСЯ
Таблица 4.3
Число пропусков занятий в первом и втором семестрах
Студент Число пропус- ков в семестре А Число пропус- ков в семестре В Студент Число пропус- ков в семестре А Число пропус- ков в семестре В
1 3 3 И 0 2
2 7 5 12 3 2
3 5 2 13 5 5
4 8 6 14 0 0
5 6 7 15 6 3
6 4 5 16 5 0
7 5 0 17 6 3
8 7 4 18 0 1
9 2 1 19 4 3
10 5 5 20 7 5
чиям между выборками (например, при использовании шкал, содержащих
всего три значения).
В данном случае одним из тестов, который можно использовать для поиска
ответа на поставленный вопрос, является тест знаков. Из всех непараметриче-
ских методов он один из наиболее простых. Основное условие его примене-
ния — наличие двух связанных выборок, образованных по принципу «до и
после» и содержащих результаты, выраженные в шкале не ниже порядковой.
Отличительная особенность теста знаков в том, что для его применения
достаточно знать всего лишь то, в какую сторону (увеличения или уменьшения)
изменились (сдвинулись) результаты второго измерения по сравнению с пер-
вым. В том случае, если второй результат больше первого, обозначим его «+»
(положительный сдвиг). Если второй результат меньше первого, обозначим
его «—» (отрицательный сдвиг). Если результат не изменился, обозначим его
«О» (нулевой сдвиг).
Затем подсчитывается количество положительных, отрицательных и нулевых
сдвигов. В дальнейшем нулевые сдвиги игнорируются, поскольку они являют-
ся признаком отсутствия изменений. Сравнение количества положительных и
отрицательных сдвигов позволяет выделить типичное направление сдвига. Если
сдвигов со знаком « + » больше, чем со знаком «—», типичное направление
сдвига положительное (в выборке «после» результаты сдвинулись в сторону
увеличения по сравнению с выборкой «до»). Соответственно, если сдвигов со
знаком «—» больше, чем со знаком «+», типичное направление сдвига отрица-
тельное (в выборке «после» результаты сдвинулись в сторону уменьшения по
сравнению с выборкой «до»).
Сдвиги в сторону, противоположную типичному направлению сдвига, на-
зываются нетипичными. Чем меньше число нетипичных и нулевых сдвигов,
98
ГЛАВА 4. СЛУЧАЙ ДВУХ ЗАВИСИМЫХ ВЫБОРОК
тем более существенны различия «до и после» между выборками. Существуют
специальные статистические таблицы для теста знаков, которые для выбран-
ного уровня значимости а показывают, при каком числе нетипичных сдвигов
различия между первой и второй выборками можно считать неслучайными.
Итак, выбираем уровень значимости а=0,05 и сформулируем нулевую и
альтернативную гипотезы.
Яо: Различия между выборками носят случайный характер: ситуация с опо-
зданиями во втором семестре не отличается от ситуации с опозданиями в
первом семестре.
Альтернативная гипотеза формулируется либо в общем виде, либо в зави-
симости от типичного направления сдвига:
Я1а: Различия между выборками носят неслучайный характер: ситуация с
опозданиями во втором семестре отличается от ситуации с опозданиями в
первом семестре (двусторонняя критическая область).
Нхь\ Различия между выборками носят неслучайный характер: опозданий во
втором семестре стало больше, чем в первом (односторонняя критическая
область, типичное направление сдвига положительное).
Я|С: Различия между выборками носят неслучайный характер: опозданий во
втором семестре стало меньше, чем в первом (односторонняя критическая
область, типичное направление сдвига отрицательное).
На основе таблицы 4.3 создадим таблицу 4.4, дополнив ее двумя новыми
столбцами.
1. Для каждой пары значений «до и после» определим и запишем в таблицу
направление сдвига результатов второго измерения («после») по сравнению с
первым («до»):
□ число пропусков во втором семестре («после») стало меньше числа про-
пусков в первом семестре («до»): А > В\
□ число пропусков во втором семестре («после») стало больше числа про-
пусков в первом семестре («до»): А < В;
□ число пропусков во втором семестре («после») равно числу пропусков в
первом семестре («до»): А =В.
2. Определим и запишем в таблицу знак сдвига (знак определяется вычита-
нием из результата «после» результата «до»).
Таблица 4.4
Расчетная таблица д ля теста знаков
Студент Число пропусков в семестре А Число пропусков в семестре В Направление изменения Знак изменения
1 3 3 А=В 0
2 7 5 А>В —
3 5 2 А>В —
4 8 6 А>В —
99
КНИГА ДЛЯ ТЕХ, КТО НЕ ЛЮБИТ СТАТИСТИКУ, НО ВЫНУЖДЕН ЕЮ ПОЛЬЗОВАТЬСЯ
Окончание табл.4.4
Студент Число пропусков в семестре А Число пропусков в семестре В Направление изменения Знак изменения
5 6 7 А<В +
6 4 5 А<В +
7 5 0 А>В —
8 7 4 А>В —
9 2 1 А>В —
10 5 5 А=В 0
11 0 2 А<В +
12 3 2 А>В —
13 5 5 А=В 0
14 1 0 0 А=В 0
15 6 3 А>В —
16 5 0 А>В —
17 6 3 А>В —
18 0 1 А<В +
19 4 3 А>В —
20 7 5 А>В —
Подсчитаем количество отрицательных, положительных и нулевых сдвигов:
□ число отрицательных сдвигов: 12;
□ число положительных сдвигов: 4;
□ число нулевых сдвигов: 4.
Исключаем из дальнейшего рассмотрения нулевые сдвиги (выборка умень-
шится с 20 до 16 значений).
Сравниваем число отрицательных и положительных сдвигов и определяем
типичное направление сдвига. Поскольку отрицательных сдвигов 12; а поло-
жительных 4, типичное направление сдвига отрицательное (количество про-
пусков занятий во втором семестре сдвинулось в сторону уменьшения).
Очевидно, что число типичных сдвигов равно 12, число нетипичных сдвигов
равно 4.
В качестве альтернативной используем гипотезу Я1с: Различия между вы-
борками носят неслучайный характер: опозданий во втором семестре стало
меньше, чем в первом (односторонняя критическая область, типичное направ-
ление сдвига отрицательное^
Если-вернуться к нулевой гипотезе, то в ней фактически говорится о том,
что с одинаковой вероятностью результаты «после» могут как возрасти, так и
уменьшиться по сравнению с результатами «до». Для проверки этого утвержде-
ния необходимо сравнить эмпирическое распределение результатов «после»
100
ГЛАВА 4. СЛУЧАЙ ДВУХ ЗАВИСИМЫХ ВЫБОРОК
(сколько из них возросло, а сколько уменьшилось) с теоретическим распреде-
лением. В данном случае мы вновь вынуждены использовать биномиальный
тест и формулу Бернулли (параграф 3.1).
Если считать, что результаты «после» распределены случайным образом, то
существует вполне определенная вероятность того, что интересующее нас со-
бытие наступит не более 4 раз из 16 (число нетипичных сдвигов из общего
числа сдвигов). Эта вероятность рассчитывается по формуле Бернулли или
находится по таблице 3 (Приложение 2). Находим в таблице для АГ=16 (размер
выборки без нулевых сдвигов) их=4 (число нетипичных сдвигов) значение
вероятностир =0,038. Поскольку это значение меньше выбранного нами уров-
ня значимости а=0,05, нулевая гипотеза отвергается и принимается альтерна-
тивная. Опозданий во втором семестре стало меньше, чем было в первом.
К сожалению, таблица 3 ограничена значением 7V=25. В случае больших
выборок приходится прибегать к вычислению z (см. ниже) и использовать
таблицу для ^-распределения.
ВКЛЮЧАЕМ КОМПЬЮТЕР...
В программе SPSS на основе числа позитивных (пр) и негативных (лл) сдвигов,
а также в зависимости от величины (лр +п„) используются следующие алгоритмы
вычислений [SPSS Statistical Algorithms, 1986]:
1. Если (пр+п„) < 25, то по формуле Бернулли рассчитывается вероятность того, что
в (Пр +п„) случаях, в каждом из которых вероятность появления события равнар =0,5,
событие наступит не более г раз, где г— min (пр, п„):
р(Х<г)=у(Пр+Пп 1(0,5)<л'+Ч
' )
2. Если {Пр +п„) > 25, вычисляется значение z:
_ _ тах(ир,ил)-0,5(ир+и„)-0,5
0,5^+ил)
В рассмотренном выше примере пр=4, пп= 12, (ир+ил)= 16, r=min(n/,, пп)=4.
Поскольку (пр+ пп) < 25, используем формулу Бернулли:
р(Х <г)=У'(Пр +Пп 1(0,5)(л₽+л") =f-^-l(0,5)16 +f—\о,5)16 +f-^-\o,5)16 +
i ) ^0!16!) (j!15! J ^2114! Jv
+р£Ц(0,5)i«+f J£-Yo,5)16 =0,0384.
(ЗПЗ! J 1^4112! J
Данное значение вероятности, разумеется, совпадает с результатом, полученным в
рассмотренном выше примере за счет использования таблицы 3 для биномиально-
го распределения.
101
КНИГА ДЛЯ ТЕХ, КТО НЕ ЛЮБИТ СТАТИСТИКУ, НО ВЫНУЖДЕН ЕЮ ПОЛЬЗОВАТЬСЯ
Создадим переменные «Первый семестр» (terml) и «Второй семестр» (term2), кото-
рые будут содержать сведения о числе пропусков занятий в первом и втором семе-
стре. Дальнейшая последовательность действий, включая получаемый результат,
показана на рис. 4.4-4.6.
Рис. 4.4. Выбор требуемой статистической процедуры
Рис. 4.5. Тест знаков: необходимые действия и настройки
102
ГЛАВА 4. СЛУЧАЙ ДВУХ ЗАВИСИМЫХ ВЫБОРОК
a. TERM2«TERM1
b. TERM2 > TERM1
С. TERM2 = TERM1
Exact Sig. (2-tailed)
a. Binomial dlstrib
Test Statistics^
TERM2-
TERM1
Уровень значимости для двусторонней критической области
(удвоенное значение вероятности р« 0,0384:0,0384x2 «0,077).
(Для односторонней критической области нулевая гипотеза
отвергается.) ________
Рис. 4.6. Тест знаков: результат
4.3. ПОМОГАЮТ ЛИ ДИЕТЫ,
ИЛИ ТЕСТ ВИЛКОКСОНА
Проблема избыточного веса, несомненно, является одной из наиболее ак-
туальной для части населения. Для ее решения люди способны идти на любые
жертвы, вплоть до рискованных операций по уменьшению размера желудка.
Сторонники менее радикальных мер готовы истязать свое тело различными
диетами во имя обретения желанных форм и охотно откликаются на призывы
попробовать очередное «чудо-средство», направленное на снижение веса.
Одна из фирм, специализирующаяся на выпуске малокалорийных продук-
- тов питания, разработала специальную диету, гарантирующую, по заверению
фирмы, снижение веса. Фирма набрала группу добровольцев, которые в тече-
ние трех месяцев питались исключительно продуктами этой фирмы в соответ-
ствии с разработанной диетой. В таблице 4.5 представлен вес участников экс-
перимента до его начала и после его завершения. Можно ли на основании
приведенных данных сделать вывод о существенном снижении веса участников
* эксперимента?
103
КНИГА ДЛЯ ТЕХ, КТО НЕ ЛЮБИТ СТАТИСТИКУ. НО ВЫНУЖДЕН ЕЮ ПОЛЬЗОВАТЬСЯ
Мы вновь встречаемся с ситуацией «до и после». Как и в предыдущем случае,
желание использовать параметрический тест Стьюдента наталкивается на факт
маленькой выборки. Несомненно, здесь также возможно применение теста
знаков, однако полученная с его помощью информация может оказаться не-
достаточной. Тест знаков выявляет сдвиг результатов в ту или иную сторону,
но ничего не говорит о том, насколько этот сдвиг выражен. Если студент в
первом семестре пропустил 7 занятий, а во втором 6, то, формально, он стал
пропускать меньше. Но вряд ли такой результат обрадует преподавателя.
Аналогичная ситуация с весом. Если после трех месяцев диеты вес со 100 кг
уменьшился до 99 кг, то формально человек похудел. Другое дело, нужна ли
кому-нибудь диета, дающая такие результаты.
Таблица 4.5
Вес участников до начала эксперимента и после его завершения
Участник Вес «до» Вес «после» Участник Вес «до» Вес «после»
1 НО 100 11 85 87
2 105 100 12 94 96
3 97 90 13 112 100
4 90 93 14 90 90
5 97 92 15 88 80
6 102 92 16 92 88
7 98 90 17 93 87
8 89 94 18 93 85
9 104 97 19 99 90
10 92 88 20 102 91
В том случае, когда важно не только выявить факт изменения результатов
«после» по сравнению с результатами «до», цо и оценить степень выраженности
этого изменения, используется один из популярных непараметрических тес-
тов — тест Вилкоксона.
Для его применения необходимо соблюдение тех же условий, что и для
теста знаков: одна и та же выборка, для которой интересующий нас показатель
измерен, как минимум, дважды — до какого-либо (экспериментального) воз-
действия и после него. Кроме этого, желательно, чтобы диапазон изменений
результатов был достаточно широким. Например, в популярном опроснике
качества жизни EQ-5D [Rabin, de Charro, 2001] используется шкала, содержащая
всего три значения. Очевидно, что диапазон возможных различий между ре-
зультатами измерений для такой шкалы будет минимальным. В подобных
случаях целесообразнее пользоваться тестом знаков.
В тесте Вилкоксона решение об отсутствии или наличии значимых различий
между двумя связанными выборками принимается не на основе сравнения
результатов в обеих выборках, а на основе сравнения рангов этих результатов.
104
ГЛАВА 4. СЛУЧАЙ ДВУХ ЗАВИСИМЫХ ВЫБОРОК
Процедуру ранжирования мы подробно рассматривали в параграфе 2.3.
Применим полученные знания для данного случая и, дополнив таблицу 4.5
новыми колонками, получим таблицу 4.6.
Таблица 4.6
Расчетная таблица для теста Вилкоксона
Участник Вес «до» Вес «после» Изменение веса Модуль изменения веса Ранг
1 ПО 100 -10 10 16,5
2 105 100 -5 5 7
3 97 90 -7 7 10,5
4 90 93 + 3 3 3
5 97 92 -5 5 7
6 102 92 -10 10 16,5
7 98 90 -8 8 13
8 89 94 +5 5 7
9 104 97 -7 7 10,5
10 92 88 —4 4 4,5
11 85 87 + 2 2 1,5
12 94 96 + 2 2 1,5
13 112 100 -12 12 19
14 90 90 0 0 —
15 88 80 -8 8 13
16 92 88 -4 4 4,5
17 93 87 -6 6 9
18 93 85 -8 8 13
19 99 90 —9 9 15
20 102 91 -11 11 18
Во-первых, определим разность между результатами «после» и результатами
«до» и запишем ее с учетом знака в дополнительную, четвертую, колонку таб-
лицы.
Во-вторых, как и в предыдущем случае, определим направление типичного
и нетипичного сдвига. Поскольку большинство значений в дополнительной
колонке отрицательно, типичный сдвиг отрицательный (у большинства участ-
ников эксперимента вес уменьшился), а нетипичный — положительный (у че-
тырех человек из 20 вес за три месяца диеты увеличился). В таблице 4.5. случаи
нетипичного сдвига выделены.
В-третьих, в новый столбец еще раз запишем значения разностей между
результатами «после» и результатами «до», 'но взятых по модулю (то есть без
учета знака).
105
КНИГА ДЛЯ ТЕХ. КТО НЕ ЛЮБИТ СТАТИСТИКУ, НО ВЫНУЖДЕН ЕЮ ПОЛЬЗОВАТЬСЯ
После этого наступает самый ответственный
—-х этап. Данные, записанные в пятом столбце, не-
J ) обходимо проранжировать от минимального зна-
) чения до максимального. При наличии нулевых
УТ“ 4» сдвигов (вес не изменился) они исключаются из
(ffiSSra "* \ ранжирования. В нашем случае имеется один ну-
'Я*/Гг Fl ) левой сдвиг (выборка уменьшится на одно значе-
/ЬД __( ние:л = 19).
ГТ) Вся подготовительная работа для использова-
jj I 1 ния теста Вилкоксона завершена.
Выберем уровень значимости а=0,05 и сфор-
мулируем нулевую и альтернативную гипотезы.
Но: После диеты изменение веса в сторону уменьшения не отличается от
изменения веса в сторону его увеличения (иными словами, снижение веса у
одних участников эксперимента компенсируется увеличением веса у других
участников).
Яр После диеты изменение веса в сторону его уменьшения превышает из-
менение веса в сторону его увеличения (то есть после диеты снижение веса у
тех, кто похудел, превышает увеличение веса у тех, кто потолстел).
Как видно из формулировки альтернативной гипотезы, для проверки будет
использована односторонняя критическая область.
Логика проверки достаточно проста. Если диеты не оказывают своего влия-
ния, то после окончания эксперимента распределение результатов с точки
зрения того, что произошло с весом (насколько он уменьшился или увеличил-
ся), должно носить случайный характер. Тогда сумма рангов для результатов,
, говорящих о сдвиге веса в одну сторону, не должна отличаться от суммы рангов
для результатов, говорящих о сдвиге веса в другую сторону.
Например, из четырех участников эксперимента двое похудели на 5 кг, а двое
потолстели на 5 кг.
Эффект от диеты (изменение веса по модулю) будет выглядеть следующим
образом:
5, 5, 5, 5.
Поскольку изменение веса одно и то же для всех участников эксперимента,
все четыре значения получат одинаковый ранг, равный 2,5:
1 2,5; 2,5; 2,5; 2,5.
Сумма рангов для тех, кто похудел, будет (2,5+2,5)=5. Для тех, кто потол-
стел, получим тот же результат.
Но если представить, что после диеты два человека потолстели на 5 кг каж-
дый, а двое похудели на 10 кг каждый, то получим другую последовательность
результатов влияния диеты (по модулю):
5, 5,10,10.
106
ГЛАВА 4. СЛУЧАЙ ДВУХ ЗАВИСИМЫХ ВЫБОРОК
Если эту последовательность проранжировать, получим следующий ранго-
вый ряд:
1,5; 1,5; 3'5; 3,5.
Сумма рангов для тех, кто похудел, будет равна (3,5+3,5)=7. Для тех, кто
потолстел, — (1,5 +1,5)=3. Поскольку 7 > 3, то сдвиг в сторону снижения веса
более интенсивен, чем в сторону увеличения.
Найдем сумму рангов для четырех значений нетипичного (положительного)
сдвига (выделено в таблице):
71 = 3 + 7+1,5 + 1,5=13.
Найдем сумму рангов для пятнадцати значений типичного (отрицательного)
сдвига:
Г2= 16,5+7+10,5+7+16,5 +13 +10,5+4,5 + 19 +13+4,5+9+13 +15+18=177.
В качестве используется меньшее из двух значений 7\ и Т2. В нашем
случае 7ЭМПИр 13.
Существует статистическая таблица для.теста Вилкоксона (табл. 5, Прило-
жение 2), содержащая нижние (минимальные) значения (в зависимости
от размера выборки и значения а), при которых различия между типичным и
нетипичным сдвигами еще могут считаться случайными. Если наблюдаемое
значение Тэмпир больше нет оснований для того, чтобы отклонить нуле-
вую гипотезу. Если меньше или равно Ткритич, нулевая гипотеза отклоня-
ется и принимается альтернативная4.
Для наших результатов (Тэмпир= 13, п = 19, а=0,05) находим втаблице 5 зна-
чение Tjcpimp! 53.
Поскольку Тэмпир меньше 7критич, нулевая гипотеза отвергается и принима-
ется альтернативная гипотеза: после трех месяцев диеты у большинства участ-
ников эксперимента произошло существенное снижение веса5.
Из табл. 5 видно, что она предназначена для выборки не более 25 человек.
В случае больших выборок приходится прибегать к вычислению z (см. ниже) и
4 В данном случае мы имеем нечастую ситуацию, когда правило принятия решения после
сравнения Т^р и носит «обратный» характер: нулевая гипотеза отвергается, когда /^„„р
меньше Т'к^кпп^
5 К сожалению, полученный результат не дает ответа на вопрос, вынесенный в название
данного параграфа. Несмотря на снижение веса после диеты, у нас нет оснований утверждать, что
снижение веса произошло вследствие диеты. Здесь возможно действие ряда других неучтенных
факторов, влияющих на вес, о которых мы ничего не знаем. Например, одновременно с диетой
участники эксперимента начали заниматься спортом или вести более здоровый образ жизни
(бросили курить, употреблять спиртные напитки и др.). Аналогичная ситуация в рассмотренном
выше примере о пропуске занятий. Несмотря на то что во втором семестре пропусков стало
меньше, неясно, произошло ли это вследствие обещаний преподавателя добавить несколько
баллов к оценке за экзамен или по другим причинам. Эти вопросы относятся к области плани-
рования эксперимента, обсуждать которые у нас нет возможности.
107
КНИГА ДЛЯ ТЕХ, КТО НЕ ЛЮБИТ СТАТИСТИКУ, НО ВЫНУЖДЕН ЕЮ ПОЛЬЗОВАТЬСЯ
использовать таблицу для z-распределения (табл. 1, Приложение 2). В том
случае, если по каким-либо причинам нет возможности применять статисти-
ческую таблицу для теста Вилкоксона,’ можно сразу переходить к вычислению
Z независимо от размеров выборки.
ВКЛЮЧАЕМ КОМПЬЮТЕР...
В программе SPSS на основе полученных из расчетной таблицы сведений о Т\ и Т2
вычисляется значение z по следующей формуле:
_min(T„T2)-^
/л(л+1)(2л+1) *
V 24
где min(rb Т2) — минимальное из двух значений 7\ иТ2;п~ объем выборки после
исключения из нее нулевых сдвигов. Подставим в эту формулу наши значения:
min(T|, Т2)= 13; л= 19.
min(7;,T2)-^
z=-----, 7----= г 4------------= -з, 30.
/л(л+1)(2л+1) fl 9(19+1) (2x19+1)
V 24 V 24
Из таблицы 1 (Приложение 2) можно найти, что этому значению z соответствует
вероятность р = 0,0005.
Переходим к программе SPSS.
Переменные «w before» и «w_after» содержат сведения о весе испытуемых до и после
диеты. Дальнейшая последовательность действий (включая получаемый результат),
необходимая для использования теста Вилкоксона, показана на рис. 4.7-4.9.
ЩNonParametr - SPSS Data Ldrtot
File Edit View Data Transform j Analyze Graphs UbCties Window Help
55: w.befote
w_before
7 110
2
3
4
5
6
7
8
9
10
11
105
97
90
97
102
98
89
104
92
85
Nonparametnc Tests
Tme Series
Survival
Multiple Response
Missing Value Analysis...
Reports
Descriptive Statistics
Compare Means
General Linear Model
Mixed Models
Correlate
Regresston
Logbnear
S Classify
~c Data Reduction
~c Scale
JC
К
c
E
87
w after
Chi-Square...
Binomial...
Runs...
1-Sample K-S...
2 Independent Semples.
К Independent Samples.
Нажать
12
13
14
96
J00
90
2 Related Sampies...
К Related Samples...
Рис. 4.7. Выбор требуемой статистической процедуры
108
ГЛАВА 4. СЛУЧАЙ ДВУХ ЗАВИСИМЫХ ВЫБОРОК
Рис. 4.8. Тест Вилкоксона: необходимые действия и настройки
a. Based on positive ranks.
b. Wilcoxon Signed Ranks Test
Рис. 4.9. Тест Вилкоксона: результат
При работе со связанными выборками может возникнуть необходимость сравнения
более чем двух выборок. В принципе, эту задачу можно решать путем последова-
тельного сравнения выборок между собой. Например, при наличии трех связанных
выборок вначале сравнить первую выборку со второй, потом первую с третьей,
потом вторую с третьей. Нетрудно видеть, что при возрастании числа независимых
выборок такой путь ведет к увеличению числа однообразных проверок.
В непараметрической статистике существует ряд методов, позволяющих анализи-
ровать несколько связанных выборок, не прибегая к процедуре их попарного срав-
нения.
Глава 5
«ЧТО ДВИЖЕТ СОЛНЦЕ И СВЕТИЛА»,
ИЛИ
СЛУЧАЙ НЕСКОЛЬКИХ
ЗАВИСИМЫХ ВЫБОРОК
5.1. ЭФФЕКТИВНЫ ЛИ ТЕЛЕФОННЫЕ ОПРОСЫ,
ИЛИ ТЕСТ КОХРАНА
Большинству владельцев телефонов знакома ситуация, когда в самый не-
подходящий момент раздается звонок и голос на том конце провода предла-
гает принять участие в очередном телефонном опросе, например по поводу
того, как поступать с бездомными домашними животными. Я в подобных
случаях под каким-либо благовидным предлогом отказываюсь от продолжения
разговора. Однако, поскольку результаты подобных опросов регулярно пуб-
ликуются в прессе, видимо, есть немало людей, согласных принимать в них
участие.'
Учитывая заметный процент отказов от участия в опросах, одна из органи-
заций, занимающихся телефонными опросами, провела исследование с целью
установить, какие факторы могут побудить людей принимать в них участие.
Было выдвинуто предположение, что начальная фаза разговора является ре-
шающей. С целью проверки данного предположения были выработаны три
стиля общения с респондентом на начальной фазе обращения к нему:
□ стиль максимального дружелюбия, радости и энтузиазма;
□ формально любезный стиль;
□ строгий, формальный и холодный стиль.
С промежутком в несколько недель три интервьюера^, В и С, представляю-
щие каждый из данных стилей, обратились по телефону к одной и той же
группе людей с просьбой принять участие в опросе. В ходе каждого обращения
фиксировалось согласие или отказ от проведения интервью.
ПО
ГЛАВА 5. «ЧТО ДВИЖЕТ СОЛНЦЕ И СВЕТИЛА». ИЛИ СЛУЧАЙ НЕСКОЛЬКИХ ЗАВИСИМЫХ ВЫБОРОК
Полученные результаты приведены в таблице 5.1, где согласие на интервью
обозначено как «1», отказ от интервью — как «О».
Можно ли на основании полученных данных утверждать, что изменение
стиля общения с клиентом сопровождается изменением его готовности принять
участие в опросе?
Таблица 5.1
Успешность интервью в зависимости от стиля интервьюера
Респондент Стиль интервью L I?
А В с
1 0 0 0 0 0
2 1 1 0 2 4
3 0 1 0 1 1
4 0 0 0 0 0
5 1 0 0 1 1
6 1 1 1 3 9
7 1 1 0 2 4
8 0 1 1 1 2 4
9 1 - 0 0 1 1
10 0 0 1 1 1
и 1 1 0 2 4
12 1 1 0 2 4
13 1 1 0 2 4
14 0 0 0 . 0 0
15 1 0 1 2 4
16 0 1 1 2 4
17 1 0 0 1 1
18 1 1 0 2 4
19 0 1 0 1 1
20 1 • 0 1 2 4
ZG=29 G{ = 12 G2=ll С3=6 ££ = 29 Е1*=55
б3! =144 6*2=121 61=36
Ответ на поставленный вопрос может быть получен с помощью теста Кохрана.
Данный тест является развитием теста МакНемара (см. параграф 4.1) и пред-
назначен для сравнения результатов более чем двух измерений, произведенных
на одной выборке в различное время или в различных условиях*.
1 Возможен иной подход к работе с зависимыми выборками. Как известно, выборки считают-
ся зависимыми, если каждому значению из одной выборки можно поставить в соответствие
единственное значение из другой выборки. Так, в рамках одного из исследований было сформи-
ровано несколько однородных выборок по 3 человека в каждой. Каждый из участников в каждой
111
КНИГА ДЛЯ ТЕХ, КТО НЕ ЛЮБИТ СТАТИСТИКУ, НО ВЫНУЖДЕН ЕЮ ПОЛЬЗОВАТЬСЯ
В тесте Кохрана, как и в тесте МакНемара,
используются дихотомические данные типа
«да» — «нет», либо данные, допускающие ди-
хотомическую категоризацию (для теста
МакНемара рассматривался пример с дихото-
мической категоризацией предродовой тре-
вожности: «предродовая тревожность высо-
кая» — «предродовая тревожность низкая»).
Если результаты каждого измерения носят
случайный характер, то числа успешных и не-
успешных обращений к респондентам в каж-
дом из столбцов таблицы не должны значи-
тельным образом отличаться друг от друга.
Аналогичным образом можно предположить,
что если изменение стиля общения не оказы-
вает своего влияния на результаты, их распре-
деление по горизонтали также должно носить
случайный характер.
Кохран предложил специальную расчетную
формулу, позволяющую одновременно оце-
нивать случайный характер результатов как по
столбцам, так и по строкам таблицы, и пока-
зал, что для проверки статистических гипотез можно использовать статисти-
ческую таблицу для теста х* 2.
' Проверка осуществляется по отношению к результатам, которые можно
условно считать «успешными». В нашем случае это число случаев, когда рес-
пондент дал согласие на участие в опросе. Такие случаи отмечены в таблице
как «I»2.
Сделаем ряд необходимых дополнений в таблицу 5.1.
1. Внизу каждого столбца запишем количество «успехов» (то есть единиц)
и обозначим их символом G.
2. Найдем сумму всех «успехов» и обозначим ее £(?.
3. Вычислим для каждого столбца значение G2.
4. Найдем количество «успехов» по строкам, обозначив их как L.
5. Для каждой строки найдем значение L2.
6. Определим сумму L и L2.
выборке получил предназначенную только для него информацию (позитивную, негативную,
нейтральную) об одном из законов, который планировался к принятию. Затем выяснялось отно-
шение к этому закону (за или против) и проверялось наличие различий в результатах для тех, кто
в каждой выборке получил соответствующую информацию (то есть сравнивались результаты тех,
кто в каждой из выборок получил только позитивную, только негативную или только нейтральную
информацию об этом законе) [по: Runyon, 1977].
2 Выбор результата, считаемого «успешным», является условным. Результаты проверки не
изменятся, если все необходимые вычисления будут проделаны для результатов, обозначенных
как «О».
112
ГЛАВА 5. «ЧТО ДВИЖЕТ СОЛНЦЕ И СВЕТИЛА., ИЛИ СЛУЧАЙ НЕСКОЛЬКИХ ЗАВИСИМЫХ ВЫБОРОК
Нами проделана вся подготовительная работа. Можно приступать к провер-
ке гипотез.
Итак, выбираем уровень значимости а=0,05 и формулируем нулевую и
альтернативную гипотезы.
Но: Вероятность согласия респондента на проведение опроса одинакова для
всех стилей общения с ним.
Hf. Вероятность согласия респондента на проведение опроса различна для
различных стилей общения с ним (двусторонняя критическая область).
Для принятия решения вычисляется значение Q по следующей формуле:
к к
(k-i)[k^G2-(^Gj)2]
п=_______&____&_____
* N N
к^Ц—^Ц
Z=1 Z-1
где N— число строк в расчетной таблице (размер выборку в нашем случае
20); к — число столбцов в расчетной таблице (число измерений, проведен-
ных на выборке; в нашем случае £=3).
Подставим в'формулу необходимые значения из таблицы 5.1:
(Л-1)[ЛУС?-(У<7..)2]
Й Й (3-l)[3(144+121+36)-(29)2]..,o/7g
’ (3х29)-55
Z=1 Z=1
Полученное значение Оэмпир сравниваем с критическим значением Хкршич,
которое находится в таблице критических значений теста %2 для выбранного
уровня значимости а и числа степеней свободы df= (к— 1) Если <23MnHp меньше
Хкригич. нет оснований отклонить нулевую гипотезу. Если 0эмпир больше или
равно х^ритич. нулевая гипотеза отклоняется и принимается альтернативная.
В нашем случае а=0,05, ^=(3 — 1) =2. В табл. 2 (Приложение 2) находим
Хкригич 5,99.
Поскольку Сэмпир = 3,875 меньше Хкригич =5,99, нет оснований отклонить
нулевую гипотезу. Готовность респондента принять участие в опросе не опре-
деляется стилем общения с ним. Возможно, более действенным фактором
будет время проведения опросов.
ВКЛЮЧАЕМ КОМПЬЮТЕР..,.
Сведения об эффективности каждого из стилей представлены в переменных «Стиль 1»
(style 1), «Стиль 2» (style2) и «Стиль 3» (style3).
Дальнейшая последовательность действий, включая результат, показана на
рис. 5.1—5.3.
113
КНИГА ДЛЯ ТЕХ, КТО НЕ ЛЮБИТ СТАТИСТИКУ, НО ВЫНУЖДЕН ЕЮ ПОЛЬЗОВАТЬСЯ
| ; NonParametr - SPSS Data Editor
File Edit View Data Transform I Analyze Graphs Utilities Window Help
G?|H|<O| EJ| Ч-l Reports ► Descriptive Statistics ► Compare Means ► General Linear Model ► Mixed Models > Correlate ► Regression ► Loglmear ► Classfy ► Data Reduction ► Scale ► mi Ш1
J35:tfyle1
stylel slyle2 vac Y*r
1 0
2 1
3 0
4 0
5 1
6 1
Г 7 1 ИНН Chi-Square...
8 0 1НПС JCiIcj * DhTu«TuoI..» Survival ► Runs...
9 1
10 0 Missing Value Analysis... 2 Independent Samples... К Independent Samples... 2 Related Samples...
11 1 Т tr
12 1 1 0
13 1 1 ° К Related Samples...
14 0 0 0
15 1 0 1
16 0 1 1
17 1 0 io1
18 1 0 f Нажать j
19 0 1 0
20 1 0 1
Рис. 5.1. Выбор требуемой статистической процедуры
Рис. 5.2. Тест Кохрана: необходимые действия и настройки
ГЛАВА 5. «ЧТО ДВИЖЕТ СОЛНЦЕ И СВЕТИЛА», ИЛИ СЛУЧАЙ НЕСКОЛЬКИХ ЗАВИСИМЫХ ВЫБОРОК
Cochran Test
Frequencies
Рис. 5.3. Тест Кохрана: результат
5.2. СТУДЕНТЫ ГОЛОСУЮТ НОГАМИ,
ИЛИ ТЕСТ ФРИДМАНА
Уже знакомый нам преподаватель предположил, что одни занятия студенты
прогуливают чаще, а другие — реже. Он связался с другими преподавателями
и в конце семестра получил данные о числе пропусков занятий у студентов
своей группы еще по двум предметам. Полученные результаты приведены в
таблице 5.2. Таблица содержит сведения о числе пропусков занятий для сту-
дентов одной группы по трем предметам: А, В, С.
Можно ли на основании полученных данных утверждать, что студенты
пропускают занятия выборочно, в зависимости от изучаемого предмета?
Ответ на этот вопрос может быть получен несколькими путями. Первый
путь связан с попарным сравнением числа пропусков по предметам А, В, С
между собой. Для этого потребуется трижды использовать, например, тест
Вилкоксона.
Существует другая возможность, предложенная Фридманом. Тест Фридмана
позволяет сравнивать результаты трех и более измерений, полученных на одной
и той же выборке. С его помощью можно определить, отличаются ли получен-
ные результаты друг от друга, без выявления направления отличий3.
3 В общем случае тест Фридмана рассматривается как непараметрический аналог двухфактор-
ного дисперсионного анализа (Two-way ANOVA by ranks). Он позволяет оценить эффект воздей-
ствия двух факторов на измеряемую величину. В нашем примере измеряемая величина — число
115
КНИГА ДЛЯ ТЕХ. КТО НЕ ЛЮБИТ СТАТИСТИКУ. НО ВЫНУЖДЕН ЕЮ ПОЛЬЗОВАТЬСЯ
Таблица 5.2
Число пропусков занятий по предметам А, Ви С
Студент Предметы Студент Предметы
А В С А В С
1 3 5 7 11 2 4 1
2 5 2 3 12 2 0 3
3 2 6 4 13 5 3 0
4 6 7 5 14 0 3 3
5 7 1 3 15 3 7 5
6 5 0 2 ' 16 0 5 4
7 0 4 3 17 3 4 6
8 4 5 6 , 18 1 6 4
9 1 2 3 19 3 5 3
10 5 7 ' 7 20 5 1 2
Тест Фридмана, как и тест Вилкоксона, также использует процедуру ран-
жирования результатов измерений, но ранжирование происходит не по верти-
кали, как в тесте Вилкоксона, а по горизонтали, от измерения к измерению.
Например, первый студент по предмету А пропустил 3 занятия, по предмету
В — 5 занятий, по предмету С — 7 занятий. Если эти результаты проранжиро-
вать, то получим ранги 1,2,3 (первый ранг приписывается наименьшему зна-
чению).
Перепишем таблицу 5.2 с указанием рангов для каждого студента. Получим
таблицу 5.3, в которой выделены значения рангов для каждого студбнта.
Если предположить, что число пропусков мало меняется от предмета к
предмету, то суммы рангов для каждого из столбцов также должны мало отли-
чаться друг от друга. В том случае, если одни предметы пропускаются чаще, а
другие реже, суммы рангов в каждом из столбцов будут существенно отличать-
ся друг от друга.
Мерой отличия сумм рангов друг от друга является значение вычисляемое
по следующей формуле:
12 к
где N— число строк в таблице (размер выборки); к—число столбцов в табли-
це (количество измерений); Rj — сумма рангов, соответственно, для первого,
второго и третьего столбцов.
пропусков занятий. Она находится под воздействием двух факторов. Первый фактор — «предме-
ты/ преподаватели», имеющий три уровня. Второй фактор — «студенты», имеющий 20 уровней.
116
ГЛАВА 5. «ЧТО ДВИЖЕТ СОЛНЦЕ И СВЕТИЛА., ИЛИ СЛУЧАЙ НЕСКОЛЬКИХ ЗАВИСИМЫХ ВЫБОРОК
Таблица 5.3
Число пропусков занятий по предметам А, В, Синх ранги
Студент А Ранг в Ранг С Ранг Студент А Ранг В Ранг С Ранг
1 3 1 5 2 7 3 11 2 2 4 3 1 1
2 5 3 2 1 3 2 12 2 2 0 1 3 3
3 2 1 6 3 4 2 13 5 3 3 2 0 1
4 6 2 7 3 5 1 14 0 1 3 2 4 3
5 7 3 1 1 3 2 15 3 1 7 3 5 2
6 5 3 0 1 2 2 16 0 1 5 3 4 2
7 0 1 4 3 3 2 17 3 1 4 2 6 3
8 4 1 5 2 6 3 18 1 1 6 3 4 2
9 1 1 2 2 3 3 19 3 2 5 3 2 1
10 5 1 7 3 6 2 20 5 3 1 1 2 2
Сумма рангов (Яу) 34 44 42
Найденное значение х?ЭМиР сравнивается с критическим значением Хгкритич>
которое находится по уже знакомой таблице для теста х2 (табл. 2, Приложение
2) для выбранного уровня значимости а и числа степеней свободы df= (к— 1).
В том случае, если х2ЭМиР меньше х2критич> нет оснований, чтобы отвергнуть
нулевую гипотезу.
В том случае, х2ЭмиР больше или равно Хгкритич. нулевая гипотеза отвергается
и принимается альтернативная.
Итак, выбираем уровень значимости а=0,05 и формулируем нулевую и
альтернативную гипотезы.
Но: Пропуски студентами занятий носят случайный характер и не опреде-
ляются изучаемым предметом.
Н]. Пропуски студентами занятий носят неслучайный характер и определя-
ются тем, какой предмет они изучают (двусторонняя критическая область).
Поданным таблицы 5.3, имеем:
#=20; Л=3;Я1=34;Я2=44; /?3=42.
Подставляем эти значения в формулу для вычисления х?:
19 к
= ^~^[(34)!+(44)2+(42)!]-Зх20х(3+1) = 2,80.
В табл. 2 для а=0,05 и df= (к-1) = (3 — 1) = 2 находим х?кРитич= 5,99.
117
КНИГА ДЛЯ ТЕХ, КТО НЕ ЛЮБИТ СТАТИСТИКУ, НО ВЫНУЖДЕН ЕЮ ПОЛЬЗОВАТЬСЯ
Так как х?Эмир=2,80 меньше хкригич=5,99, нет оснований, чтобы отвергнуть
нулевую гипотезу. Пропуски студентами занятий носят случайный характер и
не определяются изучаемым предметом.
Сейчас еще один пример.
В ходе одного из экспериментов по когнитивной психологии фиксировалось
время (в минутах), которое требуется лабораторной мыши для выхода из лаби-
ринта в четырех различных экспериментальных условиях.
Для группы из четырех мышей были получены следующие значения време-
ни в зависимости от экспериментальных условий А, В, С, D (табл. 5.4).
Таблица 5.4
Время выхода мыши из лабиринта в зависимости
от условий эксперимента
Условия эксперимента
А в С D
Мышь 1 5 3 2 4
Мышь 2 4 3 2 5
Мышь 3 6 2 3 5
Мышь 4 6 4 3 5
Проранжируем результаты в каждой строке, запишем их в новую таблицу
(табл. 5.5) и найдем сумму рангов для каждого столбца.
Таблица 5.5
Время выхода мыши из лабиринта: значения рангов
Условия эксперимента
А В С D
Мышь 1 4 2 1 3
Мышь 2 3 2 1 4
Мышь 3 4 1 2 3
Мышь 4 4 2 1 3
Сумма рангов 15 7 5 13
Выберем уровень значимости а=0,05 и сформулируем нулевую и альтерна-
тивную гипотезы.
Но: Время выхода из лабиринта носит случайный характер и не определяет-
ся условиями эксперимента.
Яр Время выхода из лабиринта носит неслучайный характер и определяет-
ся экспериментальными условиями (двусторонняя критическая область).
По данным таблицы 5.5, имеем:
Я=3; Л=4; R{=15; й2=7; Я3=5; R4= 13.
118
ГЛАВА 5. «ЧТО ДВИЖЕТ СОЛНЦЕ И СВЕТИЛА», ИЛИ СЛУЧАЙ НЕСКОЛЬКИХ ЗАВИСИМЫХ ВЫБОРОК
Подставляем эти значения в формулу для вычисления %?:
12 к
=T-i^-i?[a5)2+(7)!+(5)!+(i3)!]-3x4(4+i)=io,2.
4x4(4+l)L J
В табл. 2 для а=0,05 и df=(k-1)=(4—1)=3 находим Хгкритич=7,82.
Так как Хгэмпир= больше Хгкритич=Т>82, нулевая гипотеза отвергается и
принимается альтернативная гипотеза: время выхода из лабиринта меняется в
зависимости от экспериментальных условий.
Обратите внимание: полученный результат относится к выборке, состоящей
всего из четырех объектов! Возможность работать с малыми выборками — одно
из основных преимуществ непараметрических методов.
Рассмотрим еще один пример для теста Фридмана.
Уровень самооценки в группе наркоманов из 10 человек был измерен три-
жды: в момент оформления документов для начала лечения от наркомании в
наркологическом стационаре, после завершения лечения и в процессе после-
дующей реабилитации в дневном профилактории. В таблице 5.6 приведены
значения рангов, соответствующих первому, второму и третьему измерениям.
Таблица 5.6
Уровень самооценки: ранга значений
Испытуемый Измерение
1 2 3
1 1 3 2
2 2 2 2
3 1 3 2
4 3 1 2
5 2 1 3
6 1,5 3 1,5
7 1 2 3
8 3 2 1
9 2,5 2,5 1
10 2 3 1
Сумма рангов 19 22,5 18,5
Можно ли утверждать, что существуют значимые различия между результа-
тами трех измерений?
Выберем уровень значимости а=0,05 и сформулируем нулевую и альтерна-
тивную гипотезы.
119
КНИГА ДЛЯ ТЕХ, КТО НЕ ЛЮБИТ СТАТИСТИКУ, НО ВЫНУЖДЕН ЕЮ ПОЛЬЗОВАТЬСЯ
Но: Различия между результатами проведенных измерений отсутствуют.
Я,: Результаты проведенных измерений отличаются друг от друга (двусто-
ронняя критическая область).
Из таблицы видно, что в ней есть три случая связанных рангов (выделены в
таблице). Мы уже говорили, что многие непараметрические методы статисти-
ки чувствительны к ситуации связанных рангов. Для их учета в расчетные
формулы приходится вводить различные корректирующие поправки, услож-
няющие процесс вычислений4.
Расчетная формула для теста Фридмана, учитывающая наличие связанных
рангов, принимает следующий вид:
%? =
к
12£Лу2-ЗЯЧ(Л+1)2
I'w-ti/j'l’
Nk(k+1)+'
где gj — число групп связанных рангов в каждой строке таблицы, t — размер
каждой группы связанных рангов (сколько одинаковых рангов в нее входит).
Обратите внимание! Даже если в строке нет связанных рангов, в тесте
Фридмана каждый отдельный (несвязанный) ранг рассматривается как группа
связанных рангов, содержащая одно значение (/=1). Например, в первой
строке таблицы 5.6 нет связанных рангов. Но в соответствии с правилами ис-
пользования приведенной формулы, три отдельных ранга 1,3,2 рассматрива-
ются как три группы связанных рангов размером t= 1 (содержащих одно зна-
чение). N .
Прежде чем приступить к вычислениям, найдем значение :
N /=17=1
=(13 +р +13)+(33)+(13 +13 +13)+(13+13 +13)+(13+13 +13)+
i=i j=i
+(23+13)+(13+13+13)+(13+13+13)+(23+13)+(13+13+13) =
=3+27+3+3+3+9+3+3+9+3—66.
Приступим к вычислениям. Учтем, что Я=10; к=3; 7?i = 19; Я2=22,5;
Я3=18,5.
12£(Яу)2-ЗЯ2£(А:+1)2
v2 _ J=i__________ _
Хг ~ ( N JL ) ~
Nk(k+1)+'
4 Выше уже отмечалось, что в некоторых пособиях, где рассматриваются непараметрические
методы статистики, ситуация связанных рангов игнорируется. Это приводит к несовпадению
результатов, вычисленных вручную и полученных для тех же данных с помощью программы SPSS.
Увы, данное обстоятельство также игнорируется [см., например: Наследов, 2006, с. 183, 184].
120
ГЛАВА 5. «ЧТО ДВИЖЕТ СОЛНЦЕП СВЕТИЛА», ИЛИ СЛУЧАЙ НЕСКОЛЬКИХ ЗАВИСИМЫХ ВЫБОРОК
212[(19)2+(22,5)2+(18,5)2]-(3)(10)2(3)(3+l)2
(1О)(3)(3+1)+(10)(у6
Из табл. 2 (Приложение 2) для df=(k—1) = (3 —1) = 2 и уровня значимости
а=0,05 находим х2критич=5,99. Поскольку значение х2эмпир =1,118 меньше кри-
тического, нет оснований отвергнуть нулевую гипотезу. Между результатами
проведенных измерений отсутствуют различия.
ВКЛЮЧАЕМ КОМПЬЮТЕР....
Перенесем данные о пропусках занятий в переменные «Лекция 1» (lecturel), «Лек-
ция 2» (lecturel) и «Лекция 3» (lecture3). Дальнейшая последовательность действий
и результат показаны на рис. 5.4-5.6. На рис. 5.7, 5.8 приведены результаты теста
Фридмана для примера с мышами и случая связанных рангов.
NonPar «netr - SPSS Data Editor
File Edit View Data Transform Analyze Graphs Utilities Window Help
12 2 1
13 3 2 1
Рис. 5.4. Выбор требуемой статистической процедуры
Рис. 5.5. Тест Фридмана: необходимые действия и настройки
121
КНИГА ДЛЯ ТЕХ, КТО НЕ ЛЮБИТ СТАТИСТИКУ, НО ВЫНУЖДЕН ЕЮ ПОЛЬЗОВАТЬСЯ
Friedman Test
Friedman Test
Рис. 5.6. Тест Фридмана: результат
Рис. 5.7. Тест Фридмана (пример с мышами):
результат
)
Friedman Test
Ranks
Mean Rank
Intake Detox Day treatment 1.90 2.25 1.85
Рис. 5.8. Тест Фридмана (случай связанных рангов): результат
Этим примером мы завершаем рассмотрение ситуаций, относящихся к случаю
связанных выборок.
Перейдем к следующему разделу и рассмотрим непараметрические тесты, относя-
щиеся к независимым выборкам.
Глава 6
ОТДЕЛЕНИЕ СВЕТА ОТ ТЬМЫ,
ИЛИ
СЛУЧАЙ ДВУХ НЕЗАВИСИМЫХ ВЫБОРОК
Задача сравнения двух независимых выборок — одна из наиболее часто
встречающихся при проведении различных экспериментов и исследований.
Мужчины и женщины, контрольная и экспериментальная группа, уро-
женцы страны и иммигранты, работающие и безработные —; это далеко не
полный перечень того, каким образом могут быть получены независимые вы-
борки1.
Ниже описаны наиболее популярные непараметрические тесты, используе-
мые при работе с двумя независимыми выборками.
6.1. «НЕКОТОРЫЕ ЛЮБЯТ ПОГОРЯЧЕЕ»,
ИЛИ СНОВА ТЕСТ X2
Антон и Ричард — страстные поклонники творчества Мэрилин Монро,
готовые раз за разом смотреть фильмы с ее участием. После очередного про-
смотра бессмертной комедии «Some like it hot»2 Антон заметил, что в кино
блондинки встречаются гораздо чаще, чем в жизни. Ричард с этим не согласил-
ся, сказав, что среди девушек в университете достаточно много блондинок.
Антон возразил, что это не коренные израильтянки, а в основном девушки из
числа иммигранток. Чтобы прекратить спор, два друга решили проверить, кто
доминирует среди блондинок — коренные израильтянки или девушки, прие-
хавшие в Израиль из других стран. На следующий день в перерывах между
1К сожалению, у нас нет возможности для рассмотрения процедур, по которым из популяции
случайным образом извлекаются выборки.
2 Русскоязычному зрителю этот фильм знаком под названием «В джазе только девушки».
123
КНИГА ДЛЯ ТЕХ, КТО НЕ ЛЮБИТ СТАТИСТИКУ. НО ВЫНУЖДЕН ЕЮ ПОЛЬЗОВАТЬСЯ
занятиями они гонялись по университетскому городку за каждой девушкой,
отмечая цвет ее волос и задавая один и тот же вопрос: родилась ли она в Израиле
или иммигрировала сюда из другой страны.
Всего было опрошено 90 девушек, и результаты распределились следующим
образом (табл. 6.1).
Таблица 6.1
Цвет волос в зависимости от происхождения
Уроженки Израиля Иммигрантки Итого
Блондинки 20 18 38
Неблондинки 38 14 52
Итого 58 32 90
Можно ли на основании полученных результатов утверждать, что среди
иммигранток блондинки встречаются чаще?
Для ответа на поставленный вопрос чаще всего используется тест %2 — один
из наиболее популярных непараметрических тестов. С ним мы уже встречались,
когда рассматривали случай одной выборки (параграф 3.2). Тогда он приме-
нялся для сравнения эмпирического распределения качественных признаков
(страна-производитель автомобилей) с теоретическим распределением (рав-
номерным).
Гораздо чаще данный тест используется для сравнения между собой двух и
более эмпирических распределений качественных признаков, полученных на
независимых выборках.
В нашем примере мы имеем две независимые выборки: коренные израиль-
тянки и иммигрантки и качественный признак — цвет волос, выраженный в
дихотомической шкале наименований (блондинка или неблондинка). При этом
как число независимых выборок, так и число градаций качественной перемен-
ной может быть сколь угодно большим.
Основная идея использования теста %2 связана со сравнением наблюдаемых
(observed) частот в каждой из клеток таблицы с теоретически ожидаемыми
(expected) частотами. С опорой на имеющиеся наблюдаемые значения (О)
и вычисленные для каждой клетки таблицы ожидаемые значения (£) опреде-
ляется значение х2.
Для таблицы, содержащей г строк и к столбцов, формула для вычисления х2
выглядит так:
/=17=1 MJ
Для понимания смысла формулы представим расчетную таблицу следующим
образом (табл. 6.2).
124
ГЛАВА 6. ОТДЕЛЕНИЕ СВЕТА ОТ ТЬМЫ, ИЛИ СЛУЧАЙ ДВУХ НЕЗАВИСИМЫХ ВЫБОРОК
Таблица 6.2
Таблица для теста %2 (случай двух независимых выборок)
Выборка 1 Выборка 2 Итого
Категория 1 А (Оч) (^н) в (Оп) (£12) (Я+£)
Категория 2 С (Оя) (Ы D (O22) (Е22) (С+Р)
Итого n{=(A + O n2=(B+D) N=n} +п2
Ожидаемые (теоретические) частоты вычисляются так:
£П = (А+5)(Л+С)/М
En=(A+B)(B+D)/ N,
E2l = (C+D)(A + C)/N,
E22=(C+D)(B+D)/N.
Если эти выражения подставить в формулу для %2, то после несложных ал-
гебраических преобразований получим следующий результат (справедливый
только для таблицы размером 2*2):
2 = N(AD-BC)2
Х (Л+В)(€+Л)(Л+С)(Б+2))‘
Подставим в выражение для х2 значения, полученные Антоном и Ричардом
(А=90; Л =20; 5=18; С=38; 5=14), и произведем необходимые вычисления:
2 N(AD-BC)2 _ 90(20х14-18х38)2 =
Л (A+B)(C+£>)(A+C)(B+D) (20+18)(38+14)(20+38)(18+14) ’ '
Корректнее пользоваться другой формулой, в которую введена поправка на
непрерывность3 для таблиц размером 2x2:
N(\AD-BC\~)2
Х =(A+B)(C+D)(A+C)(B+DY
3 С поправкой на непрерывность для таблицы размером 2x2 мы уже сталкивались при рас-
смотрении теста МакНемара. Она позволяет корректировать ошибки, возникающие при исполь-
зовании непрерывного распределения х2 для анализа дискретных данных. Если эту поправку не
использовать, то значение х2 оказывается большим, чем в том случае, если эта поправка исполь-
зуется. При проверке статистических гипотез это увеличивает число случаев, при которых нуле-
вая гипотеза отвергается без должных на то оснований. К сожалению, во многих случаях иссле-
дователи поправку на непрерывность игнорируют и производят вычисления без нее.
125
КНИГА ДЛЯ ТЕХ, КТО НЕ ЛЮБИТ СТАТИСТИКУ, НО ВЫНУЖДЕН ЕЮ ПОЛЬЗОВАТЬСЯ
После всех предварительных замечаний и преобразований приступим к
формулированию нулевой и альтернативной гипотез (как и прежде, использу-
ем уровень значимости а=0,05).
Но: Среди коренных израильтянок и среди иммигранток девушки-блондин-
ки встречаются одинаково часто.
Н{: Среди девушек-иммигранток блондинки встречаются чаще, чем среди
коренных израильтянок (односторонняя критическая область).
Для проверки нулевой гипотезы вычисляется эмпирическое значение у!ЦПиГ
по приведенной выше формуле (с поправкой на непрерывность). Подставим в
эту формулу значения, полученные Антоном и Ричардом: W=90; А =20; 5=18;
C=38;Z>=14:
М|ЛР-5С|-ф2 90(|20х14-18х38|-^)2
Х "(Л+5)(С+2))(Л +С)(5+D) = (20+18)(38+14)(20+38)(18+14)=3’163’
Полученное значение Хэмпир сравниваем со значением Хкритич» которое нахо-
дим в табл. 2 (Приложение 2) для выбранного уровня значимости а и числа
степеней свободы df=(r—1)(&— 1), где г— число строк в расчетной таблице,
а к — число столбцов в ней. В нашем случае г=к=2 и df= 1.
В табл. 2 приведены значения Хкритич для различных значений уровня зна-
чимости а, соответствующих двусторонней критической области. Как мы уже
знаем, односторонней критической области с уровнем значимости а соответ-
ствует двусторонняя критическая область с уровнем значимости 2а. В нашем
случае а=0,05. Поэтому ищем в таблице значение Хкритич Для df=l и уровня
значимости 2а=0,1. Найденное значение Хкритич = 2,71.
Поскольку хэмпир > Хкритич» нулевая гипотеза отвергается и принимается
альтернативная. Девушки-блондинки встречаются чаще среди иммигранток,
чем среди коренных израильтянок4.
С таблицей размером 2x2 связан еще один показатель, называемый отно-
шением шансов (odds ratio — OR).
На основании результатов, полученных Антоном и Ричардом, можно сказать,
что шанс встретить блондинку среди иммигранток определяется как 18:14.
Шанс встретить блондинку среди коренных израильтянок будет 20:38.
Odds Ratio показывает отношение полученных результатов (отношение
шансов):
05=18:14/20:38=2,44.
Иными словами, шанс встретить блондинку среди студенток-иммигранток
в 2,44 раза выше; шанса встретить блондинку среди студенток, родившихся в
Израиле5.
4 Использование односторонней критической области, позволяющей определить направле-
ние различий между двумя выборками, возможно только для таблицы размером 2x2. Во всех
остальных случаях использования теста х1 это сделать невозможно.
s Нетрудно видеть из таблицы 6.2, что OR определяется как BC/AD.
126
ГЛАВА 6. ОТДЕЛЕНИЕ СВЕТА ОТ ТЬМЫ, ИЛИ СЛУЧАЙ ДВУХ НЕЗАВИСИМЫХ ВЫБОРОК
Приведем еще один пример для случая, когда результаты представлены в
шкале наименований, содержащей более двух категорий.
В ходе одного из исследований, проведенных центром RADAR, были полу-
чены социодемографические характерйетики израильских героиновых нарко-
манов [Isralowitz et al., 2007]. В частности, были получены данные об их семей-
ном положении и типичной занятости в течение последних трех лет. Это
позволило сформировать две независимые выборки, первая из которых вклю-
чила тех, кто на протяжении трех последних лет имел полную или частичную
занятость, а вторая тех, кто в течение последних трех лет был безработным.
В таблице 6.3 приведены данные о семейном положении для каждой из
выборок (данные только для мужчин).
Таблица 6.3
Семейное положение работающих и безработных наркоманов
Наркоманы Работающие Безработные Итого
Женатые 74 51 125
Разведенные 71 91 162
Не состоявшие в браке 79 84 163
Итого 224 226 450
Можно ли утверждать, что семейное положение членов первой выборки
отличается от семейного положения членов второй выборки?
Как и в предыдущем случае, выберем уровень значимости а=0,05 и сфор-
мулируем соответствующие гипотезы.
Яо: Семейное положение работающих мужчин-наркоманов не отличается
от семейного положения безработных мужчин-наркоманов.
Яр Семейное положение работающих мужчин-наркоманов отличается от
семейного положения безработных мужчин-наркоманов (двусторонняя кри-
тическая область).
Для вычисления %эМПИр предварительно определим значения ожидаемых
частот (табл. 6.4).
‘ Таблица 6.4
Значения ожидаемых частот
Наркоманы Работающие Безработные Итого
Женатые _ 224x125 _ £"- «0 ’62'2 Е,2 = 226x125 = 62,8 12 450 125
Разведенные 224x162.8<1.6 21 450 22 450 162
Не состоявшие в браке £ =224x163 31 450 Е= 226x163 =81,9 32 450 163
Итого 224 226 450
127
КНИГА ДЛЯ ТЕХ, КТО НЕ ЛЮБИТ СТАТИСТИКУ, НО ВЫНУЖДЕН ЕЮ ПОЛЬЗОВАТЬСЯ
Подставим значения наблюдаемых и ожидаемых частот в формулу для вы-
числения х2:
..г (74-62,2)2 (51-62,8)2 | (71-80,6)2 ,
Х Е9 62,2 62,8 80,6
, (91-81,4)2 ! (79-81,1)2 t (84-81,9)2 846
81,4 81,1 81,9
В табл. 2 находим значение Хкритич ДЛЯ а=0,05 и числа степеней свободы
df=(r-\)(к-1)=(3-1)(2—1)=2: xUk4=5,99.
Поскольку Хэмпир > Хкритич. нулевая гипотеза отвергается и принимается
альтернативная. Семейное положение работающих мужчин-наркоманов отли-
чается от семейного положения безработных мужчин-наркоманов.
ВКЛЮЧАЕМ КОМПЬЮТЕР...
В переменной «Происхождение» (origin) означим Израиль как 1, все другие страны
как 2. Переменная «Блондинка» (blond) содержит сведения о цвете волос: 1 — блон-
динка, 0 — нет. Дальнейшая последовательность действий и получаемый результат
показаны на рис. 6.1—6.36.
Щ NonPar ametr - SPSS Data Editor
File Edit View Data Transform Analyze Graphs Utilities Window Help
Г“ - f
origin blond
1 1
2 ""“Г1
3 1
4 1
5 1
6 1
7 1
8 1
9 1
10 1
11 1
12 1
13 1
14 1
15 1
16 1
17 1
18 1
Reports > l-^lr—1 r. l/sv! 5...
I De>.riptMj Statistics ►! Frequencies
Compare Means ► General Linear Model ► Descnptives... Explore... -—
Mixed Models ► Crosstabs...
Correlate Regression ► Ratio... I\
►
Log'mear ► Classfy ► Data Reduction ► Scale ► Ronparametnc Tests ► Time Series ► Survival ► Multiple Response > Missing Value Analysis...
ажать
T
1
1
1
1
1
1
1
Рис. 6.1. Выбор требуемой статистической процедуры
6 Программа SPSS предоставляет большой набор возможностей по работе с таблицами со-,
пряженности. Рассмотрение их в полном объеме выходит за рамки этой книги.
128
ГЛАВА 6. ОТДЕЛЕНИЕ СВЕТА ОТ ТЬМЫ, ИЛИ СЛУЧАЙ ДВУХ НЕЗАВИСИМЫХ ВЫБОРОК
Рис. 6.2. Тест х2 для двух независимых выборок: необходимые действия и настройки
Crosstabs
Blond *
Blond No
Yes
Расчетная
таблица
Total
Value
3.163
Origin
Israel
38
20
____58
Результаты вычислений
с использованием других
алгоритмов
TTbhfif 5 nun юл
Unear-by-Linear
Association
N of Valid Cases
.075
Exact Sig.
(1-sided)
Exact Sig.
(2-sided)
____ Полученные выше значения х2
__без поправки и с поправкой на
Chi-sqt^> непрерывность
Csymp. Sig.
(2-slded)
Уровень значимости для двух значе-
ний %2. Поправка на непрерывность дает более достовер-
ный результат. Для перехода к односторонней критической
области приведенные значения необходимо разделить на 2.
(Нулевая гипотеза отвергается.)
a. Computed only for а 2x2
b 0 cells (0%) have expected со
13.51
Рис. 6.3. Тест х2 для двух независимых выборок: результат
5 Зак 3384-
КНИГА ДЛЯ ТЕХ, КТО НЕ ЛЮБИТ СТАТИСТИКУ. НО ВЫНУЖДЕН ЕЮ ПОЛЬЗОВАТЬСЯ
Значение отношения
шансов (Odds Ratio)
Risk Estimate
95% Confidence interval
Lower Upper
Odds Ratio for Blond 4Ng/Yes) 2.443^ ) 1.009 5.911
For cohort Ungin * Israel ~"’Тз88 .985 1.958
For cohort Origin = Other N of Valid Cases .568 90 .325 .994
Рис. 6.3. Окончание
Рассмотрим еще один пример, посвященный семейному положению работающи?
и неработающих наркоманов. В случае больших выборок результаты в расчетной
таблице зачастую удобнее представлять не в виде абсолютных значений, а в виде
процентов. На рис. 6.4 и 6.5 показано, как использовать эту возможность.
Crosstabs
1. Смотри описание дей-
ствий из предыдущего
примера
ок
Pacte
Reset
5. Нажать
Marital status [mattal]
oanat.
Г Dcpiay duUeied bar
Г" Suppress tables
Counts-----
Р Observed
Г Expected
4. Нажать и вернуться
к прежнему окну
2. Нажать и перейти
к новому окну
Caiumnjs)
pb
г Lave 1 of 1
Crosstabs: Cell Display
—। r Residuals
Г" Unst
3. Установить требуемое.
Будут показаны проценты по
строкам и/или столбцам рас-
четной таблицы
Рис. 6.4. Тестх2 для двух независимых выборок: необходимые действия и настройки
130
ГЛАВА 6. ОТДЕЛЕНИЕ СВЕТА ОТ ТЬМЫ, ИЛИ СЛУЧАЙ ДВУХ НЕЗАВИСИМЫХ ВЫБОРОК
Crosstabs
Marital status * JOB Crosstabulation
Marital Married
status
Divorced
Count
% within JOB
Count 7
____________% within JCp
Never married Count Г"
________________% within Jp\
Count
___________ЧЬ Within 4OR
Total
51
22.6%
91
40.3%
84
37.1%
226
00.0%
JOB _______
Yes^
74
33.0%
71
31.7%
79
35.3%
224
4Ю.0%
Total
^425
27.МЦ
162
36.0%
163
36.2%
В соответствии с установкой показаны
проценты по столбцам
Asymp. Sifl.
(2-side$
Valye
6.84
2.714
Pearson Chi-Square
Likelihood Ratio
Linear-by-Llnear
Association
N of Valid Cases
a. 0 cells (.0
Проверяемое
значение
450
expected count less than 5. The
count is 62.22.
Уровень значимости.
(Нулевая гипотеза откло-
няется.)
Рис. 6.5. Тест x2 для двух независимых выборок: результат (случай большой выборки)
6.2. СЕКРЕТ СЕМЕЙНОГО СЧАСТЬЯ,
ИЛИ ТОЧНЫЙ ТЕСТ ФИШЕРА
После свадьбы для Фаины неприятным открытием стало то, что ее муж
храпит во сне. Заснуть рядом с ним при таком храпе было нелегко, и она ино-
гда была вынуждена уходить спать в другую комнату, что, естественно, не ра-
довало мужа. По мнению Фаины, причиной храпа была неверная поза мужа во
время сна — он предпочитал спать на спине. Фаина предпочитала спать на боку
и никогда не храпела. Муж был готов пойти ей навстречу и начать спать на боку
или на животе, но только в том случае, если она докажет ему связь между позой
во время сна и храпом. С этой целью они обзвонили своих друзей, выяснив,
храпят ли они или их мужья/жены во сне и в какой позе они предпочитают
спать.
131
КНИГА ДЛЯ ТЕХ, КТО НЕ ЛЮБИТ СТАТИСТИКУ. НО ВЫНУЖДЕН ЕЮ ПОЛЬЗОВАТЬСЯ
Полученные результаты приведены в таблице 6.5.
Таблица 6.5
Поза во время сна и храп по ночам
Храпят Не храпят Итого
Предпочитают спать на спине 8 3 11
Предпочитают спать не на спине 2 9 И
Итого 10 12 22
Убедят ли эти результаты мужа Фаины?
На первый взгляд данная задача не отличается от рассмотренных выше
примеров, в которых использовался тест х2- К сожалению, у этого теста, при
всей его популярности, есть существенный недостаток: он не предназначен
для работы с малыми выборками, содержащими (в совокупности) менее 30 зна-
чений.
В том случае, если результаты представлены в таблице размером 2x2, а чис-
ло значений меньше 30, предпочтительнее применять точный тест Фишера,
позволяющий вычислять точные значения вероятностей появления тех или
иных событий.
Представим таблицу результатов так (табл. 6.6):
Таблица 6.6
Общий вид расчетной таблицы
Храпят Не храпят Итого
Предпочитают спать на спине ос 3 В 11 (Л+5)
Предпочитают спать не на 2 9 11
спине С D (C + D)
Итого 10 (л+Q 12 (B + D) 22
Идея точного теста Фишера в следующем.
Допустим, что имеется распределение экспериментальных данных по клет-
кам таблицы сопряженности размером 2x2 (табл. 6.7). На основании этих
данных можно вычислить вероятность получения такого распределения ре-
зультатов.
Таблица 6.7
Распределения результатов для таблицы размером 2x2
А в {А + В)
С D (C+D)
(Л + 0 (B+D) N=A+B+C+D
132
ГЛАВА 6. ОТДЕЛЕНИЕ СВЕТА ОТ ТЬМЫ, ИЛИ СЛУЧАЙ ДВУХ НЕЗАВИСИМЫХ ВЫБОРОК
Вероятность вычисляется по следующей формуле:
= (Л+.В)!(С+.Р)!(Л+С)!(Л+Р)!
Р N\A\B\C\D\
Подставим в эту формулу данные из таблицы 6.12:
(Л+Д)!(С + 2))!(^+С)!(Д+Л)!_11!11!10!12!_-
Р N\A\B\C\D\ 22!8!3!2!9! ’
Однако для точного вычисления требуемой вероятности полученного ре-
зультата недостаточно. Необходимо дополнительно рассмотреть вероятности
всех теоретически возможных вариантов распределения результатов в таблице
6.5, которые носят более крайний (экстремальный) характер по сравнению с
исходным.
Вернемся к нашему примеру (табл. 6.5) и представим его в следующем
виде:
а)
8 3
2 9
10
12
11
11
22
Более экстремальные распределения результатов, не искажающие их итогов,
будут иметь такой вид:
Ъ)
9 2 11
1 10 ‘ 11
10 12 22
10 1 11
0 11 И
10 12 22
с)
Вычислим соответствующие вероятности для случаев Ь) и с):
= (Л+2?)!(С+Р)!(Л+С)!(2?+Д)! = 1ШШ0П2!
Pb N\A\B\C\D\ 22!9'.2!1!10! ’
= (Л + 2?)!(С + Д)!(Я+С)!(2?+2))!_ 1ШШ0112! ,.Q0000r
Рс N\A\B\C\D\ 22!10!1!0!11! ’
Тогда точная вероятность будет равна сумме полученных значений:
Р = Ра+Рь+Рс =0,014034 +0,000935+0,000017 = 0,014986 = 0,015.
133
КНИГА ДЛЯ ТЕХ. КТО НЕ ЛЮБИТ СТАТИСТИКУ, НО ВЫНУЖДЕН ЕЮ ПОЛЬЗОВАТЬСЯ
Для рассмотрения ситуации в общем виде представим распределение ре-
зультатов в таблице размером (2x2) следующим образом:
X г-х
С—X N—r—c+x
N-c
г
N—r
N
Тогда, в общем случае, искомое точное значение вероятности будет опре-
деляться как сумма нескольких слагаемых, каждое из которых вычисляется по
формуле:
Р=л—(fix’ гдех=0’ >(г>с)-
I с I
Вернемся к нашему примеру. Из таблицы 6.6 можно видеть, чтох=8, r= 11,
с=10 и min (г, с)=10.
Следовательно, вычисления по этой формуле начнутся со значения х=8 и
закончатся, когда х примет значение х=тin (г, с) = 10. В итоге будут получены
три значения вероятности для х=8,х=9,х=10, сумма которых даст, разумеет-
ся, тбт же результат, который был получен выше.
Несмотря на явные преимущества точного теста Фишера, особенно при
работе с малыми выборками, он не столь популярен, как тест х2, поскольку,
как видно из приведенного примера, требует большого объема дополнительных
вычислений. Поэтому при наличии достаточных по размеру выборок исследо-
ватели предпочитают применять тест х2- При наличии малых выборок требуе-
мых вычислений удается избегать за счет использования громоздкой статисти-
ческой таблицы для этого теста7.
В таблице 10 (Приложение 2) приведен фрагмент этой таблицы, относящий-
ся к рассматриваемому примеру.
Выберем уровень значимости а=0,05 и сформулируем соответствующие
гипотезы.
Но; Число случаев храпа одинаково для людей, спящих на спине, и для лю-
дей, спящих в других позах.
Н\. Число случаев храпа неодинаково для тех, кто спит на спине, и для тех,
кто спит в других позах (двусторонняя критическая область8).
Если все необходимые для проверки вычисления осуществляются вручную
(как показано выше), то получаемое в итоге точное значение вероятности р
7 В книге S. Siegel [Siegel, 1956] статистическая таблица для точного теста Фишера занимает
15 страниц.
8 Поскольку в альтернативной гипотезе не утверждается, что среди тех, кто спит на спине,
число случаев храпа больше.
134
ГЛАВА 6. ОТДЕЛЕНИЕ СВЕТА ОТ ТЬМЫ. ИЛИ СЛУЧАЙ ДВУХ НЕЗАВИСИМЫХ ВЫБОРОК
(в нашем случаер =0,015) сравнивается со значением выбранного уровня зна-
чимости а для случая односторонней критической области. Если р > а, нет
оснований отвергнуть нулевую гипотезу. Если р < а, то нулевая гипотеза от-
клоняется и принимается альтернативная.
В нашем случаер =0,015. Для перехода к двусторонней критической облас-
ти удвоим это значение. Получим р =0,030. Поскольку это значение меньше,
чем а=0,05, нулевая гипотеза отклоняется и принимается альтернативная.
Число случаев храпа неодинаково для тех, кто спит на спине, и для тех, кто спит
в других позах.
В случае использования статистической таблицы для точного теста Фишера
последовательность действий такова:
Находим в таблице 10 (Приложение 2) случай, соответствующий значениям
(А +В)=11 и (C+D)=11. В колонке «В (или А)» ищем значение В, соответст-
вующее тому, что приведено в таблице 6.6 (В=3). Поскольку этого значения в
таблице нет, используем вместо В значение А =8. Напротив значений В (или
А) в таблице приведены критические значения D (или С), соответствующие
указанным уровням значимости для односторонней критической области.
Поскольку в рассматриваемом примере используется двусторонняя критическая
область и уровень значимости а=0,05, то в таблице необходимо искать значе-
ния, соответствующие а=0,025.
Если фактическое значение D (или С), приведенное в таблице 6.6, больше
критического значения D (или С), приведенного в табл. 10, нет оснований
отвергнуть нулевую гипотезу. Если фактическое значение D (или С) меньше
или равно критическому значению D (или С), нулевая гипотеза отвергается и
принимается альтернативная.
Из таблицы следует, что для уровня значимости а=0,025 и А = 8 критическое
значение С=2. Фактическое значение С также равно двум (табл. 6.6).
Поскольку эмпирическое значение (С=2) равно критическому, нулевая
гипотеза отвергается и принимается альтернативная (для а=0,05): число слу-
135
КНИГА ДЛЯ ТЕХ, КТО НЕ ЛЮБИТ СТАТИСТИКУ, НО ВЫНУЖДЕН ЕЮ ПОЛЬЗОВАТЬСЯ
чаев храпа неодинаково для тех, кто спит на спине, и д ля тех, кто спит в других
позах.
При работе с большими выборками обычно используется другой подход,
основанный на свойствах нормального распределения. Вначале вычисляется
значение z по следующей формуле (смысл входящих в формулу обозначений
рассмотрен выше):
lrc(N-r)(N-c)
Затем по таблице ^-распределения определяется соответствующая получен-
ному значению z вероятность, которая сравнивается с выбранным уровнем
значимости а для односторонней критической области.
ВКЛЮЧАЕМ КОМПЬЮТЕР...
Создадим в программе SPSS переменные «Храп» (snoring) (1 — есть храп, 2 — нет
храпа) и переменную «Поза во время сна» (pos), где 1 означает сон на боку или жи-
воте, 2 — сон на спине.
Дальнейшие действия и результат показаны на рис. 6.6-6.8.
F
File Edit View Data Transform | Analyze Graphs Utilities Window Help
NonParametr - SPSS Data Edftor
G?|Q|© El| Reports ►
Desoptive Statstr s ►! Frequences...
2_ 1 snoring 1 Compare Means ► '' ' General Lnear Model ► —— Mixed Models ► Descr ptives... Explore... ——
Crosstabs... 1
Correlate ► Ratio... 1П
2 3 1 1 —
Regression ► Loginear > Gassify ► Data Reduction ► Scale > Nonpar ametnc Tests ► Time Ser es ► Survival ► Multiple Response ► Missing Value Analysis... —
4 6 6 1 1 1 i —> Нажать
7 1
8 1
9 1
10 1
11 2 2
12 2 2
13 2 2
14 2 1
15 2 1
16 2 1
17 2 1
18 2 1
19 2 1
Рис. 6.6. Выбор требуемой статистической процедуры
136
ГЛАВА 6. ОТДЕЛЕНИЕ СВЕТА ОТ ТЬМЫ, ИЛИ СЛУЧАЙ ДВУХ НЕЗАВИСИМЫХ ВЫБОРОК
Рис. 6.7. Точный тест Фишера: необходимые действия и настройки
Crosstabs
Count
Pos * Snoring Crosstabulation
Snonng
Pos Other
Spin
Total
Уровень значимости для односторонней (0,015)
и двусторонней критической области (0,030).
(Нулевая гипотеза отвергается.) _____
Value df AsympK \t Sig (2-sided}\ \ed) Exact Sig (1-sided)
Pearson Chi-Square Continuity Correction* Likelihood Ratio - 6.600b 4.583 1 1 1- .010 032 808-
C^Tsher's Exact Test .030^
Linear-by-ufloai Association N of Valid Cases 6 300 22 1 012
a. Computed only for a 2x2 table
b. 0 cells (.0%) have expected count less than 5xThe minimum expected count Is
5.00.
Рис. 6.8. Точный тест Фишера: результат
КНИГА ДЛЯ ТЕХ, КТО НЕ ЛЮБИТ СТАТИСТИКУ, НО ВЫНУЖДЕН ЕЮ ПОЛЬЗОВАТЬСЯ
6.3. КТО МЕНЕЕ ТРЕВОЖЕН ВО ВРЕМЯ
БЕРЕМЕННОСТИ, ИЛИ ТЕСТ МАННА-УИТНИ
Надя работает психологом в Центре матери и ребенка. Она регулярно про-
водит группы предродовой подготовки женщин, которым предстоят первые в
их жизни роды. Надя предположила, что те женщины, которые были старши-
ми детьми в своей семье и в прошлом имели опыт ухода за своими младшими
братьями и сестрами, будут иметь меньший уровень предродовой тревожности,
чем те женщины, которые были единственными или самыми младшими деть-
ми в семье и такого опыта не имели.
Для проверки этого предположения Надя сформировала две выборки.
В первую вошли шесть женщин, которые были старшими детьми в семье, во
вторую — пять женщин, бывших младшими или единственными детьми в семье.
С помощью специального опросника она получила значения их предродовой
тревожности, показанные в таблице 6.8.
Таблица 6.8
Значения предродовой тревожности
Значение предродовой тревожности
Старший ребенок в семье 73 80 77 66 62 70
Младший/единственный ребенок в семье 85 79 82 75 93
Можно ли на основании полученных данных сделать вывод о существова-
нии различий в значении предродовой тревожности между первой и второй
выборкой?
Приведенный пример типичен для ситуации с двумя независимыми выбор-
ками. Прежде всего, обратим внимание на то, что сейчас мы имеем дело с ре-
зультатами, выраженными в шкале не ниже порядковой.
В том случае, когда необходимо сравнить результаты в двух независимых
выборках (уровень измерения не ниже шкалы порядка), чаще всего использу-
ется тест Манна—Уитни. В непараметрической статистике этот тест выступает
как непараметрический аналог теста Стьюдента и не уступает ему по популяр-
ности. Тест Манна—Уитни позволяет выявлять различия между выборками,
начиная с трех значений в каждой из них9.
Как и в рассмотренном выше тесте Вилкоксона, сравнение двух выборок
основано не на сравнении результатов в каждой из них, а на сравнении рангов
этих результатов.
9 В принципе использование теста Манна—Уитни уже возможно, когда в одной выборке
всего два значения, а в другой — пять и более.
138
ГЛАВА 6. ОТДЕЛЕНИЕ СВЕТА ОТ ТЬМЫ, ИЛИ СЛУЧАЙ ДВУХ НЕЗАВИСИМЫХ ВЫБОРОК
Вначале обе выборки объединяются в одну, и происходит ранжирование
объединенных результатов, независимо оттого, к какой выборке они относят-
ся. Затем отдельно суммируются ранги результатов, относящихся к первой
выборке, и ранги результатов, относящихся ко второй выборке.
В том случае, если между выборками нет заметных различий, сумма рангов
для первой выборки и сумма рангов для второй выборки не должны сущест-
венно отличаться друг от друга.
Несмотря на простоту вычислений, использование данного теста требует
повышенного внимания и аккуратности. Иногда, чтобы не запутаться в том, к
какой выборке относятся получаемые результаты, рекомендуется применять
два набора карточек, на которых отдельно записываются данные первой и
второй выборок и которые затем помечаются различными цветами [Сидоренко,
2000].
Итак, первый шаг. Объединим обе выборки, упорядочим результаты в по-
рядке их возрастания и проранжируем их (табл. 6.9).
Таблица 6.9
Упорядоченные и проранжированные значения предродовой тревожности
Значение тревожности 62 66 70 73 75 77 79 80 82 85 93
Ранг 1 2 3 4 5 6 7 8 9 10 11
Вернемся к таблице 6.8 и напротив каждого значения в первой и второй
выборках проставим его ранг. Затем найдем сумму рангов для меньшей (Ri) и
большей (Я2) выборки. Получим таблицу 6.10.
Таблица 6.10
Предродовая тревожность: проранжированные значения
Значение предродовой тревожности
Старший ребенок в семье 73 80 77 66 62 70
Ранг 4 8 6 2 1 3 /?2=24
Младший/единственный ребенок в семье 85 79 82 75 93
Ранг 10 7 9 5 11 =42
Л| = 10 + 7 + 9+5+11=42;Л2=4+8 + 6 + 2+1+3=24.
После выполнения всех подготовительных преобразований можно присту-
пать к проверке статистических гипотез.
Выбираем уровень значимости а=0,05 и формулируем нулевую и альтер-
нативную гипотезы.
Но: Значения предродовой тревожности у женщин — старших детей в семье
не отличаются от значений предродовдй тревожности у женщин — младших
(единственных) детей в семье.
139
КНИГА ДЛЯ ТЕХ, КТО НЕ ЛЮБИТ СТАТИСТИКУ, НО ВЫНУЖДЕН ЕЮ ПОЛЬЗОВАТЬСЯ
Яр Значения предродовой тревожности у женщин — старших детей в семье
меньше значений предродовой тревожности у женщин — младших (единст-
венных) детей в семье (односторонняя критическая область).
Для проверки нулевой гипотезы вычисляются два значения:
С/| -ТЦП2 Ч--------Л1, U2 — П\П2 ч--~-----«2»
где Л| — объем меньшей выборки; и2 — объем большей выборки.
Из таблицы находим Л]=5; л2=6;/?1 = 42; 7?2=24. Подставляем эти значения
в формулы и находим:
£А1=Л1Л2+^±^-^=(5х6)ч-^)-42=3;
U2 = щп2 + =(5х6)+-(6^1)--24 = 27.
Значения Ux и U2 связаны между собой10:
Я1=П1П2-^2; У^щпг-Ui.
Из двух значений Ui и U2 выбираем меньшее 17= min (t/р Я2)=3 и обраща-
емся к статистической таблице для теста Манна—Уитни. В таблице 7 (Приложе-
ние 2) приведен фрагмент такой таблицы, соответствующий рассмотренному
примеру.
В таблице приведены крайние значения вероятностей (соответствующих
односторонней критической области), при которых для данных значений U, пх
и п2 различия между выборками считаются случайными.
Если выбранный уровень значимости а меньше приведенного в таблице
значения вероятности, то нет оснований отвергнуть нулевую гипотезу.
Если выбранный уровень значимости а равен приведенному в таблице зна-
чению вероятности или превышает его, то нулевая гипотеза отвергается и
принимается альтернативная.
Из табл. 7 для (7=3, Л] =5 и п2=6 находим/? =0,015.
Поскольку а=0,05 больше, чем />=0,015, нулевая гипотеза отвергается и
принимается альтернативная. Значения предродовой тревожности у женщин —
старших детей в семье меньше значений предродовой тревожности у жен-
щин — младших (единственных) детей в семье.
В случае отсутствия статистической таблицы для теста Манна—Уитни вы-
числяется значение z по следующей формуле:
U rvh
2
[И|И2(И,Ч-И2Ч-1)
12
10 Строго говоря, вычисляется одно значение U, которое сравнивается со значением ^2.. Если
Uоказывается больше, чем , то используется другое значение U'=snln2 — U.
140
ГЛАВА 6. ОТДЕЛЕНИЕ СВЕТА ОТ ТЬМЫ, ИЛИ СЛУЧАЙ ДВУХ НЕЗАВИСИМЫХ ВЫБОРОК
Подставим в эту формулу необходимые значения из рассмотренного при-
мера:
з 5x6
г~- 2 - 2 --2,1.91.
/5х6(5+6+1) ’
V 12 У 12
По таблице 1 (Приложение 2) для ^-распределения находим, что левее зна-
чения z=—2,191 лежит вероятность р =0,014 (левосторонняя критическая об-
ласть), что с учетом возможностей табл. 1 практически совпадает с полученным
выше значением/? =0,015. Посколькур =0,015 меньше, чем <х=0,05, нулевая
гипотеза отвергается и принимается альтернативная. Значения предродовой
тревожности у женщин — старших детей в семье меньше значений предродовой
тревожности у женщин — младших (единственных) детей в семье.
Возможен еще один подход к определению и С/2- основанный на прямом
сравнении выборок между собой и позволяющий обходиться без предваритель-
ного ранжирования результатов.
Вернемся к таблице 6.8. Рассмотрим обе выборки и сравним каждое значе-
ние в первой выборке с каждым значением во второй выборке. Определим,
сколько значений из второй выборки больше данного значения из первой вы-
борки. Например, первое значение в первой выборке — 73. Во второй выборке
все 5 значений (85, 79, 82,75,93) больше чем 73. Результат сравнения равен 5.
Запишем его в скобках рядом со значением 73 (табл. 6.11). Второе значение в
'цервой выборке — 80. Во второй выборке три значения (85,82,93) больше чем
80. Результат сравнения — 3. Продолжим эту процедуру для всех значений в
первой выборке.
После завершения работы с первой выборкой поменяем направление срав-
нения. Сейчас каждое значение во второй выборке сравним с каждым значе-
нием в первой выборке. Результаты сравнения также запишем в скобках рядом
с соответствующим значением из второй выборки.
Найдем сумму результатов сравнения первой выборки со второй (Z7|_,2)
и второй выборки с первой (t/2_>i):
[/^2=5 + 3+4 + 5 + 5 + 5=27,
[/2^=0+1+0 + 2+0=3.
Нетрудно видеть, что полученные результаты совпадают с ранее найденны-
ми значениями Ux и U2, из которых в тесте Манна—Уитни используется наи-
меньшее:
U= min(l/b [/2)=min([/I_>2, [/2_>1)=3.
Одна из типичных ситуаций, возникающих при использовании теста Манна-
Уитни, касается наличия связанных рангов. В том случае, когда в выборках
141
КНИГА ДЛЯ ТЕХ, КТО НЕ ЛЮБИТ СТАТИСТИКУ, НО ВЫНУЖДЕН ЕЮ ПОЛЬЗОВАТЬСЯ
Таблица 6.11
Сравнение выборок между собой
Значение предродовой тревожности
Старший ребенок в семье 73 (5) 80 (3) 77 (4) 66 (5) 62 (5) 70 (5) ^-2=27
Младший/единственный ребенок в семье 85 (0) 79 (1) 82 (0) 75 (2) 93 (0) t^i-з
имеются одинаковые значения, приходится использовать иной, более сложный
алгоритм действий.
Рассмотрим еще один пример.
Даниил и Юлия — студенты-психологи, интересующиеся гендерными раз-
личиями когнитивных процессов. Взяв за основу результаты психометриче-
ского экзамена (психометрия)11, они решили проверить, различаются ли эти
результаты в зависимости от фактора пола. Опросив других студентов, Даниил
и Юлия получили следующие данные (табл. 6.12).
Таблица 6.12
Результаты психометрии у мужчин и женщин
Юноши Oh=7) Девушки (/22=7)
№ Оценка по психометрии № Оценка по психометрии
1 710 1 715
2 720 2 730
3 716 3 730
4 700 4 718
5 708 5 710
6 703 6 708
7 730 7 724
Можно ли на основании полученных данных сделать вывод о существовании
различий в результатах психометрии между мужчинами и женщинами?
Объединим обе выборки и проранжируем результаты, начиная с наимень-
шего значения (табл. 6.13).
Таблица 6.13
Упорядоченные и проранжированные результаты психометрии
Оценка 700 703 708 708 710 710 715 716 718 720 724 730 730 730
Ранг 1 2 3,5 3,5 5,5 5,5 7 8 9 10 11 13 13 13
11 Комплексное стандартизированное тестирование, по результатам которого происходит
зачисление в израильские вузы. Нечто подобное внедряется в последние годы в России в виде
ЕГЭ.
142
ГЛАВА 6. ОТДЕЛЕНИЕ СВЕТА ОТ ТЬМЫ, ИЛИ СЛУЧАЙ ДВУХ НЕЗАВИСИМЫХ ВЫБОРОК
Как видно, результаты ранжирования содержат три группы связанных ран-
гов: (3,5; 3,5), (5,5; 5,5), (13,13,13) (выделены ? табл. 6.13).
Вернемся к таблице 6.4 и напротив каждого значения в первой и второй
выборках проставим его ранг. Затем найдем сумму рангов для каждой выборки.
Результаты приведены в таблице 6.14.
Таблица 6.14
Результаты психометрии: проранжированные значения
Юноши (л |=7) Ранг Девушки (л2=7) Ранг
№ Оценка по психометрии № Оценка по психометрии
1 710 5,5 1 715 7
2 720 10 2 730 13
3 716 8 3 730 13
4 700 1 4 718 9
5 708 3,5 5 710 5,5
6 703 2 6 708 3,5
7 730 13 7 724 11
» Л, =43 - «2=62
Выбираем уровень значимости а=0,05 и формулируем нулевую и альтер-
нативную гипотезы.
Но: Результаты психометрии у мужчин не отличаются от результатов психо-
метрии у женщин.
Нх: Результаты психометрии у мужчин отличаются от результатов психомет-
рии у женщин (двусторонняя критическая область12).
Для проверки нулевой гипотезы вычислим два значения:
ТТ_______ «l(«|+l) D. ТГ . «2(«2+!) D
1/1—“ /4, иг — -----К2.
Из таблицы находим пх=п2—1', R\ =43; R2 =62. Подставляем эти значения в
формулы и находим:
Ux =и[п2 + Л1(^'1)-^ =(7х7)+^?-^-43 = 34;
и2 =л1и2+'^(у1)-/?2 =(7х7)+7(72+1)-62=15.
Из двух значений Ux и U2 выбираем меньшее (U= 15) и используем его в
дальнейших расчетах13.
12 В рамках решаемой задачи не выдвигается гипотеза о том, что у одних результаты психо-
метрии лучше, а у других хуже. Для Даниила и Юлии важно проверить сам факт наличия различий
в зависимости от пола. Поэтому используется двусторонняя критическая область.
13 Здесь также можно использовать описанный выше подход, основанный на прямом сравне-
143
КНИГА ДЛЯ ТЕХ, КТО НЕ ЛЮБИТ СТАТИСТИКУ, НО ВЫНУЖДЕН ЕЮ ПОЛЬЗОВАТЬСЯ
При наличии в результатах к групп связанных рангов значение z вычисля-
ется по скорректированной формуле:
rr W2
Z= t v д
F и,л2 YN3-N
VI N(N-l) I 12 ft '
гдеЛГ=п1+л2; 7}=-*-*, — число связанных рангов в каждой из к групп.
Как отмечалось, мы имеем три группы связанных рангов. В первой группе
два связанных ранга, во второй группе также два связанных ранга и в третьей
группе три связанных ранга. Тогда А = 2;/2 =2;Г3 = 3.
к
Определим значение £7}:
/=1
J23-2) (23 - 2) (33 - 3)
и ' м 12 12 12 12
= 3.
Подставим в формулу для z все необходимые значения:
ГТ . п1п2 1 С 2х7
Z = j 2 = 2 = -1222
If п,п2 YN3-N Л 7x7 Y143-14 -А
12 ft') vv14(14+1)Jl 12 J
По таблице 1 (Приложение 2) для ^-распределения находим, что левее зна-
чения г=—1,222 лежит вероятность р =0,111 (левосторонняя критическая об-
ласть). Поскольку альтернативная гипотеза сформулирована для двусторонней
критической области, удваиваем полученное значение: р =0,222. Данное зна-
чение больше выбранного уровня значимости а=0,05, поэтому у нас нет ос-
нований отклонить нулевую гипотезу. Результаты психометрии у мужчин не
отличаются от результатов психометрии у женщин.
ВКЛЮЧАЕМ КОМПЬЮТЕР...
В программе SPSS производится вычисление значения z по одной из двух приве-
денных выше формул, в зависимости от того, имеются ли в результатах связанные
ранги или нет.
Перейдем к программе SPSS и рассмотрим первый пример. В переменной «Выбор-
ка» (sample) укажем принадлежность к первой (1) или второй (2) выборке. В пере-
менной «Тревожность» (anxiety) укажем значения предродовой тревожности для
участников обеих выборок. Дальнейшая последовательность действий и результат
показаны на рис. 6.9—6.11.
нии значений в обеих выборках. В случае совпадения сравниваемых значений результат сравне-
ния принимается равным 0,5.
144
ГЛАВА 6. ОТДЕЛЕНИЕ СВЕТА ОТ ТЬМЫ, ИЛИ СЛУЧАЙ ДВУХ НЕЗАВИСИМЫХ ВЫБОРОК
NonParametr - SPSS Data Editor
Fw Edit Vew Data Transform Analyse Graphs Utit к Window Hep
сЗ|Я|е»| ^|с -| | Reports > Descr ptrve Statistics ► Compare Means ► General linear Model ► Mixed Models > Correlate > Regression > Log near > CJassfy » Data Reduction > Scale >
29. sample
sample anxiety
1 1 7 J
2 1 Ел
3 1 7
4 1 £l
5 1 £
6| 1 7-J
7 2 Nonpar ametnc Tests ►
Time Series > Survival ► Multiple Response > Missog Value Analysis...
6 2 7
9 2 £
10 2 7 1
11 2 9T
12
13
Ch-Square...
Binomial...
Runs...
Рис. 6.9. Выбор требуемой статистической процедуры
Рис. 6.10. Тест Манна—Уитни: требуемые действия и настройки
КНИГАДЛЯ ТЕХ, КТО НЕ ЛЮБИТ СТАТИСТИКУ, НО ВЫНУЖДЕН ЕЮ ПОЛЬЗОВАТЬСЯ
Mann-Whttney Test
Ranks
__________SAMPLE N
ANXIETY 1 6
2 5
Total 11
Asymp. Sig. (2-tailed)
Exact Sig. [2*(1-tailed
Sig.)]__________________
a Not corrected for
b. Grouping Varia
Уровень значимости для
двусторонней критической области, рассчитанный
двумя различными способами. В случае малых выборок
второе значение более достоверное. Для перехода к од-
носторонней критической области приведенное значе-
ние необходимо разделить на два. (Нулевая
гипотеза отвергается.)
Рис. 6.11. Тест Манна—Уитни: результат
Для второго примера (случай связанных рангов) введем переменную «Пол» (gender),
в которой 1 соответствует мужчинам, 0 — женщинам. Результаты психометрическо-
го экзамена поместим в переменную «Тест» (test). Проделаем те же действия, что в
предыдущем примере (на этапе кодировки групп вместо обозначений 1 и 2 исполь-
зуем кодировку 0 и 1 и получим следующий результат (рис. 6.12).
Mann-Whitney Test
Ranks
Gender N Mean Rank Sum of Ranks
TEST Female Male Total 7 7 14 8.86 6.14 62.00 43.00
Test Stat tsticsb
Mann-Whitney U
Wilcoxon W
Z
Asymp. Sig. (2-tailed)
Exact Sig. (2*(1-tailed
Sig.)]
JTNot corrected for ties:
thGrouping Vanabie: Gen
TEST
15.000
43.000
-1.
.259
.222
Уровень значимости.
(Нулевая гипотеза не отвер-
гается) •
Для случая связанных рангов
это значение является менее
точным
Рис. 6.12. Тест Манна—Уитни: результат (случай связанных рангов)
146
ГЛАВА 6. ОТДЕЛЕНИЕ СВЕТА ОТ ТЬМЫ, ИЛИ СЛУЧАЙ ДВУХ НЕЗАВИСИМЫХ ВЫБОРОК
6.4. СИГАРЕТА КАК СИМВОЛ МАТЕРИНСТВА,
ИЛИ СНОВА ТЕСТ КОЛМОГОРОВА-СМИРНОВА
Среди курильщиков в Израиле не менее 20% женщин. Курят даже беремен-
ные женщины и женщины, кормящие грудью.
В одном из исследований, проведенных центром RADAR, проверялось,
приводит ли появление детей к изменению количества сигарет, выкуриваемых
ежедневно их матерями. Было опрошено 83 курящих женщин, из которых 45
имели детей и 38 не имели. Результаты опроса, отражающие количество еже-
дневно выкуриваемых сигарет, приведены в таблице 6.15.
Таблица 6.15
Наличие детей и количество ежедневно выкуриваемых сигарет
Женщины Количество ежедневно выкуриваемых сигарет Итого
Не более одной От 2 до 5 Отбдо 10 От 11 до 20 Более 20
Имеющие детей 5 13 11 9 7 45
Не имеющие детей 8 8 9 9 4 38
Итого 13 21 20 18 11 83
Можно ли на основании полученных данных сделать вывод о том, что ме-
жду женщинами, имеющими детей, и бездетными существуют различия в ко-
личестве ежедневно выкуриваемых сигарет?
В принципе, для ответа на поставленный вопрос можно использовать тест %2,
рассматривая приведенные данные как распределенные по нескольким кате-
гориям. Однако в том случае, когда полученные результаты допускают упоря-
дочивание по возрастанию (в нашем случае — по числу выкуриваемых еже-
дневно сигарет) возможно применение теста Колмогорова—Смирнова для двух
независимых выборок. Тест позволяет сравнивать распределение результатов
в двух независимых выборках, содержащих значения, выраженные в шкале не
ниже порядковой. Пример использования этого теста для случая одной выбор-
ки был рассмотрен в параграфе 3.3.
В данном случае, по аналогии с рассмотренным ранее примером, рассмат-
риваются две эмпирические кумулятивные функции распределения (значения
накопленных к данному разряду таблицы относительных частот): для
первой выборки и S^X) для второй выборки. Вычисляются величины расхо-
ждений между ними, и находится значение D=max|<yjJ.¥)-<S’%(.¥)| —макси-
мальное (по модулю) значение различий между эмпирическими кумулятивны-
ми функциями распределения для первой (щ) и второй (п2) выборки.
В таблице 6.16 показаны все необходимые вычисления для получения зна-
чения D.
147
КНИГА ДЛЯ ТЕХ, КТО НЕ ЛЮБИТ СТАТИСТИКУ, НО ВЫНУЖДЕН ЕЮ ПОЛЬЗОВАТЬСЯ
Таблица 6.16
Тест Колмогорова—Смирнова для двух независимых выборок: расчетная таблица
Женщины Количество ежедневно выкуриваемых сигарет
Не более одной От 2 до 5 От 6 до 10 От 11 до 20 Более 20 Итого
Имеющие детей 5 13 11 9 7 45
Относительная частота 5/45 13/45 11/45 9/45 7/45
Накопленная относи- тельная частота 5/45 18/45 29/45 38/45 45/45
Не имеющие детей 8 8 9 9 4 38
Относительная частота 8/38 8/38 9/38 9/38 4/38
Накопленная относи- тельная частота Sn,(X) 8/38 16/38 25/38 34/38 38/38
\S^X)-Sn,{X)\ 0,099 0,021 0,013 0,050 0,000
Выберем уровень значимости а=0,05 и сформулируем соответствующие
гипотезы.
Яо: Нет различий в количестве ежедневно выкуриваемых сигарет у женщин,
имеющих детей, и у женщин без детей.
Я|1 Существуют различия в количестве ежедневно выкуриваемых сигарет у
женщин, имеющих детей, и у женщин без детей (двусторонняя критическая
область14).
На основании таблицы 6.16 (последняя строка) находим
D = шах 15^ (X)-5^ (А') |=0,099.
Это эмпирическое значение сравнивается с критическим, которое опреде-
ляется на основе таблицы критических значений для теста Колмогорова-
Смирнова для двух независимых выборок (см. табл. 9, Приложение 2, случай
большой выборки и двусторонней критической области). Если эмпирическое
значение D меньше критического, то нет оснований отвергнуть нулевую гипо-
тезу. Если эмпирическое значение D больше критического или равно ему, то
нулевая гипотеза отвергается и принимается альтернативная.
Из табл. 9 следует, что для уровня значимости а=0,05 критическое значение
D находится по следующей формуле:
Дри™ч=1.36 = 1,36. = 0,2996.
КрИТИЧ 45x38
14 Альтернативная гипотеза не утверждает, что одни курят больше, а другие меньше.
148
ГЛАВА 6. ОТДЕЛЕНИЕ СВЕТА ОТ ТЬМЫ. ИЛИ СЛУЧАЙ ДВУХ НЕЗАВИСИМЫХ ВЫБОРОК
Поскольку эмпирическое значение D (0,099) меньше критического (0,2996),
нет оснований отвергнуть нулевую гипотезу. Женщины, имеющие детей, курят
столь же интенсивно, что и женщины без детей.
При работе с малыми выборками, в том случае, когда л j =л2=^40, исполь-
зуется другая таблица критических значений для данного теста.
Рассмотрим еще один пример.
Социальный работник, работающий с подростками группы риска, проана-
лизировал 30 личных дел подростков-правонарушителей из числа новых им-
мигрантов: 15 дел иммигрантов из бывшего СССР и 15 дел иммигрантов из
Эфиопии. Его интересовало, в каком возрасте теми и другими были соверше-
ны первые правонарушения.
Полученные результаты показаны в таблице 6.17.
Таблица 6.17
Возраст первого правонарушения
Возраст первого правонарушения
12 13 14 15 16 17 Итого
Подростки из б. СССР 0 2 1 3 6 3 15
Подростки из Эфиопии 1 4 3 2 5 0 15
Итого 1 , 6 4 5 11 3 30
Можно ли утверждать, что между двумя выборками существуют различия в
возрасте первых правонарушений?
Выберем уровень значимости а=0,05 и сформулируем нулевую и альтерна-
тивную гипотезы.
Но: Между подростками-иммигрантами из бывшего СССР и подростками-
иммигрантами из Эфиопии отсутствуют различия в возрасте первых правона-
рушений.
Ну Между подростками-иммигрантами из бывшего СССР и подростками-
иммигрантами из Эфиопии существуют различия в возрасте первых правона-
рушений (двусторонняя критическая область).
Как и в предыдущем примере, создадим расчетную таблицу .(табл. 6.18)
и вычислим значение 2)=тах|5Л|(А’)-5Л1(А’)|,, где nt =n2=N=15.
Как видно из таблицы, D=шах 15^ (X)-S^ (X) |=8/15=0,533.
Запишем полученный результат следующим образом:
где KD—числитель дроби, соответствующий значению D (в нашем случае KD=8),
N=nx =и2=15.
В таблице 8 (Приложение 2, случай малой выборки) для каждого значения
N (от 3 до 40) приведены критические значения KD для односторонней и дву- .
149
КНИГА ДЛЯ ТЕХ, КТО НЕ ЛЮБИТ СТАТИСТИКУ. НО ВЫНУЖДЕН ЕЮ ПОЛЬЗОВАТЬСЯ
Таблица 6.18
Расчетная таблица
Возраст первого правонарушения
12 13 14 15 16 17 Итого
Подростки из б. СССР 0 1 1 4 6 3 15
Относительная частота 0/15 1/15 1/15 4/15 6/15 3/15
Накопленная относи- тельная частота 5Л1 (X) 0/15 1/15 2/15 6/15 12/15 15/15
Подростки из Эфиопии 1 4 5 2 3 0 15
Относительная частота 1/15 4/15 5/15 2/15 3/15 0/15
Накопленная относи- тельная частота Sny(X) 1/15 5/15 10/15 12/15 15/15 15/15
|5Л,(Х)-5Л,(%)| 1/15 4/15 8/15 6/15 3/15 0
сторонней критических областей и соответствующих значений уровня значи-
мости а.
Если эмпирическое значение KD меньше приведенного в таблице, нет ос-
нований отвергать нулевую гипотезу. Если эмпирическое значение KD больше
или равно приведенному в таблице, нулевая гипотеза отвергается и принима-
етсяальтернативная.
Для двусторонней критической области с уровнем значимости а=0,05
и N—15, критическое значение KD—8. Поскольку это совпадает со значением
KD, полученным на основе таблицы 6.18, нулевая гипотеза отвергается. Подростки
из бывшего СССР и из Эфиопии начинают совершать первые правонарушения
в различном возрасте.
Щ NonParametr - SPSS Data Editor
He Edit View Data Transform , Analyze Graphs Utites Window Help
1
Reports
Descriptive Statistics
Compare Means
General Linear Model
Mixed Models
Correlate
Recession
Loginear
Classify
Data Reduction
Scala
Norpar amebic Tests
Tme Series
Survival
Multiple Response
Missing Value Analysis...
2 Independent Samples...
Chi-5quare... '
Bnomial...
Runs...
l-5ampie K-5...
Нажать
К Independent Samples...
2 Related Samples...
К Related Samples...
Рис. 6.13. Выбор требуемой статистической процедуры
150
ГЛАВА 6. ОТДЕЛЕНИЕ СВЕТА ОТ ТЬМЫ, ИЛИ СЛУЧАЙ ДВУХ НЕЗАВИСИМЫХ ВЫБОРОК
ВКЛЮЧАЕМ КОМПЬЮТЕР...
В переменной «Курение» (smoking) цифрами от 1 до 5 обозначим число ежеднев-
но выкуриваемых сигарет (в соответствии с градациями, приведенными в табли-
це 6.14). В переменной «Дети» (children) 0 означает отсутствие детей, 1 — их нали-
чие. Дальнейшая последовательность действий и конечный результат показаны на
рис. 6.13-6.15.
Test Typo —
Г Mann-Whjtney U
2. Перенести сюда пере-
менные «smoking»
и «children» из левого окна
Test Variable Let
smoking
Two-Independent -Samples Tests
Reset |
1. Установить настройку
для теста Колмогорова-
Смирнова
Grouping Variable
Help |
Defne Gt
| Continue
Two Independent Sampli^
3. Нажать и в новом окне вве-
Г Wald Wolfowitz
Group 1
Group 2
сти кодировку групп. В пере-
менной «children» использует-
ся кодировка 0 и 1. Ввести
ок J
Paste
4. Нажать и вернуться
к исходному окну
Cancel
Help
Two-Independent-Sample» Te*fr
Test Variable Lnt
-Тей Туре —---------s------ -------------------:-----1
Г” Mann-Whitney U Р* Kolmogorov SuanovZ
Г” Moses extreme reactions Г” WaldWoUowi>z run:
Options...
Cancel
Help
Reset
5. Нажать
Рис. 6.14. Тест Колмогорова—Смирнова для двух независимых выборок:
необходимые действия и настройки
151
КНИГА ДЛЯ ТЕХ, КТО НЕ ЛЮБИТ СТАТИСТИКУ, НО ВЫНУЖДЕН ЕЮ ПОЛЬЗОВАТЬСЯ
Two-Sample Kolmogorov-Smirnov Test
Frequencies
___________CHILDREN
SMOKING No
Yes
Total
П1П2
V(ni+«i)
Most Extreme
Differences
Проверяемое
значение
Kolmogorov-Smirnov Z
Asymp. Sig. (2-tailed)
Absolute
Positive
Negative
N_____
38
45
83,
Рис. 6.15. Тест Колмогорова—Смирнова для двух независимых выборок:
результат (смысл обозначений см. в параграфе 6.4)
D-maximum |5П1(Х)-5П.(Х)|
^=0,451
38+45
Уровень значимости
(Нулевая гипотеза
не отвергается
Для второго примера (возраст первого правонарушения) создадим переменные
«Возраст» (age) и «Происхождение» (origin), в которой 0 будет обозначать подрост-
ков из бывшего СССР, а 1 — подростков из Эфиопии.
Итоговый результат показан на рис. 6.16.
Two-Sample Kolmogorov-Smirnov Test
Рис. 6.16. Тест Колмогорова—Смирнова для двух независимых выборок:
результат (пример с правонарушителями)
152
ГЛАВА 6. ОТДЕЛЕНИЕ СВЕТА ОТ ТЬМЫ. ИЛИ СЛУЧАЙ ДВУХ НЕЗАВИСИМЫХ ВЫБОРОК
6.5. ПРОРОК ДАНИИЛ КАК ПЕРВЫЙ ДИЕТОЛОГ,
ИЛИ ТЕСТ ВАЛЬДА—ВОЛФОВИЦА
В Книге пророка Даниила дано безупречное описание эксперимента с ис-
пользованием двух независимых выборок:
«Сказал Даниил Амелсару <...>: “Сделай опыт над рабами твоими втечение
десяти дней; пусть дают нам в пищу овощи и воду для питья; и потом пусть
явятся перед тобой лица наши и лица тех отроков, которые питаются царскою
пищей...” Он послушался их в этом и испытывал их десять дней. По истечении
же десяти дней лица их оказались красивее, и телом они были полнее всех тех
отроков, которые питались царскими яствами»15.
Сейчас трудно сказать, чем питался царь Навуходоносор и его приближен-
ные, но, видимо, предложенная Даниилом овощная диета и отказ от алкоголя
в пользу воды оказались для молодых людей более полезными, чем истощающие
организм и обильно сдобренные вином царские яства.
Для достижения результата юному Даниилу понадобилось всего десять дней.
Современным толстякам и толстушкам, которые, не в пример Даниилу, реша-
ют задачу своего похудания, для того чтобы сбросить лишние 15—20 килограм-
мов своего веса, требуются недели и месяцы. Именно последнее обстоятель-
ство легло в основу исследования, посвященного проверке эффективности двух
различных диет. Для участия в эксперименте было отобрано две группы доб-
ровольцев (по 10 человек в каждой), желающих снизить свой вес не менее чем
на 20 кг. Первой группе была предложена диета А, второй — диета В. В ходе
эксперимента фиксировалось время (в неделях), которое понадобилось участ-
никам для достижения поставленной цели — снижения веса на 20 кг.
Результаты эксперимента представлены в таблице 6.19.
Таблица 6.19
Время достижения результата для двух различных диет
Диета А Время достижения результата, недели Диета В Время достижения результата, недели Диета Л Время достижения результата, недели Диета В Время достижения результата, недели
14 23 37 31
20 16 14 15
38 25 32 23
35 30 21 26
19 27 18 17
15 Дан. 1,11-15.
153
КНИГА ДЛЯ,ТЕХ, КТО Н Е ЛЮБИТ СТАТИСТИКУ, НО ВЫНУЖДЕН ЕЮ ПОЛЬЗОВАТЬСЯ
Можно ли утверждать, что две дие-
ты отличаются друг от друга по своей
эффективности?
Приведенный пример мало отли-
чается по своей сути от ранее рассмот-
ренных для двух независимых выбо-
рок. Какивслучаетеста Манна—Уитни
мы имеем две группы значений, пред-
ставленных в шкале не ниже поряд-
ковой.
Вальд и Волфовиц16 предложили
еще один тест, который в случае малых
выборок может оказаться более удоб-
ным, чем рассмотренные выше.
Если предположить, что результаты в двух выборках существенно отлича-
ются друг от друга, то при их объединении и упорядочивании (например, в
порядке возрастания результатов) практически не будет «перемешивания»
результатов одной выборки с результатами другой. Вначале будет серия данных,
относящихся к одной выборке, затем — серия данных, относящихся к другой
выборке. В том случае, если выборки различаются незначительно, в упорядо-
ченной последовательности результаты двух выборок будут следовать «впере-
мешку». Вальд и Волфовиц в своем тесте показали, до какой степени «переме-
шивание» двух выборок в упорядоченной последовательности может
считаться случайным (если «перемешиваний» слишком мало, то это говорит о
существовании значимых отличий между выборками).
Итак, выберем уровень значимости а=0,05 и сформулируем нулевую и
альтернативную гипотезы.
Но: С точки зрения времени достижения требуемого результата обе диеты
одинаковы по своей эффективности.
Ну С точки зрения времени достижения требуемого результата эффектив-
ность обеих диет различна (двусторонняя критическая область17).
На основе таблицы 6.19 объединим две выборки, упорядочим приведенные
в них результаты по возрастанию и укажем, к какой из двух диет, А или В, от-
носится каждый результат. Получим таблицу 6.20.
Таблица 6.20
Упорядоченные результаты для объединенных выборок
14 14 15 16 17 18 19 20 21 23 23 25 26 27 30 31 32 35 37 38
А А В в В А А А А В В В В В в в А А А А
16Якоб Волфовиц в 1942 г. впервые использовал термин «непараметрическая статистика».
17 В альтернативной гипотезе не утверждается, что одна из диет (например, диета В) более
эффективна, чем другая. Поэтому используется двусторонняя критическая область (утверждает-
ся различие диет по эффективности без указания направления этого различия).
154
ГЛАВА 6. ОТДЕЛЕНИЕ СВЕТА ОТ ТЬМЫ. ИЛИ СЛУЧАЙ ДВУХ НЕЗАВИСИМЫХ ВЫБОРОК
В упорядоченной последовательности результатов двух выборок можно
выделить 5 серий, говорящих о том, насколько обе выборки «перемешаны»:
ДА, ВВВ, АААА, ВВВВВВВ, АААА.
Поскольку в данном тесте мы имеем дело с сериями из нескольких одина-
ковых значений, то вновь используем таблицу 6 (Приложение 2) для теста
последовательностей. Сравниваем полученное число серий (А=5) с приведен-
ным в первой строчке значением для случая Л|®л2= 10: ЯКритиЧ = 6 (в табли-
це приведены критические значения, соответствующие уровню значимости
а=0.05).
Если эмпирическое значение R больше критического, нет оснований от-
вергнуть нулевую гипотезу. Если эмпирическое значение R меньше критиче-
ского или равно ему, нулевая гипотеза отвергается и принимается альтерна-
тивная18.
В нашем случае Яэмпир=5, Акритич =6. Поскольку Яэмпнр < Якрнтич, нулевая ги-
потеза отвергается. Диеты отличаются друг от друга по своей эффективности.
Как видно из табл. 6, она предназначена для выборок, содержащих не более
20 значений каждая. В случае выхода размеров выборок за эти пределы, необ-
ходимо использовать общую расчетную формулу для теста Вальда—Волфовица.
Если каждая выборка содержит более 30 значений, то вычисляется значение z
и используется статистическая таблица для ^-распределения (табл. 1, Прило-
жение 2). Необходимые расчетные формулы приведены ниже.
При использовании теста Вальда—Волфовица зачастую возникает допол-
нительная проблема, затрудняющая его применение.
Рассмотрим пример.
Группе детей (5 мальчиков и 5 девочек) был предложен набор из 10 голово-
ломок (популярные задачи на перекладывание спичек). За отведенное время
группа справилась с заданием следующим образом (приведено число решенных
головоломок; табл. 6.21).
Таблица 6.21
Число решенных головоломок
Мальчики Девочки
7 6
5 7
5 5
4 6
8 3
18 В данном случае мы вновь встречаемся с ситуацией, когда правило принятия решения после
сравнения и А'кри™, носит «обратный» характер: нулевая гипотеза отвергается, когда
меньше
155
КНИГА ДЛЯ ТЕХ, КТО НЕ ЛЮБИТ СТАТИСТИКУ, НО ВЫНУЖДЕН ЕЮ ПОЛЬЗОВАТЬСЯ
Если сравнить обе группы, то в них можно увидеть одинаковые (связанные)
результаты. При объединении обеих групп и упорядочивании результатов не-
ясно, в какой последовательности записывать повторяющиеся результаты,
относящиеся к разным группам.
Здесь возможны несколько вариантов:
3 4 5 5 5 6 6 7 7 8
д М М М д д д д М М
3 4 5 5 5 6 6 7 7 8
д М М д М д д д М М
3 4 5 5 5 6 6 7 7 8
д М д М М д д д М М
3 4 5 5 5 6 6 7 7 8
д М д М М д д М д М
3 4 5 5 5 6 6 7 7 8
д М д М М д д М д М
Все варианты являются равноправными, но в первом из них 4 серии, в двух
следующих 6 серий и в двух последних 8 серий. Как известно, чем больше серий,
тем сильнее «перемешаны» результаты, тем меньше шансов выявить различия
между выборками.
К сожалению, однозначного решения проблемы совпадающих результатов
не существует [Siegel, 1956]. В ряде случаев рекомендуется записать все воз-
можные варианты упорядочивания с учетом совпадающих результатов, затем
произвести статистическую проверку для каждого из них и вынести оконча-
тельное решение о судьбе нулевой гипотезы по результатам проверки [Runyon,
1977]. При этом различных вариантов записи упорядоченных результатов мо-
жет быть до нескольких десятков (в нашем простом примере их уже 5)19
ВКЛЮЧАЕМ КОМПЬЮТЕР...
В программе SPSS на основе сведений о размере выборок п1 и п2 и числе серий R
рассчитывается вероятность получения такого результата. Для этого используется
следующая формула, меняющаяся в зависимости от того, имеем ли мы дело с чет-
ными или нечетными значениями:
19 Использование программы SPSS избавляет от этих трудностей.
156
ГЛАВА 6. ОТДЕЛЕНИЕ СВЕТА ОТ ТЬМЫ, ИЛИ СЛУЧАЙ ДВУХ НЕЗАВИСИМЫХ ВЫБОРОК
Я «|
p(r^R)=7-^Y2 г
1 «1+«2 -
( th )
р(Г^ю=
V "1 J
Итоговая вероятность равна сумме «четных» и «нечетных» частей этой формулы.
В нашем примере пх =л2=Ю; R=5. Значение г меняется от 2 до 5. Если г=3, это
означает г=(2 х 2) — 1, то есть к=2. Если г=5, это означает г=(2 х 3) — 1, то есть к=3.
Кроме этого, напомним, что | а 1=———, если а > b и Iа 1= 0 , если а < b; к!= 1 х
х2хЗх ... х(к—1)£, 0! = 1. bl(a-b)l
Подставим в формулу все необходимые данные.
p(r<R)=A-S2 г
IП{+П2 “
I Л1 J
П\—1 Y
Т4 I Т4
2 Д2
г‘
«2-1
к-1
(для четных г);
(для нечетных г=2к-1).
164
,=0,00089.
184756
1
—1
2
1 * f^-iY/^-iA p^-iY^-i
Л-1 I к-2 Г к-2 к-1
( п> ) v yv ' v 7V
. . 666 = 0,00360.
184756
Объединяем «четный» и «нечетный» результаты:
p(r<R)=0,00089+0,00360=0,00449=0,004.
Кроме вычисленного значения вероятности (соответствующего односторонней
критической области), которое сравнивается с выбранным уровнем значимости а,
вычисляется значение z с учетом тех поправок, которые были рассмотрены в пара-
графе 3.4:
А-(3^+1)+о,5 5-(^1^+1)+0,5
\Л1+Л2 / ’ _ \ Ю+Ю /
12nin2(2nin2-ni -п2) pxl0xlQ(2xl0xl0-10-10)
V (л1+«2)2(л]+Л2-1) V (10+10)2(10+10-1)
=-2,527.
Если каждая выборка содержит более 30 значений, то различия между вычисленным
значением вероятности и значением вероятности, полученным на основе ^-распре-
деления (табл. 1, Приложение 2), становится несущественным.
Перейдем к программе SPSS. В переменной «Группы!» (groups) принадлежность
участников эксперимента к первой или второй группе обозначена как 1 или 2. В пе-
ременной «Время» (time) указано время (в неделях), в течение которого вес был
снижен на 20 кг. Дальнейшая последовательность действий и конечный результат
показаны на рис. 6.17—6.19.
157
КНИГА ДЛЯ ТЕХ, КТО НЕ ЛЮБИТ СТАТИСТИКУ, НО ВЫНУЖДЕН ЕЮ ПОЛЬЗОВАТЬСЯ
NonParametr - SPSS Data Editor
Fie Edt View Data Transform Analyze Graphs Utifoes Window Help
?.* • . Г Reports > Descriptive Statistics ► Corrpare Means ►
groups time General linear Model ► Mixed Models ► Correlate ► Regression ► Log! near > Classify ► Data Reduction ► Scale ►
1 1 1
2 1 2
3 1 f
4 1
5 1 1 •
6 1
7 1 Nonpar ametric Tests ►
Time Senes ► Survival ► Multiple Response ► Mtssmg Value Analysis...
8 1
9 1 2
10 1 1
11 2 2T
12 2 16
13 2 25
Рис. 6.17. Выбор необходимой статистической процедуры
Рис. 6.18. Тест Вальда—Волфовица: необходимые действия и настройки
ГЛАВА 6. ОТДЕЛЕНИЕ СВЕТА ОТ ТЬМЫ, ИЛИ СЛУЧАЙ ДВУХ НЕЗАВИСИМЫХ ВЫБОРОК
Wald-Wolfowitz Test
Frequencies
GROUPS N
TIME 1 2 Total 10 10 20
Test Statistics1**0
TIME Exact Number of Runs
a.
Number
of Runs
5*
-2.527
Exact Sig.
(1-tailed)
TZTooF
Уровень значимости для односторонней
критической области. Чтобы перейти к двусторонней
критической области, это значение необходимо
умножить на 2.
(Нулевая гипотеза отвергается.)
Рис. 6.19. Тест Вальда—Волфовица: результат
6.6. «МЕЧТАЮТ ЛИ АНДРОИДЫ ОБ ЭЛЕКТРООВЦАХ»,
ИЛИ ТЕСТ ЭКСТРЕМАЛЬНЫХ РЕАКЦИЙ МОЗЕСА
Если вы читали фантастический роман Филиппа Дика «Мечтают ли анд-
роиды об электроовцах?»20 или видели снятый по этой книге отличный фильм
«Бегущий по лезвию» (Blade Runner), с Харрисом Фордом в главной роли, то
вы, конечно, знаете, что такое тест на эмпатию Войт—Кампфа (Voigt—Kampff
Empathy Test). Именно с помощью этого теста удавалось обнаруживать на Земле
нелегальных андроидов — искусственных существ, ничем не отличающихся от
людей, кроме одной особенности: они не были способны к эмпатии. Андроидам
в определенных ситуациях удавалось имитировать эмпатию, но ее показатели,
по сравнению с показателями людей, были или неестественно низкими, или
неестественно высокими.
Предположим, что полиция задержала 9 андроидов. В таблице 6.22 приве-
дены их показатели по тесту Войт—Кампфа. В качестве контрольной группы
выступали 9 полицейских, участвовавших в задержании.
20 Philip К. Dick. Do Androids Dream of Electric Sheep?
159
КНИГА ДЛЯ ТЕХ, КТО НЕ ЛЮБИТ СТАТИСТИКУ, НО ВЫНУЖДЕН ЕЮ ПОЛЬЗОВАТЬСЯ
Таблица 6.22
Результаты теста на эмпатию
Андроиды Люди
17 27
5 20
19 20
47 18
15 29
8 32
8 28 -
52 16
39 30
Можно ли на основании полученных данных утверждать, что тест Войт—
Кампфа в состоянии эффективно выявлять андроидов?
Казалось бы, приведенный пример мало отличается от тех, которые мы уже
рассматривали для случая двух независимых выборок. Однако здесь присутству-
ет одна особенность, для учета которой Мозес предложил тест, носящий его имя.
Рассмотрим гистограммы двух распределений (рис. 6.20 и 6.21).
Оба распределения имеют совпадающие значения среднего, моды и медиа-
ны. Основное различие между ними в том, что второе распределение более
«растянуто» по горизонтальной оси (значение дисперсии для второго распре-
деления больше, чем для первого). В параметрической статистике для сравне-
ния «ширины» двух различных нормальных распределений чаще всего исполь-
зуется Гтест Фишера, основанный на сравнении дисперсий.
В случае маленьких выборок вычисление и сравнение дисперсий теряет свой
смысл, однако здесь также возникают ситуации, когда необходимо сравнить
друг с другом «ширину» распределения результатов в каждой из них. Такая
160
ГЛАВА 6. ОТДЕЛЕНИЕ СВЕТА ОТ ТЬМЫ, ИЛИ СЛУЧАЙ ДВУХ НЕЗАВИСИМЫХ ВЫБОРОК
задача становится актуальной в том случае, если у исследователя есть основания
предполагать, что в одной из выборок реакции испытуемых (респондентов),
например на экспериментальное воздействие, носят более близкий к краю
(экстремальный) характер. Такое предположение чаще всего возникает в том
случае, когда независимые выборки существенным образом отличаются друг
от друга по какому-либо показателю. Например, можно предположить, что
определенные поведенческие и эмоциональные реакции в группе женщин,
подвергшихся сексуальному насилию, будут носить более полярный характер
(от полной эмоциональной «замороженности» до бурных эмоциональных
«взрывов») по сравнению с реакциями в группе обычных женщин.
По сути дела, в тесте экстремальных реакций Мозеса одна выборка высту-
пает в качестве контрольной группы, а другая — в качестве экспериментальной.
В качестве экспериментальной группы выбирается та, в которой, по предпо-
ложению исследователя, результаты будут носить более экстремальный харак-
тер (в нашем случае это группа андроидов)21.
В качестве меры изменчивости, позволяющей сравнивать «ширину» обеих
выборок, используется один из наиболее редко применяемых статистических
показателей — размах (Span). Размах 5 определяется как разность между мак-
симальным и минимальным.значением плюс единица22: 5=Armax—Jfmin+1
(табл. 6.20 и рис. 6.22).
Размах для контрольной группы (люди): S-Xmax-Xmin+1-32-16+1-17
^min ^max
у . XX
лппп лтах л
Размах для экспериментальной группы (андроиды): S-Xmax~Xmin+l-52-5+1-48
(результаты в экспериментальной группе носят более экстремальный характер)
Рис. 6.22. Иллюстрация к тесту экстремальных реакций Мозеса
21 Если выбор сделан неудачно, будет получен результат, лишенный смысла.
22 Добавка единицы повышает точность вычисления размаха.
6 Зак. 3384
161
КНИГА ДЛЯ ТЕХ, КТО НЕ ЛЮБИТ СТАТИСТИКУ, НО ВЫНУЖДЕН ЕЮ ПОЛЬЗОВАТЬСЯ
В тесте экстремальных реакций Мозеса размах (по отношению к рангам)
вычисляется для контрольной группы. Затем, на основе значения размаха,
сведений о размере выборок и других показателях, вычисляется вероятность
получения такого результата.
Если полученное значение вероятности оказывается меньшим или равным
выбранному значению уровня значимости а, то нулевая гипотеза отвергается.
Если значение вероятности больше выбранного значения уровня значимости
а, то оснований отвергнуть нулевую гипотезу нет.
Применим тест экстремальных реакций Мозеса к нашим данным.
Выберем уровень значимости а=0,05 и сформулируем нулевую и альтерна-
тивную гипотезы.
Но: Между людьми и андроидами нет различий в значениях эмпатии.
/Г]: Значения эмпатии у андроидов носят более экстремальный характер по
сравнению со значениями эмпатии у людей (односторонняя критическая об-
ласть23).
Объединим обе выборки, расположим значения эмпатии в порядке возрас-
тания, присвоим каждому значению свой ранг24 и укажем кому — людям (Л)
или андроидам (А) — принадлежит то или иное значение (табл. 6.23).
Таблица 6.23
Упорядоченные значения эмпатии для объединенной выборки
5 8 8 15 16 17 18 19 20 20 27 28 29 30 32 39 47 52
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
А А А А Л А Л А Л Л Л Л Л Л Л А А А
На основании результатов ранжирования определяем размах для контроль-
ной группы (группы людей).
Как видно из таблицы, минимальное значение ранга в контрольной группе
равно 5, максимальное значение ранга равно 15.
Размах 5= 15—5+1 = 11.
Однако в статистике размах считается ненадежной мерой изменчивости,
поскольку он слишком зависит от колебаний крайних значений. Для придания
размаху большей стабильности в тесте экстремальных реакций Мозеса слева и
справа отбрасывается несколько крайних значений, и размах вычисляется для
оставшихся значений.
23 В этом тесте использование двусторонней критической,области невозможно.
24 В случае совпадающих значений, принадлежащих одной и той же выборке, связанные
ранги не вычисляются. Поэтому процедура ранжирования превращается в приписывание номе-
ра (по возрастающей) каждому значению эмпатии. Ситуация осложняется, если совпадающие
значения принадлежат разным выборкам. Существует ряд рекомендаций, что делать в этом слу-
чае [Siegel, 1956], но в целом такая ситуация рассматривается как нежелательная и исследователю
рекомендуется по возможности от нее избавляться. Если в двух выборках много совпадающих
значений, применение теста Мозеса становится невозможным.
162
ГЛАВА 6. ОТДЕЛЕНИЕ СВЕТА ОТ ТЬМЫ, ИЛИ СЛУЧАЙ ДВУХ НЕЗАВИСИМЫХ ВЫБОРОК
Обозначим как h то, сколько значений слева и справа будет отброшено.
Для малых выборок h обычно равно 1. В общем случае рекомендуется слева и
справа отсекать по 2,5% значений (то есть всего, слева и справа, отсекается не
более 5%).
Отбросим от рангов для контрольной группы по одному крайнему значению
слева и справа (то есть отбросим значения 5 и 15). Новое минимальное значе-
ние ранга для контрольной группы будет равно 8, а новое максимальное зна-
чение будет равно 14. Обозначим новое значение размаха как Sh. Оно будет
равно Sh = 14—7 +1 = 8.
Можно показать, что при любых размерах экспериментальной (лЭкспер)и кон-
трольной (иКонтр) группы значение размаха Sh не может быть меньше чем
(«контр ~И больше Чем («контр «экспер ~ 2Й).
Обозначим как g то, насколько наблюдаемое значение размаха 5/, больше
минимально возможного.
В нашем случае минимально возможное значение размаха равно («КОтр - 2й)=
=9-2=7.
Поскольку («контр - 2й)=7 и Sh=8, то g=Sh - («Коитр - 2й) = 8 - 7 = 1.
После проделанной подготовки можно приступить к вычислению требуемой
вероятности. Формула для ее вычисления выглядит следующим .образом:
p№^«KOHTp-2A + g) = ^
Z+Wrohtp 2 VЛэадпер+2А+1 I
I Д ^экспср~~^
^контр+^экспер
^контр
°! XL
--------, если a > b и
b'.(a-b)\
Подставляем в формулу наши данные: «КОнтр
Еще раз напомним, что
P(Sh< «контр -2A+g) =
а
b
^экспер 9, h 1 ’ 8
1= 0, если о </>.
Г^^контр 2А i
j=o( * Д «ткоир~*
I «КОНТр+^КС1Кр
I «контр
220+990
48620
=0,025.
а
b
Полученное значение вероятности меньше выбранного значения уровня
значимости а=0,05. Нулевая гипотеза отвергается, и принимается альтерна-
тивная. Показатели эмпатии в группе андроидов носят более экстремальный
(крайний) характер по сравнению с группой людей. Тест Войт—Кампфа в со-
стоянии эффективно выявлять андроидов.
163
КНИГА ДЛЯ ТЕХ, КТО НЕ ЛЮБИТ СТАТИСТИКУ. НО ВЫНУЖДЕН ЕЮ ПОЛЬЗОВАТЬСЯ
Рассмотрим еще один пример на применение теста экстремальных реакций
Мозеса [основа: Siegel, 1956].
Кира, социальный работник, работает с двумя группами женщин, недавно
переживших развод с мужем. В первую группу собраны женщины, которые
после развода стали испытывать трудности в контроле над своими агрессив-
ными импульсами по отношению к детям. Обеим группам был показан кино-
фильм — семейная драма, завершающаяся разводом супругов. После просмот-
ра в каждой из групп прошло обсуждение фильма. В ходе обсуждения Кира
фиксировала высказывания участниц групп, в которых они интерпретировали
поведение героев фильма как проявление агрессии.
В таблице 6.24 приведено количество зафиксированных высказываний для
каждой из групп.
Таблица 6.24
Число интерпретаций повеления героев фильма
как агрессивного
Группа 1 Группа 2
25 12
5 16
14 6
19 13
0 13
17 3
15 10
8 10
8 11
Кира предположила, что в первой группе (женщины, испытывающие про-
блемы контроля своих агрессивных импульсов) число агрессивно окрашенных
интерпретаций будет носить более экстремально выраженный характер, чем
во второй группе.
164
ГЛАВА 6. ОТДЕЛЕНИЕ СВЕТА ОТ ТЬМЫ, ИЛИ СЛУЧАЙ ДВУХ НЕЗАВИСИМЫХ ВЫБОРОК
Проверим это предположение с использованием теста экстремальных ре-
акций Мозеса.
Выберем уровень значимости а=0,05 и сформулируем нулевую и альтерна-
тивную гипотезы.
Но: Между женщинами первой и второй групп нет различий в числе интер-
претаций поведения героев фильма как агрессивного.
Н\: Женщины в первой группе демонстрируют более близкие к крайним
реакции в своих интерпретациях поведения героев фильма как агрессивного
по сравнению с женщинами во второй группе (односторонняя критическая
область).
Выберем в качестве экспериментальной (Э) группу 1, а в качестве контроль-
ной (К) — группу 2.
Объединим результаты обеих групп и проранжируем их (табл. 6.25).
Таблица 6.25
Упорядоченные значения числа высказываний
0 3 5 6 8 8 10 10 11 12 13 13 14 15 16 17 19 28
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
э К Э К Э э К К К А К К Э Э К э Э Э
В контрольной группе минимальный ранг — 2, максимальный ранг — 15.
Выберем h=1 и отбросим крайние ранги (2 и 15). Определим размах для
контрольной группы с новыми крайними значениями 4 и 12:
Sh=12-4+1=9.
Минимально возможное значение размаха:
(^контр 2Л) 9 2 7.
Различие между наблюдаемым размахом и минимально возможным:
g=9—7=2.
Приступаем к вычислению вероятности:
РС^Л^^контр 2A + g) — y.p+9-2-2Y9+2+l-/A -si [ A 9~z J. (9+9) 9 Г^"Дампр 2Л 2 Yn^p+2/z+l /А M)l i Д Дкспср~~* J _ I Дамир"^"^экспср J l Дсонтр J JX'HCTFL., 1^1 9
165
КНИГА ДЛЯ ТЕХ, КТО НЕ ЛЮБИТ СТАТИСТИКУ. НО ВЫНУЖДЕН ЕЮ ПОЛЬЗОВАТЬСЯ
Поскольку полученное значение больше, чем а=0,05, у нас нет оснований
для того, чтобы отвергнуть нулевую гипотезу. Между женщинами первой и
второй групп нет различий в числе агрессивно окрашенных интерпретаций
поведения героев фильма.
ВКЛЮЧАЕМ КОМПЬЮТЕР...
Создадим переменную «Группы» (groups), в которой 1 означает людей, а 2 означает
андроидов. В переменной «Эмпатия» (empathy) укажем показатели эмпатии для тех
и других.
Дальнейшие действия и конечный результат показаны на рис. 6.23-6.25.
| дропРагатеГг - SPSS Data Cdttor
Fie Edt View Data Transform | Analyze Graphs Utlibes Window Help
Reports
Descriptive Statistics
Compare Means
General Linear Model
Mixed Models
Correlate
Regression
Logbnear
Classfy
Data Reduction
Scale
Nonpar ametrk Tusts
Time Series
Survival
Multiple Response
Missing Value Analysis...
12 1 19
13
♦1-H <»|fr|
Рис. 6.23. Выбор необходимой статистической процедуры
Рис. 6.24. Тест экстремальных реакций Мозеса: необходимые действия и настройки
166
ГЛАВА 6. ОТДЕЛЕНИЕ СВЕТА ОТ ТЬМЫ. ИЛИ СЛУЧАЙ ДВУХ НЕЗАВИСИМЫХ ВЫБОРОК
Рис. 6.24. Окончание
Moses Те
______GROUPS_____
EMPATh^People (Control)
Группа, закодированная меньшим числом,
рассматривается в программе SPSS как кон-
трольная
Androids (Experimental)
Total
Observed Control
Group Span
Trimmed Control
Group Span
Outliers Trimmed from each
Размах для контрольной группы
после отбрасывания крайних
значений слева и справа
8lg. (1-tailed)
до исключения крайних значе-
нии слева и справа
Размах для контрольной группы
Sig. (1-tailed)
Уровень значимости для исход-
ного размаха и после отбрасыва-
ния по одному крайнему значе-
нию слева и справа. (Нулевая
гипотеза отвергается.)
Число значений, отбро-
шенных от размаха слева
и справа
Рис. 6.25. Тест экстремальных реакций Мозеса: результат
КНИГА ДЛЯ ТЕХ. КТО НЕ ЛЮБИТ СТАТИСТИКУ, НО ВЫНУЖДЕН ЕЮ ПОЛЬЗОВАТЬСЯ
Рассмотрим результат применения теста экстремальных реакций Мозеса для вто-
рого примера. В переменной «Группы» (groups) 1 означает представителей группы,
не имеющих проблем во взаимоотношениях с детьми после развода (контрольная
группа, закодированная меньшим числом), 2 означает представителей группы,
сталкивающихся с трудностями контроля своих агрессивных реакций по отношению
к детям (экспериментальная группа, в которой ожидаются более экстремальные
реакции). Переменная «Реакция» (reaction) показывает число агрессивно окрашен-
ных интерпретаций во время обсуждения кинофильма.
Опуская те же этапы работы с программой SPSS, которые были рассмотрены в пре-
дыдущем примере, сразу покажем конечный результат (рис. 6.26).
Moses Test
Frequencies
_____________GROUPS______________
REACTION No problem (Control)
Problem (Experimental)
Total
N____
9
9
18
Test Statistics3 6
Рис. 6.26. Тест экстремальных реакций Мозеса: результат
(пример с разведенными женщинами)
Этим примером мы завершаем рассмотрение случая двух независимых выборок
и переходим к случаю нескольких независимых выборок.
Глава 7
«ВАВИЛОНСКОЕ СТОЛПОТВОРЕНИЕ»,
ИЛИ СЛУЧАЙ НЕСКОЛЬКИХ
НЕЗАВИСИМЫХ ВЫБОРОК
7.1. ИЗ ЖИЗНИ НАРКОМАНОВ,
ИЛИ СНОВА ВЕЗДЕСУЩИЙ ТЕСТ Хг
Когда вы встречаете на улице наркомана, выпрашивающего у прохожих
мелочь на очередную дозу, часто ли вы задумываетесь о том, где он ночует, есть
ли у него семья, дети или родители? В самом деле, где и с кем живут наркома-
ны? Из каких мест они выходят утром на улицы и куда возвращаются после
захода солнца?
Ответы на эти вопросы были получены в ходе одного из исследований,
проведенных центром RADAR [Isralowitz et al., 2007]. Три группы наркоманов-
мужчин: уличные наркоманы, решившие начать лечение в наркологическом
стационаре; наркоманы, продолжающие лечение в дневном профилактории;
наркоманы, получающие метадон1, сообщили сведения о типичных условиях
своего проживания в течение последних трех лет.
Полученная информация представ-
лена в таблице 7.1.
Можно ли на основании получен-
ных данных утверждать, что в течение
последних трех лет во всех трех выбор-
ках условия проживания были различ-
ными?
В этом примере мы впервые стал-
киваемся с тремя независимыми вы-
борками. Но наши последующие дей-
1 Синтетический аналог героина. Используется в ряде стран (включая Израиль) как лекарст-
венный препарат при проведении заместительной терапии героиновых наркоманов.
169
КНИГА ДЛЯ ТЕХ. КТО НЕ ЛЮБИТ СТАТИСТИКУ. НО ВЫНУЖДЕН ЕЮ ПОЛЬЗОВАТЬСЯ
Таблица 7.1
Условия проживания респондентов в течение последних трех лет
Условия проживания Категории респондентов Итого
Уличные наркоманы Посетители дневно- го профилактория Получатели метадона
С супругом 65 24 54 143
С родителями 90 28 58 176
Отсутствие стабильных условий проживания (друзья, тюрьма, улица) 102 33 67 202
Итого 257 85 179 521
ствия мало отличаются от тех, с которыми мы уже имели дело в параграфе 6.Г,
посвященному тесту %2.
Тест %2 является универсальным тестом для данных, выраженных в шкале
наименований и представленных в виде таблицы размером (к х г), где к — чис-
ло столбцов в ней, аг - число строк (табл. 7.2). В данном случае это тест рас-
сматривается в самом общем виде, когда число независимых выборок произ-
вольно.
Таблица 7.2
Общий вид таблицы сопряженности размером (к* г)
Категории Выборки
1 2 к
1 о„ Оп О\к 7=1
2 021 022 О2к II
г О„ Ол
П\ "1
Огк ;=|
"к /=
Значение х2 вычисляется по общей формуле:
/=1 j=\ t'ij
где Еь=^-, i = (\,2,...r);j=(\,2, ...к).
N
170
ГЛАВА 7. «ВАВИЛОНСКОЕ СТОЛПОТВОРЕНИЕ». ИЛИ СЛУЧАЙ НЕСКОЛЬКИХ НЕЗАВИСИМЫХ ВЫБОРОК
После сделанных пояснений приступим к процедуре проверки.
Выберем уровень значимости а=0,05 и сформулируем нулевую и альтерна-
тивную гипотезы.
Но: В течение последних трех лет во всех трех выборках условия проживания
были одинаковы.
Ну В течение последних трех лет условия проживания были различными
для каждой из выборок (двусторонняя критическая область).
Определим по приведенной выше формуле значения ожидаемых частот Ev
(табл. 7.3), а затем вычислим значение %2. Учтем, что таблица имеет размер
(3 х 3), то есть к—г—Ъ.
Таблица 7.3
Распределение ожидаемых частот
Условия проживания Категории респондентов Итого
Уличные наркоманы Посетители дневно- го профилактория Получатели метадона
С супругом 70,54 23,33 49,13 143
С родителями 86,82 28,71 60,47 176
Отсутствие стабильных условий проживания (друзья, тюрьма, улица) 99,64 32,96 69,40 202
Итого 257 85 179 521
f (^~^)2 (65-70,54)2 (24-23,ЗЗ)2
Х ЙЙ Ev 70,54 23,33
_ (54-49,13)2 (90-86,82)2 (28-28,71)2 (58-60,47)2 _
+ 49/3 + 86^82 + 28/71 + 60,47 +
t (102-99,64)2 (33-32,96)2 (67-69,40)2
+ + 32/J6 + 6930
=1,311.
В таблице 2 (Приложение 2) находим критическое значение %2ретич для уровня
значимости а=0,05 и числа степеней свободы df=(k— l)(r— 1)=(3 —1)(3 — 1)=4:
%критич=9,49. Поскольку ХмашрО»31'1) < Х^ртич (9,49), у нас нет оснований от-
вергнуть нулевую гипотезу. В течение последних трех лет во всех трех выборках
наркоманов условия их проживания не отличались друг от друга.
Еще раза напомним, что для корректного использования теста %2 требуется
достаточная по объему выборка. Если более 20% ожидаемых частот имеют
значения меньше 5 или если хотя бы одна из ожидаемых частот имеет значение
меньше 1, применять тест %2 нельзя.
171
КНИГА ДЛЯ ТЕХ, КТО НЕ ЛЮБИТ СТАТИСТИКУ, НО ВЫНУЖДЕН ЕЮ ПОЛЬЗОВАТЬСЯ
В подобных случаях рекомендуется объединять некоторые категории, умень-
шая их количество, но увеличивая при этом значения наблюдаемых и ожидае-
мых частот в ячейках таблицы.
В качестве иллюстрации сказанного приведем еще один пример.
Представители трех групп населения (коренные израильтяне, иммигранты
из бывшего СССР и иммигранты из Эфиопии) были опрошены по поводу того,
где они предпочитают покупать овощи и фрукты (на рынке, в ближайшей
овощной лавке или в супермаркете). Наблюдаемые и ожидаемые (в скобках)
частоты распределились следующим образом (табл. 7.4).
i
Таблица 7.4
Место покупки овощей и фруктов различными категориями населения
Место покупки овощей и фруктов Тип выборки Итого
Уроженцы Израиля Иммигранты из б. СССР Иммигранты из Эфиопии
Рынок 7 (8,75) 6 (6,25) 7 (5,00) 20
Овощная лавка 6 (6,12) 5 (4,38) 3 (3,50) 14
Торговый центр 8 (6,13) 4 (4,37) 2 (3,50) 14
Итого 21 15 12 48
Как видно из таблицы, четыре из девяти значений ожидаемых частот мень-
ше 5 (это значительно больше, чем 20%). Если мы не хотим отказываться от
использования теста %2, необходимо произвести укрупнение таблицы, объеди-
нив несколько категорий. Это можно сделать несколькими путями. Например,
объединить в одну категорию иммигрантов из бывшего СССР и иммигрантов
из Эфиопии. Получим таблицу 7.5.
Таблица 7.5
Место покупки овощей и фруктов коренными жителями и иммигрантами
Место покупки овощей и фруктов Тип выборки Итого
Уроженцы Израиля Иммигранты
Рынок 7 (8,75) 13 (11,25) 20
Овощная лавка 6 (6,12) 8 (7,88) 14
Торговый центр 8 (6,13) 6 (7,87) 14
Итого 21 27 48
172'
ГЛАВА 7. «ВАВИЛОНСКОЕ СТОЛПОТВОРЕНИЕ». ИЛИ СЛУЧАЙ НЕСКОЛЬКИХ НЕЗАВИСИМЫХ ВЫБОРОК
Еще один вариант — объединить в одну категорию покупки вне рынка,
(табл. 7.6).
Таблица 7.6
Покупка овощей и фруктов на рынке и вне рынка различными категориями населения
Место покупки овощей и фруктов Тип выборки Итого
Уроженцы Израиля Иммигранты из б. СССР Иммигранты из Эфиопии
Рынок 7 (8,75) 6 (6,25) 7 (5,00) 20
Другие места 14 (12,25) 9 (8,75) 5 (7,00) 28
Итого 21 15 12 48
Какой из двух вариантов предпочтителен, решает исследователь.
ВКЛЮЧАЕМ КОМПЬЮТЕР...
Создадим переменную «Место интервью» (place), в которой 1 означает приемное
отделение наркологической клиники, 2 — дневной профилакторий и 3 — метадо-
новый центр. В переменной «Условия проживания» (living) 1 означает проживание
с супругой (супругом), 2 — проживание с родителями, 3 — другие условия прожи-
вания, включая бродяжничество.
Все остальные действия и конечный результат показаны на рис. 7.1—7.3.
NonPar ametr SPSSDataEditor
FCe Edit View Data Transform Analyze Graphs Utilities Window Help
ej| Reports > I -f-lrrl I Frequencies. .
Descriptive Statistics ►
Compare Means ► General Lnear Model ► Descrptives... Explore... J
treatm living
Mixed Models ► Crosstabs...
1 1 Correlate Regression ► Ratio... и
2 1 ► dr
3 1 Loglinear ► Classify ► Data Reduction ► Scale ► Nonparametnc Tests ► Time Senes ► Survival ► Multiple Response > Missing Value Analysis... Jtd
4 1 j\
5 1 j t_
6 1 Нажать
7 1
8 1
9 1
10 1
11 1 Т
12 1 1
13 1 1
14 1 1
15 1 1
Рис. 7.1. Выбор требуемой статистической процедуры
173
КНИГА ДЛЯ TEX, KTQ НЕ ЛЮБИТ СТАТИСТИКУ. НО ВЫНУЖДЕН ЕЮ ПОЛЬЗОВАТЬСЯ
Cnwrtabt
Cotumnfsl________________
Place of nterview [plat
R 0*4*1
1. Перенести сюда пере-
менную «living» и пере-
менную «place» из лево-
го окна
Г Duplay durteiadbar chaits
3ceb»Ucs
2. Нажать и в новом окне
установить настройку для
теста х2
F Cochran's and М
Tt^ic’THT jnr.dds а‘
ок.
Pdi’
Вер
4. Нажать
3. Нажать и вернуть-
ся в предыдущее
окно
г Layer! of 1
Nomra! by Interval---------
Г Eta
Ch-square
pNomnal-------------------
F Contingency coefficient
. F Phi and Darner’s V
F Lambda
I F Uncertainty coefficient
| Continue |
-Counts
Help |
Residuals-------------j
Г~ Unrtandaidized
F Standardized
Г Adj standardized
Рис. 7.2. Тсстх2 для нескольких независимых выборок:
необходимые действия и настройки
Г Corielabc
Ordinal -
Г Gammt
F Someri
F Kenda
Г Kenda
При необходимости можно по-
лучить данные об ожидаемых
частотах и процентах по стро-
кам и столбцам таблицы у
ГЛАВА 7. «ВАВИЛОНСКОЕ СТОЛПОТВОРЕНИЕ». ИЛИ СЛУЧАЙ НЕСКОЛЬКИХ НЕЗАВИСИМЫХ ВЫБОРОК
Crosstabs
Chi-Square Tests
Pearson Chi-Square
Likelihood Ratio
Llnear-by-Linear
Association
N of Valid Cases
a. 0 cells (.0
Проверяемое
значение x2
Asymp. Sig.
.361
л860_
.860
УаШа-J___df
.311’
308
833
521
expected count]
count!
Уровень значимости
(Нулевая гипотеза не отклоняется
Рис. 7.3. Тест x2 для нескольких независимых выборок: результат
Для примера с покупкой овощей покажем последний результат (рис. 7.4).
Chi-Square Tests
Value df Asymp. Sig. (2-sided)
Pearson Chi-Square 2.572’ 4 632
Likelihood Ratio 2.577 4 .631
Unear-by-Linear Association 2.292 1 .130
N of Valid Cases 48
Г4 ceils (44.4%) have expected countless than 5.
-minimum expected count is 3.50. —
Здесь указано, сколько ожидаемых частот имеют значение
меньше 5. Если таких частот более 20%, необходимо «укруп-
нять» расчетную таблицу
Рис. 7.4. Тест х2 для нескольких независимых выборок:
результат (пример с покупкой овощей)
175
КНИГА ДЛЯ ТЕХ, КТО НЕ ЛЮБИТ СТАТИСТИКУ, НО ВЫНУЖДЕН ЕЮ ПОЛЬЗОВАТЬСЯ
7.2. КАКОЙ КУРС ПСИХОМЕТРИИ ЛУЧШЕ,
ИЛИ ТЕСТ КРУСКАЛА-УОЛЛИСА
После окончания службы в армий Даниил решить поступать в университет
на факультет психологии. Для поступления ему нужна более высокая оценка
по психометрии, чем та, которую он получил до начала службы. С целью улуч-
шить свой результат Даниил решил пройти обучение на курсах подготовки к
сдаче психометрического экзамена. В его городе работает несколько таких
курсов, каждый из которых гарантирует успех на экзамене. Для принятия
окончательного решения Даниил опросил 14 выпускников таких курсов, что-
бы сравнить полученные ими оценки и сделать свой выбор.
В таблице 7.7 приведены оценки по психометрии 14 выпускников курсов Л,
Ди С.
Таблица 7.7
Результаты психометрии выпускников различных курсов
Курс психометрии А Курс психометрии В Курс психометрии С
710 712 727
690 • 697 732
715 700 691
720 705 692
695 722
Можно ли на основании полученных данных утверждать, что выпускники
курсов Л, В и С по подготовке к сдаче психометрического экзамена отличают-
ся друг от друга своими результатами?
Мы уже знаем, что если результаты представлены в шкалах, допускающих
ранжирование (шкала порядка и выше), то для сравнения двух независимых
выборок используется тест Манна—Уитни. Сейчас в нашем распоряжении
также данные, выраженные, как минимум, в шкале порядка, но вместо двух
независимых выборок мы имеем три2.
Как показали Крускал и Уоллис, идея проверки, лежащая в основе теста
Манна—Уитни, может быть использована и в случае нескольких независимых
выборок3.
По аналогии с тестом Манна—Уитни, все выборки объединяются в одну.
2 Разумеется, в общем случае число независимых выборок может быть любым, большим
двух.
3 Для сравнения нескольких независимых выборок чаще всего используется однофакторный
дисперсионный анализ (One-way ANOVA). Поэтому тест Крускала—Уоллиса часто называют
однофакторным дисперсионным анализом для рангов (One-way ANOVA by ranks).
176
ГЛАВА 7. «ВАВИЛОНСКОЕ СТОЛПОТВОРЕНИЕ», ИЛИ СЛУЧАЙ НЕСКОЛЬКИХ НЕЗАВИСИМЫХ ВЫБОРОК
Затем объединенные значения всех выборок ран-
жируются, после чего отдельно для каждой из
выборок суммируются ранги, соответствующие
содержащимся в выборке значениям. Если между
выборками имеются случайные различия, то сум-
мы рангов для каждой из них не будут существен-
ным образом отличаться друг от друга.
Мерой отличия сумм рангов выступает вели-
чина Н, вычисляемая по следующей формуле:
Н=
—-—Е—-з(я+1),
N(N+V)%nj
где к — число выборок; лу — объем каждой из выборок; N— объем объединен-
ной выборки (N— Znj); Rj—сумма рангов для каждой из выборок.
Приступим к процедуре проверки.
Выберем уровень значимости а=0,05 и сформулируем нулевую и альтерна-
тивную гипотезы.
Яо: Результаты психометрического экзамена у выпускников курсов А, В
и С не отличаются друг от друга.
Я,: Выпускники курсов Л, Ви С имеют различные результаты психометри-
ческого экзамена (двусторонняя критическая область4).
Вернемся к таблице 7.7. Выпишем все оценки по психометрии в порядке
возрастания и проранжируем их (табл. 7.8).
Таблица 7.8
Упорядоченные и проранжированные результаты психометрии
Оценка 690 691 692 695 697 700 705 710 712 715 720 722 727 732
Ранг 1 2 3 4 5 6 7 8 9 10 11 12 13 14
Дополним таблицу 7.7 значениями рангов для каждой выборки и найдем их
сумму. Получим модифицированную таблицу 7.9.
Приступим к вычислению Я для случая к=3, п{ =5, п2=5, л3=4, Я=14,
/?,=34,А2=39,А3=32.
17 к R?
Н=—-—У^-3(Я+1) =
Я(Я+1)£лу
(34)2 (39)2 (32)2
14(14+1)[ 5 5 4
12
-3(14+1) = 0,223.
4 Данный тест позволяет выявить различия между выборками, но не направление этих разли-
чий. С его помощью нельзя определить, в какой и^трех выборок наилучшие результаты. Для ответа
на данный вопрос необходимо попарно сравнивать выборки между собой, например, с помощью
теста Манна—Уитни.
177
КНИГА ДЛЯ ТЕХ. КТО НЕ ЛЮБИТ СТАТИСТИКУ. НО ВЫНУЖДЕН ЕЮ ПОЛЬЗОВАТЬСЯ
Таблица 7.9
Результаты психометрии и их ранги
Курс психометрии А Ранг Курс психометрии В Ранг Курс психометрии С Ранг
710 8 712 9 727 13
690 1 697 5 732 14
715 10 700 6 691 2
720 11 705 7 692 3
695 4 722 12
Сумма рангов Rj 34 39 32
Для случая /с=3, 2 < п2, л3< 5 существует специальная статистическая
таблица для теста Крускала—Уоллиса, в которой найденное значение Яэмир
сравнивается с критическим значением Якр||Т11Ч.
В общем случае (при любых значениях кн N) используется статистическая
таблица критических значений для теста х2 с (к— 1) числом степеней свободы
(табл. 2, Приложение 2). Если значение Хкритич оказывается больше вычислен-
ного значения Яэмир, нет оснований отвергнуть нулевую гипотезу. Если зна-
чение Хкритич оказывается меньше вычисленного значения Яэмир или равно ему,
нулевая гипотеза отклоняется и принимается альтернативная.
Найдем по таблице 2 значение Хкритич Для df=(k- 1) = (3—1) = 2 и а = 0,05:
Хкритич = 5,99. Поскольку это значение больше, чем Яэмир =0,223, нет оснований
отвергнуть нулевую гипотезу. Между результатами психометрического экзаме-
на у выпускников курсов А, В и С нет различий.
В рассмотренном примере выборки не содержали повторяющихся (одина-
ковых) значений. В том случае, если имеются повторяющиеся значения, для
вычисления Я используется скорректированная формула, учитывающая факт
наличия связанных рангов.
Рассмотрим еще один пример применения теста Крускала—Уоллиса для
случая связанных рангов.
Таблица 7.10
Возраст начала курения
Коренные израиль- тяне (евреи) Израильтяне — бедуины Иммигранты из б. СССР Иммигранты из Эфиопии
10 7 9 13
12 6 7 10
11 8 12 11
12 10 11 14
10 И 6 12
13 9 13 11
13 12 10 13
178
ГЛАВА 7. .ВАВИЛОНСКОЕ СТОЛПОТВОРЕНИЕ», ИЛИ СЛУЧАЙ НЕСКОЛЬКИХ НЕЗАВИСИМЫХ ВЫБОРОК
Из курящих подростков, представляющих коренных израильтян-евреев,
израильтян-бедуинов, иммигрантов из бывшего СССР и иммигрантов из
Эфиопии были сформированы четыре независимые выборки. В таблице 7.10
приведены сведения о возрасте начала курения для каждой из выборок.
Можно ли утверждать, что подростки, принадлежащие к различным куль-
турно-этническим группам, начинают курить в разном возрасте?
Поскольку алгоритм дальнейших действий нам уже известен, сразу присту-
паем к использованию теста Крускала—Уоллиса.
Выберем уровень значимости а=0,05 и сформулируем нулевую и альтерна-
тивную гипотезы.
Яо: Нет отличий в возрасте начала курения у израильских подростков — пред-
ставителей различных этнокультурных групп.
Яр Израильские подростки — представители различных этнокультурных
групп начинают курить в различном возрасте (двусторонняя критическая об-
ласть).
Как и в предыдущем примере, объединим все выборки в одну, запишем
содержащиеся в выборках значения в порядке возрастания и проранжируем их
(табл. 7.11).
Таблица 7.11
Упорядоченные и проранжированные значения возраста начала курения
Возраст 6 6 7 7 8 9 9 10 10 10 10 10 11 11
Ранг 1,5 1,5 3,5 3,5 5 6,5 6,5 10 10 10 10 10 15 15
Возраст 11 11 11 12 12 12 12 12 13 13 13 13 13 14
Ранг 15 15 15 20 20 20 20 20 25 25 25 25 25 28
Основное отличие данного примера от предыдущего — наличие большого
числа повторяющихся значений возраста, что приводит к возникновению
связанных рангов.
Заменим в таблице 7.10 значения возраста значениями соответствующих
рангов и найдем сумму рангов для каждой выборки. Получим таблицу 7.12.
В случае наличия т групп связанных рангов для вычисления Я используется
скорректированная формула:
______3(Я+1)
Я(Я+1)£Ду ?
ТУ — т ,
Zr
1 /-1 '
N3-N
где 7}=(/3/— t/) ntj — размер /-й группы связанных рангов (количество повто-
ряющихся значений), i=1,2,... т.
Вернемся еще раз к таблице проранжированных значений (табл. 7.11)
и определим размер каждой группы связанных рангов (табл. 7.13).
179
КНИГА ДЛЯ ТЕХ, КТО НЕ ЛЮБИТ СТАТИСТИКУ. НО ВЫНУЖДЕН ЕЮ ПОЛЬЗОВАТЬСЯ
Таблица 7.12
Ранги возраста начала курения
Коренные израильтяне (евреи) Израильтяне — бедуины Иммигранты из б. СССР Иммигранты из Эфиопии
10 3,5 6,5 25
20 1,5 3,5 10
15 5 20 15
20 10 15 28
10 15 1,5 20
25 ' 6,5 25 15
25 20 10 25
^ = 125 Я2=61,5 =81,5 ^4 = 138
Таблица 7.13
Размер групп связанных рангов
Возраст 6 7 9 10 И 12 13
Количество повторяющихся значений (f/) 2 2 2 5 5 5 5
6 6 6 120 120 120 120
Сейчас можно приступить к вычислению Я (учтем, что fc=4, л1=л2=
=Лз=«4=7, Я=28, ти=7):
Н=------------
Ът,
1—а_____
N3-N
12 Г1251 61,52 81,52 1 382
_ 28(28+1) L 7 1 7 1 7~~7
(6+6+6+120+120+120+120)
283-28
-3(28+1)
=8,392.
Полученное значение Яэмпир сравнивается с критическим значением Хедитич,
которое находим в таблице критических точек для теста х2 с (k—V) числом сте-
пеней свободы.
В нашем случае к— 1 =4— 1=3. Для выбранного значения уровня значимо-
сти а=0,05 и df=3 находим в таблице 2 (Приложение 2) Хкршич =7,82.
Поскольку эмпирическое значение Яэмпир (8,392) больше критического (7,82),
нулевая гипотеза отвергается и принимается альтернативная. Израильские
180
ГЛАВА 7. «ВАВИЛОНСКОЕ СТОЛПОТВОРЕНИЕ». ИЛИ СЛУЧАЙ НЕСКОЛЬКИХ НЕЗАВИСИМЫХ ВЫБОРОК
подростки — представители различных этнокультурных групп начинают курить
в различном возрасте.
ВКЛЮЧАЕМ КОМПЬЮТЕР...
В переменной «Подготовка» (training) цифрами 1,2 и 3 обозначены три различных
курса подготовки к психометрическому экзамену. В переменной «Результаты»
(results) приведены сведения о результатах психометрии улиц, вошедших в выбор-
ку. Дальнейшая последовательность действий и конечный результат показаны на
рис. 7.5—7.7.
NonParametr - SPSS Data Editor
File Edit View Data Transform Analyze Graphs Utilities
Reports
Descriptive 5tat.$bcs
Compare Means
General L near Model
Mixed Models
Correlate
Regression
Logfcnear
Classify
Data Reduction
Scale
training j results
71
62
3
1
71
2
3
Nonparametnc Tests
Window Help
£|IK| 4>|Q>|,
Chi-Square...
Binomial...
Runs...
1-Sample К-S...
2 Independent Samples...
10
11
12
13
14
15
72Т
Time Senes
Survival
Multiple Response
Missing Value Analysis...
732
691
692
Нажать
2 Related Samples.,
К Related Samples..
2
2
3
3
3
Рис. 7.5. Выбор требуемой статистической процедуры
Рис. 7.6. Тест Крускала—Уоллиса: необходимые действия и настройки
181
КНИГА ДЛЯ ТЕХ. КТО НЕ ЛЮБИТ СТАТИСТИКУ. НО ВЫНУЖДЕН ЕЮ ПОЛЬЗОВАТЬСЯ
Рис. 7.6. Тест Крускала—Уоллиса: необходимые действия и настройки (окончание)
Рис. 7.7. Тест Крускала—Уоллиса: результат
ГЛАВА 7. «ВАВИЛОНСКОЕ СТОЛПОТВОРЕНИЕ», ИЛИ СЛУЧАЙ НЕСКОЛЬКИХ НЕЗАВИСИМЫХ ВЫБОРОК
Для второго примера (случай связанных рангов) введем переменную «Происхожде-
ние» (origin), в которой цифрами от 1 до 4 закодируем принадлежность участников
опроса к коренным израильтянам (евреям), коренным израильтянам (бедуинам),
иммигрантам из бывшего СССР и иммигрантам из Эфиопии. В переменной «Воз-
раст» (age) укажем возраст начала курения. Проделаем ту же последовательность
действий (учтя на третьем этапе, что переменная origin меняется в диапазоне от 1 до
4) и получим результат, представленный на рис. 7.8.
Test Statistics*-*5
J
Chi-Square df Asymp. Sig. (§393)
a-Kruskal Wallis Test \
b. Grouping Variable* ORION
Проверяемое
значение
Уровень значимости
(Нулевая гипотеза отвер-
< гается.)
Рис. 7.8. Тест Крускала—Уоллиса: результат
(пример для возраста начала курения и связанных рангов)
7.3. ЛЕГКО ЛИ БЫТЬ ЖЕНОЙ АЛКОГОЛИКА,
ИЛИ ТЕСТ ДЖОНКХИЕРА—ТЕРПСТРА
Психологам и социальным работникам, работающим с семьями алкоголиков
или наркоманов, хорошо знаком феномен созависимости. Созависимость ха-
рактеризуется сильной эмоциональной вовлеченностью членов семьи нарко-
мана или алкоголика (родителей, супруга/супруги) в его проблему, подчине-
нием своей жизни цели решения этой проблемы, отказом от собственных
интересов, дел и планов во имя его выздоровления и др. [Москаленко, 2004].
Максим — социальный работ-
ник в дневном профилактории для
пострадавших от алкоголя и чле-
нов их семей. Он решил проверить
влияние уровня созависимости
жен алкоголиков на степень удов-
летворенности их своим браком.
Используя шкалу для измерения
созависимости [Fisher et al., 1991],
он сформировал три выборки:
группу женщин с низким уровнем
созависимости, группу с умерен-
ной созависимо’стью и группу, где
183
КНИГА ДЛЯ ТЕХ, КТО НЕ ЛЮБИТ СТАТИСТИКУ. НО ВЫНУЖДЕН ЕЮ ПОЛЬЗОВАТЬСЯ
этот показатель был сильно выражен. После формирования выборок Максим
оценил степень удовлетворенности браком (по 100-балльной шкале) предста-
вителей каждой из них. Полученные результаты показаны в таблице 7.14.
Таблица 7.14
Удовлетворенность браком у представительниц трех групп жен алкоголиков
Уровень созависимости
Низкий Средний Высокий
55 58 52
75 65 38
60 45 35
63 40 64
50 62 47
43 48
53
Можно ли на основании полученных данных утверждать, что фактор соза-
висимости влияет на степень удовлетворенности браком?
По сути дела, решаемая задача связана с выявлением значимых различий
между результатами в трех сформированных группах. На первый взгляд она
мало отличается от рассмотренного выше примера с тремя курсами психомет-
рии, где использовался тест Крускала—Уоллиса. Однако можно увидеть, что в
предыдущем примере фактор (курсы психометрии) был задан тремя ненаправ-
ленными альтернативами (курс психометрии А, курс психометрии В, курс
психометрии Q, и было не важно, в каком порядке следования этих альтерна-
тив мы будем их сравнивать (полученный результат не изменится, если в таб-
лице 7.6. курсы психометрии поменять местами).
Сейчас мы также имеем дело с тремя альтернативами (созависимость низкая,
умеренная и высокая), но, в отличие от предыдущего примера, эти альтерна-
тивы носят направленный характер и образуют упорядоченную последователь-
ность (от меньшего значения к большему), что можно учесть в процессе обра-
ботки полученных результатов.
В том случае, когда независимые выборки можно расположить в определен-
ном порядке, соответствующем упорядоченным градациям какого-либо фак-
тора, для их сравнения обычно применяется тест Джонкхиера—Терпстра5 для
упорядоченных альтернатив.
Например, в ходе одного из исследований по безопасности движения было
сформировано несколько выборок добровольцев, подвергшихся воздействию
5 Оба автора, независимо друг от друга и практически одновременно описали подход, исполь-
зуемый в данном тесте. В ряде публикаций на русском языке он упоминается как тест Джонкира—
Терпстра или тест Джонкира.
184
ГЛАВА 7. «ВАВИЛОНСКОЕ СТОЛПОТВОРЕНИЕ», ИЛИ СЛУЧАЙ НЕСКОЛЬКИХ НЕЗАВИСИМЫХ ВЫБОРОК
возрастающих от выборки к выборке доз алкоголя. В каждой выборке измеря-
лись скорость реакции, объем восприятия и другие показатели, влияющие на
безопасность дорожного движения, и проводилось сравнение результатов в
выборках между собой. В подобных ситуациях тест Джонкхиера—Терпстра
позволяет не только сравнивать выборки между собой, но и обнаруживать в
получаемых результатах определенные тенденции (тренды), являющиеся след-
ствием действия какого-либо упорядоченного по своим градациям фактора
(например, возрастающих доз алкоголя).
Используемый в тесте Джонкхиера—Терпстра подход представляет собой
развитие идей, лежащих в основе теста Манна—Уитни.
Основой для принятия решения о существовании различий между резуль-
татами в к независимых и расположенных в определенном порядке выборках
является вычисляемое значение /(см. ниже) или величина/*, вычисляемая по
следующей общей формуле:
5Х,—
A''<2A'+3)-^n’(2n;+3>
Для понимания смысла содержащихся в формуле обозначений приступим
к сравнению выборок.
Выберем уровень значимости а=0,05 и сформулируем нулевую и альтерна-
тивную гипотезы.
Яо: Между тремя группами женщин, имеющими разный уровень созависи-
мости, нет различий в показателе удовлетворенности браком.
Hi'. Между тремя группами женщин, имеющими разный уровень созависи-
мости, существуют различия в показателе удовлетворенности браком (двусто-
ронняя критическая область).
Процесс проверки сформулированных гипотез включает ряд этапов.
Вначале все к выборок попарно сравниваются друг с другом в направлении,
заданном фактором. Для случая трех выборок (к=3) первая выборка сравни-
вается со второй, затем первая выборка сравнивается с третьей, затем вторая
выборка сравнивается с третьей.
Процесс сравнения происходит в соответствии с той процедурой, которая
была описана выше для теста Манна—Уитни (параграф 6.3).
В результате каждого сравнения определяется, сколько значений во второй
из двух сравниваемых выборок больше каждого из значений в первой из них.
Например, если сравнить первую выборку со второй (табл. 7.13), то для перво-
го значения в первой выборке (55) во второй выборке можно найти три значе-
ния (58, 65,62), превышающие 55. Результат сравнения для значения 55 будет
равен трем. Если перейти ко второму значению в первой выборке (75), то во
185
КНИГА ДЛЯ ТЕХ. КТО НЕ ЛЮБИТ СТАТИСТИКУ. НО ВЫНУЖДЕН ЕЮ ПОЛЬЗОВАТЬСЯ
второй выборке нет ни одного значения, большего, чем 75. Результат сравнения
будет равен нулю.
По результатам каждого сравнения выборок находится сумма полученных
результатов, обозначенная в формуле как U^6 (табл. 7.15).
’ Таблица 7.15
Сравнение трех выборок между собой
Уровень созависимости
Сравнение первой выбор- ки со второй и третьей Низкий Сравнение второй выборки с третьей Средний Высокий
3 1 55 1 58 52
0 0 75 0 65 38
2 1 60 4 45 35
1 1 63 4 40 64
4 2 50 1 62 47
4 43 48
1 53
Цг=10 f/i3=5 1/й=15
Найдем значение J= 21/.^=+1/,3 +1/23= 10 + 5 + 15 = 30.
В том случае, если размеры сравниваемых выборок малы (не больше 8 зна-
чений в каждой), можно ограничиться полученным значением / и использовать
таблицу критических значений для теста Джонкхиера—Терпстра, где, в зави-
симости от числа сравниваемых выборок и размера каждой из них, приведены
критические значения J.
В общем случае, если предположить, что значения J имеют в популяции
нормальный закон распределения, на основе сведений о выборках вычисля-
ются среднее значение цу и дисперсия о) по следующим формулам:
к
_X* „2
#2(2#+3)-£л?(2лу+3) ,
7=1
к
где ТУ— общий объем (размер) выборки: N
>1
Подставим в формулы значения, соответствующие нашему случаю (£=3;
л1=5; л3=б; W=18):
6 Ели последовательно применить тест Манна—Уитни для трех пар сравниваемых выборок
(первая и вторая, первая и третья, вторая и третья) и в каждом случае найти значения U(см. па-
раграф 6.3), мы получим тот же результат.
186
ГЛАВА 7. «ВАВИЛОНСКОЕ СТОЛПОТВОРЕНИЕ», ИЛИ СЛУЧАЙ НЕСКОЛЬКИХ НЕЗАВИСИМЫХ ВЫБОРОК
к
6\18M^7W)=s3j50.
4 4
i Г к
№(2tf+3)-£«}(2ny+3) =
/2L j=i
= ^{182(36+3)-[52(10 + 3)+72(14 + 3)+62(12 + 3)]}=151,917.
Стандартное отклонение о, =-^о} =-7151,917 =12,325.
На завершающем этапе вычисляется /*:
----30-53,5^ 1>907
°7 k2(2tf+3)-£nJ(2«7+3) 12,325
J________>i______
V 72
Нетрудно видеть, если что если / имеет нормальный закон распределения,
то /* является аналогом z, что позволяет использовать таблицу ^-распределения
(табл. 1, Приложение 2).
Если найденному значению J* соответствует вероятность (для односторон-
ней критической области) большая, чем значение уровня значимости а, у нас
нет оснований отвергнуть нулевую гипотезу. Если соответствующая J* вероят-
ность откажется меньшей или равной значению а, нулевая гипотеза отверга-
ется и принимается альтернативная.
В таблице 1 (Приложение 2) для ^-распределения находим, что значению
£=—1,907 соответствует (приблизительно) вероятность р =0,0281. С учетом
того, что альтернативная гипотеза сформулирована для двусторонней крити-
ческой области, удваиваем полученное значение: р=0,0562.
Поскольку значение вероятности р=0,0562 больше, чем выбранный уровень
значимости а=0,05, у нас нет оснований отвергнуть нулевую гипотезу. Между
тремя группами женщин, имеющими разный уровень созависимости, нет раз-
личий в показателе удовлетворенности браком.
Рассмотрим еще один пример.
Кристина работает социальным работником в дневном профилактории для
подростков группы риска, употребляющих наркотики (преимущественно ма-
рихуану, гашиш и «экстази»). Из бесед с подростками она знает, в каком воз-
расте началось употребление, а также то, сколько правонарушений совершил
подросток в течение года.
Сформировав гомогенную по возрасту группу из 16-летних подростков,
Кристина узнала, сколько правонарушений в течение года совершил каждый
из них. Она предположила, что на число совершаемых в течение года правона-
187
КН И ГА ДЛЯ ТЕХ, КТО НЕ ЛЮБИТ СТАТИСТИКУ, НО ВЫНУЖДЕН ЕЮ ПОЛЬЗОВАТЬСЯ
рушений влияет возраст начала употребления наркотиков: чем в более раннем
возрасте началось употребление, тем большее число правонарушений в течение
года было совершено.
Связав оба показателя (возраст начала употребления наркотиков и число
правонарушений в течение года), Кристина получила следующий результат
(табл. 7.16).
Таблица 7.16
Возраст начала употребления наркотиков
и число совершенных за год правонарушений
для группы 16-летних подростков
Возраст начала употребления наркотиков
12 5 13 14 15
5 2 4
4 4 5 3
8 3 4 4
3 6 3 2
6 3 5 1
5 5 3 2
7 5 3
4 4
4
Для проверки выдвинутого Кристиной предположения выберем уровень
значимости а=0,05 и сформулируем нулевую и альтернативную гипотезы.
Но: Фактор возраста начала употребления наркотиков не влияет на число.
правонарушений, совершаемых подростками в течение года.
Фактор возраста начала употребления наркотиков отрицательно влияет
на число правонарушений, совершаемых в течение года: чем в более раннем
возрасте началось употребление, тем большее число правонарушений в течение
года было совершено (односторонняя критическая область).
Приступим к проверке. Из приведенных в табл. 7.16 значений видно, что
среди них есть совпадающие, но относящиеся к разным выборкам. Как отме-
чалось в параграфе 6.3, если в сравниваемых выборках встречаются одинаковые
значения, результат сравнения принимается равным 0,5.
С учетом последнего замечания приступим к попарному сравнению выборок
друг с другом. При наличии четырех выборок мы получим 6 результатов срав-
нения: первая выборка сравнивается со второй, третьей и четвертой; затем
вторая выборка сравнивается с третьей и четвертой, и наконец, третья выбор-
ка сравнивается с четвертой (табл. 7.17).
188
ГЛАВА 7. «ВАВИЛОНСКОЕ СТОЛПОТВОРЕНИЕ», ИЛИ СЛУЧАЙ НЕСКОЛЬКИХ НЕЗАВИСИМЫХ ВЫБОРОК
Таблица 7.17
Сравнение четырех выборок между собой
Возраст начала употребления наркотиков
Сравнение первой выборки со второй, третьей и четвертой 12 Сравнение второй вы- борки с третьей и чет- вертой 13 Сравнение третьей выборки с четвертой 14 15
3 1,5 0 5 1,5 0 5 5 2 4
5 4,5 1 4 4,5 1 4 0 5 3
0 0 0 8 7 3 3 1 4 4
7 7 3 3 0 0 6 3 3 2
1,5 0 0 6 7 3 3 0 5 1
3 1,5 0 5 1,5 0 5 3 3 2
0 0 7 0 5 3
4,5 1 4 1 4
1 4
^12=19,5 ^3=14,5 t/u=4.0 СА3=26,0 £/24 = 8,0 £/з4=14,0
Найдем значение J:
J= Un +1/13 + tZ14 + U23 + U2A + U34 = 19,5 + 14,5+4,0 + 26,0 + 8,0+14,0 = 86,0.
Вычислим значения и ст, для 7V=30; к =4; пj=6; п2=8; п3=9; л4=7:
А 4
к
4
^(2*+3)-£л2(2лу+3) =
/2L м
=^{302(60+3) -[б2(12 + 3)+82(16 + 3)+92(18 + 3)+72(14 + 3)]} = 727,917.
Стандартное отклонение с, = ^/^ = ^/727,917 = 26,980.
На завершающем этапе вычисляется J*:
_86,0-167,5_ 3021
Gj 26,980 ’ ‘
В таблице 1 (Приложение 2) для ^-распределения находим, что значению
z=-3,021 соответствует (приблизительно) вероятность р=0,00137.
7 Строго говоря, при вычислении qj, как и при вычислении J, также необходимо вводить по-
правку, учитывающую наличие в выборках совпадающих значений (здесь используется подход,
близкий к тому, который использовался в тесте Манна—Уитни при вычислении z для случая
189
КНИГА ДЛЯ ТЕХ, КТО НЕ ЛЮБИТ СТАТИСТИКУ, НО ВЫНУЖДЕН ЕЮ ПОЛЬЗОВАТЬСЯ
Поскольку это значение вероятности меньше, чем выбранный уровень зна-
чимости а=0,05, нулевая гипотеза отвергается и принимается альтернативная.
Фактор возраста начала употребления наркотиков отрицательно влияет на
число правонарушений, совершаемых в течение года: чем в более раннем воз-
расте началось употребление, тем большее число правонарушений в течение
года было совершено.
ВКЛЮЧАЕМ КОМПЬЮТЕР...
Создадим переменную «Созависимость» (codependency), в которой закодируем
низкий, умеренный и высокий уровень созависимости, соответственно, цифрами
1, 2 и 3. В переменную «Удовлетворенность» (satisfaction) поместим показатели
удовлетворенности браком для представителей каждой из выборок. Дальнейшая
последовательность действий и получаемый результат показаны на рис. 7.9—7.11.
NonPar ametr SPSS Data Editor
File Edit View Data Transform | Analyze Graphs Utilities Wndow Help
g|H|a| isj| M
’7 ... _f
codepend
1 1
2 ________£
3 1
4 1
Reports
Descrptrve Statistics
Compare Means
General Linear Model
Mixed Models
Correlate
Regression
LogJmear
Classify
5
Б
7
8
9
10
11
12
13
Time Series ►
Survival ►
Multiple Response ►
Missing Value Analysis...
Data Reduction
Scale
Nonparametnc Tests
4>|Q>|
2. Перенести сюда пере-
менную «satisfaction» и пе-
ременную «codependency»
из левого окна
Рис. 7.9. Выбор требуемой статистической процедуры
Test Lit
saUsf
Г »Ме
Reset
Cancel
l~ Medan
Test Type------
Г KrudrJ-WafcH
Growing Venable
т. Установить настрой-
ку для теста Джонк-
Х^сиера—Терпстра С
Define Range
Help
3. Нажать и в новом окне
ввести значения перемен-
ной «codependency»
Рис. 7.10. Тест Джонкхиера—Терпстра: необходимые действия и настройки
связанных рангов). Однако в связи с громоздкостью вычислительной процедуры и незначитель-
ностью вклада, который вносит данная поправка, мы ее не учитываем (она автоматически учи-
тывается в программе SPSS).
190
ГЛАВА 7. «ВАВИЛОНСКОЕ СТОЛПОТВОРЕНИЕ». ИЛИ СЛУЧАЙ НЕСКОЛЬКИХ НЕЗАВИСИМЫХ ВЫБОРОК
Several Independent Sample sj
Range for Gr<
Minimum:
xncVaru
Maximum.
3. В открывшемся окне ввести
минимальное (1)и максималь-
ное (3) значение переменной
> «codependency»
| .Continue (
Help |
4. Нажать и вернуться
в прежнее окно
Рис. 7.10. Тест Джонкхиера—Терпстра: необходимые действия и настройки (окончание)
Jonckheere-Terpstra Test3
Number of Levels in
codependency
N
Observed J-T Statistic
Mean J-T Statistic
Std. Deviation of J-T
Statistic
Std. J-T Statistic
Asymp. Sig. (2-tailed)
Рис. 7.11. Тест Джонкхиера—Терпстра: результат
J
Для второго примера создадим переменную «Старт» (start), в которой цифрами
от 1 до 4 закодируем возраст начала употребления наркотиков в соответствии с
табл. 7.15. Данные о числе правонарушений поместим в переменную «Число»
(number). Повторим те же действия, что показаны выше, учтя, что переменная «start»
закодирована числами от 1 до 4. Полученный результат показан на рис. 7.12.
191
КНИГА ДЛЯ ТЕХ, КТО НЕ ЛЮБИТ СТАТИСТИКУ, НО ВЫНУЖДЕН ЕЮ ПОЛЬЗОВАТЬСЯ
Jonckheere-Terpstra Test*
number
Number of Levels in start
N-
Observed J-T Statistic
Mean J-T Statistic
Std. Deviation of J-T
Statistic
Std. J-T Statistic
Asymp Sig. (2-tailed)
a. Grouping,
30
86.000
167.500
26.33
-3.095
.002
Рис. 7.12. Тест Джонкхиера—Терпстра: результат (пример с правонарушениями)
Результат незначительно отличается от вы-
численного вручную за счет использования
в программе SPSS более точных алгоритмов
вычислений
Уровень значимости.
(Нулевая гипотеза
отвергается.)
Тест Джонкхиера—Терпстра:
примечание
Желание использовать программу SPSS для этого теста может столкнуться
с рядом трудностей. Основу программы SPSS составляет базовый модуль, по-
зволяющий решать большинство задач статистического анализа данных.
В дополнение к базовому модулю существует большое число дополнительных
модулей, устанавливаемых отдельно и позволяющих решать более сложные и
углубленные задачи.
Одним из таких дополнительных модулей является модуль «Exact Tests»
(Точные тесты), позволяющий применять непараметрические тесты с большей
точностью (что особенно важно в случае малых выборок). Кроме этого, он
содержит ряд дополнительных непараметрических тестов, которые отсутству-
ют в базовом модуле SPSS. К числу таких тестов относится и тест Джонкхиера—
Терпстра. Поэтому перед началом работы с программой SPSS необходимо
убедиться, что в нее включен модуль «Exact Tests» (Точные тесты). Если модуль
«Exact Tests» установлен в программу SPSS, то тест Джонкхиера—Терпстра
добавляется к тестам для случая нескольких независимых выборок. В случае
отсутствия данного модуля применение программы SPSS для теста Джонкхиера—
Терпстра становится невозможным.
ГЛАВА 7. «ВАВИЛОНСКОЕ СТОЛПОТВОРЕНИЕ», ИЛИ СЛУЧАЙ НЕСКОЛЬКИХ НЕЗАВИСИМЫХ ВЫБОРОК
7.4. ЧАСТО ЛИ РОДИТЕЛИ БЫВАЮТ В ШКОЛЕ,
ИЛИ МЕДИАННЫЙ ТЕСТ ДЛЯ НЕСКОЛЬКИХ
НЕЗАВИСИМЫХ ВЫБОРОК
Тамара работает шкальным психологом и отвечает за связь школы с роди-
телями учеников. Она заметила, что одни родители (в основном матери) регу-
лярно приходят в школу, интересуются успехами своих детей, встречаются с
учителями, присутствуют на занятиях и т. п., а другие родители — крайне ред- !
кие гости в школе. Пытаясь понять, с какими факторами это связано, Тамара
предположила, что одним из факторов, определяющих интерес родителей к
школьным делам своих детей, является уровень их образования. Взяв список
учеников школы (440 человек), она сформировала выборку из 44 человек (вклю-
чив в выборку каждого десятого ученика) и узнала, сколько раз в течение учеб-
ного года их родители (матери) посетили школу. Из личного дела каждого
ученика она узнала об уровне образования его матери. Затем Тамара составила
таблицу (табл. 7.18), куда занесла сведения о числе посещений матерями шко-
лы в зависимости от уровня их образования [идея примера: Siegel, 1956].
Можно ли на основании полученных Тамарой данных утверждать, что чис-
ло случаев посещения матерями школы зависит от уровня их образования?
Данная задача мало чем отличается от рассмотренных в предыдущих пара-
графах: несколько независимых выборок и результаты, представленные в шка-
ле не ниже, чем шкала порядка. Без сомнений, здесь можно применить тест
Крускала—Уоллиса или тест Джонкхиера—Терпстра, однако эти тесты не яв-
ляются единственно возможными.
В подобных случаях используется также медианный тест для нескольких
независимых выборок8. Он менее точен по сравнению с тестом Крускала—
8 В своем первоначальном варианте медианный тест предназначался для случая двух незави-
симых выборок, но затем он был расширен на число выборок больше двух [Siegel, 1956].
7 Зак. 3384
193
КНИГА ДЛЯ ТЕХ. КТО НЕ ЛЮБИТ СТАТИСТИКУ, НО ВЫНУЖДЕН ЕЮ ПОЛЬЗОВАТЬСЯ
Уоллиса или Джонкхиера—Терпстра (там, где эти тесты выявляют различия,
медианный тест может их не обнаружить). Однако в тех случаях, когда нас не
особо беспокоит точность в принятии решений, медианный тест может ока-
заться более подходящим.
Таблица 7.18
Число посещений школы матерями в зависимости от уровня их образования
Образование матери
Незаконченное среднее Среднее Средне-специальное (техникум или колледж) Высшее
9 2 2 4
4 4 0 3
2 1 4 0
3 б 3 7
2 3 8 1
4 0 0 2
5 2 5 0
2 5 2 3
2 1 1 5
6 2 7 1
1 6
5
1
Как и во многих предыдущих случаях, проверка начинается с того, что все
выборки объединяются. Затем вычисляется медиана объединенных значений,
после чего каждое из значений сравнивается с медианой и подсчитывается,
сколько из них больше медианы, а сколько меньше медианы или равно ей.
После проведенных вычислений исходная таблица с данными превращает-
ся в таблицу размером (2х£), где к — число независимых выборок, а число 2
говорит о наличии в таблице двух категорий: «больше, чем медиана» и «равно
медиане или меньше ее». Если различия между выборками носят случайный
характер, столь же случайный характер будут носить различия между числом
значений, которые больше, чем медиана, и числом значений, которые меньше,
чем медиана (или равны ей), для каждой из выборок.
Наличие различий для таблицы размером (2*к) проверяется с помощью
теста %2 с (к— 1) числом степеней свободы.
Итак, выберем уровень значимости а=0,05 и сформулируем нулевую и
альтернативную гипотезы.
Но: Матери, имеющие различный уровень образования, не отличаются друг
от друга по числу посещений школы, в которой учатся их дети.
194
ГЛАВА 7. «ВАВИЛОНСКОЕ СТОЛПОТВОРЕНИЕ», ИЛИ СЛУЧАЙ НЕСКОЛЬКИХ НЕЗАВИСИМЫХ ВЫБОРОК
Н}: Матери, имеющие различный уровень образования, отличаются друг от
друга по числу посещений школы, в которой учатся их дети (двусторонняя
критическая область).
На первом этапе объединим все данные и вычислим медиану. Для этого
составим таблицу (табл. 7.19), содержащую сведения о числе посещений, со-
ответствующую им частоту, накопленную частоту и то, какой процент от вы-
борки составляет данное значение накопленной частоты (см. параграф 1.1).
Из таблицы видно, что в качестве медианы можно использовать значение,
равное двум посещениям (Me=2), которое делит выборку пополам (накоплен-
ная частота равна 22, что соответствует 50% всех значений)9.
Таблица 7.19
Определение медианы
Число посещений школы Частота Накопленная частота %
0 5 5 11
1 7 12 27
2 10 22 50
3 5 27 61
4 5 32 73
5 5 37 84
6 3 40 91
7 2 42 95
8 1 43 98
9 1 44 100
Итого 44
Определим для каждой выборки, сколько значений больше медианы (боль-
ше чем 2) и сколько меньше медианы или равно ей (табл. 7.20).
Таблица 7.20
Число посещений школы, больших и меньших медианы (равных ей)
Незаконченное среднее Среднее Средне-специальное (техникум или кол- ледж) Высшее Итого
Значения большие медианы 6 (5) 4 (5,5) 7 (6,5) 5 (5) 22
Значения меньшие (равные) медианы 4 (5) 7 (5,5) 6 (6,5) 5 (5) 22
Итого 10 11 13 10 44
9 С учетом ряда обстоятельств, которые мы здесь не рассматриваем, точное значение медиа-
ны равно 2,5.
195
КНИГА ДЛЯ ТЕХ, КТО НЕ ЛЮБИТ СТАТИСТИКУ. НО ВЫНУЖДЕН ЕЮ ПОЛЬЗОВАТЬСЯ
Мы получили таблицу размером (2x4).
Для перехода к тесту х2 определим ожидаемые частоты для каждой из клеток
таблицы (указаны в таблице 7.20 в скобках).
Среди ожидаемых частот нет ни одной, меньшей 5. Поэтому сразу присту-
паем к вычислению эмпирического значения х2:
v2 _(6-5)2 (4-5,5)2 (7-6,5)2 (5-5)2
Х +~бУ+~+
(4-5)2 (7-5,5)2 (6-6,5)2 (5-5)2
5 5,5 6,5 5 ’ ’
Полученное значение сравниваем с х^ритич, которое находим втаблице 2 (При-
ложение 2) для df=3 и значения уровня значимости а=0,05: Хкригич=7,82.
Поскольку Хэмпир < Хкритич, У нас нет оснований отвергнуть нулевую гипоте-
зу. Матери, имеющие различный уровень образования, не отличаются друг от
друга по числу посещений школы, в которой учатся их дети.
ВКЛЮЧАЕМ КОМПЬЮТЕР...
Создадим переменную «Образование» (educat) и закодируем в ней сведения об об-
разовании вошедших в выборку матерей цифрами от 1 (незаконченное среднее) до
4 (высшее образование) в соответствии с таблицей 7.13. В переменной «Визиты»
(visits) поместим сведения о числе посещений школы в течение года. Дальнейшие
действия и полученный результат показаны на рис. 7.13—7.15.
Q2 NonParametr - SPSS Data Editor
1 File Edit View Data Transform | Analyze Graphs Utilities Window Help
Reports
Descriptive Statistics
pg visits |2 Compare Means ► General Unear Model ► Mixed Models > Correlate ► Recession ► Logknsar ► Classify ► Data Reduction > Scale >
educat visits
1 1
2 1
3 1
4 1
5 1
6 V
7 1 Nonparametnc Tests ►
Time Senes > Survival » Multiple Response ► Missing Value Analysis...
8 1
9 1
10 1
11 7
12 2 4
13 2 1
14 2 6
15 2 3
16 2 0
17 2 2
vdr ver var
Chi-Square...
Binomial...
Runs...
1-Sample K-S...
2 Independent Samples...
И322
К Related Samples...
2 Related Samples...
Нажать
Рис. 7.13. Выбор требуемой статистической процедуры
196
ГЛАВА 7. «ВАВИЛОНСКОЕ СТОЛПОТВОРЕНИЕ». ИЛИ СЛУЧАЙ НЕСКОЛЬКИХ НЕЗАВИСИМЫХ ВЫБОРОК
Рис. 7.14. Медианный тест для нескольких независимых выборок:
необходимые действия и настройки
b. Grouping Variable: EDUCAT
Рис. 7.15. Медианный тест для нескольких независимых выборок: результат
Этим примером мы завершаем рассмотрение случая нескольких независимых вы-
борок и переходим к следующему разделу, посвященному ранговым корреляциям.
Глава 8
КОРРЕЛИРОВАТЬ ВСЕ,
ЧТО КОРРЕЛИРУЕТСЯ
В параграфе 1.6 мы уже говорили о том, что такое корреляция и коэффици-
ент корреляции. В обычной (параметрической) статистике для вычисления
коэффициента корреляции необходимо, чтобы обе коррелируемые переменные
были измерены в шкале интервалов или отношений. В непараметрической
статистике в основном используются шкалы наименований и порядка. Даже
если коррелируемые значения выражены в шкале интервалов или отношений
(например, вес), их рассматривают как измеренные в шкале порядка.
Для переменных, измеренных в шкале наименований или порядка, исполь-
зуются специальные методы, позволяющие вычислять меры связи между ними.
Из всего многообразия таких мер связи мы рассмотрим несколько наиболее
популярных*.
8.1. КРАСОТА НА ВСЕ ВРЕМЕНА,
ИЛИ КОЭФФИЦИЕНТ РАНГОВОЙ КОРРЕЛЯЦИИ
СПИРМЕНА
Борис, будущий психолог, интересуется вопросами восприятия женской
привлекательности. Он решил проверить, влияет ли на восприятие женской
привлекательности принадлежность мужчин к различным культурам. Для
проверки Борис использовал фотографии израильских «Королев красоты» за
1 Если считать, что каждая из двух коррелируемых переменных может быть выражена в шка-
ле наименований, порядка, интервалов или отношений, теоретически можно получить (4x4)
случаев для установления взаимосвязи между ними. Например, вычислить связь между полом
работника (дихотомическая шкала наименований) и размером его заработной платы (шкала от-
ношений). Подробнее об этом см.: [Glass, Stanley, 1970; Guilford, Fruchter, 1977].
198
ГЛАВА 8. КОРРЕЛИРОВАТЬ ВСЕ, ЧТО КОРРЕЛИРУЕТСЯ
последние 12 лет. Он предложил двум своим однокурсникам: студенту Л (еврей)
и студенту В (бедуин) независимо друг от друга оценить по 100-балльной шка-
ле 12 таких фотографий по степени их привлекательности (100 баллов соответ-
ствует максимальной привлекательности).
Оценки двух студентов расположились следующим образом (табл. 8.1).
Таблица 8.1
ности двумя студентами — представителями различных культур?
Для ответа на поставленный вопрос необходимо вычислить коэффициент
корреляции между оценками первого и второго студентов. Поскольку оба ис-
пользовали субъективное оценивание, полученные значения оценок относят-
ся к шкале порядка. Как уже неоднократно бывало выше, при решении постав-
ленной задачи используются не значения оценок, а их ранги.
Впервые задача вычисления коэффициента корреляции между двумя пере-
менными, представленными не своими значениями, а рангами этих значений,
была решена Ф. Гальтоном в конце XIX в. Однако такой подход к вычислению
коэффициента корреляции стал популярен после начала его повсеместного
использования Ч. Спирменом в начале XX в. Последнее обстоятельство опре-
делило то, что коэффициент ранговой корреляции носит имя Спирмена.
Для вычисления коэффициента ранговой корреляции Спирмена р исполь-
зуется следующая формула:
N
р = 1------,
И N3-N
где N— число пар коррелируемых значений, разность значений рангов
для f-той пары.
Вернемся к нашему примеру. Задача вычисления коэффициента корреляции
решается в два этапа. Вначале вычисляется само значение коэффициента кор-
реляции. Затем проверяется вероятность того, в какой степени полученный
результат может носить случайный характер (проверка значимости коэффи-
циента корреляции). Если полученный коэффициент корреляции, каким бы
199
КНИГА ДЛЯ ТЕХ, КТО НЕ ЛЮБИТ СТАТИСТИКУ, НО ВЫНУЖДЕН ЕЮ ПОЛЬЗОВАТЬСЯ
большим он ни был, не прошел проверку на значимость, использовать полу-
ченное значение нельзя. Выявленная связь носит случайный характер.
Итак, приступим к вычислению коэффициента ранговой корреляции
Спирмена.
Упорядочим оценки первого и второго студентов, например, в порядке
убывания и проранжируем их2 (табл. 8.2).
Таблица 8.2
Упорядоченные и проранжированные значения оценок
Оценка студента А 97 95 93 85 80 79 75 73 65. 60 55 40
Ранг 1 2 3 4 5 6 7 8 9 10 11 12
Оценка студента В 97 95 90 87 83 80 78 75 65 60 55 45
Ранг 1 2 3 4 5 6 7 8 9 10 11 12
Вернемся к исходной таблице 8.1 и заменим в ней оценку каждого студента
соответствующим рангом. Затем найдем разность рангов для каждой пары
значений и квадрат этой разности (табл. 8.3).
Таблица 8.3
Ранги оценок для каждого студента
Ранг студента Л 7 5 2 3 12 11 4 8 6 1 10 9
Ранг студента В 2 5 7 1 8 11 4 12 10 3 9 6
Разность рангов (d{) 5 0 -5 2 4 0 0 -4 -4 2 1 3
dl 25 0 25 4 16 0 0 16 16 4 1 9
Подставим необходимые значения в формулу для вычисления р:
N
-1 6ы^,_1 6(25+0+25+4+16+0+0+16+16+4+1+9)_п-о*
Р (123 *-12) " ’
Итак, на первом этапе мы получили значение коэффициента ранговой кор-
реляции Спирмена.
Проверим, насколько неслучайный характер носит полученный результат.
Как и во всех предыдущих случаях, выберем уровень значимости а=0,05 и
сформулируем нулевую и альтернативную гипотезы.
Но: Коэффициент корреляции между результатами оценивания женской
привлекательности представителями двух различных культур равен нулю3.
2 В данном случае все равно, в каком порядке упорядочивать результаты — либо в порядке
возрастания, либо в порядке убывания. Разумеется, что сделанный выбор должен быть одинаков
для обеих переменных.
3 Напомним, что основная идея проверки гипотез связана с поиском ответа на вопрос: спра-
ведлив ли результат, полученный на малой выборке, по отношению ко всей популяции? В данном
200
ГЛАВА 8. КОРРЕЛИРОВАТЬ ВСЕ, ЧТО КОРРЕЛИРУЕТСЯ
Hf. Коэффициент корреляции между результатами оценивания женской
привлекательности представителями двух различных культур отличен от нуля
(двусторонняя критическая область4).
Для проверки нулевой гипотезы используется таблица 11 (Приложение 2),
в которой приведены критические значения коэффициентов ранговой корре-
ляции Спирмена в зависимости от объема выборки ТУи уровней значимости а,
соответствующих односторонней и двусторонней критических областей. Если
вычисленное (эмпирическое) значение р меньше критического, нет оснований
отвергнуть нулевую гипотезу. Корреляционная связь признается недостоверной
(незначимой). Если эмпирическое значение р больше критического или равно
ему, нулевая гипотеза отвергается и принимается альтернативная. Корреля-
ционная связь признается достоверной (значимой). В случае отрицательного
значения р при проверке используется его абсолютное значение.
Находим по табл. И для 7V=12 и а=0,05 критическое значение р =0,587.
Поскольку эмпирическое значение р =0,594 больше, чем критическое значение
р =0,587, нулевая гипотеза отвергается. Существует достоверная (значимая на
уровне а=0,05) отличная от нуля корреляционная связь между результатами
оценивания женской привлекательности представителями двух различных
культур.
случае нулевая гипотеза утверждает, что если в££ студенты-евреи и в££. студенты-бедуины оценят
предложенные им фотографии, то корреляционная связь между результатами тех и других будет
равна нулю.
4 Если бы альтернативная гипотеза утверждала, что коэффициент корреляции больше нуля
или меньше нуля, использовалась бы односторонняя критическая область. В данном же случае
утверждается лишь отличие коэффициента корреляции от нуля, без указания в какую сторону.
8 Зак. 3384
201 '
КНИГА ДЛЯ ТЕХ. КТО НЕ ЛЮБИТ СТАТИСТИКУ, НО ВЫНУЖДЕН ЕЮ ПОЛЬЗОВАТЬСЯ
Рассмотрим еще один пример.
К Давиду, работающему школьным психологом, поступили жалобы от учи-
телей по поводу грубого и агрессивного поведения 12 учеников. В ходе инди-
видуальных бесед ученики были протестированы с помощью опросника,
определяющего уровень агрессивности их поведения. Давид предположил, что
истоки агрессивности детей лежат в их семьях. Он встретился с родителями
учеников и на основании этих встреч оценил степень внутрисемейного благо-
получия каждой семьи.
Полученные им результаты приведены в таблице 8.4. В обоих случаях ис-
пользовалась 100-балльная шкала. Для шкалы агрессивности больший пока-
затель соответствует большему уровню агрессии. Для шкалы внутрисемейного
благополучия больший показатель соответствует большей семейной гармонии
и благополучию.
Таблица 8.4
Уровень агрессивности и семейного благополучия для 12 школьников
Ученик Уровень агрессивности Уровень семейного благополучия
А 76 62
В 84 58
С 90 55
D 67 65
Е 64 65
F 73 70
G 84 60
н 55 79
I 67 70
J 50 79
к 62 82
L 79 70
По аналогии с предыдущим примером, упорядочим значения уровня агрес-
сивности и уровня семейного благополучия по убыванию и проранжируем их
(табл. 8.5).
Как видно из результатов ранжирования, они содержат связанные ранги.
Это обстоятельство создает определенные трудности при вычислении коэф-
фициента ранговой корреляции Спирмена.
Существует три варианта дальнейших действий:
1) использовать специальную формулу для вычисления р, учитывающую
наличие связанных рангов;
2) игнорировать наличие связанных рангов и пользоваться прежней фор-
мулой;
202
ГЛАВА «. КОРРЕЛИРОВАТЬ ВСЕ, ЧТО КОРРЕЛИРУЕТСЯ
Таблица 8.5
Упорядоченные и проранжированные значения агрессивности и семейного благополучия
Уровень агрессивности Ранг Уровень семейного благополучия Ранг
90 1 82 1
84 2,5 79 2,5
84 2,5 79 2,5
79 4 70 5
76 5 70 5
73 6 70 5
67 7,5 65 ( 7,5
67 7,5 65 7,5
64 9 62 9
62 10 60 10
55 11 58 11
50 12 55 12 .
3) отказаться от вычисления коэффициента ранговой корреляции Спирмена
и на основе имеющихся данных вычислить обычный коэффициент кор-
реляции (коэффициент корреляции Пирсона).
Покажем возможности каждого из вариантов.
Вернемся к таблице 8.4, заменим приведенные в ней значения соответст-
вующими рангами, определим для каждой пары значений разность рангов и
квадрат этой разности. Получим таблицу 8.6, в которой выделены связанные
ранги.
Таблица 8.6
Ранги значений агрессивности и семейного благополучия
Ученик Ранг уровня агрессивности Ранг уровня семейного благополучия d rf2
А 5 9 —4 16
В 2,5 11 -8,5 72,25
С 1 12 -11 121
D 7,5 7,5 0 0
Е 9 • 7,5 1,5 2,25
F 6 5 :? 1 1
G 2,5 10 -7,5 56,25
Н 11 2,5 8,5 72,25
1 7,5 5 2,5 6,25
203
КНИГА ДЛЯ ТЕХ, КТО НЕ ЛЮБИТ СТАТИСТИКУ. НО ВЫНУЖДЕН ЕЮ ПОЛЬЗОВАТЬСЯ
Окончание табл.8.6
Ученик Ранг уровня агрессивности Ранг уровня семейного благополучия d d2
J 12 2,5 9,5 90,25
К 10 1 9 81
L 4 5 1 1
519,5
Как уже говорилось, при наличии связанных рангов обычной формулой для
вычисления р пользоваться нельзя. Для этого случая необходимо использовать
другую формулу, которая выглядит следующим образом:
где -размер каждой группы связанных рангов (ко-
личество повторяющихся значений) для первого (х) и второго (у) столбцов;
N— число пар коррелируемых значений. В нашем случае 7V= 12.
В первом столбце (агрессивность) имеется две группы связанных рангов по
два значения в каждой из групп: (2,5; 2,5) и (7,5; 7,5).
Во втором столбце (семейное благополучие) имеется три группы связанных
рангов объемом едва, три и два значения: (2,5; 2,5), (5,5,5) и (7,5; 7,5).
Найдем значения Тх и Tv:
т _(23-2)+(23-2)_1. т _ (23-2)+(33-3)+(23-2)
х 12 ’ у 12
После всех пояснений приступим к вычислению р:
Между двумя показателями: уровнем агрессивности и уровнем семейного
благополучия — получена отрицательная корреляционная связь.
Рассмотрим вторую возможность. Вычислим коэффициент ранговой кор-
реляции Спирмена, игнорируя наличие связанных рангов.
N
1=1
=1_«(51ад =
(123-12)
204
ГЛАВА 8. КОРРЕЛИРОВАТЬ ВСЕ, ЧТО КОРРЕЛИРУЕТСЯ
В третьем случае вычисляется обычный коэффициент корреляции Пирсона,
используемый в параметрической статистике5: г=—0,850.
Подведем итоги.
В каждом из трех случаев были получены разные значения коэффициента
корреляции. Наибольшее отклонение от истинного значения (р=—0,842) бы-
ло в случае игнорирования связанных рангов. Это наименее желанный ва-
риант действий при использовании коэффициента ранговой корреляции
Спирмена.
Поскольку ранговая корреляция по Спирмену уходит корнями в корреляцию
по Пирсону6, между двумя значениями: р=—0,842 и г=—0,850 имеются незна-
чительные различия. Поэтому в ряде случаев (если коррелируемые значения
представлены в шкале интервалов или отношений) при наличии связанных
рангов замена коэффициента ранговой корреляции Спирмена корреляцией по
Пирсону может быть оправданной. Но в любом случае предпочтительней ис-
пользовать расчетную формулу, предназначенную для связанных рангов.
Проверим полученное значение р =—0,842 на значимость.
Выберем уровень значимости а=0,05 и сформулируем нулевую и альтерна-
тивную гипотезы.
Но: Коэффициент корреляции между уровнем агрессивности учеников и
уровнем их семейного благополучия равен нулю.
Я(: Коэффициент корреляции между уровнем агрессивности учеников и
уровнем их семейного благополучия меньше нуля (односторонняя критическая
область).
Находим в табл. 11 (Приложение 2) для N= 12 и а=0,05 критическое значе-
ние р =0,503. Поскольку эмпирическое значение |р|=0,842 больше, чем кри-
тическое значение р =0,506, нулевая гипотеза отвергается. Существует значи-
мая (на уровне а=0,05) отрицательная корреляционная связь между уровнем
агрессивного поведения учеников и уровнем их семейного благополучия (чем
более благополучна семья, тем менее агрессивно поведение ребенка).
ВКЛЮЧАЕМ КОМПЬЮТЕР...
Результаты оценивания фотографий представим в переменных «Шкала 1» (scale 1)
и «Шкала 2» (scale2). Дальнейшая последовательность действий и результат пока-
заны на рис. 8.1—8.3.
5 Вследствие трудоемкости вычисления коэффициента корреляции Пирсона мы опускаем
все промежуточные вычисления и приводим только конечный результат. Подробнее о вычисле-
нии коэффициента корреляции Пирсона см., например: [Guilford, Fruchter, 1977].
6 Коэффициент ранговой корреляции Спирмена можно рассматривать как частный случай
коэффициента корреляции Пирсона. Поэтому между двумя коэффициентами существует взаи-
мосвязь. Поскольку вычисление корреляции по Спирмену намного легче, чем вычисление кор-
реляции по Пирсону, существуют специальные переводные таблицы, позволяющие вначале
вычислить коэффициент ранговой корреляции Спирмена, а затем определить соответствующее
значение коэффициента корреляции Пирсона.
205
КНИГА ДЛЯ ТЕХ, КТО НЕ ЛЮБИТ СТАТИСТИКУ. НО ВЫНУЖДЕН ЕЮ ПОЛЬЗОВАТЬСЯ
| И NonParametr - SPSS Data Editor
File Edit View Data Transform [ Analyze Graphs Utilities Window Help
g5|H|^| ЕЦ| o|t>| 73| Reports ► Descriptive Statistics ► Compare Means ► General Linear Model ► Mixed Models ► $|F>I <»lQ>|i
123: scab!
scalel scale2 vai | var
1 75 c
Correlate ► Bivariate...
J 80 E Regression ► Partial... II
3 95 7 Loginear ► Distances... 11
4 93 c Classify ► Data Reduction ► Scale ► Nonpar ametric Tests ► Time Series ► Survival ► Multiple Response ► Missing Value Analysis... 1
5 40 7 \
6 55 c J L
7 85 E Г Нажать )
8 73 4
9 79 E
10 97 c
11 60 6^
12 65 80
13
14
15
16
17
18
19
20 •
Рис. 8.1. Выбор требуемой статистической процедуры
Рис. 8.2. Коэффициент ранговой корреляции Спирмена:
необходимые действия и настройки
ГЛАВА 8. КОРРЕЛИРОВАТЬ ВСЕ, ЧТО КОРРЕЛИРУЕТСЯ
Nonparametric Corre
Spearman's rho SCALE 1 Correlation Coefficient
Sig. (2-tailed)
_____________N_______________________
SCALE2 Correlation Coefficient
Sig. (2-tailed)
N
.594
1.000
Рис. 8.3. Коэффициент ранговой корреляции Спирмена: результат
Корреляционная матрица.
По диагонали всегда располо-
жены единицы (корреляция
переменных с самими собой)
n Is significant at the 0.05
Коэффициент корреляции и соответствующий
ему уровень значимости
(Нулевая гипотеза отвергается.)
Приведем еще один результат (рис. 8.4) для случая связи между уровнем агрессив-
ного поведения учеников и уровнем их семейного благополучия (случай связанных
рангов). Для этого сведения об агрессивности учеников поместим в переменную
«Агрессия» (aggress), а сведения об уровне семейного благополучия в переменную
«Семейная ситуация» (situat).
Correlations
AGGRESS SITUAT
Spearman's rho AGGRESS Correlation Coefficient 1.000 -.842**
Sig. (2-tailed) .001
N 12 12
SITUAT Correlation Coefficient -.842** 1.000
Sig. (2-tailed) .001
N 12 12
**• Correlation Is significant at the 0.01 level (2-tailed).
Рис. 8.4. Коэффициент ранговой корреляции Спирмена:
результат (случай связанных рангов)
8.2. ЕЩЕ РАЗ О ЖЕНСКОЙ ПРИВЛЕКАТЕЛЬНОСТИ,
ИЛИ КОЭФФИЦИЕНТ РАНГОВОЙ КОРРЕЛЯЦИИ
КЕНДАЛЛА
Неугомонный Борис не прекращает своих попыток определить, влияет ли
принадлежность к определенной этнической и культурной группе на восприятие
женской привлекательности. Он по-прежнему использует фотографии изра-
ильских «Королев красоты» за последние 12 лет.
207
КНИГА ДЛЯ ТЕХ, КТО НЕ ЛЮБИТ СТАТИСТИКУ, НО ВЫНУЖДЕН ЕЮ ПОЛЬЗОВАТЬСЯ
Устав переводить оценки в ранги, он стал просить участников исследования
не оценивать фотографии в 100-балльной шкале, а просто ранжировать их от
наиболее привлекательной к наименее привлекательной.
Два очередных студента (один коренной израильтянин, а второй — имми-
грант из Эфиопии) разложили 12 фотографий в порядке убывания привлека-
тельности изображенных на них девушек. Результаты их ранжирования пред-
ставлены в таблице 8.7.
Таблица 8.7
Существует ли корреляционная связь между результатами двух ранжиро-
ваний?
Разумеется, ответ на данный вопрос можно получить с помощью вычи-
сления коэффициента ранговой корреляции Спирмена. Однако в середине
1940-х гг. Кендалл пред ложил новый подход к определению корреляционной
связи между ранговыми переменными. В том случае, если выборка небольшая,
удобнее иметь дело с корреляцией по Кендаллу, чем с корреляцией по
Спирмену.
Идея корреляции по Кендаллу достаточно проста.
Допустим, мы упорядочили группу людей по росту — от максимального до
минимального и узнали значения веса каждого из них. Теперь можно получить
два ранговых ряда—для роста и для веса. Если предположить, что чем больше
рост, тем больше вес, то изменение рангов рос-
та будет совпадать с изменением рангов веса.
Например, первому рангу по росту будет соот-
ветствовать первый ранг по весу, второму рангу
по росту — второй ранг по весу и т. д. Однако
эта последовательность может быть нарушена
(человек может быть высоким, но очень худым,
или низкорослым, но очень тучным), и вместо
совпадения рангов для роста и веса мы получим
инверсию рангов (перестановку): например,
рост уменьшился, а вес увеличился.
Если оба ранговых ряда полностью совпада-
ют, то это соответствует коэффициенту корре-
ляции +1. Если один ряд выглядит «наоборот»
208
ГЛАВА 8. КОРРЕЛИРОВАТЬ ВСЕ. ЧТО КОРРЕЛИРУЕТСЯ
по отношению к другому, мы имеем сплошные инверсии, что соответствует
коэффициенту корреляции — 1.
В обычных случаях, если сравнивать два ряда рангов, в них встречаются как
совпадения, так и инверсии. Кендалл предложил простую формулу для вычис-
ления коэффициента корреляции на основе числа совпадений и инверсий.
Вернемся к таблице 8.7. Для студента А запишем ранги по порядку — от 1
до 12 и укажем соответствующие ранги для студента В. Получим таблицу 8.8.
Таблица 8.8
Результаты ранжирования после их упорядочивания для первого испытуемого
Ранги студента А 1 2 3 4 5 6 7 8 9 10 11 12
Ранги студента В 11 10 7 8 12 9 ~ 4 1 3 2 6 5
Процесс подсчета числа совпадений и инверсий покажем на рис. 8.5.
Ранги А 1 2 3 4 5 6 7 8 9 10 И 12
Ранги В 11 10 7 8 12 9 4 1 3 2 6 5
ц_ _9
10 - - + - -8
7 + + + -- -- '-- -з
8 + + -- -- -- -4
12 - -- -- -- -7
9 — — — — — ——6
— — — + + -1
1 + + + + +4
3 — + + + 1
2 + - + +2
6 —• -1
5 0
Итого: -32
Рис. 8.5. Подсчет суммы совпадений и инверсий рангов
Совпадения означают, что если для первого студента (студент Л) числа воз-
растают слева направо от 1 до 12, то для второго студента (студент В) эти числа
также должны меняться слева направо в сторону возрастания. Инверсии озна-
чают, что в то время, как числа для студента Л возрастают от 1 до 12, числа для
студента В уменьшаются.
Каждое из чисел для студента В Ъудцы. последовательно сравнивать с осталь-
ными числами, которые расположены правее от него. Если правее будет стоять
209
КНИГА ДЛЯ ТЕХ, КТО НЕ ЛЮБИТ СТАТИСТИКУ, НО ВЫНУЖДЕН ЕЮ ПОЛЬЗОВАТЬСЯ
большее число, обозначим это как «+»(совпадение). Если правее будет стоять
меньшее число, обозначим это как «—» (инверсия). В конце каждой строки
найдем число совпадений (количество плюсов), число инверсий (количество
минусов) и разность между ними (между количеством плюсов и количеством
минусов). Затем подсчитаем общую сумму по вертикали, которая будет равна
разности между суммой всех совпадений и суммой всех инверсий7. Обозначим
полученный результат как S:
S - (Сумма всех совпадений — Сумма всех инверсий).
Вычислим значение коэффициента ранговой корреляции Кендалла т («тау»
Кендалла) по формуле:
т= S
1лГ(ЛГ-1>
Для нашего случая S=— 32; N= 12.
S -32
j — 12(12-1) ——0,485.
Существует несколько модификаций формулы для вычисления коэффи-
циента ранговой корреляции Кендалла т, в которых используется либо значе-
ние числа совпадений, либо значение числа инверсий, либо (как в нашем
случае) как совпадения, так и инверсии. Разумеется, все они дают одинаковый
результат.
На основании рассмотренного примера можно видеть, что вычисление
коэффициента ранговой корреляции Кендалла носит более простой характер
по сравнению с вычислением коэффициента ранговой корреляции Спирмена.
Однако это справедливо только для небольших выборок. В случае возрастания
значения Nзаметно увеличивается объем вычислений (подсчет числа совпаде-
ний и инверсий) и, соответственно, возрастают затраты времени на вычисление
корреляции по Кендаллу8.
7 Нетрудно видеть, что это соответствует разности между количеством всех «плюсов» (17)
и количеством всех «минусов» (49) на рис. 8.5: S= 17—49=—32.
8 У корреляции по Кендаллу есть ряд других, более существенных достоинств, например
простота интерпретации полученного результата. Так, в частности, можно показать, что для двух
ранговых рядов вероятность совпадений равна (1 + т) / 2, а вероятность инверсий равна (1 - т)/2.
Например, если т=0,6, то это означает 80% совпадений и 20% инверсий. Иными словами, если
два студента, оценивающие женскую привлекательность, получили т=0,6, то это означает, что
их мнения относительно женской привлекательности совпадают в четыре раза чаще, чем не сов-
падают. Интерпретация коэффициентов корреляции по Пирсону или Спирмену носит не столь
явный характер. Полученный результат надо вначале возвести в квадрат, а затем сделать малопо-
нятный неспециалисту вывод относительно доли дисперсии, которая может быть объяснена
полученным результатом.
210
ГЛАВА 8. КОРРЕЛИРОВАТЬ ВСЕ, ЧТО КОРРЕЛИРУЕТСЯ
Для корреляции по Кендаллу также существует проблема связанных рангов.
Кроме этого, здесь используется иной подход к проверке значимости получае-
мых результатов.
Рассмотрим вначале ситуацию со связанными рангами.
Проверялась гипотеза о том, что успехи в изучении иврита новыми имми-
грантами связаны с уровнем развития их логического мышления, позволяю-
щего понять и использовать внутреннюю логику этого языка. Десять добро-
вольцев из числа новых иммигрантов, которые завершили стандартный курс
обучения ивриту и сдали по нему экзамен, были протестированы с использо-
ванием методик, оценивающих логическое мышление. В таблице 8.9 приведе-
ны результаты экзамена по иврйту и результаты тестирования (все в 100-балль-
ной шкале).
Таблица 8.9
Результаты экзамена по ивриту и тестированию логического мышления
Испытуемый 1 2 3 4 5 6 7 8 9 10
Иврит 83 90 75 80 93 71 83 67 85 77
Логическое мышление 95 90 73 88 93 69 88 75 64 80
Упорядочим оценки по ивриту и результаты тестирования в порядке убы-
вания и проранжируем их (табл. 8.10).
Таблица 8.10
Упорядоченные и проранжированные результаты экзамена и тестирования
Иврит 93 90 85 83 83 80 77 75 71 67
Ранг 1 2 3 4,5 4,5 6 7 8 9 10
Логическое мышление 95 93 90 88 88 80 75 73 69 64
Ранг 1 2 3 4,5 4,5 6 7 8 9 10
Заменим в таблице 8.9 результаты в 100-балльной шкале соответствующими
рангами. Получим новую таблицу 8.11.
Таблица 8.11
Ранги результатов экзамена по ивриту и тестирования логического мышления
Иврит (ранги) 4,5 2 8 6 1 9 ' 4,5 10 3 7
Логическое мыш- ление (ранги) 1 3 8 4,5 2 9 4,5 7 10 6
211
КНИГА ДЛЯ ТЕХ, КТО НЕЛЮБИТ СТАТИСТИКУ. НО ВЫНУЖДЕН ЕЮ ПОЛЬЗОВАТЬСЯ
Упорядочим значения рангов по ивриту от 1 до 10 и соответствующим об-
разом расположим значения рангов для логического мышления (табл. 8.12).
Вычислим для каждого ранга во второй строке число совпадений и инверсий.
Таблица 8.12
Упорядоченные ранги результатов экзамена по ивриту и соответствующие ранги
результатов тестирования
Иврит (ранги) 1 2 3 4,5 4,5 6 7 8 9 10
Логическое мыш- ления (ранги) 2 3 10 1 4,5 4,5 6 8 9 7
Совпадения 7 6 0 5 4 4 3 1 0 0
Инверсии 1 1 6 0 0 0 0 1 0 0
Обратите внимание! При подсчете совпадений и инверсий связанные ранги
учитываются только один раз. Например, правее ранга 2 расположено 8 значе-
ний, больших, чем 2: 3; 10; 4,5; 4,5; 6; 8; 9; 7. Но поскольку значения 4,5 и 4,5
образованы связанными рангами, они берутся в расчет только один раз. Поэтому
фактическое число совпадений для ранга 2 будет не 8, а 7.
Сумма совпадений = (7 + 6 + 0 + 5+4 + 4 + 3+ 1 +0 + 0) = 30.
Сумма инверсий = (1 +1+6 + 0 + 0 + 0 + 0+ 1 +0 + 0) = 9.
5= (Сумма совпадений — Сумма инверсий) = (30 — 9) = 21.
При наличии связанных рангов используется иная формула для вычисления
коэффициента ранговой корреляции Кендалла т:
5
т =
N(N-1)_T
У 2 x
где =-^(x(rx-1), Ty =-^ty(ty-1), (x, ty — размер каждой группы связанных
рангов (количество повторяющихся значений) в первой (х) и второй (у) строках.
В табл. 8.12 в первой строке (ранги оценок по ивриту) есть одна группа свя-
занных рангов (4,5 и 4,5). Здесь 2 „ Т, = |[2(2-1)] = I.
Аналогичная ситуация во второй строке — одна группа связанных рангов,
включающая два значения: 4,5 и 4,5. Поэтому ty=2 и Ту =^[2(2-1)] = 1.
Подставим все необходимые значения в формулу для вычисления т:
S 21 _________
10(10-1) !
t=-z~,...-
I N(N-i)_T
N 2 х
= 0,477.
N(N-\)_T
2 >
10(10-1) t
2
212
ГЛАВА 8. КОРРЕЛИРОВАТЬ ВСЕ, ЧТО КОРРЕЛИРУЕТСЯ
Проверим полученные значения коэффи-
циента ранговой корреляции Кендалла на
значимость.
Вначале проверим на значимость значение
х для первого примера (ранжирование фото-
графий): т=—0,485.
Выберем уровень значимости а=0,05 и
сформулируем нулевую и альтернативную
гипотезы.
Яо: Коэффициент корреляции между ре-
зультатами оценивания женской привлека-
тельности представителями двух различных
культур равен нулю.
Яр Коэффициент корреляции между ре-
зультатами оценивания женской привлека-
тельности представителями двух различных
культур отличен от нуля (двусторонняя кри-
тическая область).
Для проверки коэффициента ранговой корреляции Кендалла на значимость
используется несколько подходов, в зависимости от значения N.
Если Я>10, то вначале вычисляется значение z".
т
z= .
l2(2N+5)
y9N(N-l)
Затем по таблице ^-распределения (см. табл. 1, Приложение 2) определяет-
ся вероятность (для односторонней критической области), соответствующая
полученному значению. Если эта вероятность оказывается больше выбранно-
го уровня значимости "а, нет оснований отвергнуть нулевую гипотезу. Если
найденная вероятность меньше выбранного уровня значимости а или равна
ему, нулевая гипотеза отклоняется и принимается альтернативная.
Вычислим z для т=—0,485 и N= 12.
z= , Х = Г0,485—=-2,195.
|2(2N+5) 12(24+5)
5|9N(N-1) \ 108(12-1)
В таблице 1 (Приложение 2) для z-распределения, находим, что значению
г=—2,195 соответствует вероятностьр =0,0143.
В том случае, если критическая область двусторонняя (как в нашем случае),
значение вероятности необходимо удвоить: р =0,0286.
Поскольку значение уровня значимости а=0,05 больше, чем р=0,0286,
нулевая гипотеза отклоняется и принимается альтернативная. Существует
213
КНИГА ДЛЯ ТЕХ, КТО НЕ ЛЮБИТ СТАТИСТИКУ, НО ВЫНУЖДЕН ЕЮ ПОЛЬЗОВАТЬСЯ
значимая, отличная от нуля корреляционная связь между результатами оцени-
вания женской привлекательности представителями двух различных культур.
Проверим на значимость результат, полученный во втором примере (случай
связанных рангов): т=0,477.
Выберем уровень значимости а=0,05 и сформулируем нулевую и альтерна-
тивную гипотезы.
Яо: Коэффициент корреляции между уровнем знания иврита и показателя-
ми логичности мышления у новых иммигрантов равен нулю.
Hi: Коэффициент корреляции между уровнем знания иврита и показателя-
ми логичности мышления у новых иммигрантов отличен от нуля (двусторонняя
критическая область).
Для случая малых выборок (N < 10) существует специальная таблица, со-
держащая значения р (односторонняя критическая область) в зависимости от
значений т и Я (см. табл. 12, Приложение 2).
Из таблицы 12 находим, что для т=0,477 и Я=10 значение р лежит между
р =0,036 (для т=0,467) ир=0,023 (для т=0,511). Примемр =0,030. Поскольку
альтернативная гипотеза сформулирована для случая двусторонней критической
области, удваиваем это значение: р =0,060.
Полученное значение вероятности оказалось больше, чем а=0,05. Оснований
отвергнуть нулевую гипотезу нет. Коэффициент корреляции между уровнем
знания иврита и показателями логичности мышления у новых иммигран-
тов — выпускников языковых курсов незначимо отличается от нуля9.
ВКЛЮЧАЕМ КОМПЬЮТЕР...
Результаты ранжирования фотографий поместим в переменные «Ранг 1» (range 1)
и «Ранг 2» (range2). Дальнейшие действия и получаемый результат показаны на
рис. 8.6—8.8.
[ggNonParametr - SPSS Data Editor
File Edit View Data Transform | Analyze Graphs Utilities Window Help
Рис. 8.6. Выбор требуемой статистической процедуры
Reports
Descriptive Statistics
Compare Means
General linear Model
Mixed Models
9 Если мы переформулируем альтернативную гипотезу для случая односторонней критической
области (коэффициент корреляции между уровнем знания иврита и показателями логичности
мышления больше нуля), то же самое значение коэффициента корреляции окажется значимым,
поскольку 0,05 > 0,03.
214
ГЛАВА 8. КОРРЕЛИРОВАТЬ ВСЕ, ЧТО КОРРЕЛИРУЕТСЯ
Venables
Bivariate Correlations
Г One Idle
signilicenl correlations
2. Перенести сюда пере-
менные «range!» и
«гапде2» из левого окна
Conekfaon Coeffi
Г" Pearson
Test of Siqnrfcange
Twotaded
Рис. 8.7. Коэффициент ранговой корреляции Кендалла:
необходимые действия и настройки
Установлено по умолчанию.
Статистически значимые коэффици-
ента корреляции будут отмечены
звездочками
«prangel
V>tange2
3. Нажать
Будет проверена значимость
коэффициента корреляции для
односторонней или двусторонней
критической области (установлена
по умолчанию)
1. Установить настройку
для ранговой корреляции
Кендалла
Nonparametric Correlations
Correlations
Kendall's tau_b
RANGE1
RANGE2
Correlation Coefficient
Sig. (2-tailed)
N_______________________
Correlation Coefficient
Sig. (2-tailed) /
N /
RANGE1
1.000
12
-.485*
.028
12
RANGE2
-.485*
.028
12
1.000
12
*• Correlation Is significant at the
Корреляционная матрица.
Смотри пояснения в примере для
коэффициента ранговой корреля-
ции Спирмена
Рис. 8.8. Коэффициент ранговой корреляции Кендалла: результат
Рассмотрим пример со связанными рангами. В переменной «Иврит» (Hebrew)
поместим результаты экзамена по ивриту, а в переменной «Логика» (logic) — све-
дения об уровне логического мышления. Результат вычислений для случая
двусторонней и односторонней критических областей показан на рис. 8.9.
Обратите внимание! Один и тот же коэффициент корреляции, в зависимо-
сти от того, как сформулирована альтернативная гипотеза, в одном случае
признается незначимым, а в другом — значимым!
215
КНИГА ДЛЯ ТЕХ, КТО НЕ ЛЮБИТ СТАТИСТИКУ, НО ВЫНУЖДЕН ЕЮ ПОЛЬЗОВАТЬСЯ
Nonparametric
Коэффициент корреляции
незначимо отличается от нуля
Kendall's tau_b HEBREW Correlation Coefficient
1.000
377
Sig. (2-tailed)
.058
LOGIC
Sig. (2-tailed)
058
1.000
ю
Уровень значимости для
двусторонней критической области.
(Нулевая гипотеза не отвергается.)
Рис. 8.9. Коэффициент ранговой корреляции Кендалла:
результат (пример для связанных рангов)
8.3. ПОЧЕМУ ПОДРОСТКИ НАЧИНАЮТ
УПОТРЕБЛЯТЬ НАРКОТИКИ,
ИЛИ КОЭФФИЦИЕНТ КОНКОРДАЦИИ КЕНДАЛЛА
Специалисты считают, что существует несколько основных причин, по
которым израильские подростки могут начать употреблять наркотики.
Среди них:
1) сильное любопытство;
2) влияние друзей;
216
ГЛАВА 8. КОРРЕЛИРОВАТЬ ВСЕ, ЧТО КОРРЕЛИРУЕТСЯ
3) поиск возбуждения и риска;
4) бунт против взрослых;
5) недостаток уверенности в себе; | (N—y /HLivxfl
6) проблемы в семье. yy'J Y\Z
Уже знакомая нам Кристина, работающая с под- I 1у“т>~2У АД I
ростками группы риска, попросила нескольких упо-
требляющих наркотики подростков проранжировать
данный список в порядке убывания значимости при- А, Р~- ЯК. ____'
веденных в нем причин (первый ранг присваивался
наиболее значимой причине, последний, шестой ранг — наименее значимой).
Результаты ранжирования для 10 подростков приведены в таблице 8.13.
Можно ли определить, насколько совпадают мнения подростков относи-
тельно причин начала употребления наркотиков?
Для ответа на поставленный вопрос используется специальный показатель:
коэффициент конкордации10 Кендалла W, принимающий значений от 0 (пол-
ное отсутствие согласованности) до (1 полная согласованность).
Коэффициент конкордации Кендалла W определяется как отношение ре-
ального распределения рангов к идеальному (когда ранги всех испытуемых или
экспертов совпадают друг с другом).
Для нахождения коэффициента конкордации Кендалла И^проведем допол-
нительные вычисления на основе таблицы 8.13.
Таблица 8.13 Индивидуальные ранги причин начала употребления наркотиков
Подростки Причины начала употребления
1 2 3 4 5 6
А 1 4 2 3 6 5
В 2 1 3 4 5 6,
с 3 1 2 5 4 6
D 3 1 2 5 4 6
Е 2 3 1 6 4 5
F 1 4 3 2 6 5
G 1 2 3 4 5 6
Н 1 3 4 2 6 5
I 2 , 1 6 4 5 / 3
J 1 3 4 6 2 5
К, 17 23 30 41 47 52 2Х=21о
-18 -12 -5 6 12 17
324 144 25 36 144 289 5=962
10 От латинского concordate — согласованность, согласие.
217
КНИГА ДЛЯ ТЕХ, КТО НЕ ЛЮБИТ СТАТИСТИКУ, НО ВЫНУЖДЕН ЕЮ ПОЛЬЗОВАТЬСЯ
1. Для каждого столбца таблицы найдем сумму рангов (/?,), запишем ее вни-
зу соответствующего столбца и затем найдем сумму полученных значений
(ЕЛ,)-
2. Определим для каждого столбца значение (R —) и квадрат этого
у d N
значения: (Rj —&—L)2, где N—число ранжируемых объектов (в нашем случае ,
N
N=6). Полученные результаты также запишем внизу каждого столбца.
3. Найдем сумму значений (Л-^^-)2: У (Л—2l5.)2 и обозначим ее S.
N N
Коэффициента конкордации Кендалла W вычисляется по следующей формуле:
S
±k\N3-N)
где к — число испытуемых или экспертов (в нашем случае к=10).
Подставим в формулу все необходимые значения:
S
962
W--------------= -j--—-------=0,550.
' tfW-N) ±(Ю2)(63-6)
При использовании коэффициента конкордации Кендалла W также воз-
можны случаи связанных рангов, однако мы не будем рассматривать эту си-
туацию. Она описана, например, у S. Siegel [Siegel, 1956].
Полученный результат требует проверки на значимость. Для этого исполь-
зуется таблица критических знаний для теста %2.
Вначале вычисляется значение х2:
X2 =k(N—})W.
Затем полученное значение Хэмпир сравнивается с критическим значением
Х^ритич, которое находится в таблице 2 (Приложение 2), для числа степеней
свободы df=(N— 1) и выбранного значения уровня значимости а.
Если хэмпир < Х^ритич, нет оснований отвергнуть нулевую гипотезу. Если
Хэмпир > Хкригич, нулевая гипотеза отвергается и принимается альтернативная.
Выберем уровень значимости а=0,05 и сформулируем нулевую и альтерна-
тивную гипотезы.
Но: Коэффициент конкордации, полученный на основе ранжирования де-
сятью испытуемыми шести объектов, равен нулю.
Н\. Коэффициент конкордации, полученный на основе ранжирования де-
сятью испытуемыми шести объектов, больше нуля (односторонняя критическая
область11).
11 Поскольку коэффициент конкордации не может быть меньше нуля, двусторонняя крити-
ческая область здесь невозможна.
218
ГЛАВА 8. КОРРЕЛИРОВАТЬ ВСЕ, ЧТО КОРРЕЛИРУЕТСЯ
Определим значение Хэмпир:
X2=к (N-1) W= 10(6 -1) х 0,550=27,5.
Из табл. 2 находим, что для df=(N—1) = (6—1) = 5 и уровня значимости
а=0,05 Хкритич = 11,07.
Поскольку эмпирическое значение больше критического (11,07), нулевая
гипотеза отвергается и принимается альтернативная. Коэффициент конкорда-
ции Кендалла, полученный на основе ранжирования десятью испытуемыми
шести объектов, значимо отличается от нуля.
ВКЛЮЧАЕМ КОМПЬЮТЕР...
Создадим 6 переменных для каждой из причин начала употребления наркотиков:
от «Причина 1» (reasonl) до «Причина 6» (reason6) и укажем, какой ранг им присво-
ен каждым из десяти подростков. Дальнейшая последовательность действий и ко-
нечный результат показаны на рис. 8.10—8.12.
J* NonParametr - SPSS Data Editor
He Edit View Data Transform | Analyze Graphs Utilities
Reports
Descriptive Statistics
Compare Means
General Linear Model
Mixed Models
Corr date
Regression
Loghnear
Classfy
Data Reduction
Scale
Window Help
26: reasonl
1
2
3
4
5
6
7
8
9
10
11
12
reasonl
____1_
2
________3
________3
2
reason2
Nonpar ametnc Tests
13
14
15
16
17
18
19
20
reason5
6
5
4
4
4
R
reasonE
5
6
6
6
5
R
Chi-Square...
Binomial...
Runs...
I-Sample K-S...
2 Independent Samples...
К Independent Samples...
2 Related Samples...
Time Senes
Survival
Multiple Response
Missing Value Analysis..
Нажать
£|1К| <»|0>|
Рис. 8.10. Выбор требуемой статистической процедуры
219
КНИГА ДЛЯ ТЕХ, КТО НЕ ЛЮБИТ СТАТИСТИКУ, НО ВЫНУЖДЕН ЕЮ ПОЛЬЗОВАТЬСЯ
падав
*>ieaxor£
TettVanablet.
^learonl
|»>1елюп2
ф|е«тапЗ
д>1мих>4
2. Перенести сюда пере-
менные «reasonl»...
«геазопб» из левого
окна
3. Нажать
TejtType
,Г Trie
Рис. 8.11. Коэффициент конкордации Кендалла:
необходимые действия и настройки
1. Установить на-
стройку для W Кен-
далла
Kendall’s W Test
Ranks
Рис. 8.12. Коэффициент конкордации Кендалла: результат
ПРИЛОЖЕНИЯ
Приложение 1
НЕПАРАМЕТРИЧЕСКАЯ СТАТИСТИКА В ЛИЦАХ
Абрахам Вальд / Abraham Wald (1902-1950), американский математик.
Получил образование и степень доктора наук в Венском университете. В 1938 г.
был вынужден вместе с семьей эмигрировать в США, спасаясь от нацистов.
В 1940-х гг. работал вместе с Якобом Волфовицем в области математической
статистики. Одним из результатов совместной работы стал непараметрический
тест последовательностей, носящий имя своих создателей (Вальда—Волфовица
тест последовательностей). В 1950 г. трагически погиб вместе с женой в авиа-
катастрофе в Индии, куда был приглашен индийским правительством для
чтения лекций.
Франк Вилкоксон / Frank Wilcoxon (1892—1965), американский ученый, один
из создателей современной непараметрической статистики. По образованию
химик, доктор наук, много лет проработавший в химической промышленности.
Находясь под влиянием работ Фишера, начал заниматься статистикой и в 1945 г.
опубликовал статью, в которой описал два новых непараметрических теста.
Идея первого теста была впоследствии развита Манном и Уитни и привела к
созданию теста Манна—Уитни (или теста Вилкоксона—Манна—Уитни). Второй
из предложенных тестов йосит имя автора (тест Вилкоксона для двух зависимых
выборок). Вилкоксон — автор первого университетского курса по непарамет-
рической статистике и создатель первой научной школы непараметрической
статистики.
Якоб Волфовиц / Jacob Wolfowitz (1910—1981), американский математик,
профессор математики. В 1940-х гг. ввел в научный лексикон понятие «непа-
раметрическая статистика». В эти же годы плодотворно работал в области
математической статистики совместно с Абрахамом Вальдом (это сотрудниче-
ство было прервано гибелью А. Вальда в авиакатастрофе в 1950 г.). Одним из
результатов совместной работы стал непараметрический тест последователь-
ностей (Вальда—Волфовица тест последовательностей). Якоб Волфовиц — отец
Пола Волфовица, который с 2005 по 2007 г. был президентом Всемирного
Банка.
221
ПРИЛОЖЕНИЯ
Сэр Френсис Гальтон / Sir Francis Galton (1822—1911), английский ученый-
энциклопедист и исследователь. Область его научных интересов простиралась
от метеорологии до психологии. Был инициатором применения математико-
статистических методов при проведении психологических и антропометриче-
ских исследований. Заложил основы психологического тестирования, корре-
ляционного и регрессионного анализа.
Эймбел Джонкхиер / Aimable Robert Jonckheere (1920—2005), английский
психолог и статистик, доктор наук. Известен своими исследованиями в облас-
ти психологии восприятия. В 1954 г. опубликовал работу с описанием нового,
непараметрического теста для случая нескольких независимых выборок, кото-
рые могут быть расположены в определенном порядке. За два года до этого,
независимо от Джонкхиера, схожий подход описал голландский математик
Т. Терпстра. Объединение идей Джонкхиера и Терпстра привело к созданию
теста, носящего их имена (тест Джонкхиера—Терпстра для упорядоченных
альтернатив).
Сэр Морис Кевдалл / Sir Maurice George Kendall (1907—1983), английский
статистик, внесший заметный вклад в развитие математической статистики.
В 1940-х гг. разрабатывал методы ранговой корреляции. Предложил новый
подход к определению коэффициента ранговрй корреляции (коэффициент
ранговой корреляции Кендалла т). Для ситуации ранжирования одного и того
же набора объектов группой независимых экспертов разработал метод, позво-
ляющий оценивать степень согласованности их результатов (коэффициент
конкордации Кендалла).
Андрей Николаевич Колмогоров (1903—1987), российский математик, один
из создателей современной теории вероятностей, академик Академии наук
СССР. В 1930-х гг. разработал подход, позволяющий оценивать степень откло-
нения эмпирического распределения случайной величины от теоретического
распределения. Идеи Колмогорова, дополненные близкими по направлению
работами Владимира Смирнова, привели к появлению непараметрического
теста Колмогорова—Смирнова.
Вильям Кохран / William Gemmell Cochran (1909—1980), англо-американский
статистик. Родился в Шотландии, получил математическое образование в
Кембридже. С конца 1930-х гг. жил и работал в США. В качестве специалиста
по математической статистике участвовал во многих исследованиях, занимал-
ся разработкой новых статистических методов, возглавлял ряд американских
и международных статистических ассоциаций. В 1950 г. опубликовал работу,
в которой описал новый непараметрический тест, позволяющий сравнивать
результаты распределения дихотомических данных в нескольких зависимых
выборка (Q-тест Кохрана).
222
ПРИЛОЖЕНИЕ 1. НЕПАРАМЕТРИЧСКАЯ СТАТИСТИКА В ЛИЦАХ
Вильям Крускал / William Henry Kruskal (1919—2005), американский матема-
тик и статистик, доктор наук. В 1952 г. опубликовал совместную с Вильсоном
Уоллисом статью, описав метод однофакторного дисперсионного анализа для
рангов, который стал непараметрическим аналогом ANOVA (тест Крускала-
Уоллиса).
Квинн МакНемар / Quinn McNemar (1900—1986), американский психолог,
профессор психологии, автор популярного учебника Psychological Statistics,
выдержавшего в США четыре издания. В 1947 г. предложил тест для сравнения
распределения дихотомических результатов в двух зависимых выборках (тест
МакНемара).
Генри Манн / Henry Berthold Mann (1905—2000), американский математик,
профессор математики. В 1947 г. Г. Манн совместно с Р. Уитни, разработали
непараметрический тест, в основе которого лежал подход, предложенный в
1945 г. Ф. Вилкоксоном. В настоящее время тест Манна—Уитни (или тест
Вилкоксона—Манна—Уитни) является наиболее популярным непараметри-
ческим тестом для случая двух независимых выборок.
Линкольн Мозес / Lincoln Е. Moses (1921—2006), американский ученый-ста-
тистик, профессор статистики. В начале 1950-х гг. разработал непараметриче-
ский тест для сравнения результатов в двух независимых выборках, основанный
на анализе крайних (экстремальных) значений в одной из них (тест экстре-
мальных реакций Мозеса).
Карл Пирсон / Karl Pearson (1857—1936), английский математик и статистик,
один из создателей современной математической статистики. В 1901 г. осно-
вал журнал «Биометрика», который был посвящен применению математико-
статистических методов в биологических науках. Развивая идеи Гальтона,
разработал методы корреляционного анализа (коэффициент корреляции
Пирсона). Создатель одного из наиболее популярных непараметрических
тестов — теста х2.
Садней Сигель / Sidney Siegel (1916—1961), американский психолог, доктор
наук. Автор ставшей классической книги [1956], в которой были систематизи-
рованы и описаны все существующие к тому времени методы непараметриче-
ской статистики. С именем С. Сигеля связано начало широкого использования
непараметрических методов в поведенческих науках. Его имя носит один из
непараметрических тестов (тест Сигеля—Тьюки).
Владимир Иванович Смирнов (1887—1974), российский математик, академик
Академии наук СССР. В 1930-х гг. разрабатывал методы сравнения эмпириче-
ских распределений случайной величины. Объединение идей Смирнова со
схожими идеями Андрея Колмогорова привело к созданию непараметрическо-
го теста Колмогорова—Смирнова.
223
ПРИЛОЖЕНИЯ
Чарльз Спирмен / Charles Edward Spearman (1863—1945), английский психо-
лог, известный своими исследованиями в области структуры интеллекта.
В рамках проводимых исследований разработал ряд новых статистических
методов, в частности, заложил основы факторного анализа. Для целей корре-
ляционного анализа использовал коэффициент ранговой корреляции, который
впоследствии получил его имя (р Спирмена).
Тёнис Терпстра / Tennis Jannes Terpstra (р. 1926), голландский математик,
профессор математики. В 1952 г. опубликовал работу, в которой предложил
новый подход к анализу нескольких независимых выборок, допускающих
расположение в определенном порядке. В 1954 г., независимо от Терпстра,
аналогичный подход описал Э. Джонкхиер. Объединение идей Терпстра и
Джонкхиера привело к появлению нового непараметрического теста (тест
Джонкхиера—Терпстра для упорядоченных альтернатив).
Рансом Уитни / Ransom D. Whitney (1915—2007), американский математик,
профессор математики. В 1947 г. совместно со своим научным руководителем
Генри Манном опубликовал статью с описанием нового непараметрического
теста, в разработке которого использовались ранее опубликованные идеи
Ф. Вилкоксона. В настоящее время тест Манна—Уитни (или тест Вилкоксона—
Манна—Уитни) является наиболее популярным непараметрическим тестом
для случая двух независимых выборок.
Вильсон Уоллис / Wilson Allen Wallis (1912—1998), американский экономист
и статистик. В течение многих лет был экономическим консультантом ряда
американских президентов (Д. Эйзенхауэра, Р. Никсона, Д. Форда и Р. Рейгана).
Является одним из создателей (совместно с Вильямом Крускалом) метода од-
нофакторного дисперсионного анализа для рангов, который стал непарамет-
рическим аналогом ANOVA (тест Крускала—Уоллиса).
Сэр Рональд Фишер / Sir Ronald Aylmer Fisher (1890—1962), английский ста-
тистик, биолог и генетик, основатель математической теории планирования
эксперимента, создатель ряда классических методов современной статистики
(в частности, дисперсионного анализа). В непараметрической статистике ис-
пользуется предложенный им тест, позволяющий сравнивать распределение
дихотомических результатов в двух независимых выборках (точный тест
Фишера). При работе с малыми выборками точный тест Фишера предпочти-
тельней теста %1 2.
Милтон Фридман / Milton Friedman (1912—2006), американский ученый-
экономист, лауреат Нобелевской премии* по экономике за 1976 г., создатель
1 Премия по экономике не была предусмотрена в завещании А. Нобеля. Она была учреждена
в 1969 г. Банком Швеции в память А. Нобеля, и ее правильней называть Премией по экономике
памяти А. Нобеля.
224
ПРИЛОЖЕНИЕ I. НЕПАРАМЕТРИЧСКАЯ СТАТИСТИКА ВЛИЦАХ
так называемой «чикагской экономической школы». Внес большой вклад в
развитие современной экономической науки. Много внимания уделял разви-
тию экономической статистики. В конце 1930-х гг. создал тест, являющийся
непараметрическим аналогом двухфакторного дисперсионного анализа для
порядковых переменных (тест Фридмана или двухфакторный дисперсионный
анализ Фридмана для рангов).
Приложение 2
СТАТИСТИЧЕСКИЕ ТАБЛИЦЫ
Таблица 1
^-распределение2
Z 0,00 0,01 0,02 0,03 0,04 0,05 0,06 0,07 0,08 0,09
0,0 0,5000 0,4960 0,4920 0,4880 0,4840 0,4801 0,4761 0,4721 0,4681 0,4641
0,1 0,4602 0,4562 0,4522 0,4483 0,4443 0,4404 0,4364 0,4325 0,4286 0,4247
0,2 0,4207 0,4168 0,4129 0,4090 0,4052 0,4013 0,3974 0,3936 0,3897 0,3859
0,3 0,3821 0,3783 0,3745 0,3707 0,3669 0,3632 0,3594 0,3557 0,3520 0,3483
0,4 0,3446 0,3409 0,3372 0,3336 0,3300 0,3264 0,3228 0,3192 0,3156 0,3121
0,5 0,3085 0,3050 0,3015 0,2981 0,2946 0,2912 0,2877 0,2843 2,810 0,2776
0,6 0,2743 0,2709 0,2676 0,2643 0,2611 0,2578 0,2546 0,2514 2,483 0,2451
0,7 0,2420 0,2389 0,2358 0,2327 0,2296 0,2266 0,2236 0,2206 0,2177 0,2148
0,8 0,2119 0,2090 0,2061 0,2033 0,2005 0,1977 0,1949 0,1922 0,1894 0,1867
0,9 0,1841 0,1814 0,1788 0,1762 0,1736 0,1711 0,1685 0,1660 0,1635 0,1611
1,0 0,1587 0,1562 0,1539 0,1515 0,1492 0,1469 0,1446 0,1423 0,1401 0,1379
1Л 0,1357 0,1335 0,1314 0,1292 0,1271 0,1251 0,1230 0,1210 0,1190 0,1170
1,2 0,1151 0,1131 0,1112 0,1093 0,1075 0,1056 0,1038 0,1020 0,1003 0,0985
1,3 0,0968 0,0951 0,0934 0,0918 0,0901 0,0885 0,0869 0,0853 0,0838 0,0823
1,4 0,0808 0,0793 0,0778 0,0764 0,0749 0,0735 0,0721 0,0708 0,0694 0,0681
1,5 0,0668 0,0655 0,0643 0,0630 0,0618 0,0606 0,0594 0,0582 0,0571 0,0559
1,6 0,0548 0,0537 0,0526 0,0516 0,0505 0,0495 0,0485 0,0475 0,0465 0,0455
1,7 0,0446 0,0436 0,0427 0,0418 0,0409 0,0401 0,0392 0,0384 0,0375 0,0367
1,8 0,0359 0,0351 0,0344 0,0336 0,0329 0,0322 0,0314 0,0307 0,0301 0,0294
1,9 0,0287 0,0281 0,0274 0,0268 0,0262 0,0256 0,0250 0,0244 0,0239 0,0233
2 В таблице приведены значения вероятности, соответствующие площади под кривой еди-
ничного нормального распределения, находящейся справа от г.
226
ПРИЛОЖЕНИЕ 2. СТАТИСТИЧЕСКИЕ ТАБЛИЦЫ
Окончание табл. 1
Z 0,00 0,01 0,02 0,03 0,04 0,05 0,06 0,07 0,08 0,09
2,0 0,0228 0,0222 0,0217 0,0212 0,0207 0,0202 0,0197 0,0192 0,0188 0,0183
2,1 0,0179 0,0174 0,0170 0,0166 0,0162 0,0158 0,0154 0,0150 0,0146 0,0143
2,2 0,0139 0,0136 0,0132 0,0129 0,0125 0,0122 0,0119 0,0116 0,0113 0,0110
2,3 0,0107 0,0104 0,0102 0,0099 0,0096 0,0094 0,0091 0,0089 0,0087 0,0084
2,4 0,0082 0,0080 0,0078 0,0075 0,0073 0,0071 0,0069 0,0068 0,0066 0,0064
2,5 0,0062 0,0060 0,0059 0,0057 0,0055 0,0054 0,0052 0,0051 0,0049 0,0048
2,6 0,0047 0,0045 0,0044 0,0043 0,0041 0,0040 0,0039 0,0038 0,0038 0,0036
2,7 0,0035 0,0034 0,0033 0,0032 0,0031 0,0030 0,0029 0,0028 0,0027 0,0026
2,8 0,0026 0,0025 0,0024 0,0023 0,0023 0,0022 0,0021 0,0021 0,0020 0,0019
2,9 0,0019 0,0018 0,0018 0,0017 0,0016 0,0016 0,0015 0,0015 0,0014 0,0014
3,0 0,0013 0,0013 0,0013 0,0012 0,0012 0,0011 0,0011 0,0011 0,0010 0,0010
3,1 0,0010 0,0009 0,0009 0,0009 0,0008 0,0008 0,0008 0,0008 0,0007 0,0007
3,2 0,0007
3,3 0,0005
3,4 0,0003
3,5 0,00023
3,6 0,00016
3,7 0,00011
3,8 0,00007
3,9 0,00005
4,0 0,00003
227
ПРИЛОЖЕНИЯ
Таблица 2
Критические значения для распределения %2
Число степеней свободы (df) а=0,05 а=0,01 а=0,001
1 3,84 6,64 10,83
2 5,99 9,21 13,82
3 7,82 11,34 16,27
4 9,49 13,28 18,46
5 11,07 15,09 20,52
6 12,59 16,81 22,46
7 14,07 18,48 24,32
8 15,51 20,09 26,12
9 16,92 21,67 27,88
10 18,31 23,21 29,59
11 19,68 24,72 31,26
12 21,03 26,22 32,91
13 22,36 27,69 34,53
14 23,68 29,14 36,12
15 25,00 30,58 37,70
16 26,30 32,00 39,29
17 27,59 33,41 40,75
18 28,87 34,80 42,31
19 30,14 36,19 43,82 .
20 31,41 37,57 45,32
21 32,67 38,93 46,80
22 33,92 40,29 48,27
23 35,17 41,64 49,73
24 36,42 42,98 51,18
25 37,65 44,31 52,62
228
ПРИЛОЖЕНИЕ 2. СТАТИСТИЧЕСКИЕ ТАБЛИЦЫ
Таблица 3
Таблица вероятностей для биномиального теста
(указаны значения после запятой для случая р = ^ = 0,5)
\х N\ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
5 031 188 500 812 969
6 016 109 344 656 891 984
7 008 062 227 500 773 938 992
8 004 035 145 363 637 855 965 996
9 002 020 090 254 500 746 910 980 998
10 001 ОН 055 172 377 623 828 945 989 999
11 006 033 113 274 500 726 887 967 994
12 003 019 073 194 387 613 806 927 981 997
13 002 011 046 133 291 500 709 867 954 989 998
14 001 006 029 090 212 395 605 788 910 971 994 999
15 004 018 059 151 304 500 696 849 941 982 996
16 002 oil 038 105 227 402 598 773 895 962 989 998
17 001 006 025 072 166 315 500 685 834 928 975 994 999
18 001 004 015 048 119 240 407 593 760 881 952 985 996 999
19 002 010 032 084 180 324 500 676 820 916 968 990 998
20 001 006 021 058 132 252 412 588 748 868 942 979 994
21 001 004 013 039 095 192 332 500 668 808 905 961 987
22 002 008 026 067 143 262 416 584 738 857 933 974
23 001 005 017 047 105 202 339 500 661 798 895 953
24 001 003 011 032 076 154 271 419 581 729 846 924
25 002 007 022 054 115 212 345 500 655 788 885
229
ПРИЛОЖЕНИЯ
Таблица 4
Критические значения D для теста Колмогорова—Смирнова
(случай одной выборки, двусторонняя критическая область)
Размер вы- борки (N) а = 0;20 а=0,10 а = 0,05 а = 0,01
1 0,900 0,950 0,975 0,995
2 0,684 0,776 0,842 0,929
3 0,565 0,636 0,708 0,829
4 0,493 0,565 0,624 0,734
5 0,447 0,509 0,563 0,669
6 0,410 0,468 0,519 0,618
7 0,381 0,436 0,483 0,576
8 0,358 0,410 0,454 0,542
9 0,339 0,387 0,430 0,513
10 0,323 0,369 0,409 0,489
11 0,308 0,352 0,391 0,468
12 0,296 0,338 0,375 0,449
13 0,285 0,325 0,361 0,432
14 0,275 0,314 0,349 0,418
15 0,266 0,304 0,338 0,404
16 0,258 0,295 0,327 0,392
17 0,250 0,286 0,318 0,381
18 0,244 0,279 0,309 0,371
19 0,237 0,271 0,301 0,361
20 0,232 0,265 0,294 0,352
21 0,226 0,259 0,287 0,344
22 0,221 0,253 0,281 0,337
23 0,216 0,247 0,275 0,330
24 0,212 0,242 0,269 0,323
25 0,208 0,238 0,264 0,317
26 0,204 0,233 0,259 0,311
27 0,200 0,229 0,254 0,305
28 0,197 0,225 0,250 0,300
29 0,193 0,221 0,246 0,295
30 0,190 0,218 0,242 0,290
31 0,187 0,214 0,238 0,285
32 0,184 0,211 0,234 0,281
33 0,182 0,208 0,231 0,277
34 0,179 0,205 0,227 0,273
35 0,177 0,202 0,224 0,269
Больше 35 1,07 yfN 1,22 1,36 1,63
230
ПРИЛОЖЕНИЕ 2. СТАТИСТИЧЕСКИЕ ТАБЛИЦЫ
Таблица 5
Критические значения Тдля теста Вилкоксона
п Уровень значимости для односторонней критической области
0,05 0,025 0,01 0,005
Уровень значимости для двусторонней критической области
0,10 0,05 0,02 0,01
5 0 — — —
6 2 0 — —
7 3 2 0 —
8 5 3 1 0
9 8 5 3 1
10 10 8 5 3
11 13 10 7 5
12 17 13 9 7
13 21 17 12 9
14 25 21 15 12
15 30 25 19 15
16 35 29 23 19
17 41 34 27 23 ’
18 47 40 32 27
19 53 46 37 32
20 60 52 43 37
21 67 58 49 42
22 75 65 55 48
23 83 73 62 54
24 91 81 69 61
25 100 89 76 68
231
ПРИЛОЖЕНИЯ
Таблица 6
Критические значения г для теста последовательностей3
\2 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
2 2 2 2 2 2 2 2 2
3 2 2 2 2 2 2 2 2 2 3 3 3 3 3 3
4 2 9 2 9 2 3 3 3 3 3 3 3 3 4 4 4 4 4
5 2 9 2 10 3 10 3 И 3 11 3 3 4 4 4 4 4 4 4 5 5 5
6 2 2 9 3 10 3 И 3 12 3 12 4 13 4 13 4 13 4 13 5 5 5 5 5 5 6 6
7 2 2 3 И 3 12 3 13 4 13 4 14 5 14 5 14 5 14 5 15 5 15 6 15 6 6 6 6 6
8 2 3 3 11 3 12 4 13 4 14 5 14 5 15 5 15 6 16 6 16 6 16 6 16 6 17 7 17 7 17 7 17 7 17
9 2 3 3 4 13 4 14 5 14 5 15 5 16 6 16 6 16 6 17 7 17 7 18 7 18 7 18 8 18 8 18 8 18
10 2 3 3 4 13 5 14 5 15 5 16 6 16 6 17 7 17 7 18 7 18 7 18 8 19 8 19 8 19 8 20 9 20
11 2 3 4 4 13 5 14 5 15 6 16 6 17 7 17 7 18 7 19 8 19 8 19 8 20 9 20 9 20 9 21 9 21
12 2 2 3 4 4 13 5 14 6 16 6 16 7 17 7 18 7 19 8 19 8 20 8 20 9 21 9 21 9 21 10 22 10 22
13 2 2 3 4 1 5 15 6 16 6 17 7 18 7 19 8 19 8 20 9 20 9 21 9 21 10 22 10 22 10 23 10 23
14 2 2 3 4 5 5 15 6 16 7 17 7 18 8 19 8 20 9 20 9 21 9 22 10 22 10 23 10 23 11 23 И 24
15 2 3 3 4 1 6 15 6 16 7 18 7 18 8 19 8 20 9 21 9 22 10 22 10 23 11 23 И 24 11 24 12 25
16 2 3 4 1 1 6 6 17 7 18 8 19 8 20 9 21 9 21 10 22 10 23 11 23 11 24 11 25 12 25 12 25
17 2 3 4 4 5 6 7 17 7 18 8 19 9 20 9 21 10 22 10 23 И 23 11 24 11 25 12 25 12 26 13 26
18 2 3 4 5 5 О | 7 17 8 18 8 19 9 20 9 21 10 22 10 23 11 24 И 25 12 25 12 26 13 26 13 27
19 2 3 4 5 6 6 7 17 8 18 8 20 9 21 10 22 10 23 11 23 11 24 12 25 12 26 13 26 13 27 13 27
20 2 3 4 5 6 О 1 7 17 8 18 9 20 9 21 10 22 10 23 11 24 12 25 12 25 13 26 13 27 13 27 14 28
3 Приведенные в таблице значения соответствуют уровню значимости а = 0,05 для двусто-
ронней критической области и а=0,025 для односторонней критической области.
232
ПРИЛОЖЕНИЕ 2. СТАТИСТИЧЕСКИЕ ТАБЛИЦЫ
Таблица 7
Фрагмент таблицы вероятностей для теста Манна—Уитни
(значения вероятностей для односторонней критической области
в зависимости от п2 и U)4
и 1 2 3 4 5 6
0 0,143 0,036 0,012 0,005 0,002 0,001
1 0,286 0,071 0,024 0,010 0,004 0,002
2 0,428 0,143 0,048 0,019 0,009 0,004
3 0,571 0,214 0,083 0,033 0,015 0,008
4 0,321 0,131 0,057 0,026 0,013
5 0,429 0,190 0,086 0,041 0,021
6 0,571 0,274 0,129 0,063 0,032
7 0,357 0,176 0,089 0,047
8 0,452 0,238 0,123 0,066
9 0,548 0,305 0,165 0,090
10 0,381 0,214 0,120
11 0,457 0,268 0,155
12 0,545 0,331 0,197
13 0,396 0,242
14 0,465 0,294
15 0,535 0,350
16 0,409
17 0,469
18 0,531
4 В приводимом фрагменте п2 = 6.
9 Зак. 3384
233
ПРИЛОЖЕНИЯ
Таблица 8
Критические значения KD для теста Колмогорова—Смирнова
(случай двух малых независимых выборок)
N Односторонняя критическая область Двусторонняя критическая область
а=0,05 а=0,01 а=0,05 а=0,01
3 3 — — —
4 4 — 4 —
5 4 5 5 5
6 5 6 5 6
7 5 6 6 6
8 5 6 6 7
9 6 7 6 7
10 6 7 7 8
И 6 8 7 8
12 6 8 7 8
13 7 8 7 9
14 7 8 8 9
15 7 9 8 9
16 7 9 8 10
17 8 9 8 10
18 8 10 9 10
19 8 10 9 10
20 8 10 9 и
21 8 10 9 11
22 9 11 9 11
23 9 11 10 и
24 9 11 10 12
25 9 11 10 12
26 9 11 10 12
27 9 12 10 12
28 10 12 11 13
29 10 12 11 13
30 10 12 11 13
35 и 13 12 —
40 11 14 13 —
234
ПРИЛОЖЕНИЕ 2. СТАТИСТИЧЕСКИЕ ТАБЛИЦЫ
Таблица 9
Критические значения D для теста Колмогорова—Смирнова
(случай двух больших независимых выборок п j и п2, двусторонняя критическая область)
Уровень значимости D
0,05 1,36 V «1«2
0,01 1,63^
0,001 1,95 1п1+п2 N «1Л2
Таблица 10
Фрагмент таблицы критических значении D (или С) для точного теста Фишера
Сумма значений в клетках таблицы В (или А) Уровень значимости
а =0,05 а =0,025 а =0,01 а =0,005
Л+Л=10 С+2)=6 10 9 8 7 6 3 2 1 0 0 2 1 1 0 2 1 0 1 0 0
C+Z)=5 10 9 8 7 6 2 1 1 0 0 2 1 0 0 1 0 0 1 0
С+Л=4 10 9 8 7 1 1 0 0 1 0 0 0 0 0 0
C+D=3 10 9 8 1 0 0 0 0 0 0
C+D=2 10 9 0 0 0 — —
Л+Б=11 C+D=ll 11 10 9 8 7 6 5 4 7 5 4 3 2 1 0 0 6 4 3 2 1 0 0 5 3 2 1 0 0 4 3 2 1 0
235
ПРИЛОЖЕНИЯ
Окончание табл. 10
Сумма значений В(или А) Уровень значимости
в клетках таблицы а =0,05 а =0,025 а =0,01 а =0.005
Л+2? = 11 C+Z>=10 11 6 5 4 4
10 4 4 3 2
9 3 3 2 1
8 2 2 1 0
7 1 1 0 0
6 1 0 0 —
5 0 — — —
С + Р=9 11 5 4 4 3
10 4 3 2 2
9 3 2 1 1
8 2 1 1 0
7 1 1 0 0
6 0 0 — —
5 0 — — —
Таблица II
Критические значения коэффициента ранговой корреляции Спирмена
N Односторонняя критическая область Двусторонняя критическая область
а=0,05 а=0,01 а=0,001 а=0,05 а=0,01 а=0,001
4 1,000
5 0,900 1,000 1,000
6 0,829 0,943 0,886 1,000
7 0,714 0,893 1,000 0,786 0,929 1,000
8 0,643 0,833 0,952 0,738 0,881 0,976
9 0,600 0,783 0,917 0,700 0,833 0,933
10 0,564 0,745 0,879 0,648 0,794 0,903
11 0,536 0,709 0,845 0,618 0,755 0,873
12 0,503 0,671 0,825 0,587 0,727 0,860
13 0,484 0,648 0,802 0,560 0,703 0,835
14 0,464 0,622 0,776 0,538 0,675 0,811
15 0,443 0,604 0,754 0,521 0,654 0,786
16 0,429 0,582 0,732 0,503 0,635 0,765
17 0,414 0,566 0,713 0,485 0,615 0,748
18 0,401 0,550 0,695 0,472 0,600 0,728
19 0,391 0,535 0,677 0,460 0,584 0,712
20 0,380 0,520 0,662 0,447 0,570 0,696
236
ПРИЛОЖЕНИЕ 2. СТАТИСТИЧЕСКИЕ ТАБЛИЦЫ
Таблица 12
Значения коэффициента ранговой корреляции Кецдалла и соответствующие им
значения вероятности (односторонняя критическая область)
для случая маленькой выборки (7V< 10)
N т Р N т Р N т р N т Р
4 0,000 0,625 7 0,048 0,500 9 0,000 0,540 10 0,022 0,500
0,333 0,375 0,143 0,386 0,056 0,460 0,067 0,431
0,667 0,167 0£38 0,281 0,111 0,381 0,111 0,364
1,000 0,042 0,333 0,191 0,167 0,306 0,156 0,300
0,429 0,119 0,222 0,238 0,200 0,242
5 0,000 0,592 0,524 0,068 0,278 0,179 0,244 0,190
0,200 0,408 0,619 0,035 0,333 0,130 0,289 0,146
0,400 0,242 0,714 0,015 0,389 0,090 0,333 0,108
0,600 0,117 0,810 0,005 0,444 0,060 0,378 0,078
0,800 0,042 * 0,905 0,001 0,500 0,038 0,422 0,054
1,000 0,008 1,000 0,000 0,556 0,022 0,467 0,036
0,611 0,012 0,511 0,023
6 0,067 0,500 8 0,000 0,548 0,667 0,006 0,556 0,014
0,200 0,360 0,071 0,452 0,722 0,003 0,600 0,008
0,333 0,235 0,143 0,360 0,778 0,001 0,644 0,005
0,467 0,136 0,214 0,274 0,833 0,000 0,689 0,002
0,600 0,068 0,286 0,199 0,889 0,000 0,733 0,001
0,733 0,028 0,357 0,138 0,944 0,000 0,778 0,000
0,867 0,008 0,429 0,089 1,000 0,000 0,822 0,000
1,000 0,001 0,500 0,ч054 0,867 0,000
0,571 0,031 0,911 0,000
0,643 0,016 0,956 0,000
0,714 0,007 1,000 0,000
0,786 0,003
0,857 0,001
0,929 0,000
1,000 0,000
237
Приложение 3
ВСЕ НЕПАРАМЕТРИЧЕСКИЕ МЕТОДЫ
В ОДНОМ МЕСТЕ
Ниже дано краткое описание всех рассмотренных в книге непараметрических
методов статистики (за исключением методов ранговой корреляции).
Приводимые сведения не заменяет подробного описания того или иного ме-
тода, но позволяют сориентироваться в его назначении и оценить объем воз-
можных вычислений.
Описание каждого метода завершается текстом программного синтаксиса
для SPSS, обеспечивающего выполнение предусмотренных данным методом
вычислений и выдачу конечного результата. В тексте синтаксиса вместо имен
конкретных переменных используется запись «var». Если переменных несколь-
ко (к выборок), используются обозначения varb var2,..., vart.
1. Тест х2 для единственной выборки
Назначение теста. Сравнение распределения наблюдаемых частот (Оу), раз-
битых на к категорий, с распределением ожидаемых (теоретических) частот
(EJ), задаваемых соответствующим законом распределения.
В случае равномерного распределения значение ожидаемых частот для ка-
f-n
Ej~T
ждой категории определяется как
к — количество категорий.
где N— общее число наблюдений,
На основании сведений о наблюдаемых и ожидаемых частотах и числе ка-
тегорий к, вычисляется значение х2:
Л J-7
у=1 Lj
Полученное значение х2 сравнивается с критическим значением, которое
находится в таблице критических значений для теста х2 с(к—1) числом степеней
свободы.
238
ПРИЛОЖЕНИЕ 3. ВСЕ НЕПАРАМЕТРИЧЕСКИЕ МЕТОДЫ В ОДНОМ МЕСТЕ
Программный синтаксис (для случая равномерного распределения):
NPAR TEST
/ CHI SQUARE = var5
/EXPECTED = EQUAL
/MISSING ANALYSIS.
2. Тест Колмогорова^-Смирнова для одной выборки
Назначение теста. Сравнение эмпирического распределения N наблюдаемых
частот с теоретическим распределением, задаваемым соответствующей функ-
цией распределения.
Вычисляются эмпирическая кумулятивная функция распределения (ЭКФР)
и теоретическая кумулятивная функция распределения (ТКФР), которые затем
дважды сравниваются друг с другом. Вначале определяется разность между
текущими значениями обеих функций и находится максимальное положитель-
ное значение среди всех полученных (D). Затем определяется разность между
предыдущим значением ЭКФР и текущим значением ТКФР и находится наи-
меньшее отрицательное значение среди всех полученных (Р).
Оба значения сравниваются друг с другом по модулю, среди них выбирает-
ся набольшее и вычисляется значение Z для статистики Колмогорова-
Смирнова:
Z=max(|D/|,|P/|)Viv.
Программный синтаксис (для случая равномерного распределения): -
NPAR TESTS
/К-S (UNIFORM) = var
/MISSING ANALYSIS.
3. Тест последовательностей
Назначение теста. Проверка случайного характера последовательности ди-
хотомических значений.
Для анализируемой последовательности, образованной дихотомической
переменной, принимающей, например, значения 0 и 1, определяется, сколько
раз в ней встречаются значение 0 (и0)> значение 1 (nJ и количество серий г из
нулей и единиц (включая единичные значения нулей и единиц).
5 При работе с программой SPSS здесь и далее вместо «таг» или «varb var2,var*» необходи-
мо указать имя переменной (переменных), по отношению к которой будет выполнена данная
операция. Так, в параграфе 3.2, посвященном тесту х2 для единственной выборки, при переходе
к программе SPSS использовалась переменная «саге». Следовательно, для этрго примера, в запи-
си программного синтаксиса вместо «var» необходимо записать «саге».
239
ПРИЛОЖЕНИЯ
На основании полученных данных о п0, П[Иг вычисляется значение z:
2я,я2 Л_1
«|+»2
|2я,я2(2я|яг-я1-я2)
I (я|+я2)г(я,+я2-1)
В случае маленькой выборки (менее 50 значений) используются поправки:
1. Если г-| +11 < 0, формула принимает вид:
1И1+Л2 J
г-f-^+l |+о,5
(и1+л2 )
У (л|+Л2)2(А+Л2-1)
„ „ ( 2п,п-> , V п ,
2. Если г - —L-£-+1 >0, формула принимает вид:
. l«l+«2 J
г_| 2^+1 ]_0,5
(ni+ni )
/2л!л2(2И|И2-Я1-и2)
У (»|+Л2)2(«1+«2-1)
По таблице ^-распределения определяется вероятность, соответствующая
вычисленному значению г для односторонней критической области.
Программный синтаксис (для дихотомической переменной 0,1):
NPAR TESTS
/RUNS(1) = var
/MISSING ANALYSIS.
4. Биномиальный тест
Назначение теста. Сравнение частоты появления двух дихотомических пе-
ременных, имеющих вероятности р и q=(l—p), если после Nнезависимых
испытаний частота появления первой из них равна яь частота появления вто-
рой из них равна я2 (N=nl+n2).
Вероятность полученного результата рассчитывается по следующей форму-
ле (формула Бернулли), где m=min(n1, п2):
' т (N\
р(х<т)=]П .
Zojj J
В том случае, когда TV > 25, возможно применение формулы, связанной с
вычислением ?:
240
ПРИЛОЖЕНИЕ 3. ВСЕ НЕПАРАМЕТРИЧЕСКИЕ МЕТОДЫ В ОДНОМ МЕСТЕ
_(от±О,5)-Лф.
(т +0,5) используется в том случае, когда х < Np;
(т—0,5) используется в том случае, когда х > Np.
По таблице ^-распределения определяется вероятность, соответствующая
вычисленному значению z для односторонней критической области.
Программный синтаксис (для случая p=q=0,5):
NPAR TEST
/BINOMIAL (.50)= var
' /MISSING ANALYSIS.
5. Тест МакНемара для двух зависимых выборок
Назначение теста. Сравнение распределений дихотомических переменных
в двух зависимых выборках X и Y. При построении таблицы сопряженности
дихотомических признаков размером (2x2) используются только результаты,
относящиеся к несовпадающим признакам (см. рис.).
Выборка Y
0 1
Выборках 1 A в
0 c D
Если (А +Л)< 10, вероятность полученного распределения результатов рас-
считывается по формуле Бернулли для односторонней критической области:
р(х <т)=У, ( + & |(0,5)(Л+О), где т=min (Л, D).
«I ' J
' Если (A +D) > 10, то вычисляется значение %2:
(И-Д1-1)2
(Л + О)
Полученное значение %2 сравнивается с критическим значением, которое
находится в таблице критических значений для теста х2с одной степенью сво-
боды.
Программный синтаксис (var, — измерение «до», var2— измерение «по-
сле»):
NPAR TEST
/MCNEMAR= vari WITH var2 (PAIRED)
/MISSING ANALYSIS.
241
ПРИЛОЖЕНИЯ
6. Тест знаков для двух зависимых выборок
Назначение теста. Сравнение двух зависимых выборок, содержащих резуль-
таты, выраженные в шкале не ниже порядковой.
Для каждой пары значений в обеих выборках определяется направление
сдвига второго результата по отношению к первому. Определяется число по-
зитивных (лр) и негативных (л„) сдвигов. В том случае, если оба результата
совпадают друг с другом, они исключаются из рассмотрения.
Если (пр+п„) < 25, то используется формула Бернулли, по которой рассчи-
тывается вероятность того, что в (пр+п„) случаях, в каждом из которых вероят-
ность появления события равна р =0,5, событие наступит не более г раз, где
г=тт(л,,л„):
р(х < г)=У (Пр +Пп 1о,5)<"'+4
1 J
Если (лр+л„) > 25, вычисляется значение z:
~ _ тах(Лр,ли)-0,5(Лр + ли)-0,5
О,57(л,+л„)
По таблице ^-распределения определяется вероятность, соответствующая
вычисленному значению г для односторонней критической области.
Программный синтаксис (var, — измерение «до», var2— измерение «после»):
NPAR TEST
/SIGN= var2 WITH var2 (PAIRED)
/MISSING ANALYSIS.
7. Тест Вилкоксона для двух зависимых выборок
Назначение теста. Сравнение двух зависимых выборок, содержащих резуль-
таты, выраженные в шкале не ниже порядковой.
Для каждой пары значений в обеих выборках определяется разность между
ними (из второго результата вычитается первый) и ее модуль. В том случае, если
оба результата совпадают друг с другом, они исключаются из рассмотрения.
Оставшиеся л значений ранжируются (начиная с наименьшего), и определяется
сумма рангов, соответствующая случаям положительных разностей между парами
значений (Т\) и случаям отрицательных разностей между парами значений (7г).
На основании полученных данных вычисляется значение z-
min(Ti,T2)-^M
z=—. —,
/л(п+1)(2и+1)
V 24
242
ПРИЛОЖЕНИЕ 3. ВСЕ НЕПАРАМЕТРИЧЕСКИЕ МЕТОДЫ В ОДНОМ МЕСТЕ
где min(7’1, Т2) — минимальное из двух значений 7\ и Т2',п — число пар значе-
ний после исключения из них нулевых сдвигов.
По таблице ^-распределения определяется вероятность, соответствующая
вычисленному значению z для односторонней критической области.
Программный синтаксис (vari — измерение «до», var2 — измерение «после»):
NPAR TEST
/WILCOXON= varx WITH var2 (PAIRED)
/MISSING ANALYSIS.
8. Тест Кохрана для нескольких зависимых выборок
Назначение теста. Сравнение к > 2 зависимых выборок (7V—размер каждой
из них), содержащих результаты, выраженные в дихотомической шкале.
Представим имеющиеся данные в виде таблицы размером (k*N), где к—чис-
ло зависимых выборок, N— размер каждой из них (см. рис.). В каждой из к
выборок определяется число результатов (бу), условно отнесенных к категории
«успешных» (по вертикали), и квадрат этого числа (б^>. Затем для каждого из
//членов выборки определяется число «успешных» значений (1у) при переходе
от одной выборке к другой (по горизонтали) и квадрат этого числа (Lj).
Члены выборки Выборки Число «успехов» по горизонтали Квадрат этого числа
1 2 3 k
1 0 1 0 1
2 1 1 0 0 Я
3 I 0 0 1 й
...
N 0 1 1 1 l2n
К LA /«1
Число «успехов» по вертикали Gi G2 G3 Gk к YGj 7=1 N
Квадрат этого числа б? G22 G3 G* к TV 7=1 /=!
На основании данных расчетной таблицы вычисляется значение Q:
к к
(k-l)[k±G]-(£Gj)2]
п=——___________________
* N N
<=1 i=i
243
ПРИЛОЖЕНИЯ
Полученное значение Q сравнивается с критическим значением, которое
находится в таблице критических значений для теста %2 с (к— 1) числом степе-
ней свободы.
Программный синтаксис (для случая Л зависимых выборок):
NPAR TESTS
/ COCHRAN=varx var2 var3 ... vark
/MISSING LISTWISE.
9. Тест Фридмана для нескольких зависимых выборок
Назначение теста. Сравнение к > 2 зависимых выборок (N—размер каждой
из них), содержащих результаты, выраженные в шкале не ниже порядковой.
Представим имеющиеся данные в ваде таблицы размером (k*N), где к—чис-
ло зависимых выборок, 7V— размер каждой из них (см. рис.). Каждому члену
выборки i=(1,2,3,..., N) соответствует определенное значение в каждой из к
выборок (см. на рис. пример для i=3). Для каждого члена выборки проранжи-
руем эти значения по горизонтали (начиная с наименьшего) и заменим числа
соответствующими рангами.
Члены выборки Выборки
1 2 3 ... к
1 ^12 *13 %\к
2 ^21 ^22 *23 %2k
3 ^31 ^32 *33 %3к
N *ЛЧ *V2 %N3
Сумма рангов я. я2 я3
После завершения ранжирования находится сумма рангов для каждой вы-
борки (по вертикали) и вычисляется значение х?:
IT к
При наличии связанных рангов используется скорректированная формула:
к
12^Rj)2-3N2k(k+l)2
.2 _ ;=1_______________
। х;
M№+,)+L_^
244
ПРИЛОЖЕНИЕ 3. ВСЕ НЕПАРАМЕТРИЧЕСКИЕ МЕТОДЫ В ОДНОМ МЕСТЕ
где#, — число групп связанных рангов в строке z таблицы (/= 1,2,...N), tg — раз-
мер каждой группы связанных рангов (/=1,2,к).
Полученное значение %? сравнивается с критическим значением, которое
находится в таблице критических значений для теста %2 с (&— 1 j числом степе-
ней свободы.
Программный синтаксис (для случая к зависимых выборок):
NPAR TESTS
/ FRI EDMAN=var! var2 var3 ... var*
/MISSING LISTWISE.
10. Тест %2 для двух независимых выборок
Назначение теста. Сравнение двух независимых выборок объемом п{ и п2
каждая, содержащих результаты, распределенные по г > 2 качественным кате-
гориям.
Для таблицы сопряженности размером (2хг), содержащей значения наблю-
даемых частот Од, рассчитываются значения ожидаемых (теоретических) частот
е9-
Категории Выборки
1 2
1 Он 012 С.^.+Ои)
2 021 022 С2=(О21 + О22)
3 031 032 Q = (031 + 032)
1 г ОГ1 Ол Сг-(Он+Ой)
Л1 «2 Л=Л1+л2
Ед где z = (l,2, 3,..., г);у=(1, 2).
Затем вычисляется значение х2:.
Z=l ;=1 Ьд
Для таблицы размером (2x2)
А В'
С D
#ф42)-ЛС|-^)2
(А+5)(С+Р)( Л+С)(В+D)'
245
ПРИЛОЖЕНИЯ
Полученное значение %2 сравнивается с критическим значением, которое
находится в таблице, критических значений для теста х2 с (г— 1) числом степе-
ней свободы.
Программный синтаксис:
CROSSTABS
/TABLES= varx BY var2
/FORMAT= AVALUE TABLES
/STATISTIC = CHI SQ
/CELLS= COUNT
/COUNT ROUND CELL.
Программный синтаксис для подсчета процентов по столбцам и строкам:
’ CROSSTABS
/TABLES = var! BY var2
/FORMAT= AVALUE TABLES
/STATISTIC = CHISQ
/CELLS= COUNT COLUMN
/COUNT ROUND CELL.
CROSSTABS
/TABLES= varx BY var2
/FORMAT= AVALUE TABLES
/STATISTIC = CHISQ
/CELLS= COUNT ROW
/COUNT ROUND CELL.
11. Точный тест Фишера для двух независимых выборок
Назначение теста. Сравнение двух независимых выборок объемом пх и п2
каждая, содержащих результаты, распределенные по двум качественным кате-
гориям.
На основании таблицы сопряженности размером (2x2) определяется точное
значение вероятности получения представленного в таблице распределения
результатов.
X г-х
с—х N-r-c+x
с N-c N
Точное значение вероятности равно сумме нескольких слагаемых, каждое
из которых вычисляется по следующей формуле:
246
ПРИЛОЖЕНИЕ 3. ВСЕ НЕПАРАМЕТРИЧЕСКИЕ МЕТОДЫ В ОДНОМ МЕСТЕ
j>=v —I, гдех=0,1,.... min (г, с).
(N\
Для больших выборок вычисляется значение z:
|rc(N-r)(N-c)
' №(ЛМ)
По таблице ^-распределения определяется вероятность, соответствующая
вычисленному значению г для односторонней критической области.
Программный синтаксис:
Используется тот же программный синтаксис, что в тесте %2
для двух независимых выборок.
12. Тест Манна—Уитни для двух независимых выборок
Назначение теста. Сравнение двух независимых выборок объемом л( и л2
каждая, содержащих результаты, выраженные в шкале не ниже порядковой.
Результаты обеих выборок объединяются и ранжируются (начиная с наи-
меньшего). Определяется сумма рангов для первой выборки и сумма рангов
R2 для второй выборки (л(< л2). Вычисляются значения Ux = пхп2 + - R\;
Выбирается J7=min(J71, С/2) и вычисляется значение г:
' z= 1 .
1цпг(пх+пг+У)
12
При наличии к групп связанных рангов для вычисления z используется
скорректированная формула:
п ”1«2
Z= i 2 ,.
Д цпг YN3-N у у, А
12 £'J
— t •
где #=Л1 +л2; 7} = f — -, Г,- — число связанных рангов в каждой из к групп.
По таблице ^-распределения определяется вероятность, соответствующая
вычисленному значению z для односторонней критической области.
247
ПРИЛОЖЕНИЯ
Программный синтаксис:
NPAR TESTS
/М-W = varx BY var2 (0 1)6
/MISSING ANALYSIS.
13. Тест Колмогорова—Смирнова
для двух независимых выборок
Назначение теста. Сравнение двух независимых выборок объемом п{ и п2
каждая, содержащих результаты, выраженные в шкале не ниже порядковой.
Для каждой выборки вычисляются эмпирические кумулятивные функции
распределения, которые затем сравниваются друг с другом: из каждого значения
эмпирической кумулятивной функции распределения для первой выборки
5д1(х) вычитается каждое значение эмпирической кумулятивной функции
распределения для второй выборки З^х).
По результатам сравнения-определяется показатель P=max|5'nl(x)—5и2(х)|
и вычисляется значение Z для статистики Колмогорова—Смирнова:
Z=Z)
V«l+«2
Программный синтаксис:
NPAR TESTS
/К-S = магг BY var2 (0 1)
/MISSING ANALYSIS.
14. Тест Вальда—Волфовица для двух независимых выборок
Назначение теста. Сравнение двух независимых выборок объемом л1 и п2
каждая, содержащих результаты, выраженные в шкале не ниже порядковой.
Результаты обеих выборок объединяются и упорядочиваются (начиная с
наименьшего). Определяется количество серий, состоящих из значений, при-
надлежащих каждой выборке (одиночное значение, относящееся либо к первой,
либо ко второй выборке, также считается серией).
На основании сведений о числе серий R вычисляются следующие зна-
чения:
6 Для случая двух независимых выборок (тесты Манна—Уитни, Колмогорова—Смирнова,
Вальда—Волфовица, Мозеса) в переменной var2 закодировано, к какой из двух независимых'
выборок принадлежат результаты: к первой (0) или второй (1). Если используется другая коди-
ровка выборок, например 1 и 2, необходимо внести изменение в программную запись.
248
ПРИЛОЖЕНИЕ 3. ВСЕ НЕПАРАМЕТРИЧЕСКИЕ МЕТОДЫ В ОДНОМ МЕСТЕ
P(r<R)=
(для четных г);
1 А
= 1 к ,
(»1+и2 1 к-1
L щ I
к-2 +U-2 к-1
(для нечетных г=2к-1).
Итоговое значение вероятности находится как сумма соответствующих
«четных» и «нечетных» слагаемых.
Если («! +л2) > 30, предпочтительней использовать формулу для вычисления г:
«-(^24+1'1+0,5
г = , -----
У (Я1+"2)2(Л|+^-1)
По таблице ^-распределения определяется вероятность, соответствующая
вычисленному значению г для односторонней критической области.
Программный синтаксис:
NPAR TESTS
/W-W= varx BY var2, (0 1)
/MISSING ANALYSIS.
15. Тест экстремальных реакций Мозеса для двух
независимых выборок
Назначение теста. Сравнение двух независимых выборок объемом пх и п2
каждая, содержащих результаты, выраженные в шкале не ниже порядковой.
Сравниваются размахи в обеих выборках, одна из которых рассматривается
как контрольная, а другая как экспериментальная. Проверяется предположение,
что в экспериментальной выборке распределение результатов носит более
экстремальный характер.
Вероятность такого распределения вычисляется по формуле:
2й 2улжспч>+2й+1 /
^коктр+^экспср
^контр
где «контр — размер контрольной выборки, лэкспер — размер экспериментальной
выборки; Sh — размах для контрольной выборки после отбрасывания от него
249
ПРИЛОЖЕНИЯ
слева и справа нескольких крайних значений; h — количество крайних значе-
ний, отброшенных слева и справа от размаха; g — число, показывающее на
. сколько реальное значение размаха Sh для контрольной группы больше мини-
мально возможного значения размаха для этой группы, равного (иконтр—2/г).
Программный синтаксис: '
NPAR TESTS
/MOSES = varx BY var2 (0 1)
/MISSING ANALYSIS.
16. Тест x2 для нескольких независимых выборок
Назначение теста.( Сравнение к > 2 независимых выборок объемом пь
п2, ...и* каждая, содержащих результаты, распределенные по г > 2 качественным
категориям.
Для таблицы сопряженности размером (к* г), содержащей значения наблю-
даемых частот Оу, рассчитываются значения ожидаемых (теоретических) час-
тот Ef
Еу =-^-, где i=(l, 2,..., r);j=(l, 2,..., к).
N
Категории Выборки
1 2 к
1 Он чО|2 О1к J-l
2 Оц ^22 ®2к c2=toij J-l
г Ori Ол
"1 «2
Затем вычисляется значение %2:
о* cr=io. /=1
"к 7=1 ~
г к
Еу
Полученное значение %2 сравнивается с критическим значением, которое
находится в таблице критических значений для теста х2с (к— l)(r— 1) числом,
степеней свободы.
250
ПРИЛОЖЕНИЕ 3. ВСЕ НЕПАРАМЕТРИЧЕСКИЕ МЕТОДЫ В ОДНОМ МЕСТЕ
Программный синтаксис:
Используется тот же программный синтаксис, что в тесте %2
для двух независимых выборок.
17. Тест Крускала—Уоллиса для нескольких
независимых выборок
-Назначение теста. Сравнение к > 2 независимых выборок объемом пь
пк каждая, содержащих результаты, выраженные в шкале не ниже поряд-
ковой.
Результаты всех выборок объединяются и ранжируются (начиная с наимень-
шего). Для каждой выборки определяется сумма рангов, соответствующих
содержащимся в выборке значениям (7?у). Затем вычисляется значение Н по
следующей формуле:
in к D2
н=———У-^--3(^+1),
где к — число выборок; п. — объем каждой из выборок; N—объем объединен-
к
ной выборки ( N = y^rij ); Rj — сумма рангов для каждой из выборок.
При наличии g групп связанных рангов используется скорректированная
формула:
__—_y^—3(N+l)
1——
N3-N
где 7]—/3,—/,•; // — число связанных рангов в каждой изg групп.
Полученное значение //сравнивается с.критическим значением, которое
находится в таблице критических значений для теста %2 с (к— 1) числом степе-
ней свободы.
Программный синтаксис:
NPAR TESTS
/К-W= var2 BY var2 (1 k)7
/MISSING ANALYSIS.
7 Для случая к независимых выборок (тесты Крускала—Уоллиса, Джонкхиера—Терпстра и
медианный) в переменной таг2 закодировано, к какой из к независимых выборок принадлежат
результаты. Если, например, имеется четыре независимые выборки, закодированные в перемен-
ной таг2 номерами от 1 до 4, то вместо (1 к) должна стоять запись (1 4). Если используется
другая кодировка, например от 0 до 3, то запись будет (0 3).
251
ПРИЛОЖЕНИЯ
18. Тест Джонкхиера—Терпстра
для упорядоченных альтернатив
Назначение теста. Сравнение к > 2 независимых выборок объемом ль л2, —,
пк каждая, содержащих результаты, выраженные в шкале не ниже порядковой.
Выборки упорядочены в соответствии с градациями определенного фактора.
Выборки попарно сравниваются между собой (предыдущая с последующей).
Каждое значение в предыдущей выборке сравнивается с каждым значением в
последующей выборке. Определяется, сколько значений во второй из сравни-
ваемых выборок больше каждого из значений в первой из сравниваемых вы-
борок, и находится сумма этих значений U^.
Йт
парных сравнений, и вычисляется значение
т /=1
На основании сведений о выборках и вычисляется показатель J*:
м
m
______________
г'-___________1=1-
Л^^+ЗЬХ^^+З)
>1
V 72
По таблице ^-распределения определяется вероятность, соответствующая
вычисленному значению J* для односторонней критической области.
Программный синтаксис:
NPAR TESTS
/J-T= varx BY var2 (1 Jr)
/MISSING ANALYSIS.
19. Расширенный медианный тест
для нескольких независимых выборок
Назначение теста. Сравнение к > 2 независимых выборок объемом л ь ль...,
пк каждая, содержащих результаты, выраженные в шкале не ниже, поряд-
ковой.
Результаты всех выборок объединяются, и вычисляется медиана объединен-
ных значений. Для каждой выборки определяется число значений больших
медианы и меньших медианы (или равных ей).
На основании данных таблицы вычисляется значение %2:
;=1 i=i
_ rijCt
где Ev=^-
252
ПРИЛОЖЕНИЕ 3. ВСЕ НЕПАРАМЕТРИЧЕСКИЕ МЕТОДЫ В ОДНОМ МЕСТЕ
Категории Выборки
1 2 ... k
Больше медианы Он 012 0\к С,
Меньше медианы о» О-п 0-2к с2
«2 пк N
Полученйый результат сравнивается с критическим значением, которое
находится в таблице критических значений для теста %2 с {к— 1) числом степе-
ней свободы.
Программный синтаксис:
NPAR.TESTS
/MEDIAN = varx BY var2 (1 k) •
/MISSING ANALYSIS.
Приложение 4
В ЖИЗНИ ВСЕГДА ЕСТЬ МЕСТО СТАТИСТИКЕ
(Вместо домашнего задания)
Для закрепления содержащего в книге материала читателю предлагается
попробовать самостоятельно поупражняться в использовании непараметриче-
ских методов статистики на основе приведенных ниже заданий.
1. У меня зазвонил телефон...
Выберите наугад из своих записных книжек 15—20 номеров телефонов сво-
их друзей и знакомых. Сколько среди них принадлежат представителям про-
тивоположного пола? С помощью биномиального теста определите, носит ли
полученный результат случайный характер.
2. «Из всех искусств д ля нас важнейшим является кино!»
Составьте список кинофильмов, которые вы посмотрели за последние годы
(30—40 наименований), и разбейте их 4—5 категорий в соответствии с жанром
(например, боевики, комедии, фантастика и др.). Определите, сколько фильмов
попадает в каждую категорию и отличается ли полученный результат от равно-
мерного распределения.
3. Мои года — мое богатство...
Составьте список из 15—20 близких вам людей и разбейте его на на четыре
категории в соответствии с их возрастом: «младше меня», «ровесники», «стар-
ше меня», «гораздо старше меня». Определите, сколько человек попало в ту или
иную категории. С помощь теста Колмогорова—Смирнова определите, отли-
чается ли полученное вами распределение от равномерного.
4. Существуют ли договорные матчи?
Составьте список из результатов 20—30 последних игр вашей любимой спор-
тивной команды. Отметьте в списке только победы и поражения, исключите
ничейные результаты. Проанализируйте полученное чередование побед и по-
ражений и с помощью теста последовательностей определите, носит оно слу-
чайный характер или в нем можно выявить какие-либо закономерности.
254
ПРИЛОЖЕНИЕ 4. В ЖИЗНИ ВСЕГДА ЕСТЬ МЕСТО СТАТИСТИКЕ
5. От сессии до сессии живут студенты весело...
Если вы студент (студентка), то накануне сессии опросите 30—35 своих од-
нокурсников. Попросите их выбрать один из двух символов, или наи-
лучшим образом отражающий их состояние на данный момент. Проделайте то
же самое с этими же людьми после сессии и с помощью теста МакНемара
-сравните результаты «до» и «после».
6. «Жить $тало лучше, жить стало веселее!»
. Опросите труппу из 15—20 человек и узнайте, как они оценивают изменения
в своей жизни за последний год. Носят ли эти изменения позитивный, нега-
тивный или,-нейтральный характер? С помощью теста знаков определите на-
правление типичного сдвига показателей и проверьте, носит ли этот сдвиг
случайный или неслучайный характер.
7. Пустое брюхо к науке глухо
Опросите 15—20 своих друзей и знакомых из числа студентов, получающих
стипендию. Узнайте, сколько они тратят в день на питание накануне получения
стипендии и через несколько дней после ее получения. С помощью теста
Вилкоксона проверьте, оказывает ли стипендия существенное влияние на
студенческий бюджет.
8. Кто больший патриот?
Обойдите свое жилище и отметьте, сколько вещей из числа тех, которые вас
окружают, отечественного производства, а сколько являются импортными.
Включите в список 7—10 предметов (мебель, холодильник, телевизор, одежду
и др.). Попросите сделать то же самое своего друга (подругу) и с помощью
точного теста Фишера сравните оба результата.
9. Вот такое кино...
Вернитесь ко второму заданию и разбейте список из 30-40 кинофильмов не
только на 3—4 категории по жанрам, но также на две группы: «отечествен-
ный» — «зарубежный». С помощью теста %2 определите, есть ли различия ме-
жду двумя группами фильмов.
10. Краткость — сестра таланта?
Найдите в Интернете сведения о длительности 15—20 отечественных и 15—
20 зарубежных фильмов, вышедших за последнее время. Сравните полученные
результаты с помощью теста Манна—Уитни.
11. Капля никотина убивает лошадь
Сформируйте из своих друзей и знакомых группу курящих мужчин и группу
курящих женщин по 10—15 человек в каждой. Узнайте возраст начала курения
у представителей каждой из групп и с помощью теста Колмогорова—Смирнова
для двух независимых выборок сравните результаты. Можно ли утверждать, что
мужчины и женщины начинают курить в одинаковом возрасте?
255
ПРИЛОЖЕНИЯ
12. «Что-то физики в почете. Что-то лирики в загоне»
В Википедии есть страница, посвященная нобелевским лауреатам. Про-
анализируйте с помощью теста Вальда—Волфовица сведения о возрасте
лауреатов Нобелевской премии по физике и литературе за последние 20 лет.
Можно ли утверждать, что лауреаты-«физики» моложе лауреатов-«ли-
риков»?
13. Автомобиль не роскошь, а средство передвижения
Выберите 7—8 моделей автомобилей отечественного производства и срав-
ните их цены с ценами 7—8 моделей импортных автомобилей аналогичного
класса. Используйте тест экстремальных реакций Мозеса для сравнения раз-
маха цен на отечественные и импортные автомобили.
14. Понедельник — день тяжелый...
Сформируйте группу из 7—8 близких вам людей (например, родители, дру-
зья, братья и сестры). Попросите каждого из них в течение недели подводить
итог каждого прошедшего дня по принципу «удачный день» — «неудачный
день». Проанализируйте полученные результаты с помощью теста Кохрана.
Можно ли утверждать, что между разными днями недели существуют различия
с точки зрения их «удачности» и «неудачности»?
15. Понедельник — день тяжелый... (продолжение)
Через некоторое время попросите участников предыдущего опроса на про-
тяжении недели давать оценку (по 100-балльной шкале) каждому прожитому
дню. Проанализируйте полученные результаты с помощью теста Фридмана.
Можно ли утверждать, что различия в оценках разных дней недели носят не-
случайный характер?
16. Снова о физиках и лириках
Вернитесь к заданию 11. С помощью теста Крускала—Уоллиса сравните
между собой возраст нобелевских лауреатов последних лет по физике, химии,
физиологии (медицине) и литературе. Включите в каждую категорию по 7—
8 имен.
17. Друзья приходят или уходят?
Вам знаком сайт «Одноклассники»? Тогда вперед!
Задайтесь четырьмя возрастными категориями по возрастанию (например,
до 25 лет, 26—35 лет, 36—45 лет, старше 46 лет). Для каждой возрастной катего-
рии с помощью сайта «Одноклассники» случайным образом отберите'по 5—6
человек. Зайдите к каждому из них «в гости» и определите, сколько человек
входит в круг его друзей. С помощью теста Джонкхиера—Терпстра проанали-
зируйте полученные данные (число друзей для каждой выборки и соответст-
вующей возрастной категории). Можно ли говорить о существовании здесь
тенденции, связанной с изменением числа друзей с возрастом?
256
ПРИЛОЖЕНИЕ 4. В ЖИЗНИ ВСЕГДА ЕСТЬ МЕСТО СТАТИСТИКЕ
18. Храните деньги в той валюте, в которой вы их тратите
На протяжении последних 15—20 дней фиксируйте колебания курса каких-
либо двух зарубежных валют (например, доллара и евро). С помощью коэффи-
циента ранговой корреляции Спирмена определите, как колебания курса этих
валют связаны друг с другом. Проверьте полученный результат на значи-
мость.
19. Что сегодня по «ящику»?
Составьте список из 10—15 популярных телевизионных передач или сериа-
лов, которые вам знакомы. Проранжируйте список по степени привлекатель-
ности для вас включенных в него передач. Попросите сделать то же самое ва-
шего друга (подругу). С помощью коэффициента ранговой корреляции Кендалла
определите, насколько ваши мнения совпадают. Можно ли утверждать, что
полученный результат неслучаен?
20. В тиши музейных коридоров
В пятерку крупнейших музеев мира входят парижский Лувр, нью-йоркский
Метрополитен-музей, лондонская Национальная галерея, музей Прадо в
Мадриде и петербургский Эрмитаж. Если бы у вас была возможность побывать
в каждом из них, каким был бы порядок ваших предпочтений? Спросите об
этом еще у 6—7 человек и затем с помощью коэффициента конкордации Кендалла
определите, насколько совпадают ваши мнения. Проверьте полученный ре-
зультат на значимость.
БИБЛИОГРАФИЯ1
1. Берка К. Измерение: понятия, теории, проблемы. М.: Прогресс, 1987. 320 с.
2. Москаленко В. Д. Зависимость: семейная болезнь. М.: ПЕРСЭ, 2004. 336 с.
3. Наследов А. Д. Математические методы психологического исследования. Анализ и
интерпретация данных. СПб.: Речь, 2006. 392 с.
4. Сидоренко Е. В. Методы математической обработки в психологии. СПб.: Речь, 2000.
350 с.
5. AckoffR. L. The art of problem solving accompanied by AckofFs fable. New York: Wiley &
Sons, 1978.214 р.
6. Conover W. J. Practical nonparametric statistics. New York: Wiley&Sons, 1999. 584 p.
7. Fischer J. L., Spann L., Crawford D. Measuring codependency. Alcoholism Treatment
Quarterly. 1991. 8. P. 87-100.
8. Guilford J. R, Fruchter B. Fundamental statistics in psychology and education. 6th ed. New
York: McGraw-Hill, 1977. 545 p.
9. Glass G. V., Stanley J. C. Statistical Methods in Education and Psychology, Englewood
Cliffs: Prentice-Hall, 1970. 596 p.
10. Hollander M., WolfD. A. Nonparametric Statistical Methods. New York: Wiley & Sons,
1973.503 р.
11. Isralowitz R., Reznik A., Spear S., Brecht M., Rawson R. Severity of Heroin Use in Israel:
Comparisons between Native Israelis and Former Soviet Union Immigrants. Addiction,
2007. Vol. 102(4). P. 630-637.
12. Lehmann E. L., D’Abrera H. J. Nonparamertics statistical methods based on ranks. New
York: McGraw-Hill, 1975.457 p.
13. Rabin R., de Charro F. EQ-5D: a measure of health status from the EuroQol Group. Annals
. of medicine, 2001. Vol. 33(5). P. 337-343.
14. Runyon R. R Nonparametric statistics: a contemporary approach. Reading, Mass.: Addison-
Wesley Pub. Co, 1977.128 p.
15. Sheskin D. J. Handbook of parametric and nonparametric statistical procedures 3d ed.
Boca Raton: Chapman & Hall/CRC, 2004.1193 p.
16. Siegel S. Nonparametric Statistics for the Behavioral Sciences. New York: McGraw-Hill,
1956.312 р.
17. Siegel S., Castellan N. J. Jr. Nonparametric Statistics for the Behavioral Sciences. 2d ed.
New York: McGraw-Hill, 1988. 399 p.
1 Книги некоторых авторов, включенных в список, в свое время были изданы на русском
языке (Акофф, Гласс и Стэнли и др.). В связи с тем, что при работе над книгой использовались
англоязычные издания этих авторов, они помещены в английскую часть списка.
258
БИБЛИОГРАФИЯ
18. SPSS Statistical Algorithms. Chicago: SPSS Inc., 1986.225 p.
19. Handbook of Experimental Psychology / Ed. S. S. Stevens. New Yoric: Wiley & Sons, 1951.
1436 р.
20. USA Today, 22.10.2007. Available at http://www.usatoday.eom/news/health/2007-10-22-
marriage-weight_N.htm
УКАЗАТЕЛИ
Предметный указатель
А
альтернативная гипотеза 39,40,44,45
Б
биномиальный тест 56,69, 70,75,92,
101,228,240
В
вероятность ошибки второго рода 46
вероятность ошибки первого рода 42,
46,49,51
Ветхий Завет 38
взаимодействие факторов 35
внутригрупповая дисперсия 34,35
выборка 29, 37,40,45
— зависимая 38,39
— независимая 38, 39
Г
гистограмма 17,23,24,160,161
д
двухфакторный дисперсионный
анализ 115,225
— Фридмана д ля рангов 225
диаграмма рассеяния 26,27,31,32
— для негомогенной выборки 29,30
дисперсионный анализ 32, 33,35
дисперсия 11,14,15,186
Е
единичное нормальное распределение 21
3
зависимая переменная 33, 34
И
измерение 57
измерительная шкала 57, 58
К
календарное летоисчисление 66
— иудейское 66
— мусульманское 66
— христианское 66
контрольная группа 161,162,249
корреляционный анализ 26
корреляция 25,198
корреляция и причинность 27,28
коэффициент конкордации
Кендалла 56,216—220,222,257
коэффициент корреляции 26,198
коэффициент корреляции
Пирсона 26,67,203,205,223
коэффициент ранговой корреляции
Кендалла 56,207,208,210,212,213,
215, 216, 222, 237, 257
коэффициент ранговой корреляции
Спирмена 56,198-208,210,236,257
260
УКАЗАТЕЛИ
кривая Гаусса 19
критическая область 49,50,52
— двусторонняя 50,71,73,89
— односторонняя 50,51,71—73
— левосторонняя 50
— правосторонняя 50
М
медиана 11,18,20,61,194,195
медианный тест д ля нескольких
независимых выборок 55,193,197,
252
межгрупповая дисперсия 35
меры изменчивости 11,13—15
меры центральной тенденции 11,13,
20,61
„метадон 169
мода И, 18,20,61
модуль «Exact Tests» для программы
SPSS 192
Н
независимая переменная 33
нелинейная корреляционная связь 29
непараметрическая статистика 53, 55,
154
непараметрические методы статисти-
ки 49,54,55,61,64,69,120
нобелевская премия по экономике 224
нормальное распределение 19—22,53
нулевая гипотеза 39,40,44,45,46
нулевой сдвиг 98,100
О
общегрупповая дисперсия 34,35
однофакторный дисперсионный
анализ 34—36
— для рангов 176,223, 224
опросник качества жизни EQ-5D 104
относительная частота 19,82,147, 148
отношение шансов 126,130
ошибка второго рода 41,42,45,46
ошибка первого рода 41,42,45,46
П
параметрическая статистика 54, 55,
160,205
полигон 17,18
поправка на непрерывность для теста
МакНемара 94
поправка на непрерывность для теста
X2 125,126
популяция 37,40,45
правосторонняя критическая об-
ласть 50
премия по экономике памяти А.
Нобеля 224
проверка статистических гипотез 37,
38,44,45,47
программный синтаксис для SPSS 238
психометрический экзамен (психомет-
рия) 142,176
Р
равномерное распределение 76, 81,
239
размах 161,162,163,165,167,249,250
ранжирование 61—64,105,106,139,
200,2002, 208,209,211
регрессионный анализ 30
регрессия 25,30
репрезентативность выборки 37
С
связанные ранги 62,63,65,120—122,
141,143,144,146, 162, 178,179,183,
190, 202-205, 207, 211, 212, 216, 218
созависимость 183, 185, 187
среднее 11-13,18,20,23,61,186
стандартное отклонение 11,15,23
статистическая гипотеза 39
Т
таблица сопряженности 60,170
температурная шкала 66
— Кельвина 68
— Реомюра 65
261
КНИГА ДЛЯ ТЕХ. КТО НЕ ЛЮБИТ СТАТИСТИКУ. НО ВЫНУЖДЕН ЕЮ ПОЛЬЗОВАТЬСЯ
— термодинамическая 68
— Фаренгейта 66,67
— Цельсия 66,67
теоретическая кумулятивная функция
распределения 84, 239
тест Крускала—Уоллиса 55, 176, 178,
179, 181-184, 193, 194, 223, 224, 251,
256
тест Вальда—Волфовица 56, 153, 155,
158, 159,221,248,256
тест Вилкоксона 56,103,104, 106—109,
115, 116, 138,221,230,242, 255
тест Вилкоксона—Манна—Уитни 223,
224
тестДжонкира 184
тестДжонкира—Терпстра 184
тест Джонкхиера—Терпстра 56, 183—
186,190-194,222,224,252,256
тест знаков 56,97—99,102,103,104,
242,255
тест Колмогорова—Смирнова 69, 147,
222, 223, 229, 233, 234, 254
— для двух независимых выбо-
рок 56,147,148,151,152,248,255
— для единственной выборки 56,
80-86,88,239
тест Колмогорова 81
тест Кохрана 56, ПО, 111,112,114,
115,222,243, 256
тест Крускала—Уоллиса 56, 176, 178,
179,181-184, 193,194, 223, 224, 251,
256
тест МакНемара 56,91,92,94,96,111,
112,223,241,255
тест Манна—Уитни 56, 138, 140, 141,
145, 146, 154, 176, 177, 185, 186, 189,
223, 224, 232, 247, 255
тест последовательностей 56, 87-90,
155,231,239,254
тест Сигеля—Тьюки 223
тест Смирнова 81
тест Стьюдента 39,55,97,104, 138
тест Фридмана 56, 115,116,119—122,
225, 244, 256
тестх2 60,123,124, 169, 223
— для двух независимых выбо-
рок 56, 129,130,131, 245
— для единственной выборки 56,
76,79,80,237
— для нескольких независимых вы-
борок 56, 174, 175,250
— наблюдаемые частоты 77,124,
238, 245, 250
— ожидаемые частоты 77,78, 124,
171, 238, 245, 250
тест экстремальных реакций Мозеса 56,
159,161-163,165-168,223,249,256
типичное направление сдвига 98,99
тип шкалы 57,58
Тора_38
точный тест Фишера 56,131,132,134,
135,137, 224, 235, 246, 255
У
уровень значимости 43,46,47,49,50,52
Ф
Фишера F тест 160
формула Бернулли 70,71,73,92-94,
101,240,241,242
X
Хиджра 66
Ч
число степеней свободы 51
Ш
шкала Бофорта для силы ветра 60
шкала интервалов 58,65,66,198
шкала наименований 58, 59,198
шкала отношений 54,58,67
шкала порядка 58,60,62,198
шкала твердости минералов Мооса 60
Э
экспериментальная группа 161,249
эмпатия 159,162,163
эмпирическая кумулятивная функция
распределения 83,147,239,248
262
УКАЗАТЕЛИ
А ANOVA 33,34 R RADAR, исследовательский центр 8,
D Degrees of freedom (40 51 10,19,127,147,169 T
M MANOVA 33, 34 Two-way ANOVA by ranks 115 Z
О OddsRatio (OR) 126,130 One-Way ANOVA 35 One-way ANOVA by ranks 176 ^-распределение 8, 22, 23, 73, 74, 101, 108,136, 141, 144, 155, 157, 187, 189, 213, 226, 240, 241, 242, 243, 247, 249, 252 z-шкала 21,22
Именной указатель
А
Аарон 37
Амелсар 153
Б
Байрон Дж. 25
Берка К. 57
БернуллиЯ. 70,71,73,92-94,101,240-
242
Бофорт Ф. 60
Брэдбери Р. 65
В
Вальд А. 55,153, 154,155,158, 159,
221,248,256
Вилкоксон Ф. 55,103-109,115,116,138,
221,223,230,242, 255
Волфовиц Я. 55,153,154, 155,158,159,
221,248,256
Г
Гальтон Ф. 30, 199,222
Гаусс К. 19
ГоссетВ. 39
Гулливер 67
д
Даниил, пророк 153
Джонкхиер Э. 55,183—186, 190—194,
222,224, 251,252,256
ДикФ. 159
И
Иуда 37
К
Кендалл М. 55,207-213,215-220,222,
237,257
Колмогоров А. Н. 55,80,81,82,88,147,
148, 151, 152, 222, 223, 234, 239, 248,
254,255
Кохран В. 55, ПО, 111, 112,243,222,256
Крускал В. 55, 176, 178, 179,181-184,
193,223,224,251,256
М
МакНемара К., 55,91,92,94,111,112,
125,223, 241, 255
Манассия 37
Манн Г. 55,56,138,140, 141,145, 146,
154,176,177,185, 186,189,223,224,
232, 247, 248, 255
263
КНИГА ДЛЯ ТЕХ. КТО НЕ ЛЮБИТ СТАТИСТИКУ, НО ВЫНУЖДЕН ЕЮ ПОЛЬЗОВАТЬСЯ
Мозес Л. 55,159-163, 165-168, 223,
248,249,256
Моисей 37
Монро М. 123
Моос Ф. 60,61
Москаленко В. Д. 183
Мухаммад, пророк 66
Н
Навуходоносор, царь 153
НаследовА.Д. 120
Никсон Р. 224
Нобель А. 224
Ной 38
О
Омар I, халиф 66
П
Пирсон К. 26, 203, 205, 210, 223
Р
Рейган Р. 224
Реомюр Р. 65,66
С
Сигель С. 223
Сидоренко Е. В. 139
Смирнов В. И. 55,80,81,82,88,147,148,
151, 152, 222, 223, 234, 239, 248, 254,
255
Спирмен Ч. 55,198-208,210,224, 236,
257
Стивенс С. 57
Т
Терпстра Т. 55,183-186,190-194,
222,224, 251, 252, 256
Томсон У. (лорд Кельвин) 68
У
Уитни Р. 55, 56, 138, 140, 141, 145, 146,
154, 176, 177, 185, 186, 189, 223, 224,
232, 247, 248, 255
Уоллис В. 55, 176, 178, 179, 181-184,
193, 194, 223, 224, 251, 256
Ф
Фаренгейт Г. 65—67
Фишер Р. 56,131,132,134,135,137,160,
224, 235, 246, 255
Форд Дж. 224
ФордХ. 159
Фридман М. 55,115,116,119,120-122,
224, 244, 256
X
Христос 66
ц
Цельсий А. 65—67
Э
Эйзенхауэр Д. 224
А
AckoffR. L. 28
С
Castellan N. J. 55
Charro de Е 104
ConoverW. J. 55,81
F
Fisher J. L. 183
FruchterB. 198,205
G
Glass G.V. 198
Guilford J. P. 198,205
I
Isralowitz R. 127,169
R
Rabin R. 104
Runyon R. P. 112,156
S
Sheskin D. J. 83,88
Siegel S. 55,134, 156,163,193,218
Stanley J. C. 198
264
Доктор (PhD) Александр Резник работает
на отделении социальной работы Универ-
ситета Бен Гурион в Негеве (Израиль).
Область его научных интересов: сравни-
тельная аддиктология, психология меж-
культурных различий, социальная работа
с наркозависимыми в мультикультурной
среде, а также методология эксперименталь-
ных исследований в социальных науках.
Имеет более 50 научных публикаций в
России, США, Израиле и др.
Многолетний опыт научной и преподавательской деятельно-
сти А. Резника в России и Израиле включает в себя препо-
давание таких курсов, как «Математико-статистические мето-
ды в психологии», «Теория и практика психологического экс-
перимента», «Теоретические основы психологического тестиро-
вания» и др.
В настоящее время сочетает научно-исследовательскую
деятельность с консультационной в области статистики, ме-
тодов исследований и использования программы SPSS в ад-
диктологии и социальной работе.
Методы непараметрической статистики позволяют получать
обоснованные статистические выводы при наличии крайне
небольшого числа испытуемых. Кроме того, простота процесса
математической обработки результатов — в ряде случаев
необходимые вычисления можно сделать в уме.