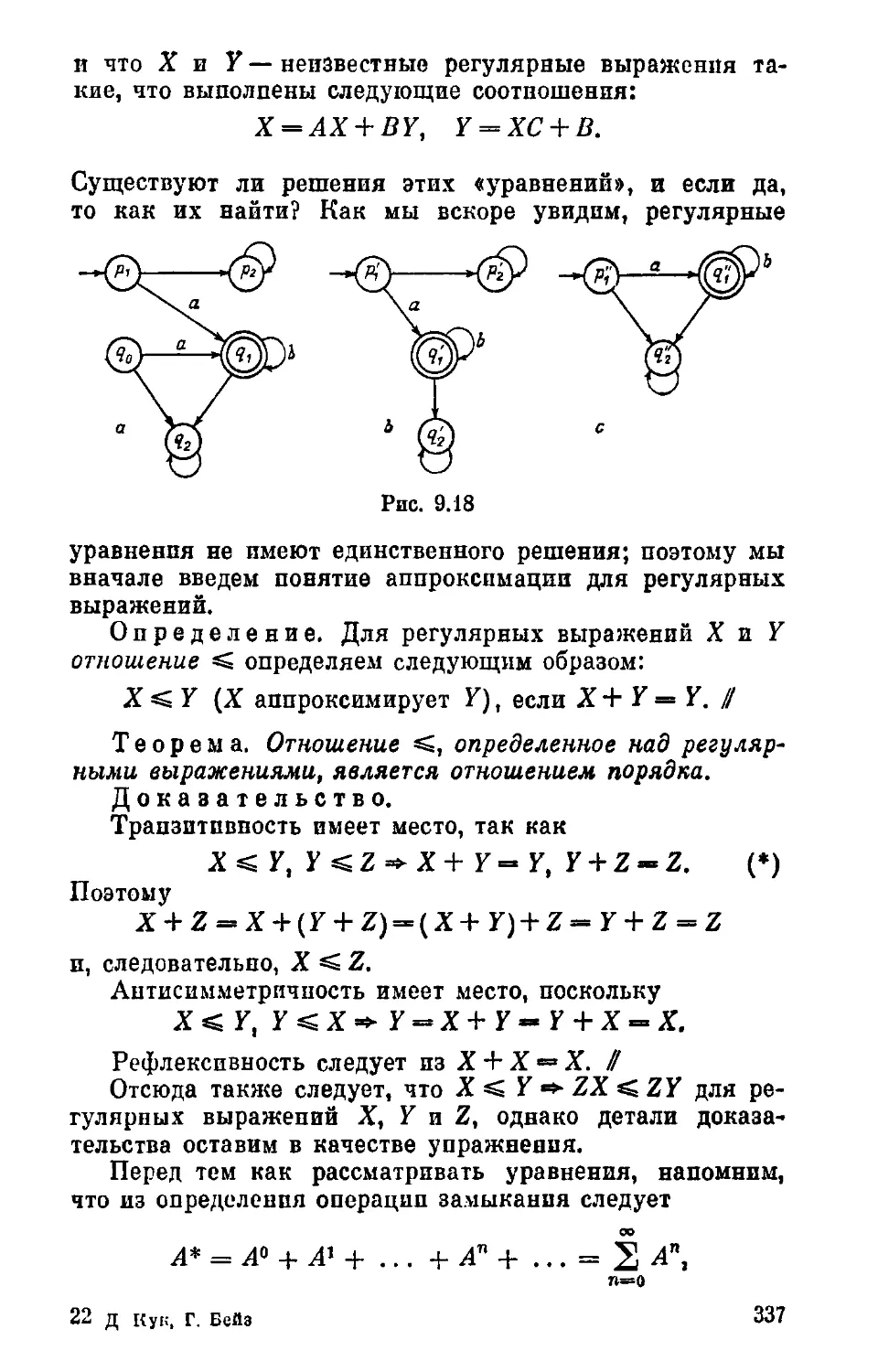
Теги: вычислительная математика численный анализ математика компьютерная математика
ISBN: 5-02-014216-6
Год: 1990
Текст
компьютерная;
математика
д.кж, rixfti
Д. КУК, Г. БЕПЗ
КОМПЬЮТЕРНАЯ
МАТЕМАТИКА
Перевод с английского Г. М. КОБЕЛЬКОВА
МОСКВА «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
1990
ББК 22.18
К89
УДК 519.6
COMPUTER
MATHEMATICS
D. J. ШОКЕ AND H. E. BEZ
Cambridge University Press
Cambridge
LONDON • NEW YORK • NEW ROCHELLE ¦
• MELBOURNE•SYDNEY
Кук Д., Бсйз Г. Компьютерная математика: Пер. с англ.—
М.: Наука, Гл. ред. физ.-мат. лит., 1990.— 384 с.—
ISBN 5-02-014216-6.
На основе фундаментальных понятий математики, введенных
в начале, математически строго описывается ряд проблем и да-
дается их решение. Изложение, где это возможно, носит строгий
математический характер. Доказательства утверждений проводят-
проводятся па конструктивном уровне. Дается большое количество при-
примеров и упражнений, результаты которых, как правило, исполь-
вуются в дальпойшем.
Для студентов, аспирантов и научпых работников, занимаю-
занимающихся вопросами компьютерной математики и ее приложениями.
Табл. 28. Ил. 164.
1602110000-056
К 053@2)-90 20ЭО
ISBN 5-02-014316-6
Cambridge University
Press, 1984
I «Наука». Физматлит,
перевод на русский язык, 1990
ОГЛАВЛЕНИЕ
Предисловие 5
Введение 7
Глава 1. Множества Ю
§ 1. Множества и их спецификация 10
§ 2. Простейшие операции над множествами ... 15
§ 3. Диаграммы Венна 22
§ 4. Подмножества и доказательства 24
§ 5. Произведения множеств 33
Глава 2. Отношения 35
§ 1. Основные понятия 36
§ 2. Графические представления 40
§ 3. Свойства отношений 43
§ 4. Разбиения и отношения эквивалентности ... 46
§ 5. Отношения порядка 50
§ 6. Отношения на базах данных и структурах данных 53
§ 7. Составные отношения 62
§ 8. Замыкание отношепий 64
Глава 3. Функции 68
§ 1. Функции и отображения 68
§ 2. Обратные функции и отображения 72
§ 3. Мощность множеств п счетность 73
§ 4. Некоторые специальные классы функций ... 83
§ 5. Аналитические свойства вещественных функций . 91
§ 6. Операции . , , 105
Глава 4. Основные понятия арифметики 114
§ 1. «Малая» конечная арифметика 141
§ 2. «Большая» конечная арифметика 119
§ 3. Двоичная арифметика , 123
§ 4. Логическая арифметика 125
Глава 5. Алгебраические структуры 134
§ 1. Алгебраические структуры и подструктуры . . . 137
§ 2. Простейшие операционные структуры .... 139
§ 3. Кольца и поля 140
§ 4. Линейная алгебра 154
§ 5. Решетки и булевы алгебры 172
§ 6. Замкнутые полукольца 192
1* 3
Глава 6. Матрицы . . ¦ ........ 195
§ 1. Матрицы и бинарные отношения на конечных мно-
' жествах 195
§ 2. Матрицы над другими алгебраическими структура-
структурами ,202
§ 3. Матрицы и векторные пространства
206
Глава 7. Теория графов 217
§ 1. Вводные понятия , *М<
§ 2. Маршруты, циклы в связность 224
§ 3. Пленарные графы 228
§ 4. Структуры данных для представления графа . , 234
§ 5. Обход графа 238
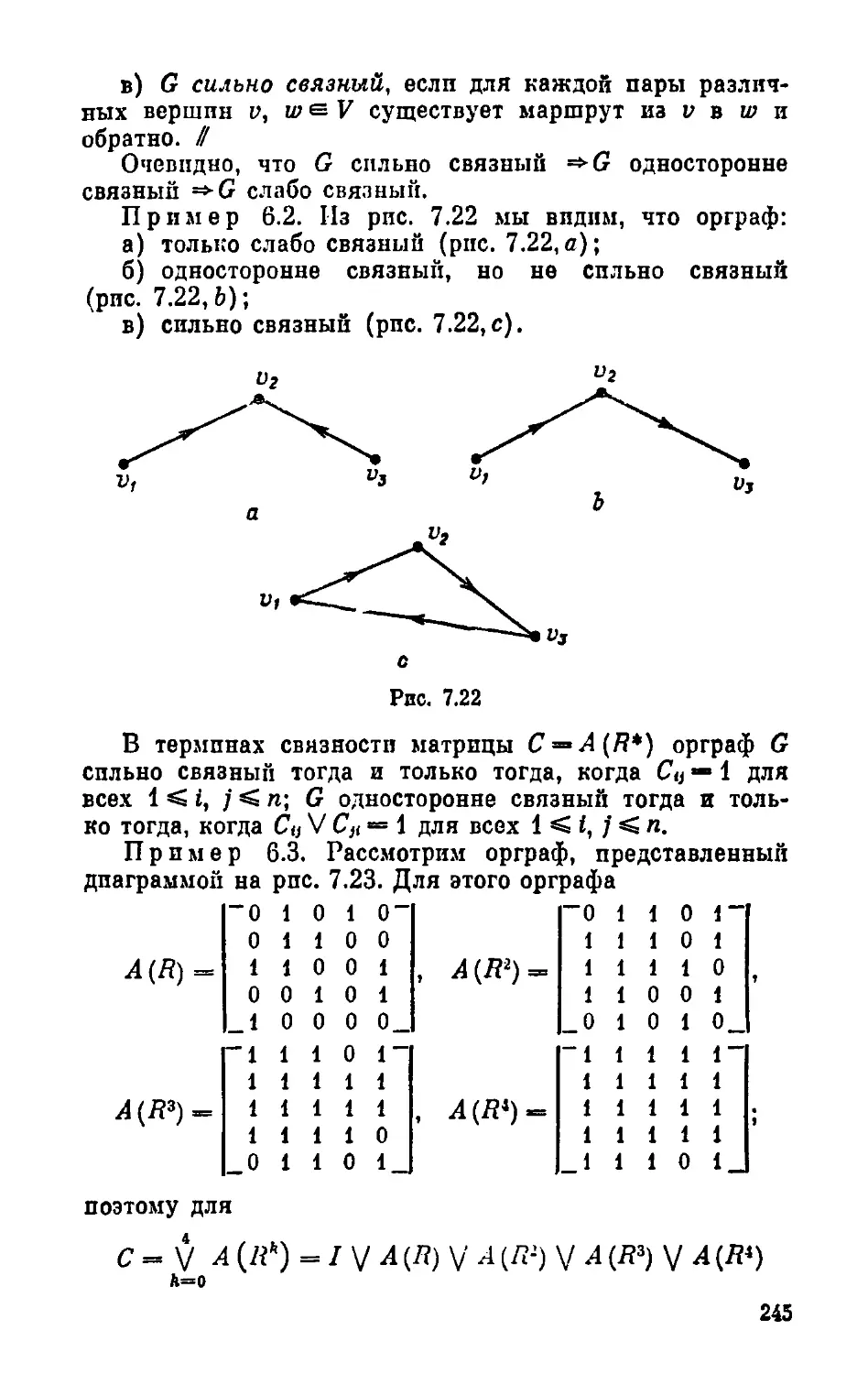
§ 6. Ориентированные графы ...,.,.. 242
Глава 8. Языки в грамматики , , 257
§ 1. Основные понятия 257
§ 2. Грамматики с фразовой структурой ..... 264
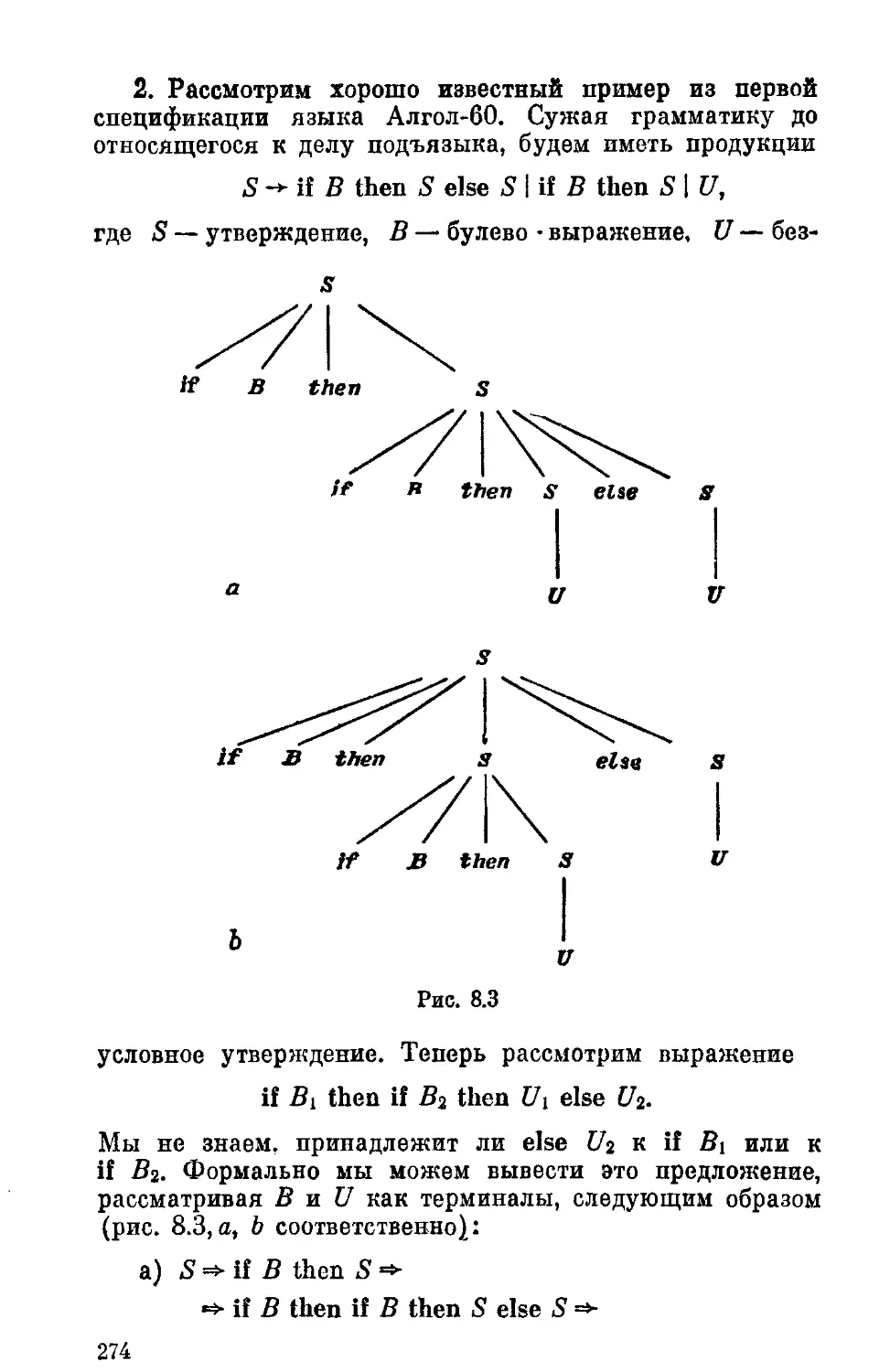
§ 3. Контекстно-свободные языки 276
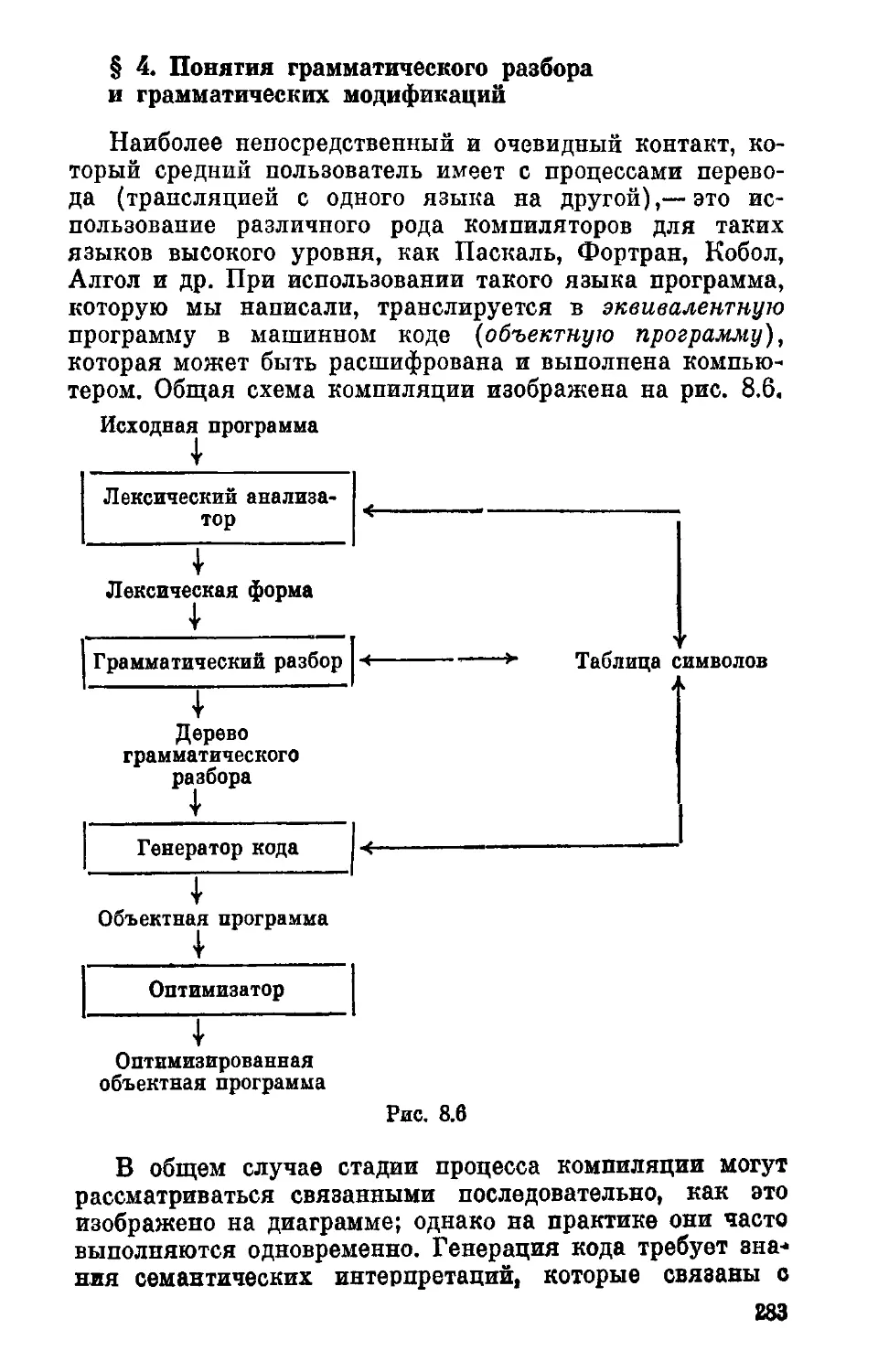
§ 4. Понятия грамматического разбора и грамматиче-
грамматических модификаций 283
§ 5. Грамматики операторного предшествования . , 298
Глава 9. Конечные автоматы . , .,.,,, 302
§ 1. Общие понятия .302
§ 2. Конечные автоматы 320
§ 3. Регулярная алгебра 335
Глава 10. Компьютерная геометрия 344
§ 1. Системы координат для подмножеств R3 . . , 345
§ 2. Преобразования . , , , 350
§ 3. Кривые и поверхности 370
Предметный указатель ...... 383
ПРЕДИСЛОВИЕ
Вычисления являются точной наукой, и си-
систематическое изучение всех аспектов, включая
такпо различные области, как разработка баз
данных, проверка систем и создание матема-
математического обеспечения, с необходимостью вы-
вызывает использование математических моделей.
С этой точки зрения многие учебные програм-
программы по вычислениям в университетах и инсти-
институтах содержат специальные курсы, знакомя-
знакомящие студентов с соответствующими математи-
математическими структурами и методами. Содержание
этой книги является таким курсом и занимает
примерно 100 лекционных часов; курс читался
студентам факультета компьютерных наук
Технологического университета в Лафбаро. Ма-
Материал книги соответствует первым двум го-
годам обучения. Лекции первого года посещают
все студенты. Курс лекций второго года явля-
является необязательным; он обеспечивает основу
для курсов, читающихся на последнем году
обучения. Содержание книги совершенствова-
совершенствовалось в течение ряда лет. В течение этого вре-
времени мы ощущали помощь многих из окружа-
окружающих нас людей, включая многочисленных
коллег (как в Лафбаро, так и в других ме-
местах) и студентов, которые помогали при
5
подготовке п проверке материала. Мы особенно
хотим поблагодарить наших жеп — Крис и Кэ-
рис — за постоянную поддержку и понимание в
течение всего процесса написания книги. Осо-
Особо благодарим Крис Кук за многочисленные
часы, которые она провела, помогая нам в со-
создании проекта рукописи, Орнеллу Ларднер за
аккуратно напечатанный окончательный вари-
вариант и Алана Бенсона, который прочитал всю
работу и сделал много конструктивных предло-
предложений. Ответственность за все оставшиеся
ошибки и неточности принадлежит исключи-
исключительно нам.
Д. Кук, Г. Вейз
Лафбаро, 1982
ВВЕДЕНИЕ
Книга в основном представляет собой курс лекций по
компьютерной математике для университетов и инсти-
институтов; однако она также может быть полезной для спе-
специалистов, работающих в этой области и желающих по-
получить более глубокие знания предмета.
Книга содержит материал из тех областей современ-
современной математики, которые имеют отношения к вычисле-
вычислениям, и, как следствие, обеспечивает читателя средством
для сжатого и точного описания многих проблем компью-
компьютерной науки. Несмотря на нашу приверженность изла-
излагать материал, непосредственно относящийся к компью-
компьютерной науке, в книге сделана попытка дать его разумное
и строгое представление, приемлемое с математической
точки зрения. Изложение по возможности носит конструк-
конструктивный характер. Везде, где возможно, в каждой новой
теме используются понятия и термины из предыдущих
тем; материал сопровождается многочисленными упраж-
упражнениями и примерами. Следует подчеркнуть, что разбор
примеров и решение упражнений являются составной ча-
частью изучения предлагаемого материала.
Преследуя эту цель, мы должны с чего-то начать. На-
Нашим исходным неопределяемым понятием является по-
понятие множества, описываемое перечислением свойств,
которыми оно обладает. Исходя из этого, можно опреде-
определить все последующие понятия конструктивным и мате-
математически приемлемым образом. Такой подход необходим,
поскольку любую ошибку легко можно проследить, вер-
вернувшись назад к неправильному предложению где-то в
цепочке рассуждений. Это также означает, что часть или
же вся рассматриваемая теория может быть запрограм-
запрограммирована.
Множества обсуждаются в гл. 1 и используются да-
далее во всей книге. Главы 2, 3 и 5—7 образуют основу
7
строгого обсуждения многих разделов компьютерной ма-
математики; материал этих глав выбран таким образом, что-
чтобы его можно было широко использовать. В гл. 4 описы-
описывается математическая модель арифметической системы,
используемой в цифровых компьютерах при работе с це-
целыми числами. Главы 8—10 связывают математическую
теорию из предыдущих глав с разделами компьютерной
математики. В частности, эдесь выделены такие области,
как теория языков, теория автоматов и компьютерная
геометрия. Эти темы отражают одновременно и интере-
интересы авторов, и их желание изложить важные разделы
современной математики, представляющие общий инте-
интерес, а не только прикладной. Другие области, где может
применяться излагаемый в книге материал, включают в
себя базы данных, сети, программную проверку и чис-
численный анализ. Главы 8—10 являются исходными для
дальнейшего изучения таких тем, как компиляция, си-
системы моделирования, теория вычислений, компьютерная
графика, вычислительная геометрия и автоматическое
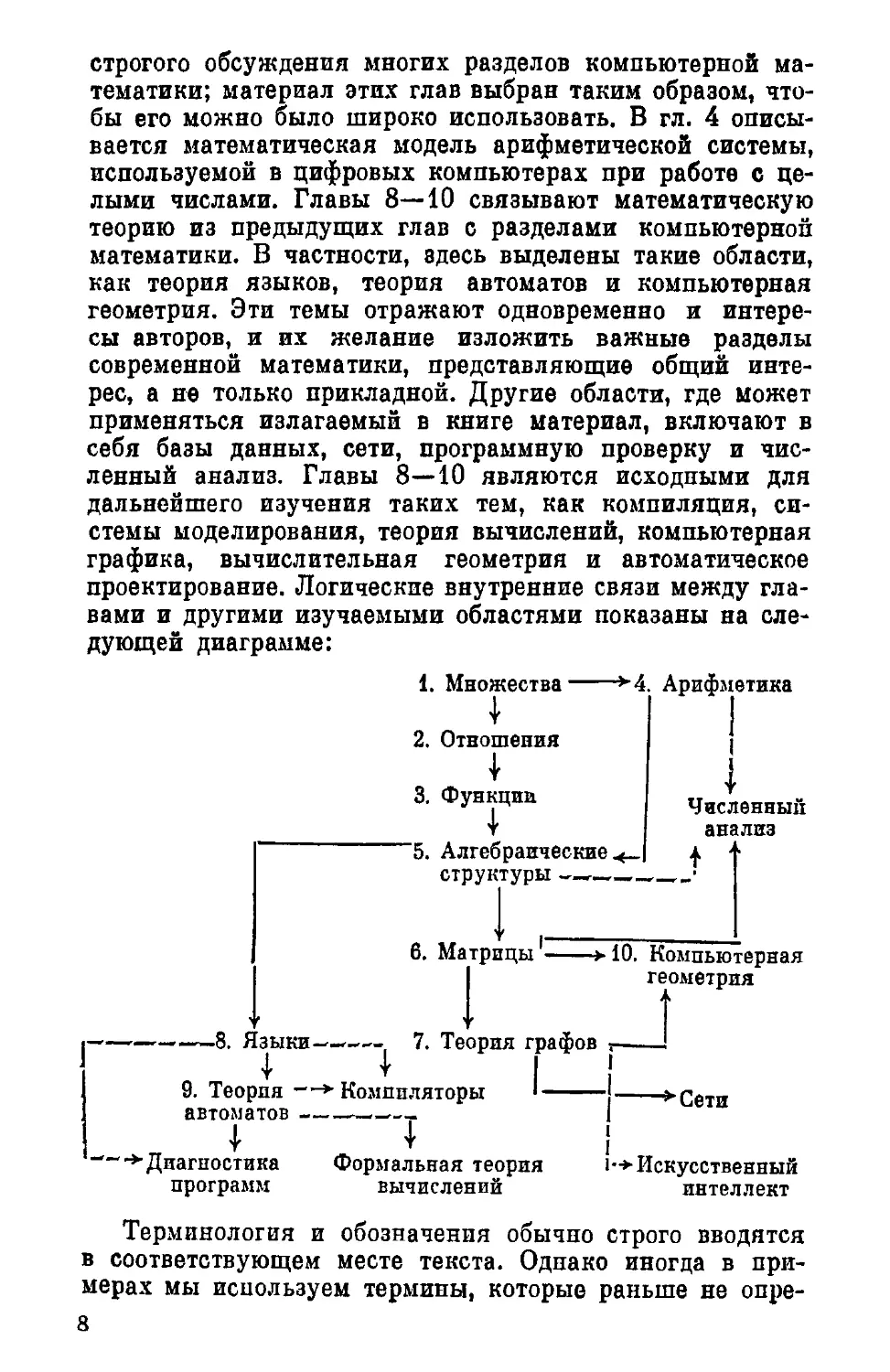
проектирование. Логические внутренние связи между гла-
главами и другими изучаемыми областями показаны на сле-
следующей диаграмме:
1. Множества >А. Арифметика
2. Отношения
\
3. Функции
Y
. Алгебраические.,
структуры ;
Численный
анализ
т
6. Матрицы
• 10. Компьютерная
геометрия
¦ 8. Языки——
7. Теория графов
9. Теория —*¦ Компиляторы
автоматов
I
'Сети
I
-—•*¦ Диагностика
программ
Формальная теория
вычислений
!•¦»¦ Искусственный
интеллект
Терминология и обозначения обычно строго вводятся
в соответствующем месте текста. Однако иногда в при-
примерах мы используем термины, которые раньше не опре-
делялись. В таких случаях обычно следует руководство-
руководствоваться интуицией, а не формальными соображениями.
Так, в одном из случаев в гл. 1 используется термин
«конечная машина», в то время как определение дано
лишь в гл. 9. В § 5 гл. 3 некоторые свойства действи-
действительных чисел используются без доказательства. Напри-
Например, мы используем неравенство треугольника |;г + уГ*5
*S \х\ + \у\, где I • I обозначает абсолютную величину
числа, в некоторых доказательствах, относящихся к пре-
пределам. При желании читатель может опустить эти дока-
доказательства до прочтения из п. 3.4 гл. 5. Повсюду в книге
символ / будет означать конец определения, примера,
доказательства и т. п., а символ #—обнаружение логи-
логической ошибки, т. е. противоречие. Также по причинам,
которые станут ясными в § 5 гл. 1, мы обычно будем ис-
использовать для обозначения операции умножения символ
* (а не X), хотя, когда мы будем иметь дело с обычны-
обычными числами, символ * иногда будет опускаться с целью
упрощения записи в больших выражениях.
ГЛАВА 1
МНОЖЕСТВА
§ 1. Множества и их спецификация
Как уже отмечалось во введении, нам хотелось бы
построить математическую теорию достаточно строго, од-
однако при этом возникают некоторые трудности с обосно-
обоснованием. Вместо этого мы начнем с описания таких на-
начальных понятий, как множество. Хотя материал может
показаться простым, это делается для того, чтобы чита-
читатель мог свободно разобрать примеры, приведенные в
конце параграфа.
Множество — это совокупность определенных различа-
различаемых объектов таких, что для любого объекта можно
установить, принадлежит этот объект данному множе-
множеству или нет.
Множество, которое подчиняется лишь такому ограни-
ограничению, может содержать объекты почти любой природы.
Например:
— множество всех подземных станций Лондона;
— множество левых ботинок;
— множество натуральных чисел: 1, 2, 3, 4 и т. д.;
— множество символов, доступных специальному пе-
печатающему устройству;
— множество кодов операций конкретного компью-
компьютера;
— множество зарезервированных слов языка Паскаль.
В конечном счете нас будут интересовать следующие
множества:
— множество идентификаторов, встречающихся в
определенной программе;
— множество операций в той же самой программе;
— множество операций, которые могут быть выполне-
выполнены после данной инструкции в той же программе.
Однако эти множества также являются достаточно
сложными для исследования. Поэтому для большинства
примеров мы будем использовать некоторые абстрактные
множества, такие как множества чисел,
10
Множества обычно обозначают прописными буквами,
например А, и специфицируют одним из двух путей. Ес-
Если множество содержит несколько элементов, то мы про-
просто записываем все его элементы. Например, если мы
определим А как множество всех целых чисел строго
между 6 и 10, то это можпо записать следующим обра-
образом:
А - {7, 8, 9}
в прочитать как
«А — множество, содержащее 7, 8, 9».
Здесь символ «=» используется в определенном смы-
смысле: А равно множеству... Далее будет использоваться
высказывание «равно ли А...». Поэтому мы должны
предложить процедуру установления справедливости это-
этого утверждения. Другими словами, множество можно
охарактеризовать определенными свойствами, и, следова-
следовательно, множество А можно определить как
А — [х; х — целое число и 6 < х < 10)
и прочитать как
«А есть множество всех х таких, что ...».
Множеству А принадлежат только те элементы, которые
являются целыми числами, большими 6 и меньшими 10,
т. е. 7, 8 и 9, и, следовательно, мы имеем 7, 8, 9, как и
ранее.
Множества часто рассматривают как «неупорядочен-
«неупорядоченные совокупности элементов», хотя иногда полезно под-
подчеркнуть, что, например,
{7, 8, 9} = {8, 9, 7} = {9, 8, 7} = ...;
мы не делаем никакой оговорки о порядке, в котором
рассматриваются элементы, поэтому было бы неправиль-
неправильным допускать какой-либо определенный порядок.
Для любого заданного объекта можно определить,
принадлежит ли он множеству А. В частности, если чис-
число принадлежит множеству, то будем говорить, что «оно
является элементом множества». Так, например, если 7
является элементом множества А, то это утверждение
может быть записано следующим образом:
Утверждение «6 не является элементом А» будем
обозначать как
11
Символ е происходит от греческой буквы е. Отрица-
Отрицание обозначается через Ф. Такое обозначение отрицания
операции (или операционного символа) является общим
в математике и часто будет использоваться в дальнейшем.
Надо подчеркнуть, что следовало бы обратить боль-
большее внимание на спецификацию множеств. Для каждого
множества должна быть записана его спецификация.
Процесс образования множества может продолжаться
бесконечно долго. В результате получается множество,
соответствующее определению. Частичная спецификация
может быть полезной в том случае, когда не ясно, при-
принадлежит данный элемент множеству или нет.
До сих пор нам встречались символы {:}, {,„}, s и Ф.
Их применение кажется достаточно простым, однако оно
требует определенных навыков, которые будут проиллю-
проиллюстрированы на следующих примерах.
Пример 1.1. Какие из приведенных определении
множества являются правильными:
A -
B =
D =
E,
U,
{x:
2,3),
6, 6, 7>,
1=1 ИЛИ
F = (множества, которые не являются элементами самих
себя) = {х: х — множество и х & хI
Если число членов множества А легко вычисляется и
среди элементов множества нет повторений, то определе-
определение верно.
Множество В выглядит также правильным, за исклю-
исключением лишь того, что число б встречается дважды. Мы
можем проверить, принадлежит ли элемент множеству
или нет. Таким образом, это наиболее важное требование
в определении множества выполнено. Следовательно, мы
может рассматривать эту запись как верную и эквива-
эквивалентную E, 6, 7}. Однако в этой ситуации возникают сле-
следующие проблемы. Если мы рассмотрим первоначальное
определение В и выбросим одно из чисел 6 из множества,
то мы, очевидно, будем иметь 6еВ и 6 & В. Возникает
противоречие. Поэтому мы будем рассматривать повторе-
повторение символов в определении множеств как упоминание
одного и того же символа, а его дублирование как недо-
12
смотр; удаление повторяющихся символов образует осно-
основу для некоторых дальнейших математических рассуж-
рассуждений.
Множество А содержит числа; это может вызвать не-
недоумение, так как числа не существуют. Более точно, мы
используем символы чисел; эти символы называются так
же, как и числа. Поэтому В — множество имен, и мы
обычно используем имена, чтобы представить объекты
(элементы), на которые ссылаемся. В вычислениях име-
имена имеют особое значение, особенно в изучении семанти-
семантики программных языков (смысла программ). Здесь не
место входить в детальное обсуждение этих проблем; до-
достаточно указать ловушки и необходимость адекватных
спецификаций рассматриваемых объектов.
Возьмем, например, множество
X = {«Введение в Паскаль»,
«Основы структурных данных», «Введение в Паскаль»}.
Это — множество названий двух книг с одним элементом,
по невнимательности записанным дважды, или же это —
множество трех книг, две из которых имеют одно и то же
название? Если верно последнее, то две книги «Введе
ние в Паскаль» следует разделить каким-либо способом.
Из данной информации нельзя выяснить правильный
ответ, поэтому в данном случае следует быть осторожным.
Определение С также справедливо как А, так как,
если х <= А, то х <? С п, если хф А, то хеС. Множество
С очень велико: оно содержит «всё», за исключением чи-
чисел 1, 2 и 3. Обозначение «всё» выделено и, как мы
скоро увидим, «опасно» с математической точки зрения.
Так как определения D, А и С представляют множе-
множества, то отсюда получаем, что определение D также спра-
справедливо. Заметим, что это — множество множеств (ниче-
(ничего неверного в этом нет!) такое, что оно имеет только
два элемента, в частпости 1 & D, даже если 1 <= А и
A s D. Это легко проверить, так как 1?> А, \ФС а
только А и С являются элементами D.
Множество Е является первым примером рекурсивно
определяемого множества; оно определяется (частично)
в терминах самого себя. Конструктивный процесс продол-
продолжается бесконечно, поэтому мы должны иметь правило
для определения элементов. Мы не можем записать их
явно. Заметим, что Е не определяется полностью в тер-
терминах Е, Мы должны знать о множестве что-то, что не
13
зависит от определения; в данном случае это то, что
1е?, Имеем:
1е?, поэтому Ш е= Е,
Ше?, поэтому Ш)}е?,
{{1}} е Я, поэтому {{{1}}} еЬт.д.
Хотя конструктивный процесс неограничен, беря любой
элемент и располагая достаточным временем, можно опре-
определить, содержится ли этот элемент в Е.
Перейдем теперь к F; это достаточно трудная задача.
Чтобы увидеть, почему F не может существовать, мы
сначала допустим существование, а затем продемонстри-
продемонстрируем, что существует особый элемент (обозначим его че-
через у) такой, что мы не можем определить, у е F или
y&F1. Вообще исследование «неудобного» примера, па
котором мы можем показать логический изъян, проводит-
проводится нелегко; однако в данном случае мы можем использо-
использовать само множество F. Чтобы прояснить дело, давайте
обозначим это множество через G. Если, как мы предпо-
предполагаем, F — искомое множество, то или G e F, или
G Ф F. Рассмотрим два возможных случая:
а) G&F. Тогда G удовлетворяет условию содержа-
содержания, т. е. G & G, и, следовательно, G Ф F;
б) G Ф F говорит о том, что G не удовлетворяет усло-
условию вхождения в F, и, следовательно, GeF.
Следовательно, во всех случаях мы приходим к про-
противоречию. Поэтому F не может существовать. Где же
была сделана ошибка? Множества множеств, вероятно,
разрешаются, и бесконечно большие множества (напри-
(например, рассмотренное выше множество Е) также разреша-
разрешаются; однако с «множеством всех множеств» нельзя ра-
работать в обычной теории множеств — это требует другого
рода математики. Эта аномалия теории множеств из-
известна как парадокс Рассела. Если мы уже имеем мно-
множество Я, то можно определить /:
J = {х: хеН и isilJ
Таким образом, мы будем использовать только мпо-
жества, которые могут быть явно записаны или же по-
построены путем хорошо определенных процессов. Поэтому
множества не так тривиальны, как они могли вначале
показаться. Однако, следуя приведенным выше правилам,
работа с ними не будет особо трудной. Попытайтесь сде-
сделать самостоятельно следующее упражнение.
14
Упражнение 1.1.
1. Рассмотреть по крайней мере две возможные ин-
интерпретации множества
{Смит, Смит, Браун}.
Определить каждую из них настолько однозначно, на-
насколько это возможно.
2. Рассмотреть следующие четыре множества. Выяс-
Выяснить, как записи этих множеств могут быть упрощены и
какие из них эквивалентны. Предложить все возможные
интерпретации, удовлетворяющие описанным выше пред-
предположениям:
а) {1, 2, 3, 4); б) {I, II, III, IV, V};
в) {1, один, one, uno, ein); г) E, V, пять, five},
3. Проверить справедливость утверждений
«Это утверждение неверно» и «я лгун».
Какие слова в утверждении требуют собственного
(т. е. математически точного) определения для того, что-
чтобы сделать ответы математически строгими?
4. Пусть X— множество A, 2), a Y — множество
{х\ х — у + z\ у, z e X). Определить в явном виде мно-
множество У. Какие это множества:
{у. у — х + z; x, z е X} и {у. х — у + z; x, z e ХI
5. Предположим, что х является элементом, а не мно-
множеством. Тогда у Ф х для любого у, и отсюда следует,
что х Ф х. Можно ли упростить множество {х, Ы, {{х}}}?
Что можно сказать относительно {х, у, {х, у)}?
6. Пусть А — множество всех целых чисел. Онисать
словами множество
X - {*: хе А и х = 1 или (х- 2)е X).
§ 2. Простейшие операции над множествами
Как мы видели из рассмотрения «ошибочного множе-
множества» F в примере 1.1 необходимо проявлять вниматель-
внимательность при определении множества. Тем не менее, строя
новые множества из старых по простым правилам, можно
безопасно получить много интересных примеров.
Позднее будут выписаны формальные правила, кото-
которым должны удовлетворять операции с множествами, а
сейчас введем некоторые обозначения. Начнем с простей-
простейших операций.
15
Определение. Пусть даны множества А и В.
Пересечением множеств А и В называется множество
всех элементов, принадлежащих А и В, в обозначается
А п В; таким образом,
А П В = {х: х&А bisB).
Аналогично объединение А и В обозначается A U В и
определяется следующим образом:
A U В •= {х: х&А или * е= В).
Значения этих обозначений нетрудно запомнить, но
иногда бывают ошибки. Один из путей запомнить, какой
символ обозначает какую операцию,— объединить сим-
символы в слова и записать « Пересечение» и «ибъединение».
Эти определения выводятся из слов «и» и «или», и, как
следствие, мы имеем
и, что, вероятно, менее очевндпо,
А\)А=А, А(\А>=А.
Эти тождества важны по двум причинам. Во-первых, из
дальнейших математических рассуждений будет видно,
что иногда следует сводить A U А (соответственно А П А),
к А или, наоборот, расширять А до A U А (соответствен-
(соответственно А ОА). Во-вторых, можно не обратить на это внима-
внимание из-за того, что, выраженные словами, эти тождества
могут казаться лишенными смысла даже тогда, когда она
логически верны.
Заметим также, что определение объединения исполь-
использует включение «или», называемое так потому, что оно
включает «и» так, что
A, 2} U {2, 3} = И, 2, 3>,
{1, 2} П {2, 3) - BJ.
Элементы в пересечении множеств (в данном случае
это — единственное число 2) включаются в объединение.
Это обычная математическая договоренность, и существу-
существует пример, в котором математическое впачеипе является
более точным, чем при общем употреблении.
Пример 2.1. В предположении, что каждый день
или дождливый, или ясный, математическим (или логи-
логическим) ответом на вопрос
«Ясно или дождливо сегодня?»
16
будет
«Да».
Оиределение. Разность множеств А а В (также
называемая дополнением В до А) записывается в виде
А\В в определяется соотношением
А\В = {х: xt=A л х&В).
Поэтому, если А = И, 2, 3} и 5 = {2, 3, 4), то А\В*={1)
и В\А = {4}.
Следующее определение включено для полноты. Хотя
мы будем редко использовать его непосредственно, одна-
однако, как мы увидим в дальнейшем, этот оператор имеет
большое значение в машинной арифметике.
Определение. Симметрическая разность множеств
А и В, т. е, А\В, определяется как
ААВ=(А UB)\(A пВ).
Возможно, читателя запутали обозначения U, П, \, Л,
или, наоборот, он поверил, что они настолько элементар-
ны, что не имеют никакого практического применения,
Следующие примеры помогут в этом разобраться.
Пример 2.2. Предположим, что мы имеем две про-
программы, называемые Р и Q, и что А — множество всех
значений данных, доступных Р, а В — множество всех
значений данных, доступных Q. Тогда А П В — множество
всех данных, доступных Р и Q; A U В — множество всех
данных, доступных по крайней мере или Р, или Q;
А\В ~ множество всех данных, доступных Р, но недо-
недоступных Q; В\А — множество всех данных, доступных Q,
но недоступных Р', ААВ — множество всех данных, до-
доступных только одной из программ Р или Q.
Чтобы полностью определить А и В, мы должпы
знать некоторые данные о вычислениях, связанные с Р
и Q. В нашем случае достаточно сказать, что они произ-
производятся на некоторой конечной ЭВМ.
Перед дальнейшим изложением будет удобно опреде-
определить два специальных множества. Первое из них «= пу-
пустое множество.
Определение. Пустое множество (обозначает-
(обозначается 0) есть множество, обладающее свойством
х & 0 при любом х.
Второе множество, определение которого зависит от
вадачи, пазывают универсальным множеством,
2 Д. Кук, Г. Бсйа 17
Определение. Универсальное множество (обозна-
(обозначается §) есть множество всех рассматриваемых в дан-
данной задаче элементов.
Ограничение <8 в этом случае помогает избежать труд-
трудностей, подобных тем, которые возникали при рассмотре-1
нии «множества» F примера 1.1; в любом случае боль-
большинство элементов несущественно в каждой данной задаче.
Например, размеры «Английского словаря», несом-
несомненно, неинтересны, если рассматривается поведение от-
отдельной программы на Фортране.
Определение. Два множества А ж В не пересека-
пересекаются, если А П В — 0.
Определение. В каждом случае, когда & задано,
определим дополнение множества А (обозначается А')
как
Из определений 0, <S и А' следует справедливость тож-
тождеств
А\)А'=>$, АПА'=*0.
В § 4 будет показано, что для данного <8 эти тождества
достаточны, чтобы однозначно определить А'.
Пример 2.3. Пусть
# = {1,2,3,4}, Л = {1,3, 4>, В = {2,3}, С = {1,4}.
Из определений легко найти, например, А', В ПС, С\А
и т. д. Однако может понадобиться исследовать более
сложные выражения, включающие две или более опера-
операций. Поскольку в этих случаях встает вопрос, как опреде-
определить порядок, в котором мы должны осуществлять эле-
элементарные операции над множествами, будем использо-
использовать скобки. Каждое выражение, заключенное в скобки,
должно быть выполнено перед тем, как его результат
может быть использован в других вычислениях. Напри-
Например, в {А П В)' пересечение ({3}) вычисляется раньше,
чем дополнение ({1,2,4}). Этого соглашения, очевидно,
достаточно. Однако, чтобы избежать такого множества
скобок, мы не будем требовать скобок, когда хотим произ-
произвести операцию дополнения перед любой из операций с
множествами {U, П, \, Д}. Поэтому ААВ' означает А Г) E')
и т. д. Следовательно,"
А ПВ' = А П A,4)-{1,4},
(А П В) ' = {3}' = {1,2,4},
18
Читатель может быть удивлен, почему изложение по-
построено на понятии множества, а не числа. Действитель-
Действительно, до сих пор мы использовали числа только как эле-
элементы множеств. Это делалось лишь для того, чтобы чи-
читатель познакомился с объектами, с которыми ему при-
придется работать. Дело в том, что существуют множества
более сложные, чем числа; мы можем получить числа из
множеств, но не па оборот. Одпако для многих приложе-
приложений последующей теории необходимо сделать точные
утверждения о пекоторых специальных множествах чи-
чисел. Чтобы обеспечить основу, с помощью которой будут
конструироваться такие множества, определим множество
N целых положительных чисел (натуральных чисел):
N = {1,2,3, ...}.
Точное определение множества N вместе с арифмети-
арифметическими операциями + и ¦ и его упорядочивание будут
даны ниже. Однако в настоящей главе мы будем предпо-
предполагать, что читатель знаком с некоторыми свойствами N.
Аналогично Z определяют как множество всех целых
чисел:
Z = {.,., -2, -1,0, 1,2,...}.
Конечно, множества N и Z не могут быть выписаны
явно (они достаточно велики), но в настоящее время мы
должны понимать «...» как «и так далее».
Рассмотрим теперь множество
А = A, 2, ..., п) = {х: х е N, Кх<п}.
Оно имеет п элементов. Будем говорить, что мощность
(или размер, норма, длина) этого множества есть п. Это
обозначается как
\А I = card (A) *=• п.
Далее любое множество В, которое имеет то же число
элементов, что и А, имеет такую же мощность, и, конеч-
конечно, эти элементы не надо пересчитывать. Для небольших
множеств достаточно легко пересчитать элементы, но для
других множеств (например, N) это может быть невоз-
невозможно. Далее мы дадим строгое, но в то же время
неформальное правило для вычисления количества эле-
элементов.
Определение. Говорят, что множество X конечно,
если X = 0 или если для некоторого neN существует
множество {1, 2, ..., п} такое, что оно имзет то же самое
2* 19
число элементов, что и X. Если X Ф 0 и никакого п не
может быть найдено, то X называют бесконечным.
Сейчас, когда мы ввели некоторые определения, мож-
можно сформулировать несколько упражнений. Чтобы сде-
сделать множества легко записываемыми, мы снова будем
использовать числа и буквы для элементов, но будем
помнить, что те же операции могут быть применены к
произвольным множествам.
Упражнение 1.2.
1. Пусть
# = {1,2,3,4}, Х={1,5),
Y = {1,2, 4}, Z = {2,5).
Найти множества:
а) ХпГ; б) (XuZ)U 7'\
в) XU(YUZ); г) (XUY)U(X\JZ);
д) (ХиУ)';е) X' П Г; ж) (ХПУ)';
a) (XU F)UZ; и) XU(FUZ); к) X\Z;
л) (X\Z)U{Y\Z).
2. Пусть
# = {а, Ь, с, d, е, /}, А = {а, Ъ, с),
В - {/, е, с, а}, С = №, е, /}.
Найти множества:
а) А\С; б) В\С; в) С\#;
г) А\В; д) Л' U В; е) ЯП Л';
ж) Л ПС; з) СП Л; и) САА.
3. Даны два произвольных множества А ж В такие,
что А П В = 0. Что представляют собой множества Л\5
и В\А?
4. Даны два произвольных множества С ж D такие,
что С П D' — 0. Что можно сказать oCflDnCUD?
5. Дано произвольное множество X. Найти множества:
а) X П Г; б) X U X'; в) Х\Х'.
6. Какие из следующих утверждений справедливы:
а) Оа0; б) 0 = {О); в) |{0}| = 1;
г) {{0» в {{{0}}}; д) |{{0}}|=2?
Это вопрос коварный. Хотя это может показаться простым
или надуманным, пустое множество и его свойства явля-
являются достаточно важными. Если вы не совсем уверены в
ответе, проработайте вопрос, используя аналогию порт-
портфеля вместо множества. Таким образом, {{}, {}} — порт-
портфель, содержащий два пустых портфеля, и, следователь-
следовательно, |{{>, {}}| =2 и т. д.
20
7. Пусть М а N — два конечных компьютера (см.
пример 2.2) с фиксированными программами. Далее
пусть А — множество значений данных, доступных М и
таких, что если х е А и машина М работает с входным
словом х, то М останавливается и выдает результат. Ана-
Аналогично пусть В — множество значений данных, которые
приводят N к остановке и выдаче результата. Если лю-
любой элемент А доступен М и N, что мы может сказать об
элементах В"} Объяснить эту ситуацию с помощью сим-
символов и пояснить бесполезность этой информации.
8. Объяснить в терминах множеств, почему пример
2.1 верен.
9. При определении операции объединения подчерки-
подчеркивалось, что мы использовали включение «или». Как
в терминах множеств можно выразить исключающее
«или»?
10. Часто в вычислениях будут использоваться ариф-
арифметические операции для образования новых множеств.
Так, если А и В — множества чисел, то
А + В = {х: х = а + Ь, ае=А, Ь^В).
Аналогично определяются операции *, —, / между мно-
множествами чисел. Найти следующие множества:
а) A,2)+ {1,3}; е) {1,2}\{1,3>;
б) {1,2} U {1,3}; ж) {2,4}/{2};
в) Н,2} • {1,3}; з) {2,4}\{2>;
г) {1,2} П {1,3}; и) {2,4}-{2}.
д) {1,2} -{1,3};
11. Для того чтобы быть в состоянии применить тех-
технику операций с множествами к конкретной задаче, мы
неизбежно должны на некотором этапе взять «нематема-
«нематематическое» утверждение и перевести его в математическое.
Обычно (но не всегда) это делает описание более ком-
компактным. Однако математическое выражение будет всегда
математически строгим, тогда как исходное выражение
может таким не быть. (Где это случается, требуется най-
найти, чего же недостает в первоначальной формулировке.)
Теперь надо:
а) попытаться сформулировать следующие утвержде-
утверждения на языке множеств:
— даны множества А, В и С', определить множество,
включающее в себя только два из этих множеств;
— решить предыдущую задачу при условии, что А, В
и С взаимно не пересекаются;
21
— даны множества У, W, Y, X и Z. Определить
множество, включающее по крайней мере два из мпожеств
V, W, X и У и не включающее Z;
б) аналогично описать словами следующие множества:
(Jf\{KUL))'U(H\L),
(PURUQ)\(Pu(Q\R))t
((E\F)U(F\E))'[)G.
§ 3. Диаграммы Веппа
Уже можно было заметить некоторые специфические
свойства операций над множествами, в особенности то
свойство, что одно и то же множество может быть опре-
определено различными путями. Далее в этой главе мы обсу-
обсудим способы доказательства этих свойств формальным
путем, однако часто полезно иметь геометрические пред-
представления множеств. Такие представления не могут за-
заменить доказательства, но могут быть полезны, чтобы
быстро и просто убедиться, справедливо ли конкретное
утверждение и, следовательно, доказательство его воз-
возможно или же оно неверно.
В этом случае можно заме-
заметить, как следует строить
пример, чтобы доказать, что
оно неверно. Диаграммы, ко-
которые мы будем использо-
использовать, называют диаграммами
Венна (по имени английско-
Рио- *'* го математика Джона Вен-
Венна) и строят, как это описано ниже.
Во-первых, начертим большой прямоугольник, пред-
представляющий ё> (рис, 1.1). Во-вторых, начертим круги
(или какие-либо другие подходящие замкнутые кривые)
внутри прямоугольника, чтобы представить множества.
Они должны пересекаться в наиболее общем случае, тре-
требуемом в задаче, и должны быть соответствующим обра-
образом обозначены (рис. 1.2). Точки, которые лежат внутри
различных областей диаграммы, сейчас могут рассматри-
рассматриваться как элементы соответствующих множеств. Если
число элементов в множествах мало, тогда отдельные эле-
элементы могут быть записаны внутри подходящих обла-
областей, как это показано в примере 3.1.
Пример 3.1. Пусть Ж = ib,c,d,e), А = {Ь, с, d),
В = {с, е}, Соответствующая диаграмма изображена па
22
рис. 1.3. Этот рисунок полностью иллюстрирует при-
пример 3.1, обеспечивая знание элементов Ж. Если же, на-
например, A s <§Г, тогда неясно, что предполагалось изобра-
вить на диаграмме. В тех случаях, когда используются
Рис. 1.2
Рис. 1.3
более сложные конструкции мпожеств, следует избегать
изображения их в виде диаграмм.
Имея построенную подходящим образом диаграмму,
мы можем заштриховать определенные области для обо-
обозначения вновь образованных множеств.
Пример 3.2. Чтобы представить множество
AU(B'uC), начнем с общей диаграммы, показанной на
рис. 1.4. Заштрихуем В' диагональными линиями в од-
одном направлении, а С диагональными линиями в другом
Рис. 1.4
Рис. 1.5
направлении (рис. 1.5). Площадь с двойной штриховкой
представляет собой множество В' П С.
На новой копии диаграммы заштрихуем эту область
горизонтальными линиями, а А вертикальными. Вся за-
заштрихованная на рис. 1.6 область представляет множе-
множество A U (В' Л С). Если в отдельных случаях мы имеем
дополнительную информацию о рассматриваемых мно-
множествах, то ее можно использовать для упрощения диа-
диаграммы Венна.
23
Пример 3.3. Пусть 4 ПВ = 0; это соответствует
диаграмме на рис. 1.7. /
Заметим, что в большинстве случаев множества со-
содержат довольно много элементов, и, следовательно, эти
элементы не могут быть представлены отдельно, Поэтому
Рис. 1.6
Рис. 1.7
более удобно в этом случае говорить о каждом из мно-
множеств как о целом и не упоминать отдельных элементов.
Упражнение 1.3.
1. Начертить диаграмму, иллюстрирующую построе-
построение множеств, рассматриваемых в задаче 1 упражне-
упражнения 1.2.
2. Как можно представить следующие множества, ис-
используя диаграммы Вениа:
Ы, {А}), {{а), Ш), {X, Y, Z],
где
Х~{х: z = l или (*-2)аД
У = Ь: z = 3 илп(*-3)е=У},
Z = {x: х = 2 или (i-2)eZ)?
§ 4. Подмножества и доказательства
Операции пересечения, объединения, разности и до-
дополнения позволяют нам формировать новые множества.
Однако, как правило, мы не можем сказать, как одно
множество соотносится с другими. Например, пусть даны
два множества X и У; пересечение X П У в некотором
смысле «меньше» (или по крайней мере не больше), чем
X. Действительно, все элементы множества X П Y при-
принадлежат также множеству X, Из этого наблюдения мож-
можно формально определить равенство множеств и различ-
различных выражений для того же самого множества. С по-
24
мощью этих определений мы также в состоянии написать
подходящие логические доказательства важных фактов,
относящихся к множествам. Эти результаты, хотя и оче-
очевидны, обеспечивают подходящие ситуации, в которых
можно ввести некоторые из основных способов доказа-
доказательств, используемых в дальнейшем.
Определение. Пусть множества А и В таковы,
что из принадлежности х е= А следует, что isfl, Тогда
говорят, что А есть подмножество В, и обозначают это как
А~В- Соответствующая диаграмма Венна изображена
на рис. 1.8. Далее, если су-
существует элемент В, кото-
который не принадлежит А, то
А называют собственным
подмножеством В и записы-
записывают в виде Ас= В. Это оз-
означает, что в некотором смыс-
смысле В больше, чем А, но, как
мы впоследствии увидим, та- Рис. 1.8
кие термины могут вводить в
заблуждение. Следовательно, при употреблении этого тер-
термина требуется проявлять осторожность. Эти отношения
могут также быть записаны в обратном порядке, или
В=>А и
тогда говорят, что В — (собственное) надмножество А.
Очевидно, что для любого множества А справедливы
следующие три соотношения:
0?Л, AsA, Л?#.
Второе из них является наиболее важным. Говорят, что
множества А и В эквивалентны (записывается как А =
= В), если
4<=Я и В^А.
Это означает, что все элементы А являются элементами
В, а все элементы В — элементами А. II
Используя определение эквивалентности множеств, до*
кажем теперь идентичность некоторых множеств, разо-
разобрав серию из пяти примеров. Они являются примерами
доказательств. Поэтому мы обязаны кратко рассмотреть
вопрос о том, почему следует заботиться о доказатель-
доказательствах в компьютерной науке. Строго говоря, как это
обычно делается, мы должны доказать что-либо только
один раз. Затем мы исходим из того, что эта часть инфор-
25
мации является правильной и, следовательно, может рас-
рассматриваться как факт. Однако, как бывает в большин-
большинстве аспектов вычислительной науки, метод, которым мы
получаем результат, по крайней мере так же важен, как
и сам результат. После анализа доказательства становят-
становятся ясными сделанные предположения и последствия, к
которым они приводят, а также становятся понятными
процессы вывода, которые можно использовать при ре-
решении других задач. (Аналогично проведению экспери-
эксперимента на ЭВМ с подобными структурами данных при их
использовании в программировании.)
Можно также заметить, что доказательства теорем
формируют основу всех решающихся автоматически за-
задач, но это будет обсуждаться позднее, Рассмотрим не-
несколько примеров.
В примере 4.1 непосредственно доказывается справед-
справедливость следующих двух соотношений:
а) Ап(В[)С)^(АпВ)\)(АГ\С);
б) (АПВ)\}(АПС)яАП{В\)С).
Каждое из этих доказательств состоит из последователь-
последовательности утверждений вида
«если Р, то Q»
(если справедливо Р, то справедливо и Q). Для удобства
запишем это утверждение как «Р =*¦ Q» и будем читать
«из Р следует Q».
Следовательно, если имеется последовательность Ро,
Ри ...,Рп такая, что Ро =*- P.,Pi •*• Р2,...,P»-i ¦»¦ Р„ (из Ро
следует Pi, из Pi следует Рг, .,., из Pn_i следует Р„), то
мы имеем прямое доказательство Ро =*¦ Р„.
Пример 4.1. Относительно множеств А, В ж С до-
докажем, что
А Г\(В[)С) = (А пВ)[)(А ПС).
Доказательство.
х<вАГ\(ВиС)°*хе2А Hie(BUC)*
(Такая группировка необходима, так как скобки означа-
означают, что объединение следует вычислить перед пересече-
пересечением.)
** хе А и (ieB или хе= С) =*¦
¦*¦ (х е А и jeS) или (х е А и х е С) «*¦
=*(геЛПЯ) или (х а А П С)— х е(А П В)\} {А П С),
26
Таким образом,
А П (В U С) s (А П 5) U (Л ПС).
Сейчас необходимо доказать включение s в обратную
сторону:
х&{А П 5) U (А О С) •+
«*• (а; е= Л П В) или (а: е Л П С) =*-
^(ге^ихеВ) или (х&А и а: е С) =>
=*- г е Л и (xefi или х е С) =*¦
=^ле4 u ieBUC^je/in(flUC).
Следовательно,
(Л ПВ)и(ЛПС)?4 п{ВиС).
Поэтому
Л П(ЯиС) = (Л ПВ)и(Л ПС). /
В этом частном случае вторая часть доказательства
точно совпадает с первой, и, следовательно, можно за-
записать
ЛП(ВиС)еЛ Д11Сит. д.
Здесь символ «¦*=*¦» («Р ¦*=*¦ Q») означает, что Р =>¦ Q и
Q =*~ Р. Он может читаться как «тогда и только тогда»
(иногда также читают «если и только если») и означает
эквивалентность двух утверждений Р и Q. Однако не
всегда так просто обратить аргумент и следствие. В об-
общем случае мы должны провести доказательства в обе
стороны раздельно. Заметим также, что эквивалентность
может быть легко получена (хотя и не доказана) из под-
подходящей диаграммы Венна, однако не всегда можно на-
начертить диаграмму, относительно которой можно быть
уверенным, что она настолько отвечает требованиям, на-
насколько необходимо. Поэтому непосредственное доказа-
доказательство необходимо. Это доказательство зависит от вну-
внутренних взаимосвязей между значениями «и» и «или» it,
следовательно, может быть выбрано для каждого случая
своим. Далее, когда будут определены некоторые алге-
алгебраические структуры, мы покажем, что это не составля-
составляет трудностей.
Примеры 4.2—4.5 также используют прямые доказа-
доказательства, однако эти доказательства записаны в несколько
другом виде.
Пример 4.2. Относительно данного множества & до-
дополнение любого множества а(А^&) единственно.
27
Доказательство. Предположим, что существует
два множества В я С, каждое из которых удовлетворяет
требованиям дополнения Л, т. е.
ЯПЛ=СПЛ = 0 и 5иЛ = СиЛ=<Г.
Тогда
д-впаг-вп(си4)-(дпс)и(впл)-
- (В П С) U 0 - 2? П С;
поэтому
z е fl =s* ж е S и zeC=*-flsBnC=*-5sS и 2? ? С.
Однако мы знаем, что В^ В, Поэтому отсюда следует,
что
ВеС,
Аналогично (меняя ролями В и С) получаем
CsB,
откуда
5 = С, т. е. В = С = Л', и Л' единственно. /
Приведенный выше пример содержит в себе основной
математический подход, употребляемый для доказатель-
доказательства единственности,— сначала предполагается, что су-
существуют два таких объекта, а затем доказывается, что
они совпадают.
В следующем примере мы опять прибегнем к предпо-
предположениям об «или», чтобы иметь возможность написать
выражение A U В U С как AU(BUC) или (Л U В) U С,
когда это будет более удобно для требуемых преобразо-
преобразований.
Пример 4.3. Дапы множества А, В я С такие, что
A UBUC = &
в А, В ж С попарно не пересекаются. Тогда
А' - В U С, В' = Л U С и С - Л U С.
Доказательство.
Л иЯиС = Л U(BUC)-ff,
Л Л(ЯиС) = (Л
Следовательно, 5UC удовлетворяет условиям для Л',
которое единственно. Поэтому Л' = В U С Аналогично
проводятся доказательства для В' и С. II
28
Пример 4.4. Для произвольных множеств X и У
справедливо соотношение
ТУ).
Доказательство. Предположим, что мы имеем
множества А, В и С из примера 4.3 и
С = DU Е и D п Е = 0.
(Диаграмма Венна на рис. 1.9 может разбить <?, как тре-
требуется.) Тогда множества А, В, D и Е взаимно не пере-
пересекающиеся и
Более того,
А' = В U С,
поэтому
А' = В U D U Е.
Сейчас легко показать, что
если положить
A~X(\Y, B = X(\Y\
A
в
Л
?
Ряс. 1.9
и Е = X' П Y', то требуемые условия будут выполнены,
и поэтому нужный результат немедленно следует из пре-
предыдущих рассмотрений. II
Пример 4.5. Для любых множеств X и У верно
соотношение
Доказательство.
х е (X П У)' <*- х е (X П Y)' U (X' П У) U (X' П Г) *=>
-** а: е (X П У)' U (ГП У) U (X' П У) U (Z' П У)
(Один член здесь продублирован. Это разрешается, так
как А = A U А для любого Л.)
U X') П У) U (ГП (У U У)) ^ х в (JT П У) U
U(A" ni?)*»jsruX'^isX'U У.
Следовательно, (X П У) - X' U У. /
Результат, полученный в примере 4.5, и подобные ему
(см, упражнение 4.5) называют законами де Моргана.
29
Они играют важную роль в математической логике. Наи-
Наиболее непосредственные приложения к вычислениям на-
находятся в области комбинаторных цепей в логике.
Последовательность примеров 4.1—4.5 иллюстрирует,
как можно развивать математическую теорию путем по-
последовательности доказательств простых теорем и выво-
выводить такие важные результаты, как законы де Моргана.
Перед тем как перейти к заключительной части этой гла-
главы, попытаемся переписать доказательства задач, разо-
разобранных в примерах 4.2—4.5, формальным образом, как
это делалось в примере 4.1. В частности, каждый шаг
должен быть проверен ссылкой на доказанный результат
из предыдущих работ или же непосредственно выведен.
Позднее мы введем необходимую терминологию, которая
позволит использовать более краткие обозначения. Дадим
сначала два определения.
Определение. Говорят, что два множества А и В
неэквивалентны, если они не эквивалентны. Это свойство
равносильно тому, что одно из множеств А\В или В\А
непусто.
Определение. Множество всех подмножеств дан-
данного множества X назовем степенью множества X и бу-
будем обозначать через &ЧА). (Некоторые авторы исполь-
используют обозначение 2х; причина этого будет ясна немного
позднее, когда мы разберем несколько примеров.) Фор-
Формально
()
В частности, заметим, что поскольку 0sX и X ^Х, то
Пример 4.6. Пусть А = {1, 2, 3}. Тогда
0>(А)-{0, {1}, {2}, C), A,2), {1,3), {2,3}, Л}. //
Завершим этот параграф упоминанием о двух косвен-
косвенных методах доказательства. Первый из них — доказа-
доказательство от противного. Вспомним парадокс Рассела (при-
(пример 1.1):
и F<?F=>Fe=F.
Если обозначить утверждение F s p через Р, то получим
Р справедливо =*-Р ложно и Р ложно =>Р справедливо.
Основой математики является предположение о том, что
не может быть утверждения, которое является истинным
и ложным одновременно (т. е. логическая система долж-
должна быть содержательной; мы отвергаем множество Рас-
30
села потому, что его определение несостоятельно в рас-
рассматриваемом смысле), и мы используем это положение
как основу доказательства от противного. Предположим,
что мы имеем совокупность высказываний Pi, Р2, ..., Рп
и хотим доказать (Pi истинно и Р2 истинно и... и Р„ ис-
истинно) =*• Q истинно, или же более просто
Если мы допустим высказывание (Pi и Р2 и ... и Р„ и не
Q), т. е. что Р], ..., Р„ истинно, a Q ложно, и отсюда
сможем вывести некоторое утверждение Р, которое одно-
одновременно является и истинным, и ложным, то логическая
система, основанная на
(Р,иР2и.,.иРп и не (?),
является недопустимой. Таким образом, доказано, что ес-
если имеет место
(Р1ИР2И...ИРП),
то мы можем заключить, что
так как предположение не Q приводит к противоречию.
Для иллюстрации вышесказанного, рассмотрим пример.
Пример 4.7. Докажем, что для произвольных мно-
множеств А и В имеет место соотношение
Доказательство. Допустим, что свойства
(т. е. определения) множеств ё>, 0 и т. д. выполнены и
что А ^ В и В' ф А. (В терминах описанной выше об-
общей ситуации Q это В' s А'.) Тогда
4sB=* если х^ А, то ieB; (*)
В' фА' =>¦ существует некоторый элемент у такой, что
Из (•) следует соотношение
уеА*>у^В=^у^В' и уе=В=*-у&В'пВ = 0
(противоречие),
Следовательно, полученное утверждение В' ф А' ложно,
и поэтому В'^А'. Аналогично можно показать, что В' s
?Л'=*-ЛеВ, и, следовательно,
31
Этот пример также распространяется и на второй ме-«
тод косвенного доказательства.
Пример 4.8. Пусть Р означает высказывание «се-
«сегодня четверг», a Q — «сегодня день недели». Тогда
(Р =*¦ Q) означает «если сегодня четверг, то это день не-
недели», а (не Q •*¦ не Р) означает «если сегодня не день
недели, то это не четверг».
Следует убедиться, что эти два высказывания эквива-
эквивалентны (т. е. что они оба одновременно являются либо
истинными, либо ложными). /
С этой точки зрения, хотя диаграммы Венна могут
использоваться для прояснения ситуации, все результа-
результаты должны быть выведены из предположений, данных в
задаче. Следует помнить, что если какое-либо утвержде-
утверждение истинно, то мы должны быть в состоянии доказать
его. Если это действительно очевидно, то мы легко дока-
докажем его, если же нет, то, по-видимому, это не так оче-
очевидно, как мы думали, и вполне возможно, что это даже
неверно.
Упражнение 1.4.
1. Доказать, что
А Л(ЯЛС) = (Л ПВ)пС.
2. Пусть дапы множества Л, В и С: С s В, Доказать,
что:
а) Л Л С s Л Л #; б) A U С s A U В;
в) А\В = А\С; г) С\А^В\А\
д) В'\А s С'\А.
3. Доказать, что если A s В, то ^(^)s^(B).
4. Показать справедливость равенства
А и(?ПС) = (Л иЯ)П(Л U С).
5. Доказать, что (A U В)' ¦= А' Л В'. (Указание:
показать, что (A U 5I1 (Л' П В') = § и (Ли В) Л
П(Л'Л5')=0-)
6. Доказать эквивалентность следующих утверждений
т. е. что из каждого следует другое:
а) Л U В - <Г; б) А'^ В; в) А' Л В' - 0.
7. Какие из следующих утверждений справедливы:
а) Ое0; б) {0} s 0; в) 0 = {0};
г) 0 5^;д) <0}s{{0}}?
Сравните ответы на этот вопрос с ответами к упражне-
упражнению 1.2,6. Существует связь между символами s и s
однако это не одно и то же. Как аналогия «портфеля»
связана с символом s ?
32
8. Показать, что для конечного множества А
12А|=2|А|.
(Указание: выписать множество А = {а\, ..., ап) и
рассмотреть его подмножества.)
§ 5. Произведения множеств
Пока мы в основном занимались построением из су-
существующих множеств множеств меньшего размера. Сей-
Сейчас будет рассмотрен один из наиболее общих способов
конструирования больших множеств. Рассмотрим для ил-
иллюстрации множество размеченных клеток шахматной
доски (рис. 1.10). Рассмотрим множество столбцов, кото-
которые обозначим буквами а, Ь, ..., h (слева направо), и
{Черные)
У77?/
ш
с2
у/Л
Ж
а Ь a d e f g Л (Белые)
Рис. 1.10
множество строк от 1 до 8 (снизу вверх). Следовательно,
каждая клетка может быть однозначно задана двумя сим-
символами: один — из множества F = {о, 6, ..., hi, другой —
из множества R «=» A, 2, ..., 8>, например ol, /7, еЗит.д.
Таким образом, из множества столбцов F и множества
строк R мы образовали множество всех клеток доски.
Этот пример содержит в себе новые идеи, которые ис-
используются при построении произведений множеств. Од-
Однако для того, чтобы быть в состоянии обобщить рассматри-
рассматриваемую ситуацию, следует быть немного более точными.
3 д. кук, г. Беаз S3
Определение. Обозначим последовательность из
п элементов х\, Х2, • ¦ ¦, х„ через (х\, хъ, ..., хп). Здесь
круглые скобки испол'зуются для того, чтобы указать на
порядок, в котором з. 1исаны элементы. Например, если
х\ Ф Х2, то последовательность (х2, х\, ..., хп) не совпа-
совпадает с исходной. Будем называть такую последователь-
последовательность набором длины га; набор длины 2 будем называть
парой.
Пусть даны п множеств А\, Ач, ..., А„', множество
всех наборов (xi, X2, ..., хп) таких, что х\ е А\, ..., х„е
е^„, называют прямым произведением А\, ..., Ап и обо-
обозначают А\ X Аз X ...X А„. Используя другие обозначе-
п
ния, это произведение запишем более кратко: II А^. //
Пример 5.1. Пусть X = {0, 1), Y = {x,\), Z =
= @, 1, 2). Тогда
ХХУ = {@,*), @,у), A,х), A,у)>,
YXX = {(x,0), (х, 1), {у, 0), (у, 1)}.
Таким образом, X X У Ф У X X. При рассмотрении
снова примера с шахматной доской становится ясно, что
будет, если написать выражение Зе. Множества F и R не
пересекаются и (е, 3)*sFXR, & C, e)<?FXR. На-
Например,
XX У = {@,0), @,1), @,2), A,0), A,1), A,2)}
и @,1) и A,0)—различные элементы XX У. Следова-
Следовательно, с математической точки зрения нам следует от-
отвергнуть запись Зе как неверную для шахматной доски. /
Мы часто будем использовать прямое произведение
для одинаковых множеств. В этом случае будет удобнее
записывать А X А X ... X А как Ап.
Упражнение 1.5.
1. Пусть Х = {а, Ь,с) и Y^{a,b,e,f). Найти XX У
и У2.
2. Доказать: при 4sXnBs7, AXB^XXY.
3. Доказать, что А Х{В П С) = (А X В)П{А X С).
4. Доказать, что для любых непустых конечных мно-
множеств А ж В выполняются соотношения:
д) АХВ =*ВХА тогда и только тогда, когда А= В.
ГЛАВА 2
ОТНОШЕНИЯ
Часто в вычислениях необходимо выбирать элементы
множеств, которые удовлетворяют некоторому «отноше-
«отношению». Это понятие довольно общее. Поэтому оно широ-
широко применимо. Естественно, что при соответствующем вы-
выборе отношения его аргументы могут быть связаны доста-
достаточно просто. Они не обязательно должны быть связаны
какой-либо простой или очевидной формулой, хотя в си-
ситуациях, когда требуется осуществить некоторые вы-
вычисления, иногда можно найти удачное описание отно-
отношения.
Перед тем как подойти к этому вопросу с математи-
математической позиции, рассмотрим несколько идей, возникаю-
возникающих из рассмотрения следующей простой ситуации (кото-
(которая также приводит к возникновению понятий отноше-
отношения). Предположим, что для некоторой конечной машины
мы имеем множество программ Р, конечное множест-
множество значений данных D и множество результатов R. Если
мы выберем конкретное значение из D, то оно может ис-
использоваться в некоторых программах из Р, и для каж-
каждой программы из Р существует совокупность значений
из D, которые в ней используются. Таким образом, мы
имеем соответствие между значениями данных и програм-
программами, и, следовательно, существуют элементы в D X Р,
представляющие интерес. Аналогично, если мы сведем
рассмотрение к р^Р, то р связывает соответствующие
значения данных из D с результатами из R. Можно рас-
рассмотреть данные, приводящие р к остановке, или резуль-
результаты, которые не могут быть получены из р. Следова-
Следовательно, мы приходим к подмножеству DX R. (При пере-
переработке данных от D к R возникают некоторые ассоциа-
ассоциации, которые могут оказаться полезными для запомина-
запоминания терминологии.)
Перейдем теперь к формальным рассмотрениям.
3* 35
§ 1. Основные понятия
п-местным отношением R на множествах А\, ..., А„
называется подмножество прямого произведения
АхХ...ХАп.
Другими словами, элементы х\, ..., хп (где Х\^А\, ...)
связаны отношением R тогда и только тогда, когда
(«1, х2, ..., хп) е R ((хи х2, ..., хп) — упорядоченный на-
набор из п элементов).
Наиболее часто встречаются отношения при п = 2; в
этом случае они называются бинарными отношениями.
Следовательно, бинарное отношение между множествами
А и В является просто подмножеством АХ В. Если эти
множества эквивалентны (скажем, равны А), то будем
говорить, что подмножество А2 определяет отношение
на А.
Отношения не являются чем-то новым. Можно по-
построить отношения, которые, несомненно, будут знакомы
читателю. Рассмотрим следующие примеры.
Пример 1.1. Пусть
А = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10>.
Тогда R ** {(х, у): х, у е А, х — делитель у и х < 5} мо-
может быть записано в явном виде:
Д = {A, 1), A,2), A,3), A,4), A,5),
A,6), A,7), A,8), A,9), A,10),
B,2), B,4), B,6), B,8), B,10),
C,3), C,6), C,9),
D,4), D,8),
E,5), E,10)}. /
Пример 1.2 (шахматы). Как и выше, пусть
F - (о, Ъ, с, d, в, /, g, h), R - {1, 2, 3, 4, 5, 6, 7, 8}
и пусть S=*FXR.
Таким образом, S — множество всех клеток, обознача-
обозначаемых парами (з, у), где x^F, у е R. Определим бинар-
бинарное отношение С (для ладьи!) на S так, что (s, f)s С
тогда и только тогда, когда s и t — элементы S и ладья
может пройти от s к t одним ходом на пустой доске. (На-
(Напомним, что ладья может изменять либо горизонтальную
координату, либо вертикальную, но не обе координаты
36
одновременно.) Поэтому С s 5X5 и
C-l((f., г.), (/„ г,)): (/.-/, и г.* г,)
пли (/. Фи и г, = г,)}. /^
На первый взгляд определение С может выглядеть
сложно, но внимательное исследование показывает, что
значение отношения находится непосредственно и вся
необходимая информация содержится в определении.
В общем случае ряд различных отношений на мно-
множестве А зависит от \А\. Большая часть этих отношении
не представляет особого интереса. Ниже приведены три
отношения, которые полезны при рассмотрении множеств.
Определение. Для любого множества А опреде-
определим тождественное отношение 1Л и универсальное отно-
отношение UЛ следующим образом:
а):
Ъ):
Таким образом, UA = А2. Так как 0 s А2, то 0 является
отношением на Л и называется пустым отношением. /
Пусть отношение R определено в соответствии с изо-
изображением на рис. 2.1. Необходимо сконцентрировать на-
наше внимание на том, что происходит на концах R, т. с.
R
Элементы А, не
включенные в R
Элементы Аи В, Элементы в,не
Включенные в R Включенные 6 R
Рис. 2.1
рассмотреть элементы А ж В, которые принадлежат R.
Они являются элементами подмножеств А и В соответ-
соответственно и, как следовало ожидать, имеют специальные
названия.
Определение. Свяжем с каждым бинарным отно-
отношением R между А и В два множества — область опре-
определения D(R) и область значений 52(Л). Они определя-
определяются следующим образом:
D(R)={z: (x, y\^R), Й(Я)={у: (z, y)^R). ff
37
Пример 1.3. Пусть отношение R такое же, как и в
примере 1.1. Тогда
S>(R)=U, 2, 3, 4, 5), #(Д) = 4. /
Пример 1.4. Предположим, что мы имеем некото-
некоторую программу. Она читает два числа из множества А •=*
«={1, 2, 3, 4, 5), обозначаемых х и у, и, если х<у, печа-
печатает число z (также из А) такое, что х ^ z< у. В любом
случае программа останавливается после считывания всех
чисел из А.
Задача определяет отношение Р, Р^АХА такое, что
Р-{((*, У), г): x<y,x^z<y).
Не все входные данные приводят к выдаче результата.
Поэтому область определения Р не совпадает е А2. Ясно,
что
Р-{(A,2), 1), (A,3), 1), (A,3), 2),
(A,4), 1), (A,4), 2), (A,4), 3),
(A, 5), 1), (A,5), 2), (A, 5), 3), (A,5), 4),
(B,3), 2), (B,4), 2), (B,4), 3),
(B,5), 2), (B,5), 3), (B,5), 4),
(C,4), 3), (C,5), 3), (C,5), 4),
(D,5), 4)};
?>(Р)-<A,2), A,3), A,4), A,5),
B,3), B,4), B,5),
C,4), C,5),
D,5)};
Хотя каждое отношение является множеством и мо-
может быть обозначено прописной буквой, существует так-
также практика обозначения отношений строчными гречески-
греческими буквами, например р, а и т. Часто используют следу-
следующие обозначения:
а) (о, Ь)е р7 т. е. (а, Ь) находится в р;
б) apb, а связано с Ъ отношением р;
в) isp(e).
Первое из обозначений является естественным (оно
следует из определений теории множеств). Второе де-
делается более разумным, если мы рассмотрим отношение
порядка (которое будет определено несколько ниже), где
R&N2 и R = {(x, у): х<у).
88
Здесь вместо 6Д7 мы можем написать 6 < 7; следова-
следовательно, мы разрешаем запись любого отношения с ис-
использованием рассмотренных выше символов, если
результирующая последовательность символов будет од-
однозначно определенной. Третья форма записи является
новой и будет преобразована к более привычным обозна-
обозначениям в гл. 3. Из заданного бинарпого отношения мож-
можно вывести ряд других отношений, большинство из кото-
которых будут обратными отношениями.
Определение. Пусть R — бинарное отношение.
Определим обратное отношение Я следующим образом:
Таким образом, R~x связывает те же пары элементов, что
и R, но «в другом порядке». II
Следовательно, если ДеЛХВ, то
Чтобы избежать использования большого количества ско-
скобок, будем также использовать обозначения S)R и 32В вме-
вместо 3){Щ и 02(Я) соответственно.
Упражнение 2.1.
1. Пусть Х = {2, 4, 6, 8} и р =={(*, у): х, у е X и
х <^ у). Выписать все элементы р и р.
2. Пусть 1? = 0>({а, Ь, с)). Найти все элементы отно-
отношений с: и ^ на <?.
3. Пусть <? = Z2 и р = {(х, у): х<у). Описать р' —
дополнение р — без исиользования отрицания отношения
«меньше».
4. Пусть а = {(х, у): xczy). Может ли о' быть опи-
описано тем же способом, что и р' в 2.1, 3? Ответ проверьте.
5. На улице есть 30 домов, пронумерованных обычным
способом: нечетные номера с одной стороны, а четные с
другой. Пусть hn обозначает жителя, живущего в доме с
номером п. Описать при помощи символов отношение N
на множестве жителей такое, что ht находится в отно-
отношении N к hh если они являются соседями.
Как будет выглядеть N, если улица является тупи-
тупиком?
6. Вернемся к множеству S клеток шахматной доски.
Отношение К связывает клетки, которые определяются
ходом копя (т. е. если копь может перейти с х на у за
один шаг). Определить К при помощи символов.
7. Пусть G — отношение на 5 такое, что xGy тогда
и только тогда, когда х есть начальная позиция (белой)
пешки, а у есть клетка, где первый ход игры заканчива-
заканчивается. Описать G, 2>(G) и &(G)
§ 2. Графические представления
При решении задачи на первом этапе часто полезно
начертить «рисунок» для того, чтобы более ясно увидеть
компоненты задачи. Особенно это полезно для описания
отношений, так как записанные в виде множества упо-
упорядоченных пар отношения нелегко расшифровываются.
Отношения — это множества, обладающие определен-
определенной структурой; их элементы имеют несколько компо-
компонент, и поэтому, в принципе, мы можем использовать диа-
диаграммы Венна для их изображения. Хотя этим методом
и можно воспользоваться, особенно при описании некото-
некоторых больших множеств чисел, существуют методы, ко-
которые более эффективны в общих ситуациях (включаю-
(включающих, в частности, бинарные отношения на небольших
множествах). В этом параграфе мы кратко рассмотрим
некоторые из них. Для описания этих методов использу-
используем множество
X — {а, Ъ, с, d)
и отношения Ix, Ux и R, где
R = {(a, Ь), (а, с), (Ъ, d), (с, е), (е, Ь)}.
Вначале рассмотрим метод, относящийся к традици-
традиционной аналитической геометрии. Начертим пару взаимно
перпендикулярных осей (ОХ — горизонтальная ось, а
OY — вертикальная ось) и на каждой отметим точки,
представляющие элементы множества X (рис. 2.2, а).
Теперь в правом верхнем координатном углу отметим
точки с координатами (х, у), у которых ieX и уеУ.
Множества, соответствующие Ix, Ux и R, изображены на
рис. 2.2, Ь, с и d.
Основной недостаток этого метода заключается в том,
что при увеличении |Х| трудно увидеть элементы в обла-
области и установить соответствие с точками, обозначающими
отношения. Чтобы преодолеть этот недостаток, можно
опустить точки и соединить стрелкой хе=2) и уей,
когда (х, у) принадлежит отношению (рис. 2.3). Ди-
Диаграмма, представляющая Ux, получилась довольно запу-
запутанной, но это естественно, поскольку число элементов в
40
Ux увеличилось. С другой стороны, отношения 1х и R
представлены наглядно, и легко увидеть их области опре-
определения и значений. Диаграмма для Ux наиболее неудоб-
неудобна в месте пересечения осей. Теперь, когда не использу-
используются координаты в областях определения и значений для
d
е
Ъ
Ь с
а
3)
с d
d
Рис. 2.2
расстановки элементов, отношения (как в первом мето-
методе) можно начертить параллельными. Поэтому, исполь-
используя параллельные вертикальные линии и двигаясь слева
направо (линия слева является областью определения),
мы получаем диаграмму, изображенную на рис. 2.4.
Здесь стрелки не требуются, так как мы знаем, что от-
отношения идут от области определения к области значе-
значений. Это приводит к двум возможностям: мы можем или
заменить стрелки прямыми линиями, или заменить две
линии, изображающие области определения и значений,
простой совокупностью точек. (Например, точка с в об-
41
d e S>
Рис. 2.3
e
d
3) с
Ъ
a
If
0
42
ласти определения является той же самой, что и точка,
представляющая с в области значений.) Это показано на
диаграмме, изображенной на рис. 2.5.
Итак, обозначены наиболее важные методы графиче-
графического изображения бинарных отношений. Они будут ис-
©
С/Мх\ /Л
(с? .-л АМЗтк / / \
Л
с*—~Н *
oR
пользоваться в оставшейся части книги. Обсуждение гра-
графических методов, связанных с соотношениями, мы про-
продолжим в гл. 7.
Упражнение 2.2.
1. Начертить диаграмму, представляющую отношение
р из упражнения 2.1, 1.
2. Начертить диаграмму, l. едставляющую отношение
N (см. упражнение 2.1, 5) на улице, имеющей десять до-
домов. Как изменится диаграмма, если улица является ту-
тупиком?
§ 3. Свойства отношений
Очевидно, что общие отношения, будучи только под-
подмножествами произведения множеств, не особенно инте-
интересны, поскольку о них можно сказать очепь мало. Од-
Однако, когда отношения удовлетворяют пекоторым допол-
дополнительным условиям, относительно них можно сделать
более содержательные утверждения. В этом параграфе
мы рассмотрим некоторые из основных свойств, которы-
которыми могут быть наделены отношения. Говорят, что свой-
свойство имеет место, если только выполнено соответствую-
соответствующее условие.
Определение. Пусть р — отношение на множест-
множестве А. Тогда:
а) р рефлексивно, если хрх для любого х^А;
б) р симметрично, если хру влечет урх;
в) р трапзитивно, если хру и уръ влечет хрг;
г) р антисимметрично, если хру и урх влекут х = у.
43
Терминология, введеппая здесь, вероятно, является
новой для читателя, однако он, по-видимому, знаком с
этими понятиями. Поясним их на следующих примерах.
Пример 3.1. Пусть
р = {(х, у): ijsNhi- делитель у),
о = {(х, у): i,yeNHi<y},
т = {(х, у): i,ye N\{1} a x я у имеют общий делитель}.
Тогда р:
а) рефлексивно, так как х/х = 1 для всех ieN;
б) несимметрично, поскольку 2 — делитель 4, но 4 не
является делителем 2;
в) транзитивно, так как если у/хeN и г/yeN, то
г) антисимметрично, так как если х/у <= N и у/х е N,
то х — у.
Аналогично о:
а) рефлексивно, так как а; < х для всех isN;
б) несимметрично, так как 2 < 3, но 3 ^2;
в) трапзитивпо;
г) антисимметрично, так как если х < у и у < х, то
х = у.
Наконец, х рефлексивно и симметрично, но не трап-
зитивно или антисимметрично. /
Пример 3.2. Пусть Р — множество всех людей, а
А и S определяются следующим образом:
А ={(х, у): х, у&Р ж х — предок у),
S — {(х, у)& Р я х и у имеют одних и тех же родителей}.
Очевидно, что А трапзитивпо, a S рефлексивно, симме-
симметрично и транзитивно. /
Заметим, что свойства симметричности и антисимме-
антисимметричности не являются взаимоисключающими. Для лю-
любого множества .X отношение 1х является симметричным
и антисимметричным. (Проверьте!) Мы можем также
иметь отношения, которые не являются ни симметрич-
симметричными, пи антисимметричными.
Пример 3.3. Пусть опять Р есть множество всех
людей. Определим отношение В такое, что хВу тогда я
только тогда, когда х является братом у. В семье, состоя-
состоящей из двух братьев р и q и сестры г, мы имеем ситуа-
ситуацию, изображенную на рис. 2.6. Отношение В не сим-
симметрично, так как рВг, но не гВр. Это отношение также
44
не является антисимметричным, так как pBq и qBp, хо-
хотя р и q различны.
В более общей ситуации мы можем интерпретировать
рассмотренные выше характеристики отношения путем
построения диаграммы:
а) отношение рефлексивно
тогда и только тогда, когда для
каждого узла (точки) на диаграм-
диаграмме существует стрелка, которая
начинается и заканчивается на
этом узле;
б) отношение симметрично то- Рис 2.6
гда и только тогда, когда для
каждой стрелки, соединяющей два узла, существует так-
также стрелка, соединяющая эти узлы в обратном на-
направлении;
в) отношение транзитивно тогда и только тогда, когда
для каждой пары узлов х и у, связанных последователь-
последовательностью стрелок от х к а\, от а\ к аг, •.., от ап-\ к а„, от
а„ к у, существует также стрелка от х к у;
г) отношение антисимметрично тогда и только тогда,
когда не существует двух различных узлов, связанных
парой стрелок.
Существует много других свойств отношений, кото-
которые можно было бы рассмотреть. Однако рассмотренные
выше свойства являются наиболее важными и будут ча-
часто использоваться в дальнейшем.
Упражнение 2.3.
1. Являются ли следующие отношения рефлексивны-
рефлексивными, симметричными, транзитивными или анситимметрич-
ными:
а) отношение на A, 2, 3, 4, 5} определяется как
{(а, Ь): а — Ъ четное);
б) отношение на {1, 2, 3, 4, 5) определяется как
{(о, Ъ): а + Ъ четное);
в) отношение на Р (множестве всех людей) опреде-
определяется как
{(о, Ъ): а и Ь имеют общего предка)?
2. Следующее утверждение ошибочно. Симметричное
и транзитивное отношение на 5 является также рефлек-
рефлексивным, так как aRb и bRa влекут aRa. Внимательно
45
изучив определения, найти ошибку. Построить отноше-
отношение на {1, 2, 3), которое является симметричным и тран-
транзитивным, но не рефлексивным.
3. Пусть р — отношение между А и В, а е А. Тогда
р(а) определено как множество {b: apb) а является под-
подмножеством В. Пусть на {—4, —3, —2, —1, 0, 1, 2, 3, 4}
определены следующие отношения:
р = {(а, Ь): а<Ь),
а-{(а, 6): Ь - К а < Ь + 2),
т = {(а, b):a2*Zb).
Какие это множества:
а) р@); б) о@); в) т@);
г) A)) A)) (
§ 4. Разбиения в отпошепия эквивалентности
Во многих вычислительных задачах берутся большие
множества и разбиваются таким образом, чтобы все ин-
интересующие нас ситуации можно было исследовать на
нескольких правильно выбранных примерах. Например,
один из путей получения качественной оценки характе-
характеристик языка программирования — это посмотреть кон-
конкретные программы, написанные на этом языке. Однако
каждый интересный язык, включая такие языки высоко-
высокого уровня, как Паскаль и Фортран, порождает бесконеч-
бесконечно много программ, и, следовательно, мы должны выби-
выбирать программы так, чтобы опи правильно отражали до-
достоинства и недостатки языка. Чтобы быть более кон-
конкретными, давайте в дальнейшем предполагать, что язык
имеет три основные управляющие структуры и четыре
метода доступа и более у него нет никаких особы к
свойств. Мы могли бы в качестве примера взять ceAib
программ, каждая из которых включает только одну ха-
характеристику языка (хотя, вообще говоря, каждая про-
программа может использовать более чем одну характеристи-
характеристику языка). Исследование этих програм тогда могло бы
покрыть большую часть свойств языка. Математически
это можно определить следующим образом.
Определение. Пусть А—непустое множество и
{Ах) — совокупность подмножеств A=1, ..., я, »sN)
таких, что
U At~A.
46
Совокупность этих подмножеств называется покры-
покрытием А. II
Пример 4.1.
{А, В) — покрытие A U В,
{A, A U В, В, С) — покрытие A U В U С. II
Используя понятие покрытия, можно обеспечить, что-
чтобы ни одно из свойств пе было пропущено, так как каж-
каждый элемент включен по крайней мере в одно из под-
подмножеств покрытия. Однако в общем случае могут
встречаться случаи дублирования. Если в дальнейшем
потребовать, чтобы элементы покрытия попарно не пе-
пересекались, то дублирования не будет. Отсюда возникает
понятие разбиения.
Определение. Разбиением непустого множества
А называется совокупность подмножеств 9*{А) таких,
что объединение всех элементов @*(А) совпадает с А п
все элементы !?(А) взаимно не пересекаются, т. е. А
разбито таким образом, что каждый элемент А содер-
содержится только в одном подмножестве разбиения. II
Пример 4.2.
{А, А'} — разбиение <§,
{А П В, А Л В', А' П В, А' П В'} - разбиение <Г,
{А\В, АПВ, В\А} — разбиение A U В. II
Разбиение определяется однозначно, и части разбиения
индуцируют особый род отношения, называемого отно-
отношением эквивалентности. Эти отношения ведут себя по-
подобно отпошению «=» между числами или множествами.
Выделяя основные свойства равенства, мы приходим к
следующему определению.
Определение. Бинарное отношение на мпожест-
ве называют отношением эквивалентности, если оно ре-
рефлексивно, симметрично и транзитивно. II
Пример 4.3. На множестве всех треугольников от-
отношение, определяемое как {(х, у): х и у имеют одина-
одинаковую площадь), является тривиальным отношением эк-
эквивалентности. Более интересно следующее отношение,
определенное на множестве всех программ: {(а, Ь): а и
Ь вычисляют одну и ту же функцию на определенной
машине). Это отношение является отношением эквива-
эквивалентности. /
Напомним, что мы рассматриваем более простые спо-
способы создания больших множеств, разбивая их на мел-
47
кие части, чем если бы в качестве этих частей брали
элементы множества. В настоящий момент у нас уже
имеется математический аппарат, однако недостает под-
подходящих простых обозначений. Сейчас это будет сделано,
после чего приведем несколько известных примеров.
Определение. Пусть р — отношение эквивалент-
эквивалентности на множестве А. Определим класс эквивалентно-
эквивалентности [х] для х <= А:
[х] = {у: xpyh
Таким образом, [х] есть множество всех элементов А,
которые р-эквивалентны х. В случаях, когда рассматри-
рассматривается только одно отношение эквивалентности, мы мо-
можем также использовать обозначение «=» (эквивалент-
(эквивалентно), поэтому
[х] = {у: хе* у),
В отдельных специальных случаях для обозначения эк-
эквивалентности иногда используют символ «~». Теперь
вместо проверки всего множества мы можем любым спо-
способом выбрать представителей (по одному от каждого
из классов эквивалентности), что упрощает вычисления.
Следующий пример иллюстрирует вышесказанное.
Пример 4.4. Пусть s — фиксированный элемент N;
отношение р. на Z:
р, = {(х, у): х — у = ns, где п е Z).
Рассмотрим случай s = 10. Тогда
[1]-{11,21,-9, 10 976 631,...},
[1066] - {66, 226, -24, ...}
и т. д.
В действительности существуют только десять раз-
различных классов эквивалентности. Целые 0, 1, 2, 3, 4, 5,
6, 7, 8, 9 принадлежат различным классам. Поэтому мы
можем использовать их в качестве представителей этих
классов. /
В вычислениях отношения эквивалентности представ-
представляют особый интерес, поскольку они ассоциируются о
различными алгоритмами, дающими один и тот же ре-
результат, или приводящими к одной и той же обработке
данных, или же представляющими одну и ту же инфор-
информацию о различных эквивалентных структурах данных.
Примером таких очевидных ситуаций является борьба с
трудностями, которые возникают ара исследования раз-
48
решимости. Такие факторы, однако, не вызывают про-
проблем, если множества образуются путем хорошо сконст-
сконструированных процессов с конечной базой. И все же ти-
типичным является случай, когда при описании даже «хо-
«хорошего поведения» требуется большое число деталей, в
связи с чем они должны быть здесь рассмотрены. Не-
Несмотря на это, мы будем возвращаться к подобным во-
вопросам в § 6 и в гл. 8 и 9.
По-видимому, наиболее известное отношение эквива-
эквивалентности знакомо читателю, хотя он мог и не внать,
что оно — отношение эквивалентности. Это отношение
связано с дробями. Рассмотрим множество ZXN. Пару
(а, Ь) мы можем рассматривать как дробь alb. Эти два
способа обозначения элементов Z X N являютея различ-
различными, но они «изоморфны». Мы будем их рассматривать
далее в § 1 гл. 5. Отметим, что можно переходить от од-
одной формы обозначения к другой.
До сих пор все было хорошо, однако существуют раз-
различные элементы в Z X N, которые желательно рассмат-
рассматривать как одни и те же, хотя записываются они по-
разному. Чтобы преодолеть эту трудность, определим от-
пошение эквивалентности на ZXN следующим образом:
(a, b)""(c, d) тогда и только тогда, когда a* d=»b« с.
Множество всех классов эквивалентности, определяемых
этим отношением на Z X N, называют рациональными чис-
числами и обозначают символом Q. Обычно выбирают тех
представителей классов, у которых самые малые а и Ь.
Следует упомянуть, что предполагается существова-
существование действительных чисел (множество действительных
чисел обычно обозначают через R). Эти числа можно
представить в форме
... О йя ... 6,2 d\ do 6i 62 •.. 6m .. ¦,
где каждое d< и 6j принадлежат множеству
{О, 1, 2, 3, 4, 5, 6, 7, 8, 9) = Z10, dn Ф О,
исключая случай п = 0. В частности, допускается беско-
бесконечная непериодическая десятичная дробь, хотя нули
перед dn обычно опускают. (Отрицательные числа пред-
представляют ненулевыми положительными числами со зна-
знаком минус.)
Заметим, что индекс отношения эквивалентности р
на множестве А — это количество частей А, индуцируе-
индуцируемых р (число р-эквивалентных классов).
4 Д. Кук, Г. Бей» 4Э
Упражнение 2.4.
1. Доказать, что любое отношение эквивалентности
порождает такое разбиение, что для любых х, у е А или
[х] = [у], или [х] П [у] = 0.
2. Пусть А — конечное множество. Какие отношения
эквивалентности дают наибольшее и наименьшее число
эквивалентных классов?
3. Если {А\, Ач. Ап) — разбиение А и А конеч-
конечное, показать, что
§ 5. Отношения порядка
Поскольку из понятия равенства (скажем, между
числами) возникает математическое понятие эквивалент-
эквивалентности, некоторые неравенства могут также использовать-
использоваться как модели для более широкого класса отношений.
Частичным порядком на множестве А назовем отно-
отношение, которое рефлексивно, антисимметрично и транзи-
тивно. Порядок (называемый также отношением поряд-
порядка) — это обобщение отношения «S на N. Поэтому мож-
можно легко проверить требуемые три свойства. Заметим,
что мы могли бы в качестве определения взять отноше-
отношение <. Тогда отношение порядка было бы только тран-
зитивно. Поэтому свойство транзитивности является наи-
наиболее важным для отношения порядка.
Определив отношение <, можно определить отноше-
отношение < следующим образом:
a<b**-a<b я аФЬ.
Аналогично, если задано <, то
Ъ ¦**¦ а = Ъ или а < Ь.
Пример 5.1. Пусть задано произвольное множест-
множество А. Тогда отношение s на {Р(А) есть тривиальное
отношение порядка. (ХеХ для всех X; если X s У и
YsX,ToX°=Y;Xs=YnY^Z^X?=Z.) II
Отношение порядка р на А называется полным, если
для любых х, у е А или хру, или урх (или же выпол-
выполняются оба).
Пример 5.2. Очевидно, что порядок на подмноже-
подмножествах данного множества не является полным. Естест-
Естественный порядок чисел на действительной оси R являет-
является полным.
50
По мере достижения прогресса в изучении матема-
математики становится ясным, что математика не набор разроз-
разрозненных идей, а совокупность связанных между собой
концептуальных понятий, которые используются во мно-
многих непохожих друг на друга ситуациях. Отсюда следу-
следует, что, если основной принцип установлен и исследован,
он фактически единым образом решает проблемы для
всех этих различных случаев. Следующий пример явля-
является простой иллюстрацией этой идеи.
Пример 5.3. На основе порядка, определенного на
N, мы можем формально получить обычные отношепия
порядка на множествах чисел Z, Q и R. (Как уже упо-
упоминалось, исследование N будет проведено в § 3 гл. 3.)
Вначале рассмотрим Z. Чтобы облегчить рассужде-
рассуждения, разобьем Z следующим образом:
Поэтому А = {—х: х е Ш. Определим отношение (кото-
(которое будем называть полным отношением порядка) на Z
рассмотрением всевозможных элементов х и у из разбие-
разбиения ОТ U @> U А).
Если х = у, то х < у и у ^ х. Пусть х Ф у. Тогда:
а) если х, у е N, то порядок в Z тот же самый, что
и в N;
б) если х, у&А, то
х < у тогда и только тогда, когда —у < — х в N
(т. е. —5 «S —4, так как 4 «S 5);
в) если х = 0 и у «= N, то х «S у;
г) если х е А а у = 0, то х «S у;
д) если «еЛ и jr«=N, то х «S у или в противном
случае у<х.
На основе порядка на Z и обычных арифметических
операций с целыми числами мы можем определить поря-
порядок на Q:
a/b < c/d тогда и только тогда, когда а • d^b • с.
Проверку этого утверждения оставляем в качестве
упражнения. Наконец, определим отношение порядка на
множестве действительных чисел R. Рассмотрим деся-
тичиые представления двух действительных положитель-
положительных чисел:
D='...0dn...d2dldQ6i82...,
C = ...OcIB...C2C1Co'Kl1B....
4» 51
Если dt =» с( и б« = 4i для всех I, то D — C и, следова-
следовательно, Z)< С и C^D. В противном случае:
а) если dn Ф 0, ст "»*• 0 и га Ф т, то D < С, если га < т,
иС<Д если m < га;
б) если л = т и d( т6 ct, но dj = Cj для всех / таких,
что i < ; «S га, то из d{ < с, следует, что D < С, и, обрат-
обратно, если d<di, то C<D;
в) если т — п и d< = c( для всех 2, но bh?"\k для не-
некоторых к и 6j = ifj для всех / таких, что 0<j<k, тог-
тогда С «S D, если if» < 6\, и I> «S С, если 6ft < fh.
Читатель может проверить это самостоятельно. Отри-
Отрицательные числа могут быть исследованы так же, как
в Z. /
Множество X вместе с отношением порядка < назы-
называется частично упорядоченным множеством (обознача-
(обозначается (X, <)). Тогда любой элемент це(Х, <) такой, что
х ^ и и у ^ и, называется верхней границей х и у. Ана-
логично* если ls(X, «S), 1 «S х и 1<у, то 1 является
нижней границей х и у. Множество всех верхних границ
х я у является подмножеством X и упорядочено отноше-
отношением <. Если существует единственный наименьший
элемент этого множества, т. е. если существует це
е(Х, <) такое, что а; < ц, у < ц и ц<м для любой
верхней границы и, то ц называют верхней гранью
(sup) х ж у. Аналогично, если существует единственная
наибольшая нижняя граница а: и у, ее называют нижней
гранью (inf) x и у. Мы отложим изучение верхней и
нижней граней до § 5 гл. 5, где будут изучаться
решетки.
Наконец, заметим, что использование естественного
порядка на R определяет новые множества. Их называ-
называют интервалами:
[а, Ь] = {х'. ieR, а «?х< Ь}
есть замкнутый интервал (отрезок) от а до Ь;
]а, Ь[ — {х: isR, а<х< Ъ)
есть открытый интервал от а до Ь. В каждом случае
числа а и Ь называются концевыми точками.
Замкнутый интервал включает в себя концевые точ-
точки, а открытый нет. Удобно также определить полуот-
полуоткрытые интервалы:
[a, b[ = {x: ieR, а <х< Ъ),
]а, 6] = {i;jeR,<i<i< Ь).
52
Для удобства будем использовать следующие обозна-
обозначения:
]—<», а] = {х: х<а),
]—«о, а[ = {ж: х<а),
[а, оо[ = {ж; а < ж),
Хотя интервалы в множества чисел в общем-то не яв-
являются центральной частью нашего рассмотрения, мы
увидим, что их удобно использовать время от времени.
Упражнение 2.5.
1. Пусть А — произвольное множество и р — отноше-
отношение на множестве &>(А)Х&>(А), определенное следую-
следующим образом:
(Р, Q)p(X, Y) тогда и только тогда, когда
(
Является ли р отношением порядка?
2. Пусть А — произвольное множество и о — отно-
отношение на iP(A)Xi?(A), определенное следующим об-
образом:
(Р, Q)o[X, Y) тогда и только тогда, когда
P^XhQsY.
Является ли о отношением порядка? Если да, то явля-
является ли этот порядок полным?
3. Пусть т и я — отношения на N2, определяемые
соотношениями:
(а, Ь)х(с, d) тогда и только тогда, когда а<с и b<d;
(а, Ь) я (с, d) тогда в только тогда, когда а^с в Ъ > d.
Являются ли т и я отношениями порядка?
4. Пусть я определено на положительных элементах
Q следующим образом:
(а/Ь)я(с, d) тогда и только тогда, когда a*d^b«с.
Показать, что я является полным отношением порядка.
§ 6. Отношения на базах данных и структурах данных
Как уже установлено, все вокруг определяется отно-
отношениями. Достаточно лишь взять отношение s на пере-
переменных {xi, ..., хп) так, чтобы можно было построить
53
множество
((xi, хг, ..., хп): s(xu x2, ..., а:») истинно).
Пусть задан набор (х\, ..., х„). Отношение
s(x\, ..., хп) можно разрешить, т. е. выяснить,
s(x\, ..., хп) истинно или ложно. Конечно, $ не обяза-
обязательно будет представлено «хорошей» формулой. Не-
Нетрудно показать, что вместо отношения $, определяюще-
определяющего множество наборов длины га, любое множество таких
наборов также определяет отношение (и содержатель-
содержательные свойства s). Эти два подхода эквивалентны.
Определение. При обработке данных наборы из
п элементов называют записями; элементы этих набо-
наборов называют полями. Записи, определяющие отношение,
обычно содержатся в файле. Если потребовать, чтобы
несколько файлов содержали совокупность записей,
удовлетворяющих некоторым отношениям, то мы полу-
получим (относительную) базу данных.
Замечание. Для случая обработки данных мы сей-
сейчас употребили термин «поле». В гл. 5 мы будем упо-
употреблять этот термин в математическом смысле, однако
в данном случае это не приводит к недоразумению.
Таким образом, это дает нам первый реальный при-
пример отношений, которые в большей мере связаны с вы-
вычислениями, в частности, с прикладными задачами. Тем
не менее краткое обсуждение некоторых простейших
свойств баз данных не только обеспечивает основу даль-
дальнейшего математического исследования отношений, но и
проясняет некоторые факторы, понимание которых необ-
необходимо для эффективного управления системами баз
данных.
Современная теория баз данных включает в себя
изучение так пазываеыых нормальных форм, однако обо-
обоснование некоторых из них очевидно лишь в простых
случаях. Мы рассмотрим только три формы для следу-
следующих задач:
— вставить новый набор из п элементов;
— удалить набор из п элементов;
— модифицировать набор, содержащий п элементов.
Начнем с простейшей нормальной формы.
Определение. Файлы в первой нормальной фор-
форме ANF), или — более просто — нормализованные фай-
файлы, имеют записи фиксированной длины, состоящие из
элементов, взятых из множеств, чьи элементы далее не
могут быть разбиты, и в каждый момент времени этот
54
файл может быть представлен как Массив значений
MXN. Каждая запись, будучи набором из п элементов,
может быть записана как строка массива. /
Пример 6.1. Рассмотрим отношение FAM1 (см.
выше), в котором мы собрали вместе родителей и детей.
Каждая запись содержит в указанном порядке фамилию
и имена отца, матери и детей. Следовательно, мы имеем
записи
(Смит, Джой, Джойс, (Сэлли, Бен))е FAM1,
(Браун, Фред, Лиза, (Люси))е FAM1.
Теперь, если мы обозначим через F и М множества от-
отцов и матерей, то из определепия следует, что
Джой (Смит) е F, Джойс (Смит) е М,
Фред (Браун) е F, Лиза (Браун) е М.
Таким образом, Люси является членом семьи Браун, но
Сэлли и Бен не являются детьми семьи Смит. Так как
в этой семье более одного ребенка, то соответствующая
вапись больше, и, следовательно, нарушены условия пер-
первой нормальной формы.
Из FAM1 мы можем получить отношение FAM2, по-
построив его из S, F, М и С, где S — множество фамилий,
а С — множество детей, путем конструирования записей:
(Смит, Джой, Джойс, Сэлли),
(Смит, Джой, Джойс, Бен),
(Браун, Фред, Лиза, Люси).
Отношение FAM2 находится в 1NF и может быть пред-
представлено при помощи табл. 2.1.
Таблица 2.1
Фамилия
Смит
Смит
Браун
Отец
Джой
Джой
Фред
Мать
Джойс
Джойс
Лива
Ребенок
Сэлли
Бен
Лижи
Однако не совсем ясно, что будет, если, например,
супруги Джонс не имеют детей? Если мы хотим иметь
в файле запись о них, то следует пересмотреть структу-
структуру файла. Это означает, что все следует начать сначала.
Введем следующую терминологию.
55
Определение. При использовании таблицы для
изображения отношения (файла с га-мерными набора-
наборами/записями, записываемыми в виде строк) столбцы на-
называются атрибутами. II
Следовательно, ФАМИЛИЯ, ОТЕЦ, МАТЬ и РЕБЕ-
РЕБЕНОК являются атрибутами различных полей в FAM2.
Для получения доступа к записям в файле используют-
используются так называемые ключи. Более точно это может быть
определено в терминах атрибутов.
Определение. Атрибут или (упорядоченное)'
множество атрибутов, чьи значения однозначно опреде-
определяют вапись в файле, называются ключом этого файла.
(Заметим, что в файле может быть много различных
ключей.) /
Каждый ключ отношения/файла FAM2 должен вклю-
включать атрибут РЕБЕНОК.
Перейдем к другим примерам.
Пример 6.2. Каждый владелец компьютера дол-
должен покупать к нему вапасные части. Поэтому мы мо-
можем рассмотреть файл, структура которого показана в
табл. 2.2,
Табджца 2.2
КОМПАНИЯ
АСЕ
IBL
DATAMETZ
PRINTAGO
WOOLIES
RTX
OXONDATA
ОТДЕЛЕНИЕ
LONDON
LONDON
BIRMINGHAM
MANCHESTER
BIRMINGHAM
LONDON
OXFORD
МЕНЕДЖЕР
SMITH
JONES
JONES
BROWN
BROWN
SMITH
WILSON
Атрибут КОМПАНИЯ является ключом в SUP1;
вся другая информация в файле доступна при посредст-
посредстве ключа. Таким образом, например, можно извлечь ат-
атрибут ОТДЕЛЕНИЕ при помощи ключа WOOLIES или
же МЕНЕДЖЕР из RTX. /
Определение. Если запись локализована с по-
помощью некоторого ключа, то поле, выделяемое из этой
записи, называется проекцией. В данном контексте про-
проекцией является «из». Будем также говорить, что эти
атрибуты зависят от ключа. И
56
На рис. 2.7 представлен графический пример зависи-
зависимостей в SUP1.
Пример 6.3. Модифицируем файл SUP1 с целью
включения туда информации об имеющихся на складе
запасных частях и об их количествах, которые отдельный
Рио. 2.7
поставщик желает продать в отдельной сделке. Вклю-
Включим в файл также код поставки, из которого мы можем
выяснить скорость и частоту поставок. Во избежание
излишней детализации введены номер компании и но-
номер запасной части (табл. 2.3). /
Таблица 2.3
КОМПАНИЯ
1
1
1
2
2
3
3
3
5
5
6
МЕСТО РАС-
РАСПОЛОЖЕНИЯ
LONDON
LONDON
LONDON
LONDON
LONDON
B'HAM
B'HAM
B'HAM
B'HAM
B'HAM
LONDON
ПОСТАВЩИК
2
2
2
2
2
4
4
4
4
4
2
ЗАП.
ЧАСТЬ
1
2
3
2
4
2
3
4
1
3
1
КОЛИЧЕСТ-
КОЛИЧЕСТВО
10
1
10
2
5
2
10
4
10
10
10
Из табл. 2.3 выясним, какие преобразования мы мо-
можем делать с SUP2, а какие нет:
а) вставка. Например, мы не можем добавить в файл
вапись, указывающую, что компания 4 (PRINTACO) на-
находится в Манчестере, без указания деталей, которые
она может поставлять;
б) удаление. Если компания 6 (RTX) прекратила
поставки запчастей 1, тогда мы обязаны удалить все
записи, относящиеся к этой компании и имеющие в по-
поле ЗАП. ЧАСТЬ код 1;
«7
в) модификация. Если код поставщика для Лондона
изменился, например, из-за транспорта, то соответствую-
соответствующее поле должно быть изменено в каждой записи, где
есть код LONDON в поле МЕСТО РАСПОЛОЖЕНИЯ.
Что можно сделать для того, чтобы уменьшить или
отодвинуть эти проблемы? С практической точки зрения
мы должны выделить информацию в SUP2 так, чтобы
по возможности избежать повторений. Таким образом,
Таблица 2.4
SUP3
Таблица 2.5
КОМПА-
КОМПАНИЯ
1
2
3
5
в
МЕСТО РАС-
ПОЛОЖЕ-
ПОЛОЖЕНИЯ
LONDON
LONDON
B'HAM
B'HAM
LONDON
ПОСТАВ-
ПОСТАВЩИК
2
2
4
4
2
КОМ-
ПА-
ПАНИЯ
1
2
3
4
5
в
МЕСТО РАСПО-
РАСПОЛОЖЕНИЯ
LONDON
LONDON
B'HAM
M'CHESTER
B'HAM
LONDON
ПО-
СТАВ-
СТАВЩИК
7
7
4
3
4
7
ЗАП. ЧАСТЬ
КОМПА-
КОМПАНИЯ
1
1
1
2
2
3
3
3
5
5
6
ЗАП.
ЧАСТЬ
1
2
3
2
4
2
3
4
1
3
1
КОЛИЧЕ-
КОЛИЧЕСТВО
10
1
10
2
5
2
10
4
10
10
10
ЗАП. ЧАСТЬ
КОМПА-
КОМПАНИЯ
1
1
1
2
2
3
3
3
5
5
ЗАП.
ЧАСТЬ
1
2
3
2
4
2
3
4
1
3
КОЛИ-
КОЛИЧЕСТВО
10
1
10
2
5
2
10
4
10
10
мы получаем возможность вставки/удаления части запи-
записи в SUP2. Возможное и, на наш взгляд, разумное раз-
разделение дается в SUP3 (табл. 2.4). Тогда остаток ин-
информации в SUP2 может содержаться в поле
ЗАП.ЧАСТЬ. Используя эту конфигурацию, можно,
например:
а) включить в SUP3 запись, означающую, что компа-
компания 4 находится в Манчестере (код поставщика 3);
68
б) удалить ссылку на компанию 6 как на поставщи-
поставщика запчасти 1, но оставить соответствующий код в SUP3;
в) изменить код поставщика для LONDON на 7 пу-
путем вамены только трех входов, соответствующих компа-
компаниям с кодом 1, а не всех шести.
Результаты этих изменений приведены в табл. 2.5.
Это уже значительно лучше, однако все же может быть
SUP3
КОМПАНИЯ ЗАП. ЧАСТЬ
КОЛИЧЕСТВО
ЗАП. ЧАСТИ
Рис. 2.8
еще усовершенствовано. Чтобы увидеть, в каком направ-
направлении продолжать исследования, отделим ключи и под-
подчиненные части (рис. 2.8). Заметим, что ЗАП. ЧАСТЬ
требует объединенного ключа.
Все не-ключи непосредственно связаны с ключом.
Это дает нам следующее свойство нормальной формы. II
Определение. Файл имеет вторую нормальную
форму BNF), если он имеет форму 1NF и неключевые
атрибуты полностью независимы от ключа. /
Пример 6.3 (продолжение). Файл SUP3 все еще
является достаточно сложным в том смысле, что для
данной записи ПОСТАВЩИК может быть установлен при
помощи исследования поля КОМПАНИЯ или же поля
МЕСТО РАСПОЛОЖЕНИЯ. Это является причиной то-
того, что в требовании а) код поставщика для Манчестера
должен быть вставлен перед записью кода 4 компании,
а требование б), возможно, потребует изменить более
одной записи для модификации единственного поля дан-
пых, относящегося к коду поставщика. На практике мы
можем убрать эту проблему проектированием SUP3 в
SUP4 и DEL (табл. 2.6). (Заметим, что коды поставщи-
поставщика, изменяемые таким образом, препятствуют той воз-
возможности, что любые другие записи в файле вызывают
противоречивую информацию. В SUP3 можно иметь за-
запись вида «ПОСТАВЩИК КОМПАНИИ 6-2» и «ПО-
59
СТАВЩМК КОМПАНИИ 1-7» на некотором этапе мо-
модификации SUP2, несмотря на тот факт, что обе компа-
компании находятся в Лондоне.)
Зависимость отношений в SUP4 и DEL изображена
на рис. 2.9. II
Нетранзитивность отношения зависимости является
внутренним свойством, из которого возникает понятие
третьей нормальной формы.
Таблица 2.6
КОМПАНИЯ
1
2
3
4
5
в
МЕСТО РАСПО-
РАСПОЛОЖЕНИЯ
LONDON
LONDON
B'HAM
M'CHESTER
B'HAM
LONDON
МЕСТО РАСПО-
РАСПОЛОЖЕНИЯ
LONDON
B'HAM
M'CHESTER
ПОСТАВЩИК
7
4
3
Определение. Файл находится в третьей нормаль-
нормальной форме CNF), если он является файлом 2NF, и каж-
каждый атрибут, не являющийся ключом, нетранзитивным
образом зависит от ключа. /
Возможен и другой путь — каждый атрибут, не яв-
являющийся ключом, зависит только от ключа и ни от че-
чего другого.
Как было отмечено ранее, существует много других
«нормальных» форм, но мы не ставим изучение файлов
1 КОМПАНИЯ
>
МЕСТО РАСПОЛОЖЕНИЯ
SUP4
МЕСТО РАСПОЛОЖЕНИЯ
ПОСТАВЩИК
DEL
Рис. 2.9
своей целью в дальнейшем. Достаточно лишь иметь в
виду, что информация в файлах является одной из реа-
реализаций математического понятия отношения.
Практическое использование отношений SUP4 и DEL
требует явной связи атрибута МЕСТО РАСПОЛОЖЕ-
РАСПОЛОЖЕНИЯ файла SUP4 с атрибутом МЕСТО РАСПОЛОЖЕ-
РАСПОЛОЖЕНИЯ файла DEL. Это — отношение эквивалентности
60
(между компонентами различных файлов, имеющих одно
и то же имя). Подобные отношения эквивалентности мо-
могут быть использованы для определения внутренних свя-
связей и других структурных данных. В качестве иллюст-
иллюстрации рассмотрим рис. 2.10. Диаграмма на рис. 2.10, а
а
Л
1
2
3
4
5
2
а
3
Ъ
S
0
с
0
а
d
0
0
е
0
1
г
3
4
5
0
е
. 0
5
Ь
3
0
в
0
2
а
г
0
d
0
Рис. 2.10
изображает дерево, диаграмма на рис. 2.10, Ь подобна
диаграмме структурных данных, а диаграммы на
рис. 2.10, cad описывают их возможные применения.
Отметим, что отношения эквивалентности различны, но
результирующие структурные связи сохраняются. С ма-
математической точки зрения это является разбиением на
классы эквивалентности. Следовательно, мы можем опре-
определить произвольное представление этого дерева как эле-
элемент множества Т = DIE, где
д = {а = (ж, а, р), Ь=*(у, b,z), c = (u, с, v),
d=(9, d, r),e=(s, e, t)),
Эти вопросы будут обсуждаться в § 4 гл. 3.
61
§ 7. Составные отношения
Подобно тому как мы устанавливали внутренние
связи в файлах, для выделения некоторых данных из
информации (например, ПОСТАВЩИК и МЕСТО РАС-
РАСПОЛОЖЕНИЯ 3 посредством файлов DEL и SUP4 в
примере 6.3) часто приходится связывать бинарные от-
отношения друг с другом. Руководствуясь предыдущими
рассуждениями, можно определить это понятие следую-
следующим образом.
Определение. Пусть заданы множества А, В и С
и отношения а между А и В и р между В и С. Опреде-
Определим отношение между А и С следующим образом: опо
действует из А в В посредством а, а затем аз В в С по-
посредством р. Такое отношение называют составным и
обозначают р ° а, т. е.
(р-о)(а)-р(о(а)). /
Следовательно, (ж, J/)s(p°o), если существует zeZ?
такое, что (х, z)&o и (г, г/)^р. Отсюда следует, что
iZ5po<, = о~'^р. Чтобы проиллюстрировать ситуацию, рас-
рассмотрим рис. 2.11. Области определения и значений а и
р заштрихованы в разных направлениях. Следовательно,
сегменты с двойной штриховкой на А, В и С представ-
представляют собой iZ5poO, 2b9 Л Ша и 32Ро„ соответственно.
Замечание. Из записи отношений о и р следует,
что они применяются справа налево. Следовательно,
(р • о) (а) означает, что вначале берется о и преобразу-
преобразуется посредством о, а затем преобразуется посредством
р. В алгебре это иногда записывают в виде аор. Следу-
Следует обращать внимание при чтении других математиче-
математических книг на то, какой порядок выполнения отношений
принят в той книге.
62
Пример 7.1. Пусть аир — отношения на N такие,
что
а = {(х, x+i): ieN), р = {(z2, х): хеШ.
Тогда
3), = {х2: х е N>, 0„ = {х: х, х + 1 е N) = N,
- {х: х е N и а; + 1 = г/2, где у е N) = {3, 8, 15, 24, ...}
(рис. 2.12). /
В случае, когда мы рассматриваем отношение на
множестве, оно может быть скомбинировано само с
N
собой. Например, используя отношения из примера 7.1,
имеем
о• а = {(ж, х + 2): хе N} и р• р = {(ж4, i):js N}.
Эти отношения можно также обозначать соответственно
о2 и р2. В общем-то эти обозначения не совсем законны
для множеств, однако их легко можно обосповать, по-
поскольку если (х, i/)eo»o, то ((х, z), (z, y))&aXa
при некотором z; никакого недоразумения при этом пе
возникает, поскольку известна структура получаемого
результата.
Используя это обозначение, мы можем определить о"
для любого neN,n>l, следующим образом:
о" = {(х, у): xoz и zan~ly для некоторого z).
Если мы вновь возьмем отношения о и р из примера 7.1,
то получим
о" = {(а:, х + п), хеЮ и р" *= {(х2П, х): jeN},
Хотелось бы рассмотреть вопрос о том, насколько в этих
63
случаях применима аналогия с умножением. Пусть А —
множество, a R— отношение на А. Тогда отношения
Ia'R, R и R°Ia эквивалентны; поэтому 1А является
тождественным отношением на А, которое ведет себя
подобно числу 1 по отношению к умножению чисел.
Чтобы дополнить аналогию, желательно было бы иметь
возможность писать JF? • JF? = /А = R • R~l. Однако в об-
общем случае этого делать нельзя. Для того чтобы иметь
такую возможность, необходимо наложить дополни-
дополнительные условия, которые мы рассмотрим в сле-
следующей главе.
Рассмотрим теперь несколько упражнений. Они изо-
изображают ситуации, которые «легко описать» в математи-
математических терминах, однако следует заботиться о том, что-
чтобы в отношение включались только те пары, которые
ему принадлежат. Мы обнаружим, что иногда полезно
воспользоваться диаграммами.
Упражнение 2.6.
1. Пусть R и S определены на Р, где Р — множест-
множество всех людей, следующим образом:
JF? =»{(ж, у): х, у sP и х является отцом у),
S «¦ {(х, у): х, у е р и х — дочь у}.
Описать явно следующие отношения:
а) Д2;б) S2; в) R'S; г) S'R;
д) S • Я; е) Я • S; ж) Д~!»5;
a) S-1 • R; и) 5 • S~l; к) 5 • Д-».
§ 8. Замыкание отношений
Понятие замыкания является фундаментальным ма-
математическим понятием и используется в большинстве
разделов математики. Чтобы проиллюстрировать это по-
понятие, рассмотрим следующий пример.
Возьмем объект хо и процесс р, который порождает
множество и определяет последовательность xi, Х2, ...
..., хп, ... такую, что
64
Множество, содержащее все элементы всех последова-
последовательностей, которые могут быть выведены при помощи
р, и начинающиеся с хо, называется замыканием процес-
процесса р относительно хо. Поэтому «ответ» будет содержать-
содержаться в р"(хо) при некотором п. Однако мы не знаем зара-
заранее значение п. Более того, если мы возьмем произволь-
произвольный элемент у из этого замыкания и выполним процесс
р, начиная с у, то не получим ничего нового. Результат
уже содержится в замыкании. Множество не может
быть расширено таким путем (оно замкнуто).
Пример 8.1. Возьмем квадрат S, размеченный, как
это показано на рис. 2.13, и определим процесс г следу-
следующим образом. Из заданного положения S процесс г по-
порождает множество всех положений, получаемых в ре-
результате поворота по часовой стрелке на прямой угол.
В
D С
Рис. 2.13
Рис. 2.14
Таким образом, г (S) дает конфигурацию, изображенную
на рис. 2.14. После применения г четыре раза, мы вер-
вернемся к положению, с которого начали, и, следователь-
следовательно, вамыкание в данном случае есть множество из че-
четырех позиций.
А В
D С
D А
D,
с в
С О
?
В А
в
A B
}¦
II
Рассмотрим теперь, что произойдет, если процесс оп-
определить при помощи отношения. (В действительности
это всегда возможно, потому что мы можем определить
подходящее отношение при помощи множества {(х, у):
уер(х), где р — изучаемый процесс).) Для построения
замыкания отношения А достаточно иметь составные
отношения А, А2, ..., Ап, ..., которые затем комбиниру-
комбинируются обычным теоретико-множественным путем.
Ъ д. Кун, г. Бейз 65
Определение. Транзитивным замыканием (или
просто аамыканием) отношения А на множестве назы-
называется бесконечное объединение
U Ап = A U A2 U A* U • • • 7/
Транзитивность замыкания отношения следует, оче-
очевидно, из его определения, однако слово «транзитивное»
часто включают, чтобы подчеркнуть различие между
этой и подобной ей операцией, которая вскоре будет оп-
определена. Транзитивное замыкание отношения А обозна-
обозначают А*.
Пример 8.2.
1. Пусть R — отношение на N такое, что R =
-{(*. У)- ух+1). Тогда Д+•={(*, у): х<у).
2. Пусть о — отношение на Q такое, что о =
= {(х, у): х<у). Тогда о+ ¦= а.
3. Пусть р — отношение на Q такое, что р «=»
«= {(х, у): х* у = 1). Тогда
р+{{х, х): х -5*0} Uр.
4. Пусть L — множество станций Лондонского метро
и в, Ъ и с — последовательные станции. Если отношение
N на L определено как N = {(х, у): х является следую-
следующей за у станцией), то (а, Ь) и (b, c)e N и (а, а),
(Ь, 6), (с, с) и (а, clejf. Следовательно N+ = UL~*
LXL II
Из этих примеров легко видеть, что замыкание отно-
отношения в общем случае не является рефлексивным. Од-
Однако иногда удобно сделать его таким. Это можно легко
сделать. Вначале мы примем удобное допущение, что
тождественное отношение на X, I «• {(х, х): * е X) яв-
является нулевой степенью произвольного отношения на
X. Таким образом, А0 = / для любого А.
Определение. Рефлексивным замыканием А * от-
отношения А называют множество
А* - 0 Ап,
Замыкания отношений связаны между собой очевидный
соотношением
ев
Пример 8.3. Используя отношения, определенные
в предыдущих примерах, получаем
/?* = {(*, y):x<y}t o* = {(x,y): х^у),
р* = р+11{@, 0)}, N*-N*. II
Практические методы получения замыканий отноше-
отношений будут обсуждаться в гл. 6, 7.
Упражнение 2.7.
1. Используя отношения R a S упражнения 2.6, опи-
описать замыкания следующих отношений:
а) Л+; б) S*; в) Л*; г) 5*;
д) (S.S-')*;e} (Д-1.Д)*;ж) E2
ГЛАВА 3
ФУНКЦИИ
Понятие функции может быть уже известным чита-
читателю, однако в этой главе мы будем рассматривать
функции как множество бинарных отношений. Собствен-
Собственно, будет дано определение функции и близкого к ней
понятия отображения и изучены различные свойства, ко-
которыми они обладают. Затем функции будут использова-
использованы для того, чтобы формализовать процесс вычислений
и дать определение мощности множества. В заключение
будут рассмотрены конкретные функции, представляю-
представляющие особый интерес, и функции, которые удобно опре-
определить с помощью операторов.
§ 1. Функции и отображения
Определение. Бинарное отношение р между
множествами А и В является функцией, если из арЬ и
аре следует, что b = с; поэтому для любого х&А суще-
существует одно у&В такое, что хру. Можно дать определе-
определение функции следующим образом:
р(я)=0 ИЛИ р (?)={#}. /
Следует помнить, что если р(х) существует (т. е.
р(х)Ф0), то этот элемент единствен. В случае, когда
р(х)Ф0, обычно опускают скобки при обозначении
множества и записывают
Функции обычно обозначают строчными латинскими
буквами /, g, h, ... или в специальных случаях особыми
сочетаниями, например sin, log, Fn, ... Если /—функция
между множествами А и В, то этот факт может быть
записан как /: А -*¦ В. В дальнейшем, если х&А и х]у,
мы будем обозначать, это соотношение следующим об-
образом:
Это обозначение часто используют для того, чтобы опи-
описать правило, определяющее функцию (если оно суще-
существует) .
Пример 1.1. Функция /: А -*¦ А, где А "={—1, 0, 1),
определяется соотношением /: ая-* х3. //
Даже когда / не является отображением (см. ниже),
мы часто будем использовать фразы типа «/ отображает
х в я3». Понятия области определения и области значе-
значений в данном случае содержательны, поскольку функция
является отношением, однако следует заметить, что об-
обратная функция может не существовать.
Пример 1.2. На множестве { — 1, 0, 1} отношение /:
х+-+ х2 является функцией, но обратной функции не су-
существует, поскольку /"'(I)*" (—1, I). II
Определение. Функция /: А -*¦ В является ото-
отображением, если ее область определения совпадает с А,
т. е. 2Dt ¦» А. Функции, не являющиеся отображениями,
называют частичными. Отображение на множество на-
навивают трансформацией {преобразованием).
Замечание. Часто терминология отличается от
принятой в этой книге, особенно в американских книгах.
Термины «функция» и «отображение» иногда использу-
используют как синонимы, а отображение в том смысле, как мы
его определили, называют полной функцией.
Конечно, каждая функция может рассматриваться
как отображение на своей области определения; иногда
это полезно, когда строятся сложные функции. Как мы
увидим в последующих параграфах, исследовать свойст-
свойства функций легче в тех случаях, если на функцию нало-
наложить некоторые условия.
Функция /: А -* R называется функцией, принимаю-
принимающей действительные значения, а функция, область опре-
определения которой совпадает с R, называется вещест-
вещественной.
Рассмотрим ограничения, которые помогут нам по-
понять, что происходит с отдельными элементами в ре-
вультате применения к ним функций. Будем занимать-
заниматься классификацией функций, определенных на множест-
множествах, и предполагать, что мы имеем мало информации об
этих множествах. Далее будут рассмотрены функции на
множествах, где определены такие операции, как сло-
сложение.
Определение. Функция /: А -*¦ В называется
сюръективной (на), если $!, = 5. Это означает, что для
данного бе В имеем f~l{b)?=0. Функция /: А -* В яв-
69
ляется инъективной, если из а\, йъ&А и
следует, что а\ = а%. II
Итак, если /: А -* В и / сюръективна, то для любого
Jefi имеем /~'(&)е &(А)\0. Это может быть проин-
проинтерпретировано следующим образом: каждая точка из В
является «острым концом» по крайней мере одной /-стре-
/-стрелы, выходящей из А. Проиллюстрировать эту ситуацию
достаточно трудно (исключая тривиальные случаи).
С другой стороны, наглядную характеристику инъек-
тивности легко дать в виде ограничения или запрета.
Рис. 3.1
Функция / не инъективна в случае, изображенном на
рис. 3.1, а.
Для сравнения на рис. 3.1, Ь изображено зеркальное
отражение, которое отличает функцию от бинарного от-
отношения.
Если /: А -*¦ В инъективна и a&2Dt, то a = /"'(/(а)).
Далее, если Ь «= 91и т. е. Ъ е 3)}-1, и в данном случае
/~1 — Функция, то Ь =/(/-'(&))•
Следовательно, если мы определим функцию 1Х: X -*¦
-*¦ X как тождественное отображение на X, т. е. 1х-
!-¦ х для всех х^ X, тогда, если / инъективна, то
Г
ГЧ-1я>,
Используя функцию / из примера 1.2, мы видим, что
/"'(/A))^ 1. Это означает, что первое из этих тождеств
в общем случае неверно, однако, как мы увидим в § 2,
вычисления становятся гораздо легче в случаях, когда
оба тождества имеют место. Прежде чем продолжить из-
изложение, обсудим терминологию, объединяющую введен-
введенные выше свойства. Функция / биективна, если она
сюръективна и инъективна. Биективное отображение на-
называют биекцией. Следовательно, используя биекцию /
между А -а В, можно брать элементы из А и переходить
в В посредством /, осуществляя некоторые вычисления,
Переход назад к А осуществляется посредством /"',
70
Термины инъекции и сюръекции также применяют-
применяются (для описания инъективного и сюръективного ото-
отображений), однако мы редко будем их использовать.
Упражнение 3.1.
1. Какие из указанных ниже отношений на множе-
множестве {—10, —9, ..., 0, 1, ..., 9, 10} являются функция-
функциями? Дать противоречащие примеры в случаях, когда от-
отношение не является функцией. (В 3.1, 1г) отношение
порядка ^ является отношением, индуцированным Z.
В 3.1, 1а)—к) \х\ определяется следующим образом:
\х\ = х, если х > 0, и |х| = —х, если х < 0.)
a) pi = {(x, у): х = у2}; б) р2 = {(х, у): х2=>у};
в) рз = {(х, у): ж = — у); г) p4 = {(z, у): х^у);
д) р5 = {(х, у): х* у = 6);
е) р6 = {(ж, у): х3 = у); ж) р7 = ((х, у): х = уъ);
в) рв = {(х, у): х-=\у\); и) рд = {(х, у): \х\*=\у\);
к) pio^iix, у): у \у\ =х» \х\).
2. Построить функцию /: А -*¦ А, где А = @, 1), не
имеющую обратной.
3. Какие из следующих функций являются отобра-
отображениями:
а) / на R определяется следующим образом:
{(х,х*): z«=R};
б) / на R определяется следующим образом:
{(*»,*): же R>;
в) / на R определяется следующим образом:
{(х, z2): zsR};
г) / на R, /: ж-»-sin(z);
д) / на R, /: х>- 1/х;
е) / на Q, /: х >-> arcsin x;
ж) /: А-*-!Р(А) определяется следующим образом:
/: х~{х};
в) /: !Р(А)-*-А определяется следующим образом:
/ =» {(ж, у): yeifl {а}}, где а — фиксированный эле-
элемент из Л?
4. Пусть /:. А -*¦ В и g: В -*¦ С— отношения. Что яв-
является областью определения g°f:
а) когда / и g — функции;
б) когда / — функция, g — отображение;
в) когда / — отображение, a g — функция;
г) когда / и g — отображения?
5. Доказать, что если функция / инъектпвна, то су^
ществует /"'.
6. Если функция / сюръективна, следует ли отсюда,
что /"' — отображение?
71
7. Построить пример, показывающий, что функция на
А — {—1, 0, 1}, определенная как /: х>-*х2, такова, что
8. Пусть /: А -*¦ В и g: В -* С — функции. Доказать,
что:
а) если / и g инъективны, то g ° / инъективна;
б) если fug сюръективны, то g• / также сюръек-
тивна.
9. Пусть /: А -*¦ В и g: В -*- С — функции и g сюръ-
ективна. Достаточно ли этого, чтобы обеспечить сюръек-
тивность g°/?
§ 2. Обратные функции и отображения
Используя результаты, полученные в предыдущем
параграфе, исследуем сложные функции. Пусть дана
функция /: А -*¦ В; в этом случае /"' является функцией
тогда и только тогда, когда / инъективна, а отображени-
отображением тогда и только тогда, когда / биективна. В большин-
большинстве рассматриваемых нами случаев / — биекция; тогда
/"' — также биекция, а функции /"'•/ и / • /"' являют-
являются тождественными отображениями.
Рассмотрим функции /: А -*¦ В и g: В -*¦ С. Тогда:
а) если / и g инъективны, то существует #•/;
б) если fug сюръективны, то также существует
g'f (см. упражнение 3.1, 8).
Обратным отношением к g'f является /~J • g~K По-
Порядок должен быть обратным, как указано на рис, 3.2.
Рис. 3.2
Заметим, что если g — отображение, т. е. 2E)S = В, то
52> s 3)g и, следовательно, 2>gef = dig. Аналогично, если
9tt^?Ds, то Sftgej — 3lg. Если fug инъективны, то су-
существует g<>f; следовательно, /~' • g~l — функция. Сум-
Суммируя вышесказанное, имеем: из &{ — &г следует, что
72
g'j: ?D, -*¦ Э1Я — отображение; если fag также инъек-
тивны, то f~l°g-u. Ыа -»¦ $Ь, — биекция. Очевидно, что
эти критерии выполняются, если / и g — биекции.
Упражнение 3.2.
1. Пусть /: А -*¦ В a g: С -*¦ В; показать следующее:
а) если / сюръективна и g — отображение, то
б) если / и g — биекции, то (g~l ° /)~' == /"' • g;
в) если 32g s &i, то (/ • /-' ¦> g) С = 9ls.
§ 3. Мощность множеств п счетность
Мы почти подошли к тому моменту, когда появляет-
появляется возможность использовать понятие биекции для фор-
формализации понятия мощности и процесса вычислений.
Вычисление важно не только само по себе, но также и
потому, что функция является вычислимой тогда и толь-
только тогда, когда связанное с ней множество счетно. Вна-
Вначале дадим определение множества N. Чтобы прояснить
наши намерения, заметим, что любое число A, 2 и т. д.)
может быть использовано двумя различными способами:
как существительное или как прилагательное, дающее
номер другого существительного. Мы будем рассматри-
рассматривать числа как существительные.
В качестве предварительного определения N по-
положим
Из этого рекурсивного определения следует, что l^N,
и если к произвольному элементу из N прибавить 1, та
полученный результат также принадлежит N. Следова*
тельно, N содержит 1, 1 + 1(=2), 2 + 1(=3), 3 + 1 (—4)
и т. д.
К сожалению, это определение неприемлемо по при-
причинам, которые будут рассмотрены ниже. Тем не менее
здесь есть несколько важных моментов. Например, так
как N (по крайней мере интуитивно) бесконечно, то мы
должны иметь механизм, при помощи которого можно
конструировать последующие элементы из конечного
множества,— другими словами, никогда не сможем напи-
написать точное представление N. Мы также должны приду-
придумать имя числу, которое называем «один», и аналогично
для «два» (сокращение 1 + 1), «три» и т, д. Конечно,
73
мы могли бы выбрать любые имена или символы для
этой цели, однако было бы неправильно использовать
неудобные обозначения. Перейдем теперь к недостаткам
данного определения. Проверка его обнаруживает, что
оно содержит два новых символа: «1» и «+»; остальные
символы известны из построения множеств. Символ «1»
можно объяснить вышеуказанным способом. Однако сим-
символ «+» означает операцию на N и, следовательно, не
может быть использован для определения N. (Операции
будут определены в § 6.)
Чтобы выйти из этого затруднения, вернемся к осно-
основам теории множеств. Напомним, что нам нужно было
построить число, которое на 1 больше максимального из
всех предшествующих чисел. Легко получить аналогич-
аналогичный процесс для множеств (называемый построением
сверхмножества с количеством элементов на 1 больше,
чем в данном множестве).
Пример 3.1. Пусть А — {х, у, z) и В = {х, у, г, А).
Тогда А^В и А&В, поэтому В\А = {А} и имеет толь-
только один элемент. II
Эта конструкция может быть перенесена на произ-
произвольное множество. Начиная от множества X, мы можем
определить последующее множество (обозначается Xе):
X9 = X U {X). Чтобы использовать этот процесс для по-
построения N, требуется некоторое начальное множество.
Выберем в качестве такого множества {0}. Оно имеет
один элемент. (Многиз авторы начинают с 0, Это по-
порождает множество @) U N. Мы не считаем 0 натураль-
натуральным числом, и в этом причина такого выбора начально-
начального элемента. Не существует универсального условия по
отношению к 0 и N. Всегда следует проверять условные
обозначения, принятые в других книгах, при обращения
к.ним.) Из {0} создадим последовательности {0}:{0}в=»
= {0, {0}}, {0}»» = {0, {0}, {0, {0}}} и т. д. Это при-
приводит к прогрессии, которая является более привлека-
привлекательной, чем 1, 1 + 1, 1 + 1 + 1, ..., по крайней мере ее
конструкция является строго определенной. Чтобы на-
навести порядок в вышесказанном, выберем временно име-
имена для этих множеств.
Переименуем {0} как 1, Iе как 2, 2® как 3 и т. д.
Тогда
1 - {0},
2 -{0,1},
3-{0, 1, 2), ...
74
Поэтому, например, множество 3 имеет три элемента.
Чтобы избежать неточности, давайте снова изменим обо-
вначения и определим множества
Nm-m»\{0}«={l, 2, .... т),
Тогда из определения следует, что Шт\=т (число т)
и что если a, beN, то a *S Ь тогда и только тогда, когда
Ne s N4. Поэтаму наша вера в упорядоченность N фор-
формально обоснована. Итак, множества N и Nm (для каж-
каждого т е N) определены и могут быть использованы в
дальнейшем. Введем некоторые понятия.
Определение. Два множества биективны (обо-
вначается X~Y), если между ними существует биек-
ция. Непустое множество конечно, если оно биективно
некоторому Nm. (meN), Если X ~ Nm, то мощность
множества (обозначается |Х|) равна тп. (Числа в дан-
данном случае используются как прилагательные. Напри-
Например, если Р — множество всех людей и XsP таково,
что X ~ Nm, то X есть множество из m людей.) Напом-
Напомним, что пустое множество 0 биективно только по отно-
отношению к себе, является конечным и имеет мощность О,
т.е. |0|=О.
Говорят, что множество счетно, если оно биективно
N. Символ Ко (алеф-нуль) часто используют для обо-
обозначения мощности N. Множество называется счетным,
если оно конечно или счетно, и может быть сосчитано с
использованием биекцпи /: N -*- X, если X счетно, или
биекция /: Nm -*¦ X, если \Х\ = пг, или /: 0 -*¦ X; 2-й эле-
элемент X является образом i отображения /. II
Перед тем как установить несколько полезных ре-
результатов, отметим одно существенное свойство мно-
множеств и биекций: отношение о, определенное на множе-
множестве S посредством
о = {(Х, У): Х~ Y},
является отношением эквивалентности, а подмножества
S, входящие в классы эквивалентности, состоят из мно-
множеств, имеющих одинаковую мощность. Следовательно,
чтобы продемонстрировать тот факт, что два множества
имеют один и тот же размер, требуется построить биек-
биективное отображение между ними.
75
Пример 3.2. Покажем, что INI ¦= |Z|. Отображение
-у-» если п нечетно,
га/2 в противном случае
является биекцией между N и Z. /
В предыдущем примере греческая буква if использо-
использовалась для обозначения биекции. Использование грече-
греческих букв q>, if, %, ... для обозначения произвольных би-
екций является общепринятым в текстах по логике и
будет здесь использоваться в этом контексте (среди дру-
других). Однако, чтобы не было путаницы с пустым множе-
множеством 0, мы будем избегать использования этих букв в
этом параграфе.
Пример 3.3. Покажем, что !N| = IQ!. Это требует
несколько более сложных рассуждений. Вначале рас-
рассмотрим счетное количество копий N, каждая из них
соответствует своему номеру п s N. Мы можем записать
это множество как N X N и упорядочить его элементы,
как указано на рис. 3.3. Такое упорядочивание является
0,1)
0,5)...
Рис. 3.3
биекцией N X N -*¦ N, задаваемой отношением (х, у) н*
•-* 2^ ' "*" ^" Каждый положительный
элемент Q может быть связан с дробью (р, q), где р и q
взаимно простые, и связан с элементом (р, q) множест-
множества N X N естественным образом, Поэтому, записывая
r = {i:*sQ, ж>0>,
получаем
iri<lNXNl-INl,
(Использование отношения «<» между этими бесконеч-
бесконечными числами не обосновано, Соотношение \А[ «S |j5|,
76
следует читать как «А биективно подмножеству 5». До-
Доказательство неочевидного факта, что это отношение яв-
является отношением порядка, лежит за пределами этой
книги.) С другой стороны, каждое р е N может быть
представлено как р/1 и, следовательно, связано с парой
(р, 1). Поэтому |N| *S |T| =S |N|, откуда следует, что
|Т| = |Nl. Для достижения нашей цели существенно
сказать следующее. Возьмем диагонально упорядоченное
множество N X N (см. рис. 3.3) и выбросим из него па-
пары, имеющие нетривиальный общий множитель. Это да-
дает метод нумерации элементов Т, однако трудно дать
формулу, которая связывала бы элементы Т с элемента-
элементами N. Теперь мы должны повторить наше рассуждение
применительно ко всем радиационным числам. Это мож-
можно сделать несколькими способами. Выберем для нагляд-
наглядности следующий. Расширяя уже полученное соответст-
соответствие между Г и N X N до оператора между Q и Z X N,
получаем
|N| = IZI < IQI < IZXNI = INXNI - |N|,
что дает требуемый результат. Построение биекщга
между Z X N и N X N оставляем в качестве упраж-
упражнения. /
Предыдущий пример несколько длинен, однако при
его рассмотрении возникло несколько важных моментов,
которые мы сейчас отметим.
1. Если S конечно и %: S -*¦ S — инъективное отобра-
отображение, тогда х биективно.
Доказательство. Пусть выполнены условия ут-
утверждения. Если 5 = 0, то требуемый результат триви-
тривиален. Если S ?* 0, тогда существует биекция -ф: N™ -»¦ 5
для некоторого m е N и отображение ip • х " ^ инъек-
тпвно: Nm -*¦ Nm и, следовательно, является биекцией.
(Доказательство этого факта оставляем в качестве уп-
упражнения.) Основная идея заключается в переупорядо-
переупорядочивании m объектов и известна под названием «прин-
«принцип раскладывания по гнездам». Даны m гнезд, каждое
в своем ящике. Любая схема переселения, при которой
в одном ящике может быть не более одного гнезда,
должна использовать все m ящиков, т. е. •ф~1°х<>11' яв"
ляется перестановкой Nm (рис. 3.4). Однако т|> — биек-
биекция; следовательно, % • \f и % также биекции. (Обратно,
если %: S -*¦ S не сюръективно, то S должно быть беско-
бесконечным.)
77
2. Множество N бесконечно, так как отображение на
N, определенное как re»-»-n + 1, инъективно, но не би-
биективно (нет элемента, отображающегося в 1). Следова-
Следовательно, обращая предыдущий результат, получаем, что N
не может быть конечным.
Подмножество А из R ограничено сверху (снизу) ес-
если существует верхняя (нижняя) граница, А ограничен-
ограниченно, если оно ограничено сверху и снизу.
3. Ограниченное подмножество из N конечно.
Доказательство. Каждое подмножество ив N
ограничено снизу нулем. Пусть A s N ограничено свер-
сверху некоторым т <= N. Определим отображение %: А -*¦ N
Рис. 3.4
так, что если А «=» {аи й2, ..., ait ..,} и ai<e2<e3<...
...<т (такой порядок возможен, так как 4eN), то
Следствием этого является соотношение x(ai)<a<, и
X, очевидно, ииъективпо. Оно также должно быть биек-
цией, т. е. %: А -* N» для некоторого п < т. Если это
не так, тогда существует аР е А такое, что %(аг)'> т и»
таким образом, ар ^%(ар)> п. Однако А ограничено т\
поэтому мы пришли к противоречию. Следовательно,
X — биекция па Nn в А конечно.
4. Каждое подмножество конечного множества ко-
конечно.
Доказательство. Пусть А = В и В конечно. Ес-
Если В = 0, то А = 0, и утверждение доказано. В против-
противном случае В ~ Nm для некоторого m e N. Тогда суще-
существует биекция х: В -> Nm. Применение х к А дает под-
подмножество из Nm и поэтому х(^) ограничено. Из слу-
случая 3 следует конечность х(^)- Потому, так как
биективно с А, то А конечно,
73
5. Прямым следствием случая 4 является тот факт,
Что любое множество, имеющее бесконечное подмноже-
подмножество, само бесконечно.
Доказывая некоторые неочевидные факты о размер-
размерностях множеств Z, Q, N, N X N, ..., разумно задаться
вопросом: существуют ли множества, мощность которых
больше мощности N? Ответ на этот вопрос утвердитель-
утвердительный. Действительно, из данного произвольного множест-
множества мы можем (используя диагональную процедуру Кан-
Кантора; см. ниже) создать множество, мощность которого
строго больше мощности N.
Мы не будем рассматривать общий случай, а ограни-
ограничимся рассмотрением удивительного примера, который
носит фундаментальный характер и соответствует целям
нашего изложения.
Пример 3.4. Покажем, что
ЦО, 1[I>IN|, [0, 1[ = {х: *eR,0«i<i}.
Доказательство (А. Кантор). Каждое число
между 0 и 1 может быть записано в виде бесконечной
десятичной дроби O.dKidnidn3... Предположим, что эти
числа могут быть перенумерованы и что п-в число име-
имеет значение, данное выше. Будем конструировать следу-
следующее число: возьмем n-ю цифру десятичной форм-j, рав-
равную я-му числу. Это дает нам число О^п^аг^зз... По-
Построим новое число: ОД 1622633..., где каждая цифра б«
отличается от соответствующей цифры d,t. Тогда это
построенное число будет отличаться от каждого числа из
первоначального перечня, а именно от «-го числа оно
будет отличаться л-й цифрой. Следовательно, мощность
[О, 1[ строго больше, чем мощность N, и счетной биекции
не существует.
Принцип построения числа О.бибгабзз... в предыду-
предыдущем доказательстве является наиболее существенным
моментом, хотя проницательный читатель может заме-
заметить, что существуют задачи, где десятичное представле-
представление чисел не единственно. Это встречается тогда, когда
представление заканчивается бесконечной последователь-
последовательностью 0 или 9. (Например, 0.3999... и 0.4000...) Чтобы
построенное число О.бпбггвзз.. • отличалось от уже вы-
выписанного списка чисел, мы можем оговорить, что б»
должны отличаться от 0, dti и 9. Соответствующие про-
проблемы возникают и в других подобных конструкциях,
однако, чтобы не отвлекать внимание от основных идей,
в большинстве случаев мы будем их игнорировать.
79
На самом деле можно показать, что [0, 1[ ~ R. Оче-
Очевидно, что R — важное множество. Поэтому его мощ-
мощность обозначают специальным символом Ki (алеф-
один). Рассмотрим теперь способы, с помощью которых
можно объединять множества и отношения между мощ-
мощностями отдельных множеств и мощностью результиру-
результирующего множества. Первый из них довольно очевиден.
Теорема. Если А~В и С ~ D,to (AXC)-(BXD).
Доказательство. Пусть %: А -*¦ В и гр: С -* D —
биекции. Тогда (а, с)>-*{%(а),%(с)) является биекцией
между АХС и BXD. И
Теорема. Если Z — конечное множество и {X, Y) —
разбиение Z, тогда \Z\ - \Х\ + |У|.
Доказательство. Так как Z конечно, то Z ~
N N
Д
Nm для некоторого
Ряс. 3.5
N и существует биек-
ция /: Z-»-Nm (рис. 3.5).
Более того, так как XsZ
и YsZ, то x(-^)sNm и
X{Y)sNm. Пусть ifi явля-
является биекцией из х(^0 в
N Pt для некоторого р\ ^
<ш, где (ti-xJW-Np,.
Аналогично пусть ifj —
биекция из х(П в Ин
для некоторого рз ^ т,
где (ifa«x)(I')-N,i. Тог-
Тогда если а: N -» N опреде-
определяется как а: х >-»¦ х + plt
то о является биекцией
между NPs и \+Pt\NPi.
Следовательно, отобра-
отображение
если
если
является инъекцией и биективно (так как Z конечно),
между ? и Npi+Pa, Таким образом, Z~NPi+Pjs, Следо-
Следовательно, m «• />i + />а и |Z| =» Ш + |У|.
Пример 3.5. Чтобы проиллюстрировать применение
предыдущей теоремы, рассмотрим случай, когда
Z - {о, 6, с, d, e, /),
X •= {Ь, е>, Y - {а, с, d, /}.
80
Тогда биекция между 2, и Ne задается следующим об-
образом:
Х-{(«,5), (Ь,1), (с, 6), (d, 3), (в, 4), (/,2)>,
и поэтому
Х(Х)={1, 4>, Х(Г) = {2,3,5,6}.
Подходящими отображениями if, являются
«.-{A, 2), D, 1)}, Ц»-{C, 1), E, 2), F, 3), B, 4)}.
Поэтому если о определяется как х *-*¦ а: + 2, то
il, 2),
«, 4,5, 61.
Комбинирование i|>i ° x и о • ф • X Дает нужный резуль-
результат. /
Предыдущий пример не является характерным в том
смысле, что он требует очень тщательных манипуляций
с биекциями. Обычно в этом нет необходимости, так как
почти всегда можно сослаться на хорошо известные ре-
результаты.
Закончим обсуждение следующим основным резуль-
результатом. Если А и В — конечные множества, то А X В ко-
конечно и \АХВ\ — \А\ • \В\. Этот результат не только
интересен сам по себе, но и дает способ для введения
доказательства по индукции.
Доказательство по индукции использует два основ-
основных понятия, содержащихся в определении N:
(I) Существует некоторый начальный элемент
(в N это 1).
(II) Для заданного утверждения, соответствующего
некоторому элементу, существует метод, позволяющий
перейти к следующему (в случае N это — создание сле-
следующего числа за наибольшим до сих пор числом, вклю-
включенным в N).
Более конкретно, если для некоторого no e N (обыч-
(обычно «о=1, но не обязательно) мы можем доказать, что
утверждение Р(по) справедливо и для любого neN
(п>ло) справедливость Р(п) влечет справедливость
Р(и+1) (здесь п +1 — следующий за и элемент), то
ваключаем, что Р (га) справедливо для всех пг > щ. Шаг
(I) является основанием индукции, шаг (II)—шагом
индукции,
в д. кукд г. Бей» 8i
Весь процесс, по существу, является прямым доказа-
доказательством
Р(по)=> . ..=> Р(т)
и, следовательно, осуществляет непосредственную про*
верку промежуточных результатов.
Рассмотрим следующий пример.
Пример 3.6. Если А и В конечны, то
UX5! = UI •\B\.
Доказательство. Поскольку А и В конечны, то
А ~ Nm с биекцией т: А -*¦ Nm и В ~ Nn для некоторых
т, п е N. Будем использовать индукцию по в- размер-
размерности В. Заметим, что от размерности А требуется ко-
конечность, так как мы предполагаем знакомство только с
умножением конечных величин.
Основание индукции. Если 5 = 0, то
и поэтому имеем тривиальное равенство
O-UI *0=UI *\В\.
Если В =» Ш, то отображение А -*¦ А X В такое, что
a >-* (а, 6), очевидно, биективно, и поэтому
Шаг индукции. Предположим, что
L4X5J = UMS»I,
где Bk s В я I5J — А е N. Тогда
UI ¦ |Bj-m»*e=N
и существует биекция if: AXBK-*- Nm+A. Если А < п, то
можно ваять подмножество В, которое имеет / ¦= А + 1
элементов. Пусть /^ = 5» U Ш, где 5» — множество из
к элементов, в пусть отображение %, %: АХ B}-*-N оп-
определяется следующим образом:
Х: XXliKlwHl m • к + т),
К (а, Ь)р— ij)(a,i), если 6е5».
Очевидно, что х является биекцией на N,,_,A+n, и
m * А + m = m • (к + 1) = m » /.
Поэтому \А X5jl'-¦ т • / -=» \А\ • |5j|. Следовательно,
тождество справедливо для всех подмножеств В, содер-
содержащихся в 5, и поэтому \А ХВ\ = \А\ • |?|. /
82
Упражнение 3.3.
1. Доказать, что отношение между множествами
{(А, В): А-В)
является отношепием эквивалентности.
2. Построить биекцию между множествами Z X N и
NXN.
3. Доказать, что если А и В — множества и A U В
конечно, то
\А\1В\ + \АПВ\~\А\ + \В\.
4. Доказать (от противного), что произвольная инъ-
инъекция Nm-*Nm (meN) является бпекцией.
5. Доказать (без использования равенства |^(/4)| =
•=2UI), что для любого конечного множества А, такого
что 1/41 > 2, справедливо соотношение \&{А) I > \А\.
6. Показать, что результат задачи 5 имеет место и
для бесконечных множеств.
7. Пусть множество {0,1}N представляет собой после-
последовательность О|, 02, из, ..¦) вщ • • •! где а,( е {О, 1). Дока-
аать, что |{0,1}N|>|N|.
8. Доказать (построением подходящих биекций и
рассуждений по индукции), что если А\, ..., Ап — ко-
конечные множества, то
U,X...X^J = Mil •...• U.I.
§ 4. Некоторые специальные классы функций
В этом параграфе мы несколько отойдем от основ-
основной темы обсуждепия для того, чтобы кратко рассмот-
рассмотреть следующие четыре важных класса функций:
подстановки, последовательности, функционалы и отобра-
отображения, сохраняющие эквивалентность. Эти функции ча-
часто используются; особо отметим их приложения к тео-
теории графов, к трассировке вычислений, к определению
языков программирования и переводу, к машинной гра-
графике.
Определение. Подстановкой множества А назы-
называется биекция на А. II
Подстановки конечных множеств представляют осо-
особый интерес в вычислениях. Когда А конечно, мы в со-
состоянии вычислить число различных подстановок А.
Пусть Ml = /i s N, Обозначим через „Р„ число таких
подстановок. Значение „Р„ легко вычислить. Можно рас-
рассматривать задачу построения биекций на А как задачу
6» 83
заполнения ящиков, пронумерованных от 1 до п
(рис. 3.6), объектами аи ..., ап. Порядок, в котором за-
заполняются ящики, несуществен (любой другой порядок
можно получить перемешиванием ящиков). Поэтому бу-
будем заполнять их слева направо. Первый ящик может
быть заполнен п способами, так как мы имеем свобод-
свободный выбор из всего множества А. Убирая выбранный
1
г
п -1
п
Рпс. 3.6
элемент из А, получим множество из п — 1 элементов.
Следовательно, второй ящик может быть заполнен п — 1
способами, третий ящик — п — 2 способами и т. д. Про-
Продолжая этот процесс, получим, что {п — 1) й ящик мо-
может быть заполнен двумя способами, а ящик с номером
п — единственным оставшимся элементом из А. Следо-
Следовательно, число различных подстановок из А равно
га • {п — 1) • {п — 2) • ... • 3 • 2 • 1.
Это произведение называется факториалом п (обознача-
(обозначается п\). Следовательно, „Рп = п\.
Так как А ~ Nn, то можно свести наше рассмотрение
к Nn. Любая подстановка на Nn должна определять об-
образ каждого элемента в Nn (который, конечно, должен
быть единственным и отличным от других). Пусть ф —
подстановка на Nn. Тогда \|з можно определить как мно-
множество из п пар следующим образом:
ф = {A, л), B, х2), .... («,*„)>,
где
{ } N
Не обязательно, конечно, должно быть Х\ = 1 и т. д.
Можно также представить ф следующим образом:
1 2 3 ...
U
Пример 4.1. Пусть о — подстановка на
_ _ П 2 3 4 5 6Х|
V5 6 3 1 4
Тогда оA) = 5, оC) = 3 и т. д. II
84
Достоинством этого обозначения является простота,
с которой могут быть вычислены сложные подстановки.
Предположим, что т|> — подстановка на Nn, определенная
выше, а х —другая подстановка на том же самом мно-
множестве. Тогда подстановка х может быть записана как
совокупность пар в порядке, определяемом х\, хг, ..., хл.
Если две последовательности записать одну над другой
(первая применяемая подстановка должна быть заиига-
на первой), то верхняя и нижняя строки дадут резуль-
результирующую подстановку.
Пример 4.2. Пусть
ра 4.1 и
( 1 2
P=U 2
о — подстановка пз прпмо-
Можно переписать р в виде
5 6 3 14
4 5 6 3 1
(
Поэтому р • о может быть вычислено следующим об-
образом:
12 3 4 5 6'
6 3 14
! 4 2 \ ^одинаковые
3 1 2
1 2 3 4 5 6\
4 5 6 3 12/
Следовательно, например,
р.оB)(~р(оB))-рF))-5 и т. д. /
Отсюда следует, что представление обратной (конечной)
подстановки получается перестановкой строк, представ-
представляющих исходную подстановку. Хотя такое представле-
представление полезно в вычислениях, оно требует много лишпего
места, особенно в тех случаях, когда многие элементы
не меняются в процессе подстановки. Существует более
простое обозначение, которое может употребляться не-
непосредственно для некоторых простых подстановок и
косвенно для всех конечных.
Определение. Пусть А = {а\, ..., ап). Подстанов-
Подстановку р называют циклом (циклической подстановкой) ,если
Р =
83
Предположим, что A s В и В конечно. Расширяя р на
все В, можно определить подстановку о так, что
fp(i), если геЛ,
I z, если же В\А.
В атом случае о ведет себя подобно р во всех случаях,
когда элементы В не остаются на месте. Применение о
к Л передвигает элементы по кругу циклическим обра-
вом, и, если известна область А, мы можем обозначить
подстановку как (fli, аг, ..., ап). Эта подстановка назы-
называется циклом длины п. II
Пример 4.3, Рассмотрим опять подстановку
(I 2 3 4 5 б\
U 2 6 1 4 5/"
Подстановка является циклом длины 5 и может быть за-
записана как
A, 3, 6, 5, 4). /
Не все подстановки являются циклами. Например, под-
подстановка о в примере 4.1 не является циклом. Напом-
Напомним, что о имела вид
/12 3 4 5 8^
\5 6 3 1 4 2/'
Поэтому оA)=5, оE)=4, оD)=1, откуда следует, что
о содержит цикл A, 5, 4). Начиная с 2, получаем дру-
другой цикл —B, 6). Таким образом, имеем о —A, 5, 4)»
•B,6) ио-B,6).A,5,4).
В действительности любая конечная подстановка мо-
может быть представлена как произведение циклов, при
этом циклы могут располагаться в любом порядке. Из
построения следует, что один элемент не может встре-
встретиться более чем в одном цикле, т. е. циклы не пере-
пересекаются.
Теорема. Каждая подстановка р на конечном мно-
множестве А выражается в виде произведения непересекаю-
непересекающихся циклов.
Доказательство. Поскольку |/4|=»neN, то
А ~ Nn. Поэтому без потери общности мы можем огра-
ограничиться рассмотрением подстановки р на Nn.
В теореме утверждается, что р = а\ • Ог °... • ог, где
каждое о\ является циклом и циклы не пересекаются.
Для доказательства теоремы построим требуемые циклы.
Сначала найдем наименьший элемент х\ е Nn такой, что
89
i и p(x) = x для всех х, l<x<ii. Еслп такого
х\ не существует, то р = / (т. е. р является тривиаль-
тривиальным пустым произведением циклов). В противном слу-
случае вычислим xi, p{x\), p2(xi), p3(xi) и т. д. Все эти
элементы находятся в N». Поэтому элементы в этой по-
последовательности должны содержать повторения. Пред-
Предположим, что p"(xi)—первый такой элемент (который
уже повторялся в последовательности). Покажем, что
р"(х\) = х\. Предположим, что это соотношение не вы-
выполняется. Тогда p'(zi) = p"(a;i) для некоторого I, 0<
<1<к. Следовательно,
Pi~1(*O-P~i#Pi(*i)-P"i#P*(*i)="P*~i(*i) и т. д.
Поэтому pl~'(x0'-pk~'(xi), т. е. p*~'(xi)= p°(zi) — xu что
противоречит минимальности к (так как к— К к). Та-
Таким образом, p*(zi) = zi, и подстановка
задает цикл внутри р.
Если все элементы ieN, такие, что p(x)?t x (будем
называть такие элементы нестационарными), содержатся
в 6], то р = Oi — единственный цикл (который, естест-
естественно, не пересекается). В противном случав найдем
следующий наименьший элемент х% е Nn такой, что
р B2)^*2 и Х2 не встречается в Оь Из xj строим множе-
множество различных степеней р:
Это цикл длины не менее 2, и он не пересекается с <Ji,
(Доказательство оставляем в качестве упражнения.)
Если все нестационарные элементы исчерпаны, то рв
¦= Oi «02 = 02 • 0i. Очевидно, что множество нестационар-
нестационарных элементов, не входящих в эти циклы, можно умень-
уменьшить, и в конце концов придем к 0. Следовательно,
р =¦ Oi • 02• 0з *. •. • о, для некоторого r^N. /
Рассмотрим теперь несколько иную ситуацию. Возь-
Возьмем множества А: \А\ *» га и 5 = Л, \В\ =г<п. Возни-
Возникает вопрос: сколько биективных функций существует
из А в В? Или, что эквивалентно, сколько существует
пнъективных отображений из В в А? Число перестано-
перестановок (без повторений) из п элементов по г обозначается
„Р, и вычисляется так же, как и „Рп, за исключением
того факта, что процесс прекращается после заполнения
г ящиков, Таким образом,
?t->n«(n—^„.«(n — r+l),
87
Легко видеть, что, продолжая процесс заполнения ящи-
ящиков, оставшиеся п — г элементов можно разместить по
последним п — г ящикам „_ГРП_Г способами. Поэтому и
TJ __^ П 71 ^^ "!
П Г == р == /„ VI-
п—тгп—г v г)>
При вычислении пР, мы находим число биективных
функций иг А в В. Подсчитаем числа таких функций.
Определение. Пусть А — конечное множество и
В s А, \А\ = п> т = \В\. Множество В называется со-
сочетанием (без повторений) из п элементов по г. Число
таких сочетаний обозначается через Стп. //
Вычисление Стп производится следующим образом.
Положим \А\ = п. Возьмем произвольное подмножество
BsA такое, что \В\ *= г. Тогда В является образом под-
подстановки из п элементов по г. Число инъектпвных функ-
функций на А, имеющих В своим образом, есть „Рг. Если /
является такой функцией и g — другая такая функция,
имеющая ту же самую область значений, то g связано
с / соотношением g = ф • /, где ф — подстановка на В.
Функции g и / определяют одну и ту же комбинацию,
и в действительности число функций, определяющих
эту комбинацию, равно числу подстановок ф на В. Сле-
Следовательно,
Р — г1 л Р
откуда
рт _ п?г п\
Поскольку относительные дополнения единственны и
\A\B\ -«п — г, то отсюда следует, что Сп = С^~т.
Вернемся теперь к математическим объектам, кото-
которые должны быть знакомы читателю, но которые, веро-
вероятно, не рассматривались как функции.
Определение. Последовательностью на множест-
множестве S называют отображение N -*¦ S.
Если о: N -¦ S — заданная последовательность и
о(п)~#в, то обычно обозначают последовательность не о,
a (sn) или (si, $2, ..., sn, ...). В этом случае sn называ-
называют л-м членом последовательности. /
Часто при изучении свойств последовательностей
возникает понятие «расстояние» между соседними эле-
элементами последовательности (скажем, sn и sn+i) и меж-
между элементами sB при п ^ щ (где щ — некоторый фикси-
фиксированный элемент N] и фиксированным элементом из S.
88
Мы вернемся к этим вопросам несколько позже, посколь-
поскольку в настоящий момент у нас в общем случае нет поня-
понятия расстояния.
Особый интерес в задачах, связанных с трансляцией
языков программирования, представляют функционалы.
Существуют функции, которые определены не на мно-
множествах простых объектов (таких, как числа), а, напри-
например, на множестве функций.
Определение. Пусть даны множества А, В и С.
Обозначим через [В -*¦ С] множество всех функций из В
в С. Функция /: А -*¦ [В -*¦ С] называется функциона-
функционалом. Следовательно, a^2),=*-f(a)—функция, п /(а):
В^С. Далее, b ^ @fw^ ]{а) (Ъ) = С. II
На первый взгляд такая комбинация, как /(а)(&),
выглядит настолько необычной, что может казаться не-
ваконной. Это в основном потому, что рассматриваемые
функции использовались как объекты особого рода, в ря-
ряде случаев отличные от элементов, которые были в об-
области определения и области значения функций. Конеч-
Конечно, множества функций могут рассматриваться так же,
как и любые другие множества.
В развитых языках программирования имена целых
переменных не отличаются от имен переменных функ-
функций и могут изучаться аналогичными способами. Хотя
эти функции являются обычно довольно сложными, язы-
языки программирования редко дают примеры важности
функционалов.
Пример 4.4. Пусть Р — множество программ, т. е.
текстов программ (строк символов), которые должны
быть обработаны компилятором. Аналогично пусть / и
О — множества соответственно входных и выходных
значений, которые доступны программе для ввода и вы-
вывода. Тогда компилятор (с соответствующего языка) яв-
является функционалом типа Р -*-[/-*- О]; для данной
реР он пытается создать машинный код, который при
выполнении будет читать is/ и выдавать оеО, Из
дальнейшего изложения будет видно, что определение
функций (или функционалов) сложности компилятора
длинное и сложное. Тем не менее эти понятия можно
изучать в более простых ситуациях.
Пример 4.5. Пусть все данные принадлежат R.
Тогда, если /: а >-*¦ [х *-*¦ а + х], то
/B): х~2 + х и /B)C) = 5,
то время как /C): г«3 + 1и /C) C)= 6 и т. д. //
89
Обращение с функционалами не вызывает трудно-
трудностей при условии, что ссылка делается на основной
функционал (т. е. А -*¦ В или А -*¦ [В-*¦ С]). Следователь-
Следовательно, в дальнейшем мы будем рассматривать их просто
как функции, имеющие нетривиальные области значе-
значений, и будем обращаться с ними соответствующим
образом.
В заключение параграфа определим функции, кото-
которые сохраняют некоторые структуры. Из дальнейшего
будет видно, что в некоторых ситуациях желательно со-
сохранить многие из алгебраических свойств, которыми
множества могут обладать. Ограничимся вначале рас-
рассмотрением простейшего случая.
Определение. Пусть X — множество, на котором
вадано отношение эквивалентности р. Тогда X разбива-
ется отношением р на р-эквивалентные классы; множе-
множество классов обозначается как Х/р.
Определение. Пусть X и Y — множества, а р* и
рг — отношения эквивалентности на них, и пусть /: X -*¦
-*¦ Y — отображение. Обозначим через / отношение
J: X/p2 -
такое, что
М
где [х] — класс эквивалентности х. Если / — функция, то
и / является отображением, сохраняющим эквивалент-
эквивалентность. В этом случае говорят, что /: X -*¦ Y индуцирует
отображение
- Y/pr. /
Наглядный способ представления такого отображения
дан на рис. 3.7.
Если рассмотреть отображение /, согласованное с
отношением эквивалентности, то можно переходить от
Х\ к у\ или через хг, используя соотношения yt f()
и xjpxXi, или через у\, используя соотношения yi
и уйртУи
Пример 4.6. Пусть Х = {1, 2, 3), У-И, 4, 9), и
пусть рх и рг таковы, что
Х/р, - {{{), {2, 3}}, У/рт - Ш>, D, 9»,
90
и /: X -*- Y такое, что х *-*¦ х%. Тогда
В этом случав B, 3} в Х/рх => 2р*3 -»¦ [2] - [3] и
«=/([3]). Поэтому / является функцией и / сохраняет
отношения эквивалентности. /
Пример 4.7. Пусть X, Y и / те же, что и раньше,
и отношение эквивалентности ах и о> индуцируют раз-
разбиения {{1), B, 3)} и {{1, 4), Ш) соответственно. В этом
случае индуцированные отношения дают
Так как 20*3, то [2] ==¦ [3] в Х/а2, но D, 9) Ф аг, по*
скольку [4] ?* [9] в У/о>. По сравнению с рис. 3.7 этот
пример дает отношения, показанные на рис. 3.8. Так как
-*-3
Рис. 3.7
Рис. 3.8
нельзя соединить стороны прямоугольника во всех слу-
случаях, то отношения эквивалентности не сохраняются. /
В гл. 5 и далее будет показано, как эти диаграммы
могут быть использованы для определения операций та-
таким образом, чтобы соединить углы прямоугольника.
После этого можно будет объединять диаграммы подоб-
подобно строительным блокам.
§ 5. Аналитические свойства вещественных функций
Этот параграф содержит материал, использующий
теорию множеств и8 гл. 1. Цель, которая при этом пре-
преследуется, состоит не в развитии техники вычислений,
а в создании строгих утверждений типа:
«Предел /(г) при х, стремящемся к 0, есть у», _
91
«Наклоп графика / в точке а равен Ь»,
«/ имеет гладкий график» и т. п.
(Два последних понятия, очевидно, относятся к графи-
графике.) Мы дадим основные определения, которые исполь-
используются при получении некоторых результатов. Этого до-
достаточно для того, чтобы проиллюстрировать доказатель-
доказательства большинства теорем.
5.1. Последовательности. Вещественной последова-
последовательностью называется отображение N на R. Последова-
Последовательность записывают в виде (а„). Если при возраста-
возрастании п члены ап становятся «близкими» к некоторому
фиксированному значению seR, то говорят, что после-
последовательность (а„) имеет предел а пли что о„ стремится
к а при стремлении п к бесконечности. Дадим строгое
определение сказанному.
Определение. Если (а„)— вещественная последо-
последовательность и для любого е > 0 существует N, е N та-
такое, что N > N, •*• \ац — а\ < е, то говорят, что (ап)
имеет предел а, и записывают это как lim an = а или
ап^-а при п-+<*>. (Здесь |х| обозначает модуль числа
Если (а„) имеет предел, то говорят, что последова-
последовательность сходится. Если последовательность не имеет
предела, то говорят, что она расходится.
Пример 5.1.
1. Последовательность (а„), где ап~=\1п, имеет пре-
предел 0; для е > 0 можно выбрать N, — любое натураль-
натуральное число, большее 1/е. Тогда
W > N, •+ \а„ - 01 = 1/N < 1/N. < е;
следовательно,
- = 0.
2. Последовательность (а„), где о„=(—1)п, расхо-
расходящаяся.
Предложение. Если (sn) и (tn)—последователь-
(tn)—последовательности и X е R, тогда (sn + fn), (sjn) и (Xsn) также яв-
являются последовательностями, и если lim sn = s и lim tn =
П-»оо 71-» 00
— t, mo:
а) lim (sn + tn) — s+t;
б) lim (sntn) = st;
62
в) lim(?.s,,) =¦ \s;
П-»оо
г) если t Ф О, то sjtn -* s/t при п -* °°.
Доказательство. Пусть е > 0. Тогда существует
Л7е s N такое, что
\sy — s\ < е/2 п \t.s — t\ < е/2
прп Л7 > Л7,. Так как прп Л' > Л',
Is* + ty — (S + t) I = Is.v - S + f.v - 11 <
^ Is.v —si + \ts — t\ <e,
то limfSft + tn) = s + t. Аналогично для случая б)
П-* ас
— St\ = Is.v^v — S.\< + S.-,t — St\ ^
Sfl ^ U.vl U.v — t\ + Is.v — S| U|.
Пусть задано е > 0. Тогда существует Л', е N такое, что
для Л' > Л7, справедливы неравенства
1 е
i
|s.v —s
2 MI-M'
Следовательно,
I вл 11 tx - 11 + | sy - s I i t\ < (I s I + 1) I f .v - 11 +
+ kv-s|l'l<4e + TT7ITT|'l<Te + Te~e'
откуда получаем (sntn) -*¦ st. Доказательство случаев в),
г) предложения оставляем в качестве упражнения. /
Определение. Пусть (ап)—последовательность
п
в R. Последовательность sn— 2 а; определяет ряд 2ал-
Прп этом sn называют п-й частичной суммой ряда. Если
последовательность (sn) сходится, то говорят, что ряд
сходящийся, и число lim sn называют суммой ряда. Оно
обозначается
а„.
5.2. Непрерывность. Понятие непрерывности почти
полностью игнорируется при изучении элементарных вы-
вычислений. В неформальной математике это понятие счи-
93
тается очевидным. Однако при начальном изучении ма-
математики достаточно трудно найти нужный путь. На са-
самом деле определение непрерывности базируется на по-
понятии предела. В этом параграфе через / будем обозна-
обозначать интервал действительной осп R. Если /: /-+R я
)(х) становится «неограниченно близким» к некоторому
числу Ъ при х, «приближающемся» к а е/, то говорят,
что предел f(x) при х, стремящемся к о, есть Ъ. Дадим
строгое определение этого понятия.
Определение. Функция /: / -¦ R имеет предел b
в точке а, если для любого е > 0 существует б, > 0 та-
такое, что
0<lx —ol <6.-»- l/(*)—ftl <e.
В этом случае будем писать
Пт/(г) = Ъ
к-кг
ИЛИ
f(x)-+ Ь при х -* а. II
Заметим, что в определение не входит значение /(х)
в точке а.
Пример 5.2.
1. lim л: = а; достаточно выбрать бв = е,
2. lim х2 «=4, поскольку
«-¦2
\х — 21 < б, *> —б. < х — 2 <
< б, о 4 — б. < х + 2 < 4 + б..
Следовательно,
1г2-41«!.г + 21 I*-21 < 6.1*+ 21 < 6.D +в.)-
Если выбрать б, = min(l, е/5), то
\х2 - 41 < 56. ^ е. //
Легко показать эквивалентность следующих утвер-
утверждений:
lim/(x) = ft, lim (/(*) — Ь) = 0,
lim/(a + A) = b, lim (/(a + h)- b) = 0,
h-»0 h-»0
Теперь мы готовы к изучению понятия непрерывно-
непрерывности для вещественных функций. Грубо говоря, функция
/:/-»• R непрерывна в точке as/, если точки, «близ-
«близкие» к а, отображаются в точки, «близкие» к /(а), Бо-
лее строго это понятие может быть определено следую-
следующим образом.
Определение. Функция /: /-»¦ R непрерывна в
as/, если
Говорят, что }(х] непрерывна, если она непрерывна в
каждой точке своей области определения. /
Из определения видно, что в данном случае требует-
требуется, чтобы f(x) была определена при х = а. Такое опре-
определение непрерывности соответствует интуитивному
представлению. Поясним его на рисунках.
На рис. 3.9, а дан график непрерывной функции f\i
[—2, 2]-*R, /i(x)~ \х\. На рис. 3.9, б представлен гра-
график функции /2: [0, 4] -*¦ R, где
при 0<х<2,
+ 1 при 2<х<4.
Функция /г непрерывна в каждой точке [0, 4], за исклю-
исключением точки х = 2, так как не существует интервала
вида 2 —б<х<2 + б, для которого |/2(з;) — /2B) 1 < 1.
(*!¦
+2 х
х
Рис. 3.9
В заключение этого раздела сформулируем без дока-
доказательства несколько утверждений. Их доказательство
можно найти в большинстве книг по математическому
анализу. Если f(x)-+ l и g(x)-+ m при х -*¦ а, то
(/ + *)(*)-/(*)+*(*)->* + ».
(fig) (•r)= l(x)li(x) -* Um при условии т ?• О,
(X/) (х)- \}{х}— М для всех X е R.
95
Отсюда следует, что если / и g непрерывны в точке а,
то непрерывными являются и функции Xf, / + g, fg, fig
при условии, что а находится в области определения
каждой из «новых» функций.
5.3. Дпфференцируемость. Графическое представле-
представление функции /: / -»• R, обсуждаемое в п. 5.2, предполага-
предполагало, что эта функция определяет некоторую другую функ-
функцию /': / -* R, где {'(а) есть «наклон» графика / в точ-
точке а. В общем случае 3)/> Е 2)/, так как на самом деле
его может не быть для всех точек 2),. В этом случае /'
не существует. Определим строго функцию /'.
Определение. Функция /: / -*¦ R дифференцируе-
дифференцируема в точке ае/, если
Л-.0
существует. Множество точек, где этот предел существу-
существует, устанавливает область определения &/> производной
/': / -*• R функции /, и
ft-»O "
Иногда производную /' записывают как dffdx. Отноше-
Отношение — h~ часто записывают в виде б//бх, где б
читают как «малое приращение». В этих обозначениях
6х-»0 °Х dX
Если / дифференцируема в точке а, то она и непре-
непрерывна в а, так как
следовательно,
(a + h)-f(a) lim h = f(a).O = 0.
Л->0 " Л-Ю
Другими словами, lim/(a + h) — f(a), и, таким образом,
/ непрерывна в а по определению. Поэтому непрерыв-
непрерывность функции является необходимым условием ее диф-
фереицируемости, но не достаточным, как показывает
следующий пример.
Пример 5.3. Функция f(x)=\x\ не дпфферепцпрус-
ма в точке х = 0, так как
/ @ + h) - f (О) _ \_h\_
h ~ h '
где
j^j f+1, если Л>0,
h = |— 1, если А < О.
Следовательно, в любом пптервале ]—А, А[, где h произ-
произвольное, функция \h\jh принимает оба значения ±1, п
поэтому предел при А -»¦ 0 по существует. /
Пример 5.4.
1. Пусть /: R -* R — постоянпая функция, т. е. /(*)=¦
¦= с для всех ieR. Тогда
/ (х + К) - / (.г) _ с —с _ Q
h h
и lim 0 = 0. Таким образом, /'(х)=0 для всех х s R. Об-
Обратно, если f'(x)=O для всех ieR, тогда /—посто-
/—постоянная.
2. Пусть f(x)= х2 для всех х е R. Тогда
f [х -г —fx)_x+i)—х_т+т —jc_ = 2x -{¦ h,
A /i A
lira Bх + А) = lim 2x + lim A = 2х.
Следовательно, /' (х)= 2х для всех ieR. II
Предложение. Если / дифференцируема в х и
?,eR, го X/ дифференцируема в х и
Доказательство.
->./'(*)• //
Следующие результаты оказываются полезными при
дифференцировании функций, которые определены че-
через другие функции.
Предложение. Если fug дифференцируемы в х,
то
а) / + S дифференцируема в х и
U+ g)'(*)-!'{*)+8'(*У.
7 Д. Кук, Г. Бойз 87
б) }g дифференцируема в х и
в) fig дифференцируема в х при g(x)?= О и
Доказательство оставляем в качестве упражнения.
Эти формулы могут использоваться при доказатель-
доказательстве некоторых, возможно, знакомых простых резуль-
результатов.
Пример 5.5.
1. Пусть /: R -ч- R, где /(*)= 1/х. Тогда
/'(г)--1/а;» и 0, = 0,-= R\{0}.
2. Пусть /: R -*¦ R задано формулой f(x) = xn (neN).
Тогда /'(*)-иж-1. //
Пред лож енпе (правило дифференцирования слож-
сложной функции). Если / дифференцируема в х и g диффе-
дифференцируема в у = 1(х), то g ° f дифференцируема в х и
Доказательство. Пусть w = g (у)— g\f{x)) =
= g° f(x)- Тогда ^°J = lim ¦— = lim ^ ^ (при условии
&УФ®) = Hm g- lim ^- (см. п. 5.1). Однако / дифферен-
дифференцируема в точке х, и поэтому
бя-Ю °х dx
аналогично
6у-»0
,. бю rf^
Поэтому
dip) = dwdj_ (g.f)'-g'(y)f'{x). II
dx dy dx кь " ь \jjj \ j и
Производную от /' записывают в виде /" плп
и называют второй производной функции /. Аналогично
производная от d"-lj/dx"-1 (ч>3) записывается как /(п)
или d"f/dx" п называется п-й производной функции /.
Если /' существует п непрерывна, то говорят, что / при-
принадлежит классу С1; /"принадлежит классу С"\ если /(в)
существует и непрерывна, и классу С°°, если /(п> суще-
существует для всех bsN,
5.4. Интегрирование. Пусть /: [о, Ь] -*• R, neN, 'h =»
= (Ь — а)/га и ar,t=»a + &/i при (К & < п. Тогда можно
определить последовательность ($Л/)):
Ы/))
ft=0
Если (sn(/)) имеет предел, то будем говорить, что / пп-
тегрируеыа па [а, Ь], и обозначать
lim
ь
\f(x
Величину J f(x) dx называют интегралом Римана функ-
а
цпи f(x) на [а, Ь].
Заштрихованная площадь на рис. 3.10 является гра-
графическим представлением Sb(f) для непрерывной функ-
функции / на [а, Ь]. Для неограниченно больших значений п
интуитивно можно ожидать,
что заштрихованная пло-
площадь будет хорошо аппро-
аппроксимировать площадь под
графиком между х = а н
х = Ь и ограниченным зна-
значением (если оно существу-
существует) этой площади.
Если &~ обозначает мно-
множество всех вещественных
функций на [а, Ь], то интег-
интегрирование может рассматриваться как функция SF -*¦ R,
область определения которой есть
1ь \
С
/e*F: J f(x)dx существует .
a J
Некоторые важные свойства интеграла приводятся ниже.
Предложение.
а) Если f непрерывна на [а, Ь], то она интегрируема
на этом отрезке;
б) если / интегрируема на [а, Ь] и х <= [а, Ь], тогда ]
интегрируема на [а, х] и [х, Ь] и
ь я ь
я
Рпс. 3.10
99
в) если f интегрируема на [а, Ь] и К ® R, тогда А,/ ин-
интегрируема на [а, Ь] и
г) если fug интегрируемы на [а, Ь], то f + g интег-
интегрируема на [а, Ь] и
ъ ъ ъ
J (/ + *)(*)<** = \j{x)dx + \g{x)dx.
Доказательство. В случае а) формальное дока-
доказательство давать но будем. Заметим, однако, что для
непрерывной функции / интуитивно ясно, что площадь
под графиком / является хорошо определенным поняти-
понятием, и, следовательно, можно ожидать, что интеграл от /
существует. Доказательства б)—г) следуют из соответ-
соответствующих свойств последовательностей. Рассмотрим, на-
например, случай г). Если fug интегрируемы па [а, Ь], то
последовательности
«п(/)-2/(**)А и *„(*)-
ft=0 h
имеют пределы. Рассмотрим последовательность sn(/) +
+ sn(g). Тогда
lim (sn (/) + sn (g)) = lim sn (/) + Km sn (g). //
Jl-»oo 1l-»oo n-»oo
Чтобы вычислить интеграл, редко используют опреде-
определение п вычисляют предел. Следующая теорема является
основной. (Она устанавливает тот факт, что интегрирова-
интегрирование и дифференцирование — взаимно обратные процессы.)
Теорема. Пусть /: [а, Ь] -*¦ R непрерывна. Опреде-
Определим функцию F: [а, Ь] -*¦ R формулой
Тогда F дифференцируема на [а, Ь] и F' •=» /.
Доказательство. Будем лишь фиксировать ос-
основные моменты доказательства. Используя результаты
100
предыдущего предложения, имеем
t+h t
f f(x)dx-\ f(x) dx
h ~ h
t t+h t
§f(x)dx + j f(x)dx~^f(x)dx
= ° L—i = 7T J H*)dx.
Рассмотрим
lira-i f f(x)dx.
h-»0 t
Из определения интеграла и его интерпретации как пло-
t+h
щади ясно, что для малых h интеграл J / (х) dx стре-
t
мится к f(t)h a
t+h
lim-i f f(x)dx = f(t).
ft-»o я у
Следовательно,
*"(*) =/(О Для всех «e[s, Ь]. /
Пусть Ф — произвольная функция, для которой Ф' =»
= /. Тогда F — Ф является постоянной, так как
( О С)
Следовательно,
(^-Ф)'@=0 для всех *е[а, 6],
и иэ п. 5.3 заключаем, что F — Ф = Л, X е R. Таким
образом,
Функцию Ф называют неопределенным интегралом от /
и обозначают J / (t) dt. Неопределенный интограл опре-
определен с точностью до постоянного слагаемого. Он опре-
определяет класс эквивалентности функций [Ф]: Ф1 ~ Фа
тогда и только тогда, когда Ф1 и Фг — неопределенные
интегралы от /.
101
П р е д л о ж е н и е. Если Ф — неопределенный интег-
интеграл от /, то
ъ
(х) dx = Ф (Ь) — Ф (а).
Доказательство.
Ф (Ь) — Ф (а) = (F (b) + l) — (F(a) + к) = F(b) — F(a) =
Ь a b
= j /(*) Жг - J /(*) Ле = j /(ж) rf*. //
а а а
Как и при исследовании дифференцирования, эти
результаты могут быть использованы для вычисления
интегралов, некоторые примеры которых даны ниже.
Пример 5.6.
1. Если F(t) = I xdx, то F'(t) = t, и неопределенные
о
интегралы от функции /: х<-+ х есть
Таким образом,
2. В более общем случае, если/:а;>-»а;"для nsZ\{—1}
t
и F (t) = J xn dx, то F' (t) = f", и неопределенный иптег-
a
рал есть
Тогда
Очевидно, что это соотношение неверно при га = — 1.
Этот случай будет рассмотрен в п. 5.5.
5.5. Некоторые специальные функции. Мы предпо-
предполагаем, что читатель внаком с геометрическими опреде-
определениями функций sin х и cos x, из которых следует, что
sin: R - [-1, 1],
cos: R -4-1, 1],
где
2>.m - S>tot = R, SZm = #co, = [-1, 1].
102
Мы также предполагаем знакомство с порподпческпмп
свойствами этих функций. Некоторые другие элементар-
элементарные свойства приведены в следующем предложении.
Предложение. Для всех х, у е R имеем:
а) sin(x + у) = sin (x)cos(у) + cos (х) sin (у);
б) sin (х — у) = sin (x) cos (г/) — cos (x) sin (у);
в) cos(x + y) = cos (х) cos (у)— sin (x) sin (у);
г) cos (ж— !/)= cos(x)cos(!/) + sin(x)sin(!/);
д) sin2 х + cos2 a; = 1;
Эти результаты непосредственно следуют из опреде-
определений. Их доказательство оставляем читателю в качест-
качестве упражнения. Мы не будем касаться обоснования этих
понятий (можио принять их в качестве допущений).
В п. 5.4 был определен j xn dx при п ?= —1. В дейст-
t
вительности интеграл \ — dx существует для всех О О
г
и равен In t. Функция In является отображением
]0, °°[ -*¦ R и обладает свойством
ln(xy) = In х + In у для всех х, у е ]0, °°[,
так как
¦у- In (xy) = — = — = -г- In х.
dx K "' ху х dx
Из результатов п. 5.4 имеем \п(ху) — 1па; = Х, где х&
е ]0, <»[ и X е R. В частности, при х = 1 имеем In г/ —
— In 1 = "к и In 1 = 0; поэтому In у = X. Следовательно,
\п{ху) = In a; + In у.
Можно показать, что In биективна и, следовательно, су-
существует функция
exp: R -> ]0, °°[
такая, что In (ехр р) = р для всех jeR и exp {In q) = q
для всех q s ]0, оо[. Из свойств функцпп In следует, что
ерх{я + у) = ехр х ехр у для всех х, jeR,
ехрО = 1,
d
-г- ехр х = ехр х.
Удобно обозначить In x через log, x, a exp x через е1.
103
Функцию log. x называют натуральным логарифмом
числа х, а функцию х *-* ех — экспоненциальной функ-
функцией.
Если при а > О функция /: ]—а, а[ -*¦ R принадлежит
С и х е ]—а, а[, то ряд
fc-0
нааывают рядом Маклорена для / в точке х. Для неко-
некоторых функций можно показать, что ряд Маклорена схо-
сходится к аначеиию функции / в точке х. Другими слова-
словами, для / имеем
"-»oo ft=0
В частности, это справедливо для функций sin x, cos x,
е*, для которых
• t \ V / 1\* **Ш _ *3 . *Ь *7 j.
sin^ = ^(-i) BА + 1I ~~ ж 31 +Ы~ 7Т+ •••»
ft—О
ft=0
для всех ieR,
Упражнение 3.5.
1. Показать, что последовательности, определенные
ниже, сходятся, и найти их пределы:
а) snai/n2;
б) *,.-Зл/(п + 3);
в) sn = 1 + 1/2".
2. Пусть (sn) и (?„)—последовательности, lim sn = s
и п ltn\ < \sn\ для всех neN, Показать, что lim?n = O,
п-»ся
3. Доказать, что если (sn) и (fn) имеют пределы s и
f соответственно, то последовательность (рп), где р„ =•
«= Xsn, имеет предел Xs. Если f ?= 0, то lim {sn/tn) = sjt.
п-*еа
4. Найти производные следующих функций (опреде-
(определить области, в которых существует производная);
104
J/,W/(J;
б) /: R\{O>-*R, где /(г) = I/a:;
в) /: R-R, где/(г)=|а:|2.
5. Показать, что если fag дифференцируемы в точ-
точке х, то:
а) / + ё дифференцируема в точке х и
(/ + *)'(*)-/'(*) + *'№
б) fg дифференцируема в точке х п
в) fig дифференцируема в точке х при g(x)?=0 и
S (*)
6. Показать, что если ак е R при O^k^Nnp'.Tl-*-
-*¦ R определено соотношением
р(х)= 2 ahxh, то р'(х)= 2 аькх4'1.
ft=0 А=1
7. Определить производные следующих функций:
а) /: R-» R, где f(x) = x sin x/ A + cosx),
б) g: R -»¦ R, где g (х) = sin х2 + х cos2 z.
8. Вычислить интегралы:
2 1 Я/2
a) j а? <?г; б) j а:1/з da;; в) j cos x dx,
1—1 О
9. Найти неопределенные интегралы:
a) ja**8 dx; б) J fj8 + 2xf + 1) dx; в) j sin a; cos x dx.
§ 6. Операции
Часто некоторые функции (такие, например, как сло-
сложение целых чисел) используются при введении более
простых обозначений. Это можно использовать для опи-
описания основных идей, изложенных в предыдущих пара-
параграфах, что, в свою очередь, позволит нам сделать дока-
доказательства более короткими и в то же время точно вы-
выделить свойства, на основе которых делаются выводы.
Более детальное исследование будет проведено в
гл. 5—8.
105
Определение. Операцией над множеством S на-
называется функция /: Sn -*¦ S, п е N. В этом определении
есть два важных момента, которые заслуживают особо-
особого упоминания. Во-первых, раз операция является
функцией, то результат применения операции однознач-
однозначно определен. Поэтому данный упорядоченный набор из
п элементов 5 функция / переводит только в один эле-
элемент 5. Во-вторых, поскольку область значений опера-
операции лежит в 5, на которое операция действует, будем
говорить, что операция замкнута на 5.
Говорят, что операция 5" -*¦ S имеет порядок п. Ог-
Ограничимся рассмотрением ситуаций, когда порядок ра-
равен 1 или 2. В этом случае операции называют мопади-
ческими (или унарными) и диадическими (или бинар-
бинарными) соответственно. Элементы набора из п элемеытоп
в области определения называют операндами. Операции
обычно обозначают символами, называемыми оператора-
операторами. В случае унарпых операций обычно символ операто-
оператора ставят перед операндом. II
Наиболее простым примером является операция из-
изменения знака на R. В предположении, что операция
сложения уже определена, —х определяет операцию
Xh+y: х + у = 0 (х отображается в у: х + у = 0).
Определение. Бинарные операции обозначают
одним из трех способов. В первом случае оператор ста-
ставится между операндами (infix), во втором — иеред опе-
операндами (prefix) и в третьем — после операндов (post-
fix). II
Пример 6.1.
о + 6 infix,
+ай prefix,
аЬЛ- postfix. II
Переход от одной формы к другой нетруден и лучше
всего описывается в терминах ориентированных графов,
которые будут обсуждаться в § 6 гл. 7.
В соответствии с большинством математических тек-
текстов, исключая некоторые работы по алгебре и формаль-
формальной логике, мы будем использовать обозначение infix.
Другие обозначения имеют то преимущество, что не тре-
требуют скобок при определении порядка вычислений слож-
сложных выражений, и это делает их особенно удобными для
автоматической обработки. Читатель может проверить
соответствие между следующими парами выражений, за-
записанными в формах infix и postfix соответственно:
106
а) a + b* c + (d + e*(j + g)),
abc * + dejg + « ++;
б) (a + b)*c + d + e*f + g,
ab + c* d + ef * + g+;
в) a+(b*(c + d)+e)*j + g,
abed + *e + f*+g+.
Пример 6.2. Рассмотрим алгебраическое выражение
и его представление на рис. 3.11, которое пазывают до-
ревом. Из свойств арифметических операций мы знаем,
что значение этого выражения молено вычислить многи-
многими способами. Однако если двигаться слева направо и
снизу вверх, то получаем
а*- Ь* с, р1 - а + a, 4*-f + g,
Здесь греческими буквами обозначаются промежуточные
результаты, за исключением р —искомого результата.
Вычисление значепия этого выражения с помощью
дерева производится очень просто, однако если работать
непосредственно с исходным выражением, то это можно
л
Рис. 3.11
сделать по-другому. Действительно, обычпо {infix) вы-
выражение, как это показано в примере, нерегулярно по-
потому, что некоторые подвыражения заключены в скоб-
скобки, а некоторые нет. Особенно такая ситуация будет на-
наблюдаться в том случае, если проинтегрировать инфор-
информацию о различных символах на дереве (поскольку на
самом деле его нет). Очевидно, что формы записи prefix
и postfix этого выражения несут больше информации.
107
Вычисление значения выражения в форме postfix осу-
осуществляется следующим образом:
fl
Р
R
Аналогично в форме prefix вычисления осуществляются
следующим образом:
Ъ
+
+
+
а
+ а
1
а
fl
«Переходы» по дереву показаны на рис. 3.12, а
(форма prefix) на рис. 3.12, Ь (форма postfix) а на
рис. 3.12, с (форма infix) со скобками:
К этим вопросам мы вернемся позднее.
Конечно, мы уже виакоыы со многими бинарными
операциями, например с арифметическими операциями
+1 •» —1 / и операциями над множествами — объедине-
объединением (U) и пересечением (fl).
Операции, определенные на конечных множествах,
часто удобнее задавать при помощи таблиц.
Пример 6.3. Пусть операция ® определена на мно-
множестве {а, Ь, с) при помощи таблицы
9
а
Ъ
с
а
а
Ъ
а
Ъ
а
а
b
с
Ъ
с
Ь
108
Следовательно,
а ® Ъ = а,
Такие символы, как © и ®, будут использоваться для
обозначения различных операций, которые будут вво-
109
диться в процессе изложения. Очевидно, что использова-
использование таблиц имеет важное значение, так как некоторые
операции, с которыми приходится иметь дело в компью-
компьютерной математике, непригодны для словесного аадания.
Обратим теперь внимание на свойства операций. Опе-
Операции вместе со своими следствиями обеспечивают ос-
основу всех алгебраических вопросов математики, так как
оии определяют порядок работы с объектами.
Определение. Говорят, что бинарная операция ®
на множестве А коммутативна, если
а®Ъ = 6 ® а для всех а, Ъ е А. //
Следовательно, обычная операция сложения на Z комму-
коммутативна, а вычитания — нот.
Определение. Говорят, что операция ® на мно-
множестве А ассоциативна, если
(а ® Ь)® с = а ® (Ь® с) для всех a,b, с^А. ff
Заметим, что в определении ассоциативности поря-
порядок операндов a, b и с сохранен (операция может быть
некоммутативной!) и использованы круглые скобки, что-
чтобы определить порядок вычислений.
Таким образом, выражение (а ® Ь) ®с требует, чтобы
сначала вычислялось а ® Ь и результат этого (скажем,
х) участвовал в операции с с, т. е. давал х ® с. Если
операция ассоциативна, то порядок вычислений несу-
несуществен и, следовательно, скобки не требуются.
Пример 6.4. Над Z имеем
но
A + 2) + 3 = 1 + 2 + 3=1 +B + 3),
A — 2)— 3 = —4 и 1 — B — 3)= 2.
Таким образом, операция вычитания не ассоциативна. II
Коммутативность и ассоциативность являются двумя
важными свойствами, которые могут быть определены
для простых операций. Перед тем как описывать свойст-
свойства, связывающие две операции, определим некоторый
термины, относящиеся к специальным элементам мно-
множеств, к которым эти операции применяются.
Определение. Пусть ® — бинарная операция на
множестве А и I e А такая, что
/ ® а = а для всех ае/1.
Тогда I называется левой единицей по отношению к ©
НО
на А. Аналогично, если существует г^А такое, что
а®г = а для всех a s A,
то г является правой единицей по отношению к ® Да-
Далее, если существует элемент е, который является и ле-
левой, и правой единицей, т. е.
е® о = а®е = а для всех eei,
то е называется {двусторонней) единицей по отноше-
отношению к ®. II
Пример 6.5. Над R 0 является правой единицей по
отношению к вычитанию и единицей по отношению к
сложению, так как
а — О = а,
но
О — а Ф а, если а Ф 0;
а + 0 = а и 0 + а~а для всех а. II
Определение. Пусть ®— операция на А с еди-
единицей е и х ® у = е. Тогда говорят, что х — левый об-
обратный элемент к у, а у — правый обратный элемент к
х. Далее, если х и у такие, что
то у называется обратным элементом к i по отношению
к ®, и наоборот. II
Замечание. В некоторых работах левые (правые)
обратные элементы относят к левой (правой) единице,
однако, как мы скоро увидим, в большинстве случаев
единицы являются двусторонними и, следовательно, не
требуется делать никаких различий. Для решения урав-
уравнений необходимо существование и единственность еди-
единиц и обратных элементов. Менее общим свойством опе-
операций является идемпотентность, хотя оно используется
в алгебре логики.
Определение. Пусть операция ® иа множестве
А и произвольный элемент х& А таковы, что х ® х =- х.
Тогда говорят, что х идемпотентен по отношению
к ®. //
Очевидно, что любое подмножество идемпотентно по
отношению к операциям пересечения и объединения.
Определение. Пусть дано множество А, на кото-
котором определены две операции ® и ©. Тогда, если
а ® (Ь ф с) = (а ® Ъ) ф (а ® с) для всех а,Ь,с е А,
то говорят, что ® дистрибутивна по отношению к (В-
111
Если сказанное выше не совсем понятно, следует
провести соответствие между этим тождеством и обыч-
обычной арифметикой на R, например,
Может вызвать удивление, что в § 5 рассматривались
только несколько специальных свойств, и можно прийти
к выводу, что практически ничего нельзя вывести иа
того факта, что множество и связанные с ним операции
обладают некоторыми из этих свойств. На самом деле
(как будет видпо из последующих глав) наиболее обще-
общеизвестная алгебра может быть построена из относи-
относительно небольшого набора основных правил. Сейчас мы
продемонстрируем, как из элементарных предположений
можно извлечь некоторые простые следствия; большин-
большинство примеров дано в виде упражнений.
Пример 6.6. Пусть © — операция на множестве А
и существует единица по отношению к ®, Тогда еди-
единичный элемент единствен.
Доказательство. Предположим, что х и у —
иицы по отношению к ®, т. е.
у ® а = а® у = а для всех игА.
Тогда х = х ® у, так как у — единица, и х ® у = у, по-
поскольку х — единица. Следовательно, х = у. /
Пример 6.7. Пусть ® — ассоциативная операция
на множестве А и е — единица по отношению к ®. Тог-
Тогда если х ^ А ъ х имеет обратный, то обратный эле-
элемент единствен по отношению к ®.
Доказательство. Допустим, что х' и х" — об-
обратные элементы к х, так что
х®х' = х'®х=>е и х ® х" = х" ® х = е.
Тогда
х' = х' ® е = х' ® (х ® х") = {х' ® х) ® х" —
— е ® х" = х'. II
Упражнение 3.6.
1. Рассмотреть указанные ниже «определения» ®#
Решить, правильно или нет каждое из них определяет
бинарную операцию, и если так, то является ли опера-
операция коммутативной. Найти, если это вовможно, единицу
а обратный элемент к х. Предполагаются выполненны-
выполненными обычные свойства арифметикн:
112
а) x © у = x — у на N;
б) х ® у = (х*у) — 1 на Z;
в) х ® у = тах{х,у) на N;
г) х® у = Ух2 + г/2 на {ж: 0<i,ieR};
д) х®у = х/у на {я: 0<а;, ieR}.
2. Определим операцию ф на множестве {а, Ь, с), как
указано ниже. Проверить, что ф ассоциативна и комму-
коммутативна и найти единичный элемент.
ф
a
с
Ь
a
Ъ
a
с
Ь
с
Ъ
a
с
a
е
Ъ
3. Предполагая обычные свойства операций +, —, •
и / на R, доказать, что операция i|>, определенная на
[1, °°[ следующим образом:
ассоциативна. Обосновать ответ.
Указание: не следует особо обращать внимание
на область определения.
4. Пусть ® — ассоциативная операция на множестве
А с единицей е такая, что каждый элемент a e А обра-
обратим и обратный обозначается через а'. Показать, что
(а ® Ь)' = V ® а'.
5. Показать, что если ®— ассоциативная операция
на множества А с единицей е такая, что a ® a = e для
каждого оеЛ, то ® коммутативна.
6. Пусть ® — ассоциативная операция на множестве
А такая, что для любых a, iei, если о © b = b ® а, то
о=>6. Показать, что каждый элемент А идемпотентен по
отношению к ©. Что можно сказать про ©¦ если опера-
операция имеет единицу?
8 д. кук, г, Бейз
ГЛАВА 4
ОСНОВНЫЕ ПОНЯТИЯ АРИФМЕТИКИ
Итак, мы определили операции и описали некоторые
их свойства. Теперь посмотрим, что можно сделать с со-
совокупностью операций, заданных на множестве.
Множество с заданными иа нем операциями называ-
называют алгебраической структурой. Некоторые из наиболее
часто встречающихся алгебраических структур будут
рассмотрены позднее. Прежде чем приступить к их рас-
рассмотрению, посмотрим на арифметику с неформальной
точки зрения. В большинстве случаев мы будем опу-
опускать формальные определения, делая ударения на
«следствия из правил», даже в тех случаях, когда это
приводит к необычным способам использования извест-
известных символов, которые обычно используются для пред-
представления десятичных чисел.
§ 1. «Малая» конечпая арифметика
Арифметику можно рассматривать как мпожество с
двумя операциями, действующими подобно сложению и
умножению. Ее можно изучать многими способами. Что-
Чтобы уяснить требования арифметической системы, при-
примем конструктивное приближение и рассмотрим целыэ
числа @, 1, 2, ...) просто как символы. В дальнейшем
будем рассматривать только конечную арифметику, в ко-
которой используется лишь конечное множество чисел;
вначале это множество будет небольшим. Подразумевает-
Подразумевается, что если А ~ Nm, то требуется т различных симво-
символов, при этом никакие комбинации символов не разреша-
разрешаются. Если используются только десятичные числа, то
т < 10. Поскольку все множества данного размера би-
биективны, то можно рассматривать только множества Nm.
Для большей наглядности рассмотрим множество Ne.
Для этого необходимо построить таблицы умножения и
сложения. Множество Ne достаточно велико для того,
чтобы изучать свойства основной структуры, Можно по*
114
думать, что для этой цели более уместным является
множество N2, однако это не так. Начнем со сложения.
Операция сложения имеет единицу, которая обычно
обозначается символом 0, однако 0 *? Ne. Поэтому будем
использовать множество Ze = <0, 1, 2, 3, 4, 5), которое
более удобно. Очевидно, что Ze ~ Ne. Поэтому можно
работать с Ze, не теряя никаких свойств. Таким образом,
к настоящему моменту мы имеем соответствующую
табл. 4.1.
+
0
1
2
3
4
5
0
0
1
2
3
4
5
1
1
2
2
'1'
3
3
а б л п ц а
4
4
4.1
5
5
Так как операция коммутативна, то таблица должна
быть симметричной. Труднее обстоит дело с ассоциа-
ассоциативностью. Если мы хотим, чтобы операция была ассо-
ассоциативной, и требуем, как обычно, существования обрат-
обратных элементов по сложению, то любой элемент должен
входить ровно один раз в каждую строку и каждый стол-
столбец. Поясним это высказывание.
Если а + Ь = а + с, то
О + b = 0 + с,
Ъ = с.
Рассмотрим теперь операцию, определенную в
габл. 4.2. Из трех возможностей для операции сложения
на Ze только С удовлетворяет всем условиям, что выгля-
выглядит несколько необычно. Операция А не коммутативна,
а в В нарушен критерий «единственности результата».
Как же построить соответствующую операцию, удовлет-
удовлетворяющую всем обсуждаемым выше свойствам? Из
дальнейшего изложения будет видно, что наиболее труд-
трудно обеспечить выполнение свойства ассоциативности.
В предложенной ниже процедуре мы используем ассо-
8* 115
циативность как основной шаг построения, и, следова-
следовательно, это свойство будет выполняться автоматически.
Шаг 1. Число 0 является единицей для операции
сложения. Поэтому полупаем табл. 4.3.
Таблица 4.2
А
0
1
?,
3
4
5
0
0
1
2
3
4
5
1
1
2
0
5
3
4
2
2
0
1
4
5
3
3
3
4
5
0
1
2
4
4
5
3
2
0
1
5
5
3
4
1
2
0
В
0
1
2
3
4
5
0
0
1
2
3
4
5
1
1
1
2
3
4
5
2
2
2
2
3
4
5
3
3
3
3
3
4
5
4
4
4
4
4
4
5
5
5
5
5
5
5
5
С
0
1
2
3
4
5
0
0
1
2
3
4
5
1
1
5
3
4
2
0
2
2
3
1
5
0
4
3
3
4
5
0
1
2
4
4
2
0
1
5
3
5
5
0
4
2
3
1
+
0
1
2
3
4
б
0
0
1
2
3
4
5
1
1
2
2
Таб
3
3
лица
4
4
4.3
5
5
Шаг 2. Определим следующую строку таблицы, удов-
удовлетворяющую условию «единственности результата».
Чтобы подчеркнуть используемую технику, специально
выберем результат, который отличается от привычного,
Возьмем
+ 10 12 3 4 5
4
Так как операция должна быть коммутативпой, аапол-
ним соответствующий столбец табл. 4.4.
Шаг 3. Заполним другие клетки таблицы, используя
ассоциативность. Проследим подробно ва каждой де-
деталью:
Ив
Здесь мы использовали соотношения 2+1 = 0 и
= х. Далее
3 + 3 = A + 1)+3=1+A + 3)=1 + 5 = 4и т. д.
Таким образом, на основе значений 1 + х получаем таб-
таблицу для операции + (табл. 4.5).
Таблица 4.4 Таблица 4.5
+
0
1
2
3
4
5
0
0
1
2
3
4
5
1
1
3
0
5
2
4
2
2
0
3
3
5
4
4
2
5
5
4
+
0
1
2
3
4
5
0
0
1
2
3
4
5
1
1
3
0
5
2
4
2
2
0
4
1
5
3
3
3
5
1
4
0
2
4
4
2
5
0
3
1
5
5
4
3
2
1
0
При выполнении процесса надо учитывать дополнитель-
дополнительные ограничения на шаге 2. Значения в нулевой строке
должны выбираться так, чтобы они «продолжали» все
Ъь. Например, начиная с 1 (как мы делали), получаем
1 + 1 = 3, 3 + 1 = 5, 5+1 = 4, 4+1 = 2,
2 + 1 = 0, 0+1 = 1.
Следовательно, прибавляя только 1, можно получить
все Ze.
Перейдем теперь к умножению. Сначала ааметим,
что единица для операции умножения должна отличать-
отличаться от нуля. В противном случае для любых х и у мы
имели бы
поэтому
х • у = х * @ + у) = (х • 0)' + (х • у) = х + (х * у),
а значит, х = 0. Поэтому 0 не является единицей для
умножения.
На самом деле нам требуется число, которое будет
порождать Ze. Следовательно, мы могли бы определить
аналогичным образом операцию умножения на основе
частичной табл. 4.6. Однако в этом случае мы не долж-
должны настаивать па выполнении критерия «единственности
результата». (В обычной арифметике не существует це-
целого числа, которое при умножении на 2 давало бы 1!
Поэтому в конечном множестве могут быть повторения.)
117
Вместо того чтобы повторять процедуру построения таб-
таблицы для умножения, вернемся к проблеме связи двух
операций — дистрибутивности умножения относительно
сложения. Эта проблема связана с ассоциативностью.
Рассмотрим (уже построенную) операцию сложения.
Таблица 4.6
Таблица 4.7
*
0
1
2
3
4
5
0
0
1
0
1
2
3
4
5
2
2
3
3
4
5
4 5
*
0
1
2
3
4
5
0
0
0
0
0
0
0
i
0
1
2
3
4
5
2
0
2
1
4
3
5
3
0
3
4
4
3
0
4
0
4
3
3
4
0
5
0
5
5
0
0
5
Заметим, что 1 + 1 = 3. Поэтому из предположения ди-
дистрибутивности получаем, что
3*0=A + 1)*0 =
Теперь 3 + 3 = 4, 3+1 = 5, 1 + 4 = 2 и 1 + 2 = 0. Дей-
Действуя как и рапее, получаем следующую операцию
(табл. 4.7).
Следовательно, начиная с почти произвольного выбо-
выбора строки в таблице, не содержащей 1 по сложению, и
накладывая ряд простых ограничений, мы приходим к
приемлемой арифметической системе. Теперь достаточно
установить, что полученная система не находится в про-
противоречии с высказанными рапее соображениями, т. е.
что 1 + 1 действительно существует. Короче говоря, если
в нормальной (бесконечной) арифметике a + b = c u cs
е Ze, то хотелось бы, чтобы и в пашей арпфметпке ответ
был с. Следовательно, мы пришли к выбору
+ 10 1 2 3 4 5
1
3
4
Недостающим элементом должен быть 0, поскольку 6 9^
0 Ze, и 0 является единственным элементом Ze, которо-
118
го нет в строке. В результате такого выбора получаем
соответствующую табл. 4.8. Она определяет так называе-
называемую арифметику по модулю 6. (Эта арифметика работа-
работает точно так же, как и обычная целочисленная арифме-
арифметика, за исключением того, что все целые числа заменя-
заменяются на остатки от деления их на 6.)
Таблица 4.8
0
1
2
3
4
5
0
0
1
2
3
4
5
1
1
2
3
4
5
0
2
2
3
4
5
0
1
3
3
4
5
0
1
2
4
4
5
0
1
2
3
5
5
0
1
3
4
0
1
2
3
4
5
0
0
0
0
0
0
0
1
0
1
2
3
4
5
2
0
2
4
0
2
4
3
0
3
0
3
0
3
4
0
4
2
0
4
2
5
0
5
4
3
2
1
Упражнение 4.1.
1. По аналогии с «естественной» арифметикой, полу-
полученной для Ze, построить аналогичную арифметику для
Zie, используя символы {0, 1, ..., 9, А, В, ..., F).
2. Построить арифметику для Ze, которая согласует-
согласуется со строкой
+ | 0 1 2 3 4 5
2 | 2 3 4 0 5 1
3. Рассматривая 1 + 3, показать, что следующая таб-
таблица приводит к противоречию:
+
0
1
0
0
1
1
1
0
2
2
3
3
3
4
4
4
5
5
5
2
§ 2. «Большая» конечная арифметика
Мы уже построили арифметику для Za. Возникает во-<
прос: как можно расширить эту систему, чтобы иметь
возможность считать после 5? Для этого достаточно
иметь множество п-значных чисел (наборов из п эле-
элементов из Ze) с арифметикой над Ze. Чтобы проиллю-
проиллюстрировать это, рассмотрим упорядоченную тройку из Ze,
т. е. элементы множества Ze X Ze X Ze. Если Ze упоря-
упорядочено обычным способом, т. е. 0<1<2<3<4<5,
тогда определим порядок на Ze X Z6 X Z6 по правилу
(а, Ь, с)<{х, и, z),
119
если а<х или а = х и b<у или а — ж, & — у и e<s.
В этом случае элементы Z\ = Ze x Ze x Z, будут упо-
упорядочены следующим образом:
@,0,0), @,0,1),..., @,0,5;,
@,1,0) @,1,5),
@,5,0),..., @,5,5),
A,0,0),..., A,0,5),
E,5,0) E,5,5).
Таким образом, существует б3 = 216 различных троек.
Поэтому нужно уметь производить арифметические вы-
вычисления над Zg в пределах от 0 до 215. В приведенном
выше упорядочивании элементов из Z|
@, 0, 5) непосредственно предшествует @, 1, 0).
@, 1, 5) непосредственно предшествует @, 2, 0)
@, 5, 5) непосредственно предшествует A, 0, 0).
Следовательно, хотелось бы, чтобы выполнялось соотно-«
шение
@, 0,5)+1-@,1,0).
Однако до сих пор не было представления 1 в Zg. И хо-
хотя это соотношение выглядит естественным, мы должны
заботиться о том, чтобы не использовать ни одного не
определенного понятия. Для облегчения описания пред-
представим Z* как А2Х А\ХАо и рассмотрим сумму (аг, аи
ао) и (fo, bu bo). Покомпонентное сложение дает (аг +
+ Ь2, а\ + Ь\, по+bo), где сложение осуществляется в Ze,
и пока, как кажется, этого достаточно.
Пример 2.1. Рассмотрим соотношение
@, 1,3)+ D, 2, 1) = D, 3, 4),
которое будет более наглядным, если записать его в виде
0, 1, 3
= 47з7Т
120
Однако
1, 2, 5 и
'2, 3. 1
= 3, 5, О
0, 0, 5
0, 0, 1 (=1?)
0, 0, 0 (=0?). //
В результате операции сложения множество Ао пере-
переходит в себя. Однако для того чтобы сумма достаточно
больших чисел (таких, как 5+1) могла бы выйти за
пределы Ао, нам необходимо производить некоторые дей-
действия в А\ и также, возможно, в Лг. (Это иллюстрирует-
иллюстрируется табл. 4.9).
Таблица 4.9
¦+
*
0
1
2
3
4
5
0
0
1
2
3
4
5
1
1
2
3
4
5
0
2
2
3
4
5
0
1
3
3
4
5
0
1
2
4
4
5
0
1
2
3
5
5
0
1
2
3
4
е
0
1
2
3
4
5
0
0
0
0
0
0
0
1
0
0
0
0
0
1
2
0
0
0
0
1
1
3
0
0
0
1
1
1
4
0
0
1
1
1
1
5
0
1
1
1
1
1
Возьмем любые два числа а и Ъ из Ъ$. Тогда их сум-
сумма (в Z) составляет
Пример 2.2. 4 плюс 4 дает 6 * A) + B) = 8 в Z.
Таблица +, дает «обычную» сумму двух элементов из
Ze, в то время как таблица +е показывает, когда необ-
необходим «переход» в следующее множество Z6, и содержит
только нули и единицы. Значения в +е ограничены, по-
потому что если
0«S х <п и 0«?у < гс,
то
0^х^х + у<х + п<п + п = 2п (и гс = 6 в Z6). II
В действительности можно получить лучшую оценку,
поскольку
и, следовательно,
Возвращаясь к суммированию (аг, аи
(b2, bu bo)
121
и обозначая ответ через (dj, di, (?o), получим
do = До "Ь «Ьо,
х\
а, + ,bi + ,хо,
если ai + А = 1 тогда 1,
иначе
,?0,
$2 == «2 "Т" »^2 "Т" i^li
Х2 = если яг + с&2 = 1 тогда 1,
ипаче (яг + .Ьг) + e*i«
Поскольку 0 < Oi + Ь, < 2гс — 1 и а:( = О или х, = 1, то
переносимый результат из а( + bt + ar<_i никогда не может
быть больше 1.
Заметим, что в наших определениях числа (О, О, О)
и (О, О, 1) в Zg действуют, как 0 и 1 в новой арифме-
тпке. Кроме этого, если хг = 5, то результат сложения
может оказаться слишком большим для Zj?. В этом слу-
случае говорят, что произошло «переполнение». Этот случай
мы обсудим более подробно в § 3 гл. 4, а до конца пара-
параграфа возможность перевыполнения будем игнорировать.
Аналогично можно использовать операции *р и *„
(таблицы произведения и переноса), заданные в
табл. 4.10 для того, чтобы производить умножение над
Zg, однако мы не будем этим заниматься.
Таблица 4.10
•
р
0
1
2
3
4
5
0
0
0
0
0
0
0
1
0
1
2
3
4
5
2
0
2
4
0
2
4
3
0
3
0
3
0
3
4
0
4
2
0
4
2
5
0
5
4
3
2
1
с
0
1
2
3
4
5
0
0
0
0
0
0
0
1
0
0
0
0
0
0
2
0
0
0
1
1
1
3
0
0
1
1
2
2
4
0
0
1
2
2
3
5
0
0
1
2
3
4
До спх пор мы рассматривали только символы, имею-
щпе впд положительных чисел. Конечно, с символами
О, 1, 2, ... можно обращаться «естественным» образом,
и, следовательно, их можно интерпретировать как неот-
неотрицательные числа. Арифметика над Ъ\ оперирует с чис-
числами от 0=@, 0, 0) до 215 = E, 5, 5), которые были
получены из последовательности (от 0 до 5) в Ze. Если
122
взять мпожество (—3, —2, —1, 0, 1, 2} вместо Ze, то по-
получим систему, которая содержит отрицательные числа,
но ведет себя странным образом.
Если мы возьмем дна множества Z6 и множество {—3,
—2, —1, 0, 1, 2), которое назовем Z^.n образуем множе-
множество Z^xZaXZ,,, то можно построить арифметику с
числами от —108 до 107. Иа самом деле арифметика
является той же самой, за исключением того, что значе-
значения 3, 4 п 5 в Ач сейчас интерпретируются как —3, —2,
—1 соответственно. Поэтому, например, (—2, 4, 2) вычис-
вычисляется в Z как
Биекция между двумя системами, определенная следу-
следующим образом:
я*-*- я в остальпых случаях,
может быть применена в любой момент при условии, что
результат вычислений не имеет цифр 3, 4 или 5 в А2.
Мы выбираем обозначения из соображения удобства, не
вводя ограничении па случаи, когда можно применять
бнекцпю или обратное отображение. Па этом этапе мы
настойчиво советуем игнорировать любые очевидные про-
противоречия, относящиеся к переполнению А2. Этот случай
будет подробно рассмотрен в последующих параграфах
на более простом примере. Отметим, что новая система
«переходит» от положительных чисел к отрицательным.
Например,
(C,0,0) в старой системе,
B, 2,5) + A,0,1)= 0 ' ,
4 ' v ; Ц— 3,0,0) в новой системе.
(В Z это дает 107+1 = -108!)
Вычисления, включающие в себя сложение и вычи-
вычитание, в новой арифметике довольно просты и зависят
от двух тождеств. Первое имеет вид
E,5,5) + @,0, 1)-@,0,0)
(E, 5, 5) эквивалентно (—1, 5, 5)), а второе — вид
(а2, аи ао) + (Ь2, bit Ьо)==E, 5, 5).
123
Они имеют место тогда и только тогда, когда
Таким образом, чтобы вычислить обратное по сложению
число к (аг, а\, а0), мы должны сначала найти число
(Ьг, bi, bo), которое называют дополнением по 5, и затем
прибавить 1=@, 0, 1). Это даст дополнение до 6. Про-
Проиллюстрируем этот процесс на следующем примере.
Пример 2.3. Найдем обратные элементы к (—3, 4,
1) и C, 4, 1).
Из 3, 4, 1
получаем 2, 1, 4 (дополнение до 5)
+ 1
2, 1, 5 (дополнение до 6)
Проверим рез} чьтат 3, 4, 1
2, 1,5
- О, О, О
Поэтому - (-3, 4, 1) - B, 1, 5). //
Таким образом, вычитание сводится к сложению с со-
соответствующим дополнением.
Пример 2.4. Вычислим A, 3, 4) —B, 1, 5).
Берем 2, 1, 5
получаем 3, 4, 0 (дополнение до 5)
результат 3, 4, 1 (дополнение до 6)
прибавим A, 3, 4) A, 3, 4)
5, 1, 5=(-1, 1,5).
Проверяя вычислеппя пад Z, получаем 58—83 = —25. /
Конечно, причиной образования так называемых допол-
дополнений до 5 и 6 является тот факт, что мы проводим вы-
вычисления над Ne (или Ze).
В общем случае, если вычисления производятся в Nm,
мы должны использовать дополнение до т — 1 и т со-
соответственно.
Надо подчеркнуть, что в вычислениях на ЭВМ мы
обычно имеем дело с "Lm для некоторых фиксированных
т и п и очень редко — с множеством Z. Таким образом,
совокупность имеющихся в нашем распоряжении чисел
всегда ограничена, и, хотя границы могут быть очень
большими, мы не должны забывать о том, что они су-
существуют. Риск тем более велик по той причине, что в
записи обычно опускают запятые и все нули, стоящие
слева от первой ненулевой цифры за исключением числа
124
(О, 0, 0). Следовательно, A, 3, 4) запишется кан 134,
@, 0, 6) как 6 и @, 0, 0) как 0.
Упражнение 4.2. Обозначим Z^xZjjT1 через Zj},~,
где
— \ in л т . I
| ° еСЛИ m четное»
если т нечетное.
in л т . I
— . • . •) °1 ¦ • • > у ~ Ч'
= | ^—, ..., 0, ..., —2— |,
Вычислить: а) 10-7; б) 17-23; в) (-8)+ (-21) в
каждой из «естественных» арифметик Z*~, Ъ\^, Zbb~, Ъ\^'
(Замечание: числа в примерах заданы над Z; по-
поэтому вначале требуется перевести их в соответствую-
соответствующую систему, а потом проводить вычисления.)
§ 3. Двоичная арифметика
Из уже построенных арифметик над ZJ}, и Z?,~ легко
выделить основы двоичной арифметики. Существуют две
так называемые двоичпые арифметики. Первая — это
знаковая и модульная форма, определенная па {—. +} X Z?,
т.е. Za (определенпое в предыдущем парагра-
параграфе) с добавленным знаком, расширяющим элементы Z?#
Знак обычно кодируют в бинариой форме: 0 для «+» и
1 для « —». Вторая арифметика (двоичная арифметика
дополнений) — это Z'2l~ с элементами {0, 1} во всех п по-
позициях. Этот вид двоичной арифметики используется в
большинстве компьютеров. Поэтому ограничим наши рас-
рассмотрения Z!,1", Чтобы сделать обсуждение более конк-
конкретным, рассмотрим Zj", элементы которого лежат в пре-
пределах от 10000 (=-16) до 01 111 (=+15) (т. е. содер-
содержит 32 = 25 различных чисел). Число —1 представляется
в Z'2~ как 11 111. Поэтому легко пайти двоичное допол-
дополнение. Для этого падо слегка изменить все двоичные
цифры, называемые битами, чтобы получить дополнение
до 1, а затем прибавить 1, чтобы получить дополнение
до 2.
Пример 3.1.
-@1011)
10100
__
10 101
125
-A0110)
-Ь 01001
_
01 01U
(=23 + 2' = 10). //
Очевидпо, что могут возникнуть проблемы, вызванные
ограниченностью чисел. Мы не можем их избежать, од-
однако следует знать, когда возможна «ошибка». Форма
дополнения делает проверку условия переполнения от-
относительно легкой, использующей только значения стар-
старшего значащего бита. (В Zip это бит с номером 24.)
Этот бит обозначает знак представляемого числа и назы-
называется знаковым битом или знаковым разрядом. Перед
тем как проверить, какое значение имеет знаковый бит,
напомним, что прибавление 1 к максимальному положи-
положительному числу в Zm~ дает максимальное отрицатель-
отрицательное число (наибольшее отрицательное число — это отри-
отрицательное число, отстоящее дальше всего от нуля). Дру-
Другими словами, числа повторяются циклическим образом.
В Z?~ мы имеем ситуацию, изображенную на рис. 4.1.
15
t
1
-16
i
i
0
i
15
i
-16
i
I
•¦2
0
1
)
15
I
-16
i
i
0
1
i
15
1
i
-16
1
I
-<t9 -4S -32 -17 -16 0 15 16 31 47 48
BZ
Рис. 4.1
Что же произойдет, если мы сложим два числа х и у,
где
— а<а;<а и —а<г/<а (в 7\~, а = 16)?
Сумма х + у будет ограничена:
2а «3 х + у < 2а - 2 < 2а - 1.
Само по себе это неравенство ничего не дает. Поэтому
мы рассмотрим три случая:
(I) если — a«Sа:<0 и — а<у <0
тогда —2а «? х + у < 0;
(II) если 0<ж<а и 0*3у <а
тогда 0^х + у^2а-2<2а-1-,
126
(Ill) если -а<х<ОшО<у<а
тогда — а < х + у < а.
Вначале заметим, что результат в случае (III) нахо-
находится в требуемых пределах п, следовательно, всегда пра-
правильный. Чтобы понять, как могут возникать ошибки в
случаях (I) и (II), необходимо вспомнить, что если ге
е Z и —2а < z < —а, то число z представимо в конечной
арифметике числом z', где z' = z + 2а и 0 < г' < а. Ана-
Аналогично, если а«?г<2а— 1, то z представимо z", где
z"=z —2а и — a«?z"<0. Следовательно, ответ будет
неправильный, если он в случае (I) положительный или
в случае (II) отрицательный.
Чтобы объяснить эти заключения в терминах свойств
знакового разряда, рассмотрим различные возможности
сложения двух чисел:
а) оба числа отрицательны;
б) оба числа положительны;
в) числа имеют различные знаки.
Анализируя эти случаи, видим, что переполнение
(ошибка переполнения) встречается тогда и только тог-
тогда, когда существует перенос в знаковый разряд или пе-
перенос из знакового разряда, но не оба вместе. Для иллю-
иллюстрации этого рассмотрим несколько примеров в Z|~.По-
Z|~.Попытаемся сопоставить эти примеры со случаями (I) —
(III) и а) — в), рассмотренными выше.
Пример 3.2. Напомним, что вычисления проводятся
Zs—.
,10101 ,11100
+ 1 1 0 1 0 +10 111
101111 110011
t. I UtJ
,1110 1 ,00101
+ 0 0 110 +00111
100011 01100
,01100
+01010 .
1 0 1 1 О" И
Вернемся теперь к умножению и делению. Сначала
рассмотрим умножение. Напомним, что в Z (или, более
точно, в Z"o для достаточно большого п) умножение на
10 можно получить «сдвигом» всех цифр на одну пози-
позицию влево и записью в 0-й позиции цифры 0. (В Zm ум-
умножение на m также всегда можно осуществить сдвигом
влево.)
127
Следовательно, мы имеем простой способ умножения
на неотрицательные степени числа 2 в Z? — сдвиг каж-
каждой цифры влево на соответствующее число позиций.
Пример 3.3. (Вычисления проводятся в Zj~.)
0 0 0 11
0 0 110
0 110 0
C)
(•2)
(.2 =
0
0
1
0
12)
0
1
0
1
1
0
1
0
0
1
0
0
1
0
0
0
1
1
1
E)
(•2)
(.2)
(•2
1
1
1
ES
1
1
0
8).
1
0
0
/
0
0
0
(-2)
(.2)
(¦2=.-8)
Из этих примеров видно, что метод также хорошо ра-
работает для отрицательных чисел, но результат будет о
ошибкой (переполнения), если на каждом этапе менялся
внак и если потом он опять изменился. Для умножения
произвольного целого числа (элемента N) используем
свойство дистрибутивности умножения по отношепию к
сложению и представим множитель как сумму степеней
числа 2.
Пример 3.4. (Вычисления проводятся в Zj~.)
(-5). 3 = (-5)«24-(-5)» 2°.
Поэтому
0 0 0 11 1 1 0 1 1
+01100 +10110
01111 11000 1./
Точно так же, как умножение производилось сдвига-
сдвигами влево, деление на положительные степени числа 2
осуществляется сдвигом вправо. (Деление на другие це-
целые числа должно получаться путем сведения к вычи-
вычитанию степеней числа 2. Этот процессе мы обсуждать не
будем.) Однако специального рассмотрения требуют от-
отрицательные числа. Отметим также, что в общем случае
ожидаемый результат (т. е. арифметически ожидаемый
результат в R) будет не целым, а дробным.
Пример 3.5. Попытаемся в Zj~ вычислить 12/4,
(—6)/2 и 7/4 сдвигом на 2, 1 и 2 позиции соответствен-
соответственно. Имеем
0 110 0 A2) 110 10 (-6)
0 0 0 1110 0 C = 12/4) 0 110 110 A3^.-6/2)
0 0 1111 G)
О 0 0 0 1 | 1 1 A» 7/4). /
128
Сдвиг на одну позицию вправо автоматически сводит
любое отрицательное число к положительному. В Ъ\"
сдвиг переводит —16 к +8. Чтобы исправить это, следует
отнять от результата число 16, что даст —8 (т. е. —16/2).
То же самое можно получить, устанавливая знаковый
разряд равным 1. Следовательно, правильный результат
достигается использованием знакового разряда, значение
которого равно 0 или 1 (в зависимости от знака числа),
для того чтобы заполнить «пропусни», создаваемые в ре-
результате сдвига вправо.
Следовательно, (—6)/2 приводит к
11101 = -3.
Действие битов (со значением 1), «выпадающих» из чис-
числа в результате сдвига вправо, должно усекать резуль-
результат. Поэтому 7/4 дает 1. Существует общепринятая прак-
практика округлять число (вверх независимо от знака) при-
прибавлением к числу утерянного последнего бита. Это со-
соответствует обычному арифметическому правилу округ-
округления, поскольку 1 в первом бите остатка представляет
собой 0.5. Следовательно, 7/4 дает 2.
Упражнение 4.3.
1. Быстрый способ вычисления дополнения до 2 от
данного битового элемента в Zj~ заключается в следую-
следующем. Начиная с правого конца, копируем все идущие
подряд нули и первую встретившуюся единицу. Затем все
оставшиеся биты изменяем. Показать, что этот способ
работает в большинстве случаев, и рассмотреть случаи,
когда он не работает.
2. Пусть в Zij~ производятся следующие вычисления.
Складывают два числа х и у (обозначим их сумму че-
через г). Если от z отнять у, то получим некоторый ре-
вультат с, а если от г отнять с, то получим некоторое
число d. Что можно сказать о с и d? Как отличаются
результаты, если вычисления производятся в Zj~?
§ 4. Логическая арифметика
Строго говоря, булева арифметика оперирует на мно-
множествах Z2 и Zj и, следовательно, включает только чис-
числа 0 и 1. Для того чтобы подчеркнуть такую структуру,
начнем с рассмотрения логической арифметики на «отно-
«относительно большом» множестве Zs. Она дает основу много-
многозначной логики. Отсюда легко получить более простой
9 д. кук, г. Бейз 139
случай Ъ% Возьмем множество Zs = @, 1, 2, 3, 4} и опе-
операции V и Л> определенные в табл. 4.11.
Таблица 4.11
V
0
1
2
3
4
0
0
1
2
3
4
1
1
1
2
3
4
2
2
2
2
3
4
3
3
3
3
3
4
4
4
4
4
4
4
Л
0
1
2
4
4
0
О
0
О
О
0
1
О
1
1
1
1
2
О
1
2
2
2
3
О
1
2
3
3
4
О
1
2
3
Упорядочивая Zs обычным образом (порядок индуциру-
индуцируется Z и R), видим, что
а V b •= max {a, b),
a/\b = min{a, b).
Обе операции коммутативны и ассоциативны, 0 является
единицей для V, а 4 является единицей для Д; Д ди-
дистрибутивна по отношению к V, но не наоборот.
Пример 4.1. Возьмем множество Zm с естественным
порядком элементов. Введем операции Д и V. Рассмот-
Рассмотрим шесть возможных случаев упорядочивания трех про-
произвольных элементов a, b, e из Zm:
(I) asSb«?c;
(II) а^с<Ь;
(III) fc«Sa<c;
(IV) 6 «S с< я;
(V) c<a<b;
(VI) c«?b<a.
Использование символа < является интуитивным, однако
может быть обосновано с помощью следующего опреде-
определения:
a ss Ь тогда и только тогда, когда о V Ь = Ь.
Для проверки условия дистрибутивности нужно показать,
что
Это можно сделать проверкой того, что обе части выра-
выражения совпадают для каждого из наборов a, b а с. Бу-
130
дем одновремеппо вычислять п сопоставлять соответствую
ющие выражения:
(I) а/
(II) а/\(Ъ\/с) = а
(III) a
(
(IV)
(
(V) a
(
(VI) а/\{Ъ\/с) = а/\Ъ = Ь,
Следовательно, Л дистрибутивна по отношению к V. /
Можно также показать (это как раз тот случай, ког-
когда мы не получаем ожидаемого результата), что V ди-
дистрибутивна по отношению к Д, т. е. что
Проверку этого свойства оставляем в качестве упраж-
упражнения.
Перед тем как закончить обсуждение общего случая,
давайте вернемся к табл. 4.11, определяющим V и Д*
Элементы, имеющие одинаковые значения в таблицах,
расположены относительно единичных элементов так, как
показано на рис. 4.2. На самом деле каждая из этих
Рис. 4.2
операций является «отражением» другой и связь, кото-
которая позволяет одну операцию менять на другую, опре-
определяется (в Z5) парами @, 4), A, 3), B, 2), C, 1),
D, 0). В сущности, это принцип двойственности, который
9* 131
будет обсуждаться в гл. 5. Возвращаясь к Ъг, имеем
V
0
1
0
0
1
1
1
1
Л
0
1
0
0
0
1
0
1
В Z2 операцию V обычно интерпретируют как или (ре-
(результат равен 1, если один из операндов равен 1, вклю-
включая случай, когда они оба равны 1). Аналогично Д чи-
читается как и. Число 0 является единичным элементом
по отношению к или, число 1 является единичным элемен-
элементом по отношению к и. Можно распространить эти ре-
результаты на более высокие размерностп (переходя от Ъг
к Zj)> расширяя компоненты и учитывая, что не сущест-
существует переноса из одной копии Z2 к другой,
П р п м е р 4.2.
0 1110 10 10 0 1
Д 0 0 11110 0 10 1
0011010000 1./
Упражнение 4.4. Определяя операции Д и V как
минимум и максимум, показать для произвольного Zn, что
ГЛАВА 5
АЛГЕБРАИЧЕСКИЕ СТРУКТУРЫ
В предыдущей главе мы уже познакомились с неко-
некоторыми способалш определения операций над множества-
множествами и научились с ними работать с целью производить
имеющие смысл вычисления. Конечно, существует мно-
много различных операций, которые могут быть определены
на множестве, и, следовательно, в некотором смысле ал-
алгебраических структур больше, чем множеств. Однако
получается так, что большинство полезных структур
(под этим мы подразумеваем структуры, которые описы-
описывают естественно возникающие явления и пригодны для
вычислении) может быть разбито на небольшое число
типов. В этой главе мы вначале введем терминологию,
которая имеет отношение ко всем алгебраическим струк-
структурам, а потом займемся некоторыми специальными
структурами, которые, на наш взгляд, ближе всего от-
относятся к вычислениям. Это нам позволит связать ранее
«оборванные» нити рассуждений, с тем чтобы приступить
к изучению структур, а также чтобы подвести серьез-
серьезный математический фундамент под оставшуюся часть
КНИГИ.
Центральное место в наших рассмотрениях занимают
поля, линейная алгебра и булева алгебра. Поля формиру-
формируют основу простой арифметики, линейная алгебра обес-
обеспечивает основу для геометрии и операций с числами,
а булева алгебра содержит в себе основные положения
элементарной логики. Разумнее начать изучение с та-
таких структур, которые могут рассматриваться как части
поля. Затем поля будут расширены до векторных про-
пространств.
Аналогично мы расширим изучение булевой алгебры,
включив решетки и свободные полукольца. Некоторые
другие структуры будут кратко упомянуты в упражне-
упражнениях к этой главе,
133
§ 1. Алгебраические структуры п подструктуры
Определение. Алгебраической структурой назы-
называется множество вместе с операциями (замкнутыми),
определенными на этом множестве. /
Обычно операции имеют некоторые характерные свой-
свойства, которые могут быть обоснованы в виде теорем п
которые используются в вычислениях. (Структуру вме-
вместе со всеми теоремами, правилами вычислений и вывода
иногда называют алгебраической системой.)
К каждой структуре применимо понятие подструкту-
подструктуры. Чтобы это продемонстрировать, рассмотрим гипотети-
гипотетическую структуру, называемую указателем. Пусть А —
указатель. Предположим, что имеется только одна опе-
операция ®, определенная на А. Следовательно, более точ-
точно это может быть записано как (А, ®), т. е. указатель
состоит из множества А с операцией ®. Теперь, если
В s А и (В, ®) также является указателем, в частно-
частности ® может быть замкнута на В, то (В, ®) называ-
называется подуказателем.
Возьмем другую структуру, состоящую пз множества
С и операции ©. (© и ® должны иметь один и тот же
порядок. Например, если одна из них является бинар-
бинарной, то и другая должна быть такой же. Можно ввести
и другие операции на С, однако в настоящее время мы
их не рассматриваем). Если существует отображение (р:
А-*-С такое, что
Ф (* ® У) = Ф (х) Ф ф (У)
для любых х и у из А, то <р называют гомоморфизмом.
Если существует гомоморфизм между Л и С, то в не-
некотором смысле образ (<f(A), ©) гомоморфизма из (А,
®) ведет себя подобно прообразу, так как мы можем
выполнить операцию ® на Л, а затем отобразить в С
(посредством <р) или сначала отобразить в С, а затем
выполнить операцию ©. В обоих случаях результат бу-
будет один и тот же. Поэтому мы можем делать так, как
нам удобнее. Эту ситуацию можно пояснить с помощью
коммутативных диаграмм, изображенных на рис. 5.1.
Диаграмма на рис. 5.1, а указывает включаемые множе-
множества или структуры, а диаграмма на рис. 5.1, Ь связывает
отдельные элементы. На рис. 5.1, Ь справа изображены
две различные формы одного и того же результата. Ком-
Коммутативность диаграммы вытекает из определения опе-
операций.
134
На самом деле мы получаем <р • ® = ф • <р, что не яв-
является в строгом смысле коммутативностью, так как ®
п © существенно различны. Однако обе части равенства
А»А
Рис. 5.1
означают комбинации операций одного и того же поряд-
порядка и, следовательно, подходят под общее определение
отображение • операция — операция • отображение.
Рассмотрим пример.
Пример 1.1. Пусть отображение 0, 0: Z -»¦ Zio — ос-
остаток от деления на 10. Тогда
0B0) = 0,
0A7) =7,...
Если мы рассмотрим простейшие системы (Z, +) и (Zio,
+ ) с операцией +, определенной естественным образом
на Z и на «единичном столбце» для Zio, то легко видеть,
что 0 является гомоморфизмом. Например,
0B4 + 38) -0F2) = 2,
0B4) + 0C8)=4 + 8 = 2 (в Zio).
В этом случае диаграмма будет выглядеть так, как это
изображено на рис. 5.2. /
Рпс. 5.2
Таким образом, гомоморфизм одной структуры в дру-
другую является отображением, которое сохраняет структуру.
Можно вводить ограничения на ранг отображения,
чтобы получить, например, сюръектпвность пли пнъек-
тивность, Поэтому, если отображение является гомомор-
135
физмом, можно надеяться, что это обеспечит механизм
перехода от структуры к структуре (и обратно!) без ка-
кой-лпбо потери информации.
Определение. Гомоморфизм, который является
инъекцией, называют мономорфизмом, гомоморфизм, ко-
который является сюръскцней, называют эпиморфизмом,
а гомоморфизм, который является бпекцней, называют
изоморфизмом. Если существует изоморфизм между дву-
двумя структурами, то говорят, что они изоморфны. II
Слово «изоморфно» означает «той же самой формы»,
п поэтому, кажется, разумно ожидать, что изоморфизм
должен быть в состоянии разделить множество всех ал-
алгебраических структур на классы эквивалентности (см.
упражнение 5.1, 2).
Пример 1.2. Структуры ({0, &), П, U) п ({0, 1}
Л» V)(cm. определснпе в § 4 гл. 4) изоморфны.
Доказательство. Пусть ф@)=О и <р(ЗГ)= 1.
Ясно, что ф — бпекцпя. Тогда
Ф @ П 0) = Ф@) = О =0Д0 = Ф@)Дф@).
ф@ Л $) = Ф@) = 0 = 0Д1 = Ф@)ЛФ(#).
Ф@ U 0) = Ф@) = 0 = ОV 0 = ф@)\/ф@),
1 = 1VI
Таким образом, ф является гомоморфизмом п, следова-
следовательно, изоморфизмом. /
В заключение отметим, что структура может быть пзо-
морфна самой себе (имеется в виду изоморфизм, отлич-
отличный от тривиального) и может также быть пзоморфна
одной из своих подструктур (это возможно лишь для
бесконечных множеств).
Определение. Если область определения и об-
область значений отображения совпадают, гомоморфизм на-
навивают эндоморфизмом, а пзоморфизм называют авто-
автоморфизмом. II
Пример 1.3. Для заданного множества А структура
(&>(А), П, 0) изоморфна (&ЧА), U, Л) с отображением
ф: X -* X',
136
Доказательство. Очевндпо, что ф ппъектпвпо п
сюръектишю. Если В, С^З>{А), то
U С) = (В U С)' = В' П С = фE)П ф(С).
Позднее мы увидим, что эти соотношения явно показыва-
показывают самодвойственность булевой алгебры множеств и ф
является автоморфизмом. II
Упражнение 5.1.
1. Показать, что две структуры (Ze, *), полученные
при решенпп задачи пз упражнения 4.1, 2 изоморфны.
2. Пусть (А,®), (В, ©) и (С, ©)—указатели,
а ф: А -*¦ В п 0: В -*¦ С — изоморфизмы. Показать, что
6"ф: А-+С, ф-1: В-+А
также являются пзоморфизмалш.
§ 2. Простейшие операционные структуры
Начнем детальное изучение алгебраических структур
с рассмотрения тех пз них, которые пмеют только одну
бинарную операцию. Где это возможно, будем в этом п
последующих параграфах представлять структуры в (при-
(приблизительно) возрастающем порядке «силы». (Говорят,
что структура А слабее структуры В, если А можно рас-
рассматривать как В «с отброшенной структурой». Как мы
увидим позже, некоторые структуры получают путем
«слияния» двух более слабых структур, и, следователь-
следовательно, строгий порядок здесь невозможен.)
Обычно каждую структуру можно определить в тер-
терминах основных свойств, а не только в терминах про-
простейших структур.
Определение. Полугруппой называется множест-
множество 5 с бинарной операцией ®, которая удовлетворяет
только требованию ассоциативности
х ® (у ® z) = (х ® у) ® г, х, у, z s 5. /
Определение. Моноидом называют множество М
вместе с бинарной операцией ® такой, что
(I) ® ассоциативна;
(II) существует и<=М такое, что
и®х = х = х®и для всех хеМ;
и называют единицей по отношению к ®, ff
137
Полугруппы и моноиды имеют особое значение при
обработке строк символов и теории языков.
Пример 2.1. Пусть А*=>{х, у, z). Рассматривая х,
у и z просто как символы, а не как имена объектов или
«переменных», получаем, что А является алфавитом. Оп-
Определим А* как множество всех строк символов, принад-
принадлежащих А. Тогда А* включает х, у, z, хх, ху, ух, xxyz,
zyx и т. д.; А* бесконечно.
На А* можно определить операцию конкатенации ©
следующим образом: если а, р е А*, то а © р = оф, т. е.
результатом является строка а и сразу же за ней за-
записанная строка §. Таким образом, имеем
xyz © 2 = xyzz, xz® yx — xzyx и т. д.
Каждая строка а имеет конечную длину, которая обо-
вначается через led и равна числу символов в а, (при
этом разрешаются повторения). Таким образом,
\х\ — 1, \ху\ = 2, \xxxzy\ = 5.
Это несколько похоже на обозначение мощности множе*
ства. Заметим, в частности, что
1*2/1=2, |{х, у) 1=2,
\yx\-2, |{jftz}|-2,
но
\хух\=3, Нх,у,х}\ = \{х,уП=2.
Поэтому нет полной аналогии, хотя существует аналогия
с пустым множеством. Для обозначения строки, анало-
аналогичной пустому множеству, будем использовать специ-
специальный символ Л, А&А*. Таким образом, |A|=O и
Л©а = сс©Л = а для всех строк а.
Следовательно, для любого алфавита А структура
(А*, ©) является моноидом, а Л — единица по отноше-«
пию к ©. /
(Может показаться, что символ • неверно употреб-
употребляется в обозначении А*, однако это не так: А* — Д*(Л),
где
R - {(а, р): р = а © а, а е А}.)
Приведенный выше пример чрезвычайно важен. Для
заданного, достаточно большого алфавита А, содержаще-
содержащего, например, все символы, доступные периферийным уст-
138
ройствам какого-либо компьютера, все языки, используе-
используемые в компьютерных системах, являются подмножеством
А*. Это понятие является основным при формальном
изучении языков (см. гл. 8).
Третьей (и последней) операционной структурой яв-
является непосредственное и естественное расширение мо-
моноида.
Определение. Группой G называют множество с
бинарной операцией ® такой, что
а) ® ассоциативна;
б) существует элемент кеС (единица по отношению
к ®) такой, что
ц ® х =• х = х®и для всех ie(J;
в) каждому элементу ieG соответствует элемент уе
<= G такой, что
х®у = и = у®х;
у называется обратным элементом к z по отношению к
В случаях, когда групповая операция обозначается
символом ®, единичный элемент обозначается 1, а об-
обратный к элементу х элемент записывается в виде х~К
Когда групповая операция обозначается символом ©, еди-
единичный элемент обозначается 0, а обратный к элементу
х элемент записывается в виде —х.
По сравнению с первыми двумя структурами группы
обладают следующими важными свойствами. Внутри
группы (G, ®) можно решить уравнение
а ® х = Ъ.
Более того, решение легко найти (однако заметим, что
для этого требуются все аксиомы группы). Если
а ® х = Ь
то
о-1 ®(а®а) = а-1 ®Ь (я е G =ф- а'1 е G),
(а-1 ® а) ® х = a-1 ® Ъ (® ассоциативна),
и ® х = а*1 ® Ъ (свойство обратных элементов),
поэтому
х = о ® Ъ (свойство единицы).
Часто к словам «группа» и «моноид» приписывают тер-
термин «коммутативный». Это просто означает, что опера-
139
ция в рассматриваемой структуре удовлетворяет свойству
коммутативности, т. е.
у ® х = х ® у для всех х, у е М или <?.
Можно сделать много полезных выводов из аксиом груп-
группы. Рассмотрим простой пример.
Пример 2,2. В группе (G, *)
(а * fc)-i = б ® a-i.
Доказательство.
(a*b)*{b-x *a-1) = a*(b*b-1)* а~] =
= а « 1 * о = а * а = 1.
Следовательно, Ь~х • а является правым обратным эле-
элементом к а * Ь. Аналогично можно показать, что он яв-
является левым обратным элементом, откуда и следует
требуемый результат. /
Группы дают нам первый пример широко используе-
используемых изоморфизмов. Эти изоморфизмы (между группами
(R, +) и (]0, <»[, *)) называют логарифмами. Они по-
позволяют выполнять умножение при помощи сложения на
основе следующего тождества:
где
ф: Xf* logj,(?) для некоторого р е] — 1, оо[.
Упражнение 5.2.
1. Доказать единственность единичного элемента и
обратных элементов в группе (G, ®).
2. В группе (G, ®) показать, что если а ® Ъ =а ® с,
то Ъ = с, а если х ® а = у ® а, то х = г/.
3. Проверить, что множество перестановок конечного
множества образует группу по отношению к операции
умножения перестановок,
§ 3. Кольца и поля
По-видимому, простые операционные структуры § 2
не были 8накомы читателю. Сейчас мы готовы исполь-
использовать свойства групп для описания арифметических
структур, обсуждавшихся 'в гл. 4. Наибольший интерес
для нас представляют поля (на текущий момент это наи-
наиболее идеальные арифметические структуры) и их клас-
классификация в тергинах размерности, Однако сначала мы
140
кратко рассмотрим структуры, которые несколько отли-
отличаются от полей и называются кольцами.
3.1. Кольца. Многие математические конструкции, ко-
которые естественно возникают в линейной алгебре (осо-
(особенно в теории матриц), являются кольцами или вклю-
включают кольца как подструктуры. Следовательно, примеры
колец часто будут появляться в этой главе и в гл. 6.
Мы уже изучили одну совокупность колец. Вернемся к
ней после введения аксиоматических понятий.
Определение. Кольцом называется множество R
с двумя определенными на нем бинарными операциями
® и © такими, что:
а) ® ассоциативна;
б) © ассоциативна;
в) © коммутативна;
г) © имеет единицу, которая называется нулем и обо-
обозначается 0;
д) существуют обратные элементы относительно ©;
е) ® дистрибутивна по отношению к ©, т. е.
х ® (у ® г) = (я ® у) ф (х ® г),
(х ф у) ® г = (х ® г) ф (г/ ® г) для всех 1,у,гей. /
Следовательно, система (Zn, •, +) при любом n<=N
является кольцом.
Будем говорить, что кольцо коммутативно, если ум-
умножение ® коммутативно, и является кольцом с едини-
единицей, если существует единица относительно умножения.
Как обычно, ее обозначают символом 1. Легко показать,
что в кольце (#, ®, ф) для любых а, Ь е R выполня-
выполняются соотношения
Здесь —а это элемент, обратный к а относительно ©;
а®(—6) записывают обычно как а — Ь, и если 1еД,
то 1 единственна.
Пример 3.1. (Zn, *, +) является коммутативным
кольцом с единицей при любом rsN. //
В системе (Zn, •, +) не всегда возможно «деление».
В этом состоит основное отличие между полем и комму-
коммутативным кольцом с единицей. Рассмотрим кольцо (Zs,
•, +). Покажем, что оно не является полем,
141
В Ъь существует 15 случаев, когда произведение двух
элементов может давать нуль, а именно:
(О, 0),
(О, 1), @, 2), @, 3), @, 4), (О, 5J,
A,0), B,0), C,0), D,0), E,0),
B,3), C,4),
C,2), D,3).
Очевидно, что существуют утверждения, которые спра-
справедливы не для всех арифметических вычислений. При
умножении выражений мы явно используем тот факт, что
о « Ъ — 0 тогда и только тогда, когда а -»0 или Ъ = 0.
В кольце (R, ®, ф) нулевые элементы хну назы-
называют делителями нуля, если их произведение равно ну-
нулю. В случае, когда R не является коммутативным коль-
кольцом, х называют левым делителем нуля, & у — правым
делителем нуля. Нетрудно показать (см. упражнение
5.3), что Z6 имеет делители нуля (так как 6 — составное
число) и что Ър не имеет делителей нуля тогда и только
тогда, когда р является простым числом.
Если в группе (G, ®)
а ® Ъ •= а ® е,
то Ъ = с. Однако в случае произвольного кольца это не-
неверно.
Теорема. Приведенное выше условие имеет место
в кольце R тогда и только тогда, когда R не содержит
делителей нуля.
Доказательство. Достаточность. Предпо-
Предположим, что R не имеет делителей нуля. Тогда, если
х®у = х®гжх?=0, то
{х ® у) — (х ® z) = (х ® у) — (х ® у) = 0,
(х ® у) — (х ® г) = (х ® у) ф (х ® (— г)) =
= (х ® (У ф (— z)) = х ® (у — z).
Поэтому х ® (у — г) = 0; но так как не существует де-
делителей нуля и хФО, то отсюда следует, что у — 2 = 0
и, следовательно, y = z. Аналогично, если y®x = z®x,
то у = z. Достаточность доказана.
Необходимость. Предположим, что из а ® Ъ =
= а®с следует равенство Ь = с, и пусть х® у=0. Тогда
х ® у = х ® 0
'см. упражнение 5.3), и если г Ф 0, то у — 0. Аналогпч-
142
но, если у Ф 0, то
я® г/ = 0 = 0® #
и по предположению х ¦=* 0. Таким образом, из х ® у = 0
следует, что или а; = 0, или y — Q.ff
Рассмотрим теперь еще одну структуру, перед тем как
перейти к изучению полей
Определение. Областью целостности называется
коммутативное кольцо с единицей, не имеющее делите-
делителей нуля, т. е. множество D с двумя бинарными опера-
операциями ® и ® такими, что:
а) сложение ® ассоциативно;
б) сложение коммутативно;
в) существует единица по сложению, обозначаемая 0;
г) существуют обратные элементы по сложению (обо-
(обозначаются {—х));
д) умножение ® ассоциативно;
е) умножение коммутативно;
ж) существует единица по умножению (обознача-
(обозначается 1);
з) умножение дистрибутивно по отношению к сло-
сложению:
(х ® (у ф г)) => (х ® у) ф (х ® г) для всех х, у, г е D;
и) если 1^0иг®у = г®г, то у *= z. II
Каждая конечная область целостности является по-
полем, однако существуют примеры бесконечных областей
целостности, не являющихся полями.
3.2. Поля. Уже работая с понятиями арифметики, мы
сталкивались с аксиоматическим определением поля.
Определение. Полем называется множество F с
двумя определенными на нем бинарными операциями —
сложением © и умножением ® (обозначается (F, ®, ф)
или же просто F), которые удовлетворяют следующим
девяти свойствам.
1. Сложение коммутативно:
х® у = у®х для всех х, y<=F.
2. Сложение ассоциативно:
х Ф (у Ф г) ¦= (х © у) ® г для всех х, у, z <= F.
3. Существует элемент в F, который обычно обозна-
обозначается символом 0, такой, что
х ® 0 = х для всех ief;
0 называется аддитивной единицей или просто нулем,
143
4. Каждому элементу x<=F соответствует элемент
у е F такой, что
х®у = 0;
у называется аддитивным обратным элементом к х а
обозначается через —х.
5. Умножение коммутативно:
х® у = у ®х для всех z,y <= F,
6. Умножение ассоциативно:
х® (У ® г) = (х ® У) ® z для всех x,y,z^F.
7. Существует элемент в F, который обычно обозна-
обозначается символом 1, такой, что 1?=0 и
х ® 1 = х для всех ief;
1 называют мультипликативной единицей или просто
единицей.
8. Каждому элементу х е F\{Q] соответствует элемент
у & F такой, что
х® у — 1;
у называется мультипликативным обратным элементом к
х и обозначается через х~1.
9. Умножение дистрибутивно относительно сложения:
х ® {у © г) = (х ® у) ф (х ®z) для всех ж, г/, z e F. И
Пример 3.2. (R, *, +) является полем, и, следова-
следовательно, (И, +) и (R\{0), •)—коммутативные группы.
(N, •, +) не является полем, поскольку не существует
ни аддитивной единицы, ни аддитивных обратных эле-
элементов. (^(А), П, U) для заданного множества А не яв-
является полем, поскольку не существует обратных эле-
элементов. /
В предыдущем определении использовались символы
® и ® для того, чтобы подчеркнуть, что операции в по-
поле могут отличаться от умножения и сложения. Однако
в дальнейшем часто будут рассматриваться поля (R, »,
+) и (Q, », +), Поэтому мы будем использовать сим-
символы * и +.
Перед тем как перейти к доказательству основных
утверждений, напомним (вместе с доказательствами) не-
некоторые важные ;ледстрия, которые непосредственно из-<
влекаются из определения поля.
Предложение. Единичный элемент в поле един-
единствен.
144
Доказательство. Предположим, что
х*е = хих*е'~х для всех х е F.
Тогда
е = е « е' = е' ¦ е = е'
Поэтому е = е' == 1.
Для операции сложения доказательство аналогично. /
Предложение. Обратные элементы в поле един-
единственны.
Доказательство. Опять рассмотрим случай опе-
операции умножения. Возьмем х е F\{Q} и допустим, что
имеется два элемента у и z таких, что
х * у = 1, ж • z = 1.
Из коммутативности следует, что
у • х — 1 = 2* я;
поэтому
у = 2/» l = r/»(z*z) = (#*z)»z = l»z = l.
Следовательно, j/ = z = x~l.
Единственность обратных элементов по сложению до-
доказывается аналогично. /
Перейдем к основным результатам.
Теорема. В поле (F, «, +) для любых а, Ъ е F
справедливы следующие утверждения:
а) а «0 = 0;
б) (-а)-в»(-1), -а(+Ь)-(-о) + (-Ь);
в) -(-а) = а, (-l).(-l)-l;
г) если а ?• 0, го (а) = а;
д) а»6 = 0=*'а = 0 или 6 = 0;
е) (-а)*(-6)= а» Ь.
Доказательство.
а) а*1 = аиа + 0 = а; поэтому
о+(а»0)-(о» 1) + (а»0)=а»A + 0)=а» 1-а.
Следовательно, а * 0 является единицей по сложению.
Она единственна; поэтому а * 0 = 0.
б) Аналогично
Ю Д. Кук, Г. Бейз 145
Таким образом, — а = а*(—1). Используя это равенство,
получаем
в) По определению
(-а)+а = 0 и (_
Но обратные элементы единственны; поэтому а = —(—а).
Таким образом, 1 = —(—1). Пусть х равно —1. Тогда
l = -(x) = z*(-l) = (-l)»(-l).
г) Заметим вначале, что а ^ О, так как в противном
случае
1 = а • а-1 - а • 0 = О,
что противоречит свойствам поля. Следовательно, а ?= О
и доказательство аналогично доказательству случая в).
д) Воэьмем а Ф 0. Тогда о определено и
Ъ =» 1 • Ь = (о » а) • Ъ = а-1 « (а • Ь) — а * 0 = 0.
е) Из случая б) следует
(-а)=а »С-1) и (-6)-Ь*(-1).
Поэтому
(-в).(-Ь)-(а.(-1)).(Ь.(-1))-
= а*((-1)*(-1))»Ь = а» 1 * 6 = а»6. /
Для упрощения записи выражений в полях примем
обычное соглашение о том, что если нет скобок, то ум-
умножение выполняется раньше сложения. Например, вы-
выражение а+ b * с оэначает а + (Ь * с),
Из аксиом поля следует разрешимость линейных
уравнений. Это — очень важное свойство, и можно при-
привести аргументы в пользу того, что оно — основное свой*
ство полей.
Линейным уравнением относительно х над полем F
называется выражение вида а • х + b = (У, где 0, а,
b&F.
Теорема. Если а?=0, то линейное уравнение а*
* х + b =• 0 имеет единственное решение в F (т. е. су-
существует только один элемент поля, при подстановке ко*
торого в уравнение получается верное равенство).
146
Доказательство.
а * х + Ь = О,
а»х+Ь+(-Ь)=О + (-Ь),
0 • х + (Ь + (—Ь)) = (—6) (ассоциативность
и свойство 0),
а * х + 0 = (—6) (по определению 0),
а • х =(—6) (свойство 0),
а-1*(а*х)=а-1 ¦•(-&) (а?=0),
(а « о)« а; =(—6) * а (ассоциативность
и коммутативность),
1 • х = (—&)• а (по определению 1),
г = (—&)*а~' (свойство 1),
Поле F эамкпуто относительно веданных операций. По-
Поэтому элемент (—Ь) • а~1 содержится в F. Этот элемент
и дает решение уравнения. Более того, так как обрат-
обратные элементы в F единственны, то — Ъ и а'1 определя-
определяются из данного уравнения единственным образом, щ
следовательно, решение единственно. /
Уравнения, которые получаются из полиномов более
высоких степеней, например квадратные уравнения
а *х•х + Ъ•х + с = 0
с коэффициентами а, Ь, с из R, в общем случае нераз-
неразрешимы в R. Для того чтобы эти уравнения были разре-
разрешимы, нужно перейти к расширению поля R — полю
комплексных чисел. Однако полиномиальные уравнения
с комплексными коэффициентами всегда разрешимы в
поле комплексных чисел: никакого более широкого поля
не требуется. Р1сследование этого интересного факта мог-
могло бы увести нас в сторону от более уместных тем.
3.3. Конечные поля. До сих пор все упоминаемые по-
поля были бесконечны (содержали множества, имеющие
мощность Хо или X i). Обсудим теперь возможность суще-
существования конечных полей — полей, содержащих конеч-
конечное число элементов. Сформулируем основные свойства
конечных полей и докажем некоторые из них (доказа-
(доказательства других лежат за пределами этой книги). Внача-
Вначале приведем некоторую дополнительную информацию.
Пусть a s F. Тогда элементы а, а + а, а + а + а, ...
являются элементами поля. Обозначим их через а, 2а,
За, ,,., па, .,, (не требуется, чтобы n<=F) соответствен-
10* 147
но. Аналогично а, а * а, а * а * я, ... также являются
элементами поля. Обозначим их через а, а2, а3, ..., а", ...
соответственно. Предположим, что а Ф 0.
Определение. Если существует целое пеN та-
такое, что па = 0 (и не существует меньшего целого reN
такого, что га — О), то га называют аддитивным порядком
а. Если существует meN такое, что ат = 1 (и не су-
существует меньшего reN такого, что а' = 1), то иг назы-
называют мультипликативным порядком а. II
Теорема. Ненулевые элементы поля F имеют один
и тот же аддитивный порядок.
Доказательство. Возьмем а, Ъ sF\{0) и пред-
предположим, что аддитивные порядки а и Ъ равны га и иг
соответственно. Тогда
пЪ = п (а » а~') ¦ Ъ = (па) • (о • 6) = 0 * а" * Ъ = 0.
Поэтому m < re. Аналогично
ига = m F * Ь) * а — (nib) * (б • а) = 0 * Ъ~х * а = 0.
Следовательно, п < т, и поэтому т = п. /I
Определение. Если в поле F все ненулевые эле-
элементы имеют аддитивный порядок п, то говорят, что F
имеет характеристику п. Если такого аддитивного поряд-
порядка не существует, то говорят, что поле имеет характери-
характеристику, равную 0. II
Если |F| = m e N, т. е. F имеет m элементов, то гово-
говорят, что F конечно. Если F имеет характеристику, рав-
равную 0, то оно должно быть бесконечным. (См. упражне-
упражнение 5.3.)
Теорема. Характеристика любого конечного поля
является простым числом.
Доказательство. Предположим, что конечное по-
поле F имеет характеристику п и п = р • q, где р, q<n и
р, gsN, Возьмем
a s F\{0>.
Тогда 0 = па *=(р • q)a-p(qa). Далее qa&F. Поэтому,
если qa = 0, выполняется соотношение п ^ q (поскольку
порядок а равен п); в противном случае qa e F\{0), по-
порядок qa также равен п и поэтому п< р. Таким обра-
образом, в обоих случаях получаем противоречие. Следова-
Следовательно, таких р и q не существует и п простое. II
Таким образом, мы получили следующий основной
результат.
Теорема. Конечное поле имеет характеристику р
(простое число) и \F\ = р" для некоторого п s N.
148
Доказательство. Мы уже знаем, что F имеет
характеристику р, причем р простое. Пусть \F\ = q. Если
р ш- q, то утверждение теоремы очевидно. В противном
случае возьмем элемент а\ е F\{Q] и положим
Т\=*{у: у = паи »eN, Кге</?}, \&"x\ = р.
Рассмотрим теперь элемент а% е F\&~i, и пусть
3^2 = (j/: у = ий| + та.2] т, га е N, 1 < га < р, 1 < /п < р).
Если ^"г = ^. то процесс заканчивается; в противном слу-
случае рассмотрим а% е F\&~2 и т. д. В конце концов (посколь-
(поскольку F конечно) процесс остановится и мы получим совокуп-
совокупность множеств {Fi, &~2, • • •. &~п для некоторого га е N.
Каждый элемент / из F единственным образом пред-
представим в виде
/ = miu\ + /П2Я2 +... + тпая,
причем 1 < irii < р для всех i = 1, ..., га. (Доказать это
в качестве упражнения.) Следовательно, существует рп
таких выражений, и, таким образом, IFI =/?". II
Итак, любое конечное поле должно иметь рп элемен-
элементов при некоторых р, п е N (р простое). На самом деле
для любых таких р и п существует поле порядка рп,
однако доказать это не совсем просто.
Рассмотрим в качестве примера поле (Z3, *, +), где
• и + определены в табл. 0.1. Нетрудно показать, что
выполнены условия 1—8 из определения поля.
Таблица 5.1
*
0
1
2
0
0
0
0
1
0
1
2
2
0
2
1
+
0
1
2
0
0
1
2
1
1
2
0
2
2
0
1
Для контраста рассмотрим соответствующую табл. 5.2
для Z4
Таблица 5.2
•
0
1
2
3
0
0
0
0
0
1
0
1
2
3
2
0
2
0
2
3
0
3
2
1
+
0
1
2
3
0
0
1
2
3
1
1
2
3
0
2
2
3
0
1
3
3
0
1
2
149
Очевидно, что не существует мультипликативного об-
обратного элемента к 2. Поэтому Z4 с естественной опера-
операцией умножения не является полем. Поле порядка 4 я-
= 22 хотя и существует, но не совпадает с Z4 (см. уп-
упражнение 5.3). Конечные поля заданного порядка стро-
строятся достаточно сложным образом — на основе теории
многочленов над другими структурами (не полями). Они
имеют важное значение в теории кодирования. Мы не
будем этим заниматься, поскольку такое приложение яв-
является довольно специальным.
3.4. Упорядоченные поля. Мы уже видели, что мно-
множество R вместе с обычными операциями сложения и
умножения определяет поле. Однако структура поля са-
сама по себе не дает какого-либо упорядочения элементов,
которое мы обычно связываем с R. Не все поля могут
быть упорядочены. Поэтому мы должны проверить, ка-
какие дополнительные условия должны быть выполнены,
прежде чем рассматривать это понятие. Обычные свой-
свойства порядка можно получить, как и ожидается, многими
способами. Начнем с определения свойства положитель-
положительности. Оно непосредственно приводит к отношению по-
порядка в поле, а затем к понятию длины. Основные ре-
результаты этого параграфа будут сформулированы в двух
теоремах, а вспомогательные результаты даны в виде
упражнений.
Определение. Говорят, что поле F упорядочено,
если оно содержит непустое подмножество Р, которое
замкнуто относительно операций сложения и умножения,
и такое, что для каждого элемента х из F имеет место
ровно одно из соотношений
х е Р\{0), х = 0, -х е Р\{0).
Р есть множество всех положительных элементов F. (На
этом этапе отметим, что 0 может как включаться в Р,
так и не включаться. Для определенности выберем слу-
случай, когда 0 включается в Р, что согласуется с изложе-
изложением предыдущей части книги.)
Если х^Р, то будем говорить, что элемент х поло-
положителен, и обозначать этот факт как х > 0. Если —х е
s Р\{0), то будем говорить, что элемент х отрицателен,
и обозначать это как х < 0. Аналогично, если х и у —
элементы F, то будем говорить, что х меньше или равно
у (обозначается х<у), тогда и только тогда, когда
у — х s P, и что х меньше у (х<у), тогда и только
тогда когда у — х^Р \{0). Символы <, ^ можно так*
150
же использовать для записи в противоположную
сторону. /
Из этих определений можно получить, что «<» явля-
является отношением порядка и выполняются все ожидав'
мые свойства.
Теорема. Пусть F — упорядоченное поле и а, Ъ, с,
def. Тогда:
а) если а < Ь и Ь < с, то а < с;
б) й<й;
в) если а < Ь и Ъ < а, то а = 6-;
г) если а?=0, то а? > 0;
д) 1>0;
е) если а < Ь, то а + с < Ъ + с;
ж) если a^buc^d, тоа + c^b + d;
з) если a<b, 0<c u d<0, то а * с «s 6 * с, b*d^
<а * d;
и) если 0 < о, то 0 < а, и если Ь < 0, го Ь < 0.
Доказательство.
а) а< Ь и 6 < с ¦> F — а)е Р, и по определению
(с — i)eP. Тогда c-a = c-i + 6-asP1 поскольку Р
замкнуто относительно сложения. Следовательно, а<с,
б) Очевидно, что а — a = 0 в Р.
в) а<Ь и Ь<а; поэтому если 6 —а=л:, то х<=Р и
—г е р, что противоречит определению Р. Поэтому х = 0
и а = 6.
г) Если а ** 0, то или а<=Р, или —а в Р. Поскольку
Р замкнуто относительно умножения, то а&Р**¦ а2 & Р
и, как показано в п. 3.2,
(-а) • (-о) — а2, откуда -а<г Р *¦ о?& Р.
д) I2 -¦ 1, поэтому из случая г) следует, что 1 > 0.
е) Утверждение непосредственно следует из соотно-
соотношения
b-a = F + c)-(a + c).
ж) Требуемый результат получаем из соотношения
(b-a) + (d-c) = (b + d)-(a + c),
используя замкнутость Р.
151
з) Утверждение доказывается аналогично, используя
следующие соотношения:
(h — a)*c = b*c — a * с
и
(Ъ — a)* {—(I) = a*d — b»d.
и) 0 < а =>- а е Р\{0). Если а = 0, то 1 = а * а ==
•= а * 0 = 0, а если а ^ Р, то из случая з) имеем 1 =
«=а~1*а<0»а = 0. В обоих случаях получили противо-
противоречие. Поэтому а" в Р\{0) и, следовательно, 0 < о.
Оставшаяся часть доказательства проводится анало-
аналогично. /
Получим похожие соотношения для понятия величи-
величины в упорядоченных полях.
Определение. Если F — упорядоченное поле, то
абсолютным значением (величиной, длиной или модулем)
называется функция
( х, если х^О
х*-* \ г,
I—х, если х<С.\).
Традиционно эту функцию обозначают как Ы (х — ар-
аргумент) и читают это как «модуль я». II
Сформулируем без доказательств основные результа-
результаты, относящиеся к функции \х\. (Доказательства остав-
оставляем в качестве упражнения.)
Теорема. Если F — упорядоченное поле и а, Ь е
е F, то:
а) \а\ =0 тогда и только тогда, когда а=»0;
б) |-ol - Ы;
в) |а»Ы = !а|.|Ь!;
г) если 0 < Ь, то \а\ ^ Ъ тогда и только тогда, когда
д) -\а\ <а«ЗЫ;
е) Па1 — 1611 < 1а±&1 < Ы + |&| (неравенство тре-
треугольника). И
Упражнение 5.3.
1. Доказать, что в кольце (R, *, +) выполняются со-
соотношения:
а) 0*а = а» 0 = 0;
б) а»(-6) = (-а)»6 = -(а»Ь);
в) (-о)«(-Ь)=й * Ь.
152
2. Показать, что если в кольце (/?, ¦, +) для каждо-
каждого а е R выполняется соотношение а • а = а, то R ком-
коммутативно.
3. Показать, что в кольце Zn делителями нуля явля-
являются только те элементы, которые имеют общие нетри-
нетривиальные множители с п. Следовательно, Zp, где р про-
простое, не имеет делителей нуля.
4. Показать, что каждая конечная область целостно-
целостности является полем.
5. Показать, что (Z, *, +) — область целостности, но
не поле.
6. Пусть р < q и (Zp, #„ +„) и (Z,, •„ +,) — обыч-
обычные системы по модулю р и q. Доказать, что, хотя они
и являются коммутативными кольцами и Zp <= Z, кольцо
(Zp, »р, +р) не является подкольцом (Z,, •„ +,). Пока-
Показать, что операции ¦, и +, не замкнуты на ZP.
7. Без использования теорем доказать, что (Ze, •, +)'
не является полем (• и + суть операции по модулю 6).
8. Доказать, что конечное поле имеет ненулевую ха-
характеристику и что поле с характеристикой 0 бесконечно.
9. Пусть aj, a2, ..., ап определены так же, как и при
доказательстве последней теоремы п. 3.3. Доказать, что
любое выражение вида
wiifli + VH2U2 + ... + т„а„
определяет некоторый элемент поля, причем такое пред-
представление единственно.
10. В поле (F, *, +) с операциями, определенными
ниже, решить систему лпнейных уравнений
х + d « у = с,
х * d + у = Ь,
•
а
Ь
с
d
а
а
а
а
а
Ь
а
Ь
с
d
с
а
с
d
Ь
d
а
d
Ь
с
+
a
b
с
d
a
a
b
с
d
b
b
a
d
с
e
с
d
a
b
d
d
с
b
a
11. Доказать, что если а * Ъ > 0, a, b&F, то пли а,
Ь > 0, или а, Ъ < 0.
12. Доказать, что в упорядоченном поле а2 + Ь2 = О
тогда и только тогда, когда а = Ъ = 0.
13. Пусть F — упорядоченное поле и a, b <= F такие,
что 0 < а < 6. Доказать, что a2 «S б2.
153
14. Доказать, что каждое поле является областью це-
целостности.
15. В упорядоченном поле, складывая неравенства
— \а\ <а< \а\ и — \а\ <-а^ \а\,
доказать, что:
а) \а±Ь\<\а\ + \Ь\;
б) 1Ы-|б||<|в±б1.
§ 4. Линейная алгебра
В большинстве элементарных учебников векторы оп-
определяют как объекты, обладающие «величиной» и «на-
«направлением». Такой подход берет начало из приложений
в геометрии и физике. Эти вопросы формально будут об-
обсуждаться в п. 4.2. Дадим более общее определение век-
вектора, для которого понятия величины и направления не-
несущественны.
4.1. Векторные пространства и линейные преобразо-
преобразования.
Определение. Пусть F — поле, а V — множество
с бинарной операцией +. Предположим, что для каждого
а е F и х е V определен элемент ах е V, Тогда, если вы-
выполнены аксиомы:
а) (^» +)— коммутативная группа;
б) для всех х, у е F и a, b*=F
(а + Ь)х = ах + Ьх,
а(х + у) = ах + ау,
(ab)x-a(bx),
lfX = X,
где If — мультипликативная единица в F, то говорят, что
V является векторным, пространством над F. Элементы V
называются векторами, операция + называется сложени-
сложением векторов, а отображение
Л: F X V ¦* V,
определяемое соотношением Л (а, х)==ах, называют ум-
умножением вектора на скаляр. II
Векторное пространство над F может рассматриваться
как тройка (V, +, Л), удовлетворяющая приведенным
выше аксиомам. Нуль векторного пространства по сложе-»
154
нию обозначают символом 0. Из аксиом следует, что
0Fx == 0 для всех х <= V,
где 0F — аддитивная единица в F, и
аО = 0 для всех а е F.
В следующих примерах будет показано, что различные
классы множеств обладают структурой векторного про-
пространства.
Пример 4.1.
1. Fn (л e N) является векторным пространством над
F с операциями
(аи ..., an) + (bh ..., bn) = (ai + 6i, .... an+bn),
а(а\, ..., an) = (aoi, ..., аа„).
Нулем Fn является вектор (О*, ,.., 0F). Элементы а\, ...
..., а„ называются компонентами вектора a = (ai, ...
..., а„).
2. Пусть ЯГ — множество всех отображений /: [a, b] -*
-*¦ R. Тогда 2Г является векторным пространством над R
с операциями
(/ + ё) (х) -/(*) + ?(а;) для всех /, g^T,
(a/) (x) = a/(x) для всех aeR,
3. Пусть ЧР, <& <=¦ 2Г — множество всех непрерывных
отображений из &~. Тогда *8 является векторным про-
пространством с операциями, определенными в ST. II
Множество U, U s V, называется векторным подпро-
подпространством пространства V, если оно является вектор-
векторным пространством с операциями из V.
Множество {(cti, ..., ап-\, О*): afs^} является век-
векторным подпространством пространства Fn\ ЧР является
векторным подпространством пространства $Г. Если U,
U = F,— векторное подпространство пространства V, то
ОеСЛ
Векторные пространства R" A<ге<4) возникнут
естественным образом в гл. 10. Операции в R" имеют гео-
геометрическую интерпретацию. Для пространства R2 это
показано на рис. 5.3. Если г = (а:, r/)<=R2, то компонен-
компоненты х и у измеряются вдоль ортогональных линий, начи-
начиная с точки пересечения О (рис. 5.3, а). Компоненты х
и у откладываются вдоль линий ОХ (ось х) и OY (ось
у) соответственно. Эти линии проведены под углом 90°
155
друг к другу, и угол между ними измеряется против
часовой стрелки от оси ОХ. Такую систему осей назы-
называют правосторонней системой координат в R2. Вектор-
Векторное сложение в R2 геометрически соответствует правилу
параллелограмма, как это показано на рис. 5.3, с.
Геометрия векторных пространств R" будет рассмат-
рассматриваться ниже, а сейчас мы введем понятия базиса и
о х
О X
Умножение Вектора г
на скаляр К I А > 7)
Сумма ВектпороВ
Рис. 5.3
размерности. Если V — векторное пространство над F и
S s V, то сумму вида
п
й
называют линейной комбинацией векторов из S. Говорят,
что конечное множество векторов {х(: 1 ^ i < k) является
линейно независимым, если
h
в противном случае множество является линейно зави-
зависимым. Подмножество S s V такое, что любой элемент V
представим в виде линейной комбинации элементов из
S, называется порождающим множеством пространства
V (или же еще говорят, что S порождает V), Упорядо-
156
ченное линейно независимое порождающее множество
пространства V называется базисом этого пространства.
Пример 4.2. В R3 вектор E, 5, У2) является ли-
линейной комбинацией векторов A, 1, 0) и @, 0, 3), так
как
E,5, /2) = 5A,1,0) + ^ @,0,3),
Множество L = {A, 1, 0), @, 0, 3)} является линейно
независимым подмножеством в R3, так как аA, 1, 0) +
+ 6@, 0, 3) = (а, а, 36) = 0 тогда и только тогда, когда
а = 0 и 6 = 0. Однако подмножество L не является бази-
базисом, поскольку оно только определяет векторное подпро-
подпространство
{(х, х, у): i,jfsR}c R».
Базис 5 = LU{A, 0, 0)} «расширяет» L до базиса
в R3. //
Легко показать, что каждый элемент векторного про-
пространства имеет единственное представление в фиксиро-
фиксированном базисе, так как если V имеет базис В = {ei, ...
..., е„} и
то
Однако В — линейно независимое множество. Поэтому
bt = at для всех i, I < i *S n.
Докажем следующий важный результат.
Предложение. Пусть S = {хь ..., хт} — порож-
порождающее множество пространства V, a L = {yi, ..., у,} —
линейно независимое множество векторов из V, Тогда
т>1.
Доказательство. Предположим, что т<1. Так
как iS порождает V, то существуют элементы аи .,., ат s
е F такие, что
+ ,.. + amxm.
Однако yi Ф 0, так как L — линейно независимое множе-
множество (см. упражнение 5.4), и, следовательно, не все
а\, ..., ат равны нулю. Для определенности положим
157
Of. Тогда
т. е. xi является линейной комбинацией {уь Х2, ..., хт).
Так как S порождает F, то по доказанному выше множе-
множество векторов (yi, X2, ..., хт} также порождает V. Анало-
Аналогично получаем, что {yi, уг, х3, ..., хд) порождает V.
Повторяя этот процесс т раз, получаем, что множество
{yi, ..., ут) порождает V. Следовательно,
Ут+1 = Рф + Р2У2 + ...+ ртУт,
где pi, ••-, J3m s F не все равны нулю (так как ym+i не
может быть равно нулю). Отсюда
Ут+1 - /»1У1 ~ Р2У2 - ... - РтУт = О,
однако последнее невозможно, потому что {yi, ..., уг) —
линейно независимое множество векторов. Следователь-
Следовательно, т>1. II
Предложение. Пусть В и В' — базисы векторно-
векторного пространства V над F. Тогда \В\ = \В'\.
Доказательство. Пусть В = {еи ..., е„} и 5' =
= [ev ... ,em}. Тогда из предыдущего предложения сле-
следует, что и ^ m и т^ п, т. е. т — п. II
Мощность базиса векторного пространства V называ-
называется размерностью V и обозначается через dim(F).
Предложение. dim(Fn)= п.
Доказательство. Определим В = {ej, ..., е„}, где
ei = @, ...,0,lF,0,...,0),
i-й разряд
и покажем, что В является базисом в Fn. Очевидно, что
п
(av ...,а„)= 2 а%еи
поэтому В порождает Fn и
п
2 !,...,ъп) — о=^ь±=оГ, ьа = of>...,bn=oF.
t=l
Следовательно, В является базисом в F" i dim(F)=*
- ISI - п. II
Из данного выше определения следует, что базис
всегда состоит из конечного числа векторов, и не во вся-
всяких векторных пространствах можно выделить базис (на-
(например, в &", Ф нет базиса). Понятия базиса и размер-
158
вости можно расширить на все векторные пространства,
однако такое обобщение нам не потребуется. Если про-
пространство V имеет базис, соответствующий данному вы-
выше определению, то говорят, что пространство имеет ко-
конечную размерность, а само пространство называется
конечномерным векторным пространством.
Рассмотрим теперь гомоморфные отображения между
векторными пространствами.
Определение. Пусть V\ и Vt — векторные про-
пространства над полем F, Говорят, что отображение
Т: Fj -*¦ V2 линейно, если
Т(х + у)=Тх + Ту, Т(ах)~а(Тх).
Если Vi —• Fi, то Т называют линейным преобразовани-
преобразованием пространства V\, II
Далее нас будут интересовать конечномерные вектор-
векторные пространства над R и линейные преобразования над
ними. В оставшейся части главы через V будем обозна-
обозначать векторное пространство, а через End(F) — множе-
множество всех линейных преобразований V (эндоморфизмов
V). Заметим, что большинство приводимых утверждений
можно представить в более общем виде.
Перейдем от алгебры V к алгебре End(F) и покажем,
что End(F) аамкнуто по отношению к естественным
операциям сложения, умножения и умножения на ска-
скаляр. Вначале заметим, что единичное отображение Iv и
нулевое отображение 0v являются линейными на V, так
как по определению
Ivx = х для всех xsV,
0vx = 0 для всех хеУ,
Следовательно, для всех х, уеКв leR имеем
U (X + у)"= X + у = 1уХ + /vy,
0v (x + у) = 0 = 0 + 0 = 0vx +
Если S, T^End(V), то сумма S + T и произведение
S'T (композиция) определяются формулами
(S+T)x=*Sx + Tx для всех xeF
E • Т) х = S (Гх) для всех х е= F.
Отметим следующие свойства End(F) относительно при-
приведенных выше операций.
159
Предложение. Множество (End(F), •, +) явля-
является кольцом с единицей.
Доказательство. Укажем основные этапы дока-
доказательства. Надо показать, что:
(I) 5, reEnd(F)^5 + reEnd(F) и S»fs
eEnd(F);
(II) (End(F), + )—коммутативная группа.
Если 5, Т, tfeEnd(F), то:
(III) S»(T»U)-{S»T)*U;
(IV) S°(T+U) = S°T + S°U;
(V) Iv*T = T°lv = T.
Имеем
(I) (S + r)(x + y)=S(x + y)+7(x + y)= Sx + Sy +
+ Tx + Ty =Ex + rx) + Ey + ry) = E + f)x+(S + T)y.
Аналогично
(S + T) {Xx) = Six + Ш - XSx + XTx =
Доказательство того, что S ° T <^End(V), оставляем в
качестве упражнения.
(II) E + (r+C/))x = 5x + (iT+C/)x = 5X + (fx+C/x)-
-(Sx + Tx)+ Ux = (S+ T)x+ Ux-*{{S + T)+ U)x.
Следовательно, операция + ассоциативна. Элемент 0v s
е End(F) удовлетворяет условию
Т + Ov = Ov + Т = Т для всех Т е End(F)'
и является аддитивной единицей End(F). Для Ге
eEnd(F) определим отображение —Г: F -*- V соотно-
соотношением
(-Т)х = -(Тх) для всех х е у.
Легко показать, что —fsEnd(F) и
Поэтому отображение —Т является аддитивным, обрат-
обратным к Т. Коммутативность (End(F), +) следует из ком-
мутативпостп (F, +).
(III) Утверждение следует из результатов гл, 3.
(IV) Для х е V имеем
(V) Утверждение очевидно. /
Пусть TsEnd(F) и A,eR. Определим отображение
Я,Г: У -»• 7 следующим образом:
(XT) х =» А, (Гх) для всех х е F.
Легко показать, что X7"eEnd(F). Отображение
Л: RXEnd(F)-*End(F),
определяемое соотношением Л (А,, Т) = ХТ, называют ум-
умножением на скаляр.
Предложение. (End(F), +, Л) — векторное про-
пространство над R.
Доказательство. Из предыдущего утверждения
следует, что (End(F), +) — коммутативпая группа; сле-
следовательно, нам надо показать, что умножение на ска-
скаляр удовлетворяет условиям
(К + р.) Т = XT + pT, X(S + Т) = XS + XT,
(Хц) Т = X (fir), 1RT = T,
где X, (i^R и S, feEnd(F). Имеем цепочку соотно-
соотношений
Остальные соотношения доказываются аналогично. II
Предложение. Операции умножения в кольце и
умножения на скаляр А в End(F) удовлетворяют соот-
соотношению
Доказательство.
11 А Кук. Р, Бейа 161
Алгебраические структуры, удовлетворяющие таким же
свойствам, как и End(F), называют линейными алгеб-
алгебрами. Дадим строгое определение.
Определение. Четверка (X, +, °, Л) называется
линейной алгеброй над R, если Л: RXI-»-Xh
(I) (X, +, Л)—векторное пространство над R;
(II) (X, », +) — кольцо;
(III) Л и • удовлетворяют условиям
X (xi • х2) = (Kxi)° х2 = xi«(Ххг)
для всех X е= R и х\, х2 «= X. II
Результаты, полученные для End(F), можно сфор-
сформулировать следующим образом.
Предложение. End(F) с введенными выше опе-
операциями является линейной алгеброй с мультипликатив-
мультипликативной единицей. II
Если TeEnd(F) и существует преобразование
S: V -*¦ V такое, что
SaT°=T°S = /у,
то (см. упражнение 5.4) SeEnd(F). Тогда Т называют
обратимым, a S — Г — обратным к Т преобразованием.
Обозначим через Aut(F) множество всех обратимых пре-
преобразований из End(F), т. е. множество автоморфиз-
автоморфизмов V.
Предложение. (Aut(F), °) является группой.
Доказательство. Так как Iv e Aut (V) и Ir °
о /v = Iv, следовательно, существует Iy1, равное Iv. Пусть
-Se Aut(F); тогда
Поэтому (S)-1 существует и совпадает с S. Следова-
Следовательно, S-1 <= Aut(V). Если теперь S, reAut(F), то
Аналогично
Поэтому (S ° Т)~1 существует, и из 5, 3reAut(F) сле-
следует, что S • Т е Aut(F). Ассоциативность операции »
уже доказана. II
4.2. Структурные изображения в R". Рассмотрим гео-
геометрическую интерпретацию пространства R", при кото-
которой понятия «направление» и «величина» для векторов
162
имеют геометрический смысл. Вернемся к геометриче-
геометрическому изображению R2. Мы видим, что если г = (х, i/)s
е R2, то расстояние от точки (я, у) до @, 0) есть
(х2 + у2I/2. Обозпачим это расстояние через llrll,
которое можно рассматривать как отображение
11-11: R2-*-R. Оно называется длиной, модулем илп
нормой. Рассмотрим точки ri=(xi, ух) и Г2=(хг, у%)
Г2-Г,
Рис. 5.4
(рис. 5.4). Пусть 0i и Ог — углы в иптерпале [0, л] меж-
между положительной полуосью ОХ и векторами ri и гг со-
соответственно. Тогда расстояние между rt и гг равно
11гг — rill, а угол между пими равен в == 02 — 0i. Имеем
cos G = cos @a — 0Х) = cos Qa cos 02 + sin 0X sin Э2 =
II MINI И Mill'.I llriliilral "
Выражение Х\Х2 + У\Уг можно использовать для вычис-
вычисления расстояний и углов в И2. Определим отображение
Ф: R2 X R2 -* II
следующим образом:
Тогда
2, cos 6 =
Угол 0 между двумя векторами в П2 определяется одно-
вначно при условии, чго 0 < 0 ^ л. Когда 6 = 0 или G =¦
¦= л, то говорят, что ri и гг параллельны (коллинеарны).
В прикладной математике удобно обозначать Ф(г1, гг)
через Г! • Г2 и называть скалярным произведением ri и т%.
Если ri Ф 0 и гг Ф 0, то ri • гг = 0 тогда и только тогда,
когда G = л/2; в этом случае говорят, что ri и гг взаимно
ортогональны, перпендикулярны или нормальны. Ниже
приведены некоторые свойства скалярного произведения.
11» 183
Предложение.
а) г • г > О и г • г = О тогда и только тогда, когда
г-@,0);
б) rj • Г2 *= гг • ri для всех ri, Г2 s R2;
в) Г|-(ra + rsj^ri Т8 + Г1-гз для всех г\, гг, Гз^И2;
г) Х(Г|-Г2)-(ЛГ|)-14-г,-(Xij), г,, r2eR', Я е R.
Доказательство.
а) Если г ¦= (х, у) е R2, то г • г = (х* + у*) > 0 для всех
х, yeR и гт = 0 тогда и только тогда, когда х — 0 и
0-0.
б) Г! • Г2 = XiX2 + У\У2 = Х2Х{ + Цгух = Г2 • Гь
Соотношения в) и г) доказываются аналогично и ос-
оставляются в качестве упражнения. /
В более общем случае, если V — векторное простран-
пространство над R и Ф: FXF-*R — отображение, удовлетво-
удовлетворяющее свойствам а) —г), то (V, Ф) становится про-
пространством, для которого могут изучаться понятия длп-
ны и угла. Отображение Ф называют внутренним про-
произведением для V, а (V, Ф)—векторным пространством
с внутренним произведением. В частности, если опреде-
определить Ф: R" X R" -*- R(n e N) соотношением
п
Ф(а,Ь)^а-Ь=» 2 аФь
где a «(at, ,.., а„), b==(&i, ..., Ъп), то отображение • бу-
будет соблюдать требуемыми свойствами. Определим длину
вектора asR" как
а косинус угла менаду двумя векторами а и Ь как
угол лежит на отрезке [0, л].
На R" могут быть определены другие внутренние про-
произведения. Внутреннее произведение, введенное выше,
называется обычным или евклидовым внутренним произ-
произведением. Оно дает те зпачения длины и угла, которые
ожидались интуитивно.
Когда п = 1, ясно, что • является лишь умножением
в R, и угол между двумя векторами определяют как
164
угол равен или 0, пли я в зависимости от знака ху.
Норма 11-11 обобщает понятие модуля |-| в R и обладает
аналогичными свойствами. Например, можно показать,
что
Hall > О для всех а е R",
ПаП = 0 тогда и только тогда, когда а = О,
ИЯа11 = МПаИ для всех aeR" n^eR,
На + Ы1 < ПаП + НЫ1 для всех a, be R".
Вектор а е R" такой, что Hall = 1 (что эквивалентно
а-а = 1), называется единичным вектором. Если as
е R"\{OJ, то а/Ы1 — единичный вектор, параллельный а.
Едиппчпый вектор обычно обозначается а.
Если В =» tei, ..., ej — базпс в R" и
О, если i Ф /,
если i = /,
то базис В называется ортопормированным. Пронорми-
Пронормированный базис в R", определенный следующим образом:
е§ — @, ..., 0, 4,0, ..., 0), 1<1<л,
1-й разряд
называется стандартным базисом' в R". В R2 и^ R3 стан-
стандартные базисы удобно записывать в виде (i, j) и (i, j,
к) соответственно. Рассмотрим следующую геометриче-
геометрическую интерпретацию этих базисов. Векторы i и j опреде-
определяют правостороннюю систему осей в R2, а третья ось^
OZ перпендикулярна плоскости, содержащей векторы i
"* j, и направлена таким образом, чтобы концы векторов
i, j и к (в указанном порядке) определяли правосторон-
правостороннее движение (рис. 5.5). Это свойство известно как пра-
правило правой руки. В системах такого типа в R3 оси на-
называются правосторонними.
Определение. Если a=(ai, a2, a3JsR3 и Ь =
= (fci, Ьг, &з)е R3, то векторным произведением а и Ь
(обозначается а X Ь) по определению называют вектор
Операция X может рассматриваться как отображение
R3 X R3 -* R8.
165
Предложение. Если a, be R3, то
а) НаХЬИ = Hall НЫ1 sin 8, где 8 — угол между а и Ь;
б) вектор а X b ортогонален векторам а и Ь.
X
-Х^'г
Рис. 5.5
Доказательство,
a) ||axb|2 ЧяА-«зЬ
= (flj + a\ + al) (б? + Ь» + Ь|) - (aA + аг\ + а3Ь3J =»
= ||a f I b Ц2 A - cos2 8) = I а ||21| b ||2 sia2 8,
б) Легко показать, что а-(аХЬ)=0 и Ь-(аХЬ)=0,
откуда и следует требуемый результат. /
Чтобы получить геометрическую интерпретацию
а X Ь, заметим, что если
а«=(вь 0, 0), Ь = (&,, 62, 0),
то
аХЬ = @, 0, й,&2);
поэтому если а\ > 0, то
|axb2|k для 62>0,
| аф21 k для Ь2 < О,
и направление а X b определено таким образом, чтобы
выполнялось правило правой руки относительно векторов
а, b и а X Ь. Это правило носит общий характер, посколь-
166
аХЬ =
ку для произвольной пары векторов в правосторонней
системе координат всегда можно выбрать способ пред-
представления векторов, который определяется векторами а
и Ь. В результате векторное произведение будет иметь
вид
а X Ь = Hall ПЫ1 sin On,
где п — единичпый вектор, ортогональный а и Ь, с на-
направлением, выбираемым по правилу правой руки. Если
аХЬ = 0, то векторы а
и Ь линейно зависимы, а у ус
если Hall >0 и ИЬН >0, то а/ /
из равенства аХЬ = 0сле- /д /
дует, что а и Ь параллель- q?-j *? /
ны. Пусть а и Ь — векто- в
ры, изображенные на „ г fi
рис. 5.6. Тогда На X Ы1 - "^ 5Ь
площадь параллелограмма
ОАСВ и аХЬ может рассматриваться как вектор пло-
площади.
Некоторые свойства векторного произведения приве-
приведем ниже; доказательства оставляем в качестве упраж-
упражнений.
Предложение.
а) аХЬ= -ЬХа;
б)
в)
г)ТхТ =
д) аХ(ЬХс) = (а с)Ь-(а Ь)с;
е) аХ(ЬХс)= b (сХа)= с(аХЬ)= -а-(сХЬ) =
¦=-Ь(аХс)=-е (ЬХа). /
Выражение аХ(ЬХс) часто называют тройным век-
векторным произведением а, Ь и с, а а (Ь Хс)— смешанным
произведением. Геометрически а-(ЬХс) означает объем
параллелепипеда с ребрами a, b и с.
Предложение. Множество {а, Ь, с) с: R3 линейно
зависимо тогда и только тогда, когда а-(ЬХс)=0.
Доказательство. IIредположим, что а, Ь и с ли-
линейно зависимы. Тогда существуют X, ц, о? R, не все
равные нулю, такие, что
Ха + цЬ + ос = 0.
167
Не ограничивая общности, предположим, что X ч* 0. Тогда
а = -Ат1 (цЬ + ос),
а • (Ь X с) = -Аг1 (цЪ + ос) • (Ь X с) =
- -К'1 [цЪ • (ЬXс) + ос • (ЬX с)] = О,
Обратно, если а•(Ь X с), то или
а) один из векторов а, Ь, с равен нулю (в этом случае
результат очевиден), или
б) вектор а ортогонален b X с.
Однако b и с ортогональны к Ь X с; поэтому а =
*= К'Ъ + (х'с при некоторых к', ц' е R и а, Ь, с линейно
зависимы. /
Закончим главу кратким рассмотрением вопросов диф-
ференцируемости «векторнозначных» функций. Пусть на
R* задана обычная норма. Определим производную функ-
функции вида
/: R - R\
Обобщая одномерный случай, скажем, что / дифферен-
дифференцируема в точке t, если существует вектор F(f) =
(F@ F@)Rn такой, что
при h -*¦ 0, или, что эквивалентно, если f имеет компо-
компоненты /i, ..., /„ такие, что
при h -*¦ 0. Очевидно, что каждая компонента должна
стремиться к нулю при А -*¦ 0, поэтому dijdt существует
тогда и только тогда, когда dfijdt, ,.,, dfjdt суще-
существуют и
dl_(dft dfn\
Другими словами, чтобы продифференцировать векторно-
вначную функцию, мы должны продифференцировать ее
покомпонентно. Например, если f: R -*¦ R3 определена со-
соотношением
f@ = Bf2, Int, sin* 0,
то
gj = ]М, -Г| 2 sin t cos t).
Пусть f: R -+ R! и g: R -*• R3. Определим функции f • g:
R -*- R и f X 0: R -*¦ R3 Пплпжпм
Пусть f: R R и g: R R. О
R -*¦ R и f X g: R -* R3. Положим
Дифференцирование этих функций производится следу-
следующим образом:
('Ч>!& + ?*
Проверку этих формул оставляем в качестве упражнения.
Упражнение 5.4.
1. Показать, что если V — векторное пространство над
полем F, то
OfX = 0 для всех х s F,
аО = 0 для всех aef.
2. Представить вектор (а, 1, 3)е R3, где це R, в виде
линейной комбинации векторов множества
5 = {A, 1,0), @,2,0), @,0,4)}
и показать, что 5 — линейно независимое множество век-
векторов. Является ли S базисом в R3?
3. Показать, что если {xi, ..., xm} — линейно незави-
независимое подмножество векторного пространства V, то х< ?• 0
при любом i, 1 «? i s? m.
4. а) Какие из следующих преобразований являются
линейными:
y) = Va + y, ay), X, oeR\{0>,
Тг(х, i/) = (x2, 0), Tt(x, y)-(x,0I
б) Определить произведения Тч. ° T$ и Т* ° Ti.
в) Доказать, что если T^End(V), то ТО = 0.
5. а) Если V — векторное пространство, то проекцией
(проектором) V называют преобразование Р: V -** V, об-
обладающее свойством
(Р ° Р) х = Рх для всех х е V.
Доказать, что преобразование Р: R2 -»¦ R2, определя-
определяемое соотношением
р(*. г/) = (т=1>(ах~ у + с)' 7^Гь^ах - ^ + с) + с)
при а, 6, с е R и а ч* Ь, является проектором в R2. При
каких условиях Р s End (R2) ?
109
б) Какие из определенных в п. 4. а) преобразований
являются проекторами?
6. Пусть Т е lCmJ(F). Нулевым подпространством
(ядром) Т называют множество Jf(T), определяемое со-
соотношением
(хе F: Гх = 0).
Доказать, что Jf(T) является векторным подпростран-
подпространством V. Доказать также, что образ Т является вектор-
векторным подпространством V.
7. Пусть V — векторное пространство над R в Ге
eEnd(F). Говорят, что Т имеет действительное собствен-
собственное значение К & К, если существует ненулевой вектор
х е V такой, что
Тх = Ях;
при этом х называют собственным вектором Т, соответ-
соответствующим собственному значению К. а) Доказать, что
если Т е End (V) такое, что
Т(х, у) = (х + ау, у),
то любой вектор вида (р, 0) при рФО является собст-
собственным вектором Т. Какие у Т собственные значения?
б) Пусть 7'eEnd(F). Обозначим через V\ множество
собственных векторов Т, соответствующих собственному
зпачеппю К. Показать, что \\ U Ш является векторным
подпространством V. Доказать аналогичное утверждение
для Jf(T).
8. Найти собственные значепия и собственные векто-
векторы преобразований Ти 712eEnd(R2):
Ti(x, V)-(-U, г), Тг(х, у)-(х, -у).
Какой геометрический смысл имеют Т\ п T^i
9. Доказать, что
а) если S, rsEnd(F), то 5«7'eEnd(F);
б) если при JeEnd(F) существует преобразование
S: V -*¦ V такое, что
то Se=End(F);
в) если f«=Aut(F), то
10. Доказать, что если n, rs, T3sR2 и AeR, то
а) Г! • (г2 + г3) = rj • г2 + Г1 • г3;
170
б) \ (г, • r2) = (to,) • г2 = г, ¦
в) |rj т21 < Иг,И llrall;
г) Иг, - г2И2 •= Иг,112 + Иг2112 - 2ЦИ Нг211 соз 9,
где 8 — угол между ri и г2;
д) |Dr,ll - llrgHI < Иц + г2Я < Иг, II + 11г2Н
(последнее неравенство известно как неравенство тре-
треугольника). Дать геометрические иллюстрации этим ре-
результатам.
В действительности вышесказанное имеет место для
любого пространства со скалярным произведением; в ча-
частности, результаты справедливы для R'(nsN) с обыч-
обычным внутренним (скалярным) произведением.
11. Вычислить единичные векторы, параллельные
а) а-A, 1, 1);
б) b-(l,/»,0),/»eR.
Определить единичный вектор, ортогональный а и Ь од-
одновременно.
12. Пусть a, b, ceRs и ^eR, Доказать, что
а) аХЬ = -ЬХа;
б) аХ(Ь + с)=аХЬ +
в) (Ха)ХЬ = аХ(М>) =
г) ГхГ = k, f хк = Г
д) аХ(ЬХс) = (ас)Ь-(а Ь)с;
е) а(ЬХс) = Ь(сХа)= с(аХЬ)= -а (с X Ь) =
•=-Ь(аХс)=-с (ЬХа).
13. Используя результаты 5.4, 12, доказать, что опе-
операция X: R3 X R3 -»¦ R3 не ассоциативна, т. е. в общем
случае аХ(ЬXс)?=(аХЬ)Хс.
14. Пусть f, g: R -»• R3. Доказать, что
в) если 111@"=" я для всех t, где а е R — постоянная,
то di/dt ортогонален к f при всех t. Провести вычисле-
вычисления при
f (О-(с cost, ssini, 0), g@. = @, 1, *)•
171
§ 5. Решетки и булевы алгебры
Булева алгебра является одним из математических
объектов, с которыми мы уже сталкивались во введении.
Мы покажем, что существует не одна булева алгебра,
а много. Следовательно, любое преждевременное исполь-
использование этого объекта может привести к недоразумению.
Тем не менее мы начнем изучение с введения более
общей структуры, называемой решеткой.
Некоторые из решеток имеют важное значение в аб-
абстрактной теории вычислений, возникшей из понятия ап-
аппроксимации. Одна программа аппроксимирует другую,
если она осуществляет те же самые вычисления на под-
подмножестве данных, доступных той программе. Если жа
рассматривать результат работы программы как множе-
множество, то одна программа аппроксимирует другую, когда
для некоторых входных данных она выдает' в качестве
результата подмножество В ^ А, где А — множество вы-
выходных дапных второй программы. Это достаточно про-
простые и, вероятно, очевидные способы аппроксимации про-
программ. При этом возникает множество элементов, свя-
связанных некоторым отношением порядка.
Вычисление является результатом выполнения про-
программы (на некоторых данных), которая написана на ка-
каком-либо языке (см. гл. 8). Для общности рассмотрений
свойства вычислений падо выводить не в терминах рас-
рассматриваемой программы, а в терминах языка, используе-
используемого для записи программы. В то же время мы должны:
быть в состоянии определить результат выполнения про-
программы «язык X» с помощью формального определения.
К сожалению, количество деталей, требующихся для
описания даже простых примеров, достаточно велико и,
следовательно, ничего не определяет. Однако в п. 5.i мы
дадим теоретические обоснования некоторых ключевых
результатов. Это будет следовать (п. 5.2) из формаль-
формального использования булевой алгебры, а затем (п. 5.3)
пз краткого рассмотрения некоторых общих приложений.
5.1. Решетки. Напоышш> что бинарпоо отпошеппе р
па мпожес!ве S является частично упорядоченным от-
отношением, если оно рефлексивно, транзитивпо и анти-
антисимметрично. Следовательно, (S, р) — частично упорядо-
чепное множество, и, если не возникает двусмысленно-
двусмысленности, р можно записать как «5, a (S, <) обозначить про-
просто через S. Частичпо упорядочппное множество называ-
называется линейно упорядоченным (или цепью), если для
172
любых i, ysS или х<у, или у<х, или же выполнены
оба эти отношения. На самом деле любой частичный
порядок можно представить в виде объединения линей-
линейных порядков. Поэтому возникает естественный и по-
полезный способ изображения отношений порядка.
Заметим, что любое конечное, линейпо упорядоченное
множество (А, <) молено представить следующим об-
образом:
здесь рефлексивность и транзитивность не требуют дока-
доказательств. Легко видеть, что рис. 5.7 является «очевид-
«очевидным» представлением (А, «?). Другими словами, мы за-
записываем А как (ai, «2, ..., a»).
Предложение. Частичное упорядочение на ко-
конечном множестве может быть представлено как объеди-
объединение линейных порядков на некоторых подмножествах.
Рис. 5.8
Доказательство этого факта оставляем в качестве уп-
упражнения. /
Используя этот результат, можно представить любой
частичный порядок (конечный или бесконечный, однако
бесконечные отношения сложно изобразить на конечных
листах бумаги за конечное время!) изображением мно-
множества соответствующей цепей. Полученная диаграмма
называется диаграммой Хасса.
Пример 5.1. Отношение р = {(х, у): х — множи-
множитель у), определенное на множестве A, 2, 3, 4, 6, 10, 12,
20}, дает диаграмму Хасса (изображенную на рис. 5.8)
и может быть разбито па линейно упорядоченные под-
подмножества {A, 2, 4, 12), A, 3, 6, 12), B, 6), (/i, 20),
B, 10, 20)). Этому разбиению эквивалентно следующее
173
множество лппейных порядков: {B, 6, 12), A, 3, 6),
A, 2, 10, 20), B, 4, 20), D, 12)}. Заметим, что по срав-
сравнению с отношениями, изображенными на диаграммах
в § 2 гл. 2, хотя ipx для всех х е {1, 2, 3, 4,6,10,12, 20}.
на этом рисуике отсутствуют восемь стрел, выходящих
пз 1. Это достигается неявным представлением свойств
рефлексивности и транзитивности. /
Пусть дано (А, «?) п BsA. Разумно задать вопрос:
будет ли В ограничено сверху (снизу) элементами мно-
множества А1 Далее мы можем искать наименьшую верх-
верхнюю грань (наибольшую нижнюю грань), которая обо-
обозначается sup (inf) (читается супремум (анфимум)).
Эти понятия были полностью определены в § 5 гл. 2.
Будем их использовать для характеристики решетки.
Определение. Решеткой называется частично
упорядоченное множество (А, <), в котором каждая па-
пара элементов имеет супремум и ипфимум. Для заданных
х, у ^ А эти грани будем записывать следующим об-
образом:
х Д У = inf ({х, у}), х V у = sup {{х, у}). II
Не всякое частично упорядоченное множество явля-
является решеткой. Например, частично упорядоченное мно-
множество нз примера 5.1 не является решеткой, поскольку
12V20 не определено.
Определив операции Д в V между парами элементов
в частично упорядоченном множестве, расширим это по-
понятие естественным образом. Положим
Л ¦х= f\xexx~iniX, V
Это обозначает sup X и inf X конечного непустого мно-
множества X.
Легко показать, чю существует много специальных
видов решеток, в которых можно производить различные
операции. Ограничимся рассмотрением трех тагшх типов.
Определение. Решетка L, обозначаемая (Ь, Д,
V), дистрибутивна, если она подчиняется дистрибутив-
дистрибутивным законам
для всех х, у, ге^ /
Не все решетки являкнся дистрибутивными,
171
Пример 5.2. Решетка, изображенная на рис. 5.9,
не является дистрибутивной, поскольку
тогда кал
Предложение. Пусть в дистрибутивной решетке
(?/, Д, V) выполнены соотношения
Тогда y = z.
Доказательство. Сначала
ааметим, что из определения inf
и sup
а) а/\Ь — ЬДа, a\Jb = b\]a\
б) a
Поэтому
у = уУ(уМ - y\/(zM - (уУ*)Л(»V*) -
- (i\/y)/\(z\/x) - *V(yA*) = *V(*A*) =z- /
Определение. Предполонщм, что (L,/\,\f) —
решетка и 0, 1 еL такие, что 0<х< 1 для всех iei
(об элементах 0 и 1 скажем немного позже). Тогда
i\/l=*l. х[\\ = х, хД0 = 0, x\JQ = x
для любого iel, Такая решетка называется решеткой
е дополнениями, если для любого isi существует х е
e L такой, что
хДа-=0, х\1~х = \
(х называют дополнением х). /
Предложение. Если (L,/\, \J)— дистрибутивная
решетка с дополнениями, то дополнения единственны.
Доказательство. Предположим, что х, у, jeL и
Тогда из предыдущего предложения следует, что у = z. I/
Третий, и последний специальный тип решеток, кото-
который мы определим, необычен в том смысле, что он не дает
нам ничего нового для конечных решеток. Чтобы подчерк-
подчеркнуть ключевой момент исследования, дадим другое опре-
определение решетки в форме предложения.
175
Предложение. L является решеткой тогда и толь-
только тогда, когда VX и /\Х существуют для любого непу-
непустого конечного подмножества X из L.
(Этот факт можпо доказать индукцией по числу эле-
элементов множества X; оставляем его в качестве упраж-
упражнения.) /
Если L — решетка и в ней определен элемент Д?, то
он обозначается символом 0 и называется наименьшим
элементом L. Аналогично, если в L существует элемент
VL, то он обозначается символом 1 и называется наи-
наибольшим элементом L; по определению V0 ¦= 0.
Определение. Решетка L называется полной, если
VX и Л^ существуют для всех подмножеств X из L. II
Все конечные решетки являются полными. Рассмот-
Рассмотрим, однако, множество Q с обычным отношением по-
порядка < и бесконечное множество аппроксимаций числа
я, каждое из которых имеет на один десятичный внак
больше. Верхпяя грань этой последовательности, очевид-
очевидно, есть л, однако л s R\Q, и, следовательно, (Q, «?)
не является полной решеткой. Решетка (R, <) является
полной, и QsR,
Можно показать, что любая решетка может быть рас-
расширена до полной решетки, однако мы не будем вани-
маться атим вопросом.
5.2. Булевы алгебры. Мы уже интенсивно занимались
алгеброй множеств и упоминали об относительно «логич-
«логичной» арифметике. Сейчас дадим формальное определение
общей булевой алгебры, названной так в честь матема-
математика XIX в. Дж. Буля. Алгебра множеств — это част-
частный случай булевой алгебры, и, хотя различные булевы
алгебры структурпо подобны, следует ваметить, что не
все они включают в себя множества обычным образом.
Определение. Булевой алгеброй называют мно-
множество 9& вместе с тремя операциями V, Л и " (V на-
называют операцией или, Д — операцией и, а " — опера-
операцией дополнения или же операцией не; кроме того, пер-
первые две операции часто называют дизъюнкцией и конъ-
конъюнкцией соответственно). Бинарные операторы V и Д
и унарный оператор " (обычно записывается над операн-
операндом, например а) вместе с двумя различными элемента-
элементами $&, которые обозначаются символами 0 и 1, удовлет-
удовлетворяют следующим аксиомам.
Для произвольных элементов о, b и с в Я:
a) aV6=.fcVa; б) a V(b V c)«=(a V 6)Vc;
i7G
в) aVO = a; г) aVa — i;
д) a/\b = b/\a; e) a/\{bДс) = (а/\Ъ)/\с;
ж) лД1=а; 8) аДа = О;
и)
Таким образом, и и или коммутативны, ассоциативны
и дистрибутивны одна по отношению к другой. Каждая
из этих операций имеет единичный элемент, и, когда
элемент комбинируется вместе со своим дополнением
посредством и/или, в результате получается единица по
отношению к или/и соответственно.
Названия операторов, использованные выше, являют-
являются именами, которые непосредственно связаны с компь-
компьютерной логикой, используемой при построении схем.
В других булевых алгебрах может быть более подходя-
подходящим читать V как объединение, наименьшая верхняя
грань или supremum, а Л как пересечение, наибольшая
нижняя грань или infimum. (Иногда операцию Д обо-
обозначают также & •) Операция а может записываться как
а' или Ч а. II
Булеву алгебру можно определить как дистрибутив-
дистрибутивную решетку с дополнением. Поэтому по аналогии с бу-
булевой алгеброй {!Р(Х), U, П, ') для данного непустого
множества X из результатов предыдущего параграфа
можно вывести ряд следствий. Доказательства некоторых
из них оставлены в качестве упражнений. Наиболее важ-
важными из этих следствий являются следующие.
Инволютивный закон (или закон двойно-
двойного отрицания). Дополнение дополнеяия х, x&SB
(т. е. в рассматриваемой булевой алгебре), есть х.
Закон поглощения. Для любых a, b eд§ спра-
справедливы соотношения
а/\(а\/Ъ)*=а, а\/
Закон идемпотентности. Любой элемент SS
идемпотентен по отношению к операциям Д и V.
Законы де Моргана. Для любых a, b e <% спра-
справедливы соотношения
Из инволютивного закона и законов Моргана следу-
следует, что если мы берем булеву алгебру & (более точно,
12 д. кук, Г. Вей» *77
C$> \Л Л> )) и образуем новую систему или путем
отображения каждого х е $ в х, или использованием
операций /\ и V, то (.$, Д, V > ~) также булева алгебра.
Этот факт иавестен как принцип двойственности. Дей-
Действительно, каждый из законов Моргана может быть
получен из других путем отображения каждого элемента
в его дополнение.
Сейчас мы выведем теорему, которая показывает,
в какой стандартной форме могут записываться булевы
выражения; непосредственным следствием этого является
утверждение, что достаточно двух операторов, чтобы
описать все бинарные функции. Как всегда, введем вна-
вначале необходимую терминологию.
Определим две общеупотребительные логические связ-
связки следующим образом. Говорят, что булевы формулы
А п В эквивалентны (записывается в виде А в* В или
А ¦»-»¦ В), если они выражают одну и ту же функцию.
В простейшем случае это — отношение эквивалентности.
Таблица 5.3
А
0
0
1
1
В
0
1
0
1
А -+В
1
1
0
1
Аналогично говорят, что формула А имплицирует фор-
формулу В (записывается*) А -*¦ В), если имеют место ус-
условия, изображенные в табл. 5.3. (Таблицы такого типа
часто называют таблицами истинности.)
Заметим, что стрелки испольвуются во многих различ-
различных контекстах. Поэтому надо обращать особое внима-
внимание на расшифровку их значения. Таким образом, А -*¦
-*¦ В это то же самое, что и {*~\A)\JB, а А «а В это
то же самое, что и (А-*¦ В)/\(В-*¦ А). Логически А-*-
-*¦ В означает «если А, то 5» (т. е. если А справедливо,
то В также справедливо и обычно так и читается. Дру-
Другие названия для символов -+¦ и ¦*-*¦ это условный и без-
безусловный операторы соответственно.
Обычно вводят операции, которые обозначают отри-
•) Это выражение навывают также импликацией,—Примеч.
ред.
178
цания бинарных связок, такие, как
Ал- В=*~\{А-+В), А \ В = ~~](A\JВ).
Сейчас можно описать все бинарпые операции {О, I}2 -*¦
-+¦ {0, 1} (здесь стрелка находится между двумя множе-
множествами и, следовательно, обозначает множества, которые
являются областью определения и множеством значений;
не следует путать с логическим оператором -»-) в крат-
краткой форме, как показано в табл. 5.4. Более того, мы
Таблица 5.4
А
В
Л.
и
и
и
и
п
и
и
0
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
1
1
1
1
0
1
0
0
1
1
0
0
1
1
1
1
0
1
0
1
0
1
0
1
Функция
А
В
А
А
А
0
Л в
А А
В
AS
А
ФВ
у в
А
И
U
и
fin
hi
fv
fii
fu
/и
0
и
1
1
1
1
1
1
1
1
1
и
0
0
0
0
1
1
1
1
0
i
0
0
1
1
0
0
1
1
1
1
0
1
0
1
0
1
0
1
Функция
А \ В
А =В
~\А
А -*В
-\в
В-+А
A f В
1
можем описать исе отображения из {О, 1}П в @, 1}, ис-
используя только \ или только \ (первая из них называ-
называется тгрихом Шеффера и обозначается «I»; в вычисли-
вычислительном контексте t называют «не и», а I называют *)
«не или»). Заметим, что операции t и 4 являются удоб-
удобными сокращениями, но они, например, неассоциативны.
Следовательно, по определению A t В t С есть (А Д В Д
ДС)\ а, например, не ((А/\В)'/\С)'. Говорят, что
множества операторов Ш и Ш адекватны. Сейчас мы
сформулируем теорему и дадим ее конструктивное дока-
доказательство, т. е. не только докажем справедливость ут-
вержденая теоремы, ио и дадим метод получения резуль-
результата.
Теорема. Любое отображение @, 1}" -*¦ @, 1} мо-
может быть представлено в виде формулы, содержащей
только оператор t или только оператор \.
Доказательство. Рассмотрим произвольное ото-
отображение /: @, 1)" -*¦ @, 1} от переменных р\, .. ., рп
(neN). Функция может быть полностью определена
•) Функция А \ В называется также стрелкой Пирса,— При-
,еч. ред.
12* 479
таблицей истинности, имеющей 2П строк*). Утвержде-
Утверждение очевидно, если в каждой строке таблицы результат
равен \ (тогда /=1) или в каждой строке результат
равен 0 (тогда / = 0). В противном случав существует т
строк таблицы, в которых результат равен 1.
Рассмотрим выражения **) В и ..., Вт\ каждое Bt
соответствует упорядоченному набору (/?л, ..., Btn), где
Bij равно или pit или ~~] р; в зависимости от того, равно
Pi единице или нулю для данной строки таблицы. Тогда
В\ = (Bhf\Bi2/\ ... Л Bin)' = Bh | Bi21 ... f Sin.
Более того, если какое-либо Вц соответствует нулю в таб-
таблице, то надо брать выражение *"] р» которое можно по-
получить при помощи тождества
Итак, утверждение доказано. В компактном виде этот
результат можно записать следующим образом:
t ( t
б) Аналогично, применяя эаконы де Моргапа к (*)
пли же рассматривая строки, содержащие нуль, получим
2"-га
i>=l
Следствием этого реаультата является тот факт, что каж-
каждое выражение выводимо, а отсюда в свою очередь сле-
следует, что число элементов в булевой алгебре, порожден-
порожденной pi, ,.., рп, равно 2", /
*) Каждая строка соответствует некоторому двоичному на-
набору длины п и содержит значения функции на этом наборе,—
Примеч. ред.
**) Пусть (оц, ..., а,„), ..., (ami, .... amn) — все наборы, па
которых функция / равна 1,1 <: т < 2". Для каждого такого набо-
набора образуем конъюнкцию Bi = Вц Д ... Д Bin> где Вц, = ph, если
а», = 1, и Bi; = ~] ph, если а,* = 0 Aс — i, .. „ п). Легко видеть,
что / = В1 V ... V Вт.— Примеч. ред.
180
Пример 5.3. Получим представление для функция
j, используя только операцию t; таблица истинности
функции / дана в виде табл. 5.5.
Таблица 5.5
X
0
0
0
О
и
0
0
1
1
г
0
1
0
1
/
0
1
1
0
X
1
1
1
1
и
0
0
1
1
Z
0
1
0
1
/
1
i
0
1
Используя описанный метод, получаем
t = {*' Ау' A*)Vi*' АуА*')У{*Ау' А*')Ч
Таким образом,
и поэтому
1 = {х' \ у' \ z)\(x \ у \ z')\{x \ у' \ z')\
где х = х \ х, у' = у t у, z ¦= г t z. В
Выражение (¦) называют дизъюнктивной нормаль'
ной формой (ДИФ)—она имеет вид дизъюнкции конъ-
конъюнкций (или от и); выражение, полученное в (•¦)*),
называется конъюнктивной нормальной формой (КНФ).
В заключение отметим, что утверждение в булевой
алгебре (логическая формула), которое всегда принима-
принимает значение 1, называется тавтологией, а выражение, ко-
которое всегда принимает значение 0, называется проти-
противоречием.
5.3. Некоторые приложения булевой алгебры. Суще'
ствуег ряд проблем, например в комбинаторике, которые
можно решить наилучшим образом в подходящей буле-
булевой алгебре. Другой путь применения булевой алгебры
заключается в моделировании реалшой ситуации, или,
*) Па самом деле конъюнктивной нормальной формой назы-
2й—m
вают выражение вида / = ,\
тсдьива теоремы,— Примеч. ред.
V ~1
(см- *•) пз доказа-
131
другими словами, в интерпретации булевой алгебры в
терминах, относящихся к рассматриваемой задаче.
Этот метод может быть применен в областях, которые
так широко распространены, что у них отсутствует клас-
классификация. Мы рассмотрим только одно приложение,
а именно комбинационные и переключательные схемы*).
Другие области приложений будут представлены в виде
отдельно выбранных примеров и упражнений.
Источник питания •" Лампа
I I
Рис. 5.10
С этой точки зрения необходимо подчеркнуть, что мы
занимаемся только некоторыми вопросами построения и
преобразования схем; формальное исследование лежит за
пределами этой книги. Сначала давайте посмотрим, как
выражения булевой алгебры могут быть использованы
для описания и определения схемы, состоящей из про-
проводников и переключателей. Схема, изображенная на
рис. 5.10, состоит из пяти переключателей, источника
питания, лампы и соединяющих проводников. Из диа-
диаграммы нетрудно видеть, что ток течет по замкнутой
цени тогда и только тогда, когда переключатель А зам-
замкнут в (или)
переключатели В ж С оба замкнуты
или
переключатели D и Е оба замкнуты.
Алгебраически это можно записать в виде
А/\((В/\С)У(О/\Е)).
Перед тем как продолжить изложение, сделаем не-
несколько замечаний о представление! элементов электри-
электрических схем с переключателями в виде диаграмм. Един-
Единственный сегмент схемы, в котором будет отличие между
рассматриваемыми примерами,— это верхняя часть схе-
схемы, содержащая переключатели; следовательно, можно
•) Эти схемы называются такжо схемами из функциональпых
элементов а коатактиьшц схемадш, соответственно,— Примеч. ред.
182
не изображать остальной части схемы. Внутри схемы не-
которые переключатели могут быть взаимосвязаны
(рпс. 5.11, а) и, возможно, могут работать так, что когда
один переключатель включен, то другой должен быть
выключен и наоборот (рис. 5.11, в). Основные методы
В
\А
В/
—«-J
I— В' А' С—J
Рис. 5.11
расположения переключателей — это последовательный
(рис. 5.11, с), что соответствует связке и (т. е. А/\В),
и параллельный (рис. 5.11, d), что соответствует связке
или (т. е. А У В), Отметим, наконец, что на диаграмме
есть совершенно лишние переключатели, и их для удоб-
удобства можно обозначать теми же «именами» (рпс. 5.11, е).
Таким образом, любую операцию в булевой алгебре
можно представить при помощи схемы и наоборот. Сле-
Следовательно, для получения эквивалентных схем надо
перейти от первоначальной схемы к соответствующему
ей выражению в булевой алгебре, затем к «более про-
простому» (или более желаемому) выражению и, наконец,
к схеме, соответствующей этому выражению.
183
Пример 5.4. Упростить схему, изображенную на
рис. 5.12. Этой схеме соответствует следующее выражение:
X/\mX'/\Y)V(Y'/\Z))/\W')\J(Z/\X/\W))=*
= Xf\((X'/\Y/\W')y(Y'/\Z/\W')y(Z/\X/\W)) =
Последнее выражение соответствует схеме, изображенной
на рис. 5,13,
I— X'
—W—,
•У-
•IV'-
Рис, 5.13
Мы уже уделили достаточно внимания схемам с пе-
переключателями. Перейдем теперь к комбинационным
схемам. Основные компоненты таких схем — элементы.
В наиболее общей форме элемент является устройством,
имеющим п входов и m выходов (m, n e N). На каждый
вход может подаваться один из двух бинарных сигналов;
представим их как 0 и 1, однако любая другая система
пз двух различных значений также нам подходит. В ре-
реальной ситуации обычно мы имеем сигналы в окрестно-
окрестности 0 вольт (например, от 0 до 0,8 вольта), которые
представляются нулем, и в другой окрестности — в рай-
районе 4 вольт (скажем, между 3 и 5 вольтами), которые
представляются единицей. Отсюда определяются выход-
выходные значения @ и 1). Можно ожидать, что нам понадо-
понадобится достаточно много различных элементов, чтобы
представить все возможные функции {0, 1}п -»¦ {0, 1>,
однако, как мы увидим далее, это не так. Схемам, не име-
имеющим временных задержек (в дальнейшем только такие
схемы мы и будем рассматривать), соответствует един-
184
ственный тип элементов. Однако это не очевидно. Струк-
Структура схем станет более ясной, если вначале мы рассмотрим
три типа элементов, изображенных на рис. 5.14. Самым
не
3-
Рис. 5.14
или
простым является элемент не; его действие определяется
тождеством
с = ""] а (с = не а),
определяемым табл. 5.6.
Таблица 5.6
INPUT(o)
0
1
OUTPUT(c)
1
0
Аналогично элементы и и или определяются табл. 5.7.
Таблица 5.7
а
0
0
1
1
INPUTS
ь
0
1
0
1
OUTPUTS
в
0
0
0
1
(е)
или
0
1
1
1
Элементы и и или могут также иметь несколько вхо-
входов; в этом случае они определяются аналогично, т. е.
выходной сигнал элемента и равен 1 тогда и только
тогда, когда на всех входах сигнал равен 1, и выходной
сигнал элемента или равен 1 тогда и только тогда, когда
какой-либо из входных сигналов равен 1. Алгебраически
выходной сигнал элемента не имеет вид: *"] (входной
сигнал), выходной сигнал элемента а имеет вид: (сиг-
(сигнал первого входа) Д (сигнал второго входа) Л••• и,
наконец, выходной сигнал элемента или имеет вид: (сиг-
(сигнал первого входа) V (сигнал второго входа) V,.. Что-
139
бы представить более сложные функции, элементы мож-
можно «соединять» различными способами.
Пример 5.5. Рассмотрим схему (более точно, часть
схемы, которая нас интересует), изображенпую на
Рис. 5.15
рис. 5.15. Возвращаясь «назад» от выходов схемы, по-
получаем
Поэтому
(по закону поглощения).
Таким образом, одно из возможных упрощений схемы
изображено на рис. 5.16. /
Рис. 5.16
Следовательно, мы можем использовать булевы вы-
выражения для анализа и упрощения сложных схем. Рас-
Рассмотренный пример показывает, как можно осуществлять
такие операции.
Существуют также устройства, которые реализуют
другие логические операции. Наиболее важными явля-
являются элементы не и и не или; опи изображены на
рис. 5.17. Используя множество таких элементов, при
помощи булевых выражений можно получить требуемую
схему непосредственно по таблице истинности.
188
Пример 5.5 (продолжение). Не останавливаясь на
формальностях, заметим, что каждое выражение в скоб-
скобках в окончательной форме / (см. выше) представляет
вход для последнего элемента на рис. 5.18 и может быть
вычислено с помощью элементов предшествующего ряда
не и
не ила
Рис. 5.17
(Части схемы, обведенные штриховыми линиями, практи-
практически не требуются, поскольку для многих электрических
элементов дополнение к выходу также доступно из
вспомогательного выхода.) Отметим, что полученная схе-
схема в общем случае не будет мипимальной в смысле чис-
числа используемых элементов. /
В завершение рассмотрим два примера, которые пока-
показывают, как булева алгебра может быть использована в
задачах иного рода.
;=fc
г^ 1
аи
Рис. 5.18
Пример 5.6. Предположим, что справедливы следу-
следующие утверждения:
а) знание структур данных необходимо для совер-
совершенствования дисциплины ума;
б) только опыт программирования может создать дис-
дисциплинированный ум;
187
в) для того чтобы написать компилятор, надо иметь
возможность анализировать задачи;
г) недисциплинированный ум не может анализиро-
анализировать задачи;
д) всякий, кто писал структурные программы, может
рассматриваться как опытный программист.
Можно ли из этих предположений определить спра-
справедливость нижеследующих утверждений:
а') опыт написания структурных программ пеобхо-
дим для того, чтобы быть в состоянии написать ком-
компилятор;
б') внание структур данных является частью опыта
программирования;
в ) анализ задач невозможен теми, кто игпорирует
структуры данных;
г') опытный программист, который писал структур-
структурные программы, в состоянии анализировать задачи и
имеет дисциплинированный ум, является программистом,
который мог бы написать компилятор?
Чтобы ответить на эти вопросы, мы могли бы иссле-
исследовать логические следствия утверждений, однаки для
того, чтобы проиллюстрировать используемую технику в
более сложных ситуациях, воспользуемся нашим знани-
знанием булевой алгебры. Сначала необходимо закодировать
наши утверждения. Пусть
& — множество всех программистов,
U — те из них, кто знает структуры данных,
У —те из них, кто имеет дисциплинированный ум,
W — те из них, кто является опытными программи-
программистами,
X — те из них, кто мог бы написать компилятор,
У — те из них, кто может анализировать задачи,
Z — те из них, кто может писать структурные про-
программы. Тогда имеем
а)
г)
a') ZaX;6')" UsW; b'J Y ^ U;
г')
Теперь видно, что а') непосредственно следует из в),
г), б) и д) до транзитивности; аналогично в') следует
из г) и а). Также
188
Таким образом, г') также справедливо. Утверждение б')
не может быть выведено из а)—д), поскольку мы только
знаем, что WsZ, и цепочка на этом заканчивается. /
Пример 5.7. Алиса сказала, что Барбара и Клара
говорят правду, а Клара сказала, что Элспет и Фиона
или обе говорят правду, или обе лгут. С другой стороны,
Деби считает, что по крайней мере или Алиса, или Бар-
Барбара говорят правду, тогда как Барбара утверждает, что
только одна из двух — Алиса или Фиона — была правди-
правдивой. Элспет считает, что Алиса и Барбара всегда говорят
правду, однако Фпона уверена, что Барбара и Клара обе
не могли сказать правду. Кому мы должны верить?
Рассмотрим множество утверждений вида
«Алпса (не) говорит правду»,
«Барбара (не) говорит правду»,
и пусть А содержит только те утверждения, в которых
Алиса говорит правду. Пусть В, С, D, Е и F определены
аналогично. Тогда, если S — непустое множество пересе-
пересечений таких, что
SsAOB'uC,
то S включает утверждения, в которых
«Алиса говорит правду»,
«Барбара лжет»,
«Клара говорит правду».
Из первого утверждения следует, что можно вывести
следующий факт: если Алиса говорит правду, то то же
самое делают Барбара и Клара. Это можно закодировать
следующим образом:
если те А, то х&ВпС;
следовательно,
AsBOC. A)
Аналогично другие утверждения могут быть записаны в
виде
Cs(EuF)U{E'uFf), B)
DsAUB, C)
Bg(EUF)\(E(\F) = (E(\F')V(E'uF), D)
EsAHB, E)
F*{B(\C)f. F)
Из B), D) п A) следует, что ВПС = 0, и поэтому А —
= 0; тогда из E) следует, что Е = 0. Эти выводы мы
смогли получить непосредственно из условий задачи. До
сих пор наши рассуждения были эффективны потому, что
мы пользовались тем, что правдивый человек говорит
правду. Однако пока мы не использовали ничего о спра-
справедливости того, что говорит лжец. Если мы ограничимся
фактором, что все, что говорит лжец, неверно, то можем
заменить множество включений из A) — F) на экви-
эквивалентные. Например, если Барбара и Клара правдивы,
то, поскольку Алиса говорит, что это так, Алпса тоже
правдива. Следовательно,
А=°ВпС, Aа)
C-{Ef\F)\$(E'{\F'), Ba)
D = AUB, (За)
B — (E(\F')\}{E'(\F), Da)
Е = А П В, Eа)
F-(BflC)\ Fа)
Как и раньше, 4 = 0ий = 0,п поэтому Алиса и Элспет
никогда не говорят правду. Из Bа), Dа) и Fа) следует,
что F = <§. Таким образом, из (За) и Dа) получаем D =
— B = F = <8, откуда с помощью подстановки в Bа) сле-
следует С = 0.
Отсюда следует, что возможно только одно утвержде-
утверждение такое, что
это означает, что Алиса, Клара и Элспет лгут, а Барба-
Барбара, Деби и Фиона говорят правду. /
Упражнение 5.5.
1. Показать, что в булевой алгебре ($, *, +, ') для
х, у, ге^5 справедливы соотношепия:
а) (х + у)*(х' + у) = у;
б) {z + x)*(z' + y) = (z*y) + (z'«x);
в) ((* •!) + (?• *'))'-(*'•*) + (/• *')•
2. Доказать, что если в {3S, », +, ') выполняются со-
соотношения x»y = x*zmx + y = x + z, ¦roy = z.
3. Из схем, изображенных на рис. 5.19 и 5.20, полу-
получить «простые» схемы, эквивалентные исходным.
190
4. Получить алгебраическое представление схемы, изо-
изображенной на рис. 5.21, и дать табличное представление
выходов х и у в зависимости от значений а и Ъ на входе.
Использовать две такие схемы для построения схемы,
соответствующей функции, определяемой табл. 5.8. Свя-
Связать это с арифметикой из § 3 гл. 4.
5. Построить схему, реализующую операцию не и, ко-
которая имеет четыре входа и выдает на выходе 1 тогда в
I
& х
&
Рис. 5.21
только тогда, когда все входы равны 0.
6. Пусть выполнены указанные здесь условия:
а) все гонщики импульсивны;
б) все хорошие программисты меланхоличны;
в) никто не может быть и импульсивным и меланхо-
меланхоличным;
г) читатель меланхоличен.
Таблица 5.8
р
0
0
0
0
Входы
Q
0
0
1
1
н
0
1
0
1
Выходы
S
0
0
0
1
г
0
1
1
0
р
1
1
1
1
Входы
Q
0
0
1
1
R
0
1
0
1
Выходы
8
0
1
1
1
Г
1
0
0
1
Является ли читатель хорошим программистом и/или
гонщиком?
191
7. Организаторы международной конференции по
компьютерам решили, что для того, чтобы на встрече не
доминировали коммерческие интересы, будет только один
магазин, которым будут пользоваться вместе все произ-
производители компьютеров. Сами производители будут ответ-
ответственны за определение того, кто принимает участие в
представительстве. Десять компаний — пять европей-
европейских и пять американских — дали знать, что они
хотят принять участие в конференции. (Обозна-
(Обозначим эти компании через А, В, С, D, Е и F, G,
Н, I, J соответственно.) Однако из-за обязательств по
контрактам и торговой политики должны появиться раз-
различные ограничения. Европейские предписания требуют,
чтобы G и / не могли одновременно принимать участие в
конференции; аналогично не могут одновременно принять
участие F, G и Л Ограничения американских производи-
производителей исключают участие А и D, пока G не примет уча-
участия; аналогично исключаются С и D. Если Е присутст-
присутствует на конференции, то должно присутствовать и /, од-
однако если они принимают участив вдвоем, то В не может
быть там. И наконец, В и С не могут вместе принимать
участие в конференции.
Может ли быть достигнуто соглашение, по которому
по три компании из каждой группы могут собраться вме-
вместе, не нарушая условий? Если так, то кто именно примет
участие?
§ 6. Замкнутые полукольца
В завершение главы мы опишем довольно узкие, но
важные структуры, которые позволяют осуществлять опе-
операции на подмножествах бесконечных множеств. Пока у
нас нет понятий матриц и графов, мы не можем начинать
обсуждение приложений, и, следовательно, мы дадим
только аксиоматическое определение и покажем принци-
принципиальную разницу между полукольцами и похожими на
них на первый взгляд полями.
Определение. Замкнутым полукольцом называет-
называется множество 5 с двумя бинарными операциями ® и ©
такими, что
а) © ассоциативна;
б) существует единичный элемент по отношению к
©, который будем обозначать символом 0;
в) ® ассоциативна;
192
г) существует единичный элемент по отношению к®,
который будем обозначать символом 1;
д) для всех х s S
е) © коммутативна:
я ® у ¦= у © х для всех х, y&S;
ж) © идемпотентна:
х © а; = х для всех ie5;
з) ® дистрибутивна относительно ©:
« ® (у ф г; = (я ® у) ф (г ® z) для всех ж, у, г s 5,
(ж ф у) • z = (ж® г) ф (г/ ® г) для всех г,у,ге 5;
и) сумма счетного числа элементов из 5 существует и
единственна, т. е. не зависит от порядка суммирования;
к) ® дистрибутивна относительно бесконечных счет-
пых сумм, т. е.
/2 «Л ® B ьЛ = S
где
1 o-i Ф о-г Ф . • • i 2 Ъ) = Ъх ф Ь2 ф ...,
... ф (я2
>i) Ф (ai
i) Ф («2 $
ф .
ф (а8
ф (а8
ф
ф ... ф ...
Эта достаточно странная структура часто использует-
используется в алгоритмах замыкания для графов (гл. 7 и 8). Что-
Чтобы проиллюстрировать результаты, которые могут быть
получены в замкнутых полукольцах, сравним системы
(Z2, », +) и (Z2, Л» V)> гДе операции определены
табл. 5.9.
•
0
1
13
0
0
0
д.
1
0
1
Кук,
+
0
1
Г, Бей»
0
0
1
1
1
0
л
0
1
0
0
0
1
0
1
Та
V
0
1
б
Л И
0
0
1
ца
1
1
1
5.9
193
Рассмотрим определение операции замыкания. Резуль-
Результат а* применения этой операции к элементу а записы-
записываем в виде
2 в1.
i-o
а°=1,
(b(Z2, Л'V) сложением является V, а умножением Л)'
В замкнутом полукольце (Z2, Д, V) такое определение
имеет смысл и допуетимо. В частности,
(в силу аксиом ж) и п)). Однако если мы попытаемся те
же самые вычисления произвести в поле (Z2, *, +), то
получим
1* = 1° +11 +12 +... = 1 +1 +1 +...
Эту сумму можно вычислить следующим способом:
1 + 1 + 1 + 1 + 1 + 1 + ... = 0 + 0 + 0 + . .. = 0
или же
1 + 1 + 1 + 1 + 1 + 1 + 1 + ... = 1 + 0 + 0 + 0 + . .. = 1,
т. е. значение суммы пе определено. Следовательно, по-
понятие такого рода замыкания не имеет смысла, если его
применять к полю Z2 (которое запрещает аксиомы ж) и
и) полукольца).
Упражнение 5.6. Проверить, что ({0, §), П, U)
является замкнутым полукольцом.
ГЛАВА 6
МАТРИЦЫ
Наше изложение теории конечных матриц (множества
матриц) является более общим, чем принятое в большин-
большинстве книг, в которых матрицы обычно определяют как
линейные преобразования на векторных пространствах,
используя знакомство с координатной геометрией. Хотя
иногда мы будем возвращаться (§ 3) к этой интерпрета-
интерпретации, в основном будем придерживаться точки зрения, что
матрицы являются реализациями абстрактных алгебраи-
алгебраических структур в вычислительных целях. Тогда алгебра
абстрактных структур определяет способы, как надо ком-
комбинировать матрицы.
Сначала мы определим (§1) матричное представление
бинарных отношений над конечными множествами. Затем
последует более общее рассмотрение требуемых свойств
абстрактной системы для того, чтобы матричная реализа-
реализация была разумной. А в завершение, используя резуль-
результаты предыдущих исследований, будет рассмотрен важ-
важный случай векторного пространства над R.
§ 1. Матрицы и бинарные отношения
на конечных множествах
Формально матрицей над множеством 5 называется
отображение
М: N,XN,h.S, p, q eN.
Обычно образ (г, /) обозначают через Мц и изображают
всю функцию массивом элементов из 5, т. е.
~М.
и
Л/
м
м22...м2д
Говорят, что эта матрица имеет р строк и q столбцов и
имеет размер pXq. Матрица размера р X q имеет р * q
13* 1У5
элементов. Когда р = <j, матрицу называют квадратной.
Множество всех матриц р X q над 5 обозначают через
Л(р, q, S). Множество М(р, р, S) будем обозначать че-
через Ж(р, S).
Рассмотрим бинарное отношение р между множества-
множествами А и В, где
А •» {аи 02, ..., а,), В =» {bi, 62, ,.., Ь,},
т. е. \A\-p, |Я1-?.
Упорядочение элементов в этих множествах выбрано
произвольно, однако, однажды выбранное, оно далее оста-
остается фиксированным. Пусть это отношение р определено
посредством выбора пар (а, Ь), где as Л, Ь&В.
Рассмотрим матрицу М над {0, 1), т. е. М: N, XN, ->
-*¦ {0, 1), и свяжем элементы М с отношением р биекцией
ф: 0>(АХВ)-+Л(р, q, Z2)
(ф отображает произвольное отношение между А и В в
матрицу р X g над {0, 1}) ;
причем
, если (аи
, если (аи
В случае, когда полезно подчеркнуть, что матрица М бы-
была получена из отношения р, мы будем обозначать ее че-
через М(р).
Пример 1.1. Возьмем случай |Л|=4, |В|=3 и
р = {(аь Ъ2), (аи Ьз), (а2, bi), (o3, bi), (а4, Ь2)У.
Тогда соответствующая матрица М имеет вид
~0
i
1
_0
1
0
0
1
1"
0
0
0_
Таким образом, мы имеем способ табулирования или
кодирования отношения и можем закодировать отношение
посредством ф или декодировать посредством ф. Этот
процесс является отображением (i, ]) в АХ В или М со-
соответственно. Такое представление более удобно, чем тео-
теоретико-множественный способ определения отношений,
поскольку с ним можно обращаться формальным образом.
Оно становится даже более пригодным для вычислений,
196
если наложить некоторую структуру на множество, из
которого получается матрица. Возьмем опять {0, 1} и
определим на этом множестве логическое сложение (или)
и умножение (и). Тогда, если М и N—матрицы pXq,
соответствующие отношениям р и о, то матрица Q, пред-
представляющая отношение т, где
т = {(а, b): {a, J)ep или (а, 6)ео),
определяется следующим образом Q,1 — (M1j или iV4)=»
¦=МЧ + Л^ (логическое сложение). Следовательно, имеет
смысл называть Q суммой матриц М и N и писать
подразумевая, что Q, М и N имеют один и тот же размер
и Q вычисляется по правилу покомпонентного сложения
Это — пример использования коммутативной диаграммы,
изображенной на рис. 6.1, где производится операция на
одном множестве с использо-
использованием операции на другом
множестве посредством под-
подходящего отображения <р.
С этой диаграммой обычно
связывается тождество
<p
(л/jv)
м+и
Рис. 6.1
С помощью этого тождества
можно дать более точное определение сложения матриц:
Пример 1.1 (продолжение). Пусть А и В те же,
что и раньше, и пусть
), (au b2), (a2, bt), (а3, Ь2)).
Тогда
-1
1
0
_0
1
0
1
0
(П
0
0
0_
Дальше будет видпо, что
, @1, b3), (a2, bi),
(аз, bi), (аз, b2), (a4f b2))
197
-1
1
1
0
1
0
1
1
1~
0
0
0
п, что эквивалентно,
Более того, если мы возьмем множество С = {с\, сг, сз,
с4, С5> и рассмотрим отображение я между В ж С, опре-
определенное следующим образом:
л = {(Ьь с\), {Ьи съ), (Ъ2, с2), (Ь3, с4), (Ьз, с5)},
то оно может быть представлено в виде матрицы Р, где
I 1 0 0 0 1"|
р= о 1 о о о ,
[.о о о 1 ij
Очевидно, что отношение я ¦> р между А и С корректно
определено и, следовательно, будет соответствовать мат-
матрице 4X5. Обозначим эту матрицу через S. Как ее можно
вычислить? Для этого надо вычислить 5У для всех i, /,
где 1 < I ^ 4, 1 < / < 5. В силу биекции 5« = 1 тогда и
только тогда, когда (а(, с3)ея«р. Однако это так, если
только существует некоторое Ь&В такое, что (а(, Ь)ер
и (Ь, с,)ел, т. е.
(ait Cj) е я »р э (а(, &!) е р и (Ь,, cj) s я
или (а(, 6г)ер и (Ь2, с^)еп,
или (а(, Ь3)^р и (Ь3, Cj)sn;
или же, что эквивалентно,
з
5ц = Мг1 * Ри + Mi2 * P2j + Mi3 * Psi - 2 M« * Ли-
ft=i
Матрица 5, вычисленная по такому правилу, называется
произведением М и Р и обозначается через Л/ * Р или
просто МР.
Рассмотрим опять естественное (коммутативное) отно-
отношение между двумя рассматриваемыми операторами
(рис. 6.2). Тогда
Замечание. Изменение порядка q> зависят от спо-
способа определения матрицы отношения; если (вместо
этого) мы определим матрицу отношения следующим
образом:
My = 1 тогда и только тогда, когда (ah b<) s p,
то изменения порядка не будет. Хотя о математической
точки зрения было бы бо-
более желательно иметь
один и тот же порядок,
это нарушило бы сложив-
сложившуюся практику. Соответ-
Соответствующие диаграммы в § 3
не меняют порядок, одна- Ш,Р) = >~М*Р
ко эти соглашения естест-
естественны для вопросов, изу-
изучаемых в этом параграфе.
Пример 1.1 (продолжение). Выполним вычисления,
соответствующие определенным выше отношениям. По-
Получаем
МР
Если матрицы Л/ и N имеют одинаковый размер, то их
сумма существует и определяется формулой
*
Рис. 6.2
-о
1
1
0
1
0
0
1
1
0
0
0
р
о
о
0
0
1
1
0
0
0
0
0
0
0
0
1
1~
0
0
1
~0
1
1
0
1
0
0
1
0
0
0
0
1
0
0
0
1
1
1
0
а если матрицы Р и М согласованы (М имеет размерность
pXq, a P — размерность q X г), то умножение матрицы
М на Р возможно и определяется следующим образом:
•*«•
Хотя матрицы рассматриваются над (Z2, Д, V), мы
используем символы • и + для того, чтобы иметь возмож-
возможность обобщения введенных выше операций (см. § 2).
С этого момента обозначения Д и V будут использовать-
использоваться лишь в тех случаях, когда общие операции им неадек-
неадекватны.
В заключительной части этого параграфа ограничимся
рассмотрением матриц, представляемых отношениями на
конечном множестве А, где \А\=п. Тогда все матрицы
согласованы и их сумма и произведение всегда опре-
определены.
Из покомпонентного определения сложения сразу сле-
следует, что сложение матриц коммутативно и существует
нулевая (п X п)-матрица 0: 0(j = 0 для всех i, }; Kl,
] < гг. С другой стороны, умножение матриц, вообще го-
говоря, некоммутативно, однако существует единица, кото-
которая называется единичной (пХп)-штрщей и определя-
определяется следующим образом: /: /«=1, если t = ), п /« = 0,
если i ?= j. Так, если X — матрица га X га и Y ¦= XI, то
j
Так как все 7PJ = 0, за исключением случая р «= /, то п
сумме все члены, исключая те, где p = j, равны нулю.
Кроме того, 1ц= 1. Поэтому
У«-Хв, т. е. У = Х.
Следовательно, Х = Х1. Аналогично 1Х~=Х; поэтому
IX = X =» Z/. //
К сожалению, обратная по умножению матрица может
не существовать; однако если она существует, то она
единственна. Если матрица имеет обратную, то она на-
называется обратимой.
Пример 1.2. Не существует матрицы X такой, что
Доказательство. Вычисление произведения дает
Г Л V Т
О X,
Следовательно, какие бы значения компонент матрицы X
не рассматривались, элемент A, \) произведения никогда
не будет равен 1, откуда и следует требуемый ре-
вультат. /
Таким образом, множество квадратных матриц задан-
заданного размера с определенными на нем операциями умно-
умножения и сложения образует кольцо.
Используя далее связь между бинарными отношения-
отношениями на множестве и матрицами над (Z2, Д, \J), дадим
следующие определения.
Транспонированной матрицей М называется матрица
Л/г такая, что
(поэтому, если Л/ получена из отношения а, то Мт может
быть получена из отношения о); транзитивное замыка~
200
ние М* и рефлексивное замыкание М* (изоморфны со-
соответственно о+ и о*) определяются следующим образом:
Л/+ - S Мп, М* ш, S Л/п,
П=1 П=0
где Л/° = 7, Л/'=Л/ и ЛГ+| = АШ" (nsN). (В некоторых
случаях эти замыкашш нельзя определить корректно
(чтобы соответствующие ряды сходились), однако над
(Za, Д, V) определение корректно, поскольку это —
замкнутое полукольцо.)
В заключение заметим, что матрицы могут быть ча-
частично упорядочены путем поэлементного сравнения, а
пменно
М <lN тогда и только тогда, когда Мц «S Nti для всех i, /.
Из данного определения следует, что
M*S.N тогда и только тогда, когда М + N «= N,
при условии что + является операцией «максимум*, по-
подобной или.
Упражнение 6.1.
1. Пусть А — копечиое множество и \А\=п, а М —
матрица над Gj2, Д, \/), соответствующая некоторому
бинарному отношению на А. Доказать, что
(Следствием этого является тот факт, что вместо полу-
полукольца (Z2, Д, V) мы можем рассматривать булеву ал-
алгебру (В, Д,\Л~0> где В = {0, 1}. Поэтому ыы часто
будем обозначать множество матриц пХп через JC{n, В)
и называть их булевыми матрицами.)
2. Доказать, что если М — конечная квадратная мат-
матрица над (Z2, Д, V)' то
Указание: см. вадачу 1.
3. Показать, что если матрица М над (Z2, Д, V)
такая, что KlM, to Mn^Mn+i для любого nsN. В ка-
качестве следствия доказать, что если М имеет размер гаХ
и р> тп, то
для некоторого q такого, что 2я > т.
4. Показать, что если существует обратная к М мат-
матрица М~1 (т. е. М~1М — ЫМ~Х = /), то она единственна.
201
Доказать также, что еслп N обратима п согласовала с
М, то
5. Доказать, что если А, В и С — согласованные мат-
матрицы такие, что
то отсюда не следует равенство В — С. II
§ 2. Матрицы над другими алгебраическими
структурами
Мы уделяем много внимания матрицам над полуколь-
полукольцами (Z2, Д, V) п (Bi Л» V» 1i) однако ничего не
сказали о матрицах, чьи элементы принадлежат другим
структурам. Сначала мы рассмотрим вопрос о том, что
надо требовать от структуры E, *, +) для того, чтобы
матрицы над 5 обладали нужными свойствами. Затем об-
обсудим технику вычислений, применяемую в ситуациях,
когда операция замыкания корректно определена.
2.1. Обобщенные матрицы. Пусть {Л, ®, ф) обозна-
обозначает множество Ж(п, E, *, +)) матриц пХп над
E, *, +) с операциями ® и ©, определенными в тер-
терминах ¦ и +. Можно легко определить матрицы над про-
произвольным непустым множеством, однако индуцирован-
индуцированные при этом операции над матрицами могут быть не-
некорректными и обладать неестественными свойствами.
Рассмотрим вначале операцию сложения.
Если М и N — согласованные матрицы над 5, тогда по
определению
Для получения © использовалась только одна операция
сложения +. Поэтому сложение матриц выполняется про-
просто. Однако для того, чтобы операция © была коммута-
коммутативна и ассоциативна, теми же самыми свойствами долж-
должно обладать (S, +). Отсюда следует, что нулевая матри-
матрица Ж существует тогда и только тогда, когда существует
двусторонняя*) единица 0 по отношению к + в S. Ана-
Аналогично существование аддитивных обратных элементов
в Ж зависит от существования аддитивных обратных эле-
элементов в 5. Поэтому сложение © на Ж всегда может быть
*} Левая и вравая,— Примеч. ред.
202
определено. Причем, хотя для того, чтобы (Ж, ©) стало
коммутативной группой, требуется вьшолнешю многих
свойств на E, +), многое можно получить даже тогда,
когда операция + не обладает достаточным набором хо-
хороших свойств.
В противоположность этому умножение в Ж требует
гораздо большего от S. По аналогии с матрицами над (Z2,
Д, V) положим
Поскольку суммирование проводится в 5, то для коррект-
корректного определения умножения в Ж необходимо, чтобы ре-
результат не зависел от порядка суммирования. Это будет
выполнено, если сложение в 5 ассоциативно.
Не следует ожидать, что умножение в Ж будет комму-
коммутативно; даже (так как (Ж, ®), вавпепт от (S, *) ц
E, +)) для того, чтобы обеспечить ассоциативность в
(Ж, ®), требуется больше, чем ассоциативность в E, *).
Рассмотрим следующий пример, в котором будут выполне-
выполнены левая и правая дистрибутивность ¦ над +, ассоциа-
ассоциативность в (S, •) и ассоциативность и коммутативность
в E,+).
Пример 2.1. Пусть М, N и Р — матрицы размерно-
размерности 1X2, 2ХЗпЗХ1 соответственно. Тогда
(
+ РЛ, * Ni2)) * P21 + ((.l/n * Nia) + (M12 * Nta)) * P81 =
- ((Л/п * Nn) * Pn) + ((.1/la * Nal) * Pn) +
+ ((Mn*N12)*P21)+ ((Mi2*N22)*P21) + ((Mn*Nls)*P31) +
(Л/1а * (iV2, • Р81))=(Л/11 * (-'Vu * Pu
+
2 /3 \
203
При проведении выкладок предполагалось, что 4- ассоциа-
ассоциативна, поэтому некоторые скобки были опущены. /
Пока все это выглядит не очень оптимистично, по-
поскольку лишь небольшое число структур может удовлет-
удовлетворять условиям, накладываемым на E, *, +). Заметим
также, что для существования единичной матрицы тре-
требуется, чтобы:
а) 0*х = 0 = а:»0 для всех x&S, где 0 —аддитив-
—аддитивная единица в S (напомним, что это условие не являет-
является аксиомой поля);
б) 5 должно иметь двустороннюю мультипликативную
единицу.
Тем не менее можно проверить, что если E, », +) —
кольцо или поле, тогда все вышеуказанпые условия вы-
выполнены и {Л, ®, ф)— кольцо.
Понятия упорядочения и замыкания матриц над бо-
более узкими структурами, такими как упорядоченные поля
и т. п., становятся слишком сложными п поэтому обсуж-
обсуждаться не будут.
Как уже отмечалось в упражнении 6.1, мы можем рас-
рассматривать Ж{п,(Z2, Д, V)) как Jt(n, В). Аналогично
мы можем обобщить вычисления на другие родственные
алгебраические структуры, однако требуется тщатель-
тщательность, чтобы сформулировать условия на то, какую си-
систему использовать. Например, из Z2 ^ Z3 путем обычного
включепия Z2 c:_> Z3(A с». В обозначает тождественное
отображение на А, где 4еВ) следует, что
А е J((n, Z2)=*-4e J({n, Z3).
Пусть теперь дана матрица из 0 и 1. Спрашивается, оп-
пределена она па {0, 1} или же на {0, 1, 2)? Это необхо-
необходимо знать для перехода к построению арифметики. Ко-
Конечно (как будет показано в § 3), все это вависит от то-
того, что мы пытаемся вычислять. Аналогичные проблемы
возникают с любыми включениями, особенно Ж(га, В),
Ж(п, Z2), Jt(n, Z), Jt{n, Zm), J((n, Q) и Ж(п, R).
2.2. Алгоритм Уоршолла. В этом разделе мы опишем
быстрый способ вычисления (транзитивного или рефлек-
рефлексивного) замыкания квадратных матриц пад (Z2, f\,\J).
Этот способ — один из вариантов метода Уоршолла; пред-
ставпм его в виде программы. Если М — матрица размер-
размерности га X п над (Z2, Д, V)> то ее можно преобразовать
в Л/+ следующим образом:
for / from I to га do
for i from 1 to ra do
204
if i + / and Mv =- 1 then
foi к from 1 to n do
л/л *- л/ft v л/,».
Чтобы вычислить Л/*, мы можем прибавить / пли в нача-
начале, или в конце, используя соотношение
Л/*
Пример 2.2. Пусть
тогда, используя
элементах:
~0
0
0
0
_0
алгоритм,
1
0
1
0
0
1
0
0
0
1
0
1
0
0
1
(Г
1
0
0
0_
заменим 0
на 1 d следующих
A, 4), A, 5), C, 4), C, 5), E, 2), E, 5), B, 2,), B, 3),
C,3).
Получим матрицу
М+= 0 1 1 1 1 . /
0
0
0
0
0
1
1
1
0
1
1
1
1
0
1
1
1
1
0
1
1
1
1
0
1
Мы не будем доказывать, что программа выполняет
нужные действия, однако отметим, что смысл программы
состоит в том, что если i?*j и Л/о = 1, то (i, j) s<jp для
некоторого р «? п, где о — отношение, порожденное М. По-
Поэтому заменим i-ю строку на дизъюнкцию i-й и /-й строк,
чтобы указать, что все, что относится к /, также относит-
относится и к t.
Очевидно, что при i •= j выполнение этого шага не да-
дает никакого выигрыша. Основная сложность проверки пра-
правильности программы — убедиться в том, что ничего не
пропущено. Читатель сможет доказать это самостоятель-
самостоятельно, прочитав гл. 7.
Метод Уоршолла дает значительный выигрыш по срав-
сравнению с прямым пспользованием определения замыкания;
он может быть еще улучшен, однако это требует исполь-
использования более сложных структур данных, и поэтому мы
не будем больше этим заниматься.
Этот метод можно многими путями приспособить для
получения различных оценок, сязанных с матрицами (от-
(отношениями), простейшим из которых является понятие
205
«расстояния» между элементами множества, связанными
отношением о. Расстояние между двумя точками хну
(d(:i, у)) равно наименьшему га такому, что neN и у е
е= о"(х). Если М — матрица, соответствующая о, то, заме-
заменяя циклы следующим образом, получим требуемый ре-
результат:
if Мц Ф 0 «hen
for к from I to га do
if MJk Ф 0 and
(Мл = 0 or Mih > Mu + A/№)
then Mik *- Мц + Mjh-
Здесь используется арифметика над Z (а не над Z2).
Пример 2.3. Применение описанпой выше процеду-
процедуры к матрице пз предыдущего примера дает
0
0
0
0
0
1
3
1
0
2
1
2
3
0
1
2
1
2
0
1
2
1
2
0
3
Упражнение 6.2.
1. Определение. Говорят, что две (пХп)-матри-
(пХп)-матрицы X и Y над полем F подобны над F, если существует
обратимая матрица Р над F такая, что
Показать, что отношение, пндуцируемое подобием на
Л(п, F), является отношением эквивалентности и что
матрица / подобна только себе.
2. Показать, что если A, B<=J[(n, F) для некоторого
beN и некоторого поля F, тогда
(А + В)т •= Ат + Вт, (АВ)Т = ВТАТ.
3. Определение. Стохастической матрицей называ-
называется действительная матрица над ({х: 0 < х ^ II, *, +)
такая, что сумма элементов в каждой строке равна 1. /
Показать, что множество 3X3 стохастических матриц
не замкпуто по отношению к сложению, но замкнуто по
отношению к умножению. Установить, какпе свойства
поля (R) при этом использовались.
§ 3. Матрицы и векторные пространства
Результаты § 2 показывают, как можно применять
матрицы для проверки выполнения отношений между ко-
конечными множествами соответствующих размеров. Цель
206
этого параграфа — показать, как использовать матрицы
над полем (И, *, +) (далее просто, 11) дли того, чюГил
выполнять некоторые преобразования, в част пост линей-
линейные преобразования в векторном пространство V над 11.
В замечании из § 4 гл. 5 было установлено, что если Ге
eEnd(l7) — множество линейных преобразовании V, то
{{х, Тх): х е Т) s V X V
является бинарным отношением над V. Мы ищем резуль-
результат применения линейного преобразования на V в
Л(п, R), где n = dim(V).
Возможны два обобщения. Первое — рассмотрение
произвольных полей, второе — линейные преобразования
между векторными пространствами произвольных размер-
размерностей, которые могут быть определены аналогичным об-
образом в Л (п, m, R). Так как эти обобщения нам не по-
потребуются, то в дальнейшем рассматривать их не будем.
3.1. Матричные представления линейных преобразова-
преобразований. Операции сложения и умножения матриц в Л (п, Г»)
неявно были определены в § 2. Если A ^ Л (п, R) имеет
элемепты Ац п^е R, определим ХА е Л (га, R) как мат-
матрицу с элементами ХАц. Эту оиерацню называют умноже-
умножением матрицы на скаляр. Поскольку Jl{n, R) играет
центральную роль в оставшейся части этой главы, то по-
полезно перечислить все его свойства относительно опреде-
определенных выше операций. Единичную матрицу в Jl(n, U)
будем обозначать через / при всех п е N.
Предложение. Jl{n, R) является линейной алгеб-
алгеброй. II
Мы не даем доказательства этого факта. Рекомендуем
вначале проверить выполнение аксиом линейной алгебры
для Л B, R), после чего будет видно, как можно постро-
построить доказательство в общем случае. Надо показать, что:
а) Л(п, R) является векторным пространством;
б) Л(п, R) — кольцо;
в) умножение матрицы на скаляр обладает следую-
следующим свойством:
Х(АВ) = {ХА)В=АA.В) для всех UR, А, В^Л(п, R).
Полезно иметь специальное обозначение для подмно-
подмножества обратимых матриц из Л(п, R). Обозначим это
подмножество через
GL(n, R) = {А е!(л, R): А~х существует).
Каждое GL(n, R), ceN, определяет группу по умн^же-
207
нию. Эти группы называют полными линейными груп-
группами.
Пусть V — векторное пространство размерности п над
R и T^End(V). Если В={еь ..., еЛ — базис в V, то
очевидно, что Tet e V для всех i, 1 < i < га. Следователь-
Следовательно, должны существовать tti e= R A < i, ] ^ п) такие, что
Пусть
Ат-
матрица
Ат
fi-e, + h
вида
=
""'и
'21
J»i
i,fi2 + .
'«-
'„...
'па •«•
(in"
t
тогда ее называют матрицей преобразования Т в бази-
базисе В. Для данного В матрица Ат единственна; таким об-
образом, мы можем определить отображение
Фв: End(F) -+J[(n, R)
следующим образом:
Так как Ат можно вычислить, то ее можно использовать
для нахождения Т.
Предложение. Пусть Т s End(V) соответствует
матрица Ат в базисе #=-{ei, ..., еп}. Тогда, если X&V —
вектор
2
{-1
то
где
Доказательство. Пусть х =
Тогда
( S *^j
Z03
Следовательно, в данном базпсе линейное преобразование
Т можно выполнить с помощью произведения АТА, где Ат
имеет размерность п X п, а Л — вектор (матрица размер-
размерности п X 1)
Ш
соответствующий х е V. На самом деле можно устано-
установить гораздо больше. Ниже мы установим важные свойст-
свойства фв.
Предложение. Отображение <pB: End (V) -*¦
-*¦ J{(n, R) является изоморфизмом линейной алгебры с
обычными операциями в End(V) и Jl{n, R) на R, при-
причем сужение фв на группу Aut(F) EEnd(I/) является
группой изоморфизмов на GL(n, R).
Доказательство. Отметим основные моменты.
Чтобы избежать большого количества индексов, ограни-
ограничимся случаем п = 2. В общем случае доказательство ана-
аналогично. Изоморфизм линейной алгебры следует пз сле-
следующих утверждений:
а) фв биективно;
б) фв(М=/;
в) фвEГ) = фвE)фв(Г) для всех S, Te End(F);
г) фв(Л5 + цГ) = Яфв(^)+Цфв(Г) для всех S, Г е
eEnd(F) и К, ц е R.
Докажем некоторые пз этих утверждений; остальные
оставим в качестве упражнений. Пусть (ei, ег) — ба-
базис в V.
а) Чтобы доказать, что фв инъективно, необходимо
показать, что
фвE) = фв(Г)=^5 = Г.
Если
Sei = Slid + S2ie2, Tei = tne{ + t2ie2,
то
Поэтому Sei — fei. Аналогично 5e2 = Te2. Следовательно,
5 и Т совпадают на базисных элементах ci и ег. Однако
для всех хе F выполняется соотношение
х = Aei + ие2;
И Д. Кук, Г. Бейз 2°9
такпм образом,
Sx = }.Scx + ц5с2 = XTei + u7e2 = 2'(?.ci + цс2) = Гх,
т. e. 5 = Г.
Доказательство сюръективиостн оставляем в качестве
упражнения.
б) /vx = х для всех х е F; следовательно,
= в! + 0е2, /ve2 = 0ех + е2,
в) Пусть
1 22
тогда
+ s2ie2) +12\ (si2ei + s22e2)
Аналогично
?22822H2.
Следовательно,
что и требовалось доказать.
г) Утверждение доказывается аналогично утвержде-
утверждению в).
Чтобы показать, что сужение фв на Aut(F) является
группой изоморфизмов, используем свойства б)—г).
Пусть Т е Aut(F); тогда
следовательно,
Т е Aut (F) -*> фа (Т) е GL (n, R),
Этот результат цграет существенную роль, так как
имеет много важных следствий. Выведем некоторые из
них. В фиксированном базисе отображение Т -*¦ Ат из
End(F) в J((ji, R) биективно (каждому преобразованию
210
соответствует единственная матрица п наоборот). Далее
Ав«т = АВАТ;
это эквивалентно тому, что диаграмма па рис. б.З комму-
татпвпа. На практике это просто означает, что матрица
произведения преобразова- е
ннй 5 • Т в End (V) может {s т ' *" S°T
быть вычислена путем ум-
умножения матрицы As на
матрицу Ат- Нет необходи-
необходимости явпо определять
& ° Т, а затем вычислять
Ав°т на основе определе- рпс_ 6.3
ния. Аналогичные резуль-
результаты получаются и для S + Т. Кроме того, для сужения
Фв на обратимые преобразования Aut(F) получаем
это означает, что для вычисления ^4r_i неооходпмо лишь
найти матрицу, обратную к Ат.
Подчеркнем еще раз, что изоморфизм срв зависит от
базпса; в другом базисе мы будем иметь другой изомор-
изоморфизм между End(F) и Ж(п, R). Таким образом, элемент
Jt(ji, R) может рассматриваться как представление эле-
элемента End(F) в фикспрованном базисе или как представ-
представление различных элементов End(F) в различных бази-
базисах. В гл. 10, где результаты этого параграфа будут при-
применяться к R" (га = 2, 3, 4), отображение <рв будет рас-
рассматриваться в стандартном базисе {ei, ..., е„}, как это
определялось в § 4 гл. 5. Для этого базиса, если х =¦
= (*,, ...,i,)sR",to
х =
-*[::]¦
Пусть отображение Т^End(V) имеет собственный век-
вектор х s V, соответствующий собственному значению
о s R. Тогда, если в базисе В = {ei, .,., ej простран-
пространства V вектор х имеет вид
п
ТО
Ат
14* 211
Поэтому координатные вектора в представлении х явля-
являются собственными векторами Ат, соответствующими то-
тому же самому собственному значению.
3.2. Некоторые другие понятия теории матриц. Опре-
Определим теперь на J{(n, R) отображение, называемое де-
термилантом (определителем):
del: J[(?i, R)-+ R.
Было бы естественным ввести это понятие и исследовать
его свойства в § 4 гл. 5, так как det не вависит от базиса.
Это означает, что если ATeJ((n, R) и Aji^J[(n, R) —
матрицы отображения T&End(V) в базисах В ж В' со-
соответственно, то det Ат = det Aft. Однако, чтобы опре-
определить det на End(F), мы должны были бы ввести поня-
понятия из тензорной алгебры. Вместо этого дадим хорошо
известное определение det на Jt(n, R) и установим не-
некоторые пз наиболее важных его свойств.
Определение det будем давать при помощи рекурсии.
Вначале определим det для случая JtA, R). Пусть
!1 °2S
тогда
det Л = ап<722 —
Если 4е1(п, R) имеет элементы оч (\<i, /*?n), то
минором элемента ak! называется матрица А{к-1) е
^Л(п— 1, R), полученная из А путем вычеркивания
к-6 строки п 1-то столбца. Теперь det: Jt(n, R)-* R мож-
можно определить рекурсивно для всех га е N как
det 4 = 2 (-l)'+ifl1ideti4(ll°.
Иногда эту формулу называют разложением по первой
строке. Можно показать, что если использовать любую
другую строку пли столбец для формирования соответ-
соответствующего выражения, то сумма будет равна det Л.
Другими словами,
2 (-1)г+гап det Л(г'°, 1
r=l
Для малых значений п каждая из этпх формул подходит
212
для непосредственного вычисления del А. Чтобы миними-
минимизировать число операций разложения, следует начинать
со строки или столбца, содержащих наибольшее количе-
количество нулей. Подчеркнем, однако, что эти разложения яв-
являются в общем случае не подходящими для вычисле-
вычисления и существуют более эффективные вычислительные
процедуры для нахождения det. Некоторые важные свой-
свойства det приведены ниже.
Предложение. Отображение det: Л(п, R)-»-R
удовлетворяет следующим условиям:
а) det / = 1;
б) det А = det Ат для всех А е Ж (п, R);
в) det Я .4 =?indet4, XeR, А еЦп, R);
г) det Л J5 = det Л det J5;
д) A^GL(n, R) тогда и только тогда, когда detАФ
4*0. //
Мы не будем давать доказательства этих утверждений.
Предлагаем читателю проверить их для JC{2, R). Заме-
Заметим также, что свойство д) характеризует GL(n, R).
Удобно выделить некоторые матрицы с «особыми»
свойствами, которые будут использоваться в дальнейшем.
Если islfrt, R) и А—Ат, то говорят, что А симмет-
симметрична; если А — — Ат, то матрица А кососимметрична.
Если
ААТ = АТА=*1 (т. е. Л-' = ЛГ),
тогда говорят, что А ортогональна. Множество всех ор-
ортогональных матриц Jf(n, R) обозначается через О(п).
Через SO(n) обозначим подмножество О(п), состоя-
состоящее из матриц с единичным детерминантом. Элементы
SO(n) называют специальными ортогональными матри-
матрицами.
Предложе п и е.
а) О(п) является подгруппой GL(n, R);
б) SO(n) является подгруппой О(п).
Доказательство.
в) Надо показать, что О(п) замкнуто по умножению
и для каждой ЛеО(п) существует обратная матрица
Л-'еО(п). Если А, Ве*О{п), то ЛАТ = ЛТА=1 и ВВТ =
= ВТВ = I; следовательно,
{АВ) (АВ)Т = АВ{ВТАТ) = А (ВВТ)АТ = ААТ - /.
213
Аналогично (АВ)ТАВ = Т, и, следовательно, АВ^О(п).
Если Ае=О(п), то
(A~1)(A-i)T'=AT(AT)T-=ATA=I.
Следовательно, Л *=О(п).
б) Доказательство в этом случае осуществляется noj
добным образом и оставляется в качестве упражнения. II
Завершим этот параграф кратким обсуждением функ-
функций от матриц. Подобно del, это следовало бы рас-
рассматривать в § 4 гл. 5. Однако у нас нет аппарата для
рассмотрения сумм с бесконечным числом слагаемых
в End (У). Результаты в Jf(n, R), приведенные ниже, до-
достаточны для наших целей.
Пусть A f=Jf(n, R), тогда матрица A2^JC{n, R)—ато
по определению матрица АА. Аналогично можно опреде-
определить Ак для всех fteN, к > 2; положим А0 = /. Следова-
Следовательно, если
р: R-*R
есть полиномиальная функция
р{х) = 2 а&1> гДе aie R и neN,
1=0
то определим p(A)^Jf(n, R) как
Р(А)= 2 м1.
1=0
Такая матрица существует, поскольку Jt(n, R) —век-
—векторное пространство. Эту идею можно обобщить. Если
/: R -*• R разлагается в сходящийся ряд
/(J
1=0
оо
то имеем смысл выражение 2 а •^'. Множество Jt(n, R)
i=0
2 2
может быть идентифицировано с R" . На Rn можно
определить норму, как указано в § 4 гл. 5. Тогда это пн-
дуцирует норму на Jt{n, R), и в этом случае бесконеч-
бесконечные суммы имеют смысл. В частности, если A^Jt(n, R),
то можно показать, что
Jim fil
всегда существует в Л{п, R) и записывается как ехрЛ
214
или же еЛ. Когда п= 1, ехр является обычной экспопеп-
циалышй функцией, однако при л > 1 функция ехр ведет
себя совершенно иным образом (см. упражнение 6.3).
Упражнение 6.3.
1. Доказать, что Ж{2, R) с обычными операциями яв-
является линейной алгеброй.
2. 1) Определить матрицы линейных преобразований
Т У _ 2х+ У'-х У ' И
пространства R2 в
а) стандартном базпее R2;
б) базпее В'={A,0), A, 1)}.
2) Вычислить координаты вектора а = (—1, 7) в бази-
базисе В' и определить вектор Т{Т2я, используя матричное
представление.
3) С помощью понятия детерминанта определить, ка-
какие из преобразований (*) обратимы. Является ли про-
произведение Т\Тг обратимым?
3. Пусть
Г1 21 ГсозЭ —sin 8"] Г 0 2]
[2 4j' [sin 8 cosej' C = [—2 0J1
Определить, является лп каждая из этих матриц сим-
симметричной, кососимметрпчной, ортогональной, обратимой.
4. Показать, что у кососпмметрпчной матрицы элемеи-
ты, стоящие на диагонали, равны нулю.
5. 1) Доказать, что собственные значения симметрич-
симметричной B X 2)-матрицы всегда действительны.
2) Доказать, что собственные числа ненулевой косо-
кососимметрпчной BХ 2)-матрицы не являются действи-
действительными.
6. Пусть А^Ж(п, R). Доказать, что
(Ла) Ь = а • {АТЪ) для всех a, be Rnf
и использовать этот факт для доказательства того, что ес-
если А симметрична, то собственные вектора, соответствую-
соответствующие различным собственным значениям, ортогональны,
7. 1) Пусть
Г 1 21
L-i 3j
d p(x) = x2 — ix + 5. Доказать, что p(A) — Q.
215
2) Использовать (**) для вычисления обратной мат-<
рицы А~1.
8. 1) Пусть
Используя индукцию, доказать, что
Г1 а~\* Г1 па
[о \\ "[о i
для всех nsN, т. е. показать, что еА = еЛ, п выписать
выражение для det еА.
2) Пусть
ГО —
A[
и X е R. Определить матрицу eVA.
9. 1) Пусть А, В^Л(п, R). Какпе должны быть вы-
выполнены условия, чтобы выполнялось соотношение
2) Использовать предыдущую формулу для доказа-
доказательства того, что ел всегда имеет обратную.
10. Пусть A^JC(n, R). След матрицы А (обознача-*
ется \хА) определяется по формуле
п
ixA= 2 Ли,
Если A^Jf(n, R) — матрица с элементами
при i = /,
при 1Фь
то, используя индукцию, показать, что
71
det А «= JJ к{ = Х]^.2 ... Х„,
т. е. доказать, что в данном случае
11. Пусть А&Л(п, R) имеет собственный вектор
хе R", соответствующий собственному значению leR.
Доказать, что х является собственным вектором еА, со-
соответствующим собственному значению е\
12. 1) Доказать, что если Ae=GL(n, R), то det Л =•
dMI
)
2) Доказать, что если А е(9(«), то det А = ± 1.
13. Доказать, что 50B) является подгруппой 0B).
ГЛАВА 7
ТЕОРИЯ ГРАФОВ
§ 1. Вводные понятия
Многие отношения на конечных множествах могут
быть изображены в виде рисунков (см. § 3 гл. 2), с кото-
которыми можно работать при помощи соответствующих мат-
матриц. Перед тем как определить конструкции этих рисун-
рисунков, необходимо быть уверенными в том, что это не по-
повлечет 8а собой никаких двусмысленностей. Введем не-
необходимые понятия.
Пусть V — конечное множество и
/у-{(у, у): deF),
Положим
T'L = F2\/V = {K, у,): v^vj
и определим на VL отношение эквивалентности следую-
следующим образом:
(уь v2)~(wu u>2), если (У1, v2) = (wu и>2)
ИЛИ (Vi, Va)*=(W2, W\).
Важное свойство отношения ~ сформулировано в сле-
следующем предложении.
Предложение. Отношение ~ является отношени-
отношением эквивалентности на FL. II
Доказательство оставляем в качестве упражнения.
Множество эквивалентных классов, определенное та-
таким образом, обозначим через У1/~. Каждый класс эквп-
валентпостп содержит ровно два элемента, так как если
(vvv2)eaVL, то [(vu v2)] = {(vu v2), (v2, v\)). Здесь
[(v\, v2)}—класс эквивалентности, содержащий (i>i, v2).
Сейчас мы в состоянии дать строгое определение графа.
Определение. Графом G называется пара G =¦
¦=(F, E), где V — непустое конечное множество вершин,
а Е — подмножество FL/~. Щ
217
Другими словами, можно сказать, что граф G есть па-
пара G = (F, Е), где V — непустое конечное множество вер-
вершин, а Е — множество неупорядоченных пар различных
вершин.
Множество Е называют множеством ребер графа, \V\
обозначает число вершин G, \Е\ — число ребер G.
Следующий результат выражает связь между графа-
графами и классами отношений на конечных множествах.
Предложение.
а) Граф G = (F, E) определяет нерефлексивное сим-
симметричное отношение на V.
б) Нерефлексивное симметричное отношение на ко-
конечном множестве V определяет граф.
Доказательство.
а) Пусть G—(V, Е) — граф. Определим отношение
R{E) на V следующим образом: V\R(E)V2 тогда и только
тогда, когда [vi, vi\^E. Отношение R(E) нерефлексивно,
так как vR(E)v тогда и только тогда, когда [у, v]^E, но
[у, v]<?E, поскольку (у, у)& V2—.R(E) симметрично для
ViR(E)v2 тогда и только тогда, когда [vi, Vz\^E, од-
однако [vu v2] = i(vu V2), (У2, Vi)} = [y2, v\]. Следовательно,
v\R{E)v2 тогда и только тогда, когда vzR{E)v\.
б) Если R — нерефлексивное симметричное отношение
на У, то R с VI.
Нерефлексивность R означает, что (у, v)&R для лю-
любого i)E V, поэтому Rcz VL.
Симметричность R означает, что (vu Уг)еД тогда
и только тогда, когда (У2, V\)^R. Определим Е формулой
E — R!~, тогда G«=(y, Е) есть искомый граф.
Графы могут быть представлены матрицами с буле-
булевыми элементами. Многие из свойств графов могут быть
определены из пх матричных представлений путем алгеб-
алгебраических преобразованпй. Это станет понятным из по-
последующего изложения.
Определение. Матрица смежности А^Ж{п, В)
графа G = (V, E), где 1У|=га, определяется следующим
образом:
fl, если [Vi,Vj]^E,
lJ \0 в противном случае.
Говорят, что вершины v( и v, являются смежными, если
Ац=\. Ясно, что Ац'=0 (?=1,..., п) и А=Ат. Таким
образом, А симметрична, и в обозначениях § 1 гл. 6 А =
= A (R(E)).//
218
Изображение графа G = (V, E) получается путем рас-
расположения различных точек на R2 для каждой v e V,
причем, если [v, w] е E, ни проводим линию, соединяю-
соединяющую вершины v -a. w.
0 1 1
А= 10 1
1 1 0
Матрица
смежности Изаоражвниа
Рпс. 7.1
Пример 1.1. Пусть
1. V = {vx, v2, v3), E =
= 3, \E\-3.
Этот граф изображен на рпс. 7.1.
2. V = {V\, V2, УЗ, Vi, V$},
E = i[vi, v2], [vu vb], [v2, vz], [v2,
[
I F|=5, |?|=
Этот граф изображен на рис. 7.2.
0 10 0 1
10 110
0 10 11
0 110 1
10 110
Матрица
смежности
v2], [v2, v3], [vu vs]), IVI
[V3, V4], [Vt, Vs]),
или
Цзо5ражэниа
Рис. 7.2
Графы являются скорее «топологическими», чем «гео-
«геометрическими» объектами, т. е. они выражают больше от-
219
ношения между вершинами, чем расположение вершил
и ребер в пространстве. Таким образом, граф может быть
изображен бесконечным количеством разных, но «экви-
«эквивалентных» способов. Однако изображения графов могут
вводить в заблуждение. Например, из пересечения двух
ребер на рисунке не следует, что точка пересечения яв-
является вершиной (см. первую диаграмму на рис. 7.2).
Ясно, что нижней (верхней) треугольной части матрицы
смежности достаточно, чтобы определить граф.
д=
Эта часть определяет в
Читатель уже энаком с понятиями подструктуры и
изоморфизма или же с эквивалентностью алгебраических
систем. Дадим следующие определения.
Определение. Говорят, что граф # = (Fi, Е\) яв-
является подграфом графа G =(V, E), если V\^V а Е\^Е.
Если V\ = V, то говорят, что Н является остовным под-
подграфом G. Если V\ — непустое подмножество вершин гра-
графа (V, Е), то подграф (Vi, E\), порожденный V\, опре-
определяют как
V\ и [у, w] ен Е. //
[v, w] s Е\
Определение.
а) Пусть Gi=(F
говорить, что G\ и G
екцпя /: V\
v, w
б) Пусть
отображение
E\) и G2 = G2, E2) — графы. Будем
эквивалентны, если существует би-
V% такая, что
vR(El)w^f(v)R(E2)f(w).
= (V, ^ — произвольный граф. Определим
6: Рч-NIHO}
следующим образом: величина б (v) равна числу ребер,
содержащих вершину x&V. Назовем б (у) степенью ве{ь
шины v.
Следующее предложение выражает два простых, но
важных факта о свойствах графов.
Предложение.
а)
220
б) В любом графе число вершин нечетной степени
четно.
Доказательство. Каждое ребро дважды входит
в сумму, откуда и следует утверждение.
в) Пусть 7,s7 — множество вершин четной степе-
степени, a Vo s V — множество вершин нечетной степени. Заме-
Заметим, что
V
следовательно,
2
t-ev
= F.
U Vo и
6(у)=- 2 «
rev.
2|*|
= 2ftH
F. П Vo =
iW+ 2
rev
- 2 6(i;]
vev.
0;
6(
0
(Ясно, что 2 б (у) = 2ft, где ft — некоторое целое.) Ta-
Tars гв
кнм образом,
т. е. четно, однако каждое 6(v) в левой части нечетно,
поэтому iVol четно. II
Во многих приложениях теории графов о топологии
графа имеется дополнительная информация, относящаяся
к V, пли к Е, или к обоим множествам одновременно.
Чтобы конкретпзпровать вышесказанное, определим по-
нятпе помеченного графа и дадим несколько примеров.
Определенпе.
1) Пусть Sv n SE — множества меток. Пометкой или
распределением меток графа G— (V, Е) называется пара
функций
/: V -»¦ Sv — распределение меток вершин,
g: E -*¦ SB — распределенпе меток ребер.
2) Пусть граф G=(V, E) помечен с помощью функ-
щш / п g, a Ci =(Vi, Ei) помечен с помощью /i и g\. Гра-
Графы G п G\ называются эквивалентно помеченными, еслп
существует бпекцпя h: V -*¦ V\, такая что
а) G и G\ эквивалентны как непомеченные графы;
б) Kv) — 1\{h{v)) для всех уеу, поэтому соответ-
соответствующие вершины имеют одну п ту же пометку;
в) g{[v, w]) = gt([h(v), h(w)]) для всех v, w&V, т, е.
соответствующие ребра имеют одну п ту же пометку.
221
помечены только вершины;
помечены только ребра. II
Часто бывают помеченными только ребра или же толь-
только вершины. Вышесказанное применимо и в этом случае.
Тогда
/: V->SV,
g = const,
/ = const,
g: E-*-SE,
Ребра илп вершины (или те и другие вместе) поме-
помеченного графа несут информацию, которая дополняет илп
заменяет обычную идентификацию с помощью имен.
Пример 1.2,
1. Пусть
V={vU V2, V3, Vi), E = {[vU V3], [v2, V3], [v3,
f: V -* (города Великобритании!, g: E -*¦ N,
Лондоп, g([vu у3])=105,
)(v2) — Кардифф, g([v2, У3])== 196,
/(уз) —Бирмингем, g([v3, V4]) —292,
/(у4) — Эдинбург.
Этот граф изображен на рис. 7.3.
2. Пусть графы
у.» ЭЗиндург
292
Бирмингем
V2,
w2,
[V\, Ы [V2,
[WU W3], [W2, W3]})
помечены так же, как указано на
рис. 7.4; Gi и G2 являются экви-
эквивалентно помеченными графами
(вершины не помечены). II
Упражнение 7.1.
1. Построить доказательство
первого предложения этого пара-
параграфа.
2. Изобразить графы, представленные следующими
матрицами смежности:
Кардифф Лондон
Рпс. 7.3
-о
1
1
0
_0
1
0
0
0
0
1
0
0
1
1
0
0
1
0
0
о-
0
1
0
0_
1
1
1
о
1110-
0 0 0
0 0 1
0 1 0
10 10
222
3. Определить матрицы смежности графов, представ-
представленных па рпс. 7.5.
120
SO и>з
Рис. 7.4
4. Начертить подграф, порожденный вершинами {V2,
$, Vi, i/'б) графа па рис. 7.5, а.
Рпс. 7.5
5. Пусть G = (V, Е)— граф и |VI == та. Какое может
быть максимально возможное значеппе \Е\7
6. Сколько существует различных графов, имеющих
п вершин? Остальные задачи этого параграфа требуют
введения некоторых дополнительных понятии.
Определение.
а) Граф G = (V, E) называется полным, если для
всех V\, V2^V имеем [vi, vi\^E. Полный граф с верши-
вершинами обозначается через К„.
б) Граф G—(V, E) называется двудольным, если су-
существует разбиение V—{V\, V2) такое, что никакие две
вершины из V\ или из Vi ые являются смежными. Дву-
Двудольный граф называется полным, если для любой пары
vi <= V\ и V2^V2 имеем [vu и^^Е. Если I Vi I = m. и
IV21 = re, то полпый двудольпый граф (V, Е) обознача-
обозначается через #,„,„. /
223
7. Изобразить граф /i5.
8. Построить пример двудольного графа.
9. а) Изобразить граф ЛГз.з-
б) Сколько ребер имеет граф Кт,п?
§ 2. Маршруты, циклы п связность
Обратим сейчас внимание на понятие маршрута в
графе. Значительная часть теории графов и ее прило-
приложений занимается вопросами существования и свойств
маршрутов. Некоторые важные свойства вытекают пз
следующих определений.
Определение.
а) Пусть G = (V, Е) — граф. Маршрутом длины к в
графе G из v в w называется последовательность <уо.
ь'1, ..., vk~> вершин (необязательно различных) и,еУ
таких, что Vo = v, vk = w, a [vt-i, vt]^E для всех i =
= 1, ..., А;. Маршрут называется замкнутым, если Vo =
= у». Маршрут называется цепью, если все его вершины
различны. Замкнутая цепь называется циклом. Цикл
называется простым циклом, если только Vo = vk, а осталь-
остальные vt различны.
б) Если существует маршрут из v в w, v, w e V, то
говорят, что w достижима из V.
в) Граф без циклов называется ациклическим.
Циклы и длины циклов были определены для случая
подстановок в § 4 гл. 3. Заметим, что понятие замкнуто-
замкнутости, в сущности, соответствует своему названию.
Определение.
а) Граф G = (V, E) называется связным, если каж-
каждая пара различных вершин может быть соединена
маршрутом.
б) Деревом называется связный ациклический граф.
в) Корневым деревом называется дерево с выделен-
выделенной вершиной, называемой корнем.
г) Остовным деревом для G — (V, E) называется
остовнып подграф, являющийся деревом.
В § 1 мы отметили, что вычисления с матрицей смеж-
смежности обнаруживают важную информацию о природе
графа. Следующие результаты являются примерами внут-
внутренних связей между алгеброй и топологией в теории
графов.
В приведенной ниже теореме п ее следствиях степени
А* вычисляются в i(n, Z), а не в М{п, В). Следова-
Следовательно, в Ах могут возникать числа, большие чем 1,
224
Теорема. Пусть А—матрица смежности графа
G=(F, E) и \V\ •= п. Тогда (A)(j есть число маршрутов
длины к от vt к v,.
Доказательство. Будем использовать индукцию
по ft. Для к = 1 маршрут длины 1 как раз является реб-
ребром G. Следовательно, результат теоремы при к = 1 вы-
вытекает из определения А. Пусть
(Л*~')о = а«, Axi = aiU
тогда
?-1
Пусть результат имеет место для ft — 1. Тогда, если a(q —
элементы матрицы Л4, то а(, — число маршрутов длины
ft — 1 от V{ к iy, по определению aqi — число маршрутов
длины 1 от v, к v,. Следовательно, ce,-,a,j — число маршру-
маршрутов длины ft из у< к V), где vq есть предпоследняя вер-
вершина маршрута.
Отсюда следует, что
п
2 чч1
9=1
есть число маршрутов длины ft от vt к vs. Это завершает
доказательство. /
Следствие.
а) Маршрут от у, к vt (i^j) в G = (V, E) существу-
существует тогда и только тогда, когда (г, ])-й элемент матрицы
порядка пХп (/г = |V\):
не равен нулю.
б) Если не использовать условие i^j, то требуемая
матрица имеет вид
Доказательство.
а) Пусть (.Vu V\, ..., Vj> — маршрут из vt в v, в G.
Если не существует повторяющихся вершин, то (так как
I V\ = п) маршрут содержит не более п — 1 ребер, п не-
необходимое утверждение следует из теоремы.
Пусть существует повторяющаяся вершина. Тогда
маршрут имеет вид
вамквутый
маршрут
15 Д. Кук, Г. Бейз 225
Если мы удалпм все такие вамкнутые маршруты, то за-
задача сведется к предыдущему случаю, когда вершины
не повторялись. Таким образом, в одну сторону требуе-
требуемый результат получен. В обратную сторону рассужде-
рассуждения очевидны.
б) Если разрешается /-»/, то существование маршру-
маршрута из Vi в v, влечет то, что существует последователь-
последовательность <у(, v\, ..., V)>. Если не существует повторяющихся
вершин (за исключением, возможно, случая Vt — Vj), тог-
тогда маршруты состоят из более чем п +1 вершин (не
более п ребер). Следовательно, (i, /)-й элемент матри-
п
цы 2-^ не равен нулю. Тогда при |V|«» n отсюда
следует
А (Д+ (?)) - A (R (Е)) V А (& (?)) V • • • V Л (Дп (?)) -
- V ^(Д
A(R*(E)) = I V А(П(Е))\/ ... у A(Rn-*(E))~
Напомним, что для произвольного бинарного отноше-
отношения R величина R+ определялась как
СО
и если R^VXV при \V\ =n, то отсюда следует (с уче-
учетом § 1 гл. 6), что
A (R+) = А+ (Д) = \/ Л (Л*).
Аналогично
А=0
В этом параграфе для упрощения обозначений будем
теперь обозначать A(Rk(E)) через A(R"), A(R+(E)) че-
через A(R+), а Л (Л*(?)) через Л(Д*). Алгоритм Уоршол-
ла требует 4л3 операции для определения Л(/?+), тогда
как при помощи приведенных выше соотношений тре-
требуется 4л4 — 7«3 операций. Можно получить и другие,
226
еще более эффективные алгоритмы для больших зпме-
ний п.
Матрицу C — A(R*) называют матрицей связи, связ-
связности или достижимости графа G=>(V, E). Маршрут из
vt к V) (t^j) существует в G тогда я только тогда, когда
(t, /)-й элемент ив С равен 1. Граф G является связным
тогда и только тогда, когда Сц •= 1 для всех 1 < i, / *S n.
Важные свойства отношения R* могут быть сформу-
сформулированы следующим образом.
Предложение. R* — отношение эквивалентности
на V.
Доказательство. Так как по определению R*
является рефлексивным эамыканпем R, то необходимо
только проверить симметричность R*. Выполнение vR*w
влечет существование маршрута <i>, Vi, ..., vk, w> <n v
к w в G, т. e.
[v, vi]e?, [i>b V2]^E, ..., [vh, w)&E.
Следовательно,
[w, vk] s E, [i\, vi-i] s ?,..., [V2, vi] e E, [tfi, v] в Е.
Таким образом,
<ш, vk, vk-u .... v2, vu v>
есть маршрут из w в у в G, откуда следует wR*v. Й
Отношение R* определяет важный класс подграфов,
который сейчас будет определен. Будут также даны не-
некоторые сопутствующие понятия; они будут важны в
дальнейшем, когда будут обсуждаться «пересечения»
графа.
Определение. Пусть (V<: К i<р) — разбиение
графа, определяемое отношением R*. Тогда говорят, что
р —число связности G. Подграфы G,, Е(), порожденные
классами эквивалентности, называют компонентами связ-
связности графа G.
Лесом называется граф, в котором каждая связная
компонента является деревом. Остовный лее для графа
G = (V, E) — это совокупность вершин разъединенных
деревьев Г, — {Vt, Е,) таких, что V -= U У\ и Е,<=Е для
всех I. (Разъединенность вершин означает, что Vt П V} =
= 0 при i ¦/¦/.)
Рисупок 7.6 иллюстрирует вышеупомянутые понятия
для графа при р -» 2.
15* 227
Упражнение 7.2.
1. Пусть G = (V, E), где V-
Ц"ь из\> [уь уз], [, У4], [уз, vt]}.
v2, v3, vj и ?
ОстпоВный. лее для графа
V, V,
Рис. 7.в
Используя матрицу смежности G, определить:
а) число маршрутов длины 2 из i>j в V2i
б) число маршрутов длины 3 из Vi в Vi\
в) является ли G связным.
2. Изобразить остовные деревья для графов из упраж-
упражнения 7.1, 3.
3. Дать матричную характеристику ацикличности в
графе.
§ 3. Пленарные графы
Исторически во многих работах по теории графов рас-
рассматривают специальный класс графов, который может
быть аккуратно представлен рисунком на плоскости R*.
В этом параграфе мы рассмотрим три важных результата,
касающихся таких графов.
3.1. Теоремы Эйлера а Куратовского.
Определение.
а) Граф G называется планарньш, если он мо-
может быть изображен на плоскости так, что его ребра не
228
пересекаются*). Такой рпсупок называют кар-
картой G.
б) Карта G нааывается связной, если G связей. II
Пример 3.1.
1. G=({y,, V2, VS, Vt), {[УЬ V2], [Vt, V3], [l>[, Vt], [V2, Vi],
[V2, v*], [vz, vt]i). Изображение и соответствующая карта
G показаны на рис. 7.7; следовательно, G — пленарный
граф.
Изображение в
Карта G
Рпс. 7.7
2. Графы, изображенные на рпс. 7.8, а в Ь обычно
обозначают через Kt и Кз,з соответственно. Позднее мы
рассмотрим доказательство того факта, что эти графы не
являются пленарными. /
Рис. 7.8
Карта делит R2 на «области»; проиллюстрируем это в
следующем примере.
Пример 3.2. Рассмотрим карту, изображенную на
рис. 7.9. Она делит R2 на четыре области; п, ъ и гз
являются ограниченными областями, а г4—«неограни-
г4—«неограниченная» область.
В оставшихся параграфах будем обозначать множе-
множество областей данной карты через Я.
*) Такой граф, изображенный на плоскости, называется пло-
плоским графом.— Примеч. ред.
22S
Теорема Эйлера. Для произвольной связной
карты
1У1-1Е1
Доказательство. Пусть IVI — 1. Тогда очевидно,
что 1?1«=0 и 1521 = 1. Следовательно, формула справед-
справедлива для \V\ = 1. Рассмотрим два возможных способа
расширения данной карты.
t-HoSoe
I peSpe
Рис. 7.9
J НоВая
Sерши на
Рис. 7.10
1) Добавим новую вершину и присоединим ее к су«
ществующей карте.
2) Соединим две существующие вершины.
Покажем, что значение IVI — \Е\ + |&| инвариантно
относительно обоих способов расширения.
В первом случае добавим новую вершину так, как,
например, это сделано на рис. 7.10. Этот процесс увели-
увеличивает IVI на 1 и \Е\ на 1, однако I&I остается тем же
самым, вследствие чего значение IVI — |?| + 1Я1 не из-
изменяется.
Рпс. 7.11
Рис. 7.12
Во втором случае соединим две вершпны, как, напри-
например, на рис. 7,11, Тогда | V1 остается тем же самым, \Е\
230
возрастает па 1, а 1521 уменьшается на 1; следователь-
следовательно, вначение 171 —|/?| + |Я| опять остается неиз-
ыенным.
Все карты могут быть получены из случая I V\ •= 1
путем выполнения 1) и (или) 2); если необходимо, то
процедура повторяется. Следовательно, так как 171 —
-1Я1 + 1Я1-2 при 171 = 1, а значение \У\-\Е\ + \Я\
остается инвариантным при выполнении 1) и 2), то мы
имеем |7| — \Е\ +1521 = 2 для всех связных карт.
Очевидно, что каждая область карты ограничена за-
замкнутым маршрутом. Ниже приведены два простых ре-
вультата (один касается ограничивающих замкнутых
маршрутов). Этих результатов оказывается достаточно
для доказательства того, что К$ и #з,з не являются пла-
нарными.
Определение. Пусть G-»G, E) — пленарный
граф. Для карты G определим степень А, области г как
длину замкнутого маршрута, ограничивающего г. /
Пример 3.3. Для карты, изображенной на рис.7.12,
имеем <i>i, v%, v\, v%, vi, v{) — граничный замкнутый
маршрут для ri, a <v\, из, иг, i>i> — граничный замкну-
замкнутый маршрут для гг. Следовательно, Дг^ ¦= 5, ДГ| =» 3. /
Предложение. Пусть G = (V, Е) — планарнып
граф. Тогда
а) 2 Дг = 21 Е | для любой карты G;
гея
б) если \V\>3, то 1ЕК31П-6.
Доказательство оставляем читателю в качестве
упражнения.
Предложение. Графы К$ и Кз,з не являются пла-
нарными.
Доказательство.
Докажем, что Къ не является пленарным. Если К$ —
пленарный граф, то из предыдущего результата следует,
что |?|<317|-6. Тогда для графа Къ с \Е\ —10 и
|У|=5 имеем 10 < 15 — 6 = 9, что неверно. Таким об-
образом, предположение, что граф Кь пленарный, неверно.
Докажем теперь, что /Сз,з по является пленарным.
Предполагая противное, имеем 2j Дг = 2|?'|. Однако в
ея
з.з никакие три врршпны не связаны одна с другой;
следовательно, Дг^4 для всех re Я. Из формулы Эйле-
Эйлера \Я\ =2+ \Е\ - 171 =2 + 9-6 = 5; следовательно,
2 Дг>5»4=20. Таким образом, 2\Е\>20, откуда
231
\E\ > 10. Поскольку последнее неравенство неверно, то
граф Кз.з не является пленарным. II
Графы Кь и Яз.з интересны тем, что они являются
существенно «единственными» неилапарными графами.
Все другпе пепланарные графы имеют подграфы «подоб-
«подобные» или Кь, или Кз.з- Перед тем как уточнить наше
утверждение, необходимо ввести два определения.
Определение.
а) Пусть G"(V, E)— граф. Элементарное стягивание
G образуется путем удаления ребра [vt, vi\ из Е, вамены
каждого и( и Vj в Е новым символом w, удаления vt и и,
па V и добавления w к V. Графически элементарное стя-
стягивание G получают путем слияния двух смежпых вер-
вершин после удалепия ребра между ними и обозначения
«составной» вершины через w.
б) Граф G называется стягиваемым к графу G', еслп
G' может быть получен из G путем последовательности
элементарных стягиваний.
Прпмер 3.4. На рис. 7.13 изображены графы G п
G', при этом G стягивается к G'. /
Рпс. 7.13
Теорема (Куратовский). Граф является планарным
тогда и только тогда, когда он не содержит подграфов,
стягиваемых к Кь или Кз.з-
Доказательство этой теоремы лежит за пределами це-
целей книги и поэтому опущено. /
Из теоремы Куратовского заключаем, что Кь и Кц
являются существенно единственными не планерными
графами. Алгоритмы, основанные на этой теореме, были
придуманы для того, чтобы определить, является ли дан-
вый граф планарным или нет.
3.2. Раскраска карт в графов.
Определение.
а) Раскраской G^(V, E) называется задание цвета
вершинам G так, что если [v, w\^E, то v в w имеют
различные цвета,
232
б) Хроматическим числом x(G) графа G называется
минимальное число цветов, требующееся для раскрас-
раскраски G. II
Теорема. x(G)^4 для всех планарных графов G. /
Эта теорема была впервые «доказана» в 1976 г. про-
проверкой на компьютере всех возможных случаев*).
Определение. Пусть М — карта. Определим кар-
карту М', называемую двойственной к М, следующим обра-
образом: выберем внутреннюю точку в каждой области М\
если две области имеют общее ребро, то проведем дугу,
связывающую выбранные внутренние точки в этих об-
областях. Этот процесс определяет М'. И
Пример 3.5. На рис. 7.14 изображена карта Л/ вме-
вместе с двойственной картой М'. II
М'
Рис. 7.14
Раскраска М' соответствует раскраске областей М
так, что области, имеющие общее ребро, имеют разные
цвета. Следовательно, мы можем переформулировать тео-
теорему о раскрашивании в четыре цвета следующим об-
образом.
Теорема. Если области карты М необходимо рас-
раскрасить таким образом, чтобы смежные области имели
различные цвета, то для этого требуется не более четы-
четырех цветов. II
Упражнение 7.3.
1. Пусть T-=(V, E) — дерево с 1VI -=га. Доказать, что
1Я1-П-1.
2. Проверить справедливость формулы Эйлера для
графов из упражнения 7.1,1.
*) До сшс пор нет уверенности в том, что эта теорема на са-
самом деле доказана.— Примеч. ред.
233
3. Пусть G = (V, ?) —пленарный граф и Л, обозна-
обозначает степень области г в карте G. Доказать, что
2 Аг-2|?-|.
те®,
4. Пусть G = (V, E) — связный пленарный граф и
IVI >3. Доказать, что
1ЯК31П-6.
5. Привести примеры, показывающие, что приведен-
приведенное в задаче 4 этого упражнения неравенство неверно
при | VI < 3.
6. Определить граф G, для которого х (?)¦=¦ 4.
7. Пусть Г —дерево. Что является значением %{Т)?
§ 4. Структуры данных для представления графа
Матрица смежности предполагает очевидный метод
представления графа в машине — на языке высокого
уровня мы можем использовать массив, чтобы хранить
элементы матрицы. Симметричпость и нулевая диагональ
сокращают необходимый объем памяти; для графа с га
вершинами требуется -тр п (га — 1) ячеек. Обычно многие
элементы матрицы равны нулю и поэтому большая часть
используемой памяти является лишней, однако, несмотря
на это, иногда матрица смежности является наиболее
удобным представлением графа. Однако для многих задач
предпочтительным является представление в виде списка
смежности. В этом случае мы свяжем список связей L,
с каждой вершиной v e V; L, является списком вершин,
смежных с v.
Рис. 7.15
Пример 4.1. На рис. 7.15 даны граф и списки, кото-
которые могут быть использованы для его представления, llj
234
Один из путей применения этих списков — это ис-
использование массивов
Е{], к), 1<Л<2, и P(i), Ki<n,
где /?(/, 1) хранит номера вершин, E(j, 2) хранит связь,
a P(i)—точки начала списка LV{ в Е.
Пример 4.2. Для графа из примера 4.1 мы можем
иметь ситуацию, изображенную на табл. 7.1.
Таблица 7.1
1
1
2
3
4
5
б
7
8
9
10
11
12
Е«, 1)
1
2
3
3
4
1
4
Е<1, 2)
6
9
10
13
0
19
0
5
2
11
35
i
13
1
3
35
36
37
т. 1)
4
1
5
i
2
3
ЕA, 2)
0
1
2
36
37
0
Если i>< не имеет смежных вершив, то установим
() Q, в противном случае E(P(i), 1) является смеж-
смежной с Vi и [t, E(P(i), 1)] является ребром графа. Ана-
Аналогично, если E(P(i), 2)^0, тогда E(E{P(i), 2), 1) яв-
является смежной с vt. Фрагмент программы, которая дает
список смежных вершин к каждой вершине, выглядит
следующим образом:
totKKn do
begin
write 'вершины смежные с вершиной' , I
k*-P(i)
while А-У=0 do
begin
write E(k, 1)
k+-E(k, 2)
end
end
Аналогичная программа может быть использована для
создания матрицы смежности М графа из представления
235
с помощью сппска связей Е, Р следующим образом:
for 1 < i, j < п do M(i, )) - О
for KKndo
begin
k+-P(i)
while к Ф 0 do
begin
M(i
к*-Е(к, 2)
end
end
Чтобы создать структуры Е и Р из Л/, можно использо-
использовать следующую программу:
for К «< га do @
for К/<га do E(i, ])
for К i ^ га do
begin
ifree *- i
for 1</<п do
begin
if M(l, /)-l then do
begin
? (ifree, i)*-j
it ]?>п do
begin
E (ifree, 2) — ifree + n
ifree *- ifree + ra
end
end
end
end
Возможно другое представление графов с помощью
сппска связей. Выбор представления во многом зависит
от используемых алгорптмов.
Представление Lv вершин, смежпых с v, в виде спис-
списка связей определяет «порядок» ребер, выходящих из v.
Рассмотрим это последнее утверждение и списки связей,
данные в начале этого параграфа, по отношению к гра-
графу. Ребра упорядочены, как показано на рис. 7.16. Граф
с упорядочиванием ребер такого сорта называют упоря-
упорядоченным графом. Дадим формальное определение,
236
Определение. Множество V ~* lvu ..., vn) вершин
р
вместе с множеством {?Cl> LVt
списков упорядоченных пар
вершин называют упорядО'
ценным графом.
Необходимо наложить
некоторые условия на спис-
списки Lv, чтобы рассматривае-
рассматриваемые структуры были графа-
графами. Эти условия следующие:
а) (у, v)&L, для любого
u , р
LVn\ упорядоченных
б) (ш, ii)
*(i(, ц?)е
, V2, V3, Vt), {((Vi, V2),
, Vi), (V2, V3), (V2,
Граф, изображенный па
рпс. 7.16, может быть запи-
записан в терминах упорядоченного графа следующим об-
образом:
1. V3), (Vi, Vt)),
Vi), (V3, V2), (V3, У4)),
l). (, V2), (Vi, Уз)))).
Упорядоченный граф определяет единственный не-
неупорядоченный граф. Обратное утверждение неверно,
поскольку в общем случае возможно много способов
упорядочения графа. Некоторые из этих упорядочений
рассматриваются в соответствии со следующим опреде-
определением.
Определение. Два упорядоченных графа G\ и G%
называются эквивалентными, если существует биекппя
/: Vi -*¦ V2 между множествами вершип и биекция сохра-
сохраняет списковую структуру. Другими словами, если
?„ = ((у, w,),
есть список ребер Gu то
(v, wk))
.... (/И./К)))
есть список ребер G2. II
Пример 4.3. Графы, изображенные на рпс. 7.17,
эквивалентны, однако они не являются эквивалентными
как упорядоченные графы. /
237
Псе понятия § 2 (маршруты, замкнутые маршруты,
связность, дерево) переносятся очевидным образом на
упорядоченные графы.
v2 J
Упражнение 7.4.
1. Записать алгоритмы данного параграфа на каком-
либо языке программирования и проверить их работу на
некоторых наборах данных.
§ 5. Обход графа
5.1. Введение. Во многих задачах, включающих гра-
графы, требуется обойти граф, т. е. чтобы каждая вершина
графа «посещалась» или «обрабатывалась» только один
раз. Таким образом, обход графа может быть представ-
представлен последовательностью вершин, соответствующих по-
порядку, в котором онп обрабатываются.
Если G—({i>i, v2, .... vHi, Е) и о: N.-+- N, — пере-
перестановка, то последовательность
определяет обход G. Ток как существует га! различных
перестановок Nn, то должно быть га! различных способов
обхода графа с п вершинами. Другими словами, суще-
существует п\ способов полного упорядочения вершин. Вер-
Вершину 1>0A, называют начальной вершиной обхода, опре-
определяемого подстановкой о.
Мы опишем здесь только два метода обхода графов.
Они могут быть полезны в приложениях. Оба метода
применяются к упорядоченным графам и позволяют
определить перестановку (или полное упорядочение вер-
вершин).
5.2. Обход графа по глубине. Пусть G •= ({у,, ..., vn),
\Lt, ..., ?„„}) ~~упорядочепнып граф. Выберем покото-
рую начальную вершину и. A <*< л) и положим оA) =
**-«. Далее вершины последовательности t определяются
233
следующим образом: v^ — первая вершпна (смежная с
уОA)) из списка смежности ^„„ц). Уо(з>— первая вершп-
вершпна из ^вО(г). которой нет еще в (, п т. д., i;0(A) — первая
вершина из LVg{h_l)t которой нет еще в t (&>4). При
этом, если встречается вершина и такая, что все верши-
вершины из Lu уже содержатся в t, то процесс повторяется из
вершины w&t, где w — последняя вершина в t такая,
что Д. содержит вершины, не входящие в t. Обход за-
заканчивается, когда никакая вершина из V\t не может
быть достигнута из вершин последовательности t.
Если граф G связный, то описанный выше процесс
определяет обход G, в противном случае — только одну
из компонент графа G (содержащую у„<1>)- Если граф G
не является связным, то для получения полного обхода G
необходимо начинать процесс в каждой связной компо-
компоненте графа G. С помощью этого метода можно опреде-
определить число связных компонент графа. Для каждого вы-
выбора начальной вершины в связном графе получен един-
единственный обход, так что возможны все п обходов по
глубине упорядоченного связного графа. Если G имеет
связные компоненты Vt (Ki<p), где UM—ra», то
определены п\ • Пг * ... • п, обходов по глубине.
С помощью следующей рекурсивной процедуры мож-
можно найти обход по глубине. Здесь t— массив длины
га=»|У|, все значения которого вначале равны 0; t[v,)
устанавливается равным 1 для обозначения того, что
вершина i\ обработана,
procedure dft(v)
«(»)«-1
process vertex v
for each w&Lv do if f(u>)' = 0 then dft(w)
end proc
Пример 5.1. Рассмотрим упорядоченный граф, изо-
изображенный на рис. 7.18. Первый обход по глубине из
начальной вершины V\ определяется следующим образом:
Vl, V2, V4, l>g, l>5, V6, V3, V7. II
5.3. Обход по ширине. Пусть G = ({vx, ..., vn}, {?Ol» •. •
• • » ?»„}) — упорядоченный граф. Выберем начальную
вершину v. и предположим, что ?»,= ((i'tl u.^), (vtl u>,),...
(, Щ))
Первые к + 1 члепов t определяются следующим об-
образом: Voti, = v., v42) =*wi, ..., v«tM.i) = wk, a vjc»+i+i)
239
является 1-й вершиной из Ь„^ не входящей в t. Это
исчерпывает Lw^ и процесс начинается над ?», и т.д.
Обход прекращается, когда все вершины, достижимые
из 1>оA), содержатся в /. Замечания из п. 5.2 о единствен-
единственности, связности и числе возможных обходов также при-
применимы к этому обходу. Обход графа по ширине можно
найти с помощью следующей процедуры: t играет ту же
роль, что и прежде, & q — оставшаяся часть в процеду-
процедурах сложения и удаления (addg в delete q соответст-
соответственно)
procedure bft(v)
*(!»)«-1
process vertex v
initialize q with v
while q + 0 do
begin
delete q(v, q)
for w e L, do
begin
if <(u>)-0 then do
begin
add q(w, q)
t(w)~l
process vertex w
end
end
end
endproc
Пример 5.2. Первый обход по ширине графа в при-
примере 5.1 с начальной вершины i>i ведается следующим
240
образом:
Vl, V2, V3, Vt, V5, V6, Vh Va. ff
5.4. Остовные леса обходов по глубине и ширине.
Пусть G = ({«;,, ..., vn), Е) — граф, a t — v0(i,, ..., У,,»,—
обход G. Тогда t определяет подмножество Е' из Е сле-
следующим образом: [v, w]^E' тогда и только тогда, когда
[v, w] используется при построении обхода. Так как для
упорядоченных графов обход t определяет аналогичным
путем подсписок Ь\ каждого списка Lv, то L\ получают
из L, удалением всех пар (v, w), которые не использо-
использованы в сечении.
Предложение. Пусть G = ({ylt.. .,v,,}, {LVi, ...
*»-^\)) —упорядоченный связный граф, а t —обход по
глубине или ширине графа G. Тогда
есть упорядоченное остовное дерево для G.
Доказательство. Так как G — связный граф, то
подграф G' также связен и является остовным для G.
Если G' содержит замкнутый маршрут, тогда некоторые
вершины появляются более одного раза в t, по так как
t — обход, то это невозможно, и G' является ацикличным
графом. Следовательно, G* — дерево. II
Следствие. Каждый связный граф имеет остовное
дерево. II
Рис. 7.19
Пример 5.3. Для графа пз примера 5.1 остовными
деревьями, определенными первичными обходами по глу-
глубине и шпрппе с начальной вершиной V\, будут деревья,
изображенные соответственно на рис. 7.19, а и 7.19, Ь.
16 Д. Кук, Г. Бейэ 2ii
Для графов, не являющихся связпыми, полные обхо-
обходы по глубине или ширине определяют остоьный лес.
Упражнение 7.5.
1. Пусть G = ({у1( ..., vb), (?v ..., LBJ) — упорядо-
упорядоченный граф, определяемый следующими списками:
\ - ((fi, v2)), LVi = ((у2, v6), (у2, y4), (v2, y3), (w2I y,)),
Определить:
а) обход по глубине с начальной вершиной i>2;
б) обход по ширине с начальной вершиной ь\.
2. Нарисовать остовные деревья, соответствующие об-
обходам упражнения 7.5.1.
3. Пусть матрица смежности графа С имеет блочную
структуру
'А1 О
А,
.0 Ар_
где каждое А( является квадратной матрицей с булевыми
элементами, а все остальные элементы равны нулю. Что
можно сказать о свойствах G1
4. Написать процедуры на каком-нибудь языке про-
программирования для определения обходов по глубине и
ширине.
§ 6. Ориентированные графы
6.1. Введение. Во многих приложениях теории графов
требуется, чтобы ребра графа имели направление. На-
Например, поток данных проходит через программу.
Определение. Ориентированный граф (орграф)
G есть пара G = G, E), где V — конечное множество
вершин, а Е — произвольное подмножество V X V. II
Предложение.
а) Ориентированный граф G=[V, E) определяет от-
отношение на V.
б) Пусть V — конечное множество. Тогда отношение
на V определяет ориентированный граф, у которого мно-
множество вершин — Vt
242
Доказательство.
а) Как и в § 1, определим Я(Е) следующим образом:
vR(E)w тогда и только тогда, когда (у, w)eE. Очевидно,
что R(E) — отношение.
б) Если R — отношение на V, то ориентированный
граф G — (V, Е), определяемый R, имеет множество ре-
бор Е, где (у, u?)s?, тогда и только тогда, когда vRw. II
Направление ребра обозначают порядком в VXV;
например, если (у, w)&E, то говорят, что ребро выходит
из у и входит в w. На диаграмме в этом случае для
указания паправлепия используют стрелки.
Пример 6.1. Пусть У — {vu vj, у3), a #i — i(vu y2),
Iv2, Vt), (vt, V[)). Тогда матрица смежности и изображе-
изображение орграфа G\ a(V, Ei) будут такими, как на рис. 7.20.
0
0
1
1
0
0
0
1
0
Матрица
спешности
Изо5ратвние
Рис. 7.20
Аналогично на рис. 7.21 приведена матрица смежпости и
изображение графа G2*=*{V, Е2), где
#2 — {(У1, У)), (V\, V2), (Vu У3), (У8, Уз), (уЗ, yl)'- /
Поскольку реберное отношение для орграфа не обя-
вательно симметрично или нерефлексивно, то, вообще
1
0
1
1
0
0
1
1
0
смежности
Изо5ражеиие
Рис. 7.21
говоря, не обязательно, чтобы А*=АТ или Ац — 0. Ребра
типа (у, у) называют петлей. Степень б (у) вершины
v&V может быть записана в виде суммы 6(у) = 6~(у) +
4 6+(у), где б" (у) — чпсло ребер, входящих в у,
а б+(у)—число ребер, выходящих из у. Множества
243
lw: (w, d)e?) и {w: (v, w)^E) называют соответст-
соответственно входящим узлом и выходящим узлом вершины
v s V. Понятия эквивалентности и пометки обобщаются
на орграфы естественным образом.
6.2. Маршруты и связность в орграфах.
Определение. Маршрутом длины к из v в w в
орграфе G*=(V, E) называется последовательность ребер
вида
(У, Wi), (l»i, W2), (W2, W3), ..., (Ы\_2, Wk-i), (Wk-U W),
т. е. вторая вершина каждого ребра совпадает с первой
вершиной следующего ребра. /
Часто удобно представлять маршрут последователь-
последовательностью вершин
v, wu и>2, ..., ц\-2, wk-\, w,
которые его определяют. Если v — w, то маршрут назы-
называют замкнутым маршрутом или циклом. Орграф без цик-
циклов называется ацикличным.
Теоремы § 2 также справедливы с аналогичными до-
доказательствами для орграфов. Определим связность или
матрицу достижимости тем же самым способом. Заме-
Заметим, однако, что для орграфов отношение R* не является
отношением эквивалентности на V и, следовательно, не
осуществляет разбиения V.
Пусть Ж) обозначает множество всех орграфов, a 'S —
множество всех графов. Мы можем определить отображе-
отображение У: ?D -*¦ д следующим образом.
Определение. Пусть G — (V, E)<=3). Тогда мно-
множество вершин F{G)^S совпадает с V, а множество
ребер F(G) определяется применением следующих опе-
операций на Е:
а) удаляются все петли из Е;
б) (у, и>) заменяются па [v, w] для всех (v, w)&E.
Тогда F(G) является графом, связанным с оргра-
орграфом G. II
Для орграфов понятие связности является более со-
содержательным, чем для графов, и имеет отношение к
проблеме обхода. Сейчас мы определим три важных тппа
связности орграфа.
Определение. Если G*={V, E)~ орграф, то будем
говорить, что:
а) G слабо связный, если граф F(G) связный;
б) G односторонне связный, если для каждой пары
различных вершин v, w e V существует маршрут из v в
w или обратно,
244
в) G сильно связный, если для каждой пары различ-
различных вершин v, w e V существует маршрут из v в w и
обратно. II
Очевидно, что G сильно связный =>G односторонне
связный =>G слабо связный.
Пример 6.2. Из рис. 7.22 мы видим, что орграф:
а) только слабо связный (рпс. 7.22, о);
б) односторонне связный, но не сильно связный
(рис. 7.22,6);
в) сильно связный (рпс. 7.22,с).
В терминах связности матрицы C = A(R*) орграф G
сильно связный тогда и только тогда, когда Сц — 1 для
всех Ki, / < п\ G односторонне связный тогда и толь-
только тогда, когда Сц V Clt = 1 для всех 1 < i, / < п.
Пример 6.3. Рассмотрим орграф, представленный
диаграммой на рпс. 7.23. Для этого орграфа
¦0 110 1-
1110 1
11110
A(R) =
A(R*) =
~0
0
1
0
_1
-1
1
1
1
_0
поэтому для
4
1
1
1
0
0
1
1
1
1
1
0
1
0
1
0
1
1
1
1
1
1
0
0
0
0
0
1
1
1
0
о-
0
1
1
0_
1-
1
1
0
1_
1 1
_0 1
0 0 1
0 1 0_
о
1111-
1111
1111
1111
1 1 0 1_
С = V Л (Rk) = / V A{R) V Л{П-) V A(R3) V A{R*)
h0
245
имеем Сц = 1 для всех 1 < i, I < 5 и, следовательно, граф
является сильно связным. Для более эффективного вы-
вычисления С можно использовать алгоритм Уоршолла. /
Если G*-(V, E) — орграф, то можно разбить V путем
определения отношения эквивалентности р следующим
Рпс. 7.23
Рис. 7.24
образом: vpw, если v=w или существуют маршруты из
v в w и обратно. Если {Vt\ 1 <{</>)— разбиение V п
{Ее 1<<<р, а ?(=(К|Х7|)ПЙ являются соответ-
соответствующими множествами ребер, то подграфы Gt-*(VU E,)
A <t<p) называются сильно связными компонен-
компонентами G.
Очевидно, что psfl* и А(р) может быть определено
из A{R*) как Л(р)у-4(Д*)цЛ4(Д*)л; граф G
сильно связный тогда и только тогда, когда G имеет
только одну сильно связную компоненту, т. е. если р — 1.
Пример 6.4. Для орграфа на рис. 7.24 имеем
A{R*).
1 1 1 И
0 110
0 0 10
00 11
А(р)
Г10
01
0 0
Loo
i 0 0 0
00
0 1 0
0 0 1
Таким образом, G<-=({y(}, 0) A<J<4) являются силь-
сильно связными компонентами графа. Й
Пусть Gwm[V, E) — ациклический орграф. Вершину
иеУ называют листом, если б+(у) — 0. Если (у, ю)е?,
то v является непосредственным предком w, a w— не-
непосредственным потомком v. Если существует маршрут
из v в w, то говорят, что v является предком w, a w —
потомком v.
Эти понятия не имеют смысла для орграфов, имею-
имеющих циклы, так как для таких графов вершина может
исходить сама из себя.
Пример 6.5. Для ациклического орграфа, изобра-
изображенного на рис, 7,25, из вершив i^, vt и v% ребра не
246
выходят, v\ является предком vs, v$ является прямым
потомком Уз п т. д.
Существует тесная связь мен;ду ациклическими ор-
орграфами и частично упорядоченными отношениями. В ча-
частности, имеет место следующий результат, доказатель-
доказательство которого мы оставляем в качестве упражнения. За-
Заметим, что для сокращения некоторых доказательств,
Рис. 7.25
приведенных ниже, частичные порядки будут основаны
скорее на отношении <, чем на отношении <, и, следо-
следовательно, являются транзитивными и нерефлексивными.
Предложение.
а) Пусть отношение < является частичным отноше-
отношением порядка на конечном множестве V. Тогда, если
Е = {(у, и?): у < w),
то пара G=»(V, E) является ациклическим графом.
б) Пусть G~*(V, E) —ациклический орграф и отно-
отношение < определяется следующим образом: v<w, если
v является предком w. Тогда отношение < является ча-
частичным отношением порядка на V. /
В терминах орграфов можно дать точное определение
структурам данных, известным как ориентированное де-
дерево.
Ориентированное дерево Т«- (V, Е) — это ациклический
орграф, в котором одна вершина у, е V не имеет предков,
а каждая другая вершина имеет только одного непосред-
непосредственного предка; уг называется корнем дерева. Бинар-
Бинарное дерево — это ориентированное дерево, в котором каж-
каждая вершина имеет не более двух непосредственных по-
потомков, т. е. б+(у)<2 для всех уе=У. Говорят, что би-
бинарное дерево является полным, если каждая вершина,
пе являющаяся листом, имеет ровно два непосредствен-
непосредственных потомка.
247
Предложеппе. Следующие утверждения эквива-
эквивалентны по отношению к орграфу C = (F, Е):
а) G является деревом.
б) Граф F(G) связный, и существует вершина vr,
которая не имеет предков, а все другие вершины имеют
только по одному непосредственному предку.
в) G имеет вершину v,, которая соединяется с любой
другой вершиной единственным маршрутом.
г) G имеет вершину v,, которая не имеет предков; все
другие вершины имеют только одного непосредственного
предка; существует маршрут к каждой вершине из v,.
Доказательство оставляем в качестве упражнения. II
6.3. Упорядоченные орграфы и обходы. Списки смеж-
смежности являются альтернативной по отношению к матрице
смежности формой представления орграфов. Заданное
списком смежности представление определяет порядок
ребер, выходящих пз каждой вершины.
Определение. Упорядоченным орграфом называ-
называется пара G ¦» (V, Е), где V — конечное множество вер-
шпн, а Е — множество упорядоченных списков ориенти-
ориентированных ребер. Элементы Е имеют вид
?. = ((", »i), ••-, (у, и;»)).
где v, Wi eV. II
Пример 6.6. Упорядоченный орграф
V2, УЗ, Vj, {((Vi, V2), (Vi, l>4), (»1, Vl)),
может быть представлен списками смежности
LVi ED-HID—ЧП>
п может быть изображен диаграммой (рис. 7.26).
243
Упорядоченный орграф G определяет единственный
неупорядоченный орграф; мы только заменяем каждый
список ((у, w\), ..., (v, wh)) множеством {(v, W\), ...
,.., (v, wk)). Орграф, определенный таким образом, на-
называют орграфом, подчиненным G. Упорядоченный
ациклический орграф является упорядоченным графом,
чьим подчиненным орграфом является ациклический ор-
орграф. Упорядоченное ориентированное дерево является
упорядоченным орграфом, чей подчиненный орграф яв-
является орпентпрованным деревом.
Пример 6.7.
T-(lvu ..., рв>, ((К v2), (vu v3)),
'«), (Уз, we),
является упорядоченным ориентированным деревом, где
V\ — корень. Опо может быть
пзображепо, как показало на
рис. 7.27. //
Упорядочеппые ориенти-
ориентированные деревья будем изо-
изображать спуском вершин
слева направо (рис. 7.27).
Если принять такое согла-
соглашение, то номера ребер
можно опускать.
Определение.
1) Пусть Sv и Se — мпожества. Пометкой упорядо-
упорядоченного орграфа G = (V, E) называется пара отображе-
отображений (/, g), где
/: V-*-Sy —пометка вершин,
g: Е -* U SE — пометка ребер.
Отображение g имеет вид
g (((v, и-,), ..., (i-, и-Л))) - (av ...,ak)(= Se-
2) Говорят, что два помеченных графа G\*=(VU E\)
п G2"=(V2, Е2) с функциями пометок (/,, gi) п (/г, gz)
соответственно эквивалентны, если существует бпекция
/г: V\ -*¦ V2 такая, что
а) ((^i w0> •••• (yi wk))&El тогда п только тогда,
249
когда
((А(»), h(wx)), ...,
(эквивалентны как упорядочепные графы);
б) /i («>)¦¦/а (Му)) для всех ye V (метки вершин сов-
совпадают) ;
в) для всех ((у, w\), (у, w%), ..., (у, wk))&Ei имеем
(h(v),h(wk))))
(метки ребер совпадают). /
Следуя § 5, определим обход орграфа как перестанов-
перестановку или полное упорядочивание вершин. Для упорядочен-
упорядоченных орграфов все делается точно так же. Для упорядо-
упорядоченных ориентированных деревьев часто полезны другие
обходы. Некоторые из них будут описаны ниже.
Определение. Пусть T^(iv\, ..., vj, E) — упо-
упорядоченное ориентированное дерево и L, = ((у, wt), ...
..., (v, wk))&E. Определим отношение < па множестве
iw\, ..., и;*) следующим образом: wt < wt тогда п только
тогда, когда i<j. Определим таким образом отношение
< для каждого списка Е. II
Предложение. Отношение < является отношени-
отношением частичного порядка на V.
Доказательство.
Из соотношения v < v следует список вида
((?. и>|), ••-. (<7, v), ..., (q, v), ..., {q, wk)),
который невозможен, так как в дереве не существует
циклов. Следовательно, v*Ф v для любого це7,
Из соотношений v<w и w<и следует, что сущест-
существуют i,ye7 такие, что
?* = ((*. и>0. •••» (х, v), ..., (х, w), .... (х, wk)),
Lv=*{{y, щ) (у, w), ..., (у, и), ..., (у, и,)).
Если хФу, то б~(ы;) = 2, что невозможно, так как Т —
дерево. Следовательно, i = yn
?»-((*, u?i), ..., (х, v), ..., (*, ш), ...
..., (х, и), .... (х, wk)),
-. е. у < и. Поэтому отношение < есть частично упорядо-
упорядоченное отношение на V. II
Отношение < сравнивает только вершины, выходя-
выходящие из одной вершины,
250
Пример 6.8. Для упорядоченного орпентпроваппого
дерева на рис. 7.28 имеем
< — {(V2, Уз), (V4, V6), (l>4, Уб), (У5, V6)} ИЛИ
V2 < УЗ, У4 < VS, У4 < Уб И Уб < Ув- /
Замечание. Обозначим множество всех спусков из
вершины уе7 через Г+(у); аналогично через Г"(у) обо-
вначим множество входов в у.
Определение. Отноше-
Отношение < называют трансверсаль-
ным порядком вершин упоря-
упорядоченного направленного дере-
дерева T = (F, E). II
Наша цель в оставшейся
части главы — вывести различ-
различные полезные методы обхода
для дерева с использованием
симметрии путей расширения
трансверсального порядка. Пе- Рис. 7.28
ред точным определением об-
обходов необходимы два результата. Пусть < определяет
отношение <, на V следующим образом: если м>< < W},
то w'i < ,w'j для всех w\ e Г+ {иц) (J {ы'Л и для всех it-;S
Г+()и{Л
Предложение.
1) <s<.;
2) <, — частично упорядоченное отношение на V.
Доказательство.
1) Утверждение очевидно.
2) а) Из у <,у следует, что или у < v, или существу-
существуют I, yeF такие, что х<у и у е Г+ (z) U {х) и у е
е Г+ (у) U {у}. Однако v < у, так как < — отношение час-
частичного порядка. Аналогично из х<у следует «"^у; сле-
следовательно, i/er+(i)UW и уеГ+({/I){у}. Однако это
означает, что 6~(у)>»2 или б~(ы;)в2 для некоторого
щбГ*(р). Это невозможно, потому что T-^iV, E) — де-
дерево. Таким образом, у <,у для всех у е 7.
б) у<,ш означает, что v<w или что существуют
х, у е V такие, что at < у и 1)еГ+(х)иЫ и w e Г+ (у) U
U {у}; ш<,ц означает, что ш<ц или что существуют
г, s&V такие, что r<s и шбГ+(г)У{г} п ue=r+(s)U
U(s>; »sr+(r)U(r) и »er(j)U(y} дают, что или
(у), у()
Следовательно, дерево имеет одну из форм, изобра-
изображенных на рис. 7.29. Если геГ+(у), то $еГ+(у) а
251
х<у дает х<, s. Однако ue=r+(s), следовательно,
з<,и, и так как v&T+(x), то, следовательно, v<, a.
Если уеГ+(г), то хе Г+ (г) и r<s дает х <.s. Однако
ила
ш
Рпс. 7.29
ser+(s)UW; следовательно, х<,и, a »sr+(i) дает
V <.U.
Следовательно, <. является отношением частичного
порядка на V. /
Иногда v<.w читают как «v находится слева от w>>.
Предложение. Пусть T = (Vt Е) —упорядоченное
ориентированное дерево. Тогда для vu Vj&V (i"*j) или
Vt <, V), или v, <, vu или же у( u vt находятся на маршруте.
Доказательство. Пусть vt, vt e V и Vt *& vt. Тогда
существует вершина у«, такая, что у(е Г+(у,)и ivt) и PjS
S r+(ye)U {Ve}. ЕСЛИ Vi^Va ИЛИ У> = Уа, ТО Vi И Vj НЭХО-
дятся на маршруте; в противном случае рассмотрим пря-
прямые спуски Ш],..., wk из va. Тогда или
для
ила
у,,
В первом случае имеем пли vt <. ^, или ^ <, vt в за-
зависимости от того, wi < ц;т или wm < w,. Во втором слу-
случае повторяем процесс из и\, пока пе будут выполнены
условия первого случая, или получаем vt = у„ или v, = va\
в этом случае V\ n t;^ находятся на маршруте. II
252
Много полезных обходов дерева определяют посред-
посредством расширения отношения <, до полного упорядочи-
упорядочивания V. Используя приведенный выше результат, надо
только расширить <„ чтобы сравнивать вершины, кото-
которые находятся на маршруте, для определения полного
порядка на V, для которого <е является подпорядком.
Определение. Пусть Т = G, Е) — упорядоченное
направленное дерево. Определим полную упорядочениость
<i на V следующим образом: если v} спускается из v{,
то vt<iVi; в противном случае vt<\Vi, если vt<,Vj. От-
Отношение <i называют предпорядком на V. II
Очевидно, что <» s <1#
Пример 6.9. Пусть Т =*(V, E)~упорядоченное на-
направленное дерево, изображенное на рис. 7.30. Тогда
предпорядок на F = la, b, с, d, e, f, g, h, 0 можно запи-
записать как
a <ib <i e
Соответствующий обход вершины имеет вид
а, Ь, е, f, с, d, g, i, h./l
Определение. Пусть Г — G, Е)— упорядоченное
ориентированное дерево. Определим отношение <2 пол-
полного порядка на V следующим образом: если vf спускает-
спускается из Vj, то i>i<2i>j; в противном случае vi<2Vj, еслп
vi<.Vj. Отношенпе <2 называют постпорядком на V. II
Очевидно, что <, s <2.
Пример 6.10. Пусть Т п V такие же, как и в пре-
предыдущем примере. Тогда постпорядок на V будет иметь
вид
253
с обходом
е, /, Ъ, с, i, g, h, d, a. i
Определение. Пусть Г — (V, E)— полное бинар-
бинарное дерево. Определим симметричный порядок <, на V
следующим образом: для каждой вершины, не являющей-
являющейся листом и имеющей прямые спуски w\. и wz (u>i < w2),
положим
w[ < ,v для всех w[ S Г+ (w,) \j {w,},
v < ,iv'2 для всех и;'г s Г+ (wt) \j {w2}. I
Порядок <, также является расширением <,.
Пример 6.11. Пусть Т — дерево, изображенное на
рис. 7.31. Тогда <, определено, как показано на рпс 7.31.
а
Рис. 7.31
Обход по предпорядку упорядоченного ориентирован-
ориентированного дерева соответствует обходу по глубине с корнем в
качестве начальной вершины.
Если Т «=G, Е) — упорядоченное ориентированное де-
дерево, то вершины Т могут быть расположены в предпо-
рядок с применением следующего алгоритма, начинаю-
начинающегося с корня:
procedure pre{v)
process v
if Ь,Ф0 do рте(w) for each bjsL,
endproc
Соответствующий алгоритм для постпсрядка имеет вид
procedure post(v)
it L, ¦=» 0 then process i>
else begin
post(w) for each w&Lv
process v
end
254
Упражнение 7.6.
1. Пусть 4б/(л, В) —матрица смежности орграфа.
Выписать выражения для функций б+ и б~ в терминах А.
2. Сколько различных орграфов может существовать
на вершинах?
3. Пусть G = (V, E) — орграф. Какое максимально воз-
возможное значение величины \Е\?
4. Пусть G = (F, Е)— орграф, где V •= {уь v2, Уз, vt, vb)
в E — i(vu v2), (v2, vz), (v3, »4), (f4, v6), (y5, y3)}. Опре-
Определить матрицы R(E+) и R(E*).
5. Дать матричные характеристики слабой, односто-
односторонней и сильной связности в орграфе.
6. Пусть G-=(V, E) — ацикличный орграф. Какое мак-
максимально возможное значение величины 1?|?
7. Доказать два последних предложения в п. 6.2.
8. Показать, что если 7" = G, Е) — полное бинарное
дерево и V обозначает множество уходов из Т, то |7'| —
-\V\V\ + i.
9. Поддеревом 7"eG', E') ориентированного дерева
T*^(V, E) называется такое ориентированное дерево, что:
в) 0^F'sF;
б) Г-ГХГПЕ;
в) ни одна из вершин VW не является спуском вер-
вершины в V. Нарисовать все поддеревья
Г —({wi, i>2, ..., v6), {{vu v2), (vu v3), (v3, vt),
{vs, Уб), (уз, vt)}).
10. Определение. Если Т — ориентированное де-
дерево, то уровень вершины определяют как максимальную
длину маршрута от этой вершины до листа. Глубина вер-
вершины — это длина пути от корня до этой вершины. Глу-
Глубиной Т называют длину самого длинного маршрута в Т.
Высотой вершины Т называют глубину Т за вычетом глу-
глубины вершины. Высота Т является высотой корня. /
Пусть Т — ориентированное дерево
l, V2), (l?l, Уз), (У1, Vt), (Уз, И8),
(уз, vt), (vt, у7), (i?5, vb), (vs, v9))),
а) нарисовать Т со значениями уровней в качестве ме-
меток вершины;
б) нарисовать Т со значениями глубин в качестве ме-
меток вершины;
255
в) нарисовать Т со значениями высот в качестве ме-
меток вершин;
г) чему равна глубина Г?
д) чему равна высота Г?
11. Пусть Т — ориентированное дерево. Разрезом С де-
дерева Т называется подмножество вершин Т таких, что
а) не существует двух вершин С на маршруте в Т;
б) пи одна вершпна не может быть добавлена к С без
нарушения а).
Определить все разрезы ориентированного дерева, изо-
изображенного па рис. 7.32.
12. Пусть Г*=G, Е)— полное бинарное дерево п
IVI—п. Показать, что существует п!/2("~1)/2 полных по-
порядков на V, которые расширяют трапсверсальный поря-
порядок <.
13. Проинтерпретировать <t, <2 и <, для бинарных
деревьев, связанных со структурой арифметических вы-
выражений, как в § б гл. 3.
ГЛАВА 8
ЯЗЫКИ И ГРАММАТИКИ
Все средства общения включают язык. Обычно мы «об-
«общаемся» с компьютером при помощи языка, который ка-
каким-либо образом записывается (перфокарты, телетайп,
экран дисплея и т. п.), и, следовательно, предложения
языка состоят из строк символов. Действительно, весь
вычислительный процесс может рассматриваться как пре-
преобразование одного множества строк в другое. Такие про-
процессы ведут себя совершенно определенным образом, и,
следовательно, с ними можно обращаться как с матема-
математическими объектами —по крайней мере строки могут
рассматриваться как элементы моноида. В этой главе мы
будем подходить к изучению языка скорее с математиче-
математической точки зрения, чем с литературной. В § 1 будет вве-
введено понятие строки и будут рассмотрены некоторые
проблемы, относящиеся к этому вопросу; в § 2 будут вве-
введены языковые структуры. Далее будут более детально
исследованы некоторые важные классы языков и рас-
рассмотрено введение в грамматической разбор,
§ 1. Основные понятия
1.1. Строки. Буква (или символ) — это простой неде-
неделимый знак, или символ; множество букв образует ал-
алфавит.
Пример 1.1.
А -{о, Ь, с), В-{0, 1),
С-{PERFORM, ADD, GIVING, TO, ...},
Е - (а, Ь, с,..., х, у, z).
Здесь мы можем рассматривать В как бинарный алфавит,
С —как алфавит языка Кобол (в котором слова типа
PERFORM не могут быть разделены), а Е — как анг-
английский алфавит.
17 Д. Кук, Г, Бейв 257
Алфавиты являются множествами, и поэтому к пим
можно применять теоретико-множественные обозначения.
В частности, если А и В такие алфавиты, что As В, то
будем говорить, что А является подалфавитом В, или что
В является расширением А.
Строки являются упорядоченными совокупностями
букв алфавита (папример, алфавита А) и, следовательно,
выглядят подобно элементам Ап = А ХА Х...ХА. Од-
Однако будет более естественным записывать пх в виде
а\п2...ап, а не (а\, аг, ..., а„). Буквы сами по себе также
являются строками для случая п = 1. Мы будем допускать
случай, когда строка не имеет букв {пустая строка), и
обозначать эту строку через Л. Заметим, что Л не являет-
является символом, т. е. А.ФА для любого алфавита А.
По аналогии с лингвистикой будем строки также назы-
называть словами. Множество всех строк (слов) над алфа-
алфавитом А называют замыканием А и обозначают А*,
так что
А* - А* \} А1 \) А* \) ...= U Ап, где 4°= {Л}.
Для удобства определим также множество непустых
строк над А следующим образом:
Л+ = Л*\{Л} = U А\
Как уже упоминалось в примере 2.1 гл. 5, основная
операция над строками называется конкатенацией; фор-
формально она может быть определена как бинарная опера-
операция © па А* следующим образом:
©: (а,Р)~оф.
Аналогично эта же операция определяется для А*. Опе-
Операция © ассоциативна, но пе коммутативна; Л является
единицей в А* по отношению к ©. Сформулируем ниже
основные свойства операции © па А* и А*.
Предложение. По отношению к операции ©
а) А* является моноидом;
б) А+ — полугруппа. II
Результат слияния строк а и {$, т. е. а{$, заключается
в следующем: строка (} записывается сразу же за стро-
строкой а. Другой способ определения строки — рекурсивный:
а является строкой над алфавитом А, если или а = Л,
или а = а$, где а^А, a {$ —строка над А. Здесь а$
означает, что буква а стоит непосредственно перед
строкой р.
258
Все слова в А" (пе (О) U N) состоят точно из п букв;
в этом случав говорят, что строка имеет длину п. Длина
а&А* обозначается как tec! и |al —п тогда и только тог-
тогда, когда as Л".
Очевидпо, что 1Л1 =0 и lal = 1 тогда и только тогда,
когда ае/1.
Если строки состоят из повторяющихся букв, то обыч-
обычно принимают сокращенные обозначения, чтобы пока-
показать, что строку следует рассматривать как произведение
(по отношению к операции конкатенации). Поэтому для
sSi4 будем писать
Л = a0, aa = a2, aan~l = a", ns N.
Будем использовать следующее обозначение для повто-
повторяющихся строк: строку ababa будем записывать как
(abJa или же как а(Ьа)г.
Этот пример иллюстрирует одну из осповных трудно-
трудностей при рассмотрении строк. Мы используем строки для
описания строк, и, следовательно, мы должны иметь воз-
возможность различать используемые алфавиты. Если при-
приведенные выше выражения рассматривались над алфави-
алфавитом А, а символов «(» и «)» в А нет, тогда смысл по-
понятен; с другой стороны, если круглые скобки есть в А,
то выражение (abJa может быть понято как (ab))a. При
условии что мы осознаем возможность таких проблем и
знаем, какие алфавиты используются, этих ошибок мож-
можно избежать, используя различные алфавиты и биекцию
между двумя алфавитами. В некоторых случаях может
быть более удобно построить мономорфизм между мно-
множествами строк, так что одно множество рассматривается
над существенно более простым алфавитом.
Пример 1.2. Пусть В = @, 1} и4 = (в, Ъ, с). Тог-
Тогда ф: А* -*¦ В*, определенное соотношением
где х, у&А* и
<р(а) = О, ф(Ь)= 10, ф(с)
является гомоморфизмом моноида (нам надо сохранять
комбинации) из А* в {0, 10, 110)* s В*. Например,
ф: аЬЬса -+ 010101100, ф: 01011010110 -* аЬсЬс.
В действительности этот метод построения может исполь-
использоваться для отображения произвольного конечного ал-
алфавита в @, 1}*. И
17« 259
Из определения длины строки следует, что если
а, Р«=Л*, то
lapl-lal + lpl, 1ап1=п1а1.
Более того, если а^А, то
При преобразовании одной строки в другую нежела-
нежелательно, чтобы вся входная строка изменялась под дей-
действием одной операции; в противном случае процесс мож-
можно было бы определить только с помощью множества
входных-выходных пар. В дальнейшем нам понадобится
понятие подстроки.
Пусть заданы строки а и j} над алфавитом А. Строка
р" называется подстрокой а, если
а — «АЛ v Л е= >d ¦
Пример 1.3. Пусть А —{а, Ь, с) и а = abac. Тогда
подстроками а являются следующие строки:
Л, а, Ъ, с, ab, Ьа, ас, aba, bac, abac.
В частности, заметим, что а является подстрокой самой
себя, а Л —подстрокой а (и любой другой строки), по-
поскольку
а = ЛаЬас -»АаАЬас = ЛаАЬАас = ЛаЛЬЛдЛс -»
«" ЛаЛЬЛаЛсЛ = аКЪас — аЛЛЬас =... /
Выделение подстроки естественно приводит к замене
подстроки другой строкой. Однако пока еще мы не до-
достигли уровня, достаточного для корректного выполнения
этой операции. Рассмотрим, что случится, если мы имеем
«функцию» /, которая замещает строку ху строкой ухх
при условии, что первая строка является подстрокой в
операнде. Тогда
Однако неясно, чтб является результатом f(xypxy). Воз-
Возможны два случая — уххрху или хурухх. Аналогично по-
получается, если мы применяем / несколько раз. Тогда
f(xypxy)=*yxxpyxx, однако, применяя / к ххуу, полу-
получаем
/ (ххуу) — хухху, f (ххуу) — ухххху или хухухх.
Таким образом, «функция» является не полностью опре-
определенной, и мы не можем поправить дело, потребовав,
260
чтобы операция изменяла все подстроки, поскольку они
могут частично перекрываться.
Ситуация еще более усложняется, если применяются
несколько замещающих функций. Необходимы средства
выбора определенной подстроки всякий раз, когда возни-
возникает такой выбор; в частности, мы будем рассматривать
подстроку, встречающуюся первой при чтении слева на-
направо.
Для формализации рассуждений будем использовать
порядковые свойства целых чисел и сами целые числа,
соответствующие длипам строк. Предположим, что а
и р" — строки над А, |а| < !рЧ и а является подстрокой [J.
Предположим, что а в р" встречается т различными спо-
способами и что |р*1 — lal =п. Тогда мы можем записать $т
различными способами:
Р — fia6i •= Tf2a62 ¦=...-= Tfmafi,,,
где if<, 6isA*, i<Km и /и < n + 1 (если a = (J, то п =
= 0; поэтому существует только одна возможность). Бу-
Будем говорить, что fi, ..., fm специфицируют различные
вхождения а в р" и что ^i дает первое вхождение, а вхож-
вхождение а непосредственно за fi является первым вхож-
вхождением.
Пример 1.4. Пусть g — функция А*-*¦ А* такая,
что {х, у, р, q)^A, и g заменяет первое вхождение ху
в строке на ухх. Тогда
g (pqxy) - pqyxx, g (xypxy) = yxxpxy,
g2(xypxy) = yxxpyxx.
Заметим также, что
ge (x2y2) — g5 (xyx7y) = g * (yx*y) = gs (ух*ух*) =
— g {уху х^) — у V,
поэтому
Перед тем как продолжить изложение, отметим, что
существует альтернативный набор терминов для буквы,
алфавита и слова; это — слово, словарь и предложение
соответственно. В некоторых контекстах эти термины бо-
более разумны, однако в этом случае необходимо проявлять
особую тщательность в использовании термина «слово»,
поскольку оно имеет два смысла.
1.2. Языки. Совокупность строк (или предложение)
называется языком, Формально язык L над алфавитом
261
А — это множество строк в А*; поэтому LsA*. Следова-
Следовательно, операции над строками индуцируют операции на
языках. Отсюда получаем L+ {транзитивное замыка-
замыкание L) и L* {рефлексивное замыкание L) следующим об-
образом:
а) L°={A};
б) если Li и L, — языки, то LtL, = {ху: ieL,, у <= Ц}\
в) Ln = Ln-4,, nsN;
г) L+ = Un>1L";
д) L* = U«>0Ln.
Сейчас обратим внимание на то, как слова могут со-
составляться в предложения, а множество всех предложе-
предложений, имеющих смысл, образует язык. Нас будут в основ-
основном интересовать искусственные языки, такие как языки
программирования или языки, описывающие правильные
математические выражения, однако вначале будет полез-
полезно рассмотреть случай английского языка. Это даст воз-
возможность сформулировать некоторые определения таким
образом, что мы сможем сделать первые шаги в теорию
языка. Возьмем предложение
«The dog bit me».
Это предложение можно рассматривать двумя способа-
способами. Во-первых, изучать его как простую совокупность
слов, каждое из которых является упорядоченной сово-
совокупностью букв; в этом случае предложение рассматри-
рассматривается синтаксически. Во-вторых, интерпретировать пред-
предложение, считая, что мы понимаем значения слов и их
внутренние связи; тогда мы получаем семантику — зна-
значение предложения. В дополнение заметим, что если мы
произносим предложение, то оно влияет на нас своим
воздействием — прагматизмом. В совокупности эти три
области образуют семиотику языка.
Пример 1.5. В языках программирования Фортран
и Кобол утверждения
А-В + С, ADD В ТО С GIVING A
имеют одинаковый семантический смысл понятий сложе-
сложения и присваивания, однако у них разный синтаксис.
Прагматически они могут быть представлены на некото-
некоторой машине как результат выполнения кода
LOAD В
ADD С
STORE A. I
262
Основным объектом нашего рассмотрения будет об-
область синтаксиса. Чтобы проиллюстрировать класс струк-
структур, которые мы будем изучать, рассмотрим диаграмму
на рис. 8.1.
Предложение
' S
Артикль Существительное
the
dog bit
Рис. 8.1
Дополнение
те
На самом деле эта диаграмма означает, что Предло-
Предложение) может быть построено путем слияния Подлежа-
Подлежащего), <сказуемого> и <дополнения>, хотя это требует
формального определения. Подлежащее состоит из <ар-
тпкля) с <существительным>, и окончательно получаем
<артикль> «the», <существительное> «dog», ..., что дает
нам предложение «the dog bit me».
Перед тем как ввести терминологию и обозначения,
необходимые для уточнения общих понятий в конкретной
ситуации, изображенной на рис. 8.1, мы установим ос-
основные цели теории языков и сделаем обзор оставшейся
части главы.
Напомним, что для заданного алфавита А язык L яв-
является произвольным подмножеством множества А*, од-
однако произвольные подмножества представляют очень не-
незначительный интерес. Мы хотим сосредоточить внима-
внимание на специальных языках, содержащих строки, которые
благодаря внешней информации об их семантике счита*
ются осмысленными или хорошо сконструированными.
Наиболее интересные языки бесконечны и, следова-
следовательно, не могут быть выписаны явно. В этих случаях на-
надо придумать способы порождения языка; грамматика G
может рассматриваться как такая порождающая система.
Сформулируем две основные задачи формальной теории
языков:
а) Как по заданной грамматике G (и связанным с ней
языком L) порождать предложения a: osi?
б) Как по заданным К А* и осе 4* устанавливать,
принадлежит ли а € L?
263
Для того чтобы проверить, входят ли эти строки в L,
надо знать, как L порождается грамматикой G. В § 2 и 3
мы опишем общие принципы грамматик с фразовой струк-
структурой, а затем подробнее рассмотрим некоторый подкласс,
имеющий большое практическое значение.
Обозначим через L(G) язык, порожденный граммати-
грамматикой G. Тогда алгоритм проверки вхождения a^L(G)
называется грамматическим разбором; он использует а
и G. Часто первоначальная грамматика не подходит для
определенной техники разбора, однако она может быть
преобразована к эквивалентному, более подходящему ви-
виду. Вопросы, относящиеся к грамматическому разбору или
модификации грамматики, будут рассматриваться в § 4.
Проводя далее идею манипулирования грамматикой G,
в некоторых весьма специальных (но обычных) ситуаци-
ситуациях можно перенести почти все (а иногда и все) трудно-
трудности грамматического разбора в анализ грамматики и, сле-
следовательно, намного упростить анализ конкретных строк.
Спецификация ограничений, которым должны удовлет-
удовлетворять эти грамматики, является более сложной. Изуче-
Изучению этих проблем посвящен § 5.
Упражнение 8.1.1. Предположим, что А и В — не-
непустые алфавиты такие, что
Ul=p, I5l=?,
и ф: А -*¦ NP, ¦$: В -*¦ Ng — биекции. Пусть %\: А* -*¦ N оп-
определено как
ХХ: ах ... ak ~ 2 ср (а,)*//'5,
а хг: В* -*¦ N определено как
Доказать, что %2~loXi является биекцией строк, и пока-
показать, как применяется это отображение. Для этого надо
найти прямые и обратные образы строк x2yxz в А* и
145332 в В*, где
А = {х, у, z), 5-{1, 2, 3, 4, 5>.
§ 2. Грамматики с фразовой структурой
2.1. Основные определения.
Определение. Грамматикой с фразовой структу-
структурой (ГФС) G называется алгебраическая структура, со-
состоящая из упорядоченной четверки (N, T, P, S), где:
264
а) N и Т — непустые конечные алфавиты нетерми-
нетерминальных и терминальных символов*) соответственно та-
таких, что N П Т = 0;
б) Р — конечное множество продукций, Р s V+ X V*,
где F = iVUr называется словарем G;
в) S&N называется начальным символом или источ-
источником. II
Предполагая, что символ -*¦ не содержится в V, соот-
соотношение (а, $)^Р обычно записывают в виде а-* р.
Понятие продукции, которую также называют прави-
правилом преобразования, должно давать возможность заме-
заменять одну строку символов другой. Терминальные симво-
символы обычно рассматриваются как неизменяемые символы.
Поэтому, возможно, определение продукции в ГФС
является чрезмерно общим. На практике соответствую-
соответствующие ограничения будут вводиться так, чтобы не нару-
нарушать постоянства терминальных символов, однако сей-
сейчас этого определения достаточно.
В качестве первого шага рассмотрим рис. 8.1 и по-
попытаемся понять, как он связан со следующими при-
примерами.
Пример 2.1. Предложение на английском языке,
приведенное ранее в качестве иллюстрации, может быть
определено в грамматике G = (N,T,P,S), где N = {(пред-
{(предложение), <подлежащее>, <артикль>, <существительное>,
<сказуемое>, Дополнение»; r = {the, dog, bit, me); P =
= { ((предложение), <существительное>, <сказуемое>, До-
Дополнение)), (<существительное>, <артикль>, Подлежа-
Подлежащее)), ((артикль) the), (Подлежащее) dog)\ ^сказуе-
^сказуемое) bit), ((дополнение) me)}; S = (предложение).
Эта частная система порождает только одно предло-
предложение «the dog bit ше» и, следовательно, может быть
заменена на
N = {(предложение)},
Р = (((предложение) the dog bit me)}
или даже на
L = {the dog bit me}.
Однако если мы в данном случае захотим расширить
язык, чтобы включить в него все предложения, начина-
начинающиеся со слов, скажем, «the lion», «the rat», «the tiger»,
*) Эти символы будут называться также нетерминалами и тер-
терминалами соответственно,— Примеч. ред.
265
со сказуемыми «ate» и «attacked» и дополнениями «you»
и «Napoleon» (тогда L будет иметь более 35 элементов),
то это может быть сделано добавлением только семи до-
дополнительных элементов к каждому из множеств Т и Р.
В этом примере размер языка составляет 4*3*3, в то
время как размер множества Р примерно равен 4 + 3 + 3.
Еще большее значение имеет тот факт, что мы можем
включить все предложения вида «the dog bit (the son
of)" Napoleon» (их бесконечное множество), добавляя к
Т и Р незначительное число элементов. II
Перед тем как описать механизм порождения пред-
предложений, мы должны упомянуть нотацию, введенную
Бэкусом (нормальная форма Бэкуса или форма Бэкуса-
Наура, БНФ). Она особенно полезна, когда мы хотим
использовать элементы из N, которые можно спутать с
элементами из Т такими, как <предложелие> и «пред-
«предложение». Эта нотация использует четыре символа:
::= (мета-присвоить), < (мета-открыть),
>(мета-закрыть), I (мета-или).
Понятия «мета-открыть» и «мета-закрыты» используют-
используются для того, чтобы выделять строки в качестве элемен-
элементов N, «мета-присвоить» заменяет символ -*-, и если
(а, Р)еР, (а, ч)еР, то это может быть записано в виде
а ::= р" I f, что читается как «а есть р* или ¦у».
БНФ впервые использовалась для определения син-
синтаксиса Алгол-60, В случае, если у читателя имеются
какие-либо сомнения в том, что БНФ способна опреде-
определить что-нибудь серьезное, рекомендуем прочитать сооб-
сообщение про Алгол-60. В работах по формальным языкам
обычно избегают длинных строк в N и, следовательно,
нотация Бэкуса не используется, за исключением сим-
символа мета-или. Обычно прописные буквы используют
для обозначения элементов N, а строчные — для элемен-
элементов Т.
Пример 2.2. Рассмотрим G=(N, Г, Р, S), где
N = {S, ТУ, T~{a,b,c,d},
P = {S-+aTd, T - ЪТI Ы сТ I с}.
Заметим, что двойное использование Т в этом примере
не вызывает никаких затруднений.
Грамматика будет порождать все строки aib, c)+d,
однако мы все еще не показали, как этого можно до-
266
стичь. Будем использовать продукции следующим об-
образом.
Пусть а, Р е V*; тогда р" прямо выводится из а, если
a = Tfap и Р = Трб, где ч, б, peF*. osF+ и о-*-ре р.
Этот факт будем записывать в виде а =*¦ р"; он может не-
неформально рассматриваться как преобразования строки
а в строку р замещением подстроки о в ос на р. (Заме-
(Заметим, что не обязательно заменять конкретное вхождение
а в а или использовать конкретную продукцию с левой
частью а. Возможны любые вариации.)
Пусть теперь а и р" — ~лова над V и существует ко-
конечная последовательность a<j, ai, ..., аг, где ao = a,
a, = f н «i-i =*-a( (i = l, ..., г). Тогда будем говорить,
*
что а порождает р" (записывается a =>¦ Р) и что вывод р*
из а реализуется следующим образом: a =*- ai ¦*• аг =*-...
,..=*¦ ar_i =*• р. Аналогично a=>-P, если вывод использует
непустую последовательность прямых выводов. Если
a^V* такое, что S=$-a, то а называют сентенциальной
*
формой. Более того, если а е Т* и S =$> а, то а является
предложением, порожденным G. Таким образом, язык
L(G), порожденный G, есть {а: а^Г* я S* •*¦ а). Там,
где G подразумевается, можно определить L(X) =
>={a: a^ 21*, X(=N и X=*-a). Поскольку, применяя про-
продукции к сентенциальным формам, можно действовать
достаточно произвольно, то возможно существование не-
нескольких допустимых выводных последовательпостей для
данного предложения в L(G), где G — конкретная грам-
грамматика. Среди этих последовательностей мы выбираем
ту, которая на каждом этане оперирует с самой левой из
возможных подстрок, в которой элементы заменяются на
элементы из Р. Такая последовательность Называется
(левой) канонической выводной последовательностью для
предложения.
Пример 2.3. Пусть
где
Р = {В-*(В)\ВВ\( )}.
Тогда предложение ( ) (( ) ( )) может быть выведе-
выведено многими способами.
267
Приведем пять из них:
2)
3) В^ВВ* 41
*>В(В) +
=4 )((
5) 2?t
=>( )(( )( ))•
Первый из этих выводов является каноническим.
2.2. Иерархия Хомского. Обсуждавшаяся до сих пор
система — сильное описательное средство, однако при
создавшемся положении вещей она является слишком
общей. Тем не менее, если наложить ограничения, мы
получим более интересный, хотя все еще достаточно мощ-
мощный математический объект. Начальные ограничения,
которые мы будем накладывать па структуру граммати-
грамматики, определяют элементы Р.
Определение (иерархия Хомского). Пусть G =
"=(N, T, P, S) является ГФС, описанной в п. 2.1. Такую
грамматику называют грамматикой Хомского типа 0.
Если все элементы Р получаются из формы а -*¦ р, где
a = fi:ry2. a fJ = 41642, "iu 42 е ^*. x&N, 6sF+, то гово-
говорят, что G является контекстно-зависимой грамматикой,
или грамматикой Хомского типа 1 (КЗГ). (В этом опре-
определении строки 4i и f2 могут рассматриваться как кон-
контекст, в котором х может заменяться посредством б.)
Другим (альтернативным) ограничением для грамма-
грамматики Хомского типа 1 является то, что в каждой продук-
продукции аир должны быть такими, что 1 < lal < |{Н. (Экви-
(Эквивалентность этих двух определений неочевидна и доказы-
доказывается ниже.) Если подстановки могут быть выполнены
268
без рассмотрения контекстов, тогда мы можем заме-
заменить «контексты» fi и f2 пустой строкой Л и получить
более слабое ограничение: если ж-> 6sP, то x^N и
беУ+.Этому ограничению удовлетворяют грамматика
Хомского типа 2. Наконец, если Р состоит только из про-
продукций вида х -*¦ б, где х s= N и б е Т U TN (так, что пра-
правая часть является или единичным терминалом, или
единичным терминалом, за которым следует единичный
нетерминал), то говорят, что G является грамматикой
Хомского типа 3. II
Часто бывает полезно использовать более общие фор-
формы внутри множества продукций, хотя формально это
и не разрешается. Хотелось бы быть в состоянии вклю-
включить пустую строку Л в качестве правой части любой
продукции. Однако, как увидим позднее, это вызывает
трудности. Такие Л-продукции крайне необходимы с об-
общей точки зрения, если только Л е L. В этом случае мы
можем добавить S -*¦ А к Р при условии, что S не встре-
встречается в правой части любой продукции. Однако в неко-
некоторых случаях необходимо разрешать также и более об-
общие Л-продукции. Чтобы различать грамматики Хомско-
Хомского и те грамматики, в которых разрешаются Л-продук-
Л-продукции, введем расширенные версии грамматик Хомского
типа 2 и 3 — контекстно-свободные и регулярные грам-
грамматики соответственно.
Языки, порожденные каким-либо из этих типов грам-
грамматик, имеют аналогичные названия. Так, структурная
грамматика порождает структурный язык, структурная
грамматика Хомского типа 1 — язык Хомского типа 1,
контекстно-свободная грамматика — контекстно-свобод-
контекстно-свободный язык, а регулярная грамматика порождает регуляр~
ный язык (или регулярное множество). Большинство
примеров этой главы будет касаться контекстно-свобод-
контекстно-свободных языков, а в гл. 9 мы сконцентрируем внимание на
регулярных языках. Одпако большинство практических
языков являются некоторыми расширениями контекст-
контекстно-зависимых языков. Чтобы указать на ограничения
контекстно-свободной грамматики, рассмотрим следую-
следующий важный пример.
Пример 2.4. {xnynzn: гее№ является контекстно-
зависимым языкол!. Предположим, что G = BV, Т, Р, S),
где
N = {S, X, У, Z), T = {x,y,z), Р = {РЬ ..., Р7),
269
Рз = xY -*¦ ху, Pi=*yY-+ уу, Рв — yZ -*¦ yz,
P6 = ZY-* YZ, P7=*zZ-+ zz.
Вначале заметим, что для любого п е N мы можем по-
получить
(Р2)
(P.)
nX (P3)
(P4)
Л- (P5)
^xnynzn; (P7)
поэтому
{xnynzn: nsN):sL(G)(
Теперь мы должны показать, что никакие другие
строки не могут быть порождены G. Хотя возможны не-
некоторые изменения в порядке применения правил (Pi),
(Pi) и {Ре), любое предложение должно выводиться по-
посредством сентенциальной формы такой, как xnYZa, где
а состоит из п — 1 символов У и Z. Для того чтобы по-
получить строку над Т, мы должны в конце концов исполь-
использовать правила (Р4), (Ръ) и (Р7), однако (Р?) может
преобразовать Z в z только в контексте zZ, а (Ре) осу-
осуществляет такую же замену в контексте yZ, Аналогично
для замены Y на у при помощи цравил (Pi) и (Ре) тре-
требуются контексты yY в xY соответственно. На этой ста-
стадии подстрока хп сосгоит только из терминалов, поэтому
на следующем шаге строка должна иметь вид x"yZa и
получаться при номощи (Рз). Однако мы знаем, что пра-
правильное предложение должно порождаться преобразова-
преобразованием из Za в У-'Z" посредством (Ре). Действительно,
только таким образом можно успешно получить строку.
Предположим, что мы имеем промежуточную подстро-
подстроку вида yYmZpY$, где р состоит из оставшихся элементов
У и Z. Из рассуждений, аналогичных приведенным вы-
выше, следует, что для получения подстроки ym+lZpY$ нуж-
270
но т раз применить (Pt). Однако, если сейчас мы ис-
используем (РБ) для получения ym+lzZp~lY$, то никаким
правилом нельзя заменить элемент Y на у (или любой
другой терминал). Единственный способ выйти из этого
положения — это р раз применить (Ре), чтобы переме-
переместить У влево и, следовательно, получить xnynzn. II
Это пример контекстно-зависимого языка, который,
как будет показано, не является контекстно-свободным.
Аналогично существуют контекстно-свободные языки,
которые не являются регулярными (см. гл. 9). Вернемся
теперь к доказательству эквивалентности альтернативных
определений контекстно-зависимых грамматик.
Определение. Грамматики G\ и Gt эквивалентны,
если
Предложение. L является контекстно-зависимым
языком тогда и только тогда, когда он может быть ло-
рожден грамматикой, у которой продукции а -*¦ \i удов-
удовлетворяют условию К \а\ < |ц|.
Доказательство. Если L — контекстно-зависи-
контекстно-зависимый язык, то существует грамматика G с продукциями
вида аА$ -*¦ oqP, где А е N, i e V+ и а, р е V* такие, что
L = L(G). Однако
loci + Ml + Ipl = Id + 1 + Ifll > 1,
= lal + \t\ + Ipl > Id + 1 + 1^1 =
Следовательно, 1 ^ la^pl < \ач$\, что и требовалось до-
доказать.
Пусть G = (Л', Т, Р, S) — грамматика, у которой про-
продукции о -*¦ |х удовлетворяют соотношению 1<|о|«3|ц|.
Мы должны создать грамматику G', эквивалентную G,
с продукциями вида аА$ -*¦ ач$.
Продукции из G имеют вид
1) А -*¦ fi ...Чр или же
2) ai... a» -*• Pi... %, где п < q и A s N, а,, $,, ъ е V.
Во всех продукциях заменим каждый встречающийся
элемент й^Г новым нетерминальным элементом Ai и
включим продукции At -*¦ а{ в G'. Продукции типа 1) те-
теперь имеют правильную форму и ввлючены в G'. Однако
продукции типа 2) необходимо модифицировать. Сейчас
они имеют вид
271
где Wt и Y{ являются нетерминальными символами новой
грамматики. Для каждой такой продукции введем новые
элементы Y\, ..., У„ не являющиеся терминалами,
и n + q новых продукций: п продукций
Yx... Yn-uWn-lWn-+Y1 ... ?n_2yn_1PFn,
Y i . . . Y n-jin-1" n "*¦ Y-i . . . In-jIn-HnJn
и q продукций
Все эти продукции имеют вид ^
Новые нетерминалы Y\, ,.., У, вынуждают приме-
применять эти продукции в написанном порядке так, чтобы
никакие из предложений, не входящих в исходный язык,
не могли быть созданы. /
В заключение этого параграфа обсудим понятие не-
неоднозначности. Классическим примером, неоднозначного
предложения является предложение
«They are flying planes».
Мы имеем две интерпретации этого предложения, зави-
зависящие от того, рассматриваем мы «are flying» как ска-
сказуемое или же «flying planes» как дополнение. Это при-
приводит нас непосредственно к точному определению не-
неоднозначности. Язык называется неоднозначным, если он
содержит неоднозначное предложение. Предложение яв-
является синтаксически неоднозначным, если оно имеет
более одного канонического вывода, в семантически неод-
неоднозначным, если для заданного канонического вывода оно
имеет более одной интерпретации. (Выводы относятся не
непосредственно к явыку, а к грамматике, порождающей
его. Следовательно, мы. должны ссылаться на неоднознач-
неоднозначную грамматику; однако существуют существенно неод-
неоднозначные языки, которые могут порождаться только не-
неоднозначными грамматиками.) Для более подробного
272
изучения семантических неоднозначностей рекомендуем
обратиться к специальной литературе о языках програм-
программирования, а сейчас проиллюстрируем синтаксические
неоднозначности двумя примерами.
Пример 2.5.
1. Пусть б-(Ш, {1, -}, (Е-Е-Е\1), Е). Тогда
а) Е*-Е-Е+-
•+1-Е+-
>*• 1-Е-Е-*
-> 1 - 1 - 1;
б) Е*-Е-Е*-
-¦-1-1-1.
Из этих последовательностей следует, что два указанных
вывода являются различными, и, следовательно, хоте-
хотелось бы придать им различные значения. В примере а)
Б - Е
Е' - Е
/W
Б - Е
Б - в
Рис. 8.2
второй знак «минус», вычисляемый вначале, дает 1;
в примере б) первый знак «минус», выполняемый пер-
первым, дает —1. (Диаграммы на рис. 8.2 иллюстрируют
различные структуры.
18 д. Кук, Г, Бева 273
2. Рассмотрим хорошо известный пример из первой
спецификации языка Алгол-60. Сужая грамматику до
относящегося к делу подъязыка, будем иметь продукции
S -*¦ if В then S else S I if В then S I U,
где S — утверждение, В — булево • выражение, U — без-
if
then
if
then
if
В then
Рис. 8.3
else
S
и
V
условное утверждение. Теперь рассмотрим выражение
if Bv then if B% then Ui else U2.
Мы не знаем, принадлежит ли else Uz к if B\ или к
if B2. Формально мы можем вывести это предложение,
рассматривая В и U как терминалы, следующим образом
(рис. 8.3,а, Ъ соответственно):
a) S => if В then S •>
*> if В then if В then S else S =»-
274
¦*¦ if В then if В then U else S •»
"> if 5 then if 5 then tf else U;
6) 5 «*¦ if В then 5 else 5 =»¦
¦*¦ if В then if В then 5 else S =>¦
«*- if 5 then if В then C/ else S =»-
•> if Д then if 5 then U else ?7. /
Упражнение 2.2.
1. Выразить явно языки, определенные следующими
грамматиками:
а) С=(«число>, {0, 1, 2, ..., 9}, Р, <число>), где
Р = «число) ¦¦0111213141516171819};
б) G=({<P>, <L>, <?>}, {0, 1, 2, ..., 9), Р, <Р>), где
Р
11213. ..819,
2. Определить грамматику С-=(#', Г', Р\ S'), экви-
эквивалентную
G=(U,5, С, S), {*, ,,!}, Р,5),
где
P = {5->4S?<7, AB-+BAz, zB-+A2Bx, A-+x,
В-*-у, С-*¦%),
с продукциями вида aQ$ -*¦ ач$ для
<?eiV', te(N'\JT')*, a, pe(JV'Uf)»,
3. Определить класс Хомского грамматики, опреде-
определенной следующим образом:
G~{{A,B,T,S},{x,y,*)tPtS),
где
Р = {S -+ хТВ \ хВ, Т^хТ/\ хА,
В -*¦ yz, Ay -*¦ уА, Az -*¦ yzz).
Используя свойство класса, к которому принадлежит G,
установить, принадлежат или нет L(G) следующие
строки:
x*yxz, z!j/2z2, xyxz.
18* 275
4. Определить последовательность разрезов представ-
представленного здесь производящего дерева, соответствующую
самому правому выводу предложения х + х * х.
/ /14
/ / * V
/' * \
X х
5. Определить порядок в множестве продукций Р та-
таким образом, чтобы была возможность канонического вы-
вывода, определяющего последовательность целых чисел в
N. Продемонстрировать две такие последовательности
для предложения «aza» в L(G\), где G\ дано ниже. Вы-
Вывести также строку над N, описывающую все выводы
+
в языке ?(С?2), т. е. показать, что А=> А подразумева-
подразумевает неоднозначность. Здесь
Gi={N,T,P,E), G2 = (N,T,P,A),
где N = {А, В, С, Е, R), Т = {a, d, e, x, z) и
Р = {А - В I Cd, В -> Вх I еС I С,
C-+A\xR, E-+aE\Ea\R, R-+z).
6. Выяснить, являются ли следующие грамматики не-
неоднозначными:
а) G~({A, В, S), {а, Ь, с], Р, S), где P = {S-+AB,
A-+a.\ab, B-*c\bc);
б) С=({<целое без знака), <число>}, D, Р, <целое без
знака)), где D = {0, 1, ..., 9} и
Р = {<целое без знака) -*¦ <число),
<число) -*¦ <число) (число), <число) -*¦ О I 1 I 2... I 9).
§ 3. Контекстно-свободные языки
3.1. Основные определения. Контекстно-свободные
грамматики (КСГ) и контекстно-свободные языки (КСЯ)
важны для практических вычислений, так как, хотя
большинство языков является некоторым расширением
конте! ;тно зависимых языков, их легче изучать как кон-
контекстно свободные языки, а затем по другим (семанти-
276
ческим) критериям отбросить некоторые из предложений.
В этих случаях на КЗГ можно ссылаться как на грам-
грамматики, специфицированные связанным синтаксисом,
а на КСГ — как специфицированные несвязанным синтак-
синтаксисом. КСГ также дают возможность прояснить вопросы,
содержащие (синтаксическую) неоднозначность.
Последовательность вывода a^L{G) может быть изо-
изображена как упорядоченное дерево (см. ниже). Корень
дерева обозначен через S, и если 5=>аеГ* и а =
¦= а\... а„, то выходы помечены по порядку at, ..., а„.
Предположим, что S =»- р1 =>- у =>- а и что [5¦*• i достигает-
достигается в результате применения продукции С -*¦ ii... ^m, где
ffSV. В дереве это представляется пометкой вершины
С и т ее преемников (точек, из которых С достигается
за один шаг) ft, ..., im. Поэтому метки могут быть оди-
одиРассмотрим грамматику с продук-
продук+ Т, Т-+1\1*Т, 1-
наковыми.
Пример 3.1.
циями
Е-Т\Е
Обычно в случае контекстно-свободных грамматик мы
будем опускать другие эле- ^
менты грамматики; первое
правило специфицирует ис-
источник, а нетерминалами яв-
ляются только символы в
левой стороне продукций,
В этом случае вывод предло-
жения х + х * х может быть
изображен так, как это еде-
лано на рис. 8.4. II
С конструктивной точки
врения это изображение на-
называется деревом вывода.
(Когда это дерево используют для того, чтобы проанали-
проанализировать, могут или не могут строки содержаться в L(G),
оно называется деревом грамматического разбора.) Легко
видеть, что предложение является неоднозначным, если
оно имеет два неизоморфных дерева вывода, и что для
контекстно-свободных грамматик канонический грамма-
грамматический разбор изоморфен любой другой схеме обхода
дерева.
Мы уже установили тот очевидный факт, что КСГ
являются более ограниченными, чем КЗГ, но тем не ме-
277
Рис. 8.4
нее они все же обладают весьма широкими изобразитель-
изобразительными возможностями.
Пример 3.2. Используя контекстно-свободные пра-
правила, можно породить:
1) все последовательности из символов А:
S*=AS\A;
2) все непустые списки из символов А, отделенные
друг от друга символами В:
S-+A] ABS;
3) те же списки, что и в примере 3.2,2, однако до-
допускается возможность пустого списка:
S -*¦ Т I Л, Т -* A I ABT;
4) все строки, начинающиеся с последовательности
символов А или В и оканчивающиеся символами С или D
соответственно:
S ч- ASC\BSD\X;
например,
S-+[S\\(S)\X.
В этих примерах А, В, С, D и X могут быть опреде-
определены дополнительно. II
3.2. Характеристические свойства. Особенностью рас-
рассмотренных выше примеров, о которых вскоре мы смо-
сможем сказать несколько больше, является свойство ре-
рекурсии (один шаг рекурсии при каждом reeN). Труд-
Трудности возникают тогда, когдэ требуется наложить неко-
некоторые ограничения на глубину рекурсии, не придумывая
новых правил для каждой допустимой глубины рекурсии.
Поскольку N я Р конечны, то очевидно, что если не раз-
разрешать никаких рекурсий, то L(G) также будет конечен,
и этот случай не очень интересен.
Прежде чем идти дальше, введем необходимую тер-
терминологию. Говорят, что грамматика G:
а) леворекурсивная, если в ней имеются выводы вида
'.а, где X (= N, а <= F1";
б) праворекурсивная, если в ней имеются выводы
вида
Х=>аХ, где X и а такие же, как и выше;
278
в) самовключающая, если она имеет выводы вида
ХХ§, где X<=N и a,Pe=F+.
Говорят, что КСГ рекурсивна, если имеется один из слу-
случаев а) — в). Из сделанных выше замечаний ясно, что
желательно бы иметь в грамматике «петли», однако не
произвольного типа. К этому вопросу мы вернемся в § 4.
Сформулируем результат о возможностях КСГ. В тео-
теории КСЯ это, вероятно, наиболее известный результат.
Его доказательство использует рекурсивные свойства
КСГ и структуру деревьев. Этот результат известен как
лемма о разрастании для КСЯ или же как uvwxy
теорема.
Теорема. Если L — контекстно-свободный язык, то
существует neN такое, что если «si u \z\>n, то z
может быть записано в виде uvwxy, где и, v, w, x, ye Г*,
vx Ф Л ы для любого i e N выполняется условие
uv'wx'y e L.
Доказательство. Поскольку L — контекстно-сво-
контекстно-свободный язык, то он может быть порожден некоторой
грамматикой G = (N, T, P, S) и не имеет продукций, за
исключением, возможно, S-*¦ А (если A^L(G)), умень-
уменьшающих длину сентенциальных форм. (Если A^L, то
S также исключают из правых частей продукций для
того, чтобы не уменьшалась длина сентенциальных форм.
В § 4 показано, что такая грамматика G может быть
найдена.)
Если G не рекурсивна, то, поскольку N и Р конечны,
L(G) также конечен, и, следовательно, теорема справед-
справедлива, если взять п большим, чем длина самой длинной
строки в L(G). С другой стороны, если G рекурсивна, то
существует дерево вывода, в котором некоторый нетер-
нетерминал, например А, встречается дважды на пути от кор-
корня к листу. Эта ситуация изображена на рис. 8.5. (Сюда
включены лишь необходимые нам свойства.)
Более того, поскольку G рекурсивна, то мы можем
добиться выполнения соотношения \uvwxy\^n, где п
больше длины самого длинного предложения, получен-
полученного путем нерекурсивного вывода (^km, где к — длина
самой длинной продукции Р, а m= \N\). Таким образом,
если z&L и \z\>n, то z должно иметь требуемый вид
для некоторых пяти строк. Тогда А=$- vAx (vx?=A, no-
279
этому \vAx\ > \А\) и A=>w. Следовательно,
А =$>¦ vlAx=> vwx
*
для любого i ^ N. Отсюда, так как ?=> иАу, имеем
* t i
S => uv wx у
для любого i e N и, таким образом,
uviwx*y s L
для любого ieN. /
Этот результат может быть использован для проверки
того, что некоторые конструкции в языках программиро-
программирования не могут быть определены с помощью КСГ. Да-
Дадим более реальный пример, который не требует энания
конкретного языка.
Пример 3.3. Грамматика из примера 2.4 порожда-
порождает язык ixnynzn: n e N}. Сейчас мы можем показать, что
этот язык является контекстно-зависимым и не может
быть порожден КСГ. Из теоремы следует, что существу-
существует некоторое достаточно большое га, при котором xnynzn
может быть записано в виде abedf (требуется очевидная
замена символов) для некоторых строк о, ..., /. Посколь-
Поскольку х и z в строке разделены, то очевидно, что строки а
и Ь не могут содержать все символы х, у и z; аналогич-
аналогично и для всех других пар из {а, Ь, с, d, /}. В частности,
по крайней мере один из символов ж, у и г не может
быть одновременно в строках Ь и d; таким образом, стро-
строка ab2cd2{, которая по теореме содержится в L, содержит
не все символы х, у и z (они также могут быть распо-
280
яожены в другом порядке, однако в дальнейшем мы не
будем рассматривать эту возможность). Следовательно,
мы не получаем тот же самый язык, из чего и следует
требуемый результат. /
Подобные противоречия могут быть получены во мно-
многих ситуациях, когда информация, содержащаяся в более
ранней части строки, влияет на требуемую структуру по-
последующей подстроки. Следующий пример является ти-
типичным в этом отношении.
Пример 3.4. Язык L = (lp: р e N, р — простое чис-
число) не является контекстно-свободным:
L = {11, 111, 11111, ...Ь
Предположим, что L является КСЯ. Так как существует
бесконечное множество простых чисел, то имеется про-
простое число q такое, что
1« = uvwxy, vx = Л,
uv'wx'y s L для всех i e N
(это следует из приведенной выше леммы). Таким об-
образом, существуют о, Ь, с, d, e такие, что
при b + d > 0 и
для всех i e N, так что q = a + b + c + d + e — простое
число и </>1, а д( = а + с + е + (b + d)i— простое число
для всех i е N. В частности, qt — простое число при i =
+ b + + d+e+l, и в этом случав
Однако q~> 1 и 6 + d+l>l; следовательно, q( не явля-
является простым числом для всех i e N, и мы получаем про-
противоречие. Поэтому L = {lp:peN, p^ простое число)
не является КСЯ. /
Этот пример также демонстрирует практическую важ-
важность связанного и несвязанного синтаксисов. Можно
придумать жесткий фиксироваввый сивтаксис, который
281
включает правильную семантику. Однако, где это воз-
возможно, часто гораздо удобнее и эффективнее разрешить
использование более широкого языка, порожденного
(обычно контекстно-свободной) грамматикой, а затем,
если необходимо, сузить множество путем дальнейшей
семантической проверки.
В примере 3.4 мы могли бы использовать правило
S-MSI11,
чтобы породить все строки 1': ?>1, и после этого про-
проверить, что «q — простое число», с помощью подходящего
арифметического алгоритма.
Короче говоря, контекстно-зависимые грамматики яв-
являются сложными и не изучены с достаточной полнотой.
С другой стороны, контекстно-свободным грамматикам
уделяется достаточно много внимания, и они составляют
основу почти всех практических компьютерных трансля-
трансляционных систем.
Упражнение 8.3.
1. Вывести КСГ, которая порождает множество всех
строк над (а, Ь}, имеющих равное количество а и Ъ.
2. Построить грамматики, порождающие следующие
языки:
а) {а3п
б) {апЬ2т-и. п, т>1);
в) {anbn: n>i), n,meN,
3. Используя лемму о разрастании, показать, что язык
не является контекстно-свободным.
4. Показать, что если L\ и L^ являются КСЯ, то та-
таким же является язык L\ U L%.
5. Доказать, что множества
ixnynzm: п > 1, т > 1}, {xmynzn: п > 1, т > 1}
являются КСЯ; показать, что если языки L\ и L^ явля-
являются контекстно-свободными, то отсюда не следует, что
язык L\ П Ьг является контекстно-свободным.
282
§ 4. Понятия грамматического разбора
и грамматических модификаций
Наиболее непосредственный и очевидный контакт, ко-
который средний пользователь имеет с процессами перево-
перевода (трансляцией с одного языка на другой),— это ис-
использование различного рода компиляторов для таких
языков высокого уровня, как Паскаль, Фортран, Кобол,
Алгол и др. При использовании такого языка программа,
которую мы написали, транслируется в эквивалентную
программу в машинном коде (объектную программу),
которая может быть расшифрована и выполнена компью-
компьютером. Общая схема компиляции изображена на рис. 8.6,
Исходная программа
I
ЛексическиЁ анализа-
анализатор
Лексическая форма
1
Грамматический разбор
\
Дерево
грамматического
разбора
1
Генератор кода
1
Объектная программа
Оптимизатор
Оптимизированная
объектная программа
Рис. 8.6
В общем случав стадии процесса компиляции могут
рассматриваться связанными последовательно, как это
изображено на диаграмме; однако на практике они часто
выполняются одновременно. Генерация кода требует эна-«
ния семантических интерпретаций, которые связаны о
283
каждой синтаксической структурой внутри программы.
Для оптимизации машинного кода необходимо знать тон-
тонкости строения машины. Мы не будем рассматривать эти
стадии, а ограничимся лишь обсуждением трансляции
ключевой программы в дерево грамматического разбора.
Ключевая (исходная) программа является просто
строкой символов. Внутри этой строки часто встречаются
некоторые комбинации символов, в которых отдельные
символы не имеют смысла, однако комбинация символов
передает смысл. (См. пример 2.1; «dog» имеет значение,
а буква «о» внутри «dog», очевидно, отдельно не несет
смысловой нагрузки.) Такие составные символы, назы-
называемые также лексемами, не являются абсолютно необ-
необходимыми и могут не использоваться в некоторых языко-
языковых трансляторах, однако обычно они существуют и ко-
кодируются одним символом (для каждой комбинации свой
символ), чтобы сократить длину исходной программы
(на данный момент в ее лексической форме) и избежать
необходимости рассматривать ненужные детали на сле-
следующих этапах. Типичными лексемами являются:
а) ключевые слова, т. е. слова с постоянным значе-
значением в языке; например,
begin
end
¦while
GOTO]
Паскаль, DO ? Фортран,
.OR. J
+,—,*,/ в большинстве языков;
б) числа 52, 31.65 и т. п.;
в) строки или последовательности символов;
г) идентификаторы, введенные программистом.
Лексемы обычно описываются
регулярными грамматиками. Следо-
Следовательно, мы свели исходную про-
проблему к грамматическому разбору
строки лексем. Графически это оз-
означает — заполнить треугольник на
рис. 8.7 таким образом, чтобы он
был совместим с продукцией правил
грамматики.
4.1. Процедуры приведения. В об-
общем случае нам не разрешается из-
изменять строку а = п\п2 ... а„; поэтому вся деятельность
до проведения процесса грамматического разбора должна
быть направлена на грамматику. Потенциально нам
284
будет необходимо осуществить достаточно сложные пре-
преобразования грамматики, чтобы проверить, что все нетер-
нетерминалы действительно можно использовать в граммати-
грамматическом разборе. Существует два варианта, в которых
нетерминалы могут не подходить для проведения произ-
произвольного грамматического разбора; опишем их формально.
Определение. Пусть G=*(N, T, P, S) есть КСГ.
Тогда говорят, что нетерминальный символ X&N яв-
является:
а) недоступным, если ХФБ и не существует вывода
вида
для а, ре7*;
б) непродуктивным, если не существует строки у s
+
е Т* такой, что X =ф- у;
в) бесполезным, если он недоступен или непродук-
непродуктивен.
Грамматика, не имеющая бесполезных нетерминалов,
называется редуцированной. II
Ясно, что бесполезные символы не играют никакой
роли в построении предложений. Хотя хотелось бы не
включать в грамматику бесполезность символов, они мо-
могут быть введены алгоритмами, предназначенными для
модификации грамматики с целью соответствия некото-
некоторым требованиям (см. ниже). Бесполезные символы не
обязательно увеличивают размер грамматического разбо-
разбора, и сейчас мы опишем процесс их удаления.
Пусть G = (N, T, P, S) есть КСГ. Определим множе-
множество N' как
где т — новый символ (т?? V), и отношение р на N' сле-
следующим образом: (А, В)^р, если А-*-аВ$&Р при
A, B&N, а, р е V*; {А, т)ер, если А-*-^^Р при неко-
некотором if e T*.
Предложение.
а) А доступно тогда и только тогда, когда A^S или
(S,A)ezp+',
б) А является продуктивным тогда и только тогда,
когда (А, т)ер+.
Доказательство.
а) А доступно тогда и только тогда, когда существует
*
вывод вида 5=*-аЛр для а, f}<=F* или, что эквивалент-
285
но, тогда и только тогда, когда существует i > О такое,
что
Когда БФ А, это имеет место лишь в случае Sp+A; по-
этому E, 4)ер+.
б) А продуктивно тогда и только тогда, когда А=$-у
для некоторого i > 0 и f е 71*, т. е. тогда и только тогда,
когда существует последовательность сентенциальных
форм ао, а\, ..., а,- таких, что
А =*- ао =*¦ ai =>...=>• а,- = у,
т. е. когда существует последовательность Л=^о, ^i,...
. -., Ai-i e TV такая, что Л{ является подстрокой af, и,
следовательно,
где р — подстрока у, т. е. AopAi, A\pA%, ..., Л(_1рт. По-
Поэтому Лр+т. /
На практике р+ моншо вычислять, используя алго-
алгоритм Уоршолла. Пусть Nu<= N — множество бесполезных
символов G и N' = N\NU, Р' = Р\Ри, где Р„ — мнозкество
продукций, содержащих элементы Nu. Тогда G' — (N', Т',
Р', S), где Т' — множество терминальных символов, по-
появляющихся в продукциях Р', эквивалентно КСГ без
бесполезных символов.
Алгоритм. Удаление бесполезных символов.
Вход: КСГ G-(tf, T,P,S).
Выход: эквивалентная КСГ G'«=(#', Т\ Р', S) без
бесполезных символов.
Метод: построить N', Т', Р', как указано выше. /
Пример 4.1. Рассмотрим грамматику
, В, С, D], 1х, у, р, q, w, a), P, А),
где
P = U-+x\yDC\D, B-+q\Bx, C-+Cx\yC, D-+Da\Cw\ph
Используем отношение р, определенное выше, и его пред-
представление в матричной фбрме:
А В С D х
M(p) = C
286
А
В
С
D
%
-о
0
0
0
0
0
1
0
0
0
1
0
1
1
0
1
0
0
1
0
1
1
0
1
0
В этом примере имеем А/(р+) = М(р) — М. Таким обра-
8ом, МАВ = Мех = 0, и поэтому В недоступно, а С непро-
непродуктивно. Следовательно, грамматика сводится к
G' = (U, D), {х,а,р},Р',А),
где
После удаления бесполезных символов каждый остав-
оставшийся нетерминальный символ X встречается по крайней
мере в одном дереве вывода (рис. 8.8) с X, связанным
вверх с 5 и вниз с некоторыми
терминальными строками fli • •. ап.
Один «очевидный» путь грам-
грамматического разбора строки —¦
это вывести все строки, отметить
их соответствующие канонические
последовательности, а затем про-
проверить предложение, сравнивая
его с каждой строкой. При совпа-
совпадении использовать выводящую
последовательность, чтобы опре-
определить дерево грамматического Рис. 8.8
разбора. Конечно, в большинстве
примеров величина \L\ бесконечна, и поэтому этот про-
процесс невозможен; однако если грамматика не имеет не-
неудачных продукций, то это приближение обеспечивает
основу техники разбора, которая, по крайней мере в ло-
локальном контексте, может использоваться на практике.
Если длина сентенциальных форм не может умень-
уменьшаться при применении G, то при проверке ae?(G),
lal=ra можно отбросить все формы (перед получением
строк над Т), чья длина превосходит п. Предложения,
длина которых не превосходит га, могут сравниваться с а
обычным путем; в разумной грамматике все такие воз-
возможные строки должны порождаться за конечное число
шагов. Сейчас мы займемся приведением грамматики и
построением ее эквивалентной версии, которая обладает
«более легким» грамматическим разбором.
Для того чтобы процесс порождения, связанный >с
данным предложением, был конечен, необходимо гаран-
гарантировать, что все последовательности вывода действи-
действительно могут быть получены. Следовательно, появление
таких ситуаций, как X -*¦ X и X -*¦ Л, представляет ин-
интерес, Записывая их непосредственно как продукции, это
287
легко обнаружить; однако более общие ситуации Х=ф-Я?
и X => Л труднее локализовать. Более того, два типа вы-
выводов связаны таким образом, как это продемонстрирова-
продемонстрировано в следующем примере.
Пример 4.2. Предположим, что включенные продук-
продукции некоторой грамматики имеют вид
X-+Y, Y^-W, Z-+V, W-+Z, V-+X.
Следуя возможной последовательностью вывода из X, по-
+
лучаем, что Х=*-Х, и, следовательно, как только X
встречается в сентенциальной форме, мы могли бы вста-
вставить прогрессию X=>Y=>W=^Z=>V=^X (снова и сно-
снова), не получая, таким образом, ничего, кроме неодно-
неоднозначности.
Как нетрудно видеть, это «петля» из нетерминалов
внутри N. Заметим, однако, что мы могли бы иметь
практически такую же ситуацию в завуалированном ви-
виде, если вместо X -*¦ Y и У -*¦ W имели бы, например,
X + AY, Y-+AWA,A-+A. II
Определение, А-продукцией является продукция
вида
КСГ G — (N, Т, Р, 5) называется А-свободной, если
а) или Р не имеет Л-продукций,
б) или существует только одна Л-продукция S -*¦ Л
и S не появляется в правой части произвольной продук-
продукции из Р.
Продукция является одиночной, если она имеет вид
X-+Y, где X, ГеЛГ.
Продукция вида Х-*-Х при X&N называется тривиаль-
тривиальной. КСГ G = (N, Г, Р, S) называется циклически сво~
водной, если не существует выводов вида X => X для лю-
любого ХеЛГ. t
Как уже отмечалось, обнаружение и удаление циклов
и Л-внводов тесно связаны. Мы начнем с места располо-
расположения всех нетерминалов, из которых может быть до-
достигнуто Л.
Замечание. Для заданной грамматики G = (N, Г,
Р, S) через Na будем обозначать множество \Х: X =>- Л/ s
sN. I
283
Алгоритм. Вычисление NA.
Вход: произвольная КСГ G = (N, T, P, S).
Выход: NA.
Метод: пусть Р = {Р , Рт}, где каждое Р« имеет
вид
тогда, рассматривая NA как «переменную» типа множе-
множества, имеем
«-IPI,
repeat (if (a* ? NA) and (p\ e tfj)
then(ArA-^An{ai}, i^ |P|J
elsei-i-1)
untiU-0. /
Алгоритм. Переход к Л-свободнрй грамматике.
Вход: произвольная КСГ G = (N, T, P, S).
Выход: эквивалентная Л-свободная КСГ G'=*(N', T,
Метод:
1) определяем #л;
2) строим Р' следующим образом:
а) Пусть А -+¦ ao5iai52a2... Bkah s P,
где й^Оипри l<i</c каждое В{ есть в Л^А, но ни один
символ в а^еР @</<к) не находится в NA. Тогда
добавим к Р' продукции вида
А ¦
где Х{ есть или 5f или Л, без добавления А -*- А к Р'
(это могло бы иметь место, если бы все а< совпали с Л),
б) Пусть S<=NA- Тогда добавим к Р' продукции
S'-+A\S,
где S' — новый символ, и тогда N'**NU {5"}; в против-
противном случае N' = N и 5' =* 5. /
Сейчас мы можем рассмотреть удаление циклов из
КСГ. Месторасположение циклов может быть легко най-
найдено выделением отношения р = {(А, В): А-*-В&Р) и
формированием замыкания р+. Тогда ясно, что произ-
произвольное X: Хр+Х должно быть в цикле. Объединим это
вместе со схемой «обратной замены», которая удаляет
19 д. кук, Г. Бевз 289
все нетерминалы внутри произвольного цикла. (Она так-
также удаляет любую тривиальпую продукцию.)
Алгоритм. Переход от КСГ к эквивалентной цик-
циклически свободной грамматике.
Вход: Л-свободная КСГ G=(N, T, P, S).
Выход: эквивалентная циклически свободная грамма-
грамматика
G' = (N\ 7", Р\ S').
(Нетерминалы G переименованы: А\ па Ап, где ra = |iV|,
S на А\, а каждую продукцию Р( выражают через
af -*• ?,.) Дополнительно мы используем множество
INCYCLES, а п нотермипалов обозначаем через
REPLACE^, где 1 *S i < п. Алгоритм будет иметь следую-
следующий вид:
1) определяем р над Nn так, что щ тогда и только
тогда, когда Аг -*¦ Aj e P;
2) пусть о = р+;
3) INGYCLES ¦- 0;
4) for i from 1 to re — 1
do (for j from i + 1 to n
do if (J Ф INCYCLES and
ioj and
№ )
then (INCYCLES ^ INCYCLES U {/},
REPLACE/-A))
5) /-0
for i from 1 to !PI
do (for all к s INCYCLES
in P, replace Ak by REPLACED
giving new P(
if (new ^^{Pi P-]
and a,i Ф ^i in new P.)
then (/ 4- / + 1, P ¦ 4- new Pj))
6) G' = (A/1 INCYCLES, Г, Р', 5). //
Говорят, что КСГ является приведенной, если она
А-свободна, циклически свободна и редуцирована. Полу-
290
чив собственную КСГ G, мы можем использовать ее для
проверки условия a«=?(G) для дапного а^Т*.
4.2. Модификации грамматического разбора. Как было
установлено во введении к § 4, задача грамматического
разбора строки состоит в заполнении треугольника вьг-
вода (рис. 8:7) с соответствующим деревом. Конечно,
в большинстве случаев это заполнение нельзя разумно
выполнить за один таг, и обычно оно получается при
помощи последовательности поддеревьев. Эти последова-
последовательности поддеревьев могут быть получены многими
способами; три наиболее используемых способа изобра-
изображены на рис. 8.9.
а,... ...а„ а,... ..-а„ a,... •¦•an
а о с
Рис. 8.9
Стратегия грамматического разбор*., изображенная на
рис. 8.9, а, называется грамматическим разбором сверху
вниз. В нем применяют продукции (в некотором выбран-
выбранном порядке) к сентенциальным формам, пытаясь рас-
расширить S внутрь строки а\...ап. При таком разборе
естественно использовать в качестве гида часть, строки
(а\...ая), чтобы управлять выводом. Для практических
рассмотрений, согласующихся с чтением а\...а„ слева
направо (рис. 8.9, Ъ) и желанием начать разбор перед
включением полной строки,, необходимо использовать на-
начало строки. Следовательно, в поиске сентенциальных
форм, которые начинаются с а\ е Т (и соответственно
исследуя терминальные строки как начальные подстроки
последовательных частей входной строки), мы должны
отвергнуть возможность выводов вида X=$»X
ре F+), Таким образом, чтобы начать разбор сверху
вниз, мы должны удалить левую рекурсию.
В общем случае это может быть сделапо с использо-
использованием процесса, аналогичного решению системы линей-
линейных алгебраических уравнений. Чаото возможно рассмат-
рассматривав одну рекурсик> за один раз а. удалять ее, ис-
19* 291
пользуя довольно простое тождество. Оправданием такого
+
подхода служит порождаемый язык. Рассмотрим X =Ф- Ха.
Путем «обратной подстановки» правых частей продук-
продукций мы можем получить прямую рекурсию как элемент
Р; таким образом, имеем X -*¦ Ха I ($. Рассматривая это
как полную грамматику над (а, р} (j$ представляет все
другие нелеворекурсивные возможности для X), очевид-
очевидным образом получаем, что
L(X)={$an: re = 0 или neW.
Это множество может порождаться также продукциями
которые не являются леворекурсивными (они праворе-
курсивны). Чтобы закончить преобразование, продукция
X -*¦ рК должна быть расширена при необходимости до
правильного числа термов.
Пример 4.3. Рассмотрим грамматику с продук-
продукциями
А -> Be \dC, В -> хА I Се, С -+ АЬ\ ш.
Она леворекурсивна, поскольку
А => Вс => Сес *> АЬес.
Путем обратной подстановки для С в В и В в А полу-
получаем
В-*хА \(Ab \w)e**B-*xA \Abe\ we,
А -* ВС | dC =s A -> {хА | Abe \ we) c\dC=s
вгА -*- хАс | АЬес \ wee \dC ^A -> A bee \ xAc | wee \ dC.
Т I "
Поэтому, используя преобразование
получаем
А -+ (хАс \wec\dC)Y**A^ xAcY I wecY \ dCY,
Y - bee Y I Л, В -* хА I Ce,
C-*Ab\w. II
Заметим, что в этом примере В может быть «выреза-
«вырезано» и может не принимать никакого участия в произ-
произвольном предложении, порожденном из корня А (следо-
(следовательно, надо удалить все следы В из грамматики),
292
Отметим также, что мы ввели Л-продукцпю. Эта про-
продукция, созданная как побочный эффект «преобразова-
«преобразования грамматического разбора», вызвала бы меньше про-
проблем, чем аналогичная продукция, встречающаяся есте-
естественным образом. Символ В может быть удален при
помощи алгоритма для удаления бесполезного символа.
Хотя обычно будет достаточно частичного удаления
отдельных леворекурсивных цепей внутри Лг, мы должны
использовать матричное обобщепие описанного процесса
для того, чтобы справиться с удалением внутренних ле-
левых рекурсий.
Напомним, что в обычном случае мы заменяем X -*¦
-*• Ха I р при помощи X — $Y, Y -* aY I Л. Если мы име-
имеем п нетерминалов Х\, ..., Х„, которые являются взаим-
взаимно леворекурсивными, так что не сводятся путем после-
последовательности обратных замен к простому случаю, тогда
мы можем представить соответствующие продукции схе-
схематически следующим образом:
Xl-»XlAn\X2A2i\...\XnAnl\Bu
Х2 -* XiA\21 X2A221 ... I XnAn21 B2,
Xn -* X{Aln I X2A2n I... I XnAnn IB,, •
где каждое Ац представляет собой остаток всех операций,
которые могут быть выведены из Xt и которые начина-
начинаются с Х(, и аналогично каждое Bs представляет все аль-
альтернативы для нетерминалов Xj, которые не начинаются
с элементов {Хи ..., XJ.
Теперь, поскольку Ais и В; являются множествами
строк, отсюда следует, что:
1) если Xs -* X,, то Л е Ац;
2) если X, -* а и а Ф Х$ для $ е- V*, то а s Bs;
3) если Xj AXjf для любого if s V*, то Ац = 0.
Следовательно, над алгебраической системой (V*,
©, I) мы можем свести эти продукции к матричной схеме
Х = ХА|В в Ж(п, G*, ©, 1))\
или, записывая альтернативный оператор I как +, к схе-
схеме
Х = ХА + В в Л(п, (F*. О, +)J.
По аналогии с простым (нематричным) случаем, о кото-
293
ром будет более подробно сказано в гл. 9, скажем, что
X = BY,
где Y=-AY + I, а I определяется на (V*, ©, +) как
т _ КЛ}' если г = /»
у~10. если
Пример 4.4. Предположим, что S = D ш G имеет
следующие продукции:
D-+Dx\Ey\Fz, Е -+Da\ Fc,
F-+Dp\Eq\Fr\w.
Таким образом, используя общую схему, получаем
X —
xj
D
E
F
-+Xi Aij
-*¦ Dx
-*¦ Da
-*Dp
1 X% A2
1 Ey
! Eg
> 1 Хз
I Fz
| Fc
| Fr
Bi
1 ip.
Итак, Xi = 2 #fcFfti. Поэтому
E -у wY4<>, F -> wY44,
следовательно.
Fn - xYn \aY2\ I />Уз! I A,
Yi2-
У21 - г/Уи I gF8i,
У22 -^ i/Fl21 дУз21 A,
У23 -*- yYi31 qY33,
Yn-+zYll\cY2i\rYtu
У32-*- гУ121 еУгг I rY32,
В этом примере преобразования производят ненужные
нетерминалы; удаляя их, получаем
D -
294
zYn I cYn I rY3U
xYn I aY2i I />У311 Л,
Y21
Изменяя соответствующим образом имена, получаем
D + wJ,
J + zK\cL\ rJ,
K-+xK\aL\pJ\A,
L-*yK\qJ.
Чтобы нагляднее показать степень трансформации,
приведем вдесь дерево грамматического разбора строки
«wcqzayx» для первоначальной грамматики (рис. 8.10, а)
и модифицированной (рис. 8.10,6) грамматик.
Рис. 8.10
Удаление левых рекурсий обеспечивает, если это воз-
возможно, вывод строки, начинающейся с требуемого тер-
терминального символа; однако это не гарантирует, что мы
получим только одну такую строку, и, следовательно, мо-
может случиться, что мы пойдем неправильным путем.
Пытаясь избежать неправильных последовательностей
грамматического разбора, мы можем явно использовать
манипуляции, уже встречавшиеся при предыдущих пре-
преобразованиях. Этот процесс называют левой факториза-
факторизацией. Процесс требует, чтобы были проведены продук-
продукции, включающие в левую часть данный нетерминал.
Затем расширяют все правые части и те, которые начи-
начинаются с общей подстроки над Т, собирают вместе.
Пример 4.5.
А - хуВ I xyBC \ yPQ \yxV^
**A-r хуВ(Л I С) I y{PQ \xV) — A -*¦ xyBAi I yA2,
293
где ^4i -*- Л I С, обычно записываемое как С I Л, и Аг-*-
-+PQ\xV. II
Заметим, что мы вновь можем ввести Л-продукщш.
Однако если в настоящий момент нет Л-продукций, то
в заключительных левофакторизованных продукциях п
грамматике не будет левых рекурсий. В этом случае сле-
следующий символ входной строки можно использовать для
того, чтобы непосредственно определить, какие альтерна-
альтернативы надо использовать для расширения нетерминалов
в сентенциальную форму. Если Л-продукции встречаются
в явном виде, то это вызывает затруднения.
В силу того что Л является ведущей подстрокой каж-
каждой строки над произвольным алфавитом, она всегда
совпадает с началом строки задания, и, следовательно,
никакие последующие альтернативы никогда не будут
рассматриваться. Здесь нет возможности входить в пол-
полный анализ проблемы, однако заметим, что если G =
= (N, T, P, S) и мы определяем
a) FIRST (а) = (г: а Л- хр\ х е= Т, р е= V*}
б) FOLLOW (а) = {х: бЛ- уахЬ, хе=Т,уЬ(= V*},
и если для каждой продукции X -*¦ ai I аг I... I а„
a) FIRST(a()nFIRST(a,) = 0, %Ф]
б) Х=ф-Л,
то
FIRST(X) fl FOLLOW(X) = 0.
В этом случае G можно использовать для предсказываю-
предсказывающего анализа (см. рис. 8.9,6). В таком анализе можно
проверять альтернативы в произвольном порядке, не
применяя Л-выводов, пока все другие возможности не
исчезли. Следующий пример иллюстрирует этот процесс.
Пример 4.6. Предположим, что единственной про-
продукцией в грамматике является
С ¦* хСх I Л.
Попытаемся провести грамматический разбор строки
«xxi>. Строка отбрасывается, хотя она и законна, потому
что мы вынуждены применить первую продукцию дваж-
296
ды, порождая таким образом неправильное продвижение,
поскольку is FIRST (С) Л FOLLOW (G) и С -* А. Это
графически изображено на рис. 8.11.
Использование грамматики С -*¦ ххС I Л (рис. 8.12) не
вызывает никаких трудностей в грамматическом разборе,
потому что сейчас хФ FOLLOW (С). II
С
хх С
/I
х х л
Рис. 8.12
Перед тем как завершить параграф, упомянем другой
основной метод грамматического разбора — снизу вверх,
в котором продукции применяют назад, пытаясь свести
строку задания к S (см. рис. 8.9, с). Этот метод приме-
применяют более широко по сравнению с методом сверху вниз;
используя некоторые модификации этого метода, можно
повысить эффективность грамматического разбора.
Упражнение 8.4.
1. Модифицировать грамматику, продукции которой
даны ниже, таким образом, чтобы она не была леворе-
леворекурсивной:
A-+Bx\Cz\w, В-+АЪ\Вс, С -*- Ах I By | Ср.
2. Пусть G = {N, T, P, S) является КСГ и символ
^e]V не является бесполезным символом G. Показать,
что существование одного из следующих выводов в G
влечет за собой неоднозначность G:
б) А=>аА\А$;
в)
г)
при f e(N\iT\* и a,
297
3. Определить Л-свободную КСГ, эквивалентную КСГ
и определенную как
G-({$}, ia,b},P,S),
где
Р - IS - aSbS \ bSaS \ Л}.
4, Пусть
G = (U, В, С, Д Е, S), {а, Ь, с), Р, 5J,
где
P~{S^A\B, A-*C\D, B-+D\E, C-*S\a\A,
D-+S\b,E-+S\c\A).
Найти приведенпую грамматику, эквивалентную G.
§ 5. Грамматики операторного предшествования
Важное подмножество КСГ содержит к себе так на-
называемые операторные грамматики. Это грамматики,
в которых все продукции такие, что никакие два нетер-
нетерминала не являются смежными в любой правой части,
н, следовательно, лежащий между ними терминал можно
представить как оператор (хотя не обязательно в ариф-
арифметическом смысле). Попытаемся определить отношения
предшествования на множестве У U {I—» Н)» гДе \~ и Ч
суть новые символы, которых нет в V и которые ограни-
ограничивают «предложение». Правила определим следующим
образом:
1. а = 6, если А -+ аа$Ьч&Р; здесь a, 4&V* и (is
е N U (Л).
+
2. а<.?,если А -*¦ ааВ$& Р; здесь B^-ybb, yeN(J {Л}
и а, р, 6 в Г*.
3. а •> 6, если Л-*аВЬреР; здесь 5 =*• уабг 6&NV
U (Л) иа,Ие У*.
+
4, J- <• аа если 5=»ааРа
5, а ¦> ^J если S=> аар, E s W U {Л}3 a s V*.
Символы<•,= и •> обозначают отношения предше-
предшествования (читается как «имеет меньшее старшинство,
чем», «имеет такое же старшинство, как», «имеет боль-
большее старшинство, чем*); при условии но не более од-
ного такого отношения справедливо между двумя произ-
произвольными операторами из Т\} {(-, -|}, соответствую-
соответствующую операторную грамматику называют грамматикой
операторного предшествования.
Хотя она и является гораздо более сложной, чем дру-
другие виды грамматик, встречавшихся до сих пор, понятие
предшествования может быть введено так, что будет
совпадать с обычным старшинством арифметических опе-
операторов и будет расширено до операторов, действия кото-
которых важны с точки зрения вычислений, одпако обычно
считаются само собой разумеющимися при вычислениях
«на бумаге».
Пример 5.1.
Е -+ Е + Т I T, Т ->Т*Р\Р, Р-*{Е)\х.
Для этой грамматики отношения предшествования при-
приведены в виде таблицы на рис. 8.13. /
+
*
)
X
+
<•
>
>
>
>
*
<
<•
•>
¦>
>
(
<¦
<•
<
)
>
>
¦>
•>
X
<
<
<
>
¦>
•>
Рис. 8.13
Для того чтобы увидеть, что происходит в действи-
действительности, рассмотрим этап внутри вывода предложения
\- х*(х + а)—\. Из правила 2 определений предшество-
предшествования видно, что для символов * и ( имеем
Т-+Т*Р, рХ{Е).
Таким образом, выполняется отношение *<•(» и поэто-
поэтому поддерево Р должно быть вычислено перед вычисле-
вычислением Т * Р; следовательно, действие, связанное с «(», ко-
которым является удаление этой и парной к ней закры-
закрывающей скобки, выполняется перед действием, обозна-
обозначенным «*». (Графически ситуацию можно представить
так, как это сделано па рис. 8.14. Здесь для правила 2
имеем Д = 7\ а^Т, а=», В**Р, Р = Л, Ч = Л, b^( a
б з= Е. Отсюда видно, что основная структура грамматик
299
операторного предшествования является простой и есте-
естественной, однако выглядит сложной при записи пз-за
общности правил.) Заменяя х целыми числами 2, 3 и 4,
А /К А
X ( + » Т * Р а « В.Р
/\ / /1\ /Т\
X X < Е ) у Ь б
а Арифметическая Ь Синтаксическая с Обща? форма
структура структура правила Z
Рис. 8.14
получаем |- 2* C + 4) -\. Записывая отношения предше-
предшествования под этим выражением, видим, как определя-
определяется порядок вычислений
\- 2 *;
<• •>:
а) выберем чпсло 2 и сохраним его в стеке:
h * ( 3 +,
<• <• <• •>;
б) аналогично удалим 3 из выражения и поместим
в стек:
b * ( + 4 ),
<• <• <• <• •>;
в) с 4 поступим подобным образом:
b * ( + ).
<• <• <• •>;
г) выполним сложение двух верхних элементов в сте-
стеке и результат оставим iau ate; удалим символ +:
b * ( ).
<• << =;
д) отбросим скобки:
Ь * -!>
< >;
300
е) произведем умножение двух верхних элементов
стека, оставляя результат в стеке; удалим символ •:
Ь Ч;
ж) останов из-за отсутствия отношений предшество-
предшествования; ответ находится в стеке.
Конечно, вместо выполнения арифметических опера-
операций мы могли бы породить код и после этого вычислить
выражение — это как раз то, что сделал бы компилятор.
Упражнение 8.5.
1. В проведенном ранее обсуждении привлекаемая се-
семантика принималась само собой разумеющейся, однако
она была тесно переплетена с грамматической структу-
структурой. Показать, что каждая из следующих грамматик яв-
является грамматикой операторного предшествования,
и исследовать, как ее внутренняя семаитика отличается
от обычных соглашений:
Р, - {Е ¦* Е • Т | Т, Т -* Т + Р I Р, Р -+ (Е) | х),
Т-Е\Т, Т-*Т*Р\Р, Р
ГЛАВА 9
КОНЕЧНЫЕ АВТОМАТЫ
Автоматом является устройство, управляющее и кон-
контролирующее само себя. Обычный компьютер с програм-
программой способен пра достаточном запасе эпергии контроли-
контролировать сам себя и, следовательно, является автоматом.
Как таковые, компьютеры изучались много лет, однако
более естественно рассматривать программу и машину,
в которой она содержится, как отдельные компоненты.
Конечно, для выполнения вычислений нам нужна не
только программа, но и машина, на которой эти вычис-
вычисления могут выполняться. Однако здесь мы не стремим-
стремимся приступать к детальпому штечению теории вычисле-
вычислений, поэтому, за исключением тех случаев, где это необ-
необходимо для полноты, мы ограничим наше внимание ма-
математическим описанном некоторых конечных машин.
Несмотря па эти замечания, мы начнем (в § 1) с об-
общего введения, которое показывает границы того, что ма-
машины могут выполнять. Далее (§ 2) мы изучим матема-
математические модели устройств (обычно их малые фрагмен-
фрагменты), а затем (в § 3) связанную с этим алгебру.
§ 1. Общие понятия
Все используемые на практике компьютерные устрой-
устройства ограничены (некоторым образом) количеством ин-
информации, которую они могут храиить,— они конечпы.
Цель данного параграфа — показать, как можно делать
утверждения о программах без утомительного рассмот-
рассмотрения синтаксических деталей; затем мы продемонстри-
продемонстрируем, что даже при отсутствии ограничения па размеры
памяти существуют задачи, которые пельзя решить.
1.1. Универсальная машина. Несмотря на использо-
использование многочисленных различных типов данных в мно-
множеств символов внутри реальных программ, для теорети-
теоретического изучения достаточно ограничиться рассмотрени-
рассмотрением программ, которые действуют на множестве V = N Ц
U {0}, Это равносильно изучению программ, вычисляю*
302
1
IL-L
щих теоретико-числовые функции, которые будут введе-
введены в § 2; наша непосредственная задача — описать идеа-
идеализированный компьютер, позволяющий запоминать эле-
элементы V, с которыми можпо осу- „
ществлять преобразования, и дать '
детальное описание того, как могут г
быть представлены программы для J
машины. *
Предположим, что машина имеет
память, состоящую из неограничен-
неограниченного числа регистров: R\, R2, R3 и
т. д., и что содержание каждого ре- R
гистра Rt есть rt e V. Это можно
изобразить так, как это сделано на
рис. 9.1.
Для более ясного изложения
удобно разрешить использование-
мйогих операцийг действующих лад
регистрами, однако па самом деле необходимы лишь две
операции:
Rn*-Rn+i, Rn*-Rn-i.
Обозначая содержимое регистра п до операции и после
через г„ и гп соответственно, можно описать результаты
выполнения этих операций следующим образом:
Рис. 9.1
/?„-«- Л,, — 1 = гп
\гп — 1, если гп>0,
10, если гп = 0.
Кроме операций, изменяющих значения регистров па-
памяти, необходимо, чтобы машина имела связь с програм-
программой для того, чтобы влиять на ее работу. Необходимой
в этом случае является только одна операция, а именно
та, которая осуществляет сравнение Rn — 0. Однако, как
и прежде, мы будем разрешать более общие формы опе-
операции такого рода. Результат Rn = 0 справедлив тогда и
только тогда, когда г„= 0, и это условие используется
для управления программами. Множество регистров
вместе с описанными выше определениями называется
машиной с неограниченной памятью (МНП).
Программы состоят из конечной совокупности опера-
операций, занумерованных от 1 до некоторого ne.N. Мы не
будем вдаваться в детали, а выведем-более общие заклю-
заключения об этих программах. Поэтому не будем давать фор-
формального определения такой структуры. Рисунков 9.2 и
зоз
9.3 достаточно, чтобы понять, какого рода конструкции
допустимы в ней.
Программа на рис. 9.2 не предназначена для выпол-
выполнения особо разумных вычислений, однако она указывает
Рис. 9.2
вид блок-схемы программы для нашей машины. Заме-
Заметим, что все это может быть записано ве обязательно
в виде рисунка. Например, можно напасать:
1: если #2 "** 0 то перейти к 4 иначе перейти к 2
2: Да *- Да — 1 (ватем перейти к 3)
3: Ri *- Ri + 1 (затем перейти к 4)
4: если Ri — 0 то перейти к 6 иначе перейти к 5
5: Rs ¦*- из — 1 (затем перейти к 2)
6: STOP
На рис. 9.3 представлена более общая форма про-
программы, в которую включены макрокоманды 1и а про-
проверки Tt. Это иогут быть стандартные команды того ти-
типа, который уже определен, или же они могут быть пред-
представлены последовательностью основных команд, кото-
604
рым для удобства чтения даны имепа (подобно подпро-
подпрограмме), детали которых уже где-то определены. Такие
последовательности будем называть макропоследователь-
макропоследовательностями.
Сейчас мы можем описать некоторые из этих макро-
последовательностей, которые обеспечат связь с после-
последующими темами, а также помогут убедить читателя,
Рис. 9.4
что наше небольшое число простых команд на самом де-
деле является достаточно мощным средством.
Пример 1.1. Bt *- О может быть реализовано сле-
следующим фрагментом программы, где метки х, у в z вы-
выбраны так, чтобы не пересекаться с другими командами
в программе:
х: если Rt ¦= 0 то перейти к z иначе перейти к у
у: Д( *- Rt — 1 (затем перейти к х)
z: ?
В терминах блок-схем этот фрагмент программы изобра-
изображен на рис. 9.4.
Пример 1.2. Сейчас, определяя макрокоманду,
удовлетворяющую предыдущему примеру, и включая в
явном виде выражения «go to» («перейти к») только тог-
20 д. кук, Г. Бей» 805
да, когда мы уклоняемся от выполнения команды «go to
next instruction» («перейти к следующей команде»), мы
можем дать раскрытие формулы Rt-*- m (для некоторого
N)
m paa
Ri
Очередное расширение множества команд требует ис-
использования «рабочей памяти». Мы будем предполагать,
что по крайней мере в простейших случаях читатель в
состоянии придумать подходящую стратегию работы с
памятью, и, следовательно, не будем специально упоми-
упоминать о том, как выбираются эти дополнительные регист-
регистры. Случаи, когда количество требуемой памяти неиз-
неизвестно (такие, как стеки и т. п.), будут рассмотрены
ниже *).
Пример 1.3. Используя Rh в качестве рабочего ре-
регистра, мы можем скопировать содержимое Rs в У?(
(Ri ¦*- R)). Делая это, мы уничтожаем содержимое /?,-, ко-
которое в дальнейшем должно быть восстановлено. Следу-
Следующая программа осуществляет требуемые вычисления:
х: if Rt — О then go to у
R}*-R]—l then go to x
y: Ri *- 0
w: il Rh — 0 then go to z
Rk ¦*- Rk — 1 then go to w
z: II
Сейчас мы вернемся к «собственно» арифметическим
вычислениям. Сложение и вычитание строятся непосред-
непосредственно, однако, поскольку в регистрах существуют огра-
*) В дальнейшем будем использовать символы: «go to z» —
«перейти к z»; «if <условие> Ihen ^оператор)»—«если (условие),
то <оператор>»; «else»—«иначе»; «шеп go to z»—«затем перейти
к г».—Примеч. пер.
зов
нпчения па значения величин, операция вычитания
должна быть несколько модифицирована. Подобным же
образом можно выполнить умножение и усеченное де-
деление.
Пример 1.4. Сложение Ri-^R, + Rk, имеющее ре-
результатом п = /•; -| rh, может быть выполнено следую-
следующим образом:
Rt - Rk
х: if /?л = 0 then go to у
Л, +- Л, + 1
Rj *~ Rj — 1 then go to x
V'
Чтобы получить полную программу в терминах основных
команд, мы должны расшифровать макрокоманду «Rj *-
*- Rh», как это было сделано в примере 1.3. С этого вре-
времени мы не будем требовать доказательства таких рас-
расшифровок.
Подобным образом «ограничеппое вычитание» Л4 ¦*-
*-Rt — Rh может быть выполнено как
Л,-Я»
х: И Rj = 0 then go to у
Rt + Rj-l
Rt *- Rt — 1 then go to x
V-
Заметим, что если первоначальные зпачепия /?< и Rk бы-
были такие, что п < гк, то после г, итераций операция Rt ¦*-
— R(— 1 не будет иметь эффекта.
Аналогично /?, ¦«- Rt* Rh может быть представлено как
Л,«-0
R,*-Rk
х: if Ri = 0 then go to у
Я, - It, - 1
Rj 4-Ri + Rt then go to x
y: Ri*-R, В
В больтшистве случаев таким же способом, каким может
быть расширепо мпожество операций над регистрами пу-
путем определения макрокоманд, можно также ввести ко-
20* 307
манды сравнения, которые на первый взгляд оказывают-
оказываются более сложными, однако в действительности строятся
из последовательностей стандартных операций и опера-
операций сравнения.
Пример 1.5. Мы можем записать операцию «if Я<>
>Rk then go to x else go to у» («если Rt>Rk, то перейти
к х; иначе перейти к у») следующим образом:
if R, — 0 then go to у else go to x
Этими операциями условного перехода мы можем до-
дополнить наше множество первоначальных арифметиче-
арифметических операций вместе с операцией деления «R( ¦*- Rt-r-Rk,
где r( = 0, если rk = О». В нашем случае этой операции
соответствует следующий алгоритм:
if Rk = 0 then go to x
y: if Ri<Rk then go to x
Rt*-R, + 1
if Ri = Rk then go to x
Rt *- Ri - Rk then go to у
RR
x: R,^R,
Из менее общего, но необходимого приложения, ко-
которое кратко приведено ниже, следуют две операции,
связанные с точностью усечения при делении целых
чисел.
Пример 1.6. Если ъ?=0, операция «если Rk — де-
делитель Rit то перейти к х; иначе перейти к у» действу-
действует следующим образом:
if Rh = 0 then go to у
Ri *- R, • Rk
if Rj = R( then go to x else go to у
При помощи этой (возможно, несколько странной) опе-
операции и операции сравнения вида Rt — т (оставленной
в качестве упражнения) мы можем проверить, является
ли п простым числом.
308
Ясно, что можно операцию «если Rt простое, то пе-
перейти к х; иначе перейти к у» смоделировать следующим
образом:
if Ri = 0 then go to у
if fit = 1 then go to у
z: if /?j = 1 then go to x
if Ri делитель Rs then go to у
Rj *- Rj — 1 then go to z
Перед последним примером этого параграфа мы дол-
должны упомянуть, как в машине вводятся данные и выво-
выводится результат. Предположим, что мы хотим вычислить
значение теоретико-числовой функции /: V -*¦ Fm. Зна-
Значения пат известны перед началом выполнения соот-
соответствующей программы; поэтому мы можем вначале вы-
выделить п регистров (в которые должны быть загружены
начальные зпачения перед началом выполнения про-
программы) для входных данных и т регистров (которые не
должны быть обязательно отличными от выбранных вна-
вначале) для выходных данных. Когда программа останав-
останавливается, мы предполагаем, что некоторый «внешний
представитель» может выдать «ответы» из соответствую-
соответствующих мест. Это, конечно, разумный путь моделирования
потоков данных в программе, поскольку точно показыва-
показывает взаимодействие операций ввода-вывода. С этими согла-
соглашениями пример 1.7 может рассматриваться или как
полная программа (в которой Rt и Rt выбраны как вход-
пые и выходные регистры), или как схема для подпро-
подпрограммы.
Пример 1.7. Последовательность команд приведен-
приведенных ниже, помещает ге-е простое число в ЛЛ где п явля-
является содержимым Ri\ предполагается, что п не равно
нулю:
(Start)
х: if /?« = 0 then go to у
Rj *¦ R, + 1
z: if R, простое then go to w
R, *- R, + 1 then go to z
309
w: Rk<-Rk — 1 then go to x
y: (stop) /
Сейчас мы объясним наш очевидный интерес к простым
числам.
1.2. Кодирование программ. Программы п. 1.1 могли
работать с элементами из V = N U {0}. Мы должны объяс-
объяснить, как в принципе можно любую программу рассмат-
рассматривать в качестве программы такого типа. Это можно
сделать, описав способы, при помощи которых различные
типы данных могут быть закодированы в элементы из V.
Для этого рассматриваем данные предложения над под-
подходящими алфавитами и, следовательно, почти как по-
постороннее следствие этого процесса получаем также ме-
метод для кодирования предложений на языках програм-
программирования, а именно сами программы.
Основное математическое средство, используемое для
этой цели, это теорема о единственности разложения, из-
известная также как основная теорема арифметики. Эта
теорема устанавливает, что произвольный элемент из V
является или 0, или 1 либо может быть выражен един-
единственным образом как произведение упорядоченных про-
простых чисел. Ясно, что если us V\{0, 1} и
п ~ ?1 * ?2 * . . . * ?i = Si * Si * ... * Sj,
где <7ь ..., g,-, s\, ..., Sj — все простые числа такие, что
?1 < ?2 «?...«??(, Si < S2 < • • • < S),
то i = / и s,t = qh для всех к, i<k<i. Напомним, что
простые числа — это элементы из N, которые делятся
только на 1 и на самих себя.
Полное доказательство этой теоремы несложно, по
его запись существенно отвлекла бы нас от основной за-
задачи. Поэтому вместо доказательства мы предлагаем рас-
рассмотреть конструкцию алгоритма (процедуры/програм-
(процедуры/программы) для выделения упорядоченных простых множителей
<7i, ..., qt для любого данного п. Таким образом, избегая
деталей ввода и вывода, мы можем использовать схему,
представленную на рис. 9.5.
Предположим теперь, что некоторая программа чита-
читает данные, которые состоят из последовательности сим-
символов алфавита А = {х, у, z). Произвольно выбирая по-
порядок ф для элементов из А, можно получить фA) = .г,
ц>B) = у, фC) = г. Если вводимая последовательность i
имеет длину п и выражается как aia2...ccn, где а,ел,
310
тогда существует последовательность
лад {1, 2, 3). Взяь первые п простых чисел р\, ..., рп, мы
можем составить число
II Pi = Pi * *...*Pn ',
назовем его Ф(о^. Пусть по соглашению Ф(Л) = 1.
Чтобы проиллюстрировать использование этой общей
формулы, закодируем строку «xyxz» посредством 1, 2, 3
Рис. 9.5
следующим образом: 2'325'73«=30870. Используя теоре-
теорему о единствецности разложения на простые множители
и тот факт, что Ф~' является биекцией, имеем, что
«a-1/.rz» является единственной строкой над А, которая
дает это значение. Следовательно, применяя Ф, мы можем
811
«обратить» вычисления, чтобы восстановить строку
«xyxzb.
При помощи этой процедуры все строки над А можно
закодировать таким образом, чтобы они имели разные
значения в множестве V. Это в силу упорядоченности,
индуцируемой Z (поскольку 7sZ), влечет упорядочен-
упорядоченность строк из А*. Например, «ху»>«ухъ.
Необходимо отметить два фактора, связанных с этим
методом. Во-первых, поскольку А конечно, в N сущест-
существуют значения, которые не являются кодами какой-либо
строки в А* (например, не существует as А* такого, что
Ф(а) = 25, так как иначе а^А: ф~1E) = о, а такого а не
существует). Во-вторых, поскольку элементы А* явля-
являются неограниченными, то таковыми являются и коды.
(Для любого п е N возьмем простое рт > п и рассмотрим
строку
a = ai... От... a,
такую, что lal >m\ тогда отсюда следует, что
Ф («) - П Pi'4
Рп: >».)
Используя методику, описанную в § 3 гл. 3, преобразу-
преобразуем кодирование Ф так, чтобы получить новое кодирова-
кодирование, которое сохраняет порядок, полученный Ф, но ис-
использует все V. Это один из тех случаев, когда трудно
дать арифметическую формулу для вычисления изменен-
измененных кодов, однако все еще достаточно легко описать спо-
способ их получения.
Очевидно, что новое кодирование Ч' с областью значе-
значений V вадается формулой ai-*-|{{3: Фф)<Ф(а)}|.
В частном случае для рассмотренного в примере множе-
множества А и его упорядочения <р первые десять значений Ф
и V приведены в табл. 9.1.
Таблица 9.1
Строка а
Ф(а)
Л
1
0
2
1
V
4
2
XX
coco
S
8
4
ух
12
5
18
в
24
7
XXX
30
8
36
9
Чтобы получить эти .коды в выполнить процедуры ко-
кодирования, требуется машина, способная понимать и со-
создавать символы вне алфавита D »= {0, 1,2,..., 8, 9), на
котором определены элементы множества V. Для этого
312
необходимо только устройство, позволяющее имитировать
действие ф (и ф~'), некоторым простым способом воздей-
воздействуя на таблицу ввода-вывода; остаток процедуры коди-
кодирования, включающий Ф п Т, можно потом учесть прп
помощи машины с неограниченной памятью.
Следовательно, любой ввод в данную компьютерную
систему может рассматриваться как конечная строка
(взятая из потенциально бесконечного множества строк
над некоторым конечным алфавитом), и если применить
описанный выше процесс к соответствующему алфавиту
А, то эту строку можно преобразовать в единственный
элемент V. Обратная процедура, примененная к получен-
полученному значению из У, дает значение над другим алфа-
алфавитом В.
Следовательно, программа Р: А* -*¦ В* похожа на со-
соответствующую программу Р': V-*¦ V, где
Р: а - Ф (Р' (Ф (а))), Р'\ п~Ф (Р (ф (и))).
Величина используемых значений даже в простых ситуа-
ситуациях делает примеры непригодными, однако связанные
[гн
[гну
Рис. 9.6
диаграммы па рис. 9.6 восстанавливают сущность пропу-
пропущенных этапов,
813
Переходы, включающие детальную спецификацию Р',
являются сложными и не обязательно соответствуют Р
«очевидным» образом. Однако если Р вычислимо, то и
Р' вычислимо.
Как отмечалось выше, мы можем также применять
такие же кодирующие процедуры к программам, и, следо-
следовательно, расширив Ч? таким образом, чтобы можно было
игнорировать семантически неверные программы так же,
как и программы, включающие синтаксические ограни-
ограничения, можно перечислить все программы для данной
системы, использующей числа из V. Мы предполагаем,
что для того, чтобы программа превосходила любое за-
заданное в V число, к ней можно добавить неограничеппое
множество кодов, которые содержат произвольно много
нулевых утверждений, таких, как Rt ¦*- Rt. Однако в
большинстве языков программирования существует мно-
много избыточности в синтаксисе; поэтому в лучшем случае
мы будем обращать внимание только на лексические зна-
знаки. Прежде чем пытаться сделать замечания общего ха-
характера, рассмотрим, что можно сделать с простым язы-
языком, который использовался ранее в машине с неограни-
неограниченной памятью. Существует четыре типа команд:
х: Rt ¦<- Л( + 1 then go to у
х: Ri*-Ri— i then go to у
x\ if Ri = 0 then go to у else go to z
x'. stop
(Без потери общности мы можем предполагать, что всо
программы начинаются с команды, помеченной индек-
индексом 1.) Все, что мы должны знать из команды х,— это,
какой тип операции должен выполняться, на каком ре-
регистре и какая команда выполняется следующей. Для
того чтобы можпо было использовать ту же самую схему
для всех команд, введем формат
(тип, регистр, правильный выход, неправильный выходJ.
Обозначая комапды «останов» («stop»), «больше», «мень-
«меньше» и «равно нулю» через 0, 1, 2 и 3 соответственно,
получаем Ф-уровневое кодирование типичных утвержде-
утверждений, как показано ниже:
Ф (R, *-Rt+ I then go to у) - г'З'б»?»
Ф (Я, - R( - 1 then go to у) = 223'5*7»
Ф(П Л, = 0 then go to у else go to г) = 233'5»7*
314
Поэтому команда Ф содержит всю информацию, необхо-
необходимую для ее выполнения или, если необходимо, для
перехода к следующему шагу выполпения программы.
Поскольку все строки в А* конечны, а блок-схема
программы для машины с бесконечной памятью сверху
не ограничена, то каждая отдельная программа имеет п
утверждений, rsN. Тогда можно распространить Ф на
программы следующим образом:
Ф(prog)-IP' .
1=1
где «prog» состоит из п помеченных утверждений, из ко-
которых i-M является s4.
Из Ф(ргод) можно получить Ф^) выделением ком-
компоненты ри и, следовательно, разлагая это- значение на
простые сомножители, мы можем узнать детали утверж-
утверждения, помеченного номером i.
Используя подходящую «урезающую» функцию W,
мы получаем кодирование, которое является биекцией
между ?Р, множеством всех программ для машины с бес-
бесконечной памятью и V.
1.3. Проблема останова. Теперь мы можем доказать,
что конструкции некоторых общих программ невозмож-
невозможны: не только потому, что мы не находим решения, но
и потому, что решенпе может не существовать. Формаль-
Формальные доказательства ограничим рассмотрением двух ос-
основных случаев. Первое из доказательств получим, ис-
исходя из начальных принципов, а затем покажем, как
второе выводится из первого, иллюстрируя, таким обра-
образом, общее использование техники сведения одних задач
к другим. После этого сформулируем перечень проблем,
относительно которых будет показано, что они неразре-
неразрешимы подобным образом.
Строго говоря, все утверждения, приведенные ниже,
относятся к программам па машине с бесконечной па-
памятью со специальным кодированием функций Чг1 и Ч'г.
Однако, задав произвольную «универсальную» машину
и подходящий язык программирования, мы в состоянии
построить адекватные кодирующие функции, и, следова-
следовательно, полученные результаты применимы и в общем
случае.
Первой задачей, относительно которой мы докажем
ее неразрешимость, является задача самоприменимости.
Теорема. Для машины с бесконечной памятью не
существует программы, которая для чюбой заданной про-
315
ераммы А при ее кодировании a*=4tl(A) будет оста-'
навливатъся с выходным значением 0, если А(а) оста-
останавливается (т. е. программа А останавливается, если
входное значение равно а), и с выходным значением 1,
если А (а) не останавливается.
Доказательство. Будем строить доказательство
от противного. Предположим, что такая программа су-
существует; назовем ее В. Итак, В (а) останавливается с
результатом, равным 0, если а приводит программу А
.... к останову, а с результатом, равным 1,
(START ^ если а не ПРИВ°ДИТ к останову А.
J Изменим программу В следующим об-
образом. Заменим команду останова услов-
| 1 1 ной петлей, так что, если выходной ре-
' I гистр имеет значение 0, мы обходим эту
команду; в противном случае — останов.
Назовем эту программу С (рис. 9.7). Име-
Имеем следующее: С{х) останавливается (и
имеет то же самое выходное значение,
что и B(z)) тогда и только тогда, когда
выходное значение равно 1.
Рассматривая С при входном значении
с==Чг(С), получаем противоречие: так
Рис. 9.7 как ^"(с) останавливается тогда и только
тогда, когда С(с) = 5(с)=1, то 5(с)=1
тогда и только тогда, когда С (с) не останавливается. От-
Отсюда следует, что С не может существовать, а поэтому и
В не существует. /
Предыдущее доказательство по стилю подобно тому,
которое использовалось, чтобы опровергнуть существова-
существование множества Рассела в примере 1.1 гл. 1. Кажется, что
оно но^ит тривиальный характер, однако, подобно многим
другим кратким математическим рассуждениям, является
достаточно тонким. Следует на это обратить внимание
перед тем, как использовать этот факт при доказательст-
доказательстве более общего результата — неразрешимости проблемы
останова.
Теорема. Для машины с бесконечной памятью не
существует программы, которая по произвольным входным
данным, представляющим программу и ее данные, будет
определять, останавливается программа на этих данных
или нет.
Доказательство. Покажем, что если бы такая
программа существовала, то мы могли бы путем выбора
правильных входных данных решить проблему самопрд-i
316
менимости. Поскольку последнее невозможно, то отсюда
будет следовать, что решение проблемы останова также
невозможно.
Очевидно, что программа требует ввода двух сортов
данных: a(=4fi(J4)) —кода программы А и а:(==Чг2(Х)),
где X — входные данные для А. Это может быть закоди-
закодировано обычным путем — с использованием двух различ-
различных простых чисел р и q. Пусть входные данные будут
p"qz, и предположим, что существует программа для ре-
решения нашей задачи; назовем ее В. Тогда B(p"qx) оста-
останавливается с результатом 1, если А(Х) останавливается,
и останавливается с результатом 0, если А (X) не оста-
останавливается. В этом случае из В можно создать новую
программу С, добавляя к началу В последовательность
команд, которые превращают содержимое i-ro входного
элемента в (pq)*. Тогда
t а а\ 1^' еслп А (а) останавливается,
w — \Р Я ) — ^ если ^ ^ не останавливается#
Следовательно, С решает проблему самоприменимости,
о которой мы знаем, что она неразрешима. Следовательно,
С не существует, а поэтому не существует и В. II
Проблема останова является классическим результа-
результатом о неразрешимости в теории компьютеров. Приведен-
Приведенное здесь доказательство использует общую технику све-
сведения одной задачи к другой. Далее показывается, что
первая задача неразрешима, поскольку если бы это было
не так, то была бы разрешима и другая задача, о которой
известно, что она неразрешима.
Используя этот принцип (и соответствующие конст-
конструкции, детали которых здесь опускаются), можно пока-
показать, что многие другие проблемы также неразрешимы.
В частности, неразрешимы следующие проблемы:
а) останавливается или нет произвольная программа,
если входное значение равно 0;
б) останавливается или нет произвольная программа
при любых входных данных;
в) выполнено ли равенство L(C)=0 для произволь-
произвольной контекстно-зависимой грамматики G;
г) выполнено ли равенство L(G\H L(G%) = 0,
где G\ в G2 — произвольные контекстно-свободные грам-
грамматики;
д) выполнено ли равенство L(G)—T*, где G = (iV, T,
Р, S) — произвольная контекстно-свободная грамматика;
317
е) выполнено ли равенство L(Gi) = Z/(G2), где G\ n
Gi — произвольные контекстно-свободные грамматики;
ж) является ли произвольная контекстно-свободная
грамматика неоднозначной.
1.4. «Расширенная» машина. Насколько реалистичной
является машина с бесконечной памятью в качестве мо-
модели компьютера? Память такой машины, очевидно, пре-
превосходит память любой существующей машины., которая
подвергается ограничениям как на число .регистров, так
и на значения, которые могут содержаться в каждом ре-
регистре. Однако эта идеализация в пределах машины с
неограниченной памятью расширяет, а пе ограничивает
возможности машины. Существуют ли аспекты в компью-
компьютерных системах, которые не могут быть смоделированы
на машине с неограниченной памятью?
Мы утверждаем, что пет. Хотя формально мы не мо-
можем доказать это высказывание, остановимся на основных
моментах такой «расширенной» машины, которая может
моделировать все нужные свойства, хотя в качестве аб-
абстрактной модели она применяется редко.
Нас будут интересовать следующие свойства:
а) большой набор операций;
б) более широкий набор внешних типов данных;
в) массивы;
г) стеки;
д) более сильные команды управления;
е) общий механизм управления;
ж) рекурсия.
В пп. 1.1 и 1.2 мы показали, как в случае а) можно
добавить арифметические операции к множеству команд,
а в случае б), добавляя простые периферийные устрой-
устройства (для того чтобы иметь возможность работать с сим-
символами, которых пет в машине с неограниченной па-
памятью), можно расширить диапазон представлений
входных и выходных данных над произвольным алфа-
алфавитом.
Остановимся па работе с массивами. Предположим, что
нам необходим массив с десятью компонентами А [1], ...
..., А [10] и что содержимое этих регистров суть а\,..., аю.
С помощью методики, которая уже использовалась, мы
можем сохранить эти значения, вводя величину
которую затем можно заподшить в одном регистре. Мы
318
уже описывали процедуру выделения каждого а< из а.
Этот метод не зависит от границы массива и поэтому
переносится иа случай работы со стеками. В стеках мож-
можно хранить результаты промежуточных вычислений, не
требуя существенно больше регистров. С помощью подхо-
подходящего механизма управления (см. ниже) мы можем так-
также поместить в стек адреса возврата из подпрограмм.
Любая программа на машине с неограниченной па-
памятью конечна, и строки программы могут быть прону-
пронумерованы (помечены) числами от 1 до п, п eN. В контек-
контексте блок-схемы программы мы можем сконструировать в
случае е) «вычисление
goto», используя таб-
табличную технику, дан-
данную выше, для того, что-
чтобы получить «go to(Rk)»,
как указано на рис. 9.8.
Используя схему
прямого кодирования
для программ Ф (а не
Чг), мы можем закоди-
закодировать всю программу
одним значением, кото-
которое запоминается в ре-
регистре. Разложение на
простые множители за-
затем может использо-
использоваться для выделения
кода «следующего ут-
утверждения». Это моде- рис
лирует свойство ж), а
вместе с использованием стеков дает возможность ре-
рекурсии з).
Следовательно, используя машину с неограниченной
памятью, можно произвести «расширение» путем добав-
добавления этих свойств. Однако в действительности такие
расширения носят лишь внешний характер, а результи-
результирующая система может быть смоделирована с использо-
ванием другой машины с неограниченной памятью, у ко-
которой блок-схема программы состоит из простых команд
увеличения, уменьшения и «равенства нулю».
Упражнение 9.1.
1. Построить на машине с неограниченной памятью
блок-схему программы, осуществляющей проверку
«Л( = т».
319
2. Спроектировать машину с неограниченной памятью,
которая, если дана программа, закодированная в До, бу-
будет выполнять эту программу. (За основу взять кодирую-
кодирующую схему из п. 1.2.)
§ 2. Конечные автоматы
Уже достаточно много сказано об универсальных ма-
машинах (их свойствах и ограничениях на эти свойства),
которые могут вычислять все, что вычисляется, и, следо-
следовательно, проводя рассуждения в обратном порядке, по-
получим, что любая вычислительная проблема, которая не-
неразрешима в такой общей системе, будет неразрешима и
в любой другой системе. Однако возникает вопрос: как это
связано с реальными компьютерами? Основная пробле-
проблема — это конечность памяти реальной машины (правда,
и ее можно несколько сгладить, используя машину с не-
неограниченной памятью, описанную в п. 1.1). Машина с
неограниченной памятью состояла из неограниченного
числа регистров, каждый из которых имел возможность
содержать любое число из множества V. Хотя, как это
следует из построений п. 1.4, мы можем обменять «ко-
«короткую и широкую» память (имеющую несколько реги-
регистров, каждый с большой емкостью) на «длинную и тон-
тонкую» память (в которой емкость каждого регистра умень-
уменьшена, зато число регистров увеличено), существенное
ограничение состоит в конечности числа различных кон-
конфигураций или состоянии, которые может принимать па-
память. Такое ограничение вызвано физическими ограниче-
ограничениями. Это понятие формирует основу нашей математи-
математической модели конечных машин.
2.1. Детерминированные машины. В соответствия с
опытом электропного машиностроения (низким уровнем
аппаратуры при построении элементов типа «не и» и т. п.,
микропроцессорных систем или универсальных цифровых
машин) наша первая модель воплощает в себе понятие
детерминизма, т. е. если некоторая ситуация достигается
более одного раза, то в каждом случае устройство ведет
себя одинаковым образом. Начнем с формального опи-
описания.
Определение. Конечным (детерминированным) ав-
автоматом М называется алгебраическая структура
M = (Q, X,t, go, F,p),
320
где Q — непустое множество состояний; 2—конечный
входной алфавит; t — отображение Q X 2 -* Q, называе-
называемое переходом (или функцией переходов); qo^Q—на-
qo^Q—начальное состояние; Fs $, F — множество заключительных
состояний (или принимающих состояний); р — функция
Q X 2 -*¦ 2, называемая функцией печати (или функцией
выходов).
(В некоторых случаях полезно модифицировать функ-
функцию выходов таким образом, чтобы она имела вид р: QX
X 2 -*¦ 2', где 2' — некоторый другой алфавит.)
Идея состоит в том, что мы начинаем из состояния до,
и если Qi^t(qo, s), то под действием входного символа s
автомат переходит в состояние gi. Аналогично, если
(go, s)s=Dp, то, когда автомат перейдет в состояние (go, s),
па выходе появится p(qo, s). Продолжая таким образом
и читая каждый раз очередной входной символ, будем пе-
переходить от одного состояния к следующему, пока или
не прочитаем символ, которого нет в 2, или входные дан-
данные будут исчерпаны — в этих случаях обработка прекра-
прекращается.
Входная последовательность называется представпмой
(автоматом М), если состояние, в которое перешел авто-
автомат М, принадлежит F. Для наглядности рассмотрим
пример. Однако прежде опишем представление М в виде
диаграммы.
Во-первых, мы представим элементы Q вершинами
ориентированного графа, которые изображаются малень-
маленькими кругами; имя состояния указывается внутри круга.
Элементы из F имеют дополнительные круги, начерчен-
начерченные вокруг маленьких кругов. Если ((qt, Sj), qk)*=t, то
проведем ориентированное ребро от д( к qk и пометим его
символом Sj. Далее, если ((qt, s,), s,)^p, то пометим реб-
ребро через Sji si. К одному и тому же ребру может быть
добавлено несколько меток. Наконец, определим до стрел-
стрелкой, входящей в до.
Пример 2.1. Рассмотрим машину, изображенную на
рис. 9.9. Предположим, что мы читаем строку «abbaa».
Ребра, обозначающие функции перехода, заставляют ма-
машину проходить через состояния qo, q\, q%, q\, g0 и gi в
указанном порядке. Легко впдеть, что, начиная с до, под
действием ? получаем
(д0, а) «¦ qv (qv b) -> q2, (g2, b) -> qlt
21 Д. Кук, Г. Б?«з 321
Однако q\ пе является заключительным состоянием, и по-
поэтому этот вход не подходит. Проверка диаграммы пока-
показывает, что строками, представимыми этой машиной, яв-
являются только те строки над алфавитом {а, Ь), в которых
имеется четное число символов а и четное число симво-
символов Ъ. У этой машины нет явного выхода; требуемая ин-
информация может быть извлечена из результирующего
состояния только после останова машины. /
Следующие два примера относятся к арифметическому
«оборудованию» и фактически порождают непосредствен-
непосредственный входной результат.
Пример 2.2. Машина, изображенная на рис. 9.10
для пары строк над {0, 1}, вычисляет и выводит их сум-
сумму. Входные данные начинаются с битов с наименьшими
@,)
it,О)-1
(ОГО):О
(О,H
(Г,0):0
И,0 it
Рис. 9.10
значениями, и пары читаются справа налево. По данным
двум и-разрядным числам эта машина вычисляет их
n-разрядную сумму. Однако она пе распознает условий
переполнения и не работает с отрицательными числами. II
Проверяя свойства функции выхода (функция выхода
имеет вид <?Х{0, I}2-»- @, 1}), полезно вспомнить факты,
322
касающиеся двоичной арифметики и описанные в § 3
гл. 4. В более сложной модели можно учнтылать условия,
при которых возможны ошибки при двоичном сложении.
Пример 2.3. Машина, изображенная на рис. 9.11,
также осуществляет двоичное сложение тем же самым
@,0):0
@,1) :
@,0):
@,1 У
A.0У-
@,1): О
1,0): О
@,1): О
11,0):О
A,1)-1
Рис. 9.11
способом, что и в предыдущем случае, за исключением
того, что она содержит два дополнительных состояния q%
и <7з, которые проверяют наличие ошибок, связанных с
внесением в знаковый бит и вынесением из знакового би-
бита соответственно. Заключительные состояния <7о и qx
обозначают выходы, в которых либо произошли оба эти
переноса одновременно, либо не произошел ни один из
них. Следовательно, эти выходы являются арифметически
правильными. /
Эти примеры показывают, что можно выполнить не-
некоторые полезные преобразования и вычисления, однако
остается открытым вопрос: насколько «сильными» явля-
являются конечные автоматы? В ответе на этот вопрос встре-
встречаются две точки зрения. Первая, хотя и нетипичная,
заключается в следующем: можно заметить, что исполь-
использованные в примерах алфавиты основывались лишь на
двух символах. Мы можем использовать любой конечный
алфавит, однако, как отмечалось в § 1 гл. 8, алфавита
размерности 2 всегда достаточно.
Вторая точка зрения заключается в том, что общая
доступная память в данное время в определенном компью-
компьютере является конечной. Если она содержит п битов, то
существует ровно 2" конечных состояний, в которых
21* 323
память может находиться. Это число может быть боль-
большим, но оно всегда конечно (см. упражнение 9.2), и, сле-
следовательно, мы имеем конечную машину.
2.2. Недетерминированные машины. Рассмотрим с ма-
математической точки зрения, что могут делать эти аб-
абстрактные машины. Чтобы упростить дело, в определении,
данном выше, будем игнорировать функцию р. Следова-
Следовательно, мы будем иметь дело только с устройствами, име-
имеющими конечное число состояний; будем их для кратко-
краткости называть КР (конечными распознавателями или ак-
акцепторами). В дальнейшем будет удобно расширить
область значений функции переходов t (см. определение)
так, чтобы выполнялось условие
t:
Следовательно, из данного состояния под действием за-
заданных входных значений машина может иметь выбор,
куда идти дальше. Это ничего не добавляет к определе-
определению, однако обеспечивает простой способ конструирова-
конструирования КР, который будет активно использоваться в этом
параграфе. Машины такого тииа называют недетермини-
недетерминированными КР.
Чтобы еще более прояснить, дело для заданного КР
М определим множество строк, представимых машиной М
(обозначим это множество через А(М)), как указано
ниже.
Пусть M = (Q, 2, t, qo, F) и seE*. Запишем s в виде
s — S\S2...sn и определим множество T(s) индукцией по
длине слова s следующим образом:
4q,sh),
где a — S\...sk-i для всех к, 1<к<п. Таким образом,
Т($) — это множество всех заключительных состояний М,
которые могут быть достигнуты под действием входной
последовательности s. Если f(s)flF = 0, то слово s пред-
ставимо; поэтому множество строк, представимых маши-
машиной Л/, имеет вид
A(M)~{s: T(s)UF?*0}.
Недетерминированные КР полезны тем, что они упро-
упрощают задачу построения сложных машин. Существенным
является то, что нам хотелось бы иметь возможность со-
собрать машины вместе таким образом, чтобы не было нуж-
нужды, по крайней мере на первом этапе, касаться вопроса,
324
является или нет результат перехода функцией или от-
отношением над (QXI,)XQ. (Напомним, что функция
Q X 2 -*¦ !?(Q) соответствует отношению QX 2 -*¦ Q.)
Введение недетерминированности не увеличивает по-
потенциала КР. От недетерминированной машины всегда
можно перейти к детерминированной, как будет показано
в следующей теореме.
Теорема. Для любого недетерминированного КР ДЛ
существует детерминированный КР M% такой, что
Доказательство. Дадим вначале общую схему
доказательства. Пусть
Мх = (<?!, 2lf tv q0, F,), a Mt = (<?2, S2, ta, q'o, Fa).
Установим вначале, что Q2 — ^(Qi) (в общем случае есо
эти состояния нам будут не нужны) и 22 = 2i. Для это-
этого, начиная с qo *= Qu рассмотрим множество всех состоя-
состояний в t{qo, Si) (для Sie2|) и назовем это множество об-
образом (><}о: si) функции h; т. е. мы переводим различные
возможности машины Л/i в единственное состояние ма-
машины Л/г. Предположим, что далее мы читаем символ sz.
В Mi это могло бы вызвать перевод состояния fi(<7o» S\)
в состояние из множества t\(t\(qo, si), S2). Множество всех
состояний, полученных таким образом, сейчас дает един-
единственное состояние в А/г, получающееся в результате при-
применения h к образу из (go> si) и S2. Таким образом, мы
приходим к конструкции переходов между состояния-
состояниями в (?г.
Так как @i конечно, то копечпо и Qz\ следовательно,
необходимо вернуться к ранее построенным состояниям,
и, таким образом, процесс в конце концов оборвется. Если
одно из «выбранных» состояний в @i было в Fi, то со-
состояние в @2 является заключительным и, следовательно
лежит в F2.
Перейдем к подробному доказательству. В соответст~
вии с описанной выше конструкцией q0 = {qo}n
f
h h)*—\ U
n
(дМзшЧ
{giu •••» It) e^2 тогда и только тогда, когда
qih s Fi при некотором к, 1 ^ А; < /.
Возвращаясь назад к определению множества А(М)
для данной машины Mi, мы ыожем расширить U и ?г,
325
чтобы получить Т\ и Т% так, как это показано ниже;
«*) = U М«.**).
(Л) = {^1, Г, (с**)- U *i(9f,**)
3()
где Ti(o) = {q) и o = Si...s»_i.
Поскольку Л(Л/)= (s: 7(s) Л F ?= 0} я существует есте-
естественное соответствие между fr\ и Fz, то мы должны лишь
продемонстрировать такое же соответствие между Т\ (s)
и T<i(s) для любого s; т. е. {..., q(, ...) *=*Ti(s) тогда и
только тогда, когда {{..., q,, ...}} = T2(s). Сделаем это
индукцией по длине s.
Если Ы — 0, то s = Л, откуда
Предположим теперь, что соответствие имеет место
для всех строк о: lol^fc—1, и рассмотрим строку ash.
По предположению индукции
{..., qt, ...} = Т\ (о) тогда и только тогда, когда
{{..., д„ ...}} = Г2(о).
Однако тогда, если q,<=t\(qi, sk), то отсюда следует, что
qi^T^aSn) и (по определению tz)
Из определения Гг и h следует, что все элементы из
^(os,,) должпы выводиться таким же образом; ноэтому
{.. .,qt, ...} = Т\ (ash) тогда и только тогда, когда
{{..., qt, ...}} = 7*2@*»).
Следовательно, 7\(s) для любого s^S* «соответствует»
^(s), и поэтому
Приведенная выше аргументация была достаточно
сложной и включала некоторое сомнительное (однако
строго определенное) понятие «соответствие», которое под-
подразумевало уровень вложения включаемых множеств.
В частных примерах мы можем обойти это путем введе-
введения подходящих имен для результирующих состояний в
детерминированной машине Л/2.
Как будет показано в последующем примере, построе-
построение Мч из М\ является непосредственный, однако, чтобы
сохранить математическую строгость, напомним вначале
320
общепринятое соглашение, связанное с функциями. В си-
силу используемых построений такое соглашение было бы
здесь неуместным, однако краткое напоминание об этой
погрешности послужит объяснением, «откуда берутся не-
некоторые множества».
Пусть задана функция /: А -*¦ В такая, что /: х~у.
Мы должны были бы писать j(x)={y), однако часто за-
запись сводится к f(x) = y.
Аналогично обычно детерминированный перенос обо-
обозначаем как
t: QX2-+Q,
где
t- {Чи sI-^-' tfa, s)*=*qi.
Однако, когда мы имеем t: QXH-* &(Q) (как в М\ и
Л/г), то мы должны заключать множества в скобки даже
тогда, когда \t(qit s) I = 1, и писать t(qi, s) = {qj). Перей-
Перейдем к примеру.
Пример 2.4. Возьмем М\ таким, как указано на
рис. 9.12, а. Тогда
U{qo, x)={qu ?2>
п q\ e F\] следовательно, получаем iq\, <7г) в ^2- Ана-
Аналогично
ti{qu x)={q0}, ti{q2, x)={q2, qs);
следовательно,
h{iq\, ?2>, x) = iqo, q2, ?з> в М2 и т. д.
Окончательно получаем ситуацию, изображенную на
рис. 9.12,6. Тогда перенумерация дает нам рис. 9.12, с. II
С этого момента мы не будем выяснять, какие маши-
машины рассматриваются — детерминированные или нет; они
всегда могут рассматриваться как детерминированные.
2.3. Составные машины. Сейчас мы в состоянии опи-
описать, как заданную совокупность КР можно «собрать вме-
вместе» для Tofo, чтобы получить некоторые корректно опре-
определенные множества строк. Основные свойства даны в
виде предложения, однако вместо формальных доказа-
доказательств мы дадим лишь описание включаемых в доказа-
доказательство построений.
Предложение. По заданным машинам
Л/, - ((?!, 2, *,, q, Fu), М2 = (<?2l S, «2, р, Ft)
327
мы можем построить машины Мз, ..., М$ такие, что
328
Построение Л/3. Машина М3 получается из М{ заменой
множества F\ заключительных состояпий на множество
Qi\F\.. Следовательно,
M3 = (QU 2, tu q, ^,VP,).
Чтобы получить М4, возьмем <?4 = Q\ X Q2, возможно,
с некоторыми подходящими переобозначениями. Пусть
г = (<7. Р)- Определим t* как
ti- ((?i. Pi), s) " (hDi, s), h(Pi, s))t
и множество
^4 = {(?,-, A): gfieFb fteF2!.
Тогда
Л/4 = (^4, S, f4, r, F4) (см. пример 2.5).
Построение М$ следует из Мг и Д/3, так как
Л (М2) \А (Mi) = Л (Л/2) П (Е*\Л (Л/,)) = А (М2) П Л (Д/3).
Построение Л/6 проводится подобно Л/4. Имеем ^а —
= Qh t6 = f4, однако
^е = ((?(, />j): д^Л или p,^F2}.
Тогда
M6=(<?6, 2, «в, г, Fe).
При построении Л/7 используется идея присоединения
выхода из М[ к входу М2. Однако при этом следует быть
внимательными, чтобы не проделать лишний шаг при
движении от М\ к М2. Итак, возьмем Qi = Q\\ 1^2 (разъ-
(разъединяющее объединение | | изменяет названия так, что
?>i и Q2 не имеют общих состояний, и использует (^ U
U Q2), множество
и добавим переходы от элементов F\ к другим состояни-
состояниям М2, а именно
t7=-*ilHaU{((grfl *). Pi), гДе ?<efb fte'«(P. s)}-
Тогда
M7 = (Q7, 2, tu q, F7).
Построение Ms проводится аналогично. Сначала не-
необходимо позаботиться о том, чтобы А°(М{)=0 было
329
представимо. Для этого добавим новое начальное состоя-
состояние и (u<?Q\) таким образом, чтобы выполнялись усло-
условия Qs — Qi U {и), F8 = F[U {и}, a ta расширим (так же,
как и h) следующим образом:
_ [h U {(("• s)' ?;). Qi е h (q, s), S e= 2),
8 ~ Ui U №u *), q), t8 (qh s) eFi.ee 2}.
Тогда
Пример 2.5. На рис. 9.13—9.15 даются последова-
последовательность диаграмм состояний для машин М\ и М2 и ре-
результирующие составные машины М3, ..., М&, которые
были построены выше. Заметим, что некоторые из этих
машин являются недетерминированными, однако от не-
недетерминированности можно избавиться при помощи пре-
предыдущих результатов. II
Построения, включающие объединение, конкатенацию
и замыкание (операция «звездочка»), обеспечивают осно-
основу алгебраических систем для описания множеств, пред-
ставимых конечными распознавателями. Эта алгебра будет
обсуждаться в § 3, а в оставшейся части этого параграфа
обратим внимание на моделирование реальных компью-
компьютеров.
2.4. Моделирование «реальных» компьютеров. Как
уже отмечалось, если данный компьютер имеет память,
состоящую из п битов, то для того, чтобы смоделировать
его поведение, вообще говоря, необходим конечный авто-
автомат с 2" состояниями. Пусть начальное состояние имеет
такую конфигурацию, что программа и значения данных
находятся в «ядре». Тогда не существует внешних сти-
стимулов, которые могли бы дать начало последовательно-
последовательности переходов. Однако рассмотрение машины в несколько
другом виде может привести к выполнению команд, ис-
использующих конечное число (уже определенных) состоя-
состояний машины.
Предположим, что память состоит из т Z-битиых
слов; тогда п = т*1. Теперь отделим программный ука-
указатель (называемый также программным счетчиком или
указателем следующей команды) от оставшейся части
машины; получим машину с n' — l*(m — i) битами па-
памяти. (Для простоты предполагается, что указатель имеет
ту же длину, что и другие компоненты памяти.) Теперь
330
Рис. 9.13
можно программный указатель рассматривать после каж-
каждого изменения состояния и его значение использовать
м5
м?
для того, чтобы осуществлять очередной переход. Таким
образом, функция перехода имеет вид
P. QXP-+QXP,
где t: (qa, рь) •-»¦ (<?е, Pd) соответствует значению указате-
указателя рь, что означаем: выделить команду из состояния да
так, чтобы перевести машину в состояние qc, а зиаадиие
332
рь в программном указателе заменить на pd. (Здесь удоб-
удобно рассматривать команду как действие, частично осу-
осуществляемое программным обеспечением, а частично —
аппаратным методом. В этой модели мы не делаем раз-
различия между ними; на практике бывает, что програм-
программное обеспечение — это просто начальные дапные, кото-
которые управляют аппаратными процессами.)
Обычно программы начинают работу с программного
указателя, установленного на определенное значение.
Начиная с этого значения, все последующие значения
порождаются автоматически при помощи описанного вы-
выше процесса до тех пор, пока не выполнится команда
останова.
Конечно, не все 2' значений, которые могут содер-
содержаться в программном указателе, должны быть верны-
верными. Часто 2' может быть больше т, и, следовательно,
2' — т значений будут неправильными адресами и будут
вызывать ошибку, приводящую к останову.
Число правильных значений, которые может прини-
принимать программный указатель, определяет число перехо-
переходов, которые могут быть нарисованы в виде стрелок из
каждого состояния. Однако это не ограничивает число
состояний, которое равно 2" .
При отсутствии дополнительной информации о моде-
моделируемой системе мы можем сказать о ней довольно ма-
мало, однако на один момент следует обратить внимание.
Если построенный нами конечный автомат останавлива-
останавливается за «короткое» время или под воздействием команды
останова, или из-за полученного неправильного значения
указателя, то результат известен. Однако если машина
333
продолжает считать в течение длительного промежутка
времени, то встает вопрос: остановится ли она когда-ни-
когда-нибудь и получим ли мы результат? Поскольку машина
конечна (и, следовательно, имеет ограниченную память),
то эта задача разрешима, однако неизвестно, как долго
ждать результат. В силу способа построения машины
пара (<7, р), являющаяся указателем состояния, единст-
единственным образом определяет последовательность состоя-
состояний, которые должны последовать за данным состоянием,
и, следовательно, повторение любой данной пары подра-
подразумевает бесконечный цикл. Поэтому, чтобы гарантиро-
гарантировать, что последовательность вычислений никогда не
остановится, мы должны обеспечить, чтобы она пересе-
пересекала заданную дугу перехода дважды. Все это требует
достаточно много времени, так как необходимо выпол-
выполнить 2"' # т — 2(*(т~1) • т команд. Даже при достаточно
малых значениях т ж I число операций очень велико,
и поэтому реальное время их выполнения требует десят-
десятков, сотен и даже тысяч лет.
Урок, который мы должны извлечь из рассмотрения
этого упражнения, заключается в том, что практически
невозможно проверить корректность программы разум-
разумных размеров, используя тестовые данные. Требуется
слишком много времени для выполнения всех прогонов
программы. Такие тестовые прогоны могут только нахо-
находить ошибки.
Упражнение 9.2.
1. Построить конечный автомат, который будет рас-
распознавать четные числа, записанные в двоичной форме
и читаемые слева направо.
2. Построить конечный автомат с входным алфавитом
{а, Ъ), который останавливается в заключительном со-
состоянии тогда и только тогда, когда входные данные не
содержат рядом двух соседних элементов а и двух со-
соседних элементов Ъ.
3. Показать невозможность построения конечного ав-
автомата, на вход которого поступают только строки над
алфавитом {а, Ы, и только те из них являются предста-
вимыми, которые и,меют равное количество символов
а и Ъ.
4. Построить (детерминированный) конечный авто-
автомат, для которого представимыми являются только стро-
строки над @, 1), состоящие из чередующихся единиц и ну-
нулей, следующих за чередующимися парами из единиц и
нулей.
334
5. Придумать конечный автомат, способный распозна-
распознавать десятичные числа, записанные в виде
±dd*. d*E±dd,
где d s {0, 1,2,..., 9).
§ 3. Регулярная алгебра
Способы комбинирования конечных распознавателей
могут использоваться для проверки аксиом множеств, из
которых могут развиваться алгебраические системы.
Классическая система, известная как регулярная алгеб-
алгебра, основана на трех операциях — объединении, пересе-
пересечении и конкатенации, определенных на множестве
строк. Уравнения в алгебре могут точно определять не-
некоторые множества строк; эти множества являются ре-
решением уравнений (п. 3.1). Результаты, вытекающие из
решений, имеют непосредственное применение к аспек-
аспектам теории языков (п. 3.2).
3.1. Выражения и уравнения. Перед тем как дать
формальное определение, мы введем две копстанты внут-
внутри системы. Существует множество строк 0 и {Л}, кото-
которые обозначим символами 0 и 1 соответственно. Мы обо-
обосновываем их использование изображением конечных
распознавателей соответственно на рис. 9.16, а н Ъ.
Рис. 9.16
Определение. Пусть X — множество строк, пред-
ставимое конечным распознавателем. Гогда X называется
регулярным выражением. Если X и У обозначают мно-
множества строк, представимых двумя определенными маши-
машинами, то (в силу определения построения конечных рас-
распознавателей) X U У (далее будем писать Х+ Y), X* и
ХУ также являются регулярными выражениями.
Разрешенные конструкции составных конечных автома-
автоматов предполагают следующие аксиомы для работы с про-
произвольными регулярными выражениями А, В и С:
3) А + А =4; 4) А + 0 = А;
335
5) A(BC) = (AB)C; 6) A\ = A = 14;
7) 40-0 = 04; 8) Л E + C) = ЛВ + AC;
9) (Л+В)С = 4Я + еС; 10) 0* = l;
11) A*=A+A*; 12) D*)* =4*.
Такую алгебраическую систему называют регулярной ал-
алгеброй.
Проверка достоверности этих аксиом требует рассмот-
рассмотрения совершенно общих случаев. Поэтому их трудно
должным образом описать. Тем не менее, чтобы обозна-
обозначить используемые ниже идеи, рассмотрим два примера,
исходя из двух аксиом, примененных к конкретному ре-
регулярному выражению.
Пример 3.1. Пусть Л=*{а6п: 0<л). Это выраже-
выражение регулярно, так как является представимым для ма-
машины М, изображенной на рис. 9.17, а.
Рис. 9.17
Используя машину, изображенную на рис. 9.16, а, ко-
которая распознает 0, и применяя подходящее построение,
получим машину, изображенную на рис. 9.17,6, которая,
очевидно, эквивалентна М. Следовательно, A=A+Q. II
Пример 3.2. Используя Л и 1, определяемые маши-
машинами, данными выше, и обычной конструкцией конкате-
конкатенации, получаем недетерминированный конечный распо-
распознаватель, изображенный на рис. 9.18, а, который будет
представлять строки в регулярном выражении 1/1. Эту
машину делаем детерминированной (рис. 9.18,6), затем
получаем машину (рис. 9.18,с), эквивалентную М, кото-
которая удовлетворяет (в данном случае) части аксиомы 6),
а именно \А — А. II
Определив регулярную алгебру, посмотрим, как ее ис-
использовать. Предположим, что А, В а С являются задан-
заданными регулярными выражениями (мпожествами строк)
336
и что X и Y — неизвестные регулярные выражения та-
такие, что выполпены следующие соотношения:
X = AX + BY, Y = XC + B.
Существуют ли решения этих «уравнений», и если да,
то как их найти? Как мы вскоре увидим, регулярные
Рис. 9.18
уравнения не имеют единственного решения; поэтому мы
вначале введем понятие аппроксимации для регулярных
выражений.
Определение. Для регулярных выражений X и Y
отношение < определяем следующим образом:
X < У (X аппроксимирует Y), если X + Y = Y. II
Теорема. Отношение «?, определенное над регуляр-
регулярными выражениями, является отношением порядка.
Доказательство.
Транзитивность имеет место, так как
X<Y, Y <Z**X+Y=*Y, Y + Z-Z. (*)
Поэтому
и, следовательно, X < Z.
Антисимметричность имеет место, поскольку
X < У, У*?Х^У = Х + У-У + Х = Х.
Рефлексивность следует из X + X =» X. II
Отсюда также следует, что X < Y => ZX < ZY для ре-
регулярных выражений X, Y и Z, однако детали доказа-
доказательства оставим в качестве упражнения.
Перед тем как рассматривать уравнения, напомним,
что из опредслснпя операцип замыкания следует
A* = A0 +
22 д кук, Г. Бейз
+ ... +Ап+ ... = 2.
337
где А0 = 1. Это соотношение оказывается полезным при
доказательстве следующих утверждений.
Лемм а. Пусть Y и Z — решения регулярного урав-
уравнения Х=*АХ + В. Тогда
а) В < У,
б) 47 «У,
в) У + Z — решение.
Доказательство.
а) Так как У — решепие уравнения X = АХ + В, то
Y — AY + В, а поэтому
Следовательно, В =S У.
б) Аналогично У + AY = (Д + AY) + AY = В + AY
= У. Следовательно, Л У ^ У.
в) Имеем
Уже достаточно много сказано о свойствах решений
уравнения, однако существует ли хотя бы одно решение?
Лемма. А*В является решением уравнения X =*
АХ + В
Доказательство. Подставляя А*В в уравнение,
имеем
А (А*В) + В = {АА* + А0) В - [ А |] Ап + А0) В -
А" + аАв = ( % Ап) В = А*В. Ц
/ I
)
1 / \П=й I
Теорема. А*В является наименьшим (по отношению
к <) решением регулярного уравнения Х — АХ + В.
Доказательство. Из лемм следует, что А*В —
решение, и если У — какое-либо другое решение, то В < У,
AB^AY^ У. Поэтому АВ ^ У, Л"Я s? У, и, добавляя
неравенства для всех п е N U (О), получаем А*В ^ У.
Следовательно, утверждение теоремы верно. /
Заметим, что А*В — это множество строк, каждая из
которых является решением уравнения; если А = {а} и
В — {М, то все строки вида а"Ь также являются решениями.
Заметим также, что так как А*В является наименьшим
решением уравнения X — АХ + В, то оно является наи-
наименьшим выражением таким, что X >->• АХ + В совпа-
совпадает с тождественным отображением. Поэтому его также
338
называют наименьшей стационарной точкой уравнепия
(или минимальной стационарной точкой).
Рассмотрев одно частное уравнение, мы сейчас можем
непосредственно получить аналогичные результаты для
других похожих уравнений; доказательства в этих слу-
случаях будем опускать.
Теорема. Для заданных регулярных выражений
А и В уравнение X = АХ + В эквивалентно паре уравне-
уравнений
в том смысле, что они имеют одно и то же наименьшее
решение, и это решение есть Х — А*В. II
Теорема. Для заданных регулярных выражений А
и В уравнение X = АХ + В эквивалентно паре уравнений
X = BY,Y='AY + 1.
(В этом случае обе системы наименьшее решение X =
-ВА*.) II
Эти две теоремы позволяют нам преобразовывать пра-
правые линейные формы (X = АХ + В) в левые линейные
формы (X ¦= ХА + В), которые соответствуют правым и
левым рекурсиям внутри регулярных грамматик. Детали
этого соответствия даны в п. 3.2, однако сначала мы обоб-
обобщим результаты на системы алгебраических уравнений.
Предположим, что Х\, • • •» Хп — неизвестные регуляр-
пые выражения и что Ац A < <, /< п) и В\, ..., Вп —
известные регулярные выражения такие, что
X, - XiAll+X2A2l + ... + ХпАа1 + Ви
Х{ - XiAu + X2A2i + ... + ХпА., + В„
х. = х\а и + х\а'2я + ..'. + xUl. + в\."
Теперь можно использовать операции, определенные на
регулярных выражениях, чтобы ввести операции на мат-
матрицах из регулярных выражений:
(С + D)y = С« + D{j,
С* = S С";
С < D тогда и только тогда, когда Cti < Т)ц для всех I, f,
22* 339
где С и D — согласованные матрицы, элементы которых
являются регулярными выражениями. Обозначив через
X «регулярную матрицу», мы можем представить приве-
приведенные выше уравнения в виде
X = ХА + В.
Применяя рассуждения, аналогичные тем, которые ис-
использовались в случае одного уравнения, можно показать,
что эта система имеет минимальную стационарную точку
ВА*, которая достигается на решениях X «¦ BY, где Y =
= AY + I; I — единичная матрица. Соответствующие ре-
результаты справедливы для правых линейных систем. Из
замечаний следует, что эти системы эквивалентны. Это
помогает удалению левых рекурсий в контекстно-свобод-
контекстно-свободных грамматиках.
Ясно, что для уравнения X ¦= ХА + В решение может
быть определено как
где
Y« = (AY + I)y = 2-A»Yw + Iy.
Пример 4.4 гл. 8 показывает, как этот результат пе-
переносится на контекстно-свободные грамматики. Преобра-
Преобразования, используемые в этом примере (хотя они и не
строго обоснованы), появились при помощи рассуждений
по аналогии. Мы завершаем этот раздел, указывая на
формальную связь между регулярной алгеброй конечных
распознавателей и регулярными грамматиками.
3.2. Представления регулярных грамматик. Напомним,
в гл. 8 структурная грамматика G = (N, T, P, S) назы-
называлась грамматикой Хомского типа 3 или (Л-свободной)
регулярной грамматикой, если все элемепты Р имели вид
А -*¦ х или А -*¦ хВ, где х = Т и А, В е N, или же (если
ЛеЬ(С)) S -*¦ Л; в этом случае S не встречается ни в
какой правой части.
Множество предложений, порожденных регулярной
грамматикой, называют регулярным множеством или ре-
регулярным языком. В настоящий момент мы в состоянии
обосновать использование дважды одной и той же терми-
терминологии и, следовательно, использовать регулярную алгеб-
алгебру в грамматиках.
Основной результат состоит из двух частей и дан в
виде теоремы с конструктивным доказательством.
Часть I является непосредственной, так как каждый пе-
340
реход определяют на всей его области определения; в
части II не обязательно, чтобы грамматика {N, 7, Р, S)
для данных X еДО а а ^ Т имела продукцию вида X -*¦ а
или X -*¦ aY при некотором У &-N.
Теорема. Множество, представимое конечным ав~
томатом, является в точности таким же, как если бы вы-
выводилось из регулярных грамматик.
Доказательство. Опишем конструкции доказа-
доказательства.
Вначале рассмотрим конечный автомат М -»(Q, 2, t,
g, F). Теперь построим регулярную грамматику G—(N,
Т, Р, S). Если ЛФА(М), то можно сделать следующее.
Пусть N — Q, Г = 2 и S = д; построим Р такое, что
e))y(Z-»e, t(X, c)flF^0}.
Если Л^А(М), то расширяем конструкцию, создавая
новый нетерминал q, полагая S = q а добавляя к Р про-
продукции
S -Л,
S-+aY (если Уе«(?, а)),
S-+ а (если t{q, a)uF = 0).
Сейчас легко показать, что для каждого х = 2* усло-
условие х& А(М) выполнено тогда и только тогда, когда х е
eL(G). Очевидпо, что если q s F, то Л представимо ав-
автоматом М и S -*¦ Л — продукция G и наоборот. Если
также а е= А (М) и \а\ ¦» п, то
а = aiu2 ... а„, а( е 2,
п поэтому существует путь в графе М, как показапо па
Рис. 9.19
рис. 9.19. Здесь A,^N (не обязательно все различны) п
Ве^ипо построению
{S -* aiAi, At -*¦ fl2^2, "., Ап-2~* aa-iAn-\, A..-\ -* ani s P
(рис. 9.20). Таким образом, a^L(G). Проводя рассу-
рассуждения в обратном порядке, аналогично получаем ?(G)s
?^ (Л/), и, следовательно, равенство доказапо,
341
Сейчас надо показать, что для данной (Л-свободной)
регулярной грамматики предложения этой грамматики
могут быть представимы некоторым конечным автоматом,
а все другие строки не представимы этим автоматом.
Возьмем G\ ={NU Т\, Ри Si) и построим М\ -=((>i, Si,
'ь 9ь ^1I как показано далее. Пусть Ъ\=*Т\ и Q\ •=•
а2
\.
On
Рис. 9.20
See
Рис. 9.21
= iVi U (т) U {л} (где т и я — специальные символы, ко-
которых нет в Ni; х представляет правильную терминаль-
терминальную строку, а л представляет ошибку), q\ — Si и Ft —
— {%). Если также As L(G\), т. е S\ -*¦ Л принадлежит
Pi, то F\ ™ {x, q\). Окончательно имеем
, а), У): X-*aY есть в Р,} U
, a), i): X-+ а есть в PJU
U {((т, а), л) для всех а <= 2i) U
, Ь), я): если X = Nx пвеХ-*ЬК для любого Y е
е yVj и не выполняется условие X -*¦ Ь есть в Р\) U
U (((п, с), я) для всех а е 2,}.
Обоснование того факта, что эта машипа представляет
L{G\), оставляем в качестве упражнения. II
Пример 3.3. Пусть задала регулярная грамматика
G -({А, В, С, D), {х, у, z), P, А), где
Р = {А -«¦ Л \хВ\ уС, B-*zB \y\ yC, C-+zD, D-+ yD\x}.
Используя описанную выше конструкцию, получим ма-
машину, изображенную на рис. 9.21. /
342
Упражнение 9.3.
1. Пусть заданы регулярные выражения А, В, С и D
такие, что А «? С и В «? С. Доказать, что
а) А + D < С + D; б) AD < CD;
в) DA < DC; г) А* < С*; д) Л + В < С.
2. Исследовать, как преобразуются результаты п. 1
данного упражнения, если А, В, С и D — регулярные
матрицы размера пХп.
3. Определить конечный автомат для языка L, опреде-
определенного как 11*01* (т. е. L — {ш <= @, 1)*: w) начинает-
начинается с 1 и имеет только один нуль. Выписать правую ли-
линейную грамматику, определяемую этим автоматом, и по-
последовательность перемещений, делающих представимой
строку 111011.
ГЛАВА 10
КОМПЬЮТЕРНАЯ ГЕОМЕТРИЯ
Эта глава дает некоторые сведения из геометрии, ко-
которые широко используются в компьютерной графике и
компьютерном вспомогательном математическом обеспече-
обеспечении; при этом делается попытка изложить все более стро-
строго и унифицировапно, чем это делается во многих книгах
по компьютерам. Мы стремимся представить серию «при-
«приемов» в некотором, очевидно, случайном порядке, а так-
также использовать концепции, развитые в предыдущих гла-
главах (особенно в гл. 1—3, 5, 6), чтобы обеспечить основу
для обсуждения выбранных тем, включающих однород-
однородные координаты, кривые и поверхности. Дано также че-
четырехмерное представление данных трехмерной геомет-
геометрии, широко используемое на практике.
Перед началом обсуждения будет полезно, чтобы чи-
читатель имел некоторое представление о разнице между
терминами «топология» и «геометрия»: геометрия изуча.
ет расстояния и углы, тогда как топология занимается
более общими свойствами. Например, две сферы с различ-
различными радиусами являются топологически эквивалентны-
эквивалентными, а геометрически — нет. Два объекта топологически
эквивалентны, если один из них может быть получен из
другого искривлением и растяжением последнего без раз-
разрыва (чтобы быть более точными, путем использования
непрерывного отображения, обратное к которому также
непрерывно), тогда как в геометрии эквивалентные объ-
объекты должны быть идентичны во всех отношениях, за ис-
исключением их положения и ориентации в пространстве.
Теория графов является частью топологии, поскольку
вершины не обладают свойством положения в простран-
пространстве и топология графа есть отношение ребер.
Обычно удобно запоминать в памяти компьютера два
различных множества данных, относящихся к рассмат-
рассматриваемому объекту,— топологические данные и геометри-
геометрические данные. Например, можно представить широкий
344
класс объектов при помощи каркасных моделей. На
рис. 10.1 дано такое представление конечного цилиндра.
Топология модели такого типа может рассматриваться
как граф и может быть представлена в виде связной спи-
списочной структуры. Геомет-
Геометрические данные могут
быть просто списком век-
векторов, определяющих по-
положения вершин в R3.
Целью разделения содер-
содержания геометрии и топо-
топологии является то, что мы
хотим преобразовать рашу
модель некоторым обра-
образом, например чтобы она
была физически меньше,
пли передвинуть ее в не- Рис. 10.1
которое новое положение,
изменив ориентацию в пространстве. Такие пре-
преобразования не изменяют топологии модели, и нам
просто изменить соответствующим образом геометри-
геометрическое множество данных. В § 1, 2 мы будем заниматься
системами координат, которые дают возможность пред-
представить геометрические данные, и некоторыми полезными
в дальнейшем множествами преобразований, которые мо-
могут применяться к геометрическим множествам данных.
§ 1. Системы координат для подмножеств R*
В общем случае система координат (координатная
система) или параметризация множества 5sR" являет-
является идентификацией каждой точки в 5 при помощи един-
единственного упорядоченного набора чисел (|i, ..., |e)sR*
(geN). В терминологии отображений система координат
для S может быть определена как непрерывная биекция
Ф: S -*¦ 91, где 3? s R4. Любое преобразование или другое
вычисление, осуществляемое на S, тогда выполняется в
терминах координат (li,..., !«)• Конкретное отображение,
которое выбирается для данной задачи, часто будет опре-
определяться геометрией пространства S. Можно показать,
что q для фиксированного 5 является постоянным для
всех систем координат и называется размерностью S.
К сожалению, в одном из приведенных ниже примеров
(однородные системы координат) требуется, чтобы & бы-
было всем пространством; кроме того, существует много по-
345
лезных подмножеств, для которых такие отображения не
существуют (например, круг или сфера). Чтобы разо-
разобраться с этим, следовало бы совершить небольшой экс-
экскурс в топологию; однако вместо этого будем надеяться,
что проведенное ниже рассуждение, несмотря на недостат-
недостатки определения, поможет хорошо разобраться в данном
вопросе.
В основном нас будут интересовать пространства раз-
размерности 3 и меньше; например, кривые являются одно-
одномерными объектами, а поверхности имеют размерность
2. В следующих примерах представлены некоторые наи-
наиболее общие координатные системы в R2 и R3, однако
там, где легко обсудить более общий случай, мы это бу-
будем делать*
Пример 1.1. Прямоугольная система координат в
Rn (neN). Если 5 = {ei, ..., е„} — базис в Rn, то каж-
каждый элемент xsR" может быть записан единственным
образом в виде
R, 1 ^ i ^ П.
Отображение Ф: R" -»• R", задаваемое как Ф(х) — (а\, ...
..., а„), определяет координатную систему в R\ Если В
ортонормирован, то соответствующие координаты назы-
называются декартовыми координатами в R". В R2 и R3 обыч-
по ортонормированный базис интерпретируют геометри-
геометрически как правостороннюю систему координат в смысле
§ 4 гл. 5. /
Следующий пример в Rn является более сложным с
математической точки зрения. Необходимо некоторое
предварительное обсуждение перед тем, как мы опишем
эту систему.
Начнем с определения отношения ~ на R"+l. Опреде-
Определим его следующим образом: х ~ у, если х = осу для не-
некоторого aeR\@1. Важные свойства этого отношения
сформулированы в следующем предложении, доказатель-
доказательство которого оставляется в качестве упражнения.
Предложение. Отношение ~ является отноше-
отношением эквивалентноеги на Rn+1.
Отношение ~ определяет следующие классы эквива-
эквивалентности:
Рп = {ZA(O}: L— одномерное векторное подпространство
R"+1, 0 — нулевой вектор в Rn+1} и {0}.
346
Очевидно, что ft =» Pn U @). Определим подмноже-
подмножество Pn.
Определение. Пусть х е II"*1 имеет вид (х\, ...
..., гп, 0), где не все г( равны нулю. Тогда [х] s P* на-
вывают бесконечно удаленной точкой. Обозначим множе-
множество всех бесконечно удаленных точек Рп через L/J, и
определим Нп как Pn\L». /
Следующий результат играет важную роль: он уста-
устанавливает координатное отображение R".
Предложение. Существует биещия 0я: Нп —¦
- R".
Доказательство. Определим отношение Q":
Нп -*¦ Rn следующим образом: Qn(l(xlt ..., хп+1)\) =
•= (я?!, ...,хп). Вначале заметим, что правая часть
хп+1
всегда определена, так как /.?> исключена из области оп-
определения (?"; следовательно, &>(Qn) = Hn. Необходимо
установить три факта:
Qn — отображение на Я";
Ф" инъективно;
Q" сюръективно.
Qn является отображением, если
Пусть (an, ..., хя+1)~{уи ..., yn+i); тогда существует
a e R\tO} такое, что xt = ayt для всех i, 1 < i < га + 1.
Тогда по определению (?"([(Zi, ..., хп+1)]) = Qn
ay)]) (ayv ..., сцг„) =(tf
•••, I/n+i)]). Следовательно, Qn — отображеппе
на Я\
^n инъективно, если (?" ([х]) ¦* Qn ([у]) => х ~ у. Запи-
Записывая выражение для х и у в виде х ={х\, ..., хп, xn+i) и
у =(уь ..., уп, yn+i), получаем
откуда Xt = (xn+\fyn4.])yi^- x~y, o = xn+i/j/n+i. Следова-
Следовательно, Qn инъективно.
Q" сюръектввпо, если для всех х={х\, ..., г„)еИп
сущестует x*sRn+1 такое, что @п([х*])=»х. Если опре-
определим х* =(х\, ..., хя, 1)е=Н"*\ тогда очевидно,, что
ф"([х*]) = х, т. е. Qn сюръективно. /
.347
Пример 1.2. Однородные координаты в n'fneNI,
Однородные координаты в R" определяют как отображе-
отображение К" на //", имеющее обратное отображение Qn, так
что Ф: R" -*¦ Н", где Ф = (^"). Другими словами, одно-
однородными координатами точки (х\, ..., i,)sR" являются
(л + 1)-мерные наборы классов эквивалентности
..., хп, 1)] = {(рхи ..., рхп, р): рФО).
Элемент из [(xi, ..., хп, 1)] называют однородным пред*
ставлением для (х\, ..., хп).
Часто бывает удобно представить в компьютере гео-
геометрические данные в однородной форме (см. § 3). Что-
Чтобы из однородных координат получить физические, осу-
осуществим отображение (хх, ..., хп+1) <— (xv ..., хп).
Сформулированное выше предложение показывает, что
все однородные представления данной физической точки
имеют те же самые физические координаты.
Чтобы прояснить ситуацию, рассмотрим геометричес-
геометрическую интерпретацию однородных координат в R. Случай
более высоких размерно-
размерностей имеет подобную гео-
Класс sxSuSa- метрическую иптерпрета-
лентпности. _ цию, однако ее нелегко
изобразить на рисунке.
Элементы Р1 являются
бесконечными линиями в
R2, проходящими через на-
"^ чало координат, однако
начало координат выбро-
выброшено (рис. 10.2). Ясно,
что единственной, беско-
бесконечно удаленной точкой
Рис. 10.2 будет ось Ох\ с выбро-
выброшенным началом коорди-
координат. Рис. 10.3 проясняет понятие «бесконечно удален-
удаленная точка в Р1». Точки на линии /,„ = [(«, 1)] явля-
являются однородным представлением п = R. Из рис. 10.3
видно, что при п -*¦ °° прямая Ln стремится к бесконечно
удаленной точке ?«. II
Пример 1.3. Полярные координаты в R2. Пусть
?sR2—полубескопечная линия L — {(х, 0): х > 0} и
(х, у) = l\2\L. Тогда, если Ф: R2\L ->- J0, »[Х]0, 2я[ опре-
определено как Ф(х, у) = (г, 6), где г = (х2 + у2I'2, а 0 =
¦¦ arctg {у/х), то Ф определяет множество полярных ко-
348
ординат в R2. Обратное к Ф отображение задается соотно-
соотношением Ф~'(г> 8) = (г cos 0, г sin 8). Геометрическая ип-
терпретация гиб дана на рис. 10.4. Исключение L из
области определения Ф часто неправильно комментиру-
комментируется в элементарных учебниках. Линию L удаляют, что-
чтобы получить непрерывность Ф.
X.
Рис. 10.3
Пример 1.4. Цилиндрические координаты в R3.
Пусть Р с R3 — полуилоскость Р = {(х, 0, z):x>Q} a
Рис. 10.4
Рис. 10.5
(х, у, z)e=R3\P. Тогда отображение Ф: R3\P -*
-*]0, °°[Х]0, 2л[XR, определяемое как Ф(а:, у, г) =
= (р, ф, г), где р = (х2 + у2I/2, 9 = arctg(i//x), опре-
определяет множество цилиндрических координат в R3\P.
Обратное к Ф отображение задается формулой Ф (р,ф,
2) = (рсозф, рэ1пф, г). На рис. 10.5 изображены величи-
величины р, ф, z, относящиеся к осям декартовой системы ко-
349
ординат. Полуплоскость Р исключена из области опреде-
определения Ф, чтобы получить непрерывность. II
Пример 1.5. Сферическая система координат в
R3\P; P определено, как в примере 1.4. Сферическую си-
систему координат определяют как отображение
Ф: RVP -* ]0, ~[ X [0, я] X ]0,2л[,
где Ф(х, у, г) = (г, 6, <р) а г -(г* + у2 + 22), 6 -
= arccos (z/r), ф = arctg(j// ).
§ 2. Преобразования
Одной из наиболее часто используемых операций над
геометрическими данными является преобразование. На-
Например, вращение трехмерного пространства R3 дает воз-
возможность рассматривать трехмерные геометрические объ-
объекты с любой удобной точки. Это может оказаться полез-
полезным при проверке геометрической целостности объекта,
или при подробном изучении какого-либо свойства, или
по какой-либо другой причине. Некоторые подходы осно-
основаны на библиотеках осповных геометрических «строи-
«строительных блоков», из которых путем преобразования мо-
могут быть построены более сложные геометрии. Они следу-
следуют из некоторых теоретико-множественных операций, ко-
которые будут построены далее. Алгоритмы для такого
типа геометрического синтеза являются весьма специаль-
специальными и не будут здесь обсуждаться, однако мы упомя-
упомянем, что обобщенная форма теоремы Эйлера для графов
может быть использована для исследования топологии
конструируемого объекта. Преобразования используются
более широко. Некоторые из наиболее употребляемых
преобразований и их линейные представления будут сей-
сейчас описаны.
2.1. Преобразования в R2. Переносом в R2 называет-
называется отображение вида Гг = г + г0 для всех г е R2, где
го е R2 — фиксированный вектор. Перенос перезлещает
всю плоскость сдвигом на фиксированный вектор и может
быть записан в координатной форме:
Т (х, у) = (х, у) + (*о, Уо) = (х + хо,у + yoj.
Обозначим через ГB) множество всех переносов па R2
и определим произведение в Г B), используя композицию
отображений. Пусть Т\ — перенос на вектор ri, а Гг —
перенос на вектор Гг. Тогда произведение Т% • Т\ опреде-
350
лим как
Т2 <¦ Т^ = Т2 (Г,г) = г + ri + г2.
Очевидно, что Г2 ° Т\ есть перенос на Г| + г2, и, следова-
следовательно, операция ° является бинарной на Г B). В дей-
действительности справедливо более сильное утверждение.
Предложение. (Т B), °) — коммутативная груп~
па нелинейных преобразований R.
Доказательство. Замкнутость относительно опе-
операции • уже доказана. Аксиомы группы следуют из груп-
групповой структуры (R2, +); например, если Tt(i ^ i ^ 3) —
переносы па гП1 то
(Т3*(Т2 о Т1))г = Г3((Г2 • Г,)г)= Г3(г + г, +г2) =
поэтому (ГB), ») ассоциативна. Единицей является пе-
перенос на вектор @, 0), а обратным переносов к Гг = г +
+ Го будет 7"г = г —го; поэтому
Т ° T't = Т'Тх = г для всех г е= R2.
Коммутативность также выполняется, поскольку
(Т2 > Т\)Т = Г + Г1 + Г2 = Г + Г2 + Г! = (Г] ° Г2) Г.
В общем случае, если Т^Т{2), то Г@, 0)=^@, 0); поэ-
поэтому начало координат смещается и, следовательно, пере-
перенос является нелинейным отображением. /
На практике это означает, что можно применить любое
число переносов к геометрическому объекту и получить
один и тот же результат. Кроме того, нелинейный харак-
характер элементов Г B) означает, что мы не можем выпол-
выполнить ТB) при помощи элементов из ЛB, R); другими
словами, уравнение
всех (х, у) е R2
не имеет решения. Следствия из этого факта будет рас-
рассмотрены ниже.
Опишем поворот в R2, используя рис. 10.6. Интуитив-
Интуитивно ясно, что поворот на угол 8, обозначаемый W(&), ото-
отображает точку (х, у) в точку (х1, у'), где llrll = llr'li = г.
Из рисунка видно, что
х = г cos 8, у = г sin 0,
*F S3 Y рлв i ft *т* flii 77 —** Y oiP (ft ~ A ^
351
Применяя тригонометрические формулы, получаем
х = r(cos6cos 0i — sin 8 sin 8t) = x cos 8 — j/sinO,
y' = zsin8 + ycosQ,
так что
W(Q) (x, y) = (x cos 0 — у sin 0, x sin 8 + у cos 0).
В матричной форме это можно записать следующим
образом:
W@) геометрически соответствует повороту вокруг нача-
начала координат О.
Следующее предложение непо-
непосредственно вьи екает из представ-
представления JCB, R) и, с нашей точки
зрения, суммирует основные свой-
свойства поворотов.
Предложение.
а) Преобразование W(Q):
х — линейно,
— ортогонально, detPF@)=l.
р
Рис 10.6 б) Множество 0^(8):
< 2п) является коммутативной
группой по отношению к композициям отображений (ум-
(умножением матриц). II
С практической точки зрения из а) следует, что для
вычисления преобразования, обратного к повороту, до-
достаточно лишь транспонировать матрицу. Часть б) озна-
означает, что любое число поворотов может применяться ч
множеству геометрических данных в любом порядке п
будет давать одинаковые результаты. На самом деле вер-
верно обратное к а) утверждение. В частности, если 1Уе
ejB, R) и выполнены условия, a) W является попо-
попоротом. Другими словами, мы можем определить поворот
в R2 как элемент группы 50B).
Хотя Т B) и iSOB) являются коммутативными груп-
группами, преобразования из Г B) не коммутируют с преоб-
преобразованиями из 50B), так как если W е 50B) и Г<=
еГB)- сдвиг па го, то мы имеем TWt = Wt + t0 и
WTt = W(г + го) =Wt + Wio?>TWT при го=И=(О, 0). На
практике это означает, что преобразования переноса и по-
поворота надо применять строго в том порядке, в каком они
ваписапы. Некоммутативность проиллюстрирована на
352
рис. 10.7, где показаны результаты применения преобразо-
преобразований Г» W(n/2) a W(n/2)« T к полусфере. Из рис. 10.7
видно, что если площадь {(х, у): 0<х<а, 0<#«?&}
соответствует экрану графического терминала, то резуль-
результат применения W(n/2)« T к полукругу даст в итоге пу-
пустой экран.
W(n/2)
С
Рис. 10.7
Группы ТB) и 50B) могут быть объединены в виде
третьего множества ЕB) преобразований плоскости, на-
называемых евклидовыми. Элементы U е ?B) имеют вид
Ux =- Wx + r0 для всех г е R2, где W е= 50B), а г0 е R2 —
фиксированный вектор. Эти преобразования часто запи-
записывают в виде пар вида (W, т0). Если (Wt, ) E2)
и (W2t Г2)е?B), то (W2, r2).(Wu r,)r = (W2,
+ rl)=*W2(Wlx + xi) + X2 = (W2Wu W2r, + r2)r, так что
(W2, r2)-{Wu r,) = (W2W,, W2Tl + r2)^EB)
и ЕB) замкнуто. В действительности имеет место следу-
следующее предложение.
Предложение. ?B) является группой по отно*
шению к операции композиции.
Доказательство. Ограничимся указанием ос-
повных моментов доказательства. Замыкание уже доказа-
доказано. Ассоциативность следует из применения преобразо-
преобразований несколько раз. Если I^GLB, R)—единица, то
справедливы соотношения
(Л 0)-(W, ro) = (W, го)-(Л 0) = (W. ro)
для всех (W, го)е?B);
следовательно, G,0) является единицей в Е B). Обратный
23 д. кук, г. Бей» 353
элемент (W, г0)"' к (W, г0) будет равен (W*, —
при (WT, -WTt0)sEB), и
(W, to)°(WT, -WTt0) = (I, 0)-(W, -WroWW, ro). /
50B) и ТB) являются подгруппами {(Т7, 0)'. W&
s5OB)} и {(/, го): гое R2} из ?B) соответственно, и
каждый элемент (W, го)^?'B) может быть представлен
следующим образом:
ЕB) — некоммутативная группа, так как
(W* пУ(Ши ii)-{WaWlt W#x + r2),
{Wu п).(ИЪ, T2) = {WlW2i ^1r2 + rI)^(W2, r2)o(T7,, r,).
В приложениях компьютерной графики часто хотят
повернуть объект около некоторой фиксированной точки,
отличной от начала координат. Например, на рис. 10.8
Рис. 10.8
полукруг повернут на я/2 около точки Р. Общая ошибка
при этом заключается в попытке применить преобразова-
преобразование W(n/2); однако это приводит к результату, изобра-
изображенному на рис. 10.9. Проиллюстрируем последователь-
последовательность преобразований поворота вокруг фиксированной
точ1И го s R2 на рис. 10.10, используя понятия ?B). Тре-
Требуемое преобразование, таким образом, будет равно
(/, гьИИЧя/2), 0).(/, -го).
Эту запись можно упростить, используя правило произве-
произведения в ЕB); получим
(W(n/2), -W(n/2)T0 + t0).
Ясно, что применять составное преобразование к множе-
множеству геометрических данных более эффективно, чем при-
применять в отдельности каждое преобразование. ЕB) дает
354
возможность расположить объект в любой точке плоско-
плоскости и в требуемой ориентации.
Множество полезных операций на плоскости включа-
включает в себя преобразование масштаба. Преобразованием
масштаба на R2 называют отображение вида
S (x, у)=*(\х, \iy), к, ц>0,
или же (в матричной форме)
Множество всех преобразований такого типа обозначается
С
Рис. 10.9
Рис. 10.10
5B). Важные свойства 5B) сформулированы в следую-
следующем предложении, доказательство которого оставляем в
качестве упражнения.
Предложение. 5B) является коммутативной
группой линейных преобразований по отношению к опе-
операции композиции. (Другими словами, 5B) является
коммутативной подгруппой GLB, R).) /
Преобразование масштаба не коммутирует с перено-
переносом, так как если Т — перенос на вектор г<> и
S(x, у) = (Яя, \iy),
то
S»T(x, y)*=S(x + xo, у + Уо)*=(к(х + Хо), ц(# + 2/o))i
T°S(x, y)-=T(hc, \iy)=-(kx + x0, \iy + yo)Ф5• Т(х, у)
в общем случае некоммутативность проиллюстрирована
23* 855
йа рис. 10.11; используются преобразование масштаба
S(x, y) = {2xt 2у)
и перенос
Г(*. ?)-(*+1, у+ 1)
единичного квадрата с вершиной в начале координат.
Аналогично можно показать, что преобразования масшта-
масштаба не коммутируют с поворотами. Доказательство этого
A,1)
S
B
,2)
*-
Рис. 10.11
и построение соответствующего рисунка, который это де-
демонстрирует, оставляем в качестве упражнения.
На практике это означает, что если преобразование
масштаба комбинируют с переносом или с поворотом, то
следует обращать особое внимание на порядок примене-
применения преобразований.
Языки высокого уровня предусматривают массивы как
структуры данных; следовательно, матричное представле-
представление всех рассмотренных выше преобразований должно
существенно упростить их применение. Например, все
произведения преобразований тогда могли бы вычислять-
вычисляться путем умножения матриц (см. гл. 6) вместо того, что-
чтобы работать с определениями этих преобразований. Нели-
Нелинейная природа переносов препятствует представлению в
Jt{2, R); однако возможно получить подходящее пред-
представление обсуждаемых выше преобразований в Jt<3, R),
358
где матрицы оперируют в пространстве Я2 однородных
координат R2. Поскольку техника получения представле-
представления в однородных координатах носит весьма общий ха-
характер и, в частности, может быть применена к преобра-
преобразованиям в R3 (где получается представление в Ж (A, R)),
мы отложим рассмотрение до описания преобразований
в R3.
2.2. Преобразования в R3. Перенос в R3 есть отобра-
отображение Т: R3 -*¦ R3 вида
Тт = г + Го для всех г е R3,
где го е R3 — фиксированный вектор. Если го = (хо, уо,
го), то перенос иа Го может быть записан в компонептной
форме как
Т(х, у, z) = (x + x0, у + Уо, z + zo).
Пусть ТC) обозначает множество всех переносов R3.
Тогда ГC) образует коммутативную группу (по отноше-
отношению к операции композиции) нелинейных преобразова-
преобразований R3, изоморфную группе (R3, +). Следствием этого
является тот факт, что последовательность переносов R3
может применяться в произвольном порядке и будет да-
давать один и тот же результат и что мы не можем выпол-
выполнить ГC) при помощи элементов из М(Ъ, R).
Рис. 10.12
N Р
Рис. 10.13
Группа поворотов в R3 имеет более сложную структу-
структуру, чем 50B). Рассмотрим поворот ^-@) на угол 0
вокруг оси, определяемой единичным вектором n e Л3,
как это изображено на рис. 10.12. Тогда
где г — пектор с концом в точке Р, а г' — преобразован-
преобразованный вектор с концом в точке Р'. Чтобы определить явно
357
VFj-(8), мы должны выразить г', как функцию г, п и б.
Ясно, что если гж — вектор, определяемый точкой N, ле-
лежащей на оси поворота, то
rw=(n; r)n,
и если Гдгр — вектор, соединяющий N и Р, то
Гд,Р = Г — Гц = Г — (П • Г) П = (П X Г) X П.
Рисунок 10.13 показывает, как выглядит поворот из
точки N в направлении начала координат О; Q — точка,
полученная поворотом точки Р на п/2 относительно оси
ON. Таким образом, И7-F)— поворот; следовательно,
0 + rjvp cos 0,
где Tno —* проекция вектора на ось NQ. Отсюда следует,
что
rNQ = n X tnp = n X ((п X г) X n) = n X г
(см. упражнепие 10.1); следовательно,
Tnp> = (u X г) sin 6 + ((n X г) X n) cos 6 =
= (n X г) sin 0 — (n X (я X г)) cos 0,
но
= г + (n X (n X г))A — cos 6) + (n X r)sin 0.
Предложение. W~ @) e SOC).
Доказательство. Некоторые детали доказатель-
доказательства будем оставлять в качестве упражнений. Запишем
W~(9) в несколько иной форме. Если nsR3 определяет
ось поворота, то определим преобразование А~: R3-»-R8
следующим образом:
А~ является непрерывным и антисимметричным (см. уп-
упражнение 10.1). Тогда
A\t - А^ (А~т) =4j(nXr) = nX(nX r);
А~ линейно и симметрично. Сейчас мы можем записать
853
W~ (8) как сумму
W~ @) = / + A _ cos 9) A\ + sin 0Л-
в М(Ъ, R). Но ЖC, R) —векторное пространство; сле-
следовательно, W~ @) линейно. Ортогональность следует из
свойств А~, так как
W~ F)г = / + A - cos 0) D)Т + sin 0 (А~у =
= I + A — cos 0) Л*- — sin 0
W~ @) Р7~ @)г = [/ + A - cos 0) А\ + sin BA~] *
* [/ + A - cos 0) А\ — sin 0A~] =
= / + [2 A — cos 0) - sin2 0] Л t + A _ cos ОJ 41 =
по (см. упражнеппе 10.1)
Следовательно,
н И7- @) ортогонально.
Доказательство того, что dot И7-@)= 1, оставляем в
качестве упражнения. /
Обратное утверждение также справедливо (см. зада-
задачу 12 упражнения 10.1); в частности, если WeS0C),
то можно показать, что существуют единичный вектор
и е R3 в угол 0 в пределах 0 «S 0 < 2п такой, что
W - W- @).
Следовательно, разумно определить повороты в R3 как
группу 50C).
Определим некоторые подгруппы 50C). Часто тре-
требуется поверпуть объект вокруг одной из декартовых осей
координат. Соответствующие матрицы могут быть полу-
получены из общего вида W~ @). Например, чтобы осущест-
осуществить поворот на угол 0 вокруг оси OZ, выберем n = k =•
¦=@, 0, 1), для которого
[О -1 01 Г-1 О ОТ
1 Оо,4-= 0-10,
0 0 0J I Э 0 0j
359
так что
'cos 0 —sin б
W-(Q)
sine cos 0
0 0
°1
Аналогично матрицы
Г1 0 0 Г cos X 0 sinxl
Wr (ф) = 0 cos Ф - sin Ф , цг- {%) = 0 10
LO sin ф cos9j L — sin x 0 cos%J
соответствуют поворотам на углы ср и % вокруг осей ОХ
и OY соответственно. Доказательство этого оставляем в
качестве упражнения. Сейчас легко показать, что
50C)—некоммутативная группа, так как в общем
случае
[WT (ф), 1У? (х)] фО, [Wr (Ф), Wt F)] ф О,
Однако все подгруппы
|^@): 0<9<2я], dgR3
коммутативны (см. упражнение ЮЛ).
С практической точки зрения из этих результатов
следует, что для обращения поворота надо просто транс-
транспонировать матрицу, и если к некоторому геометрическо-
геометрическому объекту применяют несколько поворотов, то порядок
их применения важен.
Следуя двумерному случаю, объединим ТC) и 50C)
в виде множества Е{Ъ) евклидовых преобразований R3.
Элементы ЕC) имеют вид f/r — Wt + r0 для всех reRs,
где IV е 50C) и го <s R3. Правило композиции в Е{Ъ)
записывается следующим образом:
(Wt, t2)b(Wu rt)-(W3Wu W2rl + t2);
по отношению к нему Е(Ъ) становится некоммутативной
группой нелинейных преобразований R3. Отсюда выте-
вытекают следствия, аналогичные двумерному случаю.
В частности, подчеркнем, что ЕC) не может выполнять-
выполняться в М(Ъ, R).
Преобразование масштаба в R3 является линейным
отображением вида
S(x, у, z) = (Ял-, цу, 02), (х, у, z)e R^
где Я, ц, о > 0. Множество 5C) всех преобразований
360
масштаба определяет коммутативную группу по отноше-
отношению к операции композиции.
Остальные преобразования, рассматриваемые в этом
параграфе, имеют цели и свойства, отличные от рассмот-
рассмотренных выше. Нашей целью является задача представ-
представления трехмерного геометрического объекта на двумер-
двумерном графическом терминале. С математической точки
зрения мы ищем преобразования R3 в двумерные под-
подпространства, в которых получаются необходимые гра-
графические представления нашего объекта. Напомним, что
преобразование Р векторного пространства называют
проекцией, если Р2 = Р.
Пусть объект описывается в декартовой системе коор-
координат (х, у, z) и в этой системе экран графического дис-
дисплея соответствует прямоугольному подмножеству
{(х, у): О^х^а, 0 ^ у *S b)
на плоскости ху. Простейший метод получения образа
объекта на экране — это применить преобразование
Р\т = г', где г = (а;, у, z) и т'=(х, у, 0), к множеству
геометрических данных. При условия что все значения
х а у для множества данных паходятся внутри экрана,
получаем полную картину объекта. Если некоторые зна-
значения х и(или) у находятся вне пределов экрана, то на-
надо вначале произвести подходящее преобразование мас-
масштаба. Р| — линейная проекция, так как
[1 О О"
О 1 О
0 0 0
и Р\т = Рхг для всех г е R3. Однако Pf1 не существу-
существует, так как
Г1 0 ОТ
о 1 о =0.
Lo о oj
0
0
Геометрически Pi можно получить следующим обра-
образом. Начертим линию сегмента (линию проекции) из
точки Q, определяющей положение вектора г, в точку
Q', определяющую положение г', в плоскости ху так,
чтобы линия отрезка QQ' была ортогональна плоскости
ху (рис. 10.14). Тогда ясно, что
г'-I+ (—*?)-(*, у, 0)=Р,г.
Pi называют параллельной ортогональной проекцией R3.
861
В параллельной проекции не отражается глубина полу-
получаемого образа; высота объекта появляется на экране
такой же независимо от его расстояния до плоскости ху.
Рис. 10.14
а'
Рис. 10.15
Рис. 10.16
Последнее преобразование, которое мы опишем, предна-
предназначено для того, чтобы дать глубину образа или «пер-
«перспективу». Вместо линий параллельной проекции постро-
построим линии проекции, выходящие из некоторой фиксиро-
S62
ванной точки. Определим проекцию РгГ = г', где фикси-
фиксированной точкой является конец вектора zpk (как пока-
показано на рис. 10.15) и, следовательно, точка Q отобража-
отображается в точку Q'. Рисупок 10.16 представляет вид
рис. 10.15, если смотреть вдоль оси ОХ. Очевидно, мто
или же
*р
ч'
1 -
х' =
гР
1 —
1-
у
X
-«V
Аналогично получаем
явная форма для Р% имеет вид
Предложение. Pi является нелинейной проек-
проекцией R3.
Доказательство.
Р2Ь(х, у, z) = Р2{Хх, Ху, Xz) = i_\z/2 (Хя, Ху, 0),
%Р2(х, у, z) = . 4 (Хх, Ху, 0) ФР2Х(х, у, z)
1 — Z/Zp
для произвольного X. Следовательно, Рг нелинейно.
Имеем
- о
) =
и, таким образом, Р% — проекция в R3 по определению. /
Отсюда можно сделать заключение, что Р% нельзя
включить в М(Ъ, R). В образе можно достигнуть хоро-
хорошей глубины применением Рг, при условии что выбрана
подходящая точка проекции. Па рис. 10.17 показан вид
прямоугольного параллелепипеда, полученный проекция-
проекциями Pi и Р2.
363
2.3. Однородные координаты и линейное представле-
представление. В этом разделе мы опишем технику представления
преобразований R2 и R3, рассмотренных выше, при по-
помощи элементов из ЛC, R) и Ж D, R) соответственно.
Рис. 10.17
Идея является общей и описывается в R"; мы ищем
вложение некоторых специальных классов преобразова-
преобразований R", не все из которых являются линейными, в ал-
алгебру матриц Jt{n+ \; R).
В § 1 было показано, что Qn является биекцией
Н" -*¦ R" и может быть использовано для определения
системы координат в R". Это означает, что если Т —
преобразование R", то мы можем его выразить как пре-
образовапне Нп. Другими словами, существует отобра-
отображение Т: Нп -*¦ Нп такое, что диаграмма на рис. 10.18
коммутативна. Имеем Qn ° Т — Т ° Q", но отображение Q"
имеет обратное. Поэтому мы можем записать Т =(<?")"' °
•Г» Qn. Если 5 — другое преобразование R", то
- (<?n) -1 о S - <?" о (Qn)-* oT'Qn^S-T.
Другими словами, мы можем соединить вместе диаграм-
диаграммы, не нарушая коммутативность, как это показано на
рис. 10.19. Для некоторых преобразований Т прострап-
ства R" существует линейное преобразование
TL: R"+1 -+ Rn+1
такое, что Т [х] = [TLx] для всех х е Rn+I.
TL существует для всех преобразований, рассмотрен-
рассмотренных в этой главе, и является требуемым представлением
Т в Rn+1, так как если г е R", то мы имеем
Tx = Q"of .(Q*)-*X = Q''T [г, 1]-0"[Гь(г, 1)].
Таким образом, преобразование Т получается путем при-
применения Ть к однородному представлению и последую-
последующим применением Q" для возврата к физическим коор-
координатам.
364
Чтобы иметь уверенность в том, что все работает
правильно, надо показать, что композиция S • Т соответ-
соответствует произведению матриц SLTL. Это
легко сделать, так как
Графически это означает, что мы можем
Рис. 10.19
расширить коммутативную диаграмму, изображенную на
рис. 10.19, до коммутативной диаграммы, изображенной
на рис. 10.20. Отсюда следует, что, один раз определив
матрицы Гь, SL, ..., соответствующие преобразованиям
Я"*-!
¦I ~
+ Н"-
{. _ {
-*-fl
+ R»
Рис. 10.20
Т, S, ..., которые мы хотим осуществить, мы затем со-
сохраняем их, опуская обозначения классов эквивалентно-
эквивалентности и работаем с векторами, представляющими эти клас-
классы. Произведения преобразований в R" получают путем
умножения матриц из J?(re+ I, R), примененных к векто-
векторам, представляющим классы. Все представители данно-
данного класса будут давать те же самые физические коорди-
координаты в соответствии с отображением
#i,
хп+1
Обычно выбирают вектор (г, l)<=Rn+1, чтобы предста-
представить te R". Такой выбор, очевидно, всегда возможен.
365
В следующих примерах мы получим матрицы TL для
преобразований, описанных в пп. 2.1, 2.2. Все матрицы
вычисляются в стандартном базисе.
Пример 2.1. Пусть Т: R" -*¦ R" — линейное преоб-
преобразование с матрицей Ат. Тогда матрица Th будет равна
От
^ :
о
...о i
так как если х = (r, l)e Rn+l, то
Т [х] - (^)-1.Г.?п И = (О")
[(Лгг, 1)]
Для
I, если это удобно, используют обозна-
о •
0...0 lj
\АТ 01
чение L А, Раскладывая по последней строке,
[Ат 0]
0 j = 0 тогда и только тогда, когда
[Ат 0 1—1 Г д—1 о!
0 1 ~ I а\
Пример 2.1 показывает, как применять линейные
преобразования; например, применяя преобразования к
50B), получаем представление
["cos 6 — sin 6 0
I sine cos6 О I
L 0 0 lj
в J[C, R) для матрицы
[cos6 —sine]
[sine cosBJ*
Аналогично, если W & 50C), то WL имеет вид
в JfD, R) в
\w о]-1 \wT о]
[о ij =[о ij'
Пример 2.2. Пусть Т: R" -*¦ R" — перенос
Тх — г + а для всех г «= R",
где a —(at, ..., On)s R" — фиксированный вектор. Тогда
матрица Th будет равна
_О...О 1 _
она может быть записана в более краткой форме:
[о' ;]•
Легко показать, что если х =(г, 1), то
Пример 2.3. Аналогичными вычислениями можно
показать, что преобразование (W, &)е=ЕB\ можно вы-
выполнить, используя
[|f j]eG?C,R), где Wе= 50B) и as Ra,
а преобразование (W,&)^EC) можно выполнить, ис-
используя
[J j]e<?LD,R), где W<=S0C) и агВ3.
Обратные матрицы имеют вид
\W а] \WT ~WTa]
[о ij eLo l J
каквЯB),такив?C). /
Пример 2.4. Проекция Pi: R3 -»• R3, определяемая
соотношением
Л(*»*)(*»0)
может быть выполнена в
1 О
О 1
О О
О О
R) как
О 0-
0 О
о о
-!/.„ 1_
так как если х =(r, l)e R* и г = (х, у, z), то
Р» М = (QT1-?^ Кг, 1)] =
Упражнение 10.1.
1. Показать, что группы (ТB), •) и (R2, +) изо-
изоморфны.
2. Доказать, что если
11 Oj'
то матрица поворота W(Q)fsSOB) может быть записа-
записана в экспоненциальной форме WF)*- exp{Q/}.
3. Определить евклидово преобразование, отображаю-
отображающее треугольник PQR, изображенный на рис. 10.21, о, в
треугольник P'Q'R', изображенный на рис. 10.21, Ь.
ffr=l0,2)
рЧы)
Рис. 10.21
4. Доказать, что 5B)—коммутативная подгруппа ли-
нейных преобразований R2.
5. Показать, что в общем случае элементы SB) не
коммутируют с элементами ?0B), в построить рвсунок,
демонстрирующий это.
6. Доказать, что единица нетривиальной подгруппы
SB) не коммутирует с ?0B).
7. Используя преобразование 5(х, у)'°=Cа;, 5у), изме-
изменить масштаб R2 так, чтобы точка B, 2) оставалась
фиксированной. Определить это преобразование.
8. Показать, что если neR' — единичный вектор, то
п X ((п X г)ХЪ) — пX г для всех г е= R3.
9. Пусть nsR! и А а' Н3 -* R3 определено соотноше-
соотношением А о г >= п X г для всех г е R3. Показать, что А а-*~
линейное преобразование R3, и определить матрицу Аа—
в стандартном базисе {i, j, k).
10. Используя результаты п. 9 этого упражнения и
выражение W~(Q) через А~, получить в явном виде
матричную форму поворота W~{Q) в R3. Показать, что
11. В обозначениях п. 9 показать, что для всех
rsR3 имеем
4Г = ~ 4Г> А?г = - 4Г'
для всех fteN; использовать эти результаты для дока-
доказательства равенства
12. а) Используя экспоненциальную форму Vr~
получить другое доказательство того, что
б) Если Asi(n, R), то можно показать, что
det(exp Л) =
используя этот факт, получить другое доказательство
соотношения
13. Доказать, что п является собственным вектором
W- (G) при любом 9, 0 «S 6 < 2я. Чему равно собствен-
собственное значение? Дать геометрическую интерпретацию ато-
атому результату.
14. Вывести формулу для матриц поворота
15. Показать, что все подгруппы 5~"={И^(8
изоморфны SOB\.
24 д. кук, Г. Бейз 369
16. Пусть а <= RJ — фиксированный вектор и преоб-
преобразование Т: R3 -*¦ R3 определено как
л-(^ при а'
I 0 в противном случав.
а) Доказать, что Т — нелинейная проекция в Rs.
б) Доказать, что
Т[(т, 1)]-[(*, а-г)]
для всех г е R3 при г • а Ф 0.
в) Определить матрицу 4ejfD, R) такую, что
Г[х] = [Ах] для всех х е R4, где И в ЕР.
§ 3. Кривые и поверхности
3.1. Математическое представление. Кривые и по-
поверхности образуют основу большинства вспомогатель-
вспомогательных устройств компьютера и графического математиче-
математического обеспечения. Возможны различные математические
описания одной и той же геометрической формы; неко-
некоторые из них обсуждались и доступны с точки зрения
приложений.
Если / с: R — интервал, то через и" обозначим мно-
множество всех отображений класса С1:
с: I-+ R»,
причем с' Ф 0 на /. На и" определим отношение ~ сле-
следующим образом. Пусть
*: /i -*¦ R", c2: h ¦* R4;
тогда Ci ~ cs, если существует отображение ф: /i -*¦ h из
класса С1 такое, что ci = Сг • ф и ер' Ф 0 на 1\.
Предложение. Отношение ~ является отноше-
отношением эквивалентности на к". /
Доказательство оставляем в качестве упражнения.
Пусть <&п обозначает классы эквивалентности ип/~.
Определение. Кривой в Rn называется элемент
&". II
Если с е и" и с: / -»- R", то / называют параметриче-
параметрическим пространством с, a t — параметром или координа-
координатой с. График с (graph с) определяют как множество то-
точек
ic(t): t^D.
870
Если [с] обозначает класс эквивалентности с в &*, то для
всех с\ е [с] имеем
graph C\ = graph с,
так что разумнее говорить о графике кривой [с]. Обрат-
Обратное неверно; мы можем иметь соотношение graph [c{\ =
= graph [сг], но при этом [с\] Ф [cj]. Отношение эквива-
эквивалентности ~ группирует вместе элементы и", которые
параметризуются «аналогичным» образом.
Для вычислительных целей выберем элемент с е [с]
и назовем кривую также с, хотя с точки зрения терми-
терминологии это неправильно. Это возможно при условии, что
мы понимаем разницу и проявляем осторожность, когда
это необходимо. График кривой в 9'2 является множест-
множеством точек, которые мы видим отображенными на графи-
графическом терминале. Тогда 'ё'2 — множество плоских кри-
кривых, а элементы Ф3 — множество пространственных кри-
кривых. Ч?2 и 9?3 важны для приложений, однако, где легко
провести рассуждения в более общем случае, будем это
делать.
В литературе по компьютерной графике употребляют
термины «параметрический», «явный», «неявный» по от-
отношению к различным методам определения кривых. Ес-
Если (|i, ..., ?»)— система координат в R" и элемент с«н
s хя определен при помощи п функций ?>-»-5н@
(l^i^n), то такое задание кривой называют явным
параметрическим описанием. Иногда выделяют два ти-
типа— «симметричный» и «несимметричный». Описание не-
несимметрично, если параметр является одной из коорди-
координат, т. е. t = |j для некоторого i, I ^ i ^ п. Следователь-
Следовательно, несимметричные описания имеют вид
{Ь, (Si(SO. h(l<),..., Ъ, ..., Ы1<))), b&I;
в случае W2 и декартовых координат эта вапись имеет
знакомый вид
(х, (х, у(х))), х^[х0, х\],
и кривую определяют, задавая явно у как функцию от
х. С другой стороны, мы можем описать кривую в R",
определяя подходящую функцию /: R" -»¦ R. Для фикси-
фиксированного а е R функция / определяет кривую с гра-
графиком
fill, •••! ?п) называют уравнением кривой (строго гово-
говоря, следовало бы назвать графиком кривой). В пршщипо
24* 371
уравнению такого типа можно придать явную форму,
хотя в общем случае это сделать достаточно сложно. Го-
Говорят, что кривые, определяемые такими уравнениями,
описаны неявно.
Заметим, что не все отображения /: R" -*¦ R будут за-
задавать кривые описанным выше способом. Например, по-
постоянное отображение задает все Rn. Далее функция
/: R" -*¦ R может для одних значений постоянной а вада-
вать кривую, а для других — нет, как мы это увидим
ниже.
Плоская кривая, заданная неявно уравнением вида
ах2 + by2 + сху + dx + еу + / = О,
называется квадратичной кривой (кривой второго по-
порядка).
Пусть с\\ [a, b]-*Rn и с2: [с, d]-*Rn, где a<b=>
¦=c<d и ci(b) = C2(b). Тогда а V с% определяют следую-
следующим образом:
К на [а,Ь],
на [c,d]
и называют объединением функций с\ и cj. Для симмет-
симметричных описаний, если с Ф Ъ, сг может быть параметри-
параметризовано таким образом, чтобы это условие выполнялось.
Это означает, что мы можем построить сг е [с2] такое,
что интервал для с2 начинается с Ъ. Следовательно, при
условии c\(b)= c2(b) объединение С\ V сг имеет смысл,
но может не быть, строго говоря, кривой. Проблема со-
состоит в том, что с\ V С2 может не принадлежать С.
Пример 3.1. Прямо-
(x/>i/t> линейная кривая (пря-
^l мая) может быть опреде-
лена в R2 обычным обра-
'{хв ,у0) зом как
у(х)= тпх + с,
Хо
Рис. 10.22
где m — наклон прямой,
а с — точка пересечения с осью Оу (рис. 10.22). В на-
наших обозначениях это будет
(х, (х, mx + c)), so«?z<?i;
тис могут быть заданы непосредственно, однако более
372
естественно использовать концы го = (х0, у0) и г,
= (хь #i)> откуда получаем
m = (yl — yo)/(xi — х0), c=*yi
Проблема, возникающая в несимметричных описаниях,
теперь очевидна. Эта форма не описывает вертикальную
линию (когда x<j = xi). Если вместо этого воспользовать-
воспользоваться неявной формой
(У — Уо) (*> — хо) — (yi — уо) (х — хо) = 0, х0 < х <хи
то при xi = хо получим уравнение вертикальной линии
х = хо. Неявное уравнение прямой линии в общем слу-
случае имеет вид
ах + by + с = О,
и вертикальные линии описываются этим уравнением
при b = 0.
Обычное симметричное описание может быть записа-
записано в векторной форме:
(t, ю + iu), *е[0, llri
где и — единичный вектор, u = (ri — ro)/"ri — *(>"• /
Рассмотренные выше примеры приводят к общим на-
наблюдениям о природе кривых, определенных несиммет-
несимметричным способом. Перед тем как обсуждать это, дадим
несколько необходимых определений.
Определение. Говорят, что плоская кривая
(и, (х(«), у (и))), «?/ = [«!, ив] является:
— однозначной, если для всех »i, »2s / имеем
— многозначной, если предыдущее условие не вы-
выполнено;
— замкнутой, если (х(иА), ^(мА)) = (х(ив), у(ив)). II
На рис. 10.23 проиллюстрированы все три случая.
Очевидно, что замкнутая кривая является многозначной.
Несимметричное описание (х, (х, у(х))), хо^х<х\
может определять только однозначную кривую. Это по-
потому, что у является функцией от х и, следовательно,
Xi — х2 =*¦ у (xi) = у (х2).
Вертикальная линия является многозначной кривой.
Многие приложения в компьютерной графике требу-
требуют, чтобы замкнутые и многозначные кривые были вклкь
873
чены в описания. Единственный путь достижения этого —
объединять кривые, как это описывалось ранее. При ис-
использовании несимметричных форм это не очень удобно
Однозначная
криЗаа
а
Многозначная
крибая
Ъ
Рис. 10.23
Замкнутая
кривая
о
и редко применяется на практике. Симметричные описа-
описания не имеют этого ограничения и, следовательно, явля-
являются более удобными для таких приложений. Несиммет-
Несимметричные формы обычно исполь-
используют, когда требуется одно-
однозначная кривая.
Пример 3.2. Окружность
является примером замкнутой
кривой. Рассмотрим окружность
в R2 радиуса а с центром в на-
начале координат (рис. 10.24).
Чтобы записать окружность
в несимметричной форме, необ-
необходимы две кривые: у\ (х) =¦
Рис. 10.24
¦ (а2 - х2)
,2\ 1/2
в
—a ^ x ^ i
квадрантах 1 и 2 и У2{х)=а
¦=» — {а7— х7)|/2, —а <х<а в квадрантах 3 и 4. Уравне-
Уравнение окружности в неявной форме имеет вид
или же в векторных обозначениях,
Urll - a - 0.
Это уравнение описывает всю окружность; оно может
быть записано в симметричной параметрической форме
@, a (cos 6, sin 6)), 8е [0, 2я[,
Волможно бесконечное число других симметричных форм,
374
выбор которых зависит от приложений. Для выполнепия
рисунков более предпочтительной является параметриза-
параметризация с относительно постоянным изменением r(t). Мате-
Математически это означает, что величина llr'(f)ll приблизи-
приблизительно постоянна на /. Несимметричное представление в
большинстве случаев является неудобным, так как тре-
требуется проверка, на какой ветви кривой мы сейчас на-
находимся. II
Примерами кривых второго порядка являются эллипс,
гипербола и парабола.
Если G — группа преобразований R", тогда G преоб-
преобразует $"• естественным образом. Если cs?" — кривая
и g
Например, когда G = SOB) и cef2, то график ()
является графиком с, повернутым на угол G (рис. 10.25).
G, то определим кривую gc следующим образом:
ge-(t,gt[t)), tel.
График о
а
Гра/рик W(9)e
Ь
Рис. 10.25
Уравнения обычно описывают кривые в «стандарт-
«стандартном» положении, когда ось ОХ является осью симмет-
симметрии. Чтобы получить уравнение геометрически эквива-
эквивалентной кривой в некотором другом положении и ори-
ориентации в пространстве, надо просто применить подхо-
подходящий элемент группы Е{2) к уравнению. В качестве
примера выведем уоавнение эллипса с графиком е, изо-
изображенным на рис. 10.26. В стандартном положении
(изображенном штриховой кривой на рисунке) кривая
записывается в виде
cos ф| Ь si
[0, 2я[;
375
следовательно, кривая с графиком е имеет вид
(W(Q), d)c=^, (И'(б), d)(acosф, Ьбтф)) =
*= (ф, (a cos ф cos 6 — b sin ф sin 6 + d\, a cos ф sin 6 +
+ b sin ф cos 8 + d2)), ф s [0, 2n[.
Неявные уравнения для кривых в нестандартном поло-
положении могут быть получены аналогично.
Перед тем как перейти к дру-
другой теме, упомянем один интерос-
ный факт, проверка которого осу-
осуществляется довольно легко, ког-
когда кривые заданы неявными урав-
уравнениями. Пусть /(х, у) = 0 — урав-
уравнение плоской кривой, которая
делит плоскость R2 на три части,
~^5 ~% тогда, если (х', у')—произволь-
ч^ " ная точка пространства., то знак
Рис. 10.26 /(*'» У') определяет область,
в которой лежит (х', у').
Например, возьмем уравнение окружности
тогда
/(х'« У')> 0 =>¦ (хг, у") лежит за пределами круга,
1(х\ У')*°* 0=*-(х', у') лежит на окружности, /(х', у'}<
< 0 =»¦ (х', у') лежит внутри круга.
Проверки такого типа используют в трехмерных слу-
случаях в алгоритмах удаления невидимых линий с изобра-
изображений. Исследование поверхностей может быть проведе-
проведено по аналогии с исследованием кривых. Методы пред-
представления имеют те же самые преимущества и недо-
недостатки.
Поверхности двумерны и имеют пространство пара-
параметров вида 1\ X h, где I\, h — R — интервалы. Парамет-
Параметрическое представление в общем случае имеет вид
((«, v)> r(и, v)), (и,»)е/,Х/«.
Неявное уравнение поверхности записывается в виде
/(х, у, z)=0, а поверхностью второго порядка является
поверхность, определяемая уравнением
ах2 + by2 + cz2 + dxy -Ь exz + fyz + gx + hy + iz + ] = 0,
где a, b, c, d, e, ft g,h,lt]&K
876
Пример 3.3. Пусть D = {r,: r,eR3, 0 < i
множество линейно независимых векторов. Тогда
г(u, 0)-fo + «(*i-*o)+w(rs —го), (u, y)eR
2) —
есть симметричное описание плоскости Р, проходящей
через точки D (рис. 10.27). Если q = (r2 — ro)X(ri — r0),
Рис. 10.27
Рис. 10.28
тогда n = q/Hqll — единичный вектор, ортогональный Р
(называемый нормалью). Таким образом, геР тогда и
только тогда, когда (г — Го) • п = 0, или
(х — хй)щ + (у — у0) п2 + (г — г0) п3 = 0.
Это является неявным представлением Р. /
Пример 3.4. Пусть S — сфера в R3 радиуса а с
центром в начале координат. Очевидно, что rs5 тогда и
только тогда, когда llrll = а, или же
х2 + у2 + z2 — а2 = 0.
Сферические координаты дают симметричное представ-
представление
(@, ф), a (sin 9 cos ф, sin 0 sin ф, cos 8)),
@, ф)е=[0, я]Х]0, 2n[. II
Пример 3.5. Пусть С —цилиндр радиуса а с осью
симметрии OZ. В этом случае (х, у, z) e= С тогда и толь-
только тогда, когда
Используя цилиндрические координаты, получаем сим-
симметричную форму
((ф, z), (a cos ф, a sin ф, г)).
377
Обычно рассматривают «конечный» цилиндр (рис. 10.28).
Для него уравнение будет иметь вид
Относительно уравнений поверхностей, находящихся
в нестандартном положении, можно сделать те же заме-
замечания, что и для случая кривых; надо лишь Е{2) заме-
заменить на -Е(З).
3.2. Геометрия плоских кривых. Целью данного раз-
раздела является определение понятий длины, касательной
и кривизны плоских кривых. На рис. 10.29 изображена
плоская кривая
e-(f, r@), t<=[tA,tB].
Р — произвольная точка на с, являющаяся концом век-
вектора i(t), a P' — конец вектора x(t + St), 52eR\{0).
Рис. 10.29
Пусть f>t{t) обозначает вектор РР'. Тогда, очевидно,
есть длина отрезка РР'.
Если разбить интервал [tA, tB] на много маленьких
интервалов равной длины [U-\, tt],tA = to<t\< .. .<tn =
= ta, то можно образовать сумму
n
Sab =2 ISi-if,
где Sri = r(f()—r(fj_i), которая равна длине ломаной ли-
878
нии вдоль с. Интуитивно ясно, что мы получаем аппро-
аппроксимацию кривой 5ЛВ между t(tA) и t(tB). Приближение
будет тем лучше, чем больше число разбиений отрезка
[tA, tB]. Эти интуитивные понятия приводят нас к опре-
определению длины кривой Sab:
п
SAB= lim 2 1&Ч||.
С вычислительной точки зрения эта формула трудна для
использования. Поэтому мы перепишем ее в .более удоб-
удобном виде:
lim 2 1 бг{ || = lim | | г (*,) - г (**_х) || =»
П->сх> i=l )|->сс »=1
где 6t = (tB — tA)/n. Но это по определению интеграл
?i
*А
следовательно,
?|?|*
Если i(t) — (x(t), y(t)), то формула принимает вид
'в
*А
Интуитивно ясно, что линия наклона (па рис. 10.29
это QQ') к кривой с является прямой, касающейся этой
кривой и имеющей тот же самый наклон, что и с, в точ-
точке Р. Пусть 9 — это угол между отрезком РР' и каса-
касательной QQ'. Тогда при Ы -*¦ 0 следует ожидать, что
6 -»¦ 0. Это означает, что направление бг(<) или же
bt(t)lbt стремится к направлению QQ' при б?-»-0. Дру-
Другими словами, вектор
379
параллелен QQr. Если
-Jlal*
тогда в принципе все кривые могут быть выражены в
терминах параметра длины дуги (s, t(s)), se[0, SAB].
Из определения длины дуги получаем
о
дифференцируя обе части по s, имеем
Ч§
Другими словами, dr/ds — единичный вектор, параллель-
параллельный касательной линии к r(s). Это вызывает следующее
определение.
Определение. Пусть (s, r(s)), se[0, SAB],— кри-
кривая с длиной дуги в качестве параметра. Определим
единичный вектор касательной T(s) к кривой в точке
s как
а нормальный вектор N(s) к кривой как
Базис (Т, N) образует правостороннюю систему коор-
координат в R2. Если кривая не параметризуется в терминах
длины дуги, то выражение для Т (см. упражнение 10.2)
будет иметь вид
dr III dt Л ds _ n
-г-/ -г- , если — > О,
W ~~ dr l\\ dr || ds ^ „
-r T , если -7-<0.
du /1| du |P du ^
Эти формулы неявно предполагают условия на s.
В действительности знак Т не образует класса эквива-
эквивалентности, инвариантного на 'О?2, а является функцией
выбранного параметрического представления. Даже если
параметризация осуществлена с помощью параметра —
длины дуги, она зависит от того, с какого конца мы на^
280
чтгааем измерять s. Касательное пространство к точке
кривой является классом, инвариантным на 'О?2, где ка-
касательное пространство к [с] в точке Р имеет вид
(«Т: а s R, где Т — касательный вектор в Р для неко-
некоторого с е [с]}.
Из упражнений к § 4 гл. 5 следует, что dT/ds ортого-
ортогонален к Т; следовательно, существует функция к:
[О, SAB] -*¦ R такая, что Ц?} = х (s) N (s); x (s) назы-
называют кривизной кривой r(s), a l/x(s) — радиусом кри-
кривизны r(s).
Упражнение 10.2.
1. Получить в R2 явное уравнение прямой, проходя-
проходящей через точки (—1, 3) и B, —1). Определить еди-
единичный вектор, параллельный этой прямой, и написать
уравнение в параметрической векторной форме.
2. Определить касательный и нормальный векторы Т
и N и кривизну х следующих плоских кривых:
а) окружрости — (G, a(cosOi + sinO/)), 0<9<2я;
б) эллипса —(ф, (acosq>i + bsinq>/)), 0<ф<2я;
в) параболы — (t, (at2i + 2atj)), — «><f<«>) где
а > 0 и Ъ > 0 действительные.
3. Плоская кривая определена формулой
(и, (acosK?+b(l-e-tt/2O)), 0 *? и < »,
где а > 0 и Ъ > 0 действительные.
а; Показать, что касательный вектор к кривой зада-
ется формулой Т (и) - {ij ^ u + f.-uyut •
б) Начертить кривую в интервале 0 < и < 2я.
в) Найти нормаль к кривой.
4. Начертить кривую (и, (acos и, Ь sin и, Ьи)),
—оо < и < а>, и найти выражение для касательного век-
вектора Т(и).
5. Пусть (х, (х, у(х))), хо<х<хи описывает Jmo-
скую кривую. Показать, что касательный вектор Т(х)
может быть записан как
881
и, следовательно, кривизна к(х) в точке х имеет вид
6. Получить формулы, аналогичные полученным в
п. 5, для симметричного представления (и, (х(и), #(и))),
Mo < U *S В].
7. Найти симметричное параметрическое уравнение
плоскости Р, проходящей через точки @, 1, 0),
C, —2, 0) и A, 3, 4) в R3. Показать, что нормальный
вектор будет параллелен (—4, —4, 3), и использовать
этот факт для вывода неявного уравнения для Р.
8. Поверхностью вращения называется поверхность,
являющаяся результатом вращения плоской кривой во-
вокруг некоторой фиксированной оси в R3.
а) Показать, что если плоская кривая
(и, (р(иI+ q(u)k)), ил
делает поворот па угол 2я вокруг оси OZ, то соответст-
соответствующая поверхность вращения описывается уравнением
(("» ф). (p(")cos(pi + p(u)sin(pj + g(u)k)),
где иА < и < ив, 0 < ф < 2я.
б) Использовать результаты задачи 8, а) для получе-
получения симметричных параметрических представлений сле-
следующих поверхностей:
— цилиндра; — конуса; — тора.
9. Цилиндр С\ длины 21 определяется уравнением
х1 + z2 = Ь2, —l^y^l, и пересекается с цилиндром С%
длины h, который определяется уравнением у2 + (z — а) 2=»
-»а8, 0*Zx<h, где 0<а<6, h > b.
Используя параметрические координаты
{(х, G): 0 < х < h, 0 «? 9 < 2я> на С2,
показать, что кривая, являющаяся пересечением С\ и Сг,
может быть записана как @, г@)), 0О<2я, где
,@) = ((&2-(а + asin0JI/2, acos0, a + asin0).
Показать также, что единичный касательный вектор к
кривой в точке 0 = 0 задается формулой
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Автомат конечный 320
Автоморфизм 136
Алгебра Булева 176
— линейная 162
— регулярная 336
Алгебраическая структура 134
Алфавит 138, 257
Атрибут 56
База данных 64
Базис 157
— ортонормированный 165
Биекция 70
Бит 125
Буква 257
Вектор 154
— единичный 165
— собственный 170
Вектора компонента 155
Гомоморфизм 134
Грамматика 264
— регулярная 340
— Хомского 268
Граница верхняя 52
— нижняя 52
Граф 217
— двудольный 223
— ориентированный 242
— пленарный 228
— полный 223
— , пометка 221
—связный 224
Графа ребро 218
Группа 139
Делитель нуля 142
Дерево 224
Доказательство по индукции 81
Дополнение 17, 18
Единица 111
— левая 111
— правая 111
Законы де Моргана 29
Замыкание процесса 65
— рефлексивное 201
— транзитивное 66
Запись 54
Значение собственное 170
Изоморфизм 136
— неопределенный 101
Интеграл Римана 99
Карта графа 229
Класс эквивалентности 48
Кольцо 141
— коммутативное 141
— с единицей 141
Комбинация линейная 158
Композиция 159
Конкатенация 138
Кривизна 381
Логарифм натуральный 104
Маршрут 224
Матрица 195
— булева 201
— смежности 2'8
— транспонироь аная 200
Машина с неограниченной памятью
303
Множество 10
— бесконечное 19
— конечное 19, 75
— пустое 17
— счетное 75
— универсальное 13
— частично упорядоченное 52
Моноид 137
Мощность множества 19
Набор длины п 34
Надмножество 25
Неравенство треугольника 171
Нетерминал 265
Нормаль 377
Нормальная форма дизъюнктив-
дизъюнктивная 181
— конъюнктивная 181
Область значений 37
— определения 37
— целостности 143
Объединение множеств 16
Операция ассоциатизная 110
— диадическая 106
— дистрибутивная 111
— замкнутая 106
— коммутативная НО
— монадическая 106
— над множеством 106
Определитель 212
Основание индукции 81
Отношение антисимметричное 43
— бинарное 36
— обратное 39
— порядка 51
i— полное 51
— пустое 37
— рефлексивное 43
— симметричное 43
«— составное 62
883
Отношение тождественное 37
— транзитивное 43
— универсальное 37
— вквивалентности 47
— п-местное 38
Отображение 69
— линейное 159
— тождественное 70
Перенос 357
Поворот 359
Подмножество 25
— собственное 25
Подпространство векторное 155
Подстановка 83
— циклическая 85
Подуказатель 134
Покрытие 47
Поле 54, 143
Полугруппа 137
Полукольцо замкнутое 192
Порядок аддитивный 148
Последовательность 88, 92
Предел функции 94
Принцип двойственности 178
Продукция 265
Проектор 169
Проекция 56
Произведение векторное 165
— внутреннее 164
— скалярное 163
Производная 96
Пространство векторное 154
конечномерное 159
Разбиение 47
Размерность 158, 159
Разность множеств 17
— симметрическая 17
Решетка 174
Ряд 93
— Маклорена 104
— сходящийся 93
Сочетание 88
Степень множества 30
Сумма ряда 93
Таблица истинности 178
Терминал 265
Трансформация 6»
Указатель 134
Файл нормированный 54
Функционал 89
Функция 68
— биективная 70
— ннъективная 70
— сюръективиая 69
— экспоненциальная 104
Характеристика 14S
Цикл 85, 224
— длины п 88
Число рациональное 49
— связности 227
Шаг индукции 81
Эквивалентность множеств 26
'Элемент идемпотентный 111
— обратный 111, 139
Эндоморфизм 133
Ядро 170
Научное издание
КУК Д., БЕЙЗ Г.
КОМПЬЮТЕРНАЯ МАТЕМАТИКА
Зуведующий редакцией Е. Ю. Хован
Редакторы: Е. В. Ильченко, А. В. Угольников
Художественный редактор Г. Н. Кольченко
Технический редактор С. Я. Шкляр
Корректоры: М. А. Смирнов, И. Я. Кришталъ
ИБ JA 32537
Сдано в набор 02.03.89. Подписано к печати 20.04.90. Формат 84X108/32.
Бумага книжно-журнальная. Гарнитура обыкновенная. Печать высокая.
Усл. печ. л. 20,16. Усл. кр.-отт. 20,18. Уч.-изд. л. 19,84. Тираж 23 000 вкз,
Заказ М 604. Цена 1 р. 70 к.
Ордена Трудового Красного Знамени издательство «Наука»
Главная редакция физико-математической литературы
117071 Москва В-71, Ленинский проспект, 15
4-я типография издательства «Наука»
630077 Новосибирск, 77, Станиславского, 25