Текст
Зкз. № — ______
j МИНИСТЕРСТВО АВИАЦИОННОЙ ПРОМЫШЛЕННОСТИ СОЮЗА ССР
ЦЕНТРАЛЬНЫЙ АЭРО-ГИДРОДИНАМИЧЕСКИЙ ИНСТИТУТ
л к им. проф. Н. Е. Жуковского
АЭРОДИНАМИЧЕСКИЙ РАСЧЕТ РОТОРА ГЕЛИКОПТЕРА
(Вихревая теория винта в косом потоке)
А. И. Слуцкий
ОБТЕКАНИЕ КРЫЛА ПРИ БОЛЬШИХ УГЛАХ СКОЛЬЖЕНИЯ
А. Я. Бокарева
J..
АЭРОДИНАМИЧЕСКИЙ РАСЧЕТ РОТОРА ГЕЛИКОПТЕРА
(Вихревая теория винта в косом потоке)
Л. И. СЛУЦКИЙ
КРАТКОЕ СОДЕРЖАНИЕ
В работе излагаются вихревая теория и метод аэродинамического расчета
ротора геликоптера с жестким креплением лопастей на режимах горизонтального
полета и набора высоты.
На основании результатов экспериментальных наблюдений М. Л. Миля
и М. К. Сперанского построена простая теоретическая „предельная" схема обра-
зования вихрей за ротором геликоптера в поступательном потоке, являющаяся
дальнейшим развитием и продолжением результатов Г. И. Майкапара по изучению
работы винта в косом потоке.
Построенная схема дает возможность просто получить аналитические выра-
жения вспомогательных функций для расчета индуктивных скоростей винта в ко-
сом потоке и исследовать их поведение в особых точках.
В работе приводятся графики вспомогательных функций для расчета индук-
тивных скоростей при углах атаки ротора арот = О и 15 и показывается, что без
заметной погрешности графиками функций при арот = 15° можно пользоваться для
расчета индуктивных скоростей в диапазоне углов атаки ротора — 25° <ZapoT,
“рот <25".
Расчетным путем показывается, что средние по времени скорости значи-
тельно отличаются от истинных мгновенных скоростей. Характер теоретически
рассчитанного распределения средней индуктивной скорости вдоль лопасти и ее
изменение по азимуту хорошо подтверждаются опытом.
Расчет моментов и нагрузок, выполненный по теории Глауэрта Локка и по
вихревой теории, показывает, что средние за оборот ротора величины близки по
обеим теориям, мгновенные же значения различаются очень сильно. Поэтому
в расчет мгновенных нагрузок и моментов необходимо вводить истинные индук-
тивные скорости.
L тгзг не зьшосеть
ВВЕДЕНИЕ
В настоящей работе излагается метод аэродинамического расчета воздушного
винта, работающего в потоке, скорость которого составляет с осью винта некоторый
угол z/0. В дальнейшем такой режим работы винта называется косой обдувкой
винта.
В действительности ось вращения авиационного винта лишь в редких случаях
2чно совпадает с направлением полета. Обычно она составляет с направлением посту-
пательной скорости небольшой угол, которым в расчетах пренебрегают.
Иначе обстоит дело в случае винтокрылых аппаратов—автожиров и геликоптеров,
развитию которых в последнее время уделяется большое внимание. В этом случае ось
вращающейся несущей поверхности, так называемого ротора, может образовывать
с направлением поступательной скорости любой угол 0<и<к. Вследствие этого
нарушается симметрия течения, и обтекание ротора становится нестационарным. При
этом существенно меняется картина распределения нагрузок по лопастям ротора, появ-
ляются некоторые дополнительные силы, не возникавшие ран о о 'Щь—винте- при МФ,
и весь анализ явления чрезвычайно усложняется. Инсуитуг
БИСЛИ >ТЕК>,
6
расчете винта на режимах косой обдувки приходится отказаться также от
упрощающей гипотезы плоских сечений, так как опыты показывают, что характеристики
сечений крыла, обтекаемого потоком, направленным под углом к оси, существенно
зависят от угла скоса крыла и от расстояния сечения от концов крыла.
Вопросу аэродинамического расчета ротора геликоптера посвящено много работ.
Впервые вопросами теории геликоптерных винтов начал заниматься Н. Е. Жуковский.
Однако в этих работах не рассматривалась непосредственно теория аэродинамического
расчета. Первыми работами, относящимися непосредственно к аэродинамическому
расчету винтов в косом потоке, были работы Глауэрта и Локка. В дальнейшем теорию
Глауэрта — Локка несколько усовершенствовал Уитли и затем Зиссинг. Этот же во-
прос рассматривается в работах М. Л. Миля, А. П. Проскурякова и С. Я. Стрижев-
ского.
Указанные работы Глауэрта и Локка обладают весьма существенными недостат-
ками. Помимо сложности расчетных формул они базируются на предположениях, ко-
торые вносят большие погрешности в расчет и зачастую искажают явление.
В этих работах делается допущение илй о постоянстве индуктивной скорости по
сметаемому винтом диску, или о ее воронкообразном распределении.
Это допущение явно не соответствует действительности. Чрезвычайно обширные
и интересные опыты М. Л. Миля и М. К. Сперанского, измерявших средние по вре-
мени индуктивные скорости под ротором и над ним, и опыты Росса, измерявшего
мгновенные индуктивные скорости под ротором, показывают, что они резко меняются
в зависимости от азимута лопасти и от положения точки, в которой измеряется ско-
рость, по размаху ротора.
Следующее упрощение, допускаемое в этих работах, состоит в замене действи-
тельных коэффициентов лобового сопротивления сечений лопасти сх некоторым
средним для всей лопасти значением сх0, не зависящим от угла атаки, и допущением
о линейном законе су(р). Зиссинг освобождается от этого допущения и принимает для
коэффициента лобового сопротивления профиля зависимость:
Расчет производится методом последовательных приближений, последовательно
определяя изменения, вносимые в углы атаки маховым движением лопастей. Таким
образом, все усовершенствования теории расчета ротора оставляли в стороне ее су-
щественнейший недостаток—допущение о постоянстве индуктивной скорости по диску
ротора.
Расчеты по всем указанным теориям не вносят значительных, погрешностей
в вычисления суммарных характеристик ротора, но они становятся очень неточными
при определении мгновенных сил на лопастях ротора. Между тем знание истинных
мгновенных нагрузок на лопастях ротора необходимо для правильного расчета ротора
на динамическую прочность, расчета устойчивости геликоптера и для правильного
определения углов взмаха лопастей.
Решительный сдвиг в этой области был сделан в 1946 г. Г. И. Майкапаром,
впервые предложившим применить для расчета индуктивных скоростей винта в косом
потоке вихревую теорию.
Г. И. Майкапар предложил распространить известную вихревую схему Н. Е. Жу-
ковского на случай косого обтекания винта. Эта обобщенная схема давала возмож-
ность рассчитать индуктивные скорости для любого угла атаки винта. Однако для
практического приложения эта работа требовала еще ряда дополнительных исследо-
ваний и вычислений некоторых вспомогательных функций.
В последнее время Л. С. Вильдгрубе применил вихревую теорию к расчету ро-
тора при малых углах атаки, соответствующих горизонтальному полету геликоптера.
Л. С. Вильдгрубе впервые была построена плоская вихревая схема, отражающая со-
стояние вихревой пелены за ротором, и дан практический метод расчета индуктивных
скоростей, соответствующих схеме.
В данной работе, являющейся дальнейшим продолжением и развитием результатов
Г. И. Майкапара, вычисляются индуктивные скорости для произвольного угла атаки рото-
ра арот^0 и, в частности, для предельного случая арот — 0. Для последнего случая рас-
смотрена также в качестве вспомогательного математического аппарата плоская вихревая
схема, полученная методом, отличным от применявшегося ранее Л. С. Вильдгрубе.
В работе излагается также метод аэродинамического расчета жесткого изолирован-
ного ротора и производится пример расчета.
Пользуюсь случаем выразить благодарность Г. И. Майкапару за ряд ценных советов,
а также старшим техникам Ф. Г. Клаппер и В. С. Соновой за тщательное проведение
расчетов.
2
1. РАСЧЕТ ИНДУКТИВНЫХ СКОРОСТЕЙ ПРИ арет^0 1
Рассмотрим изолированный /г-лопастный винт, вращающийся с угловой скоростью S
и помещенный в поступательный поток, скорость которого V составляет с плоскостью
вращения винта угол арот. Примем плоскость вращения винта за координатную плоскость
и направим ось Ох вдоль оси винта (фиг. 1). Очевидно, что в этом случае суммарная
скорость элемента лопасти винта будет зависеть не только от его расстояния от оси вра-
щения, но также и от углового положения лопасти. Если через г обозначить расстояние
элемента лопасти (сечения) от оси
Фиг. 1. Система координат, принятая
в исследовании
вращения и через ф — его полярный угол, то
ляющие скорости элемента лопасти будут:
О = Sr — V cos арот sin ф;
V"=VsinapoT;
VR = — V cos арот cos ф,
а полная скорость элемента лопасти:
W=V (Sr)2 + V2 - 2 IZSr cos cpoT sin ф.
состав-
СП
(2)
Из этих формул следует, что и циркуляция
скорости вокруг
соотношением
сечения лопасти, определяемая
2V = cvbW,
на
каждой лопасти и будет меняться
лопасти (изменяться по времени).
будет различна
при вращении
Таким образом, обтекание винта в этом случае
является нестационарным. Для того, чтобы несколько
упростить явление и сделать возможным его анализ,
воспользуемся обычно применяемой для решения большинства нестационарных задач
и дающей хорошее совпадение теоретических расчетов с экспериментом гипотезой ста-
ционарности. Согласно этой гипотезе аэродинамические силы, действующие на крыло при
неустановившемся движении, могут быть в каждый момент заменены теми силами, кото-
рые действовали бы на крыло, если бы оно находилось в данный момент в установив-
шемся потоке.
Допустив эту гипотезу, мы можем принять, что свободные вихри, срывающиеся
с задней кромки лопасти и уходящие в бесконечность, образуют винтовую поверхность,
которую, пренебрегая сужением струи, будем считать касающейся изнутри эллиптического
цилиндра Ось этой цилиндрической поверхности приближенно принимаем совпадающей
с направлением поступательной скорости (фиг. 2). При малом значении отношения
V cos арот
р =----, каковое имеет место для ротора геликоптера, витки вихревои линии рас-
полагаются тесно друг к другу, и подобно тому, как это сделано Н. Е. Жуковским для
винта в прямом потоке, отдельные вихри можно заменить слоем наклонных вихрей,
в свою очередь, можно разложить на два вихревых слоя (фиг. 3 — а, би а):
1) слой прямолинейных вихрей, направленных вдоль наклонной образующей
стирающихся в бесконечность;
2) слой круговых вихрей, плоскости которых перпендикулярны оси вращения
Если интенсивность свободного вихря, сходящего с элемента лопасти dr' и находя-
, й dr (г', ф) . ,
щегося от оси вращения винта на расстоянии г , будет-------ту ~ аг > то интенсивность
Cll
первого слоя вихрей будет:
а его,
и про-
винта.
а второго слоя:
— 1
— 2т.г'
k
dr(rf, ф,)
dr'
(3J
- S
Ъ~ 2кИ
k
</Г(г\4,)
dr'
(32)
1 В этом параграфе будут изложены с некоторыми дополнениями и несколько подробнее резуль-
таты, полученные Г. И. Майкапаром [2].
3
у dVt
dr'
Эти формулы имеют тот же вид, что и в случае Н. Е. Жуковского, только из-за
. dv
того, что теперь циркуляция различна на каждой лопасти, произведение —к -^заменяет-
ся суммой —
При доказательстве этих формул нам придется иметь дело с разложением вихревого
слоя на составляющие компоненты и с вычислением интенсивности составляющих. Рас-
смотрим этот вопрос несколько подробнее.
Фиг. 3. Схематизация вихревой системы винта
Вихревой слой наклонных вихрей, сходящих с лопастей винта, раскладывается на два
слоя вихрей (1) и (2). Напряжение каждого вихревого слоя можно характеризовать разры-
вом компонента скорости, лежащего в касательной плоскости и нормального к оси вих-
ревой линии1. Пусть [v], [</,], рп,] (фиг. 4,а) будут разрывы указанных компонентов ско-
рости соответствующих слоев. Если 7J, y's и 7 — напряжения соответствующих слоев, то
Из подобия треугольников, изображенных на фиг. 4,а, следует:
[-nJ: [u>] ^=V:Qr.
Обозначим Yi и 7, интенсивности слоев (1) и (2). Так как интенсивность слоя пред-
ставляет собой количество вихревых линий слоя, пересекающих единичную площадки
расположенную перпендикулярно вихревым линиям, то из фиг. 4,6 находим:
73:7]' = Sina и 78:7g= Sin а.
1 См., например, В. Ф. Дюренд. Аэродинамика, т. II. Оборонгиз, 1939 г.
4
Таким образом, окончательно получаем:
Ti: Т2 = V-
Скорость, вызываемую свободными винтовыми вихрями в некоторой точке Р (фиг. 5)
плоскости вращения винта, представим приближенно суммой скоростей, вызываемых в этой
точке обеими системами вихрей. В отличие от случая арог = -^- , когда кольцевые вихри
дают осевую и радиальную, а прямолинейные вихри—только окружную составляющую
скорости, при арот^е — обе системы вихрен дают все три составляющие скорости.
Пусть точка Р, в которой требуется вычислить индуцируемую свободными вихрями
скорость, определяется координатами 0, г, ф. Обозначим координаты элементов вихрей S
первого и второго слоев через х, г', 6. Обозначая расстояние элемента 5 от точки Р
через г, и расстояние Р от оси вращения — через г, из фиг. 5 легко получить выражения
проекций вектора гг на оси декартовых координат:
И X = X,
Г\у = Г COS ф — Р COS 0 — X ctg йрот,
И 2 = г' sin 0 — г sin ф;
Фиг. 4
длина вектора гх будет:
rj = Р 2/ cos арот (г' cos 0 — г cos ф) -ф- г- -ф- г'2 — 2rr' cos (0 — ф),
где
Проекции элементов вихрей будут:
1) элемент вихря, направленный по образующей,—
dSix = dx = dl sin apOTj dSiy = dxctgapVT) dSiz — O;
2) элемент кольцевого вихря —
dS2.v = 0,
dS2 у = r’ sin 0d0, dS2 z = r' cos 0dO.
Дифференциал скорости в точке Р от системы прямолинейных вихрей вычисляется
по обычной формуле Био—Савара:
2п со
« j k
dSi x dSi у dS\ z
Г1х ГХу Г\г
did®
rl
(4)
/ =--^~—
sin otpOT
5
Скорость от кольцевых вихрей определяется по такой же формуле, в которой
и dS} заменены на и dS.,.
Подставляя выражения проекций dS и вектора rv интегрируя вдоль прямолинейных
вихрей от 0 до оо, по кольцевым вихрям —от 0 до 2 г и суммируя затем действие всех
элементов лопасти, получим выражения для проекций скорости на ось х:
R 2п оо
_ 1 f f f cos ctpor (r'sin 0 — rsin ф) r'dldO dr'____
”и,лг — 4r J J J [/3-|-2Z cos ap0T (r'cos 0 — rcosO) + r24-r'2—2rr'cos(ф — ’
r„ 0 0
R 2т: OO
If if [r'2 — rr' cos (ф — 0) -|- lr' cos 0 cos «pOTJ dl dO dr'_
V2x 4 я J ^2J J p2/cos ap0T (r'cos 0 — r cos ф)r2-f-H2 — 2г/cos(ф— 0)]я/*
r„ oo
и аналогичные формулы для других проекций. Внутренние интегралы от 0 до оо по пе-
ременной I вычисляются непосредственно. Действительно, вводя обозначения
А = г--\-г'-— 2rr'cos(tp — 0) и В = 2 cos аРот р'cos 0 — г cos ф),
приводим их к табличным интегралам:
f dl Cl dl
J Р4-2В/4-ЛР и J Р + 2В/ + Д]^
После несложных преобразований и введения обозначений
Р = у- , /14-p2-2pcos (ф -0)
находим.
R
г 2п
cos «рот Г С р (sin ф — р sin 0) dO dp____
Vlx~ 4 т. J 11 | X pf-|- cos «p0T (p cos 0 — cos ф)] ’
r„ 0
p [cos «pOT cos 0X -)- p — cos (ф — 0)] dbd?
—ApH- COS «рот (p COS 0 — cos Ф)]
Таким же образом вычисляются проекции окружных скоростей:
£
_ sin «рот f Г _____[ 1 — р cos (Ф - 0)1 ptZ0^p
г 4 К J J X |>Y-|- COS «рот (р cos 0 — COS ф)] ’
О
R
Г 2п
sin «рОт f f_________ р sin (ф — 0) 0 d р
4 я J ^2J Д'-ф-cos ap0T (р cos 0 — cos ф)
Го О
Радиальной составляющей скорости в дальнейшем мы пренебрегаем, так как можно
показать, что для малых углов арот она мала.
6
г ведем обозначения!
2n
1 f sin ф— psinO
2n J X [JVcos а()0Т(р cos 6 — cos Ф)]
о
2n
p f cos ctpor cos 6 Л 4~ p — cos (ф — 0)
2 те J X [A' 4~ cos “pot (p cos 0 — cos tp)]
о
2r
1 f_____________1 — P cos (ф — 0;___________
2 к J x [X 4~ cos apoT (p cos 0 — cos ф)]
0
±_ f _______________Sin(O_-0)_______________
2 7Г J X -|- COS ССрот (p cos 6 — COS Ф)
0
(5i)
(52)
(5S)
(Й
Тогда для осевой и касательной составляющих индуктивной скорости, вызываемых
в точке Р плоскости ротора слоями кольцевых и прямолинейных вихрей, получаются
выражения:
k R
з =. - е У f
' аг'
'=1 Г„
. V . . , ,
г, 5^ cos аро14~ h dr,
(6.)
k R
sin «рот V [ dr(r',^.) Г ЙГ
4 nr J dr' 3 ' ‘ V
(62)
Легко убедиться непосредственной проверкой, что интегралы ik удовлетворяют сле-
дующим соотношениям:
h (0) = Л («) = Ц (0) = (п) = 0, г\ ^40 = ia , Zj ) = — 4 (4г
При р = 0
sin ф . n 1
f П , • 1л ---- ---- С), Го ---- 4 , «
1 — cos арот cos О 1 — cos арот cos -Ь
При р = по
Zi = Z» = О, z2 — О, Z4
1 Sin ССрот > ,
—;--------------------SIH ’ll .
SID Ctp0T COS ОСрот
Вычисление интегралов ik не представляет принципиальных затруднений и выпол-
няется либо графически, либо одним из методов численного анализа.
Особой точкой для интегралов/], Z2 и is является точка р = 1, 0 = ф, в которой под-
интегральная функция обращается в со и интеграл становится несобственным. Этот слу-
чай соответствует вычислению скорости в точках слоя свободных вихрей.
Интеграл /4 остается обыкновенным и при р=1.
На фиг. 6, 7, 8 и 9 приведены графики функций Zj, /,, Zs и Z4, вычисленных для ряда
значений риф при значении угла ар0Т=15о. Ниже эти графики будут использованы для
вычисления индуктивных скоростей при аэродинамическом расчете ротора.
Кроме скоростей от цилиндрических слоев свободных вихрей, должны быть под-
считаны также скорости от присоединенных вихрей. Заменять присоединенный вихрь
слоем радиальных вихрей было бы неверно-, так как вследствие изменения циркуляции
по азимуту будет переменной и интенсивность присоединенных вихрей. Мы подсчитаем
скорости, вызываемые непосредственно отдельными лопастями.
7
8
2
9
Рассмотрим элемент лопасти, находящийся на расстоянии г' от оси вращения рото-
ра (центра диска). Циркуляция скорости вокруг этого элемента будет Г(г', р). Индук-
тивная скорость в какой-либо точке лопасти равна сумме скоростей, вызываемых в этой
точке всеми присоединенными вихрями. Присоединенный вихрь в точках, расположенных
на продолжении вихря, скорости не вызывает, и, следовательно, в точках лопасти остаются
скорости от присоединенных вихрей, соответствующих другим лопастям.
Из фиг. 10 легко видеть, что эти скорости направлены в разные стороны.
Воспользуемся снова формулой Био — Савара (4).
В рассматриваемом случае имеем:
dSx= dr' costi, dSv = dr'sin 6, dSz~0,
rix = rcos p — r' cos 6, n j, = rsin p — r'sin 6, Hz —0,
Ц — > r- 4- r'2 — 2rr' cos (6 — ф).
Фиг. 10
на фиг. 10. Для скорости, индуцируемой в точке Р, по
Все обозначения указаны
лучаем выражение:
(г sin ф — г' sin б.) cos 0,- — (г cos Ф — г' cos 6,) sin О, .
----------------------------------------------и------------------—---------------------------•-------------- 1-----------------‘—dr,
— 2rr'cos (ф —
или после преобразований и выполнения интеграции:
t __ 1 V4 Г(6,- ) _______/? — rcos(6; — ф)
" — 4 -г sin (Ф - ) /1?2 4- г2 - 2/? г cos (6, - ф)
r0 — г cos (6j — ф)___________
/<+ г2 — 2 rr0 cos (6,- ^Ф)
(7)
Так как ф — 6;
2 «г
, то, например, для трехлопастного ротора получаем:
120°) —Г («4-120°)
2/?^г_
К/?Ч-г2 + Дг
2гц — г
Vfr20-\~r2-\-rr0
10
Для винта с переменной вдоль лопасти циркуляцией формула (7) будет выглядеть
так;
я
k г
Г(Ш(рМр, (7,)
Го
г
Л sin (Ф — ) г'
^(р)_ [1 +ps-2pcosCi-e/)]’/. ’ Р-’7 •
Если же присоединенные вихри заменить слоями радиальных вихрей, то скорость
была бы, как известно, равна нулю.
Эта общая схема в случае малых углов атаки ротора может быть заменена очень
простой предельной схемой, соответствующей углу атаки ротора арот = 0.
2. РАСЧЕТ ИНДУКТИВНЫХ СКОРОСТЕЙ ПРИ арот = 0
(предельная схема1)
Допустим, что угол атаки ротора арот уменьшается и достигает своего предельного
значения арот = 0. В действительности, при горизонтальном полете геликоптера ротор
наклонен к горизонту под небольшим углом порядка 7°н-1(Г. Кроме этого, за ротором
струя несколько отклоняется вниз. Однако можно предположить (и в дальнейшем это
будет подтверждено расчетами), что индуктивные скорости, рассчитанные при арот = 0,
будут очень мало отличаться от индуктивных скоростей, имеющих место при арот=10°ч-15г'.
В таком случае цилиндрический слой свободных вихрей сплющится и превратится в полу-
бесконечную полосу, ограниченную с одной стороны полуокружностью диска ротора.
Из фиг. 3, И и 12 видно, каким образом при арот = 0 пространственное обтекание ротора
Фиг. И. Предельная вихревая схема. Разложение слоя круговых вихрей
Фиг. 12. Предельная вихревая схема. Слой прямолинейных вихрей
1 Экспериментальные исследования по определению вихревой системы ротора геликоптера прове-
денные в 1947 — 48 гг. в ЦАГИ М. Л. Милем и М. К. Сперанским, и их же визуальные наблюдения ды-
мовой струи, отходящей от ротора, показали, что вихревая система за ротором при поступательном дви-
жении геликоптера близка по своей конфигурации к плоской вихревой системе крыла.
Этот факт послужил основанием для теоретического построения вихревой схемы, излагаемой в этом
параграфе.
It
схематизируется плоским: цилиндрическая поверхность, покрытая двумя слоями вихрей,
превращается в полубесконечную полосу, покрытую также двумя слоями вихрей—пря-
мых продольных и круговых. При этом часть полосы, лежащая вне окружности диска ро-
тора, будет покрыта удвоенным слоем продольных вихрей, получившимся из-за совме-
щения противоположных половин цилиндра, и слоем круговых вихрей. Окружность диска
ротора будет покрыта только одинарным слоем продольных вихрей и круговыми вихрями.
б) Полоса свободных вихрей
Простые соображения позволяют получить
дальнейшие упрощения этой схемы. Из фиг. 11
следует, что для каждого элемента кругового
вихря, составляющего с осью Оу (ось—парал-
лельная скорости полета) угол <р, найдется эле-
мент другого кругового вихря, составляющего
с осью угол — <р (это может быть доказано и
строго).
Так как направление завихренности у обоих
элементов одинаково (все круговые вихри име-
ют одно и то же направление завихренности),
то после разложения вектора вихря для каж-
дого элемента кругового вихря на две состав-
ляющие по осям Oz и Оу сохранится лишь одна
удвоившаяся составляющая вдоль оси Оу.
Таким образом, окончательно получается
следующая плоская схема вихрей за ротором
геликоптера в горизонтальном полете (фиг. 14):
а) Диск ротора покрыт слоем прямолиней-
ных вихрей и слоем круговых вихрей с цент-
рами на оси Оу.
покрыта двумя слоями прямолинейных вихрей:
одного, происшедшего от продольных вихрей на цилиндре, и второго, происшедшего
от разложения круговых вихрей’.
Для расчета индуктивных скоростей
сивность вихревых слоев. Интенсивность
и равна:
необходимо прежде всего подсчитать интен-
слоя круговых вихрей, очевидно, постоянна
k dr^i)
— S „
= 2л V dr'
i—1
Интенсивность слоя
прямолинейных вихрей1 2
(8)
при плоской вихревой схеме за ротором остаются только прямолинейные
1 То обстоятельство, что i .
свободные вихри, впервые было установлено Л. С. Вильдгрубе.
2 При предельном переходе от цилиндра, покрытого продольными вихрями, к плоской полосе интен-
сивность вихревого слоя будет меняться по его ширине.
Действительно, в случае цилиндра элемент поверхности dS = rd 01 покрыт вихрями с напряжением
1 d Г
—Зтгг'йР’’ и’ слеД°вательно> полная интенсивность элемента поверхности равна:
dr d6
~ dr' 2n dr'‘
Интенсивность слоя, т. е. суммарная интенсивность площадки с шириной, равной единице, в направ-
лении, перпендикулярном осям вихрей, равна:
dr 1
1 ~ dr' 2n r' ‘
Зависимость между шириной площадок плоского и цилиндрического слоев следующая (фиг. 13):
d$rui. СЛОЯ ^ЦИЛ. слоя cos Т ^цил. слоя
Таким образом, площадка плоского слоя с шириной, равной единице, соответствует площадке цилин-
дрического слоя с переменной шириной, зависящей от ее положения по азимуту.
Следовательно, интенсивность плоского слоя продольных вихрей по его ширине меняется по закону:
1 dr
1 2пУг'2 — г'2 dr' ‘
12
= -1 у <*Г(Ю , S
1 г dr’ |Лг»2____________Z2
(-90
Интенсивность слоя прямолинейных вихрей, получившихся от разложения круго-
вых вихрей,
. & ^dV (ф,) 1/г'з_у
? dr' ~ ' (9а)
Таким образом, распределение суммарной интенсивности обоих слоев прямоли-
нейных вихрей по ширине слоя для заданного значения г' имеет вид, показанный на
фиг. 14.
Фиг. 14. Предельная вихоевая схема Результирующие вихревые слои
Как и в случае крыла, можно предполагать, что на некотором расстоянии от рото-
ра свободные вихри, невидимому, сворачиваются в два вихревых жгута различной
интенсивности. Последнее предположение подтверждается, как уже указывалось выше,
визуальными наблюдениями М. Л. Миля и М. К. Сперанского, наблюдавших подобные
вихревые жгуты при помощи дыма, пускавшегося в отходящую от ротора струю.
Эта предельная схема дает очень простую и наглядную физическую картину вих-
реобразований за ротором в горизонтальном полете. Подтверждение теоретических
соображений экспериментом позволяет надеяться, что результаты расчетов будут близки
к действительности.
Перейдем к непосредственному расчету индуктивной скорости.
Полная индуктивная скорость w от рассмотренной в предыдущем параграфе вих-
ревей схемы (фиг. 14) представится суммой индуктивных скоростей от четырех вихре-
вых слоев:
1. Слой вихрей, расположенных по дугам окружностей радиуса г' и заполняющих
окружность, описываемую элементом ротора, находящимся на радиусе г'. Интенсивность
слоя постоянна и равна т2.
2. Слой прямолинейных вихрей, заполняющий полосу шириной 2г' и простираю-
щийся от левой половины окружности диска ротора до оо. Интенсивность слоя пере-
менна по ширине и павна
3. Слой прямолинейных вихрей, заполняющий полосу шириной 2г' и простираю-
щийся от правой половины окружности диска ротора до оо. Интенсивность слоя .
4. Слой прямолинейных вихрей, заполняющий полосу шириной 2г' и простираю-
щийся от правой половины окружности диска ротора до оо. Интенсивность слоя у*.
Кроме этого, добавляется скорость, вызванная присоединенными вихрями.
Для расчета индуктивной скорости необходимо рассмотреть последовательно каж-
дый из указанных слоев.
Однако, несмотря на простоту вычисления скоростей, индуцируемых всеми указан-
ными слоями, работа эта очень трудоемка, и оказывается более выгодным расчет нор-
мальной индуктивной скорости производить по формуле (6), совершив в интегралах
и 4 [формула (5)] предельный переход при арот -> 0. Переход к пределу вполне законен,
так как 4 и 4 являются непрерывными функциями арОт. В этом случае скорость
13
является нормальной индуктивной скоростью, а скорость = При «рот — 0 после
несложных преобразований интегралы и i2 принимают вид:
Р cos 6 — cos ф
+ р2 — 2р cos (ф — в)
d6
р sin 6 — sin ф ’
2 it
= JL f [s,л в _ slnft-B) 1_______________de____
2~J L Kl-F p2 — 2pcos('p — 0)J psin6 — sin ф
(10)
Для нормальной индуктивной скорости от свободных вихрей имеем выражение,
подобное (б^:
. R
Q Д Г d Г (/ фг ) / V . , . \ п п
—---------dr' \ Qr foi + t(*Jdr •
r 0
Интегралы (10) можно выразить через эллиптические интегралы первого и третьего
рода. Выполним преобразование этих интегралов. Начнем с интеграла z02:
__ Р Г sin 0 d 0 pf______________________sin (ф — 0) d 0______________ , ч
Z°2 ~ 2ttJ psin 0 — эшф 2~j (p Sin 0 — sin ф) /1 -]- p2 — 2p cos (ф — 0)
о 0
Первый интеграл в выражении (а) просто вычисляется хотя бы с помощью теории
вычетов. Рассмотрим два случая:
1) ф = к — а, а<^тс:
2 г. 2г.
Р Г sin 0 d 0 __ J I 1 Г sin и 6 .
2~ J p sin 0 — sin ф 2~ J p sin 0 — sin a ’
о о
2) ф = л-|-а, а<^т;
2n 2r
p Г sin0d0 ________1 Г sin a d 0
2л J p sin 0 — sin ф 2л J p sin 0 ~J- sin ф ‘
о о
В свою очередь
2n I SIH Gt - о *>
Slna r de /± у
2» J psinS + sina \0 sin2a<p2.
Следовательно,
2г. , I sin ф |
_L f /8Й1“ф-р^ Sin ’ >p'
2л J psin0 — sta'li \, . , , ,
J r r V1 SlH-'Kp.
Приведем интеграл
д = Г __ sin (Ф - 0) d 0 =
J J/1 + P2 — 2p cos (ф — 0) (p sin 0 — sin ф)
0
+ V
= 2 f sin(2X —-p)dX____________
d V1 + P2 + 2p cos (2X — ф) (sin ф 4-p sin 2X)
7C
” ~2
к эллиптическим интегралам. Здесь сделана подстановка 0 = л-(-2^.
14
Разбивая последний интеграл на сумму двух — от —
-у до 0 и от 0 до — — и за-
меняя в первом интеграле X на —X, получим:
2
_________sin (2Х — d X
|1 -|- р2 4~ 2р cos (2Х — ф) (sin 'Ь -j— р sin 2Х)
________________sin (2Х 4- ф) d X_______________
V1 + Р2 + 2р cos (2Х 4- ф) (sin Ф — р sin 2Х)
= 2/?! — 2/г2.
Сделаем в первом интеграле kx подстановку z = cos(2X— ф), а во втором z —
= со8(2Х4-ф). Проведем несколько подробнее это преобразование для первого интег-
рала kx. Для второго интеграла k2 рассуждения будут аналогичны.
Очевидно, что
2Х = ф 4- arc cos z
и
sin 2Х = sin ф z 4~ cos ф j/1 — z-.
Можно показать, что 44~Ф) — 4(к ~Ф), поэтому ограничимся только 0<ф<>.
Если в первом интеграле X изменяется от 0 до , то 0<12Х<>, а— Ф<С2Х —
£
— ФО — ф. Для того, чтобы sin (arc cos z) = + )Z1 — z2 имел в интервале интегриро-
вания постоянный знак, надо интеграл kx переписать следующим образом:
________________sin (2Х — ф) d X
+ Р2 + 2р cos (2Х — ф) (sin ф 4~ Р sin 2Х)
Ф
2
2
-Ни;
О ф
в интеграле klx sin (2Х — ф) <f0, и надо писать — — z2; в интеграле ki2 sin (2Х—-ф)>0,
и надо писать 4~ХЛ1—z‘~-
Аналогичные рассуждения применимы к интегралу k2, но его надо разбить на
сумму двух следующих интегралов:
J К1 + Р2 + 2Р cos (2^ + Ф) (sin Ф — Р sin 2^)
о
ТС ф ТС
2 “ Т “г
J = ^21 4“ ^22 >
к ф
со знаком „4-“> а в интеграле
о
2
причем в интеграле /г21 корень 1/1 — z2 следует брать
k22—co знаком „—Таким образом, после подстановки г = соз(2Х + ф) интеграл Д пред-
ставится следующим образом через интегралы km,n'.
Д =
dz
—COS ф
COS ф
— COS ф
}/1 4~ Р2 4~ 2р z [sin Ф (1 4~ Р г) — Р cos ФI V1 — г21]
1
г________________________dz____________________
J 4- р2 4-2рг[8шф(1 +pz) — р cos ф| J/1 — z2|]
COS ф
dz
j/1 4- р2 4- 2р z [sin ф (1 + р z) 4- р cos Ф ]/1 — z2|]
15
Рассмотрим подробнее один из интегралов, например /г21‘.
k21 = I _ __________. —
J V1 + р2 4-2pz[sin'}> (1 -j-pz)— рсоэф]/! — z2]
COS ф
“1
. , f (1 + pz)dz
= sin ф I ------------— r '-----------------------------k
J ]/1 + p2 -f- 2p z [p2 z2 -[- 2p sin2 ф z -f- sin2 ф — p2 cos2 ф]
COStp
—1 ________________________________
( ( Г_______________________V 1 — z2 dz_____________
f-pcos , | j/1-|-p2 4~ 2p z [p3 z2 + 2p sin2 ф zsin2 Ф — p2 cos2 Ф]
cos ф
Очевидно, что если записать
—i -i
fe2i = sin ф J Ф(2)^ + рсозф j Q(z)dz,
COS ф cos ф
где
Ф (z) = -------------------------------•
~yr 1 4- p2 — 2p z [p2 z2 -j- 2p sin2 ф z 4- sin2 ф — p2 cos2 ф]
S(z) =
___________________/1 — z2___________________
j/1 4-p2 — 2p z [p2 z2 + 2p эш2ф z4~sin2 ф — p2 cos2 ф] ’
то остальные интегралы запишутся в виде:
—cos ф —COS ф
/г,2 = sin ф J Ф(г)йг — рсоэф J Q(z)dz ,
-1 _'i
1 i
йп = sin ф J Ф (z) dz 4~ р cos ф J Q(z)dz,
COS Ф COS Ф
— COS ф -COS ф
= sin ф J Ф(г)«£г —рсоБф J Q(z)dz.
1 1
Подставляя km,n в выражение для Д, после сокращений находим:
Д = £р cos ф
—1 —COS ф 1 —COS ф
J* й (z) dz — J Й (z) dz — f Й (z) dz 4- J Й (z) dz
сойф —1 СО8ф 1
— 1
= 2p cos ф J Й (z) dz.
i
(b)
Вычислим интеграл:
__________________у 1 —z-dz_________________
Vf 4- P2 2p 2 [p2 z2 + 2p sin2 ф z 4~ sin2 ф — p2 cos2 ф]
1 r__________dz_________
P2 J ' /(l + P24-2pz)(l-^)
sin2 ф Г ____________________(1 4~ P2 4~ 2p z) dz_______________
P2 J 1 4- p2 4- 2p z [p2 z2 4~2p sin2tyz4- sin2 ф — p2 cos2 ф]
16
Сокращать числитель и знаменатель на 4- р2 2р z не следует, так как это
только усложнит вывод.
Разлагая рациональную дробь на простейшие, находим:
____________1 ~l~ 2р z 4~ р2___________ 1 ____А . В
p2z2-j-2p sin2 ф2 -{—sin2 ф — р2 cos2 ф р z — a'z—Р
где в случае р2 _> sin2 ф
р2 —f- 1 — 2 sin2 ф —2 cos ф р2 — sin2 ф
2 cos ф {/р2 — sin2 ф
р24~ 1 — 2 sin2 ф— 2cos ф р2— sin2 ф _
2 cos ф Ур2 — sin2 ф
__— sin2 ф cos ф уЛр2 — sin2
Р
— sin2 ф — cos ф V"p2 — sin2 ф
Р
Итак, можно написать:
С ч . If dz
j Й (z) dz —---I ~ ----: +
J p J ]Л(1—z2) (i-|-p 4~2pz) r
. sin2 ф Г 4 [ dz -4-B f dZ -___________
+ V I J (z-a) /(T+P+ 2Й)"(Г=г2) + J (г-?) /(1+р2 + 2Р2)(Г-7Т)
В случае p2 <f sin2 ф величины a, p и А, В будут комплексными.
Последние интегралы непосредственно выражаются через эллиптические интегралы
первого и третьего рода.
Сделаем подстановку:
z=l — 2 sin2 U, dz — — 4 sin 67 cos 67^67;
тогда:
/ — (z — l)(z 4- l)(z 4~ 1 p 2p = 2(1 4- p)sin £7cos — A2 sin2 Id,
\ ^P /
где
2 2
Подставляя в выражение для Q(z) и обозначая -------г —п» о----г = m для а, р дей-
ОС 1 м 1
2 2
ствительных и-----г = п', т.-ч = т' для а, Р комплексных, получаем:
а — 1 Р — 1
f е (z) dz = -vyt-Vt f-г dU-^ +
J P‘(l +p) J /1 — k2 sin2 U
. 2 sin2 ф_______________A________________ r____________dU___________
P8(14“P) p2 4- sin2 ф — совфт/р2 — эш2ф J (1 4~nsin2 U)^/A—/г2 sin2 67
_________________В ___ г_____________dU_____________
p2 4~ sin2 ф 4~ cos ф y p2 — sin2 ф J (1 4~m sin2 — k2 sin2 67.
Подставляя пределы и вводя обычные обозначения полных эллиптических интег-
ралов первого и третьего рода с модулем k\
7t ТС
f — = К, [---------------------dU ,. = = П (п, k),
J К1 — *2 sin2 67- J (14- n sin2 67) /1— k2 sin2 67
о о
3
17
из (а) и (Ь) находим:
. _ sin ф_____2 cosj> . 2 sin2 ф cos ф
Х V sin2 ф — р2 ^О+р) к(1+р)
X и; /?(«', k) -ф- В\ П(т', k)] (sin2ф >Р2)
4 1 + 4т£Н)/<+^П+^1 lA.n^k^B.n^k)] (81п2ф<р2).
(12)
Таким же образом после аналогичных вычислений получаем:
- 2^(Т+°р)~ [Л* п (n’’k)+в'п (т'гk)] (sin’“ >р2)
-2дпф^2|ф [А1ГЦп>k}+BiП{т,ед (sin2ф<р2)
Здесь обозначено:
р-f-sin2 ф — cos ф у/р2 — sin2 ф ’ 1 р -ф- sin2-р -ф- соэф }/р2 — sin2f
А' и В' обозначают соответствующие величины для комплексных аир.
Из формулы (12) непосредственно следует, что для sin2 ф <р2
— — а, р j — 2, т. е. кривые iV2
—---а, р I симметричны относи-
тельно прямой ios==l. Точно так же из формул (12) и (13) легко видеть, что 4i (тгф-а) =
= — 41 (я — а) и 4s (" Н~ и) = 4s (г — а)> а < • Эти соотношения очень сокращают объем
вычислительной работы. Эллиптические интегралы третьего рода с мнимым параметром
можно с помощью 0-функций Якоби привести к эллиптическим интегралам с действи-
тельным параметромх.
Особенно простую форму принимают выражения Z01 и для значений 0 = 0,
тс Зтг
-2~, л, . Эти выражения приведены в табл. 1, а графики их—на фиг. 15 и 16.
Таблица 1
i *01 *02
0 0 psi 2 + П(1 +р) К PS1
л т 1 г Р <" 1 1 1 - Р2 0 р> 1 1 1 — г. Р< 1 Vl -Р2 1 Р> 1
7 0 Р si 2 1 к(Ц-р) К
Зтс "2 V Л 1 м ( о 1^ 1 1 - 5 । “ V Л н— с—
1 См., например, И. Сомов. Основания теории эллиптических функций. С.-Петербург, 1850 г.
18
Из формул (12) и (13) следует, что г01 и Z02 обращаются в бесконечность при
р -* sin ф и при р -» 1, что соответствует приближению точки, в которой определяется ско-
рость, к вихревой линии. В этом случае модуль эллиптических интегралов k = “* 1-
Однако бесконечность эта—интегрируемая и исчезает при интегрировании по р
вдоль лопасти, которое необходимо производить при расчете индуктивной скорости
от вихревой системы всего винта с переменной циркуляцией. Относительно слагаемого
sin ф р
- это очевидно, так как при интегрировании по р получится arc sin-:——.
у sin2 ф — р2 sin г
Бесконечность в эллиптических интегралах также
интегрируемая, так как при k -* 1 можно написать:
Подставляя значение k', выделяем член, стремящийся
при р^-1 к бесконечности:
/<=1п|1-Р| + 0(1),
где 0(1) означает члены, остающиеся конечными при р-»1.
Для выделения особенностей в интеграле П(п, k) можно воспользоваться формулой
из общей теории 0=функции:
/7 (га, /г) = К-у-
Sna 6' (а) 1 . 6 {К - а)
Cn a dn а 6 (а) '2 6 (/С —f— а)
Здесь Sna, Спа, dna, 6(a)—эллиптические функции Якоби и параметр га=— &2Sna.
19
Таким образом, при р -» 1 и k-^l интеграл П(п,Щ также имеет логарифмическую
особенность:
Щп,1г)=( 1 + г ааХ$ -.Д] 1п| 1 — р| 4-0(1).
' ’ ' 1 Cn a dn а 6 (a) )
В формулы (12) и (13) входят эллиптические интегралы третьего рода. Таблиц для
этих интегралов не существует, поэтому для вычисления их пользуются некоторыми
соотношениями, выражающими эллиптический интеграл третьего рода через интегралы
первого и второго рода.
В рассматриваемом случае значения параметров п, т меняются в пределах—
щ<;4-оо, что очень затрудняет расчеты даже в случае р Х> sin2 ф. Поэтому вычисление
интегралов П затруднительно и едва ли будет короче, нежели определение i01, г’оз путем
простого численного или графического интегрирования. Однако это представление
интегралов с помощью формул (12) и (13) позволило нам выделить особенности, что
будет использовано в дальнейшем для интегрирования по р при выполнении аэродина-
мического расчета.
Заметим, что подинтегральная функция в интегралах г01 и г02 может быть сделана
конечной на всем интервале интегрирования, что очень облегчает выполнение числен-
ного или графического интегрирования.
Действительно, знаменатель подинтегральной функции обоих интегралов обра-
щается в нуль при значениях переменного
. . sin ф с . sin ф . . ,
6. = arc sin-------- и 6„ = те — arc sin------- , р > sin ф .
Р Р
При этих значениях числитель подинтегральной функции интеграла inl принимает
следующие значения:
р cos 0 — cos ф
>/1 4- р2 — 2р cos (ф—6)
(sin Ф \
arc sin-] — cos ф
Р J
п , . 8Шф
— 2р cos ф — arc sin —
pcos 0 — cos ф
’Kl + Р2 — 2р cos (ф—0)
е=оа
— Р cos
. sin Ф \
arc sin-------- ) — cos ф
Р ' — 1 2.
4 । . sin ф
cos ф 4~ arc sin —
. „ sin (ф — 6) 1 2втф
sin 0---- - ------- =----------—
]Л1 4- Р2 — 2р cos (ф—O)]e=es Р
Подобным же путем легко проверить, что числитель подинтегрального выражения
в интеграле г02 принимает в точках 0 = и 6 = 62 следующие значения:
в sin (ф — в) п
sin 6---г —- _= = О,
)41 4- Р2 — 2Р cos (Ф—Ь=®1
Таким образом, вычисление интегралов /01 и /02 проводится по следующим расчет-
ным формулам:
2-
Jp cos 6 — cos ф 1 d6
у 1 4-р2 — 2Pcos (ф-0) J р Sin б — sin ф “
О
2
JP cos 6 — cos ф 1 db
|' f+p2 — 2p cos (ф — 6) ~ J p sin 6 — sin4p
0
p COS 6 — cos Ф J
У1 4~p2 — 2рсов(ф— 0)
p cos 6 — cos Ф_1 I
/14-р2 —2рС08(ф-6) + J PSin0-Sint +
"2
db_______2 r rf6
psinS — sint J psinO — sin ф ’
20
_____5Ш(ф— 6)
]/1 -J- P2 — 2p cos (Ф — 6)
l02 ---
sin (ф — 6)
1/1 4~ P2 — 2p cos (Ф — 6)
sin 0 4"
sinfp — 6)
V1 +p2 — 2pcos (Ф—6)
_______rfe________
p sin 6 — sin ф
dh
p sin 6 — sin ф
2 sin ф
P
______tZ6_______
p sin 6 — sin ф
2к к
f . c . sin (ф — 6) ] fZ6 . 2 sin ф f db
J У14-Р2 — 2рсоэ(ф— 6) J p sin 6 — 8Шф p J p sin 6 —sin Ф
В каждом из этих интегралов подинтегральная функция конечна на всем интер-
вале интегрирования, и вычисление интегралов затруднений не представляет.
Последний интеграл вычисляется аналитически:
f = 1 ln Р + Zp2 ~ sin2 ф
J р sin 6 — sin ф sin2 ф~ sin ф
2~
При р sin ф все интегралы обыкновенные, и интегрирование выполняется непо-
средственно.
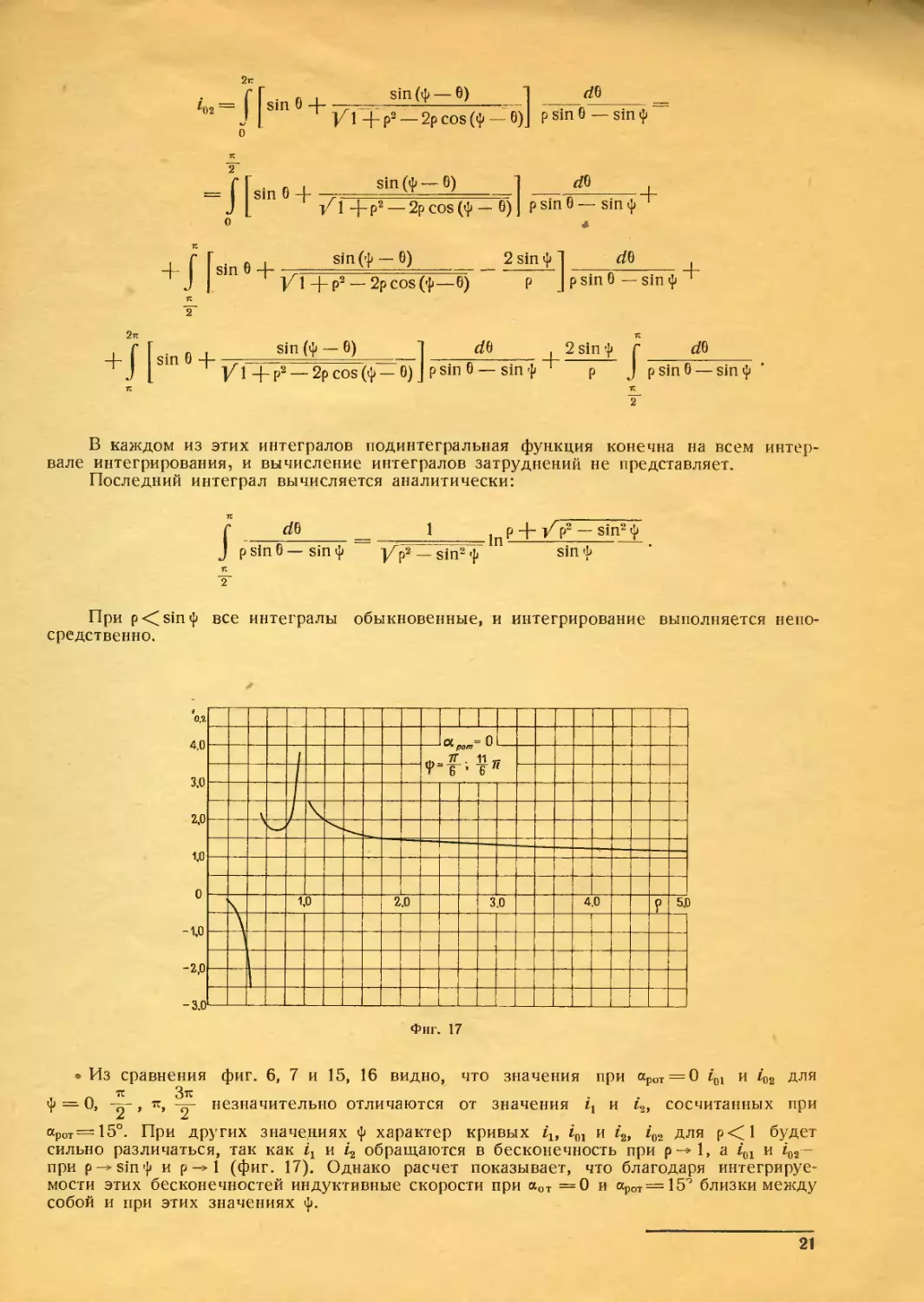
• Из сравнения фиг. 6, 7 и 15, 16 видно, что значения при арот = 0 г01 и г02 для
ф = 0, -к-, s ду незначительно отличаются от значения и t2, сосчитанных при
арот=15°. При других значениях ф характер кривых 11г t01 и i2, iB2 для Р<1 будет
сильно различаться, так как и i2 обращаются в бесконечность при р -* 1, а г01 и г02-
при р —» sin ф и р-> 1 (фиг. 17). Однако расчет показывает, что благодаря интегрируе-
мости этих бесконечностей индуктивные скорости при аот =0 и apOT=15Q близки между
собой и при этих значениях ф.
21
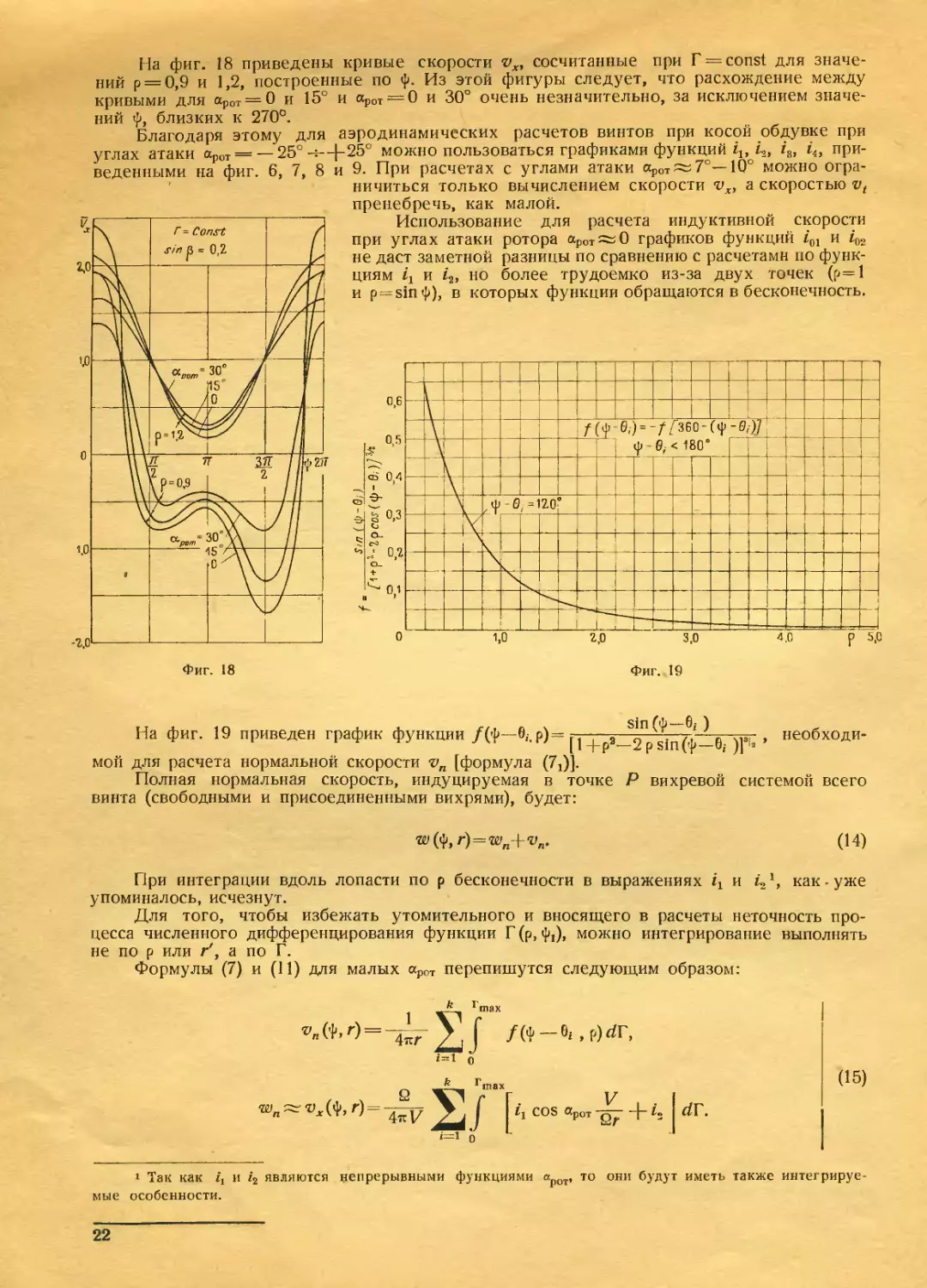
На фиг. 18 приведены кривые скорости vx, сосчитанные при Г = const для значе-
ний р = 0,9 и 1,2, построенные по ф. Из этой фигуры следует, что расхождение между
кривыми для арот = 0 и 15° и аоот = 6 и 30° очень незначительно, за исключением значе-
ний ф, близких к 270°.
Благодаря этому для аэродинамических расчетов винтов при косой обдувке при
углах атаки арот =— 25° -i—|-25° можно пользоваться графиками функций ц, rs, iis при-
веденными на фиг. 6, 7, 8 и 9. Пои расчетах с углами атаки ссрот^;7 10 можно огра-
ничиться только вычислением скорости vx, а скоростью vt
пренебречь, как малой.
Использование для расчета индуктивной скорости
при углах атаки ротора арпт~0 графиков функций /01 и i02
не даст заметной разницы по сравнению с расчетами по функ-
циям iy и i2, но более трудоемко из-за двух точек (р=1
и р=51пф), в которых функции обращаются в бесконечность.
Фиг. 19
На фиг. 19 приведен график функции /(ф—6,. р)=
sin фр—6г )
[1 +ра—2 р sin(p—
мой для расчета нормальной скорости vn [формула (7j)].
Полная нормальная скорость, индуцируемая в точке Р вихревой
винта (свободными и присоединенными вихрями), будет:
необходи-
системой всего
те(ф,г)=и/„+-ц„. (14)
При интеграции вдоль лопасти по р бесконечности в выражениях и Л \ как - уже
упоминалось, исчезнут.
Для того, чтобы избежать утомительного и вносящего в расчеты неточность про-
цесса численного дифференцирования функции Г (р, фД можно интегрирование выполнять
не по р или г', а по Г.
Формулы (7) и (11) для малых арот перепишутся следующим образом:
, P)rfr,
г)
dr.
(15)
1 Так как Zx и z2 являются непрерывными функциями арот, то они будут иметь также интегрируе-
мые особенности.
22
Здесь следует отметить, что предлагаемый метод расчета как для случая арот=0,
так и для случая ctp0T ф 0 обладает тем достоинством, что все подинтегральные функ-
g, V COS ОСрот
ции не зависят от характеристики режима работы ротора р=---~ От величины р
зависят лишь интенсивности слоев, являющиеся множителями при интегралах, входящих
в выражение скорости. Поэтому все подинтегратьные функции могут быть сосчитаны
и затабулированы один раз независимо от величины р. Это чрезвычайно сокращает расчет-
ную и вычислительную работу.
Очень просто могут быть получены также средние по времени индуктивные скоро-
сти, т. е. те скорости, которые в действительности показываются манометрами, соединен-
ными с насадками, установленными перед ротором или за ним. Действительно, так как
при изменении положения лопасти по азимуту вихревые слои остаются неизменными по
своей конфигурации и меняются лишь их интенсивности, то средняя скорость по вре-
мени (или углу) в какой-либо точке пространства получается осреднением по времени
(или углу) интенсивности слоев.
Таким образом, средняя по времени скорость в точке с координатами г, ф будет:
R 2п
~J G1C0S “рот + ) J — d'‘ dr'- (16)
г0 О
Слагаемое в выражении скорости от присоединенных вихрей при осреднении обра-
щается в нуль.
В аэродинамический расчет, однако, необходимо вводить истинные скорости, так
как использование осредненных по времени индуктивных скоростей может привести
к количественным ошибкам.
В следующем разделе этой работы, посвященном аэродинамическому расчету ротора,
будут приведены сравнительные графики средних и истинных индуктивных скоростей,
а также сравнение их с экспериментальными кривыми.
3. АЭРОДИНАМИЧЕСКИЙ РАСЧЕТ ВИНТА ПРИ КОСОЙ ОБДУВКЕ
Аэродинамический расчет винта при косой обдувке состоит из двух частей:
1) определение циркуляции Г(г'ф) по заданным геометрическим характеристикам
лопасти;
2) вычисление тяги, мощности, коэффициента полезного действия, поперечной и про-
дольной составляющих силы, развиваемой винтом.
В настоящей работе будет рассмотрен только метод расчета винта с жестко закре-
пленными лопастями. Расчет ротора с шарнирным креплением лопастей принципиально
не внесет ничего нового в метод и потребует лишь выполнения еще, возможно, одного-
двух приближений в процессе определения циркуляции. Методика определения угла
взмаха лопасти может быть оставлена той же, как и в работах Локка и Уитли, с той
лишь разницей, что вместо приближенных аналитических выражений для тяги и момен-
та, используемых в этих работах, надо будет брать интегральные выражения тяги и мо-
мента для всей лопасти.
Вторая часть аэродинамического расчета винта при косой обдувке почти ничем не
отличается от таковой для винта в прямом потоке, часть же первая содержит некоторые
принципиальные различия.
Прежде всего при косой обдувке винта нормальная к оси лопасти скорость в пло-
скости вращения
U = Qr—Vcos ссрот sin ф (17)
обращается в некоторой, определенной для каждого азимута точке в нуль. Линия ну-
левых окружных скоростей в плоскости вращения ротора определяется уравнением:
r = psin-p. (18)
Сечения лопасти, находящиеся внутри окружности (18), обтекаются обратным пото-
ком. В точках плоскости вращения ротора, в которых г = рвтф, угол притекания струй
Q * v sin арот « ~ тэ
p = arctg--— обращается в . В точках, расположенных внутри окружности ну-
К
левых скоростей, этот угол больше Так как величина р обычно бывает порядка
23
< 0,25 н-0,35, то мы не сделаем заметной ошибки в определении сил, действующих
на ротор, если исключим из рассмотрения область r<psintp. За исключением значений
60° < ф < 120°, для которых г<0,20-н0,30, для всех других ф эта область будет очень
близка к нерабочему радиусу лопасти.
Лопасти винта в косом потоке представляют собой крылья, движущиеся со сколь-
жением к направлению проекции поступательной скорости. Поэтому для расчета харак-
теристик винта нужно было бы, вообще говоря, иметь характеристики профилей, сня-
тые на крыле конечного размаха в косом потоке. Однако, как показывают опыты [9],
кривые су(а) довольно хорошо совмещаются друг с другом, если при вычислении коэф-
фициента су подъемную силу относить не к полной скорости, а к ее нормальной к про-
дольной оси крыла составляющей:
. _ 2Р
Су~~pSV2sin24 '
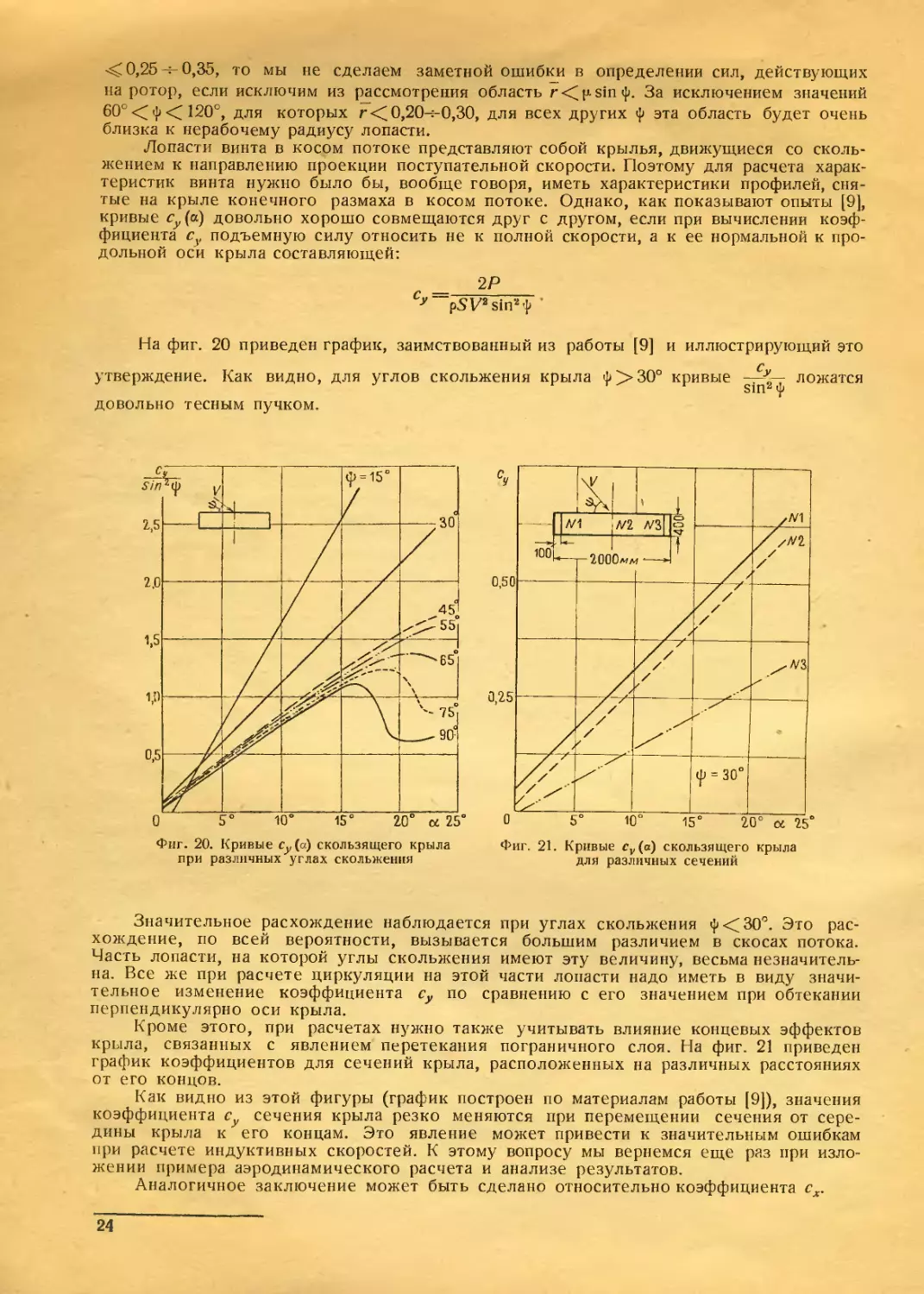
На фиг. 20 приведен график, заимствованный из работы [9]
и иллюстрирующий это
утверждение. Как видно, для углов скольжения крыла ф > 30° кривые
довольно тесным пучком.
СУ
-.„т ложатся
smz ф
Значительное расхождение наблюдается при углах скольжения ф<^30°. Это рас-
хождение, по всей вероятности, вызывается большим различием в скосах потока.
Часть лопасти, на которой углы скольжения имеют эту величину, весьма незначитель-
на. Все же при расчете циркуляции на этой части лопасти надо иметь в виду значи-
тельное изменение коэффициента су по сравнению с его значением при обтекании
перпендикулярно оси крыла.
Кроме этого, при расчетах нужно также учитывать влияние концевых эффектов
крыла, связанных с явлением перетекания пограничного слоя. На фиг. 21 приведен
график коэффициентов для сечений крыла, расположенных на различных расстояниях
от его концов.
Как видно из этой фигуры (график построен по материалам работы [9]), значения
коэффициента с сечения крыла резко меняются при перемещении сечения от сере-
дины крыла к его концам. Это явление может привести к значительным ошибкам
при расчете индуктивных скоростей. К этому вопросу мы вернемся еще раз при изло-
жении примера аэродинамического расчета и анализе результатов.
Аналогичное заключение может быть сделано относительно коэффициента сх.
24
Таким образом, в аэродинамическом расчете винта при косой обдувке для боль-
шей части лопасти можно пользоваться обычными характеристиками су и сх профилей,
полученными из испытаний крыла в прямом потоке, но при вычислении сил, развивае-
мых элементами лопасти, надо вводить не полную скорость элемента лопасти, а ее
составляющую, нормальную к оси лопасти.
При малых углах атаки ротора (apoTss7°—10°) касательной составляющей индук-
тивной скорости, как это следует из формулы (6), можно пренебречь и ограничиваться
только осевой составляющей индуктивной скорости, которая в этом случае будет
совпадать с нормальной составляющей.
После этих предварительных замечаний можно перейти к основному вопросу
аэродинамического расчета ротора — определению циркуляции и индуктивной ско
рости.
Основное интегро-дифференциальное уравнение для определения циркуляции
имеет вид:
2 Г (г, -р, ) = b (г) W„ {г, ф,- ) Т (г)-₽(г, ф,-
(19)
Здесь Wn = U = Q г — Vcos apoT sin ф означает проекцию полной скорости на нормаль
к оси лопасти (направление касательной скорости). Скорость w{r, ф; ) определяется
по (14) и (И).
В отличие от случая винта в прямом потоке искомая функция Г (г, ф, ) в уравне-
нии (17) зависит от двух переменных г и ф,- , что, естественно, усложняет задачу.
Однако, принимая снова гипотезу стационарности, можно задачу в каждый мо-
мент времени (для каждого ф; ) решать самостоятельно и рассматривать Г (г, ф; ) как
функцию только г при параметре ф, .
Для решения уравнения (19) применим метод последовательных приближений.
За нулевое приближение примем „установочную" циркуляцию, зависящую от геометри-
ческого угла атаки:
Г(0) ,р. ) b (г, ф,- ) су (г, ф,- ) (ср (г)-₽ (г, ф,- )].
Значение коэффициента су снимается непосредственно с графика кривых су(а).
По нулевому приближенье Г(0> определяем по формулам (14) и (15) нулевое при-
ближение нормальной индуктивной скорости w0 (г, ф,) (которую при малых углах атаки
ротора приближенно принимаем равной осевой индуктивной скорости ®v) и промежу-
точную величину Г<01> (г, ф;) по формуле (19):
Г<0,> (г, ф,-) —2- b (г) Wn (г, фг) су аг (г, ф)-
После этого определяется первое приближение циркуляции
Г(0) + Г<01>
2
Вообще n-е приближение циркуляции определяется по формуле:
(20)
б/П"-1)
(г ф)С L (г
, [МП ?/) Wn(r,^
где r<”-1«)=-|-Z>(r) Wn
а вычисляется по
Как указано в книге Г. Виарда „Интегральные уравнения" [10], данный процесс
построения последовательных приближений сходится очень быстро для обычных ли-
нейных интегральных уравнений. Для интегро-дифференциальных уравнений доказатель-
ства не приводятся, но расчеты показывают, что и в этом случае процесс сходится также
быстро и практически достаточно ограничиться первым или вторым приближением.
4
25
При вычислении последовательных приближений индуктивной скорости ^(г, ф)
приходится вычислять интегралы:
п R
f dr (р, ф) , г dr (р, Ф) . ,
I —d~ *01 (Р, Ф) dp и I —r02(p,<p)dp.
го го
Благодаря тому, что выявлен характер поведения подинтегральной функции
в особых точках (р— 1, p = sin'p), выполнение численного или графического интегри-
рования значительно упрощается.
Рассмотрим случаи ф = 0, , л, .
Можно написать ф —:
Zj Z
R
Для функции | составлен вычисленный с большой точностью график
J 1 + р
(фиг. 22а, и 226).
Для остальных значений ф можно написать подобные же соотношения, которые
2
вместо коэффициента — будут иметь значительно более сложные коэффициенты из-за
входящих в них эллиптических функций Якоби.
Так как выяснено, что все интегралы по р имеют только интегрируемые особен-
ности типа In 11—р| и - _ , то можно, не вычисляя всех сложных выражений с
1/1—Р2
эллиптическими функциями, интегрировать выражение (11) непосредственно графиче-
ски, выделяя малые интервалы, содержащие особенности, т. е. интегрируя по р от
f о
Ро = — До р = sin ф—е, затем от р = sin ф ф- е до р = 1 — е и от р — 1 -f- s до р — — .
Как показывают расчеты, для значений Ф = 0,
к Зя
“2*, л, численная интеграция
с выбрасыванием интервала е= 0,025—0,05 дает расхождение с формулой (21) на 5—8%,
что при малых значениях dx является пренебрежимо малой величиной.
26
Таким образом, предельная вихревая схема дала возможность аналитически иссле-
довать характер функций i01 и i02 и определить возможную погрешность при числен-
ном интегрировании с выделением интервала вокруг особой точки. Для практического
, . _ л Зк
же расчета индуктивных скоростей при малых арОт и ф^О, , ~, —- удобнее поль-
зеваться графиками функций iy и i2.
Определив из уравнений (19) и (20) циркуляцию Г(г, ф) и по формулам (14) и (15)—
скорость w, можно перейти к определению сил, действующих на винт в косом потоке.
Мощность,
потребная для вращения винта, определяется по формуле:
N==~l^~ J J Г | fdrd'\>.
° r0 -
(22)
Здесь знак „ —“ над буквой означает осреднение соответствующей величины по
времени.
Подобным же образом определяется истинная тяга винта в каждый момент:
k R
(23)
и средняя тяга по времени:
о Гп
----^-(V'4-г/Д drd^.
I"
(23,)
27
В случае винта в косом потоке, кроме силы тяги и вращающего момента, возни-
кают еще дополнительные силы, не имевшие места ранее в случае работы винта при
те
арот == 2 •
Действительно, полную аэродинамическую силу, развиваемую винтом, можно
в общем случае разложить на три следующие составляющие:
1) тягу, направленную по оси винта (ось х), — Т,
2) продольную силу (ось у) — Н,
3) поперечную силу (ось z)— S.
Аналогичное разложение будет иметь место для аэродинамического момента.
Выражение для мгновенных сил И и S будут следующие:
ft R
Cxi
Cyl
(Ut — Vh ) sin ф,- dr,
(24)
ft R
$= У о f
С XI /г т
-Vfi
i^yi
COS ф; dr.
(25)
Подобные же равенства можно написать для моментов Му и Mz:
к R
M„ =
k R
Л=У.4
ra
— Vfi —
Cxi
-------
'-yi
Cxi
Cyi
r sin ф,- dr,
(26)
(27)
4. ПРИМЕР АЭРОДИНАМИЧЕСКОГО РАСЧЕТА РОТОРА И АНАЛИЗ РЕЗУЛЬТАТОВ
В качестве объекта для проведения примерного аэродинамического расчета был
выбран трехлопастный ротор, который М. Л. Миль и М. К. Сперанский использовали
индуктивных скоростей. Лопасти ротора—трапецевид-
ные и незакрученные, угол установки <р = 7°, диа-
метр £) = 2,45 л/, профиль серии NACA 230. Отно-
сительная ширина лопасти и ее толщина приведены
на графике фиг. 23. Лопасти с шарнирным крепле-
нием.
Так'как данная работа ограничивается рассмо-
трением метода расчета применительно лишь к вин-
ту с жестко закрепленными лопастями, то естествен-
но, что нельзя ожидать полного количественного
совпадения результатов расчета и эксперимента.
Будет вполне достаточно, если подтвердится каче-
ственная картина опытного распределения скоростей
и порядок их величин.
Для расчета был выбран один из режимов,
имевших место в эксперименте: арОТ = 0, р = 0,15.
Расчет проводился при углах ф — 0; , те и
3~
~2~
7те
и2, а для остальных ази-
по графикам i01 и
4те 5те 11те
--- ------- Ы
6 ’ 3 ’ 3----6
кривые циркуляции , полученные в результате пер-
3 ’
по графикам и i2.
На фиг. 24 приведены
вого приближения, а на фиг. 25, иллюстрирующей сходимость процесса последователь-
ных приближений, приведены кривые циркуляции Г|®|, ГЭД и для значений ф =-^-
11
И 7Г.
о
На фиг. 26, 27 и 28 приведены истинные и средние индуктивные скорости на ло-
пастях ротора vx — <vx(г) при ф = const, полученные из расчета. На фиг. 27 и 28 при-
28
Фиг. 25
29
ведены для сравнения также экспериментальные кривые средних индуктивных скоро-
стей vx. Как было сказано выше, количественного совпадения не получилось, во-пер-
вых, из-за того, что в эксперименте лопасти могли совершать маховое движение и,
следовательно, имели иные углы атаки, нежели в расчете, и, во-вторых, потому, что
замеры проводились на некотором расстоянии от лопастей. Однако порядок величин
и особенно качественную картину распределения скорости теория отражает вполне
удовлетворительно.
Отметим здесь еще раз, что в аэродинамический расчет необходимо вводить не
средние, а истинные индуктивные скорости, так как иначе можно получить значи-
тельные количественные ошибки.
Фиг. 29. Истинная и средняя Фиг. 30. Истинная и средняя индуктивные скорости
циркуляции
Фиг. 31. Индуктивная скорость vx при Г = const
Как уже упоминалось выше, для точного расчета необходимо иметь величины
коэффициента су, полученные из продувок крыла конечного размаха. Отсутствие этих
величин приводит на азимуте ^ = 0 к совершенно ошибочным величинам ц*. Объяснить
это можно следующим образом.
На фиг. 15, на которой приведена функция /02, видно, что при 4* = 0 величина t02
имеет при p<Z 1, что соответствует корневым частям лопасти, большие и положитель-
ные значения (Zol=0 для ф = 0). Таким образом, неверно определенная в корне ло-
пасти циркуляция и, следовательно, производная
аг
-j- дает
ар
большие
положительные
слагающие в формулах (14) и (15), что, в свою очередь, приводит к совершенно невер-
ным величинам ъх.
На фиг. 31 приведена кривая осевой индуктивной скорости для азимутов ф = 0
и ф = сосчитанная для постоянной циркуляции. Для удобства сравнения в этом слу-
Ч'х
чае нанесены величины ; там же нанесена кривая, полученная из эксперимента.
30
Качественное совпадение и в этом случае очень хорошее. Этим, на наш взгляд,
подтверждаются соображения о том, что причиной расхождения при ф = 0 величины
vx> полученной теоретически и
ной в этом случае внутренней части лопасти
экспериментально, является незнание на наиболее важ-
истинных величин
циркуляции Г и, следовательно, производной
необходимой
коэффициентов с,,
для расчета винта
dp ’
с переменной циркуляцией.
Если воспользоваться правильными величинами cv, то кривые циркуляции в кор-
невой части лопасти должны были бы иметь вид не такой, как это изображено на
фиг. 25, а как на фиг. 32.
Неточность в определении циркуляции в корне лопасти для азимутов при-
водит к очень незначительным ошибкам, так как i2 на этой части лопасти (р<^1) мало.
Рассмотрение экспериментальных графиков показывает, что скорость гг, на ази-
муте 2~ имеет всегда тенденцию обращаться в нуль при г = р. Это подтверж-
дается и простыми теоретическими соображениями, вытекающими из рассмотрения
формул второй строки табл. 1 (стр. 18) и формул (15) *.
Фиг. 33. Истинные индуктивные скорости vx (ф) при r=const
Фиг. 34. Зависимость крутящего момента Фиг. 35. Зависимость продольной силы
для одной лопасти от азимута для одной лопасти от азимута
На фиг. 33 приведен график vx — vx(Ф) при r= const.
Составленные нами графики позволяют производить с достаточной точностью рас-
чет индуктивных скоростей и выполнять аэродинамический расчет ротора в диапазоне
углов — 25° арот 25°.
Так как ряд вспомогательных функций уже вычислен, то без особых затруднений
подобные графики могут быть составлены и для других углов атаки ротора.
На фиг. 34 и 35 приведены графики крутящего момента и продольной силы ис-
пытанной модели ротора. На графиках изображено распределение указанных величин
для одной лопасти в зависимости от ее азимутального положения. При расчете учи-
тывались только индуктивные потери, так как это дает возможность отчетливее вы-
1 На этот факт впервые указал в своем докладе Л. С. Вильдгрубе.
31
явить различие при расчетах по вихревой теории и по методу Глауэрта--Локка. Ло-
пасть в обоих случаях предполагалась жестко закрепленной.
Из этих графиков видно, что мгновенные величины нагрузок и моментов, полу-
ченные по вихревой теории, сильно отличаются от полученных по теории Глауэрта.
Средние величины, рассчитанные по обеим теориям, близки между собой.
В результате всего вышеизложенного можно заметить следующее.
Для углов атаки &рот — О И ССрот — 15° составлены графики вспомогательных функ-
ций для расчета индуктивных скоростей. Расчеты показывают, что графиками функ-
ций при арот=15° можно пользоваться для расчета скоростей в диапазоне углов
—25°<С «рот <С 25.
Разработан метод аэродинамического расчета винта в косом потоке.
Расчеты индуктивных скоростей качественно очень хорошо совпадают с экспери-
ментальными материалами, полностью отражая характер распределения скоростей по
радиусу лопасти и азимутам.
Расчеты показывают, что вихревая теория дает величины мгновенных нагрузок
и моментов, сильно отличающиеся от получаемых по теории Глауэрта—Локка. Сред-
ние величины, вычисленные по обеим теориям, близки между собой.
В аэродинамический расчет ротора необходимо вводить мгновенные индуктивные
скорости.
ЛИТЕРАТУРА
1. Н. Е. Ж у к о в с к и й. 1) Вихревая теория гребного винта, статьи 1-я и 2-я.
Дополнение проф. В. П. Ветчинкина. 2) О наивыгоднейшем геликоптерном винте,
соч., том VI.
2. Г. И. Майкапар. Приложения вихревой теории винта. Труды ЦАГИ,
вып. 613.
3. М. Л. Миль, М. К. Сперанский. Исследование поля скоростей вокруг
ротора геликоптера при осевом и косом обтекании. (Готовится к печати).
4. М. Л. Мил ь. Аэродинамика воздушного винта с шарнирным креплением
лопастей при криволинейном полете. Труды ЦАГИ № 465.
5. В. П. Ветчинки н. Новые формулы и таблицы эллиптических интегралов
и функций. Изд. ВВА, Москва, 1935 г.
6. И. П. Братухин. Автожиры. Теория и расчет. ОНТИ, 1934 г.
7. А. П. Проскуряков. 1) О коэффициенте протекания несущего винта.
2) Аэродинамический расчет несущего винта с переменным по азимуту углом уста-
новки лопастей. Труды ЛИИ, вып. 16, 1946 г.
8- С. Я- Стриже в с кий. К аэродинамике подъемного винта. Труды ВВА
им. Жуковского, вып. 116.
9. А. Я. Бокарева. Исследование обтекания крыла при больших углах
скольжения. (Здесь же).
10. Ю. С. Сикорский. Элементы теории эллиптических функций с прило-
жениями к механике. ОНТИ, 1936 г.
11. Г. Виарда. Интегральные уравнения. ГТТИ, 1933 г.
12. Н. Glauert. A General Theory of the Autogyro. R& M, №1111.
13. C. N. H. L о c k. Further Development of Autogyro Theory. Parts I and 11.
R & M, №1127.
14. 1. B. Wheatley. An Aerodynamik Analysis of the Autogyro rotor with
a comparison between calculated and experimental resalts. Report NACA, 487.
15. R. S. Ross. An Investigation of the Airflow underneath Helicopter Rotors.
I.A.S., № 12, декабрь 1946 г.
16. В. Sissingh. Beitrag zur Aerodinamik der Drehflugelflugzeuge. Jahrbuch,
Luftfahrtforschung, 1938 и 1941 .
ПРИЛОЖЕНИЕ
СХЕМК АЭРОДИНАМИЧЕСКОГО РАСЧЕТА РОТОРА
С ЖЕСТКИМ КРЕПЛЕНИЕМ ЛОПАСТЕЙ
Для практического применения изложенной теории рекомендуется следующий поря-
док расчета ротора:
1. Заданные величины, характеризующие расчетный режим работы ротора:
V [м/сек] = п [об/сек] — Н [юн] = а°от =
Р Dpot [jii] = Гр [,Н] = То,75 ==
число лопастей k =
2. Геометрические характеристики лопасти:
Таблица 1
Г 0,10 0,20 0,30 0,40 0,50 0,60 0,70 0,80 0,90 1,00
b с ?'-To,75 3. Для значений ази составляющую скорости 1 оси лопасти. мута ^0, '[ея( л 1Г г' — Р Sin 0) 5 л “б“ ’ 11 л 6 ^sin2 Тип ^чере &рот , 1 профи з До юрма. ля: л ~ У пьнук определяем к продольной
go _ _rrt„ Vsin Ирм _ V Sin Крот _____
p — arctg и arctj Qr_ Vcos apoTSin ф
5
33
Таблица 3
г' ф '—-— 0,10 0,20 0,30 0,40 0,50 0,60 0,70 0,80 0,90 1,00
0, л л 5 тс V ’ Д’ л 2тс Т ’ т и и г и
5. Для всех рассматриваемых азимутов определяем геометрический угол атаки
сечений лопасти = <р°— Р° и по графикам су(а) определяем в нулевом приближении
величину с(0', соответствующую этим значениям углов а° и толщинам с (г).
W
Коэффициент (а) определяется для тех чисел М— и Рейнольдса
bW
Re =—^-2- , которые имеют место в данных сечениях и при данных ази-
мутах.
Таблица 4
Ф г* 0,10 0,20 0,30 0,40 0,50 Л 0,60 0,70 0,80 0,90 1,о
0, л м Re
М Re
Таблица 5
ф г' 0,10 0,20 0,30 0,40 0,50 0,60 0,70 0,80 0,90 1,0
0, л аг с(П) су
л 5 л Д’ ’ Д’ “г с(0) СУ
6. Для всех рассматриваемых азимутов определяем в нулевом приближении так
называемую „установочную11 циркуляцию:
Ф) = b (г') Wn (Р,ф) <$> [а « ф) ]
Таблица 6
. ф г' 0,10 0,20 0,30 0,40 0,50 0,60 0,70 0,80 0,90 1,0
0, л л 5 л Д’ ’ Д’ л 2 л Д’ ’ Д’ г (°) р(0) г (°) 1"
34
Таблица 7
и сумму „установочных" циркуляций для всех лопастей:
ф г' 0,10 0,20 0,30 0,40 0,50 0,60 0,70 0,80 0,90 1,о
я , о>1 я о 1 w я 1 i КЗ СО _| сл ~ а я 05 а а О1| а я £ 1 ►— 1 сл I ГС OI Со «.1 . Со я и ко W (Я я 1 а 5S с и _ _ о о о, о с, £5 L_ Т- X- "и >4 >1 >4 И И К части таблиг 1ы ука зывают , ДЛЯ каких азимут ов ну> кно с? у'ММИ-
ровать циркуляции при различных положениях лопастей трехлопастного ротора.
Подобным же образом определяются значения ф в случае двух- или четырехлопаст-
ных роторов.
7. Для определения скорости vx, равной при малых углах арит нормальной скорости
w„=s‘Z/JC, по формуле (GJ должны быть вычислены для всех лопастей суммы интегралов вида:
R
Гц
В дальнейшем для сокращения расчетов мы воспользуемся соотношением
к
f d^ ) [ Z1 dr'= J ЙФ [?Г ) ’ Z1 + Zs d>J
и непрерывную функцию £Г (г'Ь*) заменим кусочно-непрерывной функцией, представ-
ляющей собой ломаную линию с вершинами в точках г'= 0,1; 0,2; 0,3 0,8; 0,9;
1,0, вписанную в кривую, выражаемую функцией Ег(^). Полученная ломаная линия
d k
будет иметь постоянную производную рр (ЕГ)1 на каждом из участков от г'=0,1 до
/'=0,2; от г'= 0,2 до г'= 0,3 и т. д. и интегралы вида / =-,(ЕГ)/(г') dr в этих пре-
/ и г
делах могут быть вычислены заранее и затабулированы. Расчеты показывают, что
замена плавной кривой 22 Г (Фо*) такой ломаной, проходящей через 10 точек, вносит
k
в расчет пренебрежимо малую ошибку. Еще большей точности можно достичь, заменяя
22 Г (ФФй ) на каждых двух интервалах г' = 0,1—0,2; 0,2—0,3 и т. д. параболой, прохо-
к
дящей через три точки, имеющие ординаты,
22Г(ФЮ-
к
равные соответствующим значениям
Вычисляем J
для всех азимутов по формуле:
Zj—- -ф 4 dr'
J = 10
Д9.10; I Д9.10/
J I л
&э юГ
Дг.зГ -ф . . . -ф
^|22 Г (г''Ь } ] = А"Г.- = К Д (22 Г } 1 =-Ю 22 [ Г } “ Г<г0 + °п. Фй )
1 л J Дг ’-л 1 л L
35
или короче
Здесь обозначено
0.2 0,3 0,4 1.0
Д’-2/= § f(r')dr', ^3f=ff(r')dr', ... Д910/ = j/(r')dr'
0.) 6,2 0.3 0,9
И
А 1,2Г =£г (г = 0,2, фй) - £ Г (г = 0,1, ф*), &2.3 = £ г (г = 0,3, Ф* ) - £ Г (г = 0,2, )
ь k k н
и т. д.
Разности Д'"’” г, и Дт>"4 затабулированы в прилагаемых таблицах V и VI для зна-
„ _ тс тс тс 2 тс 5 я
ченииф=0,-^-, -q-, , -д-и тс®; для остальных значении ф пользуемся равен-
о «5 z <5 о
ствами:
дт, (ц_ф)= _ Дт. «^(тс-^-ф), Д'”-” 1,(тс —ф) = Д'”' ”г2(тс-|-ф),
Д'”- " (ф = 0) = Д'”- " (Ф = тс) = 0.
Вычисления сводятся в таблицу:
ф = 0
(аналогично и для других ф)
Таблица 8
Дг’ 0,2—0,1 0,3-0,2 0,4-0,3 0,5-0,4 0,6—0,5 0,7—0,6 0,8—0,7 0.9-0,8 1-0,9
дг(°) Д1,2 Д2,3 Д3,4 Д4,5 Д5,6 Д6,7 Л7,8 Де,9 Д9,10
суммирование производится по последней строчке.
V
г = 0,3, — =
г
I I I Г I
Дт- % ~
F
и так далее для всех г до 1,0 через Дг=0,10.
* Для функций /3 и г4 подобные таблицы не составлены, так как для наиболее интересного случая
горизонтального полета геликоптера (арот = 10°—12°) осевая индуктивная скорость может быть принята рав-
ной нормальной скорости.
®* Множитель г получается вследствие того, что интегралы Ьт-п1 (таблицы V и V) вычислены по
переменной р, связанной с переменной г' соотношением: г' = гр и dr'—~rdo.
36
8. Для всех рассматриваемых азимутов вычисляем нулевое приближение индук
тивного скоса:
А₽(°) = arctg .
Таблица 9
ф г' 0,10 0,20 0,30 0,40 0,50 0,60 0,70 0,80 0,90 1,0
0 Д₽<°>
те
Д₽(01
л
3 др(0)
те
”2" д (°)
2 л
3 д₽(0)
5 л
ТТ др(0>
9. Для всех рассматриваемых азимутов определяем истинный угол атаки в первом
приближении аО>т = аг—Д|Э10), с графиков су (а) снимаем значения (а) в первом при-
ближении, определяем промежуточную циркуляцию П0’1* =в №пс^(а) и циркуляцию
в первом приближении Гп> = -^- [Г<0)-|- Г(01)]:
Таблица 10
Ф Г' 0,10 0,20 0,30 0,40 0,50 0,60 0,70 0,80 0,90 1,0
0 а«> ИСТ с(1> У Г(01) г(1)
ti 1® ист с(1) У р(01) Г<1)
те <й’т Г(01) Г(1)
10. Повторяем расчеты 6, 7, 8, 9 с циркуляцией Г(1) и находим циркуляцию
П2)= 2-[ГО) + Г^] и т. д. Практически в большинстве случаев можно ограничиться
первым приближением.
* Скоростью vn от присоединенных вихрей ввиду ее малости можно в расчетах, вообще говоря, пре-
небречь.
37
11. По формулам (23)—(27) определяются силы и моменты для всех азимутальных
положений лопасти и затем средние величины за оборот.
Здесь не приводится подробная схема этих вычислений ввиду их простоты.
Таблица I
Значения функции Zj
б (п + Ф) = — б (" — ф)
р " Ф 0 к “6~ а Л т 2 тс 3 5 тс “б- 1Z
0 0,000 3,058 1,674 1,000 0,584 0,272 0,000
0,20 0,000 3,259 1,780 1,045 0,620 0,280 0,000
0,40 0,000 3,112 1,915 1,115 0,655 0,300 0,000
0,60 0,000 1,995 2,210 1,255 0,705 0,325 0,000
0,80 0,000 0,641 2,400 1,535 0,855 0,407 0,000
0,90 0,000 0,099 1,500 1,910 1,115 0,542 0,000
0,95 0,000 —0,250 0,000 2,335 1,450 0,761 0,000
1,00 0,000 GO — СО от ОО ОС 0,000
1,05 0,000 —0,400 —0,245 0,000 0,655 0,500 0,000
1,Ю 0.000 —0,265 -0,190 0,000 0,155 —0,030 0,000
1,20 0,000 -0,165 —0,125 0,000 -0,035 —0,080 0,000
1,40 0,000 -0,100 —0,050 0,000 -0,030 —0,085 0,000
1,60 0,000 —0,075 —0,045 0,000 —0,020 —0,075 0,000
1,80 0,000 -0,070 —0,040 0,000 —0,010 —0,070 0,000
2,00 0,000 —0,065 —0,035 0,000 —0,005 —0,065 0,000
2,50 0,000 -0,060 —0,028 0,000 —0,003 —0,060 0,000
3,00 0,000 —0,055 —0,020 0,000 -0,002 —0,050 0,000
4,00 0,000 —0,010 -0,008 0.000 —0,001 —0,015 0,000
5,00 0,000 0,000 0,000 0,000 0,000 0,000 0,000
ПРИМЕЧАНИЯ: 1- Функцию для р> 1,4 можно принять равной нулю, так как в расчет это не
внесет заметной погрешности. 2. При р — 5 значение Z, с точностью до 3-го знака равно 0.
Таблица И
Значения функции Z2
б (« + Ф) = б (" — Ф)
р 0 я w| я в |сч 2 тс 3 5 п Т К
0 0,000 0,000 0,000 0,000 0,000 0,000 0,000
0,20 0,425 —0,040 —0,035 —0,030 —0,025 —0,020 —0,015
0,40 0,845 —0,100 0,215 -0,115 -0,040 —0,035 —0,030
0,60 1,275 0,510 -0,650 —0,237 -0,115 —0,105 —0,095
0,80 1,755 1,185 —0,895 —0,550 —0,385 —0,320 —0,280
0,90 2,010 1,590 -0,210 -1,035 —0,710 —0,535 —0,460
0,95 2,185 1,840 0,500 —1,485 0,955 —0,780 -0,600
1,00 ОО ОО ос- ОО ОО ОО
1,05 2,200 2,050 1,700 1,000 0,300 -0,050 -0,200
1,10 2,070 1,910 1,590 1,000 0,410 0,090 -0,070
1,20 1,895 1,725 1,470 1,000 0,530 0,275 0,105
1,40 1,685 1,535 1,342 1,000 0,658 0,465 0,315
1,60 1,570 1,450 1,277 1,000 0,723 0,550 0,430
1,80 1,495 1,380 1,237 1,000 0,763 0,620 0,505
2,00 1,435 1,325 1,210 1,000 0,790 0,675 0,565
2,50 1,325 1,235 1,160 1,000 0,840 0,765 0,675
3,00 1,262 1,180 1,120 1,000 0,880 0,820 0,738
4,00 1,172 1,120 1,080 1,000 0,920 0,880 0,828
5,00 1,140 1,090 1,050 1,000 0,950 0,910 0,860
38
Таблица III
Значения функции is
4 (it + ф) = /8(л — 6)
Г 0 71 Л 71 2к 5 я
р 1 6 3 2 3 6
0 29,300 6,095 1,930 1,00 0,674 0,540 0,509
0,20 20,350 6,920 2,00 1,045 0.720 0,550 0,510
0,40 15,900 9,800 2,310 1,115 0,750 0,580 0,512
0,60 11,900 11,320 3,280 1,255 0,820 0,610 0,514
0,80 8,350 10,630 5,750 1,535 0,980 0,700 0,516
0,90 6,800 8,550 7,600 1,910 1,070 0,750 0,518
0,95 6,100 6,600 6,500 2,335 1,120 0,780 0,520
1,05 4,400 3,200 2,470 0,000 —2,320 —2,750 -3,050
1,10 3,950 2,850 2,100 0,000 —2,000 —2,420 -2,820
1,20 3,150 2,370 1,700 0,000 -1,550 —2,080 —2,520
1,40 2,200 1,800 1,300 0,000 -1,200 —1,780 -2,200
1,60 1,850 1,520 1,100 0,000 —1,000 — 1,600 —1,960
1,80 1,600 1,350 0,950 0,000 -0,890 —1,420 —1,780
2,00 1,400 1,210 0,820 о.соо -0,760 — 1,280 —1,610
2,50 1,050 0,950 0,650 0,000 -0,550 —1,000 -1,280
3,00 1,000 0,770 0,520 0,000 —0,420 —0,800 -1,090
4,00 0,750 0,600 0,390 0,000 —0,300 —0,609 -0,820
5,00 0,600 0,500 0,300 0,000 —0,230 -0,520 —0,700
Таблица IV
Значения функции 4
4 (п + Ф) = — 4 (п — Ф)
0 Л 71 1 2 л 5 п Л
Р 6 3 2 3 6
0 0,000 0,000 0,000 0,000 0,000 0,000 0,000
0,20 0,000 -0,435 —0,110 -0,030 -0,006 -0,005 0,000
0,40 0,000 —2,150 —0,315 —0,100 —0,030 —0,010 0,000
0,60 0,000 —2,870 0,860 —0,265 - 0,085 -0,025 0,000
0,80 0,000 -3,120 -3,255 —0,750 - 0,195 —0,060 0,000
0,90 0,000 —3,120 —3,460 -2,250 —0,380 -0,155 0,000
0,95 0,000 3,100 —3,510 -2,640 - 0,540 —0,210 0,000
1,00 0,000 —3,065 -3,550 -2,780 0,790 —0,290 0,000
1,05 0,000 -3,000 —3,570 —2,830 -1,055 —0,360 0,000
1,10 0,000 —2,860 —3,580 - 2,850 —1,280 —0,430 0,000
1,20 0,000 —2,630 -3,560 -2,875 —1,525 —0,570 0,000
1,40 0,000 —2,330 — 3,420 —2,900 —1,730 -0,785 0,000
1,60 0,000 —2,145 —3,265 - 2,920 -1,870 —0,895 0,000
1,80 0,000 —2,005 —3,130 —2,93С -1,975 -0,950 0,000
2,00 , 0,000 —1,890 —3,040 -2,932 - 2,065 -1,000 0,000
2,50 0,000 -1,725 -2,875 —2,934 -2,220 -1,080 0,000
3,00 0,000 — 1,690 -2,775 —2,936 -2,300 —1,140 0,000
4,00 0,000 -1,680 -2,670 -2,938 —2,410 -1,240 0,000
5 00 0,000 -1,650 -2,600 —2,939 —2,470 -1,335 0,000
39
Таблица V
Г 1 1 Д2-34 Д3’4^ А4'5»! Д5’Ч Д6’7/, Д7’80 Д8’Ч д9’10/;
0,2 0,5000 —0,0896 0 Ф = 0 л тг 0 0 0 0 0
0,3 0,8980 0,1512 -0,0720 0 0 0 0 0 0
0,4 0,7780 0,4660 0,0484 -0,0600 0 0 0 0 0
0,5 0,6400 0,5700 0,2400 0,0340 -0,0560 0 0 0 0
0,6 0,5410 0,5110 0,3620 0,1485 0,0256 —0,0484 —0,0182 0 0
0,7 0,4660 0,4440 0,4120 0,2290 0,1057 0,0022 —0,0440 -0,0172 0
0,8 0,4070 0,4000 0,3800 0,3200 0,1646 0,0750 —0,0155 —0,0404 0,0145
0,9 0,3630 0,3610 0,3515 0,3220 0,2065 0,1175 0,0538 —0,0168 0,0380
1,0 0,3270 0,3235 0,3170 0,3030 0,2650 0,1540 0,0881 0,0360 0,0244
0,2 0,9500 - 0,0608 0 Ф = 0 - к со| Я О 0 0 0 0
0,3 0,6720 0,5840 -0,0560 0 0 0 0 0 0
0,4 0,4720 0,4580 0,3800 —0,0428 0 0 0 0 0
0,5 0,3700 0,4060 0,4680 0,2610 —0,0360 0 0 0 0
0,6 0,3030 0,3210 0,3620 0,3995 0,1900 -0,0320 —0,0138 0 0
0,7 0,2580 0,2665 0,2985 0,3260 0,3430 0,1300 —0,0300 -0,0128 0
0,8 0,2245 0,2300 0,2450 0,2670 0,2925 0,3000 0,0800 -0,0260 -0,0095
0,9 0,2000 0,2050 0,2120 0,2250 0,2475 0,2680 0,2670 0,0536 —0,0224
1,0 0,1800 0,1815 0,1870 0,1970 0,2130 0,2300 0,2380 0,2350 -0,0360
0,2 0,8160 0,0000 0 Ф = 0 л ~2 0 0 0 0 0
0,3 0,3876 0,5520 0 0 0 0 0 0 0
0,4 0,2760 0,3140 0,4650 0 0 0 0 0 0
0,5 0,2160 0,2352 0,2720 0,3980 0 0 0 0 0
0.6 0,1750 0,1865 0,2030 0,2380 0,3510 0 0 0 0
0,7 0,1515 0,1559 0,1660 0,1845 0,2145 0,2920 0 0 0
0,8 0,1324 0,1351 0,1424 0,1524 0,1670 0,1945 0,2650 0 0
0,9 0,1175 0,1204 0,1240 0,1298 0,1410 0,1530 0,1825 0,2400 0
1,0 0,1060 0,1070 0,1095 0,1140 0,1210 0,1300 0,1430 0,1700 0,2200
0,2 0,4570 0,0500 0 Ф = 0 2 л Т 0 0 0 0 0
0,3 0,2230 0,3400 0,0550 0 0 0 0 0 0
0,4 0,1615 0,1807 0,2820 0,0580 0 0 0 0 0
0,5 0,1280 0,1340 0,1520 0,2320 0,0600 0 0 0 0
0,6 0,1050 0,1080 0,1162 0,1320 0,2040 0,0636 0 0 0
0,7 0,0888 0,0909 0,0952 0,1030 0,1191 0,1740 0,0640 0 0
0,8 0,0776 0,0796 0,0825 0,0863 0,0936 0,1088 0,1700 0,0638 0
0,9 0,0688 0,0710 0,0728 0,0744 0,0788 0,0856 0,0996 0,1440 0,0635
1.0 0,0612 0,0630 0,0640 0,0660 0,0690 0,0730 0,0800 0,0940 0,1340
40
Окончание табл. V
Г Д1’2/! Д2’3/, д3-4/. д4’Ч Д5’% Д6’7/! Д7’Ч Д8’% дЭ.Ю/,
у 6
0,2 0,2180 —0,0640 0 0 0 0 0 0 0
0,3 0,1035 0,1730 0,0092 0 0 0 0 0 0
0,4 0,0750 0,0848 0.1400 0,0136 0 0 0 0 0
0,5 0,6580 0,0620 0,0720 0,1200 0,0198 0 0 0 0
0,6 0.0478 0,0498 0,0532 0,0635 0,1030 0,0268 0 0 0
0,7 0,0400 0,0420 0,0440 0,0486 0,0572 0,0935 0,0265 0 0
0,8 0,0350 0,0362 0,0375 0,0400 0,0437 0,0512 0,0800 0,0260 0
0,9 0,0311 0,0325 0,0336 0,0344 0,0366 0,0406 0,0482 0,0740 0,0250
1,0 0,0280 0,0286 0,0296 0,0304 0,0320 0,0384 0,0380 0,0450 0,0692
ПРИМЕМ/ ШИЕ. Ну/ 1И в столбц ах таблиц Д'"’ " Zj noj жучились в результате того, что функция
/1 для р > 1,4 принята приближенно равной нулю (см. фиг. 6). В результаты расчетов это не внесет
заметной погрешности, но значительно облегчит их выполнение.
Таблица VI
Г Д1’^ Л2’3/ a z2 Д3Л2 Д4’5/ А-' <2 д5-6/. д6,7: д7’8/2 Д8’% Д9-10 \
ф = 0
0,2 0,8150 0,9160 0,7550 0,6850 0,6500 0,6200 0,5960 0,5850 0,5750
0,3 0,3530 0,6080 0,6500 0,5400 0,4930 0,4630 0,4400 0,4260 0,4150
0,4 0,2000 0,3560 0,4850 0,5160 0,4324 0,3925 0,3670 0,3530 0,3370
0,5 0,1265 0,2100 0,3020 0,4020 0,4140 0,3540 0,3250 0,3060 0,2920
0,6 0,0870 0,14/0 0,2050 0,2700 0,3420 0,3440 0,3150 0,2790 0,2660
0,7 0,0644 0,1090 0,1500 0,1945 0,2440 0,2990 0,2950 0,2650 0,2500
0,8 0,0500 0,0824 0,1150 0,1490 0,1840 0,2220 0,2640 0,2750 0,2410
0,9 0,0388 0,0654 0,0926 0,1170 0,1190 0,1720 0,2030 0,2350 0,2360
1,0 0,0310 0,0530 0,0740 0,0952 0,1170 0,1420 0,1630 0,1880 0,2150
= ТС
0,2 0,5000 0,8290 0,7000 0,6480 6 0.6120 0,5900 0,5800 0,5700 0,5650
0,3 0,0566 0,4429 0,5980 0,4960 0,4580 0,4290 0,4150 0,3980 0,3870
0,4 —0,3000 0,1450 0,3670 0,4640 0,3870 0,3600 0,3400 0,3260 0,3150
0,5 —0,0250 0,0360 0,1660 0,3180 0,3800 0,3300 0,2980 0,2820 0,2720
0,6 —0,0176 —0,0100 0,0752 0,1660 0,2770 0,3190 0,2790 0,2600 0,2400
0,7 —0,0086 -0,0171 0,0243 0,0906 0,1600 0,2500 0,2700 0,2520 0,2320
0,8 —0,0060 —0,0150 .0 0,0474 0,0776 0,1510 0,2220 0,2490 0,2300
0,9 —0,0030 —0,0117 0,0123 0,0200 0,0610 0,1000 0,1430 0,1920 0,2270
1,0 —0,0015 —0,0090 -0,0240 0,0040 0,0350 0,0670 0,1000 0,1370 0,1830
Ф = - К т
0,2 —0,2540 0,7150 0,6240 0,5900 0,5750 0,5600 0,5450 0,5340 0,5350
0,3 —0,1270 —0,1550 0,5040 0,4330 0,4110 0,3990 0,3880 0,3780 0,3720
0,4 —0,0760 —0,1200 -0,0835 0,3900 0,3390 0,3170 0,3050 0,3025 0,2920
0,5 —0,0210 —0,0760 —0,1700 —0,0368 0,3220 0,2800 0,2620 0,2500 0,2460
0,6 —0,0100 -0,0400 -0,1000 —0,1490 -0,0140 0,2680 0,2394 0,2230 0,2170
0,7 —0,Р060 -0,0240 —0,0540 —0,1090 —0,1290 -0,0080 0,2380 0,2090 0,1970
0,8 —0,9038 -0,0130 -0,0340 —0,0670 -0,0940 —0,1110 -0,0220 0,2100 0,1890
0,9 —0,0025 —0,0110 —0,0220 —0,0422 -0,0750 —0,0976 —0,0950 -0,0270 0,1840
1,0 —0,0008 —0,0060 —0,0150 -0,0290 —0,0510 —0,0780 —0,0900 —0,0780 0,0300
6
41
Окончание табл. V1
Г а 1,2/ а z2 Д ,3«2 Д3’Ч дЧ2 Д6‘7/2 Д7’% Л8’9/ а «2 д9-’%
Ф = - nd’ я
0,2 - 0,3160 0,5000 0,5000 0,5000 0,5000 0,5000 0,5000 0,5000 0,5000
0,3 —0,0546 —0,2190 0,3330 0,3330 0,3330 0,3330 0,3330 0,3330 0,3330
0,4 -0,0260 —0,0640 —0,2150 0,2500 0,2500 0,2500 0,2500 0,2500 0,2500
0,5 0,0160 —0,0352 —0,0720 -0,1980 0,2000 0,2000 0,2000 0,2000 0,2000
0,6 -0,0085 —0,0200 -0,0365 —0,0715 —0,1845 0,1665 0,1635 0,1665 0,1665
0,7 —0,0057 —0,0166 —0,0238 —0,0386 -0,0686 -0,1860 0,1430 0,1430 0,1'430
0,8 —0,0044 —0,0087 -0,0162 -0,0250 —0,0337 -0,0724 —0,1670 0,1250 0,1250
0,9 -0.0033 -0,0066 0,0123 -0,0189 —0,0266 —0,0422 —0,0720 —0,1540 0,1110
1,0 -0,0010 -0,0050 —0,0090 -0,0136 -0,0200 -0,0290 —0,0430 -0,0740 -0,1470
2 Л т
0,2 —0,1450 0,2850 0,3790 0,4100 0,4250 0,4400 0,4550 0,4660 0.4650
0,3 -0,0233 — 0,1530 0,1620 0,2330 0,2550 0,2660 0,2780 0,2880 0,2940
0,4 —0,0090 -0,0350 —0,1450 0,1110 0,1610 0,1830 0,1950 0,1975 0,2080
0,5 —0,0040 —0,0140 —0,0380 —0,1420 0,0780 0,1200 0.1380 0,1500 0,1540
0,6 - 0,003-3 —0,0084 —0,0167 —0,0474 —0,1230 0,0650 0,0936 0,1100 0,1230
0,7 —0,0029 -0,0050 —0,0100 -0,0215 —0,0500 —0,1200 0,0500 0,0770 0,0890
0,8 -0,0025 - 0,0037 —0,0062 -0,0112 —0,0180 —0,0500 —0,1075 0,0400 0,0610
0,9 —0,0011 —0,0031 -0,0045 —0,0078 —0,0089 —0,0266 -0,0507 -0,1010 0,0360
1,0 —0,0009 —0,0020 —0,0030 - 0,0056 Ф = ’ - 0,0070 5 л 6 -0,0160 —0,0280 —0,0510 —0,0950
0,2 —0,1250 0.1710 0,3000 0,3520 0,3880 0,4100 0,4200 0,4300 0,4350
0,3 -0,0233 —0,1220 0,0680 0,1700 0,2080 0,2310 0,2510 0,2680 0,2790
0,4 —0,0090 —0,0315 -0,1175 0,0360 0,1130 0,1400 0,1600 0,1720 0,1850
0,5 —0,0040 —0,0140 —0,0440 —0,1100 0,0102 0,0700 0.1020 0,1180 0,1280
0,6 -0,0033 —0,0084 —0,0167 —0,0415 —0,1070 0,0140 0,0540 0,0730 0,0930
0,7 0,0029 —0,0050 -0,0100 —0,0186 —0,0430 —0,0915 0,0160 0,0340 0,0540
0,8 -0,0025 -0,0037 —0,0062 — 0,0112 —0,0162 -0,0424 0,0890 0,0001 0,0200
0,9 —0,0011 - 0,0031 —0,0045 -0,0078 0,0132 0,0233 —0,0444 —0,0835 —0,0050
1,0 —0,0009 -0,0020 —0,0030 —0,0056 —0,0090 л —0,0140 -0,0250 -0,0410 —0,0770
0,2 —0,1005 0,1840 0,2450 0,3150 0,3500 0,3800 0,4040 0,4150 0,4250
0,3 —0,0200 -0,1065 0,0100 0,1200 0,1670 0,1970 0,2200 0,2340 0,2450
0,4 —0,0060 -0,0265 —0,1024 —0,1600 0,0676 0,i075 0,1330 0,1470 0,1630
0,5 -0,0032 —0,0112 —0,0320 —0,0920 —0,0140 0,0460 0,0750 0,0940 0,1078
0,6 0,0027 —0,0067 -0,0143 -0,0349 —0,0830 -0,0110 0,0180 0,0540 0,0670
0,7 0,0020 —0,0029 —0,0080 —0,0172 -0,0350 —0,0772 0,0090 0,0190 0,0360
0,8 —0,0010 -0,0025 —0,0050 —0,0100 -0,0140 —0,0362 —0,0700 —0,0250 0,0090
0,9 —0,0005 -0,0022 —0,0029 —0,0058 -0,0067 —0,0200 —0,0355 —0,0644 —0,0140
1,0 —0,0001 —0,0010 —0,0020 —0,0044 —0,0070 -0,0130 —0,0210 —0.0350 —0,0620
42
ОБТЕКАНИЕ КРЫЛА ПРИ БОЛЬШИХ УГЛАХ СКОЛЬЖЕНИЙ
А. Я. БОКАРЕВА
КРАТКОЕ СОДЕРЖАНИЕ
В работе излагаются результаты испытаний модели прямоугольного крыла
методом распределения давления в большом диапазоне углов скольжения ₽.
Показано, чго при достаточно высоких углах скольжения ф >40°) простран-
ственность потока вносит существенные изменения в величину коэффициента сп
и в характер обтекания сечений.
Выводы эксперимента могут быть использованы при расчетах ротора гели-
коптера, лопасти которого работают в условиях косого потока как при малых,
так и при больших углах скольжения.
ОСНОВНЫЕ ОБОЗНАЧЕНИЯ
I — длина крыла;
Ь — хорда профиля;
с — максимальная толщина профиля;
— с
с относительная толщина профиля;
а — геометрический угол атаки профиля;
Р — угол скольжения;
V— скорость потока в трубе;
V
М=: — — число М;
а ’
Vb
Re = —----число Рейнольдса;
р — давление на поверхности профиля;
р0 — давление в потоке;
рУ2
q = —2^ —- скоростной напор;
- Р— Ро
р — -----коэффициент давления;
сп — коэффициент составляющей аэродина-
мической силы, направленной пер-
пендикулярно к хорде профиля;
ct — коэффициент составляющей аэродина-
мической силы, направленной по хор-
де профиля;
сп max — максимальное значение коэффициента
сп при заданном угле скольжения fl,
а кр - геометрический угол атаки, соответ-
ствующий г„тах .
Обтекание элементов лопасти ротора геликоптера в горизонтальном полете в
известной степени аналогично обтеканию элемента крыла при больших углах сколь-
жения. Различие заключается в том, что элемент лопасти ротора работает в условиях
переменного и нестационарного поля скоростей. Кроме того, при больших (срывных)
углах атаки под действием центробежной силы на лопастях ротора возникает эффект
перетекания пограничного слоя и оторванного воздуха вдоль лопасти.
Испытания профилей на дренированных винтах, проводившиеся в ЦАГИ [1], по-
казали, что центробежные силы не оказывают заметного влияния на характеристики
профиля при безотрывном обтекании. При срывных углах атаки сечений внутренней
части вращающейся лопасти (винта) значения коэффициента подъемной силы могут пре-
восходить соответствующие значения для невращающегося крыла.
При проведении исследований работы ротора геликоптера часто считают, что
поле скорости, в котором работают лопасти ротора, в каждый данный момент является
установившимся (гипотеза стационарности). Таким образом, в первом приближении
можно полагать, что элементы средней части лопасти ротора работают примерно в тех
же условиях, что и элементы средней части крыла.
С целью исследования физической картины обтекания элементов крыла, движу-
щегося со скольжением, и использования результатов исследования при расчетах
ротора геликоптера были проведены испытания 1 модели крыла по методу распределе-
ния давления в большом диапазоне углов скольжения 8—0-г-75° и углов атаки
а = 0 -ь 25°.
1 Эксперимент поставлен Г. И. Майкапаром.
43
Объектом испытаний было прямоугольное крыло с симметричным профилем (фиг. 1,
табл. 1), длиной (без законцовок) 7 = 2,0 м, шириной й = 0,40 м и толщиной с= 0,048 м
(с = 0,12). Для измерения давления крыло было продрепировано в семи сечениях,
расположенных симметрично относительно средины крыла: сечения 7 и 7 на расстоя-
нии 100 см от концов крыла; 2 и б—300 см, 3 и 5 — 600 см и 4 — среднее сечение
крыла (фиг. 1).
Каждое сечение имело на верхней поверхности 17 дренажных отверстий, на ниж-
ней поверхности — 15 отверстий. Коорди-
наты дренажных отверстий сечений крыла
даны в табл. 2.
Предварительно были проведены ис-
пытания при трех вариантах законцовок,
отличающихся одна от другой по форме.
Так как эти испытания показали, что форма
законцовок оказывает незначительное вли-
яние на величину коэффициента подъемной
силы даже крайнего сечения, все основные
испытания были проведены с законцовкой
1 (фиг. 1).
Законцовка 1 выступает от прямоуголь-
ной части крыла по всей длине хорды на
величину, равную половине наибольшей тол-
щины профиля; в передней части законцовка
закруглена.
Таблица 1
Координаты сечения крыла
Профиль сечения крыла
Фиг. 1
X 0,005 0,010 0,0175 0,025 0,050 0,10 0,20 0,30
У 0,0124 0,0169 0,0222 0,0261 0,0354 0,0168 0,0574 0,0600
X 0,40 0,50 0,60 0,70 0,80 0,90 1.0
У 0,0580 0,0528 0,0455 0,0366 0,0262 0,0144 0,0001
Координаты дренажных отверстий сечений крыла
Таблица 2
отверстий верхней по- верхности 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17
X 1 0 jo,03 0,05 1 0,075 0,10 1 0,15 0,20 0,25 0,30 0,35 0,40 0,50 0,60 0,70 0,80 0,90 0,93
№№ отверстий нижней по- верхности 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32
X 0,90 0,80 0,70 0,60 1 0,50 0,40 0,35 0,30 0,25 0,20 0,15 0,10 0,075 0,050 0,025
Испытания были проведены в Т-102 на специальной раме с жесткой обтекаемой
подвеской. Угол скольжения р при испытаниях изменялся вращением поворотного
круга Т-102 и определялся как угол между направлением скорости потока и перпен-
дикуляром к передней кромке крыла. Угол р считался положительным при повороте
крыла в направлении часовой стрелки (фиг. 1). Таким образом, при повороте левая
половина крыла (сечения 1, 2, 3) выступала вперед, правая (сечения 5, 6, 7) отходила
назад. Давление на поверхности крыла измерялось при помощи спиртового батарейного
манометра высотой h ==500 мм. Давление в каждой паре симметричных сечений изме-
рялось одновременно, центральное сечение 4 испытывалось отдельно.
44
Все семь сечений крыла были испытаны при скорости потока в трубе V= 50 м/сек
(число Re= 1,38-10е, число М = 0,15) и углах скольжения (3 = 0, 5', 10°, 15°, 25°, 35°,
45°, 60°, 75°.
При каждом значении угла ₽ угол атаки а менялся в пределах а = 0-г-25°.
Для определения влияния числа Re на характер обтекания профиля при больших
углах атаки были проведены испытания при скорости потока в трубе У = 35 м/сек
и И=20 м/сек (числа Re при этом Re — 0,965-10“ и Re =0,55-10е), углах скольжения
₽ = 0, 15°, 35°, 75° и углах атаки а = 13° = 25°.
При обработке материалов испытаний определялся коэффициент давления р — — Р- ,
Р^2
где р — давление на поверхности профиля, рл — давление в потоке, q —----скорост-
ной напор.
Определение коэффициента подъемной силы крыла (точнее коэффициента нормаль-
ной к хорде профиля составляющей силы, действующей на крыло) производилось пла-
ниметрированием эпюр распределения р по поверхности профиля.
р = 0°
Фиг. 2
Определение полного коэффициента подъемной силы Cj,=e„cosa — с, sin а, где
ct—коэффициент составляющей силы, направленной по хорде профиля, не проведено,
так как определение коэффициента ct по эпюре давления, полученной при малом зна-
чении числа М, недостаточно точно.
При малых значениях угла атаки а коэффициент су не будет заметно отличаться
от коэффициента сп. При больших углах атаки (а >15’) су по величине будет несколько
отличаться от коэффициента с„, но качественно изменения коэффициентов су и с„
на разных режимах обтекания крыла не будут различаться.
На фиг. 2, 3, 4, 5 и 6 приводятся эпюры давления р, полученные в испытаниях
при скорости потока в трубе V=50 м сек, углах скольжения 0=0, 35°, 45°, 60°, 75°
и углах атаки a = 2°, 10°, 16°; на фиг. 7, 8, 9, 10 и 11—при этой же скорости потока
и тех же углах скольжения р, но при ббльших углах атаки a = 19° и 25°.
45
Фиг. 3
р = ео°
Фиг. 5
Фиг. 4
Фиг. 6
Сравнение эпюр р при различных углах скольжения р и углах атаки а показывает,
что изменение угла р приводит к существенному изменению характера эпюр и вели-
чины подъемной силы.
При больших углах атаки а увеличение угла скольжения р приводит к уменьше-
нию срыва потока. Так, в сечении 4 при угле [3 = 0 и углах а. = 19° и 25° (фиг. 7) по-
лучены явно выраженные срывные эпюры распределения давления. При угле р = 35°
а—19° (фиг. 8) эпюра имеет вид досрывного обтекания, а при а = 25° срыв значи-
тельно меньше, чем при угле Р—0 и при том же угле атаки а = 25°. При еще боль-
ших значениях угла скольжения р (фиг. 9, 10 и 11) срыв совершенно исчезает как
при угле атаки а = 19°, так и при а = 25°. Подобную же деформацию эпюр р можно
видеть и на других сечениях.
Фиг. 7
Для определения порядка изменения величины коэффициента подъемной силы
с„ с изменением утла р на фиг. 12 приводятся кривые значений величины -------п—- =
cos2 р
=/(«) при p = const, полученные для сечения У. Такой способ построения оказывается
удобным, так как кривые значений
'^^р_==/(а) ПРИ Р —const совпадают в широком
диапазоне значений углов р [2]. В данном эксперименте, как показывают кривые
фиг. 12, совпадение кривых
можно наблюдать до р^40". При больших
значениях углов скольжения коэффициент значительно выше.
Сравнивая эпюры, полученные на различных сечениях при безотрывном обтека-
нии (а = 2 ; 10°; 16°—фиг. 2, 3, 4, 5 и 6) при всех значениях утла р, можно видеть,
что характер эпюр сохраняется по всему размаху крыла. Величина коэффициента
подъемной силы сп на средних сечениях крыла при малых р больше, чем коэффи-
циента сп концевых сечений крыла, что объясняется большим индуктивным скосом на
средних сечениях крыла.
При больших срывных углах атаки а (фиг. 7, 8, 9, 10 и 11) характер обтекания
меняется с изменением угла скольжения р.
47
Фиг. 8
Фиг. 10
р= 45°
Фиг. 9
Фиг. 11
При малых и средних значениях угла ₽, в том числе и при (3=0 (фиг. 7 и 8), про-
исходит неоднородное обтекание сечений: эпюры средних сечений, имеющих боль-
ший индуктивный скос, имеют вид срывного обтекания, эпюры концевых сечений—до-
срывного обтекания.
При р>35° (фиг. 9, 10 и 11)
в том, что различие в обтекании
имеют одинаковый характер для
сколько меняется вдоль размаха.
влияние большого угла скольжения р сказывается
сечений изчезает, эпюры распределения давления
всех сечений, хотя величина подъемной силы не-
7
49
Сечения 1, 2, 3, повернутые к потоку, при всех значениях >гла скольжения р,
отличных от нуля, при малых и больших значениях угла атаки а имеют большую
подъемную силу, чем сечения 5,6, 7 (фиг. 4, 5, 6, 9, 10 и 11). На фиг. 13 даны кривые
значений сп по размаху крыла при углах а=10с, 19° и углах р = 0, 35°, 45°, 60°, 75’.
Эти кривые несимметричны относительно средины крыла.
Фиг. 14
50
Нафиг. 14 приводятся эпюры/? сечения 4 при а=13°, 19°, 25° при всех иссле-
дованных значениях угла р. Эти кривые подтверждают, что при сравнительно малом
угле атаки (я = 13°) эпюры р для всех значений угла р подобны; при больших углах
атаки (а =19°, 25°) подобие эпюр нарушается при малых р и восстанавливается при
приближении угла р к значению р^25° для угла а=19° и р=^45° для угла а = 25°.
Значения - ” - для каждого сечения крыла меняются в зависимости от угла р
и от положения сечения на крыле (фиг. 15, 16, 17 и 18).
de
При углах скольжения до 45° значения - - увеличиваются к средине крыла,
но при приближении к сечению 7 снова падают, как и следует ожидать при симмет-
ричном (или близком к симметричному) положении крыла относительно набегаю-
щего потока.
de
При больших углах скольжения (р = 60°, 75°) значения —, — при переходе от се-
чения 1 к сечению 7 падают вдоль всей длины крыла.
51
На фиг. 19 показано влияние скоса потока на величину сптах и на значения акр, соот-
ветствующие сп max, при 0<40° на сечениях 3, 4, 5, 6. При углах скольжения р>40°
достигнуты.
на концевых се-
значений акр показывают, что с увеличением
Приведенные на фиг. 19 кривые
угла скольжения ₽ углы акр возрастают, а значения cnmax заметно уменьшаются.
Различное влияние скольжения вдоль крыла можно проследить и на этой фигуре:
на сечениях левой половины крыла (например, сечение 3) с„тах больше, чем на сече-
ниях правой половины крыла (сечение 5); значения акр при приближении к правому
концу крыла начинают возрастать.
52
Для определения влияния числа Re на характер обтекания профиля проведены
испытания при трех скоростях потока: И = 50, 35 и 20 м/сек (числа Re = 1,38-10®,
Re = 0,965-10е, Re = 0,55-:06). Эти испытания показали, что число Re в указанном диа-
пазоне значений не влияет на характер эпюр и величину коэффициента сп как при
безотрывном обтекании, так и при полном срыве. Влияние числа Re сказывается лишь
в некоторой задержке срыва. На фиг. 20 приводятся эпюры р сечения 4 при Р —0
а =19°, 25°; р = 35° а =19°, 22°, 25°; [3 = 75° а = 19°, 25° при трех скоростях потока.
Результаты испытаний крыла в косом потоке позволяют сделать следующие
выводы:
1. Определение коэффициента подъемной силы сп крыла, движущегося со сколь-
жением, по коэффициенту сп крыла, движущегося без скольжения, как сп ₽, 0=
= c«f1^0cos2P возможно только до [3^40°. При достаточно высоких углах скольжения
(Р>40°) пространственность потока вносит существенные изменения в величину коэф-
фициента сп. Коэффициент сп крыла, движущегося со скольжением при большом
значении угла ((3>4О”), значительно выше, чем су&_Ocos2(3.
2. Отрыв пограничного слоя при движении крыла со скольжением происходит
позднее, чем при движении без скольжения. Величина критического угла атаки акр растет
с увеличением угла (3. В вышеописанном эксперименте при (3 = 60° и [3 = 75° срыва по-
тока не было получено даже при а = 25°.
Ситах профиля с увеличением угла р падает.
3. Отрыв на передней половине крыла происходит раньше, на задней половине—
позднее.
Вышеуказанные выводы могут быть использованы при расчетах ротора геликоп-
тера, лопасти которого работают в условиях косого потока при больших углах сколь-
жения (до р = 90°).
ЛИТЕРАТУРА
1. Г. И. Майка пар. Исследование характеристик профилей при около-
и сверхзвуковых скоростях по распределению давления на лопасти воздушного
винта. Техн, отчеты ЦАГИ ftSS£?ta?5^“1948 г.
2. В. В. С тру ми нс к ий. Скольжение крыла в вязкой жидкости. Д. А. Н„
том LIV, № 7, 1946 г.
ОГЛАВЛЕНИЕ
Стр.
А. И. Слуцкий. Аэродинамический расчет ротора
геликоптера (вихревая теория винта в ко-
сом потоке).............................. 1
Введение .................................. —
1. Расчет индуктивных скоростей при арот / 0 3
2. Расчет индуктивных скоростей при арот = О
(предельная схема)........................ 11
3. Аэродинамический расчет винта при косой
обдувке -................................. 23
4. Пример аэродинамического расчета ротора
и анализ результатов...................... 28
Приложение ...............................• 33
А. Я. Бокарева. Обтекание крыла при больших
углах скольжения....................... 43
ОПЕЧАТКИ
=-:“ — -— — - ============================== - —==
Стр. Строка Напечатано Должно быть По чьей вине
5 12 ф1 12 г. 4 ,а снизу as dS = rdfrl rfx’i, ds2. ds dS = rM-\ Автора
14 9 снизу sin a db 2r. Г sin a d 6
J p sin 6-|—sin Ф 0 J p sin 0 + sin a V •
16 6 снизу A — $p cos ф [... | A = p cos ф [....] Корректора
17 9 сверху Jsw* = -y J \ fi (z) dz = - ~ J. Автора
18 2 сверху । sin ф 1 sin ф|
V sin2-^ — p2 \/ sin2 ф — p2
18 4 свс рху />j П (n, к) Bx П (in, A ) »
20 3 сверху^ снизу „ , ., ( aa n 0 v ’ 7 k Cnadiu TO(0) ~ -!'l v ($) A _ / . Sn a 6 Корректора
36 И 0 (a)J ' > '/ 1 Cn a dn a 6(a) j •
W « 4я V - " “ 4kIZ -'••• ’ Автора
37 12 сверху П‘>.1) = -£ви7л СК» («) 1(0.1) = -'-- («) Корректора
47 13 снизу Y 4 »