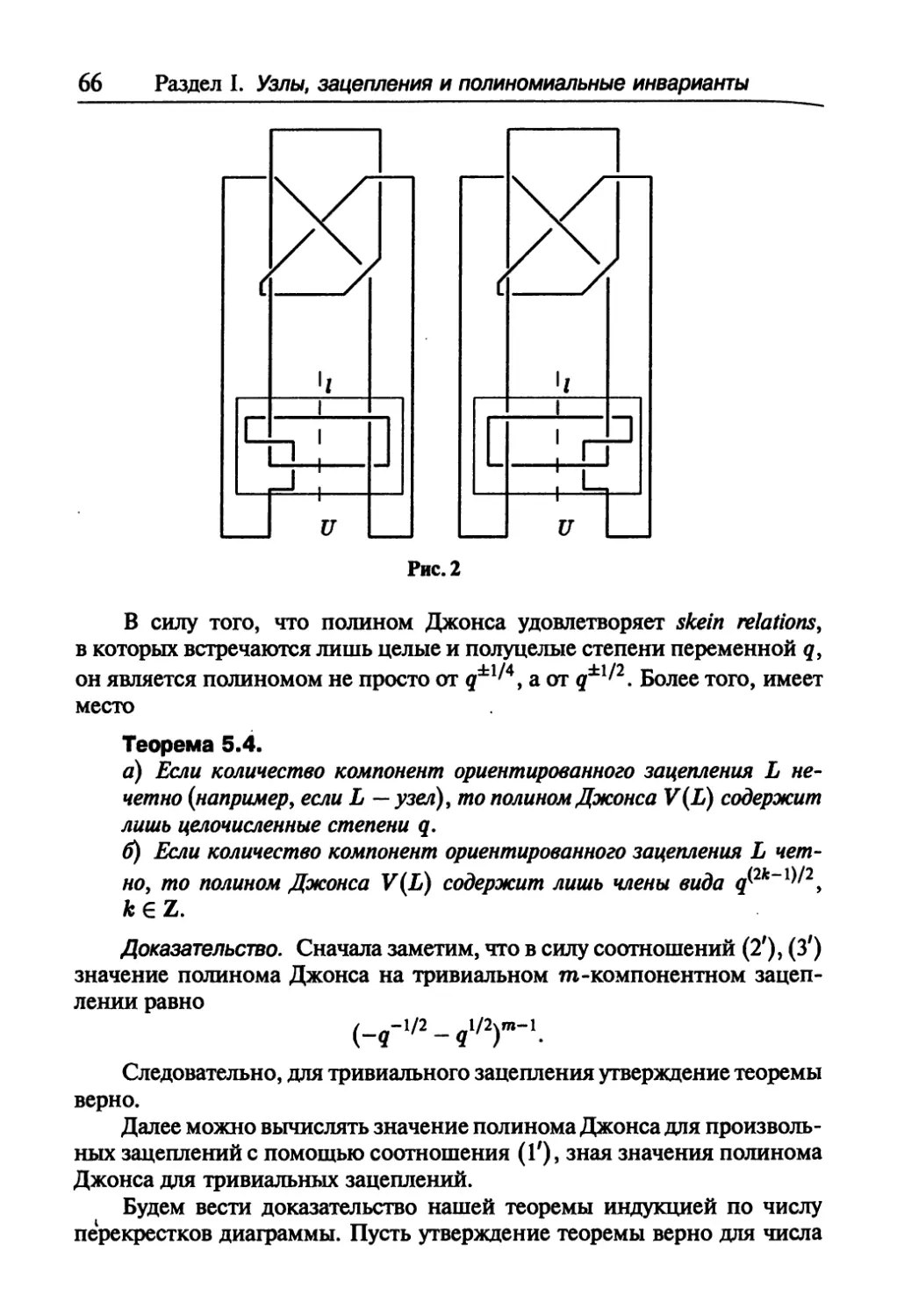
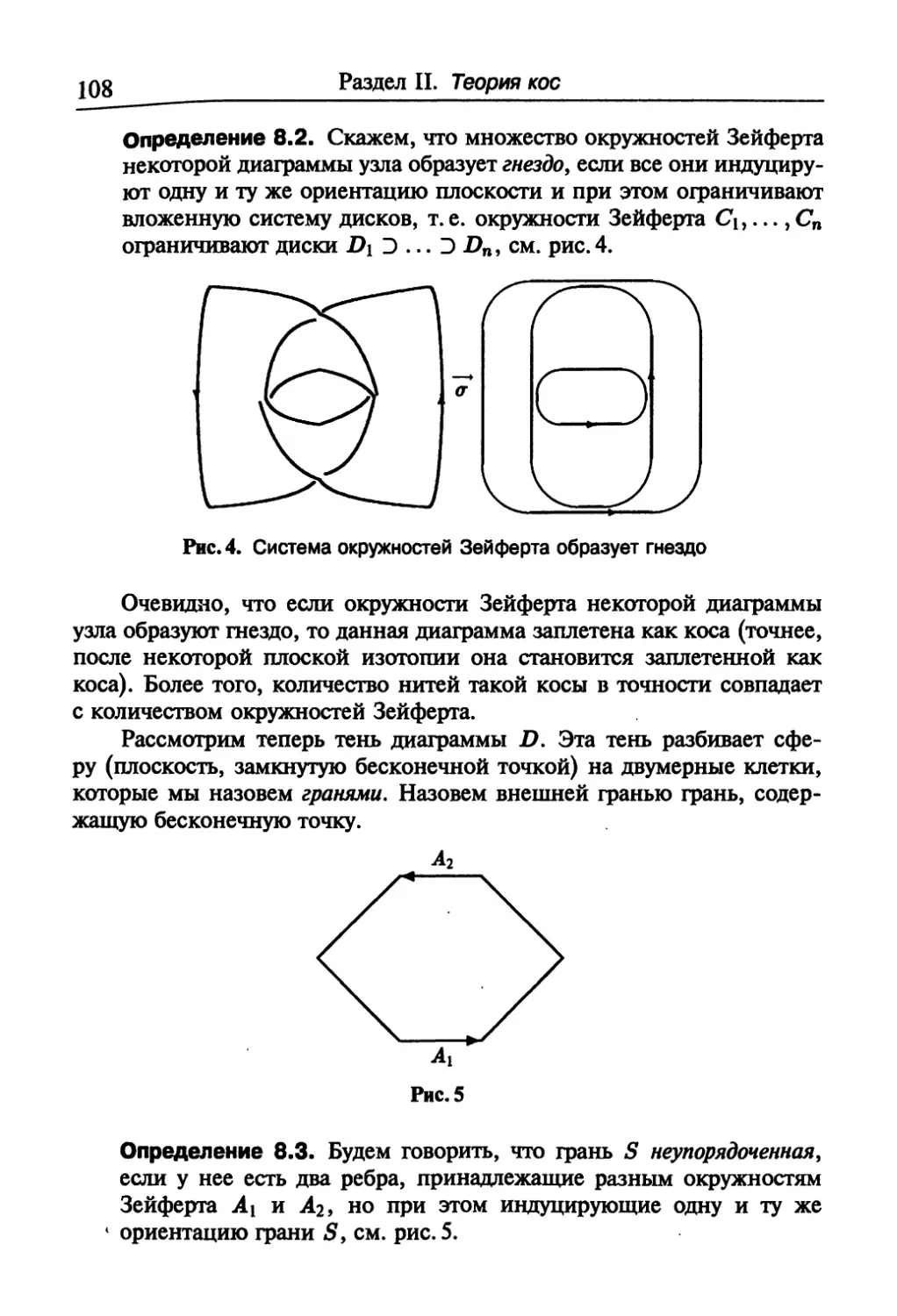
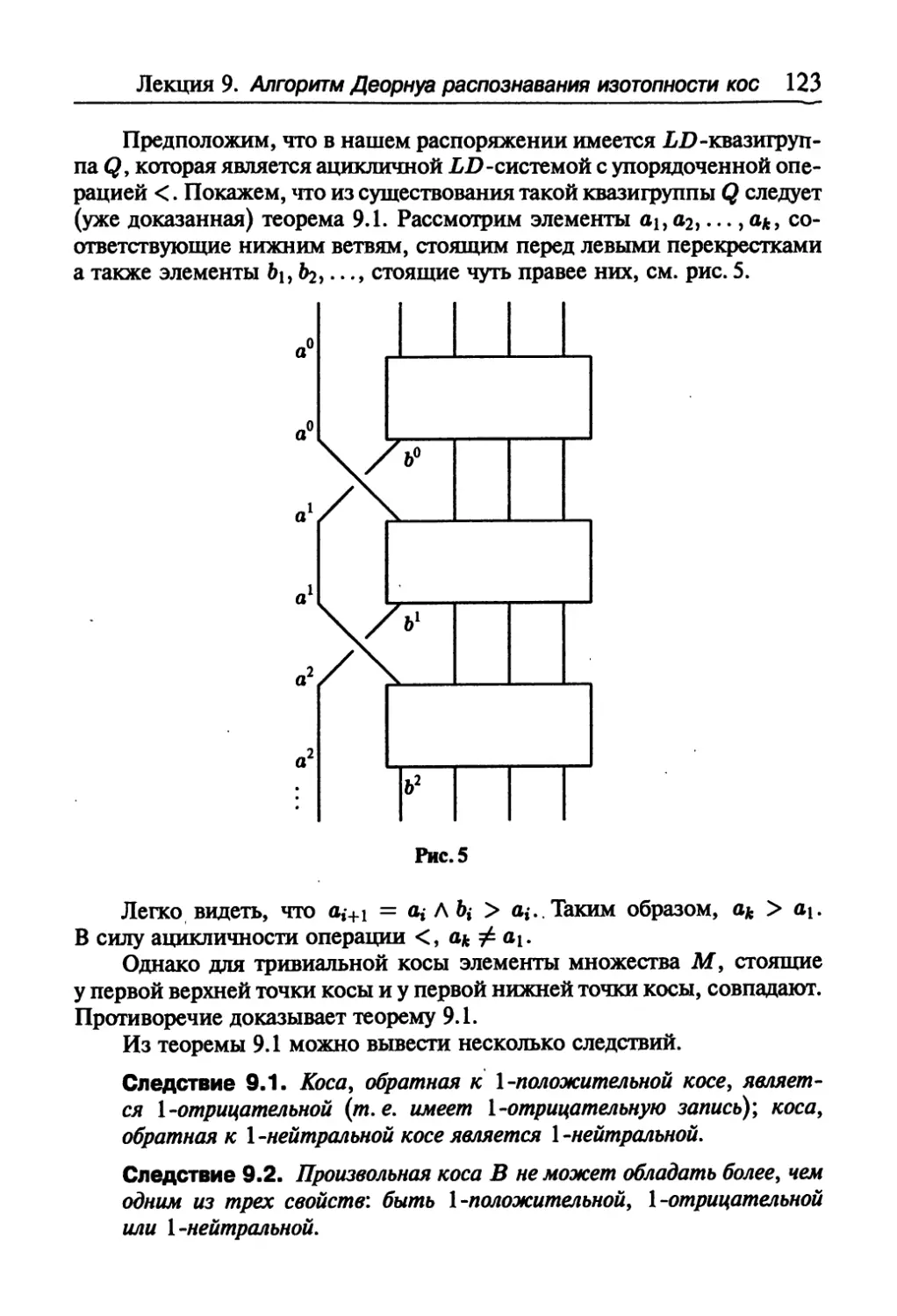
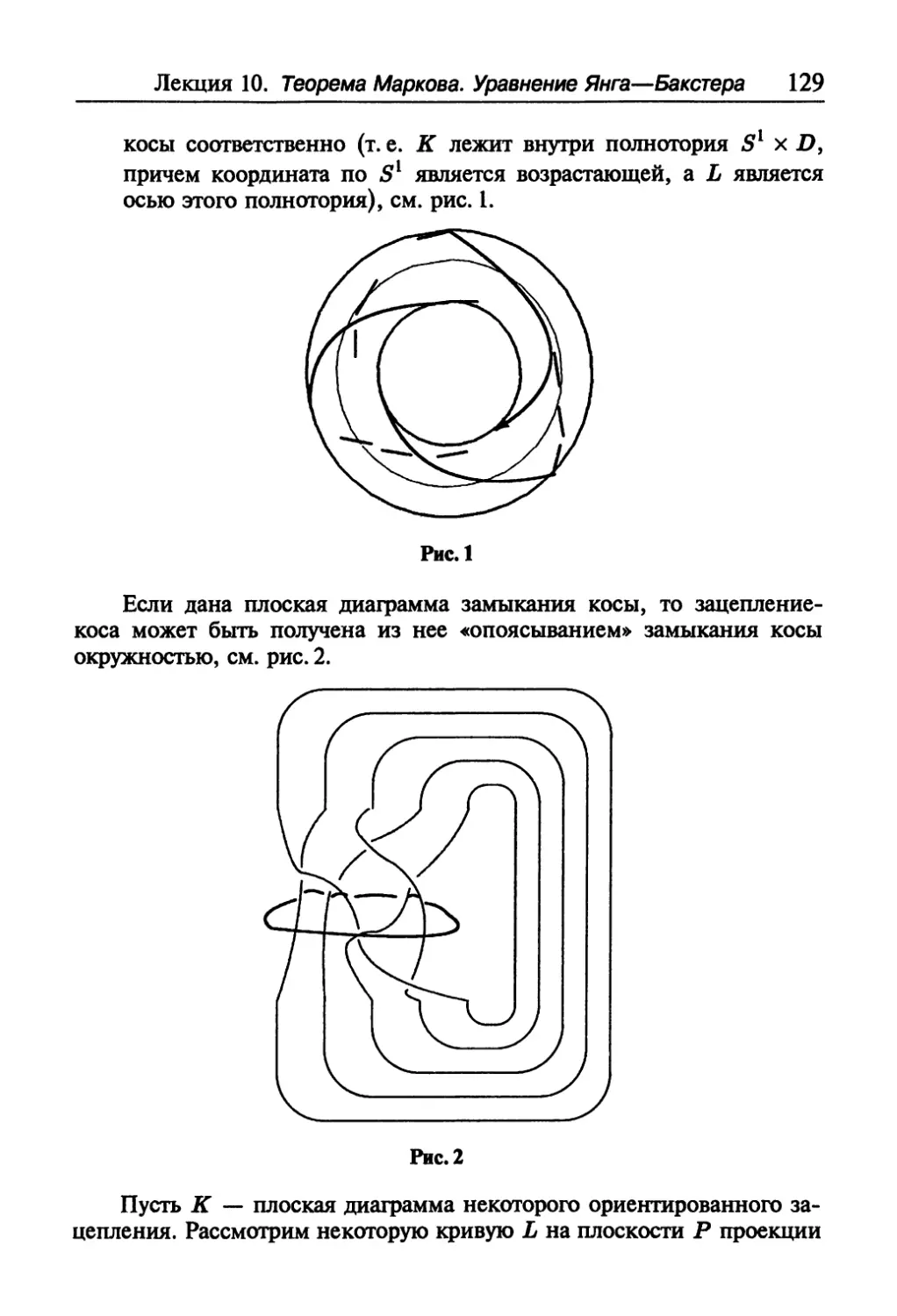
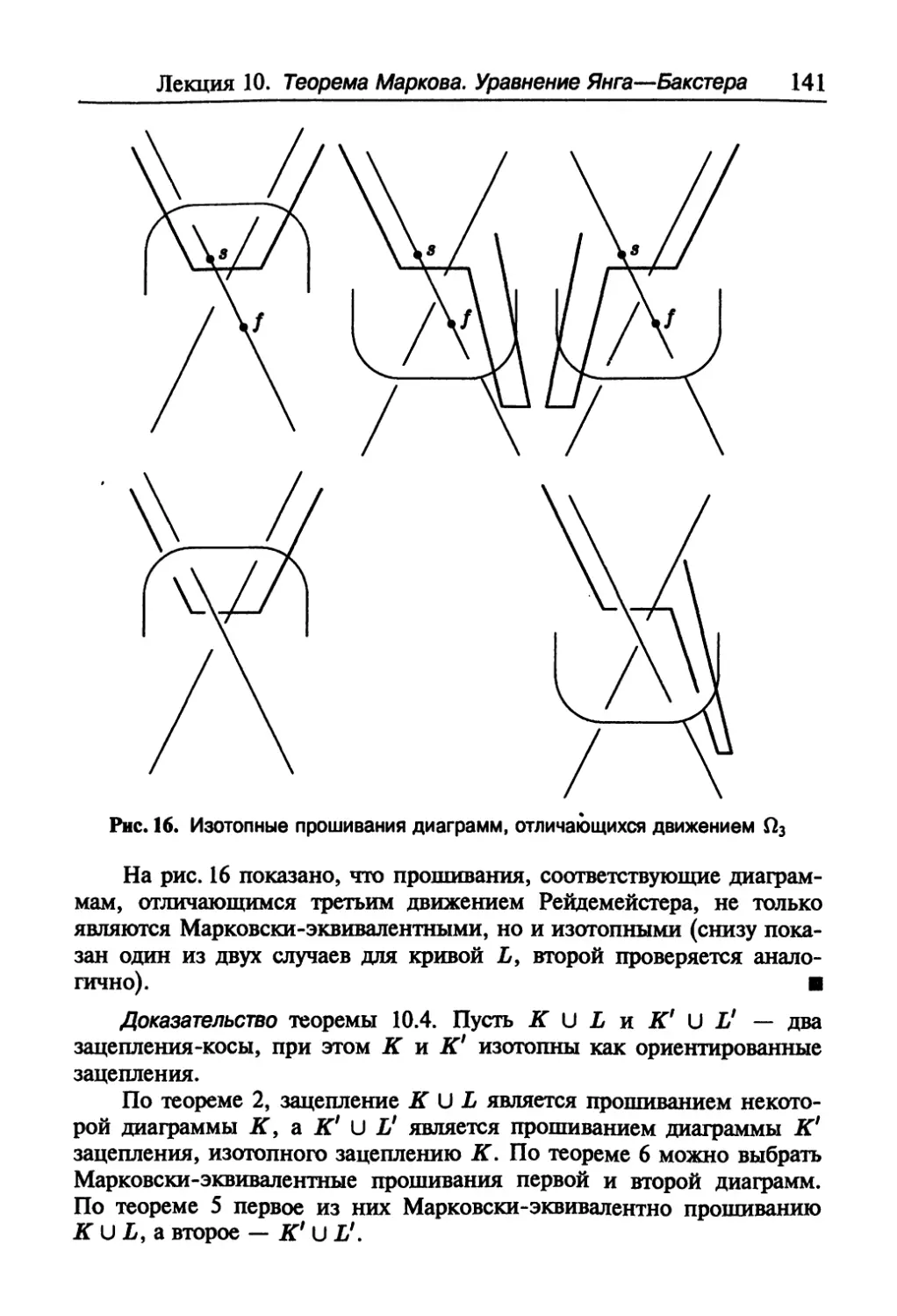
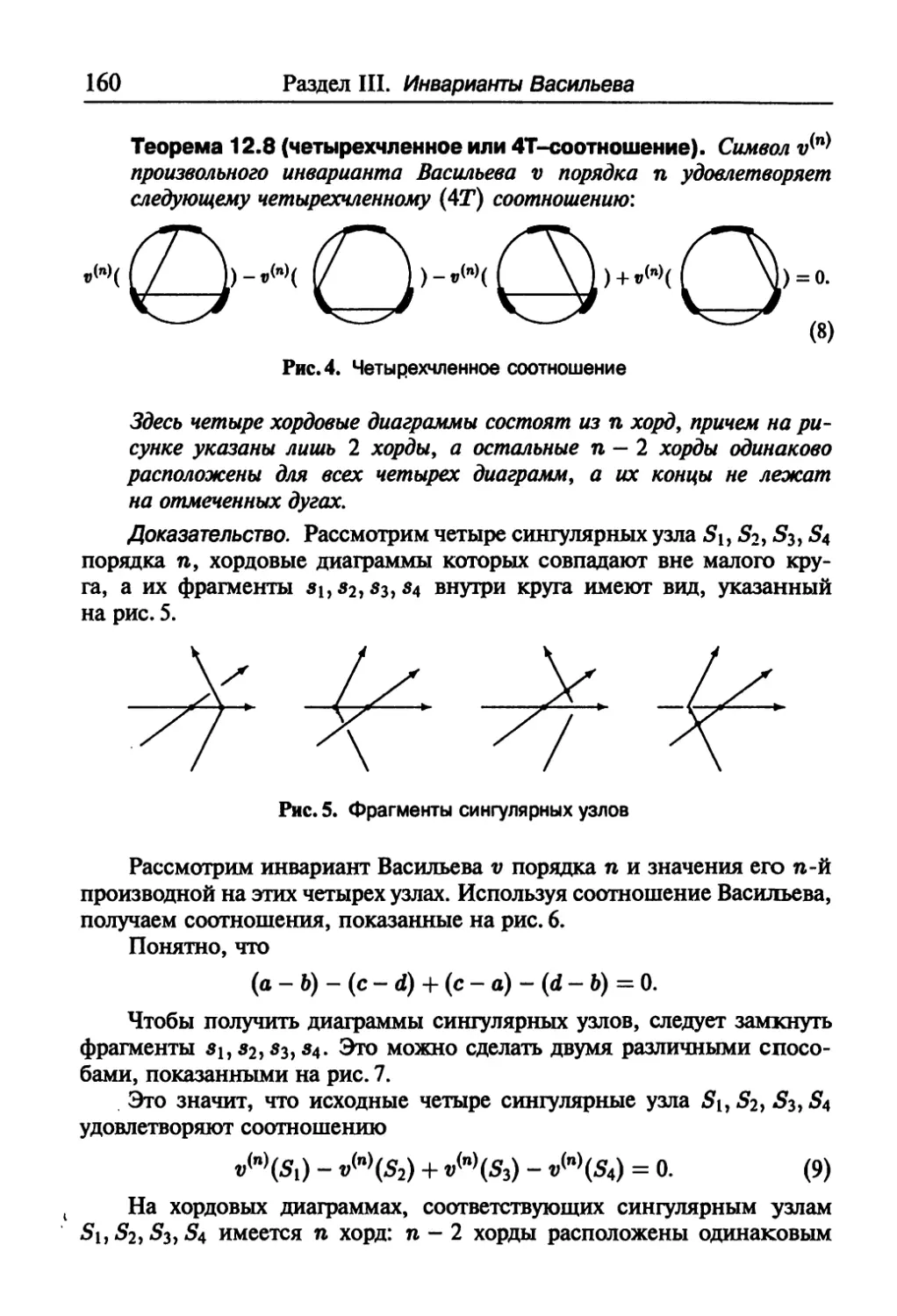
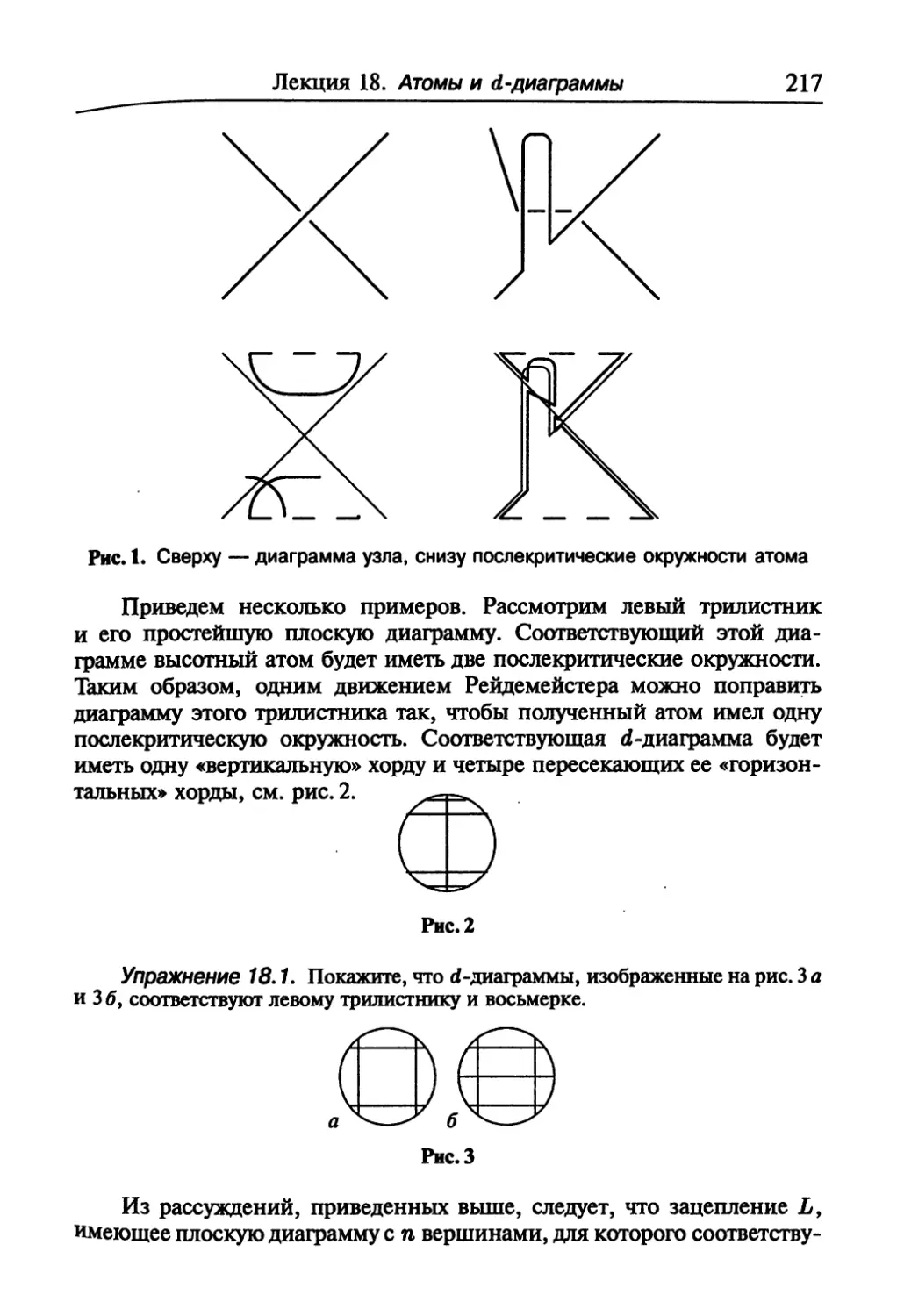
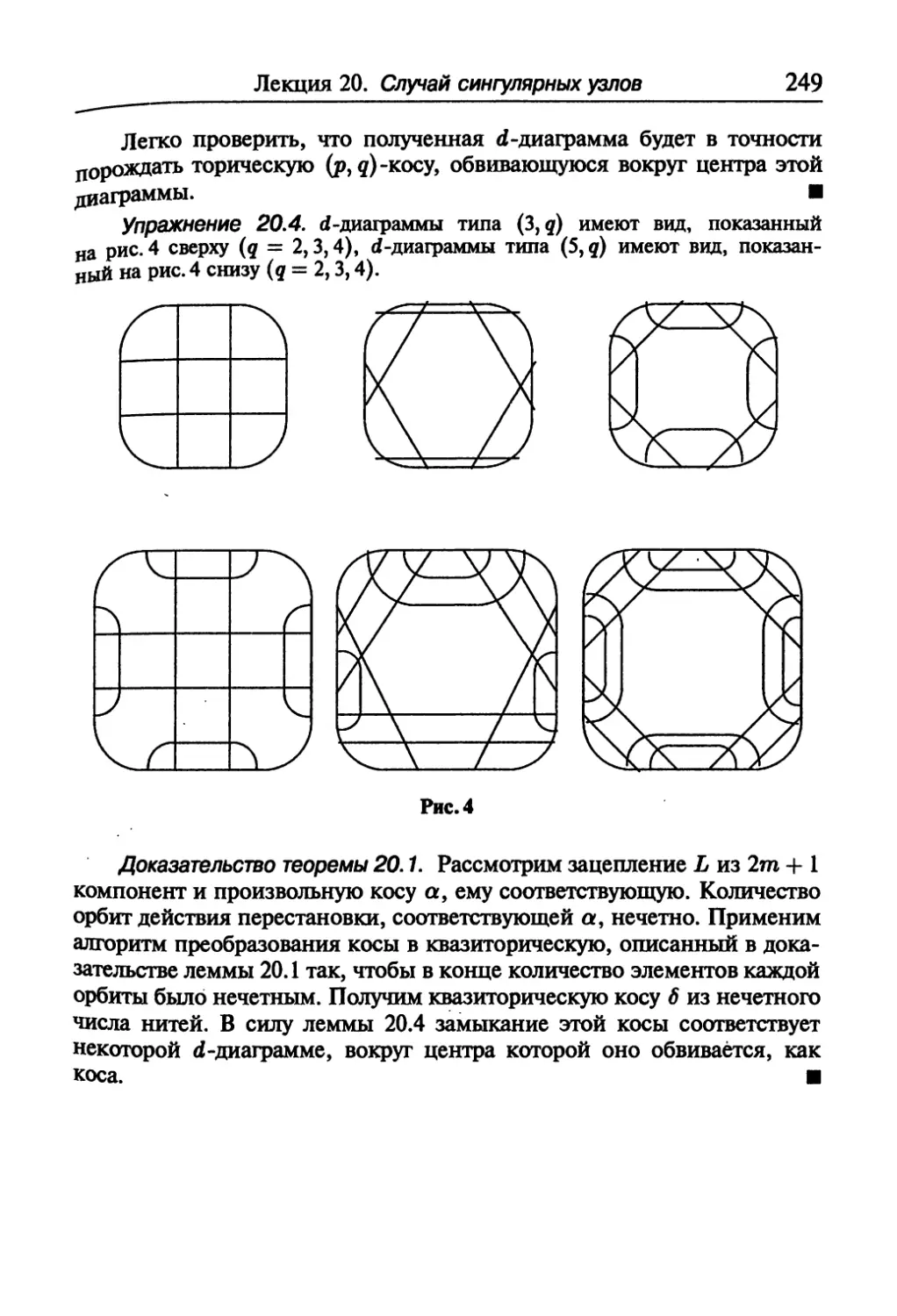
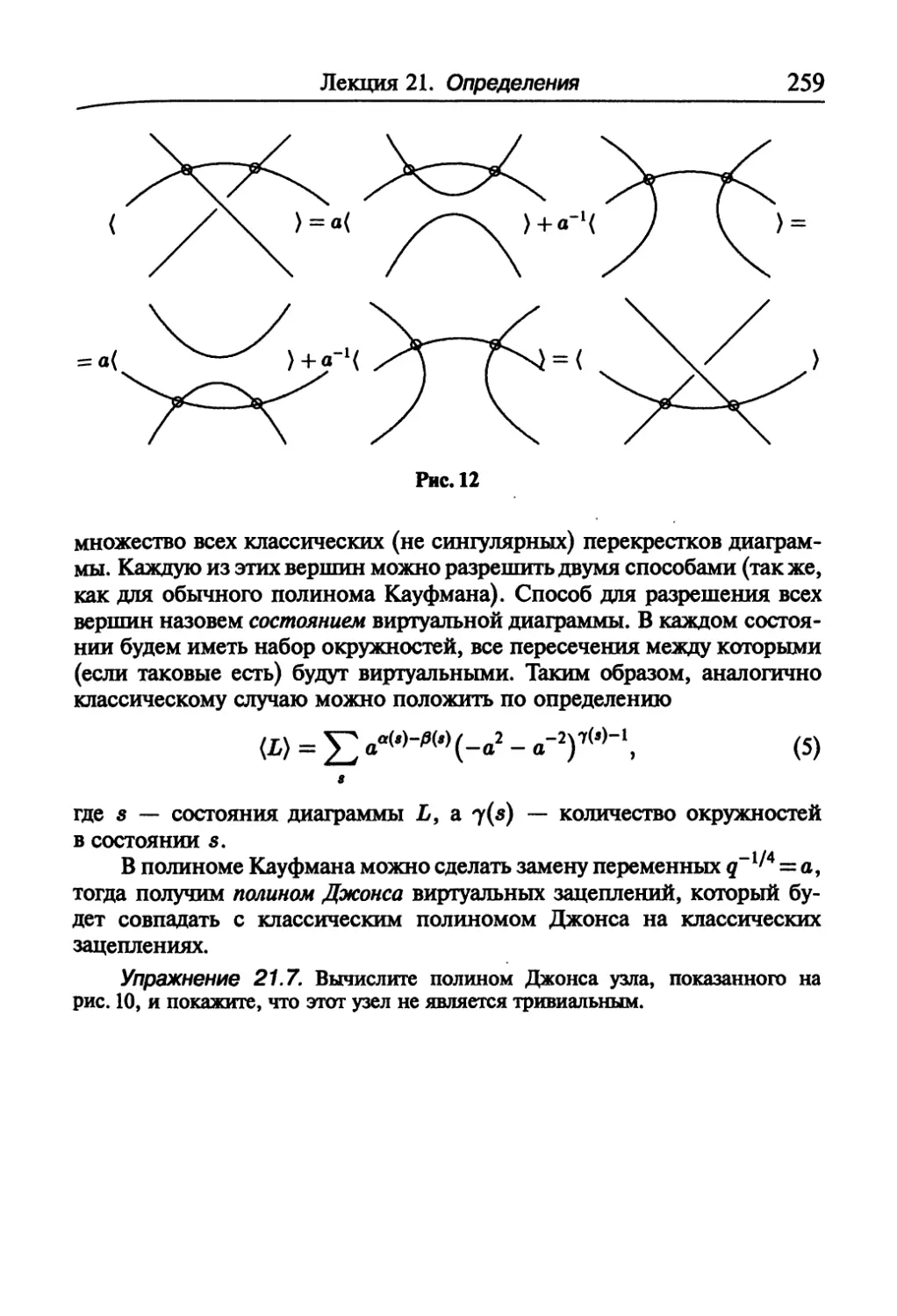
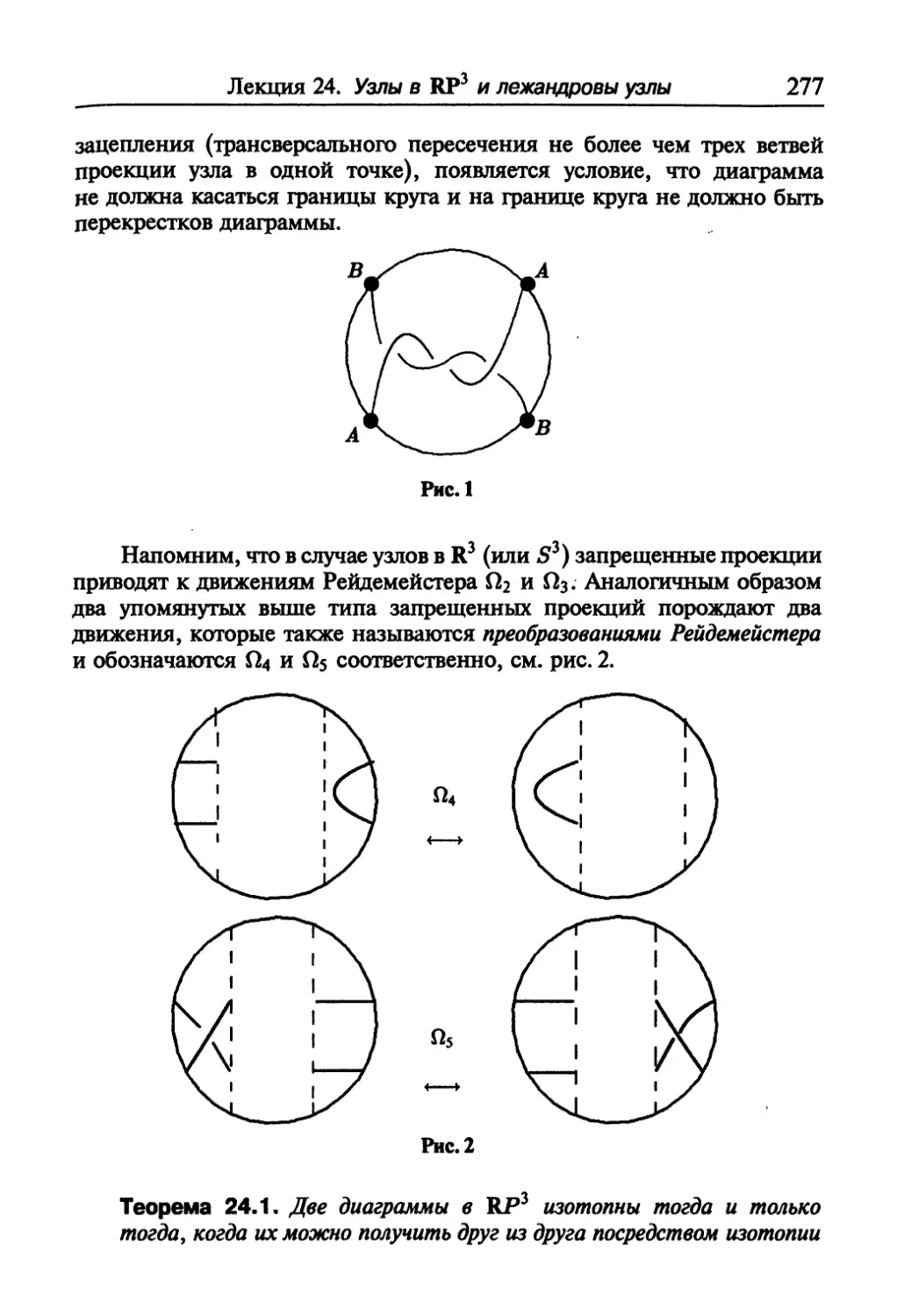
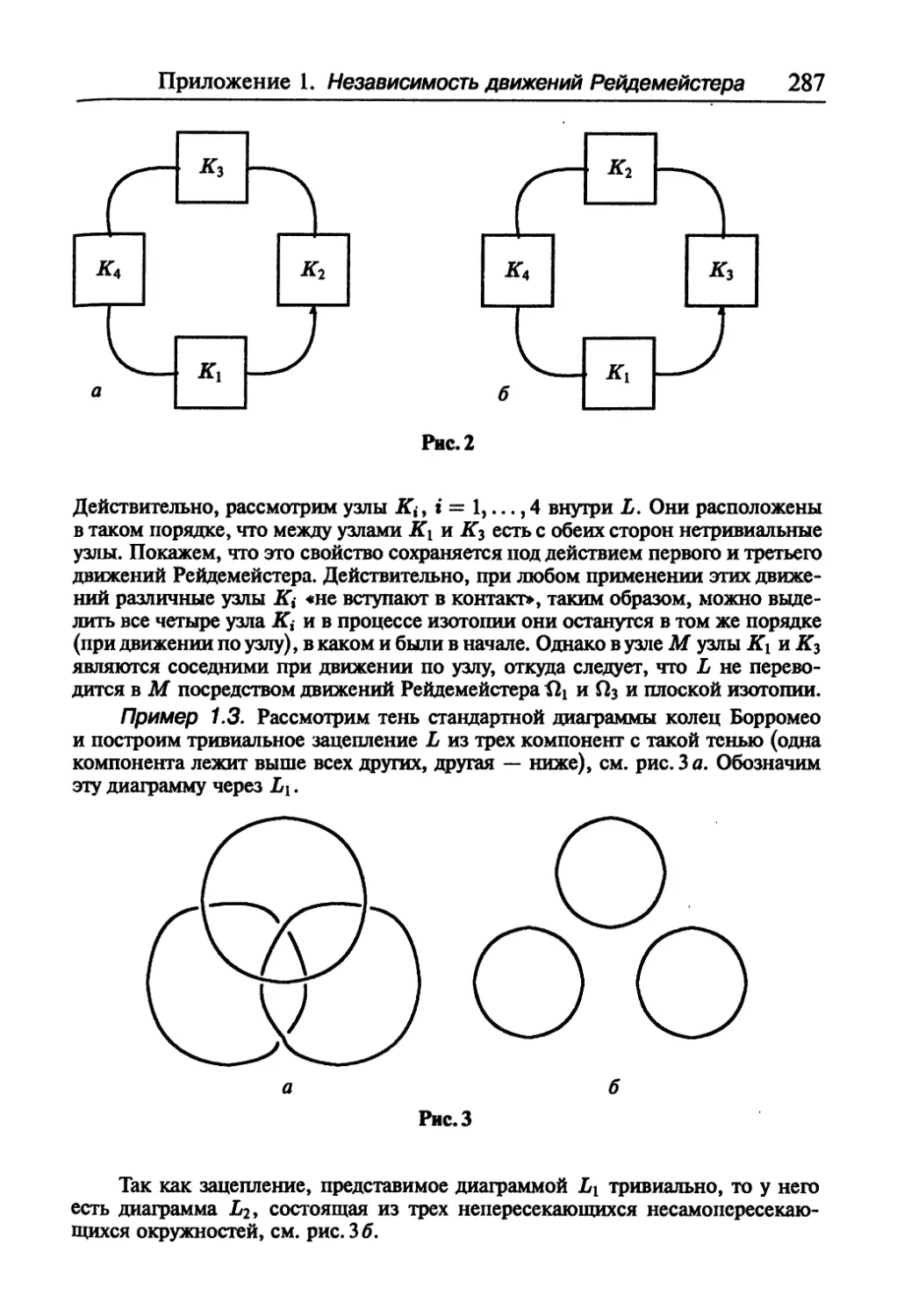
Текст
В.О.Мантуров
Лекции по теории
УЗЛ
и их инвариантов
Москва • 2001
УРСС
ББК 22.147, 22.152
Рецензенты: проф. А. Б. Сосинский и проф. А, В. Чернавский
Мантуров Василий Олегович
Лекции по теории узлов и их инвариантов. — М.: Эдиториал УРСС, 2001.
- 304 с.
ISBN 5-8360-0287-8
В книге изложены как классические результаты теории узлов, так и
знаменитые и замечательные новейшие идеи последних лет,
обуславливающие бурное развитие этой теории (полиномы Джонса, Кауфмана, HOMFLY,
инварианты Васильева, интеграл Концевича, теория Бар-Натана, теория кос,
теорема Маркова, алгоритм Деорнуа, теория виртуальных узлов). Отдельно
изложен авторский подход к разным задачам теории узлов, основанный на
понятии d-диаграммы.
Изложение не предполагает у читателя специальных знаний, за
исключением начал элементарной топологии. Книга может служить учебником
для начинающих и руководством для лиц, желающих постичь современный
уровень этого раздела математики, ознакомившись со многими строгими
доказательствами краеугольных теорем.
Группа подготовки издания:
Директор — Доминго Марин Рикой
Заместители директора — Наталья Финогенова, Ирина Макеева
Компьютерный дизайн — Виктор Романов
Главный редактор — Елена Кудряшова
Верстка — Михаил Кириллов
Корректурные работы — Борис Ветухновский
Техническая поддержка — Наталья Аринчева
Менеджер по продажам — Алексей Петяев
Издательство «Эдиториал УРСС». 113208, г. Москва, ул. Чертановская, д. 2/11, к. п.
Лицензия ИД №03216 от 10.11.2000 г. Гигиенический сертификат на выпуск книжной
продукции №77.ФЦ.8.953.П.270.3.99 от 30.03.99 г. Подписано к печати 30.05.2001 г.
Формат 60x84/16. Тираж 400 экз. Печ. л. 19.
Отпечатано в ООО «Истра». 162250, Вологодская обл., г. Харовск, ул. Герцена, 18/1.
Эдиториал УРСС
научная и учебная литература
I Г I Тел./факс: 7(095)135-44-23
Ль Тел./факс: 7(095)135-42-46
n*' I E-mail: urss@urss.ru
I J I Каталог изданий в Internet: http://urss.ni
ISBN 5-8360-0287-8
€> Эдиториал УРСС, 2001
Vous etes tous les deux tenebreux et discrets:
Homme, nul n'a sonde le fond de tes abimes,
О mer, nul ne connait tes richesses intimes,
Tant vous etes jaloux de garder vos secrets!
Charles Baudelaire,
«L'homme et la mer»
Предисловие
Теория узлов занимает в современной математике видное место,
причем самые яркие результаты в этой области были получены за
последние два десятилетия. За исследования именно в этой области,
за последние 11 лет, работы Джонса, Уиттена, Дринфельда и
Концевича были оценены высшей наградой для математиков — филдсовскими
медалями.
Целью книги является доступное для начинающих математиков
достаточно полное описание современного состояния теории узлов и кос
с полными доказательствами в таких разделах теории узлов и кос, как
полиномиальные инварианты узлов (в том числе знаменитый полином
Джонса), инварианты Васильева, интеграл Концевича, теорема
Маркова, алгоритм Деорнуа. Мы приводим также точное представление
группы кос, полученное в 1999-2000 годах в [58, 59, 8].
В книге много внимания уделяется новой теории кодирования
узлов с помощью так называемых d-диаграмм, описанной в работах
автора [105, 106, 107], а также теории виртуальных узлов,
изобретенной недавно Кауфманом [51] и бурно развивающейся в настоящее
время. В доказательствах по мере надобности используются сведения
из других — как правило, очень красивых, -— математических
теорий: мультипликативного интеграла, теории связностей, алгебр Хопфа,
LD -систем и др. Содержание книги не покрывается существующими
монографиями и учебниками по теории узлов.
Книга поделена на тематические части, первая из которых
представляет собой описание теории узлов до изобретения инвариантов
Васильева, вторая — теорию кос, третья — теорию инвариантов
Васильева, включая знаменитую конструкцию Концевича, позволяющую
представить все инварианты Васильева в виде замечательного
(мультипликативного) интеграла, четвертая — теорию d-диаграмм, ^пятая —
теорию виртуальных узлов и последняя, состоящая из одной лекции,
содержит основные конструкции двух симпатичных теорий — лежан-
дровых узлов и узлов в трехмерном проективном пространстве.
Изложение математического материала достаточно замкнуто; книга
вполне доступна студентам-математикам, начиная с младших курсов.
6
Предисловие
Настоящая книга представляет собой запись курса лекций
«Введение в теорию узлов и их инвариантов», прочитанного для студентов,
аспирантов и преподавателей механико-математического факультета
Московского государственного университета в 1999-2000 учебном году
и читаемого в 2000-2001 учебном году. Вся книга разбита на лекции —
от нулевой до двадцать четвертой в точном соответствии с тем, как они
были прочитаны.
Некоторые лекции были также прочитаны и в Институте
теоретической и экспериментальной физики, Москва, июль-август 2000.
Важную роль в написании настоящей книги сыграл семинар
«Узлы и теория представлений», который, начиная с февраля 2000 года,
автор ведет совместно с В. В. Трофимовым на
механико-математическом факультете МГУ, и на котором обсуждались актуальные задачи
современной теории узлов.
Выражаю благодарность моему отцу О. В. Мантурову и моему
научному руководителю академику А. Т. Фоменко за постоянное внимание
к моим работам, за ряд ценных замечаний и постоянную поддержку,
оказанную мне в работе над книгой.
Я благодарю своих рецензентов, А. Б. Сосинского и А. В. Чернав-
ского, способствовавших существенному улучшению текста книги.
За время написания книги для меня были полезны
обсуждения и переписка с В. А. Васильевым, В. В. Трофимовым, П. Деорнуа,
В. В. Вершининым, Дж. Бирман, X. Цишангом, В. П. Лексиным,
которым я также рад выразить благодарность.
Наконец, я благодарю своих слушателей, особенно А. В. Щепе-
тилова, за ряд важных и существенных замечаний, которые помогли
мне серьезно улучшить текст, а также И. М. Никонова, П. С.
Попова, В.В.Серегина, Е.В.Теплякова, А.С.Копылова, А.А.Гайфуллина,
М. Б. Скопенкова.
В. О. Мантуров
март 2001
Раздел I
УЗЛЫ,ЗАЦЕПЛЕНИЯ
И ПОЛИНОМИАЛЬНЫЕ ИНВАРИАНТЫ
Лекция О
Введение.
Основные определения
Теория узлов, которой посвящен настоящий спецкурс, возникла
как математическая теория в конце 18 - начале 19 века; Hai
протяжении более сотни лет ей занимались такие выдающиеся математики,
как А. Т. Вандермонд, К.-Ф. Гаусс (нашедший замечательную
электромагнитную формулу для вычисления коэффициента зацепления [37]),
Ф. Клейн, а позже — М. Ден [28]. Ее систематическое изложение
началось с восьмидесятых годов 19 века, когда математики и физики начали
составлять таблицы узлов под влиянием идей физика У. Томпсона
(впоследствии известного как лорд Кельвин), полагавшего, что
узлы должны соответствовать химическим элементам. Однако настоящие
прорывы в теории узлов начались во второй половине 20 века и связаны
в первую очередь с именами Дж. X. Конвея, В. Джонса и В. А. Васильева,
а позднее — М, Л. Концевича, В. Г. Тураева, М. Н. Гусарова.
Теория узлов происходит из красивой и на первый взгляд очень
простой топологической задачи, для решения которой, как оказалось,
требуется весьма сложный и глубокий математический аппарат,
связанный с топологией, теорией дискриминантов, теорией групп и алгебр
Ли, теорией мультипликативного интеграла, тензорной алгеброй, и др.
При этом узловая тематика является бурно развивающейся; за
последние годы важные работы в теории узлов (Джонс, Уиттен, Дринфельд
в 1990, Концевич в 1998) были оценены Филдсовскими медалями.
Кроме того, теория узлов служит для построения других теорий,
ярким примером которых является исчисление Кирби — теория
кодирования трехмерных многообразий.
Итак, начнем с определения узла. Под узлом будем понимать
непрерывное вложение окружности S1 в пространство R3 (или в
сферу 53). Наглядно узел можно представить в виде веревки с сомкнутыми
8 Раздел I. Узлы, зацепления и полиномиальные инварианты
концами. Мы можем деформировать пространство R
(соответственно 53), при этом узел будет двигаться и растягиваться (но не рваться!)
и оставаться несамопересекающимся. Более строго, два узла называются
изотопными, если один из них можно перевести в другой гладким
гомеоморфизмом объемлющего пространства R3 или 53 на себя, гомотопным
тождественному отображению в классе гладких гомеоморфизмов. При
этом хотелось бы знать, какие узлы изотопны, а какие не изотопны.
Такая задача называется задачей распознавания узлов. Можно говорить
об изотопических классах узлов. Можно также говорить об инвариантах
узлов, т. е. функциях на изотопических классах узлов, или функциях
на узлах, не меняющихся при изотопиях узлов.
Частным случаем задачи распознавания узлов является задача
распознавания тривиального узла, являющегося самым простым узлом
(узлом, представляющим границу диска, вложенного в трехмерное
пространство).
Оба эти вопроса, на первый взгляд очень простые, являются очень
трудными. На самом деле к данному моменту эти задачи уже решены,
но их решение составляет огромную книгу [41], является
алгоритмически сложным и очень трудно читается. С основными этапами решения
этой проблемы можно познакомиться в статье [116].
В данном курсе мы постараемся частично ответить на вопрос
об изотопности и неизотопности узлов. Как правило, чтобы
установить изотопность узлов, нужно перевести один узел в другой с
помощью некоторых преобразований (например, движений Рейдемейстера,
о которых будет сказано позже), а для установления неизотопности
достаточно найти инвариант, различающий эти узлы.
Обычно узлы изображаются следующим образом. Пусть дан узел,
т. е. задано отображение / : S1 —► R3. Рассмотрим некоторую плоскость
h Е R3 и проекцию узла (строго говоря, проекцию образа функции /)
на Данную плоскость. В случае плоскости общего положения, т. е. «почти
всегда», эта проекция будет представлять собой вложенный в плоскость
граф с вершинами кратности четыре. При этом в каждой вершине
графа (которую также можно назвать перекрестком) пересекаются образы
проекций разных дуг («кусочков») узла, и, если мы зададим
направление х, перпендикулярное h, то для каждой такой вершины можно будет
сказать, какая дуга проходит выше, а какая — ниже (чья координата х
больше, а чья — меньше). Отметим это на плоскости так, как показано
на рис. 1.
Такие типы символического изображения дуг узлов
называются соответственно переходами и проходами, а такой граф с
проходами и переходами называется плоской диаграммой узла. Соответственно
Лекция 0. Введение. Основные определения 9
четырехвалентный граф без указания проходов и переходов называется
тенью узла.
Рис.1
Минимальное количество перекрестков плоской диаграммы для
данного изотопического класса узла называется сложностью узла.
Итак, каждый узел допускает некоторую плоскую диаграмму с
проходами и переходами. При этом возникает естественный вопрос:
а не потеряли ли мы какую-нибудь информацию об узле, кодируя
его таким образом.
Легко можно проделать следующее
Упражнение 0.1. Узлы, имеющие в качестве плоских диаграмм
изоморфные графы с одинаковым образом расставленными проходами и переходами,
изотопны.
Приведем несколько примеров.
Пример 0.1.
Т,00<±э
Рис.2
Узел, изотопный узлу, имеющему диаграмму без пересечений (рис. 2 л),
называется тривиальным узлом. На рис. 2 б изображена другая плоская
диаграмма тривиального узла. Узел на рис. 2 в называется трилистником, а узел
на рис. 2 г называется восьмеркой. Оба эти узла — нетривиальные, при этом они
не изотопны друг другу.
Для каждого узла можно построить его зеркальное отражение —
узел, получаемый отражением данного относительно какой-либо
плоскости. Диаграммы зеркального отражения узла получаются заменой
на диаграммах исходного всех типов перекрестков (проходов на
Переходы и наоборот). Узел называется зеркальным, если он изотопен своему
зеркальному отражению.
Пример 0.2. Трилистник не является зеркальным узлом (доказательство
будет приведено позже).
10 Раздел I. Узлы, зацепления и полиномиальные инварианты
Таким образом, можно говорить о двух трилистниках — правом
и левом.
tfb rfb
Левый трилистник Правый трилистник
Рис.3
Упражнение 0.2. Показать, что восьмерка является зеркальным узлом.
Во многих задачах теории узлов рассматривают ориентированные
узлы — углы, на которых задано направление обхода, или же
отображения ориентированной окружности в R3. При этом при изотопии узлов
требуется условие сохранения ориентации.
Параллельно с теорией узлов развивалась также и теория
зацеплений, имеющая много общего в подходах с теорией узлов. Под
зацеплением будем понимать достаточно гладкое вложение нескольких
окружностей в R3, при этом требуя, чтобы образы разных точек как
одной, так и разных окружностей не совпадали. Каждый узел,
представляющий собой отображение в R3 одной из окружностей, называется
компонентой зацепления. Естественным образом определяется изотопия
зацеплений (с помощью гладкого гомеоморфизма объемлющего
пространства), плоские диаграммы зацеплений и инварианты зацеплений. При
этом для задания ориентированного зацепления нужно ориентировать все
его компоненты. Есть и другой подход к изотопии зацеплений, в
котором в процессе «изотопии» каждой компоненте зацепления
позволяется самопересекаться, но различным компонентам пересекаться нельзя.
Об этом можно прочесть в замечательной статье [68] Джона Милнора,
который ввел так называемые ^-инварианты для классификации
зацеплений с точностью до такой «изотопии». Тривиальным зацеплением из п
компонент называется зацепление, изотопное зацеплению, диаграмма
которого представляет собой п окружностей (без перекрестков).
Пример 0.3.
На рис. 4 а изображено тривиальное зацепление из двух компонент.
На рис. 46, в, г изображены зацепления, называемые зацеплением Хопфа,
зацеплением Уайтхеда и кольцами Борромео соответственно. Первые два зацепления
названы так в честь топологов X. Хопфа и Дж. Уайтхеда, а третье — в честь
итальянского рода Борромео, на гербе которого оно было изображено. Все
они — нетривиальные (это будет показано ниже, когда мы научимся считать
значения инвариантов, различающих узлы или зацепления), при этом нетрудно
заметить, что каждые две окружности из трех между собой «незацеплены».
Лекция 0. Введение. Основные определения 11
а б в г
Рис.4
Поговорим немного об инвариантах. Самым первым и самым
простым инвариантом узлов и зацеплений являлась фундаментальная
группа дополнения к узлу (зацеплению), которой будет посвящена
отдельная лекция. Этот инвариант является чисто топологическим, при этом
он очень сильный, т. е. хорошо различает узлы (в частности,
тривиальный узел и тривиальное зацепление из любого числа компонент),
но не различает некоторые неизотопные зацепления. При этом такое
«решение» проблемы распознавания узлов не является полным, так как
оно сводится к, вообще говоря, нерешаемой проблеме распознавания
групп, заданных с помощью образующих и соотношений.
В 1923 году американский математик Александер в своих работах
[2,3] ввел полиномиальный инвариант узлов и зацеплений, основанный
на фундаментальной группе дополнения к узлу.
Затем в 1932 году вышла в свет книга немецкого тополога
Рейдемейстера «Knotentheorie», в которой описывался инвариант
Александера, был приведен список движений Рейдемейстера и доказана
теорема о том, что любые две плоские диаграммы дают изотопные
узлы только в случае существования цепочки движений от одной
диаграммы к другой, а также приведена таблица изотопических классов
узлов сложности до семи включительно. Существует также английский
перевод этой книги [79]. Для доказательства инвариантности той или
иной функции на узлах, как правило, проверяют ее инвариантность
относительно движений Рейдемейстера.
Из книг, содержащих сведения об узлах «тех времен», отмечу
книги Кроуэлла и Фокса (на русском языке) [104], а также Бурде
и Цишанга [19].
Обзоры по маломерной топологии и теории узлов можно найти
в [130, 129].
Следующим этапом в теории узлов и зацеплений было
открытие полинома Конвея, см. [25], основанное на так называемых skein
relations, или соотношениях типа Конвея, при этом являющееся
комбинаторным, основанным на понятии плоской диаграммы узла. Полином
Александера мог быть также интерпретирован в соотношениях типа
Конвея, мало того, Александер (см. [2]) знал о соотношениях «типа
12 Раздел I. Узлы, зацепления и полиномиальные инварианты
Конвея», но лишь Конвей обнаружил, что skein-relations могут быть
использованы в качестве аксиоматического подхода.
Основным прорывом было изобретение полинома Джонса,
основанного на соотношениях типа Конвея. С помощью полинома Джонса
были решены некоторые важные проблемы в теории узлов, например
проблема Тейта, см. [80].
Позже появлялись другие полиномы, основанные на соотношениях
типа Конвея: Кауфмана, HOMFLYh др. При этом HOMFLY — не есть
фамилия одного автора, это — аббревиатура от первых букв фамилий
авторов Hoste, Ocneanu, Millett, Freyd, Lickorish и Yetter, см. [42].
Самым сильным из этих полиномов является полином Джонса
от двух переменных, так как каждый из оставшихся получается из него
некоторой заменой переменных, при этом полином Джонса различает
любые два узла, различаемые каким-либо из вышеперечисленных
полиномов. Существует также и полином Джонса от одной переменной,
см. [44, 45].
Задание узлов с помощью плоских диаграмм — не единственная
возможность. Рядом с теорией узлов стоит другая важная теория —
теория кос. Существуют четыре классических определения группы кос.
Косы связаны с такими красивыми алгебраическими объектами, как
полиномы комплексного переменного без кратных корней. Под косой
из п нитей понимают набор из п попарно непересекающихся
восходящих кривых, соединяющих точки А\,...,АП на одной прямой
с точками Bi,...,Sn на параллельной ей прямой. Аналогично
диаграммам узлов задаются диаграммы кос, при этом эквивалентность кос
определяется как такая изотопия, в каждый момент которой дуги
должны быть восходящими. Произведение кос а и Ь получается с помощью
пристраивания нижних вершин косы а к верхним вершинам косы Ь.
ш
Рис. 5. Замыкание косы
Легко видеть, что замыкая косу, т.е. соединяя самым простым
образом Ai с В{} i = 1,..., п, как это показано на рис. 5, мы получим
диаграмму узла или зацепления.
Лекция 0. Введение. Основные определения 13
В книге описываются три важные теоремы, связанные с косами.
Теорема Александера (см., например, [123]) утверждает, что каждый
изотопический класс узла или зацепления может быть получен
замыканием косы, теорема Артина (см. [5]) о представлении групп кос
с помощью образующих и соотношений и теорема Маркова [66] о
движениях кос, оставляющих без изменения изотопический класс узла.
На теореме Маркова основан и алгоритм Деорнуа, распознающий изо-
топность кос; этому алгоритму будет посвящена отдельная лекция. При
этом выгодное отличие теории кос заключается в том, что она —
алгебраическая, т. е. каждый узел может быть записан в виде слова (вообще
говоря, в бесконечном алфавите).
Из литературы, охватывающей все описанное выше, я рекомендую
две книги Луиса Кауфмана [47, 48], а также книги Дж. Адамса [1],
А. Каваучи [52] и (на русском языке) [94].
Предположим, что у нас есть узел и мы хотим изменить его
изотопический класс, гладко изменяя отображение окружности в R3. Без
пересечения этого сделать нельзя, поэтому самым важным является
момент пересечения. Если при таком отображении пересечение ровно
одно, в нем участвуют ровно две ветви узла и пересекаются трансвер-
сально, то такое отображение окружности в R3 называется сингулярным
узлом. Пространство сингулярных узлов называется дискриминантным
пространством.
Изучая свойства дискриминантов, В. А. Васильев ввел понятие
инвариантов конечного порядка, впоследствии получившее название
инвариантов Васильева. Изначально инварианты Васильева требовали
большого неэлементарного математического аппарата, однако
впоследствии была найдена их простая комбинаторная интерпретация, о
которой будет рассказано позднее. Далее будет также доказано, что
инварианты Васильева сильнее всех вышеперечисленных полиномиальных
инвариантов.
Изначально доказательство существования инвариантов Васильева
появилось в работе [85]; структура этих инвариантов (только для узлов)
была получена М. Л. Концевичем с помощью замечательной
конструкции знаменитого интеграла, носящего его имя. В первых версиях работы
Концевича (до публикации) была обнаружена ошибка, о чем ему
сообщил Д. Бар-Натан, после чего Концевич свою работу исправил. Эту
работу можно прочесть в [56]. При этом мы предлагаем изучать
конструкцию интеграла Концевича по статье [13]. В [13] изучены алгебры
хордовых и китайских диаграмм, а также их связь с инвариантами
представлений алгебр Ли.
Вычисление интеграла Концевича долгое время было очень
трудным делом до того, как появилась работа Ле и Мураками [63], в которой
14 Раздел I. Узлы, зацепления и полиномиальные инварианты
они, по сути дела, представляют технику такого вычисления. Она,
однако, весьма сложная, и мы ею заниматься не будем.
Есть еще один красивый способ представления всех узлов и
зацеплений, он основан на введенном в [107] понятии d-диаграммы —
окружности с двумя семействами непересекающихся хорд, ^-диаграммам
посвящена четвертая глава настоящей книги. Эта теория происходит
из теории атомов и гамильтоновых систем и позволяет построить
скобочную полугруппу узлов, описав, тем самым, все узлы и зацепления
в виде слов в конечном алфавите из четырех букв, см. [107]. В этом
состоит превосходство кодирования с помощью d-диаграмм, например,
над кодированием с помощью кос, требующим бесконечный набор
букв. Кроме того, этот способ просто и красиво обобщается на случай
сингулярных узлов, что позволяет дать описание инвариантов Васильева
в виде слов в конечном алфавите.
С помощью d-диаграмм все узлы и зацепления представляются
в виде петель на клетчатой бумаге, исходящих из начала координат
и лежащих внутри первого квадранта.
Пример 0.4.
L L L L L L L L L L L L
'- L L '_ L L L '_ '_ L L '_
i_ i_ i_ i_ i_ i_ i_ i_ i_ i_ i_ i_
i i i i i i i i i i i i
(0,0) (0,0)
Левый трилистник Правый трилистник
Рис.6
Левый трилистник может быть записан как прямоугольник 1x4, правый —
как квадрат 2x2, см. рис. 6.
Вообще, теория атомов, изначально изобретенная для
классификации гамильтоновых систем, оказывается применимой во
многих областях геометрии и топологии, например, для кодирования 3-
многообразий.
Упомяну в конце введенное Луисом Кауфманом в 1996 году
понятие виртуального узла — комбинаторное понятие, основанное на
диаграмме узла. Теория виртуальных узлов может быть интерпретирована
как «проекция» теории узлов в различных трехмерных
многообразиях. Эта теория бурно развивается и имеет много общего в подходах
с классической теорией узлов.
Лекция 1
Движения Рейдемейстера.
Арифметика узлов
В данной лекции речь пойдет об узлах, их плоских
диаграммах и движениях Рейдемейстера, а также о полугрупповой
структуре на множестве узлов, которая изоморфна полугрупповой структуре
на полугруппе натуральных чисел по умножению. Такое сходство
структур на множестве узлов и множестве натуральных чисел дает основания
говорить об арифметике узлов. Будет также дано много примеров.
Хотя сопутствующий материал по геометрии и топологии будет
рассказан и в рамках настоящего спецкурса, слушателям предлагается
ознакомиться с основными определениями, например, в [126]. С
некоторыми наглядными топологическими конструкциями читатель может
ознакомиться в [122].
§ 1. Полигональные узлы и движения Рейдемейстера
Так как узел представляет собой гладкое вложение окружности
в R3, его можно как угодно близко аппроксимировать (приблизить)
вложением замкнутой ломаной в R3, не выходя из его изотопического
класса.
Определение 1.1. Вложение замкнутой ломаной в R3 называется
полигональным (многоугольным) узлом.
Определение 1.2. Узел (зацепление) называется ручным, если он
изотопен полигональному узлу (зацеплению); в противном случае
узел (зацепление) называется диким.
Замечание 1.1. Различие между ручными и дикими узлами имеет
первостепенную важность. Почти все утверждения настоящей книги применимы
только к ручным узлам. Все С1 -гладкие узлы являются ручными,
доказательство см. в [104]. В дальнейшем мы будем предполагать все узлы гладкими и,
следовательно, ручными, если не оговорено противное.
Упражнение 1.1. Определите аккуратно полигональное зацепление.
Определение 1.3. Скажем, что два полигональных узла
(зацепления) изотопны, если одно из них может быть переведено в другое
16 Раздел I. Узлы, зацепления и полиномиальные инварианты
многократной композицией так называемой элементарной
изотопии, которая состоит в замене звена замкнутой ломаной АВ на два
звена АС и ВС при условии, что треугольник ABC не пересекает
других звеньев замкнутой ломаной данного узла, а также обратного
к элементарной изотопии преобразования, см. рис. 1.
Для полигональных узлов, как и для гладких, можно
рассматривать плоские диаграммы с проходами и переходами, при этом по графу
с проходами и переходами можно восстановить полигональный узел
с точностью до изотопии; в частности, при достаточно хорошей
аппроксимации гладкого узла полигональным плоская диаграмма будет
иметь такую же комбинаторную структуру.
Упражнение 1.2. Покажите, что все полигональные узлы с числом
звеньев, меньшим шести, тривиальны.
Упражнение 1.3. Приведите пример полигонального трилистника с
шестью звеньями.
Определение 1.4. Назовем плоской изотопией плоской
диаграммы гладкого узла (зацепления) гомеоморфизм плоскости на себя,
не меняющий комбинаторной структуры 2-комплекса,
получаемого делением плоскости графом проекции узла на клетки и
сохраняющий структуру проходов и переходов в вершинах проекции.
Замечание 1.2. Аналогично определяемая плоская изотопия полигонального
узла не должна быть чувствительна к двухвалентным вершинам; так, разбивая
ребро на два дополнительной вершиной, мы получаем диаграмму, являющуюся
плоско-изотопной исходной.
Замечание 1.3. Плоская изотопия не меняет изотопического класса узла
в пространстве R3.
Теорема 1.1 (Рейдемейстер, [79]). Две плоские диаграммы D\ и Di
гладких узлов (зацеплении) порождают изотопные узлы (зацепления)
тогда и только тогда, когда D{ переводится в Di с помощью
последовательного применения плоской изотопии и трех движений
Рейдемейстера Пь ^ ^з> см.рис.2.
Лекция 1. Движения Рейдемейстера. Арифметика узлов 17
XL
\„/ \ / \ / W
Рис.2. Движения Рейдемейстера
Одно из доказательств этой теоремы основано на понятии
коразмерности; здесь мы приведем другое доказательство, основанное
на применении полигональных узлов (зацеплений).
Доказательство. В одну сторону доказательство очевидно. Для этого
достаточно лишь проверить, что все движения Пх,£12,&з не меняют
изотопического класса узла.
Докажем утверждение теоремы в обратную сторону. Итак, пусть
два изотопных узла К\ и Кг заданы своими плоскими
диаграммами D\ и 2>2 с проходами и переходами. Тогда существует непрерывная
изотопия узла К\ в узел Ki в пространстве R3. Аппроксимируем эти
узлы полигональными узлами К[ и К'2 и рассмотрим изотопию от К[
к К'2, состоящую из элементарных изотопии [АВ] —> [j4C]U[C.B].
Без Ьграничения общности будем считать, что на каждом шаге для
соответствующего треугольника ABC звенья [DA] и [BE], выходящие
из концов отрезка [АВ], не пересекают внутренности
треугольника ABC. В противном случае этого легко можно добиться с помощью
движения £1\.
Легко видеть, что компоненты пересечения проекции треугольника
ABC с Lq, где Хо — проекция данного зацепления на плоскость ABC,
бывают верхние и нижние, т. е. соответствующие им ветви зацепления L
лежат под (или над) плоскостью ABC.
Разобьем треугольник ABC на мелкие треугольники четырех
типов, стороны которых не содержат вершин проекции Lo (см. рис. 3).
Треугольник первого типа содержит ровно один перекресток Lo, при
этом ветви Lo пересекают ровно две стороны этого треугольника.
Треугольник второго типа содержит ровно одну вершину L0 и части
выходящих из нее звеньев. Треугольник третьего типа содержит часть
ровно одного звена Lo и не содержит вершин. Наконец, треугольник
18 Раздел I. Узлы, зацепления и полиномиальные инварианты
четвертого типа не содержит ни вершин, ни ребер (на рис. 3 он не
изображен).
■•/V
А А
/ \
Первый тип Второй тип
/ У: ГТ '
ш . • • • •
/
Третий тип
Рис.3
Такую триангуляцию треугольника ABC можно построить
следующим образом. Сначала для каждого перекрестка и каждой вершины
строим треугольники первого и второго типов, а затем разрезаем
оставшуюся часть треугольника ABC на треугольники третьего и четвертого
типов.
Теперь вместо исходного элементарного преобразования
треугольника ABC будем совершать элементарные преобразования четырех
типов для маленьких треугольников. На рис. 3 видно, что движение для
треугольника первого типа соответствует комбинации третьего и вторых
движений Рейдемейстера Пз> ДОЯ треугольников второго или
третьего типа — 1^2 или плоской изотопии. Движение для треугольника
четвертого типа представляет собой плоскую изотопию.
Тем самым теорема доказана. ■
Упражнение 1.4. Покажите, что два варианта третьего движения
Рейдемейстера, показанные на рис.2, зависимы, т.е. любое из них выводится
из другого, а также второго движения Рейдемейстера.
При этом все три движения Рейдемейстера fii,ft2>^3 являются
независимыми друг от друга. Их независимость будет показана в
приложении 1.
Лекция 1. Движения Рейдемейстера. Арифметика узлов 19
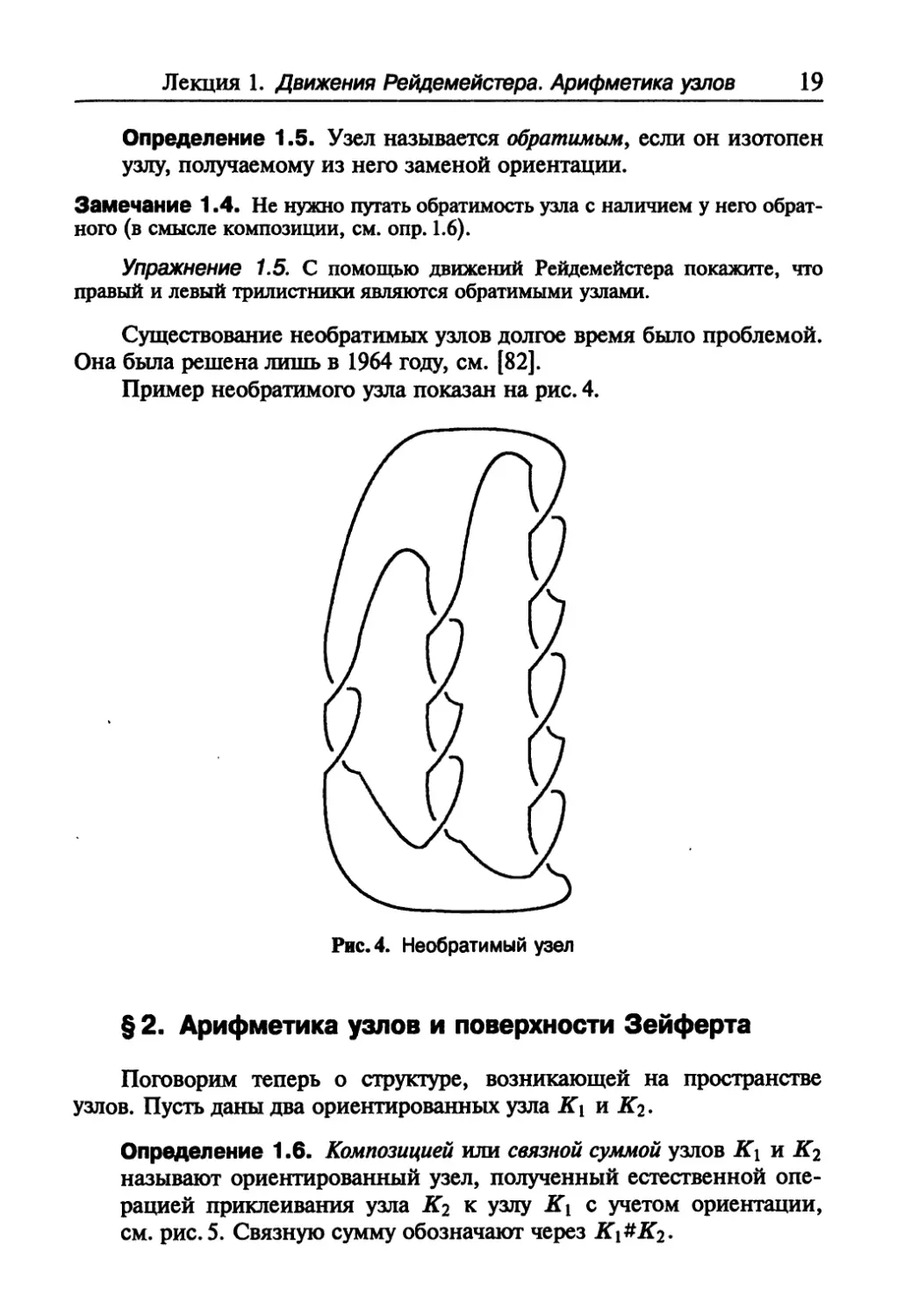
Определение 1.5. Узел называется обратимым, если он изотопен
узлу, получаемому из него заменой ориентации.
Замечание 1.4. Не нужно путать обратимость узла с наличием у него
обратного (в смысле композиции, см. опр. 1.6).
Упражнение 1.5. С помощью движений Рейдемейстера покажите, что
правый и левый трилистники являются обратимыми узлами.
Существование необратимых узлов долгое время было проблемой.
Она была решена лишь в 1964 году, см. [82].
Пример необратимого узла показан на рис. 4.
Рис.4. Необратимый узел
§ 2. Арифметика узлов и поверхности Зейферта
Поговорим теперь о структуре, возникающей на пространстве
узлов. Пусть даны два ориентированных узла К\ и Кг.
Определение 1.6. Композицией или связной суммой узлов К\ и К2
называют ориентированный узел, полученный естественной
операцией приклеивания узла Кг к узлу К\ с учетом ориентации,
см. рис. 5. Связную сумму обозначают через К\#Кг-
20 Раздел I. Узлы, зацепления и полиномиальные инварианты
К&Кг
Рис.5. Связная сумма узлов
Упражнение 1.6. Покажите, что изотопический класс полученного узла
не зависит от выбора того участка, на котором узлы подходят друг к другу.
Упражнение 1.7. Докажите, что операция конкатенации на узлах
коммутативна, т.е. для каждых двух узлов jfiTj, JiT2 узлы К^К2 и К2#Ку изотопны.
Более того, можно провести такую изотопию и на бесконечных (длинных)
R3, оба конца которого уходят
узлах, т. е. на отображениях интервала в
на бесконечность.
Тогда для каждого
Теорема 1.2. Пусть узел К\ нетривиальный,
узла К2 узел К\#К2 также нетривиальный.
Доказательство. Рассмотрим последовательность узлов
К^К2у(К^К2ЩК^К2),...7
в которой первый узел К у лежит внутри шара радиуса 1, узел К2,
следующий за ним, лежит внутри круга радиуса \, следующий узел К$ —
внутри круга радиуса |,ит.д. Тогда на ограниченном множестве можно
уместить всю бесконечную последовательность узлов, см. рис. 6.
Рис.6
Получим узел, который, возможно, будет диким, и назовем его а.
Так как Ki#K2 — тривиальный узел, то узел о — также тривиальный.
Лекция 1. Движения Рейдемейстера. Арифметика узлов 21
С другой стороны, a = K\#(K2#Ki)#(K2#K\)... В силу того, что
операция связной суммы на узлах коммутативна, узел К2#К\ — тривиален.
Следовательно, узел а изотопен К\, что противоречит предположению
о нетривиальности К\. Теорема доказана. ■
Определение 1.7. Узел К называется простым, если не существует
нетривиальных узлов Ly M, таких, что К = L#M. Остальные узлы
называются составными.
Определение 1.8- Если для узлов J5T, X, М справедливо
утверждение К = £#М, то говорят, что узлы L, М делят К.
Итак, мы установили, что в полугруппе узлов все элементы, кроме
тривиального, не имеют обратных элементов. Какими еще свойствами
обладают узлы?
Упражнение 1.8. Покажите, что любой узел вкладывается в некоторую
сферу с g ручками, точнее, любой изотопический класс узла может быть получен
в виде кривой на некоторой сфере с ручками, стандартно вложенной в R3.
Замечание 1.5. То же утверждение верно и для зацеплений.
В силу известной теоремы Жордана понятно, что в сферу (без
ручек) вкладывается лишь тривиальный узел.
Дадим теперь определение поверхности Зейферта узла [121, 104].
Определение 1.9. Пусть L — ориентированное зацепление. По-
верхностью Зейферта зацепления L называют связную компактную
ориентированную двумерную поверхность в 53, краем которой
служит зацепление L, причем ориентация L индуцирована
ориентацией поверхности.
Теорема 1.3. У любого зацепления в R3 существует поверхность
Зейферта.
Доказательство. Рассмотрим плоскую диаграмму D зацепления L.
Будем уничтожать перекрестки узла, как это показано на рис. 7.
После уничтожения получится набор замкнутых
непересекающихся простых кривых на плоскости. Эти кривые называются
окружностями Зейферта. Заклеим эти окружности дисками в трехмерном
пространстве. Хотя внутренности этих окружностей на плоскости могут
содержаться одна в другой, диски в трехмерном пространстве можно
расположить непересекающимися, приподняв внутренние точки над
плоскостью диаграммы.
В окрестности каждого перекрестка друг к другу подходят два
Диска. Выберем два отрезка на краях этих дисков и соединим диски
перекрученной полоской, краями которой служат ветви зацепления,
инцидентные этому перекрестку, см. рис. 8. На рис. 8 сверху и снизу
22 Раздел I. Узлы, зацепления и полиномиальные инварианты
лента перекручивается в разные стороны, при этом в одном случае
вертикальная ветвь расположена выше горизонтальной, а во втором —
наоборот.
j
г
Л
V
Рис. 7. Уничтожение перекрестков диаграммы
Получим некоторую (не обязательно связную) поверхность.
Соединяя связные компоненты этой поверхности тонкими трубками, будем
уменьшать число связных компонент, пока оно не станет равным
единице. ■
Осталось показать, что полученная поверхность является
ориентируемой. Действительно, рассмотрим плоскость, на которой
расположена поверхность узла и выберем на ней положительный репер. Он
порождает ориентацию для каждого диска, заклеивающего окружность
Зейферта. При этом для двух окружностей Зейферта, примыкающих
к одной вершине, такие ориентации являются противоположными
(в смысле поверхности Зейферта), так как между ними приклеена
перекрученная лента. Осталось показать, что любая
последовательность Ci,...,Cn = C\ окружностей Зейферта, в которой любые две
окружности Cj,Ct+i имеют общую вершину, имеет нечетную длину
(т. е. п — нечетно), т. е. что из любой области можно добраться до нее
самой, совершив лишь четное число перекручиваний, т. е. пройдя
лишь четное количество перекрученных лент. Это следует из того, что
Лекция 1. Движения Рейдемейстера. Арифметика узлов 23
у многоугольника с нечетным числом сторон нельзя выбрать
ориентацию сторон так, чтобы ориентации любых двух соседних сторон были
противонаправлены.
диск
J
\Г
диск
диск
А
Y"
диск
диск
^А
уг
диск
диск
у
г
диск
Рис. 8. Приклеивание полоски к дискам
Теорема 1 -4. Четность количества окружностей поверхности
Зейферта, построенной по диаграмме к-компонентного зацепления с п
пересечениями, совпадает с четностью числа п — к.
Доказательство. Пусть L — диаграмма к -компонентного
зацепления с п вершинами. Устроим разбиение поверхности Зейферта на
клетки следующим образом. Выберем сначала одномерный остов, в котором
вершинами являются перекрестки диаграммы L, а ребрами — ребра
этой диаграммы. Количество клеток такого разбиения поверхности
равно количеству окружностей Зейферта — каждая клетка заклеивает одну
окружность Зейферта. Если теперь заклеить граничные окружности
(т. е. компоненты зацепления) дисками, мы получим ориентированное
Двумерное многообразие без края, так как поверхность Зейферта была
ориентируемой. Эйлерова характеристика этого многообразия должна
быть четной. Она равна п - 2п + S + к, где 2п — количество ребер
диаграммы L, S — количество окружностей Зейферта. Учитывая четность
числа -n + S + к, получаем требуемое. ■
24 Раздел I. Узлы, зацепления и полиномиальные инварианты
Поверхность Зейферта узла К представляет собой компактную
двумерную поверхность, краем которой служит одна заузленная
окружность (сам узел К). Приклеивая к этой окружности диск, получим
сферу с некоторым количеством д ручек.
Определение 1.10. Говорят, что узел К является узлом рода д,
если д — минимальное количество ручек заклеенной поверхности
Зейферта узла К.
Замечание 1.6. На самом деле, проблема вычисления рода узла — очень
сложная, она была решена Хаксном (см. [40]), в частности, из ее решения
следует решение проблемы распознавания тривиального узла (узла рода 0)
с помощью алгоритма Хакена.
Лемма 1.1. Функция д является аддитивной, т.е. для любых двух
узлов К\УК2 верно равенство д(К{) + д(К2) = g(Ki#K2).
Доказательство. Покажем сначала, что д(К\#К2) ^ д(К\) + 0(^2)-
Рассмотрим поверхности Зейферта F\ и F2 минимальных родов
узлов К{ и К2. Без ограничения общности можно считать, что эти
поверхности не пересекаются. Два малых участка краев этих
поверхностей соединим полосой так, чтобы соблюдалось условие
ориентации. В результате получится поверхность Зейферта узла К\#К2 рода
д(Кх)+д{К2). Отсюда
д{Кх*К2)^д(Кх) + д{К2).
Покажем теперь, что g(Ki#K2) ^ 9(Ki) + 0(^2)- Рассмотрим
поверхность Зейферта F минимального рода узла К\#К2. Существует
(топологическая) сфера S2, разделяющая узлы К\ и К2 в К\#К2.
Сфера S2 пересекает F по набору замкнутых кривых
(топологических окружностей) и кривой с концами в точках А, В. Каждая
окружность делит сферу S2 на две части, одна из которых не содержит
кривой АВ. Окрестность пересечения F и S2 около каждой
окружности имеет вид цилиндра, протыкающего поверхность сферы и не
содержащего кривой АВ. Удалим из такого цилиндра его малую
цилиндрическую часть, содержащую окружность, и заклеим двумя дисками
оставшиеся части цилиндра. Если получившаяся поверхность окажется
несвязной, то возьмем ту ее часть, которая содержит узел К\#К2.
Сделав такие операции применительно к каждой окружности, получаем
замкнутую поверхность F1, содержащую узел К\#К2 и пересекающую 52
только по дуге АВ. При указанных операциях количество ручек на ка-
ркдом шаге не увеличивалось. Следовательно, (/(F') < g(F). Поскольку
род поверхности F минимален, то g(F') = g(F) = д(К\#К2).
Лекция 1. Движения Рейдемейстера. Арифметика узлов 25
Сфера S2 разбивает поверхность F1 на поверхности Зейферта для
узлов К{ и К2. Следовательно,
9{КХ) + g(K2) < g{F') = д(К{#К2),
Ч.Т.Д. ■
Из аддитивности рода узла легко следует, что у нетривиального
узла не может быть обратного, так как тривиальный узел имеет род
ноль, а все остальные узлы имеют род, больший нуля.
Упражнение 1.9. Покажите, что трилистник имеет род один и является
простым узлом.
Следовательно, каждый узел разлагается не более, чем на конечное
число простых множителей.
Для полного прояснения картины относительно арифметики узлов
нам осталось доказать еще одну лемму — об однозначном разложении
узла на множители.
Лемма 1.2. Пусть L u M — умы, а К — простой узел, делящий
L#M. Тогда либо К делит L, либо К делит М.
Доказательство. Рассмотрим узел L#M и плоскость р,
пересекающую этот узел в двух точках и отделяющую L orr М. Так как ЫМ
делится на К, то найдется двумерная сфера S2 (в топологическом
смысле), пересекающая L#M в двух точках и содержащая узел К внутри
себя. Если бы наша сфера не пересекала плоскости р, задача была бы
решена. В противном случае сфера S2 пересекает плоскость по
некоторому числу несамопересекающихся окружностей. Если эти окружности
(как узлы) незацеплены с L#M, то деформацией сферы они легко
убираются. В противном случае их также можно убрать с помощью
деформации сферы в силу простоты узла К (так как узел простой, то
внутри сферы по крайней мере с одной стороны от плоскости может
находиться лишь тривиальная его часть).
Следовательно, если узел L#M делит К, то один из узлов L или М
делит К, ч.т.д. ■
Таким образом, мы имеем:
а) Изотопические классы узлов образуют коммутативную полугруппу
с единицей относительно операции связной суммы; единицей этой
полугруппы является тривиальный узел.
б) Любой нетривиальный узел не имеет обратного в данной
полугруппе.
в) Разложение на простые множители в полугруппе узлов
единственно.
г) Количество различных простых узлов счетно.
26 Раздел I. Узлы, зацепления и полиномиальные инварианты
Последнее утверждение остается читателю в качестве упражнения.
Так как изотопических классов гладких узлов счетное число
(докажите это!), мы получаем теорему.
Теорема 1.5. Полугруппа изотопических классов узлов относительно
операции взятия связной суммы изоморфна полугруппе натуральных
чисел по умножению. При этом простым узлам соответствуют
простые числа.
При этом описанный изоморфизм — не канонический, поскольку
на множестве узлов нет канонического линейного порядка, т. е. нельзя,
например, сказать, соответствует ли простой узел трилистник простому
числу три или простому числу семнадцать.
Счетная полугруппа, обладающая свойствами а)-г), единственна
с точностью до изоморфизма, поэтому все такие полугруппы некоторым
образом «связаны» с узлами.
В [107] приведено чисто алгебраическое описание этой полугруппы,
т. е. приведен явный (конструктивный) изоморфизм этой
геометрической полугруппы и чисто алгебраически заданной полугруппы.
Лекция 2
Торические узлы и зацепления.
Простейшие инварианты
узлов и зацеплений
В этой лекции будут подробно описаны некоторые серии узлов
и зацеплений, а также приведены примеры простейших
инвариантов узлов и зацеплений. С помощью этих инвариантов можно будет
доказать, например, что трилистник не изотопен тривиальному узлу.
§1. Торические узлы
Рассмотрим узел К и вложим его в сферу с д ручками, стандартно
вложенную в R3. Очевидно, что для д = 0 существует всего один узел,
вложимый в сферу — тривиальный узел.
Упражнение 2.7. Покажите, что каждое зацепление L С R3 изотопно
зацеплению, лежащему на некотором ориентированном двумерном многообразии
(сфере с ручками), стандартно вложенном в R3.
Перейдем теперь к следующим по сложности узлам — торическим
узлам, т. е. узлам, вложимым в стандартно вложенный в R3 тор.
Рассмотрим тор как прямое произведение Sl x S1 с координатами
¥>> i> € [0) 2тг]. Его можно рассматривать также как квадрат со
склеенными противоположными сторонами, см. рис. 1.
(1к> 2тг)
¥>
(0,0) V
Рис.1. Тор
28 Раздел I. Узлы, зацепления и полиномиальные инварианты
Вложим этот тор стандартным образом в R , а именно:
(у>, г/>) —► ((R + r cos ip) cos <p,(R + r cos i/>) sin y>, r sin i/>).
Здесь R — большой радиус, а г — малый радиус тора (г < R). При
этом (р можно считать параллелью тора, а *ф — меридианом тора.
Для классификации торических узлов нам потребуется
классификация изотопических классов несамопересекающихся кривых на
двумерном торе; при этом очевидно, что кривые, изотопные на торе, будут
изотопны и во всем трехмерном пространстве.
Без ограничения общности можно считать, что рассматриваемая
нами кривая выходит и входит в точку (0,0) = (2тг, 27г). Возможно,
что наша кривая какое-то количество раз пересекает ребра квадрата.
Сосчитаем отдельно число пересечений горизонтальных ребер квадрата
и отдельно — число пересечений вертикальных ребер. При этом каждое
пересечение мы будем учитывать со знаком: проход через правую или
верхнюю стенку будем считать положительным, а проход через левую
или нижнюю стенку — отрицательным.
Таким образом, для каждой такой кривой мы имеем пару целых
(быть может, отрицательных) чисел, характеризующих данную кривую.
Упражнение 2.2. Покажите, что если оба таких числа равны нулю, то
узел — тривиальный.
Замечание 2.1. В дальнейшем будут рассматриваться только такие узлы, при
которых хотя бы одно из этих чисел не равно нулю.
Лемма 2.1. Для несамопересекающейся кривой эти числа будут
взаимно просты.
Доказательство. Предположим противное. Пусть данная несамо-
пересекающаяся кривая с проходит km раз через вертикальные стенки
и lm раз через горизонтальные, га > 1.
Рассмотрим тор как плоскость R2, профакторизованную по
решетке (2тг, 2тг). Тогда прообраз кривой с при отображении R2 —> Т2 должен
состоять из непересекающихся кривых. Так как наша кривая с — неса-
мопересекающаяся, связная компонента ее прообраза в R2, проходящая
через (0,0) не может проходить через точку (2тгк, 2*1), так как иначе
кривая на торе имела бы самопересечение в точке (0,0) = (2irky 2*1).
Значит, эта связная компонента не инвариантна относительно сдвига
на (2irk, 2irl). Кроме того, весь прообраз инвариантен относительно
сдвигов по вертикали и горизонтали на числа, кратные 2тг.
Докажем следующий факт. Плоская кривая /, инвариантная
относительно сдвига на вектор mv, га G N, m > 1 из плоскости этой кривой.
р не инвариантная относительно сдвига на v, пересекается кривой 1\
полученной из нее сдвигом на гГ. Действительно, без ограничения
Лекция 2. Торические узлы и зацепления
29
общности можно предполагать, что v = (1,0). Рассмотрим кривую I
и максимум М ординат ее точек. Очевидно, что для кривой /'
максимум ординат также равен п. Пусть (К, М) — точка, через которую
проходит кривая I. Тогда, очевидно, кривая I проходит также через
точку (К + т,М), а кривая V —через точки (К+1,М) и (JT+M-H,M).
Ясно, что отрезки кривых I и1' соединяют указанные пары точек, при
этом не пересекая линии у = М, откуда и следует то, что I и /' имеют
точку пересечения.
Прообраз кривой с состоит из пересекающихся кривых.
Противоречие завершает доказательство леммы. ■
Итак, мы доказали, что каждый торический узел проходит р раз
по параллели и q раз по меридиану тора, при этом НОД(р, q) = l.
Легко видеть, что для взаимно простых р и q такая кривая
существует: можно, например, рассмотреть кривую q<p - pt/> = 0 (mod 2?г).
Упражнение 2.3. Показать, что все кривые, соответствующие
фиксированным взаимно простым значениям р и q, изотопны между собой на торе.
Таким образом, для нахождения торических узлов нам нужно
рассмотреть пары взаимно простых чисел р и q.
Самый простой случай — когда одно из чисел р или q равно
единице.
Упражнение 2.4. Покажите, что в случае р = 1, q — любое или q = 1, р —
любое мы получаем тривиальный узел.
Следующий пример пары взаимно простых чисел р = 3, q = 2
(или р = 2, q = 3). И в том, и в другом случае узел будет изотопен
трилистнику.
(0,0) ^
Рис. 2. Трилистник на торе
Более того, имеет место
Теорема 2.1. При взаимно простых р и q торические узлы (p,q)
и (q}p) изотопны.
30 Раздел I. Узлы, зацепления и полиномиальные инварианты
Доказательство. Будем рассматривать узлы не в R3, а в 53. Как мы
знаем, на изотопность это не влияет.
Рассмотрим S3 в виде склейки двух полноторий по границе, при
которой меридиан первого полноторий соответствует параллели
второго, а параллель первого — меридиану второго. Более строго это можно
было бы написать так: S3 = {z, w € С | \z\2 + \w\2 = 1}. Эти два пол-
нотория задаются неравенствами \z\2 > \w\2 и \z\2 < \w\2, а их общий
граничный тор — уравнением \z\ = |to| = у \. При этом легко видеть,
что окружности
\w\ = у - , z — фиксированное и равное по модулю у -
и
\z\ = у - , w — фиксированное и равное по модулю у -
являются параллелью и меридианом граничного тора; при этом
параллель и меридиан двух полноторий меняются местами.
Следовательно, узел типа (р, q) в одном полноторий будет являться
узлом типа (qy р) в другом. Так как наш тор вложен в 53 стандартно,
получаем изотопию узлов (р, q) и (q,p). Ш
Торические узлы типа (р, q) имеют серию плоских диаграмм,
изображенную на рис. 3.
Замечание 2.2. Такой способ изображения узла называется изображением
узла с помощью косы (из р нитей); теория кос и точные определения будут
даны в следующих лекциях.
Аналогично торическим узлам могут быть определены и торические
зацепления — зацепления, вложимые в стандартно вложенный в R3 тор.
Каждое торическое зацепление представляет собой некоторый
набор замкнутых кривых, вложенных в тор, который в свою очередь сам
стандартно вложен в R3.
Мы уже знаем, как устроены торические узлы. Поэтому для
построения торических зацеплений нам нужно взять торический узел К
(можно считать его «прямолинейным» и нестятивающимся по тору,
с уравнением q<p - рф = 0 (mod 2ir)) и добавить в тор Т, его
содержащий, еще несколько замкнутых кривых, не пересекающих кривую
данного узла. Следовательно, нам нужно вложить некоторые кривые
вТ\К. Как известно из курса топологии. Т\К изоморфно открытому
цилиндру.
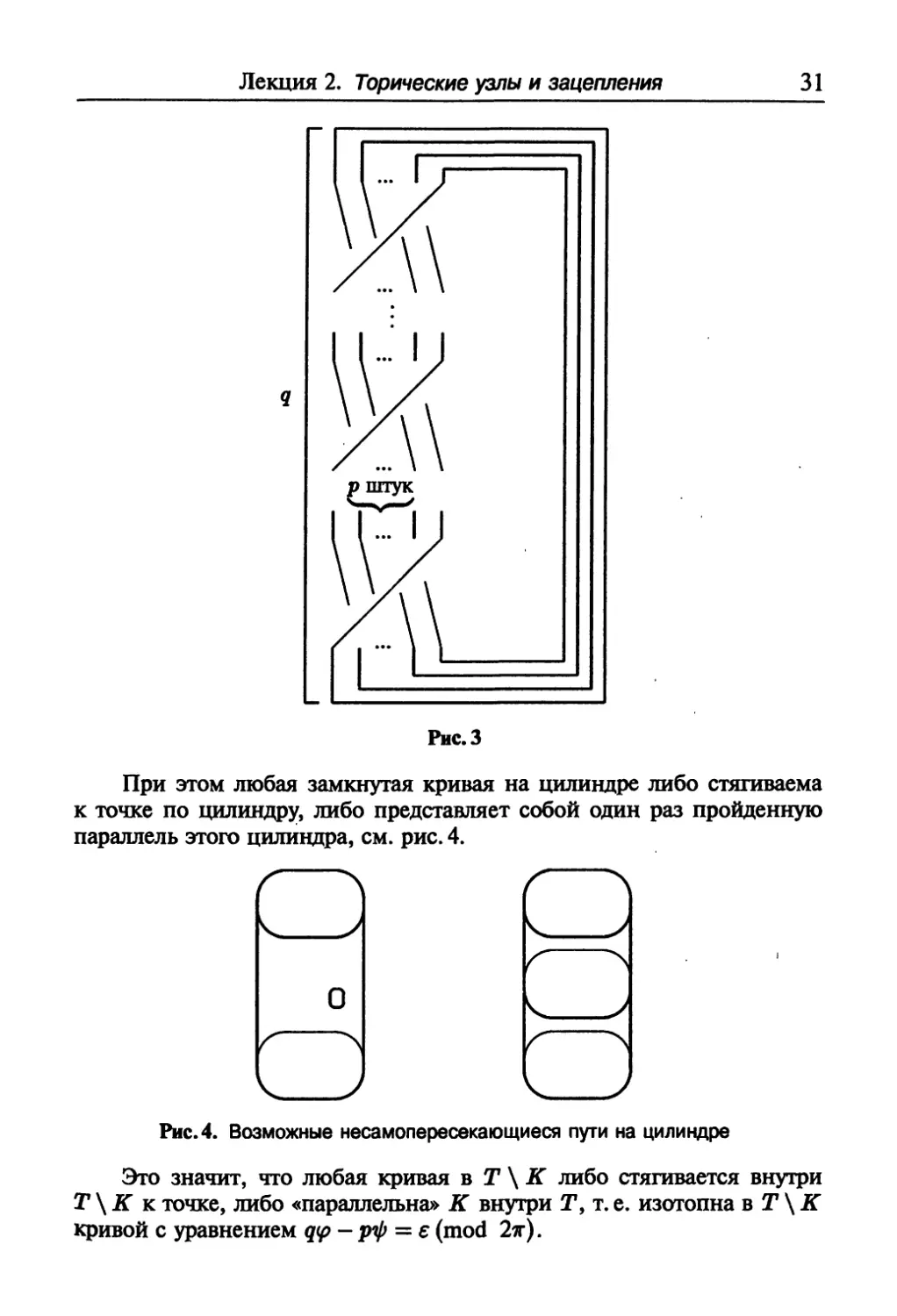
Лекция 2. Торические узлы и зацепления 31
рштук
Рис.3
При этом любая замкнутая кривая на цилиндре либо стягиваема
к точке по цилиндру, либо представляет собой один раз пройденную
параллель этого цилиндра, см. рис. 4.
К"
Л^
L
Л
N
V
N
\
Рис.4. Возможные несамопересекающиеся пути на цилиндре
Это значит, что любая кривая в Т\К либо стягивается внутри
Т \ К к точке, либо «параллельна» К внутри Т, т. е. изотопна в Т \ К
кривой с уравнением q<p - рф = е (mod 2тг).
32 Раздел I. Узлы, зацепления и полиномиальные инварианты
Следовательно, имеет место
Теорема 2.2. Любое торическое зацепление изотопно несвязной сум-
ме нескольких незацепленных отдельно стоящих тривиальных узлов
и зацепления, представляющего собой набор «параллельных», т. е.
непересекающихся и имеющих один и тот же тип (p,q), узлов
на стандартно вложенном торе.
§ 2. Простейшие инварианты узлов и зацеплений
Теперь перейдем к следующей части нашей лекции — к
простейшим инвариантам узлов и зацеплений.
Как мы уже знаем из вводной лекции, инвариант узла (или
зацепления) — это функция, определенная на узлах (или на зацеплениях,
или, быть может, только на зацеплениях с фиксированным числом
компонент), которая не меняется при изотопиях.
При этом бывают инварианты ориентированных узлов или
зацеплений, а бывают инварианты неориентированных узлов и зацеплений.
Мы будем представлять узлы и зацепления с помощью плоских
диаграмм с проходами и переходами. В силу теоремы Рейдемейстера,
для установления инвариантности той или иной функции на узлах
(зацеплениях) достаточно проверить лишь инвариантность этой функции
относительно трех движений Рейдемейстера.
Замечание 2.3. Для случая ориентированных узлов или зацеплений
движения Рейдемейстера определяются так же, как и в неориентируемом случае;
нужно лишь определенным образом ориентировать «ветви» узлов.
Сначала рассмотрим простейший целочисленный инвариант двух-
компонентных ориентированных зацеплений.
Итак, пусть дано зацепление из двух ориентированных
компонент А и В и его плоская диафамма. Рассмотрим те перекрестки
плоской диаграммы, в которых компонента А проходит выше
компоненты В. Такие перекрестки могут быть двух видов:
Каждому положительному перекрестку поставим в соответствие
число (+1), а каждому отрицательному перекрестку сопоставим (-1)
Лекция 2. Торические узлы и зацепления 33
и просуммируем эти числа по всем перекресткам, в которых
компонента А проходит выше компоненты В. Получим некоторое целое
число.
Упражнение 2.5. Покажите, что это число не меняется при движениях
Рейдемейстера.
Итак, мы имеем инвариант ориентированных зацеплений.
Определение 2.1. Назовем полученный инвариант
коэффициентом зацепления
Замечание 2.4. Этот инвариант был известен еще Гауссу, однако он вычислял
его не комбинаторным способом, а с помощью так называемой
электромагнитной формулы, получившей впоследствии его имя; это понятие обобщается
также на случай многообразий размерностей р и q в пространстве Rp+q+l.
Этот инвариант уже позволяет различать некоторые зацепления
из двух компонент.
Пример 2.1. Рассмотрим тривиальное зацепление из двух компонент
и ориентируем его компоненты произвольным образом. Тогда их коэффициент
зацепления равен нулю. Бели мы рассмотрим зацепление Хопфа, то, в
зависимости от ориентации, коэффициент зацепления будет равен ±1. Следовательно,
зацепление Хопфа не изотопно тривиальному.
Упражнение 2.6. Покажите, что коэффициент зацепления двух
параллельных торических узлов типа (1, п) равен п.
Покажем, что существуют неизотопные зацепления с одинаковым
коэффициентом зацепления.
Пример 2.2. Рассмотрим кольца Борромео — трехкомпонентное
зацепление. Для каждых двух его компонент коэффициент зацепления равен нулю,
при этом компоненты зацепления являются тривиальными узлами, хотя само
трехкомпонентное зацепление является нетривиальным. Его нетривиальность
будет показана в дальнейшем.
Построим теперь инвариант неориентированных узлов и
зацеплений, также опирающийся на понятие плоской диаграммы узла
(зацепления) с проходами и переходами, см. [123, 122].
Рассмотрим некоторый неориентированный узел (зацепление).
Определение 2.2. Назовем дугой плоской диаграммы узла (или
зацепления) проекцию ветви узла от прохода до следующего прохода,
т. е. идущую все время сверху пересекаемых ею дуг.
Теперь будем раскрашивать дуги данного узла (зацепления) в три
цвета. В каждой вершине сходятся три дуги; одна из них проходит
сверху двух остальных.
Определение 2.3. Назовем раскраску диаграммы узла
(зацепления) в три цвета правильной, если в каждой вершине сходятся
либо дуги одного цвета, либо дуги трех разных цветов.
34 Раздел I. Узлы, зацепления и полиномиальные инварианты
Теорема 2.3. Количество правильных раскрасок является
изотопическим инвариантом узла {зацепления).
Доказательство. Будем доказывать инвариантность количества
правильных раскрасок относительно движений Рейдемейстера. Более
точно: рассмотрим все движения Рейдемейстера и для каждого из них
построим однозначное соответствие между раскрасками диаграммы
«до» и диаграммы «после». В случае первого движения Рейдемейстера
возникающий перекресток всегда является одноцветным, кроме
того, существует «одноцветное второе» и «одноцветное третье» движение
Рейдемейстера.
Второе движение Рейдемейстера
■ У
У ■ у
У
.' У
1
У
У
► 1
У У
1
3
У , у
> У
У
*—> 1
У
2
3
У
У
У
У У
У
У
Третье движение Рейдемейстера
Рис.6
На рис. 6 выписаны соответствующие раскраски для ребер,
задействованных во втором или третьем неодноцветном движении Рей-
Лекция 2. Торические узлы и зацепления
35
демейстера. Все другие раскраски получаемы из данных некоторой
перестановкой трех цветов J\
Таким образом, каждой из правильных раскрасок диаграммы
до применения того или иного движения Рейдемейстера мы
однозначно сопоставили правильную раскраску после применения
движения Рейдемейстера. Следовательно, количество правильных раскрасок
не меняется при применении движений Рейдемейстера. ■
Упражнение 2.7. Посчитайте количества правильных раскрасок для
тривиального узла и для трилистника и установите, что трилистник не изотопен
тривиальному узлу.
Упражнение 2.8. Посчитайте количества правильных раскрасок для
зацепления Уайтхеда и покажите, что оно нетривиально.
Упражнение 2.9. Посчитайте количества правильных раскрасок для
тривиального зацепления из трех компонент и для колец Борромео и установите,
что эти два зацепления не изотопны.
*' Здесь цвета обозначаются цифрами 1,2,3.
Лекция 3
Фундаментальная группа
§1. Отступление.
Примеры развязывания узлов
Начнем эту лекцию с одного очень красивого примера (или задачи).
Рассмотрим произвольную диаграмму тривиального узла и
попытаемся его распутать с помощью движений Рейдемейстера. В «хорошем»
случае это можно сделать с помощью только уменьшающих количество
вершин 1-го и 2-го движений и не меняющего количества вершин
третьего движения.
Однако так бывает не всегда. А именно, существует диаграмма
тривиального узла с ненулевым количеством вершин, к которой
неприменимо третье движение Рейдемейстера, а также первое и второе
«уменьшающие» движения. Следовательно, его распутьшание нужно
начинать с увеличения количества вершин, т. е. «запутывания».
Пример 3.1. Рассмотрим диаграмму узла, показанную на рис. 1.
Очевидно, что узел, задаваемый этой диаграммой, изотопен тривиальному, так как
получается из тривиальной вытянутой окружности последовательным
применением вторых движений Рейдемейстера.
J
t
III 1
з 1
А
Рис.1
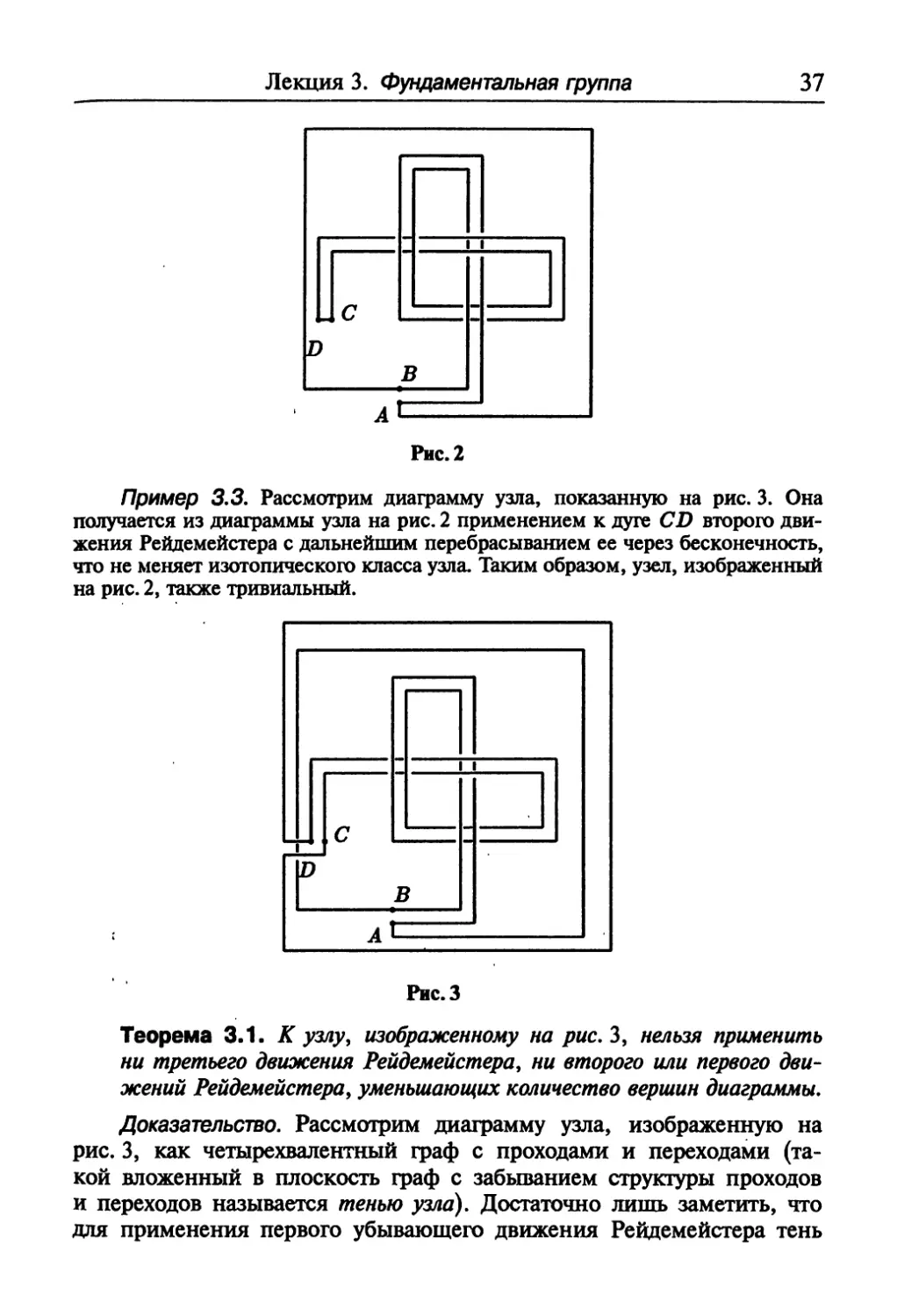
Пример 3.2. Рассмотрим диаграмму узла, показанную на рис. 2. Она.
получается из диаграммы на рис. 1 «перебрасыванием» дуги АВ через
бесконечность, что не меняет изотопического класса узла. Следовательно, узел,
изображенный на рис. 2, также тривиальный.
Лекция 3. Фундаментальная группа
37
\Цс L
i i
\р
Р 1
At
Рис.2
Пример 3.3. Рассмотрим диаграмму узла, показанную на рис. 3. Она
получается из диаграммы узла на рис. 2 применением к дуге CD второго
движения Рейдемейстера с дальнейшим перебрасыванием ее через бесконечность,
что не меняет изотопического класса узла. Таким образом, узел, изображенный
на рис. 2, также тривиальный.
11 \г 1
[р
i i
в 1
A t
Рис.3
Теорема 3-1- К узлу; изображенному на рис.3, нельзя применишь
ни третьего движения Рейдемейстера, ни второго или первого
движений Рейдемейстера, уменьшающих количество вершин диаграммы.
Доказательство. Рассмотрим диаграмму узла, изображенную на
рис. 3, как четырехвалентный граф с проходами и переходами
(такой вложенный в плоскость граф с забыванием структуры проходов
и переходов называется тенью узла). Достаточно лишь заметить, что
для применения первого убывающего движения Рейдемейстера тень
38 Раздел I. Узлы, зацепления и полиномиальные инварианты
должна содержать петли; на данном графе таких петель нет. Для
применения второго движения Рейдемейстера диаграмма узла должна
содержать двуугольники, при которых одна ветвь узла дважды
проходит над другой, в нашем случае ни один двуугольник нашей плоской
диаграммы таким свойством не обладает. Наконец, для применения
третьего движения Рейдемейстера диаграмма узла должна содержать
треугольник, ни одна ветвь которого не проходит выше двух других.
Таких треугольников у нашей диаграммы узла, изображенной на рис. 3,
нет. Этим и завершается доказательство теоремы. ■
Можно рассматривать не только плоские диаграммы узлов, но
также и сферические диаграммы. Более точно, рассмотрим двумерную сферу
как плоскость с добавленной бесконечной точкой. Можно считать, что
сам четырехвалентный граф — плоская диаграмма узла — не
проходит через эту точку. Существует изотопия, при которой какая-то
дуга проходит через бесконечность. Назовем такое движение заменой
бесконечности.
Интуитивно ясно, что замена бесконечности (перебрасывание дуги
через бесконечность) является изотопией. В действительности ее можно
осуществить последовательным применением движений Рейдемейстера.
Упражнение 3.1. Покажите это непосредственно.
Следовательно, тривиальный узел, изображенный на рис. 3, может
быть «развязан» лишь посредством применения второго движения
Рейдемейстера, уменьшающего количество перекрестков, если мы сначала
разрешим замену бесконечности. Однако узел, изображенный на рис. 4.
(связная сумма узла на рис. 3 с самим собой), уже не может быть
I I "~"| | | | ТТ
i i i i
Рис.4
Лекция 3. Фундаментальная группа
39
развязан лишь невозрастающими движениями даже с применением
замены бесконечности.
Дело в том, что если рассматривать тень узла как граф на сфере,
то в случае, изображенном на рис. 3, будет присутствовать
двуугольник, к которому применимо убывающее движение Рейдемейстера (хотя
на плоской диаграмме он и содержал бесконечную точку). Для
диаграммы узла, изображенной на рис. 4, такого двуугольника нет.
Кроме указанных выше примеров, приведем еще один (более
простой) пример тривиального узла, который является «неуменьшаемым»
даже с применением перебрасывания через бесконечность, см. рис. 5.
Этот пример придуман студентом И. М. Никоновым, слушавшим курс
лекций автора.
Б1_га^
Рис.5
§ 2. Фундаментальная группа дополнения
как инвариант узла
Перейдем к основной части нашей лекции. Речь пойдет о
фундаментальной группе дополнения к узлам (или зацеплениям) и о способах
ее вычисления.
Свойства фундаментальной группы подробно изложены в [126,127,
96, 104].
Определение 3.1. Пусть дано топологическое пространство X
и выбрана точка «о, а на окружности S1 выбрана точка а.
Рассмотрим множество непрерывных отображений /: S1 —► X, при
которых /(а) = жо- Множество изотопических классов
эквивалентности таких отображений обладает групповой структурой.
Прохождение путей одного за другим является умножением в группе,
а прохождение некоторого пути в обратном порядке представляет
обратный ему путь. Полученная группа называется
фундаментальной группой пространства X и обозначается iti(X,xo).
40 Раздел I. Узлы, зацепления и полиномиальные инварианты
Упражнение 3.2. Покажите, что для связных X группа тг^Х,^) не
зависит от выбора х0, т. е. такие группы при разных х0 изоморфны.
Замечание 3.1- Фундаментальная группа является гомотопическим
инвариантом топологического пространства.
Рассмотрим теперь некоторый узел (или зацепление) К С R3.
Пусть Мк == R3 \ К — дополнение к узлу (зацеплению) К. Ясно,
что если мы будем гладко изотопировать К в R3, дополнение к узлу
будет оставаться гомеоморфным самому себе и, следовательно,
фундаментальная группа дополнения является инвариантом изотопических
классов узлов.
В [38] показано, что дополнение к узлу (точнее, к его тонкой
трубчатой окрестности) в трехмерном пространстве является полным
инвариантом узла (с точностью до зеркального отражения).
Однако, для зацеплений аналогичное утверждение неверно.
Построение контрпримера заимствовано из [123]. Прежде, чем привести
этот контрпример, докажем следующую лемму.
Лемма 3.1- Пусть D3 С R3 — шар и Т С D3 — полноторие,
см. рис. 6. Тогда существует гомеоморфизм пространства R3 \ Т
на себя, переводящий кривые АВ и CD на рис. бае кривые АВ и CD
на рис.66 и оставляющий неподвижными точки внутри шара Х>3.
а б
Рис.6
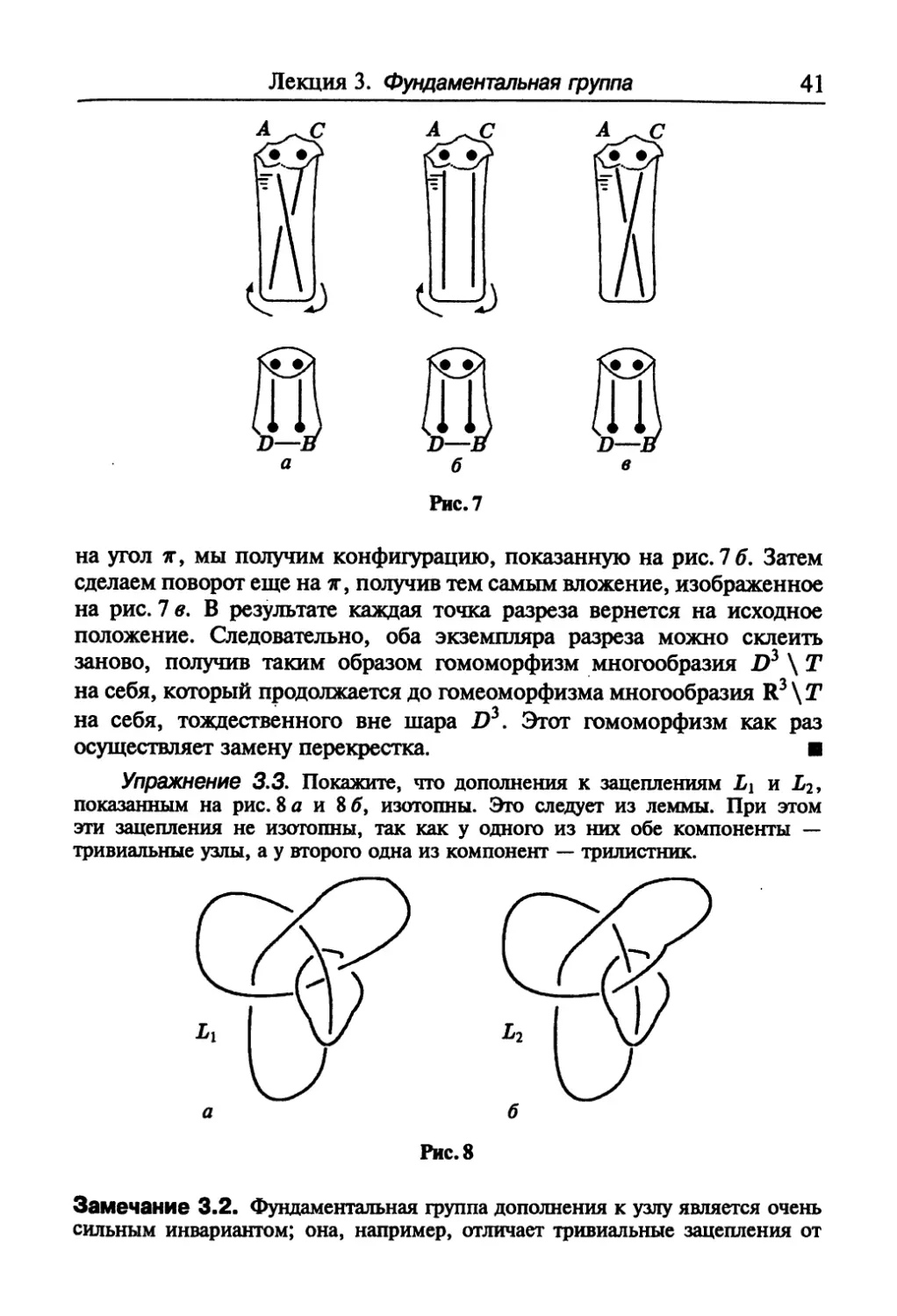
Доказательство. Для наглядности будем представлять себе
полноторие Т с внутренним диаметром большим внешнего. Таким образом,
промежуток, «окруженный» полноторием, является глубокой полостью,
см. рис. 7.
Сделаем внутри шара D3 плоский разрез в форме крута,
проходящий через эту полость так, как это показано на рис. 7 а. Будем
поворачивать верхнюю часть разреза (она представляет собой круг
с двумя отмеченными точками) в направлении, указанном стрелками;
это возможно, так как полноторие Т удалено из D*. Сделав поворот
Лекция 3. Фундаментальная группа
41
а б в
Рис.7
на угол я-, мы получим конфигурацию, показанную на рис. 7 б. Затем
сделаем поворот еще на 7Г, получив тем самым вложение, изображенное
на рис. 7 е. В результате каждая точка разреза вернется на исходное
положение. Следовательно, оба экземпляра разреза можно склеить
заново, получив таким образом гомоморфизм многообразия D3 \ Т
на себя, который продолжается до гомеоморфизма многообразия R3 \Г
на себя, тождественного вне шара D3. Этот гомоморфизм как раз
осуществляет замену перекрестка. ■
Упражнение 3.3. Покажите, что дополнения к зацеплениям L\ и L2,
показанным на рис. 8 а и 8 6, изотопны. Это следует из леммы. При этом
эти зацепления не изотопны, так как у одного из них обе компоненты —
тривиальные узлы, а у второго одна из компонент — трилистник.
Рис.8
Замечание 3.2. Фундаментальная группа дополнения к узлу является очень
сильным инвариантом; она, например, отличает тривиальные зацепления от
42 Раздел I. Узлы, зацепления и полиномиальные инварианты
нетривиальных. Это утверждает теорема Дена о том, что зацепление L из m
компонент тривиально тогда и только тогда, когда 7Ti(R3 \ L) — свободная группа
с m образующими. Хотя на самом деле такое «отличие» упирается в
проблему изоморфности групп, заданных образующими и соотношениями, которая
в общем случае не разрешима. Подробности см. в [9] и [19].
С. В. Матвеев в [116] показал, что дополнения к узлам являются
т. н. достаточно большими трехмерными многообразиями; такие
многообразия классифицированы.
В [67] он же построил полный инвариант узлов.
Упражнение 3.4. Покажите, что фундаментальная группа окружности
изоморфна фундаментальной группе дополнения к тривиальному узлу и
изоморфна Z.
Упражнение 3.5. Покажите, что фундаментальная группа дополнения
к тривиальному п -компонентному зацеплению изоморфна свободной группе
с п образующими.
Упражнение 3.6. Покажите, что фундаментальная группа букета двух
линейно-связных пространств изоморфна свободному произведению их
фундаментальных групп.
Упражнение 3.7. Покажите, что сфера с парой отождествленных точек
гомотопически эквивалентна букету сферы и окружности, тем самым
фундаментальная группа сферы с парой отождествленных точек изоморфна Z.
Существует много способов вычисления фундаментальных групп
дополнения к узлам (зацеплениям). Остановимся на двух из них.
Пусть X — топологическое пространство, причем X = Х\ U Х^\
множества Х\у Хг и их пересечение Xq открыты, линейно-связны
и непусты. Выберем в Xq точку А. Пусть фундаментальные группы
7Ti(Xi, А) и tti(X2, А) имеют копредставления < ai,... |/i = e,... > и
< &i,...|</i = е,... > соответственно. Пусть образующие группы
7Ti(Xo, А) с\, с2..., лежащие как в Ъ\(Хи А), так и в Я\(Х2, А),
выражаются в образующих группы Ki(X\, А) какс,- = Cj(ai,...), а в образующих
группы tti(X2, А) как с,- = с,(Ьь...).
Тогда имеет место
Теорема 3.2 (Теорема Ван-Кампена).
Группа Wi(X, А) допускает копредставление
< a,-, bi\fi = е,# = е, Ci(a) = Ci(b) > .
Доказательство этой теоремы довольно длинно и технически
трудно, поэтому мы его приводить не будем. См., например, [104].
Следствие 3-1- Если в условиях теоремы 2 пространства Х\ и Xi
односвязны, то и пространство X также односвязно.
{ О помощью теоремы Ван-Кампена можно вычислять, например,
фундаментальные группы двумерных ориентируемых многообразий.
Лекция 3. Фундаментальная группа
43
Теорема 3.3. Фундаментальная группа сферы с g ручками (д > 0)
имеет копредставление
< ai,6i,... I a>gibg\a\b\a\~ b{~ ...agbgag~bg~ = e>.
Доказательство. Рассмотрим данную сферу с ручками как Ад
-угольник со склеенными сторонами (крендель, т. е. сфера с двумя ручками
изображена таким образом на рис. 6).
* W,
Рис.9
Разделим это многообразие на две части, одна из которых находится
внутри большого круга на рис. 9, а другая — вне малого круга на том же
рисунке.
Первая область односвязна, вторая область стягивается на букет
из 2д окружностей, следовательно она изоморфна свободной группе
с 2д образующими аь Ьи..., аду Ьд {\
Пересечение двух областей изотопно окружности, следовательно,
его фундаментальная группа имеет один образующий элемент.
Применяя теорему Ван-Кампена, получаем, что
n\(Sg) =< ai,bi,... ,agiЪд\а,\Ъ\а\~ Ъ{~ ...agbgag~bg~ = е >,
что и требовалось доказать. ■
Мы знаем, что всякий узел (как, впрочем, и всякое зацепление)
вложим в стандартно вложенную в Rn сферу с ручками.
Следовательно, для вычисления фундаментальной группы дополнения к тому или
иному узлу можно использовать теорему Ван-Кампена, разбивая
пространство дополнения к узлу на две части, лежащие по разные стороны
от соответствующей сферы с ручками.
^ Здесь каждая буква означает обход по стороне восьмиугольника; он замкнутый, так
как все вершины склеиваются в одну точку.
44 Раздел I. Узлы, зацепления и полиномиальные инварианты
Применим теперь теорему Ван-Кампена для вычисления
фундаментальной группы дополнения к торическим узлам. Пусть К —
торический узел типа (р, </), вложенный в стандартный тор в R3.
Рассмотрим теперь R3 \ К в виде объединения пространств
(Внутреннее полноторие без К) U (Внешность тора без К).
Так как выкидывание некоторого множества на границе или точки
не влияет на фундаментальную группу трехмерного пространства, то
фундаментальная группа обоих пространств изоморфна Z (у одного
из них образующая а представляет обход вдоль параллели тора, а у
второго образующая Ь — обход вдоль меридиана тора). Их пересечение
гомеоморфно цилиндру, следовательно, его фундаментальная группа
изоморфна Z и ее образующая записывается с одной стороны как ар,
а с другой — как Ь9. Таким образом, получаем теорему.
Теорема 3.4. Фундаментальная группа дополнения к узлу типа (р, q)
имеет копредставление с двумя образующими а и Ь и одним
соотношением ар = Ь9.
Замечание 3.3. Фундаментальная группа дополнения не различает узел и его
зеркальное отражение.
Как и следовало ожидать, фундаментальные группы изотопных
узлов изоморфны, а именно: торический узел типа (р, q) имеет ту же
группу, что и узел (q>p), а группа узла типа (1,п) изоморфна
группе Z — фундаментальной группе тривиального узла. Узлы типов (р, q)
и (р, —q) являются зеркальными отражениями друг друга, поэтому их
фундаментальные группы совпадают.
Во всех остальных случаях фундаментальная группа различает то-
рические узлы, хотя доказать это не очень просто — для этого нужно
доказать неизоморфность двух групп, заданных копредставлениями.
Есть и еще один способ вычисления фундаментальной группы
дополнения к узлу (зацеплению). Он состоит в следующем.
Рассмотрим ориентированный узел или зацепление 2* и его плоскую
диаграмму. Рассмотрим некоторую точку ж, расположенную выше этой
плоскости и будем классифицировать изотопические классы петель,
исходящих из этой точки. Нетрудно заметить (проверьте это сами!),
что в качестве образующих можно выбрать петли, выходящие из
фиксированной точки х и «цепляющиеся за дуги» узла (зацепления). Для
определенности будем считать путем, соответствующим ребру, путь,
обходящий вокруг него положительно (как говорят физики, по правилу
буравчика).
Как будет видно в дальнейшем, ориентация здесь не важна.
Лекция 3. Фундаментальная группа
45
Рис.10
Перейдем теперь к нахождению достаточной системы соотношений
в этой группе.
Легко видеть, как связаны петли, зацепляющиеся за «соседние
дуги», а именно, Ь = сас"1, где дуга с разделяет дуги а и Ь и проходит
так, как это указано на рис. 11.
Рис. 11
Покажем, что все соотношения в фундаментальной группе
дополнения вытекают из таких соотношений.
Действительно, рассмотрим проекцию нашей петли на ту же
плоскость, на которую мы проектируем узел (зацепление). В процессе
изотопии петли существенны только те моменты, когда проекция
петли пересекает вершины узла. На рис. 12 изображена такая изотопия.
В процессе изотопии часть узла, соединяющая точки Р и Q, проходит
под перекрестком.
Рис.12
Легко видеть, что петля, изображенная на рис. 12 слева, задает
элемент фундаментальной группы, равный произведению cb"lc"1, а петля,
46 Раздел I. Узлы, зацепления и полиномиальные инварианты
изображенная на рис. 12 справа, задает элемент фундаментальной
группы, равный а.
Итак, копредставление фундаментальной группы дополнения к
узлу (зацеплению) получается следующим образом: дуги соответствуют
образующим, а в качестве определяющих соотношений можно выбрать
соотношения типа cac~l = b~l для соседних дуг а и Ь, разделяемых
дугой с.
Упражнение 3.8. Посчитайте фундаментальную группу дополнения к
трилистнику способом, указанным выше, и установите изоморфизм между
группами, заданными копредставлениями < о, b\aba = bob > и < с, d\c3 = d2 >.
Замечание 3.4. Группа < a, b\aba = bab > появится и в другой части теории
узлов. Она изоморфна группе кос из трех нитей.
Упражнение 3.9. Посчитайте фундаментальную группу дополнения к узлу
восьмёрке.
Докажем теперь следующую теорему.
Теорема 3.5. Для каждого узла К значение на нем инварианта рас-
красок на три меньше количества гомоморфизмов фундаментальной
группы tfi(R3 \ К) в группу 5з перестановок из 3 элементов.
Доказательство. Рассмотрим узел К и произвольную его плоскую
диаграмму. Для того, чтобы гомоморфно отобразить фундаментальную
группу яч(К3 \ К) в группу 5з, нужно найти образы всех элементов,
соответствующих дугам узла К. Предположим, что хотя бы один такой
элемент отображен в четную перестановку. Рассмотрим дугу з,
соответствующую этому элементу. Тогда любая дуга з'', заканчивающаяся
в той же вершине, что и s, также отображается в четную перестановку.
Следовательно, так как К — узел, то все его дуги отображаются в четные
перестановки. В силу того, что четные перестановки в группе 5з
коммутируют, получаем, что все дуги нашей фундаментальной группы
отображаются в одну и ту же четную перестановку. Таких отображений три.
Если же хотя бы один элемент-«дуга» отображается в нечетную
перестановку, то и все «дуги» отображаются в нечетные
перестановки. Нечетных перестановок всего три: (12), (23), (31), причем сопрягая
одну из них другой, мы будем получать третью. Это в точности
соответствует правильной раскраске ребер в три цвета, при которой ребрам,
инцидентным данной вершине, соответствуют транспозиции.
Таким образом, все гомоморфизмы фундаментальной 1руппы
iri(R*\K) в группу 5з, кроме трех, находятся в однозначном
соответствии с правильными раскрасками узла К. Ш
Отсюда получаем
Следствие 3.2. Инвариант раскрасок не различает зеркальные узлы.
Лекция 4
Полиномы Конвея и Джонса
На прошлой лекции речь шла о старинном и очень сильном
инварианте узлов — фундаментальной группе их дополнения. Однако
этот инвариант неудобен со следующей точки зрения. У одной и той же
группы могут быть разные копредставления и поэтому не всегда ясно,
изоморфны фундаментальные группы дополнения к узлам или нет.
На ближайших лекциях будут рассмотрены инварианты узлов и
зацеплений, задающиеся принципиально иным, комбинаторным
способом, основанным на диаграмме узла (зацепления). Эти инварианты —
полиномы Конвея, Джонса, Александера, Кауфмана, HOMFLY,
значениями которых являются полиномы от одной или двух переменных.
Все эти полиномы представляют собой инварианты ориентированных
узлов (зацеплений).
В этой лекции будет рассказано о трех из них — полиноме Конвея
и полиноме Джонса, названных так в честь их создателей —
английского математика сэра Джона Хортона Конвея [25] и новозеландского
математика Вогана Джонса [44, 45], а также о полиноме Кауфмана,
получающемся из полинома Джонса посредством замены переменной.
§ 1. Полином Конвея
Начнем с самого простого из инвариантных полиномов —
полинома Конвея. Несмотря на относительную простоту, открытие полинома
Конвея было значительным шагом в теории узлов. Впервые была
использована идея так называемых skein relations, что позволило
аксиоматически задавать инварианты узлов. В данной лекции я привожу
собственное доказательство корректной определенности и
инвариантности полинома Конвея.
Пусть даны три диаграммы £+, L~ и L0 ориентируемых узлов
(зацеплений), совпадающие вне кружочков, а внутри кружочков имеющие
вид, показанный на рис. 1.
Замечание 4.1. В дальнейшем две диаграммы L+ и Г, будем называть
переполюсованными по отношению друг к другу, диаграмму L0 — разведенной
по отношению к диаграммам L+ и L". При этом каждая такая тройка диаграмм
£+, L~,L° называется тройкой Конвея.
48 Раздел I. Узлы, зацепления и полиномиальные инварианты
Рис. 1
Замечание 4.2. Число компонент зацепления, имеющего диаграмму £+,
равно числу компонент зацепления, имеющего диаграмму L~ и на
единицу отличается (больше или меньше) числа компонент зацепления, имеющего
диаграмму L0. В частности, если L+ и IT задают узлы, то L° задает двухком-
понентное зацепление.
Мы хотим построить инвариант (со значениями в полиномах от
переменной х) С, который удовлетворял бы соотношению
C(L+)-C(L-) = xC(L°) (0)
для каждой тройки Конвея L+y L~, L°.
Пусть дана диаграмма ориентированного узла и выбрана точка
на ней.
Определение 4.1. Назовем диаграмму восходящей, если, стартуя
с этой точки и, следуя ориентации диаграммы, мы проходим
каждую вершину сначала снизу, а затем сверху.
Упражнение 4.1. Покажите, что узел, имеющий восходящую диаграмму,
тривиален.
Пусть некоторый ориентируемый узел (зацепление) К задан с
помощью своей плоской диаграммы.
Тогда имеет место следующая
Теорема 4.1. Всякий узел приводится к тривиальному виду заменой
некоторых типов перекрестков.
Доказательство. Для случая узла утверждение этой теоремы
следует из того факта, что любая диаграмма узла с помощью изменений
перекрестков может быть переделана в восходящую диаграмму.
В случае зацепления мы можем расположить все компоненты
зацепления «одна над другой», а затем каждую из компонент зацепления
переделываем в восходящую. ■
Теперь будем определять функцию С на диаграммах
ориентированных зацеплений. Нам нужно показать, что для построенных
многочленов выполнены следующие условия:
а) Выполнено соотношение (0).
б) Для каждой диаграммы полиномиальная функция С определена
> однозначно.
Лекция 4. Полиномы Конвея и Джонса
49
в) Полином С инвариантен относительно преобразований
Рейдемейстера.
Теорема 4.2. Существует единственная функция С, определенная
на множестве всех ориентированных диаграмм зацеплений со
значениями в полиномах от одной переменной х, равная единице на
тривиальном узле и удовлетворяющая условиям а), б), в).
Доказательство. Заметим сначала, что если такая функция
существует, то ее значение на зацеплении, одна компонента которого
не зацеплена с остальными, должно быть равно нулю.
Действительно, рассмотрим ориентированное зацепление L и две его диаграммы
с одинаковой тенью, отличающиеся одна от другой лишь в одной
вершине, в которой одна диаграмма имеет петлю в одну сторону,
а другая — в другую (так что одна диаграмма переводится в другую
последовательным применением первого движения Рейдемейстера). Так
как два узла изотопны, то разница значений полинома С на этих двух
диаграммах равна нулю. С другой стороны, в силу соотношения (0)
она равна значению полинома С на несвязной сумме зацепления L
с окружностью, умноженному на ж. В силу произвольности выбора L
получаем, что на зацеплении, одна компонента которого
представляет собой тривиальный узел и не зацеплена с остальными, значение
такой функции (если она существует) должно равняться нулю. Для
зацепления, в котором одна из компонент не зацеплена с остальными,
но не является тривиальным узлом, мы можем многократно применить
соотношение Конвея и свести это зацепление к зацеплениям с отдельно
стоящей незаузленной окружностью, на каждом из которых значение
такой функции должно быть равно нулю. Следовательно, на таких
зацеплениях полином Конвея (если существует) равен нулю.
Будем теперь задавать функцию С на диаграммах узлов и
зацеплений, исходя из того, что значение функции С на тривиальном узле
равно единице, а на тривиальном зацеплении из двух и большего числа
компонент равно нулю.
Сначала зададим значения функции С на длинных зацеплениях,
т. е. на «зацеплениях» с выделенной компонентой, концы которой
уходят в бесконечность (в (-оо, 0) — начало и в (+оо, 0) — конец,
согласно ориентации компоненты). Нетрудно заметить (это остается
в качестве упражнения читателю), что длинные зацепления задают
все изотопические классы зацеплений с отмеченной компонентой,
причем изотопным длинным зацеплениям (т. е. длинным зацеплениям,
переводимым друг в друга движениями Рейдемейстера) соответствуют
изотопные зацепления с отмеченной компонентой и наоборот. Назовем
длинным узлом длинное зацепление из одной компоненты.
50 Раздел I. Узлы, зацепления и полиномиальные инварианты
Будем называть восходящей диаграммой длинного зацепления
диаграмму, на которой все компоненты, кроме выделенной, образуют
восходящую диаграмму зацепления (в обычном смысле), при этом
выделенная компонента лежит «под» остальными компонентами, т. е.
образует проход на всех перекрестках с ними, а также выделенная
компонента является восходящей начиная с (-оо,0), т.е. «с самого
начала» в каждом перекрестке она сперва образует проход, а затем
переход. Легко видеть, что восходящая диаграмма всегда задает
тривиальное длинное зацепление (доказательство аналогично доказательству
теоремы 1).
Далее будем определять значение полинома на диаграмме
длинного зацепления следующим образом. Пусть дана диаграмма L длинного
зацепления с п вершинами. Пусть L = Lo,Lu... ,Xm —
последовательность диаграмм, каждая следующая из которых может быть
получена из предыдущей изменением одного перекрестка, причем
диаграмма Lm — восходящая.
Тогда мы знаем значение C(Lm), оно равно единице или нулю
(в зависимости от того, является L узлом или зацеплением), а с
помощью (0) мы получаем, что
m
C(L) = C(LQ) + х • ]Г) ±С(Кй), (*)
t=i
где Li отличается от JD8-+1 типом одного перекрестка, а К{ — диаграмма,
разведенная в этом перекрестке. Каждая из них имеет п — 1 вершину,
и по предположению индукции на них корректно определены значения
функции С.
Следовательно, существует не более одной функции С,
удовлетворяющей а), б), в).
Покажем, что можно корректно определить функцию С,
удовлетворяющую условиям а), б), в) на диаграммах длинных зацеплений
индукцией по числу перекрестков.
Сначала определим функцию С на диаграммах с нулем
перекрестков (на узлах — единица, на зацеплениях с двумя компонентами
и более — нуль), затем — на диаграммах с одним и двумя
перекрестками. Легко проверить, что это можно сделать корректно, причем так,
чтобы выполнялось соотношение Конвея и на изотопных диаграммах
значения функции С совпадали.
Осуществим шаг индукции.«Любую диаграмму длинного
зацепления L с п перекрестками будем сводить к восходящей
последовательности переполюсований L = Lq} L\,...,Lm, где Lm — восходящая
диаграмма. При многократном применении соотношения Конвея для
Лекция 4. Полиномы Конвея и Джонса
51
вычисления C(L) могут возникнуть следующие проблемы. Во-первых,
восходящая диаграмма Ln может быть выбрана неоднозначно, а, во-
вторых, «путь» к ней Zo, Lyy..., Lm также неоднозначен, так как можно
изменить порядок «переполюсования» перекрестков.
Покажем, что значение функции С не зависит от изменений такого
порядка.
Для этого достаточно показать, что значение функции С не
изменится, если при вычислении С переполюсование в первой, а затем
во второй вершине заменить на переполюсование сначала во второй,
а затем в первой. Выберем произвольно две вершины в качестве первой
и второй. Обозначим через KtJ, t, j G {-f, -,0} зацепление,
отличающееся от исходного только в выбранных двух вершинах, где г означает
состояние первой вершины, a j — состояние второй вершины (+
означает положительное состояние вершины, - означает отрицательное
состояние вершины, ноль — разведение перекрестка, см. рис. 1).
Согласно принятым обозначениям, в силу (0) имеем:
С(К+0) - С(МГ°) = хС(К°°),
С(К°~) - С(К°+) = -хС(К°°).
Здесь все члены С(К+0), С(К~°), С(К°~), С(К0+), С(К°°)
определены корректно в силу предположения индукции, так как количество
перекрестков в соответствующих диаграммах меньше чем п. В
частности, в верхней и нижней формулах С(К°°) означает одно и то же.
Складывая левую и правую части этих формул, получаем
С{К+°) - С{К~°) = С(К0+) - С(К°-). (**)
Рассмотрим разности значений функции С: С(К++) - С(К )
и С(К+~) - С(К~+) (исходного и дважды переполюсованного
зацеплений). Каждую из них можно вычислить двумя способами. При этом
результат вычислений для каждой разности не зависит от способа
вычисления. Действительно, в этих двух случаях получаем
С(К++) - С(К~) = С(К++ - С(К"+) + С(К~+ - С(К~) =
= xC(KQ+) + xC(K°-)
и
С(К++) - С(К~) = С(ИГ++) - С(К+~) + С(К'+) - С(К~) =
= хС(К+0) + хС(К-°).
В силу (**) правые части этих равенств совпадают.
Аналогичные выкладки справедливы для К+~ - К~+.
52 Раздел I. Узлы, зацепления и полиномиальные инварианты
Доказанное означает, что значение функции С на дважды пере-
полюсованном длинном зацеплении определено корректно, если
корректно было определено ее значение на исходном длинном зацеплении.
Диаграмма Lq может быть получена из диаграммы Lm различными
последовательностями переполюсований. Поскольку значение
функции С не изменяется при перестановке двух переполюсований в такой
последовательности, оно не изменяется при любой перестановке
переполюсований. По известному значению C(Lm) можно различными
способами найти значение C(Lo), при этом результат вычислений будет
одним и тем же.
Докажем теперь, что значение полинома С на диаграмме L не
зависит от выбора восходящей диаграммы Lm. Если Lm — длинный
узел, то это очевидно, так как у длинного узла восходящая диаграмма
единственна.
Завершим теперь шаг индукции для случая длинных зацеплений,
т. е. покажем корректность определения C(Lm) для длинных
зацеплений.
Пусть теперь Lm — длинное зацепление и 5 — его тень. Тогда
любые две восходящие диаграммы отличаются друг от друга выбором
точки на каждой компоненте, кроме выделенной, после которой
начинается восхождение, а также «перестановкой» расположения всех
невыделенных компонент одна над другой.
Рассмотрим сначала случай, когда две диаграммы Lm и Lfm
отличаются друг от друга выбором точки на одной невыделенной
компоненте о. Более того, будем считать, что на общей тени диаграмм Lm и L*m
между точками восхождения диаграмм Lm и L'm вдоль по ориентации
компоненты а расположен ровно один перекресток А компоненты а
с самой собой.
Это значит, что L'm получается из Lm переполюсованием
прохода А на переход и отодвиганием начальной точки за перекресток А,
см. рис. 2.
Рис. 2. Выделенная компонента зацепления
Легко видеть, что если развести диаграмму в точке А, то вместо
компоненты а мы получим зацепление из двух компонент, одна из
Лекция 4. Полиномы Конвея и Джонса
53
которых будет лежать сверху другой; более того, полученное
зацепление (из двух компонент) будет иметь восходящую диаграмму, см. рис. 2.
Поскольку изначальная диаграмма длинного зацепления была
восходящей, то и полученная диаграмма длинного зацепления также будет
восходящей, так как две компоненты, полученные из компоненты а,
будут находиться в том же положении относительно остальных
компонент, в каком находилась и компонента а. Следовательно, диаграмма
всего зацепления также будет восходящей. Так как зацепление имеет
п— 1 вершину, то на нем полином С определен корректно и равен нулю.
В силу соотношения Конвея получаем C(L|„) = C(Lm) + х • 0 = C(Lm).
В общем случае, когда точки восхождения не принадлежат соседним
дугам, такое переполюсование нужно проделать несколько раз, и мы
также получим C(L'm) = C(Lm). Это значит, что стартуя с любой
восходящей диаграммы длинного зацепления с тенью 5, мы будем получать
на любом зацеплении с восходящей диаграммой и тенью S значение 0.
Осталось проверить, что при перемене двух «соседних»
невыделенных компонент диаграммы Lm местами, т. е. при замене всех типов
перекрестков между этими двумя компонентами, значение функции С
не изменится. Для этого будем последовательно изменять эти
перекрестки. Разность значений функции С на диаграммах, переполюсованных
в вершине, равна в силу (0) значению функции С от диаграммы,
разведенной в этой вершине, умноженному на х. Разведенная диаграмма
имеет п - 1 вершину; на ней функция С определена корректно.
Покажем, что значение функции С на разведенной диаграмме будет равно
нулю. В таких разведенных диаграммах эти две соседние компоненты
сливаются в одну компоненту т. Хотя такая диаграмма I/ не является
восходящей, на ней выделенная компонента лежит под остальными.
Таким образом, переполюсуя перекрестки, не инцидентные
выделенной компоненте, диаграмму Lf можно свести к восходящей диаграмме,
значение функции С на которой определено корректно и равно нулю,
при этом все разведенные диаграммы будут иметь уже п - 2 вершины
и на каждой из них полином С также определен однозначно. Их можно
также свести к восходящим диаграммам, при этом получив разведенные
диаграммы с п — 2 вершинами, и т. д. Каждый раз мы будем получать
восходящие диаграммы, значение функции С на которых равно нулю,
так как у получающихся зацеплений будет более одной компоненты
(одна — выделенная и еще хотя бы одна). В конце мы получим
«полностью разведенные» диаграммы, диаграммы выделенной компоненты
и нескольких окружностей, лежащих над этой компонентой и не
имеющих перекрестков сами с собой и друг с другом. Очевидно, что такая
диаграмма является восходящей и что для таких диаграмм значение
функции С будет равно нулю.
54 Раздел I. Узлы, зацепления и полиномиальные инварианты
Следовательно, определение значения полинома С на длинном
узле (зацеплении) не зависит от выбора восходящей диаграммы с той же
тенью.
Итак, мы задали значения функции на диаграммах
ориентированных длинных узлов и зацеплений. При этом функция С удовлетворяет
соотношению Конвея, так как для любой тройки Конвея L+yL~~,L°
можно считать, что определение C(L*) происходит посредством пе-
реполюсования на LT в процессе преобразования i+ к восходящей
диаграмме.
Проверим теперь инвариантность функции С относительно
движений Рейдемейстера.
Инвариантность относительно первого движения Рейдемейстера.
Рассмотрим две диаграммы, отличающиеся друг от друга первым
движением Рейдемейстера. Тогда разница значений функции С на этих
диаграммах равна значению функции С на диаграмме зацепления,
являющейся несвязной суммой некоторого зацепления с тривиальным
узлом, что равно нулю.
Инвариантность относительно второго движения Рейдемейстера
выполняется по следующей причине: пусть диаграмма Li
некоторого зацепления с п + 2 вершинами получается из диаграммы L\ с п
вершинами применением к L\ второго движения Рейдемейстера. Тогда
изменением типов перекрестков можно превратить диаграмму L\ в
восходящую, не затрагивая двух вершин, полученных посредством второго
движения Рейдемейстера, примененного к Li. Изменим таким же
образом перекрестки для диаграммы Lj. Каждый раз как «разведенные», так
и переполюсованные диаграммы будут отличаться друг от друга
применением второго движения Рейдемейстера. Для получившихся
восходящих диаграмм значение функции С равно нулю. Все диаграммы
(образующие пары), в которых одна диаграмма переводится в другую вторым
движением Рейдемейстера, имеют соответственно п+1 и п-1 вершин.
Применим к каждой паре ту же операцию, получим пары диаграмм с п
и п — 2 вершинами. Будем продолжать эту операцию до тех пор, пока
не сведем задачу к двум диаграммам с 2 и 0 вершинами соответственно.
В этом случае равенство значений С проверяется непосредственно.
Инвариантность относительно третьего движения Рейдемейстера
также может быть доказана по индукции с помощью сведения двух
диаграмм к восходящим диаграммам, не затрагивающего трех
перекрестков, к которым и применяется движение Рейдемейстера. При
этом задача сводится к случаю пары разведенных диаграмм, количество
вершин которых после многочисленных разведений может быть
доведена до трех; в случае трех вершин равенство значений С проверяется
неЬосредственно.
Лекция 4. Полиномы Конвея и Джонса
55
Осталось проверить, что полином С определен корректно на
зацеплениях без выделенной компоненты, т. е. что при замене выделенной
компоненты зацепления значение полинома С не изменится.
Пусть С — длинное зацепление с выделенной компонентой а,
a Ca(L) — значение на нем полинома С. Выберем другую компоненту
зацепления Ь и докажем, что Сь{Ь) = Ca(L). Для этого будем перепо-
люсовывать перекрестки на диаграмме L до тех пор, пока она не станет
восходящей, причем самой нижней компонентой является а, а
следующей после нее — Ь. Обозначим получившуюся диаграмму через L1.
Значение Съ{1) получается также, если сводить диаграмму к восходящей
диаграмме L", где самой нижней компонентой является 6, а чуть выше
нее - а. Получаем Cb(L) - Ca(L) = Ch(L') - Ca(L') = Ca(L") - Св(Г),
но диаграммы L* и L" изотопны, поэтому Са(ь") = Св(Х') = 0, т. е.
Q(i) = C.(L). ■
Определение 4.2. Назовем построенный полиномиальный
инвариант С полиномом Конвея.
Замечание 4.3. Другое доказательство существования, единственности и
инвариантности полинома Конвея относительно движений Рейдемейстера будет
дано с помощью полинома Александера, получающегося из него с помощью
замены переменной.
Упражнение 4.2. Вычислите значение инварианта Конвея на правом
и левом трилистниках и убедитесь, что полином Конвея не различает эти узлы.
Упражнение 4.3. Вычислите значение полинома Конвея на восьмерке.
Упражнение 4.4. Докажите, что полином Конвея не различает зеркальных
зацеплений.
Указание 4.1. Воспользуйтесь индукцией по количеству перекрестков.
§ 2. Полином Джонса
Из того, что полином Конвея равен нулю на очень большом классе
нетривиальных зацеплений, видно, что он очень грубый и поэтому
стоило бы искать более тонкий инвариант узлов.
Один из таких инвариантов — полином Джонса.
Открытие полинома Джонса в 1985 году [44] было важной вехой
в теории узлов. Как выяснилось, полином Джонса так же, как и полином
Конвея, допускает аксиоматическое описание с помощью skein relations.
Несколько лет спустя Уиттен нашел обобщение полинома Джонса
на узлы в трехмерных многообразиях, см. [91, 7]. За эти работы Джонс
вместе с Уиттеном получили филдсовские медали.
56 Раздел I. Узлы, зацепления и полиномиальные инварианты
Замечание 4.4. Вообще говоря, полином Джонса, как и некоторые другие
полиномиальные инварианты узлов, не является полиномом в обычном смысле
слова, а является полиномом Лорана — полиномом от положительной и
отрицательной степеней переменной q112. В дальнейшем будем называть полиномы
Лорана просто полиномами.
Построение полинома Джонса начнем с того, что сопоставим
каждой диаграмме L неориентированного зацепления полином (L),
часто называемый скобкой Кауфмана (см., например, [49]).
Будем искать скобку Кауфмана как полином от трех переменных а,
Ъ, с, удовлетворяющий аксиоматическим соотношениям:
(L) = a(LA) + b(LB); (1)
(LuO) = c{L); (2)
(О) = Ь (3)
L Ъд Lb L
Рис.3
Здесь мы рассматриваем произвольные диаграммы Ь, Z/, La и Lb,
совпадающие вне кружочков, а внутри ведущие себя так, как показано
на рис. 3. Кроме того, символ О означает тривиальный узел, а символ
U — несвязную сумму.
Попытаемся теперь наложить условия на переменные а, Ъ, с
так, чтобы получающийся полином был инвариантен относительно
преобразований Рейдемейстера.
Используя соотношения (1) и (2) при применении второго
движения Рейдемейстера Пг» см. рис.4, мы получаем соотношение
(Р) = (а2 + Ь2 + abc)(Q) + ab(R),
где в диаграмме Р присутствуют две вертикальные ветви узла,
проходящие два раза одна над другой (левая над правой), в диаграмме R
эти ветви не пересекаются, а в диаграмме Q они заменены двумя
горизонтальными; в остальном все три диаграммы совпадают.
Таким образом, наш полином инвариантен относительно £2г если
и только если аЬ = 1 и а2 + Ь2 + аЬс = 0.
Поэтому положим Ь = а"1 и с = -а2 - а"2.
Следовательно, полином, который мог бы быть инвариантным
относительно Пг> единствен. Оказывается, такой полином, если он
существует, будет при этом инвариантен и относительно движения Пз-
Лекция 4. Полиномы Конвея и Джонса
57
7\ ^ V
v>=a<0>+6<0 )=
=«[«( О >+*< 0 я+*<0 >+*< О >]=
= (а2 + Ь2 + аЬс)(Ч^Х)+абЛ (>.
Рис.4
Действительно, пусть даны две диаграммы Р и Q,
получающиеся одна из другой третьим движением Рейдемейстера. Пусть А —
вершина Р и Q, через которую «проходит» ветвь узла. Применим
соотношение (1) к вершине А для узлов Р и Q. Получим два уравнения,
в левой части которых будут стоять значения (Р) и (Q), а в правой —
суммы двух слагаемых.
Далее, дважды используя инвариантность нашего полинома
относительно Ь.2 и сравнивая правые части наших соотношений, увидим,
что они совпадают. Значит, равны и левые части. Это и означает
инвариантность нашей скобки (L) относительно £2з-
Однако, когда мы исследуем наш полином на инвариантность
относительно первого движения Рейдемейстера, нас постигает неудача:
при добавлении петельки наш полином умножается либо на -а3, либо
на -о~3. Действительно, применяя соотношение (1) к вершине, в
которой есть петля, мы получим сумму из двух диаграмм, полином Джонса
на одной из которых равен р(-а2 - a~2)(L), а на другой — p~l(L), где
р = a±l в зависимости от того, какой из двух типов первого движения
мы применяем. Суммируя эти два значения, мы получаем (-а±3)(£).
Мы доказали некоторые свойства, которыми должна была бы
обладать скобка Кауфмана, исходя из аксиом, которым она
удовлетворяет. При этом мы не показали главного — того, что такой полином
существует.
Теорема 4.3. Существует единственная функция с полиномиальными
значениями, удовлетворяющая соотношениям (1)—(3).
Доказательство. Пусть дана диаграмма L неориентированного
зацепления, имеющая п перекрестков (вершин). Занумеруем все вершины
диаграммы L числами от единицы до п.
Каждому перекрестку мы можем поставить в соответствие его
состояние, т. е. сделать «разведение» двух дуг одним из двух способов,
обозначаемых буквами А и В, см. рис. 5.
58 Раздел L Узлы, зацепления и полиномиальные инварианты
Рис.5
Под состоянием диаграммы будем понимать набор состояний всех
ее перекрестков. Тогда диаграмма D может иметь 2я состояний.
Выберем состояние s диаграммы D. Пусть a(s) и p(s) — количества
перекрестков в состояниях А и В соответственно, a j(s) — количество
окружностей диаграммы D в состоянии s.
Если мы уничтожим все перекрестки диаграммы с помощью
соотношения (1), а затем воспользуемся соотношениями (2) и (3) для
вычисления полиномов полученных диаграмм, мы получим
{D) = J2 а^-^-в2 - а"2)*)"1, (4)
8
где сумма берется по всем состояниям диаграммы D.
Таким образом, мы показали единственность полинома,
удовлетворяющего аксиоматическим свойствам (1)-(3).
Заметим, что формула (4) показывает не только единственность
полинома (D), но и его существование. Действительно, мы можем
просто определить полином (D) способом (4). Тогда соотношения (2)
и (3) выполняются для такого полинома с очевидностью, а
доказательство свойства (1) следует из разбиения суммы на те слагаемые,
в которых данный перекресток находится в положении Л, и те, в
которых он находится в положении В. Из этого следует инвариантность
скобки Кауфмана относительно второго и третьего движений
Рейдемейстера. ■
Итак, корректно заданная скобка Кауфмана не инвариантна
относительно первого движения Рейдемейстера. Тем не менее по ней можно
построить полином, инвариантный относительно всех трех движений
Рейдемейстера. Рассмотрим ориентируемую диаграмму зацепления L
и сопоставим ей число w(L) следующим образом. Для каждого ее
перекрестка мы ставим в соответствие плюс или минус единицу (это число
называется local writhe number, см. рис. 6). Суммируя эти числа, мы
и получаем значение w(L).
Упражнение 4.5. Покажите, что число w(L) является инвариантом
относительно второго и третьего движений Рейдемейстера.
Относительно первого движения Рейдемейстера w(L) не является
инвариантным, а именно, оно изменяется на ±1.
Лекция 4. Полиномы Конвея и Джонса
59
Рис.6
Зададим на ориентированной диаграмме зацепления L функцию
X(L) = (-a)-3*LH\L\),
зде неориентированная диаграмма \L\ получена из диаграммы L
забыванием ориентации.
В дальнейшем будет доказана следующая теорема.
Теорема 4.4. Полином X(L) является изотопическим инвариантом
ориентированного зацепления.
Определение 4.3. Этот инвариант называется полиномом
Кауфмана.
Сначала мы определили скобку Кауфмана аксиоматически с
помощью свойств (1)-(3). Затем было показано, что такой полином (L)
существует и единствен. И уже потом мы определили полином
Кауфмана X(L) посредством (L). Впрочем, полином X(L) также допускает
аксиоматическое определение некоторыми простыми соотношениями.
Для их получения воспользуемся свойством (1) для полинома {L):
(L') = a-l(LA) + a(LB).
Умножая первое равенство на -а"1, а второе на а и складывая
левые и правые части, получим
a{L')-a-l(L) = {a2-a-2)(LB),
a(L+)-a-l{L-) = (a2-a-2)(L°),
где ориентированные диаграммы L* и L0 определяются так же, как это
было сказано в начале лекции.
Перейдем теперь непосредственно к определению полинома
Джонса. Для этого сделаем в полиноме Кауфмана X(L) замену а = q"^A
и получим полином от q±lt4.
60 Раздел I. Узлы, зацепления и полиномиальные инварианты
Определение 4.4. Этот полином обозначают V(L) и называют
полиномом Джонса ориентированного зацепления.
Упражнение 4.6. Вычислите значение полинома Джонса на кольцах Бор-
ромео и зацеплении Хопфа.
Полином Джонса удовлетворяет следующим соотношениям:
q~lV(L+) - qV(L~) = (q1'2 - <Г'/2)7(А (1')
V(LUO) = -(q-l/2 + q1/2)V(L), (2')
7(0) = 1. (3')
Соотношения, в которых три слагаемых L+, IT и L° участвуют
с коэффициентами, зависящими от переменных, называются skein
relations или соотношениями типа Конвея.
На таких соотношениях типа Конвея аксиоматически строятся
не только полиномы Джонса, Кауфмана и Конвея, но также и
некоторые другие, речь о которых пойдет на следующей лекции.
На следующей лекции также будут затронуты некоторые свойства,
которыми обладает полином Джонса.
Упражнение 4.7. Вычислите полином Джонса на правом и левом
трилистниках и покажите тем самым, что два трилистника не изотопны.
Замечание 4.5. Неизотопность двух трилистников — факт, показанный еще
Деном, см. [28].
Как мы видим, полином Джонса — достаточно сильный инвариант,
который, тем не менее, может быть довольно просто вычислен.
§ 3. Таблица узлов
Владея таким сильным инвариантом, каким является полином
Джонса, мы можем провести классификацию узлов небольшой
сложности (до 7 включительно). Более точно, узлов, у которых есть
диаграммы с числом пересечений не более семи. Мы приведем лишь таблицу
простых узлов, при этом не будем различать узел и его зеркальное
отражение, даже если они не изотопны, как в случае с трилистником.
Для классификации простых узлов перечислим сначала все возможные
плоские диаграммы узлов (с точностью до плоской изотопии) с
количеством перекрестков, меньшим семи (эта задача является простой,
но требует большого перебора; здесь она разбираться не будет). После
этого вычислим полиномы Джонса на полученных диаграммах.
Оказывается, что если двум диаграммам с числом пересечений меньшим
семи соответствует один и тот же полином Джонса, то они изотопны
Лекция 4. Полиномы Конвея и Джонса
61
с помощью преобразований Рейдемейстера.В итоге мы получаем
таблицу простых узлов с не более, чем семью перекрестками с точностью
до зеркальных отражений. Таблица простых узлов до восьми
перекрестков включительно (для которой с помощью полинома Джонса
мы провели классификацию лишь для узлов с не более, чем семью
перекрестками) приведена на рис. 7.
Рис. 7. Таблица простых узлов с не более, чем 8 перекрестками
Определение 4.5- Назовем диаграмму узла (зацепления)
альтернированной, если при движении по любой связной компоненте
проход сменяется переходом, а переход — проходом. Узел
(зацепление), имеющий альтернированную диаграмму, называется
альтернированным.
Интересно, что все диаграммы узлов с не более, чем семью
перекрестками — альтернированные, для восьми перекрестков это неверно;
мы вернемся к этому вопросу на следующей лекции.
62 Раздел I. Узлы, зацепления и полиномиальные инварианты
Составные узлы с не более, чем восемью перекрестками, также
легко пересчитываются. Они представляют собой связную сумму
трилистников (двух правых, двух левых или правого и левого), связную
сумму одного из трилистников с восьмеркой, связную сумму одного
из трилистников с узлом 5i или 52 и связную сумму двух восьмерок.
Более полную таблицу (до девяти перекрестков включительно)
можно найти в [128] или в [43].
Лекция 5
Свойства полинома Джонса,
Полиномиальные инварианты
В этой лекции речь пойдет о различных применениях полинома
Джонса, а также о других полиномиальных инвариантах, основанных
на соотношениях типа Конвея — полиномах HOMFLY и Джонса от двух
переменных. В конце лекции будет сказано несколько слов о полиноме
Кауфмана от двух переменных, который является естественным
обобщением полинома Кауфмана от одной переменной. При этом название
полинома HOMFLY является аббревиатурой, происходящей от
фамилий шести авторов, предложивших его [42]. Нужно также отметить, что
несколько позже он был переоткрыт другими авторами, см. [77].
§ 1. Свойства полинома Джонса
Напомним, что полином Джонса удовлетворяет трем
соотношениям типа Конвея:
q-W(L+) - qV(L~) = (ql>2 - <f ,/2)V(A (0
V(LuO) = -(q-l<2 + ql'2)V(L), (2')
V(0) = 1. . (3')
Сначала рассмотрим некоторые интересные свойства полинома
Джонса и красивые следствия из них.
Теорема 5.1.
а) Полином Джонса не меняется при обращении узла, т. е. при замене
направления обхода узла на противоположное.
б) При зеркальном отражении узла у полинома Джонса происходит
замена д—► q~l.
Доказательство. Утверждение пункта а) легко доказывается
индукцией по количеству перекрестков диаграммы с учетом того, что при
замене ориентации узла на противоположную положительные
перекрестки остаются положительными, а отрицательные —
отрицательными. База индукции состоит в проверке утверждения теоремы для
диаграммы узла или зацепления без перекрестков.
64 Раздел I. Узлы, зацепления и полиномиальные инварианты
Пункт б) также доказывается индукцией по количеству
перекрестков. База индукции очевидна. Пусть теперь L+,L~,L° — тройка Кон-
вея, а Z+, Ь'_, Lq — диаграммы, получаемые из 2/1", L~, L° заменой всех
типов перекрестков. Тогда очевидно, что L'-yL+,LfQ — также
тройка Конвея. По предположению индукции можно считать, что V(L' )
получается из V(L°) заменой q —► q~l. Будем также предполагать,
что аналогичное утверждение верно для диаграмм 1Г,2/~. Применим
соотношение типа Конвея (1). Получим:
V(L+) = f(V(L-) + q-l(q1'2 - q~Xl2)V(L%
V(L'+) = q-2(V(l/-) ~ q\q112 - <f ,/2M^)),
откуда видно, что V(L'+) получается из V(L+) заменой q на q~l.
Так как это утверждение верно для тривиального зацепления (и,
следовательно, для его диаграммы с произвольной тенью), то это
утверждение верно и для любой диаграммы с такой же тенью. Следовательно,
оно верно для всех узлов и зацеплений. ■
Теорема 5.2. Для произвольных ориентированных зацеплений К\
и К2 имеет место равенство V(Ki#K2) = V(K\) • V(K2).
Доказательство. Доказательство будем проводить для полинома
Кауфмана, так как он получается из полинома Джонса заменой
переменной.
Для случая полинома Кауфмана достаточно лишь заметить, что
скобка Кауфмана является мультипликативной относительно операции
взятия связной суммы (это явно следует из формулы (4.4), а число w(L)
является аддитивным относительно операции связной суммы). ■
Аналогично доказывается
Теорема 5.3. Для произвольных ориентированных узлов К\ и Кг
имеет место равенство V(KX U К2) = ~(q~l/2 + ql,2)V(Ki) • V(K2).
Замечание 5.1. Это свойство полинома Джонса точно так же доказывается
и для ориентируемых зацеплений, какую бы связную сумму мы не брали.
Пример 5.1. Рассмотрим два двухкомпонентных зацепления, показанных
на рис. 1 слева и справа. В силу замечания 1 их полиномы Джонса совпадают.
Однако эти зацепления не изотопны, так как не являются изотопными их
компоненты.
Лекция 5. Свойства полинома Джонса
65
ФсК?
РисЛ
Этот пример показывает, что полином Джонса не всегда
различает зацепления. Причина тому — неоднозначность операции взятия
связной суммы.
Впрочем полином Джонса не всегда различает и узлы. Докажем
лемму.
Пусть дана диаграмма L зацепления (узла), на плоскости которой
выделена область 17, симметричная относительно некоторой прямой i,
такая, что граница 8U представляет собой прямоугольник со сторонами,
параллельными осям координат. Пусть U пересекается с ребрами
диаграммы L только трансверсально ровно в четырех точках, две из которых
расположены на верхней стороне прямоугольника, а две — на нижней.
Предположим, что эти точки симметричны относительно прямой I.
Рассмотрим диаграмму L\ совпадающую с L вне U и полученную
из диаграммы L отражением относительно I внутри U, см. рис. 2.
Лемма 5.1 [123]. При этих условиях V(L) = V(L').
Доказательство. При симметрии относительно прямой знаки е =
±1 перекрестков диаграммы, сумма которых равна wy не
изменяются, следовательно, w(L) = w(L'). Осталось доказать неизменность
скобки Кауфмана при таком отражении. Каждому состоянию
диаграммы L естественным образом сопоставляется состояние диаграммы L1,
поэтому осталось лишь заметить, что после уничтожения
перекрестков L и L' при соответствующих состояниях диаграмм количество
связных компонент зацепления останется без изменения. Последнее
очевидно. ■
Пример 5.2. Можно показать, что узлы, изображенные на рис. 2, не
являются изотопными. Следовательно, полином Джонса не различает эти узлы.
Замечание 5.2. До сих пор неизвестно, различает ли полином Джонса
тривиальный узел, т. е. верно ли, что если V(K) = 1, то К — тривиальный
узел, см. список нерешенных проблем в приложении 2. Поэтому по полиному
Джонса нельзя понять, является узел простым или нет.
66 Раздел I. Узлы, зацепления и полиномиальные инварианты
Рис.2
В силу того, что полином Джонса удовлетворяет skein relations,
в которых встречаются лишь целые и полуцелые степени переменной q,
он является полиномом не просто от q±l^, а от q±xl2. Более того, имеет
место
Теорема 5.4.
а) Если количество компонент ориентированного зацепления L
нечетно {например, если L — узел), то полином Джонса V(L) содержит
лишь целочисленные степени q,
б) Если количество компонент ориентированного зацепления L
четно, то полином Джонса V(L) содержит лишь члены вида д^2*-1"2,
к е Z.
Доказательство. Сначала заметим, что в силу соотношений (2'), (3')
значение полинома Джонса на тривиальном m -компонентном
зацеплении равно
(_д-1/2_д1/2)Я.-1в
Следовательно, для тривиального зацепления утверждение теоремы
верно.
Далее можно вычислять значение полинома Джонса для
произвольных зацеплений с помощью соотношения (1'), зная значения полинома
Джонса для тривиальных зацеплений.
Будем вести доказательство нашей теоремы индукцией по числу
перекрестков диафаммы. Пусть утверждение теоремы верно для числа
Лекция 5. Свойства полинома Джонса
67
перекрестков меньшего п и L — диаграмма с п перекрестками. Мы
можем сводить ее к диаграмме тривиального зацепления, используя
соотношение (1'). Так как для диаграммы тривиального зацепления
утверждение теоремы верно, нам нужно проверить, что оно остается
верным и при изменении типа перекрестков.
Итак, пусть даны три диаграммы L+yL~,L°, причем £+ и L~
имеют п вершин, a L0 имеет п - 1 вершину. При этом утверждение
теоремы верно для L°, а также, по предположению индукции, и для
одной из диаграмм L+,L~. Без ограничения общности можно считать,
что эта диаграмма — L".
Для завершения доказательства теоремы осталось лишь заметить,
что:
1) количества компонент зацеплений £+ и L" совпадают,
следовательно они имеют одинаковую четность;
2) количества компонент зацеплений L+ и L0 имеют разную
четность (более того, они различаются на ±1). ■
Упражнение 5.1. Аналогичным образом покажите, что значение
полинома Конвея на зацеплениях с нечетным числом компонент (например, на узлах)
содержит только члены четной степени и наоборот, на зацеплениях с четным
числом компонент — лишь члены нечетной степени.
Определение 5.1. Определим длину полинома Джонса как
разность старшей и младшей степеней мономов, в него входящих.
Так, например, для тривиального узла существует ровно один
моном, являющийся как старшим, так и младшим, поэтому длина
полинома Джонса равна нулю.
Оказывается, длина полинома Джонса обладает рядом
замечательных свойств, из которых следует ряд красивых теорем теории узлов.
Перечислим некоторые из них.
Установим свойства значений полинома Джонса на
альтернированных диаграммах узлов и зацеплений. Диаграммы трилистника и
восьмерки являются альтернированными, см. рис. 3.
Рис.3
Теорема 5.5. Пусть диаграмма L узла (зацепления) является связной
и имеет п вершин. Тогда длина полинома Джонса V(L) меньше или
равна п.
68 Раздел I. Узлы, зацепления и полиномиальные инварианты
Доказательство. Воспользуемся тем фактом, что полином Джонса
получается из полинома Кауфмана с помощью замены переменной,
и попробуем подсчитать длину полинома Кауфмана от зацепления L.
Так как полином Кауфмана получается из скобки Кауфмана
умножением на некоторую степень а, то их длины совпадают.
Воспользуемся формулой из предыдущей лекции
<£> = £(-а)-«-«'>(-а2 - a-2?"-1, (1)
где сумма берется по всем 2П состояниям диаграммы L, a(s) и /3(з) —
количества перекрестков в состояниях а и Ъ, а у(з) — количество
окружностей диаграммы D в состоянии з.
Рассмотрим то состояние з, при котором а(з) = п, /?(з) = 0.
Тогда степень старшего члена, который дает это состояние в сумме (1),
равна 2(7(з) — 1) + п. Легко видеть, что у любого другого состояния
степень старшего члена не больше, чем 2(7(3) - 1) + п. Пусть s —
состояние, противоположное з, т.е. получаемое из з заменой всех
состояний А на Б и наоборот. Тогда минимальная степень в сумме (1)
будет равна -2(7(3) - 1) - п.
Обозначим наше множество из 7(*)+7(*) окружностей через М(L)
и заклеим эти окружности дисками. Поскольку каждая окружность
из М естественным образом отображается в тень зацепления, то при
заклеивании окружностей дисками получим некоторое двумерное
многообразие без края, которое будем называть 2-многообразием,
соответствующим диаграмме L. Воспользуемся тем фактом, что эйлерова
характеристика любого двумерного многообразия без края не
превышает двух и равна двум в случае сферы. Получим неравенство для
эйлеровой характеристики:
n-2n + 7(*) + 7(S) <2=*7(s)+7(S) ^2 + n.
Следовательно, длина скобки Кауфмана на диаграмме L не
превышает 2(7(3)+7(£) - 2) + 2п ^ 4п, отсюда длина полинома Джонса V(L)
не превышает п. ■
Существуют узлы, для которых последнее неравенство
превращается в равенство.
В силу утверждений, сформулированных по ходу доказательства
теоремы 5, для этого необходимо и достаточно выполнение следующих
условий:
1) в состоянии з, при котором а(з) = п, /3(з) = 0 (как и в
противоположном состоянии) многообразие, полученное заклеиванием кривых
из М(з) дисками, гомеоморфно сфере;
Лекция 5. Свойства полинома Джонса 69
2) члены при старшей и младшей степенях в сумме (1) не
сокращаются.
Определение 5.2. Назовем вершиной распадения диаграммы D
зацепления вершину, через которую можно провести замкнутую
кривую, пересекающую диаграмму D лишь в единственной точке —
этой вершине. В частности, вершина, из которой выходит петля
(такая, которая появляется при первом движении Рейдемейстера)
является вершиной распадения.
Теорема 5.6. Пусть связная диаграмма L с п вершинами является
альтернированной и не имеет вершин распадения. Тогда полином
Джонса V(L) имеет длину п.
Доказательство. Условие 1) выполняется очевидно: в случае
альтернируемой диаграммы окружности из М ограничивают области, на
которые тень диаграммы L делит плоскость (сферу). Поэтому, заклеивая
эти окружности дисками, мы получим сферу, тем самым условие 1)
будет выполнено.
Условие 2) докажем только для старшей степени (для младшей
доказывается аналогично). Итак, пусть з — состояние диаграммы L,
в котором п окружностей находится в состоянии А и 0
окружностей в состоянии В. Мы хотим найти состояния, дающие в сумму (1)
старший член той же степени, что и для случая состояния з. При
изменении в состоянии з некоторого набора из ife перекрестков
разница a - р уменьшается на 2fc, а количество окружностей из М
изменяется на некоторое число, четность которого совпадает с
четностью к. Действительно, изменяя состояние одного перекрестка, мы
изменяем количество элементов множества М на единицу. При этом
для того, чтобы это состояние з1 давало старший член той же
степени, необходимо, чтобы у(з') = *у(з) 4- к. Это значит, что каждый
раз, изменяя перекресток «в сторону з'», мы увеличиваем мощность
множества М на единицу. При этом, чтобы получить состояние з1,
дающее старший член той же степени, что и состояние s, нужно, чтобы
на каждом из А: шагов от з к s' количество окружностей
увеличивалось на единицу. Предположим, что такое состояние з1, отличное от з
существует. Рассмотрим «первый» перекресток fc, в котором мы
изменяем состояние диаграммы L на пути от состояния з к состоянию з1.
При изменении состояния в этом перекрестке мощность множества М
должна увеличиться, это значит, что некоторая окружность из М
два раза проходит через к. Зададим параметризацию этой
окружности параметром t Е (0,2тг). Тогда существуют пары точек, в которых
окружность самопересекается (одна из них состоит из двух прообразов
70 Раздел I. Узлы, зацепления и полиномиальные инварианты
перекрестка к). Такая вершина диаграммы как раз является вершиной
распадения. Противоречие завершает доказательство теоремы. ■
Из этой теоремы можно вывести два красивых следствия.
Следствие 5.1. Зацепление (в частности, узел), имеющее связную
альтернированную диаграмму без точек распадения, не изотопно
тривиальному зацеплению.
Доказательство. Для узла это утверждение очевидно, так как
полином Джонса тривиального узла равен единице.
Предположим, что существует альтернируемая диаграмма без
петель тривиального зацепления из п компонент. Длина полинома
Джонса такого зацепления равна п -1. Таким образом, ее количество вершин
должно быть равно п - 1. Следовательно, одна из компонент С
зацепления не имеет перекрестков с другими компонентами. Из этого
следует несвязность диаграммы. Противоречие. ■
Следствие 5.2. Если у зацепления L имеется некоторая связная
альтернированная диаграмма Den вершинами, среди которых нет
вершин распадения, то оно не имеет связных диаграмм с меньшим
числом вершин.
Хотелось бы перечислить все случаи, при которых длина полинома
Джонса того или иного зацепления равна количеству перекрестков
этого зацепления.
Из следующей теоремы следует знаменитое решение гипотезы
Тэйта, сформулированной в [80]. Эта гипотеза утверждала, что если
у простого узла есть альтернированная диаграмма, то она —
минимальна. Она существовала в нерешенном виде почти сто лет и была
доказана в 1987 году К. Мурасуги [75], а также (независимо)
Кауфманом [49] и Тилстуэйтом [49]; здесь мы приведем новое доказательство
теоремы Мурасуги, основанное на понятии d-диаграммы. Подробнее
теория rf-диаграмм изложена в четвертой часта, лекции 17-20.
Теорема 5.7. Пусть для связной диаграммы L некоторого зацепления
с п перекрестками полином Джонса V(L) имеет длину п. Тогда
диаграмма L является связной суммой нескольких альтернированных
диаграмм без вершин распадения.
Доказательство. Пусть полином Джонса от диаграммы
зацепления L с п вершинами имеет длину п. Тогда, во-первых, зацепление L
не имеет вершин распадения, так как иначе у данного зацепления есть
диаграмма сп-1 вершиной.
Во-вторых, из рассуждений, приведенных выше, следует, что имеет
место равенство
7(*) + 7(*) = 2 + я,
Лекция 5. Свойства полинома Джонса
71
где s и s — два состояния диаграммы, в первом из которых все
перекрестки находятся в состоянии А, а во втором — в состоянии В.
Следовательно, поверхность, полученная заклеиваниями циклов
состояния 8 и состояния з, гомеоморфна сфере.
Рассмотрим тень диаграммы L. Для данной тени существует
альтернированная диаграмма L* — и ей соответствуют свои состояния t
и i, — для которой поверхность, получаемая заклеиванием
соответствующих циклов, является сферой. Если диаграмма L совпадает с
диаграммой L' или с зеркальным отражением диаграммы L\ то L является
альтернированной диаграммой и теорема доказана.
В противном случае выберем обход тени S зацепления L, т.е.
замкнутый путь, состоящий из ребер тени S и проходящий каждое
ребро тени зацепления L единожды, а каждую вершину — дважды,
поворачивающий в каждой вершине с ребра на соседнее. Можно легко
показать, что такой обход существует.
Если такой путь «развести» в каждой вершине, т. е. немного
отодвинуть друг от друга две части пути, проходящие через данную вершину
и соединить точки на двух близких дугах хордой, мы получим вложение
в плоскость окружности с некоторыми хордами.
Легко видеть, что эти хорды разбиваются на два семейства —
внутренних и внешних относительно данной окружности. Все эти хорды
взаимно не пересекаются. Если же рассмотреть стандартное вложение
окружности в плоскость, а хорды изображать прямолинейными
отрезками с заданными концами, то хорды каждого из семейств не будут
пересекаться между собой. Согласно [107], такая диаграмма называется
d-диаграммой.
Обозначим эту d-диаграмму через D.
Итак, каждая плоская диаграмма J, соответствующая тени 5,
такая, что 2-многообразием, соответствующим диаграмме J,
является сфера, получается посредством вложения соответствующей d-
диаграммы D в плоскость (сферу). Действительно, каждое вложение
в сферу можно трактовать как приклеивание клеток к графу 5,
учитывающее соотношение противоположности ребер в каждой вершине.
Для того, чтобы вложить диаграмму D в плоскость, нужно ее хорды
разделить на два семейства непересекающихся хорд.
Назовем d-диаграмму связной, если для каждых ее двух хорд а и &
найдется семейство а = а^ а^ ..., а„ = Ь хорд, где каждые две соседние
хорды пересекаются между собой.
Очевидно, что если диаграмма D — связна, то ее можно вложить
в плоскость двумя способами (два семейства хорд определены, осталось
лишь выбрать, какое из них внутреннее, а какое — внешнее). Эти два
72 Раздел I. Узлы, зацепления и полиномиальные инварианты
вложения дают две альтернированные диаграммы — L1 и ее зеркальное
отражение.
Если же диаграмма D несвязна, то наша диаграмма L в точности
является связной суммой альтернированных диаграмм. ■
Аналогично доказательству теоремы 7 можно доказать следующую
теорему.
Теорема 5.8. Пусть для диаграммы L со связной тенью и п пере-
крестками многообразие; полученное заклеиванием циклов состояний s
и 8 {где все перекрестки имеют состояния А или все имеют
состояние В) гомеоморфно сфере. Тогда L представляет собой связную
сумму нескольких (возможно, одного) альтернированных зацеплений.
Из теорем 7, 8 вытекает
Следствие 5.3. Пусть L — простое зацепление, имеющее неальтер-
нированную диаграмму ll со связной тенью и с п вершинами. Тогда
длина полинома Джонса V(L) меньше п.
Пример 5.3. Теперь мы готовы привести пример неальтернированного
простого узла, т. е. простого узла, не имеющего альтернированной диаграммы.
Рассмотрим узел, диаграмма которого показана на рис. 4.
#
Рис.4
Эта диаграмма имеет 8 перекрестков, при этом значение полинома Джонса
на данном узле равно произведению значений полиномов Джонса на правом
и левом трилистнике, т. е. имеет длину 6. Это означает (в силу инвариантности
полинома Джонса), что данный узел не изотопен узлам 6i, 62,63, приведенным
на рис. 6 предыдущей лекции. С другой стороны, так как длина значения
полинома Джонса на данном узле равна шести и данный узел является
простым, то, при наличии у него альтернированной диаграммы, у него должна
была бы быть альтернированная диаграмма без петель. Такая диаграмма
должна была бы иметь шесть перекрестков. Противоречие показывает отсутствие
альтернированной диаграммы у данного узла.
Чтобы дополнить картину об альтернируемых диаграммах узлов
сформулируем еще один результат.
Теорема 5.9. От одной альтернированной диаграммы узла к другой
можно перейти последовательностью переворачиваний следующего
вида:
Лекция 5. Свойства полинома Джонса
73
Рис.5
Эта теорема долгое время также была гипотезой, предложенной
Тейтом. По-английски она называется Taitflyping conjecture. Она
просуществовала до 1993 года и была доказана в [73].
§ 2. Другие полиномы,
основанные на соотношениях типа Конвея
Поговорим теперь об инвариантах узлов от двух переменных —
полиномах Джонса, Кауфмана и HOMFLY.
Мы не будем доказывать существования, единственности и
инвариантности этих полиномов. Скажем лишь, как они строятся, т.е.
приведем их соотношения типа Конвея.
Итак, полиномы Джонса и HOMFLY от двух переменных
являются инвариантными огаосительно изотопии зацеплений функциями
со значениями в полиномах от двух переменных, их значения на
тривиальном узле равны единице, при этом они удовлетворяют следующим
соотношениям типа Конвея:
Полином Джонса X от двух переменных A, q:
1
:#(£+) - V\y/qX(L~) =
V*-i
Xtf).
Полином HOMFLY V от двух переменных x,t:
xT(L+)-tV(L-) = r(L0).
Замечание 5.3. Полином HOMFLY также иногда определяется
соотношением
xV(L+) - x"lV(L-) = yV(L°),
см. [103].
Оба эти полинома существуют и единственны в предположении их
равенства единице на тривиальном узле, верности соотношения типа
Конвея и инвариантности относительно изотопии (движений Рейде-
мейстера и плоской изотопии).
Полином Джонса от двух переменных является «самым сильным»
из всех перечисленных ранее инвариантных полиномов в том смысле,
что каждый из них легко получается их него с помощью замены
переменной.
74 Раздел I. Узлы, зацепления и полиномиальные инварианты
Это значит, что если один из вышеперечисленных полиномов
различает два неизотопных зацепления, то и полином Джонса от двух
переменных их также различает.
Упражнение 5.2. Найдите соответствующие замены переменной для:
1) полинома Конвея,
2) полинома Джонса от одной переменной,
3) полинома HOMFLY.
§ 3. Полином Кауфмана от двух переменных
Осталось сказать несколько слов о полиноме Кауфмана от двух
переменных. Как и полином Кауфмана от одной переменной, он
строится посредством некоторого полинома для диаграмм неориентируемых
зацеплений, а затем нормируется некоторым множителем.
Полином Кауфмана от двух переменных (см., например, [48]),
определяется следующим образом.
Пусть L, L\ La, Lb — четыре диаграммы неориентированного
зацепления, отличающиеся друг от друга только в небольшое кружочке,
так, как показано в предыдущей лекции.
Тогда существует единственный полином от двух переменных
D(z, а), удовлетворяющий следующим аксиомам:
D(L) - D{L') = z(D(LA) - D(LB))> (2)
Z>(0)=(l + ^), (3)
D(X#P) = aD(X), D(X#Q) = a~lD(X), (4)
где Р и Q — две петли, см. рис. 6.
Р Q
Рис. б
Этот полином D является инвариантным относительно второго
и третьего движений Рейдемейстера.
Как и в случае полинома Кауфмана от одной переменной, далее
строится полиномиальная функция на ориентируемых зацеплениях
с помощью нормировочной функции w(L), описанной в предыдущей
лекции.
Лекция 5. Свойства полинома Джонса
75
Итак, пусть дана ориентируемая диаграмма зацепления L, положим
Y(L) = a'w^D(L).
Тогда полученный полином называется полиномом Кауфмана от
двух переменных ориентируемого зацепления L,
Доказательство существования, единственности и инвариантности
полинома Кауфмана от двух переменных сложно: с помощью
соотношения (2) нельзя свести диаграмму с п перекрестками только к диаграммам
с меньшим числом перекрестков (так же, как и в случае с полиномом
Конвея). За точными доказательствами отсылаем читателя к [48].
Известно, что полином Кауфмана от двух переменных инвариантен
относительно всех трех преобразований Рейдемейстера.
Лекция 6
Полином Апександера
В настоящей лекции мы расскажем еще об одном инварианте узлов
и зацеплений — полиноме Александера. Существует много различных
интерпретаций этого полинома, но мы расскажем лишь об одной
из них — полиномиальном инварианте от одной переменной t для
ориентированных зацеплений. Этот инвариант был получен Дж. Алек-
сандером [3] с помощью интерпретации фундаментальной группы
дополнения к зацеплению, строящейся непосредственно по диаграмме
зацепления (образующие — дуги, соотношения — в вершинах
диаграммы). Существует несколько подходов к вычислению полинома
Александера, один из них изложен в [104], см. также [100].
Пусть дана диаграмма L ориентированного зацепления с п
вершинами. Рассмотрим дуги этой диаграммы. Их количество также равно п.
Действительно, в каждой вершине заканчиваются две дуги, а каждая
дуга заканчивается в двух вершинах. Занумеруем перекрестки
диаграммы числами от единицы до п произвольным образом, а дуги диаграммы
теми же числами так, чтобы дуга с номером к выходила из перекрестка
с номером к.
Построим квадратную матрицу размерап х п следующим образом.
В матрице M(L) каждой дуге диаграммы L соответствует столбец,
а каждому перекрестку (вершине) — строчка. В случае, если некоторая
дуга к не инцидентна вершине I (не проходит через нее и не
заканчивается в ней), поставим на пересечении fc-й строки и Z-ro столбца ноль,
а в противном случае поставим одну из функций от t так, как показано
на рис. 1. В этом случае двум дугам (входящей и выходящей) будет
сопоставлен один моном, а третьей (проходящей через вершину) —
полином t -1 или 1 -1. На рис. 1 на таких дугах стоят пары мономов, которые
нужно складывать — в первом случае t и -1, а во втором случае 1 и -t.
В каждой вершине сходятся три дуги. Это означает, что в каждой
строчке матрицы М(L) будут стоять три элемента, сумма которых равна
нулю.
Замечание 6.1. Вообще говоря, одна дуга может быть два или три раза
инцидентна одной и той же вершине. В таком случае на соответствующем
месте матрицы мы просто ставим сумму таких «элементов инцидентности». При
этом в этой строке будет стоять меньше трех элементов, но сумма элементов
в каждой строке всякий раз будет равна нулю.
Лекция 6. Полином Александера
77
Рис.1
Определение 6.1. Эта матрица M(L) (как, впрочем, и матрицы,
получающиеся из нее после некоторых нормировок) называется
матрицей Александера узла.
Итак, у нашей матрицы M(L) сумма элементов в каждой строке
равна нулю, или, что эквивалентно, сумма всех столбцов равна нулевому
столбцу. Следовательно, определитель det (M(L)) равен нулю. Значит,
линейная комбинация строк M(L) с некоторыми коэффициентами
равна нулю.
Так как det M(L) = 0, то строки матрицы M(L) линейно зависимы.
На самом деле, об этой зависимости можно сказать больше.
Предложение 6.1. Существуют такие целые числа аь..., ап, что
п _^
сумма YL ?*1Щ = 0, где га,- — ё-я строка матрицы М,
t=i
Доказательство. Пусть диаграмма L делит плоскость на клетки.
Сопоставим каждой клетке некоторое натуральное число следующим
образом.
«Внешней» клетке, т. е. клетке, содержащей бесконечную точку,
сопоставим число 0. Далее будем поступать следующим образом: при
переходе через дугу зацепления число, сопоставляемое клетке, будем
изменять на ±1 в зависимости от локальной ориентации компоненты
и направления движения. Если эти два вектора при переходе через
ребро образуют положительный базис, то мы прибавляем единицу,
если отрицательный — то вычитаем, см. рис. 2.
Упражнение 6.1. Проверьте, что такое сопоставление корректно, т. е. при
выходе из области U со значением п, мы вернемся в нее с тем же значением,
пройдя по любому пути.
Таким образом, в каждой вершине сходятся четыре области с
соответствующими числами fc, к + 1, к у к - 1. Сопоставим этой вершине
число к. Получим набор чисел k(v), называемых метками, где v —
перекрестки диаграммы L.
Рассмотрим матрицу М', получаемую из матрицы М умножением
строки с номером v на tk^ для всех v. Легко видеть, что сумма строк
матрицы М1 дает нулевой вектор.
78 Раздел I. Узлы, зацепления и полиномиальные инварианты
п+1
вектор
я-1
вектор f
движения 1
дуга
П
дуга
Рис. 2
Действительно, нам нужно проследить, что суммирование по
каждому столбцу (дуге) с некоторыми коэффициентами дает нуль.
Каждая дуга состоит из ребер, на которые она разбивается
вершинами, при этом каждое ребро можно рассматривать как пару
полуребер, примыкающих к вершинам. Согласно изначальному построению,
на каждом ребре стоят два монома — входящий (при одной вершине)
и выходящий (при другой вершине), первый из них равен -1 или -t,
а второй равен 1 или t. При этом, чтобы они сокращались, нужно лишь
проверить тот факт, что при умножении «перекрестков», т. е. строк
матрицы, на соответствующие tk^ эти полуребра будут попарно
сокращаться. Проверить это достаточно лишь для вершин, соседних по ребру.
Упражнение 6.2. Проверьте это аккуратно.
Таким образом, сумма ]Г) tk^m,i = б, что и требовалось
доказать. *=i ■
Перейдем к рассмотрению алгебраических дополнений к
элементам матрицы M(L).
Предложение 6.2. Все эти алгебраические дополнения отличаются
друг от друга коэффициентом ±t\l €Z.
Доказательство. Для начала напомним следующий факт: пусть
у матриц А и В размера р х р совпадают все строки, кроме первой,
у матрицы С все строки, кроме первой, совпадают с соответствующими
строками из А и В, а первая строка матрицы С является суммой
первых строк матриц А и В. Тогда det (A) + det (В) = det (С). Аналогичное
утверждение верно и для столбцов матриц.
Рассмотрим теперь нашу матрицу М(L) и два минора элементов:
rrtij и Ш{к. Обозначим через Р и Q матрицы, полученные из M(L)
вычеркиванием строки i, столбца j и строки г, столбца к
соответственно. Перенумеруем столбцы этих матриц так, чтобы все
столбцы, кроме первого, у них совпадали, а первые столбцы представляли
собой укороченные fc-йи j-й столбцы матрицы М. При такой
перестановке определители могут лишь умножиться на ±1. Обозначим
преобразованные матрицы через Р' и Q1. Пусть R — матрица, все
столбцы которой, кроме первого, совпадают со столбцами Р1 и Q',
Лекция 6. Полином Александера
79
а первый равен сумме первых столбцов Р* и Q1'. Следовательно,
det (Я) = det(P') + det(Q') = ±det(P) ± det(Q). С другой стороны,
det (R) = О, так как R — матрица, сумма элементов в каждой строке
которой равна нулю. Следовательно, такие алгебраические дополнения
могут отличаться лишь знаком.
Рассмотрим теперь две матрицы, получающиеся вычеркиванием
строки q, столбца р и строки г, столбца р соответственно. Это будут две
матрицы X и F, все строки которых, кроме одной, совпадают (и
являются укороченными строками матрицы М). Умножим все строки X иУ
на соответствующие степени t и перенумеруем их таким образом, чтобы
все строки, кроме первой, совпадали. Получим матрицы I' и У;,
определители которых отличаются от определителей X и Y умножением
на ±t\ з £ Z. Пусть Z — матрица, все строки которой, кроме первой,
совпадают со строками X1 и Y\ а первая равна сумме первых строк
матриц X1 и F'. Сумма элементов в каждом столбце Z равна нулю,
следовательно, 0 = det (Z) = det (X') + det (Y1) = ±*" det (X) ± *'2 det (Г).
Следовательно, любые два алгебраических дополнения порядка
п - 1 в матрице М отличаются друг от друга умножением на ±tl, что
и требовалось доказать. ■
Упражнение 6.3. Покажите, что у матрицы М' алгебраические
дополнения к элементам (1,1) и (Л, к) совпадают (а не отличаются знаком).
Тем самым, алгебраическое дополнение к элементу (1,1) не зависит
от перенумеровки вершин при соответствующей перенумеровке дуг.
Замечание 6.2. Вместо матрицы М можно рассмотреть матрицу М\
полученную умножением строк М на степени переменной t, такую, что сумма М!
и по строкам, и по столбцам равняется нулю. Тогда алгебраические дополнения
порядка п - 1 матрицы М' отличаются друг от друга лишь знаком.
Тем самым, каждой ориентируемой диаграмме зацепления мы
сопоставили некоторый полином, определенный с точностью до
умножения на ±tl.
Далее будем нормировать алгебраическое дополнение к первому
элементу, умножая его на некую целую или полуцелую степень t так,
чтобы младшая степень полинома отличалась от старшей знаком. При
этом мы можем рассматривать как матрицу М, так и матрицу М\
Полученный полином от положительных и отрицательных степеней t
(либо всех целых, либо всех полуцелых) мы и будем называть полиномом
Александера и обозначать через Л(£).
Пример 6.1. Вычислим значение полиномиального инварианта
Александера на восьмерке. Занумеруем дуги (арабскими цифрами) и вершины
(римскими цифрами) восьмерки так, как это показано на рис. 3.
80 Раздел I. Узлы, зацепления и полиномиальные инварианты
Вершинам I, II соответствует метка 0
Вершинам III", VI соответствует метка -1
Рис.3
Здесь числа, сопоставляемые областям, стоят в кружочках. Получим
матрицу М размера 4x4
1 0 -t t-l\
0 1 *-1 -t \
1-* -1 t 0 I
-1 1-* 0 t )
Так как вершинам J, II сопоставлена метка 0, а вершинам III и IV —
метка -1, то следует умножить третью и четвертую строки матрицы М на t~l,
оставив первую и вторую без изменения. После такой нормировки получим
следующую матрицу М':
С1 0 -t t-l
0 1 t-l -t
±-1 -I 1 0
-J 1-1 0 1
Как и следовало ожидать, сумма элементов по столбцам в последней
матрице равна нулю. Алгебраическое дополнение к ее первому элементу равно
—t+3— l/t. Это алгебраическое дополнение для матрицы М' диаграммы L будем
обозначать через 6{L) и называть полунормированным полиномом Александера
диаграммы L.
Упражнение 6А. Вычислите значение полунормированного полинома
Александера для правого и левого трилистников.
Введем следующую операцию. Пусть дана диаграмма зацепления L
и некоторая ее дуга I (будем считать, что у нее был номер один),
отделяющая область с меткой к от области с меткой к + 1. Разорвем дугу I
в произвольном месте на две дуги и поставим в этом месте вершину V.
Перенумеруем вершины дуги следующим образом. Дуга I разбивается
добавленной вершиной с номером 1 на две дуги с номерами 1
(исходящая) и 2 (вводящая), у остальных дуг и вершин номера увеличиваются
на единицу.
©
4 1
© 1
IV
©
©
©
II
3
\П ©
Лекция 6. Полином Александера
81
В дальнейшем всегда будем считать, что нумерация вершин и дуг
составлена так, что номер каждой вершины совпадает с номером
выходящей из нее дуги. Легко видеть, что при переходе от одной такой
нумерации к другой алгебраическое дополнение к элементу (1,1)
матрицы М* не меняется.
Естественно считать, что вершина V инцидентна только паре дуг,
на которые разбита дуга /, а все вершины, которые были инцидентны
дуге I, очевидным образом поделены на вершины, инцидентные дуге I
и вершины, инцидентные другой дуге.
При новых обстоятельствах построим матрицу М' от полученной
диаграммы по правилам, изложенным выше, с добавлением
следующего: строка, соответствующая добавленной вершине, содержит два
ненулевых элемента на первом и втором местах, равных +J*+1 и -£*+l,
соответствующих дугам, инцидентным точке V, исходящей и
входящей. При этом один столбец, соответствующий дуге /, разобьется на два
столбца, сумма которых равняется исходному.
В матричном виде это преобразование записывается так.
(.+»n»-(«r-rv).
где а и Ъ — столбцы длины га, a D — матрица размера га х (га - 1).
Левая матрица имеет размер га х га, а правая матрица имеет размер
(га -f 1) х (га + 1). Очевидно, что определители таких матриц равны
с точностью до умножения на J*+l (это следует из разложения по первой
строке), при этом равны и миноры соответствующих элементов. Из
этого следует инвариантность полинома Александера Д относительно
такого разбиения дуги. Меткой такой вершины будем считать число fc+1/2.
Более того, у полученной матрицы сумма элементов в каждой
строке и в каждом столбце будет равна нулю. В дальнейшем мы будем
пользоваться этим фактом и разбивать дуги в необходимом количестве.
Покажем теперь инвариантность полинома Александера Д
относительно движений Рейдемейстера (мы докажем это для некоторых
видов движений, для остальных доказательство может быть проделано
аналогично). Будем брать алгебраические дополнения, определенные
с точностью до некоторой степени t и доказывать то, что при
движениях Рейдемейстера они лишь умножаются на степень переменной t.
В силу нормировки это и будет означать инвариантность.
Итак, начнем с первого движения Рейдемейстера. При появлении
новой вершины с матрицей М1 произойдет то же, что и при разбиении
дуги, с той лишь разницей, что строка, соответствующая
появившейся вершине будет отличаться коэффициентом t±l^2 от добавляемой
82 Раздел I. Узлы, зацепления и полиномиальные инварианты
строки, соответствующей разбиению дуги. Следовательно, полином
инвариантен относительно первого движения Рейдемейстера.
Условимся, что во всех сравниваемых фрагментах диаграмм
нумерация соответствующих дуг, выходящих за пределы фрагмента,
одинакова и осуществляется, как правило, начальными членами натурального
ряда.
В дальнейшем будем считать, что мы рассматриваем минор
элемента, для которого соответствующие перекресток и дуга не участвуют
в движении Рейдемейстера (т. е. не обязательно минор,
соответствующий элементу (1,1)).
Инвариантность относительно второго движения Рейдемейстера
проверим лишь для случая, когда две ветви сонаправлены, см. рис. 4.
в,
X
©[©
© Q
4/\з
В
У
©
\>
Рис.4
Нижняя вершина на обеих диаграммах имеет номер I, верхняя —
номер II. Устроим двойное разбиение дуги, чтобы сравнивать матрицы
одинаковых размеров.
Получим две матрицы следующего вида (звездочкой обозначается
их общая часть)
*+1 Л+1 _ Л+2
tk+2_tk+l
I i
Jk+2
О -t
-t'
JH-2 Л+1
r
0
0
0
0
/ tk+1
0
0
-t
t+1
о о
о о
0
Лекция 6. Полином Александера
83
8 первой матрице сумма меток равна 2fc + 1, во второй матрице
сумма меток равна 2& + 2.
Прибавляя в первой матрице первый столбец, умноженный на
(1 - 1/4), к четвертому, получим матрицу
/ 4*+2 0 -4*+1 0 0 ... 0\
J _j*+2 f*+i о 0 0 ... 01
0
I : * I
v о )
Если первый столбец полученной матрицы разделить на 4, мы
получим в точности вторую матрицу. Следовательно, соответствующие
миноры первой и второй матрицы отличаются константой, равной
степени переменной 4, а полиномы Александера совпадают.
Упражнение 6.5. Проделайте аналогичные вычисления для случая
второго движения Рейдемейстера, когда ветви противонаправлены.
Для третьего движения Рейдемейстера (рассмотрим лишь один
случай, указанный на рис. 5) количество вершин не меняется, поэтому
не будем их учитывать. Сумма меток в правой части рис. 5 на единицу
больше, чем сумма меток в его левой части. Без ограничения
общности можно считать, что в обоих случаях на рис. 5 минимальная метка
равна нулю.
Так же, как и в случае со вторым движением Рейдемейстера,
получим две матрицы:
/1 0 0-4 4-1 0 0 ... 0\
| -1 4 0 0 0 1-4 0 ... 0 |
I 0 0 42 0 -4 t-t2 0 ... 0
0
I : * I
И
-t2
I : * I
0 0 -t 0
t t2-t о о
0 t 0 -1
t-t2 о ... o\
0 0 ... 0
l-t 0 ... 0
84 Раздел I. Узлы, зацепления и полиномиальные инварианты
Рис.5
Разделим первый столбец второй матрицы на t29 а третью строку
второй матрицы умножим на t (тем самым произведя деление минора
второй матрицы на t). Прибавим теперь к пятому столбцу второй
матрицы первый (новый), умноженный на (t - 1), а к шестому —
первый столбец (новый), умноженный на t2 -1.
Получим матрицу:
/10 0 -t t-1 0 0 ... 0\
I -1 t t2-t 0 1-* t-t2 0 ... 0 1
. 0 0 t2 0 -t t-t2 0 ... 0
0
I : * I
\° /
Прибавляя ко второй строке этой матрицы третью строку,
умноженную на (1 - t)/t, получим в точности первую матрицу. Это значит,
что минор второй матрицы равен минору первой матрицы,
умноженному на t, т. е. полином Александера не меняется при таком виде третьего
движения Рейдемейстера.
Упражнение 6.6. Проделайте аналогичные вычисления для остальных
случаев третьего движения Рейдемейстера.
Если раньше для получения значения полинома Александера мы
просто нормировали его, деля его на t в степени полусуммы
степеней старшего и младшего членов, то теперь мы будем делать иначе.
Пусть К — диаграмма узла, М'(К) — матрица Александера этой
диаграммы, в которой суммы по строкам и по столбцам равны нулю.
Рассмотрим матрицу М", полученную из М' делением на t1^2.
Разведем перекрестки диаграммы К так, как показано на рис. 6.
Лекция 6. Полином Александера
85
- X
ОС
Рис. 6
Получим некоторое количество ориентированных окружностей
Зейферта. Теперь умножим det (М"{К)) на ^А^-О-ЬЕ, где о+ —
количество окружностей Зейферта, закручивающихся по часовой
стрелке, а О- — против, а 5^ — сумма меток в вершинах диаграммы К.
Обозначим получившееся выражение через А'(К).
Так, например, для диаграммы восьмерки, показанной на рис. 3,
значение Д' будет равно —t + 3 - l/t> поскольку О- = 2, 0+ = 1,
Y2 = -2, а порядок минора равен трем. Следовательно, полином
А' отличается от полунормированного полинома 6 умножением на
r3/2+(-l/2)-(-2) = L
В конце лекции будет показано, что А'(К) = А(К), т.е. А'
совпадает с полиномом Александера.
Теорема 6-1- Полином Александера Д; удовлетворяет следующему
соотношению типа Конвея:
A'(L+) - Д'(1Г) = (*1/2 - Г1/2) Д'(£°).
Доказательство. Рассмотрим полиномы 6(L+),6(L~)y6(L0) и
перейдем к Д'(£+), Д'(2Г) и Д'(Ь°).
Мы знаем, что А' отличается от б множителем вида t8, где s —
число, определенное формулой
s=_i0rd+i(o+-o_)-x;,
где Ord — порядок минора (на единицу меньший порядка матрицы).
В нашем случае Ord, 0+, О- одинаковы для всех троек матриц
Ьл', Ь", L0; что касается £^, то
£>+) = г + 2,5, "£(!,-) = 1,5, 5>°) = 1.
86 Раздел I. Узлы, зацепления и полиномиальные инварианты
На рис. 7 приведена нумерация вершин и дуг, необходимая для
построения матриц.
После умножения первых строк этих матриц на Г"1, £°, t'^2,
получаем:
1 1
2^ ^12^ ^12 1
О 2
2 А 1/
Рис.7
Добавим к диаграммам L+ и L~ по одной вершине, а к £° — две
вершины так, как это показано на рис. 7, и будем опять сравнивать
определители матриц одинакового размера.
Получим три матрицы (соответствующие L+,L~,L°), у которых
все строки, кроме двух, одинаковые, а две оставшиеся выглядят (с
точностью до умножения этих строк во всех матрицах на некоторую
одинаковую степень переменной t) следующим образом:
t2 О 0 -t2
t-tz
-t О
О
О
о1
о
t v- -1 о
о t -t о
*
о -t о
t2 о -t2
*
t2 о
о
о
Для дальнейшего сравнения полиномов Александера умножим
первую строку первой матрицы на Г"1, а первую строку третьей — на t~1^2.
Получим три матрицы, миноры которых определят значения Д'
для L+-'°:
t О 0 -* 0 ... (Г
t-t2 t2
-t
*
О О
о
Лекция 6. Полином Александера
87
t t2 - t 0
0 t -t
*
t1'2 о -t1'2
0 t2 0
-t2 0 ..
0 0..
0 0 .
-t2 0 .
. 0>
. 0
.. 0
.. 0
Перейдем к проверке соотношения типа Конвея. Поменяем во
второй матрице строки местами (ее определитель изменит знак). Получим:
t 0 0
t-t2 t2 -t
*
0 t -t
t t2-t 0
-to..
0 0..
0 0.
-t2 0 ..
.. 0
,. 0
.. 0
.. 0
Y'2 о -t1'2 о о ... o>
0 t2 0 -t2 0 ... 0
*
Прибавим теперь в первой матрице ко второй строке первую,
умноженную на t, во второй матрице — ко второй строке первую,
а в третьей — ко второй строке первую, умноженную на t1^2.
Получим три матрицы, у которых все строки, кроме первой,
совпадают. Их общая вторая строка равна (ty t2, -t, -t2,0,..., 0). Рассмотрим
теперь первые строки всех трех матриц.
a = (t 0 0 -0 , Ь = (0 t -t 0), с = (tl/2 0 -*1/2 0) .
Получим: a + Ь = (*1/2 - Гх/2)с+ (1,*, -1, -*)> где (1, *, -1, -t) -
общая вторая строка трех матриц, умноженная на l/t.
Вспоминая, что определитель второй матрицы изменил знак,
получаем, что A'(L+) - A'(L~) = (tl/2 - Г1/2)Д'(£°). ■
Теорема 6.2. Полином А; является инвариантом зацеплений, т. е.
не меняется при движениях Рейдемейстера и разбиении дуги.
Доказательство. Будем рассуждать так же, как и при
доказательстве инвариантности полинома Д. При этом остается проверить, что
полином Д' при движениях Рейдемейстера умножается на нулевую
степень переменной t. В случае второго и третьего движений количество
окружностей Зейферта не меняется, а степень, на которую умножается
88 Раздел I. Узлы, зацепления и полиномиальные инварианты
минор, компенсируется метками в вершинах, как это было показано
ранее. Следовательно, значение полинома Александера Д' сохраняется
при втором и третьем движениях Рейдемейстера.
При разбиении дуги, находящейся между областями с метками к
и к + 1, мы имеем разложение по строке, дающее коэффициент tn+l^2,
а также метку к + 1/2, дающую коэффициент t~k+l'2. Учитывая то, что
количество окружностей Зейферта при разбиении дуги не меняется,
получаем инвариантность полинома Д' относительно разбиения строки.
В случае первого движения Рейдемейстера происходит то же, что
и при разбиении дуги, при этом одна окружность добавляется, но ее
добавление компенсируется тем, что метка в добавленной точке
отличается от метки, возникающей при разбиении дуги, на одну вторую. ■
.о
Рис.8
Заметим, что на простейшей диаграмме тривиального узла с двумя
добавленными вершинами, показанного на рис. 8, получим полином
Александера, равный 1. Действительно, соответствующая матрица
м' = г112
(-51)
Для этой диаграммы Ord =1, ^ = 1, 0+ = 1, О- = 0.
Таким образом, умножая дополнение к элементу (1,1), равное t,
на t 2 ■*■ 2 ^ = f 2+2 \ получим 1.
Отсюда получаем следствия.
Следствие 6.1. Полином Д' инвариантен относительно замены
на -t~ll2. Следовательно, его старшая степень отличается от млад-
шей знаком и он совпадает с Д.
В силу соотношения типа Конвея и того, что полином Д' равен
единице на тривиальном узле, имеем
Следствие 6.2. Полином Александера получается из полинома Конвея
с помощью замены z
Итак, мы доказали существование и единственность полинома
Конвея: для каждого ориентированного зацепления L можно по
определению Положить C{tl/1 - t~l/2) = Д(*).
Лекция 6. Полином Александера
89
Следствие 6.3. Для узлов и зацеплений с нечетным числом компонент
полином Александера инвариантен относительно t —► Г"1, а для
зацеплений с четным числом компонент он меняет знак.
Действительно, легко видеть, что L+ и L" имеют одинаковое число
компонент зацепления, а число компонент зацепления L0 отличается
от числа компонент для L+ и L" на единицу.
Следствие 6.4. Полином Александера не меняется при замене
ориентации узла (зацепления).
Доказательство. Рассмотрим две диаграммы К и К зацеплений с п
вершинами каждая, отличающиеся заменой ориентации. Без
ограничения общности можно считать, что на этих диаграммах нет разбиений
дуг. Рассмотрим матрицы Александера N(K) и N(K), отличающиеся
от М(К) и М(К) делением на t1'2, т. е. матрицы, у которых в каждой
строке стоят ±t1^2, ±t~1^2, ±(tl^2-t~1^2) и алгебраические дополнения
в них к элементу (1,1). Получим некоторые выражения, зависящие
от t^2y которые обозначим через MM(K,t1/2) и MM(K,t^2).
Полином Александера Д является функцией от tl^29 такой, что при
замене t1'2 на —t"1'2 его значение как полинома не меняется, т.е.
A(K,tl'2)=A(Ki-r1'2).
Полином Д(К\<1/2) отличается от полинома
степенью переменной t.
Изменение направления обхода индуцирует перестановку дуг, а
именно, во всякой вершине входящая дуга заменяется на исходящую
и наоборот. Эта перестановка на множестве дуг, составляющих одну
компоненту зацепления, является циклической. Четность такой
перестановки равна (-1)п~*, где з — количество компонент зацепления К
или К. __
Следовательно, ММ(КУ tl/2) = (-l)n4MM(iT, -Г1/2). При этом
Д(ЛГ, -Г"1/2) по построению отличается от ММ(К, t1^2)
коэффициентом, равным некоторой степени переменной t, умноженной на (-£^2)
в степени, равной количеству окружностей Зейферта для диаграммы К
или К. Как показано в лекции 1, количество окружностей Зейферта
имеет ту же четность, что и п — з, где з — количество компонент
зацепления.
Таким образом, мы получили, что А(К, t1^2) отличается от
Д(2Г, t1^2) лишь коэффициентом, равным степени переменной t без
знака, а поскольку у полинома Александера старшая степень от
младшей отличается знаком, то эти полиномы совпадают, ч. т. д. ■
90 Раздел I. Узлы, зацепления и полиномиальные инварианты
Замечание 6.3. Как и все остальные полиномы, основанные на соотноше-
ниях типа Конвея, полином Александера выражается через полином Джонса
от двух переменных посредством подходящей замены переменной.
Упражнение 6.7. Найдите эту замену переменной.
Кроме полинома Александера от одной переменной, аналогично
определяется полином Александера от нескольких переменных; его
описание мы опускаем, см., например, [104].
Раздел II
ТЕОРИЯ КОС
Лекция 7
Группы кос и их представления
В ближайших нескольких лекциях мы расскажем об одной
фундаментальной теории, тесно связанной с теорией узлов — теории кос.
Косы являются топологическими объектами, с помощью которых
можно кодировать узлы и зацепления. В отличие от узлов, косы допускают
естественную структуру группы.
Первоначально косы были предложены немецким математиком
Эмилем Артином. Его первая работа была на немецком, см. [5],
хотя существует и ее английский перевод, причем с более строгими
доказательствами, см. [6].
Понятие группы кос Артина имеет четыре определения, см.,
например, [131, 97, 123].
§ 1. Четыре определения группы кос
Начнем с самого простого определения косы.
1.1. Геометрическое определение
Рассмотрим в R3 две прямые у = 0,2 = 1 и у = 0,z = Оина каждой
из них набор из m точек (с абсциссами 1,..., га).
Определение 7.1. Назовем косой из га нитей набор из га
непересекающихся (гладких) путей, соединяющих точки первой прямой
с точками второй прямой (в произвольном порядке) таких, что
проекция этих путей на ось Oz представляет собой гомеоморфизм
(т. е. что пути идут строго сверху вниз).
Эти гладкие пути называются нитями косы.
Пример 7.1. Коса. (рис. 1)
92
Раздел II. Теория кос
Рис.1
Естественно рассматривать косы с точностью до изотопии. Две
косы Bq и В\ называются изотопными, если существует непрерывное
семейство кос Bti t = О, начинающееся в Бо и кончающееся в В\.
Множество классов гомотопных кос из га нитей образует группу. Для
того, чтобы перемножить косы а и Ь нужно параллельно перенести пару
прямых косы Ь так, чтобы нулевая плоскость косы Ь перешла в первую
плоскость косы а. Затем мы сотрем эти две плоскости и получим косу,
которую и будем называть произведением кос ab.
В качестве единичного элемента выберем косу, состоящую из
параллельных отрезков. Коса, обратная к данной, задается зеркальным
отражением косы относительно средней плоскости, параллельной
верхней и нижней плоскостям. Подробнее см. рис. 3.
Упражнение 7.1. Проверьте, что единичная коса и умножение в группе
кос определены корректно (в т. ч. проверьте и ассоциативность приведенного
умножения).
Определение 7.2. Группой кос Артина из га нитей называется
множество изотопических классов кос из га нитей, обладающее
описанной выше групповой структурой. Она обозначается Вг(га).
Можно рассматривать только косы, состоящие из линий,
соединяющих соответствующие точки. Такие косы называются крашеными.
Среди них есть единичный элемент и их гомотопические классы
эквивалентности образуют подгруппу в группе кос.
Определение 7.3. Эта группа называется группой крашеных кос
из га нитей и обозначается /(га).
1.2. Топологическое определение
Определение 7.4. Назовем т-конфигурационным пространством
для X множество всех неупорядоченных наборов из га попарно
различных точек в X. Оно обозначается В(Х, га).
Лекция 7. Группы кос и их представления
93
Аналогичным образом можно определить га -упорядоченное
конфигурационное пространство, оно обозначается F(Xy m).
ПустьХ = К2 = С1.
Определение 7.5. Определим группу кос из га нитей как
фундаментальную группу iri(B(Xy га)).
Определение 7.6. Фундаментальная группа *\(F(X9 га))
называется группой крашеных кос из га нитей.
1.3. Алгебро-геометрическое определение
Рассмотрим пространство всех полиномов степени га от одной
комплексной переменной z со старшим коэффициентом, равным
единице.
Оно, очевидно, изоморфно Сп, так как коэффициенты при всех
степенях этого полинома, кроме старшей, задают на нем комплексные
координаты.
Выкинем из этого пространства пространство Ето тех полиномов,
у которых есть хотя бы один кратный корень. Получим пространство
Cm\Em.
Определение 7.7. Группой кос из га нитей называется
фундаментальная группа тт^С™ \ Ет).
1.4. Алгебраическое определение
Определение 7.8. Группой кос из га нитей называется группа
с га - 1 образующей аи ..., (7m_i и соотношениями,
порожденными следующим набором: ащ — о^чт,- при \i - j\ ^ 2, ^сг^о-,- =
(7,-+1(7${Г,-+1. Эти соотношения называются соотношениями Артина.
1.5. Эквивалентность четырех определений группы кос
Теорема 7.1. Четыре определения группы кос из га нитей,
описанные выше, эквивалентны, т. е. получаемые таким образом группы
изоморфны.
Доказательство. Легче всего показать эквивалентность
топологического и алгебро-геометрического определений. Дело в том, что два
пространства — многочленов степени га без кратных корней со
старшим коэффициентом, равным 1, и неупорядоченных наборов из га
различных точек в С2 — гомеоморфны. Действительно, каждый такой
многочлен однозначно задается набором его корней. Осталось лишь
вспомнить, что фундаментальные группы гомеоморфных пространств
совпадают.
94
Раздел И. Теория кос
Покажем теперь эквивалентность геометрического и
топологического определений. Как было показано в лекции 3, фундаментальная
группа пространства не зависит от выбора начальной точки. Таким
образом, за начальную точку А неупорядоченного набора из га различных
точек на плоскости мы можем выбрать набор 1,2,..., га. Рассмотрим
пространство R3 как произведение С1 х R1.
Каждому замкнутому пути, выходящему из А и входящему в А
в пространстве Б(М), мы сопоставим набор линий в R3 следующим
образом. Каждая линия представляет собой движение точки по
комплексной прямой С1 во времени t, где t — вещественная координата,
см. рис. 2.
В
Рис.2
Итак, каждой геометрической косе мы однозначно сопоставили
топологическую косу. При этом очевидно, что изотопным
геометрическим косам соответствуют изотопные топологические косы.
Нам осталось показать лишь эквивалентность геометрического
и алгебраического определений.
Для этого введем понятие плоской диаграммы косы, аналогично
плоской диаграмме зацепления. Для этого рассмотрим проекцию косы
в общем положении на плоскость, в которой лежат две параллельные
прямые.
В общем положении получим диаграмму такого вида, как показано
на рис. 3.
Определение 7.9. Назовем плоской диаграммой косы из га нитей
расположенный внутри прямоугольника [1, га] х [0,1] на плоскости
граф со структурой, обладающий следующими свойствами:
а) в точках [0, г] и [1, г], г = 1,..., га граф имеет вершины
кратности 1, в других точках [0, t] и [1, t] вершин графа нет.
Лекция 7. Группы кос и их представления 95
б) все остальные вершины графа имеют кратность четыре;
противоположные ребра графа в таких вершинах образуют угол я\
в) уникурсалъные кривые, т. е. линии, состоящие из ребер графа,
переходящих в каждой вершине графа с ребра на противоположное
полуребро, проходят от вершин с ординатой 1 к вершинам с
ординатой 0, при этом они являются нисходящими, т. е. их проекция
на ось ординат является гомеоморфизмом.
г) в каждой не концевой вершине задана структура — какая из уни-
курсальных кривых проходит выше, а какая — ниже.
Аналогично плоской изотопии диаграмм зацеплений можно
определить плоскую изотопию диаграмм кос.
Умножение происходит посредством сжимания двух
прямоугольников по вертикали и приставления одного из них к другому.
Очевидно, что все изотопические классы геометрических кос
представляются таким образом. Более того, после небольшого шевеления
косы можно сделать так, чтобы все вершины имели различные ординаты.
Легко видеть, что каждый элемент геометрической группы кос дает
автоматическое разложение по следующим образующим: элемент <т,-,
г = 1,...,га- 1 состоит изт-2 отрезков, соединяющих точки [fc, 1]
и [ку 0], кф г, к Ф%+ 1 и двух отрезков [М]-[0,*+1], [1, г] — [0, * + 1],
из которых последний проходит выше при пересечении, см. рис. 4.
Очевидно, что разные диаграммы кос могут давать изотопные косы.
Следовательно, мы получим некоторые соотношения на сг\,..., <тт.
Предположим, что есть две изотопные диаграммы кос В\ и Бг.
Рассмотрим процесс их гладкой изотопии и его изображение на их
плоских диаграммах. В каждый момент либо происходит плоская изотопия
без изменения расположения ординат вершин, либо как минимум два
перекрестка имеют одну и ту же ординату, либо диаграмма перестает
быть регулярной. Для нас интересны те моменты, когда меняется
96 Раздел П. Теория кос
ii+1 i i+l
...
I
(Ti
...
I
...
Рис. 4. Образующие группы кос
алгебраическая запись нашей косы, т. е. изменяется выражение косы
через образующие. Без ограничения общности можно считать, что
в такой момент ровно одна пара перекрестков имеет общую ординату
(см. рис. 5 д), либо диаграмма перестает быть регулярной, причем можно
считать, что в этот момент существует ровно одна «нерегулярность». Это
либо касание двух нитей (см. рис. 5 б), либо точка тройного пересечения
(см. рис. 5 в).
Рис.5
Легко видеть, что первый случай (рис. 5 а) дает соотношение
(TiCFj = <Tj<Ti, \i - j\ ^ 2, которое называют дальней коммутативностью
(или эквивалентное ему соотношение <Tfl<rfx = aflcrf[9 \i - j\ ^ 2),
во втором случае (рис. 5 б) получаем соотношение аа~1 = 1, а в третьем
случае (рис. 5 в) получаем одно из соотношений
0W+10"» = (Ti+icriCi+i,
Лекция 7. Группы кос и их представления
97
Очевидно, что последние два соотношения эквивалентны первому,
что и завершает доказательство теоремы. ■
В группе кос из га нитей естественным образом выделяется
подгруппа крашеных кос.
Упражнение 7.2. Покажите, что I(m) — нормальная подгруппа в Вг(т),
причем факторгруппа Вг (т) \ I(m) изоморфна группе перестановок 5(ш).
Стабильная группа кос.
Для га < п группу кос Вг (га) можно считать вложенной в группу
кос Вг (п) таким образом, что последние п - га нитей являются просто
горизонтальными прямыми.
Определение 7.10. Назовем стабильной группой кос Вг предел
Вг (п) при п —> оо относительно такого вложения.
По определению группа Вг имеет копредставление с образующими
(Ть0*2,..., и соотношениями, порожденными следующим набором:
a{(rj = (jjG{ при \i - j\ ^ 2, cri<Ti+i<Ti = ov+i^-ov+i.
§ 2. Крашеные косы
Итак, крашеные косы соответствуют петлям в пространстве
упорядоченных точек на плоскости.
Для крашеных кос имеет место следующая
Теорема 7.2. У группы крашеных кос 1(тп) существует конечная
система образующих, а именно, косы
bij, l^i<j^n, (l)
см. рис. 6.
« 3
Рис. 6. Образующий элемент Ь^ в группе крашеных кос
Будем проводить доказательство индукцией по числу нитей. При
п = 2 распрямим вторую нить, т. е. сделаем изотопию, после которой
98
Раздел II. Теория кос
вторая нить будет вертикальной. При этом первая нить будет каким-то
образом «обвиваться» вокруг второй. Ясно, что полученная коса будет
изотопна степени образующей 6^ = <т\.
Предположим, что утверждение доказано для некоторого п,
докажем его для произвольной крашеной косы dn+\ из п -4- 1 нитей. Если
из нее убрать первую нить, получим некоторую крашеную косу ап из п
нитей. Рассмотрим разложение dn+\ = (dn+ian~l)an. По
предположению индукции, коса ап разлагается в произведение образующих (1).
У косы <fn+ian-1 последние п нитей незацеплены, поэтому их можно
распрямить, т. е. перевести с помощью изотопии в вертикальные
прямые. Тогда первая нить будет обвиваться вокруг них. Легко видеть, что
такую косу можно представить в виде произведения кос 6,;-. Это можно
сделать так: всякий раз, когда первая нить проходит над какой-то
нитью, первую нить нужно сразу же протащить под остальными нитями
до левого края, а затем вернуться на прежнее место под пройденными
уже вертикальными нитями, двигаясь направо, см. рис. 7.
l
Ч_1
Э
D
0"! 0*2 0*2 0*1
ЬПЬ\
12^13
Рис.7
Таким образом, и произведение кос, равное dn+i, разлагается
в произведение образующих о,-;-.
2.1. Группы крашеных кос
Приведем теперь другое описание группы крашеных кос, см.,
например, [123].
Для этого обозначим через Нп группу изотопических классов
эквивалентности гомеоморфизмов круга с п дырками, тождественных
на границе круга с дырками. Оказывается, группа крашеных кос тесно
связана с группой #„. Рассмотрим сначала группу Щ
Лекция 7. Группы кос и их представления
99
Теорема 7.3 (Теорема Александера о гомеоморфизме).
Группа #о единичная, т. е. любой гомоморфизм круга,
тождественный на границе, гомотопен тождественному отображению, причем
гомотопию можно провести в классе отображений, тождественных
на границе.
Доказательство. Рассмотрим круг \z\ ^ 1 на комплексной
прямой С1. Пусть ho — тождественное отображение этого круга на себя,
a hi — произвольный гомеоморфизм круга, тождественный на крае
круга. Согласно известной теореме, у гомеоморфизма h\ существует
неподвижная точка внутри круга. Без ограничения общности можно
считать, что эта точка совпадает с центром круга. Для t E (0,1)
построим гомеоморфизм ht следующим образом. ht тождествен в кольце
t ^ \z\ < 1, внутри кольца ht(z) = t(h\(j)). Очевидно, что ht является
гомотопией. ■
Рассмотрим теперь группу Нп. Пусть g £ Нп — некоторый
гомеоморфизм круга с п дырками, тождественный на границе круга
с дырками, т. е. на окружности круга и на границах дырок. Он
продолжается до гомеоморфизма всего круга, т. е. гомеоморфизм g можно
продолжить с границы дырки на саму дырку. Это можно сделать,
например, отобразив внутренность дырки в себя тождественно. Обозначим
этот гомеоморфизм через h{.
Согласно предыдущей теореме существует изотопия ht,
связывающая этот гомеоморфизм h\ с тождественным гомеоморфизмом ho = id.
Рассмотрим точки х\,..., хп внутри дырок. Для каждого % — 1,..., п
множество точек (£, /&*(а>о))> 0 ^ t < 1 представляет собой дугу,
соединяющую точки верхнего и нижнего оснований цилиндра / х D, где / —
временной отрезок, a D — круг, на рис. 8 указаны следы движения
отмеченных точек.
Следовательно, мы получили крашеную косу. Эта коса содержит
в себе много информации о гомеоморфизме А, но ее недостаточно,
чтобы полностью восстановить этот гомеоморфизм. Дело в том, что в
момент изотопии можно следить за движением точки на окружности,
которая, поворачиваясь, описывает путь на цилиндре, являющемся следом
этой окружности. Для полного описания изотогагческого класса этого
изоморфизма достаточно рассмотреть все такие цилиндры и на краю
каждого из них нарисовать кривую, отвечающую образу при гомотопии
точки, находящейся на краю соответствующей дырки. Крашеная коса
с такой дополнительной информацией называется утолщенной косой.
Очевидно, что гомеоморфизму круга с п дырками, тождественному
на границе, соответствует некоторая утолщенная коса.
Верно и обратное. Покажем, что каждой утолщенной косе можно
сопоставить такой гомеоморфизм.
100
Раздел II. Теория кос
\ /
Рис.8. Утолщенная коса
Без ограничения общности можно считать, что утолщенная коса
не выходит за пределы нашего цилиндра. Верхнее и нижнее основания
цилиндра являются кругами с п круглыми дырками.
Будем опускать круг с дырками так, чтобы точки внешнего края
двигались вертикально вниз параллельно оси цилиндра, а круг все
время оставался плоским. Границы дырок вслед за текущей точкой
нити будут опускаться вниз, вращаясь. Когда крут опустится до нижнего
основания, мы получим требуемый гомеоморфизм.
Пусть М2 — ориентированное двумерное многообразие (с краем
или без), а 7 — замкнутая кривая лежащая во внутренности
многообразия М2. Рассмотрим малую окрестность U кривой 7, гомеоморфную
51 х [0,1]. Пусть 7i и 72 — края этой окрестности.
Определение 7-11- Скручиванием Дена двумерной поверхности М
вдоль кривой 7 называется гомоморфизм М2 на себя, постоянный
вне U, а внутри U получающийся поворотом кривой 72 вокруг
себя на угол 27Г при закрепленной кривой 7i • На рис. 9. показано,
как скручивание Дена действует на кривые, соединяющие 7i с 72-
Рис. 9. Скручивание Дена
Лекция 7. Группы кос и их представления 101
Группа утолщенных кос является расширением группы крашеных
кос Кп. Более того, так как косы, получающиеся из тривиальной косы
некоторыми скручиваниями Дена, лежат в центре группы утолщенных
кос, группа #п является прямой суммой группы Кп обычных
крашеных кос и Zn (каждая группа Z в этом произведении соответствует
скручиваниям вдоль цилиндров).
Для полного прояснения картины осталось доказать теорему.
Теорема 7.4. Группа Нп порождена скручиваниями вдоль конечного
числа кривых, расположенных в этом круге.
Доказательство. Как было доказано ранее, группа Нп изоморфна
группе утолщенных кос. Пусть гомеоморфизму h £ Ип соответствует
утолщенная коса а'п, разлагающаяся в сумму а„-ьа, где ап е Кп,
а а£ Zn. Крашеная коса ап представима в виде произведения
образующих b{j группы крашеных кос, которые соответствуют скручиваниям
вдоль кривой, обходящей один раз точки г и j, см. рис. 10.
Рис. 10
А утолщенная коса а порождается скручиванием Дена вдоль
кривой, обходящей один раз вокруг точки а.
Суммируя сказанное, получаем утверждение теоремы. ■
Косы и узлы.
Каждой косе можно сопоставить диаграмму следующим образом.
Определение 7.12. Замыканием косы Ь называют зацепление р(Ь),
полученное из косы Ь в результате соединения верхних концов
с нижними, так как это показано на рис. 11.
При этом очевидно, что изотопным косам соответствуют
изотопные зацепления.
Некоторые косы задают узлы, а некоторые — зацепления. Для
того, чтобы разобраться в этом, нужно описать важную связь группы
кос с группой перестановок.
Дело в том, что существует естественный эпиморфизм группы кос
на группу перестановок а: Вг(п) —> 5„, а именно: каждой косе можно
сопоставить перестановку 1 -+ аь 2 -> а2> •••> п —> ап> где а,- —
абсцисса нижнего конца нити, выходящей из точки с абсциссой г.
102
Раздел II. Теория кос
Рис. 11. Замыкание косы
Пусть задана коса В. Очевидно, что для всех чисел р,
принадлежащих одной орбите естественного действия перестановки <т(В)
на множестве чисел от 1 до п, все верхние вершины с абсциссой (р, 0)
принадлежат одной компоненте зацепления.
Следовательно, получаем
Предложение 7.1. Количество компонент зацепления, получаемого
замыканием косы В, равно количеству орбит действия группы сг(В).
Так, крашеная коса из п нитей дает покомпонентное зацепление.
Упражнение 7.3. Придумайте косы, представляющие правый трилистник,
левый трилистник и восьмерку.
Зацепления разных (не изотопных) кос могут давать изотопные
узлы. Об этом и о других вопросах теории кос и пойдет речь на следующих
лекциях.
§ 3. Представление Бурау
Попробуем найти представление группы кос из п нитей исходя
из следующих соображений. Будем отображать образующие группы кос
в блочно-диагональные матрицы (п+1) х (п+1) таким образом, чтобы
матрицы, соответствующие «далеким» a^ o$, \i-j\^2, коммутировали.
Это можно сделать следующим образом. Пусть элемент <Т{ отображается
в блочно-диагональную матрицу, где в строках i, i+1 и столбцах t, t+1
стоит матрица второго порядка А, а остальные ненулевые элементы
большой матрицы расположены на диагонали.
Следовательно, соотношение дальней коммутативности
выполняется автоматически.
Лекция 7. Группы кос и их представления 103
Найдем условия, которым должна удовлетворять матрица А,
чтобы выполнялось соотношение <7t(7t+i(7i = <7i+i(Tt<rt+i. Для этого нам
придется перемножать матрицы третьего порядка.
Итак, пусть матрица А имеет вид
(;0-
Тогда для выполнения соотношения а^+хъ = tfi+i^tcri+i нужно
следующее равенство двух матриц:
р q 0\ /1 0 0\ (р q 0\ /1 0 0\ /М 0\ /р ? 0\
reO Opj гвО = 0? j reO reO .
0 0 1/ \0 г в/ \0 0 1/ \0 г в/ \0 0 1/ \0 0 1/
Таким образом, получаем равенство
p2+pqr pq + pqs q2\ (р pq q2 \
pr + prs qr + ps2 qs I = I pr qr + sp2 gs + pgs J .
г2 rs s J \r2 ts + prs s2 + sqr J
Это дает набор соотношений для р, q, r, s: pqs = prs = 0, ps2 = зр2,
(p+qr-\)p = 0, (s+gr- 1)з = 0. В таком случае, либо q = 0, г = 0,
либо ps = 0. Если g = г = 0, то все матрицы получаются диагональными,
и никакого интересного представления получиться не может.
Значит, ps=0. Будем считать, для определенности, что s = 0,р —
произвольное, не равное нулю. Тогда р -f qr = 1. В таком случае можно
выбрать р= 1-х, q = x, г = 1.
Получаем для каждого л представление группы кос из п нитей,
при котором элемент сг,- переходит в блочно-диагональную матрицу,
у которой на диагонали на местах от 1 до i - 1 и от г + 2 до п блоки
состоят из единичных матриц размера 1 х 1, а блок (2x2), стоящий
на месте (t, i -f 1) имеет вид
(1-х х\
1 0;-
Это представление можно также трактовать как представление
стабильной группы кос матрицами бесконечного размера.
Такое представление называется представлением Бурау, см. [17],
обзоры см. также в [131], [103].
§ 4. Представление Крамера—Бигелова
До недавнего времени не было известно, является это
представление точным или нет. Была доказана лишь его точность для группы кос
из трех нитей.
104
Раздел II. Теория кос
Контрпример, показывающий неточность представления Бурау
в общем случае, был построен Муди, см. [70]. На данный момент
доказано, что представление Бурау является неточным для кос начиная
с 5 нитей, см., например, обзор [84]. Для 4 нитей вопрос о точности
представления Бурау остается открытым. В [58] предъявлено
представление группы кос, которое являлось точным для кос из 4 нитей
и выдвинута гипотеза о том, что оно является точным для
произвольного числа нитей.
Совсем недавно было доказано, что это представление является
точным для группы кос из произвольного числа нитей, см. [59, 8]
и обзор [84].
Следуя [59], предъявим точное представление группы кос из п
нитей для произвольного натурального п.
Пусть R — коммутативное кольцо с единицей, a g, t £ R —
два обратимых элемента. Пусть V — линейное пространство над Д
размерности п(п - 1)/2 с образующими ж,,, 1 < г < j ^ п.
Определим действие группы кос Вг (п) на пространстве V по
следующему правилу:
**(*у) = \
"»,j
*i-U + (1 ~ q)xij
tq(q - l)xf)j+1 + qxi+ij,
tq2x,
»J
k < % - 1 или k > j;
k = i-l;
к = i < j - 1;
к = i = j - 1;
i < к < j - 1;
i <k=j -1;
k=j;
(2)
*« + '9* *(?-l)2*M+b
*«j-i+'^"'(9-l)*i-iji
(l-0)*ij+?*»j+b
где or*, fc = 1,..., (n - 1) — образующие группы кос.
To, что это отображение задает представление группы кос,
может быть проверено прямым вычислением. Доказательство точности
описанного выше представления см. в [59] или в [8].
Обозначим через Ln пространство представления Крамера—Биге-
лова (2) группы кос Вг (п). Поскольку базис пространства Ln составляет
часть базиса пространства Lnfi, то Ln С Ln+\.
Из явного вида представления (2) следует, что Ln является
инвариантным пространством этого представления группы Вг(п + 1) в Ln+\.
При переходе от матриц представления группы Вг(п) к матрицам
представления Вг (п + 1) левый верхний блок стабилизируется.
Поэтому можно говорить о бесконечномерном представлении стабильной
группы кос.
Лекция 8
Теорема Александера и алгоритм Вожеля
На прошлой лекции мы подробно познакомились с понятием косы
и с тем, как по заданной косе можно построить узел или зацепление.
Кроме того, было показано, что изотопным косам соответствуют
изотопные зацепления.
При этом неясными остались два вопроса: какие зацепления
получаются из кос и каким косам соответствуют изотопные узлы.
Первому вопросу и будет посвящена настоящая лекция.
Замечание 8.1. В дальнейшем нам будет удобно работать с
ориентированными зацеплениями, для этого мы будем задавать произвольную ориентацию
для зацепления, с которым работаем.
Упражнение 8.1. Постройте косу, порождающую зацепление, изотопное
кольцам Борромео.
§ 1. Теорема Александера
Теорема 8.1 (Теорема Александера). Любое зацепление (в том
числе любой узел) можно представить посредством замыкания косы.
Доказательство. Мы будем доказывать данную теорему для случая
ориентированных полигональных зацеплений.
Рассмотрим диаграмму ориентированного зацепления L и точку О
на плоскости диаграммы, не лежащую на ребрах диаграммы. Скажем,
что L обвивается вокруг точки О, если любое звено зацепления L видно
из точки О как ориентированное против часовой стрелки. Звенья,
видные из данной точки как ориентированные против часовой стрелки
назовем положительными; остальные звенья назовем отрицательными.
Если для зацепления L есть точка О, вокруг которой оно
обвивается, то доказательство теоремы Александера очевидно: коса получается
разрезанием диаграммы зацепления L вдоль луча, выходящего из
точки О и раздвиганием точек разреза, см. рис. 1.
106
Раздел И. Теория кос
Рис.1
Для доказательства теоремы в общем случае мы постараемся
свести наше зацепление к зацеплению, обвивающемуся вокруг некоторой
точки О. Это можно сделать с помощью трюка Александера,
который заключается в том, что некоторое отрицательное звено
(сторона АВ треугольника ABC, проекция которого содержит точку О)
заменяется на две оставшиеся стороны треугольника ABC, обе из
которых являются положительными звеньями относительно точки О,
см. рис. 2.
а б в
Рис.2
Эта операция проделывается до тех пор, пока не останется
отрицательных звеньев. В таком случае полученное зацепление будет
обвиваться вокруг точки О.
Расскажем об этой конструкции более подробно. В том случае, если
отрицательное звено АВ не содержит перекрестков, трюк Александера
производится непосредственно, см. рис. 2 а. В самом деле, можно
просто разбить звено АВ на две части и «протащить» их над точкой О.
То же самое можно сделать и в том случае, когда звено АВ содержит
один перекресток (т. е. его проекция пересекается с проекцией ровно
одного звена), причем расположено выше другого звена (рис. 26).
к-
/
а :
. с
. с
Лекция 8. Теорема Александера и алгоритм Вожеля 107
Если звено АВ содержит ровно один перекресток и при этом
расположено ниже другого звена, можно протащить АС и СВ под
этим звеном и точкой О.
Наконец, если звено АВ содержит несколько перекрестков, то его
можно разбить на меньшие звенья, каждое из которых содержит ровно
один перекресток, и повторить рассуждения, описанные выше.
Упражнение 8.2. С помощью применения трюка Александера постройте
косу, замыкание которой изоморфно связной сумме двух правых трилистников.
Описанный метод доказательства теоремы Александера, конечно,
является конкретным алгоритмом построения косы по диаграмме
зацепления. Однако этот алгоритм не является удобным для реализации
на компьютере. ■
§2. Алгоритм Вожеля
Сейчас мы опишем достаточно быстрый алгоритм представления
зацепления в виде замыкания косы, предложенный П. Вожелем [88].
Начнем с определения.
Определение 8.1. Скажем, что диаграмма зацепления заплетена
как коса, если существует точка, вокруг которой эта диаграмма
обвивается. Зацепление, диаграмма которого заплетена как коса,
очевидным образом можно представить в виде замыкания косы.
Замечание 8.2. Очевидно, что свойство диаграммы зацепления быть
заплетенной как коса не зависит от расстановки проходов и переходов, а лишь
от тени диаграммы. В дальнейшем расположение проходов и переходов
диаграммы нигде не будет использоваться.
Пусть дана ориентированная (связная) диаграмма D зацепления L.
Для нее можно корректно определить операцию уничтожения
перекрестков. Для этого просто «разведем» нашу диаграмму в каждой
вершине способом, указанным в лекции 1, получив тем самым набор
окружностей Зейферта, см. рис. 3. Это разведение в дальнейшем будем
обозначать через а.
Г~\
Г* 1
L j I I
I I у
I J
W
Рис. 3. Разведение перекрестков и окружности Зейферта
Раздел II. Теория кос
Определение 8.2. Скажем, что множество окружностей Зейферта
некоторой диаграммы узла образует гнездо, если все они
индуцируют одну и ту же ориентацию плоскости и при этом ограничивают
вложенную систему дисков, т. е. окружности Зейферта С\,..., Сп
ограничивают диски D\ Э ... Э Dn, см. рис. 4.
Рис.4. Система окружностей Зейферта образует гнездо
Очевидно, что если окружности Зейферта некоторой диаграммы
узла образуют гнездо, то данная диаграмма заплетена как коса (точнее,
после некоторой плоской изотопии она становится заплетенной как
коса). Более того, количество нитей такой косы в точности совпадает
с количеством окружностей Зейферта.
Рассмотрим теперь тень диаграммы D. Эта тень разбивает
сферу (плоскость, замкнутую бесконечной точкой) на двумерные клетки,
которые мы назовем гранями. Назовем внешней гранью грань,
содержащую бесконечную точку.
о
А{
Рис.5
Определение 8.3. Будем говорить, что грань S неупорядоченная,
если у нее есть два ребра, принадлежащие разным окружностям
Зейферта А\ и Ai, но при этом индуцирующие одну и ту же
( ориентацию грани S, см. рис. 5.
Лекция 8. Теорема Александера и алгоритм Вожеля 109
Скажем, что эти две окружности Зейферта А{ и Аг образуют
неупорядоченную грань 5.
К таким ребрам неупорядоченной грани можно применять
второе движение Рейдемейстера, как это показано на рис. 6. При этом
диаграмма становится «более упорядоченной», т. е. количество
неупорядоченных граней уменьшается.
Предложение 8.1. Если все ребра грани принадлежат ровно двум
окружностям Зейферта, то такая грань не является неупорядочен- .
ной.
Доказательство. Рассмотрим ребра этой грани. Легко видеть, что
ребра, принадлежащие одной окружности Зейферта, имеют
одинаковую ориентацию. Рассмотрим два соседних ребра, принадлежащих
разным окружностям Зейферта. Они имеют разную ориентацию.
Следовательно, любые два ребра данной грани, принадлежащие разным
окружностям Зейферта, имеют разные ориентации. Таким образом,
наша грань не является неупорядоченной. ■
Рис.6
Предложение 8.2. Если у диаграммы D зацепления L нет
неупорядоченных граней, то посредством замены бесконечности она
переводится в диаграмму, заплетенную как коса.
Доказательство. Рассмотрим некоторую грань из числа тех, на
которые тень узла разбивает плоскость. Каждые два соседних ребра этой
грани либо ориентированы одинаково и принадлежат одной
окружности Зейферта, либо ориентированы противоположно и принадлежат
разным окружностям Зейферта. Рассматривая соседние ребра,
принадлежащие одной окружности Зейферта, как одно, получим некоторый
многоугольник М. У этого многоугольника ориентации ребер
чередуются, следовательно количество его ребер четно (или же все его ребра
принадлежат одной окружности Зейферта). В силу того, что данная
грань не является неупорядоченной, все ребра данной грани
принадлежат либо одной, либо двум окружностям Зейферта. Из данного
110
Раздел II. Теория кос
утверждения следует, что каждая окружность Зейферта,
определяющая ребро многоугольника М, имеет общие вершины либо с одной
окружностью Зейферта, либо с двумя, находящимися от окружности М
по разные стороны.
Остаток доказательства оставляем читателю в качестве легкого
упражнения. ■
Алгоритм Вожеля состоит в следующем: сначала мы уничтожаем
все перекрестки, затем с помощью второго движения Рейдемейстера
избавляемся от неупорядоченных областей, и, наконец, если окружности
Зейферта не образуют гнездо, заменяем бесконечность.
Опишем этот алгоритм более подробно.
Разведем сначала все перекрестки. Получим набор окружностей
Зейферта. Пусть их з штук. Некоторые пары из них содержат ребра,
которые образуют неупорядоченную грань. Составим граф, вершинами
которого являются окружности Зейферта. Две окружности соединены
ребром в том и только в том случае, когда существует грань
(упорядоченная или неупорядоченная), которая инцидентна данным двум
окружностям.
Выкинем из нашего графа вершину (окружность Зейферта,
имеющую хотя бы одно «внешнее» ребро, т. е. ребро, инцидентное
клетке, содержащей бесконечную точку). Получим некоторый граф Гь
а остальные 5-1 окружностей перенумеруем а^ аг,..., а8-\ так, чтобы
окружности а( и а,{+1 содержали ребра, порождающие собой
неупорядоченную грань.
Рассмотрим лишь случай связного графа Т\ (алгоритм для
несвязного графа проводится последовательным применением алгоритма для
связного графа).
Будем производить следующую операцию: возьмем
неупорядоченную грань, образованную окружностями Ai и А^ и сделаем второе
движение Рейдемейстера. Получим вместо окружностей А\ и Аг две
окружности Зейферта, одна из которых лежит внутри другой, причем
новые две уже не образуют неупорядоченной грани (см. рис. 7).
Обозначим внешнюю окружность через Ai, а внутреннюю —
через А^ Так как старая окружность Аг образовывала неупорядоченную
грань с окружностью А$, то новая окружность А\ также будет
образовывать неупорядоченную грань с окружностью -4з. Проделаем
движение П2 с окружностями А\ и Аг и снова переобозначим — внешнюю
окружность через А\, а внутреннюю — через А$, и так далее. В итоге
(после 5-2 операций £2г) получим одну внешнюю окружность А\,
не образовывающую неупорядоченных граней с Аг,..., А9^.
Лекция 8. Теорема Александера и алгоритм Вожеля 111
П2
Ы
Рис.7
Теперь не будем трогать окружность А^, но проделаем те же самые
операции с окружностями (А2у А$), (А2, Ац), и т. д., затем то же с парами
окружностей л4з, -A», i > 3, и т. д. Всего мы провели ^<""1 ^ ~ ' операций.
Получим набор окружностей А\, А2, ..., -4в-ь каждая следующая
из которых лежит внутри предыдущих, причем никакие две не образуют
неупорядоченной области.
Покажем, что и оставшаяся окружность (та, которую мы выкинули
с самого начала) также не образует неупорядоченной области ни с какой
из вышеперечисленных.
Действительно, так как она имеет внешнее ребро, она могла бы
образовывать грань лишь с окружностью А\ (так как не может лежать
внутри никакой окружности).
В силу предложения 1, такая грань не может быть неупорядоченной.
Затем, в силу предложения 2, можно заменить бесконечность так,
чтобы все окружности образовывали гнездо. При этом полученная
диаграмма зацепления получится заплетенной как коса.
Таким образом, мы провели С]_2 операций для связного графа. Для
несвязного графа это количество будет равно ^ Су^, где Yl j = s - 1.
i
Очевидно, что это количество операций не превосходит ^ С]_{.
з
Теорема 8.2. Если у диаграммы зацепления D было п вершин и s
окружностей Зейферта, то:
а) алгоритм Вожеля потребует не более, чем С*_2 вторых движений
Рейдемейстера;
б) количество перекрестков у полученной косы будет не больше п +
(,_!)"(, _2).
Доказательство. Пункт 1 уже доказан.
Докажем пункт 2. Количество ветвей у зацепления, заплетенного
как коса, равно количеству его окружностей Зейферта. При применении
112
Раздел II. Теория кос
Рис. 8. Слева — плоские диаграммы узла, справа — окружности Зейферта
каждого движения Пг количество окружностей Зейферта не менялось
и оставалось равным 8. Следовательно, полученная коса будет косой
из з нитей.
Вначале диаграмма зацепления имела п перекрестков, а при
каждом движении Q.2 их количество увеличивалось на два. Поэтому
в конце их количество не будет превышать п + (s - l)(s - 2). ■
Лекция 8. Теорема Александера и алгоритм Вожеля 113
Пример 8.1. Представим теперь узел 52, изображенный на рис. 8, в виде
косы.
Для этого дважды применим второе движение Рейдемейстера, а затем
проведем замену бесконечности (см. рис. 8). (Мы применяем движения Q2
в несколько другом порядке; таким образом нам будет достаточно двух
движений ^2» а не трех.)
В итоге получим диаграмму, заплетенную как коса, см. рис. 8 внизу.
Итак, мы научились достаточно просто заплетать косы,
соответствующие тем или иным наперед заданным узлам или зацеплениям.
Остались открытыми два вопроса, связанные с узлами и косами.
1. Построить алгоритм, показывающий, изотопны две косы или нет.
2. Найти критерий того, что две неизотопные косы задают изотопные
узлы.
Этими вопросами мы и займемся на ближайших лекциях.
Лекция 9
Алгоритм Деорнуа
распознавания изотопности кос
В этой лекции речь пойдет о проблеме распознавания кос, а
именно, о том, как по буквенному (алгебраическому) заданию двух кос
понять, одинаковы они или нет.
Из теоремы Артина следует, что две косы изотопны тогда и только
тогда, когда одна из них переводится в другую посредством
конечного числа соотношений (дальней коммутативности и соотношений
типа <Ti<Ti+\<Ti = cri+1<7t-(ri+i). Однако эти соотношения не разрешают
проблемы: мы можем бесконечно долго применять эти соотношения
и не добиться успеха.
В этой лекции будет изложен точный алгоритм, полностью
решающий проблему распознавания кос — алгоритм Деорнуа, предложенный
французским математиком Патриком Деорнуа [27]. Этот алгоритм в
подробностях, а также много других интересных фактов по теории кос
можно прочесть в замечательной книге [26].
Об этом алгоритме и теории LD -множеств, которым и посвящена
книга [26], можно было бы прочитать целый специальный курс; мы
остановимся лишь на одной небольшой (практической) его части.
Замечание 9.1. Алгоритм Деорнуа, описанный в книге [123], на практике
является работающим, хотя его остановка за конечное число шагов не доказана.
Мы предлагаем другой (в некотором смысле более удобный) алгоритм Деорнуа.
Вспомним сначала, что косы, в отличие от узлов, образуют
группу. Поэтому для сравнения двух кос а и Ь достаточно проверить,
изотопна ли коса ab~l тривиальной косе.
Алгоритм Деорнуа, описанный в [26], отвечает именно на этот
вопрос.
Итак, начнем с определения.
Пусть задана алгебраическая коса в виде слова W из букв afl,
t = l,2,...,n.
Определение 9.1. Скажем, что коса W является {-положительной
(1 -отрицательной) косой, если она изотопна косе W', в выражении
которой через образующие буква <Т\ встречается в положительных
Лекция 9. Алгоритм Деорнуа распознавания изотопности кос 115
(отрицательных) степенях и не встречается в отрицательных
(положительных) степенях.
Если коса W изотопна некоторой косе W\ в разложении которой
по образующим не участвует <j\, то назовем косу W {-нейтральной.
Замечание 9.2. Поскольку изотопический класс косы состоит из большого
количества кос, a priori не исключено, что описанные выше классы
пересекаются. Оказывается, что эти классы попарно не пересекаются, см. следствие 2
теоремы 9.1.
Упражнение 9.1. Покажите, что коса, в записи которой все образующие
встречаются только в положительных степенях, не изотопна единичной косе.
Теорема 9.1. Любая I-положительная (соответственно
I-отрицательная) коса не может быть изотопна тривиальной косе.
Замечание 9.3. На самом деле, верно и более сильное утверждение: любая
коса, запись которой содержит <г*, но не содержит <Г{~е, е = ±1, не может быть
изотопна тривиальной. Это утверждение мы доказывать не будем, см [26].
Для доказательства теоремы 9.1 нам понадобится несколько
определений и небольших лемм.
Пусть дана некоторая коса Б, в записи которой участвуют только
положительные степени образующих а.
Рассмотрим ее дуги, т. е. те части нитей, которые все время
проходят снизу при перекрестках.
Мы хотим разметить косу элементами из некоторого множества М.
Это значит, что мы собираемся поставить на каждой нижней дуге
некоторый элемент из М так, чтобы:
а) дуги, исходящие из верхних точек косы, были помечены буквами —
аргументами, принимающими значения в М;
б) каждый нижестоящий элемент однозначно определялся
вышестоящими;
в) оператор /, выражающий метки нижних точек косы через метки
верхних точек косы был инвариантен относительно изотопии кос.
Для исполнения этой цели рассмотрим перекрестки косы.
Поставим в соответствие его нижним ветвям элементы а, Ъ и с
из М. Зададим формальное соотношение с = а*Ъ, см. рис. 1.
Рис.1
116
Раздел И. Теория кос
Приступим к анализу инвариантности оператора / относительно
изотопии. Известно, что всякая изотопия кос порождена двумя
преобразованиями. Эти преобразования состоят в учете формул «т,^,"1 = е,
г = 1, ...,п- 1 (ближняя коммутативность), o^+io*,- = С{+1<Г{СГ{+\9
i = 1,... 7i - 2 (дальняя коммутативность), а&} = <7j<7i, \i - j\ ^ 2,
1 < t,j ^ я — 1. Оставим без внимания «т,-^"1 = е (мы рассматриваем
лишь косы, в записи которых участвуют лишь образующие в
положительных степенях). Инвариантность относительно дальней
коммутативности выполняется автоматически по построению. Обратимся
к ближней коммутативности. Из рис. 2. следует, что
а * (6 * с) = (а * ft) * (а * с). (1)
(а*Ь)*(а*с) а*Ъ
а*(Ь*с) а*Ъ
Рис.2
Определение 9.2. Тождество (1) называется левой самодистрибу-
тивностъю, а множество М с операцией *, удовлетворяющей (1),
называется LD-системой или LD -множеством.
Замечание 9.4. Очевидно, что операции * недостаточно, чтобы определить
оператор / для всякой косы; действительно, в случае, когда в разложении косы
по образующим участвует сг,"1, неизвестно, как пометить нижестоящие точки.
В дальнейшем на множестве М мы определим другие операции, V
и Л, которых уже будет достаточно для описания всех кос. При этом
эти операции окажутся также лево-самодистрибутивными.
Очевидно, что отображение / является инвариантным
относительно дальней коммутативности (т. е. перестановки в слове-косе букв (7,-
и <Tj, где |г - j\ ^ 2. Нам осталось проверить инвариантность
отображения / относительно третьего движения Рейдемейстера, т. е. соот-
Лекция 9. Алгоритм Деорнуа распознавания изотопности кос 117
ношения а,-а,-+1а,* = a$+ia,af+i. Из рис.2 видно, что оно накладывает
условие, называемое левой дистрибутивностью (так как операция *
является дистрибутивной по отношению сама к себе).
Итак, если у нас есть лево-дистрибутивное множество, то мы
можем сопоставлять элементы этого множества ветвям положительной
косы; при этом набор элементов на нижних точках косы определяется
набором элементов на верхних точках однозначно и не меняется при
изотопии косы.
Обозначим через pi элементы из М, стоящие в верхних точках
косы, а через д,- — элементы, стоящие в нижних точках косы. Так, для
тривиальной косы pi = </,-.
На лево-дистрибутивном множестве можно определить частичное
отношение <, а именно, положим для а,с € М а < с, если ЗЬ € М:
с = а*Ь.
Определение 9-3- Назовем частично упорядоченное
лево-дистрибутивное множество М упорядоченным, если отношение <
ациклично, т. е. не существует последовательности а\ < a-i < ... <
a„ < ax.
Пример 9.1. Множества вещественных и рациональных чисел можно
снабдить некоторыми операциями, делающими эти множества
лево-дистрибутивными.
а) a*b = max(a,Ь),
б) а*6=(а + 6)/2,
в) а * Ь = (а + 1) для каждого Ь.
Позднее мы приведем доказательство ацикличности одного лево-
дистрибутивного множества. Подробное доказательство этого факта
можно найти в [26].
Приведем теперь пример ацикличной LD -системы. Для этого нам
придется вводить более сложные структуры, несущие в себе также
структуру LD -системы.
Обозначим группу кос из п нитей через Вг(п), а полугруппу
неотрицательных кос через Br (n)+. (
Определение 9-4. Пусть (М, л) — бинарная система, т. е.
множество, снабженное бинарной операцией. Определим (правое)
действие полугруппы Вг(п)+ на Мп = М х ... х М индуктивно
по правилу: для а = (аь ..., а„) „
(а)е = а, (а)а{У) = (<ц ..., а; Л ai+h a,-, at+2,. •., «n)w, (3)
где е — единица, а <г,- — образующие группы кос.
118
Раздел II. Теория кос
Перейдем теперь к раскрашиванию произвольных кос-слов (не
только положительных). Для этого (по сравнению с окрашиванием
положительных кос) нам понадобится вместо одной операции *
(обозначаемой теперь Л) ввести еще две операции: V и о. Тогда для
отрицательных перекрестков раскраска нижних точек косы будет получаться
из раскраски верхних точек косы так, как показано на рис. 3.
алЪ
аоЬ
6Va
Рис.3
Как и ранее, имеем выражение меток нижних точек через метки
верхних точек, определяющее оператор /.
Лемма 9.1- Пусть (М, Л, о, v) — тройная бинарная система.
Тогда оператор f инвариантен относительно изотопии, порождаемых
формулами С{0^1 = <r^l<Ti — ев том и только в том случае, когда
в М имеют место следующие соотношения
V ж, у G М х о у = у, х Л (х V у) = х V (х Л у) = у.
Доказательство. Следует из рис. 4. ■
аЛЪ
aob
bVa
(о ЛЬ) о a aV(bAa) (аоЬ)л(бУа) о об
Рис.4
Определение 9.5. LZ>-Система М, снабженная дополнительной
операцией V называется LD-квазигруппой, если в ней имеет место
Лекция 9. Алгоритм Деорнуа распознавания изотопности кос 119
соотношение
ж л (ж V у) = ж V (ж л у) = у
для произвольных ж, у Е М.
Замечание 9.5. Изотопия, порождаемая ближней коммутативностью,
оставляет оператор /, действующий на LD -квазигруппе М инвариантным по
определению LD -системы. Следовательно, если М — LD -квазигруппа, то
оператор / не изменяется при любых изотопиях кос.
Предложение 9.1. Пусть G — группа. Тогда бинарные операции,
определенные по правилу х А у = хух~1, х V у = х~~*ух, х о у = у,
задают структуру LD-квазигруппы на G.
Доказательство. Проверим справедливость равенств
хоу = уу
ж Л (ж V у) = ж Л (x~lyx) = хх"1ухх"1 = у,
х V (х А у) = х V (хух~1) = х~~1хух~1х = у. Ш
Таким образом, мы можем использовать систему (G,A, V),
происходящую из группы G (считая, что х о у = у Уж, у), для раскраски
кос. В частности, пусть FGn — свободная группа, порожденная
образующими {«1,..., жп}. Для слова-косы Ь из п нитей определим Ъ как
слово-косу, получающуюся из слова Ь заменой порядка букв на
противоположный.
Для заданных элементов жь ..., хп_определим элементы у\}..., уп
по правилу: (yi,... ,уп) = (жь... ,ж„)Ь. Пусть (р(Ь) — гомоморфизм
группы FGn< переводящий элемент ж,- в у,- для каждого if Тогда (р
является эндоморфизмом группы кос Вп в Aut (FGn), так как <р(Ъ~1)
совпадает с (р{Ь)'1 по построению.
Вкладывая FGn в FGn+\, мы можем перейти к прямому пределу,
который мы назовем FGoo. Таким образом, мы получаем эндоморфизм
(р : Bqo -> Aut (FGoo)- Обозначим <р(<Т{) через а,-. По построению имеем
{ж*, к < г или к > i + 1,
х{хмх^\ k = i,
Xi, ft = t+l.
Замечание 9.6. Это действие совпадает с действием образующей <Т{ группы
кос на цвета дуг, показанным на рис. 3.
Определим сдвиг sh на FGoo»переводящий ж,- в ж|+1 для каждого i.
Определим также действие sh на Aut (FGoo) по правилу: для (р £
Ax\l(FGoo) sh((p)(xi) = xi и sh((p)(xi+i) = sh(p(gt*)) для i ^ 1. Так,
например, sh (a,-) = al+i для каждого i.
120
Раздел!!. Теория кос
Тогда операция Л, определяемая по формуле <р Л *ф = <р о sh (i/>) о
а\ osh (<p~l), где значок о означает композицию отображений, является
самодистрибутивной с левой стороны, а <р — это гомоморфизм (Д», Л)
в (Aut (FGqo), Л). Заметим, что а\ коммутирует с образом
автоморфизма sh2. Для завершения доказательства самодистрибутивности
операции Л нам осталось показать, что верно следующее
Предложение 9.2. Пусть G — группа, а — фиксированный элемент
группы G, a s — изоморфизм группы G. Тогда формула х Л у =
xs(y)as(x"1) определяет левую самодистрибутивную операцию тогда
и только тогда, когда а коммутирует с образами отображения s2
и удовлетворяет соотношению
as(a)a = 8(a)as(a). (5)
Доказательство. Поскольку s — изоморфизм, получаем:
хЛ(у Az) = xs(y)s2(z)s(a)s2(y~l)as(x~'l)J
(х Л у) Л (х Л z) = xs(y)a£2(z)8(a)s2(x~l)as2(x)s(a~l)s2(y~l)8(x~~l).
Если операция Л обладает свойством левой самодистрибутивности,
то, выбирая х = у = z = 1, получаем s(a)a = as(a)as(a~l). Верно
и обратное утверждение.
Наконец, формула (5) и предположение о том, что а коммутирует
с s2(z) для каждого z влечет то, что отображение /, определенное
по формуле /(<т,) = в*"1 (о), задает гомоморфизм Д» вС ■
Итак, мы получили левую самодистрибутивную систему на
Aut (FGoo).
Теорема 9.2. Полученная система (Aut (FGoo), Л) ациклична.
Доказательство следует из двух вспомогательных лемм о
свободных редукциях, возникающих при подсчете значений оц(х). В
дальнейшем мы будем обозначать через W^ множество слов в алфавите
{ajf1,а?*1,.--}* Мы скажем, что слово из W^ свободно-редуцировано,
если оно не содержит подслов xixj1 или ж,"1»,-. Для любого w £ W^
обозначим через red(w) слово, получаемое из w последовательным
убиранием таких подслов. Таким образом, мы можем отождествить
свободную группу FGoo со множеством всех свободно-редуцированных
слов, снабженным операцией и • v = red (uv).
Определение 9.6. Для буквы х из алфавита {xfl, xfl,...} опре-
i делим Е(х) как подмножество множества FGoo, состоящее из всех
редуцированных слов, оканчивающихся буквой х.
Лекция 9. Алгоритм Деорнуа распознавания изотопности кос 121
Исследуем образ множества Е(х{ 1) под действием автоморфизма
«р.
Лемма 9.2. Предположим, что <р — произвольный элемент из
Aut(FGoo). Тогда автоморфизм sh(<p) отображает множество
Е(х^{) в себя.
Доказательство. Пусть / — гомоморфизм W<x> на себя,
отображающий Х{ в редуцированное слово (р(х{) для каждого г. Пусть w —
произвольный элемент из Е(х\1). Тогда w = ux[l, где и —
некоторый редуцированный элемент, не принадлежащий к Е(х\). Тогда
sh (f)(w) = sh (f)(u) • sh (f)(xil), т. e. red (sh (f)(u)x^1). Предположим,
что последнее слово не принадлежит Е(х^1). Это означает, что
последняя буква х~[1 сокращается с буквой жь встречающейся в sh (f)(u).
Но буква х\ в shc(f)(u) может происходить лишь из буквы х\ из и.
Таким образом, должно существовать разложение и = и\Х\иг> такое,
что red (sh (/)(г*2)) — пустое слово, т. е. sh (/)(«2) = 1. Так как sh (/) —
автоморфизм группы FGqq, то иг = 1. Это означает, что щ £ Е(х\),
что противоречит изначальной гипотезе. ■
Лемма 9.3. Автоморфизм ot\ отображает Е(х\{) на себя.
Доказательство* Пусть w — произвольный элемент из 25 (ж j"1).
По определению, w = uxj1, где и — некоторый редуцированный
элемент, не принадлежащий множеству Е(х\), a oti(w) — это red (a\(w))9
т. е.
a\(w) = red (ai(u)xiX2lXil).
Предположим, что слово из правой части не принадлежит
множеству Е {хjf1). Это означает, что х\1 в конце сокращается некоторой
буквой х\ из слова ai(u). Эта буква происходит либо из некоторого Х2,
либо из некоторого xfl в слове а\(и).
В первом случае мы запишем букву Х2, участвующую в
сокращении и выпишем и как щхгщ, где и2 — редуцированное слово,
не начинающееся сж2-1. Тогда
a\(w) = red (ai(ui)xiai(tt2)£i&2 ^Г1)»
и гипотеза состоит в том, что red (a^t^Bi&J1) — пустое слово, так
как ai(u2) = Х2Х\Х. Пусть теперь «i — автоморфизм и a^aj"1 — образ
Х21х\ относительно действия ai. Таким образом, есть единственный
возможный случай, когда и = х^1х\. Это противоречит предположению
о том, что и не начинается с scj1.
122
Раздел II. Теория кос
Во втором случае мы напишем аналогично, что u = U\x\u2, где
с = ±1. Тогда мы получаем
oti(w) = red (ai(ui)x\X2Xilai(u2)x\X2lXil),
при этом гипотеза состоит в том, что red {x\xTlai(u2)x\.xi) является
пустым словом. Из этого следует, что ct\(u2) = x\x\^ex~[l. Последнее
слово равно а\(х\~е)9 следовательно щ должно быть равно х\"е. Если
е = +1, то U2 пусто. Если е = —1, то щ = х\. В обоих случаях г*2
принадлежит Е{х\), что порождает противоречие. ■
Лемма 9-4. Предположим, что <р — автоморфизм группы FGqq,
который может быть выражен как композиция образов sh и
автоморфизма а\, причем последний встречается хотя бы раз. Тогда
(р(х\) принадлежит Е(х\1) и, в частности, автоморфизм (р не
может быть тождественным.
Доказательство. Предположение состоит в том, что <р допускает
представление вида
<р = sh ((ро) о а\ о sh (<P\)ai о... о ot\ о sh ((pp).
Тогда мы имеем sh(<pp)(x\) = Х\ и ai(x\) = х\Х2Х^1, т.е. a\(xi) Е
Е(х"{1). Тогда любое следующее отображение sh(y?*) и c*i переводят
Е(х^) вЕ(х^{). ■
Докажем теперь теорему 9.2. Мы должны показать, что в Aut (jFGqo)
невозможны равенства вида
<Р = (...(<рЛй)Л...)Л1^).
Используя определение операции Л, мы получаем представление <р
в форме
(р = (р о sh (<ро) о <*i о sh (y?i) о • о sh ((рр-\) о а\ о sh (^p),
из чего следует, что
Id = sh (^о) о «1 о sh (^>i) о • о sh (<рр-\) о ai о sh (<pp),
что невозможно в силу последней леммы.
Теперь завершим доказательство теоремы 9.1. Пусть Ь — 1-
положительная коса, т. е. коса, в записи которой встречается (Ту,
но не (7J"1. Рассмотрим автоморфизм <т(<р). Он удовлетворяет
условиям леммы 9.4, значит он не является единичным. Следовательно,
коса (р не является тривиальной.
Для наглядности можно привести также следующее доказательство.
Лекция 9. Алгоритм Деорнуа распознавания изотопности кос 123
Предположим, что в нашем распоряжении имеется
/^-квазигруппа Q, которая является ацикличной LD -системой с упорядоченной
операцией <. Покажем, что из существования такой квазигруппы Q следует
(уже доказанная) теорема 9.1. Рассмотрим элементы ai, <*2,..., а*,
соответствующие нижним ветвям, стоящим перед левыми перекрестками
а также элементы fti, &2> • • •> стоящие чуть правее них, см. рис. 5.
а0 1111
а0
i1
V
: I lb2 I I I
Рис.5
Легко видеть, что a,-+i = а,- Л fy > а,-,. Таким образом, a* > ai.
В силу ацикличности операции <, а* Ф а\.
Однако для тривиальной косы элементы множества М, стоящие
у первой верхней точки косы и у первой нижней точки косы, совпадают.
Противоречие доказывает теорему 9.1.
Из теоремы 9.1 можно вывести несколько следствий.
Следствие 9.1. Коса, обратная к I-положительной косе, являет-
ся {-отрицательной (т.е. имеет {-отрицательную запись); коса,
обратная к {-нейтральной косе является {-нейтральной.
Следствие 9.2. Произвольная коса В не может обладать более, нем
одним из трех свойств: быть {-положительной, {-отрицательной
или {-нейтральной.
X
Ч^
124
Раздел II. Теория кос
Доказательство. Предположим, что В — коса одновременно 1-
положительная и 1-отрицательная. Тогда существует 1-положительная'
запись косы В1, обратной к В. Следовательно, единичная коса ВК{
является 1-положительной, что приводит к противоречию.
Остальные случаи доказываются аналогично. ■
Следствие 9.3. Коса, изображающая тпорический узел типа (р, q)
является нетривиальной.
Мы знаем, что 1-положительные и 1-отрицательные косы не
являются тривиальными.
Все 1-нейтральные косы можно разделить на 2-положительные,
2-отрицательные и 2-нейтральные косы, где 2-положительные косы
и 2-отрицательные косы — такие, в которых не встречается
образующая <г\, а образующая (Тг встречается только в положительных
(соответственно только в отрицательных степенях). Косы, в записи
которых не встречается ни первая, ни вторая образующая, назовем
2 -нейтральными.
Аналогично теореме 9.1 можно доказать
Предложение 9.3. Любая 2-положительная или 2-отрицательная
коса не изотопна тривиальной косе.
Подобно 1-й 2-положительным (отрицательным, нейтральным
косам) можно определить к -положительные, fc-отрицательные и к-
нейтральные косы и доказать нетривиальность первых двух типов кос.
Таким образом, среди кос из п нитей, попавших под нашу
классификацию, лишь одна является тривиальной — (п — 1)-нейтральная
коса.
Теперь нужно показать, что все косы попадают под нашу
классификацию. Для этого достаточно доказать следующую теорему.
Теорема 9.3. Любая коса является изотопной либо
I-положительной, либо 1-отрицательной, либо 1-нейтральной косе.
Порассуждаем немного об этой теореме.
Пусть у нас есть алгебраическая запись некоторой косы К из п
нитей и мы хотим с помощью соотношений (т,(7у = Ojir, при \i-j\ ^2,
<Ti<Ti+i<Ti = Oi+iaiOi+i избавиться в ней либо от ai9 либо от <гГ1.
Предположим, что L — подслово в К, имеющее вид a?waCv\ где
р = ±1, а слово w содержит лишь образующие с номерами, большими,
чем г.
Определение 9.7. Такое слово называется i-ручкой.
Геометрически ручка изображается так (в случае г = 1):
Лекция 9. Алгоритм Деорнуа распознавания изотопности кос 125
Рис.6. Ручка
Для такой ручки можно провести редукцию, а именно, движение,
протягивающее t-ю нить над ближайшими перекрестками, см. рис. 7.
/
./
Рис.7. Редукция ручки
Предложение 9-4. В этом случае слово a\vG{ € перейдет в слово г/,
получаемое из слова v заменой всех вхождений <rf+x на crj^of 1<т*+х.
Доказательство. Действительно, рассмотрим редукцию ручки,
изображенную на рис. 7. Все перекрестки, лежащие справа от о^ останутся
на месте, начальный и конечный перекресток <Т\ пропадут, а
перекрестки, через которые протягивается нить, изменятся по правилу,
описанному в формулировке предложения. ■
126
Раздел И. Теория кос
Рассмотрим теперь слово К и будем последовательно редуцировать
ручки в соответствующей косе. Если процесс закончится на конечном
шаге (т.е. не останется ручек), то полученная коса будет либо 1-
положительной, либо 1-отрицательной, либо 1-нейтральной.
Покажем, что данный подход не всегда может увенчаться успехом.
Будем писать вместо образующих о^,^,... строчные латинские
буквы о, 6,..., а вместо их обратных — прописные (согласно [32]).
Пример 9.2. Рассмотрим слово аЬсВА. Оно является 1-ручкой.
Применив к нему редукцию, получим слово В(аЬсВА)Ъ, в котором 1-ручка совпадает
с изначальной. Применяя редукцию сколь угодно много раз, от этой ручки мы
не сможем избавиться.
Дело в том, что данная 1-ручка содержит внутри себя 2-ручку
и после такого редуцирования 2-ручка «вылезает наружу» и
становится 1-ручкой.
Для этой косы можно сначала сделать редукцию «внутренней»
ручки, а затем — внешней. Тогда получим а(ЬсВ)А —> (аСЬсА) -*
СЬАВс; таким образом, данная коса является 1-положительной.
К счастью, наличие внутри 1-ручки к -ручек (к > 1) является
единственным препятствием для последовательного редуцирования
косы до состояния, в котором нет 1 -ручек.
Докажем следующую лемму.
Лемма 9-5. Если внутри j -ручки нет j +1 -ручек, то после редукции
такая ручка исчезает, а на ее месте не появляется другой j-ручки.
Доказательство. Пусть и = o^va^6 — 1-ручка, е = ±1. Так
как v не содержит 2-ручек, то образующая а г входит в v либо только
в положительных степенях, либо только в отрицательных степенях.
Из предложения 2 получаем, что в тех же степенях будет входить
образующая <Т\ в слово и'у полученное из и посредством редукции.
Следовательно, слово и1 не содержит ручек. ■
Определение 9.8. Ручка, содержащая в себе другие ручки в
качество подслов, называется гнездом.
Теперь мы можем предъявить алгоритм Деорнуа.
Сначала мы проводим редукцию для внутренних ручек
(которые не являются гнездами), затем для ручек, их содержащих, и т.д.
В итоге получим косу без ручек, т.е. или 1-положительную, или 1-
отрицательную, или 1-нейтральную диаграмму.
Пример 9.3. Рассмотрим слово-косу ABacBCBaCbaa и приведем ее
к виду, не содержащему ручек.
ABacBCBaCbaa
ЬАВсВСВаСЬаа
Лекция 9. Алгоритм Деорнуа распознавания изотопности кос 127
ЬЬАВсЬАВСЬАВСЬаа
ЬЬАВсЬАВСЬАсВСаа
ЬЬАВсЬАВСЬсЬАВСа
bbABcbABCbcbbABC
Здесь подчеркнутое подслово обозначает ручку, которую мы в данный
момент редуцируем.
Полученное слово является 1-отрицательным, следовательно, наша коса
нетривиальна.
Таким образом, мы получили достаточно простой и эффективный
алгоритм распознавания кос.
Упражнение 9.2. Реализуйте этот алгоритм на компьютере.
Мы пока не доказали, что алгоритм Деорнуа заканчивает свою
работу за конечное число шагов (количество букв в слове растет и
утверждение о конечной остановке алгоритма не является очевидным).
Дело в том, что, стартуя с некоторой косы и, проводя
редуцирование ручек, мы будем всегда находиться в пределах некоторого
множества слов (кос), называемого графом Кэли. Это множество
является конечным, при этом наш обход элементов этого множества не будет
повторяться. Следовательно, за конечное число шагов алгоритм
остановится. Подробнее см. [26].
Лекция 10
Теорема Маркова.
Уравнение Янга—Бакстера
В этой лекции я расскажу еще о двух важных вопросах, связанных
с теорией кос — о теореме Маркова и об уравнении Янга—Бакстера.
§ 1. Теорема Маркова
Начнем с теоремы Маркова. В работе [115] Андрей Андреевич
Марков изложил эту теорему, однако его доказательство не
содержало деталей. Он оставил эту задачу своему ученику Н. М. Вайнбергу,
который погиб на войне вскоре после своей первой публикации [89]
на эту тему. Первое полное опубликованное доказательство
принадлежит Джоан Бирман [9], мы же будем придерживаться более поздней
работы Мортона [71], в которой изложено более простое доказательство.
Теорема Маркова отвечает на вопрос, когда замыкания двух кос
дают изотопные узлы (зацепления). При этом ответ на этот вопрос
не является алгоритмичным, т. е. приведен лишь список движений,
с помощью последовательного применения которых косы,
представляющие изотопные узлы, переводятся одна в другую, но не сказано,
в каком порядке нужно применять эти движения и когда нужно
остановиться, чтобы установить, изотопны две косы или нет.
Начнем с представления произвольного узла (или зацепления)
в виде косы, отличного от представлений, описываемых ранее в
алгоритмах Александера и Вожеля. Это представление основано на понятии
прошивания узла некоторой кривой.
Замечание 10.1. Замыкания кос мы будем рассматривать как набор кривых
внутри цилиндра, не пересекающих его ось, а осью косы будем называть кривую,
совпадающую внутри цилиндра с осью данного цилиндра и замыкающуюся
вдали от него.
Начнем с определения.
Определение 10.1. Пусть К — ориентированное зацепление в R3,
a L — некоторая незаузленная кривая. Скажем, что К
представляет собой косу относительно L или что К U L является зацеплением-
косой, если К и L образуют замыкание некоторой косы и ось этой
Лекция 10. Теорема Маркова. Уравнение Янга—Бакстера 129
косы соответственно (т. е. К лежит внутри полнотория Sl x D,
причем координата по 51 является возрастающей, a L является
осью этого полнотория), см. рис. 1.
Рис.1
Если дана плоская диаграмма замыкания косы, то зацепление-
коса может быть получена из нее «опоясыванием» замыкания косы
окружностью, см. рис. 2.
Рис.2
Пусть К — плоская диаграмма некоторого ориентированного
зацепления. Рассмотрим некоторую кривую L на плоскости Р проекции
130
Раздел П. Теория кос
диаграммы К, пересекающую эту диаграмму трансверсально и не
проходящую через ее перекрестки.
Определение 10.2. Назовем системой переходов диаграммы
зацепления К набор из двух множеств S = {з\}..., s*}, F = {/i,..., /*}
точек на ребрах диаграммы К (отличных от вершин), так, чтобы
при прохождении вдоль ориентации зацепления К точки
множества S чередовались с точками множества F, при этом участки
типа [з,/] (т.е. начинающиеся в точке из 5 и кончающиеся
в ближайшей точке из F согласно ориентации компоненты) не
содержали проходов, а участки типа [/, з] не содержали переходов,
т. е. участки [з, /] представляли собой дуги, а участки [/, з] —
верхние дуги.
Определение 10.3. Скажем, что кривая L, проекция которой
на плоскость диаграммы зацепления К является несамопересека-
ющейся, прошивает диаграмму зацепления К с заданной системой
переходов (5, F), если отрезок зацепления К проходит сверху от L
в случае, когда этот отрезок начинается в области, содержащей
точки множества 5, и проходит снизу от L в случае, если начинается
в области, содержащей точки из F, см. рис. 3.
Замечание 10.2. При этом не обязательно отрезок прохождения
кривой L через такую область содержит элементы множества S или jP.
К
К
Рис.3
Если задана диаграмма зацепления К и некоторая кривая L9
проекция которой отделяет точки множества S и точки множества F,
то на пересечении диаграммы К и проекции кривой L можно
поставить проходы и переходы так, чтобы полученная кривая ll
прошивала зацепление L.
Докажем теперь следующую теорему.
Теорема 10.1. Если кривая L прошивает зацепление К, то К
представляет собой косу относительно L.
Лекция 10. Теорема Маркова. Уравнение Янга—Бакстера 131
К
Л /з /
-^22
'1
-^1
/i j.!
/2
-U2-
1*1
Т . г
и
гт*-
L
/2
<
1
/2
*1
/з!
Рис. 4
Доказательство. Выберем систему переходов (S,F) для
диаграммы К, и кривую L, лежащую в плоскости Р диаграммы К и
разделяющую точки множества S от точек множества F. Выпрямим L
в плоскости Р посредством гомеоморфизма плоскости Р, изотопно
изменяя также и проекцию К так, чтобы L была прямой линией
внутри некоторой области, полностью содержащей К и замыкалась вне
этой области. Следовательно, точки множества S окажутся по одну
сторону от этой прямой, а точки множества F — по другую. Такой
гомеоморфизм плоскости изображен на рис. 4.
Мы можем также предположить, что все проходы и переходы
диаграммы К лежат в плоскостях, параллельных плоскости Р (в точности
над и под образами их проекций).
Изменим теперь точку зрения, предполагая, что Р — плоскость
Oxz, a L представляет собой ось Oz, замыкаясь где-то на
бесконечности.
Используем L в качестве оси цилиндрических координат. Тогда
плоскость Р будет разделена на две полуплоскости, одна из которых
будет задаваться уравнением в = 0, а другая — уравнением в = 7Г.
Построим теперь зацепление, изотопное К, следующим образом.
Расположим все нижние дуги узла К (т. е. все отрезки [/, з]) на
полуплоскостях в = -е и в = 7г + е, а верхние дуги —- на полуплоскостях
0 = екв = я — е для некоторого малого значения е. При этом над
точками из множеств 5 и F построим отрезки, проектирующиеся в одну
точку плоскости Oxz.
Дуги, в которых проекция К пересекается с прямой L, изобразим
дугами в вертикальных плоскостях (выбор того, сверху или снизу
должна проходить дуга, определяется тем, был ли в данной точке проход
или переход).
Таким образом, полярная координата в данного узла (зацепления)
К все время либо является константой, либо монотонно не убывает.
На рис. 5 и 6 показано, как по узлу, изображенному на рис. 4,
можно построить узел, полярная координата которого возрастает.
132
Раздел II. Теория кос
Рис. 5. Диаграмма зацепления, пересекающаяся с L
-Л\-
л
Рис. 6. Полярная координата возрастает при движении вдоль зацепления
После малого шевеления полученного зацепления можно сделать
так, чтобы эта координата являлась монотонно возрастающей, т. е.
чтобы зацепление (которое мы также будем называть К) представляло
собой косу относительно L. ■
Из теоремы 10.1 следует, что если некоторое зацепление К
представляет собой косу относительно некоторой незаузленной кривой L,
то К представимо посредством замыкания косы.
Теорема 10.2. Любое замыкание К косы В можно прошить
кривой L так, чтобы К являлось косой относительно L.
Доказательство. Рассмотрим В в качестве косы, проходящей от
точек на верхнем основании некоторого цилиндра к нижним точкам
Лекция 10. Теорема Маркова. Уравнение Янга—Бакстера 133
на основании того же цилиндра D2 х I. Соединим верхние точки
с нижними посредством дуг, идущих горизонтально по основаниям
и вертикально, см. рис. 7.
к
ж
Рис.7
Применим изотопию, выпрямляющую нити кос и гомеоморфно
изменяющую верхнее основание цилиндра. Получившееся зацепление,
изотопное исходному, легко прошить следующим образом. Пусть fto _
уровень, на котором лежат «нижние» вершины А\ зацепления-косы,
a hi — уровень, на котором лежат «верхние» вершины A>i. Можно
считать, что на уровнях ho и h\ лежат также другие наборы вершин, В\
и Б2, с помощью которых и происходит замыкание косы, а именно,
точки множества А\ соединяются параллельными линиями с точками
множества Ai, а точки множества В\ — с точками множества £2.
Рассмотрим теперь окружность, лежащую в плоскости на уровне h =
(hi + h-i)ll и разделяющую наборы прямых AiAi и BiBi-
Спроектируем нашу диаграмму на основание цилиндра и выберем
в качестве множества S множество Ai, а в качестве jP — множество Аг*
Легко видеть, что в таком случае проекция нашей окружности
действительно будет представлять собой прошивание диаграммы нашего
зацепления. ■
Из теорем 10.1 и 10.2 следует теорема Александера. Действительно,
мы доказали, что каждое зацепление К является косой относительно
какой-нибудь кривой, т. е. представимо посредством замыкания косы.
Сформулируем теперь саму теорему Маркова.
134
Раздел II. Теория кос
Теорема 10.3. Если замыкания двух кос А и В представляют
собой изотопные узлы (зацепления), то коса В может быть получена
из косы А последовательным применением следующих преобразований:
а) сопряжение Ь —* а~1Ъа с помощью произвольной косы а из того же
количества нитей, что и коса Ь,
б) преобразование Ь —* Ъа^1, где Ь — коса из п нитей, а полученная коса
состоит из n-f 1 нити,
в) преобразование, обратное к 2).
Доказательство необходимости двух движений Маркова очевидно.
Для этого достаточно проверить лишь изотопность замыканий кос
относительно этих движений. Для первого преобразования это видно
из рис. 8 а, для второго — из рис. 8 б (первое движение Рейдемейстера).
in
а
J i
ь
1 1
а"1
1 L
-1
а
п
Г_1
ъ
ъ\
ь
Рис.8
Переформулируем теперь сложную часть теоремы Маркова. Для
этого нам понадобится дать несколько определений.
Определение 10.4. Скажем, что два зацепления-косы К U L
и К1 U L* просто-Марковски-эквивалентны, если существует
изотопия второго из них, переводящая L1 в L, а образ К1 совпадает
с К за исключением одной дуги а — для К к а* для К', причем:
а) угловая координата постоянна на дуге а и монотонно возрастает
на дуге а',
б) На дуги а, а' можно натянуть диск, внутренность которого транс-
версально пересекает L в одной точке.
Определение 10.5. Скажем теперь, что два зацепления-косы
являются Марковски-эквивалентными, если одно переводится в другое
4 посредством многократного последовательного применения
изотопии и простой Марковской эквивалентности.
Лекция 10. Теорема Маркова. Уравнение Янга—Бакстера 135
Упражнение 10.1. Покажите, что замыкания двух кос из п нитей
изотопны в классе замыканий кос из п нитей тогда и только тогда, когда эти косы
являются сопряженными.
Лемма 10-1. Если зацепления К U L и К1 U L9 — просто-
Марковски- эквивалентны, то они являются прошитыми
замыканиями некоторых кос, которые изотопны косам /3 £ Вг (п) и /За*1 €
Вг (п + 1).
Доказательство. Пусть угловая координата, постоянная на дуге а,
равна 0о- Рассмотрим дугу «о- Без ограничения общности можно
считать, что ее координата почти везде равна во, а в некоторой малой
окрестности зацепления L1 о?о делает петлю, а также то, что эта петля
соответствует n-й (последней) нити косы а. Мы можем произотопиро-
вать наши косы К и К1 в окрестности а = $о±е таким образом, чтобы
конечные точки дуг а и а?о лежали в малой окрестности I/. После
этого утверждение леммы становится очевидным. ■
Учитывая лемму 1, мы можем переформулировать сложную часть
теоремы Маркова следующим образом:
Теорема 10-4. Пусть (3 и 7 — две косы, чьи замыкания изотопны
как ориентированные зацепления. Тогда их прошитые замыкания
являются Марковски-эквивалентными.
Для дальнейшего доказательства нам потребуется несколько
вводных лемм и теорем.
Лемма 10.2. Рассмотрим диаграмму ориентированного
зацепления К на плоскости Р с выбором переходов (5, F). Тогда прошивания
диаграммы К различными кривыми L и L1, разделяющими
множества S и F, являются Марковски-эквивалентными.
Доказательство. Основная идея доказательства заключается в
следующем: сначала мы рассматриваем случай, когда две кривые L и V
изотопны в дополнении Р \ (S U F). В таком случае они
переводятся друг в друга набором движений, каждое из которых является
Марковской эквивалентностью.
В общем случае добавляется одно движение, при котором
диаграмма L двумя ветвями проходит через точку из S (из F). Такое движение
также является Марковской эквивалентностью.
Приведем это доказательство более подробно.
а) Предположим, что L и И изотопны в Р \ (S U F). Тогда К U L
и К U L1 получаются друг из друга последовательностью
преобразований первого и второго типов, показанных на рис. 9, на которых
не появляются точки из множеств S и F.
136
Раздел II. Теория кос
(В - ®
0-
Рис.9
Первый тип представляет собой либо изотопию с помощью
второго движения Рейдемейстера, либо движение, при котором добавляются
две точки пересечения альтернированным образом. Как будет
показано далее, это движение представляет собой простую Марковскую
эквивалентность. Два прошивания, получающиеся друг из друга
преобразованием второго типа, с очевидностью изотопны, за исключением
того случая, когда их ориентации выглядят так, как показано на рис. 10.
В этом случае первое прошивание переводится во второе
последовательностью движений первого типа и изотопии, см. рис. И.
При этом нужно заметить, что проходы К под L чередуются с
переходами К над L, когда мы идем вдоль по К. Нам осталось показать,
что два прошивания, получающиеся друг из друга движением первого
типа, являются просто-Марковски-эквивалентными. Таким образом,
<3>-
Рис. 10
Лекция 10. Теорема Маркова. Уравнение Янга—Бакстера 137
Первый тип
Первый тип
Изотопия
Рис.11
часть зацепления К, изображенная на диаграмме, принадлежит либо
к одной верхней ветви, либо к одной нижней ветви. В конструкции
прошивания мы можем предположить, что две части зацепления К
на одной стороне кривой L лежат на одном и том же уровне рь (угол 0
может быть тг ± е или ±е в зависимости от стороны, с которой он
расположен). Соединим их дугой так, как это показано на рис. 12.
Рис.12
Тогда а вместе с дугой а1 из К, пересекающей L, ограничивает
диск, следовательно мы получаем простую Марковскую
эквивалентность двух прошиваний.
б) В общем случае заметим, что если кривая М1 на Р, отделяющая
набор S от набора F, изотопируется в М посредством прохождения
138
Раздел II. Теория кос
пары дуг зацепления К через некоторую точку из множества S или F
(как это показано на рис. 13), то М и М1 представляют изотопные
прошивания.
Прошивание
е-
Рис.13
Такая изотопия диаграммы L (или же наборов S и F) разбивается
на участки, между которыми происходят дискретные скачки, меняющие
комбинаторный тип взаимного расположения кривой L и наборов S
и F. Таким образом, можно рассмотреть дискретный набор таких
взаимных расположений, между каждыми двумя из которых происходит
некоторое элементарное преобразование.
Пусть S и F состоят соответственно из точек {(-1, а,)} и {(1, а*)}
для некоторых ai,...a*. Рассмотрим в качестве L часть оси Оуу
замкнутую большим полукругом так, что внутренность L содержит F.
Мы можем предположить, что К проходит параллельно оси Ох рядом
с каждой из точек 6i,..., в* множества 5.
Пусть L1 — произвольная простая замкнутая кривая,
разделяющая S и F и ограничивающая область, содержащую множество F.
Предположим, что после малого шевеления кривая L1 пересекает транс-
версально лучи у = а», х < -1, см. рис. 14. Перенумеруем пересечения
кривой L1 с каждым из лучей по убыванию координаты х. Для каждого
из лучей их количество, очевидно, будет четным. Для каждого луча
сгруппируем эти пересечения парами (1,2), (3,4),..., т. е. проведем
такую изотопию кривой L1 внутри множества Р \ (S \J F), после которой
между каждой парой точек не будет находиться перекрестков
диаграммы К. Теперь будем двигать диаграмму L1 направо так, чтобы в конце
Лекция 10. Теорема Маркова. Уравнение Янга—Бакстера 139
Рис. 14
оставить все точки слева от L. Такое передвижение будет разбиваться
на этапы, когда L* не содержит точки из 5 и моменты, при которых
L1 содержит точки из 5. В первом случае такое движение является
Марковской эквивалентностью в силу пункта а). Во втором случае
будем считать, что точки пересечения 2/ с каждым лучом исчезают
парами, т. е. кривая I/ проходит последовательно два пересечения
с одной и той же точкой $,-. Такое движение представляет собой
Марковскую эквивалентность (как показано на рис. 13).
Таким образом, прошивание с помощью кривой L' Марковски
эквивалентно прошиванию с помощью кривой, лежащей справа от всех
точек Si. Такая кривая изотопна L внутри множества P\(S[jF)9
т. е. прошивание с помощью такой кривой Марковски эквивалентно
прошиванию с помощью кривой L в силу пункта 1).
Следовательно, прошивание с помощью L Марковски эквивалентно прошиванию
с помощью кривой L, что завершает доказательство леммы. ■
Лемма 10-3. Если для диаграммы К задан выбор переходов (S,F)
и точка s на диаграмме К, не ^принадлежащая множеству F^
то существует выбор переходов (S,F), такой, что s G S,S С S
и FCF.
140
Раздел II. Теория кос
Доказательство. Если з лежит на верхней дуге разбиения (5, F), то
мы можем выбрать / непосредственно перед з относительно
ориентации К таким образом, чтобы отрезок [/, з] С К не содержал переходов.
В случае, если з лежит на нижней дуге, то мы аналогично можем
добавить / сразу после точки з, чтобы отрезок [5,/] С К не содержал
проходов. ■
Теорема 10.5. Любые два прошивания К U L и К U L1 для данной
диаграммы К Марковски-эквивалентны.
Доказательство. Сделаем выбор переходов (5, F) для прошивания
К U L и (S^F*) для прошивания К U l!. По лемме 10.3 существует
выбор переходов (S",F")> такой, что (S,F)y(S',F') D (S"yF") и два
прошивания с таким выбором переходов, первое из которых
Марковски-эквивалентно К U L, а второе — К U L1. Согласно лемме 2, эти
прошивания Марковски-эквивалентны между собой. ■
Теорема 10.6. Любые две плоские диаграммы изотопных
зацеплений К имеют Марковски-эквивалентные прошивания.
Доказательство. Для доказательства нам нужно показать, как
строить Марковски-эквивалентные прошивания для диаграмм,
получающихся друг из друга посредством движений Рейдемейстера.
Пользуясь теоремой 10.5, мы можем взять произвольный выбор
переходов. Для первых двух движений Рейдемейстера без ограничения
общности можно выбрать отделяющую кривую вне малого круга, в
котором происходит деформация (в случае первого движения внутри круга
выбираем одну вершину в, в случае второго движения все вершины
из (5, F) находятся вне круга).
Мы показали, что диаграммы зацеплений, получаемых друг из друга
первым и вторым движениями Рейдемейстера, допускают Марковски-
эквивалентные прошивания.
Для третьего движения Рейдемейстера можно выбрать одну
вершину з и одну вершину / внутри круга, а остальные — вне, см. рис. 15.
s
s
XL
U
п'
U
Рис.15
Лекция 10. Теорема Маркова. Уравнение Янга—Бакстера 141
Рис. 16. Изотопные прошивания диаграмм, отличающихся движением ft3
На рис. 16 показано, что прошивания, соответствующие
диаграммам, отличающимся третьим движением Рейдемейстера, не только
являются Марковски-эквивалентными, но и изотопными (снизу
показан один из двух случаев для кривой L, второй проверяется
аналогично). ■
Доказательство теоремы 10.4. Пусть К U L и К' U L1 — два
зацепления-косы, при этом К и К1 изотопны как ориентированные
зацепления.
По теореме 2, зацепление К U L является прошиванием
некоторой диаграммы К, а К* U L1 является прошиванием диаграммы К1
зацепления, изотопного зацеплению К. По теореме 6 можно выбрать
Марковски-эквивалентные прошивания первой и второй диаграмм.
По теореме 5 первое из них Марковски-эквивалентно прошиванию
К U L, а второе — К' U L*.
142
Раздел И. Теория кос
Следовательно, прошивание К U L Марковски-эквивалентно
прошиванию К' U L', что и завершает доказательство теоремы
Маркова. ■
Покажем теперь, как можно применять теорему Маркова. Как
известно, торические узлы типов (р, q) и (q,p) изотопны. Проведем
движения Маркова для кос, чьи замыкания изотопны трилистникам —
(2,3) и (3,2).
Пример 10.1. Действительно, первая коса из двух нитей задается
формулой <rj~3, вторая коса из трех нитей — crfVjVfVj1. Напишем
последовательность преобразований Маркова и изотопии, переводящих одну косу
в другую.
_з 2дв. _3 _1 сопр. _2 -1 _1 -1, _1 _i -к изот. кос _i _1 _1 _1
0*1 ► <Т\ 0*2 ► <Т\ 0"2 <Г\ = <У\ \<Г\ 0~2 <Г\ ) ► <Т\ (Т^ <Т\ 0"2 •
Упражнение 10.2. Проделайте аналогичную выкладку для торических
узлов типов (2,5) и (5,2).
§2. Уравнения Янга—Бакстера,
группы кос и инварианты узлов
Уравнения Янга—Бакстера являются точкой связи между теорией
узлов и физикой, хотя связь с физическими моделями мы описывать
не будем, см., например, [48].
Пусть V — конечномерное векторное пространство с базисом
еь ..., еп над некоторым полем F. Пусть R : V ®V —> V ®V —
автоморфизм.
Рассмотрим эндоморфизм
Ri:Id®...®Id®R®Id®.:.®Id: vm-^V®ny
где V®n означает n-ю тензорную степень пространства V, Id означает
тождественное отображение, а автоморфизм Ri действует на
произведении пространств V ® V, с номерами (г, г + 1).
Определение 10.6. Оператор R называется Д-матрицей, если он
удовлетворяет следующим соотношениям:
RiRi+iRi = Ri+iRjRi+i, i = 1,..., n - 1,
RiRj=RjRiy \i-j\^2.
Первое из этих соотношений называется уравнением
Янга—Бакстера, а второе является дальней коммутативностью эндоморфизмов
Ru..., Rn-\-
Уравнения Янга—Бакстера по своему виду внешне очень похожи
на соотношения Артина для группы кос: поменяв а на R, мы получим
из одного другое.
Лекция 10. Теорема Маркова. Уравнение Янга—Бакстера 143
Укажем теперь математическую связь между уравнениями Янга—
Бакстера, представлениями групп кос (для разного количества нитей)
и инвариантами узлов и зацеплений.
По любой R -матрице можно построить инвариант узлов
(зацеплений) следующим способом (придуманным В.Тураевым, [83]).
Сначала построим представление группы кос Вп в
пространстве V®n по естественной формуле: р(о{) = jR,-, где &,- — стандартные
образующие в группе кос. В силу того, что уравнение Янга—Бакстера
и дальняя коммутативность для JR-матриц повторяют соотношения
Артина и дальнюю коммутативность для кос, это отображение
действительно является представлением.
Затем для данного зацепления (узла) L находим косу Ь, замыкание
которой изотопно этому зацеплению.
Можно положить T(L) = trace (p(b)). В таком случае T(L) является
инвариантным относительно второго преобразования Маркова.
Это следует из того, что для любых квадратных матриц А и В
одинакового размера trace (4) = trace (BAB"1).
В некоторых случаях (см. [83]) T(L) является инвариантом и
относительно первого преобразования Маркова, т. е. T(L) действительно
является инвариантом зацепления.
Замечание 10.3. Численные значения полинома Джонса как инварианты
узлов могут быть получены с помощью R-матриц.
В квантовой механике встречается также квантовое уравнение
Янга—Бакстера, имеющее вид
Д12Д13Д23 = Я23Д13Д,2. (*)
Здесь матрицы Rij получаются из фиксированной матрицы R,
задающей автоморфизм R : V®n —► V®n (например, ifo = R®In,
где In — единичная матрица пхп. Решение уравнения (*) называется
квантовой R-матрицей.
Раздел III
ИНВАРИАНТЫ ВАСИЛЬЕВА
Лекция 11
Определение и основные свойства
инвариантов Васильева
§ 1. Сингулярные узлы
и определение инвариантов Васильева
Ближайшие несколько лекций мы собираемся посвятить самым
сильным из ныне известных инвариантов узлов и зацеплений —
инвариантам Васильева, которые иногда также называются инвариантами
конечного типа. До сих пор неизвестно, является ли система
инвариантов Васильева полной, т. е. всегда ли для двух неизотопных узлов
существует инвариант Васильева, их различающий. На протяжении этой
главы мы будем говорить только об инвариантах Васильева узлов, хотя
существует аналогичная конструкция и для зацеплений, дающая
замечательные результаты. В частности, инварианты Васильева различают
негомотопные зацепления, а милноровские инварианты зацеплений
сводятся к инвариантам Васильева для зацеплений, см. [16, 61]. Также
развивается теория инвариантов конечного порядка узлов в трехмерных
многообразиях, см. [62, 54].
Оригинальная работа Васильева [85] появилась в 1990 году и с
самого начала было ясно, что инварианты Васильева сильнее полиномов
Джонса и других полиномиальных инвариантов, см. [12]. Затем в
книге [86] появилась общая конструкция. Обо всем этом можно прочитать
в книге [97].
Следует заметить, что понятие инварианта конечного порядка было
введено независимо М. Н. Гусаровым [98], хотя его работа стала известна
позже.
В настоящей лекции мы опишем определение, простейшие
свойства и примеры инвариантов Васильева.
Как известно из предыдущих лекций, любую диаграмму узла
(зацепления) кожно сделать тривиальной за конечное число изменений
Лекция 11. Определение и основные свойства 145
типов перекрестков. Если мы представим изменение перекрестков как
непрерывный процесс, то самым важным окажется момент, когда две
ветви пересекаются трансверсально. Численные инварианты,
введенные Васильевым, основаны на простых соотношениях между
значениями инвариантов при таких заменах типа перекрестка. Они происходят
из замечательной конструкции вычисления когомологий пространства
узлов и теории дискриминантов, см. [97].
В этой лекции мы будем иметь дело только с инвариантами
ориентированных узлов.
Определение 11.1. Назовем сингулярным или особым узлом гладкое
отображение К: 51 —► R3, являющееся вложением всюду, кроме
конечного набора простых двойных точек (т. е. точек трансверсаль-
ного пересечения).
Упражнение 11.1. Определите аккуратно изотопию двух особых узлов
с п точками самопересечения.
Аналогично особым узлам можно определить и сингулярные или
особые зацепления, а также их изотопию.
Множество всех изотопических классов эквивалентности особых
узлов с п точками самопересечения обозначим через Хп. Так Хо —
множество изотопических классов обычных узлов. Буквой X без индекса
обозначим объединение всех множеств Хп по п от 0 до оо.
Аналогично плоской диаграмме обычного узла можно определить
и плоскую диаграмму особого узла {особого зацепления). На ней, кроме
точек прохода и перехода, есть еще точки самопересечения, которые мы
в дальнейшем будем обозначать жирными точками. Так как пересечение
двух ветвей особого узла в пространстве является трансверсальным, его
можно считать трансверсальным и на плоскости.
Пример 11.1.
Рис. 1. Особый узел с двумя точками пересечения
Упражнение 11.2. Сформулируйте и докажите аналог теоремы Рейдемей-
стера для особых узлов, т. е. классифицируйте простейшие движения, не
меняющие изотопический тип особого узла (зацепления).
Каждую двойную точку особого узла можно разрешить двумя
способами: положительно или отрицательно, см. рис. 2.
146
Раздел III. Инварианты Васильева
Рис.2. Сверху — положительное разрешение особой точки,
снизу — отрицательное
Упражнение 11.3. Покажите, что данные операции корректно
определены на изотопических классах сингулярных узлов, т. е. не зависят от того,
с какой стороны смотреть на эту точку (какую плоскость проекции выбирать).
Определение 11.2. Пусть f:Xi-*A — некоторый инвариант
особых узлов с г пересечениями со значениями в множестве А.
Производной инварианта f называется функция /': Х{+\ -—* А,
определенная соотношением Васильева:
«Х>"<Х,-ЛХ*
Рис.3
Если задан инвариант узлов /: Хо —► А, то можно определить
его производные всех старших порядков, тем самым задав
некоторый инвариант на множестве X. Такой инвариант называется
продолжением инварианта f на особые узлы.
Пример 11.2. Сосчитаем значение продолженного по Васильеву
полинома Джонса на особом узле, приведенном на рис. 1, см. рис. 4.
Определение 11.3. Инвариант f:Xo~+A называется
инвариантом Васильева порядка ^п, если его продолжение по Васильеву
на множество сингулярных узлов сп+1 вершиной тождественно
равно нулю.
Назовем инвариант Васильева порядка ^п инвариантом
Васильева порядка п, если он не является инвариантом Васильева
порядка ^п- 1.
В силу аддитивности операции взятия производной, линейная
комбинация инвариантов Васильева порядка ^п является инвариантом
Лекция 11. Определение и основные свойства 147
V"(
+V(
f
.
) = V(
'
'
1—1
1
i
)-V(
<
'
1—1
t
1
1
)-V(
'
'
i
1
i
)+
f
1 > ' 1
1
.1
) = V(
'
'
i
)-V(
'
1 1
1 tl
1
) = t + t3-tA-l
Рис.4
Васильева порядка ^п. Таким образом, для данного поля А (скажем,
R или Q) множество инвариантов Васильева порядка ^п образует
линейное пространство. Обозначим его через Vn.
Нас будут интересовать вопросы о размерности пространств Vn
и о нахождении численных значений инвариантов Васильева. Так как
V,- С Vj при % < j, то можно рассматривать лишь пространства V,/V,-i-
Определение 11.4. Символом инварианта Васильева порядка п
называется его ограничение на множество сингулярных узлов,
имеющих ровно п точек самопересечения.
Предложение 11.1. Два инварианта порядка п, имеющих один
и тот же символ, отличаются друг от друга на инвариант по-
рядка не более, чем п — 1.
Доказательство. Пусть /i и /г - два таких инварианта. Тогда
значение га-й производной инварианта /i - /2 тождественно равно нулю,
следовательно, /i - /2 является инвариантом порядка < п - 1. ■
Кроме того, имеет место
Лемма 11.1. Значение п-й производной инварианта Васильева
порядка п на особом узле порядка п не меняется при заменах типов
{не сингулярных) перекрестков.
Доказательство следует из того, что при изменении типа
перекрестка к значению инварианта добавляется значение его производной
на узле сп+1 точкой самопересечения, которое равно нулю по
определению. ■
§ 2. Инварианты порядков 0 и 1
Из леммы 11.1 следует, что для вычисления размерности
пространства Vn/Vn_i нужно найти линейно-независимые символы инвариантов
Васильева порядка п.
148
Раздел III. Инварианты Васильева
Следствие 11.1. Пространство Vo инвариантов Васильева
порядка О состоит из констант.
Доказательство. Путем замены перекрестков каждый узел можно
превратить в тривиальный, а значение инварианта Васильева порядка
нуль равно нулю на любом особом узле первого порядка. ■
Более интересным оказывается следующий факт.
Предложение 11.2. Пространство V\ совпадает с
пространством Vo, т.е. не существует инвариантов Васильева порядка 1.
Доказательство. Пусть / — инвариант Васильева порядка 1.
Рассмотрим его символ (первую производную /'). Пусть /' = к на всех
особых узлах порядка 1. Рассмотрим его значение на сингулярном
узле Р, изображенном на рис. 5.
СЮ
Рис.5
С одной стороны, это значение равно к. С другой стороны, в силу
определения инвариантов Васильева, оно должно быть равно нулю, так
как является разницей значений / на двух изотопных узлах.
Таким образом, /' = 0, следовательно, / = const, т. е. является
инвариантом порядка 0. ■
Перейдем теперь к рассмотрению инвариантов Васильева второго
порядка.
Определение 11.5. Назовем хордовой диаграммой граф, состоящий
из выделенного ориентированного цикла (окружности) и
конечного набора ребер (хорд), соединяющих точки на этой окружности
так, чтобы одна точка была инцидентна не более, чем одной хорде.
Будем рассматривать хордовые диаграммы с точностью до
изоморфизма графов, переводящих окружность в окружность с учетом
ориентации.
В силу леммы 11.1 значение инварианта порядка п не меняется
при замене типа перекрестков. Следовательно, его значение не зависит
от заузленности, а зависит лишь от порядка прохода особых точек.
Эту последовательность удобно задавать следующим образом. Пусть
дан узел к: S1 —► R3 с п точками самопересечения. Будем обходить
окружность S{ в соответствии с ее ориентацией и отмечать на нее точки,
Лекция 11. Определение и основные свойства 149
образы которых соответствуют точкам двойного самопересечения. Затем
каждую отмеченную пару точек соединим хордой, см. рис. 6.
4 5
Рис. 6. Слева — диаграмма особого узла, справа — хордовая диаграмма
Определение 11.6. Получившуюся диаграмму назовем хордовой
диаграммой порядка п. Назовем две хордовые диаграммы одного
порядка эквивалентными у если одна получается из другой
посредством диффеоморфизма окружности 51, сохраняющего
ориентацию.
Легко видеть, что каждая хордовая диаграмма соответствует
некоторому сингулярному узлу. Действительно, рассмотрим погружение
окружности в R3, при котором порядок двойных точек
соответствует данной хордовой диаграмме. Затем выберем «хорошую» проекцию
этого образа окружности на некоторую плоскость и поставим в точках
пересечения проекций разных ветвей проходы и переходы.
Следовательно, лемму 11.1 можно переформулировать на языке
хордовых диаграмм.
Лемма 11.2. Значение символа инварианта Васильева порядка п
на узле с п точками самопересечения зависит только от хордовой
диаграммы этого узла.
Следовательно, для нахождения инварианта Васильева второго
порядка нужно найти подходящую хордовую диаграмму порядка 2.
Лемма 11.3. Путем замены перекрестков любой сингулярный узел
первого порядка можно превратить в узел, изотопный сингулярному
узлу Р (рис. 5).
Доказательство. Пусть К — диаграмма сингулярного узла первого
порядка.
Рассмотрим тень этой диаграммы и зададим на ней проходы и
переходы следующим образом (не трогая сингулярную вершину). Начнем
двигаться по узлу от сингулярной вершины и, встречая какую-либо
вершину (не сингулярную) в первый раз, будем ставить проход, а второй
раз — переход. В результате получим диаграмму наподобие восходящей
диаграммы для обычных узлов.
2
1
7
5
3
64
8> 1
4 |
150
Раздел III. Инварианты Васильева
Можно увидеть, что сингулярный узел с такой диаграммой
действительно будет изотопен Р. Немного пошевелив, его можно изобразить
в пространстве следующим образом: есть отрезок вертикальной прямой
(лежащий над сингулярной точкой) и кривая, соединяющая начало
отрезка с его концом, пересекающая его однажды в промежуточной
точке t и имеющая возрастающую координату по вертикали. При этом
данный особый узел состоит из двух частей: с координатой меньше t
и с координатой больше t. Каждую из этих частей можно произотопи-
ровать до тривиального узла, тем самым показав изотопность нашего
особого узла и Р. а
§ 3. Примеры инвариантов старших порядков
Существуют две диаграммы порядка 2; две хорды одной из них (D\),
не пересекаются, а две хорды второй, (Z>2 )> пересекаются.
Упражнение 11.4. Покажите, что первая хордовая диаграмма D^ не дает
никакого инварианта Васильева второго порядка, т. е. значение второй
производной любого инварианта Васильева второго порядка на этой диаграмме равно
нулю.
Зато вторая диаграмма Di задает нетривиальный инвариант
Васильева второго порядка. Приступим к его описанию, не пытаясь пока
доказать его существование или единственность.
Пусть / — функция, значение второй производной которой на Di
равно единице (определение символа). Можно считать, что значение /
на тривиальном узле равно нулю, этого можно добиться вычитанием
из / константы, что не меняет значения второй производной /".
Оказывается, этих сведений достаточно для определения (пока
неизвестно, корректного ли) функции / на всех узлах. Действительно,
определим сначала функцию /'. Мы знаем, что /'(Р) = 0, это верно для
любого инварианта Васильева. Кроме того, мы знаем, что f"(D\) = 0,
/"(2?2) = 1- Ее™ Дан сингулярный узел первого порядка, путем замены
перекрестков его можно превратить в узел, изотопный Р. При этом
к значению функции / при каждой такой замене будет
прибавляться 0, 1 или -1, в зависимости от того, какой особый узел второго
порядка появляется при пересечении.
Аналогичным образом, зная значение / на тривиальном узле и
значения /' на всех особых узлах первого порядка, мы можем получить
значение / на всех узлах. Таким образом мы показали единственность
инварианта, равного нулю на тривиальном узле с символом, равным
нулю на Dilk единице на 2>2> но не показали существования такого
инварианта.
Лекция 11. Определение и основные свойства 151
Значит, пространство Уг либо одномерно и состоит из констант,
либо двумерно и его базис составляют единица и данный инвариант /
(если существует).
Примем на веру его существование и посчитаем его значение
на правом трилистнике, см. рис. 7. При этом вместо значения
продолжения данного инварианта / на (особом) узле а будем писать
ПРОСТО Of.
1—t I—\
Р-Ь-ГЕ
1 1 1
L 1
И*гМ
т 1
]-
I ' I I t I }
I т I I I т I
= 1.
Рис.7
Упражнение 11.5. Покажите, что значение этого инварианта на левом
трилистнике также равно единице, т. е. что он не различает правый и левый
трилистники.
Упражнение 11.6. Посчитайте значение этого инварианта на восьмерке.
Упражнение 11.7. Посчитайте значение этого инварианта на торических
узлах типа (2,п).
Точные комбинаторные формулы для доказательства
существования и построения такого инварианта будут рассмотрены позднее.
Зададимся вопросом: какие из известных нам инвариантов
являются инвариантами Васильева или выражаются через них?
Замечание 11.1. Заметим, что если мы рассматриваем инварианты со
значениями в полиномах от переменной х, то дифференцирование Васильева должно
осуществляться покоэффициентно и не связано с «обычным»
дифференцированием по переменной х. Так, если v — инвариант узлов со значениями в Ъ[х],
то (х -v)' = x-v'.
Рассмотрим, например, второй член полинома Конвея. Он,
естественно, является численным инвариантом узлов. Рассмотрим значение
производной полинома Конвея. В силу соотношения C(L+) - C(LJ) =
х C(Lo) значение производной полинома Конвея является полиномом,
кратным ж. Аналогично можно показать, что n-я производная
полинома Конвея является полиномом, кратным хп, т.е. все члены до п - 1
включительно пропадают.
Отсюда следует
152
Раздел III. Инварианты Васильева
Теорема 11.1. Для каждого к> О к-и член полинома Конвея
является инвариантом Васильева порядка не более к.
Отсюда, например, следует, что первый член полинома равен нулю
на всех узлах (так как он является константой и его значение равно
нулю на тривиальном узле).
Обратим внимание на второй член полинома Конвея. Он не
является константой на узлах, следовательно, он является инвариантом
Васильева порядка два. Следовательно, его символ пропорционален
символу /, а сам инвариант / является линейной комбинацией
второго члена полинома Конвея и константы.
Простое сравнение данного инварианта и второго члена полинома
Конвея на тривиальном узле и на трилистнике показывает, что эти два
инварианта просто совпадают.
Итак, мы установили, что существует нетривиальный инвариант
Васильева порядка два, при этом пока не ясна картина с тем, что из себя
представляет пространство Vn/Vn-i для произвольного п и какие еще
известные инварианты (кроме полинома Конвея) выражаются через
инварианты Васильева.
Кроме того, полином Конвея (а, следовательно, и все его
коэффициенты) не различают даже правого и левого трилистников. Это
побуждает искать более сильные инварианты Васильева.
Этими вопросами мы и займемся на ближайших лекциях.
Лекция 12
Инварианты Васильева
и полиномиальные инварианты
§ 1. Символы инвариантов,
происходящих от полинома Конвея
На прошлой лекции мы дали определение инвариантов
Васильева и показали, что все коэффициенты полинома Конвея являются
инвариантами Васильева. Из этого следует
Теорема 12.1. Если для двух узлов Ki и Кг С(К\) Ф С (Кг), mo
существует инвариант Васильева, значение которого на узле К\
не равно значению на узле Кг.
В таком случае можно сказать, что инварианты Васильева не слабее
полинома Конвея.
Этот факт следует из похожести skein-relation для полинома Конвея
и соотношения Васильева.
Так как n-й коэффициент полинома Конвея с„ является
инвариантом Васильева порядка не больше п, то можно попытаться,
предполагая, что инвариант имеет порядок п, найти символ этого инварианта —
значение его n-й производной.
Пусть дана хордовая диаграмма Den хордами. Проведем
рядом с каждой хордой на близком расстоянии параллельную ей хорду
и сотрем малые дуги между полученными параллельными хордами.
Построенный объект (ориентированная окружность без 2п малых дуг и п
пар параллельных дуг) допускает однозначное продолжение движения
вдоль по самому себе. Действительно, начав движение с какой-либо
точки окружности, мы доходим до начала ближайшей хорды (за
которой следует выброшенная малая дуга), затем следует поворот движения
вдоль по хорде до конца хорды и вновь поворот с движением по дуге.
В каждый момент движения существует единственная возможность его
продолжить. Ясно, что через некоторое время мы вернемся в исходную
точку. При таких обстоятельствах имеются две возможности.
1. При возвращении в исходную точку будет пройден весь объект.
2. При возвращении в исходную точку будет пройдена лишь часть
объекта.
154
Раздел III. Инварианты Васильева
За счет малого шевеления в трехмерном пространстве можно
сделать хорды объекта непересекающимися. Для этого в точках
пересечения одну хорду на малом участке нужно расположить чуть выше другой.
В этих предположениях рассматриваемый объект превращается в
одномерное многообразие m(D). Первая из описанных выше возможностей
соответствует связному многообразию, вторая — многообразию с более,
чем одной связной компонентой.
Предложение 12.1 ([23]). Значение символа с„ на D равно единице,
если m(D) имеет одну связную компоненту, и нулю, если больше
одной связной компоненты.
Доказательство. Пусть L — особый узел, хордовой диафаммой
которого является диаграмма D. Будем расщеплять его вершины и
пользоваться соотношением, полученным из skein-соотношения Конвея
и соотношения Васильева, см. рис. 1.
С(\/) = жС( |f ).
Рис.1
После n-го применения этого соотношения получим, что
значение n-й производной инварианта С на L (на D) равно значению
самого С на диаграмме, полученной из D «разведением всех сингулярных
перекрестков», умноженному на zn. При этом коэффициент с„
продолжения полинома Конвея на сингулярный узел равен значению
коэффициента со на полученной разведенной диаграмме. Это значение a priori
не зависит от замены типов перекрестков, оно равно единице на
тривиальном узле и нулю на тривиальном зацеплении с числом компонент,
большим единицы, откуда и следует доказываемое утверждение. ■
Так как на узлах (зацеплениях с нечетным числом компонент)
у полинома Конвея только члены четных степеней могут быть отличны
от нуля, Сп = 0, п — нечетно.
Этот факт можно доказать и с применением предыдущего
предложения. Пусть D — хордовая диаграмма с нечетным количеством хорд,
равным п. Предположим, что у кривой m(D), соответствующей
диаграмме D, ровно одна компонента связности. Заклеим ее диском.
Получим некоторое ориентированное (докажите это!) двумерное
многообразие с вырезанным диском. Его Эйлерова характеристика должна быть
цечетной. С другой стороны, она равна В-Р+Г = 2п-Зп+1 = -п+1.
Противоречие.
Лекция 12. Инварианты Васильева и полиномы 155
При этом для четных п существуют и такие хордовые диаграммы,
на которых Сп не равно 0.
Пример 12.1. На рис. 2 на диаграмме сверху значение с4 равно нулю,
а на диаграмме снизу значение с4 равно единице.
-4
N
^1
4J
и
Рис.2
Упражнение 12.1. Покажите, что для любого четного п значение п-й
производной инварианта с„ на диаграмме, в которой любая пара хорд
пересекается, равно единице.
Из этого упражнения следует существование инвариантов
Васильева произвольных четных порядков.
§ 2. Выражение полиномиальных инвариантов
через инварианты Васильева
Бели мы попытаемся применить формальное дифференцирование
к коэффициентам других полиномов, то потерпим неудачу, т. е.,
например, коэффициенты полинома Джонса не являются инвариантами
Васильева. Дело в том, что полином Джонса не является полиномом с
членами только положительных степеней. Он является полиномом Лорана.
Из теоремы 12.1 следует
Теорема 12.2. Полином Александера слабее инвариантов Васильева.
Доказательство. Это следует из того, что полином Александера
получается из полинома Конвея с помощью замены переменной: z —>
(tl>2-r1'2).
Следовательно, полином Конвея различает два узла тогда и только
тогда, когда их различает полином Александера. ■
Несмотря на то, что другие полиномы не получаются из полинома
Конвея (Александера) с помощью замены переменной, инварианты
156
Раздел III. Инварианты Васильева
Васильева сильнее известных нам полиномиальных инвариантов узлов.
Формулируемые далее результаты восходят к статье [12], см. также [13].
Начнем с полинома Джонса и воспользуемся следующим трюком.
Напомним, что полином Джонса удовлетворяет следующему
соотношению типа Конвея:
q~lV(L+) - qV(L~) = (ql<2 - <T1/2)V(£°).
Сделаем формальную замену переменной q = ех.
Получим:
e~xV{L+) - exV(L") = (ex - e'x,2)V(L°):
Разложим экспоненты в ряд Тейлора.
Получим в правой части сумму, делящуюся на ж, а в левой части —
производную полинома Джонса плюс нечто, делящееся на х.
V(L+) - V(L~) = x < нечто > .
Следовательно, после (п + 1)-кратного дифференцирования п-й
член ряда, выражающего полином Джонса через ж, обнуляется.
Следовательно, все члены ряда, выражающего полином Джонса, являются
инвариантами Васильева, откуда и следует
Теорема 12.3. Полином Джонса от одной переменной и полином
Кауфмана от одной переменной, получающийся из него заменой
переменной, слабее инвариантов Васильева.
Аналогично можно поступить и с полиномом Джонса от двух
переменных.
Напишем его соотношение типа Конвея.
-i=*(J+) - у/Цх(П = У^х(ь%
y/\q y/q
Сделаем замену переменных y/q = ex, y/Xq = ey и разложим наш
полином Джонса от двух переменных в двойной ряд Тейлора по а? и у.
Получим в правой части нечто, делящееся на ж, а в левой — нечто,
делящееся на ху9 плюс производная от полинома Джонса.
В итоге имеем:
X(L+) ~ X(LJ) = x < нечто > .
Таким образом, после (п+1)-кратного дифференцирования члены,
степень которых по х равна п, обнуляются и мы получаем теорему.
Теорема 12.4. Полином Джонса от двух переменных слабее
инвариантов Васильева.
Лекция 12. Инварианты Васильева и полиномы 157
Так как полином HOMFLY может быть получен из полинома
Джонса от двух переменных путем подходящей замены переменных, то
имеет место
Теорема 12.5. Полином HOMFLY слабее инвариантов Васильева.
Самый сложный и интересный случай представляет собой полином
Кауфмана от двух переменных, так как он не задается с помощью
соотношений типа Конвея, а также зависит от степеней функций z, a
и (а - aTl)/z. Для того, чтобы представить полином Кауфмана в виде
ряда из инвариантов Васильева, нужно выразить все эти функции
с помощью рядов от положительных степеней двух переменных.
Рассмотрим теперь полином Кауфмана от двух переменных,
задаваемый по формуле Y(L) = a~w^D(L), где D — функция на хордовых
диаграммах, удовлетворяющая соотношениям:
D(L) - D{ti) = z(D(LA) - D{LB)\ (1)
*0>=(l + ^), <2>
D(X#P) = aD(X), D(X#Q) = a~lD(X), (3)
где диаграммы L} L\ La, Lb совпадают вне малой окрестности
некоторой вершины, а Р и Q — правая и левая петли.
Перепишем соотношение (1) для полинома Кауфмана для Y.
Получим:
a-lY(L+)-aY(L-) = z(Y(LA)-Y(LB)). (4).
Сделаем замену переменной: р = In ((a - \)/z). Тогда через
переменные z и р можно выразить z, а, (а - a~l)/z, используя лишь
степенные ряды из положительных степеней. Действительно, z = z,
a = ^+l = 2;(H-p+...)+l,a-l = l-z(l+i>+...)+z2(l+i)+...)2+...,
(а - a~l)/z = а"1(2ер + ze2p + ...), что, очевидно, также выражается
через ряды из положительных степеней р и z.
Таким образом, значение полинома Кауфмана от двух переменных
на любом узле разлагается в ряд только по положительным степеням р
и z. С другой стороны, вспоминая, что а = 1 + z < нечтоу > и а"1 =
1 + z < пентод >, из (4) получим: Y1 = z < нечто >. При этом
все члены нашего двойного ряда, имеющие по z степень не более п,
обнуляются после п 4- 1-го дифференцирования, т.е. все члены
нашего двойного ряда для полинома Кауфмана являются инвариантами
Васильева. Тем самым доказана
Теорема 12.6. Полином Кауфмана от двух переменных слабее
инвариантов Васильева.
158
Раздел III. Инварианты Васильева
Покажем теперь, как считать продолжение на сингулярные узлы
функций, равных произведению двух функций.
Пусть даны функции / и д на диаграммах зацеплений. Тогда
можно определить производные /' и д1 на диаграммах особых узлов первого
порядка так же, как мы определяем производные инвариантов. По
индукции можно также определить продолжение функций на диаграммы
произвольного порядка.
Рассмотрим функцию fg.
Пусть дана диаграмма К особого узла порядка п. Разбиением
назовем выбор г сингулярных вершин из п имеющихся. Тогда для каждой
диаграммы К сингулярного узла пусть К\8 — диаграмма узла,
полученная из К разведением л-г выделенных вершин разбиения з
отрицательным способом, а 1^2* — диаграмма узла, полученная
разведением г выделенных вершин положительным способом.
Лемма 12.1- Пусть К — хордовая диаграмма с п хордами. Для
каждого п > О имеет место формула Лейбница:
ш(пЧк)=Е Е f(i)&u)g(n-4K2.).
i=0 *
Доказательство. Будем проводить доказательство по индукции.
Докажем сначала это утверждение для п = 1. Пусть дан особый узел
первого порядка.
Рассмотрим его диаграмму и сингулярную вершину А и распишем
соотношение Васильева в окрестности этой вершины, см. рис. 3.
Рис.3
Равенство (5) является тождеством в силу определения /' и д'.
Таким образом, мы получили утверждение теоремы для п = 1. Заметим,
что в полученной формуле вместо функций на неособых узлах можно
рассматривать и функции на особых узлах, все сингулярные вершины
которых лежат вне окрестности заданной точки. Данная формула (5)
t позволяет выразить производную произведения любых двух функций
через значения функций и их производных.
Лекция 12. Инварианты Васильева и полиномы 159
Пусть дан сингулярный узел К порядка п и выделена сингулярная
вершина. Значение (fg)n на данном узле равно разности значений
(fg)nl на ДВУХ узлах К1 и К2 порядка п - 1, получаемых
положительным и отрицательным разведением данной вершины.
По предположению индукции,
п-1
т*-Ч*) = £ £ /^У"-1-0^), (6)
»=0 s
где под s имеются в виду разбиения п - 1-го порядка.
Мы имеем
ШЧЮ = Ш^Л*1) - Ш*-1)(х2) =
= £ £(/(,)(^)/"1",)Ю - /(,)(^)5(п-,-°(^2,)).
1=0 8
Расписывая каждый член данной суммы по формуле (5) и используя
формулу (6), получаем требуемое. ■
Из леммы 12.1 вытекает
Следствие 12.1. Пусть fug — функции на диаграммах узлов
(например, инварианты), такие, что f(n+{) = 0, </*+1* = 0.
Тогда (fg){n+k+l) = 0.
В частности, произведение инвариантов Васильева порядков пик
является инвариантом Васильева порядка не больше, чем п + к.
Перейдем теперь к рассмотрению пространств Vn/Vn-i. Лемма 11.2
показала, что каждому символу инварианта Васильева
соответствует некоторая линейная функция на пространстве хордовых диаграмм,
удовлетворяющая одночленному соотношению, которую можно
также трактовать как линейную комбинацию хордовых диаграмм, среди
которых не встречаются диаграммы с изолированными хордами, т. е.
хордами, не пересекающимися с другими хордами.
Более точно это можно сформулировать так:
Теорема 12.7 (одночленное или 1Т-соотношение). Пусть Vn —
символ инварианта Васильева порядка п. Тогда для каждой хордовой
диаграммы D, имеющей хорду, не пересекающуюся с другими хордами
данной диаграммы,
Vn(D) = 0. (7)
Оказывается, существует еще одно соотношение, которому должны
удовлетворять символы инвариантов Васильева.
160
Раздел III. Инварианты Васильева
Теорема 12.8 (четырехчленное или 4Т-соотношение). Символ v^
произвольного инварианта Васильева v порядка п удовлетворяет
следующему четырехчленному (AT) соотношению:
)_„<«>( U ))-•«([ \ )) + *<*>(
Рис.4. Четырехчленное соотношение
Здесь четыре хордовые диаграммы состоят из п хорд, причем на
рисунке указаны лишь 2 хорды, а остальные п — 2 хорды одинаково
расположены для всех четырех диаграмм, а их концы не лежат
на отмеченных дугах.
Доказательство. Рассмотрим четыре сингулярных узла 5i, 52,5з, 5д
порядка п, хордовые диаграммы которых совпадают вне малого
круга, а их фрагменты si, $2,$з> *4 внутри круга имеют вид, указанный
на рис. 5.
Рис. 5. Фрагменты сингулярных узлов
Рассмотрим инвариант Васильева v порядка п и значения его га-й
производной на этих четырех узлах. Используя соотношение Васильева,
получаем соотношения, показанные на рис. 6.
Понятно, что
(а - Ь) - (с- d) + (с- а) - (d- Ь) = 0.
Чтобы получить диаграммы сингулярных узлов, следует замкнуть
фрагменты su s2, *з> 54- Это можно сделать двумя различными
способами, показанными на рис. 7.
Это значит, что исходные четыре сингулярные узла 5i, 5г, 5з, 54
удовлетворяют соотношению
v{n)(S{) - v(n)(S2) + v{n)(S3) - v{n)(S4) = 0. (9)
На хордовых диаграммах, соответствующих сингулярным узлам
5i,52,5з, 54 имеется п хорд: п - 2 хорды расположены одинаковым
Лекция 12. Инварианты Васильева и полиномы 161
) - »<"-'>(
А А А
■)=c-d,
у
*. ) = v(n-l)( / | , ) - „<»-!)( /^ >)=C-g>
) = „(»-!)(_/-у:—^ ) _ v(n-i)(_ у—*)=d-b
Рис.6. Одинаковыми буквами обозначены значения v(n_1)
на изотопных сингулярных узлах
образом и лишь две хорды отличают одну диаграмму от другой. Именно
эти хорды изображены на рис. 4. Что касается остальных, то их концы
принадлежат тем частям кругов, которые не выделены жирно.
По предположению инвариант Васильева v имеет порядок п, и это
значит, что корректно определены значения его символа на хордовых
диаграммах порядка п. Поэтому значение символа v^ на хордовых
диаграммах, соответствующих сингулярным узлам Si, S2, S3, S4, равно
значению этого же символа на самих сингулярных узлах.
Принимая во внимание формулу (9), а также произвольность
расположения оставшихся п - 2 сингулярных вершин диаграмм Si, S2,
S3, S4, получаем утверждение теоремы. ■
Итак, хордовые диаграммы с п хордами образуют линейное
пространство. Это пространство можно отождествить с двойственным ему
пространством, выбрав базис из хордовых диаграмм, и
рассматривать одночленное и четырехчленное соотношения как соотношения
162
Раздел III. Инварианты Васильева
/Л-*"1 у/у1 /ЛУ~Л /1/~л
^ИЬ \~^Г^ ?^*h \А5Г^ г
z-£-Aa \-:j.j z~h.A Л.-:^
L^^ L^V L^^ LЛ7
Рис.7
на пространстве хордовых диаграмм с п хордами. Профакторизуем
это пространство по одночленному и четырехчленному соотношениям
и обозначим полученное пространство через Д„.
Из теоремы 8 следует, что любому символу инварианта Васильева
порядка п соответствует некоторый элемент из Дп. Пока мы не знаем,
верно ли обратное, но для изучения пространств Vn/Vn-\ необходимо
изучить пространства Дп.
Пространство До состоит из одной диаграммы без хорд.
Пространство Д1 содержит только ноль в связи с одночленным соотношением.
Пространство Дг одномерно. Его базисным элементом является
диаграмма с двумя пересекающимися хордами (рис. 8).
е
Рис.8
Рассмотрим теперь пространство Дз. Существуют две хордовые
диаграммы из трех хорд, не имеющие изолированных хорд.
Однако в силу четырехчленного соотношения одна из них равна второй
с коэффициентом 2, см. рис. 9.
Итак, dim Д3 = dim Д2 = 1.
Аналогичным образом можно посчитать, что dimA4 = 3, выбрав
1 в качестве базиса диаграммы, изображенные на рис. 10.
Лекция 12. Инварианты Васильева и полиномы 163
= 2
Рис.9
Рис.10
Для этого выразим оставшиеся ненулевые диаграммы с четырьмя
хордами через три имеющиеся. Обозначим данные три диаграммы
(на рис. 10) через а,Ь и с, а остальные, показанные на рис. 11, через
dy e, / и д соответственно.
Рис.11
С помощью перебора четырехчленных соотношений можно
получить все четырехчленные соотношения в Аз. Вот они:
е = d + с,
Ь = с + /,
a = е + 6,
Ь + d = е 4- /.
Из этих соотношений видно, что диаграммы d, e, / и д
выражаются через диаграммы а, Ь и с.
Упражнение 12.2. Выведите явно эти соотношения и найдите
коэффициенты, с которыми d, е, / и д выражаются через а, Ь и с.
Таким образом, получаем, что dim А4 = 3.
В [13] и [23] приведены таблицы размерностей пространств Vn
при п до 9 и до 12 соответственно.
164
Раздел III. Инварианты Васильева
§ 3. Пример инварианта, не являющегося
инвариантом конечного порядка
Приведем пример инварианта узлов, который не является
инвариантом порядка п ни для какого натурального п, следуя [12].
Определение 12.1. Назовем числом распутывания U(K)
(ориентированного) узла К минимальное п € Z+, такое, что от узла К
можно перейти к тривиальному узлу, проходя п раз через
сингулярные узлы. Иными словами, п — минимальное число, такое, что
для узла К существует плоская диаграмма, которая переводится
в диаграмму тривиального узла заменой п перекрестков.
Очевидно, что функция U действительно является инвариантом
узлов.
Из определения следует, что число распутывания равно нулю
на тривиальном узле.
Для U, как и для любого другого инварианта, можно определить
значения производных на сингулярных узлах.
Теорема 12.9. Инвариант U не является инвариантом конечного
порядка.
Доказательство. Зададим г € N. Приведем пример сингулярного
узла, на котором U® Ф 0. Зафиксируем га > 0 и рассмотрим
сингулярный узел Ktm с 4га сингулярными вершинами, показанный на рис. 12.
X ■ X
Am вершин
Рис.12
По определению производной инварианта Васильева, значение
j7<4m) на этом узле равнс) альтернированной сумме 2<4т) слагаемых,
Лекция 12. Инварианты Васильева и полиномы 165
каждое из которых равно значению инварианта U на одном из узлов,
получаемых разведением всех сингулярных вершин узла К^т.
Заметим, что на каждом таком сингулярном узле значение
инварианта U не превосходит единицы: заменяя перекресток в точке А,
мы получим тривиальный узел. С другой стороны, узел, получаемый
из К4т разведением всех его сингулярных вершин, является
тривиальным тогда и только тогда, когда количество вершин, разведенных
положительным способом, равно количеству вершин, разведенных
отрицательным способом и равно 2га.
При разведении q вершин положительным способом, а 4га - q
вершин — отрицательным, в сумме получим знак (-1)д.
Таким образом, значение Z7^4m^(jfir4m) равно альтернированной
сумме членов 4га-й строки бинома Ньютона, за исключением члена С^щ,
U«m\K<m) = 2[C°<m-Clm + ...-C%-1].
Эта сумма, очевидно, меньше нуля, так как каждый отрицательный
член по модулю превосходит предшествующий ему положительный.
Таким образом, U{Am)(K4m) ф О, и, полагая т > г/4, получаем
U® £ 0. Таким образом, инвариант U не является инвариантом
порядка меньше *. В силу произвольности выбора числа г получаем, что
инвариант U не является инвариантом конечного порядка. ■
Замечание 12.1. Из того, что инвариант U не является инвариантом
конечного порядка не следует, что он не выражается через инварианты конечного
порядка.
Лекция 13
Алгебра хордовых диаграмм
§ 1. Структура Алгебры Хопфа на Ас и Л*
На этой лекции мы расскажем о структуре инвариантов Васильева,
а именно, об алгебраической структуре на множестве Д = Ai © Д2 0
Д3 Ф....
Дело в том, что коль скоро инварианты Васильева перемножаются,
перемножаться должны и их символы. Мы знаем, что порядок
произведения двух инвариантов меньше или равен сумме порядков. Мы
покажем, что на Д есть гораздо более сильная структура — структура
алгебры Хопфа.
Начнем с формального задания алгебраической структуры на
хордовых диаграммах. Пусть даны две диаграммы А и В. Разорвем их
в произвольных точках, не являющихся концами хорд, и соединим так,
как показано на рис. 1.
Рис. 1. Произведение хордовых диаграмм
Получим хордовую диаграмму, которая может играть роль
произведения АВ. Мы видим, что это произведение определено неоднозначно
и зависиг от выбора точек разрывания. Покажем, что по модулю
4Т-соотношения этот выбор несуществен.
Для этой цели рассмотрим теперь вместо хордовых диаграмм
дуговые диаграммы —- диаграммы, полученные из хордовых разрыванием
окружности в одной точке, отличной от концов хорд. Дуговую
диаграмму можно трактовать как диаграмму, состоящую из прямой, некоторые
точки которой соединены дугами, причем дуг конечное число, и из
каждой точки выходит не более одной дуги. При этом дуговые диаграммы
рассматриваются с точностью до положительного диффеоморфизма
прямой на себя.
Лекция 13. Алгебра хордовых диаграмм 167
На дуговых диаграммах также можно рассматривать одночленное
и четырехчленное соотношения и линейное пространство, порожденное
диаграммами и профакторизованное по этим соотношениям.
Лемма 13.1. Пусть две дуговые диаграммы D{ и D2 получаются
одна из другой перебрасыванием одного конца дуги через бесконечность.
Тогда D\ и Di равны по модулю AT-соотношения.
Доказательство. Пусть у диаграмм D\ и £>2, имеющих по п дуг,
все дуги совпадают, кроме одной дуги а, при этом один конец дуги а
у одной из диаграмм D^D2 стоит на начальном месте, а у
другой — на конечном. Перенумеруем отрезки прямой между
концами неподвижных дут слева направо: начальный отрезок, выходящий
на бесконечность, будет иметь номер 1, конечный отрезок будет иметь
номер 2п - 1. Один отрезок будет содержать неподвижный конец
дуги а. Обозначим через ск дуговую диаграмму, у которой неподвижные
концы дуг совпадают с неподвижными концами D\ и Д>, а
подвижный конец лежит на отрезке к. С помощью 4Т-соотношения
нам нужно доказать, что q - С2П-\ = 0. Перепишем с{ - с2п как
С{ — Сг + oi - сз + ... С2п-2 — С2п-\ = (*). Будем теперь группировать
члены этой суммы по четыре следующим образом: если один конец
некоторой дуги отделяет р-й отрезок от р + 1-го, а второй — q-я
от q + 1-го, то рассмотрим член Ср - Ср+ \ + cq - cg+i. Очевидно, что
равенство такой суммы нулю в чистом виде является 4Т-соотношением.
При этом суммирование по всем отрезкам таких четверок в точности
и дает сумму (*). Таким образом, (*) = 0, ч.т.д. ■
Из леммы 1 легко следует
Теорема 13.1. Описанное выше произведение хордовых диаграмм
определено корректно по модулю 4Т-соотношения.
Доказательство. Пусть А и В — две хордовые диаграммы. Выберем
пары точек из А и Б двумя способами и рассмотрим соответствующие
«произведения» АВу и АВ2. На каждой из этих диаграмм отдельно
лежит диаграмма А, разорванная в некотором месте, а отдельно — Б,
разорванная в некотором месте. Эти диаграммы А и В можно
рассматривать как дуговые диаграммы. Применяя несколько раз лемму 1,
мы видим, что дуговые диа1раммы, полученные разрыванием одной
и той же диаграммы в разных местах, эквивалентны по модулю 4Т-со-
отношения. Значит, эквивалентны и составленные из разорванных А
и В произведения АВ\ и АВ2. Ш
Определение 13.1. Назовем линейную функцию на
пространстве Ajk весовой функцией fc-ro порядка.
168
Раздел III. Инварианты Васильева
Замечание 13.1. В дальнейшем мы будем естественным образом
(посредством выбора базиса) отождествлять пространство Д и двойственное ему
пространство весовых функций на Д, если не оговорено противное. В таких
случаях будем обозначать двойственное пространство также через Д.
Мы получаем корректно определенное произведение на
пространстве Д. При этом, умножая диаграммы спит хордами, мы получим
диаграмму с п+тп хордами. Учитывая также, что IT и 4Т-соотношения
являются однородными, получаем следующую теорему.
Теорема 13.2. Пространство Д весовых функций является комму-
тативной градуированной алгеброй относительно умножения,
описанного выше. Роль единицы в этой алгебре играет хордовая диаграмма
без хорд. При этом градуировка задается количеством хорд хордовой
диаграммы.
Легко видеть, что корректность умножения не зависит от
одночленного соотношения, поэтому пространство всех хордовых диаграмм,
профакторизованное по четырехчленному соотношению, также
образует градуированную коммутативную алгебру относительно естественной
операции, описанной выше.
Обозначим это пространство через Лс.
Определим еще одну алгебру.
Определение 13.2. Назовем китайской диаграммой тривалентный
граф, у которого все вершины делятся на внешние и внутренние,
причем на графе выделен замкнутый ориентированный цикл,
содержащий все внешние вершины, а в каждой внутренней вершине
указан порядок обхода исходящих полуребер.
Определение 13.3. Если граф с выделенным ориентированным
циклом погружен в плоскость, то порядок обхода ребер при каждой
вершине определяется против часовой стрелки.
Замечание 13.2. Легко видеть, что каждая хордовая диаграмма является
также и китайской диаграммой без внутренних вершин.
Рассмотрим пространство линейных комбинаций китайских
диаграмм и профакторизуем его по следующему однородному
соотношению, называемому 5ТСГ-соотношением, см. рис. 2, на котором у самой
правой диаграммы пересечение хорд не является вершиной. Обозначим
полученное пространство через А*.
Рис.2. 5247-соотношение
Лекция 13. Алгебра хордовых диаграмм 169
Здесь жирная дуга обозначает часть выделенного цикла
(окружности), при этом имеется ввиду, что порядок исходящих полуребер
локально заимствован из плоскости, а три диаграммы, участвующие в
соотношении, не отличаются вне малой окрестности, изображенной на рис. 2.
Легко видеть, что каждая китайская диаграмма представима в
виде линейной комбинации хордовых диаграмм. Этого можно добиться
с помощью многократного применения £Т{7-соотношения (до тех пор,
пока на диаграмме остаются внутренние вершины). Из этого
следует изоморфизм профакторизованных пространств хордовых диаграмм
и китайских диаграмм.
Теорема 13-3- Пространство Ас изоморфно пространству А*.
Кроме того, из STU-соотношения следуют два соотношения в А*:
а) Антисимметрия во внутренних вершинах:
Рис.3
6) ШХ-соотношение:
Рис.4
Доказательство. Начнем с доказательства изоморфизма.
Заметим, что 5ТСГ-соотношение выражает диаграмму с к
внутренними вершинами в виде разницы двух диаграмм с А: - 1 внутренней
вершиной. Осталось лишь заметить, что если китайская диаграмма
выражалась через 5ТС/"-соотношение как линейная комбинация
хордовых диаграмм различными способами, то получающиеся комбинации
эквивалентны по модулю 4Г-соотношения. Докажем это по
индукции. Для диаграмм с одной внутренней вершиной такое равенство
в точности означает 4Т-соотношение. Предположим, что расщепление
было корректно определено для диаграмм с менее чем к внутренними
вершинами, к > 1. Пусть D — диаграмма с к вершинами. Пусть D
представляется в виде разницы диаграмм с к - 1 внутренней вершиной
170
Раздел III. Инварианты Васильева
двумя способами — разведением ребер i и j соответственно. При этом
ребра г и j выходят на окружность.
Если ребра i и j примыкают к разным внутренним вершинам,
равенство соответствующих диаграмм показано на рис. 5.
Рис.5
В случае, когда ребра i и j примыкают к одной и той же вершине,
выберем хорду /, выходящую на окружность и примыкающую к другой
вершине (если такая существует) и воспользуемся транзитивностью
равенства.
В единственном оставшемся случае (когда есть единственная
внутренняя вершина А, которой инцидентны ребра, выходящие на
окружность) существует некоторая область, содержащая все внутренние
вершины, кроме одной. Эта область имеет только одно соединение с
внешними вершинами — через внутреннюю вершину А, на которую выходят
хорды % и j. В этом случае два возможных расщепления равны в силу
корректности и коммутативности произведения, определенного на
китайских диаграммах. Действительно, в силу предположения индукции
все китайские диаграммы порядка к -1 корректно расщепляются в
сумму хордовых диаграмм, а для хордовых диаграмм данное утверждение
следует из теорем 13.1 и 13.2. Используя коммутативность
произведения, мы можем переносить вершину, на которой висит маленький
черный круг, из одной точки окружности в другую. Таким образом,
мы видим, что любое из двух расщеплений такой диаграммы дает нуль
с учетом 4Т- и 5!П7-соотношений. На рис. 6 показано, как данное
утверждение следует из корректности произведения на китайских диа-
Лекция 13. Алгебра хордовых диаграмм 171
граммах. При этом на всех диаграммах, изображенных на рис. 6, есть
еще некоторое количество хорд, которые расположены одинаковым
образом на всех диаграммах (и не изображены на рисунке).
(s) -ф -
Рис.6
Y-Y-Y-W-Y-
Рис. 7. Антисимметричность следует из 5П7-соотношения
Докажем, что из 5Т!7-соотношения следуют антисимметричность
и /ЯХ-соотношение.
Применяя многократно 5Т17-соотношение, можно свести
антисимметричность к случаю, когда все хорды, выходящие из данной
внутренней точки, кончаются во внешних точках. Тогда
антисимметричность в точности совпадает с 4Т-соотношением, см. рис. 7.
Доказательство /ЯХ-соотношения с помощью 5Т17-соотношения
сведем к случаю, когда одна вершина (скажем, левая нижняя) является
внешней. Это можно сделать, выбрав левую нижнюю вершину во всех
трех диаграммах, которые должны удовлетворять /ЯХ-соотношению
и поочередно расщеплять с помощью 5ТЕЛ-соотношения внешние
вершины так, чтобы после некоторого расщепления она стала внешней.
Тогда наше /ЯХ-соотношение будет следовать из набора /ЯХ-соотно-
шений, у которых левая нижняя вершина является внешней.
Оставшаяся выкладка показана на рис. 8. ■
172
Раздел III. Инварианты Васильева
Рис. 8. £Т!7-соотношение влечет /ЯХ-соотношение
Из изоморфизма Ас и А* следует, что на А* операция
«присоединения» одной диаграммы к другой также задает алгебраическую структуру.
При этом алгебра А* также является градуированной — степенью
китайской диаграммы является половина количества ее вершин.
Из изоморфизма Ас и А* следует, что на А* операция
«присоединения» одной диаграммы к другой также задает алгебраическую структуру.
При этом алгебра А* также является градуированной — степенью
китайской диаграммы является половина количества ее вершин.
Упражнение 13.1. Проверьте согласованность градуировок Ае и А*
относительно изморфизма, описанного выше.
На пространствах Ас и А* есть структура не только алгебры,
но и коалгебры. Это связано с тем, что если узлы можно умножать (с
помощью конкатенации), то инварианты узлов можно коумножать.
Действительно, пусть дан инвариант Васильева порядка п. Тогда в силу
формулы Лейбница его значение на сингулярном узле порядка п равно
сумме произведений значений пар инвариантов Васильева с суммарной
степенью п. В этом и заключается коумножение инвариантов Васильева.
Опишем подробнее эту структуру на примере Ас9 см. [60], а
также [13] для случая А*.
Рассмотрим некоторую хордовую диаграмму D и множество ее
хорд V(D). Пусть J С V(D) — подмножество в V(D). Это
множество определяет хордовую диаграмму Cj9 хорды которой принадлежат
множеству хорд J С V(D).
Введем копроизведение
М^)= ]£ Cj®Cvmjj
JCV(D)
где знак ® означает формальное тензорное произведение (которое
берется над полем Q или R).
Лекция 13. Алгебра хордовых диаграмм 173
Теперь нам нужно доказать, что описанное выше коумножение
согласовано с четырехчленным соотношением, т. е. если хордовая
диаграмма А равна линейной комбинации хордовых диаграмм А{ в силу
4Т-соотношения, то ее копроизведение эквивалентно сумме копроиз-
ведений диаграмм А{ в силу 4Г-соотношения.
Действительно, пусть D\ - £>2 + #з - &а = 0 — четырехчленное
соотношение для четырех хордовых диаграмм с п ребрами. Рассмотрим
альтернированную сумму fi(D\) - р(Рг) + /*(Х>з) - ^(Щ)- В каждом
члене копроизведения /i(A) две «подвижные» хорды могут оказаться
либо обе в правом сомножителе, либо обе в левом сомножителе, либо
одна в правом сомножителе, а другая в левом. Выбирая распределение
оставшихся п — 2 хорд одинаковым образом для всех D{, мы получим:
в первом и втором случае (JE?i -Е2+Еъ -E^^F и 2£® (jFi -F2+JF3 -jRj),
при этом альтернированная сумма в левом (правом) сомножителе равна
нулю в силу четырехчленного соотношения. В случае, когда пара
хорд разводится в разные сомножители, мы получаем тождественное
равенство двух пар тензорных произведений.
Определение 13.4. Коалгебра А с коумножением р, называется
кокоммутативной, если V a Е А имеет место (t(a) = £} Ь{ ® с,- =
Ее,'®*,,-.
Итак, на Ас мы получили корректно определенное коумножение.
Выбирая в качестве коединицы линейную фукцию, равную 1 на
хордовой диаграмме без хорд и нулю на любой другой хордовой диаграмме,
получаем теорему:
Теорема 13.4. Линейное пространство Ас (следовательно, и А*)
является коммутативной коалгеброй с коумножением и коединицей,
описанными выше.
Дадим теперь формальное определение алгебры Хопфа.
Определение 13.5. Пусть ЕоУЕи... — конечно порожденные
модули над полем F. Градуированный модуль Е = JEfo Ф Е\ $
Ei Ф... называется биалгеброй или алгеброй Хопфа, если у него есть
структура ассоциативной алгебры т: Е®Е—>Е9 m(Ei + Em) С
Ej+m с единичным отображением е: F -» Е, а также структура
ассоциативной коалгебры ft: Е —> Е®Е,ц(Еп) С Ео ® Еп фЕ\ ®
En-i ф ... Еп <g> Eq с коединицей е: Е -» F, удовлетворяющие
следующим условиям:
а) отображение е — гомоморфизм градуированных коалгебр,
б) отображение е — гомоморфизм градуированных алгебр,
в) отображение р. — гомоморфизм градуированных алгебр.
174
Раздел III. Инварианты Васильева
Замечание 13.3. Иногда, например, в [103], под алгеброй Хопфа
понимают биалгебру с некоторым дополнительным свойством — наличием
антипода. Мы же используем определение из математической
энциклопедии [120], в котором алгебра Хопфа и биалгебра означают одно и то же.
Об алгебрах Хопфа и квантовых группах см. [103, 31, 101].
Теорема 13.5. Пространство Ас является алгеброй Хопфа относительно
заданных на нем умножения и коумнжения, единицы и коединицы.
Доказательство. Так как единичное и коединичное отображения
являются гомоморфизмами, то достаточно лишь доказать, что
коумножение задает гомоморфизм, т. е. что V х Ф у ц(х - у) Ф 0,
причем так как коалгебра является градуированной, достаточно
доказать этот факт для х и у одного порядка. Пусть z — х - у.
Тогда fi(z) содержит член (х - у) ® 1, откуда и следует требуемое
утверждение. ■
Структура алгебры Хопфа на Ас позволяет понять некоторые
важные свойства инвариантов Васильева.
Определение 13.6. Назовем элемент р из Ас примитивным, если
1*(р) =;><8>1 + 1® р.
Пример 13.1. Любой примитивный элемент второго порядка делится
на элемент jp, показанный на рис. 9.
Рис.9. Примитивный элемент второго порядка в Ас
Действительно, пусть А и В — хордовые диаграммы второго
порядка с пересекающимися и непересекающимися хордами
соответственно. Пусть рА + qB — примитивный элемент. Тогда
ц(рА + qB) = рц(А) + q[i(B) = (рА + qB) <g> 1 + 1 0 (рА + qB) +
(р + q)C ® С, где С — диаграмма с одной хордой. Значит, р = -q,
что и требовалось доказать.
Сформулируем известную теорему о структурах алгебр Хопфа.
Теорема 13.6 ([69]). Над полем / характеристики 0 любая
коммутативная или кокоммутативная алгебра Хопфа изоморфна алгебре
многочленов от ее примитивных элементов. При этом
коммутативность влечет кокоммутативность и наоборот.
Имеет место
Лекция 13. Алгебра хордовых диаграмм 175
Следствие 13.1. Любая коммутативная алгебра Хопфа над полем
конечной характеристики не имеет делителей нуля, а в качестве
базиса можно выбрать произведение некоторого {быть может,
нулевого) числа примитивных элементов.
Таким образом, в алгебре хордовых диаграмм можно выбрать
мультипликативный базис из примитивных элементов. Он порождает другое
отождествление линейного пространства ,4£ со своим двойственным
пространством (отличное от изначального, связанного с выбором
естественного базиса из хордовых диаграмм).
Если профакторизовать алгебру Хопфа Ас по IT-соотношению,
мы опять получим алгебру Хопфа. Очевидно, что полученная алгебра
также будет коммутативной и кокоммутативной алгеброй Хопфа.
Для каждого п в пространстве хордовых диаграмм с п
хордами можно выбрать естественный базис — соответствующий мономам
в алгебре от бесконечного числа переменных.
Пусть теперь / — инвариант Васильева порядка n, a g — инвариант
Васильева порядка к.
Теорема 13.7. Произведение инвариантов Васильева fug является
инвариантом Васильева порядка п + к. Значение символа (/</)*п+**
на хордовых диаграммах с п + к хордами определяется по формуле
(/$)(n+*) = (/(,WW (О
где в правой части значения производных fn и дк рассматриваются
лишь на диаграммах с пи к хордами соответственно.
Доказательство. Очевидно, что инвариант (fg) имеет порядок
не больше п + к. Рассмотрим произвольную хордовую диаграмму D
с п+к хордами и сингулярный узел К, соответствующий этой
диаграмме. Посчитаем значение (fg)^k+n^(K) по формуле Лейбница. Получим
п+к
(fgf+k\K) = X) Е /{ЧКи)9(п+кЛК2.).
»=0 8
Так как /(n+1) = g^k+l^ = 0, то в этой сумме будут присутствовать
лишь члены, где значение производной /^п^ на сингулярном узле с п
сингулярными вершинами умножается на значение производной д^
на сингулярном узле с к сингулярными вершинами. Эти значения
можно трактовать как значения /^ и д^ на хордовых диаграммах,
соответствующих этим узлам. Очевидно, что эти диаграммы получаются
из диаграммы D разбиением множества всех хорд на два
подмножества из п и к хорд соответственно, откуда и следует утверждение
теоремы. ■
176
Раздел III. Инварианты Васильева
Формула (1) носит название формулы Концевина, см.,
например, [13].
§ 2. Таблица размерностей
пространств хордовых диаграмм
С ростом п число dim An быстро растет. Используя прямой подход,
Бар-Натан в 1993 г., добавив к оперативной памяти своего
компьютера дополнительные 32Мб оперативной памяти, сосчитал размерности
dim An, на что ему пришлось потратить несколько дней.
Приведем список размерностей пространств Vn, An и Vn —-
примитивных элементов порядка п, всего пространства хордовых диаграмм
с п хордами и инвариантов Васильева порядка до 12 (известных к
настоящему времени).
п
dimVn
dim Л»
dimV„
0
0
1
1
1
0
0
1
2
1
1
2
3
1
1
3
4
2
3
6
5
3
4
10
6
5
9
19
7
8
14
33
8
12
27
60
9
18
44
104
10
27
80
184
11
39
132
316
12
55
232
548
Ответ для п = 10,11,12 получен Яном Кнайсслером [55] в 1997 году
с применением более тонкой техники, использующей понятие
примитивного элемента, т. е. того факта, что в качестве базиса в An
можно выбрать попарные произведения базисных элементов для V%, где
£* = п.
Об оценках роста числа Васильевских инвариантов см. статьи
Дужина и Чмутова [21, 22].
Лекция 14
Формулировка теоремы
Васильева—Концевича.
Интеграл Концевича
На ближайших двух лекциях будет рассказано об интеграле
Концевича — конструкции, доказывающей сложную часть теоремы
Васильева—Концевича, а именно, строящей по каждой системе весов
некоторый инвариант Васильева.
Конструкция интеграла Концевича была введена в 1992 году [56]
как средство доказательства теоремы Васильева—Концевича.
Другие изложения понятия интеграла Концевича можно найти
в статье [13], а также (другие подходы к интегралу Концевича) в [20,
63, 76]. См. также [60, 102].
Начнем лекцию с напоминания. Пусть дан инвариант Васильева V
порядка п, тогда его (п+ 1)-я производная равна нулю, а значение п-й
производной (символ инварианта V) зависит лишь от порядка
прохождения особых вершин; следовательно, ее можно рассматривать как
функцию на хордовых диаграммах. Было доказано, что любая такая
функция удовлетворяет одночленному и четырехчленному
соотношениям. При этом любая линейная функция на хордовых диаграммах,
удовлетворяющая одночленному и четырехчленному соотношениям,
называется системой весов.
Теорема 14.1.
(1) Всякий инвариант Васильева порядка п задает весовую систему
порядка п. {В. А. Васильев)
(2) Любая линейная функция на множестве А„, т. е. любая весовая
система, происходит из некоторого инварианта Васильева порядка п.
(М.Л.Концевич.)
Первая часть теоремы, которая следует из работ Васильева [85, 86],
была доказана в предыдущих лекциях.
§ 1. Предварительный интеграл Концевича
Определение 14.1. Пополнением Л алгебры хордовых диаграмм
А называется множество всех формальных рядов вида Y^0™0™*
m
178
Раздел III. Инварианты Васильева
где Cm Е С — численные коэффициенты, a am G Аго — элементы
пространства хордовых диаграмм степени т.
Представим себе трехмерное пространство R3 как прямое
произведение комплексной прямой С с координатой z и вещественной
прямой R с координатой t.
Пусть дан ориентированный узел К в R3 = Cz x R*. Путем малого
шевеления можно, не изменяя изотопического типа данного узла,
сделать так, чтобы координата t была простой функцией Морса на К.
Это значит, что во всех точках, где t имеет нулевую производную
(скажем, по натуральному параметру), вторая производная функции t
не должна обращаться в нуль. При этом значения t в таких точках
(критические значения) должны быть различны между собой.
Определение 14.2. Предварительным интегралом Концевича узла К
называется следующий элемент пополнения Д алгебры хордовых
диаграмм:
tj некритические
при этом считается, что при «пустой» хордовой диаграмме без хорд
стоит единичный коэффициент.
Поясним подробно формулу (1).
Действительные числа Сщш и стах — минимальное и максимальное
значения функции t на узле К.
Область интегрирования представляет собой w-мерный симплекс
Cmin < £i < ... < tm < Сщах, разделенный критическими
значениями на некоторое число связных компонент. При этом Z{ и dzi под
интегралом следует понимать как функции от соответствующей
переменной U. Например, на рис. 1 показана область интегрирования
тривиального узла (ш = 2), состоящая из шести компонент.
Число слагаемых постоянно для каждой компоненты связности,
однако оно может быть различным для разных компонент. Часть узла
в полосе, заключенной между двумя критическими значениями
представляет собой набор кривых, каждая из которых однозначно
параметризована переменной Ь. Фиксируем число т и выберем т горизонтальных
плоскостей {t = £,}, г = 1,..., т, не проходящих через критические
точки и находящихся между максимальным и минимальным уровнем
высоты (затем по т будет вестись суммирование). В каждой плоскости
{t = и} С R3 выберем неупорядоченную пару различных точек (z„ U)
и (*,', U), лежащих на узле К. Обозначим через Р = {(zt-, 2,')} систему
Лекция 14. Теорема Васильева—Концевича. Интеграл Концевича 179
Сщах
с2
С\
t
— г~л
" 7""^
-/
_ ±*J
к J
/
^max
С2 U
, ^min г"
±
Cmin Cl
Рис.1
Стаз
из m таких пар для i = 1,...,га. Соединяя точки z^z\ из одной
пары для данного набора Р мы получим хордовую диаграмму, которую
обозначим через Dp. Под интегралом стоит сумма по всем системам Р
хордовых диаграмм с коэффициентами, получаемыми таким образом.
В произвольной связной компоненте области интегрирования
фиксация системы Р означает, что для каждой переменной U выбрана
некоторая пара ветвей узла К в соответствующей полосе пространства
и, следовательно, выбирая m плоскостей, мы получаем m пар точек.
По сути дела, так как хордовая диаграмма Dp не меняется внутри одной
связной компоненты, то нужно интегрировать не хордовые диаграммы,
а лишь форму (-1)А Д Г ^ > интеграл от которой по связной компо-
i=i ' '
ненте и даст коэффициент при соответствующей хордовой диаграмме
(затем эти коэффициенты суммируются, если одна и та же хордовая
диаграмма может получиться для разных компонент связности).
В примере, показанном выше, для связной компоненты {стш <
t\ < с\у С2 <t2 < Cmax} есть лишь одна пара точек на уровнях {t = ti)
и {t = t2}. Для этой компоненты сумма состоит лишь из одного
слагаемого, а для компоненты {Сщш < £i < с\у с\ < t2 < с2} у нас по-прежнему
есть лишь один выбор на уровне {t = t{}9 но плоскость {t = £2}
пересекает узел уже по четырем точкам, следовательно, мы имеем С\ — 6
возможных пар (22, z2) и общее число слагаемых равно шести. Наконец,
для компоненты {с\ < t{) t2 < с2} мы имеем тридцать шесть слагаемых:
каждому из двух сечений соответствует С\ = 6 диаграмм.
При этом легко видеть, что во всех случаях, кроме {су <t\ <
*2 < ф}, мы будем иметь хордовую диаграмму с двумя непересекающи-
180
Раздел III. Инварианты Васильева
мися хордами, которая равна нулю в силу одночленного соотношения.
Таким образом, интегрирование можно свести к интегралу по
«маленькому» симплексу {ci < t\ < t^ < C2}.
Символ I для данного выбора системы Р означает число точек
(z, ti) или (z\ ti) из Р, в которых координата t убывает при движении
по узлу в положительном направлении. На рис. 2 показано, какой
области интегрирования сколько и каких хордовых диаграмм соответствует.
Рис.2
Остались неясными следующие вопросы:
1. Имеет ли смысл ряд (1), т. е. принимают ли коэффициенты при
хордовых диаграммах конечные значения?
2. Является ли полученный элемент пополнения пространства
хордовых диаграмм инвариантом узла?
3. Какое отношение этот инвариант имеет к инвариантам Васильева?
4. Как считать этот интеграл?
В этой лекции мы не будем давать ответы на все эти вопросы
с полными доказательствами; примем на веру некоторые утверждения,
которые будут доказаны на следующей лекции.
Теорема 14.2 ([56], см., также [13]). Все коэффициенты ряда (1)
конечны.
Лекция 14. Теорема Васильева—Концевича. Интеграл Концевича 181
§ 2. Интеграл от ос и нормировка
Определение 14.3. Назовем изотопии морсовского вложения
узла, не меняющие расположения особых точек, горизонтальными
деформациями.
Теорема 14.3 ([13]). Полученный таким образом элемент Z(K)
является инвариантом узла относительно горизонтальных
деформаций, а также преобразования, указанного на рис. 3, но не инвариантен
относительно преобразования (*), указанного на рис. 4.
\У
/\
Рис.3
(*)
Рис.4
Обозначим узел, получаемый замыканием дуги на рис. 4, справа,
через А.
В частности, можно рассмотреть простейшее вложение
тривиального узла К (с одним минимумом и одним максимумом) и тривиальный
узел, показанный на рис. 5 и обозначаемый через оо. Очевидно, что
предварительный интеграл Концевича Z(K) равен единице (ряду,
состоящему из единственной хордовой диаграммы без хорд). При этом
Я(оо)*1.
Рис.5
Мы видим, что Z не является инвариантом узла.
182 Раздел III. Инварианты Васильева
С другой стороны, имеет место
Теорема 14.4- Если узел К* получается из узла К посредством
преобразования (*), то Z(K') = Z(K) • Z(oo).
Доказательство. Заметим сначала, что узел оо получается из узла А
посредством движений, не меняющих число критических точек, откуда
следует, что Z(oo) = Z(A).
Рассмотрим связную сумму узла К с «маленьким узлом» оо так,
чтобы интервал координаты t\ отвечающий А, не содержал
критических точек узла К, при этом чтобы к узлу К добавились ровно две
критические точки — один максимум и один минимум, см. рис.6.
Рис.6
В силу предыдущих теорем, интеграл Концевича от полученного
узла будет совпадать с интегралом Концевича для узла К', который
получается из узла JT#oo горизонтальными деформациями. Сравнив
теперь интеграл Концевича для данного узла и для узла К, увидим,
что каждому члену интеграла для К в интеграле для К1 соответствует
этот же член, умноженный на интеграл Концевича для А,
следовательно, Z(K') = Z(K)Z(oo), что и требовалось доказать. ■
Итак, предварительный интеграл Концевича Z(K) хотя и меняется
при преобразовании (*), но не сильно: каждый раз при добавлении
пары критических точек он умножается на Z(oo). Пусть теперь К —
морсовское вложение узла в R3, а с — количество критических точек
функции t на К.
Посмотрим теперь на предварительный интеграл Концевича как
на формальный ряд. Так как этот ряд состоит из элементов
градуированной алгебры и его начальный коэффициент равен единице данной
алгебры (хордовой диаграмме без хорд), то такие ряды можно обращать
по формуле (1 + а)^1 = 1 - а + а2 - а3 + ..., где а* — формальный
ряд для t-й степени ряда а, а также умножать. В частности, можно
обратить и Z(oo).
Лекция 14. Теорема Васильева—Концевича. Интеграл Концевича 183
W = T^Sb- (2)
Определение 14.4. Универсальным инвариантом
Васильева—Концевича узла К называется элемент пополнения алгебры хордовых
диаграмм, получаемый по формуле:
ЭД)
Z(oo)c
Замечание 14.1. Здесь степень § -1 нужна для того, чтобы в случае
простейшего вложения тривиального узла с одним максимумом и одним минимумом
мы получили 1(0) = 1.
Имеет место
Теорема 14.5. Интеграл Концевича 1(К) является инвариантом
узла.
Доказательство. Действительно, в силу теоремы 3 получаем, что
Z(K) зависит не от расположения критических точек функции t9
а зависит лишь от их количества.
Нетрудно проверить, что если два морсовских узла изотопны, то
они переводятся друг в друга движениями, не меняющими взаимного
расположения критических точек, а также движениями, показанными
на рис. 3 и 4.
Учитывая инвариантность Z(K) относительно движений, не
меняющих количества критических точек, получаем требуемое. ■
Этот инвариант !(•) называется универсальным инвариантом Васи-
льева.
Для полного прояснения картины осталось сформулировать
следующую теорему.
Пусть W — система весов степени га. Доопределим ее нулем
на хордовые диаграммы, количество хорд которых не равно т.
Теорема 14.6 ([13]). Инвариант W(I()) является инвариантом
Васильева, символом которого служит весовая система W, т.е.
V(W)(K) = W(I(K))
для каждого узла К.
Из теоремы 14.6 и следует вторая (сложная) часть теоремы
Васильева—Концевича, показывающая существование инварианта Васильева,
соответствующего произвольной системе весов.
Доказательством теорем 2,3 и 6 мы займемся на следующей лекции.
Кроме того, мы слегка затронем вопрос о сложности вычисления
интеграла Концевича для простейших узлов.
Перейдем теперь к алгебрам Ае и Л хордовых и китайских
диаграмм.
184
Раздел III. Инварианты Васильева
Как было доказано ранее, эти алгебры изоморфны,
следовательно, алгебра j£ также как и Лс наделена структурой алгебры Хопфа.
Предъявим эту структуру.
Пусть D — китайская диа1рамма, пусть V(D) — компоненты
связности этой диаграммы, т. е. компоненты связности графа,
получаемого из этой диаграммы выкидыванием ее окружности. Пусть
J С V(D) подмножество множества V(D). Это множество определяет
китайскую диаграмму cj9 компоненты связности которой принадлежат
множеству V(D), т. е. китайскую диаграмму, состоящую из окружности
диаграммы D и компонент связности графа V(D), принадлежащих
V(C).
Определим копроизведение p>(D) по формуле
/2(27) = ^2 Cj®Cv(c)\j.
JCV(c)
Пример 14.1. На рис. 7 показан пример коумножения китайской
диаграммы.
©-
О0-ФО
ОФФО
Рис.7
Теорема 14.7. Такое коумножение согласовано с коумножением для
алгебры хордовых диаграмм Лс, т.е. fi = Д.
Доказательство. Нам нужно показать, что для каждой китайской
диаграммы D ее копроизведение совпадает с линейной комбинацией
копроизведений хордовых диаграмм, на которые она раскладывается.
Будем проводить доказательство индукцией по числу п
внутренних вершин китайской диаграммы. При п = 0 утверждение теоремы
верно, так как в данном случае китайская диаграмма является хордовой
и формулы для копроизведения в точности совпадают.
Пусть данное утверждение верно для китайских диаграмм с п
внутренними вершинами. Пусть дана китайская диаграмма D с п + 1
внутренней вершиной. Покажем, что p,(D) = fi(D). В соответствии
Лекция 14. Теорема Васильева—Концевича. Интеграл Концевича 185
Рис.8
с 5!П7-соотношением диаграмма D расщепляется в разницу D+ - D-,
см. рис. 8, при этом компонента связности распадается на две. Выделим
пары компонент связности (а+, Ь+) и (а_, Ь_) на диаграммах Z>+ и Х>_,
получающиеся распадением вершины диаграммы D. У диаграмм D±
по п внутренних вершин, следовательно, для них утверждение
теоремы верно: /х(Дь) = fi(D±). Распишем теперь fi(D) = (i(D+) + /i(D-).
В этом копроизведении будут стоять члены, в которых
компоненты (а+,Ь+) (соответственно (а_,Ь_)) лежат с одной стороны
относительно знака тензорного произведения. Очевидно, что такие члены
дают в точности ji(D) (в смысле коумножения для китайских диаграмм,
определенного выше). Оставшиеся же члены в сумме будут давать нуль.
Действительно, пусть есть разделение китайской диаграммы D+ на две
диаграммы, причем компонента связности а+ принадлежит к первой
из них, а компонента 6+ — ко второй. Тогда, если разделить
диаграмму D_ «точно так же» относительно остальных компонент связности
и отнести компоненту а_ к первому члену тензорного произведения,
а компоненту Ь_ — ко второму, мы получим два совпадающих
тензорных произведения.
Суммируя сказанное, получаем утверждение теоремы. ■
Лекция 15
Интеграл Концевича —
универсальный инвариант узлов
По определению интеграл Концевича от узла К равен
*<оо)'
W = Tf^rr. О)
где Z(K) — предварительный интеграл Концевича, задаваемый по
формуле
tj некритические
Замечание 15.1. Под Zm(K) и Im(K) будем понимать m-й член интегралов
Z(K) и 1(К) соответственно.
В этой лекции мы докажем теоремы 14.2, 14.3 и 14.6 из прошлой
лекции.
Начнем с доказательства теоремы 14.2, утверждающей, что каждый
член при ненулевой хордовой диаграмме в формуле (2) конечен.
Доказательство. Пусть дано морсовское вложение узла К в R3.
Зададим некоторое га, выберем тп плоскостей, не пересекающих К
в критических точках.
Выберем хордовую диаграмму D и рассмотрим коэффициент при
ней. Он получается посредством интегрирования формы Д j)t.\Jg./t.)
по той части симплекса Сп^ < t\ < ... < tm < Сщах, которая
соответствует данной хордовой диаграмме D.
Рассмотрим особые точки данной формы. Это точки, в которых
знаменатель обращается в нуль, т. е. Zj = Zj для некоторого j. В
окрестности этих точек наш интеграл, вообще говоря, может расходиться.
Рассмотрим такую «близкую» пару Zjy z'j.
Тогда возможны два случая:
Лекция 15. Интеграл Концевича — универсальный инвариант 187
1. На дуге между Zj и zj есть концы других хорд (см. рис. 1). Тогда
область, по которой интегрируется форма с малыми значениями
знаменателя Zj - zj, имеет малость большего порядка чем Zj - zj
в силу невырожденности особой точки. Следовательно, эта часть
формулы (2) не дает особенностей.
Рис.1
2. На дуге между Zj и zj нет концов других хорд (см. рис. 2). Тогда
хорда ZjZj на диаграмме D является изолированной, следовательно,
диаграмма D равна нулю в силу одночленного соотношения.
Рис.2
Следовательно, наш интеграл всегда сходится, что и завершает
доказательство теоремы. ■
Для доказательства остальных двух теорем нам потребуется
дополнительный аппарат, называемый конструкцией Книжника—Замолодчи-
кова.
Сделаем сначала несколько напоминаний.
Определение 15.1. Пусть X — гладкое многообразие, U —
ассоциативная топологическая алгебра над R или над С с единицей.
Тогда К-связностью ft в X называется 1-форма ЙнаХс
коэффициентами из U.
Кривизной связности ft называется 2-форма Fq — dSl + ft Л Q.
188
Раздел III. Инварианты Васильева
Одномерная форма называется плоской, если ее кривизна равна
нулю.
Определение 15.2. Пусть В: I -> X — гладкое отображение
интервала [а, Ъ] в X, а П — £/-связность на X. Определим голономию
Лв,п формы £2 вдоль пути В как функцию, удовлетворяющую
дифференциальному уравнению ^Лв,л(0 = ^(#'(0)^в,п(0 t e I
с начальным условием hBjn(a) = 1.
Замечание 15.2. Нетрудно показать, что если форма О — плоская, то
значения интеграла от этой формы одни и те же на гомотопных путях от а до Ъ.
Решение такого уравнения часто существует и носит название
мультипликативного интеграла формы ft, при этом во многих случаях
голономия вычисляется по формуле:
*В,п(*)=1 + ё J (B*il)(tm)---(B*mi)- (3)
Для прояснении ситуации рассмотрим более простой и полностью
аналогичный пример.
Пример 15.1. Пусть
Y' = AY
— дифференциальное уравнение с начальным условием У(0) = 1, скажем,
в матрицах размера пхп Очевидно, что его решение y(t) будет представлять
собой произведение бесконечно большого числа бесконечно близких к единице
величин, которое называется мультипликативным интегралом и обозначается
Y(x)= f E + A(t)dt.
о
Заметим, что для вычисления Y(x) справедлива следующая итерационная
формула
х i*i
Y(x) = E+ f A(t{)dtx + / A(tY) f A(t2)dt2dtx +... , (4)
0 0 0
при условии, что ряд (4) сходится.
Действительно, при дифференцировании данного ряда каждый следующий
член суммы переходит в предыдущий, умноженный слева на А. При этом
каждый член многократного интеграла (4) можно рассматривать как интеграл
по соответствующему симплексу.
Формула (3) получается аналогично формуле (4).
О мультипликативном интеграле см. [108, 113].
Лекция 15. Интеграл Концевича — универсальный инвариант 189
Замечание 15.3. В «нормальном случае» понятно, что эта формула
действительно дает решение искомого дифференциального уравнения. Начальное
условие выполняется очевидно. Производная от m-кратного интеграла дает
(т - 1)-кратный интеграл с коэффициентом П(В).
Обозначим через V*z множество всех диаграмм, состоящих из п
восходящих упорядоченных стрелок (на рис. 3 они отмечены жирными
линиями) и отрезков, таких, что каждый конец отрезка либо лежит
на стрелке, либо является тривалентной вершиной, в которой
сходятся три конца отрезков, причем к одной точке на стрелке примыкает
не более одного конца отрезка. Будем считать одинаковыми две
комбинаторно эквивалентные диаграммы.
k i
|_z
i к
■А
Рис.3
Пусть основным полем будет С, тогда рассмотрим множество
J§z = 8рап(1>^)/{5Т(7-соотношения}. Здесь под 5247-соотноше-
нием понимается расщепления тривалентной вершины, ребро из
которой выходит на точку на одной из стрелок точно таким же образом,
как и в случае обычных китайских диаграмм. Заметим, что
STEf-соотношение задается локально на кусочках диаграмм (китайской или
из множества A%z), так что при замыкании ориентированных стрелок
из A%z в одну окружность, получая при этом китайские диаграммы,
мы получим обычное 5ТС/'-соотношение для китайских диаграмм.
Для фиксированного п на A%z можно ввести алгебраическую
структуру, понимая под произведением «приставление» одной
диаграммы к другой.
Пример 15.2. Для п = 3 пример умножения в A%z показан на рис. 4.
Для фиксированного п можно градуировать A%z половиной числа
концов отрезков.
Определим для 1 < г, j' ^ п элемент П^ £ J^z условием, что его
единственное ребро соединяет стрелки с номерами i и j.
Замечание 15.4. Легко видеть, что если {hj}f]{kyl} = 09 то П|; и fiw
коммутируют.
190
Раздел III. Инварианты Васильева
L i
/
i к
AAA
А
Рис.4
\ i
к
Рис.5
Пусть Хп — конфигурационное пространство п точек на
комплексной прямой С1. Пусть u>ij — 1-форма на Х„, задаваемая по формуле
dz{ — dzj
Wij = d(ln (zi - Zj)) = — —.
zi "~ *;'
Определим формальную связность Книжника—Замолодчикова П„
со значениями в Jfiz как Яп = Х^ &ijVij на Хп.
Теорема 15.1. Формальная связность Книжника—Замолодчикова
плоская, /и. е. £ln A iln = 0, при этом <К1п = 0.
Доказательство. Рассмотрим элемент
ilnAQn= ^2 toijtoktUijVki (5)
i<j;k<l
и множество {t,j, fc,Z}- Если это множество состоит из двух или
четырех элементов, то соответствующий член суммы равей нулю.
Следовательно, искомая сумма равна сумме по всем *,j, fc, J, где
множество {t',j,fc,I} состоит из трех элементов. Пусть, например,
{г, j, fe, J} = {1,2,3}. Рассмотрим все такие члены в сумме (5). В таком
случае получаем:
У^ toijtok№jb>kl = (^12^23 - ^23^12)^12 Л 0*23 +
{i,i,A,0={ 1,2,3} _|_ (циклические перестановки).
Лекция 15. Интеграл Концевича — универсальный инвариант 191
Используя ЗТЕГ-соотношение, получаем, что искомая сумма равна
произведению
^12з(^12 Л 072з + 0>23 Л <*>31 + ^31 Л 0712),
где Hi23 — элемент, показанный на рис. 6.
Рис.6
Упражнение 15.1 (тождество В. И. Арнольда). Покажите, что шп Ло>2з +
а>2з Л Щ\ + u>3i Л шп = 0.
Таким образом, для каждого множества из трех элементов {г, j, ft, /}
мы получаем сумму ноль, откуда и следует, что Qn Л Qn = 0. ■
Замечание 15.5. Связность П» продолжается на случай алгебры АЦ£,
порожденной диаграммами с 2п стрелками, первые п из которых идут вверх,
а остальные п — вниз. Продолжим 5ТСГ-соотношение на диаграммы с 2п
стрелками так, что знак расщепления тривалентной вершины зависит от
направлений хорд.
Положим £2ПП = .£) SiSjQijU>ij9 где 8{ равно 1 при i < n и -1
при % > п. i<i<j<n
Упражнение 15.2. Проверьте, что в таком случае связность Qnn плоская.
Перейдем теперь к доказательству теоремы 14.3 из прошлой лекции
(инвариантности предварительного интеграла Концевича относительно
непрерывных преобразований, не меняющих количества критических
точек.)
Доказательство. Докажем сначала, что предварительный интеграл
Концевича Z(K) инвариантен относительно преобразований,
оставляющих на месте критические точки.
Пусть Cmin ^ a < Ь < Сщах. Определим Z(Kt [а, Ъ]) точно так же,
как это делалось в формуле (2), заменяя лишь область
интегрирования на a < t\ < ... < tn < b, а получаемые хордовые диаграммы
на элементы алгебры Книжника—Замолодчикова. Несмотря на то, что
Z(JT, [a, b]) не будет лежать в пространстве Ас, он сходится по той же
причине, что и интеграл от узла. Так как на интервале (а, Ь) нет
критических точек, пересечение узла с полосой С х (а, Ь) представляет собой
набор кривых, касательная к которым не горизонтальна, с заданной
ориентацией. Пусть количество кривых равно 2п, причем п из них
192
Раздел III. Инварианты Васильева
являются восходящими, an— нисходящими. Зафиксируем нижние
точки <*i,..., й2п и соответствующие верхние &ь ..., &2п» причем
первые п координат отвечают восходящим кривым, а последние п —
нисходящим. Конечность этого интеграла доказывается точно так же,
как и конечность предварительного интеграла Концевича Z(K). При
этом нужно считать нулевыми диаграммы, которые имеют отдельно
стоящую хорду с концами на восходящей и нисходящей стрелке; при
построении хордовой диаграммы всего узла это будет в точности
означать одночленное соотношение.
Тогда интеграл Z(K[a, b]) можно представить как голономию
связности ilnn вдоль пути от (ai,..., а,2П) до (6i,..., bin) в силу
итерационной формулы (3). Действительно, m-й член итерационной формулы
в точности соответствует m-му члену интеграла Концевича, так как
в обоих случаях интегрируется форма
£ и^Лт^т*» (6)
р={(ч4)} i=1 3 j
при этом (-1)* соответствует знаку произведения SjSy.
Заметим также, что 5Т[7-соотношение для китайских диаграмм
совпадает с 4Т-соотношением для хордовых диаграмм. Из этого
наблюдения будет следовать, что полученный таким образом инвариант
(полный интеграл Концевича I) учитывает 4Т-соотношение.
Так как кривизна связности £2ПП равна нулю, то такой интеграл (6)
не меняется при гомотопии пути интегрирования, т. е. при
горизонтальных изотопиях в R3 части узла, заключенной в t £ (a, 6).
Также нетрудно показать, что для произвольных а < b < с
(возможно, критических) Z(K, [a, с]) = Z(K, [a, b]) • Z(K, [6, с]), откуда
следует, что интеграл Z(K), равный произведению Z(K, [с,-, c,+i]), где
с,-, Cj+i — все пары соседних критических точек, выдерживает
горизонтальные деформации на участках, не содержащих критических точек.
Рассмотрим теперь случаи, когда критические точки перемещаются
в процессе изотопии узла.
1. Критическая точка движется, но ее расположение относительно
других критических точек не меняется (см. рис. 7).
Рис.7
Лекция 15. Интеграл Концевича — универсальный инвариант 193
2. Две критические точки меняются местами (см..рис. 8).
л^-л
Рис.8
Как показано на рисунках выше, сначала можно провести
преобразование, не меняющее предварительного интеграла Концевича Z(K),
получив при этом вложение узла с узкой полоской. Покажем, что
при ее «убирании» для каждого т, га-й интеграл Концевича
изменится на бесконечно малую величину е в некоторой стандартной норме
для .4^.
Действительно, пусть К — узел, К1 — узел с добавленной
полоской. Очевидно, что разница Z(K) - Z(K*) происходит только от тех
членов, где концы хорд лежат на полоске. Предположим, что ширина
полоски равна е. Покажем, что Zm(K) - Zm(K) = 0(e).
Действительно, рассмотрим все хорды, хотя бы один конец которых
лежит на полосе. Если у самой верхней их них оба конца лежат
на полосе, то такая хордовая диаграмма равна нулю в силу одночленного
соотношения. Если хорд, оба конца которых лежат на полосе, нет, то
ситуация также простая: интеграл от члена, показанного на рис. 9,
должен иметь малость порядка е, в силу того, что при интегрировании
левого и правого слагаемого числа | отличаются на единицу, отчего
и происходит сокращение. Более строго, для любого члена существует
«симметричный» ему член, сумма с которым дает малое число.
Рис.9
Осталось рассмотреть лишь случай, когда верхняя хорда (z,-, zt')
содержит лишь один конец на полосе, а под ней лежат к хорд, оба
194
Раздел III. Инварианты Васильева
конца которых лежат на полосе: самая нижняя из них (zj^z'^), а самая
верхняя равна (zjkJ z'jk)9 см. рис. 10.
: *к
i
Рис. 10
Мы можем считать, что (z,-, zQ — единственная хорда такая, что
лишь один ее конец лежит на полосе, от убирания таких хорд наш
интеграл может лишь умножиться на некоторое число, отделенное
от нуля и от бесконечности.
Пусть 6a = \zja - ZjiJ. Тогда разница Z(K') - Z(K) ограничена
некоторой константой, умноженной на
е б\ 6k-i %
Г ddx Г d62 f d6k Г dzi - dz\
J h J 62 "' У 6k J Zi-z\ ~
0 0 0 Zjk
Действительно, последний интеграл имеет порядок малости 6к.
Следовательно, в предпоследнем интеграле 6к сокращается и он имеет
порядок бк-\9 и. т. д. Наконец, весь интеграл имеет порядок 6\ ~ е.
В силу произвольности выбора малого е, получаем инвариантность
интеграла Концевича относительно непрерывных преобразований узла,
не меняющих количества критических точек. ■
Итак, мы доказали, что I(Z) является инвариантом узла.
Докажем теперь теорему 14.6 о том, что для каждой системы
весов W функция W(I(-)) задает инвариант Васильева, символом
которого является W.
Доказательство. Выберем систему весов W степени га. Для
доказательства теоремы нужно показать, что если D — хордовая диаграмма
с га хордами, а Кв — морсовское погружение сингулярного узла
в Cz х R^, которому соответствует хордовая диаграмма D, то
I(KD) = D + (члены порядка ^ га),
Лекция 15. Интеграл Концевича — универсальный инвариант 195
где В — класс эквивалентности хордовой диаграммы D, a I(KD)
определяется как альтернированная сумма значений интеграла Концевича I
на 2т узлах, образующих сингулярный узел Кп-
Если два узла К\ и КгУ вложенные морсовским образом в Cz x R*,
совпадают везде, за исключением малого участка, на котором две ветви
узла К\ образуют переход, а две ветви узла Кг образуют проход, то
значения Z(Ki) и Z(K\) отличаются только в тех членах, в которых
спариваются точки на этих ветвях.
Сингулярный узел Kd является альтернированной суммой 2т
узлов, различающихся в малых окрестностях га точек. Заметим, что
знак этой альтернированной суммы регулируется сомножителем (-1)*
в формуле (2). По причинам, изложенным выше, Z(Kd) имеет
ненулевые коэффициенты только при тех хордовых диаграммах, которые
получаются при спаривании точек во всех этих окрестностях. Таким
образом, хордовые диаграммы с ненулевыми коэффициентами должны
иметь как минимум га хорд.
Для хордовых диаграмм с га хордами этот коэффициент не равен
нулю только для диаграммы К&. Вычислим этот коэффициент.
В каждой из га вершин мы получаем разность двух интегралов
от форм *Zy •
Эта разность равна интегралу по контуру, обходящему один раз
вокруг нуля дифференциала dz/z. По теореме Коши получаем, что этот
интеграл равен 2wi. Поскольку количество таких пар точек равно га,
коэффициенты пропорциональности перемножаются. В итоге мы
получаем коэффициент (2тг*)т, который сокращается со знаменателем
в формуле (2).
Это значит, что
Z(Kd) = D + (члены порядка ^ га).
Таккакад = ^)ТОи
I(KD) = D + (члены порядка ^ га).
Следовательно, W(I(KD)) = W(D), и инвариант Васильева W(I(-))
порядка га имеет символом весовую систему W, ч. т. д. ■
При этом вычисление интеграла Концевича является довольно
трудной задачей. В частности, трудной задачей является даже
вычисление предварительного интеграла Концевича для оо. Бар-Натан
с соавторами выдвинули гипотезу об окончательном виде этой суммы
в терминах китайских диаграмм, а не хордовых диаграмм, (см. [ 14],
формулировку можно прочесть в [102]). Эта гипотеза затем стала теоремой,
см. [15].
196
Раздел III. Инварианты Васильева
Кроме того, Ле и Мураками в работе [63] обобщили понятие
интеграла Концевича на так называемые связки — одномерные
многообразия, лежащие между двумя плоскостями и пересекающие эти плоскости
лишь в конечном числе точек. Это дало возможность предложить
технический подход к вычислению не только интеграла Концевича для
узлов, но и аналогичного интеграла для зацеплений, в частности, это
позволило доказать теорему о том, что все инварианты конечного
порядка для зацеплений также порождаются системами весов (в которых
вместо диаграмм с одной окружностью присутствуют диаграммы с
несколькими окружностями). С помощью этой техники они вычислили
интеграл Z(oo).
Лекция 16
Комбинаторные формулы
для вычисления инвариантов Васильева
Мы доказали, что для каждой системы весов W функция W (/(•)),
где J — интеграл Концевича, является инвариантом Васильева,
символом которого служит W. При этом подсчет даже первых членов
интеграла Концевича достаточно сложен, хотя и поддается технике
Ле и Мураками [63]. При этом существует и более простой способ
вычисления значений инвариантов Васильева на узлах, называемый
комбинаторными формулами. Существуют два подхода к
комбинаторным формулам. Один из них связан с так называемым «скалярным
произведением», он появился в статье О. Я. Виро и М. Поляка для
описания инвариантов Васильева второго и третьего порядка, а также
одного базисного инварианта Васильева четвертого порядка, см. [78],
эту формулу можно найти также в статье [95]. Годом раньше появилась
статья Ж. Ланна [60], в которой приводились комбинаторные формулы
для получения инвариантов второго и третьего порядков, описанные
в терминах «координат на узле». Наконец, совсем недавно появились
работы С. Д. Тюриной [124] и [125], в первой из которых она описывает
комбинаторные формулы для инвариантов Васильева второго и
третьего порядков, а во второй — для двух базисных инвариантов четверного
порядка, отличных от инварианта, описываемого в работе [78]. Таким
образом, работы [78, 124, 125] дают все комбинаторные формулы для
инвариантов Васильева порядков не выше четырех.
§ 1. Модуль Васильева
В этой лекции мы поговорим о модуле Васильева и о
комбинаторных формулах для получения инвариантов Васильева второго и третьего
порядков.
Неизвестно, различают ли инварианты Васильева все
изотопические классы узлов и зацеплений (это утверждает гипотеза Васильева).
Был введен модуль Васильева — пространство узлов и сингулярных
узлов, в котором два узла считаются различными, если их различают
инварианты Васильева порядка не выше фиксированного. При этом
каждый узел разлагается в конечную сумму образующих модуля.
198
Раздел III. Инварианты Васильева
Начнем с основных определений.
Определение 16.1. Модуль Васильева порядка п — это модуль
над кольцом Z или Q, порожденный изотопическими
классами ориентированных узлов и сингулярных узлов со следующими
соотношениями:
1. Е =-'0, где Е — тривиальный узел.
2. Соотношение Васильева.
3. Кт = 0 при га > п, где Кт — произвольный сингулярный узел
порядка т.
Тогда имеет место
Теорема 16.1 о разложении. Любой узел К в модуле Васильева п-го
порядка имеет следующее разложение
r+s
1=1
где г — размерность пространства инвариантов Васильева порядка
меньше или равного (п - 1), s — размерность пространства весовых
систем порядка n, v,- — инварианты Васильева порядка меньшего
или равного n, Ki — фиксированные (базисные) узлы, не зависящие
от узла К.
Доказательство. Заметим, что пространство инвариантов Васильева
порядка не более п имеет размерность г + з. Зафиксируем базис
v'u... ,v'r+8 в линейном пространстве этих инвариантов. Рассмотрим
изотопические классы узлов. Каждому из них можно сопоставить набор
(вектор) из г и- s значений базисных инвариантов Васильева. Так как
эти инварианты Васильева линейно-независимы, то найдутся г + s
изотопических классов узлов UTi,... ,-йГг+5, на которых получаемые
вектора v'u... ,t;J+e линейно независимы. Эти узлы можно выбрать
в качестве базиса и рассмотреть инварианты Васильева v», i = 1,...,
r + s порядка не более п, такие, что Vi(Kj) = бу. Тогда, так как модуль
Васильева n-го порядка порождается узлами ИГ,-, то
г+а
Ч.Т.Д.
■
Лекция 16. Комбинаторные формулы 199
§ 2. Комбинаторные формулы Ланна
Комбинаторные формулы, которые будут приведены ниже, дают
возможность выбрать базис в пространстве узлов, а также указать явный
вид разложения для каждого наперед заданного узла.
Итак, пусть дан ориентированный узел К с отмеченной точкой,
которая не является точкой двойной проекции, и пусть D — плоская
диаграмма этого узла. Каждой вершине х диаграммы D сопоставим два
числа 6Х и ех следующим образом:
1) Если двигаясь от отмеченной точки в направлении ориентации
узла мы сначала проходим точку х по переходу, а затем по проходу, то
6Х = 0, в противном случае 6Х = 1.
2) Двойной точке х диаграммы D сопоставим число ех = ±1
в зависимости от типа перекрестка так, как показано на рис. 1. Это
число называется local writhe number.
V
Рис.1
Пример 16.1. «Координаты» на узле восьмерка, см. рис. 2.
(Й
х
Рис.2
Здесь бх = О, 6У = 0, бг = 0, 6t = 1, ех = 1, еу - 1, ег = -1, et = -1.
Пусть дан узел К с отмеченной точкой. Тогда по координатам
на узле можно построить диаграмму Гаусса этого узла.
Определение 16.2. Гауссова диаграмма узла К с отмеченной
точкой — это ориентированная окружность (с отмеченной точкой),
у которой хордами соединены прообразы прохода и перехода точек
проекции узла. Прообразы каждой двойной точки соединены
хордой со стрелкой, направленной от прообраза точки, образующего
200
Раздел III. Инварианты Васильева
переход, к прообразу точки, образующему проход. При этом
каждая стрелка имеет знак, равный знаку local writhe number данной
вершины.
Аналогично определяется стрелочно-хордовоя диаграмма
сингулярного узла с отмеченной точкой: в обычных перекрестках ставятся
стрелки с метками, соответствующие числам е и 6, а в сингулярных
вершинах — хорды без стрелок и без меток.
Поддиаграммой Гаусса диаграммы G называется окружность с
отмеченной точкой, множество стрелок-хорд для которой принадлежит
множеству стрелок-хорд для диа1раммы G.
Пример 16.2. Гауссова диаграмма для правого трилистника показана
на рис. 3.
Рис.3
В [60] Ланн привел следующую комбинаторную формулу для
вычисления инварианта Васильева второго порядка V, равного нулю
на тривиальном узле и единице на трилистнике, для произвольного
узла К:
V(K) = - ]Г е<*> »)W(! - 6y(K))ex{K)ey{K),
х,у
где сумма берется по всем парам перекрестков (ж, у), а е(ж, у) равно
единице или нулю в зависимости от того, пересекаются ли хорды
гауссовой диаграммы, соответствующие вершинам (ж, у) или нет.
Замечание 16.1. Не любая диаграмма с хордами стрелками и со знаками
является гауссовой диаграммой некоторого узла. Пример диаграммы, не
являющейся таковой ни при какой расстановке стрелок и знаков, показан на рис. 4.
Рис.4
Упражнение 16.1. Покажите, что у гауссовой диаграммы любого узла
любая хорда имеет нечетную длину, т. е. количество вершин, находящихся
Лекция 16. Комбинаторные формулы
201
в интервале между началом и концом хорды (включая начало и исключая
конец) нечетно.
Упражнение 16.2. Покажите, что плоская диаграмма узла однозначно
восстанавливается по его гауссовой диаграмме.
§ 3. Комбинаторные формулы Виро—Поляка
Пусть К — некоторый узел с отмеченной точкой иС~ его
гауссова диаграмма. Пусть А — поддиаграмма диаграммы G. Обозначим
через (A, G) сумму знаков всех поддиаграмм G, имеющих комбинаторный
тип А у где знак поддиаграммы — это произведение знаков всех ее хорд.
Если справа вместо гауссовой диаграммы стоит стрелочно —
хордовая диаграмма, то «скалярное произведение» определяется как сумма
скалярных произведений А с диаграммами, получающимися
расщеплением «сингулярных» хорд с соответствующими знаками.
Перейдем теперь к описанию комбинаторных формул для
получения инвариантов Васильева в терминах (•, •).
Определение 16.3. Назовем инвариант / узланетным, если для
любого узла К и его зеркального образа К* имеет место
равенство f(K) = f(K*). Аналогично, инвариант называется«е«*е/я«ш#,
если для любого узла К и его зеркального образа К* имеем
/(ЛГ) = -/(**).
Упражнение 16.3. Покажите, что инвариант Васильева второго порядка,
принимающий значение 0 на тривиальном узле и 1 на трилистнике, является
четным.
Обозначим этот инвариант через t>2-
Теорема 16.2 ([78]). Если G — диаграмма Гаусса узла ИГ, тогда
имеет место тождество
v2(K) = (D,G), (1)
где D — гауссова диаграмма, показанная на рис. 5.
Рис.5
Доказательство. Непосредственно проверяется, что данная
формула для простейшей диаграммы тривиального узла дает нуль, а для
простейшей диаграммы трилистника дает единицу.
202
Раздел III. Инварианты Васильева
Осталось проверить два факта: то, что данная формула
инвариантна относительно трех движений Рейдемейстера и то, что порядок
данного инварианта равен двум (так как инварианты меньших
порядков являются константами, достаточно доказать, что порядок данного
инварианта не больше двух).
Первое движение Рейдемейстера для узлов воздействует на
гауссовы диаграммы следующим образом: к диаграмме добавляется одна
отдельно стоящая хорда. Очевидно, что она не влияет на вышеуказанное
скалярное произведение.
Второе движение Рейдемейстера состоит в добавлении
(уничтожении) двух хорд, дуга между началами которых, так же, как и дуга между
их концами, не содержит концов (начал) других хорд. Без ограничения
общности можно считать, что обе эти дуги не содержат отмеченной
точки, см. рис. 6.
ею о
а б
Рис.6
Пусть G\ и б?2 — две гауссовы диаграммы, одна из которых
получается из другой применением второго движения Рейдемейстера,
рис. 6 а или б, где количество хорд диаграммы Gi на две больше, чем
количество хорд диаграммы G\.
Очевидно, что вклад в разницу (Д G-j) - (Д G\) вносят лишь те
пары хорд диаграммы Gi, одна из которых принадлежит числу двух
добавленных. При этом пара добавленных хорд вклада не вносит. В случае
6 а это следует из непересечения добавленных хорд, а в случае 6 б —
из того, что между концами пересекающихся хорд не расположена
отмеченная точка. Если одна из добавленных хорд входит в
формулу (1) вместе с какой-либо другой хордой (не из числа добавленных),
то вторая в наборе с этими двумя также входит в эту формулу, причем
вхождения дают разные знаки и, следовательно, сокращаются.
Последнее утверждение верно как для случая, указанного на рис. 6 д, так и для
случая на рис. 6 б.
Наконец, рассмотрим третье движение Рейдемейстера. Как и в
случае со вторым движением Рейдемейстера, можно считать, что оно
происходит вне малой окрестности отмеченной точки. В
зависимости от порядка и направления хорд, возможны две принципиально
> различные ситуации на диаграммах Гаусса, см. рис. 7.
Лекция 16. Комбинаторные формулы
203
<&©@-©
а б
Рис.7
В обоих случаях изменяются лишь три хорды, указанные на
рисунке. Для каждого случая, а или б, остальные хорды одинаково
расположены на двух гауссовых диаграммах, соответствующих этому случаю.
При этом на участках, отмеченных жирным, нет концов (и начал)
хорд, кроме указанных на рисунке. Так как третье движение
Рейдемейстера не задевает отмеченной точки, то отмеченная точка лежит вне
трех участков, отмеченных жирным. При произвольном расположении
отмеченной точки вне этих трех участков видно, что пары хорд,
образованные из числа данных трех, дают одинаковый вклад до применения
третьего движения Рейдемейстера и после него. Очевидно также, что
если любая хорда с, в паре с одной из выделенных хорд а дает вклад
в (Д Gi) для гауссовой диаграммы G\ до применения третьего
движения Рейдемейстера, то хорда с в паре с хордой а', соответствующей
хорде а (т. е. соединяющей те же выделенные участки, что и хорда а'),
даст тот же вклад в (J9, Gz) для гауссовой диаграммы G2, отличающейся
от G\ применением третьего движения Рейдемейстера. Последние два
предложения одинаково применимы к случаю на рис. 7аи7б.
Утверждение о порядке инварианта докажем в общем случае.
Лемма 16.1. Пусть инвариант v задан стрелочной диаграммной
формулой (A, G), в которой диаграммы, входящие в сумму А, имеют
не более п стрелок. Тогда инвариант v имеет порядок не выше п.
Доказательство. Пусть К — сингулярный узел с (п + 1)-й точкой
пересечения, a G — его стрелочно-хордовая диаграмма. Покажем, что
(A, G) = 0. Распишем эту хордовую диаграмму как линейную
комбинацию 2n+l стрелочных диаграмм. В каждом слагаемом рассмотрим
поддиаграммы комбинаторного типа А. При этом по условию леммы
все потомки п + 1 хорды без стрелок входить в эту диаграмму не могут,
следовательно, существует по крайней мере одна хорда со стрелкой,
которая в эту формулу не входит. При ее расщеплении получаем
диаграммы, входящие в формулу с противоположными знаками, которые
при взятии скалярного произведения с А сокращаются. Следовательно,
получаем (A, G) — 0, что и требовалось доказать. ■
204
Раздел III. Инварианты Васильева
Применение леммы для п = 2 завершает доказательство
теоремы. ■
Рассмотрим теперь нечетный инвариант Васильева, равный нулю
на тривиальном узле и единице на правом трилистнике. Примем на веру
существование такого инварианта.
Предложение 16.1. Такой инвариант единственный.
Доказательство. Вычислим символ этого инварианта. Так как
размерность пространства А$ равна единице, то этот символ принимает
значение с Ф 0 на хордовой диаграмме D$, на которой одна хорда
пересекается с двумя другими, не пересекающимися между собой 1\
Так как инвариант нечетный, то его значение на левом трилистнике
равно минус единице.
Распишем соотношение Васильева для инварианта v^ третьего
порядка, см. рис. 8.
Рис.8
Получаем, что с = 2. Следовательно, любые два таких инварианта
v\ и v\ третьего порядка имеют одинаковый символ. Следовательно,
их разница является нечетным инвариантом Васильева не более, чем
второго порядка. Так как инвариант второго порядка является четным
с точностью до константы, то v\ - v\ = const. Так как они оба равны
нулю на тривиальном узле, получаем тождество. ■
Теорема 16.3 ([124]). Если G — диаграмма Гаусса узла К, тогда
имеет место тождество
v,(K) = (А + D2 + £>з + D4 + D5, G), (2)
где D{ — гауссовы диаграммы, показанные на рис. 9.
Доказательство. Покажем сначала, что правая часть в (2) не
меняется при движениях Рейдемейстера.
' Этой информации достаточно для задания инварианта. На хордовой диаграмме,
в которой каждые две из трех хорд пересекаются, он принимает значение 2с, а на осталь-
' ных диаграммах с тремя хордами — нуль.
Лекция 16. Комбинаторные формулы 205
Инвариантность правой части в (2) относительно первого и второго
движений доказывается так же, как и в случае инварианта первого
порядка (1).
Инвариантность правой части в (2) относительно третьего
движения Рейдемейстера доказывается разбором случаев а) и б) и перебором
вхождений диаграмм на рис. 9 в качестве поддиаграмм в диаграмму G,
к которой применяется третье движение Рейдемейстера. Более
подробно см. в [124].
®®еее
A D2 Di DA D5
Рис.9
Теоремы 16.2 и 16.3 являются практическими реализациями
следствия замечательной теоремы Гусарова о том, что любой инвариант
конечного порядка может быть задан такими «скалярными
произведениями». При этом узлы с отмеченной точкой можно трактовать как
длинные узлы, а диаграммы с отмеченной точкой — как диаграммы
на прямой. Более точно это можно переформулировать так
То, что степень инварианта не больше трех, и, следовательно, равна
трем, следует из леммы 16.1. ■
Теорема 16.4 (Гусаров, [39]). Любой инвариант (длинных) узлов
конечного порядка п со значениями в R может быть представлен
в форме {А, •), где А — линейная комбинация гауссовых диаграмм
на прямой с не более чем п стрелками.
Упражнение 16.4. Покажите, что инвариант Васильева третьего порядка,
задаваемый по формуле (2), действительно является нечетным.
Приведем теперь примеры разложений в модуле Васильева для
порядков 2 и 3. Эти результаты принадлежат Ланну [60].
Примеры 16.1. Для п = 2 имеет место разложение К = v2(K) -Т, где Т —
трилистник.
Для п = 3 имеет место разложение К = v3(K) • (Г + Я) - v2(K) • Я, где Т
и Я — трилистник и восьмерка соответственно.
Раздел IV
d-ДИАГРАММЫ
Лекция 17
Атомы и высотные атомы.
Основные определения
§ 1. Атомы и высотные атомы. Критерий высотности
На протяжении всего курса мы приводили различные способы
задания узлов для построения некоторых инвариантов и изучения
свойств узлов.
Однако многие из способов задания являются невыразительными
(диаграммы с проходами и переходами), содержащими лишнюю
информацию (диаграммы Гаусса) или требующими бесконечного числа
символов-переменных (стабильная группа кос).
На ближайших нескольких лекциях мы предлагаем новый способ
кодирования узлов с помощью d-диаграмм. Теория d-диаграмм
появилась и развивалась в работах автора [105, 106, 107] с 1996 года, хотя
само понятие d-диаграммы было введено в статье [107]. Связующим
звеном между понятием узла и понятием d-диаграммы является
понятие высотного атома, введенное в [105]. При этом с помощью атомов
и d-диаграмм можно построить простую кодировку всех зацеплений
словами в четырехбуквенном алфавите, как это сделано в [107].
Понятие атома было введено А. Т. Фоменко для классификации
интегрируемых гамильтоновых систем малой размерности. Начнем с
понятий атома и высотного атома, следуя [34].
Определение 17-1. Пусть М — двумерное многообразие без края,
/ — функция Морса на нем, а с — критическое значение этой
функции. Выберем е > 0, такое, что многообразие /_1([с - £>
с+е]) ^ не содержит критических точек функции / за исключением
точек, лежащих на уровне {/"^(с)}.
' Будем считать, что это многообразие с краем связно и уровень {/ = с} содержит
^ лишь седловые точки.
Лекция 17. Атомы и высотные атомы
207
Атомом называется пара (f~l([c - е, с + е]), /~1(с)) с указанием
правила вложения второй компоненты в первую.
Вторая компонента атома называется остовом атома. В силу леммы
Морса остов является графом кратности четыре.
Скажем, что атом — ориентируемый, если его первая компонента
является ориентируемой как многообразие с краем.
Вершиной атома называется вершина его остова.
Под сложностью атома будем понимать количество его вершин.
Родом атома называется род поверхности, получаемой из первой
компоненты атома заклеиванием граничных окружностей дисками.
Будем называть атомы рода нуль плоскими, ориентированные
атомы рода один — торическими, и. т. д.
У каждого атома можно рассмотреть связные компоненты его
послекритического уровня — послекритические окружности. В
дальнейшем они будут играть важную роль для построения соответствия
между атомами и узлами.
Z
Рис. 1. Пример атома с двумя вершинами
Обычно атомы рассматриваются с точностью до естественной
эквивалентности — изоморфизма.
Определение 17.2. Скажем, что два атома V{ и V2 изоморфны,
если существует изоморфизм их первых компонент, при котором
образом второй компоненты атома V\ является вторая компонента
атома V2, причем сохраняется направление роста соответствующей
функции.
Замечание 17.1. Иногда (например, в [105]) в определении атомов не
требуется сохранения направления роста функции. В этом случае соответствующие
узлы будут рассматриваться с точностью до зеркальной симметрии.
С точностью до изоморфизма атомы можно определить как графы
кратности четыре с некоторой специальной структурой на ребрах.
208
Раздел IV. d-Диаграммы
Остов атома является графом кратности четыре. Для задания атома
нужно задать его остов и поведение функции в окрестности вершин
остова. Для этого в каждой вершине нужно выделить:
1. разбиение четырех исходящих полуребер на две пары
«противоположных» (структура А).
2. разбиение четырех исходящих полуребер на две пары «соседних»
(не противоположных) полуребер, которые соответствуют «после-
критическим» уровням соответствующей функции (структура В);
другое разбиение на две пары соседних ребер соответствует «до-
критическим уровням» функции.
Замечание 17.2- Структура В включает в себя структуру А.
Упражнение 17.1. Покажите, что два атома с одинаковыми остовами
и одинаковыми структурами А и В изоморфны.
Пусть дан атом V. Если у него заклеить все послекритические
и докритические окружности дисками, то получим замкнутое
многообразие М, разбиваемое на клетки остовом атома. Если раскрасить
«послекритические» клетки черным цветом, а докритические — белым,
то многообразие М будет иметь «шахматную» раскраску: каждые две
грани, имеющие общее ребро, будут иметь разные цвета. Легко
видеть, что верно и обратное: по многообразию, которое граф кратности
четыре делит на клетки, допускающие шахматную раскраску, можно
восстановить атом. Эту конструкцию можно рассматривать как еще
одно определение атома.
Определим теперь понятие высотного атома, следуя [105].
Определение 17.3. Атом называется высотным, если он
изоморфен атому, порожденному функцией высоты на двумерном
многообразии, вложенном в R3.
Замечание 17.3. Очевидно, что любой высотный атом является
ориентируемым, а остов высотного атома является плоским графом.
Упражнение 17.2. Покажите, что все ориентируемые атомы с менее чем
тремя вершинами являются высотными.
Пример 17.1. Простейшим невысотным атомом с плоским остовом
является неориентируемый атом, обозначаемый через С в классификации [34]. Он
лежит на проективной плоскости и у него одна вершина и два ребра, у данного
атома одна докритическая окружность и одна послекритическая окружность.
Теорема 17.1 (критерий высотности атома, [105]). Атом является
высотным тогда и только тогда, когда его остов вложим в плоскость
с сохранением структуры А.
Лекция 17. Атомы и высотные атомы
209
Доказательство. Пусть атом V — высотный. Рассмотрим его
реализацию функцией высоты в R3, и пусть с — критическое значение
функции высоты. Тогда его остов является вложенным в плоскость {z = с},
рассмотрим произвольную вершину X этого остова. Предположим, что
при вложении в вершине X А-структура атома не сохранена. Это
означает, что образы двух полуребер а и Ь, являющихся соседними на атоме,
являются локально противоположными на плоскости {z = с}.
Рассмотрим угол, образованный этими ребрами на атоме. Во внутренности
этого угла лежат либо точки послекритического уровня, либо точки до-
критического уровня. Без ограничения общности предположим первое.
Обозначим два оставшихся полуребра через с и d. Угол между ними
также содержит только послекритические значения функции, z. Их
образы на плоскости {z = с} являются противоположными
полуребрами. Рассмотрим теперь проекцию послекритического уровня {z = с+е}
на плоскость {z — с}. При малом е он будет локально выглядеть так,
как показано на рис. 2.
ШЬ
a a
Рис. 2. Слева — структура В на атоме, справа — на плоскости
Очевидно, что этот атом будет самопересекающимся, что
противоречит предположению о вложенности многообразия М в R3.
Обратно, пусть остов атома V вложен в плоскость {z = с} с
сохранением структуры А. Построим реализацию атома функцией высоты
в окрестности этой плоскости. Зафиксируем е > 0. В малой окрестности
каждой вершины построим поверхность так, как показано на рис. 3.
4-
Рис. 3. Жирными линиями выделен поелекритический уровень
В остальных местах построим поверхность М идущей вертикально
от уровня {с-е} до уровня {с+е} вдоль ребер, т. е. приклеим
вертикальные ленты к уже построенным участкам поверхности в окрестностях
вершин.
210
Раздел IV. d-Диаграммы
Таким образом, получим многообразие М, вложенное в R3, краем
которого является пересечение данной поверхности с плоскостями
{z = с± е}9 а пересечение с плоскостью {z = с} является остовом
атома V. Легко видеть, что получившийся атом изоморфен атому V. Ш
Замечание 17.4. Из критерия высотности атома, в частности, следует, что
атом, остов которого вложим в плоскость с сохранением А-структуры атома,
является ориентируемым.
Пример 17.2. Простейший ориентируемый невысотный атом имеет три
вершины. Этот атом является торическим, т. е. его род равен единице. Остов
этого атома является планарным. Согласно классификации [34], этот атом
обозначается Еу. На рис.4 он изображен на торе (квадрате с
отождествленными прагивоположными сторонами); послекритический уровень атома Е\
заштрихован; вершины атома Е{ обозначены жирными точками.
Рис.4
Упражнение 17.3. Используя приведенный выше критерий высотности
атома, покажите, что ориентируемый атом Е{ действительно является
невысотным.
Замечание 17.5. Все остальные ориентируемые атомы сложности меньше
четырех являются высотными.
Среди ориентируемых атомов сложности четыре (их 58 штук) имеется семь
невысотных атомов. Все они приведены в [105].
Среди атомов больших сложностей доля невысотных возрастает и
стремится к единице при количестве вершин, стремящемся к бесконечности.
Упражнение 17.4. Постройте высотные атомы произвольного рода
т ^ 0, а также невысотные ориентируемые атомы произвольного рода n G N.
§ 2. Теорема об атомах и узлах
Пусть дан высотный атом V. Построим по нему диаграмму
некоторого зацепления следующим образом. Вложим остов атома V в
плоскость с сохранением структуры А в каждой вершине. Получим граф
кратности четыре. В каждой вершине установим правило для прохода
Лекция 17. Атомы и высотные атомы
211
и перехода следующим образом. Пусть ас и bd — две пары
противоположных полуребер. Установим переход по той из них, вращение
от которой к другой паре внутри послекритической области происходит
против часовой стрелки, см. рис. 5.
после-
крит.ур. I
после-
крит.ур.
а а
Рис. 5. Построение диаграммы узла по В-структуре атома
Получим диаграмму зацепления.
Упражнение 17.5. Покажите, что альтернированные диаграммы
зацеплений соответствуют стандартным вложениям остовов плоских атомов с
сохранением в каждой вершине В-структуры, индуцируемой из плоскости (или из
сферы), на которой расположен сам атом.
Теорема 17.2 об атомах и узлах ([105]). Построенный
изотопический класс зацепления не зависит от способа вложения в плоскость
остова атома V с сохранением структуры А.
Доказательство. Для начала сформулируем известную лемму.
Лемма 17.1.
Два плоских изоморфных графа являются изотопными в R3.
Перейдем теперь к доказательству теоремы. Рассмотрим два
вложения /i и /г остова Г атома V в плоскость Р. Рассмотрим граф Гь
получаемый из Г следующим образом: добавим в окрестности каждой
вершины Г.по одной вершине на ребрах и соединим вершины на
соседних ребрах маленькими ребрами. Вьщелим из добавленных ребер
пару, соответствующую послекритическому уровню атома V.
Очевидно, что в силу сохранения структуры А, вложения f\ и j2 графа Г
продолжаются до вложений /{ и f2 графа Г].
Будем проводить изотопию в R3 вложений /{ и f2. Без
ограничения общности можно считать, что в каждый момент изотопии малая
окрестность каждой вершины графа Г с четырьмя маленькими ребрами
лежит в плоскости, проходящей через данную вершину. В каждый
момент изотопии можно построить зацепление (с точностью до изотопии)
следующим образом. В каждой вершине графа Г произведем разведение
пар противоположных полуребер так, как показано на рис. 6 в
соответствии с выделенными ребрами графа IV Легко видеть, что такая
операция определена корректно относительно того, с какой стороны
мы смотрим на эту плоскость.
212
Раздел IV. d-Диаграммы
Г
J
Г
Рис.6. Выделенные ребра обозначены жирными линиями
Очевидно, что в начальный момент полученное зацепление будет
совпадать с зацеплением, соответствующим вложению /i, а в конечный
момент — с зацеплением, соответствующим /г. При этом ясно, что
в процессе изотопии графа зацепление также будет изотопироваться,
что и завершает доказательство теоремы. ■
Нетрудно доказать следующую теорему.
Теорема 17.3- Любой изотопический класс зацепления L может
быть получен из некоторого высотного атома V.
Доказательство. Действительно, рассмотрим произвольную
плоскую диаграмму зацепления L. Она представляет собой плоский граф Г
кратности четыре. Выберем его в качестве остова атома V. Снабдим
этот граф А-структурой, индуцированной из плоскости
(противоположными будем считать те полуребра, которые локально противоположны
на плоскости).
Выберем В-структуру для данного атома следующим образом.
Пусть из вершины X графа Г исходят четыре ребра a,b,c,d, причем
пара противоположных ребер ас образует переход, а пара
противоположных ребер Ы образует проход. Если движение от полуребра а
к полуребру d происходит по часовой стрелке, то в качестве послекрити-
ческих углов выберем ab и cd, в противном случае — ad и Ьс, см. рис. 7.
Рис. 7. Послекритический уровень справа заштрихован
Легко видеть, что построенный таким образом высотный атом V
будет порождать зацепление L. Ш
Лекция 17. Атомы и высотные атомы
213
Рассмотрим теперь произвольное зацепление L и соответствующие
ему высотные атомы. У каждого такого атома есть некоторое количество
послекритических окружностей.
В некоторых «хороших» случаях количество таких окружностей
может быть равно единице. Изобразим остов атома, его В-структуру
и образ 6 единственной послекритаческой окружности у на плоскости
так, как это показано на рис. 8.
Рис. 8. Послекритическая окружность обозначена жирной линией
К каждой вершине атома окружность послекритического уровня
подходит дважды. Рассматривая окружность 7 и соединяя на ней
прообразы пар точек подхода окружности 6 к вершинам атома, получаем
некоторую хордовую диаграмму.
Аналогичным образом строится и хордовая диаграмма для
произвольного атома с одной послекритаческой окружностью.
Определение 17.4. Назовем d-диагроммой такую хордовую
диаграмму 2\ хорды которой могут быть разбиты на два семейства хорд
так, чтобы хорды из одного семейства не пересекались.
Имеет место следующая
Теорема 17.4 ([106]). Пусть дан ориентируемый атом V с одной
послекритической окружностью. Тогда атом V является высотным
тогда и только тогда, когда соответствующая ему хордовая
диаграмма является d-диаграммой.
Доказательство. Пусть атом V является высотным. Тогда его
хордовая диаграмма С вкладывается в плоскость как граф. Окружность
этой хордовой диаграммы делит эту плоскость на две части. Некоторые
хорды находятся во внутренней части, некоторые во внешней, при
этом по построению внутренние хорды не пересекаются межу собой
и внешние не пересекаются между собой. Выбирая «внутренние» хорды
2) Безотносительно к сингулярным узлам.
214
Раздел IV. d-Диаграммы
диаграммы С в качестве одного семейства, а «внешние» — в качестве
другого, получаем, что диаграмма С является ef-диаграммой.
Обратно, пусть хордовая диаграмма С, соответствующая атому V,
является d-диаграммой. Разобьем хорды этой диаграммы на два
семейства S\ и 52.
Вложим эту диаграмму в плоскость следующим образом. Сначала
вложим окружность, а затем построим хорды из S\, а хорды из Si —
вне окружности так, чтобы хорды из одного семейства не пересекались,
см. рис. 9 а. Затем заменим каждую хорду вместе с малыми дугами,
которые она соединяет, на пару пересекающихся кривых. Таким образом
получим граф кратности четыре, вложенный в плоскость, см. рис. 96.
Рис.9
Покажем, что структура А этого графа в точности совпадает со
структурой А атома V.
Действительно, ориентируем послекритическую окружность на
атоме и ее изображение на остове. В силу того, что атом
является ориентируемым, в окрестности каждой вершины две прилегающие
к ней дуги окружности, т. е. их касательные векторы, «закручиваются»
в одну сторону относительно этой вершины.
То же самое можно сказать и об образе окружности на плоскости,
см. рис. 10.
В силу сказанного выше, образы двух противоположных
полуребер а и с атома V на плоскости являются локально противоположными.
Это означает, что остов атома V вложен в плоскость с сохранением
структуры А этого атома.
Следовательно, атом V является высотным в силу критерия
высотности, что завершает доказательство теоремы. ■
Замечание 17.6- Условие ориентируемости существенно. У атома С одна
послекритическая окружность и одна вершина. Следовательно, построенная
таким образом хордовая диаграмма будет иметь одну хорду, т. е. являться d-
диаграммой, хотя атом С является невысотным.
Пример 17.3. Рассмотрим ориентируемый атом JS?i с одной послекрити-
ческой окружностью. Ему соответствует хордовая диаграмма с тремя пересека-
Лекция 17. Атомы и высотные атомы
215
юшимися хордами, которая не является d-диаграммой. Из этого следует, что
атом Е\ является невысотным.
=*
Рис. 10. Разбиение на пары противоположных полуребер (ac)t (bd)
При этом для ориентируемого атома V с одной послекритической
окружностью такая хордовая диафамма С содержит всю информацию
об атоме, т. е. по ней восстанавливается не только его А-слруктура,
но также и его В-структура.
Действительно, рассмотрим хорду и две дуги окружности,
примыкающие к ней. Так как эта окружность является послекритической,
то послекритическим является и угол, который ее содержит. Тем са-
мым, структура В атома V однозначно восстанавливается по хордовой
диаграмме С.
Таким образом мы можем проверять высотность атомов типа 1-п,
т. е. с 1 послекритической окружностью и п докритическими, и
классифицировать их. Автором написана профамма, делающая это для
малых п, равных 4,5,6; результаты для п = 5 приведены в [106].
Лекция 18
Атомы и d-диаграммы
§ 1. Кодирование узлов d-диаграммами
На прошлой лекции мы доказали корректность построения
изотопического класса узла по высотному атому и рассмотрели случай, когда
высотные атомы имеют одну послекритическую окружность. Такие
высотные атомы кодируются d-диаграммами.
Остался открытым вопрос о том, какие изотопические классы
узлов порождаются атомами с одной послекритической окружностью,
т.е. d-диаграммами.
Теорема 18.1 ([107]). Для любого изотопического класса
зацепления L существует высотный атом V, кодирующий это зацепление
и имеющий ровно одну послекритическую окружность.
Доказательство. Рассмотрим произвольную диаграмму зацепления
L и высотный атом V\, соответствующий этой диаграмме.
Предположим, что у атома VI количество послекритических окружностей равно к.
Если * = 1, то теорема доказана.
Если к > 1, то существует вершина А атома V\, такая, что два
послекритических угла, примыкающие к данной вершине, соответствуют
двум дугам двух различных послекритических окружностей.
Действительно, если к каждой вершине примьжает дважды одна окружность
(для каждой вершины —- своя), то, в силу связности остова атома Vi,
такая окружность всего одна.
Рассмотрим такую вершину А. Подвергнем диаграмму узла второму
движению Рейдемейстера, как показано на рис. 1.
Легко видеть, что после такого движения две примыкающие
окружности преобразуются в одну, а остальные окружности останутся без
изменения. Итак, не изменяя изотопического класса зацепления, мы
уменьшим количество послекритических окружностей
соответствующего атома на единицу. Продолжая операцию до тех пор, пока количество
критических окружностей не станет равно единице, получим
утверждение теоремы. ■
Следовательно, d-диаграммы кодируют все изотопические классы
узлов и зацеплений.
Лекция 18. Атомы и d-диаграммы
217
Рис. 1. Сверху — диаграмма узла, снизу послекритические окружности атома
Приведем несколько примеров. Рассмотрим левый трилистник
и его простейшую плоскую диаграмму. Соответствующий этой
диаграмме высотный атом будет иметь две послекритические окружности.
Таким образом, одним движением Рейдемейстера можно поправить
диаграмму этого трилистника так, чтобы полученный атом имел одну
послекритическую окружность. Соответствующая d-диаграмма будет
иметь одну «вертикальную» хорду и четыре пересекающих ее
«горизонтальных» хорды, см. рис. 2.
Рис.2
Упражнение 18.1. Покажите, что с/-диаграммы, изображенные на рис. 3 a
и 3 б, соответствуют левому трилистнику и восьмерке.
Из рассуждений, приведенных выше, следует, что зацепление L,
имеющее плоскую диаграмму с п вершинами, для которого соответству-
218
Раздел IV. d-Диаграммы
ющий высотный атом V имеет ровно к послекритических окружностей,
может быть закодирован d-диаграммой с п + 2(к - 1) ребер. Легко
видеть, что суммарное количество до- и послекритических окружностей
атома V не превышает х(У) ~ п + (2я) ^ п + 2, где х(У) —
эйлерова характеристика многообразия, получаемого из V заклеиванием до-
и послекритических окружностей. Так как у атома V есть хотя бы одна
докритическая окружность, то к ^ п + 1, и мы получаем оценку для
минимального числа ребер d-диаграммы, соответствующей данному
узлу: это число не превосходит Зп.
Упражнение 18.2. Покажите, что хордовая диаграмма является d-диаг-
раммой в том и только в том случае, когда она не содержит поддиаграмм,
показанных на рис.4 (2п + 1-угольников, n G N).
Рис.4
Таким образом построено отображение множества всех d-диаграмм
на множество всех изотопических классов зацеплений. Однако это
отображение не является инъективным (например, добавление к d-
диаграмме отдельно стоящей хорды не меняет изотопический тип
зацепления).
При этом видно, что d-диаграммы кодируют не все плоские
диаграммы узлов, а лишь те из них, которым соответствуют атомы с одной
послекритической окружностью. В общем случае приходится изменять
диаграмму вторыми движениями Рейдемейстера, тем самым изменяя ее
сложность (количество вершин).
Для упрощения ситуации можно обобщить понятие d-диаграммы
следующим образом.
Определение 18.1. Назовем меченой d-диаграммой d-диаграмму,
каждая хорда которой имеет знак «+» или «-». d-диаграмму без
знаков по умолчанию считаем меченой со всеми знаками «+».
По меченой d-диаграмме можно построить диаграмму зацепления
следующим образом. Разобьем хорды данной диаграммы на два
семейства непересекающихся хорд. Вложим данную диаграмму С в плоскость,
причем хорды первого семейства поместим снаружи от окружности
данной диаграммы, а хорды второго семейства — внутри. Затем удалим
все хорды вместе с маленькими дугами и заменим их перекрестками,
причем тип перекрестка будем выбирать в зависимости от знака хорды
так, как показано на рис. 5.
Лекция 18. Атомы и d-диаграммы
219
Рис.5
Легко видеть, что в случае отсутствия меток (которое трактуется
как наличие всех положительных меток) данное правило построения
диаграммы узла будет совпадать с изначальным правилом построения
узла по атому (<£-диаграмме).
Упражнение 18.3. Покажите, что изотопичесский класс зацепления,
полученный таким образом, не будет зависеть от разбиения множества хорд на два
семейства непересекающихся хорд.
Теорема 18.2 ([64]). Любая плоская диаграмма зацепления может
быть получена из некоторой меченой d-диаграммы способом,
описанным выше.
Доказательство. Пусть L — плоская диаграмма некоторого
зацепления. Устроим обход этой диаграммы следующим образом. Выберем
вершину и исходящее из нее ребро. Начнем движение вдоль по
ребру. Попадая в вершину, будем поворачивать в произвольном из двух
направлений, не противоположных тому направлению, с которого мы
в эту вершину попали.
Упражнение 18.4. Покажите, что можно так выбрать направления
поворотов, чтобы вернуться в исходную точку, обойдя по одному разу все ребра
и по два раза все вершины.
Такой обход порождает некоторую хордовую диаграмму.
Действительно, этот обход задает окружность, проходящую по два раза все
вершины диаграммы. Отмечая на окружности хордами прообразы пар
прохождений одной и той же вершины, получаем хордовую
диаграмму С. Очевидно, что она будет d-диаграммой. Каждой хорде
диаграммы С будет соответствовать вершина плоской диаграммы L. При этом
в некоторых вершинах обход будет производиться так, как показано
220
Раздел IV. d-Диаграммы
Рис. 6. Обход для трилистника
на рис. 5 д. В этом случае сопоставим этой хорде положительную метку.
В противном случае поставим на хорде отрицательную метку.
Полученная ^-диаграмма будет кодировать диаграмму
зацепления L. ■
Упражнение 18.5. Говорят, что хорда а переполюсована, если с одной
стороны этой хорды добавлена маленькая хорда, пересекающаяся только с
хордой а.
Хорда называется дважды перепалюсованной, если с обоих ее концов
добавлены такие маленькие хорды.
Покажите, что замена отрицательной хорды на два раза
переполюсованную положительную хорду — см. рис.7 — не меняет изотопического типа
зацепления.
г
^_
л ^
J \±
Л
^
Рис.7
Таким образом, можно привести еще один способ построения
d-диаграммы без меток, соответствующей данному зацеплению.
Рассмотрим зацепление L и произвольную его плоскую диаграмму. Данной
плоской диаграмме соответствует некоторая меченая d-диаграмма.
Заменяя каждую отрицательную хорду на дважды «переполюсованную»
положительную хорду, получим d-диаграмму, кодирующую зацепление,
изотопное зацеплению L.
Лекция 18. Атомы и d-диаграммы
221
§2. d-диаграммы, хордовые диаграммы.
Реализуемость
Описанный способ построения диаграмм зацеплений по d-диа-
граммам можно рассматривать и на более простом объекте —
погружениях в плоскость гладких кривых, при которых допускаются лишь
двойные точки трансверсального самопересечения. Для этого мы
просто забываем о метках на ребрах, а на плоской диаграмме зацепления
строим самопересечение.
В терминах d-диаграмм имеет простое решение задача о
распознавании гауссовой диаграммы классического узла (о реализуемости
гауссовой диаграммы). Одно из решений этой проблемы предложено
в [95]. Остановимся на этой задаче более подробно и опишем метод ее
решения в терминах d-диаграмм.
Рассмотрим сначала плоскую замкнутую кривую и
соответствующую ей хордовую диаграмму 1\ Она строится так же, как и гауссова
диаграмма, при этом мы «забываем» о стрелках и о метках на ребрах.
Поставим задачу следующим образом. Дана хордовая диаграмма.
Является ли она диаграммой погружения кривой в плоскость?
Предположим, что ответ на этот вопрос положительный. Тогда
по кривой, погруженной в плоскость, можно построить ее хордовую
диаграмму и d-диаграмму. Для достижения обеих этих целей нужно
сделать обход этой кривой, причем в первом случае мы обходим кривую
уникурсально, переходя с каждого полуребра на противоположное,
а во втором случае — переходя с каждого полуребра на одно из соседних.
Хордовая диаграмма такой кривой восстанавливается по ее d-диа-
грамме однозначно.
Первый алгоритм (превращения d-диаграммы в хордовую
диаграмму). Пусть дана d-диаграмма D некоторой кривой К. Рассмотрим
следующий обход этой диаграммы. Выберем вершину и начнем
двигаться против часовой стрелки по дуге. Встречая вершину, перейдем
на другой конец хорды и изменим направление движения (т. е. если
мы двигались против часовой стрелки, будем двигаться по часовой
стрелке и наоборот). Будем делать так до тех пор, пока не вернемся
в начальную вершину. Легко видеть, что при этом мы единожды
обойдем каждую дугу (так как d-диаграмма является d-диаграммой кривой,
а не набора кривых). Полученный обход задает некоторую хордовую
Диаграмму L(D), в которой хордами соединены пары моментов
прохождения одной и той же хорды d-диаграммы D. Очевидно, что данная
хордовая диаграмма и будет соответствовать кривой К.
Безотносительно к сингулярным узлам.
222
Раздел IV. d-Диаграммы
Ф-®
Рис. 8. Слева d -диаграмма, справа — соответствующая ей хордовая диаграмма
Второй (обратный) алгоритм построения d-диаграммы узла по его
хордовой диаграмме несколько более сложен, так как неодаозначен (одну
и ту же плоскую диаграмму узла могут задавать разные d-диаграммы).
Рассмотрим хордовую диаграмму С некоторой кривой,
погруженной в плоскость, все самопересечения которой суть точки двойного
трансверсального пересечения.
Устроим следующий обход этой диаграммы. Выберем вершину этой
диаграммы и пойдем вдоль дуги в произвольном направлении. Встречая
вершину, перейдем на другую сторону хорды и продолжим движение
в произвольном из двух возможных направлений. При этом можно
выбрать обход таким образом, чтобы при возвращении в исходную
вершину мы обошли по одному разу каждую дугу (докажите это!).
Получим d-диаграмму D данной кривой. Очевидно, что, применяя
прямой алгоритм к кривой D, получим L(D) = С.
Замечание 18.1. Формально эти алгоритмы можно применять не только
к диаграммам погруженных кривых, а к произвольным хордовым
диаграммам. При этом нужно иметь в виду, что применение к некоторой хордовой
диаграмме С сначала второго алгоритма, а затем первого не всегда даст саму
диаграмму С.
Упражнение 18.6. Рассмотрим хордовую диаграмму, показанную на
рис. 9 а.
а б в
Рис.9
Согласно второму алгоритму, ей соответствует диаграмма, показанная
на рис. 9 б у которой, согласно первому алгоритму, соответствует диаграмма
на рис. 9 в, не совпадающая с изначальной диаграммой.
Посмотрим на причину этого несоответствия. Пусть С —
некоторая хордовая диаграмма, a L — одна из диаграмм, полученная из С
посредством второго алгоритма. Пусть диаграмма C(L) получается
из диаграммы L применением первого алгоритма. Рассмотрим
самопересекающуюся кривую, порядок противоположных полуребер которой
Лекция 18. Атомы и d-диаграммы 223
задается хордовой диаграммой С. Построение диаграммы L означает
разделение в каждой вершине четырех исходящих полуребер на две пары
соседних. Затем по этим парам соседних полуребер (по диафамме L) мы
пытаемся восстановить диаграмму С, применяя к ней первый алгоритм.
Рассматривая обход диафаммы С для получения диафаммы L
согласно первому алгоритму, зададим ориентацию дуг диафаммы С
соответственно этому обходу.
Рассмотрим хорду р диафаммы С, обозначим через р' —
соответствующую ей хорду диафаммы Z/, а через р" — соответствующую
хорду диафаммы С(Х). В ней возможны две принципиально различные
ситуации: когда в вершине на одном конце хорды сфелки сходятся,
а на другом расходятся (см. рис. 10 а) и когда на каждом из двух концов
одна стрелка входит, а другая выходит (рис. 106).
Рис.10
При этом в случае 10 а возможны два варианта локального обхода
диафаммы С, порождающего диафамму L: после дуги а идет дуга с,
после дуги Ь — d, или после а идет d, после Ь — с. В случае 10 б
возможен лишь один локальный обход: за дугой а следует d, а за дугой с
следует Ь.
Следовательно, если мы будем сфоить диафамму L с помощью
второго алгоритма, при этом будет иметь место случай, показанный
на рис. 10 а, то в диафамме C(L)9 полученной из L посредством
первого алгоритма, то сфуктура противоположных полуребер в данной
вершине кривой будет такая же, как и у исходной диафаммы С:
(ab), (cd). Таким образом, применяя первый алгоритм к диафамме L,
мы получим в вершине р" для диафаммы C(L) тот же локальный
обход, что и в вершине р для диафаммы С.
Если же имеет место случай на рис. 10 б, то у диафаммы L на одном
конце хорды, соответствующей вершине р'9 при движении против
часовой стрелки будет сначала проходиться ребро а, затем ребро d,
а на другом — сначала с, а затем d. Следовательно, при применении
224
Раздел IV. d-Диаграммы
первого алгоритма к этой диаграмме, мы получим локальный обход,
у которого на одном конце хорды р" за ребром а будет следовать
ребро с, а не Ь, как это происходит на диаграмме С.
Если же при хорде р имеет место случай, показанный на рис. 10 а,
то на диаграмме C(L) при хорде р" после ребра а будет идти ребро с,
а после ребра d — ребро с, как и при ребре р диаграммы С.
Назовем вершину источником, если обе инцидентные ей
ориентированные дуги исходят из нее, и стоком, если обе дуги входят в нее.
Таким образом, для того, чтобы первый алгоритм был обратен второму,
нужно, чтобы при таком обходе хордовой диаграммы С дуги были бы
ориентированы так, чтобы в каждой, вершине были либо две входящие
дуги, либо две исходящие, при этом каждая вершина-источник должна
соединяться ребром с вершиной-стоком и наоборот.
Легко видеть, что это достижимо тогда и только тогда, когда длина
каждой хорды диаграммы С нечетная. Более того, если длина каждой
хорды диаграммы нечетная, то любой обход и будет порождать такую
ориентацию дуг. В этом случае после применения сначала второго,
а затем первого алгоритма, мы получим диаграмму С при любом
выборе обхода для второго алгоритма.
Отсюда получаем теорему.
Теорема 18.3 (критерий реализуемости хордовой диаграммы без
меток). Хордовая диаграмма С реализует погружение без тройных
точек некоторой кривой в плоскость тогда и только тогда, когда
выполняются следующие два условия:
1. длина каждой хорды диаграммы d нечетная,
2. одна из диаграмм, полученная из С применением второго алгоритма,
является d-диаграммой.
Замечание 18.2. Легко видеть, что при выполнении первою условия теоремы
из второго условия следует, что любая диаграмма, полученная из диаграммы С
применением второго алгоритма, является d-диаграммой.
Упражнение 18.7. Диаграмма С, показанная на рис. 11, не является
гауссовой диаграммой плоской кривой, так как одна из диаграмм, получаемая
из нее применением второго алгоритма совпадает с ней самой (проверьте
это!), при этом сама диаграмма С не является d-диаграммой. Следовательно,
диаграмма С не является реализуемой гауссовой диафаммой. При этом у нее
длины всех хорд нечетные.
о
Рис. 11
Лекция 18. Атомы и d-диаграммы
225
Полученный критерий просто обобщается до критерия
реализуемости гауссовой диаграммы.
Пусть G — гауссова диаграмма, а С — хордовая диаграмма,
получаемая из нее забыванием всех меток на ребрах и ориентации
ребер. Если диаграмма С не реализует погружения без тройных точек
некоторой кривой в плоскость, то G не реализует диаграммы узла.
В противном случае по диаграмме С можно построить
некоторую d-диаграмму D, соответствующую кривой, реализуемой
диаграммой С.
Без ограничения общности будем считать, что диаграммы С и D
являются связными, т. е. от каждой хорды а любой из этих диаграмм
до любой другой хорды Ь той же диаграммы существует цепочка хорд,
соединяющих а с Ь, причем соседние хорды в этой цепочке являются
пересекающимися. В противном случае можно разбить диаграмму С
на «связные компоненты» и проверять реализуемость каждой из них.
Для дальнейшей проверки выберем разбиение ребер диаграммы D
на внешние и внутренние (для связной d-диаграммы это можно сделать
двумя способами). Затем для каждого из этих двух способов расставим
в вершинах проходы и переходы согласно меткам на хордах
диаграммы С. Эти метки задают всю информацию о плоской диаграмме и ее
проходах и переходах. Тем самым мы получаем и всю информацию
о стрелках диаграммы С Если все стрелки совпадают с
исходными (в одном их двух случаев разбиения хорд диаграммы D на два
семейства), то диаграмма является реализуемой, в противном случае — нет.
Лекция 19
Скобочная полугруппа узлов
Как мы показали на прошлой лекции, все изотопические классы
узлов задаются d-диаграммами. При этом очевидно, что такое задание
неоднозначно. В этой лекции мы перечислим достаточную систему
движений на d-диаграммах, не меняющих изотопический класс узла
(зацепления), а также построим полугруппу всех изотопических
классов зацеплений в алфавите из четырех букв. Эта полугруппа впервые
появилась в [ 107]. В данной работе мы дадим более простое ее описание.
Начнем с определения правильной двухскобочной структуры.
Определение 19-1- Назовем слово А в алфавите а из четырех
букв (,),[,] правильной двухскобочной структурой, если для
каждого начального полслова количество открывающихся круглых
скобок не меньше количества закрывающихся круглых скобок,
количество открывающихся квадратных скобок не меньше
количества закрывающихся квадратных скобок, а для самого слова А
эти неравенства превращаются в равенства.
Пусть дана d-диаграмма D и выбрана точка А на окружности
данной d-диаграммы. Разобьем хорды данной диаграммы на два семейства
непересекающихся хорд. Тогда можно построить слово в алфавите а
следующим образом. Начнем движение от точки А по окружности
диаграммы D против часовой стрелки. Встречая вершину хорды из первого
семейства, будем писать круглую скобку, а встречая хорду второго
семейства — квадратную. При этом скобка будет открывающейся, если
мы встретили начало хорды и закрывающейся, если мы встретили конец
хорды.
В результате мы получим некоторое слово а в алфавите а.
Упражнение 19.1. Покажите, что это слово будет правильной
двухскобочной структурой.
Обратно, имея некоторую правильную двухскобочную структуру а,
мы можем восстановить по ней d-диаграмму с выделенной начальной
точкой и с разбиением хорд данной диаграммы на два семейства
непересекающихся хорд.
Действительно, так как а является правильной двухскобочной
структурой, то слова, получающиеся из а отбрасыванием всех круглых
Лекция 19. Скобочная полугруппа узлов 227
(соответственно квадратных) скобок, являются правильными
скобочными структурами в обычном смысле. Это значит, что все скобки
разбиты на пары: каждой круглой открывающейся скобке
соответствует круглая закрывающаяся, а каждой квадратной отрывающейся —
квадратная закрывающаяся.
Таким образом, расставив на окружности вершины,
соответствующие скобкам, будем соединять хордами вершины, соответствующие
«парным» скобкам. При этом получившаяся хордовая диаграмма,
очевидно, является d-диаграммой.
Следовательно, все правильные двухскобочные структуры 9Дно-
значно кодируют все d-диаграммы с отмеченной точкой и
фиксированным разбиением множества хорд на два семейства непересекающихся
хорд. Забывая про разделение на семейства, получаем следующее
Предложение 19.1. Все правильные двухскобочные структуры коды-
руют все изотопические классы зацеплений с выделенной
ориентируемой компонентой и точкой на этой компоненте 1\
Упражнение 19.2. Покажите, что левый трилистник может быть
представлен как ([[[[)]]]]> правый — как (([[))]], а восьмерка — как
(([[())]]]•
Это кодирование можно перевести на более наглядный язык.
Замечание 19.1. Каждое классическое зацепление может быть задано с
помощью прямоугольной ломаной петли внутри первого квадранта плоскости Оху.
Петля выходит из (0,0) и входит в (0,0), и все ее звенья являются единичными
отрезками, горизонтальными или вертикальными. При этом каждая такая петля
задает некоторое зацепление.
Доказательство. Действительно, каждую такую правильную двух-
скобочную структуру можно трактовать как ломаную петлю такого вида,
где скобка (означает один шаг вправо,) ■— влево, [ — вверх, а ] — вниз,
см. рис. 1. При этом правильность двухскобочной структуры означает
то, что данная ломаная петля не выйдет за пределы первого квадранта
плоскости. ■
EEtt:i
(([)[)]]
(0,0)
Рис. 1. Петля и соответствующая правильная двухскобочная структура
В частности, все классы ориентированных узлов с выделенной точкой.
228
Раздел IV. d-Диаграммы
Упражнение 19.3. Что станет с зацеплением при изменении направления
обхода петли?
Легко видеть, что рассматриваемые нами объекты — зацепления
с выделенной ориентированной компонентой и отмеченной точкой
на ней2) (в дальнейшем будем называть их просто зацеплениями)
поддаются умножению. Опишем это умножение более точно.
Произведение двух элементов А и В определяется следующим
образом. Пусть А' и В' — представители классов А и В. Пусть А\9
A-i — точки на А1 в малой окрестности начальной (отмеченной) точки,
причем А\ находится после Ai относительно ориентации компоненты.
Аналогично выберем Ви В2 на зацеплении В1. Расположим А' и Б'
в пространстве незацепленным образом так, чтобы начальные точки
зацеплений А! и В1 находились на близком расстоянии. Кроме того,
потребуем, чтобы пересечение зацеплений А1 и В1 с малой
окрестностью U соответствующих отмеченных точек представляло собой два
параллельных отрезка. Потребуем также, чтобы существовала прямая I
на плоскости проекции, не пересекающая проекции А! и В1', т.е.
проекции А' и В' лежали по разные стороны от /. Удалим из А!
дугу А\А2, а из В1 дугу В\Вг и соединим отрезками точки А\ с В},
а В\ с Ai. Класс получившегося зацепления, в котором за начальную
точку выбрана А\, а ориентация в окрестности этой точки совпадает
с ориентацией А и В, назовем произведением АВ, см. рис 1.
ч3*
At
А2
1
В2
Bt
.. гР
C|J
Ai
в п
LE
ъ
АВ
Рис. 2. Произведение зацеплений
Очевидно, что такое умножение инвариантно относительно
изотопии, т. е. изотопический класс произведения не зависит от выбора
представителей изотопических классов сомножителей, а также то, что
такое умножение ассоциативно.
Следовательно, такие зацепления образуют полугруппу G
относительно такого умножения, где в качестве единицы выступает
изотопический класс тривиального зацепления.
Упражнение 19.4. Покажите, что если некоторой правильной двухско-
бочной структуре А\ соответствует зацепление Lx, а правильной двухскобочной
2* Нетрудно видеть, что так как мы рассматриваем зацепления с точностью до
изотопии, отмеченную точку можно выбирать в произвольном месте на ориентированной
компоненте.
Лекция 19. Скобочная полугруппа узлов 229
структуре А2 — зацепление L2, то конкатенации этих правильных
двухскобочных структур А\А2 (которая также является правильной двухскобочной
структурой) соответствует произведение зацеплений L\L2.
Из упражнения следует, что правильные двухскобочные
структуры образуют полугруппу относительно конкатенации, в которой роль
единицы выполняет пустое слово.
При этом понятно, что описанное кодирование не является
однозначным. В силу того, что у каждого зацепления есть много плоских
диаграмм, существует и много d-диаграмм, его кодирующих.
Следовательно, полугруппа правильных двухскобочных структур, описывающая
все зацепления, т. е. изоморфная полугруппе G, должна иметь
некоторые соотношения.
Эти соотношения должны соответствовать преобразованиям, не
меняющим изотопический класс зацепления, но меняющим
кодирующую данное зацепление правильную двухскобочную структуру.
Как уже было сказано выше, правильные двухскобочные структуры
описывают не только d-диаграммы, но также и лишнюю информацию
о них: выбор начальной точки на хордовой диаграмме и разбиение хорд
на два семейства непересекающихся хорд.
Мы можем выбрать движение, меняющее выбор начальной
точки на d-диаграмме так, чтобы соответствующая ей точка оставалась
на той же компоненте зацепления, см. рис. 3.
е-е
Рис.3
На языке правильных двухскобочных структур это движение
выражается формулой:
(А)В = (В')А\
при этом слова А и В имеют правильную ( )-структуру, а штрих
означает, что слова В1 и А' отличаются от слов А и В заменой
некоторых открывающихся скобок закрывающимися и наоборот; более
точно, если некоторая скобка из слова А закрывалась скобкой из Б,
то во второй части равенства соответствующая скобка из А1 будет
закрывающейся, а скобка из В1 — открывающейся.
На языке d-диаграмм это означает, что мы переносим начальную
точку с одной дуги на другую, соответствующую той же компоненте
связности зацепления, см. рис. 3.
230
Раздел IV. d-Диаграммы
Добавим также и движение, в котором скобки, отделяющие А
от В являются не круглыми, а квадратными. Назовем эти два движения
движениями (а).
Кроме этого, нужно учесть, что у данной d-диаграммы могут быть
различные разбиения хорд на два семейства. На языке правильных
двухскобочных структур это означает, что в подслове, которое само
является правильной двухскобочной структурой, можно заменить все
типы скобок (круглые скобки на квадратные и наоборот).
Соответствующее преобразование d-диаграмм назовем
преобразованием (6).
Таким образом, с помощью преобразований (а) и (Ь) можно
перевести друг в друга любые две скобочные структуры, отвечающие
одной и той же d-диаграмме с выделенными точками на одной и той же
«компоненте» этой (f-диаграммы.
Перейдем теперь к движениям, изменяющим d-диаграмму, но не
меняющим изотопический класс узла — к движениям, происходящим
от движений Рейдемейстера диаграмм зацеплений.
Как было показано в лекции 1, любые две диаграммы изотопных
зацеплений могут быть получены друг из друга применением конечной
последовательности движений (преобразований) Рейдемейстера. Кроме
того, каждая плоская диаграмма зацепления может быть получена из d-
диаграммы с мечеными хордами.
Пусть дана произвольная плоская диаграмма зацепления L. Ей
соответствует (вообще говоря, неоднозначно) d-диаграмма D с
мечеными хордами. Каждой такой d-диаграмме с мечеными хордами можно
однозначно поставить в соответствие обычную d-диаграмму, заменяя
каждую отрицательную хорду на положительную, «два раза переполю-
сованную».
Для удобства будем обозначать отрицательные хорды скобками [, ]
и (,). При этом такие слова легко преобразуются в обыкновенные
двухскобочные структуры по правилу (=[(]; ) = [)]; [ = ([);
Замечание 19.2. Отметим, что добавленные четыре скобки рассматриваются
не как переход к алфавиту из восьми букв, а лишь как обозначения для
комбинаций уже имеющихся скобок из алфавита а.
Каждой плоской диаграмме зацепления можно поставить в
соответствие правильную двухскобочную структуру, причем неоднозначность
данной правильной двухскобочной структуры зависит от обхода
плоской диаграммы зацепления L. Рассмотрим теперь плоскую диаграмму
1 зацепления и различные обходы данной диаграммы. Имеет место
Лекция 19. Скобочная полугруппа узлов 231
Теорема 19.1. Две меченые d-диаграммы задают обход одной и той
же плоской диаграммы зацепления тогда и только тогда, когда одна
получается из другой последовательным применением движения (0),
показанного на рис. 4.
Доказательство. Пусть L — плоская диаграмма некоторого
зацепления, D\ и Di — две меченые d-диаграммы, соответствующие ее
обходам. Это значит, что в каждой вершине диаграммы L выбраны два
«локальных» обхода, соответствующие диаграммам D\ и Z>2-
Рассмотрим множество тех вершин (пусть их количество равно п), в которых
эти обходы различаются, и множество хорд диаграммы D\,
соответствующих этим вершинам. Среди этих хорд есть по крайней мере две
пересекающиеся (иначе мы не имели бы обхода, порождающего
диаграмму Х>г). Если мы заменим обход, соответствующий диаграмме Di
в двух вершинах, соответствующих этим двум хордам, то мы как раз
произведем движение (0), а количество вершин, в которых полученный
обход отличается от обхода диаграммы 2?2, равно п - 2. Продолжая
процесс до конца, получим требуемое. ■
Это преобразование на языке правильных двухскобочных структур
представляет собой замену подслова, стоящего в одной части
формулы (0), на слово, стоящее в другой части этой формулы:
[B(C]D) = (D'[C')B'i
(0)
При этом на слова В> С, D накладывается условие, что скобки,
стоящие в формуле соответствуют друг другу так же, как если бы слова
В, С, D были пустыми.
Здесь, как и раньше, штрихи означают, что слова В\ С\ D1
отличаются от слов Б, С, D заменой некоторых (быть может, отрицательных)
открывающихся скобок на закрывающиеся и наоборот так, чтобы если
скобка в одном из подслов B,CyD закрывается скобкой в другом
подслове, то в правой части равенства открытая скобка заменяется
закрытой, так как порядок подслов меняется.
Наряду с формулой (0) справедливы также формулы, получаемые
из этой заменой скобок без черточек на скобки с черточками, а также
заменой типов скобок ()<-*[] и []*-*(); в этих уравнениях
232
Раздел IV. d-Диаграммы
на Ву С, Dy Б', С', D1 накладываются аналогичные условия. Все эти
формулы мы также будем называть нулевыми движениями (0), подобно
движениям (1), (2), (3), порожденным первым, вторым и третьим
движениями Рейдемейстера.
[B(C]D) = (D'[C,)B,l (0)
\B(C]D) = (D'iC)B'i (0)
\B(C]D) = (D,[C,)B']. (0)
Итак, с помощью преобразований (а), (Ь) и (0) мы можем
переводить друг в друга правильные двухскобочные структуры,
соответствующие3* одной и той же плоской диаграмме зацепления.
Нам осталось лишь проверить действие трех движений
Рейдемейстера на правильных двухскобочных структурах. При этом, в силу
сказанного выше, совершенно неважно, какую именно правильную
двухскобочную структуру, соответствующую данной диаграмме, мы
выбираем.
Первое движение Рейдемейстера состоит в добавлении одной
отдельно стоящей хорды (либо положительной, либо отрицательной),
см. рис. 5.
о~о
Рис.5
При этом соответствующее движение на правильных
двухскобочных структурах выглядит так:
о=[]=о=п=1, о)
это означает, что два слова, одно из которых получается из другого
вставкой (удалением) одной из четырех пар скобок, являются
эквивалентными.
Второе движение Рейдемейстера при подходящем выборе обхода
выглядит так, как показано на рис. 6 (добавление двух «параллельных»
хорд одного типа с разными знаками).
В формульном виде второе движение Рейдемейстера записывается
как
((A)) = ((A)) = А, (2)
3) Быть может, посредством диаграмм с отрицательными хордами.
Лекция 19. Скобочная полугруппа узлов 233
о-о
Рис.6
где А — слово, имеющее правильную ()-структуру или же
[[А]] = \[А]) = А> (2)
где Л — слово, имеющее правильную [ ]-структуру.
Назовем длиной движения Рейдемейстера (2) длину слова А.
Один из двух вариантов третьего движения Рейдемейстера в виде
хордовых диаграмм показан на рис. 7.
Рис.7
Здесь слева дана d-диаграмма схемы длинного зацепления до
движения Рейдемейстера, а справа — ■ d-диаграмма измененной схемы
(после движения Рейдемейстера)., На левой диаграмме
подразумеваются (но не обозначены) некоторые произвольные хорды с концами
в А, Ву С. Они же присутствуют на диаграмме в правой части рисунка.
Формулы для этих движений выглядят следующим образом:
(A(B[))]=(U)(B)), (3)
см. рис. 7, а также
UlB\))} = (U)(B)). (3)
Здесь А и В — такие слова, что все скобки, входящие в одну
из формул (3) (и не входящие ни в слово А, ни в слово В), закрывают
ДРУГ друга в таком порядке, как если бы слова А и В были пустыми.
Таким образом, получаем теорему.
234
Раздел ГУ. d-Диаграммы
Теорема 19.2. Две правильные двухскобочные структуры задают
изотопные зацепления в том и только в том случае, когда одна из них
переводится в другую посредством конечной цепочки преобразований
(а), (Ь), (0), (1), (2), (3).
Все эти преобразования, кроме (1), достаточно громоздки. Более
точно, они не являются локальными, т. е. каждое из них при
подстановке вместо пропозиционных переменных подходящих слов дает
бесконечное число различных соотношений.
Попытаемся упростить их.
Предложение 19.2. Преобразование (Ь) следует из остальных
преобразований, т. е. если одна правильная двухскобочная структура
переводится в другую движениями (а), (Ь), (0), (1), (2), (3), то это
возможно сделать лишь преобразованиями (а), (0), (1), (2), (3).
Доказательство. Без ограничения общности можно считать, что
мы имеем дело со «связной» правильной двухскобочной структурой S,
в которой хотим заменить все круглые скобки на квадратные.
Рассмотрим d-диаграмму D, которая соответствует данной
правильной двухскобочной структуре S, а также два зацепления,
порожденные этой диаграммой. Эти два зацепления D{ и D2 отличаются
лишь вложением d-диаграммы в плоскость: в одном случае
квадратные скобки соответствуют внешним хордам, а круглые — внутренним,
во втором — наоборот.
Очевидно, что полученные два длинных зацепления изотопны.
Следовательно, существует композиция движений преобразований (а),
(0), (1), (2), (3), переводящая одно длинное зацепление в другое. ■
Оставшиеся движения можно также упростить. А именно,
рассмотрим третье движение Рейдемейстера (любой из двух вариантов),
и представим его в виде композиции двух вторых движений
Рейдемейстера, третьего движения Рейдемейстера и двух вторых движений снова.
Для одного из двух вариантов это показано на рис. 8.
Здесь части диаграмм зацепления изображены жирными линиями,
а части обхода — пунктиром.
Без ограничения общности можно считать, что локально обход
данной диаграммы выглядит именно так, как показано на рис. 8. Очевидно,
что данное третье движение является локальным, т. е. две
соответствующие правильные двухскобочные структуры получаются друг из друга
заменой одного подслова конечной длины на другое. Эти два
преобразования для двух вариантов третьего движения Рейдемейстера выглядят так:
([<[[))] = (([)<[))
Лекция 19. Скобочная полугруппа узлов 235
\ \
Рис.8
(Т(ТТ)УТ = (([)([))•
В нашем распоряжении имеются движения (а), (0), (1), (2), локальная
версия движения (3).
Рассмотрим теперь движение (2). Оно происходит внутри одного
из «многоугольников», на которые тень узла делит плоскость. При этом
в движении могут участвовать «далекие» ребра этого многоугольника.
Перенумеруем эти ребра по очереди так, чтобы соседние ребра
многоугольника имели соседние номера. Будем считать, что нужное нам
второе движение должно быть применено к ребрам а и Ь с номерами 1
и п, где п — некоторое большое число, п > 3. Найдем число р,
такое, что 1 ^.р < р + 2 ^п. Рассмотрим ребра с номерами р, р + 1,
Р + 2 и устроим с помощью движения (0) такой обход диаграммы,
при котором эти три ребра обходятся по очереди (при необходимости
проделывая вторые движения Рейдемейстера, чтобы такой обход
существовал). Применим теперь второе движение Рейдемейстера к этим
Ребрам. Рассмотрим опять многоугольник, в котором находятся ребра a
и Ъ. Если теперь мы перенумеруем ребра в том же порядке, что и раньше,
236
Раздел IV. d-Диаграммы
начиная с ребра о, то ребро Ь будет иметь номер п — 1. Если п — 1 ^ 4,
то проделаем эту операцию еще раз до тех пор, пока в соответствующем
многоугольнике номера ребер а и & не будут отличаться не более чем
на два. При этом искомое второе движение Рейдемейстера будет иметь
длину не более чем два. После этого будем «убирать» вспомогательные
движения Рейдемейстера. Каждое такое убирание будет иметь длину
не более двух, см. рис. 9.
Рис.9
При этом каждое из промежуточных вторых движений
Рейдемейстера, в котором участвуют «близкие» ребра можно считать локальным
в связи с «хорошим» выбором обхода, т. е. в связи с правильным
применением преобразования (0). Локальность этого движения означает,
что между концами двух пар вставленных хорд стоит не более двух
концов хорд. На рис. 9 показано лишь одно «вспомогательное» движение
Рейдемейстера.
Таким образом, нам удалось свести второе движение к локальному
движению. Оно будет выглядеть так:
((A)) = ((A)) = А,
где А имеет правильную ()-структуру и длину не более двух; можно
считать, что А непусто и не равно (),[],[] и™ ()> и> следовательно,
состоит из одной или двух квадратных скобок любого из четырех
видов. Также нужно добавить аналогичное движение, в котором круглые
скобки заменены на квадратные и наоборот.
Итак, у нас остались лишь преобразования (а), (0), изначально
локальное преобразование (1) и локальные версии преобразований (2)
и(3).
Движение (а) из этого списка можно исключить. Для этого
достаточно доказать следующую лемму.
Лемма 19.1. Две плоские диаграммы D\ и Di изотопных зацеплений
с отмеченной тонкой можно перевести друг в друга посредством
Лекция 19. Скобочная полугруппа узлов 237
трех движений Рейдемейстера, положительных диффеоморфизмов
плоскости на себя и перебрасывания через бесконечность, при которых
отмеченная точка не совпадает с перекрестком узла.
Доказательство. Для доказательства достаточно показать, что
движение, показанное на рис. 10 а (и аналогичное ему движение, когда
Рис.10
вершина находится на верхней ветви), выражается через плоские
изотопии, движения Рейдемейстера и перебрасывания через бесконечность.
Это показано на рис. 106. ■
На рис. 10 овалом изображена область, внутри которой
заключаются все перекрестки зацепления. Рисунок 10 а иллюстрирует утверждение
леммы. На рис. 10 б показаны три преобразования, композиция которых
превращает левую схему на рис. 10 а в правую. Первое преобразование
является изотопией, выводящей часть дуги за пределы области. Второе
преобразование представляет перебрасывание дуги через бесконечность.
Следовательно, движение (б) также выражается через другие
движения, описанные выше. Действительно, вид движения (0) не зависит
от выбора начальной точки, а все движения (1), (2), (3) являются
локальными, следовательно, одинаково выглядят при «хорошем»
выборе начальной точки (вне области, в которой происходят изменения).
Нетрудно показать, что с помощью этих же движений начальную точку
можно вывести за пределы этой области.
Из теоремы 19.2, предложения 19.2 и леммы 19.1 вытекает
Теорема 19.3. Две правильные двухскобочные структуры задают
изотопные зацепления в том и только в том случае, когда одна из них
переводится в другую посредством конечной цепочки преобразований:
1. {движение 0)
[B(C]D) = (D'[C)B'i
[B(C]D) = (Dr[CJB'],
\B(C]D) = (D'[C')B'l
238
Раздел IV. d-Диаграммы
[B(C]D) = {D,[C,)B,\,
при этом на слова В, С, D накладывается условие, что скобки,
стоящие в формуле, закрывают друг друга в том же порядке, как
если бы слова Ву С, D были пустыми',
2. {первое движение Рейдемейстера)
() = [] = () = П=1;
3. (локальная версия второго движения)
(UJ) = ((А)) = А,
где А является словом из одной или двух букв с правильной структурой
квадратных скобок;
[[А]] = [[А]] = А,
где А является словом из одной или двух букв с правильной структурой
круглых скобок;
4. (локальная версия третьего движения)
(Ш1))1 = (ШШ),
(ШТШ = (([)([))•
Лекция 20
d-диаграммы, сингулярные узлы
и алгебра хордовых диаграмм
На этой лекции мы расскажем об обобщении теории d-диаграмм
на случай сингулярных узлов, а именно, мы расскажем о том, как
представить алгебру хордовых диаграмм в виде алгебры слов в некотором
алфавите, профакторизованной по некоторым соотношениям.
Кроме того, мы покажем, что все узлы могут быть заданы косами
специального вида и, как следствие, d-диаграммами специального вида.
§ 1. d-диаграммы и сингулярные узлы
Определение 20.1. Назовем d-диаграммой с тяжелыми хордами
d-диаграмму (с метками или без оных), на которой некоторые
хорды без меток выделены как тяжелые.
По ^-диаграмме с тяжелыми хордами можно построить схему
сингулярного узла (зацепления) аналогично тому, как по обычной
d-диаграмме мы строили схему классического узла (зацепления), при
этом на месте каждой тяжелой хорды вместо прохода и перехода будем
ставить пересечение узла.
Таким образом, по каждой d-диаграмме с тяжелыми хордами
получим некоторый сингулярный узел, количество сингулярных вершин
которого равно количеству тяжелых хорд данной диаграммы.
Аналогично случаю обычных зацеплений можно доказать
несколько теорем, которые мы оставляем в качестве упражнений.
Упражнение 20.1. Покажите, что изотопический класс сингулярного
зацепления не зависит от вложения <Z-диаграммы с тяжелыми хордами в плоскость
(т. е. от разбиения хорд d-диаграммы на два семейства непересекающихся хорд).
Упражнение 20.2. Покажите, что все изотопические классы сингуляр-
Нь*х узлов могут быть построены описанным выше образом по d-диаграммам
с тяжелыми хордами без меток.
Упражнение 20.3. Покажите, что все диаграммы сингулярных узлов могут
Ыть получены таким образом из d-диаграмм с метками с тяжелыми хордами.
240
Раздел IV. d-Диаграммы
Аналогично обыкновенным d-диафаммам, «J-диаграммы с
тяжелыми хордами можно описывать словами в конечном алфавите; при
этом вместо четырех скобок понадобятся восемь. Четыре из них,
соответствующие тяжелым хордам, будут крупными хордами.
Получаемые из d -диаграмм с тяжелыми хордами сингулярные узлы
(зацепления) с выделенной компонентой образуют, как и обычные
зацепления, полугруппу относительно операции связной суммы, причем
у полугруппы есть градуировка (количество сингулярных вершин).
Кроме того, из данной полугруппы введением дополнительной структуры —
алгебраической, можно построить некоторую алгебру.
Остановимся на этом более подробно. Элементами нашей
полугруппы GG будут изотопические классы сигаулярных зацеплений.
Полугрупповой операцией будет взятие связной суммы, в роли единицы
будет выступать тривиальный узел.
Определение 20.2. Назовем правильной нетырехскобочной
структурой слово в алфавите из восьми скобок (, ), [, ],
которое обладает следующими свойствами:
1. В любом начальном полслове количество открывающихся скобок
любого из двух типов (круглые, квадратные) не больше количества
закрывающихся скобок того же типа, а для самого слова эти
неравенства превращаются в равенства.
2. То же самое верно для любого из четырех подтипов скобок
(круглые, квадратные, круглые тяжелые, квадратные тяжелые).
При выполнении условий 1) и 2) каждой открывающейся
скобке однозначно соответствует закрывающая ее скобка. При этом
круглой скобке соответствует круглая, квадратной —- квадратная,
тяжелой — тяжелая.
3. Между открывающейся круглой скобкой и закрывающей ее круглой
скобкой структура круглых скобок правильная, т. е. не встречается
подслов вида ( I ).
4. То же верно для квадратных скобок.
Легко видеть, что по правильной четырехскобочной структуре
однозначно восстанавливается d-диаграмма с тяжелыми хордами и
отмеченной точкой на ней.
При этом очевидно, что конкатенации правильных четырехско-
бочных структур соответствует связная сумма (f-диаграмм с тяжелыми
хордами и, следовательно, связная сумма соответствующих
сингулярных зацеплений.
... .
Лекция 20. Случай сингулярных узлов 241
В полугруппе GG можно легко найти соотношения аналогично
тому, как это делалось для полугруппы обычных зацеплений. Не будем
приводить конкретных вычислений, приведем лишь полный список
соотношений.
1. (движение 0)
[B(C\D) =lD'[C)B'l
[B(C}D) = (D'[C')B'],
[b(c]d) =Id'[C)b],
\B(C]D) = (D'IC)B'J,
\B(C]D) = (D,[C,)Bi],
[b(c]d) =(d'[c')b'J,
[b(cJd)= (z)'Ic')b'L
[b(<7Jd) = (d'[c)b'),
[b(c]d) = (x>'[c)b'],
при этом на слова Б, С, D накладывается условие, что скобки,
стоящие в формуле соответствуют друг другу так же, как если бы
слова Б, С, D были пустыми;
2. (первое движение Рейдемейстера)
() = [] = 0 = П=1;
3. (локальная версия второго движения)
((A)) = ((A)) = А,
где А является словом из одной или двух букв с правильной
структурой квадратных скобок;
[[А}] = [[А)} = А,
где А является словом из одной или двух букв с правильной
структурой круглых скобок;
242
Раздел IV. d-Диаграммы
4. (локальная версия третьего движения)
(1Ш))Т = ((!)(!)),
(Т(ТТУ)] = (Ш(Т)),
здесь нужно добавить еще версию третьего движения, в которой
одна вершина является сингулярной;
(l(II))j=((I)(l));
5. (дополнительное движение, состоящее в «разворачивании» малой
окрестности сингулярной вершины)
(а)=(((а))),
(а)=(({А))),
где слово А имеет правильную структуру круглых скобок и
Ia| = [[ujJ],
H=l[[A]]l,
где слово А имеет правильную структуру квадратных скобок.
С помощью второго движения Рейдемейстера это движение легко
локализуется. В локальной версии этого движения слово А имеет
длину не более двух.
Полугруппа GG правильных четырехскобочных структур с
соотношениями, выписанными выше, изоморфна полугруппе всех
сингулярных зацеплений с выделенной ориентируемой компонентой.
В эту полугруппу естественно вложена полугруппа правильных
двухскобочных структур.
Кроме того, в ней естественно выделяется полугруппа К
сингулярных узлов (зацеплений с одной компонентой).
При этом сингулярные узлы можно складывать.
Действительно, введем на сингулярных узлах соотношение
Васильева (одно из соотношений, определяющее модуль Васильева),
см. рис. 0.
Лекция 20. Случай сингулярных узлов
243
х = х -х
Рис.0
На языке правильных четырехскобочных структур это
соотношение представляет собой замену пары крупных скобок (открывающейся
и соответствующей ей закрывающейся) на разницу скобок.
±\А ) = (А)- [А],
±[а\=[а]-(а].
Здесь знак ± зависит от того, какой порядок обхода стоит в
вершине, соответствующей данной паре скобок.
Групповая алгебра группы G над R или над Q, профакторизованная
по этому соотношению, изоморфна алгебре всех сингулярных узлов,
профакторизованной по соотношению Васильева.
Этот объект можно упростить следующим образом.
Посмотрим на сингулярный узел как на порядок обхода его особых
точек, забывая об его «заузленности», т. е. рассмотрим соответствующую
ему хордовую диаграмму.
Тогда мы получим, что сингулярные узлы (а следовательно, и
(f-диаграммы с тяжелыми хордами и правильные четырехскобочные
структуры) задают все хордовые диаграммы в обычном смысле. При
этом умножение правильных четырехскобочных структур согласовано
с умножением хордовых диаграмм. Следовательно, все символы
инвариантов Васильева могут быть записаны словами в конечном алфавите.
Остановимся на этом вопросе более подробно.
Если мы забываем о заузленности, а помним лишь о порядке
обхода особых точек сингулярного узла, то при замене типа нетяжелых
хорд соответствующей (^-диаграммы (положительной на отрицательную
и наоборот), хордовая диаграмма не меняется. Следовательно, нам
Достаточно использовать лишь алфавит из восьми скобок — четырех
маленьких и четырех больших.
В данной алгебре будут четыре серии соотношений (0,1,2,3),
которые будут выглядеть точно так же, как и в случае полугруппы узлов,
с той лишь разницей, что не будет играть роли знак хорды. Кроме
того, будут также алгебраические соотношения, происходящие от 1Т-
и 4Т-соотношений в алгебре хордовых диаграмм.
244
Раздел IV. d-Диаграммы
Нетрудно показать, что одночленное соотношение в терминах d-
диаграмм сводится к соотношению, в котором d-диаграмма с отдельно
стоящей тяжелой хордой полагается равной нулю, причем эту хорду
можно считать хордой из первого семейства:
0^=0, (1)
где А — правильная четырехскобочная структура.
Более подробно об одночленном и четырехчленном соотношении
см. в [64].
§ 2. Квазиторические косы
Как было показано, узлы и даже сингулярные узлы могут быть
закодированы d-диаграммами. Оказывается, для задания узлов, можно
обойтись лишь малой частью всех d-диаграмм. Об этом и пойдет речь
во второй части данной лекции.
Определение 20.3. Назовем квазиторической косу, которая
получается из стандартной диаграммы некоторой торической косы
заменой нескольких перекрестков, см. рис. 1.
Рис. 1. Квазиторическая коса
Легко видеть, что каждая квазиторическая коса из п нитей
получается произведением кос вида (о^1 ...o^Ti), j,- = ±1, т.е. квази-
Лекция 20. Случай сингулярных узлов
245
торических кос типа (га, 1). Таких кос существует Т 1 штук и можно
рассмотреть группу G с такими образующими.
Замечание 20.1- Легко видеть, что произведение квазиторических кос из п
литей является квазиторической косой из п нитей.
Верно и более сильное утверждение: все элементы этой группы G являются
квазиторическими косами из п нитей. Это следует из того, что обратный
элемент к каждой образующей выражается только через положительные степени
образующих.
Лемма 20.1. Каждый изотопический класс зацепления может быть
получен посредством замыкания некоторой квазиторической косы.
Доказательство. Зададим произвольное зацепление L. В силу
теоремы Александера существует коса В, замыкание которой изотопно
данному зацеплению L. Пусть эта коса имеет га нитей. Рассмотрим
перестановку а, соответствующую этой косе, и орбиты действия
перестановки а на множестве (1,..., п).
Эти орбиты могут содержать различное число элементов.
Рассмотрим движения Маркова, не меняющие изотопический тип зацепления,
но меняющие косу. Первое из них сопрягает косу и, значит, сопрягает
соответствующую косе перестановку. Следовательно, мощность каждой
орбиты действия этой перестановки не меняется под действием первого
движения Маркова, но сами элементы могут переходить из одной
орбиты в другую. Второе движение Маркова увеличивает количество нитей
на единицу, при этом у соответствующей перестановки элемент га + 1
попадает в орбиту, в которой лежит элемент га, а другие орбиты не
изменяются. Используя движения Маркова, мы можем перенумеровать
элементы так, чтобы самая маленькая орбита содержала элемент га,
а затем увеличить мощность этой орбиты на единицу. Применяя эту
процедуру многократно, мы можем добиться того, чтобы мощность
всех орбит совпадала.
Пусть полученная коса р имеет перестановку, действующую на
km элементов, причем каждая из к орбит этой перестановки содержит
тп элементов. Применяя к /? сопряжение, мы можем добиться, чтобы
соответствующая перестановка была равна m-й степени циклической
перестановки (12 ... km), fe,m G N. Обозначим полученную косу
через 7-
Начнем теперь изменять диаграмму косы, не меняя ее
изотопический тип.
Для завершения доказательства леммы 20.1 нам осталось доказать
следующую лемму.
Лемма 20.2. Коса из г нитей, перестановка которой является
степенью циклической перестановки (12 ... г), изотопна
квазиторической косе.
246
Раздел IV. d-Диаграммы
Доказательство. Пусть 7 — коса из г нитей, перестановка которой
равна (12 ... г)5. Рассмотрим косу у', равную j(ry 1)"*, где (г, 1) —
стандартная торическая коса из г нитей.
Тогда перестановка, соответствующая косе 7'» является
тождественной. Кроме того, если 7' изотопна квазиторической косе, то
и 7 также изотопна квазиторической косе (так как (г, I)5 является
торической косой).
Покажем, что каждая крашеная коса изотопна некоторой
квазиторической косе.
Действительно, можно выбрать образующие Ь|<7-, 1 < t < j < г
в группе кос из г нитей, как показано на рис. 2, см. лекцию 7.
* 3
L
Г.
► i
> <
► (
> 1
> i
> <
► i
> (
Рис. 2. Образующая 6,у в группе крашеных кос
Покажем, что все образующие Ь^- изотопны некоторым квазито-
рическим косам. Тем самым будет показано, что любая крашеная коса
изотопна некоторой квазиторической косе, так как квазиторические
косы образуют группу.
Действительно, Vi,j: I ^i < j ^n коса by является
произведением двух кос b\j • b%j, см. рис. 2. Рассмотрим теперь лишь нити от г-й
до j-й. Тоща можно ввести аналогичное определение квазиторических.
кос на нитях с номерами от i до j. Очевидно, что b]j и b}^ как раз
изотопны квазиторическим косам на нитях от i до j.
Для завершения доказательства леммы 20.2 и, следовательно,
леммы 20.1, нам осталось доказать следующую лемму.
Лемма 20.3. Если крашеная коса из г нитей изотопна
квазиторической косе на нитях от i-й до j-й, 1 < i < j < 2, то она изотопна
квазиторической косе в обычном смысле, на всех нитях от 1 до г.
Доказательство. Применим метод индукции по разнице r-(j-i+1).
При г = (j - i + 1) доказывать нечего. Для проведения шага индук-
Лекция 20. Случай сингулярных узлов
247
ции нам нужно показать, что при добавлении отдельно стоящей нити
к квазиторической косе мы получим косу, изотопную квазиторической.
Рассмотрим квазиторическую косу р из q нитей и добавим к ней
отдельно стоящую нить (для определенности выберем нить стоящей
справа, случай нити слева рассматривается аналогично). Пусть
изначальная коса имела ql витков, т. е. получалась из торической косы
типа (qy ql) заменой нескольких типов перекрестков. Рассмотрим тогда
крашеную торическую косу (q + 1, (q + 1)1) и на ней первые q нитей.
Они, в свою очередь, образуют крашеную торическую косу (g, ql).
Расставим перекрестки этих нитей так же, как они расставлены на косе р,
а на пересечениях последней нити с первыми нитями проведем
последнюю нить всюду сверху. Получим косу, изотопную косе р с отдельно
стоящей нитью справа, что и требовалось доказать. ■
Мы получили, что все образующие в группе крашеных кос
изотопны квазиторическим косам.
Рассмотрим произвольную крашеную косу г/>. Как показано, коса *ф
изотопна некоторой косе, выражающейся через образующие группы
квазиторических кос, быть может, в отрицательных степенях.
Следовательно, коса 'ф изотопна квазиторической косе. ■
Итак, с помощью преобразований Маркова и изотопии кос мы
получили квазиторическую косу 69 замыкание которой изотопно
узлу L. Ш
Сформулируем следующую задачу. Пусть дана d-диаграмма.
Рассмотрим зацепление, соответствующее этой d-диаграмме. Возможно,
что это зацепление обвивается, как коса, вокруг центра диаграммы.
Назовем это свойство свойством а). Оговорим несколько условий,
связанных с выполнением свойства а). Зацепление может обладать свойством
а), а может и не обладать. Будем считать, что: во-первых, концы хорд
расположены равномерно по окружности, во-вторых, ни одна хорда
не соединяет противоположные точки на окружности и, в третьих,
каждая хорда с этой диаграммы, выбранная как внутренняя, является
прямолинейной и построенные в ее окрестности две дуги не пересекают
диаметра, параллельного хорде с.
Указанных условий недостаточно, чтобы полученный узел
обвивался, как коса, вокруг центра диаграммы. Действительно, пусть D —
хордовая диаграмма и пусть о и Ъ — две пересекающиеся хорды
из разных семейств, причем их концы а\ и Ьу являются соседними
вершинами. Тогда пары дуг, соответствующие хордам а и Ь, закручены
в одну сторону относительно центра О хордовой диаграммы D, а дуга
окружности афу закручена в другую сторону относительно точки А,
см. рис. 3.
248
Раздел ГУ. d-Диаграммы
Рис.3
Будем удалять такие дуги* т. е. строить узел по d-диаграмме так,
чтобы одна половина дуги а\Ь\ удалялась вместе с хордой а, а другая —
вместе с хордой Ь.
Лемма 20.4. Каждая d-диаграмма, которой соответствует
плоская диаграмма зацепления, являющаяся замыканием стандартной
диаграммы квазиторинеской косы типа (р, q), где q — нечетное,
обладает свойством а) 1\
Теорема 20.1. Если у зацепления L нечетное число компонент,
то существует изотопное ему зацепление, полученное из некоторой
d-диаграммы и обвивающееся вокруг центра этой d-диаграммы, как
коса.
Доказательство леммы 20.4. Так как диаграмма квазиторинеской
косы получается из стандартной диаграммы торической косы заменой
нескольких перекрестков, то достаточно доказать утверждение леммы
для торических кос типа (j>, q), p — нечетное.
Соответствующая ^-диаграмма строится следующим образом.
Пусть р = 2га-f 1. Отметим на окружности 4mq точек, разбитые
на 2д групп по 2га подряд идущих точек в каждой группе.
Перенумеруем точки в каждой группе числами от 1 до 2га, причем в четных
группах будем нумеровать точки по часовой стрелке, а в нечетных —
против часовой стрелке.
Соединим каждую точку с точкой из соседней группы, имеющей
тот же номер. При этом соседнюю группу будем выбирать согласно
следующим правилам:
1. для точек с номерами одной четности из одной группы соседняя
группа выбирается одна и та же, для точек с номерами разной
четности из одной группы выбираются разные соседние группы;
2. точка с номером 1 не соединяется с непосредственно соседней
(на окружности) точкой.
1) С учетом оговорки, описанной в лемме 1.
Лекция 20. Случай сингулярных узлов
249
Легко проверить, что полученная d-диаграмма будет в точности
дорожцать торическую (р, д)-косу, обвивающуюся вокруг центра этой
диаграммы. ■
Упражнение 20.4. d-диаграммы типа (3, q) имеют вид, показанный
на рис. 4 сверху (q = 2,3,4), d-диаграммы типа (5, q) имеют вид,
показанный на рис. 4 снизу (q = 2,3,4).
л f
J Л
К
J~
Г1-
Л
Рис.4
Доказательство теоремы 20.1. Рассмотрим зацепление L из 2т + 1
компонент и произвольную косу а, ему соответствующую. Количество
орбит действия перестановки, соответствующей а, нечетно/Применим
алгоритм преобразования косы в квазиторическую, описанный в
доказательстве леммы 20.1 так, чтобы в конце количество элементов каждой
орбиты было нечетным. Получим квазиторическую косу S из нечетного
числа нитей. В силу леммы 20.4 замыкание этой косы соответствует
некоторой d-диаграмме, вокруг центра которой оно обвивается, как
коса. ■
Раздел V
ВИРТУАЛЬНЫЕ УЗЛЫ
Лекция 21
Виртуальные узлы и зацепления
и их простейшие инварианты
На ближайших нескольких лекциях мы расскажем о виртуальных
узлах (и зацеплениях) и их инвариантах. Виртуальные узлы были
изобретены Луисом Кауфманом в 1996 году, см. [50]. В отличие от обычного
узла, который представляет собой вложение окружности в трехмерное
пространство, виртуальный узел является понятием не топологическим,
а комбинаторным, хотя и допускает интерпретацию в виде «проекции»
на плоскость некоторого узла, лежащего в трехмерном многообразии
Sg х J, где Sg — сфера с д ручками, I — отрезок, т. е. гладкого
вложения окружности в данную поверхность, рассматриваемого с точностью
до изотопической эквивалентности.
Понятие виртуального узла основано на понятии виртуальной
диаграммы, которое, в свою очередь, является естественным обобщением
понятия диаграммы обычного узла.
Начнем с определения диаграммы виртуального зацепления, см.,
например, часть 3 статьи [107].
Определение 21.1. Диаграммой виртуального зацепления
называется плоский граф, все вершины которого имеют кратность четыре;
при этом в каждой вершине может быть проход, переход и так
называемое виртуальное пересечение, которое изображается
символически в виде, указанном на рис. 1.
X
Рис. 1. Виртуальное пересечение
Лекция 21. Определения 251
Все вершины на диаграмме виртуального зацепления, кроме
виртуальных, будем называть классическими.
Две диаграммы виртуальных зацеплений называются
эквивалентными, если существует последовательность виртуальных или обобщенных
движений Рейдемейстера, переводящих первую диаграмму во вторую.
Определение 21.2. Приводим список виртуальных движений
Рейдемейстера.
1. Классические движения Рейдемейстера, относящиеся к
классическим вершинам.
2. Виртуальные версии классических движений Рейдемейстера с
заменой классических вершин на виртуальные, см. рис. 2.
Рис.2
3. Версия третьего «треугольного» движения Рейдемейстера с заменой
двух классических вершин на дуге, «проходящей» через третью
вершину, на виртуальные, см. рис. 3.
Рис.3
Упражнение 21.1. Покажите, что движение, показанное на рис. 3 справа,
выражается через движение, показанное на рис. 3 слева, а также виртуальную
версию второго движения Рейдемейстера.
Замечание 21.1. Две похожие «версии» третьего движения Рейдемейстера,
п°казанные на рис. 4, являются запрещенными, т. е. не входят в список
виртуальных движений Рейдемейстера.
252
РазделУ Виртуальные узлы
Рис. 4. Запрещенные движения
Определение 21.3. Виртуальное зацепление есть класс
эквивалентности виртуальных диаграмм по виртуальным движениям Рейде-
мейстера.
Упражнение 21.2. Определите компоненту виртуального зацепления и
виртуальный узел.
Упражнение 21.3. Покажите, что виртуальное зацепление, диаграмма
которого не имеет классических вершин, изотопно тривиальному зацеплению.
Аналогично узлам и зацеплениям в R3 можно определить узлы
и зацепления в произвольных трехмерных многообразиях как
изотопические классы (гладких) вложений одной или нескольких окружностей
в данное многообразие.
На виртуальные узлы можно смотреть как на проекции узлов
в пространстве Sg х I на плоскость. А именно, пусть дано вложение
окружности (или нескольких окружностей) в Sg x J, где отрезок I
играет роль «аппликаты». Это значит, что можно рассмотреть схему
этого вложения на Sg с проходами и переходами, проектируя узел на Sg
вдоль I и указывая в точке пересечения проекции, какая ветвь узла
идет выше, а какая — ниже.
Спроектируем данную сферу с д ручками на плоскость, тем
самым проектируя на плоскость и диаграмму соответствующего узла
(зацепления). Малым шевелением такая проекция приводится в общее
положение. При проекции диаграммы в общем положении помимо
обычных вершин (проекций вершин диаграммы) возникнут также
вершины, являющиеся пересечениями проекций ребер, которые можно
трактовать как «дефект проекции». Как раз такие вершины мы объявим
виртуальными.
Нетрудно проверить, что обобщенные движения Рейдемейстера
диаграмм виртуальных узлов происходят в точности из движений
Рейдемейстера диаграмм узлов на таких поверхностях. Эти движения
изменяют диаграммы на Sg зацеплений, лежащих в Sg x I, при этом
Лекция 21. Определения
253
локально они выглядят так же, как и обычные движения Рейдемейсте-
ра на плоскости.
Упражнение 21.4. Проверьте это утверждение аккуратно.
Замечание 21.2. Виртуальные движения Рейдемейстера, вообще говоря,
создают новое огношение эквивалентности на классических зацеплениях —
виртуальную эквивалентность. При этом если два классических зацепления
получаются друг из друга последовательностью виртуальных движений
Рейдемейстера, то они изотопны. Доказательство см. в [39].
Это означает, что инварианты виртуальных узлов несут в себе
также информацию о поверхностях, в которых лежат «прообразы» этих
узлов, хотя много информации и теряется. В частности, нетривиальный
виртуальный узел не может быть проекцией тривиального узла в Sg х I.
Пример 21.1. На рис. 5 показаны примеры виртуальных узлов,
происходящих из узлов в Г2 х /.
Рис.5
Упражнение 21.5. Пусть дано виртуальное зацепление L из двух
компонент А и В, на диаграмме которого количество виртуальных перекрестков
компоненты А с компонентой В нечетно. Покажите, что зацепление L не
изотопно классическому зацеплению.
Хотя виртуальный узел (виртуальное зацепление) и является
понятием комбинаторным, можно ввести понятие фундаментальной группы
Дополнения к виртуальному узлу.
Пусть дана плоская диаграмма зацепления К. Зафиксируем
ориентацию всех компонент этого зацепления.
Определение 21.4. Назовем дугой плоской диаграммы
виртуального узла (или зацепления) проекцию ветви узла от прохода до
следующего прохода, т. е. идущую сверху или имеющую виртуальные
пересечения.
254
РазделУ. Виртуальные узлы
Рассмотрим дуги диаграммы К и обозначим их буквами, которые
выберем в качестве образующих данной группы.
На тройки букв, соответствующих дугам, примыкающим к одной
вершине, в которой перекресток является классическим, положим
соотношение Ь = cac~l, где дуга с разделяет дуги а и Ь и проходит так,
как это указано на рис. 6.
►
Рис.6
Получим некоторую группу, которую назовем фундаментальной
группой дополнения к виртуальному зацеплению.
Теорема 21.1- Фундаментальная группа дополнения к
виртуальному зацеплению определена корректно, т. е. является инвариантной
относительно виртуальных движений Рейдемейстера.
Доказательство. Нам нужно показать, что при движениях
Рейдемейстера, как классических, так и виртуальных, фундаментальная
группа дополнения не меняется. Мы покажем, что после
преобразования Рейдемейстера получится группа, отличающаяся от исходной лишь
другим копредставлением.
Более того, каждый раз новая группа будет иметь дополнительные
образующие, выражаемые через прежние образующие, или в новой
группе пропадет одна или несколько образующих, выражаемых через
остальные.
Ясно, что сама группа при этом не изменяется, так как
новые образующие, выражаемые через старые, существовали в группе
и до преобразования Рейдемейстера. Следовательно, старое и новое
копредствления задают одну и ту же группу, только в новой группе
некоторый элемент включен в число (исключен из числа) образующих
с добавлением (удалением) дополнительного соотношения.
При «чисто виртуальных» движениях Рейдемейстера, а также при
версии третьего движения Рейдемейстера с одной виртуальной
вершиной инвариантность фундаментальной группы дополнения очевидна.
Это следует из того, что не меняется количество дуг и их примыкание
друг к другу.
Рассмотрим теперь классические движения Рейдемейстера.
Первое из них разбивает одну дугу а на две а и 6, на образующие
которых накладывается соотношение Ь = <Г1 aa = а, см. рис. 7.
Лекция 21. Определения
255
Рис.7
Следовательно, эти две образующие а\ и аг равны.
Второе движение Рейдемейстера разбивает дугу а на три дуги а\,
а2 и аз, причем имеют место соотношения а{ = а3, а2 = ft_1aift, т.е.
д2 выражается через а и 6, где & — дуга, ложащаяся сверху дуги а,
см. рис.8.
Рис.8
Аналогично рассматривается другой случай дуги ft.
Рассмотрим теперь один вариант третьего движения
Рейдемейстера (вариант с противоположной ориентацией рассматривается
аналогично).
Мы имеем одну дугу а, лежащую сверху всех остальных. Она
разбивает вторую хорду ft на хорды Ь\ и &2. Кроме этого, есть еще три
ДУта сь С2, сз до применения движения и с/, сг', сз' после применения
Движения. Эти дуги лежат под дугами а и ft, см. рис. 9.
В обоих случаях получаем соотношение &2 = a\bi<L[l. Полагая
ci = q, получаем:
с2 — &2 с1&2>с3 = а1 &2 С\Ъ2<1\ = &i tti Ciaifti,
с2 = аГ с1аьсз = ^1 ai c^aiftj.
Таким образом, сз' = сз, что и требовалось доказать. ■
256
РазделУ Виртуальные узлы
Рис.9
Замечание 21.3. Полученное определение фундаментальной группы
дополнения совпадает с «настоящей» фундаментальной группой дополнения в случае
классических узлов.
Классические зацепления являются частным случаем виртуальных
зацеплений, поэтому можно говорить о виртуальной эквивалентности
классических зацеплений. С другой стороны, для классических узлов
определена обычная изотопия. В [39] доказана следующая
Теорема 21.2 (см. также [50]). Два классических узла (зацепления)
К{ и К^у являющиеся эквивалентными относительно виртуальных
движений Рейдемейстера, являются изотопными в обычном смысле.
Для доказательства этого факта используется инвариантность
некоторого обобщения фундаментальной группы, которое инвариантным
образом продолжается на виртуальные узлы.
Фундаментальная группа дополнения к сингулярному узлу
является довольно странным объектом. Например, она не инвариантна
при замене проходов на переходы, т. е. определенная нами «верхняя»
фундаментальная группа не совпадает с «нижней» фундаментальной
группой. Пример виртуального узла, для которого это явление имеет
место, показан на рис. 10.
Действительно, для образующих а, Ь, с, d, соответствующих дугам,
показанным на рис. 9, имеют место соотношения:
b = dad~\ a = bdb'\ d = bcb'\ c = dbd"\
Выбирая образующие bud, через которые выражаются
образующие а и с, получим единственное соотношение bdb = dbd. Таким
образом, фундаментальная группа дополнения к узлу, показанному
на рис. 10, изоморфна фундаментальной группе дополнения к
трилистнику.
Лекция 21. Определения 257
Рве. 10
Упражнение 21.6. Покажите, что фундаментальная группа дополнения
к зеркальному отражению этого узла изоморфна группе Z.
Следовательно узел, изображенный на рис. 10, не может быть
изотопен классическому узлу, так как обе фундаментальные группы
(верхняя и нижняя) являются инвариантными, а для классических
узлов они совпадают.
Приведем еще один пример виртуального узла со «странными»
свойствами фундаментальной группы.
Пример 21.2. Виртуальный узел, показанный на рис. 11, имеет
фундаментальную группу, изоморфную Z.
Ь
'(fb
Рис. 11
Чтобы показать, что виртуальный узел, показанный на рис. 11,
не является изотопным тривиальному узлу, нам нужно знать
некоторые другие инварианты виртуальных зацеплений. Расскажем об одном
**з них — аналоге полинома Джонса, а также о получающемся из него
заменой переменной полиноме Кауфмана.
258
РазделУ. Виртуальные узлы
Определим его аксиоматически также как и в классическом случае:
(L) = a(LA) + a-l(LB); (1)
(XuO) = (-a2-a-2)(X); (2)
<0> = i, (3)
при этом под несвязной суммой двух зацеплений будем понимать
диаграмму, состоящую из диаграмм этих зацеплений и (быть может)
некоторых виртуальных пересечений между ними, а под О ~~ узел,
не имеющий классических вершин.
Если на зацеплении L задать ориентацию, то можно посчитать его
writhe number w(L) как сумму знаков во всех невиртуальных
пересечениях.
Зададим на ориентированной диаграмме зацепления L полином
Кауфмана по формуле
X(L) = (-a)-3»M(№, (4)
где неориентированная диаграмма \L\ получена из диаграммы L
забыванием ориентации, a w — local writhe number, определенный в первой
части книги.
Теорема 21.3. Определенный выше полином Кауфмана (если
существует) является инвариантом виртуальных узлов и зацеплений.
Доказательство. Нам нужно показать инвариантность полиномов
Кауфмана относительно движений Рейдемейстера. Будем использовать
индукцию по числу классических вершин. Очевидно, что если все
вершины данного зацепления — виртуальные, то утверждение теоремы
верно.
Относительно классических движений Рейдемейстера
инвариантность доказывается так же, как в классическом случае.
При применении чисто виртуальных движений Рейдемейстера
полином Кауфмана не меняется, потому что данные движения не
затрагивают классических вершин и каждое слагаемое в сумме (4) остается
неизменным.
Перейдем теперь к версии третьего движения Рейдемейстера с
одной классической вершиной и двумя виртуальными.
Так как writhe number при этом движении не меняется, нам нужно
показать лишь инвариантность скобки Кауфмана, как это проделано
на рис. 12. ■
Доказательство существования виртуального полинома Кауфмана
проводится так же, как и в классическом случае. Итак, пусть дана
диаграмма неориентированного виртуального зацепления L. Рассмотрим
Лекция 21. Определения
259
Рис.12
множество всех классических (не сингулярных) перекрестков
диаграммы. Каждую из этих вершин можно разрешить двумя способами (так же,
как для обычного полинома Кауфмана). Способ для разрешения всех
вершин назовем состоянием виртуальной диаграммы. В каждом
состоянии будем иметь набор окружностей, все пересечения между которыми
(если таковые есть) будут виртуальными. Таким образом, аналогично
классическому случаю можно положить по определению
<£>=x;«aW"/3W(-«2-«"2)
2\7(»)-I
(5)
где s — состояния диаграммы L, а 7(5) — количество окружностей
в состоянии 5.
В полиноме Кауфмана можно сделать замену переменных q~1^ = a,
тогда получим полином Джонса виртуальных зацеплений, который
будет совпадать с классическим полиномом Джонса на классических
зацеплениях.
Упражнение 21.7. Вычислите полином Джонса узла, показанного на
рис. 10, и покажите, что этот узел не является тривиальным.
Лекция 22
Гауссовы диаграммы и инварианты
конечного порядка виртуальных узлов
На этой лекции мы продолжим рассказ о .виртуальных узлах,
а точнее, об одном способе их задания — о гауссовых диаграммах.
Кроме того, мы построим аналог инвариантов конечного порядка для
виртуальных узлов, см. [39]. Отметим, что существует альтернативное
определение инвариантов конечного порядка для виртуальных узлов.
Мы его рассматривать не будем, см. [50]. В отличие от инвариантов
конечного порядка для классических узлов, для описания их аналога
в виртуальном случае не потребуется тяжелой техники, вроде интеграла
Концевича.
Как говорилось на предыдущих лекциях, не все гауссовы
диаграммы кодируют классические узлы. Оставшиеся (нереализуемые) гауссовы
диаграммы как раз кодируют виртуальные узлы.
Пусть дана диаграмма виртуального узла V. Построим по ней
гауссову диаграмму следующим образом.
Определение 22.1. Гауссова диаграмма узла К с отмеченной
точкой — это ориентированная окружность (с отмеченной точкой),
у которой хордами соединены прообразы прохода и перехода точек
проекции узла. Прообразы каждого невиртуального перекрестка
соединены хордой со стрелкой, направленной от прообраза точки
прохода к прообразу точки перехода. При этом каждая стрелка
имеет знак, равный знаку local writhe number данной вершины. Знаки
на хордах определяются так же, как и в классическом случае.
Замечание 22.1. Для классических узлов данное определение гауссовой
диаграммы совпадает с обычным определением гауссовой диаграммы.
Итак, пусть дана гауссова диаграмма с ориентированными хордами
и метками на них. Если эта диаграмма реализуема, то она представляет
(однозначно) диаграмму некоторого классического узла; в противном
случае классический узел получен быть не может.
При этом граф кратности четыре, представимый данной гауссовой
диаграммой и не вложимый в плоскость, может быть в плоскость
, погружен. Погружение при этом можно выбрать «хорошим» образом:
Лекция 22. Инварианты конечного порядка 261
без точек тройного пересечения ребер и без прохождений образов
внутренностей ребер через образы вершин.
В точках пересечения образов ребер поставим виртуальные
вершины, а в остальных точках — проходы и переходы сообразно гауссовой
диаграмме, см. рис. 1.
Рис. 1
Таким образом, по каждой гауссовой диаграмме можно
(неоднозначно) построить некоторую диаграмму виртуального узла.
Теорема 22-1 (см. [39])- Изотопический класс виртуального узла
однозначно восстанавливается по гауссовой диаграмме.
Доказательство. Нам нужно показать, что два виртуальных узла,
которые можно построить по заданной гауссовой диаграмме, являются
эквивалентными с помощью обобщенных движений Рейдемейстера.
Рассмотрим некоторую гауссову диаграмму g и два виртуальных
узла К\ и К2, соответствующие ей. Будем считать, что на гауссовой
диаграмме g есть хорды, в противном случае это утверждение является
очевидным. Выберем на данных двух узлах точки, соответствующие
серединам дут диаграмм К\ и Ki.
Без ограничения общности можно считать, что соответствующие
точки на плоскости просто совпадают (этого можно добиться
подходящим диффеоморфизмом плоскости).
Между каждыми двумя точками данной диаграммы проходит ветвь
узла, имеющая ровно один классический перекресток с другой ветвью,
при этом тип перекрестка и порядок прохода одной ветви выше или
ниже другой одинаков, см. рис. 2. Будем также считать, что на каждой
из этих двух ветвей диаграммы К\ этот перекресток — единственный.
Без ограничения общности можно считать, что единственная
классическая вершина на двух диаграммах совпадает, более того, обе
Диаграммы совпадают вне малой окрестности данной вершины. Для
завершения доказательства осталось лишь заметить, что оставшиеся
262
РазделУ. Виртуальные узлы
КМ
Рис.2
четыре ветви на части нашей диаграммы Кг имеют лишь виртуальные
пересечения (друг с другом и с другими ветвями), следовательно, их
можно развести и получить диаграмму К\. ■
Очевидно, что любой инвариант виртуальных узлов является также
и инвариантом классических узлов.
В [39] М. Н. Гусаров, М. Поляк и О. Я. Виро ввели обобщение
понятия инварианта конечного порядка для виртуальных узлов.
Для описания таких инвариантов нам понадобятся специальные
диаграммы, представляющие собой графы кратности четыре, на
которых помимо проходов, переходов, виртуальных пересечений, будет
также и четвертый вид пересечений, называемый полувиртуальным
перекрестком.
Схематически полувиртуальный перекресток обозначается как
проход (переход), обведенный кружочком, см. рис. 3.
X
Рис.3
Полувиртуальные пересечения связаны с известными
пересечениями по формуле
х-х-х •
Рис.4
Лекция 22. Инварианты конечного порядка 263
На гауссовых диаграммах полувиртуальное пересечение
обозначается пунктирной линией. Соотношение (1) на гауссовых диаграммах
принимает вид
(--•-->н-( ) -
Рис.5
Пусть D — диаграмма виртуального узла и (di,..v,dn) —
набор из п классических вершин данной диаграммы. Для набора <т =
{(7*1,... ,(тп} из нулей и единиц определим диаграмму Dff как
диаграмму, получаемую из диаграммы D заменой всех пересечений сЦ,
для которых <г,- = 1, виртуальными пересечениями. Пусть \<г\ —
число единиц в наборе <т. Определим диаграмму с п полувиртуальными
вершинами как формальную сумму
£(-Dwiv
Такое определение согласуется с соотношением (1).
Пусть теперь К — множество всех виртуальных узлов и пусть
и: К —> G — некоторый инвариант виртуальных узлов со значениями
в абелевой группе G. Расширим этот инвариант линейно на Z[/C].
Определение 22.2. Скажем, что v является инвариантом,
конечного порядка, если v обнуляется на любом виртуальном узле с
более чем п полувиртуальными пересечениями. Минимальное n G N,
обладающее таким свойством, называется порядком инварианта v.
Заметим, что из соотношений (1) и (2) следует соотношение
х-х-х »
Рис.6
Это означает, что ограничение v1 любого инварианта v конечного
порядка для виртуальных узлов на случай классических узлов также
является инвариантом конечного порядка (в обычном смысле); при
этом степень инварианта и' не выше степени инварианта и.
264
РазделУ Виртуальные узлы
Определение 22.3. Стрелочной диаграммой (на окружности)
называется диаграмма, на которой некоторые пары точек соединены
пунктирными стрелками, при этом каждая стрелка снабжена
знаком, при этом каждая точка инцидентна не более чем одной
стрелке.
Определение 22.4. Следуя статье [39], назовем алгеброй
стрелочных диаграмм свободную коммутативную группу линейных
комбинаций стрелочных диаграмм по сложению. Термин «алгебра»
мы употребляем, так как на стрелочных диаграммах
действительно можно ввести алгебраическую структуру; этого вопроса мы
касаться не будем.
Обозначим через V множество всех гауссовых диаграмм. По каждой
гауссовой диаграмме можно получить стрелочную диаграмму, делая все
хорды данной диаграммы пунктирными. Продолжая это отображение
по линейности, мы получим отображение
г: Z[V] -> Л
Кроме данного отображения, отметим еще одно важное
отображение из множества V во множество Л, сопоставляющее гауссовой
диаграмме сумму всех ее поддиаграмм, превращенных в стрелочные.
1(D) = £ i(D').
D'CD
На языке гауссовых диаграмм это соотношение выглядит так, как
показано на рис. 7.
+
Рис.7
Предложение 22.1. Отображение Г. Z[V] —► А является
изоморфизмом. Обратное отображение I"1: А-> Z[V] определено на обра-
зующих алгебры А по формуле
Г\А) = 5>1)^VV),
А'СА
где \А - А'\ — количество стрелок диаграммы А, не принадлежащих
диаграмме А'.
Доказательство остается читателю в качестве упражнения. ■
Лекция 22. Инварианты конечного порядка 265
Гауссова диаграмма называется полувиртуальной, если все ее
стрелки являются пунктирными.
Следствие 22.1. Полувиртуальные гауссовы диаграммы образуют
базис в пространстве Z[2>].
Дадим теперь определение Алгебры Поляка.
Определение 22.5. Алгеброй Поляка V называется факторалгебра
алгебры Л по соотношениям, показанным на рис. 8.
,' = 0
Н~ £
+
= 0
е J I I I I ' I * J I L * J
.._:_[.i.J + L_._L_?J + \ в \ + Ь—4"Ч
i 1
L«6.-_
>
. »
> ■ -
+
i "i
e_
+
L . .
. »
i 1
+
I -
>
i ,
+
L ' ,
__£--
M
Рис.8
Замечание 22.2. Здесь, как обычно, считается, что части диаграмм, не
показанные на рисунке, совпадают.
Изоморфизм J индуцирует изоморфизм соответствующих факторалгебр,
который мы также будем обозначать I: Z[/C] —* V. При этом соотношения,
приведенные на рис. 8, в точности превращаются в соотношения Рейдемейстера,
переписанные на языке полувиртуальных вершин, см. рис. 9.
266
РазделУ. Виртуальные узлы
X)-
£ &• 5-
Х-Х-ХХ-
Х-Х-Х-Х
Рис. 9
Таким образом, для любой гауссовой диаграммы D виртуального узла К
диаграмма 1(D) определяет инвариант узла К со значениями в V. Более
того, так как гауссова диаграмма определяет К, инвариант 1(D) различает
виртуальные узлы.
Следовательно, получаем теорему.
Теорема 22.2. Пусть D — гауссова диаграмма виртуального узла К.
Тогда формула I: К —>V определяет полный инвариант виртуальных
узлов.
Определим теперь усеченную алгебру Vn, полагая А = О для всех
диаграмм А из алгебры V с более чем п стрелками. Обозначим через
In: K,—>Vn композицию отображения I: К —► V и проекции V —► Рп-
Определение 22.6. Пусть Р — абелева группа и р: К —► Р —
инвариант со значениями в этой группе. Назовем р универсальным
инвариантом степени п, если для каждого инварианта и: К -> G
степени не более п существует отображение 7г: Р —► G, такое, что
v = тгор.
Теорема 22.3. Отображение In: K->Vn определяет универсальный
инвариант порядка п.
Доказательство. Легко видеть, что отображение 1п переводит узлы
с более чем п полувиртуальными пересечениями в ноль. Следовательно,
/п является инвариантом степени не более п.
Лекция 22. Инварианты конечного порядка 267
Пусть v\ /С -+ G — инвариант степени не более п. Докажем, что
для отображения vol"1 существует отображение 7г, такое, что v = тгор.
В силу следствия 22.1 для любой диаграммы А ее образ Г1 {А) 6
Z[V\ может быть отождествлен с той же самой диаграммой А, но
рассмотренной как полувиртуальная диаграмма. Так как степень
инварианта v не превосходит п, то v обнуляется на всех диаграммах с более
чем п полувиртуальными пересечениями. Таким образом,
отображение uoI~l обнуляется на любой стрелочной диаграмме с более чем п
стрелками, откуда и следует утверждение теоремы. ■
Лекция 23
Виртуальные косы
§1. Основные определения
На прошлых лекциях было рассказано о виртуальных узлах,
простейших способах их задания и об их инвариантах.
На этой лекции мы поговорим еще об одном способе задания
виртуальных узлов — виртуальных косах, см., например, [87].
Начнем с определения диаграммы виртуальной косы.
Определение 23.1. Назовем плоской диаграммой виртуальной косы
из га нитей (гладкий) граф внутри прямоугольника [1, га] х [0,1]
на плоскости со следующим оснащением:
а) в точках [г, 0] и [г, 1], * = 1,..., m граф имеет вершины
кратности 1, в других точках [t> 0] и [£,1] вершин графа нет;
б) все остальные вершины графа имеют кратность четыре;
в) уникурсальные кривые, т.е. линии, состоящие из ребер графа,
переходящих в каждой вершине графа с полуребра на
противоположное полуребро, проходят от вершин с ординатой 0 к вершинам
с ординатой 1, при этом являются восходящими, т.е. их проекция
на ось ординат является гомеоморфизмом;
г) в каждой вершине задана структура — либо указано, какая из уни-
курсальных кривых проходит выше, а какая — ниже, либо
поставлено виртуальное пересечение.
Пример 23.7. Диаграмма виртуальной косы изображена на рис. 1.
Определение 23.2. Две диаграммы виртуальных кос В{ и В2
из одинакового количества нитей называются изотопными, если
существует последовательность обобщенных движений Рейдемей-
стера, переводящих диаграмму В\ в диаграмму Вг, причем после
применения каждого движения Рейдемейстера мы получаем
виртуальную косу.
Как и на классических косах (косах Артина), на виртуальных косах
также существует групповая структура. Определим ее более подробно.
Пусть дана диаграмма В виртуальной косы. Малым шевелением
(изотопией) можно добиться того, чтобы все вершины данной косы
Лекция 23. Виртуальные косы
269
Рис. 1. Диаграмма виртуальной косы
имели разные ординаты. Начнем двигаться от уровня у = О к уровню
у = 1. На участках, не содержащих вершин, мы имеем дело с набором
восходящих линий. При прохождении вершины две соседние нити
имеют пересечение (классическое или виртуальное) и меняются местами.
Следовательно, каждой диаграмме косы можно сопоставить изотопную
ей (негладкую) диаграмму косы следующего вида.
Косасостоитиз I участков с абсциссами (0, }), (}> т)> • • •» (1~Г> *)
(где I — количество перекрестков исходной косы). На каждом из
участков все линии, кроме двух, идут вертикально, а две соседние
переставляются местами так, как показано на рис. 2.
XI
а б в
Рис.2
Таким образом, каждую диаграмму виртуальной косы можно
разбить на «кусочки». Каждый из них имеет вид, показанный на рис. 2 я,
рис. 2 б или рис. 2 в.
На диаграммах виртуальных кос можно определить произведение
так же, как и на диаграммах обычных кос, приставляя нижние концы
270
РазделУ Виртуальные узлы
первой косы к верхним концам второй косы. При этом единицей будет
коса, состоящая из вертикальных нитей (без перекрестков).
Итак, каждую диаграмму косы можно разложить в
произведение кос, изображенных на рис. 2. Будем обозначать косу, показанную
на рис. 2 в, буквой Q, а косы, показанные на рис. 2а и 26, буквами <Т{
и afl соответственно (также как и в случае классических кос).
Очевидно, что произведение косы Oi на косу а,"1 будет изотопно
тривиальной (единичной) косе. Таким образом, умножение в группе
виртуальных кос будет отвечать приписыванию слов в алфавите о-,-, Q.
При этом очевидно, что Уг (? = 1.
Обращению косы будет соответствовать «отражение» ее диаграммы,
см. рис. 3.
Рис. 3. Обращение виртуальной косы
Мы показали, что виртуальные косы из п нитей образуют группу
с 2п - 2 образующими <Т{ и Q.
Теорема 23.1. Группа виртуальных кос имеет следующие
соотношения:
а) {соотношения для классических кос)
<Ti<Tj = <Tj(Ti, \i - j\ > 1, 1 < t, j < n,
^t^t+i^i = <Ti+i<W+i> l^i^n;
б) {соотношения группы перестановок)
(i = e, 1 ^ i < n,
CtCt+iC» = Ct+iCtCi+b l^i^n;
Лекция 23. Виртуальные косы
271
в) (смешанные соотношения)
*i<j = 0<7»> I* - 3\ > 1, К h J < n,
j>a/tee того, если два слова, записанные в алфавите а^ <г^1 и &
представляют изотопные виртуальные косы, то эти слова получаются
друг из друга конечной последовательностью применения
соотношений, указанных выше.
Доказательство. Необходимость этих соотношений очевидна.
Докажем их достаточность. Пусть В\ и Вг — две изотопные
виртуальные косы. Проследим за процессом их изотопии. Без ограничения
общности можно считать, что всегда за исключением конечного числа
моментов косы находятся в общем положении, т. е. все образы нитей
пересекаются трансверсально, причем не более двух нитей
одновременно и вершины (точки пересечения нитей) имеют разные ординаты.
Кроме того, можно считать, что в остальные моменты мы имеем дело
с сингудярностями коразмерности один, а именно:
1. ровно две вершины имеют одну ординату,
2. имеет место касание двух нитей,
3. имеет место точка тройного пересечения.
В случае, когда ровно две вершины имеют одну ординату, мы
имеем дело с «дальней» коммутативностью образующих с индексами
h j\ N - jl > 1» причем каждая образующая может быть как а, так и (,
см. рис. 4.
Рис.4
Возможны два случая касания двух нитей косы, соответствующие
классическому и виртуальному движениям Рейдемейстера. В одном
из которых («классическом») мы получаем соотношение я^чт,"1 = е,
а во втором («виртуальном») — соотношение (? = е, см. рис. 5.
272
РаздвлУ Виртуальные узлы
х-х-х
Рис.5
Наконец, в случае тройного касания мы имеем дело с третьим
движением Рейдемейстера, либо с классическим, либо с виртуальным,
либо с «полувиртуальной» версией, см. рис. 6.
ш ш п
ш ш е
Рис.6
В случае классического третьего движения Рейдемейстера мы
получаем три соотношения.
^t^i+i^t = <ri+i<ri<ri+h
При этом легко видеть, что второе и третье следуют- из первого.
В случае виртуальной версии третьего движения Рейдемейстера мы
, получаем соотношение
C»C»+iC» = Ct+iCtCi+i-
Лекция 23. Виртуальные косы
273
Наконец, в случае версии третьего движения Рейдемейстера с
одной классической и двумя виртуальными вершинами мы получаем два
соотношения:
CiCf'+l*7» = <7t+lCiCf+h 1 ^ * ^ П,
и
CiCi+l^f = ^t'+lCiCt+b 1 < i ^ П,
причем второе из них легко следует из первого.
Таким образом, список соотношений совпадает со списком,
предъявленным в формулировке теоремы, что завершает доказательство
теоремы. ■
Аналогично классическим косам, можно определить замыкание
виртуальной косы, см. рис. 7. При этом получившееся зацепление будет
обвиваться вокруг точки А, т.е. при некотором выборе ориентации
компонент зацепления векторное произведение вектора, выпущенного
из точки А в произвольную (фиксированную) точку зацепления Б, и
касательного вектора из точки В, все время направлено в одну сторону.
Рис.7
Замыкание виртуальной косы представляет собой диаграмму
виртуального зацепления.
При этом так же, как и в классическом случае, изотопным косам
соответствуют изотопные виртуальные узлы.
Докажем теперь аналог теоремы Александера.
274
Раздел V. Виртуальные узлы
Теорема 23.2. У каждого изотопического класса виртуальных узлов
существует диаграмма, получаемая замыканием виртуальной косы.
Доказательство. Вспомним доказательство теоремы Александера
для обычных зацеплений. В нем для заданного зацепления строится
диаграмма, обвивающаяся вокруг некоторой точки.
Для этого мы рассматриваем аппроксимацию узла ломаной, такой,
что каждое ребро данной ломаной имеет внутри не более одного
перекрестка. Затем мы заменяем каждое ребро, направленное «не в ту
сторону» на пару ребер, см. рис. 8.
о.
. с
Рис.8
Для классических зацеплений нужно рассматривать три случая:
когда данное ребро не имеет перекрестков внутри, когда оно имеет
ровно один перекресток и проходит сверху и когда оно имеет ровно
один перекресток и проходит снизу.
Для виртуальных зацеплений, помимо этих трех случаев,
добавляется еще случай виртуального перекрестка. В этом случае дугу АВ
можно «пронести» через точку О так, чтобы по ходу движения все
перекрестки, образуемые этой дугой, были виртуальными.
Упражнение 23.1. Покажите аккуратно, что этого можно достичь,
используя чисто виртуальные движения Рейдемейстера, а также одно
«полувиртуальное» движение Рейдемейстера.
В итоге получим картинку, показанную на рис. 96. ■
оф ' • # с
Рис.9
Лекция 23. Виртуальные косы
275
Мы показали, что все виртуальные зацепления задаются
замыканиями виртуальных кос.
В отличие от классического случая, для виртуальных зацеплений
до сих пор не найдено аналога движений Маркова, т. е. достаточной
системы преобразований на множестве виртуальных кос, переводящих
друг в друга виртуальные косы, которым соответствуют диаграммы
изотопных виртуальных узлов.
§ 2. Представление Бурау
Как и в случае обычных кос, виртуальные косы допускают
линейные представления. Одно из них — представление Бурау, см. [87].
Для каждого п 6 N построим представление группы виртуальных
кос из п нитей. Отобразим элемент сг{ в блочно-диагональную матрицу,
у которой на диагонали на местах от1до*-1иотг + 2доп блоки
состоят из единичных матриц размера 1 х 1, а блок (2x2), стоящий
на месте (i, г +1), имеет вид
(1-х х\
1 0J>
а элемент £• — в блочную матрицу, у которой на диагонали на местах
от1до1-1иот« + 2доп блоки состоят из единичных матриц
размера 1 х 1, а блок (2x2), стоящий на месте (г, г + 1), имеет вид
СО-
Соотношения группы виртуальных кос проверяются прямым
вычислением.
Это представление можно также трактовать как представление
стабильной группы кос матрицами бесконечного размера.
Раздел VI
ПРОЧЕЕ
Лекция 24
Узлы в RP3 и лежандровы узлы
В этой лекции мы расскажем еще о двух обобщениях теории
узлов — узлах и зацеплениях в трехмерном проективном пространстве,
а также о Лежандровых узлах (см. [102]) и простейших инвариантах
этих зацеплений.
§1. Узлыв RP3
Начнем с построения некоторого инвариантного полинома,
следуя [99], см. также [123].
Рассмотрим трехмерное проективное пространство RP3. Это
многообразие можно определить как сферу R3 с отождествленными
противоположными точками. Сфера 53 состоит из двух полусфер,
каждая из которых гомеоморфна трехмерному диску. Известно, что RP3
можно получить, отождествив диаметрально противоположные точки
края S2 = dD3. Следовательно, зацепление в RP3 можно определить
как набор гладких замкнутых кривых и дуг, лежащих в диске D3, таких,
что множество концов дуг лежит на крае 8D3 и эти концы
разбиваются на пары, являющиеся диаметрально противоположными точками
диска D3. Следовательно, зацепление в RP3 можно представить как
диаграмму в круге D29 все точки которой, попадающие на
границу 51 = 8D2, должны быть расположены центрально симметрично.
Пример такой диаграммы изображен на рис. 1.
Упражнение 24.1. Рассмотрим произвольную диаграмму зацепления в
RP3. Опишите, как выглядит диаграмма прообраза этого зацепления при
двулистном накрытии р: S3 —► RP3.
Для зацеплений в RP3 так же, как и для зацеплений в R3, будем
рассматривать лишь диаграммы общего положения. Это означает, что
помимо «обычных» условий, накладываемых на диаграмму обычного
Лекция 24. Узлы в RP3 и лежандровы узлы 277
зацепления (трансверсального пересечения не более чем трех ветвей
проекции узла в одной точке), появляется условие, что диаграмма
не должна касаться границы круга и на границе круга не должно быть
перекрестков диаграммы.
Рис.1
Напомним, что в случае узлов в R3 (или S ) запрещенные проекции
приводят к движениям Рейдемейстера ft 2 и Пз- Аналогичным образом
два упомянутых выше типа запрещенных проекций порождают два
движения, которые также называются преобразованиями Рейдемейстера
и обозначаются П4 и Qs соответственно, см. рис. 2.
Рис.2
Теорема 24-1. Две диаграммы в RP3 изотопны тогда и только
тогда, когда их можно полунить друг из друга посредством изотопии
278
Раздел VI. Прочее
диска D2, классических преобразований Рейдемейстера (2i,ft2,12з
и новых преобразований П* и ^5-
Доказательство этой теоремы полностью аналогично
доказательству классической теоремы Рейдемейстера. Оставляем его в качестве
упражнения для читателя. ■
Теперь все готово для определения аналога полинома Кауфмана
для ориентированных полиномов в RP2.
Определим сначала для диаграммы неориентированного
зацепления L в RP3 аналог скобки Кауфмана как полином, удовлетворяющий
аксиомам
< L >= a < LA > -ha"1 < LB >; (1)
< L U О >= (-a2 - a~2) <L>; (2)
< О >= 1, (3)
где диаграммы La и Lb суть разведения диаграммы L в некоторой
точке, а О означает отдельно стоящую незаузленную окружность.
Доказательство существования и единственности скобки Кауфмана
< L > полностью совпадает с доказательством аналогичной теоремы
для зацеплений в R3 (или S3).
Точно так же доказывается теорема об инвариантности полинома
< L > относительно второго и третьего движений Рейдемейстера.
Для доказательства инвариантности полинома < L > относительно
движения ^4 воспользуемся формулой
< D >= £ a*>-"9)(-a2 - a-y§)-\ (4)
в
где число j(s) определяется как количество окружностей в RP3
диаграммы L в состоянии s.
Действительно, для любого состояния s диаграммы L числа
a(s),f3(s) и 7(«) не изменяются при применении преобразования iV
Доказательство инвариантности полинома < L > относительно
движения П5 следует из серии равенств, изображенных на рис. 3.
Как и в случае зацеплений в R , полином < L > не
является инвариантным относительно первого движения Рейдемейстера,
а умножается на (—а)±3.
Определим теперь для диаграммы ориентированного зацепления L
число w(L), как и для обычного зацепления в 53 (сумма знаков
на перекрестках).
Определение 24.1. Полиномом Дроботухиной ориентированного
зацепления L в RP3 называется функция
X(L) = (-ay3w(L) < \L\ >,
Лекция 24. Узлы в RP3 и лежандровы узлы 279
где диаграмма \L\ получается из диаграммы L забыванием
ориентации.
Рис. 3. Инвариантность относительно Q5
Теорема 24.2. Полином X(L) является изотопическим инвариантом
ориентированного зацепления L в RP3.
Доказательство полностью аналогично доказательству
инвариантности полинома Кауфмана от одной переменной для зацеплений в 53.
Оно следует непосредственно из теоремы 1, определения полинома
Дроботухиной, инвариантности полинома < • > относительно
движений Пг ~ ^5 и умножения его на (-а)±3 при движении fii, а-*также
из того факта, что w(-) является инвариантным относительно
преобразований Пг - ^5 и изменяется на единицу при преобразовании 121. ■
С помощью своего полинома Ю. В. Дроботухина
классифицировала с точностью до изотопии все зацепления в RP3 с количеством
перекрестков не большим шести.
Упражнение 24.2. Покажите, что для любого зацепления L в RP3 в
полином X(L) входят лишь четные степени переменной а.
§ 2. Фронты и лежандровы узлы
Приведем теперь описание одного нового способа задания узлов,
который в последнее время привлекает все большее внимание. Будем
вести изложение следуя [102].
Рассмотрим двумерную плоскость с выделенным на ней
направлением, которое будем называть вертикальным.
280
Раздел VI. Прочее
Определение 24.2. Фронтом называется замкнутая кривая на
плоскости без вертикальных касательных, гладкая везде, за
исключением некоторого множества особенностей, при этом все
особенности этой кривой исчерпываются клювами —
полукубическими точками возврата и простыми двойными точками
самопересечения.
Полукубическая точка возврата — это точка, вблизи которой наша
кривая выглядит локально, как полукубическая парабола у2 = ж3
в окрестности начала координат.
Объясним теперь связь между фронтами и узлами и заодно
расскажем о происхождении требования отсутствия вертикальных
касательных.
Фронт — это кривая на плоскости с координатами (ж, у).
Добавляя к ним еще координату z, равную тангенсу угла наклона кривой
в данной точке, мы получим кривую в трехмерном пространстве R3.
Если на исходной кривой есть только простые двойные точки и клювы,
то полученная кривая в трехмерном пространстве будет представлять
из себя гладкий узел. При этом тангенс угла наклона определен всюду,
так как касательная к кривой не может быть вертикальной.
Если же мы откажемся от требования отсутствия вертикальных
касательных, то угол наклона кривой будет принимать значения не на
прямой, а на окружности, мы получим узел не в R3, а в
многообразии R2 х 51, представляющем собой полноторие.
Опишем теперь связь между фронтами и узлами в терминах
диаграмм.
По фронту диаграмма представляемого им узла строится
следующим образом. Все точки возврата мы просто сглаживаем, а проходы
и переходы в двойных точках устанавливаем так: ветвь кривой, идущая
из левого нижнего угла в правый верхний всегда является переходом, а
другая ветвь — проходом. Так как у фронта нет вертикальных касательных,
то такое разделение ветвей определено корректно, см. рис. 4.
х-> <- с х-
Рис.4. Построение диаграммы узла по фронту
Обратно, по диаграмме узла строится фронт узла. Для построения
приведем диаграмму в общее положение так, что в двойных точках
йи одна из касательных не будет вертикальной. После этого заменим
Лекция 24. Узлы в RP3 и лежандровы узлы 281
все точки с вертикальными касательными на точки возврата, а
двойные точки, в которых проход и переход устроены «не так как надо»,
преобразуем по правилу, указанному на рис. 5.
Рис. 5. Построение фронта по диаграмме
Таким образом, мы показали, что всякий узел можно представить
фронтом. На рис. 6 изображены фронты и диаграммы правого и левого
трилистника.
Левый трилистник Правый трилистник
Рис.6
Тот факт, что фронт левого трилистника «не симметричен» фронту
правого, следует из того, что принято соглашение о том, какой выбор
прохода по двойной точке считать правильным. Этот факт аналогичен
«асимметричности» d-диаграмм, соответствующих правому и левому
трилистнику.
Определение 24.3. Узел, представленный фронтом, будем
называть лежандровым узлом. Аналог перестроек Рейдемейстера для ле-
жандровых узлов, описывающий топологическую эквивалентность
двух таких узлов, был выписан недавно Д. Б. Фуксом и С. Л.
Табачниковым. Перестройки, описанные в следующей теореме, мы
будем называть перестройками Фукса—Табачникова.
Теорема 24.3 (доказательство см. в [36]). Два фронта
представляют эквивалентные узлы тогда и только тогда, когда от одного
282
Раздел VI. Прочее
фронта к другому можно перейти конечной последовательностью
перестроек, показанных на рис. 7.
Рис.7
Определение 24.4. Кроме приведенной выше (топологической)
эквивалентности лежандровых узлов, приведем еще одну (лежан-
дрову) эквивалентность. Скажем, что два лежандровых узла лежан-
дрово эквивалентны, если от фронта одного из них можно перейти
к фронту второго только при помощи первых трех перестроек
Фукса—-Табачникова.
В каждом классе топологически эквивалентных узлов существует
бесконечно много попарно лежандрово неэквивалентных узлов.
Например, на рис. 8 приведены два топологически эквивалентных
тривиальных узла, а также последовательность перестроек Фукса—Табачникова,
реализующая эту эквивалентность.
Далее мы покажем, что два таких узла не являются лежандрово
эквивалентными. Это значит, что в любой последовательности
преобразований Фукса—Табачникова, переводящей один узел в другой,
есть хотя бы одна перестройка типа 4).
Перейдем теперь к определению простейших инвариантов
лежандровых узлов — лежандровых инвариантов, чисел Маслова \i и Бе-
неккена /3. Эти числа не являются топологическими инвариантами
в том смысле, что значения каждого из них на двух топологически
эквивалентных узлах могут, вообще говоря, различаться.
Лекция 24. Узлы в RP3 и лежандровы узлы 283
il) 4)T
Рис.8. Топологическая эквивалентность двух тривиальных узлов
Определение 24.5. Назовем точку возврата положительной, если
в окрестности этой точки ориентация узла идет с нижней ветви
на верхнюю, и отрицательной в противном случае, см. рис. 9.
•■о- о-
Положительные точки возврата Отрицательные точки возврата
Рис.9
Определение 24.6. Числом Маслова ц(Ь) лежандрова узла L
называется половина разности между числом положительных и числом
отрицательных точек возврата фронта L.
Определение 24.7. Двойную точку фронта назовем
положительной, если ориентации двух ветвей фронта направлены в разные
полуплоскости, и отрицательной в противном случае, см. рис. 10.
XX XX
Положительные двойные точки Отрицательные двойные точки
Рис.10
В силу отсутствия у фронта вертикальных касательных такое
определение корректно.
284
Раздел VI. Прочее
Определение 24.8. Числом Бенеккена (3(L) лежандрова узла L
называется разность между числом положительных и числом
отрицательных двойных точек, увеличенная на половину общего числа
точек возврата фронта L.
Упражнение 24.3. Покажите, что числа Маслова и Бенеккена являются
лежандровыми инвариантами, т.е. что они не меняются при перестройках
Фукса—Табачникова.
На рис. 11 приведены вычисления чисел Маслова и Бенеккена для
лежандровых узлов, показанных на рис. 8. Тем самым показано, что
они не являются лежандрово эквивалентными.
р = 2,р = 5 /х= 1, /? = 4
Рис.11
В заключение приведем теорему без доказательства, проясняющую
картину лежандровой эквивалентности для тривиальных узлов.
Теорема 24.4 (Элиашберг, [33]). Два лежандровых тривиальных
узла лежандрово эквивалентны в том и только в том случае, когда
они имеют одинаковые числа Маслова и Бенеккена.
В конце отметим, что для лежандровых узлов построены и более
сильные инварианты, в частности инвариант Чеканова [24], а также
аналоги инвариантов Васильева [36]. При этом оказалось, что
инварианты р. и р также являются инвариантами конечного порядка, причем р
имеет порядок 0, а /3 — порядок 1. Более того, оказался верным
следующий удивительный факт: все инварианты конечного порядка,
кроме р и /3, являются инвариантами топологической
эквивалентности, т.е. инвариантны также и относительно четвертой перестройки
Фукса—Табачникова.
Отметим, что лежандровы узлы являются интересными не только
с точки зрения теории узлов.
Картинки, подобные фронтам, о которых говорилось в этой
лекции, естественным образом возникают в некоторых задачах геометрии
и дифференциальных уравнений. Одна из этих задач такова. На
плоскости дана гладкая овальная кривая L = L(s). Рассмотрим однопа-
раметрическое семейство преобразований этой кривой, определенное
следующими формулами:
Lt(s) = L(s) + tN(s),
Лекция 24. Узлы в RP и лежандровы узлы 285
где N(s) — единичный вектор внутренней нормали к кривой. Это
преобразование представляет собой движение, при котором каждая точка
кривой двигается внутрь в направлении нормали. В процессе
движения на гладкой кривой могут возникать особенности (точки возврата,
а затем и двойные точки). Так что понятие «фронт» можно толковать
как волновой фронт, порожденный кривой L. В геометрии и теории
дифференциальных уравнений имеется много вопросов в ситуации,
описанной выше. Подробнее см. [93].
Так, с помощью узловых свойств лежандровых узлов можно изучать
свойства (например особенности) распространения волн на плоскости
(волна задается движущимся фронтом, по которому строится лежандров
узел). Так, с помощью этой техники была решена знаменитая гипотеза
Арнольда о выворачивании эллипса.
Приложение 1
Независимость движений Рейдемейстера
Покажем, что все три движения Рейдемейстера являются
необходимыми для определения изотопности двух узлов, т. е. что для каждых
двух движений Рейдемейстера существуют две диаграммы изотопных
узлов, которые не переводятся друг в друга с помощью лишь этих
двух движений (и плоской изотопии), но без перебрасывания через
бесконечность.
По нашему мнению, изложенные ниже примеры имеют
определенное методическое значение. Нам не известны публикации, в которых
был поставлен и разрешен вопрос о независимости движений
Рейдемейстера.
Пример 1.1. Рассмотрим две диаграммы тривиальных узлов, показанные
на рис. 1 а и 1 б. На одной из них количество перекрестков четно (равно
нулю), а на другой — нечетно (равно единице). При этом применение третьего
движения Рейдемейстера к любому узлу не меняет количества перекрестков,
а применение второго движения Рейдемейстера изменяет его на два. Таким
образом, при применении лишь второго и третьего движений Рейдемейстера
и плоской изотопии четность количества перекрестков диаграммы узла
сохраняется. Следовательно, тривиальный узел на рис. 1 б не переводим этими
движениями в узел на рис. 1 а.
ОО-О
^^ а б
Рис.1
Пример 1.2.1)
Пусть KuKi^K^K^ — четыре различных простых нетривиальных узла.
Рассмотрим диаграммы узлов L = Ki#K2#K3#K4 и М = К\#КЪ#К2#К4,
показанные на рис. 2 а, 26. Так как умножение узлов коммутативно, то узлы,
задаваемые диаграммами М и L изотопны.
Покажем, что не существует изотопии диаграммы L в диаграмму М с
помощью лишь первого и третьего движений Рейдемейстера (и плоской изотопии).
Этот пример принадлежит автору.
Приложение 1. Независимость движений Рейдемейстера 287
Рис.2
Действительно, рассмотрим узлы JT,-, t = 1,..., 4 внутри L. Они расположены
в таком порядке, что между узлами Ку и Къ есть с обеих сторон нетривиальные
узлы. Покажем, что это свойство сохраняется под действием первого и третьего
движений Рейдемейстера. Действительно, при любом применении этих
движений различные узлы К{ «не вступают в контакт», таким образом, можно
выделить все четыре узла JT,- и в процессе изотопии они останутся в том же порядке
(при движении по узлу), в каком и были в начале. Однако в узле М узлы К\ и Къ
являются соседними при движении по узлу, откуда следует, что L не
переводится в М посредством движений Рейдемейстера Hi и Пз и плоской изотопии.
Пример 1.3. Рассмотрим тень стандартной диаграммы колец Борромео
и построим тривиальное зацепление L из трех компонент с такой тенью (одна
компонента лежит выше всех других, другая — ниже), см. рис. За. Обозначим
эту диаграмму через L\.
Рис.3
Так как зацепление, представимое диаграммой L\ тривиально, то у него
есть диаграмма L2, состоящая из трех непересекающихся несамопересекаю-
щихся окружностей, см. рис. 36.
288
Раздел VI. Прочее
Покажем, что диаграмма L\ не переводится в диаграмму L2 посредством
лишь первого и второго движений Рейдемейстера. Действительно, рассмотрим
произвольную плоскую диаграмму зацепления L и сопоставим ей
неупорядоченную тройку элементов из Ъг следующим образом. Определим область U,
ограничиваемую проекцией одной из трех компонент зацепления.
Зафиксируем эту компоненту I. Она делит плоскость (сферу) на клетки, которые можно
раскрасить шахматным образом. Раскрасим плоскость так, чтобы клетка,
содержащая бесконечную точку, была покрашена в белый цвет. Обозначим через U(l)
множество точек клеток, покрашенных в черный цвет, см. рис. 4.
Рис. 4. Область U заштрихована. Выделена точка пересечения в U
Посчитаем количество перекрестков, образуемых пересечением проекций
двух компонент, отличных от выбранной, находящихся внутри U, и посчитаем
его четность.
Проделаем то же для второй и для третьей компоненты. Таким образом
получим три элемента из Z2. Легко видеть, что для диаграммы Lx все эти три
элемента равны 1, а для диаграммы L2 все они равны 0.
Эта тройка чисел инвариантна относительно плоской изотопии по
построению. Покажем, что она не меняется при применении первого и второго
движений Рейдемейстера.
Легко видеть, что для первого движения Рейдемейстера, примененного
к одной компоненте зацепления Z, а также для второго движения
Рейдемейстера, примененного к двум дугам одной и той же компоненгы /, множество U(l)
меняется лишь внутри малого круга, в котором производится
соответствующее движение. Внутри этого малого круга нет проекций других компонент
зацепления. Следовательно, все три элемента из Z2 не изменяются.
В случае второго движения Рейдемейстера, которое применяется к дугам
двух разных окружностей, достаточно заметить, что появившиеся (исчезнувшие)
два перекрестка либо оба лежат в области U(l), соответствующей третьей
окружности /, либо оба не лежат в ней.
Следовательно, диаграммы Lx и L2 изотопных зацеплений не
переводятся друг в друга только преобразованиями Рейдемейстера Ql9 П2 и плоской
изотопии.
Заметим, что аналогичные утверждения встречаются в теории орнаментов,
см. гл.6 [97], а также [11, 18].
Приложение 2
Нерешенные проблемы в теории узлов
Приводим список нерешенных проблем в теории узлов.
Задачи имеют разное происхождение, почерпнуты из разных источников,
см., например, [102, 104]. Часть задач посвящена d-диаграммам,
которым мы придаем особенное значение, поскольку мы надеемся, что
методы теории d-диаграмм могут в дальнейшем сыграть значительную
роль в теории узлов.
1. Как распознать, является ли узел обратимым?
2. Пусть С(п) — число различных простых неориентированных узлов
с минимальным числом пересечений п. Как ведет себя функция
С(п) с ростом п?
3. Если некоторый узел имеет две диаграммы К+ и К-,
получающиеся друг из друга заменой одного прохода на переход, то
верно ли, что удаление этой точки приведет к распаду узла на две
компоненты?
4. Верно ли, что минимальное число перекрестков аддитивно
относительно связной суммы узлов: с(К{#К2) = с(К\) + с(К2)?
5. Существует ли нетривиальный узел, полином Джонса которого
равен единице?
В [30] показано, что если такой пример существует, то его число
перекрестков должно быть не менее восемнадцати.
6. Найти ограничение сверху на количество движений Рейдемейстера,
переводящих одну диаграмму данного узла в другую его диаграмму.
7. Найти критерий простоты узла в терминах его плоской диаграммы.
В терминах его d-диаграммы.
8. Является ли представление Бурау группы кос из четырех нитей
точным?
9. Является ли универсальный инвариант Васильева полным
инвариантом узла, т. е. верно ли, что для любых двух различных
узлов К\,К2 существует инвариант Васильева V, такой, что
V(KX) Ф V(K2)1
290
Раздел VI. Прочее
10. Верно ли, что инварианты Васильева различают обращение узла?
Иными словами, верно ли, что для каждой пары неизотопных
взаимно-обратных узлов К и К1 и инвариант Васильева v, такой,
что v(K) ф ь(К')?
И. Придумать аналог теоремы Маркова для виртуальных кос.
12. Существует ли точное представление группы виртуальных кос?
13. (Проблема Фокса.) Узел называется срезанным, если он есть
пересечение поверхности, гомеоморфной 52, вложенной в R4 и
(трехмерной) гиперплоскости. Узел называется ленточным, если он является
границей ленточного диска. Всякий ленточный узел является
срезанным.
Всякий ли срезанный узел является ленточным?
14. Описать аналог d-диаграмм для кривых, погруженных в
произвольное двумерное многообразие (то же для гауссовых диаграмм).
15. Сколько хорд нужно добавить к нереализуемой гауссовой
диаграмме, чтобы она стала реализуемой (найти разумные оценки
и построить алгоритм в терминах d-диаграмм).
16. В каждом изотопном классе зацепления существует такое,
проекция которого на подходящую плоскость имеет лишь одну точку
многократного трансверсального пересечения. Найти необходимую
и достаточную систему движений для таких диаграмм зацеплений.
17. Найти связь между диаграммами зацеплений, описанными в
предыдущем пункте, и d-диаграммами этих зацеплений.
18. Описать известные инварианты узлов в терминах диаграмм
зацеплений с единственной точкой многократного трансверсального
пересечения.
19. Придумать аналог комбинаторных формул инвариантов Васильева
узлов и зацеплений в терминах d-диаграмм.
20. Посчитать количество плоских диаграмм узлов с п перекрестками
(классов эквивалентности d-диаграмм по нулевому движению).
Литература
1. Adams С. The knot book, Freeman & Co., New York, 1994.
2. Alexander J. W. Topological invariants of knots and links, Trans. AMS. 20 (1923),
pp. 257-306.
3. Alexander J.W. A matrix knot invariant, Proc. Nat. Acad. Sci. USA 19 (1933),
pp. 222-275.
4. Alexander J. W. A lemma on systems of knotted curves, Proc. Nat. Acad. Sci.
USA 9 (1923), pp. 93-95.
5. Artin E. Theorie der Zopfe. Abh. Math. Sem. Univ. Hamburg 4 (1925), 27-72.
6. Artin E. Theory of braids, Ann. of Math (2) 48 (1947), 101-126.
7. Atiyah M. The Jones—Witten invariants of knots, Sem. Bourbaki 715 (1989-90).
8. Bigelow S. Braid groups are linear, Preprint math. GR/0005038.
9. Birman J. Braids, Links and Mapping Class Groups. Princeton, NJ: Pronceton
Univ. Press, 1974 (Ann. Math. Stud., 1982).
10. Birman /. New points of view in knot and link theory, Bull. Amer. Math. Soc.
28 (1993), pp. 253-287.
11. Bjorner A, Subspace arrangements. In: Proceedings of the First European
Congress of Mathematicians (Pfcris 1992). Boston: Birkhauser, 1993, pp. 321-370.
12. Birman /. S.y Lin X.-S. Knot Polynomials and Vassiliev's invariants, Columbia
University, preprint (1991).
13. Bar-Natan D. On the Vassiliev Knot invariants, Topology 34 (1995), pp. 423-475.
14. Bar-Natan /)., Garoufalidis S.y Rozansky L., Thurston D. Wheels, wheeling, and
the Kontsevich integral of the unknot. Preprint, 1997.
15. Bar-Natan /X, ThangL.9 Thurston D. The Kontsevich integral of the unknot, In
preparation.
16. Vassiliev homotopy string link invariants, K. of Knot Theory and its Ramif.,
1995 4 (1), pp. 13-32.
17. Burau W. Uber Zopfgruppen und gleichzeitig verdrillte Verkettungen, Abh.
Math. Sem. Univ. Hamburg, 1936, 11, pp. 179-186.
18. Bjorner A., Welker V. The homology of «k-equal» manifolds and related partition
lattices, Adv. Math., 1995, 110 (2), pp. 277-313.
19. Burde G, Zieschang #. Knots, de Gruyter, 1986.
20. Cartier P. Construction combinatoire des invariant de Vassiliev—Kontsevich des
nceuds, С R. Acad. Sci. Riris, S6r. I, Math., 1993, 316, pp. 1205-1210.
21. Chmutov S., Duzhin S. An upper bound for the number of Vassiliev knot
invariants, /. Knot Theory and its Ramifications, v. 3, 2 (1994), 141-151.
22. Chmutov £, Duzhin S. A lower bound for the number of Vassiliev knot invariants,
Topology and its Applications 92 (1999) 201-223.
23. Chmutov 5. C, Duzhin S. K, Lando S. К Vassiliev Knot Invariants I—III, Adv.
Sov. Math 21 (1994), pp. 117-147.
292
Литература
24. Chekanov Yu. Differential algebras of Legendrian Knots, Preprint 1997.
25. Conway /. H An enumeration of knots and links and some of their algebraic
properties, Computational Problems in Abstract Algebra, Pergamon Press, New
York, 1970, pp. 329-358.
26. Dehornoy P. Braids and Self-Distributivity, препринт, www.math.unicaen.fr/
~dehornoy.
27. Dehornoy P. From large cardinals to braids via distributive algebra, J. Knot
Theory Ram. 4 (1995), pp. 33-79.
28. Dehn M. Die beiden ЮееЫаШспш^еп, Math. Ann. 102 (1914), 402-413.
29. Dehn M. Uber die Topologie des dreidimensionalen Raumes, Math. Ann. 69
(1910), pp. 137-168.
30. Dasbach О. Г., Hougardy S. Does the Jones Polynomial Detect Unknottedness?
Journal of Experimental Mathematics, Vol.6, No. 1, 1997, pp. 51-56.
31. Drinfeld KG, Quantum Group, Proc. Intl. Congress Math., Berkeley, USA,
1986, pp. 789-820.
32. Epstein /)., Cannon /. Ж, Holt D. F.t Levy S. К S„ Paterson M. 5., Thurston W. P.
Word Processing in Groups, Jones and Barlett Publ., 1992.
33. Eliashberg Ya. Legendrian and transversal knot invariants in tight contact 3-ma-
nifolds // Topological methods in modern mathematics, Publish of Perish,
Houston, 1993, pp. 171-193.
34. Fomenko A, T. The Theory of Multidimensional Integrable Hamiltonian Systems
(with Arbitrary many Degrees of Freedom). Molecular Table of All Integrable
Systems with Two Degrees of Freedom, ADV. SOV. MATH. 1991. vol 6, pp. 1-35.
35. Tensor and Vector Analysis. Geometry, Mechanics and Physics, edited by
Fomenko А. Т., Manturov O.V., Trofimov V.V. Gordon and Breach Science
Publishers, 1998.
36. Fuchs /)., Tabachnikov S. Invariants of Legendrian and transverse knots in the
standard contact space, Topology, с 36, 1997, pp. 1025-1053.
37. Gauss C. F. Zur Mathematischen Theorie der electrodynamischen Wirkungen,
Werke Koningl. GeselL Wiss. Gottingen 5 (1877), s. 605.
38. Gordon G., Luecke J. Knots arc determined by their complements, /. Amer.
Math. Soc. Vol.2, 1989, pp.371-415.
39. Gussarov M,, Pblyak M., Yiro O. Finite-type invariants of Classical and Virtual
Knots, preprint October 1998 — math GT9810073.
40. Haken W. Theorie der Normalflachen, Acta Mathematicae. 105 (1961), 245-375.
41: Hemion G. The classification of knots and 3-dimensional spaces. Oxford: Oxford
Univ. Press, 1992.
42. Freyd P., Yetter &, Hoste /., Lickorish W. B. R.y Millett К. С, Ocneanu A A new
polynomial invariant of knots and links, Bull. Amer. Math. Soc. 12 (1985),
pp. 239-246.
43. Hoste /., Thistletwaite M.t Weeks J. Таблица узлов и программа KnotScape.
http://www.math.utk.edu/~ morwen
44. Jones V. F. Я A polynomial invariant for links via Neumann algebras, Bull. Amer.
v Math. Soc. 129 (1985), pp. 103-112.
Литература
293
45. Jones V. F. R. Hecke algebra representations of braid groups and link polynomials,
Annals of Mathematics. 126 (1987), pp. 335-388.
46. Jones V.F.R. On knot invariants related to some statistical mechanical models,
Pacific J. Math. 137 2 (1989), pp. 311-334.
47. Kauffinan L. H. On Knots, Annals of Math Studies, Princeton University Press,
1987.
48. Kauffinan L. H. Knots and Physics, Word Scientific, 1991.
49. Kauffinan L. H. State Models and the Jones Polynomial, Topology 26 (1987),
pp. 395-407.
50. Kauffinan L. H. Virtual Knot Theory, домашняя страница Л. Кауффмана,
http://mam.uic.edu/~kauffman.
51. Kauffinan L. H. Virtual Knots, talks at MSRI Meeting in January 1997 and AMS
meeting at University of Maryland, College Park in March 1997.
52. Kawauchi A. A survey of Knot theory, Birkhauser, 1996.
53. Thomson Ж (Lord Kelvin), Hydrodynamics, Proc. Royal. Soc. Edinburgh, 41
(1867), pp. 94-105.
54. Kalfagianni E. Finite type invariants of knots in 3-manifolds, Preprint, 1994.
55. Kneissler J. The number of primitive Vassiliev invariants up to degree twelve.
Preprint (June 1997).
56. Kontsevich M. Vassiliev's knot invariants, Adv. in Soviet Math. 16(2) (1993),
pp. 137-150.
57. Kontsevich M. Feynman diagrams and low-dimensional topology, Preprint (1992).
58. Krammer D. The braid group B4 is linear, Preprint, Basel, 1999.
59. Krammer D. Braid groups are linear, Preprint, Basel, 2000.
60. Lando S. K. Vassiliev knot invariants, Main constructions, preprint
61. Lin X.-S. Milnor link invariants are all of finite type, Columbia Univ., Preprint,
1992.
62. Lin X.-S. Finite type link invariants of 3-manifolds, Topology, 1994, 33,
pp. 45-71.
63. Le T. Q. Г., Murakami J. Representations of the category of tangles by Kontse-
vich's iterated integral, Comm. Math. Phys. 168 (1995), pp. 535-562.
64. Manturov V.O. d-Diagrams, Chord Diagrams, and Knots, Записки научных
семинаров ПОМИ 267, Геометрия и топология 5, с. 170-194.
65. Manturov О. V. Polynomial invariants of knots and links, Записки научных
семинаров ПОМИ 267, Геометрия и топология 5, с. 195-206.
66. MarkoffA. A. Uber die freie Aquivalenz der geschlossenen Zopfe, Мат. Сборник
1(1936), pp. 73-78.
67. Matveev S. V. Consturction of a complete algebraic knot invariant, Chelyabinsk
Univ. (1981), pp. 14.
68. Milnor J Link groups, Ann. math, 1954 59, pp. 177-195.
69. Milnor J., Moore J. On the structure of Hopf algebras, Ann. Math, 81 (1965),
211-264.
70. Moody J. A. The Burau representation of the braid group Bn is unfaithftil for
large n, Bull. Amer. Math. Soc, 1991, 25, pp. 379-284.
294
Литература
71. Morton Н. R. Threading knot diagrams, Math. Proc. Cambridge Phil. Soc (1986),
99, pp. 247-260,.
72. Morton H. R Problems, in Braids (Birman J., Libgober A., eds), vol. 78,
Contemporary Math., 1988, pp. 557-574.
73. Menasco W., Thistlethwaite M. A classification of alternating links, Annals of
Mathematics, Vol. 138, 1993, pp. 113-171.
74. Murasugi K. The Jones polynomial and classical conjectures in knot theory,
Topology 26 (1987), pp. 187-194.
75. Murasugi K. Jones polynomial and classical conjectures in knot theory II, Math
Proc. Cambridge Phil. Soc. 102 (1987), pp. 317-318.
76. Piunikhin S. Combinatorial expression for universal Vassiliev link invariant,
Comm. Mat. Phys., 1995, 168, pp. 1-22.
77. Przytycky J. #., Traczyk P. Invariants of Conway type, Kobe J. Math. 4 (1987),
pp. 117-139.
78. Pofyak M, Viro O. Gauss diagram formuale fot Vassiliev invariants, Int. Math
Research Notices. 1994, vol. 11, p. 445-453.
79. Reidemeister K. Knot Theory, Chelsea Publ. Co., New York, 1948.
80. Tait P. G. On Knots, Scientific paper I, pp. 273-274, Cambridge University
Press, London, 1898.
81. Thistletwaite M. A spanning tree expansion gor the Jones polynonial. Topology,
Vol.26, 1987, pp.297-309.
82. Trotter H.F. Non-invertible knots exist. Topology. Vol 2, 1964, pp. 275-280.
83. Turaev V. G. The Yang—Baxter equation and invariants of links, Inventiones
Math. (1992), pp. 527-553, Fasc. 3.
84. Turaev V. G. Faithful linear representations of the braid group, Seminaire
Bourbaki, 1999-2000,n. 878.
85. Vassiliev V. A. Cohomology of knot spaces, in Theory of Singularities and its
applications. Advances in Soviet Mathematics, vol. 1, 1990, p. 23-70.
86. Vassiliev V A. Complements of Discriminants of Smooth maps: Topology and
Applications, Revised Edition, Amer. Math. Soc, Providence, R. I., 1994.
87. Vershinin V On Homology of Virtual Braids and Burau Representation,
препринт.
88. Vogel P Representations of links by braids: A new algorithm, Comm. Math.
Helvetici 65 (1990), 104-113.
89. Weinberg N. M. Sur l'equivalence libre des tresses fermees, С R. Доклады Акад.
Наук СССР 23 (1939), с. 215-216.
90. Witten E. Physics and geometry, Proc. Intl. Congress Math., Berkeley, USA,
1986, pp. 267-303.
91. Witten E. Quantum field theory and the Jones Polynomial, Comm. Math. Phys.
121 (1989), pp. 351-399.
92. Witten E. Gauge theory, vertex models, and quantum groups, Nucl. Phys. B. 330
(1990), pp. 225-246.
93. Арнольд В. И. Особенности каустик и волновых фронтов. М.: Фазис, 1996.
$4. Атья М. Геометрия и физика узлов. М.: Мир, 1996.
Литература
295
95. Бурман Ю. М. Длинные кривые, гауссовы диаграммы и инварианты //
Мат. проев. Вып.З. 1999. С. 94-115.
96. Васильев В. А, Введение в топологию. (Библиотека студента-математика.)
М.: Фазис, 1997.
97. Васильев В, А. Топология дополнений к дискриминантам. М.: Фазис, 1999.
98. Гусаров М. Н Новая форма полинома Джонса—Конвея ориентированных
зацеплений. Зап. научн. семинаров ЛОМИ. 1991. Т. 193. геом. и топ. 1.
С. 4-9. 161.
99. Дроботухина Ю. В. Аналог полинома Джоунса для зацеплений в RP3
и обобщение теорем Кауффмана—Мурасуги // Алгебра и анализ 2 (1991).
С. 613-630.
100. Дубровин Б.А., Новиков СП., Фоменко А, Г. Современная геометрия:
Методы и приложения. Т. 1, 2. 5-е изд., испр. М.: Эдиториал УРСС, 2001.
101. Дринфельд В. Г. Алгебры Хопфа и квантовое уравнения Янга—Бакстера //
Доклады АН СССР 32. 1. 1985.
102. Дужин С. В, у Чмутов С. 2?. Узлы и их инварианты. Мат. проев. 1999. Вып. 3.
С. 59-93.
[03. Кассель К. Квантовые группы. М.: Фазис, 1999.
104. Кроуэлл Р., Фокс Р. Введение в теорию узлов. М.: Мир, 1967.
105. Мантуров В. 0. Бифуркации, атомы и узлы // Вестник МГУ. Сер. матем.
2000. N. 1.С. 3-8.
[06. Мантуров В. О. Атомы, высотные атомы, хордовые диаграммы и
узлы. Перечисление атомов малой сложности с использованием языка
Mathematica 3.0. // Топологические методы в теории Гамилътоновых
Систем. М., 1998. С. 203-212.
107. Мантуров В, 0. Скобочная полугруппа узлов // Мат. заметки. 2000. Т. 67,
вып. 4. С. 549-562.
108. Мантуров 0. В. Мультипликативный интеграл // Итоги Науки. Т. 22.
С. 167-215.
09. Мантуров О. В. Элементы тензорного исчисления. М.: Просвещение, 1992.
10. Мантуров О. В. Курс высшей математики. М.: Высшая школа, 1991.
11. Мантуров О. В, Однородные пространства и инвариантные тензоры //
Итоги науки. Проблемы геометрии. Т. 18. С. 105-142.
12. Мантуров 0. А Алгебры с неприводимой группой автоморфизмов // ДАН
СССР. Т. 281. No. 5. С. 1048-1051.
13. Мантуров О.В., Мартынюк АН Об одном алгоритме в теории
мультипликативного интеграла // Известия ВУЗов. Математика. N. 5. С. 26-33.
14. Мантуров О. В., Матвеев Н. М. Курс высшей математики. М.: Высшая
школа, 1986.
15. Марков А. А. Основы алгебраической теории кос // Труды МИАН
Т. 16 (1945). С. 1-54.
16. Матвеев С. В. Классификация достаточно больших трехмерных
многообразий // УМН. Т. 52, вып. 5. 1997. С. 147-174.
17. Матвеев С. В. Преобразования специальных спайнов и гипотеза Зимана //
Известия АН СССР 31:2 (1988). С. 423-434.
296
Литература
118. Матвеев С. В. Дистрибутивные группоиды в теории узлов // Мат. сборник.
47(1984). С. 73-83.
119. Матвеев СВ., Фоменко А. Т. Алгоритмические и компьютерные методы
в трехмерной топологии. Изд. МГУ, 1991.
120. Онищик А. Л. Хопфа Алегбра // Математическая Энциклопедия. Т. 5.
М., 1985.
121. Прасолов В. В. Поверхность Зейферта // Мат. просвещение. 3 серия, вып. 3
1999.
122. Прасолов В. В. Наглядная топология. Изд. МЦНМО, 1995.
123. Прасолов В. В., Сосинский А. Б. Узлы, зацепления, косы и трехмерные
многообразия. Изд. МЦНМО, 1997.
124. Тюрина С. Д. О формулах типа Ланна и Виро—Поляка для инвариантов
конечного порядка // Мат. Заметки. 1999. Т. 64, вып. 6.
125. Тюрина С. Д. Диаграммные формулы типа Виро—Поляка для инвариантов
конечного порядка // Успехи матем. наук. 1999. Т. 54, вып. 3. С. 187-188.
126. Фоменко А. Т. Наглядная геометрия и топология. Математические образы
в реальном мире. М.: Изд. МГУ, 1992.
127. Фоменко А. Г., Фукс Д. Б. Курс гомотопической топологии. М.: Наука, 1989.
128. Фарбер М. Ж, Чернавский А. В. Узлов теория // Математическая
Энциклопедия. Т. 5. М., 1985.
129. Цишанг X., Чернавский А. В. Геометрическая топология многообразий //
Алгебра. Топология. Геометрия. 1962 (Итоги науки и техники ВИНИТИ
РАН). М., 1963. С. 219-261.
130. Чернавский А. В. Геометрическая топология многообразий // Алгебра.
Топология. 1962 (Итоги науки и техники ВИНИТИ РАН). М., 1963. С. 161-187.
131. Чернавский А. 2*. Кос теория // Математическая Энциклопедия. Т. 3.
М., 1985.
Предметный указатель
Алгебра Поляка 265
— стрелочных диаграмм 264
— Хопфа 166
Алгоритм Вожеля 107
— Деорнуа 114
Атом 207
— высотный 208
— ориентируемый 207
Вершина атома 207
— распадения 69
Виртуального зацепления диаграмма
250
Гипотеза Васильева 197
— Тейта вторая (Tait flyping
conjecture) 73
первая 70
Гнездо 108, 126
Голономия формы 188
Граф Кэли 127
Группа кос из m нитей 92
крашеных 92
Дальняя коммутативность 142
Движение Рейдемейстера Q4> ^5 277
Движения Рейдемейстера 16
виртуальные 251
Диаграмма, обвивающаяся вокруг
точки 105
— виртуальной косы 268
— Гаусса 199
реализуемая 221
— косы 94
— плоская 9
сингулярного узла 145
сложность 9
— полувиртуальная 265
Длина полинома Джонса 67
Дуга 33
Дуговая диаграмма 166
Замыкание виртуальной косы 273
— косы 101
Зацепление 10
— виртуальное 252
компонента 252
— длинное 49
— изотопия 10
— компонента 10
— ориентированное 10
— сингулярное 145
— тривиальное 10
— Уайтхеда 10
— Хопфа 10
Зацепление-коса 128
— просто-Марковски-эквивалент-
ные 134
Зеркальное отражение 9
Изоморфизм атомов 207
Изотопия виртуальных кос 268
Инвариант Васильева конечного
порядка 144
нечетный 201
символ 147
универсальный 183
четный 201
— полный 40, 144
Интеграл Концевича 183
предварительный 178
— мультипликативный 188
Китайская диаграмма 168
Клюв 280
Кольца Борромео 10
Комбинаторные формулы 197
Конфигурационное пространство 92
Копроизведение китайской
диаграммы 184
— хордовой диаграммы 172
Коса из m нитей 91
— изотопия 94
— квазиторическая 244
298
Предметный указатель
— крашеная 92
— утолщенная 99
Косы гомотопия 92
Коэффициент зацепления 33
Кривизна связности 187
Модуль Васильева 198
Обход 71
Окружность Зейферта 21
Остов атома 207
Ось косы 128
Перекресток 8
— полувиртуальный 262
Перестройки
Фукса—Табачникова 281
Переход 8
Плоская форма 188
Поверхность Зейферта 21
Полином HOMFLY 73
— Александера 79
— Джонса 60
виртуальных зацеплений 259
— — от двух переменных 73
— Дроботухиной 278
— Кауфмана 59
— Конвея 55
Полукубическая точка возврата 280
Правильная двухскобочная
структура 226
— четырехскобочная структура 240
Представление Бурау 103
группы виртуальных кос 275
— Крамера—Бигелова 104
Примитивный элемент 174
Проективное пространство RP3 276
Произведение кос 92
Производная инварианта 146
Проход 8
Прошивание 128
Разрешение двойной точки 145
Редукция косы 125
Род атома 207
— узла 24
Самодистрибутивность левая 116
свободно-редуцированое слово 120
Связка 196
Связная сумма 19
Связность 187
— Книжника—Замолодчикова 187
Система весов 177
— переходов 130
Скручивание Дена 100
Сложность атома 207
Соотношение Васильева 146
— локальное 234
— типа Конвея 47
Соотношения Артина 93
Состояние 57
— для диаграммы виртуального узла
259
Стрелочная диаграмма 264
Стрелочно-хордовая диаграмма 200
Структура А 208
-В 208
Таблица узлов 60
Теорема Ван-Кампена 42
— Васильева—Концевича 177
— Маркова 134
— об атомах и узлах 211
Тройка Конвея 47
Трюк Александера 106
Узел 7
— восьмерка 9
— диаграмма восходящая 48
— дикий 15
— длинный 49
— зеркальный 9
— изотопия 8
— инварианты 8
— Лежандров 281
— ленточный 290
— обратимый 19
— ориентированный 10
— плоская изотопия 16
— полигональный 15
— простой 21
— ручной 15
— сингулярный 145
— срезанный 290
Предметный указатель
299
— тривиальный 9
— трилистник 9
левый 10
правый 10
Универсальный инвариант
виртуальных узлов 266
Уравнение Янга—Бакстера 142
квантовое 143
Усеченная алгебра 266
Формула Концевича 176
Фронт 280
Фундаментальная группа 39
— — дополнения к виртуальному
зацеплению 254
Функция Морса простая 178
Хордовая диаграмма 148, 149
Число Бенеккена 284
— Маслова 283
число распутывания 164
Эквивалентность лежандрова 282
1Т-соотношение 159
4Т-соотношение 160
writhe 58
i -ручка 124
d-диаграмма 70, 71, 206, 213
— меченая 218
— связная 71
— с тяжелыми хордами 239
LD -квазигруппа 118 ./
LD -система 116
Об авторе
МАНТУРОВ
Василий Олегович
Родился в Москве в 1979 году.
Окончил Независимый московский
университет в 1999 г., затем в 2000 г. — механико-
математический факультет МГУ. Аспирант
МГУ с 2000 года.
С 1999 года читает курсы и ведет
семинары на кафедре дифференциальной геометрии
и приложений МГУ.
Автор более десяти научных работ;
участник международных конференций, в том
числе ICM'98, Берлин.
Пленарный докладчик на конференции
памяти Г.Ф.Лаптева (Москва, 1999).
Основные научные интересы: теория узлов, теория атомов
(Фоменко), маломерная топология, группы и алгебры Ли, комбинаторика,
минимальные сети.
Оглавление
Предисловие 5
Раздел I.
Узлы, зацепления и полиномиальные инварианты 7
Лекция О
Введение. Основные определения 7
Лекция 1
Движения Рейдемейстера. Арифметика узлов 15
§ 1. Полигональные узлы и движения Рейдемейстера 15
§ 2. Арифметика узлов и поверхности Зейферта 19
Лекция 2
Торические узлы и зацепления.
Простейшие инварианты узлов и зацеплений 27
§ 1. Торические узлы 27
§ 2. Простейшие инварианты узлов и зацеплений 32
Лекция 3
Фундаментальная группа 36
§ 1. Отступление. Примеры развязывания узлов 36
§ 2. Фундаментальная группа дополнения как инвариант узла 39
Лекция 4
Полиномы Конвея и Джонса 47
§ 1. Полином Конвея 47
§ 2. Полином Джонса 55
§ 3. Таблица узлов 60
Лекция 5
Свойства полинома Джонса. Полиномиальные инварианты 63
§ 1. Свойства полинома Джонса 63
§2. Другие полиномы, основанные на соотношениях типа Конвея ...... 73
§ 3. Полином Кауфмана от двух переменных 74
Лекция 6
Полином Александера 76
Раздел II. Теория кос 91
Лекция 7
Группы кос и их представления 91
§ 1. Четыре определения группы кос 91
1.1. Геометрическое определение 91
1.2. Топологическое определение 92
1.3. Алгебро-геометрическое определение 93
302
Оглавление
1.4. Алгебраическое определение 93
1.5. Эквивалентность четырех определений группы кос 93
§ 2. Крашеные косы 97
2.1. Группы крашеных кос 98
§3. Представление Бурау 102
§4. Представление Крамера—Бигелова 103
Лекция 8
Теорема Александера и алгоритм Вожеля 105
§ 1. Теорема Александера 105
§ 2. Алгоритм Вожеля 107
Лекция 9
Алгоритм Деорнуа распознавания изотопности кос 114
Лекция 10
Теорема Маркова. Уравнение Янга—Бакстера 128
§ 1. Теорема Маркова 128
§ 2. Уравнения Янга—Бакстера, группы кос и инварианты узлов 142
Раздел III. Инварианты Васильева 144
Лекция 11
Определение и основные свойства инвариантов Васильева 144
§ 1. Сингулярные узлы и определение инвариантов Васильева 144
§ 2. Инварианты порядков 0 и 1 147
§3. Примеры инвариантов старших порядков 150
Лекция 12
Инварианты Васильева и полиномиальные инварианты 153
§ 1. Символы инвариантов, происходящих от полинома Конвея 153
§ 2. Выражение полиномиальных инвариантов
через инварианты Васильева 155
§ 3. Пример инварианта, не являющегося инвариантом
конечного порядка 164
Лекция 13
Алгебра хордовых диаграмм 166
§ 1. Структура Алгебры Хопфа на Ле и j£ 166
§ 2. Таблица размерностей пространств хордовых диаграмм 176
Лекция 14
Формулировка теоремы Васильева—Концевича. Интеграл Концевича .... 177
§ 1. Предварительный интеграл Концевича 177
§2. Интеграл от оо и нормировка 181
Лекция 15
Интеграл Концевича — универсальный инвариант узлов 186
Лекция 16
Комбинаторные формулы для вычисления инвариантов Васильева 197
§ 1. Модуль Васильева 197
§ 2. комбинаторные формулы Ланна 199
§3. Комбинаторные формулы Виро—Поляка 201
Оглавление
303
Раздел IV. d-Дшграммы 206
Лекция 17
Атомы и высотные атомы. Основные определения 206
§ 1. Атомы и высотные атомы. Критерий высотности .. . 206
§2. Теорема об атомах и узлах 210
Лекция 18
Атомы и d-диаграммы 216
§ 1. Кодирование узлов d-диаграммами 216
§2. d-диаграммы, хордовые диаграммы. Реализуемость 221
Лекция 19
Скобочная полугруппа узлов 226
Лекция 20
d-диаграммы, сингулярные узлы и алгебра хордовых диаграмм 239
§ 1. d-диаграммы и сингулярные узлы 239
§ 2. Квазиторические косы 244
Раздел V. Виртуальные узлы 250
Лекция 21
Виртуальные узлы и зацепления и их простейшие инварианты 250
Лекция 22
Гауссовы диаграммы и инварианты конечного порядка виртуальных узлов . 260
Лекция 23
Виртуальные косы 268
§ 1. Основные определения 268
§ 2. Представление Бурау 275
Раздел VI. Прочее 276
Лекция 24
Узлы в RP3 и лежандровы узлы 276
§ 1. Узлы в RP3 276
§ 2. Фронты и лежандровы узлы 279
Приложения 286
1. Независимость движений Рейдемейстера. , 286
2. Нерешенные проблемы в теории узлов 289
Литература 291
Предметный указатель 297
Об авторе 300