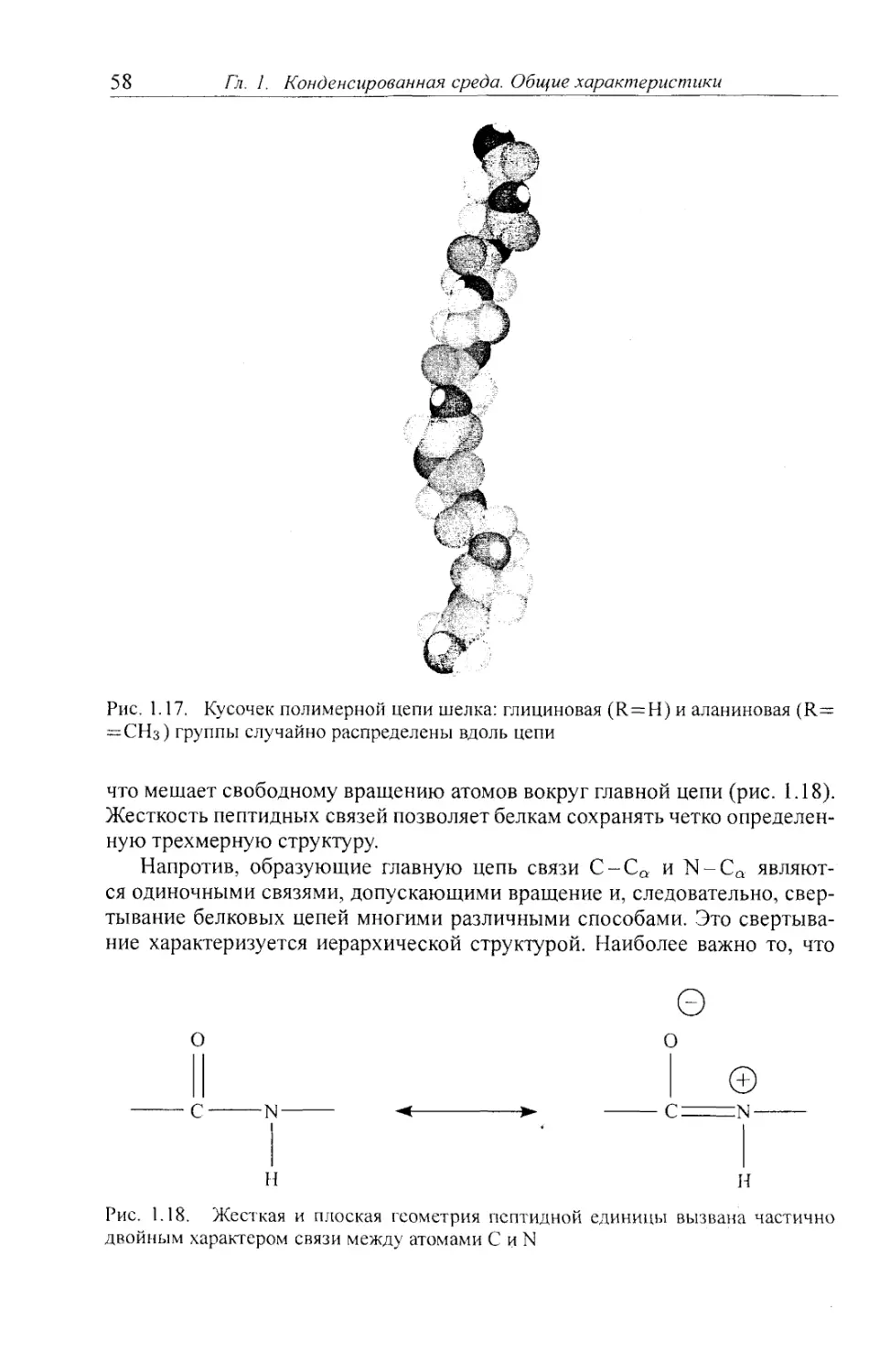
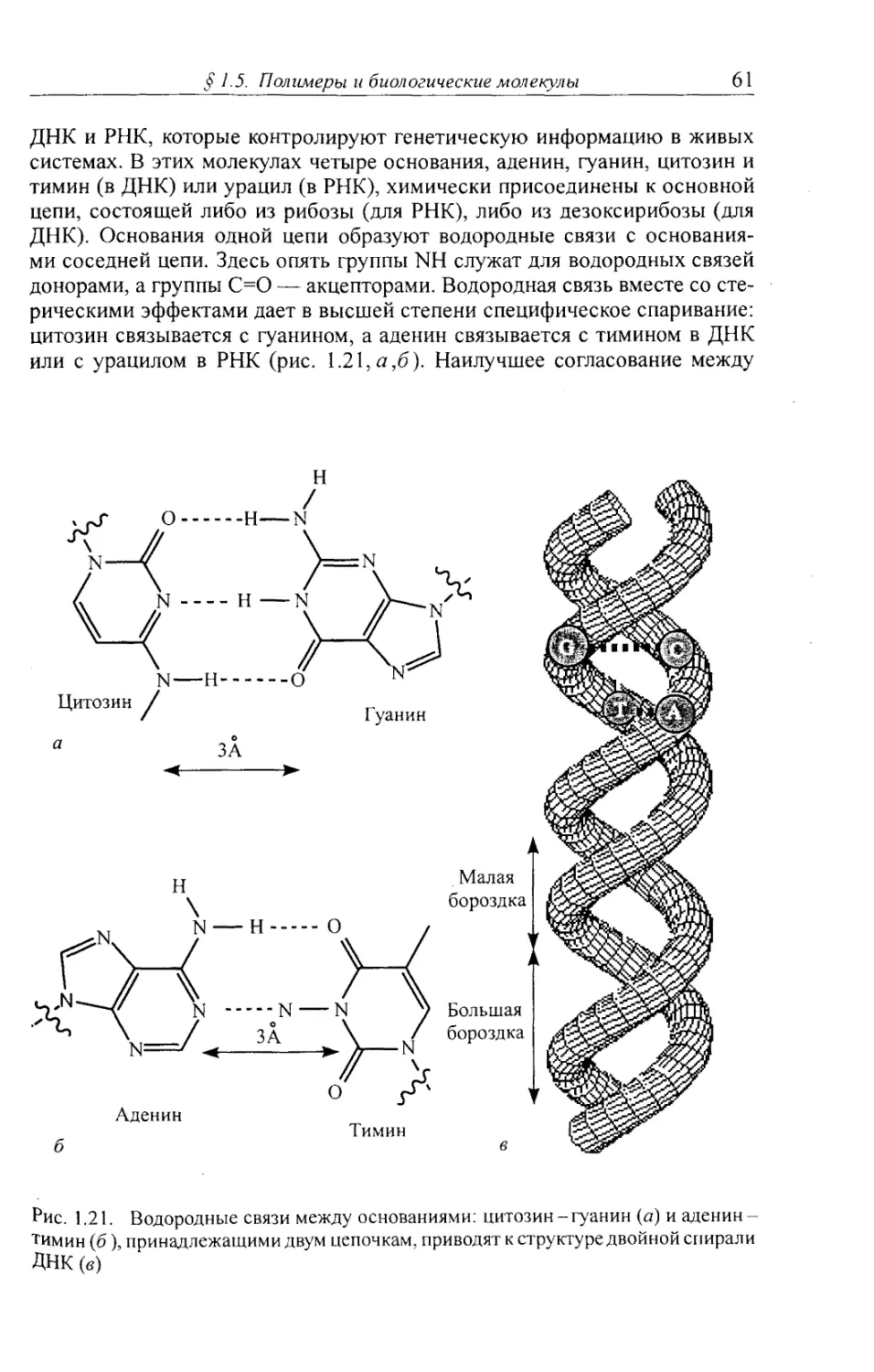
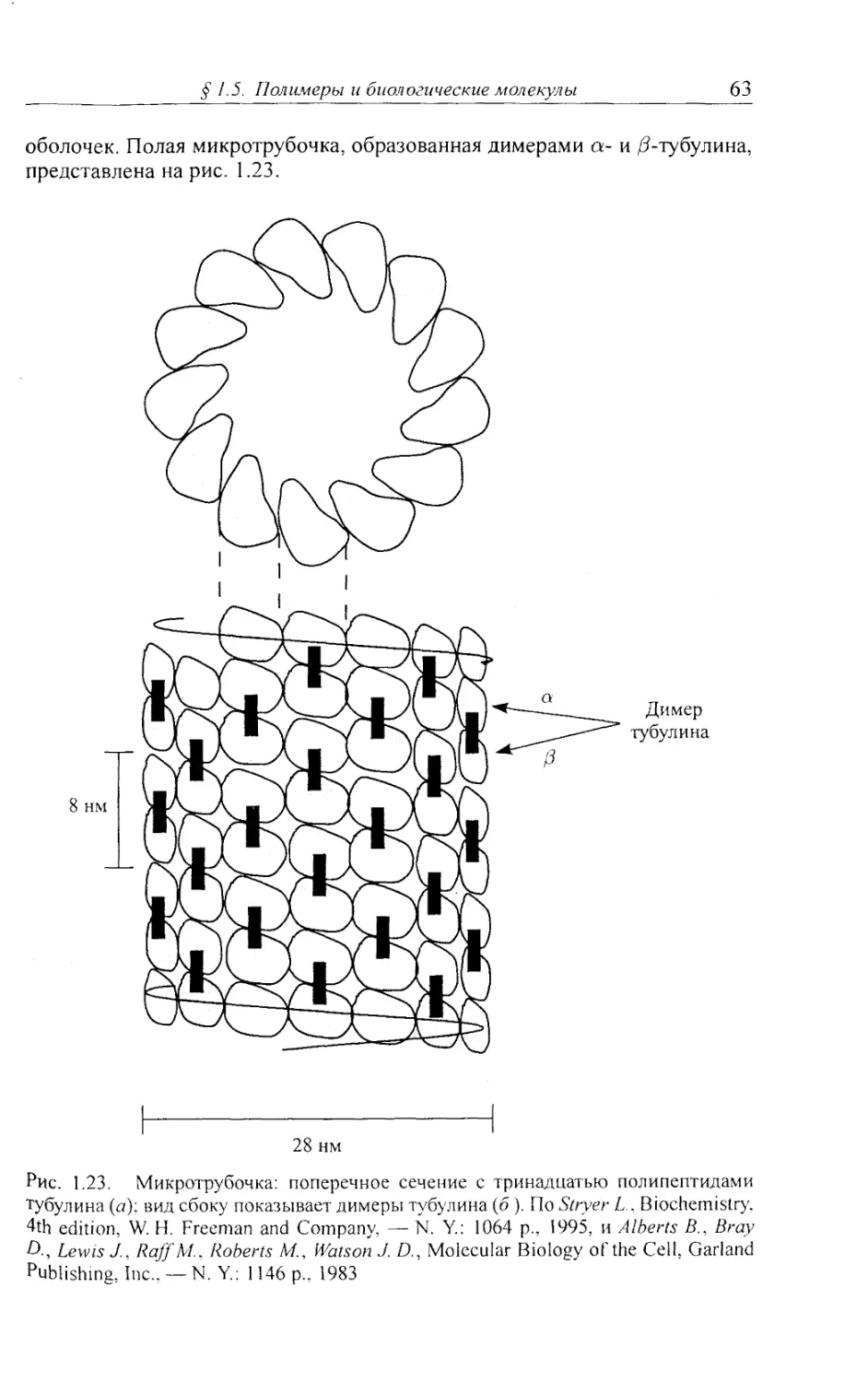
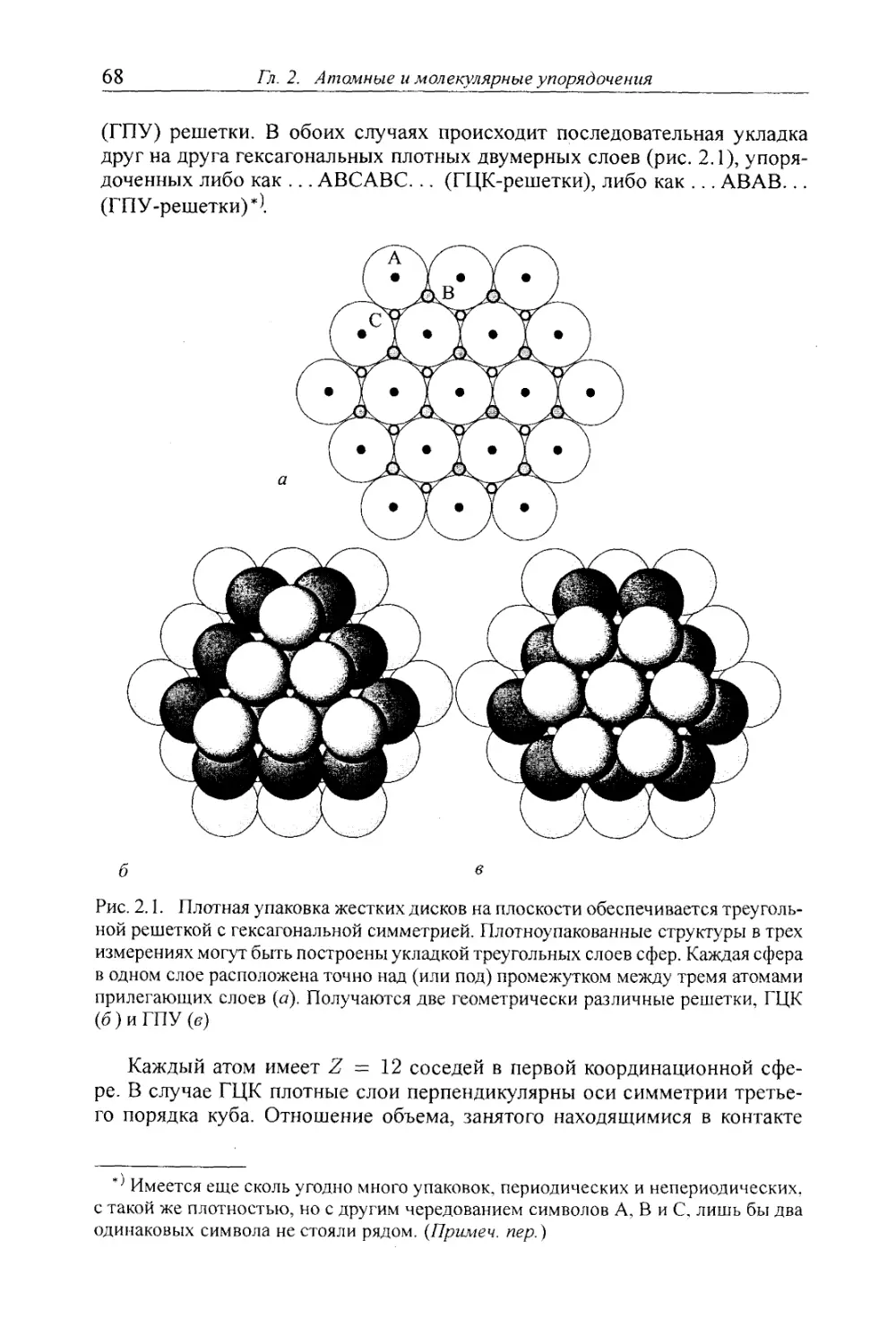
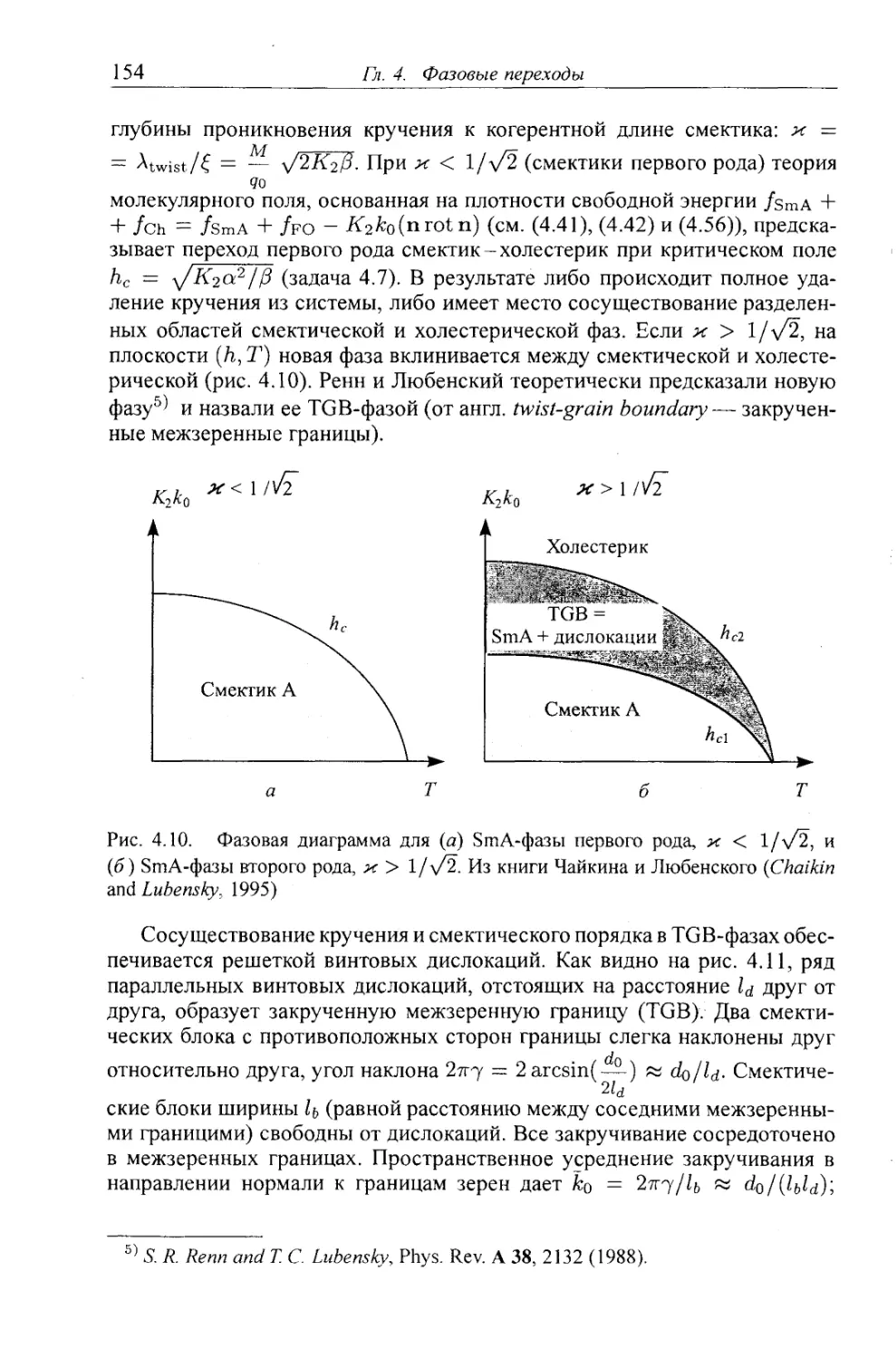
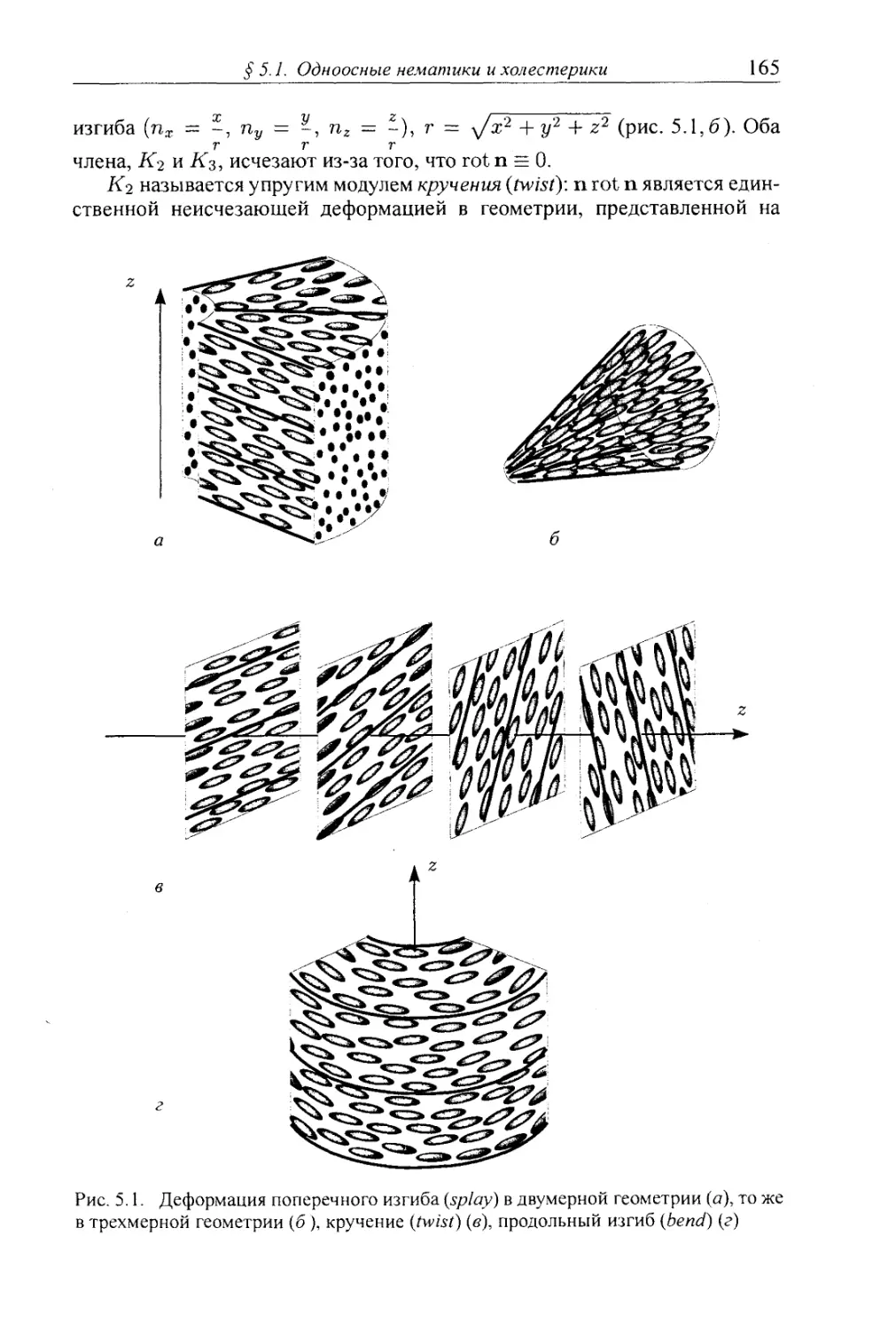
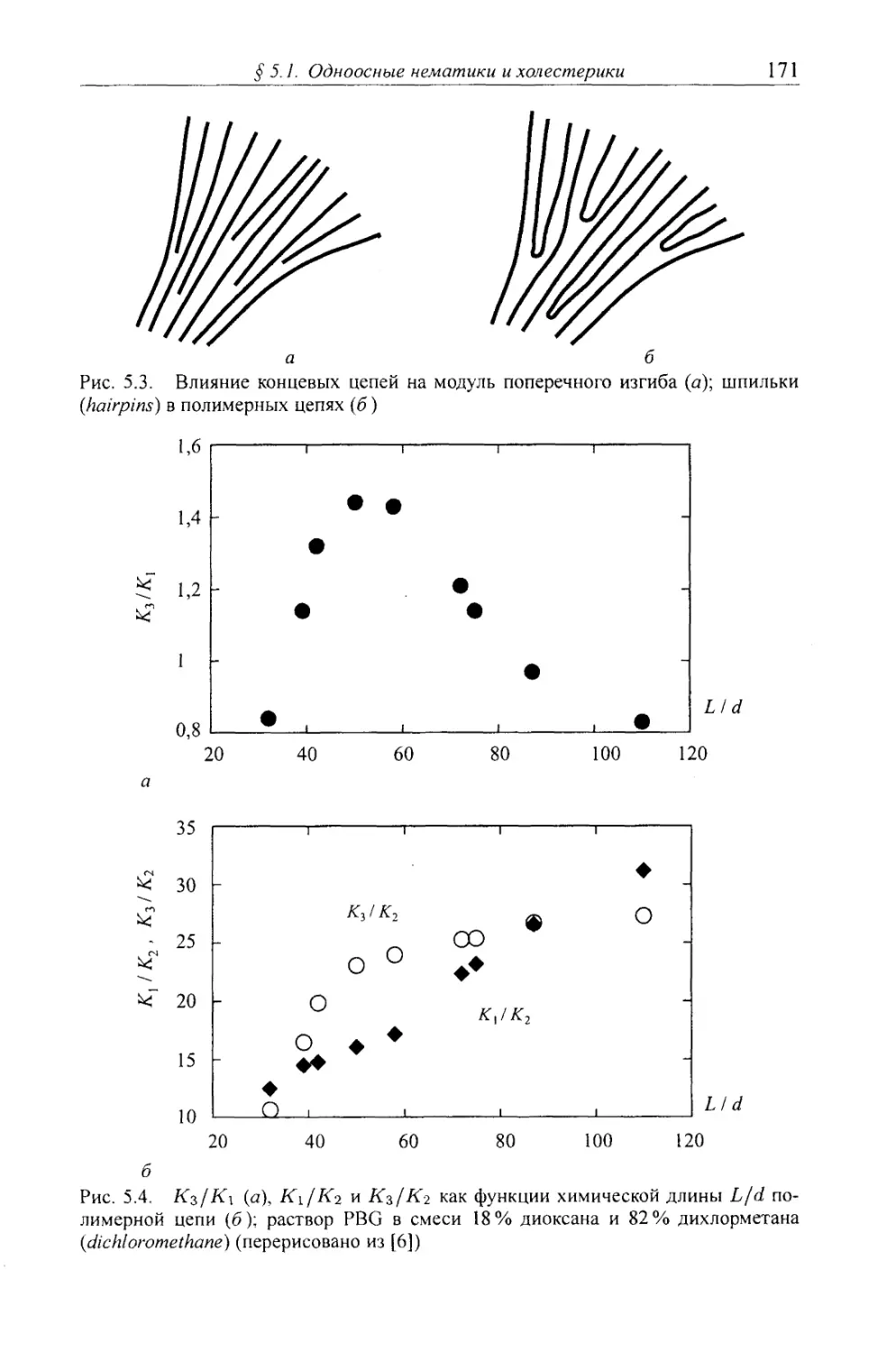
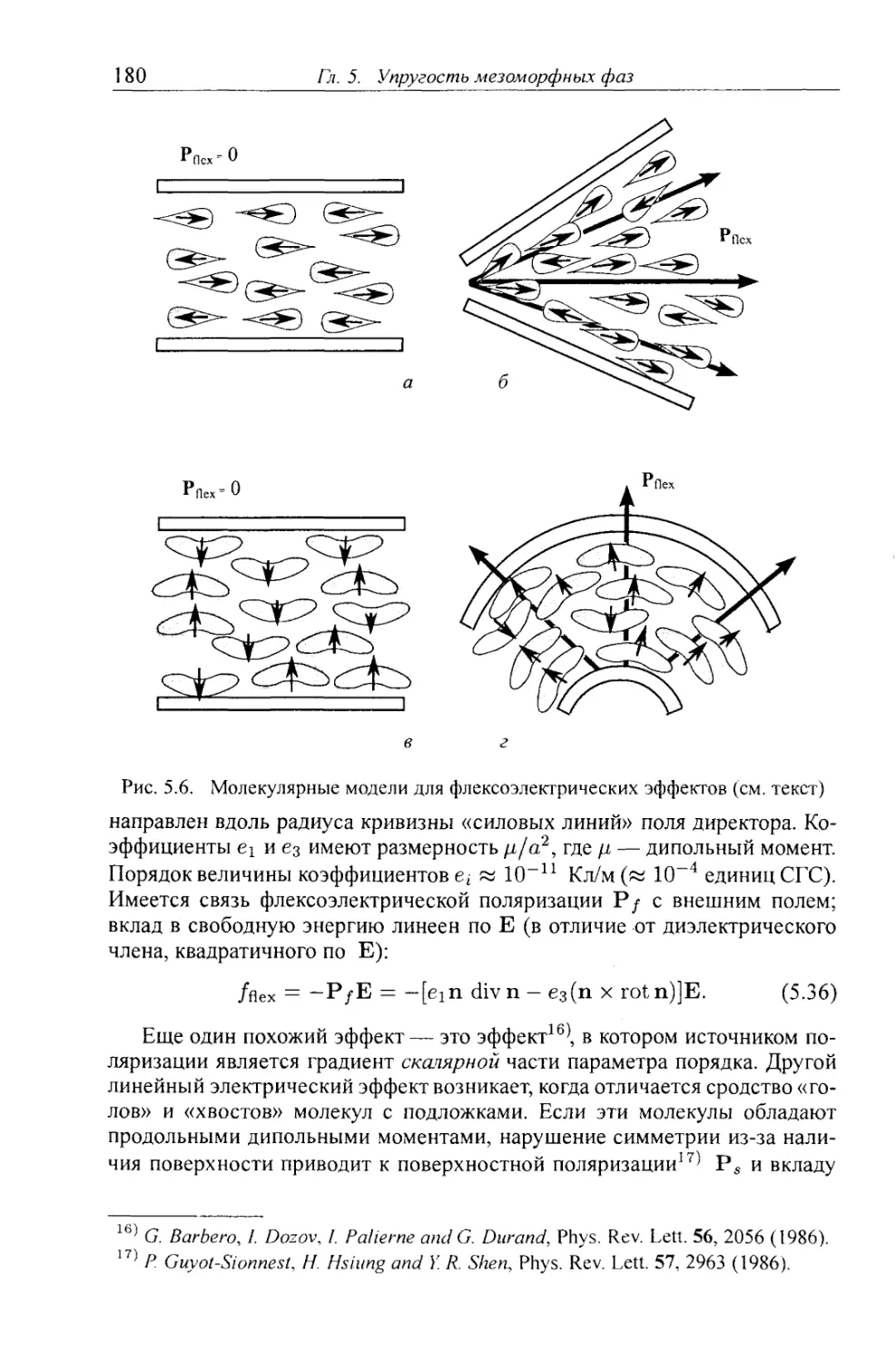
Автор: Клеман М. Лавриентович О.Д.
Теги: физика конденсированного состояния (жидкое и твердое состояние) свойства и структура молекулярных систем кристаллография физика химия биология кристаллы
ISBN: 978-5-9221-0699-3
Год: 2007
Maurice Kleman
Oleg D. Lavrentovich
SOFT MATTER
PHYSICS
AN INTRODUCTION
Foreword by J. Friedel
With 256 Illustrations, 4 in Full Color
Springer
2003
М. Клеман
О. Д. Лаврентович
ОСНОВЫ ФИЗИКИ
ЧАСТИЧНО
УПОРЯДОЧЕННЫХ
PPFTT
\^/ х I ■ 7 I
ЖИДКИЕ КРИСТАЛЛЫ, коллоиды,
ФРАКТАЛЬНЫЕ СТРУКТУРЫ, ПОЛИМЕРЫ
И БИОЛОГИЧЕСКИЕ ОБЪЕКТЫ
Перевод с английского
Е.Б. Логинова, Б.И. Островского,
Б.В. Петухова, В А. Чижикова
при участии и под редакцией
С Л. Пикина и В.Е. Дмитриенко
МОСКВА
ФИЗМАТЛИТ
2007
УДК 538.9+539.2+548 Издание осуществлено при поддержке
ББК 22.37 Р и Российского фонда фундаментальных
К 48 " * исследований по проекту 04-02-30024д
Клеман М., Лаврентович О. Д. Основы физики частично упо¬
рядоченных сред: жидкие кристаллы, коллоиды, фрактальные струк¬
туры, полимеры и биологические объекты / Пер. с англ. под ред.
С. А Пикина, В. Е. Дмитриенко. — М.: ФИЗМАТЛИТ, 2007. — 680 с. —
ISBN 978-5-9221-0699-3.
Систематически и доступно излагается одно из актуальных направлений
развития современной науки — физика частично упорядоченных сред, легко
подвергающихся изменениям под влиянием сравнительно слабых внешних
воздействий. Такие среды обычно называют «мягкой материей» (soft matter);
сейчас все знают об использовании таких материалов, например, жидких
кристаллов в дисплеях телефонов и компьютеров. Большое внимание уделяется
экспериментальным фактам, составляющим фундамент этой области естество¬
знания, которая в свою очередь лежит в основе понимания молекулярного
и надмолекулярного устройства нынешних и будущих высокотехнологичных
материалов. По сравнению с другими областями физики эксперименты здесь
не столь дорогостоящие и в большинстве случаев доступны даже для учеб¬
ных лабораторий. Изложение теории и эксперимента хорошо иллюстрировано
и сопровождается упражнениями.
Для физиков, биологов, химиков и инженеров — научных работников,
студентов и аспирантов.
В оформлении обложки использована первая абстрактная акварель Васи¬
лия Кандинского (1910) из собрания Музея современного искусства Центра
Помпиду.
Ил. 256.
ISBN 0-387-95267 5 (англ.) Springer-Verlag New York, Inc., 2003
ISBN 978-5-9221-0699-3 (русск.) © ФИЗМАТЛИТ, 2007
ОГЛАВЛЕНИЕ
Предисловие редакторов перевода 12
Предисловие Жака Фриделя 13
От редактора серии. Частично упорядоченные системы 19
Предисловие. Что такое «мягкая» материя. Цель этой книги 20
Таблица констант, перевод единиц СИ в СГС, символы соотношений ... 24
ГЛАВА 1. Конденсированная среда: общие характеристики, хи¬
мические связи и взаимодействие частиц 25
§1.1. Энтропия в неупорядоченных системах 25
§1.2. Центральные и направленные силы между атомами 27
1.2Л. Металлическая связь 27
1.2.2. Связи, образованные флуктуирующими диполями 28
1.2.3. Ковалентная связь 29
1.2.4. Ионная связь 29
1.2.5. От ионной связи к ковалентной связи в кристаллах 31
§1.3. Силы между молекулами 31
1.3.1. Электростатическая связь в диэлектрической среде 31
1.3.2. Электрические диполи 32
1.3.3. Индуцированные диполи, поляризуемость 35
1.3.4. Силы отталкивания 38
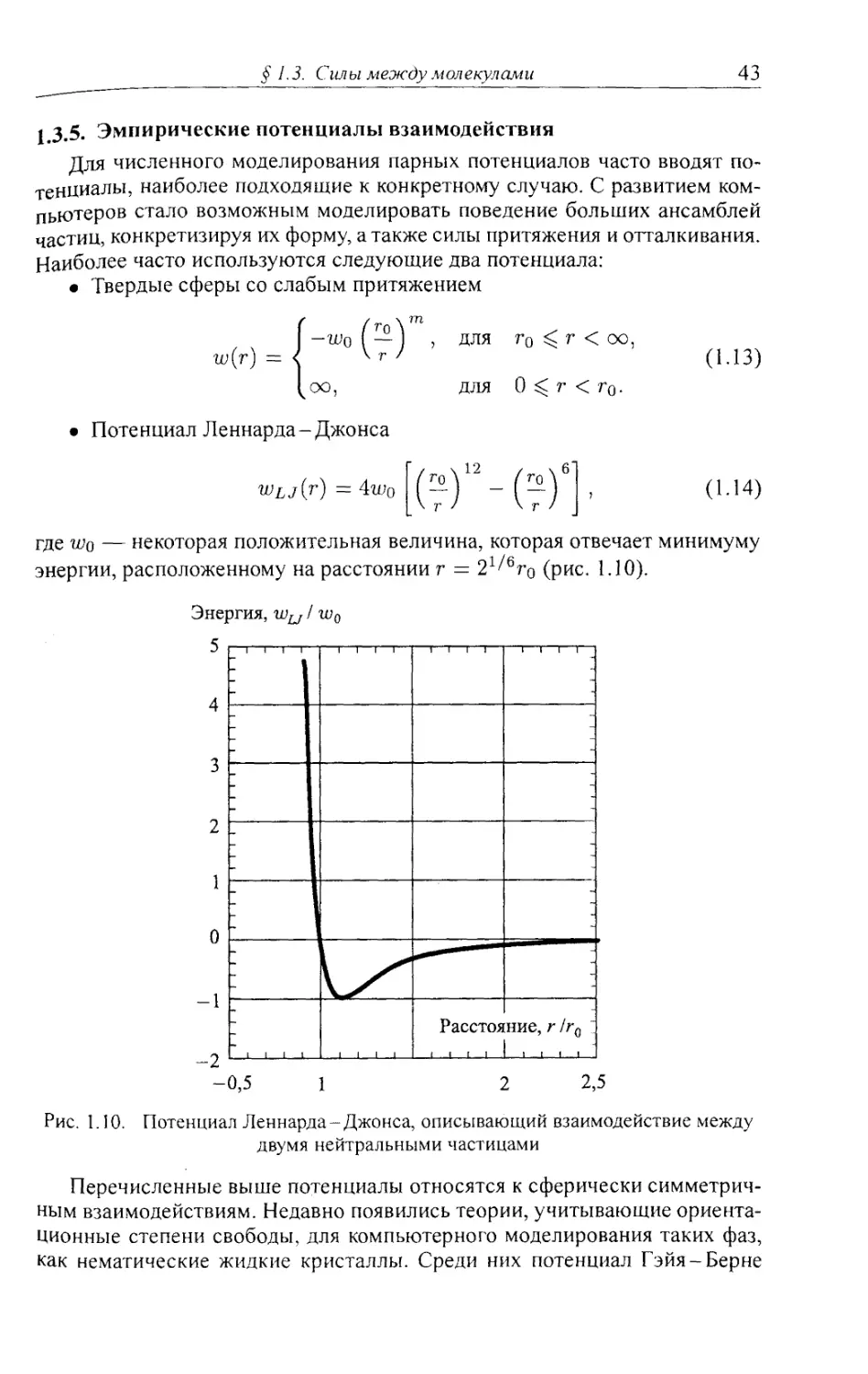
1.3.5. Эмпирические потенциалы взаимодействия 43
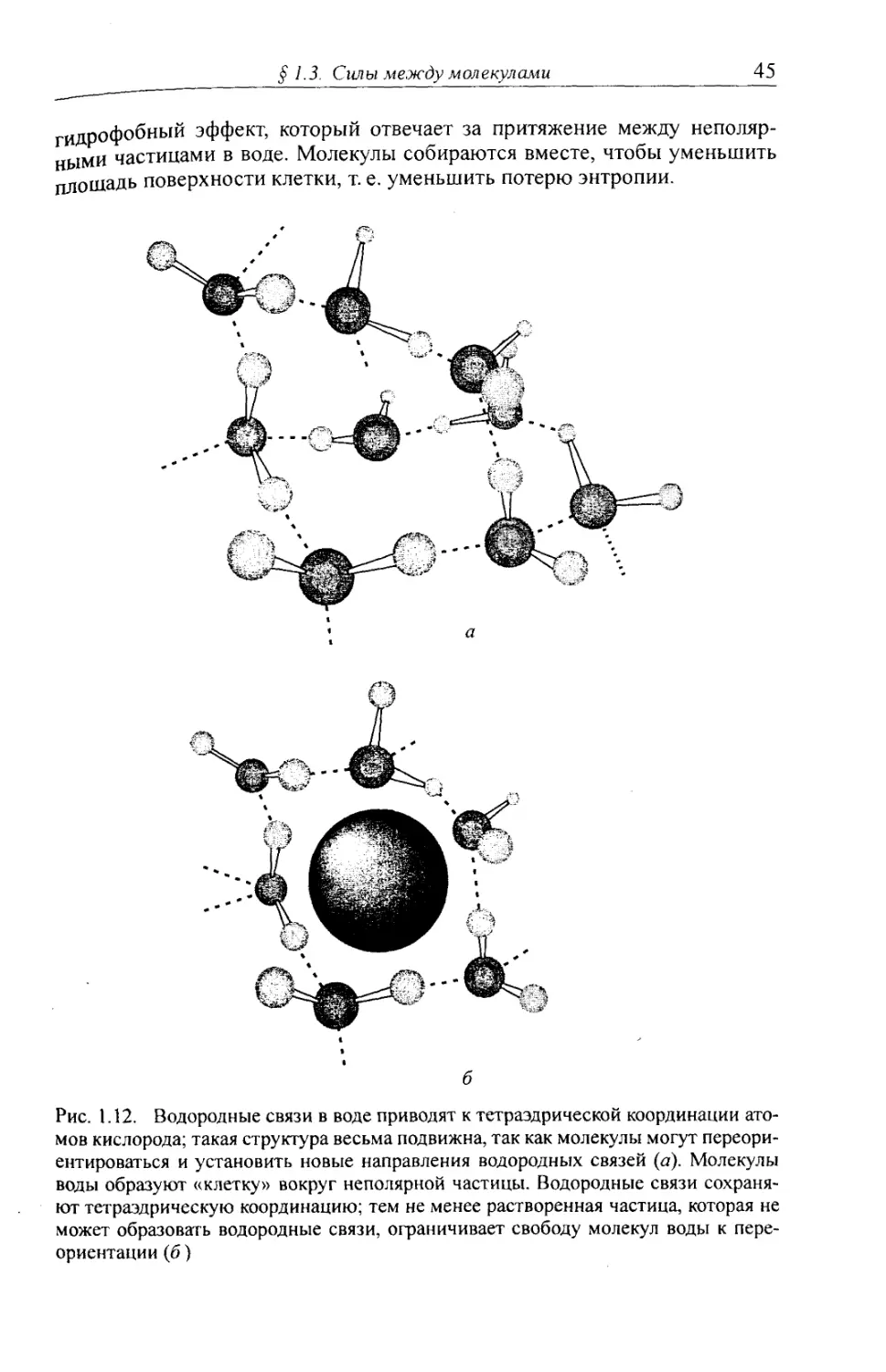
1.3.6. Вода, водородная связь. Гидрофильный и гидрофобный эффекты . 44
§ 1.4. Силы Ван-дер-Ваальса между макроскопическими частицами . 46
1.4.1. Парное суммирование молекулярных сил; константа Гамакера ... 46
1.4.2. Эффекты запаздывания 47
1.4.3. Взаимодействие Лондона в среде, теория Лифшица 51
1.4.4. Взаимодействия Казимира 52
§ 1.5. Полимеры и биологические молекулы 53
1.5.1. Синтетические полимеры 53
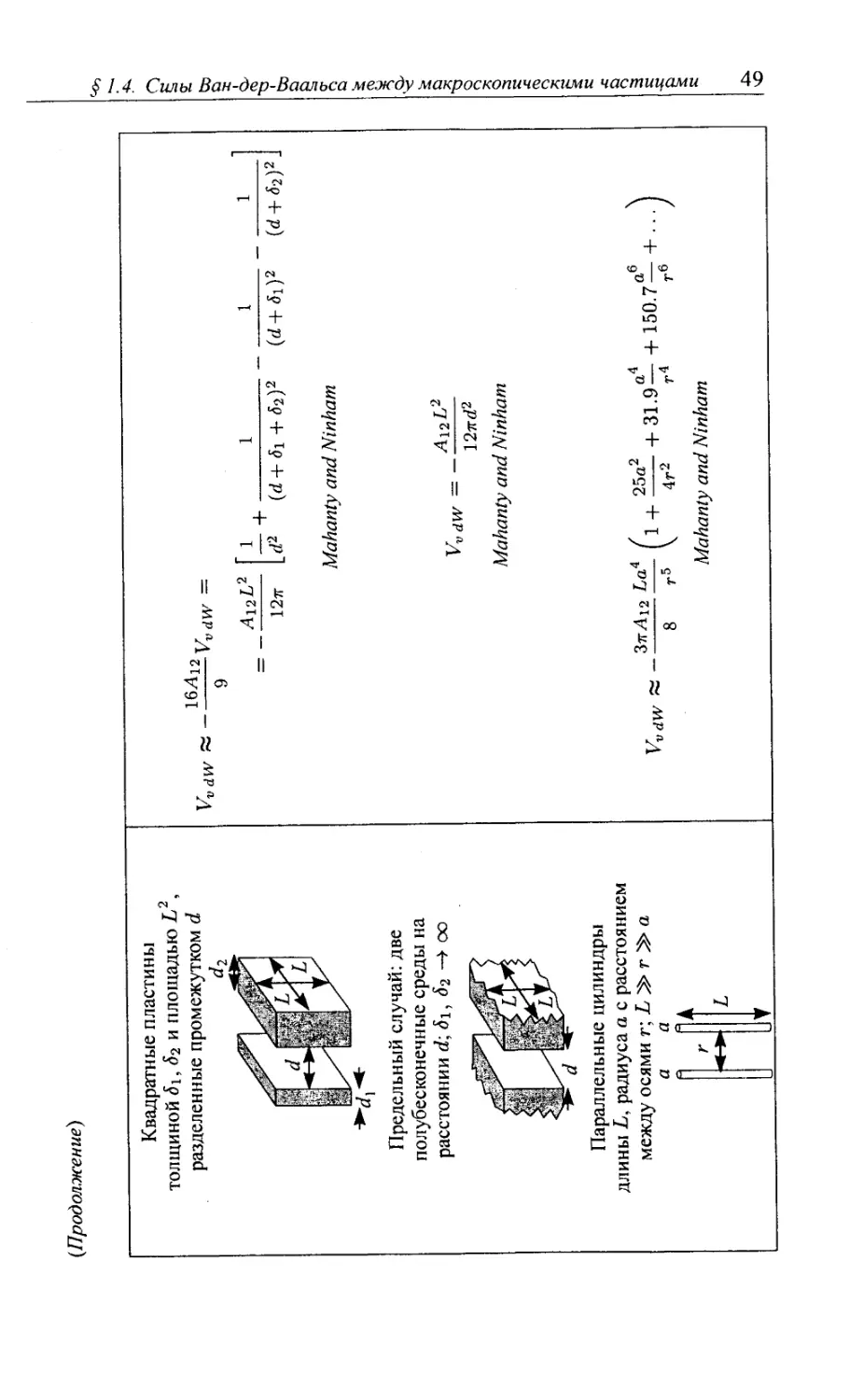
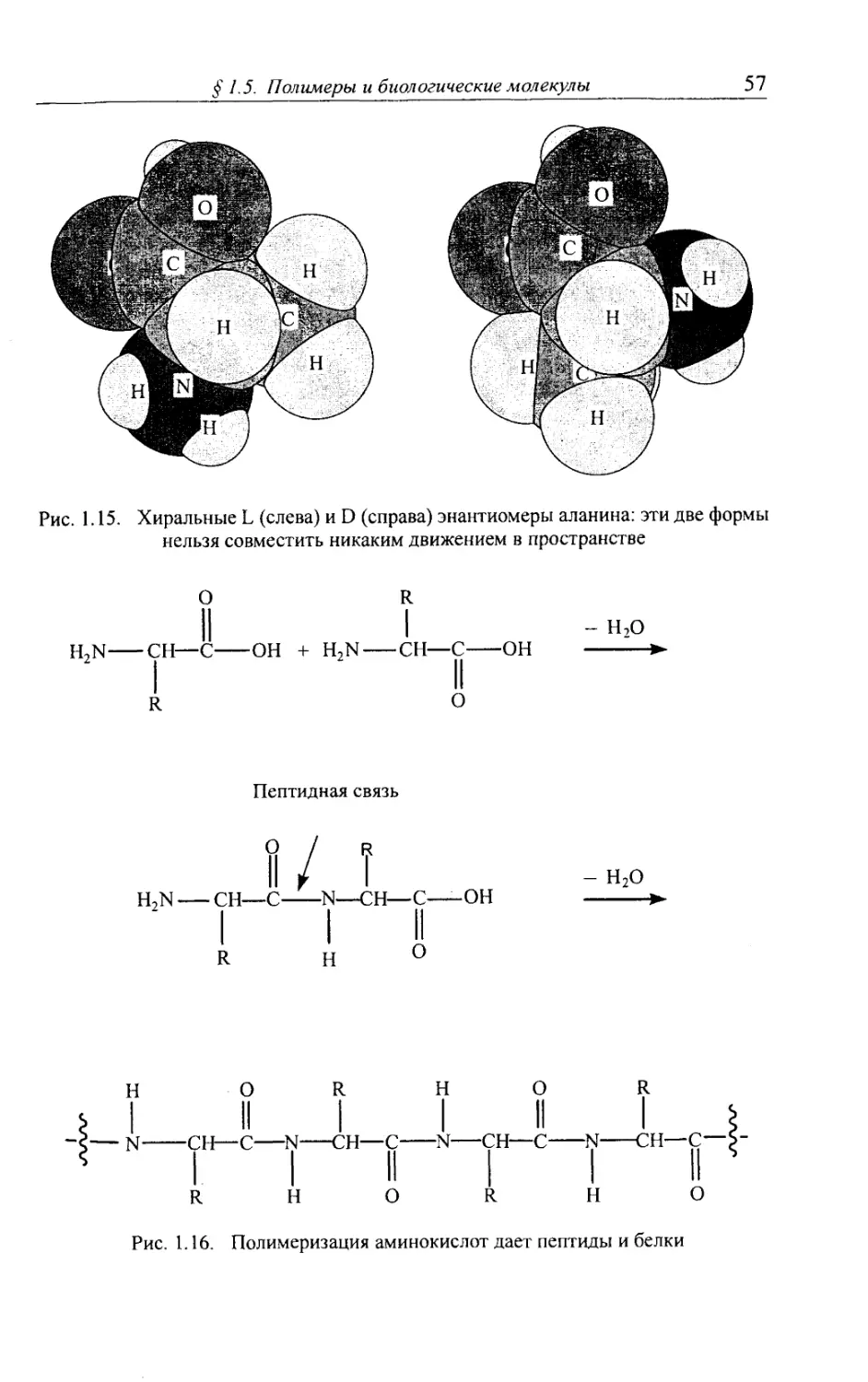
1.5.2. Аминокислоты, белки 56
1.5.3. ДНК 60
1.5.4. Ассоциация белков: вирус табачной мозаики, микротрубочки ... 62
4
Оглавление
ГЛАВА 2. Атомные и молекулярные упорядочения 67
§2.1. Атомный порядок 67
2.1.1. Плотность упаковки 67
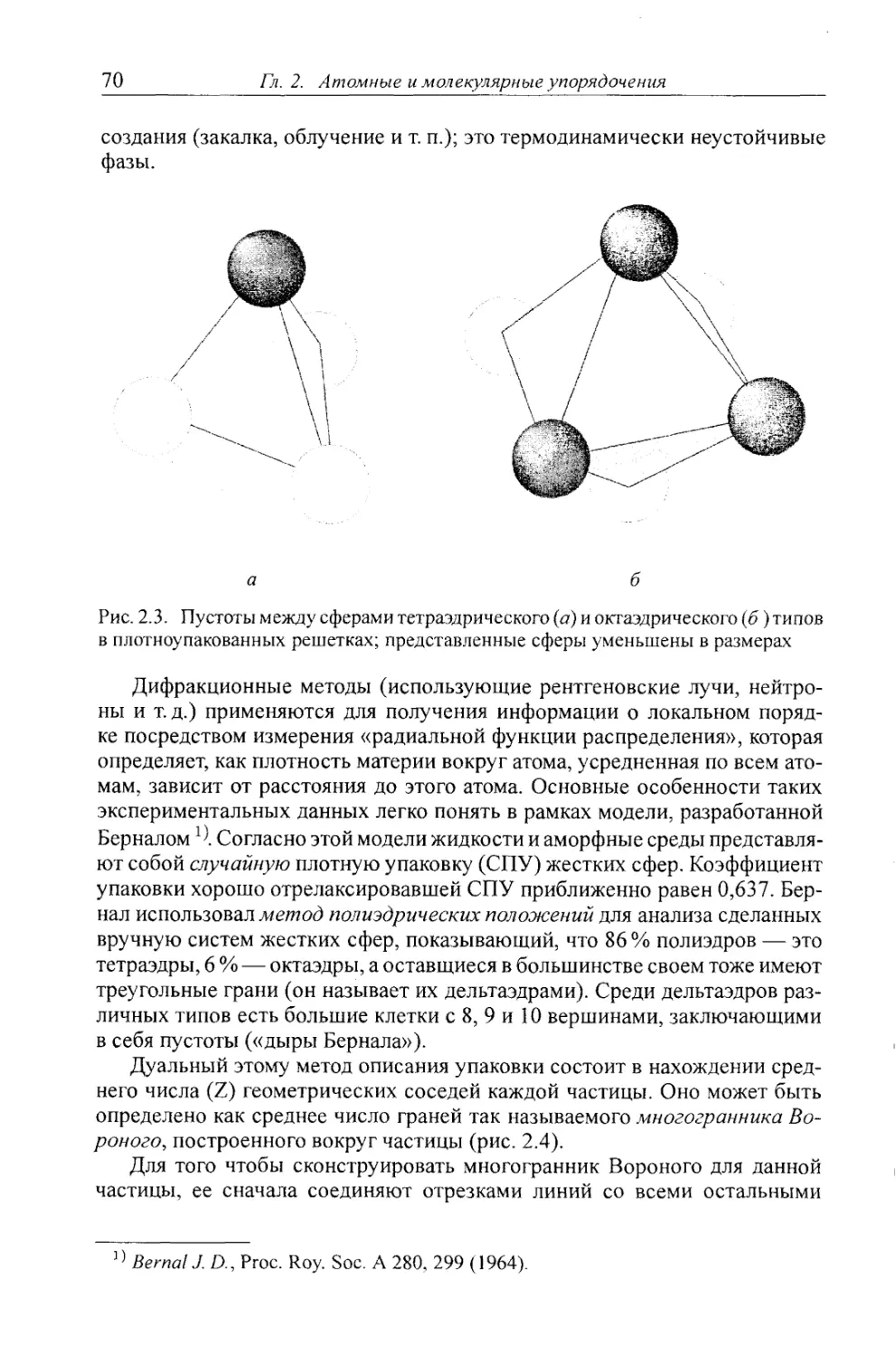
2.1.2. Жидкости и аморфные среды 69
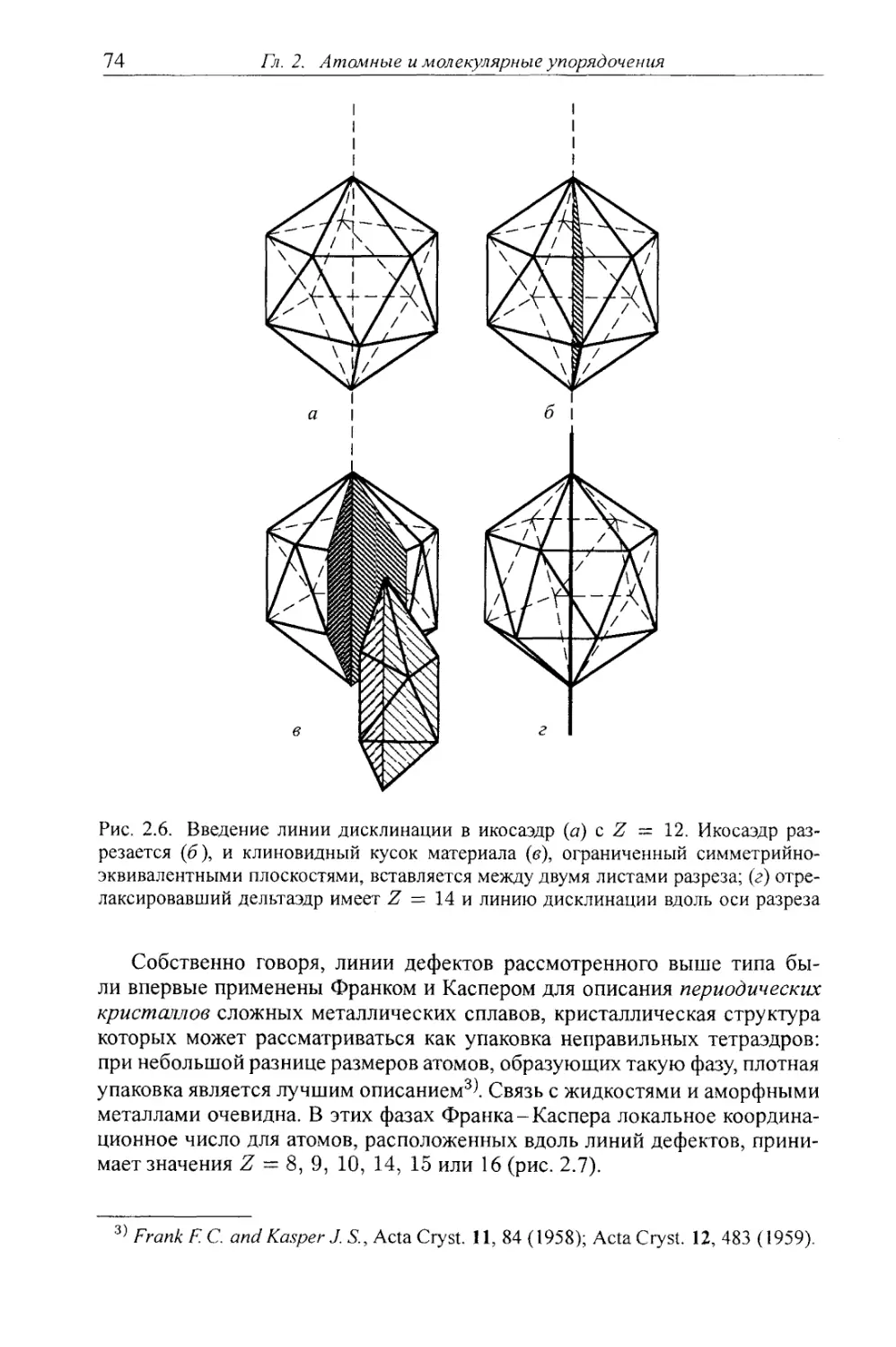
2.1.3. Геометрическая фрустрация 72
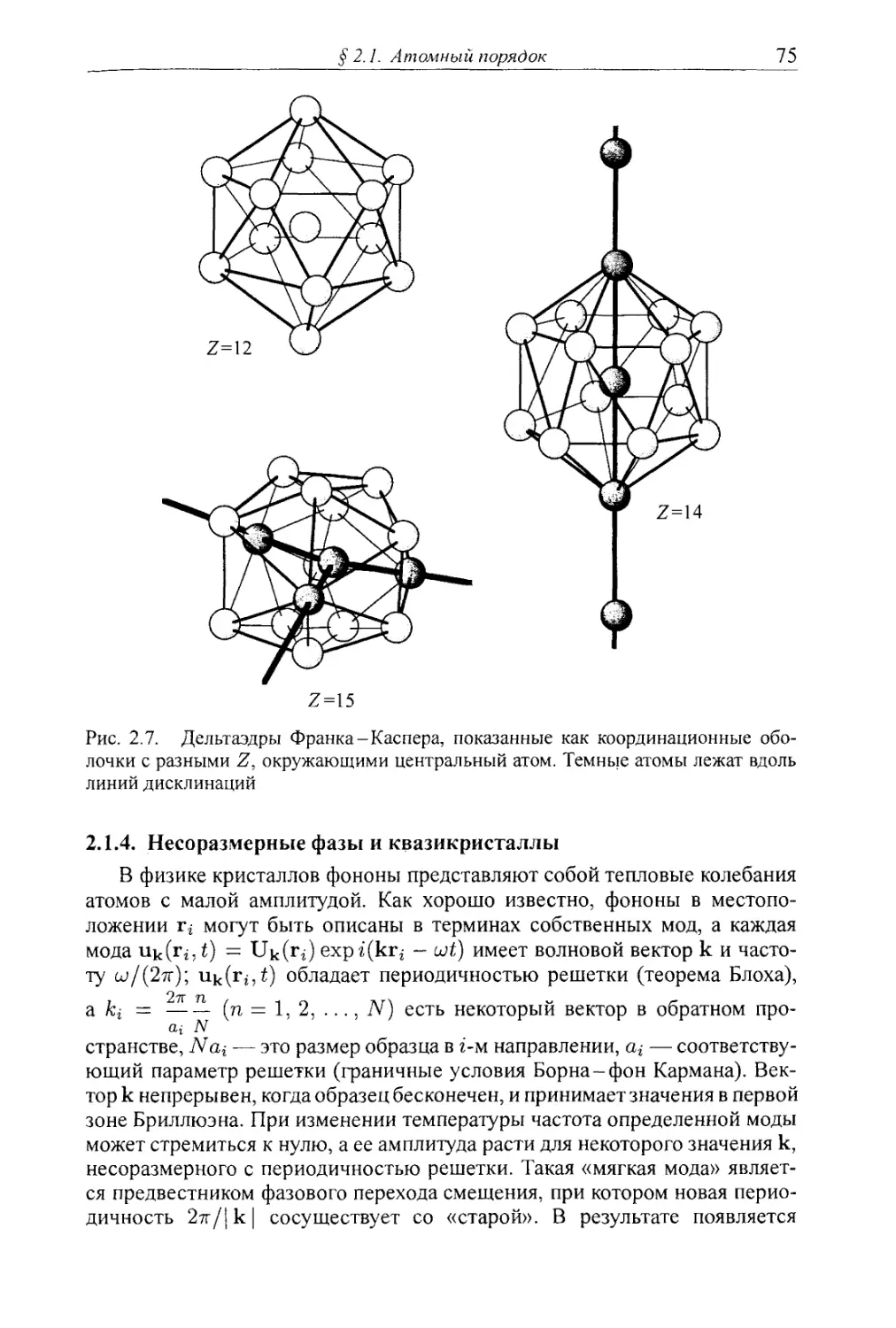
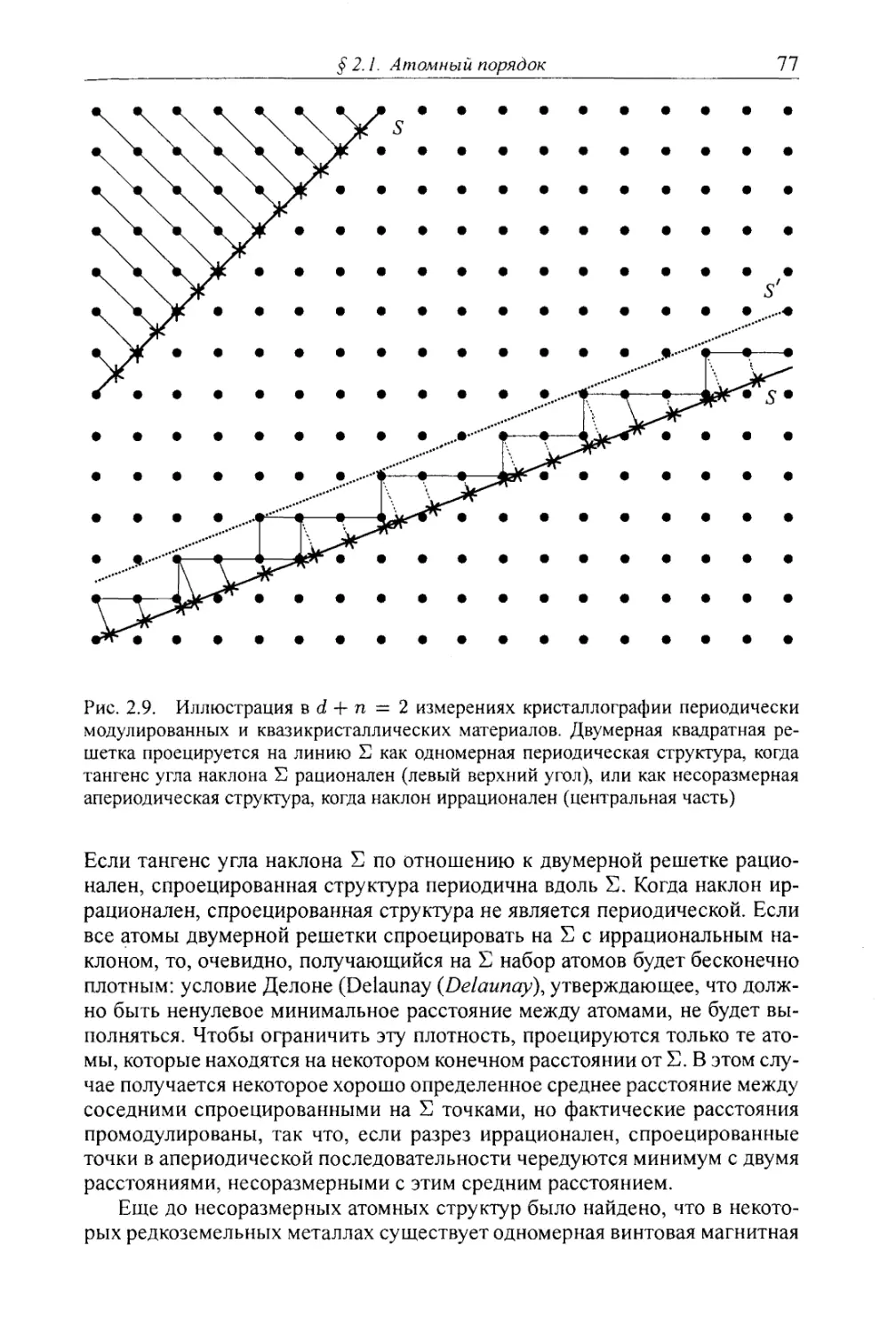
2.1.4. Несоразмерные фазы и квазикристаллы 75
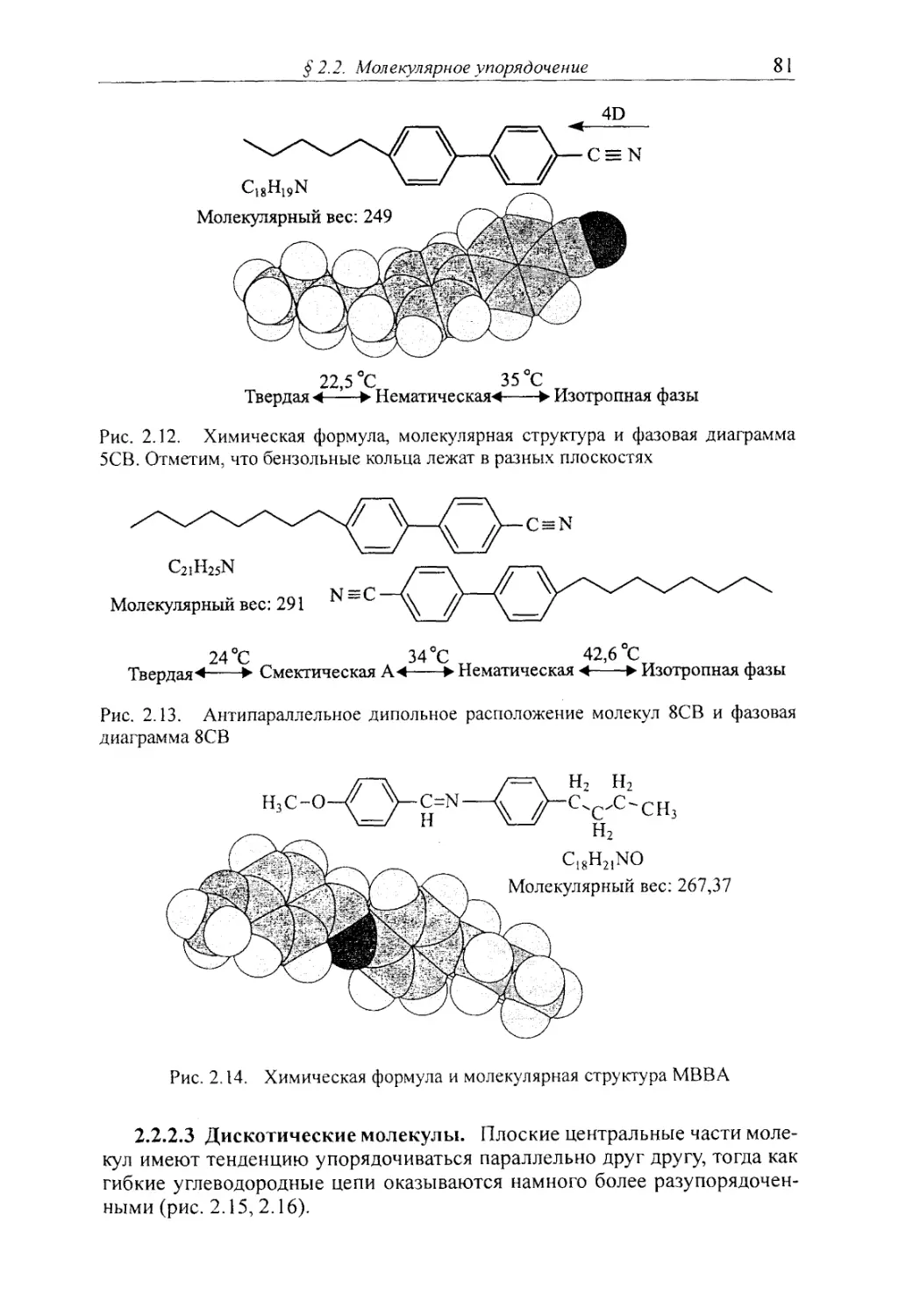
§ 2.2. Молекулярное упорядочение 79
2.2.1. Пластические кристаллы 79
2.2.2. Строительные блоки жидких кристаллов 80
ч
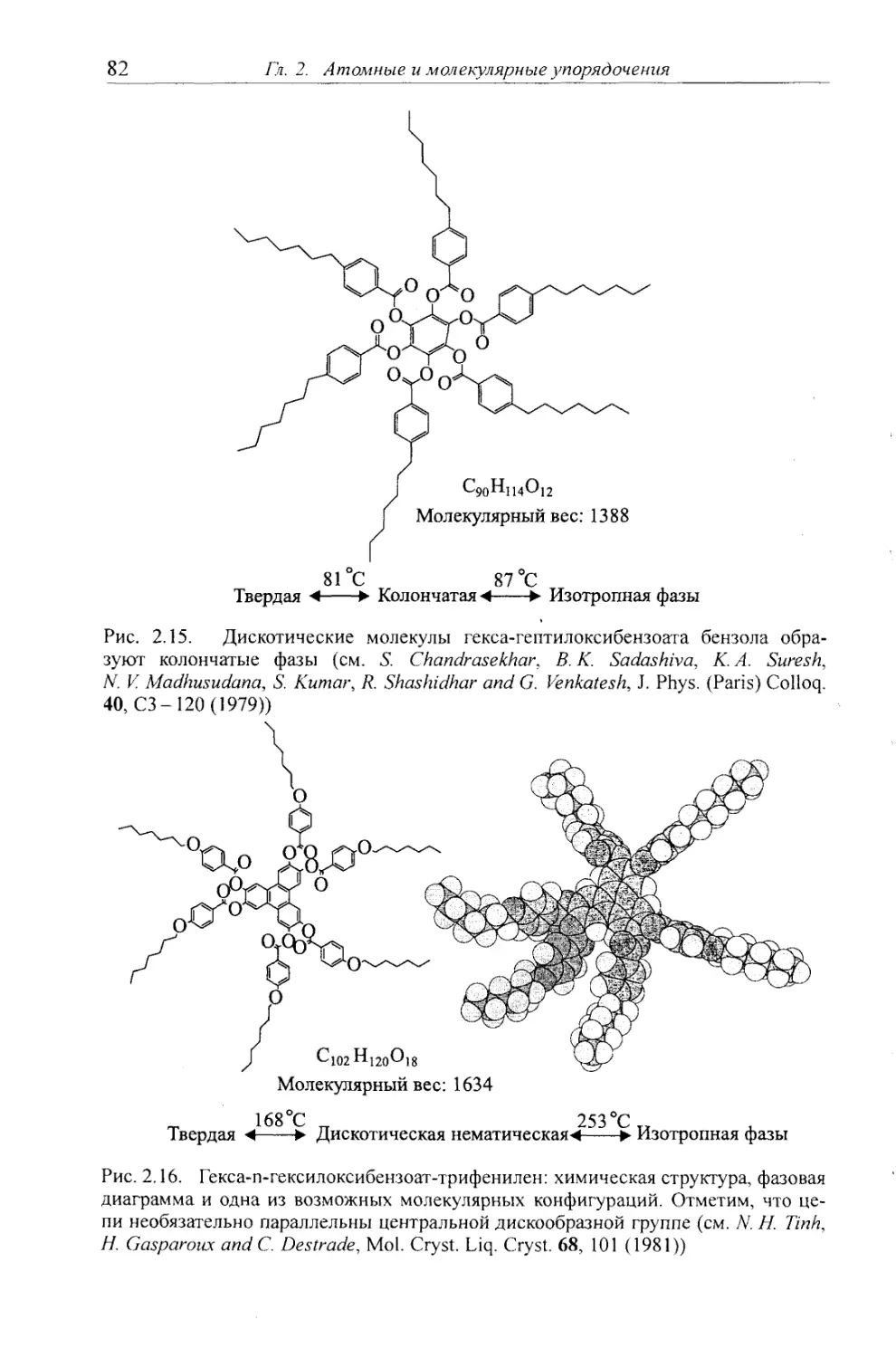
2.2.3 Классификация мезоморфных фаз 86
2.2.4 Изотропные фазы 94
/
§ 2.3. Нарушения кристаллического порядка 96
2.3.1. Слабые нарушения 96
2.3.2. Сильные нарушения 97
ГЛАВА 3. Параметр порядка: амплитуда и фаза 101
§3.1. Пространство параметра порядка 101
3.1.1. Сверхтекучий гелий 101
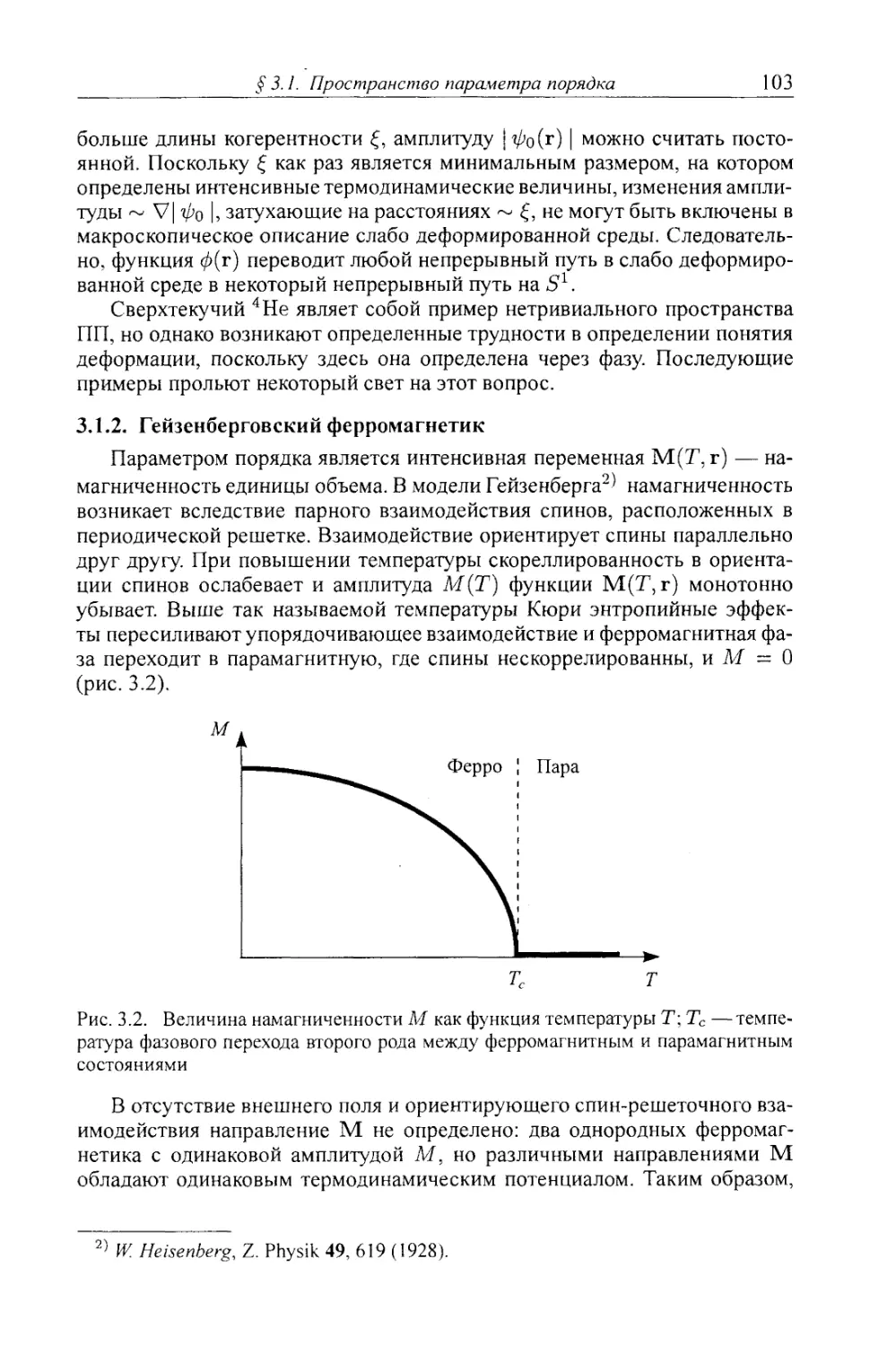
3.1.2. Гейзенберговский ферромагнетик 103
3.1.3. X-Y ферромагнетик 104
3.1.4. Одноосные нематики 105
3.1.5. Кристаллические твердые тела 107
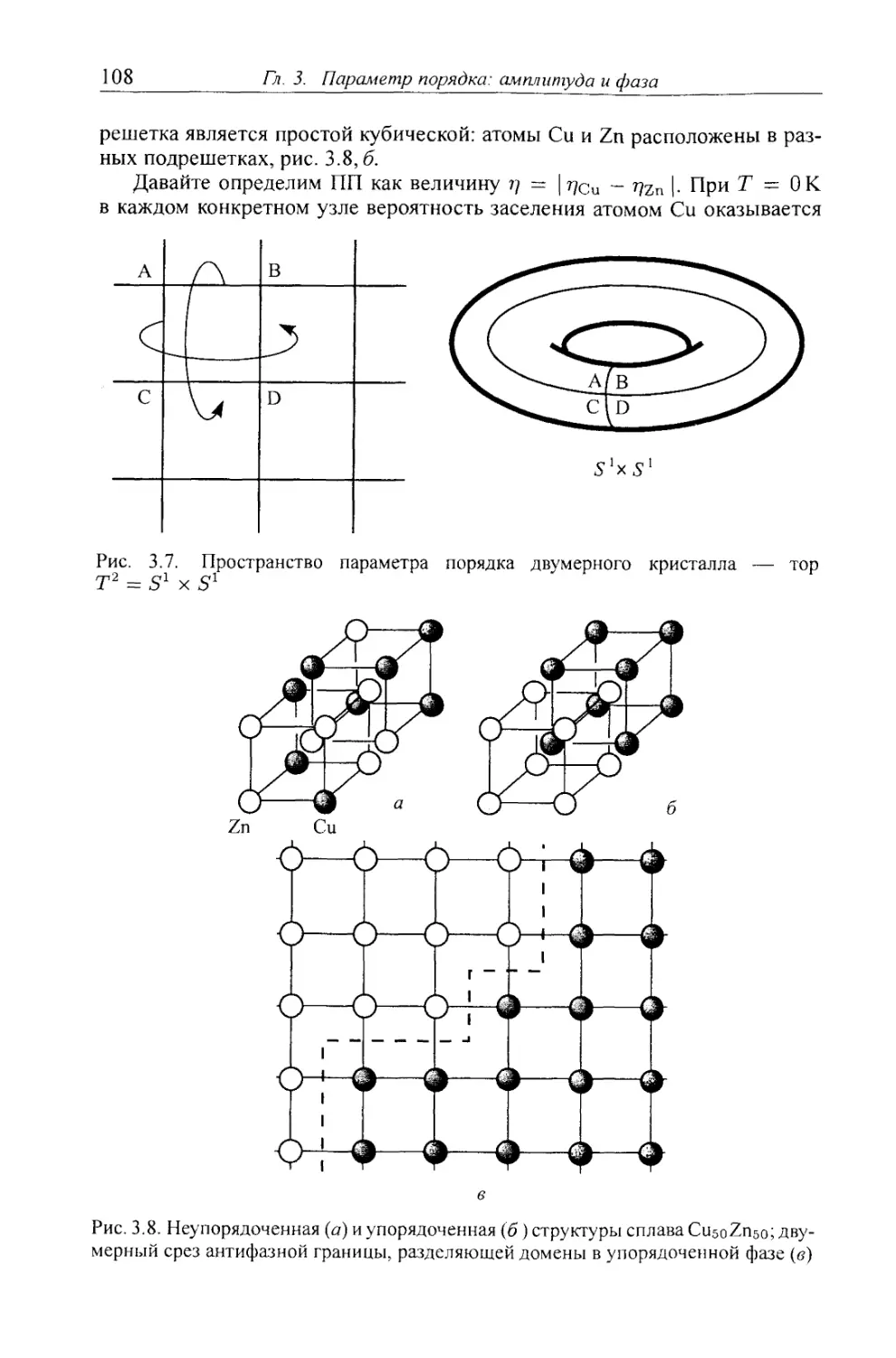
3.1.6. Переходы порядок-беспорядок в сплавах 107
§ 3.2. Характерный для жидких кристаллов параметр порядка: директор 109
3.2.1. Микроскопическое определение 109
3.2.2. Макроскопические свойства 111
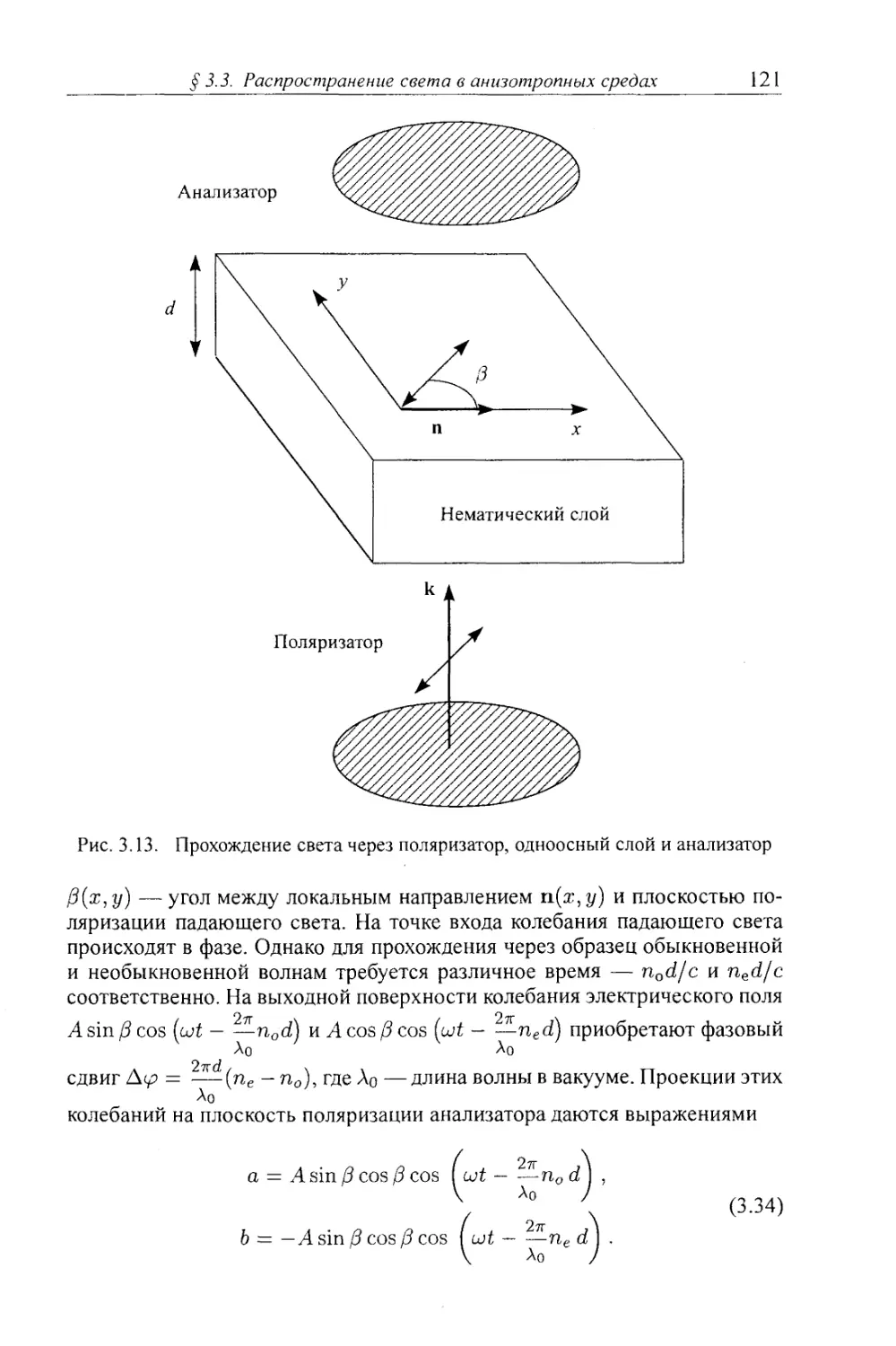
§3.3. Распространение света в анизотропных средах 115
3.3.1. Уравнение Френеля 116
3.3.2. Обыкновенная и необыкновенная волны 118
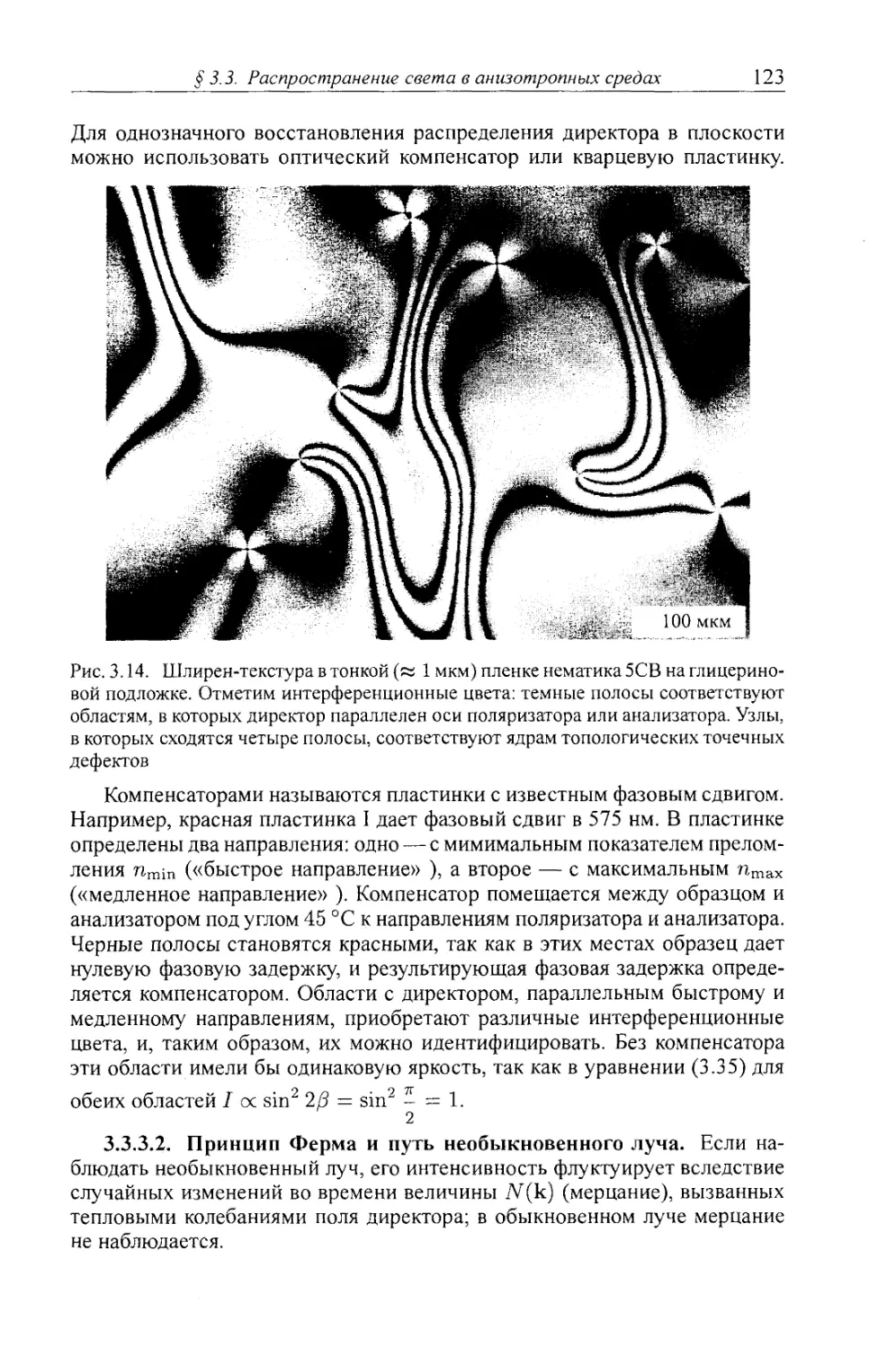
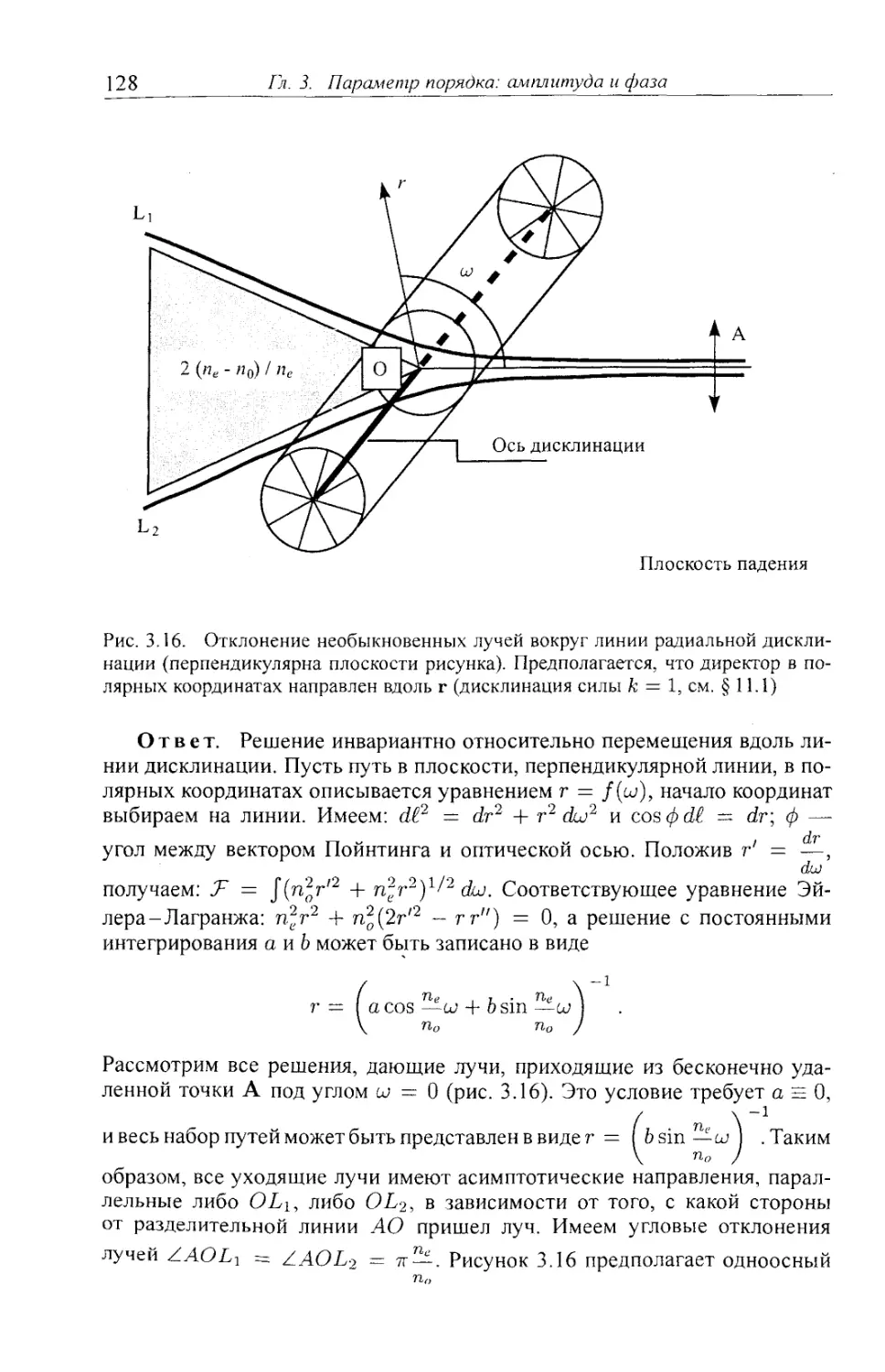
3.3.3. Наблюдения в поляризованном свете. Микроскопия 120
ГЛАВА 4. Фазовые переходы 131
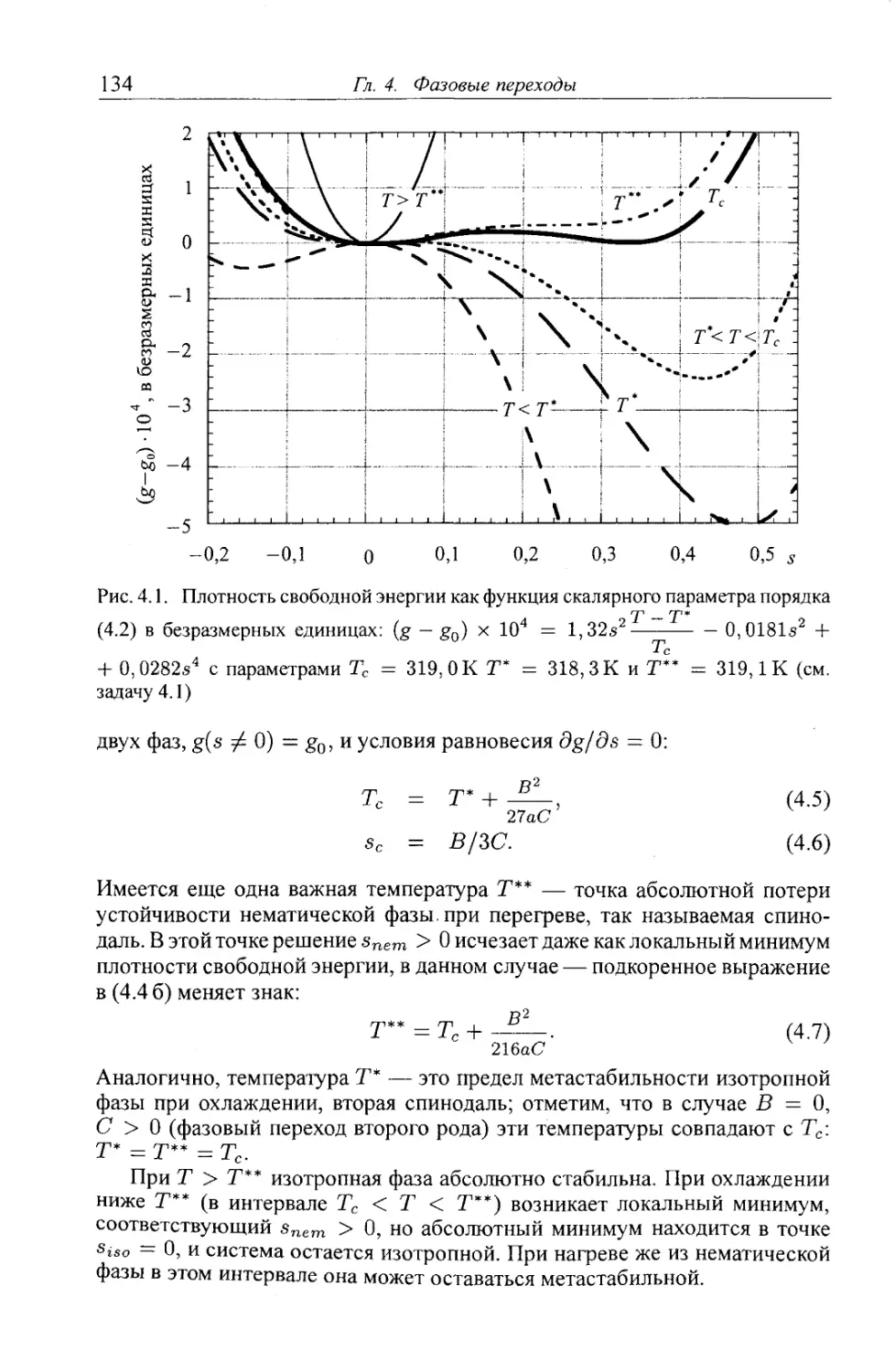
§4.1. Модель Ландау - де Жена перехода одноосный нематик - изотроп¬
ная фаза 131
§ 4.2. Нематический порядок и молекулярно-статистическая теория для
стержнеобразных молекул 136
4.2.1. Свободная энергия раствора сферических частиц 136
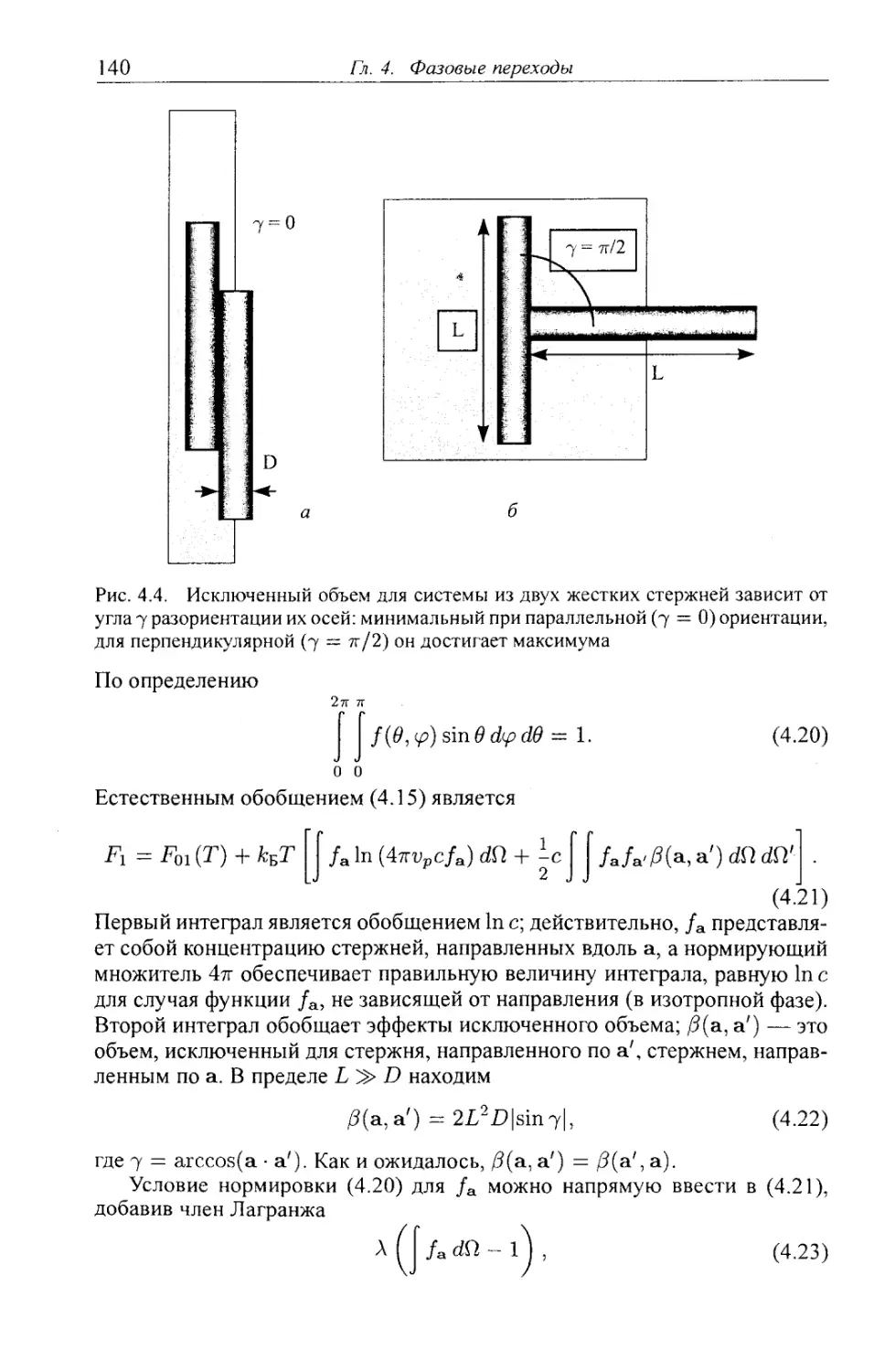
4.2.2. Свободная энергия раствора жестких стержней 139
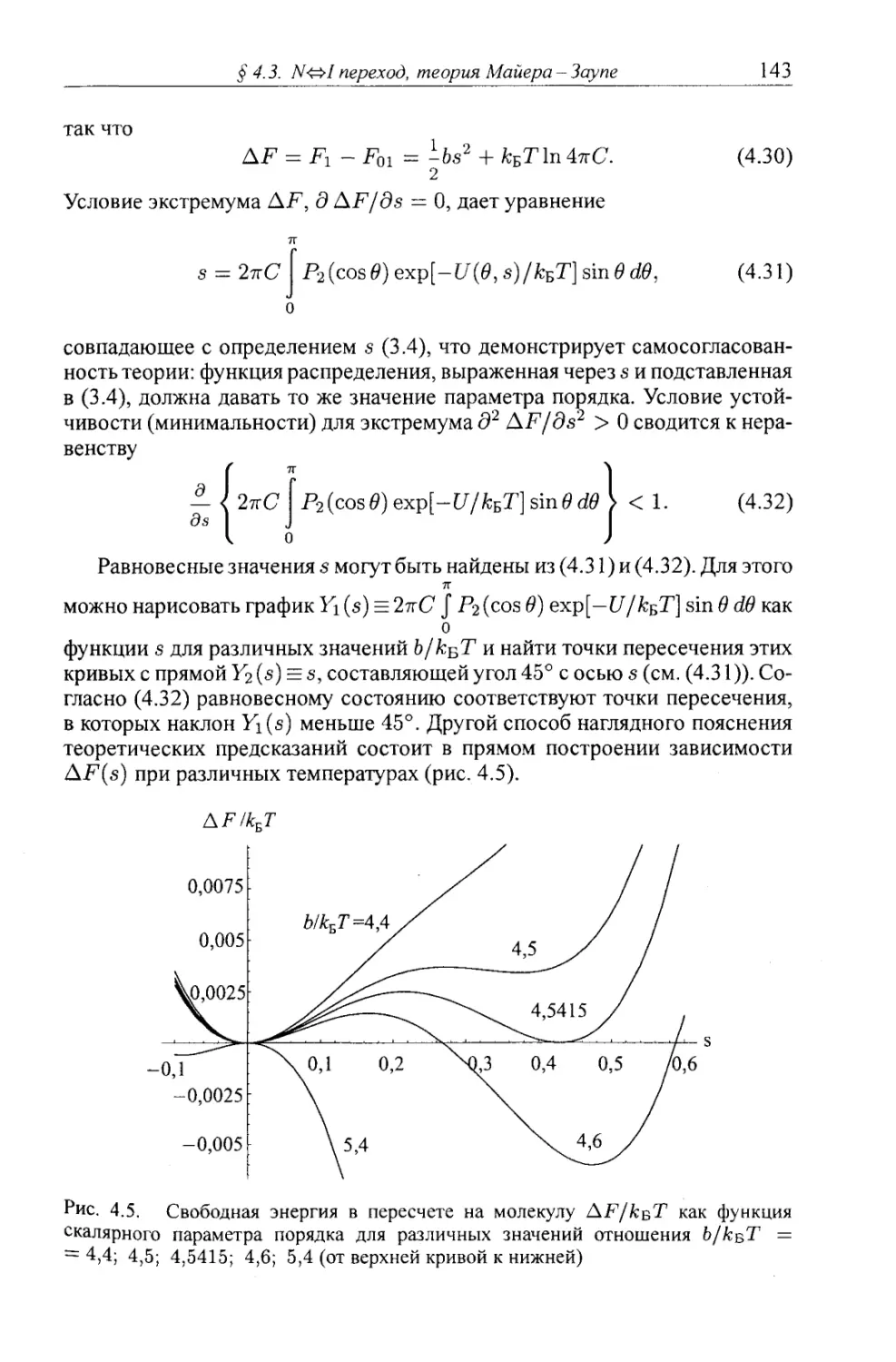
§ 4.3. Теория молекулярного поля Майера-Заупе для перехода изотроп¬
ная жидкость-нематик 142
Оглавление
5
§4.4. Переход смектик А-нематик 144
4.4.1. Параметр порядка 144
4.4.2. Разложение Гинзбурга-Ландау 144
4.4.3. Аналогия со сверхпроводниками 147
4.4.4. Характерные длины 148
4.4.5. Аномалии модулей и 150
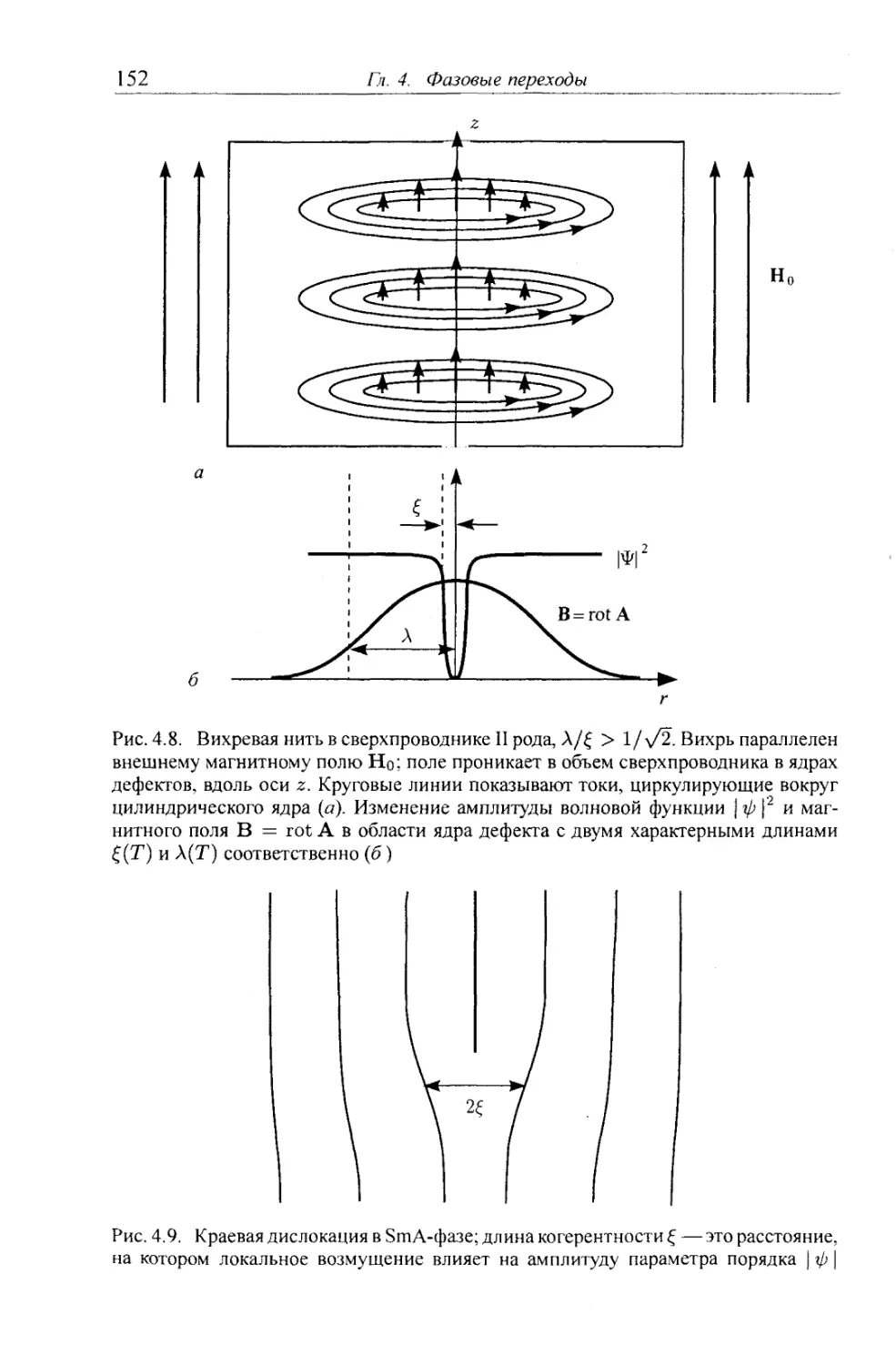
4.4.6. Фазы Абрикосова с дислокациями 151
§4.5. Модель Костерлица-Таулесса . . 155
ГЛАВА 5. Упругость мезоморфных фаз 162
§5.1. Одноосные нематики и холестерики 162
5.1.1. Плотность свободной энергии 162
5.1.2. Геометрическая интерпретация деформаций директора 164
5.1.3. Упругие постоянные материалов 167
§5.2. Слоистые фазы 172
5.2.1. Плотность свободной энергии 172
5.2.2. Деформации поперечного и седловидного изгиба 173
5.2.3. Плотность свободной энергии при малых деформациях 176
§ 5.3. Нематик во внешнем поле 177
§5.4. Типичные приложения упругости нематиков 181
5.4.1. Минимизация свободной энергии в общем случае 181
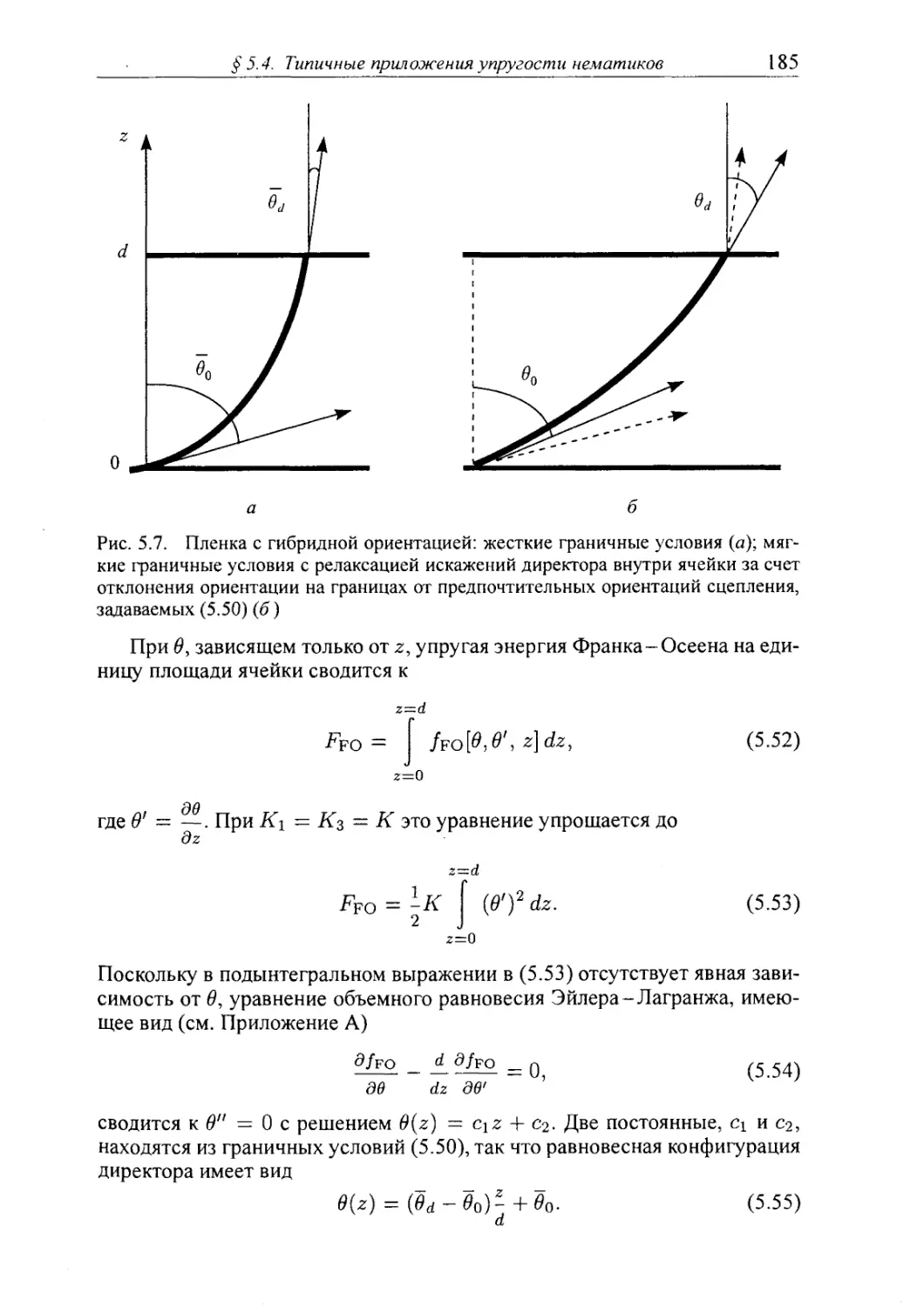
5.4.2. Нематические пленки с гибридной ориентацией 184
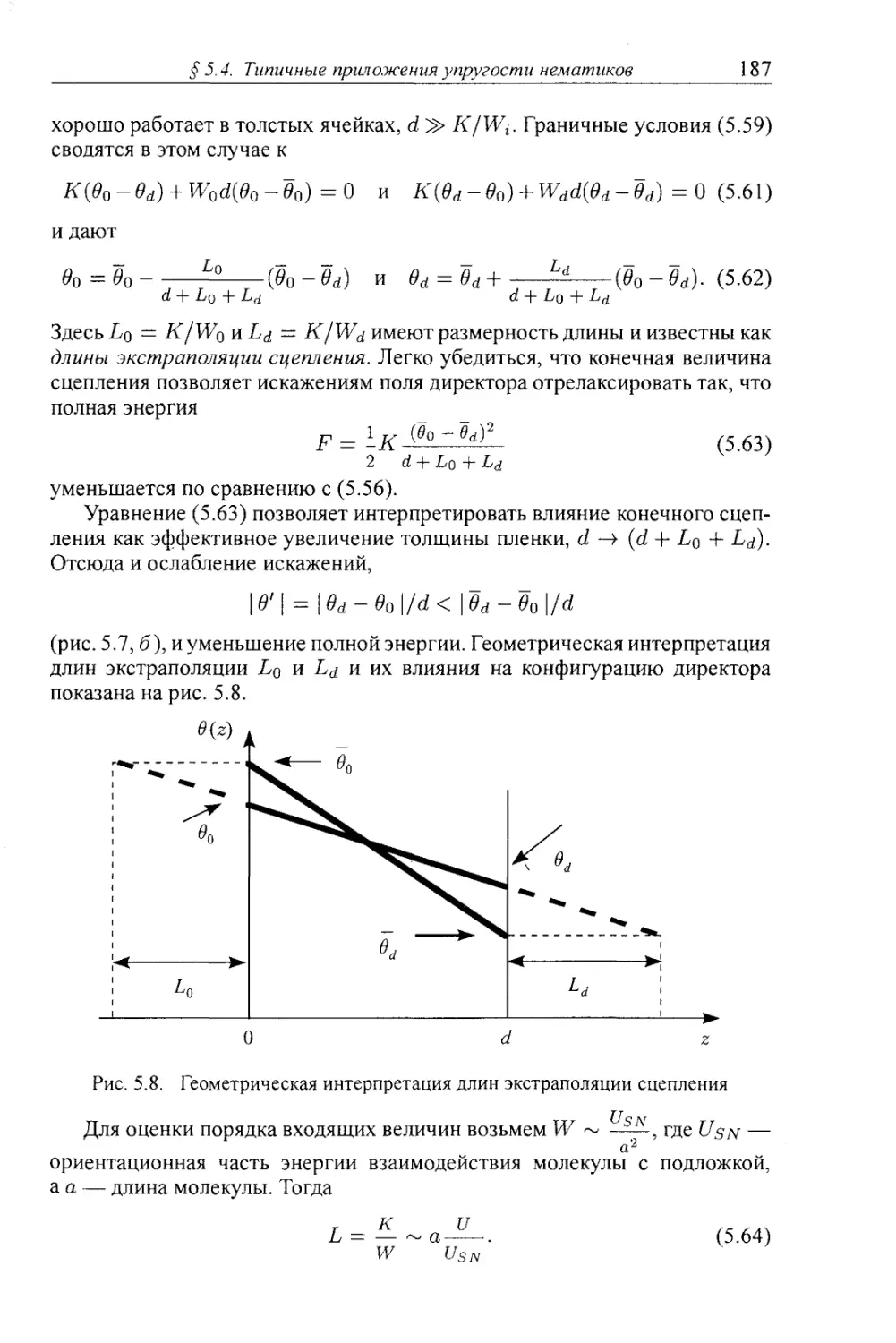
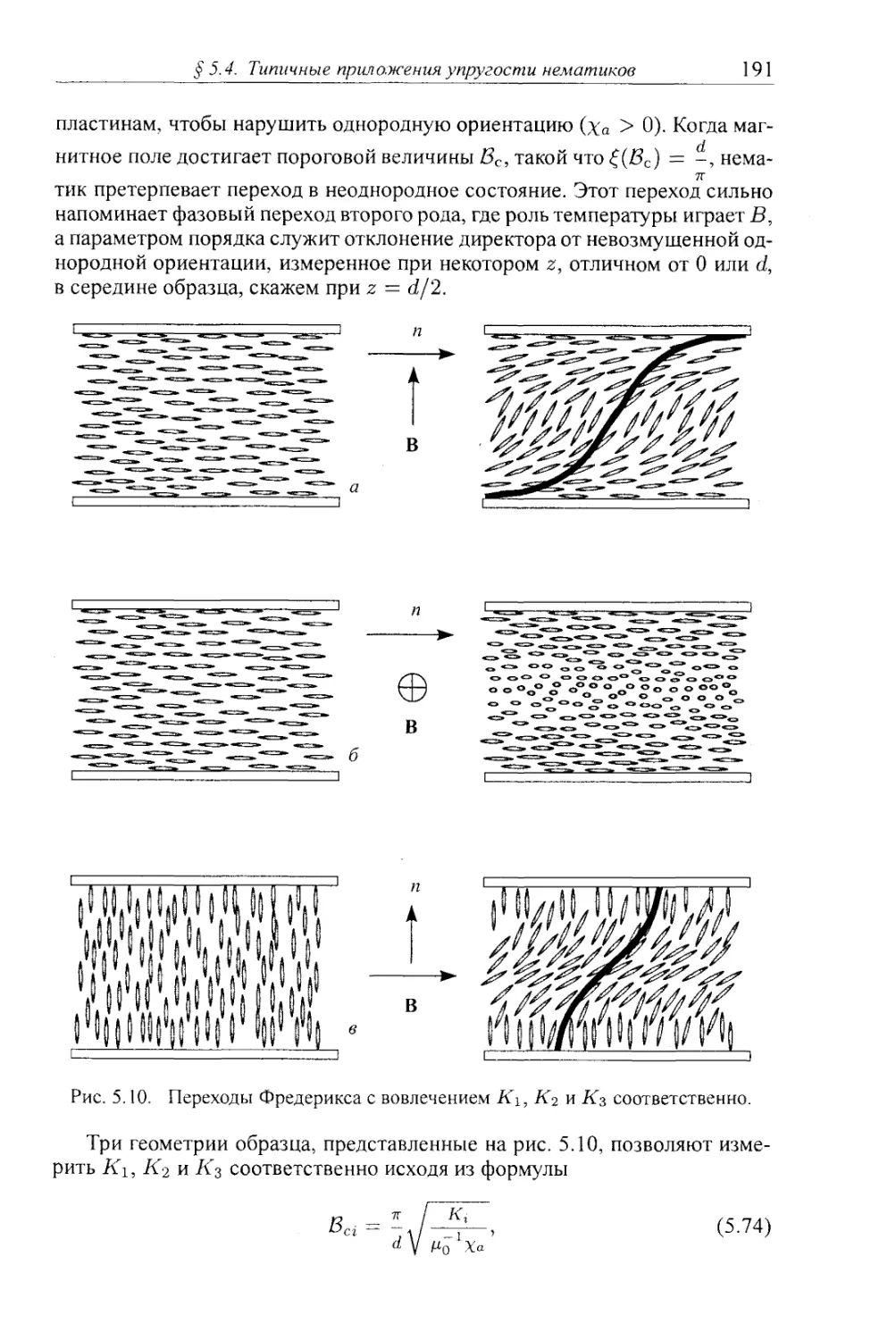
5.4.3. Эффекты во внешнем поле: характерные длины и переход Фредерикса 189
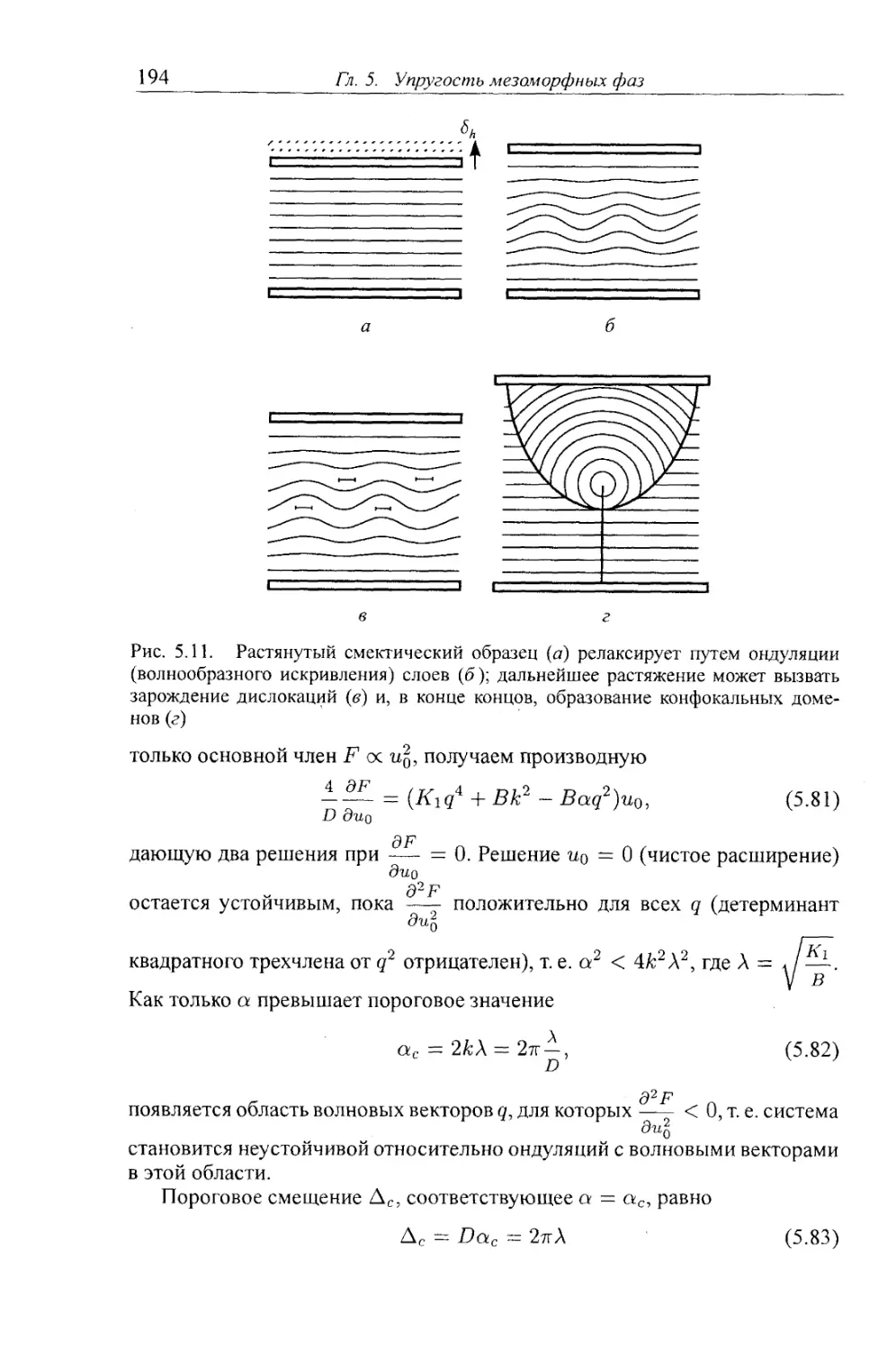
§5.5. Типичные приложения упругости смектиков 192
5.5.1. Слабо деформированная смектическая фаза 192
5.5.2. Сильно деформированные смектические фазы и топологические де¬
формации 195
§5.6. Термодинамические флуктуации 198
5.6.1. Термодинамические флуктуации в нематиках 199
5.6.2. Термодинамические флуктуации в смектиках 201
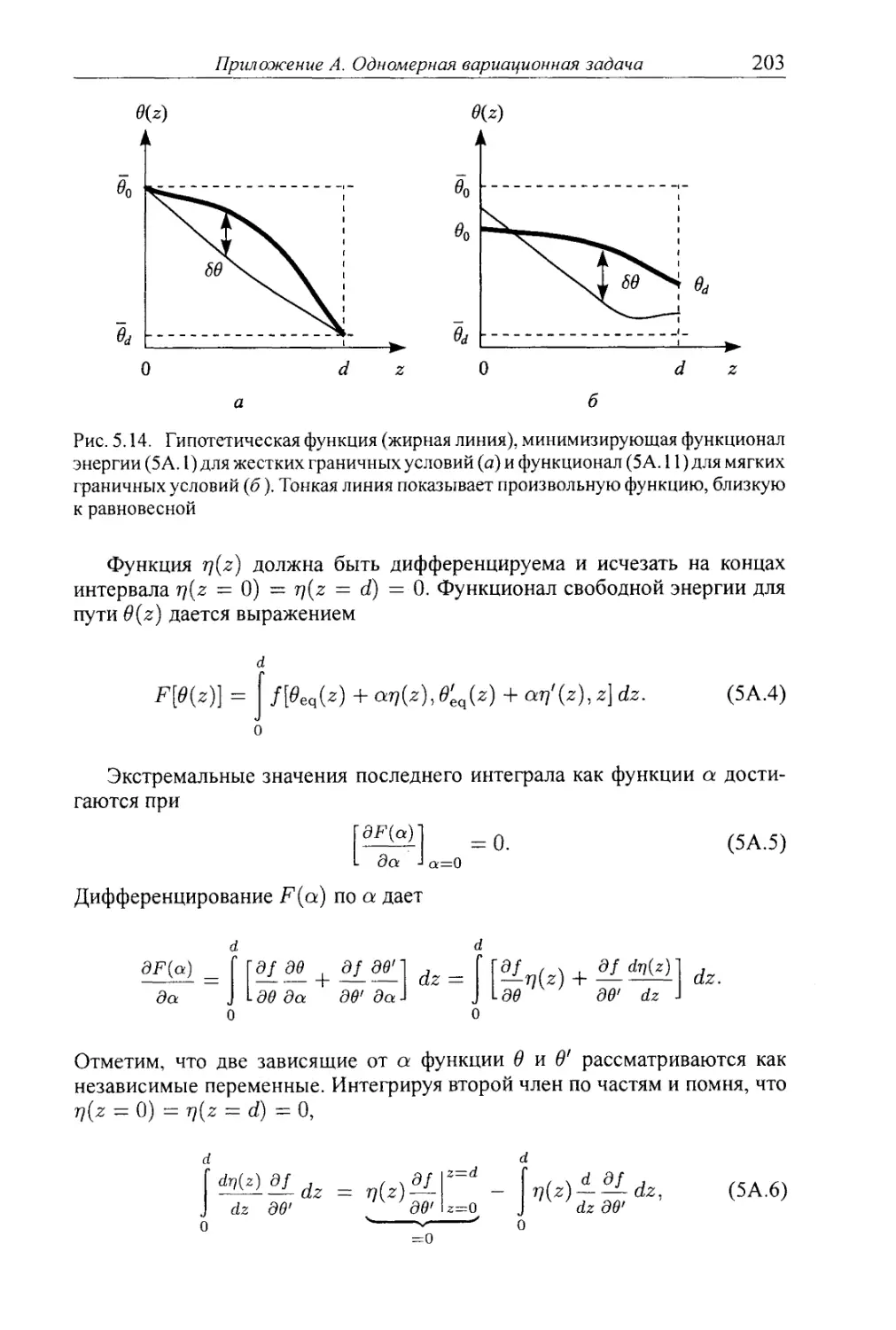
5.А. Приложение А. Одномерная вариационная задача 202
5.Б. Приложение Б. Формулы для преобразований Фурье 205
ГЛАВА 6. Динамика изотропной и анизотропной жидкостей .... 213
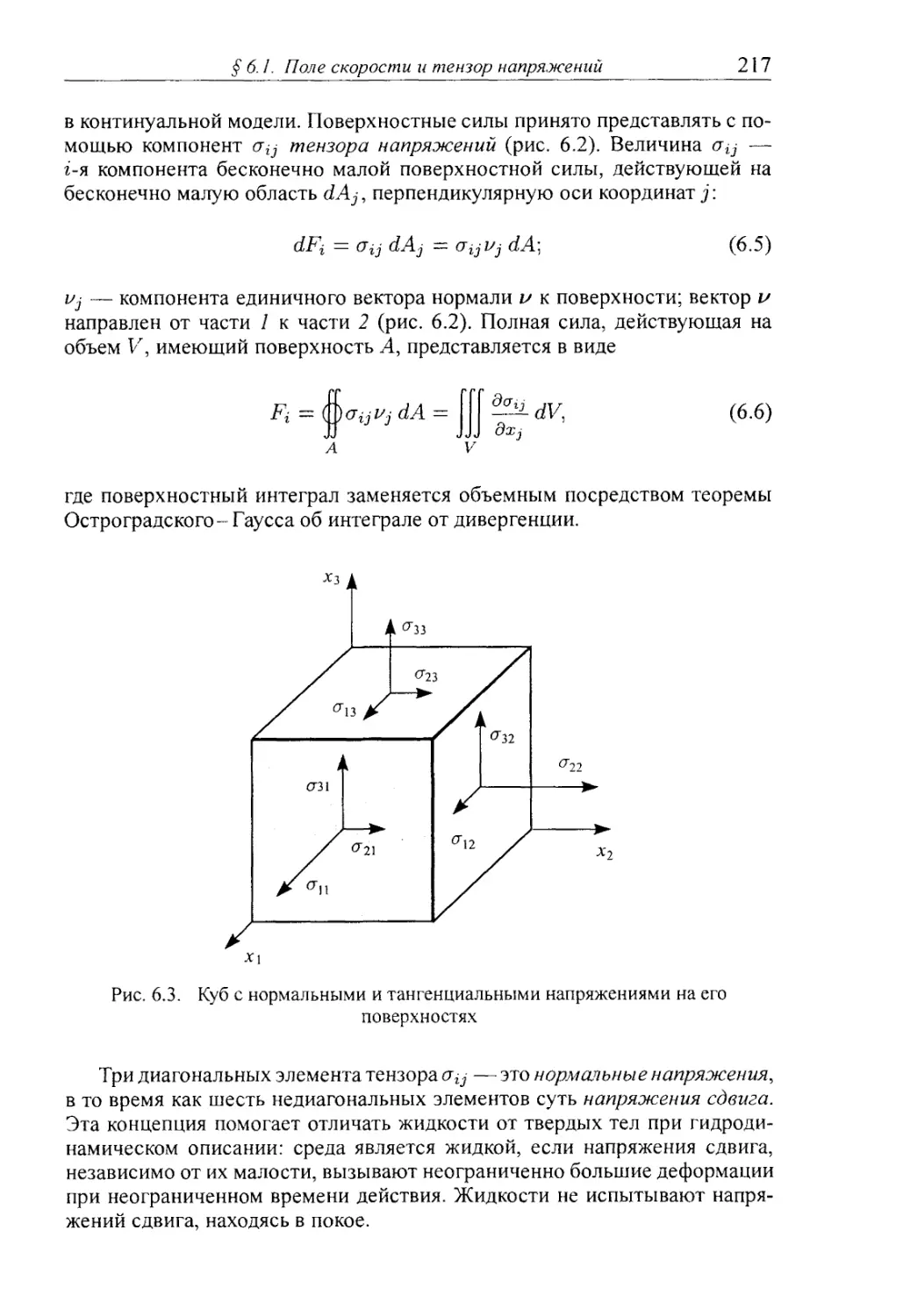
§ 6.1. Поле скорости и тензор напряжений 214
6.1Л. Материальные производные и компоненты движения жидкости . . 214
6.1.2. Объемные и поверхностные силы. Тензор напряжений 216
§6.2. Движение изотропной жидкости 218
6.2.1. Сохранение массы: уравнение непрерывности 218
6.2.2. Уравнение импульса 218
6.2.3. Уравнение баланса энергии . 220
6
Оглавление
_ ^ ~ - . . . - — , м , , - - ■ ■ ■ ■ I ■ ■ ■ I 1 I ш I ■ 1
6.2.4. Уравнение производства энтропии 221
6.2.5. Тензор вязкого напряжения 224
6.2.6. Уравнения Навье-Стокса. Число Рейнольдса. Ламинарные
и турбулентные течения 225
§6.3. Нематодинамика в модели Эриксена-Лесли 227
6.3.1. Уравнение момента количества движения 228
6.3.2. Уравнение баланса энергии 230
6.3.3. Уравнение производства энтропии 230
6.3.4. Недиссипативная динамика 232
6.3.5. Диссипативная динамика 232
§ 6.4. Нематодинамика в гарвардской теории 235
6.4.1. Динамика директора и диссипативный тензор напряжений .... 235
6.4.2. Краткое изложение положений нематодинамики 237
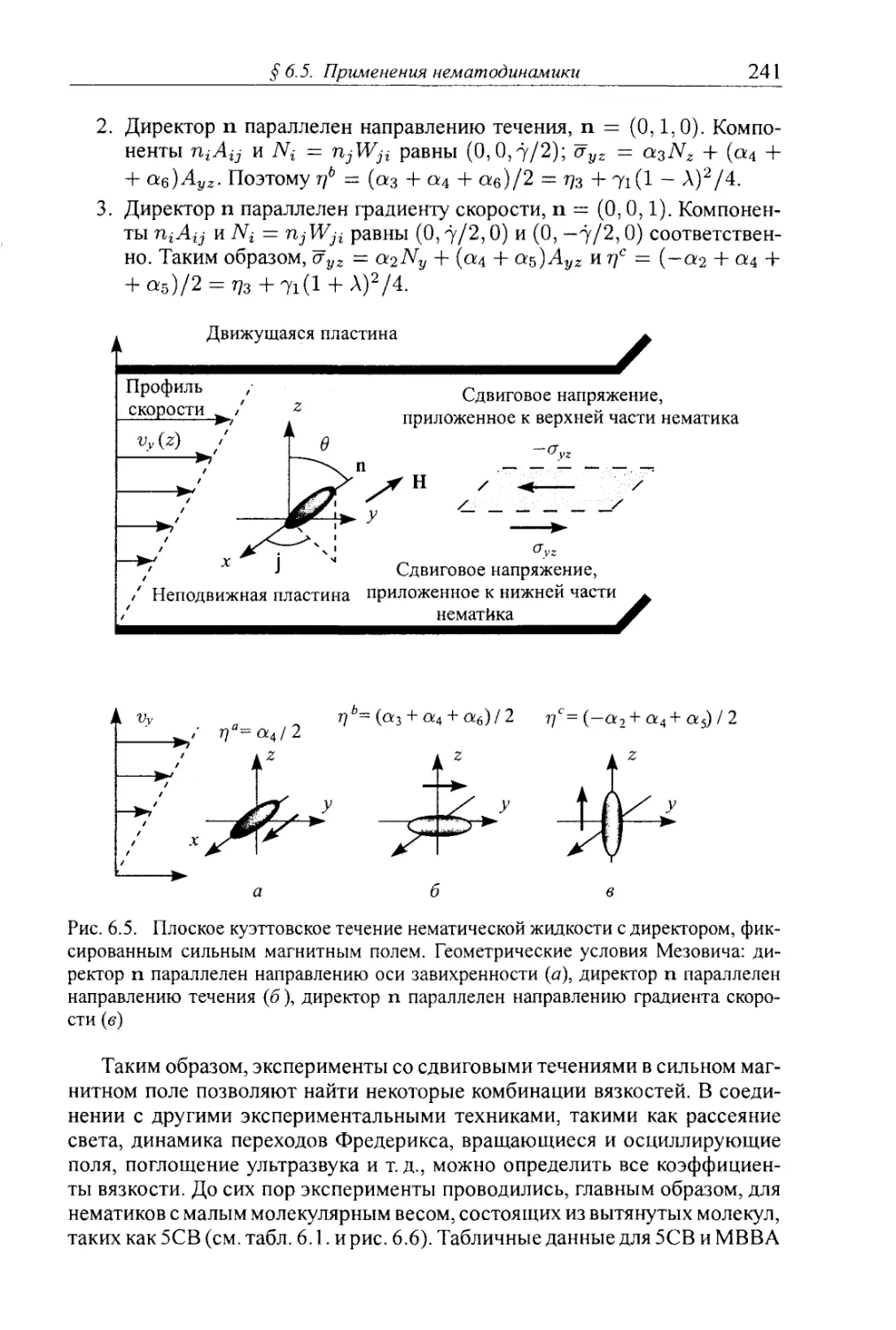
§ 6.5. Применения нематодинамики 240
6.5.1. Вискозиметрия нематика 240
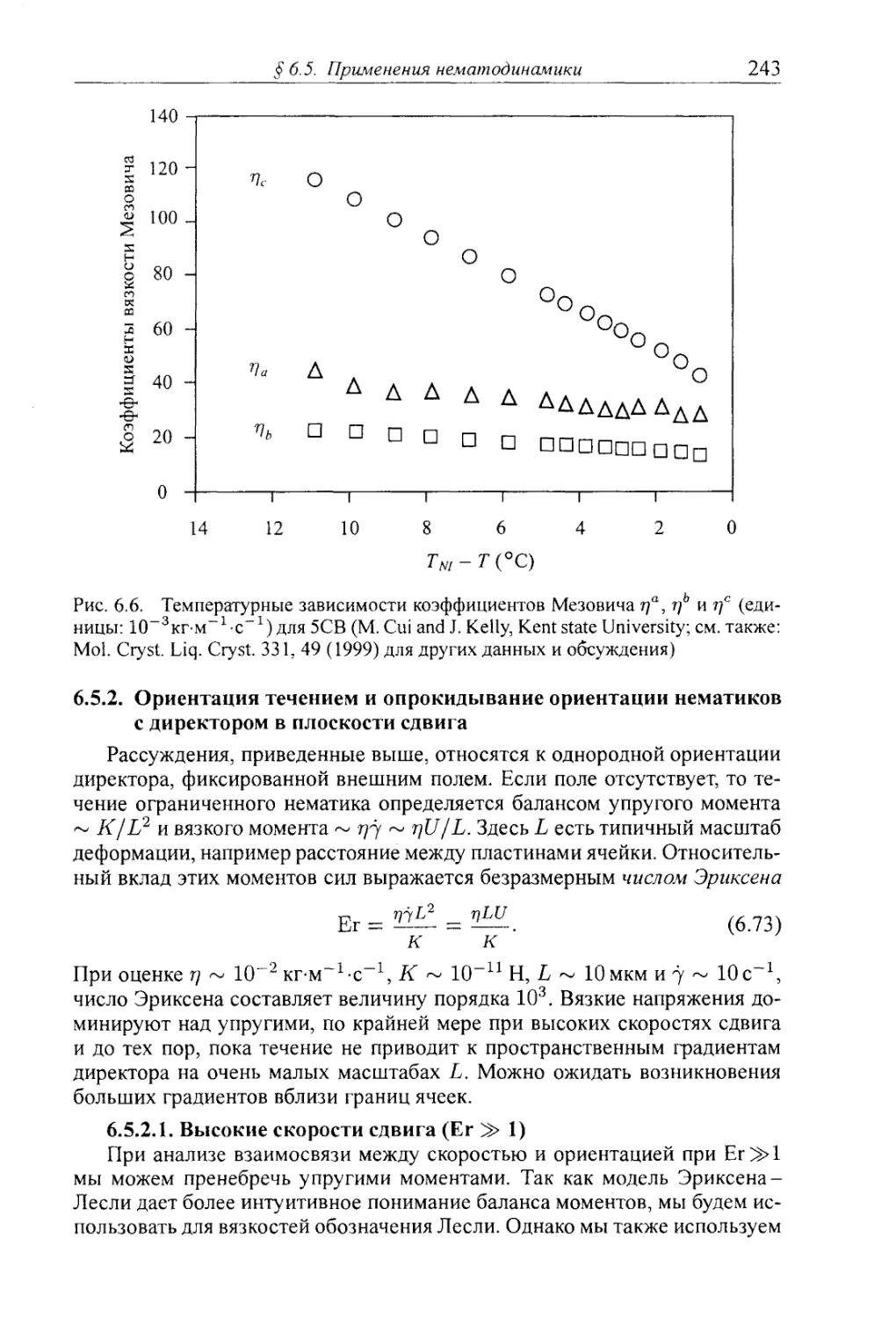
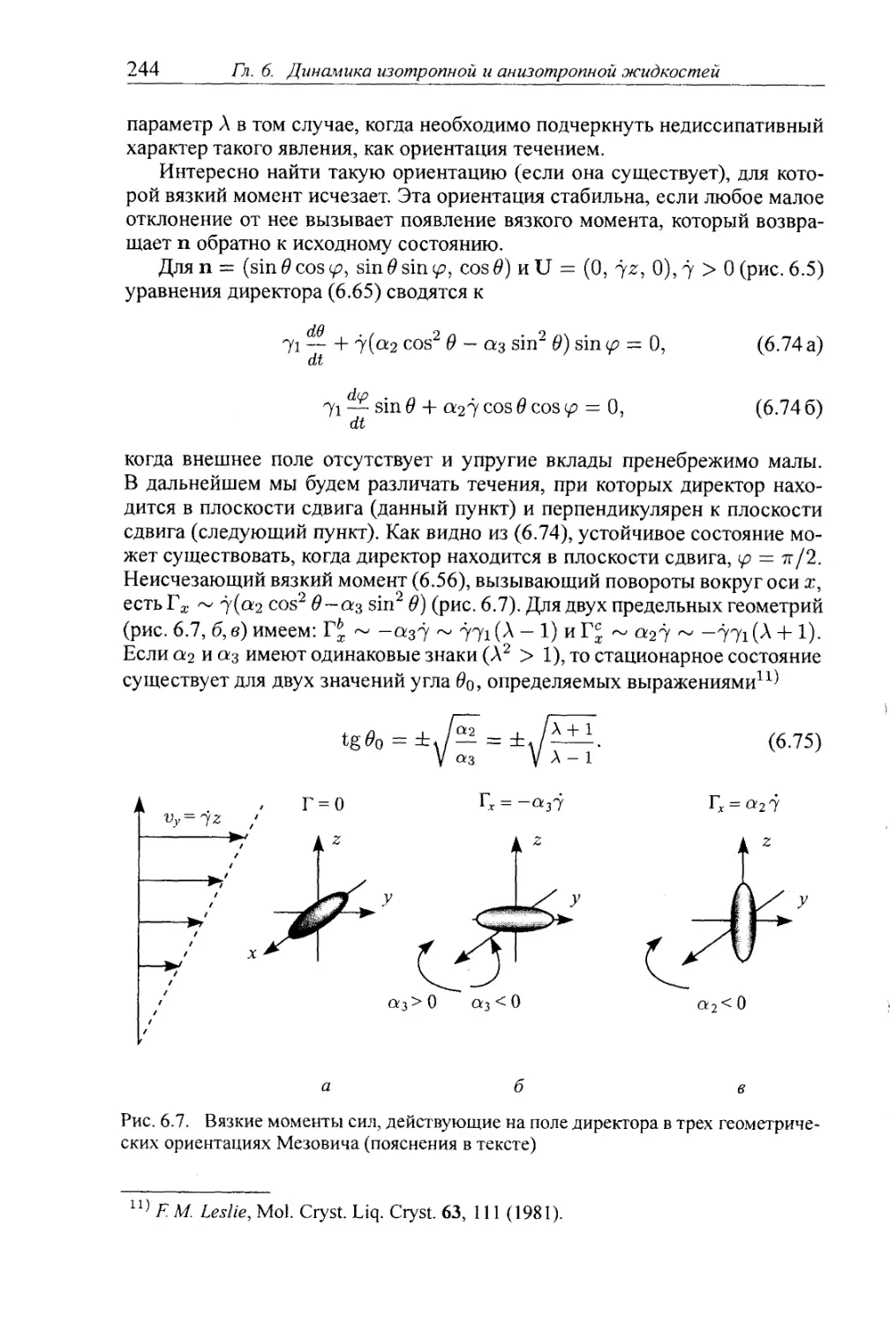
6.5.2. Ориентация течением и опрокидывание ориентации нематиков с ди¬
ректором в плоскости сдвига 243
6.5.3. Неустойчивости поля директора, перпендикулярного к плоскости
сдвига 248
§6.6. Гидродинамические моды 248
ГЛАВА 7. Фракталы и явления роста 254
§7.1. Основные концепции фракталов 255
7.1.1. Длина линии 256
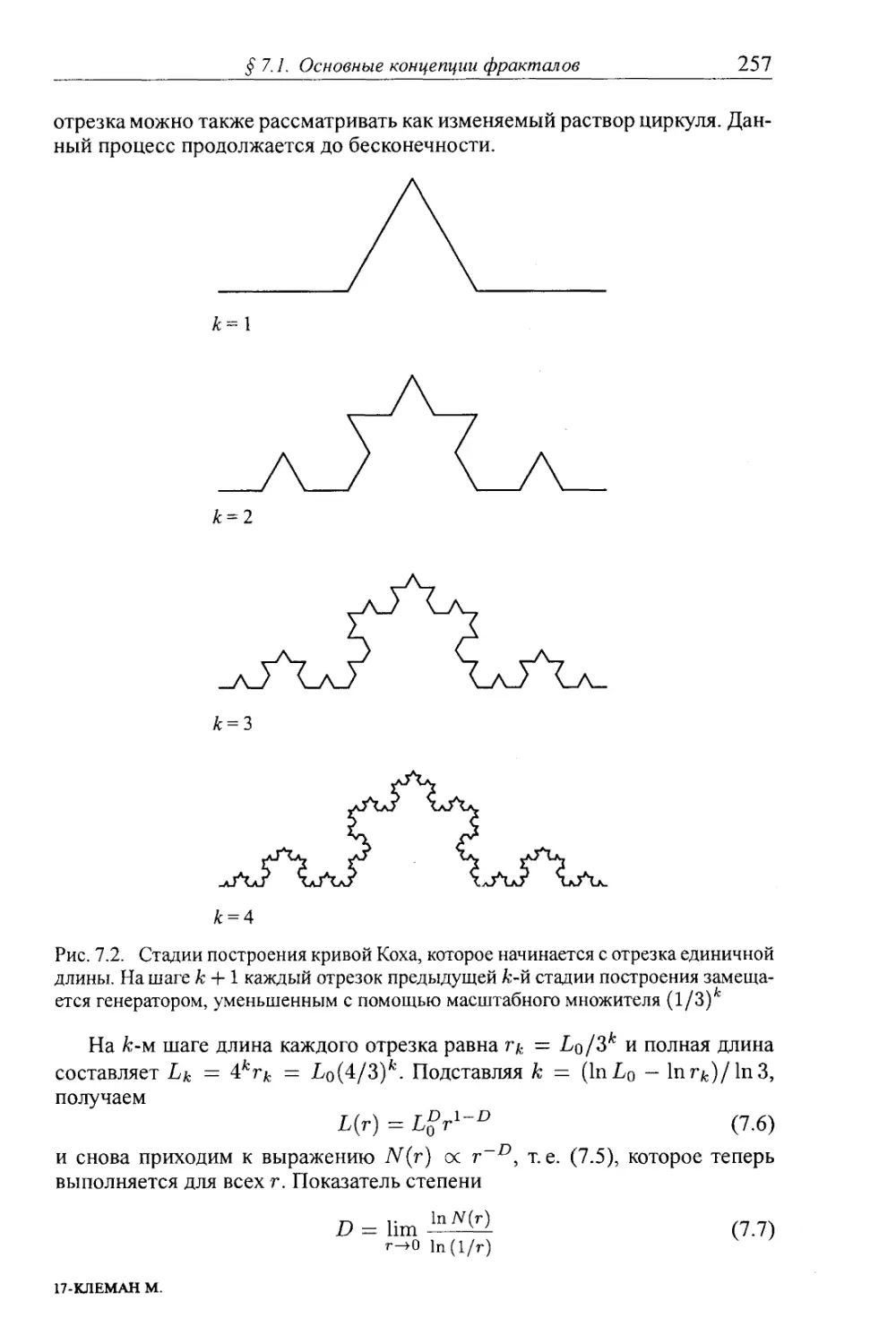
7.1.2. Кривая Коха 256
7.1.3. Самоподобие 258
7.1.4. Оценка фрактальных размерностей 259
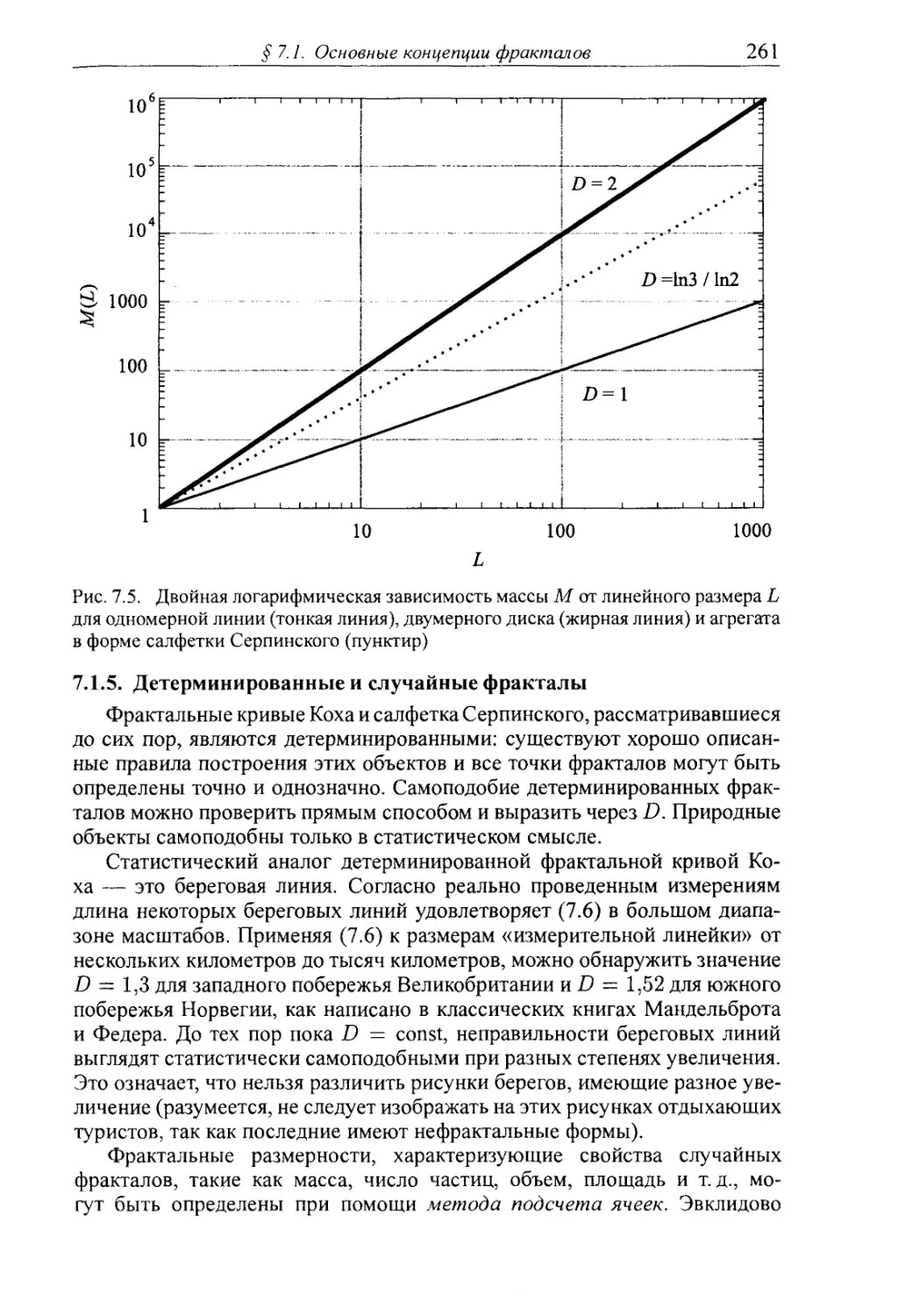
7.1.5. Детерминированные и случайные фракталы 261
7.1.6. Броуновское движение и случайное блуждание 262
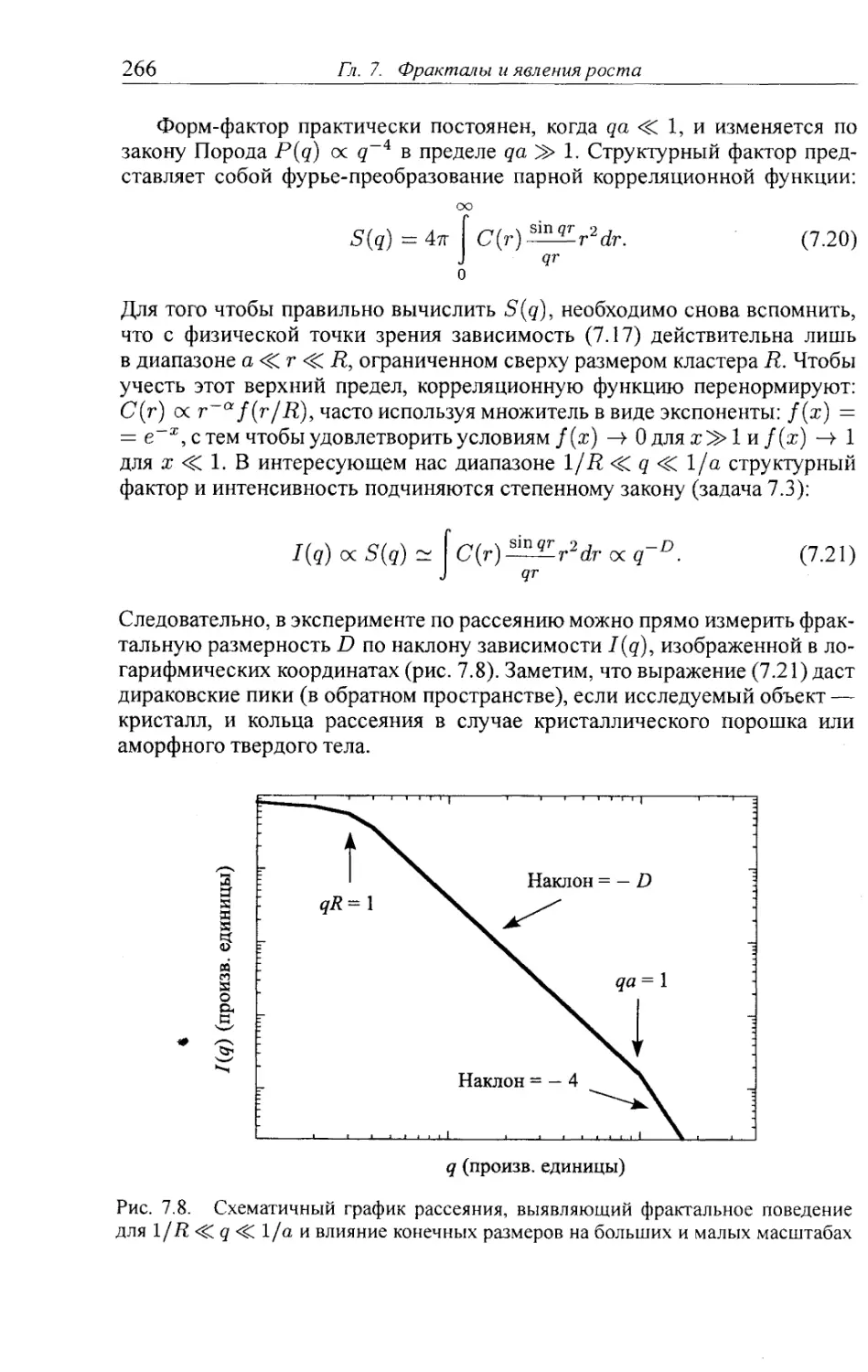
7.1.7. Парная корреляционная функция 264
7.1.8. Нижний и верхний пределы 267
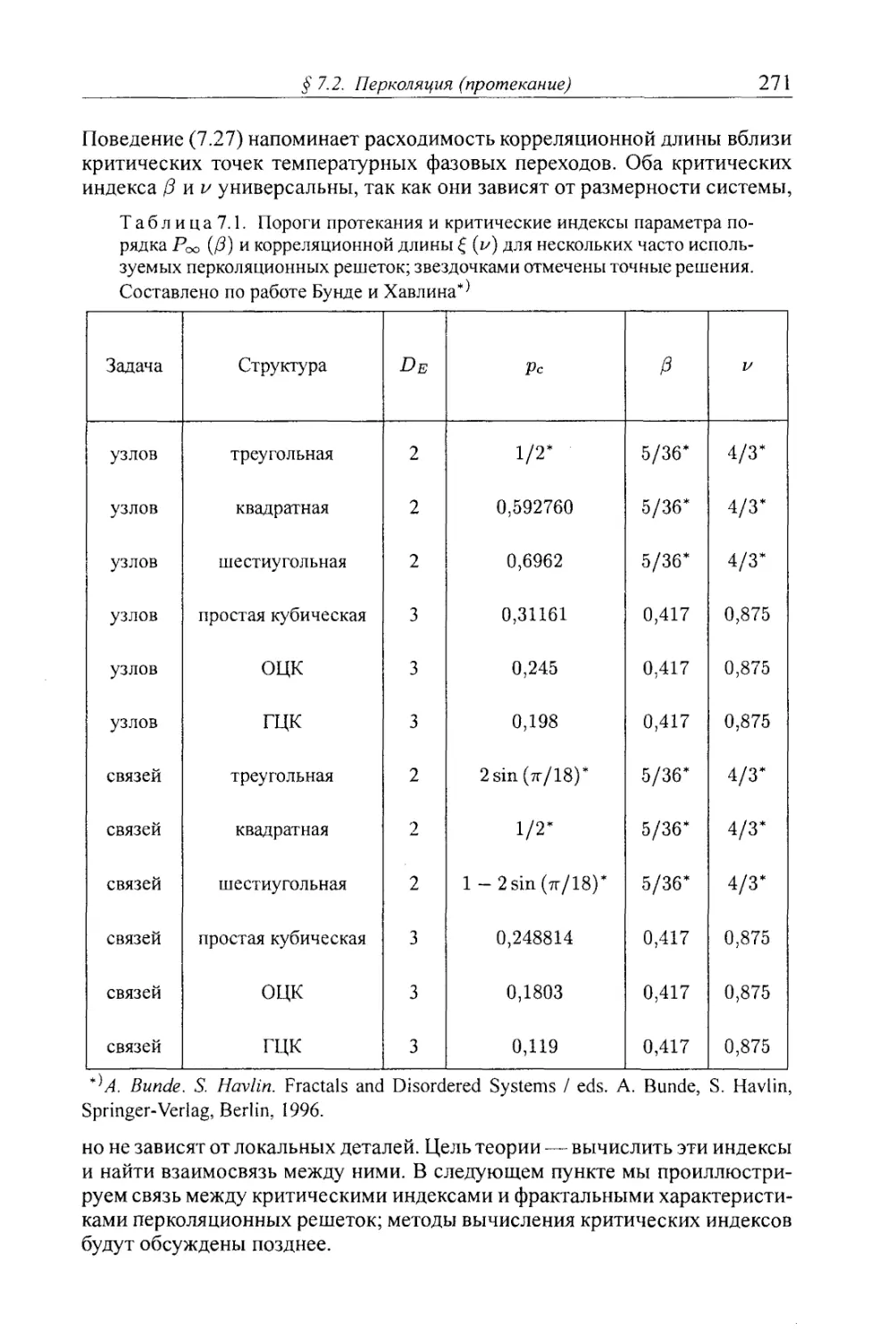
§ 7.2. Перколяция (протекание) 267
7.2.1. Геометрическое протекание 267
7.2.2 Протекание и фазовые переходы второго рода 270
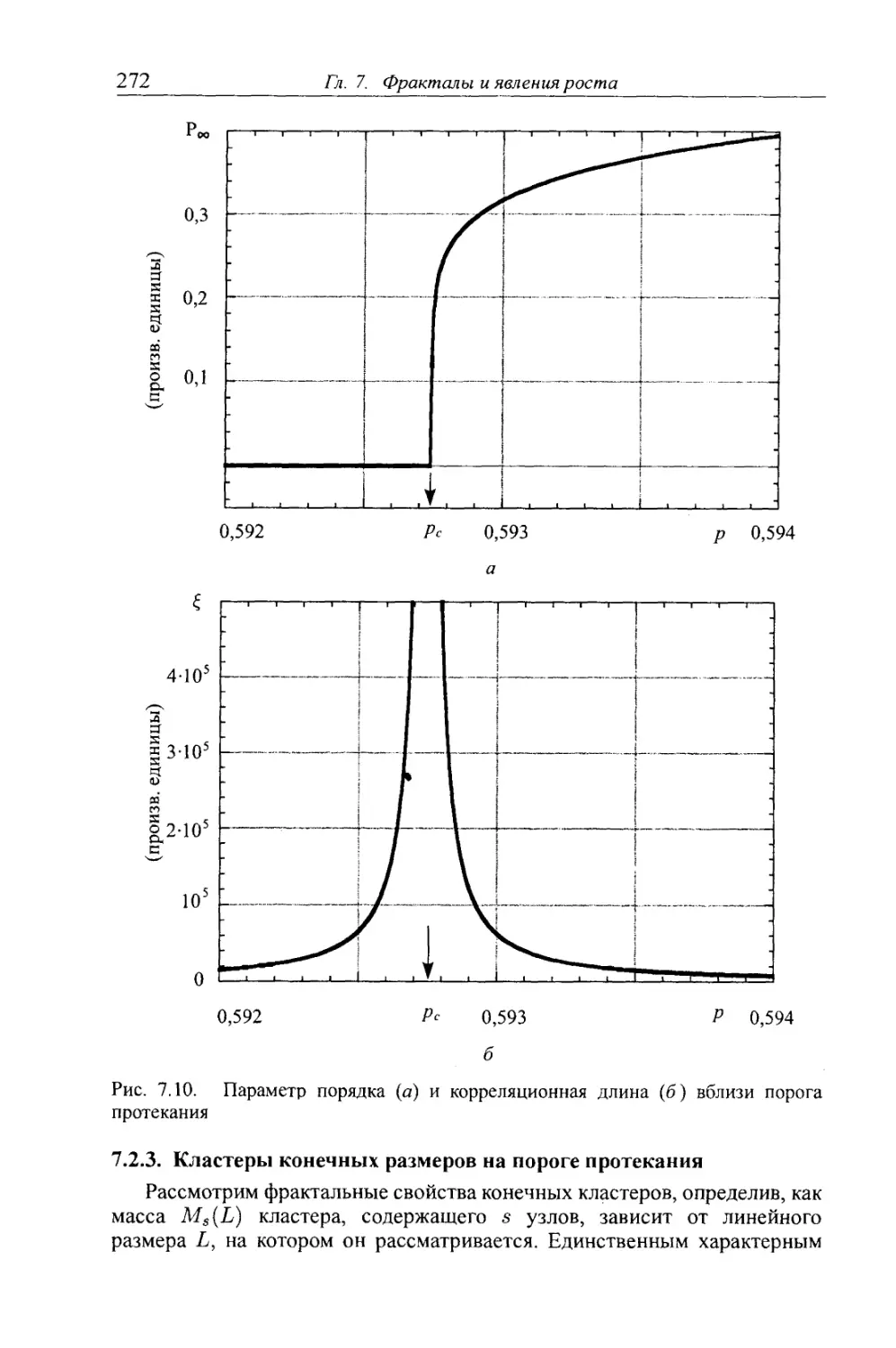
7.2.3. Кластеры конечных размеров на пороге протекания 272
7.2.4. Фрактальная размерность перколяционного кластера 274
7.2.5. Протекание на решетке Бете 275
7.2.6. Протекание и ренормализационная группа 277
§ 7.3. Агрегация 279
7.3.1. Кластер-кластерная агрегация 280
7.3.2. Модель Виттена-Сандера диффузионно-контролируемой агрегации 282
7.3.3. Непрерывная лапласова модель 283
Оглавление
1
§ 7.4. Вязкие пальцы в ячейке Хеле-Шоу 285
7.4.1. Течение в тонкой ячейке 287
7.4.2. Неустойчивость границы раздела 287
ГЛАВА 8. Дислокации в твердых телах. Пластическая релаксация 294
§8.1. Упругость дислокаций 294
8.1.1. Линейная упругость: сводка 294
8.1.2. Внешние и внутренние напряжения . . 296
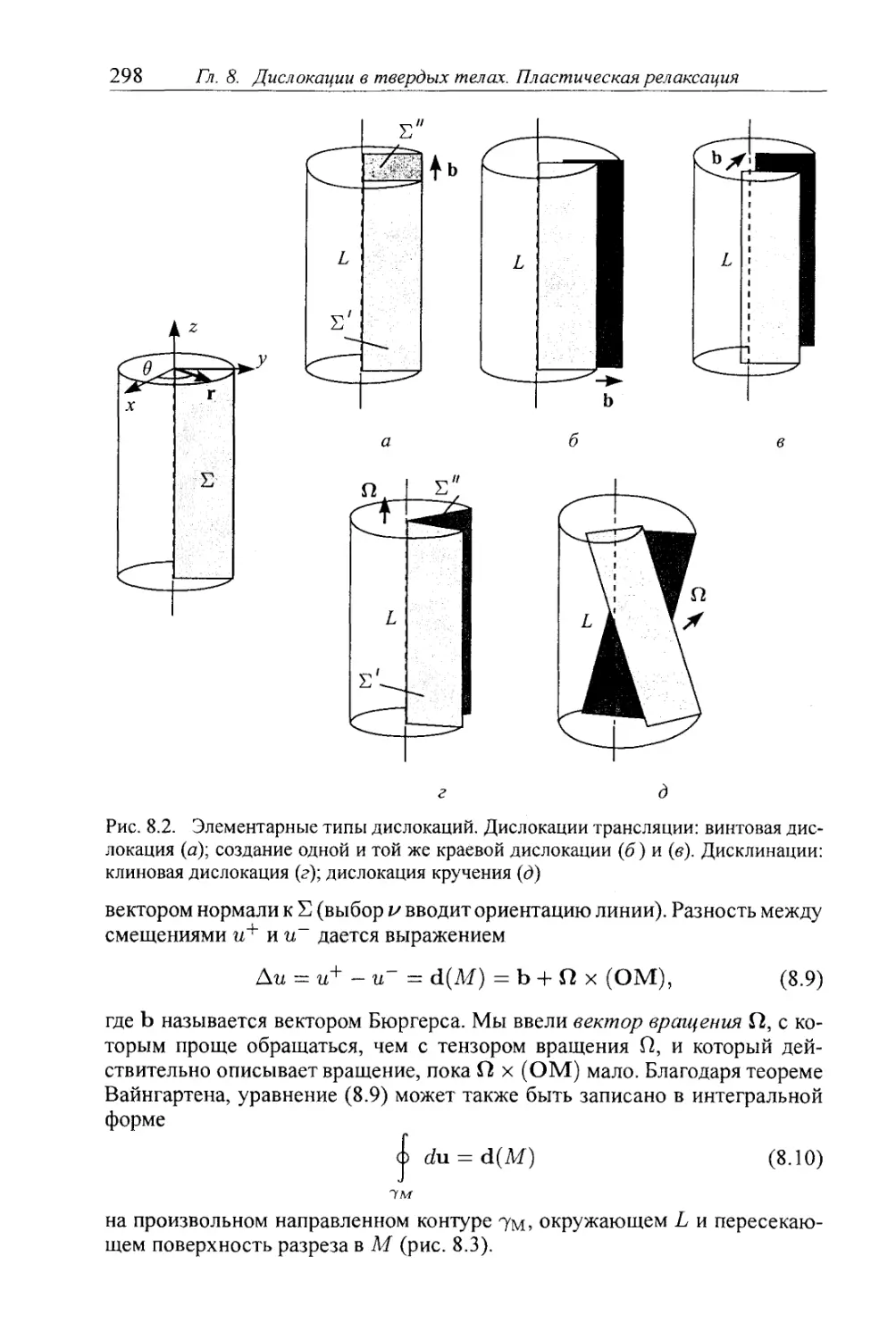
§ 8.2. Дислокации Вольтерра 297
8.2.1. Определения 297
8.2.2. Упругие поля, связанные с дефектами Вольтерра 297
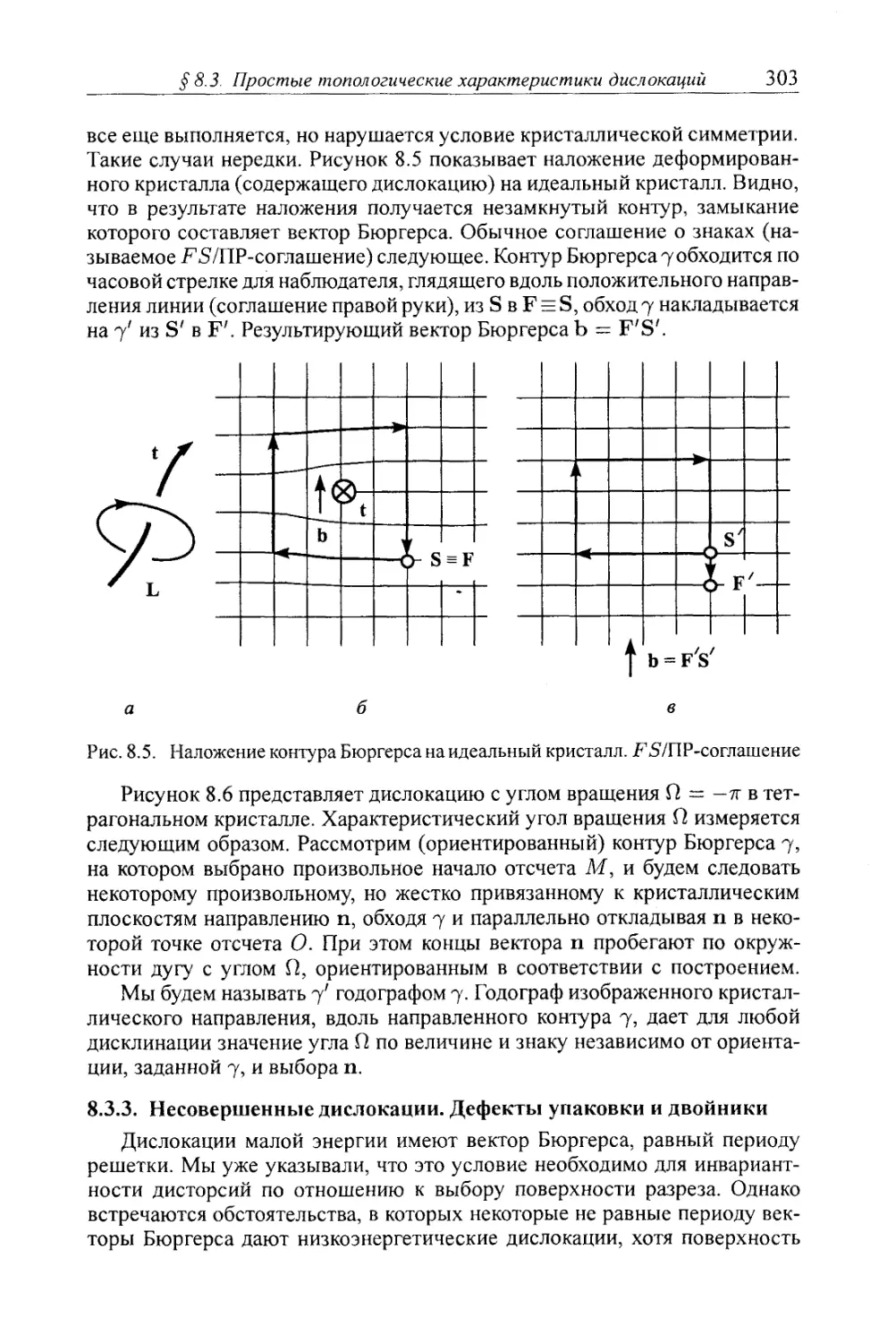
§8.3. Простые топологические характеристики дислокаций 301
8.3.1. Эквивалентные контуры 301
8.3.2. Дислокации в кристаллах 302
8.3.3. Несовершенные дислокации. Дефекты упаковки и двойники . . . 303
§ 8.4. Некоторые замечания об упругой энергии дислокаций 305
8.4.1. Стабильность 305
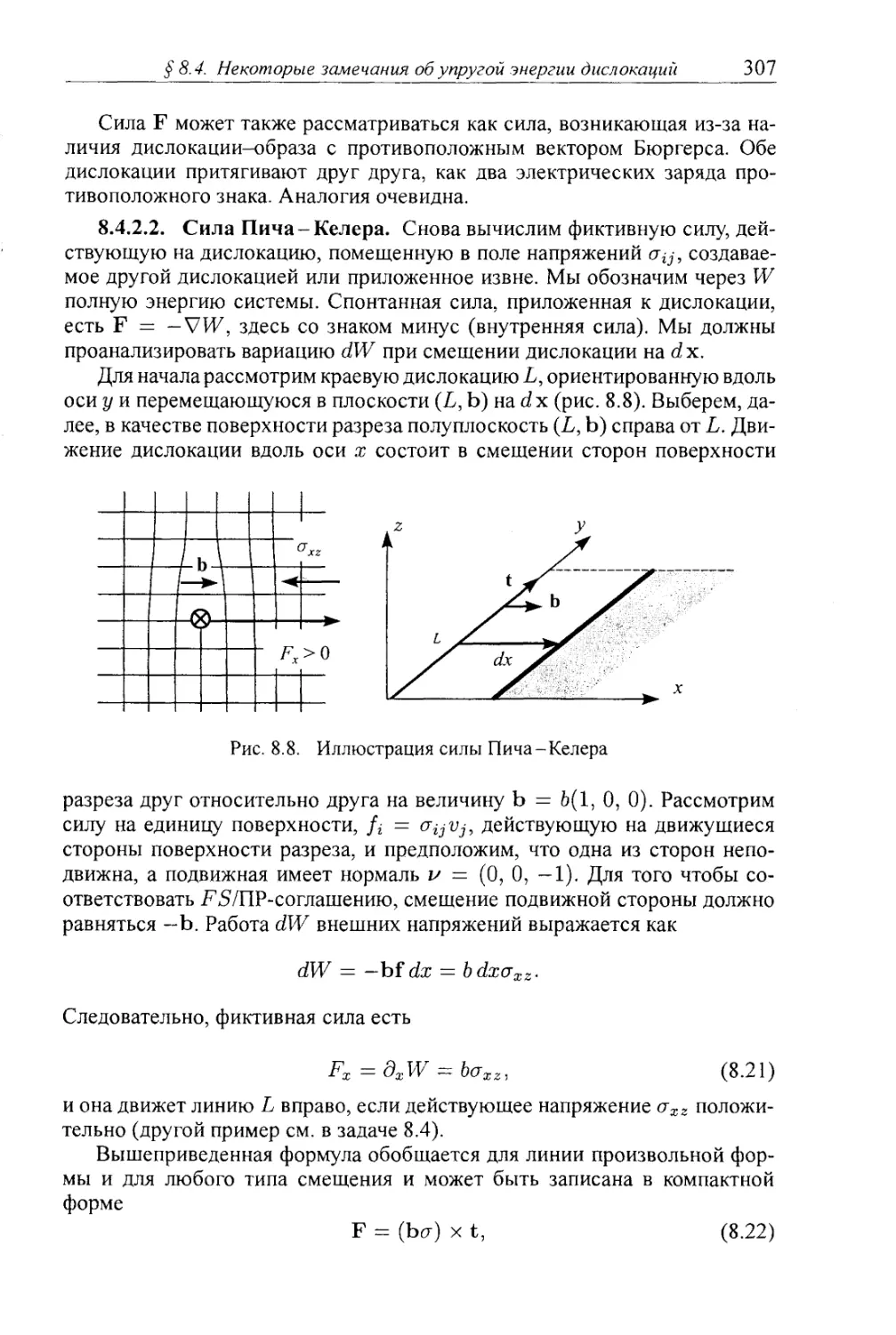
8.4.2. Силы изображения. Силы Пича-Келера 306
8.4.3. Линейное натяжение 308
8.4.4. Механизм Франка-Рида 309
8.4.5. Дислокационное ядро 310
§8.5. Подвижность дислокаций 311
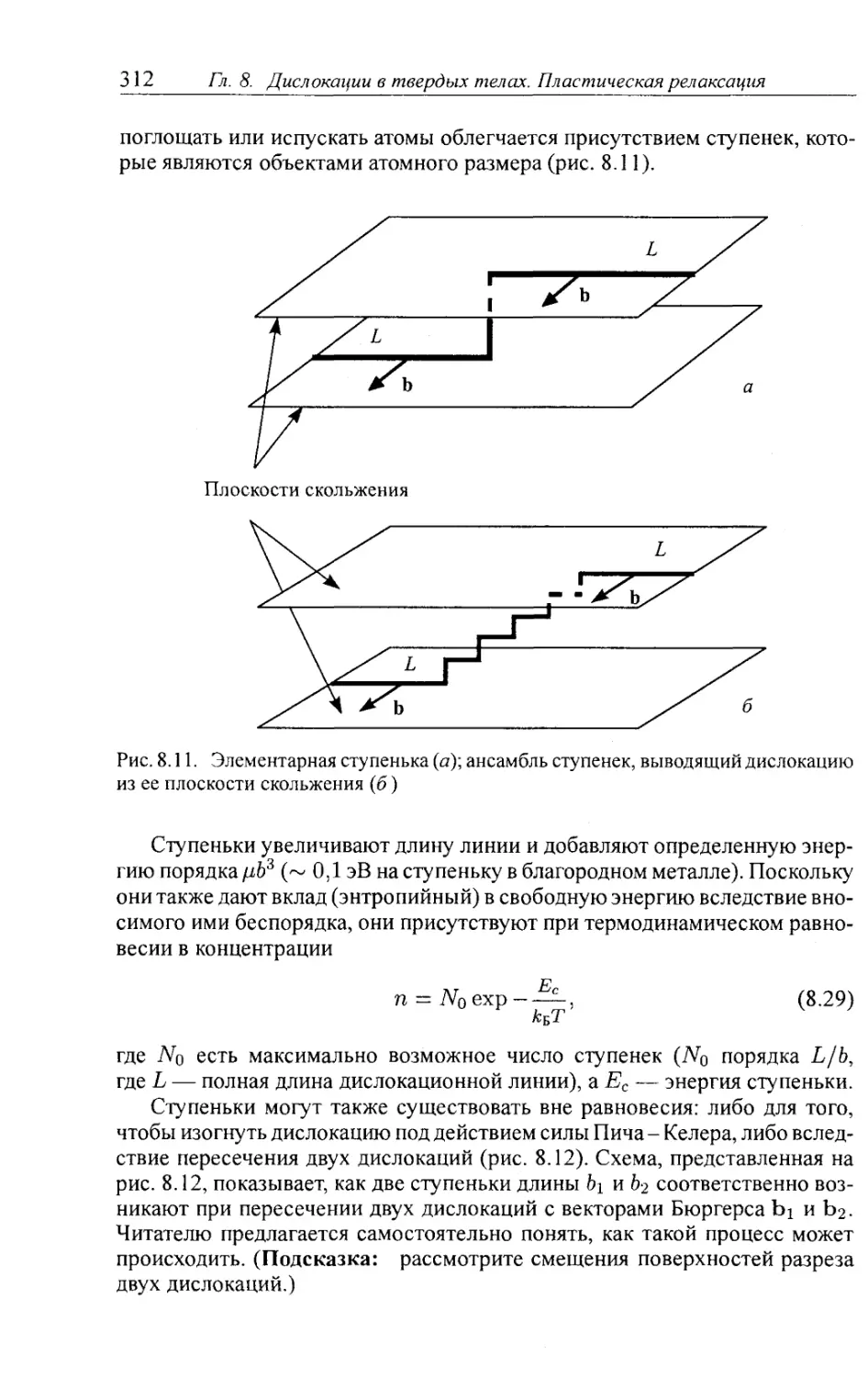
8.5.1. Элементарные перемещения дислокации 311
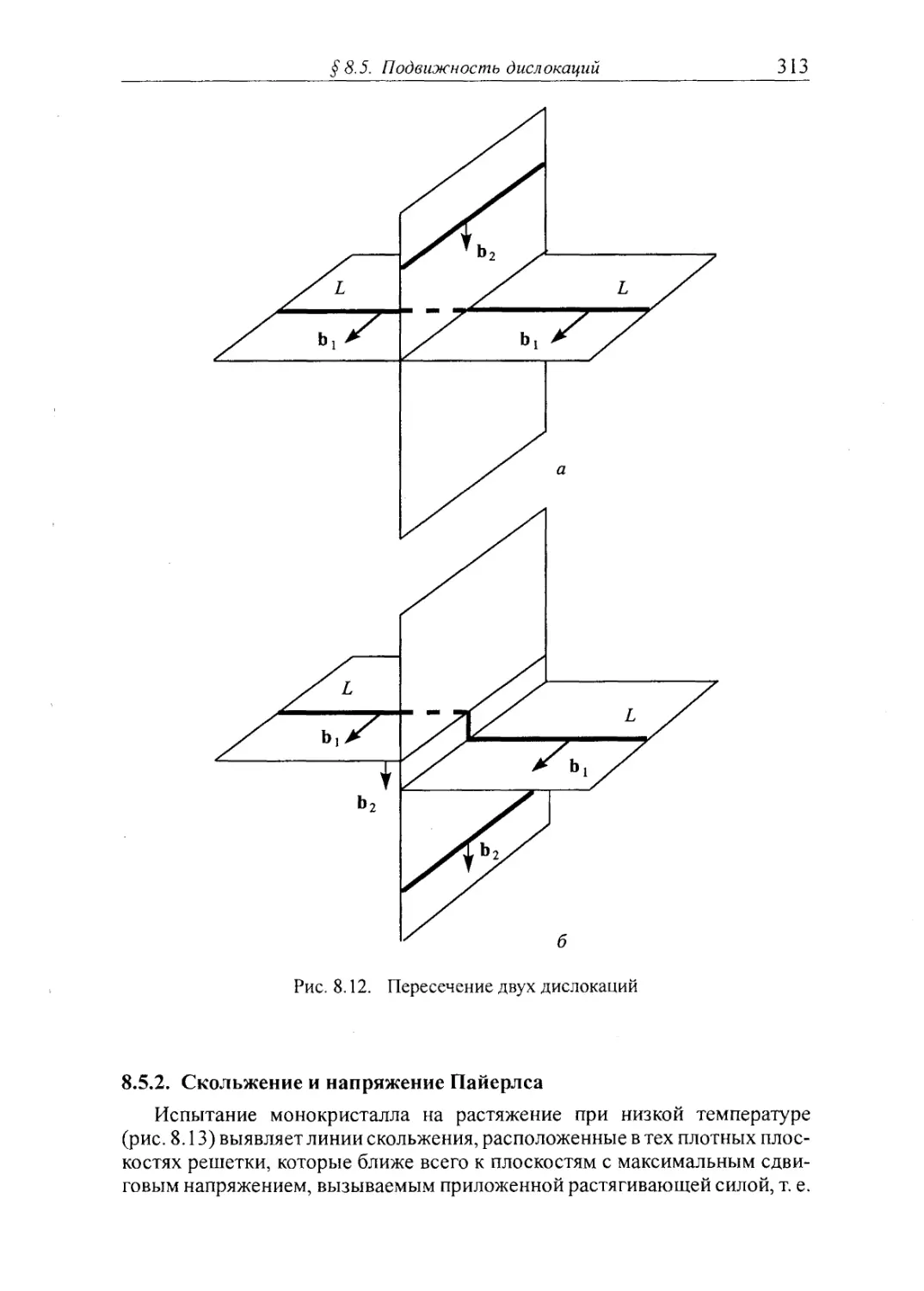
8.5.2. Скольжение и напряжение Пайерлса 313
§8.6. Точечные дефекты и переползание 318
8.6.1. Вакансии и междоузлия 318
8.6.2. Диффузия точечных дефектов и самодиффузия 319
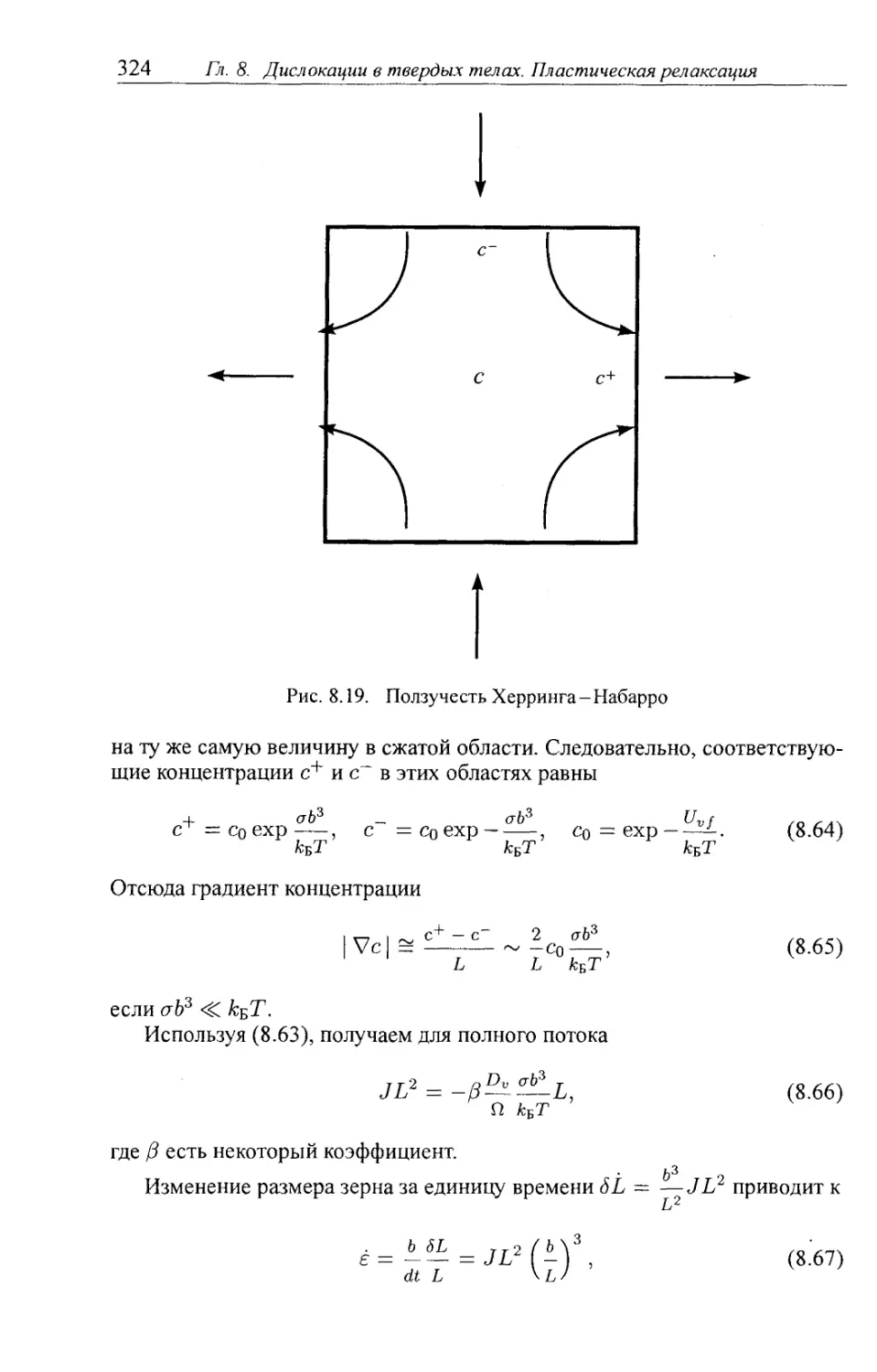
8.6.3. Ползучесть 323
§ 8.7. Ансамбли дислокаций 325
8.7.1. Сетка Франка 325
8.7.2. Субграницы 326
8.7.3. Большие разориентации, двойники и эпитаксиальные дислокации, мар-
тенситные превращения 328
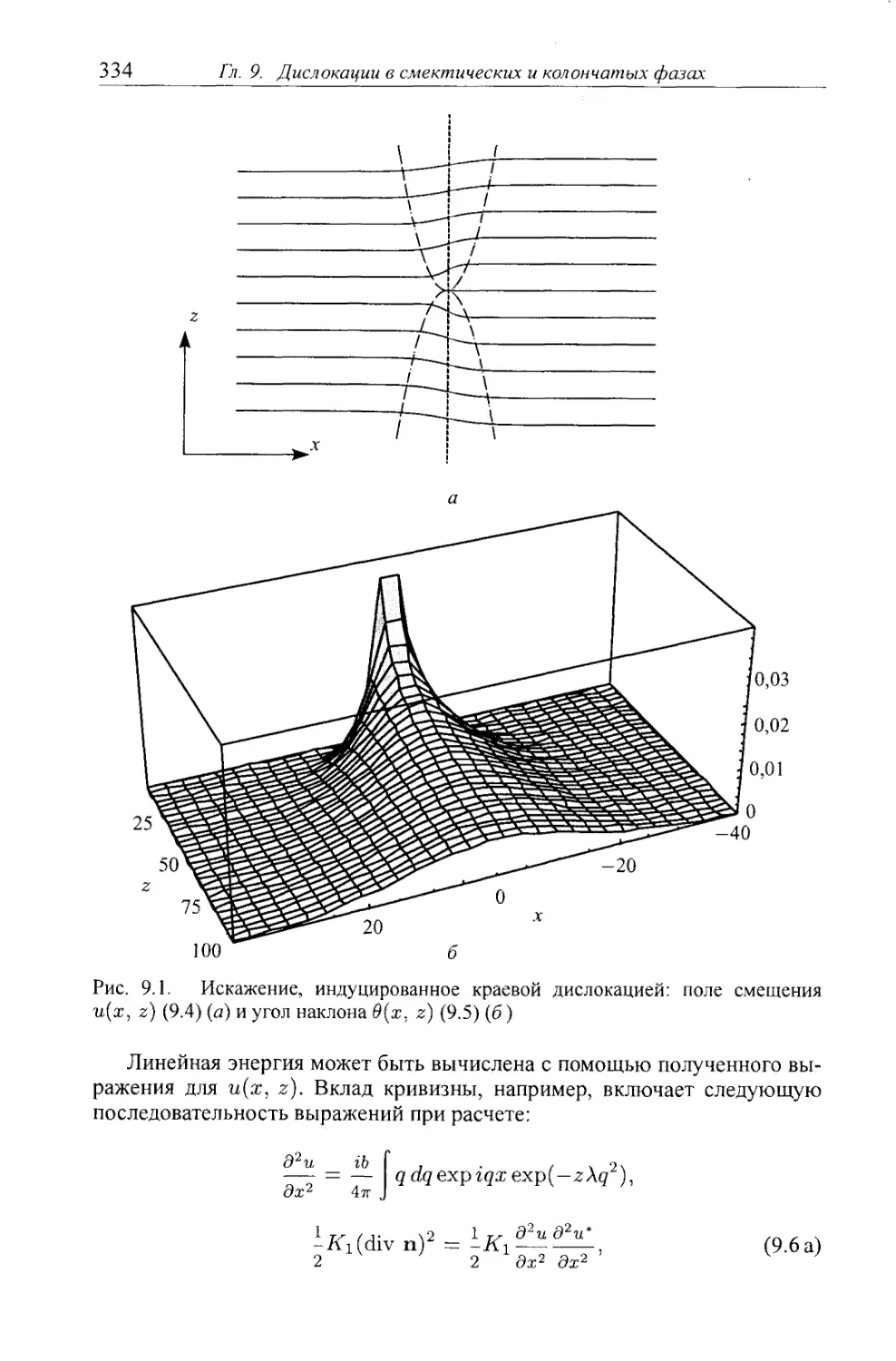
ГЛАВА 9. Дислокации в смектических и колончатых фазах 332
§ 9Л. Статические дислокации в смектиках 332
9.1.1. Краевые дислокации с малыми и большими векторами
Бюргерса 332
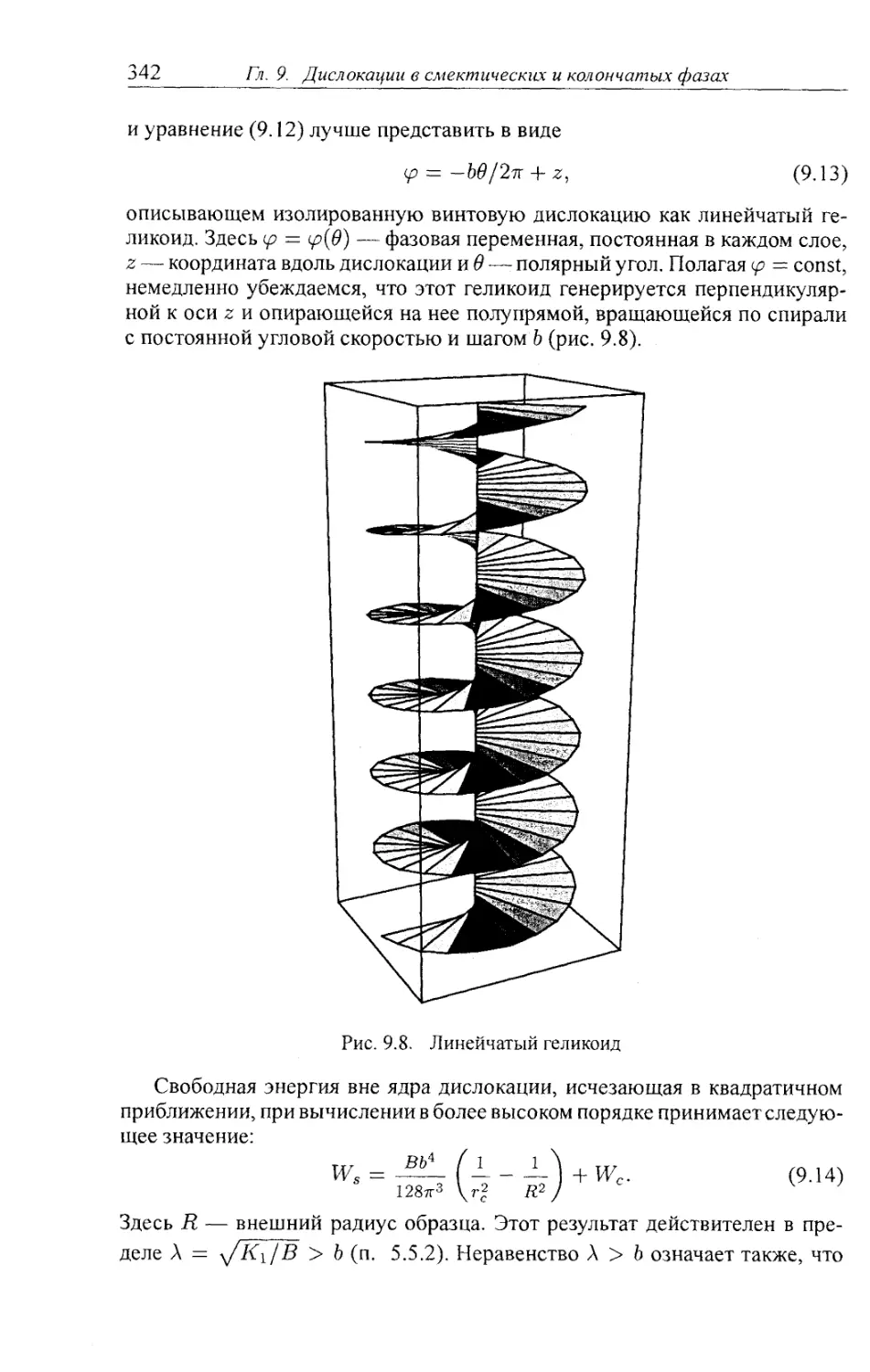
9.1.2. Винтовая дислокация 340
9.1.3. Линейное натяжение винтовой дислокации 344
8
Оглавление
9.1.4 Напряжения в SmA и сила Пича-Келера 346
§ 9.2. Дислокации в колончатых фазах 347
9.2.1. Продольные краевые дислокации в колончатых гексагональных жид¬
ких кристаллах 347
9.2.2. Поперечные краевые дислокации 348
9.2.3. Винтовые дислокации 350
9.2.4. Свободные флуктуации продольных дислокаций 352
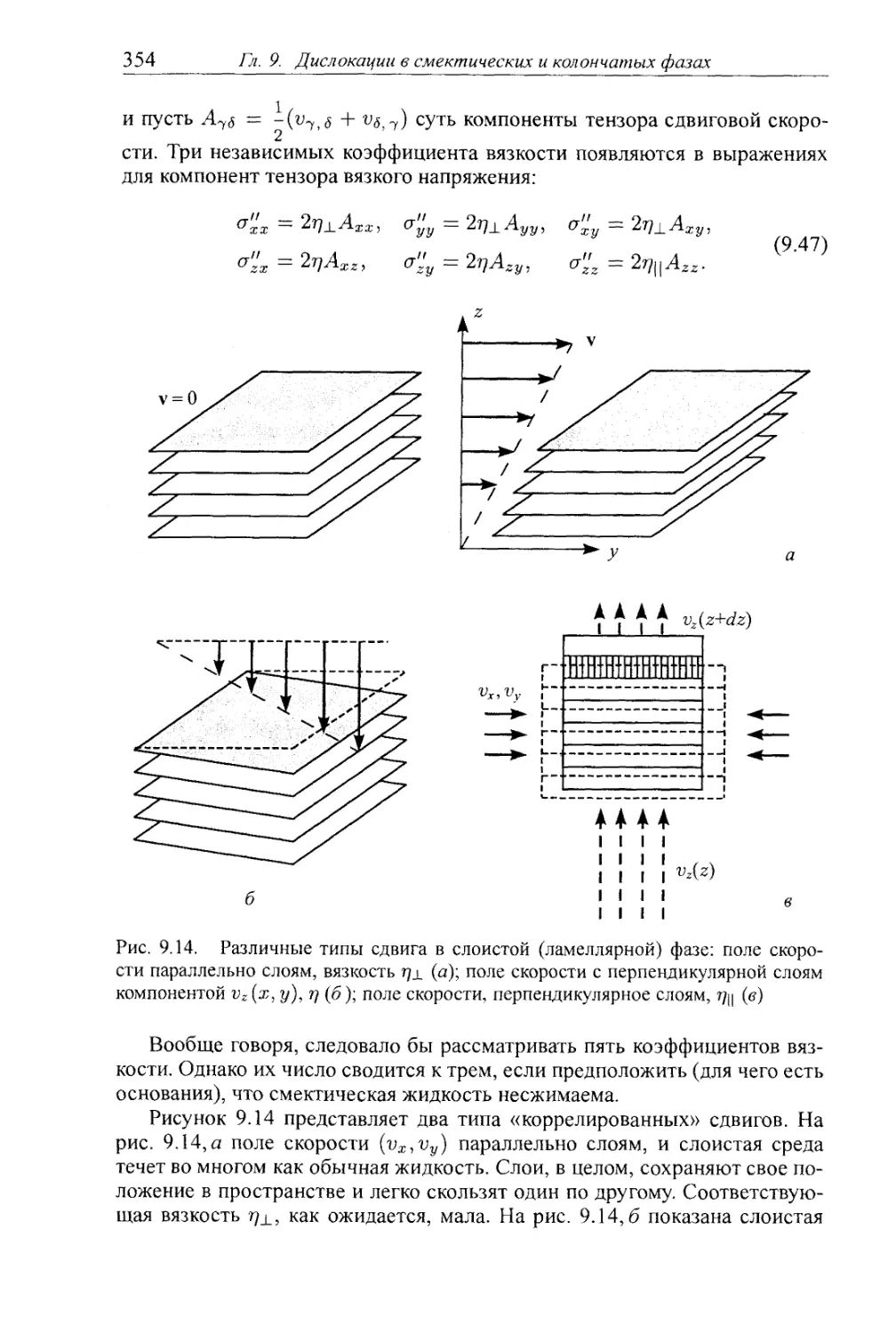
§9.3. Гидродинамика смектической фазы 353
§ 9.4. Динамические моды в смектиках 358
§ 9.5. Движение изолированных дислокаций в SmA-фазе 359
9.5.1. Краевая дислокация 359
9.5.2. Винтовая дислокация 362
§ 9.6. Коллективное поведение дислокаций и нестабильности 363
9.6.1. Общие замечания 363
9.6.2. Коллективное переползание дислокаций в SmA 364
9.6.3. Размножение краевых дислокаций 365
ГЛАВА 10. Дефекты кривизны в смектиках и колончатых фазах . . 369
§10.1. Кривизна в твердых кристаллах 369
§ 10.2. Кривизна в жидких кристаллах: общие замечания 371
§10.3. Кривизна в смектиках 372
10.3.1. Исторические замечания 372
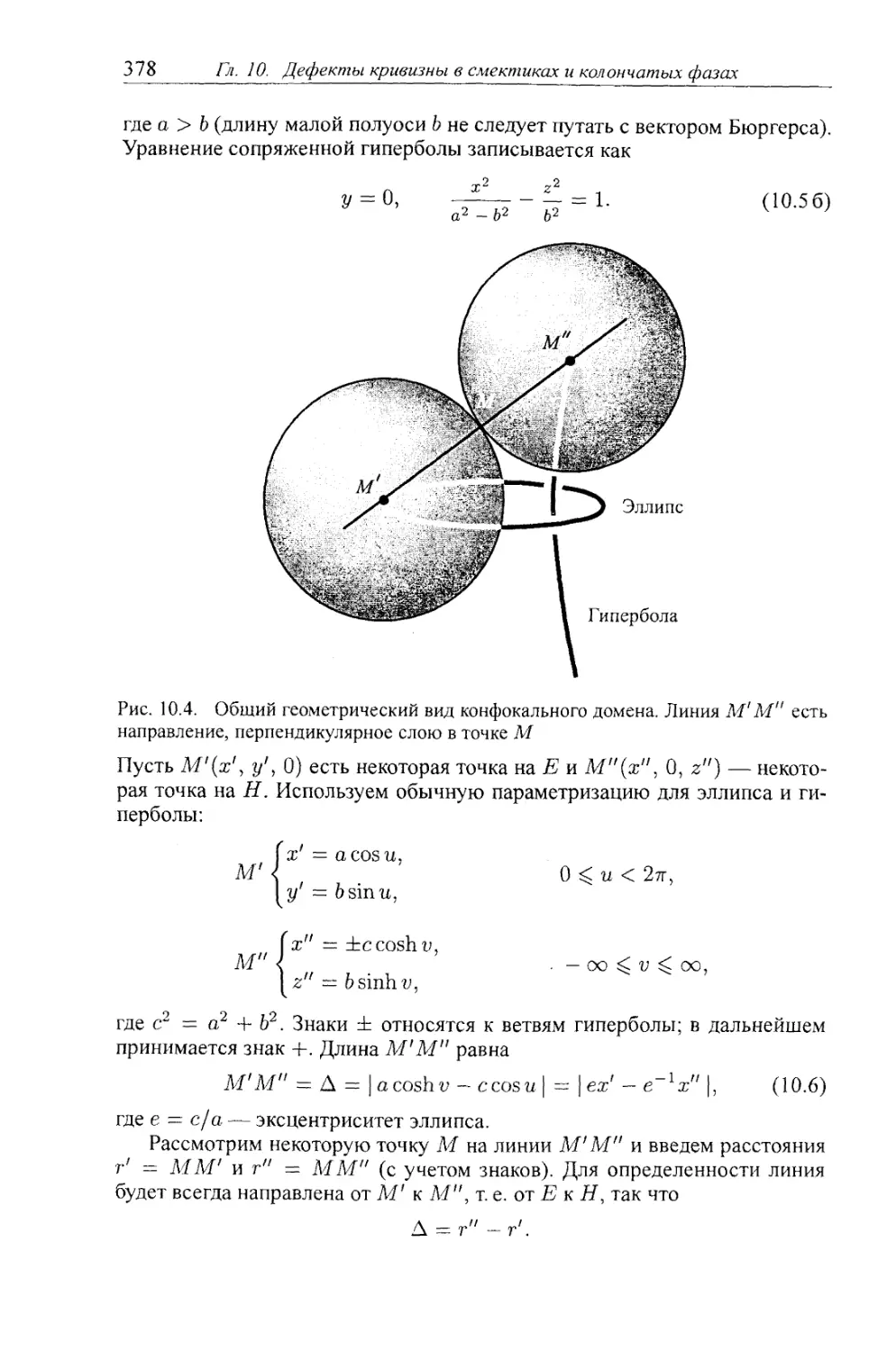
10.3.2. Конгруэнции прямых нормалей и конфокальные домены 373
10.3.3. Конгруэнции нормалей, вариации идеальных конфокальных доменов 375
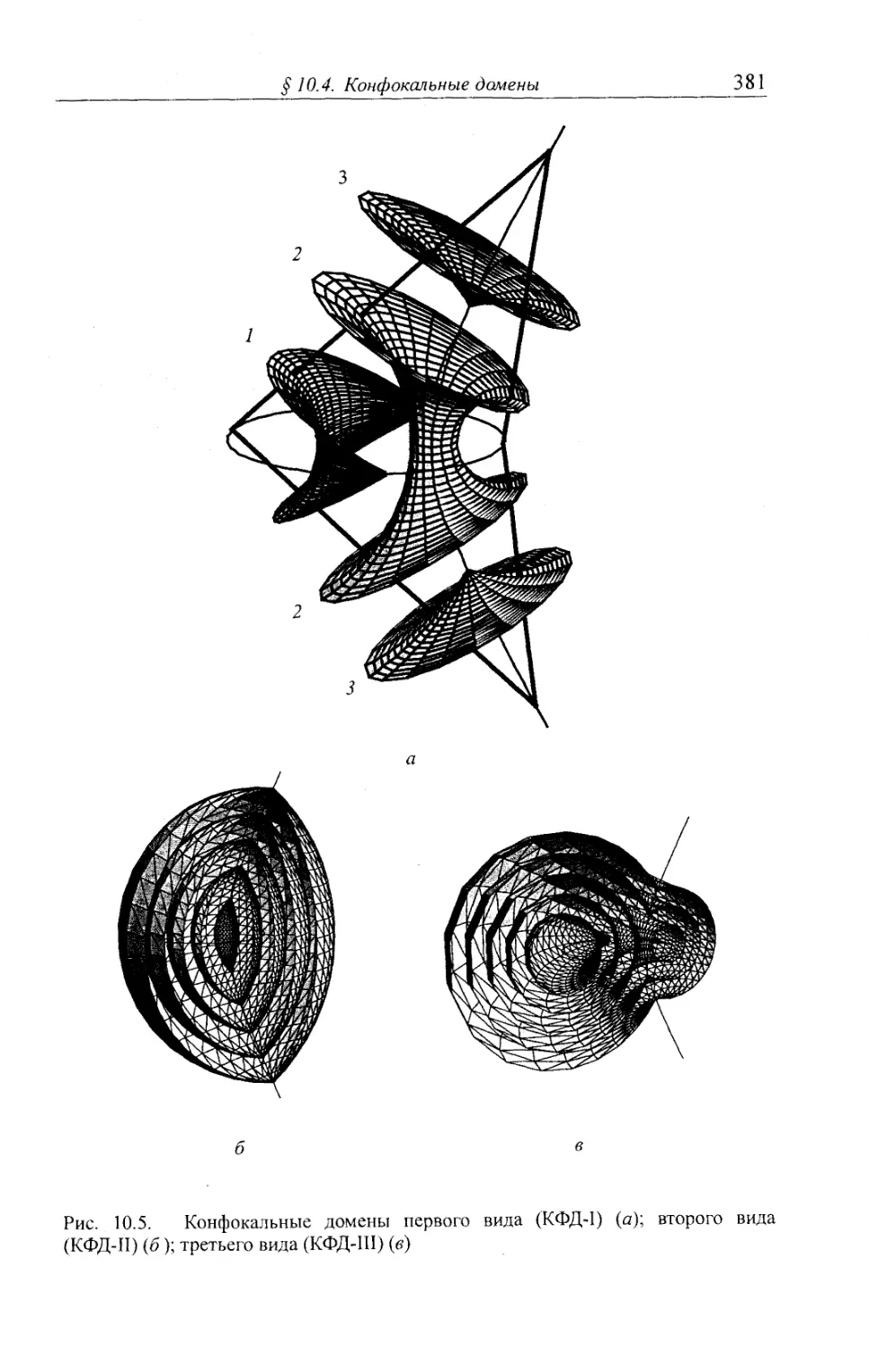
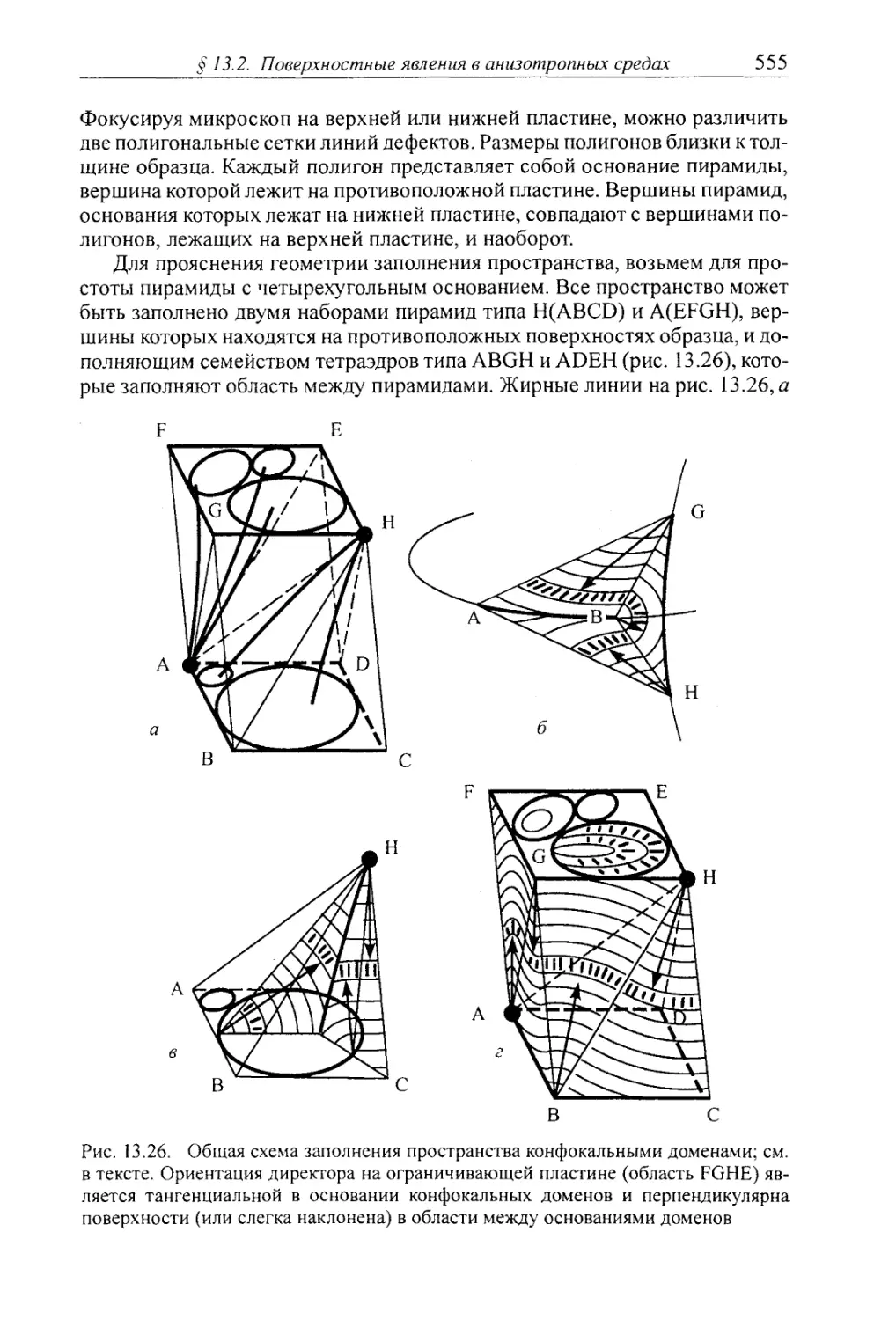
§ 10.4. Конфокальные домены 377
10.4.1. Аналитический подход: основные формулы 377
10.4.2. Различные виды конфокальных доменов 379
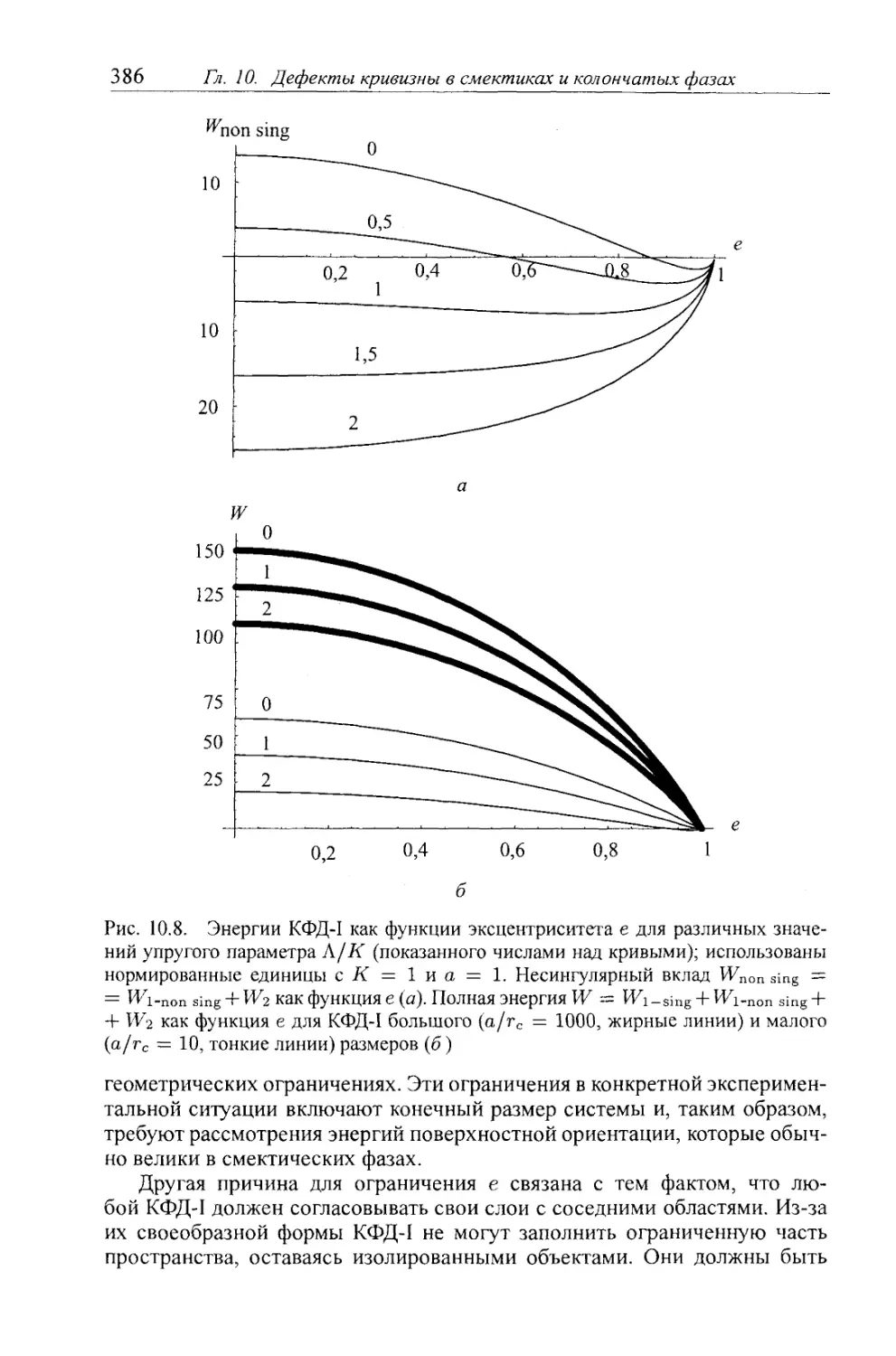
§ 10.5. Энергия кривизны КФД 383
10.5.1. КФД-I: Отрицательная гауссова кривизна 384
10.5.2. Торический КФД с отрицательной гауссовой кривизной 387
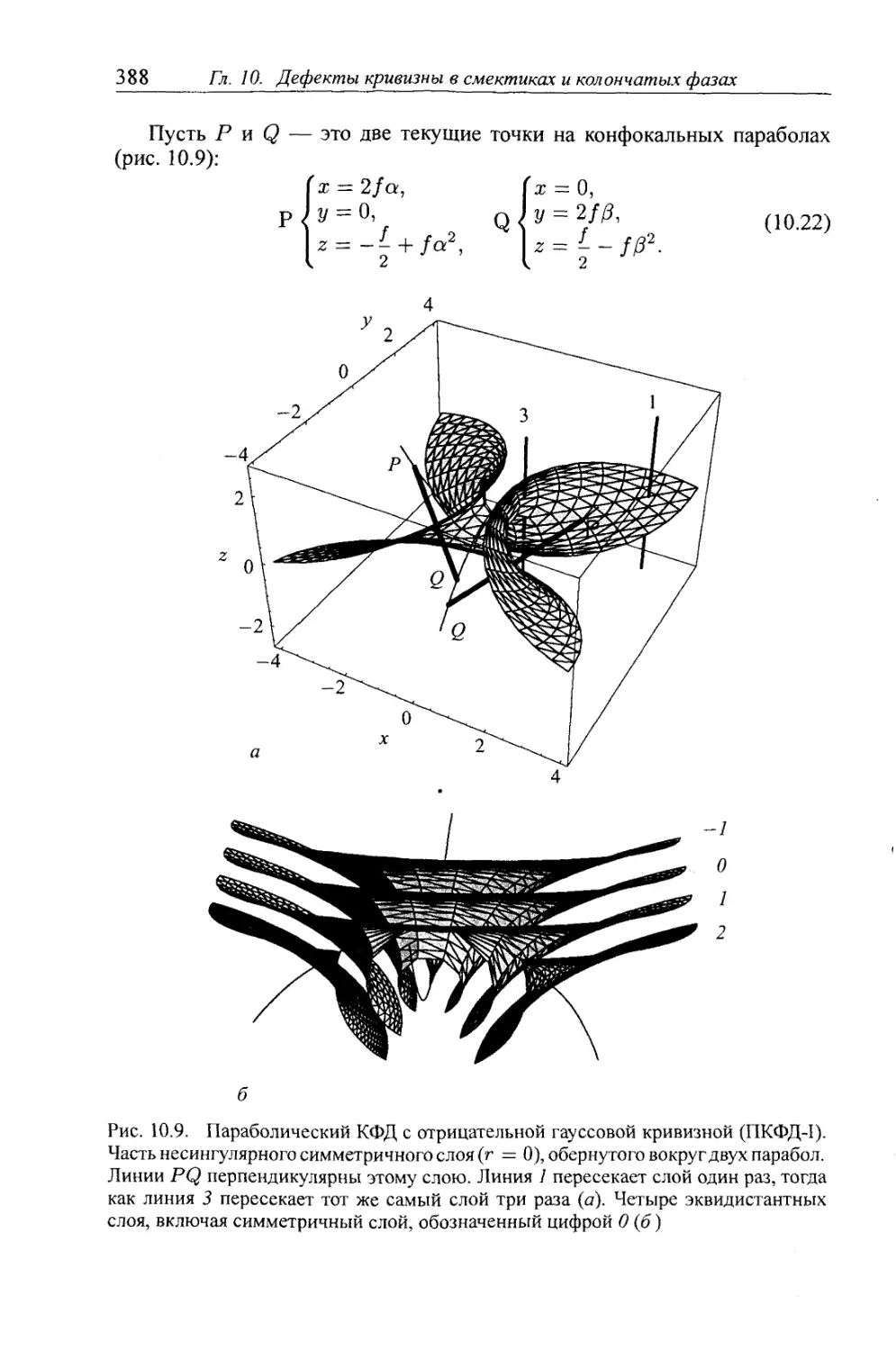
10.5.3. Параболический КФД с отрицательной гауссовой кривизной . . . 387
10.5.4. КФД-П: положительная гауссова кривизна 390
§ 10.6. Дефекты кривизны в колончатых фазах 391
10.6.1. Общее рассмотрение 391
10.6.2. Развертывающиеся домены 394
10.6.3. Классификация развертывающихся доменов 395
§10.7. КФД в лиотропных ламеллярных фазах 397
10.7.1. Маслянистые бороздки 398
10.7.2. Сферолиты 40)
Оглавление
9
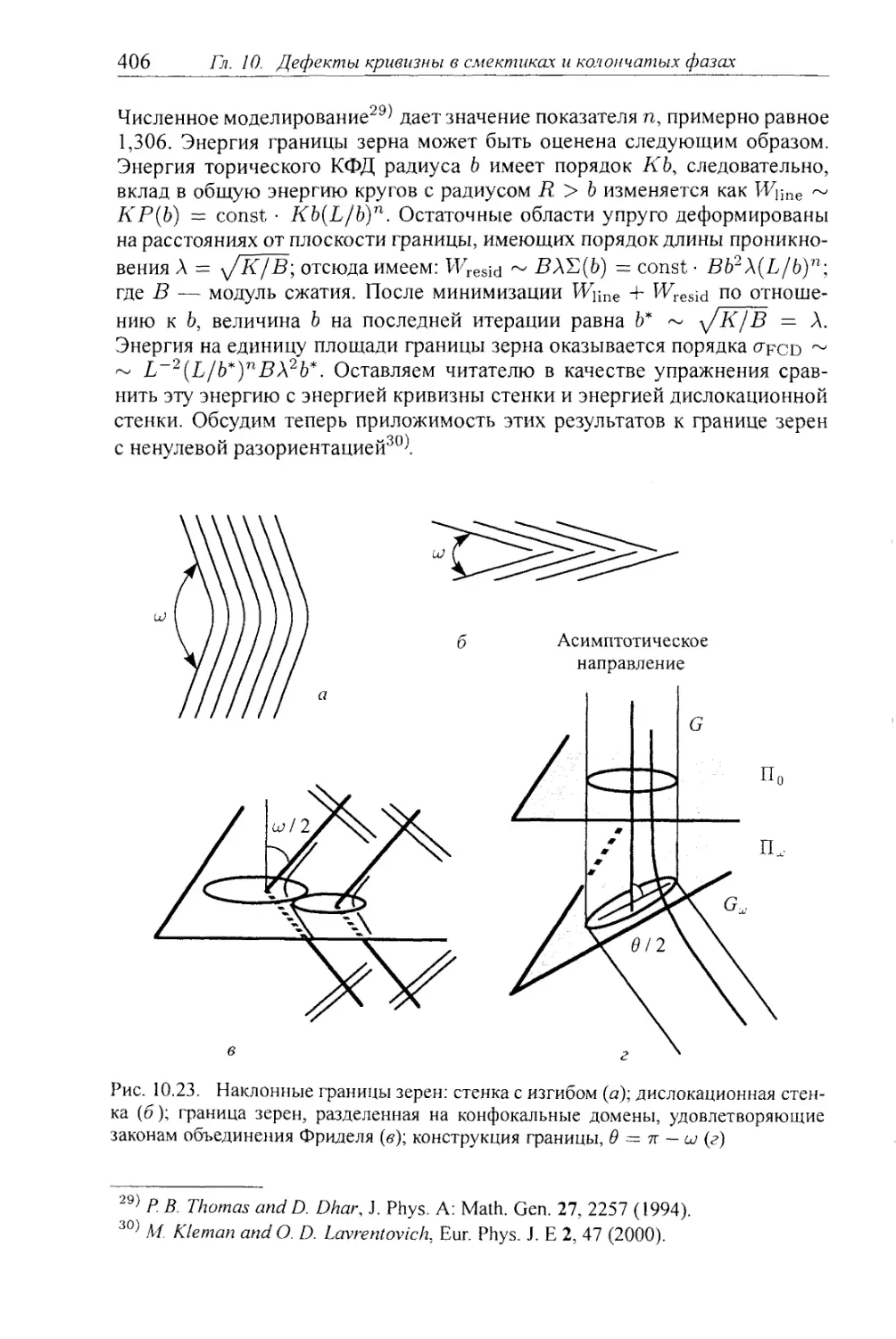
§ 10.8. Границы зерен и заполнение пространства конфокальными доме¬
нами 401
10.8.1. Конфокальные домены первого вида 402
10.8.2. Конфокальные домены второго вида 410
§10.9. Реофизика конфокальных доменов 411
10.9.1. Глобальное вязкоупругое поведение и ориентация при сдвиге ... 412
10.9.2. Текстуры 413
ГЛАВА 11. Дисклинации и топологические точечные дефекты.
Жидкостная релаксация 422
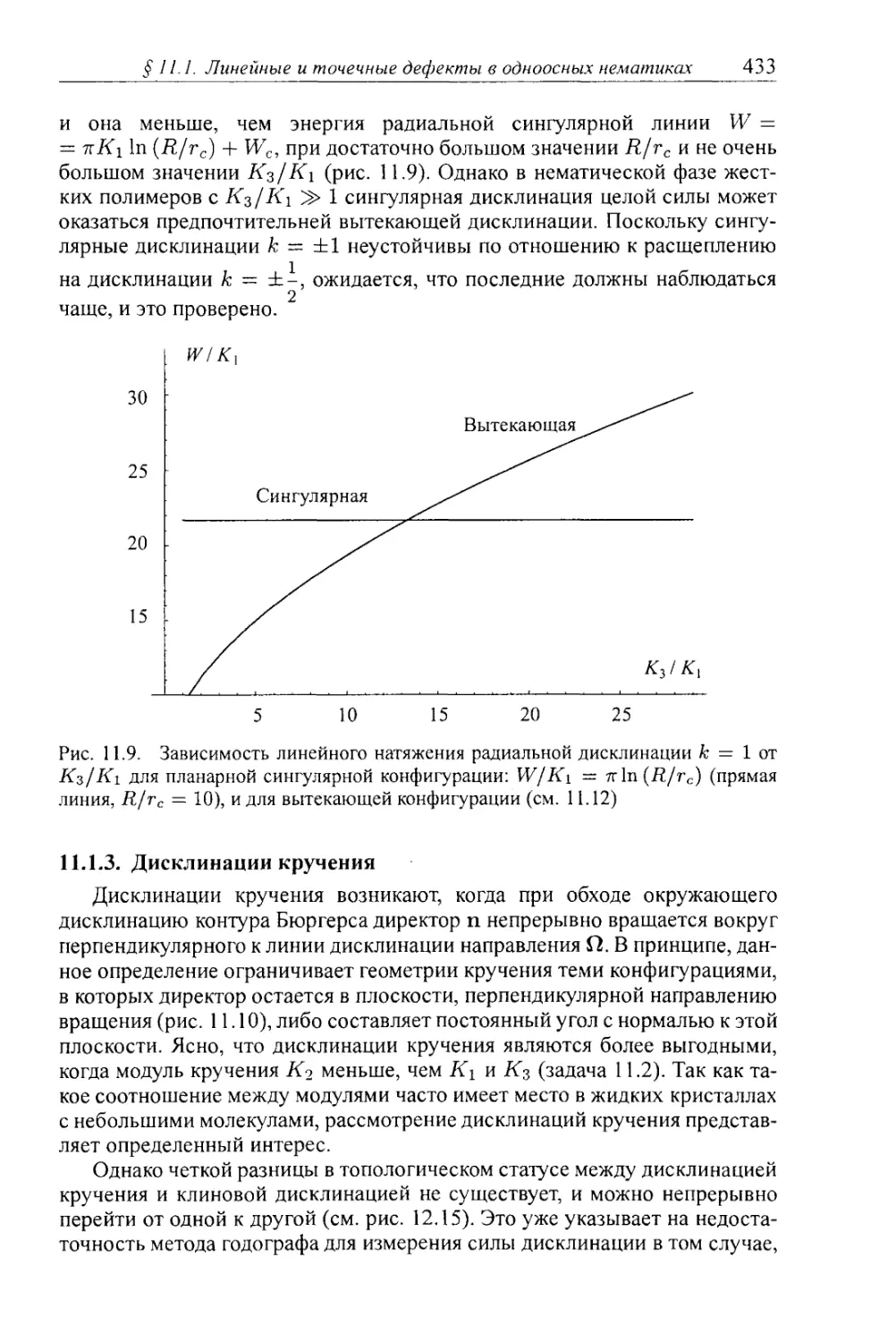
§ 11.1. Линейные и точечные дефекты в одноосных нематиках 423
11.1.1. Клиновые дисклинации в нематиках 423
11.1.2. Несингулярные дисклинации 428
11.1.3. Дисклинации кручения 433
11.1.4. Линии дефектов в жидкокристаллических полимерах 434
11.1.5. Сингулярные точки 435
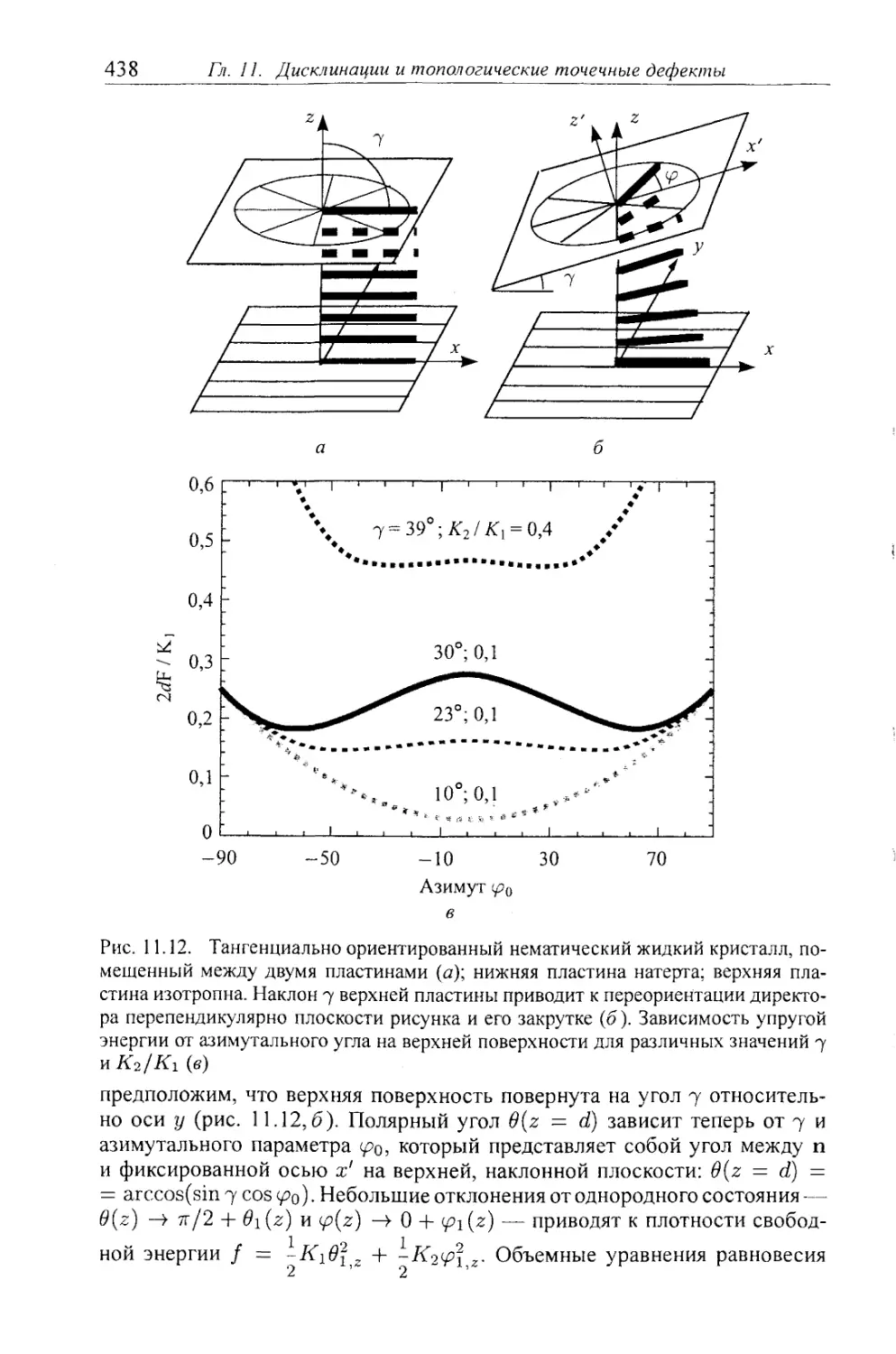
11.1.6. Закрутка вызванная ограничивающими поверхностями 437
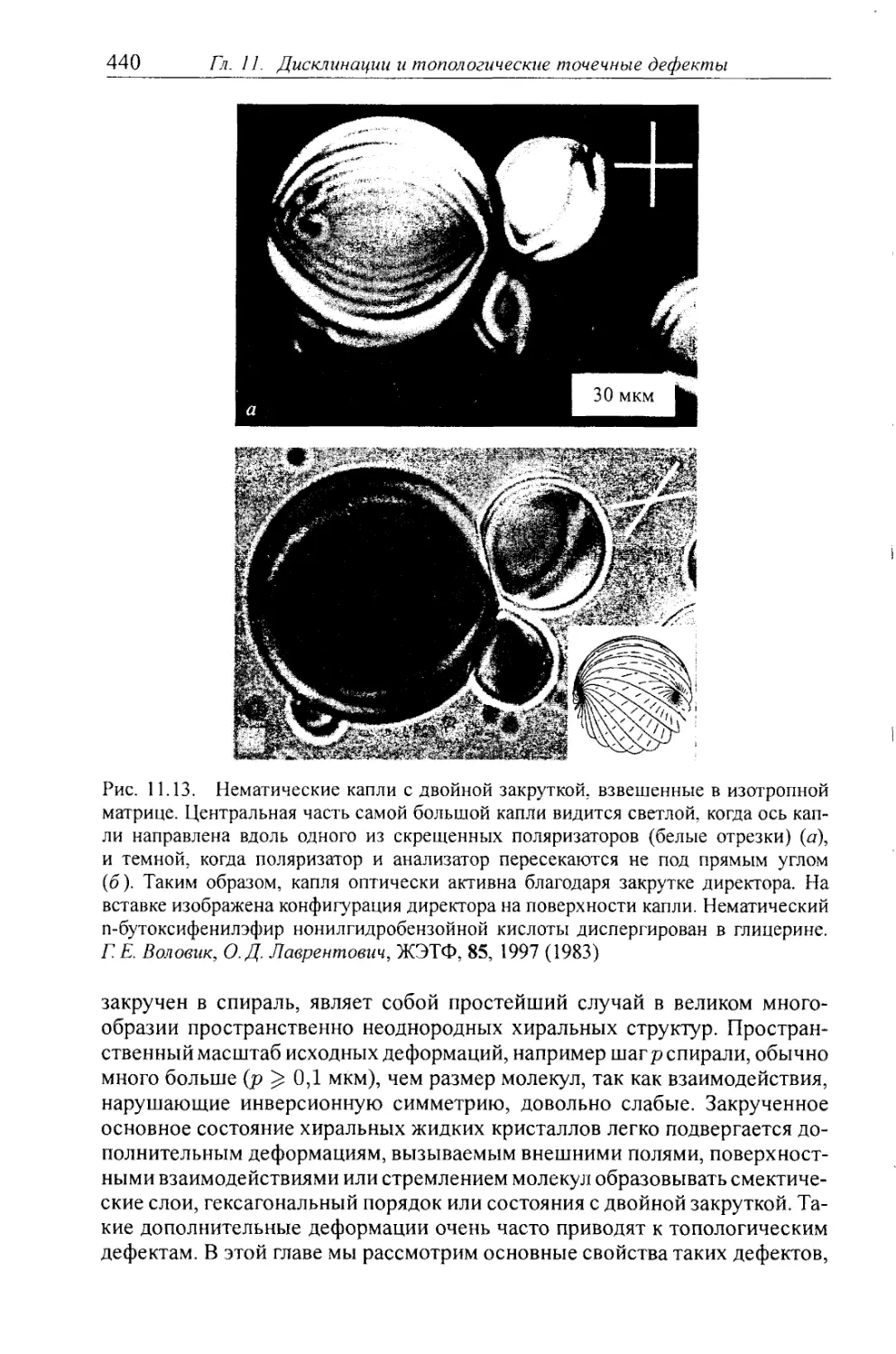
§ 11.2. Холестерики 439
11.2.1. Теория упругости на разных масштабах 441
11.2.2. Слабые деформации типа кручения: двойная закрутка 442
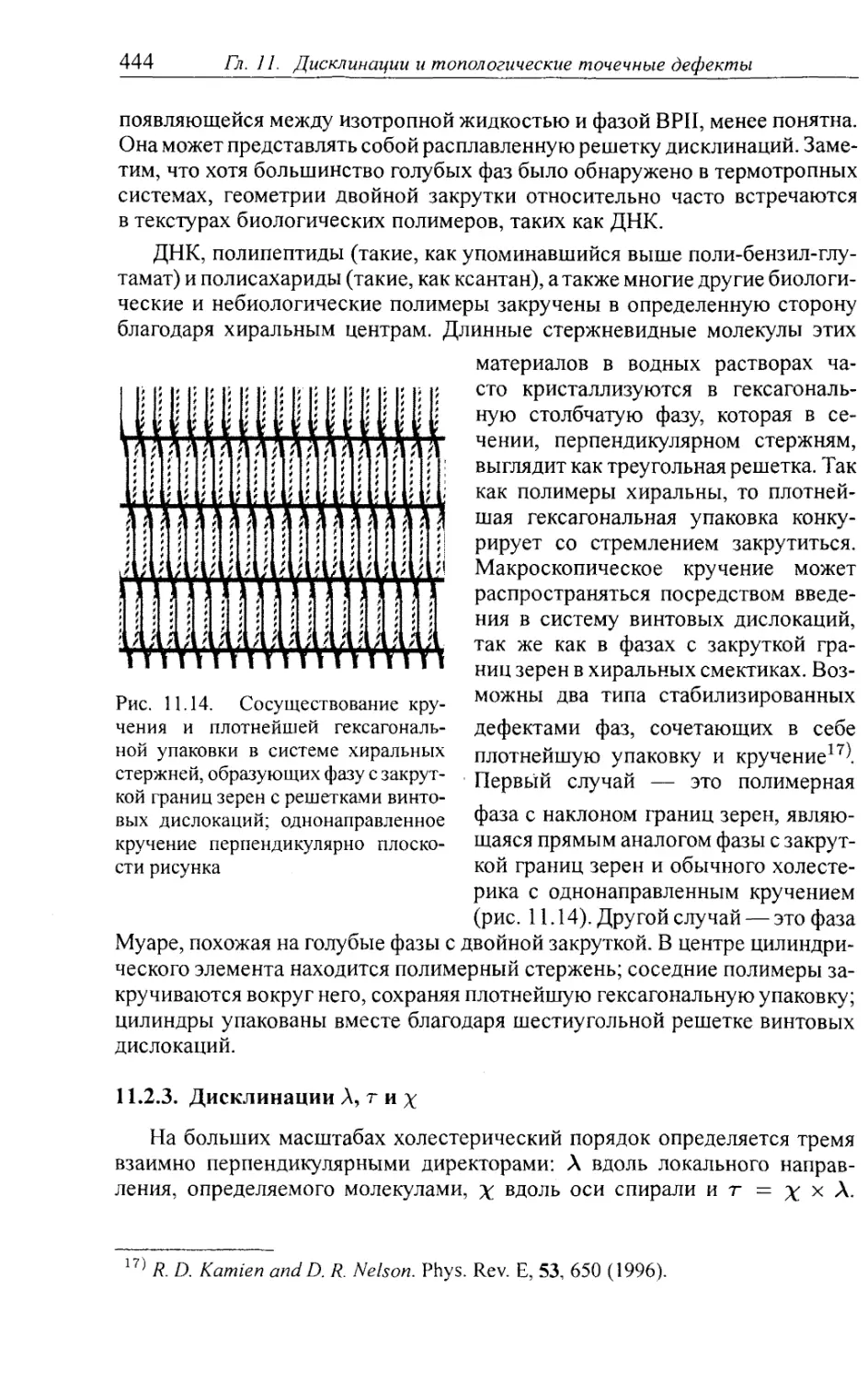
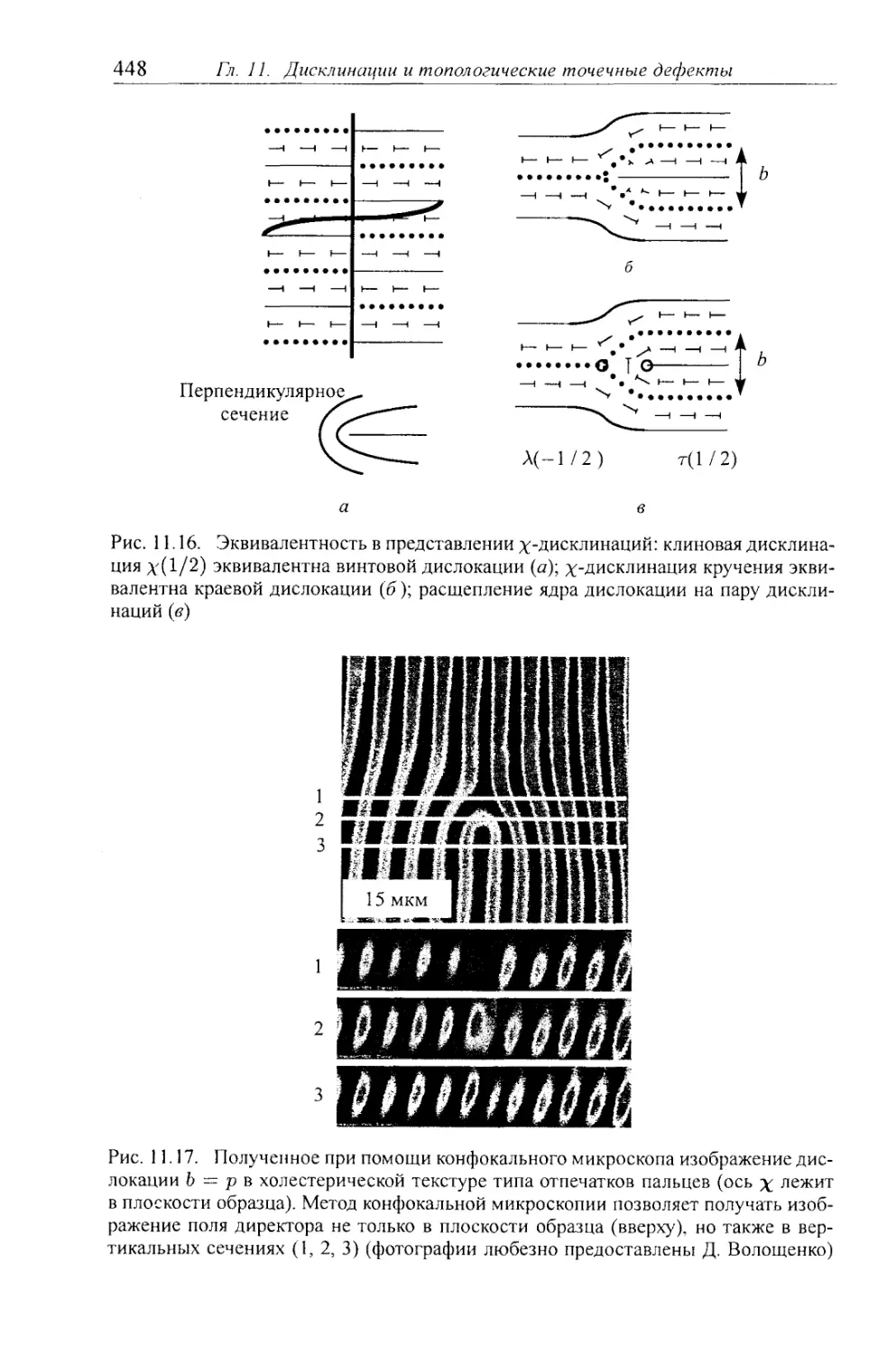
11.2.3. Дисклинации Л, г и х 444
11.2.4. Дислокации 446
11.2.5. Другие эффекты слоистой структуры 447
§ 11.3. За пределы классического процесса Вольтерра, первый шаг . . 450
11.3.1. Плотности дислокаций и дисклинаций в описании дисклинаций . . 451
11.3.2. Расширение на случай конечных дислокаций 454
11.3.3. Структура ядра и физические свойства 455
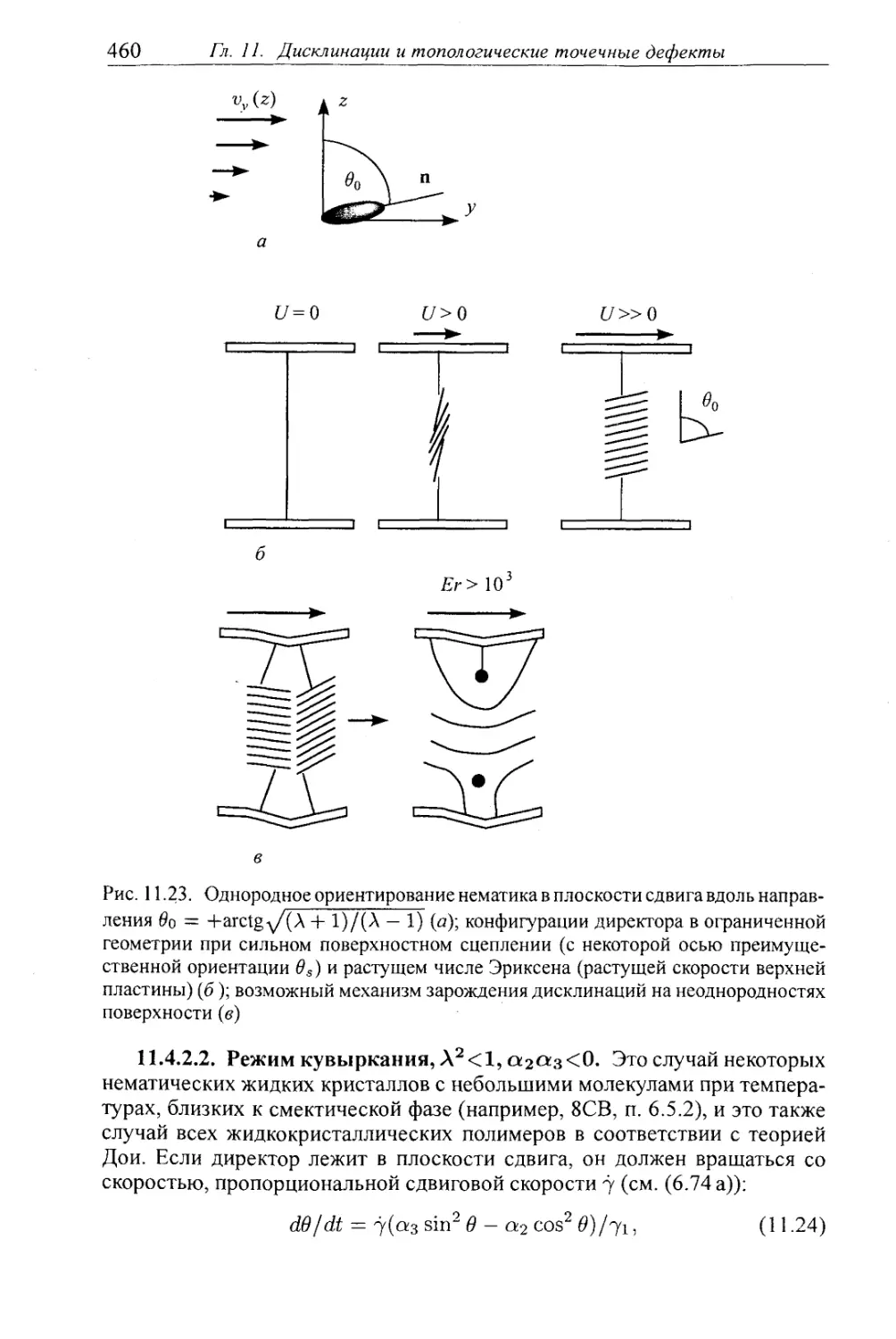
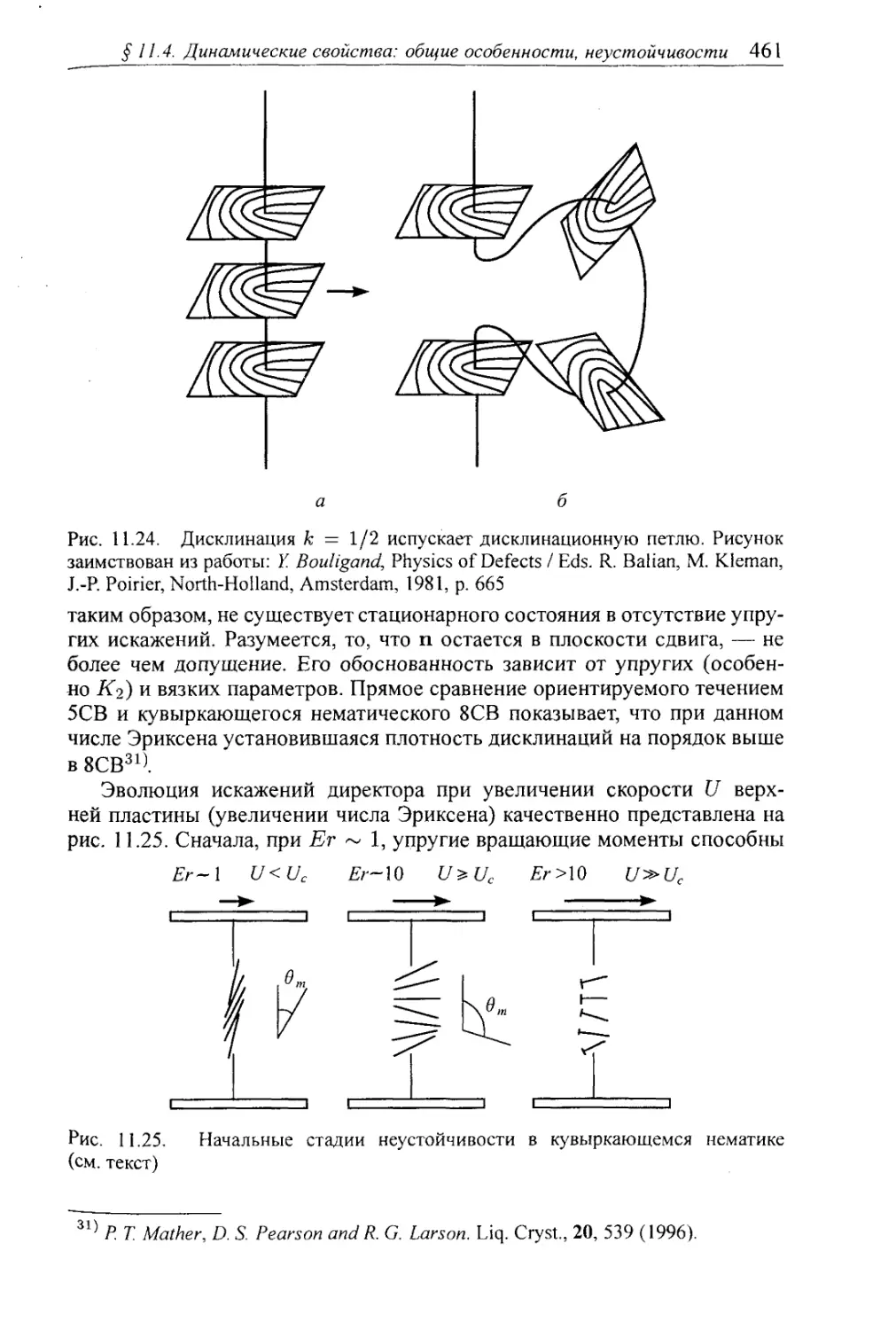
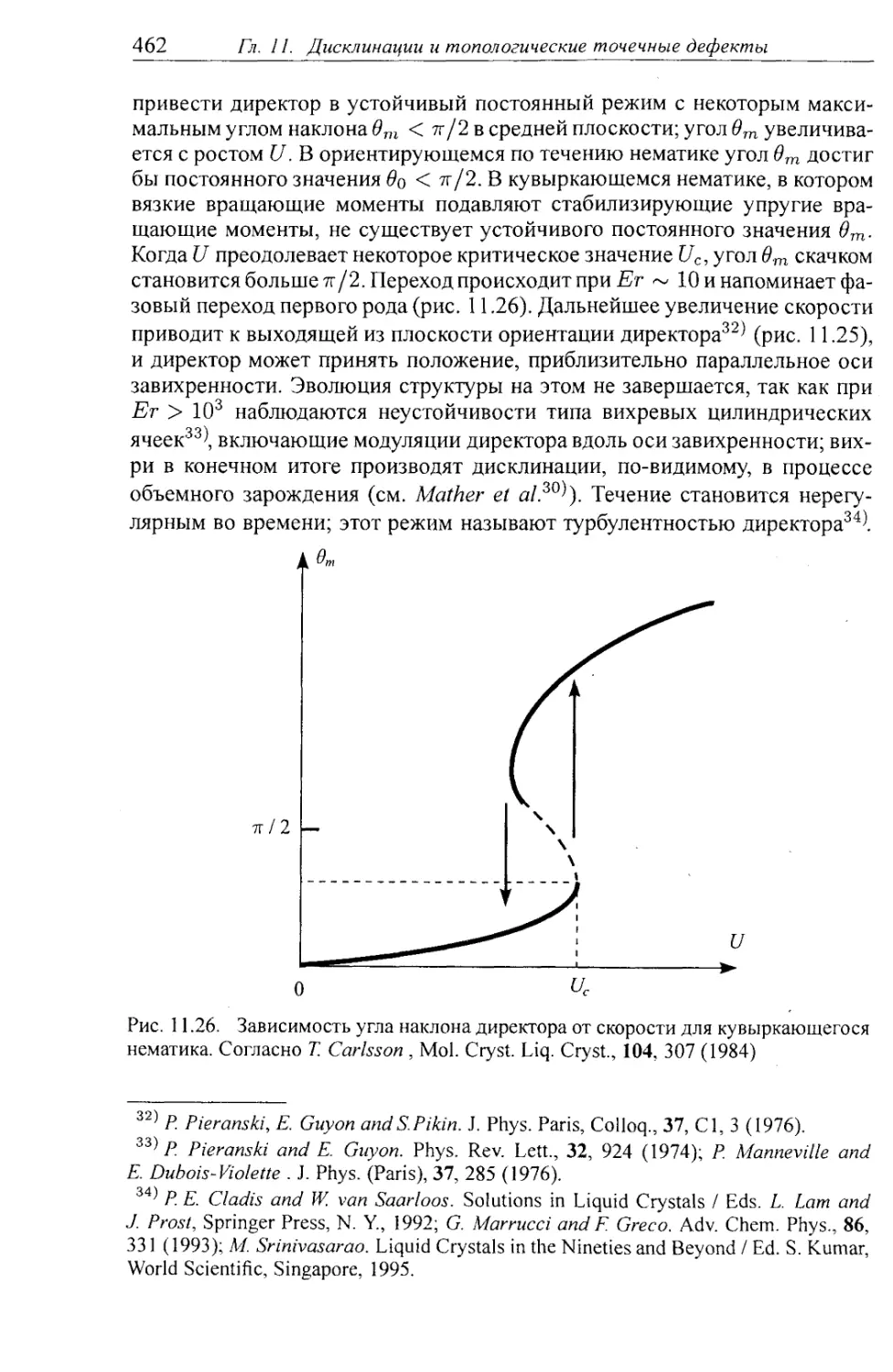
§ 11.4. Динамические свойства: общие особенности, неустойчивости . 456
11.4.1. Общие свойства 457
11.4.2. Неустойчивости в изначально бездефектных образцах 458
§ 11.5. Динамика дефектов 464
11.5.1. Отдельная дисклинация, сила лобового сопротивления 464
11.5.2. Взаимодействие и аннигиляция линейных и точечных дефектов , . 465
11.5.3. Укрупнение сеток дисклинаций 468
ГЛАВА 12. Топологическая теория дефектов 473
§12.1. Основные идеи топологической классификации 473
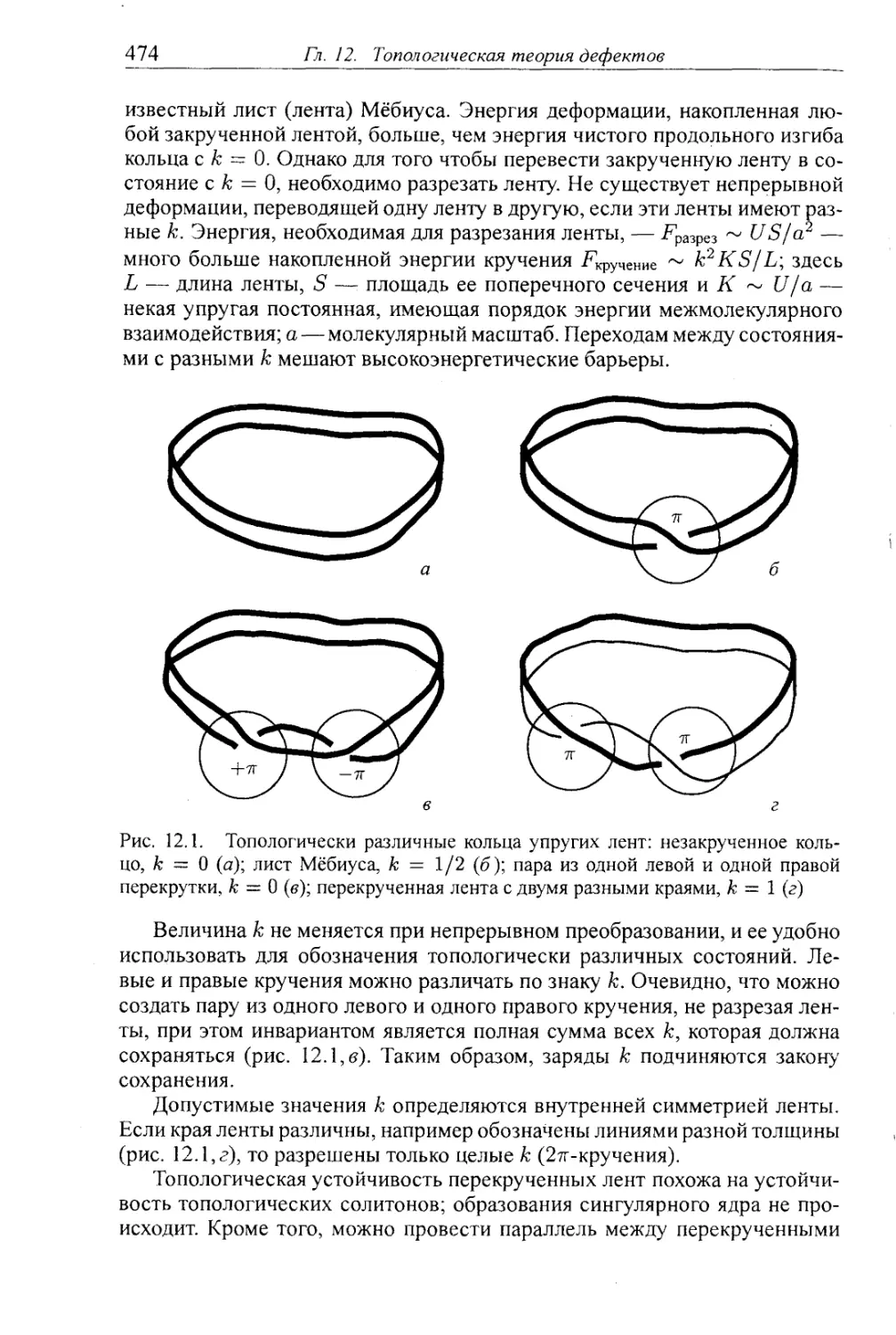
12.1.1. Топологические заряды на примере листа Мёбиуса 473
12.1.2. Некоторое отступление: ДНК и перекрученные ленты 475
12.1.3. Группы: основные определения 477
12.1.4. Общая схема топологической классификации дефектов 478
10
Оглавление
12.1.5. Пространство параметра порядка. Группы описывающие преобразо¬
вания параметра порядка 479
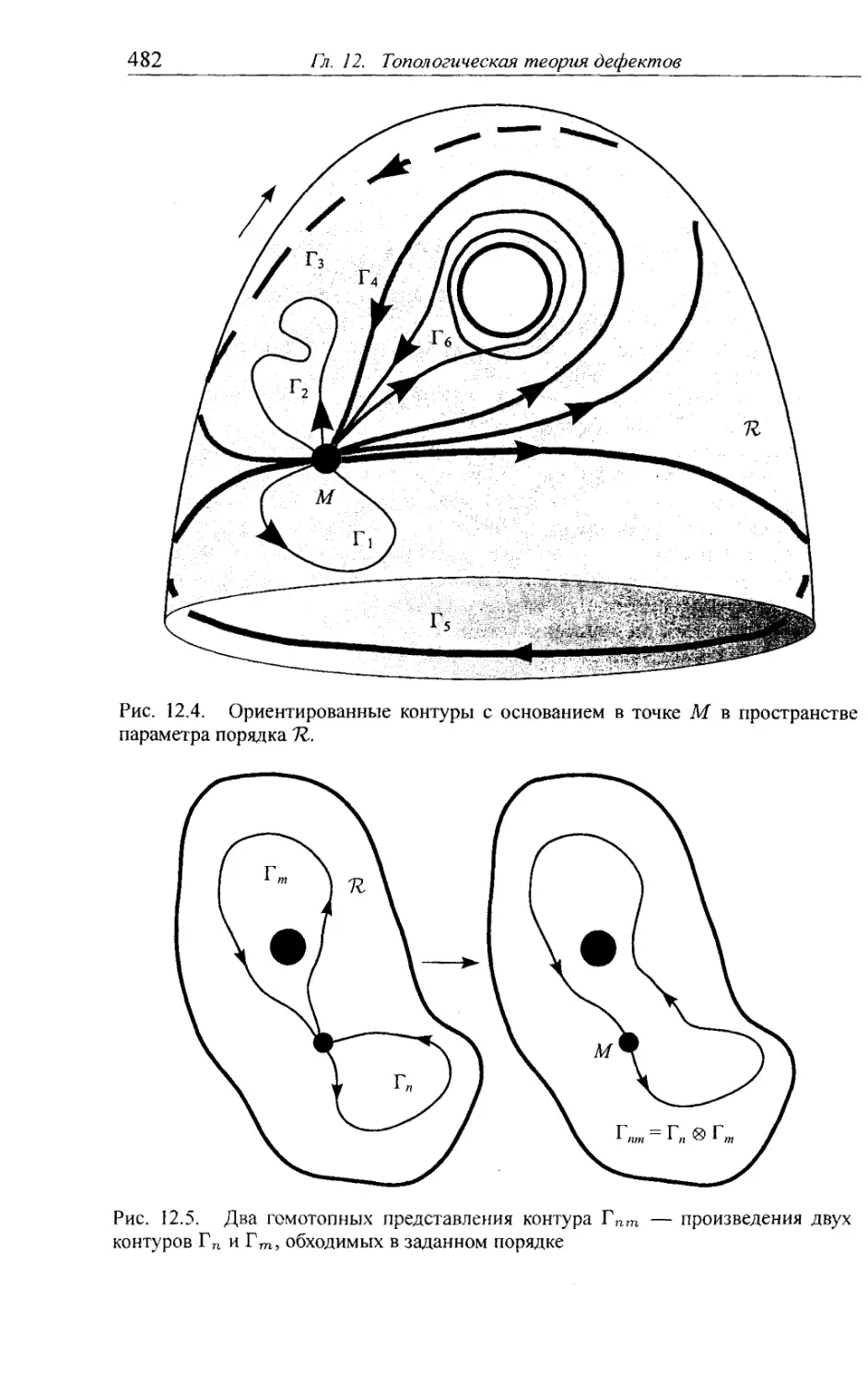
12.1.6. Гомотопические группы 481
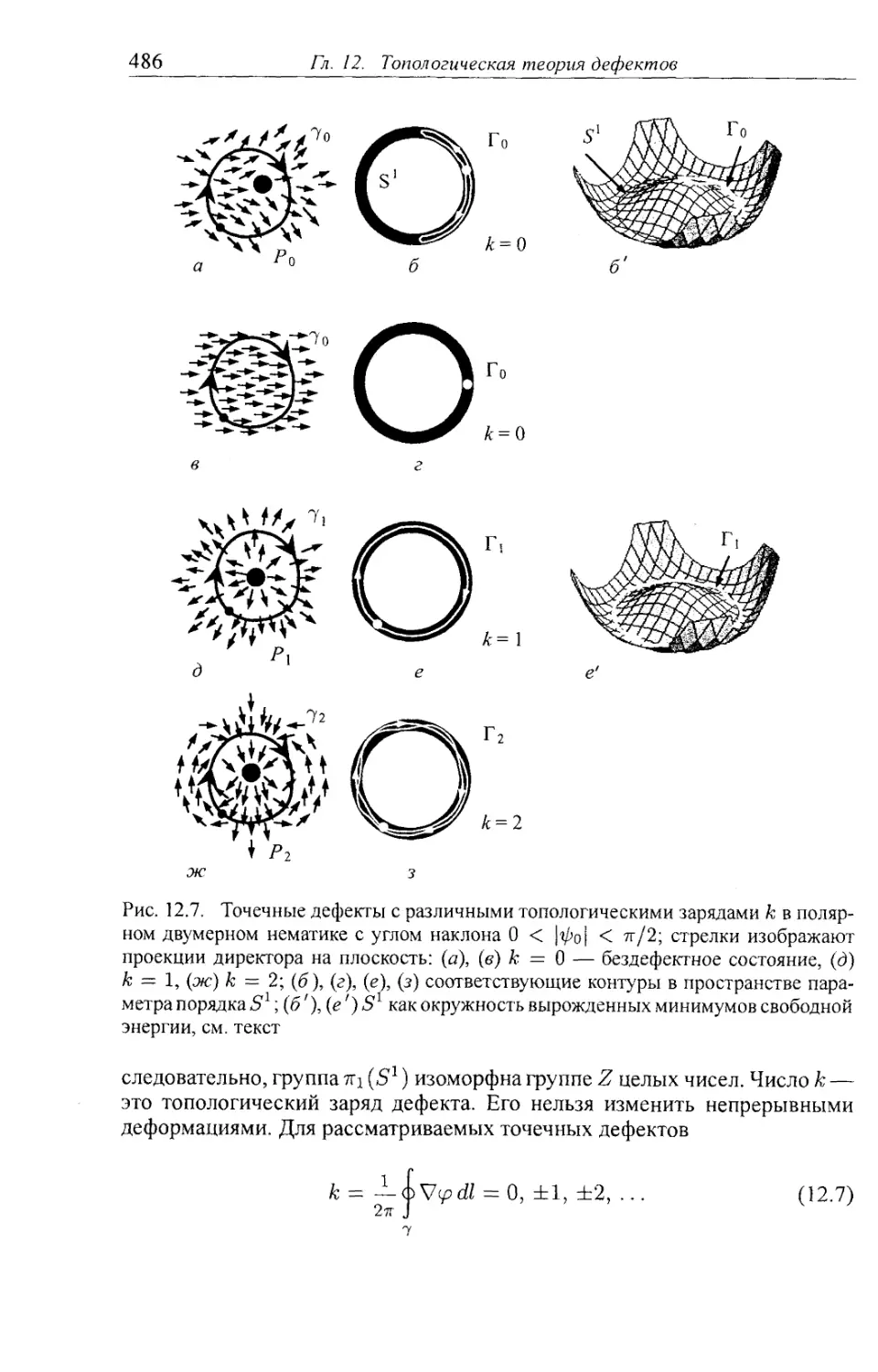
12.1.7. Точечные дефекты в двумерной нематической фазе 484
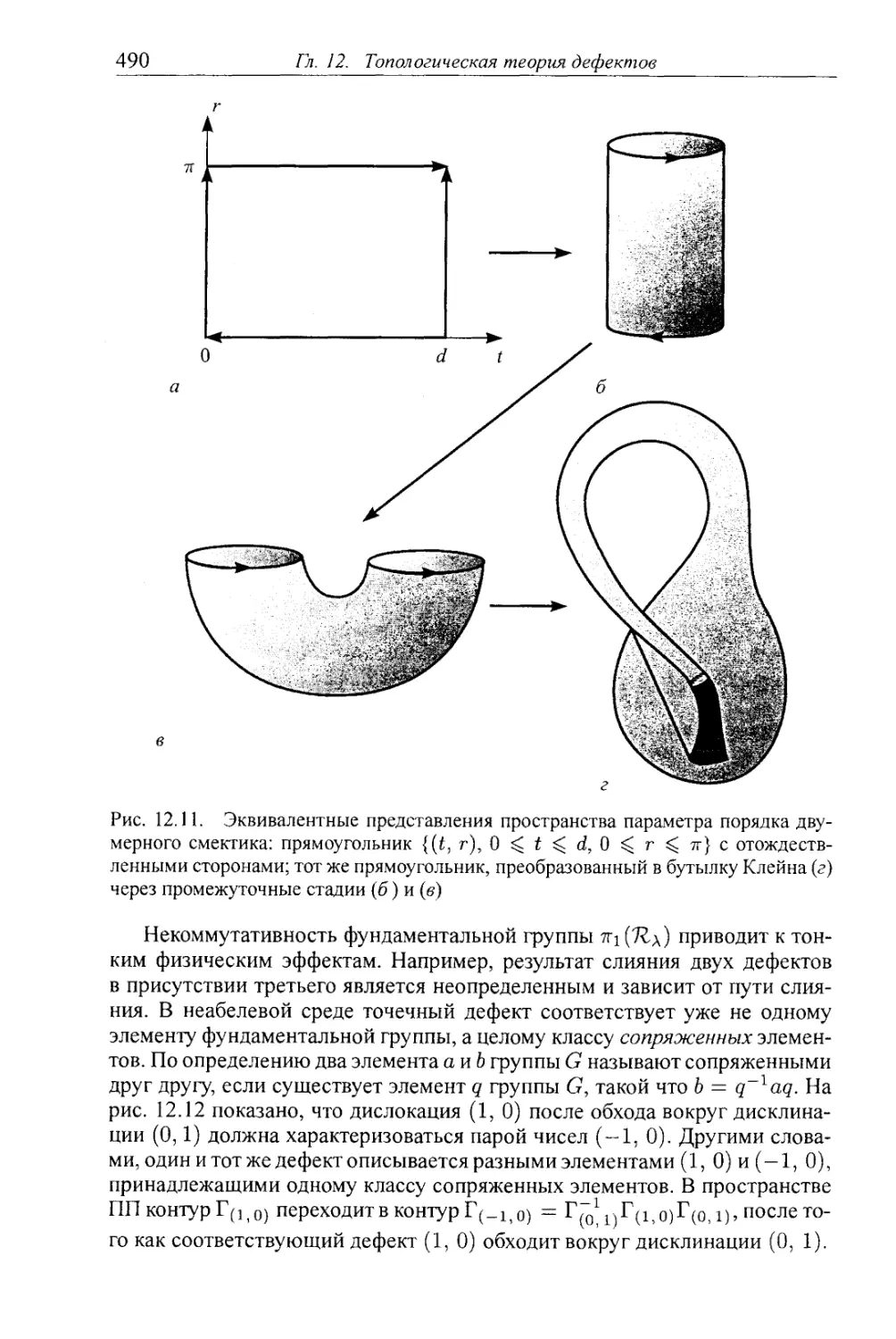
12.1.8. Точечные дислокации в двумерном кристалле 487
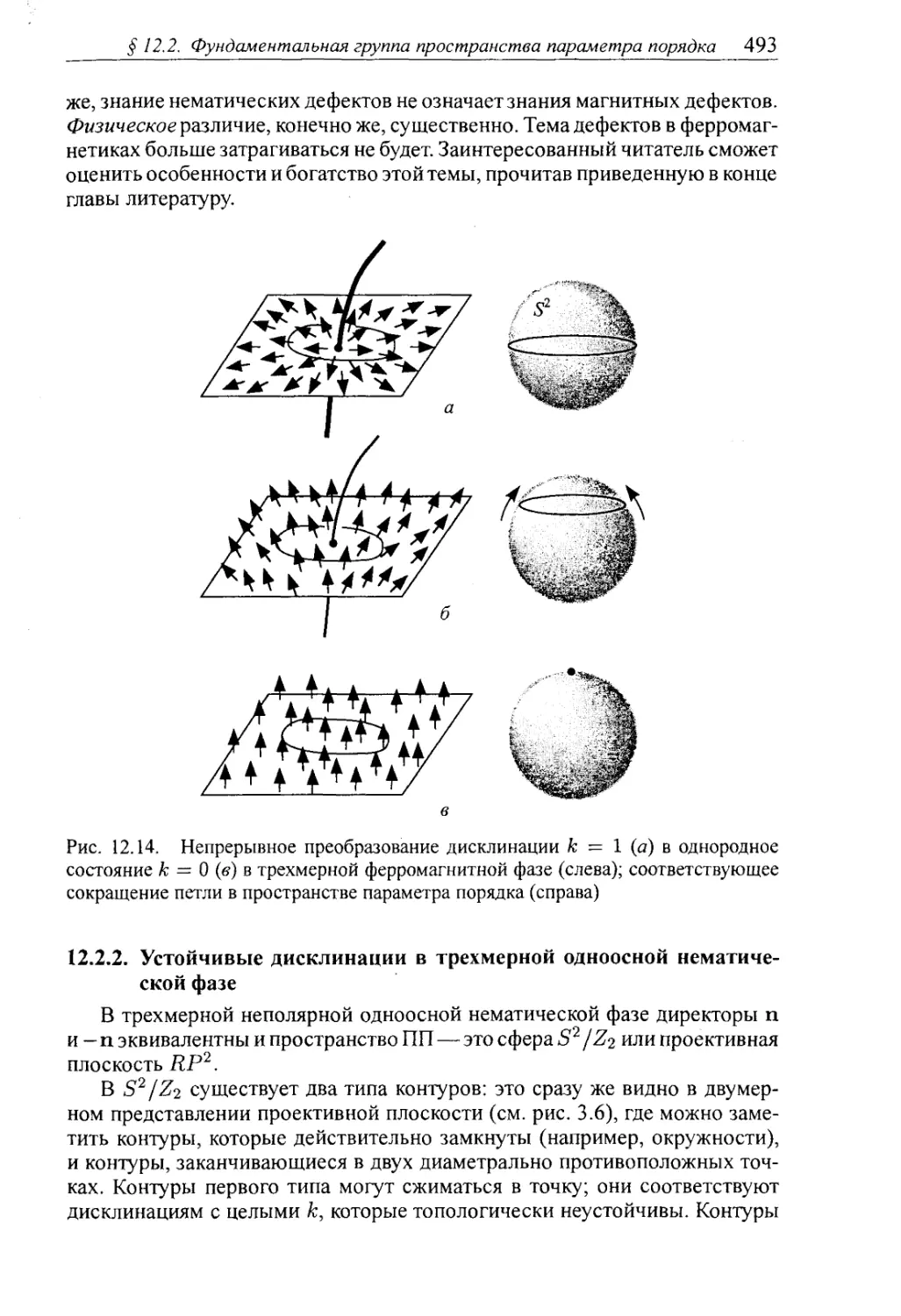
§12.2. Фундаментальная группа пространства параметра порядка . . . 492
12.2.1. Неустойчивые дисклинации в трехмерном изотропном ферромагнети¬
ке 492
12.2.2. Устойчивые дисклинации в трехмерной одноосной нематической фазе 493
12.2.3. Дисклинации в двуосной нематической и холестерической
фазах 494
§ 12.3. Вторая гомотопическая группа пространства параметра порядка 499
12.3.1. Точечные дефекты в трехмерном ферромагнетике 499
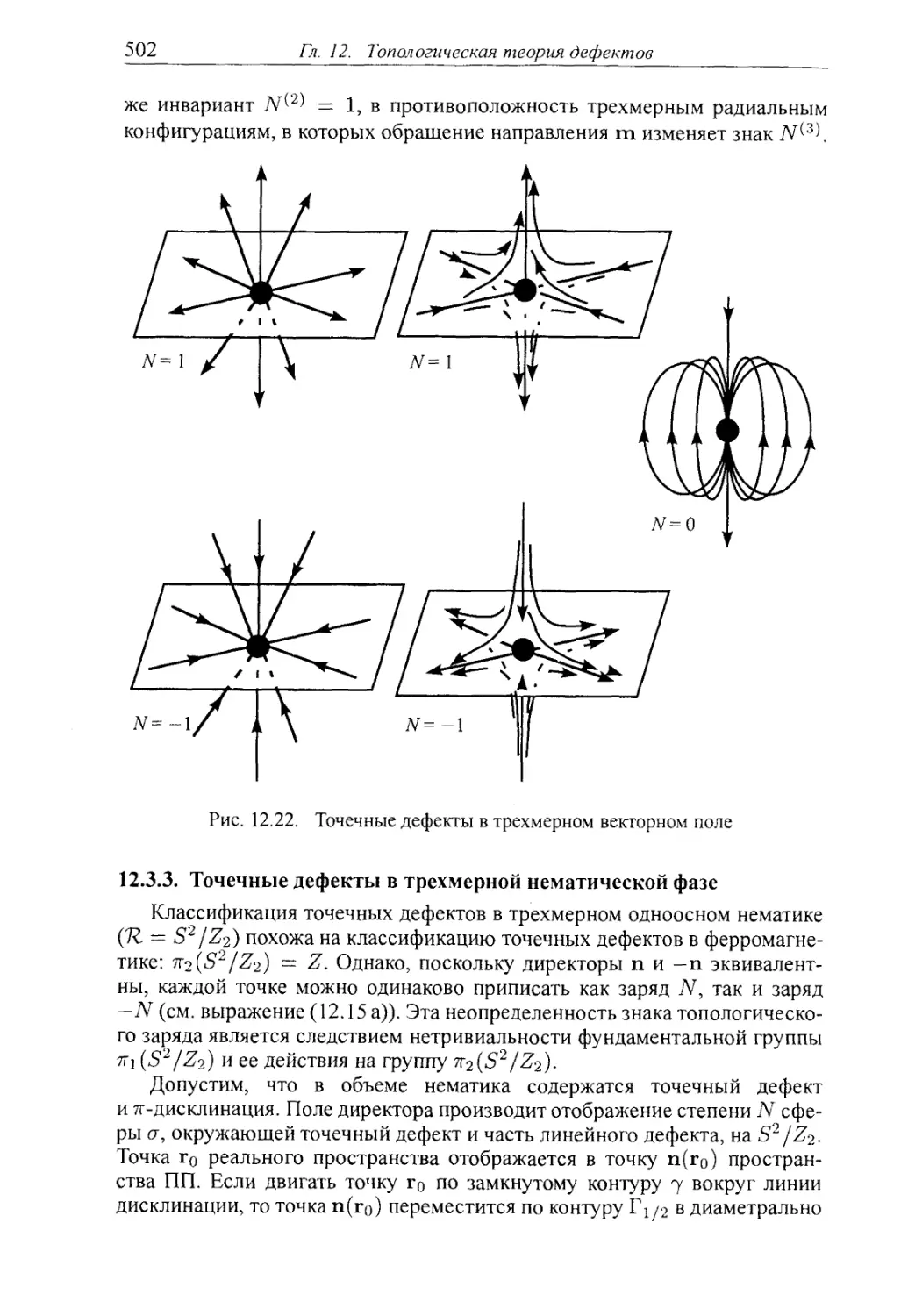
12.3.2. Топологические заряды точечных дефектов 501
12.3.3. Точечные дефекты в трехмерной нематической фазе 502
§ 12.4. Солитоны 503
12.4.1. Линейные солитоны 506
12.4.2. Части неподобные солитоны 506
ГЛАВА 13. Поверхностные явления 512
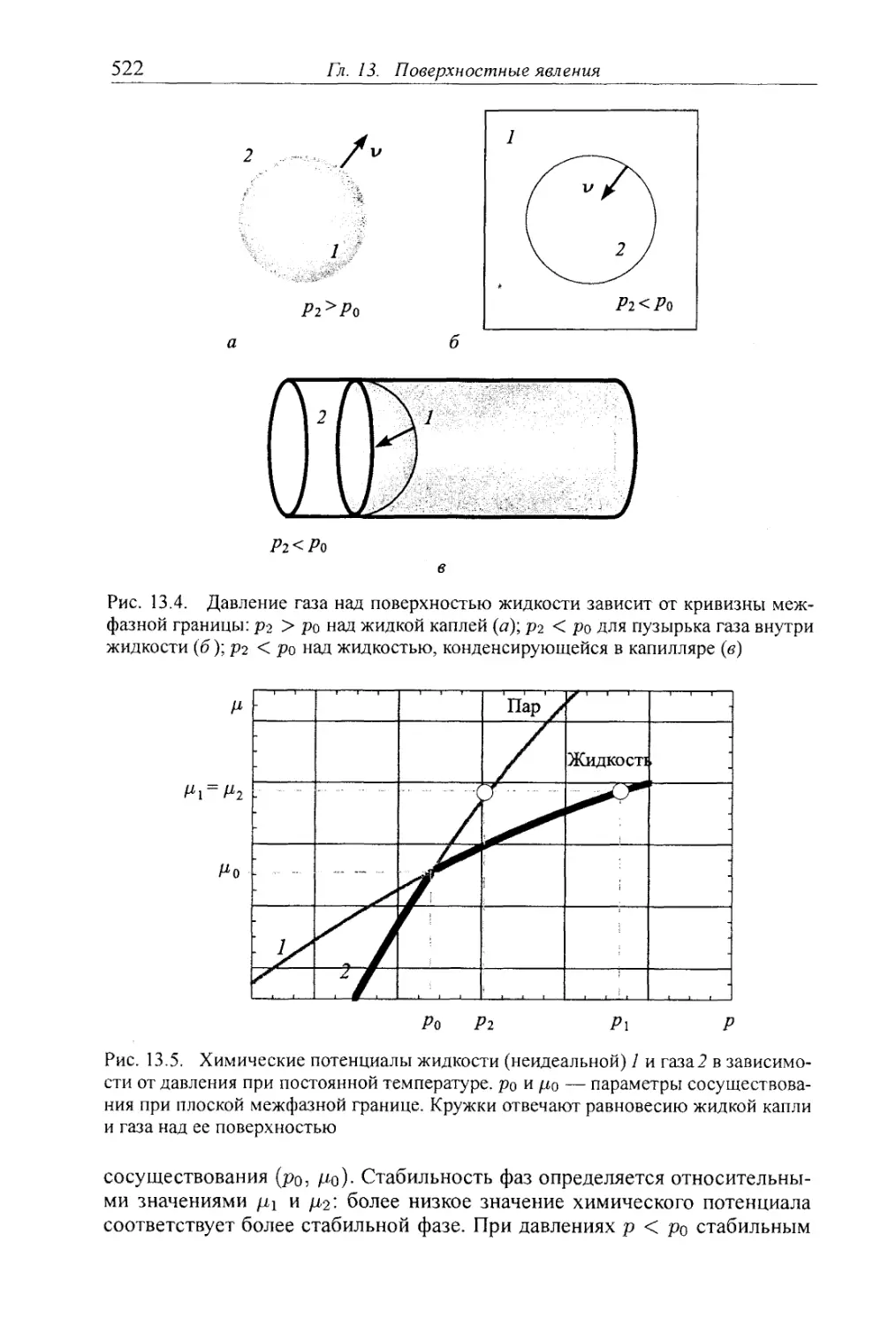
§ 13.1. Поверхностные явления в изотропных средах 512
13.1.1. Поверхностное натяжение и термодинамика плоских границ раздела 512
13.1.2. Адсорбция 515
13.1.3. Искривленные границы раздела 518
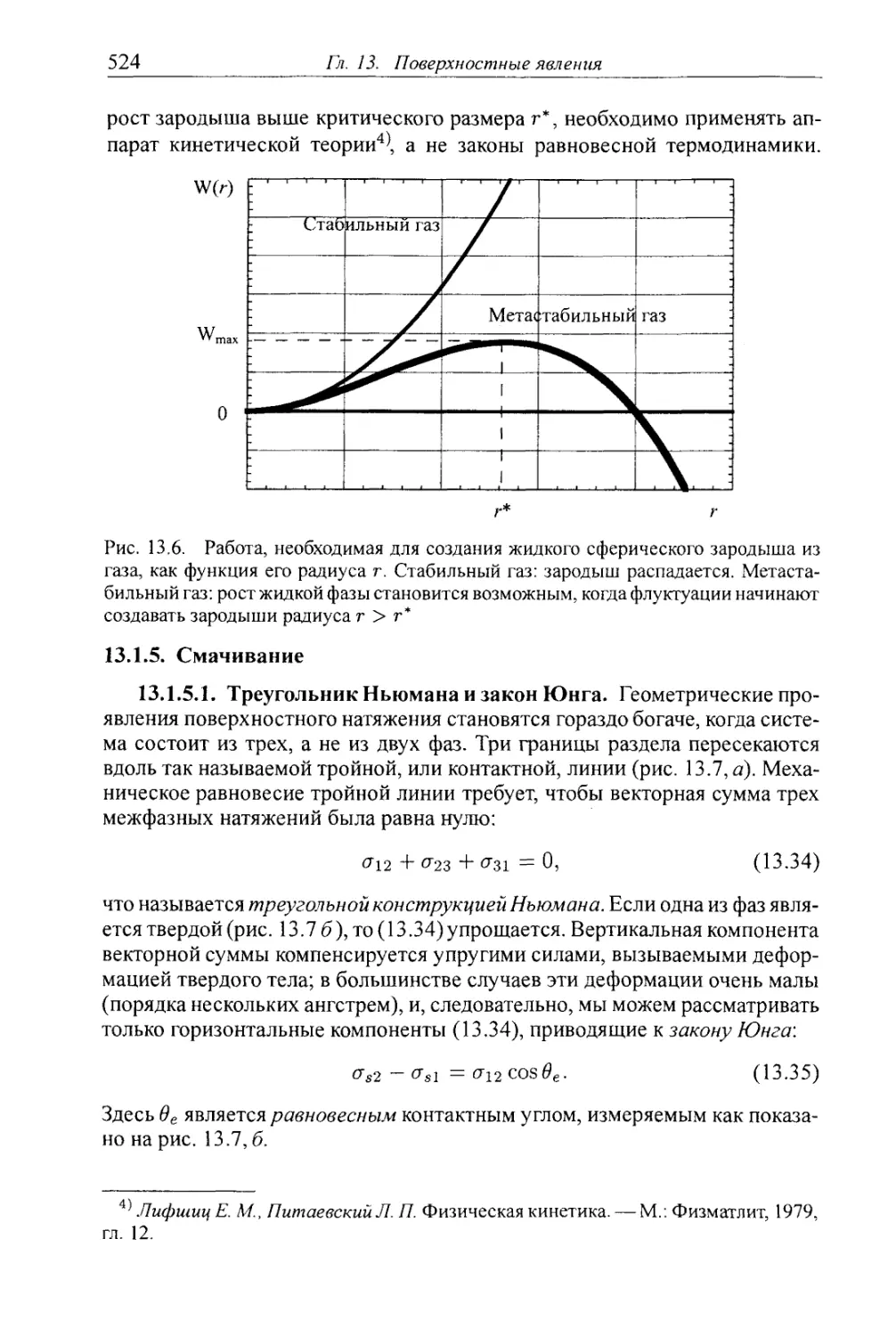
13.1.4. Поверхностное натяжение и зародышеобразование новой фазы . . 521
13.1.5. Смачивание 524
§ 13.2. Поверхностные явления в анизотропных средах 527
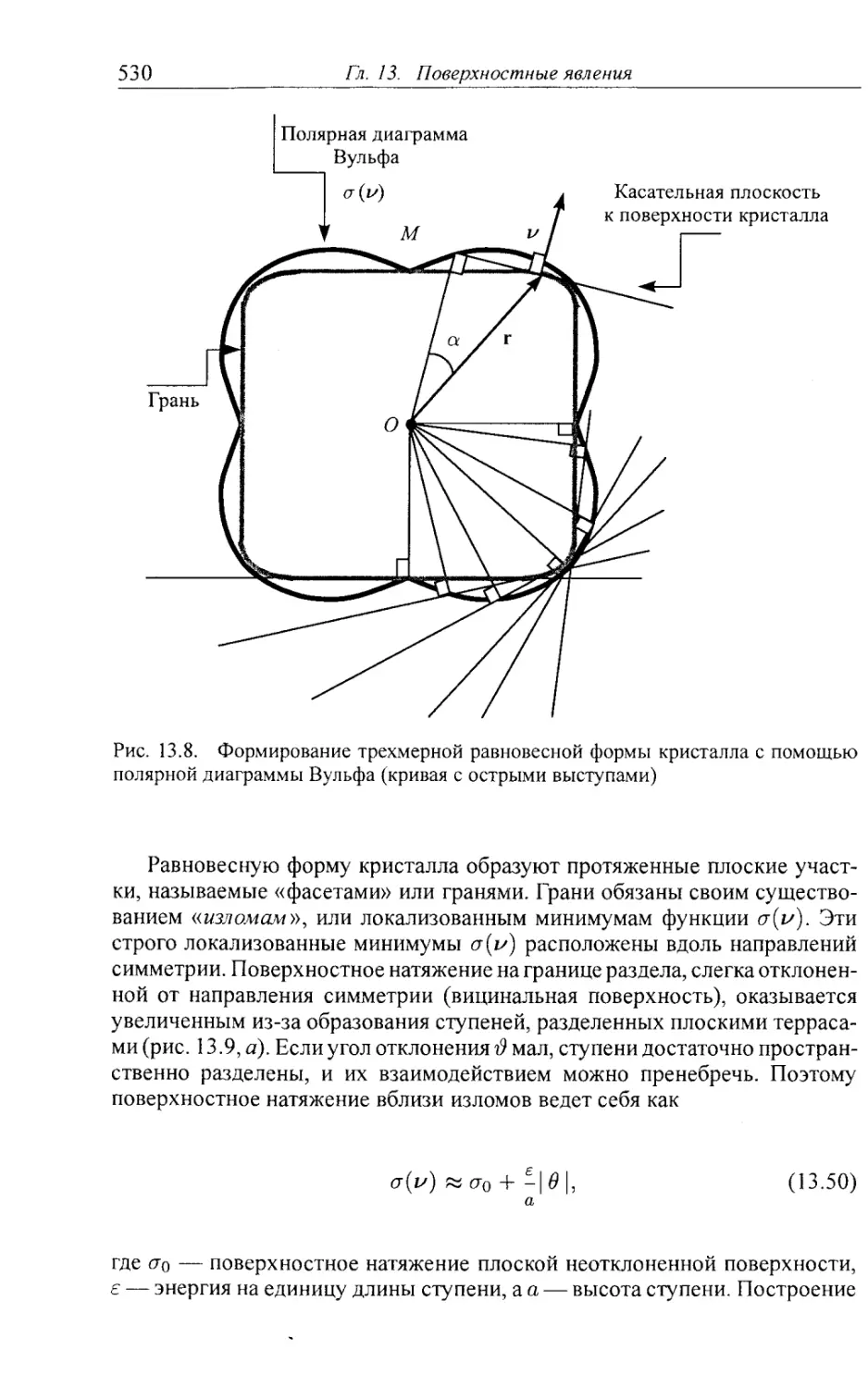
13.2.1. Равновесная форма (форма Вульфа) твердых кристаллов 528
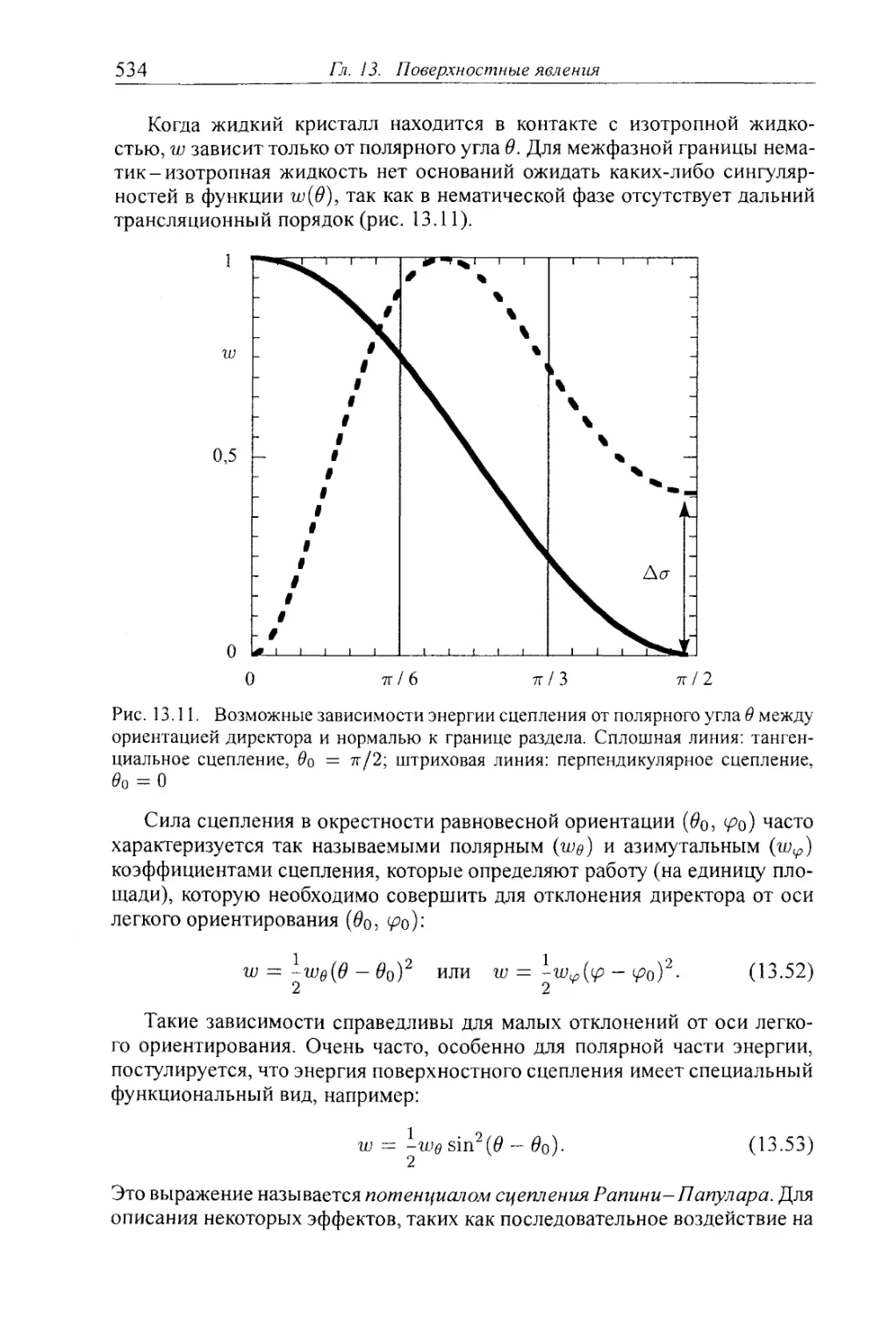
13.2.2. Поверхностное сцепление в нематических жидких кристаллах . . 532
13.2.3. Полевые эффекты в условиях конечного сцепления 535
13.2.4. Тонкие жидкокристаллические пленки; взаимодействия
Казимира 540
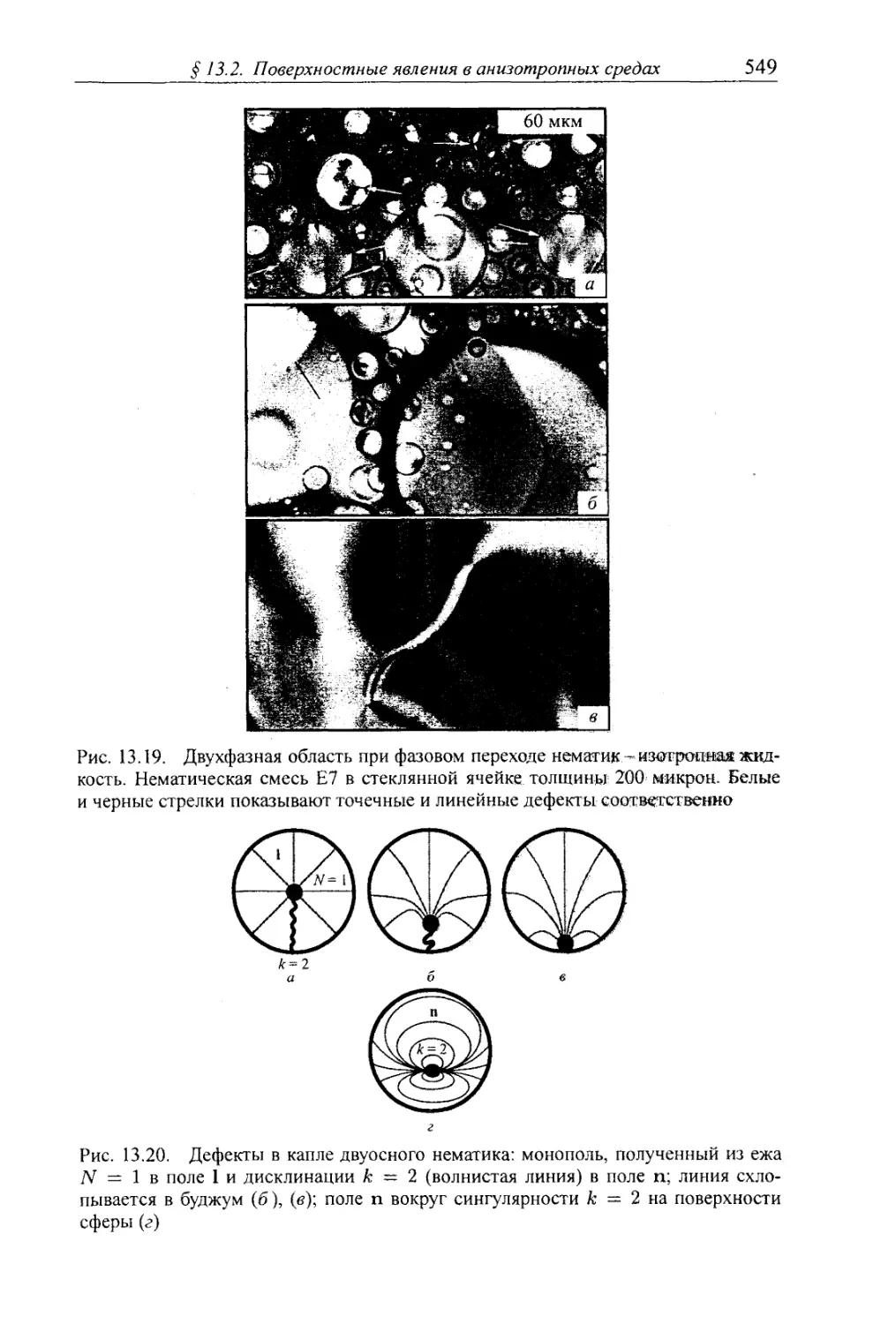
13.2.5. Топологические дефекты в больших жидкокристаллических каплях 541
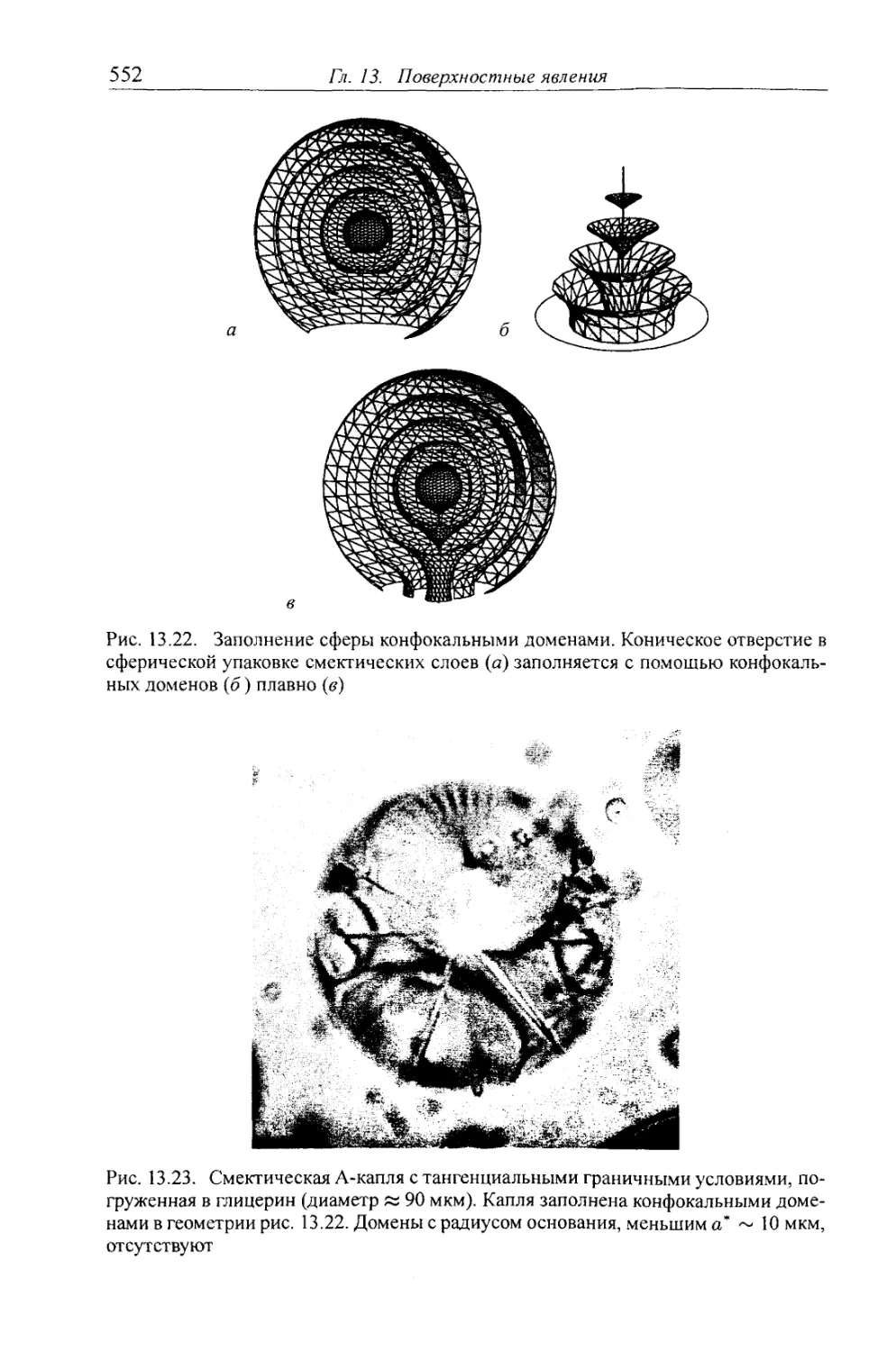
13.2.6. Капли в смектиках А 551
ГЛАВА 14. Устойчивость коллоидных систем 560
§ 14.1. Взаимодействия между твердыми поверхностями 562
14.1.1. Уравнение Пуассона-Больцмана 562
14.1.2. Фундаментальные длины в задаче Пуассона - Больцмана 564
14.1.3. Свободная энергия и тензор напряжений Максвелла 566
14.1.4. Слабые растворы электролитов 568
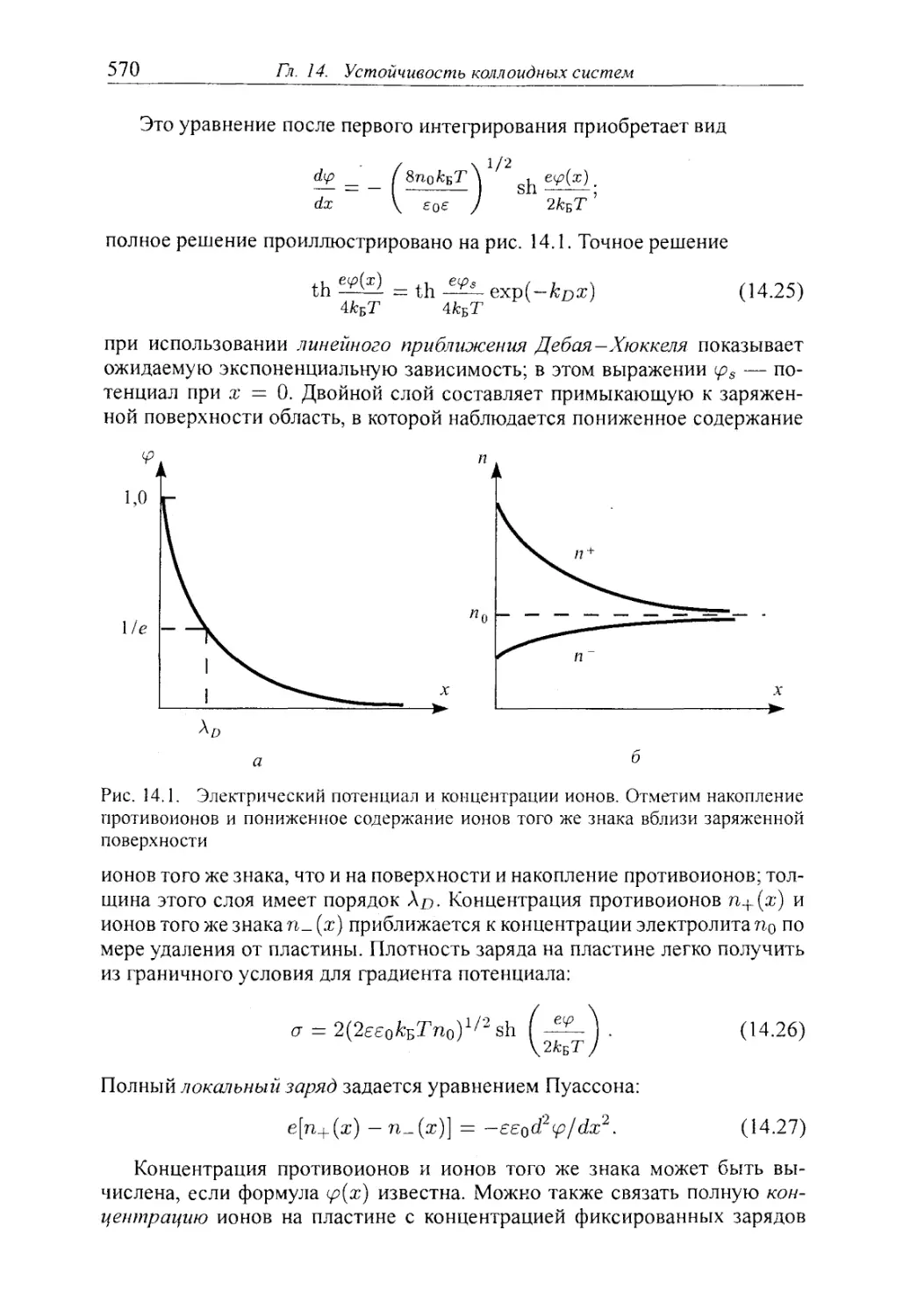
14.1.5. Сильные растворы электролитов 569
Оглавление
И
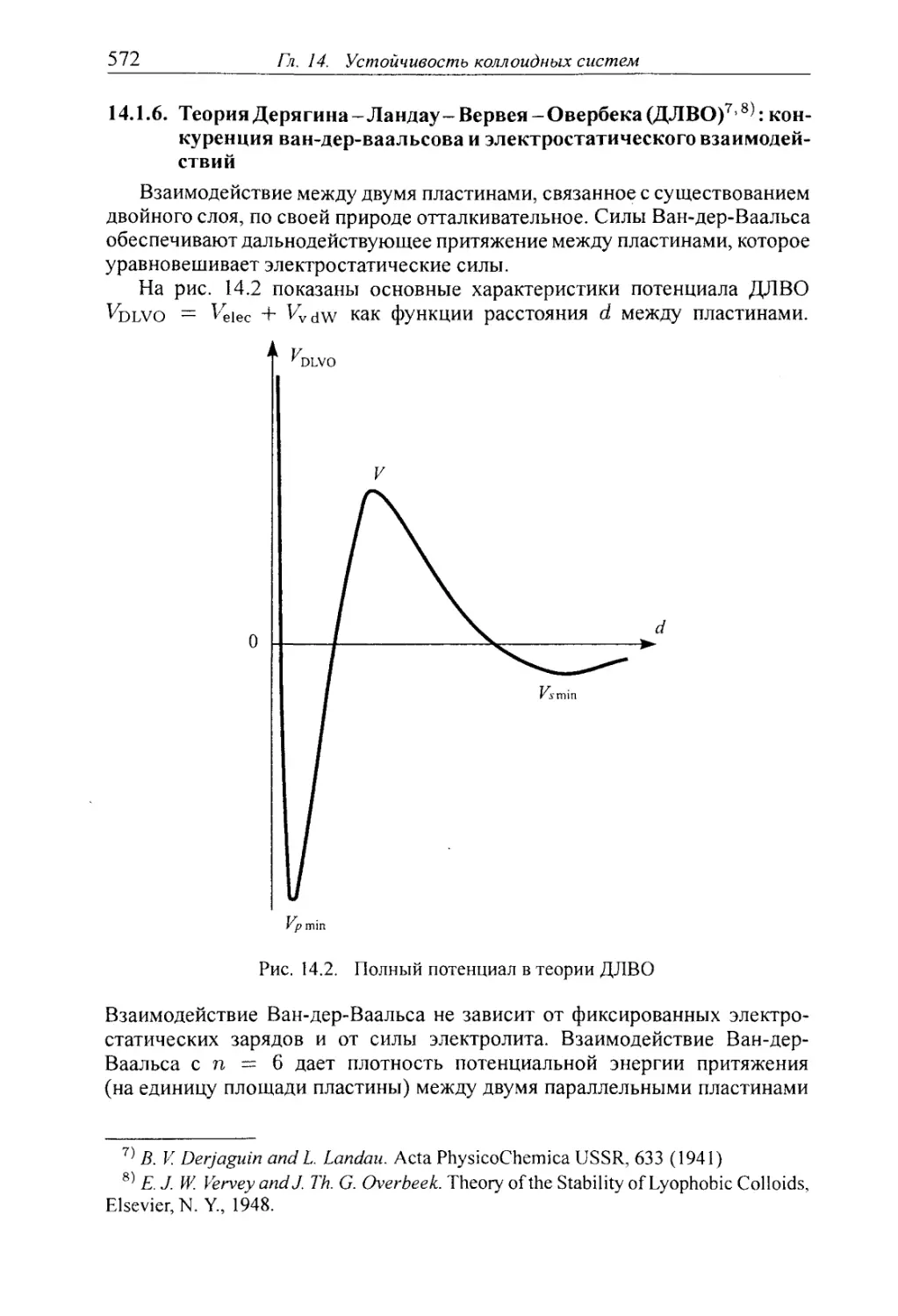
14.1.6. Теория Дерягина-Ландау-Вервея-Овербека (ДЛВО): конкуренция
ван-дер-ваальсова и электростатического взаимодействий 572
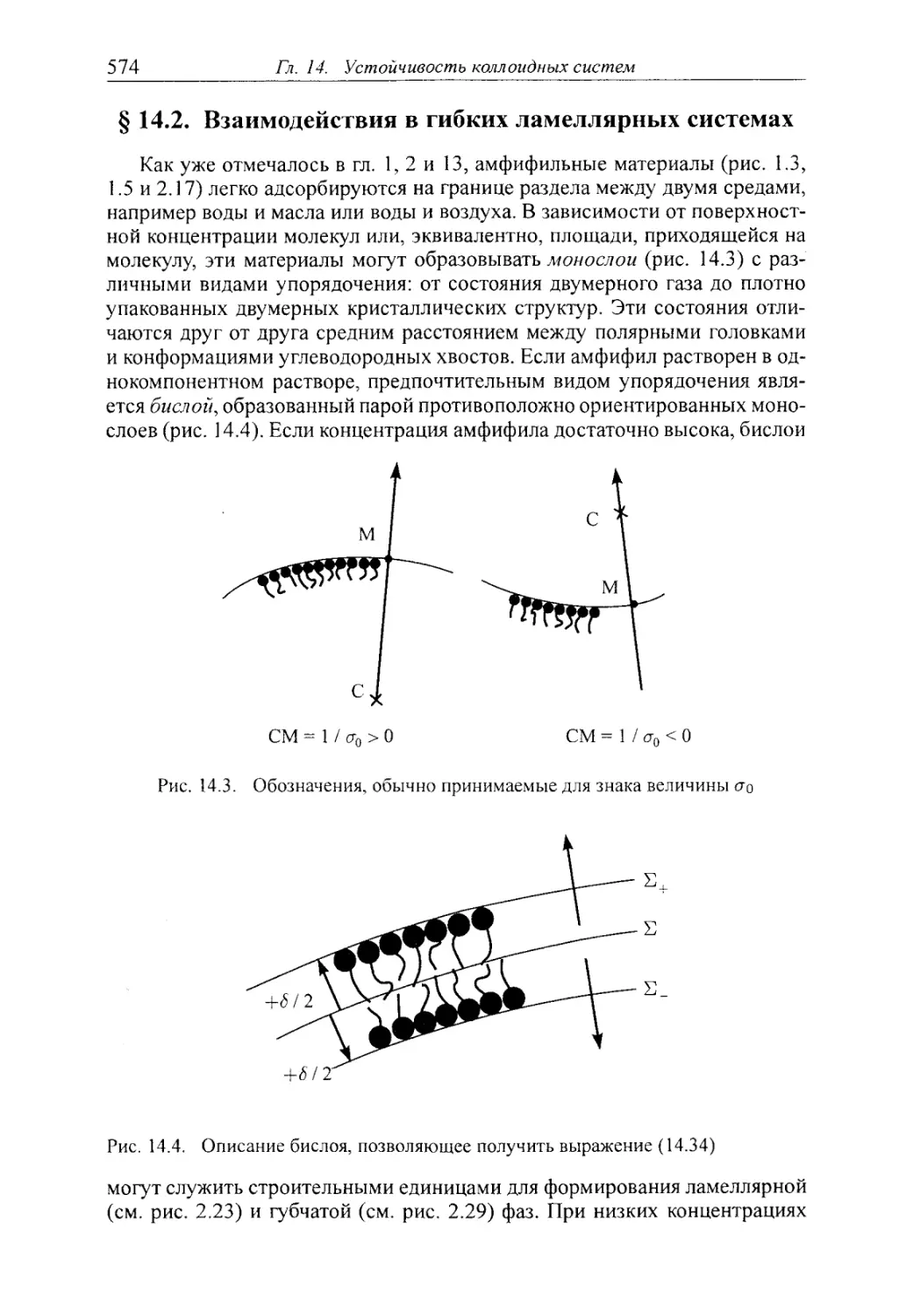
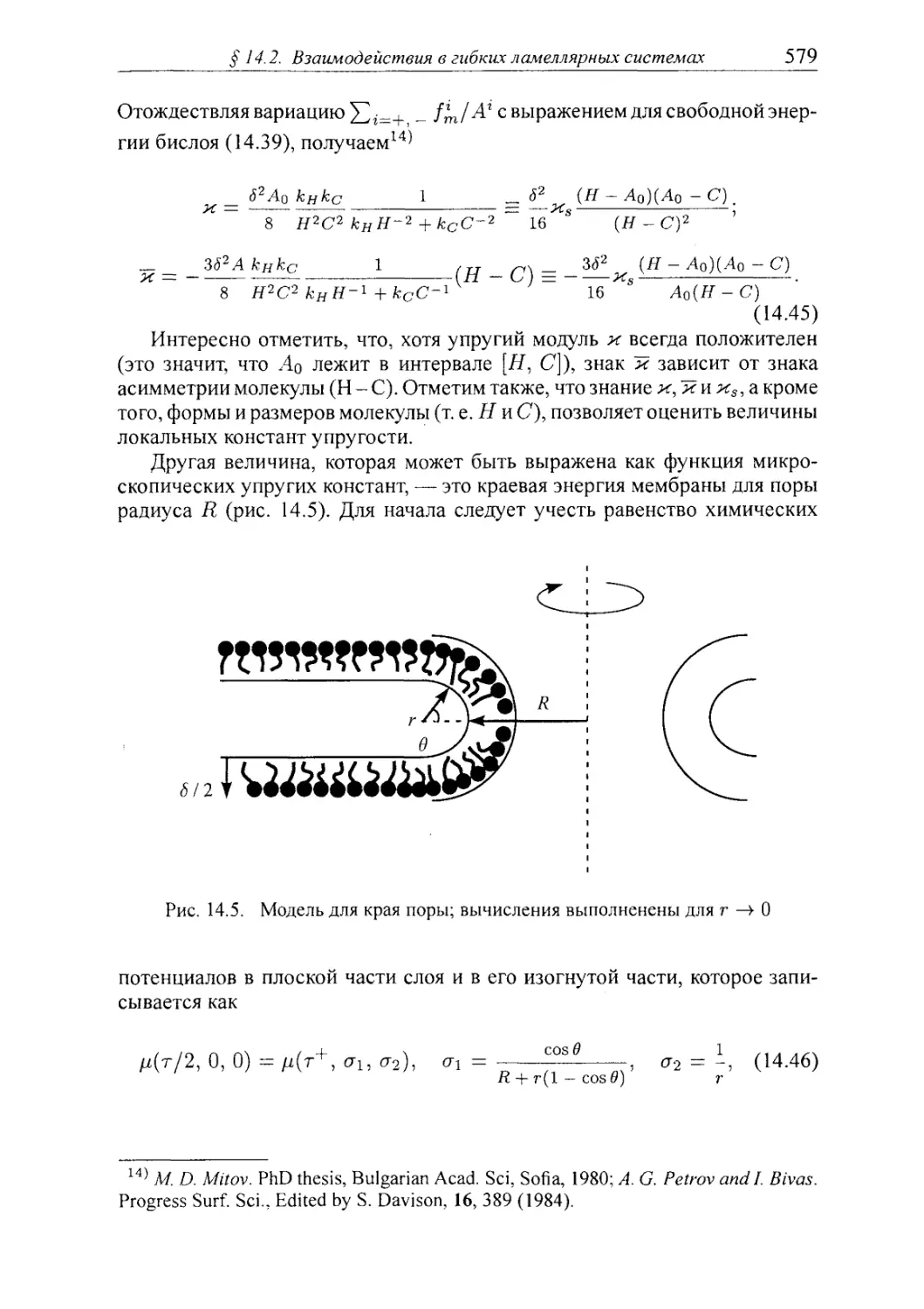
§ 14.2. Взаимодействия в гибких ламеллярных системах 574
14.2.1. Упругость нейтральных мембран 575
14.2.2. Гибкие слои и исключенный объем 583
14.2.3. Ламеллярная, губчатая и кубическая фазы; микроэмульсии .... 589
§ 14.3. Растворы коллоидных частиц; особенности устойчивости . . . 591
14.3.1. Броуновская флокуляция 593
14.3.2. Флокуляция истощения 594
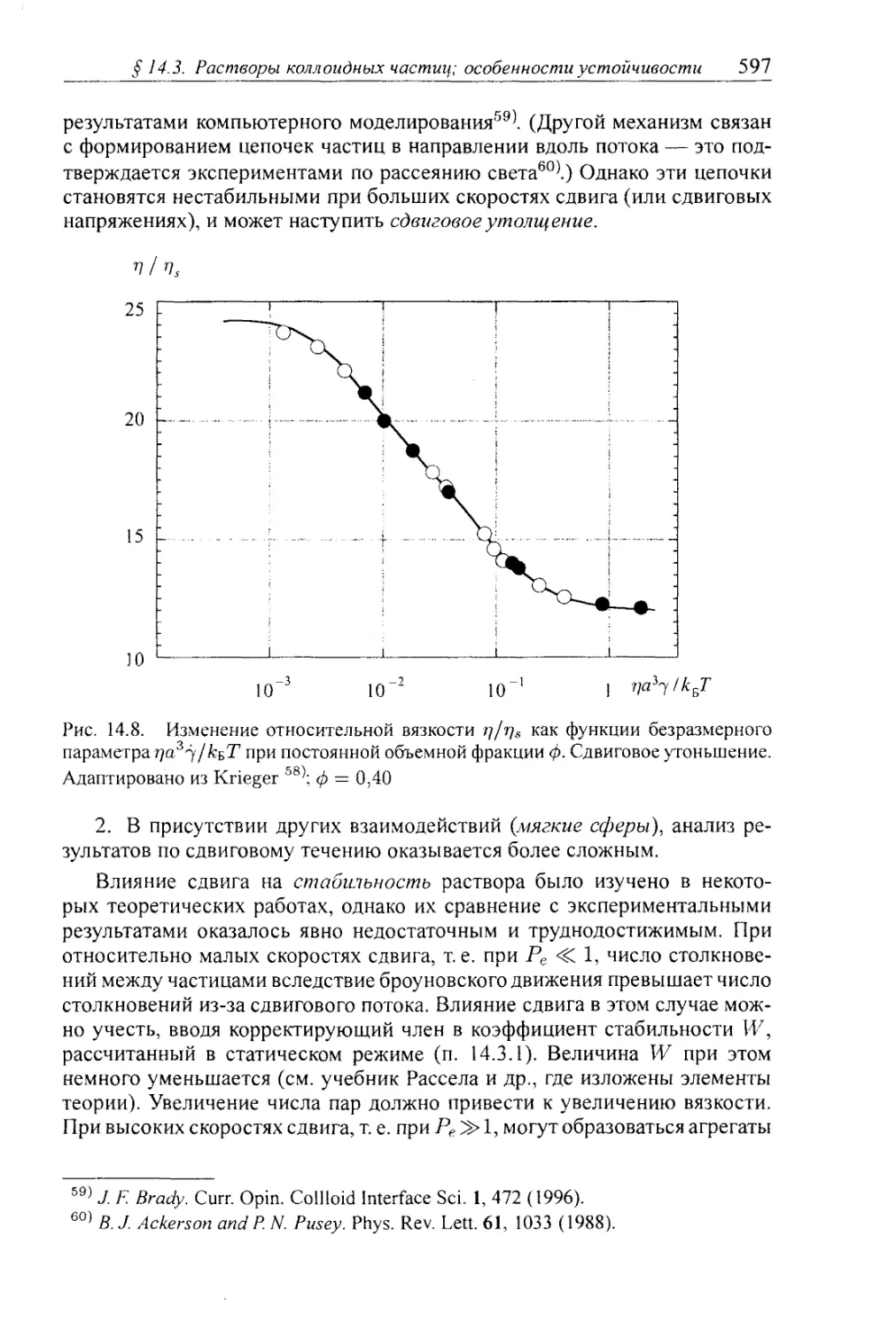
14.3.3. Стабильность в условиях сдвига; реологические свойства 596
14.3.4. Порядок против беспорядка 598
§ 14.4. Измерения взаимодействий в коллоидных системах 600
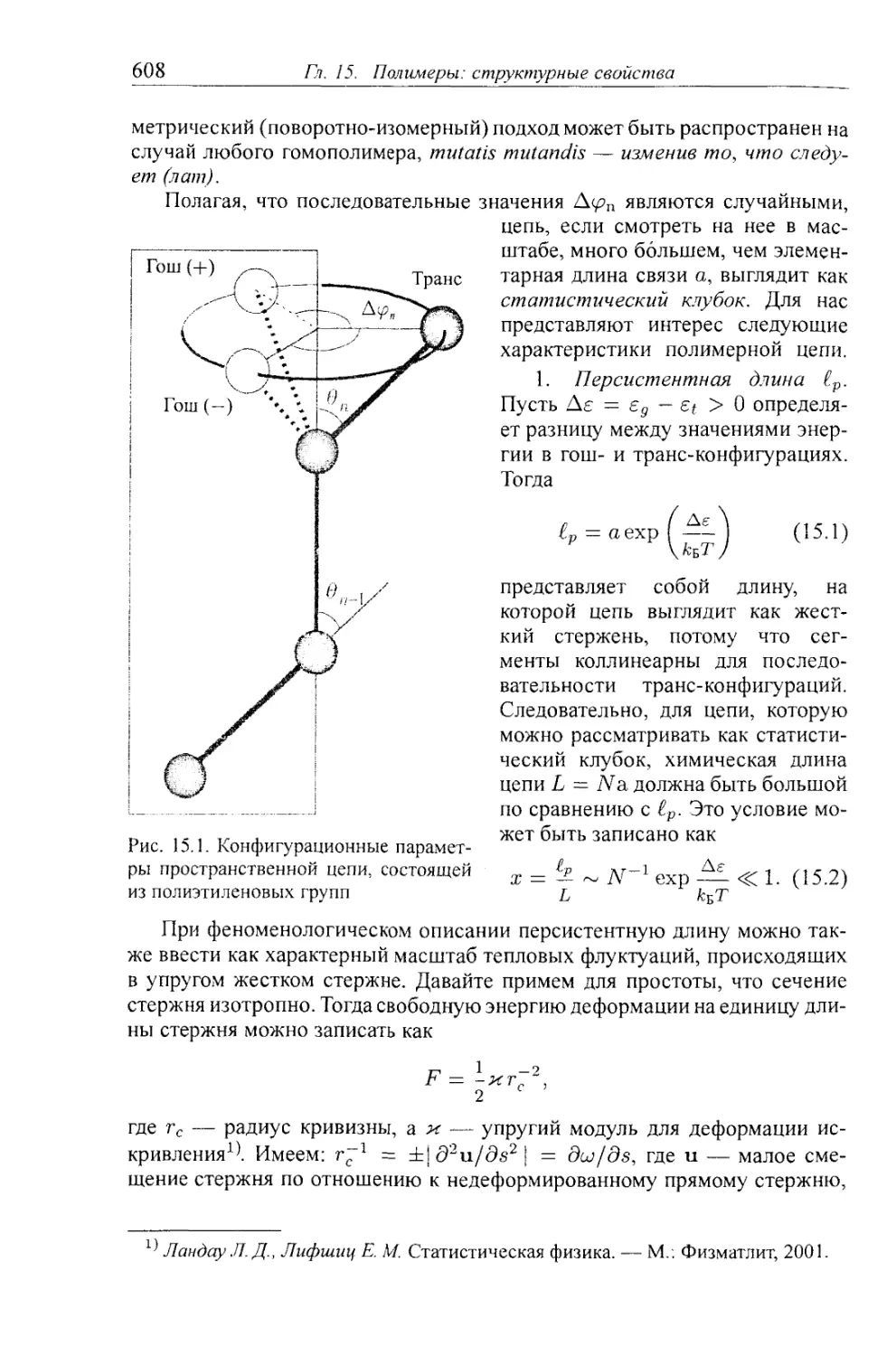
ГЛАВА 15. Полимеры: структурные свойства 606
§15.1. Идеальные цепи и цепи Флори 607
15.1 Л. Конформации одиночной цепи 609
15.1.2. Идеальная (или гауссова) цепь 610
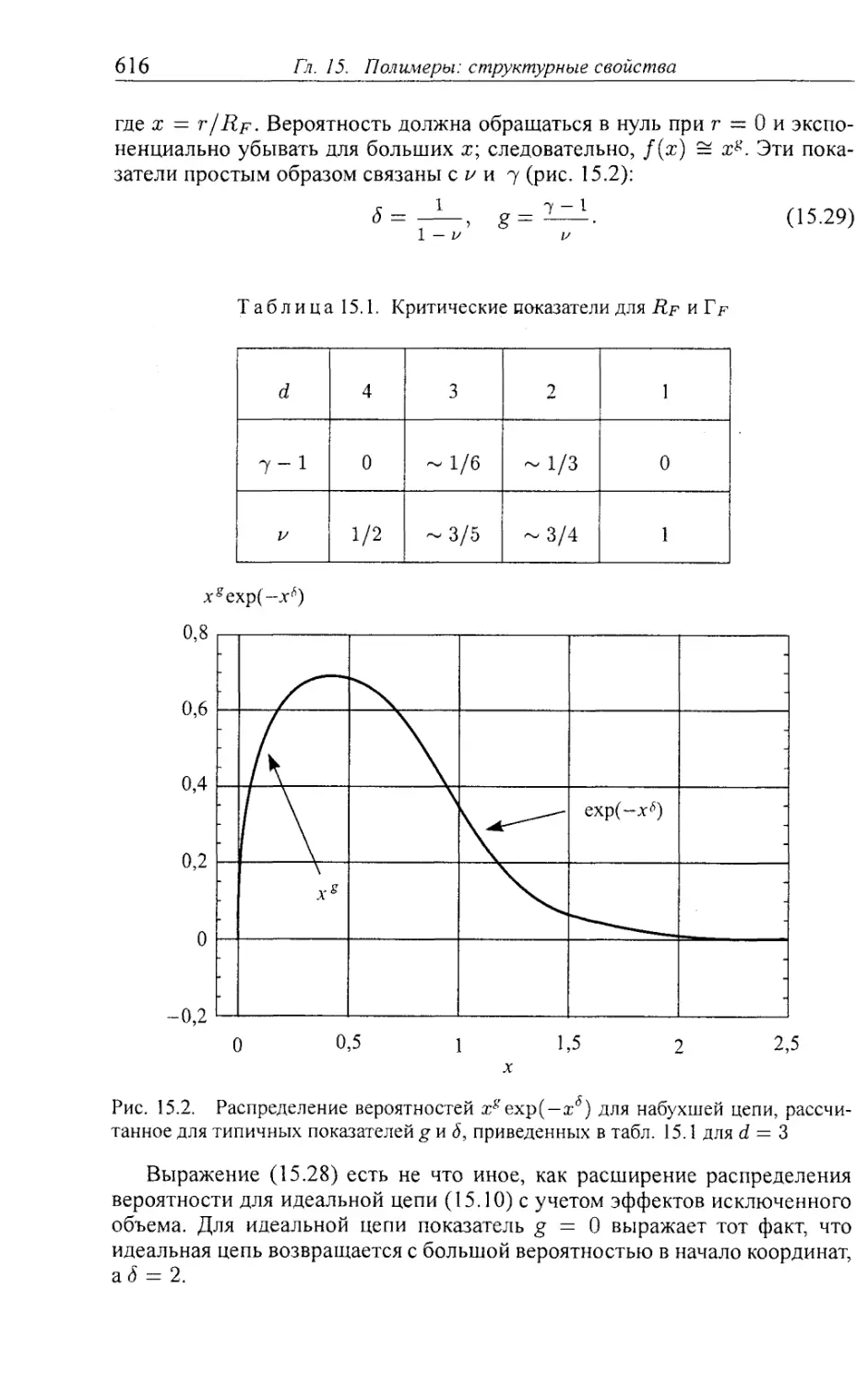
15.1.3. Парная корреляционная функция и радиус инерции 613
15.1.4. Цепь Флори 615
§15.2. Цепи во взаимодействии 619
15.2.1. Приближение среднего поля 619
15.2.2. Законы скейлинга для атермических растворов 624
§ 15.3. Фазовое разделение в растворах полимеров и полимерных смесях 627
15.3.1. Равновесные и неравновесные состояния в жидкости 627
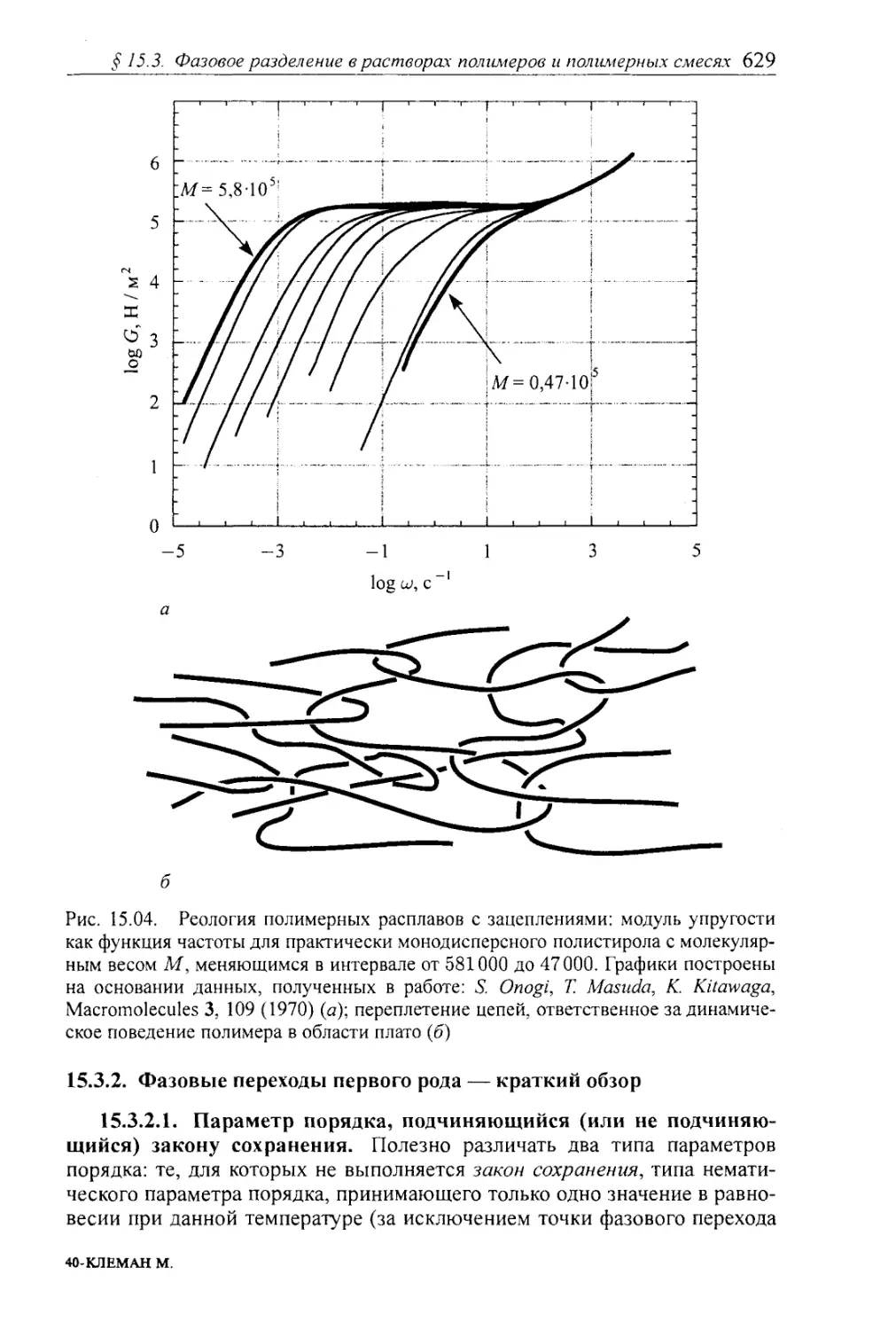
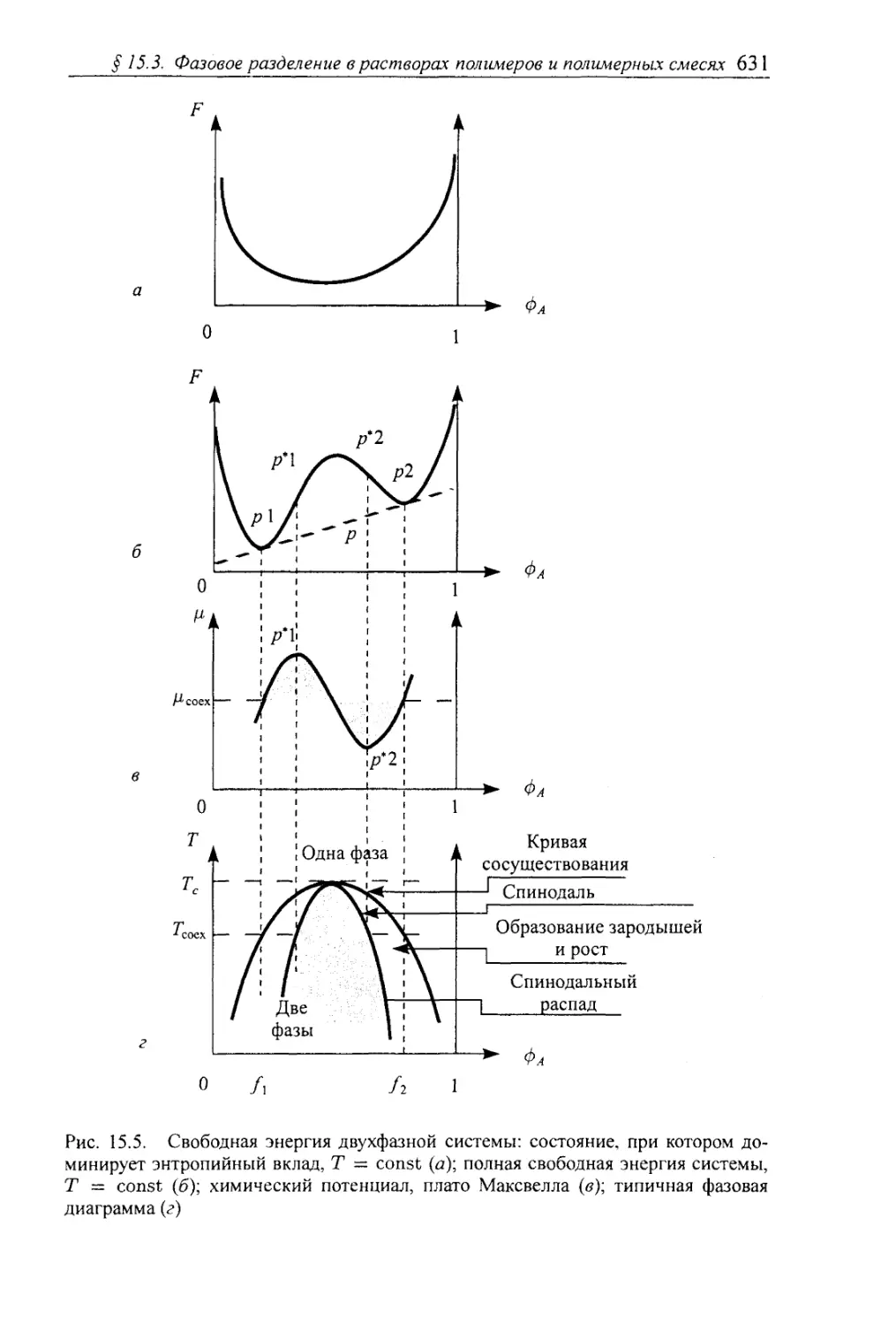
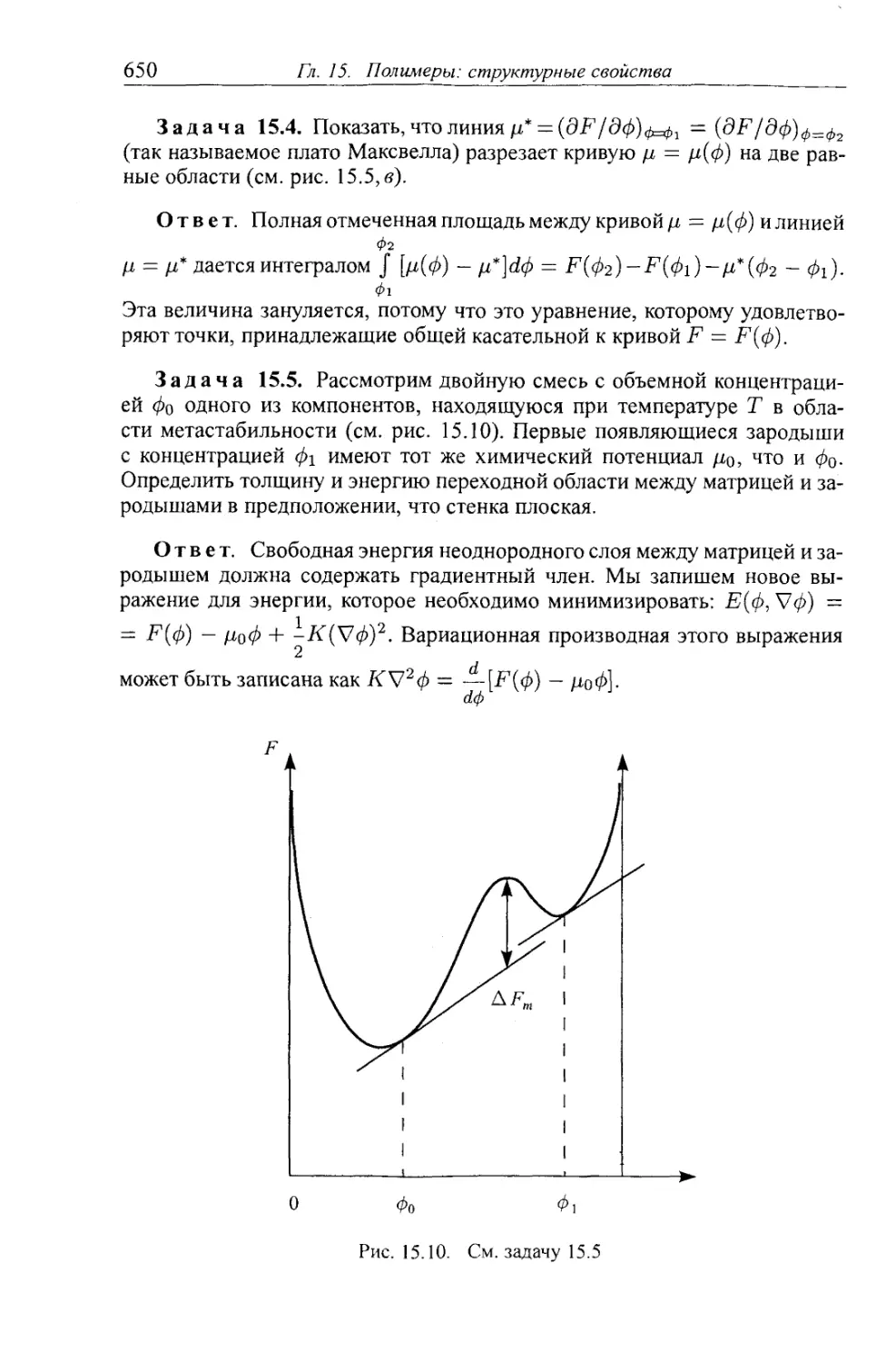
15.3.2. Фазовые переходы первого рода— краткий обзор 629
15.3.3. Смеси полимеров 634
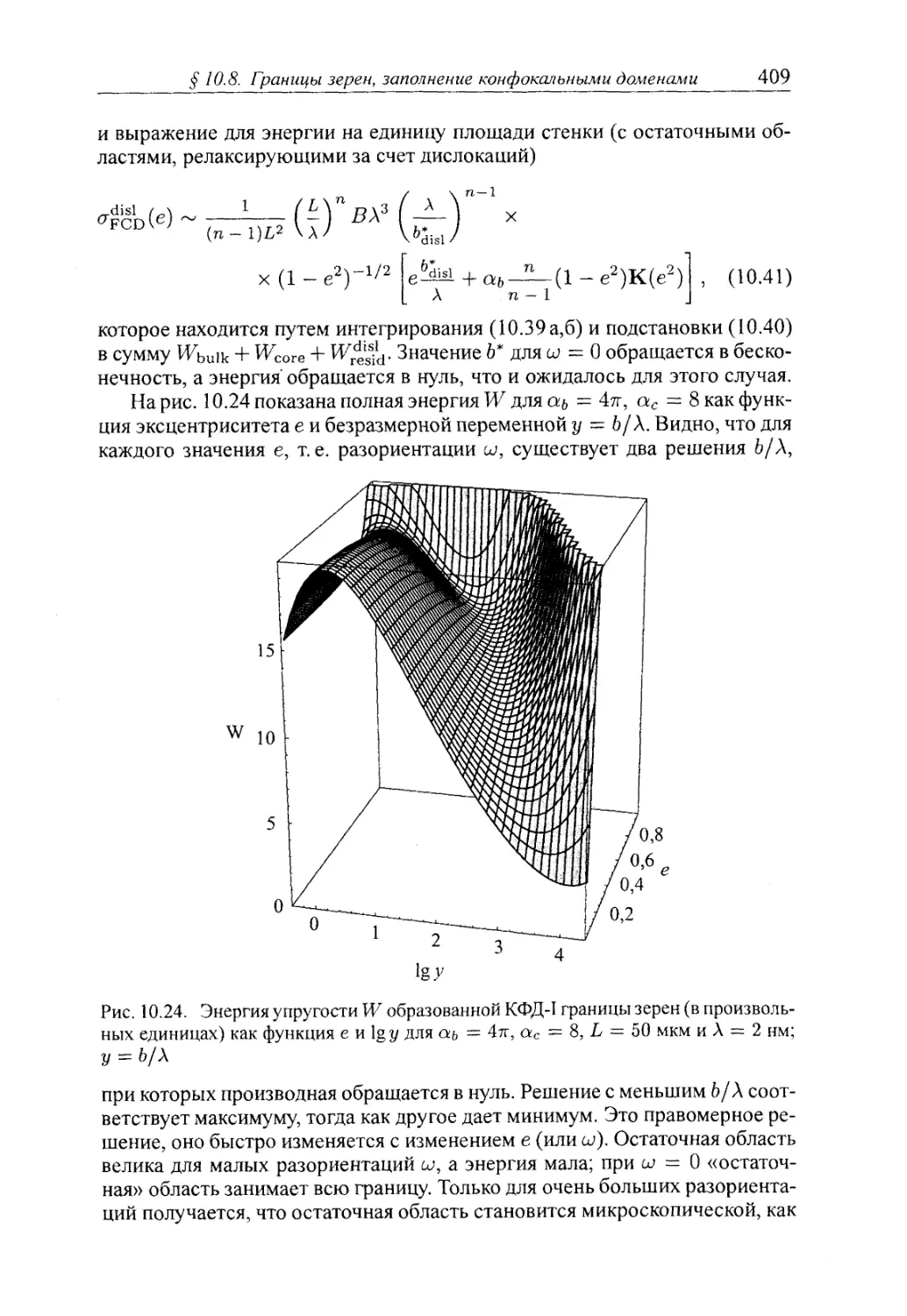
15.3.4. Микрофазное расслоение в блок-сополимерах 635
§ 15.4. Жесткие и полугибкие полимеры 638
15.4.1. Жесткие стержни 639
15.4.2. Полугибкие полимеры 639
15.4.3. Хиральность 641
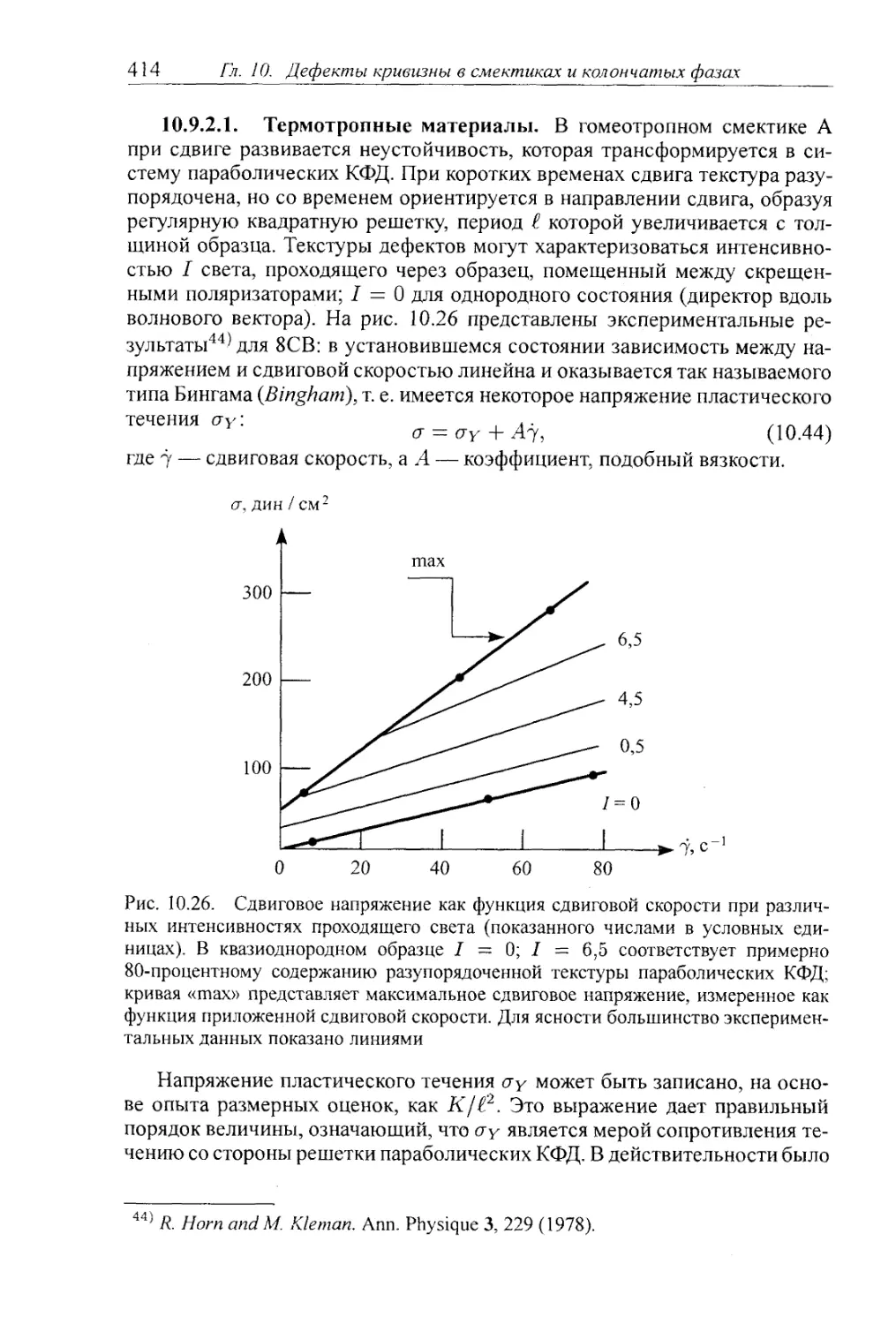
15.А. Приложение А. Центральная предельная теорема 642
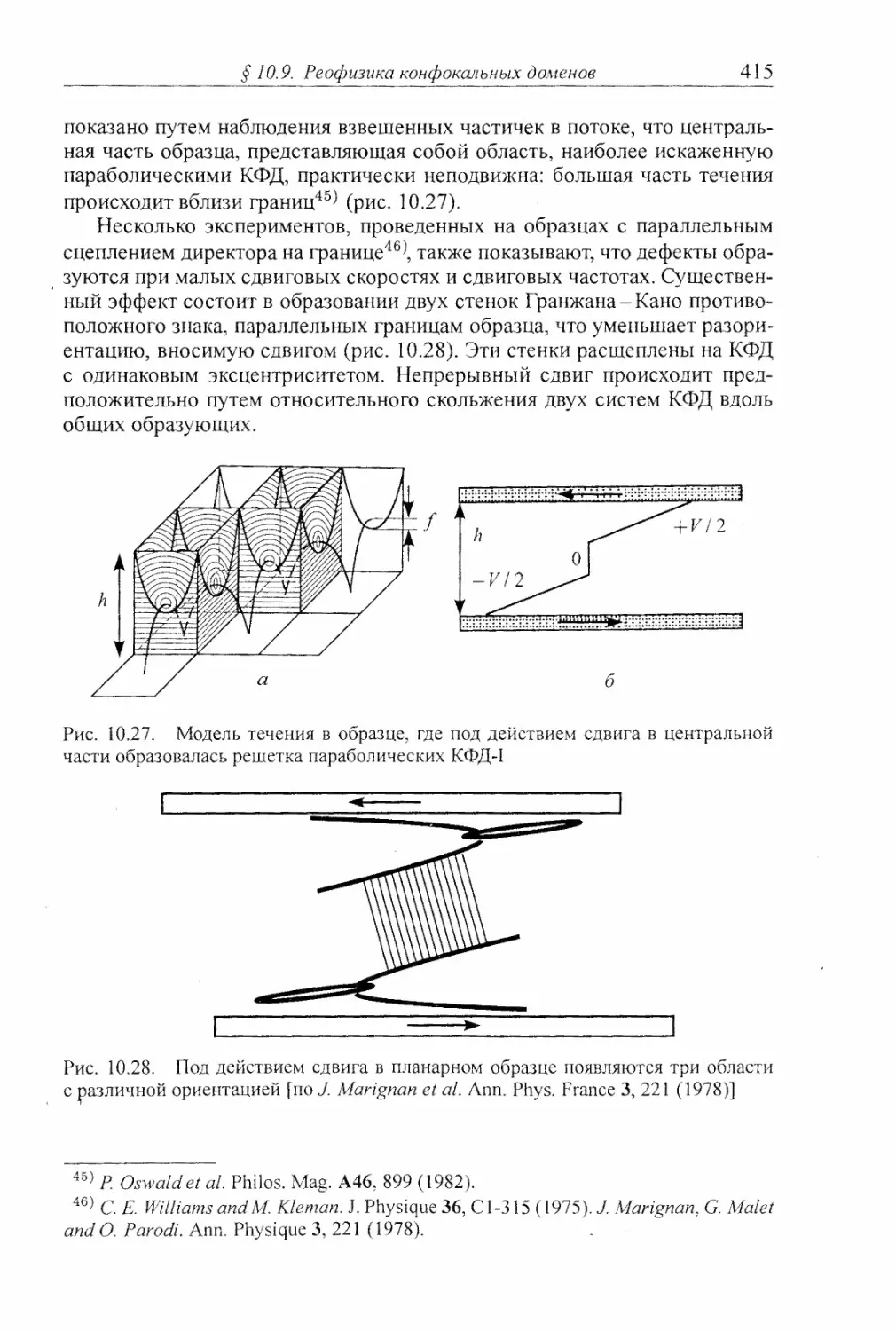
15.Б. Приложение Б. Изотермическая сжимаемость и флуктуации плотности;
статический линейный отклик 643
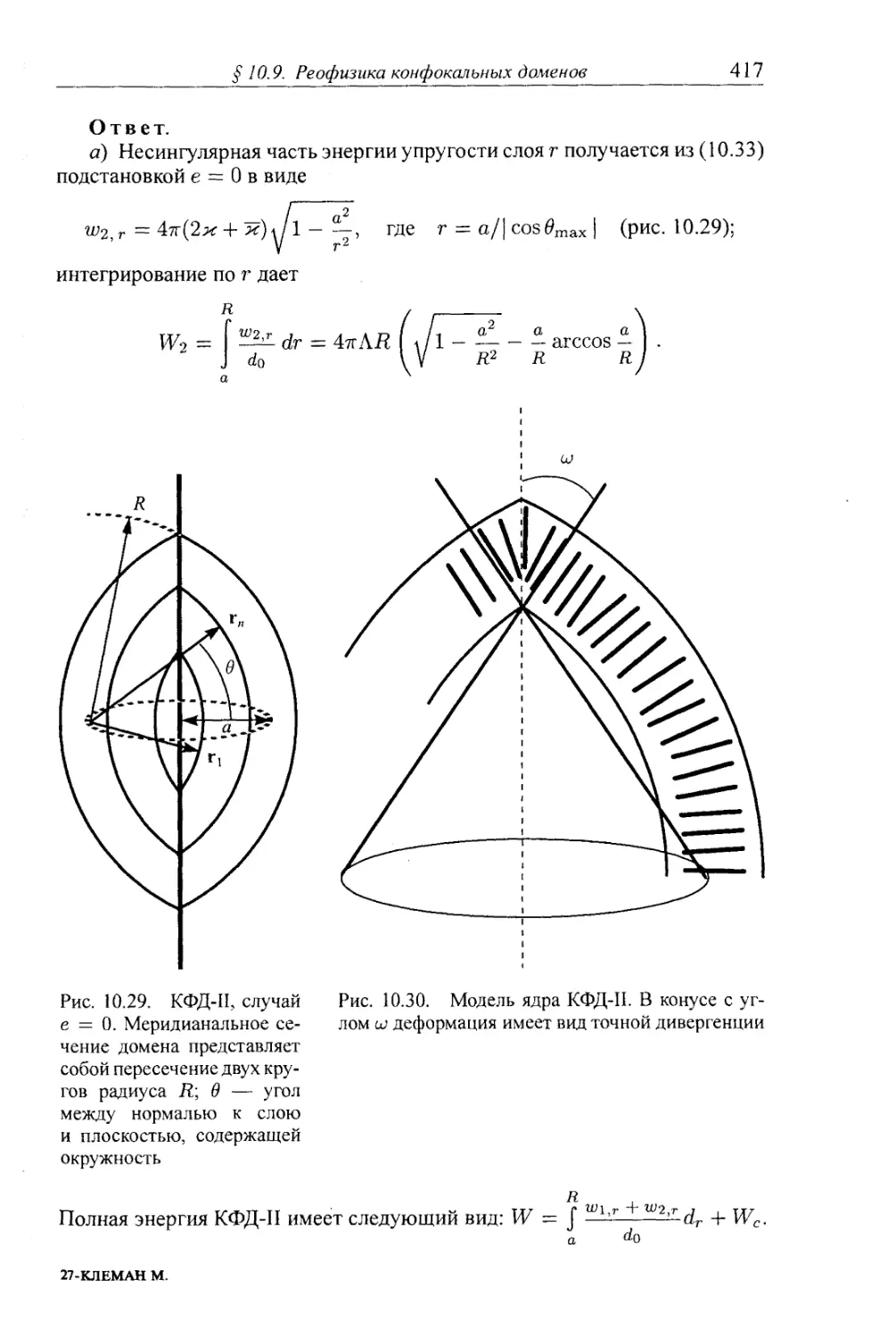
Алфавитный указатель 654
Предметный указатель 663
Предисловие редакторов перевода
Авторы книги хорошо известны своими оригинальными работами, по¬
священными изучению различных аспектов мягкой материи. Российско¬
му читателю более привычен термин частично упорядоченные среды, ис¬
пользованный в названии русского перевода книги, которая привлекла нас
фундаментальностью и обширностью излагаемого материала, а также об¬
щепризнанным авторитетом М. Клемана и О. Д. Лаврентовича. Коллектив
переводчиков и редакторов постарался как можно точнее передать суть
и дух этого уникального научного труда, который несомненно пробудит
интерес российских студентов и научных работников к изучению совер¬
шенно необычных свойств жидких кристаллов, биологических структур,
полимеров, коллоидов, гелей, сверхпрочных волокон, сложных жидкостей
с разнообразными молекулярными агрегатами, квазикристаллов и т. п. Эти
функциональные материалы имеют многочисленные практические приме¬
нения, а явления, в них наблюдаемые, дают новый импульс развитию наших
представлений о месте частично упорядоченных сред в природе и открыва¬
ют еще одну увлекательную главу в физике конденсированного состояния.
Издание этой книги стало возможным благодаря поддержке Российско¬
го фонда фундаментальных исследований. Перевод осуществлен коллек¬
тивом сотрудников Института кристаллографии РАН. Предисловия, главы
1,2 и 10 переведены В. Е. Дмитриенко, главы 3-5 — Е. Б. Логиновым, глава
6 — С. А. Пикиным, главы 7, 11 и 12 — В. А. Чижиковым, главы 8 и 9 —
Б. В. Петуховым, главы 13, 14 и 15 — Б.И. Островским.
Мы чрезвычайно признательны М. И. Монастырскому и Ю. А. Насти-
шину, внимательно прочитавшим отдельные главы перевода и сделавшим
очень ценные замечания. Мы благодарны авторам книги за помощь, ока¬
занную нам при переводе и издании. Весь русский текст прочитан и от¬
корректирован одним из авторов, О. Д. Лаврентовичем, так что является
в каком-то смысле авторизованным. Авторы внесли некоторые изменения
и уточнения по сравнению с оригинальным изданием. Комментарии пе¬
реводчиков и дополнительная литература облегчат российскому читателю
изучение затронутых в книге проблем; замеченные переводчиками и ре¬
дакторами небольшие неточности исправлены по согласованию с авторами
и не комментируются. Мы признательны Т. Я. Дмитриенко за помощь
в оформлении авторского и предметного указателей. Разумеется, все остав¬
шиеся неточности перевода остаются на совести переводчиков и редак¬
торов. Мы будем признательны читателям за комментарии и замечания,
которые можно присылать на интернет-страницу www.crys.ras.ru/labs/td/
softmatter, посвященную переводу данной книги.
С. А. Пикин, В. Е. Дмитриенко
Москва, 2006
Предисловие Жака Фриделя
Все учебники по основам физики твердого тела, начиная с книги Ф. Зей-
ца 1940 года, обычно концентрируют внимание на простых кристаллах,
в элементарной ячейке которых содержится один или несколько атомов,
связанных сильными ионными, ковалентными или металлическими свя¬
зями. Рассмотрение более слабых связей, таких как силы Ван-дер-Ваальса
в инертных газах, а также структурного или химического беспорядка
(например, сплавов или стекол) было скорее редким исключением.
Фундаментальные исследования по физике твердого тела начались за¬
долго до книги Зейца и были отмечены рядом Нобелевских премий после
Второй мировой войны. Применения их результатов включают классиче¬
скую металлургию, электронику, геологию и конструкционные материалы,
а также электронный и ионный транспорт, химию твердого тела, сегнето-
электричество и магнетизм.
Но параллельно с этим главным и широко представленным направ¬
лением — а для некоторых физических концепций и с опережением —
на протяжении всего двадцатого столетия происходило исследование и
систематическое изучение более «мягкой» материи. Находясь, главным
ч
образом, в руках физико-химиков и кристаллографов, а не физиков, эта
область науки в течение долгого времени слыла слишком сложной. Если
прогресс в исследовании полимеров был постоянным, хотя и медленным,
то в области жидких кристаллов он отсутствовал на протяжении сорока
лет, после яркого старта в 1925 г. и до конца шестидесятых, когда жидкие
кристаллы обрели новую жизнь благодаря использованию в системах отоб¬
ражения информации. Основанная на них оптоэлектроника, вообще говоря,
еще моложе.
Первоначальные научные интересы Мориса Клемана состояли в изу¬
чении магнитоупругих эффектов в ферромагнитных кристаллах и плен¬
ках. Ему удалось применить метод бесконечномалых дислокаций Кренера
(Е. Kroner) для начатого еще П. Вейсом (Р. Weiss) и существенно развито¬
го JL Неелем (L. Neel) исследования неоднородного магнетизма в стенках
и линейных и точечных дефектах. А когда П. Ж. де Жен (P.-G. de Gennes)
начал культивировать в Орсэ интерес к жидким кристаллам, было есте¬
ственно, что Клеман обратил внимание на эту область, где многие ме¬
зоскопические явления должны рассматриваться с отчасти аналогичной
точки зрения. Верный своим первоначальным интересам, Клеман сохра¬
нил в качестве главной цели рассмотрение всевозможных дефектов в таких
структурах, исследование которых было впервые начато моим дедушкой
Жоржем Фриделем (G. Friedel) и возрождено в пятидесятые годы другом
Клемана Ф. Ч. Франком (F. С. Frank). Ныне Клеман хорошо известен своими
работами по общей теории дефектов в «мягких» средах, частично изложен¬
ной в его небольшой книге (М Kleman, Points, Lines and Walls in Liquid
14
Предисловие Жака Фриделя
Crystals, Magnetic Systems and Various Ordered Media, John Wiley & Sons,
Chichester, 1983). Другой автор, Олег Д. Лаврентович, изучал в Киеве струк¬
туру жидкокристаллических капель, которые он создавал новым методом
с использованием контролируемой ориентации на поверхности, что позво¬
лило ему одним из первых обнаружить присутствие фазы с закрученными
границами зерен (TGB-фаза), предсказанной по аналогии со сверхпровод¬
никами второго рода. После продолжительной работы в группе Клемана
в Орсэ, где он в сотрудничестве с П. Болтенхагеном (Р. Boltenhagen) ис¬
следовал расщепление маслянистых бороздок на конфокальные домены,
Лаврентович стал сотрудником Кентского университета. Клеман и Лаврен¬
тович представляют и результаты своих исследований, материалы лекций
по физике «мягкой» материи. В основном же в этой книге рассматриваются
структурные свойства.
Как подробно показано в главах 1-4, типичные структуры «мягкой»
материи состоят из молекул, слабо связанных межмолекулярными силами
различного происхождения, не включающими металлические, ковалентные
и ионные связи. Таким образом, в понятие «мягкой» материи могут входить
и биологические структуры, хотя в книге они рассматриваются не очень по¬
дробно, за исключением некоторых структур, состоящих из молекул ДНК.
Из-за сложной и порою изменчивой формы молекул энтропия играет веду¬
щую роль в происхождении различных возможных форм «мезоморфных»
фаз жидких кристаллов, а также в создании искажений и дефектов. Отме¬
чается обобщение аналогичных концепций на случай жидких, аморфных
и квазикристаллических фаз в обычных твердых телах. Если же мы хотим
рассмотреть только соответствующие фазовые изменения, то нужно прежде
всего ввести параметр порядка с характерными фазой и амплитудой, плавно
меняющимися в пространстве и времени. Такой подход, ставший известным
благодаря Ландау, не учитывает локальные атомные или тепловые неодно¬
родности, но дает общий метод, применимый ко многим мезоскопическим
задачам в сверхтекучести, магнетизме и структурных фазовых превраще¬
ниях в твердых телах. Общие идеи, используемые для анализа фазовых
изменений в жидких кристаллах, аналогичны, таким образом, теоретиче¬
ским подходам, используемым в исследовании сверхпроводников и сильно
анизотропных магнетиков.
Две следующие главы описывают возможные статические или динами¬
ческие искажения в жидких кристаллах: в главе 5, посвященной упругости,
рассматриваются особенно подробно ситуации, где ведущую роль играют
граничные условия, а глава 6 представляет различные аспекты динамики
и вязкости.
Посвященная фракталам и явлениям роста глава 7 служит введением
в физику поверхностных явлений, которая представлена более подробно
далее в главе 13. Здесь снова явно различаются два подхода — статический
и динамический, — хотя эта область заслуживала бы большего внимания.
И, наконец, значительная часть книги посвящена изучению линейных
и точечных дефектов в жидких кристаллах в сравнении с классически¬
ми твердыми кристаллами. Эта обширная тематика, которой посвящены
Предисловие Жака Фриделя
15
также многие оригинальные работы авторов, освещена довольно полно
и своеобразно. В двух последних главах дан обзор коллоидов и полимеров
в доступной, хотя и конспективной манере.
В целом эта книга представляет собой хорошее введение в общие осно¬
вы изучения «мягкой» материи. Главные концепции сформулированы в про¬
стой и доступной форме. Короткие упражнения в конце каждой главы,
наряду с краткой библиографией, помогут читателям расширить свои зна¬
ния. Ядро книги составляют жидкие кристаллы, их многочисленные фазы
и возможные статические и динамические конформации с упором на роль
граничных условий и, в особенности, свободных поверхностей. Но иссле¬
дование «мягкой» материи не ограничивается рассмотрением жидких кри¬
сталлов, полимерам и коллоидам также уделено внимание, хотя и в меньшем
объеме. И еще: разнообразные концепции, развитые для изучения жидких
кристаллов, находят свои аналоги в некоторых задачах «жесткой» мате¬
рии; роль линейных и точечных дефектов в магнетизме, различные типы
дислокаций в жидких, аморфных и квазикристаллических фазах — эти раз¬
нообразные аспекты должным образом освещены, хотя и не рассмотрены
с той же глубиной.
Как справедливо отмечено авторами, замечательной чертой «мягкой»
материи является особая роль, которую играют мезоскопические расстоя¬
ния. В большинстве случаев прямые молекулярные взаимодействия явля¬
ются короткодействующими. Но способ заполнения пространства такими
молекулами различной формы, эластичности и вязкости, сохраняющими
разумно плотное и устойчивое упорядочение, может привести к набору
решений, которые будут отличаться только на больших расстояниях. В ис¬
следовании таких решений концепция длины когерентности была впервые
развита для схожих проблем магнетизма и сверхтекучести: это есть мера
величины мезоскопической области, на которой некоторый тип упорядоче¬
ния, приложенный на границе области, передается, с ослабевающей силой,
на другую границу. Однако из изучения «мягкой» материи возникло некое
новое понятие, концепция области фрустрации: во многих случаях неко¬
торое локальное либо особо устойчивое расположение атомов или молекул
не может быть далеко продолжено, так как при распространении оно со¬
здает слишком большие межмолекулярные напряжения. Примеры таких
явлений, упоминаемые в данной книге, — это двойная закрутка в холесте¬
риках и икосаэдрическая упаковка атомов в жидких, аморфных или квази¬
кристаллических фазах. В таких случаях область фрустрации ограничена
развитием и подходящим сворачиванием дисклинационных линий, как, на¬
пример, в голубых фазах. Следовательно, природа и симметрия коротко¬
действующих межмолекулярных сил может определять не только размер
сети дислокаций, но и дальнюю структуру сети. Авторы внесли большой
вклад в. само возникновение этой концепции, и, пожалуй, в этой книге она
могла бы получить большее развитие.
Как многие из их предшественников, авторы вводят линейные особенно-
/
сти (дислокации, дисклинации) с помощью процесса Вольтерра (Volterra),
а затем классифицируют возможные особенности (точки, линии, стенки)
16
Предисловие Жака Фрид ел я
с помощью топологического подхода, введенного Ж. Тулузом (G. Toulouse)
и Клеманом. Дефекты этого типа рассматриваются последовательно снача¬
ла в твердых телах, а затем в смектиках А, с их дислокациями, дискли-
нациями и конфокальными доменами. Здесь авторы недавно получили
результаты, позволившие им существенно обогатить наше понимание де¬
фектов. Затем весьма обстоятельно рассматриваются холестерики и немати¬
ки, с обсуждением жидкостной релаксации и принципиальной значимости
топологической классификации дефектов.
Несомненно, совершенно правильно подчеркнуто, что процесс Воль-
терра начинается с твердой среды, тогда как топологический подход пред¬
полагает полную вязкую релаксацию напряжений в по крайней мере ча¬
стично жидкой среде. Так как эта релаксация увеличивается от смектиков
к холестерикам и нематикам, прохождение через процесс Вольтерра кажет¬
ся все более и более искусственным, и действительно жаль, что ничего
больше не было сделано для дальнейшего изучения физических свойств
дисклинаций в нематиках, связанных с не коммутативностью их топологии:
например, что является эквивалентом «кинков» Ф. Ч. Франка, возникаю¬
щих при пересечении двух дислокаций в кристалле, когда две дисклинации
пересекаются в нематике?
Однако жидкостная релаксация, следующая за процессом Вольтерра
в «замороженной» среде, помогает нам понять некоторые характерные
особенности сингулярных линий в жидких кристаллах: она уменьшает
содержащуюся в дислокациях и дисклинациях энергию и позволяет этим
сингулярным линиям стать гибкими и подвижными; для дисклинаций она
фиксирует ориентацию поверхности разреза первоначального процесса
Вольтерра таким образом, чтобы минимизировать энергию; она дозволяет
топологическое исчезновение некоторых линий за счет вытекания в третье
измерение, создавая таким образом пары особых точек; она также допуска¬
ет, чтобы характерное вращение осуществлялось по касательной к линии
дисклинации, даже если она искривлена. Наконец, процесс Вольтерра объ¬
ясняет естественным образом, почему многие дислокационные конфигура¬
ции могут сохраняться, несмотря на то что нет топологических доводов в их
поддержку: это может относится, например, к сдвиговому скольжению при
низких температурах в аморфных твердых телах или квазикристаллах; это
может также относиться к начальным или граничным условиям, которые
могут поддерживать линии дефектов с релаксирующим или непрерывным
ядром такие, как трещины, распространяющиеся в кристалле, или дис¬
локации в трубке с нематиком при ориентации молекул перпендикулярно
поверхности трубки.
Эти замечания оправдывают, я полагаю, план, которому следуют авторы,
хотя в книге жидкостная релаксация могла бы быть введена ранее для дис¬
локаций, так же как для дисклинаций или конфокальных доменов. Непре¬
рывное распределение бесконечномалых дислокаций, производимых этой
релаксацией, представляет собой как раз ту идею, которую впервые пред¬
ложил Вольтерра для непрерывных твердых тел и которая впоследствии
Предисловие Жат Фриделя
17
была развита Дж. Ф. Наем (J. F. Nye), Б. А. Билби (В. A. Bilby) и Э. Кренером
для изгибов и кручений твердых тел.
Можно было бы сделать еще несколько пояснений, касающихся если
не существа книги, то представления материала.
• Теория Ландау, учитывающая дальний порядок при фазовых превра¬
щениях, не учитывает эффекты ближнего порядка, которые могут
оказаться существенными даже для переходов первого рода. Таким
образом, как отмечал еще в 1930 г. Ж. Фое (G. Foex), эффекты ближ¬
него порядка, наблюдавшиеся в магнитных свойствах по обе стороны
перехода нематик-изотропная жидкость, не предполагают с необ¬
ходимостью фазового перехода второго рода, эквивалентного точке
Кюри в ферромагнетике. Но эти эффекты, известные в нематической
фазе как «рои» еще до Первой мировой войны (они ответственны за
мутность нематиков и были правильно объяснены в длинноволновом
пределе де Женом), наряду с аналогичными эффектами, наблюдав¬
шимися в изотропной фазе группой Дюрана (G. Durand) в начале
семидесятых, сильно уменьшают скрытую теплоту перехода и уве¬
личивают температурные изменения эффективных параметров Лан¬
дау. Действительно, большой (оптический) диапазон этих флуктуа¬
ций ставит под вопрос сходимость разложения Ландау, которое, на
самом деле, ограничивается очень небольшой группой молекул. По¬
добным же образом ближний порядок может существовать в поли¬
мерах даже без перехода в нематическую фазу, например, как было
показано Делошем (В. Deloche), в расплавленных полимерах, а так¬
же в полимерных мембранах (использовалась резонансная техника).
Предпочитая не затрагивать подобные эффекты, авторы, вероятно,
дают слишком упрощенную картину той области, где флуктуации
несомненно важны.
• Некоторые «исторические» ссылки полезно было бы сделать более
полными. Так, ссылка на то, что дислокации в твердых телах нача¬
ли исследоваться как раз перед Второй мировой войной, по-видимо-
му, относится к фундаментальной работе, проделанной Бюргерсом
(J. W. Burgers) и Пайерлсом (R. Peierls) в 1939 г. Однако концепция
х_/
дислокационных и дисклинационных линии в непрерывных твердых
телах восходит к работам Вольтерра, выполненных перед Первой ми¬
ровой войной, а ее перенос на кристаллы относится к началу двадца¬
тых годов, в том числе многочисленные приложения к пластичности
кристаллов. С другой стороны, так называемая геометрия Кано (Cano)
с наклонной границей в смектике или в клиновидной ячейке в холесте¬
рике восходит еще к Гранжану (F. Grandjean), использовавшему рас¬
щепленные слюдяные пластинки; она была наиболее правдоподобно
интерпретирована и представлена в работе Жоржа Фриделя (рис. 8:22)
начала тридцатых годов. Кано только добавил специальный способ
упорядочения молекул в определенном направлении вдоль стеклян¬
ных обкладок.
18
Предисловие Жака Фриделя
• И, наконец, развитию исследований в области «мягкой» материи
очень способствовало перенесение идей, развитых для твердых тел,
что в книге довольно наглядно продемонстрировано. И наоборот, кон¬
цепции, развитые для «мягкой» материи, были использованы при изу¬
чении твердых тел или биологических материалов, о чем упомина¬
ется здесь в нескольких местах (что, однако, не является главным
предметом книги). Хотелось бы надеяться, что недавний прогресс,
достигнутый в тех областях исследований, где авторы были весьма
активны, найдет отражение в последующих публикациях.
В заключение я имею удовольствие представить вниманию читателей
книгу, которая в сжатой, но доступной форме освещает многие грани весьма
богатой и очаровательной области науки.
Жак Фридель
Париж, Франция
Январь 2001
От редактора серии. Частично упорядоченные системы
Многие обычные материалы не имеют ни идеального порядка, свой¬
ственного твердым телам, ни полностью случайной структуры, характер¬
ной для жидкостей или газов. Коллоиды, такие как молоко, мыло и растворы
детергентов; жидкие кристаллы, хорошо известные по плоским дисплеям;
гели; множество видов сверхпрочных волокон — все они являются частич¬
но упорядоченными системами. Такие системы не только стали важной
областью фундаментальных исследований в физике и химии, но и нашли
практические приложения в материаловедении и других прикладных дис¬
циплинах.
Данная серия включает научные монографии и учебники повышенного
уровня сложности, в которых рассматриваются на различных масштабах
(микроскопическом, мезоскопическом и макроскопическом) разнообраз¬
ные конденсированные системы, не имеющие полного дальнего простран¬
ственного и ориентационного порядков. Эти системы — некоторые из них
также называются «мягкой» материей, сложными жидкостями или сверх-
молекулярными жидкостями — включают в себя частично упорядоченные
жидкости, состоящие из молекул или агрегатов молекул, каким-либо обра¬
зом организованных на больших масштабах; жидкие кристаллы, состоящие
из мономеров или полимеров; коллоиды; молекулярные кристаллы; квази¬
кристаллы; гранулированные материалы; неупорядоченные системы и аг¬
регаты. Книги из данной серии описывают все разнообразие свойств таких
материалов, их структуру и образование, а также явление протекания (пер-
коляцию) и образование фракталов и пространственно-временных систем.
Луи Лам
Сан Хосе, Калифорния
Предисловие. Что такое «мягкая» материя
Цель этой книги
Понятие «мягкой материи» включает в себя огромное разнообразие си¬
стем, от полимеров до коллоидов, от жидких кристаллов до поверхностно¬
активных веществ и от мыльных пузырей до растворов макромолекул. Все
эти материалы становятся все более и более важными для современной про¬
мышленности. Хотя на протяжении долгого времени они были областью
исследования почти исключительно для химиков, ныне и физики проявля¬
ют к ним все более острый интерес. Действительно, системы, относящиеся
к «мягким» средам, ставят физические проблемы совершенно нового типа.
Трудно точно сформулировать, что объединяет их в единое целое (обычно
говорят о «сложных системах», и это справедливо по крайней мере в отно¬
шении их структурных свойств). Мы постараемся подробнее представить
здесь некоторые характеристики, присущие им всем.
Все системы, которые могут быть объединены под названием «мягкой
материи», относятся, за редким исключением, к органическим материалам.
В сущности, даже когда говорят о коллоидном золоте или о коллоидном
кремнеземе, скорее имеют в виду текстуру материала, а не вещество само
по себе, тогда как наука о коллоидах, в обобщенном понимании, обращается
к органическим растворам, характеризующимся дисперсией или растворе¬
нием одной фазы в другой, так что поверхностные явления оказывают¬
ся очень существенными. Сам термин коллоид является общепризнанным
и даже популярным, но никакого единого образца в его определении до сих
пор не появилось.
Таким образом, строительные блоки «мягкой» материи — это органи¬
ческие молекулы несимметричной формы, имеющие обычно сложную ар¬
хитектуру, связанные между собой довольно слабыми взаимодействиями.
Область стабильности этих фаз близка, поэтому, к комнатной температу¬
ре, и малых изменений температуры достаточно, чтобы вызвать фазовые
переходы, сопровождающиеся обычно довольно малой скрытой теплотой
или, иногда, химическим разложением. Так что можно сказать, что скорее
энтропия, чем энтальпия, является той величиной, которая должна рас¬
сматриваться в первую очередь. Биологическая материя (белки, мембраны,
ДНК и их конгломераты такие, как вирусы и микротрубочки) также вхо¬
дит в класс материалов, подпадающих под данное определение «мягкой»
материи (когда они изучаются физиками). Важной характеристикой этих
материалов является то, что in vivo они не находятся в состоянии термо¬
динамического равновесия, однако рассмотрение этого фундаментального
свойства живой материи полностью выходит за рамки данной книги.
Предисловие. Что такое «мягкая» материя. Цель этой книги 2 1
«Мягкие» среды, в частности жидкие кристаллы, демонстрируют по¬
рядок весьма своеобразной природы, промежуточный между твердыми те¬
лами и неупорядоченными фазами. Их открытие привело к существенному
развитию теории фазовых переходов и теории сингулярностей параметра
порядка, например к открытию таких замечательных стуктур, как «фазы
с дефектами» (фрустрированные фазы). Концепции, возникшие в физике
мягких сред, затем нашли применение в других областях физики (квази¬
кристаллы, аморфные среды, сверхтекучие жидкости).
Специфическая природа разупорядочения в полимерах также потребо¬
вала развития абсолютно нового типа описания случайных сред, а именно
законов подобия. Примеры новых типов фазовых переходов (например, пе¬
реход золь-гель) способствовали развитию нетрадиционных теорий в фи¬
зике разреженных сред, использующих идею фракталов.
И, наконец, следует отметить как фундаментальную, так и практиче¬
скую значимость транспортных свойств этих сред (диффузию, вязкость),
их вязкоупругих свойств (например, течение жидких кристаллов под дей¬
ствием сдвига, индуцированные сдвигом фазовые переходы, пластическая
деформация полимеров), а также поверхностные и межфазные явления
(смачивание, влияние дальнодействующих сил), которые определяют широ¬
кую область обновления мезоскопической физики, где мы находим взаимо¬
действие молекулярных и макроскопических концепций (гидродинамика,
реология, капиллярные явления). Далеко не все из этих тем освещаются
в данном учебнике, который является, по существу, введением в физику
«мягкой» материи.
Физика «мягкиой» материи — это физика конденсированного состоя¬
ния, и она идет рука об руку с физикой твердого тела. Можно ожидать, что
многие явления описываются весьма похожим, а то и идентичным образом
в обеих дисциплинах, что ведет к их взаимному обогащению. Поэтому мы
включили во вводные главы некоторое число специальных понятий, общих
для всей физики конденсированного состояния, относящихся к структуре
(расположение атомов и молекул), когезии (химическая связь), дефектам
и фазовым переходам. Однако читатель не должен ожидать, что изложе¬
ние будет совершенно одинаковым. Например, рассматривая взаимодей¬
ствие между атомами или молекулами, мы отдаем предпочтение картине
локальных химических связей, а не конфигурации бесконечной электрон¬
ной системы, которая лучше подходит для твердых кристаллов. Поэтому
традиционная классификация, подобная разделению на проводники и изо¬
ляторы, здесь едва ли подойдет.
Читатель также заметит, что мы делаем акцент на рассмотрении де¬
фектов, существенно расширяя его на случай твердых тел, для того чтобы
показать оба случая в общей перспективе. Проблема дефектов уходит кор¬
нями в начало прошлого века — жидкие кристаллы были теми материа¬
лами, для которых концепция дефектов была впервые развита, — и она
всегда представляется особенно трудной для изучения. У нас был и личный
интерес развивать данную концепцию, но он был далеко не единственным.
Общая теория дефектов сильно выиграла благодаря открытию множества
22
Предисловие. Что такое «мягкая» .материя. Цель этой книги
жидкокристаллических фаз; с другой стороны, развиваемая с недавних пор
реология сложных материалов может много почерпнуть из теории пла¬
стичности твердых тел. Некоторые подходы, хорошо изученные для случая
твердых тел, находят свое приложение в теории жидких кристаллов, при
очевидных отличиях: так, при вязкой релаксации дефектов в нематических
жидких кристаллах гистерезис оказывается намного меньше, чем при тре¬
нии в твердых телах. За исключением таких частных моментов, все наибо¬
лее существенные аспекты рассматриваются, как нам кажется, достаточно
детально, чтобы сделать доступной читателю физику «мягкой» материи
в полном объеме. Так, глава, посвященная гидродинамике нематических
жидких кристаллов, начинается с краткого изложения гидродинамики изо¬
тропной жидкости.
Несколько технических замечаний. Список литературы был сознательно
ограничен и включает учебники, обзоры и те оригинальные статьи, резуль¬
таты которых не вошли в обзоры. Каждая глава сопровождается несколь¬
кими задачами, которые либо позволяют читателям проверить понимание
концепций, развитых в данной главе, либо поднимают некоторые специаль¬
ные вопросы, не изложенные в основном тексте. В этом же состоит и роль
нескольких приложений. Мы также добавили таблицу единиц измерений.
Благодарности
Этот учебник возник в результате многолетнего сотрудничества авторов
и из их личного опыта преподавания (М. К.: в Эколь Политекник, физика
твердого тела (Орсэ) и физика жидкостей (Париж); О. Л.: междисципли¬
нарная программа по химической физике (Кентский университет, Огайо).
М. К. хотел бы поблагодарить Альберта Либшабера, Университет Рокфел¬
лера, в чьей лаборатории он нашел теплый прием и приятную спокойную
атмосферу для работы над этой книгой. Выражаем благодарность за об¬
суждения и помощь Лоику Оврэ, Паскалю Фабру, Жану-Батисту Фурнье,
Патрику Освальду, Полю Сотта и Андрэ Тьявиллю, которые были в разное
время в группе преподавателей под руководством М.К. Со своей стороны
О. Л. признателен Сергею Шияновскому, Виктору Пергаменщику и Томо-
хиро Ишикаве, помогавшим ему в преподавании данного предмета. Клодин
Фраден (из Лаборатории физики твердого тела в Орсэ) напечатала большую
часть первоначальной рукописи; авторы хотят поблагодарить ее за посто¬
янную помощь, которую она оказывала невзирая на расстояние.
Мы извлекли много пользы из конструктивных критических коммен¬
тариев Владимира Дмитриенко, Жака Фриделя, Ефима Каца, Рандалла
Камьена, Грегу ара Порта, Харальда Плейнера, Чарльза Розенблатта, Вла¬
димира Шалаева, Тима Слакина и Мадлен Вэссье. Авторы сердечно благо¬
дарят их всех.
Мы также признательны CNRS и NSF за поддержку, сделавшую воз¬
можным сотрудничество между авторами.
Предисловие. Что такое «мягкая» материя. Цель этой книги
23
Русская версия книги является полным переводом вышедшего в 2003 г.
англоязычного издания и не отличается от последнего, если не считать
некоторого числа опечаток и неясностей, исключенных или исправленных
благодаря пристальному вниманию научных редакторов и переводчиков.
Мы благодарны российским коллегам за эту возможность улучшить наш
текст.
Морис Клеман
Париж, Франция
О. Д. Лаврентович
Кент, Огайо, США
Таблица констант, перевод единиц СИ в СГС, символы
соотношений
Авогадро постоянная: N& — 6,022 х 1023 моль”1.
Больцмана постоянная: &б = 1,381 х 10-23 Дж • К-1 = 1,381 х
х 10-16 эрг • град-1.
Элементарный заряд: е = 1,602 х КГ19 Кл = 4,803 х Ю-10 СГСЭ.
Планка постоянная: h = 6,626 х 10~34 Дж ■ с = 6,626 х 10-27 эрг • с.
Электрическая постоянная:во = 8,854 х 10-12 Кл2-Дж"1-м“1 = 1ед.
СГСЭ.
1 эВ = 1,602 х 10-12 эрг = 1,602 х 10-19 Дж.
1 къТ = 4,12 х 10-14 эрг = 4,12 х 10-21 Дж ss — эВ при Т = 298 К.
40
1 кал = 4,1868 Дж.
1 эВ/молекулу = 23,042 ккал/моль = 96,472 кДж/моль.
1 Дж = 107эрг = 0,2388 кал = 6,242 х 1018 эВ.
Электрический заряд: 1 ед. СГСЭ = 3,336 х Ю~10 Кл.
1 дин = 10-5 Н.
О о
1 дин/см = 1 эрг/см = 1 мН/м = 1 мДж/м .
Электрический дипольный момент: Д = дебай;
1 Д = 10~18 ед. СГСЭ х см = 3,336 х Ю~20 Кл х см.
Давление, напряжение: Па = паскаль;
1 Па = 1 Н/м2 = 10 дин/см2.
Динамическая вязкость: Паскаль-секунда = Пахе; П = пуаз = динхс/см2;
1 Пахе =10 П.
Символы соотношений
~ «величины того же порядка», численные или алгебраические, размерные;
ос «пропорционально», пропорциональность без размерности;
= пропорциональность с размерностью;
« «приблизительно равно» в численных или алгебраических оценках; изоморфизм
групп;
~ «тождественно равно».
ГЛАВА 1
КОНДЕНСИРОВАННАЯ СРЕДА: ОБЩИЕ
ХАРАКТЕРИСТИКИ, ХИМИЧЕСКИЕ СВЯЗИ
И ВЗАИМОДЕИСТВИЕ ЧАСТИЦ
Традиционно различают три типа сред: газы, жидкости и твердые те¬
ла. В первом приближении газ характеризуется отсутствием взаимодей¬
ствия между атомами или молекулами, что приводит к статистическому
беспорядку. Это состояние регулируется условием максимума энтропии.
Газы в этой книге рассматриваться не будут. В противоположность им,
более конденсированные жидкая и твердая фазы регулируются не только
энтропией, но и межчастичными взаимодействиями. Эти состояния ста¬
билизируются за счет сложного баланса сил притяжения, ответственных
за конденсацию химических веществ, и сил отталкивания. Их равновесие
дает в результате некий локальный порядок, определенный на некоторой
характерной длине. В кристаллах этот локальный порядок воспроизводит¬
ся на расстояниях, много больших межчастичных, так что можно говорить
о дальнем порядке. Дальний порядок в кристаллических материалах опи¬
сывается в терминах элементов группы симметрии, относительно которых
он инвариантен. Независимо от типа упорядочения, все конденсированные
среды демонстрируют в жидком и твердом состояниях следующие общие
свойства.
1. Энергии взаимодействия, которые стабилизируют локальный поря¬
док, варьируются в интервале 0,1 эВ - 10 эВ на атом или молекулу. По
порядку величины это чаще всего 1 эВ.
2. Величина молярных-объемов всегда имеет один порядок, типичные
О
расстояния между атомами ~ 1 А.
3. Частоты колебаний атомных связей порядка 1013 - 1014 Гц.
Различия в этих величинах определяются природой химических связей
и молекулярной организацией.
§ 1.1. Энтропия в неупорядоченных системах
Число г] 1 способов, которыми можно ввести один атом, одну молеку¬
лу, один объект, или, как для краткости мы будем говорить, одну частицу,
в растворитель, имеющий объем V, много больший, чем объем, зани¬
маемый частицей, пропорционально V, т. е. щ = AV, где А — некото¬
рый коэффициент пропорциональности. Введем п одинаковых растворен¬
ных частиц и предположим, что А не зависит от числа уже присутствую¬
щих частиц; это тем более справедливо, чем меньше объем, занимаемый
26 Гл. 1. Конденсированная среда. Общие характеристики
п частицами, по сравнению с V. Тогда число способов ввести эти п частиц
равно
где число эквивалентных перестановок п\ учитывает, что частицы одина¬
ковы. Соответствующая энтропия S = к Б In rjn дается выражением
больших п. Свободная энергия раствора невзаимодействующих частиц за¬
писывается в виде
Здесь члены с А и е включены во внутреннюю энергию п/0(Т). Введем,
в соответствии со стандартным термодинамическим определением, «пар¬
циальное давление», связанное с растворенными частицами:
здесь с — n/V — концентрация частиц. Физический смысл р, частной про¬
изводной от свободной энергии при постоянном п, можно уяснить себе сле¬
дующим образом. Представим, что раствор частиц и чистый растворитель
находятся в контакте через мембрану, которая проницаема для растворите¬
ля, но не для частиц. Величина — р dV дает изменение свободной энергии
при обратимом процессе, когда объем раствора изменяется на бесконечно
малую величину dV. Поэтому р является нормальной силой, действующей
со стороны раствора на единицу площади мембраны и измеряемой вдоль
внешней нормали; р называется осмотическим давлением (см. также гл. 4).
Отметим, что при данной свободной энергии (1.3) уравнение (1.4) может
быть переписано как pV = RT, т. е. как уравнение состояния идеального
газа, если под V понимать объем раствора, содержащий один моль рас¬
творенного вещества; R = 8,31 Дж-моль^-К-1 — универсальная газовая
постоянная.
Уравнение (1.4) изменяется, если принять во внимание взаимодействия
между частицами и использовать так называемое вириальное разложение
где второй вириалъный коэффициент v имеет размерность объема и про¬
исходит от парных взаимодействий между частицами. Члены более вы¬
сокого порядка в уравнении (1.5) соответствовали бы взаимодействиям,
включающим три частицы, четыре частицы, и т. д. Если нет никаких даль-
нодействующих взаимодействий и частицы рассматриваются как твердые
сферы радиуса г0, то можно показать, что v — это исключенный объем:
(1.1)
S = k^nln (AVe/n)
(1.2)
7Ъ
где используется приближенная формула Inn! = nln справедливая для
е
F = U - TS = п[/о(Г) - къТЫ(У/п)}.
(1.3)
р = -(dF/dV)T,n = nkbT/V = cfcET;
(1.4)
р — скьТ(1 + cv + ...)
(1.5)
v = - х ~тг(2г0)3 — 4vp,
2 3
(1.6)
§ 1.2. Центральные и направленные силы между атомами
27
где vP — объем одной частицы (см. гл. 4). В общем случае v учитывает как
отталкивание, так и притяжение и может быть вычислен в предположении
центральных сил (т. е. в предположении, что парный потенциал взаимодей¬
ствия wi2(r) является функцией расстояния):
V
оо
1
2
г=0
[1 — ехр(—Wi-2/ksT)]4:7vr2 dr. (1.7)
Заметим, что в присутствии растворителя потенциал W12 (г) зависит не толь¬
ко от прямых взаимодействий частица-частица, но и от взаимодействий
частица-растворитель и растворитель-растворитель. Поэтому последнее
выражение справедливо, только когда растворитель можно рассматривать
как непрерывную среду, присутствие которой может быть учтено в юи{г).
Вириальное разложение используется для описания разбавленных рас¬
творов мицелл, макромолекул, белков и т. п. Рассмотрим раствор, состо¬
ящий из двух компонент, скажем растворителя А и растворенного веще¬
ства В. Пусть waa, ^вв и гиАв являются энергиями взаимодействия пар А А,
ВВ, и АВ на кратчайшем расстоянии а, которое мы считаем одинаковым для
всех пар (объем молекул, составляющих А или В, равен а3); тогда величина
w = u>ab — (^аа + ^вв)/2 является мерой эффективного взаимодействия
между частицами А и В (см. гл. 15, где также показано, что из > 0, если си¬
лами взаимодействия являются силы Ван-дер-Ваальса). В случае w > 0 при
низкой температуре молекулы А и В разделяются. Можно формально выде¬
лить две ситуации: (1) слабые притягивающие взаимодействия, w <С кьТ\
(2) сильные притягивающие взаимодействия. Эти две ситуации часто отно¬
сят к «хорошим» и «плохим» растворителям соответственно. Эффективный
исключенный объем дается выражением v = (1 — 2w/k^T)a3 (см. гл. 15).
Для плохих растворителей существует температура, при которой притяги¬
вающие и отталкивающие силы компенсируют друг друга, v = 0, и система
ведет себя как идеальный раствор невзаимодействующих частиц нулевого
объема. Условия, при которых зануляется второй вириальный коэффициент,
часто называют «тета-условиями».
§ 1.2. Центральные и направленные силы между атомами
Мы даем здесь краткий перечень понятий. Детали можно найти в учеб¬
никах, список которых приведен в конце главы.
1.2Л. Металлическая связь
Валентные электроны свободно циркулируют в металлическом кристал¬
ле, превращая его в единую гигантскую молекулу. В целом притягивающий
связующий эффект этого моря валентных электронов оказывается нена¬
правленным и приводит к плотноупакованным структурам, где каждый
28
Гл. I. Конденсированная среда. Общие характеристики
атом, рассматриваемый как сфера, окружен максимально возможным чис¬
лом атомов. Межатомные расстояния определяются отталкивающими сте-
рическими силами. Плотная упаковка является отличным приближением
первого порядка для изучения локальной структуры. Гранецентрирован-
ные кубические (ГЦК, рис. 1.1, а) и гексагональные плотноупакованные
(ГПУ) кристаллы являются наиболее плотными структурами из атомов од¬
ного размера. Объемно-центрированная кубическая структура (ОЦК) менее
компактна (рис. 1.1,6), однако в одной и той же системе она оказывается
более предпочтительной при высоких температурах благодаря большей ко¬
лебательной энтропии.
а
б
Рис. 1.1. Гранецентрированная (а) и объемно-центрированная {б) кубические
решетки
1.2.2. Связи, образованные флуктуирующими диполями
Электрически нейтральные образования, такие как атомы благородных
газов или неионизированные органические молекулы, удерживаются вме¬
сте притягивающими силами Ван-дер-Ваалъса (известными также как дис¬
персионные силы)). Для благородных газов, например аргона, в которых
совпадают усредненные позиции положительных и отрицательных заря¬
дов, эти силы были впервые исследованы Ф. Лондоном. Флуктуирующие
электрические диполи одной нейтральной частицы вызывают дипольный
момент у другой, см. п. 1.3.3. Получающаяся кристаллическая структура
является плотноупакованной, что также связано с ненаправленным харак¬
тером такой связи. Лондоновские энергии, так же как и другие ван-дер-
ваальсовы энергии, вообще-то являются малыми, часто меньшими, чем к^Т
на один атом при комнатной температуре. Соответствующие кристалличе¬
ские образования стабильны только при низких температурах, они плавятся
с малой скрытой теплотой.
§ 1.2. Центральные и направленные силы между атомами
29
1,2.3. Ковалентная связь
В паре атомов, связанных одной ковалентной связью, каждый атом по¬
ставляет один электрон для создания электронной пары, принадлежащей
двум атомам. Ковалентная структура характеризуется числом г связей, при¬
ходящихся на атом: г — 4 для С, Si и Ge; z = 2 для S, Se и Те. В первом
случае можно ожидать трехмерное (3D) атомное упорядочение (например,
две взаимопроникающие ГЦК-решетки углерода в алмазе). Во втором слу¬
чае получаются более или менее свернутые полимерные цепи, упорядочи¬
вающиеся в сильно анизотропные трехмерные кристаллы, в которых цепи
взаимно стабилизируются дисперсионными силами. Ковалентные связи яв¬
ляются сильно направленными. Их энергия высока, порядка 100 ккал/моль
~ 102 — 103 кДж/моль ~ 1 — 10 эВ на молекулу (табл. 1.1).
Таблица 1.1. Энергии типичных атомных связей
Вид связи
Структура
Энергия
на связь,
кДж/моль
Энергия
на связь,
эВ/молекулу
Ионная
Na+СГ
750
7,77
Ковалентная
С = N (пример: HCN)
870
9,02
С = О (Н2СО)
690
7,15
С - С(С2Н4)
600
6,22
О-Н (Н20)
460
4.77
С-Н (СН4)
430
4,46
С-С (С2Н6)
360
3,73
F-F (F2)
150
1,55
Металлическая
Na
109
1,13
А1
311
3,22
Водородная
N-H...0 = С;
С = 0...H-0-C
10-50
0,10-0,51
1.2.4. Ионная связь
Ионная связь возникает из-за полной передачи электронов от одного
атома к другому. Такая передача одного или нескольких электронов пре¬
вращает нейтральные атомы в ионы противоположного знака с сильным
электростатическим взаимодействием между ними. Ионные связи являют¬
ся прочными, они создают кристаллы, стабильные при комнатной темпера¬
туре. Классическим примером являются кристаллы поваренной соли с ку¬
бической структурой (хлорид натрия, NaCl, температура плавления 801 °С),
30
Гл. 1. Конденсированная среда. Общие характеристики
в которой каждый отрицательно заряженный хлор окружен шестью поло¬
жительно заряженными ионами натрия (и каждый атом натрия окружен
шестью ионами хлора (рис. 1.2)).
Рис. 1.2. Кубическая решетка NaCl
Главный вклад в энергию взаимодействия двух ионов с зарядами z\e
2
и z2e дает кулоновский потенциал wcou\ ~ ZlZ?e , который является при-
4:7T££qT
тягивающим, когда ионные валентности z\ и z2 имеют противоположные
знаки; здесь е — относительная диэлектрическая проницаемость среды,
в которой находятся ионы (называемая также диэлектрической постоян¬
ной), £0 — электрическая постоянная (проницаемость вакуума) иг — рас¬
стояние между атомами. Когда два атома подходят близко друг к другу,
преобладающим становится отталкивание.
Чтобы вычислить энергию когезии ионного кристалла, такого как NaCl,
нужно просуммировать все кулоновские энергии взаимодействия между
атомами. Энергия когезии р одного иона ze дается суммой парных потен¬
циалов взаимодействия (с противоположным знаком) этого иона с осталь¬
ными ионами zie, т. е.
= = о-8)
4:7Г££о Г{
г г
е2
Пусть \х — М , где М — постоянная Маделунга, определяемая гео-
47Т££оа
метрией упаковки атомов, и а — расстояние между двумя противополож¬
ными зарядами. Для кубической решетки NaCl имеем: М = 1,748, а —
= 0,276 нм. При £ = 1, £о = 8,854 х 10-12 Ф/м, е = -1,602 х 10~19 Кл
получается р « 1,5 х 10-19 Дж, что существенно больше тепловой энергии
к%Т и 4 х 10-21 Дж при комнатной температуре. Отсюда энергия, необхо¬
димая для диссоциации одного моля кристалла в газ ионов, оценивается как
1.3. Силы между молекулами
31
U = [iNA — 890 кДж/моль (« 8 эВ/атом), где = 6,022 х 1023 моль"1 —
это число Авогадро. На самом деле силы отталкивания несколько умень¬
шают U, однако эта поправка мала (и 15 %). Таким образом, ионные связи
очень сильны.
Может существовать и промежуточная ситуация, в которой одни и те же
атомы связаны силами смешанного типа, например ионно-ковалентными.
1.2.5. От ионной связи к ковалентной связи в кристаллах
Стандартным примером почти идеальных ионных кристаллов являются
галогениды щелочных металлов (кристаллы I-VII). Почти все они кристал¬
лизуются в ГЦК-структуру NaCl, за исключением галогенидов Cs. Дважды
ионизованые кристаллы II-VI, подобные CaSe, являются слегка ковалент¬
ными, поскольку ион Са2+ частично экранирован некоторой долей сосед¬
него электрона, той долей, которая не передана иону Se2~, и поскольку элек¬
тронное облако немного искажено вдоль направления, соединяющего Са^+
и Se2_. Эти характеристики усилены в кристаллах III-V, подобных GaAs,
где ионный обмен мал и больше электронов обобществлены между атома¬
ми. GaAs кристаллизуется в структуру цинковой обманки, которая типична
для четырехвалентных кристаллов. Подобно алмазу, структура «цинковой
обманки» состоит из двух взаимопроникающих ГЦК-решеток, каждая из
которых занята атомами разного типа.
§ 1.3. Силы между молекулами
Коль скоро главенствующие силы не являются чисто электростатиче¬
скими или ковалентными, энергии связи между частицами слабы, и мы по¬
падаем в область «мягкой материи». Преимущественные взаимодействия
здесь — экранированные ионные, дипольные и ван-дер-ваальсовы силы.
1.3.1. Электростатическая связь в диэлектрической среде
Мы часто имеем дело с атомами или молекулами, растворимыми в воде,
так что когда появляются ионы, их взаимодействие ослаблено водой из-за
ее большой диэлектрической постоянной е ~ 78. Соли, подобные NaCl,
легко растворяются в воде благодаря тому, что электрические поля сильно
ослаблены (множителем 1/е), так что энергия когезии р оказывается поряд¬
ка к^Т или даже меньше. Более того, энтропия статистической смеси ионов
также дает вклад в понижение свободной энергии. Ионные поверхностно-
активные вещества, такие как стеарат натрия, NaCi8H35 02 (рис. 1.3), тоже
легко ионизуются в воде по тому же принципу.
Отметим, что каждый гидрофильный анион стеарата натрия несет «гид¬
рофобную» углеводородную часть СпН2п+ь которая не обладает сродством
к водному окружению. Когда концентрация таких амфифилъных молекул
больше так называемой критической мицеллярной концентрации (КМК),
они формируют приблизительно сферические мицеллы. Углеводородные
хвосты оказываются скрытыми в ядре мицеллы, тогда как полярные головки
32
Гл. I. Конденсированная среда. Общие характеристики
располагаются на поверхности мицеллы, где они могут взаимодействовать
с окружающей водой и ионами противоположного знака (такими, как Na+).
Рис. 1.3 Ионное поверхностно-активное вещество: молекула стеарата натрия
растворяется в воде
По мере увеличения концентрации мицеллы могут трансформироваться в
двойные слои, простирающиеся и организующиеся в пространстве в ви¬
де разнообразных удивительных геометрических структур, которые будут
описаны позднее.
1.3.2. Электрические диполи
Молекулы «слабо» упорядоченной среды часто бывают электрически
дипольными. Асимметричные молекулы, сцепленные внутри ковалентны¬
ми связями, во многих случаях обладают постоянными электрическими
диполями. Эти диполи возникают, когда ковалентная связь соединяет два
разных атома. На рис. 1.4 показана в качестве примера молекула НС1 с ко¬
валентной связью, образованной сферически симметричной 15-орбиталью
водорода и удлиненной Зр-орбиталью хлора.
Рис. 1.4. Дипольный момент молекулы HCI. Орбитали 3р и Is дают по одному
электрону каждая. Образованная из двух электронов ковалентная связь оказывается
полярной. Электронное облако плотнее возле атома хлора
Хотя молекула электрически нейтральна, средние позиции положитель¬
ных и отрицательных зарядов не совпадают. Абсолютное значение диполь-
ного момента и — ql (заряд, умноженный на длину) измеряется в дебаях
(1 Д = 3,336-10-30 Кл-м). Дипольный момент двух элементарных зарядов,
находящихся на расстоянии 1 А, равен примерно 4,8 Д. Вектор дипольного
момента направлен от отрицательного заряда к положительному (в части
литературы по химии принято противоположное направление).
Н3С 4
О
§ 1.3. Силы между молекулами
33
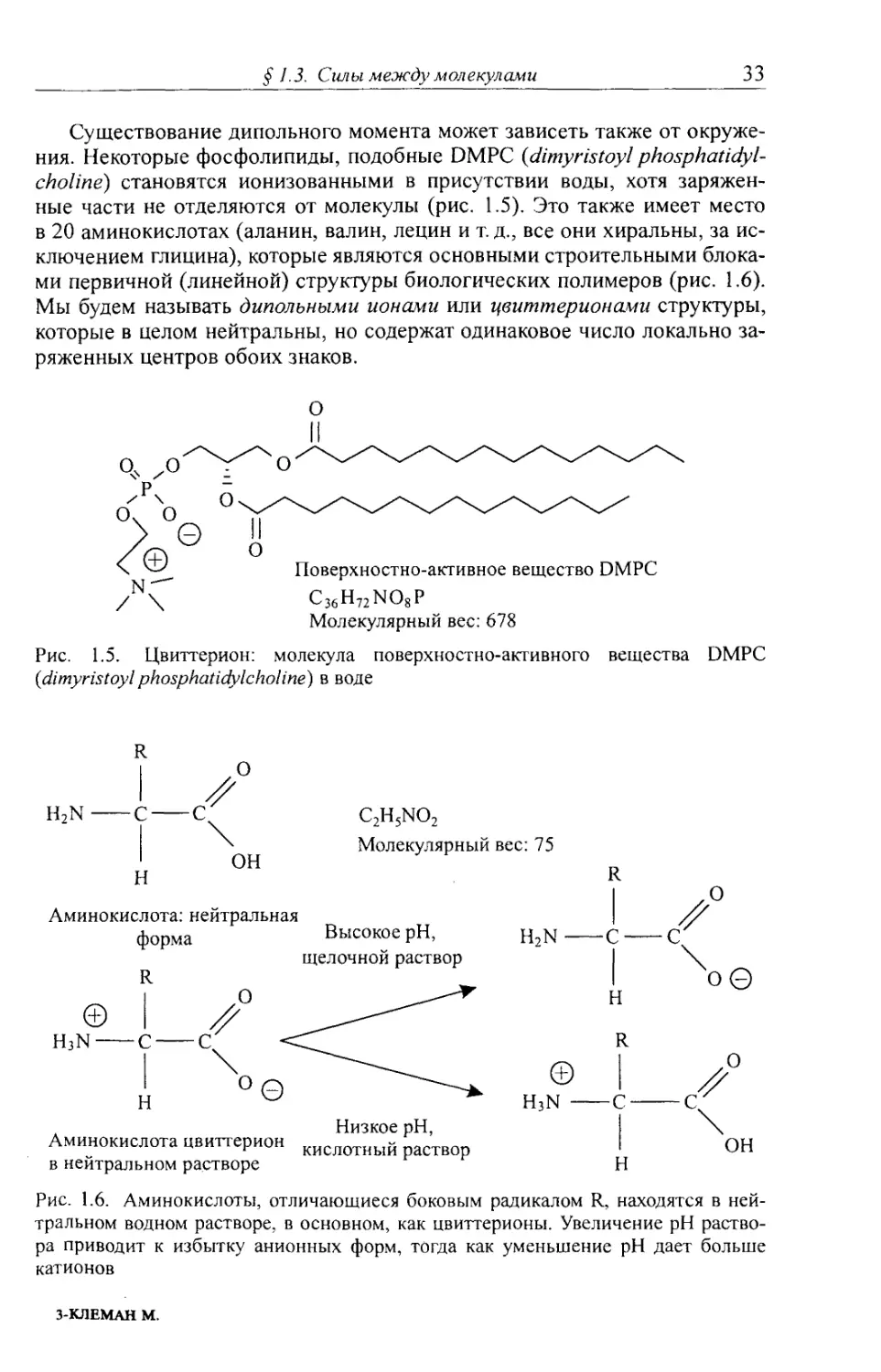
Существование дипольного момента может зависеть также от окруже¬
ния. Некоторые фосфолипиды, подобные DMPC (dimyristoyl phosphatidyl¬
choline) становятся ионизованными в присутствии воды, хотя заряжен¬
ные части не отделяются от молекулы (рис. 1.5). Это также имеет место
в 20 аминокислотах (аланин, валин, лецин и т. д., все они хиральны, за ис¬
ключением глицина), которые являются основными строительными блока¬
ми первичной (линейной) структуры биологических полимеров (рис. 1.6).
Мы будем называть диполъными ионами или цвиттерионами структуры,
которые в целом нейтральны, но содержат одинаковое число локально за¬
ряженных центров обоих знаков.
О
и
Поверхностно-активное вещество DMPC
C36H72NOgP
Молекулярный вес: 678
Рис. 1.5. Цвиттерион: молекула поверхностно-активного вещества DMPC
(<dimyristoyl phosphatidylcholine) в воде
R
H.N
С
С
О
н
он
c2h5no2
Молекулярный вес: 75
Аминокислота: нейтральная
форма
R
Высокое pH,
щелочной раствор
H,N
©
H3N
С
н
©
H3N
Аминокислота цвиттерион
в нейтральном растворе
Низкое pH,
кислотный раствор
R
С
Н
R
С
Н
С
о
0 0
С
о
он
Рис. 1.6. Аминокислоты, отличающиеся боковым радикалом R, находятся в ней¬
тральном водном растворе, в основном, как цвиттерионы. Увеличение pH раство¬
ра приводит к избытку анионных форм, тогда как уменьшение pH дает больше
катионов
З-КЛЕМАН М.
34
Гл. 1. Конденсированная среда. Общие характеристики
Дипольные моменты типичных атомных групп приведены в табл. 1.2.
Отметим, что дипольный момент зависит как от химической структуры
молекулы, так и от ее конформации.
Таблица 1.2. Дипольные моменты некоторых атомных групп и связей
Группа/связь
Дипольный
момент, Д
Группа/связь
Дипольный
момент, Д
СбНб (бензол)
0
Н2О
1,85
С02
0
NH3
1.47
у
О
О
0
СНзСООН
1.7
CH3CN
3,9
сн
0,4
CN в цианэтане
NH2 в пропиламине
C2H5CN
4,02
C3H5NH2
1.17
У
цис С — С
0.33
г*
транс С = С
0
(в цис-2-бутене)
(в транс-2-бутене)
ОН в пропаноле
С-СООН
1,7
С3Н7ОН
ОС
Взаимодействие ион-диполь играет важную роль в сольватации ионов,
т. е. в явлении кластеризации молекул-диполей растворителя вокруг иона.
Если растворителем является вода, то говорят, что ион гидратирован. На¬
пример, катион (скажем, Na+) притягивает и ориентирует соседний диполь
вдоль линии, соединяющей заряд и диполь, т. е. вдоль направления с углом
О ~ 0 (рис. 1.7). Гидратированный ион может вырасти до больших раз¬
меров. Этим объясняется зарождение капель дождя в облаках. Выигрыш
в энергии между случайно ориентированным диполем и диполем с в — О
должен быть больше или равен к^Т, чтобы стабилизировать гидратирова-
ный комплекс, который может быть очень устойчивым, если дипольный
ион мал и сильно заряжен.
§ J.3. Силы между молекулами
35
Рис. 1.7. Ионно-дипольное взаимодействие: гидратированный катион
Притягивающие взаимодействия типа диполь-диполь и свободный ди¬
поль-свободный диполь, или взаимодействие Кеезома, оказываются сла¬
бее, чем ионно-дипольное взаимодействие, и приводят к менее устойчивым
структурам. Свободный диполь — это диполь, способный принимать в про¬
странстве любые направления. Поэтому соответствующая энергия взаимо¬
действия вычисляется посредством усреднения по ансамблю ориентаций,
как в модели парамагнетизма Ланжевена:
V>d-d(r) = (1.9)
3(47Г££о)2 кБТ г6
когда /сБТ > и^/^ттееог3. Отметим, что Wd-d ос 1/Т: при повышении
температуры усиливается вращение молекул, и, следовательно, уменьша¬
ется ориентационный порядок диполей. Взаимодействие Кеезома — это
только одно из трех притягивающих взаимодействий между нейтральными
молекулами. Два других уже были упомянуты; это взаимодействие Лон¬
дона между молекулами без постоянных диполей и дебаевское взаимодей¬
ствие между постоянным и наведенным диполями. Все три изменяются с
расстоянием как 1 /г6 и имеют общее название: силы Ван-дер-Ваальса.
1.3.3. Индуцированные диполи, поляризуемость
Электрическое поле Е, либо внешнее, либо вызванное соседней моле¬
кулой, наводит на молекуле электрический диполь iiinci = a0J3, разделяя
центры положительных и отрицательных зарядов; ао — это поляризуе¬
мость молекулы. Модель, приведенная на рис. 1.8, помогает оценить этот
наведенный момент n-md в простом случае электрона, вращающегося вокруг
протона. Электрон находится под действием двух сил: силы кулоновского
притяжения со стороны заряда ядра и смещающей силы внешнего поля Е.
36 Гл. 1. Конденсированная среда. Общие характеристики
Е
Ч
Рис. 1.8. Электрическое поле наводит дипольный момент в нейтральной системе
(электрон, вращающийся вокруг протона)
Изменение кулоновской силы, вызванное смещением, оценивается как Fc =
9 '*> 1
б • GU* А
= sin# ~ = —-—, а сила со стороны поля: Fr — еЕ.
AireoR2 AiteoR3 47Г£оЯ3
В равновесии Fc — Fe и
^ind = 4тгг0Я3£ = (1-Ю)
Здесь мы полагаем, что наведенный диполь всегда ориентирован вдоль по¬
ля, и, таким образом, ао = 47г^о^3 является скалярной величиной. При
О
R = 1А, £о = 8,85 х 10“12 Ф/м получаем оценку для поляризуемости
атома или небольшой молекулы в вакууме: а0 — 10~40 К2м2/Дж. Одна-
ко молекулы большего размера могут иметь большую поляризуемость, так
как ао сх В?. Более того, если свободно вращающаяся молекула имеет
постоянный момент и, то внешнее поле ограничивает свободное враще¬
ние такой молекулы, так что усредненная по времени поляризация отлична
от нуля. В результате ориентационная поляризуемость оказывается равной
и2/ЗкБТ. Для слабополярных жидкокристаллических молекул, таких как N-
(р-метоксибензилиден)-р'-бутиланилин [N-(p-methoxybenzylidene)-pl-butyl-
aniline, МВБ А] и р-пентил-р'-цианобифенил (;p-pentyL-p'-cyanobi-
phenyl, 5СВ), типичные значения полной поляризуемости находятся в ин¬
тервале (10-100) х Ю“40 Кл2м2/Дж. Заметим, наконец, что МВВА, 5СВ
и большинство других молекул анизометричны (т. е. имеют несимметрич¬
ную форму). В результате наведенный диполь зависит от ориентации мо¬
лекулы в поле, и ее поляризуемость является тензором.
§1.3. Силы между молекулами 37
Взаимодействия ион - нейтральная молекула и диполь-нейтральная
молекула (дебаевские взаимодействия) обычно рассматриваются с исполь-
заванием представления о наведенных полем диполях. Дебаевское взаимо¬
действие изменяется с расстоянием так же, как взаимодействие Кеезома, но
не зависит от температуры. Наконец, лондоновские, или дисперсионные, си¬
пы вызываются флуктуационными взаимодействиями между нейтральны¬
ми атомами или молекулами без постоянных диполей. В действительности
эти силы не зависят от частного типа молекулы, так как флуктуации плот¬
ности заряда являются универсальным квантовомеханическим эффектом.
Поэтому лондоновские взаимодействия присутствуют в любой конденсиро¬
ванной среде; они детально рассматриваются ниже, а также в параграфе 1.4.
Сам термин «дисперсионные» происходит от дисперсии света в видимой,
УФ и ИК частях спектра, и его не следует путать с термином «дисперсия»,
описывающим коллоидные системы. Частоты, на которых электромагнит¬
ное поле вызывает флуктуирующий диполь в неполярной молекуле, — это
частоты поглощения.
Флуктуации плотности заряда наводят взаимные дипольные момен¬
ты в соседних молекулах. Притягивающий характер взаимодействия ка¬
чественно может быть выведен из того, что флуктуирующие поляризации
имеют тенденцию быть в фазе, если они направлены вдоль линии, соеди¬
няющей частицы, и в антифазе, если они лежат в перпендикулярной плос¬
кости. Лондон получил дисперсионную энергию двух нейтральных атомов,
рассматриваемых как квантовые осцилляторы, имеющие частоту и, соот¬
ветствующих электронам на 1 s-орбиталях, в виде1)
3 аца2 hv \V2 С и (л 11Л
WL И ——— г = - —, (1.11)
2(47Г£о)2 г6 + U 2) Г6
где а\ и <*2 — поляризуемости этих атомов, h = 6,63 х Ю~34 Джс — посто¬
янная Планка. Положительная константа С12 размерности Дж*м6 является
«материальным» параметром взаимодействующих частиц, не зависящим от
разделяющего их расстояния г.
Для атомов и очень малых молекул эти взаимодействия малы и вряд ли
способны сформировать устойчивые упорядоченные фазы при комнатной
температуре. Замечая, что Ц = hvi есть некоторая характерная молеку¬
лярная энергия, которую можно аппроксимировать первым потенциалом
ионизации, имеющим порядок 10"18 Дж, и полагая а.\ — а 2 — 3 х Ю-40
О
Кл м2/Дж (что соответствовало бы молекулярным радиусам Ri и 1,3 А
За2/ 3 RQl
в (1.10)), можно оценить постоянную С = ~—- rZt В (1.11) как
4(4-7Г£о)2 4
С « 0,6 х 10-77 ДЖ’М6. При расстоянии г = ЗА соответствующая энер¬
гия притяжения \wi\ « 8 х 10~21 Дж оказывается больше, чем кБТ при
^ Е London, Trans. Faraday Soc. 33, 8 (1937).
38
Гл. 1. Конденсированная среда. Общие характеристики
комнатной температуре. Следовательно, достаточно большие неполярные
молекулы могут удерживаться в конденсированном состоянии исключи¬
тельно благодаря лондоновским силам. Даже когда молекулы полярны,
лондоновские силы продолжают давать существенный вклад, 20-99% от
полной энергии. Вторым по силе взаимодействием полярных молекул ока¬
зываются обычно силы Кеезома (см. табл. 1.3).
Таблица 1.3 Парные энергии взаимодействия нейтральных молекул на рас-
О
стоянии 5 А, (данные взяты из книги: Кемпбел Дж. Современная общая хи¬
мия.— М.: Мир. 1975)
Молекула
Дипольный
момент, Д
Энергия взаимодействия (Дж/моль)
при Т = 298 К и а = 5 А
Температура
кипения. К
Wd-d
WL
Не
0
0
3
4,2
СС14
0
0
7,5 х 103
350,9
СО
0,1
о
о
и—*
290
81,0
НС1
1
71
460
189,4
1.3.4. Силы отталкивания
Взаимодействия между молекулами включают рассмотренные выше си¬
лы притяжения, а также силы отталкивания. Чаще всего силы отталкивания
вызываются электростатическим отталкиванием между частицами с заря¬
дами одного знака или короткодействующим стерическим отталкиванием.
Стерическое отталкивание возникает, в основном, из-за принципа запрета
Паули и проявляется, когда электронные облака двух частиц приближаются
друг к другу слишком близко; это взаимодействие трудно описать коли¬
чественно. В простейшей модели сферических частиц с жестким ядром
радиуса г о энергия отталкивания предполагается бесконечно большой при
расстоянии между центрами менее 2го и нулевой при расстояниях более
2го- При более реалистичном подходе потенциал отталкивания представ¬
ляется при г > 2г0 экспоненциально падающим, wvev> ос ехр(—г/const), где
§ 1.3. Силы между молекулами
39
константа положительна, или, с целью упрощения вычислений, учитываю¬
щих как силы притяжения (1.11), так и силы отталкивания, в виде
Ыгер = (1-12)
у* 1 Л
где В — некоторая положительная постоянная.
Как электростатические, так и стерические отталкивания возникают
в фазах, состоящих из поверхностей раздела, например в ламеллярной фазе
мембран. Из-за стерических сил сама форма молекул оказывает заметное
влияние на природу упаковки. Упаковка амфифильных молекул в слои или
бислои, а также в цилиндрические и сферические мицеллы весьма чув¬
ствительным образом зависит от их формы (рис. 1.9). Отметим также, что
пространственные флуктуации мембран в ламеллярных фазах являются
первопричиной специфического потенциала отталкивания (потенциала Хел-
фриха), стабилизирующего в неионных поверхностно-активных веществах
ламеллярную фазу в противовес притягивающим лондоновским силам.
В табл. 1.4 подытожена схематическая классификация молекулярных
взаимодействий в предположении, что они происходят в вакууме.
в
г
Рис. 1.9. Молекулярная форма вызывает различные геометрии монослоя
поверхностно-активного вещества: (а) плоскую, (б) цилиндрическую, (в) сфериче¬
скую и (г) седлообразную. Радиусы кривизны мембран могут отличаться от длины
молекул; см., например, (в)
Таблица 1.4. Типичные взаимодействия молекул в вакууме
40 Гл. 1. Конденсированная среда. Общие характеристики
я
Я
О-
а
н
X
<и
2
2
о
I
н
S
S
Я
о
Я
о
<D
зг
я
сх
■s-
U
н
о
Е-
Я
о
я
ffl
cd
го
Ы
cd
X
Г)
• Г4!
О
я
аг
I
х
н
X
ffl
О
et
ос
Cl
я а
О- со
w о
^ S
S «
Й «а
О- СО
с
cd
х
cd
X
О
X
Л
5 «
Я Q
U х
1
cd
е
н
о
X
<и
я
Q.
X
X
cd
m
О
о
о.
н
я
о
CJ
ы
я
я
•©<
ОС
Е?
О
я
с
ё
я s
<и
<D
э
2
cd
со
Я
и
«35
Н
X
о.
с
cd
5
и
CQ
О- <u
ас
о>
о>
со
со
S
ъ*
х
о
£
X
о
£
£
X
о
Л
К
СО
н
>5
§
2
X
cd
со
CQ
cd
X
Я
X
<D
н
о
с
IM
<и
о
U)
гН
оГ
N
СО
с^см
О
о
CS
СЧ 1—1
CS
О
3
к)
гН
ze)
Tt1
S-
h
US
СЧ
о
UJ
to
(М
ОЬ
СО
о
У
тН
со
о
и
X
со
О
О
см
Qi
Й
* И
СО
т-Ч
й
• rt
tn
СО
CN
3
о
1-4
to
э
&
1)
Я
X
о
t?
в
cd
Н
cj
и
<D
СХ
С
<и
о
X
еХ
ОС
5
cd
ас
N*
<ч
<Х>
гм
а
ОС
X
СО
н
о
«
0>
g
s
X
cd
го
И
С
X
н
см
X
о
X
X
о
S
X
о
S
>Я
3
х
«а х
— .А
uQ ed
X
X
ос
О
Н
О
о
ffl
о
О. J3
я е;
о о
* С
я £
С ■©< е*
9
cd
Э
cd
О,
ffl
О
X
ef
— о
Я ^
о о
Sffl
о
I
I
X
о <N
Н J3
о
о
с
ос
о
о
с
X
32 «
£ 3
3 я
>я
ин
*Q
х
А 1
*д cd
)Я
X
X
н
о
о
ffl
о
IX о.
О X
о
Ьй
я
С *3*
л
а
о
с
я
С*
:Я
М
►а
X
X
ос
О
ь
о
о
я
>я
-Q
X
X
ей
ffl
О <N
Си л
X с;
о о
* я
я s
•в* ч
{продолжение на следующих страницах)
§ 1.3. Силы между молекулами
41
(Продолжение)
42
Гл. 1. Конденсированная среда. Общие характеристики
♦ l-'
I
и х
й ей
3 £
2 ^
cd
со
К
L.
о;
cd
I
s 2
е &
С О
S с
э
О
О
CQ <
I
cd
У
I
0>
с*
cd
<L> К
Н I
о Ю
а. о
та с!
х о
US
cd
ь
_ о
cd н
х, о
« #■
cd
о
Си
е-
♦ с*
<и
э
2
cd
со
К
L-
W
н
Е
а-
с
cd
5
О
CQ
cd
5
§
«\
о
S
S
X
<L>
S
S
сх
с
о
Л
• Г
о
Л
CQ
о-
н
ю
S
ей
О.
cd
<D
cd
CQ
CU
(О
н
I
3
CQ
а,
ь-
и
S
cd
си
cd
CN
JI
О
X
ТТ
15
ю
о
♦ *\
*г>
ON
о
ас
о
D.
«D
е:
о
с
S
Си
К
2
S
м
Cd
£N
S
1—1
s
CN
а»
r-i
*
со
о
СМ
О
Ц)
СМ
+
СМ
см
в
Г*Ч
С
о
со
см
t-
<м
о
k)
fc
сч
оо
■ о
>S д
£> ?
§ *
Н S
о с;
СиЮ
О s
ьй а
<и
о
*
о
<=:
U
<L)
1)
SJ
к—<
О
«*4
>>
CQ
Н
CJ
о
х
-Q
cd
•т1
О
S
а
о.
о
о
Си
с
<и
s ^
w —
О s
& X
о _
KJ 5
О, S
Cd
2
о
*- Й
ё g*
и ^
cq
'Зй
Cj
б
JS
-а
л
х
cd
CQ
О
Cl
* j
* §
4 с
5 Я
S с?
>s
3
з:
cd
CQ
О
о
с
S S
S CJ
JS
N-4
•д
я
cd
CQ
о
Q.
S
=г
X
X
л
с;
о
с
S
*3
)S
-Q
I
Ж
cd
CQ
О
CU<N
S
J3
S3
=:
>4
о
с
К
s
s
n
о W
Я ОД
о н
5 о
в )2:
st: г)
►Q СЧ
Ч О
5
С S
со «J
• ^ СО
со
W
со
о
о?
cd
о
а,
о
о
со
о
X
ж
я
со,
S
с;
cd
fc
ч
О
« *
СО
<и
а.
и
щ
£
тз
cd
О
<
г-
с
о
*и
а>
тз
с
CN
о
с
1>
<и
Q
45
о
i-~
cd
С
О
-о
о
оо
О ^
С
<N
4
^ е
и*
О
Uu
(U
о
,сй
4-W
Vw
<3
U
GJ
О
cd
сл
Ё С
fc ^
С ^
о
-5;
и
-S
"<3
Q
V.
*п
S
с:
s
02
О
и
U-*
о
сл
JJ
Си
О
tC
*с
а.
с
to
КЗ
е;
D
cd
а.
го
S
и
S
I
ЬЙ
со
S
<х
S
я
К
=;
S
а
S
о
с
го
сз
X
>"Г
s
S
X
a. d-
о
^Г)
^t
гч
ON
ON
О
On
Г-
vd
oo
ON
§1.3. Солы между молекулами
43
I 3.5. Эмпирические потенциалы взаимодействия
Для численного моделирования парных потенциалов часто вводят по¬
тенциалы, наиболее подходящие к конкретному случаю. С развитием ком¬
пьютеров стало возможным моделировать поведение больших ансамблей
частиц, конкретизируя их форму, а также силы притяжения и отталкивания.
Наиболее часто используются следующие два потенциала:
• Твердые сферы со слабым притяжением
w(r)
~Wq
г о
т
ОО,
, для г0 ^ г < 00,
ДЛЯ 0 ^ Г < Го.
(1.13)
Потенциал Леннарда-Джонса
г о
Г
12
ГО
6
(1.14)
где wq — некоторая положительная величина, которая отвечает минимуму
энергии, расположенному на расстоянии г = 21/6го (рис. 1.10).
Энергия, wu / w0
5
4
3
2 :
1
О
-1
-2
—Г ■ 1 " Т" 1 " "
—г 1 Г 1-
[—1 1 Г - П—
—1—Т —ГГ
к
1
1
1
-
till
II L -Л
Расстоя
1 .-! L 1 .
[ние, г /г0 I
t t1 i.,„ 1 .
-0,5
1
2
2,5
Рис. 1.10. Потенциал Леннарда-Джонса, описывающий взаимодействие между
двумя нейтральными частицами
Перечисленные выше потенциалы относятся к сферически симметрич¬
ным взаимодействиям. Недавно появились теории, учитывающие ориента¬
ционные степени свободы, для компьютерного моделирования таких фаз,
как нематические жидкие кристаллы. Среди них потенциал Гэйя-Берне
44
Гл. 1. Конденсированная среда. Общие характеристики
(Gay-Berne), разновидность потенциала Леннарда-Джонса с параметра¬
ми, зависящими от ориентации, и потенциал Лебвола- Лашера (Lebwohl-
Lasher), в котором позиции молекул фиксированы, но отклонение от парал¬
лельного расположения молекул требует затрат энергии.
1.3.6. Вода, водородная связь. Гндрофильный и гидрофобный эффекты
Вода — это жидкость, наиболее распространенная на Земле. Это жид¬
кость исключительная по своим свойствам: очень высокие температуры
плавления и кипения, большая скрытая теплота парообразования, меньшая
плотность твердого состояния (лед) по сравнению с жидким и т. д. Все эти
особенности объясняются наличием водородных связей между молекулами
Н20. Водородная связь возникает, когда атом водорода, ковалентно связан¬
ный с сильно электроотрицательным атомом X, приобретает некоторый
положительный заряд $+, достаточно сильный, чтобы образовать по суще¬
ству электростатическую связь с другим электроотрицательным атомом У
(рис. 1.11).
<5; <5+ s; 6R+
Х-Н ... Y-R
Рис. 1.11. Водородная связь между двумя атомными группами, ХН и YR, которые
содержат сильно электроотрицательные атомы (X и Y)
Отсюда символическая запись: ХН ... Y. Обычно X, Y = 0, N, F, Cl, S.
Такая связь может соединять либо отдельные молекулы (межмолекулярная
водородная связь), либо группы внутри одной молекулы (внутримолекуляр¬
ная водородная связь). Энергия водородной связи порядка 2-10 ккал/моль
(0,1 -0,5 эВ/молекулу), что оказывается между энергиями связи Ван-дер-
Ваальса (обычно 0,01 эВ/молекулу) и ковалентной связи (~ 5 эВ/молекулу).
Важность водородных связей может быть проиллюстрирована простым
сравнением температур кипения воды (100 °С) и метана (-164°С), в ко¬
тором нет водородных связей. Водородная связь играет решающую роль
в установлении пространственной геометрии упаковки молекул; так, в воде
она приводит к локальной тетраэдрической координации атомов кислорода
(рис. 1.12, а).
Ассоциативный характер водородной связи в воде объясняет гидрофоб¬
ный эффект, т. е. очень слабую растворимость в воде неполярных молекул
(таких, как насыщенные углеводороды CH3(CH2)nCH3). Неполярные ча¬
стицы не могут участвовать в образовании водородных связей. Будучи по
одиночке изолированными в воде, такие частицы оказываются окруженны¬
ми «клеткой» из молекул воды (рис. 1.12, б). Для сохранения тетраэдриче¬
ской сетки молекулы воды, образующие клетку, должны выбрать специфи¬
ческую ориентацию, позволяющую избежать разрывов водородных связей
частицей. Такое добавочное упорядочение энтропийно невыгодно, и это
объясняет, почему неполярные частицы гидрофобны. Нужна добавочная
энергия, чтобы погрузить неполярную частицу в воду. Это тот же самый
§ 1.3. Силы между молекулами 45
гидрофобный эффект, который отвечает за притяжение между неполяр¬
ными частицами в воде. Молекулы собираются вместе, чтобы уменьшить
плошадь поверхности клетки, т. е. уменьшить потерю энтропии.
Рис. 1.12. Водородные связи в воде приводят к тетраэдрической координации ато¬
мов кислорода; такая структура весьма подвижна, так как молекулы могут переори¬
ентироваться и установить новые направления водородных связей (а). Молекулы
воды образуют «клетку» вокруг неполярной частицы. Водородные связи сохраня¬
ют тетраэдрическую координацию; тем не менее растворенная частица, которая не
может образовать водородные связи, ограничивает свободу молекул воды к пере¬
ориентации (б)
46
Гл. 1. Конденсированная среда. Общие характеристики
И, наконец, обычно говорят о гидрофильном эффекте, если молекулы силь¬
но взаимодействуют с водой. Баланс между гидрофобным и гидрофильным
взаимодействиями управляет поведением амфифильных молекул, содержа¬
щих как гидрофобную, так и гидрофильную группы.
С более общей точки зрения можно отметить, что дисперсионные взаи¬
модействия, ненаправленные (или слабо направленные, как в случае жид¬
ких кристаллов) и притягивающие, ответственны за стабильность молеку¬
лярных группировок и за их плотноупакованный характер упорядочения,
тогда как направленные водородные связи формируют их конфигурацию
и ближний порядок.
§ 1.4. Силы Ван-дер-Ваальса между макроскопическими
частицами
1.4.1. Парное суммирование молекулярных сил; константа Гамакера
Коллоидные частицы, имеющие обычно размеры от нескольких нано¬
метров до нескольких микрон, довольно часто слипаются (это называется
коагуляцией и флокуляцией). Это явление означает, что частицы притя¬
гиваются друг к другу силами, действующими на расстояниях порядка
размеров самих частиц. Уже давно было установлено, что эти дально-
действующие силы притяжения являются результатом ван-дер-ваальсовых
межмолекулярных взаимодействий, рассмотренных в предыдущих пунк¬
тах (1.3.2) и (1.3.3). Уравновешивающие их отталкивающие силы имеют
стерическое или электростатическое происхождение (см. гл. 14).
Хотя потенциал молекулярного притяжения (1.1), wl = -Ci2/r6, быст¬
ро спадает на молекулярных расстояниях, переход от микроскопических
к макроскопическим масштабам не умаляет значения сил Ван-дер-Ваальса.
Простейший способ вычислить потенциал Ван-дер-Ваальса Vv dW для двух
макроскопических частиц — это предположить попарную аддитивность
отдельных молекулярных взаимодействий, как если бы они имели место
в отсутствие всех других молекул. Более того, можно заменить в (1.1) сум¬
мирование по отдельным молекулярным взаимодействиям интегрировани¬
ем, т. е. рассматривать среду как непрерывную и содержащую некоторое
среднее число молекул на единицу объема (их плотность р равна некоторой
константе размерности м“3). Тогда энергия взаимодействия двух макро¬
скопических тел с плотностями р\, р2, занимающих в пустом пространстве
объемы Vi, V2, дается выражением
v d W
dVx
dy2^1Р2С12__
ri — Г2 I6
Здесь | ri — г2 ] — расстояние между элементами объемов V\ и V2 тел 1 и 2.
Константа С12 зависит от молекулярных параметров, таких как поляризуе¬
мость, но не от геометрии тел. Поэтому попарное суммирование позволяет
§ 1.4. Силы Ван-дер-Ваальса между макроскопическими частицами 47
представить потенциал Ван-дер-Ваальса как произведение геометрическо¬
го множителя, включающего двойной объемный интеграл:
Т/ __ ^12
VvdW —
7Г2
К/
dV\ dV'i , -
(1.16)
Г1 - Г2 °
Vi,Va
и зависящего от материальных констант множителя Р1Р2С12, зачастую
выражаемого через так называемую константу Гамакера (с размерностью
джоул ь)
Л 2 = ^2pip2Ci2, (1.17)
которая является основной величиной, характеризующей силы Ван-дер-
Ваальса. Следствием обратной шестой степени в зависимости потенциала
(1.11) от расстояния является то, что энергия взаимодействия двух тел (1.16)
остается той же самой, когда все расстояния (размеры тел и дистанции
между ними) изменяются в одно и то же число раз А: V —> Xs V, г —> Хг
(см. задачу 1.3). Так, две «молекулы» с радиусами 0,2 нм на расстоянии
1 нм взаимодействуют с такой же энергией, как и две сферы радиуса 0,2
микрона на расстоянии 1 микрон. В табл. 1.5 приведен интеграл (1.16) для
ряда простых геометрий.
1.4.2. Эффекты запаздывания
В реальности распространение электромагнитных полей занимает ко¬
нечное время. Если время распространения становится сравнимым с пе¬
риодом электронных колебаний, флуктуирующие диполи в лондоновской
картине взаимодействия становятся менее скоррелированными. При типич¬
ном периоде электронных колебаний Т = 10-16 с и скорости света с — 3 х
х 108 м/с типичное расстояние гг = сТ, на котором становятся существен¬
ными эффекты «запаздывания», оказывается равным примерно 30 нм в
пустом пространстве; оно может быть существенно меньше в среде, где рас¬
пространение электромагнитных волн происходит медленнее. Такие запаз¬
дывающие лондоновские взаимодействия имеют более крутое степенное
спадание: 1 /г7 вместо 1/г6 при г ^ т>. Чтобы увидеть это количественно2^,
заменим частоту и в потенциале (1.11) на с/А, где А — длина волны, СОСТ¬
ОЙ fac
ветствующая флуктуациям электронной плотности, так что wir — — — — •
г6 А
Для данного расстояния г флуктуации с А < г являются слишком быст¬
рыми, чтобы вызвать заметные корреляции, и от них нет вклада во вза¬
имодействие Лондона. Однако если флуктуации достаточно медленные,
А ^ г, существует хорошая корреляция между двумя электронными сис¬
темами, и «запаздывающий» потенциал зависит от расстояния как wi ~
he
. Этот эффект запаздывания, или эффект Казимира-Полдера \
г?
D. Tabor, Solids, Liquids and Gases, Cambridge University Press, 1979. p. 19-21.
H. B. G. Casimir and D. Polder, Phys. Rev. 73. 360 (1948).
Таблица 1.5. Незапаздывающие притягивающие потенциалы Ван-дер-Ваальса для пары тел различной геометрии,
находящихся в вакууме
48
Гл. ]. Конденсированная среда. Общие характеристики
•
CN
4>
ьй
cd
CQ
CQ
cd
0
Л
е:
cd
cd
CQ
1
О,
<U
i
X
cd
CQ
4
cd
5
X
X
<D
ё
с
CM
c3
+
cm
CM
CM
e
CM
Й
+
CM
<3
<3
<N
см
CM
C3
CM
fc.
+
CM
e
H
CS
CN
CM
+
CM
fc*
J
CM
CO
I
II
13
fc?
r-
m
os
oo
*n
о
ТГ
C/5
О
>Л
Oh
*4
G
s
и
CM CM
a
CM
00
+
CM CM
+
CM
CO
+
L
CO CM
<3
00 r-l
в
CM
CO
fc*
CT>
I
n
k
fc?
-C
CN
IS
+
X
1(3 I -c
CN
—,
CM
в
+
^3
CN
i-Ц
I
I
II
*
fc?
|cc
KJ
+
l«
—J
CM
<3
+
e
CN
iM
C3
+
CM
«3
1-^
в
CN
1(3
-e
+
«
CN
Й
-C I ti
+
-c
+
a
CN
+
в
см
СО
1
1
1
1
£
■
fc?
О
1
к
0
s:
-s:
1
*
s
Cu
H
a>
S
о
см
в
г-1
сз
CN
ь
в
ь.
• •
Ж
cd
sr
с;
о
>S
13
X
J3
t?
<D
Q
4)
О-
Е
£
CM
C3
• *
’§ «
^‘f-VV f .
( продолжение на следующих страницах)
§ 1.4. Силы Ван-дер-Ваальса между макроскопическими частицами 49
а
*
§
(.Продолжение)
50
Гл. 1. Конденсированная среда. Общие характеристики
1
+
(N
СМ
сз
о
п
г»*
st
G
С
§
s;
а
Ъ
s;
а
-с:
С
>« ^ at
^ I «3
Й
см
ч~
-с I (3
см
со
<М
в
(N
!
П
й:
Q
s;
’
<
"а
с
а
Ь
с
сз
-s:
I
+
<3 I *-
ю
г—
оо
CN
+
<М
е
ю
<м
г-
•г?
Cvl
CN
и
■43
-«
К
s:
£>
с
а
-с
I
+
Л
в
со
<м
1”Н
<3
-сг
СЧ
со
гг
“а
<3
-с
а;
§
"sS
s;
а
Ъ
s:
а
-s:
I
а
а
о
X
Г
О
*
£
I
Q a
* Г4
Р-+
л
Ри
п
X
S
е;
в
н
3
м
А
X
*-
я
о
а.
и
■ Г' .
3 ,5
а.^
х
К
с;
s
a
щ Г'
*т*
1 А
з в
° Л
о.А
О ^
чЗ
Q
§ 1.4. Силы Ван-дер-Ваальса между макроскопическими частицами 51
присущ дисперсионным силам, вызванным электронными флуктуациями.
Интервал, в котором замена 1 /г6 —> 1/г7 справедлива, ограничен не толь¬
ко снизу (расстоянием гг), но также сверху. Действительно, при конечных
температурах молекулы испытывают другие типы флуктуаций, например
вибрационные с характерным временем Tv и 10“13 с. Возникающее из-за
них притягивающее взаимодействие не является запаздывающим вплоть
до масштабов cTv и 30 мкм, которые много больше гг. Вдобавок другие
взаимодействия, такие как взаимодействия постоянных диполей, вовсе не
испытывают никакого эффекта запаздывания; они изменяются как ос 1/г6
и, таким образом, становятся доминирующими при г гг. Общий эффект
таков, что зависимость ван-дер-ваальсовых взамодействий от расстояния
изменяется от ос 1/г6 до ос 1/г7, а затем обратно к ос 1/г6, по мере то¬
го как увеличивается расстояние между частицами. Практически эффект
запаздывания существен в интервале 5 нм < г < 20 нм.
1.4.3. Взаимодействие Лондона в среде, теория Лифшица
Взаимодействие между молекулами или макроскопическими частица¬
ми, погруженными в раствор, отличается от их взаимодействия в вакууме.
Эффективные заряды, поляризуемости и постоянные дипольные момен¬
ты могут быть сильно изменены разделяющей средой. Модель Лондона
и ее обобщение (1.16) - (1Л 7) на макроскопические масштабы посредством
парного суммирования становятся чрезмерно сложными, когда принима¬
ются в расчет такие «многочастичные» эффекты. Эта проблема, наряду
с проблемой эффекта запаздывания, преодолевается в континуальной тео¬
рии Лифшица4 \ которая описывает раствор и взаимодействующие частицы
в терминах неких объемных свойств, частотно-зависимых диэлектрических
проницаемостей, которые заменяют индивидуальные атомные поляризуе¬
мости. Эта теория строится на квантовой электродинамике и здесь не рас¬
сматривается. На качественном уровне роль вмешательства среды может
быть проиллюстрирована в подходе Лифшица следующим образом.
Частица представляется как диэлектрическая сфера радиуса Ri с диэлек¬
трической постоянной £{. В свободном пространстве поляризуемость ча¬
стицы была бы связана с Si как а* — ^£oRf •(£* —1)/(£; + 2)51 Отметим, что
oti —У 0, когда £{ 1. Похожим образом, той величиной, которая имеет зна¬
чение для взаимодействия через диэлектрическую среду с проницаемостью
£т, была бы избыточная поляризуемость ос (£г* — ет). Когда £i = ет, ча¬
стица «пропадает» на фоне среды. Следовательно, постоянная Сп ос а\а2
и константа Гамакера А\% ос С\2 ос а\а2 должны быть пропорциональны
(^1 — £т){£2 — £т)- В результате силы Ван-дер-Ваальса, которые в ваку¬
уме всегда притягивающие, становятся отталкивающими в растворителе
Лифиащ Е. М. ЖЭТФ. 29, 94 (1955): Дзялошинскай И. Е., Лифишц Е. МПита-
евскийЛ. 11. ЖЭТФ, 37. 229 (1959) и Adv. Phys. 10, 165 (1961).
5) Ландау Л.Д., Лифишц Е. А/. Электродинамика сплошных сред. — М.: Наука.
ГРФМЛ. 1982
52 Гл. 1. Конденсированная среда. Общие характеристики
с диэлектрическои проницаемостью £т, промежуточной между диэлек¬
трическими проницаемостями двух взаимодействующих частиц, например:
Si > £т > £2* Когда взаимодействующие частицы имеют одинаковые ма¬
териальные свойства, £\ — £2, взаимодействие остается притягивающим.
Зависимость межчастичных потенциалов от расстояния в теории Лиф-
шица такая же, как и в теории, основанной на попарном суммировании; все
результаты табл. 1.5 остаются справедливыми и для взаимодействий в среде
(эффекты запаздывания естественно включаются в теорию Лифшица). Важ¬
ной и полезной особенностью является то, что теория Лифшица вычисляет
константу Гамакера из частотно-зависимых диэлектрических функций; по¬
следние отражают коллективный характер взаимодействий и могут быть
непосредственно измерены. Конечно, не следует ожидать, что теория Лиф¬
шица будет правильно работать на очень малых молекулярных масшта¬
бах, не только из-за атомарной зернистости материи, но и из-за отталкива¬
ющих сил.
Отметим, что мы рассматривали дисперсионные силы для диэлектриче¬
ски изотропных сред. Когда диэлектрические свойства анизотропны, вза¬
имодействие Ван-дер-Ваальса зависит не только от расстояния между ча¬
стицами, но и от их взаимной ориентации; это было продемонстрировано
де Женом6) на примере жидкокристаллических капель.
Лондоновские силы играют существенную роль в явлениях адгезии, по¬
верхностного натяжения, физической адсорбции, флокуляции, агрегации
частиц в воде и в формировании конденсированных макромолекул, таких
как белки и полимеры, так как эти силы являются дальнодействующими,
неэкранируемыми и в сумме дают отнюдь не пренебрежимо малую вели¬
чину. И еще эти притягивающие силы составляют один из главных вкла¬
дов в плотно упакованный характер жидкокристаллических фаз, в которых
ориентационно упорядочены анизотропные по форме молекулы с анизо¬
тропной поляризуемостью.
1.4.4. Взаимодействия Казимира
В предыдущем рассмотрении взаимодействий в среде мы не учитывали
влияния поверхностей и границ. На самом деле поверхности и границы раз¬
дела накладывают определенные ограничения на флуктуации в системе. Та¬
кие ограничения невыгодны с точки зрения энтропии. В результате система
должна подстроиться так, чтобы препятствовать этому уменьшению энтро¬
пии. Предположим, например, что флуктуации в изначально бесконечной
системе ограничены парой параллельных пластин, разделенных зазором d.
В полубесконечных областях вне пластин спектр флуктуаций непрерывен,
тогда как между пластинами моды флуктуаций становятся дискретными.
Чтобы сделать это ограниченное пространство меньше, система стремить¬
ся уменьшить d. Другими словами, это геометрическое ограничение флук¬
туаций вызывает взаимодействие между частицами. Эти накладываемые
Я G. de Gennes, С. R. Acad. Sci. 271, 469 (1970)
§ 1.5. Полимеры и биологические молекулы
53
геометрией взаимодействия, имеющие энтропийное начало, обычно на¬
зываются взаимодействиями Казимира. В 1948 г. Казимир7^ рассмотрел
электромагнитное поле между двумя параллельными электродами. Так как
электрическое поле должно зануляться на проводящей поверхности, кван¬
товые электромагнитные флуктуации в зазоре между пластинами оказыва¬
ются ограниченными, и пластины испытывают взаимодействие (в данном
случае с потенциалом притяжения ос 1/с?3). Похожие взаимодействия, как
притягивающие, так и отталкивающие, могут иметь место и в мягких сре¬
дах. В последнем случае мы имеем дело с тепловыми флуктуациями поля,
описывающего некоторый порядок в среде, а не с квантовыми флуктуаци¬
ями электромагнитного поля. Хотя и казимировские, и ван-дер-ваальсовы
(лондоновские) взаимодействия имеют флуктуационную природу, они мо¬
гут отличаться по своей величине и функциональной зависимости от рас¬
стояния. Мы вернемся к этому вопросу в п. 13.2.4; общий обзор таких
взаимодействий дан в работе Кардара и Голестаниана.8^
§ 1.5. Полимеры и биологические молекулы
1.5.1. Синтетические полимеры
Полимеры (или макромолекулы) — это молекулы, имеющие большую
молекулярную массу и состоящие из многих малых структурных единиц
(элементарных звеньев), соединенных сильными ковалентными связями.
Естественными полимерами являются белки, целлюлоза и резина. Поли¬
меры, образованные одинаковыми структурными единицами, называются
гомополимерами, тогда как сополимеры содержат больше одного типа зве¬
ньев в цепи. Геометрия макромолекулы зависит от валентной структуры
самих структурных единиц. В простейшем случае линейных полимеров,
каждое звено соединено только с двумя соседями, как в линейном поли¬
этилене на рис. 1.13, а; структурной единицей является -СН2 В разветв¬
ленных макромолекулах некоторое число структурных единиц имеет ва¬
лентность, большую чем два, и они соединены с тремя соседями или более
(рис. 1.13,6). И, наконец, некоторые полимеры имеют структуру, в которой
звенья взаимно связаны в трехмерном пространстве — сшитые полиме¬
ры, или полимерные сетки (рис. 1.13, в). Вулканизация резины дает пример
линейного полимера, «сшитого» атомами серы в полимерную сетку.
Синтез полимеров осуществляют посредством химических реакций, ко¬
торые соединяют мономеры в макромолекулу. Структурная единица макро¬
молекулы может иметь такую же химическую формулу, как и мономер. Так
происходит при реакции полимеризации, при которой мономеры последо¬
вательно присоединеняются к растущей полимерной цепи. Другим типом
7) Casimir Н. В. G., Ргос. К. Ned. Akad. Wet. 51, 793 (1948).
8* Kardar М. and Golestanian /?., Rev. Mod. Phys. 71, 1233 (1999).
54 Гл. 1. Конденсированная среда. Общие характеристики
в
Рис. 1.13. Полимеры различной геометрии: (а) линейные, (б) разветвленные и (в)
сшитые в трехмерную сетку
реакций является поликонденсация, при которой теряются некоторые ато¬
мы, присутствовавшие в мономере. Подобные реакциии, как правило, дают
побочный продукт, например воду, как в случае полимеризации аминокис¬
лот в пептиды и белки. Помимо ковалентных связей, другие молекулярные
взаимодействия, в особенности водородные связи, играют важную роль
в организации биологических молекул и полимеров, таких как аминокис¬
лоты и белки. Эти вопросы обсуждаются в следующем пункте.
Очевидно, что геометрия макромолекулы играет важную роль в макро¬
скопических упорядочениях. Если макромолекула имеет достаточно регу¬
лярное строение (как, например, линейные полимеры), в системе часто
возникает ориентационный порядок, при котором молекулы выстроены
§ 1.5. Полимеры и биологические молекулы
55
параллельно друг другу вследствие стерических и дисперсионных взаи¬
модействий. Этот ориентационный порядок может быть дальним; в этом
случае при высоких температурах мы имеем дело с жидкокристаллическим
упорядочением в полимерах (гл. 2 и 3). Кевлар является хорошо известным
примером нематического жидкокристаллического полимера при температу¬
рах выше 300 °С, дающим материалы необычайной прочности при быстром
охлаждении до комнатной температуры. Ориентационный порядок в по¬
лимерах может также осуществляться лишь на ближнем уровне: так как
жесткость полимерной цепи конечна, макромолекула может сворачиваться
или изменять свою ориентацию в пространстве, чтобы избежать контактов
с другими цепями. В результате ориентационно упорядоченные области
прерываются неориентированными частями. С другой стороны, довольно
часто макроскопический порядок в линейных полимерах оказывается даже
сильнее, чем простое параллельное выстраивание цепей — структурные
звенья, принадлежащие параллельным цепям, упаковываются в периоди¬
ческую решетку. Однако кристаллиты имеют обычно размер, существен¬
но меньший, чем длина растянутой макромолекулы, и структура в целом
представляет собой перемежающиеся кристаллические и аморфные обла¬
сти (рис. 1.14). При повышении температуры эта кристаллическая (или,
точнее, полукристаллическая) структура плавится. При понижении темпе¬
ратуры полимеры с более или менее протяженными аморфными областями
переходят в застеклованное состояние с неподвижными цепями.
Рис. 1.14. Полимеры часто имеют ближний ориентационный и кристаллический
порядок
56 Гл. I. Конденсированная среда. Общие характеристики
Линейные и разветвленные полимеры растворяются в подходящих рас¬
творителях. Напротив, трехмерные сетки не так-то легко растворить; вме¬
сто этого они поглощают растворитель и набухают. Ясно, что свойства
полимеров изменяются и по мере увеличения их молекулярного веса в про¬
цессе полимеризации. Наиболее драматичные изменения можно наблюдать
в процессе сшивки линейных полимеров: по мере увеличения молекуляр¬
ного веса в некоторой четко определенной точке гелеобразования поли¬
мер переходит из состояния вязкой жидкости в упругий гель. Мы вернемся
к физическим свойствам полимеров в следующих главах (главным образом,
в гл. 15).
1.5.2. Аминокислоты, белки
Аминокислоты — это азотсодержащие мономеры, из которых построе¬
ны биополимеры, такие как пептиды (содержащие не более ста амино¬
кислотных субъединиц) и белки (с большим числом субъединиц). Общее
устройство всех 20 обнаруженных в белках аминокислот представляет со¬
бой центральный атом углерода С (часто обозначаемый Са) с четырьмя
группами, прикрепленными тетраэдрическим образом. Три из этих групп —
общие для всех аминокислот: атом водорода Н, карбоксильная группа СООН
и аминогруппа NH2 (см. рис. 1.6). Единственное различие между аминокис¬
лотами заключается в четвертой группе — в цепи радикала R. R-цепи могут
быть гидрофильными (например, R = СН2 — ОН, серин; R = СН2 — SH,
цистеин), гидрофобными (R = СН3, аланин; R = СН2 — (СН3)2) валин),
отрицательно заряженными (R = СН2 — СОО”, аспарагиновая кислота)
или положительно заряженными (R = СН2)4 — NHj, лизин). Во всех при¬
мерах четыре группы, прикрепленные к центральному атому углерода Са,
химически различны. Такая тетраэдрическая организация не имеет плос¬
кости симметрии; атом Са с четырьмя различными группами называется
асимметричным углеродом. Существует только одна аминокислота, глицин,
в которой R=H, и, следовательно, две группы идентичны. Поэтому все ами¬
нокислоты, за исключением глицина, могут существовать в двух различных
формах, называемых L- и D-энантиомерами, которые являются зеркальны¬
ми изображениями друг друга (рис. 1.15); такие аминокислоты называются
хиральными. Это свойство придает хиральным аминокислотам оптическую
активность (если только материал не содержит L- и D-энантиомеры в рав¬
ной пропорции). Найденные в природе белки составлены исключитель¬
но из L-аминокислот; механизм нарушения симметрии в процессе эволю¬
ции остается неясным, но, как давным-давно заметил Пастер, отсутствие
у биологических объектов зеркальной симметрии в совокупности с тем
фактом, что большинство биологических объектов относится к L-типу, по-
видимому указывает на уникальный и редкий источник жизни.
При синтезе белков аминокислоты соединяются пептидными связями.
В этой реакции освобождается одна молекула воды на каждую аминокис¬
лоту (рис. 1.16 и 1.17).
Четырехатомная пептидная единица (СО -NH) является плоской и жест¬
кой, из-за того что связь между С и N имеет частично двойной характер,
§ 1.5. Полимеры и биологические молекулы 57
Рис. 1.15. Хиральные L (слева) и D (справа) энантиомеры аланина: эти две формы
нельзя совместить никаким движением в пространстве
О
R
Н,0
h2n—сн—с—он + h2n—сн—с—он
R
О
Пептидная связь
О
H2N
СН—С
R
- Н,0
N—СН—С—ОН
R
Н
О
Н
О
R
Н
О
R
N
СН—С N СН—С N СН—С N СН—С
R
Н
О
R
Н
О
Рис. 1.16. Полимеризация аминокислот дает пептиды и белки
58
Гл. 1. Конденсированная среда. Общие характеристики
. .А. > Ь*
V . '
Рис. 1.17. Кусочек полимерной цепи шелка: глициновая (R=H) и аланиновая (R=
= СНз) группы случайно распределены вдоль цепи
что мешает свободному вращению атомов вокруг главной цепи (рис. 1.18).
Жесткость пептидных связей позволяет белкам сохранять четко определен¬
ную трехмерную структуру.
Напротив, образующие главную цепь связи С-Са и N-Ca являют¬
ся одиночными связями, допускающими вращение и, следовательно, свер¬
тывание белковых цепей многими различными способами. Это свертыва¬
ние характеризуется иерархической структурой. Наиболее важно то, что
0
О О
С N ► C=N
н н
Рис. 1.18. Жесткая и плоская геометрия пептидной единицы вызвана частично
двойным характером связи между атомами С и N
§ 1.5. Полимеры и биологические молекулы
59
кажущиеся нерегулярными белки имеют замечательную регулярную осо¬
бенность, называемую вторичной структурой, в противоположность пер¬
вичной структуре, которая понимается как последовательность аминокис¬
лот. Вторичная структура происходит от двух строительных элементов:
а-спиралей и /3-слоев. Эти обозначения отражают порядок, в котором дан¬
ные формы были открыты Лайнусом Полингом.9^
Вторичная структура возникает благодаря водородным связям меж¬
ду группами NH и С = 0, принадлежащим разным пептидным единицам.
В а-спирали каждая группа С^О n-го аминокислотного остатка связана
с группой NH (п-Н)-го остатка (рис. 1.19, а). Главная цепь свернута в виде
спирали так, что п-я единица ложится близко к (п+3)-й и (п+4)-й еди¬
ницам. Например, а-кератин, белок, найденный в коже, ногтях, волосах
/
RHC
/
/
\
/
RHC
RHC
RHC
CHR
RHC
\
\
\
/
с=о,
/
Ч
с=а
с=о «н-
N
Н N
*Н-
/
/
\
\
С
/
О
N
Н N
\
\
\
/
\
CHR
CHR
CHR
RHC
CHR
О
/
/
/
\
/
С
N
•Нн11шО==С
\
N
-Н
\
\
/
N Н
N
-H«uii«o==C
/
RHC
RHC
/
/
\
RHC
CHR
RHC
\
N
/
Н
\
\
\
/
\
с=о
с=о
N
С
О
н
/
/
ч
/
\
/
N
\
Н N
\
Н N
\
С==0,,,,,пН N
CHR
CHR
CHR
RHC
/
\
CHR
О
/
/
С
\
N
/
*0=с
■н
\
л''
>0:
/
\
/
С
N Н'",,1,0=С
N
■н*
\
/
N
/
/
\
RHC
RHC
RHC
CHR
\
N
/
Н
RHC
\
С
н
/
о
ч
■N
''И-
о
\
/
\
ч
N
/
с=о,,,,,н,н-
N
Н N
\
CHR
\
\
\
С
/
/
с
о
N
CHR
CHR
RHC
/
/
/
\
\
CHR
/
а
б
Рис. 1.19. Правая а-спираль полипептидной главной цепи, стабилизированная
водородными связями (показаны тонкими линиями) между n-м и (п -Ь 4)-м ами-
О
нокислотными остатками. Диаметр спирали порядка 5 А. На один оборот спирали
приходится примерно 3,6 остатков. Боковые R-группы ориентированы во внешнюю
область спирали (я). Схема структуры /5-слоя, образованного водородными связями
между белковыми нитями. Нити могут быть или параллельными (три нити в левой
части), или антипараллельными (три нити в правой части) (б)
Pauling L. , The Nature of the Chemical Bond. 3rd edition, Cornell University Press,
Ithaca, — N. Y.: 1960. Л. Полинг. Природа химической связи.— М.-Л.: Госхимиздат,
1947.
60 Гл. 1. Конденсированная среда. Общие характеристики
и перьях, образует а-спирали. В /?-слоях главная цепь остается почти пол¬
ностью растянутой; водородные связи возникают между группами NH
и С = 0, принадлежащими разным полипептидным нитям (рис. 1.19,6).
Эти нити могут быть химически связаны и принадлежать одной и той же
главной цепи. Обращение направления нитей обеспечивается резкими 180-
градусными поворотами, в которых п-я группа СО связывается с (п + 3)-й
группой NH; /5-слои имеются, например, в белках шелковых нитей. Отме¬
тим, что /3-слои, образованные хиральными аминокислотами, имеют закру¬
ченные нити. Обычно одна молекула белка содержит как а-спирали, так и
/0-слои.
Вторичная структура совместно со сложным взаимовлиянием гидро¬
фобных, гидрофильных, водородных и ван-дер-ваальсовых взаимодейст¬
вий приводит к более высоким уровням конформационной иерархической
организации — так называемым третичной и четвертичной структурам.
Как уже отмечалось, боковые R-группы аминокислот бывают разных ти¬
пов: полярные и неполярные. Так, белковая глобула, растворимая в воде,
организуется таким образом, чтобы скрыть гидрофобные R-группы внутри
и выставить гидрофильные R-группы снаружи на границе раздела белок-
вода. Напротив, белки, встроенные в клеточные мембраны, обладают гид¬
рофобными сторонами, чтобы соответствовать гидрофобному окружению
внутри липидного бислоя (рис. 1.20).
Рис. 1.20. Мембранные белки имеют гидрофобные боковые стороны, чтобы соот¬
ветствовать гидрофобной части липидного бислоя; части с гидрофильной поверх¬
ностью находятся вне мембраны
Такая сложная трехмерная иерархия белков делает возможным их био¬
логическое функционирование: химически и геометрически различные ме¬
ста и углубления на белковой глобуле селективно реагируют на окружаю¬
щие молекулы.
1.5.3. ДНК
В отличие от взаимодействий Ван-дер-Ваальса, водородные связи весь¬
ма специфичны. Чтобы образовать водородную связь, две молекулы долж¬
ны обладать необходимыми группами, и они должны иметь подходящую
форму и взаимную ориентацию, как видно на примере а-спирали. Водо¬
родные связи также формируют наиболее важные биологические молекулы,
§ 1.5. Полимеры и биологические молекулы
61
ДНК и РНК, которые контролируют генетическую информацию в живых
системах. В этих молекулах четыре основания, аденин, гуанин, цитозин и
тимин (в ДНК) или урацил (в РНК), химически присоединены к основной
цепи, состоящей либо из рибозы (для РНК), либо из дезоксирибозы (для
ДНК). Основания одной цепи образуют водородные связи с основания¬
ми соседней цепи. Здесь опять группы NH служат для водородных связей
донорами, а группы С=0 — акцепторами. Водородная связь вместе со сте-
рическими эффектами дает в высшей степени специфическое спаривание:
цитозин связывается с гуанином, а аденин связывается с тимином в ДНК
или с урацилом в РНК (рис. 1.21,а,б). Наилучшее согласование между
Н
yS
J \
N
О
/
Н N
//
N Н
N Н
Цитозин ^
а
О
ЗА
Н
\
N
Н
N
N
/
ЗА
Аденин
б
Тимин
А
Малая
бороздка
Большая
бороздка
▼
в
Рис. 1.21. Водородные связи между основаниями: цитозин-гуанин (а) и аденин-
тимин (6), принадлежащими двум цепочкам, приводят к структуре двойной спирали
Днк (в)
62
Гл. 1. Конденсированная среда. Общие характеристики
этими взаимно комплементарными основаниями обеспечивается, когда две
соседние цепи закручиваются одна вокруг другой (рис. 1.21, в). Отметим,
что направление водородной связи перпендикулярно оси двойной спира¬
ли. Последовательность оснований вдоль цепочки сохраняет генетическую
информацию, записанную с помощью четырехбуквенного алфавита.
1.5.4. Ассоциация белков: вирус табачной мозаики, микротрубочки
Свернутые белки содержат набор химически и геометрически различ¬
ных мест, способных выборочно связывать окружающие молекулы. По¬
этому белки могут служить строительными блоками для образования над¬
молекулярных структур, таких как ферменты, рибосомы и вирусы. Такая
ассоциация основана на нековалентных связях и поэтому легко контро¬
лируется и модифицируется. Так, вирус табачной мозаики (ВТМ) имеет
форму жесткого стержня, и длину стержней ВТМ можно контролировать
лабораторными методами. Растворы ВТМ образуют жидкокристаллические
структуры10^ и служат отличной моделью для изучения природы ориента¬
ционного порядка.
Белки сами по себе могут образовывать различные надмолекулярные
единицы. Представим, например, что белковая глобула имеет на внешней
поверхности два подходящих друг к другу места. Сцепление таких взаимно
комплементарных мест может привести к образованию белковых диполей,
цепочек (рис. 1.22), плоских слоев и даже сферических и цилиндрических
а
б
Рис. 1.22. Сборка белковых глобул в димеры (а) и цепи (б)
10) Klug A., Fed. Proceed. 31, 30 (1972).
§ 1.5. Полимеры и биологические молекулы 63
оболочек. Полая микротрубочка, образованная димерами а- и /3-тубулина,
представлена на рис. 1.23.
28 нм
Рис. 1 .23. Микротрубочка: поперечное сечение с тринадцатью полипептидами
тубулина (а): вид сбоку показывает димеры тубулина (б). По Stryer L.. Biochemistry,
4th edition, W. H. Freeman and Company, — N. Y.: 1064 p., 1995, и Alberts Я, Bray
A, Lewis J., Raff М., Roberts М., Watson J. D., Molecular Biology of the Cell. Garland
Publishing, Inc., — N. Y.: 1146 p., 1983
64 Гл. I. Конденсированная среда. Общие характеристики
Задача 1.1. Вычислить второй вириальный коэффициент для следу¬
ющих потенциалов:
а) с жестким ядром w\2 (г)
О, г > 2г0,
сю, г < 2го;
б) с жестким ядром и притяжением W12(г)
в) Леннарда-Джонса (г) — 4 wq
Ответы
Г о
12
оо, 0 < г < ri,
-Wo, ri <г < г2,
О, г2 < г;
го
a) v
1 ^Г° - 1
- J [1 — ехр(—W12/къТ)]4:7Гг dr = ——£■
б) V
г=О
27rrJ
1
1 ) (еш°/къТ - 1)
1
в)
V
167ГГ0 4к;о
оо
J
/сБТ xi0
12
6
-Ж
12
Ж
6
ехр
4шо
1
/с бТ \ £
12
£
где х = го/г; раскладывая ехр
4iuo
V
167ГГ
оо
£БТх6
271+1
в ряд, получаем
-Е
а
п
п=0
4 wo
кБТ
а
п
2 р ( 2п — 1
4 п!
x2dx,
(см.1^).
Задача 1.2. Реальные газы обычно не подчиняются закону Бойля-
Мариотта pV = const, полученному для идеального газа без взаимодей¬
ствий. Уравнение Ван-дер-Ваальса, записываемое для одного моля неиде¬
ального газа как (р + —)(V — Ь) = ЯТ, учитывает как притягивающие, так
У 2
и отталкивающие силы посредством двух феноменологических парамет¬
ров: а и Ь. Силы притяжения отвечают за фазовый переход газ-жидкость,
который предсказывается уравнением Ван-дер-Ваальса. В некоторых слу¬
чаях это уравнение может быть использовано для описания растворов, на¬
пример больших (в молекулярном масштабе) коллоидных частиц, диспер¬
гированных в воде; двумерная версия уравнения Ван-дер-Ваальса часто
n) Reichl L.E., A Modern Course in Statistical Physics, Edward Arnold, Kent, U.K.,
1980, p. 364.
§ 1.5. Полимеры и биологические молекулы
65
используется для монослоев поверхностно-активных веществ, а). На¬
пишите уравнение Ван-дер-Ваальса для а молей, 6). Найдите второй
вириальный коэффициент и тета-температуру, при которой он зануляется
(известную для газов как температура Бойля Тб), в). Опишите пове¬
дение произведения pV при изотермическом сжатии, когда температура
системы ниже и выше температуры Бойля Тб. г). Напишите уравнение
Ван-дер-Ваальса для двумерной системы площади 5, испытывающей по¬
верхностное давление П.
Ответы
а) + (У - = &RT; поправка к давлению пропорцио¬
нальна а2, так как вероятность взаимодействия частиц пропорциональна
числу парных столкновений, т. е. квадрату их концентраций.
б) w = ТБ “
R V КГ / Rb
в) pV монотонно увеличивается при Т > Тв и немонотонно (с мини
мумом) при Т < Тб .
г) (П + А) (5 - Ъ) = RT.
S2
~ 1 , ТУ- - ~ dVidVz
Задача 1.3. Как изменяется энергия взаимодеиствия
| П — Г2 |Q
(см. (1.16)) между двумя элементами объема dV2 и dV\, когда все расстояния
(размеры частиц и дистанция между ними) изменяются в А раз?
Ответ. Энергия изменяется как А6
— а
Задача 1.4. Постройте потенциал Лебволя-Лашера (Lebwohl-
Lasher) vjll = — woT^cos#) как функцию угла в между осями двух ча¬
стиц; P2(cos#) = -(Зсов2# - 1) является полиномом Лежандра второго
порядка hwq — положительная константа. Может ли этот потенциал опи¬
сывать сегнетоэлектрическое состояние?
Ответ. Подробное обсуждение моделей Лебволя-Лашера, Гея-Берне
и других см. в работе: Advances in the Computer Simulations of Liquid
Crystals, Edited by Pasini P. and Zannoni C., NATO Science Series, Ser. C:
Math, and Phys. Sciences, 545, 430 p., Kluwer Acad. Publ. (2000).
Задача 1.5. Вычислите потенциал Ван-дер-Ваальса для взаимодей¬
ствия двух сфер и двух плоско параллельных пластин различной толщины.
Ответ. Табл. 1.5; детали вычислений см. в работе Mahanty J.
и Ninham В. W. (1976).
Задача 1.6. Вычислите потенциал Ван-дер-Ваальса (1.16) для двух
различных частиц 1 и 2 в растворе (диэлектрические постоянные, соответ¬
ственно, si ф и ет) и покажите, что притяжение между ними слабее,
5-КЛЕМАН М.
66 Гл. 1. Конденсированная среда. Общие характеристики
чем среднее арифметическое притяжений между парами подобных частиц
(1,1) и (2,2); расстояние между частицами одно и то же во всех случаях.
Ответ. Дисперсионная энергия зависит от — (ei — ет)(б2 — ет) Для
различных частиц и от -fa - ет)2 и -(е2 - ет)2 для подобных частиц
(через постоянную Гамакера); заявленный результат следует из того, что
(с с ^ \ ^ (£l-£m)2 + (f2-£m)2 D
~ £т ){£2 “ £т) < . В много компонентой сме-
2
си имеется эффективный притягивающий потенциал Ван-дер-Ваальса, ко¬
торый дает тенденцию к их объединению; подробное обсуждение этого
вопроса см. в книге Israelachvili (1992). Обратите внимание, однако, что
этот результат не всегда правилен (Е. И. Кац, частное сообщение). Мож¬
но представить, например, что ситуации г\ Ф е2 и е\ ~ е2 соответству¬
ют различным режимам взаимодействия Ван-дер-Ваальса (запаздывающее
и незапаздывающее). Вообще, следует помнить, что такие взаимодействия
зависят от величины е в целом диапазоне частотного спектра, а не при
одной специфической частоте.
Литература для дальнейшего чтения
1. В. Alberts, D. Bray; J. Lewis, M Raff, К. Roberts and J. D. Watson. Molecular
Biology of the Cell, Garland Publishing, Inc., — N. Y.? 1983.
2. C. Branden and J. Tooze. Introduction to Protein Structure, Garland Publishing,
Inc., N. Y., and London, 1991.
3. Paul J. riory. Principles of Polymer Chemistry, Cornell University Press, Ithaca,
1953.
4. P. C. Hiemenz. Principles of Colloid and Surface Chemistry, 2nd edition, Marcel
Dekker, Inc., — N. Y., 1986.
5. J. N. Israelachvili. Intermolecular & Surface Forces, 2nd Edition, Academic
Press, — London, 1992.
6. J. Mahanty and B. W. N inham. Dispersion Forces, Academic Press, — London,
1976.
7. C. Tanford. The Hydrophobic Effect: Formation of Micelles and Biological Membra
nes, John Wiley & Sons, — N. Y., 1980.
8. P. Schuster, G. Zundel, and C. Sandorfy. The Hydrogen Bond, vols. 1, 2, 3, North-
Holland, Amsterdam, 1976.
9. L. Stryer. Biochemistry, 4th edition, W. H. Freeman and Company, —N. Y., 1995.
10. E.J. W. Verwey and J.Th.G. Overbeek. Theory of the Stability of Lyotropic
Colloids, Elsevier, —N. Y., 1948.
Дополнительная литература
1. Волъкенштейн М. В. Биофизика. —М.: Наука, ГРФМЛ, 1981.
2. Бараш Ю. С. Силы Ван-дер-Ваальса. —М.: Наука, ГРФМЛ, 1988.
ГЛАВА 2
АТОМНЫЕ И МОЛЕКУЛЯРНЫЕ
УПОРЯДОЧЕНИЯ
Мы не будем здесь детально рассматривать кристаллическое упоря¬
дочение атомов. В большинстве учебников по физике конденсированного
состояния можно найти описание 14 решеток Бравэ (групп параллельных
переносов и точечной симметрии решеток) и 230 пространственных групп
Шенфлиса-Федорова (полный набор элементов симметрии кристалла).
Эти группы исчерпывают все возможные группы с трехмерной периодич¬
ностью. В классической кристаллографии теми элементами, на которых
базируются группы симметрии, являются атомы; они могут быть, в об¬
щем, представлены точками или, когда картина описания требует более
сложных деталей, распределением плотности материи. Из-за большой (по
сравнению с к^Т) энергии связи положения атомов можно считать фик¬
сированными, и операции симметрии можно легко представить как пере¬
мещения кристалла как целого (параллельные переносы, повороты). Такие
операции симметрии не являются определяющими для физики мягких сред.
В мягких средах упорядочение связано со специфическими особенностями
в молекулярных формах, и текучесть, а следовательно и энтропия, явля¬
ются более существенными характеристиками. Сначала мы покажем, как
концепция атомного порядка может быть распространена на случаи, когда
учитывается конкретная форма атомов, уже не рассматриваемых в каче¬
стве точек, и каким образом такое расширение может быть естественно
включено в описание «сложных» мягких сред.
§ 2.1. Атомный порядок
«
2.1.1. Плотность упаковки
Наше обсуждение химических связей показывает в первом приближе¬
нии, что структуры в конденсированных средах являются такими упаков¬
ками, плотность которых ограничена стерическими препятствиями до тех
пор, пока направленные связи (преимущественно ковалентные) не ста¬
новятся определяющими. Регулярные решетки из жестких сфер с макси¬
мально возможной плотностью называются плотными упаковками. В двух
измерениях, например, наиболее плотная регулярная плотная упаковка дис¬
ков обеспечивается в треугольной решетке с параметром решетки, равным
диаметру диска; это также наиболее плотная из всевозможных двумерных
упаковок, включая случайные и апериодические упаковки. Такая решетка
обладает гексагональной симметрией; каждый диск касается шести других.
В трех измерениях существуют два типа периодического атомного по¬
рядка, обеспечивающие наибольшую из известных плотность — это гра-
нецентрированная кубическая (ГЦК) и гексагональная плотноупакованная
68
Гл. 2. Атомные и молекулярные упорядочения
(ГПУ) решетки. В обоих случаях происходит последовательная укладка
друг на друга гексагональных плотных двумерных слоев (рис. 2.1), упоря¬
доченных либо как ... АВСАВС... (ГЦК-решетки), либо как ... АВАВ...
(ГПУ-решетки) *)
а
б в
Рис. 2.1. Плотная упаковка жестких дисков на плоскости обеспечивается треуголь¬
ной решеткой с гексагональной симметрией. Плотноупакованные структуры в трех
измерениях могут быть построены укладкой треугольных слоев сфер. Каждая сфера
в одном слое расположена точно над (или под) промежутком между тремя атомами
прилегающих слоев (а). Получаются две геометрически различные решетки, ГЦК
(б) и ГПУ (в)
Каждый атом имеет Z = 12 соседей в первой координационной сфе¬
ре. В случае ГЦК плотные слои перпендикулярны оси симметрии третье¬
го порядка куба. Отношение объема, занятого находящимися в контакте
Имеется еще сколь угодно много упаковок, периодических и непериодических,
с такой же плотностью, но с другим чередованием символов А, В и С, лишь бы два
одинаковых символа не стояли рядом. (Примеч. пер.)
§ 2.1. Атомный порядок
69
сферами, к полному объему (коэффициент упаковки) составляет pfcc —
= Рнср — 0,74048. Разумеется, для систем, находящихся при конечной
температуре, это значение достижимо только при бесконечном давлении.
Центры 12 сфер, находящихся в контакте с данной сферой, лежат в вер¬
шинах некоторого координационного многогранника (полиэдра), а именно
кубооктаэдра (рис. 2.2), имеющего 14 граней (восемь правильных треуголь¬
ников и шесть квадратов); все ребра одинаковы (кубооктаэдр представляет
собой пример попу правильного многогранника. На координационной сфере
у каждого атома есть четыре соседа.
Рис. 2.2. Кубооктаэдр для упаковки типа ... ABC...
Рассмотрим два соседних последовательных слоя А и В; центры пустот,
лежащие в серединной плоскости между слоями, могут быть двух типов.
1. Тетраэдрические положения являются центрами упаковки четырех
сфер, находящихся во взаимном контакте (например, три из слоя А, одна
из В); центры этих сфер — вершины правильного тетраэдра (рис. 2.3, а),
2. Октаэдрические положения являются центрами упаковки шести сфер,
находящихся во взаимном контакте (например, три из слоя А, три из В);
центры этих сфер — вершины правильного октаэдра (рис. 2.3, б).
Важно осознавать, что тетраэдрические положения обеспечивают наи¬
большую плотность, возможную для любых многогранников (определяе¬
мую как коэффициент упаковки для внутренней части многогранника); по¬
этому в ГЦК- и ГПУ-решетках наблюдается пространственная модуляция
плотности на характерных микроскопических расстояниях.
2.1.2. Жидкости и аморфные среды
И в жидкостях, и в аморфных телах локальный порядок может быть
определен как упорядочение ближайших (и следующих за ближайшими) со¬
седей. В любой жидкости плотность флуктуирует только локально и имеет
хорошо определенное пространственно усредненное значение; это термо¬
динамически устойчивая фаза. Напротив, глобальные упорядочения в стек¬
ле или аморфном метачле критическим образом зависят от условий их
70
Гл. 2. Атомные и молекулярные упорядочения
создания (закалка, облучение и т. п.); это термодинамически неустойчивые
фазы.
а б
Рис. 2.3. Пустоты между сферами тетраэдрического (а) и октаэдрического (б) типов
в плотноупакованных решетках; представленные сферы уменьшены в размерах
Дифракционные методы (использующие рентгеновские лучи, нейтро¬
ны и т.д.) применяются для получения информации о локальном поряд¬
ке посредством измерения «радиальной функции распределения», которая
определяет, как плотность материи вокруг атома, усредненная по всем ато¬
мам, зависит от расстояния до этого атома. Основные особенности таких
экспериментальных данных легко понять в рамках модели, разработанной
Берналом Ч Согласно этой модели жидкости и аморфные среды представля¬
ют собой случайную плотную упаковку (СПУ) жестких сфер. Коэффициент
упаковки хорошо отрелаксировавшей СПУ приближенно равен 0,637. Бер¬
нал использовал метод полиэдрических положений для анализа сделанных
вручную систем жестких сфер, показывающий, что 86 % полиэдров — это
тетраэдры, 6% — октаэдры, а оставшиеся в большинстве своем тоже имеют
треугольные грани (он называет их дельтаэдрами). Среди дельтаэдров раз¬
личных типов есть большие клетки с 8, 9 и 10 вершинами, заключающими
в себя пустоты («дыры Бернала»).
Дуальный этому метод описания упаковки состоит в нахождении сред¬
него числа (Z) геометрических соседей каждой частицы. Оно может быть
определено как среднее число граней так называемого многогранника Во¬
роного, построенного вокруг частицы (рис. 2.4).
Для того чтобы сконструировать многогранник Вороного для данной
частицы, ее сначала соединяют отрезками линий со всеми остальными
Bernal J. D., Proc. Roy. Soc. А 280, 299 (1964).
§2.1. Атомный порядок
71
частицами системы, затем добавляют плоскости П, которые перпендику¬
лярны серединам этих отрезков и, наконец, отбирают те плоскости П,
Рис. 2.4. Многогранник Вороного для разупорядоченной системы
которые образуют границу наибольшего многогранника, не пересекающе¬
гося ни с какой другой плоскостью П. Для твердых кристаллов много¬
гранник Вороного есть не что иное, как хорошо известная ячейка Виг¬
нера-Зейтца; как уже отмечалось, в ГЦК- и ГПУ-решетках число граней
в многограннике Вороного равно числу атомов, находящихся в контакте
с данным атомом, т. е. Z = 12. Вообще же число граней есть мера для чис¬
ла ближайщих соседей, независимо от того, находятся ли они в контакте
в модели жестких сфер.
Анализ Вороного делает упор на среднее число граней (Z) ячейки
Вороного и на частоты /р, с которыми встречаются грани с р-ребрами. Если
бы упаковка была идеально икосаэдрической (мы скоро увидим, почему
интересно рассмотреть икосаэдры), то мы бы имели (Z) — 12 и /5 — 1 (все
ячейки Вороного были бы тогда додекаэдрическими). Отрелаксированная
модель СПУ, предложенная Финнеем (Finney) дает /з = 0,02, /4 = 0,2,
/5 = 0,43, /6 = 0,32 и f7 — 0,03. Среднее число ребер (р) у грани довольно
просто связано с (Z) (см. Коксетер2^), если использовать соотношение
Эйлера - Пуанкаре (Euler - Poincare) для многогранника (ячейки Вороного):
v-e + f = 2, (2.1)
2) Coxeter И. S. М, 111. J. Math. 2, 746 (1958).
72
Гл. 2. Атомные и молекулярные упорядочения
где v — число вершин, е — полное число ребер и / — число граней. При¬
меним соотношение (2.1) к правильному многограннику с q — 3 ребрами,
сходящимися в каждой вершине. Легко получить соотношение между чис¬
лом граней / и числом ребер р на каждую грань, а именно / = 12/(6— р).
Мы используем то же самое соотношение для связи между средними зна¬
чениями (Z) и (v) в набоое ячеек Босоного:
1 9
(Z) = -Ц-г. (2.2)
6 - (р)
Модель СПУ для хорошо отрелаксировавшей системы мягких сфер дает
(Р) 5,12 и (Z) та 13,6. Неотрелаксировавшая (менее компактная) СПУ
дает большие значения, чем отрелаксировавшая. Отметим, что для объ-
емноцентрированного кубического (ОЦК) кристалла такие же вычисления
дают (р) «5,14 при Z = 14, т. е. большие значения, чем для отрелак¬
сировавшей СПУ. Эти данные указывают на тот факт, что коэффициент
упаковки уменьшается, когда число соседей увеличивается. Компактность
среды, которая лежит в основе (мета) стабильности металлических стекол,
требует высоких коэффициентов упаковки.
2.1.3. Геометрическая фрустрация
Тетраэдрические расположения атомов, дающие наиболее компактные
локальные упаковки, и дефекты в таких упорядочениях, которые допуска¬
ют разнообразие координационных чисел, являются главными составными
частями для описания случайных упаковок одноатомных жидкостей и ме¬
таллических стекол. В этих случаях ожидается локальная икосаэдрическая
симметрия, так как центрированный правильный икосаэдр состоит из два¬
дцати одинаковых тетраэдров, имеющих одну общую вершину в центре
икосаэдра (рис. 2.5).
а
б
в
Рис. 2.5. Тетраэдрический и икосаэдрический порядок: а) пять правильных тет¬
раэдров, имеющие общее ребро, не могут заполнить пространство без фрустрации;
верхние грани тетраэдров на рисунке не показаны; б) пять искаженных тетраэдров
с осью симметрии пятого порядка; в) икосаэдр с одной из осей симметрии пятого
порядка
§2.1. Атомный порядок
73
На самом деле икосаэдрический порядок слегка отличается от плот¬
ной упаковки в том смысле, что двенадцать одинаковых сфер, находящиеся
в контакте с центральной сферой того же радиуса, не находятся в кон¬
такте друг с другом. Такой ансамбль из тринадцати сфер стабилизируется
в результате равновесия между (неблагоприятной) энергией упругих иска¬
жений тетраэдра и (благоприятной) энтропией колебаний. На самом деле,
в идеальном икосаэдрическом кластере из тринадцати атомов расстояние
между центральным атомом и атомами в вершинах примерно на 5 % короче,
чем расстояние между соседними атомами в вершинах, отсюда и давление
на центральный атом, дающее упругую энергию. Напротив, увеличенное
расстояние между поверхностными атомами дает некоторую выгодную по¬
верхностную энтропию.
Несмотря на это отклонение от плотной упаковки, локальная плотность
икосаэдрического упорядочения больше, чем в плотноупакованных ГЦК-
и ГПУ-структурах. Поэтому есть основания считать, что икосаэдрическое
упорядочение имеет меньшую энергию, чем ГЦК и ГПУ Вычисления для
малых совокупностей атомов с парным потенциалом Леннарда- Джонса
подтверждает это заключение.
Проблема состоит в том, что нельзя заполнить пространство периоди¬
чески с помощью икосаэдров из-за их симметрии пятого порядка, которая
запрещена для периодических покрытий пространства. Попытка последо¬
вательно распространить икосаэдрический порядок исходя из локального
икосаэдрического кластера приводит к нарушениям порядка (перекрытия
атомов или вакансии, потеря позиционных корреляций). Это пример до¬
вольно часто встречающегося в мягких средах и сложных системах явле¬
ния, которое называется геометрической фрустрацией. В данном случае
оно является причиной колебаний координационного числа возле среднего
значения (Z), которое ближе к 14, чем к 12 (см. выше). Причина, по которой
происходит положительная сверхкоординация, а не отрицательная, очевид¬
ным образом связана со знаком упомянутых выше отклонений от плотной
упаковки.
Было предложено и более усовершенствованное количественное рас¬
смотрение этого вопроса; оно основывается на введении концепции ис¬
кривленного кристалла, см.: Клеман, 1989. В предположении что структура
полностью тетраэдрическая, теория искривленных кристаллов показывает,
что тетраэдры упаковываются, главным образом в форме центрированных
икосаэдров (Z — 12), за исключением определенных атомных направлений,
которые можно понимать как линии дефектов идеальной икосаэдрической
структуры. На рис. 2.6 показано, как эти линии могут быть получены из
идеального икосаэдра в так называемом процессе Вольтерра (он будет де¬
тально рассмотрен в гл. 8). В показанном здесь случае процесс Вольтерра
преобразует Z = 12 в Z = 14. Заметим, что процесс состоит в добавлении
сектора икосаэдра с угловым размером 27г/5 между двумя листами раскры¬
того разреза вдоль поверхности Е с последующей упругой релаксацией
среды. Это наше первое знакомство с пока плохо определенным понятием
дефекта, в данном случае с линией дисклинации.
74
Гл. 2. Атомные и молекулярные упорядочения
Рис. 2.6. Введение линии дисклинации в икосаэдр (а) с Z = 12. Икосаэдр раз¬
резается (б), и клиновидный кусок материала (в), ограниченный симметрийно-
эквивалентными плоскостями, вставляется между двумя листами разреза; (г) отре-
лаксировавший дельтаэдр имеет Z — 14 и линию дисклинации вдоль оси разреза
Собственно говоря, линии дефектов рассмотренного выше типа бы¬
ли впервые применены Франком и Каспером для описания периодических
кристаллов сложных металлических сплавов, кристаллическая структура
которых может рассматриваться как упаковка неправильных тетраэдров:
при небольшой разнице размеров атомов, образующих такую фазу, плотная
упаковка является лучшим описанием3). Связь с жидкостями и аморфными
металлами очевидна. В этих фазах Франка-Каспера локальное координа¬
ционное число для атомов, расположенных вдоль линий дефектов, прини¬
мает значения Z — 8, 9, 10, 14, 15 или 16 (рис. 2.7).
3) Frank F. С. and Kasper J. S., Acta Cryst. 11, 84 (1958); Acta Cryst. 12, 483 (1959).
§2.1. Атомный порядок
75
Z=15
Рис. 2.7. Дельтаэдры Франка-Каспера, показанные как координационные обо¬
лочки с разными Z, окружающими центральный атом. Темные атомы лежат вдоль
линий дисклинаций
2.1.4. Несоразмерные фазы и квазикристаллы
В физике кристаллов фононы представляют собой тепловые колебания
атомов с малой амплитудой. Как хорошо известно, фононы в местопо¬
ложении Ti могут быть описаны в терминах собственных мод, а каждая
мода Uk(r;, t) = Uk(r^) ехрг(кг* — ut) имеет волновой вектор к и часто¬
ту о;/(27г); обладает периодичностью решетки (теорема Блоха),
2тт п
a ki — (гг = 1,2, - -., iV) есть некоторый вектор в обратном про-
ai N
странстве, Na,i — это размер образца в г-м направлении, аг- — соответству¬
ющий параметр решетки (граничные условия Борна-фон Кармана). Век¬
тор к непрерывен, когда образец бесконечен, и принимает значения в первой
зоне Бриллюэна. При изменении температуры частота определенной моды
может стремиться к нулю, а ее амплитуда расти для некоторого значения к,
несоразмерного с периодичностью решетки. Такая «мягкая мода» являет¬
ся предвестником фазового перехода смещения, при котором новая перио¬
дичность 27г/| к | сосуществует со «старой». В результате появляется
76
Гл. 2. Атомные и молекулярные упорядочения
«несоразмерная фаза» (примеры: тиомочевина SC(NH2b, естественный
минерал калаверит и т. д.). Такое явление можно также понимать как моду¬
ляцию периодичности с несоразмерным периодом.
На рис. 2.8 показано, как одномерная периодическая структура с ато¬
мами, регулярно расположенными в точках хп = па (а — это период,
ап — целое число), может быть модулирована соразмерным и несораз¬
мерным образом. Атомные сдвиги в обоих модулированных состояниях
а
а • • •—• • •—• • • • • • • • • х
м^
б •• » • •—• •—• ► X
Рис. 2.8. Одномерная периодическая структура из атомов, расположенных в точ¬
ках хп = па (а), и две ее модулированные версии с атомными смещениями
~ sin (27Гахп/а): соразмерная модуляция, а = 0,6, периодическая структура
с элементарной ячейкой в пять раз больше, чем в исходной цепи (б); несоразмерная
модуляция, а = 0,62 близка к иррациональному числу т”1 = (у/Е — 1)/2; нет
периодичности (в)
описываются одинаковой функцией ~ sin (2тгахп/а). Когда число а < 1
рационально, модулированное состояние по-прежнему периодично, с уве¬
личенной элементарной ячейкой. Когда а < 1 иррационально, структура
не имеет периода и называется «несоразмерной». Несоразмерные состоя¬
ния могут возникать, когда силы сцепления действуют в противоположных
направлениях: например, ближайшие соседи отталкиваются, а следующие
за ними атомы притягиваются. В действительности несоразмерные моду¬
ляции довольно часты и либо действуют на атомы непосредственно, как в
рассмотренном выше случае, либо опосредованно, через связь с волнами
зарядовой плотности [пайерлсовская (Peierls) неустойчивость] или с вол¬
нами спиновой плотности.
Модулированные кристаллы в d измерениях (которые в строгом смысле
не являются кристаллами; в них существует своего рода «беспорядок», так
как окружение данного типа атомов непрерывно меняется в пространстве)
получили кристаллографическое описание путем погружения в простран¬
ство размерности d+n, где п — число модуляций. Эта идея иллюстрируется
рис. 2.9 для случая d= 1 и п = 1. «Физическое пространство» Е (в данном
примере Е — это линия) получается как некоторый разрез двумерной квад¬
ратной решетки, и одномерная модулированная структура на Е является
проекцией атомов двумерного кристалла. Этот метод разреза и проекции
(cut-and-project method) предложен голландской школой кристаллогафииЧ
4) Р. М. de Wolff Acta Cryst. A30, 111 (1974); N. G. De Brujn., Proc. Konig. Ned. Akad.
Weten A84, 39 (1981); Janssen T., Acta Cryst. A42, 261 (1985).
§2.1. Атомный порядок
11
Рис. 2.9. Иллюстрация в d + п — 2 измерениях кристаллографии периодически
модулированных и квазикристаллических материалов. Двумерная квадратная ре¬
шетка проецируется на линию Е как одномерная периодическая структура, когда
тангенс угла наклона Е рационален (левый верхний угол), или как несоразмерная
апериодическая структура, когда наклон иррационален (центральная часть)
Если тангенс угла наклона Е по отношению к двумерной решетке рацио¬
нален, спроецированная структура периодична вдоль Е. Когда наклон ир¬
рационален, спроецированная структура не является периодической. Если
все атомы двумерной решетки спроецировать на Е с иррациональным на¬
клоном, то, очевидно, получающийся на Е набор атомов будет бесконечно
плотным: условие Делоне (Delaunay (Delaunay), утверждающее, что долж¬
но быть ненулевое минимальное расстояние между атомами, не будет вы¬
полняться. Чтобы ограничить эту плотность, проецируются только те ато¬
мы, которые находятся на некотором конечном расстоянии от Е. В этом слу¬
чае получается некоторое хорошо определенное среднее расстояние между
соседними спроецированными на Е точками, но фактические расстояния
промодулированы, так что, если разрез иррационален, спроецированные
точки в апериодической последовательности чередуются минимум с двумя
расстояниями, несоразмерными с этим средним расстоянием.
Еще до несоразмерных атомных структур было найдено, что в некото¬
рых редкоземельных металлах существует одномерная винтовая магнитная
78
Гл. 2. Атомные и молекулярные упорядочения
структура5^, несоразмерная с параметром решетки, возникающая благодаря
конкуренции между антиферромагнитными взаимодействиями с ближай¬
шими соседями и ферромагнитными со следующими за ближайшими.
Частный случай несоразмерности имеет место в квазикристаллах,
представляющих собой большое семейство металлических сплавов, как
например AIMn, AlFeCu и AlLiCu, имеющих локальный икосаэдрический
порядок без кристаллической периодичности, но сохраняющих дальние
икосаэдрические корреляции. То есть некристаллографическая симметрия
вызывает несоразмерность. Другие некристаллографические симметрии,
встречающиеся в природе, — это пентагональная, октагональная, декаго-
нальная и додекагональная. Квазикристаллы с почти свободными электро¬
нами, подобные AlLiCu, стабилизируются, по-видимому, за счет такого зна¬
чения числа валентных электронов на атом6\ которое приводит к провалу
в плотности состояний вблизи уровня Ферми в соответствии с механиз¬
мом устойчивости, рассмотренным для более простых сплавов Джоунсом
и Юм-Розери (Jones, Hume-Rothery) много лет назад.
Исходные экспериментальные данные для несоразмерных фаз и квази-
кристаллических сплавов — это их дифракционные картины. Брэгговским
рефлексам на этих картинах присваиваются индексы с несоразмерным ба¬
зисом, например, как в вышеприведенном случае d = 1, п = 1 и двух
несоразмерных периодов a mb, дифракционные пятна оказываются в поло¬
жениях qim = 27г(£/а + т/Ь). Целые числа (индексы) £ и т могут быть,
очевидно, выбраны таким образом, что qem принимает значение сколь угод¬
но близкое к наперед заданному: т. е. дифракционная картина является всю¬
ду плотной. Однако для экспериментатора она не выглядит непрерывной,
потому что, как следует из вычисления дифракционной картины, брэггов¬
ские пятна имеют сильно различающуюся интенсивность. Физическими
примерами являются: 1) покрытие Пенроуза (рис. 2.10, а), которое похо¬
же на наблюдаемые двумерные декагональные кристаллы; дифракционная
картина (всюду плотная) может быть получена как линейная комбинация
базисных векторов, направленных вдоль ребер правильного пятиугольника
(рис. 2.10,6); 2) икосаэдрическое покрытие, дифракционная картина кото¬
рого есть линейная комбинация шести базисных векторов, направленных
из центра к вершинам правильного икосаэдра. Введенный выше для случая
несоразмерных структур метод разреза и проекции может быть распро¬
странен на случай квазикристаллов, например пентагональных с d = 2,
п — 2 (следовательно, пентагональный квазикристалл представляет собой
двумерный разрез четырехмерного кристалла, атомные поверхности кото¬
рого являются двумерными объектами) и икосаэдрических с d = 3, п = 3.
Некоторые из фаз Франка и Каспера могут рассматриваться как рацио¬
нальные аппроксиманты квазикристаллов, соответствующий разрез еще
Yoshimori A., J. Phys. Soc. Japan 14, 807 (1951); Villain X, Chem. Phys. Solids 11,
303 (1959); Kaplan T. A., Phys. Rev. 116, 888 (1959).
6') FriedelJ., Helv. Phys. Acta 61, 538 (1988).
§2.2. Молекулярное упорядочение
19
рационален, но близок к иррациональному. Поэтому локальная икосаэдри-
ческая симметрия еще присутствует, но среда периодична.
а б
Рис. 2.10. Покрытие Пенроуза (а). Компьютерное моделирование растущего
икосаэдрического квазикристалла (б) (предоставлено В.Е. Дмитриенко); отметим
додекаэдрическую огранку
§ 2.2. Молекулярное упорядочение
Все сказанное выше о позиционном упорядочении относилось к сфе¬
рическим частицам. Так как молекулы несферичны, они устанавливают не
только трансляционный, но и ориентационный порядок. Для некоторых
интервалов температур или концентраций системы из несферических мо¬
лекул образуют мезофазы (фазы, «промежуточные» между регулярными
кристаллами и изотропными жидкостями), в которых либо сохраняется по¬
зиционный порядок, но теряется ориентационный (пластические кристал¬
лы), либо ориентационный порядок сохранятся, но позиционный теряется
частично или полностью (жидкие кристаллы).
2.2.1. Пластические кристаллы
Пластические кристаллы состоят из почти сферических молекул. Их
несферичность позволяет определить для каждой позиции «молекулярные
оси», но анизотропия взаимодействия слишком мала, чтобы предотвратить
свободное вращение молекул при повышенных температурах: хотя поло¬
жения молекул скоррелированы, ориентации их осей не скоррелированы
(рис. 2.11).
Типичными примерами являются кристаллы СЬ, а также недавно от¬
крытые кристаллы, строительными блоками которых служат фуллерены
(fullerenes) с химической формулой Сбо, названные в честь Бакминстера
Фуллера (Buckminster Fuller). В фуллеренах атомы углерода расположены в
вершинах многогранника, и каждый имеет три связи с соседними атомами
углерода в том же многограннике. Каждая связь может рассматриваться как
80
Гл. 2. Атомные и молекулярные упорядочения
ребро этого многогранника, который состоит из 20 шестиугольников и 12
правильных пятиугольников,
в предположении, что все ребра
«
одинаковые.
2.2.2. Строительные блоки
жидких кристаллов
Жидкие кристаллы состоят
из сильно анизотропных моле¬
кул: удлиненных (каламитиче-
ские молекулы) или дискообраз-
ных (дискотические молекулы).
Чаще всего внутренняя часть
мезогенных молекул жесткая
(фенильные группы), а внешняя
часть — гибкая (алифатические
углеводородные цепи). Такой
двойственный характер строе¬
ния в целом объясняет как
существование стерических вза¬
имодействий (между стерж¬
необразными или дискообраз¬
ными сердцевинами молекул),
дающих ориентационное упорядочение, так и текучесть мезоморфных фаз.
Вот несколько типичных примеров.
2.2.2.1 р-Пентил-р'-Цианобифенил (5СВ) и р-Октил-р'-Цианобифе-
нил (8СВ). Наиболее изученные одно компонентные жидкие кристаллы,
цианобифенилы, являются в настоящее время важнейшими материалами,
используемыми для жидкокристаллических дисплеев, благодаря своей хи¬
мической устойчивости и высокой диэлектрической и оптической анизо¬
тропии. Впервые они были синтезированы Грэем71 На рис. 2.12 показана
молекула 5СВ.
Концевая цианогруппа дает большой продольный дипольный момент
(~ 4 Д). Из-за сильных диполь-диполь ных взаимодействий такие моле¬
кулы образуют антипараллельные конфигурации. Этот эффект особенно
выражен в смектической фазе соединения 8СВ, где каждый смектический
слой образован парой молекул. Толщина такого слоя оказывается прибли¬
зительно в 1,4 раза больше длины одной молекулы 8СВ (рис. 2.13).
2.2.2.2 М-(р-Метоксибензилиден)-р'-Бутиланилин (МВВА). МВВА
(рис. 2.14) дает другой пример хорошо изученного соединения, образую¬
щего нематическую фазу при комнатной температуре. Эта молекула менее
полярна, чем молекула 5СВ.
Рис. 2.11. Пластические кристаллы: пози¬
ционное упорядочение частиц без ориента¬
ционного порядка. В среднем восстанавли¬
вается сферическая симметрия
7) GrayG. W., J. Phys. 36, Cl, 337 (1975).
§2.2. Молекулярное упорядочение
81
c18h19n
Молекулярный вес: 249
22,5 °С 35 °С ут
Твердая <4 ► Нематическая^ ► Изотропная фазы
Рис. 2.12. Химическая формула, молекулярная структура и фазовая диаграмма
5СВ. Отметим, что бензольные кольца лежат в разных плоскостях
C21H25N
Молекулярный вес: 291
N=С
24 °С
34 °С
42,6 С
Твердая^ ► Смектическая А< ► Нематическая < ► Изотропная фазы
Рис. 2.13. Антипараллельное дипольное расположение молекул 8СВ и фазовая
диаграмма 8СВ
Н.С-0
сн
c18h21no
Молекулярный вес: 267,37
Рис. 2.14. Химическая формула и молекулярная структура МВВА
2.2.2.3 Дискотические молекулы. Плоские центральные части моле¬
кул имеют тенденцию упорядочиваться параллельно друг другу, тогда как
гибкие углеводородные цепи оказываются намного более разупорядочен-
ными (рис. 2.15, 2.16).
82
Гл. 2. Атомные и молекулярные упорядочения
Твердая < ► Колончатая А ► Изотропная фазы
*
Рис. 2.15. Дискотические молекулы гекса-гептилоксибензоата бензола обра¬
зуют колончатые фазы (см. S. Chandrasekhar, В. К. Sadashiva, К. A. Suresh,
N. V Madhusudana, S. Kumar, R. Shashidhar and G. Venkatesh, J. Phys. (Paris) Colloq.
40, C3 — 120 (1979))
168°c тт 253°стл ,
Твердая < ► Дискотическая нематическая^ ► Изотропная фазы
Рис. 2.16. Гекса-п-гексилоксибензоат-трифенилен: химическая структура, фазовая
диаграмма и одна из возможных молекулярных конфигураций. Отметим, что це¬
пи необязательно параллельны центральной дискообразной группе (см. N. Н. Tinh,
И. Gasparoux and С. Destrade, Mol. Cryst. Liq. Cryst. 68, 101 (1981))
§2.2, Молекулярное упорядочение
83
2.2.2.4 Амфифильные молекулы, полимеры. Перечисленные выше
соединения дают термотропные мезофазы, т. е. фазы с одним компонен¬
том (хотя возможны и смеси), фазовые переходы которых могут быть вы¬
званы изменением температуры. Лиотропные мезофазы возникают, когда
анизометрические амфифильные молекулы (мыла, фосфолипиды и различ¬
ные типы поверхностно-активных молекул, включая те, что используются
в косметической промышленности) добавляются в раствор, такой как вода,
рассол или масло. Амфифильные молекулы имеют две резко отличающие¬
ся части: (полярную) гидрофильную головку и (неполярный) гидрофоб¬
ный олеофильный хвост — обычно алифатическую углеводородную цепь.
На рис. 2.17 изображена общая молекулярная структура фосфолипидов, ко¬
торые присутствуют в мембранах биологических клеток. Две алифатиче¬
ские цепи нужны для того, чтобы поперечное сечение молекулы не слишком
менялось от полярной головки к алифатической части. Строительные блоки
лиотропных фаз являются совокупностью многих амфифильных молекул
(мицелл), а не отдельных молекул. Такая архитектура молекулы приводит
к относительной устойчивости различных молекулярных агрегатов.
В качестве примера рассмотрим водный раствор амфифильных моле¬
кул с одним хвостом (скажем, додецилсульфат натрия). При концентрациях
выше определенной критической мицеллярной концентрации (КМК) эти
молекулы образуют агрегаты различной формы (рис. 2.18). Простейшей
формой ассоциации являются сферические мицеллы, размер которых из-
О о
меняется с размером молекул, т.е. оказывается между 20А и БОА. Такая
геометрия позволяет гидрофобным цепям избежать контактов с водой. Сме¬
шивание различных амфифильных соединений может приводить к образо¬
ванию анизометрических мицелл.
При более высоких концентрациях такого ПАВ можно получить ци¬
линдрические мицеллы (бесконечные цилиндры), двойные слои, обращен¬
ные цилиндры и обращенные мицеллы. Эти сложные элементы являются,
в свою очередь, строительными блоками для различных фаз, имеющих
дальний порядок, которые рассматриваются ниже в этой главе.
Искуственные макромолекулы, собранные из мезогенных мономеров,
либо соединены подобно цепи (рис. 2.19, а), либо образуют гребнеобраз¬
ную полимерную цепь (рис. 2.19,6). Такие молекулы также могут быть
строительными блоками для жидкокристаллических фаз. Биологические
полимеры (ДНК, поли-7-бензил-(лево или декстро)глутамат, ксантан и др.)
образуют жидкокристаллические фазы в растворах in vitro вследствие жест¬
кости их молекулярного остова. Некоторые вирусы сильно анизометриче¬
ской формы, подобные вирусу табачной мозаики (ВТМ), также образуют
в растворах лиотропные жидкокристаллические фазы.
Интересный пример лиотропного мезоморфизма представляют так на¬
зываемые хромонические жидкие кристаллы (по аналогии с нематика¬
ми, смектикам и дискотеками назовем их хромониками). Это семейство
включает ряд красителей, лекарств, нуклеиновых кислот, антибиотиков,
канцерогенов и противораковых средств. Их молекулы подобны дощечкам
84
Гл. 2. Атомные и молекулярные упорядочения
Углеводородный
хвост
н3с
J \
Н3С
J \
сн2
сн2
н2с
н2с
сн2
сн2
Н2Сч
Н2Сч
сн2
сн2
Н2С^
н2сч
р Н2
,сн2
Н2С
H2Cs
сн2
сн2
н2сх
Н2С^
сн2
сн2
Н2С^
н2сч
сн2
сн2
Н2сч
Н2С
сн2
сн,
у ^
H2Cv
н2сч
сн2
сн2
/
/
о
II
п
С =0
\
Ох
/
0
/
сн
-сн2
г
Полярная
головка
Н7С
“ I
О
®о-р=о
г
о
© х
а
б
в
СН2
СН
HsN^ ЧСОО
© 0
сн2
сн2
NH
©
©
сн2
сн2
I
N
Н3С
\
сн
сн
Рис. 2.17. Молекулярная структура фосфолипидов: фосфатидилсерин (а), фосфа-
тидилэтаноламин (б) и фосфатидилхолин (лецитин) (в). Число углеродных атомов
в алифатических цепях меняется обычно от 16 до 20. Эти два хвоста могут быть
различной длины
§2.2. Молекулярное упорядочение
85
а
в
Рис. 2.18. Сферическая мицелла (а\ цилиндрическая мицелла (б), обращенные
сферические мицеллы (<?) и анизометрическая мицелла (г)
а
к
о
Рис. 2.19. Полимеры с мезогенными группами в основной цепи (а) или с боковыми
мезогенными фрагментами (б) способны образовывать термотропные и лиотроп¬
ные жидкокристаллические фазы
86
Гл. 2. Атомные и молекулярные упорядочения
или дискам (а не стержням) с полярными группами на переферии, спо¬
собствующими растворению, и с ароматическим цетральным ядром. Со¬
единение таких молекул, вызванное, главным образом, последовательным
наложением ароматических центральных ядер, приводит к цилиндрической
укладке и другим геометриям, отличным от мицелл, образованных стерж¬
необразными молекулами ПАВ8).
2.2.3. Классификация мезоморфных фаз
Мезоморфные фазы (также называемые жидкими кристаллами) явля¬
ются промежуточными между жидкостями и твердыми телами. Они де¬
монстрируют большое разнообразие возможных структур, причем многие
из них могут проявиться в одном и том же материале (полиморфизм).
Существует четыре основных типа жидкокристаллических фаз, класси¬
фицируемые согласно размерности трансляционных корреляций между
образующими единицами: нематики (нет трансляционной корреляции),
смектики (одномерные корреляции), колончатые фазы (двумерные корре¬
ляции) и различные трехмерно скоррелированные структуры, такие как
кубические фазы.
2.2.3.1 Нематики. Одноосные нематики, обозначаемые N, являются
оптически одноосными фазами (рис. 2.20). Направленный вдоль оптиче¬
ской оси единичный вектор п называется директором. Даже если состав¬
ляющие единицы полярны (как молекулы 5СВ), молекулярные перевороты
п
А
t
-п
а
б
Рис. 2.20. Одноосные нематики, каламитики (а) и дискотеки (б), могут рассматри¬
ваться как система удлиненных стержней или дисков с осями а, ориентированными
преимущественно вдоль общего директора п. Направления п и — п эквивалент¬
ны, даже если молекулярная ось а является настоящим вектором. Составляющие
единицы на этом рисунке представляют собой либо отдельные молекулы (в случае
термотропных нематиков), либо мицеллы (в случае лиотропных нематиков)
8) J. Lydon, Curr. Opin. Colloid Interface Sci. 3, 458 (1998).
§2.2. Молекулярное упорядочение
87
и преимущественное сцепление голова к голове устанавливают центро¬
симметричное (в среднем) упорядочение в нематическом объеме. Таким
образом, п и — п являются эквивалентными обозначениями, п= — п. Дирек¬
тор является осью непрерывной вращательной симметрии: точечная груп¬
па симметрии фазы N такая же, как у однородного кругового цилиндра,
а именно D^oh (другое обозначение этой симметрии, введенное Междуна¬
родным союзом кристаллографов, оо/тт). Молекулы нематика, которые
анизометричны по форме, направлены в среднем параллельно п, причем
это усреднение проводится по всем «направлениям» отдельных молекул.
Трудность состоит в однозначном определении этого направления для каж¬
дой отдельной молекулы. Тем не менее процесс усреднения имеет смысл,
так как ориентация п вполне определенно измеряется экспериментально
(например, как направление оптической оси; см. гл. 3). Приемлемый выбор
характерного направления в индивидуальной молекуле может быть сделан,
в случае каламитиков, вдоль некоторой задающей ориентацию осей хими¬
ческой связи в стержнеобразной молекуле (рис. 2.20, а) или вдоль некоторой
химической «нормали» к диску в случае дискотиков (рис. 2.20, б).
Другое уже упомянутое свойство нематических фаз — это их жид¬
костная природа: центры тяжести молекул не скоррелированы. Поэтому
непрерывная евклидова группа смещений R3 входит в их полную группу
симметрии.
В двуосных нематиках NB точечная группа симметрии такая же, как
у призмы (рис. 2.21). Встречаются фазы Ng довольно редко: они наблюда¬
лись для анизотропных мицелл, бананообразных молекул и некоторых ме-
зогенных полимеров, и их наиболее правдоподобной симметрией является
симметрия прямоугольной призмы. Фаза Nb может быть описана тремя
директорами: n. t и m - п х t, такими что п = — п, t = — t, и m = — m.
п
А
in
t
Рис. 2.21. Двуосная нематическая фаза
88
Гл. 2. Атомные и молекулярные упорядочения
Когда составляющие блоки (молекулы или агрегаты) хиральны, т. е.
не эквивалентны своему зеркальному отражению, то нематическая фаза
может иметь закрутку (рис. 2.22). Тогда она называется холестерической
фазой N*.
Рис. 2.22. Холестерическая фаза: закрученный нематик
Поворот на некоторый угол а вокруг холестерической оси с эквивален¬
тен переносу на ра/27т, где р — шаг холестерической закрутки, который в
два раза больше периода вдоль оси с. Фаза N* может быть охарактеризо¬
вана тремя директорами: п «вдоль» локальной молекулярной оси, с вдоль
оси спирали (которая также является оптической осью, если шаг много
меньше длины волны света) и ш = п х с «перпендикулярно» как п, так
и с. Эти три директора образуют триаду направлений ((п = — п, с = —с,
m = —m)), которая поворачивается с шагом спирали. Как Nb, так и N*
являются жидкими фазами (нет корреляций в положениях молекул).
2.2.3.2 Смектические фазы. Смектики представляют собой слои¬
стые фазы с квазидальним одномерным упорядочением центров молекул в
направлении, перпендикулярном слоям. Этот позиционный порядок, в от¬
личие от обычных трехмерных кристаллов, не является истинным дальним
порядком: как было показано Ландау9^ и Пайерлсом,10] флуктуационные
смещения слоев в одномерной решетке расходятся логарифмически с ро¬
стом линейных размеров образца. Однако этот эффект заметен на масшта¬
бах порядка 1 км или более; типичные образцы тоньше, 10 - 100 мк или даже
9) Landau L. D., Phys. Z. Sowjet Union 2, 26 (1937).
10) Peierls R. E., Annales de 1’Institut Henri Poincare 5, 177 (1935).
§2.2. Молекулярное упорядочение
89
меньше. Внутри слоя расположение молекул либо подобно жидкостному,
либо имеется упорядочение ориентационных связей, либо упорядочение,
подобное твердотельному. Хотя структуры последнего типа обладают нену¬
левыми упругими константами сдвига, эти константы много меньше, чем
в обычных трехмерных кристаллах. До конца не ясно, сохраняют ли эти
структуры, называемые смектиками В, Е, G, Н, J и К, настоящий дальний
порядок расположения молекул в направлении, перпендикулярном слоям.
В дальнейшем мы не будем рассматривать эти фазы.
Смектики с жидкими слоями бывают трех представленных ниже типов.
• Смектик A (SmA) является одноосной средой с оптической осью,
которая перпендикулярна слоям; директор п направлен по нормали к слою
(рис. 2.23, а). В слоях нет дальнего позиционного порядка; каждый слой
является двумерной жидкостью. В лиотропных кристаллах фаза с такой же
симметрией называется La (рис. 2.23, б).
п
Л
▼
п
а б
Рис. 2.23. Термотропная смектическая фаза А с периодической модуляцией плот¬
ности (а); Лиотропная фаза Ьа с бислоями ПАВ, разделенными водой; слой воды
может быть много толще, чем бислой ПАВ (б)
• Смектик С (SmC) также состоит из одномерно уложенных жидких
слоев, однако это двуосная фаза, потому что длинные оси а молекул накло¬
нены по отношению к нормали t к слоям (рис. 2.24). Оси а усредняются
в «нематический» директор п, если не обращать внимания на слои. Обра¬
зованная п и t так называемая плоскость наклона, содержащая оптические
оси, является плоскостью зеркальной симметрии. Другой операцией сим¬
метрии является поворот на угол 7г вокруг оси С2, которая перпендикулярна
плоскости наклона. Из-за слоистой структуры поворотные оси симметрии
второго порядка С2 лежат и в плоскости слоя, и в плоскости между дву¬
мя слоями. Комбинация зеркального отражения и поворотной оси второго
порядка дает инверсионную симметрию.
90
Гл. 2. Атомные и молекулярные упорядочения
а б
Рис. 2.24. Смектическая фаза С (нехиральная): общая структура (а); элементы
симметрии (б), см. текст
Три операции симметрии (зеркальное отражение, поворот вокруг осей
С2 и инверсия) приводят к интересным свойствам единичного вектора v,
задаваемого проекциями молекул на смектические плоскости. Этот вектор
и не директор, и не вектор. Поворот на угол 7г вокруг оси Сг, рассматривае¬
мый в лабораторной системе координат, переводит v в — v (и t в —t). Так как
SmC после такого поворота неотличим от исходного состояния, то это под¬
разумевает «директорный» характер v, v = —v. Рассмотрим теперь поворот
на угол 7г вокруг нормали к слоям t, которая не является осью симметрии.
Такой поворот переводит v в — v в лабораторной системе координат, но
два эти состояния с очевидностью неэквивалентны, потому что молекулы
наклонены в противоположных направлениях. Таким образом, этот пово¬
рот не отождествляет состояния v и —v. Этот двойственный характер v
отражается на природе топологических дефектов (см. п. 12.1.7).
Другой тонкий вопрос связан с ориентационным порядком вдоль С2.
Из-за слоистой структуры SmC поворот на угол 7г вокруг «нематического»
директора п не является разрешенной операцией симметрии, в противопо¬
ложность фазе N. Тем не менее из-за зеркальной симметрии нет электри¬
ческой поляризации вдоль С2. Эта ситуация изменяется, когда молекулы
хиральны (см. следующий абзац).
• Смектик С* (SmC*), состоящий из хиральных молекул, является хи¬
ральной версией SmC. Направление наклона молекул прецессирует вокруг
нормали к слоям (рис. 2.25). Хиральность устраняет зеркальную и ин¬
версионную симметрии, так как зеркальное отражение и инверсия изме¬
нили бы направление закрутки спирали (с правой на левую или наобо¬
рот). Поэтому, как было отмечено Мейером1 ^ симметрия не запрещает
R. В. Meyer, L. Liebert L. Strzelecki and P. Keller, J. Phys. (Paris) Lett. 36. L69
(1975).
§2.2. Молекулярное упорядочение
91
электрическую поляризацию р вдоль оси С2, перпендикулярной плоскости
наклона. В неискаженном геликоидальном SmC* локальная плоскость на¬
клона поворачивается от слоя к слою, и то же делает вектор поляризации р
(рис. 2.25). Суммарная поляризация Р, усредненная по области с размером,
много большим, чем шаг геликоида, обращается, таким образом, в нуль.
Однако, если поместить очень тонкий слой
SmC* между двумя жесткими пластинами,
параллельными плоскости рис. 2.25, кото¬
рые способствуют ориентации молекул в их
плоскости, то спираль может быть раскруче¬
на. Такая «стабилизированная поверхностью»
сегнетоэлектрическая пленка имеет ненуле¬
вую суммарную поляризацию Р, направлен¬
ную либо к читателю, либо от него. При-
кладывая электрическое поле определенной
полярности к ограничивающим поверхно¬
стям, можно обратить направление Р и, сле¬
довательно, изменить направление наклона
в на —в. Такая переориентация приводит к
резким изменениям оптического пропуска¬
ния, когда пленка помещается между скре¬
щенными поляризаторами (см. п. 3.3.3). Этот
эффект, открытый Кларком и Лагерволом12\
используется при конструировании быст¬
родействующих информационных дисплеев.
Недавние достижения в создании новых ме-
зогенных соединений (например, синтез бана-
но-подобных молекул) дали смектические
фазы с большим разнообразием сегнетоэлек-
трических свойств; некоторые из этих фаз
являются антисегнетоэлектриками или сегне-
тиэлектриками (последние названы так по ана¬
логии с ферримагнетиками), см. книги Chirality in Liquid Crystals (2000)
и L. M. Blinov, V. G.Chigrinov, Electrooptic effects in liquid crystal materials,
Springer, 1996.
Для некоторых смектических фаз с жидкими слоями характерен гексаго¬
нальный порядок в ориентации связей в слоях. Они называются гексатиче-
скими смектиками или гексатиками. Например, в гексатическом смектике В
молекулы нормальны к слоям и не имеют позиционного порядка в слоях, как
и в SmA. Однако они имеют дальнее гексагональное упорядочение в ориен¬
тациях направлений, которые соединяют молекулы (упорядочение связей)
(см. гл. 4). Наклоненные версии гексатика В называются гексатическими
смектиками F и I. Отметим, что в А, С, С* и гексатических смектиках слои
А
Шаг
▼
А
t
Рис. 2.25. Хиральный смею
тик С* (SmC*) с периоди
ческой в пространстве пре
цессией наклоненных моле
кул вокруг нормали к слоям
12) N. A. Clark and S. Т. Lagerwall, Appl. Phys. Lett. 36, 899 (1980).
92
Гл. 2. Атомные и молекулярные упорядочения
не скоррелированы между собой в плоскости слоев; эти фазы были исполь¬
зованы как модельные системы для проверки различных теорий двумерных
сред.
2.2.3.3 Колончатые фазы. Колончатые фазы характеризуются двумер¬
ным дальним позиционным порядком с трансляционными симметриями.
Гексагональные колончатые фазы часто образуются колонками дискотиче-
ских молекул (рис. 2.26) или лиотропными цилиндрами. Другие двумерные
симметрии (например, тетрагональная) основательно не исследованы, так
как они наблюдаются достаточно редко.
а б
Рис. 2.26. Термотропная гексагональная колончатая фаза, образованная дискооб¬
разными молекулами. Межмолекулярные расстояния случайны вдоль колонн, но
фиксированы двумерной решеткой в перпендикулярной плоскости (а). Лиотропная
гексагональная колончатая фаза, образованная цилиндрическими мицеллами (б);
показан двумерный срез, перпендикулярный цилиндрам
2.2.3.4 Трехмерные фазы
• Лиотропные кубические фазы образованы бислоями, которые прости¬
раются в трех пространственных измерениях. Этот случай лиотропиков был
изучен очень детально: поверхность середины бислоев близка к некоторой
периодической минимальной поверхности, т. е. поверхности, главные кри¬
визны которой, (Т\ и сг2, во всех точках равны и противоположны по знаку:
сг\ -f 02 = 0. Это условие минимизирует энергию кривизны бислоев (основ¬
ные понятия о геометрии поверхностей и теория упругости будут даны в
последующих главах). Полная геометрия этих кубических фаз слишком
сложна, чтобы рассматривать ее во всех деталях; отметим только, что их
периодическая организация относится к слоям, а не к отдельным моле¬
кулам, которые достаточно свободны, чтобы перемещаться внутри слоев.
§2.2. Молекулярное упорядочеиие
93
В настоящее время известно по крайней мере три типа лиотропных куби¬
ческих фаз; одна из них показана на рис. 2.27.
• Голубые фазы образованы хиральными молекулами, которые орга¬
низованы пространственно неоднородным образом исходя из следующих
принципов. Пусть По есть некото¬
рый директор, например вдоль оси
Z на рис. 2.28. В локальном состоя¬
нии с наименьшей энергией хираль¬
ные молекулы в окрестности п0 имеют
тенденцию спирально поворачиваться
при смещении вдоль всех направле¬
ний, перпендикулярных п0, а не толь¬
ко вдоль одного направления с, как
в холестерической фазе N*. Такая гео¬
метрия, называемая двойной закрут¬
кой, энергетически предпочтительнее
одномерной закрутки, по крайней ме¬
ре для некоторых хиральных молекул.
Однако по мере того как увеличивается
расстояние от директора no ||Z, холе-
Рис. 2.27.
фаза
Лиотропная кубическая
стерические цилиндрические оболоч¬
ки становятся более плоскими, и двойная закрутка плавно исчезает. Даль¬
ние конфигурации директора становятся ближе к одномерной фазе N*,
и энергетическая выгода уменьшается. Таким образом, двойная закрутка
не может распространяться на все трехмерное пространство. Типичный
радиус энергетически выгодной цилиндрической области вокруг оси по
равен полушагу р/2. Вдобавок, эти цилиндры конечного радиуса не мо¬
гут заполнить пространство непрерывно. Эта ситуация напоминает явле¬
ние фрустрации, уже встречавшееся в фазах Франка-Каспера. Согласно
наиболее современным моделям голубых фаз эти фрустрации снимаются
линейными дефектами (дисклинационного типа), либо регулярно располо¬
женными, либо разупорядоченными, так же как в фазах Франка-Каспера
и металлических стеклах. На рис. 2.28 показано, как три цилиндра двойной
закрутки образуют сингулярность в области, где они соединяются.
Голубые фазы типа BPI и ВРИ представляются в виде правильной сети
линий дисклинаций с периодичностью порядка р. Действительно, трех¬
мерно периодическая структура этих фаз проявляется в ненулевых модулях
сдвига, в способности к росту ограненных монокристаллов и в возможно¬
сти брэгговских отражений в видимой части спектра (что естественно, так
как р имеет порядок нескольких десятых микрона). Последнее объясняет
и их название: в поляризационном микроскопе эти фазы часто выглядят
голубыми. Обычно они существуют в очень узком интервале температур
(~ 1 К) между изотропной фазой и холестерической фазой N*. Третья из
обнаруженных фаз, BPIII, обычно встречающаяся между изотропным рас¬
плавом и ВРИ, пока недостаточно понята. Она может быть расплавленной
94
Гл. 2. Атомные и молекулярные упорядочения
решеткой дисклинаций. Отметим, что, хотя большинство голубых фаз на¬
блюдалось в термотропных системах, геометрии с двойной закруткой могут
встречаться и в растворах биологических полимеров, таких как ДНК.
Рис. 2.28. Голубые фазы образованы областями с двойной закруткой; показаны три
такие области с сингулярностью, которая снимает фрустрацию между ними. Два
цилиндра с двойной закруткой соответствуют друг другу, если наклон директора на
их поверхности равен 7г/4, однако место, где все три цилиндра встречаются, име¬
ет особенность. В современных моделях такие особенности образуют сеть линий
дисклинаций. Кружок обозначает «ядро» дисклинации; на вставке показаны линии
директора вокруг ядра
2.2.4. Изотропные фазы
Термин изотропые объединяет следующие фазы.
• BPIII. Эта фаза имеет на малых масштабах такое же молекулярное
упрядочение с двойной закруткой, как BPI и BPII, но предполагается, что в
ней цилиндры образуют случайную систему длинных гибких взаимопере-
плетающихся «червей».
• Фазы ассоциированых коллоидов. Мицеллы, представляющие собой
замкнутые конструкции из молекул ПАВ, либо сферические, либо червеоб¬
разные, размеры или распределение размеров которых находятся в термо¬
динамическом равновесии с растворителем (а). Изотропная губчатая фа¬
за Ьз, которая по современным представлениям описывается как двойной
слой ПАВ, распространяющийся случайным образом на все пространство
и делящий раствор на пару непрерывных связных областей; эту термо¬
динамическую фазу иногда называют «ночной кошмар водопроводчика»
(рис. 2.29) (б). Микроэмульсии, состоящие из монослоя ПАВ, распростра¬
няющегося случайным образом на все пространство и разделяющего два
р! 2
Т
А
§ 2.2. Молекулярное упорядочение
95
раствора разной природы, такие как вода и масло (в); это опять-таки термо
динамическая фаза.
• Коллоидные растворы (макромолекул, белков или биологических по
лимеров) и расплавленные полимеры (см. гл. 15).
t
L
N
ч
t
6
'.V:\
ГЛ V>,
vy1А
V к
Y
Г:
< ,
t
'v.
I
Рис. 2.29. Модель лиотропной губчатой фазы: двойной слой, делящий раствор на
пару непрерывных связных областей
Объектами вышеприведенной классификации являются фазы в термо¬
динамическом равновесии. Для растворов предполагается «хороший» рас¬
творитель. Термин раствор не будет использоваться для метастабильных
дисперсий (в «плохом» растворителе).
В вышеприведенных примерах растворитель является изотропной жид¬
костью. Последние десятилетия были временем взрывного роста интереса
к мезоморфным растворителям. Мезоморфные растворители очень необыч¬
ны, так как они навязывают растворенным частицам свой ориентацион¬
ный (нематики) и позиционный (смектики) порядок. Например, ориенти¬
руя молекулы красителя в нематической матрице, можно получить систему
с электрически переключаемым дихроизмом. Добавление растворенных ча¬
стиц в смектическую массу может привести к наномасштабной сегрегации:
в зависимости от химического сродства с хозяином растворенная части¬
ца может оказаться либо внутри смектических слоев, либо между ними13).
Многообразие явлений становится еще богаче, когда растворяют мономер
в жидкокристаллической матрице и затем полимеризуют его в этой мат¬
рице. Хотя полное описание композитных материалов полимер-жидкий
кристалл все еще отсутствует, их широко известные представители, такие
13) См., например: М. A. Glaser, In Advances in the Computer Simulations of Liquid
Crystals, Edited by P. Pasini and C. Zannoni, NATO Science Series, Ser. C: Math, and
Phys. Sciences, v. 545, p. 263, sec. 4.2 (2000).
96
Гл. 2. Атомные и молекулярные упорядочения
как диспергированные в полимерах жидкие кристаллы и стабилизируемые
полимерами жидкие кристаллы 14\ уже нашли практические применения,
главным образом в индустрии дисплеев.
§ 2.3. Нарушения кристаллического порядка
Мы будем проводить разграничение между возмущениями малой энер¬
гии, которые могут релаксировать к равновесию за конечное время, и боль¬
шой энергии, которые создают особености параметра порядка (это понятие
будет определено позднее).
2.3.1. Слабые нарушения
Тепловые флуктуации малой амплитуды, имеющие большую по сравне¬
нию с атомными и молекулярными расстояниями длину волны I = 27г/| к
и малые по сравнению с атомными и молекулярными частоты, являют¬
ся слабыми возмущениями. Такими слабыми возмущениями могут быть
фононы в кристаллических твердых телах, спиновые волны в ферромагне¬
тиках и флуктуации оптической оси в нематиках (рис. 2.30). Флуктуации
представляются как суммы собственных мод,
и0(т) = £>0(k,r) ехрг(кг - cot), (2.3)
к
частоты которых и и волновые векторы к зависят от природы упорядочения
и от симметрии.
о—о- о-
о—о— о
О—Ю—*• О-*-
а б
Рис. 2.30. Флуктуации: продольная фононная волна атомных смещений, стрелки
показывают направление и амплитуду смещений (а); флуктуации поля директора
(оптической оси) в одноосном нематике (б )
Любое навязанное системе слабое возмущение можно рассматривать
как некоторую сумму независимых собственных мод. Слабые возмущения
принадлежат миру «линейной физики», и они не изменяют порядок, потому
14^ Liquid Crystals in Complex Geometries Formed by Polymer and Porous Networks,
Edited by G. P. Crawford and S. Zumer, Taylor & Francis, 1996, 506 p.
§ 2.3. Нарушения кристаллического порядка
97
что к = | к | меньше, чем 2тх/а\ атомы, молекулы или спины реагируют
совместно.
Мягкие моды возникают, когда для некоторого специального значения к,
скажем кс, и вблизи некоторой температуры Тс частота этих мод со —> О,
а амплитуда возмущения остается конечной; они являются предвестника¬
ми фазовых переходов второго рода с изменением симметрии. Они уже
упоминались ранее в п. 2.1.4.
2.3,2. Сильные нарушения
По определению, сильные нарушения — это нарушения, «ломающие»
параметр порядка. Они могут быть подобны точкам (точечные дефекты
в твердых телах, особые точки в нематиках и т. п.), линиям (дислокации
в твердых телах, линии вихрей в сверхтекучей фазе 3Не, дисклинации
в жидких кристаллах, особые линии в конфокальных доменах и т. п.) или
поверхностям (границы зерен в твердых телах и смектиках, стенка Блоха
в ферромагнетиках и т. п.). В духе подхода к дефектам, пользующегося
популярностью у металлургов, на некотором расстоянии от дефекта рас¬
смотрение по-прежнему является линейным. То есть оно может быть про¬
ведено в пределах слабых нарушений, которые подразумевают сохранение
параметра порядка и кооперативный линейный отклик, но требуется другое
описание вблизи дефекта, где параметр порядка действительно «сингуля¬
рен». Эта область называется «ядром» дефекта.
Сильные нарушения также можно разделить на термодинамические (са¬
мопроизвольные, или спонтанные) и привнесенные. Спонтанными силь¬
ными нарушениями являются, например, точечные дефекты в кристал¬
лах (вакансии и межузельные атомы, рис. 2.31). Они распределены по
решетке случайно, и это ведет к их устойчивости за счет энтропии бес¬
порядка, которая конкурирует с их (положительной) внутренней энергией
Рис. 2.31. Точечные дефекты в кристалле, вызванные межузельным атомом (а)
и вакансией (б)
7‘КЛЕМАН М.
98
Гл. 2. Атомные и молекулярные упорядочения
(необходимой для их создания). Еще один пример дают некоторые мо¬
дели перехода твердое тело-жидкость, которые предполагают, что жид¬
кое состояние дает о себе знать в твердом теле посредством спонтанного
размножения линий дислокаций, опять-таки стабилизируемых своей эн¬
тропией беспорядка. Другие примеры, встречающиеся в мягких материа¬
лах, рассматриваются ниже. И, наконец, некоторые периодические фазы
фрустрированного типа, такие как фазы Франка-Каспера и голубые фа¬
зы, часто описываются в терминах дефектов, внутренняя энергия которых
должна быть отрицательна, так как они не вносят энтропии беспорядка.
Привнесенными сильными нарушениями являются, например, нерав¬
новесные точечные дефекты, возникающие в результате радиационных по¬
вреждений; дислокации в твердых телах, получающиеся в процессе роста
или механической обработки; дисклинации, которые рождаются, изменяют
форму и исчезают в жидких кристаллах под действием сдвиговых тече¬
ний; стенки Блоха в ферромагнетиках, которые участвуют в структурных
изменениях под действием магнитного поля.
Эти сильные нарушения затрагивают многие физические явления, в осо¬
бенности необратимые (зависимость деформации от напряжения в твердых
телах, гистерезис магнитных явлений, диссипативные процессы при тече¬
нии в жидких кристаллах), как на мезоскопических расстояниях (где эти
особенности появляются), так и на макроскопических масштабах (на ко¬
торых эти сингулярности объединяются в более или менее определенные
текстуры).
Одной из целей этой книги как раз и является изложение концептуаль¬
ных подходов к классификации различных типов сингулярностей в упо¬
рядоченной среде (эта классификация зависит от симметрии параметра
порядка) для осмысления и понимания поведения сингулярностей при раз¬
нообразных воздействиях.
Задача 2.1.
а) Показать, что точное значение коэффициента упаковки для ГЦК-
решетки равно 7гд/2/6;
б) Медь имеет ГЦК-структуру, вычислить ее плотность, принимая
О
атомный радиус равным 1,28 А.
Задача 2.2. Показать, что в упорядоченных плотно упакованных
структурах имеется в два раза больше тетраэдрических пустот, чем ок¬
таэдрических.
Ответ. Каждый атом окружен двенадцатью атомами в вершинах ку-
бооктаэдра с шестью квадратными гранями и восемью треугольными гра¬
нями. Это верно и для ГЦК-, и для ГПУ-решеток. Следовательно, к каждому
атому прикреплено шесть октаэдров и восемь тетраэдров. Каждый октаэдр
включает шесть вершин, а каждый тетраэдр — четыре вершины. Поэтому
среднее число тетраэдров на атом равно двум, октаэдров — одному.
§ 2.3. Нарушения кристаллического порядка
99
Задача 2.3.
а) Показать, что для любого многогранника v — е + / = 2 (число вер¬
шин v, ребер е, граней /). Подсказка: создать произвольный многогранник
из любого данного многогранника, добавляя или убирая, в зависимости
от ситуации, грани, ребра и вершины. Эта формула известна как теорема
Эйлера-Пуанкаре,
б) Используя результат (а), доказать (2.2).
4 р 6 р
в) Показать, что в правильном многограннике v = , е = ,
6 — р б — р
если число ребер на вершину q = 3.
Ответ
б) Пусть (Z) = (/) есть среднее число граней на ячейку Вороного.
Тогда имеем: {Z){p) = 2(e) и q(v) — 2(e). Отсюда, используя результат (а),
(Z) = 2 + М1^1(1 _ (2/д)), т, е. (Z) = — ; = 3 дает (2.2).
w 2 2q-q{p) + 2{p)
Задача 2.4. Найти геометрию фуллерена, описанного в тексте, ис¬
пользуя вышеприведенную теорему Эйлера-Пуанкаре.
Задача 2.5. Покажите, что интенсивность дифракционных пятен од¬
номерного квазикристалла (рис. 2.9) дается выражением
Iq^AqA\= —sin
q±w
<l±w
где q±_ — модуль компоненты вектора q = щ + qj_ в перпендикулярном
пространстве, a w — ширина полосы.
Ответ. Вычисляем дифракционную амплитуду Aq = ^2N exp г^цЛ^ц,
где йдгц являются одномерными координатами в физическом простран¬
стве узлов Rn двумерной решетки. Брэгговские отражения от квазире¬
шетки являются проекциями брэгговских отражений от двумерной обрат¬
ной решетки. Отсюда qR^ = Q\\Rn\\ + QxRnl — 0(mod 2n); вследствие
этого амплитуда может быть записана как Aq = ехР ~^4i.Rnl, где
Rn± — это перпендикулярные компоненты проекций узлов Rjy, лежащих
в полосе (рис. 2.9). Проекции узлов Rnl заполняют перпендикулярное
пространство плотно и однородно по причине иррациональности направле¬
ния проекции. Поэтому последняя сумма может быть заменена интегралом
по ширине полосы w:
W
Aq = У' exp -iqxR
■N -L
N
exp -iq±ydy,
О
из которого легко получить выражение для Iq. Хотя отражения плотно за¬
полняют физическое обратное пространство, немногие из них достаточно
интенсивны для наблюдения, так как Iq осциллирует между нулевым зна-
чснисм и максимумами при Qj_ ^
n/а, дц та т/а (п и т — целые числа)
100
Гл. 2. Атомные и молекулярные упорядочения
и уменьшается очень быстро с ростом q±. Разумеется, результаты такого ро¬
да применимы и к реальным квазикристаллам при внесении необходимых
изменений [с?ц = 2(D = 4); d\\ — 3(D = 6)].
Литература для дальнейшего чтения
1. Н. Ашкрофт, Н. Мермин. Физика твердого тела / Пер. с англ. под редакцией
М.И. Каганова. Т. 1,2. —М.: Мир, 1979.
2. Chirality in Liquid Crystals, Edited by H.-S. Kitzerow and C. Bahr, Springer, —
N. Y.: 2000.
3. H. S. M. Coxeter. Regular Polytopes, Dover Publications, New York, 1973.
4. F. C. Frank. Supercooling of Liquids, Proc. Roy. Soc. A215, 43 (1952).
5. J. Friedel. Helv. Phys. Acta 61, 538 (1988).
6. P. G. de Gennes and J. Frost. The Physics of Liquid Crystals, 2nd Edition,
Clarendon Press, Oxford, 1993. См. перевод первого издания: П. Ж. де Жен.
Физика жидких кристаллов. Пер. с англ. под редакцией А. С. Сонина. —
М.: Мир, 1977.
7. G. W. Gray and J' W. Goodby. Smectic Liquid Crystals. Textures and Structures,
Leonard Hill, Glasgow, 1984.
8. J.-P. Hansen. Theory of Simple Liquids, Academic Press, N. Y., 1986.
9. C. Janot. Quasicrystals: A Primer, Clarendon Press, Oxford, 1992.
10. M. Kleman. Curved Crystals, Defects and Disorder, Adv. in Physics 38, 605 (1989).
11. A. G. Petrov. The Lyotropic State of Matter. Molecular Physics and Living Matter
Physics, Gordon and Breach Science Publishers, Amsterdam, 1999.
12. Physics and Chemistry of Finite Systems: From Clusters to Crystals, vols. I and
II, edited by P. Jena, S.N. Khanna, and B.K. Rao, NATO ASI Series, Series C:
Mathematical and Physical Sciences, Vol. 374, Kluwer Academic Publishers, 1992.
13. Physics of Complex and Supermolecular Fluids, S. A. Safran and N. A. Clark, eds.
Wiley, N. Y., 1987.
14. S. A. Safran. Statistical Thermodynamics of Surfaces, Interfaces and Membranes,
Addison-Wesley, Reading, MA, 1994.
15. R. Zallen. The Physics of Amorphous Bodies, John Wiley & Sons, 1983.
Дополнительная литература
1. Беляков В. А, Дмитриенко В. Е. Голубая фаза жидких кристаллов, УФН. 1985.
Т. 146. С. 369.
2. Сонин А. С. Введение в физику жидких кристаллов. — М.: Наука, 1983.
3. Сонин А. С. Лиотропные нематики. УФН. 1987. Т. 153. С. 273.
4. Чандрасекар С. Жидкие кристаллы / Пер. с англ. — М.: Мир, 1980. 344 с., ил.
5. L. М. Blinov and V G. Chigrinov. Electrooptic Effects in Liquid Crystal Materials,
Springer series on partially ordered systems, —N. Y.: 1994.
ГЛАВА 3
ПАРАМЕТР ПОРЯДКА: АМПЛИТУДА И ФАЗА
Понятие параметра порядка возникло при попытках описания фазо¬
вых переходов порядок-беспорядок в сплавах, а именно для определения
степени упорядочения (см. п. 3.1.6). Впервые введенное Горским, а так¬
же Брэггом и Вильямсом для описания переходов порядок-беспорядок
в сплавахЧ это понятие в современном виде было развито Ландау для фе¬
номенологического описания фазовых переходов. Точнее, оно служит для
описания дальнего порядка в пространственном распределении структур¬
ных (кристаллографических) или термодинамических (магнитных, диэлек¬
трических и др.) свойств, однородно повторяющихся в данной системе.
Соответствующие термодинамические величины являются интенсивными.
Противоположное понятие ближнего порядка связано с термодинамиче¬
скими флуктуациями, которые особенно важны вблизи перехода второго
рода А о В (см. гл. 4). Флуктуации, развивающиеся, скажем, в высокотем¬
пературной фазе А, предваряют характер упорядочения фазы В. Важной
величиной, относящейся к этой теме, является размер областей флуктуа¬
ций или длина когерентности £. Тот же термин длины когерентности (или
корреляционной длины) используется для обозначения размера области ис¬
кажения в распределении параметра порядка в фазе В, вызванного локаль¬
ным возмущением (гл. 5, § 5.6), например размера центральной области
(ядра) дефекта, где распределение параметра порядка имеет особенность.
Интуитивное представление о параметре порядка можно получить на
ряде простых примеров: так, нематическая фаза является более упорядо¬
ченной, чем изотропная, в которую она переходит выше некоторой темпера¬
туры «просветления» Тс. В каждом случае выбор измеряемой физической
величины, наиболее адекватно описывающей степень порядка (так что ее
амплитуда соответствует «степени порядка»), является важным и деликат¬
ным вопросом.
Кроме амплитуды, параметр порядка может обладать еще и другой ха¬
рактеристикой — параметром вырождения (называемым также фазой),
которая учитывается значительно реже. Нас будут в равной степени инте¬
ресовать как амплитуда параметра порядка, так и параметр вырождения.
Последующие примеры прояснят различие между ними.
§ 3.1. Пространство параметра порядка
ЭЛЛ. Сверхтекучий гелий
Параметром порядка является волновая функция Бозе-конденсата:
ф — \ ф0\ ехр {ф. (ЗЛ)
^ W. Gorsky, Z. Phys. 50, 64 (1928); W. L. Bragg and E.J. Williams, Proc. Roy. Soc.
London, A 145, 699 (1934).
102
Гл. 3. Параметр порядка: амплитуда и фаза
Амплитуда \г[>о(Т,Р)\ измеряется концентрацией составляющей 4Не,
«сконденсированной» — эти атомы являются бозонами — в сверхтекучее
состояние. Величина | фо(Т, Р) \ зависит от температуры и давления и ис¬
чезает при температуре перехода из сверхтекучего в нормальное состояние
и выше. На графике (рис. 3.1) представлена «энергия конденсации» Лан¬
дау ^cond (| Фо |), минимум которой дает термодинамический потенциал при
равновесном значении | фо(Т, Р) | . Из квантовой механики хорошо извест¬
но, что изменение фазы ф в пространстве означает наличие потока частиц
j ос 1(фЧф* — ф*\7ф). Таким образом, в равновесии фаза должна быть
постоянной во всем образце, но термодинамический потенциал не зависит
от значения этой постоянной: два идеальных образца сверхтекучего 4Не
с различными фазами, находящиеся при одинаковых температуре и давле¬
нии, обладают одинаковыми значениями термодинамического потенциала.
Другими словами, каждое значение фазы соответствует некоторой реализа¬
ции равновесного состояния, так что ф является параметром вырождения.
А
р
cond
Рис. 3.1. Пространством параметра порядка для сверхтекучего 4 Не является окруж¬
ность S1 радиуса | фо (Т, Р) |, представляющая собой круговое «дно» графика сво¬
бодной энергии как функции параметра порядка = | фо{Т, Р) | ехр %ф. Все состоя¬
ния на этой окружности соответствуют одному и тому же равновесному значению
| фо(Т, Р) |, обладают одинаковой свободной энергией, но отличаются по фазе ф
Поскольку ф(г) определена по модулю 27т, она может рассматриваться
как «угол», и область изменения ф(т) может быть представлена окружно¬
стью S1 радиуса | фо(Т, Р) | (рис. 3.1). Любая точка, принадлежащая 51, со¬
ответствует идеальному равновесному состоянию с фазой ф. S1 называет¬
ся «пространством параметра порядка» (пространство ПП) сверхтекучего
4Не. Другое название пространства ПП — «пространство вырождения».
Используя терминологию, принятую в этой книге, сверхтекучее состоя¬
ние с изменяющимся в пространстве параметром вырождения ф(г) будем
называть «деформированным» состоянием. До тех пор пока эти деформа¬
ции являются слабыми, т. е. область существенного изменения ф(т) намного
§ 3.1. Пространство параметра порядка
103
больше длины когерентности амплитуду | ^о(г) | можно считать посто¬
янной. Поскольку f как раз является минимальным размером, на котором
определены интенсивные термодинамические величины, изменения ампли¬
туды ~ V| фо |, затухающие на расстояниях ~ £, не могут быть включены в
макроскопическое описание слабо деформированной среды. Следователь¬
но, функция ф(т) переводит любой непрерывный путь в слабо деформиро¬
ванной среде в некоторый непрерывный путь на S1.
Сверхтекучий 4 Не являет собой пример нетривиального пространства
ПП, но однако возникают определенные трудности в определении понятия
деформации, поскольку здесь она определена через фазу Последующие
примеры прольют некоторый свет на этот вопрос.
3.1.2. Гейзенберговский ферромагнетик
Параметром порядка является интенсивная переменная М(Т, г) — на¬
магниченность единицы объема. В модели Гейзенберга2^ намагниченность
возникает вследствие парного взаимодействия спинов, расположенных в
периодической решетке. Взаимодействие ориентирует спины параллельно
друг другу. При повышении температуры скореллированность в ориента¬
ции спинов ослабевает и амплитуда М(Т) функции М(Т, г) монотонно
убывает. Выше так называемой температуры Кюри энтропийные эффек¬
ты пересиливают упорядочивающее взаимодействие и ферромагнитная фа¬
за переходит в парамагнитную, где спины нескоррелированны, и М = 0
(рис. 3.2).
Рис. 3.2. Величина намагниченности М как функция температуры Т; Тс —темпе¬
ратура фазового перехода второго рода между ферромагнитным и парамагнитным
состояниями
В отсутствие внешнего поля и ориентирующего спин-решеточного вза¬
имодействия направление М не определено: два однородных ферромаг¬
нетика с одинаковой амплитудой М, но различными направлениями М
обладают одинаковым термодинамическим потенциалом. Таким образом,
2) W. Heisenberg, Z. Physik 49, 619 (1928).
104
Гл. 3. Параметр порядка: амплитуда и фаза
в ферромагнетике параметром вырождения является направление М. Все
возможные ориентации М могут быть взаимно-однозначно представлены
точками на сфере радиуса М (Т), которую мы обозначим как 52. Таким об¬
разом, два состояния с разной ориентацией М отображаются двумя точками
на S2 (рис. 3.3). Если магнитное состояние «деформировано» таким обра¬
зом, что при переходе в образце от точки к точке вдоль некоторого пути 7
М непрерывно меняется при неизменной величине М, то отображение 7 на
S2 больше не является точкой, а представляет собой плавный путь Г. Сфера
S2 является пространством ПП для гейзенберговского ферромагнетика.
4
4 4
4
4
4
4 4
4
4
А
4
А
4
А
4
А
4
4
4
4
Т
4
7
4
Т
4
Т
4
/
4
4
4
4
4
Ж Ж Ж '
*
Ж
Ж "А
Ж
*
ж
Ж
Ж Ж
А.
4.
ж
Ж
А Ж
Ж
*
ж
Ж
Ж Ж
Ж
Ж Ж Ж
Рис. 3.3. Гейзенберговский изотропный ферромагнетик: разные направления век¬
тора намагниченности соответствуют различным точкам в пространстве параметра
порядка S2
3.1.3. X-Y-ферромагнетик
Рассмотрим двумерную решетку, в каждом узле которой содержится по
спину. В основном состоянии все спины параллельны и лежат в плоско¬
сти ху. Параметром порядка является двумерный вектор намагниченности,
вместо которого можно использовать комплексное число, абсолютная вели¬
чина которого зависит от температуры, а фаза ф(х, у) является параметром
вырождения и взаимно-однозначно соответствует различным ориентациям
§3.1. Пространство параметра порядка
105
вектора намагниченности. Таким образом, как и в случае сверхтекучего
4Не, пространство ПП представляет собой окружность S1 (рис. 3.4).
а
б
S
в
S
Рис. 3.4. X-Y-модедь: парамагнетик (а), однородное (б) и неоднородное (в) ферро¬
магнитные состояния. Для однородного ферромагнетика путь 7 в образце отобража¬
ется в единственную точку в пространстве параметра порядка, а в неоднородном —
в путь Г
3.1.4. Одноосные нематики
Амплитуда параметра порядка нематика будет строго определена в этой
главе несколько позже. Пока же примем амплитуду как температурно¬
зависимую скалярную величину s(T), исчезающую в изотропной фазе,
Т > Тс (рис. 3.5), и равную единице в случае ориентации всех молекул
строго в одном направлении, что при отличной от нуля температуре нико¬
гда не происходит. В реальных системах вследствие тепловых флуктуаций
s(T) всегда лежит в интервале s(Tc) < s(T) < 1.
А
Нематик
Изотропная
фаза
Тг
Т
Рис. 3.5. Типичная температурная зависимость скалярного параметра порядка при
переходе первого рода нематик-изотропная фаза
106
Гл. 3. Параметр порядка: амплитуда и фаза
Параметром вырождения является директор п(г) — усредненная ори¬
ентация молекул в некотором макроскопическом объеме, по крайней мере
порядка 3 (объем когерентности), с центром в точке г и достаточно малом,
чтобы считать п(г) неизменным (сравните с нашими рассуждениями отно¬
сительно сверхтекучей фазы 4Не). Таким образом, параметр порядка может
быть записан как sn(r) в форме, аналогичной ферромагнетику. Однако име¬
ется существенное отличие: два идеальных ферромагнетика, намагничен¬
ных в противоположных направлениях, являются разными реализациями
равновесного состояния М ф —М, в то время как sn(г) и — sn(r) пред¬
ставляют собой одну и ту же реализацию равновесной нематической фазы.
Для построения пространства ПП начнем со сферы S2 радиуса s(T).
Поскольку п эквивалентно — п, две противоположные точки на сфере отоб¬
ражают одно и то же нематическое состояние, и при определении про¬
странства ПП одноосной нематической фазы мы должны их отождествить
(рис. 3.6, а). Все пары отождествленных точек взаимно-однозначно отоб¬
ражают возможные реализации равновесия одноосной нематической фазы.
S IZ
RP
а
б
Рис. 3.6. Пространство параметра порядка для одноосной нематической фазы: на
сфере S2 содержит вдвое больше точек, чем требуется, поскольку каждая реализа¬
ция идеальной нематической фазы представлена парой противоположных точек;
сфера с отождествленными антиподными точками обозначается как S2/Z2, где
Z2 — абелева группа из двух элементов (а); полусфера с отождествлением про¬
тивоположных точек на границе (б); эта же полусфера, сплюснутая до диска, без
изменения топологических свойств (в)
Способ визуализации этой процедуры представлен на рис. 3.6. Разре¬
жем S2 по любому большому кругу и оставим одну полусферу. Любая точка
полусферы, за исключением граничных, взаимно-однозначно отображает
идеальный нематик, на границе же мы все еще должны отождествлять диа¬
метрально противоположные точки (рис. 3.6, б). Эта абстрактная процедура
становится более прозрачной, если отбросить метрические свойства скон¬
струированного нами «многообразия» («manifold») и сконцентрироваться
на его «топологических» свойствах; тогда мы свободны деформировать по¬
лусферы произвольным образом без введения разрезов или разрывов. Здесь
важен тот факт, что отображение различных реализаций поля директора на
§3.1. Пространство параметра порядка
107
пространство ПП однозначно соответствует таким плавным деформациям.
На самом деле, в дальнейшем нас будут интересовать только топологиче¬
ские свойства пространства ПП.
Таким образом, можно трансформировать полусферу в круг с отож¬
дествленными парами диаметрально противоположных точек на границе,
рис. 3.6,в. В результате получаем замкнутое многообразие, так называе¬
мую поверхность Боя (Boyd), реализация которой в трехмерном эвклидо¬
вом пространстве содержит самопересечения3), которые при использова¬
нии топологических свойств поверхности можно не учитывать. Действуй
мы в четырехмерном пространстве, эти самопересечения отсутствовали
бы. Найденное нами многообразие называется проективной плоскостью
и обозначается RP2. Отметим, что пунктирная линия на рис. 3.6, в является
замкнутой линией на RP2. В дальнейшем это замечание повлечет за собой
целый ряд существенных следствий.
3.1.5. Кристаллические твердые тела
Параметром порядка является функция плотности р(г) — скалярная
функция, обладающая трехмерной периодичностью:
где суммирование производится по всем векторам обратной решетки к.
Амплитуда ПП дается набором всех рь • Параметр вырождения может быть
введен следующим образом: переместим исходный кристалл на постоян¬
ную величину. Полученный таким образом кристалл является новой реа¬
лизацией той же системы в равновесии и отличается от исходного только
трансляцией. Таким образом, пространством ПП является ячейка Браве
с отождествлением границ, отстоящих на вектор решетки а;. В двумерном
случае, рис. 3.7, отождествление дает многообразие в виде двумерного то¬
ра Т2 = S1 х S1. Это пространство ПП описывает реализации кристалла,
отличающиеся на трансляцию; мы не будем рассматривать симметрию от¬
носительно поворотов, учет которой чрезвычайно усложняет пространство
ПП. Прямое обобщение на трехмерный случай дает трехмерный тор Т3 для
пространства ПП, ограниченного трансляциями (в отсутствие поворотных
элементов симметрии).
3.1.6. Переходы порядок-беспорядок в сплавах
При высоких температурах сплав CusoZnso (латунь) образует ОЦК-
решетку, узлы которой равновероятно заняты атомами Си или Zn: rjcu =
= Vzn = 1/2 (рис. 3.8,а). В наиболее упорядоченной ситуации (0К)
(3.2)
к
См. наглядное представление поверхности Боя в книге: Д. Гильберт,
С. Кон-Фоссен. Наглядная геометрия/ Пер. с нем. — 3-е изд. — М.: Наука, 1984.
С. 315-319.
108
Гл. 3. Параметр порядка: амплитуда и фаза
решетка является простой кубической: атомы Си и Zn расположены в раз¬
ных подрешетках, рис. 3.8, б.
Давайте определим ПП как величину 7/ — | г}Си — г\ъn I- При Т = 0К
в каждом конкретном узле вероятность заселения атомом Си оказывается
А
В
-5
С
D
1„ о1
SlxS
Рис. 3.7. Пространство параметра порядка двумерного кристалла
Т2 = Sl х S1
тор
Zn
Си
О
О
о
о
о
<?
6
о
0-1
о
г
о
в
Рис. 3.8. Неупорядоченная (а) и упорядоченная (б) структуры сплава CusoZnso; дву¬
мерный срез антифазной границы, разделяющей домены в упорядоченной фазе (в)
§ 3.2. Характерный для жидких кристаллов параметр порядка: директор 109
либо rjcu = 1, либо rjcu = 0; следовательно 7? = 1. Между 0 К и тем¬
пературой фазового перехода Тс величина ту изменяется в пределах от I
до 0. В высокотемпературной фазе г) = 0. Отметим, что, хотя фазовый пе¬
реход и происходит непрерывно, при Т — Тс происходит кардинальное
изменение симметрии, причем группа симметрии низкотемпературной фа¬
зы является подгруппой высокотемпературной. Это является характерной
чертой фазовых переходов второго рода, то же справедливо и для перехо¬
дов нормальная-сверхтекучая жидкость и парамегнетик - ферромагнетик,
с которыми мы уже встречались.
Теперь рассмотрим ОЦК-решетку из узлов, занятых атомами Си и Zn
в полностью упорядоченном состоянии. Имеется два способа заселения
узлов с г] — 1, но с разными t)qu (т]си = 1 или 0), соответствующие двум
возможным доменам. Если оба домена присутствуют в одном образце, то их
разделяет стенка из дефектов (антифазная граница, рис. 3.8,в). Простран¬
ство ПП (ограниченное рассмотрением фиксированной решетки узлов) со¬
стоит из двух точек.
§ 3.2. Характерный для жидких кристаллов параметр
порядка: директор
3.2.1. Микроскопическое определение
Интуитивно директор п(г) одноосного нематика можно себе предста¬
вить как результат усреднения ориентации осей а индивидуальных моле¬
кул. Противоположные направления +а и —а должны быть взяты с оди¬
наковой микроскопической вероятностью, поскольку в нематической фазе
противоположные направления молекул не различаются. Для того чтобы
обеспечить непрерывность функции п(г), усреднение должно быть про¬
изведено по объему: (а) большему по сравнению с молекулярными раз¬
мерами, но (б) малому по сравнению с характерными размерами дефор¬
мации нематической фазы. Подобные требования постоянно встречаются
при описании квазиравновесных систем: первое условие уточняет понятие
«макроскопический», а второе позволяет рассматривать локальное термо¬
динамическое равновесие.
Представленная выше интуитивная картина полезна, но не вполне обо¬
снована, поскольку отсутствует последовательное определение молекуляр¬
ных осей а, возможно, за исключением абсолютно жестких неполярных
молекул, как, например, вирус табачной мозаики (ВТМ). Тем не менее цен-
тросимметричность нематической фазы требует составления параметра по¬
рядка из четных по а величин. Таким образом, собственный нематический
параметр порядка определяется как симметричный тензор второго ранга Q с
нулевым шпуром (см. п. 3.2.2). Директор п определяет направления главной
оси тензора Q (в такой одноосной нематической фазе Q имеет цилиндриче¬
скую симметрию). Заметим, что директор п представляет собой прекрасно
наблюдаемую макроскопическую величину, а именно оптическую ось од¬
ноосного нематика.
110 Гл. 3. Параметр порядка: амплитуда и фаза
Понятие «директора» сохраняет смысл и в других жидкокристалличе¬
ских фазах. Это очевидно в случаях смектика А и холестерика, являющегося
(в равновесии) ничем иным, как деформированным, а именно закрученным,
нематиком. В случаях смектических SmC- и 8тС*-фаз (рис. 2.24 и 2.25)
имеются некоторые тонкости, которые обсуждались в пп. 2.2.3.2.
После этих замечаний вернемся к одноосной нематической фазе. Ди¬
ректор п не несет в себе информации о степени ориентационного упо¬
рядочения. Выберем ось Z вдоль директора п и определим направления
в пространстве с помощью полярного 0 и азимутального ip углов. Пусть
/(0, <р) dft — вероятность найти молекулярную ось а внутри телесного
угла бЮ = sin# d0 dtp вокруг направления (О, ф). В силу эквивалентности
-haи — ав объеме нематика, }{0,ф) = /(7г —0, <р + 7г). Очевидно, что /(0, <£>)
не зависит от азимутального угла поэтому 9/(0, ф)/дip = 0. Поскольку
все ориентации молекул содержатся в интервале 0 ^ 0 < 7Г, нормировка
функции /(0, <р) = /(0) записывается в виде
С
7Г
f>n п
)/(0, (/?) dVt ~ 2п
/(0) sin в d0 = 1. (3.3)
о
Выше температуры перехода нематик - изотропная жидкость, в изо¬
тропной фазе, /(0) не зависит от угла и ниже точки перехода имеет макси¬
мум при 0 = 0. Степень ориентационного порядка измеряется величиной s,
впервые введенной Цветковым4):
7Г
i(3cos2 0 — 1) = 27Г
2
^2(cos 0)/(0) sin 0 d0, (3.4)
о
1
где Р2 (cos 0) = - (3 cos2 0 — 1) — полином Лежандра второго порядка, а уг-
ловые скобки означают усреднение по всем ориентациям молекул. В изо¬
тропной фазе все пространственные ориентации молекул равновероятны;
следовательно /(0) = —, и из (3.3) и (3.4) следует s = 0. Для максималь-
47Г
но упорядоченного состояния единственной ориентацией молекул является
0 = 0, следовательно /(0) = —£(0), где 6(0) —^-функция Дирака, и s = 1.
471-
Скаляр s может использоваться в качестве амплитуды параметра порядка:
его часто называют скалярным параметром порядка.
Отметим, что, если /(0) ориентирована случайно в направлении, пер-
7Г 1
пендикулярном п, и локализована, т. е. 0 = -, из (3.4) получается s = —
2 2
V. N. Tsvetkov, Acta Physicochim. USSR 16, 132 (1942).
§ 3.2. Характерный для жидких кристаллов параметр порядка: директор 1 1 1
так что s изменяется от 5 = — - до s — 1. Однако при s < 0 физическая
2
1
картина существенно меняется, например s — — - соответствует равнове-
2
роятному распределению молекулярных осей в плоскости, перпендикуляр¬
ной директору (рис. 3.9); такое распределение может быть реализовано на
поверхности жидкого кристалла.
Рис. 3.9. Распределение молекулярных осей в состоянии со скалярным параметром
1
порядка s = —
2
Типичная экспериментальная зависимость s(T) для термотропного
нематического материала схематично представлена на рис. 3.5. Для прямого
измерения 5 может быть использован метод ядерного магнитного резонан¬
са (ЯМР), спектры которого отражают движение ядер (обычно водорода
или дейтерия), усредненное как на молекулярном (вокруг оси а), так и на
макроскопическом (вокруг директора п) уровнях. Имеется также множе¬
ство косвенных методов измерения s, основанных на соотношениях между
макроскопическими свойствами нематической фазы и параметром порядка.
3.2.2. Макроскопические свойства
Макроскопические свойства нематической фазы, такие как диэлектри¬
ческая и магнитная проницаемость, измеренные в различных направлениях,
зависят как от директора п, так и от скалярного параметра порядка s. Мы
рассматриваем одноосный нематик и используем единицы СИ5^, придер¬
живаясь обозначений, принятых в книге Джэксона (Jackson, 1998).
3.2.2.1. Диэлектрические свойства. Электрическое поле Е, прило¬
женное к диэлектрической среде, вызывает образование локальных диполь-
ных моментов и, таким образом, создает электрическую поляризацию Р.
Функциональная зависимость Р(Е) определяется свойствами материала
Система СИ основана на метре, килограмме, секунде и ампере для электри¬
ческого тока, так что она является МКСА-системой. В этой системе введены две
постоянные, а именно «магнитная проницаемость вакуума» (магнитная постоянная)
р,0 = 47г х 10~7 Гн/м и «диэлектрическая проницаемость вакуума» (электрическая
постоянная) eq = 8,8541878 х 10“12 Ф/м, связанные соотношением 1/(до£о) = с2,
где с = 2,99792458 ... х 108м/с — скорость света в вакууме.
112
Гл. 3. Параметр порядка: амплитуда и фаза
и, вообще говоря, неизвестна. Однако можно разложить Р в ряд по степе¬
ням Е:
Р = Р0+ (д*Л
ЗЕ
)
• Е -j-..., (3.5)
Е=0
где Ро — вектор спонтанной поляризации. В ориентационно упорядочен¬
ной среде поляризация Ро могла бы быть отличной от нуля вследствие раз¬
личных явлений, таких как флексоэлектрический эффект (возникновение
поляризации вследствие ориентационной деформации п = п(г)); эффект
появления поляризации, вызванной неоднородностью скалярного парамет¬
ра порядка s — s(г); поверхностная поляризация, вызванная нарушением
симметрии между п и -п на поверхности. Мы полагаем Р0 = 0. Для
слабых полей, разложение (3.5) можно ограничить линейным членом
Pi — (3.6)
где ctij — компоненты тензора диэлектрической проницаемости а,
а бо — диэлектрическая постоянная5^ . Заметим, что векторы Р и Е, вообще
говоря, ориентированы по-разному. В изотропной среде все направления эк¬
вивалентны, и поляризация Р параллельна Е. Вспомнив, что электрическая
индукция является векторной суммой электрического поля и наведенной
поляризации, D = е0Е + Р, получаем
D{ = £о Ei + EoaijEj — £o{$ij + OLij)Ej — eoSijEj, (3.7)
где £ij — компоненты тензора относительной диэлектрической восприим¬
чивости ё, a Sij - ^-символ Кронекера.
Тензор Sij симметричен относительно перестановки индексов; в декар¬
товой системе координат с осью Z вдоль директора п он диагонален. Два
главных значения, соответствующие главным осям, перпендикулярным п,
совпадают вследствие цилиндрической симметрии одноосного нематика.
Так что в этой системе координат
(3.8)
В произвольной системе координат Е{3 ~ £_]_(% 4- где еа = ец —
~ £± - - диэлектрическая анизотропия жидкого кристалла. Диэлектриче¬
ские проницаемости ец и е^ зависят от частоты. На оптических частотах
£|) и е± напрямую связаны с показателями преломления среды (п. 3.3.2).
Низкочастотные проницаемости £ц и е± обычно имеют порядок (1 ... 10),
а диэлектрическая анизотропия может быть как положительной, так и от¬
рицательной, в зависимости от структуры молекул. Например, для 5СВ
(рис. 2.12)еа « 13, а для МВВА еа « —0,7 при 25 °С; имеются материалы,
у которых £а меняет знак при изменении температуры, см. книгу Блинова
и Чигринова, 1994, и Блинова, 1978.
§ 3.2. Характерный для жидких кристаллов параметр порядка: директор 1 13
3.2.2.2. Магнитные свойства. Внешнее магнитное поле с индукцией В,
будучи приложенным к жидкому кристаллу, наводит в нем намагниченность
М = - Н, где ро — магнитная проницаемость вакуума, а Н, явля¬
ясь аналогом электрической индукциии D, называется напряженностью
магнитного поля; В часто называется плотностью магнитного потока. Для
слабых полей намагниченность можно считать линейно зависящей от поля,
Mi = Xij Hj' Намагниченность может быть записана и через компоненты
вектора В :
Mi — (Лд Xij$j: (3*9)
где г, j = х, у, z]\ij — Xji—компоненты симметричного тензора магнит¬
ной восприимчивости х- Последнее выражение записано в предположении
малости эффектов локального поля, что оправдано малостью Xij (~ Ю”5
в единицах СИ, в единицах СГС Xij меньше в 47т раз).
Как и для диэлектрической проницаемости, два главных значения х сов¬
падают вследствие цилиндрической симметрии. Соответственно в системе
координат с осью г вдоль п тензор х можно записать в виде
/Хх 0 0 \
х= о XX о . (3.10)
V о 0 х\\/
В произвольной системе координат Xij = Xx^ij+Xa^i^j, гдех<г = Х|| —
— Х± — анизотропия магнитной восприимчивости. В типичных нематиках,
таких как 5СВ или МВВА, хц < 0и%± < 0 — материал является диамагне¬
тиком, т. е. намагниченность противоположна приложенному полю. Пара¬
магнитные жидкие кристаллы могут быть получены путем синтеза метал¬
лосодержащих молекул. Ферромагнитной мезофазы в однокомпонентном
веществе до сих пор обнаружено не было, однако ферромагнитные мезофа¬
зы могут быть получены путем добавления в жидкий кристалл маленьких
(но макроскопических) ферромагнитных частиц. В дальнейшем мы огра¬
ничимся рассмотрением диамагнитных материалов. Как правило, диамаг¬
нитная анизотропия положительна, Ха > 0, и п ориентируется вдоль поля.
Причиной являются круговые орбитальные токи в ароматических кольцах
молекул, таких как 5СВ (рис. 2.12) и МВВА (рис. 2.14), дающие большой
отрицательный вклад в магнитную восприимчивость в направлении, пер¬
пендикулярном плоскости колец (а значит, и длинным осям молекул), т. е.
I X_l | > \х\\ I-
Анизотропия макроскопических свойств вызвана ориентационным упо¬
рядочением жидких кристаллов. Измерения анизотропии позволяют опре¬
делить степень ориентационного порядка s. Магнитные измерения особен¬
но удобны по сравнению с диэлектрическими вследствие пренебрежимой
малости эффектов локального поля. Это нетрудно понять, если вспомнить,
что величины магнитной восприимчивости (~ 10-5) намного меньше 1,
и можно написать
+ Xij)Hj — ^0(1 + Х± )Hi + Mo XaninjHj'
(3.11)
114
Гл. 3. Параметр порядка: амплитуда и фаза
Соотношение между s и анизотропиеи магнитнои восприимчивости
нетрудно установить, если ввести тензор магнитной восприимчивости к*
индивидуальной молекулы. В силу крайней слабости межмолекулярного
магнитного взаимодействия, макроскопическая восприимчивость может
быть получена суммированием молекулярных восприимчивостей с учетом
функции распределения молекул по ориентациям f(9) (для диэлектриче¬
ской восприимчивости такое суммирование даст неверный результат из-за
сильного влияния на молекулярный диполь окружающих диполей). В ре¬
зультате суммирования получаем (см. задачу 3.2)
Xa = N(*'{l-*'±)s, (3.12)
где N — число молекул в единице объема, х|| и — молекулярные
восприимчивости вдоль оси молекулы и в перпендикулярных направлениях
(вырожденные на нулевой частоте).
Таким образом, степень упорядочения нематической системы может
быть определена через макроскопическое свойство. В изотропной фазе
Ха = 0 и s = 0. Пусть Trx = Ххх + Хуу + Xzz; можно построить сим¬
метричный тензор с нулевым шпуром
Qij = Q (xij - ^ijTry?). (3.13)
Нетрудно убедиться, что Tr Q — QXx + Qyy + Qzz — 0. В изотропной
фазе все компоненты Q исчезают, а в одноосной нематической фазе они
пропорциональны s:
0 0
-Ха/з 0 ) . (3.14)
0 2Ха/3
Величина множителя Q значения не имеет, для удобства мы можем
выбрать(2 = N~l(x'n —Учитывая, что Xij = получаем
Qij = s(T) [щщ - -Sij) . (3.15)
Тензорный параметр порядка позволяет описать также и двуосную нема¬
тическую фазу:
Qij = s (jbiTij - +p{klj - rriimj), (3.16)
где (n, 1, m — [nl]) — три ортогональных директора, ар — «параметр дву-
осности»; р = 0 в одноосной фазе.
Анизотропия жидких кристаллов и возможность их ориентирования
внешним электрическим или магнитным полем нашли многочисленные
§ 3.3. Распространение света в анизотропных средах
115
практические применения. Любая жидкокристаллическая ячейка ограни¬
чена, например, парой параллельных стеклянных пластинок. Ориентирую¬
щее влияние подложек может предотвращать переориентацию директора в
слабом внешнем поле. Однако если поле превышает некоторую пороговую
величину, оно в конце концов преодолевает как связь директора с подлож¬
кой, так и объемную упругость нематика и переориентирует директор. Это
явление называется эффектом Фредерикса и впервые было открыто в маг¬
нитном поле6) (см. также п. 5.4.3 и 13.2.3). После удаления поля связь
с поверхностью восстанавливает первоначальное распределение директо¬
ра. Таким образом, при наличии связи с поверхностью можно переключать
ориентацию директора с помощью внешнего поля. Эффект Фредерикса,
в основном его диэлектрический вариант, используется во многих электро-
оптических устройствах (дисплеях, оптических затворах и т. д.). Обычно
слой жидкого кристалла помещается между двумя прозрачными электро¬
проводящими пластинами (например, стекло с покрытием из смеси окислов
индия и олова), покрытыми подходящим ориентирующим слоем (например,
буферной полимерной пленкой). Напряжение, прикладываемое к образцу,
управляет распределением директора, а значит, и оптическими свойствами
ячейки. Заметим, что имеется множество факторов, таких как нелокаль¬
ный характер распределения электрического поля в искаженном жидком
кристалле, конечная электропроводность, флексоэлектричество (см. § 5.3),
поверхностная поляризация (п. 13.2.3) и т.п., значительно усложняющих
электрические эффекты в нематиках по сравнению с их магнитными двой¬
никами.
§ 3.3. Распространение света в анизотропных средах;
приложение к полю директора
Оптические наблюдения анизотропных сред, таких как кристаллы и жид¬
кие кристаллы, внесли огромный вклад в понимание структуры и свойств
конденсированного состояния. Знаменитые исследования Леманом текстур
под микроскопом 7) нашли свое практическое осуществление в определе¬
нии фаз и структур Жоржем Фриделем81 Тонкие (несколько микрон) слои
жидкого кристалла между стеклянными пластинами легко приготавливают¬
ся; большое двупреломление этих материалов приводит к хорошему кон¬
трасту между областями с различной ориентацией оптической оси (которая
в одноосных нематиках и смектических A-фазах совпадает с директо¬
ром). Большинство жидкокристаллических фаз легко идентифицируется по
^ V Frederiks and V Tsvetkov, Sov. Phys. 6, 490 (1934); V Freedericksz and V. Zolina,
Trans. Faraday Soc. 29, 919 (1933).
O. Lehmann, Fliissige fCristalle; W. Engelmann, Leipzig, 1904; Fliissige Kristalle
und die Theorie des Lebens; J. Ambr. Barth, 1908.
G. Friedel. Les etats mesomorphes de lamatiere, Ann. de Phys. 18, 273 (1922).
116
Гл. 3. Параметр порядка: амплитуда и фаза
наблюдению текстур и дефектов в скрещенных поляроидах. Более того,
приложением к ячейке жидкого кристалла электрического поля можно из¬
менить распределение директора, а следовательно, как только что указы¬
валось, и соответствующие оптические свойства. Поэтому для понимания
дальнейшего материала крайне важно усвоить основы теории распростра¬
нения света в анизотропных средах.
3.3.1. Уравнение Френеля
Распространение света в однородной среде описывается уравнениями
Максвелла, которые в отсутствие свободных зарядов и токов выглядят в си¬
стеме СИ следующим образом:
v х е = ~дв/ы, (3.17)
V х н = эв/dt, (3.18)
VB = О, (3.19)
VD = 0. (3.20)
Эти уравнения должны быть дополнены соотношениями, описывающи¬
ми отклик среды на электромагнитное поле распространяющейся
волны (так называемыми материальными уравнениями). Поскольку нас ин¬
тересуют линейные эффекты, когда поляризация и намагниченность, инду¬
цированные полем, пропорциональны полю, материальными уравнениями
могут служить соотношения (3.7) и (3.11). Отметим, что задача распростра¬
нения света соответствует высокочастотному (~ 1015 Гц) электромагнит¬
ному полю. Диэлектрическая восприимчивость зависит от частоты, и ее
величина на оптических частотах (порядка единицы) обычно существенно
меньше, чем статические или низкочастотные (си ~ 103 Гц) значения, осо¬
бенно для материалов, состоящих из полярных молекул. Причина состоит
в том, что в низкочастотную восприимчивость существенный вклад вносят
процессы переориентации постоянных молекулярных диполей, практиче¬
ски не участвующие в отклике на оптических частотах (так, например, для
воды статическая диэлектрическая проницаемость е « 78, а на оптических
частотах 5 « 1,78). К тому же в отсутствие поглощения все компоненты
Eij вещественны. Более того, всеми магнитными эффектами можно прене¬
бречь, положив М = 0, и (3.11) сводится к В = /аоН.
Рассмотрим монохроматическую плоскую волну Е(г, t) — Е0 ехр(гк х
х г - icot), H(r, t) = ... и т. д. Здесь г — радиус-вектор точки наблюдения,
со — частота, а к — волновой вектор. В непроводящей среде к = 2тг/Х — и/и
является вещественным числом, Л — длина волны, a v — ее фазовая ско¬
рость. Уравнения Максвелла принимают вид
к х Е —
= и В,
(3.21)
к х Н г
= cjD,
(3.22)
кН г
- 0,
(3.23)
kD =
= 0.
(3.24)
§ 3.3. Распространение света в анизотропных средах
117
Последняя система уравнений означает взаимную перпендикулярность
векторов k, D и Н. Кроме того, Н JL Е. Так как Н перпендикулярно трем
векторам k, D и Е, эти векторы лежат в одной плоскости. Поток энергии
задается вектором Пойнтинга S — [Е х Н]. В общем случае в анизотроп¬
ной среде направления векторов S и к не совпадают (рис. ЗЛО). Фаза волны
изменяется в направлении к, а энергия переносится в направлении S. В изо¬
тропной среде оба направления совпадают.
Рис. ЗЛО. Ориентация векторов, описывающих монохроматическую плоскую вол¬
ну в анизотропном диэлектрике с различающимися направлениями электрического
поля Е и индукции D. Закрашенная плоскость, перпендикулярная векторам Н||В,
содержит векторы Е, D, S и к. Направление к, вдоль которого изменяется фаза
волны, не совпадает с направлением S. — [Ex Н] распространения энергии S _L Е,
ak±D
Исключая Н из (3.21) и (3.22), получаем
wVoD = к2Е - k(Ek). (3.25)
Это уравнение должно быть совместимо с материальным уравнением (3.7),
D = еЕ. Следовательно
(N4rj - N{Nj - ei3)Ej - 0, (3.26)
где был введен вектор «показателя преломления» N = к—— , направ-
UJ^/SQflO
ленный вдоль к. Длина N этого вектора называется показателем прелом¬
ления данной волны в данной среде; она обратно пропорциональна фазо¬
вой скорости и волны, распространяющейся в среде. Поскольку к = и/и,
а 1 / о До — скорость света с в пустоте, то N = с/ v.
118
Гл. 3. Параметр порядка: амплитуда и фаза
Условием существования нетривиального решения однородной систе¬
мы линейных уравнений (3.26) является обращение в нуль детерминанта.
Это условие приводит к известному уравнению Френеля, которое в системе
главных осей тензора е выглядит следующим образом:
Det (k,cj) = N2(exN2 + eyNy + £ZN2)-
— [£xN2(£y + Ez) + SyNy (ex 4- £z) + £ZN2 (ex + Ey)\ + ExEyEz = 0.
(3.27)
В одноосной среде г содержит только две независимые величины, е
и уравнение Френеля принимает вид
И Е±
Det(k,w) = (TV2 -e±)(e{lN2z +e±(N* + N2y) -£||ex) = 0.
(3.28)
3.3.2. Обыкновенная и необыкновенная волны
Из уравнения (3.28) следует, что в одноосной среде поверхность показа¬
телей преломления £ (называемая еще поверхностью волновых векторов),
являющаяся поверхностью четвертого порядка в пространстве показателей
преломления, распадается на сферу радиуса N2 — е± и эллипсоид враще-
дг2 ДГ2 + N2
ния — + — - = 1. Имеются две точки, в которых эти поверхности
£||
касаются; ось, соединяющая эти точки, является оптической осью немати¬
ка. Таким образом, имеются две волны, распространяющиеся в одноосной
среде. Для одной из них, так называемой обыкновенной волны (оволны),
нематик ведет себя как изотропная среда с показателем преломления п0 =
= у/ё±. Вторая волна — это необыкновенная волна (е-волна) с показате¬
лем преломления N, зависящим от направления распространения. Вводя
угол в между оптической осью и волновым вектором k, N2 = N2 cos2 в,
N2 + N2 = N2 sin2 в, получаем эффективный показатель преломления
необыкновенной волны как функцию направления луча в:
1 cos2 6 sin2 в ATfn\ П°Пе /л ллч
7^ = ~Г + —Г' или = /2 (3'29)
N2(9) п20 п2 у п\ cos2 в + п£ smJ в
где пе — у/Щ — необыкновенный показатель преломления.
Если пе < п0, то сфера находится снаружи эллипсоида (оптически
отрицательный нематик, обычный случай для веществ, состоящих из дис¬
кообразных молекул); при пе > п0 сфера находится внутри эллипсоида (оп¬
тически положительный нематик, типичная ситуация для стержнеобразных
молекул), рис. 3.11. При распространении волны вдоль оптической оси ско¬
рости обыкновенной и необыкновенной волн совпадают, и они становятся
неразличимыми. Показатели преломления п0 и пе обратно пропорциональ¬
ны соответствующим фазовым скоростям v световых волн в среде.
§ 3.3. Распространение света в анизотропных средах
119
►
Оптически отрицательный
кристалл
а
Оптически положительный
кристалл
б
Рис. 3.11. Поверхности показателей преломления для оптически отрицательного
(а) и оптически положительного (б) кристалла
Поскольку к = w/i/, то п0 — с/и0 и пе = с/ие. Типичные термотроп¬
ные нематики имеют дву преломление пе — п0 « 0,1 — 0,2, в лиотропных
системах оно обычно несколько меньше.
Используя уравнения (3,26), можно найти поляризации обыкновенной
и необыкновенной волн (рис. 3.12). Без потери общности будем считать
векторы к и N лежащими в плоскости xz (т. е. Ny = 0). Тогда два решения
уравнения (3.26) имеют следующие поляризации:
Рис. 3.12. Поверхности показателей преломления для оптически отрицательного
одноосного кристалла с указанием направлений волнового вектора к, вектора Пойн-
тинга (луча) S, электрического поля Е и индукции D для обыкновенной (окруж¬
ность) и необыкновенной (эллипс) компонент
120
Гл. 3. Параметр порядка: амплитуда и фаза
1. о-волна поляризована вдоль оси у, нормальной к оптической оси п
и волновому вектору к:
Е(х0) = 0, Е{уо) ф 0, Е[о) = 0. (3.30)
Поскольку Dx = е±Е^ = 0, Dy = £±Е^ ф 0 и Dz — ецЕ^ = 0
для о-волны D||E и S||k, групповая и фазовая скорости совпадают, равны
= с/п0 и не зависят от направления распространения;
2. е-волна имеет компоненты
Е^ф О, Е^= 0, Е^ф 0, (3.31)
где
E(ze) N? -s± £j_ TV
X
4e) NxNz eu Nz
(3.32)
Уравнение (3.32) показывает, что Е-вектор е-волны направлен по ка-
N2 N2
сательной к эллипсоиду оптической индикатрисы —- + —— = 1. Чтобы
е± £ 11
убедиться в этом, достаточно вспомнить, что уравнение касательной к кри¬
вой, задаваемой уравнением ip(Nx, Nz) — 0, имеет вид tga — —
d(p/dNz
= — — —, где а — угол между касательной и осью х. Направление S легко
£\\ Nz
найти из условия перпендикулярности векторов S и Е:
£_l Nx ^
"ы = —ТГ* (3.3л)
£ц Nz
3.3.3. Наблюдения в поляризованном свете. Микроскопия
Заметим, что директор всегда лежит в плоскости поляризации е-волны
и перпендикулярен вектору Е для о-волны. Это правило весьма полезно
при наблюдениях в поляризованном свете.
3.3.3.1. Интенсивность проходящего света. Шлирен-текстура. Рас¬
смотрим слой нематика, заключенный между двумя стеклянными пластин¬
ками и помещенный в скрещенные поляроиды. Директор ориентируется
в плоскости слоя (рис. 3.13) и изменяется в зависимости от координат
в плоскости ху (предполагается, что директор не зависит от вертикальной
координаты z). Луч света падает на ячейку перпендикулярно, вдоль оси 2.
Поляризатор, расположенный между источником света и образцом, пре¬
образует падающий свет в линейно поляризованный. В нематике линейно
поляризованная волна с амплитудой А и интенсивностью /о = А2 расщеп¬
ляется на обыкновенную и необыкновенную волны со взаимно перпендику¬
лярными поляризациями и амплитудами A sin/3 и A cos/? соответственно,
§ 3.3. Распространение света в анизотропных средах
121
Анализатор
d
Рис. 3.13. Прохождение света через поляризатор, одноосный слой и анализатор
fi(x,y) — угол между локальным направлением п(ж, у) и плоскостью по¬
ляризации падающего света. На точке входа колебания падающего света
происходят в фазе. Однако для прохождения через образец обыкновенной
и необыкновенной волнам требуется различное время — n0d/c и ned/c
соответственно. На выходной поверхности колебания электрического поля
A sin (3 cos (u)t - ~n0d) и A cos (3 cos (yjt - ^-ned) приобретают фазовый
сдвиг A(p
27id
Ao
Ao
(ne — n0), где Ло —длина волны в вакууме. Проекции этих
колебаний на плоскость поляризации анализатора даются выражениями
а = A sin /? cos (3 cos (cot — ~no d ] ,
b = — A sin f3 cos /3 cos ( cot
2n
Ao
(3.34)
nP d
122
Гл. 3. Параметр порядка: амплитуда и фаза
Сложение двух колебаний с одинаковой частотой А\ cos (cot 4- <pi) и
А2 cos (ut + ip2) дает колебание Л cos (tut + ф) с амплитудой, определяе¬
мой уравнением А2 = А\ + А\ + 2А1А2 cos (чр\ — <р2). Таким образом,
анализатор преобразует зависящую от (х, у) разность фаз в интенсивность
прошедшего света 1(х, у) = А2. Из (3.34) получаем для интенсивности
света, прошедшего через скрещенные поляроиды и нематический образец:
J = Jo sin2 2/3 sin
7id / \
— (Пе ~ П0)
Ао
(3.35 а)
В последнем уравнении предполагается, что вектор п перпендикулярен
оси z. Если п составляет с осью z постоянный угол 0, то (3.35 а) принимает
вид [см. (3.29)]:
/ = /0 sin2 2/3 sin
7ГЙ / п0пе
I - —. --г.. —
Aq V Vnl cos2 ^ sin2 ^
(3.35 6)
Разумеется, для описания оптических свойств систем со сложной конфигу¬
рацией директора и нетривиальной геометрией (например, внутри капель
жидкого кристалла или ячеек, управляемых полем) требуется более основа¬
тельный подход; интересующиеся решением подобных задач могут найти
их в многочисленных обзорах, см., например, книгу Блинова и Чигринова
(1994).
Уравнения (3.35) являются основополагающими при идентификации
жидкокристаллических текстур. Во-первых, заметим, что фазовый сдвиг, а
значит и I, зависит от Ао* В результате при освещении образца белым светом
получаем цветное изображение текстуры (рис 3.14). Наиболее яркие интер¬
ференционные цвета наблюдаются при (ne - n0)/d «(1ч- 3)Ао. Для ти¬
пичных значений (пе - п0) и 0,2, Ао и 500 нм, диапазон толщин, дающих
насыщенные цвета, составляет d & (1 4* 10) мкм. Во-вторых, наклон 0 ди¬
ректора кардинально меняет фазовый сдвиг. При n\\z (так называемая го-
меотропная ориентация, 0 = 0) образец выглядит черным: распространя¬
ется только обыкновенная волна и, согласно (3.35 б), / = 0. В-третьих, при
в > 0, но /? = 0, ±7г/2,... текстура все равно выглядит черной, I = 0 даже в
монохроматическом свете. В образце с искажениями директора в плоскости
п(х, у), как только п (или его горизонтальная проекция) становится парал¬
лельным или перпендикулярным оси поляризатора, прошедшая световая
волна становится либо чисто необыкновенной, либо чисто обыкновенной,
и соответствующая область текстуры выглядит черной. Рисунок 3.14 как раз
и является примером такой текстуры с темными «полосами погасаний». По¬
лосы сходятся в центрах топологических дефектов. Текстура с дефектами
и темными полосами и называется шлирен-текстурой.
В принципе, вращая скрещенные поляроиды, можно полностью восста¬
новить распределение директора в шлирен-текстуре. Правда, здесь имеется
неоднозначность: поскольку I ~ sin2 2/?, реконструкция приводит к двум
возможным вариантам распределения директора — /3(х, у)и(3(х, 2/) + 7г/2.
§ 3.3. Распространение света в анизотропных средах
123
Для однозначного восстановления распределения директора в плоскости
можно использовать оптический компенсатор или кварцевую пластинку.
Рис. 3.14. Шлирен-текстура в тонкой (« 1 мкм) пленке нематика 5СВ на глицерино¬
вой подложке. Отметим интерференционные цвета: темные полосы соответствуют
областям, в которых директор параллелен оси поляризатора или анализатора. Узлы,
в которых сходятся четыре полосы, соответствуют ядрам топологических точечных
дефектов
Компенсаторами называются пластинки с известным фазовым сдвигом.
Например, красная пластинка I дает фазовый сдвиг в 575 нм. В пластинке
определены два направления: одно — с мимимальным показателем прелом¬
ления птin («быстрое направление» ), а второе — с максимальным nmax
(«медленное направление» ). Компенсатор помещается между образцом и
анализатором под углом 45 °С к направлениям поляризатора и анализатора.
Черные полосы становятся красными, так как в этих местах образец дает
нулевую фазовую задержку, и результирующая фазовая задержка опреде¬
ляется компенсатором. Области с директором, параллельным быстрому и
медленному направлениям, приобретают различные интерференционные
цвета, и, таким образом, их можно идентифицировать. Без компенсатора
эти области имели бы одинаковую яркость, так как в уравнении (3.35) для
4 *) _ « О 7Г
обеих областей I ос sin 2р = sin - — 1.
2
3.3.3.2. Принцип Ферма и путь необыкновенного луча. Если на¬
блюдать необыкновенный луч, его интенсивность флуктуирует вследствие
случайных изменений во времени величины N(к) (мерцание), вызванных
тепловыми колебаниями поля директора; в обыкновенном луче мерцание
не наблюдается.
124
Гл. 3. Параметр порядка: амплитуда и фаза
Принцип Ферма гласит, что из всех возможных путей между точками А
и В свет выбирает тот, для которого интеграл
в
Т
N(k,r)dr (3.36)
минимален вдоль того пути, по которому действительно распространяется
энергия (т. е. вдоль огибающей вектора Пойнтинга S); здесь dr — вектор,
касательный к пути. Теперь разовьем некоторые идеи по использованию
принципа Ферма для вычисления пути необыкновенного луча, ограничи-
ваясь одноосной средой.
Согласно (3.36), обыкновенный луч, для которого 7V(k) = п0, распро¬
страняется по прямой в слабо деформированном нематике, слабо в смыс¬
ле малости градиента директора по сравнению с обратной длиной волны
света, что соответствует условиям применимости геометрической оптики.
В данном случае волновой вектор к, вектор Пойнтинга S и элемент пути
dr колинеарны. С другой стороны, распространение необыкновенного луча
значительно сложнее, поскольку к уже не направлен вдоль векторов S и dr
и использование (3.36) становится проблематичным. К счастью, если пе¬
реформулировать принцип Ферма через скорости распространения света,
ситуация сразу становится определенной: интеграл Ферма Т на самом деле
пропорционален продолжительности пути между А и В (для обыкновенно¬
го луча n0 = c/vо, см. ниже), и в действительности принцип Ферма требует
минимальности времени прохождения пути. Таким образом, принцип Фер¬
ма может быть переформулирован как минимальность интеграла
в
Т
-М, (3.37)
S
А
где s — s(t,r) — отношение (скалярной) групповой скорости к скорости
света (т. е. величина s пропорциональна вектору Пойнтинга), at = dr/dl —
единичный вектор, касательный к пути. Введем вектор луча s, направ¬
ленный вдоль вектора Пойнтинга S, модуль же определяется из условия
sN = 1. Легко показать, что | s | = 5. Соотношение sN = 1 подчеркивает
сопряженный характер входящих в него величин. Вектор S перпендикуля¬
рен оптической индикатрисе (рис. 3.12):
N2 Jsf2 + TV2
й*. + v = 1. (3.38)
£ j_ £\
Таким образом, sx = Nx/e\\,sy = Ny/e\\^sz = Nz/e±_, что удовлетворяет
условию sN = 1. Подстановка в (3.38) дает
£LS2z +£||(S2 +Sy) = 1,
(3.39)
§ 3.3. Распространение света в анизотропных средах
125
откуда можно получить уравнение, сопряженное к (3.29), в виде
— — п20 cos2 ф + п2 sin2 ф. (3.40)
S2
Здесь ф — угол между вектором Пойнтинга и оптической осью. Заметим,
что s, к и оптическая ось лежат в одной плоскости.
Выражение (3.40) для s записано в системе координат, связанной с глав¬
ными осями индикатрисы; но для деформированного жидкого кристал¬
ла их следует переписать в лабораторной системе координат в виде s =
= s(t, г). При этом уравнение для пути получается интегрированием урав¬
нений Эйлера-Лагранжа, соответствующих минимуму интеграла Ферма:
0(0 _ ± 3(0 _ 0) j — 15 2, 3, (3.41)
дх{ di dti
вместе с подходящими граничными условиями (см. задачу 3.3).
3.3.3.3. Разное. Наблюдаемая в поляризованном свете картина очень
чувствительны к деформациям кручения. Рассмотрим вкратце так называе¬
мую планарную холестерическую текстуру: директор однороден в плоско¬
сти ху, но закручен вдоль нормальной к ячейке оси z (см. рис. 2.22). Про¬
стой режим «захвата поляризации волны», называемый режимом Могена9\
возникает, когда шаг геликоидальной структуры много больше длины вол¬
ны света, точнее р Ао (пе — п0), где пе и п0 — локальные показатели
преломления вдоль и поперек директора соответственно. Если падающий
свет (на входе в образец) поляризован вдоль директора или перпендику¬
лярно к нему, то прошедший свет остается линейно поляризованным, но
с плоскостью поляризации, повернутой на угол 7, где 7 — угол разворота
директора на противоположных пластинах. Если же шаг холестерической
спирали порядка Ао, р = Ао/п (п — это некоторое усредненное значение
показателя преломления), то наблюдается брэгговское отражение; холесте¬
рические образцы в отраженном свете выглядят окрашенными. Наконец,
при коротких шагах геликоида холестерик ведет себя как оптически ак¬
тивная среда с огромной вращательной способностью. Все эти эффекты
широко используются во множестве оптических приложений закрученных
нематиков и холестериков, например принцип действия дисплеев на «твист-
ячейках» основан на управляемом электрическим полем режиме Могена.
Взаимодействие света и структур, относящихся к мягкой материи, не
ограничивается проиллюстрированным выше пассивным влиянием среды
на состояние световой волны. Кроме этого имеются эффекты нелинейной
природы, в которых прохождение света вызывает изменение состояния сре¬
ды. Так, широко известны явления самофокусировки и самодифракции све-
W KJ
тового пучка при распространении в нелинейной среде, генерация второй
гармоники и другие преобразования частот и т. д. Эти эффекты можно на-
С. Mauguin. Bull. Soc. fr. Miner. Cristallogr. 34, 3 (1911).
126
Гл. 3. Параметр порядка: амплитуда и фаза
блюдать как в изотропной, так и в анизотропной среде. Имеются также
и нелинейные оптические явления, подразумевающие ориентационный по¬
рядок. Мы лишь перечислим некоторые из них, отсылая читателя к обзорам
Khoo (1995) и Simoni (1997).
1. Оптический эффект Фредерикса, т. е. переориентация директора
в электрическом поле распространяющегося светового пучка10).
2. Тепловые эффекты при распространении света. Их значение повыша¬
ется вследствие узости температурного интервала стабильности жидкокри¬
сталлических фаз; небольшие изменения температуры вызывают радикаль¬
ные изменения показателей преломления или даже фазовые превращения.
3. Изменения конформации молекул, вызванные освещением, как на¬
пример цис-транс изомеризация (рис. 3.15), способные приводить к кар¬
динальным изменениям фазовой диаграммы материала. Например, стерж¬
необразные транс-том&ръ\ дигептилазобензола (diheptylazobenzene),
показанные на рис. 3.15, способны образовывать жидкокристаллическую
фазу, в то время как r/wc-вариант — нет.
4. Фотоиндуцированная полимеризация и ориентационное упорядоче¬
ние полимеров при освещении поляризованным светом.
5. Эффект «гость-хозяин»: «чужие» молекулы или частицы могут
быть сориентированы жидкокристаллической матрицей. Если «гостем» яв¬
ляется молекула красителя, то эффект может быть использован в элек-
трооптических приборах. Флюоресцентные красители позволяют создавать
изображения трехмерных распределений директора (так называемая флю¬
оресцентная конфокальная поляризационная микроскопия11).
Задача 3.1.
а) Найти пространство параметра порядка для смектика С.
б) Сравните параметр порядка смектика С и двумерного нематика с мо¬
лекулами, параллельными границе.
в) Как изменяется пространство параметра порядка ферромагнетика
при приложении сильного магнитного поля?
10^ A. Saupe, Deformation of a nematic liquid crystal by polarized light, subm. to Phys.
Rev. Lett, on July 17, 1969; published in «Dynamics and Defects in Liquid Crystals»,
edited by P. E. Cladis and P. Palffy-Muhoray, Gordon and Breach Science Publishers,
Amsterdam, p. 441 (1998); B. Ya. Zel ’dovich, N. F. Pilipetskii,A. V. Sukhov, N. V Tabiryan,
JETP Lett. 31, 263 (1980); A. S. Zolot'ко, V. F. Kitaeva, N. Kroo, N. I. Sobolev, L. Csillag,
ibid. 32, 158 (1980); /. C. Khoo and S. L. Zhuang, Appl. Phys. Lett. 37, 3 (1980).
/. /. Smalyukh, S. V Shiyanovskii and O. D. Lavrentovich, Chem. Phys. Lett. 336, 88
(2001).), см. рис. 11.17.
§ 3.3. Распространение света в анизотропных средах
127
Транс
УФ
Тепловые
возбуждения
Рис. 3.15. Транс- и гшоизомеры мезогенной молекулы дигептилазобензола.
Переходы из транс- в г/ис-конфигурацию могут вызываться коротковолновым (уль¬
трафиолетовым) излучением. Тепловая релаксация или длинноволновое излучение
восстанавливают т/?аяс-конфигурацию
Задача 3.2. Доказать справедливость соотношения Ха — Х\\ ~ Х± =
= N(x|| — уравнение (3.12).
Ответ. Предположим, что молекулы представляют собой жесткие ци¬
линдры с осью а, ориентированной вдоль оси z* некоторой системы коорди¬
нат xlyfz*. В этом базисе ненулевые компоненты • тензора молекулярной
восприимчивости — это х!х,х, — dyiyt = Vl, m!z>z* = Х||. Компоненты тен¬
зора молекулярной восприимчивости в лабораторной системе координат
xyz с осью z, ориентированной вдоль п, могут быть найдены из законов
преобразования xaj3 = cos (а, a') cos (/?, где cos (а, а') — направ¬
ляющие косинусы углов между координатными осями двух систем. Мак¬
роскопическая магнитная восприимчивость системы из N молекул опреде¬
ляется усреднением молекулярных восприимчивостей с функцией распре-
27Г 7Г
деления /(#, ц>)\ \а,в — N J dtp J яар(0, ф)1{в,ф) sin в dO. Используя (3.4),
о о
получаем: = х\\ ~ Х± = N(^\\ - ^х)5-
Задача 3.3. Рассчитать пути необыкновенных лучей вблизи линии
радиальной дисклинации силы к = 1. Плоскость падения и направление
поляризации света перпендикулярны линии дисклинации, рис. 3.16 (адап¬
тировано из статьи Гранжана12)).
12^ F. Grandjean, Bull. Soc. Prang. Mineralogie, 42, 42 (1919).
128
Гл. 3. Параметр порядка: амплитуда и фаза
Плоскость падения
Рис. 3.16. Отклонение необыкновенных лучей вокруг линии радиальной дискли¬
нации (перпендикулярна плоскости рисунка). Предполагается, что директор в по¬
лярных координатах направлен вдоль г (дисклинация силы k = 1, см. § 11.1)
Ответ. Решение инвариантно относительно перемещения вдоль ли¬
нии дисклинации. Пусть путь в плоскости, перпендикулярной линии, в по¬
лярных координатах описывается уравнением г = /(cj), начало координат
выбираем на линии. Имеем: dl2 = dr2 4 г2 du2 и cos <j)dl = dr; ф —
dir
угол между вектором Пойнтинга и оптической осью. Положив г' = —,
duj
получаем: Т = J(n2r/2 4 п^г2)1/2 duj. Соответствующее уравнение Эй¬
лера-Лагранжа: n2r2 4- п2(2г'2 — гг") = 0, а решение с постоянными
интегрирования а и Ъ может быть записано в виде
х
| Tig , Т ■
г = I a cos —си 4 о sin —и;
V По
Рассмотрим все решения, дающие лучи, приходящие из бесконечно уда¬
ленной точки под углом со — 0 (рис. 3.16). Это условие требует а ~ О,
и весь набор путей может быть представлен в виде г = ( b sin — со ] . Таким
V по J
образом, все уходящие лучи имеют асимптотические направления, парал¬
лельные либо OLb либо OL2, в зависимости от того, с какой стороны
от разделительной линии АО пришел луч. Имеем угловые отклонения
лучей ZAOL-i = ZAOL2 = 7г~. Рисунок 3.16 предполагает одноосный
П„
§ 3.3. Распространение света в анизотропных средах
129
оптически положительный нематик; в область между ОЬ\ и OL2 не попа¬
дает ни один луч.
Задача 3.4. Из уравнения (3.27) можно вывести оптические свойства
двуосной среды, у которой различны все три главных значения диэлек¬
трической проницаемости, например: ех < £у < ez- Для волны, распро¬
страняющейся в плоскости х,у, Nz = 0, уравнение (3.27) принимает вид
(.N2 - ez){exNl + еуЩ — ехеу) = 0 и имеет два решения: окружность
дг2 iV2
N = ez и эллипс — -Ь —- = 1. Поскольку ех < еу < ez, эллипс распо¬
ложен внутри окружности. Пользуясь тем же приемом, находим решения
для плоскостей xz и yz. В плоскости yz окружность находится внутри эл¬
липса, а в xz они пересекаются. Поверхность волновых векторов содержит
четыре пересечения в плоскости xz, по одному в каждом квадранте. В этих
точках пересечения имеется только одно значение показателя преломления,
соответствующие направления называются оптическими осями двуосного
кристалла (рис. 3.17). Найти угол х между этими двумя оптическими осями
и ОСЬЮ Z.
Рис. 3.17. Поверхность показателей преломления для двуосной среды. Пунктирная
линия показывает ориентацию оптической оси
Задача 3.5. Найти интенсивность света, прошедшего через систему
из двух параллельных поляризаторов и помещенного между ними слоя
нематика с ориентацией директора в плоскости слоя.
9-КЛЕМАН М.
130
Дополнительная литература
Задача 3.5. Рассчитать компоненты тензора диэлектрической про¬
ницаемости для хирального нематического жидкого кристалла с полем ди¬
ректора n — {cos qz, sin qz, 0}, где q = 27г/р и p — шаг геликоида дирек*
тора, закрученного вдоль оси z.
Ответ. Из Sij — £±Sij -b £a^i^j имеем: exx = e± + £acos2 qz =
= e(l -f 6 cos 2qz)\ eyy ~ e± + ea sin2 qz — e(l — S cos 2qz)\zzz —
Sxy = Syx - £aswqzcosqz — s8sin2qz, и = eyz = ezy = 0,
где £ = (<Sj{ + £±_)/2 и S = (ец -£±)/(e\\ +£±). Здесь и e±_ — про¬
ницаемости в направлениях, параллельном и перпендикулярном директору
соответственно. Для хирального смектика С* аналогичные вычисления бы¬
ли выполнены Берреманом131
Литература для дальнейшего чтения
1. L. М. Blinov and V G. Chigrinov, Electrooptic Effects in Liquid Crystal Materials,
Springer series on partially ordered systems, N. Y., 1994.
2. P. M. Chaikin and Т. C. Lubensky. Principles of Condensed Matter Physics, Camb¬
ridge University Press, 1995.
3. D. Demus and L Richter. Textures of Liquid Crystals, Verlag Chemie, Weinheim,
N. Y., 1978.
4. P. G. de Gennes and J' Prost. The Physics of Liquid Crystals, Oxford Science
Publication, Clarendon Press, Oxford, 1993.
5. J. D. Jackson. Classical Electrodynamics, 3rd Edition, John Wiley & Sons, Inc.,
N. Y., 1998.
6. N. H. Hartshorne and A. Stuart. Crystals and the Polarising Microscope, 2nd
edition, Edward Arnold & Co., London, 1950. 476 p.
7. I.-C. Khoo. Liquid Crystals: Physical Properties and Nonlinear Optical Phenomena,
John Wiley & Sons, Inc., N. Y., 1995. 298 p.
8. Ландау Л. Д., Лифшиц E. М. Теоретическая физика. Т. VII. Электродинамика
сплошных сред. 5-е изд., стереот. — М.: Физматлит, 1982. 624 с.
9. Ландау Л. Д., Лифшиц Е. М. Теоретическая физика. Т. VI. Статистическая
физика. 5-е изд., стереот. — М.: Физматлит, 2001. 583 с.
10. F. Simoni. Nonlinear Optical Properties of Liquid Crystals and Polymer Dispersed
Liquid Crystals, World Scientific, Singapore, 1997. 260 p.
11. R. E. Stoiber and S. A. Morse. Microscopic Identification of Crystals, Ronald, 1972.
12. The Optics of Thermotropic Liquid Crystals, Edited by S. Elston and R. Sambles,
Taylor & Francis Ltd., London, 1998.
Дополнительная литература
13. Беляков В. АДмитриенко В. Е., Орлов В. П. Оптика холестерических жидких
кристаллов, — УФН. 1979. Т. 127. С. 221.
14. Блинов Л. М. Электро- и магнитооптика жидких кристаллов. ■— М.: Наука,
1978.
13) D. W. Berreman, Mol. Cryst. Liq. Cryst. 22, 175 (1973).
ГЛАВА 4
ФАЗОВЫЕ ПЕРЕХОДЫ
Вещество может существовать в различных состояниях, или фазах, от¬
личающихся типом упорядоченности, плотностью и т. п. Переходы между
фазами сопровождаются особенностями в поведении термодинамических
потенциалов, таких как потенциал Гиббса G или свободная энергия Гельм¬
гольца F, а также их производных. Фазовый переход называется перехо¬
дом первого рода, если в точке перехода первая производная потенциала
(например, энтропия, плотность) претерпевает скачок. В этих случаях теп¬
лота перехода отлична от нуля. Если первые производные непрерывны, но
вторые производные (например, теплоемкость, сжимаемость) расходятся
в точке перехода, то это переход второго рода. Ко второй категории при¬
нято относить все непрерывные фазовые переходы, не сопровождающиеся
выделением теплоты перехода. Хотя при фазовых переходах второго ро¬
да термодинамический потенциал изменяется плавно, симметрия системы
изменяется скачком.
Для описания появления ориентационного и частичного трансляцион¬
ного порядка в мягком теле используются три различных теоретических
подхода. Феноменологические теории используют идею Ландау о возмож¬
ности разложения свободной энергии в ряд по степеням параметра порядка,
малого в окрестности перехода. В этих теориях используются симметрий-
ные соображения, что обычно накладывает довольно сильные ограничения
на возможный вид разложения, однако попытки придать физический смысл
коэффициентам этого разложения (т. е. связать их с параметрами меж-
молекулярного взаимодействия) нередко сталкиваются с немалыми труд¬
ностями. Ко второй категории относятся молекулярно-статистические по
своей природе теории, основывающиеся на выборе модели межмолекуляр-
ного взаимодействия. Так, например, модель жестких стержней Онсагера
подчеркивает межмолекулярное отталкивание и связанные с ним эффек¬
ты ориентационно-зависимо го исключенного объема. Напротив, модель
Майера-Заупе основана на анизотропном ван-дер-ваальсовом притяже¬
нии. Наконец, методы ренорм-группы позволяют кардинально расширить
теории фазовых переходов с учетом критических флуктуаций (в общих чер¬
тах этот подход представлен в гл. 7). Как отмечалось в гл. 3, эти флуктуации
тесно связаны с понятием ближнего порядка.
§4.1. Модель Ландау -де Жена перехода
одноосный нематик-изотропная фаза
В феноменологической теории Ландау исследование фазового перехо¬
да состоит из трех основных этапов: 1) поиск подходящего параметра
порядка; 2) разложение свободной энергии в окрестности перехода по сте¬
пеням (малого) параметра порядка; 3) нахождение минимума свободной
132
Гл. 4. Фазовые переходы
энергии как функции параметра порядка при различных температуре, дав¬
лении и т. п^_
Тензор Q, введенный в п/п. 3.2.2.2 полностью описывает симметрию
нематика и может быть выбран в качестве параметра порядка для пере¬
хода изотропная жидкость-нематик N<=>1. Он был использован де Женом
для построения разложения Ландау плотности свободной энергии (Гиббса)
в окрестности перехода:
g(T) — go + -A(T)QapQpa — ~B(T)QaisQi31QyaJr
2 3
H- ~C(T)Q0ipQ(XfiQ1$Q15 + ..., (4.1)
4
где g0 — плотность свободной энергии изотропной фазы, а по повторяю¬
щимся индексам производится суммирование. Отметим, что мы использу¬
ем строчные буквы, например g(T), для обозначения плотности энергии
и прописные, например G(T) = J g(T) dV, для самой энергии. Здесь сле¬
дует сделать важное замечание относительно термодинамического смысла
G, применимое ко многим ситуациям, обсуждаемым в этой книге. Очень
часто при анализе перехода NOI или других явлений в мягких средах плот¬
ность g связывают либо с термодинамическим потенциалом Гиббса G, ли¬
бо со свободной энергией Гельмгольца F, или просто с некой абстрактной
«свободной энергией», не делая между ними различия. Вспомним, что си¬
стемы, находящиеся при постоянных температуре Т и давлении Р, стре¬
мятся к минимуму G. При постоянных температуре Т и объеме V следует
минимизировать F = G — PV. Реальные эксперименты происходят при
Р = const и Т ~ const, в то время как компьютерное моделирование
проще при V = const и Т = const. Если изменение плотности (объема)
в экспериментальной системе мало, разность в теоретических результатах,
полученных из минимизации G или F, также мала. Переход N<£>1 как раз
попадает в эту категорию, поскольку скачок плотности при атмосферном
давлении мал, около 0,3 %, так что в разложении (4.1) отсутствуют члены,
зависящие от плотности, a g может считаться плотностью как G, так и F.
Каждый член в разложении (4.1) инвариантен не только относительно
операций симметрии нематической фазы, но также относительно всех опе¬
раций, меняющих «фазу» параметра порядка (в смысле § 3.1), таких как
произвольные пространственные вращения. Отличительной чертой этого
разложения является наличие кубического члена, нечетного по скалярно¬
му параметру порядка s, а значит, оно неинвариантно при преобразова¬
нии Qa,/3 т. е. 5 —>> — s. Как уже отмечалось, нематические
состояния, описываемые s и ~s, отличаются существенно, преобразова¬
ние s —у —s не является разрешенным. Таким образом, условие Ландау не
соблюдено, следовательно переход N<^>1 должен быть первого рода, что
и подтверждается многочисленными экспериментами. Напротив, в гейзен¬
берговском ферромагнетике состояния М и — М вырождены и кубиче¬
ский член в разложении Ландау отсутствует. Условие Ландау гласит, что
§4.1. N<^>1 переход, модель Ландау ~де Жена
133
необходимым (но не достаточным) условием перехода второго рода явля¬
ется симметрийно обусловленное отсутствие членов третьего порядка в
разложении свободной энергии, т. е. В = 0. Фактически, широко известно,
что точка Кюри является переходом второго рода.
Коэффициенты А, В и С в разложении Ландау-де Жена (4Л) зависят
от температуры. Ясно, что коэффициент А должен быть положительным
в высокотемпературной изотропной фазе и отрицательным в низкотемпе¬
ратурной области в нематической фазе: А > 0 позволяет найти минимум
при 5 — 0, а в случае А < 0 минимум находится при s ^ 0. Простейшая
зависимость А(Т) подобного рода является линейной: А(Т) = а(Т - Г*).
Если бы переход был переходом второго рода, его температура в точности
равнялась бы Т*. В имеющемся случае перехода первого рода смысл Т*
слегка отличается: как будет видно из дальнейшего — это температура
абсолютной потери устойчивости изотропной фазы при охлаждении. Для
дальнейшего упрощения модели коэффициенты а, В и С предполагаются
положительными постоянными, не зависящими от температуры.
Подстановка (3.15) в (4.1) приводит к выражению
g = go + -a(T-T*)s2---Bs3 + -Cs\ (4.2)
3 27 9
которое должно быть проминимизировано по s. Уравнение dg/ds = 0 мо¬
жет быть записано в виде
а(Т - T*)s - -Bs2 + -Cs3 = 0 (4.3)
и имеет три решения, два из которых соответствуют:
siso — 0 (изотропная фаза), (4.4 а)
_ в
$пет —
4 С
1 + </1_24а(Г-Г>)С
В2
> 0 (нематическая фаза). (4.4 б)
Третье решение
в
S3 = —
4 с
должно быть отброшено. Оно соответствует либо максимуму энергии (4.2),
либо, при температуре Т < Т* (53 < 0), локальному минимуму (рис. 4Л).
Поскольку при Т < Т* решение snem > 0 дает абсолютный минимум
свободной энергии, состояние 53 < 0 в равновесии не достигается.
Температура перехода Тс и соответствующая величина sc > 0 параметра
порядка определены из условия равенства плотностей свободной энергии
24а(Т ~Т*)С
В2
134
Гл. 4. Фазовые переходы
х
cd
EJ
S
X
Я
е*
X
3
в
о-
(D
S
3
а
го
0)
ю
QQ
ГЧ
^г
О
о
Ьо
2
1
О
1
-2
-3
-4
5
0,2 -0,1
0
0,1
0,2
0,3
0,4
0,5
Рис. 4.1. Плотность свободной энергии как функция скалярного параметра порядка
(4.2) в безразмерных единицах: (g — g0) х 10
1,32s
2 Т
Т
+ 0, 0282s4 с параметрами Тс
задачу 4.1)
Г,
319, 0К Т
318,ЗК и Т
С
* *
- 0,0181s2 +
= 319,1 К (см.
двух фаз, g(s Ф 0) — g0, и условия равновесия dg/ds = 0
Т,
т* +
в
27 аС
в/за
(4.5)
(4.6)
Имеется еще одна важная температура Т** — точка абсолютной потери
устойчивости нематической фазы, при перегреве, так называемая спино-
даль. В этой точке решение snem > 0 исчезает даже как локальный минимум
плотности свободной энергии, в данном случае — подкоренное выражение
в (4.4 б) меняет знак:
т** =ТС + —. (4.7)
216аС
Аналогично, температура Т* — это предел метастабильности изотропной
фазы при охлаждении, вторая спинодаль; отметим, что в случае В — 0,
С > 0 (фазовый переход второго рода) эти температуры совпадают с Тс:
О ф
При Т > Т** изотропная фаза абсолютно стабильна. При охлаждении
ниже Т** (в интервале Тс < Т < Т**) возникает локальный минимум,
соответствующий snem > 0, но абсолютный минимум находится в точке
Siso — 0, и система остается изотропной. При нагреве же из нематической
фазы в этом интервале она может оставаться метастабильной.
§ 4.1. N&I переход, модель Ландау ~де Жена
135
В интервале Т* < Т < Тс минимум в SiS0 = 0 становится локаль¬
ным, а в snern >0 — абсолютным. Соответственно стабильной становится
нематическая фаза, а изотропная может (при охлаждении) оставаться ме-
тастабильной. В системе, находящейся в метастабильной фазе, переход
в равновесную (стабильную) осуществляется путем образования и роста
зародышей, например в интервале Т* < Т < Тс, нематических капель в ме¬
тастабильной изотропной фазе. Наконец, при Т — Т* минимум в SiSO =
= 0 становится точкой перегиба, а ниже — максимумом. Соотвественно
при Т < Т* единственной стабильной фазой является нематическая. От¬
метим, что для разложения (4.2) в области Т < Т* имеется локальный
минимум при s3 < 0. Казалось бы, он может соответствовать некоторо¬
му метастабильному состоянию, однако для этого состояния отсутствует
область стабильности. Более того, наличие этого состояния является свой¬
ством разложения (4.2), и для других переходов первого рода (для которых,
например, В = 0, С < 0 и учтен член шестой степени) оно может отсутство¬
вать, в то время как наличие метастабильных фаз и спинодалей является
общим свойством фазовых переходов первого рода.
У внимательного читателя могут возникнуть возражения относитель¬
но применимости самого разложения (4.1) по степеням параметра порядка
для переходов первого рода. Разложение Ландау хорошо обосновано для
фазовых переходов второго рода, где параметр порядка непрерывно меня¬
ется от 0 до малых значений в упорядоченной фазе. Частичное обосно¬
вание разложения (4.1) следует из того обстоятельства, что переход N<^1
является слабым переходом первого рода, близким ко второму. В экспери¬
менте слабость перехода проявляется в малости (меньше кБТ на молеку¬
лу) теплоты перехода и в сильных предпереходных явлениях (например,
в рассеянии света) в довольно широком температурном интервале. Тео¬
ретически слабость перехода связана с малостью коэффициента В, что
делает осмысленным разложение (4.1). Относительную малость В можно
наглядно проиллюстрировать, используя безразмерные единицы. Для объ¬
емной плотности энергии [g] = [Дж/м3] обезразмеривающим множителем
является [RTp] — [(Дж • моль-1 ■ К~1) • К • (моль/м3)] = [Дж/м3], где
R — универсальная газовая постоянная, а р — число молей на единицу
объема. Обычные экспериментальные системы, как, например, магнетики,
имеют безразмерные коэффициенты Ландау порядка единицы. В жидких
кристаллах эксперименты дают В, С и 0,1 или меньше (см. задачу 4.1).
В результате, вследствие близости перехода ко второму роду (малое В
и большая длина когерентности) выше Nc существенную роль играют эф¬
фекты ближнего порядка. Это приводит к таким макроскопическим явле¬
ниям, как дву преломление, индуцированное электрическим (эффект Керра)
или магнитным полем.^ Физическая причина малости коэффициента В
остается загадкой.2)
L) P. G. de Gennes, Mol. Cryst. Liq. Cryst, 12, 193 (1971).
См. обзор P. H. Mukherjee, J. Phys.: Condens. Matter 10, 9191 (1998).
136
Гл. 4. Фазовые переходы
§ 4.2. Нематический порядок
и молекулярно-статистическая теория
для стержнеобразных молекул
Эта приближенная теория была развита Онсагером 3) и заложила кра¬
еугольный камень теории растворов. Она рассматривает жесткие продол¬
говатые частицы и применима к растворам жестких полимеров (например,
поли-7-бензил-Ь-глутамата в диоксане) или анизотропных вирусов (вирус
табачной мозаики). Фазовый переход описывается как результат стериче-
ского отталкивания (эффект исключенного объема).
4.2.1. Свободная энергия раствора сферических частиц
Этот более простой случай позволит нам познакомиться со статисти¬
ческим описанием эффектов исключенного объема. Рассмотрим раствор п
невзаимодействующих твердых шаров, плавающих в расворителе, состоя¬
щем из N частиц (атомов или молекул), с общим объемом V. Чистый раство¬
ритель обладает свободной энергией Гельмгольца FS0\V(T). Растворенные
шары добавляют к этой свободной энергии следующие вклады.
• Вклад энтропии беспорядка к^Т In п\ « пкБТ In
е
• Химический потенциал пр(Т) внедренных шаров; этот вклад про¬
порционален п.
• Возмущение энтропии вследствие невозможности для частиц, поме¬
щенных в раствор, занимать часть общего объема У, занятую другими
частицами. Это возмущение подразумевает стерическое взаимодей¬
ствие между двумя, тремя и т. д. частицами и должно принимать вид
ряда из членов ос п2, ос п3 и т. д. Наибольший член этого ряда может
быть записан в виде n2k^Tv/2, где v обладает размерностью объема
и, как мы увидим ниже, является исключенным объемом.
4.2.1.1. Исключенный объем. Пусть vs — объем одной частицы рас-
47Г о
творителя, a vp = —г*5 — объем одной растворенной частицы. Общий
3
объем равен V = Nvs + nvp. Будем вводить растворяемые частицы по
одной так, чтобы на каждой стадии общий объем оставался равным V
и выполнялось соотношение nvp «С Nvs.
Введение первой растворяемой частицы может быть осуществлено rji
различными способами, где
т/l = AV. (4.8)
3') L Onsager, Ann. N.Y. Acad. Sci. 51, 627 (1949).
§ 4.2. N<=>1 переход, теория Онзагера
137
Вторая частица вводится в частично занятый объем V — и, где и — объем,
исключенный первой частицей, а именно и = ~(2г)3 (рис. 4.2). Следова¬
тельно,
Щ = A(v - и),
и после многократного применения этих рассуждений
щ = A(V - 2и), ..., Tji = A{V - (i - l)it).
(4.9)
(4.10)
2 г
Рис. 4.2. Исключенный объем для сферических частиц радиуса г: расстояние между
центрами двух твердых сфер не может быть меньше 2г
Таким образом, общее число способов введения п частиц есть
П
7
^ГЬ
п\
1—1
AnVn
п\
п— 1
1 -
1=1
ги
V
(4.11)
где п\ — число перестановок п тождественных частиц.
Соответствующая энтропия смешения дается выражением
П— 1
Smix/kE = lnW = nlnA + n\nV - - У' г-Inn!,
\/ * ^
г-1
(4.12)
• w
где мы заменили In (1 — —) на . Для п > 1 (4.12) упрощается до
V V
1 V) —
и 2 л п
п In AV — —п —п In-
2V е-
(4.13)
Мы намерены принимать во внимание только разность Д5П1|Х(п, V) =
~ Sm\x(n, V) — 5miX(0, V) — 5miX(n, uvp) энтропии конечного состояния
{и, У) и суммы энтропий начальных состояний (0, V) и (n, nvp). Основной
138
Гл. 4. Фазовые переходы
вклад состояния (п, nvp) сводится к устранению члена п In -. Несложные
вычисления дают
Д»$ггцх(и, V) —
1 V , и
п in — + —п
и 2
— П
* 71V
2v
V
2V
(4.14)
В случае идеального раствора теплота смешивания отсутствует. Свободная
энергия на растворенную частицу
*i = *oi (Т)
TAS
mix
Foi (Т) + кБТ (In vpc + - uc + const
n
(4.15)
n/V
концентрация частиц. Последнее уравнение позволяет
где с =
проиллюстрировать идею осмотического давления, введенную в гл. 1.
4.2.1.2. Осмотическое давление. В типичном эксперименте по ос¬
мотическому давлению раствор с концентрацией с отделяется от чистого
растворителя полупроницаемой мембраной, проницаемой для растворите¬
ля, но непроницаемой для частиц растворенного вещества (рис. 4.3). Пред¬
положим, что мембрана сместилась так, что объем раствора изменился
Рис. 4.3. Полупроницаемая мембрана, «прозрачная» для молекул растворителя
и «непрозрачная» для растворенных молекул
на величину dV. Изменение свободной энергии Ftot = nFi = cVF\ может
быть записано как
dF
tot
Pos dV,
(4.16)
что означает
Pos
( dFtot \
\ dV )
T,n
(4.17)
Очевидная интерпретация (4.17) — это то, что pos представляет собой дав¬
ление, приложенное к полупроницаемой мембране, осмотическое давление.
Отметим, что оно не сбалансировано давлением в чистом растворителе за
§ 4.2. N<=>1 переход, теория Онзагера
139
мембраной (рис. 4.3), поскольку Fbehind = 0 вследствие выбора в (4.17)
точки отсчета энергии. В результате получаем
Pos - къТ {с + ]л1С2^ , (4.18)
где v = -и = 4vp — исключенный объем, пересчитанный на одну молекулу,
2
введенный в (1.5), (1.6).
Замечание. В физической химии принято выражать термодинамические
) , где G — неко-
/ nj:T
торая термодинамическая функция, а щ — концентрация г-й компоненты
смеси. Такими парциальными величинами являются химические потенциа¬
лы растворителя /^solvent и растворенного вещества //о, solute, дающиеся вы¬
ражениями /isolvent = МО, solvent (^) ^ т ? Msolute ~ О , solute (Т)
dN
— х —. Легко убедиться, что свободная энергия nFi является суммой
дтг
парциальных величин:
n[Fi -Foi(r)] = -Т (dASmi*N+ dAS™*n) . (4.19)
V dN дп /
4.2.2. Свободная энергия раствора жестких стержней
Уравнение (4.13) для энтропии системы твердых шаров показывает
невыгодность исключенного объема с точки зрения энтропии. Однако для
удлиненных частиц эффекты исключенного объема становятся ориента¬
ционно-зависимыми (рис. 4.4). Очевидно, что для параллельных стержней
исключенный объем меньше, чем для перпендикулярных. В результате, эн¬
тропийный эффект исключенного объема ведет систему к ориентационно
упорядоченному состоянию. В этом состоит основная идея теории немати¬
ческого упорядочения Онсагера.
Рассмотрим жесткие цилиндрические стержни длины L и диаметра D,
так что L^> D. Такой раствор с чисто отталкивательным взаимодействием
имел бы переход N <=> I при фЬ/D ^ 4, где ф = c7rLD2/4 — объемная
доля растворенных частиц. Как и выше, с — n/V.
Определим угловое распределение стержней, используя функцию плот¬
ности распределения
ш
f(6, tp) dfl = /а sin# dip dO,
которая выражает вероятность ориентации стержня внутри малого телесно¬
го угла dQ, = sin в dtp dO вокруг направления а с полярными углами (0, <р).
, . dG
функции смесей через парциальные величины
дпi
140
Гл. 4. Фазовые переходы
0
а
б
Рис. 4.4. Исключенный объем для системы из двух жестких стержней зависит от
угла 7 разориентации их осей: минимальный при параллельной (7 = 0) ориентации,
для перпендикулярной (7 — 7г/2) он достигает максимума
По определению
27Г тт
ГШ А
/(#, ф) sin в dipdO — 1.
(4.20)
о о
Естественным обобщением (4.15) является
Fx = F01(T) + кБТ
1
/а In (47Гг>рс/а) dQ, + -с
г* л
/а/а'/3(а, a') dfl ddf
(4.21)
Первый интеграл является обобщением In с; действительно, /а представля¬
ет собой концентрацию стержней, направленных вдоль а, а нормирующий
множитель 47г обеспечивает правильную величину интеграла, равную In с
для случая функции /а, не зависящей от направления (в изотропной фазе).
Второй интеграл обобщает эффекты исключенного объема; /?(а, а') — это
объем, исключенный для стержня, направленного по а\ стержнем, направ¬
ленным по а. В пределе L^> D находим
j3(а, а') — 2L2£>|sin7|,
(4.22)
где 7 = arccos(a -а'). Как и ожидалось, /?(а, а') = /?(а', а).
Условие нормировки (4.20) для /а можно напрямую ввести в (4.21),
добавив член Лагранжа
А
(4.23)
§ 4.2. N^l переход, теория Онзагера
141
где Л — множитель Лагранжа. Минимизируя сумму выражений (4.21)
и (4.23) по неизвестной функции /а, получаем уравнение
In (47rvcpfa) = -A - 1
/5(а, а')/а' бйУ,
(4.24)
в которое физические величины L, с, D входят в виде безразмерного про¬
изведения:
с/?(а, а7) — 2cL2 L>| sin7
8 , L
-ф —
n D
sin 7
(4.25)
Тривиальное решение /.
l
47Г
, описывающее изотропную фазу, удовле¬
творяет уравнению (4,24) при определенном значении А. Остальные реше¬
ния найти сложнее, и аналитические решения неизвестны. Онсагер исполь¬
зовал вариационный метод с пробной функцией /а = —-—ch(acos$),
47г sh а
удовлетворяющей условию нормировки (4.20). Здесь в — угол между а и
осью нематика, а а — вариационный параметр, исчезающий в изотропной
фазе и большой в нематической; в точке сосуществования апет = 18,84.
Можно заметить, что при больших а пики пробной функции при 9 — 0
и в — 7г обостряются. В точке сосуществования объемные доли нематиче¬
ской и изотропной фаз равны фПет = 4,5 D/Ьиф{ = 3,3 D / L соответствен¬
но; эти величины означают, что переход имеет место при весьма больших
отношениях L/D. Более того, оценки показывают, что при L/D ^ 10 сле¬
дует учитывать члены более высокого порядка (ос с2 и выше) в вириальном
разложении. Таким образом, модель Онсагера не может претендовать на
точное описание низкомолекулярных термотропных нематических фаз, где
обычно L/D < 10. К тому же система Онсагера атермальна: фпет, Ф1 не за¬
висят от температуры.
Теория Онсагера была усовершенствована Флори для описания полу-
жестких молекул, которые располагались в узлах решетки с периодом,
равным персистентной длине, и им разрешалось иметь зигзагообразную
форму. Теория Флори оказалась более успешной при описании концентри¬
рованных растворов, и для точки сосуществования она давала значения
Фпет — ~ 12,5, «8, большие, чем теория Онсагера.
D D
Эксперименты, проведенные на растворе поли-7-бензил-Ь-глутамата в
диоксане, подтвердили, что переход I<^>N происходит при критической объ¬
емной доле фс, линейно зависящей от отношения L/D, так что фсЬ/D —
= const. Однако численные коэффициенты не столь хорошо согласуются
с теорией. Отличия, главным образом, связаны с пренебрежением силами
притяжения (например, ван-дер-ваальсовыми силами) и эффектами поли¬
дисперсности.
142
Гл. 4. Фазовые переходы
§ 4.3. Теория молекулярного поля Майера - Заупе для
перехода изотропная жидкость — нематик
Теория Майера-Заупе — это аналог теории молекулярного поля Вейса
для ферромагнетиков. Здесь предполагаются ван-дер-ваальсовы межмоле-
кулярные взаимодействия. Силы отталкивания и эффекты исключенного
объема не рассматриваются. В парном взаимодействии молекул, располо¬
женных в точках г и г', учитывается вклад UTT> = I?p2(cos7)/| г — г'
где 7 — угол между молекулярными осями а и а'. Знак потенциала де¬
лает энергетически выгодной параллельную ориентацию молекул. Вме¬
сто вычисления взаимодействия данной молекулы со всеми остальными
в теории Майера-Заупе предполагается, что каждая молекула находится
в некотором среднем потенциале, создаваемом остальными молекулами
и получающемся усреднением по их положениям и ориентациям меж-
молекулярного взаимодействия. Усреднение по положениям дает посто¬
янную b = ^2ЛВ/\ г - г; |6) , в то время как усреднение по ориентациям
ТI
с функцией распределения/(0, ф) приводит к выражению (Рг (cos 7))| —
= SF2 (cos 0), где (0, ф) — полярные координаты вектора а в системе коор¬
динат с осью Z, направленной вдоль директора, a s — скалярный параметр
порядка. Таким образом, эффективный потенциал записывается в виде
U = — 6sP2(cos0). (4.26)
При данном потенциале функция распределения дается выражением
/(0, <р)=С exp[-U(в, s)/kBT], (4.27)
где
7Г
С”1 = 2тг
ехр[— U(в, s)/k^T] sin в dO
О
Выражение (4.27) позволяет найти значения s, соответствующие миниму¬
му свободной энергии на молекулу Fi(s Ф 0) - F0i(s = 0) — Е — TS.
Внутренняя энергия Е получается усреднением эффективного потенциала
(4.26) с функцией распределения f(0,ip):
E=--bs2, (4.28)
множитель 1/2 возникает вследствие двухкратного учета каждого парного
взаимодействия при суммировании. Ориентационная энтропия в пересчете
на молекулу дается выражением
5 = ~h
/(0, ф) In [47г/(0, ф)} d£t — —bs2/Т — /сБ In 47гС, (4.29)
§ 4.3. I переход, теория Майера - Заупе
143
так что
AF — F\ — F(
i = -bs2 + къТ\п^С.
2
Условие экстремума ДF, д AF/ds — 0, дает уравнение
(4.30)
7Г
2тг С
■^2(cos в) ехр[—[/(#, ^)/^бТ] sin 0 d0,
(4.31)
J
о
совпадающее с определением s (3.4), что демонстрирует самосогласован-
ность теории: функция распределения, выраженная через s и подставленная
в (3.4), должна давать то же значение параметра порядка. Условие устой¬
чивости (минимальности) для экстремума д2 AF/ds2 > 0 сводится к нера¬
венству
7Г
д
ds
2тхС
Р% (cos в) ехр[—U/к^Т] sin 0 d0 > < 1.
(4.32)
о
Равновесные значения s могут быть найдены из (4.31) и (4.32). Для этого
7Г
можно нарисовать график Yi (s) = 2л С f Р2 (cos в) ехр [—17/к^Т] sin в dO как
о
функции s для различных значений Ь/к^Т и найти точки пересечения этих
кривых с прямой 1г(з) = s, составляющей угол 45° с осью s (см. (4.31)). Со¬
гласно (4.32) равновесному состоянию соответствуют точки пересечения,
в которых наклон Yi(s) меньше 45°. Другой способ наглядного пояснения
теоретических предсказаний состоит в прямом построении зависимости
AF(s) при различных температурах (рис. 4.5).
AF/bT
0,0075
s
-0,005
Рис. 4.5. Свободная энергия в пересчете на молекулу AF/ksT как функция
скалярного параметра порядка для различных значений отношения Ь/квТ =
= 4,4; 4,5; 4,5415; 4,6; 5,4 (от верхней кривой к нижней)
144
Гл. 4. Фазовые переходы
Значения свободной энергии в двух минимумах при 5 — 0 и s ф О
сравниваются при температуре Тдг/ — &/(4,5415&б), а соответствующее
значение параметра порядка Sjv/ ~ 0,429, что, в общем, соответствует
экспериментальным значениям, представленным в литературе.
§4.4. Переход смектик А-нематик
4.4.1. Параметр порядка
Как уже отмечалось, параметр порядка смектической A-фазы содержит
две различные составляющие:
• нематическая составляющая с амплитудой s и фазой п.
• составляющая, связанная с модуляцией плотности вдоль оси г:
Р=^Рк ехр(—гк • z), (4.33)
1 27т
где к = m—и, m — целое, и — единичныи вектор нормали к смектиче-
do
ским слоям, a do — межслоевое расстояние. Обозначим соответствующий
и w 2тг
элементарный волновой вектор как qo = — •
do
Рассмотрим слегка деформированный смектик. Деформация описыва¬
ется полем смещений u — uz, так что материал, находившийся до дефор¬
мации в точке г, перемещается вг' = г — и. Следовательно, плотность
в точке г может быть записана в виде
р(г) = ^2 рк exP[“*k(r “ u)] = Ро + Pi ехр[—iqo(r - u)] + ... =
к
Ро + pi exp (lip) exp(—iq0 • r) + ..., (4.34)
где мы ввели фазу (р = qo ■ и, которая является параметром вырождения;
меняясь в интервале [0,27г], она описывает все возможные положения смек¬
тических слоев по отношению к начальной фазе ц> — 0. Таким образом,
описывающий слои смектический параметр порядка — это комплексное
число:
ф = ф0ехр({р). (4.35)
4.4.2. Разложение Гинзбурга-Ландау
Образование в нематической фазе смектических кластеров, размер ко¬
торых расходится при Т —> Тс, приводит к радикальным изменениям неко¬
торых материальных параметров, таким как неограниченное возрастание
упругих модулей, отвечающих за кручение (twist) и продольный изгиб
(bend) поля директора, или расходимость шага холестерической спирали
в хиральных нематиках. Для описания этих и других явлений мы присту¬
пим теперь к описанию феноменологической картины Гинзбурга-Ландау
этого перехода.
§ 4.4. Переход смектик Л - нематик
145
Для начала рассмотрим смектический параметр порядка отдельно, для
о разложение свободной энергии Гинзбурга-Ландау выглядит следу ю-
обоазом:
него
щим образом:
/SmA = а\ф
+ 1
dip
+ 1
2
4
2Мц
dz
2 М±
У±Ф\ +■■■, (4.36)
где а = а(Т — Тс), положительные коэффициенты а, /?, Мц и М±_ не зависят
от температуры; V
х
(
д д
,0), I V±1р
dip
+
— |2. В (4.36) чле-
ду
дх ду ' ' ' дх
ны нечетного порядка отсутствуют, так что переход может быть переходом
второго рода. Отличительной чертой разложения (4.36) является наличие
градиентных членов, позволяющих учесть изменение ф в пространстве.
Коэффициенты 1 /М± и l/Мц описывают (анизотропную) жесткость смек¬
тической фазы для деформаций вдоль слоев и по нормали к слоям. Мы рас¬
сматриваем флуктуационные деформации с малой амплитудой и большими
длинами волн, так что амплитуда параметра порядка фо предполагается по¬
стоянной. Получающееся в результате выражение
1
2 М
д-ф
dz
2
1 dip дф
1
2М\\ dz dz
2 М
<9гЛ
dz)
(4.37)
представляет собой вклад в энергию сжимаемости, обычно записывае-
в традиционной свободной энергии смектической фазы
мый как ~В
ди \
2 V dz )
(п. 5.2.3), соответствующий модулю Юнга
В
1
I 2 2
ФоЯо'
м
(4.38)
Ниже будет показано, что введение в (4.36) нематического параметра по-
1
рядка перенормирует член
В нематической фазе 5 достигает максимального значения в точке пе¬
рехода в смектическую фазу, поскольку смектическая фаза, как правило,
появляется при понижении температуры. Можно предположить, что непо¬
средственно перед переходом (чуть выше Тс) нематическая фаза хорошо
упорядочена и имеет s порядка 1. В таком случае параметр s практически
не зависит от температуры сразу ниже Тс в смектической фазе. Напротив,
директор п0 = (0,0,1) может испытывать флуктуации 6n = (5пх, Sny, 0),
п = по + 8п, которые, как и флуктуации ф, должны быть приняты во
внимание.
Свободная энергия Гинзбурга-Ландау должна быть инвариантна отно¬
сительно одновременного поворота директора п и нормали к слоям v\
п
(6пх, 6пу, 1), V
du
dx
(4.39)
146
Гл. 4. Фазовые переходы
здесь эти переменные рассматриваются как независимые. При поворотах на
бесконечно малый угол О <С 1 наклон директора Sn = (8пх, Sny) эквивален¬
тен смещению слоев и = —х 6пх — у 8пу вдоль оси г. В заданной системе
координат это смещение эквивалентно изменению фазы (р —» ip + qou, так
что ф —> фо exp (i(f) exp (go и) и
С уточненным таким образом градиентным членом свободная энергия Гинз-
бурга-Ландау приобретает вид
Отметим, что малый угол между пи v может быть выражен через компо¬
ненты векторного произведения
Таким образом, член | (V_l — iqo 6п)ф |2 представляет собой квадрат угла
между пи г/, умноженный на q%.
Полная плотность свободной энергии получается добавлением к fsmA
свободной энергии Франка -Осеена, описывающей деформации
директора:
где К2, К$ и К\ — постоянные упругости для деформаций кручения
(twist), продольного (bend) и поперечного (splay) изгибов соответствен¬
но (см. п. 5.1.1). Таким образом, в окрестности перехода полная плотность
свободной энергии /tot = /smA + ho Для малых искажений директора
принимает вид
(4.40)
2
Умножая это выражение на iq^> видим, что | (Vj_ — Що 8п)ф | есть не что
иное, как
v х niqоф
/ко = -i^i(divn)2 + -7^2(п • rotn)2 + ~К$(п х rotn)2, (4.42)
2 2 2
/tot = <*| ф I2
+ -Ki(div<5n)2 + -K^n ■ rot<5n)2 + -K3 ( — <5n) . (4.43)
2 2 2 V dz /
§ 4.4. Переход смектик А - нематик
147
4.4.3. Аналогия со сверхпроводниками
Как заметил де Жен4\ сумма /tot = /smA + ho (4.43) очень похожа на
функционал Гинзбурга-Ландау, описывающий фазовый переход нормаль¬
ный металл - сверхпроводник:
/super — /normal Ос\ф\ — j ф | ~
2 4т
А \
—«V — 2е — ) ф +
he)
+ (rot А)2 _ Н0rot А ^ 44^
87Г 47Г
Здесь использована гауссова система единиц (сантиметр, грамм, секунда), а
для упрощения сопоставления с /tot — в качестве функционала /suрег взят
термодинамический потенциал Гиббса. Параметр порядка ф сверхпровод¬
ника в (4.44) — это волновая функция когерентного ансамбля куперовских
пар, А — векторный потенциал магнитного поля, Н0 — напряженность
внешнего магнитного поля, отличная от локального магнитного поля с ин¬
дукцией В = rot А, т и е — масса и заряд электрона, ас — скорость
света в вакууме. В предположении М = Мц = М± соответствие нематик-
сверхпроводник осуществляется заменой
h2/(2т) 1/M, 2e/hc дсь А ^ <5п; (4.45)
член (rot А)2/(87г) соответствует слагаемым, ответственным за деформа¬
цию кручения и продольного изгиба в упругой энергии Франка-Осеена,
1 /(47т) К2, Конечно, аналогия не полная. Например, /super не содер¬
жит членов, отражающих анизотропию упругих модулей К2 Ф К% и нет
члена, соответствующего члену с дивергенцией, (div<Sn)2. С другой сто¬
роны, в /tot, представленной в (4.43), отсутствует аналог члена Н0 rot А,
описывающего взаимодействие с внешним полем; так что переход смек¬
тик - нематик аналогичен переходу сверхпроводник - нормальный металл
в отсутствие внешнего магнитного поля Но = 0.
Первое, что приходит на ум при сравнении (4.43) и (4.44) — это воз¬
можность появления в смектиках аналога эффекта Мейснера - Оксенфельда
(Meissner-Ochsenfeld), согласно которому магнитное поле выталкивается
из сверхпроводника; т. е. В = rot А = 0. Аналогичным образом смектиче¬
ская фаза запрещает деформации продольного изгиба и кручения, в которые
входит rot п. Причина самая простая: при деформации обоих типов нару¬
шается эквидистантность смектических слоев (а при поперечном изгибе —
нет). Хорошей рабочей моделью для иллюстрации этого явления может
служить толстая стопка бумаги.
Для определения распределений смектического параметра порядка и ди¬
ректора следует проминимизировать свободную энергию (4.43) по двум
P. G. de Gennes, Solid State Comm. 10, 753 (1972).
148
Гл. 4. Фазовые переходы
функциям: ф(г) и <5п(г). В результате получаются два уравнения (в случае
сверхпроводников они называются уравнениями Гинзбурга-Ландау) объ¬
емного равновесия, позволяющие определить две характерные длины: дли¬
ну когерентности, общепринятое обозначение £, и глубину проникновения,
обозначаемую А. Как и в сверхпроводниках, предсказания модели Гинзбур¬
га-Ландау для смектиков сильно зависят от соотношения этих длин.
4.4.4. Характерные длины
4.4.4.1. Длина когерентности. Градиентный член типа | \7ф |2 в (4.43)
и (4.44) препятствует резким пространственным изменениям параметра по¬
рядка. Проминимизируем J (/smA + /fo) dV по функции ф*(т), комплекс¬
но сопряженной к ^(г). Вариационная задача дает следующее уравнение
равновесия в объеме (задача 4.6):
2
аф -f /3| ф \2ф — —— ( — ) — —-—(Vx — Що 8п)2ф = 0. (4.46)
2Mi I V dz / 2 Мх
Из последнего уравнения получаем выражения для длин когерентности:
£|| = ~~т== и 1 . (4.47)
у/2\а\М±
При Т > Тс эти длины являются размерами смектических кластеров в нема¬
тической фазе, £jj — вдоль директора, a £_l — в поперечных направлениях.
При Т < Тс это расстояния, на которых спадают возмущения амплиту¬
ды параметра порядка; например, длины когерентности задают в смек¬
тике размер ядра дислокаций, которые будут рассмотрены ниже в этом
пункте. При Т Тс длины когерентности стремятся к бесконечности.
4.4.4.2. Глубина проникновения. Теперь предположим, что при по¬
стоянном фо поле директора подвергается возмущению, а именно дефор¬
мации кручения, продольного или поперечного изгиба. Кручение и про¬
дольный изгиб включают в себя rot п / 0 и несовместимы со слоистой
структурой смектика, в то время как поперечный изгиб совместим. Дли¬
на, на которую деформации кручения или продольного сдвига проникают
в смектическую фазу, называется глубиной проникновения (рис. 4.6).
Уравнение, минимизирующее J (/smA + /fo) dV по <5п, может быть
существенно упрощено, если предположить, что Мц = Mj_, и записать сво¬
бодную энергию Франка -Осеена в сокращенной форме: /ро = -/f(rotn)2,
отражающей тот факт, что нас интересуют только деформации продоль¬
ного изгиба и кручения. Равенство нулю вариационной производной от
J —(Vj_ — iqo 6п)ф -К(rot£n)2 dV по Sn дает условие объемного
v
- 2М 2
§ 4.4. Переход смектик А - нематик
149
равновесия по отношению к отклонениям поля директора £п(г)
уравнение объемного равновесия (задача 4.6):
второе
J
г 90
.2
(■ф*v-ф - ipVip*) -^6п\ф
гм м
(4.48)
///////////
///////////
\\n\U\llll
/II
А
у
Рис. 4.6. Глубина проникновения деформации продольного изгиба Л в смектиче¬
ской A-фазе. Слои параллельны подложке. Слабая деформация продольного изгиба,
задаваемая подложкой, проникает в объем смектика на расстояние Л
Введенный здесь вектор
j — К rot(rot <5п)
(4.49)
является аналогом вектора плотности тока в сверхпроводнике: в отсутствие
связи со смектическим параметром порядка j . параллелен директору.
Уравнение (4.48) наводит на мысль о характерной длине
1
Яо
МК
Ф
ЯО
мк$
а
где амплитуда | ф | параметра порядка заменена ее значением у/ а //?
в недеформированном смектике. С учетом четырех различных комбинаций
Му, М± и К2, имеется четыре глубины проникновения:
Л
,-L
1
2,3
ЯО
Щ\,±К 2,3/3
(4.50)
а
Пятая важная глубина проникновения следует из соотношения членов, свя¬
занных с поперечным изгибом и сжимаемостью:
Л
М\\К 1
<70
Ф
К1
В
(4.51)
150
Гл. 4. Фазовые переходы
4.4.5. Аномалии модулей К2 и К3
Как уже упоминалось, деформация поперечного изгиба директора внут¬
ри смектических кластеров, возникающих в объеме нематика при Т > Тс,
не нарушает эквидистантности и параллельности слоев. Рассмотрим те¬
перь деформации кручения (К2) и продольного изгиба (К3) некоторой
амплитуды | 80 |, где £0 — угол между нормалями к слоям на противо¬
положных границах кластера (рис. 4.7). Ненулевое значение \60\ вызывает
Л
Рис. 4.7. Смектический кластер в нематической матрице, подверженной деформа¬
ции продольного изгиба директора
сжатие/растяжение слоев. Таким образом, энергетический прбигрыш из-
за искажений внутри кластеров можно оценить либо через сжимаемость
В(8в)2£? ~ M^ip^qKSO)2^, либо, эквивалентно, через упругость по от¬
ношению к искривлению 6iir[rot(£n)]2£3 ~ 5К(50)2£, где 6К — прира¬
щение упругой константы Франка К, вызванное наличием смектических
слоев. Сравнивая обе оценки, заключаем, что 6К в?
ГЧ-/
М\
нахождения ф$ заметим, что флуктуация, приводящая к возникновению
смектического кластера объема £3, требует затраты энергии | а || ф |2£3
rss
ksT, т.е. Щ
А
М
£ 6к^Т/\а\ ос £ 1 (см. (4.47)). Таким образом, 5К
Ф1(? ос £. Детальные вычисления, учитывающие разницу между £
и £_l, дают следующую перенормировку К2 и К%:
К2,3-> + 6K2t3; SK2 cxfi/f||, 5К3 <х£
(4.52)
Таким образом, модель предсказывает неограниченное возрастание упру¬
гих постоянных, ответственных за кручение и продольный изгиб, по мере
§4.4. Переход смектик А-нематик
151
приближения к смектической фазе; напротив, упругая константа Кь ответ¬
ственная за поперечный изгиб, не перенормируется из-за возникновения
смектических кластеров.
4.4.6. Фазы Абрикосова с дислокациями
Вернемся к эффекту Мейснера-Оксенфельда. В присутствии слабого
внешнего поля Н0 в объеме сверхпроводника магнитная индукция остается
равной нулю, В = rot А — 0. Однако достаточно сильное поле проника¬
ет в сверхпроводник. Это может произойти двумя различными способами.
В сверхпроводниках первого рода поле, превышающее так называемое кри¬
тическое поле, проникает в объем материала, разрушая сверхпроводимость.
В сверхпроводниках второго рода до перехода в нормальное состояние по¬
ле проникает частично, вдоль так называемых вихревых нитей (рис. 4.8).
Вихревые нити составляют периодическую решетку и образуют термодина¬
мически стабильную фазу, которая называется смешанным состоянием или
фазой Абрикосова. Смешанное состояние претерпевает переходы второго
рода: в сильном поле — в нормальное состояние, а в слабом — в обычное
сверхпроводящее состояние без вихрей.
«Ядро» вихря находится в нормальном состоянии. По мере удаления от
ядра магнитное поле быстро убывает, и материал становится сверхпрово¬
дящим. Имеет место квантование магнитного потока через поверхность £,
ограниченную замкнутым контуром 7, охватывающим всю сингулярную
область:
л А
B-dE = oA-dl = N—, (4.53)
J 2е
7
здесь первое равенство следует из теоремы Стокса, преобразующей поверх¬
ностный интеграл в интеграл по контуру. Квант потока равен а N
целое число.
Таким образом, фазовые диаграммы сверхпроводников первого и вто¬
рого рода в плоскости (Но, Т) существенно различаются. Параметр, опре¬
деляющий род сверхпроводника, — это температурно-независимое отно¬
шение и = А/£:
• к < 1/\/2; сверхпроводники I рода; промежуточная (смешанная)
фаза отсутствует;
• к > 1/\/2; сверхпроводники II рода; в магнитном поле выше так на¬
зываемого нижнего критического поля существует смешанное состоя¬
ние, в котором нормальный металл в ядрах вихревых нитей сосуще¬
ствует со сверхпроводящей матрицей. Выше верхнего критического
поля фаза Абрикосова переходит в нормальный металл.
В смектиках аналогом вихревых нитей являются винтовые и краевые
дислокации. Дислокации вносят продольный изгиб и кручение в систему
смектических слоев. Например, единичная краевая дислокация, показан¬
ная на рис. 4.9, создает продольный изгиб поля директора. В присутствии
152
Гл. 4. Фазовые переходы
к к
к к
Н
о
а
б
Рис. 4.8. Вихревая нить в сверхпроводнике II рода, А/£ > 1/\/2. Вихрь параллелен
внешнему магнитному полю Но; поле проникает в объем сверхпроводника в ядрах
дефектов, вдоль оси z. Круговые линии показывают токи, циркулирующие вокруг
цилиндрического ядра (а). Изменение амплитуды волновой функции | ф |2 и маг¬
нитного поля В = rot А в области ядра дефекта с двумя характерными длинами
£(Т) и А(Т) соответственно {в)
Рис. 4.9. Краевая дислокация в SmA-фазе; длина когерентности f —это расстояние
на котором локальное возмущение влияет на амплитуду параметра порядка | ф
§ 4.4. Переход смектик А - нематик
153
дислокаций фаза <р параметра порядка перестает быть однозначной функ¬
цией координат. При обходе вокруг единичной дислокации изменяется
на 27г, как и в случае вихря. Эквивалентом квантования магнитного потока
является условие
oSndl^do, (4.54 а)
7
где do — межплоскостное расстояние в смектике. В более общем виде
o6ndl = Nd0, (4.546)
7
где N — число (со знаком) единичных дислокаций, пересекающих пло¬
щадь Е, ограниченную контуром 7. Похожим образом ядра дислокаций
являются областями с rot п ф 0; «нормальное» ядро дислокации находится
в состоянии с | ф | =0.
Теперь перейдем к интригующему вопросу: при всем сходстве смектика
со сверхпроводником — между параметрами порядка ф и дефектами (вих¬
ревые нити и дислокации) существует ли жидкокристаллический аналог
фазы Абрикосова, в которой продольный изгиб или кручение сосуществу¬
ют со слоистостью смектика? Для утвердительного ответа на этот вопрос
требуется жидкокристаллический аналог внешнего магнитного поля Но
в сверхпроводнике (в нулевом поле Но = 0 фаза Абрикосова отсутствует).
Как уже упоминалось, в плотности свободной энергии (4.42) нематического
жидкого кристалла отсутствует член, соответствующий Но rot А в (4.44).
Потерянная связь должна быть пропорциональна rot п, а не (rot п )2. Эле¬
гантный и эффективный способ создания внутреннего источника деформа¬
ции rot п ф 0 состоит в превращении нематического жидкого кристалла
в холестерический простым добавлением хиральных молекул.
Если нематический жидкий кристалл хирален (хиральные мезогенные
молекулы или хиральные добавки), то обычно равновесное распределение
директора является геликоидальным с шагом геликоида Р и осью, скажем,
вдоль оси z:
n = (sin 27rz/P, cos 27rz/P, 0). (4.55)
Хиральность приводит к появлению дополнительного члена в плотности
свободной энергии Франка-Осеена для холестерика:
/сh = Sfo - K2ko(nrotn), (4.56)
где /ро дается выражением (4.42), а к0 в равновесии равно ко = 27г/Р
(см. § 5.1). Таким образом, холестерическая фаза является аналогом нор¬
мального металла во внешнем магнитном поле со следующим соответстви¬
ем: h = К2ко О Н0 и К2ко (п rot n) f* Но rot A <<p[0JleM>>? С0ПрЯжен-
47Г
ным кручению (nrotn), является хиральность h. Параметром Гинзбур¬
га-Ландау, определяющим вид фазовой диаграммы, является отношение
154
Гл. 4. Фазовые переходы
глубины проникновения кручения к когерентной длине смектика: ус =
Ц = — у/2К20. При ус < 1/^/2 (смектики первого рода) теория
Яо
молекулярного поля, основанная на плотности свободной энергии /smA +
+ fch - /smA + /fo - K2k0(nrot n) (см. (4.41), (4.42) и (4.56)), предска¬
зывает переход первого рода смектик-холестерик при критическом поле
hc — yjK2a2 / (3 (задача 4.7). В результате либо происходит полное уда¬
ление кручения из системы, либо имеет место сосуществование разделен¬
ных областей смектической и холестерической фаз. Если к > 1/V2, на
плоскости (/г, Т) новая фаза вклинивается между смектической и холесте¬
рической (рис. 4.10). Ренн и Любенский теоретически предсказали новую
фазу5) и назвали ее TGB-фазой (от англ. twist-grain boundary —
ные межзеренные границы).
закручен-
К,к
2Л0
X < \ /
€
х>\!
€
Холестерик
б
Т
Рис. 4.10. Фазовая диаграмма для (а) SmA-фазы первого рода, к < 1/>/2, и
(б) SmA-фазы второго рода, х > 1/\/2. Из книги Чайкина и Любенского (Chaikin
and Lubensky, 1995)
Сосуществование кручения и смектического порядка в TGB-фазах обес¬
печивается решеткой винтовых дислокаций. Как видно на рис. 4.11, ряд
параллельных винтовых дислокаций, отстоящих на расстояние Id друг от
друга, образует закрученную межзеренную границу (TGB). Два смекти¬
ческих блока с противоположных сторон границы слегка наклонены друг
относительно друга, угол наклона 2тгу = 2arcsin(—) « do/Id- Смектиче-
2ld
ские блоки ширины (равной расстоянию между соседними межзеренны-
ми границими) свободны от дислокаций. Все закручивание сосредоточено
в межзеренных границах. Пространственное усреднение закручивания в
направлении нормали к границам зерен дает ко = 2п'у/1ь do/(hldy,
S. R. Renn and Т. С. Lubensky, Phys. Rev. А 38, 2132 (1988).
§ 4.5. Модель Костерлица - Таулесса
155
шаг структуры Р = 2п/к0 = /ь/7. Интересно, что можно классифициро¬
вать TGB-фазы как соизмеримые и несоизмеримые, в зависимости от того,
является ли 7 = 1ъ/Р рациональным или иррациональным числом. Среди
соизмеримых версий TGB можно найти обладающие «квазикристалличе-
скими» симметриями, когда TGB-фаза инвариантна относительно поворота
(вокруг оси кручения) на угол 27r/Q, где Q = 5 или Q > б.
Стопка слоев
смектика А
Закрученные межзеренные границы
Винтовые дислокации
Рис. 4.11. TGB-фаза: стопки смектических слоев, разделенные межзеренными
границами, принимающими на себя все закручивание соседних стопок. Закрученная
межзеренная граница может состоять из винтовых дислокаций. Из книги Чайкина
и Любенского (Chaikin and Lubensky, 1995)
§ 4.5. Модель фазовых переходов Костерлица-Таулесса
Система, обладающая позиционным или ориентационным порядком,
при переходе в изотропную фазу теряет это упорядочение. Однако даже
до перехода порядок может быть частично разрушен такими дефектами,
как дислокации и дисклинации. Заманчивая идея рассмотреть плавление
как процесс зарождения и размножения дефектов. Конечно, у такого под¬
хода имеются и ограничения. К примеру, если число дефектов становится
действительно большим, упорядоченная матрица перестает существовать,
и само определение дефекта оказывается под вопросом. Тем не менее при
рассмотрении начальных стадий плавления идея с физической точки зрения
выглядит привлекательной. Костерлиц и Таулесс6^ разработали двумерную
6) J. М. Kosterlitz and D. J. Thouless, J. Phys. С 5, LI24 (1972); С 6, 1181 (1973).
156
Гл. 4. Фазовые переходы
модель дислокационного плавления, упрощенную версию которой мы сей¬
час рассмотрим.
Не вдаваясь в детальное описание свойств дислокаций (они будут рас¬
смотрены в гл. 8), отметим только, что в двумерной решетке дислока¬
ции — это точечные дефекты, вызывающие поле деформаций Vu ос 1 /г
и обладающие упругой энергией
Е — К
R
— + Есоте — Kin + Есоте, (4.57)
^ Т core
Т core
где К — некоторая упругая постоянная, интегрирование ведется от радиуса
гСоге «ядра» дефекта до некоторого макроскопического размера R, это либо
расстояние между дислокациями, либо размер системы для изолированной
дислокации; Есоге — энергия ядра. Если N — число дефектов на единицу
площади, то R — 1/y/~N.
Теперь рассмотрим ансамбль дефектов как «газ» с поверхностной плот¬
ностью N частиц на единицу площади. Имеется 7VSites = 1/гсоге узлов,
доступных для дефектов. Энтропия газа дефектов определяется числом
различных размещений N дефектов по A^tes узлов:
■^sites- ^, 7^ Л г -^sites
s = кв In « kzN In (4.58)
N\(Nsites - N)l N
(приближение следует из формулы Стирлинга и справедливо при iVSites
>N).
Таким образом, свободная энергия газа дефектов равна
F = E- TS = N\n - 2 АбГ) + NEC0Te. (4.59)
Легко заметить, что начиная с некоторой критической температуры
Т>ТС = K/2ks минимум свободной энергии становится отрицательным,
и кристалл плавится. Выше температуры плавления Тс имеется конечное
равновесное число дислокаций
N = —— ехр
&Т 2
core
core
^/сБ(Г-Гс)_
(4.60)
в то время как ниже Тс дислокации в равновесии отсутствуют.
§ 4.5. Модель Костерлица — Таулесса
157
Задача 4.1. Найти коэффициенты Ландау в (4.2) в безразмерных еди¬
ницах (см. текст) и температуры Т** и Т* для нематического соединения
МВВА, используя Тс = 319,0 К, плотность при Тс 1,09 г • см~3 и экспери¬
ментальные данные7^: аТс = 43,1 Дж • см"3, В = 2,66 Дж • см-3 и С —
2,76 Дж • см
-з
Ответ. Обезразмеривающим фактором для объемной плотности энер¬
гии служит RTcpc, где рс — отношение плотности к молекулярному весу,
^ з
для МВВА рс и 1?Q9r см •- * 67,37г • моль*1 та 4,1 х 103моль/м3. Таким
образом, в безразмерных единицах аТс/3 = 1,32; В/27 ~ 0,0181; С/9 =
= 0,0282, Г* = 318, ЗК и Г** = 319,1 К (см. рис. 4.1).
Задача 4.2. В задаче 4.1 коэффициенты Ландау находились из изме¬
рений температуры перехода, параметра порядка, теплоты перехода и т. д.
На основе теории Ландау -де Жена найти: a) snem как функцию Т** — Т
и б) теплоемкость ср в нематической фазе как функцию Т** — Т и ее скачок
в точке перехода; в) скачок энтропии и г) теплоту перехода.
О т в е ты
a) s
пет
В
4 С
б) ср — — Т
&) S'lSO S
+v
^3a(T** -
2C
\ _ o?T
ar2
К 2C
о
l
1 4- ^ (гр** _ ТЛ —1/2
2 \/баС
и 2а2Тс/С.
пет
дТ
аВ
2
Т—Т.
С
27 С2
сьВ^Т
г) H[so - Япет = Tc(Siso " ^пет) = ■ ° | Подробности СМ. В КНИГе
Анисимова (1991).
27 С2
Задача 4.3. В модели Онсагера найти скалярный параметр порядка
как функцию а.
Ответ. 5 = 1 — 3 cth— + —; s = 0,85 при а = 18,84.
а а2
Задача 4.4
а). Найти теплоту перехода в теории Майера-Заупе.
б). В предположении о малости параметра порядка выразить коэффи¬
циенты А, Б, С теории Ландау-де Жена через параметр Майера-Заупе b
(см. обзор8)).
О т в е ты
а) В пересчете на молекулу bs2/2 « 0,42/сБТс.
7^ К Poggi, J. С. Filippini and R. Aleonard, Phys. Lett. 57A, 53 (1976).
M. J. Stephen andJ. P. Straley, Rev. of Mod. Phys. 46, 617 (1974).
158
Гл. 4. Фазовые переходы
б) А = —
2 Т
Задача 4.5. Обычно рацемические смеси, содержащие одинаковое
количество правых и левых (L и D) энантиомеров, не проявляют макроско¬
пической хиральности. Однако если взаимодействие между молекулами
одинаковой и противоположной хиральности существенно отличается, то
можно ожидать расслоения раствора и образования больших хиральных
областей. В 1988 г. Андельманом и де Женом9) было рассмотрено попарное
группирование в хиральных монослоях.
Рассмотрим хиральную молекулу, состоящую из центрального атома
углерода и четырех разных групп, присоединенных к нему по вершинам
тетраэдра. Одна из групп представляет собой углеводородную цепь, вытал¬
киваемую из воды, три остальные — А, В и С (например, А, В, С — NH2,
СНз, Cl, F, CN и т. д.), находящиеся в контакте с водой, рис. 4.12, а.
Рис. 4.12. Поверхностно-активные хиральные молекулы (L-энантиомер (а)) в за¬
висимости от взаимодействия трех гидрофильных групп могут образовывать на
поверхности воды либо гомохиральные (б), либо гетерохиральные (в) пары
У пары молекул взаимодействуют две пары групп, касающиеся друг
друга, как показано пунктирными линиями на рис. 4.12, б, в. Если энергии
парного взаимодеиствия групп wAB, wаа, ^ас и т.д. известны, то стрем¬
ление системы к образованию гетерохиральных (L, D) или гомохиральных
(L, L) димеров может быть установлено путем сравнения соответствующих
парных статистических сумм Zld и Zll.
а) Используя обозначения = exp(-i^-/к^Т), найти статистические
суммы для (L, L) и (L, D) пар.
б) В предположении что группы В и С обладают противоположными
электрическими зарядами, так что /вв = fee = 0, /вс > 1, и что части¬
ца А безразлична к обеим заряженным группам, /Ав = /ас ~ v, найти
А
А
С
А
А
А
а
б
в
предпочтительный тип димеров.
D. Andelman and P. G. de Gennes, C. R. Acad. Sci. 307, Ser. II, 23 (1988).
§ 4.5. Модель Костерлица — Таулесса
159
(в-ж) Найти тип димеров, когда в) одинаковые группы предпочитают
не взаимодействовать друг с другом, fti — 0; г) группа А индифферентна;
т. е. fAj = / = const; д) группы А, В и С несут ненулевые заряды а, Ь и с
соответственно; а + b + с — 0; е) все взаимодействия — лондоновского типа
с потенциалом Wij — — Uctiaj, где U — положительная постоянная, такая
что UaiOLj/к^Т 1; (ж) температура очень высока, к^Т
Отв еты
я) Zll = /вс + /ас + /ав + 2/ав/сс + 2/аа/вс + 2/дс/вв, Zld —
— /вв/сс + /аа/вв + /аа/сс + 2/ас/вс + 2/дв/вс + 2/ав/ас-
б) Обозначая/аа - и, находим AZ = = /|с + 2/вс(и-2и),
и димеры становятся гомохиральными (AZ > 0) для любого значения
/вс > 2(2^ — и). С другой стороны, если силы притяжения действуют
только между одинаковыми группами, так что fij = 0 при i ф j, тогда
AZ = -/вв/сс - /аа/вв - /аа/сс < 0 и образуются гетерохиральные
димеры.
в) Область гетерохиральности — внутри конуса вращения, касающе¬
гося плоскостей /ав = 0, /вс = 0, /Ас = 0.
г) Гомохиральные при /вс > /вв, fee-
д) Гомохиральные.
гетерохиральные димеры.
ж) —> 0: быстрые тепловые вращения молекул делают их эффек¬
тивно нехиральными.
Задача 4.6. Вывести уравнения (4.46) и (4.48).
Ответ. Варьирование J (/smA + /fo) dV по отношению к ф* (г) при¬
водит к выражению
и I \ 3 (аА - ав)2(ав - Qc)2(Qc - ад)2 х
2
dV аф 6ф* + /3\ ф \2ф 8ф* +
dip \ / д \
dz) V dz )
2 М
V
160
Гл. 4. Фазовые переходы
Для преобразования члена V 8ф* вводим г/ = (Vj_ — iqo 8п)ф и используем
равенство \7(г}8ф*) = rjV 8ф* 4- 8ф*\/т]. В результате имеем
8ф* dV
V(t? 8ф*) dV
6ф*Чг) dV
v
V
V
а вариация приобретает вид
ог]6ф* dS
ёф*Х7г] dV,
5
V
V
аф + /?| ф 12ф +
2Mj| V dz
Н — (Vi - iqo Sn)2ф
2Mj_
О
1
Эф
5ф* dV+
+ -i-(Vi - iqo^n)ф
2M\ i \0z/ 2Af I
cfy>* = 0.
Условие обращения в нуль объемной вариации приводит к (4.46), а поверх¬
ностной — к граничному условию
— (Р^) + rrr-(V
2 Мп Яг
2МХ
Jl
гд0 6п)ф
t
0, где t — единичный вектор нормали к смектическим слоям.
Применение аналогичной процедуры к упрощенной версии свободной
энергии
— (V - iqo 5п)ф + -K(rot8n)
12 М 2
dV
v
приводит к (4.48); для упрощения текущего выражения К rot rot S(Sn) мож¬
но использовать тождество brota — a rot b = div [а х Ь], где а = 8(8п)
и b = rot 8п.
Задача 4.7. Найти критическое поле для перехода смектик А - нема¬
тик в материале первого рода с к < 1 /л/2-
Ответ. hc — y/K2a2/(3. Вычисления нижнего и верхнего критиче
ских полей в смектиках второго рода можно найти в книге Чайкина и Лю
бенского (Chaikin and Lubensky, 1995).
Литература для дальнейшего чтения
161
Литература для дальнейшего чтения
1. М. A. Anisimov Critical Phenomena in Liquids and Liquid Crystals. Gordon and
Breach, Philadelphia, 1991.
2. P. M. Chaikin and Т. C. Lubensky. Principles of Condensed Matter Physics. Cambrid¬
ge University Press, 1995.
3. P. G. de Gennes and J. Prost. The Physics of Liquid Crystals, Oxford Science
Publication. Clarendon Press, Oxford, 1993.
4. Ландау Л.Д., Лифшиц E.M. Теоретическая физика. Т. VI. Статистическая
физика. — 5-е изд., стереот. — М.: Физматлит. 2001. 584 с.
5. Phase Transitions in Liquid Crystals, Edited by S. Martellucci and A. N. Chester,
NATO ASI series. Series B, Physics, v. 290.
6. V V Schmidt. The Physics of Superconductors. Berlin: Springer-Verlag, 1997.
7. H. E. Stanley. Introduction to Phase Transitions and Critical Phenomena. Oxford
University Press, N. Y. 1987.
8. G. Vertogen and W. H. de Jeu. Thermotropic Liquid Crystals, Fundamentals, Sprin¬
ger Series in Chem. Phys. V. 45. Berlin: Springer-Verlag, 1988.
Дополнительная литература
1. Пикин С. А. Структурные превращения в жидких кристаллах. — М.: Наука,
1981.
11-КЛЕМАН М.
ГЛАВА 5
УПРУГОСТЬ МЕЗОМОРФНЫХ ФАЗ
§ 5.1. Одноосные нематики и холестерики
5.1.1. Плотность свободной энергии
Состояние деформации нематической или холестерической фазы при
постоянной температуре описывается с помощью поля директора п(г).
Свободная энергия, связанная с деформацией, с необходимостью зависит
дть'
от градиента директора Vn, компоненты которого —1 будем обозначать
dxj
как riij. Такие искажения директора предполагаются не слишком резкими,
1 ni,j I ^ (5-1)
а
где а — характерная молекулярная длина. Такое предположение дает сле¬
дующие преимущества.
• В каждой точке г хорошо определен «касательный» (к траектории
директора) идеальный (жидкий) кристалл с ориентацией п(г), харак¬
терный размер которого достаточно велик, чтобы сделать возможным
непрерывное описание среды.
• Хорошо определено локальное значение параметра порядка s[T(r)],
однозначно зависящего от температуры Т(г).
• В каждой точке г симметрийные свойства «касательного» жидкого
кристалла должны быть отражены в плотности свободной энергии
/(г), которая зависит не только от п(г), но и от его пространственных
производных Vn. Важно, что энергия / должна быть инвариантна от¬
носительно любого изменения ориентации директора п и значений
его производных Vn, разрешенных симметрией. Эта инвариантность
ни в коей мере не является тривиальной и должна рассматриваться
как принцип, которому можно было бы присвоить имя Нолла (прин¬
цип инвариантности материи), и он оказывается гораздо глубже, чем
инвариантность разложения Ландау, которое (в простейшем случае)
не зависит от производных.
Таким образом, свободная энергия образца нематика или холестерика
должна быть инвариантна относительно любой операции, сохраняющей
локальную ориентацию директора п.
1. Инвариантность относительно преобразования п —> — п, общая
операция для нематической и холестерической фаз. Отметим, что это пре¬
образование симметрии не является ни пространственным преобразовани¬
ем, которое перемещает вещество, ни операцией инверсии; эта операция
§ 5.1. Одноосные нематики и холестерики
163
действует в пространстве параметра порядка и не затрагивает реальных
молекул.
В случае нематиков имеются дополнительно:
2. центр инверсии в любой точке;
3. инвариантность относительно любого поворота вокруг п.
А в случае холестериков имеем:
2*. отсутствие центра инверсии. Такая операция превращала бы, ска¬
жем, правый холестерик в левый;
3*. инвариантность относительно поворота на угол 7г вокруг директо¬
ра п, оси геликоида х и поперечной оси т = х х п-
Заметим, что голубые фазы, обладающие локальной двойной закрут¬
кой, инвариантны относительно замены п -4 — п и операций симметрии
соответствующих пространственных групп.
В силу малости riij как в нематиках, так и в холестериках в разложении
свободной энергии можно ограничиться членами, квадратичными по Vn.
Единственными скалярными инвариантами, линейными по явля¬
ются divn = n^i и nrotn = Здесь eijk — полностью анти¬
симметричный единичный псевдотензор (тензор Леви-Чивита) с компо¬
нентами £'123 = ^231 = £312 = 1, ^132 = ^213 — ^321 = ~1 И £ijk = 0, еСЛИ
хотя бы два индекса совпадают. В компонентах векторное произведение
записывается как [а х b]* = £ijk&jbk\значит, [rot n]i = [V х n]* = eijk^kj-
Поскольку divn нечетна по п, ее следует исключить из разложения сво¬
бодной энергии. С другой стороны, (div п)2 разрешена как для немати¬
ков, так и для холестериков. Более того, nrotn меняет знак при инверсии
(;х —> —х: у —у —у, z -4 — z\ так что этот член может появиться в разло¬
жении свободной энергии для холестерика, но не для нематика. Наконец,
квадратичный скаляр (rot п)2 появляется в обеих фазах.
Поскольку в правой части равенства (rot n)2 = (n rot n)2 + (nx rot n)2
оба слагаемых являются инвариантами, свободная энергия нематика, огра¬
ниченная первыми производными, может быть записана в виде
/ро = ijK^Mivn)2 + -К2(п ■ rotn)2 + -К3(п х rotn)2. (5.2)
2 2 2
Плотность свободной энергии (5.2) называется свободной энергией
Франка-Осеена с упругими постоянными Франка К2, (все три
являются положительно определенными). Мы уже использовали их при
анализе перехода N о SmA (п. 4.4.2). В холестерической фазе наличие
члена n rot п приводит к плотности энергии в виде
/ро = -Ki(divn)2 + -К2(п • rotn + g0)2 + -Кз(п х rotn)2, (5.3)
2 2 2
27Г -
где qo = —, а р, как будет видно из дальнейшего изложения, представляет
164
Гл. 5. Упругость мезоморфных фаз
собой шаг холестерическойшаг спирали; в наших обозначениях qo положи¬
телен для правых холестериков и отрицателен для левых при условии, что
используемая система координат — правая.
В используемом приближении выражения (5.2) и (5.3) являются полны¬
ми, но только если пренебречь дивергентными членами1
Лз + /24 — К13 div (n div n) — K24 div (n div n + n x rot n). (5.4)
Член с множителем K2а может быть преобразован в квадратичную форму из
первых производных, см. (5.7) ниже, в то время как член с К13 пропорцио¬
нален вторым производным riijk ив принципе мог бы быть сравнимым
с /fo ос rii jTik i. Тот факт, что эти члены представляют собой дивергенции
некоторых векторов, позволяет по теореме Остр о граде ко го - Гаусса преоб¬
разовать интеграл по объему J (/13 + /24) dV в поверхностный интеграл:
Кхз div gi3 dV
К24 div g24 dV = K13 (\)v • gi3 dA-
i^24 Qv • g24 dA, (5.5)
A
где gi3 = n div n, g24 — n div n + nxrotn, a v — единичный вектор
внешней нормали к поверхности А. Однако преобразование (5.5) в интеграл
по поверхности не является основанием для того, чтобы пренебречь дивер¬
гентными членами (5.4) (впредь мы будем использовать для этих членов
название «поверхностные», принятое в отечественной литературе). Энер¬
гетические интегралы (5.5), вообще говоря, линейно зависят от размера
деформированной области, как и интегралы J /ро dV. Отметим, что преоб¬
разование (5.5) возможно только в случае постоянных К13 и К24. Основное
различие между /fo и (/13 + /24) проявляется при вычислении равновес¬
ного распределения директора путем минимизации функционала полной
свободной энергии J (/fo + /13 + /24) dV: члены с К13 и К24 не входят
в вариационные производные Эйлера-Лагранжа в объеме. Однако они мо¬
гут вносить свой вклад в энергию и влиять на равновесное распределение
директора через граничные условия на поверхности А.
5.1.2. Геометрическая интерпретация деформаций директора
5.1.2.1. Объемные члены. К\ называется упругим модулем попереч¬
ного изгиба (splay). Деформация поперечного изгиба div п не исчезает в
двух геометриях, представленных на рис. 5.1 а и б: div п — - для двумерно-
г
го поперечного изгиба (пх = cos пу = sin у?, nz = 0) в цилиндрических
2
координатах (г, </?, z) (рис. 5.1, а) и div п = - для трехмерного поперечного
Г
1} J. NehringandA. Saupe, J. Chem. Phys. 54, 337 (1971); 56, 5527 (1972).
§ 5.1. Одноосные нематики и холестерики
165
изгиба (пх = пу = nz = -), г = л/ж2 + у2 4- г2 (рис. 5.1,6). Оба
г г г
члена, К2 и Кз, исчезают из-за того, что rot п = 0.
К2 называется упругим модулем кручения (twist): n rot п является един¬
ственной неисчезающей деформацией в геометрии, представленной на
А
а
б
в
А
г
Рис. 5.1. Деформация поперечного изгиба (splay) в двумерной геометрии (а), то же
в трехмерной геометрии (б), кручение (twist) (в), продольный изгиб (bend) (г)
166
Гл. 5. Упругость мезоморфных фаз
рис. 5 Л, в, иллюстрирующем правостороннее закручивание директора (пх=
q, 2тг
= cos qz, пу = sin qz, nz = 0). Здесь q ~ ~ ~ — > 0, a — суммарный
d p
угол закручивания всего образца, d — его толщина, а р — шаг геликоида.
Заметим, что nrotn + q = 0; q — —nrotn — волновое число, связанное
с шагом; отсюда следует интерпретация qo\ свободная энергия (5.3) холе¬
стерика зануляется при nrotn = —go в идеальной холестерической фазе.
Теперь пора сделать одно важное замечание относительно геометриче¬
ского смысла уравнения n rot п=0. Это необходимое и достаточное условие
для того, чтобы «силовые линии» директора были перпендикулярны некото¬
рому семейству поверхностей. «Достаточность» очевидна: предположим,
что п таков, что его можно записать в виде
п = ±Чф/\Щ\, (5.6)
т. е. перпендикулярен семейству поверхностей ф(х, у, z) — const с различ¬
ными значениями константы; 1/| Х7ф\ — это нормирующий множитель,
введенный, чтобы удовлетворить условию п2 — 1. Уравнение (5.6) дает
n rot п = 0: закручивание исчезает. Следовательно, в слоистых фазах, даже
деформированных, закручивание отсутствует.
Кз называется упругим модулем продольного изгиба (bend): n х rot п —
единственная неисчезающая деформация в геометрии, представленной на
рис. 5.1,г (пх = sin(р,пу = cosip,nz = 0) и |n х rotn| = Такой про-
Г
дольный изгиб имеет точный геометрический смысл в любой искаженной
конфигурации: n х rot п — это вектор, направленный по главной нормали
к «силовой линии» директора в точке М. Длина этого вектора равна кри¬
визне - в данной точке (рис. 5.2). Если n х rot п = 0, то «силовые линии»
г
прямолинейны.
5.1.2.2. Поверхностные члены. Геометрический (и физический)
смысл поверхностных членов намного сложнее.
К24 называется упругим модулем седловидного изгиба (.saddle-splay) по
причине, которая прояснится при обсуждении аналогичного модуля для
слоистых фаз. Если п зависит только от одной декартовой координаты,
член с множителем К%4 тождественно исчезает. Седловидный изгиб отсут¬
ствует в двумерном поперечном изгибе (рис. 5.1, а), но не в трехмерном:
2
div (n div n + п х rot п) = — на рис. 5.1,6. Важно понять, что другой сед-
2
ловидный изгиб скрыт в плотности свободной энергии /ро (5.2), как видно
из тождества
(div n)2 + (rot n)2 = TiijTiij + div (n div n + n x rot n). (5.7)
§5.1. Одноосные нематики и холестерики
167
Рис. 5.2. Геометрический смысл n х rot п
if 13 часто называют упругим модулем смешанного продольно-попереч¬
ного изгиба (mixedsplay-bend). Его геометрический смысл становится более
понятным, если рассмотреть поверхностную плотность энергии, получаю¬
щуюся из поверхностных членов:
5i3 + ^24 = ^13(^n) div и — i^24^(ndivn 4- n x rot n). (5.8)
Поверхностная плотность, связанная с членом К24, содержит производ¬
ные только в направлениях, касательных к поверхности А, в то время как
поверхностная плотность, связанная с членом Кi3, кроме того, с необходи¬
мостью содержит производную по нормали к А2\
Для скаляра div п отсутствует простое образное представление для ха¬
рактерных искажений в нематиках и холестериках, но в слоистых фазах
геометрическая интерпретация существует.
5.1.3. Упругие постоянные материалов
5.1.3.1. Низкомолекулярные жидкие кристаллы. Модули Кь К2,
Кз, K\z и имеют размерность силы, т. е. они могут быть выражены как
отношение энергии U к длине а. Единственными типичными энергиями в
упорядоченной среде являются энергии межатомного или межмолекуляр-
ного взаимодействия, причем наиболее характерными являются взаимодей¬
ствия ближайших соседей. Очевидно, эти энергии не могут быть намного
больше к&Тс, где Тс — температура «прояснения», при которой плавится
нематическая фаза. В случае низкомолекулярных нематиков Тс лежит в об¬
ласти комнатных температур или немного выше, скажем 400 К, и разумной
оценкой является U та 5 х 10"21 Дж или 5 х 10"14 эрг. Единственными ха¬
рактерными длинами являются молекулярные или атомные размеры. Взяв
а ~ 1 нм, a U из оценки, приведенной выше, получаем: та — та 0,5 х
а
х КГ11 Н, или 0,5 х 10_6 дин. Такие величины чаще всего и получаются
2) VM. Pergamenshchik, Phys. Rev. Е48, 1254 (1993); Е49, 934 (Е) (1994).
168
Гл. 5. Упругость мезоморфных фаз
при измерении Кг, К2 и Кз (например, с помощью перехода Фредерикса,
п. 5.4.3) в термотропных нематиках. Так, для 5СВ1^
Ki = 0,64 х НП11 Н; К2 = 0,3 х ИГ11 Н; К3 = 1 х НП11 Н.
Как правило, наименьшим из коэффициентов является К2. В результате
закручивание часто встречается в деформированных нематических образ¬
цах, так, например, в каплях нематика можно видеть закрученные структу¬
ры (см. п. 11.1.6).
Совсем мало известно о К24 (см. данные Кроуфорда (Crawford4^))
и практически ничего не известно о К\3. Как показал Эриксен (J. L Erick-
sen2)), требование n = const в нематике с q — 0 и К\з — 0 приводит
к 0 < К2\ < К\ или 0 < Кш24 < К2 (меньше наименьшего из них).
5.1.3.2. Полимерные жидкие кристаллы. Здесь не встретишь про¬
стоты низкомолекулярных жидких кристаллов, но, с другой стороны, мож¬
но ожидать необычной связи коэффициентов с конформациями мол екул\ эта
область до сих пор открыта для исследований. Обычно К2 остается меньше,
чем К\ и Кз. Такое соотношение интуитивно оправдано, поскольку моле¬
кулярная длина L априорно не играет большой роли в деформации чистого
закручивания. С другой стороны, К\ и К3 модифицируются кардинально.
Однако имеются немногочисленные точные теоретические исследования
и недостаточное количество экспериментальных результатов, касающихся
величин Ki, К2 и Кз в различных полимерах. При этом следует разли¬
чать два типа полимерных жидких кристаллов (подробности можно найти
в обзорных статьях6^).
Раствор жестких полимеров. Как уже упоминалось, это, например,
многочисленные полимеры биологического происхождения в растворе или
вирусы, как вирус табачной мозаики в воде; полиамиды в серной кислоте
имеют нематическую фазу, элементы которой используются как волокна для
тканей. В этих случаях переход в нематическую фазу согласуется с моделью
Онсагера. В онсагеровской модели жестких стержней К\ и К2 слабо меня¬
ются при разбавлении раствора, поскольку стержни не очень мешают друг
другу при поперечном изгибе или закручивании. Деформация продольного
изгиба, напротив, обещает6) сильные эффекты взаимного расталкивания.
Измерения Ki/xa из эффекта Фредерикса (ха — это диамагнитная или
Обзор современных данных можно найти в книге: L.M. Blinov and V.G.
Chigrinov, Electrooptic Effects in Liquid Crystal Materials, Springer series on partially
ordered systems, N. Y., 1994.
4) G. P. Crawford, in Physical Properties of Liquid Crystals: Nematics, Edited by D. A.
Dunmur, A. Fukuda and G. R. Luckhurst, INSPEC, The Institution of Electrical Engineers,
London, U. K. (2001), p. 230.
2) J. L. Ericksen, Inequalities in liquid crystal theory, Phys. Fluids 9, 1205 (1966).
S. D. Lee and R. B. Meyer, in «Liquid Crystal 1 inity in Polymers», Edited by A. Ciferri,
p. 343, VCH Pub. 1991; Liq. Cryst. 7, 15 (1990).
§ 5. L Одноосные нематики и холестерики
169
диэлектрическая анизотропия), а также Ki/rj из неупругого рэлеевского
рассеяния (здесь г} — это вязкость) показывают возрастание Кi и с ро¬
стом молекулярного веса Mw ос — и объемной доли молекул Ф = -d2Ln
d 4
(bud — длина и диаметр молекулы, а п — число молекул в единице объе¬
ма). Аналитическое решение7^, полученное в пределе большого скалярного
п Т/- 7 /сБТ т L 0 Т г Т г 4 /сБТ т q / L ч з
параметра порядка 5 —1, = Ф та 37^2, ^з = Ф (-) ,
87г d d 37Г2 d d
показывает, что К3 возрастает намного быстрее, чем с возрастанием
объемной доли.
Численные результаты, полученные в рамках модели Флори -Онсагера,
модифицированной для учета изменения исключенного объема с деформа¬
цией, приведены в табл. 5.1.
Таблица 5.1. Численные результаты для коэффициентов Франка, полу-
11 Л
ченные в модели Флори-Онсагера" (размерность 10” Н или 10 дин)
s = 0,7
s = 0,8
s = 0,9
Ki
1,8
2.1
3,3
K2
0,6
0,69
1,1
K3
8,0
14,0
43,0
Кг/К2
3
3
3
K3/K2
13
21
39
*G. Strajer, S. Fraden and R. B. Meyer, Phys. Rev. A 39, 4828 (1989); R. B. Meyer
et aL, Faraday Discuss. Chem. Soc. 79, 1.25 (1985).
Полугибкие полимеры. Две особенности, характерные как для лио¬
тропных, так и для термотропных полимерных жидких кристаллов, прояв¬
ляются с возрастанием молекулярного веса, а именно:
• с возрастанием L концентрация концов цепей убывает, что оказывает
прямое влияние на величину модуля поперечного изгиба К\. Вклад
концов цепей в полную свободную энергию обусловлен, во-первых,
их упругой деформацией (настоящей, как в кристаллических твердых
телах), а во-вторых, их энтропией, которую можно оценить в пред¬
положении, что концы цепи образуют идеальный газ. Упругая часть,
вычисленная де Женом8\ дает вклад в К\, пропорциональный L2.
С другой стороны, можно порассуждать о возможности деформации
7) Т. Odjit Liq. Cryst. 1, 553 (1986).
P. G. de Gennes, Mol. Cryst. Liq. Cryst. Lett. 34, 177 (1977).
170
Гл. 5. Упругость мезоморфных фаз
поперечного изгиба без изменения плотности (и без упругих деформа¬
ций), как на рис. 5.3, а: V-образная полость между двумя стержнями
заполняется введением между ними конца третьего стержня. Тогда
основной эффект обеспечивается изменением энтропии и приводит
к вкладу в Ki9\ имеющему порядок — Ф (Ф — это объемная
доля в случае лиотропных полимерных жидких кристаллов или по¬
стоянная для термотропных). Другой способ релаксации деформаций
поперечного изгиба состоит во введении «шпилек» («hairpins»), как
на рис. 5.3,6. В пределе бесконечной длины цепей любая деформа¬
ция поперечного изгиба оказывается запрещенной, а К\ стремится
к бесконечности;
• деформации продольного изгиба, напротив, не нуждаются в изме¬
нении плотности. Соответствующий упругий модуль связан с пер¬
систентной длиной £р, ус = к^Т£р (см. § 15.1). Доводы, основан¬
ные на масштабной инвариантности, позволяют написать выражения
для упругих постоянных Франка. Основное предсказание7^ состоит
в том, что величина Кз « Ф — становится независящей от длины
d d
цепи, в предположении, что L £р. На рис. 5.4 приведены экспе¬
риментальные данные для поли-7-бензил-Ь-глутамата (poly-y-benzyl-
L-glutamate, PBG). Молекулы PBG образуют жидкокристаллические
фазы в своей расширенной а-спиральной конформации в различных
органических растворителях, таких как m-крезол, диоксан, бензол,
О
хлороформ и т. п. Как правило, в этих растворах PBG £р « 103А, в то
О
время как d « (15 — 25)А, а Ф = 0,1 — 0,2. Заметим, что макси¬
мум в зависимости К3/К1 на рис. 5.4 а достигается при L/d яз 50,
или L и 103 А, что блестяще согласуется с результатами прямых
измерений £р. Однако измеренное отношение К2/К1 не совпадает
с теоретическим значением 1/3.
Совсем мало измерений проведено в термотропных полимерных жид¬
ких кристаллах. Здесь сошлемся на работу Жень Миня и Клемана (Zheng
Min и Kleman)l0\ где показано, что в полиэфире, главная цепь которого
образует нематическую фазу, модуль К\ крайне велик (примерно в 10
раз больше) по сравнению с низкомолекулярными нематиками, в то вре¬
мя как К2 и К% имеют величины, более близкие к обычным. Ядра дефектов
(дисклинаций) в этом соединении демонстрируют молекулярное упорядо¬
чение, подтверждающее сильную анизотропию коэффициентов Франка1 Ч
R. В. Meyer, in Polymer Liquid Crystals, Edited by A. Ciferri, W. R. Krigbaum and
R. B. Meyer, Academic Press, N. Y., 1982, p. 133.
10) Sun Zheng Min andM. Kleman, Mol. Cryst. Liq. Cryst, 111, 321 (1984).
n) G. Mazelet andM. Kleman, Polymer 27, 714 (1986).
§5.1. Одноосные нематики и холестерики
171
б
Рис. 5.3. Влияние концевых цепей на модуль поперечного изгиба (а); шпильки
(hairpins) в полимерных цепях (6)
k fn
20
40
60
80
100
Lid
120
а
V 04
L М
ьГ
б
Рис. 5.4. Kz/K\ (а), К\/1<2 и Къ/К^ как функции химической длины L/d по¬
лимерной цепи (б); раствор PBG в смеси 18% диоксана и 82% дихлорметана
(dichloromethane) (перерисовано из [6])
172
Гл. 5. Упругость мезоморфных фаз
§ 5.2. Слоистые фазы
5.2.1. Плотность свободной энергии
Параметр порядка фазы SmA содержит как нематическую часть (при¬
шедшую от нормального к слоям директора п(г)), так и часть, связанную
с одномерной кристалличностью. Отсюда сразу следует выражение для
свободной энергии. «Объемная» нематическая часть (5.2) приводит к той
же свободной энергии, а именно
fi = -Ki(divn)2 + ~Кз(п х rotn)2, (5.9)
без члена, ответственного за кручение, о чем было сказано выше. Кристал¬
лическая часть дает
Н=-в( ^1±] = 1ву2, (5.10)
2 \ do } 2
где do — равновесный период слоистости, d — фактическое межслоевое
расстояние, измеренное вдоль п (в приближении непрерывной среды d яв¬
ляется непрерывной функцией г), а В — модуль Юнга одномерного твер¬
дого тела.
Обсудим члены К2 и Кз подробнее. Проведем замкнутую петлю в слег¬
ка деформированном смектике. Суммарное число пересеченных (в алгеб¬
раическом смысле, с учетом направления пересечения) слоев в точности
равно нулю и может быть записано в виде ™ § ndlb если слои подверже¬
но
ны деформации изгиба, но без сжатия или растяжения. Следовательно, по
теореме Стокса § nd£ = J rot ndS = 0, что дает rot n = 0 т. е.
nrotn = 0 (5.11а)
(отсутствует закручивание поля директора) и
п х rotn = 0 (5.11 б)
(отсутствует продольный изгиб поля директора). Равенство (5.11а) уже
изучалось, и оно остается в силе даже при сжатии или растяжении слоев.
Уравнение (5.116) декларирует прямолинейность «силовых линий» поля
директора (поля нормалей к слоям) (линии - = 0) и параллельность слоев
г
(см. задачу 5.1). Если это не так, то имеется вклад в /2, меняющийся от
точки к точке. Сравним вклады /2 и К%. Имеем
{1<з} __ ^3 (п х rot п)2 ^ Кз_ 1
{/•2} В 72 В г 2
Заметим, что — = A3, где Аз — некоторая характерная для материала дли-
в
на, которая должна быть сравнима с межслоевым расстоянием. Поэтому
§ 5.2. Слоистые фазы
173
отношение ~“~у = (—) действительно очень мало (радиус кривизны г —
величина макроскопическая). Вклад К%, связанный со сжатием слоев, пре¬
небрежимо мал по сравнению со вкладом от В, имеющим ту же природу.
Плотность свободной энергии (5.9) и (5.10) сводится в итоге к выра¬
жению
/ = - К\ (div п)2 -Ь - Б72. (5.12)
2 2
Отношение Кг к В определяет важную шкалу длин
Л = y/Ki/B, (5.13)
называемую «глубиной проникновения»; величина Л имеет порядок меж-
слоевого расстояния, но по мере приближения к переходу SmA-нематик,
она неограниченно возрастает. Для низкомолекулярных SmA ожидается
величина К\ того же порядка, что и в высокотемпературной нематической
фазе. При Л ~ d0 и (1-гЗ) нмиХ! « Ю"а Н находим: В « 1064-107 Н/м2,
т. е. величина модуля сжимаемости здесь в 103 104 раз меньше, чем в твер¬
дых телах.
5.2.2. Деформации поперечного и седловидного изгиба
Теперь приступим к анализу другого выражения для плотности свобод¬
ной энергии:
/ = -К{аг 4- сг2)2 + Kaia2 + -В'у2, (5.14)
2 2
отличающегося от предыдущего (5.12) учетом поверхностного члена, свя¬
занного с седловидным изгибом К; упругая постоянная поперечного из-
1 1
гиба обозначена как К (вместо КА. Параметры о\ — — и а2 =
Ri R2
главные значения тензора кривизны смектического слоя в точке г, что
позволяет интерпретировать деформацию слоев через главную кривизну
Я = i(<7i -f сг2) и гауссову кривизну G = о\о2. Выражение (5.14) вер-
2
но для сильно искривленных слоев со слабой «твердотельной» дефор¬
мацией. Для положительной определенности плотности свободной энер¬
гии слоистой фазы (5.14) значение К должно лежать внутри интервала
—2К < К ^ 0 при положительном К.
Для начала покажем, что
div n = ±((Ji + а2). (5.15)
Здесь нам потребуются некоторые понятия теории поверхностей. Слои
можно представлять как поверхности. Рассмотрим такую поверхность Е в
окрестности точки М (рис. 5.5). В плоскости, касательной к £ в точке М,
выбраны ортогональные оси М#ь Мх2, а ось М'z направлена по нормали
174
Гл. 5. Упругость мезоморфных фаз
а
Рис. 5.5 Элемент поверхности в окрестности точки касания М: эллиптическая
точка (а); гиперболическая, или седловая, точка (б)
(произвольно ориентированной). В окрестности точки М уравнение по¬
верхности имеет вид
но можно выбрать направления осей xi и х2 так, чтобы перекрестный член
исчез:
Этот выбор определяет главные направления в М. Любая плоскость, содер¬
жащая Mz, пересекает £ по параболе (с точностью до третьего порядка)
с вершиной в точке М. Главные плоскости х2 = 0 и х\ =0 дают пара¬
болы с кривизнами в точке М: l/Ri и l/R2 соответственно. Легко пока¬
зать, что R\ и R2 являются экстремумами радиусов кривизны в точке М
всех парабол, получающихся наложением условия х2 — р,х\ на (5.17), где
/1 — изменяющийся параметр. Мы будем различать следующие два случая.
• Если знаки R\ и R2 совпадают, то элемент поверхности полностью
находится по одну сторону от касательной плоскости, а все центры
кривизны находятся между С\ и С2, двумя главными центрами кри¬
визны в точке М. Два радиуса кривизны MCi — jRi и МС2 = R2
являются алгебраическими длинами (со знаком). Гауссова кривизна
G — а\о2 положительна. В этом случае М называется эллиптической
z = ах\ + 26^1 х2 + сх 2 + О (ж3)
(5.16)
(5.17)
§ 5.2. Слоистые фазы
175
точкой. В окрестности М поверхность выглядит как эллиптический
параболоид (рис. 5.5, а).
• Если знаки R\ и R2 противоположны, элемент поверхности пересека¬
ет касательную плоскость, и все центры кривизны находятся снаружи
сегмента Ci С2. В этом случае М называется гиперболической точкой,
а поверхность локально выглядит как седло (рис. 5.5,6). Гауссова
кривизна G = <J\o2 отрицательна.
Директор нормален к поверхности,
n = ±V0/| V01, где ф = -z +- (— + — ) ,
2\R1R2J
и имеет компоненты
1
„=±и Х2 _Л(1 + ^+АУ^ (5Л8)
IЯ1 я2 /V R\ щ)
а в точке М получаем искомый результат:
divn = ± ( — -j~ — ) . (5.19)
\Ri R2J
Заметим, что div п не зависит от распределения п вне Е.
Классическим результатом теории поверхностей является запись гаус¬
совой кривизны в виде
G — oia2 = - div (n div n -b n x rot n). (5.20)
Это выражение связывает гауссову кривизну в смектиках с нематическим
поверхностным членом (5.4). Оно объясняет исчезновение седловидного
изгиба в геометрии двумерного продольного изгиба: поверхность, нормаль¬
ная к п, имеет нулевую гауссову кривизну.
В физике слоистых сред приняты обозначения: К\ — К и —2К24 — К,
как в (5.14).
Теперь рассмотрим единичный слой, или мембрану, толщины do и вве¬
дем модули изгиба для этой мембраны:
>с ~ К do^ х — К do- (5.21)
Свободная энергия на единицу площади может быть записана в виде
/с = -х{(Т1 + <Т2)2 + Л0\0ъ (5.22)
в предположении, что данная мембрана не связана с другими слоями, так
что Б-члены отсутствуют. Мы еще будем иметь возможность убедиться
в том, насколько важную роль играет это выражение для свободной энергии
176
Гл. 5. Упругость мезоморфных фаз
при изучении поверхностно-активных веществ в растворителях. Уравнение
(5.22) давно известно как выражение для энергии на единицу площади
в механической теории оболочек12\ с соответствием
^ EhZ - ^ ~Eh* ГС 004
ус ус ^ (5.23)
12(1 — is2) 12(1 + is)
где Е — модуль Юнга, a h — толщина оболочки. Заметим, что в этой тео¬
рии порядок величин хих одинаков. Это замечание остается в силе и для
мембран из поверхностно-активных веществ, материальные постоянные
которых могут выражаться через механические взаимодействия на моле¬
кулярном уровне13^ (см. гл. 14). И, наконец, поскольку <7i<T2 ~ я2, вклад
члена, связанного с гауссовой кривизной, в плотность свободной энергии /
сравним с таковым от члена, связанного с главной кривизной.
5.2.3. Плотность свободной энергии при малых деформациях
Теперь рассмотрим случай, когда слои лишь слегка изогнуты, так что
их деформация может быть описана одной скалярной переменной, компо¬
нентой смещения v(x, у, zq) слоев вдоль нормали к неискаженным слоям,
выбранной как ось z. Слой, первоначально находившийся в позиции zq,
в результате деформации находится в положении г = z0 -f- v(x, у, z0).
Следовательно, zo = г — v(x, у, z0), что может быть переписано с исполь¬
зованием новой переменной для смещения и(х, у, z):
zq = z — и(х, ?/, z). (5.24)
Уравнение деформированного слоя ф(х, у, z) — zo, где ф(х> у, z)
— z - и(х, у, z), а директор п = ±Уф/1 Уф | записывается в виде
„ = ±<5-^(1 + ^), + i_I
дх V dz J ду V dz) 2
(525)
с точностью до второго порядка. С той же точностью (задача 5.4)
ди
7 = ^
- r(Vxu)2, (5.26)
где член (Vj_u)2 = (^~) Учитывает эффективное сжатие слоев
12^ А. Е. И. Love, The Mathematical Theory of Elasticity, Dover, 1944, article 298.
13^ A. G. Petrov and A. Derzhanski, J. Physique Fr. 3, C3-15 (1976).
§ 5.3. Нематик во внешнем поле
177
при наклоне на малые углы ди/дх,ди/ду. Плотность свободной энергии
с точностью до членов второго порядка имеет вид
f =Y-Kl{Axu)2 + \в(д^)\ (5.27)
2 2 V oz /
д2 О2
где А± — —г + —г. Однако имеется немало интересных явлений, таких
дх2 ду2
как ондуляции слоев, вызванные полем или напряжениями (см. п. 5.5.1),
которые не могут быть надлежащим образом описаны в рамках квадра¬
тичной формы (5.27), и приходится возвращаться к нелинейным членам,
возникшим в (5.26):
/ = -КАА±и)2 +1-в\~- ~(Vxu)2
2 2
dz 2
-* 2
(5.28)
В большинстве случаев, представляющих практический интерес (вклю¬
чая ондуляции слоев), член седловидного изгиба исчезает либо из-за нуле¬
вых главных кривизн, либо из-за взаимной компенсации вкладов от обла¬
стей с противоположным знаком гауссовой кривизны.
§ 5.3. Свободная энергия нематика во внешнем поле
Явления, вызванные электрическим полем, обычно исследуются в гео¬
метрии, когда жидкий кристалл заключается между двумя стеклянными
пластинами. Внутренние поверхности пластин покрываются прозрачным
электропроводящим материалом, таким как смесь окислов индия и олова
(indium tin oxide, ITO). Более того, на электроды часто наносят специальное
покрытие (какой-нибудь полимер, например полиамид, слой поверхностно¬
активного вещества и т. д.), ориентирующее директор в определенном на¬
правлении, называемом «направлением сцепления» или «легкой осью».
Имеется четыре основных механизма взаимодействия жидкого кристал¬
ла с приложенным электрическим полем: (а) диэлектрический, (б) флексо-
электрический, (в) через поверхностную поляризацию двойного слоя ионов
или просто из-за нарушения поверхностью симметрии (на границе п ф — п)
и (г) обусловленное движением электрических носителей — ионов. Во из¬
бежание излишнего усложнения материала мы пока опустим явления, свя¬
занные с флексоэффектом (они будут рассмотрено позже), и предположим,
что жидкий кристалл является идеальным изолятором, а поверхностная
поляризация типа (в) на подложках отсутствует.
Предположим, что ячейка подключена к внешнему источнику, поддер¬
живающему постоянное напряжение между подложками. Диэлектрическая
связь подразумевает, что молекулы жидкого кристалла стремятся сориен¬
тироваться таким образом, чтобы компонента тензора молекулярной поля¬
ризуемости вдоль поля была максимальна. Чтобы найти равновесную ори¬
ентацию поля директора во внешнем электрическом поле, следует найти
минимум упругой энергии Fpo “ J /fo dV, дополненной:
178
Гл. 5. Упругость мезоморфных фаз
энергией электрического поля
14)
Fe
}е dV
1
ED dV,
(5.29 а)
вариация которой при малых переориентациях молекул записывается
в виде
SF
1
Е
Е5П dV\
(5,296)
свободной энергией, связанной с изменением зарядов на электродах в
связи с переориентацией директора п. Для поддержания постоянного
напряжения на ячейке источник электрического напряжения затра¬
чивает дополнительную энергию SFq. Она равна работе (с противо¬
положным знаком), необходимой для поддержания постоянного на¬
пряжения при изменении электрическй индукции SD, изменяющего
поверхностную плотность заряда на пластинах на величину (—SDZ)
(индекс «z» означает компоненту D по нормали к пластинам):
5F,
G
ГЧ А
ф SDZ dA
if К
Л
div (ф 5D) dV,
(5.30 а)
где мы применили теорему Остроградского-Гаусса. Здесь ф — элек¬
трический потенциал, a dA — элемент поверхности электрода. По¬
скольку div (ф5Т5) — ф divJD + Е — —Уф и divJD = 0
(свободные заряды отсутствуют), получаем
SFg
ESB dV = -25Fe*
(5.306)
Минимум полной объемной свободной энергии достигается, когда
5Fpо + SFe Н- SFq = S(Ffo ~ Fe) — 0.
(5.31)
Энергия Fe может быть выражена через компоненты напряженности по¬
ля и тензора диэлектрической проницаемости е (см. гл. 3). Представляя
электрическую индукцию как сумму двух компонент, перпендикулярной п
и вдоль п, т. е. D = £0£±Ех + £о£цЕц = £о£±Е -f £0^a(En)n (причем
£а — £\\ — получаем
ED = £о£±Ё2 + £:0ea(nE)2.
(5.32)
14^ J. D. Jackson, Classical Electrodynamics, John Wiley & Sons, Inc.. N. Y., 3rd edition,
1999, Chapter 4; В. И. Сугаков, E. М. Верлан. Гидродинамика жидких кристаллов. —
Киев: Изд-во КГУ, 1978.
§ 5.3. Нематик во внешнем поле
179
Опуская ориентационно-нечувствительный член в правой части, приходим,
наконец, к выражению для свободной энергии нематика, дополненной ди¬
электрическим членом:
/ = /fo - }е - /fo - -е0£а(пЕ)2. (5.33)
В одноосном нематике с еа > 0 директор п ориентируется вдоль Е; в случае
£а < 0 имеется вырождение по направлениям п в плоскости, перпендику¬
лярной Е.
Аналогичные рассуждения, проведенные для магнитного поля, дают
M = Mo1XxB + M0-1Xa(Bn)n (5.34)
для намагниченности, производимой магнитным полем с индукцией В.
в
Соответствующая плотность энергии Зеемана — это интеграл — J М • dB.
о
Свободная энергия в присутствии магнитного поля принимает вид
/ = /FO - -Но1Ха(пВ)2. (5.35)
2
Как и в предыдущем случае, не зависящий от п член опущен. Анизотропия
восприимчивости Ха обычно положительна для стержнеобразных немати¬
ческих фаз, а для дискотических — отрицательна, так что имеется вырож¬
дение по направлениям директора в плоскости, перпендикулярной В.
Как уже отмечалось, эффекты в электрическом поле сильно усложняют¬
ся механизмами, отличными от простой диэлектрической связи, рассмот¬
ренной выше, а именно: флексоэлектричеством, поверхностной поляриза¬
цией и свободными ионами.
Флексоэлектричество15'1 в жидких кристаллах — это аналог пьезо¬
эффекта в трехмерных кристаллах. (Точнее, прямым кристаллофизиче¬
ским аналогом флексоэффекта в жидких кристаллах является неоднород¬
ный вариант пьезоэффекта, см.: В. С. Машкевич, К. Б. Толпыго, ЖЭТФ 32,
520 (1957); К. Б. Толпыго, ФТТ 4, 1765 (1962); Ш. М. Коган, ФТТ 5, 2829
(1963). — Примеч. пер.). Кривизна поля директора вызывает электрическую
поляризацию среды. Этот эффект можно проиллюстрировать на примере
деформаций в нематике, состоящем из анизометрических (грушеобразных
или бананоподобных, рис. 5.6) молекул, обладающих постоянными диполь-
ными моментами. Например, поперечный изгиб нематика из грушеобраз¬
ных молекул с постоянными диполями вдоль оси приводит к макроскопи¬
ческой электрической поляризации Pi = ein(divn). Продольный изгиб
нематика из бананоподобных молекул с постоянными диполями, перпен¬
дикулярными оси, вызывает поляризацию Рз = e3(rotn х п), где вектор
rot п х п
15) R. В. Meyer, Phys. Rev. Lett. 22, 918 (1969).
180
Гл. 5. Упругость мезоморфных фаз
в г
Рис. 5.6. Молекулярные модели для флексоэлектрических эффектов (см. текст)
направлен вдоль радиуса кривизны «силовых линий» поля директора. Ко¬
эффициенты ех и ез имеют размерность p/а2, где р — дипольный момент.
Порядок величины коэффициентов е* та 10-11 Кл/м(та 10~4 единиц СГС).
Имеется связь флексоэлектрической поляризации Р/ с внешним полем;
вклад в свободную энергию линеен по Е (в отличие от диэлектрического
члена, квадратичного по Е):
/flex = -Р/Е = —[ein divn - e3(n х rot n)]E. (5.36)
Еще один похожий эффект — это эффект16^ в котором источником по¬
ляризации является градиент скалярной части параметра порядка. Другой
линейный электрический эффект возникает, когда отличается сродство «го¬
лов» и «хвостов» молекул с подложками. Если эти молекулы обладают
продольными дипольными моментами, нарушение симметрии из-за нали¬
чия поверхности приводит к поверхностной поляризации17^ Ps и вкладу
16-> G. Barbero, /. Dozov, I. Palierne and G. Durand, Phys. Rev. Lett. 56, 2056 (1986).
17^ P. Guyot-Sionnest, H. Hsiung and Y. R. Shen, Phys. Rev. Lett. 57, 2963 (1986).
§ 5.4. Типичные приложения упругости нематиков
181
(—PSE) в плотность поверхностной свободной энергии. Поверхностная
поляризация другого рода возникает из-за двойных слоев, образованных
вследствие селективной адсорбции ионов поверхностью. Ионы всегда при¬
сутствуют в жидких кристаллах либо как остатки химического синтеза,
либо из-за инжекции из электродов под действием приложенного напря¬
жения. Множество гидродинамических эффектов возникает, когда ионные
токи вовлекают жидкий кристалл в движение.
§ 5.4. Типичные приложения упругости нематиков
5.4.1. Минимизация свободной энергии в общем случае
Определение равновесного распределения директора из минимизации
функционала свободной энергии является классической задачей вариацион¬
ного анализа181 Сначала мы дадим общую схему, а потом проиллюстрируем
ее примерами.
5.4.1.1. Общие положения. Пусть F = f / dV — полная свободная
энергия нематической или холестерической фазы в объеме V. Впослед¬
ствии / принимается в виде (5.2), возможно, с добавлением полевых чле¬
нов (5.33), (5.35) или других членов. Задача минимизации состоит в поиске
распределения директора п(г), соответствующего минимуму F при физи¬
ческих условиях, таких как ориентация директора на поверхности, форма
образца и т. п.
Рассмотрим произвольную вариацию <5п(г), такую что п' = п(г) +Sn(r)
приводит к возрастанию полной свободной энергии F1. Задача минимиза¬
ции состоит в вычислении SF = F' — F:
SF =
*
' -
d df
Slli dV -f
Л
df
_дп{
dxj driij _
9nt,j
SriidAj, (5.37)
v
и требовании SF = 0 при любом выборе 5п(г). Выражение (5.37) получа¬
ется после интегрирования по частям, что позволяет в объемном интеграле
избавиться от производных 8щ^ и иметь только сами Зщ; ценой является
появление поверхностного члена.
Более того, в данном случае следует ввести дополнительный член в ва¬
риацию F:
8F
L
XniSriidV, (5.38)
происходящий из условия нормировки для п:
-А(п2 — 1) = О, (5.39)
2
18) Вариационные вычисления: см., например: Arfken G., Mathematical Methods for
Physicists, Academic Press, Inc., San Diego, 1985, Chapter 17.
182
Гл. 5. Упругость мезоморфных фаз
где так называемый множитель Лагранжа А — неизвестная функция коор¬
динат (не имеющая ничего общего с глубиной проникновения в слоистых
фазах).
Объемный и поверхностный члены в (5.37) должны трактоваться по-
разному.
В объеме. Так как вариация <5п(г) может быть выбрана произвольно
2
(но с соблюдением условия нормировки п' = 1 с точностью до величин
первого порядка, имеющего вид п • 8п = 0), рассмотрим поле <Sn, исчезаю¬
щее везде на поверхности и в объеме, за исключением бесконечно малого
объема dV, расположенного в некоторой точке г, где Sn постоянна. Таким
образом, получается
hi = -8L + A._2L = \ni. (5.40)
дп{ dxj driij
Эти уравнения должны выполняться в любой точке г образца, они назы¬
ваются уравнениями минимума Эйлера-Лагранжа. Вектор h называется
молекулярным полем. Уравнения (5.40) должны быть дополнены условием
нормировки (5.39) и граничными условиями, которые мы сейчас и рассмот¬
рим.
На границах. Условия на границах могут определяться либо усло¬
виями, относящимися к значению п на поверхности, либо условиями,
касающимися значений внешних моментов или сил, приложенных на гра¬
нице. В эксперименте чаще всего встречается первый случай, с п на грани¬
це, обусловленным обстоятельствами физико-химической природы. Тогда
с необходимостью имеем: Sn£ = 0, и поверхностные члены в (5.37) исчеза¬
ют тождественно; они играют роль математического выражения граничных
условий. Теперь рассмотрим случай внешних моментов С, приложенных
к директору на поверхности, на единицу площади, так что момент, дей¬
ствующий на элемент dA поверхности, дается произведением CdA. Работа,
производимая этим моментом при повороте директора на угол 8w, дается
выражением С8и> dA. Но | 5и> | — это угол между п и п'ц = n + т. е.
8пs = о; х П£. (5.41)
Следовательно, свободная энергия возрастает на величину
SF
ext
tOjCj dA. (5.42)
Определив dAj = Vj dA, где и — единичный вектор внешней нормали
к поверхности, и подставляя (5.41) в поверхностный член в (5.37), получаем
уравнение
^Р ^ ^Р ’ ^ipq^q^j ^ ~~ 0) (5*43)
driij
§ 5.4. Типичные приложения упругости нематиков
183
справедливое при любых значениях величины ир, которая является вирту¬
альным поворотом. Следовательно,
Ср — ~ ■ ISj € ipqTlq. (5.44)
dni,3
Это равенство выражает тот факт, что в равновесии полный момент, дей¬
ствующий на директор на поверхности, равен нулю. Эти уравнения опи¬
сывают упругую релаксацию директора на поверхности, и в них можно
включить поверхностные члены К13 и К2±, если они присутствуют в плот¬
ности свободной энергии / (эти члены не влияют на уравнения Эйлера-
Лагранжа в объеме). Включение члена К\% нетривиально, поскольку он
содержит производные по нормали к поверхности. Процедура должна учи¬
тывать то обстоятельство, что некоторые параметры жидкого кристалла,
такие как скалярный параметр порядка и плотность, изменяются на некото¬
ром ненулевом расстоянии возле поверхности19). В оставшейся части главы
будет предполагаться Кх3 — 0.
5.4.1.2. Особые случаи и упрощающие предположения. Уравнение
(5.40) решалось при некоторых специальных предположениях, таких как
(1) изотропная упругость с одинаковыми постоянными Франка —
= К2 — К% — К или (2) планарная геометрия искажений (п остается
параллельным некоторой плоскости). Нередко оба эти условия использо¬
вались одновременно. Хотя они и далеки от действительности, они тем не
менее облегчают качественное понимание специфических сторон настоя¬
щей упругости кривизны, а также некоторых свойств дефектов. Заметим,
что предположению (1) низкомолекулярные жидкие кристаллы следуют в
большей степени, чем полимерные: очень часто, К\ действительно и К3,
за исключением окрестности фазового перехода N—SmA, где К% расходит¬
ся. К тому же К2, как правило, меньше, чем К\ или К%. Следовательно,
деформации закручивания являются предпочтительными^0); поскольку эти
деформации образуют локальную ось геликоида, предположение (2) также
выглядит как нечто выполнимое на макроскопическом уровне. Ситуация
(2) рассмотрена в задаче 5.2. Ниже мы вкратце обсудим подход изотропной
упругости.
При К\ — К2 = К% = К свободная энергия в присутствии магнитного
поля записывается в виде
/ = ^[(divn)2 + (rot n)2] - -HolXa(Bn)2, (5.45)
2 2
или, в компонентах,
f = ~К \riq,pTlq,p "Н {j^p^q.q) ,р {^p^q, р) ,q } —Mo Xa^iTl{13jTlj , (5.46)
2 2
19) V.M. Pergamenshchik, Phys. Rev. E58, R16 (1998); Phys. Lett. A243, 167 (1998);
У. M. Pergamenshchik and S. Zumer, Phys. Rev. E59, R531 (1999).
20) С. Mauguin. Bull. Soc. Fran$. Miner. Crist. 34, 71 (1911).
184
Гл. 5. Упругость мезоморфных фаз
где использованы обозначения Б — | В |. В (5.46) имеются два поверхност¬
ных члена:
(прпя^я)1р “ div (ndivn), ~{npnq>p),q = div (n x rotn)
[см. также (5.4)], которые не играют роли при минимизации F = j f dV
в объеме, поскольку, как уже говорилось, с помощью теоремы Остроград¬
ского-Гаусса они могут быть преобразованы в интеграл по поверхности.
Следовательно, пока нас не интересуют поверхностные члены, мы можем
писать
/ = ^-Kviq^pTiqp ^Хо(Вп)^ = l-K(VnVnT)- -^^(Bn)2, (5.47)
Z Z Z £
и уравнения Эйлера-Лагранжа принимают простой вид
К Ап + /i^~1Xa(Bn)В = Ап. (5.48)
5.4.1.3. Параметризация директора. Практический способ учесть
условие п2 = 1 в задаче минимизации состоит в параметризации директора
с помощью полярного 0 и азимутального ip углов,
n = (sintfcosc/?, sin 0 sin 9?, cos#), (5.49)
вместо использования множителя Лагранжа. В общем случае и в, и (р зави¬
сят от всех трех декартовых координат, но условие n2 = 1 удовлетворяется
всегда. В следующем пункте мы воспользуемся угловой параметризацией
при нахождении равновесного п(г) для так называемых гибридно ориен¬
тированных нематических пленок.
5.4.2. Нематические пленки с гибридной ориентацией
5.4.2.1. Фиксированные граничные условия. Нематический слой
(рис. 5.7 а) заключен между двумя плоскими пластинами л = 0 и z — d, на
которых ориентация директора строго фиксирована по физико-химическим
причинам:
9(z = 0) = во, 0(z = d) = §d. (5.50)
Директор предполагается лежащим в вертикальной плоскости xz, ip = 0:
n — [sin0(z)3 0, cos0(z)]. (5.51)
Поскольку в (5.51) закручивание отсутствует, приближение изотропной
упругости сводится к Ki — = К, что недалеко от действительности,
и мы это приближение здесь используем.
§ 5.4. Типичные приложения упругости нематиков
185
а
б
Рис. 5.7. Пленка с гибридной ориентацией: жесткие граничные условия (а); мяг¬
кие граничные условия с релаксацией искажений директора внутри ячейки за счет
отклонения ориентации на границах от предпочтительных ориентаций сцепления,
задаваемых (5.50) (б)
При в, зависящем только от z, упругая энергия Франка-Осеена на еди¬
ницу площади ячейки сводится к
z=d
Ffo
(5.52)
J
z=0
ao
где 6f = —. При K\ — Kz — К это уравнение упрощается до
dz
z—d
Ffo = -К
2
(.в'f dz.
(5.53)
z—0
Поскольку в подынтегральном выражении в (5.53) отсутствует явная зави¬
симость от в, уравнение объемного равновесия Эйлера-Лагранжа, имею¬
щее вид (см. Приложение А)
d/FO
дв
d д/го
dz дв(
о,
(5.54)
сводится к в" = 0 с решением 9(z) = C\z + с2. Две постоянные, сi и со,
находятся из граничных условий (5.50), так что равновесная конфигурация
директора имеет вид
6{z) = {6d - во) - + во- (5.55)
d
186
Гл. 5. Упругость мезоморфных фаз
Упругая энергия нематической пленки на единицу площади с конфигура¬
цией директора (5.55),
(5.56)
Ffo = -К^в° вл)2,
2 d
зависит от разности \во — 0&\ в ориентации директора на границах.
5.4.2.2. Нежесткие граничные условия. При выводе (5.55) предпола¬
галось бесконечно сильное взаимодействие с поверхностью, поддерживаю¬
щее ориентацию директора на поверхности, строго фиксированной вне за¬
висимости от упругих искажений в объеме (см. (5.50)). На самом деле сила
молекулярного взаимодействия с пластинами конечна. Полная энергия мо¬
жет быть уменьшена, если понизить сильные упругие напряжения в объеме
за счет некоторых отклонении направлении директора на поверхностях от
выделенных осей во и в а. Энергия, вносимая этими отклонениями на по¬
верхности, описывается «потенциалом анизотропного сцепления» fs, ко¬
торый является функцией величины отклонения; например, fsо(#о — #о)-
Свободная энергия на единицу поверхности гибридной ячейки принима¬
ет вид
d
F
/fo[0? в'} dz + /s0(#0 — во) + fsd{e<l — 0d)
(5.57)
J
0
Для нахождения равновесного угла 0(z), минимизирующего функцио¬
нал (5.57), снова начинаем с уравнения Эйлера-Лагранжа (5.54), имеющего
все тот же вид в" = 0. Его решение может быть записано в виде [ср. с (5.55)]
o(z) = (ed
во) - + $0-
d
(5.58)
Постоянные интегрирования во и в^ отличающиеся от во и 8$, являются
фактическими углами ориентации директора на подложках, поскольку эти
углы определяются балансом упругих напряжений и сил связи через новые
граничные условия (см. Приложение А):
df FO
+
Со
О
1
II
о
к
dfvo
_l_ dfsd'
L д01
de J
z 0
1 дв'
dO J
0.
z~d
(5.59)
Предположим, что отклонения от направлений сцепления во and ва ма¬
лы, так что в разложении поверхностного потенциала достаточно оставить
первый неисчезающий член:
fsi = -WiiOi-Oi)2,
2
0, d.
(5.60)
Здесь W — так называемый коэффициент анизотропии сцепления, завися¬
щий от пары жидкий кристалл-подложка (п. 13.2.2). Приближение (5.60)
§ 5.4. Типичные приложения упругости нематиков
187
хорошо работает в толстых ячейках, d K/W{. Граничные условия (5.59)
сводятся в этом случае к
K(Oo-9d) + Wod(9o-0o)=Q и K(ed-0o) + Wdd(6d-0d) =0 (5.61)
и дают
во — во —
Lq
d + Lq + Ld
(во - ed) И ed = ed +
L
d
d + Lq + Ld
(i9o-0d). (5.62)
Здесь I/q = К/Wo и Ld = if/Wd имеют размерность длины и известны как
длины экстраполяции сцепления. Легко убедиться, что конечная величина
сцепления позволяет искажениям поля директора отрелаксировать так, что
полная энергия
2 d -j- Lq + Ld
(5.63)
уменьшается no сравнению с (5.56).
Уравнение (5.63) позволяет интерпретировать влияние конечного сцеп¬
ления как эффективное увеличение толщины пленки, d —> (d 4- L0 -f Ld).
Отсюда и ослабление искажений,
O'
0d ~ Оо \ /d < | 6d - во \/d
(рис. 5,7, 5), и уменьшение полной энергии. Геометрическая интерпретация
длин экстраполяции Lq и Ld и их влияния на конфигурацию директора
показана на рис. 5.8.
0
d
z
Рис. 5.8. Геометрическая интерпретация длин экстраполяции сцепления
Для оценки порядка входящих величин возьмем W
&SN
а
2
, где Usn
ориентационная часть энергии взаимодеиствия молекулы с подложкой,
а а — длина молекулы. Тогда
L
к и
— ^ а —
И/ Usn
(5.64)
188
Гл. 5. Упругость мезоморфных фаз
Случаи, когда L порядка нескольких длин молекул, будем называть сильным
сцеплением (strong anchoring): W (10 3 —10 2) Дж/м2 — (1-10) эрг/см2.
Слабое сцепление (weak anchoring) относится к длинам L, лежащим в «опти¬
ческом диапазоне»: 0,1-1 мкм. Экспериментальные значения лежат в диа¬
пазоне W ~ (10“6 — 10“3) Дж/м2.
5.4.2.3. Равновесие моментов. Вернувшись к граничным условиям
(5.59), мы хотим рассмотреть их с точки зрения равновесия моментов. Для
простоты, опять используем приближение К\ — К3 = К и начнем, как
и выше, с выражения SF — 6FV0\ + 8FSUTf:
rfifi
SFvo\ = —К —бвйг; (5.65)
2
SFsmf = -K(-) 5в0 + к(~) 66d +
V dz'Q \dz' d
+ Wo(0o - во) 6в0 + Wd(0d - ed) 86d, (5.66)
где 6в = arf{z) — виртуальный поворот директора, как и ранее. В величине
<5^surf можно распознать произведения поверхностных моментов на углы
поворота; например, 1¥о(во — во) — это внешний момент, приложенный
_ QQ
нижней подложкой к нематику. Поскольку Wo(0o — во) — К(—)о = 0, то
dz
дв
К(—)о следует интерпретировать как момент, действующий на директор
dz
на поверхности г = 0 со стороны внутренних напряжений. Эта величи-
о л л J
на в точности равна Су = —— nz пх из (5.44) с v — (0, 0, -1).
dvix,z dnz>z
дв
Аналогично, — К(—)d является моментом, приложенным внутренними на-
dz
пряжениями к директору на поверхности z ~ d, где v — (0, 0, 1). Заметим,
что эти два упругих момента в точности противоположны. Рассмотрим
тонкий слой материала между z и z + Sz. Очевидно, что полная вариация
энергии этого слоя 8F \ zz+dz есть
§F\z+dz = _к(дв\ SQz + Km\ 6(ez+Sz). (5.67)
\dz'z \dz/z+Sz
d^6 dd
Поскольку из минимума SFV0\ получается — — 0, производная — по-
dz2 dz
стоянна. Следовательно, момент, приложенный внешними напряжениями,
возникшими в области ниже г, к поверхностному директору v — (0, 0, -1),
равен К ( — V Аналогично, момент, приложенный внешними напряжени-
V dz /
ями, возникшими в области ниже z -h Sz, к поверхностному директору над
(дв \
— ): нематики передают
dz '
§5.4. Типичные прил оже н ия у пру г ост и немат шов
189
моменты. Мы еще вернемся к тому понятию «напряжения», на которое
сослались выше.
5.4.3. Эффекты во внешнем поле: характерные длины и переход Фре¬
дерикса
В геометрии рис. 5.9, изображающей полубесконечный объем нематика,
А
▼
Рис. 5.9. Конкуренция сильного планарного сцепления и приложенного
магнитного поля
мы предположим бесконечно сильное сцепление на плоской границе z — О,
так что граничным условием при z — 0 является n = (1, 0, 0). Магнитное
поле В = (0, Б, 0) стремится закрутить директор. Уравнение Эйлера-
Лагранжа имеет вид
К2~^ +/XoIXa£2sin0cos0 = 0 (5.68)
(см. задачу 5.2). Это же уравнение следует из условия баланса момен¬
тов, приложенных к тонкому слою материала z, z + dz. Полный момент,
190
Гл. 5. Упругость мезоморфных фаз
приложенный к материалу внутренними напряжениями, есть
0, 0, #2 0). (5.69)
Аналогично, полный момент, приложенный магнитным полем, направлен
по оси г:
(М х Н) = (0, 0, /iQ1XaB2sm9cos9) , (5.70)
откуда следует (5.68).
В (5.68) появляется характерная длина £, называемая магнитной длиной
когерентности (magnetic coherence length):
(5.71)
Проинтегрировав (5.68), получаем
£— = ±cos6, (5.72)
OZ
где постоянная интегрирования выбрана так, чтобы удовлетворить уело-
7г дО
виям в = ±-, — = 0 при z —> оо. Теперь найдем решение уравнения
2 dz
(5.72), удовлетворяющее условию в = 0 при 0 = 0. Имеются два таких
решения:
z = +оо, & = -, tg (- + = ехр (5.73 а)
2 \24/ £
г = — оо, 0 =—- tg (--f= ехр—(5.736)
2 V2 4/ f
отличающиеся только направлением закручивания. Директор поворачива¬
ется спирально от0 = Одо# = ±~ (физически эти два граничных значения
не отличаются) либо по правой, либо по левой спирали. Приведем типич¬
ные значения: для К2 = 10"11 Н, Ха = Ю-6 (единиц СИ) и В = 1Т
получаем £ « 3 мкм, т. е. вполне макроскопическую длину. Эффект сильно¬
го сцепления при г = 0, противостоящего магнитному полю, выправляется
на макроскопической, наблюдаемой длине.
В более общем случае ожидается, что возмущение директора магнит¬
ным полем происходит в области с типичным размером £ = —. —^—, где
Ха
Ki — относящиеся к данной задаче коэффициенты Франка или некоторая
их комбинация.
Важным приложением подобных явлений служит переход Фредерикса
(см. рис. 5.10 и задачу 5.8, а). Нематический слой толщины d помещается
между двумя параллельными предметными стеклами, обеспечивающими
сильное сцепление (W —¥ оо), так что директор п однородно ориентиро¬
ван в плоскости ячейки. Магнитное поле прикладывается перпендикулярно
§ 5.4. Типичные приложения упругости нематиков
191
пластинам, чтобы нарушить однородную ориентацию (ха > 0). Когда маг¬
нитное поле достигает пороговой величины Вс, такой что £(#с) — -> нема-
7Г
тик претерпевает переход в неоднородное состояние. Этот переход сильно
напоминает фазовый переход второго рода, где роль температуры играет Б,
а параметром порядка служит отклонение директора от невозмущенной од¬
нородной ориентации, измеренное при некотором г, отличном от 0 или d,
в середине образца, скажем при z — d/2.
п
а
А
в
п
6
0
В
л О ° €> о О
О
О
<3> <1> о
о о
О О
А
в
б
Рис. 5.10. Переходы Фредерикса с вовлечением Кi, К2 и Кз соответственно.
Три геометрии образца, представленные на рис. 5.10, позволяют изме
рить К1, К2 и К% соответственно исходя из формулы
В
7Г
сг
К,
-Г
d V /“о Ха
(5.74)
192
Гл. 5. Упругость мезоморфных фаз
причем BCi — критическое поле, выше которого параметр порядка отли¬
чен от нуля. Формула выведена в приближении бесконечного сцепления
с поверхностью; конечное сцепление снижает BCi (п. 13.2.3).
§ 5.5. Типичные приложения упругости смектиков
5.5.1. Слабо деформированная смектическая фаза
В этом пункте мы рассмотрим смектическую фазу, лишь слегка дефор¬
мированную по отношению к планарному основному состоянию. Искаже¬
ния описываются функцией смещения и(х, у, z), а плотность свободной
энергии дается выражением (5.27). Соответствующее дифференциальное
уравнение Эйлера-Лагранжа для функции и(х, у, г) может быть записано
в виде
2 ^д2и
В — =0, (5.75)
dz2
д2 д2
где Д]_ = (— + —) . Заметим, что два члена в (5.75) отличаются в следу-
дх2 ду2
ющем: упругий член, отвечающий за искривление слоев, содержит частные
производные четвертого порядка; с другой стороны, член, ответственный
за сжатие слоев, содержит только вторые производные, как и в классиче¬
ской теории упругости. Присутствие члена, ответственного за искривления,
делает упругость весьма необычной.
5.5.1.1. Влияние флуктуаций слоев на дальний порядок. Рассмотрим
полубе с конечный смектик, ограниченный плоскостью z = 0 и занимающий
полупространство z < 0, на границах которого имеется статическая дефор¬
мация и(х, у, 0), которую мы представим в виде интеграла Фурье:
и(х, у, 0)
Uq ехр zq • г d2q, q = (<7*, , 0). (5.76)
Поскольку уравнение (5.75) линейное, компоненты Фурье независимы. По¬
этому рассмотрим только одну qx -компоненту, которую обозначим и —
= uq cos qx, и будем искать решение (5.75) в виде
и — uq cos qx exp(z/L), (5.77)
удовлетворяющем граничным условиям и(х — 0) = uq cos qx и u(z
-> — оо) = 0. Без труда находим
L = ^"2 = i- (5J8)
Пусть A ~ q~l — характерная длина деформации границы. Выражение
§5.5. Типичные приложения упругости смектиков 193
(5.78) говорит о том, что влияние возмущений распространяется на расстоя¬
ния, намного превышающие Л: (L = А—), где Л — некоторая микроско-
Л
пическая длина; так что L Л. Это кардинально отличается от того, что
происходит в трехмерных кристаллах, где поверхностное возмущение с ха¬
рактерным размером Л внутри материала спадает на расстояниях L — Л,
т. е. возмущения локализованы в объеме Л3 ; ясно, что причина этого от¬
личия лежит в порядке дифференциального уравнения Эйлера. Результат
L ~ А для кристаллических твердых тел известен как один из «принципов»
теории упругости, принцип Сен-Венана (Saint-Venant). Слоистые среды, об¬
ладающие упругостью, отвечающей за искривление слоев, не подчиняются
принципу Сен-Венана.
5.5Л.2. Изгибовая неустойчивость при растяжении. Рассмотрим
макроскопический образец смектика, помещенный между двумя строго па¬
раллельными жесткими пластинами. Слои параллельны пластинам, а сцеп¬
ление с поверхностью для простоты выберем бесконечно сильным. При
равновесном расстоянии D между пластинами система предполагается сво¬
бодной от напряжений. Теперь увеличим это расстояние на малую величи¬
ну А, так что D D + А, не меняя числа слоев. В чисто упругом процессе
деформация свелась бы к однородному расширению слоев, описываемому
смещением как функцией координат: u(z) = az, а — Слои накапливают
1 1 Л ^
(позиционную) упругую энергию -Ba2D — — на единицу площади
ячейки. Однако по достижении некоторой критической величины А = Дс
энергетически выгодным становится неоднородное искривление слоев по
сравнению с однородным расширением. Вычислим значение Ас и длину
волны такой деформации искривления, для простоты предполагая дефор¬
мацию одномерной (рис. 5.11, а, б).
Полная деформация, соответствующая волнообразному искривлению
слоев, может быть записана в виде
и — az + uo cos gxsin kz, (5.79)
где щ — малая величина. Оказывается, что для вычисления амплитуды он¬
дуляции нам придется ввести в плотность свободной энергии нелинейный
член (см. задачу 5.4 и уравнение (5.28)):
/ = ~КХ ( — )2 + -В
2 V дх2) 2
ди\ 1 /дик 2
dz* 2 Vдх
(5.80)
Вычисляя полную энергию на единицу длины в направлении х, т. е.
2тг fq D
F = — J / dx f dz, где D = -, получим выражение, зависящее от и0
2тг о 0 k
и а, которое предстоит минимизировать по ио. Заметим, что минимизация
F по а бессмысленна, поскольку выражение для F не содержит внешне¬
го воздействия, вызывающего относительное смещение пластин. Оставляя
13-КЛЕМАН М.
194
Гл. 5. Упругость мезоморфных фаз
<5*
и,, — - —: ~п
а
б
Рис. 5.11. Растянутый смектический образец (а) релаксирует путем ондуляции
(волнообразного искривления) слоев (б); дальнейшее растяжение может вызвать
зарождение дислокаций (е) и, в конце концов, образование конфокальных доме¬
нов (г)
только основной член F ос получаем производную
4 dF
D 8uq
дающую два решения при
(KiqA + Вк2 - Baq2)u0,
(5.81)
OF
= 0. Решение щ = 0 (чистое расширение)
д2 F
остается устойчивым, пока положительно для всех q (детерминант
dul
квадратного трехчлена от q2 отрицателен), т. е. а2 < 4к2Х2, где А
Как только а превышает пороговое значение
Кг
в
а
2кХ = 27г
Л
D
(5.82)
появляется область волновых векторов q, для которых
d2F
dul
< 0, т. е. система
становится неустоичивои относительно ондуляции с волновыми векторами
в этой области.
Пороговое смещение Дс, соответствующее а = ас, равно
Д
С
Da
27гА
(5.83)
§ 5.5. Типичные приложения упругости смектиков
195
и не зависит от толщины образца, а порядок величины Л — это длина моле¬
кулы. Для D = 100 мкм типичное значение ас = 6х 10~5, что соответству¬
ет напряжениям ис — Вас х 102 Н/м2. Таким образом, механическая
неустойчивость возникает при малых приложенных напряжениях.
При А < Ас имеем ио = 0. Вычисление ио выше порога требует
учета члена более высокого порядка Uq в разложении F(uq) (см. (5.80)),
что дает
ио = -А ( ) , (5.84)
т. е. медленное возрастание щ с ростом А > Ас выше порога. Но как только
щ достигает некоторой величины порядка толщины слоя, может включать¬
ся новый механизм релаксации, а именно рождение краевых дислокаций в
областях максимального расширения, рис. 5.11, в (см. статьи Хэлфриха и
Юро21)). При дальнейшем повышении напряжения дислокации трансфор¬
мируются в параболические конфокальные домены (рис. 5.11 ,г), описанные
в гл. 10.
Экспериментальное исследование такой дилатационной неустойчиво¬
сти было проведено методом упругого рассеяния света, что дает возмож¬
ность прямых измерений А = k/q2. Подробности см. в статьях22^
5.5.2. Сильно деформированные смектические фазы и топологические
деформации
Два примера, изученные выше, ставят на одну доску «упругость искрив-
1 1
ления» fc = -Кi(divn)2 и «упругость положения» /р = -By2. Нетрудно
убедиться, что они вносят одинаковый вклад в общую деформацию как
в первом примере, так и выше порога неустойчивости во втором.
Доводы, основанные на скейлинговых оценках, показывают, что такой
паритет вовсе не является обязательным. Пусть L — характерный размер
деформированной области, и предположим, что таков же размер этой обла¬
сти во всех трех пространственных измерениях. Соответствующие энергии
оцениваются как
Fc = KiL и Fp = BL3, (5.85)
т.е. Fc/Fp = (Х/L)2. Следовательно, доля энергии упругости искрив-
ления оказывается тем больше, чем меньше L, а для энергии упругости
справедливо обратное положение. Таким образом, можно заключить, от про¬
тивного, что в реальных ситуациях искажения типа искривления превали¬
руют на больших масштабах (L > А), а искажения позиционного типа (типа
сжатия-растяжения) превалируют на малых масштабах (L < А), тогда как
21) W. Helfrick Appl. Phys. Lett. 17, 531 (1970); J. P. Hurault, J- Chem. Phys. 59, 2086
(1973).
22^ M. Delaye, R. Ribotta and G. Durand, Phys. Lett. A44, 139 (1973); N. A: Clark and
R. B. Meyer, Appl. Phys. Lett. 30, 3 (1973).
196
Гл. 5. Упругость мезоморфных фаз
на микроскопических масштабах (L — Л) их вклад сопоставим. Кроме то¬
го, это указывает на важность явлений неустойчивости на всех масштабах,
поскольку в двух примерах, отмеченных выше:
• на больших масштабах ожидается 7 = 0, т. е. все слои имеют одина¬
ковую толщину, а значит параллельны друг другу. В общем случае
граничные условия могут быть удовлетворены только путем образо¬
вания крупномасштабных дефектов, в данном случае конфокальных
доменов;
• на малых масштабах ожидается о\ + а2 = 0, т. е. слои искривляются,
принимая форму минимальных поверхностей. Это ограничение так¬
же приводит к специфическим неустойчивостям, таким как винтовые
дислокации, что мы увидим позже.
Проведенный анализ не принимает во внимание члены К\3 и К24. Как
уже отмечалось, в слоистых фазах член n х rot п оказывается почти нуле¬
вым, так что члены К13 и К24 типа div (n div п) не могут быть разделены.
Ожидается, что соответствующий модуль К, определяющий член с гаус¬
совой кривизной в (5.14) и способный изменяться в слоистой фазе в диа¬
пазоне —2К < К ^ 0, может иметь разумную величину ~ (~К). Вклад
в энергию от К является топологическим свойством рассматриваемого объ¬
ема, он принимает новое значение каждый раз, когда сильная деформация
или фазовый переход меняют топологию слоев. Примеры представлены на
рис. 5.12. Например, геометрия рис. 5.12, а показывает слегка деформиро¬
ванные слои на фоне жесткой планарной геометрии. Каждый слой имеет
выпуклости и впадины, образующие области с противоположной гауссовой
кривизной. Поскольку сг\о2 — это член типа седловидного изгиба, полная
гауссова кривизна должна обращаться в нуль:
aicr2dS = 0. (5.86)
F2,=K
На рис. 5.12, б показаны флуктуации сферы, дающие в сумме нуль, но
этот же интеграл теперь может быть вычислен на идеальной сфере, что дает
F24 (сфера) = 47vK, (5.87)
в то время как по тем же причинам на флуктуирующем полном торе
(рис. 5.12, в):
F24 (тор) = 0, (5.88)
поскольку области положительной и отрицательной гауссовой кривизны
в среднем компенсируются. Заметим, что флуктуации не ограничиваются
малыми значениями: любая поверхность, «гомотопная» сфере, как, скажем,
очень вытянутый эллипсоид, дает тот же интеграл Гаусса -Боннэ, что и сфе¬
ра. Это топологическое свойство интеграла справедливо также и для тора
или любой другой замкнутой поверхности.
§ 5.5. Типичные приложения упругости смектиков
197
а
б
в
г
Рис. 5.12. Иллюстрации теоремы Гаусса-Боннэ; флуктуирующий слой с нуле¬
вой средней гауссовой кривизной (а), флуктуирующая сфера (б), флуктуирующий
тор (<?), отрицательный полутор, расширенный до бесконечности (г)
Теперь рассмотрим полутор с положительной гауссовой кривизной. Его
можно преобразовать в сферу (склеивая две окружности по краям полутора)
без изменения интеграла J dH — 4тг.
Таким образом, флуктуирующий полутор с отрицательной гауссовой
кривизной, расширенный до бесконечности (рис. 5 Л 2,г), таков, что
^24 (отриц. полутор) = —4.7тК. (5.89)
В общем случае теорема Гаусса-Боннэ соотносит интеграл от гауссо¬
вой кривизны по замкнутому многообразию с эйлеровой характеристи¬
кой х этого многообразия:
(5.90)
Эта величина определена в задаче 5.5. Вместо эйлеровой характеристики
используется еще и род, представляющий собой число ручек замкнутого
O<7l02 ~ 27гх
198
Гл. 5. Упругость мезоморфных фаз
многообразия: g — 1 для тора, который является также сферой с одной
ручкой, g — 2 для тора с двумя отверстиями (крендель, или сфера с двумя
ручками, рис. 5.13), и т. п. Между этими величинами имеется соотношение
X = 2(l -g). (5.91)
Рис. 5.13. Тор с двумя отверстиями, g — 2, ^ = —2
Возвращаясь к физике, отметим, что знак К играет чрезвычайно важную
роль в слоистых системах, особенно лиотропных, где преимущественное
присутствие внутренних мицелл или полуторов с отрицательной гауссовой
кривизной может привести к эффектным фазовым переходам. Важными
примерами являются кубическая и губчатая £3-фазы, представляющие со¬
бой фазы, в которых бислои везде имеют отрицательную гауссову кривизну.
Рассмотрение этих фаз будет проведено позднее.
§ 5.6. Термодинамические флуктуаций
Как гласит принцип равнораспределения энергии, г термодинамиче¬
ском равновесии при Т / О К, любая система испытывает флуктуации
с энергией на степень свободы. Амплитуда этих флуктуаций лег¬
ко может быть рассчитана исходя из разложения свободной энергии по
фурье-компонентам фазы параметра порядка. Действительно, предполага¬
ется, что амплитуда параметра порядка не затрагивается флуктуациями,
если система находится далеко от фазового перехода. Любое однородное
изменение фазы параметра порядка (т. е. с волновым вектором q = 0) не ме¬
няет свободную энергию идеальной системы. Поэтому следует ожидать, что
в упруго деформированной системе длинноволновые флуктуационные мо¬
ды этих «непрерывных переменных, нарушающих симметрию», постоянно
возбуждаются с энергией в пределах ~к^Т и постоянно исчезают. Другими
словами, мы изучаем эти флуктуации на нулевой частоте и — 0. Более по¬
дробное обсуждение их низкочастотной динамики под действием внешних
полей (которые могут вносить энергию ^>-къТ на степень свободы) будет
проведено в следующих главах. 2
§ 5.6. Термодинамические флуктуации
199
5.6.1. Термодинамические флуктуации в нематиках
Нематики являются мутными средами: из-за флуктуаций направления
директора они сильно рассеивают свет231 Для объяснения наблюдаемых
эффектов рассеяния достаточно непрерывной теории этих флуктуаций241
Мы будем предполагать однородную ориентацию образца вдоль оси z.
Интересовать нас будут (малые) флуктуации Sn = (пх(г), пу(г), 0) дирек¬
тора п = (пж(г), пу(г), 1). Разложим пх(г), пу(г) на фурье-компоненты
(см. Приложение Б к данной главе) и выразим через эти компоненты плот¬
ность свободной энергии (5.2). Например, для div п получаем
div n = iV~l ^exp(iq ■ г)[qxnx(q) + qyny(q)] (5.92)
а для квадрата
(divn)“ = (div n) (div n)* =
= V~2 ^exp[?(q - q')r]fenx(q) + 9!/n9(q)][^na:(q') + q'yny{q')]*,
q>q'
другими словами,
(div n)2dr = V 1 ^ | qxnx(q) + qyny(q) (2. (5.93)
v
Наконец, после проведения подобной процедуры для всех членов, получаем
fFodr = iy 1 ] Kl I ЯхПх(сi) -b qyny(q) |2 +
2
v q
+ K2 | qxny(q) - qynx(q) |2 + K3q2z (| nx (q) |2 + | ny(q)
Разложим £n(q) на поперечную Sni и продольную Sn2 компоненты
(Sn = Siii + Sn2,SniSn2 = 0) так, что \qxnx(q) + qyny(q)|2 - (q2x +
+ qy)Sn\ = q\_Sn\. Для поперечной компоненты qxny(q) - qynx(q) есть
^-компонента векторного произведения Sn х q, умноженная на q±, т. е.
Яхпу(ч) — Чупх{ц) |2 = q\_Sn\. Таким образом,
fpodr = V-1 {чЦКгдп\ + К25п\) + ^К3(6п\ + (5.94)
V
q
23) Orsay Liquid Crystals Group, Phys. Rev. Lett. 22, 1361 (1969).
24) P.-G. de Gennes, C. R. Acad. Sci. Paris 266, 15 (1968).
200
Гл. 5. Упругость мезоморфных фаз
Диагональность jv foodr (отсутствие перекрестных членов) следует из то¬
го обстоятельства, что фурье-компоненты являются нормальными коорди¬
натами системы, что позволяет применить теорему о равнораспределении
энергии:
(<5n2) = VkbT/iqlK, + Ч\Кг), (5.95 а)
(<5n2) = VkBT/{qlK2+q\K3), (5.95 6)
где угловые скобки {) означают усреднение по статистическому ансамблю.
Эти выражения используются при вычислении интенсивности рассея¬
ния света на флуктуациях ориентации директора. Распространение света
чувствительно к электрическому полю, излучаемому микроскопическими
диполями, наведенными в молекулах электрическим полем падающего све¬
та. Мы не будем приводить здесь анализ этих явлений, выполненный в книге
де Жена и Проста.
Приведенные уравнения нетрудно модифицировать с учетом присут¬
ствия магнитного поля, так что они могут быть использованы для описания
радиуса корреляций ориентаций (п.;(г)п;(г')). При поле В, направленном
вдоль оси г, находим
(Snl) = VkET/ (q\Ki + q\K3 + цц1 Ха®2'} , (5.96a)
(<5n2) = VkBT/ {q\K2 + qjK3 + ^lXaB2) . (5.966)
Вычисление корреляционной функции
(Пг(г)пДг')) = V~2 ]Г(п*(я)Пг(-я')) exp [i(qr - q' • г')] (5.97)
q>q'
провести нетрудно, если вспомнить, что фурье-компоненты с различными
волновыми векторами являются разными нормальными координатами (сте¬
пенями свободы) системы, а потому корреляция между ними отсутствует
(диагональность выражения (5.94)). Следовательно,
(ni(q)ni(-q')) = (К^)|2)<5ч+ч,,0
И
(nj(r)nj(r')) = V 2V](|ni(q)|2)exp{iq(r-r')}. (5.98)
Вычисление производится подстановкой в выражение (5.98) для
(n^(r)nj(г')) вычисленных ранее в (5.96) величин (<5п2) и (5п2) и в конце
концов приводит к следующему выражению для корреляционной функции
(в предположении равенства всех трех упругих модулей Франка):
(пг(0)пг(11)) ос ^expj-^ } , (5.99)
§ 5.6. Термодинамические флуктуации
201
где £ — —, / магнитная длина когерентности, введенная в (5.71)
Я V
В нулевом поле корреляции медленно (как Rrl) спадают с расстоянием
5.6.2. Термодинамические флуктуации в смектиках
Вычисление тепловых флуктуаций в недеформированном смектике про-
изводится согласно той же логике. Исходя из (5.27) получаем
u(q)D = Щ , (5.100)
Bq2z +Kq\ (q2± + £“2)
где введен вклад от магнитного поля вдоль оси z (^-зависимый член). Сред¬
ний квадрат флуктуаций дается выражением
м2(0)) = in-L; (5.101)
4тг\/ В К do
где do — нижний размер обрезания, взятый равным периоду (межслоевому
расстоянию). При уменьшении магнитного поля до нуля логарифмический
член расходится; фактически в образце размера L и нулевом магнитном
поле последнее выражение заменяется на
(ц2(0)) = fcEX_ln —■ (5.102)
N ' Атг^/ВК d0
Таким образом, средний квадрат флуктуаций слоев расходится. Это так
называемая теорема Пайерлса-Ландау о разрушении одномерного даль¬
него позиционного порядка (или невозможности существования одномер¬
ных кристаллов). Несмотря на то что расходимость сказывается только при
очень больших размерах системы (при К — 10“11 Н, к^Т = 4 • 10~21 Дж=
— 4 * 10~14 эрг, sjК!В ~ do ^ 1 нм, получаем \J(и2(0)) ~ do только
при L ~ 10 км), мы заключаем, что настоящий дальний трансляционный
порядок в смектиках отсутствует.
Рентгеновский структурный фактор показывает степенной спад, в то
время как в трехмерных кристаллах он содержит (5-образные пики. Зави¬
симость интенсивности рентгеновского рассеяния от волнового вектора
рассеяния дается преобразованием Фурье фактора Дебая -Уоллера25^:
G(R) = exp -igg(Ju(R) - u(0) |2 ) , (5.103)
25) A. Caille, C. R. Acad. Sci. Paris 274B, 891 (1972).
202
Гл. 5. Упругость мезоморфных фаз
где корреляционная функция смещений записывается в виде
u(R) — u(0)
(2тг)
rfq \ I «(я) I2) t1 - ехР {-щ ■ R-)]
кьТ
4 ni/КВ
X
0.
(5.104)
Вычисление зависимости интенсивности рассеяния от волнового век¬
тора рассеяния дает
/(q) ос
Qz ~
n _2+7?
" Яо ,
Q± :
-o,
Q±.
—4+2ry
У
qz =
f i
О
(5.105)
где г]
8тг ^КВ’
до = 2тт/йо.
5.А. Приложение А. Одномерная вариационная задача
Минимизация функционала типа (5.52)
z~d
F
f[0,0',z] dz (5А.1)
2 — 0
— это простейшая стандартная задача вариационного анализа (см. ссыл¬
ку 18^)5 поскольку подынтегральное выражение зависит только от одной
функции 0(z) только одной переменной г. Ниже мы рассмотрим два случая:
жесткие граничные условия, когда оба граничных значения фиксированы:
0(z = 0) = So, 0(z = d) = 0d, (5A.2)
и мягкие граничные условия без конкретизации физического смыс¬
ла задачи.
5.АЛ. Фиксированные граничные условия
Все возможные функции 0(z) могут рассматриваться как пути, соеди¬
няющие две точки: (z ~ 0, 0 = 0О) и (z = d, 0 ~ 0d) (рис. 5.14, а). Пусть
0eq{z) — путь, минимизирующий (5А.1). Любой другой, но близкий путь
0{z) может быть представлен в виде: 0eq(z)+50(z), где 60(z) —мысленные
повороты директора, эквивалентные произвольной вариации Srii в общей
схеме (п. 5.4.1). Вариация 60 (z) обычно представляется в виде произве¬
дения oi.rf(z), где новая неизвестная функция rj(z) описывает деформацию
пути, а малый параметр а — амплитуду вариации:
o(z) = 0eq(z) + arj(z)
(5А.З)
Приложение А. Одномерная вариационная задача
203
0{z)
А
а
о
в,
О
d
О
а
d
б
Рис. 5.14. Гипотетическая функция (жирная линия), минимизирующая функционал
энергии (5 А. I) для жестких граничных условий (а) и функционал (5 А. 11) для мягких
граничных условий (б). Тонкая линия показывает произвольную функцию, близкую
к равновесной
Функция 7](z) должна быть
интервала rj(z = 0) = r](z = d)
пути 0(z) дается выражением
дифференцируема и исчезать на концах
= 0. Функционал свободной энергии для
d
F\e{z))
f[eeq{z) + аф),в' (z) + aT}'(z),z] dz.
(5A.4)
0
Экстремальные значения последнего интеграла как функции а дости¬
гаются при
aF(a)
da
о
(5А.5)
а=0
Дифференцирование F(a) по а дает
d
d
dFja)
да
'д/ дв df дв'‘
dz —
>
\df r,(z) + df dv(z) 1
dz
■ de da d6’ da -
1дв дв' dz
0
О
Отметим, что две зависящие от а функции в и в1 рассматриваются как
независимые переменные. Интегрируя второй член по частям и помня, что
rj(z — 0) = T)(z — d) — 0,
d
d
djr,iA^Ldz
dz дв'
r]{z)
df
дв
f
z=d
r}(z) — ^~ dz,
dz дв’
(5A.6)
204
Гл. 5. Упругость мезоморфных фаз
получаем
d
ч
d df'
о
1дв
dz дв' -
rf(z) dz = 0
(5А.7)
о
Отметим соответствие между (5А.5) и требованием SF
в пп. 5.4.1.1. Умножая (5А.7) на а, получаем
0 в общей схеме
d
Л
'df _ d df 1
89 dz -
- a
'dF(a)'
J
- de dz дв' J
- da J
SF = 0
а=0
(5А.8)
о
Условия экстремума как в форме (5А.7), так и в форме (5А.8) могут удовле¬
творяться для произвольной т](z) (59 (z)) только при выполнении условия
d_l
дв
d df
dz дв
/
О,
(5А.9)
которое и является дифференциальным уравнением Эйлера- Лагранжа для
нашей одномерной задачи. Его решение представляет собой семейство
функций 9 — 9(z, Ci, С2) с двумя произвольными постоянными интегри¬
рования, которые могут быть найдены из граничных условий (5А.2).
Если явная зависимость f от z отсутствует, можно найти первый инте¬
грал уравнения Эйлера-Лагранжа (5А.9)
в9
ЁЛ
дв'
/ = const
(5А.10)
(см. задачу 5.3).
5.А.2. Нежесткие граничные условия
Энергия, подлежащая минимизации, содержит поверхностный член:
d
F
/[0, 9l,z] dz -f До(0o ~ 0o) + fsd{9d — 0rf)*
(5A.11)
о
Как и выше, разность 89 = 9(z ) 0eq(z) = ar}(z) может быть опи¬
сана новой функцией r](z), которая на сей раз не обязательно исчезает на
границах (рис. 5.146). Поскольку
dfso(Oo)
da
~fso[0o,eq + <*Ф = 0)] = Г](0) ^
da dd о
имеем
dF(a)
да
df дв , df дв
/ -
+
- дв да дв' да -
о
dfso
d6 о
Т)( 0) +
dfsd
ded
ri(d).
(5A.12)
Приложение Б. Формулы для преобразований Фурье
205
Интегрирование по частям второго члена в объемном интеграле дает усло¬
вие экстремума в виде
d
df
d df
- dO dz dO' -
r](z) dz +
df dfs0
de
de -
z=0
7/(0) +
0
df + df^
i de
de j
z~d
77(d) = 0. (5A.13)
Таким образом, для нахождения семейства решений в виде в =
= 6(z, ci, с2) все еще следует пользоваться уравнениями Эйлера-Лаг¬
ранжа (5.54), но теперь постоянные интегрирования с\ и с2 находятся из
следующих граничных условии:
г df
dfso'
— 0 и
Г df
I
+
= 0
L дв'
de J
z=0
ldef
de J
z=d
(5.1)
Вместо решения этих уравнений можно было подставить функцию в =
= 0(z, ci, с2) в выражение (5.11) для F, проинтегрировать, а затем найти
минимум интеграла по с\ и с2.
5.Б. Приложение Б. Формулы для преобразований Фурье
Пусть т(г)
непрерывная наблюдаемая величина, определенная в
объеме V. Обычно предполагается, что этот объем представляет собой
параллелепипед со сторонами L\, L2, L3 и периодическими граничными
условиями. Значит, V — LiL2L3 и
т(х, у, z) = т(х + Ьг, у, z)
(5Б.1)
Ниже приводятся формулы, которые мы постоянно будем использовать
в дальнейшем изложении:
т(г) = V 1 У^ ехр(гдг)ш(д),
q
т( д)
dr ехр(—гдг)т(г),
v
У%хр[-гд(г - г')] = VS(г - г'),
(5Б.2а)
(5Б.2 б)
(5Б.2 в)
drexp[ir(q - q')] = K(5qq<
(27r)3(5(q - q')
v
(5Б.2 г)
206
Гл. 5. Упругость мезоморфных фаз
I 27т 2тг 27г в —* —
где q = ( —ni, —-n2, —?^з J — набор волновых векторов, обеспе-
L1 Ь‘2 L з
чивающий удовлетворение условий (5Б.1), (ni, 77,2, пз — целые числа);
(5qq/ — S — символ Кронекера, равный 1 при q = q' и 0 в остальных
случаях; <5(q — q') — трехмерная (5-функция Дирака.
В пределе V —> оо сумма по q преобразуется в интеграл
Y-+V
dq , (5Б.З)
(2тг)
а (5Б.2 а) и (5Б.2 б) дают
m(r)
rfq
(2тг)
exp(iqr)m (q),
(5Б.4)
dqexpj— iq(r — г')1 = (2тг)35(г — г').
(5Б.5)
Все эти выражения написаны для трех измерений. Размерность простран¬
ства проявляется в показателе степени при множителе 2тт. Так что все вы¬
ражения можно непосредственно расширить на любую размерность.
Задача 5.1. Доказать, что п х rotn направлен по главной нормали
к «силовой линии» поля директора и по модулю равен 1/г, т. е. совпадает
с кривизной.
Ответ, п х rot п в компонентах может быть записан в виде (п х
X rotn)^ £'ijkWjj£'kpq'Rjq,p' ПОСКОЛЬКУ Eijk&kpq ~ ^ipSjg SiqSjpi ПОЛуЧаеМ
(n х rotn); = —rtjUij. Следовательно, n x rotn = —nVn = — —, где
ds
s — криволинейная абсцисса вдоль «силовой линии» поля директора, ори¬
ентированная в направлении вектора п. В соответствии с формулой Френе
dn v
имеем: — =
ds г
Задача 5.2. Планарные искажения поля директора. Предположим,
что к нематической ячейке с корфигурацией директора
п — (пж, ny,0) = (cos#, sin#, 0)
приложено магнитное поле в плоскости ху В = (Вх, Ву, 0). Здесь 0 =
= 0(х, у, z) — угол между осью х и директором. Записать: а) плотность
упругой энергии и б) уравнение Эйлера-Лагранжа задачи в приближении
к, = к3 = К.
Приложение Б. Формулы для преобразований Фурье
207
Ответ.
а) Плотность упругой свободной энергии
2
/ро = 1(Кг sin2 е + К3 cos2 0)( — \ +-(Кг cos2 в + К3 sin2 в)
2 V дх / 2
дв
ду
+
+ i(tf3 -tfi) sin20— — + -^2 Г
9. Вт, dv 2 V
2 ' <9х ду
<70
<90
<9z
(5.106)
При К\ = — К формула упрощается, так что полная плотность сво¬
бодной энергии с учетом двумерного магнитного поля В = (Вх, Ву,0)
становится равной
f=-K
2
дв
дх
дв
ду
+ -К>2 (q0 —
дв_
dz
-~№о гХа(Вх cos# + Ву sin#)2. (5.107)
б) Плотность свободной энергии (5.107) интегрируется в полную энер¬
гию вида
jp ? Itedydz.
дх оу oz
Любая вариация в меняет /, но не элемент объема. Поэтому уравнение
Эйлера-Лагранжа может быть записано в виде
д_1
дв
д df d_df_ д_д1
дх двх ду дву dz d6z
0,
т. е.
Но1 Ха [(-В2 - -В2) sin 20 - 2BxBycos29] -
- 2
К
д2 д2
~г
dx2 dy
d2
dz2
0 = 0. (5.108)
Задача 5.3. Доказать, что первый интеграл уравнения Эйлера -
Лагранжа для функционала (5.52) имеет вид (5АЛО), если в подынтеграль¬
ной функции отсутствует явная зависимость от координаты z.
208
Гл. 5. Упругость мезоморфных фаз
Ответ. Обозначим G = в' — — /. Тогда
дв'
dG
- 0,f — -f в' ~ } - —
dz дв' dz \дв'/ d*
в" + O' — (—] - — 0l - d/ g"
56», <*г V00'/ £<9 56"
0'
1
dz V дв' /
и(? = const, если справедливо уравнение Эйлера-Лагранжа.
Задача 5.4. Показать, что в смектической A-фазе дилатация слоев
с точностью до второго порядка может быть записана в виде
d-*, = fdu\ 1
d0 \дг/ 2
Ответ. Пусть z0 = г - и (ж, ?/, г) — уравнение деформированного
слоя с координатой z0 до деформации. При переходе по пути длины d
вдоль п от одного деформированного слоя к следующему эта величина
увеличивается на do (d—это величина do после деформации). Раскладывая
в ряд Тэйлора это смещение, переносящее точку из слоя zq на слой z0 4- do,
получаем: zq + d0 = zo -f dn • Vzo. Следовательно,
d- do l ^ i
7 = = -1 + « -1 +
do | Vzq I riz — n • Vu
Искомый результат получается из выражения для директора
п — ди/дх(\ -f du/dz)y —ди/ду( 1 + du/dz), 1 — - (V±u)2 j ,
записанного с точностью до второго порядка.
Задача 5.5. Исходя из теоремы Эйлера - Пуанкаре, приведенной в за¬
даче 2.3 гл. 2, доказать, что для полиэдра рода g имеется следующее обоб¬
щение:
Xg = v - е + f - 2{1- g).
Подсказка: разрезать исходный полиэдр, следуя теореме Эйлера - Пуанка-
ре, вдоль двух многоугольников, не имеющих общих ребер, и ввести поли¬
тизированную «ручку», объединяющую границы этих многоугольников.
После этого легко показать, что эйлерова характеристика xi = 0 независи¬
мо от способа проведенной полигонизации.
Чтобы показать идентичность этого результата уравнению (5.91), тре¬
буется глубоко вникнуть в дифференциальную геометрию поверхностей.
Задача 5.6. Исходя из (5.22), /с = -х(<т\ + <т2)2 + >ссг\сг2, вывести
условие устойчивости в виде неравенств на модули кривизны х и х слои¬
стой, мицеллярной и губчатой фаз.
Приложение Б. Формулы для преобразований Фурье 209
Ответ. Уравнение (5.22) может быть представлено как сумма двух
членов с положительными выражениями для кривизн:
/с = - \(к+ -5?) (<71 + О'г)2 - -Ус(<Т 1 - <72)2
2 LV 2 > 2
х
а) Если оба коэффициента положительны, а именно х + -х > 0,
х < 0, основному состоянию соответствуют о\ +0*2 = 0, <т\ — а2 — 0, т. е.
слоистая фаза.
I
б) Если х+ -х < 0, х < 0, энергия неограниченно убывает, и основ-
ное состояние отсутствует для больших значений | сгх -h сг2 |, crj. — о2 = 0.
Таким образом, можно ожидать некоторой стабилизации для G > 0, напри¬
мер в мицелярной фазе.
в) Если х -1- -х > 0, х > О, энергия неограниченно убывает и основ-
ное состояние отсутствует для сгх + а2 = 0 и больших значений \а\ — а2
т. е. при возрастающей кривизне а — \ <7\ | = | а2 |. В этом случае мембрана
является минимальной поверхностью. В действительности можно ожидать
некоторого отталкивания, стабилизирующего систему при конечной кри¬
визне и ненулевом значении G < 0, например в губчатой фазе, по другим
причинам, таким как взаимодействия Хелфриха (см. п. 14.2.2).
1
г) Случай х Н- -х < 0, х>0, приводит к противоречиям.
2
Задача 5.7. Применив метод фурье-компонент, изложенный в тек¬
сте, показать, что вклад дивергентных членов в полную энергию тепловых
флуктуаций равен нулю. Почему именно этого результата и следовало ожи¬
дать как для нематиков, так и для смектиков?
Задача 5.8. Показать, что наблюдение перехода Фредерикса в смек¬
тической A-фазе с сильным планарным сцеплением и магнитным полем В,
параллельным слоям, затруднено (призрачный переход)26^.
Ответ. Представим плотность свободной энергии
/ = Itf(divn)2 + 1в(d-=^) - Vo_1Xa(Bn)2
2 2 \ do / 2
как функцию угла 0 между нормалью к деформированному слою и невоз¬
мущенным направлением. Напомним, что В и В (или В — | В |) обозначают
две совершенно разные величины: модуль одностороннего сжатия (Юнга)
и магнитную индукцию соответственно. Получаем
/ = -К COS2 0 ( —) + -В( 1 - COS0)2 - -/Iq lXaB2 sin2 0.
2 V dx' 2 2
26^ A. Raping J. de Phys. (Paris) 33, 237 (1972).
210
Гл. 5. Упругость мезоморфных фаз
Ось х направлена вдоль слоев, перпендикулярно границам ячейки, а ось г —
перпендикулярна невозмущенным слоям.
а) Предполагая искажения малыми и разлагая / до второго порядка
по 9, приводим свободную энергию к виду
1 ( йв\2
что дает уравнение Эйлера-Лагранжа
— + —в = о
dx2 £2
(где С — —гг— — магнитная длина когерентности), решение которого
В V Мо Ха
0 — 9м cos - для В > Вс 71 1 К
£ Г V Мо Ха
(Подсказка: L — толщина ячейки, при В = Вс выполняются условия силь¬
ного сцепления, 9м — это значение 9 на серединной плоскости ячейки),
Вс — критическое поле перехода Фредерикса. Это решение применимо
и к нематической фазе.
б) Для того чтобы оценить 9м, учитываем и член сжимаемости. Пер¬
вый интеграл уравнения Эйлера-Лагранжа, минимизирующий /, пред¬
ставляет собой выражение
2
2К cos2 9 ~ 2В (cos 9м — cos 9) +
\ dnr: /
+ (^о lXaB2 + £)(sin2 9м - sin2 9).
гч u dO
Этот первый интеграл удовлетворяет соотношению
= 0. Величина
м
dx
в правой части положительна в силу положительности левой части. По¬
скольку 0 < cos 9м ^ cos 9, получаем
cos9М > ^1 4- М° Х*В ^
-1
Последнее неравенство можно переписать в виде
cos Ом > ( 1 + ^) - 1 -
где А — микроскопическая длина (глубина проникновения де Жена), а f —
макроскопическая длина. Малость их отношения затрудняет наблюдение
изменений в ориентации директора.
Приложение Б. Формулы для преобразований Фурье
211
Задача 5.9. Найти равновесную конфигурацию директора в гибридно¬
ориентированной пленке (5.51) с бесконечно сильным сцеплением (5.50)
при К\ ф Кз.
Ответ. Записываем выражение для свободной энергии,
/ = -(Кп sin2 в + Кгъ cos2 в){в')2 = 1-К{в){в')2,
2 2
и видим, что явная зависимость от z отсутствует. Первый интеграл уравне¬
ния Эйлера-Лагранжа K(0)(6f)2 = с2, где с — постоянная, определяемая
из граничных условий (5.50),
ви d
JK{x)dx
во 0
с dz.
Отсюда получаем усредненное по толщине ячейки равновесное распреде
ление наклона:
ZC
х/ВД dx
в
о
Задача 5.10. При рассмотрении нематических пленок с гибридной
ориентацией и сильным сцеплением (п. 5.4.2 и задача 5.9) мы предполагали,
что директор не выходит из вертикальной плоскости и искажения в плос¬
кости ячейки отсутствуют («однородная гибридная пленка»). Используя
одно константное приближение в упругой энергии Франка -Осеена, пока¬
зать, что искажения поля директора в плоскости ячейки могут уменьшить
упругую энергию гибридной пленки.
Ответ. Один из простейших способов — сравнить упругие энергии
пленок, ограниченных в горизонтальной плоскости коаксиальными цилин¬
драми с радиусами R > г. Сначала рассмотрим однородную гибридную
пленку с двумерными искажениями (пх, пу, nz) = [sinaz, 0, cosaz], где
а — постоянная, определяемая разностью полярных углов на противопо¬
ложных подложках и толщиной пленки, скажем а — —. Упругая энергия
з 2d
такой пленки FpQmo = —— (R2 — г2). Теперь возьмем набор (nr, nz) =
8d
= [sin az, 0, cos az] в цилиндрических координатах (г, (/?, z), который опи¬
сывает трехмерное поле директора, искаженное в плоскости пленки. Упру-
гая энергия этой искаженной пленки
rndist грЬото ,
^FO — ^FO Н
—tt(R — г) -f (йп —
г -1
т. е. Fдействительно может быть меньше, чем FpQno однородной
FO
пленки.
212
Гл. 5. Упругость мезоморфных фаз
Литература для дальнейшего чтения
1. P.G. de Gennes and J. Prost. The Physics of Liquid Crystals, 2nd Edition,
Clarendon Press, Oxford, 1993. См. перевод первого издания: П.Ж. Де Жен.
Физика жидких кристаллов / Пер. с англ. под редакцией А.С. Сонина. —
М.: Мир, 1977.
2. G. Vertogen and W. de Jeu. Thermotropic Liquid Crystals, Fundamentals, Edited
by V. Goldanskii, F. Shafer, and J. Toennies, Springer Series in Chemical Physics,
vol. 45, Berlin: Springer-Verlag, 1988.
3. L M. Blinov and V. G. Chigrinov. Electrooptic Effects in Liquid Crystal Materials,
Springer, N. Y. 1996.
4. F. C. Frank. Discuss. Faraday Soc. 25, 19 (1958).
5. R. Barberi and G. Barbero. The Physics of Liquid Crystalline, Edited by I.-C.
Khoo and F. Simoni, Gordon and Breach Science Publishers, Philadelphia, 1988.
6. G. Barbero andL R. Evangelista. An Elementary Course on the Continuum Theory
for Nematic Liquid Crystals. Series on Liquid Crystals, Edited by H. C. Ong, World
Scientific, Singapore, 2001.
Дополнительная литература
1. Пикин С. А. Структурные превращения в жидких кристаллах. —
М.: Наука, 1981.
ГЛАВА 6
ДИНАМИКА ИЗОТРОПНОЙ
И АНИЗОТРОПНОЙ ЖИДКОСТЕЙ
Статическая континуальная теория позволяет найти равновесные кон¬
фигурации поля параметра порядка с помощью минимизации подходяще¬
го функционала свободной энергии. Если система слегка возмущена, она
обычно релаксирует назад к этому равновесному состоянию. Большин¬
ство возмущений релаксирует быстро, за характерное время столкновений
между молекулами (которое составляет величину порядка 10~1О-10-14 с
для классических жидкостей). Однако некоторые переменные, называе¬
мые гидродинамическими переменными, релаксируют медленно. Класси¬
ческим примером является плотность массы: частота си (обратное время)
звуковых волн стремится к нулю, когда их длина становится бесконечной,
L оо, согласно закону дисперсии и ~ c/L, где с — скорость звука.
В общем случае плотности сохраняющихся переменных (масса, импульс
и энергия) являются гидродинамическими переменными. В среде с нару¬
шенными непрерывными симметриями, такой как нематические жидкие
кристаллы, имеется другой класс гидродинамических переменных, кото¬
рый был рассмотрен в гл. 3, а именно параметры вырождения (или фазы
параметра порядка).
Представим, например, волну переориентации нематического директо¬
ра как возмущение однородного состояния n = const. Если L —> ос, это
возмущение становится просто другим однородным состоянием с другой
ориентацией n' = const. Оно практически никогда не релаксирует назад
к первоначальному состоянию, так как оба эти состояния имеют одинако¬
вую энергию. Если длина L конечна, но все еще является макроскопической,
то время релаксации конечно, но все еще больше, чем времена молеку¬
лярных столкновений. Ориентация директора, которая представляет собой
фазовую переменную параметра порядка нематика, является независимой
гидродинамической переменной. Напротив, амплитуда параметра порядка
не является гидродинамической переменной. Она должна релаксировать
к локальному равновесному состоянию, даже если длина волны возмуще¬
ния бесконечно велика, L —у оо.
Гидродинамика изучает процессы, которые осуществляются на про¬
странственных и временных интервалах, много больших, чем
характерные молекулярные масштабы: на гидродинамически малых интер¬
валах времени dt и расстояния dr происходит множество актов молекуляр¬
ных столкновений, которые приводят к локальному равновесию в системе.
Это позволяет оперировать полевыми переменными (такими, как дирек¬
тор, скорость, плотность и т. д.), усредненными по многим частицам, чтобы
характеризовать состояние элементарного объема, локализованного в мо¬
мент времени t в точке пространства г. Положение г может быть задано
в фиксированной лабораторной системе отсчета посредством, например,
214
Гл. 6. Динамика изотропной и анизотропной жидкостей
декартовых координат х2, £3. Этот подход называется эйлеровым. При
альтернативном лагранжевом подходе следуют за выбранной частицей, пе¬
ремещая систему координат вместе с этой выбранной частицей.
Движущаяся однокомпонентная изотропная жидкость описывается сле¬
дующими пятью полями: тремя компонентами локальной скорости v(r, i)
и двумя термодинамическими компонентами, обычно плотностью массы
p(r, t) и плотностью энергии. Так как процессы являются медленными,
можно использовать подходящее термодинамическое уравнение состояния,
чтобы выразить любую термодинамическую величину через две вышеупо¬
мянутые. Мы начнем наше рассмотрение с гидродинамики такой простой
однокомпонентной жидкости. Остальная часть главы посвящена гидроди¬
намике нематической фазы, у которой имеются две дополнительные пере¬
менные, а именно две компоненты директора (третья компонента исключа¬
ется уравнением п2 — 1).
§ 6.1. Поле скорости и тензор напряжений
6.1.1. Материальные производные и компоненты движения жидкости
6.1.1.1. Материальная производная. Предположим, что некоторый
параметр а движущейся жидкости (например, плотность или компонента
скорости) изменяется в пространстве и во времени. Изменения наблюдаемо¬
го параметра а (г, t) являются различными для стационарного наблюдателя,
находящегося в точке г, и для наблюдателя, который движется вместе с вы¬
бранной материальной частицей. Для стационарного наблюдателя скорость
изменения да/dt вызвана исключительно локальными изменениями наблю¬
даемой величины. Для движущегося наблюдателя имеются дополнительные
изменения: в течение интервала времени dt элемент жидкости переносится
в новое положение r+dr, где значение параметра а, вообще говоря, отлично
от значения последнего при г, t:
a(r + dr, t + dt) -a(r, t) = dt (— -h ^ - (5 j)
\dt dx, dt J \ dt 8x4
Vi — dxi/dt суть компоненты скорости частицы в точке г в момент време¬
ни t. Здесь и далее мы используем эйнштейновское правило суммирования
по индексам, которые появляются дважды в выражении. Деля обе части
уравнения (6.1) на dt, получаем важное определение материальной произ¬
водной:
± + vVa. (6.2)
dt dt
Величина vVa вносит существенную нелинейность в уравнения гидро¬
динамики: свойство жидкости а переносится со скоростью v, которая сама
является свойством жидкости.
§6.1. Поле скорости и тензор напряжений
215
6.1.1.2. Компоненты движения. Локальное движение жидкости мож¬
но разложить на четыре различные компоненты: (1) чистая трансляция,
(2) вращательное течение наподобие вращения твердого тела, не приводя¬
щего к деформациям, (3) сдвиговые деформации и (4) деформации расши¬
рения или дилатация.
Рассмотрим две близкие частицы жидкости, находящиеся в точках Мо
и Mi. В некоторый момент времени t эти частицы разделены расстоянием dr
и движутся со скоростью v и v + dv (рис. 6.1.). Скорость Mi по отношению
д*и * *
к Мо есть инкремент dvj = j = 1, 2, 3, который сочетает эффек¬
те i
ты (2) - (4) вращений и деформаций; чистая трансляция (1) задается величи¬
ной v. Чтобы разделить твердотельные вращения (2) и деформации (3), (4),
v + d\
Рис. 6.1. Относительное движение двух близких частиц жидкости
тензор градиентов скорости dvj/dxi представляется в виде суммы Aij + Не¬
симметричной Aij и антисимметричной частей:
Ац = Ал = i ( р- + ^ ] , (6.3)
2 \ dxj дх{
Wij = -Wji = i ( ^ | . (6.4)
dxj dxi
Тензор называется тензором скорости деформации (или скорости на¬
пряжений). Диагональные элементы А^ описывают дилатацию (4): если,
например, частицы М\ и Мо разделены на оси х\, то Ац — dv\jdx\ есть
скорость растяжения, приходящегося на единицу расстояния такого разде¬
ления. Недиагональные элементы Ац пропорциональны скорости сдвига
в направлении i для двух частиц Mi и Мо, разделенных по направлению j,
и, таким образом, представляют движение сдвига (3). Наконец, тензор W\j
описывает твердотельные движения (2) частицы Mi вокруг частицы Мо
и часто выражается через угловую скорость из — -V х v в виде =
= —£ijk^k, где Si3k — это компоненты тензора Леви-Чивита, равные 1,
216
Гл. 6. Динамика изотропной и анизотропной жидкостей
если ijk — 123, 231, 312, и —1, если ijk = 321, 213, 132, или 0, если
любые два индекса одинаковы. Как уже отмечалось в гл. 5, компоненты
векторного произведения суть [а х b]* — Cijk.ajbkl следовательно, [V х
ха]* = EijkCik j, где а н j — да^/dxj. Отметим также полезное соотношение
£ipq£ikl — 8рк Sql Sp[ 6qk*
6.1.2. Объемные и поверхностные силы. Тензор напряжений
Изменение в состоянии движения жидкости может быть вызвано двумя
типами сил, называемыми объемными силами и поверхностными силами
(рис. 6.2.). Некоторые силы (например, электростатического происхожде¬
ния) могут быть представлены в каждой из этих двух форм.
Нормаль к поверхности,
направленная от «/»
Сила, действующая
на«/> со стороны <2>
М
‘.Г.'.*.; ч;. •.> ■ . .. • • •
S&3„'■'*" *&У • / ••• •
~ >•>. Mi/-.1:
• ^ •• Г Л М. - - , ♦ - .V . - V . I
•ч* * * **, * s - * чл * 'П? • ' v-V .. ' ■■ ■ ? •
2
pgdV
Рис. 6.2. Объемная сила pgdV, действующая на малый элемент объема, и по¬
верхностная сила dF, действующая на малый элемент поверхности с единичным
вектором нормали и
6.1.2.1. Объемные силы Объемные силы проникают в весь объем
системы и действуют на все ее элементы. Очевидным примером является
гравитация. Объемная сила, действующая на элементарный объем dV, про¬
порциональна этому объему и может быть записана в виде pg dV, где g есть
сила, действующая на единицу массы.
6.1.2.2. Поверхностные силы Поверхностные силы вызваны прямы¬
ми молекулярными взаимодействиями, которые включают в себя взаимо¬
действия между соседними областями одной и той же среды. Поверхност¬
ная природа этих сил обусловлена очень малым радиусом молекулярных
взаимодействий по сравнению с характерными масштабами возмущений
§ 6. /. Поле скорости и тензор напряжений
217
в континуальной модели. Поверхностные силы принято представлять с по¬
мощью компонент <Jij тензора напряжений (рис. 6.2). Величина Oij —
i-я компонента бесконечно малой поверхностной силы, действующей на
бесконечно малую область dAj, перпендикулярную оси координат j:
dFi = &ij dAj — atjvj dA; (6.5)
Uj — компонента единичного вектора нормали v к поверхности; вектор v
направлен от части 1 к части 2 (рис. 6.2). Полная сила, действующая на
объем V, имеющий поверхность А, представляется в виде
Fi = QvijVj dA
да
дх
dV,
(6.6)
Л
V
где поверхностный интеграл заменяется объемным посредством теоремы
Остроградского-Гаусса об интеграле от дивергенции.
Рис. 6.3. Куб с нормальными и тангенциальными напряжениями на его
поверхностях
Три диагональных элемента тензора — это нормальные напряжения,
в то время как шесть недиагональных элементов суть напряжения сдвига.
Эта концепция помогает отличать жидкости от твердых тел при гидроди¬
намическом описании: среда является жидкой, если напряжения сдвига,
независимо от их малости, вызывают неограниченно большие деформации
при неограниченном времени действия. Жидкости не испытывают напря¬
жений сдвига, находясь в покое.
218
Гл. 6. Динамика изотропной и анизотропной жидкостей
§ 6.2. Движение изотропной жидкости
Конечной задачей динамики жидкости является нахождение плотности,
трех компонент скорости, а также плотности энергии как функций от вре¬
мени и пространственных координат. Пять динамических уравнений для
этих пяти неизвестных следуют из законов сохранения массы, импульса
и энергии.
6.2.1. Сохранение массы: уравнение непрерывности
Рассмотрим объем жидкости V0, ограниченный поверхностью Ао. Ин¬
декс «О» означает, что объем зафиксирован в пространстве. Масса жидко¬
сти в этом объеме в любой момент времени равна объемному интегралу от
ее плотности: JJJ p(r, t) dV. Скорость вытекания массы через замкнутую
Vb
поверхность Ло равна <Ц> p\v dA. Скорость, с которой масса уменьшается
Aq
д
внутри объема, равна — — JJJ р dV. Поскольку масса не может произвольно
dt v0
возникать, то мы получаем
9 ' pdV + (
JJ
dt
Vo Л о Vo
) р\и dA — — + divpv ) dV = 0. (6,7)
Последнее уравнение справедиво для любого объема жидкости Vo. Поэтому
выполняется уравнение
др_
dt
V/>v, (6.8)
называемое уравнением сохранения массы, которое известно также как
уравнение непрерывности. Чтобы представить его в лагранжевой форме,
т. е. при следовании за частицей жидкости, необходимо продифференциро¬
вать второй член в (6.8) и применить определение материальной производ¬
ной (6.2). В результате получаем
J = -pVv, (6.9)
at
т. е. скорость изменения плотности dp/dt равна произведению плотности р
и скорости расширения объема Vv, взятому с противоположным знаком.
Для несжимаемой жидкости, р(г, t) — const, уравнение непрерывности
имеет простой вид
Vv = dvk/dxk = 0. (6.10)
6.2.2. Уравнение импульса
Лагранжев подход открывает прямой путь к выводу динамических урав¬
нений для импульса и энергии. Выбирается материальный объем V, ограни¬
ченный поверхностью А, который движется с жидкостью (таким образом V
§ 6.2. Движение изотропной жидкости
219
и А могут зависеть от времени), и к этому движущемуся объему применяют¬
ся основные законы механики. Уравнение импульса следует из принципа,
аналогичного второму закону Ньютона в механике: скорость изменения им¬
пульса частицы, — JJJ pv dV, равна результирующей силе, действующей на
dt у
частицу:
d
dt %
PVi dV = I I p9i + ^ I dV. (6.11)
dxj
Чтобы получить баланс импульса в дифференциальной форме, необходи¬
мо провести дифференцирование в левой части (6.11) под интегралом. Эта
операция недопустима, так как объем интегрирования зависит от времени.
Заметим, однако, что интегрирование по объему можно заменить на ин¬
тегрирование по массе, р dV = dm. После этого область интегрирования
(масса движущейся частицы) становится постоянной, и изменение порядка
операций допустимо:
— dm=\p — dV. (6.12)
dt J dt
Так как объем V произволен, лагранжева форма уравнения импульса имеет
вид
р ^ = ?pL + pg.. (6.13 а)
dt dxj
d
р\ dV = —
l i
v dm =
dt .
dt J
В эйлеровой форме получаем уравнение
^ — (-aij + PViVj) + pg{, (6.136)
at dxj
где величина pVi — плотность импульса, а (—+ /л{Vj) — тензорный
поток импульса, называемый также тензором потока импульса.
Заметим, во-первых, что вклад источника одинаков в обоих уравнениях
(6.13); это замечание справедливо для всех законов сохранения. Во-вторых,
имеется аналогия между (6.13 6) и законом сохранения массы (6.8). Правая
д
часть уравнения (6.13 б) содержит дивергенцию — потока {—crij + pviVj)
dXj
и источник импульса pg{, который не имеет эквивалента в (6.8), где для про¬
стоты мы не вводим никакого источника материи, обусловленного диффу¬
зией. Таким образом, уравнения (6.13 б) и (6.8) могут рассматриваться как
частные примеры «уравнения баланса»
^(density) __ __^*v (f[ux) ^ (sources), (6.14)
dt
которое иллюстрирует универсальную структуру всех законов сохранения.
Вывод уравнения баланса наглядно иллюстрирует рис. 6.4. Пусть х есть
220
Гл. 6. Динамика изотропной и анизотропной жидкостей
массовая плотность некоторой величины X (например, полного импуль¬
са, кинетической энергии и т. д., отнесенных к единице массы), опреде¬
ленной в объеме Vo, ограниченном фиксированной поверхностью Ао. Из¬
менение JJJ д— dV величины X вызывается двумя факторами:
потоком
Ко dt
ф (-ЛЛ •v)dA = - JJJVo (V ■ Jx) dV величины X через поверхность Ао
Aq
(поток Jx вычисляется по отношению к единичной площади, нормальной
к J*, за единицу времени) и производством (или уничтожением) величи¬
ны X в объеме Vo, которое есть объемный интеграл от всех «источников».
Уравнение (6.14) является дифференциальной формой баланса.
Нормаль к поверхности,
направленная от «/>
• • •• ' * * * -■
х
и источники
•• й
. й Л, . »
• V;?
* .'.л ;
т.*
Рис. 6.4. Количество величины X в объеме Vo изменяется благодаря ее потоку
через ограничивающую поверхность Ао и ее производству в объеме Fo
6.2.3. Уравнение баланса энергии
Рассмотрим полную энергию жидкости, состоящую из кинетической
энергии ее макроскопического движения и удельной внутренней энергии
микроскопических движений, которые не исчезают даже в покоящейся жид¬
кости. В дальнейшем мы будем обозначать через е полную энергию, а через
2
и — внутреннюю энергию, отнесенные к единице массы, так что е = — +
2
+ и. Изменение полной энергии со скоростью (задача 6.1), определяемое
выражением
pedV= \р- (— + и) dV,
dt V 2 /
вызвано работой, совершаемой над системой, и потоком тепла. Работа за
единицу времени (мощность), совершаемая объемными и поверхностными
§ 6.2. Движение изотропной жидкости
221
силами, есть JJJ p(gv) dV +§ (F • v) dA. Тепло, получаемое за единицу
у л
времени, равно $ (—Jqv) dA, где Jq — поток тепла.
А
Следовательно,
p—dV= | р(g ■ v) dV + ([
dt
V V A A
)(Fv) dA 4- (’)(—Jqu) dA, (6.15)
или, в локальном (лагранжевом) виде:
р— = + Ji) + pgivi- (6.16 а)
dt dxj
Потоки энергии и источники могут быть также записаны в эйлеровом виде
[ср. с (6.14)]:
д д
ре = [vi(-crij + peSij) + Л) + pgiVi. (6.166)
dt dxj
Поучительно разделить изменения кинетической и внутренней энергий.
Записывая скорость изменения кинетической энергии в виде Р~(~) ~
/ dvi \ dvi
= Vi(p—)> где величина р—^ выражается посредством уравнения им-
dt dt
пульса (6.13а), и исключая этот член из (6.16а), получаем уравнение для
внутренней энергии:
fj')/ fill’ д
p™=(Tijm L. (6.17)
dt dxj dxj
Удельная внутренняя энергия контролируется, таким образом, работой по¬
верхностных сил и потоком тепла; работа объемных сил изменяет только
кинетическую энергию.
6.2.4. Уравнение производства энтропии
Тот факт, что градиенты скорости (член aijdvi/dxj) вызывают изме¬
нение внутренней энергии, представляется естественным: молекулярные
взаимодействия и перемещения между соседними областями жидкости,
движущимися с различными скоростями, приводят к внутреннему трению
и, таким образом, к диссипации энергии. Это явление в точной форме опи¬
сывается вторым принципом термодинамики, с одной стороны, и уравне¬
ниями Онсагера — с другой.
6.2.4.1. Второй принцип. В необратимом процессе изменение энтро¬
пии системы
dS = dS{r) +dSid) (6.18)
обусловлено двумя вкладами: обратимым изменением dS^ и необратимым
(диссипативным) изменением dS^. Если система замкнута (обменивается
222
Гл. 6. Динамика изотропной и анизотропной жидкостей
теплом, но не веществом с окружающей средой), то dS^ — —, где dQ
Т
есть полное тепло, поступающее в систему. Величина dS^ может содер¬
жать дополнительные вклады, если система открыта и обменивается также
веществом с окружающей средой. В самой общей форме1 ^ второй прин¬
цип термодинамики гласит, что для всех систем, открытых, закрытых или
изолированных, изменение dS^ всегда является положительным:
dS(d)>0. (6.19)
Даже если система разделена на малые части, производство энтропии в каж¬
дой из этих частей является, тем не менее, положительным. Это позволяет
записать второй принцип в локальной форме как уравнение баланса:
+ VJS = а = — > 0. (6.20)
dt Т
Здесь мы вводим локальные (зависящие от координат и времени) величины:
энтропию единицы массы $ ~ s(r, t), так что S — JJJ ps dV nds = ds^ +
Vo
-f dsds^ > 0; поток энтропии Js (предполагается векторной величи¬
ной), связанный с обратимыми процессами, dS^/dt = <$ (-JV) dA. Ис-
Ао
точник энтропии а (называемый также производством энтропии) на едини¬
цу объема часто выражается с помощью эквивалентной записи 2 Д/Т, где R
есть диссипативная функция. Чтобы найти 2R/Т явно в терминах парамет¬
ров, характеризующих вязкое трение и, например, теплопроводность, мы
dps
вычисляем — на основе первого принципа термодинамики.
dt
Дифференциал внутренней энергии ри единицы объема (подразумева¬
ется, что dV = 0) можно на самом деле записать в виде
d(pu) = (idp + Td(ps), (6.21)
где температура и химический потенциал единицы массы определяются
стандартным образом как Т = (ди/ds)p)A ц — (дри/dp)ps соответственно.
Путем деления последнего уравнения на элемент времени dt (достаточ¬
но большой по сравнению с молекулярными временами, чтобы сохранить
применимость гидродинамического приближения) мы получаем уравнение
скорости изменения энтропии ps:
TfM =р^ - (6.22а)
dt dt dt
^ D. Kondepudi and I. Prigogine, Modem Thermodynamics, John Wiley & Sons,
Chichester, 1998.
§ 6.2. Движение изотропной жидкости
223
где сделана подстановка d(pu)/dt = pdu/dt 4- udp/dt. Преобразуя соотно¬
шение
d(ps)/dt = d(ps)/dt + v • V(ps) = d(ps)/dt + div (psv) — ps div v
с помощью (6.2) и используя уравнение непрерывности (6.9), уравнение
(6.22 а) можно записать в виде
+ Т div (psv) = р— H-pdiv v, (6.22 6)
dt dt
где p = —pu + pp + Tps есть давление. Результат (6.17) для pdu/dt и со¬
отношение — VJ9 = V * позволяют придать уравнению
(6.226) вид
d(ps)
+ V (psv + —) = aiJ ' + J9V (1) . (6.23)
dt \ TJ T dx j \T/
Сравнивая последнее с (6.20), находим локальное производство энтропии
2R _ ajj +p$ij dvj _ dT „ 24л
T ~ T dxj T2 dXj ’
вызванное вязким трением (первый член) и необратимым тепловым пото¬
ком (второй член). Другие процессы, такие как химические реакции или
диффузия, могут также вносить вклад в производство энтропии.
6.2.4.2. Соотношения взаимности Онсагера. Отметим, что члены
в (6.24), отвечающие за производство энтропии, имеют определенную
структуру. Они являются произведениями некоторых потоков Ja (таких,
как поток импульса или поток тепла J9), характеризующих необратимые
процессы, и некоторых «термодинамических сил» Fa, которые управляют
течением. В нашем примере (6.24) «силами» являются градиенты скорости
и температуры. Мы можем записать феноменологическое соотношение
^ = ^FaJa. (6.25)
а
В равновесии, когда R = 0, потоки и силы исчезают. Если система не
находится в равновесии, но близка к нему, так что все процессы имеют ма¬
лые амплитуды, то можно предположить, что потоки Ja будут линейными
функциями от сил Fa:
J“=]TLa^. (6.26)
/3
Уравнения (6.26) называются феноменологическими (а также кинетически¬
ми) уравнениями; хорошо известными примерами являются закон Ома для
224
Гл. 6. Динамика изотропной и анизотропной жидкостей
электрической проводимости, закон Фика для диффузии и закон Фурье для
теплопроводности.
На значения феноменологических коэффициентов Ьар накладывают¬
ся определенные ограничения. Во-первых, заметим, что (6.26) приводит
к квадратичному выражению 2R/T = для производства
энтропии (6.25). Таким образом, коэффициенты Ьа$ должны быть таковы,
чтобы второй принцип R > О выполнялся для всех значений сил Fa, т. е. ве¬
личина R является положительно определенной. Например, значения Laa
должны быть положительными. Во-вторых,
^а/3 — Lpa. (6.27)
Соотношения (6.27) суть знаменитые соотношения взаимности Онсагера,
которые берут начало в обратимых по времени свойствах процессов на
микроскопических масштабах. Если система подвергается действию маг¬
нитного поля или испытывает угловое вращение, то
Lap( В) = Lj3a(-~ В), (6.28 а)
LajS(fi) =Lpa(-Sl). (6.286)
Отметим, что вклады в производство энтропии за счет тепла и напряже¬
ний не дают перекрестных членов в уравнении (6.24), так как соответствую¬
щие потоки имеют разный тензорный характер. Можно записать выражение
для потока тепла в изотропной среде в виде Jq = —кVT, он вызван силой
Yq = V Это явление носит название молекулярной теплопроводно¬
сти, ах — коэффициент теплопроводности.
6.2.5. Тензор вязкого напряжения
Если при движении жидкости отсутствует диссипация (идеально те¬
кучая жидкость), dS^/dt = 0, то согласно (6.24) мы должны получить
соотношение Oij = — р 5^. В более общем случае диссипативного процесса
представим тензор напряжений в виде суммы обратимой части сг^ = —pSij
и необратимой части о^, т. е. + о . Необратимая часть
называется тензором вязкого напряжения. Когда вязкие напряжения запи¬
сываются в виде линейных функций от градиентов скорости (случай малых
отклонений от равновесия), соответствующая диссипативная функция име¬
ет вид
2 R = aW^= ЪдЧ' (629)
13 dxj dxj dxi
Априори имеются 54 коэффициента Щы • Последующие рассмотрения сво¬
дят это число к 2 в случае изотропной жидкости. Заметим, во-первых, что
(d)
значения сг>. должны исчезать, если отсутствует относительное движе¬
ние (и, таким образом, трение) между элементами жидкости, т. е. когда
§ 6.2. Движение изотропной жидкости
225
v = const (это автоматически следует из (6.29)), или если жидкость вра¬
щается как твердое тело с постоянной угловой скоростью ик Примером
такого вращения вокруг оси г является поле скоростей^, Vy)=(—oJy, шу).
Очевидно, что для такого течения dvy/dx = ~dvx/dy. Поэтому среди че¬
тырех компонент движения, рассмотренных в начале данной главы, лишь
дилатация (3) и сдвиг (4), характеризуемые симметричным тензором Aijy
могут вызвать внутреннее трение. Эти величины суть единственные ком¬
бинации градиентов скорости, которые должны появиться в уравнениях
Онсагера и, таким образом, могут быть записаны в виде <х-^ = ifcjkiAki.
Вследствие симметрии по отношению к перестановкам i о j, к «-»• /,
и ij *4 Ы (соотношения Онсагера) изотопная жидкость характеризуется
только двумя независимыми коэффициентами вязкости:
дхк \дх{ dxj 3 dxk
— ^ &ijAkk (.Aij — S{j Afck у • (6.30)
Скалярные величины <; и г} — это динамическая объемная вязкость и ди¬
намическая сдвиговая вязкость. Оба коэффициента должны быть положи¬
тельными, г) > 0 и с > 0, чтобы выполнялся второй закон термодинамики.
Объемная вязкость исчезает в двух важных предельных случаях: в идеа¬
льном газе и в несжимаемой жидкости, т. е. когда течение не вызывает
дилатации (6.10). Жидкость может рассматриваться как несжимаемая, если
скорости меньше, чем скорость звука (около 1,5 км/с в воде при 15 °С).
Жидкости, которые удовлетворяют линейному уравнению (6.30), на¬
зываются ньютоновскими, — по образцу ньютоновского закона вязкости,
выведенного для простого одномерного сдвигового течения. Для поля ско¬
ростей [0, vy(z), 0] этот закон принимает вид
№ = я ■ (6.31)
dz
В ньютоновской жидкости, такой как вода или воздух, в широком интервале
значений градиентов скорости вязкость не зависит от напряжения сдвига
в жидкости. Жидкости, состоящие из длинных вытянутых молекул (поли¬
меры), и эмульсии (например, кровь) обычно не являются ньютоновскими:
связь между напряжениями сдвига и градиентами скорости в них не явля¬
ется линейной.
6.2.6. Уравнения Навье-Стокса. Число Рейнольдса. Ламинарные
и турбулентные течения
Подставляя (6.30) в уравнения количества движения (6.13), мы получаем
хорошо известные уравнения Навье-Стокса
— + (vV)v = g- ^V2v, (6.32)
dt op
15-КЛЕМАН M
226
Гл. 6. Динамика изотропной и анизотропной жидкостей
которые выполняются в случае несжимаемой жидкости, ^ = 0, и в случае,
когда динамическая вязкость г] не изменяется в пространстве (несмотря на
возможные градиенты температуры и давления). Уравнение (6.32) следует
дополнить уравнением непрерывности (6.10) и соответствующими гранич¬
ными условиями, чтобы получить полную систему уравнений, имеющую
однозначное решение. Подходящим граничным условием является так на¬
зываемое условие отсутствия проскальзывания, которое отражает тот экс¬
периментальный факт, что скорость жидкости на твердой границе равна
скорости границы.
Несмотря на все упомянутые выше упрощения, уравнения Навье-
Стокса являются заметно нелинейными благодаря члену (vV)v и поэто¬
му чрезвычайно трудны для решения. Для каждой конкретной задачи по-
лезныи первый шаг состоит в анализе относительной важности величин,
входящих в (6.32). В большинстве случаев можно определить наибольшую
скорость U в системе и некоторую характерную длину L. Величины U и L
вместе с кинематической вязкостью г}/р составляют безразмерную комби¬
нацию, называемую числом Рейнольдса:
Re = (6.33)
V
которое указывает на относительную важность инерциального вклада
(vV)v и вязкого вклада (??/p)V2v в (6.32). Если эти вклады оценить соот¬
ветственно как (vV)v U2/L и (т]/p)V2v (:г)/p)U/Ь2, то их отношение
и есть число Рейнольдса. Течения при низких и высоких числах Рейнольдса
имеют существенные различия и часто называются ламинарным и турбу¬
лентным режимами соответственно.
Если число Рейнольдса мало (благодаря большой вязкости, медленному
течению или малому масштабу длины), то член (v • V) v пренебрежимо мал
по сравнению с вязким вкладом. Если, кроме того, рассматриваются стацио¬
нарные (не зависящие от времени) решения, то dv/dt — 0, и инерциальный
вклад в целом (~ dv/dt) может быть опущен. Уравнения Навье-Стокса
становятся (в отсутствие объемных сил) много проще:
77 V2 v = Vp, (6.34)
что позволяет найти некоторое количество аналитических решений. Одним
из них является формула Стокса для силы сопротивления Fdrag, которую
оказывает ламинарное течение с постоянной скоростью U на сферу ради¬
уса a: Fdrag = 67T77aU. Вывод этой формулы довольно громоздкий (см.,
например, книги Ландау и Лифшица, а также и Бачелора СBatchelor).
Стационарное течение при низких числах Re обычно устойчиво по
отношению к малым возмущениям. Если такие возмущения появляются,
вязкое демпфирование возвращает систему в исходное состояние. Однако
при увеличении Re вязкое демпфирование может оказаться недостаточным
для преодоления возмущений, усиливаемых нелинейными членами. Дви¬
жение жидкости становится турбулентным с многочисленными вихревыми
областями.
§ 6.3. Иематодинамика в модели Эриксена-Лесли
227
Переход от ламинарного режима к турбулентному и поведение жидкости
при хорошо развитой турбулентности составляют две чрезвычайно слож¬
ные темы (именно вследствие нелинейного характера уравнений Навье-
Стокса). Турбулентность уже давно называют единственной остающейся
большой проблемой классической физики. Попытки понять это явление
ведут к формулировке основных принципов нелинейной науки, которая
возникла в течение нескольких последних десятилетий.
§ 6.3. Иематодинамика в модели Эриксена - Лесли
Взглянем снова на общую схему вывода гидродинамических уравне¬
ний для изотропной жидкости. Мы определили пять сохраняющихся ве¬
личин (масса, энергия, импульс) и записали пять законов сохранения для
их плотностей. Затем мы рассмотрели термодинамику жидкости, слегка
выведенной из состояния равновесия, и вычислили производство энтро¬
пии как сумму вкладов, каждый из которых является произведением «по¬
тока» и «термодинамической силы», вызывающей этот поток. Затем мы
предположили, что потоки являются линейными функциями от сил, при¬
чем коэффициенты пропорциональности — это вязкости или коэффициент
температуропроводности. Симметрийное рассмотрение установило, какие
вязкости являются независимыми параметрами.
Похожая схема может быть применена к гидродинамической теории
любой системы, включая нематические жидкие кристаллы. Важным отли¬
чием является то, что нематическая жидкость имеет нарушенную ориен¬
тационную симметрию, и, таким образом, директор п становится новой
гидродинамической переменной (с двумя независимыми компонентами).
Исторически теория гидродинамики нематической жидкости была сфор¬
мулирована с использованием двух различных подходов.
1. Макроскопическая гидродинамическая теория Эриксена -Лесли2)
основана на классической механике. Уравнение динамики директора
выводится из сохранения момента количества движения. Этот под¬
ход — основа для многих экспериментов, он используется в боль¬
шинстве учебников. Однако не ясно, как модель Эриксена-Лесли
может быть применена к другим упорядоченным системам, например
к SmA, где переменной нарушенной симметрии является смещение
слоев, а не повороты директора.
2. Гарвардская модель3) основана на общей идее, что уравнения макро¬
скопической динамики должны получаться путем усреднения
микроскопических (молекулярных) взаимодействий в системе.
J. L. Ericksen, Trans. Soc. Rheol, 5, 22 (1961); F.M. Leslie, Arch. Ration. Mech.
Analysis 28, 265 (1968) and Continuum Mech. Thermodyn. 4, 167 (1992).
3 ^
; D. Forster, Т. C. Lubensky, P. C. Martin, J. Swift and P. S. Pershan, Phys. Rev. Lett.
26, 1016 (1971).
228
Гл. 6. Динамика изотропной и анизотропной жидкостей
Гидродинамические уравнения строго выводятся путем выявления
с самого начала гидродинамических переменных, как сохраняющих¬
ся, так и относящихся к типу нарушенной симметрии. Каждая гидро¬
динамическая переменная удовлетворяет «уравнению баланса» (6.14),
которое представляет собой либо закон сохранения (для плотностей
массы, энергии, импульса), либо динамическое уравнение для пе¬
ременных нарушенной симметрии. Термодинамические потенциалы
зависят от гидродинамических переменных. Например, возмущения
директора входят в упругую энергию Франка-Осеена. Уравнение
производства энтропии теперь содержит члены, зависящие от дирек¬
тора, и число независимых коэффициентов вязкости и температуро¬
проводности возрастает.
Эти две теории не вполне эквивалентны. Например, имеется тонкая про¬
блема числа и природы независимых вязкостей; смотри детальное обсуж¬
дение в работе Плейнера и Бранда4^. Здесь мы рассматриваем оба подхода,
начиная с модели Эриксена-Лесли.
6.3.1. Уравнение момента количества движения
Новой переменной является директор п (две независимые компоненты;
скалярный параметр порядка принимает свое статическое значение s(T) —
— const). Два уравнения динамики директора выводятся из закона сохране¬
ния момента импульса. Что касается остальных переменных, то уравнение
непрерывности для массы остается таким же (6.9), как и для изотропной
жидкости; уравнение количества движения выглядит так же, как (6,13), но
в тензоре напряжений теперь надо учитывать наличие ориентационного по-
»
рядка; ориентационный порядок вносит также новые вклады в уравнение
энергии (6.16).
Момент импульса элемента объема dV в нематике рассматривается как
сумма макроскопического «внешнего» вклада dMext — г х (pv) dV, где г
есть расстояние элемента от некоторой точки отсчета, и микроскопического
«внутреннего» вклада, связанного с вращениями директора, который после
усреднения по большому ансамблю молекул дает чистый момент импульса
на континуальном уровне: dMmt = ICldV, где I — момент инерции еди-
d it
ницы объема и ft = [п х —] — локальная угловая скорость директора. По
dt
порядку величины момент инерции одной молекулы равен mi а2, где т\ —
масса молекулы, а — ее размер. Если N молекул идеально ориентированы
параллельно друг другу, то их полный момент инерции равен Nmia2. Та¬
ким образом, момент инерции единицы объема мал, I ~ ра2 (задача 6.4).
Инерциальными вкладами можно пренебречь при низкочастотных движе¬
ниях, но они включены в уравнения ради полноты рассмотрения.
4) Н. Р lei пег and Н. R. Brand, in Pattern Formation in Liquid Crystals, Edited by
A. Buka and L. Kramer, Springer, N. Y., (1995), p. 15.
§ 6.3. Нематодинамика в модели Эриксена —Лесли
229
Закон сохранения момента количества движения М гласит, что скорость
изменения dM/dt равна сумме объемных и поверхностных моментов сил.
Объемные моменты сил существуют благодаря полю тяжести и внешним
полям, способным переориентировать директор. Для элемента dV гравита¬
ционное поле создает момент [г х pg] dV; мы исключим его, помещая начало
координат в центр тяжести системы. Остающийся вклад равен [n х G\dV,
где сила G может переориентировать директор благодаря анизотропии ве¬
щества. Здесь мы ограничимся лишь рассмотрением диамагнитного эффек¬
та, Gk = p^XaKjBjBk, где В{ суть компоненты индукции В приложен¬
ного магнитного поля, Ха — анизотропия магнитной восприимчивости.
Включение электрического поля является более тонкой проблемой из-за
эффектов флексоэлектричества, ионов и т. д. Ч
Имеются два типа поверхностных моментов сил. Во-первых, имеется
обычный момент [г х dF] благодаря напряжениям ОкР, действующим на
элемент площади v dA, с компонентами [г х dF]i = p£ijkXj&kpVp dA. Этот
момент не исчезает даже в изотропной фазе. Второй тип поверхностных
моментов сил обусловлен исключительно ориентационными взаимодей¬
ствиями. Он связан с поверхностной ориентацией директора и может быть
выражен как через «тензор момента напряжений» в виде dli = lijVj dA,
так и через тензор «напряжений директора на поверхности» ТкР в виде
[п х dt]i — SijkTijTkpVp dA. Мы будем использовать второе представление,
так как оно явно включает директор. Связь между т*р и искажениями ди¬
ректора будет пояснена позже.
Таким образом, закон сохранения момента количества движения в ин¬
тегральной форме имеет вид
J {[г х pv] + /[п х n]} dV = J [п х G] dV -f (
v v А
~){[г х dF] -h [п х dt]}. (6.35)
Здесь точка — другое обозначение материальной производной n = dn/dt,
а в дифференциальной форме
P^ijk^j^k IZijk'ft'jfi'k — к “Ь &ijk {%j@kp “Ь TljTkp)- (6.36)
OX p
Дифференцируя последний член и замечая, что комбинация (pi)k —
— дакр/дхр) должна исчезать в силу сохранения импульса (6.13), получаем
уравнение для внутреннего момента количества движения — так называе¬
мое уравнение динамики директора:
д
I^ijkTljU'k — £ijk^ljGk ^ijk&jk £ijk (TljTkp)• (6.37)
дх
p
230
Гл. 6. Динамика изотропной и анизотропной жидкостей
6.3.2. Уравнение баланса энергии
Уравнение баланса энергии для нематической жидкости получается из
«изотропного» уравнения (6.16 а) с помощью добавления членов, связан¬
ных с ориентационным порядком:
гии и теперь должна содержать вклад от плотности энергии нематика (5.35),
/ — /fo - -Ро 1Ха(Вп)2, где /fo есть упругая энергия Франка-Осеена,
определяемая выражением (5.2). Правая часть в уравнении (6.38) дополне¬
на мощностью ориентационных сил (второй член) и мощностью тензора
директора на поверхности. Наконец, в анизотропной среде температурный
градиент может вызывать поток тепла в направлении, отличном от направ¬
ления градиента, Jj — — XjSdT/dxSi и коэффициент температуропровод¬
ности Xjs становится тензором второго ранга. В одноосном нематике тензор
Xjs имеет две независимые компоненты, >гц и к_L, так что XjS = >c\\Ujns -f
+ Kl Sj-g, где Sj~s ~ Sjs —rijns есть поперечный символ Кронекера. В начале
следующего раздела мы временно опустим вклад температуропроводности,
так как целью станет выяснение структуры тензоров сг^ и .
6.3.3. Уравнение производства энтропии
На данный момент у нас нет информации о возможной структуре тензо¬
ров (Tij и Tij. Чтобы ее получить, мы рассмотрим уравнение производства
энтропии, как это было сделано для изотропной жидкости.
Снова выделяем вклад внутренней энергии в (6.38). Умножая уравнение
импульса (6.13) на и уравнение момента импульса (6 2 7) на fU, получаем
два уравнения, которые, если их сложить, приводят к выражению
PQiVi 4- Gihi + JL-(yi(Tij + fiiTij) =
dxj
d ^ j fc / У- Л \
(Tij TijTfcp j (6.39)
dxj dxp
rjxeftjk = eijk{li — антисимметричный тензор вращения. Подставляя (6.39)
в (6.38), получаем
du / ч j jij. ^ f . лч.
P — ®ij H” bljk&jk Tlj7~kp~ • (6.40)
dt dxj dxp
С другой стороны, величина pdu/dt может быть найдена из термоди¬
намических рассмотрений, подобных тем, что были использованы для изо¬
тропной жидкости. Важное отличие заключается в том, что внутренняя
энергия единицы объема должна также включать плотность внутренней
d v . Т d О?
р + I
dt 2 dt 2
§ 6.3. Нематодинамика в модели Эриксена - Лесли
231
энергии Франка-Осеена / (в которой фигурируют модули Франка при
постоянных объеме и энтропии), так как директор может испытывать воз¬
мущения. Следовательно, d(pu) ~ p,dp + Td(ps) + d/, и скорость изменения
энергии pdu/dt = d(pu)/dt — udp/dt может быть представлена в виде
ptL = fa-u)±+T±(P8) + dl (6.41)
at dt dt dt
где р — (dpu/dp)ps^n — химический потенциал единицы массы и Т —
— (ди/дз)р>п. Преобразуя d(ps)/dt с учетом определения материальной
производной (6.2) и используя уравнение непрерывности (6.9), получаем
диссипативную функцию
2R = р— +pdiv v — —. (6.42)
dt dt
Скорость изменения плотности энергии / равна
+ а/ щ***, (6.43)
dt drii dt d(drii/dxj) dt dxj dt dtdxj
где мы ввели два новых обозначения: — /1q 1Xa{njBj)Bj
дПг drii
Я f it
= - . Полезно представить df /dt в терминах тензора flij и его
d(drii/dxj)
производных, преобразуя величину — с помощью (6.2) в выражение
dt dxj
д drii dvv дп{ i/i/ гл
_ —и используя соотношение ащ/аъ = —*нкПк,
dxj dt dxj дхр
dl = -ФАм - Try — (iliknk) - тгij рг-р-. (6.44)
dt dxj dxj oxp
С помощью подстановки (6.40) и (6.44) в (6.42) диссипативная функция
может быть переписана в виде
И 7Xij
2R — (<Jjk Н" р Sjk + Крк ~ ) "Ь Qjk \ Cjk + ф^к + TTjp —“ ) +
дхь \ dxj J \ охр J
+ —^(njTj.p - HjTTkp). (6.45)
дхр
При наличии температурных градиентов член
вую часть уравнения (6.45), причем = —*CjSdT/dxs, как было показано
в п. 6.3.2.
дТ
— — дает вклад в пра
т ) дх
232
Гл. 6. Динамика изотропной и анизотропной жидкостей
6.3.4. Недиссипативная динамика
Проанализируем уравнение (6.45) сначала для недиссипативного про¬
цесса. Все три выражения в скобках должны исчезнуть, чтобы равенство
R — 0 выполнялось для любых значений dvj/dxk, Qjk и d£ljk/dxp:
ajk = -Р sjk ~ Kpk , (6.46 a)
dXj
Sijk^jp i (6.466)
J dxp
— £ij k^lj^kp * (6.46 b)
Мы используем тензор Леви-Чивита, чтобы подчеркнуть, что во втором
и третьем членах в (6.45) значимую информацию содержат только антисим¬
метричные части выражений в скобках: так как есть антисимметрич¬
ный тензор, любая симметричная часть в скобках исчезает при умножении
на ftjfc.
6.3.5. Диссипативная динамика
В (6.46 в) и последующих выражениях мы будем предполагать, что ди¬
ректор на поверхности фиксирован (сильное сцепление), так что необрати¬
мая часть тензора «напряжений директора на поверхности» т*р равна нулю:
(г)
Ткр — Ткр •
Уравнение (6.46 а) побуждает нас определить тензор напряжений
Эриксена
ajk = -ptjk - TTpfc (6.47)
дх,
содержащий два вклада: напряжение невязкой жидкости и напряжение из-
за искажений директора (без диамагнитного вклада). Напряжение Эриксена
не зависит от диссипативных эффектов и обычно меньше, чем вязкие на¬
пряжения.
Подставляя (6.46) в (6.45), записываем диссипативную функцию в виде
2 R = Ацс№ + (Uij + Wijplf = AijWff + ttiMf. (6.48)
Здесь мы представляем градиенты скорости в виде dvi/dxj — Aij -f Wij
и вводим тензор напряжений а^ — ас симметричной
частью W— (т^ и антисимметричной частью о[^ = Наконец, мы
вводим обозначение -1-
Тензор напряжений оц включает диссипативные эффекты. Первый член
Aij^ij в (6.48) это диссипация за счет сдвигового течения. Во втором члене
антисимметричный тензор W\j определяет угловое вращение системы как
целого, наподобие твердого тела. Если — -V х v — угловая скорость
§ 6.3. Нематодинамика в модели Эриксена -Лесли
233
такого вращения, то = —ekij^k- Таким образом, второй член в (6.48)
равен €kij{^k — Wk)o^ и представляет собой диссипацию, вызванную от¬
носительным вращением директора.
Феноменологические уравнения (6.26) принимают форму
= VijkiMi + Vijkfikh = VijkiAki + Vijkfiki- (6.49)
Вязкости riijki могут зависеть от компонент директора. Так как нематик яв¬
ляется центросимметричной средой, коэффициенты щы должны быть ин¬
вариантны при преобразовании п = — п. Коэффициенты r)\jkl должны быть
симметричны по отношению к операциям г j и к «-> /, в то время как
коэффициенты rjj2kl должны быть симметричны по отношению к операции
г о j и антисимметричны по отношению к операции к *4 /, и т. д., чтобы
отразить симметрию тензоров ст, Аы и Пм. Более того, если нематик
является несжимаемым, то модель Эриксена-Лесли требует, чтобы любой
член, содержащий след Арр или произведение 5ыАц в тензоре напряжений,
обращался в нуль (см. также критическое обсуждение в 4^). Члены дыА^
не дают вклада в производство энтропии, так как SkiAijAki = AijAkk —
= 0. Все эти требования выполняются для следующего вида тензоров
—(s) —(а)
^ = ахщп^ПкщАы -Ь $ik SjiAki *f Q--^~ a*-(tiunjnk + Sjtni7ik)Aki +
Q3 + Ot2
т^(а) _ a5 — a6 (x ^ ^ ^ 4 L &2 —
0"■ j —
(fili'H'j'ft'k fikj'H'i'H'l') Akl H“ (^li'TljTlk ~b &kj'ftji'n,l)Qkl •
2 (6.50)
Шесть коэффициентов а* называются коэффициентами вязкости Лесли.
Их размерность в системе СИ есть [кг м'_1-с"1], а в системе СГС — [пу¬
аз]; 1 пуаз = 1 г-см^-с"1 = 0,1 кг-м”1^”1. Только пять из шести коэф¬
фициентов являются независимыми. Согласно соотношениям взаимности
Онсагера г)\?к1 = и
0^2 + СКЗ = ^6 “ <^5) (6.51)
Последнее соотношение известно как соотношение Пародий Наконец, по¬
ложительная определенность производства энтропии накладывает допол¬
нительные ограничения, такие как аз > а2 (см. задачу 6.6). В модели
Эриксена-Лесли несжимаемая нематическая жидкость характеризуется,
таким образом, пятью независимыми коэффициентами вязкости.
5) О. Parodi, J. Phys. (Paris) 31, 581 (1970).
234
Гл. 6. Динамика изотропной и анизотропной жидкостей
Диссипативный тензор напряжений и динамика директора часто
описываются в терминах вектора N, характеризующего относительную
скорость вращения директора:
N — п — о; х п или г Nj = —Uk^tjk — nk^lkj- (6.52)
Тензор напряжений выражается через N и Ац как
Oij = агщп^игцАы + a2rijNi + a3n*iV;- -f а4Л^- +
~h ot§TijTipApi -Ь ckqTiiTipApj, (6.53)
в то время как уравнения директора (6.37) с помощью (6.52) и (6.46) преоб¬
разуются к виду
I~[п х п] = [п х h] 4- Г. (6.54)
dt
Здесь
hi = ^ + Но 'xainjB^Bi + —{ df-FO ) (6-55)
дх, dm л. \ j дХ' уд(дщ/дх.^ I
— это молекулярное поле, которое включает как чисто упругий (/fo), так
и диамагнитный эффекты, а выражение
Г — (а2 — аз)[п х N] + (as — аб)[п х Ап] (6.56)
представляет собой момент вязких сил. Заметим, что уравнения (6.37) и
(6.54) предполагают, что внутренний угловой момент IsijkrijUk не сохра¬
няется. Величина {—SijkVjk) есть источник внутреннего углового момен¬
та. Разумеется, изменения величины ISijkUjfik возможны только за счет
внешнего углового момента peijkXjVk - такой же член £ijk&jk, но с проти¬
воположным знаком, входит в уравнение для pSijkXjVk [которое находится
вычитанием (6.37) из (6.36)]. Поэтому полный момент количества движения
сохраняется, как и должно быть.
При низкочастотных возбуждениях инерциальным вкладом можно пре¬
небречь, и (6.54) сводится тогда к
[п х h] + Г — 0, или [nxh]-[nx (7XN + 72 An)] = 0, (6.57)
где мы ввели две комбинации коэффициентов вязкости, которые будут по¬
лезны для обсуждения в следующих разделах:
71 = аз ~ > 0 и 72 = #6 ~ <^5 = ос2 + а3. (6.58)
В стационарном случае, когда производные по времени отсутствуют, урав¬
нение директора (6.57) представляет собой просто уравнение Эйлера-
Лагранжа [n х h] = 0 для равновесного поля директора п(г).
§ 6.4. Иематодинамика в гарвардской теории
235
§ 6.4. Иематодинамика в гарвардской теории
Согласно общей схеме, очерченной в § 6.3, мы определяем семь незави¬
симых гидродинамических переменных: плотность р, плотность импульса
pv, плотность энергии ре и две компоненты директора п. Законы сохране¬
ния для первых пяти переменных имеют ту же самую форму (6.9), (6.13)
и (6.16), что и для изотропной жидкости. Моменту импульса не уделяется
особого внимания. Сохранение момента импульса всегда гарантировано,
если тензор напряжений симметричен. Фактически, требование для aij
является более мягким. В законе сохранения (6.13) для плотности импуль¬
са наблюдаемой величиной является не тензор напряжений, а дивергенция
д(т'1
этого тензора —Требуемая симметрия может быть восстановлена до-
9Xj дх k
бавлением к несимметричному тензору члена ——, где Xijk — произ-
дхк
вольный тензор, антисимметричный по отношению к двум его последним
индексам j и к, т. е. Xijk = ~Xikj■ Новый симметричный тензор напряже-
« - дуак дац дац
нии а^ = Oij + — ■- удовлетворяет соотношению —- = —так что
дхк dxj dxj
и импульс, и момент импульса сохраняются6).
6.4.1. Динамика директора и диссипативный тензор напряжений
Недостающее «уравнение баланса» для директора должно связывать
производную по времени п с градиентами скорости Wij и молекуляр¬
ным полем h{, определенным уравнением (6.55). Вывод уравнений дина¬
мики директора облегчается тем фактом, что нормировка n2 = 1 приводит
к равенству пп = 0.
Во-первых, вспомним, что в состоянии равновесия молекулярное по¬
ле ориентирует директор п параллельно себе. Поэтому в выражении для
молекулярного поля (6.55) величиной, представляющей интерес, является
вектор ш = h — n(nh), перпендикулярный rx, пт = 0. Компоненты векто¬
ра ш могут быть записаны с помощью поперечного (5-символа Кронекера
в виде mi — 8+jhj. Зависимость щ от hj в уравнении динамики описьь
J
вается, таким образом, членом (—где скаляр 71 имеет размерность
71
г» • ®v3
вязкости. Во-вторых, связь между щ и градиентами скорости —- должна
дхк
осуществляться посредством тензора третьего ранга а именно: щ —
= Kjk—-• Так как = 0, то у тензора \jk должны быть только две
дхк
независимые компоненты. Мы разделяем на симметричную и антисим¬
метричную части, так что hi — X\fkAjk + X^Wjk. Поскольку вращения
1 4.
нематика как целого с угловой скоростью и) = - rot v переориентируют
2
Р. С. Martin, О. Parodi and P. S. Pershan, Phys. Rev. A6, 2401 (1972).
236
Гл. 6. Динамика изотропной и анизотропной жидкостей
все поле директора (без энергии диссипации), то антисимметричный вклад
\[jl Wjk должен быть просто равен EijkUjUk = WikUk ■ Симметричная часть
может быть записана с коэффициентом — Л где Л есть некоторый
безразмерный параметр.
В итоге уравнения динамики директора выглядят следующим образом:
— = Wikiik + A S±Ajknk + — 6-jhj. (6.59)
dt 7i
Сравнение с (6.56) и (6.57) оправдывает обозначения, введенные ранее
в (6.58). Как и в (6.57), диамагнитный эффект включен в молекулярное
поле h. В правой части уравнения (6.59) вследствие эквивалентности п
и — п отсутствуют члены, пропорциональные VT.
Производство энтропии вычисляется так же, как это делалось в преды¬
дущих параграфах. Оно равно (см. задачу 6.5)
2 R = (r\f')Aij+Nihi, (6.60)
т. е. совпадает с (6.48), когда опускается инерциальный вклад (и им следует
пренебречь в гидродинамическом пределе). Как уже упоминалось, тензор
напряжений может быть сделан симметричным без видоизменения зако¬
на сохранения импульса (и при гарантировании сохранения момента им¬
пульса)6^.
Величины N = п - о; х п и <т\^ в (6.60) — это рассматриваемые
потоки, в то время как hi и Ац являются силами. Как обычно, мы полагаем,
что потоки являются линейными функциями от сил. Поэтому мы можем
записать N = -i-h, т. е. имеется единственный скалярный диссипативный
71
коэффициент 7i, связанный с относительными вращениями директора N.
Для диссипативного тензора напряжений cr\fs^ = ЩыАы коэффициенты
вязкости образуют тензор rjijki, который зависит от компонент директора щ
и от Sij. Рассматривая симметрии тензоров и Аы и симметрию Онса¬
гера щи = Vkiij, находим пять независимых комбинаций щ и 5^: 5^ Ski,
&ik Sjl “b Sjk &ih TliTlj Ski TbfaTli Sij, TliTbk Sj[ TljTlk Sn + 7Xifll Sjk + TijTli Sik
и niUjrikni. В результате получаем
aij’S) = 2%Ац + 2(щ - т)(щпкА^к + nkrijAik) + (щ - i)2) 8цАкк +
+ 2(771 +rj2 - 2щ)щп^пкщАк1 + (775 - щ + г/2)(ЩП] Akk +
+ nkni6ijAki). (6.61)
Ограничения на величины 77 изложены в задаче 6.6.
§ 6.4. Нематодинамика в гарвардской теории
237
Отметим, что до сих пор мы не использовали условие несжимаемости.
Для несжимаемого нематика, А^к — 0, мы получаем: щ ~ г}2 и щ — 03\
и остаются независимыми только три коэффициента вязкости.
6.4.2. Краткое изложение положений нематодинамики
Для удобства мы резюмируем ниже все существенные уравнения, ис¬
пользуемые в модели Эриксена-Лесли и гарвардской модели для описания
нематика в движении. Объемные силы учитывают диамагнитный эффект
в молекулярном поле h, но не включают гравитацию.
Имеются семь неизвестных переменных: (1) плотность массы р(г, t),
(2) три компоненты поля скоростейу (г, t) илиплотностиимпульсару(г, t),
(3) плотность энергии и (4) две компоненты поля директора п(г, t). Эти пе¬
ременные находятся из семи уравнений:
1) уравнения сохранения масды (6.10)
др
dt
dpvj.
dxi
(6.62)
2) трех уравнений для сохраняющихся компонент импульса,
dpvi
dt
d
дх
+ pvivj)
(6.63)
В модели Эриксена-Лесли обратимая часть тензора напряжений пред-
(г)
ставляется в виде тензора напряжений Эриксена , а диссипативная
часть — посредством уравнений (6.50) или (6.53); в гарвардской модели
диссипативная часть дается выражением (6.61);
3) уравнения баланса энтропии
dps d ( Jf
+ ( pSVi +
dt
dxi
T
2 R
T
(6.64 a)
где увеличение энтропии либо равно нулю для обратимого процесса, либо
положительно,
2 R
(г'и)Ли + .V; h,
13
j? dr
T dx.
>o,
(6.64 a)
для необратимых процессов; поток тепла здесь = -
+Xj_ S^)dT/dxs;
4) уравнения динамики директора в виде (6.57) либо (6.59)
[и х h] — [п х (71N + 72Ап)] = 0,
N = А[Ап — п(пАп)] + —[h — n(hn)].
(х П{П8 +
(6.65 а)
(6.65 6)
238
Гл. 6. Динамика изотропной и анизотропной жидкостей
Эти обозначения подразумевают соотношения [А-п-п(пАп)]^ = Aijrij —
— UirijAjknk и N = fi — о; х п.
Если сравнить диссипативные тензоры в (6.53) и в (6.61), то
получается, что вязкости Лесли связаны с гарвардскими вязкостями несжи¬
маемого нематика следующими соотношениями:
ai - 2(771 + 772 - 2773) - 71 А2, а2 = -71(1 + А)/2,
«з = 7i(l - А)/2, 0:4=2772, а5 = 2(773 - 772) + 7iА(А + 1)/2,
а6 = 2(773 - т) + 7iA(A - 1)/2. (6.66)
Соотношение Пароди (6.51) выполняется, а6 - — аз + а2 = у2. Безраз¬
мерный параметр А в (6.65 б) (гарвардская модель) не дает вклада в про¬
изводство энтропии (6.60) и, таким образом, является недиссипативным,
несмотря на тот факт, что этот параметр представляет собой отношение
двух диссипативных величин в модели Эриксена-Лесли:
A=_2i = 2l±^i. (6.67)
71 02 — «3
Можно показать, что число коэффициентов вязкости в модели Эрик¬
сена-Лесли также сводится к трем, когда возмущения директора малы.
В этом случае мы можем опустить величину ф{ в определении молеку¬
лярного поля (6.55) и записать: hi — ditij/dxj. Тензор (?ij, который появ¬
ляется в (6.53) в модели Эриксена-Лесли, переписывается в виде
@ ij OLiTliTljTb^Tli Afci OC/^Aij ~\~ (jl/jWjpApi + TliTlp Apj)
71
+ (6.68)
71 9xk 71 dxk
din'
ec^.* исключить Ni — —- - WikUk, используя (6.59) и обозначения (6.58).
_
Тензор <Jij, таким образом, расщепляется на истинно диссипативную часть
= airiinjrikmAki + aiAij + аза5 ~ Q2C*6 (njnpApi + щпрАрj) (6.69)
71
с тремя независимыми вязкостями и не диссипативную часть
- Ьт* + Ьтг*- (6-щ
2 \ дхк дхк J 2 дхк 2 дхк
Диссипативная часть является симметричной, в то время как недиссипатив-
(г\
ная часть несимметрична. Однако, как уже указывалось, тензор <т) • может
§ 6.4. Иематодинамика в гарвардской теории
239
быть преобразован в симметричный тензор, например в виде
a^’s) = -- (nj^ +гц^)
2 \ дхк дхк )
да^
что не изменяет физически важную величину —-— — —— в законе
dxj dxj
сохранения импульса. Преимущество такого преобразования заключается
в том, что симметричная форма тензора напряжений автоматически приво¬
дит к сохранению момента импульса.
Таким образом, в пределе малых возмущений обе модели дают одина¬
ковые результаты, хотя точное соответствие все же отсутствует. Например,
сравнивая (6.69) с гарвардской моделью несжимаемого нематика (6.61),
находим: а\ — 2(r]i + щ — в то время как согласно (6.66) имеем:
аг — 2(771 4- г}2 — 2773) — 71 Л2. Как утверждают Плейнер и Бранд4), рас¬
хождения в определениях коэффициентов вязкости в этих двух моделях
могут быть вызваны неполнотой тензора напряжений в модели Эриксе¬
на-Лесли. В следующем параграфе мы частично будем использовать язык
коэффициентов Лесли (со ссылкой только на соотношения (6.66)), так как
это упрощает обозначения в балансе моментов.
Мы завершаем этот краткий обзор перечислением проблем, являющихся
общими для обеих гидродинамических моделей.
Если частоты движений являются высокими, то вся теория должна быть
модифицирована, с тем чтобы она включала динамику скалярной части па¬
раметров порядка (см. обзор Бериса и Эдвардса7^). Соответственно является
важным параметр, называемый числом Деборы (Deborah):
De = 7 г, (6.72)
где 7 есть характерная сдвиговая скорость, а г — характерное молекуляр¬
ное время релаксации. В жидких кристаллах с малым молекулярным весом
De <С 1. Для полимерных жидких кристаллов время т может быть большим,
и De может быть величиной порядка единицы; в этом режиме течение из¬
меняет скалярный параметр порядка. В этой главе рассматривается случай
малых De.
Обе теории ограничиваются рассмотрением течений, не имеющих ка-
ких-либо топологических дефектов, таких как ежи, дисклинации и т. д. Ес¬
ли подобные дефекты присутствуют, то искажения ориентации директора
охватывают все пространство вырождения (см. гл. 12), т. е. усреднение поля
директора на расстояниях, больших, чем расстояния между дефектами, дает
7) А. N. Beris and В. J. Edwards, Thermodynamics of Flowing Systems with Internal
Microstructure, Oxford University Press, N. Y., 1994.
1 d , x
—^ji) 4"
2 dxk
+ -rii~{wkj + njk), (6.71)
2 dxk
240
Гл. 6. Динамика изотропной и анизотропной жидкостей
нулевой результат; директор более не является гидродинамической пере¬
менной. Движение с топологическими дефектами может быть рассмотре¬
но с использованием формализма «гидродинамических» скобок Пуассона,
как предложили Дзялошинский и Воловик8). Однако простые случаи мо¬
гут быть изучены с помощью менее сложного формализма, предложенно¬
го для рассмотрения подвижности дефектов в твердых телах (см. гл. 11).
Наконец, отметим, что гарвардская модель нематодинамики представляет
собой только один пример общей гидродинамической теории систем с на¬
рушенной симметрией6^. Кац и Лебедев (1994) рассмотрели ее применения
к смектическим и колончатым фазам, свободно подвешенным пленкам,
ленгмюровским монослоям и мембранам.
§ 6.5. Применения нематодинамики
6.5.1. Вискозиметрия нематика
Анизотропия вязких свойств нематической жидкости может быть про¬
иллюстрирована путем измерения эффективных вязкостей для различных
ориентаций директора по отношению к направлению течения. Рассмотрим
плоское куэттовское течение нематика, заключенного между двумя пласти¬
нами, при z — 0 и г = d (рис. 6.5). Верхняя пластина движется с постоянной
скоростью U вдоль оси у, нижняя пластина неподвижна; сдвиговое течение
определено как [0, vy(z), 0]. Жидкости прилипают к твердым подложкам,
так что vy z_d — U и vy z_Q — 0. Предположим, что директор фиксирован
в пространстве и во времени сильным магнитным полем, n(r, t) = const,
и немятик удовлетворяет закону вязкости Ньютона (6.31), aydJ — 77—, где
dz
(d)
аyZ есть постоянное напряжение сдвига, передаваемое через нематическую
жидкость, а г] — постоянный эффективный коэффициент вязкости. Инте¬
грируя последнее уравнение и используя граничные условия, мы находим,
что скорость является линейной функцией от координаты г: vy = jz, где
7 — U/d есть постоянная сдвиговая скорость с размерностью с-1. Опреде¬
лим tj как функции от коэффициентов Лесли щ и гарвардских вязкостей щ
для следующих трех наиболее часто встречающихся на практике условий
ориентации директора по отношению к сдвиговому течению, известных
как геометрические условия Мезовича.
1. Директор п перпендикулярен направлению течения и градиенту ско¬
рости, и = (1,0,0). Тогда riiAij — 0, iV* = rikWki = 0, и тензор
напряжений сводится к ayz — a^Ayz = 047/2, т. е. г)а = а±/2 — г)2.
Вязкий момент (6.56) исчезает, Г = 0, т. е. нематик ведет себя как
изотропная жидкость с эффективной вязкостью а±/2 = 772.
I. Е. Dzyaloshinskii and G. Е. Volovik, Ann. Phys. N. Y., 125, 67 (1980); Г. E. Воловик
и E. К Кац. ЖЭТФ 81, 240 (1981).
§ 6.5. Применения нематодинамики
241
2. Директор п параллелен направлению течения, п = (0,1,0). Компо¬
ненты UiAij и Ni ~ njWji равны (0,0,7/2); ayz = a^Nz -f (а4 +
+ a6)Ayz. Поэтому r]b = (a3 + a4 + ae)/2 = ffo + 7i(l - A)2/4.
3. Директор n параллелен градиенту скорости, n ~ (0, 0,1). Компонен¬
ты riiAij и Ni = rijWji равны (0,7/2,0) и (0, —7/2,0) соответствен¬
но. Таким образом, = а2Л^ + (a4 + a§)Ayz и rjc = (~a2 + a4 -f
4 )/2 = 773 + 7i(l + A)2/4.
Движущаяся пластина
Профиль
скорости
(г)
/
Сдвиговое напряжение,
приложенное к верхней части нематика
а
VZ
н
/
/
/
/
а
VZ
Сдвиговое напряжение,
/ Неподвижная пластина приложенное к нижней части
нематйка
A tv
>>
/
/
/
X
7]b= (a3 + ai4 + a6)/2
а
б
77c=(-a2 + a4+a5)/2
в
Рис. 6.5. Плоское куэттовское течение нематической жидкости с директором, фик¬
сированным сильным магнитным полем. Геометрические условия Мезовича: ди¬
ректор п параллелен направлению оси завихренности (а), директор п параллелен
направлению течения (б), директор п параллелен направлению градиента скоро¬
сти (в)
Таким образом, эксперименты со сдвиговыми течениями в сильном маг¬
нитном поле позволяют найти некоторые комбинации вязкостей. В соеди¬
нении с другими экспериментальными техниками, такими как рассеяние
света, динамика переходов Фредерикса, вращающиеся и осциллирующие
поля, поглощение ультразвука и т.д., можно определить все коэффициен¬
ты вязкости. До сих пор эксперименты проводились, главным образом, для
нематиков с малым молекулярным весом, состоящих из вытянутых молекул,
таких как 5СВ (см. табл. 6.1. и рис. 6.6). Табличные данные для 5СВ и МВВА
242
Гл. 6. Динамика изотропной и анизотропной жидкостей
показывают, что отношение г\ь jrf мало, « 0,18, что является объяснимым
результатом, если трение коррелирует с поперечным сечением молекул,
которое находится на пути потока. Для полимерных лиотропных жидких
кристаллов, таких как поли-7- бензол-глютамат(РВО), растворенных в сме¬
си метилхлорида и диоксана9), это отношение еще меньше, г}Ь/rjc « 0,005.
О дискотических материалах известно мало. Основное различие между ни¬
ми и обычными каламитическими материалами заключается в величине
параметра Л: А ~ — 1 для дискообразных молекул, и Л ~ 1 для стержнеоб¬
разных молекул10^. Предположим, что директор в равновесии ориентирован
вдоль оси z. Тогда в каламитическом нематике переориентация стержнеоб¬
разных молекул вдоль п вызывается, главным образом, градиентами скоро¬
сти dvxjdz и dvy/dz. Напротив, переориентация дисков перпендикулярно
п вызывается градиентами dvz/dx и dvz/dу. Данные для каламитических
нематиков подтверждают, что А ~ 1, причем обычно этот параметр немного
больше единицы (см. табл. 6.1 и рис. 6.6).
Таблица 6.1. Типичные значения вязкостей пентилцианобифенила
(5СВ) (из книги: L. Ы. Blinov and V. G. Chigrinov. Electrooptic Effects in
Liquid Crystal Materials, Springer, N. Y, 1996, 464 p); МВВА при 25 °C
(из книги: W. H. de Jeu. Physical Properties of Liquid Crystalline Materials,
Gordon and Breach Science, N. Y., 1980) и PBG из
Вязкости,
10"3 кг • м~1 • с-1
(или 10“2 пуаз)
5 СВ
МВВА
PBG
0.1
-11
-18 ±6
-3660
0*2
-83
-109 ± 2
-6920
аз
-2
-1 ±0,2
18
OL\
75
83 ±2
348
OLb
102
80 ±15
6610
а 6
-27
-34 ±2
—292
G. Srayer, S. Fraden and R. B. Meyer, Phys. Rev. A 39, 4828 (1989).
10^ Г. E. Воловик. Письма ЖЭТФ. 31, 297 (1980).
§ 6.5. Применения нематодинамики
243
140
сЗ
Т
S
CQ
О
сп
120 -
Vc
О
100 _
о
о
К
н
о
о
го
и
О
80 -
О
О
О
О
3 60 -
о
J5
Н
X
0>
S
а
S
-Qi
D
О
о
о
40
Па
А
О
О
А
А А Д д
О
20 -
Ъ □ □ □ □
ДДДддА Адд
□ □ □□□□□□□□□
0
14
12
10
8
6
4
2
0
Тт-Т{° С)
Рис. 6.6. Температурные зависимости коэффициентов Мезовича г}а, т}Ь и 7]с (еди¬
ницы: 10 кг-м -с ) для 5СВ (М. Cui and J. Kelly, Kent state University; см. также:
Mol. Cryst. Liq. Cryst. 331, 49 (1999) для других данных и обсуждения)
6.5.2. Ориентация течением и опрокидывание ориентации нематиков
с директором в плоскости сдвига
Рассуждения, приведенные выше, относятся к однородной ориентации
директора, фиксированной внешним полем. Если поле отсутствует, то те¬
чение ограниченного нематика определяется балансом упругого момента
~ К/L2 и вязкого момента ~ 777 ~ rjU/L. Здесь L есть типичный масштаб
деформации, например расстояние между пластинами ячейки. Относитель¬
ный вклад этих моментов сил выражается безразмерным числом Эриксена
Ег
7/7L2 nLU
к
к
(6.73)
При оценке т\ ~ 10~2 кг-м'1-с-1, К ~ 10”11 Н, L ~ 10мкм и 7 ~ Юс-1,
число Эриксена составляет величину порядка 103. Вязкие напряжения до¬
минируют над упругими, по крайней мере при высоких скоростях сдвига
и до тех пор, пока течение не приводит к пространственным градиентам
директора на очень малых масштабах L. Можно ожидать возникновения
больших градиентов вблизи границ ячеек.
6.5.2.1. Высокие скорости сдвига (Ег > 1)
При анализе взаимосвязи между скоростью и ориентацией при Ег^>1
мы можем пренебречь упругими моментами. Так как модель Эриксена-
Лесли дает более интуитивное понимание баланса моментов, мы будем ис¬
пользовать для вязкостей обозначения Лесли. Однако мы также используем
244
Гл. 6. Динамика изотропной и анизотропной жидкостей
параметр Л в том случае, когда необходимо подчеркнуть недиссипативный
характер такого явления, как ориентация течением.
Интересно найти такую ориентацию (если она существует), для кото¬
рой вязкий момент исчезает. Эта ориентация стабильна, если любое малое
отклонение от нее вызывает появление вязкого момента, который возвра¬
щает п обратно к исходному состоянию.
Дляп = (sin в cos ip, sin^sin^, cos#) hU = (0} jz, 0),7 > 0 (рис. 6.5)
уравнения директора (6.65) сводятся к
7i “ + 7(а2 cos2 в — а3 sin2 в) sin <р = 0, (6.74 а)
dt
7i —sin^-{-a27cos0cos(/? = 0, (6.746)
dt
когда внешнее поле отсутствует и упругие вклады пренебрежимо малы.
В дальнейшем мы будем различать течения, при которых директор нахо¬
дится в плоскости сдвига (данный пункт) и перпендикулярен к плоскости
сдвига (следующий пункт). Как видно из (6.74), устойчивое состояние мо¬
жет существовать, когда директор находится в плоскости сдвига, ip = 7г/2.
Неисчезающий вязкий момент (6.56), вызывающий повороты вокруг оси х,
есть Гх ~ 7(а2 cos2 O—a^ sin2 в) (рис. 6.7). Для двух предельных геометрий
(рис. 6.7, б, в) имеем: Гьх а37 ~ 77! (А - 1) и Тсх ~ а27 ~ -771 (A -f 1).
Если а.2 и аз имеют одинаковые знаки (А2 > 1), то стационарное состояние
существует для двух значений угла во, определяемых выражениями11)
tgi9°= ± = ± (6-75)
Гг = -<*з7
Гг = а27
У
а б
в
Рис. 6.7. Вязкие моменты сил, действующие на поле директора в трех геометриче
ских ориентациях Мезовича (пояснения в тексте)
F. М. Leslie, Mol. Cryst. Liq. Cryst. 63, 111 (1981).
§ 6.5. Применения нематодинамики
245
Обычно для нематиков со стержнеобразными молекулами, таких как
МВВА и 5СВ, а2 < 0, величина Л лежит в интервале 1,01 < Л < 1,1 (см.
табл. 6.1), и направление переориентации в геометрии показано на рис. 6.7, в,
что представляется логичным для продолговатых молекул, расположенных
вертикально в плоскости течения Куэтта. Ситуация с коэффициентом аз
является более сложной, так как он может изменять знак от отрицательного
к положительному, т. е. Л изменяется отА>1кА<1. Такое поведение на¬
блюдалось вблизи температур фазовых переходов N-SmA и N-твердое тело.
Например12^, Л — 0,27 для нематика 8СВ при температуре 34 °С. Различ¬
ные знаки произведения а2аз приводят к совершенно разному поведению
течения.
1. Ориентация течением: Л2 > 1, а2аз > 0.
Если Л > 1, стабильное стационарное решение соответствует зна¬
ку плюс в (6.75): флуктуация директора 66 будет вызывать момент
Гх ~ (—27азу/ск2/аз) 66 ~ 77iл/А2 - 166, восстанавливающий
угол в®, как показано на рис. 6.8. Этот режим называется режимом
«ориентации течением». Директор должен быть ближе к оси у, чем
к оси z, тг/4 < во < 7г/2, так как требование положительного про¬
изводства энтропии устанавливает неравенство аз — а2 >0 (см. за¬
дачу 6.6.). Действительно, для 5СВ и МВВА отклонения от «идеаль¬
ной» ориентации 6о = 7г/2 вдоль потока малы и составляют примерно
1 -10 градусов.
Напротив, для дискотических молекул аз > а2 > 0, Л < — 1
стабильное стационарное решение отвечает знаку минус в (6.75)
(рис. 6.8); —7г/4 < #о < 0, и, как ожидается, диски не должны сильно
отклоняться от плоскости ху.
2. Опрокидывание: Л2 < 1,а2аз < 0.
Уравнение (6.75) не имеет действительных решений: п вращается
в плоскости сдвига, что называется режимом опрокидывания. Пе¬
риод времени, необходимый для поворота на угол тг, вычисляется
2тг
с помощью интегрирования выражения (6.74 а): Т = — - , т. е.
'ys/l — Л2
он обратно пропорционален скорости сдвига. Опрокидывание легко
порождает линии дисклинаций.
В действительности при а2а^ < 0 уравнения (6.65) имеют ста¬
ционарное решение с малой амплитудой, если число Ег меньше неко¬
торого критического значения Егс « 4,8(—а2/а^)112\ при Ег ^ Егс
происходит опрокидывание директора (С. А. Пикин. ЖЭТФ 65, 2495
(1973); С. А. Пикин. Структурные превращения в жидких кристал¬
лах. — М.: Наука, 1981). Вблизи температуры Т{, при которой у ко¬
эффициента аз происходит инверсия знака, аз = а'3 (Т* — Т), должна
12^ Н. Kneppe, F Schneider and N. К. Sharma, Вег. Bunsenges. Phys. Chem. 85, 784
(1981).
246
Гл. 6. Динамика изотропной и анизотропной жидкостей
иметь место сингулярная температурная зависимость критической
скорости: Vc ~ (Т{ — Т)"1//2. Эти выводы были подтверждены экс¬
периментально в работе: Р. Pieranski, Е. Cugon, S.A.Pikin, J. Phis.
(France) Coll., 37, Cl - 3 (1976). (Примеч. ред.)
О
fN
5
j_>
X
s
fc*
i-T
-4
-8
-40
0
40
80
в
Рис. 6.8. Вероятные угловые зависимости вязкого момента = 7(0:2 cos2 в —
— аз sin2 в) для ориентированных течением каламитических (сплошная линия)
и дискотических (пунктирная линия) нематиков; 7 = Юс"1; коэффициенты вяз¬
кости указаны на графике. Открытые кружки соответствуют стабильным стацио¬
нарным ориентациям директора, закрытые кружки — нестабильным ориентациям
Опрокидывание особенно существенно для жидкокристаллических по¬
лимеров, так как эти материалы, как правило, отвечают неравенству
<^2«з < 0. Течение ЖК-полимеров имеет характерные отличия от течения
изотропных полимеров. Наиболее сильным отличием является эффект от¬
рицательной первой разности нормальных напряжений Nx = сгуу — azz, где
сгуу — нормальное напряжение в направлении скорости, azz — нормальное
напряжение в направлении градиента сдвига. Когда течение неньютонов¬
ской жидкости происходит в реометре конус-пластина, вдоль оси вращения
имеет место осевая нагрузка. Обычно для изотропного полимера эта на¬
грузка стремится отделить пластину от конуса, что означает Ni > 0. Кисс
и Портер13^ обнаружили, что для некоторых скоростей сдвига Ni < 0
в ЖК-полимере PBG механизм этого явления тесно связан с жидкокри¬
сталлическим характером PBG и опрокидыванием. В обычной изотропной
полимерной жидкости сдвиг увеличивает ориентационный порядок моле¬
кул s вдоль направления течения. Упругий отклик жидкости заключается
в восстановлении случайной ориентации, s = 0, и, таким образом, в оттал¬
кивании конуса от пластины вдоль оси z. В ЖК-полимере s не равен нулю
уже в невозмущенном состоянии. Сдвиг может здесь вызвать опрокидыва¬
ние и, значит, уменьшить s. Упругий отклик привел бы к восстановлению
13^ G. Kiss and R. S. Porter. J. Polym. Sci., Polym. Symp. 65, 193 (1978).
§ 6.5. Применения нематодинамики
247
более высокого значения $ и, таким образом, к подтягиванию конуса и пла¬
стины ближе друг к другу14).
6.5.2.2. Низкие скорости сдвига (Er <С 1). Рассмотрим теперь стаци¬
онарный режим при малых числах Эриксена, когда упругие моменты пре¬
пятствуют переориентациям директора151 Если директор находится в плос¬
кости сдвига, а течение происходит вдоль оси у, то уравнение для момента
сил (6.57) имеет вид
(К\ sin2 9+ К3 cos2 9) ^ + (К3 - Кх) sin 9 cos 9
dz2
дв
dz
dv
dz
-(аз sin2 в — а2 cos2 в) = 0, (6.76)
а уравнение для импульса есть
d
dz
где -L/2 ^ г ^ L/2 и
OZ -I
о,
(6.77)
•ц(9) = Qi sin2 9 cos^ 9 + ri° sin'* 9 + rf cos2 9.
Интегрирование уравнения для импульса приводит к выражению
(6.78)
Щ)Ъ.
dz
и ~ const.
(6.79)
Уравнения (6.76) и (6.79) можно линеаризовать, когда сдвиг мал. Пред¬
положим также, что поверхностное сцепление на границах устанавливает
«планарную» ориентацию директора п = (0, 1, 0), в = тх/2. Линеаризо¬
ванное уравнение (6.79) для импульса:
b dv
у
dz
а
(6.80)
имеет решение vy = 7z, где 7 = а/ту6, в то время как линеаризованное
уравнение (6.76) для момента сил,
К1
d2e
d?
(6.81)
дает в качестве решения следующий профиль полярного угла в поперек
ячеики:
0 — !L _ Q3^2
2 8/^1
1
2 z\2
L /
(6.82)
14^ G. Marrucci and P. L. Maffettone, Mocromolecules 22, 4076 (1989); R. G. Larson,
Ibid. 23,3983 (1990).
15) E. Dubois-Violette and P. Manneville, in Pattern Formation in Liquid Crystals, Edited
by A. Buka and L. Kramer, Springer-Verlag, N. Y., 1995, Chapter 4.
248
Гл. 6. Динамика изотропной и анизотропной жидкостей
Сравнение результатов для малых и больших значений числа Эриксе¬
на показывает очевидное неньютоновское поведение нематических жидко¬
стей. Для планарной нематической ячейки кажущаяся вязкость изменяется
от г)\ до rj{0o) при увеличении скорости сдвига. Хотя локально соотно¬
шение между напряжениями и деформациями принимает линейный вид,
переориентация, индуцированная течением, делает эффективную вязкость
зависящей от величины напряжения. Не только течение может вызывать
возмущения ориентации директора, но и изменения директора могут инду¬
цировать течение. Эти «эффекты обратного потока» существенно влияют
на работу нематических дисплейных устройств.
6.5.3. Неустойчивости поля директора, перпендикулярного к плоско¬
сти сдвига
Очевидное стационарное решение системы уравнений (6.74) есть в =
— 7г/2 и <р = 0. Оно соответствует геометрии (а), т. е. условиям, когда ди¬
ректор перпендикулярен плоскости сдвига (рис. 6.7, а). Вязкий момент ис¬
чезает, когда п = (1, 0, 0);т. е. нематик ведет себя как изотропная жидкость
с эффективной вязкостью щ/2, что было установлено выше. Однако когда
с*2 и аз имеют одинаковый знак, первоначальная ориентация n = (1, 0, 0)
неустойчива по отношению к флуктуациям директора (рис. 6.9)161 А имен¬
но, малое отклонение 6nz > 0 ведет к появлению вязкого момента Tz —
= —а27 8nz > 0 (рис. 6.9 а). Когда а2 < 0, этот момент сил поворачивает
директор вокруг оси г и создает компоненту 6пу > 0. При появлении конеч¬
ного значения 5пу возникает другой момент сил: Гу = а3 jSny (рис. 6.9, б).
Если аз < 0, данный момент сил усиливает начальное отклонение Snz > 0,
и директор отклоняется к плоскости yz. Конечно, если поверхностное сцеп¬
ление удерживает п = (1, 0, 0) на границах, то неустойчивость возникает
только в том случае, когда скорость сдвига превышает некоторое пороговое
значение, определяемое балансом вязкого и упругого моментов (см. задачи
6.7, 6.8).
§ 6.6. Гидродинамические моды
Исследование линеаризованных версий уравнений гидродинамики спо¬
собствует пониманию природы малых движений при низких частотах (со —»
0) и больших длинах волн (| q | -* 0). Число уравнений баланса (к = 5
для изотропной жидкости, к — 7 для нематика) равно числу независимых
переменных. Разлагая в ряд потоки в уравнениях баланса, можно ожидать
такое же число линеаризованных дифференциальных уравнений со = со (q)
первого порядка по производной d/dt. Производя замену d/dt —> —ico и
приравнивая нулю детерминант получившейся системы уравнений, при¬
ходим к дисперсионному уравнению Yln=о Сп{ч)иП = 0, где Сп(q) суть
16) Р. Pieranski and Е. Guy on, Solid State Comm. 13, 435 (1973).
§6.6. Гидродинамические моды
249
А
Tz = ~а2'У fin
а
Гу = — а37 <5лгv
0!3> О
б
Рис. 6.9. Неустойчивость Пьеранского-Гийона в поле директора, первоначально
перпендикулярного плоскости сдвига (рисунок из работы16^)
полиномы порядка п по вектору q. Корни этого уравнения, или «моды»,
разделяются на диссипативные моды (с обозначением D), означающие про¬
изводство энтропии, и недиссипативные моды, называемые также распро¬
страняющимися модам'и (с обозначением Р). Тот же самый аналитический
подход позволяет найти функции отклика (действительные и мнимые части
восприимчивостей) и корреляционные функции. Эти величины непосред¬
ственно поддаются экспериментальному изучению. Эксперименты по рас¬
пространению ультразвука дают действительные части восприимчивости,
изменения таких транспортных коэффициентов, как вязкости и коэффици¬
енты диффузии, определяют мнимые части восприимчивости, рассеяние
света и нейтронов дает сведения о корреляционных функциях.
В изотропных жидкостях, где число переменных равно пяти (плот¬
ность р, три компоненты скорости v и температура Г), продольные (вдоль v)
и поперечные (перпендикулярно v) моды расщепляются. Определяются
следующие пять мод.
Две Р-моды:
to — ±cq - i^q2, где благодаря спариванию со сдвигом и тепловой
диффузией возникает вклад в затухание моды, которым часто пренебре¬
гают. Р-моды всегда действуют попарно вследствие инвариантности соот¬
ветствующих гидродинамических уравнений по отношению к обращению
времени.
Три D-моды:
со = —ixthQ2 — тепловая диффузия; зависимость от iq2 есть харак¬
теристика сохраняющейся переменной, которая удовлетворяет уравнению
диффузионного типа,
со = —i-q2 —две поперечные сдвиговые моды, соответствующие двум
р
различным поляризациям.
250
Гл. 6. Динамика изотропной и анизотропной жидкостей
В нематиках имеются две дополнительные D-моды благодаря «нару¬
шающим симметрию» непрерывным переменным, связанным с директо¬
ром, а именно,
FC
две D-моды: и = —i—q2, где К — соответствующий коэффициент
Г}
Франка, г) — вращательная вязкость.
Важно отметить, что коэффициенты диффузии, связанной с вращением
директора, DTOt = —, и диффузии, связанной со сдвигом материи, Dsh =
V
= -, не имеют одинакового порядка величины: обычно — — « 10-4
Р Dah г)2
в термотропных нематиках. Релаксация завихренности (сдвига) является
быстрым процессом по сравнению с релаксацией ориентации директора.
Эксперименты по рассеянию света дали богатые данные об этих медленных
ориентационных модах (вязкости, постоянные Франка).
Задача 6.1. Показать, что — JJJ ар dV ~ JJJ р~ dV, где а есть ха-
dt у у dt
рактеристика жидкости, зависящая от времени и координат.
Ответ. Используйте то обстоятельство, что pdV есть постоянная
масса элемента жидкости.
Задача 6.2. Записать уравнение момента количества движения для
нематической жидкости в эйлеровой форме для случая отсутствия объем¬
ных сил.
$ ^
Ответ. — (Я);) + -—{IfliVp—EijkTijTkp) = —SijkGjk Для внутренней
dt охр
части и Sijk~(pxjVk) + 6ijk — (pXjVkVp — Xj<JkP) = eijuOjk для внешней
dt dxp
части; ни одна из частей не сохраняется сама по себе из-за наличия вкладов
«источников» в правых частях; однако эти источники компенсируют друг
друга при их включении в уравнения, так что полный момент импульса
сохраняется.
Задача 6.3. Рассмотреть закон сохранения момента импульса для изо¬
тропной жидкости и показать, что он приводит к симметрии тензора напря¬
жений: оц — Gji.
Ответ. Скорость изменения момента импульса любого материаль¬
ного элемента равна сумме моментов, создаваемых объемными и поверх¬
ностными СИЛаМИ. р (SijkXjVfc) P^ijkXjQk ^ijk^kp)^ ГДе Xj
dt dxp
координата положения элемента по отношению к началу отсчета; век¬
торные произведения, такие как [г х v], выражаются через компоненты
[г х v], = EijkXjVk- Так как dxj/dxp = SjP, то —(х:1акр) = ак} +
дхр
I дакр г
+ Xj—и уравнение момента импульса может быть переписано в виде
dxp
г dvk da кг, _
£ijkXj[p— ~ Р9к — —-J = £ijk&kj‘ Уравнение импульса показывает, что
dt dxp
§6.6. Гидродинамические моды
251
член в скобках исчезает. Таким образом, Sijk^kj — 0, т. е. сг^р = арк.
Задача 6.4. Вычислить момент импульса единицы объема жидкого
кристалла как функцию от скалярного параметра порядка s ^ 1.
Ответ17). Микроскопическая плотность момента импульса р равна
сумме моментов импульса pk = i^k отдельных молекул, расположенных
в точках Tk(i)\ /л(г, t) — ^2k Iuik 8(г — r^); I — та2 есть момент инер¬
ции молекулы массы т с характерным размером а. Пусть е* есть единич¬
ный вектор вдоль оси молекулы. Тогда угловая скорость имеет компоненты
(ojk)i = [efcx—= [ekxukxek]i = (ojk)j[6ij~(ek)i(ek)j], и,такимобра-
dt
30M,jUj(r,t) = ^2kI(oJk)j[Sij - (ek)i(ek)j]5(r-rk). Усреднение по малому
объему дает: //*(г, t) — ^k /y(r, r, t), где fty(r, () = [nx —
771 fc dt
есть угловая скорость директора и выражение
тк
111 <5ij - а(г, t)
TliTlj Sij
3
определяет локальный момент инерции; (...) обозначает среднее по моле¬
кулярному ансамблю. Так как векторы ft и п взаимно перпендикулярны,
riinjQ,j = 0 и зависимостью 5 от координат и времени можно пренебречь,
12 1
получаем: pi — р — (- + момент инерции единицы объема есть
m3 3
2/2 1 n
величина порядка ~ pa 4- -s).
3 3
Задача 6.5. Записать выражение (6.48) 2 R = Ajk&^k + (Г2?'&Н-И/
в терминах вектора N относительной скорости вращения директора (6.52)
и молекулярного поля (6.55).
Ответ. Записываем (ttjk + Wjk)o$ = £ijk{^i ~ Ui){&jk ~
затем используем (6.466), чтобы найти Sijk&jk и уравнение директора
Q
ввир,е l£ijkrijnk = £ijkrijGk-£ijk<yjk+£ijk—(njTkp) = 0, это уравнение
дхр
справедливо, когда инерциалъные члены пренебрежимо малы. В результате
имеем: 2R — Ajk^^ + Njhj (см. также (6.60)).
Задача 6.6. Найти ограничения на коэффициенты вязкости в модели
Эриксена-Лесли и в гарвардской модели исходя из требования
положительной определенности производства энтропии, что соответствует
диссипации.
17) Сугакое В. И., Верлан Е.М.. Гидродинамика жидких кристаллов. — Киев:
Изд-во К ГУ, 1978.
252
Гл. 6. Динамика изотропной и анизотропной жидкостей
Подсказка. Упростить (6.48) и (6.60), направив одну из осей координат
вдоль п.
Ответ. Выберем ось х в декартовой системе координат вдоль дирек¬
тора п. Тогда из (6.48), (6.50) и (6.51) находим производство энтропии
2R — (ос\ 4- а4 4- а$ 4- qiq)A^x 4* cx^Aij Aij 4-
+
(2a4 4" ОС 5 4“ OtQ )Axi Axi 4" 2 (ag ^5) Axi^xi (03 a2
где i и j принимают значения у и z\ здесь нет суммирования по индексу х.
Требование 2R > 0 означает, что а\ + а4 4 > 0; а4 > 0; 2а4 4-
4- «5 + аб > 0; аз — а2 > 0 и (2а4 4- аз 4 аб)(аз — а2) — (а6 — as)2 > 0.
Подобным же образом в гарвардской модели имеем: г/2 ^ 0, щ ^ 0, т?4 0,
щ(2гц + щ) > (т/5 - т)2, и 2(771 + Г}5) -Щ+Т]2 ^ 0.
Задача 6.7. Рассмотреть нематическую жидкость в планарной ячейке
толщины L в режиме плоского куэттовского течения. Найти критическую
скорость сдвига, при превышении которой ориентация п = (1, 0, 0) —
— const становится неустойчивой. Предположить, что (1) а2 и а3 имеют
одинаковый знак, (2) поверхностное сцепление бесконечно сильно, (3) те¬
чение имеет форму [0, 7z, 0], где 7 > 0 есть скорость сдвига.
Ответ18). Для малых флуктуаций пу и nz уравнения баланса момента
импульса принимают вид
( \dnz ТуГ d2nz , . Л
(а3 - а2) — - К± —— 4- аз7Пу - 0,
dt dz1
(а2 - а3)^- + К2д-~- - a2jnz = 0.
at dz1
Отыскивая решения в виде пу — пуо ехр(iqz) и nz = nzо ехр(гд^), где q =
= 7t/L, находим: a37ny0 + Kiq2nz0 = 0 и K2q2nyo 4* a27n2o = 0. Из усло¬
вия совместности этой линейной системы двух алгебраических уравнений
получаем: 7crit = -- \/-Kl ^2-(-)2. Условие неустойчивости может быть
7i у — 1 L
записано в виде: Ег > 7г2, где Ег — —— Л- есть число Эриксена
2 у КгК2
данной задачи.
Задача 6.7. Рассмотреть те же условия, в том числе геометрические,
что и в задаче 6.7, но с включением магнитного поля В = (В, 0, 0), стабили¬
зирующего первоначальную ориентацию директора п = (1, 0, 0) = const.
Найти критическую скорость сдвига, при превышении которой директор
становится неустойчивым.
18) Р Pieranski and Е. Guyon. Phys. Rev. A 9, 404 (1974); P. Manneville and E. Dubois-
Violette, J. Phys. (Paris) 37, 285 (1976).
Литература для дальнейшего чтения
253
Ответ. Добавление магнитного стабилизирующего момента сил
rmag — Но 1Ха(п х В)пВ приводит к условию совместимости
а2а37с2 = {Кгп21Ь2 + ^1Х2аВ2) (К2тг2/Ь2 + ^\2аВ2) ,
аналогичному условию в задаче 6.7. Если поле является слабым, однород¬
ное возмущение ориентации директора появляется выше значения
2 I К1 К 2 / 7Г \ о
7crit = —\ ——(—) * В сильном магнитном поле порог равен 7crit =
71 у А2 — 1 L
2 и, 1 Y2 В2
— — - — - Выше порога появляется система полос, ориентированных
71 у/Х2 -1
вдоль направления течения (см. Дюбуа-Виолетт и Манневиль15\ Пьеран-
ский и Гийон18)).
Литература для дальнейшего чтения
1. Ландау Л. Д., Лифшиц Е. М. Механика. — М.: Наука. Гл. ред. физ.-мат. лит.
1965. 204 с., ил.
2. G. К. Batchelor. An Introduction to Fluid Dynamics, Cambridge University Press,
1970.
3. M. J. Stephen, J. P. Straley. Physics of Liquid Crystals, Rev. Mod. Phys. 46, 617
(1974).
4. Pattern Formation in Liquid Crystals, Edited by A. Buka and L. Kramer, Springer-
Veri ag, N. Y., 1995.
5. Hydrodynamics and Nonlinear Instabilities, Edited by C. Godreche and P. Manne-
ville, Cambridge University Press, 1998.
6. S. R. de Groot and P. Mazur. Non-Equilibrium Thermodynamics, Dover Publica¬
tions, Inc., N. Y, 1984.
7. Гроот С. P. де, Мазур П. Неравновесная термодинамика. — М.: Мир, 1964.
8. D. Forster. Hydrodynamic Fluctuations, Broken Symmetry, and Correlation Functi¬
ons, W. A. Benjamin, Inc., Reading, MA, 1975.
9. Кац E. И., Лебедев В. В.. Динамика жидких кристаллов. — М.: Наука. 1988.
Е. I. Kats and V V. Lebedev. Fluctuational Effects in Dynamics of Liquid Crystals,
Springer-Verlag, N. Y., 1994.
10. R. G. Larson. The Structure and Rheology of Complex Fluids, Oxford University
Press, 1999.
11. F.M. Leslie. Adv. Liq. Cryst. 4, 1 (1979).
12. G. Marrucci and F. Greco. Flow Behavior of Liquid Crystalline Polymers, Adv.
Chem. Phys. LXXXVI, Edited by I. Prigogine and S. A. Rice, John Wiley & Sons,
Inc., p. 331 (1993).
13. PC. Martin, O. Parodi and P. S. Pershan. Phys. Rev. A6, 2401 (1972).
14. L. C. Woods. The Thermodynamics of Fluid Systems, Clarendon Press, Oxford,
1975.
Дополнительная литература
1. Пикин С. А. Структурные превращения в жидких кристаллах. — М.: Наука,
1981.
ГЛАВА 7
ФРАКТАЛЫ И ЯВЛЕНИЯ РОСТА
Эвклидова геометрия описывает мир как узор из простых форм (шаров,
треугольников, линий и др.) с интуитивно понятным представлением о раз¬
мерности: 0 — для точки, 1 — для линии, 2 — для плоскости и т. д. Однако
эта классическая картина не в полной мере отображает Природу, так как
«облака — не шары, горы — не конусы, береговые линии — не окружно¬
сти, древесная кора не гладкая, а молния не распространяется по прямой
линии»1). Бенуа Мандельброт, открывший новое семейство форм и введший
для них термин «фракталы», предлагает следующее — одно из возможных
определений: «фрактал — это форма, части которой каким-либо образом
подобны целому»2^.
В математике понятия фрактала и фрактальной размерности применяют
к структурам, которые обладают детерминированным или статистическим
свойством самоподобия, сохраняющимся на любых масштабах увеличения.
Фрактальная размерность служит показателем в степенном законе вида
M(Ar) = А DM(r), (7.1)
который показывает, каким образом изменяется «свойство» М данного
фрактала, например его м хса, если характеристический пространственный
размер фрактала увеличивается в А раз: г Хг. Заметим, что показатель
степени А не зависит от г, что подчеркивает существование самоподобия на
любых масштабах. Нормальные однородные объекты (называемые также
компактными) удовлетворяют (7.1), причем в этом случае D — «обычная»,
целочисленная размерность (1, 2, 3 и т.д.). Однако самое удивительное
здесь то, что в действительности существуют удовлетворяющие (7.1) объ¬
екты (фракталы), для которых D — дробное число. В простейшем случае,
если рассматривать г как единицу длины, а А — L — как измеренный
в этих единицах размер фрактала, то «свойство» фрактала зависит от его
размера L следующим образом:
М ос Ld, (7.2)
где, например, D = 1,42 или D = In 3/In 2 = 1,58496 ... показывает, что
рассматриваемый фрактал не является ни линией, ни поверхностью. Здесь
символ сх означает пропорциональность.
В физике идея бесконечного самоподобия ограничена тем, что межча-
стичные взаимодействия различаются на разных масштабах, например на
^ В. В. Mandelbrot. The Fractal Geometry of Nature, W. H. Freeman and Company,
N. Y., 1983, p. 1 (Перевод: Мандельброт Б. Фрактальная геометрия природы, М.:
Институт компьютерных исследований, 2002, с. 13.)
21
’ Мандельброт Б. 1987, цитата из: J. Feder. Fractals, N. Y. and London: Plenum
Press, 1988, p. 11.
§7.1. Основные концепции фракталов
255
субатомном и сверхатомном. Тем не менее многие физические системы
на самом деле обладают свойством самоподобия, хотя и в ограниченном
диапазоне масштабов. К ним можно отнести агрегаты коллоидных частиц,
полимеры (см. также гл. 15), гели, скомканные мембраны сурфактантов,
пористые среды, броуновское движение, турбулентные потоки, системы
фокальных конических доменов в смектических жидких кристаллах (гл. 10
и п. 13.2.6) и даже колонии бактерий. Геометрия этих систем, часто основан¬
ная на случайных процессах, таких как броуновское движение, довольно
запутанна; понятие фрактальной размерности помогает выразить, смоде¬
лировать и истолковать как саму геометрическую сложность, так и ее физи¬
ческие следствия. Кроме того, идея фрактала и степенной закон типа (7.1)
устанавливают сходство между явлениями роста (формированием структу¬
ры) во множестве равновесных (например, перколяция) и сильно неравно¬
весных (например, диффузионно-контролируемая агрегация и эффект вяз¬
ких пальцев) процессов. Такая связь обладает эвристической значимостью,
так как в настоящее время еще нет теории, способной исходя из первых
принципов описывать, например, диффузионно-контролируемую агрега¬
цию, являющуюся существенно неравновесным и нелокальным процессом.
Мы начнем с рассмотрения классических фракталов, таких как кривая
Коха, и объектов считающихся фракталами, таких как береговые линии,
и затем перейдем к рассмотрению ряда физических явлений: перколяции,
случайного блуждания, диффузионно-контролируемой агрегации и эффек¬
та вязких пальцев в ячейках Хеле-Шоу (названных так в честь британского
инженера Генри Хеле-Шоу, который в конце XIX в. наблюдал формирова¬
ние разветвленных структур, впрыскивая менее вязкую жидкость в плоскую
ячейку, заполненную более вязкой жидкостью). Для некоторых из пере¬
численных явлений фракталы не являются обязательными: вязкие пальцы
не всегда обладают фрактальной структурой. Существует и другая объеди¬
няющая тема, оправдывающая рассмотрение фракталоподобных агрегатов
и эффект вязких пальцев в рамках одной главы: в обоих случаях мы име¬
ем дело с неустойчивостью фронта роста, когда небольшие возмущения
фронта (поверхности раздела) начинают расти гораздо быстрее соседних
участков. Физическое описание неустойчивости поверхности роста осно¬
вано на уравнении Лапласа с подходящими граничными условиями.
§ 7.1. Основные концепции фракталов
Многие природные объекты могут быть приближены простыми эвкли¬
довыми фигурами, такими как нульмерные точки, одномерные прямые,
двумерные плоскости или трехмерные шары. Некоторые объекты не укла¬
дываются в эту схему. Их размерность D отличается от эвклидовой раз¬
мерности пространства, в которое они вложены, и от того, что может быть
названо «топологической размерностью». Возьмем кривую на плоскости.
Минимальная эвклидова размерность De пространства, содержащего кри¬
вую, равна 2. Топологическая размерность Dt равна 1. Однако ни De,
ни Dt не позволяют дать определение длины кривой L. Как мы измеряем L?
256
Гл. 7. Фракталы и явления роста
7.1.1. Длина линии
Для измерения L можно разбить линию на N меньших частей (исполь¬
зуя, например, циркуль) и затем заменить каждую часть отрезком прямой
длины г (раствор циркуля). Если линия кривая, то измеренная длина зави¬
сит от г:
L(r) — rN(r). (7.3)
Если мы имеем дело с отрезком прямой длины Lo, то зависимость N (г)
ясна:
N(r)=L0r~\ (7.4)
где показатель степени — 1 очевидно связан с топологической размерно¬
стью Dt — 1. Однако если линия кривая, то уменьшение шага циркуля
может привести к увеличению длины Ь(г) (рис. 7.1). Число N(r) может
расти с уменьшением г быстрее, чем г-1; например, N может подчиняться
степенному закону с D, большим, чем топологическая размерность Dt = 1:
N(r) ос r-jD, (7.5)
по крайней мере в некотором диапазоне значений г. Однако даже если
линия кривая, но гладкая и дифференцируемая, то в пределе г 0 можно
снова получить D = Dt = 1. С математической точки зрения, такая линия
не является фракталом, и следует подумать о более изощренных примерах,
для которых D > Dt — 1 даже при г 0. Один из таких примеров — это
троичная кривая Коха.
Рис. 7.1. Измерение длины кривой циркулями с разными растворами
7.1.2. Кривая Коха
Построение кривой Коха начинается с инициатора — отрезка прямой,
например длины Ь0. Срединная треть инициатора заменяется ребрами
равностороннего треугольника (рис. 7.2). В результате получается так на¬
зываемый генератор, состоящий из N = 4 отрезков, каждый длиной г\ =
= L0/3, так что полная длина составляет Li = 47*1. На следующем шаге
каждый из этих четырех отрезков рассматривается как исходный и замеща¬
ется генератором, уменьшенным умножением на 1/3. Полная длина стано¬
вится равной Ь2 = 16г2 > где r2 — Lq/9 — длина новых отрезков; длину
§7.1. Основные концепции фракталов
257
отрезка можно также рассматривать как изменяемый раствор циркуля. Дан
ный процесс продолжается до бесконечности.
лАл.
к = 4
Рис. 7.2. Стадии построения кривой Коха, которое начинается с отрезка единичной
длины. На шаге к + 1 каждый отрезок предыдущей /с-й стадии построения замеща¬
ется генератором, уменьшенным с помощью масштабного множителя (l/3)fc
На к-м шаге длина каждого отрезка равна г* =
составляет = 4— Lo(4/3)fc. Подставляя к
Lq/3
к
получаем
L(r)
и полная длина
(InLo - In rfc)/In 3,
(7.6)
и снова приходим к выражению N(r) ос г D, т. е. (7.5), которое теперь
выполняется для всех г. Показатель степени
D = lira
г—»0 1п(1/г)
(7.7)
17-КЛЕМАН М.
258
Гл. 7. Фракталы и явления роста
является константой, D — — « 1,26186, которая больше топологической
In 3
размерности Dt = 1. Фрактальная размерность D кривой Коха является
дробной, отсюда возникает термин «фрактал» (от ma.fractio (дробь) и, как
предложил сам Мандельброт, от лат. fractus (сломанный) — примеч. пер.).
Если прервать итерации на каком-то конечном шаге к, то получаю¬
щуюся структуру называют иногда предфрактальной. В этом смысле все
физические фракталы — предфракталы. Какая-нибудь кривая, вроде рас¬
смотренной в п. 7.1.1, может не быть фрактальной в строгом математиче¬
ском смысле; однако если такая кривая представляет физический интерес
(например, траектория движения) и подчиняется масштабному закону типа
(7.5) или (7.6) при изменении длины на несколько порядков, то можно пред¬
положить существование некой причины такого поведения и опереться на
фрактальное описание для лучшего проникновения в суть проблемы.
Численное значение D показывает, как далеко кривая Коха отклоняется
от прямой линии и насколько эффективно она заполняет плоскость. Что¬
бы проиллюстрировать это, можно модифицировать правила построения
кривой, а именно изменить угол у основания треугольника. На рис. 7.3
б
Рис. 7.3. Кривые Коха с разными углами у основания треугольника: а—угол 0,157
рад, D к 1,0045; б — угол 1, 5 рад, D и 1,8205
изображены две кривые (на шаге к ~ 5) с D « 1,0045 и D « 1,8205. Чем
блил^е D к 1, тем кривая Коха ближе по внешнему виду к прямой, и чем
ближе D к 2, тем более плотно кривая заполняет двумерную плоскость
(см. задачу 7.1).
7.1.3. Самоподобие
Фрактальная природа кривой Коха связана с ее самоподобием. На каж¬
дом шаге А; + 1 на рис. 7.2 кривая предыдущего шага к заменяется на N — 4
§ 7.1. Основные концепции фракталов
259
свои точные копии, уменьшенные с помощью масштабного множителя Л =
= 1/3. Мы можем использовать даже меньшие копии, получаемые на шаге
к + п, где п > 1. Тогда, для того чтобы перестроить конфигурацию ша¬
га к, понадобится N — Ап копий, уменьшенных с помощью масштабного
множителя Л = (1/3)п. Масштабный множитель может быть записан как
Л = (l/TV)1/-0, (7.8)
где
D = — In N/ In\(N) (7.9)
есть «размерность подобия», в нашем случае равная фрактальной размер¬
ности. Аналогично, отрезок прямой самоподобен с размерностью подобия
D = 1, так как он может быть собран из N ему подобных частей, умень¬
шенных с помощью масштабного множителя Л = (l/N)1/1 = (1 /TV).
7.1.4. Оценка фрактальных размерностей
Структуры с фрактальными свойствами часто являются результатом аг¬
регации. Агрегация — это вызванный силами притяжения процесс фор¬
мирования макроскопических структур (агрегатов) из меньших частей, ко¬
торые сами могут быть агрегатами или элементарными частицами. Если
этот процесс необратим, т. е. однажды соприкоснувшись частицы не могут
оторваться друг от друга, то получаемый агрегат отличается от компактной
«эвклидовой» структуры, например кристалла, выращенного в равновес¬
ных условиях. Отличие заключается в том, что агрегаты содержат большие
пустоты, которые становятся все менее и менее доступными для новых ча¬
стиц по мере роста агрегата: более вероятно, что частица будет захвачена
переферийной ветвью, чем то, что она избежит любых контактов и заполнит
вакансию вблизи центра агрегата. Данный эффект называют «самоэкрани-
рованием». По мере роста агрегата самоэкранирование приводит к фор¬
мированию все больших и больших пустот; существование пустот на всех
масштабах делает агрегат фрактальным.
Хотя в природе агрегация включает случайные процессы, будет полез¬
ным начать с рассмотрения детерминированной агрегации, приводящей
к еще одному классическому фрактальному объекту в математике — так
называемой салфетке Серпинского; позже в этой главе мы вернемся к фи¬
зическим примерам.
Пусть элементарной частицей («атомом») процесса агрегации является
черный треугольник с единичной длиной ребра (L = 1) и единичной массой
М = 1. В соответствии с правилами, предложенными Стенли3), три тре¬
угольника соединяются вместе, образуя новый равносторонний треуголь¬
ник с длиной ребра L = 2 и массой М = 3. На шаге к+1 три точные копии
агрегата, полученного на предыдущем шаге к, соединяются в больший
Н. Е. Stanley. Fractals and Disordered Systems/ eds. A. Bunae, S. Havlin, Springer-
Verlag, Berlin, 1996.
260
Гл. 7. Фракталы и явления роста
агрегат, имеющий линейный размер 2k+1 и массу М — 3fc+1 (рис. 7.4).
Масса и длина ребра связаны степенным законом
с показателем степени D = In 3/ In 2 и 1,585. Этот показатель снова не ра¬
вен ни единице, ни двум, но он явно имеет сходство с целыми размерностя¬
ми масс эвклидовых фигур. Если закон роста выбрать иначе, D изменится.
Например, если треугольники могут соединяться только вершинами своих
оснований вдоль прямой линии, то D = 1; если треугольники склеиваются
своими сторонами и сочленяются в вершинах, то D = 2. Если для салфетки
Серпинского построить график М (L) в двойном логарифмическом масшта¬
бе, получится прямая с наклоном D « 1,585, промежуточным между 1 и 2
(рис. 7.5). Интересен и важен тот факт, что выражение (7.10) предполагает
убывание плотности р фрактала с ростом его размера. Если нарисовать сфе¬
ру радиуса г вокруг любой точки фрактала, то средняя плотность внутри
этой сферы зависит от г следующим образом:
Самоподобие салфетки Серпинского проявляется в присутствии дыр
(белых областей на рис. 7.4) на каждом масштабе длин. Именно самопо¬
добная и полая структура фракталов приводит к степенному закону с фрак¬
тальной размерностью в (7.10) и (7.11).
M(L) ос Ь°
(7.10)
р(г) ос rD De
(7.11)
k= 1 k=2
k= 3
k = 4
Рис. 7.4. Агрегация маленьких треугольников в салфетку Серпинского
§7.1. Основные концепции фракталов
261
10 100 1000
L
Рис. 7.5. Двойная логарифмическая зависимость массы М от линейного размера L
для одномерной линии (тонкая линия), двумерного диска (жирная линия) и агрегата
в форме салфетки Серпинского (пунктир)
7.1.5. Детерминированные и случайные фракталы
Фрактальные кривые Коха и салфетка Серпинского, рассматривавшиеся
до сих пор* являются детерминированными: существуют хорошо описан¬
ные правила построения этих объектов и все точки фракталов могут быть
определены точно и однозначно. Самоподобие детерминированных фрак¬
талов можно проверить прямым способом и выразить через D. Природные
объекты само подобны только в статистическом смысле.
Статистический аналог детерминированной фрактальной кривой Ко¬
ха — это береговая линия. Согласно реально проведенным измерениям
длина некоторых береговых линий удовлетворяет (7.6) в большом диапа¬
зоне масштабов. Применяя (7.6) к размерам «измерительной линейки» от
нескольких километров до тысяч километров, можно обнаружить значение
D — 1,3 для западного побережья Великобритании и D = 1,52 для южного
побережья Норвегии, как написано в классических книгах Мандельброта
и Федера. До тех пор пока D = const, неправильности береговых линий
выглядят статистически самоподобными при разных степенях увеличения.
Это означает, что нельзя различить рисунки берегов, имеющие разное уве¬
личение (разумеется, не следует изображать на этих рисунках отдыхающих
туристов, так как последние имеют нефрактальные формы).
Фрактальные размерности, характеризующие свойства случайных
фракталов, такие как масса, число частиц, объем, площадь и т.д., мо¬
гут быть определены при помощи метода подсчета ячеек. Эвклидово
262
Гл. 7. Фракталы и явления роста
пространство размерности De, в которое вложен фрактал, покрывается
сеткой, составленной из ячеек с линейным размером е. Подсчитывается
количество непустых ячеек, и затем эта процедура повторяется для разных
значений е, различных ориентаций ячеек и положений начала координат.
Каждая непустая ячейка имеет объем sDe и массу М(е) = ре°Е, где р —
константа, характеризующая материал, из которого сделан объект. На рас¬
стоянии не больше г от любой непустой ячейки находятся N ос (г/е)° яче¬
ек, покрывающих объект. Их общая масса (объем) равна M(r) = NM(e),
или
М(г) ос (r/e)DM(e). (7.12)
Если увеличить г в Л раз, то масса объекта заключенная внутри сферы
радиуса Лг < L0, будет равна
M{\r) = \DM{r). (7.13)
Если D > Dt (и обычно D < De, см. задачу 7.2), то объект является
фрактальным с фрактальной размерностью D, определенной в (7.7). Урав¬
нение (7.13) говорит о том, что масса фрактала внутри сферы радиуса L
изменяется по закону М(Ь) ос LD, как в (7.10). Возвращаясь к приме¬
ру с салфеткой Серпинского, можно рассматривать N(e) = 3k в (7.7) как
число треугольников с линейным размером е = (1/2)к, необходимое для
покрытия салфетки на к-м итерационном уровне; в результате получаем:
D = In 3/ In 2, что уже было найдено ранее.
На рис. 7.6 явно видны различия и сходство между детерминированны¬
ми и случайными фракталами, которые могли бы сформироваться
в процессах агрегации. Согласно схеме построения исходный квадрат раз¬
бивается на девять одинаковых квадратов меньшего размера, четыре из
которых затем выбрасываются. Эта четверка может быть выбрана детер-
минированно (рис. 7.6, а) или случайно (рис. 7.6,6). Несмотря на внеш¬
ние различия, в обоих случаях фрактальная размерность одинакова —
D — In 5/In 3 и 1,465, так как необходимо одно и то же число квадратов
для покрытия двух объектов с одинаковой эвклидовой площадью.
7.1.6. Броуновское движение и случайное блуждание
Броуш&ское движение небольших (микронного размера) частиц, взве¬
шенных в изотропном растворителе, — это один из простейших приме¬
ров случайных фракталов. Броуновская частица находится в непрерывном
и неравномерном движении по зигзагообразной траектории (рис. 7.7) благо¬
даря флуктуационному движению молекул растворителя и их столкновени¬
ям с частицей. Из-за того что частица явно скачет в случайных направлени¬
ях, а каждый скачок имеет некую характерную среднюю длину а = \J(г2 ),
броуновское движение часто называют случайным блужданием. Покажем,
что соотношение между числом скачков N и средним расстоянием R, про¬
ходимым броуновской частицей, является фрактальным.
§ 7.1. Основные концепции фракталов 263
б
Рис. 7.6. Детерминированный (а) и случайный (б) кластеры (рисунок заимствован
из Т. Vicsek. Fractal Growth Phenomena, World Scientific, Singapore, 1992)
Рис. 7.7. Траектория броуновской частицы в двумерной плоскости
Накопленное за N прыжков смещение равно сумме R^v = 2^n=i Гп*
Среднее полное смещение R = ^(R?N) растет линейно с числом скачков,
так как любые два прыжка нескоррелированы:
/V N
п, т п>гп
264
Гл. 7. Фракталы и явления роста
Таким образом, соотношение между числом скачков («массой») и средним
пройденным расстоянием («радиусом») записывается как
Это означает, что броуновское движение имеет фрактальную размерность
D — 2. Данное заключение, очевидно, будет действительным для любого
вмещающего пространства с размерностью De ^ 2.
Модель случайного блуждания может быть использована в качестве
сильно идеализированной модели линейного полимера в хорошем раство¬
рителе. В такой модели каждый шаг случайного блуждания можно рас¬
сматривать как мономер полимерной цепи, предполагая, что любые два
соседних звена направлены в произвольных направлениях; более того, по¬
лимер может иметь самопересечения, как и броуновская траектория. Более
реалистичная модель полимера — это модель случайного блуждания без са¬
мопересечений. Очевидно, что если случайное блуждание без самопересе¬
чений является фрактальным, то его фрактальная размерность должна быть
меньше посчитанного выше значения D = 2. Действительно, вычисления
в приближении среднего поля приводят к формуле Флори: D = + 2,
3
т. е. D — 4/3 для De = 2 и D — 5/3 для Де — 3; более подробно данный
вопрос рассмотрен в книге Гуйе (Gouyet, 1996) и ниже в гл. 15. Формула
Флори, однако, не описывает более высокие размерности (De ^ 5), для
которых D приближается к 2.
В заключение этого пункта отметим, что идею случайного блуждания
можно распространить на объекты с Dt = 2, описывающие другие системы
из мира мягких веществ, а именно мембраны. Тепловые флуктуации стре¬
мятся смять мембрану, которая принимает форму случайной поверхности
без самопересечений. Для отдельной мембраны в пространстве с размер¬
ностью De — 3 было найдено значение D « 2,5.
7.1.7. Парная корреляционная функция
Уравнение (7.13) можно непосредственно применить к эксперименталь¬
но наблюдаемой фрактальной структуре, если есть хорошая микрофото¬
графия фрактала. Однако во многих случаях такие фотографии непросто
получить; кроме того, разрешение снимков, очевидно, ограничено. Стати¬
стическое самоподобие природных фракталов может быть подтверждено
экспериментах по когерентному рассеянию света, рентгеновского излуче¬
ния и нейтронов. Эти эксперименты дают возможность понять структурные
свойства на многих порядках масштаба длины от 1А до 1 мкм и позволяют
проверить масштабно-инвариантную симметрию. Измеряемые в них вели¬
чины прямо связаны с так называемой парной корреляционной функцией.
Парная корреляционная функция кластера (агрегата) из N одинаковых
частиц,
N = (R/a)2.
(7.15)
О
(р(г + г')р(г'))
<р(г')>
(7.16)
§ 7.1. Основные концепции фракталов
265
есть вероятность того, что точка, находящаяся на расстоянии г от занятого
узла г', принадлежит этому же кластеру. Здесь р — локальная нормиро¬
ванная плотность, т. е. р(г) = 1, если положение г занято, и р(г) = О
в противном случае. Для корреляций, зависящих только от расстояния, но
не от направления, можно заменить г —» г. Общая масса М (или чис¬
ло частиц N) представляет собой интеграл от корреляционной функции:
Г
М(г) ос J C(x)dPEx. Если объект фрактальный, т. е. М(г) ос rD, то корре-
о
ляционная функция должна иметь вид
С (г) ос г-а, (7.17)
где а — нецелое положительное число, меньшее D#:
а — De ~ D\ (7.18)
сравните это с выражением (7.11) для плотности.
Степенная зависимость (7.17) означает, что корреляционная функция
инвариантна (с точностью до постоянного множителя) относительно из¬
менения масштаба с помощью произвольного масштабного множителя А:
С(Хг) = \~аС(г). (7.19)
Другими словами, не существует характеристического масштаба длин, что
поразительным образом контрастирует с корреляционной функцией разу-
порядоченной среды с ближним порядком, например поликристалла, сос¬
тоящего из маленьких разориентированных микрокристаллитов, или
аморфного твердого тела, в которых пики корреляционной функции при¬
ходятся на значения г, соответствующие ближайшим или следующим за
ними соседям.
В экспериментах по рассеянию образец исследуется при помощи колли¬
мированного монохроматического пучка, при этом наблюдается рассеяние,
вызванное колебаниями свойств, таких как показатель преломления (рассе¬
яние света), электронная плотность (рентген) или ядерные плотности (ней¬
троны). Для рентгеновского и нейтронного рассеяний исследуемые мас¬
штабы гораздо больше длины волны пучка и, следовательно, необходимо
использовать малоугловое рассеяние. В случае упругого рассеяния интен¬
сивность излучения, рассеянного на некий малый угол в, определяется пе¬
реданным импульсом (разностью между волновыми векторами падающей
и рассеянной волн) а = — sin где Ао — длина волны. Размер частиц а
А0 2
обычно достаточно мал по сравнению с Ао, чтобы оказывать влияние на
картину рассеяния. Для того чтобы учесть этот эффект, предполагают, что
частицы представляют собой одинаковые сферы, и выражают I(q) в ви¬
де произведения форм-фактора P(q), описывающего рассеяние от незави¬
симых рассеивателей-сфер, и структурного фактора S(q), описывающего
корреляции между сферами.
2 66
Гл. 7. Фракталы и явления роста
Форм-фактор практически постоянен, когда qa <С 1, и изменяется по
закону Порода P(q) ос q~A в пределе qa 1. Структурный фактор пред¬
ставляет собой фурье-преобразование парной корреляционной функции:
S(q) — 47Г
сю
Sin qr 2
О
С (г) ——*-r dr. (7.20)
Для того чтобы правильно вычислить S(q), необходимо снова вспомнить,
что с физической точки зрения зависимость (7.17) действительна лишь
в диапазоне а<гСЛ, ограниченном сверху размером кластера R. Чтобы
учесть этот верхний предел, корреляционную функцию перенормируют:
С (г) ос r~a f(r/R), часто используя множитель в виде экспоненты: f(x) =
= е_ж, с тем чтобы удовлетворить условиям f(x) 0 для х^> 1 и }(х) —> 1
для х <С 1. В интересующем нас диапазоне 1/Я<дС 1/а структурный
фактор и интенсивность подчиняются степенному закону (задача 7.3):
I(q) ос 5(g)
С (г) -1П qr г2 dr ос q D. (7-21)
qr
Следовательно, в эксперименте по рассеянию можно прямо измерить фрак¬
тальную размерность D по наклону зависимости 7(g), изображенной в ло¬
гарифмических координатах (рис. 7.8). Заметим, что выражение (7.21) даст
дираковские пики (в обратном пространстве), если исследуемый объект —
кристалл, и кольца рассеяния в случае кристаллического порошка или
аморфного твердого тела.
q (произв. единицы)
Рис. 7.8. Схематичный график рассеяния, выявляющий фрактальное поведение
для 1/Я 1/а и влияние конечных размеров на больших и малых масштабах
§ 7.2. Перколяция (протекание)
267
7.1.8. Нижний и верхний пределы
Фракталы, образованные агрегацией частиц, имеют естественную ниж¬
нюю границу масштабной инвариантности — это размер а одной частицы.
Это может быть, например, молекулярный размер мономера в полимерной
сети. Верхняя граница — это размер кластера. Однако в некоторых случаях
определение нижнего и верхнего пределов не так очевидно.
В §10.8 будет идти речь о том, что основания фокальных конических
доменов в смектических полигональных текстурах образуют фрактало¬
подобную картину, похожую на аполлониевы упаковки окружностей.
Иерархия доменов обладает масштабно-инвариантными свойствами соот¬
ветствующей асимптотической аполлониевой фрактальной салфетки, но
только в ограниченном диапазоне масштабов г* < г < Lq, где Lo — верх¬
ний предел, например толщина смектического образца, иг* ~ K/W —
нижний предел, определяемый отношением коэффициента упругости к ани¬
зотропии поверхностной энергии. Этот нижний предел обычно гораздо
больше характерного молекулярного размера.
§ 7.2. Перколяция (протекание)
7.2.1. Геометрическое протекание
Рассмотрим квадратную решетку. Ячейки этой решетки заполнены с ве¬
роятностью р (пусты с вероятностью 1 —р). Соседние заполненные ячейки
(черные на рис. 7.9), имеющие общие стороны, образуют связанный кла¬
стер. Если р« 1, то кластеры маленькие и изолированные (рис. 7.9, а).
Когда р увеличивается от 0 до 1, растет и масса самых больших класте¬
ров (рис. 7.9,6). Существует значение 0 < р < 1, при котором возникает
единственный кластер, связывающий противоположные стороны решетки
(рис. 7.9, в). Когда размер решетки Lq —> оо, этот перколяционный кластер
бесконечен; значение рс, при котором появляется бесконечный кластер, на¬
зывают порогом протекания или критической вероятностью. Численные
расчеты (выполненные, разумеется, на конечных решетках) позволяют за-
КЛЮЧИТЬ, ЧТО Рс ^ 0,59275 для кластеров, образованных соседними узлами
на двумерной квадратной решетке, как на рис. 7.9; эти вычисления также
показывают, что кластеры представляют собой фрактальные распределения
занятых ячеек.
Изображенная на рис. 7.9 модель — лишь один из многочисленных ва¬
риантов геометрического протекания, отличающихся по типу решетки или
по алгоритму определения связанных кластеров. Также различают протека¬
ние по узлам (рассмотренное выше) и протекание по связям между узлами.
Первым прообразом теории протекания (по связям) стала теория полиме¬
ризации, развитая Флори в 1940-х годах.
Перколяционные модели позволяют понять физику многих явлений,
таких как фазовые переходы изолятор-проводник и золь-гель, полиме¬
ризация, распространение эпидемий, поведение разреженных магнитных
268
Гл. 7. Фракталы и явления роста
и пористых систем и т. д. Например, можно представить, что пустые ячейки
(см. рис. 7.9) принадлежат непроводящей матрице, а занятые (черные) —
представляют собой проводящие зерна в этой матрице. При малой концен¬
трации зерен, р < рс, система является изолятором, тогда как при р > рс
ишлшлшт
ш ш тт
тштт mi ■ ■ •■■■ ■■■ ттш ■■■ т тш
■■а ■■ ттшш ■■■ ■■ ivii шшш 1вяявм«в1
шшштш тттттт ттш ш т тт вяв ■ тшшт тш
в тшишт ш аая вв явяв ттш тшш ттш* тшшт
вв тш тш ш т тш т штшшт яв тшшт» ш ш
вввя штштшт ттш тш вявв ттшш тшш я шш
ш ш ив II в sb шв штшшш тш шшшшшш
а
р = 0,3
:■ * ВДОД j--
■ ■■ ■. ■■ - -.-«и ■*>..
I
С
и,:-.* I ij- .уйнС"1
в
р = 0.4
I
■
4
. Л . 7
: '>•
.■ 'л
. j : . .
'; >
Ь‘1
■I
I
L
•• .
v *
I
Л *
г,. ,Д . ....
I
. У.*
б
р = 0,6
Р = 0,7
Ф
Рис. 7.9. Перколяционные решетки для различных вероятностей заполнения р
система является проводником. Таким образом, рс — это точка фазового
перехода. К примерам, более близким к области физики мягких веществ,
относятся переход золь-гель (гелеобразование) и процесс полимеризации.
Золь — это система, в которой отдельные частицы рассеяны в некой жид¬
кой среде. Если частицы держатся отдельно друг от друга, вся система
ведет себя как жидкость. Гелеобразование заключается в установлении свя¬
зей (химических, электростатических, ван-дер-ваальсовых или имеющих
другую природу) между этими частицами. Когда связная решетка связей
становится достаточно большой, чтобы распространиться (протечь) через
§ 7.2. Перколяция (протекание)
269
всю дисперсионную среду, система переходит в гель, и у нее появляет¬
ся некоторая упругость. Иллюстрациями этого процесса служат варка яиц
и вулканизация каучука.
Приведенные выше примеры показывают, что для анализа перколяцион-
ных явлений важно знать линейный размер конечных кластеров. Кластеры
конечных размеров существуют как при р < рс, так и при р > рс, распола¬
гаясь в пустотах, оставленных бесконечным перколяционным кластером.
Два параметра (можно ввести и другие) подходят для описания системы:
радиус инерции Rs и длина связности
Rs — это среднеквадратичный радиус кластера, состоящего из s узлов,
измеренный от центра масс г о этого кластера. Если гг — положение г-го
1 3
узла, то г0 = - Ti и
5 г=1
я* = - ~ г°)2 = А X! fo ~ г^2- (7-22)
S Т” 2S* ГТ*.
г=1 ij = l
Во второй части (7.22) Rs выражается через расстояния между всеми па¬
рами узлов кластера (задача 7.4). Величина 2Щ — это средний квадрат
расстояния между двумя узлами кластера. Связность £ (или, по-другому,
длина корреляции) — это среднеквадратичное расстояние между парами
узлов, принадлежащих одному кластеру, усредненное по всем кластерам
ограниченного размера:
3
£.< s2n*
(7.23)
где ns — число кластеров размера s в расчете на узел решетки. Иными сло¬
вами, ns — это число кластеров размера s на решетке Lq х Lq, поделенное
на Lq. Выражение (7.23) учитывает, что любой случайно выбранный узел
решетки принадлежит кластеру размера s с вероятностью w(s) = sns, так
как существует s различных способов, которыми этот узел может входить
в данный кластер.
По мере приближении ркрс конечные кластеры увеличиваются в раз¬
мере; длина корреляции £, представляющая собой радиус тех кластеров,
которые вносят наибольший вклад в это увеличение, обращается в бес¬
конечность в точке рс. Когда £ расходится, то исчезает типичная длина,
которая могла бы характеризовать масштабные зависимости физических
свойств системы. Подобно фрактальным структурам в §7.1, эта система вы¬
глядит одинаково при разных увеличениях. Свойства системы становятся
нечувствительными ко многим локальным деталям, таким как небольшие
изменения межчастичных взаимодействий, структуры решетки и т. д., кото¬
рые не влияют на поведение системы на больших масштабах. Это свойство
приводит к универ сальности критических индексов, описывающих расхо¬
димость параметров вблизи рс. Эти универсальные индексы зависят от
270
Гл. 7. Фракталы и явления роста
рассматриваемой модели и размерности системы, но не зависят от деталей
локальной структуры.
7.2.2. Протекание и фазовые переходы второго рода
Приведенные выше рассуждения показывают, что данная перколяци-
онная модель имеет особенности объединяющие ее как с фракталами, так
и с температурными фазовыми переходами.
Вблизи точки перехода р — рс геометрическое протекание можно опи¬
сать тем же языком, что и фазовый переход второго рода, скажем пере¬
ход из парамагнитного высокотемпературного состояния в ферромагнитное
низкотемпературное состояние. Аналогом температуры Т является вероят¬
ность р занятости узла; аналогом параметра порядка, например намагни¬
ченности М(Т), — вероятность Роо(р) того, что случайно выбранный узел
принадлежит бесконечному кластеру:
р-рс^Тс-Т, (7.24)
Роо(р) ^М(Т). (7.25)
В магнитных материалах намагниченность исчезает при критической
температуре Тс согласно степенному закону М(Т) ос (Тс — Т)& с критиче¬
ским индексом j3. Непосредственно выше порога протекания, 0 < р—рс <С 1,
параметр порядка Роо(р) ведет себя аналогичным образом (рис. 7.10а):
Рос (р) ОС (р - Рс)0. (7.26)
Разумеется, Роо(р < рс) — 0, из-за того что при р <рс существуют только
кластеры конечных размеров.
Значения критического индекса /3 различаются в случаях с магнетиз¬
мом и протеканием. Например, теории среднего поля предсказывают, что
в двумерном случае /3 = 1/8 для магнитов и /3 = 5/36 для протекания.
Значения /3 также различаются в двумерных и трехмерных системах. Тем
не менее, если система (магнитная или перколяционная, двумерная или
трехмерная) выбрана, то критический индекс /3 есть более универсальная
величина,^ем порог протекания рс (см. табл. 7.1). Например, /3 останется
постоянной, если перейти от протекания по узлам к протеканию по свя¬
зям или изменить локальную структуру решетки, например с треугольной
на квадратную. В противоположность этому рс различно во всех выше¬
перечисленных случаях (табл. 7.1). Хотя рс и /3 можно всегда оценить при
помощи компьютерного моделирования, аналитические решения доступны
лишь в нескольких особых случаях. Один из этих случаев — решетка Бете,
или дерево Кейли, использованное Флори при создании модели гелеобра-
зования в полимерах; мы рассмотрим эту модель в п. 7.2.5.
Длина корреляции £ также расходится, когда р приближается к рс (свер¬
ху и снизу) (рис. 7.10,6), с некоторым новым критическим индексом и:
£сх|р-рс| "
(7.27)
§ 7.2. Перколяция (протекание)
271
Поведение (7.27) напоминает расходимость корреляционной длины вблизи
критических точек температурных фазовых переходов. Оба критических
индекса 0 и v универсальны, так как они зависят от размерности системы,
Таблица 7.1. Пороги протекания и критические индексы параметра по¬
рядка Р0о {/3) и корреляционной длины £ (г/) для нескольких часто исполь¬
зуемых перколяционных решеток; звездочками отмечены точные решения.
Составлено по работе Бунде и Хавлина*-1
Задача
Структура
De
Рс
/5
и
узлов
треугольная
2
1/2*
5/36*
4/3*
узлов
квадратная
2
0,592760
5/36*
4/3*
узлов
шестиугольная
2
0,6962
5/36*
4/3*
узлов
простая кубическая
3
0,31161
0,417
0,875
узлов
оцк
3
0,245
0,417
0,875
узлов
ГЦК
3
0,198
0,417
0,875
связей
треугольная
2
2 sin (7г/18)*
5/36*
4/3*
связей
квадратная
2
1/2*
5/36*
4/3*
связей
шестиугольная
2
1 — 2 sin (тг/18)*
5/36*
4/3*
связей
простая кубическая
3
0,248814
0,417
0,875
связей
ОЦК
3
0,1803
0,417
0,875
связей
ГЦК
3
0,119
0,417
0,875
Bunde. S. Havlin. Fractals and Disordered Systems / eds. A. Bunde, S. Havlin,
Springer-Verlag, Berlin, 1996.
но не зависят от локальных деталей. Цель теории — вычислить эти индексы
и найти взаимосвязь между ними. В следующем пункте мы проиллюстри¬
руем связь между критическими индексами и фрактальными характеристи¬
ками перколяционных решеток; методы вычисления критических индексов
будут обсуждены позднее.
272
Гл. 7. Фракталы и явления роста
л
TS
К
ж
S
5
со
со
К
О
Он
с
£
4-ю
^т
1 з-ю5
К
П
V
ю
со
Я г
8.2'Ю
с
10
5
о
0,592
а
Р
0,593
б
Р 0,594
Рис. 7.10. Параметр порядка (а) и корреляционная длина (б) вблизи порога
протекания
7.2.3. Кластеры конечных размеров на пороге протекания
Рассмотрим фрактальные свойства конечных кластеров, определив, как
масса MS(L) кластера, содержащего $ узлов, зависит от линейного
размера L, на котором он рассматривается. Единственным характерным
§ 7.2. Перколяция (протекание)
273
масштабом длин конечного кластера является его радиус инерции Rs. Пред¬
положим сначала, что L 2Rs; в этом случае масса равна s, MS(L) ос s,
и не зависит от L. На длине, меньшей этого размера, L <С Rs, кластер про¬
являет себя как самоподобный объект: MS(L) ос Ld, как в (7.10). Так как
Rs — единственная длина, характеризующая кластер, то можно ожидать,
что Ms зависит от L только через безразмерное отношение L/R8, и можно
записать для обоих случаев соотношение
MS(L) ос R°m(L/Rs), (7.28)
где функция т{х) постоянна при ж>1и меняется по закону т(х) ос х°
при х С 1. Так как s ос М, когда L 2RS, то число узлов и линейный
размер конечного кластера связаны типично фрактальным соотношением
$ ос R® или Rs ос s1^, (7.29)
что было подтверждено многочисленными компьютерными моделирова¬
ниями.
Вероятность w(s) того, что случайно выбранный узел принадлежит кла¬
стеру размера s, также подчиняется степенному закону. Рассмотрим ре¬
шетку Lo х L0 на пороге протекания и уменьшим ее в b раз до решетки
(Lo/b) х (Lo/b). Радиус инерции кластера уменьшается с Rs(s) до jRs(s') —
= Rs (s) /Ь, где s* — число узлов «нового» кластера. В соответствии с (7.29),
s' = s/bD. Вероятность w(s) для исходной решётки можно выразить через
соответствующую ей вероятность w(s') уменьшенной решетки как
w(s) = b~2w(s') = b"2w(s/bD). (7.30)
Множитель b~2, где 2 — эвклидова размерность решетки (De = 2), воз¬
никает из-за того, что каждый узел решетки (Lq/Ь) х (Lo/b) соответствует
b2 узлам исходной решетки Lq х Lo. Для того чтобы удовлетворить (7.30),
w(s) и s должны быть связаны степенным законом
w(s) — sns ос sl~T (7.31)
с критическим индексом, полностью определяемым размерностями D и De :
t = De/D + 1. (7.32)
Мы заменили показатель степени 2 на De, так как результат остается спра¬
ведливым для решеток с DE < 6. Для размерностей De ^ 6 имеет место
особая, на удивление простая, ситуация: все модели теории протекания да¬
ют одни и те же критические индексы, которые могут быть определены точ¬
но из теории среднего поля для решетки Бете (см. п. 7.2.5). Посредством г
размерности D и De определяют все остальные критические индексы при
Р = Рс
Теперь вычислим средний размер S конечных кластеров. Он может быть
S max
выражен суммой S = Y1 гДе ^тах ~ максимальный размер класте-
5=1
ра и wJ(s) — вероятность того, что занятый узел принадлежит кластеру из s
274
Гл. 7. Фракталы и явления роста
узлов. Очевидно, что при р и рс максимальный размер кластера на огра¬
ниченной решетке Lq х Lq есть smax ос Lq . Так как любой узел заполнен
с вероятностью р w рс, можно установить связь между w (s) и вероятностью
w(s) — sns, рассмотренной выше: pcw ж w. Следовательно,
^гпах
1
Рс s=l
Заменяя суммирование интегрированием и учитывая (7.31), находим
max
S ос
s2 Тds ~ s3maL ос LlD De (7.34)
max ^ О
1
(заметим, что 3 — т > 0, так как D не может быть меньше 1 для двумерной
перколяционной модели). Этот результат отличается от закона масштабной
инвариантности для наибольшего кластера: smax ос Lq.
7.2.4. Фрактальная размерность перколяционного кластера
На пороге протекания рс бесконечный перколяционный кластер содер¬
жит дырки всех возможных размеров, так как корреляционная длина £
расходится согласно (7.27). Выше рс длина £ конечна (рис. 7.106) и со¬
ответствует линейному размеру наибольших «дыр», оставленных перколя-
ционным кластером. Это значит, что при р > рс перколяционный кластер
самоподобен только на масштабах длин L < £ и однороден на больших
масштабах L > £. Пример такой структуры представлен на рис. 7.11. При
L < £ и L > £ масса бесконечного кластера по разному зависит от длины:
М{Ь) ос Ld, L<£, (7.35 а)
М(L) ос PqoLDe , L > £. (7.35 б)
При L = £ эти два выражения должны давать одно и то же зна¬
чение массы: PoqLDe ~ (р — pc)^£De ~ £D- Однако согласно (7.27)
£ а \р — pc\~v- Следовательно, *
D = DB-~, (7.36)
V
что связывает фрактальную размерность перколяционного кластера с /3
и v. Критические индексы /3 и v являются универсальными постоянны¬
ми в обсуждавшемся выше смысле; по этой причине размерность D тоже
универсальна. При /3 = 5/36 и v — 4/3 получаем: D = 91/48 « 1,8958.
В двух последних пунктах показано, что критические индексы связа¬
ны между собой, но ничего не говорится о том, как можно получить их
§7.2. Перколяция (протекание)
275
численные значения. В следующих двух пунктах мы рассмотрим два теоре¬
тических подхода к получению аналитических результатов; более подробно
об этом можно прочесть у Стоффера и Аарони (1992) и Гуйе (1996).
Рис. 7.11. Периодическая решетка, сложенная из салфеток Серпинского размера
~ £ (адаптировано из A. Bunde, S. Havlin. Fractals and Disordered Systems / eds.
A. Bunde, S. Havlin, Springer-Verlag, Berlin, 1996)
7.2.5. Протекание на решетке Бете
Как уже говорилось, порог протекания рс и критический индекс /3 могут
быть вычислены точно, когда протекание имеет место на решетке Бете, так¬
же называемой деревом Кейли. Чтобы построить дерево Кейли, начинают
с одного узла и присоединяют к нему 2 связей одинаковой длины. Конец
каждой связи представляет собой новый узел, к которому также присоеди¬
нены z связей, и т. д. (рис. 7.12). Любые два узла соединены только одним
составленным из связей путем. Дерево Кейли похоже на настоящее дерево
тем, что его ветви не образуют петель и, следовательно, они остаются стати¬
стически независимыми; это как раз и есть то свойство, которое позволяет
нам провести точные вычисления.
Рассмотрим дерево Кейли как перколяционную решетку: каждый узел
заполнен с вероятностью р. Определим вероятность существования (бес¬
конечного) пути из занятых узлов, ведущего от некого «исходного» узла
к периферии (рис. 7.12). Разумеется, все узлы дерева Кейли являются эк¬
вивалентными, за исключением узлов, близких к периферии, которые мы
не рассматриваем. Когда мы движемся вдоль ветвей дерева, в каждом узле
всегда есть (z — 1) связей, ведущих к (z — 1) соседним узлам (z-я связь —
это та, что привела нас в данный узел). Так как узлы заполняются с ве¬
роятностью р, среднее число связанных узлов, по которым можно продол¬
жить путь, равно (z — 1 )р. На каждом шаге среднее число узлов решетки,
276
Гл. 7. Фракталы и явления роста
связанных с «исходным» узлом, изменяется в (z — 1)рраз. Если (z — l)p< 1,
то нет шансов обнаружить бесконечный путь. Поэтому порог протекания
решетки Бете определяется из условия (г — 1)рс = 1 как
Для дерева Кейли с z = 3 (рис. 1Л2)рс — 1/2; то же значение характеризует
протекание по узлам в треугольной решетке.
Рис. 7.12. Решетка Бете 02 = 3 в каждом узле (кроме поверхностных). Каждое
новое поколение соседей показано на одной оболочке; выбранный центр концентри¬
ческих оболочек не имеет особого физического значения, так как все узлы внутри
решетки эквивалентны. Пустые узлы обозначены белыми кружками, занятые —
черными. Стрелками показан один из возможных путей соединения занятых узлов
Вычислим теперь критический индекс /3, описывающий критическое
поведение Роо(р), т.е. вероятность, что узел принадлежит бесконечному
кластеру из связанных между собой заполненных узлов (см. (7.26)). Для
рассмотрения вероятностей различных состояний, в которых может нахо¬
дится выбранный узел и его окружение, применяют приближение среднего
поля. Рассмотрим некий узел, пустой или занятый, с числом z выходящих
из него связей, ведущих к соседним узлам. Вероятность того, что выбранная
связь не соединена с бесконечным кластером, обозначим как Q, 0 ^ <2^1.
Исходный узел не принадлежит бесконечному кластеру (с вероятностью
1 — Роо), когда (а) этот узел пустой (с вероятностью 1 — р) либо (б) когда
этот узел заполнен, но все его г связей не ведут к бесконечному кластеру
(с вероятностью vQz\ поскольку нет петель, то связи статистически неза¬
висимы и вероятности Q умножаются друг на друга). Следовательно,
Рс = 1/Сг - 1)
(7.37)
1 - Роо - (1 - р) + pQz
(7.38)
§ 7.2. Перколяция (протекание)
277
Можно найти другое выражение для Q, изучив, что происходит в со¬
седних узлах. Связь не будет включена в бесконечный кластер (с вероятно¬
стью Q) в двух случаях. Во-первых, если соседний узел (конец выбранной
связи) пустой; вероятность этого (1 — р). Во-вторых, даже если соседний
узел заполнен (с вероятностью р), другие (z — 1) связей, исходящие из
этого соседнего узла, могут быть не соединены с бесконечным кластером
(вероятность Qz_1). Вероятность второго события pQz~l. Полностью Q
записывается в виде суммы
Q = (l-p)+pQz~1. (7.39)
Если z = 3, то решение для р < рс = 1/2 — это Q = 1 и Р,*, = 0; для
р> рс = 1/2 — это Q = (1 -р)/р и
Роэ =Р~ (7-40)
pi
Используя разложение в ряд Тэйлора вблизи порога протекания рс = 1/2
по степеням (р — 1/2), получаем
Роо =6(р-рс), (7.41)
т. е.
/3 = 1. (7.42)
Отсюда следует, что ни /3 = 1, ни другие критические индексы не зависят
от числа ближайших соседей z дерева Кейли, откуда вытекает универсаль¬
ность критических индексов. В противоположность этому, порог протека¬
ния (7.37) существенно зависит от г.
Можно ли результаты, полученные для модельного дерева Кейли, рас¬
пространить на обычные перколяционные решетки? Существенным упро¬
щающим элементом в вышеприведенных вычислениях было отсутствие
петель. Действительно, дерево Кейли имеет бесконечную размерность (для
того чтобы увидеть это, вычислите отношение числа поверхностных уз¬
лов к числу внутренних узлов дерева Кейли большого размера). В низко¬
размерном включающем пространстве петли в перколяционных решетках
встречаются часто, так как не хватает «свободного пространства», которое
позволило бы разным ветвям избегать друг друга. Однако если размерность
Dе растет, вероятность образования петель убывает и даже становится рав¬
ной нулю при некоторой критической размерности Dе,с — б. Таким обра¬
зом, при De ^ 6 точное решение приближения среднего поля для решетки
Бете можно приписать любой перколяционной модели. Хотя число 6 может
показаться слишком большим, для того чтобы представлять практический
интерес, некоторые теоретические заключения можно сделать,используя
тейлоровское разложение вблизи De,c — б.
7.2.6. Протекание и ренормализационная группа
Решетка Бете — одна из немногих моделей, дающих точные значения
критических индексов. Во множестве случаев мощным инструментом для
278
Гл. 7. Фракталы и явления роста
оценки критических индексов, и иногда даже для получения точных ре¬
зультатов, является метод ренормализационной группы. Он был развит для
изучения критических явлений при температурных фазовых переходах4^,
но может также применяться к явлениям протекания, так как в основе ре¬
нормализационной идеи лежат самоподобие и соотношения масштабной
инвариантности, подобные (7.28). Ниже приводится оценка критического
индекса v связности £ (см. выражение (7.27)) для протекания на треуголь¬
ной решетке (рис. 7.13).
О
О
О
•
• о
•
•
о
•
•
о
•
о-
•
о-
о-
о-
•
о- о
•
•
• о
•
•
о
•
•
о
•
о-
•
о-
Ъ-
о-
•
о- о
•
•
• о
•
•
о
•
•
о
•
о*
•
Ъ-
Рис. 7.13. Ренормализация треугольной решетки в реальном пространстве. Боль¬
шими кругами показаны сверхузлы, замещающие по три исходных узла. Сверхузлы
считаются занятыми, если заполнены по крайней мере два исходных узла
Как известно, порог протекания треугольной решетки в точности равен
Рс = 1/2 (см. табл. 7.1). Перенормируем решетку, замещая каждую тройку
соседних узлов (образующих треугольник) одним сверхузлом (рис. 7.13).
Сверхузел считается заполненным, если замещаемый треугольник является
«связным», т. е. если все три исходных узла, или по крайней мере два из
них, заполнены. Вероятность того, что все три вершины заняты, равна р3.
Вероятность того, что две данные вершины из трех заняты, равна р2(1 — р).
Принимая во внимание, что таких пар три, можно найти вероятность р'
того, что сверхузел занят:
рг = р3 + Зр2(1 - р). (7.43)
^ К. G. Wilson and J. В. Kogut. Phys. Rep. С, 12, 75 (1974). Обзор по мас¬
штабной инвариантности и универсальности в статистической физике содержится
в L.P. Kadanoff, Physica А, 163, 1 (1990).
§ 7.3. Агрегация
219
Перенормировку можно повторять, каждый раз увеличивая единицу
длины в одно и то же число раз b (в нашем примере b = \/3). Максимальное
значение Ъ ограничено тем требованием, что единица длины перенорми¬
рованной решетки должна быть много меньше £, для того чтобы можно
было использовать свойства самоподобия и масштабной инвариантности.
Напомним, что £ устанавливает верхний предел длин для самоподобия пер¬
коляционных кластеров (рис. 7.11),
В общем случае р* для перенормированной решетки не обязано сов¬
падать с р для исходной решетки. Только на пороге протекания долж¬
но выполняться точное равенство: р* = р — рс. Преобразование (7.43)
сохраняет только три значения р, называемые стационарными точками:
р* = 0; 1/2; 1; их можно получить, полагая р* = р в (7.43). Предельные
значения 0 и 1 представляют собой тривиальные случаи, но значение р* =
= 1/2 не тривиально, потому что совпадает с точным значением рс — 1/2
для треугольной решетки. В принципе от данной модели нельзя ожидать
точного результата, так как преобразование (7.43) не является точным: пе¬
ренормировка иногда изменяет связность кластеров, соединяя изначально
не связанные кластеры или разбивая единый исходный кластер.
Теперь вернемся к корреляционной длине £. Если самоподобие исход¬
ной и перенормированной структур сохраняется, то
№) = £(Р), (7-44)
что можно переписать, используя (7.27):
Ь(р'- РсГ1’= (Р ~ РсГ1'■ (7.45)
Равенство (7.44) имеет место, когда £ исчезает (для случаев р* = ОД) или
когда £ -» оо (для случая р* = 1/2). В окрестности рс можно линеаризовать
(7.43): р' = р*+А(р—р*) + . - -,где А = dp'/dp вычисляется ю (7.43). Кроме
того, взяв логарифм от обеих частей (7.45), можно выразить критический
индекс v вблизи рс как
- = —. (7.46)
v In Ь
При А = 6р—6р2 = 3/2 и b = л/З получаем: v — - 1пЗ/(1пЗ—1п2) = 1,355,
очень близкое к точному значению и = 4/3.
§ 7.3. Агрегация
Агрегация частиц приводит к различным результатам в зависимости от
того, происходит ли она в равновесных условиях или вдали от равновесия,
как обсуждалось в п. 7.1.4. Если частицы, добавляемые к растущему аг¬
регату, могут изменять свое положение и находить наиболее подходящие
позиции, минимизируя поверхностную энергию, в результате получится
компактный, нефрактальный объект. Если добавляемые частицы необрати¬
мо приклеиваются в том месте, где они впервые ударились о поверхность
280
Гл. 1. Фракталы и явления роста
растущего агрегата, то агрегат может принимать крайне неправильную фор¬
му с многочисленными дырами. В отличие от протекания, агрегация пред¬
ставляет собой нелокальный процесс. Из-за эффекта самоэкранирования
вероятность обнаружения частицы в некоторой точке г зависит не только
от г, но также от структуры агрегата в целом, т. е. от состояния системы
вдали от г. На сегодня не существует общей схемы описания нелокальных
и идущих вдали от равновесия процессов, таких как агрегация. Имеющи¬
еся аналитические подходы помогают понять физику роста, но не могут
дать всей картины, например, не могут вычислить значения фрактальных
размерностей. Вместо этого процесс роста можно описать алгоритмом, на¬
бором правил. Эти правила устанавливают:
1) тип объекта, добавляемого к растущему агрегату; объект может
быть (1а) отдельной частицей (агрегация частиц в кластер, или частично¬
кластерная агрегация) или (16) другим агрегатом, обычно сравнимого раз¬
мера (кластер-кластерная агрегация);
2) способ сближения объектов; траектории объектов могут быть (2а)
броуновскими или (26) линейными (баллистическими); вдобавок,
объект может вращаться;
3) когда два объекта сталкиваются друг с другом, существуют три
основные возможности: (За) они приклеиваются друг к другу сразу и
навсегда; не существует отталкивающих сил, способных предотвратить
соединение; скорость агрегации ограничена временем, необходимым для
того, чтобы два объекта смогли найти друг друга; как правило, это время
определяется диффузией, и агрегация называется диффузионно-контроли¬
руемой; (36) небольшие отталкивающие силы препятствуют немедленной
агрегации, и образование постоянной связи происходит после нескольких
столкновений; такая агрегация называется реакционно-контролируемой;
(Зв) связь не является постоянной, и существует конечная вероятность от¬
соединения (обратимая агрегация).
Комбинации вышеперечисленных правил приводят к многообразию
структур (см. табл. 7.2).
7.3.1. Кластер-кластерная агрегация
Кластер-кластерная агрегация экспериментально реализуется в колло¬
идных суспензиях крошечных (нанометры и микроны) частиц, взвешен¬
ных в жидкости, например в воде. Коллоидные частицы подвержены силам
взаимодействия двух типов: ван-дер-ваальсово притяжение (гл. 1) и элек¬
тростатическое отталкивание (гл. 14). На поверхности частиц обычно на¬
ходятся электрические заряды, причины возникновения которых — иони¬
зированные химические группы или адсорбированные ионы. Например,
силикатные частицы, образованные мономерами SiC>2, несут на себе от¬
рицательно заряженные поверхностные группы ОН~ и SiO2-. Облако по¬
движных положительных ионов (противо ионов) в растворе экранирует
§ 7.3. Агрегация
281
Таблица 7.2. Экспериментальные примеры и фрактальные размерности D
различных типов агрегации; собрано из Гуйе (1996)
тип
частично-кластерная (la)
кластер-кластерная (16)
диффузионно¬
контролируемые
электролитическое осаждение,
коллоиды и аэрозоли
2a+3a
пробой диэлектрика,
(экранированные)
рост колоний бактерий
1,44(Ds = 2)
1,72 (De = 2)
1,75 (De = 3)
2,50(Де = 3)
реакционно¬
контролируемые
эпидемии, опухоли,
коллоиды и аэрозоли
2а+3б
лесные пожары
(частично экранированные)
«•
2,00(1^ = 2)
1,59 (De = 2)
3fiO(DE = 3)
2,11(De =3)
баллистические
осаждение, напыление
аэрозоли в вакууме
26+36
2,00(De - 2)
1,55(Дб = 2)
3fiO(DE = 3)
1,91 (De = 3)
поверхностные заряды; таким образом, формируется двойной электриче¬
ский слой (гл. 14). Отталкивание между двойными электрическими слоями
препятствует тесному контакту частиц. Однако потенциальный барьер мо¬
жет быть понижен, например уменьшением поверхностного заряда или
добавлением в раствор соли. Когда потенциальный барьер меньше
ван-дер-ваальсовы силы притягивают частицы друг к другу, и те быстро
собираются вместе, образуя сильные связи Si-О-Si. Сначала образуются
дублеты, затем квадруплеты и т. д. Данный процесс классифицируется как
диффузионно-контролируемая кластер-кластерная агрегация. Если экрани¬
рование не является полным и потенциальный барьер остается большим
к^Т, агрегация относится к медленному реакционно-контролируемому ти¬
пу. Оба типа агрегации могут быть реализованы в одной и той же си¬
стеме в зависимости от степени экранирования5^. Кластеры, образован¬
ные в результате реакционно-контролируемой агрегации, более компактны,
М. Y Lin, Н. М. Lindsay, D. A. Weitz, R. С. Ball, R. Klein and P. Meakin. Proc. Roy.
Soc., A423, 71 (1989).
282
Гл. 7. Фракталы и явления роста
т. е. имеют большую фрактальную размерность, чем кластеры, образован¬
ные в результате диффузионно-контролируемой агрегации.
Кластер-кластерная модель является более подходящей, чем частично¬
кластерная модель, для описания агрегации коллоидов и их ближайших
двойников — аэрозолей (частицы в газовой среде). Однако существует
много других процессов, не обязательно включающих присоединение ча¬
стиц, которые описываются частично-кластерной моделью. Широко изве¬
стен частично-кластерный алгоритм диффузионно-контролируемой агре¬
гации, предложенный Виттеном и СандеромЧ
7.3.2. Модель Виттена-Сандера диффузионно-контролируемой агре¬
гации
Данная модель предписывает следующие правила роста. Начинают с од¬
ного заполненного узла. Вторая частица выпускается вдали от этого узла,
и затем ей позволяют совершать случайное (броуновское) движение до тех
пор, пока она не пристанет к частице-зародышу или не забредет так далеко
от исходной частицы, что ее можно будет рассматривать как безвозвратно
потерянную. Как только частица ударяется о зародыш, она перестает дви¬
гаться. Эмиссия случайно блуждающих частиц продолжается до тех пор,
пока агрегат не достигнет желаемого размера.
Этот простой алгоритм дает в результате неожиданно сложные и хоро¬
шо организованные агрегаты; один из них показан на рис. 7.14. С точки
зрения статистики, самоподобная и открытая структура агрегатов являет¬
ся следствием эффекта самоэкранирования: узлы, расположенные дальше
от центра, обладают большей вероятностью захватить новые частицы. Для
того чтобы сделать видимой эту особенность, можно пометить частицы,
присоединяемые на разных стадиях, с помощью различных цветов или
оттенков серого, как на рис. 7.14. Видно, что частицы, выпущенные на
поздних стадиях, редко проникают внутрь кластера.
Фрактальная размерность кластера, полученного с помощью компью¬
терного моделирования диффузионно-контролируемой агрегации, может
быть определена из корреляционной функции или из зависимости радиуса
инерции от числа частиц. Моделирование обычно показывает, что обе функ¬
ции подчиняются степенному закону: С (г) ос r~a, Rs ос sl^D (см. (7.17)
и (7.29) соответственно). Для кластеров на плоскости а = De - D и
« 0,3, и, таким образом, D « 1,7; в трехмерном пространстве D ы 2,5
(см. табл. 7.2). Однако расширенные моделирования на очень больших мас¬
штабах показывают, что показатели данных степенных законов не являются
точными константами, а представляют собой функции от отношения r/Rs\
т. е. С (г) ос r-Q(r/Rs)m q физической точки зрения это можно объяснить
уменьшением зоны роста в сравнении с полным размером кластера, по
мере того как кластер становится все больше и больше.
Т. A. Witten andL. М. Sander. Phys. Rev. Lett., 47, 1400 (1981).
§ 7.3. Агрегация
283
8 Л !• • л Фш Л
' Л—"%Л I* Ч
•т и *г®
8» *
«1мП 14t *|
«•I «I *1 гт
Ч • I 4е •
« т 1|4м /I
% L Ч1* ^
« •«. •«•па #г
•• в п t "*Я«Г •«“
^-Ь*| «Ьь *»£ „ь
«I • • tt«M • 9м «I9
8«n£«SM6S%3 |e| >tM
. " *~,8.А-йм«,Тй
S • • • *8* i t
••••** If. ИГ т9т ПтГ
тт м®®®»®»#.. л/ш ш ••
•Г Лт * •«!ГЭ»1 Sot •
id 1и»Ы *ш
* $ * г"** wa
• •г г •* • !*#•?••
"Г»!*- м, 1Я*.Чп .V Г1и
Sl# flmJ « 'Пкиит! I
W-Л • АГЛ ••«J- П f *4. •
»t§ * & Г ©»8o«S* t> i •*
•4 •*! fi *1«4<1 I* «4м «•!*
« •_ • • • «er-Cog в®® • •
* •»• «** tr 1 • It
n « trar t.
«IS m>4i
4 ГГ*
-JT
11Ф»
а
Рис. 7.14. Агрегат из 1500 частиц, полученный с помощью компьютерного мо¬
делирования диффузионно-контролируемой агрегации. Общее число выпущенных
частиц равно 12 421. Использован алгоритм Гэйлорда и Веллина (1995)
7.3.3. Непрерывная лапласова модель
Разветвленные структуры, напоминающие кластеры диффузионно¬
контролируемой агрегации, образуются при росте деревьев и снежинок,
кристаллизации тонких пленок, электролитическом осаждении и пробое
диэлектрика, и даже при росте колоний бактерий и нейронных структур.
Многие, если не большинство, из этих структур не удовлетворяют опреде¬
лению фрактала на разумных масштабах длины.
284
Гл. 7. Фракталы и явления роста
Как уже было сказано, не существует общей теоретической схемы, для
того чтобы описать далекие от равновесия ростовые процессы, такие как
диффузионно-контролируемая агрегация, и для того чтобы получить, на¬
пример, аналитическое выражение фрактальной размерности исходя из
первых принципов. В некоторых моделях фрактальную размерность мож¬
но получить в виде аналитического выражения, но эти модели предполага¬
ют определенные упрощения. Например, можно рассматривать растущую
верхушку как конус7) и связать D с углом этого конуса. Тем не менее да¬
же в случае, когда аналитическое решение недоступно, поведение системы
все еще может быть понято и предсказано, если известен алгоритм роста.
Вышеприведенная модель Виттена - Сандера — один из таких алгоритмов.
Детальное рассмотрение этой модели показывает, что данный алгоритм
можно приблизить непрерывной моделью, а именно уравнением Лапла¬
са с подходящими граничными условиями, описывающими движущуюся
границу растущего агрегата. Еще более интересно то, что множество дру¬
гих ростовых явлений являются вариациями на одну объединяющую тему:
уравнение Лапласа с (различными) граничными условиями. Рассмотрим
модель диффузионно-контролируемой агрегации8 \
Пусть р(г, t) — вероятность того, что случайно блуждающая частица
находится в положении г в момент времени t. Эта вероятность зависит от
вероятности p(r + a, t — 1) обнаружить частицу в соседнем узле г + а
в предыдущий момент времени t — 1, усредненной по всем z соседним
узлам (z — 4 для двумерной решетки):
p(r, t) = -V^r + a, t-l). (7.47)
Z
а
Если частицы выпускаются равномерно, то не должно быть временной
зависимости: р(г, t — 1) — р(г, t). Тогда
Р(г) = ~У^Р(г + а)’ (7.48а)
г
а
что для двумерного случая записывается как
P(h j) = ]\p(i ~ 1, j)+p(i + 1. j) +P{i, j ~ 1) +P(i, j + 1)]- (7.486)
4
Уравнение (7.3.3) есть дискретная форма уравнения Лапласа (задача 7.5):
V2p(r) = 0 (7.49 а)
или, в двумерном случае,
^ + ^= 0. (7.496)
дх2 ду2
7') L. A. Turkevich and Н. Scher. Phys. Rev., АЗЗ, 786 (1986).
^ T. A. Witten and L. M. Sander. Phys. Rev., B27, 5686 (1983).
§7.4. Вязкие пальцы в ячейке Хеле -Шоу
285
Скорость роста v± (г) в незанятом узле г на поверхности А кластера про¬
порциональна вероятности прихода в эту точку случайно блуждающей ча¬
стицы:
(символ _L означает, что мы интересуемся компонентой v, перпендикуляр¬
ной поверхности А. Во всех узлах, принадлежащих агрегату р ~ 0: части¬
цы адсорбируются, как только достигают агрегата, и не могут проникать
внутрь. С другой стороны, вдали от агрегата р(т) есть некая константа —
р(т -> оо) — const, при условии что поток новых выпущенных частиц со¬
храняется постоянным. Следовательно, правая часть (7.50) пропорциональ¬
на градиенту р(г) и (7.50) можно рассматривать как дискретное приближе¬
ние уравнения, описывающего движение гладкой непрерывной границы:
где Т> — коэффициент диффузии и и — нормаль к А.
Тот факт, что диффузионно-контролируемая агрегация может быть при¬
ближена уравнением Лапласа (7.3.3) с граничным условием (7.51), имеет
важное эвристическое значение, так как многие ростовые явления могут
быть описаны этой общей моделью. Различие заключается в граничных
условиях. В следующем параграфе мы рассмотрим двумерный эффект вяз¬
ких пальцев в ячейке Хеле-Шоу.
Ячейка Хеле-Шоу состоит из двух горизонтальных прозрачных пла¬
стин линейного размера w, расположенных на высоте z = — Ь/2и z = Ь/2.
Ячейка очень тонкая: b <С w, так что число Рейнольдса мало (см. § 6.2).
Ячейка заполнена вязкой жидкостью, такой как масло или глицерин. Через
отверстие в ячейку вдувается обладающая низкой вязкостью текучая сре¬
да (воздух), замещающая имеющую высокую вязкость жидкость. Течение
можно рассматривать как двумерное ламинарное течение (или потенциа¬
льное течение со скоростью, удовлетворяющей условию V х V = 0). Мно¬
гочисленные эксперименты, самые известные из которых были выполнены
Саффманом и Тэйлором9^, показывают, что движущаяся граница раздела
между двумя текучими средами является неустойчивой. Малые флуктуа¬
ции на границе раздела (выпуклости) вырастают в устойчивые «пальцы»
(рис. 7.15). Толщина пальцев меняется с изменением скорости; при высоких
скоростях палец может разветвляться и делиться.
Структуры, образующиеся в ячейках Хеле-Шоу, оказываются различ¬
ными в зависимости от нескольких факторов. Среди этих факторов есть
(7.50)
а
(7.51)
§ 7.4. Вязкие пальцы в ячейке Хеле-Шоу
91 P. G. Saffman and G. I. Taylor. Proc. Roy. Soc., A 245, 312 (1958).
286
Гл. 7. Фракталы и явления роста
Ъ
f
I Ввод
а
б
Рис. 7.15. Вязкие пальцы в ячейках Хеле-Шоу прямоугольной (а) и круглой (б)
формы
интуитивно «очевидные» такие как скорость вдувания, поверхностное на¬
тяжение, вязкость, форма ячейки Хеле-Шоу (например, прямоугольная или
круглая).
Одним из наиболее интересных экспериментальных открытий10) явля¬
ется то, что структуры сильно зависят от граничных условии на границе
раздела двух сред. Так, если ячейка Хеле-Шоу заполнена пористым ма¬
териалом, например случайно упакованными шарами, получаемая в итоге
структура является фракталом, поразительно похожим на агрегаты, обра¬
зованные в результате диффузионно-контролируемой агрегации. В отсут¬
ствие пористои среды положение менее ясное: в некоторых случаях вытал¬
кивающая среда принимает компактную форму, тогда как в других случаях
форма становится фрактальной, что наводит на мысль о том, что возможны
все комбинации этих двух типов поведения. И снова не существует общего
аналитического решения задачи Лапласа, способного предсказывать фрак¬
тальную структуру и фрактальную размерность. Таким образом, реальные
эксперименты остаются важным инструментом исследования форм роста.
Ниже мы рассмотрим лишь самое начало неустойчивости вязких паль¬
цев, предполагая, что все отклонения границы раздела от прямой линии
малы. Цель — показать физический механизм неустойчивости роста, при
которой небольшие выступы на поверхности раздела растут гораздо быст¬
рее соседних участков.
10') J. D. Chen and D. Wilkinson. Phys. Rev. Lett., 55, 1892 (1985); K. J. Malfiy, J. Feder
and T.Jfissang, ibid., p. 2688.
§ 7.4. Вязкие пальцы в ячейке Хеле -Шоу
287
7.4.1. Течение в тонкой ячейке
При малом числе Рейнольдса уравнение Навье-Стокса для двумерного
поля скоростей [vx(z), vy(z), 0] сводится к уравнению
= i = x> У' <7-52)
OZ1
*
где rj — сдвиговая вязкость, р — давление, которое не нужно путать с рас¬
сматривавшейся выше вероятностью (хотя обе эти величины удовлетворя¬
ют уравнению Лапласа и, следовательно, играют схожую роль, как будет
показано в дальнейшем); х и у — декартовы координаты в плоскости ячей¬
ки. Гравитационные эффекты отсутствуют, из-за того что ячейка горизон¬
тальна. Уравнения (7.52) можно проинтегрировать, используя в качестве
граничных условий отсутствие проскальзывания на границах ячейки —
±6/2
0:
локальной силе:
Vi = - (Z2 - U2) Vip. (7.53)
27? ^ 4 /
Для дальнейшего анализа полезно ввести среднюю (по оси z) скорость U
1 6/2
с компонентами Ui = - J Vi(z)dz, так как U прямо пропорциональна
ь -Ь/2
U (x,y) = -—Vp(x,y). (7.54)
12г?
(Последнее уравнение применяется к течениям сквозь пористые среды;
в этом случае его часто называют законом Дарси.) Условие несжимаемости
VU ~ 0 теперь означает, что давление удовлетворяет уравнению Лапласа
на плоскости (сравните с (7.49 б) для вероятности):
^ + ^=0. (7.55)
дх2 ду2
7.4.2. Неустойчивость границы раздела
Мы обозначаем цифрой 1 менее вязкую среду (воздух), вытесняющую
более вязкую среду 2 (рис. 7.15). Когда движущаяся граница раздела остает¬
ся прямой в горизонтальной плоскости, ее положение задается выражением
х — Ut. Движение поддерживается градиентами давления, которые нахо¬
дятся из уравнения (7.54):
Vi =Ро~ ~ Ut); j = 1, 2; (7.56)
Ъ1
ро — не зависящая от х постоянная. Предположим, что есть небольшое
возмущение, периодическое вдоль оси у, с волновым числом q и амплиту¬
дой А:
х(у) = Ut + A(t) cos qy. (7.57)
288
Гл. 7. Фракталы и явления роста
Когда А ф 0, давления pi и р2 должны испытывать периодические возму¬
щения ~ cos qy подобно профилю границы раздела сред:
Pj =Ро- - ut) + Bj(x, t) cos qy. (7.58)
62
Зависимости амплитуд Bj(x, t) от координаты x должны иметь фор¬
му ехр (qx) или ехр (—qx), так как pi и р2 с возмущениями ~ ехр (—iqy)
должны удовлетворять уравнению Лапласа (7.55). Естественно будет пред¬
положить, что вдали от границы раздела давления должны оставаться ко¬
нечными; следовательно,
Bi(x> t) = Bi(t) exp(gx); B2(x, t) = Лг(£) exp(—gx). (7.59)
Амплитуды Bi(x, t) и В2(ж, t) можно определить из условий на границе.
Во-первых, существует условие непрерывности, которое требует, чтобы
нормальные компоненты скорости равнялись друг другу и скорости Un
границы раздела сред:
Un = - —(Vpi)„ = - — (VP2)„. (7.60)
12r)i 12772
Если амплитуда A(t) в (7.57) мала, то
Un « U + — cos qy. (7.61)
dt
Из (7.54), (7.58), (7.59) и (7.61), пренебрегая членами второго порядка ма¬
лости ~ А2 и ~ АБ, находим следующее приближение для уравнения
(7.60):
= (7.62)
dt 12т 12*72
Другое граничное условие устанавливает связь между скачком давления
Ар — pi — р2 на границе раздела сред и средней кривизной этой грани¬
цы (см. гл. 13). Обе главные кривизны могут быть ненулевыми: граница
раздела искривлена в вертикальной плоскости xz с радиусом Rxz «6/2
и в горизонтальной плоскости ху с некоторым радиусом Rxy, который
становится конечным, когда различные участки границы перемещаются
с разной скоростью. Предполагая, что текучая среда 2 смачивает пластины
ячейки Хеле-Шоу, в то время как текучая среда 1 их не смачивает, и пре¬
небрегая любым влиянием, которое движение границы может оказывать на
геометрию смачивания, записываем
§ 7.4. Вязкие пальцы в ячейке Хеле -Шоу
289
Хотя первый («вертикальный») вклад в (7.63) часто больше второго вклада,
он не зависит от х и у и, следовательно, не влияет на неустойчивость
в плоскости. Второй член важен, так как он стремится распрямить границу
раздела. При l/Rxy ~ —д2х(у)/ду2, где х(у) определяется в (7.57), этот
член дает вклад
Др = aq2A(t) cos qy. (7.64)
С другой стороны, из выражений (7.58) следует, что
Ар
1 9/7
— (rii-r)2)A(t)+Bi(x,t)-B2(x,t) cos qy. (7.65)
b1
Сравнение (7.64) и (7.65) приводит к равенству
Bi(x, t) - В2(х, t) = A(t) - щ) + aq2 . (7.66)
L Ь
Исключая Вi(x, t) и B2(x, t) из уравнений (7.62) и (7.66), находим окон¬
чательное выражение
дА _ - т) - <гд3ь2 (7 67)
dt 12(771 + 7?2)
Когда 7]i > г}2 (более вязкая среда толкает менее вязкую), граница разде¬
ла сред устойчива при любых q. Однако когда щ > *7ь любое возмущение
с достаточно большой длиной волны Л > Лс,
Лс = 7Tbi 17777^ Т’ ^7'68^
ш(т]2 - т)
будет неустойчивым: амплитуда А возмущения растет со временем. Са¬
мая быстрорастущая мода соответствует длине волны А/ = \/ЗАс. Как по¬
казывают многие эксперименты, периодичность неустойчивости границы
раздела в ячейке Хеле-Шоу, как и ожидается, близка к Л/.
Если (малой) вязкостью выталкивающей среды 1 можно пренебречь, то
\s « -g=, (7.69)
у NCap
где Ncap = Пщ/а — безразмерное «капиллярное число». Увеличивая Ncap,
можно значительно уменьшить длину Л/, которая является аналогом харак¬
терного размера частиц, образующих кластеры в процессе диффузионно¬
контролируемой агрегации.
Будет поучительно получить качественное физическое объяснение эф¬
фекта вязких пальцев исходя из уравнения (7.54) и геометрии границы
раздела (см. рис. 7.16, а, где тонкие линии представляют собой изобары,
19-КЛЕМАН М.
290
Гл. 7. Фракталы и явления роста
образованные возмущением границы раздела). Пусть разница давлений
(pi — Р2) между «вводом» и «выводом» постоянна. В текучей среде 1 с низ¬
кой вязкостью градиенты давления малы, как следует из (7.54); мы можем
предположить, что давление внутри области /, включая вершину самого
большого пальца, остается постоянным. Тогда наибольшие градиенты дав¬
ления Vp ~ (pi - Р2) /(^£вывод “ ^вершина) в вязкой среде 2 возникают как
раз у вершины пальца. Согласно (7.54) вершина должна двигаться быстрее,
чем остальная граница раздела. Из этого следует, что небольшое начальное
возмущение развивается в быстро увеличивающийся палец (рис. 7.16,5).
Поверхностное натяжение играет стабилизирующую роль, стремясь пони¬
зить градиенты давления (см. 7.63).
Стремление выступающих возмущений увеличивать градиенты поля
характерно для многих систем, образующих узорчатые структуры. Вместо
изобар тонкие линии (см. рис. 7.16) могут представлять собой изотерми¬
ческие линии вблизи границы раздела кристалл-расплав (при неустойчи¬
вости Маллинса -Секерки11)), вероятность (диффузионно-контролируемая
агрегация), эквипотенциальные линии и т. д.
а б
Рис. 7.16. Малое возмущение границы раздела сред увеличивает градиенты поля
(давления), это наиболее заметно на вершине выступа (а); в результате в данном
месте граница раздела ускоряется (б)
Как уже было отмечено, эффект вязких пальцев в ячейках Хеле-Шоу,
заполненных пористым материалом, приводит к вполне определенной фрак¬
тальной структуре, в то время как в «традиционных» ячейках редко обра¬
зуются хорошо развитые фракталы. Разница может заключаться в «случай¬
ном» характере граничных условий, устанавливаемых пористой средой.
Случайным образом меняющийся размер пор отличается от (постоянной)
характеристической длины волны Лс, определяемой капиллярными эффек¬
тами в традиционной ячейке. Проницаемость зависит от размера пор: в уз¬
кие поры трудно проникнуть, так как капиллярное давление связано с раз¬
мером поры.
За дача 7.1. Определите аналитическую зависимость фрактальной
кривой Коха от угла /3 у основания треугольника.
u) W. W. Mullins andR. F. Sekerka. J. Appl. Phys., 34, 323 (1963).
§ 7.4. Вязкие пальцы в ячейке Хеле -Шоу
291
Ответ. D
In 4
In [2(1 + cos fi)\
(см.: G. Baumann (1996)).
Задача 7.2. Может ли фрактальная размерность быть больше эвкли¬
довой размерности вмещающего пространства? Приведите примеры.
Ответ. Да. Начнем с прямой линии, и на каждом итерационном шаге
будем замещать отрезки прямой, например, 18 отрезками, как показано на
рис. 7.17. На следующем шаге линия начнет самопересекаться. Размерность
подобия больше, чем 2: In 18/ In 4 и 2,1.
Рис. 7.17. См. задачу 7.2
Задача 7.3. Докажите, что 5(g) ос q D при q 1/R (см. выражение
(7.21)).
Ответ. 5(g) ос q~°T(D - 1)sin[tt(D - 1)/2].
Задача 7.4. Докажите вторую часть (7.22).
Ответ. Получим искомый результат, проделав следующие преобра¬
зования:
^ (ri - г,-)2 = ^2 [(г* - Го) - (г
i,j=1
3
го)1
г,.7 = 1
В
г=1
го)2 + - Го)
i=i
го);
г=1
j = l
последний член равен нулю по определению центра масс (г0
1 s
- £ Гг).
292
Гл. 7. Фракталы и явления роста
3 а д а ч а 7.5. Докажите, что уравнение Лапласа (7.49 б) можно прибли¬
зить дискретным выражением (7.48 б) в двумерном случае.
Совет. Приблизьте частные производные конечными разностями.
Задача 7.6.
а) Определите фрактальную размерность ковра Серпинского (рис. 7.18).
б) Губка Менгера — это фрактал, построенный в трехмерном простран¬
стве по правилам, похожим на правила построения ковра Серпинского.
Начинают с куба линейного размера 1. Каждая грань куба делится на де¬
вять одинаковых квадратов. Через центральный квадрат каждой стороны
высверливают сквозное отверстие. Оставшиеся 20 кубов, имеющие линей¬
ный размер 1/3, снова сверлят подобным образом. Стороны исходного куба
имеют узор, в точности повторяющий ковер Серпинского. Вычислите раз¬
мерность подобия губки Менгера.
О т в е ты
а) D = In8/ 1пЗ « 1,9;
б) D = In 20/In3 « 2, 7.
Задача 7.7. Напишите компьютерные программы для построения де¬
терминированных кривых Коха и их случайных аналогов (а); перколяцион¬
ных структур (б); кластеров диффузионно-контролируемой агрегации (в).
k=1 к=2 к=3 к=4
Рис. 7.18. Построение ковра Серпинского
Литература для дальнейшего чтения
1. J. Feder. Fractals, Plenum Press, N. Y. and London, 1988, 283 p.
2. Fractals. Selected Reprints, Ed. A. J. Hurd, American Association of Physics
Teachers, College Park, Maryland, 1989, 139 p.
3. J.-F. Gouyet. Physics and Fractal Structures, Springer-Verlag, Berlin, 1996, 234 p.
4. Introduction to Nonlinear Physics, Ed. Lui Lam, Springer-Verlag, N. Y., 1997,
417 p.
5. The Fractal Approach to Heterogeneous Chemistry. Surfaces, Colloids, Polymers,
Ed. D. Avnir, John Wiley & Sons, Chichester, 1989, 441 p.
Литература для дальнейшего чтения
293
6. В. В. Mandelbrot. The Fractal Geometry of Nature, W. H. Freeman and Company,
N. Y., 1983. (перевод: Мандельброт Б. Фрактальная геометрия природы. —
М.: Институт компьютерных исследований, 2002).
7. Solids Far from Equilibrium, Ed. С. Godreche, Cambridge University Press,
Cambridge, 1992.
8. D. Stauffer and A. Aharony. Introduction to Percolation Theory,. Taylor & Francis
Ltd., London, 1992.
9. D. Bensimon, L. P. Kadanoff S. Liang, B. Shraiman and C. Tang, Rev. Mod. Phys.
58, 977(1986).
10. J. S. Langer, Rev. Mod. Phys., 52, 1 (1980).
11. H. Gould and J. TobochniL An Introduction to Computer Simulation Methods:
Application to Physical Systems, 2nd Edition, Addison-Wesley Publishing
Company, Reading, MA, 1996.
12. R. J. Gaylord and P. R. Wellin. Computer Simulations with Mathematica: Explo¬
rations in Complex Physical and Biological Systems, Springer-Verlag, N. Y., 1995.
13. G. Baumann. Mathematica in Theoretical Physics, Springer-Verlag, N. Y., 1996,
Ch.7, 348 p.
14. #. Lauwerier. Fractals: Endlessly Repeated Geometrical Figures, Princeton
University Press, Princeton, New Jersey, 1991, 209 p.
ГЛАВА 8
ДИСЛОКАЦИИ В ТВЕРДЫХ ТЕЛАХ.
ПЛАСТИЧЕСКАЯ РЕЛАКСАЦИЯ
Дислокации ответственны за пластическую деформацию таких кристал¬
лических материалов, как металлы, и играют важную роль при росте кри¬
сталлов, в электрических свойствах полупроводников, при радиационном
повреждении (вследствие взаимодействия с точечными дефектами) и т. д.
Их теоретическое предсказание датируется годами перед Второй мировой
войной, а их визуальное наблюдение с помощью различных техник, в основ¬
ном электронно-микроскопических, было осуществлено в 50-е годы. Дис¬
локации являются важной составляющей физической металлургии. Они
несут внутренние напряжения и «топологически» связаны с симметрией
кристалла. Именно эта двойная природа дислокаций делает их источниками
пластической деформации. Их топологические свойства были полностью
признаны с появлением общей классификации топологических дефектов
в упорядоченных средах, которая охватывает сверхтекучие жидкости, маг¬
нитные системы и жидкие кристаллы. Хотя дефекты и обусловленные ими
текстуры в жидких кристаллах наблюдались с помощью оптических мик¬
роскопов много раньше, чем в твердых телах, только в последние десять
лет были предприняты исследования влияния структуры и текстуры на
реологические свойства. Хорошее знание основ физики дефектов в твер¬
дых телах полезно при изучении реологических свойств и нестабильностей
в мезоморфных материалах.
§ 8.1. Упругость дислокаций
8.1.1. Линейная упругость: сводка
Рассмотрим стержень длины £ с площадью сечения S, находящийся
под действием силы F = aSz (z есть единичный вектор вдоль оси стерж¬
ня), приложенной к одному концу стержня, в то время как второй конец
удерживается неподвижным. Длина стержня увеличивается на величину и,
пропорциональную I (рис. 8.1). Обозначим е = и/£. До тех пор пока сила
F = |F| мала (условие будет уточнено позднее), выполняется линейное
соотношение (закон Гука):
а = Ее, (8.1)
где о представляет собой компоненту растягивающего напряжения, дей¬
ствующего на внешнюю поверхность St, а Е—модуль сдвига, являющийся
материальным параметром. Следовательно, и(£) — Fi/SE.
Пусть S+, представляют собой верхнюю и нижнюю поверхности
воображаемого сечения стержня в произвольном месте. Напряжение о вы-
ступает как сила на единицу площади, с которой нижняя часть стержня дей¬
ствует на верхнюю часть, будучи приложенной к S+. Происходит передача
§8.1. Упругость дислокаций
295
силы, и е(М) = и(М)/£(М). Относительное смещение, или деформация,
имеет то же самое значение е — ujt в любой точке стержня М. Энергия, за¬
пасенная в стержне при обратимом упру¬
гом смещении от Ы — 0 до 51 = и7 есть
▲
w
S
сг(х) du(x)
S£
ае
о
о
F^aS
(здесь а(х)
О ^ х ^ 1)
объема:
ах
du(x)
etdx,
или, в расчете на единицу
w/Sl
~ае = | Ее2.
(8.2)
Приведенные выше обозначения обобща¬
ются на тензор напряжений сг^* и тензор
деформаций е^-,
,-:Г
Л.-
fisV
;*ЖГ
А v
Л-
' . j
'■А
• •,
■ч а,
*- ■
'ial
' ViVl
Ш-1Х -
eij
2 j + г) J
(8.3)
'•«r'
таким образом, что:
1) бесконечно малый участок поверх¬
ности dS с внешней нормалью v есть
место приложения инфинитезимальной
силы
:rrrx,vr.
V '» к?.* : ...
(Г* . 4. ■
■&
"ZS*
Л
*1
/
/ + и
Y Т
<№
(8.4)
Рис. 8.1. Деформация стержня
под действием силы F, приложен¬
ной к одному из его краев
действующей на материю снаружи (рис. 6.2). Мы используем в (8.4) обыч¬
ное соглашение Эйнштейна о суммировании по повторяющимся индексам.
Компонента dFi вдоль элемента поверхности, т. е. dFi(Sik — щщ), назы¬
вается сдвиговым напряжением; компонента dFi вдоль нормали к поверх¬
ностному элементу, т. е. (dFi/)^, есть растягивающее напряжение (если
скалярное произведение (dFu) положительно) или сжимающее напряже¬
ние (если скалярное произведение (dFu) отрицательно). Условия равно¬
весия применительно к малому объему вещества приводят к следующим
уравнениям:
ai j, j
0; в компактном обозначении: Уст
0 (полная сила отсутствует),
(8.5 а)
сг
нет полного скручивающего усилия;
(8.5 6)
2) энергия квадратична по деформациям, как в (8.2), это является
следствием закона Гука, который гласит, что до тех пор пока силы малы,
выполняется линейное соотношение между напряжениями и деформа¬
циями:
— & ijkl&kl‘
<?ij
(8.6 а)
296 Гл. 8. Дислокации в твердых телах. Пластическая релаксация
Так как и ец — симметричные тензоры, мы получаем: Cijki =
= Cjtki — Cijik = Cjuk, поэтому имеется только 36 независимых упругих
коэффициентов. Это число уменьшается при наличии симметрий в материа¬
ле, так как запасенная плотность упругой энергии а^е^/2 должна быть
инвариантна во всех системах координат, не меняющихся под действи¬
ем преобразований симметрии (это обстоятельство будет позднее проил¬
люстрировано на конкретных примерах). В результате имеются только
два независимых упругих коэффициента Ламэ А и р в изотропной среде,
так что
o'ij — 2peij -f A div u, (8.6 б)
где div u = еп + в22 + е^з = модуль Юнга Е — р(ЗХ + 2р)/(Х -f р).
Определяют также безразмерный коэффициент Пуассона v — A/(2(A-f ^)),
обычное значение которого в твердых телах и 0,3.
При этих условиях мы находим, что уравнение (8.5 а), выраженное в тер¬
минах смещений щ, принимает форму
р Ди + (А + р) grad div и — 0, (8.7)
в случае, когда не приложены другие силы. В динамическом режиме добав¬
ляются силы инерции:
р Ди + (А + р) grad div и = (8.8)
dt2
где р — плотность массы.
Приближение линейной упругости достаточно для описания физиче¬
ских свойств дислокаций, и мы в дальнейшем им ограничимся.
8.1.2. Внешние и внутренние напряжения
Обычно уравнения (8.5) дополняются условиями на поверхности образ¬
ца Sb, состоящими либо в задании внешних сил, либо в задании смещений.
Эти два типа условий могут применяться в различных участках поверхно¬
сти Sb. Существует общая теорема, которая гласит, что дифференциальные
уравнения (8.5) имеют единственное регулярное решение, если только пол¬
ные приложенные силы J fappdSb и результирующее кручение обращаются
Sb
в нуль. Непрерывные напряжения, отвечающие регулярному решению, суть
внешние напряжения.
Однако существуют сингулярные решения даже при GijVj = 0 во всех
точках, если среда не является просто связной, т. е. когда имеются внутрен¬
ние границы, которые не учитываются в вышеуказанных граничных усло¬
виях. Очевидным примером является сферическая каверна с внутренним
давлением, действующим на ее поверхности. Однако этот случай может
быть охвачен простым расширением обычных методов, и не этот случай
мы имели в виду. Что требует отдельного рассмотрения, так это дислока¬
ции Вольтерра, которые отвечают намного менее тривиальному случаю
внутренней несвязности.
§ 8.2. Дислокации Вольтерра
291
§ 8.2. Дислокации Вольтерра
8.2Л. Определения
Процесс Вольтерра. Элементарные типы дислокаций представлены на
рис. 8.2. Их можно получить следующим образом. Разрежем образец вдоль
поверхности Е (называемой поверхностью разреза), ограниченной лини¬
ей L (представляющей собой петлю или бесконечную линию); переместим
две стороны Е' и Е" разреза на некоторую величину относительного сме¬
щения, которое может быть представлено как сумма перемещения b и вра¬
щения П. Мы будем обозначать как П: ОМ преобразование вектора ОМ
под действием матрицы вращения П, где О есть фиксированная начальная
точка, не меняющаяся при вращении, а М — вращающаяся точка Е. Сме¬
щение d(М), которое переводит М в М' (ММ' =d(M)=b + fi: ОМ),
является жестким в том смысле, что оно сохраняет углы и расстояния. Те¬
перь добавим материал в недеформированном состоянии, чтобы заполнить
пустоту, оставленную трансляцией и вращением, или устраним материал
в областях перекрытия; склеим снова стороны Е' и Е" разреза нового ма¬
териала; позволим среде упруго релаксировать. Такой процесс, конечно,
не имеет смысла вдоль L, и, следовательно предполагается, что вдоль L
исключена некоторая цилиндрическая область. К этой области «ядра» вы¬
шеупомянутый процесс неприменим.
Процесс Вольтерра совместим с условиями свободной границы образ¬
ца, но он неизбежно вводит напряжения. Они называются внутренними
н апряжениями.
1. Ядро. Ясно, что эти напряжения и деформации увеличиваются при
подходе к области ядра. Размер гс ядра выбирается так, чтобы поля напря¬
жений и деформаций были физически осмысленными в упругой области
за гс, где справедлив закон Гука. Они растут вблизи гс, и их аналитическое
продолжение сингулярно внутри области ядра.
2. Теорема Вайнгартена. Упругие напряжения и деформации
несингулярны на Е (в действительности, на Е' и Е"), если d(М) является
жестким смещением. Следовательно, окончательный результат не зависит
от конкретного выбора Е.
Рисунки 8.2, а, б я в представляют трансляционные дислокации: сме¬
щение сводится к чистой трансляции либо в направлении L (рис. 8.2, а,
винтовая дислокация), либо перпендикулярно L (рис. 8.2, б, в, краевые дис¬
локации). По теореме Вайнгартена, дислокации рис. 8.2, б и рис. 8.2, в тож¬
дественны. Рисунки 8.2, г и д представляют дислокации вращения, называе¬
мые также дисклинациями. Ясно, что твистовая дисклинация (рис. 8.2, д)
поднимает нетривиальную проблему ее конструирования, к которой мы еще
вернемся. Имеются также случаи смешанных дислокаций и дисклинаций.
8.2.2. Упругие поля, связанные с дефектами Вольтерра
Сначала общее замечание: граничные условия для уравнений упруго¬
сти должны быть записаны на поверхности разреза Е. Пусть и является
298 Гл. 8. Дислокации в твердых телах. Пластическая релаксация
п
г.
швшш
L
Е
/
а
б
в
L
г д
Рис. 8.2. Элементарные типы дислокаций. Дислокации трансляции: винтовая дис¬
локация (а); создание одной и той же краевой дислокации (5) и (в). Дисклинации:
клиновая дислокация (г); дислокация кручения (д)
вектором нормали к S (выбор и вводит ориентацию линии). Разность между
смещениями и+ и и дается выражением
Аи
и
+
и
а(м) = ъ + пх (ом),
(8.9)
где b называется вектором Бюргерса. Мы ввели вектор вращения ft, с ко¬
торым проще обращаться, чем с тензором вращения ft, и который дей¬
ствительно описывает вращение, пока ft х (ОМ) мало. Благодаря теореме
Вайнгартена, уравнение (8.9) может также быть записано в интегральной
форме
о du = d(M)
(8.10)
7м
на произвольном направленном контуре 7м, окружающем L и пересекаю¬
щем поверхность разреза в М (рис. 8.3).
§ 8.2. Дислокации Вольтерра
299
Ум
Рис. 8.3. Направленные контуры ум, приводящие к одному и тому же значению
интеграла (8.11)
Мы приведем ниже некоторые результаты, касающиеся классических
случаев (более детальное рассмотрение дано в учебниках, указанных в кон*
це этой главы).
8.2.2.1. Винтовые дислокации. Мы будем использовать цилиндри¬
ческие координаты, изображенные на рис. 8.2. Полное поле напряжений
в конечном образце (цилиндре радиуса R) может быть представлено как
сумма поля сг, которое исчезает на бесконечности и сингулярно на линии,
и поля которое регулярно всюду и сокращает силы, создаваемые син¬
гулярным полем о на границе г — R, т. е. (а 4- а')и — 0 в любой точке
на границе, v есть единичный вектор, перпендикулярный границе. Линей¬
ная упругость допускает, конечно, такую линейную суперпозицию. Пусть
uscrew = u + и' есть полное поле смещения. Оба поля, и и, и и', подчиня¬
ются уравнению (8.8) в случае изотропной упругости, а для сингулярной
части, кроме того, выполняется соотношение (8.10), которое сводится к
о du — b,
(8Л1)
7
где 7 — произвольная замкнутая петля, обходящая однократно вокруг оси z.
Очевидным решением для и является
и
27Г
4irr
ere
Vz6
fib
27ГГ
(8.12)
все прочие компоненты исчезают. Отметим, что поля деформации и, сле¬
довательно, напряжения исчезают на бесконечности, но не исчезают на
300 Гл. 8. Дислокации в твердых телах. Пластическая релаксация
границе г — R. По этой причине и должно быть дополнено полем релак¬
сации и', которое создает противоположно направленные поверхностные
силы на границе и регулярно всюду в объеме. Мы не будем рассматри¬
вать здесь это поле релаксации. Вычисленная без учета релаксации энергия
сингулярного поля есть, согласно общему выражению для упругой энергии
деформированной среды,
w = -
2
(8.13)
что равно - J (o-0Ze0Z + сгzgеze)r dr d6
2
fib2 , R
— In — на единицу длины ли-
47Г гс
нии, где интеграл берется по области rc ^ г ^ R. Энергия релаксации,
/
соответствующая напряжению а 9
(Xbr
7Г Я2
, добавляет член того же по¬
рядка величины, хотя и меньший. Получаем
Wel = ^ ( In й
47Г
(8.14)
Отметим три обстоятельства.
1). Зависимость энергии от 6, вследствие которой можно ожидать, что
реальные дислокации будут иметь наименьшие из возможных векторов
Бюргерса. Действительно, (26)2 > 262, поэтому каждая дислокация с век¬
тором Бюргерса 2Ь стремится расщепиться на две дислокации с векторами
Бюргерса Ь.
2). Дислокацией ощущается слабая логарифмическая зависимость от
размеров области.
3). Помимо релаксационных членов выражение
также дополнено энергией окрестности «ядра» (г <
будут в деталях рассмотрены в дальнейшем.
(8.14) должно быть
гс). Все эти пункты
8.2.2.2. Краевая дислокация Предполагая, что среда бесконечна, и,
следовательно, забывая о релаксационных эффектах, мы имеем (см. также
задачу 8.1) (рис. 8.2,6):
и
X
2тг
в+
sin 2 в
4(1 — I/)
и
У
и
0,Wel
27Г
1 — 2v , cos 29
In ПГ +
2(1 -и)
R
4(1-И
47г(1 — и) rc
(8.15)
8.2.2.3. Смешанная дислокация. Пусть /3 есть угол между линией L
и вектором Бюргерса Ь. Вычисление поля смещений и легко выполняется с
использованием принципа линейной суперпозиции, учитывая, что b имеет
винтовую компоненту b cos /3 и краевую компоненту b sin р. Энергии также
аддитивны, но это следует не из принципа суперпозиции, а из факта, что
§ 8.3. Простые топологические характеристики дислокаций
301
эти две компоненты дислокации не взаимодействуют (см. задачу 8.2). Мы
находим, с включением поверхностной релаксации при г = R,
^Ап*-Л, где I = cos2/3 + ^. (8.16)
Wel =
4пК \ гс J К 1 — v
8.2.2.4. Клиновая дисклинация. Расчет был сделан Тимошенко
(рис. 8.2,г). Для дисклинации с (малым) утлом П = \ft\ (8.10) сводится к
о du = ft х ОМ,
7М
где ft направлен вдоль линии дисклинации, О является произвольно вы¬
бранной начальной точкой на линии, М лежит на поверхности разреза.
Получаем
ГГ —
С) —
27Г(1 — I/)
(Твв = (In
27Г(1 — is) \
®zz ~ v(oTT "Ь &гв ” &6z ~ &zr — 0)
(Ш}2 /^9 9\ I w 4R2r2
In
Т
+
г2
' с
In
Гс)
R
г2
R >
г
-\-
г2
1 с
In
Гс
+
R
г2
R
= 1 '■ (8Л7)
Эта энергия много больше, чем для трансляционной дислокации. Сле¬
довательно, дисклинации трудно встретить в реальных твердых средах,
кроме тех случаев, когда они образуют пары противоположного знака. Мы
упоминали об их существовании в фазах Франка и Каспера и о возможном
их существовании в аморфных средах. В обоих случаях дисклинации об¬
разуют взаимосвязанные сетки, напряжения в которых компенсируются на
малых расстояниях.
§ 8.3. Простые топологические характеристики
дислокаций
8.3.1. Эквивалентные контуры
Из вышесказанного очевидно, что дислокация, характеризуемая своим
топологически инвариантным вектором Бюргерса Ь, — это линия, кото¬
рая должна либо замыкаться сама на себя, либо оканчиваться на другой
дислокации или границе образца, либо уходить в бесконечность.
Контур Бюргерса 7м — это направленный путь обхода, окружающий L
один раз и не проходящий через область ядра. В этом смысле образец
с цилиндрической областью ядра является несвязной средой, потому что
302 Гл. 8. Дислокации в твердых телах. Пластическая релаксация
не все контуры, которые могут быть проведены в образце, эквивалентны
при гладких преобразованиях (гладких деформациях контуров и гладких
смещениях). Но все контуры 7м, переводимые один в другой посредством
гладкого преобразования, дают одно и то же значение интеграла (8.11).
Правило узла (рис. 8.4)
£ъг = о (818)
9
г
есть прямое следствие эквивалентности контуров в вышеуказанном смыс-
ле. Отметим, что в (8.18) все дислокации направлены к узлу или все на¬
чинаются в узле, b изменяет знак, если ориентация линии изменяется на
противоположную.
Рис. 8.4. Иллюстрация к формуле (8.18)
8.3.2. Дислокации в кристаллах
В кристаллах интерес представляют только те смещения d(М) поверх¬
ности разреза, которые отвечают кристаллической симметрии, потому что
в этом случае шаг «склеивания» в процессе Вольтерра эквивалентен восста¬
новлению атомных или молекулярных связей: верхняя и нижняя поверхно¬
сти разреза не вносят никакой кристаллической сингулярности, если d(M)
расщепляется на решеточную трансляцию и решеточное вращение. Более
того, применима теорема Вайнгартена, так что поверхность разреза не несет
какой-либо упругой сингулярности. Такая дислокация является «совершен¬
ной». Говорят о «несовершенной» дислокации, если условие Вайнгартена
§ 8.3. Простые топологические характеристики дислокаций
303
все еще выполняется, но нарушается условие кристаллическои симметрии.
Такие случаи нередки. Рисунок 8.5 показывает наложение деформирован¬
ного кристалла (содержащего дислокацию) на идеальный кристалл. Видно,
что в результате наложения получается незамкнутый контур, замыкание
которого составляет вектор Бюргерса. Обычное соглашение о знаках (на¬
зываемое FS/ПР-соглашение) следующее. Контур Бюргерса 7обходится по
часовой стрелке для наблюдателя, глядящего вдоль положительного направ¬
ления линии (соглашение правой руки), из S в F = S, обход 7 накладывается
на 7' из S' в F'. Результирующий вектор Бюргерса b = F'S'.
| b = FV
а б в
Рис. 8.5. Наложение контура Бюргерса на идеальный кристалл. FS/ПР-соглашение
Рисунок 8.6 представляет дислокацию с углом вращения О, ~ — тг в тет¬
рагональном кристалле. Характеристический угол вращения fl измеряется
следующим образом. Рассмотрим (ориентированный) контур Бюргерса 7,
на котором выбрано произвольное начало отсчета М, и будем следовать
некоторому произвольному, но жестко привязанному к кристаллическим
плоскостям направлению п, обходя 7 и параллельно откладывая п в неко¬
торой точке отсчета О. При этом концы вектора п пробегают по окруж¬
ности дугу с углом Q, ориентированным в соответствии с построением.
Мы будем называть 7' годографом 7. Годограф изображенного кристал¬
лического направления, вдоль направленного контура 7, дает для любой
дисклинации значение угла П по величине и знаку независимо от ориента¬
ции, заданной 7, и выбора п.
8.3.3. Несовершенные дислокации. Дефекты упаковки и двойники
Дислокации малой энергии имеют вектор Бюргерса, равный периоду
решетки. Мы уже указывали, что это условие необходимо для инвариант¬
ности дисторсий по отношению к выбору поверхности разреза. Однако
встречаются обстоятельства, в которых некоторые не равные периоду век¬
торы Бюргерса дают низкоэнергетические дислокации, хотя поверхность
304 Гл. 8. Дислокации в твердых телах. Пластическая релаксация
Рис. 8.6. Дислокация с углом вращения П = — 7г в тетрагональной решетке и стро¬
ение «годографа» 7' контура вращения для измерения П
разреза сохраняет свою индивидуальность и, следовательно, обладает неис¬
чезающей поверхностной энергией. Так происходит в хорошо известной
ГЦК-решетке (см. § 2.1), где правильная упаковка плоскостей (111), т. е.
... ABC : ABC А ..может быть модифицирована ценой небольшого про¬
игрыша в энергии, давая, например, ... ABC | ВСАВ ... Скольжение на
b (А В вдоль направления [110]), очевидно, не является периодической
трансляцией в ГЦК-решетке. Если такой плоский дефект ограничен конеч¬
ной частью Е плоскости несовпадения, граница между Е и остальной плос¬
костью является несовершенной дислокационной линией с вектором Бюр¬
герса Ь. Детальное описание всей «зоологии» несовершенных дислокаций
выходит за рамки этой книги, так как само понятие несовершенства дис¬
локаций еще не* нашло применения в физике мягкой материи. Решетки
... ABC ABC А ... и ... АСВАСВ ..., очевидно, одинаковы, но в зеркаль¬
ной симметрии. Последовательность дефектов упаковки в параллельных
сопряженных (111) плоскостях переводит одну решетку в другую. Такая
упаковка дает пример двойника ... АВСЦВАС ...
Двойной вертикальной чертой в этой последовательности отмечена га-
битусная плоскость двойника. Напротив, повторное двойникование на двух
сопряженных плоскостях создает дефект упаковки.
Понятие дефекта упаковки и его соотношение с двойникованием обоб¬
щается и на другие решетки, не являющиеся ГЦК-решетками.
§ 8.4. Некоторые замечания об упругой энергии дислокаций
305
§ 8.4. Некоторые замечания об упругой энергии
дислокаций
8.4.1. Стабильность
Согласно уравнениям (8.14)—(8,16) упругая энергия дислокации (на
единицу длины) имеет порядок величины pb2, так как логарифмический
фактор оказывается порядка нескольких единиц в широком интервале до¬
пустимых значений Rn гс.
Расстояние R может быть оценено как среднее расстояние между дис¬
локациями. Действительно, внутренние напряжения, как полагают, флук¬
туируют на масштабе среднего расстояния между дислокациями, образую¬
щими (в хорошо отожженном материале) сетку (сетку Франка), в которой
дислокации противоположных знаков, т. е. несущие противоположные на¬
пряжения, находятся приблизительно на среднем расстоянии 2R. Типич¬
ный порядок величины R составляет порядок нескольких десятков нано¬
метров в деформационно упрочненных материалах или нескольких микрон
в хорошо отожженном монокристаллическом металле. Позднее мы рас¬
смотрим гс.
Согласно выражениям (8.14) и (8.15), величина рЬ3 есть типичная энер¬
гия дислокационной линии, приходящаяся на межатомное расстояние вдоль
линии. В ГЦК-металле Al, pb3 ~ 2,2 эВ (р — 2,7 х Ю10 НУм2, b — -[110],
2
Ь — 0,29 нм). В оливине, ромбоэдрическом смешанном силикате Mg и Fe,
наиболее распространенном в земной коре минерале, имеем: рЬ3 ~ 52 эВ
(р = 8х Ю10 Н/м2, b = —[110], fe = 0,48 нм). Энергии ядер, как мы увидим,
2
имеет тот же порядок величины. Таким образом, полная энергия дислока¬
ционной линии, измеренная на атомную или молекулярную длину вдоль
линии, значительна и, самое меньшее, имеет тот же порядок величины,
что и энергия связи. Следовательно, за исключением специальных случаев,
дислокация является неравновесным объектом, так как прирост энтропии
благодаря создаваемому дислокациями беспорядку мал, кроме, быть может,
окрестности точки плавления.
Для реальной дислокации модуль вектора Бюргерса принимает наи¬
меньшее возможное значение, допускаемое кристаллическими трансляция¬
ми, т. е. b = — [110] в ГЦК-решетке, b — -[111] или [100] в ОЦК-решетке
2 2
и т. д. Как упоминалось выше, причина заключается в том, что дислокация
с вектором Бюргерса 2Ь имеет энергию, в четыре раза большую, чем дис¬
локация с вектором Бюргерса Ь, и стремится расщепиться на две элемен¬
тарные дислокации, если только положительная энергия взаимодействия
между ними не превысит удвоенную энергию элементарной дислокации.
Аналогично, дислокация b = bi -f b2, где bi и Ъ2 суть два элементарных
(различных) вектора Бюргерса и fe2 — fe2 Н- fe2 + 2b!b2, стремится рас¬
щепиться на две дислокации Ьх и Ь2, если скалярное произведение bib2
положительно, так что дислокации bi и Ь2 отталкиваются. Если b*b2 < 0,
306 Гл. 8. Дислокации в твердых телах. Пластическая релаксация
они притягиваются.
8.4.2. Силы изображения. Силы Пича-Келера
8.4.2.1. Силы изображения. Существующие из-за свободных границ
релаксационные вклады, упомянутые в предыдущем пункте, могут быть
описаны как результат дислокаций-образов, расположенных вне образца.
Простейший случай представляет винтовая дислокация +Ь, параллельная
плоской границе S (рис. 8.7).
!!.
!1
F
+Ь
-ь
• t
!1
It'
L
V
!;
ir
S’
Рис. 8.7. Сила изображения для винтовой дислокации. Дислокация притягивается
к свободной границе
Легко проверить, что винтовая дислокация —Ь, помещенная симмет¬
рично по отношению к срединной плоскости 5, создает поле смещений
ъе
uimage = ——, которое вызывает напряжения erim, точно уравновешиваю-
27Г
щие напряжения от реальной дислокации на S: (сг + crim) v — 0, где v —
нормаль к S. Следовательно, u + uim = ^-(6 - 0im) представляет собой
2п
поле смещений винтовой дислокации +Ь, изолированной в полупростран¬
стве. Получаем
Wp = — In —
Аж
(8.19)
Гс
где L — расстояние между дислокацией и плоскостью S (см. задачу 8.3).
Так как энергия ядра, очевидно, не зависит от положения линии L, мы
видим, что энергия винтовой линии уменьшается, когда она приближается
к свободной границе. Этот эффект может быть описан фиктивной силой
Т-] . W*.. / u r\ I u
F — +——, направленной вдоль и. Знак + указывает, что эта сила, деи-
9L
ствующая на линию со стороны внешней среды, такова, что дислокация
притягивается к свободной границе:
F
fib2
4ттЬ
(8.20)
§ 8.4. Некоторые замечания об упругой энергии дислокаций 307
Сила F может также рассматриваться как сила, возникающая из-за на¬
личия дислокации-образа с противоположным вектором Бюргерса. Обе
дислокации притягивают друг друга, как два электрических заряда про¬
тивоположного знака. Аналогия очевидна.
8.4.2.2. Сила Пича- Келера. Снова вычислим фиктивную силу, дей¬
ствующую на дислокацию, помещенную в поле напряжений сг^-, создавае¬
мое другой дислокацией или приложенное извне. Мы обозначим через W
полную энергию системы. Спонтанная сила, приложенная к дислокации,
есть F = — VW, здесь со знаком минус (внутренняя сила). Мы должны
проанализировать вариацию dW при смещении дислокации на dx.
Для начала рассмотрим краевую дислокацию L, ориентированную вдоль
оси у и перемещающуюся в плоскости (L, Ь) на dx (рис. 8.8). Выберем, да¬
лее, в качестве поверхности разреза полуплоскость (L, Ь) справа от L. Дви¬
жение дислокации вдоль оси х состоит в смещении сторон поверхности
Рис. 8.8. Иллюстрация силы Пича-Келера
разреза друг относительно друга на величину b = 6(1, 0, 0). Рассмотрим
силу на единицу поверхности, fi = действующую на движущиеся
стороны поверхности разреза, и предположим, что одна из сторон непо¬
движна, а подвижная имеет нормаль v = (0, 0, —1). Для того чтобы со¬
ответствовать ^5/ПР-соглашению, смещение подвижной стороны должно
равняться —Ь. Работа dW внешних напряжений выражается как
dW = —bf dx — bdxaxz.
Следовательно, фиктивная сила есть
Fx = dxW = Ьахг, (8.21)
и она движет линию L вправо, если действующее напряжение crxz положи¬
тельно (другой пример см. в задаче 8.4).
Вышеприведенная формула обобщается для линии произвольной фор¬
мы и для любого типа смещения и может быть записана в компактной
форме
F = (Ьсг) х t, (8.22)
308 Гл. 8. Дислокации в твердых телах. Пластическая релаксация
где t — единичная касательная к линии. В этом уравнении b действует на
первый индекс тензора <т, т. е. (Ьог)^ = &;сг^, как в (8.21). Это замечание
имеет значение, когда <т^ ф ctji из-за наличия кручения. Полное выраже¬
ние с индексами имеет вид F* — £kpqbi(7iPtq, но сила Пича-Келера часто
используется в простой форме (8.21), описывающей сдвиг в «плоскости
скольжения» (L, Ь). Компонента axz — сдвиговое напряжение, действую¬
щее в этой плоскости.
Из формулы (8.22) легко видеть, что две параллельные прямые дисло¬
кации притягиваются, если имеют противоположные векторы Бюргерса,
и отталкиваются, если их векторы Бюргерса совпадают.
8.4.2.3. Стабильность дислокации вблизи поверхности. Зарождение
дислокаций. Уравнение (8.20) может быть интерпретировано с исполь¬
зованием формулы Пича-Келера как произведение напряжения, создава¬
емого изображением, на вектор Бюргерса. Отсюда а — Напряже-
47тЬ
ния такого порядка необходимо приложить, чтобы удерживать дислока¬
цию внутри материала на расстоянии L от границы. Для L — а, т. е. на
межатомном удалении, получаем: сгтах — ~ — (приблизительно
47Г а 47г
103 кГ/мм2, или Ю10 Н/м2). Говоря иначе, (ттах является напряжением,
необходимым для создания дислокации на границе идеального кристалла.
В действительности пластическая деформация материала начинается при
напряжениях, которые в типичных случаях в 103 раз меньше. Так как пла¬
стическая деформация требует наличия многих свежих дислокаций, необ¬
ходимо понять, почему существующие дислокации могут размножаться
при очень малых напряжениях. В этом заключается роль механизма Фран¬
ка-Рида (см. ниже).
8.4.3. Линейное натяжение
Энергия прямой дислокационной линии пропорциональна ее длине.
Энергия искривленной дислокационной линии также, в первом прибли¬
жении, пропорциональна ее длине, если радиус кривизны линии больше,
чем Я, — типичное расстояние между соседними линиями. Искривленная
линия имеет, следовательно, тенденцию выпрямиться, чтобы уменьшить
свою длину. Такая тенденция может быть описана в терминах линейного
натяжения г, которое есть отношение приращения упругой энергии SW =
= rSt к приращению длины St. Разумное приближение для г дает линейная
энергия, а именно г ~ fib2. Эта идея будет несколько подробнее изложена
в п. 9.1.3. и задаче 9.2.
Рассмотрим сегмент линии, закрепленный на концах и искривленный
под действием фиктивной силы F (рис. 8.9). Линия приобретает кривиз¬
ну р-1, что является результатом равновесия между F и линейным натяже¬
нием. Получаем (задача 8.5)
F = т/р.
(8.23)
§ 8.4. Некоторые замечания об упругой энергии дислокаций
309
F
Рис. 8.9. Иллюстрация формулы (8.23)
8.4.4. Механизм Франка-Рида
Рассмотрим прямолинейный сегмент дислокации АВ длины 2£, закреп¬
ленный в точках А и В (А и В, которые могут быть местами нахожде¬
ния примесей, преципитатов, пересечений с другими дислокациями и т. д.
(рис. 8.10, позиция (а)). Сегмент легко движется в своей плоскости скольже¬
ния под действием силы Пича-Келера F = сгЪ на единицу длины. Сегмент
г ab
принимает равновесный радиус р —
ab а
Начнем с малого <т. Для а = 0 в итоге имеем: р~1 =0. Радиус кривизны
поначалу уменьшается при возрастании а до значения
рс = - = (8.24)
2 сг с
достигаемого при ас = 2pb/t (рис. 8.10, позиция (с)). Вследствие закреп¬
ления радиус кривизны не может уменьшаться, но он не может и увели¬
чиваться, так как большее значение радиуса соответствует меньшим зна¬
чениям напряжения а < ос. Следовательно, положение а = ас, р = i/2
нестабильно и длина дислокации спонтанно увеличивается до новой по¬
зиции (d), где сегменты противоположных знаков (по-прежнему принад¬
лежащие той же дислокации) сближаются и, следовательно, сильно при¬
тягивают друг друга (позиция (е)). Этот процесс приводит к образованию
петли оторвавшейся от сегмента АВ, (позиция (f)). Сегмент восста¬
навливается и растет снова, выталкивая петлю поскольку она является
дислокацией того же знака. Работа механизма повторяется, давая после¬
довательность петель Li, Ь2 ... до момента, когда их суммарные напря¬
жения не погасят приложенное напряжение до уровня ниже критического,
310 Гл. 8. Дислокации в твердых телах. Пластическая релаксация
равного ас. Заметим, что ас ~ оЪ/£ мало в хорошо отожженном мате¬
риале, в котором мало дислокаций и мало точек закрепления. Принимая
£ ~ 10~6 м, b ~ 10-9 м, получаем: ас ~ 10“3//. Однако ас должно
быть больше, чем напряжение Пайерлса ап, которое возникает вследствие
противодействия движению со стороны решетки (см. анализ ар ниже).
Рис. 8.10. Механизм Франка-Рида. Стрелки показывают вектор Бюргерса
8.4.5. Дислокационное ядро
Решение проблемы атомного или молекулярного устройства ядра дисло¬
кации значительно продвинулось благодаря доступной в наши дни могуще¬
ственной вычислительной технике. Кроме того, высокоразрешающая элек¬
тронная микроскопическая техника позволяет прямую визуализацию ядер
краевых дислокаций в ковалентных структурах наподобие Ge. То, о чем
пойдет речь, устарело во многих отношениях, но по-прежнему обладает
некоторыми преимуществами, в частности простотой. Энергия ядра Wc
заведомо лежит между энергией переохлажденной жидкости при темпера-
иЬ2
туре твердого тела, часто оцениваемой как Ws « , и энергией однородно
деформированного твердого тела (е
Отсюда
47Г г,
следовательно, Wu
гs-/
/ib2
87Г
)•
^ < wc <
8тг 5
§ 8.5. Подвижность дислокаций
311
Принимая ес и ОД, типичное значение, за которым деформация не может
56
больше рассматриваться как упругая, мы оцениваем гс ~ ~ 0,86. Можно
2тс
также использовать феноменологический подход к решению этой задачи.
Пусть fc есть плотность энергии ядра. Имеем
wt0t = In — + тггс2/с, (8.25)
4 ттК егс
%
dWtot П / м
с минимумом, определяемым условием = 0 (это действительно ми-
дгс
d2Wtot ^ m
нимум, так как > 0), т. е. при
дг2
о = Jib2 _ (g 26)
8тг 2Kft
Отсюда получаем энергию ядра на единицу длины дислокации:
Wc = (8.27)
8тг К
т. е. того же порядка, что и упругая энергия вне ядра. Здесь К= 1 для вин¬
товой дислокации п К — I — v для краевой дислокации. Отметим, что Wc
не зависит от /с. Для этой модели ядра полная энергия может быть запи¬
сана как
Wtot=-^(ln —+ -). (8.28)
4тгК V егс 2
§ 8.5. Подвижность дислокаций
8.5.1. Элементарные перемещения дислокации
Имеются два типа элементарных движений: скольжение и пере¬
ползание.
8.5.1.1. Скольжение. Скольжение происходит в «плоскости» сколь¬
жения (по теперешней терминологии), т. е. по поверхности, определенной
линией дислокации и вектором Бюргерса. Как будет показано ниже, сколь¬
жение реализуется по наиболее плотноупакованным плоскостям. Это дви¬
жение консервативно, так как для перемещения ядра сквозь среду оно
не требует ничего кроме локальных смещений атомов. Мы упоминали
скольжение, когда рассматривали силу Пича-Келера. Скольжение наблю¬
дается при низких температурах. Это согласуется с тем, что оно не требует
большой энергии активации.
8.5.1.2. Переползание. Всякое другое движение называется перепол¬
занием. «Чистое» переползание происходит перпендикулярно плоскости
скольжения. Переползание требует диффузии атомов на большие расстоя¬
ния, и оно не является консервативным. Возможность для дислокации
312 Гл. 8. Дислокации в твердых телах. Пластическая релаксация
поглощать или испускать атомы облегчается присутствием ступенек, кото
рые являются объектами атомного размера (рис. 8.11).
Плоскости скольжения
Рис. 8.11. Элементарная ступенька (я); ансамбль ступенек, выводящий дислокацию
из ее плоскости скольжения (6)
Ступеньки увеличивают длину линии и добавляют определенную энер¬
гию порядка fib3 (~ 0,1 эВ на ступеньку в благородном металле). Поскольку
они также дают вклад (энтропийный) в свободную энергию вследствие вно¬
симого ими беспорядка, они присутствуют при термодинамическом равно¬
весии в концентрации
п ~ No ехр
К
кБТ
(8.29)
где N0 есть максимально возможное число ступенек (7V0 порядка L/Ъ,
где L — полная длина дислокационной линии), а Ес — энергия ступеньки.
Ступеньки могут также существовать вне равновесия: либо для того,
чтобы изогнуть дислокацию под действием силы Пича- Келера, либо вслед¬
ствие пересечения двух дислокаций (рис. 8.12). Схема, представленная на
рис. 8.12, показывает, как две ступеньки длины bi и Ъ2 соответственно воз¬
никают при пересечении двух дислокаций с векторами Бюргерса bi и b2.
Читателю предлагается самостоятельно понять, как такой процесс может
происходить. (Подсказка: рассмотрите смещения поверхностей разреза
двух дислокаций.)
§8.5. Подвижность дислокаций
313
Рис. 8.12. Пересечение двух дислокаций
8.5.2. Скольжение и напряжение Пайерлса
Испытание монокристалла на растяжение при низкой температуре
(рис. 8.13) выявляет линии скольжения, расположенные в тех плотных плос¬
костях решетки, которые ближе всего к плоскостям с максимальным сдви¬
говым напряжением, вызываемым приложенной растягивающей силой, т. е.
314
Гл. 8. Дислокации в твердых телах. Пластическая релаксация
▼
О
Рис. 8.13. Растягивающее на¬
пряжение
близко к плоскостям, составляющим угол
45° с осью растяжения. Эти плотные плос¬
кости являются, как легко понять, плос¬
костями скольжения и размножения дис¬
локаций. Но не сразу очевидно, почему
направления смещения являются плотны¬
ми направлениями в этих плотных плоско¬
стях. Скольжение начинается при значении
сдвигового напряжения ое, называемом на¬
пряжением течения. Модель Пайерлса объ¬
ясняет три факта: 1) движение дислокаций
облегчено по плоскости, в которой ее яд¬
ро «размазано», такие плоскости являются
плотными; 2) направление смещения явля¬
ется плотным направлением; 3) напряжение
течения есть напряжение, необходимое для
преодоления энергетических барьеров, со¬
здаваемых изменениями энергии ядра при
движении дислокации через неэквивалентные положения в решетке, что
эквивалентно силе трения.
8.5.2.1. Модель критического сдвигового напряжения Френкеля
Эта теоретическая модель описывает свободную от дислокаций среду
(рис. 8.14). Она предполагает, что сдвиговое напряжение а действует
Рис. 8.14. Модель скольжения Френкеля
в определенной плоскости Р, вдоль которой верхняя часть кристалла про¬
скальзывает на длину и относительно нижней части. Когда и достигает
величины периода решетки 6, на пересечении Р с границей образца возни¬
кает линия скольжения. Рассмотрим сперва малые и < Ъ. Тогда мы можем
записать
= /А (8.30)
а
а
согласно закону Гука. Так как напряжение а периодично с периодом 6, мож¬
но ожидать, что разумным приближением для больших и будет выражение
а
цЬ . 27TU
— sin
2тта
(8.31)
§8.5. Подвижность дислокаций
315
которое согласуется с (8.30) для малых и. Теоретическое напряжение Френ-
ab
келя есть максимальное значение сг, а именно ар — —, которое дает
2-7Г а
порядок величины напряжения, необходимого при этом виде скольжения.
Полученное таким образом напряжение течения ар в 103 или в 104 раз
больше экспериментальных значений. Тем не менее формула Френкеля все
же имеет некоторую ценность. Во-первых, она говорит, что чем меньше от¬
ношение Ь/а, тем меньше ар. Расстояние а между атомными плоскостями
максимально, когда эти плоскости наиболее плотно заселены. Следователь¬
но, наиболее плотные плоскости являются наилучшими для скольжения.
Эти предсказания находятся в согласии с экспериментами. Далее, эта тео¬
ретическая модель вводит интересную концепцию поверхностной энергии
7(и) такой, что
а(и) Su — ёу (8.32)
есть работа внешнего напряжения, когда смещение и увеличивается на
величину 5и. Интегрируя (8.32), получаем
7(ti) = J^L (i - COS —) , (8.33)
4тг2а V b /
исчезающее при и = 0. Если поверхность разреза несовершенной дислока¬
ции с вектором Бюргерса (3 лежит в ее плоскости скольжения, эта поверх¬
ность разреза приобретает энергию на единицу площади, равную у(/3).
Такая конструкция является одной из иллюстраций дефекта упаковки.
8.S.2.2. Непрерывная модель Пайерлса. Если исходить из концеп¬
ции поверхностной энергии, разумно ожидать, что вектор Бюргерса покоя¬
щейся дислокации «размазывается» в ее плоскости скольжения,что приво¬
дит к протяженному ядру. Анализ дислокации с уширенным ядром может
быть произведен следующим образом (рис. 8.15).
• Энергия ядра Wc считается энергией дефекта упаковки того же разме¬
ра, если предположить, в духе Френкеля, что несовпадение в основ-
4-00
ном ограничено плоскостью скольжения. Отсюда Wc = J 7(и) dx,
—00
где и(±00) = =F-.
2
• Напряжение а (и) в любой точке х на этой плоскости, в от¬
сутствие внешнего напряжения, есть сумма напряжений, создавае¬
мых инфинитезималъными дислокациями с векторами Бюргерса
db(x') = — du(V), расположенными в х1. Каждая из этих краевых дис¬
локаций создает в х инфинитезимальное сдвиговое напряжение
\i du(x')
2ттК х — х'
такое что в аналогии с приведенным выше анализом напряжения
316 Гл. 8. Дислокации в твердых телах. Пластическая релаксация
Френкеля мы имеем в точке х
dj ( ч /х
о[х) -
du 2 тгК
Мх') (8з4)
X — х' ,
где dry /du принимает значение, следующее из (8.33). Решение этого
интегро-дифференциального уравнения хорошо известно:
✓
tg— = —(x0-x), (8.35)
Ь а
где хо есть центр дислокации. Из уравнения (8.35), дающего распре¬
деление смещения в плоскости скольжения, легко видеть, что ядро
распределено на длине порядка L ~ что скоро будет доказано.
Рис. 8.15. Расщепление ядра дислокации в ее плоскости скольжения
Переходя теперь к полной энергии, мы можем установить (задача 8.7),
что энергия ядра расходится. Этот недостаток модели будет устранен в сле¬
дующем разделе. Мы примем временно выражение Wc = 7шахЬ, которое
по-прежнему приписывает ядру большую энергию, растущую пропорцио¬
нально ширине ядра, как и должно быть. Мы оцениваем упругую энергию
(вне ядра) из (8.16), а именно: We\ — —— In —, т. е. меньшей, чем в стан-
47тК L
дартной модели In поскольку ядро велико. Следовательно, из¬
менение энергии по отношению к стандартной модели есть
AW - 7тахЬ - In — = In —. (8.36)
4ттК 26 47r2a АттК 2b
Находя минимум энергии W = Wei -f Wc по отношению к L, получаем
L=—, AW = --^-ln—, (8.37)
К 4пК 2 ЪК
что дает значение L, близкое к результату расчета в дискретной моде¬
ли, приведенной ниже. Заметим, что величина AW в (8.37) показывает
§ 8.5. Подвижность дислокаций
317
предпочтение больших значений а и малых значений Ь, как в модели Френ¬
келя, что согласуется с опытом.
8.5.2.3. Дискретная модель Пайерлса. Не говоря уже об отмеченных
радикальных предположениях, непрерывная модель еще и не предсказыва¬
ет никакой зависимости энергии от положения дислокации хо, следователь¬
но, никакого трения. Модель может быть улучшена вычислением относя¬
щейся к ядру поверхностной энергии несовпадения J 7(a) dx с помощью
суммирования £ 7(un) по всем ячейкам дефекта упаковки в предположе¬
нии, что ип(х = nb) принимает то же значение, что в (8.35). Эта процедура
также дает конечное значение для поверхностной энергии, которое мы за¬
пишем как W — Wei + Wc + Д AW. Дополнительный энергетический вклад
Д Д W выражается в виде
AAW = -^cos^exp- —. (8.38)
2ттК Ь КЬ
Следовательно, напряжение Пайерлса есть
1 (дА AW \ (I 2па
ар = 7 ( — = ^ехР--—• (8-39)
дх0 J max К КЬ
Напряжение Пайерлса ир экспоненциально уменьшается с ростом от¬
ношения а/Ь и, очевидно, много меньше, чем теоретическое напряжение
Френкеля, с которым оно должно сравниваться. Например, в ГЦК-решетке
скольжение по плотноупакованной плоскости L{lll} с а/b = (2/3)х/2 дает
величину <тр ~ 10-3// Для краевой дислокации (К = 1 — v) и ар ~ 10~2ц
для винтовой дислокации (К = 1).
8.5.2.4- Кинки. Дислокация, которая первоначально не лежит в до¬
лине потенциального рельефа V, где AAW = 0, принимает извилистую
форму с длинными участками вдоль долин и пересекающими гребни Н
укороченными участками, называемыми кинками. Такая форма дислокации
изображена на рис. 8.16, где можно видеть отдельные и парные кинки.
Эти кинки играют важную роль в процессах деформации, когда дис¬
локации движутся под действием приложенного напряжения. Определим
несколько величин, представляющих интерес для этих явлений. Мы назо¬
вем микродеформацией смещение кинков вдоль линии (рис. 8.16) и мак¬
родеформацией — смещение линии перпендикулярно самой себе. При
достаточно низких температурах напряжение Пайерлса для микродеформа¬
ции am меньше, чем для макродеформации ор. Макродеформация требует
рождения пар кинков (энергия рождения UJdd), что увеличивает эффектив¬
ное напряжение течения. При высоких температурах скорость дислока¬
ций лимитируется перемещением кинков. Эта схема действительна для
ГЦК-металлов и ковалентных материалов, но с некоторыми вариациями,
зависящими от структуры и вида химической связи. Низкотемператур¬
ное скольжение затруднено в ОЦК-металлах, ионоковалентных структурах
и для определенных систем скольжения в гексагональных металлах. Мы
318 Гл. 8. Дислокации в твердых телах. Пластическая релаксация
не будем углубляться в эти концепции, представляющие интерес лишь для
твердых тел.
При достаточно высокой температуре, обычно при Т ^ Тт/2, где Тт
есть температура плавления, пластическая деформация твердых тел проис¬
ходит главным образом за счет неконсервативного движения дислокаций,
которое требует диффузии атомов на большие расстояния. Этот механизм
включает точечные дефекты, вакансии и междоузлия. Ползучесть, т. е. де¬
формация, развивающаяся во времени под действием постоянной нагрузки,
есть типичное следствие легкой диффузии при высоких температурах.
8.6.1. Вакансии и междоузлия
Рисунок 2.31 схематически иллюстрирует дефекты, называемые вакан¬
сией и междоузлием в кристалле. При условии постоянства полной массы
энергия образования вакансии UVf есть энергия, необходимая для переноса
какого-либо атома из объема кристалла в положение более низкой энергии
на его поверхности. Энергия Uvf имеет порядок энергии сублимации Es,
потому что в обоих случаях должно быть разорвано одно и то же чис¬
ло связей. Электронная и упругая релаксации вокруг вакансии несколько
уменьшают Uvf по сравнению с Es:
Энергия образования междоузлия Uif много больше и имеет главным
образом упругую природу (внедрение в матрицу сферы радиуса b):
Существует равновесная концентрация с = n/N точечных дефектов, кото¬
рая возникает из баланса между их внутренней энергией Uf и их трансля¬
ционной энтропией. Простое вычисление свободной энергии ансамбля N
атомов дает
Рис. 8.16. Кинки на дислокационной линии
§ 8.6. Точечные дефекты и переползание
(8.40)
Uif ~ fib3.
(8.41)
F = N{c(Uf - TSf) + kbT[c\nc + (1 - с) In (1 - с)]}, (8.42)
§ 8.6. Точечные дефекты и переползание
319
где Sf есть энтропия образования (изменение колебательных мод соседних
атомов, модификация ближнего порядка и пр.), которой, в общем, можно
пренебречь
с — ехр — ■ ехр — (8.43)
кБ квТ
где вклад 5/ мал (ехр(5//А:в) ~ 1)- Подставляя в (8.43) численные значе¬
ния, получаем, что концентрация вакансий (Uf = Ufv) мала при комнатной
температуре (с ~ 10”17), но велика вблизи точки плавления Tm(c ~ 10-4).
Концентрация междоузлий мала во всем интервале температур.
Точечные дефекты могут образовываться неравновесным способом, ли¬
бо при радиационном повреждении (образование пар Френкеля, состоящих
из одной вакансии и одного междоузлия), либо при низкотемпературном де¬
формационном упрочнении. Вакансии, созданные равновесно при высокой
температуре, могут быть заморожены с понижением температуры. Вакан¬
сии, созданные неравновесно, могут находиться или в дисперсном виде,
или в виде кластеров (например, дислокационных петель). Их энергией
миграции (Uvm = Uvf) нельзя пренебречь.
С другой стороны, междоузлия легко диффундируют и исчезают, либо
аннигилируя с вакансиями, либо выходя на границы зерен или поверхность
образца. В ГЦК-металлах междоузлия, созданные облучением, стремятся
собраться в небольшие подвижные петли.
Понятие точечного дефекта типа вакансии или междоузлия в равной сте¬
пени применимо к жидким кристаллам с преимущественно позиционным
порядком, таким как SmB, где движением точечных дефектов объясняет¬
ся пластическая деформация. Неравновесные точечные дефекты не играют
роли, так как их диффузионная подвижность очень велика. Гетеромеждоуз¬
лия обычны в жидких кристаллах, в которых составляющие молекулярные
блоки обычно термически- или фотонестабильны. Подвижность точечных
дефектов ответственна за неустойчивость роста Муллинса-Секерки, про¬
являющейся при направленном росте изотропных фаз гексагонального ко¬
лончатого SmA или нематика.
Концы колонок в колончатых фазах, концы полимерных цепей в жид¬
кокристаллических полимерах и т. д. являются характерными примерами
точечных дефектов в жидких кристаллах.
8.6.2. Диффузия точечных дефектов и самодиффузия
8.6.2.1. Диффузия и случайные блуждания. Диффузия вакансии
в кристалле происходит прыжками из одной ячейки в другую. В большин¬
стве случаев допускают, что эти прыжки являются элементарными прыжка¬
ми в соседнюю позицию со смещением г0, которое принимает z значений
по числу соседей. Мы предполагаем, что а2 = Tq одинаково для всех этих г
значений. Конечно, когда мы говорим о движении вакансии, в действитель¬
ности это соседний атом смещается в положение вакансии, которая, следо¬
вательно, перемещается на место, освобожденное атомом. Пусть гп — это
320 Гл. 8. Дислокации в твердых телах. Пластическая релаксация
положение, достигнутое вакансией после п прыжков. Имеем
гп+1 = гп + г0 (8.44)
и, взяв среднеквадратичное значение, получаем
(rn+i) = (rn) + 2 (rnro) + Го- (8.45)
Это уравнение упрощается, если прыжки не скоррелированы,что имеет
место, когда дефект по меньшей мере так же симметричен, как и кристал¬
лическая ячейка, в которой он сидит. Следовательно, (гпг0) = 0 и (8.45),
используемое как рекуррентное соотношение, приводит к
(Г2„) = nrl, (8.46)
где п, число прыжков, есть также мера времени диффузии t, за которое
вакансия уходит на расстояние L — (г2)1/2. Обсуждаемые явления харак¬
теризуются коэффициентом диффузии
Dv = —, (8.47)
который согласно (8.46) постоянен:
Т2 п2
£>„ = — = —. (8.48)
t Т
Здесь т — временная характеристика одного прыжка. Пусть v& есть ти¬
пичная для решетки атомная частота порядка дебаевской частоты (vd ~
~ 1013 с”1 в кристалле). Число эффективных элементарных прыжков для
данной позиции пропорционально vd и г, числу доступных соседних по¬
зиций. Их частота изменяется, следовательно, согласно (8.48) как
i/d = Bzi/Dex —. (8.49)
кБТ а2
Здесь Uvm есть энергетический барьер, который вакансия должна преодо¬
леть, а В — численный коэффициент. Следовательно, микроскопическое
выражение для Dv можно записать в виде
Dv = Bza2vD exp — (8.50)
kLT
Коэффициент Dqv — Bza2vD имеет порядок нескольких единиц в системе
CGS (Dqv = 1см2с-1). Принимая Uvm ~ 1 eV, находим: Dv ~ 10_15см2с“1
в твердом теле.
8.6.2.2. Соотношение Эйнштейна для вакансий. Предположим что
на точечный дефект действует сила F, помогающая набрать активационную
энергию Uvm прыжка, понижая высоту барьера на Fa/2. В направлении
§ 8.6. Точечные дефекты и переползание
321
вдоль F эффективная энергия миграции есть Uvm — Fa/2, в противопо¬
ложном направлении она равна Uvm -f Fa/2. Число эффективных прыжков
в направлении F в единицу времени есть, следовательно,
Sv = ид { ехр - — ехр — - ) . (8.51)
2 къТ 2 кБТ
Это выражение принимает во внимание только прыжки вперед-назад. Пусть
aF к^Т. Разлагая экспоненты, получаем дрейфовую скорость вдоль F :
v = 8va = Vd—-> (8.52)
квТ
которую мы запишем в сжатой форме
mk^T — DV: (8.53)
где га — v/F называется подвижностью точечного дефекта. Уравнение
(8.53) есть знаменитое соотношение Эйнштейна.
8.6.2.3. Самодиффузия атомов матрицы. Атомы матрицы движутся,
меняясь местами с вакансиями. Мы введем коэффициент самодиффузии
атомов, который пропорционален концентрации вакансий cv:
D"CVDV. (8.54)
Коэффициент D измеряют, помечая некоторую долю атомов матрицы (на¬
пример, радиоизотопным методом). Их временная эволюция подчиняется
второму закону Фика:
— = Z?V2c (8.55)
dt
(который будет доказан ниже). Решение может быть выражено как функция
безразмерной величины
' х1
(8.56)
е
4 Dt
Например, если при t — 0 все помеченные атомы находятся в плоскости х =
= 0 {с(0, 0) = 1, с(ж, 0) = 0}, в последующие моменты времени решением
является
ОО
с(£)
ехр —£2 d£ = со erfc(£), (8.57)
С
где erfc(z) = 1 — erf(z), erf (z) — функция ошибок (рис. 8.17).
Для того чтобы вывести закон Фика, обобщим сначала соотношение
Эйнштейна на случай самодиффузии. Заметим сперва, что помеченные ато¬
мы образуют практически идеальный раствор среди непомеченных атомов,
если их плотность достаточно мала и если они не взаимодействуют. Соот¬
ветствующая свободная энергия есть преимущественно энтропия и нет ни¬
какого существенного специфического химического взаимодействия между
21-КЛЕМАН М.
322 Гл. 8. Дислокации в твердых телах. Пластическая релаксация
изотопами. Поэтому
F() = NkET[c\nc + (1 — с) In (1 — с)], (8.58)
что дает химический потенциал на атом
ц = = квТ\п~ ~ А:бТ1пс (8.59)
N дс 1 — С
и спонтанную силу, действующую на меченый атом:
F = -Vn= - —Vex, (8.60)
где х — единичный вектор в направлении F.
с(х)
c{x)+fxdx
X
х + dx
Рис. 8.17. Второй закон Фика
Соотношение Эйнштейна теперь записывается как
= -Dvcv~ = -D — , (8.61)
С С
где v — скорость меченого атома и D — коэффициент диффузии. Это
и есть первый закон Фика, который соотносит поток меченых атомов J =
= cv с градиентом концентрации.
Второй закон Фика является прямым следствием. Рассмотрим, напри-
мер, баланс входящих и выходящих атомов в слое толщины dx в положе¬
нии х. Согласно (8.61)
f)c f)
- = J, (8.62)
dt дх
т. e. получаем одномерный вариант уравнения (8.55). Одномерное уравне¬
ние легко обобщается на полное трехмерное (8.55).
Заметим, что законы Фика могут быть применены к любому типу ато¬
мов, дефектов или «частиц», если только справедливо (8.59) и используется
правильный коэффициент диффузии. Например, законы Фика применимы
к вакансиям с D = Dv. Отметим также, что (8.59) не зависит от точного
определения концентрации, которая может быть атомной, весовой и т. д.
Например, принимая в качестве с объемную долю с = пП, где П — объем
частицы и J = vc/П = vn — поток частиц через единицу поверхности
§ 8.6. Точечные дефекты и переползание
323
в единицу времени, получаем наиболее удобную формулу для дальнейшего
использования
J = ——Vc. (8.63)
п
8.6.3. Ползучесть
При высокой температуре дефект может течь под действием постоянно¬
го приложенного напряжения сг0 > ау, превышающего предел текучести.
Типичный эксперимент по ползучести состоит в записи деформации £ как
функции времени (рис. 8.18).
а
▼
►
1
1
'
Л
<7
t
Рис. 8.18. Эксперименты по ползучести. Принципиальная схема испытания (а);
логарифмическая ползучесть при низких температурах и три стадии ползучести
при высоких температурах (6)
При низких температурах ползучесть является логарифмической и ско¬
рость деформации убывает с увеличением времени: ё ~ t~l. При более
высоких температурах или высоком напряжении в типичном случае су¬
ществуют три стадии: /3-ползучесть с убыванием скорости деформации;
линейная х-ползучесть; третичная ползучесть с ускорением деформации,
оканчивающимся разрушением.
Модель линейной ползучести Херринга-Набарро исходит из того, что
образец состоит из зерен (типичного размера L), не содержит дислока¬
ций, за исключением, может быть, границ зерен, и что границы зерен,
испускают или поглощают точечные дефекты (рис. 8.19) под действием
приложенного растягивающего или сжимающего напряжения <х. Вакансии
мигрируют из сжатых областей в растянутые. Энергия образования ва¬
кансии в сжатой области увеличивается на величину ab3 и уменьшается
324 Гл. 8. Дислокации в твердых телах. Пластическая релаксация
1
А
Рис. 8.19. Ползучесть Херринга-Набарро
на ту же самую величину в сжатой области. Следовательно, соответствую¬
щие концентрации с+ и с~ в этих областях равны
.4"
аб3
с0 ехр ,
къТ
cq ехр
<тЬ3
hT
со = ехр
Отсюда градиент концентрации
и,
vf
кБТ
(8.64)
Vc
2 сгЬ3
~ —Со j
L L ksT
если ab3 <С А:бТ.
Используя (8.63), получаем для полного потока
JL
П ЛБГ
где /? есть некоторый коэффициент.
Изменение размера зерна за единицу времени SL
(8.65)
(8.66)
L2
JL2 приводит к
§ 8.7. Ансамбли дислокаций
325
или, с П = 63,
е = (5cqDv~^—. (8.68)
k^T L2
Уравнение (8.67) имеет форму уравнения потока с вязкостью ц = а/ё:
т] = Р'-^-квТ (8.69)
Dvn
(где /?' — 1/(со/3) имеет порядок 1013 пуаз для L ~ 10 мкм, Т = 750 К,
D = 10“10см2с-1 и П = 10~23см3. Этот порядок величин встречается,
например, при стекловании. При высоких напряжениях или высоких тем¬
пературах твердое тело ведет себя как жидкость.
Отметим далее, что жидкость соответствовала бы L3 = П, т. е.
т1 ~ к^Т/(Dva), что дает правильный порядок величины с тем же значени¬
ем D, что указано выше. Мы напомним также, что вязкое движение сфе¬
рической частицы радиуса а в жидкости с коэффициентом диффузии Dv
дается формулой Стокса - Эйнштейна (которая является точной в рамках
уравнений Навье - Стокса):
Vse = — ■ (8.70)
67xDva
Аналогия с вышеприведенной формулой очевидна.
§ 8.7. Ансамбли дислокаций
8.7.1. Сетка Франка
В хорошо отожженном кристалле плотность дислокаций может быть на¬
много уменьшена за счет разнообразных процессов движения дислокаций
под действием их взаимных напряжении или термонапряжении; дислокаци¬
онные петли могут стянуться в нуль, а дислокации противоположных зна¬
ков аннигилировать. Типичная остаточная плотность составляет от 104 до
106 дислокаций на см2 (ср. от Ю10 до 1012 в деформационно-упрочненном
материале).
Сетка Франка в хорошо отожженном кристалле является низкоэнерге¬
тической конфигурацией, составленной из дислокационных сегментов, ко¬
торые сходятся в узлах с автоматическим выполнением условия Кирхгофа
bi = 0 (рис. 8.20).
В узле соединяются по меньшей мере три дислокации с различными
векторами Бюргерса. Равновесие линейных натяжений, если оно имеет ме¬
сто, приводит к дополнительному условию
1>=0, (8.71)
326 Гл. 8. Дислокации в твердых телах. Пластическая релаксация
f
/
/
/
/
I
Рис. 8.20. Тройной дислокационный узел и равновесие линейных натяжений
где Ti — Titi есть вектор, направленный вдоль внешней касательной t$
к дислокационной линии Li в точке слияния, а т* — линейное натяжение.
Избыточные дислокации, создаваемые пластической деформацией, на¬
пример благодаря мельницам Франка-Рида, индуцированным внешним
напряжением на сегментах сетки Франка, все имеют одинаковый знак
и не могут собираться в сетку Франка. Они создают «полигонизированную»
структуру субграниц (дислокационных стенок), расположенных вдоль сте¬
нок сетки Франка. Эти субзеренные границы являются причиной легкой
разориентации в порядка ~ b/t, где £ есть расстояние между одинаковыми
дислокациями.
Сетка Франка и полигонизированная структура дают в картине рент¬
геновской дифракции монокристаллов уширенные пики Лауэ, благодаря
которым эта разориентация может быть измерена (типично от 1 до 30 уг¬
ловых минут для блоков порядка 10_3 см). Эта блочная структура известна
также как мозаичная структура.
8.7.2. Субграницы
Угол разориентации из-за наличия стенки дислокаций может быть вы¬
числен следующим образом. Рассмотрим (рис. 8.21) замкнутую петлю Г,
окружающую сегмент стенки <5L, который пронизывают несколько дис¬
локаций с суммарным вектором Бюргерса (5Ь. Наложим петлю Бюргер¬
са Г на идеальный кристалл, Г —У у. Образ 7 является, вообще говоря,
разомкнутым контуром, замыкание которого равно 6Ъ. Но это замыкание
§ 8. 7. Ансамбли дислокаций
327
а
б
Рис. 8.21. Контур Бюргерса для субграницы
пропорционально длине 6L = |<5L|, если та же самая дислокационная кон¬
фигурация повторяется вдоль стенки. Следовательно, можно записать <5Ь =
= в х 6L, где в есть вектор вращения, перпендикулярный 6Ъ, являющийся
мерой разориентации при прохождении любой петли, окружающей сегмент
стенки, параллельный 5L.
Рассмотрим два простых примера субграниц.
1. Наклонная субграница, разориентация в которой параллельна плос¬
кости границы. Это может быть достигнуто набором параллельных краевых
дислокаций, векторы Бюргерса которых перпендикулярны границе. Такие
наклонные границы встречаются в геометрии Гранжана-Кано в холесте¬
риках или смектиках (рис. 8.22). В обоих случаях фиксирующие припо¬
верхностные условия задают ориентацию слоев, параллельную границам
образца, обычно границы образуют клин с углом в порядка 10-4 ради¬
ан. Эта разориентация релаксирует за счет наклонной границы субзерна
в срединной плоскости образца. Отсюда расстояние £ между дислокациями
с векторами Бюргерса b есть £ ~ Ъ/в.
Рис. 8.22. Дислокационная модель наклонной субграницы в смектическом клине
В твердом кристалле наклонная граница образуется слиянием двух иде¬
альных решеток, ограниченных плоскостью, расположенной под малым уг¬
лом ± 0/2 к общей плоскости скольжения, соединенных вместе вдоль этой
328 Гл. 8. Дислокации в твердых телах. Пластическая релаксация
плоскости, которым предоставлена возможность релаксировать. Ожидает¬
ся, что дальнодействующие напряжения дислокаций исчезают на больших
расстояниях, что и было точно доказано. Напряжение заключено в неко¬
торой параллельной границе области, толщина которой равна по поряд¬
ку величины расстоянию между дислокациями и вне которой напряжение
убывает экспоненциально. Энергия, ассоциированная с дислокациями, мо¬
жет в таком случае вычисляться как сумма отдельных энергий дислока¬
ций, сконцентрированных в цилиндрах радиуса £/2. Энергия на единицу
площади стенки равна, следовательно,
Е(в) = —^—в In —. (8.72)
47г(1 — и) 2 гсв
Выражение (8.72) имеет максимум при в ~ Ь/(2егс). Это, видимо, подтвер¬
ждается экспериментальными данными.
2. Субграница кручения, разориентация в которой перпендикулярна
плоскости границы. Такая ситуация может быть порождена одним или
несколькими наборами винтовых дислокаций с различными векторами Бюр¬
герса. В смектиках, параметры которых повторяются только в одном на¬
правлении, такие границы кручения образуются единственным набором
параллельных дислокаций. Напомним, что согласно хорошо установлен¬
ной модели, TGB-фазы образуются параллельными границами кручения
(см. рис. 4.11). Как ожидается, в гексагональных колончатых фазах имеется
три набора винтовых дислокаций в границах кручения, перпендикулярных
колоннам.
В твердом кристалле граница кручения без дальнодействующих напря¬
жений должна состоять из двух наборов винтовых дислокаций с непарал¬
лельными векторами Бюргерса (Франк).
Отметим, что три субграницы с энергией Et на единицу площади, сли¬
вающиеся вдоль линии, должны быть такими, чтобы F. -f Е2 + Ез = О, где
Е* = Ем, vi есть единичный вектор в плоскости субграницы г, перпен¬
дикулярный линии слияния. Это равновесие «поверхностных натяжений»
имеет место в хорошо отожженном кристалле.
8.7.3. Большие разориентации, двойники и эпитаксиальные дислока¬
ции, мартенситные превращения
Можно ожидать, что расщепление границы разориентации на дислока¬
ции имеет физическое оправдание, когда расстояние £ между дислокациями
больше, чем диаметр ядра (порядка 2Ь). Уравнение (8.72), таким образом,
справедливо (приблизительно) для в ^ 25°. При превышении этого зна¬
чения энергия стенки практически постоянна, так как переустройство ато¬
мов имеет место в полосе атомного размера и не очень сильно зависит
от разориентации. Однако энергия стенки резко уменьшается для некото¬
рых специальных значений разориентации и особых ориентаций стенки,
соответствующих двойникованию между двумя решетками (см. п. 8.3.3).
Примечательно, что энергия стенки очень резко увеличивается при малых
§ 8. 7. Ансамбли дислокаций
329
отклонениях от условий двойникования. Это происходит благодаря появ¬
лению двойникующих дислокаций, которые создают дальнодействующие
напряжения (некогерентные двойники), плотность и природа которых за¬
висят от величины отклонения. Такие дислокации сродни несовершенным
дислокациям (см. подробнее в учебнике Фриделя и текущей литературе).
Эпитаксия есть общее название для явлений, сопутствующих легко¬
му сопряжению двух типов кристаллов вдоль плоскости, для которой они
имеют равные (совершенная эпитаксия) или почти равные двумерные
параметры решетки. Когерентное двойникование есть специальный случай
совершенной эпитаксии, когда имеется только один тип кристалла и две
решетки сохраняют общие элементы симметрии кристалла. Любое откло¬
нение от совершенной эпитаксии обычно релаксирует посредством возник¬
новения на границе эпитаксиальных дислокаций.
В заключение стоит упомянуть, что при фазовом превращении внутри
кристалла с созданием зародыша новой фазы посредством локального пе¬
реустройства атомов, границы между двумя фазами часто могут содержать
дислокации, перемещения которых важны для понимания роста второй фа¬
зы. Это называется мартенситным превращением.
Задача 8.1. Проверьте выражение (8.15) и вычислите поля дефор¬
маций и напряжений краевой дислокации. Проверьте, что они убывают
как 1/г. Вычислите дилатацию и покажите, что она в среднем исчезает.
Ответ.
цЬ sin# fib cos в fiisb sin#
(Jrr = (70$ = —— , (Тгв — —— ~ j &zz — ““ ~— ~
27t(1 — v) r 27t(1 — v) Г 7г(1 — is) r
(7rr + CfQQ + СГ
2Z
(5 = (Тц/\ + 2 n
<Tj* г A ^ х у oiii v л
crr — вQQ — - - 1 &ZZ O,
2 \x 47t(1 — v) r
2тг(1 -
V) т
fib sin в 1 + и
7Г
Г 1 — V
Ь
X — 2г^ sin в
27Г
1 — и г
6(1-
■ 2и) sin в
•>
ere
COS в
7г( 1 — v) r
Задача 8.2. Вычислите энергию взаимодействия параллельных крае¬
вой и винтовой дислокаций.
Ответ. Пусть а\]\ — напряжения, создаваемые по отдельности
J +J
каждой из дислокационных линий Ь2 независимо от присутствия дру¬
гой. При наличии обеих дислокационных линий полное напряжение, в соот¬
ветствии с законом Гука, вычисляется как сумма • Полная энергия
330 Гл. 8. Дислокации в твердых телах. Пластическая релаксация
(см. (8.13)) W = i J (а^ 4- +е-^)б?1/ может быть расщепле-
2
на на три части: собственные энергии двух линий: Wi — ~ J dV
и W2 ~ ^ J vjpeip dV, и энергию взаимодействия W[nt = i +
-\-a^e^)dV = \ ~
1 13 13 ' j 13 l3
Поля напряжений двух параллельных винтовой и краевой линий соглас¬
но (8.12) и (8.15) ортогональны (без общих компонент). Более того, дила-
тация, производимая винтовой дислокацией, равна нулю. Следовательно,
равна нулю и энергия их взаимодействия.
Задача 8.3. Докажите эквивалентность двух выражений для энер¬
гии взаимодействия между двумя дислокациями с поверхностями разреза
Хл и 5^2 и Напряжениями и W-mt = Saij^eif dV и W-mt =
= - § (LSj■
Ответ. Тензоры и являются симметричными. Свертка сим¬
метричного тензора с антисимметричным равна нулю. Следовательно, мож-
(2) 1 / (2) - (2)\ (2) . (2) (2) , (2)
но заменить ^[и]1- + •) на е\-} + ~ u-J (где тензор =
= — и^1) антисимметричен) в произведении а^е^\ Следующий
шаг заключается в замене объемного интеграла поверхностным (по двум
сторонам поверхности разреза которые разделены постоянным векто¬
ром Ь2). Действительно, имеем: где вто-
ij J
рое слагаемое в правой части уравнения исчезает аналогично (8.5 а). Оста¬
ется только применить теорему Гаусса. Более подробно выкладки см. в кни¬
ге Набарро.
Задача 8.4. Краевая дислокация с вектором Бюргерса Ь, направлен¬
ным по оси z, лежит вдоль оси у и подвержена воздействию продольного
сжатия вдоль z. Какова воображаемая сила, действующая на дислокацию,
и в каком направлении движется дислокация?
Ответ. Внешнее продольное сжатие вдоль оси г может быть описа¬
но тензором напряжения с единственной компонентой azz < 0. Применяя
формулу Пича-Келера, получаем: F = b(azz, 0, 0). Дислокация движет¬
ся вправо, если b > 0. Действительно, такая краевая дислокация создает
дополнительный полу слой в плоскости ху (х > 0), если вышеуказанные
данные соответствуют соглашению FS/ПР.
Задача 8.5. Докажите (8.23).
Ответ. Пусть dO есть угол, под которым дуга ds видна из центра
кривизны. Радиус кривизны р — ds/dO будем считать намного большим
Литература для дальнейшего чтения
331
по сравнению с дугой ds. Тогда линейное натяжение на обоих концах ду¬
ги, спроектированное в середине дуги на радиус, имеет суммарную ком¬
поненту 2тsin (d0/2) и rdO, противодействующую силе Пича-Келера F
в соответствии с (8.23).
Задача 8.6. Вычислите радиус ядра гс пустой дислокации. Покажите,
что условие гс > а означает, что Ь^> а.
Ответ. Энергия ядра пустой дислокации в первом приближении про¬
порциональна площади его границы, скажем, Wc = 27ггс7, где 7 ~ (ла.
nb2 1 f)2
Минимизация Wei + Wc дает: гс = ■ - ~ , определяя действи-
S^K'y 8ir2K а
тельный радиус пустого ядра, если гс > а, т. е. b > 27г\/2К а.
Задача 8.7. Покажите, что энергия ядра Wc = j(x) dx в непре¬
рывной модели Пайерлса расходится.
Ответ. Энергия ядра может быть записана как
-6/2
ГТГ ub2 (2пи\ dx ,
IVс = I 1 — COS 1 — du,
J 47г2а V b ' du
+ &/2
где — = —J¥L(i + tg2 —) может быть получено из (8.35). Полагая t =
du 2 Kb b
-OO ^
= tg 7ти/b, находим: Wc oc J —— dt, где интеграл, очевидно, расходится.
-j-oo 1 + t2
Литература для дальнейшего чтения
1. Ландау Л. Д., Лифшиц Е. М. Теория упругости. 3-е изд. — М.: Наука. Гл. ред.
физ.-мат. лит, 1965. —204 с., ил.
2. J. Friedel. Dislocations, Pergamon, N. Y., 1964. [Перевод: Фридель Ж.
Дислокации. — М.: Мир, 1967. — 643 с.].
3. J. P. Hirth and J. Lothe. Theory of Dislocations, Second Edition, John Wiley,
N. Y., (1982). [Перевод первого издания: Xupm Д., Лоте И. Теория дислока¬
ций. — М.: Атомиздат, 1972. — 598 с.].
4. F. R. N. Nabarro. Theory of Crystal Dislocations, Oxford University Press, 1967.
5. Report on the Conference on «Defects in Crystalline Solids» held at the H. H. Wills
Laboratory, University of Bristol, The Physical Society, London, 1955.
6. Dislocations in solids, V. 1-8, Edited by F. R.N. Nabarro, North-Holland,
Amsterdam, 1975.
Дополнительная литература
1. Орлов А. И. Введение в теорию дефектов в кристаллах. — М.: Высшая школа,
1983. — 144 с.
2. Лихачев В. А., Хайров Р. Ю. Введение в теорию дисклинаций. — JL: Изд-во
ЛГУ, 1975. — 183 с.
ГЛАВА 9
ДИСЛОКАЦИИ В СМЕКТИЧЕСКИХ
И КОЛОНЧАТЫХ ФАЗАХ
Вследствие трансляционной симметрии одномерные (смектические)
и двумерные (колончатые) позиционно упорядоченные жидкие кристал¬
лы могут содержать дислокации с различными характеристиками. Сильно
зависящие от вектора Бюргерса упругие и пластические свойства таких
дислокаций, взаимосвязь с дисклинациями и т. д. существенно отличают
их от прообразов в трехмерных твердых кристаллах. Эти дислокации за¬
служивают детального изучения также из-за их роли в комплексных фазах
с термодинамическими дефектами, таких как TGB-фазы (смектики с пери¬
одическими субграницами кручения), уже упоминавшиеся выше, или муа¬
ровые фазы (колончатые фазы с периодическими субграницами кручения),
существование которых было недавно предсказано.
Мы ограничимся рассмотрением простейших случаев одномерных или
двумерных жидких кристаллов, а именно SmA- и колончатых фаз гексаго¬
нальной симметрии. В SmA картина слоев не усложнена дополнительным
упорядочением, как, например, в SmB или SmC, а параметр порядка сводит¬
ся к нематической компоненте (директор п идентичен нормали к слою и)
и компоненте плотности массы, описывающей одномерное периодическое
возмущение массы вдоль оси г. Элементарными дефектами являются, сле¬
довательно, дисклинации (сингулярности поля директора) и дислокации
с векторами Бюргерса b = ndou (сингулярности одномерного твердого
тела), а также их комбинации. Здесь do — период повторяемости смекти¬
ческой фазы, а п — целое число. Для двумерных колончатых фаз с гекса¬
гональной симметрией выражение для плотности свободной энергии, учи¬
тывающее члены разложения по деформациям до второго порядка, имеет
цилиндрическую симметрию и, следовательно, может быть легко проана¬
лизировано.
§ 9.1. Статические дислокации в смектиках
9.1.1. Краевые дислокации с малыми и большими векторами
Бюргерса
9.1.1.1. Малые векторы Бюргерса. Рассмотрим дислокацию, распо¬
ложенную вдоль оси у. Если вектор Бюргерса мал (п= 1,2,...), упругое поле
может быть изучено в приближении малой деформации в терминах поля
смещений и(х, г), которое нечетно по zl\ Выберем поверхность разреза
вдоль полуплоскости г = 0, х > 0, и рассмотрим полупространство z > 0.
^ P. G. de Gennes, Comptes Rendus Acad. Sci. (Paris) 275B, 939 (1972).
§9.1. Статические дислокации в смектиках
333
Граничные условия имеют вид
z = 0; и(х < 0) = 0; и(х > 0) = (9.1)
Мы ищем решение дифференциального уравнения Эйлера-Лагранжа
К\ А2±и = которое соответствует функционалу упругой энергии
dz2
в его линейной форме (5.27). Граничные условия могут быть выражены
в виде интеграла Фурье:
и(х, 0) = - + 6
+ оо
dq
4 47г
iq
ехрiqx, (9.2)
— со
где мы использовали тот факт, что интеграл от дельта-функции $(ж) являет-
1 d
ся ступенчатой функцией Н(х) = — J — ехр iqx, такой что Н(х < 0) =
2тг „оо iq
— —1/2, Н(х > 0) — +1/2.
Мы можем, следовательно, записать общее решение и (х. z) как
+оо
( \ b I &
w(x, 2;) = - +
4 47г
—gq(z)expiqx. (9.3)
iq
— оо
Используя уравнение Эйлера - Лагранжа, находим: g?(2;) = ехр (—Ад2 2),
где А = у/ЩрЗ, так что
+оо
xfVXz
и(х, z)
4 47Г
ехр(г</:г — Ад г) -
4\/7г
ехр(—t2/4) dt. (9.4)
ОО
— ОО
Поэтому выражение для угла 6(х) между 1/, нормалью к слою, и осью z
может быть записано как
в(х)
ди
b
дх 4\Лr\z
ехр
х
4Xz
(9.5)
Эта величина медленно убывает с увеличением z (на типичном расстоя¬
нии х2/(4Л)), быстро уменьшаясь с ростом х внутри параболы х2 = ±4z\
и принимая значения, близкие к нулю, вне этой параболы (рис. 9.1). Пусть £
есть длина, вдоль которой ядро уширено по оси х. Соответствующее воз¬
мущение вдоль направления z простирается, согласно (9.5), на расстоя¬
ние £2/(4А).
334
Гл. 9. Дислокации в смектических и колончатых фазах
А
X
а
б
Рис. 9.1. Искажение, индуцированное краевой дислокацией: поле смещения
и(х7 z) (9.4) (а) и угол наклона 9(х, z) (9.5) (б)
Линейная энергия может быть вычислена с помощью полученного вы¬
ражения для и(х, z). Вклад кривизны, например, включает следующую
последовательность выражений при расчете:
д2
и
ib
дх2 4тг
\d
q dq ехр iqx ехр(—z\q2)^
* is (А' \2 1 т/ д2и д2и*
-Ki(div n) — -Кл —
2 2 дх2 дх2
(9.6 а)
§9.1. Статические дислокации в смектиках
335
д2и* д2и
где —— комплексно сопряжено
дх2
дх2
1
2 J
i^i(div n)2 dx dz
К ib2
167Г „
О о
q dqexp— 2z\q dz
К ib2
32тгЛ
dq
Kib2
8Л^
(9.6 6)
где принято gmax — ±27г/£. Вышеприведенное выражение есть результат
интегрирования в верхней полуплоскости и должно быть умножено на 2.
Вклад сжатия -В
2
ди
dz
равен вкладу кривизны для каждой моды q, и энер-
гии мод складываются аддитивно. Поэтому
W.
к ib2
2А£
+ W,
-b2- + Wc,
2 £
(9.7)
где Wc есть энергия ядра, пока неизвестная. Слагаемое Bq2/2 в послед¬
нем выражении сродни найденному для трехмерных твердых тел, и оно
свидетельствует о том, что малые векторы Бюргерса предпочтительней.
До сих пор мы предполагали, что нелинейный член (ди/дх)2 в плотно¬
сти упругой энергии (5.28) мал: <с 1. Однако отношение ——-—
\ди/дг\ \ди/дг\
имеет порядок b/Х независимо от значения z внутри параболы х2 = ±4zX
(см. рис. 9.1). Следовательно, линейная теория оправдана только для
b С Л, в то время как в общем случае b ~ Л, и нелинейными членами нель¬
зя пренебрегать. К счастью, задачу нахождения дислокационного профиля
по плотности энергии (5.28) с нелинейным членом (ди/дх)2 по-прежнему
можно решить аналитически 2) (задача 9.1):
и(х, z) = 2А In
X
/ у/Х
1 +
ехр(6/4Л) — 1
2л/7Г
ехр(—t2/4) dt
ОО
(9.8)
Наиболее заметное отклонение от линейной модели имеет место при
X < Ь. Условие X < b естественно выполняется в случае холестериков,
даже для элементарных дислокаций: в крупномасштабной (coarse-grained)
модели де Жена-Любенского А = у/К~/В
v
2тс
^ЗКз/8К2 обычно мень¬
ше, чем шаг р. Дислокация b = р в холестерической текстуре отпечатков
пальцев показана на рис. 9.2. Смещение слоев достаточно хорошо описы¬
вается уравнением (9.8), что позволяет экспериментально определить А.
Качественно разница между линейным и нелинейным описанием дислока¬
ционного профиля проявляется в положении точек перегиба д2и/дх2 = 0.
Е. A. Brener and V. I. Marchenko, Phys. Rev. E 59, R4752 (1999).
336
Гл. 9. Дислокации в смектических и колончатых фазах
Согласно линейной модели точки перегиба находятся на оси х — 0, в то
время как в нелинейной модели они расположены при х < 0.
5
4
3
2
1
Jv -ум/ь лл_
■JA ■ :v;vv»;v;-:i
1 : ' уV' V/, vs
,'XV ' ss **. ,
* i V-’" • T . f ж^.-^у.^ул’.у/ * • "s , s,,, ^ <
•:. *•. v ^ ■. W' '/“v- Л ^ . ... +ib t,'.
ss. < ((( v
v • / ’ ****.» ^ c
<Y 'V. ( „
.:. . ‘w v*>
a
/w<
5
4
3
2
1
15mkm
<u
к
a
CD
g
t?
о
к
<t>
о
щ
л
X
X
Н
о<
1)
PQ
140
120 -
100 -
80 -
20
о о
•&
-G—©—©—0—0—0—©
0—0—©—0—©—О-
■G—О О—©—©—6Э©
о -е—е—в—е—своое
OOOtiiO &■' О С
—о ^ о о ^
ооееэ—е—©—©—©—©
—О О—О - 'О о
3
оошэооооэ—©—©—о о о
2
-100
-50
0
50
100
Горизонтальное положение, мкм
б
Рис. 9.2. Дислокация в текстуре «отпечатков пальцев» холестерического жидкого
кристалла с шагом р = 15 мкм (а); Дислокационный профиль, описанный нели¬
нейной теорией (9.8) с Л = 2,65 мкм в качестве подгоночного параметра. Жирная
линия отмечает точки перегиба (б), (см. Т. Ishikawa and О. D. Lavrentovich, Phys.
Rev. Е 60, R5038 (1999).)
§ 9.1. Статические дислокации в смектиках
337
Краевые дислокации с малыми векторами Бюргерса наблюдаются в тон¬
ких слоях SmA, например в тонких свободно подвешенных пленках и в го-
меотропных клиньях. Свободно подвешенная на отверстии пленка имеет на
краю отверстия мениск материи, который действует как резервуар3^. Кри¬
визна этого мениска является источником перепада лапласовского давления
Ар = 'j/R (7— поверхностное натяжение) между жидкокристаллической
материей и окружением, которое вытягивает материю из пленки к резервуа¬
ру. Этот дренаж происходит посредством движения петель краевых дисло¬
каций, из-за наличия активационного барьера легче образующихся в плен¬
ке (рис. 9.3) при высоких температурах, до тех пор, пока толщина пленки
не становится равной лишь нескольким слоям.
Рис. 9.3. Свободно подвешенная смектическая пленка с Краевой дислокацией
Гомеотропные клинья были описаны в п. 8.7.2. Дислокации имеют еди¬
ничный вектор Бюргерса (п — 1), пока их удаление от клина меньше,
чем некоторое значение г*, затем происходит переход к большим векторам
Бюргерса, которые увеличиваются с г. Расстояние между соседними дисло¬
кациями также увеличивается с г (см. рис. 9.4 и работу Наллета и Проста4)).
9.1.1.2. Большие векторы Бюргерса. Дислокации с макроскопиче¬
скими векторами Бюргерса, достаточно большими, чтобы их можно было
определить с помощью оптической поляризационной микроскопии, обна¬
руживаются как в термотропных, так и в лиотропных системах. Объясне¬
ние заключается в специфической модели ядра, которое расщеплено на две
дисклинации противоположного знака (рис. 9.5, а). Модель дает £ ~ Ь/2.
Следовательно, упругая энергия (9.7) вне ядра увеличивается пропорцио¬
нально 6, а не Ь2. Стабильность дислокаций была бы практически не за¬
висящей от величины вектора Бюргерса, если бы эта внеядерная энергия
давала главный вклад в полную энергию.
P. Pieranski et al. Physica A 194. 364 (1993).
F. Nallet andJ. Prost, Europhys. Lett. 4, 307 (1987).
338
Гл. 9. Дислокации в смектических и колончатых фазах
Рис. 9.4. Дислокации, наблюдаемые в гомеотропном клине лиотропной фазы La.
(С разрешения К. Бланка)
ь
ъ
Рис. 9.5. Расщепление ядра дислокации с большим вектором Бюргерса (а); мо¬
дель краевой дислокации с исчезающей твердотельной упругостью (6). Отметим
появление сингулярной стенки
Именно вклад ядра приводит к зависимости стабильности от вектора
Бюргерса. Согласно дисклинационной модели, представленной на рис. 9.5, а,
возрастает вклад упругости изгиба в полный баланс энергий, так как теперь
энергия ядра может быть записана в виде
Wc = ]п - - + т,
2 2d0
(9.9)
§ 9.1. Статические дислокации в смектиках
339
Энергия ядра тс двух дисклинаций Ь\ и £2 имеет порядок К\ и не зависит
от Ь. Отметим, что разность
Wc{2b) - 2WС{Ъ)
7Г К
— In
4dn
(9Л0)
отрицательна для Ь > 4do. Следовательно, разность энергий (9.10) лога¬
рифмически уменьшается с увеличением Ъ. Большие векторы Бюргерса
оказываются предпочтительней.
Так как вышеприведенные вычисления упругой энергии вне ядра про¬
изводились в приближении малых возмущений, наши заключения должны
быть справедливы, если b велико, Ъ ^ А. Действительно, как мы уже пока¬
зали в п. 5.4.2, пока характеристическая длина (роль которой теперь игра¬
ет Ъ) превышает А (т. е. практически для любого вектора Бюргерса, боль¬
шего с/о), мы ожидаем, что вклад упругого изгиба преобладает над вкладом
упругого сжатия. Полное исчезновение вклада упругого сжатия подразуме¬
вает, что слои становятся параллельными. Это достигается, как видно на
рис. 9.5, б, за счет появления сингулярной стенки. Модель, представленная
на рис. 9.5, б, есть крайний случай нелинейного дислокационного профиля,
рассмотренного выше для элементарных дислокаций при Ъ ^ А с дефект¬
ной стенкой, являющейся аналогом места расположения точек перегиба на
рис. 9.5, б.
Дисклинационная модель ядра, обосновываемая здесь энергетическими
соображениями, также имеет значение для описания холестериков
(см. рис. 9.2, а, рис, 11.17) и лиотропных кристаллов. В последних она
допускает полное разделение растворителя и бислоев (рис. 9.6). В этом
случае модель справедлива даже для малых векторов Бюргерса.
Наиболее частым проявлением краевых дислокаций с большими векто¬
рами Бюргерса являются маслянистые бороздки, нередко присутствующие
в холестериках (п. 10.7.1,11.2.5.3) и в толстых образцах гомеотропных смек¬
тиков. Согласно модели Жоржа Фриделя, маслянистые бороздки состоят
Рис. 9.6. Краевая дислокация в лиотропной фазе La
340
Гл. 9. Дислокации в смектических и колончатых фазах
из пар дислокаций (больших) противоположных векторов Бюргерса. Каж¬
дый элемент пары, вероятно, возник в результате слияния дислокаций с
малыми векторами Бюргерса одного знака (как показано выше, дислока¬
ции с большим вектором Бюргерса Ъ = ndo могут быть предпочтитель¬
ней по сравнению с дислокациями малого вектора Бюргерса n*do, ^Г, щ =
= п), возникшими при создании образца. Маслянистые бороздки являют¬
ся типичными дефектами лиотропных фаз. Специальная топология ядра
краевых дислокаций противоположного знака в этих фазах делает труд¬
ной аннигиляцию дислокаций противоположного знака даже для малых п.
Следовательно, имеет место преимущественное образование дислокаций с
большими п. Другая особенность маслянистых бороздок состоит в частом
возникновении продольной нестабильности, которая иногда даже расщеп¬
ляет бороздку на ряд конфокальных доменов; это явление будет изучено
в гл. 10.
9.1.2. Винтовая дислокация
Уравнение Эйлера - Лагранжа
т. е. винтовую дислокацию с той же конфигурацией, что и в твердом теле.
Можно легко проверить (это оставляется читателю в качестве упражнения),
что упругая энергия линии, вычисляемая с точностью до членов второго
порядка по деформациям, исчезает, но существует энергия ядра Wc. Вин¬
товые дислокации имеют, следовательно, малую энергию Ws = Wc. Они
наблюдаются в различных системах вода-ПАВ с помощью электронной
микроскопии замороженных расколотых образцов, которые легко расщеп¬
ляются вдоль границ парафиновых цепей. Винтовые дислокации прони¬
зывают поверхности раскола и создают вдоль них ступени, которые соби¬
раются в «ручьи», как в обычных кристаллах (рис. 9.7). Их также можно
наблюдать с помощью оптической поляризационной микроскопии в гомео-
тропных образцах термотропных SmA вблизи перехода в SmC5\ где они
закрепляют краевые дислокации. Наконец, дислокационные линии с ма¬
лым углом отклонения от направления вектора Бюргерса, вероятнее все¬
го, состоят из длинных сегментов чисто винтового характера, связанных
небольшими краевыми сегментами, вследствие большого линейного натя¬
жения винтовых дислокаций (см. п. 9.1.3).
Тг А 2 7-> д2и
К Д1 и = В —
(9.11)
dz2
имеет решение вида
(9.12)
R. В. Meyer, В. Stebler and S. Т. Lagerwall, Phys. Rev. Lett. 41, 1393 (1978).
§9.1. Статические дислокации в смектиках
341
4 мкм
а
б
Рис. 9.7. Винтовые дислокации, ступени и «ручьи» (rivers) на поверхности раскола
лиотропной фазы СпЕОб (с разрешения М. Allain) (а); картина раскола в ламел¬
лярном образце, где винтовая дислокация выходит на поверхность, зарождается
ступенька, удлиняющаяся по мере распространения разрыва (б)
В действительности (9.12) является точным решением задачи ми¬
нимизации плотности упругой энергии (5.12), / = -К\(divn)2 + -By2,
включающей вклады, определяемые кривизной и дилатациейЧ Это реше¬
ние, для которого div п = 0, т. е. оно представляет собой некую минималь¬
ную поверхность. Смещение и не является наиболее удобной переменной,
6) М. Kleman, Phil. Mag. 34, 79 (1976).
342
Гл. 9. Дислокации в смектических и колончатых фазах
и уравнение (9.12) лучше представить в виде
<р = -Ьв/2тх + z, (9.13)
описывающем изолированную винтовую дислокацию как линейчатый ге¬
ликоид. Здесь ip = ip(Q) — фазовая переменная, постоянная в каждом слое,
z — координата вдоль дислокации и в — полярный угол. Полагая (р = const,
немедленно убеждаемся, что этот геликоид генерируется перпендикуляр¬
ной к оси г и опирающейся на нее полупрямой, вращающейся по спирали
с постоянной угловой скоростью и шагом'& (рис. 9.8).
Рис. 9.8. Линейчатый геликоид
Свободная энергия вне ядра дислокации, исчезающая в квадратичном
приближении, при вычислении в более высоком порядке принимает следую¬
щее значение:
Ws = (- - 2Л + Wc. (9.14)
128тг3 \г2 В?) 4 }
Здесь R — внешний радиус образца. Этот результат действителен в пре¬
деле А = а/ К i /В > Ь (п. 5.5.2). Неравенство А > Ь означает также, что
§ 9. /. Статические дислокации в смектиках
343
рассматриваемые векторы Бюргерса малы, типичное значение есть b = do.
Условие Л > do хорошо выполняется вблизи перехода смектик - нематик,
так как в нематической фазе В = 0.
Вышеприведенный анализ верен, когда вектор Бюргерса достаточно
мал. Уже подчеркивалось (см. также п. 5.5.2), что как только любая харак¬
теристическая длина в геометрии образца, например 6, превышает Л, упру¬
гий вклад, связанный с дилатацией, становится преобладающим, и слои
предпочитают укладываться параллельно друг другу. Следовательно, усло¬
вие равенства нулю производной от смещения вдоль нормали к слоям,
ди/дп = 0, приближенно выполняется, в то время как условие divn =
= 0 не выполняется. Как мы увидим в следующей главе, условие ди/дп = 0
дает точную геометрию дефектов, конфокальных доменов, но оно может
приблизительно выполняться также в других геометриях, и такой геомет¬
рией является гигантская винтовая дислокация (рис. 9.9, а)7\ в противопо¬
ложность винтовой дислокации с малым вектором Бюргерса, рассмотрен¬
ной выше.
а б
Рис. 9.9. Модель укладки слоев в гигантской винтовой дислокации (а); гигантская
винтовая дислокация в термотропном смектике (б). (С разрешения К. Бланка)
Начнем с линейчатого геликоида Но с шагом р — b = ndo. Эта по¬
верхность очерчивает один из слоев винтовой дислокации. Другие слои
Нп уложены вдоль поверхностей, параллельных Но, так что ди/дп — 0.
Поверхности Нп более не являются минимальными, но они близки к та¬
ковым, потому что минимальна поверхность Я0. Другими словами, вклад
7) С. Е. Williams, Philos. Mag. 32, 313 (1975).
344
Гл. 9. Дислокации в смектических и колончатых фазах
сжимаемости в плотность своооднои энергии исчезает полностью, а вклад
кривизны остается малым.
Эта укладка может реализовываться до тех пор, пока слои физически
не сталкиваются. Более точно, так как слои Нп параллельны, их нормали
(т. е. поле директора) представляют собой прямые линии и огибают фокаль¬
ную поверхность F, состоящую из двух листов. Эта геометрическая задача
является в действительности аналогом задачи, встречающейся в геометри¬
ческой оптике: нормали — лучи света, а слои — поверхности постоянной
фазы. Два листа — это геометрическое место точек двух центров кривизны
параллельных поверхностей Н0 (все пересечения параллельных слоев Нп
с общей нормалью имеют общий центр кривизны). Поверхность F дает
естественную границу укладки Нп. В действительности, имеется по одно¬
му спиральному клювоподобному {caspidal) краю на каждом листе F, ска¬
жем Ь\ и Z/2, и эти клювоподобные края порождают две физические линии
дефектов, вокруг которых слои складываются за поверхностью F в фор¬
ме двух дисклинационныхлиний мощности к — ±1/2. Эта примечательная
мода расщепления винтовой дислокации с большим вектором Бюргерса
действительно наблюдается в термотропном SmA (см. рис. 9.9, б, где хоро¬
шо видны эти две спиральные линии L\ и Li). Еще более примечательно,
что существование таких линий можно предположить в текстурах конден¬
сированных хромосом прокариотных микроскопических морских водорос¬
лей, где ДНК является холестериком8^ Здесь слои холестерика повторяют¬
ся с периодом р/2, хромосома ограничена двойной спиральной складкой,
и вне этой области слои отсутствуют, а нити ДНК изгибаются вокруг линий
к =1/2 4
Для полного понимания вышеприведенного рассмотрения требуется
ввести концепцию виртуальной поверхности, которая проиллюстрирова¬
на на рис. 9.10 (для двумерного случая). Часть виртуальной фокальной по¬
верхности слева (справа) от излома касается нормалей к параллельным сло¬
ям, принадлежащим правой (левой) части рисунка, и пересекается слоями,
принадлежащими левой (правой) части рисунка. Эта многолистная геомет¬
рия может быть развернута в однолистную заменой сингулярной фокаль¬
ной поверхности ее срединной поверхностью, на которой левые и правые
части слоев встречаются под углом (который может быть малым). Наи¬
более сильная сингулярность, которая остается, — это излом фокальной
поверхности. Рассмотренный выше клювообразный излом, около которого
слои образуют дисклинацию с к — 1/2, как раз является сингулярностью
такого типа.
9.1.3. Линейное натяжение винтовой дислокации
Пусть, как в п. 8.4.3, г — линейное натяжение дислокации. Если при¬
нимать во внимание изменение линейной энергии W(а) с ориентацией а,
F. Livolant and Y Bouligand, Chromosoma 80, 97 (1980).
M Kleman, Physica ScriptaT19, 565 (1987).
§ 9.1. Статические дислокации в смектиках
345
Параллельные
слои
Нормали
к слоям
Виртуальная фокальная
поверхность
Сингулярная плоскость,
на которой слои имеют излом
Рис. 9.10. Схематическое представление возникновения виртуальной фокальной
поверхности в двумерном случае
линейное натяжение г может быть записано (задача 9.2) как
г
w + ?^) .
да2 / а=0
(9.15)
Для большинства твердых тел, даже сильно анизотропных, вклад
d2w
да2
мал
по сравнению с ИЛ Это не так в случае рассматриваемой здесь винтовой
дислокации. Можно показать, что поле смещений, создаваемое линией,
отклоненной от оси г на малый угол а, может быть записано как
/ \ Ь , _ 1 у — az
и{х, у, z) = —tg
27Г
(9.16)
X
Энергия на единицу длины линии есть
W(a)
ВЬ2 2. R
a In
87Г
(9.17)
следовательно
г
ВЬ2 , R
In —
47Г Гг
(9.18)
Линейное натяжение велико, вследствие чего дислокация остается пря¬
мой вдоль оси z, если к линии не приложена конфигурационная сила Fconf.
В противном случае она искривляется между точками закрепления с ра¬
диусом кривизны
(9.19)
Р
г
F,
conf
Здесь Fconf — сила на единицу длины линии.
346
Гл. 9. Дислокации в смектических и колончатых фазах
9.1.4. Напряжения в SmA и сила Пича-Келера
Для того чтобы определить поле напряжений в смектической фазе, мы
поступим так же, как в случае твердого тела. Ограничимся малыми дефор¬
мациями слоев. Тогда полную свободную энергию F можно выразить в
виде
F
fdV
^(Дхи)2*^^)2
2 2 V dz /
dV,
(9.20)
Рассматривая в качестве исходного состояние с деформацией и(г), подчи¬
няющейся уравнению Эйлера-Лагранжа, введем малое поле смещений Su,
которое увеличивает F: F F + SF, где
SF
(Кг А\и- В
д2
и
dz2
6u dV+
В— dSs - Ki — (A±u) dSi
dz dx
Кг A\u
Ki— (A±u)dS2 S- Su
dy
dSi + S
5u
dy
dS‘
(9.21)
Выражение (9.21) для добавки к свободной энергии включает:
• объемные вклады, которые в сумме зануляются вследствие уравнений
Эйлера-Лагранжа;
• поверхностные члены двух типов: поверхностные силы и поверх¬
ностные моменты сил.
9.1.4.1. Поверхностные силы. Первый поверхностный интеграл в
(9.21) представляет собой работу внешних сил при перемещении грани¬
цы на 6и. Так как поле смещений 5и может быть выбрано каким угодно,
предположим, что оно исчезает в некоторой произвольной части объема
системы. В таком случае внешние силы являются компонентами тензора
напряжений, действующего на границу оставшейся части. Следовательно,
в любой точке объема имеем
d
а
ZX
dx
zy
Ki~(A iu);
dy
a
zz
в
du
dz
(9.22)
Все другие компоненты а исчезают. Тензор напряжений не симметричен,
и его антисимметричная часть может быть выражена через моменты вра¬
щения, которые и приводят к наличию в выражении (9.21) поверхностных
членов второго типа.
Заметим, что наше определение напряжений таково, что силы на едини¬
цу площади, действующие на поверхность с внешней нормалью могут
быть записаны как fj — (JjiVi. Уравнение Эйлера-Лагранжа может быть
выражено через напряжения как
оZX,X O' zy, у Н- СГ
zz^ г
0.
(9.23)
§ 9.2. Дислокации в колончатых фазах
347
дъь ди
9.1.4.2. Поверхностные моменты сил. Таккакп = (——, — —, 1), мы
дх ду
можем записать последний интеграл в (9.21) как
К\ /\\и (5пх dS\ + 6пу dS2). (9.24)
С учетом соотношения Scv = Sn х п имеем
Snx SS\ + ёпу SS2 — Sn ■ SS — (n x dS) Su(9.25)
Отсюда поверхностные моменты сил в расчете на единицу площади, при¬
ложенные в точке поверхности с внешней нормалью v, равны
С = К\ Д^_гт х и, (9.26)
При заданном поле напряжений сила Пича-Келера равна
FPK = (Ьст) х t, (9.27)
где при вычислении Ьст нужно принимать во внимание, что b сворачивает¬
ся по первому индексу компонент тензора напряжений; t есть единичная
касательная к линии, как в (8.23).
§ 9.2. Дислокации в колончатых фазах
Колончатые гексагональные жидкие кристаллы являются двумерными
твердыми телами в плоскостях, перпендикулярных колонкам, и возможные
векторы Бюргерса принадлежат этой двумерной гексагональной решетке.
Плотность упругой свободной энергии может быть записана как
/ = 2fl (иху — Ux^xUyyy) + ^Ux'x Uviv) 2^3 (ux,zz Uy,zz) j
(9.28)
где и = (их, и у) — вектор смещения в гексагональной плоскости, иху —
= ~(их,у ~^иу, х), Ц — модуль сдвига, BL — Л + 2^ —модуль сжимаемости
и Кз есть модуль изгиба Франка. Мы предполагаем, что колонки релакси-
руют подобно двумерной жидкости, следовательно, вклада смещения uz
в плотность свободной энергии нет. Мы также предполагаем, что Vu мало,
что дает п — (—uX}ZJ —uyiZ-> 1) для директора вдоль колонки.
9.2.1. Продольные краевые дислокации в колончатых гексагональных
жидких кристаллах
Линии дислокаций, параллельных колонкам, не создают никакой из-
гибной деформации, следовательно, плотность свободной энергии в этом
случае аналогична имеющей место для двумерного твердого тела. Приме¬
нимо выражение (8.15), и линейная энергия (включающая поверхностную
348
Гл. 9. Дислокации в смектических и колончатых фазах
релаксацию
Wiong = -^Ц ( In — + - | , (9.29)
47г(1 — и)
где v — коэффициент Пуассона. Предполагая, что глубина проникновения
(Кз/ц)1/2 имеет порядок параметра решетки а, имеем оценку ц « К$/а2,
т. е. Wiong К3(Ь/а)2. Для b — а это тот же порядок, что и энергия
дисклинации, типичное значение которой составляет 0,01 эВ на молекуляр¬
ную длину £, измеренную вдоль линии (£ ~0,2 нм, а ~3 нм в термотропной
фазе). Это сравнимо с къТ при комнатной температуре, так что ожидаются
заметные энтропийные эффекты в противоположность обычным кристал¬
лам, и в конечном счете полная свободная энергия оказывается равной
W^iong (9.30)
а
становясь отрицательной при достаточно высокой температуре. Жидкий
кристалл в этой фазеа плавится благодаря размножению дефектов (см. § 4.5).
Этот процесс подобен плавлению твердых тел.
Приведенное рассмотрение, конечно, очень грубое. Оно не принимает
во внимание другие типы дислокаций (винтовые дислокации, поперечные
краевые дислокации), которые имеют совсем иную природу. Линейная энер¬
гия дислокации общего типа в колончатой фазе значительно варьируется
с изменением направления линии и включает деформацию изгиба, т. е. зави¬
сит непосредственно (не через от модуля Франка К%. Если р достаточно
мало по сравнению с А, можно ожидать, что продольные дислокации будут
иметь меньшую линейную энергию, и тогда вышеприведенные аргументы
будут верны. Если \х и А сравнимы, винтовые дислокации преобладают.
Краевые продольные дислокации во многом сродни краевым дислока¬
циям в твердых телах. Более своеобразный характер имеют поперечные
и винтовые дислокации.
9.2.2. Поперечные краевые дислокации
Для краевой дислокации, расположенной вдоль оси х и имеющей вектор
Бюргерса 6, единственным существенным смещением является иуу причем
производные иу по х равны нулю. Плотность свободной энергии записы¬
вается как
f=-(X + 2M)K,)2 + -К3(иу,гх)2, (9.31)
2 2
так что сама свободная энергия J / dV минимальна при
(А + 2^)— = К3 ^. (9.32)
' ду2 dz4
§ 9.2. Дислокации в колончатых фазах
349
Это уравнение сродни уравнению краевой дислокации в смектике. Сле¬
дуя подходу, примененному в аналогичном случае в п. 9.1.1, и используя
симметрию у —» —г/, мы запишем решение, например для у > 0, в виде
/ ч Ь Ь
иу{У> г) = т + —
4 47Г
—g(y, q) ехр igz,
щ
g(y. 9) = ехр -92г/Л3
(9.33)
(9.34)
для дислокации с вектором Бюргерса (0,6,0) и g(0, q) = 1. Здесь Лз =
= лУКз/(\ + 2//) есть глубина проникновения соответствующей изгиб-
ной деформации (ср. с Ai = yjKi/B в смектиках). Угловая деформация
записана как
uv z колонок вне дислокационного ядра (рис. 9.11) может быть
0{z)
47г(Аз2/)1/2
ехр
4 Азу
(9.35)
а
b
/
/
/
/
ь
/
/
/
/
Рис. 9.11. Поперечная краевая дислокация
Отметим, что в этом вычислении мы пренебрегли вкладом деформации
поперечного изгиба в плотность свободной энергии
/splay
-Кг
2
д2
и
У
дудг
(9.36)
Такое приближение тем более оправдано, что колонки теперь удерживаются
почти параллельно и нет свободных концов. Для колончатых фаз ожидается
К\ ЙТ3, и, как следствие, исчезновение деформации divn. Это прибли¬
жение заведомо не работает в области ядра. Добавляя /spiay в свободную
350
Гл. 9. Дислокации в смектических и колончатых фазах
энергию, получаем вместо (9.34)
g{y, я) = ехр [-д2уЛ3(1 + q2h\) 1/2
(9.37)
где Ai = \JK\j(А + 2/i) есть новая глубина проникновения (Ai Л3).
Очевидно с первого взгляда, что снаружи области |д|_1 > Ai различие
мало и выражение (9.35) справедливо. Напротив, для l^l-1 <С Ai получаем
g(y, q) = ехр - qy
Аз
Ai
(9.38)
откуда
и
У
- 4- — arctg - —
4 27г у Ai
(9.39)
Область ядра, в которой концы колонок свободны, ожидается, таким обра¬
зом, большой, порядка Ai.
По аналогии со смектическим случаем можно ожидать, что
trans
£_l
соге>
(9.40)
где £_l есть истинный размер ядра в направлении г.
9.2.3. Винтовые дислокации
Рассмотрим винтовую дислокацию, вытянутую вдоль направления х.
Существенными смещениями являются их и иу, вследствие однородности
д/дх — 0. Плотность свободной энергии записывается как
/
(А + 2(i){uy,y) -Ь и(их,у) + ~К\
А £ £
+ -к3
2
д2и
у
X
dydz
+ -К2 ' дЧ
2 V dzdy
~Ь
д2
и
х
dz2
+
д2
и
у
dz2
(9.41)
Замечаем сразу, что их и иу расцеплены. Рассмотрим вклад их. Получа¬
ем после минимизации
а2
U
X
ду
к<
дАи^ -гг дАих
dz2dy
+ К-.
dz4
(9.42)
Отметим, что можно выбрать иу = 0, так как вектор Бюргерса направлен
вдоль х: нет деформации поперечного изгиба, но имеется кручение. Вы¬
числение производится, как в предыдущем пункте, и дает
g(y, q) = ехр i -q2yA'3 (l + q2A^
1/2
(9.43)
§ 9.2. Дислокации в колончатых фазах
351
где Л2 — у/Кч!\*> и A3 = л/K^JJl. Разумно предположить, что в колон¬
чатых системах К2 К$, потому что деформация кручения не позволя¬
ет колонкам держаться параллельно и эквидистантно. Из (9.43) следует,
так же как из вышеприведенного обсуждения выражения (9.37), что кру¬
чение сконцентрировано в области ядра (рис. 9.12). Как будет показано
в гл. 11, возможной моделью твистовой гексагональной фазы, изображен¬
ной на рис. 11.14, является периодическая решетка винтовых дислокаций1
Примечательной чертой такого ядра является отсутствие на колонках
какой-либо физической сингулярности. Отметим также, что ступенька эле¬
ментарной длины на винтовой дислокации создает одну обрезанную ко¬
лонку. Появление соответствующей плотности таких ступенек на винтовых
дислокациях может быть на практике способом пластической релаксации
приложенных напряжений.
Линейная энергия дислокации имеет вид
Wscrew = ~1ЛЬ2^ + Were, (9.44)
2
где £j_ — размер ядра в направлении z.
Рис. 9.12. Винтовая дислокация в колончатой фазе. Физической сингулярности на
колонках нет
10^ R. D. Kamien and D. R. Nelson, Phys. Rev. Lett. 74, 2499 (1995).
352
Гл. 9. Дислокации в смектических и колончатых фазах
9.2.4. Свободные флуктуации продольных дислокаций
Флуктуации линии дислокации сродни образованию пар кинков, изу¬
ченному в гл. 8 (п. 8.5.2). Воспользуемся этой аналогией для описания
термически активированного скольжения. Так как дислокации различных
типов в колончатой фазе обнаруживают сильно анизотропные свойства,
соотношение энергии Udd образования пары кинков и U™, энергии пере¬
мещения кинков, в основном зависит от этой анизотропии. Например, если
ji достаточно мало, т. е. Аз = а, где а есть молекулярная
длина, мы ожидаем, что Wscrew > W\onz. При таком соотношении наибо-
-С
лее вероятна большая энергия UJdd (кинки являются сегментами винтовых
дислокаций) по сравнению с Udl. Следовательно, предел текучести для
скольжения продольных дислокаций будет «низкотемпературного» типа,
в терминах классического анализа для металлов. Однако зарождение пар
кинков есть термически активированный процесс, и мы ожидаем, что они
появляются во множестве благодаря согласованному тепловому движению
молекул и снижают сопротивление Пайерлса-Набарро. Вычисление про¬
изводится следующим образом.
Рассмотрим пару кинков длины 21, зарождающихся под действием внеш¬
него напряжения а < ар (рис. 9.13). Требуемая энергия есть разность
Минимумы
потенциала
Максимумы
потенциала ^ т ~ ^
^ ::
"-.Г—
Потенциальная энергия
как функция положения
Рис. 9.13. Термически активированное скольжение против силы
Пайерлса - Набарро
между энергиями состояний с парой кинков (зарождение которых требует
увеличения поверхности разреза на площадь порядка Ы) и прямой дисло¬
кации, т. е.
и (а) я 2Wscrew ^, (9.45)
^СГ
ГДе t(j — "^/^^screw j {о р (j).
В этом уравнении, как можно ожидать, напряжение Пайерлса ар выра¬
жается так же, как в твердом теле, см. формулу (8.39). Подставляя порядки
§9.3. Гидродинамика смектической фазы
353
величин, получаем для а = 0:
*7(0) и 2цЬ2 (^.)1/4ехр—
(1 - и)Ь
(9.46)
X- С- типичные значения £(х—о 100 нм для b « 3 нм, Аз = b и U(0) порядка
к^Т для /х ^ 107Н/м2 (108 дин/см2). Следовательно, можно ожидать, что
флуктуации продольных дислокаций в большинстве термотропных колон¬
чатых гексагональных жидких кристаллов будут свободными.
В этом параграфе развивается теория гидродинамики слегка деформи¬
рованной совершенной смектической фазы (т. е. в приближении слабых
возмущений). Затем, в §9.4 кратко описываются, без деталей, ламелляр¬
ные динамические моды (малой амплитуды). Гидродинамическая теория
далее применяется к движению краевых дислокаций с малыми векторами
Бюргерса, для которых точная модель ядра не требуется (§9.5). Сразу мож¬
но утверждать, что переползание, представляющее собой смещение дисло¬
каций в плоскости слоев перпендикулярно вектору Бюргерса, происходит
легче, чем скольжение, в противоположность случаю твердых тел. Такое по¬
ведение имеет место благодаря тому обстоятельству, что скольжение делает
необходимым разрыв слоев (особенно трудный в лиотропных смектиках), а
переползание этого не требует. Наконец, в § 9.6 рассматривается поведение
макроскопических образцов при простом сдвиге или сжатии; те немногие
эксперименты, которые были проведены, выявили интересное коллектив¬
ное движение дефектов, размножение дислокаций и нестабильности по
отношению к образованию дефектов другой природы (см. гл. 10).
Теория движения дислокаций может быть выражена либо на языке, за¬
имствованном из металловедения и использующем, тем самым, концепции,
развитые в науке о твердых материалах (таких как диффузия в случае пере¬
ползания краевых дислокаций), либо на языке гидродинамики, либо на том
и другом. То, что в описании смешиваются концепции, заимствованные из
обеих теорий, является одной из по настоящему притягательных особенно¬
стей динамики дефектов в ламеллярных фазах. Гидродинамические свой¬
ства слоистых материалов весьма примечательны. Можно различать кор¬
релированное (рис. 9.14, а, б) и некоррелированное (рис. 9.14,в, рис. 9.15)
движение молекул и слоев. В первой группе слои следуют движению мо¬
лекул, которые могут считаться составляющими обычную (анизотропную)
жидкость. Можно, следовательно, ожидать наличия трех различных вяз¬
костей ?7j_, т) и щ. Пусть v — (vx, vyi vz) есть скорость жидкости (мы
предполагаем, что жидкость слегка возмущена по отношению к идеально¬
му смектику, направление z выбрано вдоль невозмущенного директора),
§ 9.3. Гидродинамика смектической фазы
23-КЛЕМАН М.
354
Гл. 9. Дислокации в смектических и колончатых фазах
и пусть — -(vy,<s + 7) суть компоненты тензора сдвиговой скоро-
сти. Три независимых коэффициента вязкости появляются в выражениях
для компонент тензора вязкого напряжения:
®хх ^'П^-^xx'i ® уу ^VJ-Ayy, ОХу — 2,T)j_Axy:
(9.47)
v"x = 2V Axz, <?"у = Ч-nAzy, cr”z = 2щАгг.
^'x ? ^ v
6
\—
\
b-
I
I
I
I
г -
I
I
I
I
Г~
I
A A A A
LJ I J.
vz(z+dz)
I
I
1
I
4—I
к
- *
I
1
1 t
1 1
1 1
1 1
1 1
A I
I 1
II ( \
I 1 Vz(z)
I I
I I
в
Рис. 9.14. Различные типы сдвига в слоистой (ламеллярной) фазе: поле скоро¬
сти параллельно слоям, вязкость г}± (а); поле скорости с перпендикулярной слоям
компонентой vz(x, у), г) (б); поле скорости, перпендикулярное слоям, щ (в)
Вообще говоря, следовало бы рассматривать пять коэффициентов вяз¬
кости. Однако их число сводится к трем, если предположить (для чего есть
основания), что смектическая жидкость несжимаема.
Рисунок 9.14 представляет два типа «коррелированных» сдвигов. На
рис. 9.14,а поле скорости (vx,vy) параллельно слоям, и слоистая среда
течет во многом как обычная жидкость. Слои, в целом, сохраняют свое по¬
ложение в пространстве и легко скользят один по другому. Соответствую¬
щая вязкость г)_l, как ожидается, мала. На рис. 9.14,6 показана слоистая
§ 9.3. Гидродинамика смектической фазы
355
конфигурация, вовлеченная в движение, контролируемое вязкостью г]. Слу¬
чай с вязкостью щ, иллюстрируемый рис. 9.14,в, несколько более сложен.
Он реализуется, если dvz/dz ф 0, но вследствие условия несжимаемости
div v — 0 отличны от нуля vZ: vy, т. е. имеется связь с другими вязкостями.
Вообще говоря, такой поток будет значительно изменять толщину слоев,
если слои и молекулы движутся сообща. Однако большое изменение тол¬
щины слоев энергетически невыгодно. Следовательно, ожидается, что этот
тип движения связан с потоком материи сквозь слои или, эквивалентно,
с движением слоев сквозь жидкость (рис. 9.14, в), что напоминает (тер¬
мически активированную) диффузию вакансий и межузельных атомов в
кристаллах.
Движение жидкости сквозь слои называется просачиванием1 Ч Из об¬
щих соображений ожидается, что щ велико по сравнению с т] иг/i.
Очень простое «некоррелированное» движение молекул и слоев выгля¬
дит так. Предположим, что слои фиксированы в пространстве и что пер¬
пендикулярно к ним приложен градиент давления др/дг. Возникает слабое
течение сквозь слои со скоростью
где Ар есть так называемая константа просачивания. По размерности
для движения молекул перпендикулярно слоям, и а есть длина, сравнимая
с квадратным корнем из площади пересечения молекул с двухслойной по¬
верхностью. В действительности, просачивание есть медленный процесс,
как мы покажем ниже, и любое движение, рассматриваемое на временах
rq < 1/(АpBq2) , где q~l есть характеристическая длина движения, не
относится к этому типу (задача 9.3). В любом реальном движении суще¬
ствуют коррелированные и некоррелированные процессы в соответствии
с изучаемыми пространственными и временными масштабами.
Разовьем эти понятия. Имеются две существенные скорости.
1. Скорость v молекул, которая удовлетворяет закону сохранения:
в отсутствие дилатации.
Основополагающее уравнение, выражающее сохранение импульса, бы-
(9.48)
Ар ~ а2т]р 1, где, как ожидается, г)р должна быть (большой) вязкостью
div v — О
(9.49)
ло выведено Мартином и др.121 Оно может быть записано как
р— = — Vp -f div o' + div сг".
dt
(9.50)
u) W. Helfrich. Phys. Rev. Lett. 23, 372 (1969).
12^ P. Martin, O. Parodi and P. Pershan. Phys. Rev. A6, 2401 (1972).
356
Гл. 9. Дислокации в смектических и колончатых фазах
Величины, фигурирующие в правой части этого уравнения, имеют следую¬
щий смысл:
а) а' есть тензор упругих напряжений, создаваемых деформированны¬
ми слоями согласно уравнениям (9.22). Величина div сг', которая является
действующей на слои возвращающей силой в расчете на единицу объема
и исчезает в покое, равна
div о> = fo, О, В— - KV^u) . (9.51)
V dz2 /
Введем обозначение
В— - KV4,u = g.
dz2 х
б) а есть тензор вязких напряжений, который можно принять сим¬
метричным, так как кручение уже присутствует в а'. Векторная величина
div а" представляет собой силу трения на единицу объема.
в) р — это давление.
2. Скорость слоев (0, 0, й), направленная в принятой здесь картине ма¬
лых возмущений вдоль нормали к невозмущенным слоям. Относительная
скорость й — vz сопряжена с д, следовательно, источник энтропии может
быть записан как
Tcrirr = о"А + g(ii - vz), (9.52)
где, простоты ради, мы опустили транспортные вклады, подобные нагреву
электрическим полем. Получаем
®а(3 ” ^■otfi'ydA'y 6) ^ Vz — Apg. (9.53)
Тензор Ла/з7£ сводится к трем независимым коэффициентам вязкости,
определенным соотношениями (9.47). Второе уравнение в (9.53) легко при¬
водится к (9.48), если слои удерживаются фиксированными, поток стацио¬
нарен, а вязкие напряжения пренебрежимо малы. Уравнение (9.48) анало¬
гично закону Дарси для пористой среды, который утверждает, что скорость
жидкости пропорциональна перепаду давления (см. п. 7.4.1). В этом случае
смектическая фаза выступает как свой собственный фильтр.
С микроскопической точки зрения коэффициент просачивания связан
с активационным переходом молекул из одного слоя в другой. Применим
к этому процессу закон Эйнштейна (8.53). Сила, действующая на молекулу,
есть gujm, где сот — a2 do — молекулярный объем. Отсюда
u-vz = -~guJm = a pg, (9.54)
/сБГ
так что
Ар = (9.55)
kT
§ 9.3. Гидродинамика смектической фазы 357
где Dи есть коэффициент диффузии молекул сквозь слои.. Коэффициент
просачивания может быть измерен в экспериментах по наблюдению по¬
движности краевых дислокаций (см. ниже). Следующий мысленный экс¬
перимент, при котором слои жестко закреплены перпендикулярно стенкам
цилиндрического капилляра радиуса L и подвержены воздействию посто¬
янного градиента давления р1 — др/дх, также, в принципе* позволяет из¬
мерить коэффициент просачивания (рис. 9.15). Поток предполагается по¬
стоянным и слои фиксированы, так что й — 0. Уравнение Навье-Стокса
(9.50) с пом о шью соотношения (9.54) может быть записана как
v
X
V
р' + п
д2
V
дх2
о
(9.56)
XIX
Р+¥*г
Az
р
А
dz
▼
Рис. 9.15. Мысленный эксперимент по измерению Хр
Уравнение (9.56) есть не что иное, как обобщение соотношения (9.48) на
случай, когда слои не остаются плоскими. Мы ищем решение, не завися¬
щее от координаты z (следовательно, член щд2vz jдz1 в уравнении (9.56)
не появляется). Этим решением будет
v
р'Хр (1 -
ch хх
ch xL
)
(9.57)
где ус 2 — Xprj. Заметим, что величина х 1 фигурирует здесь в качестве
толщины граничного слоя (см. рис. 9.15 и работу Кларка13^).
13) N. A. Clark. Phys. Rev. Lett. 40, 1663 (1978).
358
Гл. 9. Дислокации в смектических и колончатых фазах
§ 9.4. Динамические моды в смектиках
В смектиках существует шесть мод, т. е. одной модой больше, чем в изо¬
тропной жидкости. Эта добавочная мода есть фаза слоев. Большие пово¬
роты директора исключены в этой модели, использующей приближение
малых возмущений для свободной энергии (см. учебник де Жена и Про¬
ста).
• Четыре Р-моды:
cj = ±ci<7 — первый звук, связанный с вариацией плотности р\ фазо¬
вая скорость Сх = у/А/р\
и = ±c2q — второй звук, относящийся к вариации толщины слоев
при постоянной плотности р; с2 — у/В/р sin ф cos ф, где ф есть угол
между направлением q = (q cos ф, q sin ф) и слоем. А и В — упругие
модули.
• Две D-моды:
и = -ixthq2 — теплопроводность;
и = — ivq2 — поперечная сдвиговая мода.
Две ситуации, в которых вектор q либо параллелен, либо перпендику¬
лярен слоям, являются особыми, потому что для этих значений ф две анизо¬
тропные распространяющиеся (Р) моды исчезают. Шесть мод заменяются
в этом случае следующими модами.
1) — Направление q перпендикулярно директору (параллельно слоям):
а) две Р-моды:
сj = ±ciq± — первый звук.
б) четыре D-моды:
to = -i—q2± — волнообразное движение слоев, напоминающее мед-
ленную моду в нематике (задача 9.4),
to — —ixtkq2 — теплопроводность, связанная со звуковой модой,
и; = —ii/q2 — поперечная сдвиговая мода,
и) — ~iv'q^ — продольная сдвиговая мода, связанная со звуковой модой
t *7
V^V ОС
р
2) Направление q параллельно директору:
а) две Р-моды:
UJ — —
=*= ciQ\ \ — первый звук; с\ — у/ А/р.
§ 9.5. Движение изолированных дислокаций в SmA-фазе
359
б) четыре D моды:
CJ
со
iBXpq2| — мода просачивания (задача 9.3),
iKXthQu — теплопроводность, связанная со звуковой модой,
и) — —
ivq^
поперечная сдвиговая мода:
IV
2
gjj — продольная сдвиговая мода, связанная со звуковой модой
§ 9.5. Движение изолированных дислокаций в SmA-фазе
и
это полное (за исключе-
9.5.1. Краевая дислокация
9.5.1.1. Переползание. Пусть и — о1 4- а
нием собственного) напряжение, в поле которого находится краевая дисло¬
кация. Действующая сила Пича-Келера согласно уравнению (9.27) равна
F — h(azytz &zztyi ®zz^x &zytxi &zxty Gzy^x)’ Мы будем предпо¬
лагать, что дислокация ориентирована вдоль оси у (tx = 0Т ty = 1, tz = 0).
Рассмотрим следующую простую модель14) (см. рис. 9.16), в которой
дислокация символизируется полубесконечной жесткой пластиной исчезаю¬
щей толщины, движущейся со скоростью — V в смектическом образце,
х
Рис. 9.16. Модель переползания краевой дислокации
покоящемся на бесконечности, или, эквивалентно, пластину, покоящуюся
в смектическом образце, движущемся со скоростью + V на бесконечности.
Вдоль пластины образуется граничный слой толщины <5(ж), и мы будем
в дальнейшем предполагать, что <5(+оо) = Ь/2, Тремя уравнениями, опи¬
сывающими рассматриваемую задачу, являются: закон Дарси, уравнение
Навье-Стокса и уравнение непрерывности. Слои предполагаются фикси¬
рованными, а молекулы проникают сквозь них (й = 0). Поэтому можно
ожидать выполнения соотношений
vz=Xp~, vzx = VS, (9.58)
ОХ о2
14^ Orsay Group on Liquid Crystals, J. de Physique 36, С1-305 (1975).
360 Гл. 9. Дислокации в смектических и колончатых фазах
где мы ограничиваем себя порядками величин различных переменных. Эти
уравнения дают 82{х) ~ х~1х, т. е. 4х
ваемое пластиной с каждой стороны, есть
max
хсг. Полное трение, испыты-
X
max
axz
О
S(x)
dx ~ rjxbV.
(9.59)
Эта сила трения уравновешивается силой Пича-Келера bazz. Отсюда на¬
ходим, что подвижность дислокации т
ся как
V/a
к 1 / (277) оценивает-
ZZ
т ~ Ар>с ~ (Лрг) х)
1\1/2
Т>\\oj
m
k^T do
(9.60)
Такое выражение для подвижности применялось в двух вариантах изме¬
рений коэффициента просачивания (задача 9.6) в клиньях Гранжана-Кано
с гомеотропными граничными условиями: либо при измерении времени от¬
жига образца из наиболее неупорядоченного состояния в состояние с един¬
ственной границей15), либо при измерениии времени релаксации тс меж-
зеренной границы, движущейся под действием напряжения afzz (см. ниже
выражение (9.66)). Типичным значением оказывается Хр ~ 10-13 см2/пуаз
в термотропном SmA, в котором 77 ~ 1 пуаз. Это значение находится в согла¬
сии с величиной Z}||, измеренной с использованием ЯМР или квазиупругого
рассеяния нейтронов1 Ч
Вышеприведенное выражение для подвижности (9.60) не зависит от
вектора Бюргерса Ъ. Отметим, что закон Дарси (первое соотношение в (9.58))
получен из г-компоненты уравнений Навье-Стокса в предположении, что
вклад вязких напряжений мал по сравнению с вкладом градиента давления
dp/dz. Простое вычисление показывает, что это предположение эквива¬
лентно неравенству 6 < х, т. е. х > . Следовательно, расчет непри¬
меним вблизи ядра дислокации. Но эта область в точности та, где имеет
место диффузия молекул от дислокации, и это главный эффект, рассматри¬
ваемый в модели подвижности дефекта в металловедении. Пусть vm есть
скорость молекул, диффундирующих из одного слоя в другой. Согласно
соотношению Эйнштейна (8.53) vm может быть записано как
v
771
■^j | fm
къТ
(9.61)
где fm есть сила, действующая на молекулы вследствие приложения на¬
пряжения azz. По порядку величины fm ~ ozza2. Так как скорость V
дислокации связана с vm соотношением сохранения потока Vb = vma,
15^ W.K. Chan and W. W. Webb, J. de Physique 42, 1007 (1981).
16) G. T. Kruger, Phys. Rep. 8, 231 (1982).
§ 9.5. Движение изолированных дислокаций в SmA-фазе
361
получаем
т = — =* “Ъа?- = (9.62)
°zz Ь к%Т Ь къТ d0
Это выражение сродни оценке (9.60), отличаясь лишь наличием фактора
а/6, учитывающего вектор Бюргерса. Разница несущественна для малых
векторов Бюргерса, но эффект ядра становится значительным для боль¬
ших Ь.
9.5.1.2. Скольжение. Как уже утверждалось, скольжение происходит
труднее, чем переползание. Элементарные краевые дислокации при движе¬
нии изменяют конфигурацию ядра от изображенной на рис. 9.17, а к изобра¬
женной на рис. 9.17, в через энергетически отличающуюся промежуточную
конфигурацию. Скольжение требует разрыва слоев, в то время как для пе¬
реползания нужна диффузия или просачивание, в жидкости два последних
процесса происходят легко. Энергия, участвующая в разрыве слоя в ламел¬
лярной фазе, может быть оценена в термотропной фазе с использованием
аргументов, подобных примененным Френкелем для вычисления напряже¬
ния сдвига в твердых телах (см. гл. 8 и книгу: Фридель Ж.. Дислокации,
гл. 5). Это приводит к напряжению разрыва ар ~ К do/а3 и к активацион¬
ной энергии Пайерлса - Набарро порядка Kdl/a2 на единицу длины линии.
Следовательно, «быстрое» скольжение, т. е. скольжение без термической
активации, требует силы Пича-Келера, действующей на дислокацию, по
меньшей мере порядка Fc = К do/а2 и В do.
а
б
в
Рис. 9.17. Дислокации в соседних потенциальных ямах (а) и (в). Промежуточное
состояние (б)
362
Гл. 9. Дислокации в смектических и колончатых фазах
Предшествующее рассмотрение предполагало, что линия движется це¬
ликом параллельно самой себе. Но скольжение дислокаций с малым векто¬
ром Бюргерса может также происходить активируемыми прыжками конеч¬
ных сегментов дислокационной линии (кинков винтового характера) меж¬
ду эквивалентными конфигурациями низкой энергии. Краевые дислокации
с большими векторами Бюргерса, ядра которых расщеплены на две дискли¬
нации, не должны быть подвижны иначе как под действием относительно
высоких напряжений. Их движение подразумевает движение дисклинаций,
которое не может происходить без рождения и аннигиляции элементарных
краевых дислокаций, т. е., в данном случае, без обмена такими дислока¬
циями между двумя дисклинациями. Наконец, в лиотропных кристаллах
скольжение может быть результатом сложного взаимодействия между мем¬
бранами, включая образование перемычек под действием напряжения.
9.5.2. Винтовая дислокация
Поле скоростей и структура слоев винтовой дислокации, ориентиро¬
ванной, например, вдоль оси г и движущейся с постоянной скоростью
перпендикулярно винтовой оси, были вычислены путем решения гидро¬
динамических уравнений17^. Согласно Плейнеру, такое движение не вовле¬
кает диффузию молекул, если только дислокация не осциллирует. Более
того, просачиванием можно пренебречь, и молекулы текут внутри слоев,
приобретая малую z-компоненту скорости вследствие винтовой геометрии.
Движению противодействуют: а) сила торможения F^r, подобная силе, дей¬
ствующей в простой жидкости на твердый цилиндр радиуса гс (радиус ядра)
(эта сила дается формулой Осеена, приведенной ниже), и б) сила трения
F*c, специфическая для винтовой структуры:
Ft = 1 4ЭТ7?Х l/ Re , (9.63 а)
7 _ 1п —
2 4
= <9-636)
47Г^
где 7 = 0,577... — постоянная Эйлера и Re — pTcV/v± — число Рей¬
нольдса потока. Формула Осеена (и вся теория движения винтовой дисло¬
кации) справедлива для малых чисел Рейнольдса, т. е. для довольно малых
скоростей V < rj±rcf р. Гидродинамическая величина радиуса ядра гс счи¬
тается большей, чем его величина в покое.
Винтовая дислокация в сдвиговом потоке а"у = 777 со скоростью сдви¬
га 7 испытывает силу Пича- Келера FPK = (bcr"y, 0, 0) = (6777, 0, 0),
перпендикулярную плоскости сдвига у z. Она приобретает, следовательно,
А
скорость V вдоль х, вычисляемую из баланса сил и Fx — F£c + F£r.
17) Н Pleiner, Phil. Mag. A 54, 421 (1986).
§ 9.6. Коллективное поведение дислокаций и нестабильности
363
Эта скорость мала по сравнению с любой скоростью vy ~ jd, связанной
со сдвигом, где d есть характерный размер образца. В результате дислокация
тоже вытягивается вдоль направления сдвига, оставаясь прикрепленной
своими концами к границам образца.
§ 9.6. Коллективное поведение дислокаций
и нестабильности
9.6.1. Общие замечания
Несколько экспериментов, часть которых детально описана ниже, про¬
демонстрировали переползание краевых дислокаций в смектиках А и роль
винтовых дислокаций. Наблюдаемые явления остаются довольно просты¬
ми до тех пор, пока: а) используются хорошо ориентированные образцы
и б) напряжения не слишком велики (по сравнению, например, с Bdo/L,
где L есть характерный макроскопический размер образца). При быстро
меняющихся напряжениях часто наблюдаются неустойчивости. Например,
линейная волнистость, изученная в п. 5.5.1, переходит в краевые дисло¬
кации, переползание которых способствует релаксации приложенных на-
пряжений181 А при более высоких напряжениях появляются конфокальные
домены, иногда в виде регулярных картин, чаще всего в нерегулярном рас¬
положении; конфокальные домены будут рассмотрены в следующей главе.
В нескольких случаях наблюдалось коллективное скольжение краевых
дислокаций, приводящее к большим неустойчивостям и образованию кон¬
фокальных доменов (также см. следующую главу).
Смектики В (SmB) являются трехмерными упорядоченными твердыми
телами, характеризуемыми слабой связью между слоями и, следовательно,
большой анизотропией вязкоупругих постоянных. Их пластические свой¬
ства могут обсуждаться во многом на языке чисто металловедческих кон¬
цепций, по крайней мере когда речь идет о простой геометрии. Например,
в смектической В фазе бутилоксибензилиденанилина (называемом также
40.8) для объяснения ползучести под действием сжимающих напряжений
<jzz привлекается активированная диффузия вакансий. Под действием по¬
стоянного сдвигового напряжения а, приложенного параллельно слоям, тот
же самый SmB обнаруживает также стационарную ползучесть19)
j = j ехр — ехр , (9.64)
khT къТ
которая интерпретировалась как результат активированного скольжения ба¬
зисных дислокационных линий (параллельных слоям и с вектором Бюргер¬
са (50, принадлежащим двумерной гексагональной решетке слоев, S0 есть па¬
раметр решетки внутри слоев SmB), пересекающих «лес» дислокационных
18^ R. Bartolino and G. Durand, Phys. Rev. Lett 39, 1346 (1977).
19) P. Oswald, J. Physique 46, 1255 (1985).
364
Гл. 9. Дислокации в смектических и колончатых фазах
линий, перпендикулярных слоям. Величина U есть активационная энер¬
гия, необходимая для перерезания «дерева», а сгП — это работа напряже¬
ния в одном элементарном прыжке базисной дислокации от одного дерева
к следующему. Активационный объем ft велик (~ 105 молекулярных объ¬
емов). Он равен О = LSodo, где L есть среднее расстояние между двумя
соседними деревьями. Однако из-за того что в SmB часто наблюдаются
дефекты упаковки, разумно предполагать, что базисные дислокации рас¬
щеплены на частичные, разделенные расстоянием 1$. Все эти рассуждения
типичны для описания (двумерного) твердого тела. Следует также иметь
в виду, что вся тема пластической деформации «упорядоченных» смектиков
все еще пребывает в начальной стадии развития, и мы не будем настаивать
на справедливости приводимых рассмотрений.
9.6.2. Коллективное переползание дислокаций в SmA20)
Мы рассмотрим клин Гранжана-Кано с углом а (см. п. (8.5) при го-
меотропных граничных условиях. В срединной плоскости находится гра¬
ница наклона, образованная краевыми дислокациями, разделенными рас¬
стоянием I = Ь/а. Будем предполагать, что дислокации элементарны (6 =
= do) и клин идеален в том смысле, что в нем нет других дефектов. Под
действием сжимающего напряжения сг0 = 033 дислокации согласованно
переползают, чтобы дать напряжению отрелаксировать. Дислокации пере¬
ползают вправо или влево в соответствии с направлением, вдоль которого
слои добавляются или устраняются. Пусть х есть смещение дислокации.
Тогда имеем
сг = а0 — —ах. (9.65)
L
Здесь L толщина образца. Так как угол а очень мал (обычно 10 ~3 рад), мож¬
но пренебречь изменением толщины образца. Пусть v — та есть скорость
дислокации: v — dx/dt. Поэтому
a(t) = сг0ехр — £/тс, тс = L/mBa. (9.66)
Эти уравнения действительны до тех пор, пока напряжения достаточно ма¬
лы и дислокации движутся параллельно друг другу. Такие эксперименты
определяют величины В(= Lao/do) и ш, т. е. либо коэффициент само-
диффузии, либо коэффициент просачивания. Температурная зависимость
m ~ ехр (—U/къТ) дает энергию активации самодиффузии.
При достаточно высоких напряжениях, выше некоторого напряжения
течения егс21) с типичной величиной порядка 10~5£, т. е. довольно малого,
образец деформируется с экспоненциально нарастающей скоростью дефор¬
мации ё — ёо ехр (t/т), где т уже не равно тс, а ведет себя более сложным
20^ P. Oswald and М. Kleman, J. Physique Lett. 45, L319 (1984).
21) Впервые отмечено в работе R. Bartolino and G. Durand , Mol. Cryst. Liq. Cryst.
40, 117(1977).
§ 9.6. Коллективное поведение дислокаций и нестабильности
365
образом (см. п. 9.6.3). Простейшая интерпретация экспоненциального ро¬
ста ё заключается в том, что плотность дислокаций, первоначально равная
ро = а/Ь, увеличивается со временем. Из простых геометрических сооб¬
ражений следует (см. задачу 9.7), что скорость деформации ё изменяет¬
ся как
pbv.
(9.67)
Это выражение, связывающее скорость деформации с плотностью движу¬
щихся дислокаций и их скоростью, известно как соотношение Орована.
Так как v = тег и Ъ постоянны, только увеличение р может объяснить
экспоненциальное поведение.
До сих пор не было произведено систематического изучения сгс, что мо¬
жет быть связано с затруднениями из-за зарождения дефектов на свободных
границах.
9.6.3. Размножение краевых дислокаций
Эксперимент показывает, что время релаксации т (ё = ёо ехр (t/r), вве¬
денное в предыдущем параграфе, изменяется последовательными скачками
при увеличении приложенного напряжения. Обозначим порядковый номер
прыжка через р. Прыжки могут характеризоваться двумя величинами:
1) числом слоев Np = pNi, вовлеченных в прыжок р, Np пропорцио¬
нально р;
2) временем релаксации 1/т = 1/тс + 1/тр, где гр ~ р
-1
Эти результаты были объяснены на основе нестабильности винтовой
дислокационной линии, которая принимает геликоидальную форму под
действием сжимающей (или расширяющей) деформации у = SL/L
(рис. 9.18). Геликоидальная форма соответствует устранению (при сжатии)
или добавлению (при расширении) лишнего слоя на площади 7гг2, ограни¬
ченной цилиндром, в который вписана линия геликоида, заданная уравне¬
нием z = 1/0/27гр. Шаг есть L/р, ив образце толщины L укладывается р
▼
7
а
б
Рис. 9.18. Геликоидальная нестабильность винтовой дислокационной линии при
сжатии
366
Гл. 9. Дислокации в смектических и колончатых фазах
оборотов на 27г. Хиральность спирали зависит от знаков деформации 7
и вектора Бюргерса Ь. Нестабильность была проанализирована в статиче¬
ском пределе22^.
Задача 9.1. Используя плотность энергии (5.28) с сохраненным
нелинейным слагаемым (ди/дх)2, покажите, что выражение (9.8) описы¬
вает профиль и(х, z) краевой дислокации с вектором Бюргерса Ь.
Ответ. Варьирование свободной энергии (см. работу2))
1
В [du/dz — (ди/дх)2/2]2 + К (д2и/дх2)
приводит к уравнению Эйлера - Лагранжа А д*и - д2и + 2 (д%)дгдхи 4-
-f- (d%u)dzu - !(3^)2<92u = 0. Выражая все длины в единицах А = yjK/B
и предполагая, что поле смещений и(х, г) зависит только от одной пере¬
менной v — х/л/z, приходим к дифференциальному уравнению для поля
деформации (f = du/dv
tfl V2 / . 2 I З'У / , 3 2 / /Г\ ТЛ 1 \
р -~(р 4- —{р + (р + —(pip + -ip р . (9.Р1)
4 4 2 2
Замечая, что (9.Р1) удовлетворяется при ip' = ~-(v(p + (^?2), находим
общее решение
_ 2ехр(—у2/А)
J ехр( —t2/4) dt + С
— ОО
с постоянной интегрирования С, определяемой из условия и(х оо)
ОО
и (я -00) = J ipdv = Ь/2. Восстанавливая первоначальные пере-
ОО
менные, получаем выражение (9.8).
Задача 9.2. Докажите соотношение (9.15).
Ответ. Рассмотрим сегмент винтовой дислокационной линии дли¬
ны £ с энергией £W(a)a=о, ориентированный вдоль оси z. Флуктуация
Z — 1
этого элемента меняет его длину на £ + 8£ и энергию на j W (a) ds,
2=0
где ds « dz( 1 + ot2/2), т. е. (5£ = - J а2 dz. Среднее значение флуктуации
есть (а) = 0, так что J a dz = 0. По определению линейного натяжения
z—t
тё£ = J W(a) ds — £W(0). Достаточно разложить W(а) в ряд Тейлора
z-о
22^ Я Oswald and М. Kleman, J. Physique Lett. 45, L-319(1984); L. Bourdon. M. Kleman,
Lejcek and D. Taupin, J. Physique 42, 261 (1981).
§ 9.6. Коллективное поведение дислокаций и нестабильности 367
около а = 0 и получить
(\*т( ^ 1 d2W(a),
т = (W{a) + -_i-i)a=0.
aar
Задача 9.3. В режиме чистого просачивания (т.е. когда vz = 0)
и в предположении, что смещение слоев и(г, £) одномерно (ди/дх =
= ди/ду — 0), покажите, что u(г, t) подчинено простому диффузионному
закону с коэффициентом диффузии Dj_ = ВХр. Каково типичное время
релаксации для просачивания флуктуаций с длиной волны
д2и
Ответ. Согласно уравнению (9.53) мы имеем: й = Apg и g — В —.
dz2
д2и
Отсюда й = АРВ —. Это выражение имеет форму уравнения диффузии
dz2
для смещения слоев с = ВАр. Характеристическое время просачивания
есть D± q z =
XpBq
Задача 9.4. Докажите, что волнистая мода слоев, напоминающая
медленную моду в нематиках, релаксирует с частотой и = —iKq\/rj.
Ответ. Рассмотрим моду и = uoexpi(qx — ut). Уравнения (9.53)
и (9.50) могут быть записаны как g = —KqAu = \~1(й — vz) и pvz =
— ^.1jq2Vz g Пренебрегая инерциальным членом (так как число Рей¬
нольдса мало) и более высокими степенями q (предполагая, что длина вол¬
ны велика по сравнению с микроскопическими размерами), получаем после
устранения vz\ г]й + Kq2u = 0.
Задача 9.5. Докажите (9.66) (вычислив время релаксации).
Задача 9.6. Покажите, что подвижность для переползания краевой
дислокации с малым вектором Бюргерса контролируется просачиванием.
Ответ. Начнем с модели дислокационной подвижности, рассмот¬
ренной в п. 9.5.1. Согласно результатам задачи 9.3 релаксационная частота
просачивания есть ~ АрВх/х, если принять, что q\\(ж) ~ 1/8(х). Мате¬
рия, переносимая просачиванием вдоль центрального слоя (представляемо¬
го здесь пластиной бесконечно малой толщины), диффундирует вдоль этого
слоя с релаксационной частотой cjdiff(^) ~ v/(Px2)' Это уравнение получе¬
но из выражения для поперечной сдвиговой моды (см. § 9.4) с q±(x) ~ 1/х.
Легко увидеть, что использование разумных экспериментальных значений
констант (например, г? « ОД пуаз, х"1 и 5 • 10“7 см, В и 107 дин/см2)
ПРИВОДИТ К > 1.
Задача 9.7. Докажите соотношение Орована23) (9.67) для скольже¬
ния и для переползания.
23'> Е. Orowan, Nature 149, 643 (1942).
368
Гл. 9. Дислокации в смектических и колончатых фазах
Ответ. Рассмотрим элемент вещества в виде параллелепипеда, под¬
верженного простой сдвиговой деформации exz ~ Vx/L в плоскости ху
(рис. 9.19, а) или сжатию (растяжению) вдоль направления z: ez — Vz/D
(рис. 9.19, б). Считаем, что образец реагирует на эти действия только дви¬
жением дислокаций (пластическая деформация).
Скольжение. Дислокации с вектором Бюргерсаb = (b, 0, 0) распо¬
ложены, например, вдоль направления у. При каждом смещении дислока¬
ции на Ах средняя сдвиговая деформация элемента вещества изменяется
на величину A^tot — pbAx. Если N — pDL дислокаций (с плотностью р)
сдвигаются на одно и то же расстояние за одно и то же время, средняя
сдвиговая деформация есть A^tot = pbAx, и она отвечает скорости сдви¬
га exz = dAstot/dt. Формула Орована получена для случая медленного
изменения плотности дефектов.
Переползание. Дислокации с вектором Бюргерсаb = (6, 0, 0) рас¬
положены, например, вдоль направления у в плоскости yz. Смещение дис¬
локаций в плоскости ху требует диффузионного движения молекул к дис¬
локациям или от них. Эти молекулы поставляются (или захватываются)
либо на большом масштабе (например, на границах), либо за счет встреч¬
ного движения другой дислокациц. Второй случай определенно встречается
в трехмерных твердых телах, в то время как первый случай осуществляется
в ламеллярных фазах. В обоих случаях полное количество вещества посто¬
янно и полная дилатация отсутствует, как это и должно быть при чисто
сдвиговой деформации (ех + еу + ez — 0). Получаем окончательно, если
дислокации не размножаются, что ~ pbv.
1. J. Friedel. Dislocations. Pergamon, New York, 1954; J. de Physique C3-40, 45
(1979). [Перевод: Ж. Фридель. Дислокации. —М.: Мир, 1967. — 643 с.]
2. P. S. Pershan. J. Appl. Phys. 45, 1590 (1974).
3. R. Holyst and P. Oswald. Int. J. Mod. Phys. B9, 1515 (1995).
4. J.-P Poirier. Plasticite a haute temperature des solides cristallins, Eyrolles, Paris,
Рис. 9.19. См. задачу 9.7
Литература для дальнейшего чтения
1976.
ГЛАВА 10
ДЕФЕКТЫ КРИВИЗНЫ В СМЕКТИКАХ
И КОЛОНЧАТЫХ ФАЗАХ
Как смектики A (SmA), так и колончатые фазы обладают дискретной
симметрией параллельных переносов (трансляций) (в SmA имеется од¬
но направление таких переносов, в колончатых фазах — два). Вот поче¬
му в этих фазах обнаруживаются дислокации, т. е. дефекты, нарушающие
трансляционную симметрию. Дефекты, включающие другие виды нару¬
шения симметрии, также могут существовать; например, дисклинации или
топологические особые точки, нарушающие поворотную симметрию.
Дислокации сопровождаются протяженными полями деформаций, опи¬
сание которых (см. две предыдущие главы) зависит от конкретных значений
упругих постоянных и, таким образом, изменяется от материала к материа¬
лу. Однако бывают случаи, для которых искажения на больших расстоя¬
ниях практически не зависят от материала, например, когда дислокации
одного знака собираются в стенку (это хорошо известно для трехмерных
кристаллов, см. гл. 8) или в ситуациях, где работает только кривизна. Этот
последний случай тем более важен для смектиков и колончатых фаз, по¬
скольку эти фазы подобны жидкости в одном или в двух измерениях. Ценой
небольшого проигрыша в энергии слои в фазе SmA могут принимать любую
форму при постоянной плотности и толщине. Похожим образом колонки,
например дискотической гексагональной фазы, могут изгибаться при по¬
стоянной плотности. В обоих случаях мы интересуемся текстурами, в ко¬
торых локальный порядок сохраняется, т. е. слои или колонки сохраняют
эквидистантность, когда подвергаются искривлению или изгибу. Постав¬
ленная таким образом задача приобретает чисто геометрический характер
и имеет решения с нульмерными (точки), одномерными (линии) или дву¬
мерными (стенки) сингулярностями. Решение для смектиков уже известно
в течение более восьмидесяти лет и заключается в так называемых кон¬
фокальных доменах, набор одномерных особенностей которых состоит из
пары сопряженных конических сечений11 Колончатые фазы были иссле¬
дованы сравнительно недавно: одномерная особенность так называемых
развертывающихся доменов представляет собой заостренный край развер¬
тывающейся поверхности.
§ 10.1. Кривизна в твердых кристаллах
Кривизна как одна из типичных мод деформации была впервые
введена для твердых кристаллов2^ и имеет отношение главным образом
^ G. Friedei, Annales de Physique Fr. 18, 273 (1922).
2) J. F. Nye, Acta Met. 1, 153 (1953).
370
Гл. 10. Дефекты кривизны в смектиках и колончатых фазах
к геометрии. Решетка Бравэ трехмерного кристалла задается тройкой векто¬
ров а, Ь, с, которую можно деформировать двумя способами: изменяя углы
между направлениями а, Ь, с и разрешая изменяться их длинам | а |, | b
Такие деформации можно выразить посредством тензора малых деформа¬
ций eij. Предположим для простоты, что локальная тройка векторов явля¬
ется прямоугольной, и тогда компоненты в связанной с этой тройкой
системе координат таковы, что диагональные компоненты еаа,... соответ¬
ствуют относительным изменениям длин векторов а,..., а недиагональные
компоненты еаъ • • • соответствуют поворотам этих векторов. Такое описа¬
ние деформации является локальным; тем не менее оно также определяет
небольшой поворот от одной тройки к другой. Запишем этот поворот как
du)i — Kjidxj. (10.1)
В этом выражении Kji, так называемый тензор искривления (tensor
of contortion), может быть легко получен из антисимметричной части тен¬
зора дисторсии 0ji = дщ/dxj, которую можно записать как и\ =
= -(ди^/дх^ — дщ/дх2) и т. д., т. е. через вектор малых поворотов
1 1
ш = - rotu; u>i = -£ijkuk,j. (10.2)
2 2
Это выражение напоминает завихрение при движении жидкости (см. гл. 6).
Получается, следовательно, что (см. задачу 10.1)
Kji — duji/dxj — -CikiPji.k — £iki££j,k- (10.3)
2
Рассмотрим теперь некоторое обобщение тензора искривления, которое
может быть легко понято на следующем двумерном примере, когда семей¬
ство параллельных атомных слоев деформируется в процессе, называемом
одиночным скольжением (single glide) (рис. 10.1). На больших масштабах
результат выглядит как некоторая кривизна слоев. Но на малых масштабах
жесткость решетки и требование малости упругой энергии приводят к мно¬
жеству краевых дислокаций, число которых (на единицу площади) равно
1 /bR, где R — радиус кривизны и b — модуль вектора Бюргерса. В пределе,
когда вектор Бюргерса b —у 0, это число становится бесконечным, а дефор¬
мация eij обращается в нуль. Величина а = 1/R называется плотностью
дислокаций; она также является единственной значимой компонентой К =
= Кзз — 1/R тензора искривления для этого процесса. Стоит напомнить,
что все дислокации имеют одинаковые знаки; опять-таки подчеркнем, что
рассматриваемый в целом эффект является чисто геометрическим и не под¬
разумевает знания материальных констант. Также отметим, что компонента
К = 1/R становится бесконечной в фокальной плоскости F данного набо¬
ра параллельных слоев. Эта фокальная область содержит в себе дисклина-
цию, так как нормали к слоям поворачиваются вокруг F. Вся геометрия
в целом может также рассматриваться как расширенная граница зерен.
§ 10.2. Кривизна в жидких кристаллах: общие замечания
371
Рис. 10.1. Слои (или плоскости решетки) L подвергаются искривлению; слои М
остаются плоскими, но заканчиваются дислокациями с векторами Бюргерса, парал¬
лельными слоям L. Плоскость F является особой фокальной плоскостью
Этот двумерный анализ может быть распространен на трехмерный слу¬
чай31 В присутствии дислокаций обобщенный тензор искривления записы¬
вается как
Kji — ^ik£^£j,k ~ OLij + - {<*11 + а22 + ^зз)^'? (Ю-4)
где aij — это плотность дислокаций, параллельных направлению г, век¬
торы Бюргерса которых направлены вдоль направления j. В (10.4) ясно
прослеживаются два источника кривизны. Один из них связан с упругими
деформациями и не интересует нас. Другой является геометрическим след¬
ствием дислокаций и может быть назван кривизной Ная (Nye’s curvature)
(задача 10.2).
§ 10.2. Кривизна в жидких кристаллах: некоторые общие
замечания
Это рассмотрение кривизны в твердых телах может быть рас¬
пространено на жидкие кристаллы. В них полезно различать два типа век¬
торов Бюргерса: конечные векторы Бюргерса, связанные с дискретными
^ В. A. Bilby, L.R.T. Gardner and Е. Smith, Acta Met. 6, L9 (1958). E. Kroner,
Kontinuums Theorie der Versetzungen und Eigenspannungen, Springer, N. Y., (1958).
E. Kroner, Continuum Theory of Defects, in Physics of Defects. Ed. by R. Balian.
M. Kleman, T. P. Poirier. Les Houches, North Holland, 1980. p. 215-384.
372
Гл. 10. Дефекты кривизны в смектиках и колончатых фазах
трансляционными симметриями, и бесконечно малые векторы Бюргерса,
связанные с непрерывными трансляциями.
Как мы уже знаем, конечные дислокации существуют в смектиках и ко¬
лончатых фазах. Поэтому, как и в твердых кристаллах, можно ожидать, что
трехмерные распределения дислокаций конечной силы будут неустойчи¬
вы по отношению к полигонизации, т. е. по отношению к формированию
наклонных (или закрученных, или смешанных) границ, на которых дис¬
локации одного знака собираются вместе и на которых слои резко пово¬
рачиваются на угол, пропорциональный содержанию дислокаций в стенке
(см. гл. 8 и §10.8).
Дислокации с бесконечно малыми векторами Бюргерса присущи только
жидким кристаллам. Было показано4\ что в нематике искажения поля ди¬
ректора могут быть описаны посредством чистого тензора искривления Kji
при ец = 0 (последнее условие гарантирует постоянную плотность массы
и отсутствие упругой энергии, связанной с самими плотностями дислока¬
ций), т. е. на языке бесконечно малых дислокаций. Хотя использование это¬
го языка не является абсолютно необходимым, он имеет то преимущество,
что устанавливает связь между полем искажения анизотропной жидкости
и полем кривизны в твердом теле. Мы вернемся к случаю нематиков (и хо¬
лестериков) в следующей главе, где обсудим связь между плотностями бес¬
конечно малых дислокаций и дисклинациями. Что касается смектических
и колончатых фаз, то в них такие дислокации имеют векторы Бюргерса, на¬
правленные либо вдоль слоев (смектики), либо вдоль колонок (колончатые
фазы). Поэтому они характерны для изгиба слоев или колонок. Отметим,
что жидкостная релаксация, которая приводит к изменению кривизны поля
директора при постоянной плотности массы, может быть описана как изме¬
нение поля искривления, т. е. как движение бесконечно малых дислокаций.
Чистое искривление (ец = 0), которое как раз и является предметом этой
главы, невозможно в трехмерном твердом теле.
§ 10.3. Кривизна в смектиках
10.3.1. Исторические замечания
В начале прошлого века Жорж Фридель, осуществив с помощью оп¬
тического микроскопа наблюдения того, что впоследствии было названо
смектическими фазами A (SmA), сделал вывод, что эти фазы являются
слоистыми. Дифракционные методы еще не были изобретены, и открытие
слоистости в то время основывалось только на видимых геометрических
свойствах линейных сингулярностей смектиков А. Эти особенности возни¬
кали в виде пар конических сечений — эллипса Е и одной ветви гипербо¬
лы Н, — расположенных в двух ортогональных плоскостях таким образом,
что вершина любого из них находится в фокусе другого.Заключение
4) М. Kleman, Phil. Mag. 27, 1057 (1973), J. de Phys. 34, 931 (1973).
G. Friedel and F. Grandjean, Bull. Soc. Franc. Miner. 33, 192, 409 (1910).
§ 10.3. Кривизна в смектиках
373
Ж. Фриделя основывалось на замечательной догадке, что наблюдаемые ко¬
нические сечения являются фокальными линиями, т. е. что они составляют
геометрическое место точек центров кривизны симейства параллельных
поверхностей, расположенных вдоль физических слоев. Такая (ограничен¬
ная) область пространства, где искривленные слои проявляются через при¬
сутствие пары конических сечений, называется «конфокальным доменом»,
КФД (focal conic domain).
Будучи объектом исследований, который все еще привлекает много вни¬
мания, особенно в лиотропных фазах, конфокальные домены являются,
по-видимому, старейшим объектом в физике дефектов. Заметим, что одна
из главных черт теории дефектов, а именно то, что полное знание дефек¬
тов в некоторой упорядоченной среде достаточно для понимания природы
(скалярной, векторной и т. п.) ее «параметра порядка», была очевидна уже
ее основателям; однако важность этого открытия не была оценена до со¬
здания топологической теории дефектов (см. гл. 12). Смектики А, конеч¬
но же, не являются единственной средой, где знание КФД очень полезно.
Похожие геометрии возникают в других смектических фазах, таких как
SmC, SmC* 6) или даже упорядоченные смектики, а также в везикулах7).
Тема конфокальных доменов рассматривалась неоднократно в превос¬
ходных обзорных статьях; кроме исторической фундаментальной статьи
Ж. Фриделя, заслуживают упоминания статья Брэгга8) и статья Булигана9),
который переработал эту тему и внес вклад в ее обновление. С тех пор было
выполнено еще какое-то количество экспериментальных и теоретических
работ; эта вспышка интереса к предмету, так давно установленному, спу¬
стя восемьдесят лет после открытия конфокальных доменов, связана с его
внутренней красотой, вызывающей восхищение.
Пункт 10.3.2 является непосредственным введением к § 10.4, посвя¬
щенному КФД. В § 10.3 описаны общие свойства различных пучков норма¬
лей, а не только нормалей к семействам параллельных плоскостей, которые
встречаются в КФД.
10.3.2. Конгруэнции прямых нормалей и конфокальные домены
Нормали к некоторому семейству параллельных поверхностей являют¬
ся прямыми линиями и образуют «конгруэнцию» прямых нормалей, т. е.
пучок нормалей зависит только от двух параметров, например от двух ко¬
ординат точки на произвольно выбранной из этого семейства поверхности.
Единственным отличным от нуля градиентом директора п (направленного
вдоль нормалей) является div п. Как хорошо известно, такая же ситуация
L. Bourdon. М. Kleman andJ. Sommeria, J. de Phys. 43, 77 (1982).
7-) см., например, В. Fourcade, M. Mutz and D. Bensimon, Phys. Rev. Lett. 68, 2551
(1992).
W. Bragg, Trans. Faraday Soc. 29, 1056 (1933).
9-) Y. Bouligand, J. Physique 33, 525 (1972).
374
Гл. 10. Дефекты кривизны в смектиках и колончатых фазах
возникает в геометрической оптике: прямые нормали напоминают лучи
света в среде с постоянным показателем преломления, а поверхности на¬
поминают волновые фронты, и такая конгруэнция огибает две «фокальные
поверхности» Fi и F2, на которых кривизна слоев а1 или сг" становится
бесконечной и, следовательно, соот¬
ветствующая плотность энергии / =
К(а{ + сг")2 + Ксг'а" тоже ста-
1
С-ух:'..
в Fft
V »
Рис. 10.2. Текстуры конфокаль¬
ных эллипсов и гипербол в смек-
тических образцах, наблюдаемых
в плоскости эллипсов (а); в произ¬
вольной наклонной плоскости (6);
в плоскости гипербол (<?)
новится бесконечной. Здесь К и К
упругие постоянные деформаций попе¬
речного изгиба и седловидного изги¬
ба соответственно, сг' и <т" — главные
значения кривизны (см. ниже уравне¬
ние (10.14)). Эта энергия, конечно же,
уменьшается, если Fi и F2 вырождают¬
ся в линии. Тогда из теоремы Дюпена
(см.: Дарбу, 1954) следует, что одна из фо¬
кальных линий (скажем Fi) есть эллипс,
а другая — гипербола, фокусы которой
являются вершинами кривой Fi и кото¬
рая лежит в плоскости, перпендикуляр¬
ной плоскости эллипса Fi. И наоборот,
фокусы Fi являются вершинами F2. Слои
согнуты в циклиды Дюпена, т. е* такие
поверхности, линии кривизны которых
являются окружностями. Эти сопряжен¬
ные эллипс и гипербола легко наблю¬
даются в поляризационном микроскопе
(рис. 10.2), а конфокальный домен, кото¬
рый они несут, может быть сделан види¬
мым посредством конфокальной микро¬
скопии.
Наблюдаемые
эксцентриситеты
эллипсов имеют широкую область зна¬
чений 0 ^ е < 1, в зависимости от па¬
раметров материала, граничных условий
и геометрии системы. Частный случай,
соответствующий эллипсу с нулевым
эксцентриситетом, е — 0, — это пара,
состоящая из окружности и прямой линии. Такой домен называется ториче-
ским КФД. КФД можно также образовать вокруг пары парабол10'1; однако па-
роболический КФД не является предельным случаем е = 1 эллиптически-
гиперболического КФД и имеет другие упругие свойства (см. п. 10.4.3).
10^ С. S. Rosenblatt, R. Pindak. N. A. Clark andR. В. Meyer, J. Physique 38, 1105 (1977).
§ 10.3. Кривизна в смектиках
375
Можно задаться вопросом, почему наиболее часто наблюдаемые фо¬
кальные домены не те, в которых особенности сильно редуцированы, на¬
пример до одной точки (в этом случае слои являются концентрическим
сферами). Такие «сферолиты», как особый тип фокальных доменов, дей¬
ствительно наблюдаются, когда упругая константа седловидного изгиба К
имеет подходящее значение (см. (10.34)).
Целью настоящей главы является полный обзор аналитических основ по
данной тематике, подкрепленный описанием нескольких недавно исследо¬
ванных физических ситуаций. Однако мы не будем доказывать ни теорему
Дюпена, ни теорему о циклидах; заинтересованных читателей отсылаем
к книгам по геометрии (Дарбу, Гильберт и Кон-Фоссен).
10.3.3. Конгруэнции нормалей, вариации идеальных конфокальных
доменов
Малые вариации идеальных конфокальных доменов, образованных кон-
груенциями прямых нормалей, могут быть проанализированы с использо¬
ванием понятий коикруэиция нормалей и конкруэнция прямых линий. В кон-
круэнции нормалей молекулы уже не упорядочены вдоль прямых линий и
слои уже не параллельны, т. е. n х rot п ф 0, nrot п = 0. В конкруэнции
прямых линий понятие слоев исчезает, т.е. nrotn / 0, n х rotn = 0.
В обоих случаях энергетические соображения способствуют тому, чтобы
Fi и F2 оставались линиями, но уже нет геометрических препятствий для
того, чтобы они стали поверхностями; могут существовать смешанные си¬
туации.
Конгруэнция нормалей упруго искажена, но это искажение может отре-
лаксировать путем возникновения некоторого числа дискретных краевых
дислокаций (рис. 10.3). Такая ситуация возникает в холестериках11 \ где
замечено, что дислокации часто подвержены полигонизации. Изменение
формы Fi и F2 по сравнению с идеальными коническими сечениями до¬
пускает более легкое заполнение пространства, чем при идеальных КФД
(см. ниже).
В случае конгруэнции прямых линий можно по-новому ввести физиче¬
ское понятие слоев: величину nrotn можно рассматривать как плотность
дискретных винтовых дислокаций одного знака, наложенных на набор сло¬
ев (рис. 10.3,6). Если они испытывают полигонизацию, возникает ситуа¬
ция, напоминающая закрученную границу зерен. Однако полигонизация
необязательна, потому что слои в своих ближних окрестностях оказываются
изогнутыми почти как минимальные поверхности (следовательно, энергия
кривизны исчезает) и потому что их упругая энергия мала.
Гигантские винтовые дислокациии, наблюдавшиеся в смектиках А12),
являются замечательным примером топологии, где сохранены постоян¬
ные расстояния между слоями, но тем не менее фокусы представляют
Y. Bouligand, J. Physique 38, 1011 (1973).
12) С. Williams, Phil Mag. 32, 313 (1975).
376
Гл. 10. Дефекты кривизны в смектиках и колончатых фазах
Слои Краевые
дислокации
М
н
а б
Рис. 10.3. Краевые дислокации в фокальном домене; С' и С" — части фокальных
линий (а). Типичная ситуация, в которой должны появляться винтовые дислока¬
ции (б)
собой поверхности. Однако наблюдаемые особенности остаются линия¬
ми, составленными из пары спиралей, которые являются острыми краями
эволюты геликоида, порождаемого прямой линией (для этих целей была
предложена концепция «виртуальной поверхности», см. гл. 9). Все слои
параллельны этому геликоиду, шаг которого равен вектору Бюргерса дис¬
локации (см. рис. 9.9). Физическая часть таких фокальных листов редуци¬
руется в линию, а остальная является «виртуальной». Это происходит из-за
того, что некоторые области пространства по нескольку раз перекрываются
плоскостями 'Em, параллельными геликоиду, и, таким образом, приходится
делать выбор, чтобы исключить некоторые части плоскостей которые
близки к эволютам (определение £м см. в §10.4.1). Другие фокальные
домены с виртуальными фокальными листами были предложены сравни¬
тельно недавно13^ в связи с наклонными граничными условиями, встреча¬
ющимися в некоторых случаях; та же самая проблема граничных условий
может также привести к фокальным доменам с «канальными» поверхностя¬
ми14) (когда только одна из фокальных поверхностей вырождается в линию,
а другая частично виртуальна или невиртуальна).
Теорема Дарбу является общей для конгруэнции прямых линий и кон¬
груэнции прямых нормалей, но она неприменима к конгруэнции норма¬
лей. Теорема утверждает, что в данной конгруэнции прямых линий D две
плоскости, касающиеся фокальных поверхностей F\ и F2 вдоль любой ли¬
нии D, ортогональны. Ж. Фридель заметил, что в смектиках А наблюдаемые
в оптический микроскоп фокальные линии, относящиеся к одному и тому
13^ J. В. Fournier. Phys. Rev. Lett. 70, 1445 (1993).
14) J. Sethna and M. Kleman. Phys. Rev. A26, 3037 (1982).
§10.4. Конфокальные домены
377
же конфокальному домену, всегда пересекаются в проекции под прямыми
углами, и заключил, что линии молекулярных расположений удовлетворяют
теореме Дарбу. Эта геометрия не наблюдается столь же хорошо в холесте¬
риках, где идеальная геометрия КФД существенно нарушена.
Выше были описаны (малые) изменения сопряженных конических сече¬
ний с использованием плотности дискретных дислокаций (в смысле Ная).
Подобным же образом можно использовать плотности недискретных дис¬
локаций, для того чтобы описать кривизны в идеальных конфокальных
доменах путем введения подходящего тензора искривлений Kji, Однако
эта процедура здесь непосредственно не приложима, так как кривизны
велики, а обсуждавшаяся выше теория справедлива лишь при малых кри¬
визнах. Расширение понятия тензора искривления на большие кривизны
см. в работе Билби151 Заметим, что наше «эмпирическое» описание дефек¬
тов прокладывает путь к пониманию более абстрактных калибровочных
теорий, в которых дислокационным плотностям придается статус плотно¬
стей калибровочных полей161
§ 10.4. Конфокальные домены
10.4.1. Аналитический подход: основные формулы
В любом КФД слои обворачиваются вокруг двух сопряженных линий,
а именно эллипса Е и одной ветви гиперболы Н, таким образом, что они
везде перпендикулярны прямым линиям, соединяющим произвольную точ¬
ку М7 на эллипсе с произвольной точкой М" на гиперболе (рис. 10.4).
Любая точка М на линии М'М" есть ортогональное пересечение этой ли¬
нии с некоторой однозначно определяемой поверхностью («слоем») Ем,
всюду перпендикулярной двухпараметрическому семейству линий М'М",
называемому конгруэнцией. Все параллельные поверхности Ем, ортого¬
нальные М'М", имеют одни и те же центры кривизны М' и М". Кривизны
(т'| = 1 /М'М или сг" — 1 /М"М становятся бесконечными, когда М
приближается либо к М', либо к М". Соответственно, поверхности Ем
сингулярны в М' и М", где плотность энергии растет неограниченно. До¬
кажем, что каждый слой является (общей) огибающей семейства сфер, цен¬
трированных на Е и Н, и что он характеризуется некоторым скалярным
параметром г.
Пусть Е и Н — сопряженные эллипс и гипербола, расположенные в двух
перпендикулярных плоскостях, и уравнение эллипса в стандартных обозна¬
чениях имеет вид
2 = 0, f! + »! = l) (10.5а)
а2 Ь2
15) В. A. Bilby. Progr. Solid Mech., 1, 329 (1960).
16) L. Dzyaloshinski andG. Inlovik. .1. Physique 39,493 (1978). B. Julia andG. Toulouse,
J. Physique Lett. 40, L-395 (1979).
378
Гл. 10. Дефекты кривизны в смектиках и колончатых фазах
где а > Ь (длину малой полуоси b не следует путать с вектором Бюргерса).
Уравнение сопряженной гиперболы записывается как
У = О,
X
а2 — b2 62
1
Эллипс
Гипербола
(10.56)
Рис. 10.4. Общий геометрический вид конфокального домена. Линия М' МИ есть
направление, перпендикулярное слою в точке М
Пусть М'(х', у*, 0) есть некоторая точка на Е и М"(ж", 0, zn) — некото¬
рая точка на Н. Используем обычную параметризацию для эллипса и ги¬
перболы:
М'
a cos иу
6sinu,
0 ^ и < 27г,
М
//
х
Z
н
и
±ccosh v
b sinht>,
где с2 = а2 4- Ь2. Знаки ± относятся к ветвям гиперболы; в дальнейшем
принимается знак +. Длина М'М" равна
М'М" = Д
a cosh v — с cos и
ех
!
e~lx”
(10.6)
где е = с/а — эксцентриситет эллипса.
//
Рассмотрим некоторую точку М на линии М1 М" и введем расстояния
г — ММ1 и г" — ММ" (с учетом знаков). Для определенности линия
будет всегда направлена от М' к М", т. е. от Е к Н, так что
§ 10.4. Конфокальные домены
379
Для такой ориентации М'М" введем теперь параметр г, определен-
ный как
V = ex' — г; г" = е~1хп — г. (Ю.7)
Каждому значению г ставится в соответствие поверхность Е(г), и легко по¬
казать, что линия М'М" перпендикулярна £(г) в точке М. Действительно,
пусть
Sr(M') = (X - х')2 + (У - у')2 + - г'2 = 0 (10.8 а)
является уравнением сферы с центром в М', проходящей через М, и, ана¬
логичным образом,
5Г(М") = (X - а:")2 + У2 + (Z - г")2 - г"2 = 0 (10.86)
является уравнением сферы с центром в М", проходящей через М. Сферы
Sr(Mf) являются огибающими для некоторой поверхности, которая есть в
точности £(г). Действительно, точка контакта Sr(Mf) со своей огибающей
принадлежит одновременно Sr(Mf) и следующей производной поверх¬
ности:
dSAMJl = ^ = y'x + (e2 _ jyy- _ ey'r = o, (10.9)
dM’ dx' dxf dx’ dyf
и далее простые вычисления показывают, что точка М принадлежит пере-
dS
сечению Sr(Ml) и ———Очевидно также, что М принадлежит Пересе-
dMf
чению Sr{Mn) и dSA4 \ Поэтому £(г) является геометрическим местом
dMn
точек общих огибающих для Sr(M') и Sr(Mn), а М* и Мп являются ее
центрами кривизны в М. Поверхность £(г) везде перпендикулярна линии,
соединяющей произвольную точку М' на Е с произвольной точкой М
на Н\ поэтому она как раз и есть искомая поверхность. К тому же £(г) яв¬
ляется циклидой (т. е. ее линии кривизны — окружности), так как полный
контакт Sr(M') (соответственно, Sr(M")) с £(г) есть окружность Cr(М')
(соответственно, СГ(МП)), вдоль которой пересекаются Sr(Ml) (соответ¬
ственно, 5Г(М")) и - (соответственно, dSr-tM^~).
dM' dM"
Отметим следующее геометрическое свойство, которое мы здесь не до¬
казываем, но используем постоянно: М' является вершиной конуса враще¬
ния с основанием СГ(М'), который лежит на Я; соответственно М" являет¬
ся вершиной конуса вращения с основанием СГ(М"), который лежит на Е.
//
10.4.2. Различные виды конфокальных доменов
На рис. 10.4 был показан случай, когда физический слой пересекает
линию М'Мп между М1 и М". Согласно теории конгруэнций прямых ли¬
ний, центрами кривизны цикл ид в точке М являются М1 и М", которые
находятся на фокальных линиях. На этом рисунке кривизны а( и сг" имеют
противоположные знаки, и поэтому циклида оказывается в точке М гипер¬
болической (седловая точка), см. рис. 5.5,6. В зависимости от положения
380
Гл. 10. Дефекты кривизны в смектиках и колончатых фазах
точки М и от гауссовой кривизны слоев можно охарактеризовать различные
типы КФД (рис. 10.5).
10.4.2.1. Конфокальные домены первого вида (КФД-I). Если физи¬
ческая часть слоя расположена между М' и М", получаются конфокальные
домены первого вида (КФД-I), рис. 10.5, а. В этой геометрии & а" < 0. Цик-
лиды Дюпена в КФД-I обладают некоторыми деталями, изменяющимися в
зависимости от положения М на сегменте М*Ми: или Ем заканчивается
на эллипсе двумя точечными особеностями (слой 1 на рис. 10.5, а), или Ем
не имеет особенностей и выглядит как половина тора (слой 2), или она
заканчивается на гиперболе и имеет форму сфероида (ограниченного той
его частью, где сг'сг" < 0) с двумя точечными особенностями на гиперболе
в виде зубцов (слой 3). Очевидно, что и эллипс, и ветвь гиперболы являются
линейными дефектами, и поэтому оба видимы.
Различные проекции любого КФД-I, наблюдаемые в поляризационном
микроскопе, удовлетворяют теореме Дарбу^ которая утверждает, что ор¬
тогональные проекции на любую плоскость сопряженных эллипса и ги¬
перболы пересекаются под прямыми углами (см. рис. 10.2 и рис. 10.6).
Экспериментальные наблюдения удивительно хорошо согласуются с этим
свойством и дают, таким образом, подтверждение геометрической модели
Фриделя.
С аналитической точки зрения для КФД-I г' < 0 и г" > 0; следова¬
тельно, г удовлетворяет неравенству
с cos u < г < achv. (10.10)
Весь набор значений г для полного КФД-I (показанного на рис. 10.5, а) лежит
в интервале [—с, -f оо). Специальные значения г соответствуют следующим
ситуациям:
г — —с, циклида Дюпена вырождается в точку в вершине эллипса,
противоположной физической ветви гиперболы.
-с < г < +с, циклида Дюпена имеет две особые точки на эллипсе
(получающиеся при г' = 0) и никаких на гиперболе, слой 1 на рис. 10.5, а.
с < г < -ha, циклида Дюпена не имеет особых точек; полная циклида,
т. е. собранная из частей сг'сг" < 0 и a'cr" > 0, гомотопна тору, слой 2 на
рис. 10.5, а. Средняя циклида Дюпена Tq — ас уникальна: согласно гипо¬
тезе Вилмора (Willmore), полная циклида г0 (тороидальная поверхность)
отвечает абсолютному минимуму энергии кривизны -xj (сг' -b <т")2 dE.
г > а, особые точки только на гиперболах, слой 3 на рис. 10.5, а.
10.4.2.2. Конфокальные домены второго вида (КФД-II). КФД-П
имеют положительную гауссову кривизну, г'г" > 0. Такой домен полу¬
чается, когда физическая часть нормали к Ем располагается вдоль полу-
бесконечной линии с началом в М! (рис. 10.5,6). В этом случае циклиды
выглядят как мяч для регби с двумя коническими пиками на гиперболе.
Эллипс теперь виртуален, и только гипербола видима в микроскоп. После¬
довательное наложение таких циклид может покрыть все пространство.
§ 10.4. Конфокальные домены
381
Рис. 10.5. Конфокальные домены первого вида (КФД-I) {а); второго вида
(КФД-Н) (б); третьего вида (КФД-Ш) (V)
382
Гл. 10. Дефекты кривизны в смектиках и колончатых фазах
а
в
Рис. 10.6. Теорема Дарбу: проекции КФД-I, наблюдаемые в поляризационный
микроскоп в плоскости эллипса (а), в произвольной плоскости (б% в плоскости
гиперболы (с)
С аналитической точки зрения имеем: г' < 0 и г" < 0, так как точка М
расположена вне М*М" и направления ММ1 и ММ" противоположны
направлению М'М". Поэтому вдоль данной нормали (u,v) выполняется
следующее неравенство:
г > a cosh г;,
(10.11)
и весь набор значений г для полного КФД-П лежит в интервале [a, -boo).
Для г — а циклида Дюпена редуцируется в вершину F физической ветви
гиперболы.
10.4.2.3. Конфокальные домены третьего вида (КФД-Ш). КФД-Ш
формируются циклидами как с положительной, так и с отрицательной гаус¬
совой кривизной (рис. 10.5, в).
10.4.2.4. Полезные формулы. Во всех трех случаях могут быть ис¬
пользованы следующие формулы для главных кривизн, определенных через
обратные радиусы кривизны:
сг
/
1
1
V
с cos и — г
3
сг
н
1
и
a cosh v — г
(10.12)
\
Отметим также, что бесконечно малый элемент поверхности d£(г) —
= АВ du dv циклиды Е (г) может быть представлен как функция главных
кривизн (рис. 10.7). Рассмотрим бесконечно малое изменение величины и,
ди, вдоль линии главной кривизны, соответствующей постоянному значе¬
нию v. Точка М смещается из М в M+5UM, а М' в М'+Й^М'; г1 изменяется,
но М" и г" остаются неизменными. Имеем
A du
диМ
д
Г
/
и
А
М'М
ba
//
а — а
и
du, В dv = ±
Ъа’
dv.
а
а
п
Следовательно,
<Щг)
а’а"
(сг' — а")
и\2
du dv
(10.13)
§ 10.5. Энергия кривизны КФД
383
КФД-1
SVM
км
КФД-II
Рис. 10.7. Бесконечно малые элементы поверхности d£ циклид Дюпена в случае
КФД-I и КФД-П. dE = I <5„ II Su
§ 10.5. Энергия кривизны конфокальных доменов
Энергия кривизны КФД определяется как интеграл по объему КФД от
плотности энергии /, связанной со средней и гауссовой кривизнами:
1
/ = -К{о' + а")1 + Ка'а".
Удобно разбить этот интеграл на две части:
W
fdEdr = Wi + W2,
(10.14)
(10.15)
Wi
=F-КУ
2
a'an du dv dr
e2)a
du dv dp
(e cos и — p)(cosh v — p)
(10.16a)
384
Гл. 10. Дефекты кривизны в смектиках и колончатых фазах
w2 = Т(К + 2 К)Ь
a' a" du dv dr
/М2
(а' — а")
=рЛ(1 - е2)а
du dv dp (Ю.166)
(cosh v — e cos и)2 *
где A = К + 2K, p = r/a, e — эксцентриситет и a —- большая полуось
эллипса; верхний знак соответствует КФД-I, а нижний — КФД-П. Отметим,
что члены и с К, и К’ дают вклады в «топологию», так как они появляются
в W2, который является интегралом типа Гаусса “Боне.
10.5.1. КФД-I: Отрицательная гауссова кривизна
Член W2 может быть легко проинтегрирован по области параметров
с cos и < г < achv, 0 ^ и < 27т, —00 ^ v < 00 и записан в точной форме
= —47гЛа(1 — е2)К(е2), (10.17)
1 dt
где К(х) = J — полный эллиптический интеграл первого
о у/(1 - t2)( 1 -xt2)
рода. Величина W2 отрицательна, когда Л > 0, что выполняется, если
К > —2К. Отметим, 4tj для того, чтобы плотность свободной энергии
(10.14) была положительно определенной в ламеллярной фазе, К должно
находиться в интервале -2К ^ К < 0. Это также означает 0 < Л ^ 2К
(.К всегда положительно).
Член W\ сингулярен вблизи эллипса и гиперболы, где г —> с cos и и г —>
-» a ch и. Рассматриваемая феноменологическая теория не может быть при¬
менена в этих областях, и следует ограничить интегрирование на некоторой
пороговой длине, называемой радиусом ядра. Предположим, что радиус яд¬
ра не зависит от слоя (т. е. не зависит от г):
cutoff — achv — г с вблизи гиперболы,
^cutoff = с cos и Л'г с вблизи эллипса.
Очевидно, что это предположение чересчур упрощает ситуацию. Например,
оно не принимает во внимание, что слои, которые пересекают гиперболу
вдали от эллипса, почти не имеют сингулярностей. Более того, вблизи ядра
дефекта может меняться межплоскостное расстояние (критическое обсуж¬
дение см. в работе Фурнье17^).
17^ J. В. Fournier. Phys. Rev. Е 50, 2868 (1993)
§ JO.5. Энергия кривизны КФД
385
Интегрирование по р разбивает W\ на сингулярную W^ijSing и несингу-
лярную Wit non sing части:
t^i-sing = 47г^о(1-е2)К(е2)1п-, (10.18 а)
Гс
Wi -non sing = 4пКа(1 - е2)К(е2) In (ly/l - е2 ) , (10.186)
где г с имеет обычно порядок межплоскостного расстояния. Должна быть
еще добавлена некоторая характерная энергия ядра, которая не может быть
вычислена из (10.14) аналитически: Wi-sing —^ Wi-sing + Wcore> где энергия
Wcore пропорциональна длине дефекта. Мы не учитываем Wcоге; в некото¬
рых случаях это может быть оправдано тем, что параметр гс может быть пе¬
ренормирован таким образом, чтобы Wcore оказалась величиной в
Общая энергия кривизны КФД-I W = Wi-non sing + ^l-sing + W2, пред¬
ставленная как функция большой полуоси а и эксцентриситета 0 < е < 1,
принимает довольно компактную форму18):
W = 47га(1 — е2)К(е2)
гг т 2ay/l ? »
К In А
Гс
(10.19)
Заметим, что a\/l — в2 = 6, где b — малая полуось; А — 2К 4- К.
Зависимость W(K) довольно очевидна: чем больше К, тем меньше
энергия, просто по причине отрицательного знака гауссовой кривизны цик-
лид Дюпена в КФД-L Еще одно замечание касается суммы двух несингу¬
лярных членов W^i-nonsing + ^2 при а = const. Когда А увеличивается,
положение минимума этой суммы смещается от е —>> 1 к е —0 (рис. 10.8).
Достижение суммой HVnonsing + И^2 минимума при малом эксцентриси¬
тете е —у 0 конкурирует, разумеется, с ростом Wi-5[ng при е -» 0, таким
образом, минимум энергии кривизны может быть достигнут при е, суще¬
ственно отличном от 1, только когда домены очень малы, а/гс ~ 10, и когда
константа седловидного изгиба близка к своему верхнему пределу К = 0,
налагаемому положительной определенностью / в (10.14). Вообще говоря,
для достаточно большого домена с а/тс > 10 энергия кривизны становится
минимальной только при е —> 1. Однако было бы ошибкой сделать вывод на
основе (10.19), что КФД-I имеет тенденцию увеличивать как можно больше
свой эксцентриситет. В реальных образцах КФД редко бывают изолирован¬
ными; их упругая энергия — только часть общей энергии, которая включает
энергии поверхностной ориентации, дислокаций, изменения межслоевого
расстояния и тому подобные вклады, которые будут рассмотрены ниже.
Во-первых, заметим, что графики на рис. 10.8 соответствуют а — const.
Объемы КФД-I с одинаковыми а, но разными е, очевидно, различны; уве¬
личение е означает уменьшение малой полуоси b. Соответственно энергии
кривизны двух КФД с различными е должны сравниваться при добавочных
18^ М. Kleman and О. D. Lavrentovich. Phys. Rev. E61, 1574 (2000).
25-КЛЕМАН М.
386
Гл. 10. Дефекты кривизны в смектиках и колончатых фазах
W
non smg
а
W
0,2
0.4
0,6
0.8
1
б
Рис. 10.8. Энергии КФД-I как функции эксцентриситета е для различных значе¬
ний упругого параметра А/К (показанного числами над кривыми); использованы
нормированные единицы с К = 1 и а = 1. Несингулярный вклад Wnon sing =
= Wi "■non sing + VK2 как функция e (а). Полная энергия ~ VTi-smg + W^i -non sing +
4- W2 как функция е для КФД-I большого (а/гс = 1000, жирные линии) и малого
(а/гс — 10, тонкие линии) размеров (б)
геометрических ограничениях. Эти ограничения в конкретной эксперимен¬
тальной ситуации включают конечный размер системы и, таким образом,
требуют рассмотрения энергий поверхностной ориентации, которые обыч¬
но велики в смектических фазах.
Другая причина для ограничения е связана с тем фактом, что лю¬
бой КФД-I должен согласовывать свои слои с соседними областями. Из-за
их своеобразной формы КФД-1 не могут заполнить ограниченную часть
пространства, оставаясь изолированными объектами. Они должны быть
§ 10.5. Энергия кривизны КФД
387
внедрены в окружающую матрицу смектических слоев, которые могут быть
плоскими или искривленными. Если КФД-I с малым эксцентриситетом
внедрен в систему плоских слоев, то, как видно из рис. 10.5, а, имеющийся
внутри КФД-I наклон смектических слоев (по отношению к горизонтальной
плоскости) требует некоторого набора согласовывающих дислокаций вне
КФД-I. Полный вектор Бюргерса этого набора равен 2ае. Таким образом,
хотя тенденция е —> 1 благоприятна с точки зрения кривизны слоев внутри
КФД-I, противоположная тенденция е —> 0 благоприятствует уменьшению
линейного натяжения ~ у/ВКае дислокаций вне КФД-1. Данное взаимо¬
действие между КФД и дислокациями играет важную роль в структуре
пространственно упорядоченных систем КФД, таких как маслянистые бо¬
роздки или наклонные границы зерен, которые будут рассмотрены в этой
главе. В общем и целом, задача нахождения равновесного е требует учета
энергий дислокаций, сжимаемости и поверхностной ориентации в допол¬
нение к энергии кривизны.
10.5.2. Торический КФД с отрицательной гауссовой кривизной
Энергия кривизны (10.19) принимает очень простую форму для тори-
ческих КФД-I, или ТКФД, в которых эллипс вырождается в окружность,
а гипербола — в прямую линию, е = 0:
W
а
2тг"а I 1Пп - +/Пп 2 - Л
Гс
(10.20)
Заметим, что для Л/К = In 2 « 0,693 энергия сводится к сингулярному
члену. Радиус ядра один и тот же вдоль всего круга. В случае Л/К > 1 ~f
+ In 2 легко видеть, что W принимает минимальное значение для решения
д\у п
уравнения в частных производных — = U:
да
а = г с ехр ( — — In 2 — 1) . (10.21)
Энергия кривизны (10.20) отрицательна для этого значения а/гс
(W^min = “27т2аК). Энергия ядра ТУС, которая положительна и изменяет¬
ся пропорционально а, имеет тот же порядок величины. Более детальное
рассмотрение должно включать более точное вычисление Wc.
10.5.3. Параболический КФД с отрицательной гауссовой кривизной
Этот случай нам приходится рассматривать отдельно, так как он анали¬
тически не следует из общего случая; здесь приводятся соответствующие
результаты.
388
Гл. 10. Дефекты кривизны в смектиках и колончатых фазах
Пусть Р и Q
(рис. 10.9):
это две текущие точки на конфокальных параболах
х
р )У
2fa,
0,
-И*2,
Q
X
У
0,
2 fP,
0
2
(10.22)
4
б
Рис. 10.9. Параболический КФД с отрицательной гауссовой кривизной (ПКФД-1).
Часть несингулярного симметричного слоя (г = 0), обернутого вокруг двух парабол.
Линии PQ перпендикулярны этому слою. Линия 1 пересекает слой один раз, тогда
как линия 3 пересекает тот же самый слой три раза (а). Четыре эквидистантных
слоя, включая симметричный слой, обозначенный цифрой 0 (6)
§ 10.5. Энергия кривизны КФД
389
Здесь / — расстояние от фокусов парабол до их вершин (не следует путать
с обозначением / для плотности свободной энергии). Расстояние PQ равно
PQ = f(l + a2 +(32),
(10.23)
а радиусы кривизны (измеряемые вдоль линии, ориентированной; от Р к Q)
равны
Ra — РМ
1
(Та
2 + -
R
/з
MQ
1
г,
т - r >
(10.24)
о . 1
< сг + -
где —(/? +-)<-< сг + * для параоолических первого вида
2 / 2
(ПКФД-1) с < 0. Равенства здесь запрещены, потому что при них кри¬
визна бесконечна; исключенные области вблизи точек Р и Q представляют
собой область ядер.
Розенблат и др.10), наблюдавшие ПКФД-1, показали на серии диаграмм,
что ПКФД-1 продолжается на все пространство: на большом расстоянии от
фокусов (| r/f | 1)) слои практически плоские и перпендикулярны общей
оси парабол. Когда | r/f | > 1/2, Е(г) пересекает одну из парабол в двух
точках, в которых кривизна неограниченно возрастает. Слои с | r/f | < 1/2
не имеют точечной сингулярности: они не пересекают параболы, а скорее
обертывают их, образуя седловины; циклида Дюпена г = 0 симметрична
относительно плоскости z = 0 с поворотом на 7г/2 при переходе от области
z > 0 к области z <0. Используя определение циклид как огибающих для
сфер (см. выше (10.8) и (10.9) для общего случая), находим, что циклиды
могут быть выражены аналитически параметрическими уравнениями
х = а(р Л-г — z),
У = P(p-r + z),
z — ах — /Зу — г.
Элемент области d£(r, а, /3) записывается как
(10.25)
da d/3
СГаЯ/З | (1 + а2 + I32)2
(10.26)
а энергия ПКФД-1 имеет вид
W
4А
da d{3 dr
(1 + а2 4- /З2)2
+ 2 К
da d(3p2
&а&(3
dr.
(10.27)
Мы не будем приводить здесь полное выражение для W. Достаточно
отметить, что:
• топологический член суммируется в — 47гЛр в континуальном преде¬
ле (p^>d) для слоев с | r/f | < 1/2: каждый слой дает топологический
вклад ос (—47т). Для | r/f | ^ 1/2 топологический вклад расходится
390 Гл. 10. Дефекты кривизны в смектиках и колончатых фазах
логарифмически с размером домена 2L, измеренным вдоль оси г,
который сопоставим (при L, большем, чем /) с максимальным значе¬
нием г. В итоге имеем
Wtopol « —4тгЛ/ ^1 + 2 In у V (10.28)
член с К дает несингулярный конечный вклад при |г//| < 1/2,
а именно:
WK-non sing = 2тг3х/, (10.29)
и некоторый сингулярный вклад при | г/f | ^ 1/2. Так как эффекты
кривизны уменьшаются, с увеличением г, кривизна этих поверхно¬
стей оказывается величиной небольшого порядка в области вне ядра
радиуса гс. Считая гс постоянным на сегментах парабол порядка /,
при условии, что сингулярность пренебрежимо мала вне этих сегмен¬
тов, можно ожидать, что
Wk-non sing ~ К\п2 (10.30)
Т
' С
Опять-таки, сумма вкладов (10.28), (10.29) и (10.30) не учитывает энер¬
гию ядра. По-прежнему имеется необходимость в более полном рассмот¬
рении всех этих энергий.
10.5.4. КФД-Н: положительная гауссова кривизна
Выберем область изменения г > a ch v и введем также нижний радиус
обрезания гс, связанный с максимальным значением v на каждой поверх¬
ности £(г) соотношением г = a chvmax + гс, и верхний радиус обрезания
Гщах = +Д. Это последнее условие означает, что КФД-II ограничен цик-
лидой с параметром г = R. Так как слои имеют положительную гауссову
кривизну, диклида является замкнутой поверхностью нулевого рода с дву¬
мя особыми точками в противоположных точках гиперболы. Вне КФД-Н
слои приспосабливаются к граничным условиям несколькими возможны¬
ми способами (см. задачу 10.3).
Вычислим сначала энергию слоя с параметром г. Соответствующие
области изменений для v и и таковы:
1 < chv < г/а\ 0 < и < 2тг. (10.31)
Энергия упругости слоя разбивается аналогично (10.5)
w
fd£ = wi>r + tu2,r, (10.32)
§ 10.6. Дефекты кривизны в колончатых фазах
391
где
Wl r = \JT-±± th
\/r2 — e 2 a2 \/r 2 — а 1 V t — a
1 i (r — rt
- arcch
r2 - a2
w2,r = 47t(2x+ x) J —„ , ■ (10.33)
e2a2
В этих уравнениях — iftjfo, a do — периодичность слоев.
Выражения в (10.33) должны быть еще проинтегрированы по интервалу
R
г с < г < R, где г с зависит от г, однако общая энергия J dr(u)i,r Н- W2,r)
а
может быть приемлемым образом оценена, если принять rc = const. Осо¬
бый простой случай е — 0 рассматривается в задаче 10.3. Главный резуль¬
тат, который легко проверить, заключается в том, что энергия упругости,
запасенная в сферолите (также называемом луковицей) радиуса R, равна
W = 4тгА R = 4тг(2 К + K)R. (10.34)
§ 10.6. Дефекты кривизны в колончатых фазах
10.6.1. Общее рассмотрение
Обозначим t(r) единичный вектор, расположенный в точке г и направ¬
ленный вдоль физической колонки. Предполагается, что колонки в искажен¬
ном состоянии не ломаются. Это значит, в силу сохранения потока колонок,
что
div t = 0. (10.35)
Так как мы рассматриваем состояние с чистой кривизной, колонки
остаются параллельными в таком искаженном состоянии. Можно визуа¬
лизировать это свойство параллельности на поверхностях Е, образуемых
некоторым однопараметрическим подмножеством колонок. Определение
таких поверхностей можно дать в континуальном пределе, так как расстоя¬
ние а между колонками мало по сравнению с их длиной. На любой из этих
поверхностей ортогональные к колонкам траектории являются геодезиче¬
скими линиями, так как эти траектории ортогонально пересекают некото¬
рую систему параллельных колонок (этот результат относится к свойству
фронтальности геодезических линий; доступный и наглядный обзор этой
геометрической концепции, равно как и других, затронутых в этой главе,
см. в книге Гильберта и Кон-Фоссена).
Две различные поверхности, Е* и Ej, пересекаются вдоль колонки и со¬
ставляют в этом пересечении постоянный угол; этот угол равен углу в неис¬
каженном состоянии, что требуется в ситуации с чистой кривизной. Здесь
мы используем теорему Иоахимшталя, утверждающую, что для двух по¬
верхностей, пересекающихся под постоянным углом, линия пересечения
является линией кривизны либо на обеих поверхностях, либо ни на одной.
392
Гл. 10. Дефекты кривизны в смектиках и колончатых фазах
Если пересечение не является линией кривизны, то, как показывает де¬
тальный анализ, невозможно избежать некоторой закрутки q — — t rot t,
которая с необходимостью сопровождается упругими искажениями. Но это
как раз то, чего хотелось бы избежать. Поэтому единственное решение —
это колонки, направленные вдоль некоторой линии кривизны на любой
поверхности Е; что означает, что ортогональные к колонкам траектории
являются одновременно геодезическими линиями и линиями кривизны.
Поэтому они являются плоскими кривыми, поскольку тот факт, что они яв¬
ляются линиями кривизны, означает, что их геодезическое кручение должно
зануляться, а то, что они являются геодезическими линиями, означает, что
их геодезическое кручение равно их естественному кручению191 Следо¬
вательно, колонки перпендикулярны некоторому семейству плоскостей П
в ситуации с чистой кривизной, которая также означает, что каждая по¬
верхность Е порождается некоторой плоской кривой с неизменной формой
(геодезической линией), движущейся таким образом, что скорости всех ее
точек нормальны к плоскостям П, которые содержат эту плоскую кривую.
Поверхности Е называются поверхностями Монжа, по имени знаменитого
геометра, который впервые детально изучил их.201
На рис. 10.10 представлены две бесконечно близкие плоскости П;
прямая D — линия их пересечения, которая огибает пространственную
кривую L, когда плоскость П движется. Бесконечно малое движение плос¬
кости П можно разделить на чистое вращение вокруг D, а именно dtp,
и движение dip вокруг нормали к П, проходящей через точку контакта D с L.
Рис. 10.10. Расположение колонок между двумя бесконечно близкими плоскостя¬
ми П; на каждой плоскости существует идеальная гексагональная решетка. Подроб¬
ности в тексте
19^ См.: Darboux или Hilbert and Cohen-Vossen.
2°) G. Monge. Applications de Panalyse a la geometrie, Paris, 1807.
§ 10.6. Дефекты кривизны в колончатых фазах
393
Рассмотрим теперь произвольную колонку21^: ее центр кривизны лежит
на D, ее соприкасающаяся плоскость перпендикулярна D, а кривизна — =
R
t х rott — | d(p/ds |, где s — криволинейная абсцисса вдоль колонки.
Что же касается dip, то эта величина связана с кривизной L в точке М
ее контакта с D, т. е. 1 /р — \d^/da\, где а — криволинейная абсцисса
вдоль L. Соприкасающаяся плоскость для линии L в точке М есть П.
Между L и произвольной колонкой существует соотношение взаимности,
а именно
Р Т
т
R
(10.36)
где Тит — это кручение, соответственно колонки и кривой L, ориентиро¬
ванных по движению плоскости П. Кривизна колонок 1 /R становится бес¬
конечной на D, геометрическое место точек которой есть, следовательно,
дефект кривизны системы. Это геометрическое место точек представляет
собой развертывающуюся поверхность и в то же время границу области
существования колонок (рис. 10.11). Мы называем эту область разверты¬
вающимся доменом21\
Рис. 10.11. Построение развертывающейся поверхности, образуемой касательны¬
ми к пространственной кривой L, которая называется острым краем (<cuspidal edge)
развертывающейся поверхности
2I) Детальное аналитическое рассмотрение см. в работе: М. Kleman. J. de Phys. 41,
737 (1980).
394
Гл. JO. Дефекты кривизны в смектиках и колончатых фазах
10.6.2. Развертывающиеся домены
Сначала рассмотрим случай, когда развертывающаяся поверхность пред¬
ставляет собой круговой цилиндр радиуса а; кривая L сводится к точке
на бесконечности в направлении образующих цилиндра. Рассмотрим кру¬
говое сечение этого цилиндра; плоскости П пересекают это сечение по
касательным к окружности радиуса а, и колонки являются эвольвентами
этой окружности (рис. 10.12). Ясно, что такая конфигурация есть как раз
дисклинационная линия силы k — -f 1 с ядром радиуса гс, с необходимо¬
стью большим, чем а, так что можно ожидать пустое ядро или, по меньшей
мере, ядро, в котором колонки имеют ориентацию, совершенно отличную
от внешней, например параллельно образующей цилиндра. Такие объекты
наблюдаются в очень тонких образцах дискотических фаз, в которых колон¬
ки ориентируются параллельно поверхности (рис. 10.13). Линии с к — 1/2
более многочисленны, чем с к = 1, и можно показать экспериментально,
что они имеют геометрию с половиной ядра. На рис. 10.13 есть и пример
линии с к = 1, но ее ядро расширено (задача 10.4); более подробный анализ
см. в работе Освальда и Клемана221
0С
Рис. 10.12. Поперечное сечение развертывающегося домена, эквивалентного
дисклинации с силой, равной единице, а — радиус развертывающейся поверхности
и г с — радиус ядра. Колонки являются эвольвентами окружности
22) P. Oswald and М. Kleman. J. Phys. 42, 1461 (1981).
§ 10.6. Дефекты кривизны в колончатых фазах
395
Среди прочих простых развертывающихся доменов рассмотрим такой,
в котором заостренный край (cuspidal edge) L является точкой на конеч¬
ном расстоянии, а развертывающаяся поверхность представляется конусом
вращения. Можно показать, что колонки являются сферическими кривы¬
ми (центрированные в L сферы являются в этом случае поверхностями
Монжа), которые оказываются траекториями, ортогональными к набору
Рис. 10.13. Тонкая капля дискотической гексагональной фазы (Cs гексаалкокси
производная трифенилена, растекшаяся по стеклянной подложке, показывает воз-
никновение многочисленных дисклинационных линий половинной силы, которые
имеют геометрию полуразвертывающихся доменов (колонки ориентированы ча¬
стично вдоль эвольвент, а частично вдоль прямых)
больших окружностей (последние служат здесь геодезическими линиями),
нанесенных на сферу и касающихся в двух точках пересечения конуса и сфе¬
ры (рис. 10.14). Колонки легко получаются из эквидистантности и симмет¬
рии относительно оси сердцевины. Отметим, что решение может быть либо
правосторонним (как на рис. 10.14), либо левосторонним, что означает воз¬
можность задания хиральности в системе колонок без закрутки.
10.6.3. Классификация развертывающихся доменов
По определению развертывающуюся поверхность S можно развернуть
на плоскости Р путем чистых изгибов без растяжения. При таком отоб¬
ражении острый край L становится линией L в этой плоскости, а прямые
линии D (см. рис. 10.11) отображаются в одну из полупрямых D\ и D-2
прямой D, выходящих из точки контакта М на линии L.
Длины и углы сохраняются, что означает одинаковые кривизны линий L
и L в соответствующих точках. Следовательно, L и L отличаются толь¬
ко некоторой функцией кручения г(<т), которая может быть выбрана про¬
извольно.
Так как любая функция т{а) может быть выбрана для построения L,
то ясно, что еще один способ отображения развертывающегося домена на
396
Гл. 10. Дефекты кривизны в смектиках и колончатых фазах
плоскость Р состоит в его раскручивании (а не выпрямлении), т. е. в умень¬
шении т(сг) непрерывным образом без изменения кривизны р{о) вплоть до
зануления т{а). Любая промежуточная ситуация в ходе этого процесса со¬
ответствует некоторому развертывающемуся домену с таким же представ¬
лением на плоскости Р. В частности, конечное состояние на Р представляет
собой развертывающийся домен, в котором все плоскости, касающиеся 5,
лежат на Р. Это также означает, что гексагональное расположение колонн
в любой плоскости П отображается на то же самое расположение на Р
(рис. 10.15), тогда как каждая физическая колонна становится прямой ли¬
нией, перпендикулярной Р.
Рис. 10.14. Сингулярная точка в качестве развертывающегося домена. Колонки на¬
правлены вдоль сферических кривых, соединяющих одну точку на (нижнем) круге
пересечения сферы и фиксированного конуса со второй точкой на другом (верхнем)
круге пересечения. Другие колонки на той же сфере получаются путем аксиаль¬
ной симметрии. Заметим, что концы колонок перпендикулярны фиксированным
конусам, как и требуется. Этот конус действительно является развертывающейся
поверхностью, связанной с сингулярной точкой. Должны быть рассмотрены кон¬
центрические сферы; две такие сферы показаны на рисунке
Заметим, что возможность аналитического процесса раскрутки не озна¬
чает, что можно непрерывно уменьшить до нуля энергию развертывающе¬
гося домена посредством похожего физического процесса, так как раскрут¬
ка — это неконсервативный процесс.
Рисунок 10.15 соответствует выпуклой замкнутой кривой L. Легко пред¬
ставить поднятие в пространство двух листов соответствующей разверты¬
вающейся поверхности. Ситуация становится более сложной, если L имеет
асимптоты, точки изгиба, окончания. Тогда необходимо разделить L на
простые выпуклые дуги Li и поднимать каждую из них. Этот случай пред¬
ставлен на рис. 10.16.
§ 10.7. КФД в лиотропных ламеллярных фазах
397
Рис. 10.15. Представление развертывающегося домена на Р. Линия L является
отображением L; каждая плоскость П отображается на Р. Гексагональные распреде¬
ления на плоскостях П отображаются в одно и то же гексагональное распределение
на Р независимо от выбора П
Рис. 10Л 6. Выпуклая дуга Li и ее прямая и обратная концевые касательные разде¬
ляют внешнюю часть на различные секторы. Сектор 1 охватывается направленными
вперед полукасательными и поднимается к одному листу поверхности 5; подобным
же образом сектор 2 (обратные полукасательные) поднимается к другому листу по¬
верхности S
§ 10.7. КФД в лиотропных ламеллярных фазах:
маслянистые бороздки и сферолиты
Лиотропные жидкие фазы и термотропные смектики А дают различ¬
ные текстуры дефектов, возникающих в обоих случаях из-за упорядоче¬
ния КФД. Так как большинство примеров, которые могут быть найдены
398
Гл. 10. Дефекты кривизны в смектиках и колончатых фазах
в литературе, посвящены термотропным смектикам А, мы сосредоточимся
в этом параграфе на некоторых специальных текстурах КФД, встречающих¬
ся в лиотропных системах чаще, чем в термотропных.
10.7.1. Маслянистые бороздки
Маслянистые бороздки являются наиболее распространенными струк¬
турными дефектами в ламеллярных фазах, особенно лиотропного типа
(рис. 10.17). Они появляются как длинные полосы со сложной внутренней
структурой и разделяют однородные области со слоями, параллельными
границам образца (так называемое гомеотропное упорядочение в случае
смектика А).
Рис. 10.17. Маслянистые бороздки, содержащие КФД-I. Каждая из них состо¬
ит из цепочки доменов, а зазор между доменам заполнен краевыми дислокация¬
ми. Материал: СрС1/гексанол/рассол — 14,8/15,2/70. Толщина образца 130 мкм.
Предоставлено П. Болтенхагеном23)
Эти маслянистые бороздки, впервые описанные Жоржем Фриделем,
представляют собой краевые дислокации с большими векторами Бюргер¬
са, сравнимыми с толщиной образца. Дислокации с малыми векторами
Бюргерса появляются в образце как результат капиллярного заполнения
материалом пространства между стеклянными пластинами и собираются
вместе в течение нескольких часов, образуя дислокации с большими векто¬
рами Бюргерса. Как уже отмечено в п. 9.1.1, современная модель предпо¬
лагает, что маслянистая бороздка состоит из двух дислокаций с большими
(иногда порядка толщины образца) векторами Бюргерса противополож¬
ного знака, см. рис. 11.18, 11.19. В лиотропных фазах большая активаци¬
23^ P. Boltenhagen, О. D. Lavrentovich and М. Kleman, J. Phys. II France 1, 1233 (1991).
§ 10.7. КФД в лиотропных ламеллярных фазах
399
онная энергия топологической природы (две жидкие среды) удерживает
противоположные дислокации от коллапса.
Энергия упругости, запасенная в маслянистых бороздках, часто умень¬
шается за счет ращепления бороздки на серию КФД; см. другие модели
неустойчивости маслянистых бороздок в работах: Колье и др.24\ Ро251
Рис. 10.18. Общая структура маслянистой бороздки, состоящей из конфокальных
доменов вида I, объединяемых краевыми дислокациями
Эллипсы КФД лежат в плоскости наблюдения, и их длинные оси перпен¬
дикулярны маслянистым бороздкам. Топологические соотношения между
КФД и дислокациями, которые разрешают такое расщепление, не будут
в этой книге подробно рассматриваться. Мы лишь ограничимся замечани¬
ем о том, что сингулярности в КФД имеют дисклинационный характер, и как
таковые подвержены топологическому взаимодействию с дислокациями со¬
гласно правилам, обсуждавшимся в гл. 9, 12. Заинтересованный читатель
найдет детальное рассмотрение этого вопроса в работе Бурдона и др.2Ч
24) С. Colliex, М. Kleman and М. Veyssie, Eighth Int. Congress on Electron Microscopy,
Camberra, 1, 718 (1974).
25) J. Rault, Comptes Rendus Acad. Sci. (Paris) B280, 417 (1975),
26^ L. Bourdon, M Kleman andJ. Sommeria, J. de Phys. 43, 77 (1982).
400 Гл. 10. Дефекты кривизны в смектиках и колончатых фазах
Рис. 10.19. Конфокальные домены вида II. Материал: СрС1 /гексанол/ рас¬
сол = 12,5/7,5/80. Предоставлено П. Болтенхагеном (см. P. Boltenhagen, О. D. Lav-
rent ovich and М. Kleman, Phys. Rev. A 46, R1743 (1992))
Интервалы между КФД заполнены либо сегментами дислокаций
(рис. 10.17), либо КФД меньшего размера. Самые большие КФД имеют
геометрические особенности, которые напрямую связаны с вектором Бюр¬
герса /3 (здесь /3 — ndo кратно периоду фазы La, не путать с параметром [3
параболических КФД; в большинстве случаев выполняется соотношение
(3 — Ь\ — 62, означающее, что эта дислокация является суммой дислокаций
противоположного знака, &i, —62, векторы Бюргерса которых имеют поря¬
док размеров образца). Наибольшие КФД имеют главную ось а — (Ь± +62) /2
(т. е. покрывают всю внутреннюю дислокационную область), меньшую ось
\/&1&2 и эксцентриситет е — (bi + b2)/\ |.
Рисунок 10.18 иллюстрирует эти характерные особенности. Плоскость,
содержащая эллипс, всегда параллельна слоям, принадлежащим гомеотроп-
ной области. Перефокусируя микроскоп, можно следовать линии сингуляр¬
ности, которая лежит в вертикальной плоскости, содержащей главную ось
эллипса, и проходит через фокус эллипса. Эта линия является одной из
ветвей гиперболы. Между скрещенными поляризаторами фокус эллипса
выглядит как центр темных секторов (рис. 10.17). Домены являются КФД
первого вида.
Устойчивость краевой дислокации относительно расщепления на КФД
была теоретически изучена в работе Болтенхагена и др231 Имеется два глав¬
ных упругих вклада в эту устойчивость: (1) образование КФД-I уменьшает
энергию упругости, так как ослабляется сжатие слоев, (2) КФД-I содер¬
жат слои с отрицательной гауссовой кривизной, что уменьшает энергию,
если величина А = 2К + К положительна. Важным элементом устойчи¬
вости может быть (в представленном на рис. 10.17 случае) близость к губ¬
чатой фазе; это единственная область на фазовой диаграмме, где видны
КФД-I. Поверхностная ориентация (гл. 13) тоже влияет на устойчивость,
поскольку большие КФД-I требуют больших наклонов слоев на границах
(см. рис. 10.18).
§ 10.8. Границы зерен, заполнение конфокальными доменами
401
10.7.2. Сферолиты
Сферолиты возникают, когда ламеллярная фаза, образованная, напри¬
мер, в смеси CpCl/гексанол/рассол, находится вблизи мицеллярной фазы,
состоящей из глобулярных или палочкообразных мицелл. При наблюдении
в поляризационный микроскоп обнаруживаются текстуры, разительно от¬
личающиеся от текстур, когда-либо найденных в смектикоподобных фазах.
Видны двупреломляющие удлиненные домены, расположенные на разных
уровнях внутри окружающей матрицы, которая также является двупрелом-
ляющей (рис. 10.19). Меридианальное сечение границы каждого из этих до¬
менов имеет форму пересечения двух окружностей одинакового радиуса R
(см. ниже рис. 10.29). В таких доменах оптическая ось перпендикулярна
доменной границе. Наблюдения приводят к заключению, что эти домены
являются КФД второго вида (рис. 10.5, б), в которых слои обернуты вокруг
двух сопряженных линий, а именно окружности и прямой. Эта окружность
виртуальна, и в микроскоп видна только прямая линия.
Такие домены нестабильны, и со временем они релаксируют в сфери¬
ческие. В этом процессе виртуальная окружность схлопывается в точку,
число же слоев, составляющих домен, сохраняется.
В отличие от случая КФД-I, в КФД-И слои имеют положительную гаус¬
сову кривизну. Это, вероятно, связано с отрицательным значением К, кото¬
рое было оценено различными способами. Ниже будет показано, что поло¬
жительная кривизна может быть также связана со способами приготовления
образца, которые всегда включают сдвиг: КФД-П в этом случае являются
результатом гидродинамической неустойчивости. Эти две причины не яв¬
ляются взаимоисключающими: в смектиках А сдвиговые неустойчивости
дают параболические КФД-I (см. § 10.8).
§ 10.8. Границы зерен и заполнение пространства
конфокальными доменами
КФД имеют нетривиальную форму, и ими нельзя покрыть простран¬
ство. Так как наблюдается их объединение в крупномасштабные кластеры,
то возникает вопрос, какими законами регулируется этот процесс и как
органинизованы слои между доменами, т. е. на меньших масштабах. Здесь
будут рассмотрены примеры с обычными КФД-I и КФД-Н271 Случай то-
рических КФД-I является простым, так как двумерная периодическая сеть
эквивалентных торических КФД может заполнить пространство с некото¬
рыми промежутками, где слои параллельны и планарны и плавно стыкуют¬
ся частями торов с отрицательной гауссовой кривизной (рис. 10.20).
Случай параболических КФД-I был изучен экспериментально и теоре¬
тически10); каждый параболический КФД-I заполняет все пространство,
27-) М. Kleman, J. de Phys. 38, 1151 (1977).
402 Гл. 10. Дефекты кривизны в смектиках и колончатых фазах
и слои практически плоские (см. выше) на некотором расстоянии от оси
парабол; поэтому происходит практически плавное согласование одного
параболического КФД-I с другим, коль скоро их оси параллельны.
10.8.1. Конфокальные домены первого вида
10.8.1.1. Законы объединения Фриделя. Обычно в поляризацион¬
ный микроскоп наблюдаются не изолированные КФД, а целые ансамбли
контактирующих доменов. Эти ансамбли были очень подробно описаны
Жоржем Фриделем, который установил геометрические законы, которым
они подчиняются1^.
Рис. 10.20. Конфокальный домен с основанием в виде окружности, встроенный
в систему горизонтальных плоских слоев
Домен называется полным, если физически существуют все его слои
с отрицательной гауссовой кривизной, связанные с парой сопряженных ко¬
нических сечений. Полный КФД ограничен двумя полубесконечными кру¬
говыми цилиндрами, которые имеют в качестве общего основания эллипс,
и образующие которых параллельны асимптотам гиперболы. На рис. 10.5, а
показаны только те части циклид Дюпена, которые находятся внутри этих
цилиндров. Неполные домены могут быть либо законченными, либо фраг¬
ментированными. Законченный домен ограничен двумя круговыми конуса¬
ми, которые имеют в качестве общего основания эллипс и вершины которых
лежат на физической ветви гиперболы, обычно по разные стороны от плос¬
кости эллипса (например, точка М" на рис. 10.4 могла бы быть одной из
таких вершин). Наибольший из возможных законченных доменов получа¬
ется перенесением вершин в бесконечность на асимптоты, т. е. это полный
домен. Домен будет называться фрагментированным, если эллипс не полно¬
стью физичен. В таком случае домен ограничен еще двумя листами конуса
вращения, вершины которых лежат на эллипсе.
§ 10.8. Границы зерен, заполнение конфокальными доменами
403
Нижеследующие законы объединения доменов имеют простой геомет¬
рический смысл. Как будет понятно, они физически соответствуют тенден¬
ции заполнять пространство таким образом, чтобы обеспечивать непрерыв¬
ность слоев от одного домена к другому и сохранять постоянную толщину
слоев. Конечно, эти требования не могут быть выполнены повсюду, и на¬
блюдаются многочисленные несогласования. Например, как уже было от¬
мечено, КФД-I не могут укладываться согласно этим законам. Но в целом
они допускают корректный анализ укладки слоев на больших масштабах,
особенно в термотропных образцах.
Чаще всего наблюдается экспериментальная ситуация в термотропных
системах — это когда два КФД касаются друг друга вдоль двух образующих
и конические сечения, образующие эти домены, попарно контактируют, т. е.
пары конических сечений либо прерывают друг друга, либо оказываются
касательными друг к другу. Согласно Фриделю, это означает, что контакт
между двумя КФД подчиняется описываемому ниже «закону соответствую¬
щих конусов». Если же два КФД касаются только по одной образующей,
содержащиеся в них конические сечения не контактируют попарно. Фри-
дель обобщает свои данные следующим образом.
Закон непроникновения: два КФД не могут проникать один в
другой; если они находятся в касательном контакте в точке М,
то они касаются один другого по крайней мере по одной обра¬
зующей, общей для двух ограничивающих конусов.
Этот «закон» непроникновения имеет экспериментальную природу; его
физический смысл заключается в том, что взаимодействия между КФД
имеют стерическую природу.
Закон соответствующих конусов (ЗСК): когда два конических
сечения, С\ и С2, принадлежащие двум различным КФД (КФД-1
и КФД-П), находятся в контакте в точке М, два конуса вращения
с общей вершиной М, которые лежат на двух других конических
сечениях, С[ и С2, этих двух КФД, совпадают. Поэтому С[ и С2
имеют две точки пересечения, Р и Q, на этом общем конусе,
и линии PM hQM являются двумя образующими этого конуса,
по которым соприкасаются два КФД.
Закон соответствующих конусов имеет гораздо более широкий смысл,
чем закон непроникновения; он имеет физическое содержание, которое бу¬
дет рассмотрено в следующем подпункте, и геометрическое содержание,
на котором остановимся теперь. Если два КФД находятся в контакте в двух
точках, подобных М и Р (чтобы упростить рассмотрение, читатель мо¬
жет представить С\ и С2 в виде двух эллипсов, а С[ и Q в виде двух
гипербол (рис. 10.21), но результат не зависит от такой конкретизации),
то действительно два конуса вращения с общей вершиной М, лежащие,
соответственно, на С[ и идентичны, потому что у них одна и та же
ось (касательная к С\ и С2 ъ точке М) и общая точка Р. Так как они
404
Гл. 10. Дефекты кривизны в смектиках и колончатых фазах
совпадают, то кривые С{ кС2, находясь на одном и том же конусе, имеют
две точки пересечения: Р и Q. Другими словами, два КФД, имеющие общую
образующую и два контакта на своих порождающих конических сечениях,
удовлетворяют ЗСК.
Закон соответствующих конусов приводит к геометрической конструк¬
ции, изображенной на рис. 10.21. Если два касающихся конических сечения
лежат в одной плоскости, то тройки точек М, F2 и М, F2 лежат на
прямых линиях; Fi, F/ nF2,F2— это фокусы С\ и С2 (задача 10.5). Точка А
на рис. 10.21, а является общей проекцией двух пересечений, Р и Q, кри¬
вых С[ и С2.
Проекция Р на Q q
а б
Рис. 10.21. Закон соответствующих конусов: вид в плоскости эллипсов (а) и трех¬
мерный вид (б)
10.8.1.2. Границы зерен. Аполлониева упаковка. Так как слои пер¬
пендикулярны линиям, соединяющим эллипс с гиперболой, то они пере¬
секают линию контакта между двумя КФД без сингулярностей, если
соблюдаются законы Фриделя. Особенно простой тип группирования кон¬
фокальных доменов встречается на границах зерен (рис. 10.22, 10.23, в, г):
вместо дислокаций, как на рис. 10.23,6, граница заполнена эллипсами с
одинаковыми эксцентриситетами и параллельными длинными осями. В
результате соответствующие гиперболы имеют параллельные асимптоты.
Угол между асимптотами в соседних зернах измеряет разориентацию этих
зерен, так как слои перпендикулярны асимптотическим направлениям. «Об¬
щие вершины» находятся по обе стороны границы на бесконечности, так
что домены являются полными (рис. 10.22, 10.23, в, г).
Но по-прежнему остается много вопросов. Каково распределение эл¬
липсов по размерам? Ясно, что с целью уменьшения области границы,
§ 10.8. Границы зерен, заполнение конфокальными доменами
405
которая не занята эллипсами, т. е. не принадлежит никакому КФД и, соот¬
ветственно, энергия которой не просто энергия кривизны, нужно ввести
меньшие эллипсы между и в контакте с большими. Такое «итеративное
заполнение» должно дать минимум энергии границы, что требует локаль¬
ного соблюдения законов Фриделя при контактах; типичный же размер
остающихся вне КФД включений получается путем глобальной минимиза¬
ции энергии.
Эта проблема обсуждалась Бидо и др.28^ для особенно простого слу¬
чая границы зерен с зануляющейся разориентацией, когда гиперболы
вырождаются в прямые линии, эллипсы — в окружности, а КФД ста¬
новятся торическими. Торические КФД, построенные из компланарных
соприкасающихся окружностей, тривиально удовлетворяют законам Фри¬
деля. Задача далее сводится к двум следующим шагам: итерации в ком¬
пактном заполнении плоскости кругами (в математике это известная задача
Аполлония: на каждом шаге итерации радиусы вновь вводимых кругов,
касающихся уже присутствующих, уменьшаются) и вычисление размера
остающихся зазоров, так чтобы полная энергия минимизировалась. Неиз¬
вестными являются: а) число кругов радиуса R > 6, когда итерация дости¬
гает кругов радиуса 6, обозначим это число g(b); б) полный периметр этих
кругов Р(Ь)\ в) остаточная не покрытая кругами поверхность £(&). Пусть
L — размер наибольших кругов; можно ожидать, что искомые величины
алгебраически зависят от безразмерного числа L/b:
g(b) — const • ; P(b) = const • b ^ j ; S(6) = const • b2 .
(10.37)
Рис. 10.22. Граница зерен, разделенная на конфокальные домены; гиперболы лежат
в плоскости рисунка, а эллипсы перпендикулярны ей (предоставлено Клер Мейер)
28 ^ R. Bidaux, N. Boccara, G. Sarma, L. de Seze, P. G. de Gennes and О. Parodi,
J. Physique 34, 661 (1973).
406
Гл. 10. Дефекты кривизны в смектиках и колончатых фазах
Численное моделирование29^ дает значение показателя п, примерно равное
1,306. Энергия границы зерна может быть оценена следующим образом.
Энергия торического КФД радиуса b имеет порядок КЬ, следовательно,
вклад в общую энергию кругов с радиусом R > Ь изменяется как Wyme ~
КР(Ь) = const • Kb(L/b)n. Остаточные области упруго деформированы
на расстояниях от плоскости границы, имеющих порядок длины проникно¬
вения Л = s/WjB; отсюда имеем: H^esid ~ ВХЕ(Ь) = const • Bb2X(L/b)n;
где В — модуль сжатия. После минимизации W\\ne -f- I^sid по отноше¬
нию к Ь, величина Ъ на последней итерации равна b* ~ yjK/B — А.
Энергия на единицу площади границы зерна оказывается порядка crFCD ~
~ L~2(L/b*)nBX2b*. Оставляем читателю в качестве упражнения срав¬
нить эту энергию с энергией кривизны стенки и энергией дислокационной
стенки. Обсудим теперь приложимость этих результатов к границе зерен
с ненулевой разориентацией30^
LJ
б
а
в
Асимптотическое
направление
Рис. 10.23. Наклонные границы зерен: стенка с изгибом (а); дислокационная стен¬
ка (5); граница зерен, разделенная на конфокальные домены, удовлетворяющие
законам объединения Фриделя (в); конструкция границы, в — л -си (г)
29) Р. В. Thomas and D. Dhar, J. Phys. A: Math. Gen. 27, 2257 (1994).
30/ hi Kleman and O. D. Lavrentovich, Eur. Phys. J. E 2, 47 (2000).
§ 10.8. Границы зерен, заполнение конфокальными доменами
407
Рассмотрим систему полных КФД, опирающихся на аполлониево по¬
крытие. Их граница представляет собой систему параллельных цилиндров
вращения С, касающихся по общим образующим G, рис. 10.23, г. Пере¬
сечем этот систему плоскостью под углом cj/2 к плоскости П0, со¬
держащей аполлониево покрытие. Легко показать, что набор эллипсов Еи
с эксцентриситетом eu = sin со/2 на пересечении С и является правиль¬
ным набором конических сечений, удовлетворяющих закону соответству¬
ющих конусов. В самом деле, любой конус вращения, лежащий на каком-
нибудь эллипсе, имеет свою вершину на сопряженной гиперболе; любой
цилиндр С, лежащий на принадлежащей П0 окружности, является таким
конусом; поэтому асимптотические направления ориентированы вдоль G
и вдоль направления зеркально симметричного G относительно плос¬
кости nw. Полуцилиндры вращения с образующими G и G^, лежащие на
эллипсах касаются, в случае верхних полуцилиндров, по тем же обра¬
зующим G, что и полные КФД, опирающиеся на аполлониево покрытие,
и касаются по зеркальным образующим в случае нижних полуцилин¬
дров. Поэтому каждый полный КФД на граннце зерен с разориентацией со
касается его соседних полных КФД по двум образующим (рис. 10.23, в) и на¬
ходится в однозначном соответствии с некоторым полным торическгш
доменом, принадлежащим аполлониеву покрытию.
Уравнения (10.37) модифицируются следующим образом:
g(b) = const • ; P(b) — const • Е(е2)(1 — e2)~l^2b ;
Е(6) = const ■ (1 - е2)“1/262 (^)", (10.38)
где Ъ — половина меньшей оси эллипса (радиус окружности становит-
1
ся половиной меньшей оси при косом сечении); Е(х) = J (1 — £2)-1/2 х
о
х (1 — xt2)1/2 dt — полный эллиптический интеграл второго рода; пери¬
метр эллипса равен 4аЕ(е2) = 46Е(е2)/cosе2 ~ sin2 -; отношение
2 2
площадей при косом сечении равно у/l— е2 — cos
Чтобы вычислить энергию стенки, необходимо уравнение (10.19) для
энергии кривизны W изолированного КФД-I и оценка энергии ядра. Пред¬
положим, что радиус ядра постоянен вдоль эллипса (гс А = s/K/B)
и что энергия ядра равна К на единицу длины вдоль эллипса, в то время
как полная энергия ядра вдвое больше энергии ядра эллипса; тогда энергия
ядра одной конфокальной пары равна примерно 8аХЕ(е2). Таким образом,
энергия стенки включает следующие три вклада:
L L
W]
bulk
dg(x)W(x) ~аьК{ 1-ег)
- *2x1/2
Г, \ П , о ч X
In 2- — 2
n(-) dxK(e )
X
A
408
Гл. 10. Дефекты кривизны в смектиках и колончатых фазах
L
L
W.
core
dg(x)wcore(x) ~ асК( 1 - е2) 1/2Е(е2)
x—b
vrdis.1j
r resid
rs-/
eBAE(fe) = Б62Ле(1 - ег)
2л —1/2 /М
n
(10.396)
(10.39b)
где аь и ас — численные константы.
Получить выражения (10.39 а, б) довольно просто, а вот (10.39 в) требует
комментария. Остаточные области являются кусочками границы и поэтому
должны принять вид либо стенки изгиба (рис. 10.23 а) (когда разориента¬
ция uj велика), либо дислокационной стенки (рис. 10.23 б) (когда разориен¬
тация мала). Обсудим первый сценарий, когда энергия релаксирует через
краевые дислокации. Второй сценарий будет рассмотрен в задаче 10.6.
Сама возможность релаксации через дислокации вытекает из того фак¬
та, что сингулярные линии в КФД являются на самом деле изогнутыми (не
прямыми) дисклинациями, которые, согласно общему анализу3Ч являются
окончанием дислокаций. Как показано Болтенхагеном и др.2Ч дислокации,
прицепленые к эллипсу изолированного КФД с параметрами а ие, име¬
ют полный вектор Бюргерса 2ае. Предположим теперь, что ядро каждого
сегмента дислокации с вектором Бюргерса 2ае протянулось на сходное рас¬
стояние гс — 2а. Такое предположение тем более справедливо, что вектор
Бюргерса велик, и имеет то преимущество, что дает некоторое (малое) на¬
тяжение w дислокационной линии, которое изменяется пропорционально
вектору Бюргерса32^, а не квадрату вектора Бюргерса, т. е. w ~ В Хае =
= ВХЬе/у/1 — е2. Мы должны вычислить общую длину таких дислокаций,
что мы и сделаем. Площадь каждого связного элемента, остающегося в
промежутке между КФД, на стадии «Ь» итеративного процесса имеет по¬
рядок ~ ab. Можно убедиться в правильности этой оценки, рассматривая
четыре одинаковых эллипса (а, е), находящиеся в симметричном попарном
контакте; между ними заключена «остаточная» площадь, равная (4 — n)ab.
Поэтому число связных остаточных элементов изменяется как ~ Е(Ь)/аЬ =
= (1 -e2)-1/262(L/6)n/ab = (L/b)п. Длина сегмента дислокации в связном
элементе изменяется пропорционально b; следовательно, общая остаточная
энергия дается выражением (10.39 в). Отметим, что это выражение приво¬
дит К занулению Wresid при и = 0.
Теперь, минимизируя полную энергию W = Wbulk + Wc0re + ^resid по
отношению к 6, получаем минимальное Ь\
ь*
disi
А
1
ГЧ-/
е 2
)К(е2)
2 Ъ*
In disi
А
2
+ асЕ(е2)}, (10.40)
31) J. Friedel and М. Kleman. J. de Phys. 30, C4:43 (1969).
32^ M. Kleman. Points, lines and walls, John Wiley & Sons, Chichester, 1982.
§ 10.8. Границы зерен, заполнение конфокальными доменами
409
и выражение для энергии на единицу площади стенки (с остаточными об¬
ластями, релаксирующими за счет дислокаций)
^FCD (е)
1
п
rsJ
(п - 1)L2
х (1 - е )
-) " ВХ3
А/
2л —1/2
А
71—1
^disl
X
(1 “ ez)K(e2)
A
Tl — 1
(10.41)
которое находится путем интегрирования (10.39 а,б) и подстановки (10.40)
в сумму Wbuik + Wcore + W^esfd* Значение b* для со — 0 обращается в беско¬
нечность, а энергия обращается в нуль, что и ожидалось для этого случая.
На рис. 10.24 показана полная энергия W для аь = 47т, ас = 8 как функ¬
ция эксцентриситета е и безразмерной переменной у = b/Х. Видно, что для
каждого значения е, т. е. разориентации со, существует два решения 6/А,
W
Рис. 10.24. Энергия упругости W образованной КФД-I границы зерен (в произволь¬
ных единицах) как функция е и lg у для аь = 47т, ас = 8, L = 50 мкм и А = 2 нм;
У = ь/х
при которых производная обращается в нуль. Решение с меньшим Ь/X соот¬
ветствует максимуму, тогда как другое дает минимум. Это правомерное ре¬
шение, оно быстро изменяется с изменением е (или си). Остаточная область
велика для малых разориентаций со, а энергия мала; при си = 0 «остаточ¬
ная» область занимает всю границу. Только для очень больших разориента¬
ций получается, что остаточная область становится микроскопической, как
410
Гл. 10. Дефекты кривизны в смектиках и колончатых фазах
в аполлониевой модели. Мы предлагаем в качестве упражнения сравнить
энергию границы зерен, образованной КФД-I, с энергией дислокационной
границы зерен (при больших и) и изгибной границы зерен (при малых cj),
см. задачу 10.6.
Рассмотренная выше модель КФД объясняет ту хорошо известную экс¬
периментальную особенность, что остаточная область границ зерен в смек¬
тиках имеет микронные размеры, т. е. макроскопична. Та же характерная
ситуация с большими остаточными областями встречается в других ти¬
пах упаковок, например на границах раздела между смектической фазой
и другой фазой33) (которая может быть изотропной фазой того же смекти¬
ческого соединения34)). Такие границы часто бывают покрыты эллипсами
и гиперболами из-за специальных свойств сцепления на границе. Обсуж¬
дение этого будет продолжено в п. 13.2.6, где будет рассмотрено значение
ориентационной зависимости поверхностного сцепления.
10.8.2. Конфокальные домены второго вида
Плотная упаковка «луковиц» наблюдалась в подвергнутых сдвигу лио¬
тропных Ьа-фазах35). Луковицы остаются после прекращения сдвига, и их
размер зависит критическим образом от скорости сдвига. Следовательно,
такое заполнение не является интерактивным.
Хотя неясно, наблюдалось ли итеративное заполнение пространства
в смектической фазе, но рассмотрение такой возможности представляет
определенный интерес, так как многие электронно-микроскопические ис¬
следования лиотропных фаз обнаружили наличие упаковки сферолитов,
имеющих различные размеры: от макроскопических (несколько микрон)
до микроскопических (десятки и сотни ангстрем); например, вблизи фа¬
зового перехода La ~ Li36) или после встряхивания сильно растворенной
фазы La.
Имеется несколько существенных различий в заполнении пространства
посредством КФД-I и КФД-Н. Прежде всего, КФД-I конической формы име¬
ет объем abL и простирается на весь образец (толщины L). Основание
КФД-I часто располагается на поверхности образца. Вот почему анизо¬
тропия поверхностной энергии так важна для ситуации с КФД-I (п. 13.2.6).
Напротив, КФД-П имеет замкнутую форму с характерным объемом а3, где а
может быть много меньше L. Поэтому физический предел для итеративного
процесса определяется исключительно объемными свойствами ламелляр¬
ной фазы.
33) О. D. Lavrentovich. Sov. Phvs. JETP 64. 984 (1986); Mol. Cryst. Liq. Cryst. 151,
417 (1987).
34^ J. B. Fournier and G. Durand. J. Phys. II France 1, 845 (1991).
35) P. Sierro and D. Roux. Phys. Rev. Lett. 78, 1496 (1997).
36^ P. Boltenhagen, M. Kleman and O. Lavrentovich. J. de Physique II (France) 4. 1439
(1994).
§ 10.9. Реоф изика конф окал ьных доменов
Наибольшие сферолиты имеют макроскопический размер R А (опре¬
деляемый, например, размером образца или скоростью сдвига) и искажа¬
ют ламеллярную матрицу. Энергия Wb сжимаемости слоев вне сферолита
радиуса R изменяется как BXR2, если среднее расстояние между сферо-
литами больше R2/А, и как BR3, если расстояние меньше R, (в последнем
случае относительное изменение расстояния между слоями е. имеет поря¬
док единицы). Эти искажения могут уменьшиться за счет меньших КФД-Н,
лежащих между большими КФД-II, так как геометрия КФД-II предпола¬
гает только деформации кривизны и энергию ~ Аа. Такой итерационный
процесс прекратится на масштабах а*, которые уже не обеспечивают выиг¬
рыша в энергии при замене изменения расстояния между слоями кривиз¬
ной. Чтобы определить а*, введем число сфер gрадиуса R ^ а, уложенных
в объеме L3, g ~ (Ь/а)7. Остаточный объем (который не занят КФД-Н)
есть V^a) ~ L7a3-7. Тогда полная свободная энергия изменяется как
W(p) ~ ALV“7 + BLV"7. (10.42)
Здесь 7 не является универсальной константой, в отличие от показате¬
лей степени, встречающихся в двумерной аполлониевой задаче заполнения
плоскости кругами. Но в некоторых конкретных экспериментальных слу¬
чаях получается значение у « 2,8371 Эта величина в действительности дает
минимум W(p), когда А > 0, и физический предел для итераций:
а* = у/(7 — 1) Л/(3 — у) В. (10.43)
Таким образом, итерации идут вниз до очень малого масштаба ~ Л, как
и в модели Бидо с соавторами для заполнения с КФД-I. Трудно вообразить
какой-нибудь другой предел для итераций, так как при балансе вкладов от
кривизны и изменения расстояний между слоями единственная характерная
длина есть Л.
Покрытие пространства сферолитами оказывается (мета)стабильным,
если величина А ~ 2К + К отрицательна и достаточно велика. Слияние
двух соседних сферолитов затруднено из-за необходимости создания между
ними энергетически невыгодного «мостика» с отрицательной гауссовой
кривизной (рис. 10.25).
§ 10.9. Реофнзика конфокальных доменов
Реологические свойства связаны с микроструктур ой только когда обра¬
зец совершенен, т. е. остается в основном состоянии по ориентационному
порядку после приведения в движение. Например, если градиент скорости
перпендикулярен слоям (скорость направлена в плоскости слоя), подверг¬
нутый сдвигу образец чувствует микроструктурную вязкость, связанную
37) R. Omnes. J. Physique France 46, 139 (1985).
412
Гл. 10. Дефекты кривизны в смектиках и колончатых фазах
с межплоскостным трением. Но даже такое простое течение может приве¬
сти к неустойчивости при еще очень низких скоростях сдвига. Нелинейное
поведение, которое затем наблюдается, может быть связано с дефектами
соответствующей структуры, подобными дислокациям или КФД. Теория,
описывающая возникновение этих нестабильностей и их рост, является еще
развивающейся областью38^ 391 Поэтому данный параграф будет в основ¬
ном посвящен экспериментальным результатам. С экспериментальной точ¬
ки зрения лиотропные и термотропные системы демонстрируют похожее
поведение при низких частотах (или низких скоростях сдвига), но дают
различные текстуры при высоких скоростях сдвига.
Рис. 10.25. Слияние КФД-Н с центрами в точках А через три КФД-I: АВОС,
ACOD, ABOD
10.9.1. Глобальное вязкоупругое поведение и ориентация при сдвиге
Хорошо известно, что в линейной вязкоупругой жидкости измерение
низкочастотной зависимости комплексного модуля G* = G' -Ь iGn дает
G1 « т/гоД G" « t)gj, где г — наибольшее время релаксации данного
материала, связанное с процессами молекулярной релаксации. Такое пове¬
дение зафиксировано, например, в высокотемпературных сополимерах, где
типичные частоты релаксации г-1 имеют порядок нескольких обратных
38^ S. I. Ben-Abraham and P. Oswald. Mol. Cryst. Liq. Cryst. 94, 383 (1983).
39^ R. Ribotta and G. Durand. J. Physique 38, 179 (1977).
§ 10.9. Реофизика конфокальных доменов
413
секунд или более, что сопоставимо с частотами, доступными измерению
с помощью реометров. Подобное поведение прекращается, когда материал
охлаждается до макроскопически упорядоченной фазы: времена релакса¬
ции теперь зависят от коллективных мод, и нет наибольшего времени ре¬
лаксации. Зависимости G'(и>), Gn (и) должны в таком случае быть связаны
со структурой упорядоченной фазы.
Как показано Ларсоном и др.40), такое поведение характерно для мно¬
гих ламеллярных фаз с очень разной молекулярной структурой, подобных
блок-сополимеру полистирол-полиизопрен и термотропному материалу
8СВ. В обоих случаях Gf(uj) и G"(cj) реагируют одинаковым образом на
перемену температуры, величины сдвига или продолжительности прило¬
жения сдвига. Указанные факты связаны с тем, что различные ламелляр¬
ные образцы рвлаксируют похожим образом при увеличении температуры
или при долгодействующем сдвиге. Другими словами, независимо от ти¬
па образца плотность дефектов является главным фактором, влияющим на
вязкоупругие свойства.
Другой глобальный эффект от изменения температуры и скорости или
продолжительности сдвига — это ориентация образца. Согласно боль¬
шинству авторов41), ламеллярные фазы ориентируются так, что директор
перпендикулярен как течению, так и направлению сдвигового градиента
(см. рис. 6.5, а) при достаточно низких скоростях непрерывного сдвига (или
при низких частотах) и при достаточно высоких температурах. После про¬
межуточной области скоростей сдвига, в которой директор ориентируется
в направлении сдвигового градиента (см. рис. 6.5, в, слои в это время па¬
раллельны сдвигающимся обкладкам), при больших скоростях сдвига снова
происходит переход к ориентации, изображенной на рис. 6.5, а. Эти эффек¬
ты относят к нелинейному взаимодействию сдвига с флуктуациями42) 43).
10.9.2. Текстуры
Текстуры лиотропных и термотропных ламеллярных фаз имеют суще¬
ственно различный внешний вид при сдвиге, хотя принципы, лежащие
в основе связи между сдвигом и флуктуациями, одни и те же. Это про¬
исходит потому, что, как уже утверждалось, дефекты, хотя и одной тополо¬
гической природы, имеют тем не менее разные типы физической реализа¬
ции. Вдобавок, условия сцепления на поверхности могут иметь различную
природу и противодействовать (сильно или нет) объемным эффектам.
40) R. G. Larson. К. I. Winey, S. S. Patel, Н. Watanabe and R. Bruinsma. Rheol Acta 32,
245 (1993).
41) см. например К. A. Koppi et al. J. Phys. II (France) 2, 1941 (1992); C. R. Safinya
et al. Science 261, 588 (1993); P. Panizza et al. J. Phys. II, France 5, 303 (1995).
42) R. F. Bruinsma and C. R. Safinya. Phys. Rev. Lett. A43, 5377 (1991).
43) M. Goulian and S. T. Milner. Phys. Rev. Lett. 74, 775 (1995).
414
Гл. 10. Дефекты кривизны в смектиках и колончатых фазах
10.9.2.1. Термотропные материалы. В гомеотропном смектике А
при сдвиге развивается неустойчивость, которая трансформируется в си¬
стему параболических КФД. При коротких временах сдвига текстура разу-
порядочена, но со временем ориентируется в направлении сдвига, образуя
регулярную квадратную решетку, период £ которой увеличивается с тол¬
щиной образца. Текстуры дефектов могут характеризоваться интенсивно¬
стью I света, проходящего через образец, помещенный между скрещен¬
ными поляризаторами; / = 0 для однородного состояния (директор вдоль
волнового вектора). На рис. 10.26 представлены экспериментальные ре¬
зультаты44) для 8СВ: в установившемся состоянии зависимость между на¬
пряжением и сдвиговой скоростью линейна и оказывается так называемого
типа Бингама {Bingham), т. е. имеется некоторое напряжение пластического
течения сгу: Л .
а — aY + А 7, (10.44)
где 7 — сдвиговая скорость, а А — коэффициент, подобный вязкости.
а, дин / см2
300
200
100
7, с
-1
0
20
40
60
80
Рис. 10.26. Сдвиговое напряжение как функция сдвиговой скорости при различ¬
ных интенсивностях проходящего света (показанного числами в условных еди¬
ницах). В квазиоднородном образце / = 0; I = 6,5 соответствует примерно
80-процентному содержанию разупорядоченной текстуры параболических КФД;
кривая «гпах» представляет максимальное сдвиговое напряжение, измеренное как
функция приложенной сдвиговой скорости. Для ясности большинство эксперимен¬
тальных данных показано линиями
Напряжение пластического течения ау может быть записано, на осно¬
ве опыта размерных оценок, как К/£2. Это выражение дает правильный
порядок величины, означающий, что <гу является мерой сопротивления те¬
чению со стоооны оешетки папаболических КФЯ. В действительности было
44^ R. Horn and М. Kleman. Ann. Physique 3, 229 (1978).
§ 10.9. Геофизика конфокальных доменов
415
показано путем наблюдения взвешенных частичек в потоке, что централь-
ная часть образца, представляющая собой область, наиболее искаженную
параболическими КФД, практически неподвижна: большая часть течения
происходит вблизи границ45^ (рис. 10.27).
Несколько экспериментов, проведенных на образцах с параллельным
сцеплением директора на границе46), также показывают, что дефекты обра¬
зуются при малых сдвиговых скоростях и сдвиговых частотах. Существен¬
ный эффект состоит в образовании двух стенок Гранжана-Кано противо¬
положного знака, параллельных границам образца, что уменьшает разори-
ентацию, вносимую сдвигом (рис. 10.28). Эти стенки расщеплены на КФД
с одинаковым эксцентриситетом. Непрерывный сдвиг происходит пред¬
положительно путем относительного скольжения двух систем КФД вдоль
общих образующих.
Рис. 10.27. Модель течения в образце, где под действием сдвига в центральной
части образовалась решетка параболических КФД-1
Рис. 10.28. Под действием сдвига в планарном образце появляются три области
с различной ориентацией [по J. Marignan et ai Ann. Phys. France 3, 221 (1978)]
45) P. Oswaldetai Philos. Mag. A46, 899 (1982).
46^ С. E. Williams andM. Kleman. J. Physique 36, С1-315 (1975). J. Marignan, G. Malet
and O. Parodi. Ann. Physique 3, 221 (1978).
416
Гл. 10. Дефекты кривизны в смектиках и колончатых фазах
10.9.2.2. Лиотропные материалы. Наиболее показательная разни¬
ца между лиотропыми и термотропными текстурами при наличии сдвига
состоит в появлении в первых из них сферолитов (луковиц). Образование
таких КФД-Н также наблюдалось в разбавленных образцах47). Они обра¬
зуют плотные регулярные упаковки, характерная протяженность которых
(размер луковиц К) связана со скоростью сдвига R ос 1 / л/т* Тот факт,
что некоторые разбавленные лиотропные материалы предпочитают КФД-И
(луковицы), а не КФД-I выше порога сдвиговой неустойчивости, который,
вероятно, одинаков в обоих случаях, пока в достаточной мере не понят.
Задача 10.1. Доказать(10.3).
Ответ. Так как тензор еца антисимметричен по отношению к любой
паре индексов, свернутое произведение вида £гы^ы = 0, если тензор aki
симметричен (аы = Щк)• Следовательно, = 0. Поэтому можно
записать -eikiPij, к = -£iki(Pij, к + Pji, к) и отождествить -{fa + /3#) с ец.
2 2 2
Задача 10.2. Доказать соотношение между тензором искривления
и плотностью дислокаций (10.4).
Ответ. Доказательство получено Наем2); см. также К R. N. Nabarro,
Theory of Crystal Dislocations, Oxford, 1967, p. 45.
Задача 10.3. Пункт 10.5.4 представляет собой сводку результатов,
требующих особого внимания читателей, так как для доказательства боль¬
шинства формул даны лишь несколько советов. Здесь предложено упражне¬
ние, завершающее список (наблюдаемых) случаев, изученных в этой главе.
Рассмотрим КФД-П с симметрией вращения (е = 0, а = Ь, а < г < R),
рис. 10.29.
а) Показать, что главные кривизны и бесконечно малый элемент поверх-
1 cos 0
ности можно записать как сг' = -уа1! — , е£Е — 2тгг(г cos# — a) d6.
г г cos 9 ~ а
Вывести несингулярную энергию кривизны w2,r слоя г и соответствующий
несингулярный вклад в полную энергию КФД-Н. Оценить энергию ядра
в модели на рис. 10.30. Показать, что энергия ядра обращается в нуль при
а 0. Вычислить полную энергию КФД-И (луковицы), когда а -> 0.
б) Оценить энергию деформации матрицы, соответствующую введе¬
нию КФД-П в гомеотропную область (рис. 10.31).
47) О. Diat andD. Roux. Langmuir 11, 1392 (1995).
§ 10.9. Реофизика конфокальных доменов
417
Ответ.
а) Несингулярная часть энергии упругости слоя г получается из (10.33)
подстановкой е = 0 в виде
w2,
47г(2>гг + х)\ 1
интегрирование по г дает
я
Л
w,
а
а
где г = а/1 cos#
^ dr = 4тгЛД
do
1
шах
(рис. 10.29);
а
R2
а а
— arccos —
R R
и
Рис. 10.29. КФД-Н, случай Рис. 10.30. Модель ядра КФД-IL В конусе с уг-
е = 0. Меридианальное се- лом ш деформация имеет вид точной дивергенции
чение домена представляет
собой пересечение двух кру¬
гов радиуса R; в — угол
между нормалью к слою
и плоскостью, содержащей
окружность
R w -j- U)
Полная энергия КФД-Н имеет следующий вид: W = J — —dr 4- Wc.
a dO
27-КЛЕМАН М.
418
Гл. 10. Дефекты кривизны в смектиках и колончатых фазах
По аналогии с нематической фазой с деформацией скоса, плотность энер¬
гии ядра имеет порядок К sin2 со, где и — угол между нормалью к слоям
и линией дефекта. Энергия ядра линейного дефекта записывается как
R
а
dr — Ка
2 R — а — do/2
R(a c/q/2)
Когда а О, W —у 4nAR. Этот случай чаще всего наблюдается в экспери¬
ментах.
б) Плотность энергии такой деформации имеет вид и>в = ’
где и — перпендикулярное смещение (в направлении z) слоев от перво¬
начального положения, соответствующего плоским слоям. В очень упро-
щенной модели и может быть взято в виде: и = Rt cos qx cos hy exp( — —),
L
c q
7Г
2 Ri
и h
IT
2 Rt
. Отсюда получается: 1/L = A(q2 + h2), где A
= VK/B.
Интегрирование плотности энергии, связанной с деформацией матри¬
цы, в пределах —Ri < х < Ri\ —Rt <у < Rt\ —оо < z < оо дает энергию
в виде
WB
7Г
BAR? ( ?± + ^
Ri Rt
Я,
8
Энергия Wв имеет минимум, когда Ri
домена (луковицы).
Rt, т. е. в случае сферического
Рис. 10.31. Деформация гомеотропной области из-за введения КФД-Н с симметрией
вращения
§ 10.9. Реофизика конфокальных доменов
419
Задача 10.4.
а) Вычислить энергию дисклинации силы k = 1 в колончатой гексаго¬
нальной фазе для следующих трех случаев: 1) пустое ядро, 2) изотропное
ядро, 3) заполненное ядро.
Подсказка: единственный существенный объемный вклад — это вклад
от кривизны колонок. Обозначения ниже такие же, как и на рис. 10.12.
б) Вычислить энергию дисклинации к = 1/2, предполагая, что ядро
заполнено.
в) Рассмотреть устойчивость линии к — 1 по отношению к расщепле¬
нию на две линии к — 1/2 (см.: Освальд и Клеман22)).
Ответ.
а) к = 1. Пусть 7he—это поверхностная плотность энергии для пустого
ядра. Находим
1) Whc = — In R ~а + 2тг7hcrc,
2 rf - а2
что должно быть минимизировано по отношению к гс и а и должно удо¬
влетворять гс > а;
2) Whc - In + 2тт'у1гс + wc,
2 г2 — а2
АН АТ * гг ^
с « , где Дл — это энтальпия перехода, 1С — температура
Тс
перехода в изотропную жидкость и АТ — Тс — Т. Получаем
а — 0, гс - — ( J-yf + 2wcK3 - 7*
2wc \ v
3) 7 = 7o + Л7 sin2 9с;
существует два решения:
а = 0, гс = ^ и ге = —а = г '70 + 2А7
270 4(70 4- А7) V а 7
б) к = 1/2. Есть два решения:
а = 0, г
#з
С
70 (1 + 2 / 7Г) + 2А7/7г
И
^3 _ / 70 (1/2 + 2/7г) 4- А7(1 - 1 /тг)
гс = , а — г
8[7о(1/2 + 2/7г) 4- А7/2] У Л7(1/2 — 1/тг)
Задача 10.5.
а) Доказать утверждение из пп. 10.8.1.1, связанное со случаем, когда
конические сечения С\ и С2 компланарны.
б) Доказать, что если два КФД имеют только одну общую образующую,
то они не находятся в контакте по двум коническим сечениям.
420 Гл. 10. Дефекты кривизны в смектиках и колончатых фазах
Ответ.
а) Точка М является вершиной общего конуса вращения, лежащего
на конических сечениях С[ и С2 (рис. 10.21). Но С[ (соответственно, С2),
будучи сопряженным к С\ (соответственно, к С2), проходит через фокус С\
(соответственно, С2). Поэтому F\MFи F[MF2 являются образующими
этого общего конуса.
Замечание: общая касательная к С\ и С2 в точке М является осью
этого конуса.
Задача 10.6. Сравнить энергию границы зерен, образованную КФД,
с энергией: а) дислокационной границы зерен (малые w) и б) границы зерен
с искривлением (большие со), рис. 10.23.
Ответ.
а) При малой разориентации та дислокационая модель, что наблюдает¬
ся в клине Гранжана-Кано, имеет энергию на единицу площади порядка
tfdisi ~ В Ае, практически не зависящую от вектора Бюргерса (предполагаю¬
щегося малым) дислокаций. Сравнивая эту энергию с
_disl ^ BA3 / L чП / А \n~-l
apCD ~ !Т{х} ’
где А/Ь* ~ е (см. (10.40)), получаем
^disi /Le\2 п
disl ^ V а /
FCD А
исключением
преимущество при малых е.
б) При больших разориентациях со (или малых 9 = 7г — а;) остаточные
области заполнены изгибными стенками. Соответствующий вклад вычис¬
ляется тем же способом, что и в (10.39в). Он имеет вид
Cld ~ 2В62Л
^ е Arc cos е
у/l — е2
L
п
Здесь было использовано следующее точное выражение для энергии изгиб-
ной стенки48^, справедливое для всех углов:
—
в\ в
- cos
2/ 2
где в = 7Г - СО. Минимизируя полную энергию W = Wbulk + Wcore + ^esid
относительно Ь, получаем соответствующую минимуму величину b,
bcurv 1 п v
~ — х
А 2 ^>/l — е2 — eArc cos 2 — п
х {а6(1 -е2)К(е2) [in - 2] + асЕ(е2)},
L L \ J ✓
48) С. Blanc and М. Kleman, Eur. Phys. Journ. B10, 53 (1999).
Литература для дальнейшего чтения
421
и энергию на единицу площади разделенной на КФД стенки, в которой
остаточные области релаксируют посредством искривления слоев:
rurv ( \
^fcdIw
L
П
(■п - 1 )L2 V А
В А
А
п— 1
6*
^curv
2 fo*
^ucurv
A
1
e Arc cos e
y/l — e2
-f
n
n
1
\/l - e2K(e2)
Зависимость VF от эксцентриситета и отношения 6/А показывает, что оста¬
точные области имеют макроскопические размеры. Две модели остаточных
областей разделенной на КФД стенки, с дислокациями и искривлением, яв¬
ляются дополнительными, первая более пригодна при меньших е, а вто¬
рая — при больших е. Наконец, можно сравнить энергию чисто изгибной
ВХв3 « БА(1 — е2)3/2 с энергией разделенной на КФД
стенки crcurv и
границы
curv / L \П / А \
FCD ~ -jyij)
п
11
в
при
ь*
А
—У
12 асп
(2 — п)#3
чтобы увидеть, что
Crcurv
а
curv
FCD
-)
А/
2— п
о
7-Зп.
т. е. за исключением очень больших образцов модель с чистым искривле
нием без КФД более благоприятна при больших е.
Литература для дальнейшего чтения
1. G. Darboux, Theorie Generate des Surfaces, Chelsea Publishing, N. Y., 1954.
2. J. D. Ferry, Viscoelastic Properties of Polymers, 3rd edition, John Wiley & Sons,
N. Y, 1980.
3. G. Friedel, Annales de Physique (Paris) 18, 273 (1922).
4. £>. Hilbert and S. Cohn- Geometry and the Imagination, Chelsea Publishing,
N. Y., 1952. [Перевод с немецкого издания: Д. Гильберт, С. Кон-Фоссен.
Наглядная геометрия / Пер. с нем. — 3-е изд. — М.: Наука, 1984 ~ 344 с.]
5. М. Kleman, Points, Lines and Walls, John Wiley & Sons, Chichester, 1983.
Дополнительная литература
1. А. С. Сонин. Введение в физику жидких кристаллов. — М.: Наука, 1983.
ГЛАВА И
ДИСКЛИНАЦИИ И ТОПОЛОГИЧЕСКИЕ
ТОЧЕЧНЫЕ ДЕФЕКТЫ.
ЖИДКОСТНАЯ РЕЛАКСАЦИЯ
Дислокации в кристаллических твердых телах представляют собой про¬
стые примеры топологических особенностей: трансляционная симметрия
нарушается вдоль линии, и векторы Бюргерса соединяющихся дислока¬
ций линейно складываются; с другой стороны, это сложные физические
объекты, наиболее важные свойства которых связаны с необратимыми яв¬
лениями, сопровождающими пластические деформации.
Жидкие кристаллы, с их непрерывными симметриями и физическим
преобладанием корреляций ориентаций молекул над корреляциями место¬
положений, обнаруживают удивительно сложное и широкое разнообразие
топологических особенностей. Как и в случае дислокаций, роль этих де¬
фектов в необратимых явлениях физически весьма значима; однако дефор¬
мация течения {реология) гораздо менее понятна, чем пластическая дефор¬
мация. Кроме того, отметим, что в жидких кристаллах и, в более общем
контексте, в анизотропных жидкостях, магнитных системах и спиновых
стеклах особенностями являются дефекты разных размерностей, не только
линейные, но также точечные дефекты, стенки и «конфигурации» (стенки,
топологические солитоны).
Дислокации поворота, чаще называемые дисклинациямщ ^— это линей¬
ные дефекты, вдоль которых нарушается поворотная симметрия. Эти дефек¬
ты чаще всего встречаются в одноосных нематиках (рис. 11.1) и в текучих
средах с директорами (холестерики, двуосные нематики и т. д). Другими
топологическими дефектами в одноосном нематике являются точечные де¬
фекты. В отличие от их тезок в твердых кристаллах (не являющихся топо¬
логическими дефектами), они искажают порядок во всем объеме системы.
В принципе, дисклинации можно классифицировать по элементам пово¬
ротной симметрии упорядоченной среды. Придерживаясь определения и
правил построения дефектов, инспирированных процессом Вольтерра для
дислокаций (гл. 8), легко понять тип привносимых линейным дефектом
искажений в случае, когда вектор поворота (аналог вектора Бюргерса;
ft = Hz/; v2 = 1) направлен вдоль линии дефекта1 \ Такие линии представ¬
ляют собой клиновые дисклинации в нематиках (см. п. 11.1.1). Напротив,
дисклинации, линии которых не параллельны U (например, дисклинации
кручения в нематиках, п. 11.1.3) нельзя получить простым использованием
процесса Вольтерра. Превосходные иллюстрации процесса Вольтерра для
клиновых дисклинаций и дисклинаций кручения, которые можно найти
F С. Frank И Disc. Faraday So с., 25, 19 (1958).
§ 11.1. Линейные и точечные дефекты в одноосных нематиках
423
в литературе2^, демонстрируют эту трудность. Обсуждение данного вопроса
мы откладываем до §11.3. Для него окажется полезным введенное в гл. 10
понятие непрерывной плотности дислокаций. Другие методы, имеющие
более общую топологическую природу, необходимы для досконального по¬
нимания дисклинаций с несингулярным ядром (п. 11.1.2, 11.2.3) и особых
точек; эти методы охватывают дефекты всех размерностей и применимы
ко всем упорядоченным средам. Они будут детально рассмотрены в гл. 12.
Рис. 11.1. Тонкие и толстые линии дисклинаций и особая точка (белая стрел¬
ка), наблюдаемые в объеме нематического образца при помощи поляризационного
микроскопа
§ 11.1. Линейные и точечные дефекты в одноосных
нематиках: статические свойства
11.1.1. Клиновые дисклинации в нематиках
Клиновая дисклинация в твердом теле может быть построена с помо¬
щью процесса Вольтерра; здесь слово «клиновая » означает, что ось враще¬
ния направлена вдоль линии дисклинации (рис. 11.2). Хотя умозрительно
подобные объекты представляются возможными, существует очень малая
вероятность экспериментального обнаружения изолированных клиновых
дисклинаций из-за значительной упругой энергии, которой они обладают.
Дисклинации кручения, ось вращения которых перпендикулярна линии
дисклинации, еще труднее построить, причем даже мысленно, как уже бы¬
ло упомянуто ранее. Начиная с этого места дислинации в твердом теле
будут рассматриваться только в виде пар дисклинаций противоположного
знака, взаимодействующих на коротких расстояниях. Мы упоминали о су¬
ществовании таких пар в фазах Франка-Каспера, а также об их возможном
2) W.F. Harris, Disclinations // Sci. Am., 237, 130 (1977).
424 Гл. 11. Дисклинации и топологические точечные дефекты
существовании в аморфных средах. В обоих случаях дисклинации проти¬
воположных знаков образуют взаимосвязанные сетки.
Рис. 11.2. Клиновая дисклинация с углом 7г в твердом теле
В жидких кристаллах дисклинации являются обычными объектами. На
рис. 11.3 показано построение Вольтерра клиновой дисклинации с углом 7г
в нематике. Здесь можно увидеть полуплоскость разреза £, угол 7г между
ее раскрытыми краями, введение дополнительного однородного вещества
в двугранный угол и, наконец, завершающую процесс упругую релаксацию.
Сила к клиновой дисклинации — это отношение к — а/где а — угол
поворота (с учетом знака) директора после обхода окружающего дискли-
нацию контура Бюргерса (рис. 11.3, г). Это также угол, на который были
раскрыты края разреза S. Знак а определяется сравнением направлений об¬
хода контура Бюргерса и годографа Г директоров (рис. 11.3, г). Рассмотрим
(ориентированный) контур Бюргерса 7, на котором выбрана произвольная
точка начала обхода М; каждый директор п, который мы встретим при
обходе 7, будем смещать в начало координат при помощи параллельного
переноса. Множество концов пробегает дугу окружности с углом а, ори¬
ентированную в соответствии с построением. Эта дуга и есть годограф Г
(см. также §8.3 и рис. 8.6). В примере, представленном на рис. 11.3, кон¬
туры Г и 7 ориентированы в противоположном направлении, отсюда знак
минус, добавленный к силе к: хотя ориентация контура Бюргерса 7 про¬
извольна, знак к не произволен. Таким образом, на рис. 11.3 изображено
§ 11.1. Линейные и точечные дефекты в одноосных нематиках 425
построение дисклинации силы fc = —Тот же результат получится, если
выбрать противоположное направление обхода на рис. 11.3, г. Отметим, что
в ходе данного процесса Вольтерра был введен клин вещества. Наоборот,
дисклинация fc — -получается удалением клина вещества.
2
а
б
в
г
о
Рис. 11.3. Процесс Вольтерра и контур Бюргерса для клиновой дисклинации
fc = —1/2 в нематике: полуплоскость разреза Е, край которой совпадает с пря¬
мой L (а), раскрытие краев £ на угол 7г и введение дополнительного вещества (б),
упругая релаксация (в), контур Бюргерса 7 и его годограф Г (г)
Примеры клиновых дисклинаций приведены на рис. 11.4; все силы крат¬
ны ±~. В качестве упражнения читателю предлагается убедиться, что силы
всех этих дисклинаций можно получить построением годографа директо¬
ров. Обратим внимание также на дополнительное правило: две параллель¬
ные дисклинации k = и к = —~ складываются на расстоянии в fc = О
2 2
(используйте метод годографа). Метод годографа всегда предоставляет спо¬
соб измерения сил к клиновых дисклинаций, какие бы они ни были, в то
время как процесс Вольтерра не дает ясного значения для дисклинаций с
высокой силой |fc| ^ 1.
Дефектные конфигурации директоров на рис. 11.4 являются двумерны¬
ми (векторы п лежат в плоскостях, перпендикулярных оси дисклинации),
и незакрученными. Эта планарная модель дисклинации была использована
426
Гл. 11. Дисклинации и топологические точечные дефекты
£=1/ 2, с = 7г/ 4
к= 1/2, с = О
к=Ъ!2,, с = О
X
\
X
X
X
1
\
1
1
•
1
1
• г
1
/
1
f
?
/
ч х
\
\
\
4
4
4
N
4
4
4
4
V.
х
4
ч
X
X.
X.
X
ч
ч
ч
\
s
1
i
r
г
;
(
1
V
V
X
\
У
1
1
1
.
1
1
t
/
t
{
/
/
/
\ X
\
\
\
4
\
\
4
4
\
4
4
V
4
X
X
X
-
X
w.
w
X
4
4
V
«
\
X
i
•
1
t
i
/
1
V
S
\
1
1
\
1
ь
.
J
\
<
/
!
(
/
/
/
V \
\
Ч
\
4
\
\
\
4
4
4
4
4
4
V»
х*
х>
X
-
-W
-
*х
4
ч
\
«
S
i.
;
•
i
{
/
/
/
\
ч
\
X
\
N
X
1
1
[
1
J
! /
/
/
}
/
/
/
X \
\
\
\
\
4
\
\
4
4
4
4
4
V
4
X
Х>
*х
у
г*
—
-
4
Ч
ч
ч
X
1
1
t
/
i
/
/
/
\
ъ
X
X
X
\
1
1
)
; ;
/
t
/
/
/
/
X X
\
\
\
\
4
4
4
V
4
4
4
4
X
ч
-
X.
-
-
У
/
wv-
-•
ч
ч
\
V
1
I
I
у
/
f
/
/
/
\
ч
\
Ч
V
к
\
•i
1
1
1
\
/ t
/
/
/
/
/
/
X X
К
X
V
\
4
4
\
4
4
4
*ч
4
V.
X
-
X,
•-
У
/
s'
W.
-
X
ч
ч
V
•
i
/
/
/
/
у
У
\
ч
\
X
\
X
к
1
1
1
1
г
1
t
1
; /
/
/
/
/
/
/
^ 1
\
X
\
\
\
4
\
V
/
/
У
У
-
-
4
ч
X
1
{
/
/
/
/
у
у
у
ч
ч
ч
ч
ч
\
\
X
«,
Г
1
/
/ /
✓
/
/
/
г
1
Ч 1
\
\
\
X
к
к
I
4
\
4
v
X
-
•-
-
—
—
-
/
/
/
/
У
у
-
-
V .
х
ч
1
\
f
/
у
У
у
У
s’
у
\
ч
ч
ч
ч
S
\
\
1
1
t
J
/
/ /
/
/
/
/
/
/
1 1
1
1
I
V
4
\
4
4
-
••
-
-
—
-
-
—
/
/
/
/
/
/
У
-
4
у
•
/
/
x'
✓
s'
✓
ч
ч
ч
ч
\
\
\
\
*>
1
i
/
/ /
/
/
/
/
/
/
1 1
1
1
1
I
4
\
X
\
*4
-
•
-
-
•-
'
-
г
/
1
/
i
/
/
✓
ь.
X
/
у
✓
-
-
ч
ч
ч
ч
\
\
ч
\
Ч
/
/
/
/ /
/
/
/
/
/
/
к
1
L
1
в
5
i
4
X
--
—
—
-
•-
-
••
-
-
•
—
i
)
г
j
1
■
f
1
/
/
t
✓
-
-•
-
-
-
—
-
-
-
✓
/
✓ /
J
г
/
/
/
/
(
г
{
•
i
i
}
/
в>
1
1
\
*
\
X
ч
ч*
w
4w
,w
ч
ч
ч
ч
ч
ч
ч
ч
4
ч,.
\
ч
4
ч
ч
4
ч
4
ч.
■-
у
У У
у
У
✓
/
/
/
: г
1
t
j
j
'
1
(
/
/
-•
-
-
V-
—
-
-
••
-
1
•
X
X
\
Ч
ч
ч
•-
X
»
X
S
4
X
x*
-
-
-•
4
4
ч
4
ч
4
■s.
• ^
—•
—
-
у- ✓
X
у
у
S
У
/ >
1
J
i
i
t
/
/
/
N
N
ч
\
\
ч
4
X.
—
у
У
X
%
4
4
x
X,
4
•x
4
4
4
V.
'ч
“V.
■ч.
—
-•
-
✓ Г
✓
X
✓
/
г
У
1 1
(
1
i
/
I
/
/
/
/
✓
У
>•
-
-
-
-
-
-
-•
—
ч
\
ч
ч
ч
ч
-
-
у
/
1
X
4
V
4
4
4
X.
X
ч
*ч
*х
4
_
...
—
w*"
X
✓
у
У"
1 1
1 *
/
t
1
t
/
/
/
/
/
У
ч
Ч
ч
х
ч
X.
—
-
-
У
/
t
s
V
4
\
4
4
4
X
V.
4
4
4
к ^
W
-•
—
-•
г- ^
-
✓
! J
;
i
f
t
/
/
/
/
У
-
-
ч
Ч
4
у
/
i
;
4
4
\
4
4
ч
г*
у*
/ f
/
!
/
/
/
/
/
/
/
У
✓
✓
,^г
ч
х
х
X
-
-
-
У
/
/
/
i
s
X
4
\
V
ч
V
—
--
*р
ш»
''
: *
/
!
/
/
/
/
/
/
/
/
У
✓
4
х
X,
•-
—
—
-
-
У
/
/
i
\
\
X
4
v
ч
/ t
/
/
/
/
/
/
/
*"
/
/
S
S'
✓
■х
■*“
••
—
—
*
У
/
/
/
I
1
s
4
»
\
ч
( /
/
/
/
/
/
/
/
/
f
У
✓
У
s'
/•
, *
*
w-r
/
/
i
1
i
\
Ч
/
с
1
5
с
1
[
J
Ч
\
Ч
\
\
V
X
\
1
1
1
i
•
/
/
/
/
/
/
/
\
\
ч
\
V
\
\
X
»
1
1
J
/
/
/
/
/
/
/
/
ч
Ч
ч
\
ч
ч
X
X
1
\
1
:
/
/
;
/
/
у
У
У
ч
ч
ч
\
\
\
\
X
1
\
J
1
/
/
/
/
✓
У
У
У
4
ч
ч
\
\
ч
ч
\
X
\
i
/
/
/
/
/
/
У
У
X
4
4
4
ч
\
\
ч
X
\
1
<
/
/
/
/
у
у
У
У
X
X
X
X
4
ч
4
\
ч
\
1
J
/
/
/
у
у
у
У
W*
X
X
X
X
4
4
ч
\
X
1
1
/
/
г
У
s'
✓
-
-
*х
-
х
х
4
\
1
1
\
/
✓
у
-
-
-
-
' ч
-
-
-
х
ч
\
X
t
/
т г
-
-
-
-
-
—
-
-
—
-
-
-
-
4
/
-
-*
-
-
-
-
•-
-
—
—
^ V
-•
-■
—
—
—
/
ч
-
—
—
-
—
—
/
X
У
/
У
1
Ч
ч
4
4
X
4
*-
•-
■*-
-■
s'
у
/
/
/
4
(
i
1
1
V
ч
ч
4
4
4
X
-
-
✓
У
У
У
/
/
/
/
\
ч
X
\
ч
4
Ч
4
X
X
-
X
X
г*
/
У
/
/
/
/
/
1
\
X
\
ч
\
\
Ч
4
X
X
X
У
/
У
/
/
Г
/
!
*
\
1
X
ч
Ч
Ч
\
4
4
ч
4
У
г"*
/
/
/
/
/
/
г
1
>.
\
N
ч
Ч
ч
Ч
4
ч
ч
У
У
/
/
/
/
/
/
J
1
\
1
S
ъ
ч
ч
ч
Ч
\
ч
4
У
/
/
*
/
/
/
/
‘
*
i
1
X
\
ч
\
ч
Ч
ч
S
4
/:= 1, с = 7г / 4
£ = 1, с = 7г / 2
X
х
4
4
Ч
ч
\
ч
X
\
\
1
1
1
1
У
✓
у
/
X
4
4
4
4
ч
\
_
-W
X
х
х
ч
4
\
ч
ч
ч
ч
1
1
\
1
1
1
1
У
у
✓
У'
✓ ^ . . - - ^ ч
X
4
4
4
Ч
\
Ч
W
X
х
х
ч
\
ч
ч
ч
X
\
\
•
г
г
\
/
У
у
/
У
у. ^ ^ ^ Ч
X
4
4
Ч
Ч
ч
ч
-W
х-
х.
4
Ч
ч
ч
\
1
\
)
1
*
1
1
/
/
У
У
У
4
Ч
4
ч
ч
V
ч
—
•-
X
4
Ч
ч
ч
X
X
•
1
j
1
j
(
}
/
/
/
/
У
У
✓ ^ ^ 4
4
ч
Ч
ч
ч
ч
ч
W-
—
-
—
-
-
X
х
Ч
V
ч
S
1
1
<
1
1
/
!
/
/
/
/
/
/
У
^ ^ ^ ^
Ч
ч
ч
\
ч
\
ч
.г*
-
х
ч
ч
\
•»
1
1
t
/
t
/
t
/
/
/
г
/
/
У
ч
ч
Ч
ч
ч
г
ч
—
—
X
ч
\
X
1
г
t
/
/
/
У
/
/
1
(
/
/
/
Ч
ч
X
X
X
X
г
✓
-•
-
-
4
ч
’|
f
1
/
s
/
/
/
/
/
(
1
/
/
/
t
/ / ^ - 4 4
Ч
ч
\
•
X
i
У
У
w’
-
X
ч
*
/
i
/
/
/
/
/
/
/
f
г
Г
f
{
/
/ / / - " 4 4 '
•
X
X
I
I
S
У
У
✓
/
/
У
-
!
/
/
/
/
/
У
/
/
/
/
г
\
г
1
1
Г
; / . , 4 ' 1 '
\
S
•
•
]
’
У
/
/
/
/
/
/
/
i
-
X*
У
У
у
У
У
/
У
У
\
1
1
1
1
1 * V ч ' '
j
}
г
>
i
I
/
/
/
/
<
/
1
Ч
X
...
у
>
✓
У
У
У
У
1
1
ь
1
!
S
X
X Ч ч - - ' / ''
1
i
/
i
t
•
\
1
1
/
/
/
/
t
1
►
\
\
4
-
—
-
У
✓
У
У
\
\
X
\
\
ч
Ч V 4 ^ ^ /
/
f
/
1
/
/
*
/
/
/
4
1
i
1
\
Ч
4
\
\
X
ч
Ч
\
Ч4-.---^У
/
/
/
f
/
/
/
t
t
г
\
;
1
\
ч
ч
X
-
-
—
**
Ч
Ч
ч
ч
ч
ч
4 чх.-' ш- г* ' У
/
/
/
i
/
/
/
(
»
э
1
1
1
1
1
\
Ч
ч
Ч
ч
\
ч
ч
4
у
/
/
г
/
/
/
*
1
i
1
\
*
\
\
ч
ч
4
х
-
-•
--
*-
\
V
ч
ч
4
4
ч - - - - ^ у
У
/
/
f
/
/
/
г
:
1
)
:
X
>
\
ч
ч
ч
X
—
—
—
<—•
—
Ч
\
ч
ч
Ч
4
X'-- — • ^ х
У
У
/
У
/
/
/
*
i
\
ч
X
X
ч
\
ч
ч
4
X
-
—
-
—
—
ч
ч
ч
ч
4
X
Ч - - - -
у
/
У
/
у
/
1
i
ч
L
\
X
X
ч
\
ч
ч
4
4
X
X
—
--
—
V
ч
4
4
х
' ц
-К - _
X"
/
У
/
у
У
Аг — — 1 ? с = 7г /2
ч ч ч X
ч \ V ч
\ \ Ч ч
\ \ ч ч
\ ч
ч ч
\ \
X X
\ X
I
I j
\
ч
V
X
I
i
г
*ч 4 X
\ S ч
S v v
Ч Ч Ч
\ S ^
Ч Ч
Ч Ч
Ч \
\ Ч
X
X
/
/ / /
/ / /
/ / /
/ / /
/ / /
/ / / / s
/ У / s У
ч s
ч S
ч Ч
N Ч
\ \
I \ \ \
; г 1 i
i i / /
/ f / /
///'
/ / / '
///S'
//s''
' У У У •
-XX'/'Z'////
-*^'У'УУ/ /
^ ^ У У У У У / /
^^yyy////
^ у у у / r // /
у У У / f //( t
* у / / / / /
у у //// f
/
/
/
/
/ /
/ /
/
t
i
/
/
/
/
;
/
J
I r r
/
;
/
/
S 1 I
4 \ 4
4 4 \
ч 4 \
—.4 4
1
X
4
\
4
i I 1 I I
\
\
ч \ 4
4 \
4 4
ч V
V
\
4
\
x ч 4 4 \
■x 4 ч 4 \
x X 4 Ч 4
Ч Ч 4 N 4
\ \
\ X
X \
4 V
\ \
ч 4
ч ч
k~ 2, с = 7Г / 2
S V
4 \
ч 4
ч ч
\ \
\ \
4 4
ч 4
ч ч
I I
у *
V \
4 \
ч 4
1
\
\
\
*
x
\
4
4
4
4 4V
•* ' .• I-
У У У У У У
//////
///ft:
> • , S \ \
• ■ v \ ч
• X V 4 \ ч k
\ Ч Ч \ ч x .
\ \ V 4 *4. ta, _
Ч 4 4 4 ^ .
V \ 4 *4 N. -
Ч 4 N V ^ _
/
/
/
f
f
i
/
у
/
/
у
✓
✓
/
✓
✓
у
^ X
^ - 4 s
^ S. ч Ч 4
_ ^ V s 4
_ x ч 4 \
^ 4 Ч Ч V
4 \ I
4
4
X
4
4
\
4
X
1
4
4
4
\
4
4
4
4
4
X
t
/
I J
/ /
s s
/
/
/
f
/
\
4
4
\
I
; S
i r
t t
/ t
/ /
s s
i
/
/
/
/
/
/
/
> \
\
t \
• I
/ •
/ I
I )
/ I
\
\
X
4
4
4
5
V
4
4
4
4
4
4
4
X 4
N X
4
4
\
\
4
4
\
ч 4
Ч ч
k~ —2, с ~ ix 12
4 4
4 4
\
\
\
X
4
\
4
I
I,
4
4
4
\
X
4
4
4
/ /
I I
/
/
t
/
/ /
/
/
/
4 ч
Ч ч
4 4
X \
I 1
} }
/ f
/ у
4
X
/
/
/
/
/
f
/
/
/
f
4
\ 4
/
/
/
/
t
i•
i
4
\
4
; \
\
X
4
1
\
4
\
1 s. \
1 V \
X S N
% V 4
\ ч ^
Ч ч 4
Ч ч ^
\
\
4
4
\
4
4
4
4
4
4
ч %
4 4
Ч ч
4 V
4
4
4
\
4
\
4 \
\ 4
4 \
V \
X 1
: 1
4
\
X
4
X
\
I
r
t
f
/
^ 4
J--*
/ “
' —
/ "
/ -*
/ -•
/
• > ** / / / s
//////
1 Г /• / / /
\ ^ i I • i
\ \ \ • i !
4 4 \ \
^ 4 4 \
- .4 ч 4
---44
- — ^ 4
/
1
X
\
\
\ X
\ \
4 \ \
ч 4 \
4 4 S
/
/
i
i
I
[
\
4
\
4
Рис. 11.4. Конфигурации директора nx = cos (kO + c), ny — sin (кв + с) для кли¬
новых дисклинаций с разными значениями силы к и постоянной с; в — arctg(y/a:)
Франком1^ для вычисления упругих энергий дисклинаций в предположе¬
нии К\ = Кз — К. Компоненты директора записываются как
п
х
COS (р, п
У
smtp, nz
о,
(ii.i)
где <р является функцией декартовых координат ж, у или полярных коорди¬
нат г, 0.
Уравнение Эйлера-Лагранжа совпадает с двумерным уравнением Ла¬
пласа для электростатики:
Ду, = + ** = О,
дх2 ду2
которое в полярных координатах записывается как
(11.2 а)
г дг
г2 дв2
(11.2 6)
§ ILL Линейные и точечные дефекты в одноосных нематиках
427
Мы ищем сингулярные решения, которые могут быть двух типов:
ip = Ав -Ь В(г, в), (р = Сlnr + D(r, в), (11-3)
где В и D — гармонические функции, А и С — постоянные. Нас инте¬
ресует первый тип решений, который дает дислокации поворота. Заметим,
что решение второго типа описывает вращение директора, бесконечно по¬
вторяющееся при движении вдоль направления в = const. В силу правила
годографа имеем
о dip = 27гfc, (11.4)
V
где интеграл берется по контуру, охватывающему начало координат. Сле¬
довательно,
.4 = А;, (11.5)
где fc — четное либо нечетное кратное величины ±-. Читатель может легко
проверить, что решение
ip — кв + В(г, 0) (11.6)
удовлетворяет всем топологическим требованиям, предъявляемым к дис¬
клинации в начале координат; необходимо также, чтобы В (г, в) была гар¬
монической функцией, не имеющей особенности в начале координат. Энер¬
гия, приходящаяся на единицу длины дисклинации -К J(Vcp)2dxdy, равна
W = тгКк21п- + Шс, (11.7)
Гс
где rcnWc — радиус и энергия ядра дисклинации. Это выражение полно¬
стью совпадает с выражением для энергии винтовой дислокации в твердом
теле и имеет то же толкование. Двумерный анизотропный случай (Кх ф К^)
должен приводить к такому же выражению, в котором К = К{К\, К%)
представляет собой функцию от К\ и Къ. Заметим, что вклады в энергию,
соответствующие и К и (см. выражение (5.4)), равны нулю в случае
планарной дисклинации. Коэффициент к2 показывает, что энергия вне ядра
дисклинации к ~ ± 1 будет в два раза больше суммы энергий двух дискли¬
наций к = ±~; поэтому ожидается, что в модели Франка дисклинация
2
к = ± 1 должна расщепляться на пару дисклинаций к = ±i.
Вклад ядра нельзя изучать в упругом приближении Франка-Осеена,
так как градиенты директора слишком велики. В простейшей модели мож¬
но предположить, что в ядре сохраняется одноосный порядок и что ампли¬
туда 5 параметра порядка уменьшается до нуля на корреляционной длине
£ ~ гс. Полное вычисление изменения s возможно, например, в рамках
теории Гинзбурга-Ландау. Ограничение, накладываемое на эти вычисле¬
ния, заключается в том, что модель Гинзбурга-Ландау действует, когда
типичные градиенты Vs < s/£. В случае более сильных градиентов пред¬
почтительнее использовать вычисления из первых принципов.
428
Гл. 11. Дисклинации и топологические точечные дефекты
В модели изотропного ядра, s(г —> 0) -> 0, радиус гс можно грубо
оценить следующим способом. Пусть k^{T^j — Т) — оценочная энергия,
приходящаяся на одну степень свободы; Т^[ — точка просветления. Так
как количество степеней свободы пропорционально числу молекул, Wc про¬
порционально г2: Wc ~ -ks{Tjsfi — T)7rr2cpNA/M, где р — плотность массы
нематика, М — масса молекулы и N а — число Авагадро. Минимизация
полной энергии (1 1 .7) дает
rc~kj — , Шс~жк2К. (11.8)
PNAkE(TNI -т)
Следовательно, в нематической фазе радиус гс имеет тот же порядок, что и £,
т. е. равен нескольким молекулярным длинам; гс расходится при Т ->• Тдг/.
Вторая модель ядра дисклинации снимает ограничение одноосности и
учитывает двуосный порядок. Параметр порядка нематического жидкого
кристалла, как было показано в гл. 3, является симметричным бесследовым
тензором второго ранга Q. Одноосный порядок соответствует случаю, когда
два собственных значения Q являются вырожденными. В общем случае все
три собственных значения различны и
Qij = s (riiTij - - т*тД (11.9)
где n, 1, т = n х 1 — набор ортогональных единичных векторов и р —
«параметр двуосности»: р = 0 в одноосной фазе, см. (3.3). Сильные иска-
жения в ядре можно ослабить, варьируя s и р, вместо того чтобы полагать
s = 0 и р = 0. Двуосная модель ядра изображена на рис. 11.5. Вдали
от ядра нематик является одноосным: s ф 0, р — 0. Одноосный порядок
также наблюдается в самом центре, причем локальная оптическая ось на¬
правлена вдоль дисклинации. Две одноосные области разделены двуосным
кольцом31
11.1.2. Несингулярные дисклинации
Полученный выше результат, согласно которому дисклинации к = ± -
2
обладают меньшей энергией, чем любые другие дисклинации, и упругая
энергия пропорциональна к2, предполагает, что в одноосном нематике «по-
луцелые» дисклинации встречаются часто, а дисклинации к ~ ± 1 — ред¬
ко. Экспериментальная ситуация является более тонкой, как показывают
наблюдения шлирен-текстур. Мы сначала обсудим случай жидких кристал¬
лов, имеющих небольшие молекулы.
Люксютов И. Ф. ЖЭТФ, 75, 358 (1978); N. Schopol and T.J. Sluckin, J. Phys.
(France), 49, 1097 (1988).
§ ILL Линейные и точечные дефекты в одноосных нематиках
429
Рис. 11.5. Двуосная структура ядра дисклинации к = 1/2. Перерисовано у Люк-
сютова3)
Шлирен-текстуры образуются, когда образец нематика зажат между дву¬
мя стеклянными пластинами и директор лежит параллельно поверхности
или слегка наклонен по отношению к ней. Искажения директора, оставляю¬
щие его в плоскости, ведут к появлению полос погасания (см. гл. 3). В об¬
разцах с тангенциальными граничными условиями наблюдаются дефекты
в виде центров, из которых выходят две или четыре полосы погасания.
Можно предположить, что эти центры представляют собой концы планар¬
ных дисклинаций, которые видны сверху. Учитывая, что полоса погасания
соответствует области, в которой п направлен параллельно либо перпенди¬
кулярно поляризации падающего света (п. 3.3.3), легко найти соотношение
между \к\ и числом N полос погасания, скрепленных в данном центре:
|fc| — iV/4. (11.10)
Таким образом, в центрах с четырьмя полосами погасания можно узнать
дефекты с к = ±1, а в центрах с двумя полосами погасания — дисклинации
к — ±-.
2
Прежде всего, неожиданным является то, что в образце с тангенциаль¬
ными граничными условиями количество дефектов с к — ±1 сравнимо
I
с числом дефектов с к = ±~. Более того, когда директор на ограни-
чивающих образец пластинах становится слегка наклоненным (в резуль¬
тате изменения характера сцепления, вызванного изменением темпера¬
туры), дисклинации к = ±- перестают существовать как изолирован-
ные объекты и вызывают появление стенки (рис. 11.6, б, в). Дефекты с
к — ±1, напротив, выживают. Различие проистекает из того факта, что
430
Гл. П. Дисклинации и топологические точечные дефекты
при наклонном поверхностном упорядочении проекция директора п<
< 1 на поверхности уже не обладает свойством эквивалентности п
<
ns. При переходе через стенку ns переориентируется в — ns, причем
= 1 (за-
п
Рис. 11.6. Нематическая шлирен-
текстура, содержащая дефекты с к =
= — 1 и fc = 1/2. Скрещенные поля¬
ризаторы. Поверхностная ориентация
директора тангенциальна в случае (а)
и слегка наклонена в случае (б). При¬
крепленная к дисклинации fc — 1/2
стенка отмечена стрелкой. На схеме
(в) изображено поверхностное поле ди¬
ректора текстуры (б); маленькие стрел¬
ки показывают наклоненные директо¬
ры. Фотографии любезно предоставле¬
ны Ю. А. Настишиным
в центре самой стенки
темненная область на рис. 11.6, в).
Для fc — ±1 тот факт, что ns и —ns
неэквивалентны, не имеет большого
значения, так как ns —> ns при со¬
вершении полного обхода вокруг де¬
фекта.
Второе замечательное различие
между дисклинациями к — ±1 и fc —
±-,
2
которое также не предска¬
зывается планарной моделью Фран¬
ка, обнаруживается, когда одну из
пластин слегка сдвигают (рис. 11.7).
После разделения в плоскости на¬
блюдения пара центров с N = 2
всегда выглядит так, как будто цен¬
тры соединены тонкой нитью (яд¬
ром дисклинации), которая сильно
рассеивает свет. В противополож¬
ность этому, пары с N = 4 по¬
лосами погасания разделяются без
сохранения какой-либо видимой осо¬
бенности между центрами: иска¬
жения вдоль воображаемой линии,
соединяющей два центра, кажут¬
ся размытыми и распределенными
по объему. Единственные особен¬
ности — это два поверхностных
точечных дефекта. Сдвиговый экс¬
перимент помогает понять приро¬
ду дисклинаций, представленных на
1
рис. 11.1: дисклинации к — ±- (N ~
2
= 2) выглядят «тонкими», тогда как
дисклинации fc = ±1 (iV = 4) выгля¬
дят «толстыми». Мы увидим, что тол¬
стые дисклинации к ~ ±1 не соот¬
ветствуют планарной модели, так как
конфигурация директора не является
плоской, по крайней мере в одноос¬
ных нематических жидких кристал¬
лах с небольшими молекулами.
§ ILL Линейные и точечные дефекты в одноосных нематиках
431
Рис. 11.7. Сдвиг шлирен-текстуры выявляет, что центры с двумя секторами пога¬
сания (черные стрелки) являются концами тонких сингулярных дисклинаций, в то
время как центры с четырьмя секторами погасания (белые стрелки) представляют
собой лишь особые точки без каких-либо сингулярностей в объеме
Клиновая дисклинация силы к — 1с радиальным п (рис. 11.8, а) может
потерять сингулярность ядра за счет «вытекания в третье измерение»4^:
на центральной оси директор п параллелен линии дисклинации, однако на
периферии он сохраняет радиальную ориентацию (рис. 11.8,6). Эту геомет¬
рию легко наблюдать в капилляре, где перпендикулярное (т. е. радиальное)
сцепление обеспечивает наличие дисклинации к = 1; центральная линия
размыта и часто обнаруживает точечные сингулярности, соответствующие
областям перехода от вытекания вверх к вытеканию вниз (рис. 11.8, в).
Вытекание директора вдоль линии дисклинации может снять сингу¬
лярность с ядра любой дисклинации с целым к. На рис. 11.8 вытекание
заменяет чистый поперечный изгиб (а) комбинацией поперечного и про¬
дольного изгибов (б). Если бы дисклинация относилась к круговому типу
(к — 1, с — 7г/2 на рис. 11.4), она могла бы вытечь посредством замещения
чистого продольного изгиба комбинацией продольного изгиба и кручения.
В противоположность этому, «полуцелые» дисклинации обязательно явля¬
ются сингулярными. Данный результат станет более ясным в гл. 12.
Упругая энергия, приходящаяся на единицу длины «целой» дисклина¬
ции с вытекающим ядром, пропорциональна К\к\ и не зависит от размера R
системы (задача 11.1):
W = ЗтгК'\к\, (П.11)
4) Р Е. Cladis and М. Kleman. J. Phys., 33, 591 (1972); R. Meyer. Phil. Mag., 27, 405
(1973).
432
Гл. 11. Дисклинации и топологические точечные дефекты
а
б
в
Рис. 11.8. Центральные сечения цилиндров с сингулярной (а) и несингулярной
вытекающей (б) дисклинациями к — 1; противоположные направления вытекания
приводят к сингулярным точкам — гиперболическим и радиальным «ежам» (в)
где К* — некая функция от К2 и К%. Ясно, что вытекание обычно
энергетически выгодно (сравните (11.11) и (11.7)), но оно может быть невы¬
годным, если упругие константы слишком сильно различаются. В жидких
кристаллах с небольшими молекулами, где К2 и К% имеют одинако¬
вый порядок величины, вытекание выгодно, за исключением того случая,
когда R не намного больше, чем гс (размножение дисклинаций с изотроп¬
ным ядром вблизи точки просветления).
Однако в жидкокристаллических полимерах К\, К2 и К$ могут сильно
различаться и природа искажения (т. е. преобладание кручения, продоль¬
ного или поперечного изгибов) играет решающую роль. Когда К3 > Ki,
что имеет место в некоторых жидкокристаллических полимерах, главным
образом в лиотропных растворах жестких стержней5\ а также во многих
жидких кристаллах с небольшими молекулами, энергия радиальной выте¬
кающей конфигурации записывается как (задача 11.1)
W = ттКх 2 +
arcsin /3
J7^
P=J\- Кх/Кг,
(11.12)
5) S. D.Lee andR. B.Meyer. J. Chem. Phys., 84, 3443 (1986).
§ 11.1. Линейные и точечные дефекты в одноосных нематиках
433
и она меньше, чем энергия радиальной сингулярной линии W =
= лК\ In (R/rc) + Wc, при достаточно большом значении R/rc и не очень
большом значении Kz/K\ (рис. 11.9). Однако в нематической фазе жест¬
ких полимеров с K^jK\ 1 сингулярная дисклинация целой силы может
оказаться предпочтительней вытекающей дисклинации. Поскольку сингу¬
лярные дисклинации к = ±1 неустойчивы по отношению к расщеплению
на дисклинации к — ±—, ожидается, что последние должны наблюдаться
2
чаще, и это проверено.
Рис. 11.9. Зависимость линейного натяжения радиальной дисклинации к = 1 от
Kz/Ki для планарной сингулярной конфигурации: W/Ki = 7г1п(Д/гс) (прямая
линия, R/rc = 10), и для вытекающей конфигурации (см. 11.12)
11.1.3. Дисклинации кручения
Дисклинации кручения возникают, когда при обходе окружающего
дисклинацию контура Бюргерса директор п непрерывно вращается вокруг
перпендикулярного к линии дисклинации направления 17. В принципе, дан¬
ное определение ограничивает геометрии кручения теми конфигурациями,
в которых директор остается в плоскости, перпендикулярной направлению
вращения (рис. 11.10), либо составляет постоянный угол с нормалью к этой
плоскости. Ясно, что дисклинации кручения являются более выгодными,
когда модуль кручения К2 меньше, чем К\ и Кг (задача 11.2). Так как та¬
кое соотношение между модулями часто имеет место в жидких кристаллах
с небольшими молекулами, рассмотрение дисклинаций кручения представ¬
ляет определенный интерес.
Однако четкой разницы в топологическом статусе между дисклинацией
кручения и клиновой дисклинацией не существует, и можно непрерывно
перейти от одной к другой (см. рис. 12.15). Это уже указывает на недоста¬
точность метода годографа для измерения силы дисклинации в том случае,
434
Гл. П. Дисклинации и топологические точечные дефекты
когда конфигурация не является планарной. Возможно следующее обоб¬
щение (Булиган): к каждой точке контура крепится соответствующий этой
точке директор и рассматривается лента, образованная контуром с при¬
крепленными к нему директорами. Она представляет собой ленту Мебиуса
(имеющую только одну сторону), когда | k | = 1 /2, т. е. когда полный поворот
составляет ±тг. Отметим, что поскольку зеркальный образ ленты Мебиуса
не эквивалентен исходной ленте, то хиральность ленты отражает не ска¬
лярное свойство дисклинации (рис. 11.10). Об этом будет более подробно
говориться в гл. 12.
Рис. 11.10. Дисклинация с закруткой директора на угол 7г. Инвариантность ленты
Мебиуса к — 1/2 по отношению к изменению ее положения
11.1.4. Линии дефектов в жидкокристаллических полимерах
Указанные выше различия между дисклинациями в жидкокристалли¬
ческих полимерах и жидких кристаллах с небольшими молекулами рас¬
пространяются и на структуру ядер. Четкие экспериментальные данные
о структуре ядер дисклинаций кручения |fc| = - и клиновых дисклина-
ций к = были получены для коллоидных растворов вируса табачной
мозаики методом электронной микроскопии с предварительным стеклова¬
нием и приготовлением реплик на свежих сколах образца. Ядро дисклина¬
ции кручения невелико, порядка длины вируса, и на ядре вирусные час¬
тицы скачком меняют ориентацию на угол тт/2. С другой стороны, ядро
клиновой дисклинации достаточно крупное (несколько длин вирусов);
§ ILL Линейные и точечные дефекты в одноосных нематиках
435
видно, что стержневидные частицы ориентированы вдоль линии дискли¬
нации6) и они разворачиваются в направлении, перпендикулярном ядру,
таким образом, что полная конфигурация имеет хорошо известную сим¬
метрию третьего порядка, ожидаемую из стандартной модели дисклинации
к — — Аналогичные заключения можно вывести также из наблюдений
2
нематической фазы полиэфира с мезомофной главной цепью, проведенных
методом оптической микроскопии7^: даже на таком масштабе клиновые
дисклинации к — — ^ обнаруживают симметрию третьего порядка и по¬
движность, более низкую, чем у клиновых дисклинаций к — + - , у которых
2
другой оптический контраст. В результате данного исследования было сде-
, 1
лано заключение о том, что клиновые дисклинации к = — - описываются
2
той же моделью, что и в случае с вирусом табачной мозаики, в то время как
7 , 1
молекулы в ядре клиновои дисклинации к = +- перпендикулярны направ-
2
лению ядра. Так как ожидается, что коэффициент вращательной диффу¬
зии DT01 ~ К /г] гораздо меньше коэффициента трансляционной диффузии
^trans ~ v/p (V — вязкость, р — плотность массы), то это могло бы объ¬
яснить различие в подвижности дисклинаций. Моделирование клиновых
дисклинаций к ~ — ^ в полимерах методом Монте-Карло ясно показа¬
ло наличие двуосного кольца на ядре дисклинации8^ и симметрию третьего
порядка; детали сильно зависят от отношения упругих постоянных, которое
определяется отношением длины стержневидных молекул к их диаметру.
11.1.5. Сингулярные точки
Сингулярные точки возникают либо в объеме (рис. 11.1, 11.8, в), либо
на поверхности (рис. 11.7). Точечные дефекты в объеме называют «ежа¬
ми», тогда как точечные дефекты на поверхности называют «буджумами»;
причина использования такой терминологии станет ясна в гл. 13. Практи¬
ческий способ наблюдения объемных и поверхностных точечных дефектов
заключается в том, чтобы диспергировать капельки нематика в изотропной
жидкости (такой, как глицерин или вода) (см. рис. 11.13). Как будет пока¬
зано в п. 13.2.5, точечные дефекты появляются в равновесном состоянии
таких капелек благодаря граничным условиям и топологическим ограниче¬
ниям. Точечные дефекты могут развертываться в дисклинационные петли
(рис. 11.11).
6') J. А. N. Zas adz inski, М. J. Sam топ. R. В. Meyer, M. Cahoon and D. L. D. Caspar II
Mol. Cryst. Liq. Cryst., 138, 211 (1986).
7-) G. Mazelet and M. Kleman 11 Polymer, 27, 714 (1986).
S. D. Hudson and R. G. Larson H Phys. Rev. Lett., 70, 2916 (1993).
436
Гл. 11. Дисклинации и топологические точечные дефекты
а
б
Рис. 11.11. Точечный дефект — радиальный еж в одноосном нематике (а) —
развертывается в дисклинационную петлю (б)
Энергия сингулярных точек пропорциональна K"R, где R — макро¬
скопическая длина, например расстояние между последовательно располо¬
женными сингулярными точками вдоль линии дисклинации, и К" — некая
зависящая от геометрии комбинация коэффициентов Франка. Плотность
К"
энергии Франка, которая пропорциональна
, не расходится на ядре:
R
К
и
г2 dr
K"(R - гс)
(11.13)
Г
г2 ~
' с
Однако ядро существует, так как, топологически, нет способа избежать
сингулярности и сохранить одноосный порядок. Предположим, что ядро
представляет собой сферу радиуса гс, имеющего по крайней мере порядок
длины молекулы, с постоянной плотностью энергии г > 0 (или изотропное
или двуосное ядро9)). Минимизируя полную энергию, получаем радиус
2г
энергию сингулярной точки Wp — Kff(R - —),
3
т. е. энергия меньше, чем KnR.
До сих пор во всех вычислениях мы пренебрегали существованием
дивергентных упругих членов (см. гл. 5). Однако вклад таких членов стано¬
вится существенным, когда деформации не являются плоскими. Это случай
целых дисклинаций с вытекающим ядром, и это также случай точечных
1X \1 £ j
дефектов. Например, упругие энергии «радиального» f п — 5 ’
и «гиперболического» ( п
(-£, -у, -Z)
yjX2 ~\~ у2 + Z'
у/х2 + у2 + г
«ежей» записываются как
VFr = 8тг R(KX - #24) и Wh
81TR ( *1 +
V 5 15 3
(11.14)
9) Е. Penzenstadler and H.-R. Trebin. J. Phys. France, 50, 1027 (1989).
§ 11.1. Линейные и точечные дефекты в одноосных нематиках
437
Предполагается, что модуль Кц равен нулю. Отметим разницу в знаках
членов с 1^24- Различия в упругих постоянных могут служить важным фак¬
тором для устойчивости ежей по отношению к петлям дисклинаций1
11.1.6. Закрутка, вызванная ограничивающими поверхностями
В следующем параграфе мы рассмотрим холестерическую фазу, которая
представляет собой, грубо говоря, закрученную версию нематической фа¬
зы. Полезно обсудить деформации кручения, которые появляются в ограни¬
ченных нематических образцах даже в отсутствие химической хиральности
молекул. Чистое кручение можно получить, если поместить нехиральный
нематический жидкий кристалл между двумя параллельными натертыми
твердыми поверхностями и затем вращать одну из пластин в ее плоскости.
Подобная структура является оптически активной; кручение поддержива¬
ется поверхностным азимутальным сцеплением.
Можно было бы ожидать, что если разрешить вращение директора п
в плоскости одной из пластин (отсутствие азимутального сцепления), то
кручение и оптическая активность исчезнут. К удивлению, совсем дру¬
гое поведение можно наблюдать, помещая капельки нематика на натер¬
тую пластину и оставляя верхнюю поверхность нематика свободной: по¬
саженные капли обнаруживают значительную оптическую активность1 Ч
Данное явление нетрудно объяснить, если принять во внимание тот факт,
что свободная поверхность лежащей капли обычно искривлена. Градиенты
толщины приводят к появлению вращающего момента, устанавливающе¬
го ориентацию директора в плоскости образца, причем даже в том слу¬
чае, когда образец ограничен изотропной средой; это явление называют
«геометрическим эффектом сцепления» 12\ Например, клиновый профиль,
изображенный на рис. 11.12,6, заставляет п выстраиваться перпендикуляр¬
но градиенту толщины (скажем, вдоль оси у на рис. 11.12,6), уменьшая
таким образом упругую энергию поперечного изгиба. Когда одна из пла¬
стин натерта вдоль направления, отличающегося от у, конкуренция между
геометрической и физико-химической осями преимущественной ориента¬
ции может приводить к закручиванию.
Для того чтобы показать это, вычислим энергию, приходящуюся на
единицу площади клина, пренебрегая искажениями директора в плоско¬
сти ячейки. Параметризуем директор через полярный угол в и азиму¬
тальный угол ср следующим образом: (пх, пу, nz) = [sin 9(z) cos (p(z),
sin 0(z) sin v?(z), cos 0(г)]. На нижней пластине 0(z = 0) = 7г/2 и cp(z =
= 0) = 0. На верхней пластине директор расположен тангенциально к по¬
верхности. Если две ограничивающие поверхности параллельны, то в со¬
стоянии равновесия Q(z) = 7г/2 и <p(z) = 0 (рис. рис. 11.12, а). Теперь
10) Н. Mori and Н. Nakanishi. J. Phys. Soc. Japan, 57, 1281 (1988); O. D. Lavrentovich,
T. Ishikawa and E. M. Terentjev. Mol. Cryst. Liq. Cryst, 299, 301 (1997).
D. Meyerhofer, A. Suss man and R. Williams. J. Appl. Phys., 43, 3685 (1972).
12) O. D. Lavrentovich. Phys. Rev. A, 46, R722 (1992).
438 Гл. 11. Дисклинации и топологические точечные дефекты
0,6 г
0,5
0,4
Uh
(N
0
90
а
б
39 ; К21 К[ = 0,4
30°; 0,1
6?
* *
50
10 ; 0,1
ь
* ■%: ^ & i:_ v>. ?s: $ ^
I L„ I I L
-10
Азимут ipQ
в
г
зо
70
Рис. 11.12. Тангенциально ориентированный нематический жидкий кристалл, по¬
мещенный между двумя пластинами (а); нижняя пластина натерта; верхняя пла¬
стина изотропна. Наклон 7 верхней пластины приводит к переориентации директо¬
ра перепендикулярно плоскости рисунка и его закрутке (6). Зависимость упругой
энергии от азимутального угла на верхней поверхности для различных значений 7
и К2/К1 (в)
предположим, что верхняя поверхность повернута на угол 7 относитель¬
но оси у (рис. 11.12, б). Полярный угол 6(z = d) зависит теперь от 7 и
азимутального параметра (ро, который представляет собой угол между п
и фиксированной осью х' на верхней, наклонной плоскости: 0(z = d) =
= arccos(sin 7 cos <£>o) • Небольшие отклонения от однородного состояния —
0(z) -> 7г/2 + в\ (z) И ip(z) “->• 0 + (fi(z) — приводят к плотности свобод¬
ной энергии /
-K\B\ Z + z. Объемные уравнения равновесия
2 2
§ 11.2. Холестерики
439
Oi,zz = 0 и <fi,zz — 0 вместе с вышеприведенными граничными условия¬
ми дают следующее выражение для энергии на единицу площади12):
F — — [arcsin(sin7cos(/?o)]2 -f —
2d 2d
Согласно последнему уравнению, равновесный азимутальный угол на верх¬
ней поверхности может быть отличен от нуля (рис. 11.12 в). Это предпо¬
лагает закрутку и, следовательно, оптическую активность лежащей капли.
Угол закрутки растет по мере убывания отношения К2/Кi, поэтому дан¬
ный эффект может быть сильно выраженным в нематических полимерах,
таких как полибензилглутамат, где отношение K2fK\ имеет порядок 0,1
и меньше.
Релаксация поперечных и продольных изгибов за счет кручения —
обычное явление в материалах с малым К2. Хорошо известный пример —
это периодическая картина из полос, которая появляется в геометрии
перехода Фредерикса с поперечным изгибом в полимерных нематиках
с небольшим (меньше 0,33) отношением К2/Ку. Поле, приложенное пер¬
пендикулярно к плоской нематической ячейке, служит причиной появления
полосатых структур13), состоящих главным образом из кручения, а не из од¬
нородного поперечного изгиба, наблюдаемого в обычных материалах.
Особенно отчетливо релаксацию за счет кручения демонстрируют сфе¬
рические капли нематика с тангенциальными граничными условиями, взве¬
шенные в изотропной матрице (глицерин) (рис. 11.13). Линии директора
соединяют два точечных дефекта, буджума, находящихся в полюсах кап¬
ли. Однако вместо наивной картины чистого поперечного и продольного
изгибов, когда линии представляют собой меридианы, лежащие в плоско¬
стях с постоянным азимутальным углом, наблюдается закрученная струк¬
тура. Линии директора наклонены по отношению к меридианальным плос¬
костям. Этот наклон уменьшается при приближении к оси капли. Таким
образом, каждая капля закручена и оптически активна, несмотря на нехи¬
ральную природу молекул как нематика, так и матрицы. Разумеется, в таком
дисперсионном образце присутствует одинаковое количество капель с ле¬
вой и правой закруткой.
Капли на рис. 11.13 в действительности обнаруживают двойную закрут¬
ку, а не простую закрутку в одном направлении. Двойная закрутка будет
рассматриваться в п. 11.2.2 в связи с модулем К2± седловидного изгиба.
§ 11.2. Холестерики
Поле директора основного состояния хиральных фаз не является од¬
нородным, потому что у молекулярных взаимодействий отсутствует ин¬
версионная симметрия. Холестерическая фаза, в которой директор п
13) F. Lonberg and R. В. Meyer. Phys. Rev. Lett., 55, 718 (1985).
440
Гл. 11. Дисклинации и топологические точечные дефекты
Рис. 11.13. Нематические капли с двойной закруткой, взвешенные в изотропной
матрице. Центральная часть самой большой капли видится светлой, когда ось кап¬
ли направлена вдоль одного из скрещенных поляризаторов (белые отрезки) (а),
и темной, когда поляризатор и анализатор пересекаются не под прямым углом
(б). Таким образом, капля оптически активна благодаря закрутке директора. На
вставке изображена конфигурация директора на поверхности капли. Нематический
n-бутоксифенилэфир нонилгидробензойной кислоты диспергирован в глицерине.
Г. Е. Воловик, О. Д. Лаврентович, ЖЭТФ, 85, 1997 (1983)
закручен в спираль, являет собой простейший случай в великом много¬
образии пространственно неоднородных хиральных структур. Простран¬
ственный масштаб исходных деформаций, например шагр спирали, обычно
много больше (р ^ 0,1 мкм), чем размер молекул, так как взаимодействия,
нарушающие инверсионную симметрию, довольно слабые. Закрученное
основное состояние хиральных жидких кристаллов легко подвергается до¬
полнительным деформациям, вызываемым внешними полями, поверхност¬
ными взаимодействиями или стремлением молекул образовывать смектиче¬
ские слои, гексагональный порядок или состояния с двойной закруткой. Та¬
кие дополнительные деформации очень часто приводят к топологическим
дефектам. В этой главе мы рассмотрим основные свойства таких дефектов,
§ 11.2. Холестерики
441
как дисклинации и дислокации в чистых холестериках. О топологических
свойствах будет сказано больше в гл. 12. Даже на простейшем уровне про¬
блема дефектов в случае холестериков гораздо сложнее, чем для одноосных
нематиков, так как свойства дефектов на масштабах, меньших р и больших р
различаются.
11.2.1. Теория упругости на разных масштабах
Существует два взаимодополняющих способа описания искажений в хо¬
лестерической фазе в зависимости от величины отношения L/p, где L —
характерный масштаб деформаций или размер жидкокристаллического об¬
разца. Мы различаем слабо закрученные (L/p <1)и сильно закрученные
(L/p^> 1) холестерики. Упругость слабо закрученных холестериков описы¬
вается уравнением (5.3). Любая слабая деформация | Vn| <С qo должна вести
себя так же, как в нематике. Другими словами, существует очень слабое раз¬
личие между слегка закрученным нематиком и холестериком, наблюдаемы¬
ми на масштабах, меньших, чем шаг спирали. И действительно, оптические
наблюдения холестериков с большим шагом в образцах размера L < р об¬
наруживают толстые и тонкие дисклинации, как в нематиках (рис. 11.1).
Собственно холестерические свойства преобладают на масштабах L
р. Эти свойства распадаются на две категории: слоистость структуры
(с периодом р/2), которая приводит к появлению свойств, аналогичных
свойствам смектиков, и существование локальной триады директоров, как
в двуосных нематиках. Поэтому можно одновременно ожидать появления
дислокаций, конфокальных доменов (см. гл. 10) и дисклинаций трех ти¬
пов. Это действительно так, однако реальная ситуация оказывается более
тонкой, как мы увидим в п. 11.2.3.
Упругие свойства слоистой структуры холестерика при L ^ р были
феноменологически описаны в рамках подхода, использованного для ла¬
меллярных фаз (гл. 5). Здесь снова возможны две ситуации. Во-первых,
«слои» холестерика могут быть лишь слегка изогнуты и сохранять тополо¬
гию плоских поверхностей. Плотность свободной энергии, описывающая
растяжение и сжатие слоев и небольшие наклоны, выражается через поле
смещения и(х, у, z) следующим образом:
/ = 1к (— + — ^ + -В
2 \ дх2 ду2 J 2
где введены перенормированные постоянные В = K2ql и К =
8
эта модель крупномасштабных искажений называется моделью де Жена-
Любенского.
Если отклонения от плоской геометрии существенны, то уместнее ис¬
пользовать главные кривизны ai и о2 слоев:
ди
dz
I f ди
1 I ди
дх
ду
, (11.15)
/ = -К(сг\ -f <т2)2 + -Bj2,
2 2
(11.16)
442 Гл. 11. Дисклинации и топологические точечные дефекты
где 7 = |р — Ро|/Ро — относительное растяжение (сжатие). В модели круп¬
номасштабных искажений энергия искривления Fc ~ КL, тогда как энер¬
гия растяжения (сжатия) Fp ~ BL3. Следовательно, Fp/Fc (L/p)2 » 1.
Другими словами, при L/p^> 1 теория рассматривает холестерическую сре¬
ду как систему равноудаленных (и, следовательно, параллельных) слоев с
преобладающими деформациями типа искривления. Как правило, гранич¬
ные условия могут удовлетворяться только при появлении крупномасштаб¬
ных дефектов, таких как конфокальные домены и маслянистые бороздки.
11.2.2. Слабые деформации типа кручения: двойная закрутка
Можно задаться вопросом: какова роль члена 7^24 в слабо закрученном
холестерике. Ответ состоит в том, что этот член способствует образованию
двойной закрутки14^. Пусть по — некий директор, направленный, например,
вдоль оси z (см. рис. 2.28). В локальном состоянии с наименьшей энергией
хиральные молекулы, находящиеся вблизи от по, стремятся повернуться
по спирали вдоль всех направлений, перпендикулярных п0. Двойная за¬
крутка является энергетически более выгодной, чем одномерное кручение,
по крайней мере для некоторых хиральных материалов.
В цилиндрических координатах простая конфигурация с двойной за¬
круткой записывается как
пг — 0, по — — sin ф(г), nz = cos/0(r), (11.17)
причем -0(0) = 0. Свободная энергия равна
г 1 ту* f di) 1 • / / \2 , 1 TS sin4 'Ф К24 d / . 2 1\
/ = - К2 ( qo — — — - sm ф cos ф j -f -К з — — (sin ф).
2 V dr r / 2 r2 r dr
(11.18)
Член Кi3 отсутствует, так как div n = 0. Интегрируя /, находим вклад члена
К24 в энергию цилиндра вещества радиуса R:
R
F2a — ~К24
27Г —(sin2 ф) dr = —27ri^24 sin2 ф(И). (11.19)
dr
о
Этот вклад отрицателен при любых значениях ф(В) Ф тгп, если К24 по¬
ложителен. В этом случае зарождение холестерической геометрии с двой¬
ной закруткой является предпочтительным, в особенности когда коэффи¬
циент К\ велик по сравнению с К$. Двойная закрутка может наблюдаться
в несингулярных дисклинациях силы fc = 2 в холестерических сферолитах
(часто наблюдаемых в биополимерах), что будет обсуждаться позднее.
Другой пример двойной закрутки встречается в хромосоме микроско¬
пической морской водоросли — Prorocentrum Micans (динофлагеллатные
14) М. Kleman. J. Phys. (Paris), 46, 1193 (1985); J. Phys. Lett., 46, L-723 (1985).
§ 11.2. Холестерики
443
хромосомы)15^. По предположению Клемана16), структура содержит две
дисклинации к — -, которые закручиваются по спирали вокруг оси хромо-
сомы. Геометрия двойной закрутки имеет ограниченный размер, за предела¬
ми которого двойная закрутка уменьшается и фрустрации в системе стано¬
вятся слишком большими. Слои имеют отрицательную гауссову кривизну.
Весьма вероятно, что данная геометрия является более предпочтительной,
чем геометрия сферолитов, когда Кх меньше так как дисклинации
к ~ ~ вызывают поперечный изгиб.
Наконец, если коэффициент К24 положителен и очень велик, цилиндри¬
ческая геометрия может стать устойчивее, чем холестерическая фаза: так
возникают голубые фазы. На рис. 2.28 по мере удаления от оси z холесте¬
рические цилиндрические оболочки становятся более плоскими и двойная
закрутка плавно исчезает. Вдали от оси распределение директора стано¬
вится похоже на одномерное кручение обычной холестерической фазы;
выигрыш в энергии уменьшается. Таким образом, двойная закрутка не мо¬
жет распространяться на все трехмерное пространство. Типичный радиус
цилиндрической области вокруг п0, в которой сохраняется выигрыш в энер¬
гии, равен половине шага спирали р/2. (В этом состоит причина того, что
мы рассматриваем двойную закрутку как слабо закрученную структуру;
такое рассмотрение не противоречит тому, что голубые фазы обычно встре¬
чаются в материалах с коротким, субмикронного размера, шагом спирали.)
Далее, эти цилиндры конечного радиуса не могут заполнять пространство
непрерывно. Согласно современным моделям голубых фаз, эта фрустрация
снимается дисклинациями, распределенными периодически либо беспо¬
рядочно. На рис. 2,28 показано, как три цилиндра с двойной закруткой
порождают сингулярность в области, где они соединяются. Следует выска¬
зать предостережение в отношении интерпретации плоских дисклинаций
как источника седловидного изгиба. Как уже было показано в п. 11.1.1, со¬
ответствующие К24 яК13 члены не дают вклада в упругую энергию прямой
плоской дисклинации. Оба члена исчезают при интегрировании плотности
энергии по азимутальному углу вокруг ядра дисклинации. Неисчезающая
энергия седловидного изгиба может возникать вблизи мест пересечения
дисклинаций или из-за точечных дефектов, если таковые имеют место.
Голубые фазы BPI и ВРИ обычно представляют в виде периодических
решеток дисклинаций с периодом порядка р. Действительно, трехмерная
периодическая структура этих фаз проявляется в их ненулевых модулях
сдвига, способности вырастать в виде хорошо ограненных монокристал¬
лов, а также в брэгговских отражениях в видимой части спектра (что
является естественным, так как р имеет порядок нескольких десятых
долей микрона). Структура третьей из найденных фаз (BPIII), обычно
15) F. Livolant and Y. Bouligand. Chromosoma, 80, 97 (1980).
16) M. Kleman. Physica Scripta, T19, 565 (1987).
444 Гл. 11. Дисклинации и топологические точечные дефекты
появляющейся между изотропной жидкостью и фазой BPII, менее понятна.
Она может представлять собой расплавленную решетку дисклинаций. Заме*
тим, что хотя большинство голубых фаз было обнаружено в термотропных
системах, геометрии двойной закрутки относительно часто встречаются
в текстурах биологических полимеров, таких как ДНК.
ДНК, полипептиды (такие, как упоминавшийся выше поли-бензил-глу-
тамат) и полисахариды (такие, как ксантан), а также многие другие биологи¬
ческие и небиологические полимеры закручены в определенную сторону
благодаря хиральным центрам. Длинные стержневидные молекулы этих
материалов в водных растворах ча¬
сто кристаллизуются в гексагональ¬
ную столбчатую фазу, которая в се¬
чении, перпендикулярном стержням,
выглядит как треугольная решетка. Так
как полимеры хиральны, то плотней¬
шая гексагональная упаковка конку¬
рирует со стремлением закрутиться.
Макроскопическое кручение может
распространяться посредством введе¬
ния в систему винтовых дислокаций,
так же как в фазах с закруткой гра¬
ниц зерен в хиральных смектиках. Воз¬
можны два типа стабилизированных
дефектами фаз, сочетающих в себе
плотнейшую упаковку и кручение17\
Первый случай — это полимерная
фаза с наклоном границ зерен, являю¬
щаяся прямым аналогом фазы с закрут¬
кой границ зерен и обычного холесте¬
рика с однонаправленным кручением
(рис. 11.14). Другой случай — это фаза
Муаре, похожая на голубые фазы с двойной закруткой. В центре цилиндри¬
ческого элемента находится полимерный стержень; соседние полимеры за¬
кручиваются вокруг него, сохраняя плотнейшую гексагональную упаковку;
цилиндры упакованы вместе благодаря шестиугольной решетке винтовых
дислокаций.
11.2.3. Дисклинации Л, г и х
На больших масштабах холестерический порядок определяется тремя
взаимно перпендикулярными директорами: Л вдоль локального направ¬
ления, определяемого молекулами, х вдоль оси спирали и г = \ х Л.
Рис. 11.14. Сосуществование кру¬
чения и плотнейшей гексагональ¬
ной упаковки в системе хиральных
стержней, образующих фазу с закрут¬
кой границ зерен с решетками винто¬
вых дислокаций; однонаправленное
кручение перпендикулярно плоско¬
сти рисунка
17) R. D. Kamien and D. R. Nelson. Phys. Rev. E, 53, 650 (1996).
§ 11.2. Холестерики
445
Можно сразу же предположить, что должно быть три класса полуцелых
дисклинаций, обозначим их С\, СТ и Сх, которые соответствуют вращени¬
ям двух из трех директоров на угол 7г при обходе вокруг ядра дисклинации.
Например, дисклинации класса С\ (А-дисклинации) связаны с вращени¬
ем % и т, тогда как директор Л остается несингулярным и направлен вдоль
линии дисклинации (рис. 11.15). Кроме того, должен существовать класс
дисклинаций с целой силой с вращениями на угол 2тг, который обозначается
А(-112)
А(1/ 2)
А(1 /2)
а
б
Рис. 11.15. Дисклинации А и г в холестерической фазе
как Cq. В отличие от своих аналогов в одноосных нематиках, эти дискли¬
нации не могут вытекать в третье измерение. Действительно, если один
из трех директоров вытекает (рис. 11.8,6), два других все еще остаются
сингулярными. И лишь дисклинация с вращением на угол 4тг, т. е. \к\ = 2,
становится топологически неустойчивой и может непрерывно трансфор¬
мироваться в однородный холестерик. Мы обозначим класс таких дискли¬
наций Со.
Замечательное различие между устойчивыми 2 7г-дисклинация ми и неус¬
тойчивыми 47г-дисклинациями станет понятным в гл. 12, где мы рассмотрим
дисклинации в двуосных нематиках: обе фазы имеют одинаковую топо¬
логическую классификацию дефектов. Различие между устойчивыми 2тг-
и 7Г-дисклинациями можно проиллюстрировать на примере х-дисклинации
446
Гл. 11. Дисклинации и топологические точечные дефекты
(отсутствие сингулярности в поле директора х)* Предположим, что х_
дисклинация перпендикулярна равноотстоящим холестерическим слоям.
При приближении к ядру упругая энергия, которая имеет порядок
~ К(Vn)2, возрастает до тех пор, пока на расстоянии ~ р она не становит¬
ся сравнимой с разницей (~ К/p2) между энергиями холестерического и
нематического состояний. На расстояниях, меньших р, имеет место нема¬
тический порядок. Следовательно, 27г-дисклинации с целыми к должны
иметь толстое ядро с диаметром порядка р, которое является несингуляр¬
ным с нематической точки зрения: директор однороден (вытекает в третье
измерение) внутри цилиндра с диаметром ~ р. В противоположность этому,
параметр порядка х-дисклинации с полуцелым к сингулярен как в одноос¬
ном нематике, так и в холестерике.
Энергия 7г-дисклинаций сильно зависит от того, как искажается триада
Л, х, т. Три директора имеют разный физический смысл и различную энер¬
гию искажения. Только Л является настоящим директором, тогда как г их
представляют собой «нематериальные» директоры; сингулярности СТ и Сх
обходятся обычно энергетически дороже, чем С\. Ядра А-дисклинаций
имеют радиус р («толстые» дисклинации) (рис. 11.15, а, б, г), в то время
как г-дисклинации («тонкие» ) обладают молекулярными размерами (или
несколько большими, что обсуждалось выше) (рис. 11.15 в). Таким образом,
линейные натяжения дисклинаций отличаются на величину ~ К In где
а
а имеет порядок 1-10 размеров молекул.
Дисклинации А и г часто встречаются в текстурах типа отпечат¬
ков пальцев, в которых ось х лежит в плоскости образца. На основании
сделанной выше оценки энергии можно было бы ожидать, что А-дефекты
встречаются чаще. Однако это заключение может измениться в случае
двуосного холестерика: тогда все три директора могут иметь одинаковую
энергетическую значимость. Изучение холестерических текстур биологи¬
ческих полимеров ДНК, полибензилглутамата и ксантана показывает, что
А-дисклинации действительно встречаются часто18). С другой стороны,
r-дисклинации часто появляются в паре с А-дисклинациями, замещая х-
дисклинации с полуцелыми к.
11.2.4. Дислокации
Повороты на угол птт вокруг оси х эквивалентны трансляциям п(р/2)х*
По этой причине х-дисклинации можно эквивалентным образом трактовать
как дислокации19) с длиной вектора Бюргерса
Ъ=-кр. (11.20)
Значения вектора Бюргерса приведены в табл. 11.1, в которой представле¬
на окончательная классификация всех линейных дефектов в холестериках.
18) F. Livolant. J. Phys., 47, 1605 (1986).
19) К Bouligand and М. Kleman. J. Phys. (France), 31, 1041 (1970).
§ 11.2. Холестерики
447
На рис. 11.16, а изображена клиновая дисклинация х(1/2) (X меняется
непрерывно). Она может быть построена с помощью процесса Вольтерра,
проведенного вдоль линии дисклинации с раскрытием краев разреза на
угол 7г: каждый слой холестерика дает двумерную конфигурацию k = i,
которая вращается по спирали вдоль дисклинации с шагом р.
Таблица 11.1. Классификация Вольтерра линейных дефектов в холестериках;
п — целое число
Со
Со
Сл
Сг
Сх
Ь = —2 пр
Ь = —(2 п + 1)р
Ь ~ — ^71 + Р
А(2 тъ)
А(2тг + 1)
ЧП+9
т(2п)
т(2п 4-1)
r(”+D
х(2 п)
Х(2п + 1)
x(n+i)
Эквивалентность винтовых дислокаций и клиновых х-дисклинаций, по¬
казанная на рис. 11.16, а, может быть распространена на краевые дислока¬
ции (рис. 11.17)и х-дисклинации кручения и даже дальше — на смешанные
дислокации и дисклинации по той простой причине, что соответствующие
процессы Вольтерра одинаковы.
Важным свойством х-дислокаций является их способность расщеплять¬
ся на комбинацию А- и т-дисклинаций. Например, х-дисклинация класса
Сх может расщепиться на пару дисклинаций А и г (классы С\ и СТ соот¬
ветственно). Пример изображен на рис. 11.16,6, в: ядро расщепляется на
А(—1/2) и т( 1/2), разнесенные на расстояние р/4; вектор Бюргерса равен
Ь — р/2, т. е. удвоенному расстоянию между дисклинациями. В холестери¬
ческих жидких кристаллах с небольшими молекулами линейные дефекты
Ь = р/2 обычно расщепляются на пару т(—1/2) А(1/2). На рис. 11.17 пока¬
зана дислокация с b = р, расщепленная на пару А(—1/2)А(1/2).
11.2.5. Другие эффекты слоистой структуры
11.2.5.1. Конфокальные домены и полигональные текстуры. В хо¬
лестерических жидких кристаллах с небольшими молекулами наиболее ча¬
сто встречаются домены, аналогичные конфокальным доменам первого ви¬
да в смектиках (гл. 10). В этом случае слои имеют отрицательную гауссову
кривизну, но их толщина изменяется (в противоположность смектикам)
448
Гл. 11. Дисклинации и топологические точечные дефекты
Перпендикулярное
сечение
b
Ъ
Л(-1 / 2)
т( 1/2)
а
в
Рис. 11.16. Эквивалентность в представлении х-Дисклинаций: клиновая дисклина¬
ция х(1/2) эквивалентна винтовой дислокации {а)\ х-Дисклинация кручения экви¬
валентна краевой дислокации (6); расщепление ядра дислокации на пару дискли¬
наций (<?)
Рис. 11.17. Полученное при помощи конфокального микроскопа изображение дис¬
локации b — р в холестерической текстуре типа отпечатков пальцев (ось х лежит
в плоскости образца). Метод конфокальной микроскопии позволяет получать изоб¬
ражение поля директора не только в плоскости образца (вверху), но также в вер¬
тикальных сечениях (1, 2, 3) (фотографии любезно предоставлены Д. Волощенко)
§11.2. Холестерики
449
ценой умеренного проигрыша в энергии кручения К2. Эти так называе¬
мые полигональные текстуры реже встречаются в растворах биополимеров
(ДНК, полипептиды и др.), так как в данном случае благодаря жесткости
длинных молекул к этому кручению прибавляется существенный вклад от
продольного изгиба Кг, а также некоторый вклад (не слишком большой) от
поперечного изгиба К\ (см. ниже).
11.2.5.2. Сферолиты Робинсона. Наиболее жесткие холестерические
биополимеры имеют другие типы слоистых текстур—так называемые сфе¬
ролиты Робинсона: слои близки к концентрическим сферам (положительная
гауссова кривизна). В ориентациях молекул должна присутствовать сингу¬
лярность, так как невозможно нарисовать непрерывное поле директора на
сфере. В этом легко убедиться на примере полей параллелей и меридианов:
оба поля имеют сингулярность k = 1 в каждом из полюсов, и полная сила
этих сингулярностей равна к = 2 (см. рис. 11.13 и пп. 13.2.5.1). Можно
показать, что все поля на сфере характеризуются такой же полной силой.
Возвращаясь к сферолитам, отметим, что поверхностные сингулярности
обязательно должны продолжаться в объем образца, и, действительно, на¬
блюдения показывают, что поверхность и центр сферы соединены либо
двумя радиальными линейными дефектами к = 1, либо одним радиальным
линейным дефектом к = 2.
11.2.5.3. Маслянистые бороздки. Маслянистые бороздки и жидкие
кристаллы были открыты одновременно. В 1888 г. Ф. Рейнитцер, изучая
холестерилбензоат, заметил вытянутые «жидкие» включения в холестери¬
ческом образце201 Маслянистые бороздки, как и конфокальные домены,
встречаются во многих слоистых жидких кристаллах. В плоской ячейке
со слоями, параллельными ограничивающим пластинам, маслянистые бо¬
роздки появляются в виде длинных лент, разделяющих идеальные области
плоских слоев (рис. 11.18). Их внутренняя структура достаточно сложна.
Согласно модели, предложенной Г. Фриделем2Ч маслянистые бороздки об¬
разованы парами краевых дислокаций с (большими) противоположными по
знаку векторами Бюргерса nd, n'd; таким образом, суммарный вектор Бюр¬
герса равен Ь = (n — n*)d\ здесь d — характерное межслоевое расстояние,
такое как толщина слоя смектика А или половина шага спирали в холе¬
стерике. Дислокация с большим вектором Бюргерса b = nd может затем
расщепиться на две дисклинации противоположного знака, как показано
в гл. 9. Простейшая разновидность маслянистой бороздки изображена на
рис. 11.19: две параллельные дисклинации к — 1/2 со стенкой между ни¬
ми. Полный вектор Бюргерса равен нулю. Поперечные бороздки отсутству¬
ют, так что гауссова кривизна равна нулю всюду, за исключением, может
быть, концов (где кривизна отрицательна). Маслянистые бороздки обыч¬
но не имеют свободных концов и завершаются в узлах, как на рис. 11.18;
20^ F. Reinitzer Я Monatsh. Chem., 9, 421 (1888).
21) G. FriedelH Ann. Phys. (Paris), 18, 237 (1922).
29-КЛЕМАН М.
450
Гл. 11. Дисклинации и топологические точечные дефекты
полукруглые концы могут наблюдаться у растущих маслянистых бороздок,
например, когда приложено поле.
Рис. 11.18. Плоская холестерическая текстура с сетью маслянистых бороздок. Боль¬
шая часть маслянистых бороздок обладает нулевым суммарным вектором Бюргерса
и разделяет области одного цвета; если две смежные области отличаются цветом,
то b ф 0 (см. цветную вклейку)
Рис. 11.19. Маслянистая бороздка с нулевым вектором Бюргерса, состоящая из
двух дисклинаций
§ 11.3. За пределы классического процесса Вольтерра,
первый шаг
Приведенное выше представление дефектов в нематиках и холестериках
начинается с использования в нематиках процесса Вольтерра для твердых
тел, однако вскоре уходит в сторону более интуитивного рассмотрения, все
§ 11.3. За пределы классического процесса Вольтерра, первый шаг 45 1
же сохраняя классификацию Вольтерра по элементам группы симметрии.
Данный выбор является следствием нескольких недостатков, связанных
с применением процесса Вольтерра к средам с непрерывной симметрией.
На рис. 11.3 был продемонстрирован процесс Вольтерра для клино¬
вых дисклинаций \к\ = 1/2, однако не вполне ясно, как распространить
данный процесс на углы, большие или равные 2к. Далее, дисклинации кру¬
чения нельзя построить с помощью процесса Вольтерра, за исключением
локальных областей. Последнее утверждение хорошо проиллюстрировано
рисунками Харриса21 Наконец, «вытекание в третье измерение», очевидно,
не следует из анализа Вольтерра.
Таким образом, встает вопрос о том, можно ли классифицировать дис¬
клинации по векторам вращения группы симметрии (такая классификация
традиционно связана с процессом Вольтерра), и если можно, то каким об¬
разом необходимо видоизменить процесс Вольтерра. Ответ состоит из двух
частей.
1. Оставаясь в рамках классификации Вольтерра, необходимо изме¬
нить процесс Вольтерра, и здесь ключевыми составляющими станут по¬
нятия непрерывных плотностей дислокаций (см. § 10.2) и непрерывных
плотностей дисклинаций. При таком рассмотрении подвижность и гиб¬
кость дисклинаций трактуются как результат вязкой релаксации указанных
плотностей (Ж. Фриде ль). Эти плотности станут предметом рассмотрения
в следующих пунктах.
2. Классификация Вольтерра дефектов должна быть пересмотрена, на¬
пример для того, чтобы включить в общую картину возможное вытекание
ядра, существование точечных дефектов и т. п. Этот расширенный анализ
требует топологического рассмотрения (см. гл. 12).
11.3.1. Плотности дислокаций и дисклинаций в описании дисклина¬
ций
Следующий подход был впервые введен Фриделем и Клеманом22).
11.3.1.1. Плотности дислокаций. Рассмотрим сначала прямую кли¬
новую дисклинацию L в нематике, и сместим ее на расстояние 6 таким
образом, чтобы она оставалась параллельной самой себе (рис. 11.20, а).
Допустим также, что при этом смещении вектор вращения ft — Vtu не дви¬
жется. С точки зрения процесса Вольтерра, это эквивалентно смещению
краев поверхности разреза по отношению друг к другу на дополнительную
величину 2 sin — {у х (5), т. е. введению дислокации с вектором Бюргерса
b = 2 sin — {у х <5), перпендикулярным этой дисклинации. В твердом теле
2
такой процесс потребовал бы большой энергии, и поэтому он запрещен.
В нематике вязкое расщепление дислокации на бесконечно малые дефекты
22^ J. Friedel and М. Kleman // J. Phys. Paris, Colloq., 30, C4, 43 (1969); NBS Special
Publication, 317, 607(1970).
452
Гл. 11. Дисклинации и топологические точечные дефекты
dh уменьшает упругую энергию, и это в действительности является тем
процессом, благодаря которому П следует за линией дисклинации в ее но¬
вое положение. Движение дисклинации в жидкой среде сопровождается
характерным процессом испускания (поглощения) дислокаций.
Рассмотрим теперь искривленную линию дисклинации (рис. 11.20, б).
Искривленные дисклинации существуют в нематике в состоянии покоя,
также наблюдается движение дисклинаций во время изменения формы.
Мы покажем, что гибкость нематической дисклинации совместима с век¬
тором вращения Q, изменяющимся по положению (но не по направлению)
от точки к точке вдоль линии L. Рассмотрим две бесконечно близкие точки
Р hQ = Р -b tds на L. Бесконечно малая дислокация, вводимая для изме¬
нения положения S7 из Р в Q согласно приведенным выше рассуждениям
о поверхности разреза равна
где М — произвольная точка на поверхности разреза. Можно считать, что
эта дислокация прикреплена к дисклинации. В сравнении с результатом
Рис. 11.20. Плотности бесконечно малых дислокаций. Смещение клиновой дискли¬
нации, при котором дисклинация остается параллельной самой себе (а) (для просто¬
ты предполагается, что угол Q небольшой); плотности дислокаций прикрепленных
к искривленной дисклинации (б); М — произвольная точка на поверхности разреза;
плотности дислокаций и дисклинаций (в)
обычного процесса Вольтерра новая форма линии дисклинации получает¬
ся благодаря вязкой релаксации плотностей бесконечно малых дислокаций
dh = dg(M) — dp(M), которые допускаются симметрией нематической
фазы. Эта релаксация оптимизирует энергию, переносимую дисклинацией.
Процесс Вольтерра, определенный в гл. 8, не подходит для данной гео¬
метрии, так как его использование возможно только в том случае, когда
вектор поворота П неподвижен в пространстве. Видоизмененный процесс
dq(M) -dp(M) = 2sin-(i/ х QM) - 2sin -{и x PM)
2 2
2 sin —{y x t)ds, (11.21)
2
. a
a
6
в
§ 11.3. За пределы классического процесса Вольтерра, первый шаг 453
Вольтерра, который учитывает изменение положения вектора ft вдоль дис¬
клинации, заключается в относительном повороте директора на угол S7 при
переходе от одного края к другому в каждой точке поверхности разреза без
относительного смещения этих двух краев.
Подобные возможности существуют не для всех дисклинаций в холесте¬
рике. Легко показать, что А- и г-дисклинации должны лежать в плоскости
холестерика и быть прямолинейными, параллельными либо перпендику¬
лярными директору, как на рис. 11.15. С другой стороны, %-дисклинации
могут иметь любую форму благодаря существованию непрерывных смеще¬
ний в плоскости холестерика и, следовательно, бесконечно малых дислока¬
ций, которые делают возможным искривление х-дисклинации.
Заметим, что полный набор плотностей дислокаций, прикрепленных
к искривленной дисклинации, имеет тот же статус, что и плотности дис¬
локаций, на которые мы ссылались в § 10.2. Знание этих плотностей эк¬
вивалентно знанию искажения поля директора, которое не является един¬
ственным и зависит от граничных условий, материальных параметров и т. п.
Плотности дислокаций могут, разумеется, иметь любую пространственную
зависимость от их точек прикрепления на L (рис. 11.20, б).
11.3.1.2. Плотности дисклинаций. Предположим, что ftp ф S7q
(S7i/p ф fluq) (рис. 11.20 б). Векторы Ир и fig почти равны для двух
бесконечно близких точек Р и Q, и можно записать, что jz^p х i/g
= sin (da) ~ da. Директор нематика представляет собой ось бесконеч¬
но малой поворотной симметрии dft = dfln\ спиральная ось холестерика
представляет собой ось бесконечно малой трансляционно-поворотной сим-
2тг
метрии dh, dft = — — db. Других непрерывных поворотных симметрий
v
в этих фазах нет. Мы обобщаем (11.21) на случай Л = 7г, т. е. для дисклина¬
ций с минимальной силой в нематиках и холестериках. Произведение двух
поворотов на угол 7г вокруг двух различных осей есть сумма смещения, уже
учтенного в (11.21), и вращения на угол 2da вокруг оси, перпендикулярной
ftp и flQ и пересекающей оси данных поворотов. После несложных вычис-
2
лений находим, что dft = —Г2р х ftQ (мы положили ft = it и). В нулевом
7Г2
приближении ось dft проходит через Р или Q. В итоге, разницу смещений
поверхности разреза в точках Р и Q можно записать как
dQ(M) — dp(M) = dfl х PM-2sin-(iv xt)ds
2
(11.22)
т. e. как сумму бесконечно малой дислокации dh = — 2 sin — (и х t)ds (как
и ранее) и бесконечно малой дисклинации dft. В этих выражениях вновь
ft ~ ТТ.
Пусть L — искривленная линия дисклинации в нематике и вектор fl
всюду направлен по касательной к L. Так как вектор dft должен быть на¬
правлен вдоль п, то директор в недеформированном нематике перпендику¬
лярен дисклинации, которая, таким образом, является локально клиновой
454
Гл. 11. Дисклинации и топологические точечные дефекты
(рис. 11.21). Заметим, что директор поворачивается на угол J da = 2к
при обходе некоторой петли вокруг L (например, петля у на рис. 11.21).
Следовательно, ожидается, что ограниченная петлей L поверхность прон¬
зена дисклинацией |fc| = 1, которая в случае на рис. 11.21 является «выте¬
кающей».
Бесконечно малые дисклинации в холестериках, разрешенные симмет¬
рией, — это дефекты, связанные с непрерывными вращениями вокруг
оси х, спаренными с непрерывными смещениями вдоль того же направ¬
ления. Взаимодействуя с х-дисклинацией, эти дефекты могут преобразо¬
вывать ее в дислокацию посредством вязкой релаксации (п. 11.2.4).
11.3.2. Расширение на случай конечных дислокаций
Линия А- или г-дисклинации силы \ k\~- должна быть прямой, однако
пара А- или т-дисклинаций противоположного знака, Q и — О, спаренных на
коротком расстоянии d в одной холестерической плоскости и параллельных
друг другу, может принимать более общие формы, правда, ценой некото¬
рых плотностей дефектов, прикрепленных к дисклинациям и распростра¬
няющихся в ленточную область между ними. Эти плотности не являются
Рис. 11.21. Замкнутая клиновая дисклинация в нематике
настоящими плотностями с точки зрения симметрий, но представлены лишь
в ограниченной внутренней области между дисклинациями. Детальный
анализ показывает22 \ что предпочтительными являются спиральные фор¬
мы. Структуры сечений таких пар уже были показаны на рис. 11Л 6. Общий
случай схематически изображен на рис. 11.22. При постоянном векторном
§ 11.3. За пределы классического процесса Вольтерра, первый шаг 455
Рис. 11.22. Расщепление дислокации на две дисклинации противоположного знака.
Волнистыми линиями показаны плотности дефектов
произведении г/ х d пара эквивалентна одной дислокации с вектором Бюр¬
герса
b = 2z/xd. (11.23)
Так как b квантуется, то расстояние d между дисклинациями также может
принимать дискретный набор значений.
Расщепление ^-Дисклинаций наблюдалось в клиньях Гранжана-Кано
(см. рис. 8.22): одна из дисклинаций всегда относится к A-типу, т. е. не несет
с собой существенной сингулярности. Первые дислокации вблизи центра
клина обладают маленькими векторами Бюргерса (6 — р/2), тогда как с уда¬
лением дислокаций от центра b увеличивается.
11.3.3. Структура ядра и физические свойства
В твердых телах движение дислокаций затруднено решеточным трени¬
ем (обычно анизотропным), так что если приложено небольшое или даже
исчезающе малое напряжение, то дислокация не принимает форму с ми¬
нимальной энергией. Это решеточное трение возникает из-за структуры
ядра (п. 8.5.2). Движение дисклинации имеет другую природу. Оно связано
с испусканием и поглощением дислокаций и с тем, как данный механизм
соотносится со структурой ядра подвижной дисклинации. Эта тема очень
слабо изучена. Измерения23^ скорости Uo дисклинации кручения в нема¬
тике под действием магнитного поля и наблюдения ядра показывают, что
ядро достигает больших размеров (порядка 0,04 d, d — толщина образца;
дисклинация параллельна границам образца). Такое огромное подвижное
ядро предполагает значительную перестройку поля директора. Большой
радиус ядра, по-видимому, соответствует модели, согласно которой вяз¬
кая диссипация, вызванная локальным вращением директора, имеет место
23) J. A. Geurst, А. М. Spruijt and G. J. Gerritsma. J. Phys. (Paris), 36, 653 (1975).
456
Гл. 11. Дисклинации и топологические точечные дефекты
лишь в объеме материала, вне области ядра. Другие модели, принимающие
во внимание другие диссипативные процессы (обратное течение, изотерми¬
ческую релаксацию параметра порядка в ядре и пр.), приводят даже к еще
большим ядрам24). На самом деле эксперименты с движущимися дисклина-
циями обнаруживают некоторое количество характерных длин, связанных
с ядром25). Простые рассуждения, основанные на размерности, приводят
нас к выводу, что длина, на которой исчезает любая вызванная движением
дислокации турбулентность течения, имеет порядок величины rv = 2i//U0,
где v — кинематическая вязкость движения текучей среды. Мы можем
представить образование этой турбулентности как процесс, происходящий
вследствие изменения конфигурации директора в ядре, связанного с испус¬
канием и поглощением плотности дислокаций со скоростью db/dt « U0.
Если идея об испускаемых и поглощаемых дислокациях верна, то область
размера rv превращается в след дисклинации, похожий на вихревой слой
с эффективной толщиной (vr/Uo)1/2, где О < г < гv. Таким образом,
ядро движущейся дисклинации должно сильно отличаться от статического
ядра. Более того, согласно предположению Фриделя26), ядро может обнару¬
живать продольную неустойчивость. Отношение rv/Rc, где Rc « K/jU0
представляет собой длину, на которой исчезают переориентация директо¬
ра и диссипация, достаточно велико; поэтому дислокационный механизм
воздействует на большую область. Не будем затрагивать здесь другие ха¬
рактерные длины.
В холестериках испускаемые и поглощаемые дислокации могут быть
конечными x-Дис локациями, как было отмечено Франком (см. работу Фри¬
деля и Клемана22)). Данный явление сродни, таким образом, тому, что
имело бы место в твердых телах, если бы в них присутствовали дискли¬
нации.
§11.4. Динамические свойства: общие особенности,
неустойчивости
Вследствие чего в жидкокристаллических образцах возникают топо¬
логические дефекты, такие как дисклинации и точечные сингулярности?
Можно выделить две группы причин. Во-первых, дефекты могут существо¬
вать как особенности равновесного состояния системы, примером служат
точечные дефекты в свободно взвешенных нематических каплях
(см. рис. 13.13). Равновесные дефекты могут также образовываться меха¬
ническими примесями, воздушными пузырьками и др. Например, сфери¬
ческий воздушный пузырек с перпендикулярной ориентацией директора
24) О. Parodi, G. Durand, G. Malet and J. J. Marignan. J. Physique Lett., 43, L727
(1982).
25) M. Kleman. The relation between core structure and physical properties, Dislocations
1984 / Eds. P. Vayssiere et ai., Editions du CNRS 1984,1.
26) J. Friedel. J. Physique Coll., 40, C3, 45 (1979).
§ 11.4. Динамические свойства: общие особенности, неустойчивости 457
действует как радиальный точечный дефект. Для того чтобы полные то¬
пологические инварианты не менялись (см. гл. 12), такой дефект должен
сопровождаться еще одним дефектом, например гиперболическим (ради¬
ально-гиперболическая пара изображена на рис. 11.8, в). Чтобы вызвать
появление равновесных топологических дефектов, жидкокристаллическая
капля (либо механическая частица внутри жидкого кристалла) должна быть
достаточно большой, больше K/w, где w — характерная сила сцепления на
поверхности капли или частицы (см. гл. 13). Во-вторых, причиной появле¬
ния дефектов могут служить происходящие вдали от равновесия процессы,
такие как закалка (термическая или давлением) изотропной среды в жидко¬
кристаллическое состояние; дефекты могут быть также вызваны течением
жидкого кристалла в режимах с большими числами Эриксена. Эти спосо¬
бы образования дефектов еще малопонятны. Кроме очевидного научного
интереса, проблема образования дефектов имеет практическое значение,
например для обработки высокопрочных жидкокристаллических полиме¬
ров, которые должны быть хорошо ориентированными и не иметь дефектов.
Далее мы рассмотрим процессы течения, относящиеся к проблеме тополо¬
гических дефектов.
11.4.1. Общие свойства
В нематодинамике модель Эриксена-Лесли и гарвардская модель
(гл. 6) предполагают отсутствие дефектов параметра порядка (дисклинаци-
онных линий или точечных дефектов). Таким образом, эти модели хорошо
подходят для описания стационарных неустойчивостей вблизи порогов, ко¬
гда амплитуда параметра порядка не возмущается течением, т. е. пока число
Деборы De = jтг 1 (см. уравнение (6.73)). Здесь 7 — типичное значение
сдвиговой скорости в образце, тг — время молекулярной релаксации. Ста¬
ционарные неустойчивости ориентации директора хорошо видны в поля¬
ризационном микроскопе, и поэтому они были изучены в тонких образцах,
расположенных между двумя равномерно сдвигаемыми параллельными
пластинами. В данной главе мы будем использовать только эту геометрию.
В наиболее общем случае поведение неустойчивостей является нели¬
нейным выше порога, который часто становится видимым благодаря по¬
явлению дисклинаций. Собственно говоря, параметр порядка нарушается
вдоль этих дисклинационных линий как по фазе, так и по амплитуде, од¬
нако эту новую ситуацию можно теоретически описать, по крайней мере
в принципе, распространяя методы, развитые для дисклинаций в состоянии
покоя, на динамические задачи; т. е. уравнения гидродинамики, собранные
в п. 6.4.2, все еще остаются верны вне ядер дисклинаций, пока число De
достаточно мало.
Выше значения De и 0,1, какова бы ни была природа появляющих¬
ся топологических дефектов, уравнения Лесли-Эриксена уже не действу¬
ют и амплитуда параметра порядка становится связанной со скоростями
деформации и вращения директора. Этот режим достигается в жидко¬
кристаллических полимерах, для которых время тг велико при умерен¬
ных значениях сдвиговой скорости. Например, в 13-процентном водном
458
Гл. 11. Дисклинации и топологические точечные дефекты
растворе полибензил(правый)-глутамата с молекулярным весом М =
— 298000, найдено27^ значение тг «0,1 с; следовательно, небольшой сдви¬
говой скорости 7 « 1с-1 достаточно, для того чтобы сделать уравнения
Лесли-Эриксена неприменимыми. Они заменяются молекулярной теори¬
ей Дои для полимеров28).
Хотя состояния с большим числом Деборы обычно описывают, исполь¬
зуя функции значения De, другие безразмерные величины также оказы¬
ваются востребованными, когда применимы уравнения Лесли-Эриксена:
число Рейнольдса Re = и число Эриксена Ег = (см. уравнение
г) К
(6.73)). Здесь U —; характерная скорость, например скорость верхней пла¬
стины относительно нижней, и d — характерная длина, такая как толщина
образца; К я г] — комбинации модулей Франка и вязкостей Лесли. Так как
7 ~ U/d есть соответствующая сдвиговая скорость, т. е. соответствующая
частота, то интересно переписать число Рейнольдса в виде Re = тцп7 и
число Эриксена в виде Ег = T&ngj, где тцп = ~d2 — это характерное
время передачи импульса, a rang = ~d2 — характерное время переда-
чи углового момента. Заметим, что Re 1 для рассматриваемых тонких
образцов. Поскольку отношение
Re _ rlin _ рК
Ег Tang Г)2
чрезвычайно мало, то именно ориентация директора управляет динамиче¬
скими процессами и именно Ег является числом, существенным в данной
ситуации. Отметим также, что (1) число Эриксена Ег одновременно явля¬
ется отношением вязкого вращающего момента к упругому вращающему
моменту Франка; (2) в режиме Дои отсутствует франковская упругость
и число Деборы не зависит от d; следовательно, в режиме Дои отсутствует
зависимость от толщины образца.
В жидких кристаллах с небольшими молекулами тг « 10_8с, и дина¬
мический режим Дои не может быть достигнут при обычных сдвиговых
скоростях. В жидкокристаллических полимерах, наоборот, наблюдаются
как динамическая область Дои, так и область Лесли-Эриксена.
11.4.2. Неустойчивости в изначально бездефектных образцах
Течение нематической среды практически всегда приводит к сложной
трехмерной конфигурации директора, которая в итоге может порождать то¬
пологические дефекты несмотря на исходную геометрию: директор может
выстраиваться однородно в плоскости сдвига или быть перпендикуляр¬
27) R. G. Larson and D. W. Mead. Liq. Cryst., 15, 151 (1993); 20, 265 (1996).
28) M. Doi and S. F Edwards. The theory of polymer dynamics, Oxford University Press,
N. Y., 1986.
§ 11.4. Динамические свойства: общие особенности, неустойчивости 459
ным ей (см. рис. 6.7, 6.9 в гл. 6). Основной вопрос заключается в том,
как в точности зарождаются и развиваются дефекты. На него нет ясного
ответа. Теоретические модели освещают только начальные этапы возник¬
новения неустойчивостей; большая часть новых результов идет от экспе¬
риментов. Ниже мы приводим краткое обобщение известных данных, огра¬
ничиваясь тем случаем, когда невозмущенный директор лежит в плоскости
сдвига, образованной скоростью и градиентом скорости, В этой геомет¬
рии мы различаем «ориентируемые течением» нематики и «кувыркающие¬
ся» нематики в соответствии со значением недиссипативного коэффициен¬
та А или знаком произведения двух коэффициентов Лесли (пп. 6.4.2,
6.5.2).
11.4.2.1. Режим ориентирования течением, А2>1, а2О:3>0. Дирек¬
тор принимает постоянную ориентацию с нулевой вязкостью в плоскости
сдвига, близкую к направлению течения (для стрежневидных молекул). Это
случай большинства жидких кристаллов с небольшими молекулами, таких
как 5СВ. Течение выстраивает п вдоль оси
Оо — +arctgy[А 4- 1)/(А — 1)
(рис. 11.23 и уравнение (6.75)). Когда нематик ограничен двумя пластинами
с сильным сцеплением, конфигурация директора определяется равновеси¬
ем сил упругости, вязкости и поверхностного сцепления, что схематически
изображено на рис. 11.23 б. При больших Ег преобладают вязкие вращаю¬
щие моменты и директор имеет постоянную ориентацию во почти везде,
исключая тонкие приграничные слои. Так как для многих ориентирую¬
щихся по течению нематиков угол во близок к тг/2, существует вероят¬
ность того, что в поверхностной области директор будет проворачиваться
I
и образовывать дисклинации с к — ±-; этому процессу могут способ-
ствовать неровности ограничивающей пластины, отклоняющие локальную
ось преимущественной ориентации от вертикальной оси z (рис. 11.23, в).
Эксперименты29^ определенно показывают, что тонкие дисклинации в фор¬
ме замкнутых петель образуются на ограничивающих пластинах начиная
со сдвиговых скоростей 7 и 1с-1. Интересно, что могут также наблю¬
даться толстые дисклинации, образующиеся в объеме образца30). Если по¬
явилась одна дисклинация, то она может испускать другие дисклинацион-
ные петли (рис. 11.24). Петли растягиваются по течению и кувыркаются;
при 7 « 10 с-1 все поле видимости покрыто ячеистой сеткой взаимодей¬
ствующих дисклинаций. Когда сдвиг прекращается, эта сетка релаксирует
с сокращением размеров ячеек и их свертыванием в точечные дефекты.
29) D. J. Graziano and М. R. Mackley. Mol. Cryst. Liq. Cryst., 106, 103 (1984).
30'1 P. T. Mather, D. S. Pearson and R. G. Larson. Liq. Cryst., 20, 527 (1996).
460 Гл. 11. Дисклинации и топологические точечные дефекты
Vv (z)
а
У
и=о
б
в
и>0
и» о
] с
с
в
о
Ег> 10
Рис. 11.23. Однородное ориентирование нематика в плоскости сдвига вдоль направ¬
ления во ~ +arctg^/(A -hi)/(Л — 1) (а); конфигурации директора в ограниченной
геометрии при сильном поверхностном сцеплении (с некоторой осью преимуще¬
ственной ориентации 0S) и растущем числе Эриксена (растущей скорости верхней
пластины) (б); возможный механизм зарождения дисклинаций на неоднородностях
поверхности (в)
11.4.2.2. Режим кувыркания, Л2 <1, а2аз<0. Это случай некоторых
нематических жидких кристаллов с небольшими молекулами при темпера¬
турах, близких к смектической фазе (например, 8СВ, п. 6.5.2), и это также
случай всех жидкокристаллических полимеров в соответствии с теорией
Дои. Если директор лежит в плоскости сдвига, он должен вращаться со
скоростью, пропорциональной сдвиговой скорости 7 (см. (6.74 а)):
dQ/dt — 7(аз sin2 в — а2 cos2 6)/71,
(11.24)
§ 11.4. Динамические свойства: общие особенности, неустойчивости 461
а
б
Рис. 11.24. Дисклинация к = 1/2 испускает дисклинационную петлю. Рисунок
заимствован из работы: Y. Bouligand, Physics of Defects / Eds. R. Balian, M Kleman,
J.-P. Poirier, North-Holland, Amsterdam, 1981, p. 665
таким образом, не существует стационарного состояния в отсутствие упру¬
гих искажений. Разумеется, то, что п остается в плоскости сдвига, — не
более чем допущение. Его обоснованность зависит от упругих (особен¬
но К2) и вязких параметров. Прямое сравнение ориентируемого течением
5СВ и кувыркающегося нематического 8СВ показывает, что при данном
числе Эриксена установившаяся плотность дисклинаций на порядок выше
в 8СВ311
Эволюция искажений директора при увеличении скорости U верх-
ней пластины (увеличении числа Эриксена) качественно представлена на
рис. 11.25. Сначала, при Ег ~ 1, упругие вращающие моменты способны
Er~\ U<UC
Ег~\О U&U,
£У>10
£/»£/,
1
Рис. 11.25.
(см. текст)
Начальные стадии неустойчивости в кувыркающемся нематике
31 ^ Р. Т. Mather, D. S. Pearson and R. G. Larson. Liq. Cryst., 20, 539 (1996).
462
Гл. 11. Дисклинации и топологические точечные дефекты
привести директор в устойчивый постоянный режим с некоторым макси¬
мальным углом наклона вш < 7г/2 в средней плоскости; угол 9Ш увеличива¬
ется с ростом U. В ориентирующемся по течению нематике угол вт достиг
бы постоянного значения во < тг/2. В кувыркающемся нематике, в котором
вязкие вращающие моменты подавляют стабилизирующие упругие вра¬
щающие моменты, не существует устойчивого постоянного значения вт.
Когда U преодолевает некоторое критическое значение 17с, угол вт скачком
становится больше тт/2. Переход происходит при Ег ~ 10 и напоминает фа¬
зовый переход первого рода (рис. 11.26). Дальнейшее увеличение скорости
приводит к выходящей из плоскости ориентации директора32) (рис. 11.25),
и директор может принять положение, приблизительно параллельное оси
завихренности. Эволюция структуры на этом не завершается, так как при
Ег > 103 наблюдаются неустойчивости типа вихревых цилиндрических
ячеек33), включающие модуляции директора вдоль оси завихренности; вих¬
ри в конечном итоге производят дисклинации, по-видимому, в процессе
объемного зарождения (см. Mather et а/.30)). Течение становится нерегу¬
лярным во времени; этот режим называют турбулентностью директора34).
Рис. 11.26. Зависимость угла наклона директора от скорости для кувыркающегося
нематика. Согласно Т. Carlsson , Mol. Cryst. Liq. Cryst., 104, 307 (1984)
32) P. Pieranski, E. Guyon andS.Pikin. J. Phys. Paris, Colloq., 37, Cl, 3 (1976).
33) P. Pieranski and E. Guyon. Phys. Rev. Lett., 32, 924 (1974); P. Manneville and
E. Dubois-Violette . J. Phys. (Paris), 37, 285 (1976).
34) P. E. Cladis and W. van Saarloos. Solutions in Liquid Crystals / Eds. L. Lam and
J. Prost, Springer Press, N. Y., 1992; G. Marrucci and F Greco. Adv. Chem. Phys., 86,
331 (1993); M. Srinivasarao. Liquid Crystals in the Nineties and Beyond / Ed. S. Kumar,
World Scientific, Singapore, 1995.
§ 11.4. Динамические свойства: общие особенности, неустойчивости 463
Эволюция текстуры наблюдалась во многих жидкокристаллических поли¬
мерах, таких как растворы поли-бензил-глутамата в метакрезоле. Высокие
вязкости жидкокристаллических полимеров делают число Эриксена боль¬
шим даже при низких сдвиговых скоростях. В результате дисклинации на¬
блюдаются в изобилии как в лиотропных, так и термотропных35^ жидкокри¬
сталлических полимерах. Образованию дисклинаций обычно предшествует
появление несингулярных квазиодномерных текстур — «полос» и «лент»
(табл. 11.2). Полосы ориентированы по направлению течения, тогда как
ленты — перпендикулярно.
Таблица 11.2. Структуры, образуемые в сдвигаемых растворах поли-бензил-
глутамата (R. G. Larson, Spatio-Temporal Patterns in Nonequilibrium Complex
Systems / Eds. P. E. Cladis and P. Palffy-Muhoray, Addison-Wesley, MA, p. 219 (1995))
Число Эриксена, Ег
Число Деборы, De
Структура
Условие течения
102-103
<1
полосы
установившийся сдвиг
О
т <
А
<1
пригггл
кратковременное,
JlCrl 1 Ь1
во время сдвига
> ю3
ленты
кратковременное,
после сдвига
>103
О
ry As
полосы
установившийся сдвиг
Эволюция текстур дефектов, по крайней мере с несколькими исходны¬
ми дефектами в состоянии покоя, наблюдалась в сополиэфирах и растворах
биополимеров. Пока еще неясно, соответствуют ли эти наблюдения области
сдвигов Дои, которая, как показано выше, достигается при умеренных сдви¬
говых скоростях в полимерах с высокими молекулярными весами. После
стадии очень медленного сдвига, на которой дефекты удлиняются в на¬
правлении сдвига и не взаимодействуют (что, несомненно, соответству¬
ет области Лесли-Эриксена), сперва наблюдается так называемая червяч¬
ная текстура — разновидность разупорядоченной полидоменной текстуры
на масштабе нескольких микрон с размножением дефектов; в этом режи¬
ме первая разница нормальных напряжений Ni отрицательна (п. 6.5.2.1);
отрицательное значение Ni могло бы служить указанием на режим Дои.
При больших сдвигах величина Ni снова резко увеличивается и достига¬
ет положительных значений; соответствующая «упорядоченная текстура»
является дву преломляю щей и становится однородной для самых высоких
35 ^ Т. De’ Neve, P. Navard and M. Kleman. J. Rheol., 37, 515 (1993).
464 Гл. 11. Дисклинации и топологические точечные дефекты
сдвиговых скоростей. Весьма вероятно, что «червячная текстура» свиде¬
тельствует о турбулентности директора.
§ 11.5. Динамика дефектов
11.5.1. Отдельная дисклинация, сила лобового сопротивления
Первым шагом в анализе динамики отдельной дисклинации может стать
упрощение описания как динамики, так и упругости. Предположим, что
1) скорость дефекта слишком низка, для того чтобы вызывать течение нема¬
тической среды; 2) дисклинация относится к планарному типу (11.1) и все
упругие постоянные равны К. Предположение (1) сводит уравнения дирек¬
тора (6.65) к
df д
drii dxj
df
^d(dnifdxj) _
Ъ — (11.25 a)
dt
и уравнения (6.20), (6.25), (6.646) для скорости диссипации энергии на
единицу объема к уравнению
TV = 71 > ^ . (11.26а)
dt
Здесь / — плотность упругой энергии Франка-Осеена, 71 = аз — а2 —
вязкость кручения, Т — абсолютная температура, о — скорость увеличения
энтропии на единицу объема. Согласно (11.25 а) скорость изменения упру¬
гой свободной энергии в точности компенсируется диссипацией за счет
вязкости. Предположение (2) приводит к еще большему упрощению36):
^ + ^ = 21^, (Ц.256)
дх2 ду2 К dt
Та = 'yi(—)- (11.266)
V dt /
Если дисклинация медленно перемещается в направлении х со скоростью
и — const, то решение (11.25 б) есть приблизительно
ip & k arctg —-—, (11.27)
х — ut
т. е. дисклинация сохраняет свою постоянную геометрию, описываемую
уравнением (11.6), в котором в = arctg-. Диссипация энергии на единицу
X
36) Н. Imura and К. Окапо. Phys. Lett., 42А, 403 (1973); P. G. de Gennes. Molecular
Fluids, Proc. Les Houches Summer School / Eds. R. Balian and G. Weill, Gordon and
Breach, London, 1976.
§ 11.5. Динамика дефектов
465
длины вычисляется как интеграл
£ = 71
—) dx dy « 7T7ifc2u2 In —. (11.28)
dt / r
С
Таким образом, коэффициент трения 77 = E/ia2 и сила лобового сопротив¬
ления /drag = S/w, которую испытывает дисклинация,
Г] = ТГ7! fc2 In —, /drag =ir-fik2win—, (11.29)
Гс ГС
логарифмически расходятся с ростом размера R системы. На первый взгляд
логарифмическая расходимость является естественным свойством данной
задачи: такой же логарифмический член присутствует в выражении (11.7)
для статической упругой энергии дисклинации. Однако более точный ана¬
лиз37) показывает, что сила лобового сопротивления не расходится с ро-
3 б
стом R, поскольку на больших расстояниях, R > Rc « ——, переориента-
71 и
ция директора и диссипация энергии практически исчезают, так что
/drag = 7T7iA:2nln —, (11.30)
Ег
где Ег — 7iигс/К — это число Эриксена данной задачи. Похожее уточне¬
ние было сделано38^ для линейного натяжения W движущейся дисклина-
1 1
ции: W и nKk2 In —. По существу, результат (11.29) соответствует Ег =
Ег
~ 0. Заметим, что как в (И .29), так и в (11.30) мы пренебрегаем диссипаци¬
ей на ядре; следовательно, эти выражения применимы при R гс и Ег 1.
11.5.2. Взаимодействие и аннигиляция линейных и точечных дефектов
11.5.2.1. Линии. Описанную выше модель можно сразу же приме¬
нить к динамике аннигиляции двух дисклинаций с силами противополож¬
ных знаков. Потенциал взаимодействия (на единицу длины) двух плоских
дисклинаций с силами к\ и к2, разнесенных на расстояние L в системе
с поперечным размером R, определяется выражением (задача 11.4)
W12 = 7tK(ki -f к2)2 In — — 27rKkik2 In —. (11.31)
rc 2 rc
Две дисклинации противоположной силы, к\ = —к2 — /с, притягиваются
друг к другу с силой /12 = —dW/dL:
/12 = —2тгКк2/Ь. (11.32)
37^ G. Ryskin and М. Kremenetsky. Phys. Rev. Lett., 67, 1574 (1991).
38^ C. Denniston. Phys. Rev. B, 54, 6272 (1996).
466
Гл. 11. Дисклинации и топологические точечные дефекты
3 б
Уравнивая /12 с силой лобового сопротивления /drag = 2ityik2u\n —
Ег
(11.30), получаем, что две дисклинации будут приближаться друг’к дру¬
гу по закону
L2 и const х — (to — t) (11.33)
71
до аннигиляции в момент времени t — to-
Аналогия между (11.32) и силой Пича-Келера в твердых телах была
рассмотрена Эшелби39). Хотя сила Пича-Келера представляет собой фик¬
тивную конфигурационную силу, /12 является реальной силой, и в состоя¬
нии равновесия она должна компенсироваться внешней силой, действую¬
щей на дисклинацию.
11.5.2.2. Точки. Результат (11.32) также применим к точечным дефек¬
там в двумерном пространстве, но не к точечным дефектам в трехмерном
пространстве. Размерный анализ40) наводит на мысль о том, что точечные
дефекты, имеющие упругую энергию ~ КR, когда они изолированы, долж¬
ны взаимодействовать посредством линейного потенциала W12 ~ KL (как
кварки). Более точный анализ показывает, что два точечных дефекта свя¬
заны солитонной «струной» примерно постоянной толщины; вне струны
директор практически однороден. Если дефекты разнесены на большое рас¬
стояние L гС9 то энергия пары дефектов определяется упругой энергией
W ~ L, запасаемой в струне. Таким образом, в первом приближении сила
притяжения между двумя простыми точечными дефектами в трехмерном
пространстве не зависит от L41)*.
/12 = -4тг К (11.34)
(заметим, что /12 имеет размерность настоящей силы). Сила лобового со¬
противления /drag зависит от геометрии области, в которой присутству¬
ют искажения директора и происходит диссипация энергии. Так как на
конфигурацию директора сильно влияют граничные эффекты, то ситуа¬
ция не вполне ясна; результаты могут различаться, например, когда L > R
и когда L ~ R; здесь R — поперечный размер, например радиус цилиндри¬
ческого капилляра.
11.5.2.3. Эксперименты. Динамика планарных линейных дефектов,
наблюдаемых в нематических ячейках МВВА, находящихся в сильном элек¬
трическом поле (что обеспечивает планарную конфигурацию директора
повсюду в объеме)42), удовлетворяет (11.33). В случае точечных дефектов
имеет место более тонкая ситуация, так как большинство исследований
39) J. Eshelby. Phil. Mag. А, 42, 359 (1980).
40) W. F. Brinkman and P. E. Cladis. Phys. Today, 35, 48 (1982).
41) .S. Ostlund. Phys. Rev. B, 24, 485 (1981).
42) H. Orihara, T. Nagaya and Y. Ishibashii. Formation, Dynamics and Statistics of
Patterns / Eds. K. Kawasaki and M. Suzuki, World Scientific, Singapore, vol. 2, 1993.
§ 11.5. Динамика дефектов
467
было выполнено в капиллярных трубках, где сказывалось влияние ограни¬
чивающих стенок. Когда L ~ R, динамика следует закону L ос (to — t)l/2\
в случае L^> R есть указания на линейную зависимость43).
Линейный закон L ос (to — t), служащий отличительной особенно¬
стью линейного потенциала W\2 ~ КL, наблюдается для пар поверхност¬
ных точечных дефектов — буджумов, связанных 27г-«струнами» в пленках
толщины ~ (1—10) мкм, помещенных между двумя изотропными среда¬
ми и имеющих гибридную ориентацию на границах44) (рис. 11.27). На¬
блюдаемые в эксперименте струны имеют приблизительно постоянную
х
Рис. 11.27. Струны, соединяющие пары точечных дефектов - буджумов в гибрид¬
но ориентированной нематической пленке 5СВ, расположенной на глицериновой
подложке44^
толщину D\ следовательно, диссипация энергии должна происходить толь¬
ко внутри области характерного размера D: /drag ~ Dyiu. При /12 ~ К
43) A. Pargellis, N. Turok and В. Yurke. Phys. Rev. Lett., 67, 1570 (1991).
44) О.Д. Лаврентович, С. С. Рожков. Письма в ЖЭТФ, 47, 210 (1988).
468
Гл. 11. Дисклинации и топологические точечные дефекты
струна должна укорачиваться без ускорения:
L « const х JLfto — t)y (11.35)
Dji
что наблюдалось экспериментально, по крайней мере, для L > D. Тот
факт, что толщина струны постоянна, является следствием геометрического
сцепления (см. ссылку [12] и обсуждение в п. 11.1.6 эффектов, связанных
с градиентами толщины пленки)4Ч
11.5.3. Укрупнение сеток дисклинаций
Динамика отдельной дисклинации позволяет рассмотреть, по крайней
мере качественно, динамику укрупнения дефектов. Как уже было замечено,
плотные сетки дисклинаций могут образовываться сильным течением ли¬
бо быстрым охлаждением изотропной среды до нематического состояния.
Какова могла бы быть зависимость плотности дисклинаций от времени?
Давайте сперва рассмотрим значительно более простую задачу об от¬
дельной сокращающейся в размерах дисклинационной петле. Для того что¬
бы получить грубую оценку зависимости радиуса R петли от времени, при¬
равняем вязкую силу лобового сопротивления r}dR/dt к упругой энергии
R
W/R, W = 7rk2K In —, приходящейся на единицу длины искривленной
гс
дисклинации:
W dR (
— = -7/ — . (11.36)
R dt
Интегрирование показывает, что петля сокращается согласно закону46^
Д=А/—(i0-t) (11.37)
Л
(to > t — момент времени, в который петля исчезает), который, видимо,
отвечает эксперименту47^.
Подобным образом можно рассмотреть48) ячейку сетки дисклинаций
в трехмерном пространстве с характерной длиной сегментов f. Плотность
дисклинаций на единицу площади равна р ~ £-2. Скорость потери энергии
в единице объема равна Wup/t; = W2p2/rj. Если приравнять это значение
к производной по времени от линейного натяжения, приходящегося на еди¬
ницу объема, Wр, придем к уравнению
— = -const х — р2, (11.38)
dt г]
45^ D. R. Link, М. Nakata, К Takanishi, К. Ishikawa and Н. Takezoe. Phys. Rev. Lett.,
87, 195507 (2001).
46^ G. J. Gerritsma, A. Geurst and A. M. Spruijt. J. Phys. Lett. A, 43, 356 (1973).
47^ W. Wang, T. Shiwaku and T. Hashimoto. J. Chem. Phys., 108, 1618 (1998).
48') 1. Chuang, R. Durrer, N. Turok and B. Yurke. Science, 251, 1336 (1991).
§ 11.5. Динамика дефектов
469
лли, после интегрирования,
р= ^ Г", (11.39)
const X W
где показатель степени v = 1. Последний результат, по-видимому, описыва¬
ет экспериментальную ситуацию, по крайней мере для сетки протяженных
сингулярных дисклинаций, образовавшихся во время быстрого охлажде¬
ния изотропной фазы до нематического состояния 48\ Он также является
точным аналогом результата, полученного Фриделем при анализе роста
мозаичной структуры дислокаций в кристаллах49^. Общая теория возник¬
новения крупнозернистых структур во время фазовых переходов рассмат¬
ривается в обзорной статье Брэя.
Задача 11.1. Рассмотрим одноосный нематический жидкий кристалл
в круглом капилляре (рис. 11.8,6). Предполагается, что стенки удержива¬
ют директор перпендикулярно цилиндрической границе. Линиям дирек¬
тора позволено вытекать вдоль оси z, так что директор может быть па¬
раметризован в цилиндрических координатах как nr = cosx(^), Пц? = ^
nz = sinx(r), где \ — это Угол между директором и плоскостью (г, <р);
граничные условия записываются в виде: x(r ~ R) — 0 и х(г — 0) — ^/2-
Используя выражение (5.2) для плотности свободной энергии, найдите рав¬
новесное распределение директора и энергию, приходящуюся на единицу
длины конфигурации, если
а) К, = К3 = К\
б) К\ ф (P. Е. Cladis and М. Kleman, J. Physique, 33, 591 (1972);
R. Meyer, Phil. Mag., 27, 405 (1973)).
Ответ
а) Учитывая, что
j. 1 d(rnT) . dv t cosy
divn — ~ — — — sinx— + -
dr dr
И
, d(nz) dx
rOt<o n = — - COSX —,
V dr dr
получим выражение для упругой энергии на единицу длины:
W = -К
2
R 2-п
2
dx\ , cos х 1 ■ о
1 н — - sm 2х
dr J r2 r dr
0 О
г dr
d(f.
В задачах с цилиндрической симметрией часто бывает полезным перейти
49) J. Friedel. Dislocations, Pergamon Press, Oxford, 1964, p. 239.
470
Гл. IJ. Дисклинации и топологические точечные дефекты
от г к новой переменной f: г — Интеграл для энергии тогда имеет вид
In R
W = ттК
(х'У2 + cos2 х- х' sin 2x1 df,
— ОО
где х = dx!d£.
Уравнение Эйлера-Лагранжа в этом случае имеет вид: х
Первое интегрирование дает
Ь(!)2 = cos2 х -f const.
!f
cosxsmx-
(11.40)
В соответствии с граничными условиями £ -оо в центре капилляра.
Это является возможным, когда х! = 0 при х 7г/2; следовательно, по¬
стоянная интегрирования равна нулю. Выбирая одно из двух возможных
направлений вытекания, например х! — ~ cos X? находим из уравнения
R
о
-dq
Я
dp
cos р
(11.41)
X
равновесное решение
Я _ 1 -h tg (х/2)
1 - tg (х/2)
или х = 2 arctg
R ~ г
R + г
(11.42)
Это решение удовлетворяет обоим граничным условиям и описывает глад¬
кую переориентацию директора на угол тт/2 при переходе от оси к стенке
цилиндра. Энергия на единицу длины равна
W = ЗтгК.
б) Аналогом первого интеграла (11.40) будет выражение
(11.43)
/\2
(х‘)
К г cos2 х
К\ sin2 х + Kz cos2 х
-f const,
(11.44)
приводящее к решению
R
о
1
dq = —
у/sin2 р -f (К3/К1) cos2 р
cos р
dp
(11.45)
х
Если > К1, то решение можно записать в виде
R
02 sin х
In — = ■■ И _ arcsin(/3 sin х) - - In ^ ±; (j j щ
r л/l — (32 2 yj\ — fi2 sin x + \/l — /32 sin x
§ 11.5. Динамика дефектов
471
где Р = у/l — К\ /К3. Энергия на единицу длины в этом случае равна
W — nKj f 2 + -arcsl?l ^ , (11.47)
Заметим, что при замене К\ —> К2 и при (разумном) допущении > К2
последняя формула описывает круговую дисклинацию fc = 1, с = 7г/2
(рис. 11.4), вытекающую посредством деформации кручения. Наконец, при
проведении вычислений мы пренебрегли вкладом (5.4) седловидного из¬
гиба К24, который становится ненулевым для вытекающих дисклинаций.
Включение этого члена позволяет оценить К24 (D. W Allender, G. P. Craw¬
ford andJ. W Doanef/Phys. Rev. Lett., 67,1442 (1991); R. D. Polak, G. P. Craw¬
ford,, В. С. Costival, J. W Doane and S. Zumer !! Phys. Rev. E, 49, R978 (1994)).
Отметим также, что выражения (11.43) и (11.11) несут вклады от дивер¬
гентного члена, скрытого в объемной плотности (5.7).
Задача 11.2. Образование дисклинационных петель может ослаб¬
лять закрутку, навязанную нематическому образцу, зажатому между соот¬
ветствующим образом ориентированными стенками. Рассмотрим петлю L
в нематическом образце, находящемся между двумя параллельными пла¬
стинами с сильным однонаправленным поверхностным сцеплением в плос¬
кости пластин. Пусть d — это толщина образца и а = qd — угол между
двумя направлениями сцепления. Предполагается, что упругость изотроп¬
на (К = К\ — К2 — Кз) и что деформация имеет место в плоскости,
параллельной направлениям сцепления. Показать, что
к
а) угол поворота директора можно записать как <р(г) = -П(г) + qz +
+ const, где П(г) — телесный угол, под которым петля видна из точки г;
УГ ^
б) энергия петли равна Fioop = K(-^L — 7гд£), где L — собственная
индуктивность петли L, рассматриваемой как замкнутый электрический
контур, и £ — площадь проекции L на плоскость вращения.
Ответ. J. Friedel and P.-G. de Gennes, С. R. Acad. Sci. Paris B, 268,
257 (1969). Начнем с построения электромагнитной аналогии для уравне¬
ния КА<р(г) — 27rfcJ(L). Так как угол ip(г) удовлетворяет гармоническому
уравнению Ду?(г) = 0 повсюду, кроме линии L, мы вводим бездивергент-
ный вектор магнитного поля Н = —KVy>(r). Решение гармонического
уравнения сингулярно на L: ср(г) = — П(г) + ф{т), где ^(г) — несингу-
Атг
лярная часть решения гармонического уравнения, учитывающая граничные
условия; при этом J J rotHdS = — J VtpdL — — 2кк. Поэтому j — 2тгк.
Задача 11.3. Можно ли оценить коэффициент Wa полярного сцепле¬
ния из рис. 11.6, б, если известно, что ячейка заполнена 5СВ и ее толщина h
составляет примерно 5 мкм?
Ответ. Да. Пусть So 1 — равновесный угол между директором
и подложкой; в центре стенки $о = 0. При небольшом наклоне потенциал
472
Гл. 1I. Дисклинации и топологические точечные дефекты
поверхностного сцепления равен Wa(S — Jo)2/2. Если искажения дирек¬
тора происходят в плоскости, перпендикулярной стенке, как предлагает
рис. 11.6, в, то упругая энергия на единицу длины стенки равна 2Khb\jd
(d — толщина стенки) и энергия сцепления равна WaS^d/Z. Миними-
б h
зируя полную энергию, находим: Wa = . Оценивая из фотографии
d2
d ~ Юмкм, получаем: Wa ~ 10~6 Дж/м2.
Задача 11.4. Покажите, что энергия двух планарных дисклинаций
дается выражением (11.3\)Wl2 = 7rK(ki+k2)2 In R / г c-2ix К к\к2 h\L/2rc.
Указание. Используйте суперпозицию решений <р = к arctg - + const:
х
ip = ki arctg -—— -f const.
, Jb JU 'i
г
См.: С. E Dafermos. Quart. J. Mech. Appl. Math., 23, 549 (1970).
Литература для дальнейшего чтения
1. A. Bray, Adv. Phys., 43, 357 (1994).
2. Chirality in Liquid Crystals / Eds. C. Bahr and H.-S. Kitzerow, Springer Verlag,
Ser. «Partially Ordered Systems», N. Y., 2000.
3. T. De’ Neve, M. Kleman and P.Navard, C. R. Acad Sci. Paris, 316, serie II, 1037
(1993).
4. M Doi and S. F. Edwards. The theory of polymers dynamics, Clarendon Press,
Oxford, 1986.
5. Formation and Interaction of Topological Defects, vol. 349 of NATO Advanced
Study Institute, Series В: Physics/Eds. A.-C. Davis and R. Brandenberger, Plenum.
N. Y., 1995.
6. M Kleman. Points, Lines and Walls in Liquid Crystals, Magnetic Systems and
Various Ordered Media, John Wiley & Sons, Chichester, 1983.
7. Defects in Liquid Crystals: Computer Simulations, Theory and Experiments /
Eds. O. D. Lavrentovich, P. Pasini, C. Zannoni and S. Zumer, Kluwer Academic
Publishers, The Netherlands, 2001.
8. S. Chandrasekhar and G. S. Ranganath, Adv. Phys., 35, 507 (1985).
9. P. Navard, J. Polym. Sci.: Polym. Phys. Ed., 24 , 435 (1986).
10. R. Ribotta and A. Joets, Cellular Instabilities / Eds. J. E. Weisfreid and Z. Zaleski,
Springer, N. Y., 1984.
ГЛАВА 12
ТОПОЛОГИЧЕСКАЯ ТЕОРИЯ ДЕФЕКТОВ
В третьей главе мы рассмотрели понятие параметра порядка, его ам¬
плитуду и фазу. Параметр порядка представляет собой непрерывное поле
(скалярное, векторное, тензорное и т. д.), описывающее состояние системы
в каждой точке. В общем случае параметр порядка — это функция коор¬
динат, ^(г). Возможны два вида искажений ф(г): искажения, содержащие
сингулярности, и искажения без сингулярностей. На сингулярностях функ¬
ция гр не определена. В трехмерной среде сингулярные области могут быть
нульмерными (точки), одномерными (линии) и двумерными (стенки). Это
и есть дефекты. Если неоднородное состояние невозможно уничтожить
(т. е. его нельзя привести к однородному состоянию), непрерывно изменяя
параметр порядка, то его называют топологически устойчивым состояни¬
ем или, проще, топологическим дефектом. Если неоднородное состояние
не содержи? сингулярностей, но при этом его невозможно непрерывно де¬
формировать до однородного состояния, то говорят, что система содержит
топологическую конфигурацию (или солитон).
Очень часто задачи, включающие дефекты, слишком сложны для ана¬
литического рассмотрения в рамках теории упругости. Трудности происте¬
кают либо из сложности функционала свободной энергии (двуосные нема¬
тики, смектик С, анизотропные фазы сверхтекучего гелия-3 и т. д.), либо из
сложности конфигурации дефекта (например, пересечение дисклинаций).
Даже в том случае, когда решения существуют, они основаны на некоторых
допущениях и, следовательно, могут сильно зависеть от модели.
Адекватное описание дефектов в упорядоченных конденсированных
средах требует введения нового математического аппарата, а именно тео¬
рии гомотопий, являющейся частью алгебраической топологии. Именно
язык топологии позволяет связать характер упорядочения среды с типами
возникающих в ней дефектов, обнаружить законы распада, слияния и пере¬
сечения дефектов, проследить их поведение во время фазовых переходов
и т. п. Ключевое положение занимает понятие топологического инварианта
(его также часто называют топологическим зарядом), присущего каждому
дефекту. Устойчивость дефекта гарантирована сохранением его топологи¬
ческого инварианта. Понятие топологического инварианта может быть про¬
иллюстрировано следующим простым примером.
§ 12.1. Основные идеи топологической классификации
12.1.1. Топологические заряды на примере листа Мёбиуса
Рассмотрим множество упругих лент, свернутых в кольца. Каждая лен¬
та характеризуется числом к, которое учитывает, сколько раз концы ленты
были перекручены на угол до того момента, когда лента была склее¬
на в кольцо (рис. 12.1). Кольцо с к ~ 1/2 (рис. 12.1,6) — это хорошо
474
Гл. 12. Топологическая теория дефектов
известный лист (лента) Мёбиуса. Энергия деформации, накопленная лю¬
бой закрученной лентой, больше, чем энергия чистого продольного изгиба
кольца с к ~ 0. Однако для того чтобы перевести закрученную ленту в со¬
стояние с к = 0, необходимо разрезать ленту. Не существует непрерывной
деформации, переводящей одну ленту в другую, если эти ленты имеют раз¬
ные к. Энергия, необходимая для разрезания ленты, — разрез ~ US/a2 —
много больше накопленной энергии кручения учеНие ~ k2KS/L\ здесь
L — длина ленты, S — площадь ее поперечного сечения и К ~ U/а —
некая упругая постоянная, имеющая порядок энергии межмолекулярного
взаимодействия; а — молекулярный масштаб. Переходам между состояния¬
ми с разными к мешают высокоэнергетические барьеры.
Рис. 12.1. Топологически различные кольца упругих лент: незакрученное коль¬
цо, к ~ 0 (а); лист Мёбиуса, к = 1/2 (б); пара из одной левой и одной правой
перекрутки, к = 0 (в); перекрученная лента с двумя разными краями, к = 1 (г)
Величина к не меняется при непрерывном преобразовании, и ее удобно
использовать для обозначения топологически различных состояний. Ле¬
вые и правые кручения можно различать по знаку к. Очевидно, что можно
создать пару из одного левого и одного правого кручения, не разрезая лен¬
ты, при этом инвариантом является полная сумма всех к, которая должна
сохраняться (рис. 12.1, в). Таким образом, заряды к подчиняются закону'
сохранения.
Допустимые значения к определяются внутренней симметрией ленты.
Если края ленты различны, например обозначены линиями разной толщины
(рис. 12.1, г), то разрешены только целые к (27т-кручения).
Топологическая устойчивость перекрученных лент похожа на устойчи¬
вость топологических солитонов; образования сингулярного ядра не про¬
исходит. Кроме того, можно провести параллель между перекрученными
§ 12.1. Основные идеи топологической классификации
475
лентами и сингулярными дефектами. Представим себе окружность, описан¬
ную вокруг 7г-дисклинации в одноосном нематическом жидком кристалле
(см. рис. 11.10). Последовательность молекул с центрами на этой окруж¬
ности образует лист Мёбиуса с к — 1/2. При одном обходе окружности
директор п переходит в — п, что является возможным благодаря тому, что
нематик в объеме вне ядра центросимметричен: директоры п и — п экви¬
валентны. Число к будет оставаться равным 1/2, если мы выберем другой,
больший или меньший, радиус окружности (см. рис. 11.10). Таким обра¬
зом, вся конфигурация директора может быть охарактеризована значением
к — 1/2. На ядре дисклинации мы обнаруживаем сингулярность: если
окружность стягивается в точку, то в этой точке представлено бесконечное
число ориентаций директора. Если дисклинация была создана в ферромаг¬
нетике, то лента Мёбиуса с к = 1/2 вокруг нее невозможна, так как вектор
намагниченности не обладает свойственной директору симметрией между
началом и концом директора.
Подводя итог, можно заключить, что топологически устойчивые дефек¬
ты и конфигурации («топологические перекрутки») удовлетворяют следую¬
щим общим правилам.
1. Виды дефектов связаны с типом упорядочения системы.
2. Дефекты характеризуются квантованными инвариантами (топологи¬
ческими зарядами) к.
3. Процессы слияния и распада дефектов описываются как некото¬
рые операции (например, сложение), примененные к их зарядам к; зако¬
ны сохранения топологических зарядов контролируют результаты слияния
и распада.
Топологические инварианты к образуют группы. Так как понятие груп¬
пы является важным для гомотопической классификации дефектов, мы
кратко рассмотрим его в следующих пунктах. Однако до этого мы скажем
несколько слов о, вероятно, самых интригующих перекрученных лентах —
молекулах ДНК.
12.1.2. Некоторое отступление: ДНК и перекрученные ленты
Перекрученные ленты с разными к имеют отношение к задаче о строе¬
нии и репликации двуцепочечных молекул ДНК. Две цепочки закручены
в спираль, в которой на каждые 10,5 пар нуклеотидов приходится круче¬
ние на угол 27г (см. рис. 1.21). Во многих организмах, начиная от вирусов
и прокариот и заканчивая некоторыми эукариотами, молекулы ДНК образу¬
ют замкнутые петли. Топологически эти петли напоминают перекрученные
ленты с двумя различными краями и целым значением Ьк, которое мы
будем называть числом зацеплений двух цепочек (рис. 12.2). Величина Lk
сохраняется при любом изменении формы молекулы ДНК, не разрывающем
Цепочек. Если значение Ьк близко к Lko = l/p (I — полная длина ДНК,
а р и 3,4 — шаг спирали (см. рис. 1.21), то кольцо ДНК расслаблено и оно
может лежать на плоской поверхности без искривлений. Часто Ьк ф Ьк$\
476
Гл. 12. Топологическая теория дефектов
концы расслабленной двойной спирали ДНК могут быть дополнительно
перекручены (или раскручены) на несколько оборотов ±2п до их соеди¬
нения в кольцо. Таким образом, введенное искажение релаксирует двумя
способами. Во-первых, может измениться число пар нуклеотидов, приходя¬
щихся на шаг спирали; кольцо останется плоским, и число зацеплений будет
равно числу оборотов одной цепочки вокруг другой; тогда Lk будет равно
к — определенной ранее топологической перекрутке. Во-вторых, может
закрутиться ось двойной спирали, оставляя число пар, приходящихся на
шаг спирали, нетронутым. Такая сверхзакрученная ДНК не остается более
плоской и извивается в трех измерениях, подобно покоробленной перекру¬
ченной ленте. В любом случае, хотя к и Lk остаются нетронутыми и они
все еще равны целым числам топологической природы, полная геометрия
(и, следовательно, энергия «перекрученной» ленты и способ, которым она
релаксирует) зависит от упругих свойств молекулы, и ее удобнее описы¬
вать, введя два геометрических параметра: кручение Tw и искривление Wr.
Кручение можно записать как
в
Lk(Q d) = 5
Рис. 12.2. Числа зацеплений пар ориентированных кривых
Tw — — oft(s) ds,
(12.1)
где fl(s) — скорость, с которой каждая из цепочек оборачивается вокруг оси
двойной спирали. Эта величину можно определить также и для открытой
ленты; параметр Тw может принимать любое значение, и мы назовем его
§ 12.1. Основные идеи топологической классификации
477
геометрическим кручением. Однако если ось двойной спирали плоская, то
Lk — Tw = к. Искривление Wr кривой С — понятие куда более тонкое.
Введенное Фуллером искривление равно усредненному числу самопересе¬
чений (со знаком) плоских ортогональных проекций кривой С (замкнутой
или разомкнутой); в контексте ДНК оно описывает продольный изгиб оси
двойной спирали. Подобно Tw, искривление Wr может принимать любое
значение. Имеет место соотношение
Lk = Tw + Wr, (12.2)
где Lk (для двух ориентированных кривых С иС^ий^г (для ориентиро¬
ванной кривой С) задаются двойными интегралами:
Lk = — О —r^s ^ - [ds х ds1];
4тг .j |r(s) — r(s')|3
°Z (12.3)
Wr — — О -г(з) TJ(S*L [ds x ds*}.
4n
cc
r(s) — r(s*)|3
Здесь С — ось двойной спирали, С' — любая из цепочек, а г(5) — точка
на кривой С, абсцисса которой равна 5. Искривление Wr исчезает, ко¬
гда С представляет собой плоскую кривую. Заметим для примера, что на
рис. 12.2,6 Lk(C, С") — 0, так как две кривые можно распутать, если
разрешить имеющей форму восьмерки линии пересечь саму себя; такие
пересечения не влияют на приведенный выше интеграл Lk.
Для того чтобы разделить цепочки ДНК во время репликации, необхо¬
димо изменить число Lk (см. задачу 12.1). Это может быть сделано непо¬
средственно, при помощи топоизмераз, разрезающих одну или обе цепоч¬
ки. В других случаях репликация происходит через локальное связывание
молекулы ДНК с белками, которое создает зоны отрицательной и положи¬
тельной сверхзакрутки.
12.1.3. Группы: основные определения
Рассмотрим множество (конечное или бесконечное, дискретное или
непрерывное) G элементов а, Ь, с, ..для которых существует опера¬
ция 0, определенным образом сочетающая элементы. Множество G явля¬
ется группой тогда и только тогда, когда удовлетворяются следующие тре¬
бования.
1. Любые два элемента а, b из множества G можно сочетать операци-
ей
2. Данная операция является ассоциативной: (а 0 6) 0 с = а 0 (Ь 0 с).
3. Существует единичный элемент I множества G, такой что для любого
элемента а выполняется условие а 0 J = I 0 а = а.
4. Для каждого элемента а найдется обратный элемент, обозначаемый
а-1, такой что а 0 а^1 — а^1 0а — /.
478
Гл. 12. Топологическая теория дефектов
Простым примером группы является ряд Z всех целых чисел с опе¬
рацией сложения ((8) 4-). Действительно, аксиома (2) выполняется при
сложении целых чисел; единичный элемент —- это 0; обратный к а эле¬
мент — это —а.
Группы бывают коммутативные (называемые также абелевыми) и неком¬
мутативные (неабелевы). В абелевых группах а® b = Ъ®а для любой пары
элементов. В неабелевых группах a <g) b ф b 0 а. Группа целых чисел яв¬
ляется абелевой. Группы могут содержать ограниченное число элементов
либо бесконечно много элементов. Конечные и счетные бесконечные груп¬
пы называются дискретными. Группа сложения Z целых чисел является
дискретной..
Подгруппой Н группы G называют подмножество элементов из G, кото¬
рое также является группой. Если hi — элементы подгруппы Н и g — про¬
извольный элемент G, то множество элементов — произведений g 0 —
левым смежным классом по подгруппе Н, а множество hi 0 g называет¬
ся правым смежным классом по подгруппе Н. Легко доказывается, что
два смежных класса gx 0 hi и g2 0 hi, образованные элементами g1 и g2
группы G, либо совпадают, либо вовсе не имеют общих элементов. Дру¬
гими словами, данная подгруппа Н делит группу G на непересекающиеся
смежные классы, образующие пространство смежных классов (или ор¬
биту), обозначаемое как G/Н. Пространство смежных классов не обяза¬
тельно является группой. Однако если подгруппа Н является нормальной
(или инвариантной), что означает, что левый и правый смежные классы
содержат одинаковые элементы для каждого g из группы G, то простран¬
ство смежных классов G/Н имеет структуру группы и называется фактор¬
группой.
Две разновидности групп важны для топологической классификации
дефектов данной упорядоченной среды, обе связаны с параметром порядка.
1. Непрерывная, как правило, группа G, элементы которой находятся
в соответствии со всеми допустимыми преобразованиями параметра поряд¬
ка. Группа симметрии Н представляет собой подгруппу этой непрерывной
группы.
2. Дискретные гомотопические группы, связанные с топологической
структурой пространства параметра порядка.
Ниже мы остановимся на этом вопросе более подробно. Сперва же
построим схему топологической классификации дефектов.
12.1.4. Общая схема топологической классификации дефектов
Гомотопическая классификация дефектов в упорядоченных средах
включает следующие три шага.
Во-первых, определяется параметр порядка (ПП) ф системы. В неодно¬
родном состоянии ПП представляет собой функцию координат: ф(г).
Во-вторых, определяется пространство 1Z параметра порядка (или вы¬
рождения), т. е. множество всех возможных значений ПП, не изменяющих
§ 12.1. Основные идеи топологической классификации
479
термодинамические потенциалы системы. Функция ф(г) отображает точки
реального пространства, занятого средой, на 7Z.
Представляют интерес отображения г-мерных сфер, окружающих де¬
фекты в реальном пространстве. Точечный дефект в двумерной системе
и линейный дефект в трехмерной системе можно окружить линейным кон¬
туром, г = 1; точечный дефект в трехмерной системе можно окружить
сферой, г = 2; дефект-стенку можно «окружить» двумя точками (г = 0),
расположенными по разные стороны стенки.
В-третьих, определяются гомотопические группы 7гД7£). Элементами
этих групп служат отображения г-мерных сфер, окружающих дефекты в ре¬
альном пространстве, на пространство ПП. Для того чтобы классифициро¬
вать дефекты размерности t' в t-мерной среде, необходимо знать гомотопи¬
ческую группу TTi(7Z), где г = t — tf — 1.
С одной стороны, каждый элемент гомотопической группы соответ¬
ствует классу топологически устойчивых дефектов; все эти дефекты экви¬
валентны в том смысле, что они переходят друг в друга при непрерывных
деформациях. С другой стороны, элементы гомотопических групп пред¬
ставляют собой топологические инварианты, или топологические заряды
дефектов. Бездефектные состояния (например, ф(г) = const) соответствуют
единичному элементу гомотопической группы и нулевому топологическо¬
му заряду.
12.1.5. Пространство параметра порядка. Группы, описывающие пре¬
образования параметра порядка
Изотропная ферромагнитная фаза Гейзенберга с единичным вектором
намагниченности d в качестве параметра порядка служит примером среды,
пространство ПП которой легко определяется с помощью качественных
рассуждений. Эта фаза изотропна в том смысле, что в ней пренебрегают
связью между d и кристаллографическими осями. Любое вращение во¬
круг фиксированного d переводит систему саму в себя. Концы векторов d
с различными ориентациями в пространстве образуют сферу 52. Таким об¬
разом, очевидно, что пространство ПП есть сфера 52. Для многих других
сред ситуация не настолько ясна. Далее мы проиллюстрируем общий метод
определения пространства ПП, проливающий некоторый свет на взаимо¬
связь между симметрией упорядоченной среды и пространством ПП.
Рассмотрим непрерывную группу трехмерных вращений. Эта группа
представляет собой часть полной эвклидовой группы смещений и пово¬
ротов, сохраняющей инвариантным термодинамическое состояние систе¬
мы. Трехмерные вращения можно однозначно описать вектором к, кото¬
рый параллелен оси вращения и имеет абсолютное значение, равное углу
поворота ip. Повороты вокруг всех осей, проходящих через одну общую
точку, образуют группу, называемую группой чистых вращений трехмер¬
ного эвклидова пространства. Эту группу можно представить в виде шара
радиуса 7г, обозначаемого как 50(3) и состоящего из точек <^k/|k|, где
—7г ^ р ^ 7г. Две диаметрально противоположные точки на поверхности
480
Гл. 12. Топологическая теория дефектов
такой сферы тождественны: повороты на угол 7г вокруг противоположно
направленных осей дают одинаковый результат.
В принципе, 50(3) может служить пространством ПП для ферромагне¬
тика Гейзенберга. Однако существуют множества точек в 50(3), соответ¬
ствующие неразличимым устойчивым состояниям ферромагнетика. Так как
любое вращение вокруг d переводит систему саму в себя, все точки ip d,
принадлежащие любому фиксированному радиусу шара 50(3), описыва¬
ют неразличимые состояния. Из-за этой симметрии шар 50(3) «сводится»
к сфере 52 поворотами, не меняющими параметр порядка d. Данный про¬
цесс называется факторизацией группы 50(3) по группе 50(2) двумерных
вращений вокруг фиксированной оси d (рис. 12.3). Группа 50(2) является
подгруппой 50(3). Пространство ПП ферромагнетика представимо в виде
сферы 52 = 50(3)/50(2), где 50(3)/50(2) есть обозначение простран¬
ства смежных классов группы 50(3) по подгруппе 50(2). Заметим, что 52
является лишь одним из множества примеров. Общие определения приво¬
дятся ниже.
Если среда — одноосный нематик, то направления d и — d эквивалент¬
ны, и происходит дополнительная факторизация 52 множеством, состоя¬
щим из двух диаметрально противоположных точек на 52. Пространство
ПП одноосного нематика есть множество 1Z = 50(3)/(50(2) х Z2) =
- 52 /Zo , также называемое проективной плоскостью RP2 (см. гл. 3). Z2 —
это группа двух чисел — Ои1: 0 + 0 = 0, 0 + 1 = 1, 1 + 0 = 1, 1 + 1 = 0.
Символ х обозначает прямое произведение двух групп 50(2) и Z2. Пря¬
мым произведением двух групп, скажем G и X1, называется множество
G х Т пар (g, t), представляющее собой группу по отношению к следую¬
щей операции: (g1? ti) 0 (g2, t2) =
= tel *1 ® Ы*
Приведенные выше примеры поз¬
воляют сделать следующее обобщение
теоретико-группового описания про¬
странства ПП.
Параметр порядка непрерывной
идеально упорядоченной среды можно
связать с «термодинамической» груп¬
пой G (которая обычно представляет
собой эвклидову группу) с элемента¬
ми g, преобразующими данное значе¬
ние фо параметра порядка в другое
значение gipo, для которого термо¬
динамические потенциалы системы
остаются прежними. Повороты идеаль¬
ного ферромагнетика как целого яв¬
ляются преобразованиями такого типа.
Среди элементов g могут быть преобра¬
зования, сохраняющие не только энергию, но также значение параметра
порядка: gHi^o = фо. Эти элементы образуют подгруппу Н группы О,
Рис. 12.3. Факторизация группы
50(3) чистых вращений по группе
вращений 50(2) дает в результате
сферу 52
§ 12.1. Основные идеи топологической классификации
481
называемую группой изотропии фо или малой группой фо. Тогда простран¬
ство ПП представляет собой пространство смежных классов
К = G/H. (12.4)
Заметим, что в общем случае 7Z не является группой. Более того, су¬
ществует некая произвольность в выборе группы G (но не 72-!). Группа G
может быть «больше» или «меньше», однако соответствующая подгруппа
изотропии Н должна в итоге приводить к тому же 72. = G/H. Если G —
это полная эвклидова группа, то Н — группа симметрии упорядоченной
среды.
12.1.6. Гомотопические группы
Гомотопическая группа описывает топологию пространства ПП. Здесь
мы кратко рассмотрим некое абстрактное пространство ПП 72, и группу
ориентированных контуров (петель) в нем, образующих так называемую
фундаментальную, или первую гомотопическую, группу.
Предположим, что 72. — связная поверхность: любые две точки на
72, можно связать кривой. Выберем произвольную точку М, принадле¬
жащую поверхности, и построим ориентированные непрерывные конту¬
ры, начинающиеся и заканчивающиеся в М (рис. 12.4). Контур считается
«ориентированным», если задано направление обхода. Среди контуров есть
такие, которые могут переходить друг в друга непрерывным преобразова¬
нием, например контуры Fi и Г2 или контуры Г3 и Г4 на рис. 12.4. Говорят,
что эти контуры гомотопны, или что они принадлежат одному гомотопиче¬
скому классу. Если 72. представляет собой простую связную (т. е. состоящую
только из одного куска и не имеющую дыр) поверхность, то любой контур
можно сжать в точку М; следовательно, все контуры принадлежат одному
гомотопическому классу. Если 72, не является простым связным множеством
(один из примеров — это окружность S1, другой приведен на рис. 12.4), то
существуют различные классы гомотопных контуров. Например, контуры
Г3 и Г5 на рис. 12.4, окружающие разные «дырки», или контуры Г4 и Гб,
которые окружают одну дырку, но разное число раз, относятся к разным го¬
мотопическим классам. Контуры из разных гомотопических классов нельзя
связать непрерывным преобразованием.
Можно определить произведение двух контуров Гп и Гт как контур Гnm,
который получится, если сначала обойти контур Гп, а затем контур Гт:
Гпт = Гп 0 Гт. На рис. 12.5 показаны два гомотопных представле¬
ния Гпт. Подобно произведению отдельных контуров, можно определить
произведение гомотопических классов как множество произведений пред¬
ставителей этих классов. Эта идея позволяет придать множеству контуров
структуру группы, причем в качестве групповой операции используется
произведение гомотопических классов. Элементами группы являются го¬
мотопические классы. Класс контуров, сжимаемых в одну точку, служит
единичным элементом группы. Каждый класс имеет обратный элемент —
это то же самое множество контуров, но с противоположной ориентацией.
31-КЛЕМАН М
482
Гл. 12. Топологическая теория дефектов
Рис. 12.4. Ориентированные контуры с основанием в точке М в пространстве
параметра порядка 71.
Рис. 12.5. Два гомотопных представления контура ГПт — произведения двух
контуров Гп и Гт, обходимых в заданном порядке
§ 12.1. Основные идеи топологической классификации
483
Произведение классов удовлетворяет ассоциативному закону. Таким обра¬
зом, множество гомотопических классов контуров образует группу, назы¬
ваемую фундаментальной группой множества 7Z с основанием в точке М
и обозначаемую rci(7Z, М), или просто фундаментальную группу ni(TZ)
множества 7Z. Последнее упрощение, заключающееся в пренебрежении
точкой основания, возможно, когда множество 7Z связно. Если вместо М
в качестве точки основания в связном множестве 1Z выбрать другую точку,
Mi, то полученная в результате группа 7Ti(7Z, Mi) будет изоморфной ко¬
пией 7г 1 (7£, М). Групповой изоморфизм — это взаимнооднозначное отоб¬
ражение одной группы на другую, сохраняющее операцию группы. Таким
образом, связное пространство ПП 7Z можно охарактеризовать единствен¬
ной абстрактной группой которую также называют первой гомо¬
топической группой, для того чтобы отличать ее от n-х гомотопических
групп тгп(7г), которые будут рассмотрены позднее.
Рис. 12.6. Контуры в пространстве 1Z параметра порядка (плоскость с двумя про¬
битыми дырками). Точка основания М. Контуры Гз(— Ti 0 Г2) Ф Г£(= Г2 <8> Г1)
принадлежат неабелевой фундаментальной группе (1Z)
484
Гл. 12. Топологическая теория дефектов
Фундаментальная группа щ (TV) может быть абелевой или неабелевой
в зависимости от пространства ПП 1Z. Если 1Z — плоскость с одной про¬
битой дыркой (гомеоморфная окружности 51), то группа tti(7Z) абелева
(рис. 12.5). Если 7Z — плоскость с двумя пробитыми дырками (гомеоморф¬
ная фшуре «8»), то фундаментальная группа неабелева: Гт<£)Гп ф Гп<£>Гт.
Как показано на рис. 12.6, не существует непрерывного перехода от Г3 =
= Гх 0 Г2 к Г3 ~ Г2 0 Гх; М — фиксированная точка на Гз и Г3.
На этом мы закончим рассмотрение пространства ПП и гомотопических
групп, необходимых для понимания общей схемы классификации тополо¬
гических дефектов. Для того чтобы проиллюстрировать указанную схе¬
му, мы сперва рассмотрим точечные дефекты в двумерных нематической,
смектической и кристаллической фазах, классифицируемые при помощи
фундаментальной группы. Эти примеры требуют сравнительно простого
топологического рассмотрения. В общем случае для получения гомотопи¬
ческих групп из структуры G/Н необходимы более изощренные теоретико¬
групповые методы.
12.1.7. Точечные дефекты в двумерной нематической фазе
В нашей модели двумерного нематика центры тяжести молекул лежат в
одной плоскости, в то время как директор п образует угол о < IV’ol ^ тг/2
с нормалью и к плоскости. В качестве параметра порядка можно выбрать
либо единичный вектор т = п — и (пи), представляющий собой проек¬
цию п на плоскость, либо волновую функцию ф = \фо\ ехр(гср), где \фо \ —
полярный и (р — азимутальный углы наклона молекулы. Плотность сво¬
бодной энергии однородного состояния не зависит от угла (р и может быть
представлена как некая функция модуля |^о|? например
^cond = Л\ф\2 + BIV’I4 (12.5)
(сравните с описанием сверхтекучего гелия; п. 3.1.1). Пространство ПП 7Z
зависит от модуля |^о|.
1. Если 0 < \фо\ < тг/2, то 1Z = S1. Фаза (р может меняться от 0 до
и каждая точка окружности S1 соответствует некоторому значению ср. На
рис. 12.7, б' окружность S1 соответствует минимуму плотности свободной
энергии Fconcj (см. также рис. 3.1).
2. Если \фо | = тг/2, то 1Z = S1 /Z2. Любые две диаметрально противо¬
положные точки окружности отождествляются благодаря эквивалентности
директоров п и —п в нематике. Топологически S1 и S1 jZ2 эквивалент¬
ны. Однако, как мы увидим, существует важное физическое отличие между
дефектами в случаях 0 < \фо\ < 7г/2 и |^о| = тг/2.
3. Если |^о| = 0, то 7Z является точкой.
Неоднородность азимутальной ориентации молекул приводит к появле¬
нию дополнительного градиентного члена в энергии:
Fconi = А\ф\2 + ВЩ* + - К\V ф\\
(12.6)
§ 12.1. Основные идеи топологической классификации
485
где К — упругая постоянная плоских деформаций поперечного и продоль¬
ного изгибов. Плотность энергии (12.6) определяет масштаб длины, на¬
зываемый длиной когерентности £ = у/К/А. Если характерный масштаб
искажений много больше £, то угол наклона близок к своему равновесному
значению |^o,eq| = у/—А/2В и неоднородность затрагивает только изме¬
нения азимутального угла <р(х, у). Функция (р(х, у), или, что то же самое,
функция т(х, у), отображает двумерное пространство (х: у) в Л. Изучение
отображений замкнутых контуров, окружающих точечные дефекты двумер¬
ной системы, позволяет определить, являются ли дефекты устойчивыми.
В качестве примера рассмотрим устойчивость трех разных точек: Ро,
Pi и Р2 в поле г для случая 0 < \фо\ < тг/2 и, следовательно, 7Z = S1
(рис. 12.7).
Окружим «подозрительную» точку ориентированной петлей, такой как 70
вокруг точки Ро на рис. 12.7, а. Отображение г (ж, у) рисует соответствую¬
щую ориентированную петлю на S1, такую как Го на рис. 12.7, б. Петлю Го
можно непрерывно сжать в точку, оставаясь при этом на окружности S1
(рис. 12.7, г); следовательно, гладкая перестройка векторного поля т(я, у)
в реальном пространстве приводит к однородному состоянию т(ж, у) =
= const (рис. 12.7, в). Таким образом доказано, что исследуемый дефект Ро
является устранимым, или топологически неустойчивым.
Другая ситуация имеет место в случае радиальной конфигурации т(я, у)
(рис. 12.7, д). Петля Г1 пробегает всю окружность S1 и не может непре¬
рывно сжаться в точку. Для того чтобы уничтожить дефект (рис. 12.7, д),
необходимо разрушить конденсированное состояние вдоль целой линии
с началом в точке Р\ (чтобы разрезать Гi) либо разрешить существенные
отклонения угла наклона от \фо,щ\ (чтобы отделить Т\ от окружности S1).
Оба случая требуют преодоления значительного энергетического барьера,
намного превосходящего энергию искажений, не выходящих из плоскости.
Другими словами, дефект на рис. 12.7, д устойчив. Дефект Р2 (рис. 12.7, ж),
контур которого Г2 дважды пробегает S1, также является устойчивым: его
нельзя перевести ни в однородное состояние, ни в радиальный дефект.
Построенная схема устанавливает соответствие между топологически
устойчивыми дефектами и контурами сингулярности Гk, k раз обходящими
51 в заданном направлении. Все точечные сингулярности разделяются на
классы, каждый из которых соответствует своему собственному классу го¬
мотопных контуров Г^. Множество классов Г^ образует фундаментальную
группу 7т 1 (S1). Она удовлетворяет определению группы: любые два конту¬
ра Vk и Гп, могут сочетаться, образуя третий контур Г^п = Г&ГП (начиная
с этого момента будем пользоваться упрощенной записью произведений,
опуская знак ®). Эта операция ассоциативна; существует особый, экви¬
валентный точке контур Го, представляющий собой единичный элемент;
контуры Г^ и Г_£, пробегающие S1 в противоположных направлениях,
являются обратными друг другу: Г*Т_*; = Го. Наконец, группа Ki(Sl)
является абелевой.
Каждый элемент 7Ti(51) может быть помечен целым числом /с;
486
Гл. 12. Топологическая теория дефектов
б
Г
о
к — О
б'
Г
о
к = О
в
г
Г
к = 1
Г
к —2
е'
Л/Л
t//V
Рис. 12.7. Точечные дефекты с различными топологическими зарядами к в поляр¬
ном двумерном нематике с углом наклона 0 < |^о| < 7г/2; стрелки изображают
проекции директора на плоскость: (а), (в) к = 0 — бездефектное состояние, 0)
к = 1, (ж) к = 2; (б), (г), (е), (з) соответствующие контуры в пространстве пара¬
метра порядка S1; (б(е') S как окружность вырожденных минимумов свободной
энергии, см. текст
следовательно, группа 7Ti (S1) изоморфна группе Z целых чисел. Число к —
это топологический заряд дефекта. Его нельзя изменить непрерывными
деформациями. Для рассматриваемых точечных дефектов
к
1
27Г ,
О\7(pdl = 0, ±1, i2,
(12.7)
§ 12.1. Основные идеи топологической классификации
487
Когда |^о| = тг/2, пространство вырождения есть множество 1Z =
= S1 /Z2, топологически эквивалентное S1. Следовательно, в случае \фо\ =
7г/2 имеется столь же много (т. е. бесконечно много) топологически раз¬
личных дефектов, что и в случае 0 < \фо\ < 7г/2. Однако эти два множества
дефектов отличаются физически: в случае \фо\ = 7г/2 допустимо нечет¬
ное число вращений на угол п и, таким образом, к может быть целым
или полуцелым (рис. 12.8, а). Контур Г_!/2, соединяющий диаметрально
противоположные точки окружности на рис. 12.8,6, является замкнутым
и не может сжаться в точку; (ср. с рис. 12.8, г).
Наконец, в случае |^о| — 0 дефекты отсутствуют вовсе и фундаменталь¬
ная группа тривиальна, тг\ (0) = 0.
rZ Л , .
«*4‘444si
S1Z2
» \.,.А »>\
а
б
Рис. 12.8. Дефект к = —1/2 в двумерном неполярном нематике
12.1.8. Точечные дислокации в двумерном кристалле
Как было установлено в гл. 3, пространство ПП двумерного кристал¬
ла есть прямое произведение двух окружностей, или тор: 71 = Sl х S1
(мы пренебрегаем поворотной симметрией) (см. рис. 3.7 и рис. 12.9). Лю¬
бое смещение в плоскости двумерной кристаллической решетки как целого
приводит лишь к другому представлению кристалла, но не меняет его тер¬
модинамических потенциалов. Если вектор смещения совпадает с базис¬
ным вектором решетки, то это преобразование переводит кристалл в точно
такое же состояние. Отождествление границ двумерной ячейки Бравэ при¬
водит к тору в качестве пространства вырождения.
Перечисленные основные типы петель, которые не могут быть сжаты
в точку на торе: петли, обходящие «маленькую» окружность (рис. 12.9, г);
петли, обходящие «большую» окружность (рис. 12.9, ё) и их комбинации.
Эти петли соответствуют точечным дислокациям. Каждая дислокация ха¬
рактеризуется парой топологических инвариантов (кх, ку), которые пока¬
зывают, сколько раз петля обходит «маленькую» и «большую» окружности
соответственно:
^(S1 х S1) = 7Ti(S1) х ^(S1) = Z х Z = (kx, ky). (12.8)
Числа (kx, ky) суть не что иное, как х- и ^/-координаты вектора Бюр¬
герса Ь, выраженного в единицах базисных векторов решетки (аж, ау):
b — кх S-x ку&у.
488
Гл. 12. Топологическая теория дефектов
s' X s'
а
б
в
г
д
1 .1 1 _
(1,0) _
/
\
(
ш'\
...
ч
✓
г ■
Рис. 12.9. Точечные дислокации в двумерном кристалле с пространством параметра
порядка 7Z — S1 х S1
Двумерный смектик можно представить как двумерную среду с од¬
номерной волной плотности. Близкая экспериментальная модель — это
покрытая рябью ламеллярная лиотропная фаза Рр> , составленная из распо¬
ложенных один над другим бислоев лецитина с дополнительным трансля¬
ционным порядком вдоль одного из двух направлений внутри мембраны.
Упорядочение в плоскости делает такие мембраны жесткими; в принци¬
пе, можно разбавлять фазу Рр и наблюдать поведение одного отдельного
бислоя. Бислои фазы Рр обнаруживают два типа гофрированных в плоско¬
сти сверхмолекулярных структур: A-фазу и (А/2)-фазу (рис. 12.10). Гребни
и впадины мембраны равноотстоят друг от друга, и их можно рассмат¬
ривать как двумерную смектическую фазу. Различие между двумя фазами
заключается в том, что «слои» А-фазы имеют одинаковую толщину d, тогда
как в (А/2)-фазе перемежающиеся нечетные и четные «слои» имеют раз¬
ную толщину; такой асимметричный профиль наблюдается у хиральных
поверхностно-активных веществ.
§ 12.1. Основные идеи топологической классификации
489
Рис. 12.10. Молекулярная структура бислоев с Л- и (А/2)-упорядочениями фа¬
зы показанная в сечении, сделанном плоскостью, перпендикулярной бислоям.
Стрелками показаны периоды структур
Для того чтобы определить пространство вырождения симметричной
A-фазы, нужно рассмотреть как трансляционную, так и поворотную сим¬
метрии. Смещение t вдоль нормали к слоям, кратное периоду d, и поворот г,
кратный 7г, переводят систему саму в себя. Таким образом, пространство
ПП представляет собой прямоугольник {(£, г), 0 ^ t ^ d, 0 ^ г ^ 7г}
(рис. 12.11, а). Точки (t,r) внутри прямоугольника соответствуют различ¬
ным представлениям двумерного смектика; все эти представления имеют
одинаковую энергию. Стороны прямоугольника отождествляются по пра¬
вилам (0, г) (d, г) и (£, 0) -» (d - t, 7г), как показано стрелками на
рис. 12.11, а. Отметим, что после поворота на угол тт смещение t перехо¬
дит в d—t. Благодаря этой тонкости получаемое пространство вырождения
представляет собой бутылку Клейна (рис. 12.11), а не тор. Фундаментальная
группа бутылки Клейна является неабелевой и изоморфной полупрямому
произведению группы Ztr, описывающей трансляции, и группы Zrot, опи¬
сывающей вращения (обе группы изоморфны Z):
ttiCR-a) = г A Zrot. (12.9)
Следовательно, каждый точечный дефект в A-фазе соответствует паре чи¬
сел (n, га). Элементы (п, 0) соответствуют точечным дислокациям с век¬
тором Бюргерса b = nd, а элементы (0, га) — точечным дисклинациям
с целыми (четные тп) и полуцелыми (нечетные га) силами. Здесь значе¬
ния га выбраны в два раза большими обычных значений к для лучшего
представления сочетаний дефектов. Закон сочетания для полупрямого про¬
изведения отличается от закона для прямого произведения. Если п\ и п2 —
две трансляции, a mi и га2 — два поворота, то закон сочетания имеет вид:
(пь mi)(n2, га2) = (щ +min2, m\ + т2).
490
Гл. 12. Топологическая теория дефектов
7Г
0
d
л'-
S. t '
Ч . :^г^.Жг‘-
Г
а
б
в
г
Рис. 12.11. Эквивалентные представления пространства параметра порядка дву¬
мерного смектика: прямоугольник {(£, г), 0 ^ t ^ d7 0 ^ г ^ 7г} с отождеств¬
ленными сторонами; тот же прямоугольник, преобразованный в бутылку Клейна (г)
через промежуточные стадии (б) и (в)
Некоммутативность фундаментальной группы тг\ {И\) приводит к тон¬
ким физическим эффектам. Например, результат слияния двух дефектов
в присутствии третьего является неопределенным и зависит от пути слия¬
ния. В неабелевой среде точечный дефект соответствует уже не одному
элементу фундаментальной группы, а целому классу сопряженных элемен¬
тов. По определению два элемента а и Ь группы G называют сопряженными
друг другу, если существует элемент q группы G, такой что Ь = q~laq. На
рис. 12.12 показано, что дислокация (1,0) после обхода вокруг дисклина¬
ции (0,1) должна характеризоваться парой чисел (—1, 0). Другими слова¬
ми, один и тот же дефект описывается разными элементами (1, 0) и (—1, 0),
принадлежащими одному классу сопряженных элементов. В пространстве
ПП контур Г(10) переходит в контур F(_li0) = 0)Г(0} после то¬
го как соответствующий дефект (1,0) обходит вокруг дисклинации (0, 1).
§ 12.1. Основные идеи топологической классификации
491
(-1,0)
Рис. 12.12. Превращение дислокации (1, 0) в антидислокацию ( — 1, 0) после оги¬
бания ею дисклинации в двумерной смектической Л-фазе
В абелевой среде и Г(0?1) коммутируют, и, следовательно, F(li0)
и Г(_1;о) были бы гомотопными; однако в некоммутативном случае Г(1}0)
иГ(__1)0) негомотопны.
Так как один и тот же дефект может соответствовать разным элемен¬
там класса сопряженных элементов неабелевой группы 7Ti, слияние двух
дефектов не определено однозначно. Например, дислокация (1,0) и «анти¬
дислокация» (—1,0) при слиянии либо аннигилируют (рис. 12.13,6), либо
образуют двойную дислокацию (2,0), если точка (—1,0) обходит вокруг
дисклинации (0, 1/2) по пути к месту слияния (рис. 12.13,в). Результат
определяется не перемножением отдельных элементов группы гомотопии,
(1,0) (-1,0)
(0, 0)
б
а
(2, 0)
в
Рис. 12.13. Результат слияния дислокаций (1, 0) и (—1, 0) (а) в двумерной смекти¬
ческой Л-фазе зависит от пути слияния вокруг дисклинации: однородное состояние
(0, 0) (б); двойная дислокация (2, 0) (е)
492
Гл. 12. Топологическая теория дефектов
как в случае абелевых сред, а всеми результатами перемножения клас¬
сов сопряженных элементов. Таким образом, для того чтобы предсказать
результат слияния, необходимо знать глобальную конфигурацию парамет¬
ра порядка; знания локальной топологии вокруг дефектов недостаточно.
Другая разновидность фазы Рр> — (А/2)-структура — по внешнему
виду мало отличима от A-структуры (см. рис. 12.10): всего лишь исчезает
ось симметрии второго порядка С2. Однако теперь пространство параметра
порядка есть двумерный тор Т2. Следовательно, фундаментальная группа
7Г1 (7гА/2) = х Zrot (12.10)
представляет собой прямое произведение групп и является коммутативной:
результат слияния двух дефектов всегда однозначно определен. Более того,
в противоположность A-фазе, в (А/2)-фазе отсутствуют отдельные дискли¬
нации с нечетными т.
Простые примеры А- и (А/2)-фаз также обнаруживают некоторую
ограниченность теории гомотопий в применении к классификации дефек¬
тов в средах с нарушенной трансляционной симметрией. Согласно теории
гомотопий (выражения (12.9) и (12.10)), в слоистых системах могут суще¬
ствовать дисклинации с любым целым т. В действительности дисклинации
с тп, не равными 1 или 2 (fc ^ 1/2, 1), нарушают равноудален но сть слоев
и, следовательно, энергетически невыгодны.
§ 12.2. Фундаментальная группа пространства параметра
порядка. Линейные дефекты
Фундаментальная группа систематизирует топологически устойчивые
точечные дефекты в двумерных упорядоченных средах и топологически
устойчивые линейные дефекты в трехмерных средах.
12.2.1. Неустойчивые дисклинации в трехмерном изотропном ферро¬
магнетике
Пространство ПП изотропного ферромагнетика Гейзенберга — это сфе¬
ра S'2. Рассмотрим дисклинацию в векторном поле намагниченности. Ори¬
ентированная петля, окружающая ядро дисклинации в реальном простран¬
стве, отображается векторным полем в пространство ПП и, таким образом,
создает контур на сфере S2. Очевидно, что любой нарисованный на сфере
контур можно сжать в точку. Следовательно, 7ri (S2) = 0: любую дисклина¬
цию в трехмерном изотропном ферромагнетике можно непрерывно преоб¬
разовать в однородное состояние (рис. 12.14).
Топологическая простота пространства ПП вовсе не свидетельствует
о том, что вопрос о дефектах в ферромагнетике тривиален. Существуют
интересные сходства между дефектами (точечными и линейными) в нема¬
тиках и ферромагнетиках, так как параметры порядка выглядят очень похо¬
же: вектор — в случае ферромагнетика, директор — в нематике. Но опять
§ 12.2. Фундаментальная группа пространства параметра порядка 493
же, знание нематических дефектов не означает знания магнитных дефектов.
Физическое различие, конечно же, существенно. Тема дефектов в ферромаг¬
нетиках больше затрагиваться не будет. Заинтересованный читатель сможет
оценить особенности и богатство этой темы, прочитав приведенную в конце
главы литературу.
Рис. 12.14. Непрерывное преобразование дисклинации k = 1 (а) в однородное
состояние к — 0 (в) в трехмерной ферромагнитной фазе (слева); соответствующее
сокращение петли в пространстве параметра порядка (справа)
12.2.2. Устойчивые дисклинации в трехмерной одноосной нематиче¬
ской фазе
В трехмерной неполярной одноосной нематической фазе директоры п
и — п эквивалентны и пространство ПП—это сфера S2 /Z2 или проективная
плоскость RP2.
В S2 /Z2 существует два типа контуров: это сразу же видно в двумер¬
ном представлении проективной плоскости (см. рис. 3.6), где можно заме¬
тить контуры, которые действительно замкнуты (например, окружности),
и контуры, заканчивающиеся в двух диаметрально противоположных точ¬
ках. Контуры первого типа могут сжиматься в точку; они соответствуют
дисклинациям с целыми fe, которые топологически неустойчивы. Контуры
Г
в
494
Гл. 12. Топологическая теория дефектов
второго типа не могут быть сжаты в точку: при любых непрерывных дефор¬
мациях концы этих контуров остаются в диаметрально противоположных
точках. Эти контуры соответствуют полуцелым fc.
Легко видеть, что все контуры, соответствующие полуцелым к, могут
переходить друг в друга (рис. 12.15). Следовательно, есть только один класс
топологически устойчивых дисклинаций в одноосной нематической фазе:
тп (S2 /Z2 ) = Z2.
Законы сохранения просто представляются в терминах к: 1/2 + 0
и 1/2+ 1/2 = 0.
(12.11)
= 1/2
Щ>/
V* ч А >
1 1
1 1
J* JL
J. J.
т т
т т
т т
1
2
3
п ,1 \\
//I I w
►i-#-
* У к * Д
4
5
Г
3
■fj
-I*..
4- • ’ .
У • 1 ' ' - 4 Ч*. : ^,ч
i “ " ;■- gfr i-t s
•Л'.лм.М-lw- S4Wk„.AHMA...sA .«|V •*
г
-1/2
Рис. 12.15. Непрерывное преобразование дисклинации fc = 1/2 в дисклинацию
к = —1/2 в реальном пространстве (в верхней части рисунка) и соответствующее
2
преобразование контуров в пространстве ПП RP
12.2.3. Дисклинации в двуосной нематической и холестерической
фазах
Двуосный нематический порядок определяется тройкой взаимно пер¬
пендикулярных векторов: 1 (эквивалентен —1), п (эквивалентен — п) и [nl]
(эквивалентен — [nl]). Пространство ПП есть группа G = 50(3) вращений
тройки векторов 1, n, [nl], факторизованная по состоящей из четырех эле¬
ментов точечной группе D<i поворотов на угол 7г вокруг направлений 1, п
И^: Яьх = 50(3)/г>2. (12.12)
Любые две диаметрально противоположные точки на поверхности 50(3)
тождественны: повороты на угол 7Г вокруг противоположно направленных
§ 12.2, Фундаментальная группа пространства параметра порядка 495
осей дают один и тот же результат, как уже было показано в п. 12.1.5. Сле¬
довательно, 50(3) можно эквивалентным образом представить как проек¬
тивное пространство RP3 = 53 /Z2 или как трехмерную сферу в четы¬
рехмерном пространстве, диаметрально противоположные точки которой
тождественны: 50(3) = 53/Z2 (сравните с одноосным нематиком с про¬
странством ПП RP2 = S2 /Z2).
Теперь самое время сделать несколько представляющих общий инте¬
рес замечаний, которые будут полезны в применении к средам, ПП кото¬
рых представляет собой локальную тройку (двуосные нематики, холесте¬
рики). Стандартный метод вычисления гомотопических групп в контексте
упорядоченных сред заключается в том, чтобы поднять топологическое
пространство G в простое связное пространство G (называемое универ¬
сальным покрытием пространства G), т. е. такое, что 7Гх (О) = 0. В этом
процессе каждая точка g € G поднимается до множества из п точек g-
(п не зависит от g). И наоборот, проецирование на G любой точки g- € G
и Vi-окрестности точки g* отображает g- и Ц в g и F-окрестность точки g.
Путь 7ij в пространстве G из точки g{ в точку g • отображается на замкну¬
тую петлю в О, т. е. соответствует одному элементу группы 7гi(G, g);
следовательно, п — это индекс фундаментальной группы или одной из ее
подгрупп (Массэй). Отметим также, что подгруппа Я С G поднимается
в подгруппу Я С О с соотношениями вида g{hj = /р; g0 hj: fp € G, если
gh = /; g, ft, / (E G. Простой иллюстрацией рассмотренных выше свойств
служит одномерная окружность G = 51; ее универсальное накрытие — это
спираль (ть = оо), которую, простоты ради, можно представить имеющей
тот же радиус, что и окружность, и находящейся над ней, для того что¬
бы сделать видимым процесс проецирования, хотя необходимо помнить,
что это представление не имеет никакого отношения к рассматриваемым
здесь топологическим свойствам. Наконец, рассмотрим подгруппу Я С G,
представляющую собой результат поднятия подгруппы Я С G. Фундамен¬
тальная группа 7Гх(G/H) = 7Ti(G/H), так как одинаковы пространства
смежных классов: 7Z = G/H — G/Я. Теперь рассмотрим множество, по¬
лученное отождествлением любой точки g из G со всеми точками h gh:
h 6 Я, принадлежащими подгруппе, сопряженной точке g 6 G. Ясно, что
это множество представляет собой 71. Кроме того, 7Г1(С/Я) = Я в силу
того, что G — простое связное множество; полное доказательство требует
более изощренных методов и выходит за рамки этой книги.
Универсальное накрытие проективной плоскости — это сфера 52; ана¬
логично, универсальное накрытие 50(3) — это S3. В обоих случаях п = 2.
Рассмотрим G = 53; группа симметрии тройки директоров D2 представ¬
ляет собой абелеву подгруппу 50(3) с четырьмя элементами, которые мы
обозначим как /, г, j и р с соотношениями: г2 = I, ij = —ji = р, где
I — единичный элемент, а каждый из оставшихся элементов представляет
собой поворот на угол 7г вокруг одной из трех перпендикулярных осей. Ре¬
зультат поднятия D2 в 53 есть группа из восьми элементов. Мы назовем эти
496
Гл. 12. Топологическая теория дефектов
элементы I, г, j и р (так же, как и раньше), добавив дополнительные эле¬
менты J, —г, — j и — р, обозначение которых соответствует тому, что они
один за другим были на тех же самых «нитях» подняты над 50(3) (следова¬
тельно, они имеют ту же геометрическую интерпретацию). Этого достаточ¬
но, чтобы получить новые групповые соотношения, вспоминая замечание
из предыдущего абзаца (а именно: g{hj = /р; gi: hj,fp е G, если gh ~
= fig, ^^ / £ G). Группа из восьми элементов, обозначаемая Q, неабелева
и подчиняется правилам умножения
и = -ji = р, ip = -pi = г, рг = -гр = j,
(12.13)
JJ = I, и = jj =рр = j, ijp - j.
Это группа кватернионов. Окончательно находим
7T1(SO{3)/D2) = ТГ i(S3/<2) = (5- (12.14)
Элементы группы кватернионов образуют пять классов сопряженных эле-
ментов: С0 = {/}, Со = {./}, Сх = {г, -г}, Су = {j, -j} uCz = {р, -р}.
Дисклинации в двуосных нематиках резко отличаются от дисклина¬
ций в одноосных нематиках. В двуосных нематиках имеется четыре класса
(а не один) топологически устойчивых дисклинаций, связанных с четырьмя
(исключая Go) из пяти классов сопряженных элементов группы Q. Соот¬
ветственно, топологический заряд может принимать значения /, J, (г, — г),
С?\ “Л (р? ”Р) с правилами умножения (12.13). Различные дисклинации
показаны на рис. 12.16. Сила к может быть как полуцелой (повороты ди¬
ректора на угол 7г при обходе вокруг ядра, классы Ох, Су и Cz\ так и целой
(повороты на угол 27т, класс Go). Сингулярное ядро 27г-дисклинации нель¬
зя уничтожить с помощью «вытекания в третье измерение», в отличие от
случая одноосного нематика (рис. 2.16,12.17). В противоположность этому,
47г-дисклинации (класс Go), |fc| — 2, топологически неустойчивы. Эта по¬
разительная разница между 27т- и 47г-дисклинациями проиллюстрирована
на рис. 12.17.
Слияние и распад дисклинаций в двуосном нематике подчиняются пра¬
вилам умножения, относящимся не к самим элементам, а к их классам.
Результаты приведены в табл. 12.1.
Если две дисклинации, принадлежащие разным классам, сливаются,
то образуется дисклинация, принадлежащая классу, который является про¬
изведением первых двух классов. Результат слияния дисклинаций одного
и того же класса, Сх, Су или Сл, неоднозначен: может образоваться либо
тривиальная несингулярная конфигурация (класс Go), либо дисклинация из
класса С о, в зависимости от пути слияния по отношению к другим линей¬
ным дефектам системы.
Упомянутые особенности слияния дисклинаций проистекают из неком-
мутативности группы Q. Другое эффектное следствие некомутативности
проявляется при запутывании дисклинаций в двуосных нематиках.
§ 12.2. Фундаментальная группа пространства параметра порядка 497
а б
Рис. 12.16. Поля директоров п (длинные стержни) и 1 (короткие стержни) для то¬
пологически устойчивых дисклинаций в двуосном нематике: к — 1/2, класс Cz (а)',
к = 1, класс Со (б). Показаны сечения, перпендикулярные осям дисклинаций
: 1 Ддл.
•а ' :• -^:jC_‘ ^ v
.
■ ля *■'*« як
а
б
в
Рис. 12.17. Замкнутые контуры Гг (а) и Г2 (б, в), соответствующие дисклинациям
|А:| = 1 и |/с| = 2 в пространстве ПП двуосного нематика. Оба контура соединяют
диаметрально противоположные эквивалентные точки на поверхности 50(3). Кон¬
тур Fi невозможно непрерывно сжать в точку. Контур Г2 пробегает между двумя
диаметрально противоположными точками дважды (б) и может плавно покинуть
эти точки и сжаться в точку (в)
Таблица12.1. Правила умножения пяти классов сопряженных элементов груп¬
пы кватернионов, управляющие слиянием и распадом дисклинаций в двуосном
нематике
Со
Со
сх
Су
cz
Со
Со
С0
сх
Су
cz
Со
Со
Со
сх
Су
cz
сх
сх
сх
Со или Со
cz
Су
Су
Су
Су
cz
Со или Со
сх
cz
Cz
cz
Су
сх
Со или Со
498
Гл. 12. Топологическая теория дефектов
На рис. 12.18, а изображены две запутанные дисклинации. Вопрос в том,
могут ли непрерывные изменения директора перевести систему к рас¬
цепленной конфигурации (рис. 12.18,6), если мы требуем, чтобы концы
дисклинаций оставались зафиксированными.
Для того чтобы найти ответ на этот вопрос, начертим три контура 71, 72
и 7з из точки М реального пространства: 71 и 72 окружают дисклинации,
а 73 окружает запутанный участок (рис. 12.18). Их образами в простран¬
стве ПП будут какие-то контуры Гь Г2 и Г3. Очевидно, что дефекты можно
расцепить только в том случае, когда контур Г3 гомотопен нулю. Если
это не так, то разделение дисклинаций оставит топологически нетриви¬
альный след в пространстве, а именно третью дисклинацию (рис. 12.18, в).
Результат зависит от природы сцепленных дисклинаций. Можно показать
(рис. 12.19), что контур Г3 гомотопен произведению 1Г^"1; элемент
такого вида называют коммутатором в фундаментальной гомотопической
группе. В случае абелевых групп коммутатор представляет собой единич¬
ный элемент, так как 1^2 = Г2Г1. Это не так для неабелевых групп;
в частности, для группы Q контур Г3 может принадлежать либо классу
Со (ГхГаГ^ГГ1
1), либо классу Со (Г^ГгГ^ :Г2 1
— 1). Последняя
ситуация имеет место, когда две запутанные дисклинации принадлежат
разным классам из набора Сх, Су, Cz. Таким образом, после прохождения
двух различных дисклинаций |fc| = 1/2 друг через друга, они оказываются
связанными дисклинацией |fc| — 1 из класса Со.
7з
а
б
в
Рис. 12.18. Запутывание дисклинаций в двуосном нематике (а); топологически
тривиальный случай (6); нетривиальный случай (в)
Топологическая классификация дефектов в двуосных нематиках может
быть приложена к холестерикам, если шаг спирали холестерика много мень¬
ше характерного масштаба деформаций, как было показано в гл. 11, где
ради удобства мы использовали те же обозначения для классов дискли¬
наций. Однако приведенная выше топологическая классификация непри¬
менима в своем наиболее общем виде к грубозернистой картине холесте¬
риков, учитывающей высокую энергетическую стоимость изменения шага
спирали.
§ 12.3. Вторая гомотопическая группа пространства параметра порядка499
Рис. 12.19. Непрерывные деформации контура 73 с рис. 12.18 в произведение
контуров 717271 72~:, демонстрирующие тот факт, что образ Гз контура 73 в про¬
странстве ПП гомотопен произведению ГхГгГ^Гз1- На шаге (г) происходит объ¬
единение четырех отмеченных кружками точек
§ 12*3. Вторая гомотопическая группа пространства
параметра порядка и точечные дефекты
Точечные дефекты в трехмерных упорядоченных фазах классифициру¬
ются по элементам второй гомотопической группы.
12.3.1. Точечные дефекты в трехмерном ферромагнетике
В трехмерном изотропном ферромагнетике поле намагниченности ш(г)
может содержать сингулярные точки, в которых направление m точно
не определено. Для того чтобы пролить свет на топологическую устой¬
чивость такой точки, ее окружают замкнутой поверхностью а (рис. 12.20).
Радиус сферы должен быть много больше размера ядра точечного де¬
фекта. Функция m(r) отображает поверхность а на некую поверхность
в пространстве ПП 1Z — S2 (рис. 12.20). Если полученную поверхность Е
можно сжать в одну точку (рис. 12.20 а), то точечный дефект является
топологически неустойчивым. Если Е обернута N ф 0 раз вокруг сфе¬
ры £2, то точечная сингулярность представляет собой устойчивый дефект
с топологическим зарядом N ф 0. Например, на рис. 12.20,6 изображен
500
Гл. 12. Топологическая теория дефектов
радиальный «еж», m(r) = r/|r|, для которого Е полностью покрывает S2
один раз (N = 1). Классы всех образов Е (включая поверхности, гомотоп¬
ные одной точке) образуют вторую гомотопическую группу П2 (S'2), которая
в случае ферромагнетика изоморфна группе целых чисел Z. Топологиче¬
ский заряд N точечного дефекта также называют степенью отображения о
на S2. Число N показывает, сколько раз вектор m обегает сферу S2 при
движении по замкнутой поверхности сг. В приведенном выше примере
ш(г) = г/|г| и N = 1; если обратить ориентацию вектора т, т. е. взять
m(r) = -г/|г|, то степень отображения также поменяет знак: iV = —1.
Когда точечные дефекты объединяются, заряды N суммируются.
а
б
Рис. 12.20. Топологическая устойчивость точечного дефекта в ферромагнетике
(область ядра (черный шар), окруженная замкнутой поверхностью а): неустойчи¬
вый точечный дефект (а); топологически устойчивый точечный дефект (б )
В противоположность группам группы тт2{1Z) всегда абелевы,
т. е. умножение классов поверхностей Е коммутативно. На рис. 12.21 пред¬
ставлена непрерывная деформация, обосновывающая соотношение Ei Е2 =
= Е2Еь
§ 12.3. Вторая гомотопическая группа пространства параметра порядка501
а бег
Рис. 12.21, Умножение классов поверхностей, например Ei и £2, является коммута¬
тивной операцией: £1 £2 = £г£1. Стрелка в (в) показывает деформацию вращения.
Перерисовано у Минеева
12.3.2. Топологические заряды точечных дефектов
Топологический заряд точечного дефекта в трехмерном поле единично¬
го вектора ш определяется аналитически как интеграл1 ^ по сфере а:
ДГ(Э)
1
1
dm
dm
m
X
47Г „
_du\
du2
dui du<i
(12.15а)
а
Интеграл содержит якобиан перехода от координат и\ и u2 на сфере сг
к компонентам вектора ш, параметризующим поверхность £, покрываю¬
щую N раз пространство ПП S2. Если векторное поле параметризовано
как {пх, nyj nz} = {sin# cos у?, sin в sin у?, cos в}, где углы в и у? являются
функциями двух угловых сферических координат ui и u2, то
2тг
7Г
дг(з)
1
du
47г ь
О
дв dip
дв dip
dui ди2 ди2 dui
sin в du\.
(12.15 6)
0
Для радиального ежа, как и ожидается, = 1. Различные трехмерные
точечные дефекты изображены на рис. 12.22.
Подобным способом можно определить топологический заряд поля дву¬
мерного единичного вектора т с компонентами т1 (/) и г2 (/) как интеграл по
координате I вдоль контура вокруг дефекта (сравните с равенством (11.4)):
27Г
О Т
1 dr
dl
r2^) dl
dl
(= 0, ±1, ±2, ...).
(12.16)
Заметим, что две двумерные радиальные конфигурации — «сток» (вектор г
направлен к ядру) и «источник» (г направлен от ядра) — имеют один и тот
х) М. Kleman. Phil. Mag., 27, 1057 (1973); N. D. Mermin and T.-L. Ho. Phys. Rev.
Lett., 36, 594(1976).
502
Гл. 12. Топологическая теория дефектов
же инвариант = 1, в противоположность трехмерным радиальным
конфигурациям, в которых обращение направления ш изменяет знак N^3\
Рис. 12.22. Точечные дефекты в трехмерном векторном поле
12.3.3. Точечные дефекты в трехмерной нематической фазе
Классификация точечных дефектов в трехмерном одноосном нематике
{К = S2/Z2) похожа на классификацию точечных дефектов в ферромагне¬
тике: 7t2(S2 jZ2) — Z. Однако, поскольку директоры п и —п эквивалент-
ны, каждой точке можно одинаково приписать как заряд JV, так и заряд
—N (см. выражение (12 Л 5 а)). Эта неопределенность знака топологическо¬
го заряда является следствием нетривиальности фундаментальной группы
7Ti(S2/Z2) и ее действия на группу tt2(S2 jZ2).
Допустим, что в объеме нематика содержатся точечный дефект
и 7г-дисклинация. Поле директора производит отображение степени N сфе¬
ры сг, окружающей точечный дефект и часть линейного дефекта, на S2/Z2.
Точка го реального пространства отображается в точку п(го) простран¬
ства ПП. Если двигать точку го по замкнутому контуру 7 вокруг линии
дисклинации, то точка п(го) переместится по контуру Гх/2 в диаметрально
§ 12.4. Солитоны
503
противоположную точку — п(г0) и N поменяет знак (рис. 12.23). Контур
Г1 /2? соединяющий п(г0) и —п(г0), представляет собой нетривиальный
элемент группы K\{S2jZ<i) = Z2. Если бы контур был единичным
элементом группы, то степень отображения сохранила бы знак.
S2/ Z
Рис. 12.23. Действие фундаментальной группы тт\ на вторую гомотопическую груп¬
пу 7Г2 в одноосном нематике: движение точки го в реальном пространстве вокруг
7г-дисклинации переводит точку п(го) образа в диаметрально противоположную
точку — п(го)
Таким образом, если — нетривиальная группа, то каждая то¬
чечная сингулярность соответствует нескольким элементам (N и — TV в
нашем случае) группы 7г2(72), а не одному элементу группы 7г2(72.) (N или
—Аг). Эти элементы переходят один в другой при движении точек образа
вдоль контуров, являющихся нетривиальными элементами группы 7Ti(7Z).
Слияние двух точечных дефектов N\ и iV2 в присутствии дисклинации
может приводить к дефекту с зарядом \Ni ~Ь iV2| или \Ni — TV21 в зависи¬
мости от пути слияния. Благодаря этому свойству в нематической системе
с 7г-дисклинацией могут аннигилировать все ежи или, по крайней мере, все
кроме одного с N = 1 (если суммарный заряд нечетный).
§ 12.4. Солитоны
12.4.1. Плоские солитоны. Возьмем одноосный нематик, помещен¬
ный в плоский капилляр, обе поверхности которого устанавливают пла¬
нарное сцепление в одном направлении h. Директор в объеме должен быть
ориентирован вдоль h: n = ±h. Другими словами, взаимодействие со стен¬
ками сжимает пространство ПП нематика в одну точку. Допустим, что в об¬
разце существует вертикальная дисклинация к = ±1/2. В присутствии
дисклинации невозможно сохранять однородную конфигурацию n = ±h:
на некоторой поверхности, ограниченной с одной стороны данной дискли-
нацией, директор поворачивается на угол 7г (рис. 12.24, а). Толщина стенки
504
Гл. 12. Топологическая теория дефектов
определяется из условия равновесия упругой энергии и энергии поверх-
ностного сцепления. Если мы запишем энергию стенки в виде
F
Kd
+ wp,
(12.17)
то равновесная толщина стенки ро будет равна
Ро
Kd\*/2
(12.18)
W
Здесь d — это толщина капилляра, К
и W
упругая постоянная нематика
2
— это коэффициент сцепления (размерности Дж/м ), вычисляемый
как энергия на единицу площади, необходимая для отклонения директора
от «легкой оси» n = ±h на угол 7г/2. Такие стенки с несингулярной кон¬
фигурацией директора называются плоскими солитонами топологическо¬
го типа.
n = ± h
= h
m = —h
7n
a
lilw
7m
6
n= ± h
= —h
Рис. 12.24. Топологически устойчивый плоский солитон в одноосном нематике
(а, б); доменная стенка Блоха в анизотропном ферромагнетике с осью «легкого
намагничивания» (<?, г)
Рассматриваемый солитон не только сохраняет постоянную толщину, но
также обладает нетривиальным топологическим зарядом. Действительно,
рассмотрим отображение проходящей сквозь солитон линии уп на про¬
странство ПП (рис. 12.24, а). Концы линии отображаются в диаметрально
§ 12.4. Солитоны
505
противоположные точки n = ±h, в то время как линия уп отображается
на замкнутый контур Гп, соединяющий эти точки на 52/Z2 (рис. 12.24, б).
Этот контур нельзя сжать в точку никакими непрерывными преобразова¬
ниями, что определяет топологическую устойчивость плоского солитона.
В общем случае классы гомотопных отображений линии 7, проходящей
сквозь плоский солитон, образуют относительную гомотопическую груп¬
пу 7г! (71,71), где 7Z — это область возможных значений параметра порядка
вдали от ядра солитона, уменьшенная по сравнению с 7Z дополнительным
взаимодействием (внешнее поле, граничные условия и т. п.). Если 7Z состоит
из одной точки, как в рассматриваемом случае, группа 71*1 (7Z, 7Z) совпада¬
ет с фундаментальной группой 7Гх (7Z). Таким образом, солитонные стенки
в нематиках находятся во взаимно однозначном соответствии с порождаю¬
щими их дисклинациями и описываются той же группой ni(S2 /Z2) = Z2.
Если 7Z не является точкой, то для того чтобы найти ki(7Z, 7Z), сперва
находят ni(7Z), а затем исключают из ni(7Z) элементы, соответствующие
7Ti (7Z). Другими словами, нужно найти фактор-группу группы тг\ (7Z) по ее
подгруппе, представляющей собой образ гомоморфизма tti(7Z) щ(7Z):
7г 1 (7Z: 1Z) = 7гх (7Z) / Im [7Г1 (7Z) —> 7Г1 (7Z)}. (12.19)
Существуют другие примеры стенок, отличные от рассмотренного вы¬
ше плоского солитона, которые появляются в средах с несвязной обла¬
стью 7Z (рис. 12.24, в). Рассмотрим, например, ферромагнетик, в котором
дополнительное взаимодействие между вектором намагниченности и кри¬
сталлической решеткой является анизотропным. В равновесии вектор m
ориентирован вдоль особой кристаллографической оси, например m = ±h.
Состояния m = h и ш = —h различны, в отличие от нематической фазы.
Следовательно, 7Z понижается со сферы S2 до множества из двух точек:
m = ±h (рис. 12.24, г). Множество несвязанных частей пространства ПП 7Z
обозначается как 7Го(7Z). В нашем случае 7Го(т = ±h) — Z2 и любые две
доменные стенкк могут сливаться, образуя однородное состояние. Альтер¬
нативный подход заключается в использовании относительной фундамен¬
тальной группы 7Ti(7Z, 7Z) = 71*1 (S'2, m = ±h); однако поскольку 7Z —
несвязное множество, то ni ('1Z, 7Z) больше не является группой. Доменные
стенки типа Блоха и Нееля, которые обеспечивают соединение различных
частей несвязного пространства ПП, могут быть названы «классическими
доменными стенками», чтобы отличать их от солитонных стенок, оканчи¬
вающихся на линейных дефектах. Эта терминологическая разница имеет
физическое основание: для того чтобы убрать стенку, связанную с линей¬
ной сингулярностью, достаточно создать кольцо дисклинаций в плоскости
стенки. Последнее, расширяясь, «пожирает» стенку; в то же время для то¬
го чтобы убрать классическую стенку, необходимо преодолеть значительно
больший энергетический барьер и преобразовать параметр порядка в целом
полупространстве по одну сторону от стенки.
506
Гл. 12. Топологическая теория дефектов
12.4.1. Линейные солитоны
Аналогично тому, как дисклинация во внешнем поле может порождать
плоский солитон, точечный дефект может порождать линейный солитон
(рис. 12.25). Линейные солитоны описываются классами отображения пе¬
ресекающей солитон поверхности сг в пространства ПП TZ и 1Z, т. е. эле¬
ментами относительной группы 7Т2 (7Z, 7Z). Если одноосный нематик орие-
тирован магнитным полем В вдоль оси h||B, то TZn сводится к одной точке
и 7Г'2(TZjv, 72-дг) = 7^2(TZn) = 7Г2(S2/Z2) — Z\ классификация линейных
солитонов, таким образом, совпадает с классификацией ежей.
В
А
Отображение в
SliZ2
Отображение в
п
h
n = h
Рис. 12.25. Линейный солитон, заканчивающийся в точечном дефекте (радиальный
еж в нематическом жидком кристалле). Магнитное поле В направлено вдоль оси h.
См. текст
12.4.2. Частицеподобные солитоны
Распределение параметра порядка в частицеподобных солитонах зави¬
сит от всех трех координат. Эти солитоны описываются группой 7Г3 (TZ, 7Z)
гомотопических классов отображений трехмерного шарообразного объе¬
ма D3, содержащего солитон, в пространство 1Z. Здесь граница шарооб¬
разного объема — сфера сг — отображается в суженное пространство 7Z.
Если 1Z состоит из одной точки, то частицеподобный солитон описывается
группой тгз(7Z). Шарообразный объем D3, все точки поверхности сг кото¬
рого эквивалентны, гомотопен трехмерной сфере S3 в четырехмерном про¬
странстве. Таким образом, элементами группы 7г3(7Z) служат отображения
53 -» 7Z. Особые случаи S'3 —> S2 и S3 —> S2/Z2 называются отображения¬
ми Хопфа и соответствуют 7г3(52) = 7г3(52/^2) = Z (рис. 12.26).
В одноосном нематике частицеподобный солитон означает конфигу¬
рацию директора, искаженную в области конечного размера, вне которой
поле директора однородно. Как правило, такие солитоны неустойчивы по
§ 12.4. Сояитоны
507
отношению к уменьшению размера с последующим исчезновением на раз¬
мерах меньших длины когерентности £. Уменьшение размера L —>> [iL
О < 1) влечет за собой увеличение плотности упругой энергии в 1 j у?
раз и изменение объема солитона в fi3 раз, так что полная упругая энергия
уменьшается: F —у Fp. Стабилизации частицеподобных солитонов могут
способствовать дополнительные взаимодеиствия, в частности спиральное
закручивание структуры. В слабозакрученной холестерической смеси Бу-
лиган наблюдал два сцепленных дисклинационных кольца ki = к2 — 1,
каждое из которых само по себе топологически неустойчиво, из-за чего
все точки ядер дисклинаций отображаются в одну единственную точку
пространства вырождения S2 /Z2. Переходя от одного кольца к другому,
директор претерпевает вращение на угол 180°, и кольца могут рассмат¬
риваться как обратные отображения двух диаметрально противоположных
точек на сфере S2. Очевидно, что эту конфигурацию невозможно перевести
в однородное состояние, так как кольца сцеплены: при попытках расцепить
кольца они должны были бы пересечься и в конфигурации возникли бы
сингулярности. Число зацеплений колец, в данном случае равное единице,
совпадает с инвариантом Хопфа, который представляет собой элемент гру п-
пы 7r3(52/Z2) = Z. Устойчивость конфигурации как целого определяется
сохранением инварианта Хопфа.
Рис. 12.26. Нетривиальная текстура Хопфа в трехмерном векторном поле, показан¬
ная в вертикальном сечении. Векторное поле направлено на север всюду вне сферы
и в начале координат. Вертикальная ось служит осью поворотной симметрии. При
движении вдоль любого радиуса из центра к поверхности сферы вектор повора¬
чивается на угол 2'nr/R вокруг радиуса. Длина стрелок пропорциональна длине
проекции векторов на плоскость ху
508
Гл. 12. Топологическая теория дефектов
Задача 12.1. Склейте бумажную ленту с 27г-закруткой. Раскрасьте
края полоски разными цветами. Представьте, что лента — это модель про¬
стой петли двойной спирали молекулы ДНК. ДНК должна дублироваться
при каждом делении клетки. Две цепочки исходной молекулы ДНК должны
разделиться, и затем каждая из них должна синтезировать себе новую пару,
для того чтобы образовать двуцепочечную ДНК. Попытайтесь подготовить
бумажную ленту к «репликации», разрезав ее вдоль центральной линии;
в реальной ДНК это соответствует разрыву водородных связей между па¬
рами оснований. Повторите разрезание вдоль центральной линии два раза.
Опишите топологию структур, получающихся в результате каждого ша¬
га. Сравните поведение в случае лент с 2тг-, 7г-закруткой и незакрученной
ленты.
Подсказка. Упражнение должно демонстрировать необходимость то-
поизомеров, придуманных Природой для того, чтобы изменять топологию
двойной спирали ДНК, разрезая одну или обе ее цепочки.
Задача 12.2. Число зацеплений Lk двух кривых — это целое чис¬
ло (12.3), не меняющееся, когда кривые деформируются, не пересекая
друг друга. Вычислите число зацеплений пары окружностей х2 + у2 — 1
и (у - I)2 + z2 - 1.
Ответ. Lk = 1. Параметризуем окружность х2 + у2 = 1 как
rc/(s') = (coss', sins', 0), 0 ^ sf ^ 27r;
затем увеличим окружность (у - l)2 + z2 = 1 (не пересекая первой окруж¬
ности) таким образом, чтобы ее можно было параметризовать как гс($) =
= (0, 0, s), —оо < s < оо. Согласно (12.3)
Lk = -
ОО 2 7Г ОО
г
47Г
ds dsf 1
(l + s 2)3/2 2
=1.
J
(1 +s2)3/2
— oo 0 —oo
Задача 12.3. Пусть G — это группа преобразований g, трансформи¬
рующих данное значение параметра порядка ф в другое значение ^ф, для
которого термодинамические потенциалы системы остаются неизменны¬
ми. Пусть Н — это множество преобразований^, не меняющих параметр
порядка: gнф = ф. Докажите, что Н является подгруппой G.
Ответ. E^Hg^ и gH2 не меняют ПП, то gHlg]^2 тоже не меняет ПП.
Задача 12.4. Найдите пространства ПП и фундаментальные группы
трехмерного смектика А и смектика С (М. Kleman and L. Michel H J. Phys.
Lett., 39, L-29 (1978)).
Ответ. Ввиду сложности пространств ПП смектических фаз А и С,
прямой алгебраический метод вычисления сложен. Можно использовать
интуитивную графическую схему.
§ 12.4. Солитоны
509
Функции плотности Sm А и Sm С являются модулированными вдоль
нормали к слоям с периодом do, имеющим порядок длины молекулы (или
больше, как в некоторых разбавленных лиотропных ламеллярных фазах).
Внутри слоев плотность постоянна и молекулы либо расположены перпен¬
дикулярно слоям (SmA), либо наклонены (SmC). Ориентационный поря¬
док в Sm А и Sm С, как и в нематической фазе, описывается директором п.
Принимая во внимание также трансляционный порядок, пространство ПП
фазы SmA можно представить как заполненный тор: 7ZA = (S2/Z2) х S1.
Вертикальные сечения тора в форме двух кругов эквивалентны полусфе¬
рам S2/Z2, растянутым в диски, точки которых характеризуют ориентацию
директора п. Точки вдоль больших окружностей тора соответствуют точ¬
кам вдоль отрезка [0, do], замкнутого в окружность S1, В (S2 fZ2) х S1
существуют два типа элементарных контуров, негомотопных нулю: кон¬
туры, соединяющие диаметрально противоположные точки дисков S2/Z2
(описывающие дисклинации), и контуры, обегающие вокруг дырки тора
(описывающие дислокации). Фундаментальная группа яч (72,а) = ягС^1) х
х 7Ti(52/Z2) = Z х Z2 состоит из элементов (6, к), где b — целое число,
а к равно 0 или 1/2. Комбинации дислокаций и дисклинаций с одновременно
ненулевыми b и к называются «дисгирациями».
Для смектической фазы С параметр порядка легко представить, исполь¬
зуя соотношение 72. д — IZc/S1, которое означает, что каждая точка 72 д со¬
ответствует в 7Zc целому семейству S1 точек, определяющих ориентацию
наклоненных молекул в плоскости слоев смектика С. Прямые вычисления
показывают, что tti(7Zq) = Z Л Z4, где Z4 — (/, а, а2, а3) — это группа
вычитаний по модулю 4 с единичным элементом I.
Задача 12.4. Неограниченный двуосный нематик содержит 7г-дис-
клинацию Сх и 27г-дисклинацию Со. Найдите способ уничтожить дискли-
нацию С о. __
Подсказка. Расщепите дисклинацию Со на две (какие?) и сведите их
вместе (вдоль каких путей?).
Задача 12.5. Определите относительную гомотопическую группу
7Г1 (72,, 72.), где 71 — это тор S1 х S1 и 71 = S1.
Ответ. Im[7Ti (72,) 7Г1 (Я)] = 7Гх (72) = Z, 7г± (7Z, 7Z) = Z х Z/Z — Z
(VP. Mineyev andG. Е. Volovik ii Phys. Rev. B, 18, 3197 (1978)).
Задача 12.6. Вычислите топологический заряд следующих вектор¬
ных полей на плоскости:
а) (я, -у)/\/х2 +у2-
б) (-х, ~у)/^х2 + у2;
в) (х2 - у2, 2ху)/{х2 + у2)',
г) (х2 - у2, -2ху)/(х2 + у2)'
д) (а:3 — Зге у2, —у3 + Зх2у)/(х2 + у2)3/2.
510
Гл. 12. Топологическая теория дефектов
Подсказка. Параметризуйте векторное поле, используя координату
0 ^ I ^ 27г на окружности (cos/,sin/). Например, поле (д) принимает
форму (cos3/, sin3/).
Ответ, а) — 1; б) 1; в) 2; г) —2; д) 3.
Задача 12.7. Вычислите топологические заряды и упругую энергию
следующих двух ежей в нематическом объеме радиуса R:
П1 = (ж, у, z)/\/x2 + у2 + z2 и n2 = {-x,-y,z)/\/x2 +у2 + Z2".
Используйте плотность свободной энергии Франка-Осеена с упругими
постоянными
Ki ф К2 ф Кг ф К2±, Кхз = 0.
Ответ. См. (11.14) в гл. 11.
Литература для дальнейшего чтения
Общие курсы
1. М. Kleman. Points, Lines and Walls in Liquid Crystals, Magnetic Systems and
Various Ordered Media, John Wiley & Sons, Chichester, 1983.
2. T. FrankeL The Geometry of Physics: An Introduction, Cambridge University
Press, 1997.
3. D. J. Thouless. Topological Quantum Numbers in Nonrelativistic Physics, World
Scientific, Singapore, 1998.
Узлы и ленты
1. Louis H. Kauffman. Knots and Physics, 3rd Edition, World Scientific, Singapore,
2001.
2. W. F. Polh, J. Math. Mech., 17, 975 (1968).
3. J. H. White, Am. J. Math., 91, 693 (1969).
4. F.B. Fuller, Proc. Nat. Acad. Sci. USA, 68, 815 (1981).
5. DNA Topology and Its Biological Effects / Eds. N. Cozzarelli and J. C. Wang,
Cold Spring Harbor Laboratory Press, 1990.
Геометрия и алгебраическая топология
1. D. Hilbert and S. Cohn-Vossen. Geometry and the Imagination, Chelsea Publishing,
N. Y., 1952.
2. N. Steenrod. Topology of Fiber Bundles, Princeton University Press, 1951.
3. W. S. Massey. Algebraic Topology: An Introduction, Harcourt, Brace & World,
Inc., N. Y., 1967.
Обзоры по приложениям теории гомотопий к дефектам в упорядочен¬
ных средах
1. N. D. Mermin, Rev. Mod. Phys., 51, 591 (1979).
2. L. Michel, Rev. Mod. Phys., 52, 617 (1980).
3. V. P. Mineev, Sov. Sci. Rev. A, Vol.2 / Ed. I. M. Khalatnikov, Chur, London,
Harwood Academic, N. Y., 1980.
4. H.-R.Trebin, Adv. Phys., 31, 194 (1982).
Литература для дальнейшего чтения
511
Топологическая устойчивость
1. G. Toulouse and М. Kleman, J. Phys. Lett. (Paris), 37, L-149 (1976); M. Kleman,
J. Phys. Lett. (Paris), 38, L-199 (1977).
2. Г. E. Воловик, В. П. Минеев, Письма в ЖЭТФ, 24, 605 (1976); ЖЭТФ, 72, 2256
(1977).
3. Y Bouligand, Physics of Defects / Eds. R. Balian, M. Kleman and J.-P. Poirier,
North-Holland, Amsterdam, 1981, p. 665.
4. M. Kleman andL. Michel, Phys. Rev. Lett., 40, 1387 (1978).
5. Y. Bouligand, B. Derrida, V Poenaru, Y. Pomeau and G. Toulouse, J. Phys. (Paris),
39, 863 (1978).
Сравнение с экспериментами в жидких кристаллах
1. Курик М. В., Лаврентович О, Д., УФН, 154, 381 (1988).
Двуосные нематики
1. G. Toulouse , J. Phys. Lett. (Paris), 38, L-67 (1977).
Дефекты в анизотропных сверхтекучих жидкостях
1. G. Е. Volovik. Exotic Properties of Superfluid 3He, World Scientific. Singapore,
1992.
Дефекты в ферромагнетиках
1. M. Kleman. Dislocations, disclinations and magnetism, Dislocations in Solids 5 /
Ed. F.R.N.Nabarro, North-Holland, Amsterdam, 1980.
2. M. Kleman. Magnetization processes in ferromagnets, Magnetism of Metals and
Alloys I Ed. M.Cyrot, North-Holland, Amsterdam, 1980.
3. A. P. Malozemoff and J. C. Slonczewski. Magnetic Domain Walls in Bubble
Materials, Academic Press, N. Y., 1979.
Дополнительная литература
1. Монастырский М. И. Топология калибровочных полей и конденсированных
сред. — М.: ПАИМС, 1995.
2. Фоменко А. Т. Наглядная геометрия м топология: Математические образы в
реальном мире. — 2-е изд. — М.: Изд-во МГУ, Изд-во «ЧеРо», 1998. —416 с.
3. Дж. Франсис. Книжка с картинками по топологии. Перев. с англ. — М.: Мир,
1991. — 240 с., ил.
ГЛАВА 13
ПОВЕРХНОСТНЫЕ ЯВЛЕНИЯ
Реальные образцы конденсированных фаз с необходимостью имеют
границы. Наиболее очевидно эффекты ограничения проявляют себя на ло¬
кальном уровне: молекулярные взаимодействия в объеме и на границах раз¬
личны. Эти отличия ведут к локальным изменениям, которые обычно про-
исходят на расстояниях порядка нескольких атомных радиусов. Поскольку
отношение объема к поверхности растет с увеличением размера системы,
при рассмотрении достаточно больших систем локальными поверхност¬
ными эффектами часто пренебрегают. Однако могут существовать и гло¬
бальные последствия поверхностных взаимодействий. Например, ограни¬
ченные объемы жидких кристаллов в равновесии содержат топологические
дефекты, стабильность которых определяется исключительно поверхност¬
ными условиями, как на рис. 11.13. В этой главе мы будем рассматривать
поверхностные эффекты как в изотропной, так и в анизотропной средах.
Монослои и бислои поверхностно-активных веществ описаны в гл. 14.
§ 13.1. Поверхностные явления в изотропных средах
13.1.1. Поверхностное натяжение и термодинамика плоских границ
раздела
Понятие поверхностного натяжения проще всего проиллюстрировать
на примере границы раздела жидкость-газ. В объеме жидкости средняя
сила, действующая на молекулу, усредняется до нуля на шкалах времени,
больших времени релаксации молекулярного окружения. На поверхности
средняя сила не исчезает (рис. 13.1). Для увеличения поверхностной обла¬
сти необходимо совершить работу по переносу молекул из объема к поверх¬
ности. Работа dW, необходимая для увеличения площади поверхности на
небольшую величину dA, пропорциональна dA: dW — adA. Положитель¬
но определенный коэффициент о называется поверхностным натяжением.
В термодинамическом описании границ раздела часто используется вве¬
денное Гиббсом понятие «разделяющей поверхности», позволяющее ис¬
ключить микроскопические детали. Наиболее часто разделяющая поверх¬
ность рассматривается как математическая плоскость нулевой толщины,
расположенная где-то в межфазной области (рис. 13.1). Две объемные фа¬
зы, скажем 1 и 2, предполагаются однородными вплоть до разделяющей
поверхности. Поскольку свойства двух фаз изменяются при пересечении
границы раздела, действительные значения экстенсивных термодинамиче¬
ских величин Ф (таких, как внутренняя энергия или энтропия) необязатель¬
но равны сумме объемных значений величин Фх + Ф2 двух однородных фаз.
Исключение делается для полного объема системы
У-Ух+У2,
(13.1)
§ 13.1. Поверхностные явления в изотропных средах
513
г А
2
а
б
Рис. 13.1. Граница раздела жидкость-газ (а) и изменения концентрации частиц
поперек межфазной границы (б). Молекулярные силы в объеме и на поверхности
различны. Позиция разделяющей поверхности Гиббса (штриховая линия) может
быть задана, исходя из определения, что заштрихованные области в ((б)) равны;
т. е. имеются частицы типа 1 и типа 2, но нет поверхностных частиц
если толщина разделяющей поверхности предполагается нулевой. Чтобы
компенсировать разницу, вводят поверхностную «избыточную» величину
где 01 и 02 вычисляются на единицу объема, а А является площадью кон¬
такта, Заметим, что Vl, V2, и следовательно, С surf, зависят от действитель¬
ной позиции разделяющей поверхности. Эта неопределенность не имеет
значения во многих практических случаях и ее можно избежать, если, по¬
мимо поверхностного избыточного объема, положить какую-либо другую
избыточную величину равной нулю. Например, если поверхностное избы¬
точное число частиц iVSUrf равно нулю, то V\ и V2 однозначно определяются
из (13.1) и из уравнения для полного числа частиц:
Здесь ci и с2 являются объемными плотностями (обычно называемыми
концентрациями) числа частиц, рассчитанных для бесконечно протяжен¬
ных фаз 1 и 2 соответственно.
Найдем поверхностные избыточные величины термодинамических па¬
раметров для однокомпонентной двухфазной системы в контакте с резер¬
вуаром при фиксированной температуре Т и химическом потенциале /х.
Согласно первому началу термодинамики, дифференциал внутренней энер¬
гии Е системы имеет вид
ф _ 0! Vi -h 02^2 + Я sur f А
(13.2)
N ~ C\V\ + C2V2.
(13.3)
dE = —pdV + TdS -f p dN -f a dA
(13.4)
33-КЛЕМАН M.
514
Гл. 13. Поверхностные явления
где р — давление и S — энтропия. В (13.4) отсутствуют члены, отнесенные
явно к определенной фазе, потому что в равновесии
— Т2 — То; pi — р2 — Ро; fJ'i = М2 = l^o
(13.5)
(нижний индекс «О» означает, что условия записаны для плоской границы
раздела с нулевой кривизной; см. ниже). Исключая из обеих частей (13.4)
член d(TS Ч- fiN), мы получаем большой термодинамический потенциал
ft — Е — TS — pN с естественными параметрами V, Т, р и, соответствен¬
но, А:
dft = -pdV ~SdT -Ndp, + odA,
ft
pV -f a A;
(13.6)
(13.7)
последнее уравнение получено после дифференцирования внутренней энер¬
гии Е = — pV + TS + //iV + а А. Для однородных фаз 1 и 2 fli — —pV\
и — —pV2. Следовательно, поверхностный избыток ft surf — П — fli — ft2
большого термодинамического потенциала равен
surf
(7 А,
(13.8)
независимо от положения разделяющей поверхности.
Поверхностные избытки других величин могут быть найдены из стан¬
дартных термодинамических соотношений, например, связывающих сво¬
бодную энергию Гельмгольца F и потенциал ft: F — ft + N р. Для энтропии
дП \ -гг О (dfl surf \
J поверхностный избыток surf = — ^ ~~~~ J равен
S
дТ * д, А
^surf
А
да\
дТ
)
ОТ /
(13.9)
Если NSUTf
дП
Surf
О, то
т
S
surf
-А
da
dT
поскольку
да
О, ив этом случае
da
да
д/л J т dT \dT'v
Качественно можно связать температурную зависимость а со структу¬
рой границы раздела жидкость-газ. Поскольку расстояния между частица¬
ми вблизи поверхности увеличиваются, взаимодействия между ними стано¬
вятся слабее, и мы можем ожидать положительный поверхностный избыток
энтропии, S surf > 0. Следовательно, а уменьшается с ростом температуры,
что наблюдается во многих системах, включая органические и металличе¬
ские жидкости (например, олово). Однако в некоторых случаях само при¬
сутствие межфазной границы индуцирует дополнительное упорядочение,
§ 13.1. Поверхностные явления в изотропных средах
515
например осцилляции плотности вдоль нормали к границе раздела, уве¬
личение ориентационного порядка анизометричных молекул или полярное
расположение молекулярных диполей. Тогда 5surf < 0 и а возрастает с
ростом температуры. При достаточно высоких температурах, вблизи кри¬
тической точки, где граница между жидкостью и газом исчезает (а = 0),
эффекты пространственной делокализации нарастают, и <т(Г), следователь¬
но, снова уменьшается. Инверсия наклона da/dT часто наблюдается вблизи
фазовых переходов в жидких кристаллах. Если возможное влияние упру¬
гих деформаций в эксперименте исключено, эти результаты свидетельству¬
ют о том, что поверхностная область более упорядочена по сравнению
с объемом.
13.1.2. Адсорбция
Равновесное распределение химических объектов становится простран¬
ственно. неоднородным в присутствии границ раздела. Чужие молекулы
могут быть исторгнуты из объема к поверхности для уменьшения поверх¬
ностного натяжения. Это явление, называемое адсорбцией, играет важную
роль в коллоидных системах.
Рассмотрим двухфазную систему, содержащую к компонент. Это может
быть, к примеру, водный раствор этанола и глицерина в равновесии с его
газовой фазой. Выражение (13.6) в этом случае обобщается до
к
dSl = -pdV - SdT - ^2 Ni dm + a dA. (13.10)
i=l
Дифферецируя (13.7) и вычитая результат из (13.10), получаем уравнение
Гиббса -Дюгема
к
SdT -V dp + ^Nidm + Ada = 0. (13.11)
i=1
Аналогичные уравнения для объемных фаз 1 и 2 имеют вид
к к
Si dT — Vi dp + Nit i dpi = 0, S2 dT ~ V2dp + N{} 2 d\i{ — 0.
i=l i= i
(13.12)
Вычитая оба выражения (13.12) из (13.11) и используя обозначения Ssurf —
~ S - Si - S2i A^surf = i ~ Nii2, V - Vi - V2 = 0, приходим
к уравнению адсорбции Гиббса
к
da =-^ dT-Vr;, surf dm, (13.13)
л S'
где Г., surf = Niy surf M представляет собой избыточное число молекул ком¬
поненты i на единицу площади.
516
Гл. 13. Поверхностные явления
Для двух компонента о го раствора при постоянной температуре уравне¬
ние адсорбции Гиббса сокращается до
da = -Гф-Г'ф', (13.14)
где Г и \х относятся к растворенному веществу, а Г' и р! — к растворите¬
лю. Соотношение (13.14) между сг и Г неоднозначно, поскольку и Г, и Г'
неизвестны. Однако можно легко увидеть, что относительная адсорбция
(задача 13.2)
Relative = Г - Г'С-^- (13.15)
с[ - 4
выражается исключительно через экспериментально измеряемые величи¬
ны, такие как V, А, концентрация растворителя с и концентрация раство¬
ренного вещества с' в объеме фаз 1 и 2. Если поместить разделяющую
поверхность таким образом, чтобы поверхностный избыток массы раство¬
рителя был равен нулю, то уравнение адсорбции Гиббса выглядит как
da — —Г dp (13.16)
(черта отвечает выбору Г' = 0)). В равновесии химический потенциал
раствора р должен быть однородным во всей системе. Это обстоятельство
может быть использовано для того, чтобы выразить р через концентрацию
растворенного вещества в одной из фаз, например в жидкости, используя
общее термодинамическое соотношение
d{i — v dp, (13.17)
справедливое при постоянной температуре. Здесь v представляет собой
объем, приходящийся на одну частицу растворенного вещества и равный
vi = 1/ci в фазе 1. Если раствор является очень разбавленным и ведет себя
как идеальный, то dp, — кБТ dIn ci [см. (1.4) в гл. 1] и
Г = —2- —. (13.18)
кьТ dc 1
Согласно (13.18) различают два типа растворенных веществ:
а) поверхностно-активные агенты (или сурфактанты), которые умень¬
шают поверхностное натяжение, da/dci < 0, и скапливаются на границе
раздела (положительная адсорбция, Г > 0) ) (рис. 13.2);
б) поверхностно-неактивные агенты, которые увеличивают поверх¬
ностное натяжение, da/dci > 0, и вытесняются с поверхности (отрицатель¬
ная адсорбция, или десорбция, Г < 0)). В воде поверхностно-активными
агентами являются спирты (например, этанол), белки и, в особенности, ам¬
фифильные молекулы, содержащие полярную и неполярную части, такие
как молекулы в составе мыла и детергенты. Сильно полярные электроли¬
ты (такие, как NaCl), диссоциирующие на ионы, являются поверхностно¬
неактивными на границе раздела жидкость-газ.
§ 13.1. Поверхностные явления в изотропных средах
517
т-9--ф-Ф -Ф
f
И'
Л
V*'
Ф
Я
б
Рис. 13.2. Адсорбция на границе раздела жидкость-газ. Поверхностно-активные
молекулы растворенного вещества (темные сферы) скапливаются в межфазной об¬
ласти (перерисовано из D. Н. Everett) (а). Схематический концентрационный про¬
филь растворенного вещества (б). Пленка из адсорбированных молекул растворен¬
ного вещества толкает плавающий барьер в сторону чистого растворителя (в)
Если поверхностное натяжение не изменяется значительно с концентра¬
цией (слабая адсорбция), тогда можно разложить функцию cr(ci) « ао +
4- о\с\ для малых с\ (ао является поверхностным натяжением чистого рас¬
творителя; а 1 — некоторая константа). В этом случае выражение (13.18)
описывает адсорбированное растворенное вещество как двумерный иде¬
альный газ:
7г = Г къТ, (13.19)
где двумерное «давление» 7г дается разностью поверхностных натяжений:
тг — ао ~ а
(13.20)
518
Гл. 13. Поверхностные явления
Полупроницаемый барьер, плавающий на поверхности растворителя
и отделяющий область чистого растворителя от области, занимаемой адсор¬
бированным растворенным веществом, испытывает действие силы,
пытающейся расширить область адсорбата (рис. 13.2,в). Эксперименты
с плавающими барьерами подтверждают справедливость (13.19) для низ¬
ких концентраций; для более высоких концентраций (13.19) может быть
модифицировано в двумерный аналог уравнения Ван-дер-Ваальса.
Экспериментальная установка, показанная на рис. 13.2,в и известная
как ленгмюровская ванна, широко используется в современных техноло¬
гиях молекулярной самоорганизации, основанных на нековалентной ассо¬
циации молекул в агрегаты нанометрового размера. Монослой адсорби¬
рованного поверхностно-активного вещества (ленгмюровский монослой)
может быть сжат из газовой фазы в различные конденсированные фазы
за счет сдвига барьера и уменьшения площади пленки. Окуная и извлекая
гладкую пластинку, можно перенести на нее этот монослой. Такая проце¬
дура может быть многократно повторена для создания стопки монослоев.
Пленки, перенесенные из ванны на твердую подложку, называются плен¬
ками Ленгмюра-Блоджетт (Langmuir-Blodgett). Эти пленки могут быть
полярными (оси, соединяющие головы и хвосты молекул сурфактанта, ле¬
жащих в соседних монослоях, ориентированы в одном направлении) или
неполярными. Интересным и простым вариантом этой техники являет¬
ся так называемый метод послойного электростатического переноса1 ^ 2\
Пластина с электрически заряженной (скажем, отрицательно) поверхно¬
стью погружается непосредственно в раствор соединения, содержащего
заряды, такого как полиэлектролит. Полиэлектролит — это полимер, со¬
стоящий из противоположно заряженных структурных единиц. Например,
положительно заряженная группа ковалентно связана с макромолекулой,
в то время как отрицательно заряженная группа диссоциирует при раство¬
рении полиэлектролита в воде. Электростатическое взаимодействие такого
полимера с отрицательно заряженной подложкой фиксирует адсорбирован¬
ный слой. После этого остатки полимера и ионов противоположного знака
смываются. Процедура повторяется путем погружения пластины в раствор
второго полиэлектролита с электрической полярностью, противоположной
полярности первого полимера. Эта техника позволяет проводить сборку
монослоев красителей, белков, наночастиц SiC>2 и т. д.
13.1.3. Искривленные границы раздела
13.1.3.1. Уравнение Лапласа-Юнга. Предположим, что жидкая кап¬
ля 1 окружена газом 2. Система замкнута и поддерживается при посто¬
янных температуре и полном объеме. Какова равновесная форма жидкой
капли? Ответ следует немедленно, если представить термодинамический
потенциал в духе подхода Гиббса как сумму объемной и поверхностной ча-
1} R. К. Her. J. Colloid Interface Sci. 21, 569 (1966).
G. Decker, J. D. Hong, and J. Schmitt. Thin Solid Films, 210/211, 831 (1992).
§ 13.1. Поверхностные явления в изотропных средах
519
стей. Равновесие достигается, когда поверхностный вклад а А минимален
(в отсутствие испарения). При фиксированной температуре натяжение а
в изотропной системе (жидкость-газ) является постоянной величиной, и,
следовательно, равновесие требует минимума межфазной площади А. Ми¬
нимальную площадь среди тел с фиксированным объемом имеет сфера.
Механическое равновесие границы раздела накладывает определенные
условия на давление в сосуществующих фазах. Если межфазная грани¬
ца плоская, тогда р\ = р2. Однако если граница раздела фаз искривлена,
ее искажение изменяет площадь поверхности. Изменение поверхностной
энергии есть a dA, или, если объем 1 представляет собой сферу радиу¬
са г, это изменение равно 8тгаг dr. Условие равновесия: —pi d\\ — р2 dV2 +
+ a dA = 0, где dV\ = — dV2 — 4nr2 dr, приводит к уравнению Лапла¬
са —Юнга
Pi-P2 = -. (13.21)
Г
Для поверхности произвольной формы, характеризуемой двумя главными
значениями кривизны, г”*х и локальное избыточное давление опре¬
деляется средней кривизной (l/rmax 4- l/rmin):
Pi — Р2 = сг ( + —— ) — сг div г/, (13.22)
\ тmax rmin J
где v представляет собой единичный вектор, перпендикулярный поверхно¬
сти. Здесь и далее в тексте для определенности вектор v направлен из фазы 1
в сторону фазы 2, а радиус кривизны положителен, когда центр кривизны
находится в фазе 1.
Уравнение Лапласа-Юнга описывает многочисленные явления, такие
как капиллярный подъем жидкостей и форма мыльных пленок, натянутых
на проволочный каркас (рис. 13.3).
Рис. 13.3. Иллюстрация явлений, описываемых уравнением Лапласа-Юнга: ка¬
пиллярный подъем (а); мыльная пленка между двумя коаксиальными кольцами
принимает форму катеноида с нулевой средней кривизной (б)
520
Гл. 13. Поверхностные явления
13.1.3.2. Капиллярный подъем и капиллярная длина. Рассмотрим
цилиндрический капилляр небольшого внутреннего радиуса г, погружен¬
ный в тарелку большого радиуса г (рис. 13.3 а). Тарелка заполнена
жидкостью, которая смачивает стенки капилляра. Поверхность жидкости,
следовательно, будет вогнутой. Скачок давления поперек этой поверхности,
Ар = pi — р2 , также называемый капиллярным давлением, определяется
уравнением Лапласа-Юнга (13.21). Высота h подъема жидкости в капил¬
ляре выше уровня плоской поверхности жидкости в тарелке такова, что Ар
уравновешивается гидростатическим давлением столба жидкости в капил¬
ляре, Ар = Apgh. Здесьg~— ускорение свободного падения, а Ар — разни¬
ца плотностей жидкости и воздуха. В дополнение, равенство 2о/г = Apgh
определяет характерную длину капиллярности:
На масштабах длин х Хс эффектами гравитации можно пренебречь, как
если бы система была в состоянии невесомости; для длин х^>\с, гравитация
является доминирующей.
13.1.3.3. Мыльные пленки и минимальные поверхности. Если
мыльная пленка, натянутая на проволочный каркас, не образует замкнутую
поверхность, то перепад давления поперек пленки будет равен нулю. Это
возможно только тогда, когда средняя кривизна пленки равна нулю в каждой
точке (13.22); т. е. когда пленка образует минимальную поверхность. Три¬
виальным примером является плоская поверхность l/rmax = l/rmin = 0.
Если пленка натянута между двумя слегка разведенными коаксиальными
кольцами, она образует катеноид, l/rmax = -l/rmin ф 0 (рис. 13.3,6),
13.1.3.4. Уравнение Кельвина. Вернемся к проблеме двух сосуще¬
ствующих фаз, т. е. жидкой капли / в газе 2 при постоянной температуре.
Механическое равновесие определяется (13.21), в то время как условия
химического равновесия имеют вид
Заметим, что два химических потенциала отвечают двум различным давле¬
ниям. Условия (13.21) и (13.24 а) позволяют вывести уравнение Кельвина5
которое описывает, как равновесное давление поперек искривленной меж-
фазной границы меняется с изменением кривизны.
Вначале мы перепишем (13.24а) в виде
(подстрочный индекс «0» отвечает плоской границе раздела), или, исполь¬
зуя (13.17), как
(13.23)
Ml(Pl) = М2 (Р'2 ) •
(13.24 а)
Ml (Pi ) - IM> (Р<> ) = Р-2 (Р2 ) - IM) (/>())
(13.246)
Pi
Vi dp — v2 dp.
(13.25)
P 0
P 0
§ 13.1. Поверхностные явления в изотропных средах
521
В жидкости 1 объем v\ в минимальной степени зависит от давления, что
позволяет проинтегрировать левую часть (13.25) с v\ =const:
pi
Vi dp = Vi (pi — po)
(13.26)
PO
Правая часть (13.25) может быть упрощена в случае, когда газ2 является
идеальным газом, см. (1.4):
Р 2
Р2
v2 dp
^dp=kBT ln^
(13.27)
V
PO
Po
Po
Используя новый эквивалентный вид уравнения Лапласа-Юнга,
Pi -Ро=Р2~Ро +
2а
(13.28)
и замечая, что при не очень высоких температурах v\ <^v2 и, следовательно,
в соответствии с (13.25) рг — Ро р2 — ро, в конечном счете приходим
к соотношению
V2 2аы
кБТ In
(13.29)
Ро
3 х 10 29 м3 при
что и представляет собой уравнение Кельвина. В общем случае коэффи¬
циент 2/г сферической кривизны в (13.29) должен быть заменен средней
кривизной межфазной границы 2/г —> (l/rmax + 1 /гт-ш).
Уравнение Кельвина (13.29) предсказывает, что давление газа вокруг
жидкой капли больше, чем над плоской границей раздела (рис. 13.4, а). На¬
оборот, для газового пузырька в жидкости, или для газа, находящегося в
контакте с жидкостью в капиллярной трубке, как показано на рис. 13.4, б, в,
давление понижается. Разница в давлении становится заметной для субмик-
ронных масштабов. Капля воды (сг w 0,07 Дж/м2 и Vi
комнатной температуре) радиуса г — 1 мкм изменяет давление газа только
на 0,1 % , в то время как для г — 0,01 мкм получаем р2/ро « 1,1. Разумеет¬
ся, на меньших масштабах длин справедливость многих допущений (таких,
как независимость а от г) перестает быть очевидной.
13.1.4. Поверхностное натяжение и зародышеобразование новой фазы
Концепция поверхностного натяжения между двумя фазами призвана
помочь понять явления переохлаждения и перегрева и механизм зародыше-
образования при фазовых переходах первого рода. Рассмотрим, для приме¬
ра, конденсацию жидкости 1 из ее газа2 в интервале температур Т и давле¬
ний р ниже критической точки.
Рисунок 13.5 схематически показывает, как химический потенциал газа
и жидкости изменяется с давлением при постоянной Т в окрестности точки
522
Гл. 13. Поверхностные явления
2
I '
а
С
Л
А
, и*
/и
•Г-'Ь
.* С*»*-
• < •»
' ' Ч
<: .
"У. ■ ..
i
, , *А , ,s>
. . .
/>2>Ро
б
Pi < Ро
в
Рис. 13.4. Давление газа над поверхностью жидкости зависит от кривизны меж-
фазной границы: pi > ро над жидкой каплей (а); р2 < ро для пузырька газа внутри
жидкости (б); р2 < ро над жидкостью, конденсирующейся в капилляре (в)
Рис. 13.5. Химические потенциалы жидкости (неидеальной) 1 и газа2 в зависимо¬
сти от давления при постоянной температуре, ро и до — параметры сосуществова¬
ния при плоской межфазной границе. Кружки отвечают равновесию жидкой капли
и газа над ее поверхностью
сосуществования (ро, До)* Стабильность фаз определяется относительны¬
ми значениями рь\ и /х2: более низкое значение химического потенциала
соответствует более стабильной фазе. При давлениях р < ро стабильным
§ 13.1. Поверхностные явления в изотропных средах
523
является газ. Если давление поднять вышеро, газ становитсяметастабиль-
ным, Р2(р) > №\{р)’ ^ принципе, газ должен трансформироваться в ста¬
бильную жидкость, позволяя зародышам жидкости расти. Однако, посколь¬
ку зародыши жидкости появляются внутри газа, возникает поверхностная
область и поверхностная энергия, связанная с образованием зародыша. Эта
избыточная поверхностная энергия препятствует фазовому переходу.
Рассмотрим работу, необходимую для создания сферического зароды¬
ша, как функцию его радиуса г. Эта работа определяется тремя вкладами,
которые отвечают; а) созданию границы раздела, б) компенсации разницы
давления, и в) компенсации разницы химических потенциалов двух фаз:
W(r) = 4тгг2(7 - -nr3(pi -р2) + —7ГГ3 - М2СР2)]. (13.30)
3 3г>1
где 47гг3/3i>i — число частиц в фазе 7. Уравнение (13.30) упрощается, если
химические потенциалы берутся при одном и том же давлении р2 фазы 2.
Раскладывая ^i(pi) в ряд Тейлора: ^i(pi) « fi2{p2)+vi(pi ~ Р2), получаем
W(r) = Ажг2а + — 7гг3 [/xi(рг) - /^(Ы] • (13.31)
Зг?1
Поведение зародыша зависит от баланса между поверхностным чле¬
ном — г2 и объемным членом ~ г3 (рис. 13.6). Поверхностный член
положителен по определению. Поэтому, когда > /^(р), любой заро¬
дыш должен распасться. Объемный член становится отрицательным, когда
р>2 (рг) > (Р2), и доминирует над поверхностной энергией, но только для
зародышей, больших чем
г* = — . (13.32)
/^2 {Р2 ) - Ml(P2)
Большие зародыши, г > г*, расширяются до тех пор, пока вся система
не перейдет в жидкое состояние. Амплитуда потенциального барьера со¬
ставляет 1/3 поверхностной энергии зародыша:
wmax = -7ГОТ*2, (13.33)
3
и может быть представлена как свободная энергия активации термически
возбужденного зародыша. Вероятность флуктуационного возникновения
зародыша размера г* пропорциональна exp( — Wmax/k^T). Скорость, с ко¬
торой зародыши возникают в единицу времени в единице объема, есть
J = cbexp(—WmdiX/ksT), где b — кинетический фактор, который доста¬
точно трудно вычислить. Его значение оценено для многих жидкостей как
b ~ 101Ос-1. Время, необходимое для образования новых растущих за¬
родышей в объеме V, равно т = 1/JV. Для реалистических значений
переменных V ~ 1 см3, г — 1 с и с — 1021 см-3 находим, что газ переста¬
ет быть метастабильным при WmAX ^ 71 к^Т. Для того чтобы проследить
524
Гл. 13. Поверхностные явления
рост зародыша выше критического размера г*, необходимо применять ап¬
парат кинетической теории4^ а не законы равновесной термодинамики.
Рис. 13.6. Работа, необходимая для создания жидкого сферического зародыша из
газа, как функция его радиуса г. Стабильный газ: зародыш распадается. Метаста-
бильный газ: рост жидкой фазы становится возможным, когда флуктуации начинают
создавать зародыши радиуса г > г*
13.1.5. Смачивание
13.1.5.1. Треугольник Ньюмана и закон Юнга. Геометрические про¬
явления поверхностного натяжения становятся гораздо богаче, когда систе¬
ма состоит из трех, а не из двух фаз. Три границы раздела пересекаются
вдоль так называемой тройной, или контактной, линии (рис. 13.7, а). Меха¬
ническое равновесие тройной линии требует, чтобы векторная сумма трех
межфазных натяжений была равна нулю:
^12 + 023 + СГ31 = О, (13.34)
что называется треугольной конструкцией Ньюмана. Если одна из фаз явля¬
ется твердой (рис. 13.7 б), то (13.34)упрощается. Вертикальная компонента
векторной суммы компенсируется упругими силами, вызываемыми дефор¬
мацией твердого тела; в большинстве случаев эти деформации очень малы
(порядка нескольких ангстрем), и, следовательно, мы можем рассматривать
только горизонтальные компоненты (13.34), приводящие к закону Юнга:
(7s2 - <7 si = сг12 COS ве . (13.35)
Здесь ве является равновесным контактным углом, измеряемым как показа¬
но на рис. 13.7, б.
4) Лифшиц Е. М., ПитаевскийЛ. П. Физическая кинетика. — М.: Физматлит, 1979,
гл. 12.
§ 13.1. Поверхностные явления в изотропных средах
525
^23
2
а
2
1
2
3
б
2
1
«*«% >.<*>:> *г«.• \ «•> x't.wv; • •
в
Рис. 13.7. Трехфазная система в состоянии частичного (а, б) и полного (<?, г)
смачивания. Подложка представляет собой или жидкость (а, в) или твердое те¬
ло (б, г)
Уравнение Юнга (13.35) предсказывает две различные ситуации: а) ча¬
стичное смачивание с конечным контактным углом 0 < 9е < 7г, определен¬
ным из (13.34) или (13.35); жидкость 1 на рис. 13.7, а, б имеет вид капли,
форма которой определяется капиллярными и гравитационными силами;
и б) полное смачивание, ве — 0, когда жидкость растекается вдоль поверх¬
ности раздела (рис. 13.7,в,г). Важным параметром, позволяющим разли¬
чить две эти ситуации, является параметр растекания Sspr, определяемый
как разница между свободными энергиями непокрытой подложки (индексы
5 или 5), находящейся в прямом контакте с фазой 2, и подложки, покрытой
плоским протяженным (строго говоря, бесконечно протяженным, см. ниже)
слоем жидкости 7:
S
spr
<Js2 “ (cFsl + G12), ИЛИ S
spr
сг23 - (031 + а 12). (13.36)
Случай Sspr > 0 соответствует полному смачиванию, 5spr < 0 отвечает
частичному смачиванию с cosOe = 1 + Sspr/cr12. Знак 5spr может быть
изменен на обратный вследствие изменения температуры, что отвечает так
называемому переходу смачивания.
Сделаем несколько замечаний по поводу (13.34) и (13.35). Прежде всего,
обе формулы описывают небольшую область около тройной линии, и они
не учитывают объемные силы типа гравитации. Сила тяжести влияет на
центральную часть сидящей капли, когда характерный размер капли срав¬
ним с капиллярной длиной Ас (задача 13.5). Равновесная форма частично
смачивающих капель, размером меньших Ас, представляет собой сфериче¬
скую шапочку: гидродинамическое давление внутри капли уравновешива¬
ется, и кривизна поверхности остается постоянной и удовлетворяет зако-
526
Гл. 13. Поверхностные явления
ну Лапласа-Юнга (13.22). Похожие на линзы жидкие капли, плавающие
на поверхности другой жидкости, ограничены двумя усеченными сферами.
Второе замечание состоит в том, что приведенные выше классические урав¬
нения неприменимы вблизи «ядра» тройной линии, на расстояниях, сравни¬
мых с молекулярными размерами. «Микроскопический» контактный угол
может отличаться от «макроскопического» контактного угла, определяемо¬
го уравнениями (13.36) или (13.35). В третьих, следует иметь в виду, что рав¬
новесный контактный угол трудно измерить экспериментально, особенно
на твердых подложках. Наблюдаемый контактный угол в обычно отвечает
метастабильному состоянию, застабилизированному за счет поверхност¬
ной шероховатости, химических примесей и т. д. Как следствие, величина
угла в зависит от истории образца: различают контактный угол в а > 0е,
получаемый на надвигающейся жидкой капле, и возвратный контактный
угол Or < ве, образующийся, когда капля отходит назад.
13.1.5.2. Расклинивающее давление. Для тонких жидких пленок,
в субмикронном и нанометровом диапазонах, энергия системы начина¬
ет зависеть от их толщины. Это является следствием дальнодействую-
щих сил, определяемых ван-дер-ваальсовыми взаимодействиями (гл. 1)
и электрическими двойными слоями (гл. 14), а также короткодействующих
(стерических) молекулярных сил. Например, приращение свободной энер¬
гии Гиббса (связанной со свободной энергией Гельмгольца соотношением
G = F + PV) может быть представлено в виде
где А и h — площадь и толщина пленки соответственно. Величиной, кото¬
рая может быть измерена в эксперименте, является расклинивающее давле-
П(/г) — это давление, которое необходимо приложить, чтобы воспрепят¬
ствовать тенденции пленки 1 к утолщению, т. е. к разделению («расклини¬
ванию») двух прилегающих фаз 2 и 3. Положительное П(А) способствует
утолщению пленки 7, в то время как отрицательное U(h) стремится сде¬
лать пленку тоньше; U(h) 0, когда h ^ оо, и П(h) -» 5spr, когда h -> 0.
Например, незапаздывающие дальнодействующие силы Ван-дер-Ваальса
дают следующий вклад в расклинивающее давление:
ОО
СО
^surf(^) ^surf(^ оо)
4~ П(^) dz — cfs\ + (7\2 + П(г) dz, (13.37)
A A
h
h
ние, введенное Дерягиным5}
(13.38)
(13.39)
см., например: Дерягин Б. В. Теория устойчивости коллоидов и тонких пле¬
нок. — М.: Наука, 1986.
§ 13.2. Поверхностные явления в анизотропных средах
527
где Ан является константой Гамакера, определямой диэлектрическими про¬
ницаемостями всех трех фаз; в первом приближении Ан ос (е3 — е\) х
х (б2 — £i) (см. § 1.4). На молекулярной шкале короткодействующие стери-
ческие силы могут вызвать осцилляторное поведение П(й). Немонотонное
поведение П(/г) также может наблюдаться и на промежуточных шкалах
длин вследствие конкуренции электростатических и ван-дер-ваальсовых
сил. Концепция расклинивающего давления может быть приложена и к
упорядоченным жидкостям, в которых имеются дополнительные источни¬
ки дальнодействующих взаимодействий (п. 13.2.4).
Расклинивающее давление играет определяющую роль в режиме пол¬
ного смачивания. На практике полный объем растекающейся жидкости яв¬
ляется конечным и смачивающая пленка принимает форму «блина». Пре¬
небрегая краевыми эффектами и силой тяжести, толщину пленки можно
определить из баланса параметра растекания Sspr и П(h) > 0. Избыточная
энергия слоя толщины h и площади А, рассчитанная для границы раздела
пар-твердое тело, равна А(—5 + J П(г) dz). Минимизируя эту энергию
h
с ограничением постоянного объема: Ah = V = const, получаем уравне¬
ние, определяющее толщину пленки:
Например, когда расклинивающее давление определяется незапаздываю¬
щими силами Ван-дер-Ваальса (13.39), из (13.40) следует
(константа Гамакера Ан должна быть отрицательна, для того чтобы фа¬
зы 2 и 3 отторгали друг друга). Эта минимальная толщина hc может быть
значительно больше, чем молекулярный размер, невзирая на тот факт, что
Sspr > 0 (полное смачивание).
Мы не будем здесь рассматривать динамику смачивания. Один из наи¬
более интересных эффектов в динамике заключается в том, что для 5spr > 0
растекающаяся пленка содержит микроскопическую часть толщины /гс, ко¬
торая распространяется впереди макроскопического края; этот микроско¬
пический «язык» называется предшествующей пленкой. Мы отсылаем чи¬
тателя к обзорам де Жена, а также Леже и Джоанни, в которых можно найти
как статические, так и динамические аспекты смачивания.
§ 13.2. Поверхностные явления в анизотропных средах
ОО
S = hcTl(hc) + П(г) dz.
(13.40)
(13.41)
В анизотропных средах поверхностное натяжение а зависит от ориен¬
тации границы раздела по отношению к осям симметрии, таким как кри¬
сталлографические оси в твердом кристалле или ориентация директора
528
Гл. 13. Поверхностные явления
в нематическом жидком кристалле. К тому же создание новой границы раз¬
дела в жидких и твердых кристаллах вызывает искажения параметра поряд¬
ка как на поверхности, так и в объеме. Величины типа плотности свободной
энергии Гельмгольца начинают зависеть от искажений параметра порядка.
Следовательно, равновесная форма и внутренняя конфигурация параметра
порядка ограниченной анизотропной системы определяются минимумом
суммы поверхностного и объемного членов:
где / представляет объемную плотность свободной энергии.
Для изотропных жидких капель о ~ const, и минимизация поверхност¬
ной области приводит к сферической форме поверхности. Можно также
представить себе твердый кристалл, имеющий форму сферы, в котором
расположение атомов на поверхности отвечает возможному минимуму сг.
Эта конфигурация неизбежно будет искажена в объеме. Энергия дефор¬
мации растет с размером кристалла быстрее, чем поверхностная энергия,
и сферический кристалл будет энергетически очень невыгоден. Следова¬
тельно, равновесная форма твердого кристалла должна быть рассмотрена
исходя из предположения, что деформации в объеме отсутствуют, / — О
в (13.42). Форма кристалла определяется зависимостью сг от кристаллогра¬
фических направлений. Жидкие кристаллы оказываются наиболее трудным
случаем, потому что как поверхностная, так и объемная энергии зависят от
молекулярного порядка (в отличие от изотропных жидкостей, где отсут¬
ствует упругость в объеме). В отличие же от твердых тел, предположение
/ = 0 не может быть использовано в случае жидких кристаллов, посколь¬
ку энергия объемных деформаций, проинтегрированная по пространству,
= КR, оказывается меньше, чем суммарная поверхностная энергия = oR2
для достаточно большого размера R системы. Таким образом, в общем
случае оба интеграла в (13.42) должны быть приняты во внимание.
13.2.1. Равновесная форма (форма Вульфа) твердых кристаллов
Рассмотрим для начала форму твердых кристаллов. Пусть г = г(х, у)
определяет поверхность твердого кристалла в прямоугольных координатах
ху у, z. Единичный вектор, перпендикулярный этой поверхности, имеет
вид
а элемент поверхностной области dA ~ wz2 + z2 + 1 dxdy\ здесь =
= dzjdx и zy — dz/dy. Равновесие достигается, когда интеграл поверх-
F — Fs + Fv — Оо dA + f dV,
(13.42)
— zyj + k
(13.43)
ностнои энергии
(13.44)
§ 13.2. Поверхностные явления в анизотропных средах
529
имеет экстремум при условии, что объем кристалла остается постоянным:
V
и* л
z dx dy = const,
(13.45)
или, иначе говоря, когда достигается безусловный экстремум следующего
интеграла:
F* - 2XV
Г% А
<j{y)Jz\ + + 1 — 2z\ dxdy,
(13.46)
где Л — множитель Лагранжа. Уравнение Эйлера-Лагранжа имеет вид
a d(a\/zl + z'y + l) а а(сгУ21 + zy +!)
2 A -j-
0.
dx
dz
X
dy
dz
(13.47)
у
Можно проверить, что одно из его решений может быть представлено в виде
A (z
zxx
zvV)-
(13.48)
Замечая, что
VX
z - zxx — ZyU
z'l + 2,2 + 1
У
выражение (13.48) может быть переписано в виде
<*(у)
А
v г,
(13.49)
где г — (xi + у} + zk) — радиус-вектор, проведенный из начала координат
в точку отсчета вектора нормали и на поверхности кристалла.
Уравнение (13.49) объясняет, как получить равновесную форму кри¬
сталла, если известна диаграмма о (и) (диаграмма Вульфа на рис. 13.8)
в полярных координатах. Вначале соединим начало координат О с любой
точкой М на кривой а(г^), полученной следующим образом: направление
ОМ есть v ; длина пропорциональна cr(iv), скажем, | ОМ | = cr(i/)/A. Че¬
рез точку М проведем плоскость, перпендикулярную ОМ. Операция по¬
вторяется для всех точек диаграммы Вульфа cr(i/). Семейство получаемых
плоскостей и представляет собой равновесную форму кристалла: (13.49)
удовлетворяется для любого радиуса-вектора г, проведенного из начала ко¬
ординат к поверхности кристалла, vv — | г | cos a — | ОМ
углом между г и ОМ (рис. 13.8).
, где а является
530
Гл. 13. Поверхностные явления
Полярная диаграмма
Вульфа
Касательная плоскость
к поверхности кристалла
Рис. 13.8. Формирование трехмерной равновесной формы кристалла с помощью
полярной диаграммы Вульфа (кривая с острыми выступами)
Равновесную форму кристалла образуют протяженные плоские участ¬
ки, называемые «фасетами» или гранями. Грани обязаны своим существо¬
ванием «изломам», или локализованным минимумам функции <т(г/). Эти
строго локализованные минимумы а(и) расположены вдоль направлений
симметрии. Поверхностное натяжение на границе раздела, слегка отклонен¬
ной от направления симметрии (вицинальная поверхность), оказывается
увеличенным из-за образования ступеней, разделенных плоскими терраса¬
ми (рис. 13.9, а). Если угол отклонения д мал, ступени достаточно простран¬
ственно разделены, и их взаимодействием можно пренебречь. Поэтому
поверхностное натяжение вблизи изломов ведет себя как
а(и) « <т0 + £ в з (13.50)
а
где сто — поверхностное натяжение плоской неотклоненной поверхности,
е — энергия на единицу длины ступени, а а — высота ступени. Построение
§ 13.2. Поверхностные явления в анизотропных средах
531
г
Рис. 13.9. Ступени на поверхности кристалла при Т = 0 (а) и Т > 0 (б). Эволюция
равновесной формы кристалла (<?) и сечения полярной диаграммы Вульфа в зависи¬
мости от температуры (г). Острые выступы и грани исчезают в точке Tr фазового
перехода от огранения к шероховатости (перерисовано из С. Rottman, М. Wortis)
Вульфа преобразует сингулярности функции а (у) в плоские грани поверх¬
ностной формы кристалла. Заметим, что существуют участки на кривой
которые не участвуют в формировании внешней формы кристалла.
Соответствующие кристаллографические ориентации запрещены на по¬
верхности кристалла, и поверхностное натяжение для этих ориентаций
не может быть измерено. Выраженное огранение поверхности кристал¬
ла последовательно исчезает с ростом температуры. Это происходит из-за
того, что тепловые флуктуации разрушают края ступеней (рис. 13.9, б). Эн¬
тропийный вклад уменьшает свободную энергию ступеней. Изломанные
532
Гл. 13. Поверхностные явления
участки становятся все более мелкими, и плоские грани сокращаются. При
некоторой температуре, называемой температурой перехода от огранения
к шероховатости (различной для различных кристаллографических ориен¬
таций), энтропия поверхностных флуктуаций берет верх над поверхност¬
ным натяжением, грани исчезают, и соответствующие области кристалла
становятся однородно закругленными (рис. 13.9, в, г). Теоретический под¬
ход к переходу огранение ~ шероховатость6^ имеет много общего с двумер¬
ным переходом Костерлица-Таулесса (см. § 4.5). Этот переход происходит
при температуре Тд = 2аа2/к , где а является (температурно зависимым)
поверхностным натяжением, а а — высотой ступенек, т. е. периодичностью
решетки в направлении, перпендикулярном грани. Переход к шероховато¬
сти имеет также практическое значение для понимания процесса роста
кристаллов.
В этом разделе рассмотрены равновесные формы кристаллов, учитываю¬
щие также флуктуации при Т > 0. Для таких внешних форм должна рабо¬
тать обсуждавшаяся ранее теория роста, но она дает большие пересыщения.
В действительности, на эксперименте, как раз малые пересыщения являют¬
ся скорее правилом, чем исключением. Это является следствием дефектов,
пронизывающих поверхность; в частности, дислокации с винтовой ком¬
понентой, перпендикулярной поверхности, содержат (ростовую) ступень,
представляющую собой область легкого роста кристалла, поскольку такие
ступени являются самовоспроизводящимися местами для присоединения
атомов. Эти ступени служат центрами кристаллизации. Дополнительные
детали см. в статье Бартона и др.7)
13.2.2. Поверхностное сцепление в нематических жидких кристаллах
Анизотропные взаимодействия между молекулами жидкого кристалла
и окружающей средой вызывают два основных эффекта: 1) модификацию
жидкокристаллической структуры в окрестности границы раздела и 2) сня¬
тие вырождения в ориентации директора в объеме. Примерами структур¬
ных перестроек типа (1) являются: а) периодические модуляции плотно¬
сти (рис. 13.10,а), которые в некоторых случаях похожи на наблюдаемые
в смектиках (аналогичные модуляции плотности были обнаружены так¬
же и для обычных жидкостей); б) полярное упорядочение молекулярных
диполей, которое снимает вырождение п и — п вблизи границы раздела
(рис. 13.10, б); и в) модификация скалярного параметра порядка (который
может стать как больше, так и меньше, чем в объеме).
Явления второго типа обычно называют эффектами сцепления. Они
обусловлены тем, что поверхностное натяжение, определенное как по¬
верхностное приращение термодинамического потенциала, зависит от
6) S. Т. Chui andJ. D. Weeks. Phys. Rev. В14, 4978 (1976).
7^ W. K. Burton, N. Cabrera and F. C. Frank. Phil. Trans. Roy. Soc. A243, 299 (1951).
§ 13.2. Поверхностные явления в анизотропных средах
533
а б
Рис. 13.10. Модификации жидкокристаллического порядка поверхностью; перио¬
дическая модуляция молекулярной плотности с одновременным возрастанием ска¬
лярного параметра порядка (а); полярное упорядочение молекулярных диполей,
приводящее к поверхностной электрической поляризации Р5 (б). Пространствен¬
ное изменение скалярного параметра порядка (а) также приводит к появлению «ор-
доэлектрической» поляризации
ориентации директора8). Для искривленных ограничивающих поверхно¬
стей выделенные направления сцепления могут быть обусловлены объем¬
ной упругостью жидкого кристалла. Представим, например, слой нематика
между двух плоских пластин, которые обеспечивают тангенциальную ори¬
ентацию директора. Когда пластины параллельны друг другу, равновесной
ориентацией является ориентация директора параллельно пластинам. Од¬
нако когда пластины наклонены по отношению друг к другу, равновесное
состояние достигается, только когда директор перпендикулярен градиенту
толщины (п. 11.1.6). Подобное «геометрическое сцепление» может давать
вклад в искажение поля директора в образцах с искривленными поверхно¬
стями (свободно подвешенные пленки, пленки на жидких или твердых под¬
ложках). Другой фактор, имеющий существенное значение в случае, когда
жидкий кристалл ориентирован натертой полимерной пленкой, это прямое
ван-дер-ваальсово взаимодействие между молекулами жидкого кристалла
и полимера.
Поверхностная ориентация директора характеризуется полярным уг¬
лом в и азимутальным углом fi. Выделенное направление (#о, <fio), миними¬
зирующее функцию а (в, (р), называется «осью легкого ориентирования».
Таким образом, а(0, ip) можно представить как сумму поверхностного
натяжения <т(0о, <^о), отвечающего равновесной ориентации, и функции
энергии сцепления w($, ip), которая в общем случае неизвестна и зависит
от деталей молекулярных взаимодействий на границе раздела:
а(0, (fi) = сго(0о, <Ро) + w{0 — во, (р — фо). (13.51)
8) В качестве обзора по гиббсовской термодинамике на границе нематика см.:
Н. Yokoyama. in Handbook of Liquid Crystal Research, Edited by P. J. Collings and
J. S. Patel, Oxford University Press, N. Y., 1997.
534
Гл. 13. Поверхностные явления
Когда жидкий кристалл находится в контакте с изотропной жидко¬
стью, w зависит только от полярного угла в. Для межфазной границы нема¬
тик-изотропная жидкость нет оснований ожидать каких-либо сингуляр¬
ностей в функции w(Q), так как в нематической фазе отсутствует дальний
трансляционный порядок (рис. 13.11).
Рис. 13.11. Возможные зависимости энергии сцепления от полярного угла в между
ориентацией директора и нормалью к границе раздела. Сплошная линия: танген¬
циальное сцепление, во = 7г/2; штриховая линия: перпендикулярное сцепление.
Сила сцепления в окрестности равновесной ориентации (#о7 щ) часто
характеризуется так называемыми полярным (г^) и азимутальным (w^)
коэффициентами сцепления, которые определяют работу (на единицу пло¬
щади), которую необходимо совершить для отклонения директора от оси
легкого ориентирования (0о, <Л))*
Такие зависимости справедливы для малых отклонений от оси легко¬
го ориентирования. Очень часто, особенно для полярной части энергии,
постулируется, что энергия поверхностного сцепления имеет специальный
функциональный вид, например:
0,5
w
0
0
7Г / 6
7Г / 3
7Г / 2
в о = 0
w — -we sin2 (в — во).
2
(13.53)
Это выражение называется потенциалом сцепления Рапини- Папул ара. Для
описания некоторых эффектов, таких как последовательное воздействие на
§ 13.2. Поверхностные явления в анизотропных средах
535
ориентацию или зависимость потенциала сцепления от координат в плоско¬
сти подложки, удобнее использовать бесследовый координатно-зависимый
симметричный тензор9^ wap(r):
W = --'^2,wa0{T)nanp. (13.54)
2 «,/3
В нематической фазе коэффициенты сцепления с поверхностью обыч¬
но гораздо меньше, чем энергия (на единицу площади), необходимая для
расширения площади поверхности при сохранении равновесной ориента¬
ции директора. Типичные значения коэффициента поверхностного натяже¬
ния для границы раздела жидкого кристалла цианобифенила и глицерина
составляют ао ~ (10~3 — 10-2) Дж/м2, в то время как полярный коэффи¬
циент сцепления для той же границы раздела we ~ (10-5 — 10“6) Дж/м2.
На границе раздела нематик - изотропная жидкость в 5СВ10^ угол во — 64 °,
ао ~ 2 х 1СГ5 Дж/м2, в то время как wq « 5 х 10 ~ 7 Дж/м2. Как поверх¬
ностное натяжение, так и коэффициенты сцепления зависят от темпера¬
туры. Коэффициенты сцепления уменьшаются с увеличением температу¬
ры Т, потому что нематический скалярный параметр порядка уменьшается.
Температурная зависимость ао может быть более сложной. В изотропных
жидкостях ао обычно монотонно уменьшается с ростом температуры Т.
В жидких кристаллах функция ао(Т) может быть немонотонной, особенно
в окрестности фазовых переходов.
Обычно различают три типа полярных ориентаций на границе раздела
изотропная жидкость-нематик: 1) перпендикулярная, во = 0; перпенди¬
кулярное сцепление также называют «гомеотропным» в случае плоской
границы раздела; 2) наклонная коническая, 0 < во < 7г/2; и 3) танген¬
циальная, Оо = 7г/2. Оси легкого ориентирования, лежащие в плоскости
границы раздела, могут быть получены для анизотропной подложки, на¬
пример для кристаллической. Ниже мы рассмотрим роль поверхностного
сцепления для двух эффектов, индуцируемых полем, а именно для перехода
Фредерикса и совместного эффекта флексоэлектрической и поверхностной
поляризаций.
13.2.3. Полевые эффекты в условиях конечного сцепления
13.2.3.1. Переход Фредерикса. В п. 5.4.3 мы рассматривали индуци¬
рованную полем переориентацию директора в объеме нематической ячей¬
ки, известную как переход Фредерикса. Переход Фредерикса имеет строго
определенный порог в тех случаях, когда директор п первоначально на¬
ходится в планарной или гомеотропной ориентации, а внешнее поле В
перпендикулярно п или параллельно ему. Неустойчивость имеет место
S. V Shiyanovski, A. Glushchenko, Yu. Reznikov, О. D. Lavrentovich and J. L. West.
Phys. Rev. E 62, R1477 (2000).
10) S. Faetti. Mol. Cryst. Liq. Cryst. 179, 217 (1990).
536
Гл. 13. Поверхностные явления
в геометрии В||п, когда диамагнитная (диэлектрическая) анизотропия яв¬
ляется отрицательной, Ха < 0, и в геометрии BJLn , когда %а > 0. По¬
рог перехода (5.74) был рассчитан исходя из предположения, что директор
находится в сильном сцеплении с ограничивающими пластинами при г =
= 0 и г = /г, где h — толщина ячейки. Рассмотрим теперь, как конечное
сцепление модифицирует результат (5.74) в геометрии, когда п = (0, 0, 1)
и В — (Б, 0, 0); Ха > 0.
Запишем директор в виде n = [sin 6(z), 0, sin0(z)]. Вблизи порога пе¬
рехода искажения слабы, < 1, и свободная энергия (рассчитанная на
единицу площади) записывается в упрощенном виде
h
F
1
2
о
Къ(-) - -1
dz /
2 л2
Мо ХаВ в
, 1
dz+-we6
&
(13.55)
z=h
Соответствующее уравнение Эйлера-Лагранжа имеет вид
?— + е
dz2
о,
где £
ляется
1
в
к 3
М0
магнитная длина когерентности. Его решением яв-
в(г)
С\ cos - + С2 sin -.
£
(13.56)
Здесь константы интегрирования С\ и С2 определяются граничными усло¬
виями для момента кручения:
dd
dz
2=0
+ U>e0\z=o = о,
Кг
М
dz
z—h
+ WqQIz-Ii — 0.
(13.57)
Система уравнений (13.57) дает отличные от нуля коэффициенты С\ и С2,
когда
ctg
h
Кз
2£ wet
(13.58а)
Используя определение В^ для порогового значения поля (5.74) в ячейке с
бесконечно сильным сцеплением, последний результат можно переписать
как
ctg
7Г В
W
tyK^B
W
2 В
hw@ Boo
(13.586)
где Bw является порогом перехода Фредерикса для конечных we. Разло¬
жение (13.58 а) в ряд по малому параметру (1 — Bw/В^) дает выражение,
которое может быть легко интерпретировано:
В
w
1 -
В
ОО
2Кг
hwQ
1
2 L
h
W
(13.58 в)
§ 13.2. Поверхностные явления в анизотропных средах
537
где Lw — Къ /we — характерная длина сцепления, с которой мы уже встре¬
чались в гл. 5. Полярный коэффициент сцепления we может быть измерен
путем сравнения значений порога перехода Фредерикса в толстой и тонкой
ячейках11^. Для жидкого кристалла МВВА, ориентированного гомеотропно
с помощью слоя поверхностно-активного вещества (ПАВ), w$ уменьшается
от б х 10-5 до 1 х 10-5 Дж/м2, когда температура приближается к точке пе¬
рехода нематик-изотропная жидкость. Эксперименты также показывают,
что скалярный параметр порядка вблизи слоя ПАВ, гомеотропно ориен¬
тирующего нематик, немного выше, чем в объеме. Поверхностная область
при этом может напоминать смектик12^.
13.2.3.2. Флексоэлектрический эффект и поверхностная поляри¬
зация. Переход Фредерикса является объемным эффектом: максимальное
отклонение директора для симметричной ячейки происходит в централь¬
ной плоскости ячейки, при z — /г/2. Диамагнитный эффект, рассмотренный
выше, имеет диэлектрическую аналогию; пороговое электрическое поле
может быть оценено с помощью замены ц$1ХаВ2 £о£аЕ2 (для более
точных вычислений следует учитывать, что электрическое поле в ячейке
с искаженным директором является неоднородным). Электрическое поле
вызывает не только диэлектрические, но и другие типы эффектов, такие
как полярные (т. е, зависящие от полярности приложенного поля) флексо-
электрические и поверхностно-поляризационные неустойчивости. Эти две
неустойчивости представляют особый интерес при изучении поверхност¬
ных явлений, потому что максимальные искажения директора происходят
на ограничивающих поверхностях13) z = 0, h.
Мы рассматриваем ту же гомеотропную ячейку, что и в предыдущем
подпункте: п = (0, 0, 1). Электрическое поле Е = (О, О, Е) приложе¬
но вдоль ориентации директора. Если материал является диэлектрически
положительным, еа > 0, следует ожидать отсутствие какого-либо откли¬
ка, поскольку Б||п. Однако простой эксперимент показывает, что низ¬
кое постоянное напряжение, порядка одного вольта, приложенное к го-
меотропной ячейке, заполненной, например, нематическим жидким кри¬
сталлом 5СВ, вызывает искажение директора вблизи одного из электродов
(рис. 13.12). Возможный механизм этого явления связан с вкладами флек-
соэлектричества/flex = — Р/Е = — [eindiv п — ез(п х rot п)]Е и поверх¬
ностной поляризации (—PSE) в плотность свободной энергии. Оба вклада
линейны по Е и усредняются до нуля, когда приложенное поле является
высокочастотным. Однако когда поле постоянно или является низкочастот¬
ным переменным, как флексоэлектрическая, так и поверхностная поля¬
ризации могут вызвать неустойчивость в гомеотропной ячейке, а имен¬
но: возрастание поверхностного полярного угла от нуля до некоторого
и) С. Rosenblatt. J. Phys. (France) 45, 1087 (1985).
12) С. Rosenblatt. Phys. Rev. Lett. 53, 791 (1984).
13) W. Helfrich. Appl. Phys. Lett. 24, 451 (1974).
538
Гл. 13. Поверхностные явления
значения Os. Например, если поверхностная поляризация направлена в сто¬
рону ограничивающих плоскостей, постоянное поле (0,0, Ере), действую¬
щее вдоль оси z, будет вызывать отклонение директора вблизи пластины
с z = 0 и увеличивать гомеотропную ориентацию у пластины с z ~ h
(рис. 13.12). Экспериментальная проверка этого полярного эффекта не так
проста, поскольку он может быть замаскирован другими полевыми эф¬
фектами, такими как инжекция ионов с электродов ячейки или периоди¬
ческое движение нематической жидкости, т. е. электрогидродинамическая
неустойчивость.
а
б
Рис. 13.12. Полярная поверхностная нестабильность в гомеотропной нематиче¬
ской ячейке с еа >0: взаимодействие флексоэлектрической поляризации (двойная
стрелка) и поверхностной поляризации (одиночная стрелка) с приложенным по¬
лем Edc (я); текстура гомеотропного слоя жидкого кристалла 5СВ выше порога
полярной неустойчивости (б)
Для проверки природы электрооптических эффектов в гомеотропной
ячейке можно использовать одновременное воздействие переменного (Е\с)
§ 13.2. Поверхностные явления в анизотропных средах
539
и постоянного (£Ьс) полей14). Совместный момент кручения, вызываемый
флексоэлектрической и поверхностной поляризациями, может быть оценен
как (—e*Evc)Os, где е* = е\ + ез + | Р5 |. Положительный знак | Р5 | отве¬
чает случаю, когда поверхностная поляризация способствует отклонению
директора на аноде. Дестабилизирующему моменту кручения (~~е*c)0s
составляют конкуренцию: а) момент кручения поверхностного сцепления
wqOs — K6S/LW и б) диэлектрические моменты кручения, связанные с по¬
стоянным KOs/^ос и переменным Кв§/£ас электрическими полями. Здесь
£dc
К
£Q€aE^Q
И £аС
К
SQSaEл
АС
представляют собой соответствующие длины когерентности. Имеется так¬
же момент кручения упругих сил, который может быть опущен в случае
толстой ячейки, h £дс 3 Сое* Уравнение для совместного момента круче¬
ния на поверхности имеет вид
?АС ?DC L
О,
W
и из него получается порог поверхностной полярной неустойчивости:
Бос,
1
th
е* - у/ео€аК
\JКео£а | ЕаС | 4 We
(13.59)
Важной особенностью является то, что порог полярной нестабильности
Euc,th возрастает с увеличением | ЕАс |; Для электрогидродинамических
эффектов порог не должен возрастать с увеличением | Еас |- Эксперимен¬
ты действительно подтверждают существование полярного поверхностно¬
го эффекта с £?DC,th — I Вас |- Другим важным следствием (13.59) явля¬
ется возможность измерения длины сцепления и е*. Для этого необходи¬
мо сравнить порог Е^с th для случая, когда отсутствует переменное поле,
с порогом Еоc,th, измеренным, когда ячейка находится под действием ста¬
билизирующего переменного поля:
L
W
£ас
£pC,th
Е°
DC, th
-l;
\Jso£aK! f 1 4-
Eac
Эксперименты14) дают L
W
1 мкм и e
^DC,th ^DC.th
5 x 10 3 (единицы СГС) для
(13.60)
жидкого кристалла 5СВ, гомеотропно ориентированного слоем силиконо¬
вого эластомера. Полная флексоэлектрическая и поверхностная поляриза¬
ция е* = е\ +ез 4-1 Ps | отличается от чисто флексоэлектрического парамет¬
ра (ei 4- ез). Следовательно, вклад поверхностной поляризации в полную
14^ О. D. Lavrentovich, V G. Nazarenko, V. V. Sergan and G. Durand. Phys. Rev. A 45,
R6969 (1992).
540
Гл. 13. Поверхностные явления
поляризацию может быть значительным. Более подробный анализ и обзор
эффектов электрического поля можно найти в книге Пикина15^
13.2.4. Тонкие жидкокристаллические пленки; взаимодействия
Казимира
Как уже отмечалось в п. 13.1.5, дальнодействующие взаимодействия ти¬
па сил Ван-дер-Ваальса играют важную роль в поведении систем с проме¬
жуточными характерными длинами, лежащими в интервале от 1 микрона до
нескольких нанометров. Если пленка является упорядоченной, например,
отвечает нематической фазе, то имеются дополнительные дальнодейству¬
ющие взаимодействия, дающие вклад в расклинивающее давление. Наибо¬
лее очевидный эффект определяется балансом сил сцепления и упругости.
Например, если нематическая пленка имеет различные оси легкого ориени-
тирования на двух противоположных поверхностях, искажения директора
в объеме стремятся увеличить толщину подобной гибридно ориентирован¬
ной пленки, добавляя положительный член neiastic(fr) ~ K/h2 к расклини¬
вающему давлению (задача 13.6). Аналогичным образом пространственные
искажения директора препятствуют плотному контакту двух сферических
частиц в нематическом растворе. Кроме того, даже если распределение
директора является пространственно однородным, имеется другой универ¬
сальный источник дальнодействующих взаимодействий, например силы
Казимира (п. 1.4.4).
Взаимодействия Казимира происходят из-за энтропийно невыгодных
ограничений, которые геометрия системы накладывает на термические
флуктуации параметра порядка. Например, в плоском нематическом слое
с бесконечно сильным сцеплением, которое удерживает директор перпенди¬
кулярно пластинам, п = (0, 0, 1) = const. В таком слое отсутствует упругая
энергия искажений. С другой стороны, поверхностное сцепление подавляет
ряд флуктуирующих мод ориентации директора в объеме. Система стремит¬
ся уменьшить объем, в котором эти ограничения осуществляются, и пла¬
стины притягивают друг друга. Потенциал этого притяжения должен быть
пропорционален кБТ, так как эффект вызван термическими флуктуациями.
Кроме того, взаимодействие должно быть пропорционально площади пла¬
стин А. Чтобы получить правильную размерность, мы приходим к тому, что
потенциал может быть приближенно записан как (—к^Т) A/h2, т. е. он изме¬
няется с разделяющим пластины расстоянием ~ l/h2. Эта оценка оказыва¬
ется качественно правильной, если использовать одно константное прибли¬
жение нематической теории упругости. В общем случае упругие константы,
описывающие флуктуации с волновыми векторами, перпендикулярными
и параллельными пластинам, не равны друг другу, и амплитуда взаимо¬
действий Казимира должна быть умножена на фактор (К^/Кг + К2/Кi).
1 г \
J Пикин С. А. Структурные превращения в жидких кристаллах. — М.: Наука.
1981. — 336 с.
§ 13.2. Поверхностные явления в анизотропных средах
541
Тщательные рассчеты16) показывают, что потенциал притяжения имеет вид
<гя(3) къТА К3 К2
16тг К2 \КХ Ki
Здесь — дзета-функция Римана, о?(3) ~ 1,202 ... Используя определе¬
ние (13.38), находим, что вклад сил Казимира в расклинивающее давление
гомеотропной нематической пленки:
является отрицательным (гибридная ориентация нематической пленки мо¬
жет обеспечить положительный знак вклада сил Казимира). В смектике А,
ориентированном аналогичным образом, со слоями, лежащими параллель¬
но пластинам, зависимость расклинивающего давления от расстояния меж¬
ду пластинами имеет иной функциональный вид. Это связано с тем, что
в плотности упругой энергии смектика имеется характерный масштаб длин
Л = y/Ki/B. Как следует из вычислений Аджари и др.16\
Строгая экспериментальная проверка взаимодействий Казимира в жид¬
ких кристаллах (или других упорядоченных средах) в настоящее время
отсутствует.
13.2.5. Топологические дефекты в больших жидкокристаллических
Равновесие ограниченного образца жидкого кристалла определяется
минимумом полной энергии, которая включает объемный упругий и по¬
верхностный члены. Под последним подразумевается как поверхностная
«изотропная» энергия, так и энергия анизотропного сцепления. Поскольку
общее решение проблемы минимизации неизвестно, часто используют раз¬
личные приближения, основанные на качественном сравнении различных
членов. Для нематического образца с характерным размером R (напри¬
мер, капля, находящаяся в некоторой матрице) соответствующие оценки
составляют KR, аоВ? mveR2; обычно we ао. Объемная упругая энергия
линейно зависит от R, что снова приводит к характерной длине сцепле¬
ния Lw = К/we, являющейся важным параметром. Нематические капли
любого разумного надмолекулярного размера, «подвешенные» в различных
жидкостях (вода, глицерин), практически сферичны. Внутренняя структура
капли различна для случаев /?> Lw и R <С Lw. Сравним два экстремальных
(13.61)
(13.62)
каплях
16^ A. Ajdari, В. Duplantier, D. Hone, L Peliti and J. Prost. J. Phys. II France 2, 487
(1992).
542
Гл. 13. Поверхностные явлення
состояния капли с перпендикулярным сцеплением n||i/: а) пространствен¬
но однородная ориентация директора, n = const, нарушающая граничные
условия; б) структура, имеющая вид ежа, п\\и (рис. 13.13). Энергия од¬
нородной структуры определяется сцеплением с поверхностью, SttwoR2/3
(в приближении Рапини-Папулара (13.53)), в то время как энергия струк¬
туры, имеющей вид ежа (11.14), SttKR, является чисто упругой. Таким
образом, капля малого размера, R Lw, предпочитает быть однородной,
n « const, в то время как капля большого размера, R Lw, должна иметь
структуру типа ежа. Стабильные топологические дефекты являются харак¬
терной особенностью жидкокристаллических капель, что будет показано
в следующем подпункте.
©
—н—
К / w$
О
К/ а0
R
Рис. 13.13. Большие и малые нематические капли, имеющие перпендикулярное
поверхностное сцепление
13.2.5.1. Топологические законы сохранения. Когда нематическая
капля имеет большой размер, R^> K/wq, ориентация директора на поверх¬
ности задана равновесным полярным углом во. Для типичных значений
полярного коэффициэнта сцепления wg ~ (10-5 - 10~6) Дж/м2 и модуля
упругости К та 10-11 Н те капли, размер которых значительно превыша¬
ет микрон, являются «большими». Даже не решая проблему минимизации,
можно установить общие топологические свойства подобных структур, при
условии что во фиксировано. Эти возможности вытекают из двух теорем
дифференциальной геометрии, а именно теоремы Гаусса-Бонне и теоремы
Эйлера-Пуанкаре. Эти теоремы позволяют связать полный заряд точечных
дефектов в векторном поле с эйлеровыми характеристиками ограничиваю¬
щей поверхности, что будет показано ниже171
В ограниченном образце нематика может быть два типа топологических
дефектов: те, что находятся в объеме, и те, что на поверхности. Точечные
дефекты в объеме представляют собой ежи (гл. 11, 12). Линейные дефек¬
ты в объеме, образующие замкнутые петли, могут быть рассмотрены как
ежи с увеличенным ядром. На поверхности могут быть другие типы то¬
чечных дефектов — «буджумы» (рис. 13.14, рис. 13.15). Буджумы могут
17^ Воловик Г. Е., Лаврентович О. Д. ЖЭТФ 85, 1997 (1983).
§ 13.2. Поверхностные явления в анизотропных средах
543
С = 1/2
С = cos2 (вй/2)
С = 1
а
б
в
Рис. 13.14. Точечные дефекты - буджумы с С = cos2(#o/2)? к = 1 и N = 1 для
различных углов «легкого» сцепления с поверхностью: во = 7г/2 (а), 0 < во <
< 7г/2 (б) и #о = 0 (в). Верхняя часть рисунка а: проекционное поле т с /е = 1 на
поверхности нематика. Средняя часть: векторное поле п в объеме нематика. Ниж¬
няя часть рисунка: элементы поверхности сферы параметра порядка S2, площадь
которых равна С в (13.63). Эскиз Г. Е. Воловика
С=-1 /2
а
С = —sin2 (0О/2)
б
тшшштг
\
/
б
Рис. 13.15. Точечные дефекты-буджумы сС = — sin2(0o/2), к -
тех же углов «легкого» сцепления с поверхностью, что и на рис. 13.
0 < во < 7г/2 (б) и #о =0 (<?). Эскиз Г. Е. Воловика
= 1 и N = 0 для
14: 0О = тг/2 (а),
быть охарактеризованы некоторым «двумерным» топологическим заря¬
дом /с, определенным как показатель поверхностной проекции поля т ~
= n — см. (12.4). Однако буджумы вызывают также искажения
544
Гл. 13. Поверхностные явления
внутри среды. Например, дефект, показанный на рис. 13.14,а напомина¬
ет половинку радиального ежа. Можно приписать ему «объемную» ха¬
рактеристику С = 1/2. Эта характеристика не является, строго говоря,
топологическим зарядом: ее можно использовать только в тех случаях, ко¬
гда условия сцепления достаточно сильны, чтобы ограничить сингулярное
ядро, где условия сцепления не могут быть удовлетворены, небольшой
областью. Чтобы избежать неопределенности со знаками, будем рассмат¬
ривать п как вектор и исключим дисклинации из этой картины. Когда в$
изменяется от 7г/2 до нуля, буджум постепенно трансформируется в ежа
с С = N — 1 (рис. 13.14). Противоположный сценарий, т. е. постепенное
исчезновение буджума, С -> 0, показан на рис. 13.15. В принципе, любой
буджум может быть охарактеризован с помощью «объемного» заряда N,
в дополнение к поверхностному заряду к. Для определения N достаточно
окружить буджум полусферой из объема нематика и вычислить интеграл
(12.15), введенный в гл. \21В\ по этой полусфере. Получающаяся вели¬
чина С связывает N, к и «угол легкого ориентирования» на поверхности
(n v — cos$o)):
с- 1
%
dU2
>
п
’ дп
дп
X
47Г „
К.
ди\
ди2 _
dux
к ,
-(11 V
2
1) + TV.
(13.63)
Из (13.63) находим топологический заряд N буджума, потому что к
определяется независимо как показатель поверхностной проекции поля
т — n — Заметим, что буджумы с нецелым числом С ни при ка¬
ких условиях не могут покинуть поверхность и уйти в объем нематика
(в отличие от них, ежи могут располагаться в любой точке пространства,
включая поверхность нематика).
Последовательно используя определенные выше параметры С, можно
найти законы сохранения для зарядов к и N. Представим себе, что име¬
ется р точечных дефектов на поверхности капли и q ежей в ее объеме.
Окружим все дефекты в объеме поверхностью 71, и всю поверхность нема¬
тика, включая буджумы, — поверхностью 72, как показано на рис. 13.16.
Полный топологический заряд ежей, окруженных 71, равен Полный
*
г
заряд дефектов, окруженных 72, равен сумме параметров буджумов Cj
и параметра Cs поверхности капли, который отличен от нуля из-за кри¬
визны границы раздела. Вычисляя интеграл (12.15) по поверхности капли
с исключенными буджумами, находим
С
— П V.
(13.64)
18) М. Kleman. Phil. Mag. 27, 1057 (1973).
§ 13.2. Поверхностные явления в анизотропных средах
545
Параметр Cs равен умноженному на — пи/Ак интегралу от гауссовой
кривизны поверхности, который равен 47т в случае сферы единичного ра¬
диуса. Теперь, поскольку между 71 и 72 дефекты отсутствуют, два полных
Р+Я
топологических заряда Na и X^6=i + С8 (взятые с противополож-
а=р+1
ными знаками) равны:
Р+Я Р
£ Na = -^Cb-Cs. (13.65)
а—р+1 6=1
Рис. 13.16. Ограниченная система, содержащая ежи (заполненные круги)
и буджумы (полуокружности)
Данные выше определения параметров С и Cs ведут к равенству
р
р+я
р
Р+Я
Y,Cb + Ca+ Y, Na = ~ )(nv-l) + '£iNa-l
0.
6=1
a~p+1
6=1
a=l
(13.66)
Последнее уравнение накладывает следующие ограничения на поверхност¬
ные двумерные заряды к и объемные трехмерные заряды N:
v
£> = 2
6=1
(13.67)
35-КЛЕМАН М.
546
Гл. 13. Поверхностные явления
(справедливое для любых Оо ф 0)) и
р+ч
(13.68)
а=1
Уравнение (13.67) есть не что иное, как теорема Эйлера-Пуанкаре,
которая гласит: сумма показателей гладкого (за исключением конечного
числа изолированных сингулярных точек) векторного поля т на замкнутой
поверхности равна эйлеровому параметру х этой поверхности:
Как уже отмечено в конце гл. 5, параметр Эйлера х Для любой сфериче¬
ской поверхности равен 2.
Уравнение (13.68) является следствием теоремы Гаусса-Бонне. Дей¬
ствительно, полный «объемный» заряд не зависит от «угла легкого ориен¬
тирования» и, следовательно, должен быть равен интегралу (13.63), взято¬
му по ограничивающей поверхности системы, где n = v во всех точках.
Результат интегрирования тогда является гауссовой кривизной ограничи¬
вающей поверхности, что делает интеграл равным половине эйлерового
параметра вследствие теоремы Гаусса-Бонне (5.81), т. е.
Согласно (13.67)-(13.70) большие нематические капли в условиях рав¬
новесия должны содержать топологические дефекты. Тривиальные при¬
меры включают каплю с перпендикулярным сцеплением, содержащую еж
N= 1, и каплю с тангенциальным сцеплением, в которой имеется па¬
ра буджумов fci = к<2 — 1 на полюсах (см. рис. 11.13). Промежуточные
поверхностные ориентации могут еще и индуцировать дисклинации.
13.2.5.2. Упругие взаимодействия. Топологические ограничения
(13.67)-(13.70) и ориентационная упругость жидких кристаллов приво¬
дят к специфическому типу коллоидных взаимодействий, возникающих,
когда твердые или жидкие частицы диспергированы в жидкокристалли¬
ческой матрице191 Если диспергированные частицы достаточно велики,
R^> K/wq, они играют роль «зародышей» топологических дефектов, внед¬
ренных в нематическую матрицу. Например, каждая диспергированная ча¬
стица, имеющая радиальное сцепление, эквивалентна радиальному ежу
с N — 1 в нематической матрице. Такая частица может быть воздушным
v
(13.69)
&=i
Р+7
(13.70)
а=1
19) P. Pieranski, P. Cladis and М. Kleman. С. R. Acad. Sci. 273, 275 (1971).
§ 13.2. Поверхностные явления в анизотропных средах
547
пузырьком или каплей воды с растворенным поверхностно-активным ве¬
ществом, которое способствует ориентации директора п перпендикулярно
границе раздела нематик - вода. Предположим, что имеется много частиц
с радиальным сцеплением, диспергированных в одном очень большом
нематическом объеме (сферическая капля). Поскольку полный топологи¬
ческий заряд нематика должен быть равен 1, каждая частица, добавляемая
внутрь нематической капли вслед за первой, должна создавать
ориентационный дефект в исходной матрице. Одна из простейших воз¬
можностей, удовлетворяющая этим общим топологическим ограничениям,
состоит в создании гиперболических ежей, сопровождающих каждую ча¬
стицу в нематическом хозяине (рис. 13.17). Эти дефекты нематической мат¬
рицы не позволяют диспергированным частицам плотно приблизиться друг
к другу, и тем самым создают барьер отталкивания против коагуляции20).
Рис. 13.17. Сферы с перпендикулярным поверхностным сцеплением (открытые
круги) создают связанные друг с другом гиперболические ежи (ядра показаны
сплошными кругами) в поле директора нематической матрицы, что позволяет со¬
хранить полный топологический заряд
13.2.5.2. Рост нематической фазы. Законы сохранения, задаваемые
уравнениями (13.67) — (13.70), могут влиять на протекание поздних стадий
фазового перехода первого рода из изотропной в нематическую фазу, про¬
исходящего посредством зарождения нематических капель. Капли растут за
счет присоединения молекул из окружающей изотропной матрицы и путем
их слияния. На ранних стадиях капли малы, и, следовательно, поле дирек¬
тора в них практически однородно. В то же время ориентации директора
в различных каплях нескоррелированы. Когда несколько таких доменов
встречаются, имеется шанс, что их взаимная разориентация достаточна для
образования дефекта в точке соединения (рис. 13.18). Этот механизм рабо¬
тает для фазовых переходов как первого, так и второго рода. (Хотя новая
20^ P. Poulin, Н. Stark, Т. С. Lubensky and D. A. Weitz, Science 275 1770 (1997).
548
Гл. 13. Поверхностные явления
фаза возникает приблизительно одновременно для фазовых переходов вто¬
рого рода, различным частям может не хватить времени для согласования и
для создания пространственно однородного состояния). Похожий механизм
был предложен в качестве космологической модели структуры вселенной.
а
б
Рис. 13.18. Возможный механизм формирования дефектов (Киббл21^): по-разному
ориентированные монодомены упорядоченной фазы (а) могут формировать топо¬
логические дефекты при слиянии (б)
Другой механизм имеет место, когда размер растущих капель пре¬
вышает характерный размер ~ K/wq. Топологические дефекты появля¬
ются в каждой капле вследствие сцепления с поверхностью и топологи¬
ческих ограничений, рассмотренных выше. Это проиллюстрировано на
рис. 13.19, а, б, где можно увидеть нематические капли размером значи¬
тельно больше микрона, содержащие стабильные топологические дефекты.
Наличие дефектов обусловлено сцеплением с поверхностью, которое спо¬
собствует наклонной конической ориентации директора. Большинство де¬
фектов, кроме тех, концы которых захвачены на противоположных стенках
ячейки (рис. 13.19, в), исчезает, когда капли становятся достаточно больши¬
ми, чтобы заполнить все пространство между стеклянными ограничиваю¬
щими стенками.
13.2.5.3. Монополи: ежи с присоединенными дисклинациями. Осо¬
бенно интересные следствия топологических теорем (13.67)—(13.70) име¬
ют место, когда параметр порядка характеризуется более чем одним век¬
торным полем. Рассмотрим, например, гипотетический фазовый переход
из одноосной в двуосную нематическую фазу в сферической капле. Пусть 1
является директором, характеризующим обе фазы, и п — директор, кото¬
рый появляется только в двуосной фазе; li_n. Предположим, что окружаю¬
щая среда создает перпендикулярную ориентацию 1 на поверхности, так
что точечный дефект AT = 1 существует где-то в объеме, в соответствии
с (13.68). Положение ежа определяется упругими константами нематика.
Если константа поперечного изгиба относительна мала, еж будет находить¬
ся в центре сферы (рис. 13.20, а). Ориентация директора п в двуосной фазе
21) TW.B. Kibble, J. Phys. A Gen. Phys. 9, 1387 (1976).
§ 13.2. Поверхностные явления в анизотропных средах
549
Рис. 13.19. Двухфазная область при фазовом переходе нематик - изшродшя жад¬
ность. Нематическая смесь £7 в стеклянной ячейке толщины: 200 микрон. Белые
и черные стрелки показывают точечные и линейные дефекты соответственно
г
Рис. 13.20. Дефекты в капле двуосного нематика: монополь, полученный из ежа
N = 1 в поле 1 и дисклинации к = 2 (волнистая линия) в поле п; линия схло-
пывается в буджум (б), (в); поле п вокруг сингулярности к = 2 на поверхности
сферы (г)
550
Гл. 13. Поверхностные явления
тангенциальна к поверхности сферы. Следовательно, поле директора п
должно подчиняться теореме Эйлера-Пуанкаре (13.67) и, соответствен¬
но, должно содержать или две сингулярности с к = 1, или одну с к — 2
(рис. 13.20,г). Радиальный еж с присоединенной линией дефектов напоми¬
нает магнитный монополь Дирака2 2\ в котором радиальный «еж» вектора
магнитной индукции сопровождается струной (дисклинацией) векторного
потенциала (оба векторных поля перпендикулярны друг другу). Существует
способ уменьшить энергию системы, сдвигая 1-ежа в сторону поверхности
и таким образом уменьшая длину линейной дисклинации (рис. 13.20,6).
Получающаяся сингулярность на поверхности (рис. 13.20,в) является од¬
новременно ежом в 1-поле и буджумом с к — 2 в n-поле. Топологиче¬
ская возможность того, что линейный дефект схлопнется в точечную син¬
гулярность на поверхности, была впервые осознана Мерминым, который
рассматривал капли сверхтекучей анизотропной A-фазы в 3Не, имеющей
параметр порядка, аналогичный тому, что в двуосном нематике. Мермин
назвал сингулярность «буджумом»23^ (персонаж из произведения Льюиса
Кэррола «Охота на Снарка»).
Еж с присоединенными дисклинациями может оказаться стабильным
в отношении буджума, если имеется некоторый механизм, препятствую¬
щий схлопыванию дисклинаций. Жидкие кристаллы, имеющие слоевую
структуру (например, холестерики с коротким шагом и смектики С), об¬
ладают подобным стабилизирующим механизмом. Представим, например,
холестерическую каплю с концентрической сферической упаковкой слоев
(рис. 13.21). Нормаль 1 к слоям образует «радиального ежа». Тогда поле
Рис. 13.21. Холестерический монополь в капле (сферолит Робинсона), содержащий
дисклинацию к = 2 в поле директора. Радиус капли около 30 микрон
22>} Р. А. М. Dirac. Proc. Roy. Soc. (London) А 133, 60 (1931).
23^ N. D. Mermin. Boojums all the way through, Cambridge Univ. Press, 1990.
§ 13.2. Поверхностные явления в анизотропных средах
551
директора, тангенциальное к слоям, должно содержать одну дисклинацию
к — 2 или две дисклинации к\ = к2 = 1. Любая попытка уменьшить эти
линии нарушает эквидистантность слоев.
13.2.6. Капли в смектиках А
Хорошо известная особенность «сидячих» (т. е. прикрепленных к твер¬
дой поверхности) капель SmA, в противоположность свободно подвешен¬
ным, состоит в том, что их свободная поверхность имеет грани. Их слои
параллельны горизонтальной поверхности, и искривленная поверхность
капли приспосабливается к этому, создавая ступеньки, известные как тер¬
расы Гранжана. Как и в твердых кристаллах, наличие граней означает излом
в зависимости а (пи) при во = 0: w(9) та wq\ в | для 0 < \9\<С 1. Коэффици¬
ент сцепления велик, поскольку наклоненные слои не могут заполнить про¬
странство без создания дислокаций или ступеней: wq ~ В d (или we ~ сто),
где В — коэффициент сжимаемости SmA, a d — период слоев. В общем
случае ожидается, что в SmA-фазе поверхностное натяжение <т(ш/) ведет
себя немонотонно, имея два минимума: при 6 — 0и# = 7г/2и выраженный
максимум u>max ~ В d между ними. Для многих материалов равновесная
поверхностная ориентация на границе раздела SmA — изотропная жид¬
кость является тангенциальной, в — тг/2. Тангенциальное сцепление на
замкнутой поверхности, очевидно, не совместимо с однородной структу¬
рой в объеме. Как мы увидим ниже, можно снова провести различие между
двумя предельными случаями: «большие» капли, R > К/Дет, и «малые»
капли, R < К/Лет, где Да = сг±(в = тт/2) (в — 0) представляет собой
анизотропию поверхностной энергии (меньшую, чем wmax) • Малые капли
имеют однородную структуру и форму Вульфа. Большие капли содержат
конфокальные домены (КФД), в которых поверхностную ориентацию уда¬
ется сохранить за счет объемных искажений, не требующих больших затрат
энергии (рис. 13.22, рис. 13.23).
Представим себе большую каплю SmA со сферической упаковкой слоев
и вырежем из нее круговой конус с вершиной в центре сферы (рис. 13.22, а).
Теперь заполним отверстие круговым конусом, принадлежащим к КФД
(рис. 13.22, б, в). Основание КФД изменяет перпендикулярную поверхност¬
ную ориентацию в тангенциальную, и тем самым уменьшает поверхност¬
ную энергию системы на величину ~ тга2(а± — <7ц). Вследствие того что
нормали к слоям являются одновременно нормалями для КФД и сфериче¬
ских слоев, смектические слои плавно пересекают коническую поверхность
между областью со сферической упаковкой и КФД. Упругая энергия КФД,
имеющая порядок Ка, — единственная энергетическая плата, необходимая
для согласования граничных условий.
Сколько конусов должно быть удалено из сферы и заменено КФД?
Мы можем начать с нескольких максимально возможных доменов радиуса
flmax < R, затем заполнить пространство между ними меньшими доме¬
нами и т.д. (рис. 13.24). Получающаяся поверхностная картина представ¬
ляет собой апполониево заполнение сферы кругами. Если тангенциальное
сцепление является бесконечно большим, последовательные заполнения
552 Гл. 13. Поверхностные явления
Рис. 13.22. Заполнение сферы конфокальными доменами. Коническое отверстие в
сферической упаковке смектических слоев (а) заполняется с помощью конфокаль¬
ных доменов (6) плавно (<?)
Рис. 13.23. Смектическая A-капля с тангенциальными граничными условиями, по¬
груженная в глицерин (диаметр та 90 мкм). Капля заполнена конфокальными доме¬
нами в геометрии рис. 13.22. Домены с радиусом основания, меньшим а* ~ 10 мкм,
отсутствуют
§ 13.2. Поверхностные явления в анизотропных средах
553
будут продолжены до тех пор, пока минимальное основание домена не до¬
стигнет молекулярного размера Л = у/К/В (см. гл. 5, 10). Однако если
((jj_ — сгц) является конечным, предел итераций, определяемый балансом
поверхностной энергии ~ a2(aj_ — сгц) и энергии кручения ~ Ка мельчай¬
шего из ФКД, составит24^
К/(а±_ - а ),
(13.71)
что может быть гораздо больше Л. Зазоры, размер которых меньше а*
заполнены слоями со сферическим изгибом.
А
м
• _ У: •
N • . •• •• > •••. ” f -
• •: ' 4 --г s - r • * •• . ,
’.if- . > • « • ^ ' •
* y: • ’ ’ '• v- . . * •
Рис. 13.24. Апполониево заполнение поверхности с помощью серии конфокальных
доменов. Основания доменов (черный цвет) заменяют невыгодное перпендикуляр¬
ное сцепление (белые зоны) на благоприятное тангенциальное сцепление
Максимальный размер КФД атах в процессе заполнения также ограни¬
чен. Это связано с тем, что угловые отклонения ~ a/2R от строго танген¬
циальной ориентации в основании КФД возрастают с увеличением размера
домена а. Основание самого большого домена, показанного на рис. 13.23,
реструктурировано, что позволяет избежать возникающих угловых расхо¬
ждений. Этот дисбаланс стремится уменьшить размер самых больших до¬
менов,25) атах < R-
Упаковка смектических слоев в плоских образцах с пластинами, обес¬
печивающими тангенциальное сцепление, часто похожа на упаковку сло¬
ев в сферических каплях. Разумеется, абсолютный минимум свободной
энергии в плоских ячейках отвечает однородной структуре со слоями, пер¬
пендикулярными пластинам. Однако история образца (фазовые переходы,
24) Лаврентович О. Д. ЖЭТФ 91, 1666 (1986).
J. В. Fournier and G. Durand. J. Phys. II France 1, 845 (1991).
554
Гл. 13. Поверхностные явления
течения вещества) могут приводить к метастабильным текстурам КФД,
часто называемым полигональными текстурами. Например, когда смек¬
тическая A-фаза образуется непосредственно из изотропного расплава,
первичные КФД формируются посредством «столбиков», «батоннетов» —
зародышей SmA-фазы, растущих из изотропного расплава, и затем за¬
крепляются на пластинах. Рассмотренная выше модель сферической капли
является только первым шагом в понимании особенностей КФД, образую¬
щихся из батоннетов, что было впервые описано Фриделем и Гранжаном261
Усложнение возникает из-за того, что батоннеты имеют вытянутую, отлич¬
ную от сферической форму вследствие малости поверхностного натяжения
на границе раздела смектик А - изотропный расплав.
Рисунок 13.25 показывает типичную полигональную текстуру SmA.
Рис. 13.25. Полигональная текстура в смектической А-ячейке с вырожденными
тангенциальными граничными условиями. Полигоны заполняются эллиптически¬
ми основаниями ряда конфокальных доменов, итеративно уменьшающихся в раз¬
мерах. Понижение температуры от (а) 40° С до (б) 21 °С приводит к уменьшению
характеристического размера обрезания а* ~ К/ Да, так что малые конфокальные
домены исчезают. Материал: СНР20(СбН4)СН = N(C6H4)C4H9
26 ^ G. Friedel and F. Grandjean. Bull. Soc. Fr. Mineral. 33, 409 (1910).
§ 13.2. Поверхностные явления в анизотропных средах
555
Фокусируя микроскоп на верхней или нижней пластине, можно различить
две полигональные сетки линий дефектов. Размеры полигонов близки к тол¬
щине образца. Каждый полигон представляет собой основание пирамиды,
вершина которой лежит на противоположной пластине. Вершины пирамид,
основания которых лежат на нижней пластине, совпадают с вершинами по¬
лигонов, лежащих на верхней пластине, и наоборот.
Для прояснения геометрии заполнения пространства, возьмем для про¬
стоты пирамиды с четырехугольным основанием. Все пространство может
быть заполнено двумя наборами пирамид типа H(ABCD) и A(EFGH), вер¬
шины которых находятся на противоположных поверхностях образца, и до¬
полняющим семейством тетраэдров типа ABGH и ADEH (рис. 13.26), кото¬
рые заполняют область между пирамидами. Жирные линии на рис. 13.26, а
Рис. 13.26. Общая схема заполнения пространства конфокальными доменами; см.
в тексте. Ориентация директора на ограничивающей пластине (область FGHE) яв¬
ляется тангенциальной в основании конфокальных доменов и перпендикулярна
поверхности (или слегка наклонена) в области между основаниями доменов
F
Е
а
А
В С
В
с
556
Гл. 13. Поверхностные явления
показывают линии дефектов, которые могут быть выявлены под микроско¬
пом. (Тонкие линии не связаны с сингулярностями директора п и служат
только для выявления структуры). Наблюдаемые линии дефектов представ¬
ляют собой эллипсы и гиперболы внутри пирамид, так же как и стороны
полигонов. Стороны полигонов образуются верхними и нижними ребра¬
ми тетраэдров. Эти ребра являются частями большего размера пар ги¬
пербола-эллипс: каждый тетраэдр является частью одного большого КФД
(рис. 13.26,6).
Из вышеизложенного следует, что проблема заполнения пространства
в полигональной текстуре сводится к проблеме заполнения пирамид. Это
заполнение происходит аналогично рассмотренному выше заполнению ка¬
пель. Эллипсы семейства КФД, последовательно итеративно заполняющих
пространство, вписываются в полигоны. Внутри эллипсов ориентация яв¬
ляется тангенциальной (рис. 13.26,в,г). Гиперболы всех этих КФД сходят¬
ся в вершине пирамиды (точки А, Н, рис. 13.26,а,в). Остающиеся зазоры
внутри пирамид заполнены слоями со сферической кривизной с центром в
вершине пирамиды (рис. 13.26, в). На поверхности образца области между
различными КФД имеют нормальную (или слегка наклоненную) ориен¬
тацию молекул (рис. 13.26, б). Последовательное итеративное заполнение
обрывается на некотором а*, определенном как в (13.71), но с модифи¬
цированными численными константами. Рисунок 13.25 показывает, что а*
может быть функцией температуры. По мере понижения температуры мель¬
чайшие КФД исчезают, главным образом вследствие возрастания упругой
константы поперечного изгиба К.
Заметим, что слои SmA плавно переходят от одной пирамиды к другой
через тетраэдры: в плоскости пересечения (АВН на рис. 13.26,г) слои как
пирамиды H(ABCD), так и тетраэдра ABGH имеют общий центр кривиз¬
ны (точка Н). Таким образом, изогнутые смектические слои заполняют все
пространство, сохраняя неизменным свой период и удовлетворяя гранич¬
ным условиям за счет образования дефектных структур с размерностью,
меньшей двух.
Задача 13.1. Найти поверхностный избыток свободной энергии
Гельмгольца (а) и внутренней энергии (б) для однокомпонентной системы
с двумя сосуществующими фазами 1 и 2.
Ответ
я) ^surf — о A -f //iVsurf; если положение разделяющей поверхности
фиксировано за счет выбора ArSUrf = 0, то поверхностное натяжение рав¬
но поверхностному избытку свободной энергии Гельмгольца на единицу
■Fsurf
площади а —
Л
б) -Esurf — СУ А TSsurf /^^Vsurf •
Задача 13.2. Выразить относительную адсорбцию (13.15) через экс¬
периментально измеряемые величины, такие как V, А, концентрация с'
растворителя и концентрация с растворенного вещества в объеме фаз 1 и 2.
§ 13.2. Поверхностные явления в анизотропных средах
557
Ответ. См., например: Problems in Thermodynamics and Statistical
Physics, Edited by P.T. Landsberg, PION, London, 1971. [Перев. на рус¬
ский язык: Задачи по термодинамике и статистической физике / Под. ред.
И. П. Базарова. — М.: Мир, 1974.]
Используя N — N\ + N2 4- АТ, сперва получаем: Г=(N ~~ Vi ci — V2 с2) / А
и затем, исключая V\ wV2,
Г relative
А
N - Vci - (N* - Vc[)
Cl — С 2
7
/
C'l c2
Задача 13.3. Найти давления pi,p2 и химические потенциалы pi и р2
двух фаз, находящихся в равновесии, для случая, когда фаза 1 представляет
собой сферу большого радиуса г.
Ответ. Для большого радиуса кривизны параметры системы должны
быть близки кро и /хо * Раскладывая и р2 в ряд в окрестности (напри¬
мер, р\ — ро + (pi — po)vi + •. •) и используя уравнение Лапласа - Юнга,
получаем
. 2а V2 , 2а г»1
Pi = РО + , Р2 = РО +
ГУ 2 — Г V2 — Vl
И
. 2a V1V2
pi _ р2 — Мо +
Г V — V1
Задача 13.4. Некоторые параметры (какие?), определяющие кри¬
тический радиус г* образования зародышей новой фазы (13.32), трудно
измерить экспериментально. Выразить г* через величины, которые мож¬
но действительно измерить: ро, р2> Щ, и v2, предполагая, что химические
потенциалы и давления двух фаз несильно отличаются от ро и ро-
Ответ. Используя решение предыдущей задачи, получаем
* 2а vi
Г — .
р2 ~р0V2- VI
Задача 13.5. Большая капля помещена на твердую поверхность в ва¬
кууме. Силы гравитационного притяжения делают поверхность капли плос¬
кой в центральной части (блин). Уравнивая капиллярные и гравитационные
силы, оценить толщину центральной части капли в зависимости от капил¬
лярной длины и контактного угла.
Ответ. Сочетая уравнение равновесия между капиллярными и гра¬
витационными силами, Ssрг + ~pgh2 — 0, где Sspr < 0 дается выражением
2
(13.36), и закон Юнга (13.35), получаем: h = \/2Acsin (6е/2), где Ас опре¬
делено (13.23).
558
Гл. 13. Поверхностные явления
Задача 13.6. Рассмотрим гибридно-ориентированную нематичес¬
кую пленку, в которой поле директора искажено в плоскости, перпенди¬
кулярной поверхности пленки вследствие разницы в направлениях поляр¬
ного сцепления во и Od на двух ограничивающих поверхностях z = 0 z = h
(см. п. 5.4.2). Предполагая, что все упругие модули Франка равны К и что
1
потенциалы сцепления имеют вид: fSi — -Wi(0i — в{) , г — 0, /г, найти
расклинивающее давление, вызванное искажениями директора в пленке
толщины h^> К/Wi.
Ответ.
11(h) = -К
1 ту ( Он
h -f- K/wq -f К
Ответ может быть иным для пленок малой толщины h < K/wiy посколь¬
ку в тонких пленках происходят ранообразные структурные превращения
[см. обзор: О. D. Lavrentovich and V М. Pergamenshchik, Int. J. Mod. Phys.
B9, 251 (1995)].
Задача 13.7. Полубесконечный объем нематика ограничен поверх¬
ностью с синусоидальным профилем: г — и sin (qx), и q~l. Молекуляр¬
ные взаимодействия ориентируют директор параллельно подложке. Вы¬
числите упругую энергию деформации в одноконстантном приближении
для следующих конфигураций поля директора: а) п ~ (пх, 0, nz), б)
п=(0, 1,0).
Ответ. См.: D. W. Berreman, Phys. Rev. Lett. 28, 1683 (1972).
а) Пусть ф — малый угол между директором и осью х. Плотность
свободной энергии
К
приводит к уравнению Эйлера - Лагранжа
д2 'ф d2ip _ q
дх2 dz2
решение которого имеет вид: ф — uqexp(-zq) cos (qx). Энергия на едини¬
цу площади равна = Ku2q3 /4.
б) Ify) = 0. Если вертикальная плоскость, содержащая директор,
повернута на угол ip относительно оси у, то энергия становится равной
F = Ku2q3 cos2 ф/4.
Задача 13.8. Используя (12.4) и (13.63), найти топологические заря¬
ды к, N и параметры С для буджумов на рис. 13.14, 13.15.
Ответ. А; = 1 для всех конфигураций, за исключением тех, что по¬
казаны в частях (в) рисунков. Чтобы найти N, запишите поле директора
в виде
n = [sin в (и) cos ip\ sin в(и) sin ip\ cosO(u)].
Литература для дальнейшего чтения
559
Для буджума на рис. 13.14 в (и) — 2(тг — во)и/тг + 2 Оо — 7г, для буджума
на рис. 13.15 в (и) = 20ои/тт — 2во. Интегрирование по 0 ^ и < 27т
и 7г/2 ^ и < 7г дает: С = cos2(#o/2), С — — sin2(#o/2), TV = 1, TV = О
соответственно.
Литература для дальнейшего чтения
1. A. W. Adamson and А. Р Gast, Physical Chemistry of Surfaces, John Wiley & Sons,
Inc., N. Y., 1997, 784 p.
2. Блинов Л. M, Кац E. К, Сонин А. А. Поверхностные явления в термотропных
жидких кристаллах. УФН, 152, 449 (1987).
3. P.S. Drzaic, Liquid Crystal Dispersions, Series on Liquid Crystals, vol. 1, Edited
by H.L. Ong, World Scientific, Singapore, 1995, 430 p.
4. D. H. Everett, Basic Principles of Colloid Science, Royal Society of Chemistry,
London, 1988, 244 p.
5. P G. de Gennes, Rev. Mod. Phys. 57, 827-863 (1985).
6. C. Isenberg. The Science of Soap Films and Soap Bubbles, Dover, 1992.
7. B. Jerome, Rep. Prog. Phys. 54, 391 (1991).
8. Ландау Л.Д., Лифшиц E. М. Статистическая физика. 3-е изд. — М.: Наука.
Главная редакция физико-математической литературы. 1976.
9. L. Leger and J\ F. Joanny, Rep. Prog. Phys. 431 -486 (1992).
10. P. Nozieres, Shape and growth of crystals, in: Solids Far From Equilibrium, Edited
by C. Godreche, Cambridge University Press, Cambridge, 1992.
11. PS, Pershan, Liquid Crystal Surfaces, J. Phys. (France) 50, Coll. C7, C7-1 (1989).
12. J. S. Rowlinson and B. Widom, Molecular Theory of Capillarity, Oxford University
Press, N. Y. and London, 1982.
13. T.J. Sluckin and A. Poniewierski, in Fluid Interfacial Phenomena, Edited by
C.A. Croxton, John Wiley & Sons, N. Y., 1986, Chapter 5.
14. J. D. Weeks, The roughening transition, in Ordering in Strongly Fluctuating
Condensed Matter Systems, Edited by T. Riste, Plenum Press, N. Y., 1980, p. 293.
Дополнительная литература
1. Веденов А. А. Физика растворов. — М.: Наука, 1984.
2. Гегузин Я. Е. Капля. — М.: Наука, 1973.
3. Дерягин Б. В., Чураев Н. В., Муллер В. М. Поверхностные силы. — М.: Наука,
1985.
4. Дерягин Б. В. Теория устойчивости коллоидов и тонких пленок. — М.: Наука,
1986.
ГЛАВА 14
УСТОЙЧИВОСТЬ КОЛЛОИДНЫХ СИСТЕМ
Микроскопическая устойчивость «мягких» материалов (жидких кри¬
сталлов, коллоидов и полимеров) — проблема, имеющая много граней.
В случае термотропных жидких кристаллов природа взаимодействий
достаточно хорошо известна (стерические силы отталкивания, ван-дер-
ваальсовы силы притяжения, дипольные взаимодействия), хотя здесь ма¬
ло что проработано в деталях. Стоит отметить, что благодаря возможно¬
стям современных компьютеров можно проводить подробные вычисления
методом Монте-Карло термодинамических функций и фазовых перехо¬
дов, используя потенциалы Лебвол-Лашера или Гэй-Берна, упомянутые
в п. 1.3.5, а также осуществлять моделирование жидкокристаллических
молекулярных структур на основе твердых эллипсоидов со стерическим
отталкиванием. Некоторые из этих вычислений уже принесли интересные
результаты (см. обзор Пелковитца1)).
Коллоидные системы — обозначение, относящееся ко множеству раз¬
личных диспергированных систем. Отличительной особенностью послед¬
них является то, что один из компонентов раствора — растворенное
вещество — образует частицы размера г, настолько малого, что поверх¬
ностные эффекты (сх г2) доминируют над объемными (сх г3). Стабиль¬
ность коллоидных суспензий зависит, следовательно, от таких величин, как
поверхностное натяжение, электростатические взаимодействия, включаю¬
щие поверхностные заряды растворенного вещества и электролитический
состав растворителя, а также от взаимодействий Ван-дер-Ваальса. К это¬
му необходимо также добавить броуновское движение, поскольку части¬
цы обычно достаточно малы, чтобы участвовать в термической диффузии.
Название «коллоидные системы» также дается системам, в которых ча¬
стицы растворенного вещества имеют только два малых измерения (на¬
пример, стержни поли-7-бензил-/,-глутамата {poly-^-benzyl-(L)-glutamate,
PBLG), полугибкие полимеры, стеклянные волокна) или одно малое изме¬
рение (т. е. пленки поверхностно-активных веществ, пластинки глины или
слюды). Частицы растворенного вещества в определенном интервале кон¬
центраций могут самоорганизовываться в различные упорядочные фазы,
часто называемые лиотропными жидкими кристаллами. Этим они отлича¬
ются от термотропных жидких кристаллов, которым не нужен растворитель
для образования мезоморфного состояния в определенном интервале тем¬
ператур. Например, агрегаты молекул поверхностно активного вещества
могут образовывать нематическую фазу (когда частицы представляют со¬
бой эллиптические мицеллы), колончатую фазу (в случае цилиндрических
^ R, A. Pelcovits. Theory and Computation, in Handbook of Liquid Crystals Research,
Edited by R. J. Collins and J. S. Patel, Oxford University Press, N. Y., 1997.
561
мицелл), ламеллярную фазу (когда агрегаты являются непрерывными бис¬
лоями) и другие фазы.
В данной главе не рассматриваются подробно коллоидные системы как
таковые (в гл. 13 обсуждаются некоторые подходы, как относящиеся к кол¬
лоидам, так и имеющие более общее значение) и основное внимание будет
уделено свойствам лиотропных систем. Здесь возможности для теоретиче¬
ского описания гораздо богаче, чем в термотропных системах (хотя зна¬
чительные успехи в численных расчетах до сих пор отсутствуют). Меж-
молекулярные силы и силы, действующие между коллоидными частицами,
имеют различное происхождение: электростатическое, дипольное, ван-дер-
ваальсово, энтропийное (последнее есть следствие больших флуктуаций
в мембранах — эффект, отсутствующий в собственно коллоидных раство¬
рах). Имеются также силы отталкивания более сложной природы, обуслов¬
ленные присутствием растворителя — так называемые сольватационные
силы (или гидратационные силы — в тех случаях, когда растворителем
является вода).
Эта глава содержит краткое введение в проблему электростатических
сил, действующих между жесткими заряженными поверхностями типа пла¬
стин и сфер (уравнение Пуассона-Больцмана), и их конкуренции с силами
Ван-дер-Ваальса (теория Дерягина-Ландау-Вервея-Овербека (ДЛВО),
см. п. 14.1.6). Этот предмет в течение долгого времени относился к компе¬
тенции коллоидного сообщества, и ему посвящена многочисленная литера¬
тура. Поведение нежестких флуктуирующих поверхностей стало изучаться
сравнительно недавно. Здесь возникают две предельные ситуации, которые
будут последовательно рассматриваться:
а) в присутствии слабого электролита электростатические силы рас¬
пространяются на большие расстояния и в определенной мере ослабляют
флуктуации, внося таким образом вклад в величины к и >с (см. (5.21),
(5.22));
б) в присутствии сильного электролита заряды экранированы, что спо¬
собствует развитию флуктуаций большой амплитуды, дающих вклад в си¬
лы отталкивания между соседними мембранами. Теория Хелфриха явилась
ключевой в понимании этих процессов и прошла успешную эксперимен¬
тальную проверку.
Вследствие разнообразия предмета обсуждения и трудностей, крою¬
щихся в применяемых подходах, мы опустили полный вывод некоторых
важных формул.
Наконец, в этой главе будут рассмотрены, хотя и менее подробно, си¬
стемы, образованные составными блоками нулевой размерности — части¬
цами. Некоторые из них являются коллоидными кристаллами. Достаточно
детально эти фазы описаны в ряде превосходных учебников. Системы, об¬
разованные одномерными составными блоками, — нематическая упаковка
полимеров, гексагональные фазы, изотропные растворы вирусов типа ВТМ
и т. д. кратко представлены в следующей главе.
562
Гл. 14. Устойчивость коллоидных систем
§ 14.1, Взаимодействия между жесткими поверхностями
Модели, которые будут рассмотрены ниже, содержат определенные
упрощения. Предполагается, что кроме электростатических взаимодейст¬
вий, отсутствуют молекулярные взаимодействия между заряженными
частицами. Кроме того, дискретный характер и конечный размер ионов
не учитываются. Эти предположения удовлетворяются в случае малых кон¬
центраций зарядов. Следовательно, можно принять континуальное описа¬
ние среды, где заряды распределены непрерывно во всем пространстве.
14.1.1. Уравнение Пуассона-Больцмана
Начнем с геометрии жесткого тела (в виде сферы, полубесконечной
среды, ограниченной плоскостью, и т. д.), на поверхности которого нахо¬
дятся фиксированные заряды и которое погружено в электролитический
растворитель с известной степенью диссоциации. Обычно растворителем
является вода. Будучи чистой, она содержит Н+ и ОН” ионы в равных
молярных концентрациях 10~7 М вдали от заряженной поверхности (М —
обозначение для единиц моль/дм3). Концентрация ионов (число ионов, при¬
ходящихся на единицу объема) составляет п+ = п~ — 10_т АГд на дм3
при комнатной температуре (N\ — число Авогадро). Это малые концен¬
трации по сравнению с обычными концентрациями в воде противоионов,
компенсирующих поверхностные заряды, или по сравнению с концентра¬
циями ионов в электролитах (см. задачу 14.1). В дальнейшем пf и nj бу¬
дут обозначать концентрацию положительных (отрицательных) ионов ти¬
па i(j) в присутствии заряженной поверхности (поверхностная плотность
зарядов a), zf отвечает положительной валентности катионов, a zj —
отрицательной валентности анионов. Поэтому полная плотность зарядов
где е равно заряду электрона и имеет положительный знак. Полный заряд
системы равен нулю, следовательно
где а/е — концентрация поверхностных ионов на единицу площади.
Как мы увидим ниже и как этого следовало ожидать, ионы, знак кото¬
рых противоположен зарядам, находящимся на поверхности, собираются
в большом количестве вблизи поверхности, образуя так называемый двой¬
ной слой. В теории это описывается следующим образом: наличие зарядов
приводит к появлению электрического поля Е = — (ip — электрический
в некоторой точке г в растворе имеет вид
(14.1)
р(г) dV + a = 0
(14.2)
§ 14.1. Взаимодействия между твердыми поверхностями
563
потенциал), которое уудовлетворяет уравнению Пуассона:
—div Е = У'2ср = —-р(г), (14.3)
его
где е — диэлектрическая проницаемость растворителя (равная 78,5 для во¬
ды и 2,0 для циклодекана), £q — диэлектрическая проницаемость вакуума.
Мы будем использовать единицы СИ; для возвращения к электростати¬
ческим СГС-единицам необходимо заменить величину £о, где-бы она ни
появлялась, на 1 /4 7г.
Распределение р(г) задается электрическим потенциалом. При этом хи¬
мический потенциал заряженной частицы с валентностью z может быть
записан в виде
р = ро -f ezip, (14.4)
где ро — химический потенциал системы в отсутствие электрического по¬
тенциала. В большинстве реальных систем концентрация заряженных ча¬
стиц мала, так что они образуют разбавленный идеальный раствор, для
которого химический потенциал может быть представлен в виде
= кБТ\пп. (14.5)
Для системы, находящейся в равновесии, химический потенциал р, прихо¬
дящийся на частицу, есть величина постоянная, и мы получаем уравнение
Больцмана:
&Z g LD / Л A f \
Щ = nij0exp-—(14.6)
kfoT
где riit о — концентрация частиц в точках с <р ~ 0, для удобства взятых на
бесконечности («резервуар»), в том случае, когда имеется одна единствен¬
ная жесткая граница.
Уравнение Пуассона-Больцмана (ПБ) получают подстановкой (14.6)
в (14.3):
VV = y^ni.oexp-^^. (14.7)
еео къТ
1
Это дифференциальное уравнение должно быть дополнено законом сохра¬
нения заряда (Г4.2) играничнымиусловиями, которые обычно записываются
в одном из следующих видов.
1. Фиксированный потенциал: ср — const (например, на бесконечности
Ч> = 0).
2. Фиксированные заряды: —Es п = — = —.В этом уравнении нор-
Эп ££о
маль п к поверхности направлена наружу, в сторону растворителя.
Уравнение ПБ в общем случае трудно решить, за исключением несколь-
ких специальных ситуации, когда валентности заряженных частиц одни
и те же и заряженные границы имеют простую геометрию (сферы или
изолированная плоскость, или две плоскости, разделенные раствором, в
564
Гл. 14. Устойчивость коллоидных систем
который не добавлен электролит). Решения, полученные в этих простых
случаях, свидетельствуют о существовании двух фундаментальных длин:
длины Гоу и- Чепмена Ъ и длины Дебая -Хюккеля А#. Физическая интер¬
претация этих длин имеет важное значение и позволяет рассматривать, по
крайней мере на качественном уровне, поведение самых сложных систем21
14.1.2. Фундаментальные длины в задаче Пуассона-Больцмана
14.1.2.1. Длина Гоуи-Чепмена для слабых электролитов. Рассмот¬
рим плоскую бесконечную заряженную поверхность в контакте с раство¬
рителем без добавления электролита. Это может быть заряженная сторо¬
на жесткой мембраны, образующая границу непроводящей среды. Тогда
в растворе (помимо Н+ и ОН“)) присутствуют лишь ионы, являющиеся
противоионами ионов, находящихся на поверхности. Мы будем полагать
поверхностную плотность заряда а отрицательной, поскольку в большин¬
стве систем, представляющих практический интерес, фиксированные на
поверхности ионы заряжены отрицательно. Кроме того, все валентности
положим равными единице. Ось х направлена перпендикулярно границе
раздела. Тогда уравнение ПБ может быть записано в виде
d?<p eno ew
— ехр
dx2 ЕЕ о &БТ
где по — отсчетная концентрация противоионов (для которой потенциал
принимается равным нулю), и объемная плотность противоионов меняет¬
ся по закону п(х) = п0 ехр(—е<р/к^Т). Легко проверить, что решением
уравнения является
ф) = in (^±1 ] . (14.8)
Поскольку — = - — (граничные условия для фиксированных заря-
дх Ж-и ЕЕ о
дов), имеем
b = (14.9)
(7
В (14.8) £ — произвольная длина, которая позволяет добавить любую кон¬
станту к потенциалу. Она должна быть выбрана в соответствии с величиной
исходной концентрации противоионов. Соответствующие вычисления дей¬
ствительно показывают, что произведение no£2 = —ob/e. Это выражение
может быть также записано в виде
п0(2 = —. е= — , (14.10)
2п£ АкеоекьТ
где £, так называемая длина Бьеррума (Bjerrum), является расстоянием,
за пределами которого чисто электростатическое взаимодействие между
P. Pincus, J.-F. Joanny and D. Andelman. Europhysics Lett. 11, 763 (1990).
§ 14.1. Взаимодействия между твердыми поверхностями
565
двумя зарядами начинает слегка размываться их броуновским движением.
В этих условиях заряды не могут рассматриваться как неподвижные, и эн¬
тропийные эффекты должны быть учтены; величина I в воде составляет
О
порядок 7А.
Длина Гоу и- Чепмена Ь отвечает толщине слоя раствора, контактирую¬
щего с границей раздела и содержащего половину полного числа проти¬
воионов. Ее типичное значение для воды при плотности сг, равной одному
элементарному заряду, приходящемуся на 0,16 нм2 (т. е. I Кл/м2 в единицах
ккТ
СИ), и — 25,69 мВ при комнатной температуре (298 К), составляет b =
е
= 4 • 10“2 нм, т. е. она представляет собой весьма малую область, вплотную
примыкающую к пластине. Плотность противоионов меняется по парабо¬
лическому закону:
п(х)
2тг£(х + Ь)2
(14.11)
(задача 14.1). Логарифмическая расходимость (14.8) не имеет большого
физического смысла — для образца конечного размера она исчезает.
14.1.2.2. Длина экранирования Дебая - Хюккеля для сильных элек¬
тролитов. Противоположная ситуация возникает, когда граница раздела
контактирует с сильным электролитом, например 1 моль/л NaCl в воде.
Пусть по = п+(оо) = п_(оо) представляет собой плотность ионов каж¬
дого знака, присутствующих в растворе. Вычисления легко провести, если
эти ионы и противоионы имеют одинаковую валентность, — положим ее
равной единице. Следовательно, нужно решить следующее уравнение ПБ:
VV=—sh^i, (14.12)
£о£ къТ
где теперь п0 — концентрация электролита в резервуаре. В случае, ко¬
гда возможна линеаризация (приближение Дебая-Хюккеля), т. е. при Ч> <
< к^Т/е (« 25 мВ при комнатной температуре, «0,9-10 4 в единицах
СГС), мы получаем
V2<р = = к20ф) с kD = А^1 = 7 , (14.13)
££окЪТ \££окь1. /
т. е. экспоненциальное уменьшение (р(х) = <ps ехр(—х/Х&) с характерной
длиной А о; <Ps — потенциал заряженной границы раздела. Заметим, что
kjj = SttEtiq. Длина Дебая-Хюккеля Ад, также называемая длиной Дебая,
определяет характерное расстояние, на котором электростатические эффек¬
ты, вызванные заряженной плоскостью, экранированы. В общем случае она
может быть выражена как
ad = ('l&miV‘/!. (14.14)
££оквТ
566
Гл. 14. Устойчивость коллоидных систем
Типичное значение А# для сильного электролита (1 моль/л NaCl) составляет
1 нм при комнатной температуре. Более детальное обсуждение уравнения
(14.12) дано ниже в п. 14.1.5.
14.1.3. Свободная энергия и тензор напряжений Максвелла
14.1.3.1 Свободная энергия и «расклинивающее» давление. Плот¬
ность свободной энергии электрического двойного слоя (на единицу пло¬
щади границы) имеет следующее выражение:
С
Л
Fe 1
dcr'ipAa'),
(14.15)
о
где интегрирование проведено по всем (жестким) заряженным поверхно¬
стям. Величина da/ips(a/) определяет работу, которую необходимо совер¬
шить для переноса заряда da' из точки с потенциалом V — 0 в точку
с потенциалом V = (ps(af). Эту величину можно также получить, если за¬
писать свободную энергию в виде суммы избыточной электростатической
объемной энергии однородной системы,
1
bulk
£6о
Ё2 d\
/
1
-еео
2
(W)2 dV,
(14.16)
и избыточной конфигурационной энтропии ионов в растворе по отношению
к ионам в резервуаре, которая в случае двух типов ионов противоположного
знака и одинаковой валентности записывается как
К
entropy
ккТ
EUi ill
1
П;
п0
У" rii + 2?г0
dV.
(14.17)
Полная энергия представляет собой Fe\ = Fbuik -Ь Entropy (подробнее
см. работу: Голдстейн и др.3^).
Если раствор помещен между двумя идентичными заряженными пла¬
стинами, суммарные силы электростатического и осмотического происхо¬
ждения таковы, что вызывают отталкивание между пластинами. Если одна
из пластин закреплена, то сила, действующая на другую, имеет вид
Pd
dFe i
д d
Т, ni
где d
расстояние между пластинами. Пусть п(х = 0) является пол¬
ной плотностью частиц в плоскости, расположенной посередине между
^ R. Е. Goldstein, A. I. Pesci and V. Romero-Rochin. Phys. Rev. A41, 5504 (1990).
§ 14.1. Взаимодействия между твердыми поверхностями
567
пластинами, х — 0. Можно показать4^, что общее выражение для «раскли¬
нивающего» давления pd записывается как
Pd = кБТ п(* = 0)-У п*.о • (14.18)
Эту величину можно интерпретировать как избыточное осмотическое
давление ионов в срединной плоскости по отношению к осмотическому
давлению в резервуаре ро — к^Тщ — кьТ Y^ini,o- Это видно из формы
(14.18), напоминающей уравнение Вант-Гоффа для осмотического давле¬
ния. Отметим, что именно вследствие электростатического потенциала, pd
не равно давлению в резервуаре.
В случае когда в растворе нет электролита, п(х = 0) сводится к плотно¬
сти противоионов и — 0. Тогда pd можно также выразить
как функцию плотности противоионов ns = п(х = 0) + а2
2s£Qk^T
(задача 14.2):
Pd = къТп(х = 0) = кБТ ( п
I
14.1.3.2. Тензор напряжений Максвелла; продольное и попереч¬
ное давления. Полное «осмотическое» давление pd в приведенном вы¬
ше уравнении (14Л 8) содержит два члена, один из которых имеет чисто
осмотическую природу, а другой обусловлен электростатическими заряда¬
ми. Присутствие двух подобных членов может стать более понятным, если
рассмотреть электростатические силы, действующие на ионы в растворе.
Эти силы могут быть представлены в континуальном пределе с помощью
тензора напряжения (тензора Максвелла)
= £со fEi(r)Ej(r)'- -E2(r)Sij) -p(r)6ij. (14.19)
^ 2 '
Вывести этот тензор весьма непросто. Его компоненты определяются сле¬
дующими силами (на единицу объема):
1) силой, вызванной электрическим полем, р(r)E = ££0EdivE, дей¬
ствующей на свободные заряды р(т) (также записываемой в виде eeoEVE
или (eeoEkdiEi);
2) силой Р VE (или (P{diEk)), действующей на заряды, обусловленные
поляризацией среды рр(г) = —VP, также вызванной электрическим полем;
3) силой, связанной с локальным избытком осмотического давления
р(г), которое должно существовать в среде для данной концентрации ионов
J. Israelachvili, Intermolecular and Surface Forces, 2nd edition, Academic Press,
N. Y., 1992.
568
Гл. 14. Устойчивость коллоидных систем
в точке г. Более детальное изложение заинтересованный читатель найдет
в книгах51
Продольное напряжение. Локальный избыток осмотического давле¬
ния р(г) таков, что р(х) = к^Т(п(х) - п0), где п0 — пг, о- Компонента
= 0. Легко видеть, что а^х не зависит от х, поскольку это первый интеграл
общего уравнения ПБ. Продольное напряжение есть не что иное, как рас¬
клинивающее давление, взятое с обратным знаком.
Поперечное напряжение. Другая сила, которая также представляет
интерес, — поперечная сила pt{x), т. е. компоненты а^у и взятые с от¬
рицательным знаком. Рассматривая, как и раньше, плоские заряженные
пластины, получаем
pt{x) = р(х) + -ssqE2, (14.20)
2
что также можно записать в виде
Pt(x) = pd + ££0Е2, (14.21)
т. е. величина pt зависит от х.
14.1.4. Слабые растворы электролитов
Вначале рассмотрим случай слабых электролитов, когда эффект экрани¬
рования фиксированных зарядов мал (большая дебаевская длина), а затем
перейдем к противоположному случаю сильных электролитов. В обзорной
статье Андельмана6) можно найти детальное описание различного рода ре¬
шений уравнения Пуассона-Больцмана в зависимости от величин безраз¬
мерных длин = —ц& = ~(d — расстояние между двумя пластинами).
d d
Нас в основном будет интересовать поведение системы при изменении ве¬
личины Для больших значений экранировка фиксированных зарядов
мала, и можно ожидать, что электрический потенциал будет убывать алгеб¬
раически с ростом расстояния. В противоположном случае можно ожидать
экспоненциальной зависимости.
Для иллюстрации этих общих качественных соображений рассмотрим
две параллельные мембраны, несущие равный заряд и находящиеся на рас¬
стоянии d друг от друга. При этом электролита в растворе нет. Соот¬
ветствующее уравнение Г1Б и граничные условия могут быть записаны
^Ландау Л. Д, Лифщиц Е. М Электродинамика сплошных сред. Наука. Главная
редакция физико-математической литературы. М.: — 1957; W. В. Russel, D. A. Saville
and W. R. Scholwalter, Colloidal Dispersions, Cambridge Monographs on Mechanics and
Applied Mathematics, 1991.
D. Andelman. Electrostatic Theories of Membranes: the Poisson-Boltzmann theory,
Handbook of Biological Systems 1, 577 (1994).
§ 14.1. Взаимодействия между твердыми поверхностями
569
в виде
d2V _ е е<р(х) dip
—- — - —п0 ехр — —, —
dxz ££q ккТ dx
а (14.22)
где по — концентрация противоионов при х — 0 в срединной плоскости,
равноудаленной от мембран. Вследствие симметрии задачи мы выберем
у>(0) — 0. Легко проверить, что решением уравнения является
<р — ^£- in cos2 кьх} (14.23)
где А;2 = 27гпо^ и ио = ~ki~ ctg (kid/2) — концентрация противоионов
е
в срединной плоскости. Общее выражение для расклинивающего давления
есть p(d) = ksTuQ. Из граничного условия и определения b (14.9) мы также
находим: k^dtg (kid/2) = d/ b. Отметим, что при к l 1, т. е. для больших
расстояний между мембранами, это соотношение дает к^Г1 => Ь\ в противо¬
положном случае, kid<^ 1, мы получаем к^1 => \Jdbf 2. Рассмотрим два
эти случая.
1) Режим Гоу и- Чепмена: k^d^> 1, или, эквивалентно, d/b^> 1 с ма¬
лым 6, т. е. имеем большую поверхностную плотность заряда на мем¬
бране. Для полностью ионизированной мембраны типичные значения а
О _>
могут составить одну единицу заряда на 9А2, т. е. и 1,78 Кл/м ; это дает
О
b < 1А. Следовательно, большая часть мембран в растворе, не содержащем
электролит, находится в этом режиме. «Расклинивающее давление» имеет
d
вид Pd — к^Т —потенциал отталкивания Ve\ = - J dxfp(xr) ведет себя
как d
_i 2 id2
ОО
2) Режим идеального газа: ki d<C 1, или, эквивалентно, d/b<^ 1; поверх¬
ностная плотность заряда мала и противоионы равномерно распределены
с концентрацией пи-. Сила, удерживающая мембраны на удалении,
d
имеет вид и к^Т ~—, а потенциал отталкивания логарифмически зави-
тг bdi
сит от d\ при этом электростатический потенциал убывает алгебраически:
(р и — к^Тк\х2/2е.
Получение обоих результатов не представляет большой сложности.
14.1.5. Сильные растворы электролитов
Рассмотрим изолированную пластину в электролитическом растворе,
состоящем из моновалентных ионов. Это первый шаг в развитии теории
двойного слоя в присутствии сил Ван-дер-Ваальса. Положим, для начала,
что эти силы отсутствуют. Уравнение (14.7) принимает вид (14.12), т. е.
dV = 2eno gh Мх)
dx2 £q£ к^Т
570
Гл. 14. Устойчивость коллоидных систем
Это уравнение после первого интегрирования приобретает вид
”1 / О
dip
dx
полное решение проиллюстрировано на рис. 14.1. Точное решение
при использовании линейного приближения Дебая—Хюккеля показывает
ожидаемую экспоненциальную зависимость; в этом выражении (ps — по¬
тенциал при х = 0. Двойной слой составляет примыкающую к заряжен¬
ной поверхности область, в которой наблюдается пониженное содержание
Рис. 14.1. Электрический потенциал и концентрации ионов. Отметим накопление
противоионов и пониженное содержание ионов того же знака вблизи заряженной
поверхности
ионов того же знака, что и на поверхности и накопление противоионов: тол¬
щина этого слоя имеет порядок \]j. Концентрация противоионов п+(х) и
ионов того же знака п_ (я) приближается к концентрации электролита п0 по
мере удаления от пластины. Плотность заряда на пластине легко получить
из граничного условия для градиента потенциала:
Концентрация противоионов и ионов того же знака может быть вы¬
числена, если формула (р(х) известна. Можно также связать полную кон¬
центрацию ионов на пластине с концентрацией фиксированных зарядов
th = th exp(-kDx)
АкьТ АкъТ
(14.25)
п
к
1,0
\(е
а
б
а — 2(2е£окьТпо)1^2 sh
Полный локальный заряд задается уравнением Пуассона:
е[п+(ж) — п_(ж)] = ~££od2(p/dx2.
(14.26)
(14.27)
§ 14.1. Взаимодействия между твердыми поверхностями
571
(соотношение Грэхема (Grahame)). Действительно, имеем
dn+(x)
dx
dn_ (х)
dx
е ( dip \
По — ( — ехр
к%Т V dx /
+ П0
к^Т \ dx
.Л
кьТ)
кБТ
(14.28)
т. е., добавляя эти две производные, полагая п
(14.24), получаем
dn(x)
dx
ее о d ( dp
2
2kвТ dx \dx
+ n_ и используя
Уравнение (14.29) легко интегрируется и дает для х ~ О
(14.29)
«
77-0 +
а
9
*2,££окТ
(14.30)
Уравнение (14.30) связывает концентрацию ионов вблизи пластины с их
концентрацией в резервуаре. Оно имеет тот же вид, что и для раство¬
ра, не содержащего электролит, заключенного между двумя пластинами
(см. задачу 14.1), но по имеет другой смысл.
Давайте теперь обсудим некоторые приближения уравнения (14.25), ко¬
торое может быть переписано в виде
ер)
2 къТ
(I +
In
V
ехр(-кпх) th ( —)
\4 квТ)
1 — ехр( — крх) th ( е(?-~ )
V 4 к^Т )
(14.31)
1. Линейный режим Дебая-Хюккеля получают при
ер
4 кБТ
«С 1 .
2. Для
e(ps
> 1 потенциал может быть записан в виде
е<р
In
4/сбТ
1 + ехр(—к&х)
1 — ехр(—к&х)
-1
2 кБТ
, т. е. он не зависит от потенциала поверхности.
3. Upux^>kD мы получаем
ер)
4 th (
ехр(—кох), т. е. убы-
къТ \±къТ)
вание потенциала вдали от границ всегда экспоненциальное. Если, кроме
e(ps > 1, потенциал поверхности </?s,eff5 экстраполированный из обла-
того,
4 кЕТ
сти, удаленной от границы, является величинои постоянной, независимой
^9^3, eff
от заряда пластины,
4 кът
1.
572
Гл. 14. Устойчивость коллоидных систем
14.1.6. Теория Дерягина -Ландау-Вервея-Овербека(ДЛВО)7,8^: кон¬
куренция ван-дер-ваальсова и электростатического взаимодей¬
ствий
Взаимодействие между двумя пластинами, связанное с существованием
двойного слоя, по своей природе отталкивательное. Силы Ван-дер-Ваальса
обеспечивают дальнодействующее притяжение между пластинами, которое
уравновешивает электростатические силы.
На рис. 14.2 показаны основные характеристики потенциала ДЛВО
^dlvo = Kiec + Vv dw как функции расстояния d между пластинами.
Рис. 14.2. Полный потенциал в теории ДЛВО
Взаимодействие Ван-дер-Ваальса не зависит от фиксированных электро¬
статических зарядов и от силы электролита. Взаимодействие Ван-дер-
Ваальса с п = 6 дает плотность потенциальной энергии притяжения
(на единицу площади пластины) между двумя параллельными пластинами
В. V Derjaguin and L. Landau. Acta PhysicoChemica USSR, 633 (1941)
^ E.J. W. Vervey andJ. Th. G. Overbeek. Theory of the Stability of Lyophobic Colloids,
Elsevier, N. Y., 1948.
§ 14.1. Взаимодействия между твердыми поверхностями
573
толщины S с молекулярной плотностью р в виде
т/ тгС62р
VvdW = --
2dA
если 5 d, А = тт2Ср2 — константа Гамакера, см. уравнение (1.17), или
в виде
Т/ _ пСР
^vdW — -
2d2
если 8 > d, смотри табл. 1.5.
Главными особенностями рис. 14.2 является наличие двух минимумов,
очень глубокого основного минимума, отвечающего крайне малым рас¬
стояниям (< Л£>), и промежуточного максимума, который задает энер¬
гетический барьер отталкивания. В действительности основной минимум
не является бесконечно глубоким вследствие короткодействующих гидра-
тационных или сольватационных сил.
Для d Хо, т. е. в случае сильных электролитов, электростатические
силы пренебрежимо малы, и коллоидные объекты (в виде пластинок в вы¬
шеприведенных примерах, а также сферические или цилиндрические ча¬
стицы) должны слиться вместе, за исключением ситуации, когда в системе
реализуется вторичный минимум (см. рис. 14.2). Другой случай, который
будет рассматриваться в § 14.2, — когда заряженные поверхности являются
гибкими (мембраны вместо жестких пластин), так что силы отталкивания
энтропийной природы становятся определяющими.
Для d С \&, т. е. в случае слабых электролитов, поверхности сильно от¬
талкиваются, и можно ожидать существования сильного энергетического
барьера между заряженными частицами. Наиболее глубокий основной ми¬
нимум при этом может не достигаться, и система сохраняется в состоянии
кинетической стабильности, в положении более слабого минимума.
Все промежуточные ситуации также могут быть реализованы в систе¬
ме. Одним из наиболее интересных свойств теории ДЛВО является пе¬
реход из состояния кинетической стабильности, при котором энергети¬
ческий барьер достаточно высок (> к^Т), в состояние агрегации, когда,
например, концентрация электролита возрастает. Этот переход был объек¬
том многочисленных исследований для системы сферических заряженных
частиц (см. § 14.3), где агрегаты могут образовывать хлопья (floes), раз¬
мер которых связан с областью действия реальных сил притяжения между
частицами. Наоборот, в случае мембран эти эффекты агрегации не явля¬
ются определяющими из-за короткодействующих сил отталкивания другой
природы, а именно связанных с энтропийными силами, характерными для
флуктуирующих мембран. Эти силы, описываемые потенциалом Хелфриха
^Неь также быстро меняются на малых расстояниях (Vjiei = Р(кьТ)2/хdp)
и могут уравновесить силы Ван-дер-Ваальса (Kdw ) в этом диапазоне
(константа Гамакера и (к^Т)2/>с сравнимы по величине).
574
Гл. 14. Устойчивость коллоидных систем
§ 14.2. Взаимодействия в гибких ламеллярных системах
Как уже отмечалось в гл. 1, 2 и 13, амфифильные материалы (рис. 1.3,
1.5 и 2.17) легко адсорбируются на границе раздела между двумя средами,
например воды и масла или воды и воздуха. В зависимости от поверхност¬
ной концентрации молекул или, эквивалентно, площади, приходящейся на
молекулу, эти материалы могут образовывать моносл о и (рис. 14.3) с раз¬
личными видами упорядочения: от состояния двумерного газа до плотно
упакованных двумерных кристаллических структур. Эти состояния отли¬
чаются друг от друга средним расстоянием между полярными головками
и конформациями углеводородных хвостов. Если амфифил растворен в од¬
нокомпонентном растворе, предпочтительным видом упорядочения явля¬
ется бислой, образованный парой противоположно ориентированных моно¬
слоев (рис. 14.4). Если концентрация амфифила достаточно высока, бислои
С -
м
СМ = 1 / а0 < О
Рис. 14.3. Обозначения, обычно принимаемые для знака величины а о
СМ - 1 / сг0 > О
Е
Е
Е
Рис. 14.4. Описание бислоя, позволяющее получить выражение (14.34)
могут служить строительными единицами для формирования ламеллярной
(см. рис. 2.23) и губчатой (см. рис. 2.29) фаз. При низких концентрациях
§ 14.2. Взаимодействия в гибких ламеллярных системах
575
бислои могут принимать форму замкнутых везикул со сферической, торо¬
идальной топологией или даже с топологией более высокого рода91 Раз¬
личные геометрии везикул можно найти даже в пределах одного и того
же топологического класса. Хорошо известным примером является двоя¬
ковогнутая дискоидная форма ограничивающей мембраны эритроцитов.
Она переходит в эллипсоидальную, когда эритроциты путешествуют по
кровяным сосудам или когда клетка становится дефектной. Оказывается,
что основным фактором, определяющим форму бислоев, является их упру¬
гость. Основные понятия упругости бислоев рассматриваются ниже. Мы
рассматриваем только жидкие мембраны (монослои, бислои), у которых
отсутствуют упругие модули сдвига в плоскости слоя, а также нет коопе¬
ративного наклона углеводородных хвостов. Единственные деформации,
представляющие интерес, это тангенциальные сжатия и растяжения, кото¬
рые изменяют площадь, приходящуюся на молекулу, и изгиб (кривизну)
мембраны.
14.2.1. Упругость нейтральных мембран
14.2.1.1. Феноменологическое описание. В этом подпункте обсужда¬
ются микроскопические модели, позволяющие оценить материальные кон¬
станты свободной мембраны. В соответствии с предложением Хелфриха10^
плотность свободной энергии изгиба (на единицу площади .монослоя), за¬
писывается как функция средней Н = (ai + <j2)/2 и гауссовской G = о\о2
кривизн:
1 9
/ = -*т{° 1 + 02 - СГ0) + ТстО\02 (14.32)
2
(нижний индекс означает «монослой»). Это выражение аналогично введе-
ному в гл. 5, за исключением дополнительного слагаемого, отвечающего
спонтанному изгибу <7о, который учитывает диссимметрию монослоя. Ес¬
ли, по определению, ориентация монослоя задается направлением от непо¬
лярных алифатических цепей к полярным головкам, то изгиб <то берется
положительным, когда «внешняя» сторона изогнутого монослоя является
стороной, занимаемой полярными головками (рис. 14.3). Исходя из размер¬
ных соображений, модули хт и кт имеют вид уст — К d0, х.т — К do, где
К, К — упругие модули Франка и do — длина порядка толщины монослоя.
Отметим, что изгиб, принимаемый свободной мембраной, определяется
не его, а величиной (Teq — аi ~ а2, которая отвечает минимуму /, а именно:
creq = ao *та__ , (14.33)
2>Сгп
В. Fourcade, М. Mutz and D. Bensimon. Phys. Rev. Lett. 68, 2551 (1992).
10^ W. Helfrich. Z. Naturforsch. 28, 693 (1973).
576
Гл. 14. Устойчивость коллоидных систем
к которому должно быть добавлено условие стабильности d2f/da2q > О,
т. е. 2усш + хт > 0, так как устп > 0.
Очевидно, что бислой, образованный двумя химически идентичными
монослоями, не имеет спонтанного изгиба. Связь между материальными
параметрами х, ус для бислоя и усш, может быть записана в виде
где 6 — эффективная толщина бислоя, представленного на рис. 14.4 вместе
с другими обозначениями, необходимыми для вывода выражения (14.34),
которые будут детализированы ниже.
Мы полагаем, что бислой может быть представлен в виде ряда парал¬
лельных физических поверхностей с центральной непрерывной поверх¬
ностью Е, которая охватывает концы углеводородных цепей, и внешними
поверхностями и £_, являющимися огибающими для полярных голо¬
вок. Изгиб бислоя будет, по определению, описываться поверхностью £.
Пусть 6/2 является (положительным) расстоянием от S, на котором выра¬
жение (14.32) применяется для каждого из монослоев. Мы исходим из того,
что в системе нет иных взаимодействий между монослоями, кроме тех, что
задаются геометрией плотной стерической упаковки молекул. Имеем
где знак + относится к «верхнему» монослою, а знак — к «нижнему». От¬
метим, что мы выбрали один и тот же знак для спонтанного изгиба, это
означает, что два монослоя ориентированы в противоположных направле¬
ниях. Теперь можно показать (задача 14.3), что
где 2Я — о\ 4-02, G = aicr2, а величины со штрихом относятся к тем же
переменным, описывающим поверхность, смещенную вдоль нормали на
алгебраическую длину Л, взятую с определенным знаком в зависимости от
направления. Следовательно,
ус — 2 ус т 7 ус — 2 ( ус гп <5 сг о У^тп)
(14.34)
dl,' = dZ,(l + 2H\ + G\2)
Н' = Н{ 1 - 2НХ) + GX,
G' = G{ 1 - 2ЯЛ),
(14.366)
(14.36b)
(14.36 а)
/+
2
1
§ 14.2. Взаимодействия в гибких ламеллярных системах
511
f— — —^т
2
+ Xw(7i<T2 ^1 + (сгг 4- a2)-j (14.37)
и
/d£ = /+d£++/_ d£_.
(14.38)
Оставляя только члены первого порядка по 5, получаем
X 2
/ = -х(сг I + а2) + ХСГ х (72,
2
(14.39)
(14.40)
Рассмотрим поправку к модулю седловидного изгиба х; может
быть очень малым, как это часто предполагается в L^-фазе, находящейся
на фазовой диаграмме вблизи губчатой фазы L3. В этом случае поправка до¬
минирует над исходной величиной кт; она дает положительное значение 3?,
если спонтанный изгиб отрицателен — ситуация, которая способствует по¬
явлению губчатой фазы11).
14.2.1.2. Микроскопические модели; модель Петрова-Держанско-
го-Митова. Для того чтобы связать материальные константы жидких
мембран с их микроскопическими параметрами, были предложены раз¬
личные модели. Мы рассмотрим здесь основные элементы модели Пет¬
рова-Держанско го-Митова (ПДМ). Эта модель, наряду с другими, типа
модели Израелишвили - Митчела - Нинхама (ИМН)12\ довольно подробно
разобрана в книге Петрова131
В подходе болгарской школы исходным является выражение для сво¬
бодной энергии монослоя, приходящейся на одну молекулу:
Im = kf(lF _1)2 + Т (^-1)2’ (14'41)
где кн (соответственно кс) — упругая константа, характеризующая взаи¬
модействие между полярными головками (углеводородными цепями), Л#
(соответственно Ас) — площадь сечения и Н (соответственно С) — пло¬
щадь сечения молекул в отсутствие взаимодействий. Целью подобного под¬
хода является установление связи между упругими константами и спонтан¬
ным изгибом монослоя с микроскопическими параметрами, в особенности
с их анизотропией. Результат зависит от деталей строения молекулы, кото¬
рое используется в модели.
11'1 G. Porte, J. Appell, P. Bassereau andJ. Marignan. J. Physique France 50, 285 (1989).
12^ J. Israelachvili, D. J. Mitchel and B. W. Ninham. J. Chem. Soc. Faraday Trans. II 72,
1525 (1976).
13) A. G. Petrov. The Lyotropic State of Matter, Gordon and Breach, 1999.
37-КЛЕМАН M.
578
Гл. 14. Устойчивость коллоидных систем
Рассмотрим вначале отдельный монослой толщины 6/2. Мы определяем
сечения полярных головок на расстоянии 6/2 от поверхности Е, образован¬
ной концами цепей, и сечения цепей на расстоянии <5/4 от Е. Соотношения
между изгибами монослоя (измеряемыми на поверхности Е) и площадью
сечений согласно (14.36а) имеют вид
где А — средняя площадь сечения приходящаяся на одну молекулу на по¬
верхности Е.
Для монослоя, удерживаемого в плоском состоянии (А# = Ас — А),
равновесная площадь, отвечающая минимуму /ш, составляет
Эта величина не совпадает со средней площадью сечения для монослоя.
Дело в том, что монослой, вследствие асимметрии двух его сторон, име¬
ет спонтанный изгиб ао. Тем не менее соотношение (14.43) может быть
напрямую использовано для описания бислоя, образованного двумя моно¬
слоями, цепи которых заканчиваются на одной и той же поверхности Е.
Уравнения (14.42) применимы к обоим монослоям бислоя. Энергия, прихо¬
дящаяся на единицу площади бислоя, изотропно растянутого на величину
е ~ (Л — Ао)/Ао, может быть записана, с учетом членов до второго порядка
включительно, как — 2Д/т/Ло — >cse2 /2.. Константа растяжения к8
может быть легко получена из Д/т — fm(A) - fm(Ao). Соответствующее
напряжение имеет вид г = д/ы^/де — xse, и
Теперь мы должны подставить (14.42) в (14.41), поскольку бислой изо¬
гнут. В дальнейшем мы будем исходить из того, что растяжение отсутствует,
поскольку бислои являются жидкостными. Это условие может быть запи-
пряжение, которое развивается в монослое i — -Ь, —. Мы также полагаем,
что два монослоя могут обмениваться молекулами друг с другом (с пе¬
реворотом). Следовательно, химический потенциал является одним и тем
же в двух монослоях; т. е. р{г\ а\, а\) = — r+ А+ = /“ — т~ А~.
Ан — А 1 -Ь
(01 4- сг2) +
<7lCT2
(14.42)
Ас — А 1 ~Ь
(“) (&1 + а2) +
(14.43)
(14.44)
сано как г = г+ + г =0. Здесь г1 = д/гш/дег представляет собой на-
§ 14.2. Взаимодействия в гибких ламеллярных системах
519
Отождествляя вариацию fm/ с выражением для свободной энер¬
гии бислоя (14.39), получаем14^
62Aq кнкс
1 = 6^ (Я-Ло)(Ло -С).
8 Н2С2 кнН~2 + ксС~2 ~ 16 S (Я-С)2 ’
3Ь2 А кнкс
8 Н2С2 кнН~1 +ксС~1Х ' 16 “ Ао(Н-С)
(14.45)
Интересно отметить, что, хотя упругий модуль я всегда положителен
(это значит, что Ао лежит в интервале [Я, С]), знак ~к зависит от знака
асимметрии молекулы (Н - С). Отметим также, что знание х,хих5,а кроме
того, формы и размеров молекулы (т. е. Я и С), позволяет оценить величины
локальных констант упругости.
Другая величина, которая может быть выражена как функция микро¬
скопических упругих констант, — это краевая энергия мембраны для поры
радиуса R (рис. 14.5). Для начала следует учесть равенство химических
812
шшш
R
Рис. 14.5. Модель для края поры; вычисления выполненены для г О
потенциалов в плоской части слоя и в его изогнутой части, которое запи¬
сывается как
ц(т/2, 0, 0) = м(т+, СГ2), (71
COS в 1 ,1 Л лгх
, СГ2 = (14.46)
R -j- r( 1 — cos в) г
14^ М. D. Mitov. PhD thesis, Bulgarian Acad. Sci, Sofia, 1980; A. G. Petrov and I. Bivas.
Progress Surf. Sci., Edited by S. Davison, 16, 389 (1984).
580
Гл. 14. Устойчивость коллоидных систем
т. е. позволяет получить величину т
+
функцию
жения г, которое пытается открыть пору. Сила (на единицу длины линии),
действующая на край мембраны, дается интегралом
+ Л-/2
7(г, R) = lim(r
г —У 0
т+(т, R, г, в) dd),
(14.47)
— 7г/2
вычисление которого дает разложение 7 по степеням S/R с коэффициента¬
ми 7ь зависящими от микроскопических упругих констант:
7 = 7о 1 +
т
ТО
“7i [ 1 +
г
Т1
R
+
(14.48)
14.2.1.3. Микроскопические модели; модель Хелфриха. Модель
Хелфриха15) (развитая далее Шлейфером и др.16)) связывает величины
и сто с распределением напряжений в монослое:
0
xpt{x)dx, хт
x2pt(x) dx,
1
т
dptjx)
дН
(14.49)
#->о
Первая и вторая формулы справедливы для плоского бислоя, третье вы¬
ражение применимо для изогнутой поверхности со средней кривизной Н.
Подынтегральные выражения должны включать в себя все силы, действую¬
щие в системе, в частности те, что были рассмотрены в п. 4.1.3. Принцип
вычислений заключается в следующем (см. также Сафран17)). Вариация
свободной энергии изотропной сжимаемой жидкости, изменяющей объ¬
ем от Vo до V, есть AF — — f p(V')dV', где p(V') представляет собой
давление в состоянии Vq ^ V1 ^ V. Это выражение обобщается на случай
анизотропной жидкости (и твердого тела) в виде AF = J V'a'^de^. Отме¬
тим, что dVf = Vde^; — компоненты тензора упругой деформации.
В случае двумерной изотропной мембраны, как уже указывалось, соответ¬
ствующие компоненты тензора напряжений о'ц выражаются функциями
продольного и поперечного «давлений», р\ и р*. Продольное давление на¬
правлено против сил, действующих вдоль нормали к мембране, которые
15) W. Helfrich. Amphiphilic mesophases made of defects, in Physics of defects, Edited
by R. Balian, M. Kleman, and J, P. Poirier, Les Houches, North-Holland, Amsterdam,
1980, 714.
16^ /. Szleifer, D. Kramer, A. Ben Shaul, W. H. Gelbart and S. A. Safran. J. С hem. Phys.,
92, 6800 (1990).
17^ S. A. Safran. Adv. in Phys. 48, 395 (1999).
§ 14.2. Взаимодействия в гибких ламеллярных системах
581
пытаются изменить толщину мембраны. Поперечное давление действует
против сил, которые изгибают мембрану и изменяют ее локальную поверх¬
ность. Кроме того, вычисления предполагают, что полный объем мембраны
не меняется. При этих условиях величина AF, рассчитанная на единицу
площади мембраны, имеет вид (14.39), с упругими модулями, записывае¬
мыми как в (14.49). Продольного давления при этом не возникает, так как
мы ожидаем, что оно исчезает в случае изолированной мембраны.
Эти формулы с успехом использовались для вычисления вкладов элек¬
тролита в растворе и заряженных слоев в упругие модули как для изолиро¬
ванных мембран18\ так и для ламеллярных систем15). При этом для запи¬
си поперечного напряжения pt(x) использовались величины, приведенные
в (14.21). Согласно (14.49) эти добавки к упругим модулям выражаются как
произведение разницы давления на куб характеристической длины. Напри¬
мер15), в случае добавленного электролита можно ожидать, что характерная
длина есть не что иное, как дебаевская длина Ад, разница давлений имеет
характерный масштаб к^Т/Ъ2£ в пределе слабых зарядов, а модули оказы¬
ваются порядка k^TX3D/b2£. Последней величиной, как мы увидим ниже,
можно явно пренебречь по сравнению с другими вкладами. Отметим, что
повторяющееся расстояние в системе (период слоев) в данном случае не иг¬
рает роли. С другой стороны, в случае, когда электролит не добавляется,
но имеются сильные поверхностные заряды, давление имеет характерный
масштаб k^T/dPl, характерной длиной является период слоев, а модуль
имеет вид кБТd/i.
14.2.1.4. Экспериментальные значения. Упругая константа растя¬
жения ks связывает компоненту т тензора двумерного изотропного на¬
пряжения с относительными изменениями площади мембраны е\ т —
= kse (т обычно называется натяжением — это двумерное давление, взятое
с обратным знаком). Величина была измерена в гигантских бислоевых
лецитиновых везикулах. Метод измерений состоит в надувании везикул
с помощью контролируемого повышения давления при сохранении моле¬
кулярного состава везикул19). Типичные значения xs составляют 140 мН/м
для лецитина, однако для мембран красных кровяных телец эта величи¬
на оказалась 450 мН/м. Более подробное обсуждение микромеханических,
а также термоупругих свойств лецитина и биомембран можно найти, на¬
пример, в работах20)21).
Модуль изгиба я был определен из флуктуаций формы трубчатых
и сферических везикул. В случае длинных, имеющих двойную цепь ли¬
пидов14) обычно получают величины порядка Юк^Т. В то же время для
мембран, образованных молекулами с короткими цепями и некоторых
18) И. N. W. Lekkerkerker. Physica А159, 319 (1989); Physica А167, 384 (1990).
i9^ R. Kwok and E.A. Evans. Biophys. J. 35, 637 (1981).
20) E. A. Evans and R. Skalak. Crit. Rev. Bioeng., 3 and 4, 181 (1979).
21^ V A. Parsegian, N. Fuller andR. P. Rand. Proc. Nat. Acad. Sci. USA 76, 2750 (1979).
582
Гл. 14. Устойчивость коллоидных систем
смесей величина к составляет только 0, lk^T. Такие низкие величины я
означают, что тепловой энергии достаточно для возбуждения больших флук¬
туаций формы амфифильных пленок 22^ 23\ (См. недавний обзор 171)
Модель Петрова-Держанского-Митова предсказывает, что знак моду¬
ля седловидного изгиба к зависит от анизотропии формы молекул (Н -
— С)/С. Если сечение полярных головок больше, чем сечение углеводород¬
ных цепей, можно ожидать я < О для бислоя. Отметим, что такая ситуация
способствует положительной спонтанной кривизне монослоя, что и было
обнаружено в эксперименте. Этот вывод также согласуется с соотноше¬
нием (14.34), которое предсказывает, что бислоевая константа упругости
седловидного изгиба меньше, чем удвоенный модуль седловидного изгиба
монослоя при ао > 0. Наоборот, можно ожидать, что к > 0 , когда спон¬
танный изгиб отрицателен, т.е. когда сечение полярных головок меньше,
чем сечение углеводородных цепей. Это типично для некоторых разбух¬
ших коллоидных растворов сурфактантов. Например, считается, что в це-
тилпиридиний хлориде, с добавкой гексанола в качестве дополнительного
поверхностно-активного вещества, цепи проникают друг в друга (боль¬
шие (7), в то время как полярные головки показывают увеличение площади
конденсации с возрастанием концентрации спирта. Этот процесс управля¬
ет переходом из ламеллярной £а-фазы при низких концентрациях алкоголя
в губчатую Ьз-фазу при повышенном содержании спирта241 В этой системе
величина я контролирует стабильность дислокаций с большими векторами
Бюргерса (маслянистые бороздки) относительно их расщепления в конфо¬
кальные домены: топология ядра дефекта разная в этих двух случаях, что
предполагает существенную роль х2Ъ\ Величина 3<т может быть получе¬
на для масляно-солевых сурфактантных смесей, образующих разбавленные
капельные микроэмульсии (с радиусом в несколько нанометров), если из¬
вестны межфазное натяжение, модули изгиба и радиус капель (системы
типа ЛОТ (sodium di -2 - ethylhexyl sulfosuccinate)—соль-масло26^).
Были изучены многочисленные лиотропные системы27), с доминирую¬
щими электростатическими силами (SDS - вода- пентанол, SDS - вода - гек-
санол) или доминирующими силами, связанными с флуктуациями
мембран (ЯА^-соль-додекан или пентанол); здесь SDS (sodium dodecyl
sulphate) — додеци л сульфат натрия. Профили рассеяния, полученные
22^ R. М. Servuss, W. Harbich and W, Helfrich. Biochimica et Biophysica Acta 436, 900
(1976).
23) F. Brochard andJ. F. Lennon. J. Physique (Paris) 36, 1035 (1975).
24^ G. Porte, J. Appel, P. Bassereau andJ. Marignan. J. Phys. France 50, 1335 (1989).
25^ P. Boltenhagen, O. Lavrentovich andM. Kleman. J. Phys. II, France 1, 1233 (1991).
26^ H. Kellay, J. Meunier and B. P. Sinks. Phys. Rev. Lett. 70, 1485 (1993).
27^ D. Roux, C. R. Safinya and F. Nallet. Lyotropic lamellar LQ phases’, in Micelles,
Membranes, Microemulsions, and Monolayers, Edited by W. M. Gelbart, A. Ben-Shaul,
and D. Roux, Springer-Verlag, N. Y., 1994.
§ 14.2. Взаимодействия в гибких ламеллярных системах
583
в экспериментах, позволили провести четкое различие между этими двумя
категориями ламеллярных систем. Были также исследованы промежуточ¬
ные случаи между электростатическими силами и силами флуктуационной
природы (смотри ниже).
Показатели степени Кайе, описывающие форму крыльев диффракци-
онных пиков от ламеллярной фазы (см. п. 5.6.2), позволяют напрямую из¬
мерить величину VКВ. С другой стороны, в случае £а-фазы измерение
периодичности как функции разбавления раствора дает величину к « К do
(см. (14.60)). Следовательно, К может быть измерено двумя независимыми
способами. Кроме того показатель Кайе, согласно теории, ведет себя по-
разному с изменением d0 в зависимости оттого, имеют ли силы отталкива¬
ния в мембранах преимущественно электростатическую или энтропийную
(смотри ниже) природу 27\
Представленный ниже список микроскопических констант для лецити¬
на, взятый из диссертации Митова и из статьи Петрова и Держанского28),
был критически отобран этими авторами из различных измерений16) 2°)29)
(к = 0, 26 х 1(Г19 Дж, = 0,14 ± 0.2 Дж/м2, 70 = 0, 23 х 10“n Н):
кц = 19,1 х 10~21 Дж, кс = 32, 3 х 10~21 Дж,
Я = 90,2 х Ю“20 м2, С = 66,2 х Ю“20 м2.
Величина 3? может быть рассчитана на основе этих значений микроскопи¬
ческих констант с помощью (14.45): х « 0, 25 х 10~19 Дж. Величины того
же порядка были получены и в результате оптико-микроскопических на¬
блюдений неустойчивости седловидного изгиба в мембранах30) и «ручек»
между мембранами31).
14.2.2. Гибкие слои и исключенный объем
Устойчивость фаз L\ (мицеллярной), La и L3 (губчатой) может быть
рассмотрена на феноменологическом уровне с использованием выражения
для плотности поверхностной свободной энергии изолированной мембра¬
ны (смотри (14.39)). Ламеллярная фаза La стабильна в интервале значений
2>г -Ь 3? > 0, х < 0. Мы не обсуждаем здесь устойчивость губчатой L3
и мицеллярной фаз. Как флуктуации в мембранах вписываются в эту кар¬
тину?
Уравнение (14.39) имеет тот же вид, что и классическое выражение для
плотности поверхностной свободной энергии твердой оболочки, в которой
28^ Петров А. Г. Держанский А. Журнал Всесоюзного химического общества
им. Д. И. Менделеева 28, 197 (1983).
29) W. Harbich and W. Helfrich. Z. Naturforsch. 34a, 1063 (1979).
30^ A. G. Petrov, M. D. Mitov and A. Derzhanski. Phys. Lett. 65A, 374, (1978).
31^ W. Harbich, R. M. Servuss and W. Helfrich. Z. Naturforsch. 33a 1013 (1978).
584
Гл. J 4. Устойчивость коллоидных систем
отсутствуют растяжения, со следующим взаимным соответствием:
Eh3 — Eh3 / Л
к ? ус <=> -- - (14.50)
12(1-/у2) 12(1+ и)
где h — толщина оболочки, Е — модуль Юнга и v — коэффициент
Пуассона32^. Основные различия между этими двумя случаями заключа¬
ются в следующем:
1. Нерастяжимость твердой оболочки ограничивает ее возможные де¬
формации теми, при которых сохраняются длины и углы, т. е. при которых
сохраняется гауссова кривизна G — Это условие не является столь
строгим для мембран; нерастяжимость заменяется условием сохранения
площади div = 0, а гауссова кривизна может изменяться за счет диф¬
фузии.
2. Известно, что бислои подвержены значительным тепловым флук¬
туациям, которые должны быть усреднены в нашем широкомасштабном
описании. Например, в тех случаях, когда электростатические взаимодей¬
ствия экранированы в сильных растворах электролитов, величина к имеет
порядок не более чем к^Т. Соответственно, модуль изгиба х и модуль сед¬
ловидного изгиба к перенормированы тепловыми флуктуациями33). Инте¬
грирование J / dAp полной поверхностной энергии должно проводиться по
средней поверхности Ар, усредненной с учетом термических флуктуаций.
14.2.2.1. Длина когерентности де Жена. Вначале мы рассмотрим слу¬
чай изолированной плоской мембраны (не взаимодействующей с другими
мембранами) площади А — L2, поверхность которой искажена тепловы¬
ми флуктуациями. Как было показано де Женом и Топеном34), подобная
свободная мембрана имеет конечную длину персистентности
4тг/ Л Л Г~ Л \
= а ехр ——, (14.51)
акБТ
так что имеет смысл говорить о плоской мембране до тех пор, пока ее
размер L ^ £*.. В этом выражении а — коэффициент порядка единицы,
а а — поперечный размер молекулы сурфактанта, образующего мембрану.
Вывод этого выражения приведен ниже.
Для того чтобы упростить вычисления, положим, что амплитуды флук¬
туаций малы. Мы можем, следовательно, записать плотность свободной
32^ А. Е. Н. Love. A Treatise on the Mathematical Theory of Elasticity, Dover, 1944,
article 298.
33^ В качестве обзора смотрите, например: Statistical Mechanics of Membranes and
Surfaces, Edited by D. Nelson et al. World Scientific, Singapore, (1989). Основные
результаты для >c и 5?, полученные методами ренормализационной группы, были
недавно подвергнуты сомнению в работе Helfrich, Eur. Phys. J. Bl, 481 (1998).
34^ P. G. de Gennes and C. Taupin. J. Phys. Chem. 86, 2294 (1982).
§ 14.2. Взаимодействия в гибких ламеллярных системах
585
энергии системы в приближении малых смещений, т. е. в виде /bend =
= ^>с(ихх + иуу)2. В том же приближении интегрирование свободной
энергии может быть проведено не по истинной площади мембраны, а по
спроецированной, плоской средней поверхности. Также нет необходимости
учитывать вклад деформаций седловидного изгиба, поскольку флуктуации
не изменяют топологию поверхности. Давайте теперь запишем полную
энергию в терминах фурье-компонент смещения и(т) = A"1 ^uqexp(iqr)
q
(где — и*). Мы получаем
fhend^Y
1
-X
2
(J^XX "J- 'U’yy)^ d
A
-1
u4u
-q
q
A
-i
xEq
и
2
Используя теорему о равнораспределении энергии, получаем
кБТ = A xxq4
и,
2
(14.52)
(14.53)
и, проводя простое интегрирование по всем модам,
(к (г)2)
1
л
u(r)2d2v
-Е
А2
q
u(q)
1 квТ
А ус
Ез
q
(14.54)
После того как эти общие формулы получены, мы можем вычислить
парную корреляционную функцию ориентации директора:
£п(г) = (ОО + р) - п(р))
2 ((|п(г)
(п(г + р)п(р))). (14.55)
Эта корреляционная функция определяет средний угол ф между двумя нор¬
малями к поверхности мембраны на расстоянии г. Действительно,
gn(r) — 2(1 — (cosф(г))) « {Ф2{г)) • Так как п = {—ди/дх, —ди/ду, 1},
имеем
gjr)
А2
и
2
1 — cos qr)
кьТ
& а — In
4:7ГУС
г
а
(14.56)
Первое соотношение в (14.56) достаточно легко получить. Для того что¬
бы вывести второе соотношение, необходимо быть внимательным в сум¬
мировании, которое, как обычно, заменяется интегрированием. Мы имеем,
(кТ/itx) In (Jmax/Qmin■ УчИТЫВаЯ,
непосредственно: 2A 2Eq2{|uq|2)
что Jcosqrdfl — j cos (qr cos 6) dO = 2ix Jo(qr), вторую часть интеграла
получаем в виде: —(кТ/пя) J dqJo{qr)/q , где интегрирование проведено
от qm-mr = 27ir/L до qmeiXr = 2пт/а. Jo(qr) представляет собой функцию
Бесселя нулевого порядка. Верхний предел в интеграле велик, в то время
как нижний меньше 2тт. Следовательно, мы интегрируем от qm\nr = 27rr/L
586
Гл. 14. Устойчивость коллоидных систем
до оо и получаем: —(кТ/тгх) J dqJo(qr)/q = (kTt/пя) In (qminr/2) + чле¬
ны, которыми можно пренебрегать до тех пор, пока величина qminr =
= 2?xrjL меньше единицы. В результате мы имеем выражение (14.56), где
а — некоторый коэффициент порядка единицы. Важный результат состоит
в том, что ведущий член в корреляционной функции очень слабо зависит от
размера системы. Если мы зафиксируем г = так 4Togn(r) и (Ф2{т)) бу¬
дет порядка единицы, т. е. угол будет велик, то из этого следует, что нормали
к поверхности мембраны могут считаться некоррелированными. Отсю¬
да возникает понятие персистентной длины де Жена-Топена. Свободный
бислой является «жестким» на коротких расстояниях (L < £„) и сильно
искажен на больших масштабах (L > £**); разумеется это не исключает
существования (малых) тепловых флуктуаций на меньших расстояниях.
Коэффициент а у разных авторов имеет различные значения; Хел-
фрих35) — а = 1; де Жен и Топен — а = 2; вычисления с помощью
методов ренормализационной группы дают а = 3 (см. обзор Дэвида36^).
14.2.2.2. Избыточная площадь у флуктуирующих мембран. Пусть Ар
представляет собой среднюю площадь37^, А — действительная площадь, а
АА — А — Ап — избыточная площадь мембраны размера L(A — L2),
ДЛ(г)
Р
рис. 14.6. Относительная локальная избыточная площадь есть
nz — 1
ГЧ>
rs^
1 г / dil \ 9]
-Г (т-)" + (т-)' , где z
А(г)
единичныи вектор, перпенди-
2 “'дх ду
кулярный поверхности мембраны. Следовательно, полная относительная
избыточная область может быть записана в терминах фурье-компонент сме¬
щений:
ДЛ A'2 2 2
q
А.
и
т. е.
АЛ
А
кБТ
In
Qm ах
47Г >С Qm\n
(14.57)
А
Рис. 14.6. Средняя Ар и действительная (молекулярная) А площади гибкой мем¬
браны
35) W. Helfrich. Z. Naturforsch. ЗЗА, 305 (1978).
36' F David. Statistical Mechanics of Membranes and Surfaces, edited by D. Nelson &
al., World Scientific, Singapore, (1989) 157.
37^ Также называемую площадью проекции, потому что этот теоретический подход
справедлив и для квазиплоских поверхностей.
§ 14.2. Взаимодействия в гибких ламеллярных системах
587
Отметим, что это выражение справедливо для свободной мембраны до тех
пор, пока Ар меньше, чем А* — поскольку искажения поверхности раз¬
мера А* являются независимыми. Эти соотношения выполняются и в тех
случаях, когда мембрана не является свободной, например, если она явля¬
ется составной частью фазы La. Обозначим Ар = Согласно (14.54),
среднеквадратичное смещение и2т в направлении, перпендикулярном мем¬
бране, имеет величину порядка ~ {к^Т/х)£^_. Если взять um ~ d, то
для можно получить следующую оценку38^:
X
^ = c\l~d’ 04.58)
где с — коэффициент, величина которого у разных авторов различна. На¬
пример, у Голубовича и Любенского39) с = (32/37Г)1/2 « 1,84.
Напомним, что <р$ является объемной концентрацией мембран (поверх¬
ностно активного вещества) в ламеллярной фазе, а 6 — толщина бислоя.
Имеем
y?s = (14.59)
dAp
где необходимо положить А = А*. Используя (14.57) с <7max = 27г/а, qm[n =
получаем
p \ 47г>£ \ a у k^T p J J \ 47тус \ a у k^T
(14.60)
Эта логарифмическая поправка к линейному закону разбавления была
с успехом использована для измерения модуля изгиба40).
Согласно Дэвиду41), флуктуации перенормируют упругие модули сле¬
дующим образом:
*(L) = x(i-^ln-), 5?(1) = зг( 1+iMiin-). (14.61)
V А-кус а / V б7гх а /
Здесь х — так называемый затравочный упругий модуль изгиба, ко¬
торый связан с упругими свойствами среды на молекулярном масштабе
длин.
38} W. Helfrich and R. М. Servuss. II Nuovo Cimento 3D, 137 (1984).
39^ L. Golubovic and Т. C. Lubensky. Phys. Rev. В 39, 12110 (1989).
40 ^ D. Roux, F. Nailet, E. Freys singe as, G. Porte, P. В as sere au, M. Skouri and
J. Marignan.Porte, G. Europhys. Lett. 17, 575 (1992).
41^ F. David. Statistical Mechanics of Membranes and Surfaces, D. Nelson & al. eds,
World Scientific, Singapore, (1989) 157.
588 Гл. 14. Устойчивость коллоидных систем
14.2.2.3. Интерпретация флуктуирующих мембран как идеального
газа локальных изгибов (лоскутков); энтропия отталкивания Хелфри-
ха. Мы полагаем, что в свободной мембране лоскутки площади А* —
= образуют двумерный идеальный газ. В терминах плотности энер¬
гии это можно интерпретировать как появление поверхностного натяжения
7 = *бГ/£.
В случае ламеллярной фазы поверхностная плотность лоскутков состав-
2
ляет . Будем описывать явления с точки зрения теории среднего поля.
Представим себе, что флуктуации данной мембраны задевают две соседние
мембраны, которые предполагаются неподвижными. Объемная плотность
лоскутков в интервале толщины 2d составляет
n(d)
1 с"2 кБТ
2 2d3 ус
Согласно закону Бойля - Мариотта, соответствующее давление есть
p(d) = п{й)къТ =
2 ус d?
а энергия взаимодействия этих флуктуаций с любой из двух соседних мем
бран представляет собой следующую величину:
d
p(d') dd! = —М2
4с2 *d2
ОО
т. е. мембраны на расстоянии d друг от друга испытывают действие потен¬
циала отталкивания
т/ _ 1 (къТ)
геР
4с" н dЛ
2
(см. 42)). Этот результат можно получить иначе, если обратить внимание
на то, что каждый лоскуток обладает тепловой энергией возбуждения к^Т
(на каждый флуктуационный изгиб приходится две степени свободы, по¬
скольку лоскутки ограничены двумерной геометрией поверхности). Эта
энергия делится поровну между двумя соседними поверхностями, т. е. на
каждого соседа приходится энергия, равная -k^Tn{d) d.
Предположим, что потенциал Vrep является функцией расстояния А =
= d + и между мембранами, причем d — равновесное расстояние, а и —
малое смещение:
_ 1 (кеТ)2
гер “ 4с2 хДЗ ‘
42) W. Helfrich. Z. Naturforsh. 33а, 305 (1977).
§ 14.2. Взаимодействия в гибких ламеллярных системах
589
По определению модуля сжимаемости имеем
4с2 >«Д3
1 (къТ)2 _ 2
Следовательно,
(14.62)
^Д2 Д—d с2 >fd3
Многие авторы используют для коэффициента 3/с2 значение Хелфриха
97г2/64.
Другой способ, позволяющий понять, отчего зависит В, заключается
в следующем. Длина проникновения в направлении, перпендикулярном
слоям, имеет величину порядка £j_/A (поскольку деформации распростра¬
няются в плоскости слоев на расстояние £j_)) и не должна превышать рас¬
стояния d между слоями. С другой стороны, не имеет смысла этой величине
быть меньше периода слоев. Следовательно, можно записать, используя
представленную выше, в гл. 5, модель: £2 /А = d, где А = у/К/В =
= yfxjdB. Это уравнение дает
Полное теоретическое обоснование рассмотренных выше вопросов из-
14.2.3. Ламеллярная, губчатая и кубическая фазы; микроэмульсии
Относительная устойчивость различных фаз, составленных из бислоев,
была рассмотрена в задаче 5.6. Мы напомним соответствующие результаты,
которые зависят от знаков модулей изгиба х и х, т. е.от макроскопических
материальных параметров системы. Имеются три области стабильности.
1. Для х + ~х > О, х < 0, гауссова кривизна исчезает и ламеллярная
фаза является устойчивой.
цательной; в то же время можно сделать среднюю кривизну равной нулю.
При этих условиях бислой принимает форму минимальной поверхности.
Вариант (1) также включает фазу, образованную цилиндрическими бис¬
лоями, типа гексагональной фазы. Подобные фазы обычно состоят из мо¬
нослоев, как, например, в мицеллярной фазе (вариант (2)). В обоих случаях
следует ожидать, что хш < 0. Отметим, что х также обязательно имеет
ложено в работах 41^42\
2. Для х + -х < 0, х < 0, гауссова кривизна должна быть положи-
2
тельна и устойчивой является мицеллярная фаза.
3. Для х + -х > 0, х > 0, гауссова кривизна должна быть отри-
590
Гл. 14. Устойчивость коллоидных систем
отрицательный знак, если спонтанный изгиб монослоя является положи-
тельным (см. (14.34)).
Случай, при котором гауссова кривизна должна быть отрицательна,
представляет больший интерес. Он дает два подкласса, кубическую и губ¬
чатую фазы, причем обе они обнаружены экспериментально.
Кубические фазы. Эти фазы уже были отмечены в классификации ме-
зомофных фаз (гл. 2) и известны для умеренно разбухших поверхностно¬
активных веществ43^. Строго доказано44), что минимальная поверхность
может быть периодической и в трехмерном пространстве, без взаимных пе¬
ресечений. Из экспериментов известны три кубические фазы, называемые,
соответственно, G (пространственная группа IaSd), D (пространственная
группа РпЗгп), и Р (пространственная группа /шЗт), но, в принципе, их
может быть гораздо больше. Мы отсылаем читателя к соответствующей
литературе45). Стабильность кубических фаз, очевидно, связана с тополо¬
гическим выигрышем, из-за наличия «ручек» (перемычек между поверх¬
ностями), и исчезновением энергии искажения (минимальная поверхность,
+ 0*2 = 0)). Было высказано предположение, что переход из ламеллярной
фазы в кубическую может быть изучен в рамках теории Ландау46).
Губчатая фаза. Фаза L3 обнаружена в разбухших лиотропных систе¬
мах, для которых, как уже отмечалось, энергия изгиба очень мала {х та k^T).
Принятая в настоящее время модель губчатой фазы представляет собой би-
континуальную неупорядоченную фазу растворителя, состоящую из двух
областей растворителя, разделенных случайно распределенным бислоем,
аналогично модели для микроэмульсий. Чисто математически можно пока¬
зать, что для неупорядоченного бислоя его центральная поверхность может
быть приблизительно минимальной. Устойчивость системы обеспечивается
трансляционной энтропией конфигураций «ручек», а энергия искривления
оказывается малой47).
Наконец, микроэмульсии представляют собой термодинамически ста¬
бильные фазы, состоящие по крайней мере из трех компонентов: масла,
воды и сурфактанта (наиболее часто с добавкой спирта с короткой угле¬
водородной цепочкой в качестве дополнительного сурфактанта). Поверх¬
ностно активные вещества образуют монослой, который отделяет масло от
43^ Стронциево мыло со структурой Ia3d: V Luzzati and P. A. Spegt. Nature 215, 701
(1967); липидо-водные системы со структура Ia3d: V Luzzati, A. Tardieu, T. Gulik-
Krzywicki, E. Rivas and F. Reiss-Husson, Nature 220. 485 (1968).
44) A. И. Sc hoe n. NASA report TN D —5541 (1970).
45^ См., например, специальный выпуск Journal de Physique on Geometry and
Interfaces, colloquium C7 51, (1990).
46^ D. M. Anderson, S, M. Gruner and S. Leibler. Proc. Natl. Acad. Sci. USA 8, 5364
(1988). W Helfrich and H. Rennschuh, J. de Phys. 51, C7-189 (1990).
4T) М. E. Cates, D. Roux, D. Andelman, S. T. Milner and S. A. Safran. Europhys. Lett. 5,
733 (1988).
§ 14.3. Растворы коллоидных частиц; особенности устойчивости 591
воды. Различают глобулярные (по большей части сферические) микро¬
эмульсии, которые достаточно хорошо исследованы, и фазы Винзора, строе¬
ние которых аналогично неупорядоченным биконтинуальным системам,
впервые изученные Скривеном48) и Талмоном и Прагером49). Микроэмуль¬
сии могут характеризоваться как положительной гауссовой кривизной (мик¬
рокапли), так и отрицательной гауссовой кривизной (структуры, схожие
с губчатыми фазами). Существует определенное мнение50\ что фактором,
позволяющим разделить глобулярные и неупорядоченные биконтинуаль-
ные микроэмульсии, является величина спонтанного изгиба его. Этот па¬
раметр велик в глобулярных системах, но мал и ассоциируется с малым
модулем изгиба хт в случайных биконтинуальных системах. Для объясне¬
ния стабильности микроэмульсий был предложен целый ряд теоретических
моделей. Их детальное изложение представлено в5Ч
§ 14.3. Растворы коллоидных частиц; особенности
устойчивости
Предшествующие параграфы были в основном посвящены мембранам,
но были также рассмотрены свойства поверхностей, у которых средняя кри¬
визна мала по сравнению с обратным расстоянием между двумя коллоид¬
ными объектами в растворе. Центральным среди полученных результатов
является теория ДЛВО, учитывающая конкуренцию между дисперсионны¬
ми силами притяжения (силы Ван-дер-Ваальса модифицированные, если
это необходимо, с учетом эффектов запаздывания на больших расстояни¬
ях; см. гл. 1 и задачу 1.6) и электростатическими силами отталкивания.
На первый взгляд эти результаты могут быть использованы для описания
умеренно концентрированных растворов частиц. Однако нередко возни¬
кают ситуации, выявляющие существенные различия. Частицы конечных
размеров, о которых идет речь, не обладают той же топологией, что и бес¬
конечные мембраны в разбухших сурфактантах. Кроме того, поскольку ча¬
стицы имеют небольшие, конечные размеры (обычно в интервале от 50 нм
до 1 мкм ), броуновское движение становится важным фактором, опреде¬
ляющим их стабильность и кинетические свойства. Вопросы, связанные
с коллоидными растворами, уже в течение долгого времени имеют боль¬
шую технологическую значимость: молоко, тушь, краски и т.д. являют¬
ся коллоидными растворами частиц. Следствием этого явилось огромное
48) L. Е. Scriven. Nature 63, 123 (1976)
49^ К Talmon and S. Prager. J. Chem. Phys. 69, 2984 (1978)
5°) L. Auvray. The structure of microemulsions: experiments’ in Micelles, in Membranes,
Microemulsions, and Monolayers, Edited by W. M. Gelbart, A. Ben-Shaul, and D. Roux,
Springer-Verlag, N. Y., 1994.
51 * Membranes, Microemulsions, and Monolayers, Edited by W. M. Gelbart, A. Ben-
Shaul, and D. Roux, Springer-Verlag, N. Y., 1994.
592
Гл. 14. Устойчивость коллоидных систем
число опубликованных экспериментальных результатов, а также появление
уже в начале двадцатого века значительных теоретических работ, например
трудов Смолуховского и Эйнштейна. Предмет был глубоко изучен во мно¬
гих блестящих научных статьях и монографиях, поэтому мы ограничимся
здесь достаточно упрощенным рассмотрением, в котором акцент будет сде¬
лан на анализе устойчивости растворов коллоидных частиц.
Различают коллоидные растворы нескольких типов в зависимости от
природы сил отталкивания между частицами.
1. Взаимодействие твердых сфер представляет большой теоретиче¬
ский интерес и может быть экспериментально реализовано с помощью
калиброваных кварцевых сфер, покрытых тонким органофильным слоем,
диспергированных в неполярном растворителе, показатель преломления
которого совпадает с показателем преломления кварца52\ В этих условиях,
естественно, ни ван-дер-ваальсово, ни электростатическое взаимодействия
не играют роли. Броуновское движение должно уравновесить процесс се¬
диментации (выпадения осадка), следовательно частицы должны быть до¬
статочно малы (a4ApgfksT < 1; радиус а ^ 1 мкм), где Ар — разница
плотностей частиц и растворителя).
2. Электростатические силы отталкивания, которые можно модели¬
ровать с помощью заряженных частиц в электролите. Примером могут слу¬
жить полимерные калиброваные заряженные сферы в электролите, часто
называемые латексными растворами — слово латекс ранее ассоциирова¬
лось с соком гевеи, из которого вырабатывался натуральный каучук.
Мы напоминаем, что потенциал ДЛВО (см. рис. 14.2) показывает глу¬
бокий основной минимум (когда расстояние между объектами чрезвычай¬
но мало), отделенный от второго минимума барьером, величина которого
уменьшается с увеличением концентрации электролита. Расстояние, на ко¬
торое сближаются две мембраны, в принципе отвечает второму минимуму
Клтп- В случае когда электростатическое отталкивание велико, это про¬
исходит потому, что активационный барьер отталкивания чрезвычайно вы¬
сок. Когда же барьер оказывается разрушенным в присутствии электролита,
это происходит за счет расталкивающих мембраны флуктуаций Хелфриха.
С другой стороны, в случае частш\ основной минимум Vpmin достигается
гораздо легче, если активационный барьер Vmax уже преодолен, потому что
контакт должен осуществляться только в одной точке. Такое агрегирован¬
ное состояние необратимо, если | Vpmin \/k^T достаточно велико — время
выхода является величиной порядка a2D~1 ехр(| V^mm \/k^T), где D —
коэффициент диффузии.
3. Частицы с полимерным покрытием. В этом случае отталкивательное
взаимодействие устанавливается между полимерными покрытиями частиц
(см. гл. 15).
С. G. de Kruifet ai in Complex and Supramolecular Fluids, Edited by S. A. Safran
and N. A. Clark, Wiley-Interscience, N. Y., 1987, p. 673.
§ 14.3. Растворы коллоидных частиц; особенности устойчивости 593
При достаточно больших концентрациях или в присутствии спе¬
циального вещества, которое уменьшает силы отталкивания (например,
электролит или полимер, добавленные в раствор (см. п. 14.3.2)), части¬
цы могут сформировать кристалл, стекло или напоминающую твердое
тело гель-фазу. Суммируя вышеизложенное, можно заключить, что физика
коллоидных частиц — это конкуренция агрегации и растворения, порядка
и беспорядка. Это как раз те темы, которые мы рассмотрим в дальнейшем.
Похожая ситуация, но усложненная эффектами анизотропии, возника¬
ет в коллоидной структурной физике, когда частицы представляют собой
жесткие стержни (типа вирусов табачной мозаики) или полугибкие полиме¬
ры (типа ДНК, биополимеров и т. д.) Эта ситуация будет кратко рассмотрена
в следующей главе.
14.3.1. Броуновская флокуляция
Флокуляция — характерный термин, часто используемый, чтобы объ¬
единить различные явления, приводящие к появлению пористых, слабо
связанных агрегатов, или хлопьев (floes). Она происходит, например, ко¬
гда контакты между частицами обеспечиваются броуновским движением,
а основной минимум достаточно глубок по сравнению с &БТ. При этом
силы притяжения являются большими, а большинство контактов между
частицами необратимы.
Быстрая броуновская флокуляция. Она имеет место, когда одновре¬
менно с глубоким основным минимумом максимум парного отталкиватель-
ного потенциала Vrmax пренебрежимо мал по сравнению с к^Т. При этом
единственным процессом, лимитирующим контакты, является диффузия.
Рассмотрим одну частицу, считающуюся неподвижной, и определим чис¬
ло контактов С, которое она испытывает в единицу времени. Это число
можно оценить, используя первый закон диффузии Фика (см. гл. 8). Другие
частицы движутся изотропно вокруг пробной частицы, так что имеем
C = tor2cD — , (14.63)
dr
где г с та 2а — расстояние, при котором другие частицы (того же радиуса а)
касаются пробной частицы, и D — коэффициент диффузии. Эффективный
dn п
градиент концентрации можно записать как — та -, где п — плотность
dr а
частиц. Следовательно, кинетическое уравнение, описывающее уменьше¬
ние числа индивидуальных частиц, имеет вид
— = —167laDn2. (14.64)
dt
Плотность частиц уменьшается наполовину за время t* та (STrDano) ^1,
которое для D — к^Т/(6жг}а) (закон Стокса) составляет, самое большее,
несколько секунд при исходной концентрации частиц по та 1012 см“3. Та¬
ким образом, кинетика агрегации очень велика.
594
Гл. 14. Устойчивость коллоидных систем
Коэффициент стабильности. В большинстве случаев столь большие
скорости агрегации не достигаются. Это частично связано с тем, что коэф¬
фициент диффузии не подчиняется закону Стокса на коротких расстояни¬
ях между частицами (когда течение растворителя затруднено), и, помимо
всего, с тем, что на коротких расстояниях действуют силы отталкивания.
Для того чтобы количественно описать этот эффект, вводят коэффициент
стабильности W = Jq/J, где Jo — 16тraDn2 — броуновская скорость
агрегации индивидуальных частиц, а J — истинная скорость, определяе¬
мая деталями парного потенциала взаимодействия. Пусть V(г) — парный
потенциал взаимодействия между двумя частицами, т = (67varj)~1 — их
подвижность, D = ткьТ — коэффициент диффузии согласно соотноше¬
нию Эйнштейна. Выражение (14.63) принимает вид
Полагая, что процесс агрегации носит установившийся характер (С — кон¬
станта), это уравнение можно проинтегрировать и получится
где по — концентрация частиц вдали от данной частицы, помещенной в
начало координат, а граничное условие имеет вид: п{2а) = 0. Из (14.66)
можно вывести выражение для W = Jq/J. Приблизительная формула,
используемая в случае электростатического отталкивания:
позволяет получить для коэффициента стабильности значения вплоть до
к дискуссии о структурных свойствах ДОА (диффузионно-ограниченная
агрегация) в гл. 7.
14.3.2. Флокуляция истощения
Две коллоидные частицы в растворе, содержащем частицы меньшего
размера, испытывают действие сил притяжения, природа которых была
впервые осознана Асакурой и Оосавой54) для случая, когда малые частицы
(14.65)
п(г) = п0ехр(-У(г)/кБТ) +
Г
сехр (-У(т)/кБТ)
47г D
А у!
ехр(-У(г')/к^Т)^, (14.66)
ОО
W = {2ак0у1 exp(Vmax/kBT)
(14.67)
W ~ 105, если Утах/к^Т ~ 15, с ко ~ Ю8 м !. Такие величины и были
получены в эксперименте.
Форма хлопьев. Часто она фрактальная531 Мы отсылаем читателя
53) см., например, S. Dimon et al. Phys. Rev. Lett. 57, 595 (1986).
54^ S. Asakura and F. Oosawa. J. Chem. Phys. 22, 1255 (1954).
§ 14.3. Растворы коллоидных частиц; особенности устойчивости 595
являются макромолекулами. Это явление, называемое флокуляцией исто¬
щения, может быть качественно объяснено следующим образом. Пусть п —
плотность субчастиц: рассмотрим область размера h, площади А, в кото¬
рую малые частицы не могут проникнуть, поскольку h меньше или того же
порядка, что и размер субчастиц (рис. 14.7). Уравне¬
ние адсорбции Гиббса (13.13) может быть применено в
этом случае с 2ГЛ = — nhA, где Г — избыточное число
(в данном случае отрицательное) субчастиц на единицу
площади в зазоре:
da
dfi
г (h).
(14.68)
Сила, с которой одна частица действует на другую,
составляет / = — 2 — . Полагая, что раствор субчастиц
dh.
идеальный, т, е. ц = кБТ In с+const представляет собой
химический потенциал субчастицы, получаем
/ = -скБТА.
(14.69)
Рис. 14.7. Меха¬
низм флокуляции
истощения.
Перерисовано из
D. И. Everett, Basic
Principles of Col¬
loid Science. The
Royal Society of
Chemistry, 244 p.,
1988
цепь принима-
Коллоидные частицы находятся, следовательно, под
действием осмотического давления posm = скБТ. Зазор
между ними является областью, запрещенной для про¬
никновения субчастиц, как если бы они были отделены
от объема раствора полупроницаемой мембраной.
Эти рассуждения можно распространить на по¬
лимеры в растворе, которые не адсорбируются на
поверхности коллоидных частиц, с некоторой мо¬
дификацией величин коэффициентов в приведен¬
ной выше формуле. Как мы увидим в сле¬
дующей главе, изолированная гибкая полимерная
ет форму неупорядоченного (статистического) клубка как след¬
ствие конкуренции между энтропией системы и исключенным
объемом взаимодействий. Область в пространстве, занимаемая полимер¬
ным клубком, имеет типичный радиус Rq• Если две частицы разделены
зазором, меньшим чем ~ 2Rq, то макромолекулы, находящиеся в этой
области, оказываются сжатыми, что приводит к некоторому уменьшению
энтропии в системе. Величина энтропии может быть восстановлена за счет
исхода макромолекул из этой области. Этот эффект, связанный с внутренни¬
ми степенями свободы субчастиц, дает дополнительный вклад в флокуля¬
цию истощения, описанную выше для случая недеформируемых субчастиц,
и был учтен в работе Жоанни и др.551
55^ J.-F Joanny, L. Leibler and P. G. de Gennes. J. Poly. Sci.: Poly. Phys. Ed. 17, 1073
(1979).
596
Гл. 14. Устойчивость коллоидных систем
14.3.3. Стабильность в условиях сдвига; реологические свойства
При низких скоростях сдвига и низких объемных концентрациях ф
эффективная вязкость rj стабильного раствора удовлетворяет соотношению
Эйнштейна56^
-2-= 1 + 2.5 ф + 0(ф2), (14.70)
Vs
где 7]s представляет собой вязкость растворителя. Это увеличение вязкости
происходит из-за дополнительной диссипации энергии вследствие искаже¬
ния поля потока 7 — const вокруг частиц, к которым молекулы растворите¬
ля как бы «прилипают»; здесь 7 — характерная сдвиговая скорость (§ 6.4).
Члены более высокого порядка в (14.70) становятся существенными при
увеличении концентрации частиц: они отвечают взаимодействиям, вклю¬
чающим пары (ф2), триады (ф3) частиц и т.д. Стабильность в условиях
сдвига и вязкоупругое поведение коллоидных суспензий критически зави¬
сят от природы взаимодействий между частицами и от их концентрации
(подробности изложены в учебниках Рассела и др., а также Ларсона). Ко-
эффициенты при ф“,ф и членах более высокого порядка в (14.70) зависят
от природы этих взаимодействий.
1. В случае твердых сфер эффект парных взаимодействий при низких
объемных концентрациях ф был рассчитан Батчелором57);
2- = 1 + 2,5ф + 6,2ф2 + 0(ф3), (14.71)
Vs
и нашел подтверждение в экспериментах. Для всех объемных концентраций
размерный анализ предполагает существование связи между безразмерным
отношением ц/ц8 и безразмерным числом Пекле: Ре — a27/D, потому что
в системе нет других взаимодействий кроме тех, что обусловлены эффек¬
тами исключенного объема58). Число Пекле представляет собой отноше¬
ние времени а2 /£), характеризующего броуновское движение, к времени,
определяющему приложенный сдвиг, при постоянных концентрациях. Дей¬
ствительно, экспериментально было показано, что изменения r]/r]s могут
быть отложены вдоль одной и той же кривой как функция безразмерного
параметра rja^j/k^T, эквивалентного Ре (рис. 14.8). Мы видим, что эффек¬
тивная вязкость при постоянной объемной концентрации уменьшается при
увеличении скорости сдвига (так называемое сдвиговое утоныиение). Эта
зависимость экспериментально прослеживается для ф ^ 0,3. Сдвиговое
утоныиение связано с исчезновением вклада броуновского движения в дис¬
сипацию энергии при высоких напряжениях сдвига, что подтверждается
56^ A. Einstein. Ann, der Physik, 19, 289 (1906); English translation in Investigations on
the Theory of the Brownian Movement, Dover, 1956.
57) G. K. Batchelor. J. Fluid Mech. 83, 97 (1977).
58^ I. M. Krieger. Adv. Colloid Interface Sci. 3,111 (1972).
§ 14.3. Растворы коллоидных частиц; особенности устойчивости 597
результатами компьютерного моделирования59^. (Другой механизм связан
с формированием цепочек частиц в направлении вдоль потока — это под¬
тверждается экспериментами по рассеянию света601) Однако эти цепочки
становятся нестабильными при больших скоростях сдвига (или сдвиговых
напряжениях), и может наступить сдвиговое утолщение.
V I vs
Рис. 14.8. Изменение относительной вязкости r\jr\s как функции безразмерного
параметра при постоянной объемной фракции ф. Сдвиговое утоньшение.
Адаптировано из Krieger 58\ ф = 0,40
2. В присутствии других взаимодействий (мягкие сферы), анализ ре¬
зультатов по сдвиговому течению оказывается более сложным.
Влияние сдвига на стабильность раствора было изучено в некото¬
рых теоретических работах, однако их сравнение с экспериментальными
результатами оказалось явно недостаточным и труднодостижимым. При
относительно малых скоростях сдвига, т. е. при Ре < 1, число столкнове¬
ний между частицами вследствие броуновского движения превышает число
столкновений из-за сдвигового потока. Влияние сдвига в этом случае мож¬
но учесть, вводя корректирующий член в коэффициент стабильности W,
рассчитанный в статическом режиме (п. 14.3.1). Величина W при этом
немного уменьшается (см. учебник Рассела и др., где изложены элементы
теории). Увеличение числа пар должно привести к увеличению вязкости.
При высоких скоростях сдвига, т. е. при Ре ^> 1, могут образоваться агрегаты
59^ J. F Brady. Curr. Opin. Collloid Interface Sci. 1, 472 (1996).
60 ^ B. J. Acker son and P. N. Pusey. Phys. Rev. Lett. 61, 1033 (1988).
598
Гл. 14. Устойчивость коллоидных систем
большего размера, стабильность которых отвечает вторичному минимуму
потенциала ДЛВО (меньшие скорости сдвига) или основному минимуму
(большие скорости сдвига).
В случае стабильных растворов заряженных частиц теория6 ^ предска¬
зывает, что для малых ф вязкость может быть описана аналогично случаю
твердых сфер, но с эффективным диаметром частиц deff, учитывающим
диапазон действия сил отталкивания (подробности изложены в учебнике
Ларсона). Мы получаем
Л
Vs
1 + 2,50 +
2,5 + —
40 V а /
Ф2 + 0(ф3)
(14.72)
При низкой ионной силе теория предсказывает de^ 2а. Показатель степе¬
ни равен 5, следовательно, обеспечивает быстрое возрастание эффективной
вязкости с увеличением объемной фракции вследствие электростатических
взаимодействий, что было обнаружено в эксперименте. При больших объ¬
емных долях, скажем ф > 0,1, и высоких скоростях сдвига гидродинами¬
ческие взаимодействия становятся более существенными, по сравнению
с электростатическими, de^ уменьшается, и мы получаем величины вязко¬
сти, близкие к тем, которые можно было бы ожидать для системы твердых
сфер.
14.3.4. Порядок против беспорядка
Коллоидные системы дают замечательные примеры фазовых переходов,
представляющих фундаментальный интерес. В отличие от твердых тел,
в коллоидах достаточно легко изменить характер взаимодействий в одной и
той же системе. Это дает большое разнообразие объемных фаз: от газовой
фазы до трехмерной кристаллической организации62^. К числу подробно ис¬
следованных модельных систем относятся суспензии частиц золота, квар¬
ца, полистирола в воде, полиметилметакрилата (ПММК) в масле, двойные
коллоидные смеси типа частиц ПММК в полистироле и т. д. Во всех указан¬
ных случаях размер частиц достаточно мал, так что броуновское движение
способно эффективно предотвратить седиментацию. Ниже мы кратко обсу¬
дим влияние сил отталкивания на стабильность коллоидных кристаллов.
Недавние эксперименты63^ выявили существование сил притяжения между
одинаковыми зарядами в коллоидных средах с пространственными огра¬
ничениями; возможно, эти силы способствуют кристаллизации коллоидов.
Сказанное выше означает, что теория коллоидных растворов и коллоидных
кристаллов переживает период полного обновления.
61} W. В. Russel. J. Fluid Mech. 85, 209 (1978).
62^ А. P. Gast and W. В. Russel. Physics Today, December 1998, p. 24.
63^ J. C. Crocker and D. G. Grier. MRS Bulletin 10, 24 (1998).
§ 14.3. Растворы коллоидных частиц; особенности устойчивости 599
14.3.4.1 Силы отталкивания; твердые сферы
В основе понимания конкуренции между порядком и беспорядком ле¬
жит энтропия. В среде, где действуют исключительно силы отталкивания,
типа системы твердых сфер, причиной кристаллизации (так называемо¬
го перехода Кирквуда-Алдера) является то, что энтропия колебаний ча¬
стиц в их ячейках при упорядочении может быть больше, чем энтропия
трансляции в жидком состоянии. Такой переход можно сравнить с моделью
Онзагера фазового перехода жидкость - нематик в системе жестких стерж¬
ней (см. гл. 4), в которой также определяющими являются взаимодействия
отталкивания и связанные с ними эффекты ориентационно-зависящего ис¬
ключенного объема. Переход Кирквуда-Алдера был рассчитан методами
молекулярной динамики64^ и экспериментально обнаружен65^ в суспензии
сфер из полистирола в жидкости, выбранной таким образом, чтобы при¬
тяжения Ван-дер-Ваальса были подавлены. При переходе кристаллизации
объемные доли составляют для жидкости фущ = 0,494 , а для кристалла
фСТ = 0,545. Структура является ГЦК, хотя этот переход происходит при
объемных плотностях, гораздо меньших, чем в состоянии плотнейшей упа¬
ковки фсг = 0,74. Однако плотнейшая упаковка может быть достигнута
непрерывным образом за счет повышения давления. Переход в застекло-
ванное состояние был обнаружен при — 0, 58661 Мы отсылаем читателя
к учебнику Рассела и др., где изложены детали соответствующей статисти¬
ческой теории.
14.3.4.2. Силы отталкивания; мягкие сферы. Силы отталкивания
могут быть изменены на дальнодействующие, если поместить на части¬
цы постоянные электрические заряды. При этом толщина двойного слоя
является тем минимальным расстоянием, на которое две частицы могут
сблизиться. Другая возможность состоит в закреплении полимерных цепей
на частицах (графт-полимер), так что две полимерные щетки не проникают
друг в друга (см. гл. 15). Переходы по-прежнему осуществляются за счет
изменения энтропии, с той существенной разницей по сравнению с твер¬
дыми сферами, что покрытые полимером или заряженные частицы имеют
больший эффективный радиус, так что переход Кирквуда-Алдера проис¬
ходит при меньших объемных плотностях.
Случай заряженных частиц был рассмотрен выше (п. 14.3.3). Эффек¬
тивная объемная доля составляет: фе$ = 0(deff/2a)3, что для слабых элек¬
тролитов может быть гораздо больше, чем ф. Полистироловые сферы при
очень низкой ионной силе образуют радужные ОЦК-фазы при ф ^ 0,01,
в то время как ГЦК-фазы образуются при больших ф. Аналогичным обра¬
зом, белки могут кристаллизоваться при очень небольших объемных долях
растворенного вещества.
64 ] В. J. Alder, IV. G. Hoover and D. A. Young. J. Chem. Phys. 49, 3688 (1968).
65* S. Hachisu and Y. Kobayashi. J. Colloid Interface Sci. 46, 470 (1974).
66^ P. N. Pusey and W. van Megen. in Complex and Supramolecular Fluids, Edited by
S. A. Safran and N. A. Clark, Wiley-Interscience, N. Y., 1987, p. 673.
600
Гл. 14. Устойчивость коллоидных систем
Обладая кристаллическими свойствами, коллоидные кристаллы име¬
ют предел текучести и пластические свойства, связанные с движением дис¬
локаций67). Однако кристаллы, полученные таким образом, являются очень
мягкими и легко плавятся при сдвиговой деформации68\
§ 14.4. Измерения взаимодействий в коллоидных
системах
Силы, действующие на коллоидные частицы, весьма малы. Например,
сила, действующая между двумя сферами радиуса а « 10"5 м с одним
элементарным зарядом на 0,16 нм2 (т. е. q « 1 Кл*м-2 в СИ-единицах),
кБТ
— = 25,69 мВ, ко ~ Ю-9 м"1 и h « 10 а, определяется выражением69)
е
—2'К£Ео(кьТ/ze)2aq2 In (1 — ехр —hko)
и имеет величину порядка одного фемтоньютона (10”1й Н)). Кроме того,
весьма сложно обращаться с такими малыми объектами. Однако в послед¬
нее время были достигнуты значительные успехи — например, созданы
атомно-силовой микроскоп для измерения сил и оптический пинцет для
манипуляции с частицами или биополимерами. Конечно, были развиты
и специальные методы проведения точных измерений в коллоидных си¬
стемах. Мы кратко опишем те из них, что приобрели важное значение за
последние двадцать лет. Мы уже упоминали технику пипеточного удаления
для измерений механических свойств однослойных везикул.
Осмотическое напряжение (ОН). Исследуемый образец погружается
в раствор декстрана, полиэтиленгликоля и т. д., фактически в любой рас¬
твор, содержащий большие молекулы, которые не могут проникать в об¬
разец. В то же время растворитель может свободно циркулировать между
двумя средами. Осмотическое давление окружающей среды в этом случае
передается механически на исследуемый образец. Этот метод, например,
позволяет измерять силы, действующие между слоями в ламеллярной фазе
в зависимости от периода структуры. ОН-метод позволил провести пря¬
мые измерения потенциала ДЛВО между бислоями поверхностно актив¬
ного вещества70^. Интегрирование давления по расстоянию между слоями
позволяет получить потенциал взаимодействия.
Поверхностно-силовой аппарат (ПСА). ОН-метод позволяет исследо¬
вать только оггалкивательную часть потенциала взаимодействия. С другой
стороны, поверхностно-силовой аппарат позволяет восстановить полную
67^ М. Jorand, F. Rothen and P. Pieranski. J. Physique, 46, C3-245 (1985).
68^ A. J. Ackerson andN.A. Clark. Phys. Rev. Lett. 46, 123 (1981).
69^ Russel et aL textbook, p. 559.
70^ Y.-H. Tao, D. F. Evans, R. P. Rand and V. A. Parsegian. Langmuir 9, 223 (1993).
§ J4.4. Измерения взаимодействий в коллоидных системах
601
потенциальную кривую взаимодействия (см. учебник Израелашвили, с. 41).
Образец помещается между парой атомно-гладких слюдяных цилиндров,
пересекающихся под прямым углом. Аппарат измеряет отношение силы,
действующей между слюдяными цилиндрами, к их радиусу. Это отноше¬
ние зависит от минимального расстояния между цилиндрами и должно
рассматриваться как функция числа слоев, если вещество находится в ла¬
меллярной фазе. ПСА также использовался для изучения структурных сил
в мицеллярных системах71 X Точность метода составляет величину поряд¬
ка 10 пН, сравнимую с точностью ОН. Для сравнения возможностей ПСА
и ОН, см. публикацию Тао и др.701 ПСА специально разработан для измере¬
ний сил притяжения, например константы Гамакера72). Необходимо однако
отметить, что флуктуации бислоев сильно гасятся контактом с ограничи¬
вающими поверхностями и эффектами сцепления. С другой стороны, при
очень малых расстояниях между цилиндрами ПСА позволяет определить
молекулярную структуру растворителя, а также установить отклонения на
малых расстояниях от стандартных моделей; переход из губчатой в ла¬
меллярную фазу, индуцированный ограничивающими поверхностями, был
изучен подобным образом73 \
Атомно-силовая микроскория (ACM). Этот метод позволяет одно¬
временно получать изображения непроводящей поверхности на атомном
уровне — путем сканирования вдоль поверхности непроводящим наконеч¬
ником (tip), смонтированным на кантилевере (cantilever), с разрешением
в несколько ангстрем, — и измерять силы, действующие между наконечни¬
ком и исследуемым атомом или молекулой на поверхности, в пиконьюто¬
новом (10-12 Н) диапазоне74).
Оптический пинцет7о1 Микроскопические частицы могут быть пой¬
маны в ловушку, создаваемую электромагнитным потенциалом лазерного
света, и затем ими можно манипулировать в трехмерном пространстве.
Эта техника позволяет изучать взаимодействие между двумя независимо
пойманными частицами или прослеживать движение частиц. При исполь¬
зовании второго метода определяют траектории частиц, из которых затем
можно рассчитать парную корреляционную функцию
g(r) ~ I
Г
2
dtp
Г
0
dr'pO' - г, t)p(r\ t),
71 ^ P. Richetti and P. Kekicheff Phys. Rev. Lett. 68, 1951 (1992).
72^ J. N. Israelachvili and P. M. McGuiggan. Science 241, 795 (1988).
73^ D. A. Antelmi, P. Kekicheff and P. Richetti. J. Phys. II France 5, 103 (1995).
74) D. Sarid. Scanning Force Microscopy with Applications to Electric, Magnetic, and
Atomic Forces, Oxford University Press, 1991.
75) A. Ashkin, J. M. Diedzic, J. E. Bjorkholm and S. Chu. Opt. Lett. 11, 288 (1986).
602
Гл. 14. Устойчивость коллоидных систем
N
где р(г, t) = *52 &(? — yi(t)) — функция траекторий N частиц. Из парной
корреляционной функции с помощью формулы g(r) = ехр[-\/(г)//свТ]
можно получить потенциал парного взаимодействия V (теория стохастиче¬
ских процессов в жидкостях изложена в76)). Этот метод измерений потен¬
циала был впервые использован для определения потенциала притяжения
между полистироловыми сферами микронных размеров, помещенными
между двумя пластинами. Траектории полистироловых сфер фиксирова¬
лись с помощью видеомикроскопических наблюдений77). Использование
оптического пинцета позволило изучить взаимодействие изолированных
пар частиц78), и получить согласие с теорией ДЛВО, с учетом того что
некоторые параметры, типа фиксированных зарядов сфер, были подогна¬
ны63).
Задача 14.0.
а) Вычислить n0f2 (14.10), используя условие сохранения заряда (14.2).
б) Определить, в какой мере можно пренебречь присутствием в воде
свободных Н+ и ОН~ ионов в вычислениях, приводящих к выражению
(14.11).
Ответ.
б) Концентрация противоионов велика вблизи заряженной пластины,
и уменьшается с увеличением расстояния х от пластины. Концентрация
противоионов — это величина порядка концентраций ионов Н+ и ОН“
(т. е. 10“7 Nav/дм3)) для х та (10~7 Nav ■ 1000/27г^)1/2(в единицах СИ)
та 2•10~6 м = 2 мкм.
Задача 14.1. Выразить плотность противоионов на границе как функ¬
цию плотности противоионов в центральной плоскости между двумя оди¬
наково заряженными пластинами в случае, когда раствор не содержит элек¬
тролита.
Ответ. Уравнение ПБ (р" = ~(епо/££о) ехр(—е^р/к^Т), которое мо¬
жет быть записано как <//' ~ —еп(х)/££о, где п(х) — плотность противо-
2 к^Т
ионов, легко трансформируется в уравнение d(<pf)L/dx = • dn(x)/dx
его
после умножения обеих частей на . Пусть начало координат выбрано в
центральной плоскости. По симметрии задачи, ipl(x — 0) = 0 и п(х) =
= п(0) + (££о/2кБТ)((рг)2. Используя граничные условия на заряженных
пластинах, можно получить: п$ — п(0) + (еео/2&бТ)а2. Поэтому можно
76'1 J.-P. Hansen and 1. R. McDonald. Theory of Simple Liquids, 2nd edition, Academic
Press, N. Y., 1986.
77) G. M. Kepler and S. Fraden. Phys. Rev. Lett. 73, 356 (1994).
78^ J. C. Crocker and D. G. Grier. Phys. Rev. Lett. 73, 352 (1994).
§ 14.4. Измерения взаимодействий в коллоидных системах
603
также выразить p(d) в следующем виде:
p(d) — кьТп(х — 0) = k^T(ns — {eeol2k^T)a2)
Задача 14.2. Решить уравнение ПБ для заряженной сферы радиу¬
са а в приближении Дебая-Хюккеля. Вычислить связь между плотностью
поверхностного заряда а и потенциалом ip(a) = (ps на поверхности.
Ответ. Мы полагаем, что электролит содержит ионы с валентностя¬
ми Z{, концентрация которых равна п^о- В приближении Дебая-Хюккеля
нелинейное уравнение ПБ
2^n,i0Zi ехр
г dr dr eso \ кБТ
г
сводится к простому виду
I d 7 2 ( \
-—г — = kD<p(r),
г ат ат
где кр — обратная дебаевская длина (14.14). Мы использовали здесь усло¬
вие нейтральности = 0-
ф
г
Наиболее общим решением уравнения Дебая-Хюккеля является
rtp(r) = Aexp(—ki)r) + В ехр(-Ькрг), с условием, что потенциал зану-
ляется на бесконечности и принимает заданное значение на поверхности
сферы. Мы получаем
<p(r) = Ifs - ехр[~kD{r - а)].
Г
т=а
Граничные условия для зарядов могут быть записаны как а = —seq —
dr
следовательно, а — еео — (1 + кра). Полный заряд q — 4iта2а частицы
а
оо
противоположен полному заряду в растворе: — q — J Airpr2 dr. В итоге мы
а
получаем
ips = +
Атг££оа 47Г££о(а + Ад)
Задача 14.3. Доказать (14.36).
Ответ. Когда область = dxi dx2 преобразуется с помощью бес¬
конечно малой величины A, а{ -Л а[ и / (1 -Ь Асг^) и dxi —У dx\ и
dxi(l + A ai). Эти выражения зависят от знака.
Задача 14.4. Рассмотрим две мембраны, связанные друг с другом
и расположенные вдоль некоторого элемента площади (см. рис. 14.9). Они
604
Гл. 14. Устойчивость коллоидных систем
разделяются вдоль некоторой линии L, перпендикулярной рисунку, и обра¬
зуют угол 2$0 на асимптотическом расстоянии от линии L. Пусть 7соь есть
выигрыш энергии на единицу площади при установлении контакта между
двумя мембранами, и 7 — поверхностное натяжение мембран.
Рис. 14.9. См. задачу 14.4
а) Показать, что пара связанных мембран обладает поверхностным на¬
тяжением т =■ 27 — 7сoh ■ Мы будем полагать, что эта величина является
положительной.
б) Выразить как функцию 7 и 7соь-
в) Доказать следующее выражение для свободной энергии, приходя¬
щейся на единицу площади мембраны вдали от области контакта:
fs = (1/2)х d2d/ds2 -f 7(cosi9 — cos^o),
где 5 — абсцисса, измеренная вдоль свободной мембраны в плоскости, пер¬
пендикулярной L. Найти первый интеграл уравнения Эйлера-Лагранжа,
соответствующий этой плотности энергии, и показать, что мембрана экс¬
поненциально стремится к своему асимптотическому направлению $о на
длине порядка $о —
Ответ
б) 27(1 - COSI?o) = 7coh*
в) Заметим, что
7(cos$ — cos^o) = jAAp/A,
где А Ар — величина, противоположная вариации площади проекции мем¬
браны на направление д — 0; это выражение, которое является двумерным
эквивалентом классического трехмерного выражения —pdV/V, предпола¬
гает, что $ и малы; (1/2)x(d$/ds)2 H-7(cosi9o — cosi9) = 0; подробности
см. в работе: W. Helfrich andR.-M. Servuss, II Nuovo Cimento, 3D, 137 (1984).
Литература для дальнейшего чтения
605
Литература для дальнейшего чтения
Мембраны
1. A. W. Adamson and А. РGast. Physical Chemistry of Surfaces, John Wiley &
Sons, Inc., N. Y., 1997, 784 p.
2. Micelles, Microemulsions, Membranes and Monolayers, Edited by W. Gelbart,
A. Ben-Shaul, and D. Roux, Springer-Verlag, N. Y., 1994.
3. Physics of Amphiphilic Layers, Edited by J. Meunier, D. Langevin, and N. Boccara,
Springer-Verlag, N. Y., 1987.
4. Samuel A. Safran. Statistical Thermodynamics of Surfaces, Interfaces, and Memb¬
ranes, Frontiers in Physics, Addison-Wesley Publishing, Reading, MA, 1994.
Наука о коллоидах
1. D.F. Evans and H. Wennerstrom. The Colloidal Domain: where Physics, Biology,
and Technology meet. Wiley-VCH, N. Y., 1994.
2. R. J. Hunter. Foundations of Colloid Science, Oxford University Press, Oxford,
1986.
3. J. N. Israelachvili. Intermolecular and Surface Forces, 2nd edition, Academic
Press, N. Y, 1992.
4. R. G. Larson. The Structure and Rheology of Complex Fluids, Oxford University
Press, N. Y, Oxford, 1999.
5. D. Myers. Surfaces, Interfaces, and Colloids, 2nd edition, Wiley-VCH, N. Y.,
1999.
6. W. B. Russel, D. A. Saville, and W. R. SchowalterColloidal Dispersions, Cambri¬
dge University Press, Cambridge, 1995 (reprinted).
7. E. J. W. I ei'vey and J. Th. G. Overbeek. Theory of the Stability of Lyophobic
Colloids, Elsevier, N. Y., 1948.
Дополнительная литература
1. ВеденовА.А. Физика растворов. — М.: Наука, 1984.
2. Дерягин Б. В., Чураее Н. В., МуллерВ. М. Поверхностные силы. — М.: Наука,
1985.
3. Дерягин Б. В. Теория устойчивости коллоидов и тонких пленок. — М.: Наука.
1986.
4. Измайлова В. Н., ЯмпольскийГ. П., Сумм Б. Д. Поверхностные явления в бел¬
ковых системах. — М.: Химия, 1988.
5. Фролов Ю. Г. Курс коллоидной химии. —М.: Химия, 1989.
6. Фридрихсберг Д. А. Курс коллоидной химии.—Л.: Химия, 1995.
7. Щукин Е.Д., Перцев А. В., Амелина Е. А. Коллоидная химия. 3-е изд. —
М.: Высшая школа, 2004.
ГЛАВА 15
ПОЛИМЕРЫ: СТРУКТУРНЫЕ СВОЙСТВА
Для полимеров характерно большое разнообразие химических струк¬
тур, начиная от биополимеров типа ДНК, ксантана, целлюлозы, белков
и волокон актина вплоть до синтетических полимеров типа полиэтиле¬
на (ПЭ), полибутадиена (ПБ), полистирола (ПС), полиметилметакрилата
(ПММА) и т. д., представляющих колоссальный интерес для промышленно¬
сти. Полимеры применяются в самых различных видах: в растворах, в виде
гелей, резины, синтетических тканей, литых деталей и т. д.
В первой части этой главы отражено влияние разработанного де Женом
классического подхода к физике полимеров. Мы убеждены, что простей¬
ший путь описания фундаментальных свойств полимеров как в растворе,
так и в их расплавах состоит в использовании соотношений подобия (Скей-
линговых соотношений), которые являются основными характеристиками
цепей с большой степенью полимеризации (СП) N. Хотя математика здесь
является довольно простой, физические последствия такого подхода весьма
глубоки — совершенно невозможно получить реалистические скейлинго-
вые законы без тщательного анализа физических свойств макромолекул.
Здесь не сильно помогает стандартный подход, основанный на использова¬
нии выражений для плотности свободной энергии системы, часто приме¬
няемый вслепую, как черный ящик, из которого результаты выскакивают
как по волшебству. С другой стороны, нелинейные эффекты или явления,
описываемые методом ренормализационной группы, которые в обычных
теориях удается рассчитать только в результате серьезных усилий, при
скейлинговом подходе получаются самым естественным путем. Все это
говорится вовсе не потому, что мы недооцениваем обычные подходы, ко¬
торые совершенно необходимы, когда приходится оперировать материаль¬
ными константами среды. В первой части этой главы мы сосредоточим¬
ся на замечательных физических эффектах в гибких полимерах, которые
сродни критическим явлениям, проявляющимся при фазовых переходах.
Физические свойства описываются в терминах конформаций гибких це¬
пей как функции молекулярной массы полимера (часто выражаемой как
число мономеров N на цепь), объемной концентрации мономеров с = n/V
(п мономеров в объеме V), температуры и т.д. При описании фазовых
переходов в полимерах аналогом температуры является величина 1/N. Мы
также найдем аналоги для критических показателей, часть которых может
быть интерпретирована как фрактальные размерности.
Цепи в расплаве близки по своим свойствам к идеальным цепям, рас¬
смотренным в первой части главы, и их физика может быть описана в рам¬
ках теории среднего поля. Следовательно, мы представим классическую
теорию Флори - Хаггинса для расплавов полимеров и их смесей и, в част¬
ности, рассмотрим явления фазового разделения в смесях, что типично
для полимеров. Это как раз разделы, посвященнные упорядоченным фазам
§ 15.1. Идеальные цепи и цепи Флори
607
двублочных сополимеров, где мы возвращаемся к структурному описанию
конденсированных сред — одной из важнейших тем данной книги.
Наконец, в этой главе единым образом обсуждаются жесткие и полугиб¬
кие полимеры, которые включают все биополимеры, некоторые анизотроп¬
ные вирусы и синтетические полимеры. Последние используются как ткани
или составные элементы высокопрочных материалов, механические свой¬
ства которых определяются тем, что они имеют тенденцию к образованию
жидкокристаллических фаз при высокой температуре или ориентируются
под действием сдвига.
Мы отсылаем читателя к имеющейся обширной литературе за подроб¬
ными описаниями микроскопических динамических свойств полимеров
(времена релаксации, процессы диффузии, и т.д.), (например: М. Doi,
S. F. Edwards, 1988. [Пер. на русск. язык: Дои М., Эдвардс С.. Динамическая
теория полимеров / Пер. с англ. под ред. С. И. Кучанова, В. А. Кислова. —
М.: Мир, 1998]. Макр о скопические ре о логические свойства полимеров, как
в растворе, так и в форме упорядоченных или разупорядоченных расплавов,
составляют такую большую область исследований, что мы предпочитаем
оставить ее полностью в стороне. Современное изложение этих вопросов
можно найти в книге Ларсона (1999). По сходным причинам мы не каса¬
лись здесь вопросов кристаллизации. Эта тема рассмотрена в гл. 4 книги
Штробля (1996). Мы также рекомендуем интересный обзор Келлера по
складывающимся полимерным цепям.
§ 15.1, Идеальные цепи и цепи Флори
Мы ограничим наше рассмотрение гибкими полимерами, образующими
основную цепь (линейные полимеры), прототипом которых является поли¬
этилен [—СНг—|п- Другими стандартными примерами являются
полиоксиэтилен [-0-СН2-СН2-]п, полидиметилсилоксан
СНз
Si
СНз
полистирол
- СН2 - СН -
Ф
(Ф = фенильное кольцо) и т. д
П
О
Каждый из этих полимеров может быть представлен как последователь¬
ность связей, соединяющих элементарные мономерные звенья. В простей¬
шем случае полиэтилена, который мы будем рассматривать в качестве
модельного, изменение угла между последовательными атомами углерода
можно определить как А0п — вп ~ вп~] = 0, Atpn = 0, ±120° (рис. 15.1);
Афп = 0 называется ш/?щус-конфигурацией; Aipn — ±120 — гош-конфигу-
рацией. Эти состояния обладают различными энергиями. Подобный гео-
608
Гл. 15. Полимеры: структурные свойства
Гош (+)
метрический (поворотно-изомерный) подход может быть распространен на
случай любого гомополимера, mutatis mutandis — изменив то, что следу¬
ет (лат).
Полагая, что последовательные значения А(рп являются случайными,
цепь, если смотреть на нее в мас¬
штабе, много большем, чем элемен¬
тарная длина связи а, выглядит как
статистический клубок. Для нас
представляют интерес следующие
характеристики полимерной цепи.
1. Персистентная длина iv.
Пусть Ае = £9 — et >0 определя¬
ет разницу между значениями энер¬
гии в гош- и транс-конфигурациях.
Тогда
Гош (—)
£
р — а ехр
Ае
кБТ
(15.1)
представляет собой длину,
которой цепь выглядит как жест¬
кий стержень, потому что сег¬
менты коллинеарны для последо¬
вательности транс-конфигураций.
Следовательно, для цепи, которую
можно рассматривать как статисти¬
ческий клубок, химическая длина
цепи L — N а должна быть большой
по сравнению с 1Р. Это условие мо¬
жет быть записано как
на
1
Рис. 15.1. Конфигурационные парамет¬
ры пространственной цепи, состоящей
из полиэтиленовых групп
х
I
р
L
N
^хр — <1. (15.2)
к^Т
При феноменологическом описании персистентную длину можно так¬
же ввести как характерный масштаб тепловых флуктуаций, происходящих
в упругом жестком стержне. Давайте примем для простоты, что сечение
стержня изотропно. Тогда свободную энергию деформации на единицу дли¬
ны стержня можно записать как
F
1 -2
-КГ
2
с
где г с
радиус кривизны, ах — упругий модуль для деформации не¬
малое сме-
кривленияЧ Имеем: гс 1 = ±\d2\i/ds2 \ = duj/ds, где и
щение стержня по отношению к недеформированному прямому стержню,
^ Ландау Л. Д., Лифшиц Е. М. Статистическая физика. — М.: Физматлит, 2001.
§ 15.1. Идеальные цепи и цепи Флори
609
расстояние, измеренное вдоль стержня, иси — угол отклонения стерж¬
ня. Используя преобразование Фурье свободной энергии стержня длины L:
х ь
F = - J xr2 ds, а затем применяя теорему о равнораспределении энергии
2 о
и суммируя по всем модам, легко получить средний квадрат угла:
(ш2)=2 ^L. (15.3)
Считая (coscj) % 1 — LkвТравным нулю, что эквивалентно условию,
при котором элементы стержня при <s = 0 и s = L ориентационно нескор-
релированы (см.: Ландау и Лифшиц1)), мы получаем: £р — В конечном
/сБТ
счете плотность свободной энергии может быть записана как
F = -кБТ£рг~2. (15.4)
2
Разумеется, это выражение для свободной энергии справедливо для L < iv.
Для длин L > 1Р цепь является гибкой, и ее свободная энергия записывается
в совершенно другом виде (см. ниже).
2. Персистентное время тр, т. е. время, характеризующее изменение
конформации. Пусть АЕ — активационная энергия (энергетический ба¬
рьер), необходимая для транс-, гош-изомеризации. Имеем
A f?
т. = т0 ехр . (15.5)
/сбТ
Цепь проявляет себя гибкой в любом эксперименте, продолжительность
которого г > тр. Характеристическое время то связано с тепловыми коле¬
баниями цепи и является величиной порядка 10“12 с.
15.1.1. Конформации одиночной цепи
На одну связь в цепи приходится три вращательных изомерных состоя¬
ния: £, g+, и g~. Следовательно, для цепи полиэтилена с СП, равной N,
можно насчитать 3^ различных конфигураций. Некоторые из них, как по¬
казано ниже, обладают специфическими свойствами.
I. Спиральная конфигурация. Это конфигурации цепи, в которой все
мономерные единицы повторяются периодически и геликоидально вдоль
направления удлинения цепи (наиболее часто такая повторяющаяся струк¬
тура имеет спиральную форму, отсюда и название). Спиральная конфигура¬
ция имеет минимальную внутреннюю энергию и встречается в кристаллах
полимеров. Для ПЭ это полностью Аиряис-состояние: цепь имеет зигзагооб¬
разную структуру в направлении своего удлинения, а не истинную трехмер¬
ную геликоидальную структуру. Политетрафлуороэтилен (ПТФЭ) образует
настоящую спираль, близкую к полному транс-состоянию, но отличаю¬
щуюся от него закруткой вдоль цепи, вызываемую стерическим отталки¬
ванием между соседними атомами фтора. Для полиоксиметилена (ПОМ)
39-КЛЕМАН М.
610 Гл. 15. Полимеры: структурные свойства
существует несколько спиральных состояний, отвечающих минимуму энер¬
гии, которые различаются видом закрутки полностью г<?ш-конфигураций.
2. Конфигурации клубка. В дальнейшем нас будут интересовать только
молекулы, которые являются динамически подвижными, т. е. макромоле*
кулы, у которых химическая длина aN велика по сравнению с lv и ко¬
торые наблюдаются в течение времени, гораздо большего чем тр. Подоб¬
ные молекулы образуют 3N конфигурационных состояний. В этом случае
свойства системы не зависят от локальных масштабов и на детали хими¬
ческого строения можно просто не обращать внимания. С другой стороны,
все «мезоскопические» свойства системы зависят от N в соответствии со
скейлинговыми законами такими, как
Rg ос aNv, (15.6)
где, в данном примере, Rq — так называемый радиус инерции (строгое
определение которого будет дано ниже), т. е. характерный радиус стати¬
стического клубка, в который сворачивается полимерная цепь, помещенная
в подходящий растворитель. Следующий пункт посвящен вычислению по¬
казателя степени v в различных теоретических моделях.
15.1.2. Идеальная (или гауссова) цепь
15.1.2.1. Средний размер идеальной цепи. Положим, что N элемен¬
тарных сегментов (иногда в дальнейшем называемых для простоты связя¬
ми) образуют полимерную цепь. Будем считать, что ориентации различных
сегментов не зависят друг от друга. Подобная цепь называется идеальной.
Вектор, соединяющий начало цепи с ее концом, может быть записан как
N
Г = £а<. О5'7)
г-1
Возводя г в квадрат и проводя усреднение по всем возможным конфигура¬
циям, мы получаем
<г2> = Еа? + 2£<а^> = ^2> (15-8)
i гфj
потому что ориентации двух сегментов i и j между собой не коррелируют.
Следовательно, среднее расстояние между концами цепи, которое также
можно назвать средним размером идеальной цепи, есть
R0 = (г2)1/2 = aN1/2, (15.9)
и v = 1/2 для идеальной цепи. Отметим, что этот показатель степени не за¬
висит от размерности окружающего пространства. Скейлинговый закон
§ 15. L Идеальные цепи и цепи Флори
611
(15.9) остается неизменным, если ввести взаимодействия между различны¬
ми связями вдоль самой цепи (называемыми короткодействующими взаи¬
модействиями, чтобы подчеркнуть разницу с дальнодействующими взаи¬
модействиями между связями, относящимися к различным цепям).
Можно показать, что, в силу центральной предельной теоремы (см. при¬
ложение 15. А), вероятность Рдг (г) того, что цепь, имеющая N связей, окан¬
чивается в точке г, отвечает гауссовому распределению:
\ 3/2
\ 3 г
2
P"W=I2-^J ('510)
Другой вывод этого распределения предложен в упражнении (задача 15.1).
Вероятность Рлг(г) определяется отношением числа конфигураций Гдг(г),
необходимых для того, чтобы привести цепь из фиксированного начала
координат в точку г, к общему числу конфигураций Гд? — ГдКг)- Эн-
тропия идеальной цепи представляет собой S — кБ In IV (г), следовательно
5(г) — k^lnPj^ + &б 1пГдг, (15.11)
откуда получаем с точностью до аддитивной константы выражение
S(v) =(15.12)
2 Rq
которое зависит только от модуля г = | г |. Энтропия увеличивается с умень¬
шением г, из чего можно заключить, что идеальная цепь представляет собой
компактный объект со многими пересечениями.
15.1.2.2. Свободная энергия. Свободная энергия цепи имеет чисто
энтропийную природу и может быть записана как
F(r) = Fo + -кЕТ^-. (15.13)
2 R%
Пусть к изолированной цепи приложена внешняя сила f. Если предполо¬
жить, что под действием внешней силы расстояние между концами цепи
изменится от г до г 4- dr, то работа, проделанная внешней силой, есть f dr.
Эта величина должна соответствовать возрастанию свободной энергии, т. е.
f dr — dF и
f^dF/dr. (15.14)
В результате зависимость между приложенной силой и производимой ею
«деформацией» приобретает вид
Г = /-Щ=, (15.15)
Зк%Т
т. е. цепь удлиняется в направлении вдоль линии действия силы f. Это
совпадает с удлинением струны с упругой константой Зк^Т/Щ.
Де Жен показал, что выражение (15.15) может быть получено напрямую
исходя из законов подобия. Предполагается, что удлинение цепи зависит
612
Гл. 15. Полимеры: структурные свойства
только от f,k^T и невозмущенного размера До- Предположим, что искомая
зависимость удовлетворяет закону подобия, т. е. что имеется некоторый
показатель степени такой, что
/ \771
Г =* До ( ] . (15.16)
\*БТ J
Так как растягивающая сила одинакова вдоль всей цепи, то удлинение долж¬
но быть пропорционально числу связей N. Согласно выражению (15.9), это
предполагает m = 1, и удлинение является линейной функцией силы. От¬
сюда и получаем требуемое выражение, постоянный множитель в котором,
разумеется, не может быть получен на основе изложенного выше подхода.
15.1.2.3. Модель Рауза (Rouse). Выскажем некоторые соображения
относительно динамических режимов. Для прояснения ситуации полезно
сравнить выражение (15.13) с выражением (15.4), которое описывает упру¬
гость в масштабе, меньшим персистентной длины, т. е. применимо к стерж¬
необразному полимеру (§ 15.4).
В приближении жесткого стержня уравнение динамики макромолеку¬
лы может быть записано в виде: rjdu/dt + кБТ£рд4и/дs4 = 0, который
позволяет получить частоты релаксационных мод: oo(q) та k^T£pq4/77, где
27Г(?~1 > Ер. Это уравнение показывает, что суммарная упругая сила, дей¬
ствующая в системе, уравновешивает силу вязкого сопротивления, пропор¬
циональную скорости локальных смещений. Типичное значение частоты
составляет 108 Гц.
В случае идеальной изолированной цепи уравнение динамики (уравне¬
ние Рауза) имеет вид
фr/dt - (3kbT/R0)d2r/ds2 = 0.
Опять-таки, это уравнение показывает, что упругая сила (Зк^Т / Rq) д2 г /ds2
уравновешивает силу вязкого трения m~ldr/dt, где m та 1/туДо—подвиж¬
ность сферы радиуса До, а т/ — вязкость растворителя. Характеристические
частоты, отвечающие различным модам, имеют вид uj(qn) Ri kbTql/Rov
с qn — пДДоЛ^1/2),п — 1, 2, N. Самые малые частоты, порядка
10~7 Гц (для До = 10 нм и N = 100) отвечают движению цепи как
целого. Это как раз тот предел, для которого модель Рауза более или ме¬
нее применима, если считать раствор разбавленным. Модель Рауза была
усовершенствована за счет учета гидродинамических взаимодействий, т. е.
влияния движения одного элемента цепи на другие. Однако она не отвечает
реальной ситуации, когда полимерные цепи переплетены друг с другом.
15.1.2.4. Упругость резины. Уравнение (15.13)— простейшее пред¬
ставление энергии, используемое для объяснения упругих свойств резин2\
состоящих из сшитых полимерных цепей (т. е. являющихся полимерными
L. Treloar. The Physics of Rubber Elasticity, Clarendon Press, Oxford, 1975.
§ 15.1. Идеальные цепи и цепи Флори
613
сетками). Мы сразу приведем окончательный результат3^: напряжение в си¬
стеме, определяемое симметричным тензором а, может быть выражено
через компоненты деформации Е в виде: о — GET.E, где G — Ncik^T —
упругий модуль (Nci —объемная плотность полимерных сшивок). По опре¬
делению, = дхз/дх[, где xj (соответственно, ir')) — положение мате¬
риальной точки после (соответственно, до) деформации. Представление
деформации через так называемый тензор Фингера (Finger), В = ЕТ.Е
справедливо для больших деформаций и сводится к традиционному тензору
деформации для малых деформаций. Тензор Фингера принимает простой
вид в случае чистой деформации растяжения, Bij — А2 5^, где величи¬
ны Ai представляют собой относительные удлинения в трех ортогональных
направлениях, причем А1А2А3 = 1, так как объем системы остается неиз¬
менным (см. также: М. Warner and Е. М. Terentjev, 2003).
15.1.3. Парная корреляционная функция и радиус инерции
Важным понятием, относящимся к полимерной цепи, является парная
корреляционная функция g(r), которая описывает зависимость плотности
связей от г в предположении, что первый мономер помещен в начало коор¬
динат. Интеграл от этой функции есть общее число связей в цепи, что дает
ее естественную нормировку
N
g(r)ddr. (15.17)
В соответствии с (15.9) для идеальной цепи имеется в среднем п(г) ос г2/а2
связей в сфере радиуса г. Следовательно,
g(r) = sM ~ 7“ ~-Г <15Л8>
47гг^ ar azr
в трехмерном случае; для пространства размерности d объем сферической
оболочки пропорционален И"1, так что
*(г)~ТТ-7- (15Л9)
a*ra~z
Приведенные выше оценки справедливы до тех пор, пока г ^ До- Для
больших значений г следует ожидать более быстрое, экспоненциальное
убывание функции g(r).
Фурье-образ 5(q) функции g(r) может быть измерен с помощью экспе¬
риментов по рассеянию рентгеновских лучей или нейтронов при волновом
векторе рассеяния q = к' — к, где к и к' — волновые векторы падающей
3) R. Larson. Constitutive Equations for Polymer Melts and Solutions, Butterworths,
N. Y., 1988.
614
Гл. 15. Полимеры: структурные свойства
и рассеянной волн соответственно (| к'
к |):
S(q)
g(r) expzqr dг
(15.20)
последнее выражение справедливо, пока qRo > 1. Заметим, что предел 5(g)
при q — 0 известен из (15.17):
5(q 0) N.
(15.21)
Для того чтобы получить более точные результаты, рассмотрим цепь из
N сегментов, причем сегмент п расположен в точке тп. Плотность связей
gn(r) при гп + г представляет собой gn(г) = £mMriJ Wrn + г - rm)), где
угловые скобки означают усреднение по ансамблю сегментов. Кроме того,
g(r) = ^ Е„£„М- В итоге получаем
g(r)
N
LL№+r
П
**m)) 5
(15.22a)
пфт
S( q)
1 a'
N V
(exp[«q(r„ - rm)])
(15.226)
п ф m
Выражение для фурье-образа корреляционной функции может быть разло¬
жено в ряд для малых | q(rn - гш) |. Очевидно, что (гп — гт) = 0. Вводя
определение
р2
HG
1
2 N2
((г„ - гт)2 ),
(15.23)
п т
получаем
S(q) = 5(0) (l - l-q2R2G +
(15.24)
для размерности пространства d ~ 3. Радиус инерции можно также выра¬
зить в виде
R%
1
N
N
£ ((r" -
cm
)2>>
(15.25)
n=l
где rcm = N 1 Y^n rn — координата центра масс системы.
Уравнения (15.22) — (15.24) являются весьма общими. Их можно исполь¬
зовать и для случая идеальной цепи. Для достаточно больших
п — т
име¬
ем ((г
П
Гт)2)
п — т
а2, т. е. Rг
G
^Е
сумму интегралом, можно получить
2 N2
m, п
п — т
а2. Заменяя
Д2 = In а2.
6
(15.26)
§ 15.1. Идеальные цепи и цепи Флори
615
15.1.4. Цепь Флори
В рассмотренной выше модели не учитывается самое простое из воз¬
можных атермических взаимодействий в системе — влияние исключенного
объема. В модели идеальной цепи различные ее сегменты могут занимать
одни и те же точки в пространстве, так как энтропия имеет максималь¬
ное значение при г = 0. Радиусы инерции были измерены в разбавленных
растворах полимеров (разбавленных настолько, чтобы отдельные клубки
не взаимодействовали друг с другом) самыми разными методами, вклю¬
чая рассеяние света, вискозиметрию, измерение коэффициентов диффу¬
зии, а также были рассчитаны методами компьютерного моделирования.
Во всех случаях значение критического показателя v оказывалось ближе
к 0,6, чем к 0,5. То есть реальная изолированная полимерная цепь, как и
следовало ожидать, оказывается более разбухшей, чем идеальная цепь. Для
пространства размерности d = 2 численное моделирование дает и & 0,75.
Теория Флори4), учитывающая эффекты исключенного объема, позволяет
получить результаты, очень близкие к этим экспериментальным значениям.
Теоретические подходы к описанию реальных полимерных цепей со¬
стоят в следующем. Идеальную цепь можно представить в виде траектории
случайного блуждания на решетке с координационным числом г (числом
ближайших соседей). При этом полное число путей длины N, включая са¬
мопересечения, есть zN. Реальная цепь также представляется траекторией
случайного блуждания, однако в отличие от идеальной цепи эта траек¬
тория не может себя пересекать. То есть для реальной полимерной цепи
адекватной математической моделью являются случайные блуждания без
самопересечений. Полное число путей из N шагов в этой модели в асимп¬
тотическом пределе (при больших N) ос zNTf, где z, согласно данным
модельных расчетов, несколько меньше, чем г, а ос ЛГ7”1. Показатель 7
является аналогом критического показателя для восприимчивости в тео¬
рии фазовых переходов и зависит только от размерности пространства d
(см.: деЖен, 1979). Важным универсальным показателем является и пока¬
затель v для Rp (радиус Флори для набухшей цепи, см. табл. 15.1):
Другим полезным критическим показателем является 6. Этот показа¬
тель позволяет точно описать как эффект исключенного объема, заставляю¬
щий конец цепи отодвигаться от начала координат, так и эффект «клетки»,
вследствие которого конец цепи загоняется внутрь клубка. Запишем вероят¬
ность jP/v (г) того, что цепь Флори с фиксированным началом заканчивается
в точке г, в виде
Rf ос aN1', TF ос ЛГ7-1.
(15.27)
PN(г) = — f(x) ехр -Xs
ftp
(15.28)
4) P. J. Flory. Principles of Polymer Chemistry, Cornell University Press, Ithaca, N. Y.,
1971.
616
Гл. 15. Полимеры: структурные свойства
где х = г/Др. Вероятность должна обращаться в нуль при г — 0 и экспо¬
ненциально убывать для больших х; следовательно, f(x) = х8. Эти пока¬
затели простым образом связаны с и и 7 (рис. 15.2):
<5=—, g=l^±. (15.29)
1 — U I/
Таблица 15.1. Критические показатели для Rf и Tf
d
4
3
2
1
7 - 1
0
- 1/6
- 1/3
0
V
1/2
- 3/5
- 3/4
1
xgexp(— лг***)
х
Рис. 15.2. Распределение вероятностей xgexp(—xs) для набухшей цепи, рассчи¬
танное для типичных показателей g и <5, приведенных в табл. 15.1 для d = 3
Выражение (15.28) есть не что иное, как расширение распределения
вероятности для идеальной цепи (15.10) с учетом эффектов исключенного
объема. Для идеальной цепи показатель g = 0 выражает тот факт, что
идеальная цепь возвращается с большой вероятностью в начало координат,
а (5 = 2.
§ 15.1. Идеальные цепи и цепи Флори
617
1. Теория Флори и показатель скейлингового закона. Пусть с = NR~d
представляет собой среднюю объемную концентрацию связей в клубке,
занимающем сферический объем радиуса R. Плотность свободной энергии
клубка содержит два вклада:
а) член, отвечающий исключенному объему,
fex = \квТ(с2)у, (15.30)
где v есть объем мономера в пространстве размерности d. Член (с2) по
сути определяет число парных взаимодействий между связями. Это можно
показать следующим образом. Пусть kETvS(vi — г j) есть энергия взаимо¬
действия (стерического) между связями i и j. Полная свободная энергия
может быть записана в виде U — -к^ТьУ2- - <5 (г* — г А Далее, мы введем
2 —**
локальную плотность связей: с (г) — j 6(r — rj) и запишем: <5 (г* — г^) =
= J 5(г{ — г) 5(r — Tj)ddг. Это дает
Будем считать с2 (г) величиной постоянной (с = N/Rd) и равной ее средне¬
квадратичному значению в (15.30). При таком допущении мы фактически
пренебрегаем эффектами корреляций и переоцениваем энергию взаимодей¬
ствия.
б) упругий вклад энтропийной природы, для которого мы полагаем, что
цепь является идеальной:
fei — Fei/Rd = kT^^-. (15.31)
Na2
Как и ранее, при таком допущении пренебрегают корреляциями между
связями и переоценивают полную энергию взаимодействий.
Минимизируя полную энергию клубка F = Fex -f Fei Ftdfex “b Fei,
мы получаем
v — —-—; (15.32)
d + 2
3 3
т. e. щ 1/2 = -• Эти значения чрезвычайно близки к эксперименталь-
5 4
ным данным.
Развитые в последнее время теории полностью подтверждают справед¬
ливость соотношений подобия. Теорема «п = 0» де Жена5) устанавлива¬
ет, что проблема конформации цепи с исключенным объемом (случайные
5-) P. G. de Gennes. Phys. Lett. A38, 339 (1972); см. также: П. деЖен. Идеи скейлинга
в физике полимеров, пер. с англ. / Под ред. И. М. Лифшица. — М.: Мир, 1982.
618
Гл. 15. Полимеры: структурные свойства
блуждания без самопересечений) формально аналогична проблеме корре¬
ляций n-мерных спинов в ферромагнетике при п = 0! Эта замечатель¬
ная аналогия позволяет установить формальные связи между показателями
для случайного блуждания без самопересечений и критическими показа¬
телями для такого ферромагнетика. Аналогом относительной температуры
(Т - Тс)/Тс служит TV"1, а аналогом корреляционной длины является ра¬
диус инерции R ос aNv. Численные расчеты, сделанные в рамках теории
ренормализационной группы, позволили оценить показатель v для про¬
странств различной размерности. Результаты расчета оказались очень близ¬
ки к результатам и, получающимся в теории Флори, хотя и дают несколько
меньшие значения.
2. Концепция блоба (или бусин). Возвращаясь обратно к выражению
(15.28) и вычисляя вклад энтропии в свободную энергию полимерного
клубка, получаем
F = кБТ[ ) + Fq, (15.33)
т. е. растяжение клубка
г ¥ RF [ (15.34)
под действием приложенной силы /. Как и ранее, мы полагаем, что растя¬
жение клубка пропорционально N, что позволяет получить
6=—. (15.35)
\ — V
Это выражение, как и ожидалось, дает 5 — 2 для идеальной цепи.
Заметим, что выражение (15.34) фактически вводит новую длину £ —
= кБТ// такую, что
(15.36)
П
где
(15.37)
Величина п, следовательно, — это характерное число связей, принадлежа¬
щих блобу размера f. Выражение (15.36) говорит нам, что растяжение цепи
есть не что иное, как число блобов N/n, умноженное на типичный размер
блоба (рис. 15.3).
3. Случай d ^ 4 (приближение среднего (или самосогласованного) по¬
ля). Результаты Флори предсказывают среднеполевые значения критиче¬
ских показателей (v — 1 /2) для размерности пространства, равной 4. Такое
поведение характерно для идеальной цепи. Аналогичные результаты полу¬
чаются для целого интервала значений d ^ 4 в теории «п = 0». Заметим,
§ 15.2. Цепи во взаимодействии
619
что из выражений (15.30) и (15.31) можно получить
F,
СХ
F.
ei
V
а1
дг2 —d/2^
(15.38)
если Fex присвоено его среднеполевое значение. Это отношение стремится
к нулю при d > 4: член, отвечающий исключенному объему, становится
пренебрежимо малым — свойство, типичное для идеальной цепи.
Рис. 15.3. Разбиение набухшей цепи на последовательность бусин (или блобов)
под действием приложенной силы
§ 15.2. Цепи во взаимодействии
Давайте с самого начала проведем различие между двумя предельными
случаями. В сильно разбавленном растворе каждая цепь ведет себя ин¬
дивидуально, независимо от других цепей. Если цепь является «набух-
шей», то растворитель считается хорошим; радиус инерции цепи меняется
по закону, описываемому теорией Флори (Rq ос 7V3/5). С другой сторо¬
ны, в отсутствие растворителя каждый мономер полимера, представляю¬
щего расплав, находится под действием сил притяжения Ван-дер-Ваальса
(из-за присутствия связей в других соседних цепях) и под действием сил
отталкивания (из-за наличия связей в той же самой цепи), которые в дру¬
гих условиях ответственны за набухание цепи. Эти взаимодействия пол¬
ностью компенсируют друг друга на шкале порядка нескольких мономе¬
ров, поскольку флуктуации плотности в расплаве чрезвычайно малы. Из
этого следует, что каждая цепь должна вести себя в расплаве как иде¬
альная цепь {Rq ос iV1/2), что и было подтверждено в эксперименте.
Цель этой главы состоит в том, чтобы предложить несколько способов
описания взаимодействующих цепей в ситуациях, отличающихся от рас¬
смотренных выше предельных случаев. Для начала следует рассмотреть
среднеполевой подход Флори-Хаггинса, а затем подход, основанный на
законах скейлинга.
15.2.1. Приближение среднего поля
15.2.1.1. Свободная энергия Флори-Хаггинса 4) Ч Представим се¬
бе, что мономеры полимерной цепи расположены в узлах решетки (с ли¬
нейным размером а) и будем считать, что каждая связь занимает объем а3.
Р. М. Huggins. J. Phys. Chem. 46, 1712 (1942)
620
Гл. 15. Полимеры: структурные свойства
Пусть ф — доля позиций, занятых мономерами, а (1 - ф) —доля мест, заня¬
тых растворителем. Мы предполагаем, что каждая молекула растворителя
также имеет объем а3. Объемная плотность мономеров есть с — фа~3. По
Флори—Хаггинсу энтропия смешения <Smix полимерного раствора может
быть записана как
<^mix — ^Б-^tot
In ф -f (1 - ф) In (1 - ф)
(15.39)
где A^tot есть полное число узлов и N — число мономеров в цепи.
1. Вывод выражения (15.39). Справедливость приведенного выше
выражения можно обосновать следующим образом. Предположим, что два
химических вещества ведут себя как идеальные газы, термодинамические
потенциалы которых складываются аддитивно. Химический потенциал г-го
компонента
pV
Pi - -AfcTln -5- + fi(T), (15.40)
Ni
где Vi — полный объем, занятый веществом г, и iV* — число молекул
типа г. Заметим, что с помощью выражения (15.40) можно вывести закон
Бойля -Мариотта. Действительно, свободная энергия системы имеет вид
Fi = PiNi, и парциальное давление компонента i есть pi — -dFi/dVi —
= k^T(Ni/Vi). Аналогичным образом парциальная энтропия компонента г
есть Si = —OFi/dT, т. е.
Si = hNiln ^ - NifliT). (15.41)
Ni
Когда два компонента смешиваются, оба они занимают полный объем V =
— V\ + V2. Следовательно, полная энтропия системы принимает вид
S - к Б
iVi In — + N2 In —
N! N2
+ s(T),
где s(T) — некоторая аддитивная функция, пропорциональная Эн¬
тропия смешения есть Smix = S — S\ - S2, где Si, i = 1, 2, даются
выражением (15.41), т. e.
Smix = -ks^Njlnvj, (15.42)
где Vi = Vi/V — объемная доля компонента г. Уравнение (15.39) непосред¬
ственно следует из (15.42), если произвести замену N1 = —Ntot и N2 =
N
— (1 — ф)Ntot. Энтропия смешения, приходящаяся на узел решетки, есть
^mix/site — к
— In ф + (1 — ф) In (1 — ф)
IN
(15.43)
§ 15.2. Цепи во взаимодействии
621
2. Члены взаимодействия. К энтропийному члену (15.43) добавля¬
ем член, отвечающий парным взаимодействиям, который включает па¬
ры мономер-мономер, мономер-растворитель и растворитель-раствори¬
тель, т. е.
^/site = -&бТ [химФ2 + 2xms0(1 — Ф) + Xss(l ” Ф)2] * (15.44)
Обратите внимание на схожесть (15.44) с выражением (15.30). Коэффици¬
енты Xij являются безразмерными. Энергия смешения представляет собой
^/site — Ф&/вИе{Ф — 1) (1 — 0)^/site(0 ” 0), Т. е.
^mix/site = кБТхФ(1 ~ 0), (15-45)
гдех = Xms - - (xss + Хмм) называется параметром взаимодействия Фло-
ри. Парные взаимодействия Xij по большей части обусловлены притяже¬
ниями Ван-дер-Ваальса и пропорциональны соответствующим поляризуе¬
мостям, т.е. хмм ос — xms ос -am«s, Xss ос -а|. Следовательно,
в общем случае величина х положительна. Складывая (15.43) с (15.45),
получаем
= ±1пф + (1-ф)1п(1-ф)+ХФ(1-Ф)- (15-46)
кБТ N
3. Хороший растворитель и плохой растворитель. Когда силы при¬
тяжения малы, т. е. х 0? мы имеем так называемый режим хорошего
растворителя. Сильные взаимодействия притяжения соответствуют режи¬
му плохого растворителя. Этот вывод можно сформулировать более точно,
анализируя поведение свободной энергии (15.46) при малых ф :
F,
^^1 = ±\пф+-ф2(1-2х) + -ф3 + .-- (15.47)
кЕТ N 2 6
Отметим, что линейные члены в разложении (15.47) были опущены, так
как они не дают вклада в свободную энергию смешения (см.: де Жен,
1979). Это уравнение можно сравнить с выражением для свободной энер¬
гии, полученным нами ранее, при рассмотрении эффектов исключенного
объема (гл. 4). Поскольку с = 0а_3, выражение (15.47) можно перепи¬
сать как
/mix/site _ ^Ьс+ 1ус2 + _ (15.48)
къТ N 2
ГДе /mix/site = ^mix/site/^3 есть не что ИНОе, КаК ПЛОТНОСТЬ СВ060ДН0Й
энергии, a v = (1 - 2х)а3 представляет собой исключенный объем. Режим
хорошего растворителя отвечает условию v > 0,х < 1/2. Режим плохого
растворителя отвечает ситуации х > 1/2.
622
Гл. 15. Полимеры: структурные свойства
4. ©-температура. Температура, при которой 1 — 2\ — О, называется
тэта-температурой. Она может быть оценена из выражения для х- Дей¬
ствительно, следует ожидать, что взаимодействие Ван-дер-Ваальса слабо
зависит от температуры, поэтому
(ам — as)2 г\ (ам — »s)2
X ОС — И 0 ОС V '
&Б Т &Б
Так как взаимодействия при 0-температуре исчезают, можно ожидать, что
цепь будет вести себя как идеальная. Этот результат можно понять, исполь¬
зуя подход Дои (Doi), который рассмотрен в задаче 15.2. В этой задаче для
получения условия идеальности цепи при 0-температуре вместо объема
v = а3 вводится объем Флори-Хаггенса v = (1 - 2х)а3, который обра¬
щается в нуль при 0-температуре. При Т < 0 система находится в обла¬
сти плохого растворителя, и размер полимерной цепи меньше, чем радиус
инерции идеальной цепи. При этом в системе превалирует притяжение: по¬
лимерная цепь сжимается, образуя плотную глобулу. Переход от области
хорошего растворителя к области плохого растворителя через 0-точку (т. е.
при понижении температуры) является скачкообразным. Он называется пе¬
реходом клубок - глобула.
5. Атермический режим. Условие х — О отвечает максимально воз¬
можному значению г>, т. е. v = а3, что соответствует ситуации, когда рас¬
творитель и мономеры химически схожи.
15.2.1.2. Осмотическое давление. Осмотическое давление, обуслов¬
ленное присутствием полимера, есть
osm = - (^) , (15.49)
р
дУ 7 Nmono
где Nmono = Уфа . Дифференцирование в (15.49) выполнено при усло¬
вии: dNmonoINmono=dV/У+йф/ф - 0; кроме того, Ftot = ^mix/site^/a3 =
./mix/site^ • Следовательно,
= (15.50)
Оф I ф
a Posm = — + ln— ф-хф2- (15.51)
k^T N 1 — ф
Рассмотрим свойства полимерных растворов различных концентраций.
а) Разбавленный раствор, ф —> 0,ф<^ 2N~l. Разложение в ряд выраже¬
ния (15.51) дает
Posm « ksT (- + —) . (15.52)
\N 2 /
Осмотическое давление зависит от молекулярного веса полимера и пропор¬
ционально числу клубков, которые образуют идеальный газ клубков. Член,
§ 15.2. Цепи во взаимодействии
623
отвечающий исключенному объему, пренебрежимо мал, пока 2N~l > ф,
т. е. для клубков малого размера или при очень малых концентрациях. Рас¬
смотрим теперь случай полуразбавленных растворов, в которых клубки
перекрывают друг друга.
б) Полуразбавленный раствор, 2А/'-1 < ф<^1. Уравнение (15.51)теперь
сводится к
Posm ~ —VC2, (15.53)
2
т. е. для больших N осмотическое давление становится независимым от
степени полимеризации. Условие перехода между двумя режимами малых
концентраций (от разбавленного к полу разбавленному) будет уточнено ни¬
же с помощью соотношений подобия. На самом деле этот переход не про¬
исходит при концентрации ф ~ iV_1, как можно было бы полагать исходя
из изложенных выше аргументов.
в) Предел высоких концентраций, ф ~ 1. Подходящей переменной
для описания свойств концентрированного раствора является доля узлов,
заполненных растворителем, ф3 = 1 — ф. Давайте введем осмотическое
давление растворителя ps — понятие, которое не имеет явного физического
смысла, но может быть формально использовано:
, dFtot ^ квТ
dV/NsoW аЗ I \2N
{ф'+<Я (^7-х) + •••}• (15-54)
Член, отвечающий исключенному объему, исчезает для бесконечно длин¬
ных полимерных цепей, когда растворитель является атермическим. Как
уже отмечалось выше, атермические молекулы растворителя подобны мо¬
номерам полимерных цепей. Следовательно, величина а3 /(2АГ), которая
фигурирует в (15.54) в качестве исключенного объема мономеров, также
является исключенным объемом для молекул растворителя. Поэтому мож¬
но ожидать, что в пределе ф —ь 1, который отвечает расплаву полимера,
взаимодействия, связанные с исключенным объемом, исчезают и восста¬
навливаются условия, отвечающие поведению идеальных цепей, как уже
отмечалось во введении к этой главе. Следовательно, можно ожидать, что
модель Флори - Хаггинса будет верна и для высоких концентраций поли¬
меров с большой степенью полимеризации. В самом деле, модель Флори -
Хаггинса достаточно успешно используется для описания плотных смесей
полимеров (с небольшим содержанием или полным отсутствием раствори¬
теля). Эта модель оказывается вполне состоятельной при описании явлений
сегрегации, стабильных или метастабильных состояний, кривой спинодали
и ряда других явлений в расплавах полимеров.
15.2.1.3. Сжимаемость; измерение исключенного объема. Важная
теорема статистической физики связывает фурье-образ корреляционной
функции плотности, т. е. функцию рассеяния (или, как ее часто называют,
структурный фактор), с изотермической восприимчивостью среды:
624
Гл. 15. Полимеры: структурные свойства
(15.55 а)
где S(q) = a3 J dr exp(zqr){c(0)c(r) — с2) — функция рассеяния, а с
объемная плотность частиц. Вывод выражения (15.55 а) можно найти в при¬
ложении 15.Б. Уравнение (15.55 а) может быть также записано в очень удоб¬
ном виде
где свободная энергия, приходящаяся на частицу, выражена как функция
объемной концентрации (15.46). Эту формулу можно применить к слу¬
чаю разбавленного раствора (ф = са3 —>■ 0). Используя выражение (15.52)
для осмотического давления, которое мы представляем в стандартном виде
что, в случае достаточно длинных цепей (когда N велико) предоставля¬
ет способ экспериментального определения величины A<i — второго ко¬
эффициента вириального разложения свободной энергии, т. е. исключен¬
ного объема.
15.2.2. Законы скейлинга для атермических растворов
При использовании подхода Флори-Хаггинса полимерные компонен¬
ты и растворитель рассматриваются как идеальные газы, что позволяет
рассчитать их энтропию. При этом эффекты исключенного объема в рас¬
чет не берутся. В этом разделе мы обсудим случай атермических растворов
(X = 0) с иной перспективы — исходя из законов теории подобия. Изучение
свойств атермических растворов имеет существенное значение, поскольку
это как раз та ситуация, когда в системе нет других взаимодействий, кроме
как связанных с исключенным объемом — так называемый чистый случай.
Следовательно, подход Флори-Хаггинса должен быть совершенно неудо¬
влетворителен. Мы сравним эти два подхода.
15.2.2.1. Критическая концентрация для полуразбавленного рас¬
твора. Будем называть раствор разбавленным, когда полимерные клубки
не находятся в контакте. Пусть с* ~ N/RdF — средняя концентрация мо¬
номеров (сегментов) в клубке. Мы используем в качестве радиуса клубка
радиус Флори, потому что условие х ~ 0 означает, что полимер находится в
режиме хорошего растворителя. Ясно, что клубки вступают в контакт друг
с другом при с > с*. Давайте оценим объемную долю, отвечающую с*. Мы
имеем
(15.556)
1
с
+ А2С2 + ..можно получить
N
S(q - 0)
1 1
(15.56)
а3с TV-1 + 2сАг
§15.2. Цепи во взаимодействии 625
*
Для пространства размерности d = 3, с N = 104 и I/ — 3/5 получаем ф
~ 10"3. Таким образом, клубки начинают контактировать друг с другом в
хорошем растворителе уже при малых концентрациях.
В случае с > с* раствор называют полу разбавленным. Обращает на се¬
бя внимание отличие полученного выше результата (13.57) от определения
полу разбавленного режима, полученного нами в рамках теории Флори-
Хаггинса, ф* = N~1. Определение перехода от разбавленного раствора
к полуразбавленному по Флори-Хаггинсу совпадает с новым определе¬
нием (15.57) при dv = 2, т. е. для размерности d — 4 (где v — 1/2,
см. табл. 15.1); это как раз та граничная размерность, начиная с которой
работает приближение среднего поля. Де Жен обратил внимание на то,
что, поскольку в полуразбавленном растворе цепи взаимно проникают друг
в друга, нет возможности указать, какому клубку принадлежит тот или иной
мономер, выбранный наугад. Следовательно, конформационные свойства
цепей не должны зависеть от N в этоы универсальном режиме. Интересно
посмотреть, как эта новая ситуация скажется на осмотическом давлении
в системе.
1. с < с*. Выражение (15.52) для осмотического давления может быть
улучшено за счет добавления члена, отвечающего исключенному объему,
пропорциональному Rj?, т. е.
Р osm — — + А2(? + . . . , (15.58)
къТ N
где А2 ос Nl~dv. Этот скейлинговый закон был подтвержден эксперимен¬
тально с большой точностью.
2. с > с*. В этом режиме осмотическое давление, следуя аргументам
де Жена, не должно зависеть от N. Однако, с другой стороны, оно должно
стремится к c/N при с с*. Поэтому запишем его в виде
1 Posm ОС - (15.59)
кБТ N \С
где показатель х получают из условия независимости осмотического дав¬
ления от N. Используя (15.57), получаем
du
X — И —~Рosm ос а~аф^ - 1. (15.60)
du - 1 къТ
Как и ранее, полученное в приближении среднего поля предсказание
Флори - Хаггинса р osm ос ф2, оказывается справедливым при d — 4. При
d — 3 величина показателя у = --- — — 9/4 хорошо подтверждается в
эксперименте. Величина показателя у ~ 9/4 отличается от среднеполевого
значения 2, и это различие становится весьма заметным при очень малых ф.
‘/ГКЛЕМАН М.
626
Гл. 15. Полимеры: структурные свойства
15.2.2.2. Внутренняя энергия полуразбавленных растворов.
Рассмотрим отдельное звено в решеточной модели, в котором с вероятно¬
стью ф находится мономер. Условная вероятность того, что соседняя связь
будет занята другим мономером, составляет не ф, а величину фу~1. Эту
условную вероятность можно получить, если проанализировать выраже¬
ние (15.60). Действительно, осмотическое давление обусловлено парны¬
ми взаимодействиями в газе мономеров, и величина показателя, равная 2,
получается только в приближении среднего поля (член ф2 в выражении
для плотности энергии; каждый участник парного взаимодействия играет
зеркальную роль по отношению к другому). Для размерности d ф 4 чис¬
ло эффективных пар мономеров составляет не ^ ф2, а соответственно,
эффективное число молекулярных пар типа мономер-растворитель есть
ф( 1 — фу~1), и внутренняя энергия раствора может быть записана как
^mix/site = кьТХФ( 1 - ФУ~1). (15.61)
Это выражение справедливо в режиме хорошего растворителя.
15.2.2.3. Корреляционная длина в полуразбавленных растворах.
Флуктуации плотности при с — с* имеют характерную длину £, равную
радиусу Флори Rp. Используя тот же метод, что и раньше, т. е. подбирая
такой показатель степени тп в выражении
t*£RF(*^\ , (15.62)
при котором величина £ не зависит от N, мы получаем из (15.27), (15.57),
и (15.62):
тп — —--—, £ = аф~т. (15.63)
dis — 1
Осмотическое давление легко можно выразить как функцию корреляци¬
онной длины: рosm — исходя из того что «блобы» размера £ ведут
себя как независимые объекты. Давайте предположим на время, что все
мономеры в блобе принадлежат одной и той же цепи. Это предположение
выглядит разумным, поскольку согласно (15.63) размер блоба £ меньше,
чем радиус Флори. Число мономеров в «блобе» можно теперь оценить как
что также равно c£d. Следовательно, плотность мономеров
в блобе равна их плотности в растворе, и блобы можно рассматривать как
объекты, плотно заполняющие пространство. Можно далее рассматривать
блобы, принадлежащие одной и той же цепи, как исходные элементы —
«сверхсегменты» расплавленного полимера, в котором «сверхцепи» (т. е.
цепи, имеющие конформацию блобов) ведут себя как идеальные. Следова¬
тельно, радиус сверхцепи меняется как
= ajV1/2^-1/2)/(d*'-l)) (15.64)
§ 15.3. Фазовое разделение в растворах полимеров и полимерных смесях 627
и, как и ожидалось, оказывается меньше, чем радиус Флори.
Так как флуктуации плотности имеют размер можно ожидать, что
полуразбавленный полимер ведет себя в отношении частиц, пересекающих
его, как сито с размером ячейки f. Это свойство было успешно использова¬
но для измерения £ и скейлинговых показателей. Мы рекомендуем посмот¬
реть фундаментальную работу Дауда и др.7) по нейтронному рассеянию
в полимерных растворах, где представлены результаты измерений радиуса
инерции, корреляционных длин и осмотической сжимаемости.
§ 15.3. Фазовое разделение в растворах полимеров
и полимерных смесях
15.3.1. Равновесные и неравновесные состояния в жидкости
Полимеры в плохих растворителях, а также смеси полимеров имеют тен¬
денцию к фазовому расслоению. Рассмотрим смесь двух типов полимеров,
А и В, со степенями полимеризации соответственно Na м Nb. Используя
подход Флори-Хаггинса, выражение для свободной энергии (15.46) можно
обобщить на случай смеси двух полимеров:
/ш = Fro'x^lte = In фА + ^g- In фв + хФаФв, (15.65)
кът N А N в
где fm есть безразмерная плотность свободной энергии и Фа + Фв = 1-
Если величина х положительна и достаточно велика, то ожидается, что
энергия будет уменьшаться, если Фа (или фв) мало, а фв (или Фа) велико.
Это как раз и происходит, когда полимер находится в плохом раствори¬
теле (Ng = 1, х велико). Альтернативно, за исключением случая, когда
величина х исключительно мала, практически невозможно образовать од¬
нородную смесь двух полимеров при сравнимых по величине объемных
фракциях. Как мы увидим ниже, несовместимость двух полимеров может
быть использована для получения разнообразных структур, аналогичных
тем, что образуются при растворении поверхностно-активных веществ в во¬
де (лиотропные фазы), т. е. происходит фазовое разделение в микроскопи¬
ческом масштабе (микрофазное расслоение).
Фазовые переходы расслоения являются фазовыми переходами первого
рода. Для них характерны скачкообразные изменения термодинамических
параметров, описывающих состояние системы, скрытая теплота перехода
и такие гистерезисные явления, как переохлаждение и перегрев. В част¬
ности, хорошо известно, что если переохлаждение велико, т. е. если сис¬
тема остается разупорядоченной (например, в расплавленном состоянии)
до области очень низких температур, то вязкость может возрасти до таких
^ М. Daoud, J. P. Cotton, В. Farnoux, G. Jannink, G. Sarma, //. Benoit. R. Duplessix,
C. Picot and P. G. de Gennes. Macromolecules 8, 804 (1975).
628
Гл. 15. Полимеры: структурные свойства
больших значений (г] > 1013 Р), что система не может закристаллизоваться
за сколь угодно длительное время. В итоге мы получаем застеклованное
или аморфное состояние.
Подобные гистерезисные нелинейные явления тем более характерны
для полимерных систем, где кинетика фазовых переходов контролируется
медленными процессами диффузии. Необходимо отметить, что все харак¬
терные времена в полимерах значительно больше, чем в атомных (низкомо¬
лекулярных) сплавах, и возрастают существенно нелинейно с увеличением
молекулярного веса М; например, коэффициент диффузии растет прибли¬
зительно как М3)4). Имеются и дополнительные сложности, связанные с ре¬
альной полидисперсностью полимерных цепей. В дальнейшем мы не бу¬
дем рассматривать подобные неравновесные процессы или транспортные
свойства полимеров. В частности, мы не будем обсуждать сложные кине¬
тические и структурные явления, связанные с кристаллизацией полимеров.
Вне нашего внимания остаются и гели — «замороженные» неупорядочен¬
ные сетки из гибких полимерных цепей, которые могут быть сшиты друг
с другом или необратимым образом — за счет химических связей, как в ре¬
зине, или обратимым — так называемый физический гель (см. задачу 15.6
в качестве иллюстрации).
Фактически динамика расплавов и концентрированных полимерных
растворов демонстрирует три различных режима в зависимости от ха¬
рактерного времени наблюдения. Эти режимы схематически показаны на
рис. 15.4, а, где отложен модуль упругости G' как функция частоты (G' —
= ReG*(u>), G*(u) = сг/е, а = aoexpiout — зависящее от времени на¬
пряжение сдвига, а е — ео expi(ujt — ф) — сдвиговая деформация). Отли¬
чительной особенностью этого графика является наличие плато. Величину
модуля в области плато, G'0 ~ рек^Т, можно связать с плотностью зацепле¬
ний ре или эффективных сшивок, определяющих плотность препятствий,
которые испытывает цепь при своем движении вследствие переплетений
с другими цепями (см. рис. 15.4,5). В области частот, отвечающей пла¬
то, вязкоупругие свойства полимера такие же, как у обычной резины. При
более высоких частотах наблюдается поведение, отвечающее полимерно¬
му застеклованному состоянию — внутренние релаксационные процессы
в цепи (транс-гош-переходы и т.д.). Наконец, при низких частотах поли¬
мерный расплав ведет себя как жидкость, и можно считать, что G1 ~ и2.
Отсылаем читателя к книге Ларсона, где дано современное изложение
реологических (длинномасштабных) свойств полимеров, а также к книгам
Дои, Эдвардса и де Жена, в которых представлена динамическая теория
полимеров. Мы ограничимся здесь рассмотрением свойств полимерных
смесей, которые в обычных условиях эксперимента ведут себя подобно
жидкостям. Следовательно, рассматриваемые нами термодинамические со¬
стояния полимерных систем являются равновесными. Эти состояния осо¬
бенно интересны с концептуальной точки зрения: даже вблизи критиче¬
ских точек их можно рассматривать в рамках теории среднего поля Флори-
Хаггинса. Однако прежде чем перейти к этому, необходимо сделать краткий
экскурс в теорию фазовых переходов первого рода.
§ J5.3. Фазовое разделение в растворах полимеров и полимерных смесях 629
6
5
fS
2 4
X
сз 3
3
2
1
-113 5
log CJ, с _|
б
Рис. 15.04. Реология полимерных расплавов с зацеплениями: модуль упругости
как функция частоты для практически монодисперсного полистирола с молекуляр¬
ным весом М, меняющимся в интервале от 581000 до 47000. Графики построены
на основании данных, полученных в работе: S. Onogi, Т. Masuda, К. Kitawaga,
Macromolecules 3, 109 (1970) (а); переплетение цепей, ответственное за динамиче¬
ское поведение полимера в области плато (б)
15.3.2. Фазовые переходы первого рода — краткий обзор
15.3.2.1. Параметр порядка, подчиняющийся (или не подчиняю¬
щийся) закону сохранения. Полезно различать два типа параметров
порядка: те, для которых не выполняется закон сохранения, типа немати¬
ческого параметра порядка, принимающего только одно значение в равно¬
весии при данной температуре (за исключением точки фазового перехода
40-КЛЕМАН М.
630
Гл. 15. Полимеры: структурные свойства
в случае фазового перехода первого рода), и те, для которых справедлив за¬
кон сохранения, например плотность при фазовом переходе жидкость - газ,
или концентрация каждого компонента А или В в бинарной смеси. В подоб¬
ных случаях параметр порядка может иметь два значения и в системе при
любой температуре сосуществуют две фазы. Каждая фаза занимает объем,
определяемый условием сохранения полного числа частиц. Например, для
двойной смеси имеем
т. е. два уравнения для двух неизвестных величин V\ и V2. Фазовый пере¬
ход с необходимостью является переходом первого рода, за исключением
некоторой критической температуры, при которой Фа, i = Фа, 2-
15.3.2.2. Свободная энергия двойной смеси. В этом подпункте мы
рассмотрим случай бинарной смеси, при этом предполагается, что компо¬
ненты А и В образуют идеальные смеси в каждой из фаз р! и р2. В от¬
сутствие взаимодействий выражение для свободной энергии на частицу
содержит только энтропийную часть, что может быть записано как
Кривая для свободной энергии при любой температуре имеет вогнутую
форму с единственным минимумом в точке
Естественно ожидать, что подобное решение существует при высоких тем¬
пературах, когда вклад энтропии в свободную энергию является определяю¬
щим. Однако при низких температурах в свободной энергии доминиру¬
ет член, отвечающий за взаимодействие частиц, который может изменить
кривую F = Г(фд) таким образом, что она из чисто вогнутой (рис. 15.5, а)
станет кривой с двумя минимумами (рис. 15.5, б).
15.3.2.3. Фазовое разделение. Давайте сосредоточим внимание на сме¬
сях с концентрациями ф\ и 02, которые отвечают точкам касания двойной
касательной к кривой свободной энергии. Эти две смеси могут сосуще¬
ствовать, потому что химические потенциалы /л(ф,Т) = dF/Эф в точках
pi и р2 равны друг другу. На рис. 15.5, в показан химический потенциал
системы как функция ф. Отметим, что при данной температуре условию
равновесия отвечает не минимум свободной энергии F = F(0), а минимум
потенциала С(ф) = F(0) - [л(Т)ф; в этом выражении /л(Т) есть химиче¬
ский потенциал, отвечающий условию сосуществования фаз. На рис. 15.5, в
отложен наклон р(ф) свободной энергии F(0) как функция объемной до¬
ли ф при данной постоянной температуре, т. е. химический потенциал всех
смесей при температуре Т. Химический потенциал /i(T), отвечающий сосу¬
ществованию фаз, представлен горизонтальной линией, которая рассекает
кривую fi = р(ф) на две равные области (задача 15.4).
ФаАТ)У1 + Фа,2(Т)У2 = фАУ, Vi+V2 = У,
(15.66)
F = kBT Ы фА + {1 ~ фл)1п(1 - фА)
Na Nb
(15.67)
Фа/0- - Фа) = ехр{NBX - JV*1)-
§ 15.3. Фазовое разделение в растворах полимеров и полимерных смесях 63 1
а
Ф.
б
в
соех
о
Г
г
г,
соех
о
Одна фаза
А
h
1
Фа
Ф
Кривая
сосуществования
Спинодаль
Образование зародышей
и рост
Спинодальный
распад
ф
1
Рис. 15.5. Свободная энергия двухфазной системы: состояние, при котором до¬
минирует энтропийный вклад, Т = const (а); полная свободная энергия системы,
Т — const (б); химический потенциал, плато Максвелла (<?); типичная фазовая
диаграмма (г)
632
Гл. 15. Полимеры: структурные свойства
Если концентрация исходной смеси ф находится между точками ф\ и ф2,
система распадается на фазы р 1 и р2 в соотношении х, таком, чтобы вы¬
полнялись условия ф = хф\ + (1 — х)02> F — + (1 “ X)F2. Легко
показать, что минимизация F при условии, что химические потенциалы
в точках ф\ и </>2 равны, дает: С(ф\) — С(ф2), т. е. в точности условие, от¬
вечающее плато Максвелла, независимо от х. Представляющая точка ряда
сосуществующих фаз находится в точке р (рис. 15.5, б). Мы замечаем, что
эта точка находится ниже соответствующей точки на кривой свободной
энергии при той же самой исходной концентрации, т. е. фазовое разделе¬
ние выгодно для системы. С другой стороны, если концентрация исходной
смеси ф' находится вне интервала ф\ — 02, расслоения системы на две
различные фазы не происходит.
Откладывая вместе пары сосуществующих фаз при различных темпе¬
ратурах, можно получить фазовую диаграмму. Типичный вид кривой со¬
существования фаз показан на рис. 15.5, г, с критической температурой Тс
и критической концентрацией фс. Мы также нанесли на этот график положе¬
ния точек перегиба р* 1 и р*2 на кривой свободной энергии, так называемой
кривой спинодали.
15.3.2.4. Возможные сценарии фазового разделения: спинодальный
распад или расслоение с образованием зародышей и ростом новой
фазы. Переход из высокотемпературной однородной смеси ф, Тн в низ¬
котемпературную двухфазную систему ф\, ф2, 7} происходит различным
образом, в зависимости от положения р средней концентрации ф0 по отно¬
шению к кривой спинодали. Такое разделение прослеживается по крайней
мере на первом этапе процесса фазового расслоения (рис. 15.6). Еслир нахо¬
дится внутри кривой спинодали, где d2F/дф2 < 0, система является
нестабильной и фазовое расслоение происходит по механизму спинодаль-
ного распада. Если р находится между спинодалью и кривой сосущество¬
вания, d2F/дф2 ^ > 0, система является метастабильной и фазового
расслоения не происходит, пока не возникают зародыши с концентрацией
ф\ или </>2. Соответствующий процесс образования зародышей и роста но¬
вой фазы обсуждался в п. 13.1.4. Ниже мы рассмотрим упрощенную теорию
спинодального распада81
Разложим свободную энергию в окрестности концентрационной точ¬
ки 0о ■
F = F(0o) + (Ф ~ Фo)Fl + (ф — фо)2F2 -Ь ... (15.68)
Химический потенциал может быть записан как
// = F\ -Ь 2(0 — 0о)^2 + ... (15.69)
Рассмотрим эффект флуктуаций состава смеси: частицы смещаются вслед¬
ствие градиента химического потенциала / — —дц/дх = —2Г2дф)дх.
8)J. W. Cahn. J. Chem. Phys. 42, 93 (1965).
§ 15.3. Фазовое разделение в растворах полимеров и полимерных смесях 633
Образование
зародышей и рост
\ .
: X ч -
* • •
. 4
ч Л
\.У V'
* * '-у*.
> '
-ч.. 'КТш ^ • 1. - . .
/ч*7. *: .'V ч.. ;
- о .
.! %•> >чч««. •
- «ЦТ
• л
. V -
ч * .
'W- <*ч.-
' * .. У 4 . Т
' -ч'л • :ч" ^
v-ur* •i-.-'vV
ГЛ. "ч-.; * *•*? v-
•• :- ' " V :
л : ,г-Лл v;-
; I
% Ш ,
• •<• ч. < •• •
. *'
V-
• --х.
Спинодальный
распад
; ;:'л> '
wi s ... j.
. 4 -V .... Ъ* •
v>.N. ’ :. *>. -,T N-''*-N Г-
•s .. .. • **г*ч \:.. . * • . — > V- •
%y ".£» . ' ... -V.*- s.f 4 ^wTjj 4 ^
. •:»;: o. ^.Vi \ % 1♦ ”s *.»vVi'Vs .. w•' . ^ ''
■; , -ЙТ-
—>:S<* • j v-s . . '■■.^Sfb-r **-'
\. ,.:•£*•:*- v • '■ . _ ••• - * *^4.
Л . . . ' ’
V? ^ • •
: . -fi v
. ^' . хуЛлг-г; fv ,. ••. . „ • '^'v.cV^^ n.
V v . -• •.'
Vi?.-.-.-"' •.'«•' - t'iS/jr-.у:-- T
1 :. .-:
• ? - i.. ,
;V .r; * . . '*/***« . ' * *
fe :• v- . * *??** '>.* ' - •'.'. • ■'• ■ •'•'
- • >-.? •- Г '■#&*^ЕЖ** >-
Рис. 15.6. Структурные изменения в расслаивающейся двойной смеси, состоящей
из «черных» и «белых» компонентов, для двух возможных сценариев: образование
зародышей и рост (верхняя серия) и спинодальный распад (нижняя серия). От¬
тенки серого цвета приближенно соответствуют концентрации компонентов смеси.
Укрупнение областей, занимаемых сосуществующими фазами, на поздних стадиях
расслоения происходит из за положительной межфазной энергии
Согласно соотношению Эйнштейна, скорость частиц может быть записа¬
на как
и
fD_
кБТ
2 F,
D дф
к^Т дх
(15.70)
где D
коэффициент диффузии. С другой стороны, закон сохранения
числа частиц может быть записан в виде
дф
dt
д(фи)
дх
(15.71)
Предполагая малые флуктуации ф вблизи фо (ф = фо + бфо ехр i{ut
— qx)), мы получаем линеаризированное по 8 уравнение
дф
dt
-2
0qF2D д2ф
къТ дх'2
(15.72)
и дисперсионное уравнение
IU)
2*o£VD 2
къТ
(15.73)
Таким образом, если F2 < 0 (внутри спинодальной кривой), любая сколь
угодно малая флуктуация будет экспоненциально увеличиваться со вре¬
менем. При этом флуктуации состава с меньшими длинами волн растут
быстрее. Обратная картина наблюдается в «метастабильной» области, где
флуктуации убывают со временем. В этом последнем случае только зароды¬
ши, радиус которых превышает критический размер, могут расти, как было
634
Гл. 15. Полимеры: структурные свойства
показано в п. 13.1.4. Соответственно, этот рост сопряжен с преодолением
энергетического барьера (энергии зародышеобразования).
Интенсивность и волновой вектор флуктуаций в спинодальном режиме
могут быть изучены напрямую с помощью экспериментов по рассеянию;
обнаружено, что позиция пика сдвигается с течением времени к меньшим
углам рассеяния, т. е. как и ожидалось, в сторону больших длин волн.
Известно большое число прямых наблюдений двух режимов фазового
расслоения в полимерах. Когда расслоение идет по механизму образования
зародышей, в начале процесса наблюдается формирование сферических ка¬
пель, случайно распределенных в матрице и имеющих состав, «противопо¬
ложный» составу матрицы. В случае спинодального распада наблюдаются
взаимопроникающие непрерывные домены. По мере развития расслоения
домены увеличиваются в размерах и их границы становятся более резкими.
Процессы спинодального распада в полимерах подробно описаны в книге
Штробля (Strobl).
15.3.3. Смеси полимеров
Кривые сосуществования фаз и спинодали отвечают условиям
dfm/дф = 0 и д2 fm/дф2 — 0 соответственно. В критической точке, где
эти две кривые сходятся, также выполняется условие д3/т/дф3 = 0. Рас¬
смотрим вначале, для простоты, случай, когда два полимера в смеси име¬
ют одну и ту же степень полимеризации N — Na = Nb. Температура
включена в параметр взаимодействия Флори: х ос Т-1; это справедли¬
во, если определяющую роль в системе играют взаимодействия Ван-дер-
Ваальса. Используя уравнение (15.65), можно последовательно получить
выражения:
- для кривой сосуществования фаз,
д/т/дф=-Ь (-4-) + (1-2ф)Х = 0; (15.74а)
N \1-фУ
- для кривой спинодали,
д2 fm/дф2 = -(- + —) - 2х = 0; (15.746)
N \ф 1~ф)
- для критическая точки,
фс — 1/2, Хс = 2/АГ. (15.74в)
Решения уравнения (15.746) являются действительными при условии
NX > 2. Оно одновременно является и условием существования кривой
спинодали. Фазовое расслоение происходит при х > Хс> т. е. при условии,
которое легко выполнить, поскольку Хс очень мало, когда N велико. В сме¬
сях полимеров очень сложно получить сверхмалые значения х и сегрегации
практически невозможно избежать.
§ 15.3. Фазовое разделение в растворах полимеров и полимерных смесях 635
В общем случае Na ф Nb легко получить
, NlJ2 „ (<2+<2)2
Фа,с= 1/2в ху2, 2Хс=-^— S-J-. (15.75)
na +К NaNb
Этот результат означает, что если Na и Nb очень отличаются, величина Хс
может быть достаточно велика, и расслоения можно не допустить (напри¬
мер, для малых Na и больших Nb Хс~ 1 /Na)-
Критические флуктуации могут быть рассмотрены в так называемом
приближении случайных фаз (ПСФ); этот метод первоначально был создан
для описания почти свободных электронов в металлах9) и затем расширен
на случай (почти идеальных) полимерных цепей в расплавах 101 Основы
этого метода изложены в Приложении 15.Б (15Б.22). Для нас здесь важно
то, что фурье-трансформанта парных корреляций флуктуаций плотности
пропорциональна интенсивности рассеяния. Мы получаем
1 1 +—^ г - 2v, (15.76)
s{q) <pAg{^A, q) <i>Bg{NB, я)
где g(NA, q) (соответственно, g(Ns, q)) — фурье-образ парной корре¬
ляционной функции для изолированной цепи А (соответственно, В); эта
функция описывает интенсивность рассеяния одной идеальной цепью из
мономеров А (соответственно, В). Уравнение (15.76) есть обобщение выра¬
жения (15Б.22) на случай двойных систем. Поскольку при q = Qg(NA,0) =
— Na, g(NB, 0) = NB, выражение (15.76) становится идентичным фор¬
муле (15.746), и мы окончательно получаем
1 1 + — 2х=^2-. (15.77)
5(0) ЛтаФа МвФв дф2
Это выражение согласуется с общим термодинамическим соотношением
(15.55 6). Таким образом, интенсивность малоуглового рассеяния расхо¬
дится при q -* 0 не только в критической точке расслоения, но и вдоль всей
кривой спинодали.
15.3.4. Микрофазное расслоение в блок-сополимерах
Один из способов, позволяющих удержать вместе несовместимые поли¬
мерные цепи, — это химически соединить их концы. В результате получа¬
ются так называвемые блок-сополимеры. Фазовое расслоение при этом про¬
исходит только в микроскопическом масштабе, а получающиеся
макроскопические фазы по своей структуре аналогичны фазам, образуе¬
мым поверхностно-активными веществами в присутствии растворителя
D. Pines. Elemementary Excitations in Solids, W.A. Benjamin, N. Y., 1963.
i0) P. G. de Gennes. Rep. Progr. Phys. 32, 187 (1969).
636
Гл. 15. Полимеры: структурные свойства
(рис. 15.7). Микрофазное расслоение в полимерных расплавах по сути явля¬
ется фазовым переходом первого рода, индуцированным флуктуациями1
ПИ-сферы
ПС-сферы
ПИ-УБДА
ПИ-, ПС-ламеллы
ПС-УБДА
Рис. 15.7. Различные морфологии двублочных сополимеров полистирола (Г1С) —
полиизопрена (ПИ) в зависимости от объемной концентрации ПС фps (ПС показан
черным цветом). Данные взяты из работы15^
Морфология расслоения зависит от величины отношения Na/Nb. Сле¬
дует ожидать, что образующаяся фаза будет ламеллярной, если N^/NB « 1
(если положить для простоты, что объемы, занимаемые мономерами двух
полимерных цепей, равны: va = у в )• При Nb Na предпочтительной
является мицеллярная фаза (например, сферы полимера А в непрерывной
матрице полимера В). Объемно-центрированная кубическая мицеллярная
фаза действительно была найдена в целом ряде блок-сополимеров, на¬
ряду с колончатой гексагональной и ламеллярной фазами (рис. 15.7)121
Эта последовательность фаз в интервале концентраций 0 ^ Фа ^ 0,5
G. Н. Fredrickson and К. Binder. J. Chem. Phys. 91, 7265 (1989).
12) G. E. Molau. in Block Polymers, Edited by S.L. Aggarwal, Plenum Press, N. Y.,
1970, p. 79.
§ 15.3. Фазовое разделение в растворах полимеров и полимерных смесях 631
коррелирует с уменьшением средней кривизны так называемой межблоч¬
ной разделяющей поверхности, т. е. поверхности между цепями А и В (оч +
-Ьсг2 — 2R^1 для мицеллярной фазы, а\+сг2 = Rд1 для колончатой фазы и
сг 1 ~\~(Т2 = 0 для ламеллярной фазы )131 Здесь Ra есть не что иное, как радиус
1 /2
инерции для идеальной цепи А (например, Ra = )), однако истин¬
ная периодичность в системе определяется балансом между поверхностной
энергией межблочной границы и упругой энергией растяжения цепей, ко¬
торая имеет такой же вид, как, например, для резины (см. задачу 15.7). На
фазовых диаграмах блок-сополимеров между ламеллярной и колончатой
фазами также наблюдались кубические биконтинуалъные фазы. Структура
этих фаз описывается той же пространственной группой симметрии, что
и структура алмаза, которую можно представить себе состоящей из двух
идентичных гранецентрированных решеток, смещенных одна относитель¬
но другой. При этом стержни, образованные, например, цепями А-типа,
имеют тетраэдрическую координацию в точках соединения — так назы¬
ваемая упорядоченная биконтинуальная двойная алмазная структура, или
УБДА141 Можно ожидать, что средняя кривизна этих кубических фаз явля¬
ется промежуточной между средней кривизной ламеллярной и колончатой
фаз. Однако их стабильность с необходимостью требует учета, помимо от¬
меченных выше упругих и поверхностных сил, также вкладов, связанных
с изгибной деформацией, описываемой модулями хих.
Известно также большое количество других фаз, образованных более
сложными блочными (триблочные и т. д.) или гребнеобразными сополиме¬
рами. В качестве обзора теоретических и экспериментальных исследований
фаз блок-сополимеров см. работу Бейтса и Фредриксона15).
Многочисленные исследования, как экспериментальные (по большей
части электронная микроскопия в сочетании с моделированием контраста),
так и теоретические, были посвящены изучению границ зерен в ламел¬
лярных блок-сополимерах (полистирол-полибутадиен16); полистирол-
полиэтилен, полистирол-пропилен17)). Гидо и др.16) обнаружили суще¬
ствование двух типов закрученных границ зерен, а также ряда симметрич¬
ных и асимметричных наклонных границ. В случае закрученных границ
межблочная разделяющая поверхность остается непрерывной в области
13^ Е. L. Thomas, D. М. Anderson, С. S. Henkee andD. Hoffman. Nature 334, 598 (1988).
14) Е. L. Thomas, D. В. Alward, D. J. Kinning, D. C. Martin, D. L. Handlin and
L.J. Fetters. Macromolecules 19, 2197 (1986).
15) F S. Bates and G. H. Fredrickson. Ann. Rev. Phys. Chem. 41, 525 (1990).
16^ (a) S. P. Gido, J. Gunther, E. L. Thomas andD. Hoffman. Macromolecules, 26, 4506
(1993); (b) 5. P. Gido and E. L. Thomas, Macromolecules 27, 849 (1994); (c) P. Gido
and E. L. Thomas, Macromolecules 27, 6137 (1994); (d) B. L Carvalho, R. L. Lescanec
andE.L. Thomas, Macromol. Symp.,98, 1131 (1995).
17) Y. Nishikawa, H. Kawada, H. Hasegawa and T. Hashimoto. Acta Polymer. 44, 192
(1993).
638
Гл. 15. Полимеры: структурные свойства
стенки и стремится принять форму минимальной поверхности. Две воз¬
можные морфологии отвечают или двойной периодической поверхности
Шер ка (во всем интервале закрутки 0 ° — 90 °) или участку правой спирали
(в диапазоне малых углов). Шевронная наклонная граница эквивалентна
симметричной закрученной стенке — малоугловой наклонной границе —
описанной в гл. 10. В случае омега-симметричных наклонных границ, кото¬
рые возникают при больших углах наклона, искажения стенки релаксируют
за счет появления периодических вспучиваний межблочной границы. Про¬
стейшим типом асимметричной стенки является Т-стенка. Различные виды
наклонных стенок показаны на рис. 15.8.
а б в
Рис. 15.8. Наклонные стенки в ламеллярной фазе двублочных сополимеров: шев¬
ронная или изгибная стенка (а); омега-стенка (б); Т-стенка (<?) (заимствовано из
работы Гидо и Томаса16^)
§ 15.4. Жесткие и полугибкие полимеры
Мы перейдем теперь к рассмотрению свойств линейных полимеров,
которые отличаются от изученных ранее величиной отношения ip/d, где
d обозначает теперь диаметр поперечного сечения молекулы. Для гибких
полимеров величина £p/d составляет от 3 до 5 и персистентная длина срав¬
нима с длиной мономера. С другой стороны, вирусы со спиральной сим-
метрией18\ полипептиды, ДНК, эфиры целлюлозы или ароматические по¬
лиэстеры характеризуются величиной tp/d « 20 - 200. Такие полимерные
цепи принято называть жесткими. Экстремальный случай представляют
волокна актина, имеющие большое биологическое значение, поскольку они
присутствуют в клетках всех живых существ. Актин является глобулярным
белком (« 42 000 Да), который образует широкие (d « 7 нм) и длинные
(молекулярная длина до L = 50 мкм) полугибкие волокна (1Р/d составляет
от 1500 до 3000). Основываясь на достаточно грубой классификации, мы
будем различать макромолекулы, являющиеся жесткими стержнями, для
которых L < и полугибкие полимеры с L > ip.
18) D. L. D. Caspar and A. Klug. Cold Spring Harbor Symp. Quant. Biol. 27, 1 (1962).
§ 15.4. Жесткие и полугибкие полимеры
639
15.4.1. Жесткие стержни
Жесткие стержнеобразные полимеры отличаются от полугибких поли¬
меров рядом особенностей, которые перечислены ниже.
• Радиус инерции меняется линейно с изменением молекулярного
веса.
• Динамические макроскопические свойства характеризуются больши¬
ми временами релаксации и меньшими коэффициентами диффузии.
• Высокая молекулярная анизотропия позволяет с гораздо меньшими
усилиями достичь однородной ориентации в изотропной фазе под
действием сдвига, магнитного или электрического полей.
• По мере увеличения концентрации взаимодействие между стержнями
приобретает все большее значение. В конце концов может произой¬
ти переход в жидкокристаллическое состояние, для которого, как уже
обсуждалось в гл. 4, характерно преобладание эффектов исключенно¬
го объема (энтропийных сил). Исторически фазовые переходы такого
типа впервые наблюдались Берналом и Фанкухеном в растворах рас¬
тительных вирусов19^. Изучение фазовых диаграмм вирусов до сих
пор является многообещающей областью исследований. Сюда отно¬
сится изучение вируса табачной мозаики (ВТМ)20) 2Х\ вирусов /J,
рЛ22) и даже смеси ВТМ и сферических коллоидов23).
Разбавленные, полуразбавленные и концентрированные растворы жест¬
ких стержнеобразных полимеров были предметом многочисленных теоре¬
тических и экспериментальных исследований (структурные и динамиче¬
ские свойства), В качестве обзора рекомендуем книгу Дои и Эдвардса и их
статью24).
15.4.2. Полугибкие полимеры
В случае полугибких полимеров необходимо ввести в рассмотрение но¬
вую характерную длину £е, которая называется длиной отклонения (deflec¬
tion length), и задает расстояние между точками контактов цепи с окружа¬
ющими цепями25) 26)(рис. 15.9).
19^ J. D. Bernal and I. Fankuchen. J. Gen. Physiol. 25, 111 (1941).
20) A. Klug. Fed. Proceed. 31, 30 (1972).
21^ R. В. Meyer, in Dynamics and Patterns in Complex Fluids, Edited by A. Onuki and
K. Kawasaki, Springer Proceed. Phys. 52, 62 (1990).
22) S. Fraden. in Observation, Prediction, and Simulation of Phase Transitions in
Complex Fluids, Edited by M. Baus, L. F. Rull,and J. P. Ryckaert, NATO-ASI- Course
CXXIX, Kluwer Acad. Pub., 113 (1995).
23^ M. Adams, Z Dogic, S. L. Keller and S. Fraden. Nature 393, 349 (1998).
24^ M. Doi andS.F Edwards. J.Chem. Soc., Faraday Trans. 74, 1802, 1818 (1978).
25) T. Odijk. Macromolecules 19, 2313 (1986).
26) A. N. Semenov. J. Chem. Soc., Faraday Trans. 82, 317 (1986).
640
Гл. 15. Полимеры: структурные свойства
Рис. 15.9. Характерные длины в полуразбавленном растворе полугибких поли'
меров (модель трубки). Окружающие полимерные цепи (обозначены крестами) за
ключают данную цепь в область, напоминающую изогнутую трубку
Пусть cs = ^—концентрация цепей в среде объема V, содержащей пь
цепей длины L. Давайте также введем концентрацию мономеров, которая
в данном случае отвечает концентрации сегментов длины £р, т. е. с = пь L
V tp
в соответствии с обозначениями, использовавшимися до сих пор. Объемная
плотность длины цепей есть р = csL — civ, а среднее расстояние между
цепями составляет £т — р~1/2. Однако не следует путать это расстояние
с поперечным размером трубок, внутри которых флуктуирует цепь.
Рассмотрим сегмент цепи длины L Средний угловой разброс сегмента
и среднее поперечное смещение составляют соответственно (см. § 15.1)
e{i) И 2 - , <5(£) ~ ев{£) ~ £3/2С1/2. (15.78)
Число цепей, которые проникают в трубку длины £ и ширины 6(£), есть
Ns — 5(£) х £ х р. Задавая А^5 — 1, можно оценить длину свободного
сегмента:
£е ~ ер(рф-2/5, (15.79)
и поперечный размер трубки:
8е ~ 1Р(ре2р)-3/5- (15.80)
Наше рассмотрение неявно предполагает, что длина отклонения и размер
трубки меньше, чем персистентная длина: £е < £р, 8е < £р. Это означа¬
ет, что р£2 > 1, т. е. 1 /(L£2) С с8. Последнее условие, накладываемое на
концентрацию, должно также выполняться для полуразбавленного режима
О О Q
(cs > 1 /Rq9 т. е. L£* < Rq ), для того чтобы иметь взаимодействие между
цепями. Понятие длины отклонения расширяет на область полимеров по¬
нятие лоскутов (patches) Хелфриха (п. 14.2.2), которое было введено для
мембран.
§ 15.4. Жесткие и полугибкие полимеры
641
Динамические свойства этого полуразбавлеиного режима были недавно
исследованы для волокон актина как экспериментально27^ 28^, так и теоре-
тически29) 301 Однако в целом это направление исследований еще остается
малоизученным.
При более высоких концентрациях, вследствие взаимодействий, обу¬
словленных эффектами исключенного объема, возможен переход в жид¬
кокристаллическую фазу. Мы уже сталкивались с подобным переходом в
системе жестких стержней (гл. 4). В случае полугибких полимеров фазо¬
вый переход первого рода из изотропной в нематическую фазу получен3 ^
при Рпет ~ 6,7/(£pd). Интересно сравнить это решение с результатом
Онзагера для жестких стержней: рПет ~ 4,3/(Ld).
15.4.3. Хиральность
Многие полугибкие полимеры — в основном, биополимеры — являют¬
ся хиральными и вследствие этого обладают интересными структурными
свойствами. Среди них следует отметить иерархическую структуру и при¬
роду дальнего порядка. Мы ограничимся здесь несколькими замечаниями
и ссылками на предмет, изучение которого со времен открытия Био (Biot)
вращения плоскости поляризации света прогрессировало с безудержной
энергией 32\
Иерархический порядок был обнаружен в случае конформаций белко¬
вых макромолекул (§ 1.5) и в волокнистых биологических тканях33^ типа
кологена34), a-кератина35^ и целлюлозы. Фибриллярная упаковка придает
этим структурам замечательные механические свойства, поэтому крайне
важной задачей является изучение природы подобной организации как для
практических биологических целей, так и для возможного получения схо¬
жих синтетических материалов. Очевидно, что возникновение подобных
структур определяется химической природой макромолекул, однако часто¬
та появления гексагональных фибриллярных ансамблей в биологических
27^ A. Ott, М. Magnasco, A. Simon and A. Libchaber. Phys. Rev. E48, R1642 (1993).
Л Q Ч
' В. Schnurr. F Gittes. F. C. Mackintosh and C. F. Schmidt. Macromolecules 30, 7781
(1997).
29^ H. Isambert and A. C. Maggs. Macromolecules 29, 1036 (1996).
30^ D. C. Morse. Macromolecules 31, 7030 (1998).
31^'A. R. Khokhlov and A. N. Semenov. Physica 108A, 546 (1981); Sov. Phys. Uspekhi
31,988 (1988).
32>> Т. C. Lubensky, R. D. Kamien and H. Stark, preprint, University of Pennsylvania,
1995.
33-) D. A. D. Parry and P. M. Steinert. Intermediate Filament Structure, Springer-Verlag,
N. Y, 1995.
34) L. J. Gathercole and A. Keller, in Structure of Fibrous biopolymers, Edited by
E. D. T. Atkins and A. Keller, Butterworth, London, 1975; in The Periodontal Ligament
in Health and Disease, Edited by В. К. B. Berkovitz, Pergamon, Oxford, 1982.
35^ F. Briki, B. Busson andJ. Doucet. Biochim. Biophys. Acta 1429, 57 (1998).
642
Гл. 15. Полимеры: структурные свойства
объектах указывает на существенность вклада стерических взаимодействий.
Как было показано Клеманом36), плотная упаковка молекул спиральной
формы поднимает интересные вопросы фрустрации, сходные с эффектами
конформации двойной закрутки, которую мы обсуждали в § 11.2. Подобные
процессы могут лежать в основе иерархии волокнистых структур.
Те же аргументы, связанные с фрустрацией, должны быть приняты во
внимание при описании дальнего порядка, наблюдаемого в фазах, обра¬
зующихся в растворах биополимеров37) 38\ типа ДНК, ксантана, поли-7-
бензил-Ь-глутамата и т. д. Наконец, недавние экспериментальные исследо¬
вания гексагональных фаз ДНК под давлением, выявившие их гексатиче-
скую структуру, и теоретический анализ гексагональных фаз полимеров39)
в очередной раз указали на решающую роль вклада хиральности40).
15.А. Приложение А* Центральная предельная теорема
Центральная предельная теорема утверждает, что сумма N случайных
независимых переменных Xi(i = 1, ..., N) является гауссовой случайной
переменной, когда N стремится к бесконечности, при условии, что момен¬
ты (хсуществуют. Гауссова случайная переменная £ — это переменная,
которая подчиняется закону вероятности экспоненциального типа (15А.7).
Мы имеем: сг2 = J €2p(£)d£\ величина а называется стандартным отклоне¬
нием.
N
Пусть X = £ хi. Его среднеквадратичное значение — {X2)~(52%iXj).
1 itj
Так как переменные являются независимыми, имеем: (xiXj)^ — 0. Пред¬
положим теперь, что все среднеквадратичные значения {х2) = а2. Опреде¬
лим £ = TV-1/2X. Получаем
(t2)=v\ (15А.1)
т. е. среднеквадратичное значение (£2) не зависит от N.
Назовем характеристической функцией <p$(k) случайной переменной £
фурье-трансформанту ее функции распределения, т. е.
<Pt(k) = (exp(ik£))
ехр(г&£)р(£) (15А.2)
36) М. Kleman. J. Phys. Lett. 46, L723 (1985), Physica Scripta T19, 565 (1987).
37) F. Livolant. J. Physique 48, 1051 (1987).
38^ F. Livolant and Y. Bouligand. J. Physique 47, 1813 (1987).
39) /?. Podgornik, И. H. Strey, K. Gawrish, D. C. Rau, A. Rupprecht and V. A. Parsegian.
Proc. Nat. Acad. Sci. U.S.A. 93, 4261 (1996).
40) R. D. Kamien andD. R. Nelson. Phys. Rev. E53, 650 (1996).
Приложение Б. Изотермическая сжимаемость, флуктуации плотности 643
Применяя обратное фурье-преобразование, запишем
ехр(—ik€)ipz(k) dk. (15А.З)
Используя написанное выше выражение для £, получаем
N
(k) = ^exp (ikN — ^ / 5 (15А.4)
поскольку все Х{ имеют одно и то же распределение вероятности.
Пусть N стремится к бесконечности, и можно разложить характеристи¬
ческую функцию (p(kN~1^2) в ряд по kN~1/2:
2
ip{kN^2) = 1 - — {х2) + ... = 1 - —а2 + 0(k3N~3//2). (15А.5)
2 N 2 N
Отсюда получаем выражение
(ft {к) = Jim
к ^ о
1 - — а2
2N
N к2а2
— ехр , (15А.6)
фурье-трансформанта которого есть
= (15А'7)
15.Б. Приложение Б. Изотермическая сжимаемость
и флуктуации плотности; статический линейный отклик
1. Изотермическая сжимаемость по определению есть
1
dv\
Хт = — I — j * (15БЛ>
V\dpJN,T
Мы докажем, что
N , (15Б.2)
\r)N / V Т
сХт \dN/V,T
где р — химический потенциал и с = N/V — плотность числа объектов
(частиц, связей и т.д.). Необходимость использования выражения (15Б.2)
для сжимаемости станет понятна ниже.
Мы начнем с выражения для свободной энергии Гельмгольца F —
= F(T, V, N). Имеем
р ~ —(8F/dV)T, N> № — (9F/dN)T,v.
644
Гл. 15. Полимеры: структурные свойства
Отсюда, поскольку вторые производные равны,
—) = • (15Б.З)
dV / Т, TV V ON ' T,V
Соотношение Гиббса - Дюгема, записанное при постоянной температуре,
имеет вид: V dp ~ N dp, т. е.
v(^-) =n(^-) . (15Б.4)
V dN / т, V V dN ' Ту V
Теперь, используя выражение для свободной энергии Гиббса G =
= G(T, р, N) = Np, получаем
И(д1л/д V)TtN = (dG/dV) T,N = (dG/dp)TtN(dp/dV)T,N
v(dP/dv)T,N,
что дает
n(Sj) =-—■• (15Б-5>
\dV/T,N XT
С учетом (15Б.З) и (15Б.4) мы получаем искомое выражение (15Б.2).
2. В этом Приложении мы используем статистическую сумму для
большого канонического ансамбля и выражение (15Б.2), чтобы доказать
важное термодинамическое соотношение
{N2) ~ {N)2 = сАъТхг- (15Б.6)
(N)
Флуктуации числа частиц нетрудно рассчитать с помощью большой
статистической суммы, которую можно записать как
°° N
Т ^-ZN(V, Г), (15Б.7)
^о N'
гдеас = Х^ехр(/3р) — так называемая активность, Хав = \/2тгрН2/т —
тепловая длина волны де Бройля, /? — 1/ksT и Zn{V, Т) — конфигураци¬
онный интеграл (пропорциональный канонической статистической сумме),
ZN(HN,T) = ехр(-/ЗЯлг(гъ - rjv.Pi, •••, Pjv)) drN dpN).
Тепловое среднее любой переменной, описывающей состояние системы,
) ^*2> • - • о Pl^ Р2j • - * 5 РЛГ)
Приложение Б: Изотермическая сжимаемость и флуктуации плотности 645
(обозначенной как ^(г^; р^)), может быть записано с помощью большой
статистической суммы в виде
°° N
N=0
(Л) = i Y] А(rN; pN) exp(-pHN) drN dp
“ N\ K
N
oo
E Тг(Аехр(-/ЗЯ* -h /3/хЛГ))
^ . (15Б.8)
E Тг(ехр(-/?Ядг +PljlN))
N=0
Большая статистическая сумма связана с большим потенциалом
П(Т? V, (л) = —pF соотношением 5 = ехр(—/ЗП). Таким образом, мы
получаем важное соотношение
05В.9)
(N) (N) д\х
В термодинамическом пределе (для бесконечной системы) имеем N =
= (N). Следовательно, с учетом (15В.2) получаем выражение (15Б.6).
3. Общее выражение для функций отклика41^ 42\ Мы хотим описать
изменения набора переменных А#(® = ш, п, ...), определяющих состоя¬
ние системы, в условиях, когда к системе приложены небольшие поля F#,
сопряженные Ащ. Гамильтониан возмущенной системы записывается как
Н = Докажем следующее соотношение:
Xmn - Р({Ат ~ (Ат)){Ап - {Ап))) = (АтАп) - (Ат)(Ап), (15Б.10)
где Хтп — -dAm/dFn|F _0 — восприимчивость, характеризующая воз¬
действие поля, Ат — тепловое среднее, рассчитанное на основе гамиль¬
тониана возмущенной системы и (Ат) — тепловое среднее, отвечающее
невозмущенному гамильтониану. При этом восприимчивость не зависит от
величины поля возмущения.
По определению имеем
j = Тг(Л.ехР (-£#)).
Тг(ехр(-/ЗЯ))
41) Я. £. Stanley. Introduction to Phase Transitions and Critical Phenomena, Oxford
University Press, Oxford, 1971.
42^ L. E. Reichl. A Modern Course in Statistical Physics, Arnold, London, 1991.
646
Гл. 15. Полимеры: структурные свойства
следовательно,
F.= о
Тг Ат Ап ехр(-/ЗЯдг)
Тг ехр(—/ЗЯдг)
(15Б.11)
В качестве примера, иллюстрирующего использование этого метода, рас-
смотрим случай, когда переменной, характеризующей состояние системы,
является полное число частиц А = N. При этом AF — —Np. В результате
мы имеем
откуда можно восстановить выражения (15Б.9) и (15Б.6).
4. Парные корреляционные функции плотности. Вместо парной корре¬
ляционной функции некоторой переменной, характеризующей состояние
системы, мы можем использовать соответствующую парную корреляцион¬
ную функцию плотности. Плотность а., отвечающую переменной Аф, мож¬
но определить с помощью интегрального соотношения Ат — Ja9dr. Мы
также имеем: (а.) = Am/V> Тогда можно переписать выражение (15Б.10)
в виде
где £а#(г) — а.(г) — (а.). Переход от двойного интеграла к одинарному
в этом выражении стал возможен, потому что в однородной системе пар¬
ные корреляции между значениями некоторой переменной в точках гиг7
зависят только от расстояния г — г' между этими точками. Следовательно,
можно ввести корреляционную функцию
Soft (г) = (Saa(r) Sab( 0)) = (ao(r)at(0)) - {аа)(аь) (15Б.14)
Xnn = d(N)/dv = р «N2) - (7V)2)
(15Б.12)
Хтп = Р ((ат(г) - (ат))(а„(г') - (a„)))drdr'
(ЗУ (6am(r) San(0)) dr, (15Б.13)
и ее фурье-трансформанту
Sab(q) = ехр(—iq • r)Sa6(r) dr.
(15Б.15)
Таким образом, мы можем записать восприимчивость в виде
Нш ^ = PSab(q = 0).
(15Б.16)
Приложение Б: Изотермическая сжимаемость и флуктуации плотности 647
5. Рассмотрим теперь более подробно флуктуации плотности.
Величина
N
Ф) =У2 S(t- rm)
т.—I
есть плотность числа частиц в некоторой точке г для набора из N иден¬
тичных частиц (или связей, как в случае полимерных цепей), находящихся
в точках гш и занимающих объем V. Тепловое усреднение плотности да-
N
ет: с — ( S(r - rm)) = N/V. Нас интересует корреляционная функция
т=1
плотности (15Б.14)
5(г) — (<5с(0) ёс(г)) = (с(О)с(г)) - с2, (15Б.17)
где 6с(г) = с(г) — с . Определим фурье-трансформанту этой функции как
S (q) = а
ехр(—iqr)S(r) dr, (15Б.18)
где коэффициент а3 (объем частицы) был введен для того, чтобы сделать
величину S(q) безразмерной. Уравнение (15Б.16) в приложении к флуктуа¬
циям плотности приобретает вид
къТса\Т = с“15( q = 0). (15Б.19)
(см. (15.55)). Давайте введем фурье-образ плотности
c(q)
с(г) exp(-iq • r)dr = ^ exp(-zq • rm).
m
Интенсивность рассеяния в обратном пространстве (структурный фактор
системы) можно записать как корреляционную функцию этой величины:
7(q)
exp[-jq(r0 - r/g)](c(ra)c(r/3)) dra drp
(c(q)c(-q)) = V(a~3S(q) + (2tt)3c2 J(q)). (15Б.20)
Мы можем спокойно забыть о члене с дельта-функцией, который соответ¬
ствует рассеянию в направлении падающего пучка и экспериментально не
регистрируется43). Таким образом, эксперименты по рассеянию выявляют
43^ J.-P. Hansen and I.R. McDonald. Theory of Simple Liquids, 2nd edition, Academic
Press, N. Y., 1991, p. 99.
648
Гл. 15. Полимеры: структурные свойстса
эффекты длинноволновых флуктуаций (при q = 0) и, в частности, поведе¬
ние сжимаемости.
Парная корреляционная функция, введенная в п. 15.1.3
s(r) = <15Б-21>
тфп
связана с S(г). Начнем со следующего соотношения (где г = га — г#)):
(S( Та - гт)5(гр - г„)) = У* УШг0 + г - гт) 6{т0 - г„)) +
ГО п гпфп
+ - гт) 6(гр - гт)),
та
и преобразуем его правую часть. Первый член в правой части может быть
записан как
1
v J
dr0 +г - rm) Нгв - rn)) = 7- Y] У2 ^(Гп+г -Гт^’
/ V
тпфп тфп
а второй член — как с2 (см. п. 15.1 .4, где приведен вывод этого равенства).
В конечном счете мы получаем полезные выражения
с#(г) = 5(г) и </>g{ q) = 5(q), (15Б.22)
где ф = са3 есть объемная доля частиц.
Задача 15.1. Показать, что вероятность Pn(t) того, что идеальная
цепь из N связей, зафиксированная в начале координат, имеет завершение
в точке г, удовлетворяет дифференциальному уравнению
^(r) = -V2Pn( г)
dN 6
в предположении, что N велико. Используйте решеточную модель для по¬
лимерной цепи.
Ответ. Положим, что связи в полимере а; (г — 1, 2, ..., z) распо¬
ложены вдоль ребер регулярной решетки с координационным числом 2.
Очевидно,что
Z
Р(Т, 7V) = iVp(r-ai,iV-l).
2 *
Приложение Б: Изотермическая сжимаемость и флуктуации плотности 649
Разложим это выражение в ряд по векторам а;, величина которых мала по
сравнению с г:
р/ 1 ЛГ \ _ ту f АТ\ дР дР , 1 д2р
Ьг> N 1) A ) — —— &ia ^га^г/З
ON дга 2 дгадгр
1 б
Поскольку ага ~ 0 и - ^2 aiaaip = &2 z исчезает из суммы, и мы
г z i 3
получаем требуемый ответ (адаптировано из Doi, Introduction to Polymer
Physics).
Задача 15.2
а) Показать, что в решеточной модели с координационным числом г
число конфигураций идеальной цепи, состоящей из N сегментов, с одним
концом, закрепленным в начале координат, и другим, находящимся между
г | и | г + dr|, есть Wid dr, с Wid = zN 47rr2 Pjy (г).
б) Пусть вероятность отсутствия перекрывания для двух сегментов
объема v = а3 для цепи с радиусом инерции R равна 1 — a3/R3. Пока¬
зать, что вероятность отсутствия перекрывания два на два для N сегментов
ДГ2дЗ
(вообще говоря, неидеальной) цепи есть p(R) = ехр(— ) (N велико).
2 ^
в) Показать, что максимальное значение числа конфигураций для
неидеальной цепи из N сегментов получается для величины г = R ос
ос Nv(u ~ 3/5) (адаптировано из Dor, Introduction to Polymer Physics).
Ответ
б) p(R) = (1 — a3/pft)N{N~-i)/2 ^ exp(—N2a3/2R3)\
в) величина, которую необходимо сделать здесь максимальной, есть
W
p(r)Wid. Получаем: (Д/Д^)5 - (R/Rid)3 = '^-N1/2, где Rid
16
= (27Va2/3)1/2.
Задача 15.3. Вычислить три показателя степени для радиуса Фло-
ри Rp ~ v^apNu в рамках теории Флори, сформулированной на основе
теории подобия. Вычислить при тех же предположениях концентрацию
перекрывания с* и корреляционную длину £ в полуразбавленном режиме.
Ответ. Начните с выражений (15.30) и (15.31) для энергии полимер¬
ного клубка. Минимизация по отношению к R позволит получить
1 2 3
(1 = -—р = —v
d 2 d -1- 2 с? 4“ 2
Кроме того, с* = N1 */da2dl(d~{~2}v d/(d+2)?x>e> ф* — N1 vd(a/v)d/^+2)5
и т. д.
41-КЛЕМАН М.
650
Гл. 15. Полимеры: структурные свойства
N
Задача 15.4. Показать, что линия р* — (dF/дф)ф=ф1 — (8F / дф)ф=ф2
(так называемое плато Максвелла) разрезает кривую р = р(ф) на две рав¬
ные области (см. рис. 15.5, в).
Ответ. Полная отмеченная площадь между кривой р = р(ф) и линией
02
р = р* дается интегралом J [/л(ф) - р*]с1ф = F {ф2) ~ F (ф\) - р* (ф2 ~ фг).
Ф\
Эта величина зануляется, потому что это уравнение, которому удовлетво¬
ряют точки, принадлежащие общей касательной к кривой F = Ё(ф).
Задача 15.5. Рассмотрим двойную смесь с объемной концентраци¬
ей 0о одного из компонентов, находящуюся при температуре Т в обла¬
сти метастабильности (см. рис. 15.10). Первые появляющиеся зародыши
с концентрацией ф\ имеют тот же химический потенциал ро, что и фо-
Определить толщину и энергию переходной области между матрицей и за¬
родышами в предположении, что стенка плоская.
Ответ. Свободная энергия неоднородного слоя между матрицей и за¬
родышем должна содержать градиентный член. Мы запишем новое вы¬
ражение для энергии, которое необходимо минимизировать: Е(ф, V</>) =
— Р(ф) — роф 4- -К(\7ф)2. Вариационная производная этого выражения
может быть записана как КУ2ф — ~[F(</>) — роф].
йф
Рис. 15.10. См. задачу 15.5
Приложение Б: Изотермическая сжимаемость и флуктуации плотности 651
В плоском случае, который реализуется, когда радиус кривизны заро¬
дыша много больше, чем толщина стенки, получаем первый интеграл
2
-к(^) = F(</>) - цоФ + const = h(4>). (15Р.1)
2 V dx /
Производная должна обратиться в нуль при х = ±оо. Следовательно, в до¬
полнение к условию (Iq = ц(Фо) = m(0i)j мы также имеем
Р(фо) - ЦоФо = F{<t>i) - fi0Фг.
(15Р.2)
Это означает, что, если стенка плоская, система находится на кривои сосу¬
ществования и ро — №(Т) \ уравнение (15Р.2) представляет собой условие
для плато Максвелла. Интегрирование (15Р.1) дает: х — J <1фу/кЩЩ.
Энергия на единицу площади есть
+ оо
+ сю
ф 2
7
с1хЕ(ф, Уф)
К
— ОО
dxK(V4>)
2
(1ф^2К}г(ф).
ОО
Ф1
Эти две величины могут быть оценены, если взять для Ь(ф) его значение
в максимуме на кривой свободной энергии между концентрациями фо и фх;
обозначим Ahm — AFm — роФт\ в итоге имеем
1
Фо)^кЩ
mi т •
(15Р.З)
Задача 15.6. Пусть гель приготовлен путем добавления полуразбав-
ленного раствора полимера в хороший растворитель. При этом полимерные
цепи набухают. N — среднее число мономеров между узлами полимерной
сетки. Зацепления отсутствуют. Гель погружен в хороший растворитель
в избытке и имеет параметр взаимодействия Флори х* Показать, что сво¬
бодная энергия системы, приходящаяся на ячейку, в единицах к^Т записы¬
вается как
/ = (1 - Ф) In (1 - Ф) +хФ(1~Ф) +
2 N R*
где ф — объемная доля мономера в геле, Rq = Na2.
В условиях, когда разбухание уравновешивается, строение геля опре¬
деляется плотно упакованными полимерными клубками, которые не про¬
никают друг в друга. Выразить / как функцию только одной перемен¬
ной ф. Вычислить феq и размер Req клубков в условиях уравновешива¬
ния разбухания. Учесть, что фец < 1, и ввести параметр исключенного
652
Гл. 15. Полимеры: структурные свойства
объема v = а3(1 — 2%). Показать, что результат соответствует переходной
концентрации с* для раствора в хорошем растворителе.
Как изменится свободная энергия системы, если растворителем явля¬
ется расплав полимера, степень полимеризации которого равна числу Р
мономеров и имеющего ту же химическую природу, что и клубки геля?
Пусть Р мало по сравнению с N. Выразить феq и Req как функции N
и Р. Показать, что при Р порядка 7V1/2 клубки геля являются идеальными.
Что происходит при Р ~ N ?
Задача 15.7. Вычислить период слоев d в ламеллярной фазе дву¬
блочных сополимеров, полагая N = NA = Nb, v = v>a — vb- Поверх¬
ностная энергия 7 межблочной разделяющей поверхности предполагается
известной.
Связать поверхностную энергию 7 с параметром Флори - Хаггинса х
и с толщиной 5 переходной области между цепями А и В.
О т в е т. С помощью выражения (15.31) упругую энергию, приходящую¬
ся на единицу объема системы, можно записать как fei k^T сР / (N2 a2 v);
поверхностная энергия на единицу объема есть /surf « 2j/d. Сумма этих
двух вкладов имеет минимум при d « [7N2a2v/(kBT)]1^3. Поверхностная
энергия пропорциональна числу контактов между мономерами различного
типа в области перехода, т. е. 7 « xksT 5/v. Порядок величин: используйте
величину <5, имеющую порядок нескольких длин мономеров.
Литература для дальнейшего чтения
1. J. des Cloizeaia and G. Janninck. Polymers in Solution, Their Modelling and
Structure, Oxford University Press, 1990.
2. M.Doi. Introduction to Polymer Physics* Oxford Science Publications, 1995.
3. M Doi and S. F Edwards. The Theory of Polymer Dynamics, Oxford Science
Publications, 1988.
4. P. J. Flory. Principles of Polymer Chemistry, Cornell University Press, Ithaca,
N. Y., 1953.
5. P-G. de Gennes. Scaling Concepts in Polymer Physics, Cornell University Press,
Ithaca, N. Y., 1979. [П. де Жен. Идеи скейлинга в физике полимеров / Перев.
с англ. под ред. И. М. Лифшица. — М.: Мир, 1982.]
6. N. G. van Катреп. Stochastic Processes in Physics and Chemistry, North-Holland,
Amsterdam, 1981.
7. A. Keller. Chain-Folded Crystallization of Polymers from Discovery to Present
Day: A Personalized Journey, in Sir Charles Frank, an Eightieth Birthday Tribute,
Edited by R. G. Chambers et al., Adam Hilger, 1991.
8. R. G. Larson. The Structure and Rheology of Complex Fluids, Oxford University
Press, N. Y. and Oxford, 1999.
9. G. Strobl. The Physics of Polymers, Concepts for Understanding Their Structures
and Behavior, Springer, N. Y., 1996.
Литература для дальнейшего чтения
653
Дополнительная литература
1. Волькенштейн М. В. Конфигурационная статистика полимерных цепей. —
М. - Л.: Изд-во АН СССР, 1959.
2. Бирштейн Т.М., Птицын О. Б. Конформации макромолекул. — М.: Наука,
1964.
3. Плате Н.А., Шибаев В. П. Гребнеобразные полимеры и жидкие кристал¬
лы, — М.: Химия, 1980.
4. Жидкокристаллический порядок в полимерах / Под ред. А. Блюмштейн. Пе-
рев. с англ. — М.: Мир, 1981.
5. Гросберг А.Ю., Хохлов А. Р. Статистическая физика макромолекул. —
М.: Наука, 1989.
6. Гросберг А. Ю., Хохлов А. Р. Физика в мире полимеров. Библиотечка «Квант»,
выпуск 74. — М.: Наука, 1989.
7. Жидкокристаллические полимеры с боковыми мезогенными группами / Под
ред. К. Макардл. Перев. с англ. — М.: Мир, 1992.
8. Хохлов A. R, Кучанов С. И. Лекции по физической химии полимеров. —
М.: Мир, 2000.
9. Паташинский А. 3., Покровский В. Л. Флуктуационная теория фазовых пе¬
реходов.— М.: Наука, 1982.
10. М. Warner and Е. М. Terentjev. Liquid crystal elastomers, Clarendon Press,
Oxford, 2003.
АЛФАВИТНЫЙ УКАЗАТЕЛЬ
Abrikosov, А. А., 151, 153
Ackerson, В. J., 597, 600
Adams, М., 639
Adamson, A. W., 559, 605
Aggarwal, S. L., 636
Aharony, А., 275, 293
Ajdari, А., 541
Alberts, В., 63, 66
Alder, В. J., 599
Aleonard, R., 157
Allain, М., 341
Allender, D. W., 471
Alward, D. B., 637
Amelina, E. A., 605
Andelman, D., 158, 564, 568, 590
Anderson, D. М., 637
Anisimov, M. A., 157, 161
Antelmi, D. A., 601
Apollonius, 405, 551
Appell, J., 577, 582
Arfken, G., 181
Asakura, S., 594
Ashkin, A., 601
Auvray, L., 22, 591
Avnir D., 292
Avogadro, 428, 562
BahrC., 100, 472
Balian, R., 580
Ball, R.C., 281
Barash, Yu. S., 66
Barbero, G., 180, 212
Bartolino, R., 363, 364
Bassereau, R, 577, 582, 587
Batchelor, G. K., 226, 253, 596
Bates, F. S., 637
Baumann, G., 291, 293
Baus, М., 639
Belyakov, V. A., 130
Ben Shaul, A., 580, 591, 605
Ben-Abraham, S. I., 412
Benjamin, W. A., 253
Benoit, H., 627
Bensimon, D., 293, 373, 575
Beris, A.N., 239
Bernal, J. D., 70, 639
Berne, 43, 65, 560
Berreman, D. W., 130
Bessel, 585
Bethe, 275
Bidaux, R., 405
Bilby, B.A., 17,371,377
Binder, K., 636
Bingham, 414
Binks, B, R, 582
Biot, J.-B., 641
Birshtein, Т. М., 652
Bivas, I., 579
Bjerrum, 564
Bjorkholm, J.E.,601
Blanc, C., 338, 343, 420
Blinov, L. М., 91, 112, 122, 130, 168,212,
559
Bloch, 505
Blodgett, 518
Blumshtein, A., 652
Boccara, N., 405, 605
Boltenhagen, R, 14, 400, 410, 582
Boltzmann, 563, 568
Bonnet, 542
Born, 75
Bouligand, Y., 344, 373, 375, 434, 443,
446, 507, 511, 642
Bourdon, L., 366, 373
Boyd, 107
Boyle, 588
Bragg, W. L, 78, 101,373
Brand, H. R., 228
Branden, C., 66
Brandenberger, R., 472
Bravais, 487
Bray, A., 469, 472
Bray, D., 63, 66
Brener, E.A., 335
Briki, F., 641
Brillouin, 75
Алфавитны й указ am ел ь
655
Brinkman, W. F., 466
Brown, 262, 282, 597
Bruinsma, R., 413
Buka, A., 228, 247, 253
Bunde, A., 259
Burgers, 17,298,332,335,337-340,343,
344, 347, 348, 350, 353, 360, 362, 363,
366,367, 451,487
Burton, W. K., 532
Busson, B., 641
Cabrera, N., 532
Cahn, J.W., 632
Cahoon, М., 435
Caille, A., 583
Campbell, J. A., 38
Cano, 17, 327, 360,364
Carlsson, Т., 462
Caroll, L., 550
Carvalho, B. L., 637
Casimir, H. B. G., 47, 53, 540, 541
Caspar, D. L. D., 435, 638
Cates, М. E., 590
Cayley, 277
Chaikin, P.M., 130, 154, 161
Chan W.K.. 360
f
Chandrasekhar, S., 472
Chapman, 564, 565
Chen, J. D., 286
Chigrinov, V.G., 12, 112, 122, 130, 168,
212
Chizhikov, V. A., 12
Chu, S., 601
Chuang, I., 468
Chui, S.T., 532
Churaev, N. V., 559, 605
Ciferri, A., 168, 170
Cladis, P. E., 431, 462, 466, 469, 546
Clark N. A., 91, 195,357, 374
Cohn-Vossen, S., 107, 392, 421, 510
Colliex, C., 399
Collings, P J., 560
Cooper, 147
Costival, В. C., 471
Cotton, J. P., 627
Couette, 240, 245
Coxeter, H. S. М., 71
Cozzarelli, N., 510
Crawford, G. P., 168, 471
Crocker, J. C., 598, 602
Croxton, C. A., 559
Csillag, L., 126
Cugon, E., 246
Cui, М., 243
Curie, P., 17, 133
Dafermos, C. F., 472
Daoud, М., 627
Darboux, G., 375 -377, 392, 421
Darcy, 287, 356, 359, 360
David, F., 586, 587
Davis, A.-C., 472
Davison, S., 579
de Broglie, 644
de Brujn, N.. G., 76
de Gennes, P.-G., 13, 17, 52, 130, 131,
135, 158, 161, 169, 199,212, 332, 335,
358, 405, 464, 471, 527, 559,. 584, 586,
595, 606, 611, 615, 617, 625, 627, 628,
635, 652, 661
de Groot, S. R., 253
De Jeu, W.H., 161, 212
De Kruif, C. G., 592
de Seze, L., 405
de Wolff, P. М., 76
De’Neve, Т., 472
Deborah, 457, 458
Debye, 320, 564, 565, 570, 581, 603
Decher, G., 518
Delaunay, 77
Delaye, М., 195
Deloche, B., 17
Demus, D., 130
Denniston, C., 465
Derjaguin, В. V., 526, 559, 561, 572, 605
Derrida, B., 511
Derzhanski, A., 176, 583
des Cloizeaux, J., 652
Destrade, C., 82
Dhar, D., 406
Diat, О., 416
Diedzic, J.M., 601
Dimon, S., 594
Dirac, P. А. М., 110, 266, 550
Dmitrienko, V. E., 12, 22, 130
Doane, J. W., 471
Dogic, Z., 639
Doi, М., 458, 460, 463, 472, 607, 622,
628, 639, 649, 652
Doucet, J., 641
656
Алфавитный указатель
Dozov, I., 180
Drzaic, P. S., 559
Dubois-Violette, E., 247, 462
Duhem, 515, 644
Dunmur, D. A., 168
Dupin, 374
Duplantier, B., 541
Duplessix, R., 627
Durand, G., 17, 180, 195, 363, 364, 410,
412, 456, 539, 553
Durrer, R., 468
Dzyaloshinskii, I. E., 51, 240, 377
Edwards, B. J., 239
Edwards, S. R, 458, 472, 607, 628, 639
Elston, S., 130
Einstein, A., 214, 295, 321, 325, 356, 360,
592, 596, 633
Ericksen, J.L., 168, 227, 228, 232, 237,
239, 245, 457, 458, 461, 463, 465
Eshelby, J., 466
Euclid, 254, 255, 479
Euler, 333, 340, 346, 362, 366, 536, 604
Evangelista, L. R., 212
Evans, D. F., 581, 600, 605
Evans, E. A., 581
Everett, D. H., 559
Fabre, P., 22
Faetti S., 535
Fankuchen, I., 639
Famoux, B., 627
Feder,J., 254, 261,286, 292
Fedorov, 67
Ferma, 123, 124
Fermi, 78
Ferry, J.D., 421
Fetters, L. J., 637
Fick, 321,322
Filippini, J. C., 157
Flory, Paul J., 66, 141, 169, 264,267, 270,
606, 615, 618, 620, 622, 623, 628, 649,
651,652
FoexG., 17
Fomenko, A. Т., 511
Forster, D., 227, 253
Fourcade, B., 373, 575
Fourier, 333, 585, 609, 635, 647
Fournier, J.-B., 22, 376, 384, 410, 553
Fraden, S., 242, 602, 639
Fradin, Claudine, 22
Francis, G. K., 511
Frank, F.C., 13, 16, 74, 146, 150, 163,
170, 183, 200, 212, 301, 308, 326, 347,
348, 422, 423, 426, 436, 458, 532, 558,
575
Frankel, Т., 510
Frederiks (Freedericksz), V. K., 115, 168,
209, 439, 535, 537
Fredrickson, G. H., 636, 637
Freeman W. H, 63
Frenkel, J. (Yakov), 315, 317, 361
Fresnel, 116, 118
Freyssingeas, E., 587
Fridrihsberg, D. A., 605
Friedel, G., 13, 17, 22, 78, 329, 331, 339,
361, 368, 369, 372, 373, 376, 380, 398,
402 - 405,408,421,449,451,456,469,
471, 554
Frolov, Yu. G., 605
Fukuda, A., 168
Fuller, Buckminster, 79
Fuller, F. B., 510, 581
Fuller, N., 581
Gardner, L. R. Т., 371
Gasparoux, H., 82
Gast, A. P., 598, 559, 605
Gathercole, L. J., 641
Gauss, 382, 542, 545, 575
Gay, 43, 65, 560
Gaylord, R. J., 293
Geguzin, Ya. E., 559
Gelbart, W. H., 580, 591,605
Gerritsma, G. J., 455, 468
Geurst, J. A., 455, 468
Gibbs, W., 131, 132, 147, 512, 516, 518,
644
Gido, S. P., 637
Ginzburg, V. L.„ 144, 147, 427
Gittes, F., 641
Glaser, M. A., 95
Glushchenko, A., 535
Godreche, C., 293
Goldanskii, V, 212
Goldstein, R. E., 53, 566
Golestanian, R., 53
Golubovic, L., 587
Goodby, J. W., 100
Gorsky, W., 101
Алфавитный указатель
657
Gould, Н„ 293
Goulian, М., 413
Gouy, 564. 565
Gouyet, J.-F., 264, 275, 292
Grahame, 571
Grandjean, R, 17, 127,327,360,364,373,
551, 554
Gray, G. W., 80
Graziano, D. J., 459
Greco, R, 253, 462
Grier, D.G., 598, 602
Grosberg, A. Yu., 652
Gruner, S. М., 590
Gulik-Krzywicki, Т., 590
Gunther, J., 637
Guyon, E., 248
Guyot-Sionnest, P., 180
Hachisu, S., 599
Hamaker, H. C., 66, 527, 573, 601
Handlin, D. L., 637
Hansen, J.-P., 647
Harbich, W., 582, 583
Harris, W. R, 423
Hartshorne, N. H., 130
Hasegawa, H., 637
Hashimoto, T.; 468. 637
Havlin, S., 259
Heisenberg, W., 103, 479, 480
Hele-Shaw, H., 255, 285, 288, 289
Helfrich W., 195, 209, 355, 537, 561, 575,
580,582 - 584,586 - 588,590,604,640
Helmholtz, 643
Henkee, C. S., 637
Herring, 323
Hiemenz, R C., 42, 66
Hilbert, D., 392, 510
Hirth, J. R, 331
Ho, T.-L., 501
Hoffman, D., 637
Holyst, R., 368
Hone, D., 541
Hong, J. D., 518
Hooke, R, 295, 297,314, 329
Hoover, W. G., 599
Horn, R., 414
Hsiung, H., 180
Huckel, 564, 565, 570, 603
Hudson, S. D., 435
Huggins, P.M., 606, 620, 622, 623, 628,
651
Hume-Rothery, 78
Hunter, R. J., 605
Hurault, J. P., 195
Hurd, A. J., 292
Her, R. K., 518
Imura, H., 464
Isambert, H., 641
Isenberg, C., 559
Ishibashi, Y., 466
Ishikawa, K., 22, 336, 468
Ishikawa, Т., 468
Israelachvili, J.N., 42, 66, 567, 601, 605
Izmaylova, V. N., 605
J0ssang, Т., 286
Jackson, J. D., Ill, 130, 178
Jannink, G., 627, 652
Jena, P., 100
Janot, C., 100
Janssen, Т., 76
Joachimstahl, 391
Joanny, J. F., 527, 559, 564, 595
Joets, A., 472
Jones, 43
Jorand, М., 600
Julia, B., 377
Kadanoff, L. P., 293
Kamien, R. D., 22, 351, 444, 641, 642
Kaplan, T. A., 78
Kardar, М., 53
Kasper, J. S., 74, 301, 423
Kats, E. I., 22, 240, 253, 559
Kauffman, L. H., 510
Kawada, H., 637
Kawasaki, K., 466, 639
Keesom, 35, 37
Kekicheff, P., 601
Kellay, H., 582
Keller, A., 641,652
Keller, P., 90
Keller, S. L., 639
Kelvin, 520
Kepler, G. М., 602
Kerr, 135
Khairov, R. Yu., 331
Khalatnikov, I. М., 510
658
Алфавитный указатель
Khanna, S.N., 100
Khokhlov, A. R., 643, 652
Khoo, I.C., 126
Kibble, T. W. B., 548
Kinning, D. J., 637
Kirehhoff, 325
Kirkwuud, 599
Kiss, G., 246
Kitaeva, V. F., 126
Kitawaga, K., 629
Kitzerow, H.-S., 100
Klein, R., 281
Kleman, М., 12, 13, 16, 170, 341, 344,
364,366,371 -373,376,385,393,394,
398-401, 406, 408, 410, 414, 415,
419 - 421,431,43 5,442,443,446,451,
456, 469, 472, 501, 508, 510, 546, 580,
582
Klug, A., 62, 638, 639
Kneppe, H., 245
Kobayashi, Y., 599
Koch, 255, 256, 258, 290
Koehler, 346, 347, 359-362
Kogut, J. B., 278
Kondepudi, D., 222
Koppi, K. A., 413
Kosterlitz, J. М., 155
Kramer, D., 580
Kramer, L., 228
Kremenetsky, М., 465
Krieger, L М., 596
Krigbaum, W. R., 170
Kroner, E., 13,371
Kroo, N., 126
Kruger, G. Т., 360
Kuchanov, S. I., 652
Kumar, S., 82
Kurik, М. V., 511
Kwok, R., 581
Lagerwall, S., 91, 340
Lagrange, 182, 333, 340, 346, 366, 536,
604
Lam, Lui, 292
Lame, 296
Landau, L. D., 14, 17, 51, 88, 101, 102,
130, 131, 144, 147, 161, 162, 201,226,
331,427, 559, 561,590, 608, 661
Landsberg, R Т., 557
Langer, J. S., 293
Langevin, D., 605
Langmuir, 518
Laplace, 255, 337
Larson, R. G., 247, 253, 413, 435, 458,
596, 598, 605, 607, 628, 652
Lasher, 44, 65, 560
Laue, 326
Lauwerier, H., 293
Lavrentovich, O. D., 12,14, 126,336,385,
406, 410, 437, 467, 511, 535, 539, 542,
553, 558, 582
Lebedev, V. V., 240, 253
Lebwohl, 44, 65, 560
Lee, S. D., 432
Legendre, 65, 110
Leger, L., 527, 559
Lehmann, O., 115
Leibler, L., 595
Leibler, S., 590
Lejcek, L., 366
Lekkerkerker, H.N. W., 581
Lennard, 43
Lescanec, R. L., 637
Leslie, F. М., 227,228,237,239,244,253,
457-459, 463
Levi-Civita, 163, 215
Lewis, J., 63, 66
Liang, S., 293
Libchaber, A., 22, 641
Liebert, L., 90
Lifshitz (Lifshits), E. М., 51, 130, 161,
226, 331, 559, 608
Likhachev, V. A., 331
Lin, M.Y., 281
Lindsay, H. М., 281
Link, D.R., 468
Li volant, F., 344, 642
Loginov, E. B., 12
Lonberg, F., 439
London F., 37
Lothe, J., 331
Love, A.E.H., 176,584
Lubensky, T.C., 130, 154, 161. 227, 335,
441,442, 547, 587, 641
Luckhurst, G. R., 168
Luzzati, V., 590
Lydon, J., 86
Lyuksyutov, I. F., 428
Mackintosh, F. C., 641
Алфавитный указатель
659
Mackley, М. R., 459
Madelung, 30
Madhusudana, N. V., 82
Maffettone, P. L., 247
Maggs, A. C., 641
Magnasco, М., 641
Mahanty, J., 65, 66
Maier, 142
Malet, G., 415. 456
Mal^y, K. J., 286
Malozemoff, A. P.. 511
Mandelbrot, Benoit B., 254, 261, 293
Manneville, P., 247, 462
Marchenko, V. I.. 335
Marignan, J., 415, 456, 577, 582, 587
Mariotte, 588, 620
Marrucci, G., 247, 253, 462
Martin, D. C.. 637
Martin, P.C., 227, 235, 253, 355
Massey, W. S., 495, 510
Masuda, Т., 629
Mather, P. Т., 462
Mauguin, C., 125, 183
Maxwell. 567, 632, 649
Mazelet, G., 170, 435
Mazur, P., 253
McDonald, I. R., 647
McGuiggan. P М., 601
Mead, D. W., 458
Meakin, P., 281
Meissner, 147
Mendeleiev, D., 583
Menger, 292
Mermin, N. D., 501, 510, 550
Meunier, J., 582, 605
Meyer, R. B., 90, 170, 179, 195, 242, 340,
374, 431, 432, 435, 439, 469, 639
Meyerhofer, D., 437
Michel. L., 508. 510
^ s у
Miezowicz, 240
Milner, S. Т., 413, 590
Mineev, V. P., 510
Mitchel, D. J., 577
Mitov. M. D., 579, 583
Molau, G. E., 636
Mobius, 474, 475
Monastyrskii, M. L, 12, 511
Monge, G., 392
Mori, H., 437
Morse, D. C., 641
Mukherjee, P. H., 135
Morse, S. A., 130
Muller, V. М., 559, 605
Mullins, W.W., 290, 319
Mutz, М., 373, 575
Myers, D., 605
Nabarro, F. R. N., 323, 331, 352, 361, 416
Nagaya, Т., 466
Nakanishi, H., 437
Nakata, М., 468
Nallet, F., 337, 582, 587
Nastyshyn, Yu. A., 12
Navard, P., 472
Navier, 325, 357, 359, 360
Nazarenko, V. G., 539
Neel, L., 13,505
Nehring, J., 164
Nelson, D. R., 351, 444, 586, 642
Neumann, 524
Newton, 225, 240
Ninham, B. W., 65, 66
Nishikawa, Y., 637
Noll, 162
Nye J. F., 17
Nozieres, P., 559
Ochsenfeld, 147
Odjik, Т., 169, 639
Okano, K., 464
Ohm, 223
Onsager, L., 131, 139, 141, 157, 168, 169,
221, 224, 599, 641
Onuki, A., 639
Oosawa, J., 594
Orihara, H., 466
Orlov, A.N., 331
Orlov, V. P., 130
Orowan, E., 365, 367, 368
Orsay Liquid Crystals Group, 199
Oseen, 362
Ostlund, S., 466
Ostrovskii, В. I., 12
Oswald, P., 22, 363, 364, 366, 368, 394,
412,415,419
Ott, A., 641
Overbeek, J. Th. G., 66, 572, 605
Palffy-Muhoray, P., 126, 463
Palierne, I., 180
660
Алфавитный указатель
Panizza, P., 413
Papoular, 534, 542
Pargellis, A., 467
Parodi, O., 233, 235, 253, 355, 405, 415,
456
Parry, D. A. D., 641
Parsegian, V. A., 581, 600, 642
Pasini, R, 65
Pasteur, 56
Patashinskii, A, Z., 652
Patel, J. S., 560
Patel, S. S., 413
Pauli, 38
Pauling, L.? 59
Peclet, 596
Peach, 346, 347,359-362
Pearson, D. S., 459, 461
Peierls, R.E., 17, 76, 88, 201, 310, 314,
317,352,361
Pelcovits, R. A., 560
Peliti,L., 541
Penrose, 78
Penzenstadler, E., 436
Pergamenschik, V. М., 22, 167, 183, 558
Pershan, P. S., 227, 235, 355, 368, 559
Pertzev, A. V., 605
Pesci, A. I., 566
Petrov, A. G., 176, 579, 583
Petukhov, В. V., 12
Picot, C., 627
Pieranski, Pawel, 246,248, 337, 462, 546,
600
Pikin, S. A., 12, 161, 212, 245, 246, 253,
462, 540,
Pilipetskii, N. F., 126
Pincus, P., 564
Pindak, R., 374
Pines, D., 635
Pitaevskii, L. P., 51, 524
Plane, K., 37
Plate, N. A, 652
Pleiner, H., 22, 228, 362
Poenaru, V.? 511
Podgornik, R., 642
Poggi, Y, 157
Pohl, W.F., 510
Poincare, 71, 208, 542, 546, 550
Poirier, J.-P, 368, 580
Poisson, 348, 563, 568, 570, 584
Pokrovskii, V. L., 652
Polak, R.D., 471
Polder, D., 47
Pomeau, Y., 511
Poniewierski, A., 559
Porod, 266
Porte, G., 22
Porter R. S., 246
Poynting, 117, 128
Poulin, P., 547
Prager, S., 591
Prigogine, I., 222
Prost, J., 130, 161,200,212,337,358,541
Ptitzyn, О. B., 652
Pusey, P. N., 597
Raff, М., 63, 66
Rand, R. P., 581, 600
Ranganath, G. S., 472
Rao, В. K., 100
Rapini, 534
Rault, J., 399
Rayleigh, J. W., 169
Read, 309, 310
ReichI, L. E., 64, 645
Reinitzer, F., 449
Reiss-Husson, F., 590
Renn, S. R., 154
Rennschuh, H., 590
Reynolds, 362, 367, 458
Reznikov, Yu., 535
Ribotta, R., 195,412, 472
Rice, S. A., 253
Richetti, P., 601
Richter, L., 130
Riemann, 541
Riste,T., 559
Rivas, E., 590
Roberts, K., 66
Romero-Rochin, V., 566
Rosenblatt, C., 22, 374, 537
Rothen, F., 600
Rottmann, C., 531
Rouse, 612
Roux, D., 410, 416, 590, 591, 605
Rowlinson, J. S., 559
Rozhkov, S. S., 467
Rull, L. F., 639
Rupprecht, A., 642
Russel, W. B., 568, 598, 600, 605
Ryckaert, J. P., 639
Алфавитный указатель
Ryskin, G., 465
Sadashiva, В. К., 82
Saffman, P. G., 285
Safinya, C. R., 413, 582
Safran, S. A., 580, 590, 605
Saint-Venant, 193
Sambles, R., 130
Sammon, M. J., 435
Sander, L. М., 282, 284
Sandorfy, C., 66
Sarid, D., 601
Sarma, G., 405, 627
Saupe, A., 126, 131, 142, 157, 164
Saville, D. A., 568, 605
Scher, H., 284
Scherk, 638
Schmidt, C.F., 641
Schmidt. V. V., 161
Schmitt, J., 518
Schneider, F., 245
Schnurr, B., 641
Schoen, A. H., 590
Schdnflies, 67
Schopol, N., 428
Schowalter, W. R., 568, 605
Schukin, E. D., 605
Schuster, P., 66
Scriven, L. E., 591
Seitz, F., 13
Sekerka, R.F., 319, 290
Semenov, A. N., 639, 641
Sergan, V. V., 539
Servuss, R. М., 582, 583, 587, 604
Sethna, J., 376
Shafer, F., 212
Shalaev, V., 22
Sharma, N. K., 245
Shashidhar, R., 82
Shen, Y. R., 180
Shibaev, V.P., 652
Shiwaku, Т., 468
Shiyanovskii, S. V., 22, 126, 535
Shraiman, B., 293
Sierpinski, 529
Sierro, P., 410
Simon, A., 641
Simoni, E, 126, 130
Skalak, R., 581
Skouri, М., 587
661
Slonczewski, J. C., 511
Sluckin, Т., 22, 428, 559
Smalyukh, 1.1., 126
Smith, E., 371
Smoluchowski, М., 592
Sobolev, N. I., 126
Sommeria, J., 373
Sonin, A. A., 559
Sonin, A. S., 421
Sotta, P., 22
Spegt, P. A., 590
Spruijt, A. М., 455, 468
Srinivasarao, М., 462
Stanley, H.E., 161, 259, 645
Stark, H., 547, 641
Stauffer, D., 275, 293
Stebler, B., 340
Steenrod, N., 510
Steinert, Р. М., 641
Stephen, M. J., 157, 253
Stirling, 156
Stoiber, R. E., 130
Stokes, 325, 357, 359, 360, 593
Straley, J. P., 157
Strayer, G., 242
Strey, H. H., 642
Strobl, G., 607, 634, 652
Stryer, L., 63, 66
Strzelecki, L., 90
Stuart, A., 130
Sugakov, V. G., 178
Sukhov, A. V., 126
Summ, B. D., 605
Suresh, K. A., 82
Sussman, A., 437
Suzuki, М., 466
Swift, J., 227
Szleifer, I., 580
Tabiryan, N. V., 126
Tabor, D., 47
Takanishi, Y., 468
Takezoe, H., 468
Talmon, Y., 591
Tanford, C., 66
Tang, C., 293
Tao, Y.-H., 600
Tardieu, A., 590
Taupin, C., 584, 586
Taupin, D., 366
662
Алфавитный указатель
Taylor, 366
Taylor, G. I., 285
Terentjev, E. М., 437, 613, 652
Thiaville, A., 22
Thomas, E. L., 637
Thomas, P. B., 406
Thouless, D. J., 16, 155, 510
Timoshenko, 301
Tinh, 82
Tobochnik, J., 293
Toennies, J., 212
Tooze, J., 66
Toulouse, G., 377, 511
Trebin, H.-R., 436
Treloar, L., 612
Tsvetkov, V.N., 110, 115
Turkevich, L. A., 284
Turok, N., 467, 468
Van der Waals, 13, 131, 142, 13,533,560,
572, 591, 599, 622
Van Kampen, N. G., 652
Van Megen, W., 599
Van Saarloos, W., 462
Vant’Hoff, 567
Vedenov, A. A., 559, 605
Venkatesh, G., 82
Verlan, E. М., 178
Vertogen, G., 161,212
Verwey, E. J. W., 66, 561, 572, 605
Veyssie, М., 22
Vicsek, Т., 263
Villain, J, 78
Volkenshtein, М. V., 66, 652
Voloschenko, D., 448
Volovik, G. E., 240, 377, 509, 511, 542
von Karman, 75
Volterra, V., 15-17, 296, 302, 422, 423,
447, 451
Wang, J. S., 510
Wang, W., 468
Warner, М., 652
Watanabe, H., 413
Watson, J. D., 63, 66
Webb W. W., 360
Weeks, J. D., 532, 559
Weiil, G., 464
Weingarten, 297, 298, 302
Weisfreid, J. E., 472
Weiss, P., 13, 142
Weitz, D. A., 281, 547
Wellin, P. R., 293
Wennerstrom, H., 605
West, J. L., 535
White, J.H., 510
Widom, B., 559
Wigner, 71
Wilkinson, D., 286
Williams, С. E., 343, 375, 415
Williams, E. J., 101
Williams, R., 437
Willmore, 380
Wills, H. H., 331
Wilson, K. G., 278
Winey, K.I.,413
Winsor, 591
Witten, T. A., 282, 284
Woods, L. C., 253
Wortis, М., 531
Wulff, 551
Yampolskii, G. P., 605
Yokoyama, H., 533
Yoshimori, A., 78
Young, 145, 584
Young, D. A., 599
Yurke, B., 467, 468
Zaleski, Z., 472
Zallen, R., 100
Zannoni, C., 65
Zasadzinski, J. A. N., 435
Zeeman, 179
ZePdovich, B. Ya, 126
Zheng-Min, Sun, 170
Zhuang, S. L., 126
Zolina, V., 115
Zolofko, A. S., 126
Zumer, S., 183, 471
Zundel, G., 66
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
а-кератин, 641
а-спираль, 59, 60
/?-слой, 59
Т-стенка, 638
5СВ, р-пентил-р'-цианобифенил, CisHigN,
36, 86, 112, 113, 241, 245, 461, 471,
537, 539
8СВ, р-октил-р'-цианобифенил, C21H25N,
80,413,414, 460, 461
Абрикосова фаза, 151, 153
Авогадро постоянная, 31, 428, 562
Агрегат, 255, 259, 280, 282, 285, 518,
560, 573, 593, 597
Агрегация, 52, 259, 267, 279, 280, 573,
593, 594
— диффузионно-контролируемая, 255,
280, 282-284, 289, 594
-диффузионно-контролируемая кластер-
кластерная, 282-284
— кластер-кластерная, 280, 282
— частично-кластерная, 282
— эффект самоэкранирования, 259
Аденин, 61
Адгезия, 52
Адсорбция, 515, 517
— относительная, 516, 556
— отрицательная, 516
— положительная, 516
— уравнение Гиббса, 516
Актина волокна, 606, 638, 641
Активационный
— объем,364
— энергия, 364, 592, 609
Алифатическая цепь, 80, 83, 575
Алмаз, 29, 637
Аминогруппа NH2, 56
Аминокислоты, 33, 54
— аланин, 33
— аспаргиновая кислота, 56
— валин, 33
— глицин, 33, 56
— лецин, 33
— лизин, 56
— серин, 56
— хиральные, 56
— цистеин, 56
Аморфные среды, системы, 69,424,628
Аморфное твердое тело, 265
Амфифильные молекулы, 83, 516, 574
— гидрофильная головка, 83
— гидрофобный хвост, 83
Анализатор, 121, 123
Анионы, 562
Анизотропные жидкости, 422
Анизотропное сцепление, 247,429,431,
437, 457, 504, 532, 535, 536, 541, 544,
546, 548, 553
— (бесконечно) сильное, 188, 189, 193,
211,471,536, 540
— геометрическое, 437, 468, 533
— коэффициент, 471, 504, 534,535, 537,
542, 551
— направление, 177, 186
— потенциал, 186, 472, 533, 535
— потенциал сцепления Рапини-Па-
пулара, 534, 542
— сила, 534, 540
— характерная длина, 537, 539, 541
Антибиотики, 83
Антисимметричный тензор вращения,
230
Аполлониево заполнение, 267, 551
Атермические взаимодействия, режи¬
мы, растворы, 615, 622-624
Атомно силовая микроскопия ACM,
600, 601
Баланса уравнение, 219, 220, 228, 230
— для энтропии, 222
Батоннеты, 554
Белки, 20, 27, 52-54, 60, 516, 518, 606
— вторичная структура, 59, 60
— глобула, 60, 62
— первичная структура, 59
— синтез, 59
664
Предметный указатель
— третичная структура, 60
— четвертичная структура, 60
Бензол СбНб, 34
Бернала дыры, 70
Бете решетка, 270, 273, 275, 277
Бинарная смесь, система, 630
Биополимеры, 56, 442, 449, 463, 600,
606, 607, 641, 642
Бислой, 39, 92, 561, 574-576, 589
— модули упругости х, 3<, 576, 579,
581,583
— случайный, 590
— устойчивость, 589
Ближний порядок, 55, 101
Блоб, 618, 626
Блок-сополимеры, 413, 635-637
Блоха стенка, 505
— теорема, 75
Блуждание без самопересечений, 615,
618
Бойля - Мариотта закон, 64, 588, 620
Бойля температура, 65
Больцмана уравнение, 563
Большой потенциал, 645
Борна-фон Кармана граничные усло¬
вия, 75
Боя поверхность, 107
Браве ячейка, 107
Броуновское движение, 255, 262, 264,
282, 560, 565, 591 -593, 596-598
Брэгговские рефлексы, 78
Бьеррума длина, 564
Бюргерса
— вектор, 298, 300, 303, 305, 311, 325 -
327,330,332,337,340,347 -349,353,
360, 361, 363, 366, 368, 387, 422, 446,
451,455, 487
бесконечно малый, в жидких кри¬
сталлах, 372
большой, в смектиках, 332, 337 —
340, 344, 362, 398, 582
——малый, в смектиках, 332, 335, 337,
339, 340, 343, 353, 361, 362, 367, 455
— контур, 301, 424, 433
Вайнгартена теорема, 297, 298, 302
Вакансии, 73, 318, 319, 321, 355, 363
Валентность, 78, 562-564
Ван-дер-Ваальс, 44
— силы, 27, 131, 526, 533 560, 561, 569,
572, 591, 619
— уравнение, 64, 518
Вант Гоффа уравнение, 567
Везикула, 575, 581, 600
Вейса теория молекулярного поля, 142
Взаимодействия, атомные и молекуляр¬
ные, 25, 26
— Ван-дер-Ваальса, 31, 60, 526
— водородная связь, 44
— дипольные, 31
— ион-диполь, 34
— ион-нейтральная молекула, 37
— Казимира, 52
— отталкивательное, 38
— экранированное ионное, 31
Вигнера - Зейтца ячейки, 71
Вилмора гипотеза, 380
Винзора фаза, 591
Вириальный коэффициент второй, 26,
27, 65, 624
Вириальное разложение, 26, 141
Вирус, 20, 62, 607, 638
Вирус табачной мозаики (ВТМ), 62, 83,
109, 136, 168, 434, 435, 593,639
Вискозиметрия, 615
Вихревая нить, 151
Внутренняя энергия, 512
Вода, 561, 562, 574
— диэлектрическая постоянная, 563
Водородная связь, 44, 59
Воздух, 574
Вольтерра, 15
для дисклинаций, 73
для дислокаций, 296, 297
— процесс в жидких кристаллах, 451
— процесс в твердых телах, 16
в холестериках, 447
Восприимчивости показатель, 615
Вращение плоскости поляризации, 641
Вторичный минимум, 573, 592
Второй закон термодинамики, 225
Вулканизация, 53, 269
Вульфа
— построение, диаграмма, 529, 531 54
— форма, 551
Вырождения параметр, 101, 102, 104,
106, 107,213
Вытекание в третье измерение, 431,432,
436, 445, 446, 451, 454, 469, 470, 496
Предметный указатель
665
Вязкие пальцы, 255, 285, 289
Вязкости коэффициенты, 225, 226
— в гарвардской модели, 228
—динамическая объемная вязкость, 225
— кинематические, 456
— Лесли, 238-240
— нематические, 459
— относительной вязкости, 596
— смектические, 353, 354
— Эйнштейна соотношение, 596
Вязких напряжений тензор, 224
— смектический, 356, 360
Газ, 25
— двумерное газообразное состояние,
517, 574
Газовая постоянная, 26
Галогениды щелочных металлов. 31
✓
Гамакера постоянная, 46, 51, 66, 527.
573, 601
Гарвардская модель гидродинамики, 227,
237, 238, 457
Гаусса-Бонне теорема, 196, 542, 546
Гауссова кривизна, 173, 176, 196, 380,
545, 575, 584, 589
отрицательная, 175, 196, 198, 382,
385, 400, 401, 411, 443, 447, 590, 591
— положительная, 174, 380, 390, 401,
449, 591
Гексатическое упорядочение
— в ДНК, 642
— в смектиках В, F и I, 91
Гелеобразования точка, 56, 268
Геликоид, 342, 376
Геликоидальные конфигурации, моле¬
кулы, 609, 642
Гель, 19, 593, 606, 628, 651
Гельмгольца свободная энергия F, 131,
132,514, 526, 556, 643
Геодезическая линия, 391, 395
Гиббса - Дюгема соотношение, 515,644
Гиббса свободная энергия G, 131, 132,
147, 644
Гиббса уравнение адсорбции, 516, 595
Гибкие полимеры, главные цепи, 606,
607, 628
Г ибридно-ориектированный нематиче¬
ский слой, 184, 211, 467, 540, 558
Гидратированньлй ион, 34
Гидродинамические переменные, 213,
227, 228, 235
Гидрофильный эффект, 44, 46
Гидрофобный эффект, 44, 45
Гинзбурга-Ландау модель, 427
Гинзбурга-Ландау параметр, 153
Гинзбурга-Ландау разложение, 145,
147, 148
Гиперболическая точка на поверхности,
175, 379
Глины пластинки, 560
Глицерин, 515, 535
Глобула, 60, 622
Годограф, 303, 424, 433
Голубые фазы, 93, 163, 443, 444
Гомополимеры, 53
— линейные, 53
Гомотопическая группа, 478, 479
Гомотопический
— вторая гомотопическая группа, 499,
500
— дефектов классификация, 475, 478
— класс, 481
— относительная гомотопическая груп¬
па, 505, 506
— первая гомотопическая группа, фун¬
даментальная группа, 481, 484, 485,
487, 489, 490, 492, 495, 498, 502, 505,
508
— третья гомотопическая группа, 507
Гость-хозяин эффект, 126
Гоуи- Чепмена длина, 564, 565
Гранжана-Кано клин, 327, 360, 364,
420, 455
Графт-полимер, 599
Гребнеобразные сополимеры, 637
Группа, 475, 477
— группа изотропии, 481
— евклидова, 480
— кватернионов, 496
— коммутативная (абелева), 478, 492
— коммутатор, 498
— малая группа, 481
— некоммутативная (неабелева), 478,
490
— полупрямое произведение, 489
— пространство смежных классов, 478,
480, 481
— прямое произведение, 480
— сопряженности класс, 490, 491
666
Предметный указатель
Группа 50(2), 480
Группа 50(3), 480, 496
Групповая скорость, 120
Грэхэма сооотношение, 571
Гуанин, 61
Губчатая фаза, 208, 400, 574, 577, 582,
583, 590, 601
Гука закон, 294, 297, 314, 329
Гэя-Берне потенциал, 44, 65, 560
Дальний порядок, 101, 641
Дарбу теорема, 376, 377, 380
Дарси закон, 287, 356, 359, 360
Двойная закрутка (деформация), 15, 93,
439, 440, 442-444, 642
Двойники, 304, 329
Двойной спирали ось, 476, 477
Двупреломление, 115, 119, 135
Дебай, 35
— взаимодействие, 35, 37
—Дебая - Хюккеля длина, 564,565,581
— линейное приближение, 570, 603
— частота, 320
Деборы число De, 239, 457, 458
Де Жена-Любенского крупномасштаб¬
ная модель, 335, 441, 442
Де Жена-Топена длина персистентно¬
сти, 584
Дезоксирибоза, 61
Делоне условие, 77
Дельтаэдр, 70
Дендритов рост, 283
Десорбция, 516
Дефект, 72
— топологический, 90, 122
— ядро, 101
Деформация, 93
— двойной закрутки, 93, 163, 439, 440,
442-444
— изгиба поперечного, 147, 148, 151,
164, 170, 179, 350
— изгиба продольного, 144, 147, 148,
150, 151, 166, 170, 179, 431,432, 439,
485
— изгиба седловидного, 166, 175, 374,
443, 577
индуцированная ограничениями,
437
— кручения, 144, 146-148, 151, 154,
350,351,431,432, 442, 443
релаксация, 439
Деформированное состояние, 102
Диамагнитный, 536, 537
Дивергентные (упругие) члены, 164,209,
436, 471
Дигептилазобензол, 126
Дилатация, 208, 215, 225, 329, 343
Динамический модуль упругости, 628
Диполь
— наведенный (индуцированный), 35
— постоянный, 35, 37
— свободный, 35
— флуктуирующий, 47
Дипольный ион, 33
Дипольный момент, 28, 32. 34, 80, 179
Дирака магнитный монополь, 550
Директор, 86, 106, 109-111, 122, 424-
427,429-431,433,434,437-439,442,
443, 445, 446, 448, 449, 453, 455-
462,464 - 466,469 -471,484,493,502,
503, 506, 542
— в голубых фазах, 93
— в двуосном нематике, 87, 114
— в смектике С, 89, 90
— в холестерике, 88, 439, 441, 444
Директора поле, 107
Директора уравнение динамики, 229,
234-237
Дисклинация, 73, 127, 155, 239, 245,
332, 419
— аннигиляция, 465
— в двуосном нематике, 496
— взаимодействие, 459, 465
— в нематиках, 455
диссипации процессы, 455, 456
клиновая, 424, 425, 431, 434, 435
кручения, 422, 433, 434, 451, 455
несингулярное ядро, 423
планарная модель, 425, 427, 430,
435
полуцелая, 428, 431
сеть дисклинационная, 459, 468,
469
сила, 424, 425, 453, 454, 465, 489,
496
толстая, 430, 459
тонкая, 430, 459
— — целая, 428, 431, 493
ядро, 427, 428, 430, 431, 434, 455,
456, 465
Предметный указатель
667
— в твердых телах, 423
клиновая, 423
— в холестериках, 422, 498
X линия, 446, 447, 453, 454
X линия, расщепление на Л и г,
447
Л линия, 444—447
— — т линия, 446, 447
полуцелая, 445
сила, 449
целая, 445
ядро, 445, 446
— зарождение, 462
— испускание-поглощение дислокаций,
452, 455
— петля, 437, 459, 468
— плотность, 468
—~ связь с дислокациями, 451, 452
Дискотический, 394
— колончатая фаза, 369
— нематик, 242
Дислокация, 155, 156, 305, 309, 332,
369-372
— бесконечномалая (инфинитезималь-
ная), 13, 16, 315, 452
— Вольтерра процесс, 297, 302
— вязкая релаксация, 451, 452, 454
— в кристаллах, 302
несовершенная, 302, 315, 329
совершенная, 302
с углом вращения, 303
— в смектиках, 153, 195
винтовая, 151, 154, 196, 328, 337,
340-343,348, 362
винтовая, геликоидальная неста¬
бильность, 365
винтовая, гигантская, 343, 375
винтовая, линейное натяжение,
340. 344
*
винтовая, ступени, «ручьи», 340,
341
краевая, 151, 195, 332,334, 337-
339, 361,366, 408
краевая, нелинейная теория, 335
— — краевая, переползание, 353, 359,
361, 364, 363, 367
краевая, подвижность, 357, 360,
367
краевая, расщепление ядра, дис-
клинационная модель, 337, 338, 362
— — краевая, размножение, 365
краевая, скольжение, 361 -363
—- — краевая, энергия ядра, 335
— в твердых телах, 294, 296
двойникующие, 329
винтовая, 297, 306, 311, 317, 329
вращения, 297
краевая, 307, 310, 317, 327, 329
смешанная, 297
—- — трансляции, 297
эпитаксиальная, 329
ядро, 297, 301, 310, 311, 314, 316
— в холестериках, 335, 336
— —винтовая, 350
— в колончатых фазах, 347, 348
краевая, 447
краевая, поперечная, 348, 349
— — краевая, продольная, 347, 348
— — краевая, свободные флуктуации,
352
скольжение, 352
эквивалентность с \ линиями,
447
— в твердых телах, 315
— кинк, 317, 352, 362
— Кирхгофа условие, 325
— линейное натяжение, 308, 326, 344
345, 366, 387
— механизм Франка-Рида, 326
— мозаичная текстура, 469
— Пайерлса модель, 314, 331
— Пайерлса напряжение, 310, 317
— Пича-Келера силы, 308, 309, 311,
312,330, 331,347,359-362
— переползание, 311,353,359,363,364,
367, 368
— пересечение дислокаций, 312
— петля, 325
— плотность, 370-372, 375, 377, 416,
423, 451 -453, 456
— связь с дисклинациями, 332
— скольжение, 31 1, 353, 361, 367
Френкеля модель, 315, 317
— скольжения плоскость, 327
— соглашение о знаках, 303, 307, 330
— ступенька, 312
— ядро, 148, 156, 300, 306
Дисперсия, 28, 37
Дисплей, 19, 91, 115, 125
Диссипативная функция R, 222, 224
\ф
668
Предметный указатель
Диэлектрическая постоянная
— вакуума, 563
— воды, 563
Диэлектрическая проницаемость, 30,51,
111, 116
Диэлектрической проницаемости тен¬
зор а], 112
Диффузии коэффициент, 320, 325, 592 -
594,615, 628, 633,639
Диффузии коэффициент в смектиках,
357, 367
Диффузия, 219, 318, 584
ДЛВО (Дерягина-Ландау-Вервея-
Овербека) теория, 561, 572, 573, 591,
592, 598, 600, 602
ДНК, 14, 20, 83, 344, 444, 446, 475, 477,
508, 606, 638, 642
— гексагональные фазы, 642
— репликация, 475, 477, 508
Додецилсульфат натрия, 83, 582
Додецилсульфат натрия-вода-гексанол
или пентанол, 582
Доя молекулярная теория, 458
Дюпен
— теорема, 374, 375
— циклиды, 374, 380, 382, 385, 389, 402
Жесткие полимеры, жесткие стержни,
607, 608,612, 638, 639
— динамики уравнение, 612
— радиус кривизны, 608
— свободная энергия, 608, 609
Жидкий кристалл, жидкокристалличе¬
ские фазы, 110
Жидкокристаллические полимеры,
168-170
Жидкокристаллические структуры, 62
Жидкостная релаксация, 16, 372
Закрученная граница, 14, 154, 332, 372,
375, 637
Закрученный нематик, 125, 437
Запаздывания эффект, 47, 591
Запутывание, 628
— дисклинаций, 496, 498
Зародышеобразование, 34, 135, 521,
523, 632
— энергия, 634
Заряда закон сохранения, 563
Заряды
— поляризационные, 567
— свободные, 567
Зеемана энергия, 179
Зерен граница, 154, 319, 370
— в блок-сополимерах, 637
— в колончатых фазах, 444
— в смектиках, 360, 404, 406, 410, 420
— — Аполлониево покрытие, 407, 410,
551
дислокационная граница зерна,
410, 420
—^— наклонная граница зерна, 387
стенка кривизны, 420
— муаровая фаза с границами зерен,
332, 444
Золь-гель переход, 21, 267
Идеальная цепь, 606, 610, 615, 618,619,
648
— динамическая модель Рауза, 612
— радиус инерции, 614, 622
— свободная энергия, 611
— тэта-температура, 622
— удлинение, 611, 612
— энтропия, 611
Идеальный раствор, 138, 563, 595
Иерархия структур, 60, 641
Избыточная площадь, 586
Изломы, 344, 530
Изомеризация
— транс-гош, 609
Изотропная фаза, 110, 132, 134, 140,
141
Изотропная упругость (одноконстант¬
ное приближение), 184, 540, 558
Изотропный ферромагнетик, 499
Израелашвили - Митчела - Нинхама
модель (ИМН), 577
Икосаэдр, 72
Икосаэдрическое упорядочение, 15, 71,
73, 78
Индия и олова окисел, 177
Инверсионная симметрия, 439
Ионы, 562, 564-567, 603
Исключенный объем, 26, 27, 131, 136,
139,142, 169,596,599,615-617,619,
621,623,624, 639, 641,651
Искривление, 369-372, 377, 416, 421
Истощения флокуляция, 595
Йоахимшталя теорема, 391
Предметный указатель
669
Казимира взаимодействия, 540, 541
Казимира-Полдера эффект, 47
Кайе показатели степени, 583
Каламитический нематик, 87, 242
Калаверит, 76
Капиллярная длина, 520, 525
— эффекты гравитации, 525, 557
Капиллярное давление, 290, 520
Капли, 442
— в биополимерах, 442
— в двойных смесях, 634
— в двуосных нематиках, 548
— изотропные, 528
— луковицы, 391, 410, 416, 418
— нематические, 135, 439, 456, 541,
542, 544, 546 “548
— Робинсона сферолиты, 449
— смектические, 551, 556, 557
Карбоксильная группа СООН, 56
Катионы, 33, 562
Квазикристалл, 14-16, 19, 21, 78
Квазикристаллы, 75
Кварки, 466
Кварц, кремнезем SiCh, 20, 280, 598
Кватернионов группа, 496
Кевлар, 55
Кеезома силы и взаимодействия, 35, 37
Кейли дерево, 275-277
Кельвина уравнение, 520, 521
Керра эффект, 135
Кинк, 16, 352
Клейна бутылка, 489
Клубок, 608, 624, 625, 649, 651
Клубок - глобула переход, 622
Когерентности длина, 101, 148, 539
— магнитная, 536
Кологен, 641
Коллоиды, 20, 282, 526, 560, 561, 598
Коллоидные кристаллы, 561, 598
— ГЦК, 599
— ОЦК, 599
Коллоидные растворы, 434, 582, 591,
592, 598
Колончатая фаза, 86, 92, 240, 328, 332,
347-349,351 -353,369,372,419,560,
636. 637
А
— термотропная гексагональная, 332,
347
Компоненты движения (жидкости), 214,
215
Конгруэнции. 374
— линий, 374
— нормалей, 375, 376
— прямых линий, 375, 376, 379
— прямых нормалей, 373
Конфокальная микроскопия, 126
Конфокальные домены, 369, 373-375,
377, 378, 400, 403, 410, 441, 551, 553,
554, 556
— в лиотропных фазах, 397
— в холестериках, 441, 442
— законы объединения, 403
— заполнение пространства, 555, 556
— КФД-I (первого вида), 380, 400, 403,
407.410.416
— КФД-И (второго вида), 380, 382, 401,
410.411.416
— КФД-Ш (третьего вида), 382
— неполные, 402
фрагментированные, 402
— ГТКФД (параболические), 195, 374,
389, 401,402,414
— полные, 402, 404
— реофизика, 412-414
— связь с дислокациями, 385
— ТКФД (торические), 374, 401, 405,
406
— эксцентриситет, 378, 385, 386, 404,
409,415, 421
Координационное число, 72, 73, 615,
648, 649
Корреляционная длина, 279, 427, 618,
626, 627, 649
Корреляция одномерная, 86
Костерлица-Таулесса модель, 155,156,
532
Коха кривая, 255, 256, 258, 290
Коэффициент зацепления, 475,476,507,
508
Краситель, 126, 518
Краски, 591
Кривизна, 173
— главные кривизны, 173,288,374,416,
441
— в твердых кристаллах, 369-371
— спонтанная кривизна, 575 - 578, 582,
590, 591
Кривизны дефекты, 393
— в колончатых фазах, 394
— в смектиках, 369
670
Предметный указатель
кривизны свободная энергия, 383
острый край, 376
— — развертывающиеся домены, 396
эвольвенты, 394
Кристалл, 79
— жидкий, 79, 80
— искривленный, 73
— пластический, 79
Критическая мицеллярная концентра¬
ция (КМК), 31, 83
Критические явления, 606
— показатели, 270, 271, 273, 276, 277,
279, 606,615,618
— универсальность, 269-271, 274
Кронекера дельта Sij, 206, 230
Кручение (деформация), 88, 431, 432
— вызванное ограничивающими поверх¬
ностями, 437
— лент Tw, 476, 477
— релаксация, 449, 471
Ксантан, 83, 444, 446, 642
Кубическая фаза, 92, 590, 636
— биконтинуальная, 92, 590, 637
Кубооктаэдр, 69
Кувыркания режим
— кувыркающиеся нематики, 245, 459,
462
Кулона потенциал, 30
— сила, 35
Куперовские пары, 147
Куэтта течение, 240, 245
Кюри температура (Кюри точка, 17,133
Лагранжа и Эйлера подходы, 214, 219
Лагранжа множитель, 141, 182, 184
Лагранжа условие, 140
Ламинарное течение, 227, 285
Ламэ коэффициенты, 296
Ландау разложение, 131, 135, 162
Ландау-де Жена модель (теория), 157
Ланжевена модель парамагнетизма, 35
Лапласа давление, 337, 520
Лапласа уравнение, 255, 284, 285, 288
Лапласа-Юнга уравнение, 519-521,
526, 557
Латекса раствор, 592
Латунь (сплав Cu5oZn5o), 107
Лебволя-Лашера потенциал, 44, 65,
560
Леви-Чивита тензор, 163,215
Легкого ориентирования ось (направ¬
ление анизотропного сцепления), 177,
504, 533
Ленгмюра ванна, 518
— Ленгмюра-Блоджетт пленка, 518
— монослой, 240, 518
Леннарда-Джонса потенциал, 43, 44
Лесли - Эриксена
— уравнения, 457
область применимости, 457, 458
Лецитин, 488, 581, 583
Лиотропные мезофазы, лиотропные
жидкие кристаллы, 83
Липидный бислой, 60
Лифшица теория, 51, 52
Локальный порядок, 69
Лондоновские (или дисперсионные)
взаимодействия и энергия, 37
Луковицы, 391, 410, 416, 418
Магнитная проницаемость вакуума ро,
111
Магнитной восприимчивости тензор х,
113
Маделунга постоянная, 30
Майера-Заупе модель, 157
Макромолекула, 53
Максвелла плато, 632, 649, 650
Максвелла тензор напряжений, 567
Максвелла уравнения, 116
Маллинса-Секерки неустойчивость,
290,319
Мартенситный переход, 329
Масло, 574
Маслянистые бороздки, 14, 339, 387,
398, 399, 442, 449, 582
Материальная производная, 214
Материальные уравнения, 116
Мёбиуса лист (лента), 434, 474, 475
Межблочная разделяющая поверхность,
637,651
Междоузлия, 318
Мезофазы, мезоморфные фазы, 79
Мезовича геометрии, 240
Мейснера-Оксенфельда эффект, 147,
151
Мембрана, изолированная, свободная,
575, 584, 587
— двумерный идеальный газ, 588
Предметный указатель
671
— де Жена—Топена длина персистент¬
ности, 584, 586
— избыточная площадь, 586
— краевая энергия, 579
— микроскопические упругие констан¬
ты, 577, 579, 581, 583
— свободной энергии плотность, 575,
577, 584
— связанные мембраны, 603, 604
Мембранные белки, 60
Менгера губка, 292
Мениск, 337
Микроскопия оптическая, 120,337,340,
372, 374,376,380, 401,435
Микротрубочки, 20, 62
Микрофаз расслоение, 627, 636
Микроэмульсии, 590, 591
— глобулярные, 591
Минимальная поверхность, 341, 343,
375, 520
— геликоид, 342
— катеноид, 520
Мицелла, 27, 32, 39, 83, 85
— обращенная, 83
Мицеллярная фаза, 208, 583, 589, 601,
636
Многогранник Вороного, 70
Могена режим, 125
Модель Виттена-Сандера, 284
Молекула
— дискотическая, 81, 92
— хиральная, 93
Молекулы
— дискотические, 80
— каламитические, 80
Молекулярное поле h, 182, 234
Молекулярной динамики моделирова¬
ние, 599
Молоко, 19, 591
Момент количества движения (импуль¬
са), 228, 234, 236, 239
Монжа поверхности, 392, 395
Мономеры, 53
Монополь. 550
ж
Монослой, 574, 576
— кривизны модули, 575
Монте-Карло вычисления, 435, 560
Мыло, 19, 20, 516, 520, 590
Муаровая фаза с границами зерен, 332,
444
«Мягкие среды», 13-15, 18-21,31,53,
67, 125, 131, 264, 304, 560
Навье—Стокса уравнения, 225,226,325,
357, 360
Намагниченность, 113, 270
Наночастицы, 518
Напряжение
— нормальное, 217
— растягивающее, 294, 295
— сдвига, 217, 295
— сжимающее, 295
Напряжения тензор а г/, 217, 228, 234,
235, 239
— в смектиках А, 346
— необратимая часть, 224
— обратимая часть, 224
Насыщенные углеводороды, 44
Нееля стенка, 505
Нематическая фаза, 86, 87, 101, 112,
132, 135
— двумерная, 484
— двуосная, 87, 114, 422, 441, 445, 473,
494, 496, 498
пространство параметра порядка,
495
фундаментальная группа, 494,495,
496
— дискотическая, 87
— жидкие кристаллы с малыми моле¬
кулами, 432, 433, 460
— жидкокристаллический полимер, 432,
434, 439, 458, 460
— закрученная, 88
— каламитическая, 87
— одноконстантная упругость, 464,469
— одноосная, 105, 106, 109, 110, 114,
115
Неньютоновская жидкость, 248
Необыкновенная (световая) волна,
118-120, 122, 124, 127
Непрерывности уравнение (закон сохра¬
нения массы), 218, 223, 228, 231
Несжимаемая жидкость, 225, 354, 355
Несоразмерная модуляция (фаза), 75,
77
Нестабильность растяжения (ондуля¬
ции), 193
Неупорядоченная биконтинуальная
фаза, 590
672
Предметный указатель
Низкомолекулярные жидкие кристаллы,
167, 170, 460
Нолла принцип инвариантности, 162
Нормальных напряжений разница, 463
Ньюманатреугольная конструкция, 524
Ньютона закон вязкости, 225, 240
Ньютоновская жидкость, 225
Оболочка, нерастяжимая, твердая, 584
Обратного потока эффекты, 248
Обыкновенная (световая) волна,
118-120, 122, 124
Огранка, 530, 531
Односвязный, 481, 495
Омега стенка, 638
Ондуляция слоев, 177, 193
Онсагера
— взаимности соотношения, 223 -225,
233, 236
— модель (теория), 131, 139, 141, 157,
168, 599, 641
Оптическая активность, 437, 439
Оптическая ось, 88, 109, 115
Оптические компенсаторы, 123
Оптический Фредерикса эффект, 126
Оптический пинцет, 600
Ориентационный порядок, 35, 54, 62,
79, 80, 90
Ориентированные контуры, 481
Орована соотношение, 365, 367, 368
Осмотическое давление, 26, 138, 567,
568, 595, 600, 622, 623
— скейлинг, 625
Осмотического напряжения техника,
600
Основной минимум, 573, 592, 593
Остроградского - Гаусса теорема, 164,
184, 330
Отклонения длина, 639, 640
Относительная скорость вращения ди¬
ректора N, 234
Отпечатков пальцев текстура, 335, 336,
446
Отсутствия проскальзывания условие,
226, 287, 596
Отталкивания потенциал (Хелфриха),
39, 561, 588
Отталкивания силы, взаимодействия,
28, 560, 592, 594, 598
— короткодействующие, 573
— электростатические, 583, 591, 592
— энтропийные, 573, 583, 588
Пайерлса-Ландау неустойчивость, 88,
201
Пайерлса модель, 314
Параллельное сцепление, 551
Параметр порядка, 14,21, 101, 192, 270,
332, 473, 478
— амплитуда, 101, 105, 107, 110, 144,
149, 198,213
— пространство, 101-107, 109, 478,
480,481,484,487,492 -494,501,502,
504, 506, 508
— скалярный в жидких кристаллах, 110,
142, 169, 183, 228
— смектика А, 144
—тензорный в жидких кристаллах, 109,
114
— фаза, 102, 104, 144, 198,213
Парная корреляционная функция, 601,
613, 646
— фурье преобразование S(q). 585,613,
614. 635
✓
Пароди уравнение, 238
Парциальное давление, 26, 620
Паули принцип запрета, 38
Пекле число, 596, 597
Пептиды, 63
Пептидная связь, 56
Первая разность нормальных напряже¬
ний. 246
а
Первичная структура биополимеров, 33
Первый ионизационный потенциал, 37
Перегрев, 134, 521, 627
Переохлождение, 521, 627
Переход от огранения к шероховатости,
532
Перколяция (протекание), 19, 255, 267,
269, 270, 274, 275, 279
— порог протекания (критическая ве¬
роятность), 267, 270, 273, 275-278
Перпендикулярное сцепление, 357,535,
542, 546-548, 551
Персистентная длина, 141,170,608.612,
638, 640
Персистентное время, 609
Петрова - Держанского - Митова модель.
577
— упругие модули, 582, 583
Предметный указатель
673
Пипеточного удаления техника, 600
Пича-Келера сила, 308, 309, 311, 312,
331
— в нематиках. 466
— в смектиках, 347. 359-362
J у
Планка постоянная, 37
Пластическая деформация, 294,308,364,
422, 600
Плоская монохроматическая волна, 116
Плотности флуктуации, 619, 626, 627,
643
— корреляционная функция плотность -
плотность, 635
Плотные упаковки молекул спиральной
формы, 642
Поверхностная поляризация, 177, 179,
535, 537, 539
Поверхностно-активное вещество, сур¬
фактант, 20, 65, 176, 177, 488, 516,
518, 537, 546, 560, 582, 584, 587, 590,
591,600, 627, 635
— ионное, 31
— неионное, 39
Поверхностно-силовой аппарат (ПСА),
600
Поверхностное натяжение, 52,290,328,
337, 512, 515-517, 521, 524, 530-
533, 535, 554, 556, 560, 588, 604
Поверхностные моменты сил, 229
— в нематике, 183, 188
— в смектике, 346, 347
Поверхностные силы, 216, 300
— в смектике, 346
Поверхностный избыток, 513, 556
— большого потенциала, 514
— свободной энергии Гельмгольца, 556
— энтропии, 514
Поверхность коэффициента преломле¬
ния (поверхность волновых векто¬
ров), 118, 129
Поворота вектор, 422
Пойнтинга вектор, 117, 128
Ползучесть, 318, 323. 363
— Херринга-Набарро модель, 323
Поли-7-бензил-(лево или декстро) глу-
тамат, 83, 136, 141, 170,439,444, 446,
458, 560, 642
Полиамиды, 168
Полибутадиен, 606, 637
Полидиметилсилоксан, 607
Полидисперсность, 628
Полимеризация, 53, 56, 267
— степень, 606, 623, 627, 634, 651
Полимерные
— расплавы, 626-628
динамический модуль упругости,
628
— — запутанность, 628
Полимеров конфигурации
— гош. 607
— клубок, 610
— полностью гош, 610
— полностью транс, 609
— спираль, 609
— транс, 607
Полимеры, 52, 444
— биополимеры, 444,446,449,463,641
—жидкокристаллические, 607,639,641
— кристаллические, кристаллизация,
607, 609, 628
— покрытия, 592
— разветвленные, 53
— решеточная модель, 648, 649
— синтетические, 53, 607
— сшитые в трехмерную сетку, 53
Полиметилметакрилат, 598, 606
Полиоксиметилен, 609
Полипептид, 60, 63, 444, 638
Полистирол ПС, 599, 602, 606, 637
Политетрафлуороэтилен, 609
Полиэлектролит, 518
Полиэтилен, 606, 607, 609
Полиэфиры, 170, 435
Полосы погасаний, 122
Полугибкие полимеры, 169, 560, 593,
607, 638, 639, 641
Полукристаллический порядок, 55
Полупроницаемая мембрана, 138, 595
Полупроницаемый барьер, 518
Полуразбавленного раствора режим,
625, 640, 641, 649
—- внутренняя энергия, 626
— скейлинг, 624, 625
— Флори - Хаггинса, 623
Поляризатор, 123, 129
Поляризуемость, 35, 36, 46
— избыточная, 51
Полярная головка, 31, 83, 574, 575, 578,
582
Полярный электролит, 516
674
Предметный указатель
Поперечный изгиб (деформация), 449
Порода закон, 266
Порядок-беспорядок
— переход, 107
— порядок против беспорядка, 593
Потенциал взаимодействия, 27
— Ван-дер-Ваальса, 47,48,65,526,533,
560, 561, 572, 621
— Гэя- Берне, 560
— жесткого ядра, 64
— Лебволя-Лашера, 560
— Леннарда-Джонса, 64, 73
— отталкивающий, 39
Предфрактал, 258
Предшествующая пленка, 527
Преломления показатель, 112, 117, 118.
125, 126
Принцип линейной суперпозиции, 300
Притягивающие
— взаимодействия, 27, 621
— силы, 25, 27, 28, 39, 560, 573, 591,
593, 594, 598, 601,619,621
Проективная плоскость RP2, 107, 480,
493, 495
Проективное пространство RP3, 495
Проникновения глубина, 148, 154, 589
— колончатые фазы, 348-352
— смектические, ламеллярные фазы,
335, 336, 339, 366, 409, 411, 421, 553
Проницаемость свободного простран¬
ства (электрическая постоянная) £о,
30
Просачивание, 355, 356, 359-362, 364,
367
Просветления температура, 101, 428,
432
Противоионы, 562, 564, 565, 567, 569,
570, 602
Пуассона «гидродинамические» скоб¬
ки, 240
Пуассона коэффициент, 348
Пуассона отношение, 296
Пуассона уравнение, 563, 570
Пуассона-Больцмана уравнение, 561,
563, 568
Равновесие моментов, 188, 189, 243
Равнораспределение, теорема о равно¬
распределении, 200, 585
Радиус инерции, 269,273,610,614.619,
622, 627, 637, 639, 649
Радиусы кривизны, 174
Разбавленный раствор, 612, 615, 619.
622, 624
— Флори-Хаггинса, 623, 625
Разбухшие поверхностно-активные ве¬
щества, сурфактанты, 590
Развертывающиеся домены, 393, 395,
396
Разделяющая поверхность, 512-514,516,
556
Размерность, 254
— Евклидова, 254, 255, 260, 262, 273,
291
— подобие, 259
— топологическая, 255
— фрактальная, 254, 255, 258, 259, 262,
264, 266, 274, 280, 282, 284, 286
Расклинивающее давление, 526, 527,
540, 541, 558, 567-569
Раскол, 340
Расплавленные полимеры, 17, 626
Рассеяние, 613, 615, 623, 627, 634
Раствор
— идеальный, 27
Растворенное вещество, 26, 516, 560
Растворитель, 25, 27, 516, 560
— плохой, 27, 621, 622. 627
— хороший, 27, 264, 619, 621, 622
Растяжения упругая константа >rs, 581
Рауза модель, 612
Резина, 53, 592, 606, 612, 628, 637
Рейнольдса число Re, 362, 367
Рейнольдса число Re, 226,285, 287,458
Релаксация
— молекулярная, 412, 457, 607, 639
— параметра порядка в ядре, 456
— транс-гош переходы, 628
Ренорм-группы теория, 131, 278, 606,
618
Реологические свойства
— конфокальных доменов, 411, 414
— полимеров, 607
Реология, 422
Решетка. 28
— Бравэ, 67, 370
— гексагональная плотноупакованная
(ГПУ), 28, 68, 69
Предметный указатель
675
— гранецентрированная кубическая
(ГЦК), 28, 67, 69, 304, 317, 599
— объемно-центрированая кубическая
(ОЦК), 28, 72, 107,305,317
— треугольная, 270
Рибоза; рибосомы; РНК, 62
Рост, 524, 532, 632
Ростовые явления, 255
Ручки, 197, 208, 583, 590
Самоподобие, 254, 258, 260, 261, 273,
278, 282
Сверхпроводник, 147, 149
Сверхпроводники, 147
— второго рода, 14, 151
— первого рода, 151
Сверхтекучие жидкости, 21, 294
— гелий-3 3Не, 473, 550
— гелий-4 4Не, 103. 106
у s
Света рассеяние, 615
Свободная энергия
— кривая, 630
— плотность, 335, 344, 347, 366, 606
в колончатой фазе, 332, 347-350
в полимерных смесях, 630, 632
“—в смектиках, 342, 346
Свободно подвешенные пленки, 337,533
Связь, 25
— водородная, 61
— ионная, 29
— ионно-ковалентная, 31
— ковалентная, 29, 31, 53
— металлическая, 27
Сдвиг, 225, 596
— в смектике А, 411, 413
— сдвиговое утоныиение, 597
— стабильность, 596, 597
Сдвига плоскость, 244
Сдвига скорость, 239, 412
Сегрегация, 623, 634
Седловидный изгиб (деформация), 173,
175,375, 443,471
Седловидного изгиба неустойчивость,
583
Сен-Венана принцип, 193
Серпинского ковер, 292
— салфетка, 259, 260, 262
Сетчатое строение, 628
Симметрия, 15, 25, 72, 109, 131, 155,
162, 198, 213, 227, 294, 329, 332, 451,
475, 479, 489
— икосаэдрическая, 79
— инверсионная, 89
— непрерывная поворотная, 87, 453
— непрерывная трансляционная, 87
— поворотная, 89, 107, 422, 530
— точечная, 67, 87
— трансляционная, 67,92,332,422,492
Сингулярность, 16,21,93, 151,299,332,
338, 344, 351, 369, 372, 384, 385, 387,
389, 390, 399, 400, 404, 427, 431, 433,
436, 443, 445, 446, 449, 471, 473, 474,
496, 499, 503, 505, 534, 544, 546, 556
Скейлинг, масштабная инвариантность,
195, 264, 267, 274, 278, 606, 610, 617,
619, 625, 627
Скорости деформаций (напряжений) тен¬
зор Aij, 215
Скорость света в вакууме, 147
Случайное блуждание, 255, 615
Случайной фазы приближение, 635
Случайные плотные упаковки (СПУ),
70, 71
Случайная переменная, 642
Слюды пластинки, 17, 560
Смачивание, 21, 288, 525, 527
— смачивания переход, 525
Смектик двумерный, 488
Смектическая фаза, 86
Смектическая А-фаза, 110, 115,332,369,
508
— динамические моды, 358
— первого и второго рода, 154
— полигональная текстура, 554
— фундаментальная группа, 509
Смектическая В фаза, 363
— пластичности свойства, 363, 364
Смектическая С фаза, 373, 508
Смектическая С* фаза, 90, 373
Смектические кластеры, 150, 151
Смектические фазы, 88, 240, 556
— батоннеты, 554
Снежинка, 283
Солитон, 422, 466, 473, 474, 504, 505,
507
Сольватация ионов, 561
— силы, 561, 573
Соляная кислота НС1, 32
676
Предметный указатель
Сополимеры, 53, 412
Сопротивления сила, 465, 466, 468
Соразмерная модуляция, 76
Сосуществование, сосуществования ли-
ния, 630, 632, 634, 650
Спин, 103, 104,618
Спинодальный распад, кривая, спино-
даль, 134, 623, 632-635
Среднего поля теория, 618, 625, 628
Средняя кривизна, 288, 575, 637
Статистический клубок, неупорядочен¬
ный клубок, 595, 608, 610
Стекло, 593, 628
— волокна, 560
— переход, 599
Степенной закон, 254, 256, 260, 266,
273, 282
Стерические взаимодействия, 28,39,46,
55, 67, 136, 560, 576, 609, 617, 641
Стокса закон, 593
Стокса теорема, 151, 172
Стокса формула, 226
Субграница, 326-328, 332
Твердые сферы, 26, 43, 560, 592, 598
Температура, 27, 156, 513, 606, 630, 632
— тэта, 27, 622
Текстура, 20, 294, 344, 397, 413
— планарная холестерическая, 125
— полигональная, 267, 449, 554, 556
— шлирен, 120, 122, 428
Теорема п = 0, 617
Теплопроводности коэффициент ж
(тензор), 224, 227, 228, 230
Тепловые флуктуации, 101, 198, 352,
413, 523, 531, 540
— мембран, 264, 561, 573,583, 584,586,
601
— полимеров, 608, 640
—- перенормировка упругих констант,
587, 588
Термотропная мезофаза, термотропный
жидкий кристалл, 83, 111, 119, 141,
169, 170,337, 348, 560
Тетраэдр, 72, 73, 158, 555, 556
Тетраэдрическая сеть, 44
Тетраэдрические позиции, 69
Течением ориентируемые нематики, 459
Тимин, 61
Тиомочевина SC(NH2b, 76
Топологический дефект, 294
— дефекты, 195, 239,422, 440,456,473,
479, 542, 546
— заряд, 473, 475, 479, 486, 500, 502,
509, 543, 544, 547, 558
— инвариант, 301, 457, 473, 475, 487
— классификация, 16, 478, 498
— конфигуруция, 473
— кручение, 475, 476
— подход, 16
— устойчивость, 473-475, 485, 492-
494, 496
Тор, 107, 487
Точечные дефекты, 422, 431, 435, 443,
451,485, 486, 500-502
— в нематиках, 456, 502, 542
буджум, 435, 439, 542, 544, 546,
550, 558, 559
еж, 435, 501, 542, 544, 546, 548,
550
ядро, 436
— в твердых телах, 294, 318-321, 323
— в трехмерном ферромагнетике, 499
Транс-гош изомеризация, 609, 628
Транс-изомеры, 126
Транс-цис изомеризация, 126
Трансляционное упорядочение, 79
Трение, 455, 465
Трехмерная сфера S3 в четырехмерном
пространстве, 495, 506
Триблочные сополимеры, 637
Тубулин, 63
Турбулентность, 227, 255
Тушь, 591
Углеводородный хвост, 31, 574, 575
Угловой момент, 234
Универсальное накрытие, 495
Упаковки дефекты, 304, 315, 317, 364
Упорядоченная биконтинуальная двой¬
ная алмазная структура, 637
Упорядоченная текстура, 463
Упорядочение в ориентациях связей, 91
Упругая энергия в твердых телах, 300
Упругие константы/модули, 146, 150,
169, 190
— изгиба ус, 561, 577, 579, 582-584,
586, 587, 589, 590, 637
— изгиба >ст, 575, 576
— изгиба поперечного, 149
Предметный указатель
677
— изгиба поперечного Кi, 146, 163,
164, 167-170, 183, 195
— изгиба продольного Кг, 146, 163.
168, 172, 173
— изгиба седловидного, 166
— изгиба седловидного Кi3, 164, 168,
175, 183, 196, 427
— изгиба седловидного Кчъ, 437, 439
— изгиба седловидного Kjm, 442
— изгиба седловидного К, 198, 374,
375, 384
— изгиба седловидного 561, 579, 583
— изгиба седловидного хт, 575, 580,
582, 589
— изгиба смешанного поперечно-про-
дольного #13, 164, 167, 183, 196, 437
— кручения #2, 163, 165, 167, 168
— растяжения 578, 579
Упругие константы/модули (сжатия/
растяжения)
— в колончатых фазах, 347-349
— в смектических, ламеллярных фа¬
зах, 333, 335, 341 -343, 346, 356, 358,
364, 366, 408,411,421,583, 589
— в твердых телах, 296
— в холестериках, 441
Урацил, 61
Устойчивость, 560
— в коллоидных системах, 560, 573,
576, 583, 589, 590
— в термотропных жидких кристаллах,
560
— коэффициент, 594, 597
Фаза Р/5/, 488
Фаз разделение, 158, 606, 627, 632, 634,
636
Фазовая диаграмма, 151, 577, 632, 639
Фазовая скорость, 116, 120
Фазовое расслоение, 635
Фазовые переходы, 83, 126, 155, 267,
606
— второго рода, 131
— второго рода, Ландау, 109, 151, 191,
270
— в коллоидах, 598
— Кирквуда-Алдера переход, 599
— Ландау-де Жена модель, 131
— ламеллярная-кубическая, 590
— Майера-Заупе модель, 131, 142
— нематик-изотропная фаза, 110, 547
космологическая модель, 548
— нематик - изотропная фаза стержней,
599, 641
— Онсагера модель, 131, 139, 168, 599,
641
— Онсагера модель (теория), 136
— первого рода, 17, 131, 135, 627, 628,
630, 636, 641
критическая точка, температура,
628, 630, 632, 634
сосуществование, 628, 630, 632
спинодаль, 623, 632, 634
— слабые первого рода, 135
— смектик А-нематик, 144, 160, 245
— смектик А-холестерик, 154
Ферма интеграл, 124
— принцип, 123
Ферменты, 62
Ферми уровень, 78
Ферромагнетик, 103, 106, 109, 475, 480
— Гайзенберга типа, 103, 480
— типаХ Y, 104
Ферромагнитная фаза, 103
Фика закон, 224
— второй, 321, 322
— первый, 322
Фингера тензор, 613
Флексоэлектрический эффект, 112, 115,
177, 179, 229, 535, 537, 539
Флокуляция, 52, 593
— броуновская, 593
— истощения, 595
Флори модель, 615, 618
— взаимодействия параметр, 621, 634,
651
— исключенный объем, 615-617
— радиус, 615, 624, 626, 627, 649
— свободная энергия, 617, 618
— среднее поле d — 4, 618
— цепь, 615
— энтропия, 617
Флори - Хаггинса модель, 606,619,622 -
625, 628
— осмотическое давление, 622,624,625
— свободная энергия, 620, 627
— Флори параметр взаимодействия, 621,
634
— энергия смешения, 621
— энтропия смешения, 620
678
Предметны й указател ь
Фокальная
— линия, 373
— поверхность, 344, 370, 374
виртуальная, 344, 345
Фосфолипиды, 33, 83
Фрактал, 254, 256, 258-260, 283, 290
— детерминированный, 262
— случайный, 262
Франка сетка, 326
Франка (упругие) коэффициенты (кон¬
станты, модули), 200
Франка-Каспера
— дельтаэдры, 75
— фаза, 74, 93
Франка-Осеена (упругая) энергия,
146-148, 153, 163, 185, 211, 228, 230,
231,427, 464
Фредерикса эффект (переход, индуци¬
рованный полем), 115, 168, 190, 439,
535, 537
— в смектиках А, 209
Френеля уравнение, 116, 118
Френкеля модель (скольжения), 316,317
Фрустрация, 15, 21, 72, 73, 93, 443, 642
Фуллерены, 79
Характеристическая функция, 642, 643
Хеле-Шоу ячейка, 255, 285, 288, 289
Хелфриха модели мембран, 561
— упругая модель, 575
— флуктуации, 592
— энтропийная модель, 39
Химический потенциал, 136, 139, 222,
513, 516, 520, 521, 557, 563. 578, 595,
620, 630, 632, 643, 649
Хиральность, 90,153, 159,366,395,434,
641, 642
Хиральные молекулы, 88, 90, 93, 153,
442
Хиральные энантиомеры (L и D), 56,
158
Хлопья, 573, 593
Хлорид натрия, 29
Холестерическая фаза (жидкий кристалл),
88, 93
Холестерический, 125,441-444
— крупномасштабная энергия де Же¬
на-Любенского, 335
— полигональные текстуры, 449
— текстура отпечатков пальцев, 335,
336, 446
— фаза (жидкий кристалл), 153, 162,
163, 166, 181,439, 443,447
— фундаментальная группа, 498
— шаг спирали, 88, 91, 125, 130, 153,
164, 166, 335, 336, 440, 441, 498, 550
Хопфа инвариант, 507
Хопфа отображение, 506
Хромонические жидкие кристаллы, 83
Хромосома, 344
— прокариотных водорослей, 334, 443
Цвиттерион, 33
Целлюлоза, эфиры целлюлозы, 53. 606,
638,641
Центральная предельная теорема, 611
Центральный атом углерода CQ, 56
Цетилпиридиний хлорид, гексанол, во¬
да, 582
Цинковой обманки (сфалерита) струк¬
тура, 31
Цитозин, 61
Червячная текстура, 463
Шевронная стенка, 638
Шенфлиса - Федорова группы, 67, 637
Шерка двойная переодическая поверх¬
ность, 638
Шлирен-текстура, 428, 429
— взаимодействие, потенциал взаимо¬
действия, 592, 596
— энтропия, 136, 139
Эйлера характеристика х, 197, 542, 546
Эйлера-Лагранжа уравнение, 125,128,
184, 186, 189, 192, 204, 205, 208, 210,
234, 333, 340, 346, 366, 426, 470, 529,
536, 558, 604
Эйлера - Пуанкаре соотношение, 71,208,
542, 546, 550
Эйнштейна закон для подвижности, 356,
360, 594, 633
Эйнштейна соотношение для вакансий,
321
Эластомеры, 539, 652
Электрическая проницаемость вакуума
£о, 111
Предметный указатель
679
Электрические двойные слои, 177, 181,
526, 562, 569, 599
— плотность свободной энергии, 566
Электрические диполи, 32
— постоянные, 32
— флуктуирующие, 28
Электролит. 560, 562,564,565, 567,569,
570, 572, 573
— сильный, 561, 565, 566, 568, 573, 584
— слабый, 561, 568, 573
Электронная микроскопия, 294, 310,
340, 434, 637
Электрооптические эффекты, 538
Электроотрицательные атомы, 44
Электростатические взаимодействия,
560, 561, 564, 567, 572
— потенциал, 567, 569, 584, 594
Эллипс, гипербола, сопряженные, 377
Эллиптическая точка на поверхности,
175
Энантиомеры L и D, хиральные, 56, 158
Энергии Лондона, 28
Энергия активационная, 361, 364
Энтропии производство а, 221-224,
227, 230, 236, 249, 464
Энтропийные силы, 573, 583
Энтропия, 25, 26, 28, 52, 67, 595, 599
— бинарной смеси, 630
— ориентационная, 142
— смешения, 137, 620
— трансляционная, 590
Эпитаксия, 329
Эриксена-Лесли модель, 227,233,237,
238, 243, 457
Эриксена тензор напряжений схг^, 237,
239
Эриксена число Ег, 243, 245, 458, 461,
465
Этиловый спирт, 516
Юнга закон, 524, 525, 557
Юнга модули В, Е, 145, 172, 209, 296,
584
Научное издание
КЛЕМАН Морис
ЛАВРЕНТОВИЧ Олег Дмитриевич
ОСНОВЫ ФИЗИКИ ЧАСТИЧНО УПОРЯДОЧЕННЫХ СРЕД:
ЖИДКИЕ КРИСТАЛЛЫ, КОЛЛОИДЫ, ФРАКТАЛЬНЫЕ СТРУКТУРЫ, ПОЛИМЕРЫ
И БИОЛОГИЧЕСКИЕ ОБЪЕКТЫ
Редактор Н.Б. Бартошевич-Жагель
Оригинал-макет: В.И. Шутов
Оформление переплета: А.Ю. Алехина
Подписано в печать 28.12.06. Формат 60x90/16. Бумага офсетная.
Печать офсетная. Уел. печ. л. 42,5. Уч.-изд. л. 46,8. Тираж 300 экз
Заказ №. 2688.
Издательская фирма «Физико-математическая литература»
МАИК «Наука/Интерпериодика»
117997, Москва, ул. Профсоюзная, 90
E-mail: fizmat@maik.ru, fmlsale@maik.ru;
http://www.fml.ru
Отпечатано с готовых диапозитивов
в ОАО «Ивановская областная типография»
153008, г. Иваново, ул. Типографская, 6
E-mail: 091-0l8@adminet.ivanovo.ru