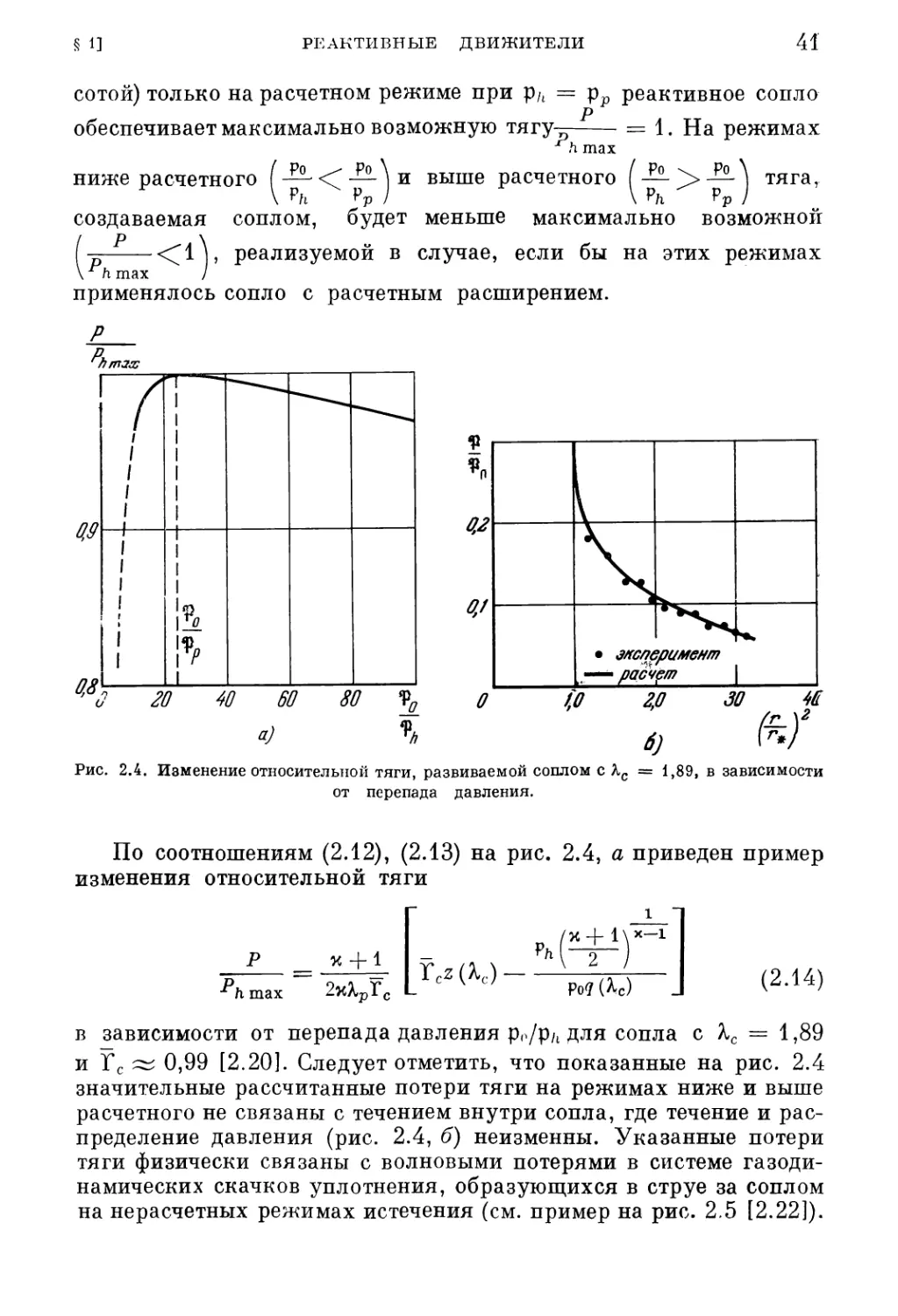
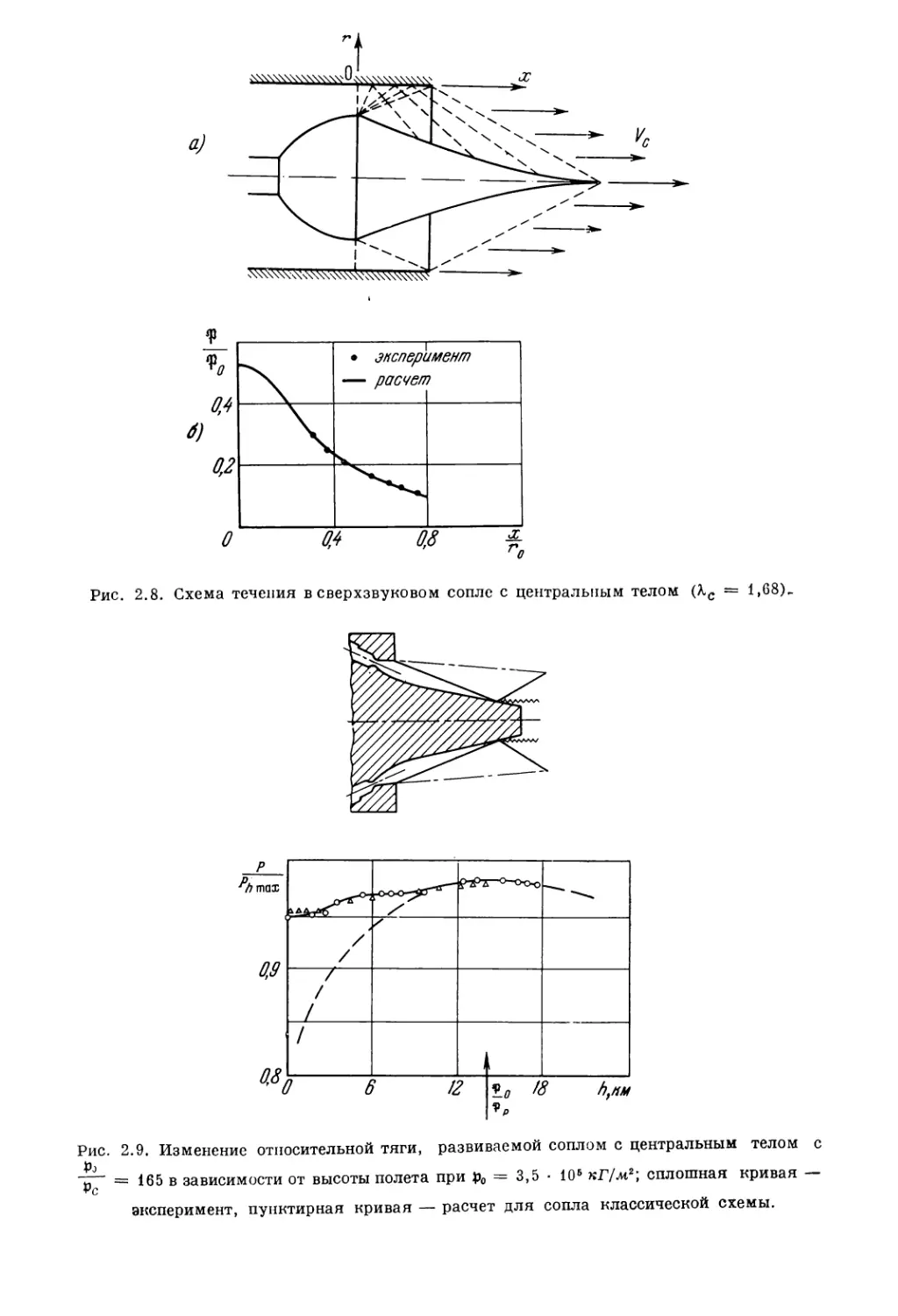
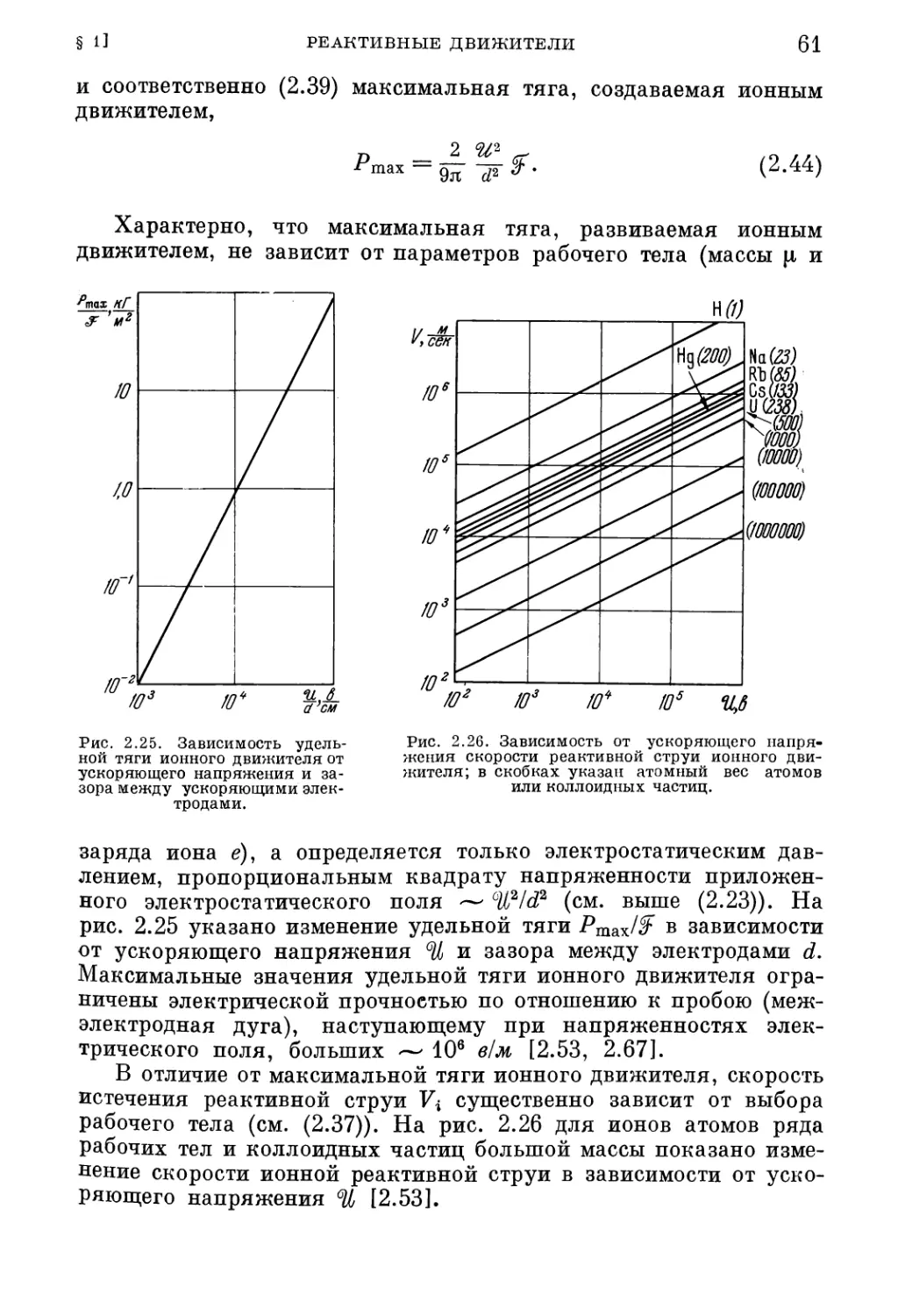
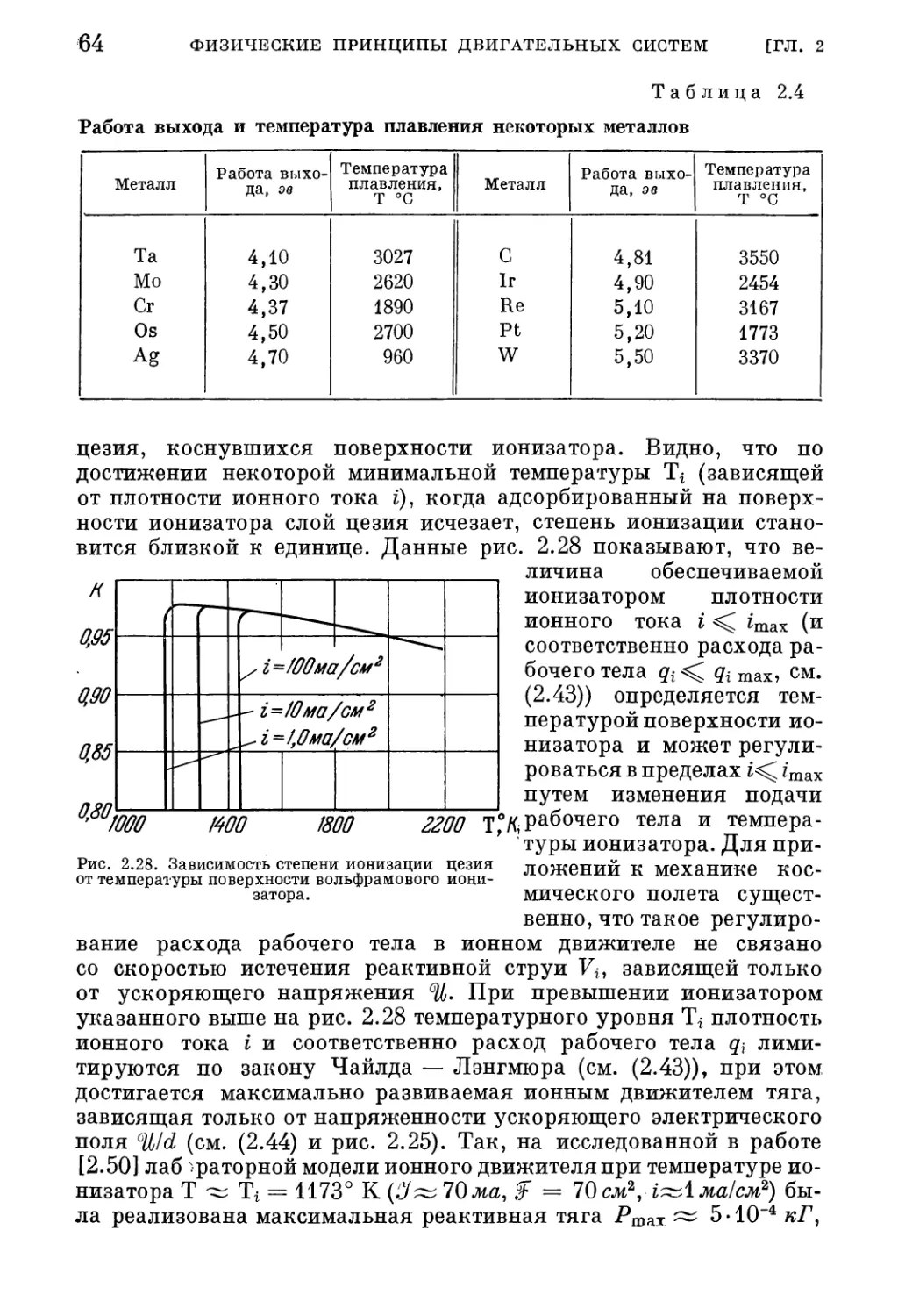
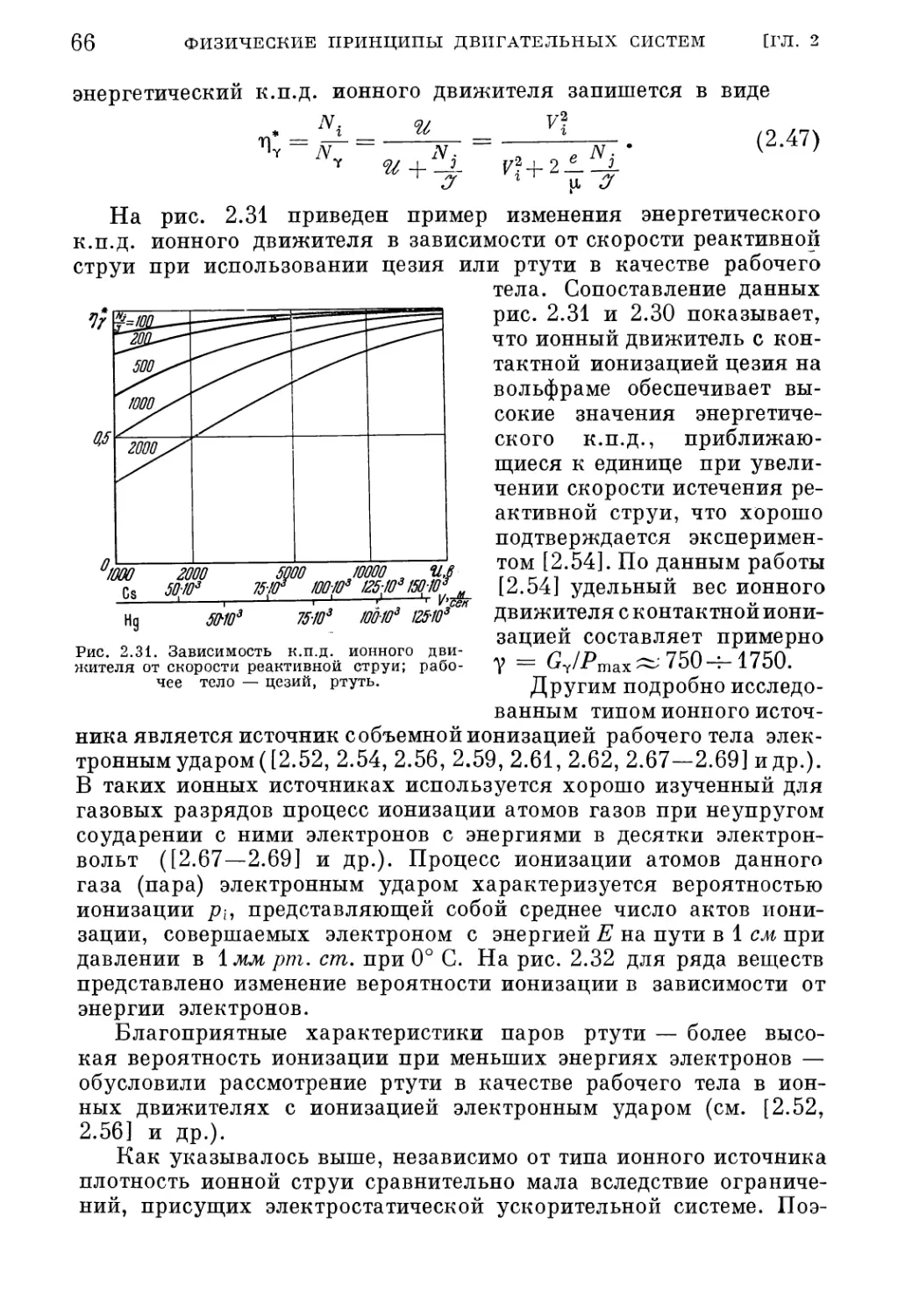
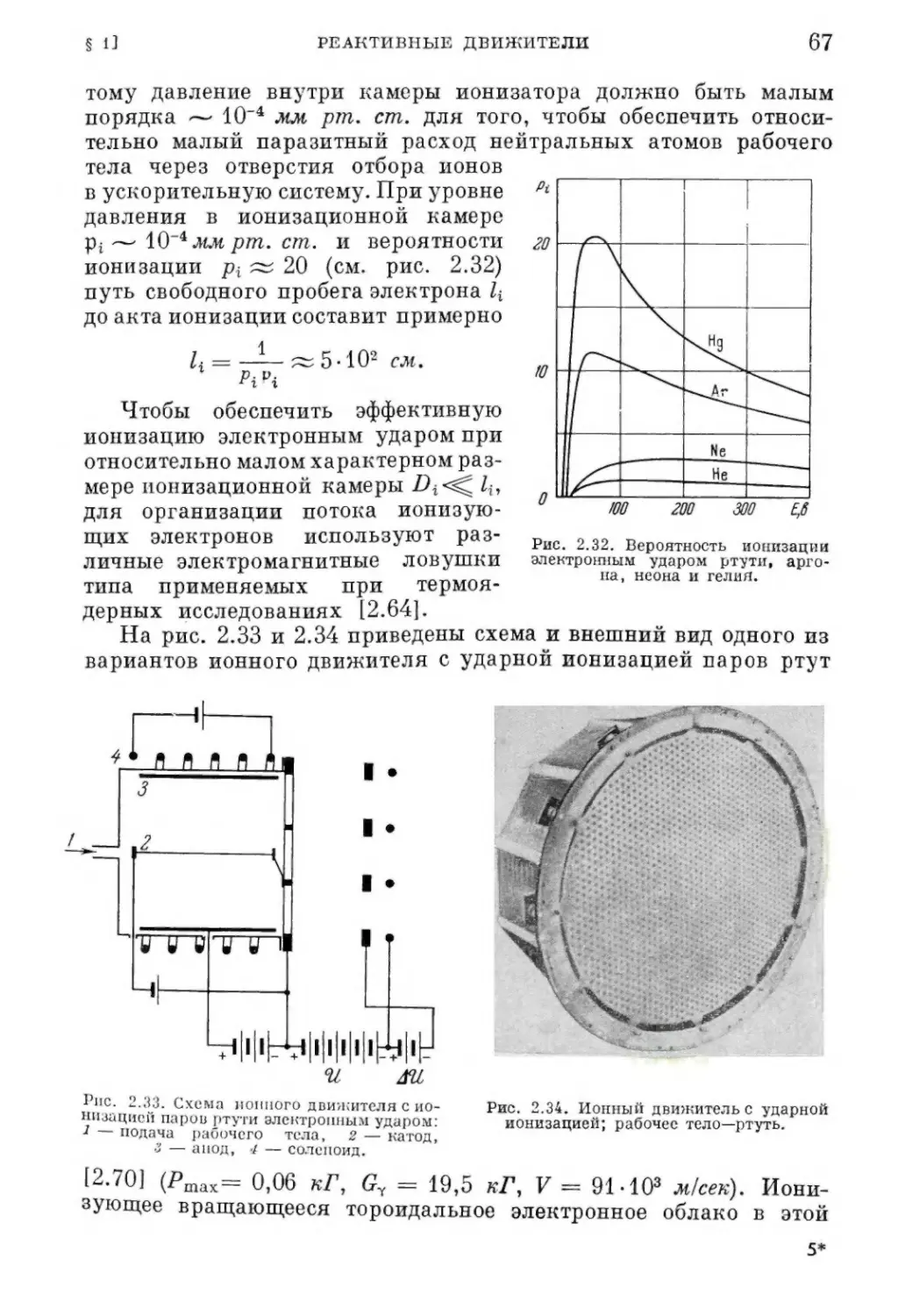
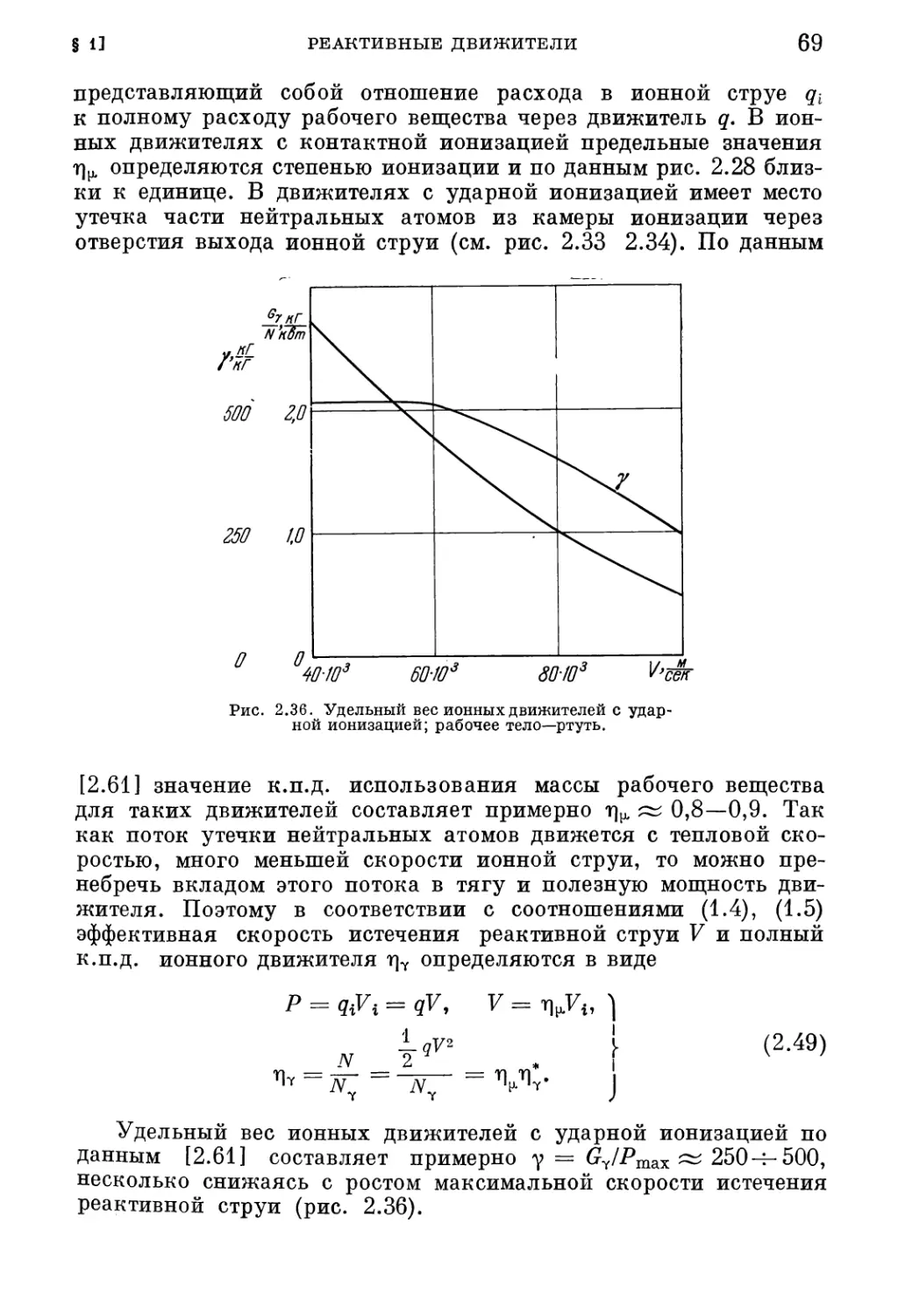
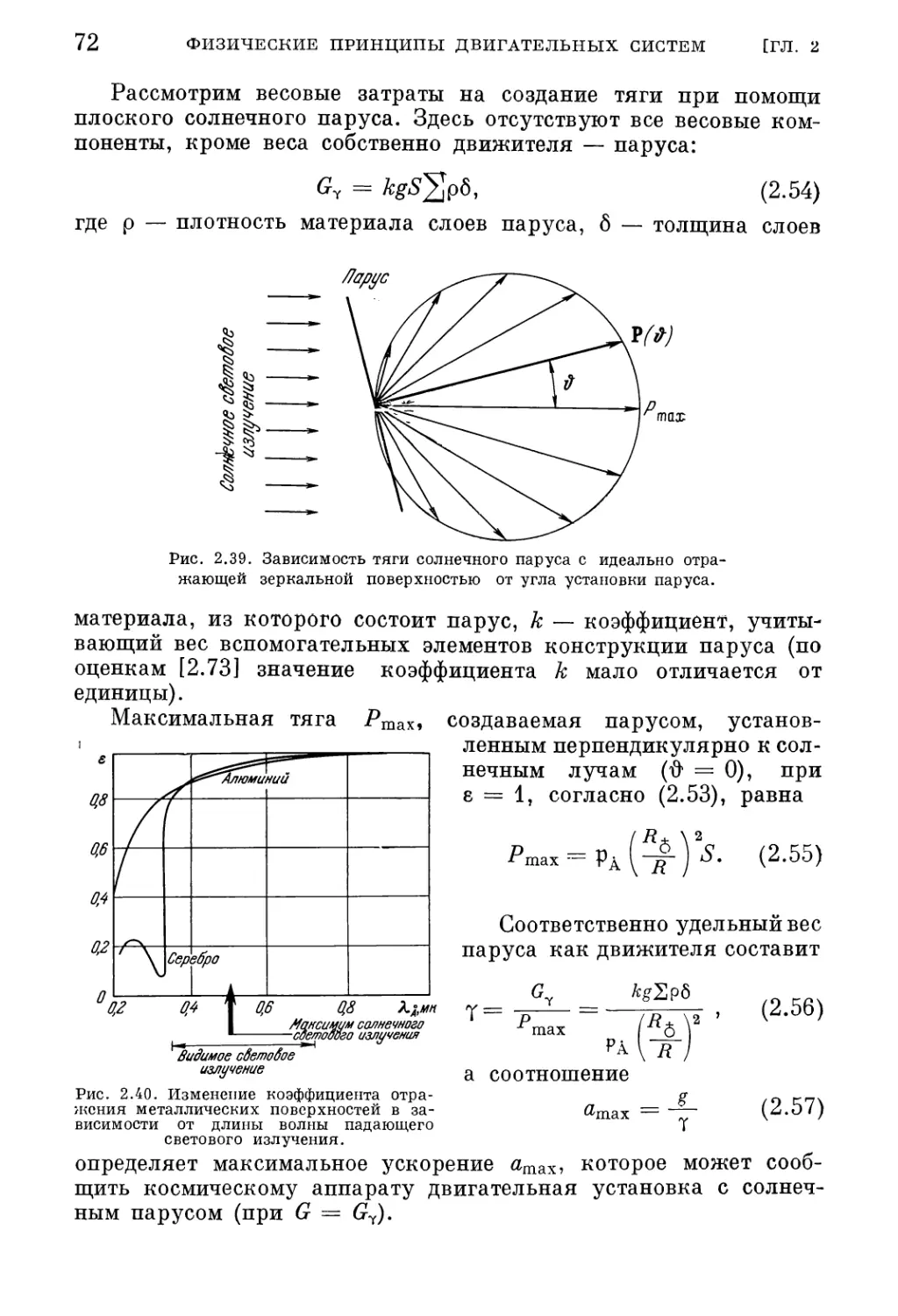
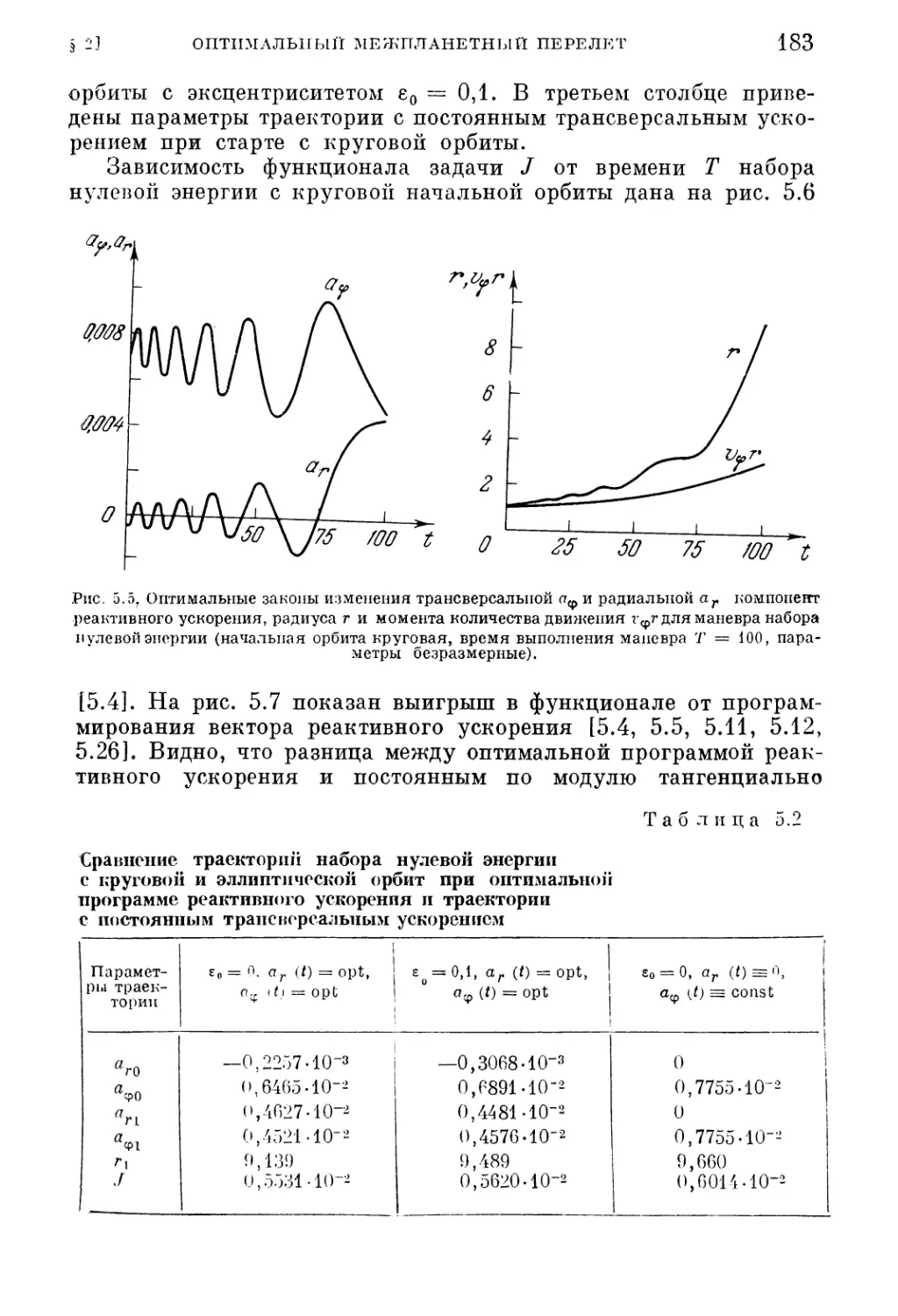
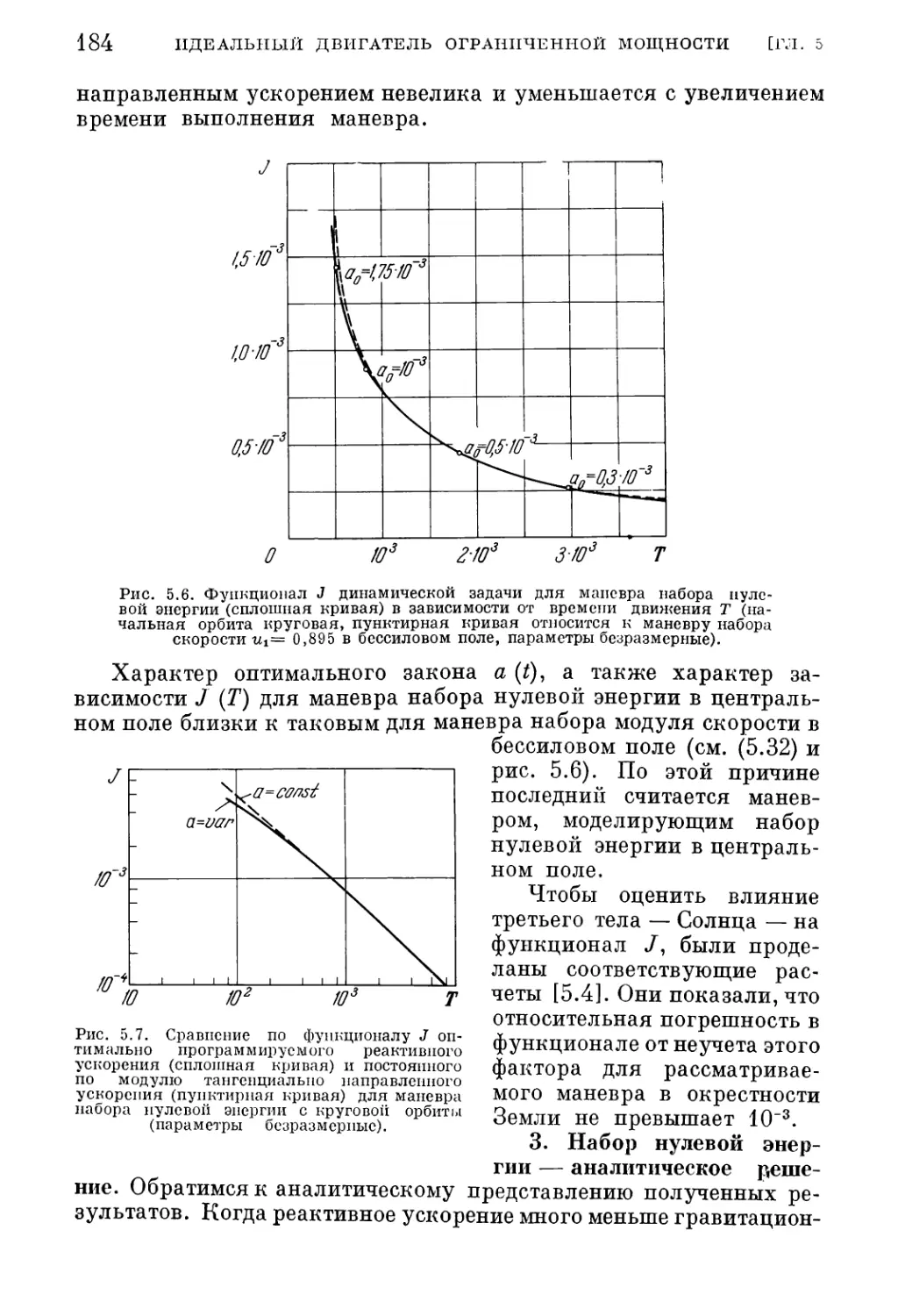
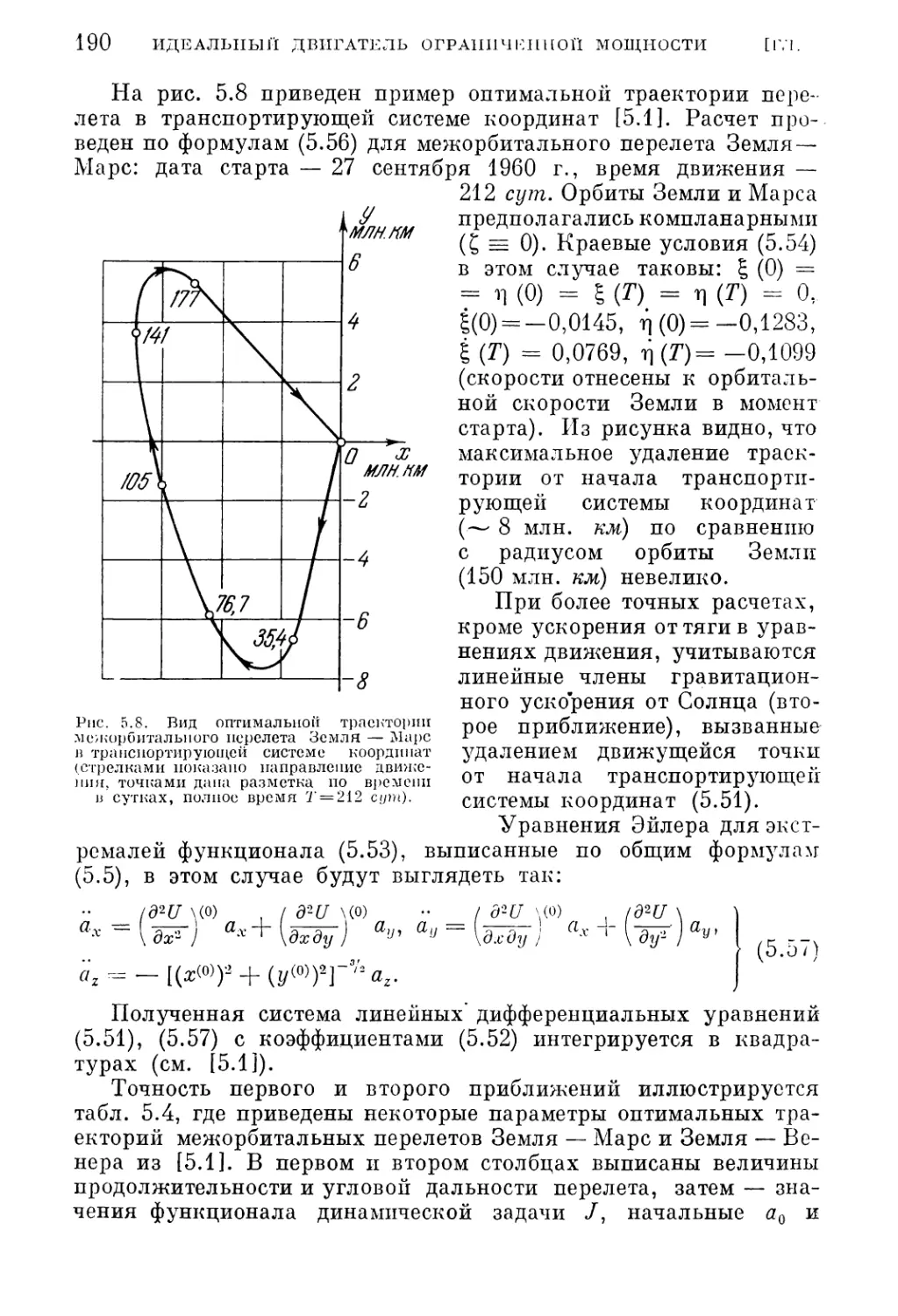
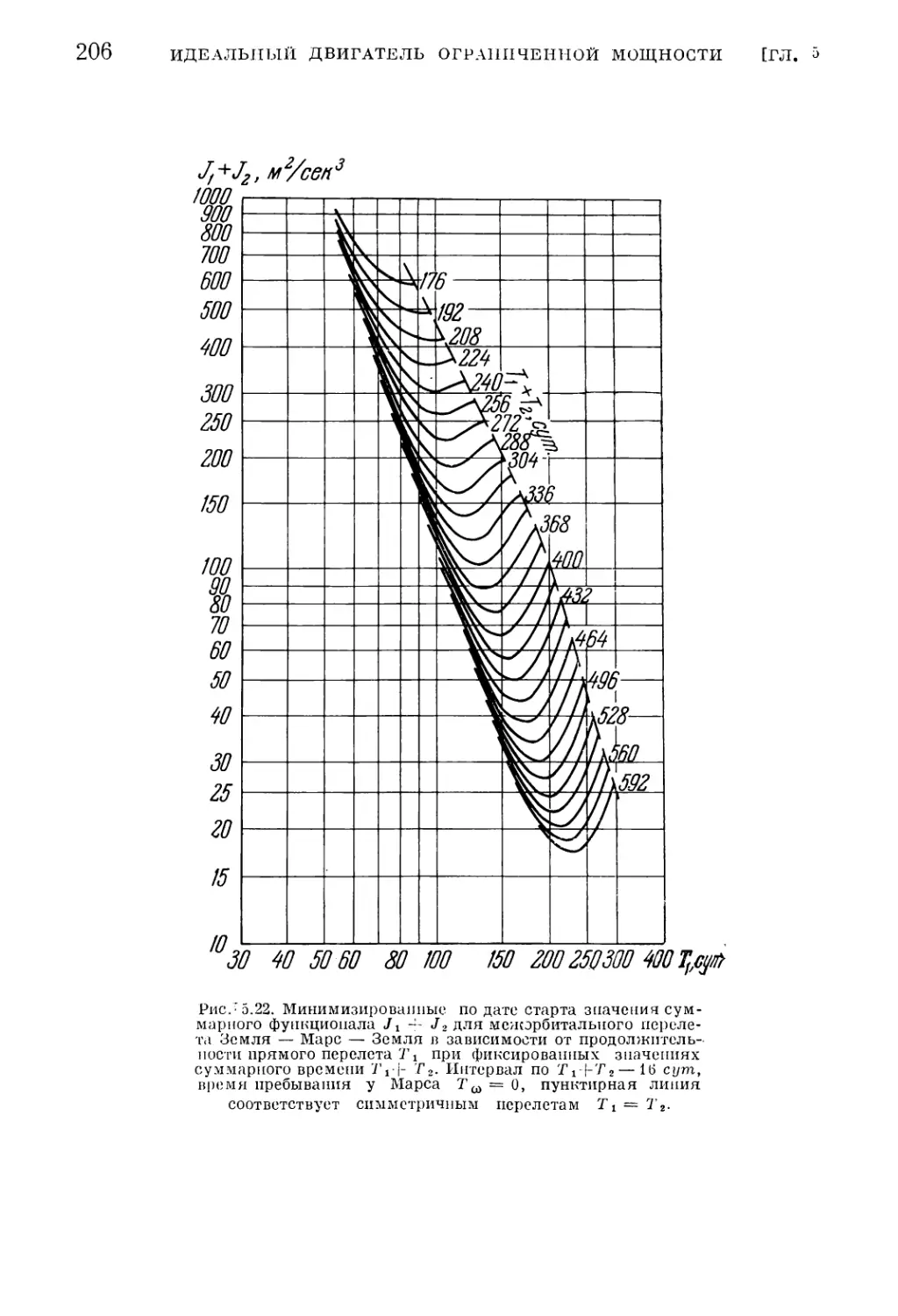
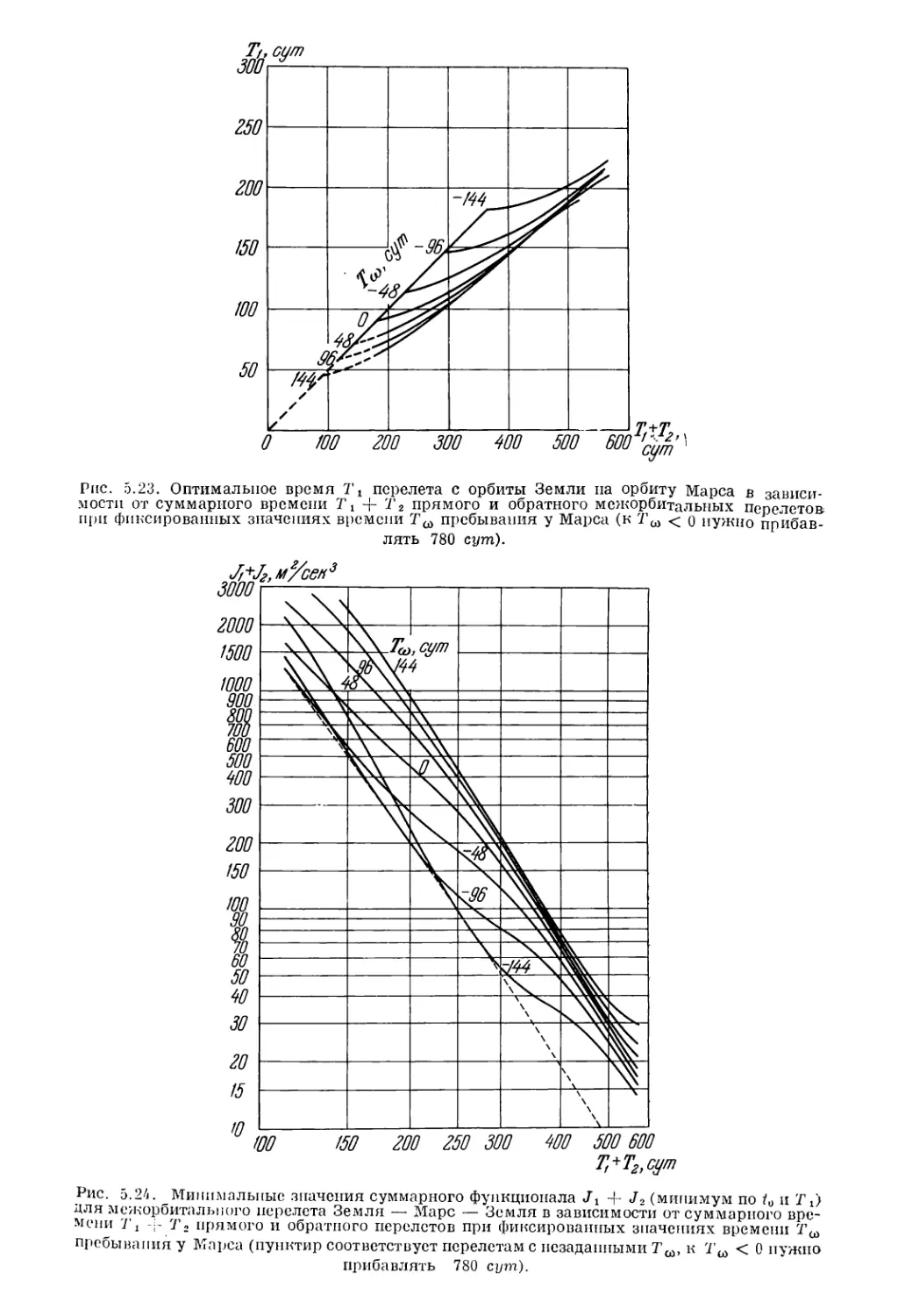
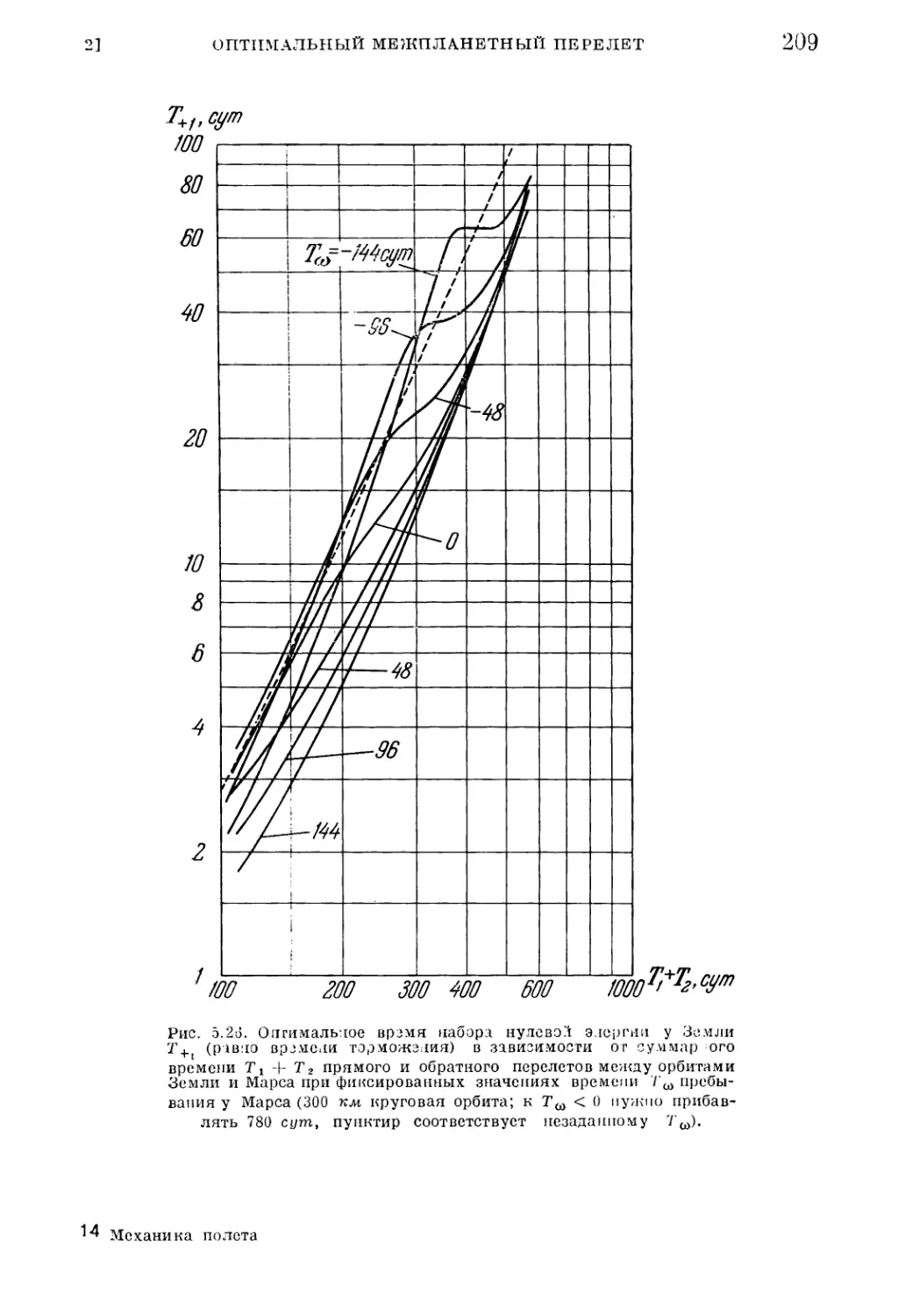
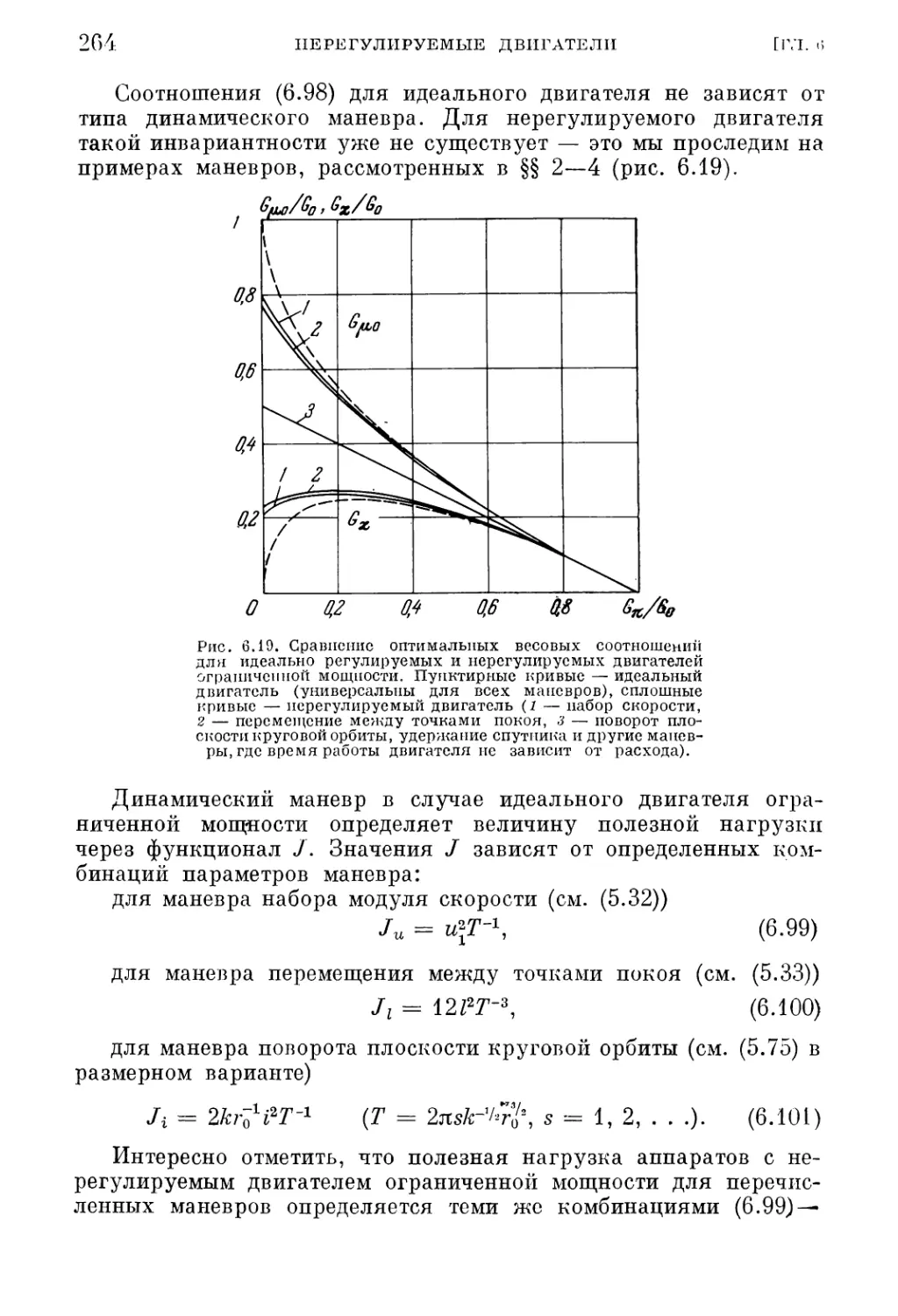
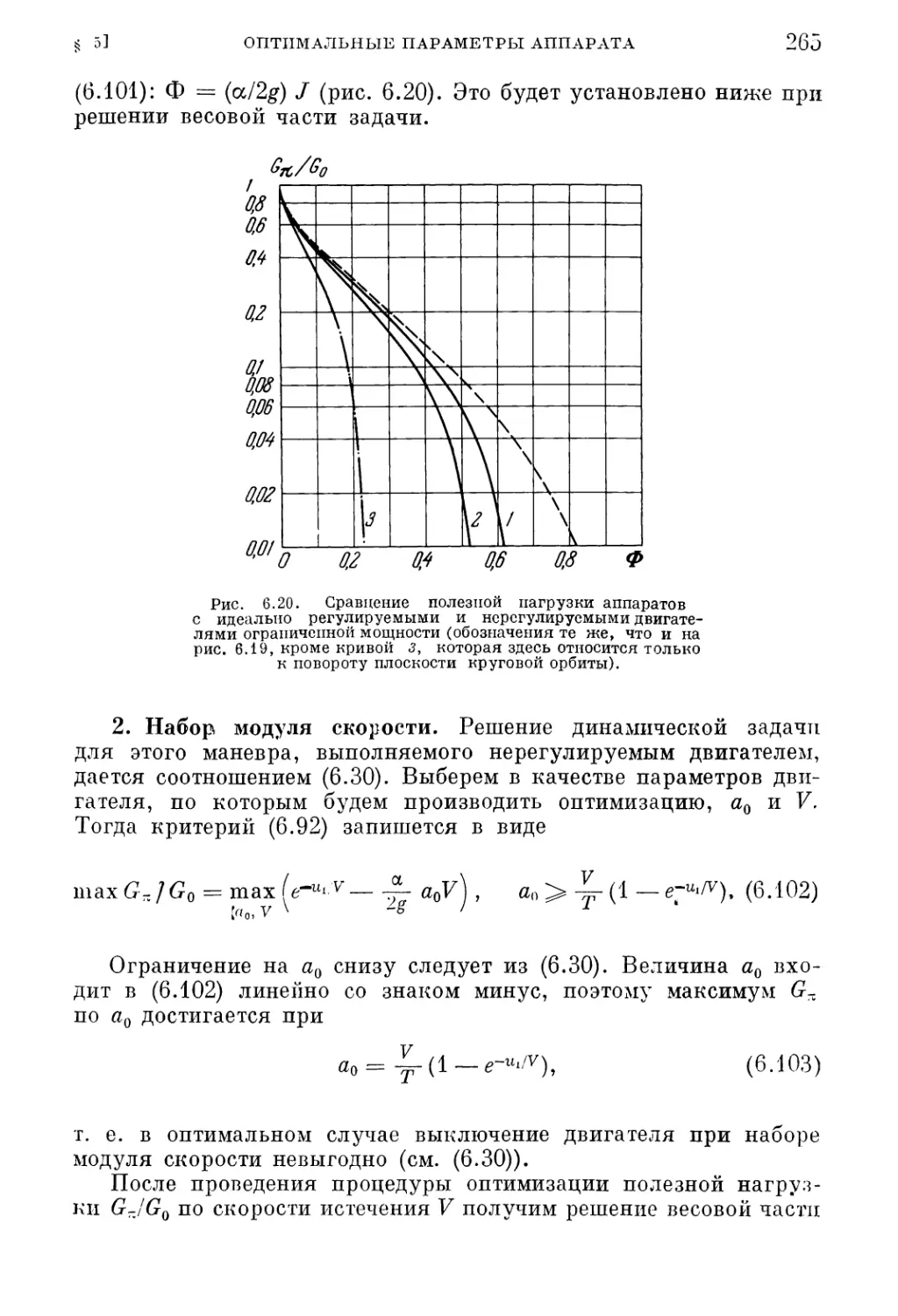
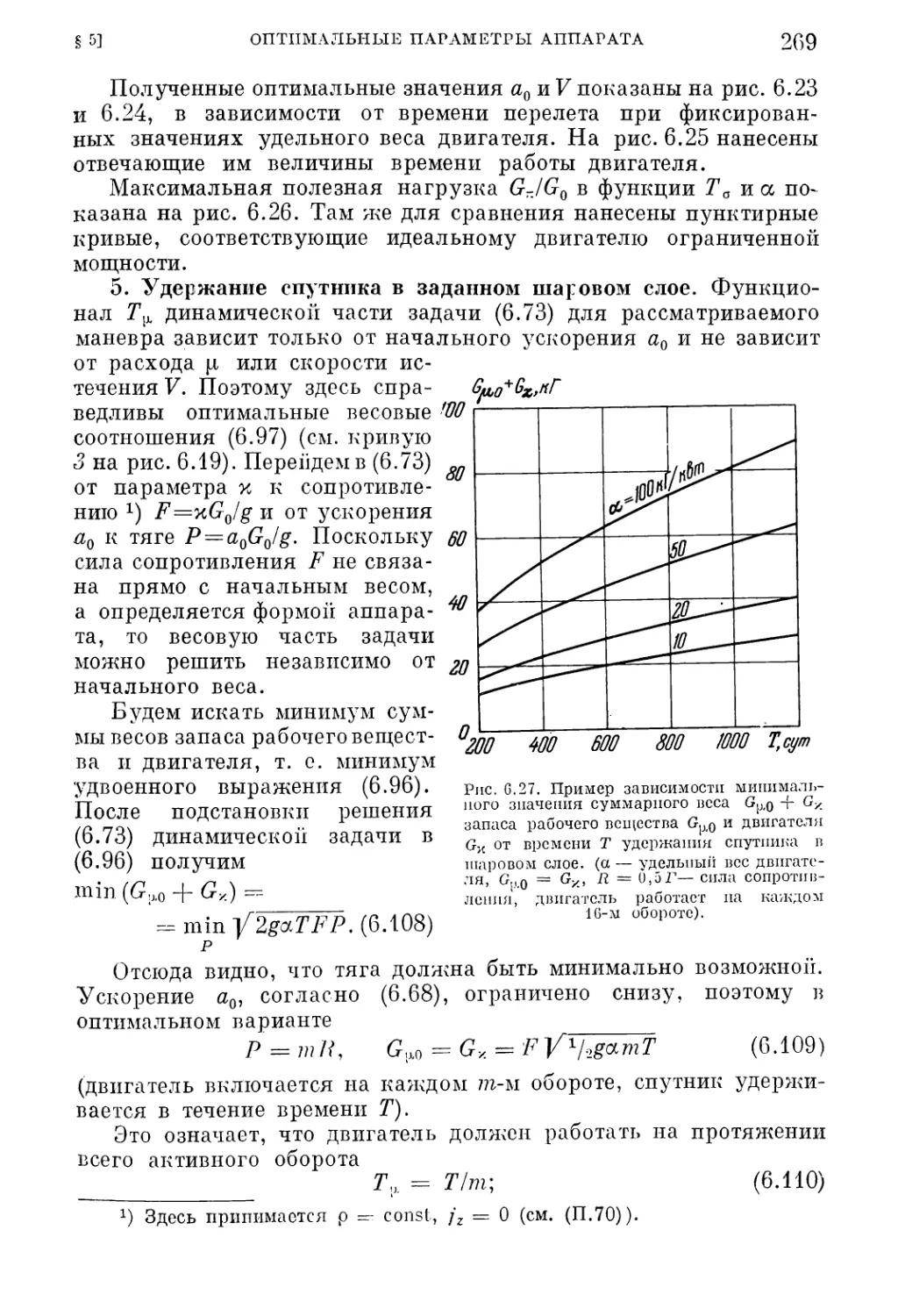
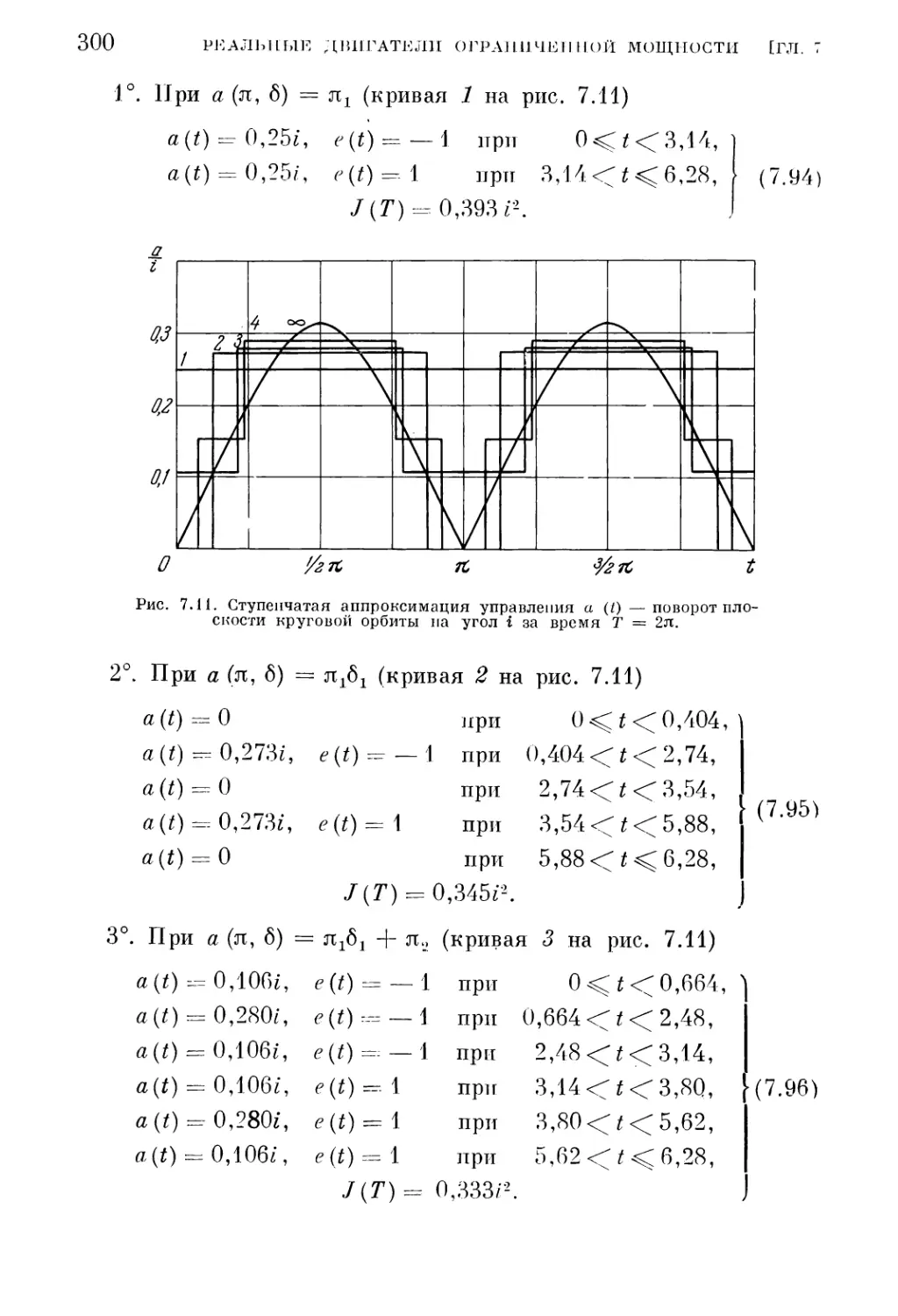
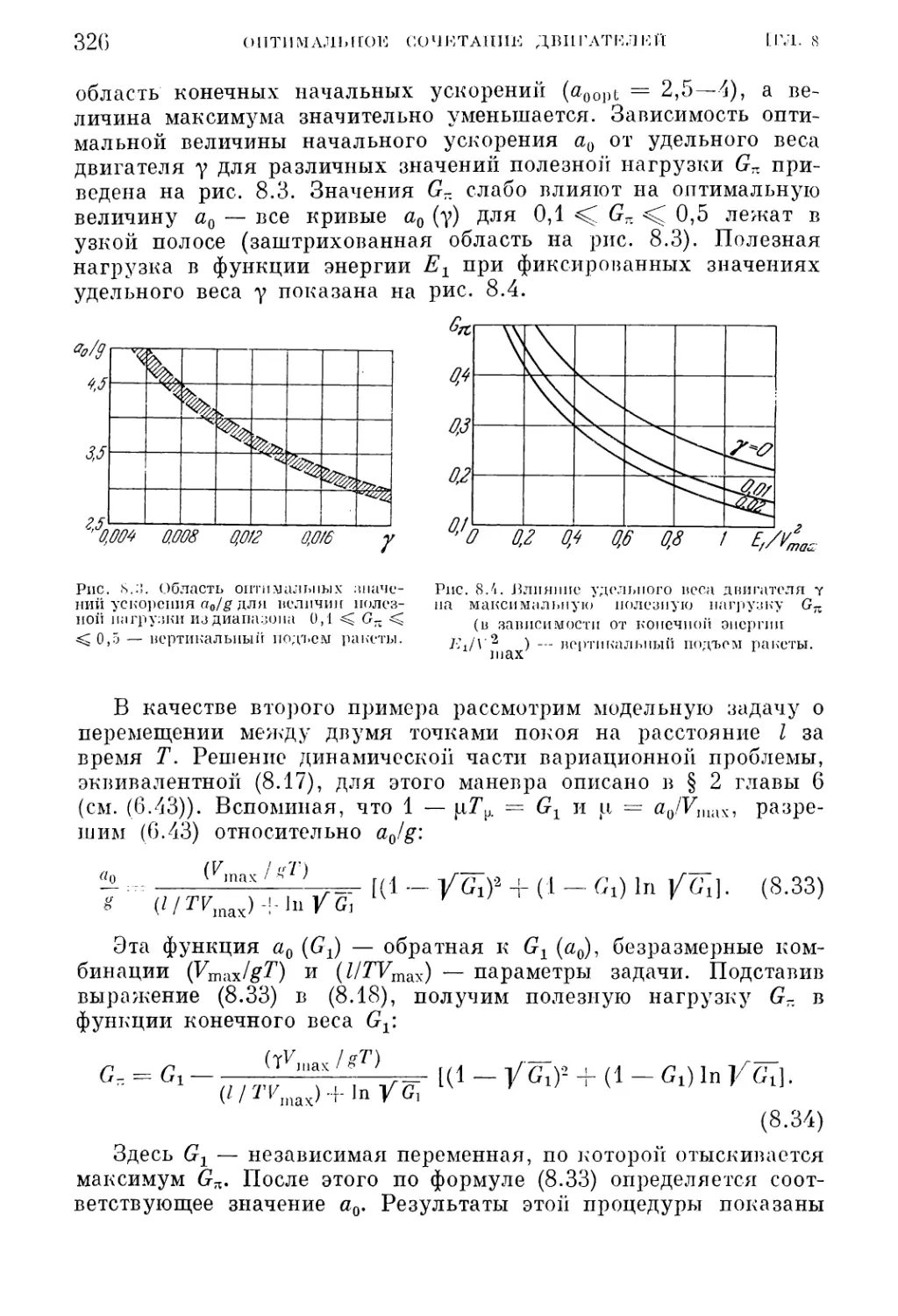
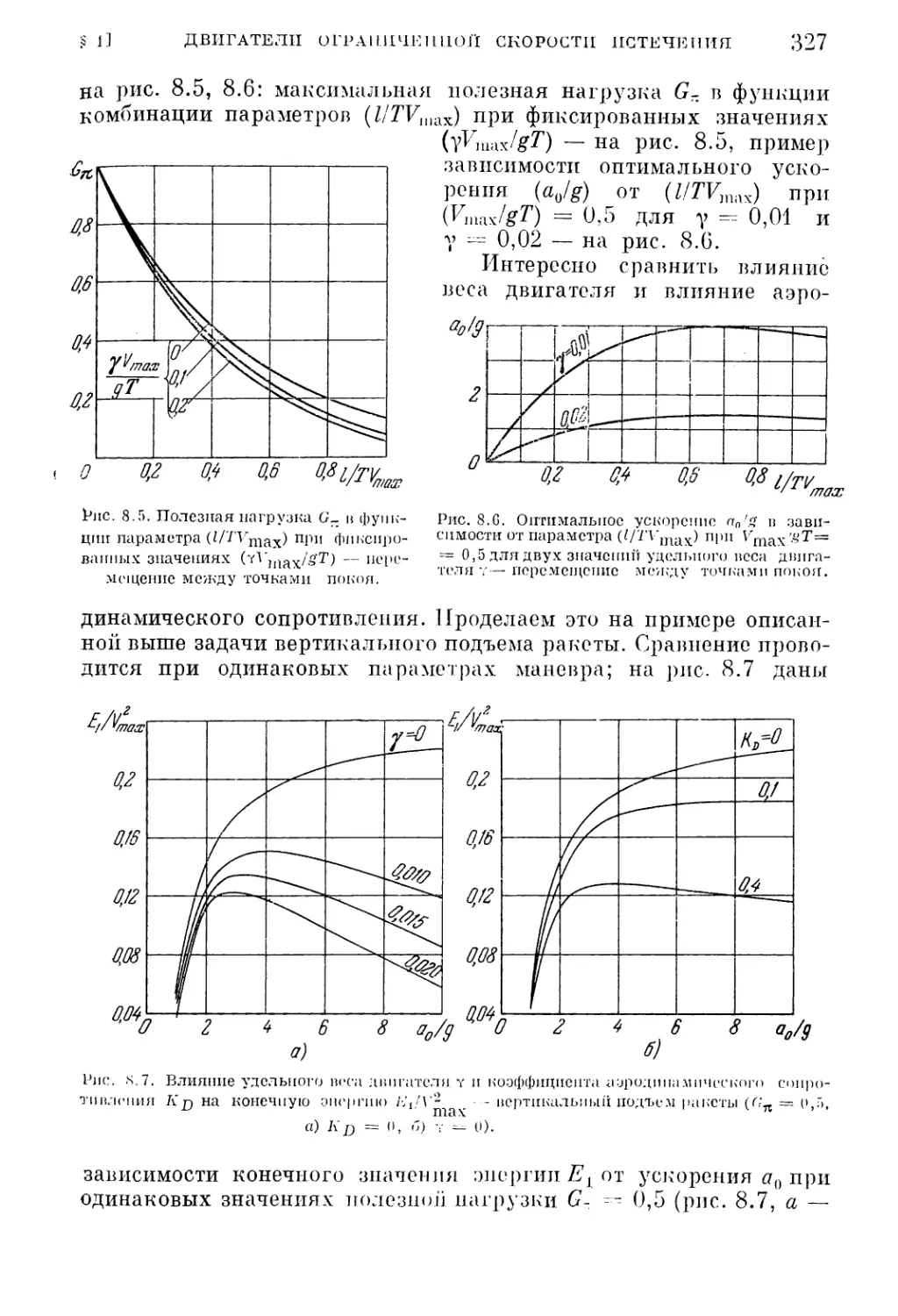
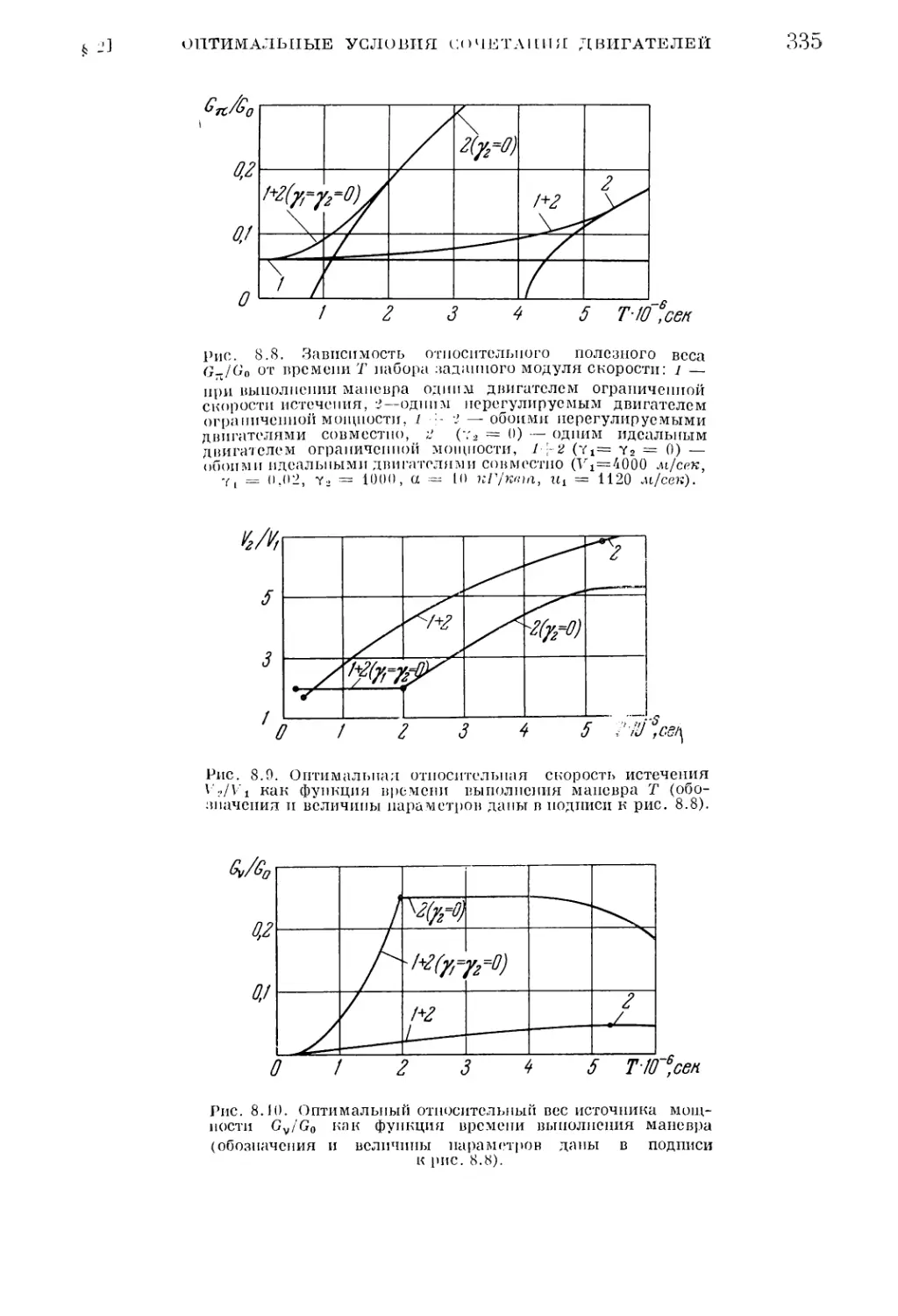
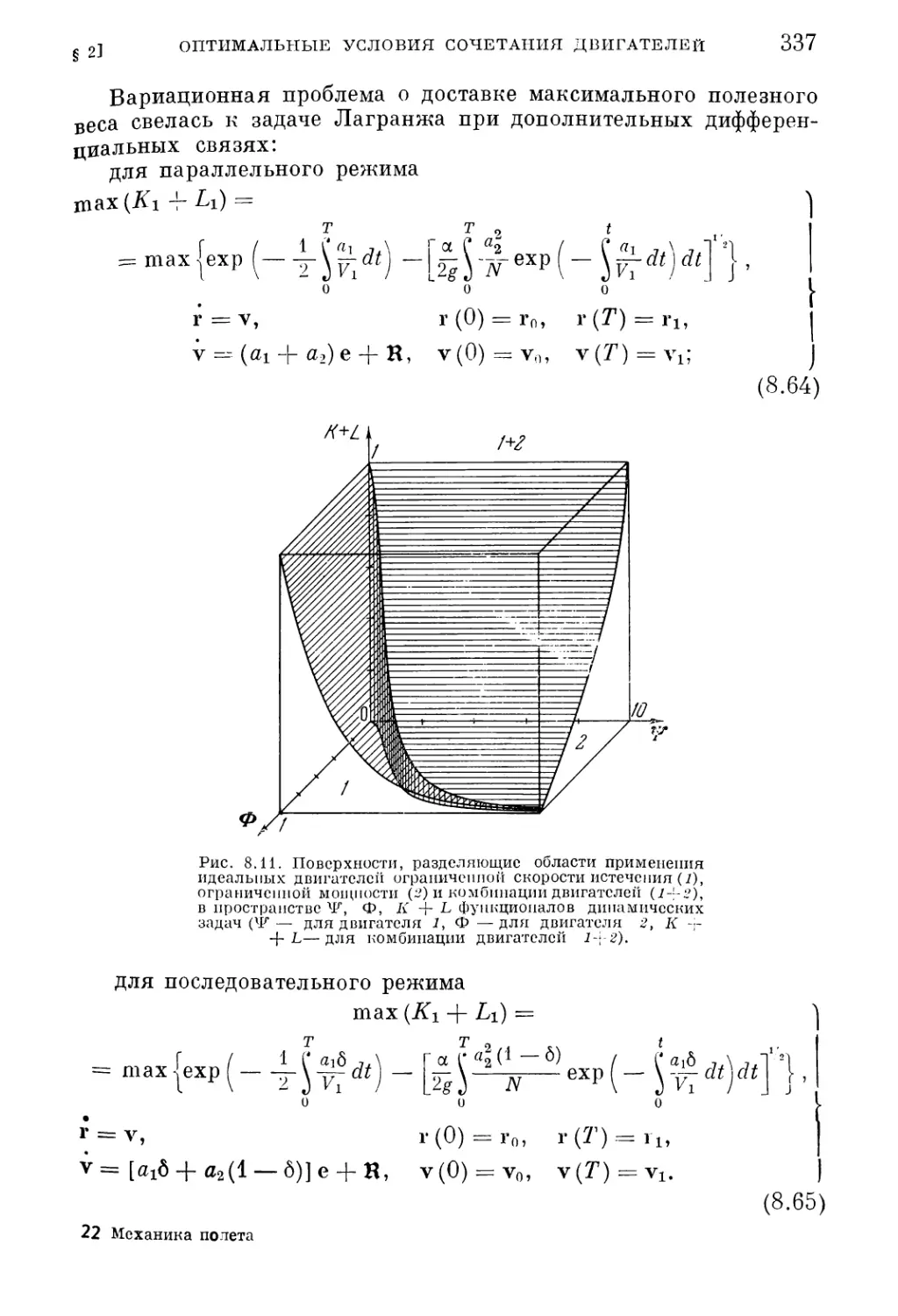
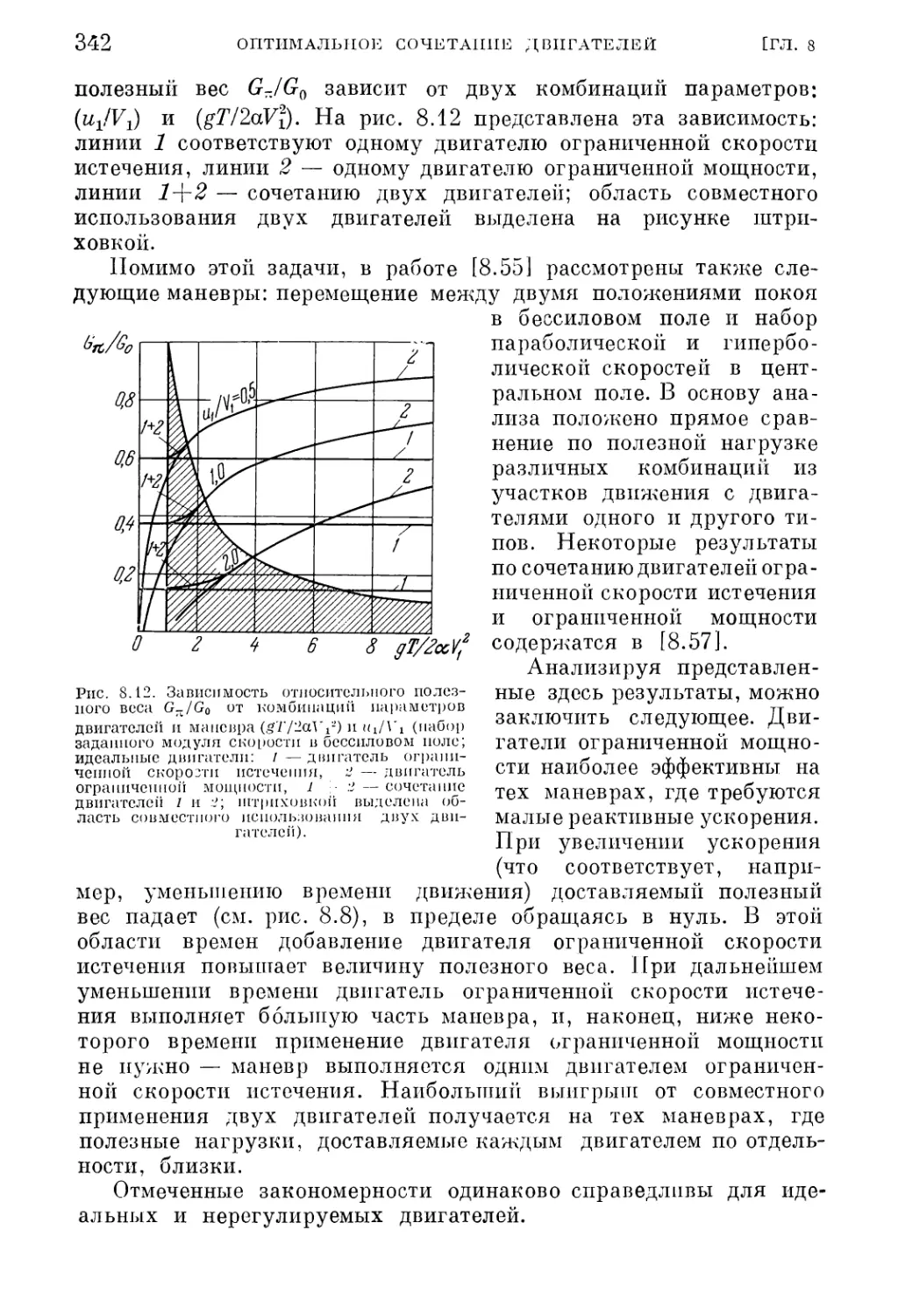
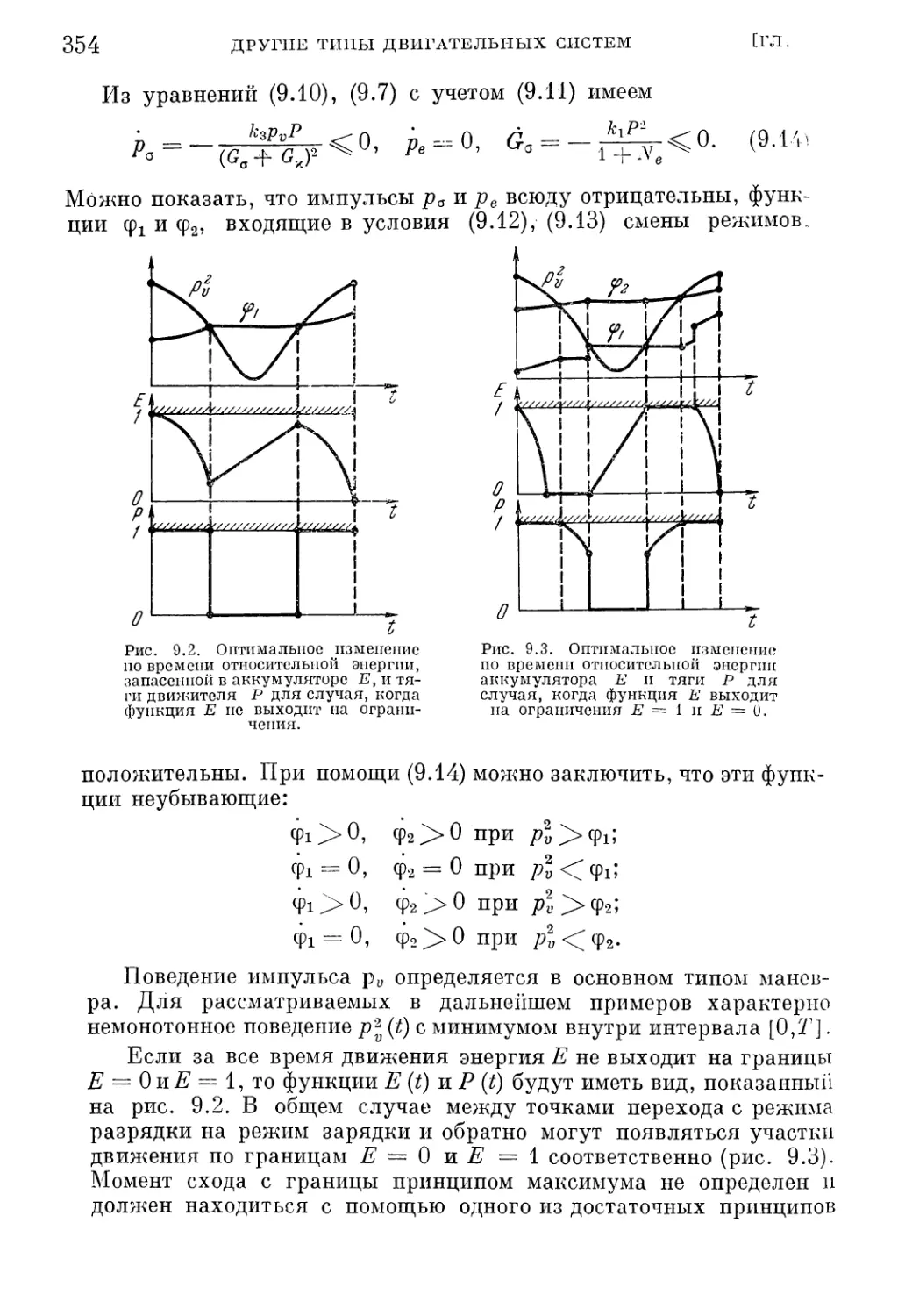
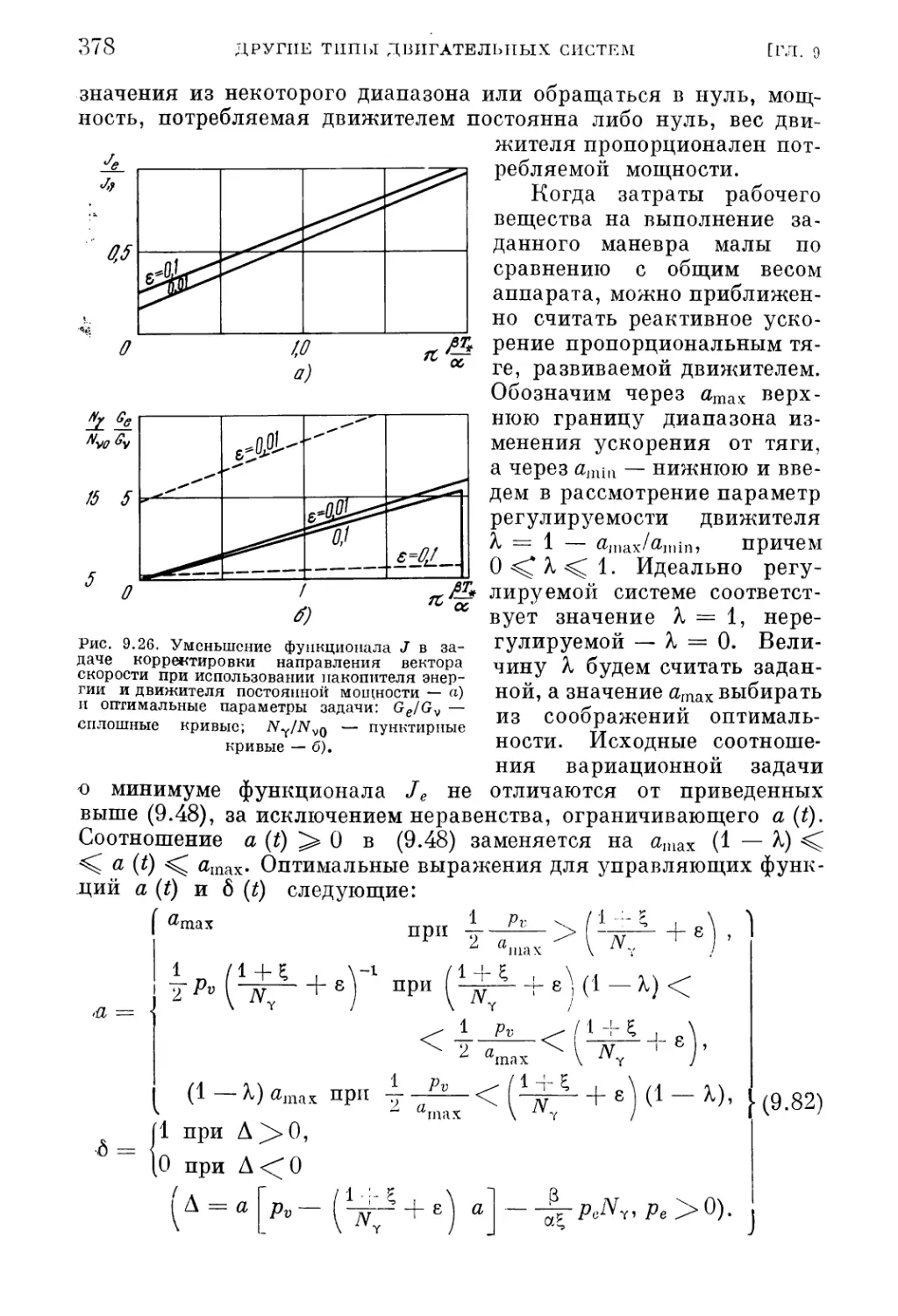
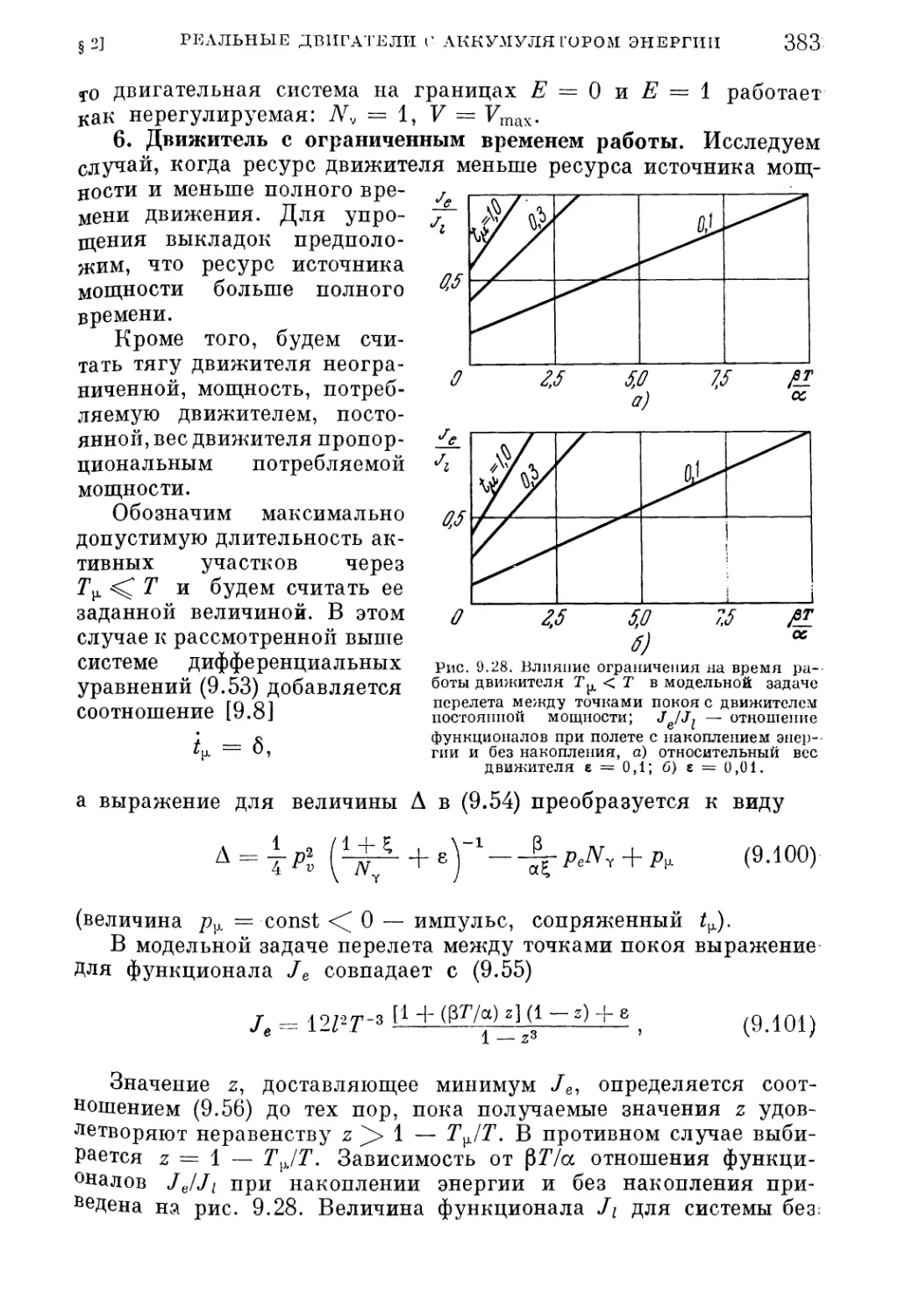
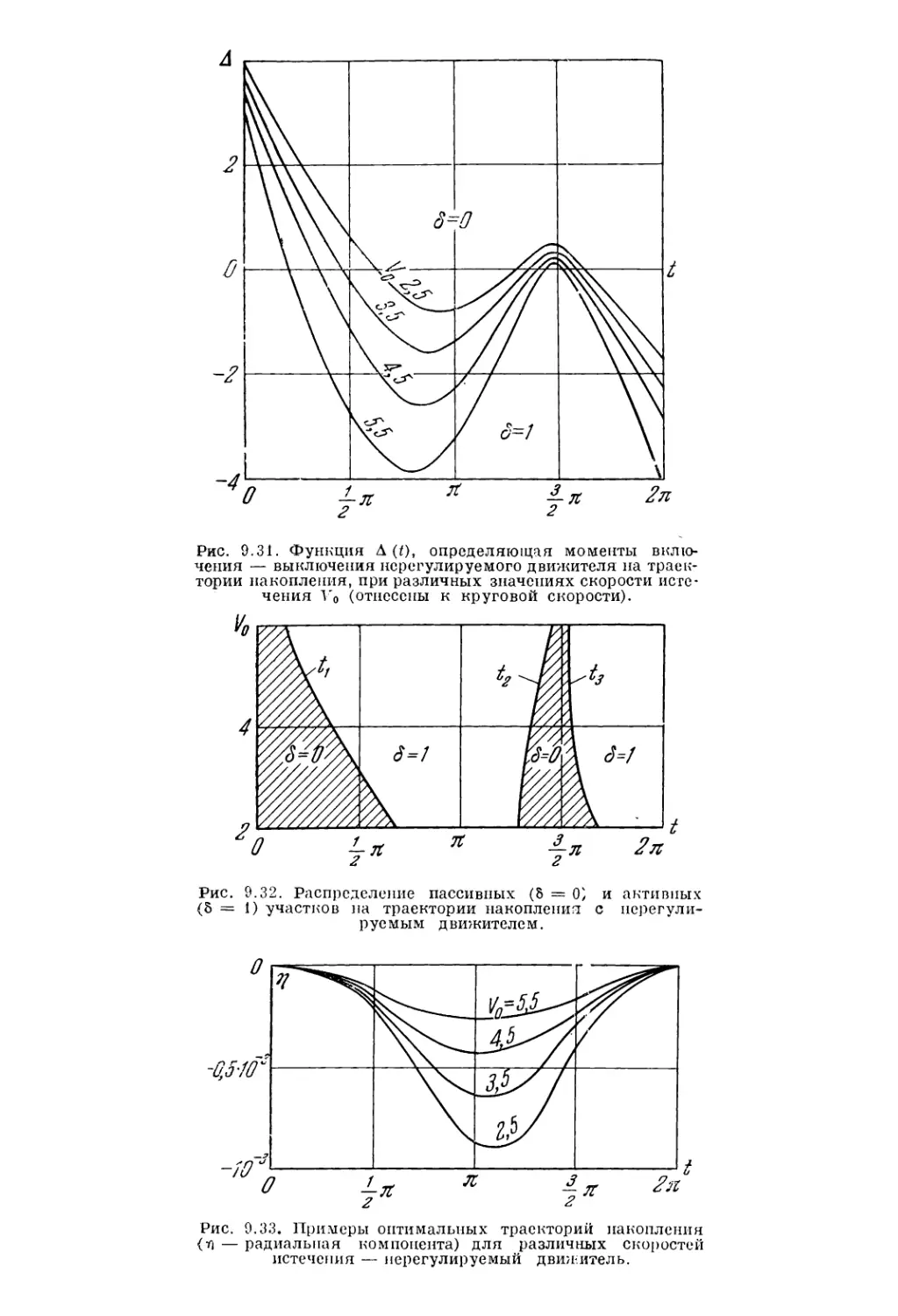
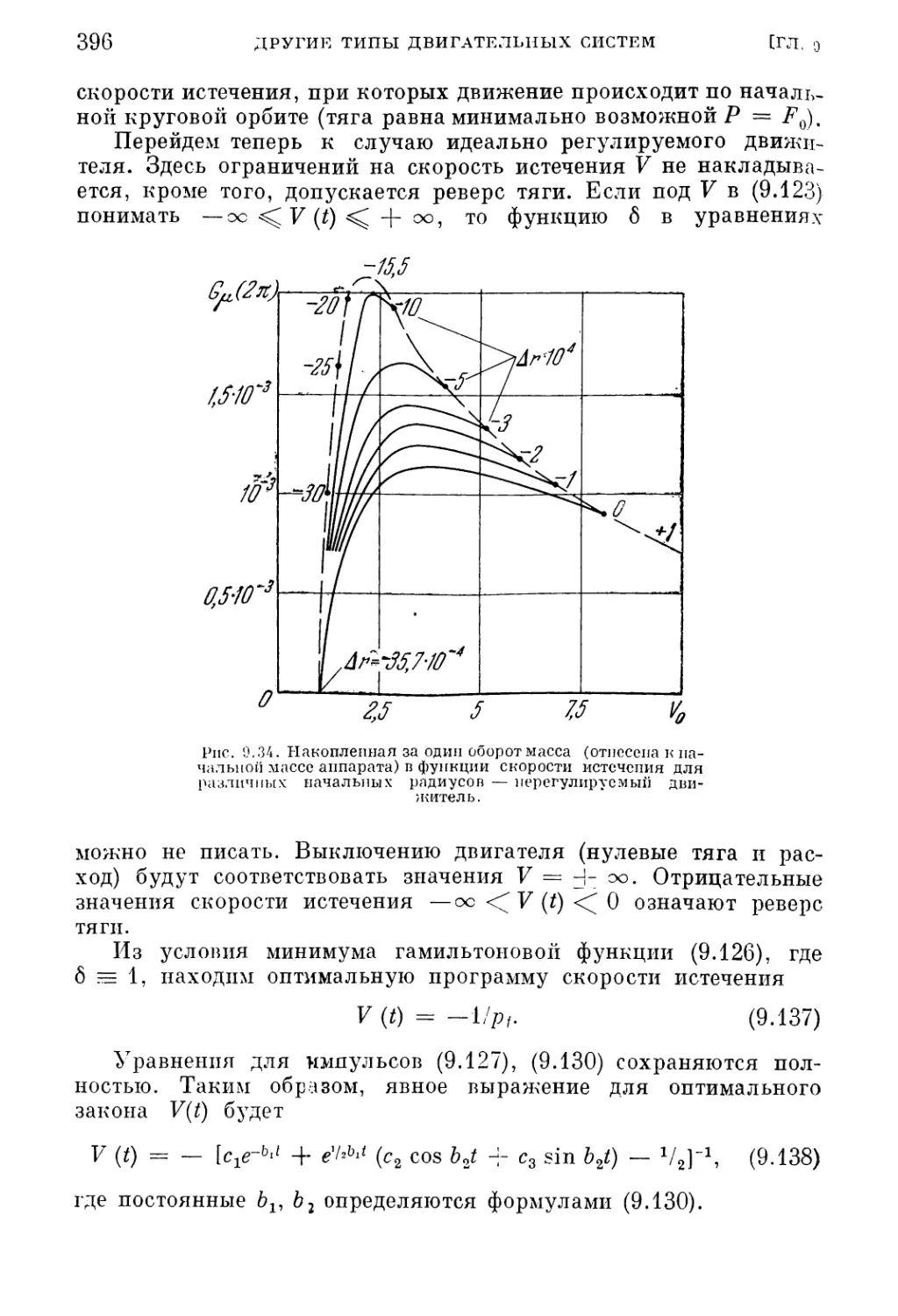
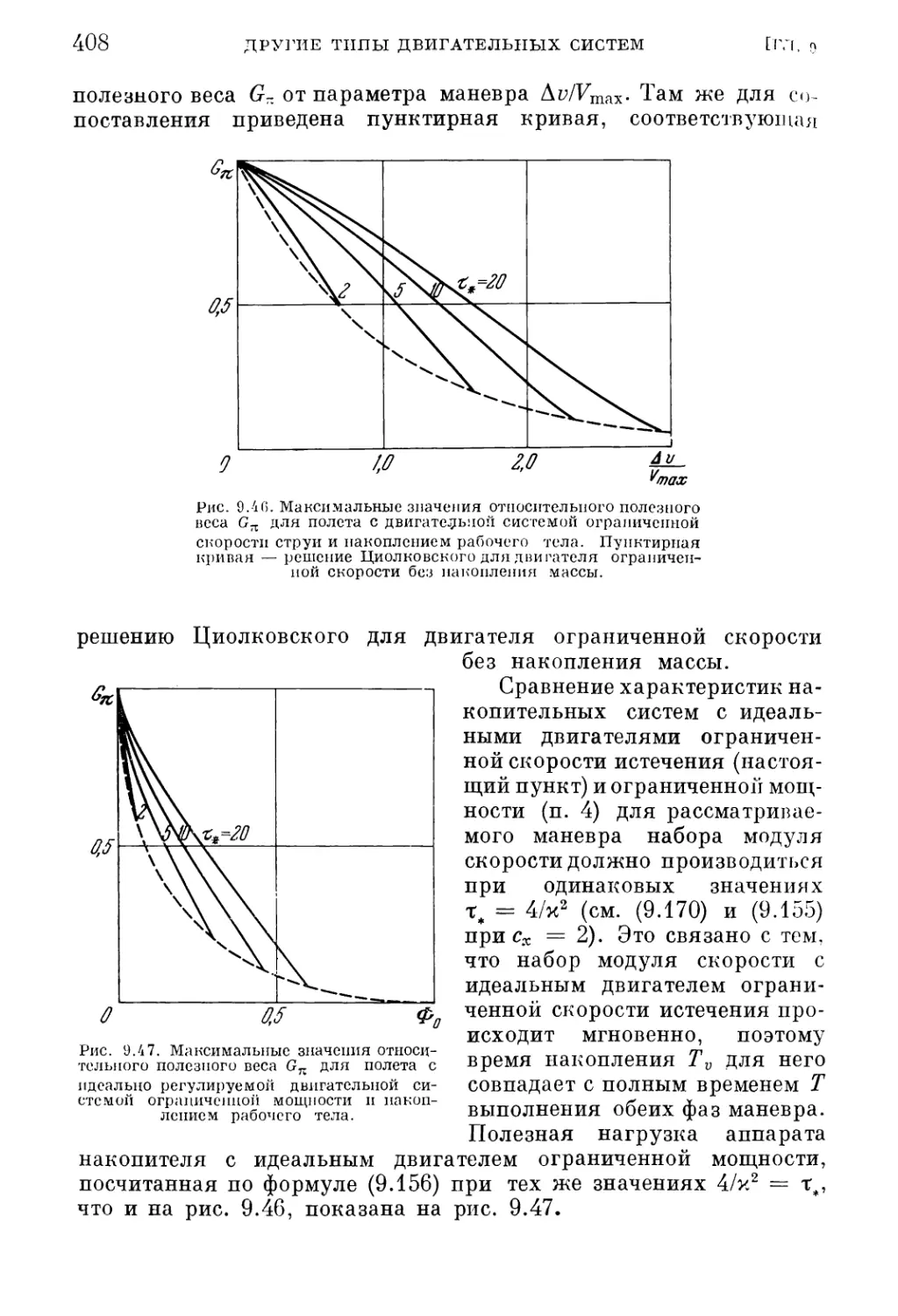
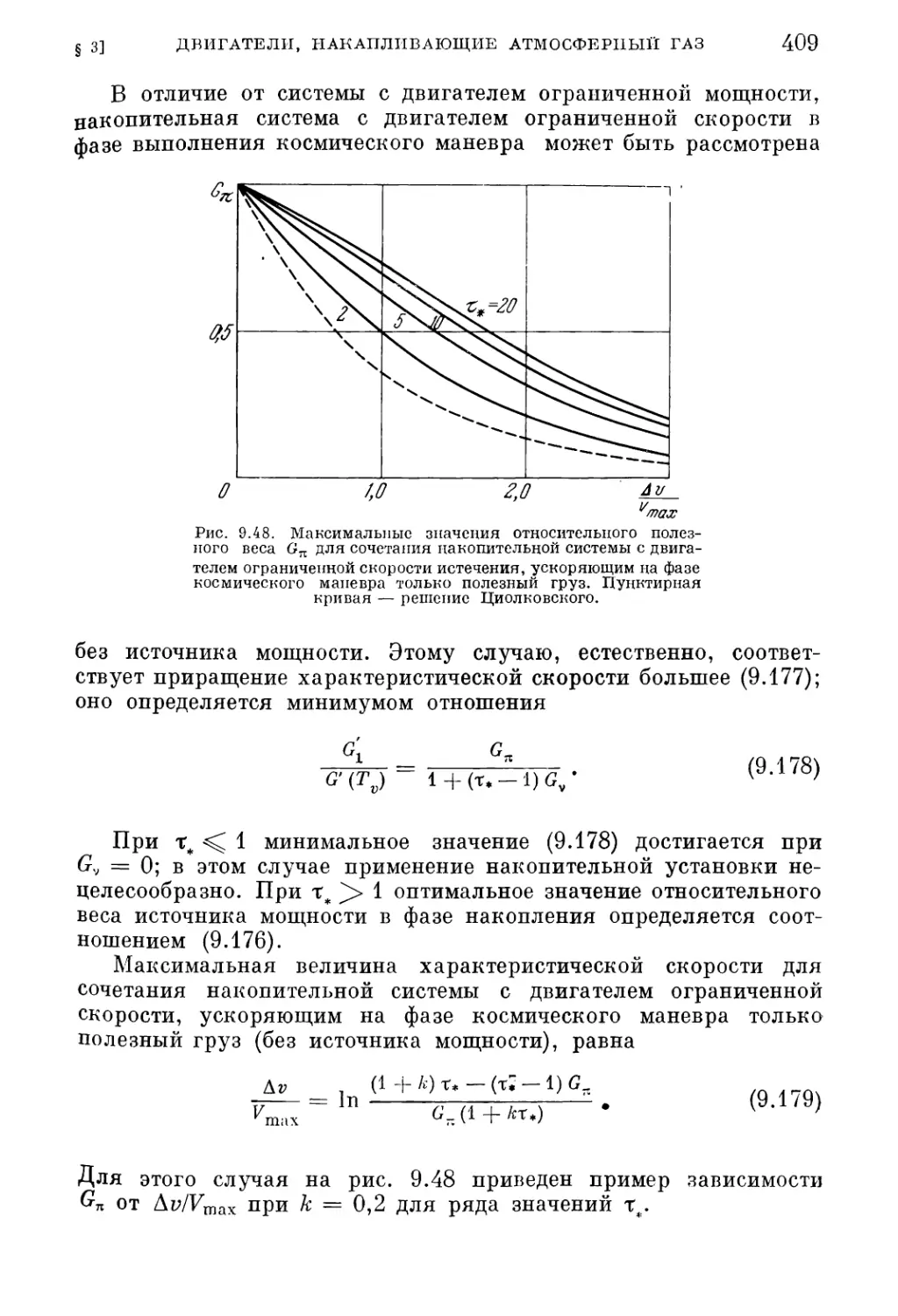
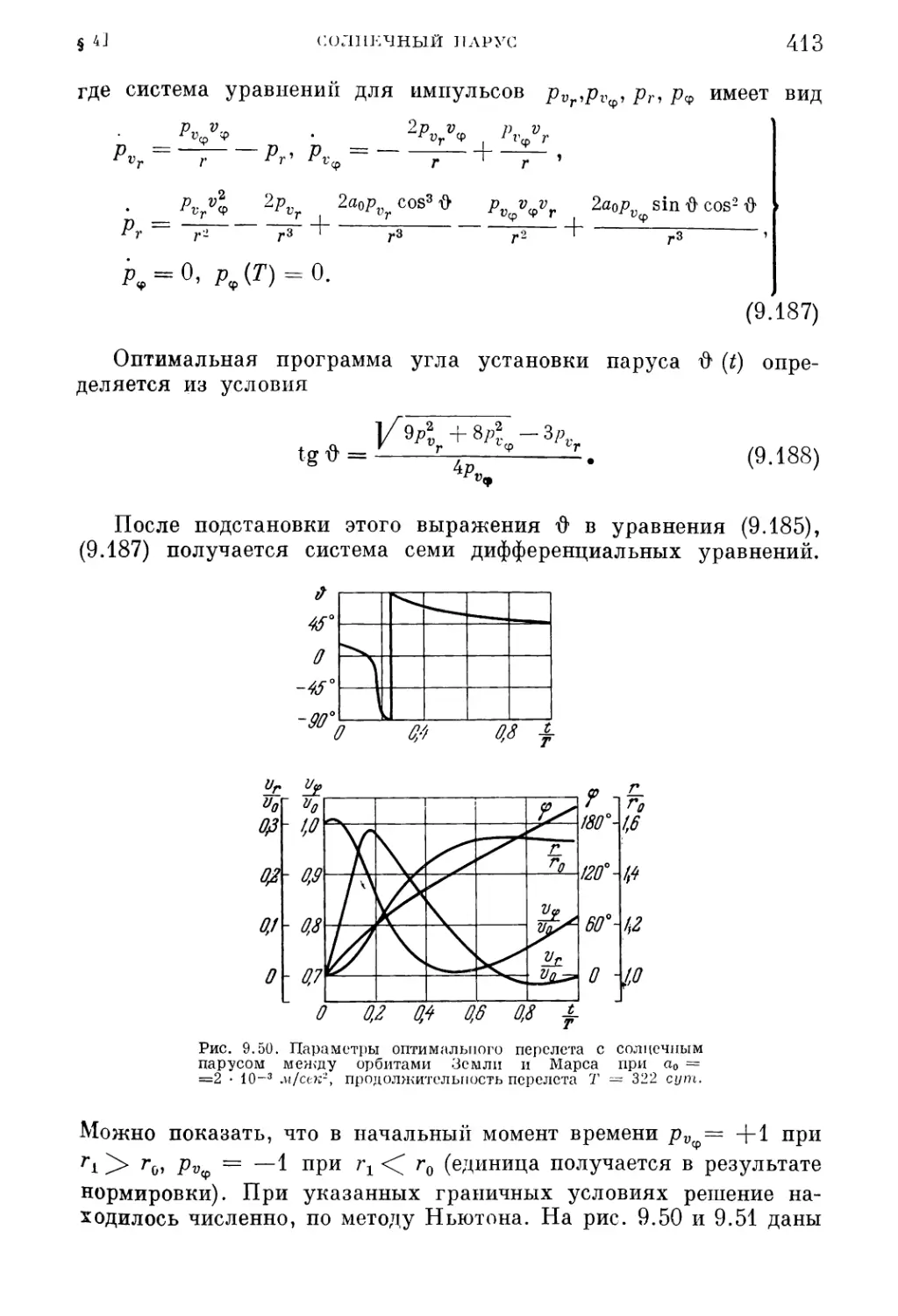
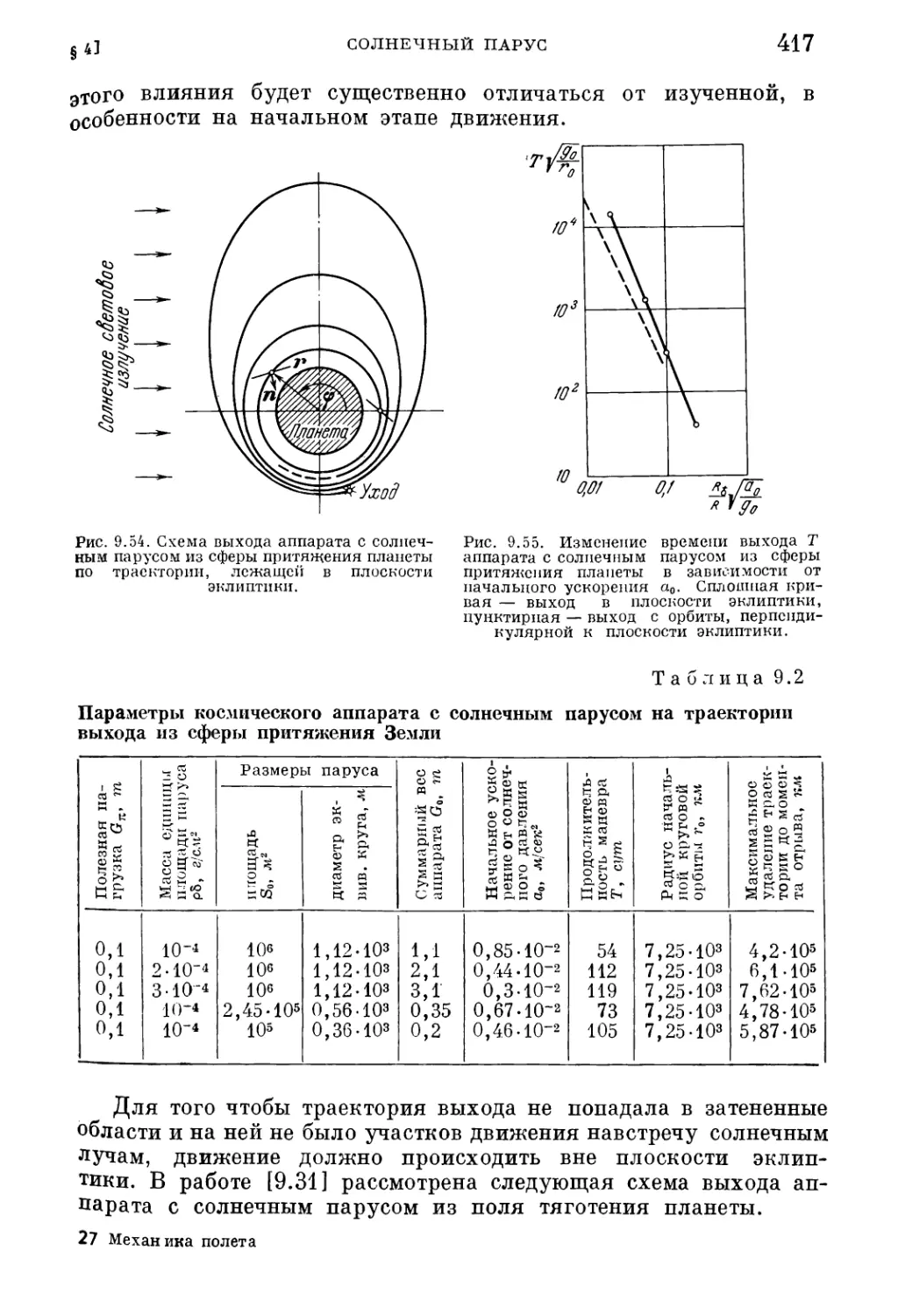
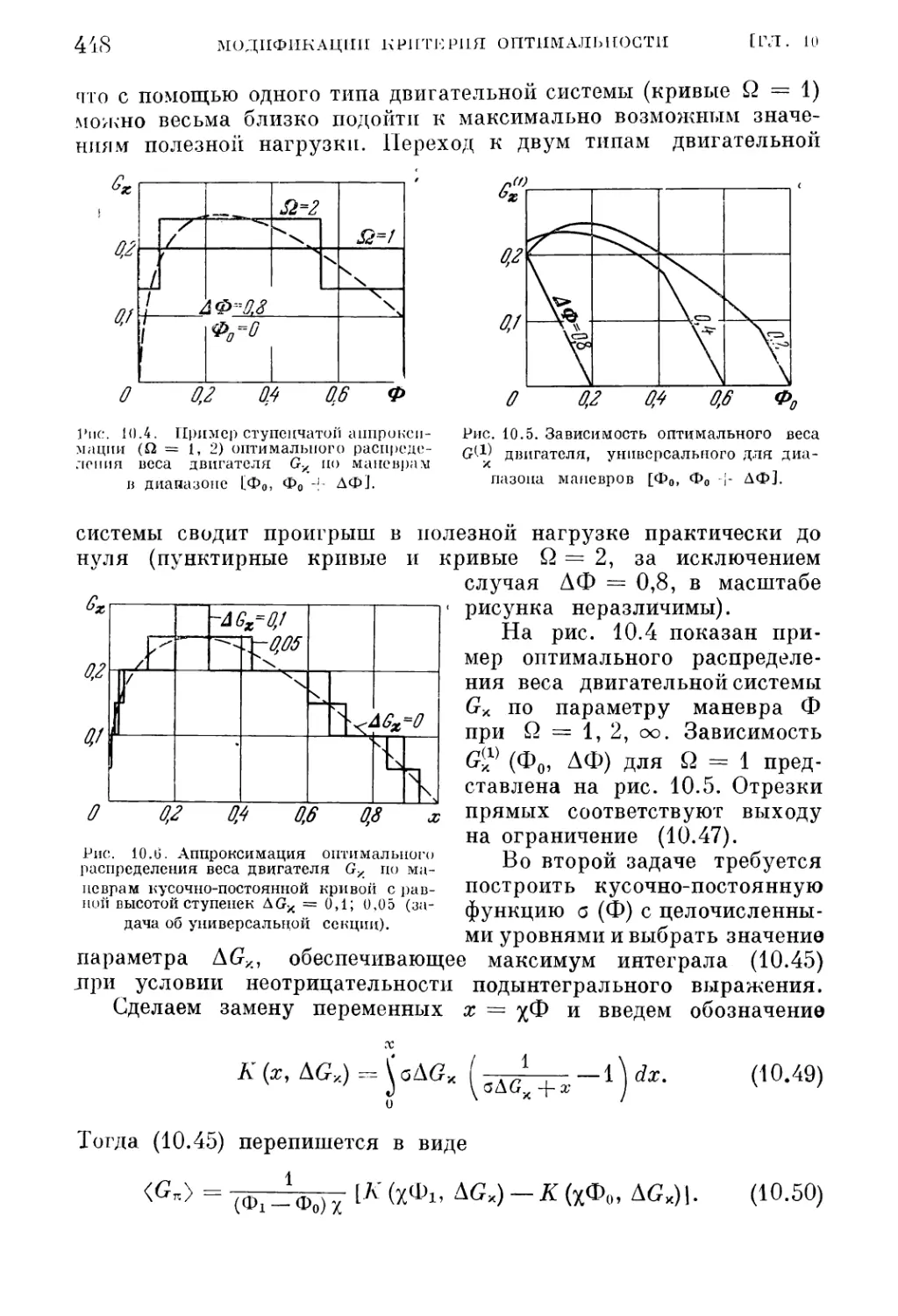
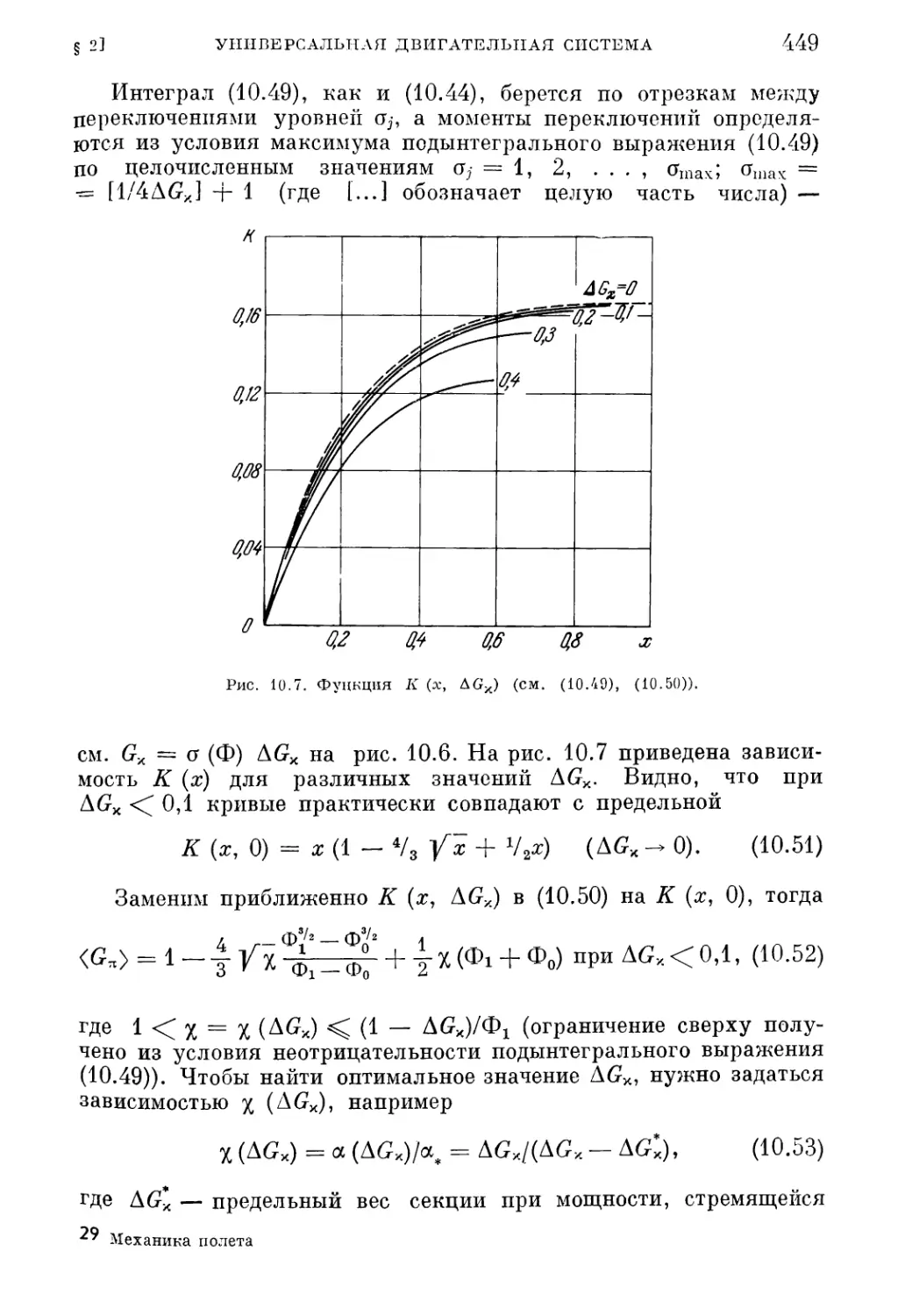
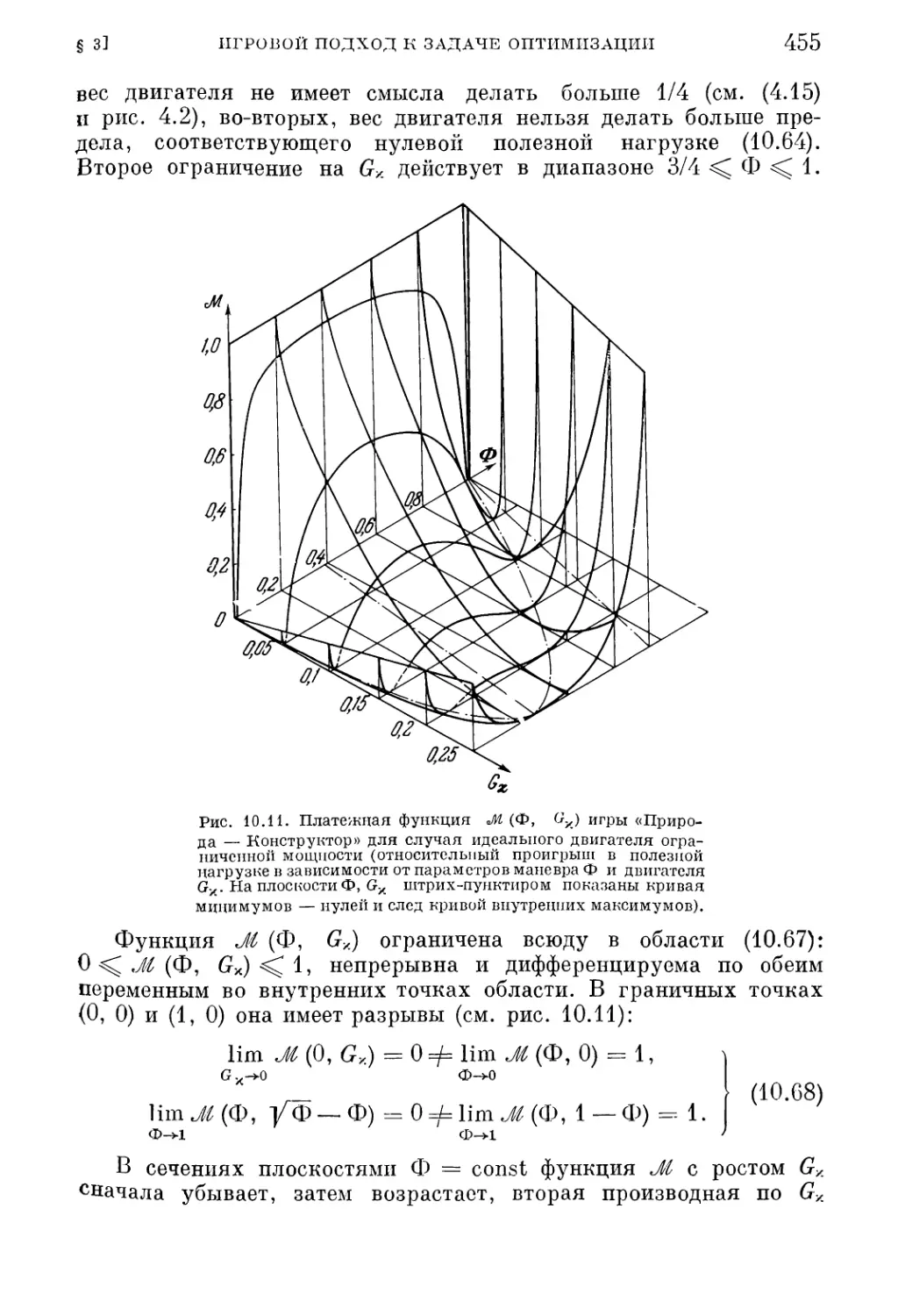
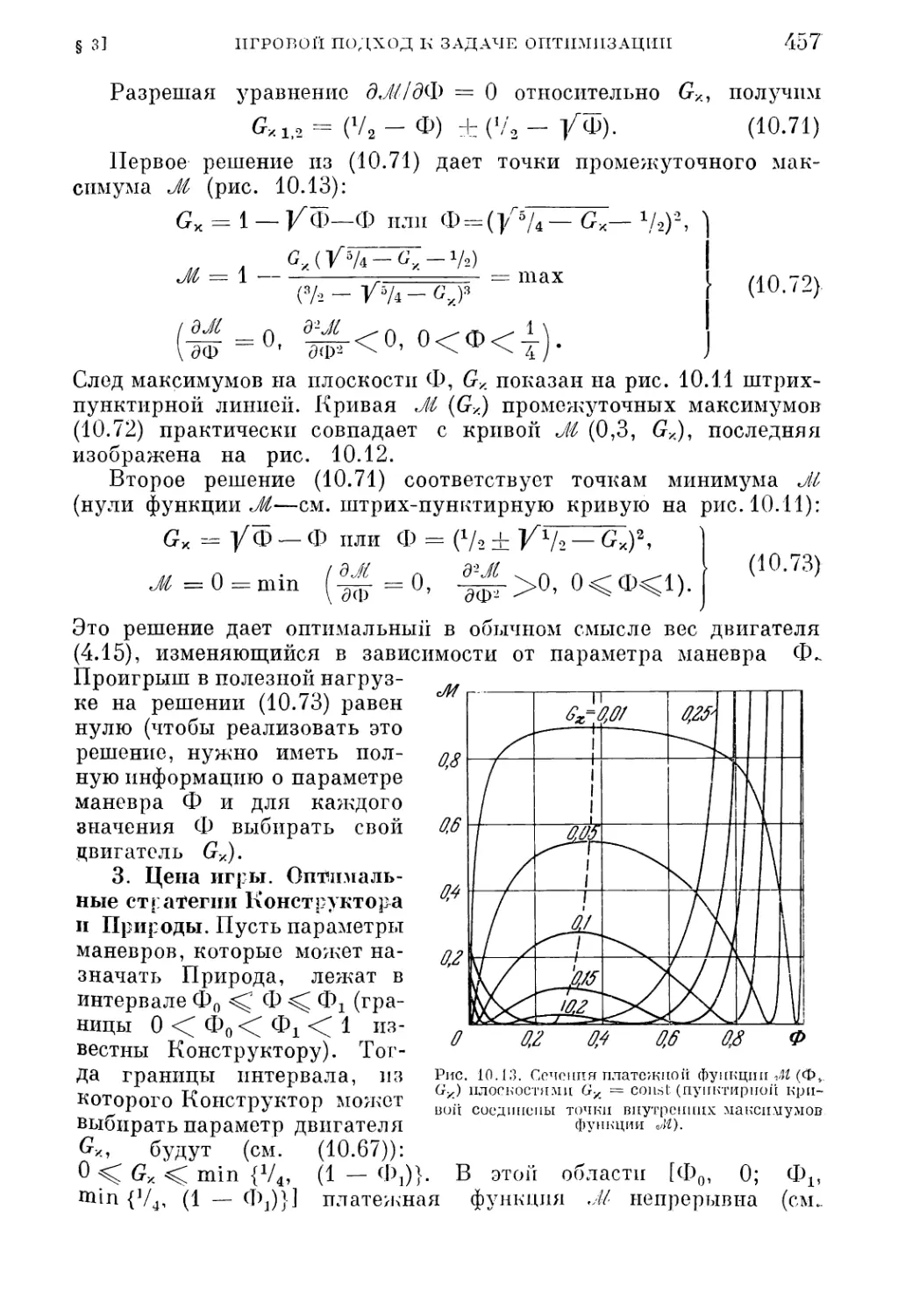
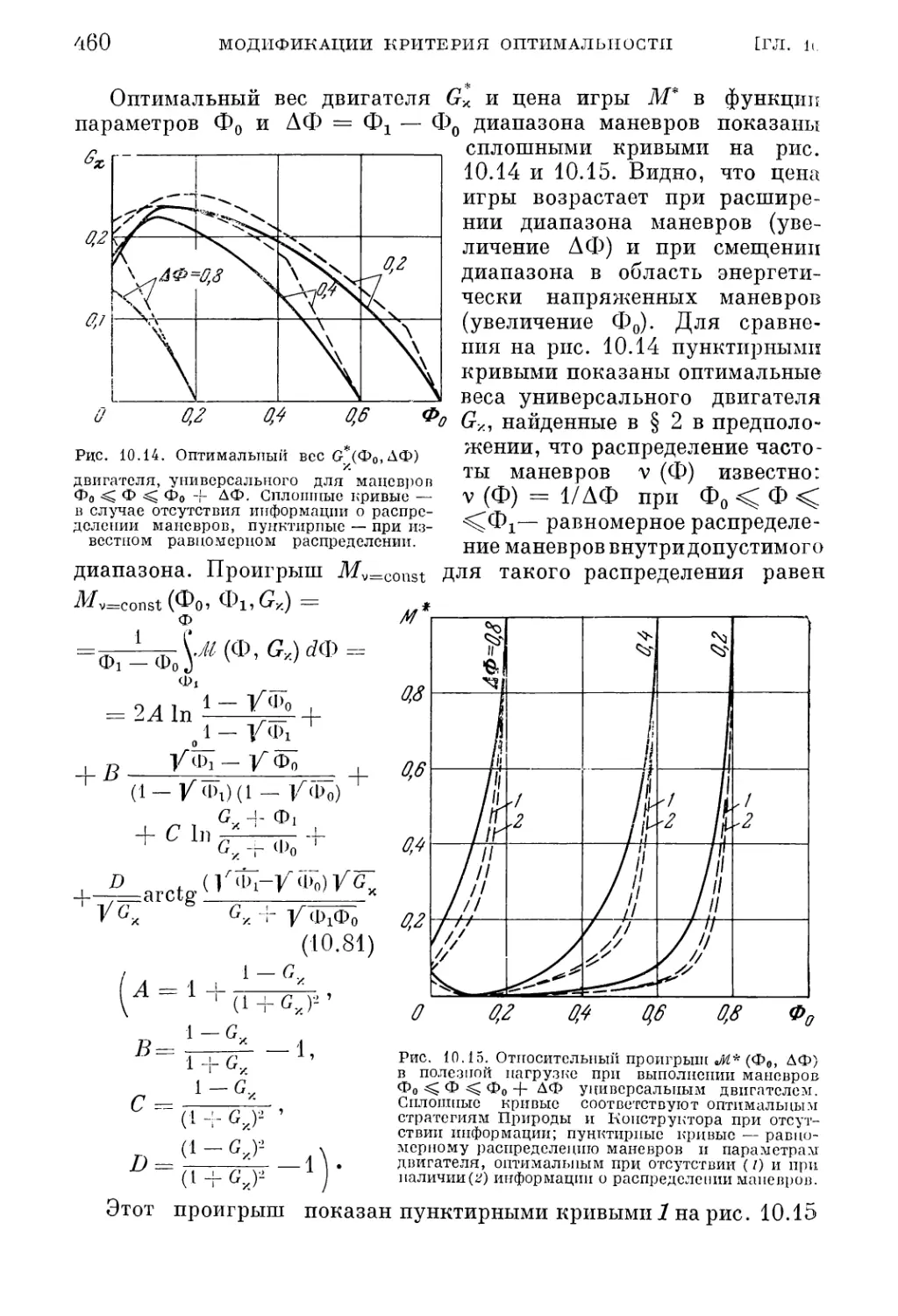
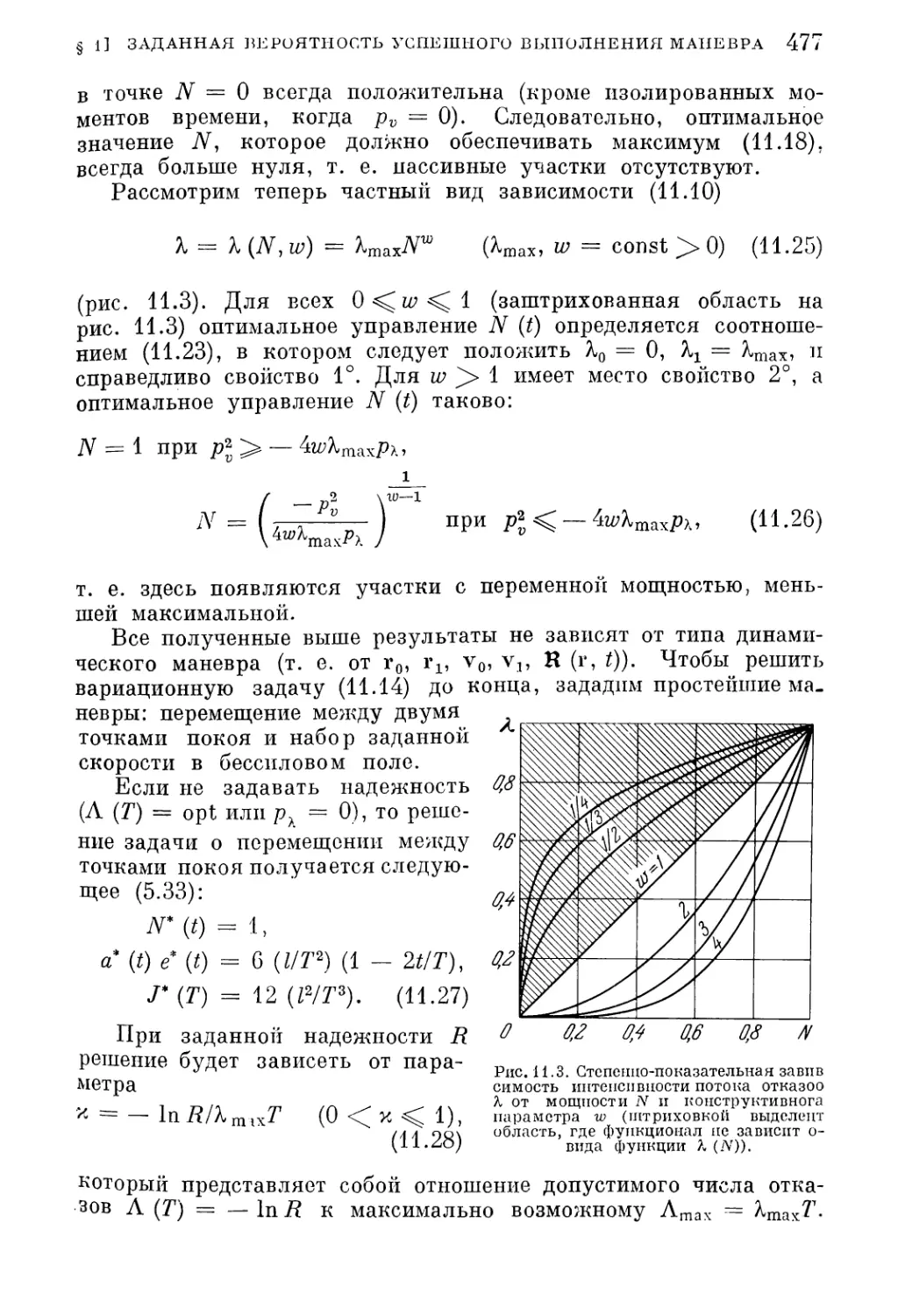
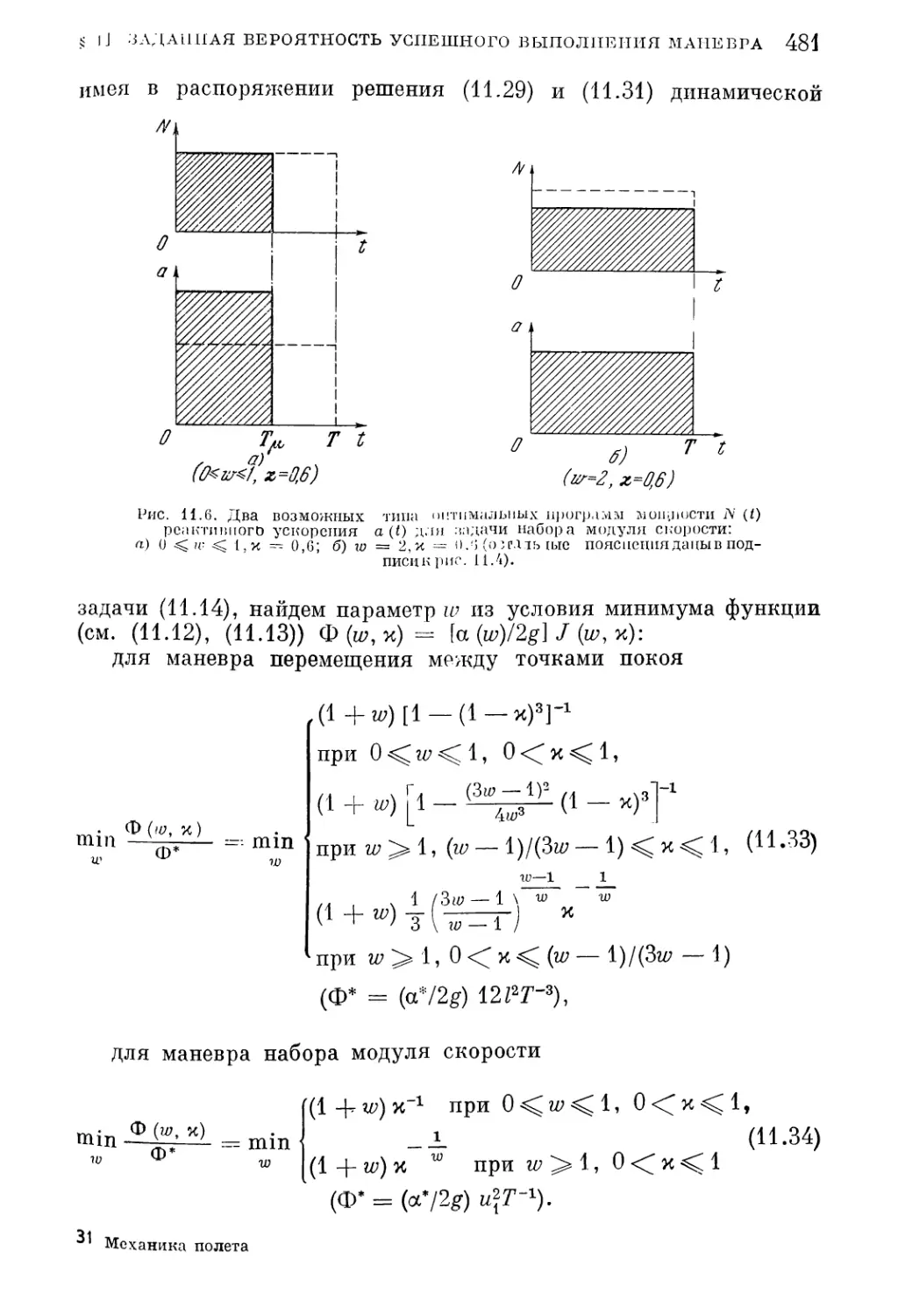
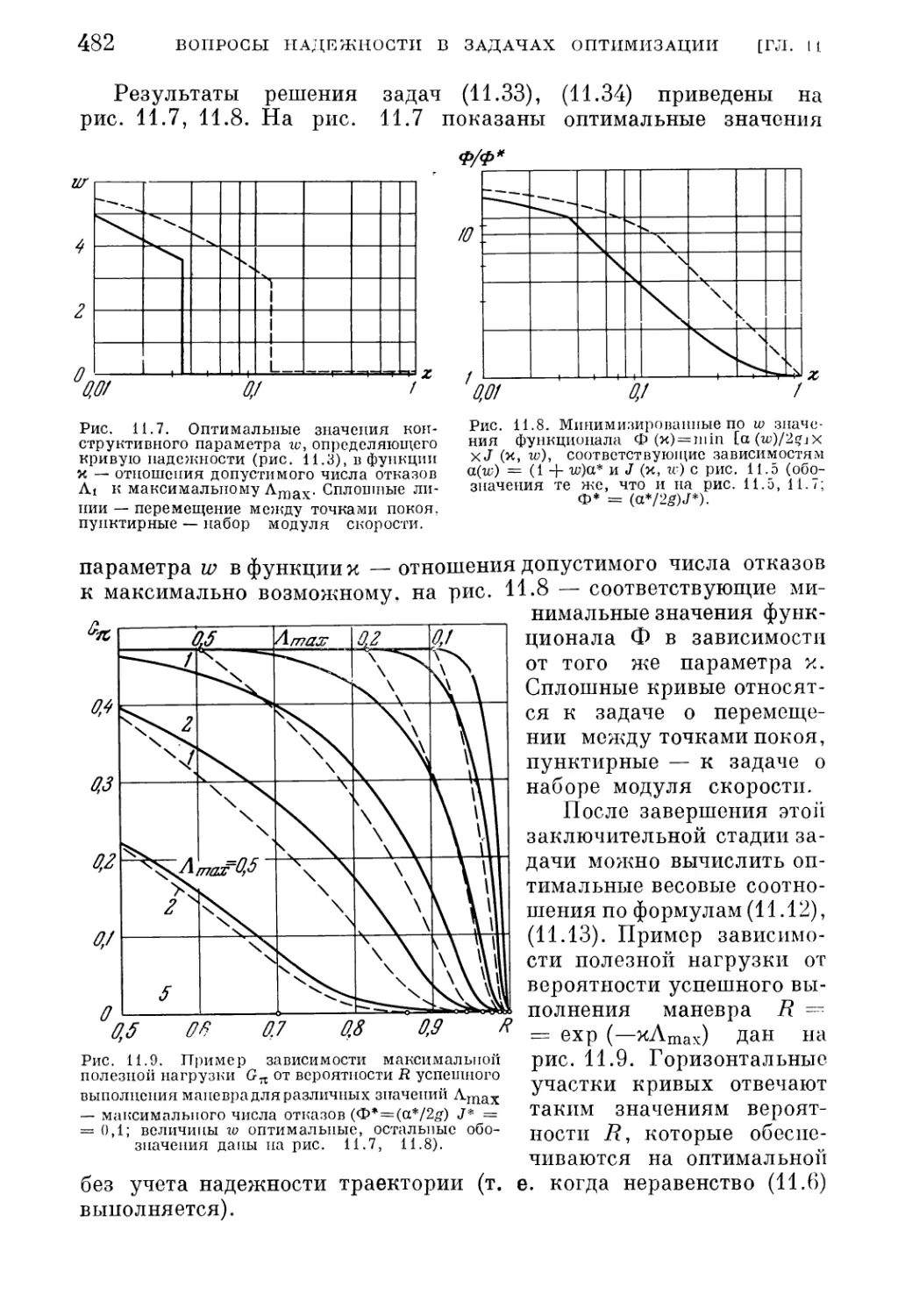
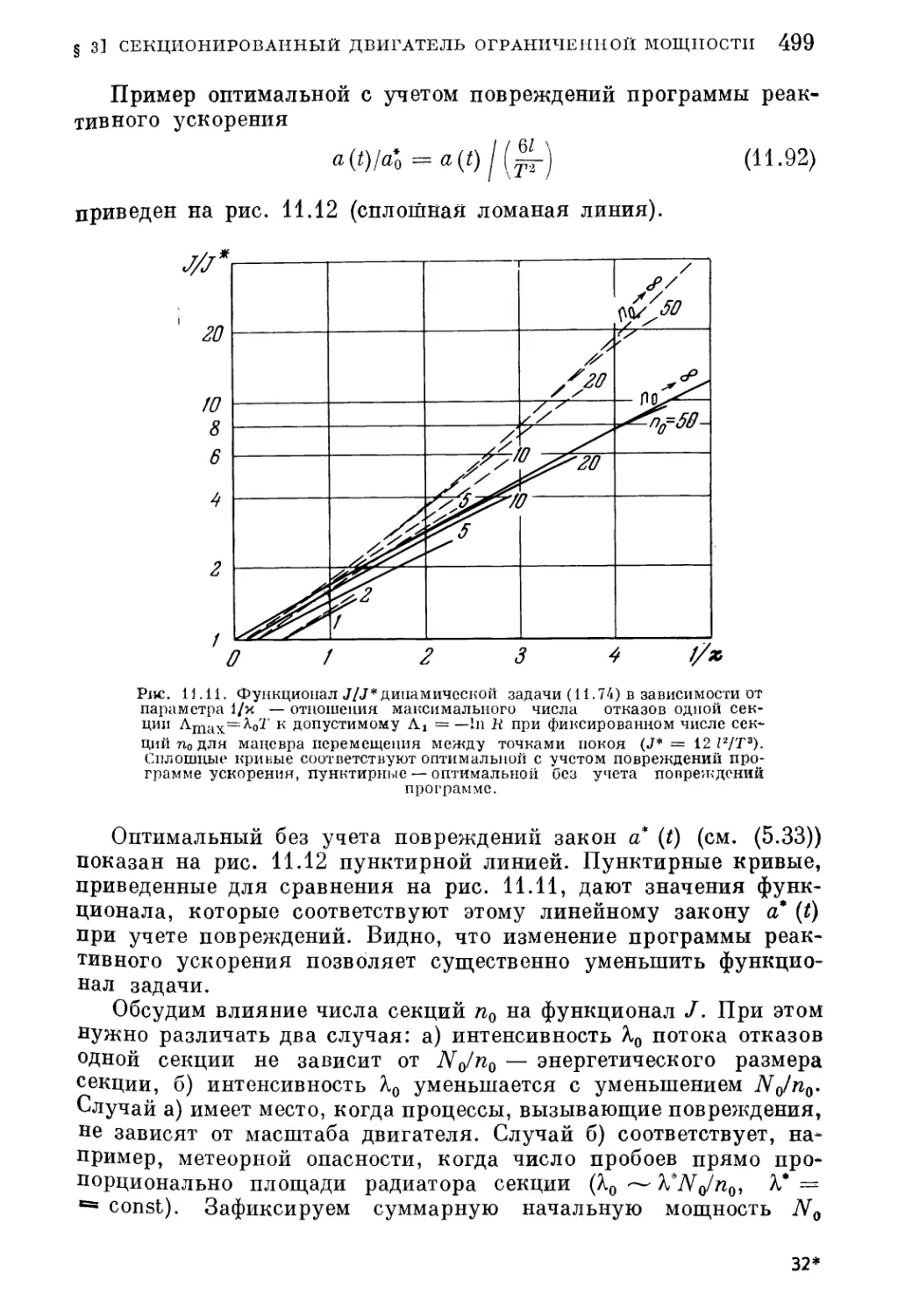
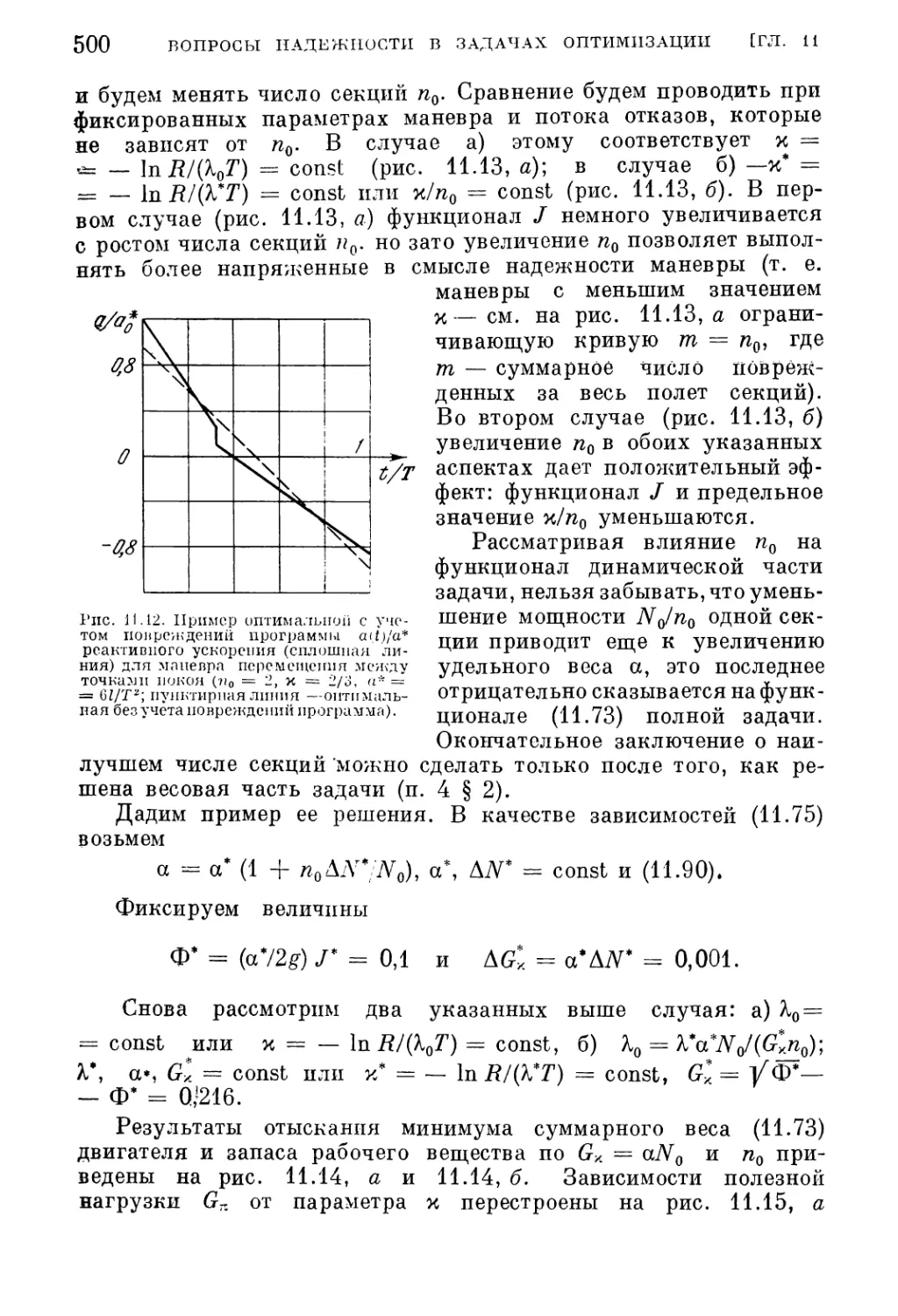
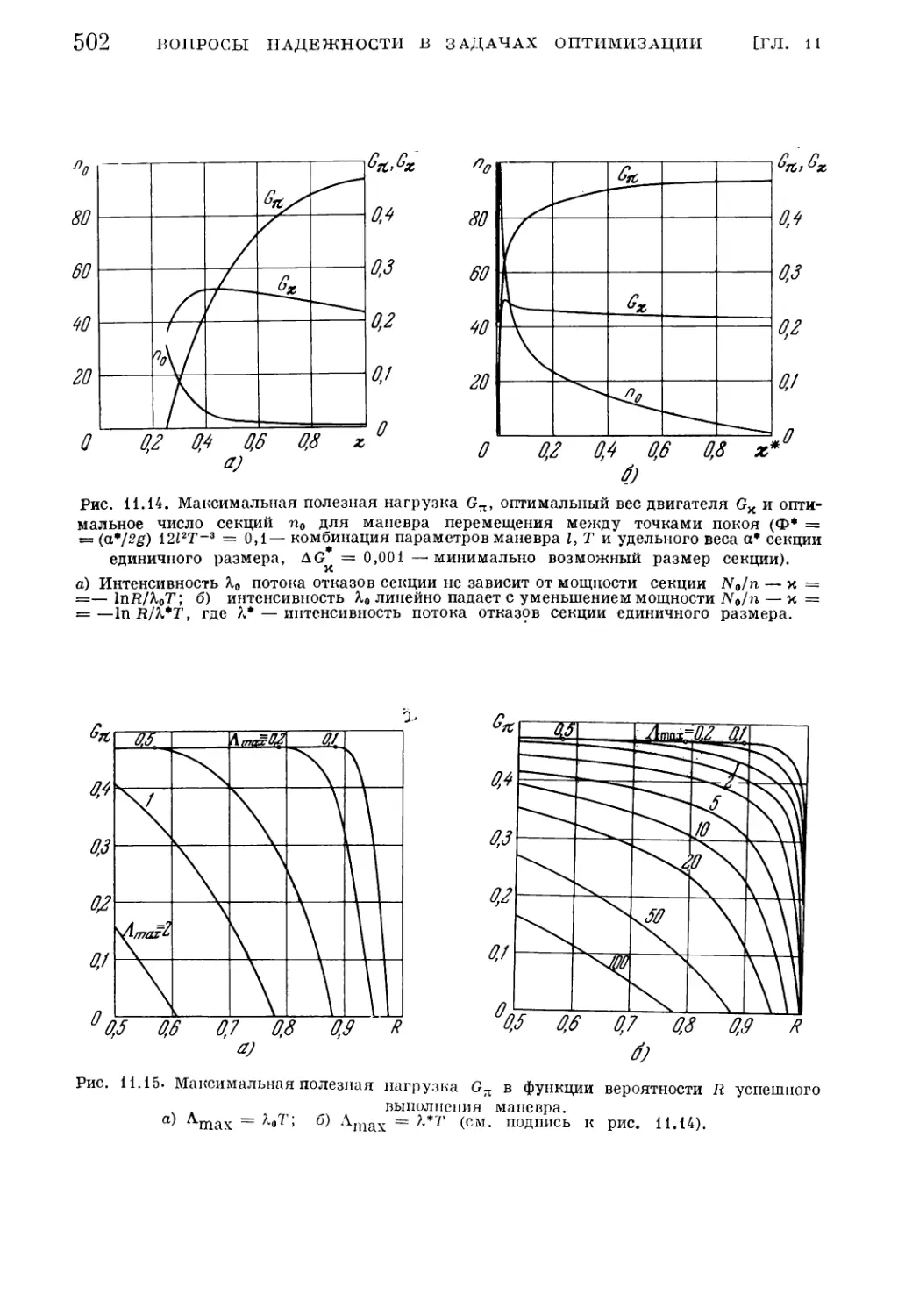
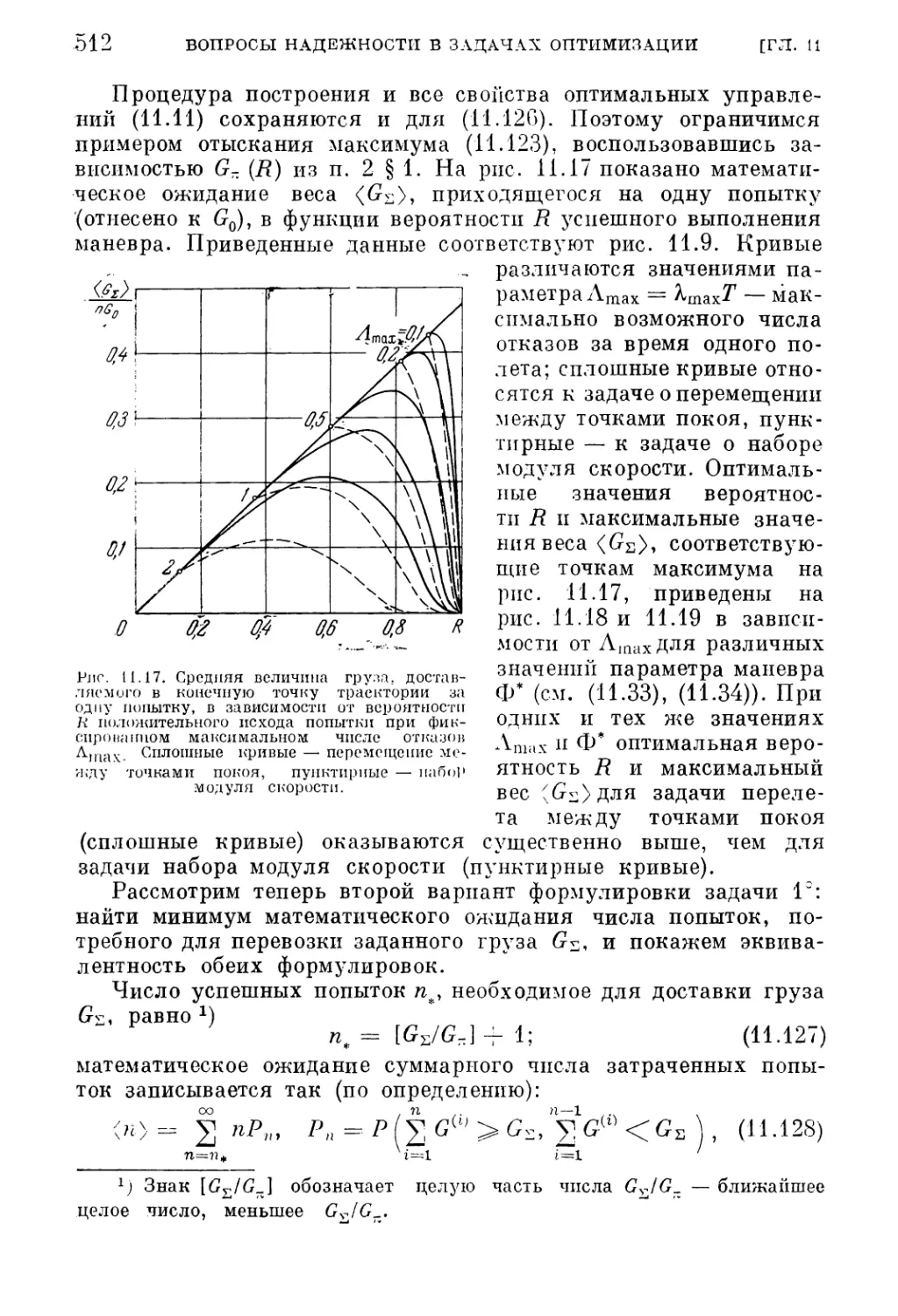
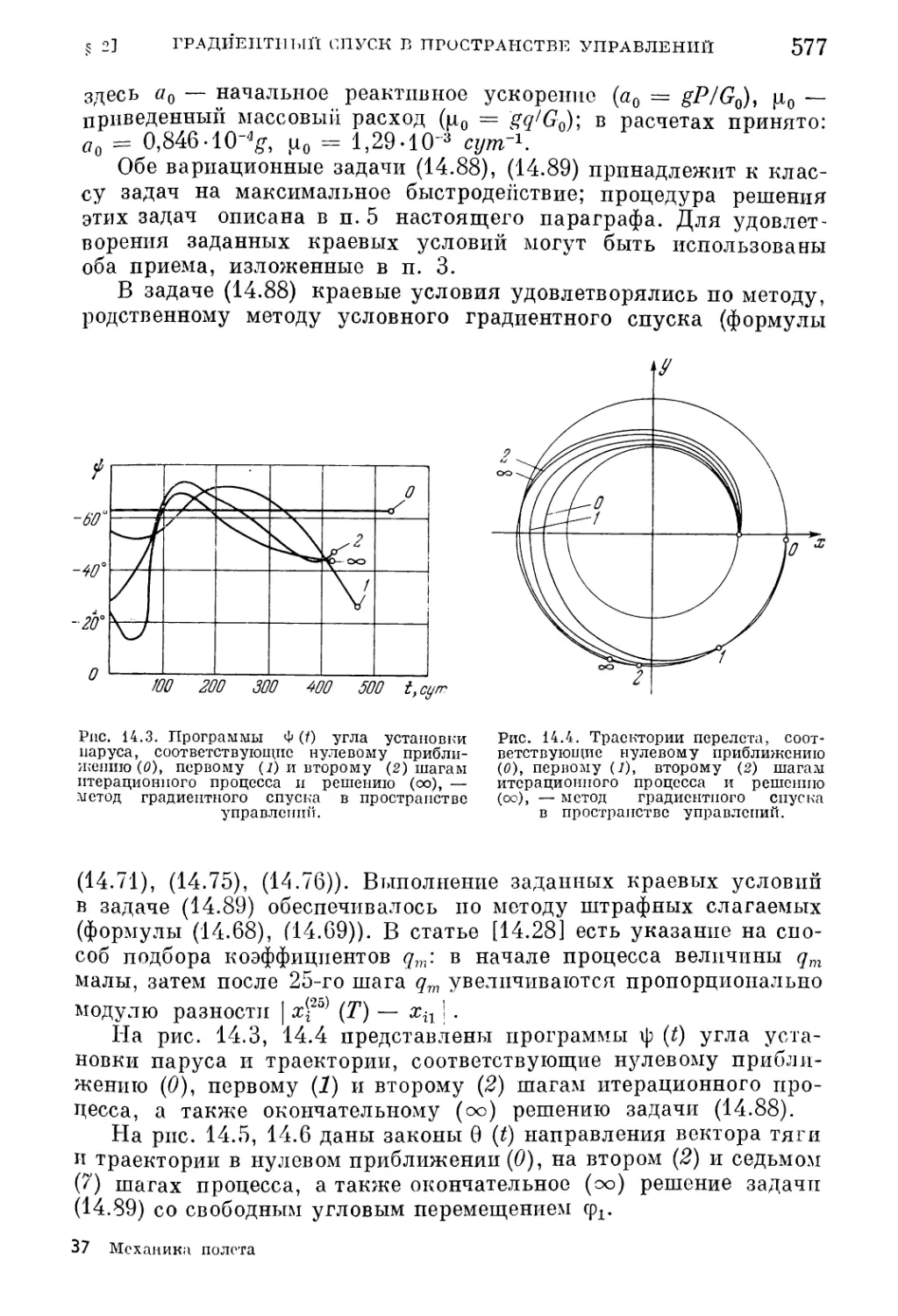
Текст
<гР о*
X У У
-U ЛУ
* <v
<; о
dax *
* ж
.<Х 0Л
«. <5>*
# *«■
eV ^ -ч ♦
<Cv (v \
^ \^>>>
XX XxV ХУ X+*
XVX XVV ееХ *'X
># ^ >>. *в У УУУУ
Г 50 # Л <&
У У У У
У Л* л 3
S* *° £
«?* °л л* ж л?
У У
/ ' У УУ\
У У У ь*кЛ .*
<г* ^ л, . J
? XX XV ^
X «ч ^
> X
У
. w\
X „ * *[Л О X
* &3* >\
Лч X v£
X <$ д*
? .X О* Qs
а
»* .0 * . *
Л. ГРОЛЗОВСКИ
Ю.Н. ИВАНОВ
В. В. ТОКАРЕВ
И
В книге систематизированно из¬
лагается механика космического
полета. Предметом этого раздела
механики является совместное ре¬
шение проблем выбора оптималь¬
ных весовых параметров космиче¬
ского аппарата, оптимального уп¬
равления его двигательной систе¬
мой и определение оптимальных
траекторий полета.
Название книги отражает совре¬
менное состояние механики косми¬
ческого полета, которая получила
наибольшее развитие примени¬
тельно к двигательным системам
«малой тяги» — развивающим тягу,
меньшую веса аппарата (плазмен¬
ные и ионные двигатели, солнеч¬
ный парус и др.). Для этих систем
вследствие большого веса двига¬
тельной установки оптимизация
параметров двигателя совместно
с выбором оптимальных управле¬
ний и траекторий полета особен¬
но существенна.
Книга рассчитана на научных ра¬
ботников, инженеров, аспирантов
и студентов старших курсов. У чита¬
теля предполагается знание основ
вариационного исчисления, однако
книга позволяет пользоваться
главными результатами, опуская
разделы, посвященные вариаци¬
онному анализу.
Г. Л. ГРОДЗОВСКИЙ
ю. Н. ИВАНОВ
В. В. ТОКАРЕВ
МЕХАНИКА
КОСМИЧЕСКОГО
ПОЛЕТА
С МАЛОЙ ТЯГОЙ
ИЗДАТЕЛЬСТВО «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
м ° С К В А 1966
6Т5.2
Г 86
УДК 629.195
2-6-5
179—66
ОГЛАВЛЕНИЕ
Предисловие
Введение . .
И
13
ЧАСТЬ I
ФИЗИЧЕСКИЕ ПРИНЦИПЫ И ОБОБЩЕННЫЕ ПАРАМЕТРЫ
КОСМИЧЕСКИХ ДВИГАТЕЛЬНЫХ СИСТЕМ
Г л а в jl 1
Основные параметры и состав космических
двигательных систем
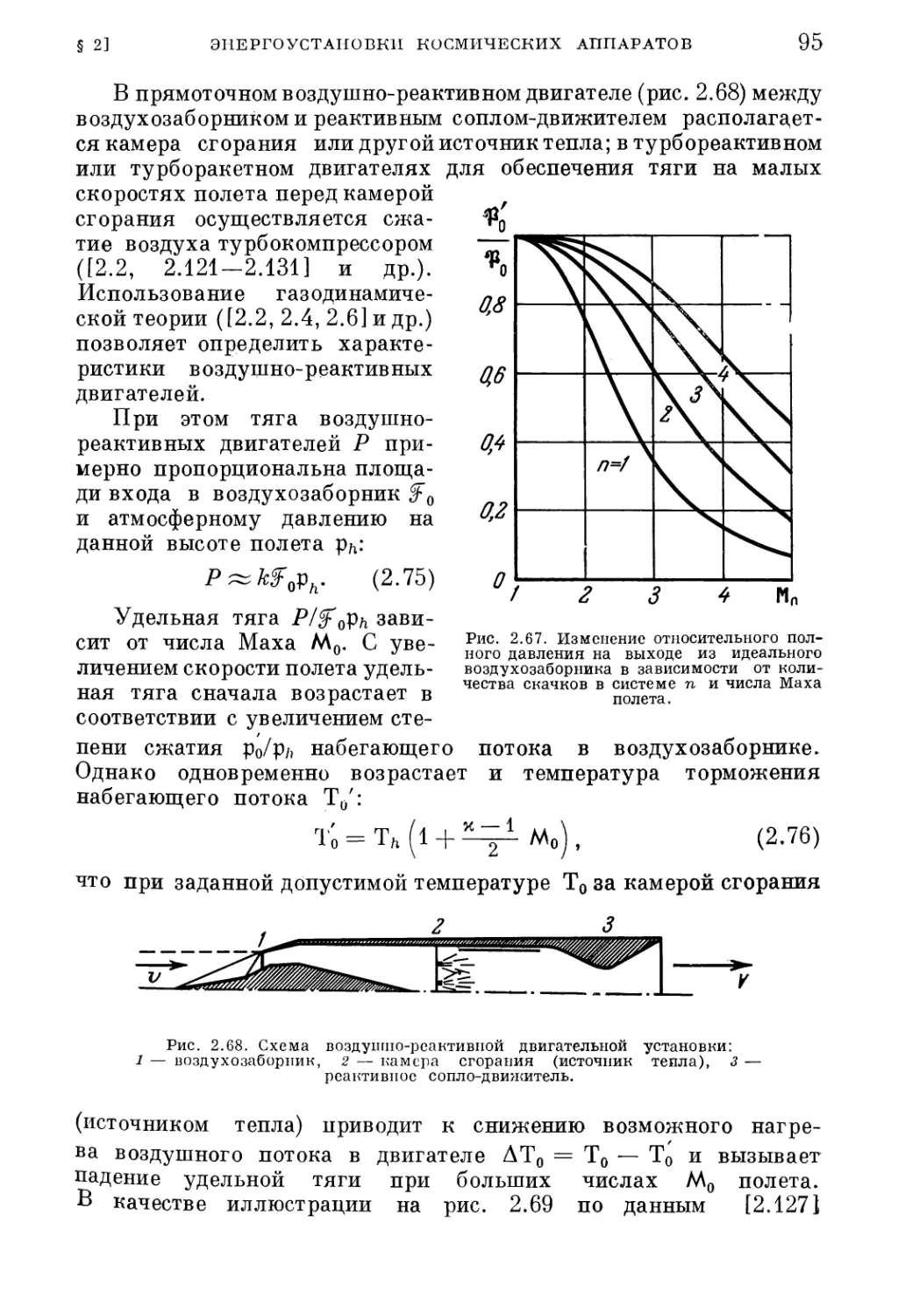
§ 1. Основные параметры космических двигательных систем
§ 2. Состав космических двигательных систем
§ 3. Условия космического полета . . . . .
21
23
25
1. Гравитационные поля (25). 2. Параметры окружающей среды (30). 3. Ме¬
теорные потоки (33).
Глава 2
Физические принципы элементов космических
двигательных систем
§ 1. Реактивные движители 3Q
1. Реактивная тяга и внешнее сопротивление (36). 2. Реактивные сопла. Дви¬
жители ЖРД (37). 3. Высокотемпературные тепловые реактивные движители
(47). 4. Электродинамические и электростатические реактивные движители
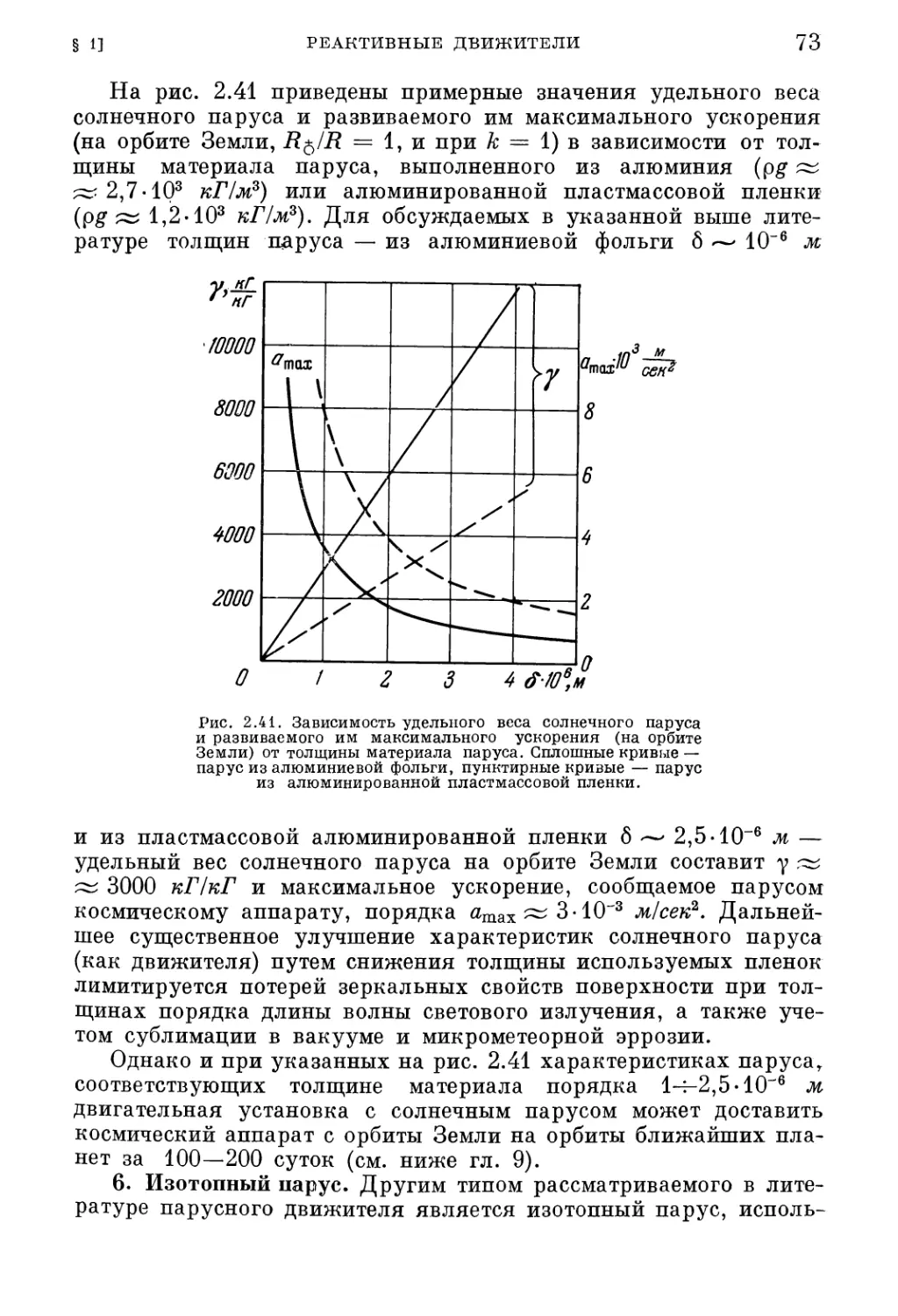
(53). 5. Солнечный парус (70). 6. Изотопный парус (73).
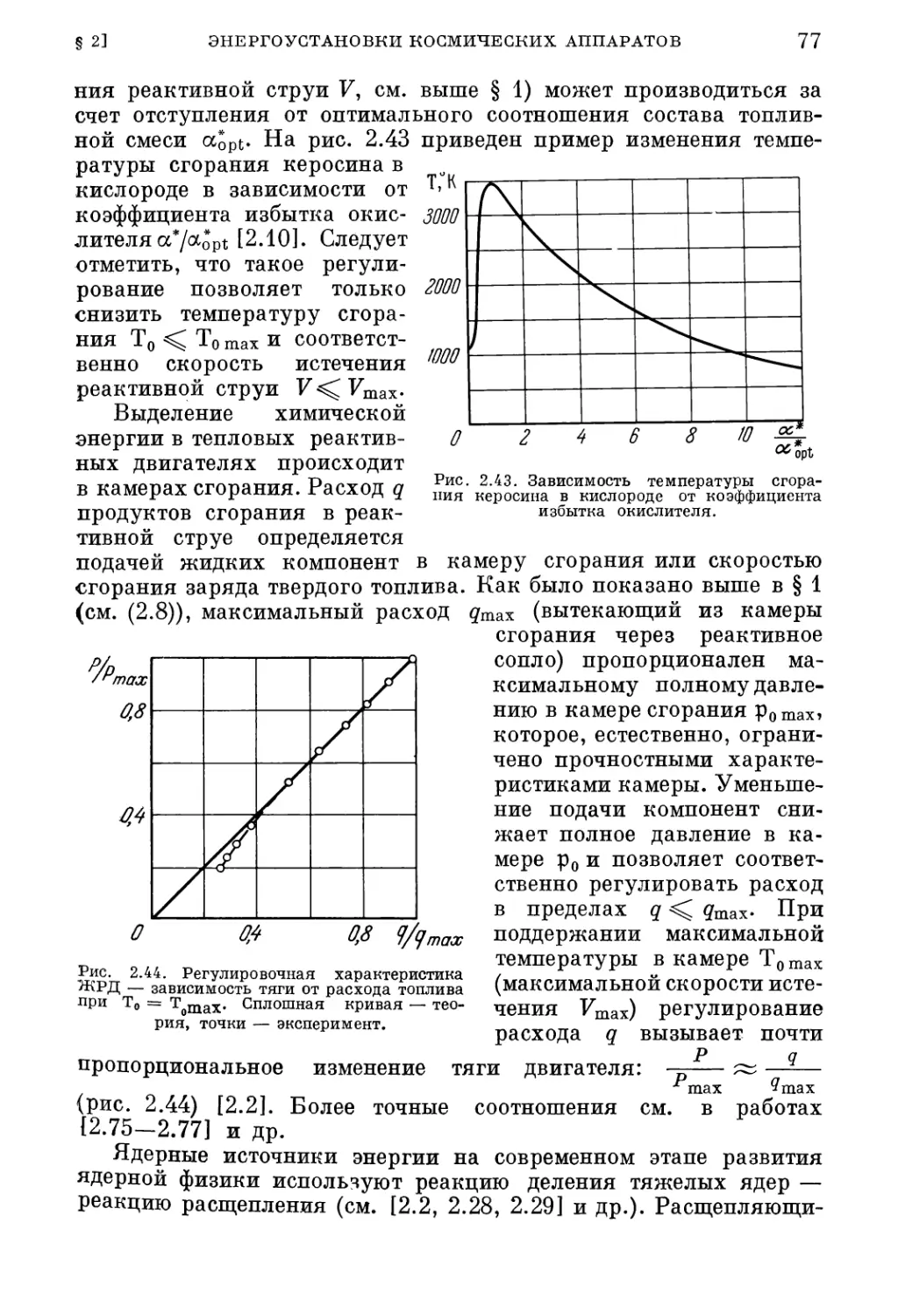
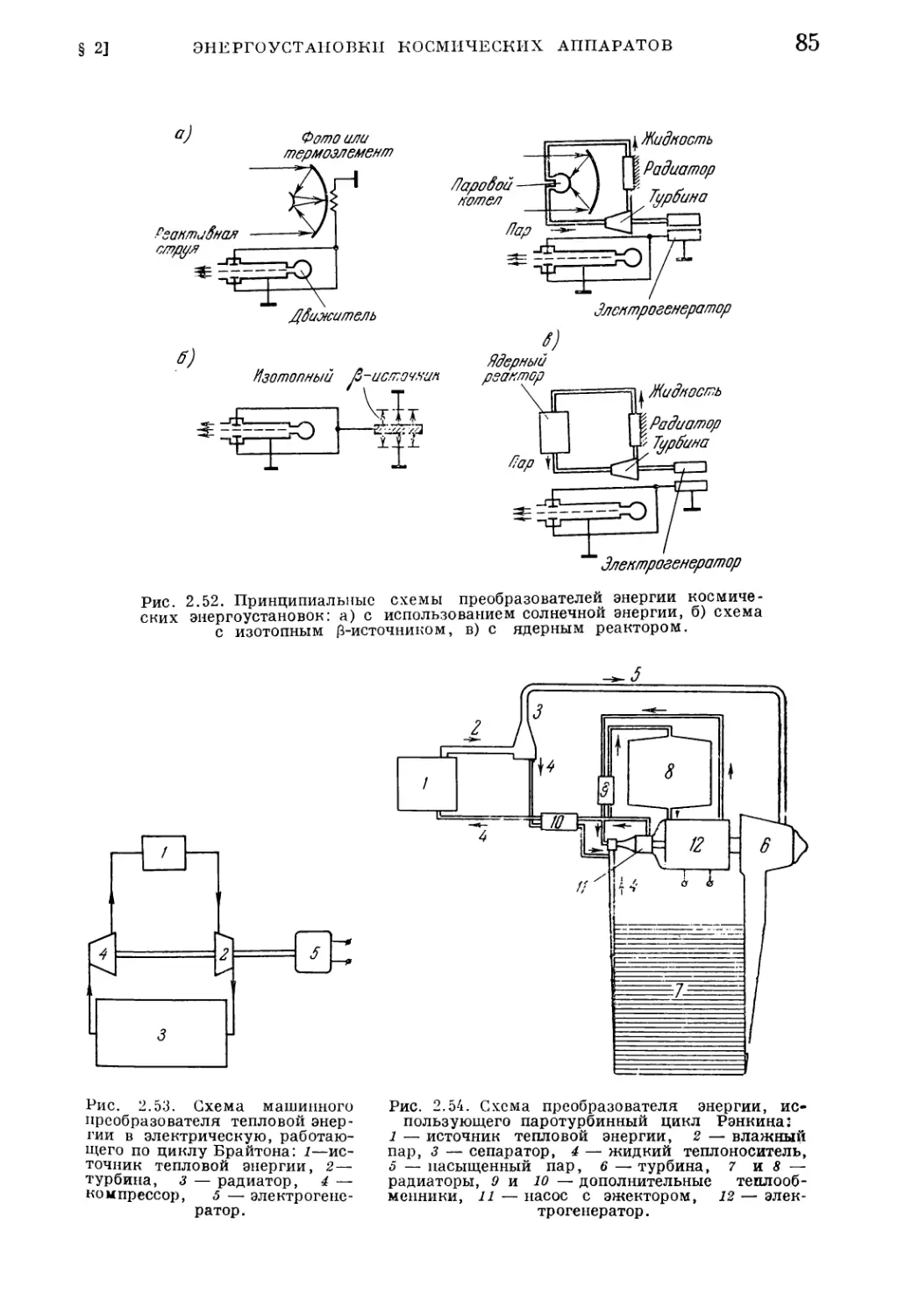
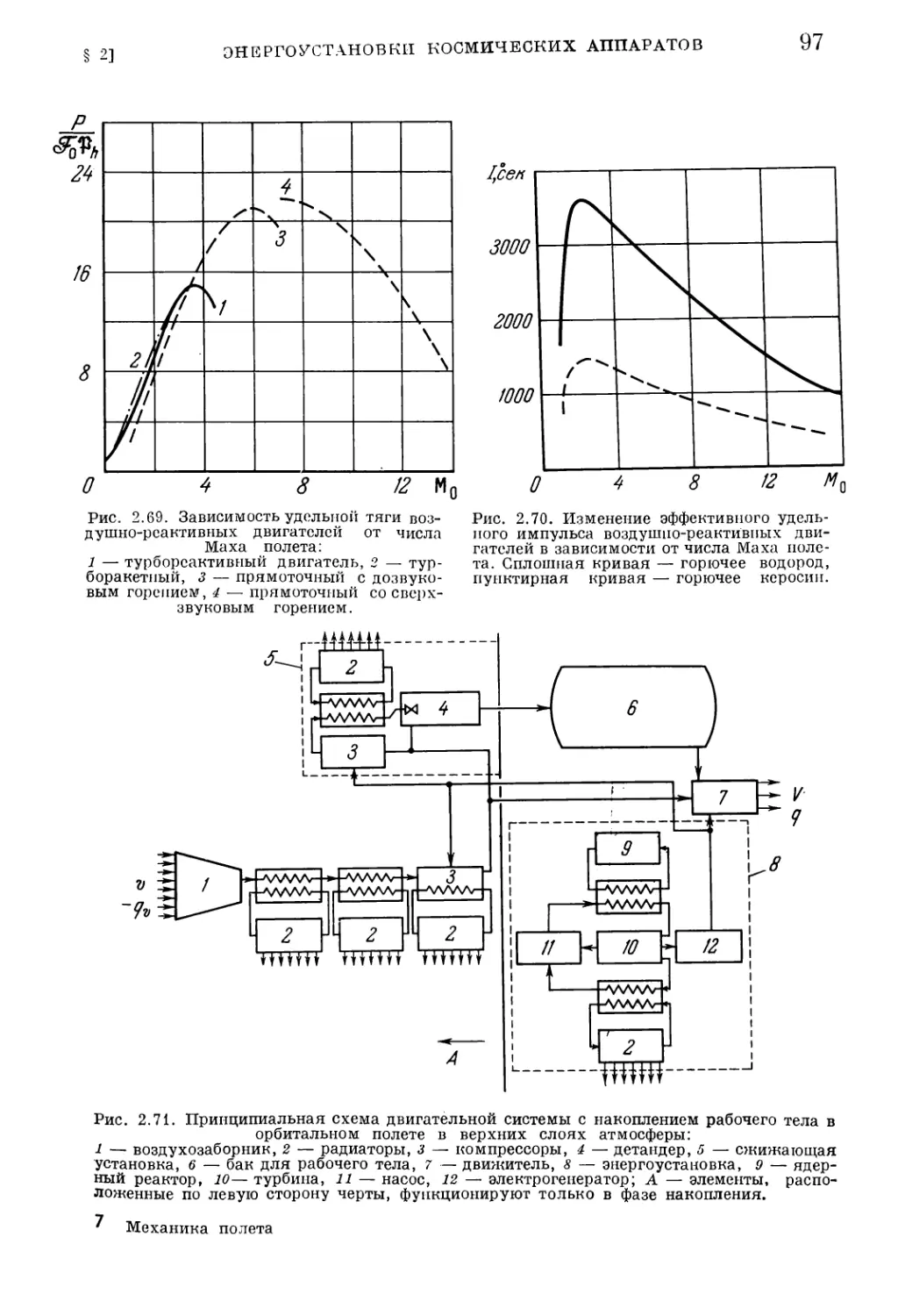
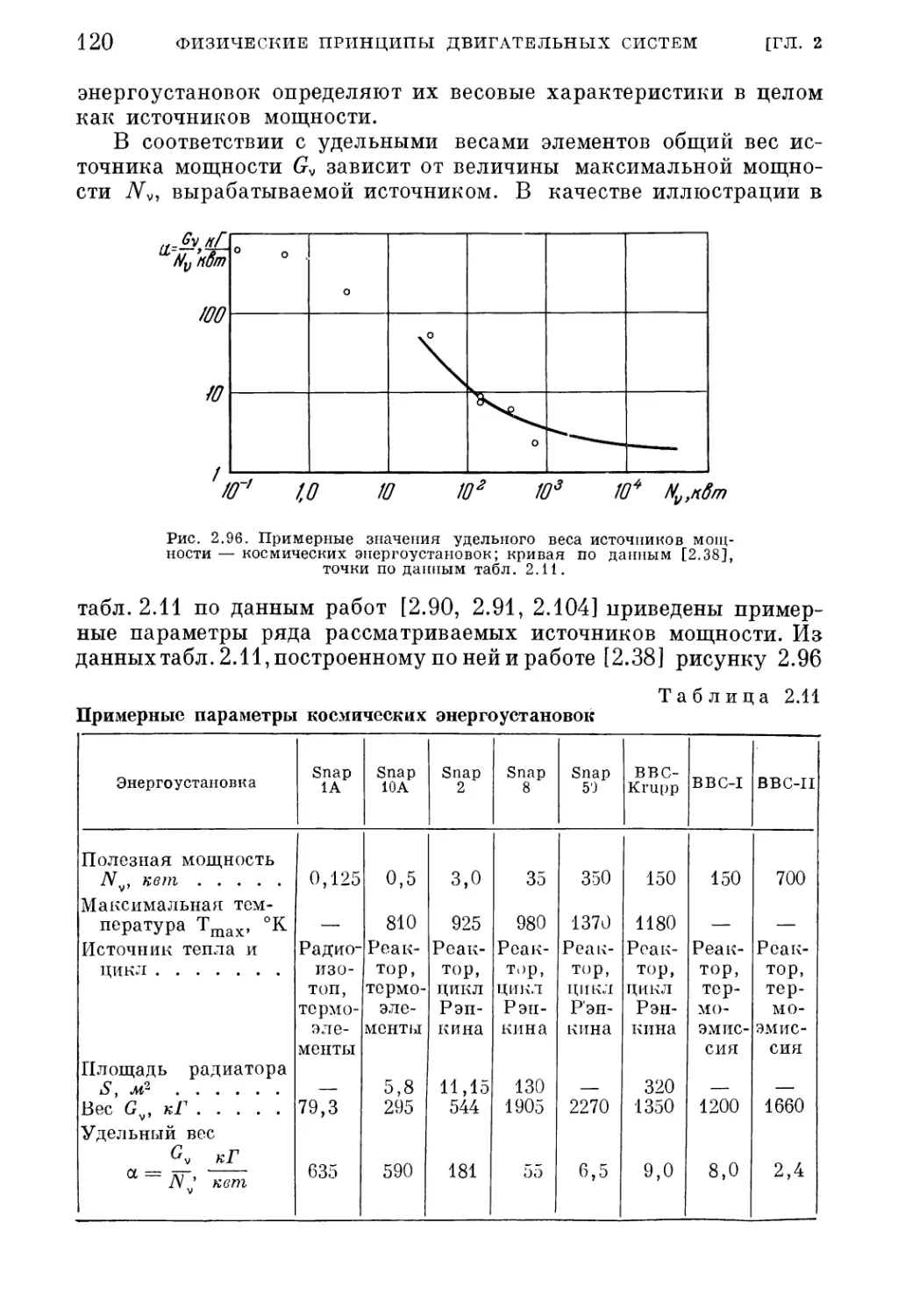
§ 2. Энергоустановки космических летательных аппаратов
1. Источники энергии (76). 2. Системы преобразования энергии (83). 3. Акку¬
муляторы энергии (90). 4. Системы подачи и хранения рабочего тела (92).
5. Энергоустановки с забором рабочего тела из внешней среды (93). 6. Внешнее
сопротивление двигательной установки при полете в атмосфере (98).
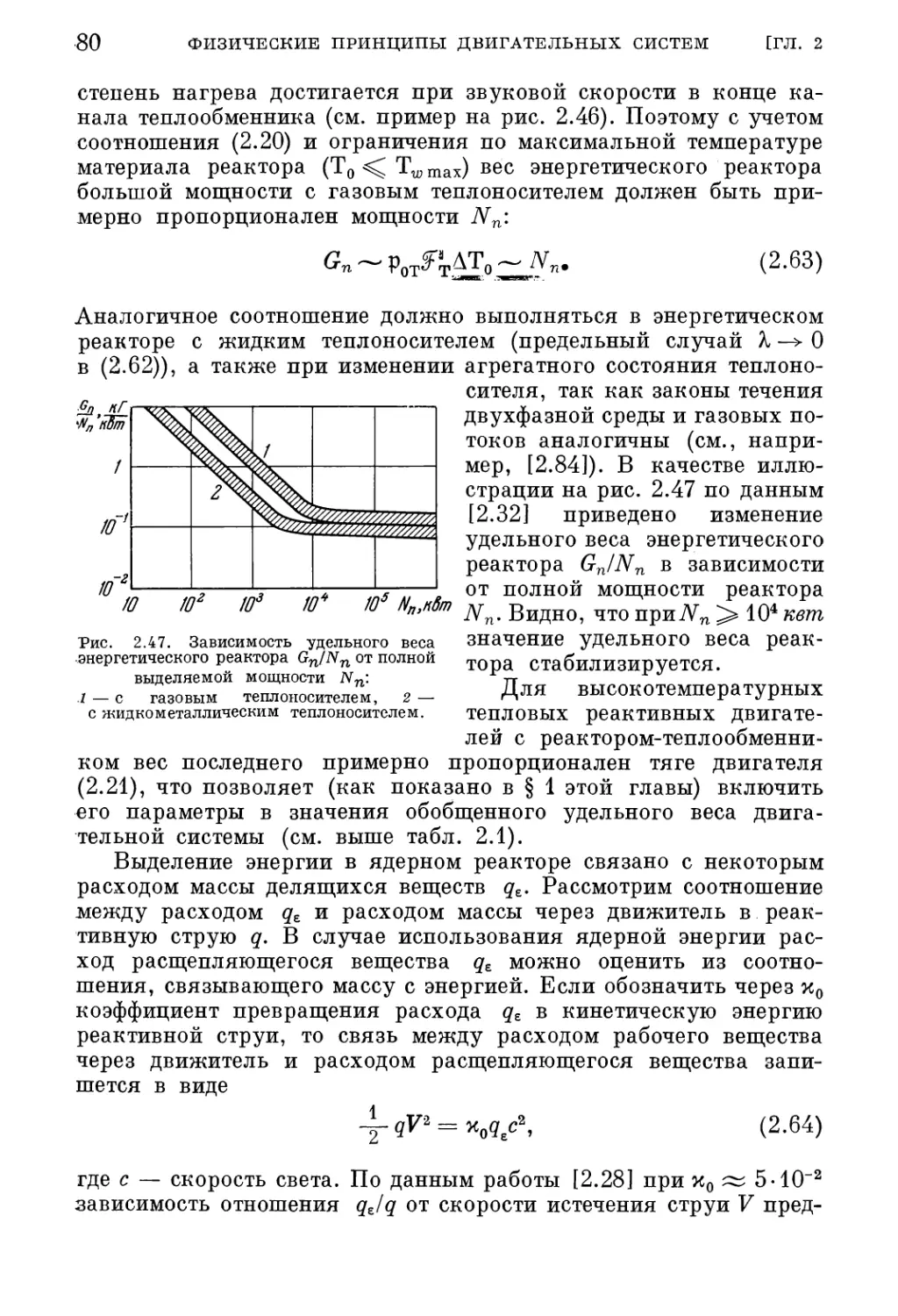
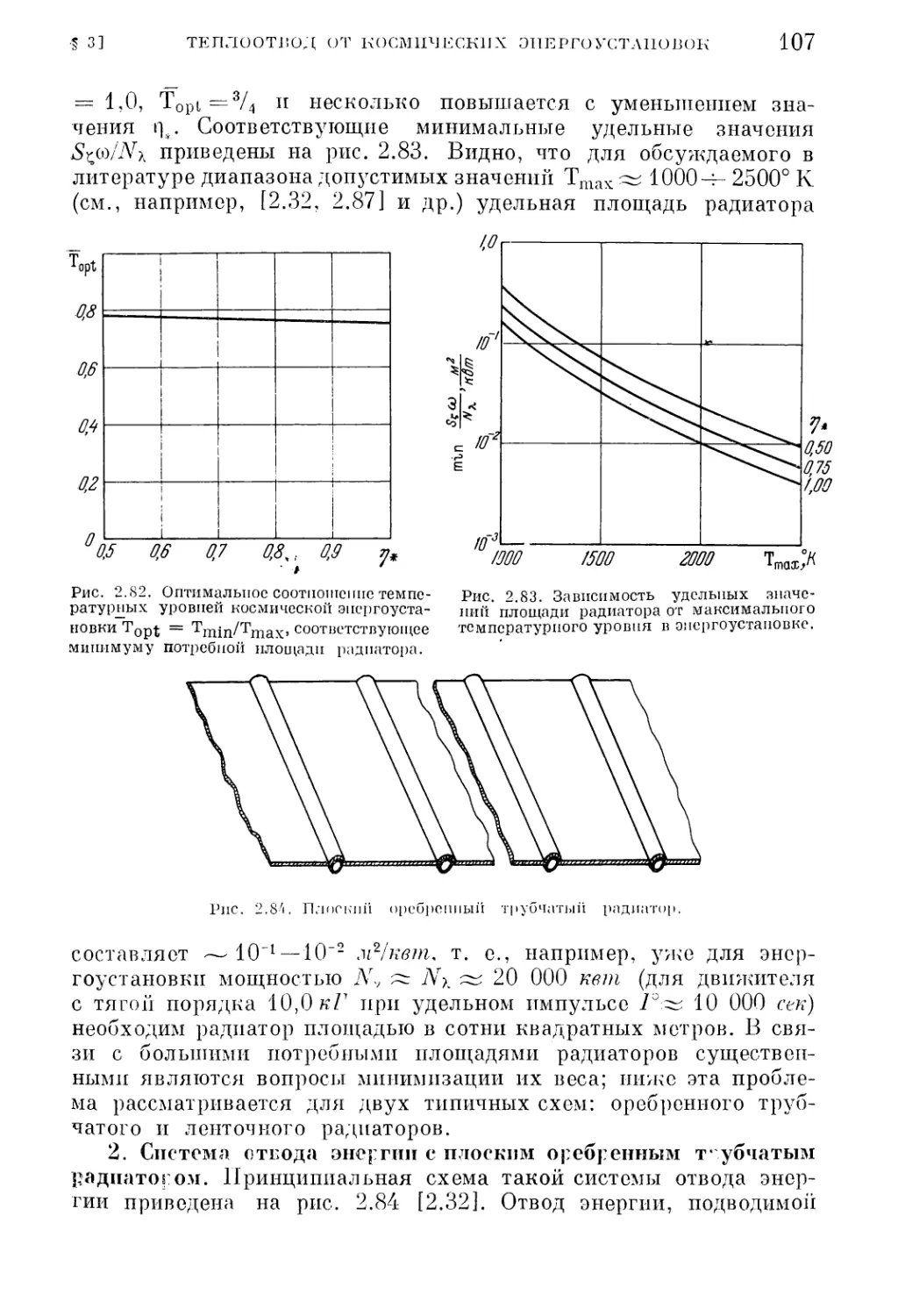
§ 3. Теплоотвод от космических энергоустановок 104
1. Радиационные системы отвода-энергии (104). 2. Система отвода энергии с пло¬
ским оребренным трубчатым радиатором (107). 3. Система отвода энергии со
звездообразно оребренным трубчатым радиатором (114). 4. Система отвода энер¬
гии с ленточным радиатором (116). 5. Весовые характеристики космических
энергоустановок — источников мощности (119).
4
ОГЛАВЛЕНИЕ
Глава 3
Обобщенные параметры космических двигательных систем
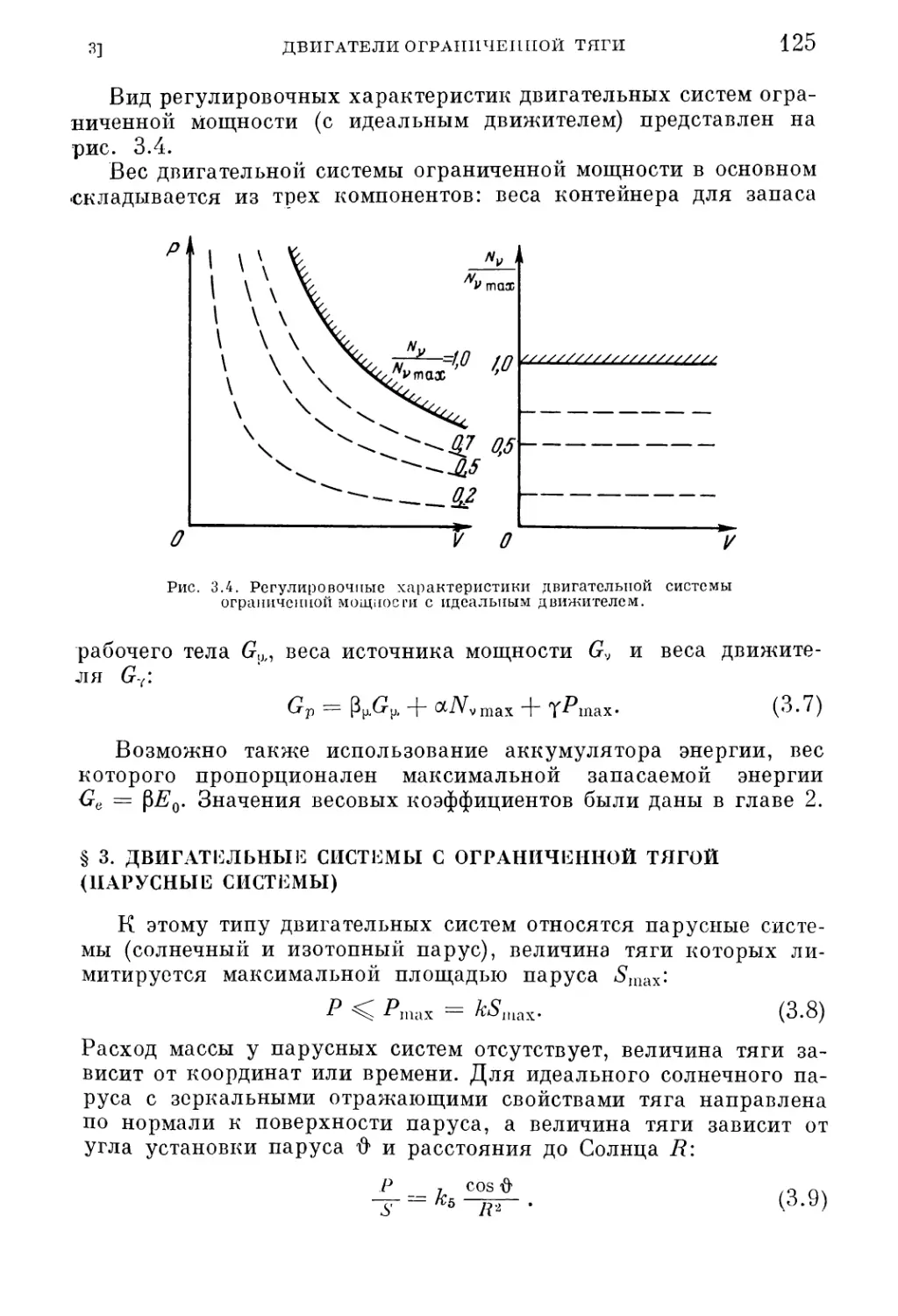
§ 1. Двигательные системы с ограниченной скоростью истечения
реактивной струи
§ 2. Двигательные системы ограниченной мощности
§ 3. Двигательные системы с ограниченной тягой (парусные системы)
ЧАСТЬ II
ПРОБЛЕМЫ ОПТИМИЗАЦИИ
Глава 4
Идеальный двигатель ограниченной мощности —
разделение вариационной задачи,
оптимальные весовые соотношения
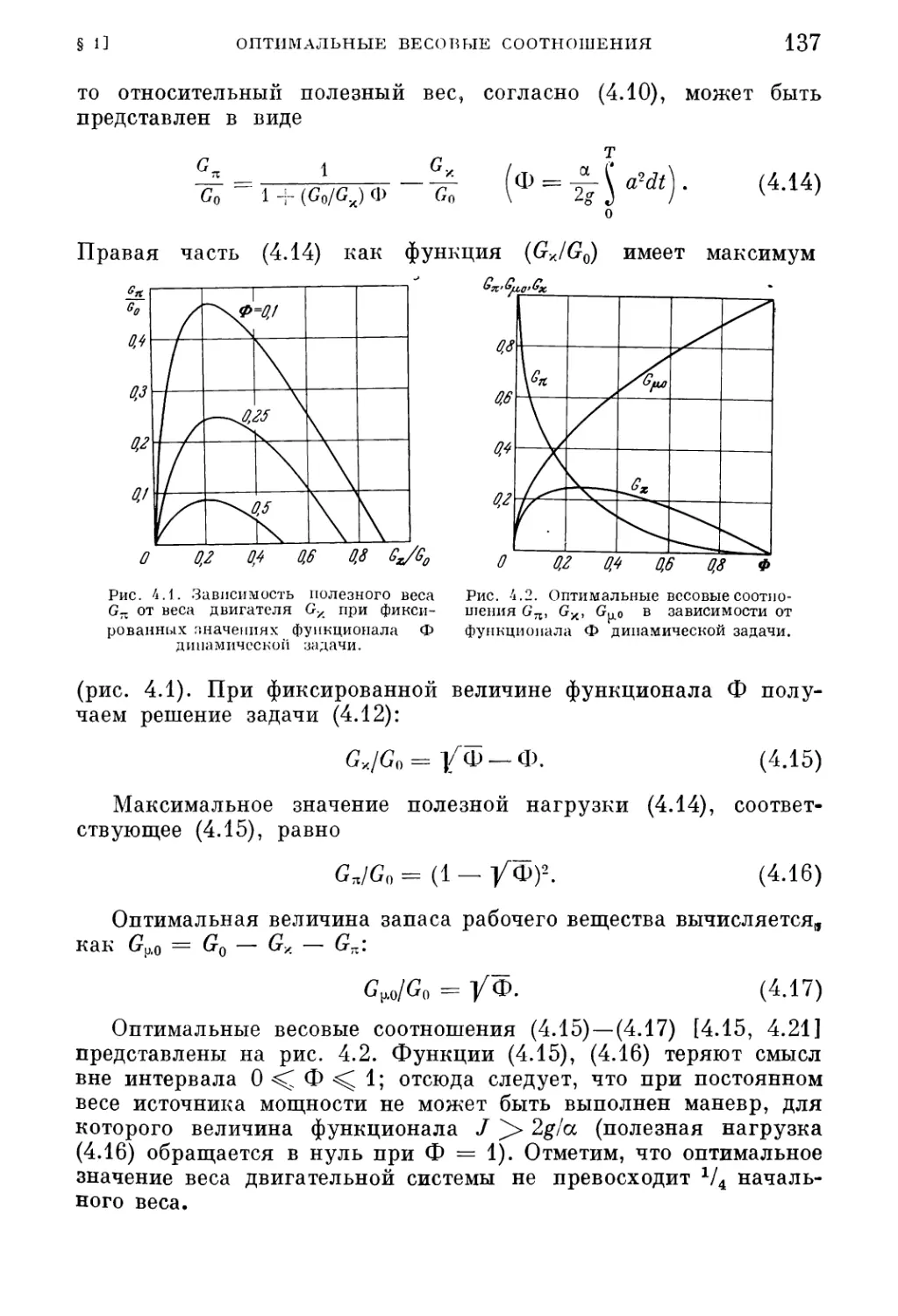
§ 1. Оптимальные весовые соотношения при постоянном и ступенчато
изменяемом весе двигателя
1. Разделение задачи, управление мощностью (134). 2. Оптимальные весовые
соотношения (136). 3. Ступенчатое изменение веса двигателя (а139).
§ 2. Оптимальная программа изменения веса двигателя
1. Формулировка задачи (142). 2. Разделение вариационной задачи (144).
3. Решение весовой части вариационной проблемы (146). 4. Ступенчатая аппро¬
ксимация оптимального управления весом двигателя (149).
§ 3. Использование сбрасываемых секций двигателя в качестве рабо¬
чего вещества
1. Постановка задачи (151). 2. Состав оптимального управления (152). 3. Чере¬
дование оптимальных программ для расходов (155). 4. Разделение задачи
на весовую и динамическую (159). 5. Решение весовой части задачи (161).
6. Ступенчатое уменьшение веса двигателя (165).
Глава 5
Идеальный двигатель ограниченной мощности —
оптимальные программы
реактивного ускорения
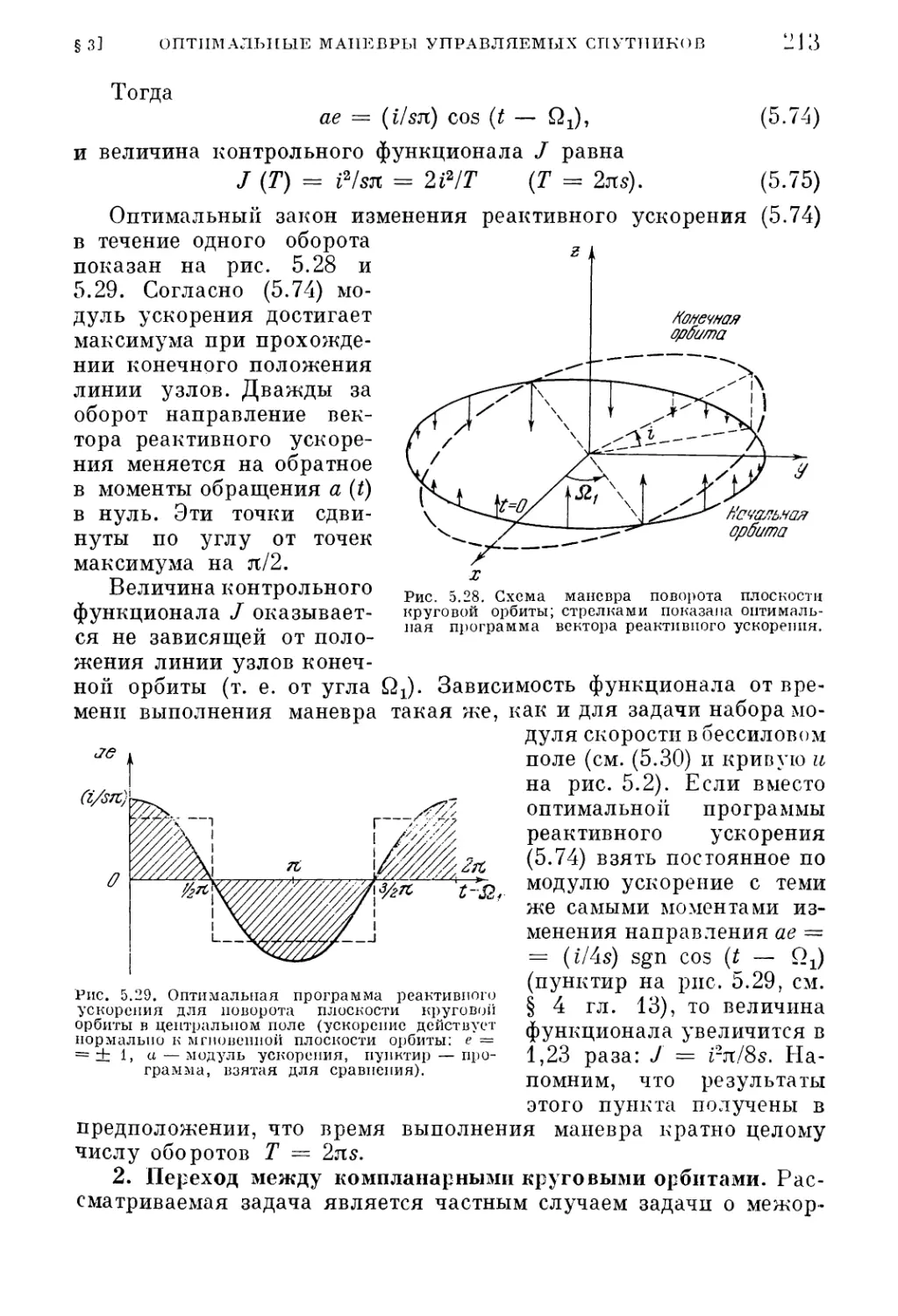
§ 1. Уравнения экстремалей и их свойства
1. Уравнения экстремалей, общий случай (169). 2. Первые интегралы уравне¬
ний экстремалей для пространственного движения в центральном поле (169).
3. Уравнения экстремалей — плоское движение в центральном поле (170).
4. Свойства уравнений (5.13) (171). 5. Особая точка уравнений (5.13) (172).
6. Интегрирование в окрестности особой точки (173). 7. Связь параметров начала
и конца траектории (174). 8. Уравнения экстремалей — плоское движение в поле
двух центров (175). 9. Аналитические решения — плоскопараллельное поле (175).
10. Аналитические решения, однородное центральное поле (177). И. Аналити¬
ческое решение, центральное поле (178).
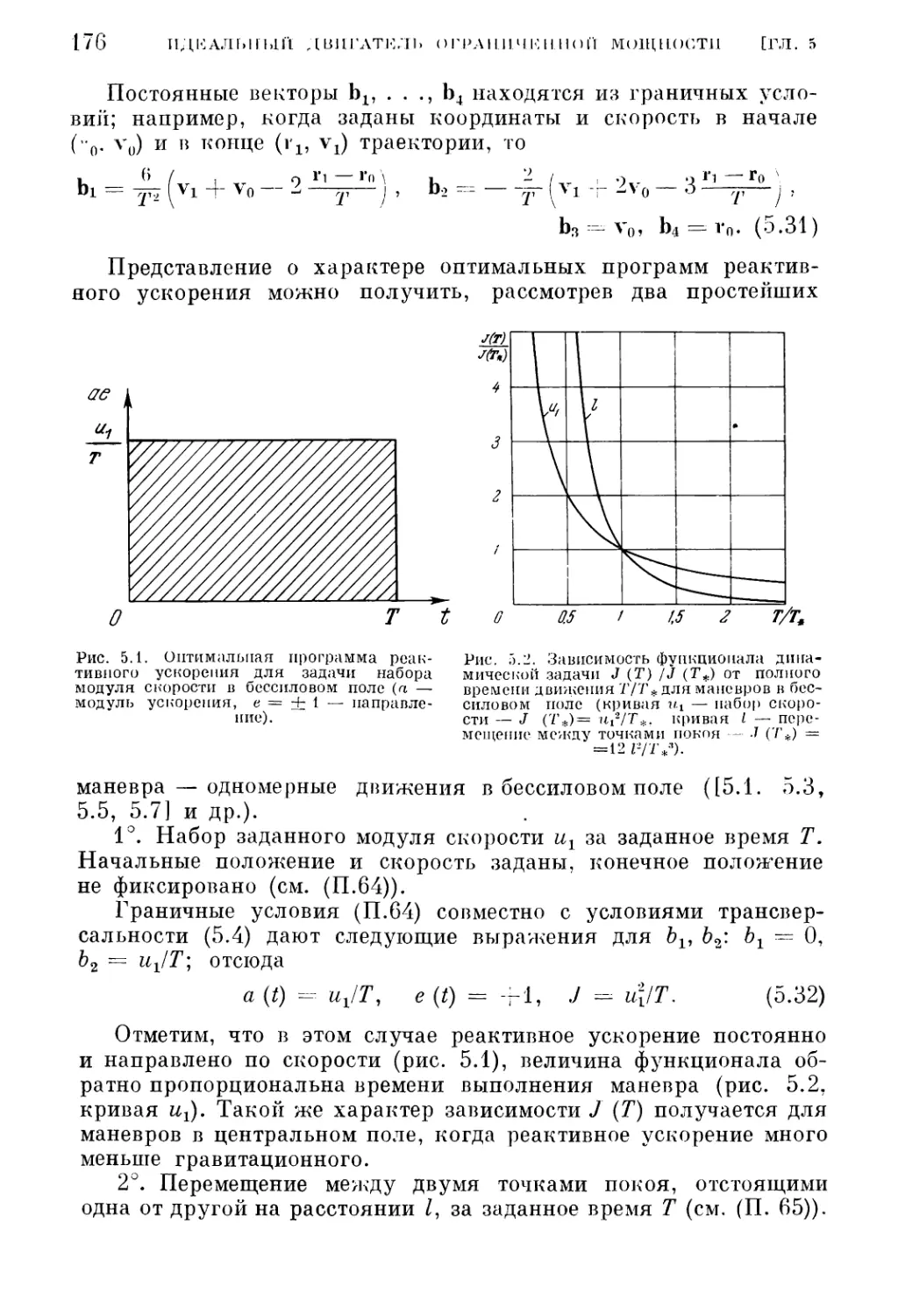
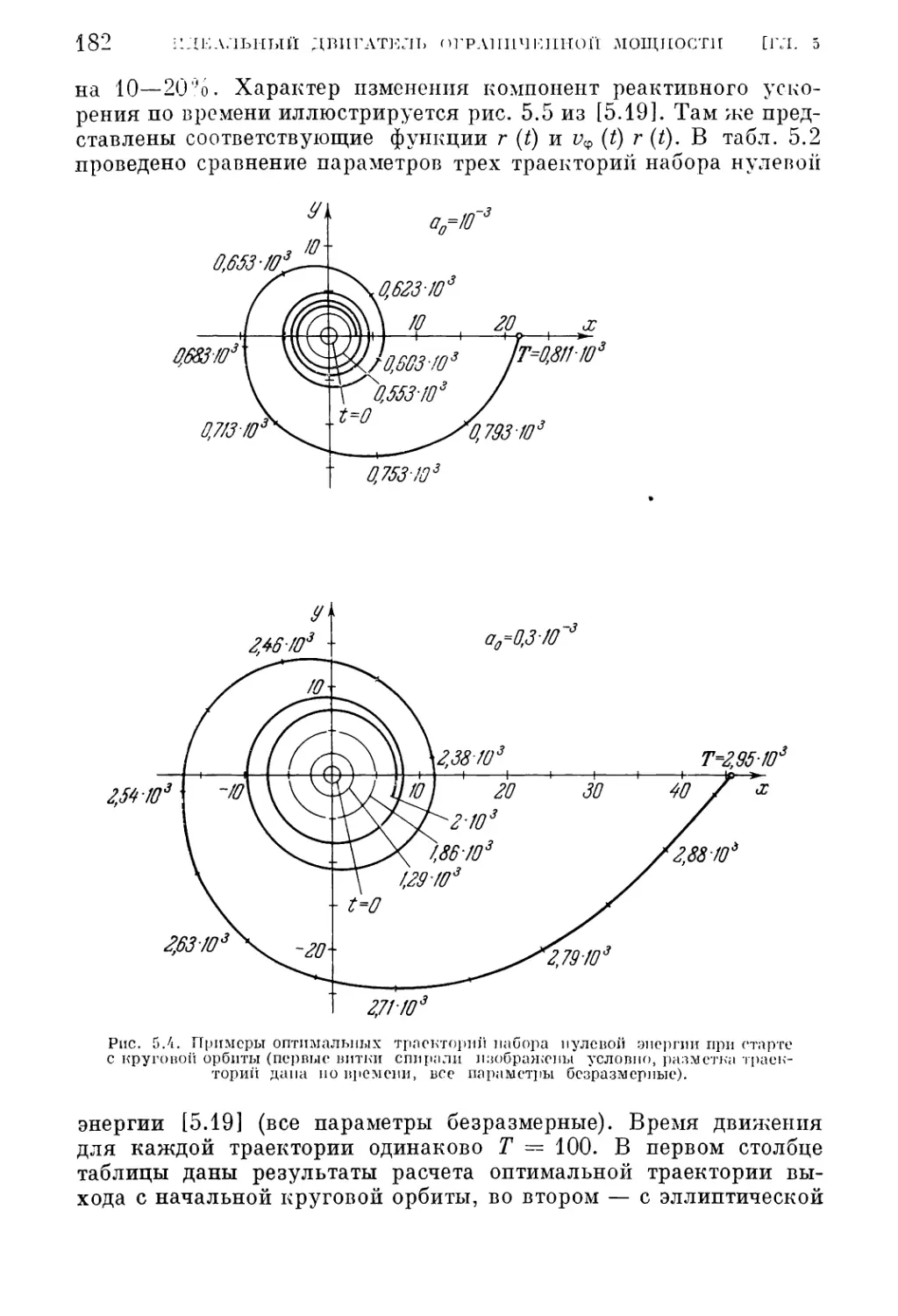
§ 2. Оптимальный межпланетный перелет с идеальным двигателем
ограниченной мощности
1. Набор нулевой энергии (179). 2. Набор нулевой энергии — численные резуль¬
таты (181). 3. Набор нулевой энергии — аналитическое решение (184). 4. Меж-
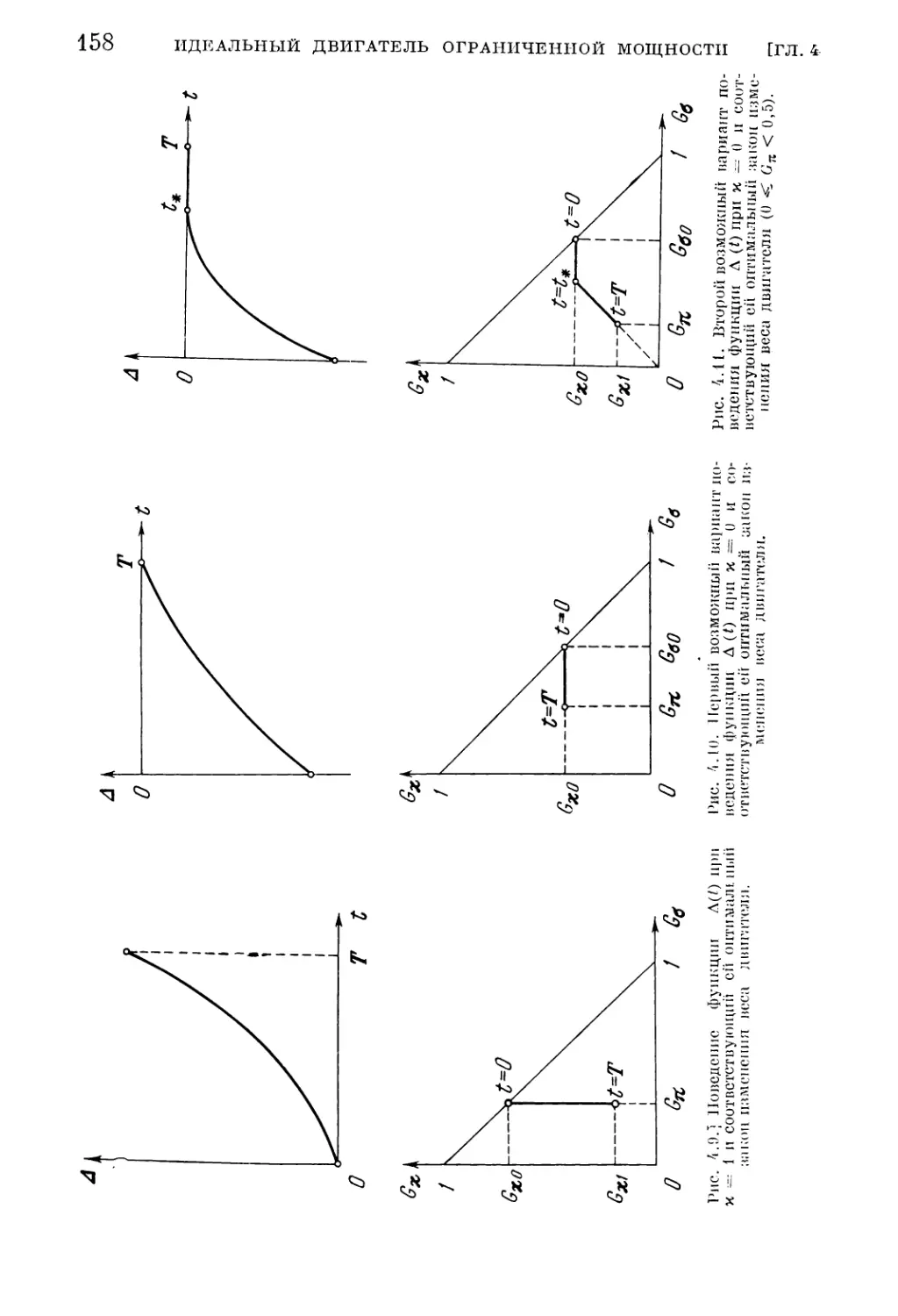
ОГЛАВЛЕНИЕ
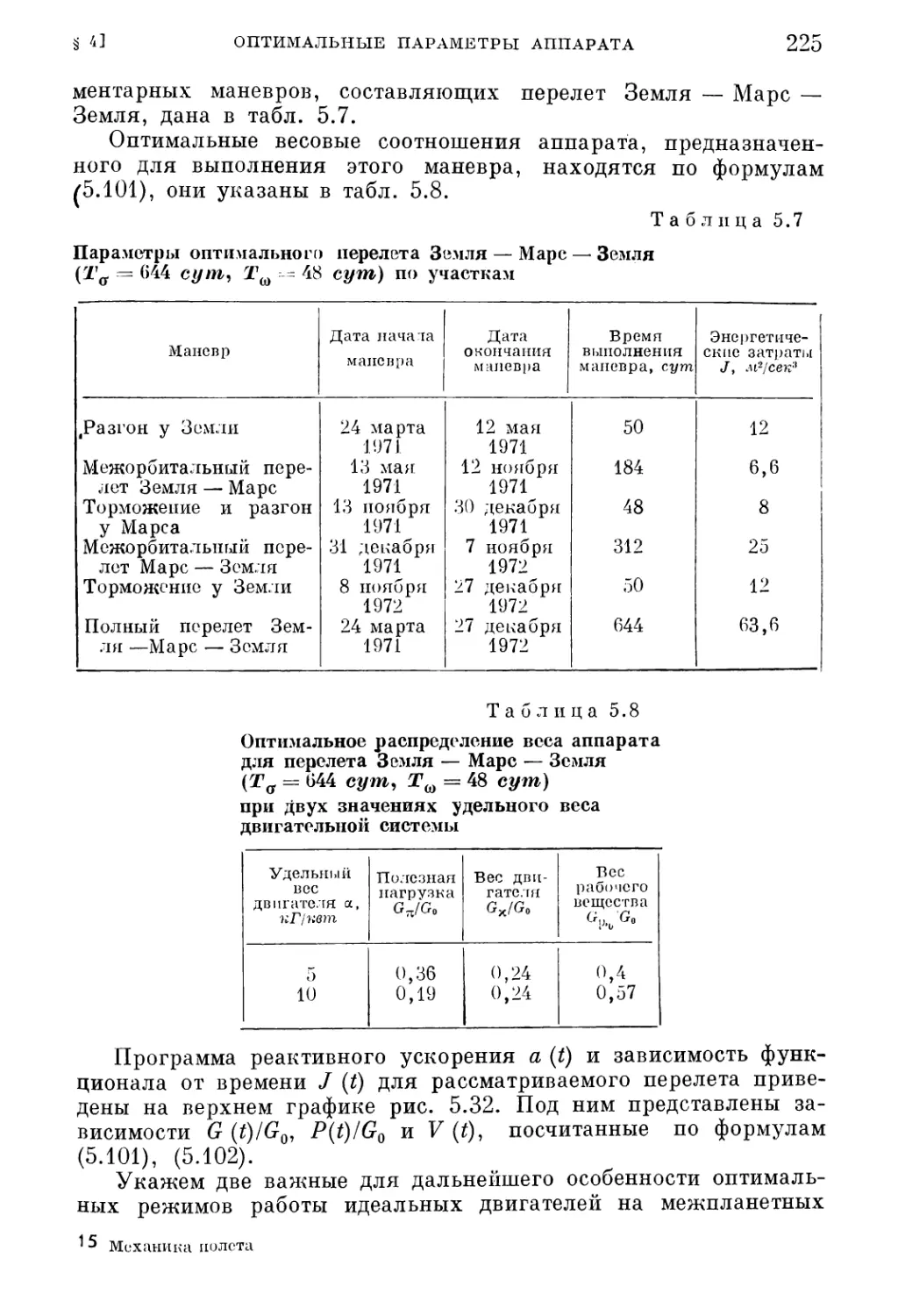
5
орбитальный перелет (186), 5, Решение краевой задачи (5.48) — метод транс¬
портирующей траектории (188). 6. Решение краевой задачи (5.48)—численные
результаты (192). 7. Межпланетный перелет с возвращением (202).
§ 3. Оптимальные маневры управляемых спутников с идеальным
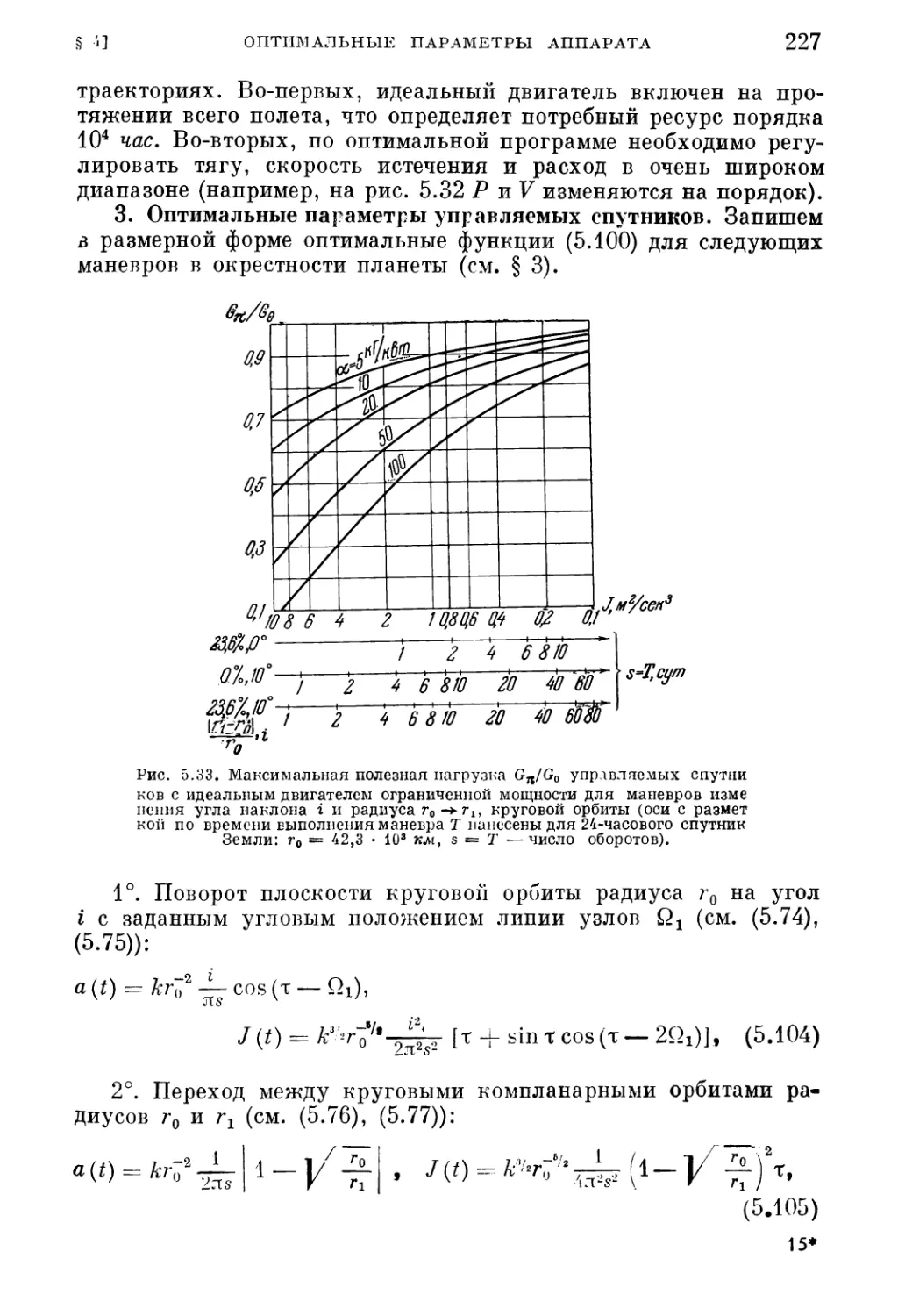
двигателем ограниченной мощности 211
1. Поворот плоскости круговой орбиты (211). 2. Переход между компланар¬
ными круговыми орбитами (213). 3. Переход между некомпланариыми кру¬
говыми орбитами разных радиусов (217).
§ 4. Параметры аппарата с идеальным двигателем ограниченной мощ¬
ности 221
1. Расчетные формулы (221). 2. Оптимальные параметры межпланетных аппа¬
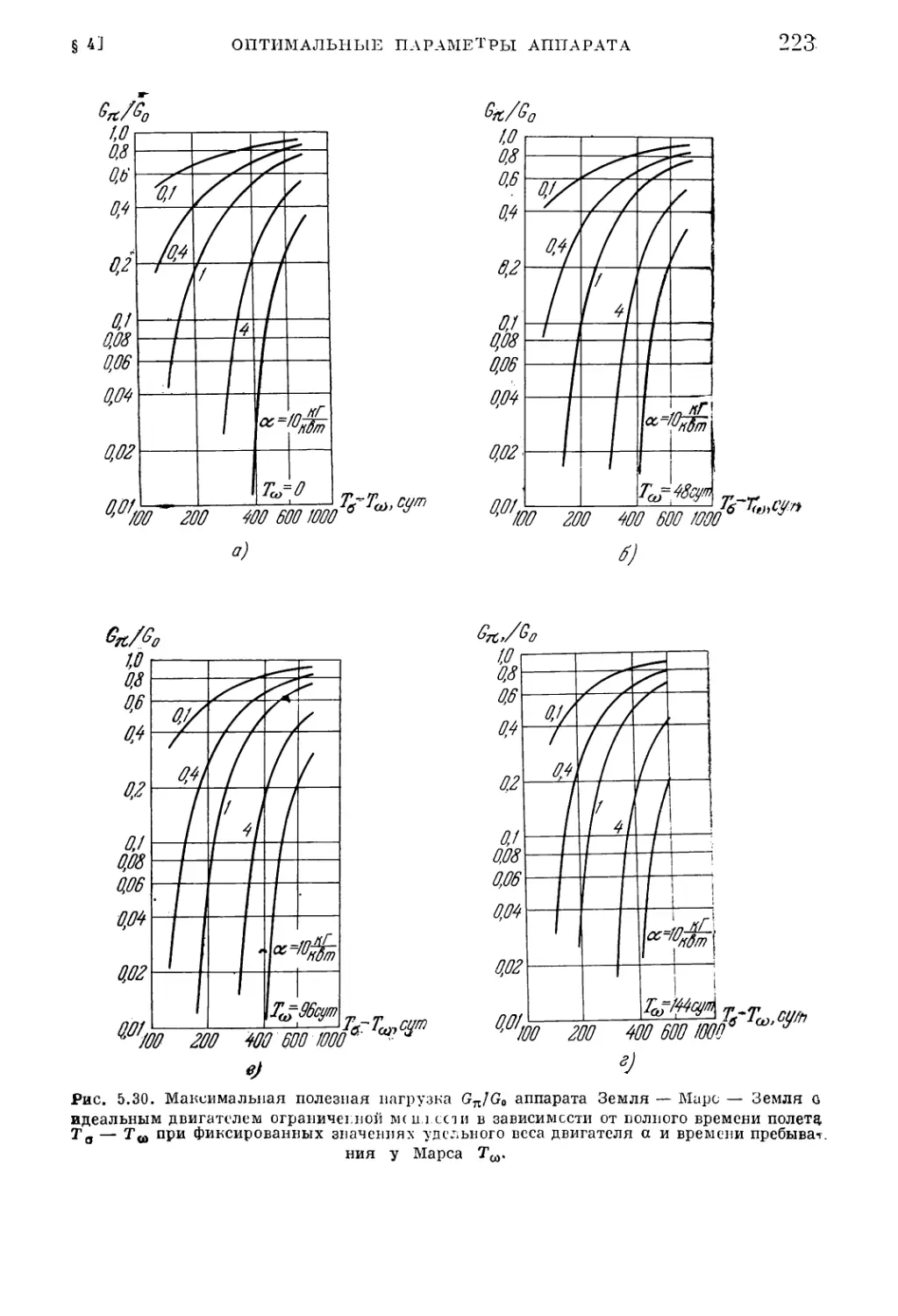
ратов (222). 3. Оптимальные параметры управляемых спутников (227).
Глава 6
Нерегулируемые двигатели — разделение
вариационной задачи,
оптимальные программы вектора тяги
§ 1. Разделение вариационной проблемы на весовую и динамическую
части 230
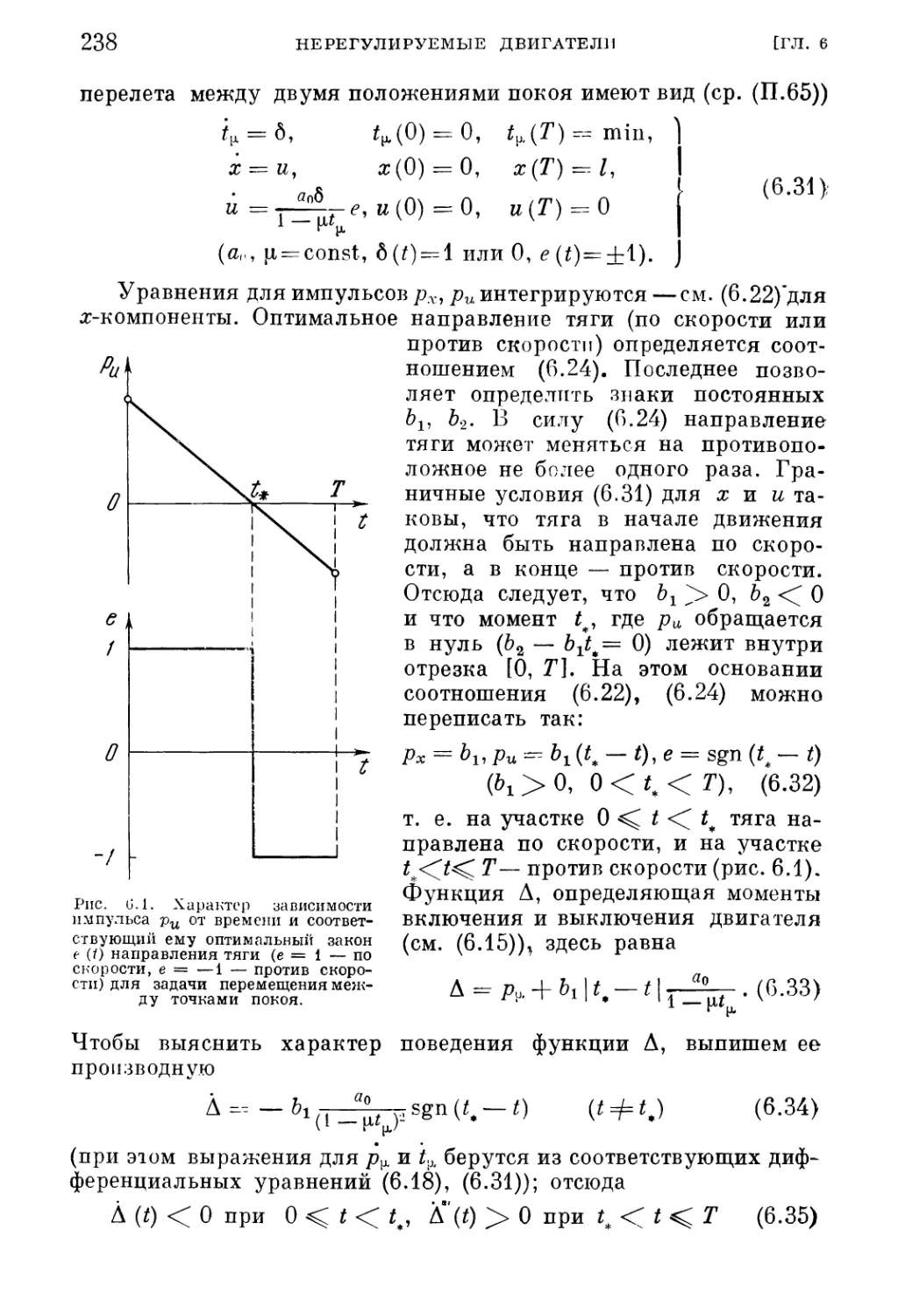
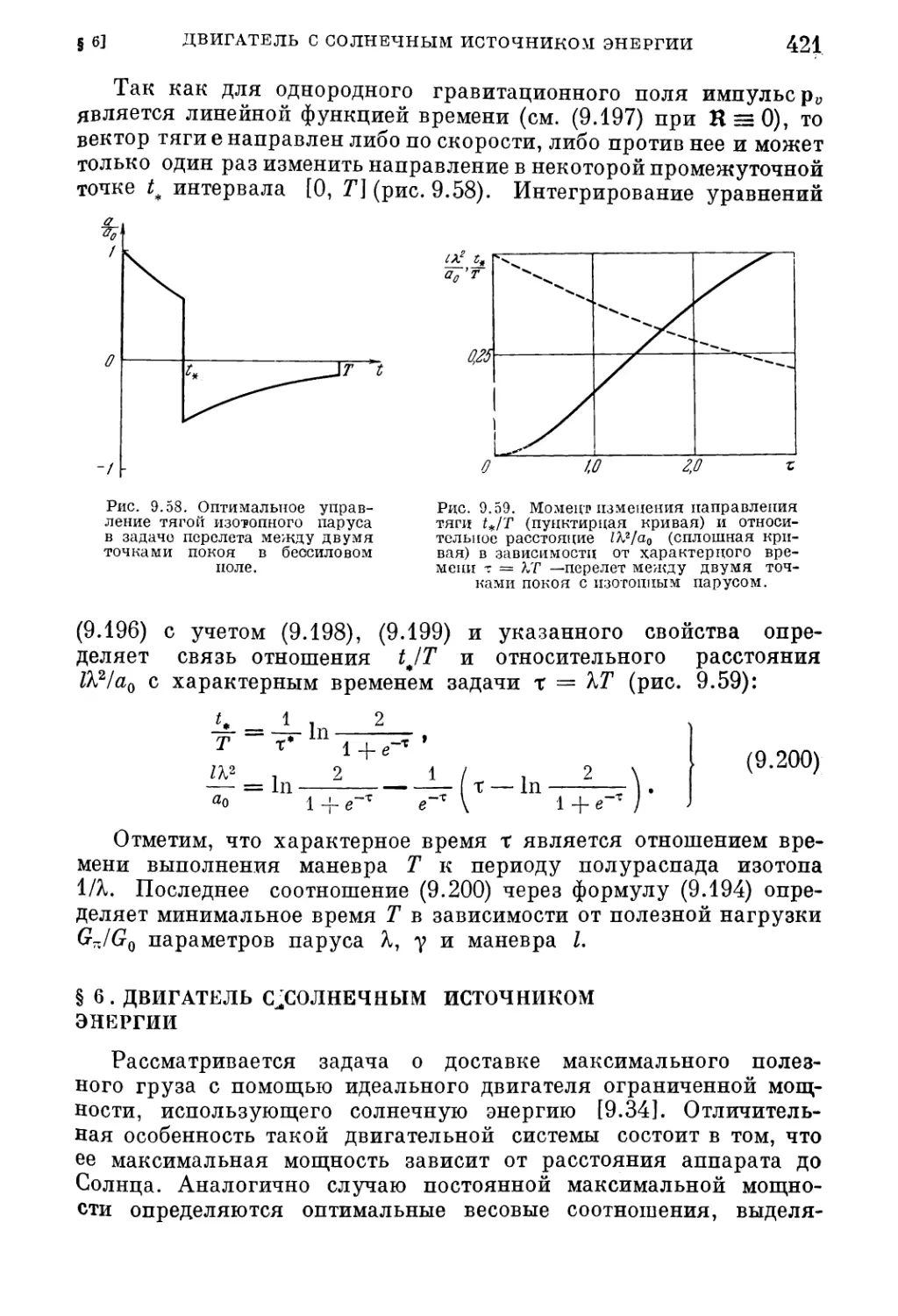
1. Формулировка з!дачи (23)). 2. В лд?лэ шз дя пмической чазгл задач л (231).
§ 2. Уравнения для оптимальной программы вектора тяги. Модельные
задачи 233
1. Произвольное гравитационное поле (233). 2. Центральное поле (234).
3. Плоскопараллелыюе поле (236). 4. Набор модуля скорости в бессиловом поле
(236). 5. Перемещение между точками покоя в бессиловом поле (237).
§ 3. Оптимальный межпланетный перелет с нерегулируемыми дви¬
гателями 240
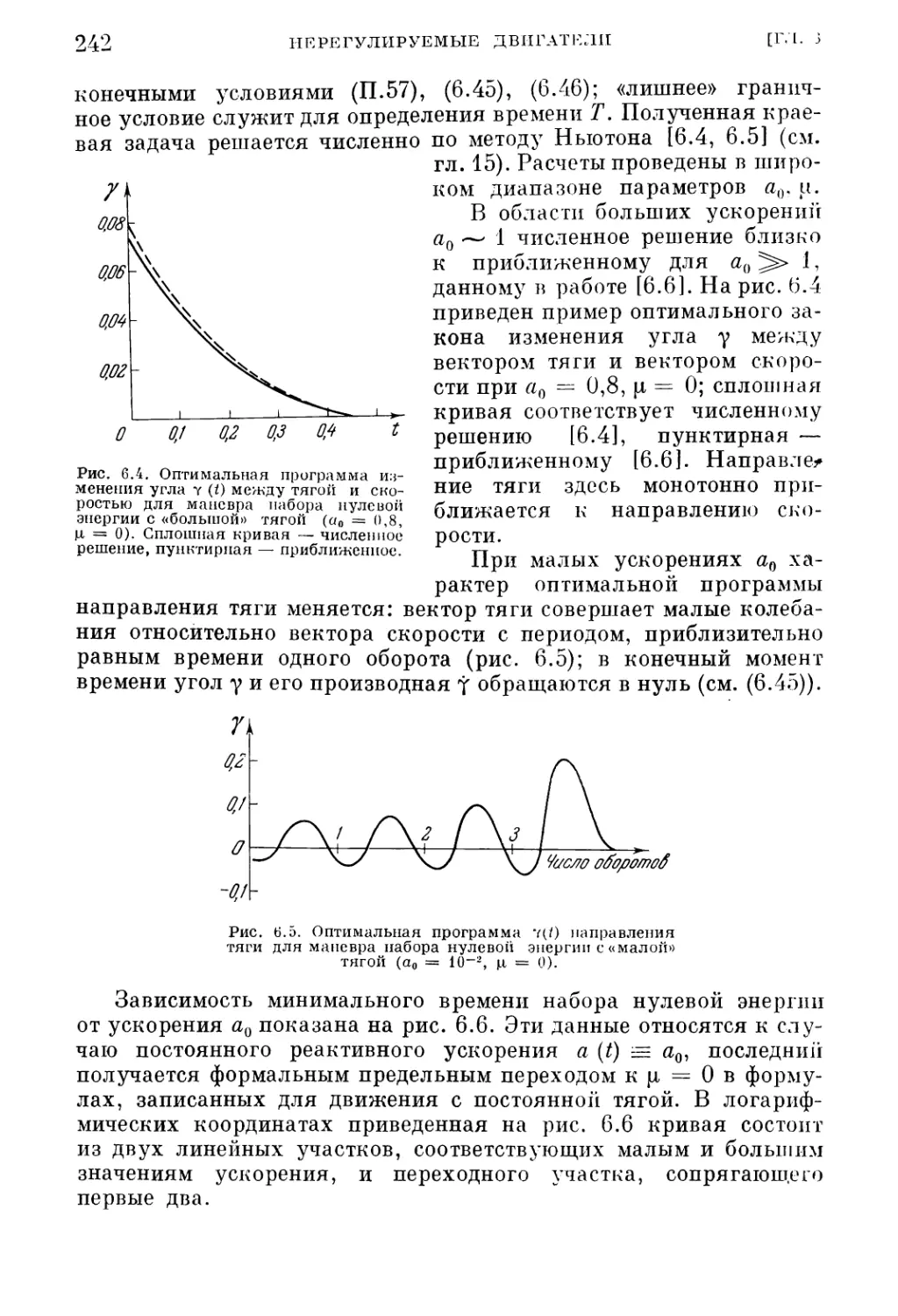
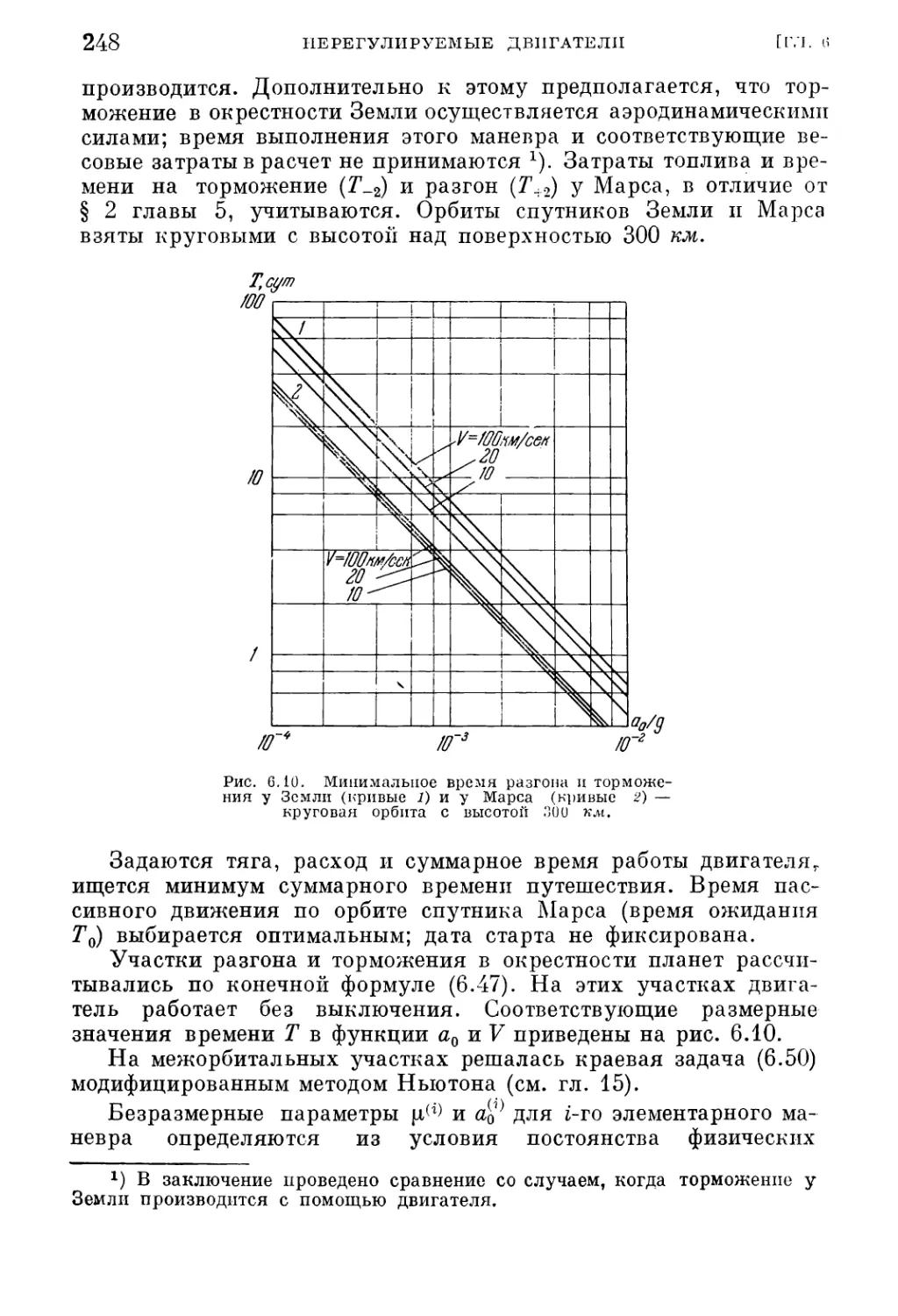
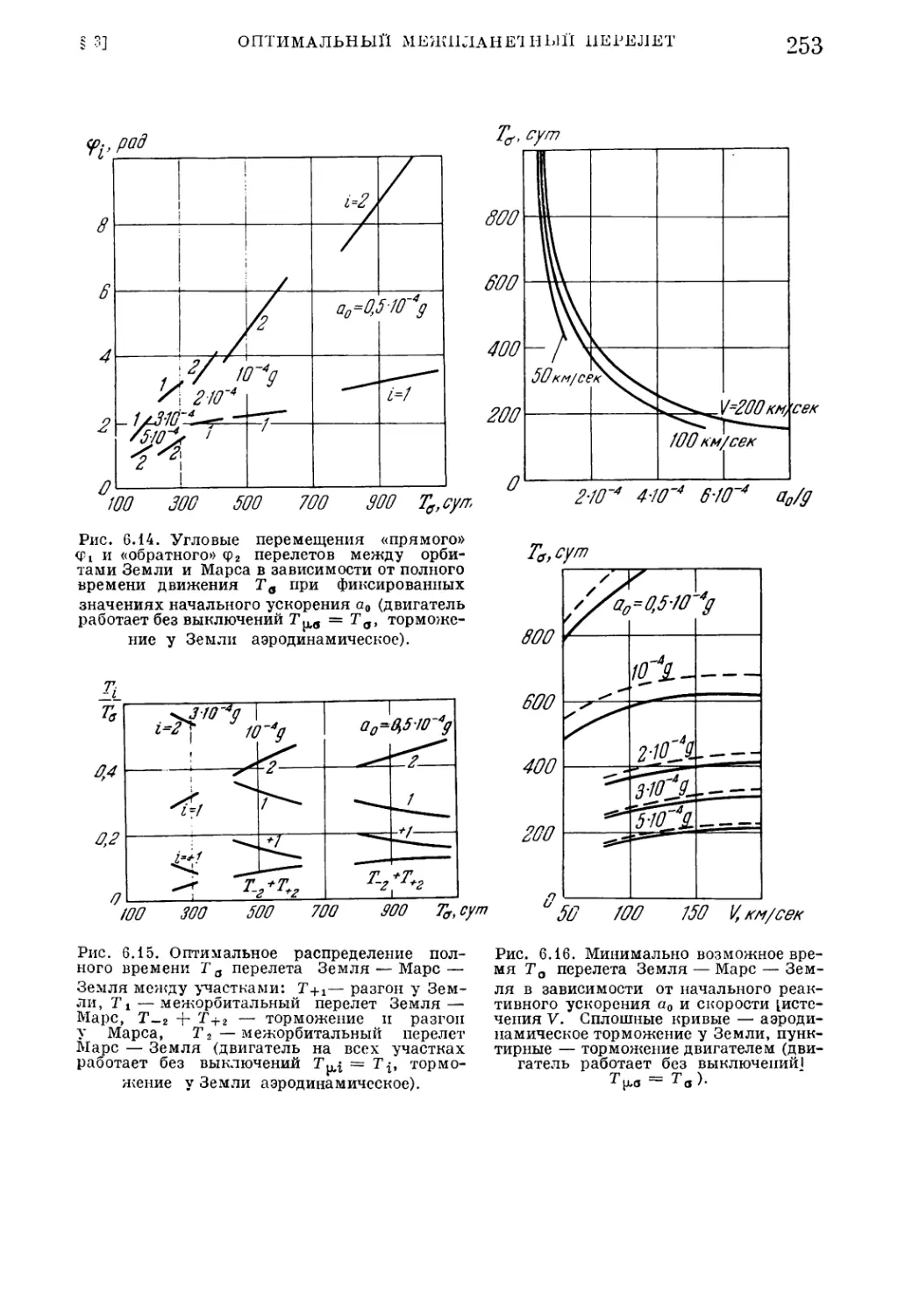
1. Набор нулевой энергии (241). 2. Межорбитальный перелет (244). 3. Межпланет¬
ный перелет с возвращением (247).
§ 4. Оптимальные маневры управляемых спутников с нерегулируе¬
мыми двигателями 254
1. Удержание спутника в заданном шаровом слое (254). 2. Поворот плоскости
круговой орбиты (258).
§ 5. Параметры аппарата с нерегулируемым двигателем ограниченной
мощности 262
1. Расчетные формулы (262). 2. Набор модуля скорости (265). 3. Перемещение
между точками покоя (266). 4. Межпланетный перелет Земля — Марс (267).
5. Удержание спутника в заданном щаровом слое (269). 6. Поворот плоскости
круговой орбиты (270).
Глава 7
Реальные двигатели ограниченной мощности
§ 1. Дополнительные весовые компоненты 273
1. Учет веса баков (273). 2. Учет веса движителя (276).
6
ОГЛАВЛЕНИЕ
§ 2. Заданное время работы двигателя 280
1. Общая методика (281). 2. Применение общей методики к изучаемой проблеме
(283). 3. Маневры в бессиловом поле (284). 4. Поворот плоскости круговой
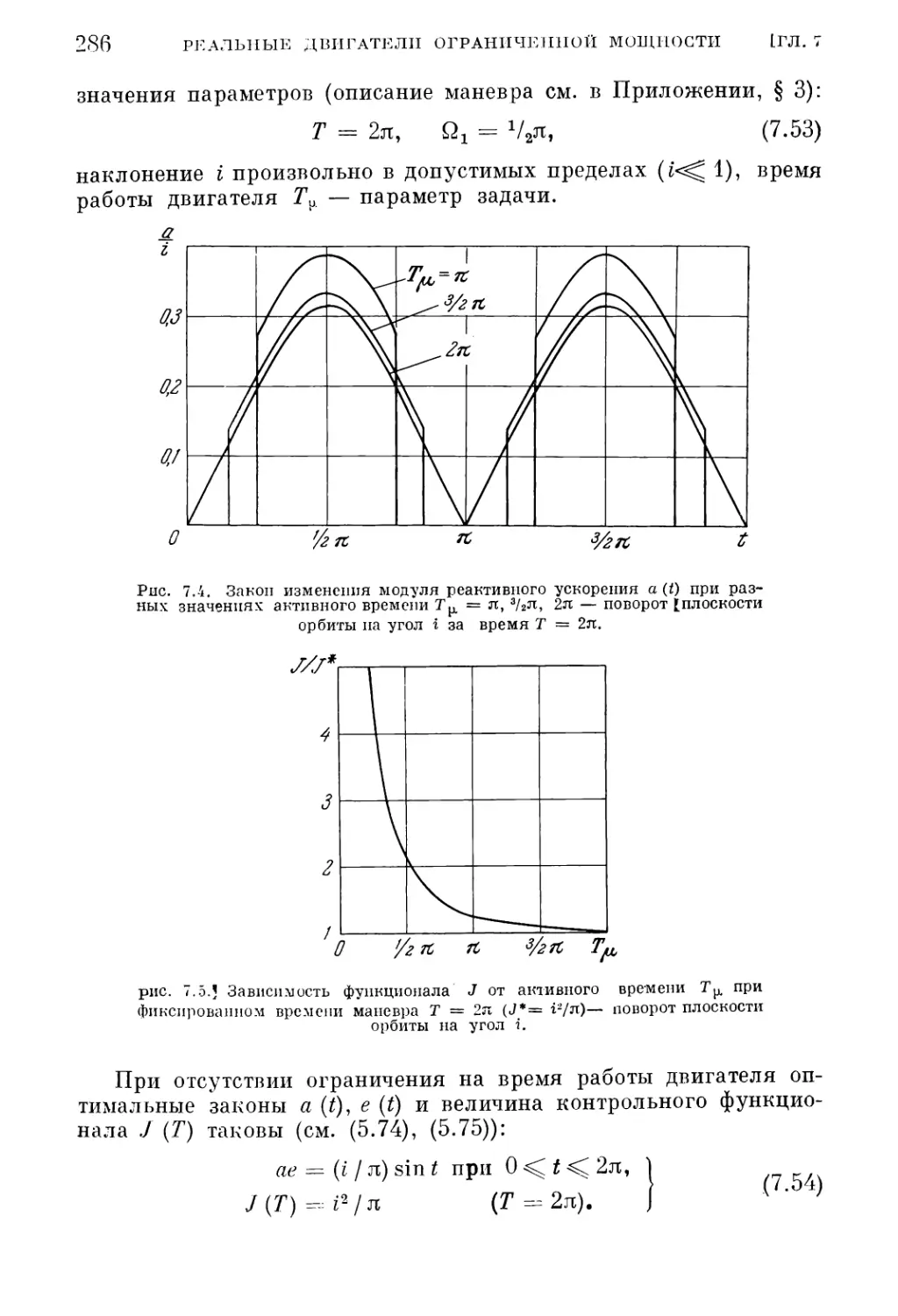
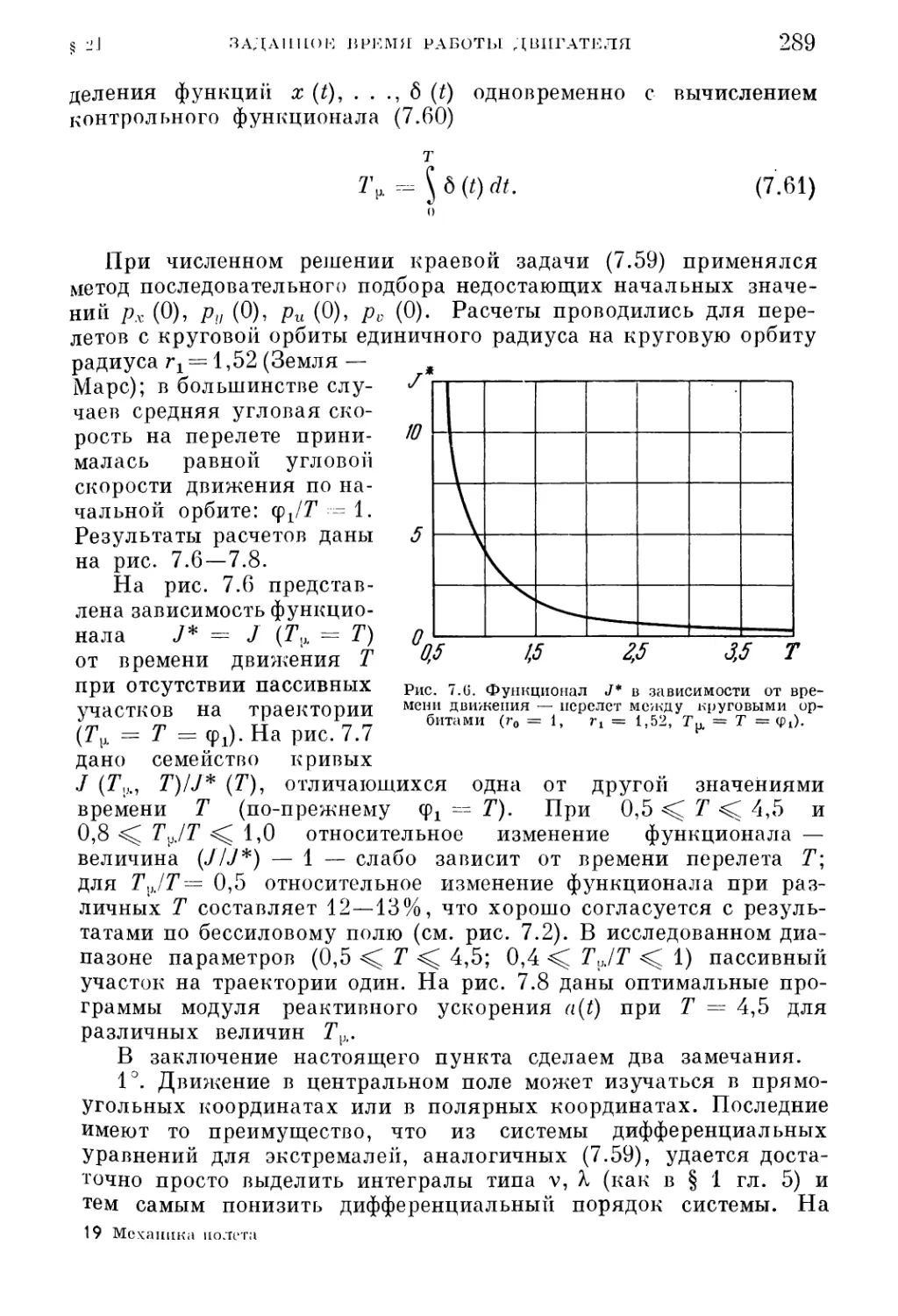
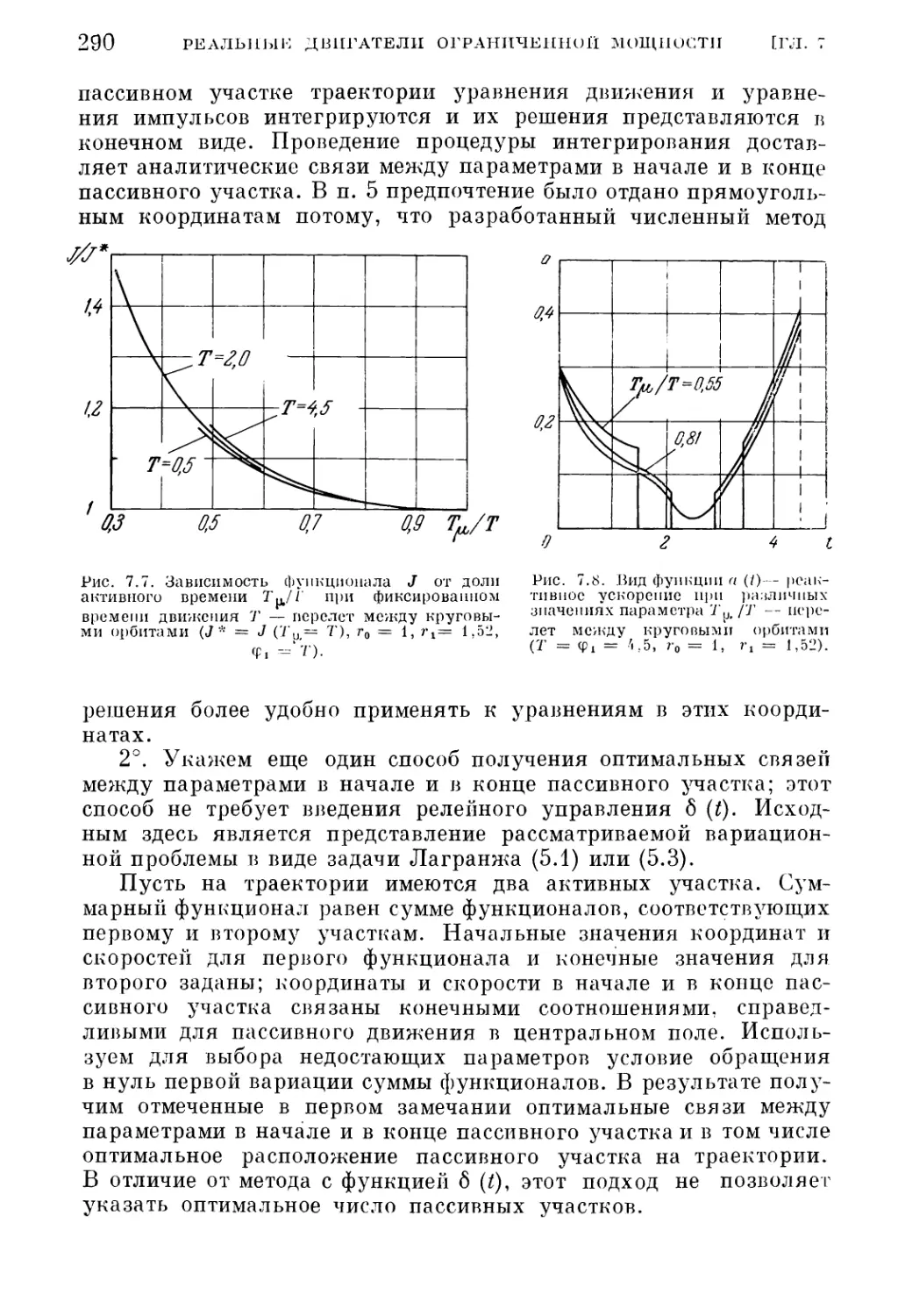
орбиты (285). 5. Межорбитальный перелет (287).
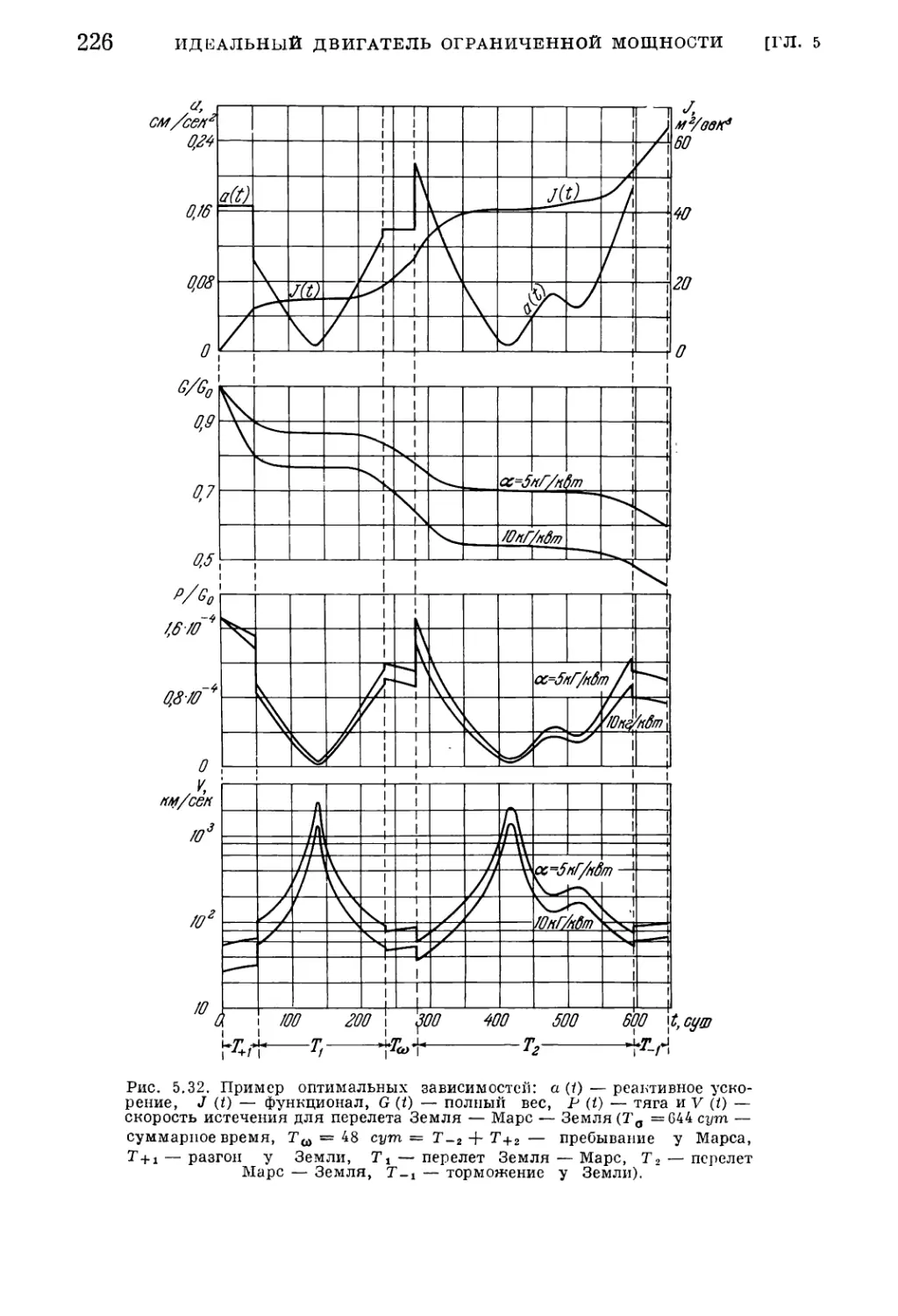
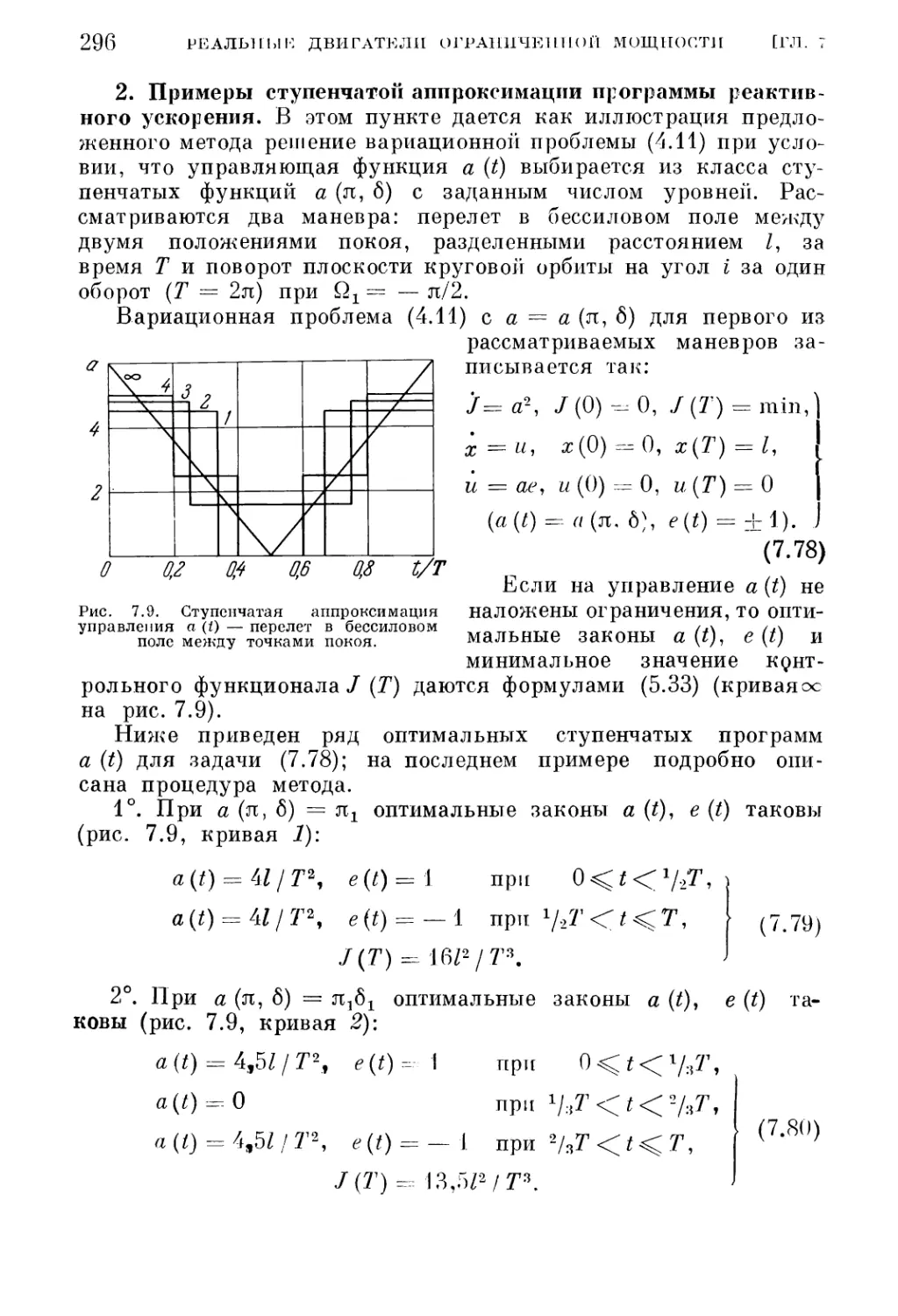
1. Общая методика (291). 2. Примеры ступенчатой аппроксимации программы
реактивного ускорения (295). 3. Формулировка задачи аппроксимации программы
тяги с учетом веса движителей (331). 4. Ступенчатая программа тяги с опти¬
мальным числом уровней для межорбитального перелета (304).
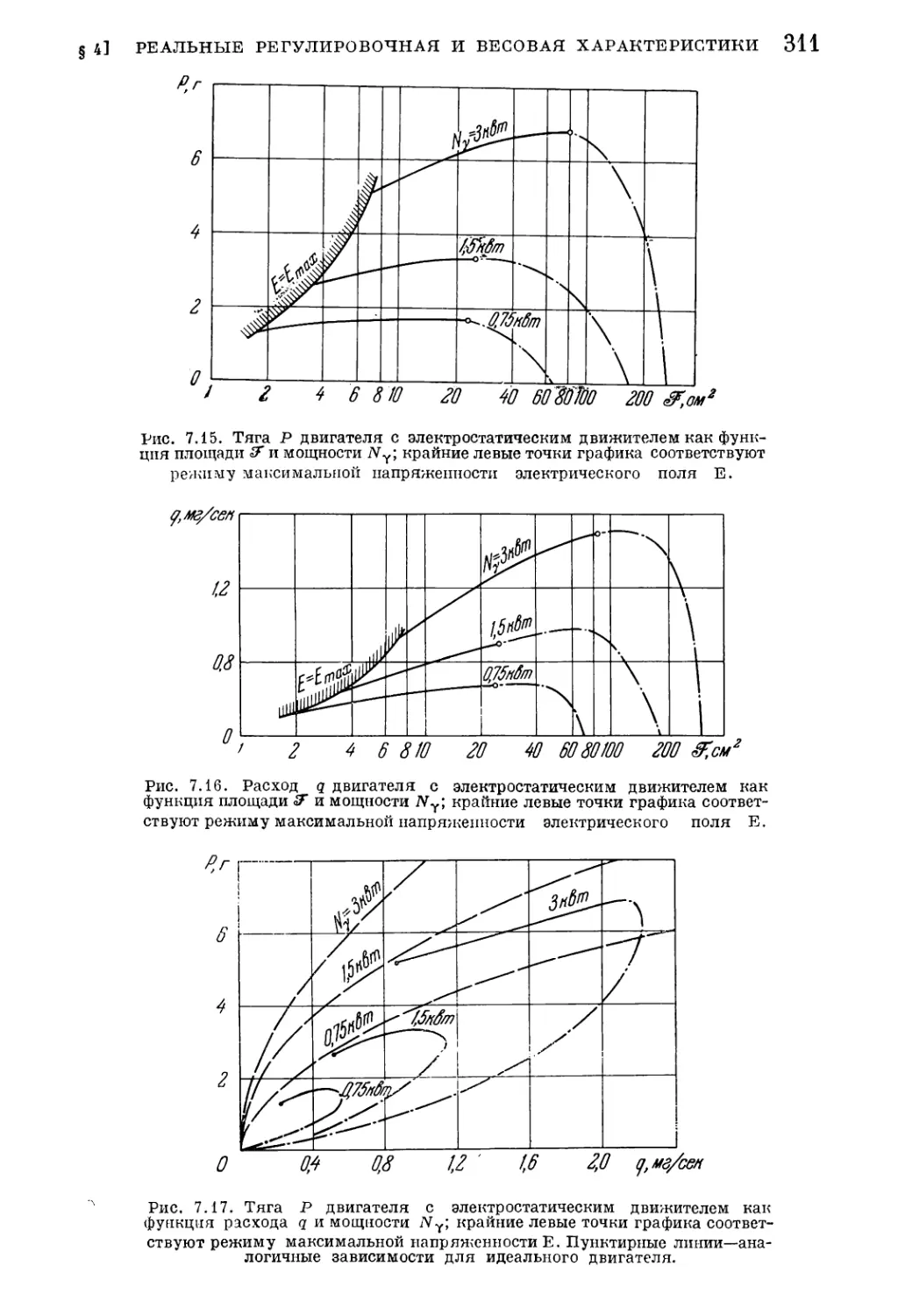
§ 4. Реальные регулировочная и весовая характеристики 309
1. Характеристики двигателя с электростатическим движителем (309). 2. Оп¬
тимальные программы регулирования реальных двигателей (310). 3. Оптималь¬
ные параметры нерегулируемых реальных двигателей (314).
Глава 8
Двигатели ограниченной скорости истечения.
Оптимальное сочетание двигателей
ограниченной скорости истечения
и ограниченной мощности
§ 1. Особенности характеристик и оптимальных режимов работы
двигателей ограниченной скорости истечения 318
1. Характеристики двигателей ограниченной скорости истечения (318). 2. Осо¬
бенности оптимальных режимов работы идеальных двигателей ограниченной
скорости истечения (318). 3. Учёт веса двигателя (321).
§ 2. Оптимальные условия сочетания двигателей ограниченной ско¬
рости истечения и ограниченной мощности 328
1. Общие оптимальные условия сочетания (328). 2. Оптимальные условия со¬
четания нерегулируемых двигателей (330). 3. Оптимальные условия сочетания
идеальных двигателей (334).
§ 3. Области применения двигателей ограниченной мощности . . . 343
1. Набор параболической скорости (344). 2. Перелет между круговыми орбитами
(345). 3. Межпланетный перелет Q возвращением (347). 4. Замечания (348).
Глава 9
Двигательные системы с накоплением энергии и массы.
Двигатели, тяга и мощность которых
зависят от координат и времени
§ 1. Двигатели ограниченной мощности с аккумулятором энергии —
1. Регулировочная и весовая характеристики (350). 2. Формулировка вариа¬
ционной проблемы. Состав оптимального управления (351) 3. Идеально регули¬
руемая двигательная система (355). 4. Маневры перемещения между точками
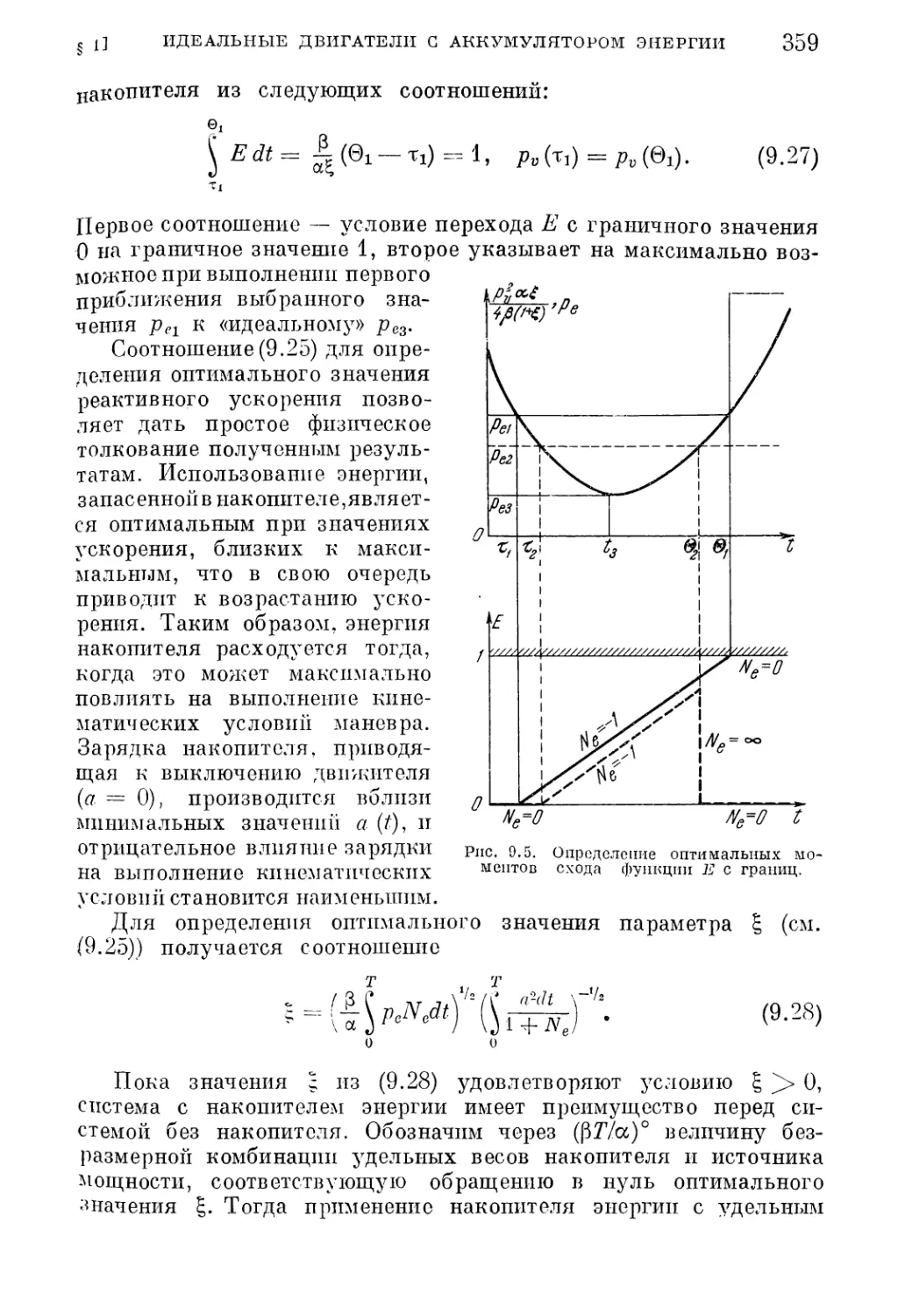
покоя и поворота плоскости круговой орбиты (360).
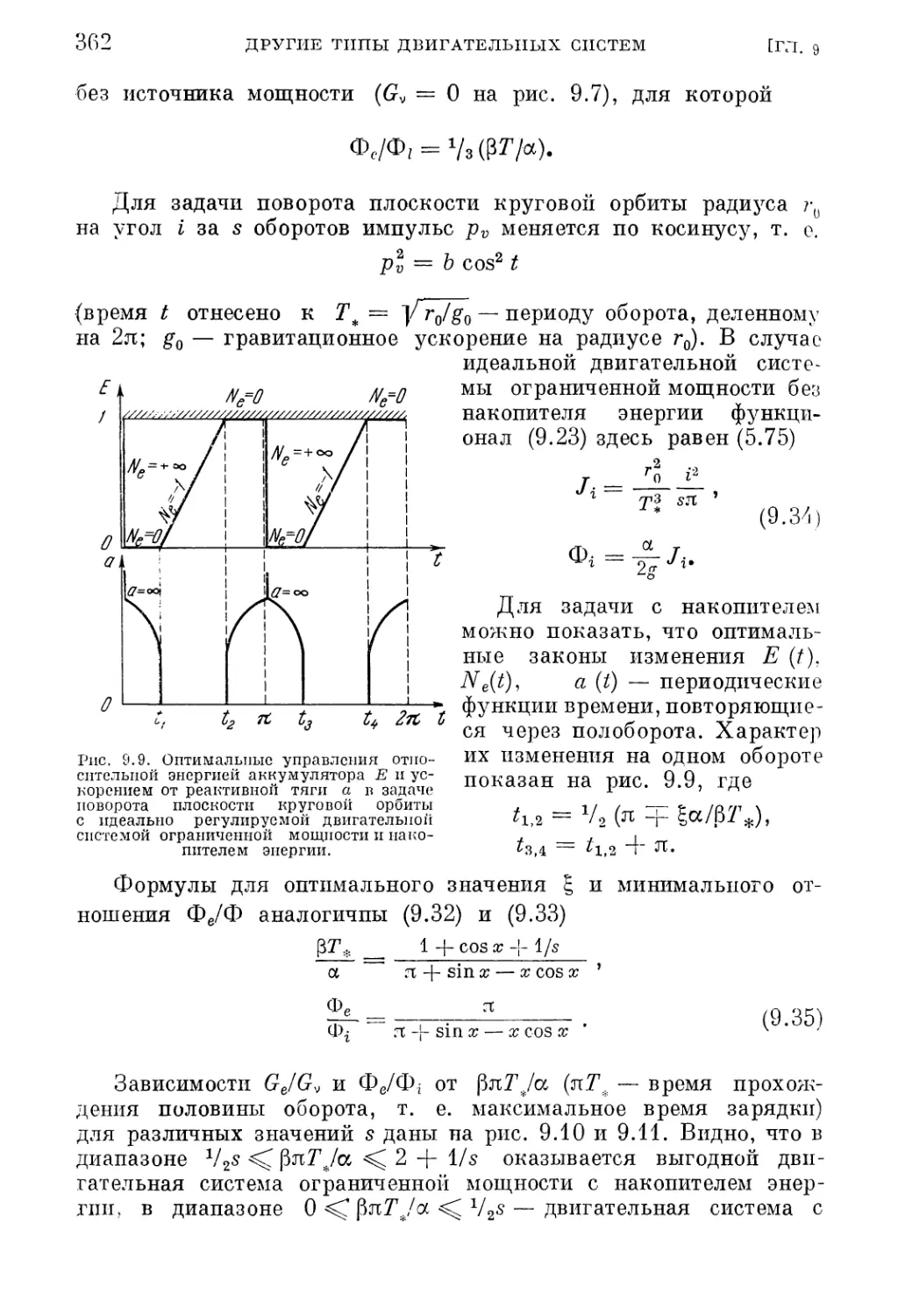
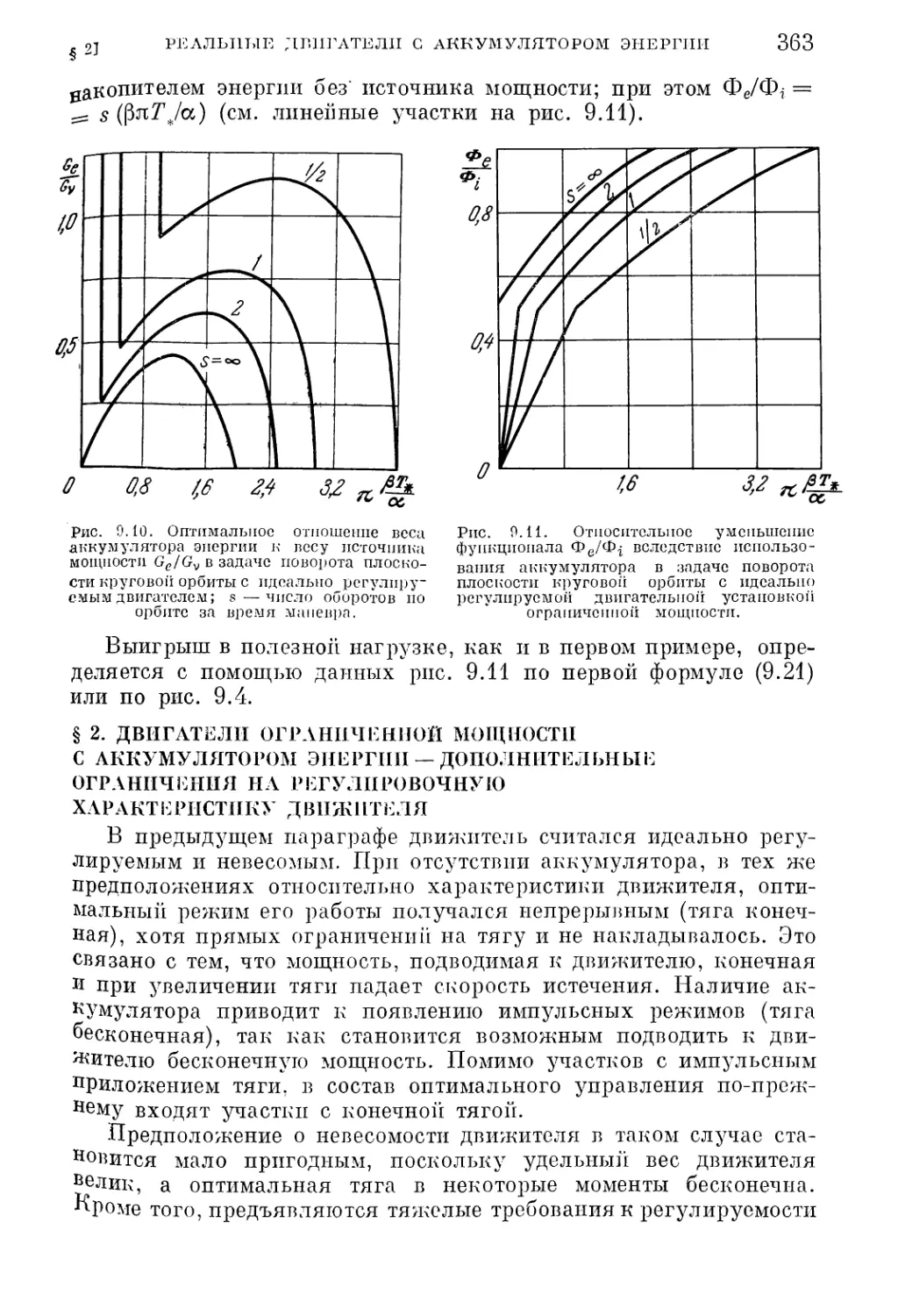
§ 2. Двигатели ограниченной мощности с аккумулятором энергии —
дополнительные ограничения на регулировочную характеристику
движителя 363
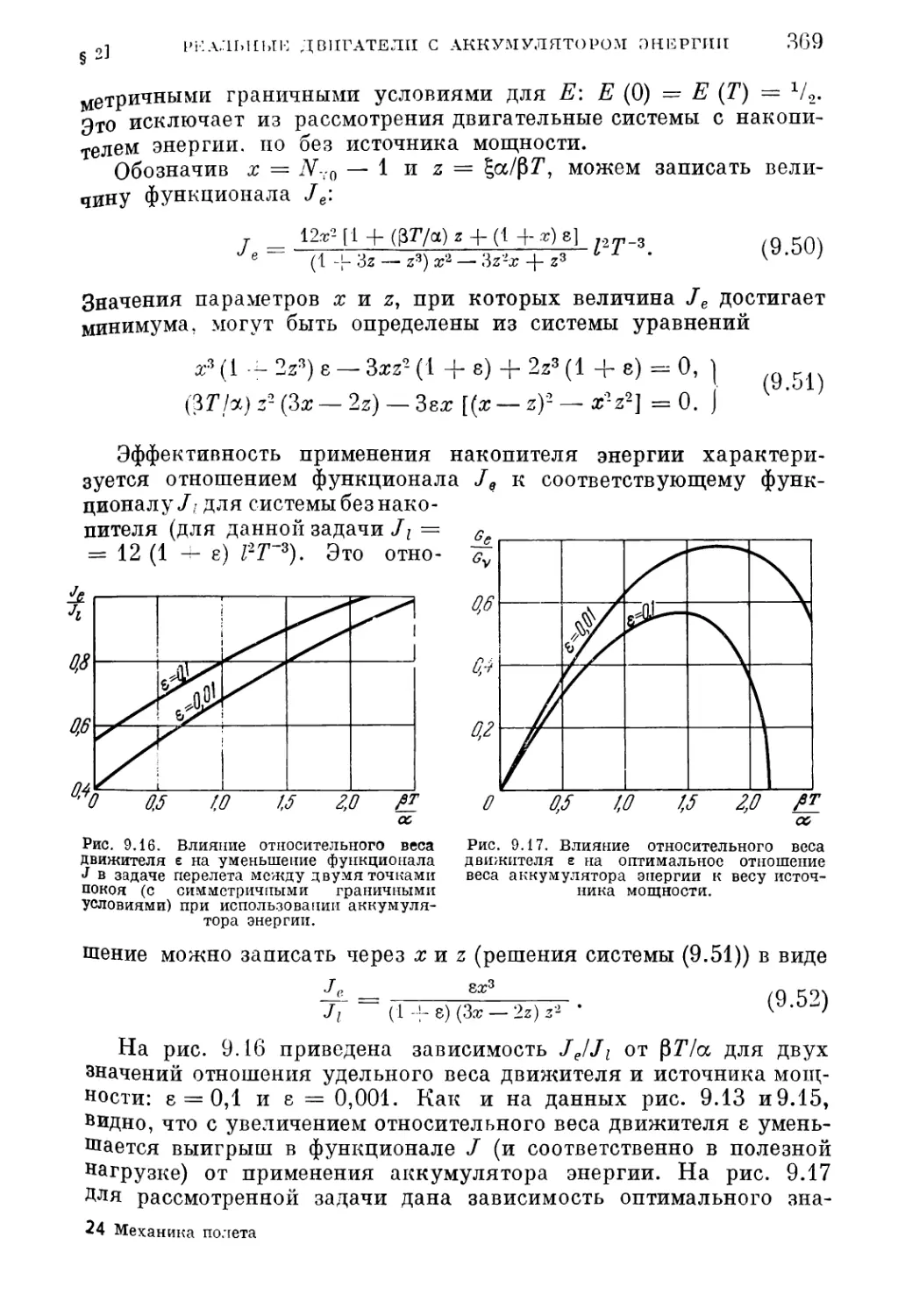
1. Нерегулируемый движитель (364). 2. Движитель ограниченной мощности (368).
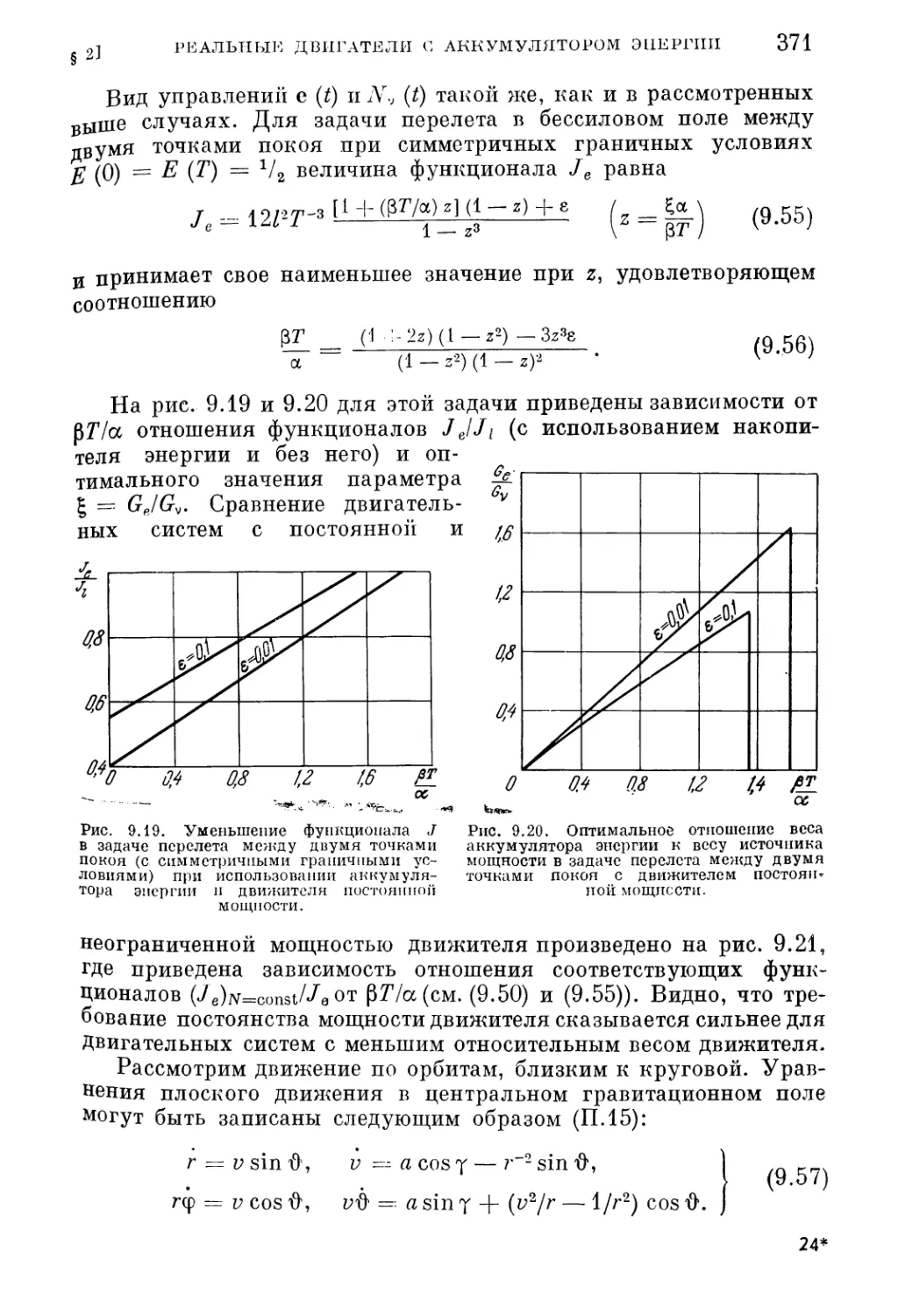
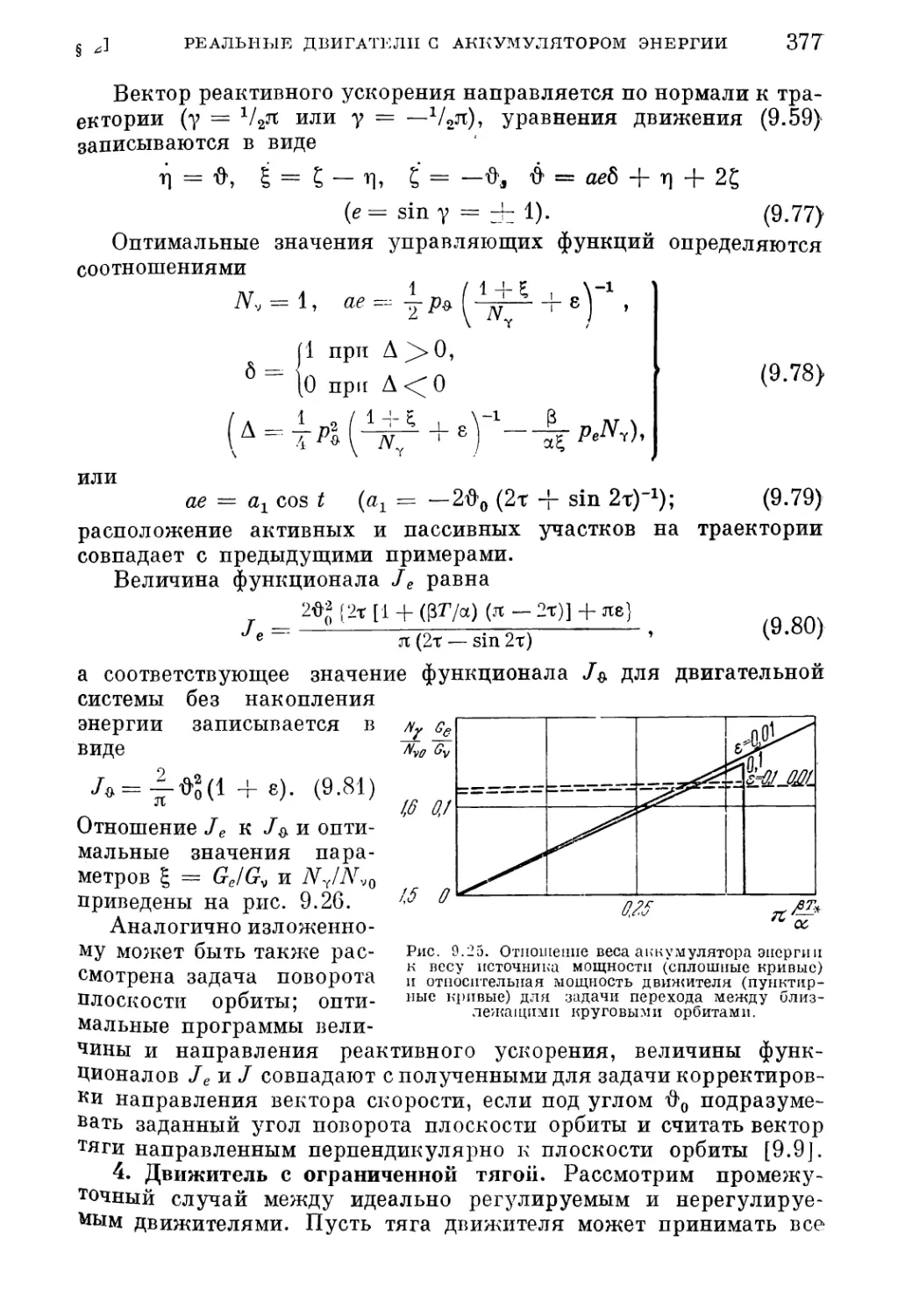
3. Движитель постоянной мощности (370). 4. Движитель с ограниченной тягой i
§ 3. Оптимальная ступенчатая программа тяги
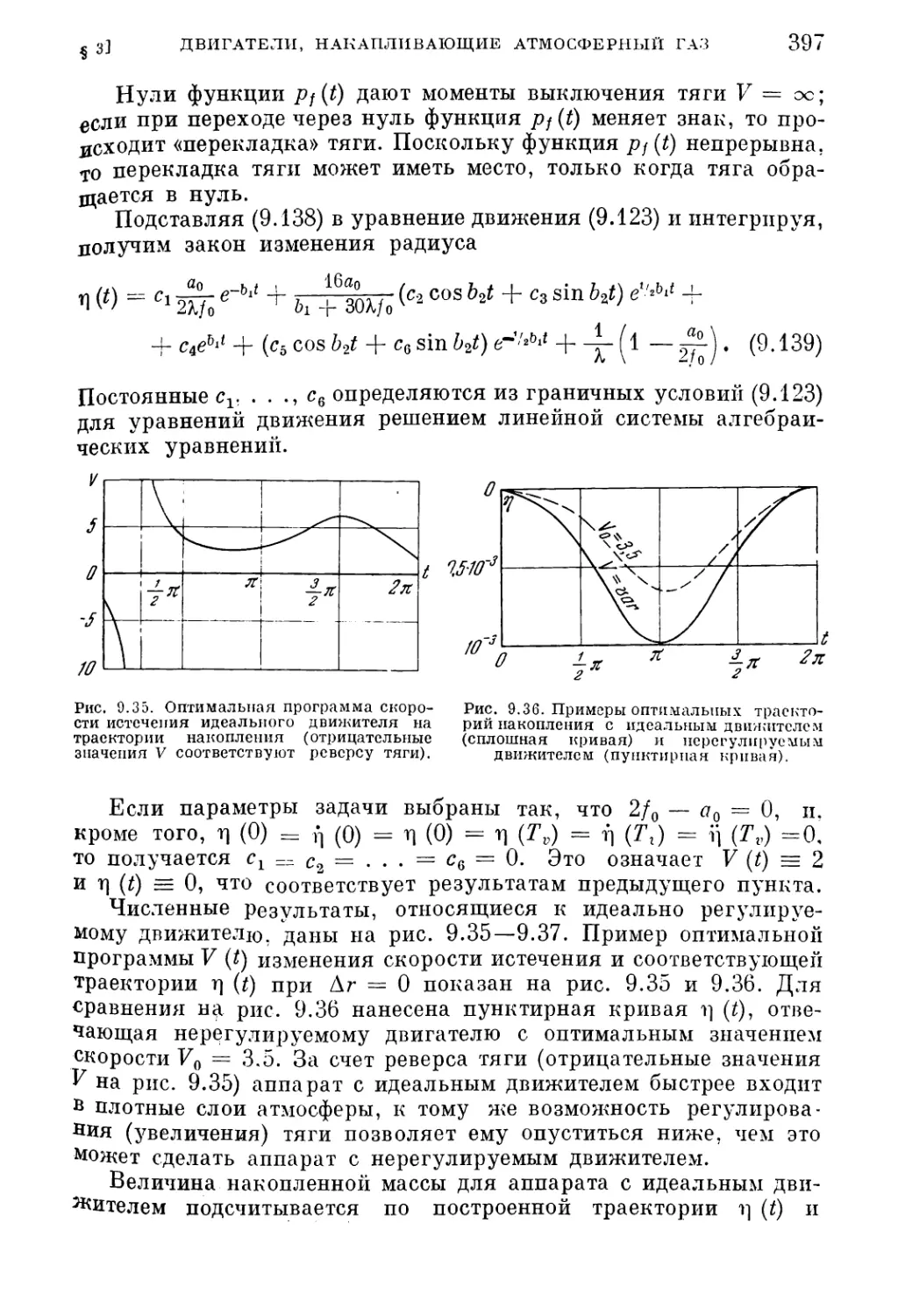
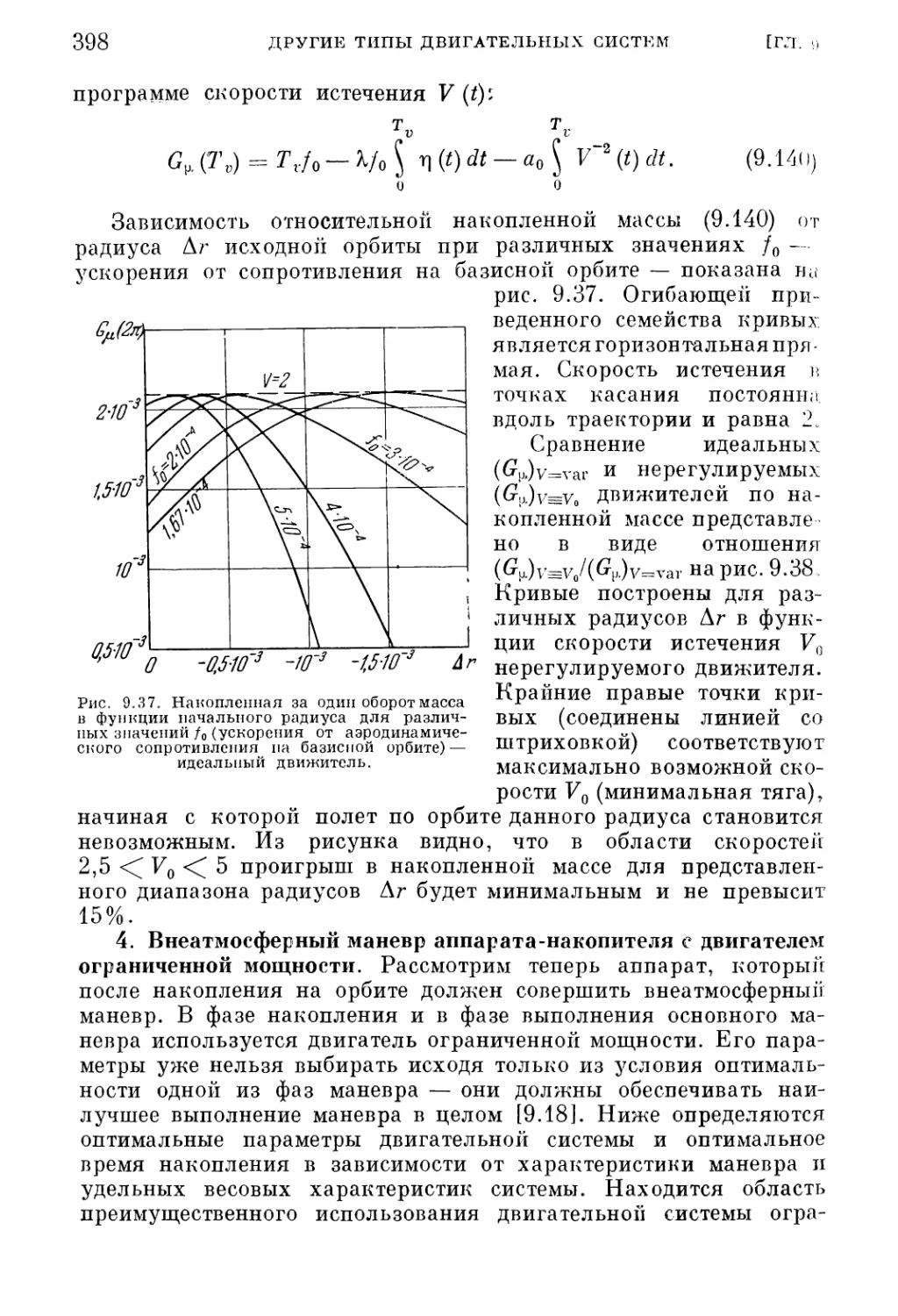
291
идеальный случай .
349
ОГЛАВЛЕНИЕ
7
(377). 5. Движитель ограниченной скорости истечения (380). 6. Движитель
с ограниченным временем работы (383).
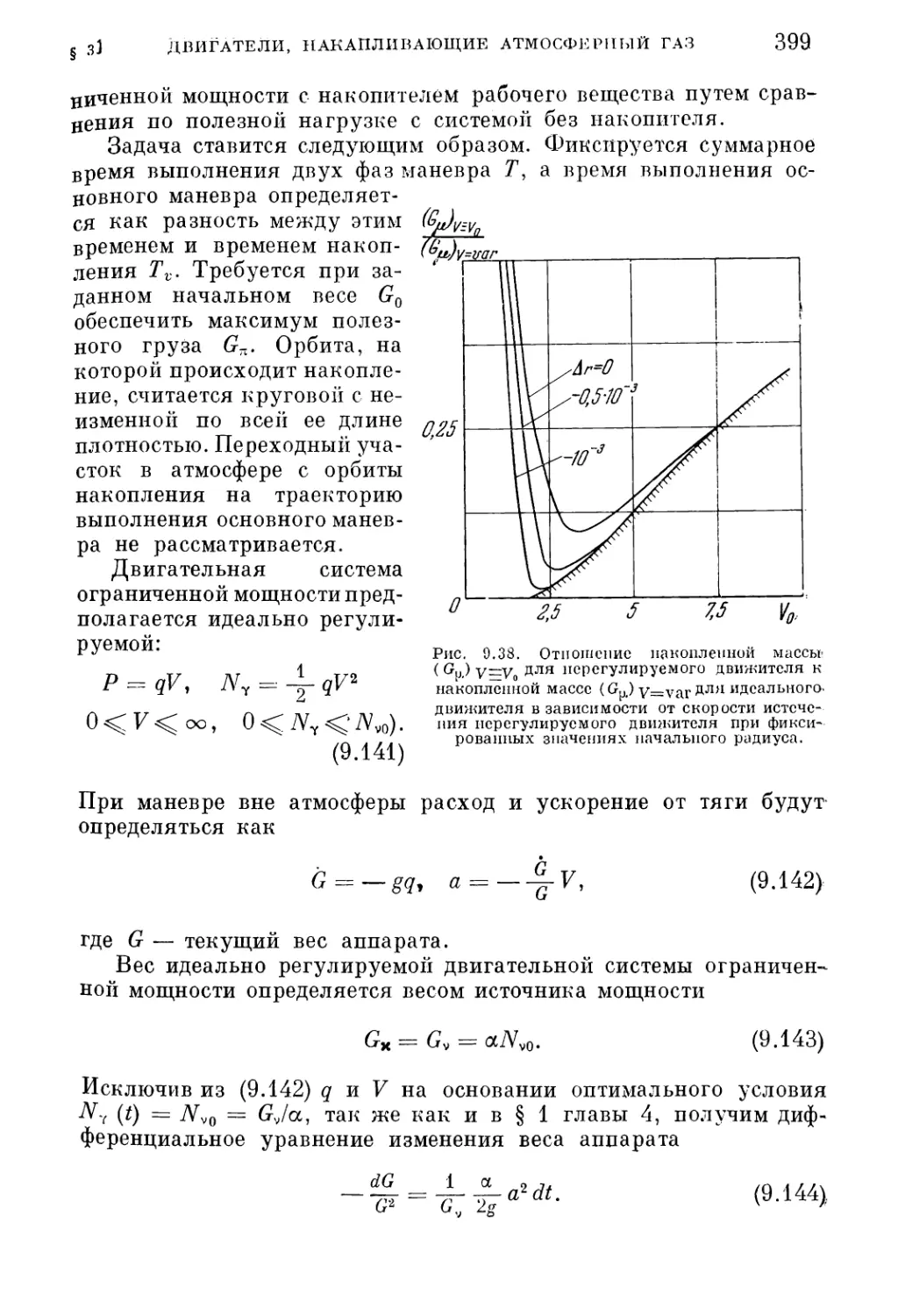
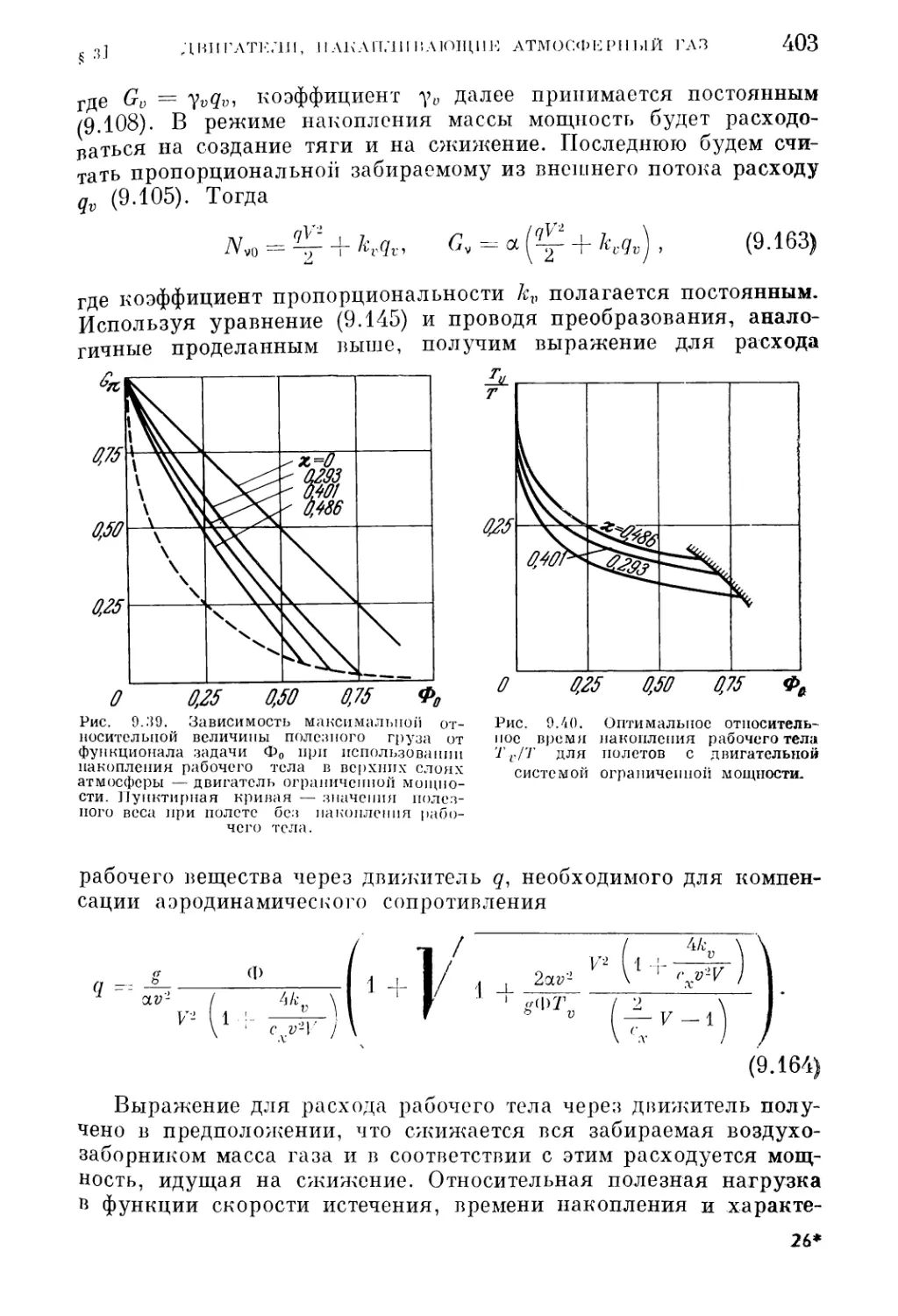
§ 3. Двигательные системы с накоплением атмосферного газа . . • 384
1. Характеристики двигательной установки с накопителем рабочего вещества (385),
2. Накопление в стационарном режиме(387). 3. Накопление в нестационарном ре¬
жиме (389). 4. Внеатмосферный маневр аппарата-накопителя с двигателем огра¬
ниченной мощности (398). 5. Внеатмосферный маневр аппарата с двигателем
ограниченной скорости истечения при использовании накопления (406).
§ 4. Солнечный парус 410
1. Постановка задачи оптимизации полета с солнечным парусом (410). 2. Пе¬
релет космического аппарата с солнечным парусом между орбитами планет (411).
3. Выход космического аппарата с солнечным парусом из сферы притяжения
планеты (416).
§ 5. Изотопный парус 419
1. Основные характеристики изотопного паруса и формулировка вариационной
задачи (419). 2. Состав оптимального управления (420). 3. Модельная задача (420).
§ 6. Двигатель с солнечным источником энергии 421
1. Формулировка задачи оптимизации (422). 2. Оптимальные весовые соотноше¬
ния и расчетное расстояние до Солнца (423). 3. Уравнения оптимальной траекто¬
рии (426). 4. Приближенный метод построения оптимальной траектории (427).
5. Расчет межорбитального перелета с помощью транспортирующей траектории
(429).
§ 7. Двигатель с изотопным источником энергии 431
1. Характеристики двигателя и формулировка вариационной задачи (431).
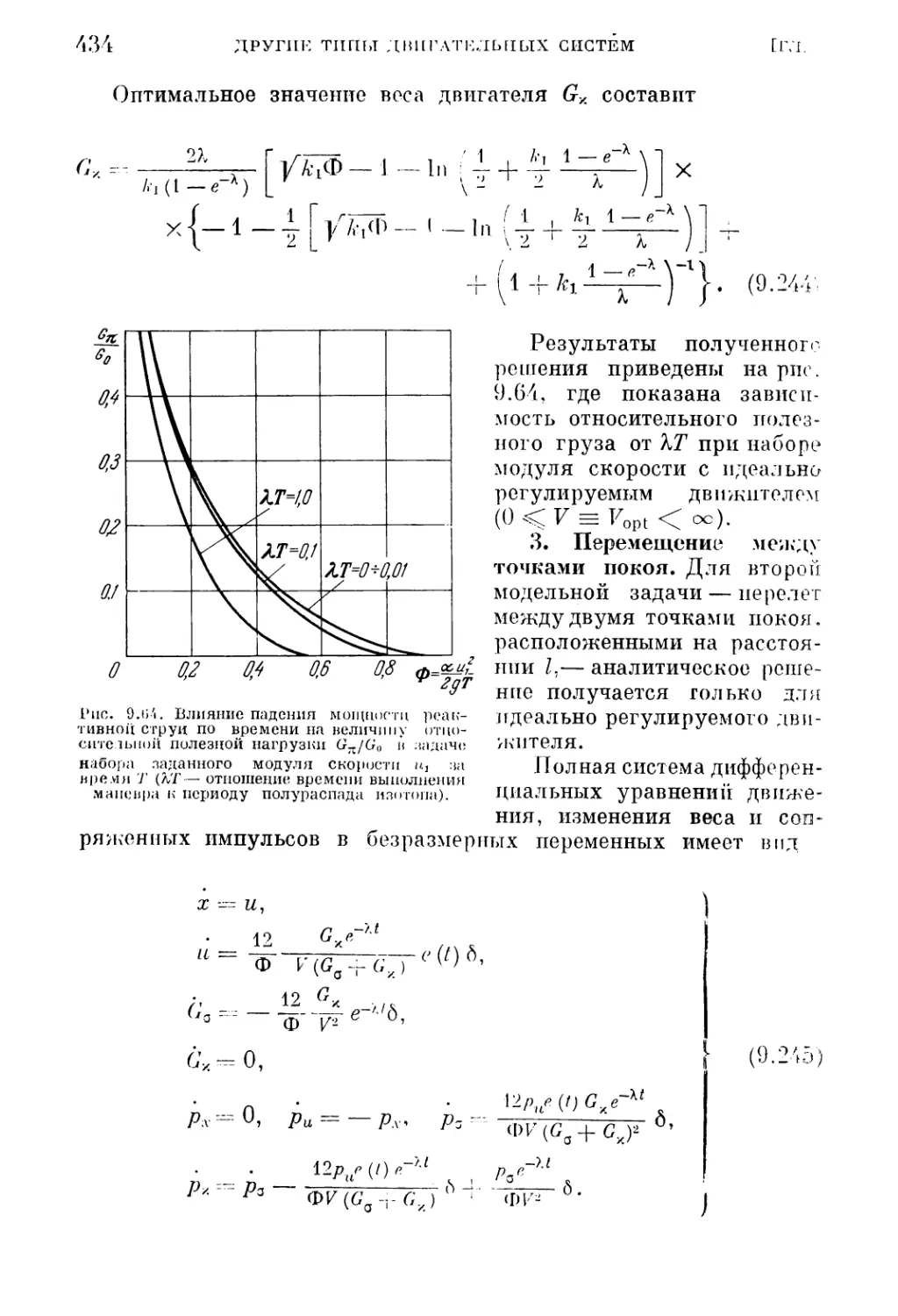
2. Набор модуля скорости (432). 3. Перемещение между точками покоя (434).
Глава 10
Модификации критерия оптимальности
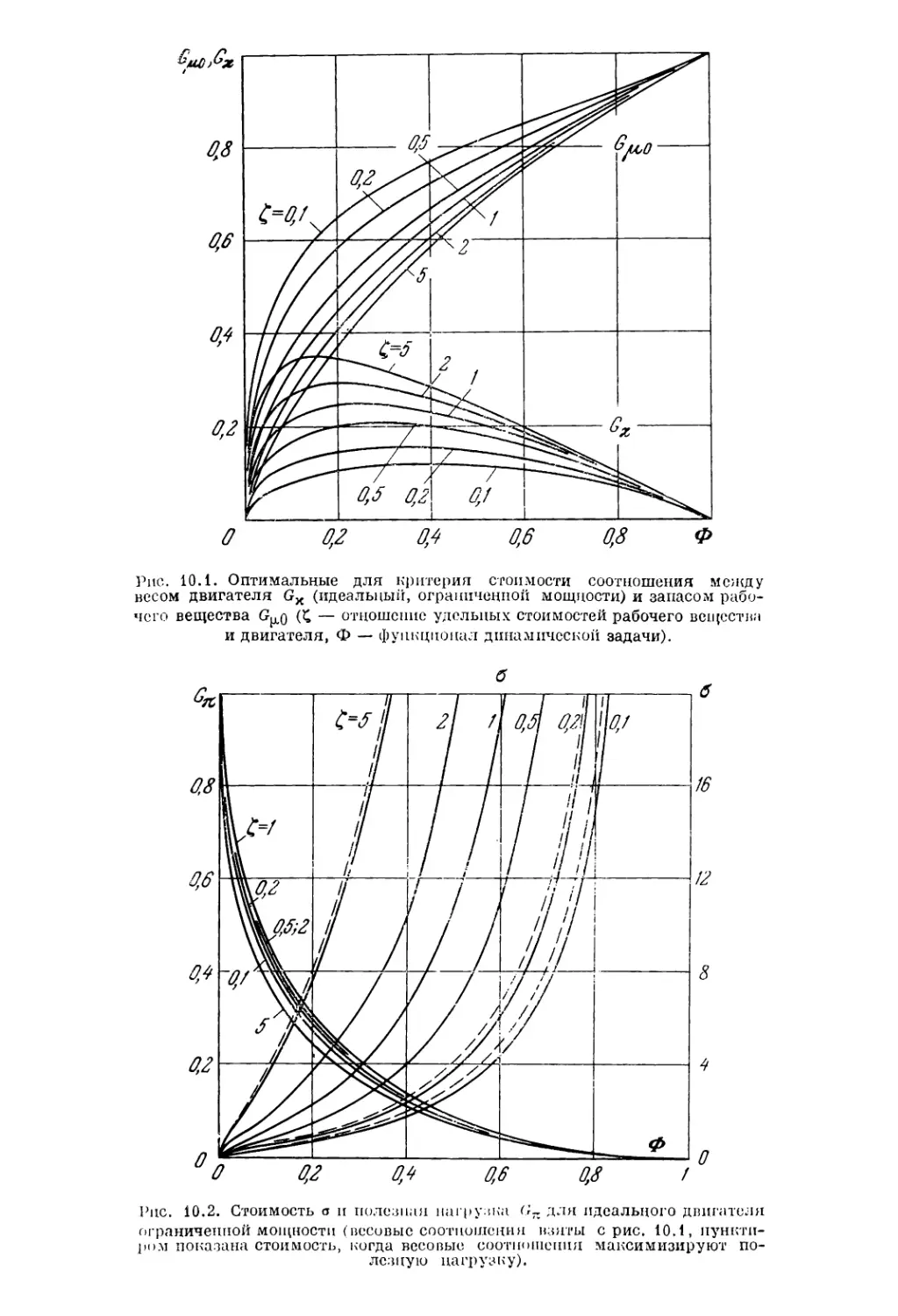
§ 1. Минимизация стоимости выполнения маневра 436
1. Формула стоимости (436). 2. Критерий оптимальности (437). 3. Форму лировка
вариационной задачи (437). 4. Идеальный двигатель ограниченной мощности (438).
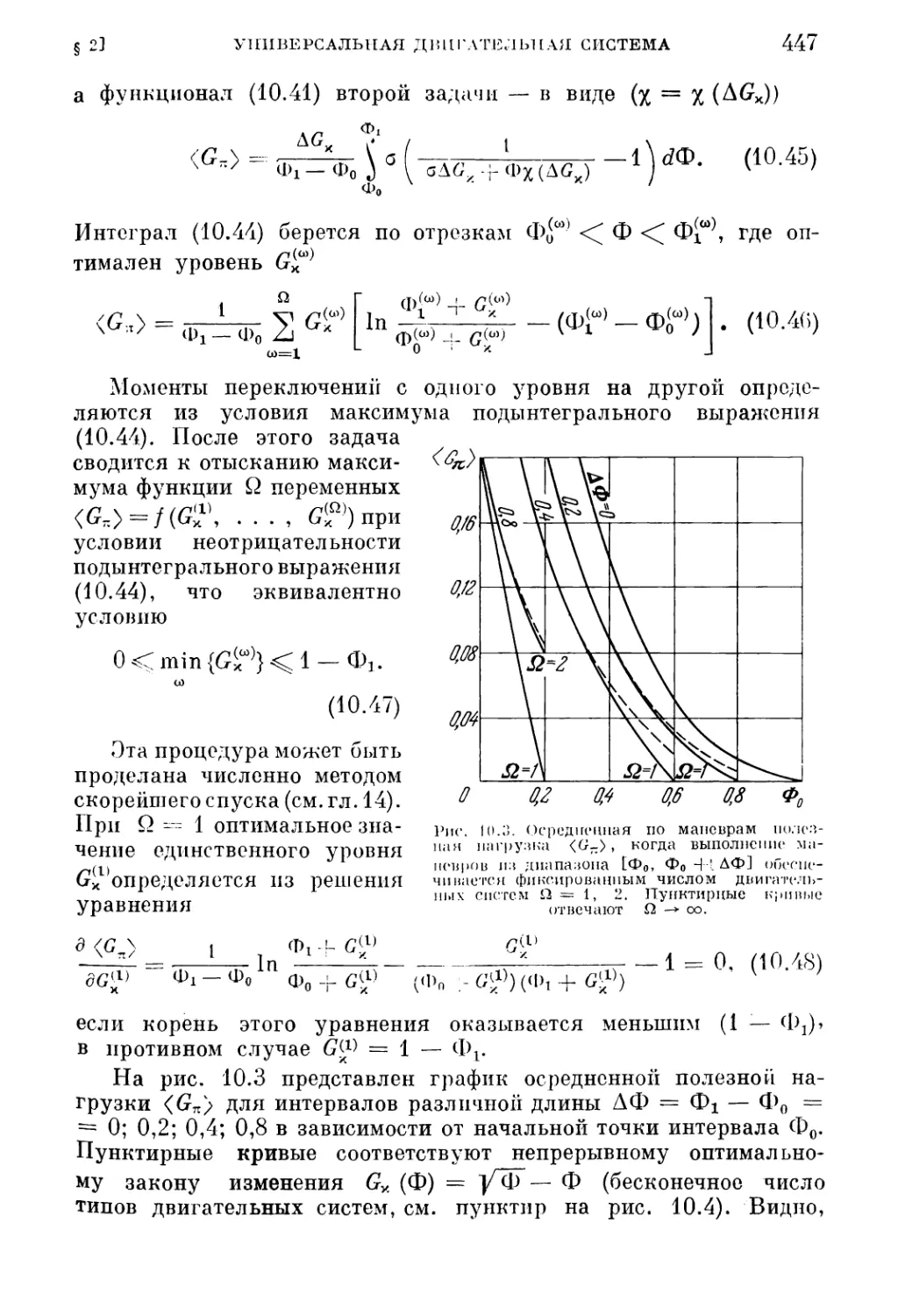
§ 2. Двигательная система, универсальная для заданного класса
маневров 440
1. Общая постановка задачи (440). 2. Критерий оптимальности (442). 3. Фор¬
мулировка задачи для заданного числа типов систем (443). 4. Формулировка
задачи об универсальной секции (444). 5. Идеальный двигатель ограниченной
мощности (445).
§ 3. Игровой подход к задаче выбора оптимальных параметров двига¬
тельной системы 451
1. Постановка задачи (451). 2. Платежная функция (454). 3. Цена игры.
Оптимальные стратегии Конструктора и Природы (457).
§ 4. Запас рабочего вещества, оптимальный для заданного маневра при
фиксированных параметрах двигателя • • • .'462
1. Формулировка вариационной проблемы (462). 2. Идеальные двигатели ог¬
раниченной мощности и ограниченной скорости истечения (463). 3. Нерегули¬
руемые двигатели (466).
8
ОГЛАВЛЕНИЕ
Глава И
Вопросы надежности в задачах оптимизации
§ 1. Оптимальное управление при заданной вероятности успешного
выполнения маневра 470
1. Формулировка вариационной проблемы (470). 2. Двигатель ограниченной
мощности (473). 3. Двигатель ограниченной скорости истечения (483).
§ 2. Секционированный двигатель ограниченной мощности — форму¬
лировка и уравнения вариационной проблемы 486
1. Ожидаемые моменты повреждений (487). 2. Вероятность реализации ожидае¬
мых моментов повреждений (488). 3. Весовые соотношения (492). 4. Форму¬
лировка задачи ( 493). 5. Уравнения вариационной задачи (494). 6. Непрерыв¬
ная аппроксимация ступенчатого закона повреждений (495).
§ 3. Секционированный двигатель ограниченной мощности — приме¬
ры решения для модельных маневров 497
1. Ступенчатый закон повреждений (497). 2. Непрерывный закон повреждений
(503). 3. Движение с возвращением (503). 4. Движение с заданным активным
временем (504). 5. Нелинейная зависимость мощности от числа работающих
секций (506).
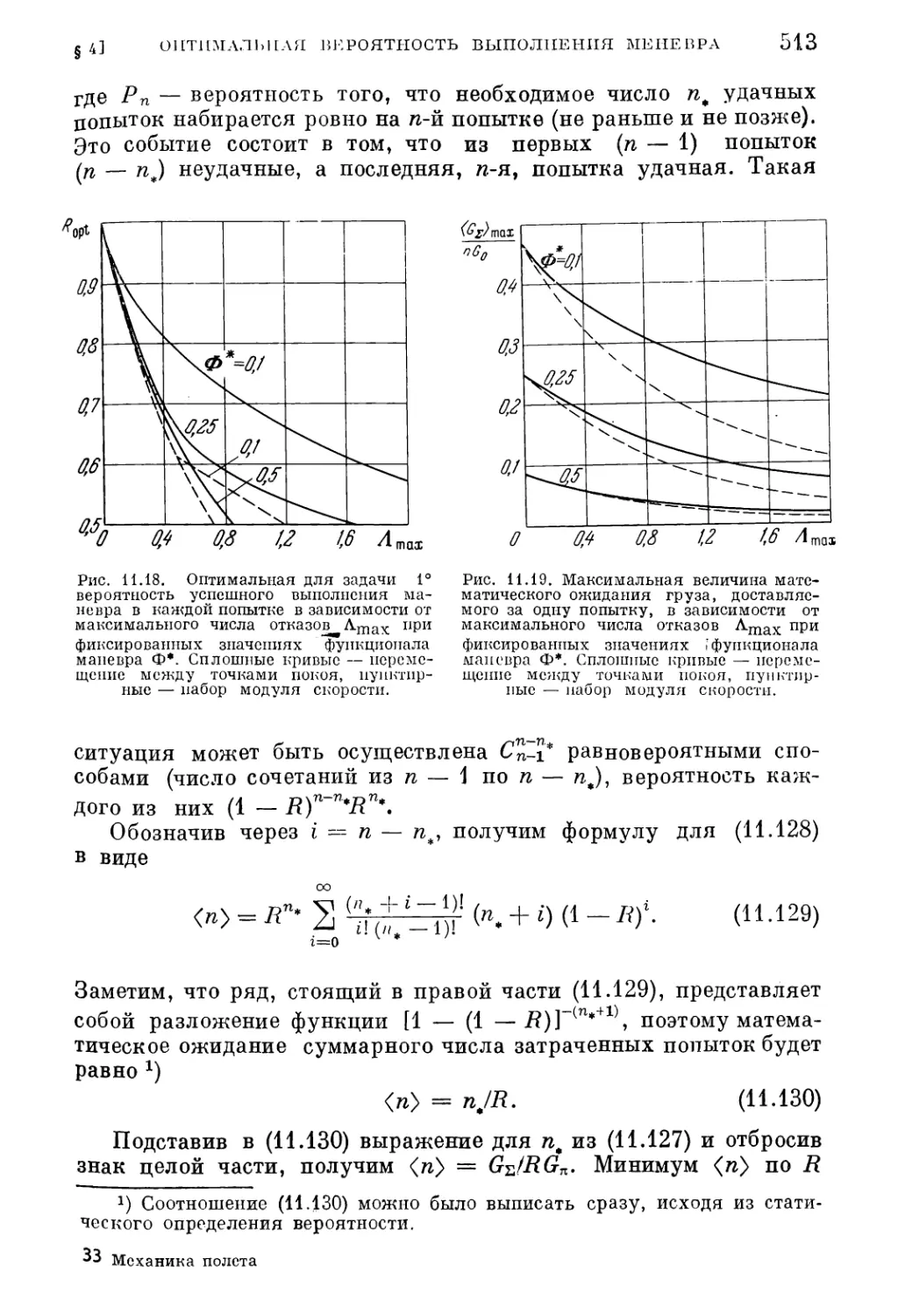
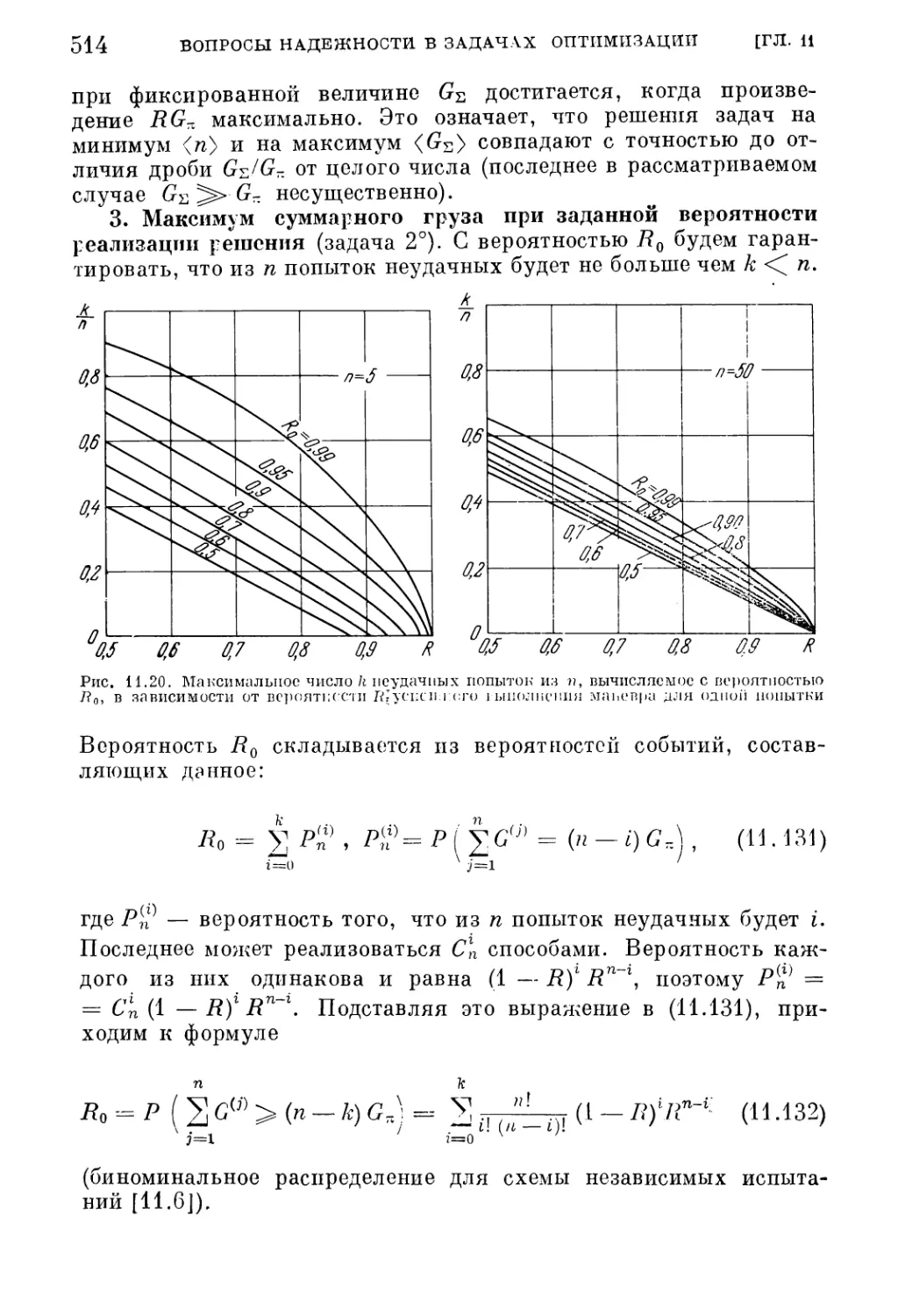
§ 4. Оптимальная вероятность выполнения маневра 508
1. Формулировка транспортной задачи (509). 2. Максимум математического
ожидания суммарного груза (510). 3. Максимум суммарного груза при задан¬
ной вероятности реализации решения (514).
Глава 12
Весовые затраты на коррекцию траектории
§ 1. Ошибки реализации программы реактивного ускорения и откло¬
нения от расчетной траектории 518
1. Ошибки в реактивном ускорении (518). 2. Среднеквадратичные величины от¬
клонений от расчетной траектории (519).
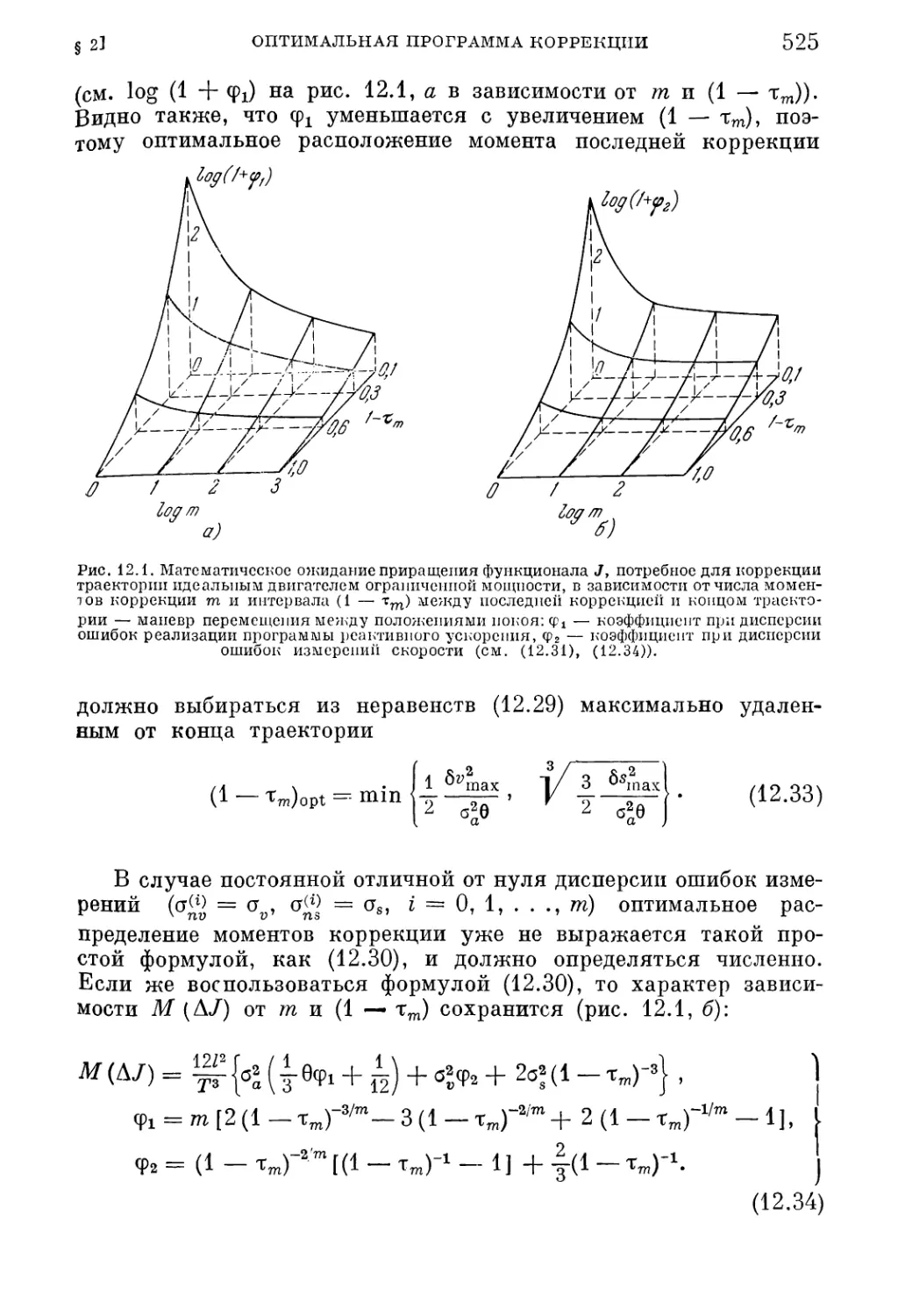
§ 2. Оптимальная программа коррекции 520
1. Измерения координат и скорости (520). 2. Оптимальные поправки к про¬
грамме реактивного ускорения (521). 3. Приращение функционала (522).
4. Оптимальные распределения моментов коррекции (524).
Ч'А С Т Ь III
ПОСТРОЕНИЕ ОПТИМАЛЬНЫХ РЕШЕНИЙ
Глава 13
Аналитические решения уравнений динамики
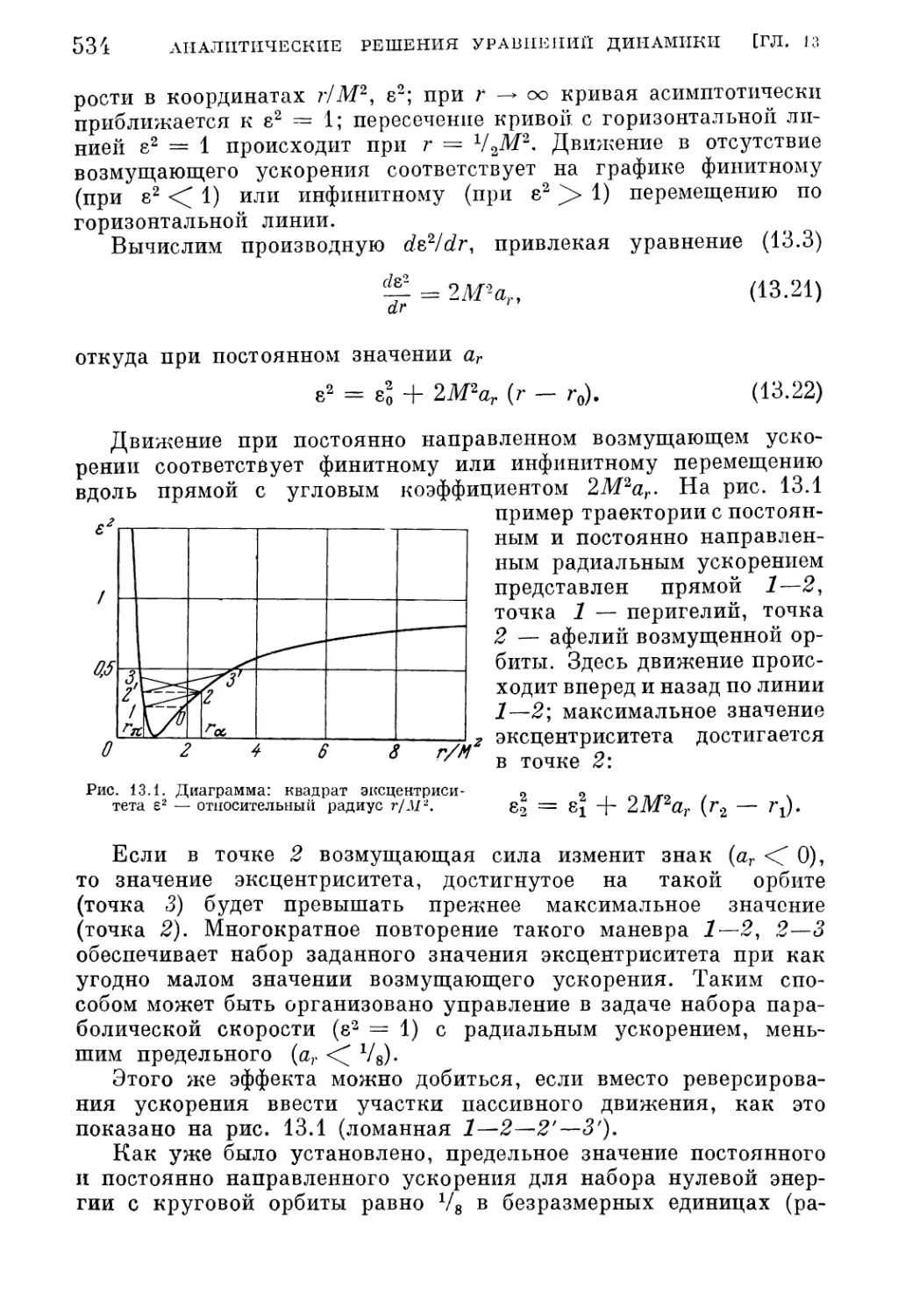
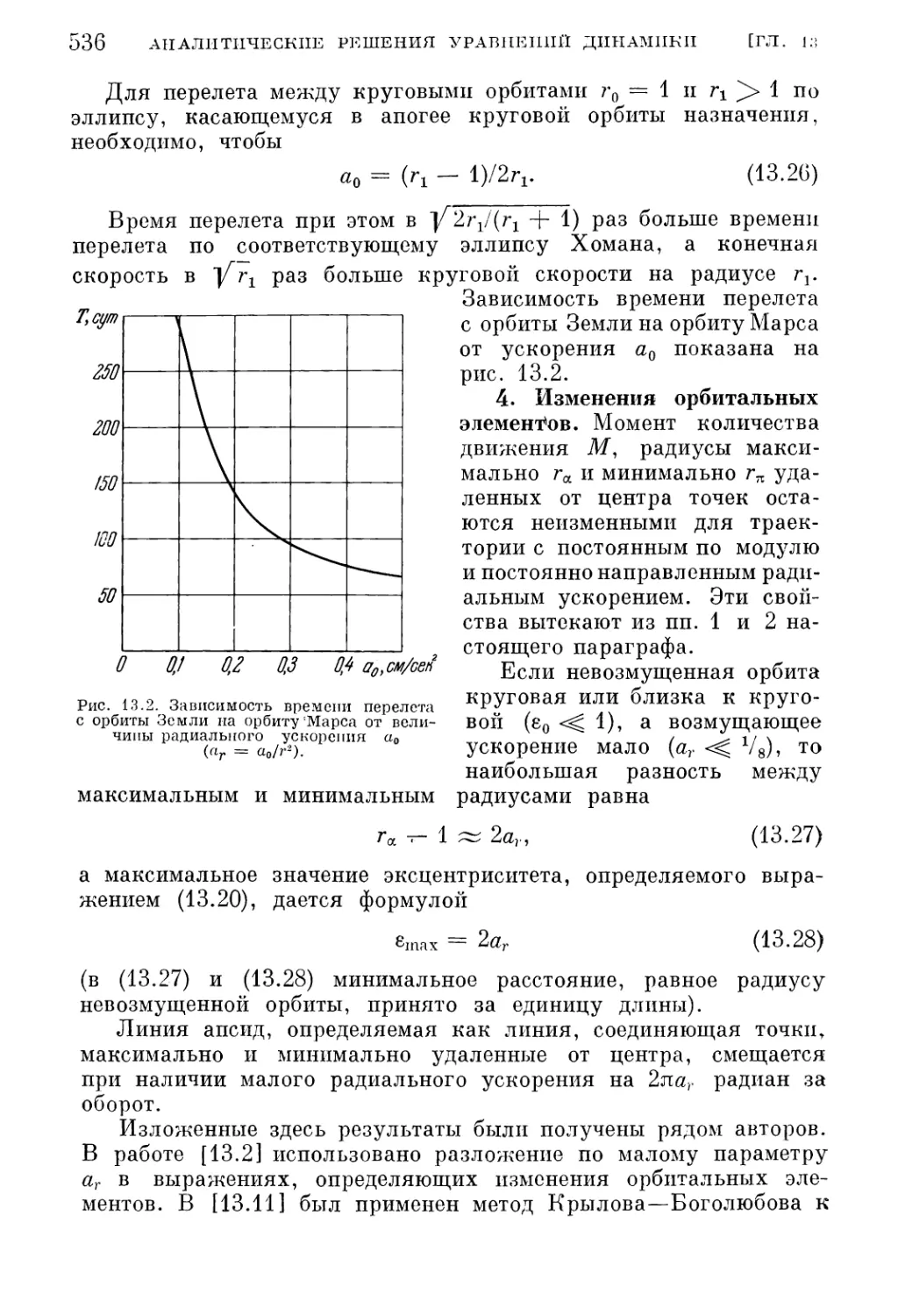
§ 1. Радиальное ускорение (яф = 0 в (П. 9)) 530
1. Уравнения и интегралы движения (530). 2. Набор параболической скорости
(532). 3. Межорбитальцый перелет (535). 4. Изменения орбитальных эле¬
ментов (536).
ОГЛАВЛЕНИЕ
9
§ 2. Трансверсальное ускорение (аг = О в (П. 7)) 537
1. Уравнения движения (537). 2. Набор параболической скорости (537).
3. Представление решения в виде рядов (538). 4. Изменение орбитальных эле¬
ментов (539).
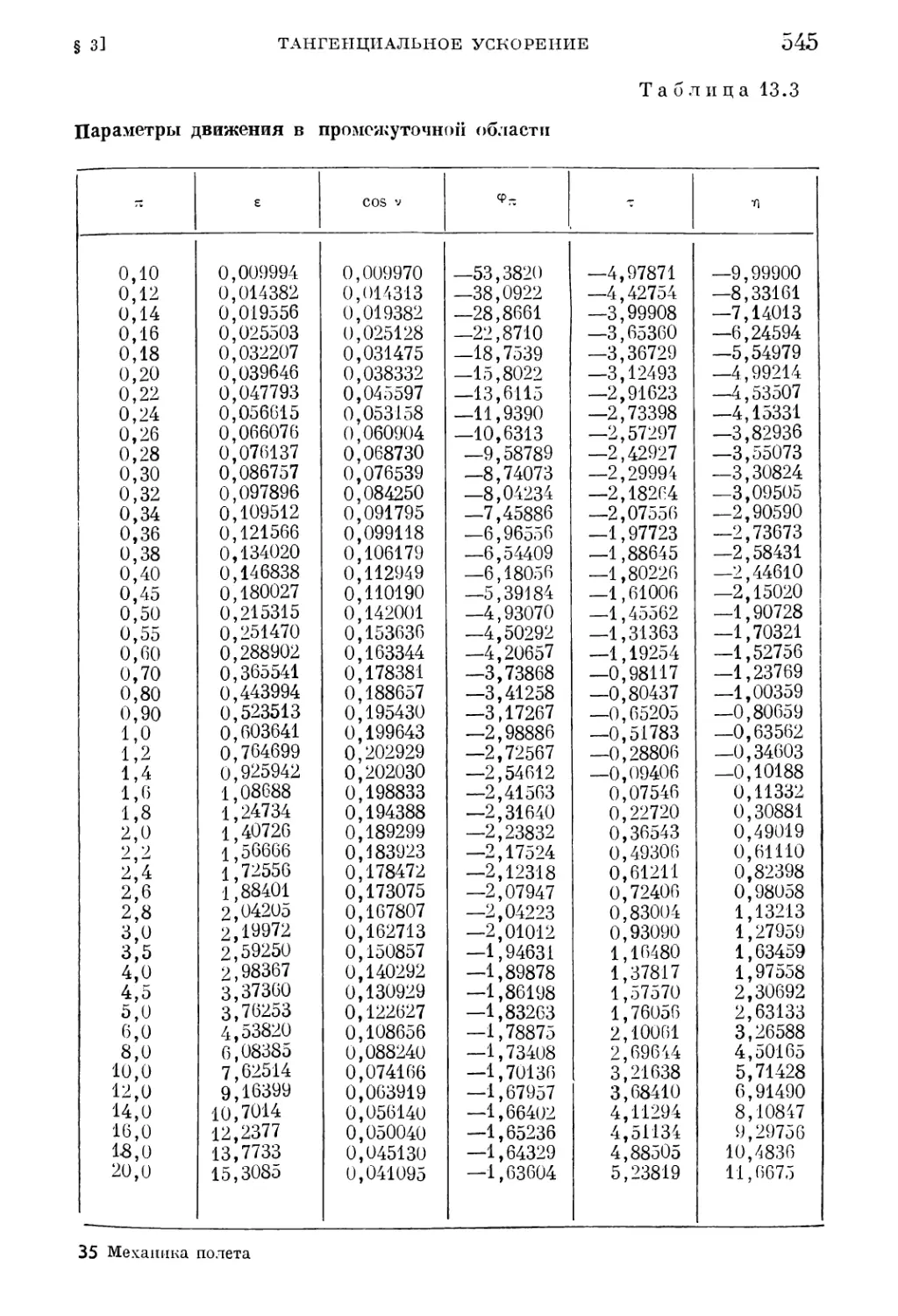
§ 3. Тангенциальное ускорение (у = 0 в (П. 16)) 533
1. Уравнения и интеграл движения (539). 2. Приближенные решения уравне¬
ния (13.48). (540). 3. Асимптотические решения задачи о разгоне (541).
4. Движение по логарифмической спирали (548).
1
§ 4. Нормальное ускорение (т = уяв (П. 14)). Бинормальное ускоре¬
ние (aR = 0, аф — 0 в (П. 37)) 549
1. Уравнения и интегралы движения с нормальным ускорением (549). 2. Свой¬
ства траекторий движения с нормальным ускорением (550). 3. Уравнения и ин¬
тегралы движения с бинормальным .ускорением (550). 4. Свойства траекторий
движения с бинормальным ускорением (552).
§ 5. Постоянный вектор ускорения (ау = а2 = 0, ах = а = const в
(П. 3)) . . ’ 553
1. Уравнения и интегралы движения (553). 2. Классификация плоских траек¬
торий (554).
Глава 14
Функциональные численные методы построения
оптимальных решений
§ 1. Градиентный спуск в фазовом пространстве 558
1. Алгоритм метода (558). 2. Вычислительная процедура (561). 3. Обоб¬
щения алгоритма (562). 4. Пример (564).
§ 2. Градиентный спуск в пространстве управлений 567
1. Алгоритм метода для задач со свободным правым концом траектории (568).
2. Ограничения на управляющую функцию (570). 3. Алгоритм метода для задач
с фиксированными начальной и конечной точками траектории (571). 4. Обобщения
процедуры для произвольных краевых условий (574). 5. Алгоритм метода для
задач со свободным правым концом и свободным временем движения (574). 6. При¬
меры (576). 7. Ограничения на фазовые координаты (578). 8. Численный метод,
основанный на принципе максимума JT. С. Понтрягина (582).
§ 3. Функциональный метод Ньютона 585
1. Алгоритм метода (585). 2. Пример (587).
Глава 15
Конечномерные численные методы построения оптимальных решений
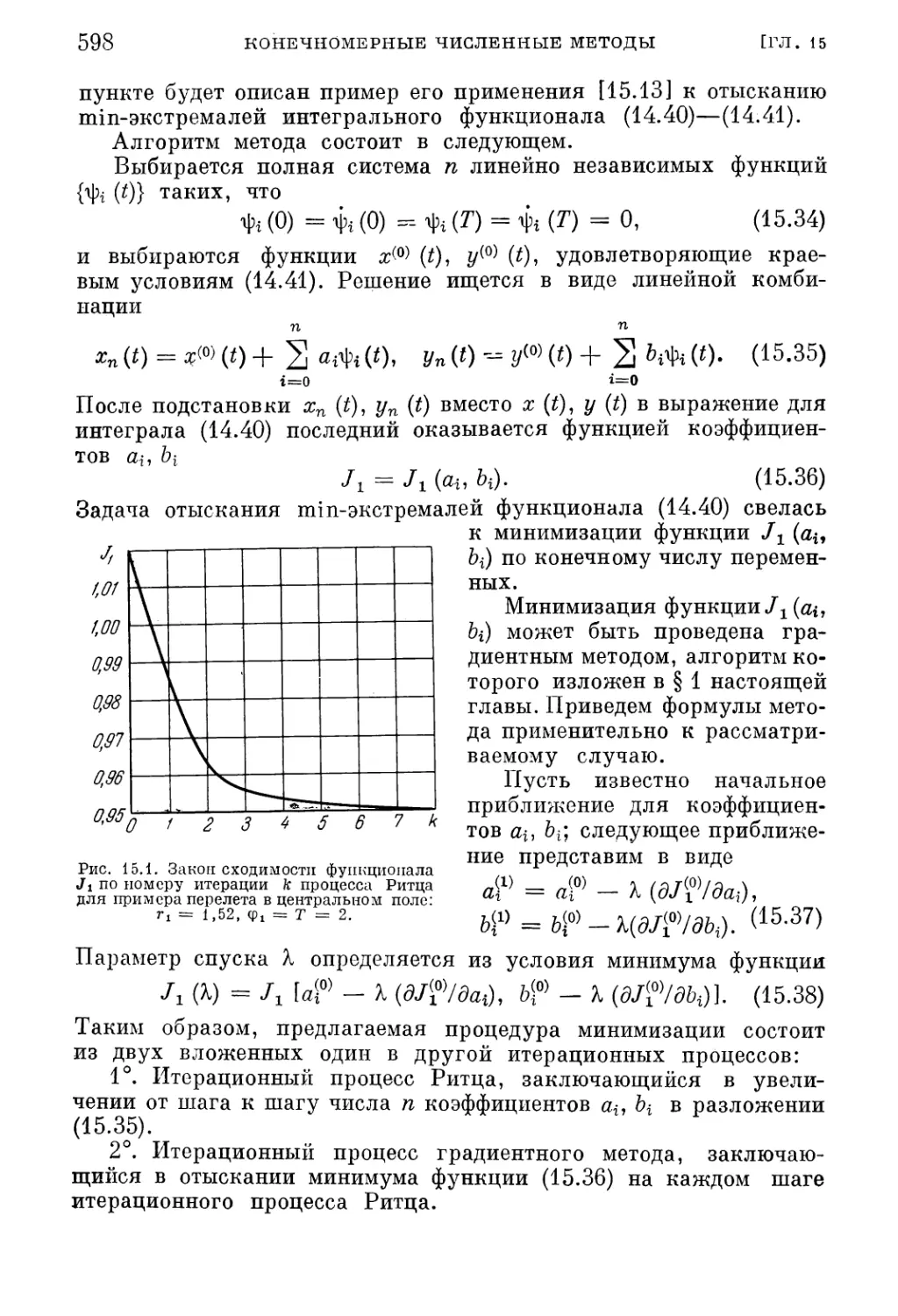
§ 1. Минимизация функции при дополнительных условиях .... 591
1. Градиентный метод (592). 2. Метод Ньютона (594).
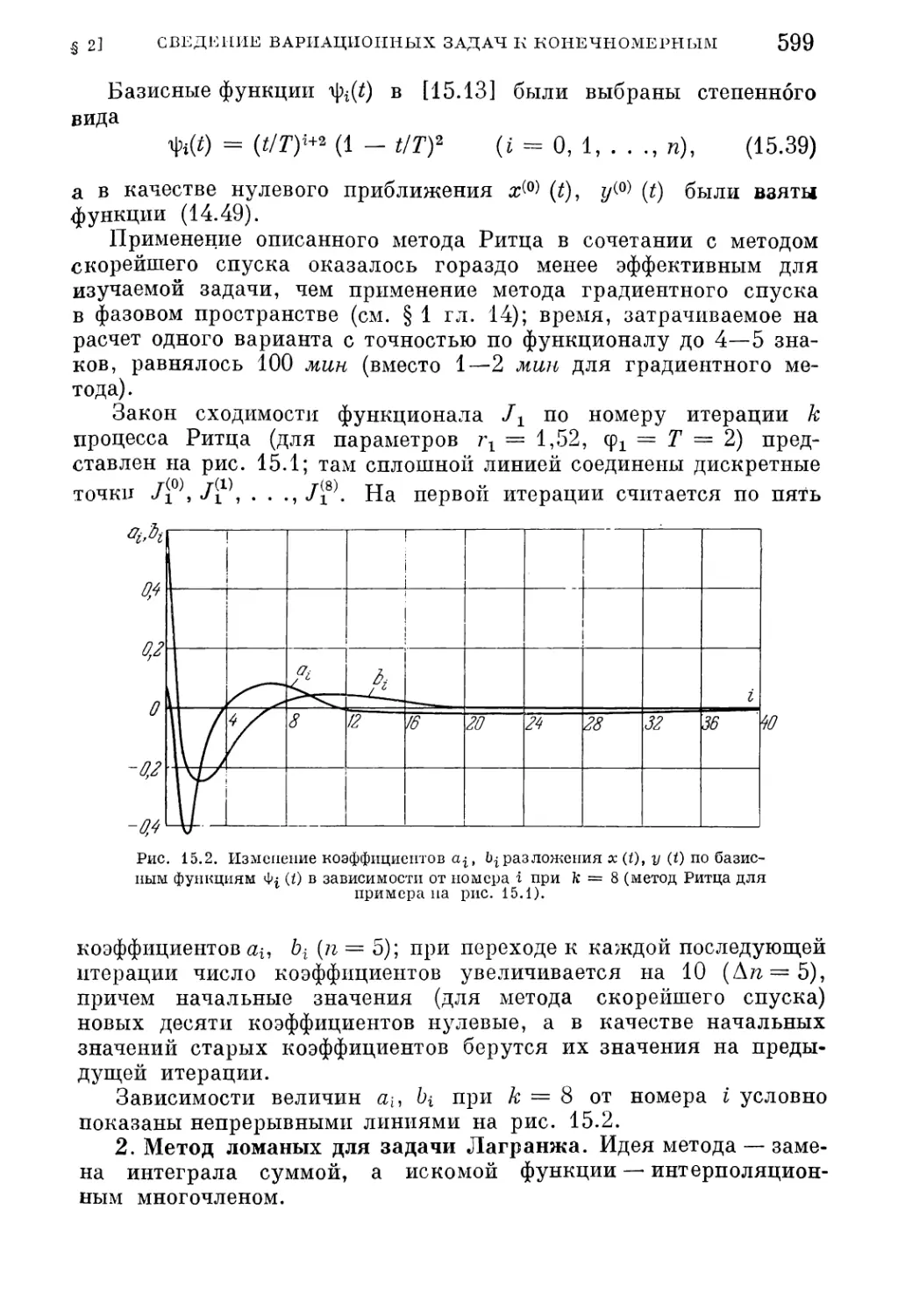
§ 2. Сведение вариационных задач к конечномерным . 597
1. Метод Ритца с определением коэффициентов по градиентному методу (597). 2. Ме¬
тод ломаных для задачи Лагранжа (599). 3. Метод ломаных для задачи Майера
(601). 4. Подбор недостающих начальных значений в краевой задаче (603).
10
ОГЛАВЛЕНИЕ
П р и л о ж е ни е
Описание динамических маневров
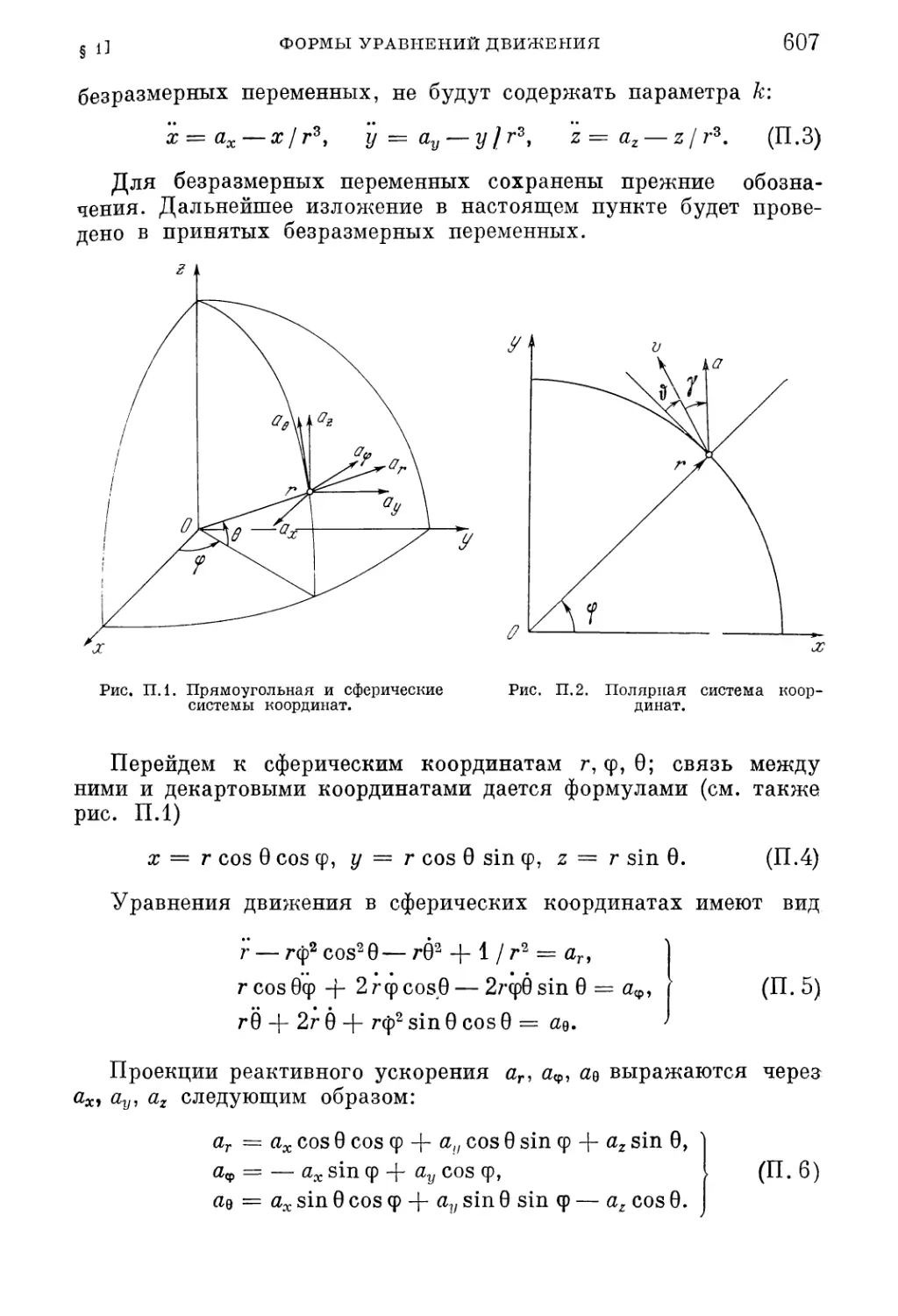
§ 1. Формы уравнений движения 606
1. Уравнения движения в центральном поле (606). 2. Уравнения движения
в поле двух центров (617). 3. Уравнения движения в модельных полях (618).
§ 2. Межпланетный перелет 619
1. Разбиение межпланетного перелета на элементарные маневры (619). 2. Межпла¬
нетный перелет с возвращением (621). 3. Модельные маневры (622).
§ 3. Эволюции спутника 623
1. Удержание спутника в заданном шаровом слое (623). 2. Поворот плоскости
круговой орбиты спутника поперечной тягой (629).
Основные обозначения 631
JI итература 638
Именной указатель . » . . 673
ПРЕДИСЛОВИЕ
В этой книге читателям предлагается систематизированное
изложение результатов исследований, заложивших основу нового
раздела механики космического полета. Предметом этого раз¬
дела является совместное решение проблем выбора оптимальных
весовых параметров космического аппарата, оптимального управ¬
ления его двигательной системой и определение оптимальных тра¬
екторий полета, обеспечивающих доставку максимального по¬
лезного груза. Необходимость совместного рассмотрения ука¬
занных трех составных частей проблемы обусловлена большим
относительным весом и широкими возможностями регулирова¬
ния параметров перспективных видов космических двигательных
систем: химических реактивных двигателей (при большой тяго-
вооруженности), тепловых ядерных реактивных двигателей, элек-
трореактивных двигателей и др.
К настоящему времени теоретические исследования по механи¬
ке космического полета двигателями «малой тяги» настолько
продвинулись, что можно говорить об определенных итогах проде¬
ланной работы. Однако материалы по этому вопросу опубликованы
в виде сотен статей в различных научных журналах. Предлагаемая
читателю книга является первой попыткой систематизированного
изложения основных вопросов механики космического полета.
Авторы, естественно, не ставят перед собой задачи исчерпывающего
освещения всех известных работ в этой области, хотя и сочли
целесообразным привести подробную библиографию.
В первой части книги рассмотрены физические принципы
космических двигательных систем и указаны обобщенные харак¬
теристики основных типов двигательных систем, необходимые для
дальнейшего анализа.
Задачи оптимизации параметров космических аппаратов с
различными типами двигательных систем изложены во второй
части книги, где последовательно рассмотрена механика полета
с двигательными системами ограниченной мощности, ограничен¬
ной скорости истечения и тяги, с нерегулируемыми и регулируе¬
12
ПРЕДИСЛОВИЕ
мыми двигательными системами, с накоплением энергии и массы.
Особо рассмотрены вопросы оптимального сочетания на косми¬
ческом аппарате различных типов двигательных систем, опти¬
мальная коррекция космического полета и влияние надежности
двигательной системы на оптимизацию параметров аппарата.
В третьей части книги обсуждаются вопросы построения тра¬
екторий оптимальных с позиций механики космического полета.
В ней излагаются аналитические решения и численные методы
построения траекторий.
Основные разделы иллюстрированы примерами характеристик
перелетов на планеты солнечной системы, маневров управляемых
спутников планет и полетов в однородных гравитационных полях;
эти примеры раскрывают требования к двигательным системам и
возможности космических полетов.
Книга рассчитана на научных работников, инженеров, аспи¬
рантов и студентов старших курсов; у читателей предполагается
знание основ вариационного исчисления. Однако книга позво¬
ляет пользоваться основными результатами, если даже разделы,
посвященные вариационному анализу, будут при чтении опущены.
В связи с большим объемом книги работа между авторами была
распределена следующим образом: главы 1, 2, 3 и 9 подготовлены
Г. JI. Гродзовским, главы 7, 8, 13, 14, 15 и Приложение —
Ю. Н. Ивановым, главы 4, 5, 6, 10, И, 12 — В. В. Токаревым.
Авторы считают своим приятным долгом выразить благодар¬
ность В. В. Белецкому, Ю. Е. Кузнецову и Ф. JI. Черноусько,
прочитавшим книгу в рукописи и сделавшим ряд полезных заме¬
чаний. Авторы благодарны JI. А. Арцимовичу, В. А. Егорову,
В. К. Исаеву, Г. Е. Кузмаку, А. И. Курьянову, А. И. Лурье,
Н. Н. Моисееву, Г. П. Свшцеву, Л. А. Симонову, В. В. Сонину,
Г. Г. Черному, Л. М. Шкадову, Т. М. Энееву за обсужде¬
ния затронутых в книге вопросов. Авторы особо признательны
Л. И. Седову и Д. Е. Охоцимскому, внимание которых к работе
авторов во многом способствовало появлению данной книги.
Мы будем благодарны читателям за все замечания и пожела¬
ния по этой книге.
Г. Гродзовский
Ю. Иванов
Москва, 1966 г. 5. Токарев
ВВЕДЕНИЕ
Прогресс космической ракетной техники вызывает к жизни
новые разделы механики. Сформировавшаяся на рубеже XIX
и XX столетий идея применения реактивных двигателей для вы¬
хода в космос стимулировала развитие механики космического
полета (И. В. Мещерский, К. Э. Циолковский, Р. Годдард,
Ф. А. Цандер, Г. Оберт, В. Гоман, Р. Эно-Пельтри, С. П. Ко¬
ролев и др. [1.1—1.9]). Эта наука изучает движение космических
аппаратов как тел переменной массы с целью определения усло¬
вий доставки максимального полезного груза.
Решающая роль здесь принадлежит типу двигательной си¬
стемы. На первом этапе развития механики космического полета
наиболее подробно исследовался полет аппаратов с тепловыми
химическими реактивными двигателями, для которых характерен
малый удельный вес двигательной системы (отношение веса
двигательной системы к развиваемой максимальной тяге —
порядка единиц процентов). При умеренной тяговооруженности
(отношение тяги к весу ракеты) для таких ракет было допустимо
в первом приближении пренебрежение весом двигательной
системы, и задача оптимизации сводилась к отысканию условий
наименьшей затраты топлива на совершение заданного космиче¬
ского маневра *). На основе формулы Циолковского последнее
условие сводится к минимизации простого кинематического пара¬
метра, так называемой характеристической скорости, что тре¬
бует только определения оптимальных траекторий с указанием
на них моментов и направления приложения импульсов тяги.
Эти задачи подробно изложены в известных работах и моно¬
графиях по ракетодинамике [1.10—1.59] и др.
Развивающиеся перспективные виды космических двигатель¬
ных систем (солнечный парус, электрореактивные двигатели,
тепловые ядерные реактивные двигатели и др.) отличаются боль¬
шим относительным весом и широкими возможностями регули¬
рования параметров (скорости истечения, расхода массы и др.).
Перспективность использования таких двигательных систем опре¬
деляется малым расходом массы на единицу тяги для электро-
*) Выбор числа ступеней ракет, т. е. учет последовательно сбрасывае¬
мых баков, вес которых пропорционален запасу топлива, не изменял прин¬
ципиально указанную постановку.
14
ВВЕДЕНИЕ
реактивных и ядерных тепловых двигателей (вследствие боль¬
шой скорости истечения реактивной струи) или отсутствием
расхода массы для солнечного паруса. Технический прогресс
последних лет в области ядерной энергетики, электрических
ускорителей, технологии тонких пленок и др. поставил на оче¬
редь дня проблему научной и технической разработки указанных
перспективных двигательных систем. А с увеличением тягово-
оруженности недопустимо пренебрежение весом двигательной
системы и для тепловых химических реактивных двигателей.
В этой связи получил развитие новый раздел механики косми¬
ческого полета, рассматривающий в совокупности: оптимальные
соотношения между весовыми компонентами ракеты с учетом веса
основных элементов двигательной системы, оптимальное управ¬
ление и регулирование двигательной системы и оптимальные
траектории космического полета [1.60].
В механике космического полета задача о нахождении условий
доставки максимального полезного груза выделяется в силу ее
определяющего влияния на идеологию компоновки и управления
космическим аппаратом. С этим аспектом неизменно связана
постановка задач в плане оптимизации траектории движения,
управляющих параметров и весовых компонентов двигательной
системы. Указанная постановка основной задачи механики кос¬
мического полета органически связана с характеристиками дви1
гательных систем.
В современной литературе обсуждается большое число типов
космических двигательных систем. Основные перспективные виды
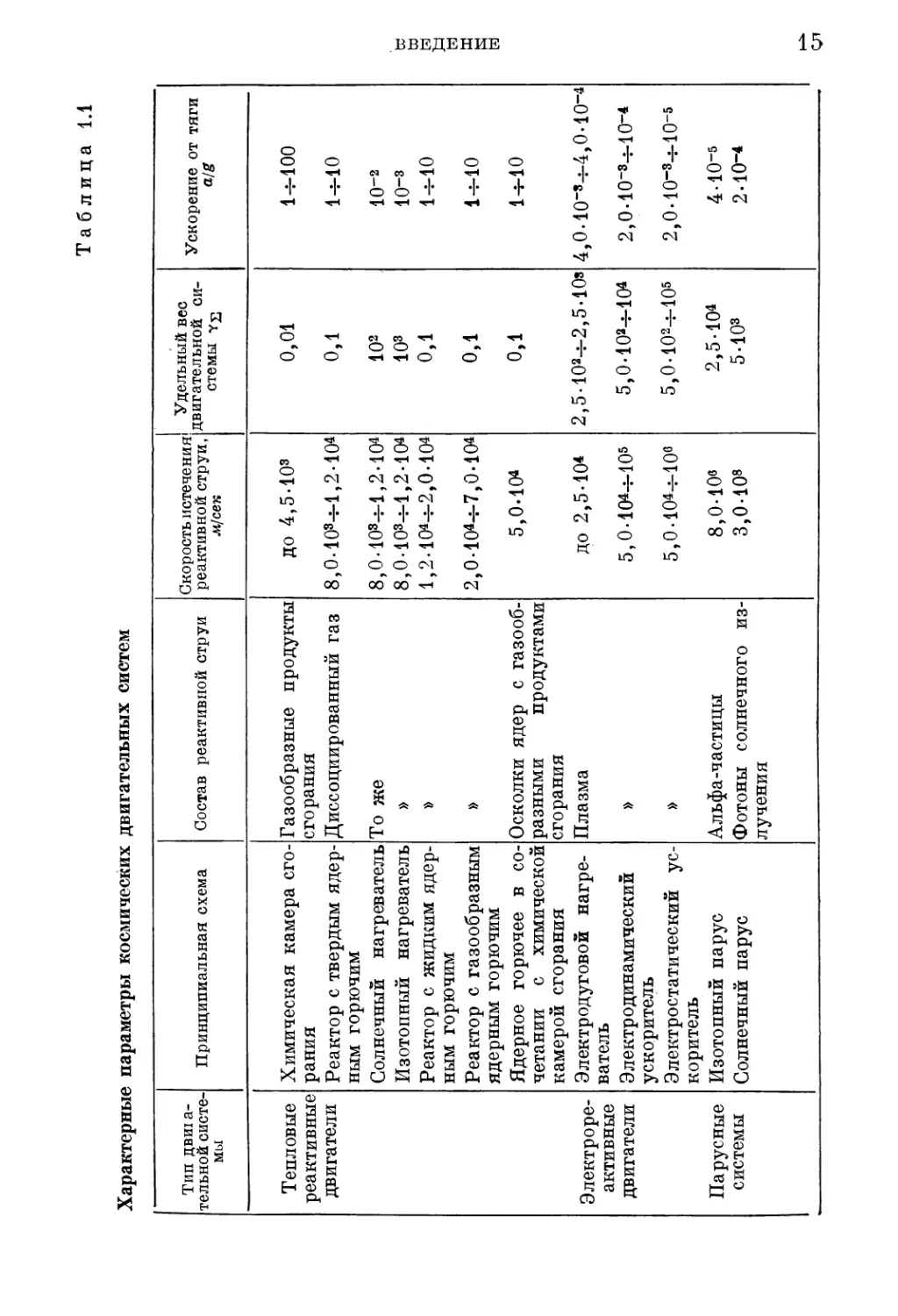
указаны в табл. 1.1 ([1.61—1.67] и др.),где приводятся некоторые
характеристики систем: характерные значения скорости истечем
ния реактивной струи F, удельного веса двигательной системы
(веса двигательной системы, отнесенного к создаваемой тяге)
и ускорения аппарата от реактивной тяги а; характеристики дви^
гательных систем в таблице расположены в порядке возрастания
скорости истечения реактивной струи.
Приведенные в табл. 1.1 характерные значения удельного веса
двигательной системы ys объясняют сложившуюся в последние
годы терминологию: двигатели большой тяги и двигатели малой
тяги. Верхний предел ускорения от реактивной тяги атах дости¬
гается в том случае, когда вес двигательной системы становится’
преобладающим по сравнению со всеми остальными компонен¬
тами веса космического аппарата: тогда атах —^ g/ys (g — уско¬
рение силы тяжести на поверхности Земли). Если то amax>g;
если YsJ>1,to атаХ<С g. Соответственно первые называются двига¬
телями большой тяги, а вторые — малой тяги (правильнее —'
большого и малого ускорения оттяги (рис. 1.1)). Следует отметить,
что большие значения удельного веса для двигателей малой тяги
не являются отличительным качеством физических принципов,.
Характерные параметры космических двигательных систем
ВВЕДЕНИЕ
15
со
рг
К
vo
сС
н
о 50
S« и
«2
• 3 g я
д ф о
В Ен н
аз оз о
И Си
к ж
S s
К
оз ft
а ен
О О
go 8
S 9 ^
о э
о Ё
о. К
о а
к ®
о а
И
И
В
ВТ
в
в
ft
к
И« а
о
о
+ +
т ?
о о
+ + +
ю
1
7
О
о
жН
жН
СЧ
о
о
о
ю
<of
2Ь
жН
+
сч
о
жН
о
о
о
о
жН
‘ ю
ю
о
к
ъ
s s s
гН
^Г-1
жН
ж-t
ж-t
СЧ
<М
С\1
О
О
ъ
гН
r-i
жН
ftT
жН
+
+
•I-
•I*
•I-
О
<Ь
£>
£> 6
s>
ю
н-Н
жН
жН
жН
О
О
О
СЧ
О
00
00
00
счГ
Ю
<оГ
о
«■
о
ю
о
ю
° Я
00 со
а
н
и
«
о
Рн
н
со
сс
ft
5Н
а
к
к
сс
m
о
Рн
J К I
Л к »
VO к о
Я * §
9 ft о
ж ° К
сс г. ,и.
ф
а
и
со
СС
ф
8
о
Е-
\о
||
о о
Рн
РнИ
ф
н
W
н н 5
§Й«
ISS.S
| § g И
О ftp н
§ К й
§ w Й
U С« Лф
Рн Рн
ф
gas
а в 1=3
п и ф
2 н ж
R н 2
Н у Ь
§й§
Ь £ В
Рн М-
ф 2 и
РнЭ ч
о и ф
Рн 5 Й
н н 2
® И g
CD
а а
К а
О ф
>>> н
2
сС н
е °
ВВЕДЕНИЕ
Рис. 1.1. Космические двигательные системы; 1—5— двигатели
большой тяги: 1 — химическая камера сгорания, 2 — нагрев в
реакторе с твердым ядерным горючим, а — то жес жидким ядер-
ным горючим, 4— то же в сочетании с химической камерой сгора¬
ния, 5 — нагрев в реакторе с газообразным ядерным горючим;
6—12—двигатели малой тяги: 6—с солнечным нагревателем, 7 — с
изотопным нагревателем, 8 — электродуговой, 9 — электродинами¬
ческий, Ю — электростатический, 11 — изотопный парус,
12 — солнечный парус.
ВВЕДЕНИЕ
17
а характеризуют лишь современную оценку уровня разработки
таких двигательных систем. Поэтому распространенный сейчас
термин «малая тяга» в значительной степени условен. Однако
авторы сочли целесообразным сохранить этот сложившийся тер¬
мин и в названии книги, так как механика космического полета
наибольшее развитие получила сейчас применительно к двига¬
тельным системам «малой тяги», для которых роль веса двига¬
тельной установки особенно существенна.
С точки зрения механики космического полета, определяющее
значение имеют две характеристики двигательной установки:
возможность управления реактивной тягой и весовые затраты
на реализацию тяги (потребный запас рабочего вещества и вес
двигательной системы).
Выяснение этих вопросов находится в центре внимания пер¬
вой части книги, при обсуждении физических принципов и ос¬
новных характеристик космических двигательных систем, знание
которых необходимо для последующего подхода к задачам ме¬
ханики космического полета.
Движение космического аппарата исследуется как движение
материальной точки. Вопросы, связанные с движением аппарата
вокруг центра масс, в книге не затрагиваются, с ними можно
ознакомиться в монографии [1.68] и др.
К траектории движения космического аппарата обычно
предъявляется требование, чтобы она начиналась в заданной точке
фазового пространства (т. е. при заданных координатах и проек¬
циях скоростей) и за фиксированное время достигала другой задан¬
ной точки в фазовом пространстве. Это требование может быть
удовлетворено не единственным образом. Из всего многообразия
траекторий, соединяющих за фиксированное время две заданные
точки в фазовом пространстве, выбирается такая траектория,
которая отвечает движению космического аппарата с максималь¬
ным полезным грузом при фиксированном стартовом весе. Это—
постановка основной вариационной задачи механики косми¬
ческого полета об определении оптимальных управлений двига¬
тельной системой и оптимальных соотношений между весовыми
компонентами аппарата, обеспечивающих движение по указан¬
ной оптимальной траектории.
Вместо приведенной выше может быть сформулирована вторая
вариационная постановка, эквивалентная первой: требуется опре¬
делить оптимальные управления и построить траекторию, со¬
единяющую за минимальное время две заданные точки фазового
пространства и обеспечивающую движение аппарата с заданными
стартовым и полезным весами. Вторая постановка может ока¬
заться удобнее в тех случаях, когда нет уверенности относитель¬
но энергетической выполнимости маневра в рассматриваемом
Диапазоне времен перелета.
2 Механика полета
18
ВВЕДЕНИЕ
Кроме этих двух основных вариационных постановок, в механике
космического полета формулируются частные постановки, соот¬
ветствующие отдельным типам космических маневров: меж-
орбитальный перелет, задача выхода из гравитационного поля
планеты, эволюции в окрестности планеты и др. Вариационные
формулировки этих задач не требуют выполнения всех граничных
условий по координатам и скоростям — задаются не все коор¬
динаты и скорости, а только часть их или комбинации. Свободные
граничные условия в этом случае определяются из соображений
оптимальности траектории.
В ходе изложения будет акцентироваться внимание на форму¬
лировках вариационных задач и их связи с приведенными выше
двумя основными постановками.
ЧАСТЬ I
ФИЗИЧЕСКИЕ ПРИНЦИПЫ
И ОБОБЩЕННЫЕ ПАРАМЕТРЫ
КОСМИЧЕСКИХ
ДВИГАТЕЛЬНЫХ СИСТЕМ
2*
ГЛАВА 1
ОСНОВНЫЕ ПАРАМЕТРЫ И СОСТАВ
КОСМИЧЕСКИХ ДВИГАТЕЛЬНЫХ СИСТЕМ
§ 1. ОСНОВНЫЕ ПАРАМЕТРЫ КОСМИЧЕСКИХ
ДВИГАТЕЛЬНЫХ СИСТЕМ
Принципы работы и характеристики космических двигатель¬
ных систем подробно изложены в известных монографиях, об¬
зорах и учебниках ([1.61 — 1.67] и др.). Ниже основные фи¬
зические принципы и обобщенные параметры космических
двигательных систем излагаются в объеме, необходимом для
подхода к задачам механики космического полета. В соответствии
с указанным во введении в механике космического полета весо¬
вая проблема (например, задача о нахождении условий доставки
максимального полезного груза) выделяется в силу ее определяю¬
щего влияния на параметры космического аппарата. Весовые
затраты, необходимые для реализации полета космического аппа¬
рата, во многом определяются его двигательной системой. Сред¬
ством, обеспечивающим активное управление движением центра
масс космического аппарата является реактивная тяга Р, созда¬
ваемая его двигательной системой.
Движение центра масс космического аппарата под действием
тяги в гравитационном поле может быть описано векторным диф¬
ференциальным уравнением (см., например, [1.60])
^-G(*)r' = P + -i-G(0K + F, (1.1)
где G (t) — вес аппарата, г (t) — радиус-вектор в инерциальной
системе координат, Р — вектор тяги: Р = Ре, е — единичный
вектор направления тяги, H(r, t) — вектор ускорения от гра¬
витационных сил, t — время, F — вектор внешних сил, дейст¬
вующих на аппарат (сопротивление среды и др.), определяемый
внешними условиями полета.
Полная система уравнений, описывающих поведение косми¬
ческого аппарата, складывается из векторного уравнения дви¬
жения (1.1) и связей между весовыми характеристиками и пара¬
метрами двигательной системы. При оптимизации параметров
космического аппарата управляющими функциями являются
вектор направления е реактивной тяги и параметры двигательной
системы, определяющие величину тяги Р и вес G.
22 основные параметры и состав двигательных систем [гл. 1
Создание реактивной тяги Р связано с расходом массы через
движитель q (например, массы отбрасываемого рабочего тела).
Полный расход массы равен
dm . , л с\\
Qo — — Q Qe Qvi (1 -2)
где m = Gig, qE — расход массы при выработке энергии, qv —
расход, забираемый из внешней среды.
Собственный вес двигательной системы Gv (t), величина реак¬
тивной тяги Р (t) и расход массы на создание тяги q (t) являются
основными параметрами космической двигательной системы.
Значение текущего веса аппарата G(t) можно представить в виде
G (t) = Ga (t) + (0» (1-3)
t
где Ga (t) = G0 — Gy (t) — g ^ qa (t) dt, G0 — начальный вес ап-
o
парата.
При этом конечное значение Ga (в конечной точке пути t = Т)
можно отождествить с полезным грузом Gn. Из соотношений
(1.1), (1.2) и (1.3) видно, что основные параметры двигательной
системы определяют движение космического аппарата; указан¬
ные параметры Gp (£), Р (t), q (t) и вектор направления тяги е
являются управляющими функциями в задачах оптимизации
космического полета.
С указанными параметрами Р (t) и q (t) связаны зависимые
параметры средней эффективной скорости истечения и эффектив¬
ной мощности реактивной струи. Частное от деления Р на q, имею¬
щее размерность скорости, можно характеризовать как среднее
эффективное значение скорости реактивной струи V (для полетов
без забора массы рабочего тела из внешней среды и для дореля-
тивистского уровня скоростей)
V = Plq, (1.4)
Тягу, приходящуюся на единицу весового расхода, характери¬
зует отношение 1° = V/g, имеющее размерность времени (напри¬
мер, сек). Величину 1° принято называть удельным импульсом
двигательной системы.
Соответственно (1.2) и (1.4) эффективное значение мощности
реактивной струи будет равно
N = \qVK (1.5)
Отметим, что отношение N к величине мощности Nni вырабатывае¬
мой энергоисточником двигательной системы, характеризует
§ 2] СОСТАВ КОСМИЧЕСКИХ ДВИГАТЕЛЬНЫХ СИСТЕМ
23
коэффициент полезного действия двигательной системы
Ч = (!-6)
Возможные регулировочные характеристики основных пара¬
метров космических двигательных систем Gp (t), Р (t), q (t) и
взаимосвязь между ними, естественно, определяются типом дви¬
гательной системы, физическими принципами ее работы. Для
определения обобщенных параметров рассмотрим состав косми¬
ческих двигательных систем.
§ 2. СОСТАВ КОСМИЧЕСКИХ ДВИГАТЕЛЬНЫХ СИСТЕМ
Обобщенный состав космической двигательной системы при¬
веден на рис. 1.2. Исходным элементом двигательной системы явля¬
ется источник энергии; завершающим элементом является реак¬
тивный движитель, где часть выработанной источником энергии
Рис. 1.2. Состав космической двигательной системы.
превращается в кинетическую энергию направленного движения
реактивной струи. Если виды энергии, выделяемой источником и
потребляемой движителем, различны, то между источником энер¬
гии и движителем включается энергопреобразователь. В паузах
работы двигательной системы часть выработанной источником
энергии может накапливаться в аккумуляторе энергии. Масса
рабочего тела, расходуемая на создание реактивной тяги, пода¬
ется в движитель системой подачи из контейнеров (баков). При
полете в среде с ощутимой плотностью масса рабочего тела может
пополняться через заборное устройство и накопительную систему.
24 ОСНОВНЫЕ ПАРАМЕТРЫ И СОСТАВ ДВИГАТЕЛЬНЫХ СИСТЕМ [ГЛ. 1
Последняя согласует параметры поступающего рабочего тела
с условиями в контейнерах (баках).
В результате отличия энергетического коэффициента полезного
действия двигательной системы от единицы значительная часть
вырабатываемой энергоисточником мощности должна быть от¬
ведена от двигательной системы системой отвода энергии.
Естественно, что указанные составные элементы присущи не
всем типам космических двигательных систем, в которых возмож¬
ны различные сочетания элементов в рамках рассмотренного
обобщенного состава.
С позиций механики космического полета характерными пара¬
метрами источника энергии являются вырабатываемая им мощ¬
ность Nn (t) (существенна возможность регулирования выделяемой
мощности), собственный вес энергоисточника Gn (Nn, t) и рас¬
ход массы qe при выработке энергии. Характерными параметра¬
ми преобразователя энергии являются отношение вырабатывае¬
мой им полезной мощности Nv (t) к входной мощности Nn (t)r
которое можно характеризовать как коэффициент полезного
действия энергопреобразователя т]х (А^), а также вес энерго¬
преобразователя GT (7V\, max) • Характерными параметрами акку¬
мулятора являются величина запасаемой им энергии Е, макси¬
мальные величины потребляемой Ртах и полезной выделяемой
ЕШ\а мощности (точка обозначает дифференцирование по време¬
ни t), а также собственный вес аккумулятора Ge (Pmax)* Харак¬
терными параметрами накопителя рабочего тела с заборником
являются qv — расход массы и привносимая забираемым рабочим
телом мощность Nqv, мощность, расходуемая накопителем Nv(qv),
и вес накопителя с заборником Gv (qv max). Характерным пара¬
метром контейнеров (баков) для рабочего тела является их вес
G$ (t), зависящий от величины запаса рабочего тела Gv, (t) =
— Ga (t) — G„ (cm. (1.3)).
Характерными параметрами системы подачи рабочего тела
являются подаваемый ею расход массы д, потребляемая мощность
Nq (q) и собственный вес Gq (qmах). Характерными параметрами
реактивного движителя являются создаваемая им тяга Р (t),
потребляемые им мощност N (Р) и расход массы q (Р), а также
собственный вес движителя GY (Ртах, А^таЦТ
Разность между мощностью, вырабатываемой энергоисточ¬
ником Nn плюс привносимой забираемым рабочим телом Nqv,
и полной мощностью реактивной струи движителя Nx должна
быть выделена системой отвода энергии.
Характерным параметром последней являются ее вес G^ (N^), где
NK = Nn + Nqv-Nx.
Указанные характерные составные элементы космической
УСЛОВИЯ КОСМИЧЕСКОГО ПОЛЕТА
25
двигательной системы определяют ее основные параметры:
Р(!)> tfo(t) = q + qe — qv,
Gv (0 = Gn G^ Ge Gv G$ -f- Gq + Gy -f- G
Параметры составных элементов космических двигательных
систем, естественно, зависят от физических принципов их рабо¬
ты, что будет подробно рассмотрено в последующих главах. Су¬
щественное влияние на параметры космической двигательной
системы оказывают внешние условия космического полета; да¬
дим краткую характеристику этих условий.
} (1.7)
§ 3. УСЛОВИЯ КОСМИЧЕСКОГО ПОЛЕТА
1. Гравитационные поля. Силы гравитационного поля опре¬
деляют основное внешнее воздействие в космическом полете. Для
типичного случая космического перелета, когда гравитационные
массы можно считать сферическими, вектор ускорения от гра¬
витационных сил (см. (1.1)) будет равен [1.69]
H = =-gradtf, (1.8)
г
где U — потенциал поля тяготения, / — универсальная грави¬
тационная постоянная, 991* — величина массы гравитационного
центра, Ri — вектор расстояния до центра гравитационной
массы.
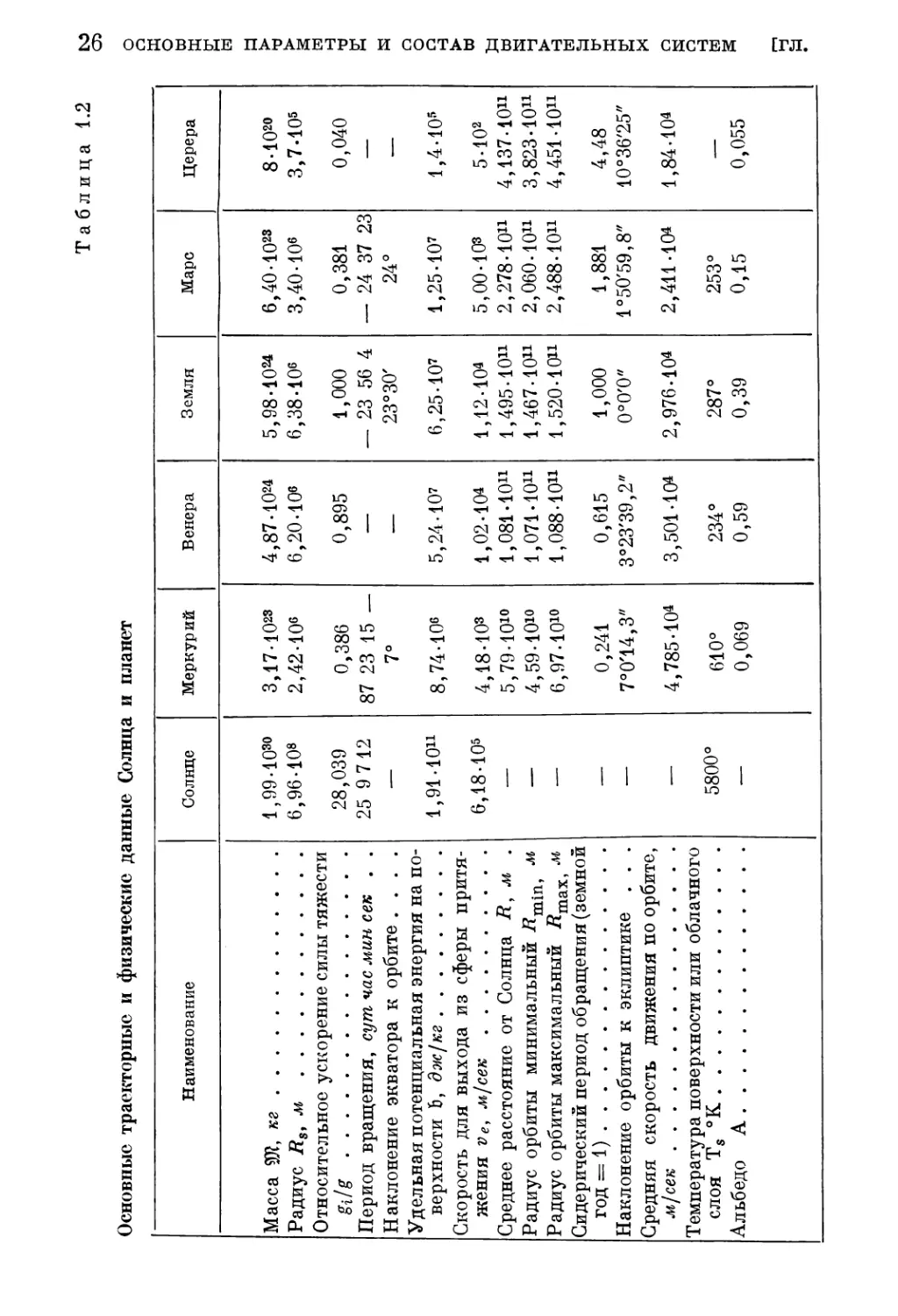
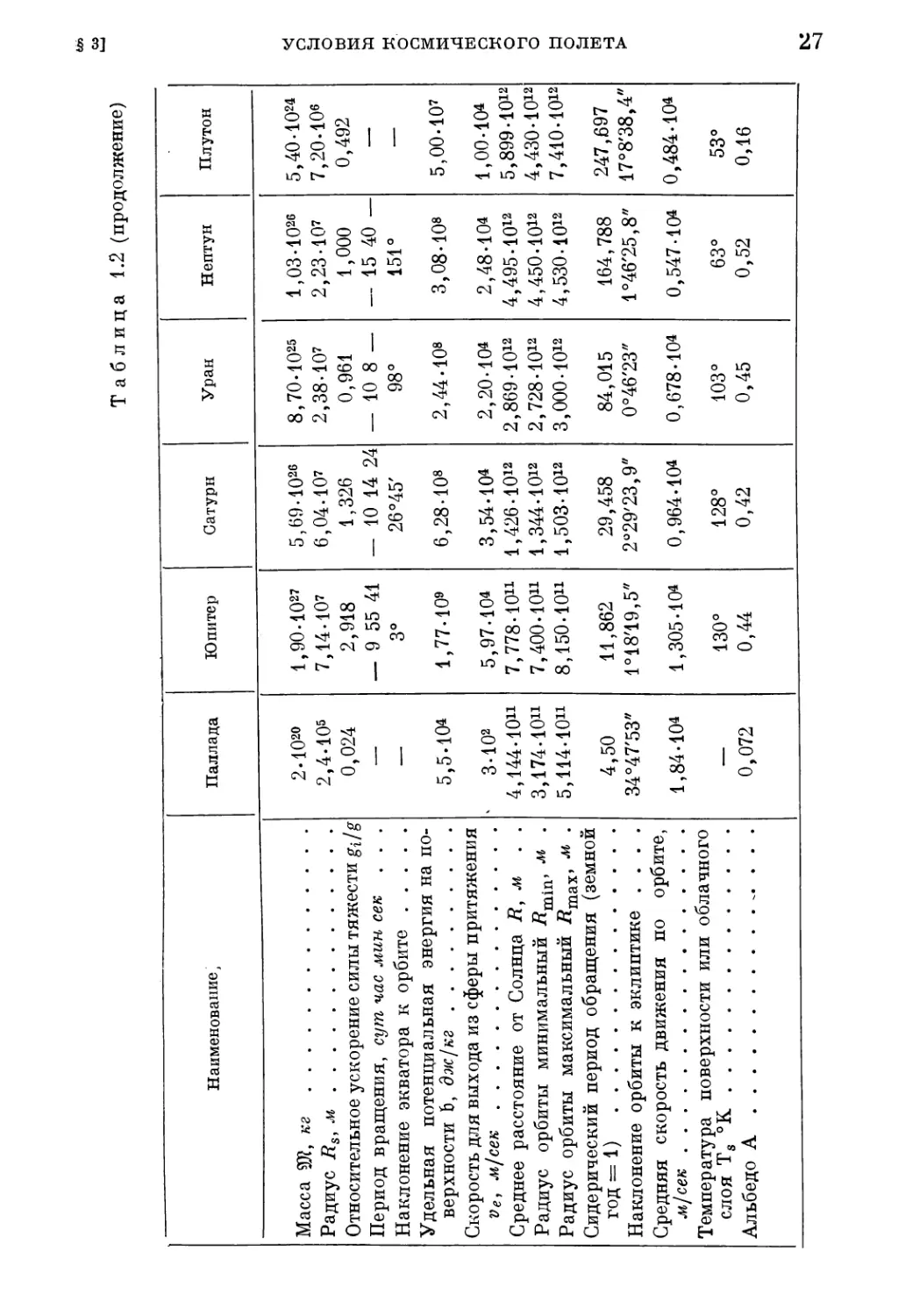
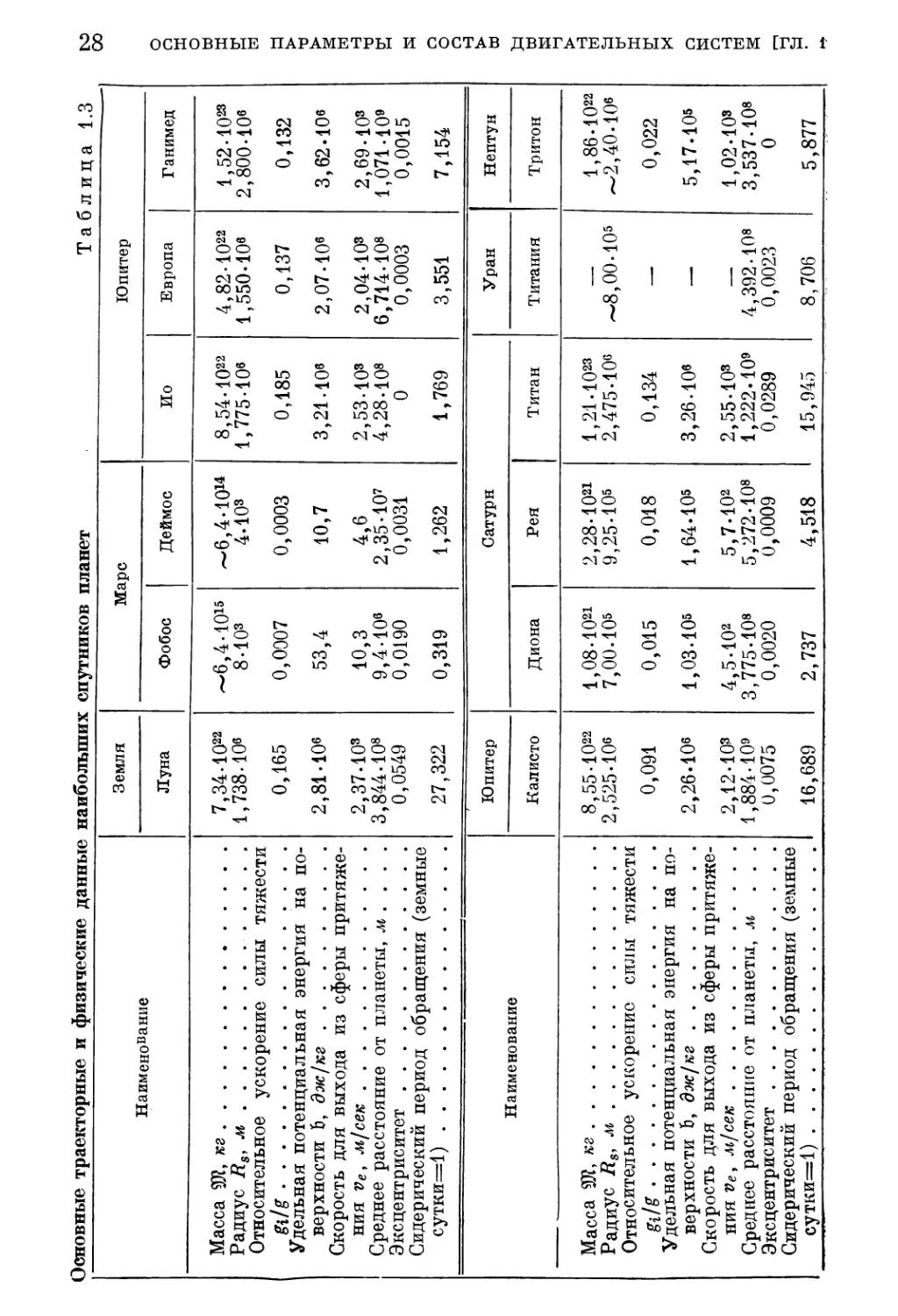
В табл. 1.2 и 1.3 приведены значения Ж* для небесных тел
солнечной системы, а также их основные траекторные и физиче¬
ские данные [1.70]. При движении вблизи планет следует учиты¬
вать несферичность поверхности и гравитационного поля. Так,
например, для Земли потенциал тяготения в точке, расположен¬
ной на геоцентрической широте <р, может быть записан в виде
и = т
1 + т (%Т ^ — 3 sit[2 + ТГ (%)3 (3 sin ф — 5 sinS ф) +
+ ж(%)4(3 — 30й1п2ф + 35sin4cp) + ..(1.9)
где Rs = 6,37815 * 106 м — экваториальный радиус; /, /г, кг —
коэффициенты второй, третьей и четвертой зональных гармоник,
/ = 1623-10"6, h = 6,0-10-6, кг = 6,4-10"6.
Движение космического аппарата в гравитационном поле при
отсутствии других сил, действующих на аппарат (Р = 0, F = 0
в (1.1)), как известно, является консервативным движением (см.,
например, [1.71—1.72]), для которого полная энергия остается
неизменной.
Основные траекторные и физические данные Солнца и планет
26 ОСНОВНЫЕ ПАРАМЕТРЫ И СОСТАВ ДВИГАТЕЛЬНЫХ СИСТЕМ [ГЛ.
а
В"
В
Е
VO
аЗ
Е-
1Л
1Г_
О
о
о
Ю
СМ
НИ
&
О
О
О
со
ч-Н
чН
ч-н
00
О
Ю
о
чН
ЧР
О
чН
ю
чеН
О I
1
Ч-Н
г-
СО
Ч"Н
чР
CD
1 о
1>
-
1 ЧР^
СО
СМ
Ю
СО
4ft
1
00
л
о
Ю
ч-Н
00
ЧР
чр~
о
00
о
СО
чн
чР~
СО
чР~
О
ч-t
чН
со
со
см
гН
I-H
гН
V.
са
«о
г-
&
о
О
о
оо
о
О
чН
о
чН
чН
чН
чН
чн
чн
00
со
о
ЧН
ч-н
00
03
СО
ЧР
00
о
00
00
ю
О
О
ЧР
см
ю
О
CD
00
чР
чР
сГ
см
см
о
см
О
чГ
чН
LO
CD
СО
I
чН
ю
см
см
см
чН
чР
см"
СО чН
Ю
СМ О
00 00
оз со
4jt
О CD
О ю
о
- со
чН СМ
Ю 1> о
03 со ОТ
чР ч}< ю
о *
о о
чь
^ о
нК
о
чН
о
03
CD
tr—
СО
00
аз
см
О
см"
1>- О
00 см
ю
03
00
• ч-Н чН 00
СМ оо В- 00
о о о о
чН 03
CD СО
° см
о
со
&
О ОЗ
чР LO
со
см о
я
Он
X»
к
а
в
к
В
1> см
■чн чр
CD Ю
00 чн
СО О
~ со t>
о см
о
ч-Н
чр
со"
см"
С*.
00
00
о
сс
00
CM
rH
О
О
03 чН
О
ч-t
ч-н
8^ 1
чН
03
CD
- 03 I
чН
ОЗ
03
00
ОЗ
CM vo
ч-н
CD
CM
чН
о о о о
00 03 03 1>-
-н 1> Ю о:
^ LO ^ CD
о о
о
4J1
О
чН
03
о
CD
VO
О
О
00
чН
с^
ч?
CD
О
о
чн
00
Ч-Н
CD
о
о
00
2
§
и
к
ЕН
ф
й
В
н
а
Е
£
о
ф
к
и
ф
Рн
с
s'4 &
о к
сб >i о
о R о
О « и
®2 « н
S о. о
S *
5S3 В
о
и
сб
н
В
5
Рн
ф
I и
со
В
сб
к
в
Е
В
ЕН
в
Рн
и
а
Рн
ф
>е<
CJ
со
к
со
5 3
' Й в
' I 0)
, g, к
я w
, w ф
ВС w
э О 2
к w
- Рн В
) ф б
fcj к
Сб
и
о
a s
в ^
*
и ^ и -
8« в *
S к Е
н н « а
и о ^
gg s«
5 " § а
а Рн 2 w
а
а;
к 3
в
в
Е
Сб
а
в
в
в
а
(В
о
а §
aS
05 ^
а
ЕН
w Н
сб VD
Рн ft
ф
Ф О
и fc
вс в
Ф и
Рн сб
и Он
»в в
а ®
в &
В сб
Е Рн
сс VO
2 О
В tf
^ о
в
Рн
ф
в
рВ
в
в
О "
Ф ч
в
в
ф
в
ЕС _
сб Н
Он о
ф
в
• VO
Рн
ф о
В о
в в
В S
в в
в в
в ф
® й
м к
&
a *
в g
vo 5
Рн О
О Рн
и §
§ °
м в
и к »
о м ^
В Wo
2 ф ^
м ft
М а
о
и
о
в
в
сб
Е
VO
о
в
Е
в
в
Ен
о
о
в
XI
Рн
ф
в
о
сбо
Таблица 1.2 (продолжение)
3]
УСЛОВИЯ КОСМИЧЕСКОГО ПОЛЕТА
27
и
и
cd
£
я
«о
Г*
5>
тН
г-1
о
о
Г4
о
о
4Н
О
4ТН
см
05 I
4ГН
1 ^
4гН
05
4^
о
4тН
о
о
О
ЧР 1
1 я
О
05
со
4Н
см
о"
о
О
00
ЧР
но
t-
но
4тН
по
чР~
Г»
S
05
00
тН
СО
со
•
о
СО
1>
0°
4t<
00
53
4ГН
чг
СМ
t—
4Н
4f
О
О
(О
(М
с»
1
00
са
(N
-г-t
<N
rH
00
00
S
О
О
о
О
О
о
О
О
о
00
4Г-1
4Г-1
4гН
о
о
4ГН
4Г-1
4Г-1
4Г1
ио
о
см
о
тН
00
00
см
со
ю
СО
СО
Ю
Ю
ио
О
О
чГ
со
чР
ЧР
со
О
(N
*ЧН
4ГН
4Н
о
чг
05
ио
со
СО
ио
сГ
4f
4f
ио
4ГН
СМ
1
со
см
»•
° |
о
1
4f
4f
ЧГ
О О •'Н
н CD 00 О
• о 00
О 00 - О 05
1> СО о н
00 см~ I
о
<М N <N
I—I г-1 гН
ООО
о 05 00 о
СМ СО СМ О
с* °° ч ®
см см со
Li J
ч—t см
°° о
о
г-н
о
ио
00
со
чГ
с^
о
со
4ГН
о
о"
05 чР
о о
со чР
СМ 4Г-1
со
- о
о о
00
см
со
чр СО чр СО
ю см ^ о
со ю
СО ~ #ч л
й
05
ъ
00
4гН
ио
со
о
см
ЧР
СМ
чР
00
ЧР
05
см
о
см
со
см
05
см
05
сГ
4Г-1
o'
и
а
Й f чр
О О 00
4Н "Ж тН НО
• 05 НО о
о чР со
05 4ГН см 05
-71>Г I
00 о о
05 С'- о но
st< -н
И0
о
см
4ГН
СО
05
о
чР
00
4Г1
ио
о
чр
00
о
со
4Г^
со
4Г-1
o'
4Г-1
о
4ГН
4Ж
ч
4
05
к
® О чР
О - g
Y ЧР -
^ CsT0
S
<м
о
о
о
4ТЧ
о
4гН
О
5:
СО
ИО
411
О
4ГН
см
ио
1гГ
4Г-1
со
Чр
4Г-1
чр
4^
4Н
ио
чр
ЧР
о
ЧР
ЧР
оо
1 °.
О
ЧР
со
ПО
СО
4Г^
W
<х>
S
а
ч
к
Ъо
к
о
я
cd
я
я <*}
Я *
н £
я
Я
В
о
0
а
к
(О
ft
о
Я •
а .
и
ф .
* .
я
н .
а
ft .
а
VO
ft
о
а
51 а
М
ф ф
S ч
у
S к
>5 Я
- ft
о
н
■05
о
OS >>
о к
га й
^ Рн О G К
ft S
о cd
я
а
и
ft
ф
н ' ч '
® . Э •
ft
«•>§<•
g . W .
и
л 2 .
гг ®
cd со .
а ^ о •
Я со и
ф а •
ЕН * и
с ^
н а 5
§ S- «
ы О и <Ъ
So
И В gY
3 X о
? Ао. «
ttf cef
§■ ’Э
я ^
к *
§ й
° §
• JH
а о
s а
- S
и ф
cd СО
CS я
а
>я я
ф
н
а
VO
ft
о
я
OS
ft
Cd VO
2 s
s s
я
* 4
о A
H н
о a
О VO
я ft
ft о
Ф
ф о
Я
« в
Ф чс
ft Cd
" 1-Г
О В
я °
5 н
S ft
^ ф
а н
Ен
а
VO
ft
О Ф 4Н
F и
О Н II
Ь ftfcf
а ф в
« « 2
cd Я
Рч о
>Я
а
я
а *
м л
а н
VO о
ft О
о ft
ф
а
я
ф
я
о
я
я
Я ft
Д а
я ^
ж ^
Я о
tt""*
и
ft •
ф
я •
о
Я •
cd ^
ft° .
b ад<:
Н г.
я ^ о
ft м «
ф я ф
я 2 vo
§о й
ф и я
н с
Основные траекторные и физические данные наибольших спутников планет
28
ОСНОВНЫЕ ПАРАМЕТРЫ И СОСТАВ ДВИГАТЕЛЬНЫХ СИСТЕМ [ГЛ. 1
cd
£Г
К
R
ю
8 CO
О О
см
со
О
ео л
О О Ю
чН •чгН
со
чгН
чН ч—( чгН
CSJ О
ч-н
•
• • О
ю
СМ
03 ч-н о
чгН
ю о
о
со
CD t>* -
-00
-о о
Г-
Ч—1 «ч
см
со
см -
<N
со ео
со
ео оо
О О
О
О О СО
чН чН
СО
чгН
ч-н ч-н О
ч-Н
чгН
• • О
ю
СМ О
!>•
ю
оо ш
О
О
О ч-н ~
»-ю
^JH ~
чН
см~
-Г- О
СМ -
со
СО
(М
<м со
О О
Ю
со
О
ео оо
О О
03
чгн ч-Н
00
чН
чгН чН
со
^ Ю
чгН
• • О
чгН
СО 00
LQ
О
см
LO см
ч-Н
-t>-
оо -
чн
СО
см~^
о
Го
о
|>
О Ч-Н
чгН СО
см
^ г
о
СО • О
со
о
о
-Ю о
см
со^
)
чгН
^ со -
о"
-о
см
чгН
ю
2со
V о
о
"Г
со
о о
СО -гН 03
03
о
ч-н
о
со"
0^0
со
со*4 00
ю
чгН «- —
о
03 о
о
&
N СО
оо
ю
со
о
ео оо
О О 03
СМ
Ч-Н чгН
со
чгН
чгН ч-н
СМ
ч-н
• • LO
со
^ 00
чгН
t^sfO
СО со
о
00
СО ^ -
-1>-
t" -
ч-н
см
-00 О
СМ -
со
см
Н fcf R" © El
м © о fc[
и PR К °
или
ь2
Ч-Н ^
СО О
00 ^
см
in
о
00
ео О
О чН
Е—
см
Ч-Н
чН .
с~—
о
• t^o
00
t"-
СМ СО
о"
ч-н
<э ю
ю
ю
ЧГН СО
щ
О
00
О
ч-н
ч-н СО
• 0-1
со
Я 1
| 1 см о
о
о 1
1 1 О30
со -
00
-о
00
)
К+1-
8 о
со
о
со О
О ЧН
о
О ^ 03
ю
Ч-н •
СО
чгН
чН • ОО
. ю
ч-н
• см СМ
03
чН t'-
СО
ю см о
»ч
СМ ^
о"
СМ
ю см -
ио
- -о
чН
ч-н СМ
со
СМ чгН
(М ю
О о
00
ю
о
сз О
О чН 03
00
ч-н ч—н
чН
чН
чН • О
ч-н
• СМ О
Ю
00 ю
1> о
см см
о"
со
-0-1 -
оГоз"
-е-Н
ю -о
Ю
гН
сз л
1П
00
о о
ю
О
<м О О
чН Ч-Н
ч-н
чгН
ОчНСМ
чгН • О
00
00 о
СО
• Ю о
1>-
° °л
о"
О
Ю f— -
чгН t>-
чН
—1>* о
^ со
см"
(М
С<1 о
О о
чН
со
О
ео. а
О О Ю
03
чгН ч-Н
03
чгН
Ч-Н ч-Н t>-
00
Ю LQ
• • О
со
СО
СМч^О
ю см
о"
см
ч-н 00 -
СО
-ю
-оо о
ч-н
00 -
см
см
см -
• у
. н
ф
• *
• к
н
о
Р
С
ф
о
а
« ag
OR
Cd J
о R О
2 ww
cd cd н
J^PhO
ф
‘ Й
. a
H
. К
Он
• К
• Я
. P
Ф
.►©<
о
со
• И
Р со cd
Ч * «
cd ^ ~
Г
И
Ф „
HsO ^
Н g
О g
W g
3 7- о
R Й x
£c§ Я
^ n
H
• К
a
• ф
. S’
cd
• pH
VO
• О
• fct
. o
a
• Ph
Ф
ш l_l
Ен 5H
_ а н ^
- cd p
Рн а О II
£ E4 8
^ О Ен а м
Ф w H §
к а © p g
gsss*
УСЛОВИЯ КОСМИЧЕСКОГО ПОЛЕТА
29
Для движения в гравитационном поле, описываемого урав¬
нениями (1.1) (1.8), в случае отсутствия других сил (r=R)
полная энергия движения будет равна
*=~г(т — 2/-^) =const” (1Л0)
где у = г — скорость движения.
При движении в поле тяготения превалирующего действия
одного небесного тела (в так называемой, сфере притяжения
этого небесного тела) урав¬
нение (1.10), естественно,
упрощается:
2
\ /^ = const. (1.11)
г
Значение удельной потен-
циальноиэнергии Ь =
г
на поверхности небесного
тела при R{ = Rs характе¬
ризует энергетические за¬
траты, необходимые для
выхода из сферы притяже¬
ния данного тела. Эти же
энергетические затраты
можно охарактеризовать
минимальным потребным
значением начальной ско¬
рости, необходимой для вы¬
хода из сферы притяжения
ve= У2f$Ri/Rs. Значения Ь
и ve дяя небесных тел сол¬
нечной системы также при¬
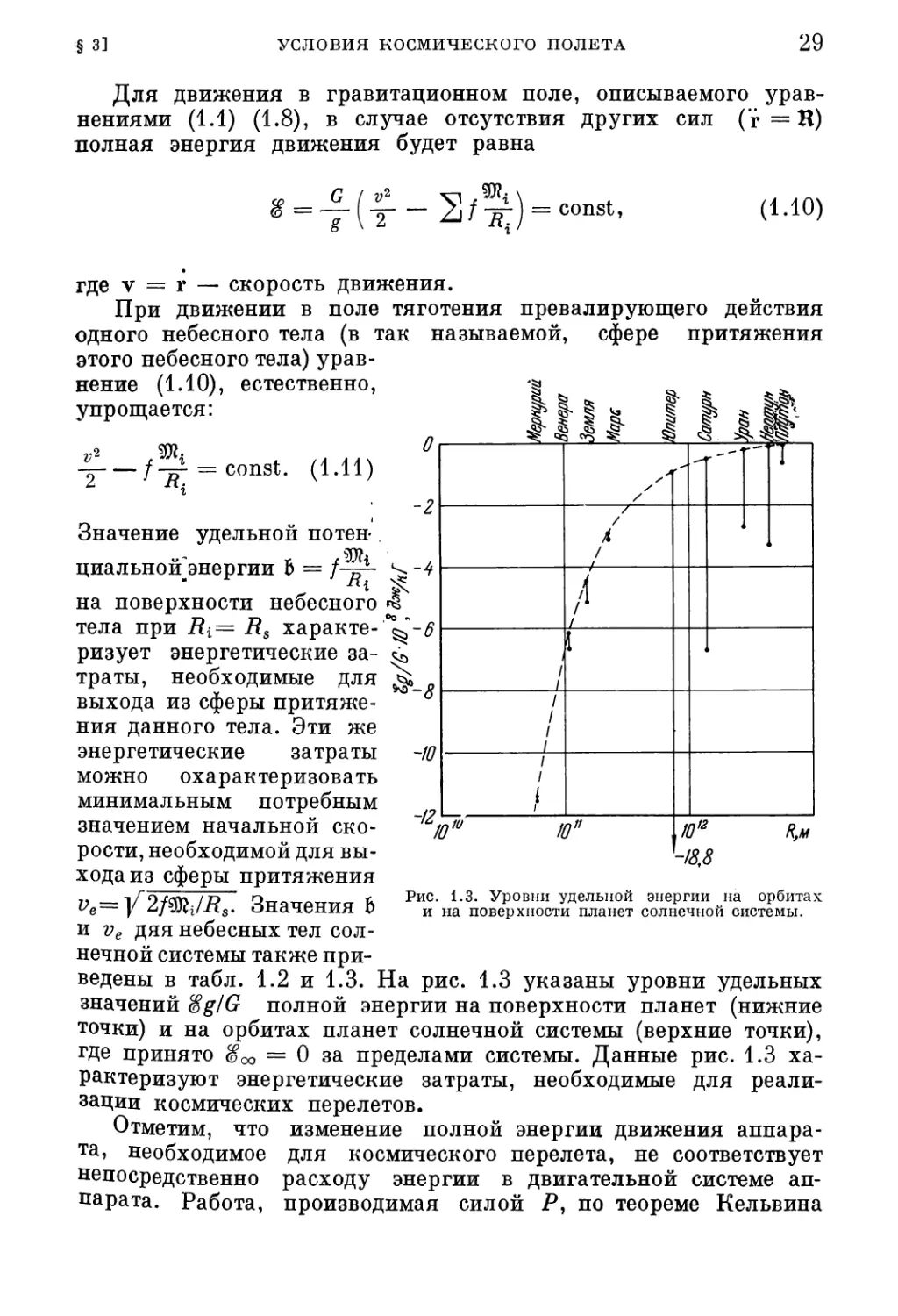
ведены в табл. 1.2 и 1.3. На рис. 1.3 указаны уровни удельных
значений SgIG полной энергии на поверхности планет (нижние
точки) и на орбитах планет солнечной системы (верхние точки),
где принято (осо 0 за пределами системы. Данные рис. 1.3 ха¬
рактеризуют энергетические затраты, необходимые для реали¬
зации космических перелетов.
Отметим, что изменение полной энергии движения аппара¬
та, необходимое для космического перелета, не соответствует
непосредственно расходу энергии в двигательной системе ап¬
парата. Работа, производимая силой Р, по теореме Кельвина
Is
&-8
tils. f I § Й*
UV4 ск 2$ о* 9
Ю11
л
/
/
/
I
/
/
4
/
/
/
/1
/
/
/
I
/
/
/
/
/
/
1
1
Ю12
-18,8
Я,м
Рис. 1.3. Уровни удельной энергии на орбитах
и на поверхности планет солнечной системы.
30 ОСНОВНЫЕ ПАРАМЕТРЫ И СОСТАВ ДВИГАТЕЛЬНЫХ СИСТЕМ [ГЛ. 1
составит
(1.12)'
Следовательно, работа, производимая реактивной тягой за
заданный промежуток времени (что связано с заданным расходом
энергии в двигательной системе), существенно зависит от скорости
движения космического аппарата в период действия тяги. Поэ¬
тому из приведенных общих соображений следует целесообраз¬
ность включения двигательной системы в областях гравитацион¬
ного поля, где скорость движения аппарата максимальна (подроб¬
нее см., например, [1.4]).
2. Параметры окружающей среды. Для обобщенного косми¬
ческого перелета с поверхности планеты старта через космическое
пространство к поверхности планеты назначения характерно
существенное изменение вдоль траектории полета плотности,
давления и температуры внешней среды,—параметров, определяю¬
щих вектор действующих на аппарат внешних сил F (см. (1.1)),
и возможности пополнения массы рабочего тела забором из внеш¬
ней среды. Особенно существенное значение для механики полета
эти параметры имеют в непосредственной близости к поверхности
планеты, в ее атмосфере. Величины плотности и давления в ат¬
мосферах планет резко падают с высотой. На рис. 1.4 [1.73] при¬
ведено распределение плотности р, давления и температуры
Th по высоте h в атмосфере Земли; там же нанесены определяе¬
мые высотой значения скорости звука а и кинематической вяз¬
кости V.
В межпланетном пространстве плотность газовой среды в ос¬
новном определяется корпускулярным излучением Солнца: по¬
током протонов (ионизованные атомы водорода) с энергией по¬
рядка 1 кэв (скорость го = 4,5-10ъ м!сек), интенсивность которого
в период спокойного Солнца составляет (см. [1.74])
где R — расстояние до Солнца, R§ = 1,495• 1011 м — средний
радиус орбиты Земли.
Соответственно (1.13) плотность распределения протонов
равна
Корпускулярный поток Солнца оказывает на элементы космиче¬
(1.13)
(1.14)
УСЛОВИЯ КОСМИЧЕСКОГО ПОЛЕТА
31
ского аппарата давление, соответственно (1.13), порядка
р3»рэП)2^2-10-8^укг/ж2 (1.15)
и подводит мощность порядка
9^^5-Ю вт/м2. (1.16)
Следует отметить, что в период активного Солнца по данным
[1.74] интенсивность корпускулярного излучения может воз¬
расти на два-три порядка.
/),КМ
ю~7
10'"
гоо°
ю5
ю~9
т°
ю~3
10'7
600°
10~1
10~5
800°
10
/О'3
1000°
103
10'1
1200°
рм/м3
ТД
ь
100
ю-*
200
ю~3
300
10~2
400
10ч
500
1
сЛС/сеп
ч^Усеп
Рис. 1.4. Изменение давления, плотности и температуры с высотой в ат¬
мосфере Земли; пунктир — скорость звука и кинематическая вязкость.
Основной энергетический поток в межпланетном пространстве
составляет электромагнитное излучение Солнца, имеющее ма¬
ксимум в видимой области светового излучения на длине волны
— 5500 А [1.75].
Спектр солнечного светового излучения непрерывный (рис. 1.5),
большая часть его соответствует излучению черного тела при тем¬
пературе Tq ^ 5800° К. Мощность потока солнечного светового
излучения составляет
3?А
:1400 (^-V2
вт/м2.
(1.17)
32 ОСНОВНЫЕ ПАРАМЕТРЫ И СОСТАВ ДВИГАТЕЛЬНЫХ СИСТЕМ [ГЛ. *
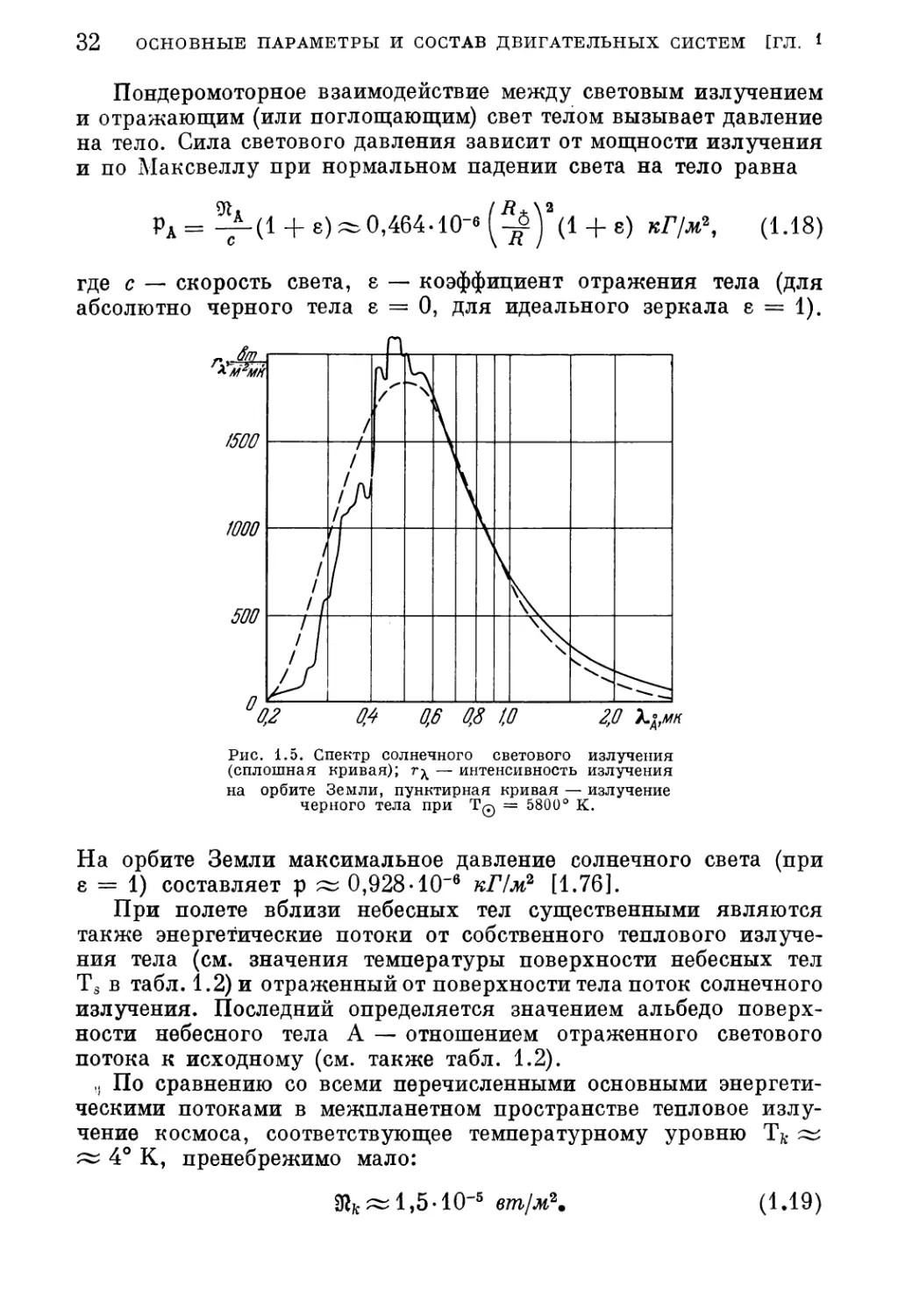
Пондеромоторное взаимодействие между световым излучением
и отражающим (или поглощающим) свет телом вызывает давление
на тело. Сила светового давления зависит от мощности излучения
и по Максвеллу при нормальном падении света на тело равна
РА = -—-(1 + е)^ 0,464-10 6 (1 + е) кГ/м2, (1.18)
где с — скорость света, е — коэффициент отражения тела (для
абсолютно черного тела е = 0, для идеального зеркала е = 1).
на орбите Земли, пунктирная кривая — излучение
черного тела при Tq = 5800° К.
На орбите Земли максимальное давление солнечного света (при
е = 1) составляет р ж 0,928-10'6 кГ/м2 [1.76].
При полете вблизи небесных тел существенными являются
также энергетические потоки от собственного теплового излуче¬
ния тела (см. значения температуры поверхности небесных тел
Т3 в табл. 1.2) и отраженный от поверхности тела поток солнечного
излучения. Последний определяется значением альбедо поверх¬
ности небесного тела А — отношением отраженного светового
потока к исходному (см. также табл. 1.2).
,, По сравнению со всеми перечисленными основными энергети¬
ческими потоками в межпланетном пространстве тепловое излу¬
чение космоса, соответствующее температурному уровню ^
~ 4° К, пренебрежимо мало:
3ifc ^ 1,5-10"5 вт/м2.
(1.19)
3]
УСЛОВИЯ КОСМИЧЕСКОГО ПОЛЕТА
33
Баланс суммарного воздействия всех отмеченных энергетиче¬
ских потоков и внутренней энергии (рассеиваемой телом) опре¬
деляет тепловой режим тела в космическом полете. Например,
максимальная эффективная температура Тт абсолютно черной и
теплопроводной сферы, движущейся вблизи поверхности небес¬
ного тела и не имеющей внутренних источников энергии, может
быть оценена соотношением
Ъ (i + A)Ti +
т, -
C0S гр4
4я ls
(1.20)
полета являются радиационные
RijiM
где со@ — угол, под которым видно Солнце, cos — угол, под кото¬
рым видно небесное тело.
Наряду с энергетическими потоками существенными для про¬
блем механики космического
потоки в космосе, представ¬
ляющие биологическую опас¬
ность и требующие опреде¬
ленных весовых затрат на
защиту. Помимо указанного
выше корпускулярного излу¬
чения Солнца, существен¬
ными являются космические
лучи, образованные ядрами
атомов с энергиями до
~ 1017 эв; удельная мощность
потока космических лучей
— 7-10"6 вт/м2, интенсив¬
ность ~ 6-103 м~2-сек~г.
Магнитное поле у небес¬
ного тела приводит к обра¬
зованию специфических маг¬
нитных «ловушек», сущест¬
венно усиливающих радиа¬
ционные потоки. Например,
у Земли такие «ловушки»
образуются магнитным полем относительно небольшой интен¬
сивности, которое оказывает малое силовое воздействие непос¬
редственно на летящий космический аппарат. Так, на геомаг¬
нитном экваторе горизонтальная составляющая магнитного поля
Земли достигает — 3,1-10"5 вб/м2, на геомагнитных полюсах вер¬
тикальная составляющая равна— 6,3*№~ъвб/м2. Однако это поле
является причиной образования у Земли радиационных поясов
с высокой интенсивностью заряженных частиц (рис. 1.6), пред¬
ставляющих значительную биологическую опасность [1.62].
3. Метеорные потоки. Движущиеся в солнечной системе ме¬
теорные потоки могут потребовать существенных весовых затрат
3 Механика полета
Рис. 1.6. Радиационные пояса Земли; контуры
соответствуют постоянной интенсивности за¬
регистрированных частиц.
34 ОСНОВНЫЕ ПАРАМЕТРЫ И СОСТАВ ДВИГАТЕЛЬНЫХ СИСТЕМ [ГЛ. 1
на защиту от них элементов космического аппарата, а характер
распределения интенсивности метеорных потоков в солнечной
системе может оказать влияние на выбор целесообразных траек¬
торий полета.
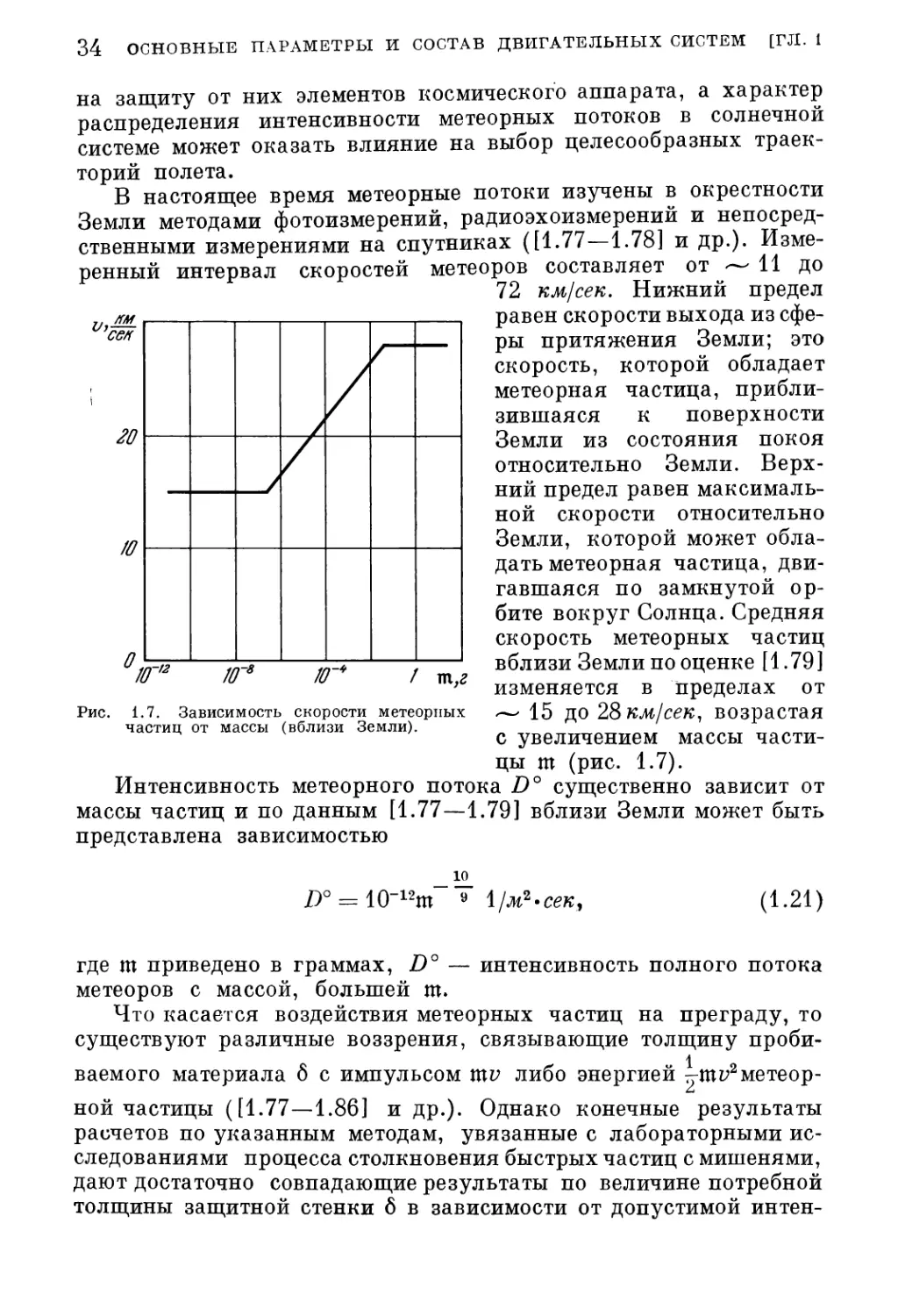
В настоящее время метеорные потоки изучены в окрестности
Земли методами фотоизмерений, радиоэхоизмерений и непосред¬
ственными измерениями на спутниках ([1.77—1.78] и др.). Изме¬
ренный интервал скоростей метеоров составляет от 11 до
72 км/сек. Нижний предел
равен скорости выхода из сфе¬
ры притяжения Земли; это
скорость, которой обладает
метеорная частица, прибли¬
зившаяся к поверхности
Земли из состояния покоя
относительно Земли. Верх¬
ний предел равен максималь¬
ной скорости относительно
Земли, которой может обла¬
дать метеорная частица, дви¬
гавшаяся по замкнутой ор¬
бите вокруг Солнца. Средняя
скорость метеорных частиц
вблизи Земли по оценке [1.79]
изменяется в пределах от
— 15 до 28 км/сек, возрастая
с увеличением массы части¬
цы ш (рис. 1.7).
Интенсивность метеорного потока D° существенно зависит от
массы частиц и по данным [1.77—1.79] вблизи Земли может быть
представлена зависимостью
Рис. 1.7. Зависимость скорости метеорных
частиц от массы (вблизи Земли).
[)° = 10 12щ 9 1 /м2*сек
(1.21)
где ш приведено в граммах, D° — интенсивность полного потока
метеоров с массой, большей ш.
Что касается воздействия метеорных частиц на преграду, то
существуют различные воззрения, связывающие толщину проби-
ваемого материала б с импульсом mv либо энергией -mi>2метеор¬
ной частицы ([1.77—1.86] и др.). Однако конечные результаты
расчетов по указанным методам, увязанные с лабораторными ис¬
следованиями процесса столкновения быстрых частиц с мишенями,
дают достаточно совпадающие результаты по величине потребной
толщины защитной стенки 6 в зависимости от допустимой интен-
УСЛОВИЯ КОСМИЧЕСКОГО ПОЛЕТА
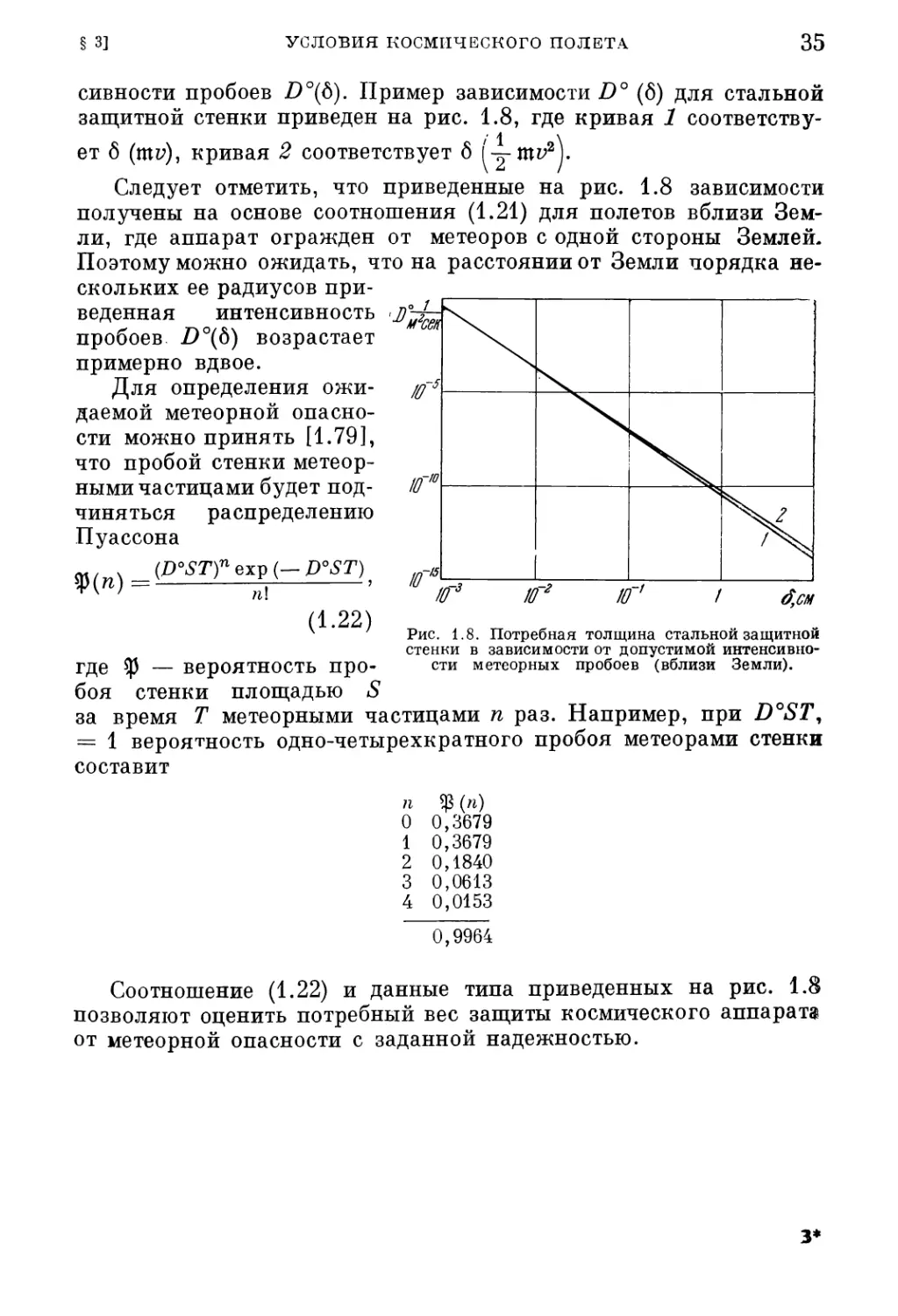
35
сивности пробоев D°{6). Пример зависимости D° (б) для стальной
защитной стенки приведен на рис. 1.8, где кривая 1 соответству¬
ет б (шу), кривая 2 соответствует б mz;2).
Следует отметить, что приведенные на рис. 1.8 зависимости
получены на основе соотношения (1.21) для полетов вблизи Зем¬
ли, где аппарат огражден от метеоров с одной стороны Землей.
Поэтому можно ожидать, что на расстоянии от Земли порядка не¬
скольких ее радиусов при¬
веденная интенсивность
пробоев D°{б) возрастает
примерно вдвое.
Для определения ожи¬
даемой метеорной опасно¬
сти можно принять [1.79],
что пробой стенки метеор¬
ными частицами будет под¬
чиняться распределению
Пуассона
y(r)_ (D°ST)n exp (— D°ST)
(1.22)
t0~3 /Г НГ* /
Рис. 1.8. Потребная толщина стальной защитной
стенки в зависимости от допустимой интенсивно¬
сти метеорных пробоев (вблизи Земли).
где ф — вероятность про¬
боя стенки площадью S
за время Т метеорными частицами п раз. Например, при D°ST,
= 1 вероятность одно-четырехкратного пробоя метеорами стенки
составит
¥(*)
0,3679
0,3679
0,1840
0,0613
0,0153
0,9964
Соотношение (1.22) и данные типа приведенных на рис. 1.8
позволяют оценить потребный вес защиты космического аппарата
от метеорной опасности с заданной надежностью.
3*
ГЛАВА 2
ФИЗИЧЕСКИЕ ПРИНЦИПЫ ЭЛЕМЕНТОВ
КОСМИЧЕСКИХ ДВИГАТЕЛЬНЫХ СИСТЕМ
§ 1. РЕАКТИВНЫЕ ДВИЖИТЕЛИ
1. Реактивная тяга и внешнее сопротивление. Реактивный
движитель является завершающим элементом двигательной си¬
стемы, в котором полезная часть выработанной источником энер¬
гии, превращаясь в кинетическую энергию направленного дви¬
жения реактивной струи, создает реактивную тягу Р. Сумма
реактивной тяги и внешних сил, действующих на летательный
аппарат от сопротивления среды, равна интегралу по замкну¬
тому контуру (например, по контуру аппарата) от составляющих
давлений р, напряжения трения т° и изменения количества дви¬
жения:
Р + FK = {I^cos^, x)dqx + [р cos (гс, х) + T°sin(72, х)] dS}, (2.1)
где п — направление нормали к контуру, тяга направлена по оси х.
При полете в атмосфере условились (см., например, [2.1]) в ка¬
честве силы внешнего сопротивления Fx принимать интеграл на¬
пряжения трения и давления, избыточного йад атмосферным рл,
по внешнему контуру аппарата АА^Ё^В вне реактивных струй и
расхода qVl забираемого из внешнего потока (рис. 2.1, а и б):
в
= 5 К** — Р/г) cos (72,#) -{- T°sin (72, х)] dS, (2.2)
и А
Тогда по определению (2.1), (2.2), с учетом отсутствия расхода
(Яг — 0) по контуру аппарата АВ, реактивная тяга при полете в
атмосфере равна (см., например, [2.2] и др.)
А
Р = ^ [Vi cos (Vi, х) dqi + (р — р„) cos (п, х) <?£] =
В
= qVc + (Vc — Ph)fc — qvV, (2.3)
где рс, Vс средние давления и скорость в сечении реактивной
струи по В А, $ с — площадь сечения реактивной струи.
РЕАКТИВНЫЕ ДВИЖИТЕЛИ
37
Такое общепринятое разделение силы, действующей на реак¬
тивной аппарат, на тягу и сопротивление, естественно, является
условным. Так, например, сила донного давления на участках
аА и ЪВ (рис. 2.1) аппарата, во многом определяемая реактивными
струями ([2.1] и др.), т. е. тягой, при указанном разделении от¬
носится к силе сопротивления. Однако принятое разделение между
тягой и сопротивлением имеет определенный физический смысл,
четко переходит в предельные случаи (отсутствие сопротивления
или тяги), а некоторая возможная корреляция между ними долж¬
на быть учтена при детальных анализах.
*)
At
Рис. 2.1. Схемы реактивных аппаратов: а) без забора;
б) с забором расхода qv из внешнего потока.
При полете в космосе, где сопротивление среды практически
отсутствует (F = 0), выражение для реактивной тяги упроща¬
ется; при ph — 0 и qv = 0
Рк — (?^с + Рс^с* (2-4)
2. Реактивные сопла. Движители ЖРД. В тепловых реактивных
двигателях движителем, создающим тягу, является реактивное
сопло, превращающее тепловую энергию газа в кинетическую
энергию направленной газовой струи. Физические принципы
работы реактивного сопла как движителя могут быть в основном
пояснены на основе газодинамической теории ([2.2—2.12] и др.).
Мерой тепловой энергии газа является так называемая тем¬
пература торможения Т0 — температура газа при отсутствии на¬
правленной скорости течения, V0. Максимально возможная
скорость направленного движения газа Fmaxmax, естественно, рав¬
на средней скорости теплового движения молекул покоящегося
газа; для совершенного газа значение Fmaxmax определяется извест¬
ным газодинамическим соотношением
F„
(2.5)
38
ФИЗИЧЕСКИЕ ПРИНЦИПЫ ДВИГАТЕЛЬНЫХ СИСТЕМ
[ГЛ.
где к — показатель адиабаты, равный для одно-, двух- и много¬
атомных газов соответственно 1,66, 1,40 и 1,33, Я — газовая
/ -|/х+1
постоянная. Эта максимальная скорость значительно (в I/
г X — \
раз) больше критической скорости звука в газе:
т/ 2Х
:а*~ V х + 1
Л;
поэтому для достижения больших скоростей истечения реактив¬
ные сопла должны быть сверхзвуковыми. Классическая схема
сверхзвукового осесиммет¬
ричного сопла представлена
на рис. 2.2.
В соответствии с газоди¬
намической теорией одномер¬
ных газовых течений ([2.4,
2.6] и др.) относительная ско-
-1 Ус
рость газа Ас = — на срезе
я*
идеального сверхзвукового
сопла без потерь и с равно¬
мерным осевым потоком оп¬
ределяется отношением пло¬
щади критического сечения
сопла (узкое сечение, где скорость газа равна критической
скорости звука aj к площади среза сопла fc
Рис. 2.2. Классическом схема течения в
сверхзвуковом реактивном сопле.
q {К) = К 1
и + 1
1 1 Рт-1)* 1 =
£•
&г.
(2.6)
Показано, что для газового потока с расходом q полный импульс
равен
ЛбГ х -|- 1
г = qV + pf
2х
qa„z (X),
(2.7)
1
где z (X) = X + « . По уравнению расхода для одномерных га¬
зовых течении величина расхода газа через идеальное реактивное
сопло составит
1 1
2 \х_1 Ро /ЛЧ5Г Ро-^, ( 2 \*-1
■о - фТо «• (х + 1) > (2.8)
q =
мт{
1 1
*-1 /к . 1^-1
U + 1
где q(X) = .. j ^ 2
заторможенного газа на входе в сопло.
Поэтому в соответствии с уравнениями (2.7), (2.8) величина ре¬
активной тяги, создаваемой идеальным соплом при полете в космосе
р0 — полное давление
РЕАКТИВНЫЕ ДВИЖИТЕЛИ
39
которая совпадает с величиной полного импульса газового по¬
тока Г на срезе сопла (ср. (2.4) и (2.7)), будет равна
1
р* = Г С = Voft (^l)K_1 2(Ьс). (2.9)
Отметим, что тяга, создаваемая реактивным соплом при по¬
лете в вакууме (2.9), не зависит от температуры газа Т0 и опре¬
деляется только полным давлением газа р0, площадью критиче¬
ского сечения и степенью расширения сопла fc / (опреде¬
ляющей Кс и z (К))- С увеличением степени расширения идеаль¬
ного сопла при фиксированных р0 и создаваемая им реактив¬
ная тяга в вакууме непрерывно растет, достигая теоретически
максимума при $оо, когда скорость истечения газов из
сопла становится максимально возможной:
P)cmax = Pof»(^q7l) ( ) (2'10)
при Vc— ГтаХ} max — у . в реальных соплах за счет
потерь на трение газового потока о стенки чрезмерное расшире¬
ние сопла нецелесообразно, так как при больших степенях рас¬
ширения дополнительные потери на трение при дальнейшем рас¬
ширении (и соответственно увеличении площади поверхности) пре¬
валируют над приростом тяги от расширения сопла. Аналогично
влияет и учет инерциальных сил при ускорении аппарата. Учет
потерь на трение газа в сопле определяет рациональную степень
расширения реактивного сопла (и соответственно ^CoPt)> при
которой реализуется тяга до — 95% Р/cmax (см., например, [2.7 —
2.11] и др.). Газодинамические принципы и вариационные про¬
блемы построения оптимальных контуров сверхзвуковых реак¬
тивных сопел рассмотрены в работах [2.13—2.21] и др. С учетом
указанных потерь импульса Гс в реальных соплах максимальная
тяга, развиваемая соплом при полете в вакууме, определится
соотношением
1
Ртах = Z(^copt)* (2.11)
Последнее соотношение показывает, что для фиксирован¬
ных р0 и f * максимальная тяга, развиваемая реактивным соп¬
лом при полете в вакууме, также фиксирована. Температура
газа на входе в сопло Т0 при фиксированных р0 и $л определяет
40
ФИЗИЧЕСКИЕ ПРИНЦИПЫ ДВИГАТЕЛЬНЫХ СИСТЕМ [ГЛ. 2
расход газа через сопло (см. (2.8)); с увеличением температуры
газа Т0 при постоянной тяге уменьшается расход газа q и соот¬
ветственно увеличивается удельный импульс двигательной си¬
стемы.
Для нахождения величины реактивной тяги, создаваемой
соплом при полете в атмосфере (для простоты рассматривается
случай qv = 0), необходимо из определенного значения тяги в
вакууме (2.11) вычесть член, учитывающий влияние атмосфер¬
ного давления р/г (см. (2.3)); тогда
rQz(K)--
Ph
х + 1
1
х—1
(2.12)
род (К)
Подчеркнем, что тяга, развиваемая реактивным соплом при
фиксированных значениях р0, §^ и Яс, возрастает с увеличением
высоты полета примерно на
— 10—30%, достигая макси¬
мального значения Ртах в
космосе.
Зависимость газодинами¬
ческих функций z (кс) и q (кс)
от Хг приведена на рис. 2.3.
Эти функции изменяются по
Хс так, что для фиксирован¬
ных значений р0, рл, §^ ре¬
активная тяга Р достигает
максимума при такой степени
расширения сопла и
таком соответствующем зна¬
чении скорости истечения
vc (Хс) = Vp (hp), при кото¬
рых статическое давление в
струе на срезе сопла рс рав-
Рис. 2.3. Изменение газодинамических функ¬
ций г (Я) ид (Я) (Я— относительная скорость).
но атмосферному давлению: при рс = ph
2х
Рh max — "ГcPcS'^p % ^
1
х—1
(2.13)
где
i —1
■р) =
Ph
Ро
Это так называемый расчетный режим работы сопла. Для
фиксированного сопла (fJS'c = const) при изменяющихся пере¬
падах давления р0/Рл (например, р0 = const, рл изменяется с вы-
а)
б)
«)
Рис. 2.5. Картина течения за соплом на режиме выше расчетного
а) цветной теплеровский снимок; б) снимок с оптической решеткой; в) то же
без потока.
§ 1] РЕАКТИВНЫЕ ДВИЖИТЕЛИ 41
сотой) только на расчетном режиме при ph = рр реактивное сопло
Р
обеспечивает максимально возможную тягу— = 1. На режимах
h max
ниже расчетного (— <^ — ]и выше расчетного тяга,
\ Pfi Рр I \ Ph Рр I
создаваемая соплом, будет меньше максимально возможной
[р—^реализуемой в случае, если бы на этих режимах
V h max I
применялось сопло с расчетным расширением.
£
р
hmazc
Рис. 2.4. Изменение относительной тяги, развиваемой соплом с Яс = 1,89, в зависимости
от перепада давления.
По соотношениям (2.12), (2.13) на рис. 2.4, а приведен пример
изменения относительной тяги
h max
х + 1
2хХрГс
Г cz(K)~
?h
и +1 \ x-i
Ро? (Хс)
(2.14)
в зависимости от перепада давления p( /p/t для сопла с Хс = 1,89
и Гс^ 0,99 [2.20]. Следует отметить, что показанные на рис. 2.4
значительные рассчитанные потери тяги на режимах ниже и выше
расчетного не связаны с течением внутри сопла, где течение и рас¬
пределение давления (рис. 2.4, б) неизменны. Указанные потери
тяги физически связаны с волновыми потерями в системе газоди¬
намических скачков уплотнения, образующихся в струе за соплом
на нерасчетных режимах истечения (см. пример на рис. 2.5 [2.22]).
42
ФИЗИЧЕСКИЕ ПРИНЦИПЫ ДВИГАТЕЛЬНЫХ СИСТЕМ
[ГЛ. 2
При реальных течениях газа неизменность сверхзвукового
потока внутри реактивного сопла классической схемы, с учетом
которой определяется относительная тяга по формуле (2.14)
О)
Рис 2.6. Схема истечения из сверхзвукового сопла на режиме ниже расчетного: а) те¬
чение без отрыва; б) течение с отрывом потока от стенок сопла.
(см. пример на рис. 2.4), имеет место во всем диапазоне режима
выше расчетного и в значительном диапазоне режима ниже рас¬
четного вблизи расчетного зна¬
чения перепада давления на
сопле. С уменьшением перепада
давления на сопле ро/р/г на ре¬
жиме ниже расчетного возра¬
стает перепад давления р/г/рс в
газодинамическом скачке уплот¬
нения на срезе сопла (так как
отношение давлений рс/Ро =
= const); после достижения кри¬
тического значения (Рь/рс)к ин¬
тенсивный скачок уплотнения
вызывает отрыв пограничного
слоя на стенках сопла и измене¬
ние картины течения внутри
сопла (см. схемы течения на
рис. 2.6 [2.23]). Приведенные
на рис. 2.7 по данным [2.23,
2.24] значения критического
перепада давления в скачке
уплотнения (ph/Vc)k иллюстри¬
руют для сопла классической
схемы ширину безотрывного
диапазона перепадов давления
на сопле на режиме ниже рас¬
четного, где сохраняется неиз¬
менным сверхзвуковое течение внутри сопла и где справедливо
определение потерь тяги по формуле (2.14).
Рис. 2.7. Изменение критического перепа¬
да давления в скачке уплотнения, вызы¬
вающего отрыв турбулентного погранично¬
го слоя на срезе сопла, в зависимости от
относительной скорости потока на срезе.
РЕАКТИВНЫЕ ДВИЖИТЕЛИ
43
После наступления отрыва потока в сопле давление на стенках
сопла в зоне отрыва повышается (по сравнению с расчетным дав¬
лением) и соответственно уменьшаются потери тяги. Это явле¬
ние особенно сильно проявляется в сверхзвуковых соплах с
центральным телом. На расчетном режиме и на режимах выше
расчетного течение в сверхзвуковом сопле с центральным телом
(рис. 2.8, а [2.20]) принципиально не отличается от течения в
сверхзвуковом сопле классической схемы. Однако на режимах
ниже расчетного попадающий и отражающийся от центрального
тела скачок уплотнения (идущий от среза обечайки сопла) вы¬
зывает существенное повышение давления на центральном теле
(рис. 2.8, б), интенсифицирующееся отрывом потока при взаимо¬
действии скачка уплотнения и пограничного слоя. Такие сопла
имеют небольшие потери тяги на режиме ниже расчетного. На
рис. 2.9 показан пример характеристики реактивного сопла с
центральным телом с = 165 [2.25]; пример компоновки ра¬
кеты с таким соплом см. в [2.26].
В целом в рамках газодинамической теории величина реак¬
тивной тяги, создаваемой соплом как движителем, определяется
по формуле (2.12) с учетом указанных поправок на влияние отры¬
ва потока на режимах ниже расчетного (включаемых, например,
в величину потерь импульса сопла Гс). Результаты, полученные
в газодинамической теории, справедливы для химических теп¬
ловых реактивных двигателей, при температурном уровне кото¬
рых влияния диссоциации, ионизации и рекомбинации газового
потока (не учтенные в изложенной теории) не являются опреде¬
ляющими. Типичным представителем таких космических двига¬
телей являются жидкостные реактивные двигатели, у которых
реактивное сопло является стержневым конструктивным элемен¬
том (см. пример на рис. 2.10) [2.27]. Вследствие конструктивной
и газогидродинамической взаимосвязи элементов у ЖРД нецеле¬
сообразно раздельно анализировать вес сопла (движителя),
камеры сгорания и системы подачи рабочего тела.
Согласно соотношениям (2.11), (2.12) максимальная тяга
ЖРД пропорциональна полному давлению газа в камере сгора¬
ния р0 и площади критического сечения сопла
Pi nax~Pof*. (2.11')
Вес сопла-движителя (являющегося одновременно системой
отвода энергии, см. рис. 2.10) из условий статической прочности
должен был бы быть пропорционален произведению РоЗГ*2, одна¬
ко из-за улучшения конструктивных качеств с увеличе¬
нием размеров двигателя вес возрастает медленнее, чем куб ха¬
рактерного размера, примерно пропорционально p0.?v Ана¬
логично изменяется и вес камеры сгорания ЖРД, являющейся
Рис.
Рис.
pj _
Рс =
Ф_
%
0,4
б)
0,2
О 0,4 0,8 £
Т О
2.8. Схема течения в сверхзвуковом сопле с центральным телом (А.с = 1,68).
;.9. Изменение относительной тяги, развиваемой соплом с центральным телом
165 в зависимости от высоты полета при р0 = 3,5 • 10Б кГ/м2’, сплошная кривая
эксперимент, пунктирная кривая — расчет для сопла классической схемы.
РЕАКТИВНЫЕ ДВИЖИТЕЛИ
45
энергоисточником и энергопреобразователем (см. ниже § 2 гл. 2).
Вес системы подачи рабочего тела должен быть пропорциона¬
лен расходу д, величина последнего по соотношению (2.8) также
Горючее
Окислитель
Рис. 2.10. Жидкостный реактивный двигатель RL10A-3 второй сту¬
пени ракеты «Сатурн» 1; горючее — жидкий водород, окислитель —
жидкий кислород:
1 — охлаждаемая излучением часть сопла, 2 — охлаждаемая горючим
часть сопла, 3 — камера сгорания, 4 — система подачи горючего
и окислителя.
пропорциональна произведению p03v Поэтому для ЖРД примерно
можно считать
(Gy + G^ + Gn + Gx + Gq) —
и с учетом (2.11')
Gy + Gr + Gn -f Gx + Gq ^ T^max>
(2.15)
(2.16)
G — C*
где y== -OL удельный вес двигателя (для ЖРД Ge = 0 и
Gv = 0).
46
ФИЗИЧЕСКИЕ ПРИНЦИПЫ ДВИГАТЕЛЬНЫХ СИСТЕМ
[ГЛ. 2
На рис. 2.11 в качестве примера приведены значения удель¬
ного веса двигателей ракет «Сатурн» (см. [2.11, 2.27] и др.); ука¬
занные там же данные двигателя ракеты V-2 иллюстрируют про¬
гресс в улучшении весовых характеристик ЖРД за последние
20 лет. Приведенные на рис. 2.11 характеристики подчеркивают
малые значения удельного веса химических тепловых реактивных
двигателей на жидком топливе.
7tw
т
0,02
0,01
0 5 10 20 50 /00 200 500 PmJ0~‘«r
Рис. 2.11. Зависимость удельного веса ШЕД от
величины развиваемой им максимальной тяги (пунк¬
тирная кривая — двигатели 1 — 4 ракет «Сатурн»):
1 — RL10A-3 (Н2 + 02), 2 — J-2 (Н2 + 02), 3 —
Н-1 (керосин + 02), 4 — F-1 (керосин + 02), 5 —
двигатель ракеты V-2 (этиловый спирт 75% + 02).
Важным параметром реактивного сопла как движителя явля¬
ется средняя эффективная скорость истечения струи из сопла V
и связанная с нею величина удельного импульса двигательной
системы 1°. По соотношениям (2.8), (2.12) и (1.4) эти параметры
равны (при qa = q)
(2Л7)
При фиксированных параметрах реактивного сопла и высоты
полета эффективная скорость истечения струи (и соответственна
удельный импульс) определяются составом (к) и температурой
торможения газового потока Т0. Максимальная скорость истече¬
ния для тепловых реактивных двигателей ограничена, например,
для химических двигателей максимальной температурой, дости¬
жимой при химических реакциях Т0 тах (см. ниже § 2), возмож¬
ностью выбора горючего и окислителя с малым значением молеку¬
лярного веса продуктов сгорания (увеличение газовой постоян¬
ной^) и допустимой температурой конструкции. Поэтому тепло-
±i
2к
rcz(?o-
РлНг
Ро7 (К)
/
3
___ д
■
—
.л
2
§ 1]
РЕАКТИВНЫЕ ДВИЖИТЕЛИ
47
вые реактивные двигатели можно классифицировать как двига¬
тельные системы с ограниченной скоростью истечения струи:
Как следует из соотношения (2.18), с увеличением высоты
полета максимальная эффективная скорость истечения из сопла
возрастает (соответственно с ростом тяги, см. (2.12)) примерно
на 10—30% [2.27]. Характерными являются точка старта на
поверхности Земли и полет в космосе. Например, для указанных
на рис. 2.11 двигателей ракет «Сатурн» максимальные значения
скорости истечения струи и удельного импульса составляют [2.27]:
для ЖРД стартовых ступеней на компонентах керосин + 02
при h = 0 Fmax о — 2550 м/сек, 10° ^ 255 сек; в вакууме Fmax =-
= 2800 м/сек, 1° ^ 280 сек;
для ЖРД космических ступеней на компонентах Н2 + Оа
при h = 0, Fmax о = 3200 м/сек, 10° х 320 сек; в вакууме Fmax =
= 4200 м/сек, /° ж 420 сек.
На рис. 2.12 по этим данным, соотношениям (2.12), (2.18)
и данным рис. 1.4 приведено примерное изменение с высотой полета
тяги, эффективной скорости истечения струи и удельного им¬
пульса высотного ЖРД.
3. Высокотемпературные тепловые реактивные движители. Для
получения величин эффективной скорости истечения и удельного
импульса больших, чем достижимые в химических тепловых реак¬
тивных двигателях, в литературе обсуждается ряд тепловых дви¬
гательных систем с нагревом рабочего тела до высоких темпера¬
тур электрическим разрядом либо в теплообменнике, обогревае¬
мом ядерным или изотопным реактором, или солнечной энергией
1 и
F< Fj
max —
0 10 20 30 40 hunt
Рис. 2.12. Относительное изменение с высотой полета
тяги, эффективной скорости истечения струи и удель¬
ного импульса высотного ЖРД.
48
ФИЗИЧЕСКИЕ ПРИНЦИПЫ ДВИГАТЕЛЬНЫХ СИСТЕМ [ГЛ. 2
([2.28 2.41] и др.)* Характерной особенностью таких двигатель¬
ных систем является очень высокая температура Т0 газового
потока на входе в реактивное сопло. При высокой температуре
Ю* 2'Ю* Т0,7<
Рис. 2.13. Доля тепловой энергии газового потока в зависимости
от температуры тормошения при £0 = Ю4 кГ/м2.
га*
ю*
°И03 8-/03 12:Ю3 Ю-Ю3 Утах ,м/сен
400 800 /200 /600 fan
Phj. 2.14. зависимость максимальной эффективной скорости истечения струи и удель¬
ного импульса в вакууме от температуры торможения «замороженного» газового потока.
нагрева газа перед соплом большая часть подводимой к движи¬
телю энергии (1 — г]Т) Nx расходуется на диссоциацию и иониза¬
цию газового потока. Долю тепловой энергии потока характе¬
ризует к. п. д. г]Т, зависимость которого от температуры для раз¬
личных рабочих тел приведена на рис. 2.13 [2.39]. Для нижней
оценки величины эффективной скорости истечения струи и удель-
РЕАКТИВНЫЕ ДВИЖИТЕЛИ
49
ного импульса высокотемпературных движителей принимается
(см., например, [2.33, 2.39] и др.), что за короткое время расши¬
рения газа в сопле энергия ионизации и диссоциации не успевает
выделиться (так называемое «замороженное»
состояние потока). Тогда величина эффек¬
тивной скорости истечения струи и удель¬
ного импульса может быть оценена по фор¬
муле вида (2.17) с учетом к. п. д. цт, если
принять Т0 мерой полной энергии газа:
1 -I
Гсг(Я.с) •
2 )
Ро<7 (А,с)
/»=Х.
g
(2.19)
На рис. 2.14 по данным [2.39] приведено
изменение максимальной эффективной скоро¬
сти истечения струи и удельного импульса
в вакууме для высокотемпературных реак¬
тивных двигателей в зависимости от темпе¬
ратуры торможения газового потока для
различных рабочих тел. Отчетливо видны
преимущества водорода как рабочего тела, обеспечивающего
Рис. 2.15. Схема теп¬
лового РД с ядсрным
реактором:
1 — реактивное сопло,
2 — ядерный реактор-
теплообменник, з— си¬
стема подачи рабочего
тела.
7 6 5
Рис. 2.16. Схема изотопного теплового РД:
1 — трубопровод системы охлаждения, 2 — тепловая изоляция, 3 — канал теплообмен¬
ника для нагрева рабочего тела, 4 — реактивное сопло, 5 — капсула с радиоактивным
изотопом, 6' — клапан системы подачи. 7 • — подача рабочего тела.
высокие скорости истечения при наименьшем потребном нагреве
газа. Величина тяги таких двигательных систем (не зависящая
4 Механика полета
50
ФИЗИЧЕСКИЕ ПРИНЦИПЫ ДВИГАТЕЛЬНЫХ СИСТЕМ [ГЛ. 2
от температуры газового потока — см. выше) определяется по
формуле (2.12).
Примеры схем высокотемпературных тепловых реактив¬
ных движителей с теплообменниками, нагреваемыми ядерным?
реактором [2.41], изотопным реактором [2.40] или концент¬
рированным солнечным излучением [2.39], приведены на рис.
2.15-2.17.
Рис. 2.17. Схема теплового реактивного движителя с солнечным нагревом:
1 — подвод рабочего тела (водород), 2 — дефлектор газа, 3 соединение
кварцевой прозрачной сферы с соплом, 4 — реактивное сопло, 5 и 6 — ось
вращения и цапфа системы ориентации движителя, 7 — пористый тепло¬
обменник — приемник лучистой энергии, 8 — многослойный , экран,
9 — кварцевая прозрачная сфера.
В этих движителях высокотемпературный газовый поток образу¬
ется в теплообменнике и разгоняется до больших скоростей
истечения в реактивном сопле. Аналогично случаю ЖРД из-за
взаимосвязи целесообразно совместно анализировать веса теп¬
лообменника и сопла. Обобщенная газодинамическая схема теп¬
ловых реактивных движителей с теплообменниками приведена на
рис. 2.18. Типовой канал теплообменника, в котором происходит
нагрев газового потока до заданной температуры торможения на
входе в сопло Т0, представлен эквивалентной трубкой диаметром
D и длиной^. Как будет показано ниже (§ 2 гл. 2), заданная сте¬
пень нагрева газового потока определяет потребное число калиб¬
ров каналов теплообменника LID = кт. С учетом эррозионной
РЕАКТИВНЫЕ ДВИЖИТЕЛИ
51
стойкости толщину стенки каналов (трубки) б для оценки примем
пропорциональной полному давлению: б —» р0. Тогда вес тепло¬
обменника будет пропорционален
Gx - f TLZ)6nT-p0TrT, (2.20)
где &т— фронтальная площадь теплообмен-
ника, пт—— число трубок теплообмен¬
ника на единицу фронтальной площади. По
уравнению расхода р0т^“т — Ро^*> поэтому с
учетом соотношения (2.13) вес теплообмен¬
ника пропорционален максимальной тяге
движителя
Gx Pof. Р maxi (2.21)
и аналогично (2.16) для высокотемператур¬
ных тепловых РД с теплообменником
Gyт = Gy + + Gq ^ YTPmaxi (2.22)
где ут — обобщенный удельный вес движи¬
теля. У ядерных тепловых РД с увеличе¬
нием мощности вес делящегося вещества —
энергоисточника (Gn) возрастает незначи¬
тельно и составляет малую долю веса двига¬
теля, поэтому для ядерных двигателей
ж С?£ (Ge ^ 0, Gv = 0). Для изотопных и
солнечных тепловых двигателей вес энер¬
гоисточника является существенной частью
и определяется по данным § 2 этой главы.
Примерные значения обобщенного удельного
веса ут тепловых реактивных движителей
с теплообменниками указаны в табл. 2.1 [2.32, 2.39, 2.40].
Величина максимальной эффективной скорости истечения струи
и удельного импульса для тепловых РД с теплообменниками, есте¬
ственно, зависит от максимально допустимой температуры нагрева
газа Тошах (см. (2.19) и рис. 2.14), которая ограничивается
допустимой для материалов движителя температурой. Пример¬
ные свойства некоторых высокотемпературных материалов
для тепловых РД с теплообменниками приведены в табл. 2.2
[2.29].
Указанный в табл. 2.2 максимально допустимый уровень тем¬
пературы стенок теплообменника теплового РД порядка 2800° К
ограничивает максимальную скорость истечения реактивной струи
в движителях с теплообменником: для водорода (оптимальное
рабочее тело — см. рис. 2.14) в вакууме Fmax ~ 8000 м/сек,
1° ж 800 сек.
4*
иЛодача рабочего
тела
mm
V
Рис. 2.18. Газодинами¬
ческая схема теплового
реактивного движителя
с теплообменником; Q—
тепловой поток от энер¬
гоисточника (ядерный
реактор, изотопный ре¬
актор , концентратор сол¬
нечного излучения).
52
ФИЗИЧЕСКИЕ ПРИНЦИПЫ ДВИГАТЕЛЬНЫХ СИСТЕМ [ГЛ. 2
Таблица 2л
Значения обобщенного удельного веса
для высокотемпературных тепловых реактивных
движителей с теплообменниками
Тип движителя
Gyt «г
-мпах К1
С теплообменником, нагреваемым ядер¬
ным реактором
С теплообменником, нагреваемым изотоп¬
ным реактором
С теплообменником, нагреваемым концен¬
трированным солнечным излучателем
*) Включая вес концентратора солнечной энер
—5-10-®
—100
—150*)
ГИИ.
Таблица 2.2
Свойства некоторых высокотемпературных материалов
для тепловых РД с теплообменниками
Материал
ВеО
Графит
W
Точка плавления, °К ......
Плотность при 20°С, кГ/м3 . . .
Кратковременная прочность на
разрыв, кГ/см2
2800
2,7-103
70-^-280
при 1500°К
3900 (субли¬
мирует)
1,7-Юз
210—420
при 2780° К
3650
19,1-Юз
350-630
при 2780° К
Значительно более высокие температуры нагрева и скорости
истечения струи реализуются в электротермических реактивных
движителях с нагревом рабочего тела электрическим разрядом —
дугой. Принципиальная схема электродугового движителя [2.36]
показана на рис. 2.19. Дуга, стабилизированная закруткой пода¬
ваемого рабочего тела или магнитным вращением, обеспечивает
большой градиент температуры газа по радиусу и позволяет на¬
гревать рабочее тело до температур в десятки тысяч градусов при
допустимых температурах стенок движителя (см. [2.42—2.45]
и др.)» что может обеспечить скорость истечения реактивной струи
ДО Fmax ~ 25 000 м/сек, 1° ^ 2500 сек [2.38]. Удельный вес элек¬
тродугового движителя по данным [2.33] составляет примерно
РЕАКТИВНЫЕ ДВИЖИТЕЛИ
53
у = Gy/Pmax ^ 10. Максимальная температура нагрева струи,
как и у других типов тепловых РД, лимитируется допустимой
температурой материала стенок движителя. Однако предельный
уровень нагрева рабочего тела в электродуговом движителе зна-
Рис. 2.19. Схема электродугового теплового реактивного
движителя: 1 — вводы системы охлаждения.
чительно выше, чем в химическом РД или тепловом РД с тепло¬
обменником. Важным параметром является к.п.д. движителя
т]^ = N/Ny: отношение мощности направленного движения реак¬
тивной струи N к мощности
Ny, потребляемой движителем.
По данным [2.46] при регули¬
ровании величины скорости ис¬
течения струи V и расхода рабо¬
чего тела q к.п.д. электродуго¬
вого движителя сохраняется
примерно постоянным, несколь¬
ко снижаясь с увеличением V
(рис. 2.20). Эти качества позво¬
ляют при ограниченной мощно¬
сти питания движителя Ny эф¬
фективно регулировать скорость
истечения реактивной струи V
при примерно постоянной по¬
лезной мощности струи N, что
в ряде случаев целесообразно с позиций механики полета (см,
ниже).
4. Электродинамические и электростатические реактивные
движители. Эти движители позволяют регулировать скорость
истечения реактивной струи V в практически неограниченном
Диапазоне вплоть до уровня релятивистских скоростей.
4000
8000 V,M/c
сен
Рис. 2.20. Экспериментальная характери¬
стика электродугового движителя; ра¬
бочее тело гелий.
54 ФИЗИЧЕСКИЕ ПРИНЦИПЫ ДВИГАТЕЛЬНЫХ СИСТЕМ [ГЛ. 2
Тепловые реактивные движители создают тягу в результате
воздействия газодинамического давления на стенки движителя.
Одновременно с воздействием газодинамического давления газо¬
вый поток в тепловом РД отдает стенкам движителя тепловую
энергию, что и лимитирует, как указывалось выше, эффективную
скорость истечения и удельный импульс таких движителей. Элек¬
тродинамические и электростатические движители используют
воздействие соответственно магнитного или электростатического
давления на стенки движителя, что практически снимает тепло¬
вое ограничение на эффективную скорость истечения реактивной
струи.
Подробно принципы работы электродинамических и электро¬
статических РД изложены в литературе [2.32, 2.36, 2.38, 2.47—
2.62]. Рассмотрим свойства таких движителей. Величины маг¬
нитного Рн и электростатического рв давления, как известно,
определяются соотношениями [2.63]
г> _ 112 _ Е2 /о 9Ч\
Рн — 8л ’ Ре - 8Я ’ (2.23)
где Н — напряженность магнитного поля, Е — напряженность
электрического поля. Величина напряженности магнитного поля
Н лимитируется силой электрического тока, используемого для
создания магнитного поля. Так, например, в технике использу¬
ются магнитные поля напряженностью Н ^ 1 тл = 10 ООО гс,
что соответствует магнитному давлению рн~4*104 кГ!м2. Ве¬
личина напряженности электрического поля Е лимитируется
условиями электрического пробоя диэлектрика (в том числе и
вакуума) между проводниками; в технике используются напря¬
женности электрического поля Е ^ 106 в!м ^ 30 ед. GGSE, что
соответствует электростатическому давлению Рв ~ 0,4 кГ/м2.
Из сопоставления указанных уровней магнитного и эле¬
ктростатического давления следует, что электродинамические
движители по сравнению с электростатическими могут обла¬
дать значительно большими значениями тяги на единицу
площади миделя движителя. Электродинамические движи¬
тели в литературе (см., например, [2.32, 2.36, 2.38, 2.57] и др.)
рассматриваются как импульсного, так и непрерывного действия.
На рис. 2.21 приведена принципиальная схема простейшего им¬
пульсного электродинамического ускорителя «рельсового» типа,
который был исследован в Институте атомной энергии АН СССР
в 1953 г. как плазменный инжектор для изучения термоядерных
процессов [2.64]. В этом ускорителе конденсатор С0 разряжа¬
ется на тонкую металлическую проволоку aft, натянутую между
двумя параллельными жесткими проводниками («рельсами»).
При замыкании разрядника Р проволочка практически мгновен¬
но испаряется и пар ионизуется, превращаясь в отрезок плазмен¬
РЕАКТИВНЫЕ ДВИЖИТЕЛИ
55
ного шнура. Вследствие взаимодействия электрического тока,
проходящего по плазме, с магнитным полем подводящих прово¬
дов возникает электродинамическая сила, которая ускоряет плаз¬
менный сгусток вдоль «рельсов», а приложенное к проводникам
магнитное давление определяет реактивную тягу. Основные свой¬
ства импульсного электродинамического ускорителя плазмы мо¬
гут быть описаны следующей теоретической моделью [2.64—2.66]:
масса ускоряемого плазменного
сгустка т принимается постоян¬
ной по времени разгона, урав¬
нение движения записывается в
виде
d2x 1 /ип dX / л о / \
тЧё=2С)1ь' <2-24>
где Cf — сила тока в цепи,
X — величина самоиндукции
контура, ось х направлена
вдоль «рельсов»; принимается
также, что омическим сопротив¬
лением электроцепи (включая
плазменный шнур) можно пренебречь. Тогда напряжение на
электродах «рельсов» % определится соотношением
% = Щр-. (2.25)
Уравнение энергии (разрядки конденсатора емкостью С0) замыка¬
ет систему
J = _C0^. (2.26)
При разгоне плазменного сгустка по «рельсам» самоиндукция
контура возрастает линейно по х
X = Х0+ Ь±х, (2.27)
где Х0 — начальная самоиндукция контура при t = 0 и х = 0;
dX
Ь±= = const. С учетом (2.27) решению подлежит следующая
система уравнений:
d2X 1 дупт
mdi?=2C,bl'
6)! d л
с начальными условиями: при t
= %Q, Cf = 0,
_ r d<U
(2.28)
dx
= 0^ = 0J=^ = 0J =
Рис. 2.21. Принципиальная схема импульс¬
ного электродинамического движителя:
Со — конденсатор, Р — разрядник.
56
ФИЗИЧЕСКИЕ ПРИНЦИПЫ ДВИГАТЕЛЬНЫХ СИСТЕМ [ГЛ. 2
При рассмотрении импульсного электродинамического уско¬
рителя как движителя важным параметром является к.п.д. пре¬
образования начальной запасенной в конденсаторе энергии Е =
= уCq%* в кинетическую энергию направленного движения
плазменного сгустка
N mV2
^— жг ~
(2.29)
• у Сйч\-
Целесообразно ввести в рассмотрение безразмерные переменные
t ж, <U 1й dU Cf
ОС — ОС , t — - i
^0 V%oCo
% = СП- * У = —— = Л
«о dt П» VColSSo
(2.30)
Тогда решение системы уравнений (2.28)
d2x
dl2
= е(^У
V dt I
dt
dx
*(0)=0, ^(0) = 0, <M(0)=1,
dt
(i + *)
dt _
q
dl
(2.28')
зависит только от одного основного безразмерного параметра 6:
ъ\с\и\
0 =
2 mSSo ’
(2.31)
через который выражается и к.п.д. движителя
"г-4>{§У- <2-29')
В работах [2.65—2.66] приведены решения системы уравне¬
ний (2.28'). Сопоставление их с экспериментом показало, что
изложенная теория удовлетворительно описывает основные свой¬
ства импульсных электродинамических ускорителей. Из формул
(2.30), (2.28'), (2.31), (2.29') следуют широкие регулировочные
возможности импульсного электродинамического движителя. Так,
например, при постоянстве безразмерной скорости (dxldt)т в
конце разгона сгустка плазмы и 0 = const при регулировке будет
постоянным к.п.д. движителя = const. Рассмотрим в качест¬
ве регулируемого параметра число импульсов движителя в се¬
кунду к; тогда расход рабочего тела q и мощность струи движителя
N определятся соотношениями
q=km, N=y]yk^,
(2.32)
§ 1] РЕАКТИВНЫЕ ДВИЖИТЕЛИ 57
а выражение для основного безразмерного параметра 0 запишется
в виде
b*NC0
e-«S^-consl' (2'33)
При постоянных значениях зазора между электродами («рель¬
сами») Ъх = const, параметров питающей электрической цепи
Рис. 2.22. Коаксиальный импульсный электродинамический ускоритель плазмы:
1 — подача рабочего тела, 2 — соленоид привода клапана подачи, 3 — клапан подачи
рабочего тела, 4 — коаксиальные электроды («рельсы») ускорителя.
Х0 = const и °Ц0 = const, в рассматриваемом примере регулиро¬
вания, если емкость конденсатора С0 и число импульсов в секунду
к изменяются по закону
Со- q, (2.34)
то регулирование скорости истечения струи V будет происходить
при постоянной мощности струи N = const и постоянной мощно¬
сти, потребляемой движителем, Ny = const; тогда
V=Y Щ—Уь p = qV~yf.' (2-35)
При этом максимальное значение потребной емкости конден¬
сатора С0 соответствует минимуму скорости истечения реактивной
струи V. Регулирование частоты импульсов выброса плазменных
сгустков к может осуществляться, например, клапанной системой
подачи газообразного рабочего тела (см. на рис. 2.22 схему иссле¬
дованного коаксиального импульсного электродинамического
ускорителя [2.64]). При коаксиальном расположении «рельсов»
58
ФИЗИЧЕСКИЕ ПРИНЦИПЫ ДВИГАТЕЛЬНЫХ СИСТЕМ [ГЛ. 2
радиуса гг и г2 значение погонной индуктивности движителя
равно
Ъг = In IL .
п
У импульсных электродинамических движителей получены
скорости выброса плазменных сгустков реактивной струи до
— 2-105 м/сек (см. [2.33, 2.38] и др.) при удельном весе движителя
Q
порядка у = -р Y ~ 10-1-100 кГ/кГ [2.36]. В это значение не вклю-
^шах
чен вес конденсатора, который хотя и является накопительным
элементом системы (см.
ниже § 2), но служит не¬
отъемлемой частью им¬
пульсного движителя.
Пример схемы электро¬
динамического движителя
непрерывного действия
[2.33] рассмотрен на
рис. 2.23. Предваритель¬
ной ступенью в этой схеме
является электродуговой
подогреватель, обеспечи¬
вающий начальную иони¬
зацию и электропровод¬
ность рабочего тела—плазмы, поступающей в собственно электро¬
динамический ускоритель. В последнем системой электродов и элек¬
тромагнитов устанавливается скрещенное электромагнитное поле,
ускоряющее плазму как проводник. Можно считать, что ускоряе¬
мый газ — рабочее тело — представляет собой нейтральную плазму
с электропроводностью а*. Разность потенциалов между верх¬
ним и нижним электродами (рис. 2.23) создает в канале ускорителя
алектрическое поле с напряженностью Е, благодаря которому
возникает электрический ток через плазму плотностью i. Взаимо¬
действие магнитного поля Н (перпендикулярного Е) и электри¬
ческого тока i вызывает приложенную к плазме ускоряющую
силу Fx, действующую перпендикулярно i и Н:
(2-36)
где Fx — сила, действующая на единицу массы плазмы, р —
плотность плазмы.
По результатам расчетов, приведенным в работе [2.33], такой
движитель при V = 2-104 м/сек и Ny = 4800 кет имеет к.п.д.
Q
% ~ 0,8 и удельный вес порядка у = -р -Y- ^ 10 кГ/кГ. Ре"
max
V-н
1вШВ1
1
/
Рис. 2.23. Схема электродинамического движи¬
теля с непрерывным истечением плазменной
реактивной струи:
2 — ВВод рабочего тела в дуговой ионизатор, 2 —
анод электродинамического движителя, 3— катод,
4 — катушка электромагнита.
РЕАКТИВНЫЕ ДВИЖИТЕЛИ
59
гулирование движителя может осуществляться изменением маг¬
нитного и электрического поля, что, согласно уравнению (2.36),
изменяет ускоряющую силу, действующую на плазму в движителе.
В литературе ([2.30—2.33, 2.36, 2.38, 2.45, 2.57] и др.) опи¬
сано много разновидностей электродинамических движителей
с импульсным или непрерывным ускорением реактивной плазмен¬
ной струи, которые принципиально не отличаются от рассмотрен¬
ных выше двух основных схем. С точки зрения механики полета
основным общим свойством
электродинамических движи¬
телей следует признать воз¬
можность регулирования в
широком диапазоне скорости
истечения реактивной струи.
Этим основным свойством об¬
ладают и электростатиче¬
ские — ионные движители.
В отличие от электродина¬
мических движителей, уско¬
ряющих квазинейтральную
плазму, электростатические
движители ускоряют заря¬
женные частицы — ионы и
электроны, которые после
ускорения смешиваются в
квазинейтральную реактив¬
ную струю (см. [2.31, 2.32,
2.36, 2.38, 2.47—2.56, 2.58-
2.62] и др.). На рис. 2.24 приведена обобщенная схема электро¬
статического движителя, состоящего из источника ионов, уско¬
рительной электростатической системы и источников электро¬
нов: на схеме % — разность потенциалов ускоряющего ио¬
ны электрического поля, потенциал А% прикладывается для
предотвращения обратного потока электронов.
При электростатическом ускорении заряженных частиц, имев¬
ших нулевую начальную скорость, конечная скорость V{ опре¬
деляется разностью потенциалов ускоряющего поля %, которую
прошла частица
Рис. 2.24. Обобщенная схема электростатиче¬
ского движителя: 1 — подача рабочего тела,
2 — ионизатор рабочего тела, з — электроста¬
тическая ускорительная система, 4 — эмиттер
электронов.
F,_/ .
(2.37)
где е — электрический заряд частицы, ц — масса частицы.
Расход рабочего тела соответствует электрическому току О
потока заряженных частиц
qi = У, (2.38)
60
ФИЗИЧЕСКИЕ ПРИНЦИПЫ ДВИГАТЕЛЬНЫХ СИСТЕМ
[ГЛ. 2
и соответственно тяга Р{ и мощность струи N{ равны (для ионов i)
Из условия квазинейтральности реактивной струи в электроста¬
тическом движителе потоки ионов и электронов должны создавать
одинаковый ток (Cfi = CfE) и иметь одинаковую скорость (F* = Fe);
поэтому
Для однозарядных ионов отношение массы электрона к массе
иона порядка fxe/jm, ж Ю-5, что позволяет, согласно соотноше¬
ниям (2.40), пренебречь вкладом электронов в тягу и мощность
электростатического движителя. Превалирующее влияние ион¬
ного потока определило и название электростатического движи¬
теля как ионного движителя. Реактивная тяга ионного движителя
по закону Чайлда—Ленгмюра (см., например, [2.67]) лимити¬
руется возможной плотностью ионного тока i = Cf/f, создавае¬
мого электростатической ускорительной системой (f — площадь
сечения ионной струи). Это ограничение связано с тем, что элек¬
тростатическое давление пространственного заряда потока одно¬
именно заряженных ионов противодействует ускоряющему воз¬
действию электрического поля. Потенциал в каждой точке элек¬
трического поля % связан с плотностью пространственного заряда
pi соотношением
Для плоского случая с учетом (2.37) параметры ионного по¬
тока находятся интегрированием следующего дифференциального
уравнения:
где i — -д~ = —Pi^i, с начальными условиями: при х = О
% = 0, d%!dx = 0.
После интегрирования определяется величина максимально
возможной плотности ионного тока imax, создаваемой электроста¬
тической ускорительной системой с ускоряющим напряжением %
и расстоянием между ускоряющими электродами d:
V2% = — 4яр|.
(2.41)
(2.42)
§ 1] РЕАКТИВНЫЕ ДВИЖИТЕЛИ 61
и соответственно (2.39) максимальная тяга, создаваемая ионным
движителем,
= (2.44)
Характерно, что максимальная тяга, развиваемая ионным
движителем, не зависит от параметров рабочего тела (массы ц и
Рис. 2.25. Зависимость удель- Рис. 2.26. Зависимость от ускоряющего напря-
ной тяги ионного движителя от жения скорости реактивной струи ионного дви-
ускоряющего напряжения и за- жителя; в скобках указан атомный вес атомов
зора между ускоряющими элек- или коллоидных частиц,
тродами.
заряда иона ё), а определяется только электростатическим дав¬
лением, пропорциональным квадрату напряженности приложен¬
ного электростатического поля — %2‘!d2, (см. выше (2.23)). На
рис. 2.25 указано изменение удельной тяги Ртах/^ в зависимости
от ускоряющего напряжения % и зазора между электродами d.
Максимальные значения удельной тяги ионного движителя огра¬
ничены электрической прочностью по отношению к пробою (меж-
электродная дуга), наступающему при напряженностях элек¬
трического поля, больших — 106 в!м [2.53, 2.67].
В отличие от максимальной тяги ионного движителя, скорость
истечения реактивной струи V\ существенно зависит от выбора
рабочего тела (см. (2.37)). На рис. 2.26 для ионов атомов ряда
рабочих тел и коллоидных частиц большой массы показано изме¬
нение скорости ионной реактивной струи в зависимости от уско¬
ряющего напряжения % [2.53].
62
ФИЗИЧЕСКИЕ ПРИНЦИПЫ ДВИГАТЕЛЬНЫХ СИСТЕМ [ГЛ. 2
В целом данные рис. 2.25 и 2.26 указывают на большие регу¬
лировочные возможности ионного движителя. Подчеркнем, од¬
нако, что соотношение (2.44) определяет максимально возможную-
Рис. 2.27. Схема лабораторной модели ионного движителя с контактной
поверхностной ионизацией:
1 — охлаждение кожуха вакуумной камеры, 2 — весы для измерения
тяги, з — окно для наблюдений, 4—5 — система подачи рабочего тела це¬
зия, 6 — экранирующая сетка, 7 — ускоряющая сетка — эмиттер электро¬
нов, 8 — вольфрамовый ионизатор, 9 — нагреватель ионизатора, 10 — за¬
пирающая сетка.
тягу, создаваемую ионным движителем, при условии, что макси¬
мально возможная плотность ионного тока imax (2.43) и соответ¬
ственно расход рабочего тела q{ max обеспечиваются источником
РЕАКТИВНЫЕ ДВИЖИТЕЛИ
63
ионов. Поэтому характеристики ионных движителей во многом
определяются характеристиками ионных источников.
Наряду с электродуговыми источниками ионов (типа рас¬
смотренных выше электротермических движителей) в литературе
[2.31, 2.32, 2.36, 2.38, 2.47-2.56, 2.58-2.62, 2.67-2.69] под¬
робно рассмотрены два типа ионных источников: с контактной
поверхностной ионизацией (см. на рис. 2.27 [2.50] схему лабора¬
торной модели) и с объемной ионизацией электронным ударом
(см. ниже).
В ионных источниках с поверхностной ионизацией (рис. 2.27)
используется свойство образования положительных ионов рабочих
тел с малой энергией ионизации при контакте с нагретой поверх¬
ностью ионного источника, выполненного из материала с большой
работой выхода электронов.
Энергия ионизации атома рабочего тела соответствует энер¬
гии, потребной для удаления внешнего электрона атома. Работа
выхода материала ионизатора соответствует энергии поглощен¬
ного электрона. Вероятность актов ионизации рабочего тела —
поглощения внешних электронов атомов рабочего тела при кон¬
такте атомов с поверхностью ионизатора — увеличивается с
ростом разницы между работой выхода и энергией ионизации.
Эта разница наибольшая у пары Cs — W [2.53, 2.68] (см. данные
табл. 2.3 и 2.4, где работа выхода и энергия ионизации указаны
в электрон-вольтах).
После контакта атома рабочего тела с поверхностью иониза¬
тора образовавшиеся ионы должны иметь достаточную для отхода
тепловую энергию, иначе адсорбированный на поверхности слой
атомов рабочего тела снижает работу выхода и соответственно
ионизацию. На рис. 2.28 приведена величина степени ионизации
К цезия на вольфраме в зависимости от температуры вольфра¬
мовой поверхности Т, где степень ионизации К представляет
собой отношение числа образующихся ионов к числу атомов
Таблица 2.3
Энергия ионизации некоторых элементов
Элемент
Атомный вес
Энергия ио¬
низации, эв
Элемент
Атомный вес
Энергия ио¬
низации, 9в
Не
4,003
24,50
Li
6,940
5,36
Кг
83,800
13,90
Na
22,991
5,12
Н
1,008
13,50
К
39,100
4,32
С
12,011
11,20
Rb
85,480
4,16
Hg
200,610
10,39
Cs
132,910
3,87
64 ФИЗИЧЕСКИЕ ПРИНЦИПЫ ДВИГАТЕЛЬНЫХ СИСТЕМ [ГЛ. 2
Таблица 2.4
Работа выхода и температура плавления некоторых металлов
Металл
Работа выхо¬
да, эв
Температура
плавления,
Т °С
Металл
Работа выхо¬
да, эв
Температура
плавления,
Т оС
Та
4,10
3027
С
4,81
3550
Мо
4,30
2620
1г
4,90
2454
Сг
4,37
1890
Re
5,10
3167
Os
4,50
2700
Pt
5,20
1773
Ag
4,70
960
W
5,50
3370
цезия, коснувшихся поверхности ионизатора. Видно, что по
достижении некоторой минимальной температуры Т\ (зависящей
от плотности ионного тока i), когда адсорбированный на поверх¬
ности ионизатора слой цезия исчезает, степень ионизации стано¬
вится близкой к единице. Данные рис. 2.28 показывают, что ве¬
личина обеспечиваемой
ионизатором плотности
ионного тока i ^ гтах (и
соответственно расхода ра¬
бочего тела qi<^ щах, см.
(2.43)) определяется тем¬
пературой поверхности ио¬
низатора и может регули¬
роваться в пределах /тах
путем изменения подачи
0,95
0,90
0,85
0,80.
■■/00ml
у/см2
ъ=Юма/см2
Ома/см2
7000
то
/800
Рис. 2.28. Зависимость степени ионизации цезия
от температуры поверхности вольфрамового иони¬
затора.
туры ионизатора. Для при¬
ложений к механике кос¬
мического полета сущест¬
венно, что такое регулиро¬
вание расхода рабочего тела в ионном движителе не связано
со скоростью истечения реактивной струи У*, зависящей только
от ускоряющего напряжения %. При превышении ионизатором
указанного выше на рис. 2.28 температурного уровня Т* плотность
ионного тока i и соответственно расход рабочего тела q% лими¬
тируются по закону Чайлда — Лэнгмюра (см. (2.43)), при этом
достигается максимально развиваемая ионным движителем тяга,
зависящая только от напряженности ускоряющего электрического
поля %/d (см. (2.44) и рис. 2.25). Так, на исследованной в работе
[2.50] лаб 'раторной модели ионного движителя при температуре ио¬
низатора Т ^ Тг = 1173° К (J^70 ма, f = 70 см2,л^\ма!см2) бы¬
ла реализована максимальная реактивная тяга Ршат ~ 5-10"4 кГ,
1]
РЕАКТИВНЫЕ ДВИЖИТЕЛИ
65
соответствующая напряженности ускоряющего электриче¬
ского поля %/d х 3000 е/см. Скорость истечения реактивной струи
ионного движителя в этих опытах составляла Viж 70 000 м/сек
(удельный импульс 1° ж 7000 сек).
В ионном движителе с поверхностной ионизацией мощность
излучения с нагретой поверхности ионизатора Nj является основ¬
ным видом потерь [2.53]. По своей природе эти потери
: N i = асоТ tf
(2.45)
связаны с плотностью ионного тока i (Т{ = / (i)), с площадью се-
чения реактивной струи f и не зависят от скорости истечения
струи (от ускоряющего напря¬
жения %). По данным [2.53] для
Ш
200
100
50
20
\
N
ч
\>
ч
\
\
s
1 г
5 Ю 20 50 b1,
Рис. 2.29. Потери на излучение с поверх¬
ности нагретого ионизатора при контакт¬
ной поверхностной ионизации цезия на
вольфраме.
Рис. 2.30. Изменение удельных потерь
мощности в ионном движителе с контакт¬
ной ионизацией цезия на вольфраме в за¬
висимости от максимальной плотности
ионного тока; на кривой отмечено значе¬
ние гшах, ограниченное условиями пробоя
%
max '
* 10 000 е[при d =1 смщ
ионизации цезия на вольфраме зависимость удельных потерь
Nj/f (в вт/см2) от плотности ионного тока i (ма/см2) может быть
аппроксимирована следующим соотношением (рис. 2.29):
lg jp- = 0,20 -j- 0,22 lg г. (2.46)
Рассматриваемые потери мощности в ионном движителе удоб¬
но отнести к полному току О ионной струи; при размерности Nj/Cf,
выраженной в эв/ион (в электрон-вольтах на ион—в вольтах),
численно это значение Nj/Cf указывает эквивалентную разность
потенциалов для каждого иона, соответствующую потерям мощ¬
ности в движителе (рис. 2.30). С учетом значения полезной
разности потенциалов %, ускоряющей ионный поток (см. (2.37)),
5 Механика полета
66
ФИЗИЧЕСКИЕ ПРИНЦИПЫ ДВИГАТЕЛЬНЫХ СИСТЕМ
[ГЛ. 2
энергетический к.п.д. ионного движителя запишется в виде
N, 9/ V?
VI
. 2 — —L '
LL У
(2.47)
На рис. 2.31 приведен пример изменения энергетического
к.п.д. ионного движителя в зависимости от скорости реактивной
струи при использовании цезия или ртути в качестве рабочего
тела. Сопоставление данных
* г.
7/
рис. 2.31 и 2.30 показывает,
что ионный движитель с кон¬
тактной ионизацией цезия на
вольфраме обеспечивает вы¬
сокие значения энергетиче¬
ского к.п. д., приближаю¬
щиеся к единице при увели¬
чении скорости истечения ре¬
активной струи, что хорошо
подтверждается эксперимен¬
том [2.54]. По данным работы
[2.54] удельный вес ионного
движителя с контактной иони¬
зацией составляет примерно
у = GT/Pmax^ 750-ч-1750.
Другим подробно исследо¬
ванным типом ионного источ-
V’jwT
Рис. 2.31. Зависимость к.п.д. ионного дви¬
жителя от скорости реактивной струи; рабо¬
чее тело — цезий, ртуть.
ника является источник с объемной ионизацией рабочего тела элек¬
тронным ударом ([2.52, 2.54, 2.56, 2.59, 2.61, 2.62, 2.67—2.69] идр.).
В таких ионных источниках используется хорошо изученный для
газовых разрядов процесс ионизации атомов газов при неупругом
соударении с ними электронов с энергиями в десятки электрон-
вольт ([2.67—2.69] и др.)* Процесс ионизации атомов данного
газа (пара) электронным ударом характеризуется вероятностью
ионизации рп представляющей собой среднее число актов иони¬
зации, совершаемых электроном с энергией Е на пути в 1 см при
давлении в 1 мм pm. cm, при 0° С. На рис. 2.32 для ряда веществ
представлено изменение вероятности ионизации в зависимости от
энергии электронов.
Благоприятные характеристики паров ртути — более высо¬
кая вероятность ионизации при меньших энергиях электронов —
обусловили рассмотрение ртути в качестве рабочего тела в ион¬
ных движителях с ионизацией электронным ударом (см. [2.52,
2.56] и др.).
Как указывалось выше, независимо от типа ионного источника
плотность ионной струи сравнительно мала вследствие ограниче¬
ний, присущих электростатической ускорительной системе. Поэ¬
РЕАКТИВНЫЕ ДВИЖИТЕЛИ
67
Pi
тому давление внутри камеры ионизатора должно быть малым
порядка — 10"4 мм рт. ст. для того, чтобы обеспечить относи¬
тельно малый паразитный расход нейтральных атомов рабочего
тела через отверстия отбора ионов
в ускорительную систему. При уровне
давления в ионизационной камере
pi — 10~*мм рт. ст. и вероятности 20
ионизации pi ^ 20 (см. рис. 2.32)
путь свободного пробега электрона li
до акта ионизации составит примерно
1
: 5-Ю2 СМ.
Г\
ч»
/
/*=
Ne
Не
200
р• Р.
*4 г
Чтобы обеспечить эффективную
ионизацию электронным ударом при
относительно малом характерном раз¬
мере ионизационной камеры Di<^ 1\,
для организации потока ионизую¬
щих электронов используют раз¬
личные электромагнитные ловушки
типа применяемых при термоя¬
дерных исследованиях [2.64].
На рис. 2.33 и 2.34 приведены схема и внешний вид одного из
вариантов ионного движителя с ударной ионизацией паров ртут
V
Рис. 2.32. Вероятность ионизации
электронным ударом ртути, арго¬
на, неона и гелия.
3
£
VU U
НФМИФЙЙ
и ш
Рис. 2.33. Схема ионного движителя с ио¬
низацией паров ртути электронным ударом:
i — подача рабочего тела, 2 — катод,
з — анод, •! — соленоид.
[2.70] (/>тах= 0,06 кГ, Gy = 19,5 кГ, V = 91 • 103 м/сек). Иони¬
зующее вращающееся тороидальное электронное облако в этой
5*
Рис. 2.34. Ионный движитель с ударной
ионизацией; рабочее тело—ртуть.
68
ФИЗИЧЕСКИЕ ПРИНЦИПЫ ДВИГАТЕЛЬНЫХ СИСТЕМ
[ГЛ. 2
схеме формируется электромагнитной ловушкой, образованной
радиальным электрическим полем (центральный катод — цилинд¬
рический анод в камере) и продольным магнитным полем (от внеш¬
него соленоида). Источником ионизующих электронов является
размещенный в камере накаленный катод; приложенный к
аноду камеры потенциал в несколько десятков вольт обеспечи¬
вает электронам энергию, необходимую для ионизации, а небольшое
продольное магнитное поле соленоида предотвращает прямое
попадание электронов на
анод. Пары рабочего тела
(ртути) ионизуются элект¬
ронными ударами при про¬
хождении сквозь вращаю¬
щееся электронное обла¬
ко. Дальнейшее ускорение
ионной струи осуществля¬
ется так же, как в указан¬
ной выше на рис. 2.24 обоб¬
щенной схеме электроста¬
тического движителя. Ре¬
гулирование параметров
ионного движителя с удар¬
ной ионизацией проводит¬
ся аналогично рассмотрен¬
ному выше управлению
параметрами ионного дви¬
жителя с контактной иони¬
зацией.
Как указано в табл. 2.3,
потенциал ионизации для
ртути составляет 10,39 в. Однако при ударной ионизации только
часть столкновений электронов с атомами приводит к образованию
ионов [2.67] (рис. 2.35). Кроме того, в ионизационной камере
имеют место потери ионов на стенки камеры, уход электронов на
анод и дополнительно часть энергии должна быть затрачена на
нагрев катода, питание соленоида. В результате по исследова¬
ниям [2.52, 2.56] удельные потери мощности в ионном движителе
с ударной ионизацией паров ртути значительно превышают
потенциал ионизации и составляют примерно NjICf ^ 500 в, что
все же обеспечивает высокие значения энергетического к.п.д.
движителя t]y (см. рис. 2.31).
Для движителей с ударной ионизацией принято оценивать
к.п.д. использования массы рабочего вещества
Рис. 2.35. Вероятность ионизации при каждом
столкновении в зависимости от энергии элек¬
трона.
РЕАКТИВНЫЕ ДВИЖИТЕЛИ
69
представляющий собой отношение расхода в ионной струе qL
к полному расходу рабочего вещества через движитель д. В ион¬
ных движителях с контактной ионизацией предельные значения
rjjj, определяются степенью ионизации и по данным рис. 2.28 близ¬
ки к единице. В движителях с ударной ионизацией имеет место
утечка части нейтральных атомов из камеры ионизации через
отверстия выхода ионной струи (см. рис. 2.33 2.34). По данным
Рис. 2.36. Удельный вес ионных движителей с удар¬
ной ионизацией; рабочее тело—ртуть.
[2.61] значение к.п.д. использования массы рабочего вещества
для таких движителей составляет примерно ^ 0,8—0,9. Так
как поток утечки нейтральных атомов движется с тепловой ско¬
ростью, много меньшей скорости ионной струи, то можно пре¬
небречь вкладом этого потока в тягу и полезную мощность дви¬
жителя. Поэтому в соответствии с соотношениями (1.4), (1.5)
эффективная скорость истечения реактивной струи V и полный
к.п.д. ионного движителя rjY определяются в виде
P = qiVi = qV, 7=тц^|, 1
1 ?F2 I (2.49)
N 2 4 . I V
T1y — iVv W J
Удельный вес ионных движителей с ударной ионизацией по
данным [2.61] составляет примерно у = GT/Pmax ^ 250-^-500,
несколько снижаясь с ростом максимальной скорости истечения
реактивной струи (рис. 2.36).
70
ФИЗИЧЕСКИЕ ПРИНЦИПЫ ДВИГАТЕЛЬНЫХ СИСТЕМ
[ГЛ. 2
Изложенное показывает, что с точки зрения механики полета
электростатические движители обеспечивают в широких преде¬
лах регулирование скорости реактивной струи V и тяги Р при
высоком значении к.п.д.
5. Солнечный парус. Движительным элементом двигательной
системы с солнечным парусом является зеркальная поверхность,
создающая тягу отражением солнечного светового излучения
(рис. 2.37). Идея использования для межпланетных полетов
давления солнечного света давно
^=а=^^^олнечнь/и оирус-зерналн- привлекала сравнительной про¬
стотой реализации. Первое серьез¬
ное исследование этой проблемы
принадлежит Ф.А. Цандеру [2.71]
(1924—1925 гг.). Для создания тяги
он рассматривал использование
зеркал, выполненных из тонких
алюминиевых листов. Исследова¬
ния Ф. А. Цандера показали прин¬
ципиальную возможность реали¬
зации межпланетных полетов при
использовании давления солнечно¬
го света. Так, при толщине алю¬
миниевого зеркала в одну тысяч¬
ную миллиметра космический ап¬
парат весом в 1 тонну может осу
ществить перелет с орбиты Земли
на орбиту Марса примерно за 300
Рис. 2.37. Схема аппарата с солнеч- СуТОК| при ЭТОМ ВвС паруса СОСТа-
ным парусом. вит — 400 кГ, а его площадь
~ 0,15 -106 ж2, что соответствует
круглому парусу диаметром ~ 450 м.
Солнечный парус как движитель создает тягу, используя по¬
ток энергии и массы электромагнитного излучения Солнца (см.
выше формулы (1.17), (1.18)). При взаимодействии потока сол¬
нечного светового излучения с поверхностью паруса происходит
изменение вектора количества движения потока фотонов.
В соответствии с формулой (1.18) величина тяги, создаваемая
освещенным Солнцем плоским парусом площадью S, будет равна
[2.72]
P = -|-Pa(^) SУ 1 + 2ecos2(ni) (n-i)e’ (2.50)
а направление тяги будет заключено между нормалью к те¬
невой стороне паруса п и направлением солнечного светового
Солнечное сбетобое
излучение
1]
РЕАКТИВНЫЕ ДВИЖИТЕЛИ
71
излучения i (рис. 2.38):
nP = arcsin — (1 s) sin (п0 ^ (2.51)
V 1 -j- е2 +2е cos 2 (ni)
гд еп — единичный вектор направления нормали к поверхности,
i — единичный вектор направления солнечного светового излу-
чения, ni, nP — углы между векторами п и Р, п и i соответ¬
ственно, (n-i) — скалярное произведение единичных векторов
п и i (т. е. косинус угла между ними (n-i) = cos й).
Управляющим параметром сол¬
нечного паруса как двигательной
системы является угол установки ^
паруса ft, от регулирования кото-
рого зависят направление и ве-
личина тяги. §
Однако при полном поглоще-
нии света поверхностью паруса ^
{при е = 0), согласно (2.50), (2.51), ^
1 [R±\2
р 0 = — Р 1-^1 iS'coS'O'i, (2.52) Рис. 2.38. Направление тяги солнеч-
2 та \ Н 1 ного паруса.
т. е. в предельном случае тяга полностью поглощающего паруса
всегда направлена по солнечному световому излучению, незави¬
симо от угла установки паруса.
В случае идеально отражающей зеркальной поверхности (при
8 = 1) максимальная величина тяги плоского паруса возрастает
вдвое, а направление тяги совпадает с нормалью к теневой стороне
паруса, и им можно управлять, изменяя ориентацию паруса от¬
носительно солнечного светового излучения (рис. 2.39):
Ре=1= Ра(~Д*") ^С08*п- (2.53)
Все современные исследования по солнечному парусу (см.
ниже главу 9) ограничиваются этим простейшим случаем. До¬
полнительные возможности управления тягой, создаваемой сол¬
нечным парусом, появляются при рассмотрении системы зеркал,
установленных под разными углами к направлению солнечного
светового излучения (см. работу Ф. А. Цандера [2.71]).
Следует отметить, что металлические поверхности алюминия и
серебра (рассматриваемые как материалы или покрытия для сол¬
нечного паруса) обладают коэффициентом отражения солнечного
светового излучения, близким к единице (рис. 2.40), что оправ¬
дывает проведение предварительного анализа характеристик сол¬
нечного корпуса в идеальной постановке при е = 1 [2.32].
72
ФИЗИЧЕСКИЕ ПРИНЦИПЫ ДВИГАТЕЛЬНЫХ СИСТЕМ
[ГЛ. 2
Рассмотрим весовые затраты на создание тяги при помощи
плоского солнечного паруса. Здесь отсутствуют все весовые ком¬
поненты, кроме веса собственно движителя — паруса:
Gy = kgS^ рб, (2.54)
где р — плотность материала слоев паруса, б — толщина слоев
&
1
1
Г
1'
1.
Рис. 2.39. Зависимость тяги солнечного паруса с идеально отра¬
жающей зеркальной поверхностью от угла установки паруса.
материала, из которого состоит парус, к — коэффициент, учиты¬
вающий вес вспомогательных элементов конструкции паруса (по
оценкам [2.73] значение коэффициента к мало отличается от
единицы).
~ создаваемая парусом, установ¬
ленным перпендикулярно к сол¬
нечным лучам ('0* = 0), при
е = 1, согласно (2.53), равна
Максимальная тяга
. = Pj
-f)s-
(2.55)
Соответственно удельный вес
паруса как движителя составит
Т =
А#2рб
^шах
Ра
а соотношение
dr.
R
(2.56)
= (2.57)
Рис. 2.40. Изменение коэффициента отра¬
жения металлических поверхностей в за¬
висимости от длины волны падающего
светового излучения.
определяет максимальное ускорение атах, которое может сооб¬
щить космическому аппарату двигательная установка с солнеч¬
ным парусом (при G = Gy).
РЕАКТИВНЫЕ ДВИЖИТЕЛИ
73
На рис. 2.41 приведены примерные значения удельного веса
солнечного паруса и развиваемого им максимального ускорения
(на орбите Земли, R$/R = 1, и при к = 1) в зависимости от тол¬
щины материала паруса, выполненного из алюминия (pg ^
я^2,7-103 кГ/м3) или алюминированной пластмассовой пленки
(рg ^ 1,2-103 кГ/м3). Для обсуждаемых в указанной выше лите¬
ратуре толщин паруса — из алюминиевой фольги б — 10~6 ж
Рис. 2.41. Зависимость удельного веса солнечного паруса
и развиваемого им максимального ускорения (на орбите
Земли) от толщины материала паруса. Сплошные кривые —
парус из алюминиевой фольги, пунктирные кривые — парус
из алюминированной пластмассовой пленки.
и из пластмассовой алюминированной пленки б ~ 2,5 -10-6 м —
удельный вес солнечного паруса на орбите Земли составит у ^
х 3000 кПкГ и максимальное ускорение, сообщаемое парусом
космическому аппарату, порядка атах ж 3-10~3 м/сек2. Дальней¬
шее существенное улучшение характеристик солнечного паруса
(как движителя) путем снижения толщины используемых пленок
лимитируется потерей зеркальных свойств поверхности при тол¬
щинах порядка длины волны светового излучения, а также уче¬
том сублимации в вакууме и микрометеорной эррозии.
Однако и при указанных на рис. 2.41 характеристиках паруса,
соответствующих толщине материала порядка 1—^-2,5 • 10-6 м
двигательная установка с солнечным парусом может доставить
космический аппарат с орбиты Земли на орбиты ближайших пла¬
нет за 100—200 суток (см. ниже гл. 9).
6. Изотопный парус. Другим типом рассматриваемого в лите¬
ратуре парусного движителя является изотопный парус, исполь¬
74
ФИЗИЧЕСКИЕ ПРИНЦИПЫ ДВИГАТЕЛЬНЫХ СИСТЕМ [ГЛ. 2
зующий для создания тяги реакцию от одностороннего вылета
а-частиц радиоактивного распада [2.32, 2.38]. Хотя радиоактив¬
ные изотопы (см. ниже табл. 2.8 в § 2) могут явиться источниками
как а-частиц (ионы гелия), так и |3-частиц (электроны) больших
.энергий, рассмотрение а-излучателей предпочтительнее вследствие
значительно большей массы а-частиц и мень¬
шей проникающей способности. Последнее
свойство особенно важно, так как по сути
определяет возможности изотопного паруса
как движителя, основной проблемой кото¬
рого является обеспечение одностороннего
вылета а-частиц, образующих реактивную
струю. На рис. 2.42 приведена принципиаль¬
ная схема изотопного паруса [2.32], исполь¬
зующего радиоактивный изотоп Ро210 (а-излу-
чатель). Парус представляет собой тонкий
слой изотопа Ро210 толщиной б*, нанесенный
и С **
на пластмассовую пленку толщиной о —
поглотитель частиц. Реактивная струя изо¬
топного паруса представляет собой поток
положительно заряженных а-частиц; поэтому
должна осуществляться нейтрализация реак¬
тивной струи подводом электронов, как в
ионных движителях. Основные параметры
элементов изотопного паруса представлены
в табл. 2.5.
Как видно из табл. 2.5, толщина пластмассовой пленки 6**
выбирается равной пути пробега а-частицы в пластмассе, что
существенно снижает поток а-частиц за пластмассовой пленкой.
Таблица 2.5
Параметры изотопного паруса
р* — плотность Ро210, г/см2
9,2
та — масса а-частицы, г
1
— — период полураспада Ро210, сут
6 J.IO'2*
138
—постоянная распада Ро210, 1 /сек
5,8-10—8
Еа —энергия а-частицы для Ро210, дж ....
8,5- IO-13
Пробег а-частицы в Ро210, м
6,5*10-6
6* — толщина слоя Ро210, м
6,5-10—7
р** — плотность пластмассы, г/см2
2,0
Пробег а-частицы в пластмассе, м
3*10-5
б** — толщина пластмассовой пленки, м . . .
3*10-5
2 /
Рис. 2.42. Схема изотоп¬
ного паруса:
1 — слой Ро210 — а -из¬
лучатель, 2 — пластмас¬
совая пленка — погло¬
титель а-частиц.
РЕАКТИВНЫЕ ДВИЖИТЕЛИ
75
б* — толщина слоя Ро210 — выбирается в —10 раз тоньше пути
пробега а-частиц в Ро210, что обеспечивает вылет из паруса в сто¬
рону слоя изотопа примерно половины образующихся а-частиц
[2.32]. Расход массы в реактивной струе изотопного паруса опре¬
деляется числом а-частиц, образующихся при радиоактивном
распаде
q = К S8*m(Xe~Xxt, (2.58)
где А — атомный вес изотопа, А* — число Авогадро, S — пло¬
щадь поверхности паруса; остальные обозначения указаны в
табл. 2.5. jj
Скорость реактивной струи определяется энергией а-частиц
Еа; эффективное значение скорости струи V, осредненное по полу¬
сфере, равно половине истинной скорости а-частицы:
7 = 4- (2.59)
Соответственно (2.58) и (2.59) тяга, развиваемая изотопным
парусом, составит
p = qV= Хт . (2.60)
При указанных в табл. 2.5 параметрах удельная тяга, удель¬
ный вес и скорость струи для рассмотренного примера изотоп¬
ного паруса равны
ж 2,6 • 10'VмкГ/м2, т = -р^2- ~ 25 ООО,
^ max
7^8-10 «м/сек, Жи^Е~5.10-и^^
Y г
(2.61)
В целом с позиций механики полета изотопный парус явля¬
ется движителем с почти постоянной тягой, медленно изменяю¬
щейся по времени, и практически нулевым расходом массы (2.61).
Помимо рассмотренных выше типов реактивных движителей
космических двигательных систем, в литературе обсуждаются и
движители более далекой перспективы (фотонные, термоядерные
и др.) с начальными соображениями о которых можно познако¬
миться, например, в работе [2.32].
76
ФИЗИЧЕСКИЕ ПРИНЦИПЫ ДВИГАТЕЛЬНЫХ СИСТЕМ
[ГЛ. 2
§ 2. ЭНЕРГОУСТАНОВКИ КОСМИЧЕСКИХ ЛЕТАТЕЛЬНЫХ
АППАРАТОВ
1. Источники энергии. Для космических летательных аппара¬
тов рассматривается использование химических источников энер¬
гии, ядерных и радиоизотопных источников энергии и солнечной
энергии ([2.2, 2.7—2.11, 2.27—2.33, 2.38] и др.).
Источником химической энергии являются вещества, способ¬
ные вступать в экзотермические реакции. Наиболее распростра¬
ненная из таких реакций—окисление (горение), в которой участ¬
вуют горючее и окислитель. Экзотермической является также
реакция разложения некоторых веществ, которая используется
в двигателях с унитарным рабочим телом. При использовании
химической энергии в тепловых реактивных двигателях основ¬
ными параметрами с позиций механики полета являются состав
и температура продуктов реакции, определяющие максималь¬
ную скорость истечения реактивной струи (см. выше § 1). Важ¬
ными являются также исходные параметры топлив (агрегатное
состояние, плотность и др.), связанные с весовыми параметрами
системы подачи и хранения рабочего тела. В качестве иллюстра¬
ции в табл. 2.6 по данным [2.11, 2.30, 2.74] указаны основные
характеристики некоторых типов ракетных топлив.
При использовании химической энергии регулирование тем¬
пературы продуктов сгорания Т0 (и соответственно скорости истече-
Таблица 2.6
Основные характеристики некоторых ракетных топлив
Максимальная вели¬
чина удельного им¬
пульса при
р0 = 35-104 кГ/м2,
1° сек
Плот¬
Оптимальное
соотношение
состава топ¬
Темпера¬
тура сго¬
Топливо
на уровне
моря при
* = 8
в космосе
при
ЭГС1&*=2,Ъ
ность
Р, кг/м3
ливной смеси
aopt
рания
Т0 °С
Жидкий кислород + ке¬
росин
261
324
1010
2,25
3200
Жидкие 02 + Н2 ...
357
441
256
3,5
2480
Жидкие F2 + Н2 . . . .
364
447
304
4,0
2600
Азотная кислота + не¬
симметричный диме-
тилгидразин ....
246
304
1210
2,4
2820
Однокомпонентное топ¬
ливо Н202 90% . . .
137
167
1390
740
Твердое топливо-балли-
стит IPN
200—230
—*
1610
—
2900
ЭНЕРГОУСТАНОВКИ КОСМИЧЕСКИХ АППАРАТОВ
77
ни я реактивной струи V, см. выше § 1) может производиться за
счет отступления от оптимального соотношения состава топлив¬
ной смеси c&opt* На рис. 2.43 приведен пример изменения темпе¬
ратуры сгорания керосина в
кислороде в зависимости от
коэффициента избытка окис¬
лителя a*/&opt [2.10]. Следует
отметить, что такое регули¬
рование позволяет только
снизить температуру сгора¬
ния Т0 <; Т0 max и соответст¬
венно скорость истечения
реактивной струи VFmax.
Выделение химической
энергии в тепловых реактив¬
ных двигателях происходит
в камерах сгорания. Расход д
продуктов сгорания в реак¬
тивной струе определяется
подачей жидких компонент
Рис. 2.43. Зависимость температуры сгора¬
ния керосина в кислороде от коэффициента
избытка окислителя.
в камеру сгорания или скоростью
сгорания заряда твердого топлива,
(см. (2.8)), максимальный расход
Как было показано выше в § 1
дтах (вытекающий из камеры
сгорания через реактивное
сопло) пропорционален ма¬
ксимальному полному давле¬
нию в камере сгорания р0тах>
которое, естественно, ограни¬
чено прочностными характе¬
ристиками камеры. Уменьше¬
ние подачи компонент сни¬
жает полное давление в ка¬
мере р0 и позволяет соответ¬
ственно регулировать расход
в пределах q < gmax. При
поддержании максимальной
температуры в камере Тотах
(максимальной скорости исте¬
чения Fmax) регулирование
расхода q вызывает почти
р п
пропорциональное изменение тяги двигателя: -
(рис. 2.44) [2.2]. Более точные соотношения см.
[2.75—2.77] и др.
Ядерные источники энергии на современном этапе развития
ядерной физики используют реакцию деления тяжелых ядер —
реакцию расщепления (см. [2.2, 2.28, 2.29] и др.)* Расщепляющи¬
Рис. 2.44. Регулировочная характеристика
ЖРД — зависимость тяги от расхода топлива
при Т0 = ТоП1аХ. Сплошная кривая — тео¬
рия, точки — эксперимент.
max ^max
в работах
78
ФИЗИЧЕСКИЕ ПРИНЦИПЫ ДВИГАТЕЛЬНЫХ СИСТЕМ
[ГЛ. 2
мися материалами являются изотоп урана U-235 и плутоний
Ри-239, получающийся в специализированных реакторах. Де¬
ление ядра расщепляющегося материала происходит при про¬
никновении в его ядро свободного нейтрона; ядро переходит в
возбужденное состояние, равновесие ядра нарушается и оно
делится на «осколки» с вылетом двух-трех вторичных нейтронов;
последние поддерживают цепную реакцию. Основная часть
Рис. 2.45. Схема энергетического ядерного Л реактора:
А — активная зона, В — кожух, С и D — входной и выходной кол¬
лекторы теплоносителя; 1 — монтажная плита, 2 — замедлитель
нейтронов, 3 — отражатель нейтронов, 4 — регулирующий стер¬
жень, 5 — тепловыделяющий элемент.
энергии деления ядра (свыше 80%) соответствует кинетической
энергии разлетающихся «осколков», которая превращается в теп¬
ловую энергию при задержании «осколков» деления элементами
реактора, например тепловыделяющими элементами (рис. 2.18).
Мощность Ж/г, выделяемая реактором, может регулироваться
путем воздействия на параметры цепной реакции, которая за¬
медляется, например, при введении в реактор регулирующих
стержней из поглощающих нейтроны веществ (кадмий, бористая
сталь). Принципиальная схема энергетического реактора с твер¬
дыми тепловыделяющими элементами приведена на рис. 2.45 [2.2].
В литературе ([2.32, 2.37, 2.38] и др.) рассматриваются также
жидкофазные и газофазные реакторы.
Критическая масса расщепляющегося материала, необходи¬
мая для цепной реакции, составляет примерно Gn х 5,0—200 кГ
[2.32] и не зависит от мощности реактора. Поэтому основной вес
энергетического реактора большой мощности составляет система
ЭНЕРГОУСТАНОВКИ КОСМИЧЕСКИХ АППАРАТОВ
79i
теплоотвода, типичными элементами которой являются образуе¬
мые тепловыделяющими элементами каналы теплообменника,
обеспечивающего заданную степень нагрева теплоносителя (см.
рис. 2.18, 2.45). Движение газового теплоносителя в канале
постоянного сечения хорошо описывается теорией одномерного*
стационарного течения вязкого газа с использованием данных
гидродинамической теории теплообмена [2.4, 2.78—2.83]. При
использовании известной связи между коэффициентом теплоот¬
дачи кг и коэффициентом гидравлического сопротивления £
/[
к± == g
дифференциальные уравнения движения газа в трубе с учетом тре¬
ния и конвективного теплообмена записываются в виде
с. dx
Ь ”
(А,2 —1 )ldl
X2
х + 1
+ г*’1 2ч
W
Т0
•lj(V-+l)
<*То , £ /Тц? л \ dx ^ ЛЁ1/Т» \
Т0 2 V То ) D 2 \ Т0 1
X
ч + 1
X
(Я2 — 1 )ЫЯ
(2.62)
лГ
где р — плотность, ср — теплоемкость при постоянном давлении,.
W — скорость потока газа, X — приведенная скорость, D —
диаметр трубы, — темпера¬
тура стенки трубы, Т0 — тем¬
пература торможения газового
потока, фх = [1 — 1,74 Re-1'8 х
X (Рг—1) ] —коэффициент, учи¬
тывающий отличие числа Пра-
ндтля Рг от единицы, Re —
число Рейнольдса.
Решения системы (2.62) хо¬
рошо согласуются с экспери¬
ментом.
На рис. 2.46 дан пример со¬
поставления теоретических дан¬
ных [2.80] и эксперимента [2.82]
по течению газа вдоль нагревае¬
шь
2000
\ft,OT\
ь
120 ^
9П°
г
OU
40-—
><
г
*
9
0,8
ол
О 80 160 240 320 400 x/D
Рис. 2.46. Изменение давления, темпера
туры и приведенной скорости газового^
потока при течении вдоль нагреваемой
трубы. Сплошные кривые — теоретическое
решение, точки — эксперимент.
мой трубки. Анализ решений системы (2.62) указывает на прямую
связь заданной степени нагрева газового потока ДТ0/Т0 и потреб¬
ного числа калибров канала теплообменника LID. Максимальная
80
ФИЗИЧЕСКИЕ ПРИНЦИПЫ ДВИГАТЕЛЬНЫХ СИСТЕМ [ГЛ. 2
степень нагрева достигается при звуковой скорости в конце ка¬
нала теплообменника (см. пример на рис. 2.46). Поэтому с учетом
соотношения (2.20) и ограничения по максимальной температуре
материала реактора (Т0 Т^щах) вес энергетического реактора
большой мощности с газовым теплоносителем должен быть при¬
мерно пропорционален мощности Nn:
Gn-V^Wo^n. (2.63)
Аналогичное соотношение должно выполняться в энергетическом
реакторе с жидким теплоносителем (предельный случай X 0
в (2.62)), а также при изменении агрегатного состояния теплоно¬
сителя, так как законы течения
двухфазной среды и газовых по¬
токов аналогичны (см., напри¬
мер, [2.84]). В качестве иллю¬
страции на рис. 2.47 по данным
[2.32] приведено изменение
удельного веса энергетического
реактора Gn/Nn в зависимости
Рис. 2.47. Зависимость удельного веса
•энергетического реактора Gn/Nn от полной
выделяемой мощности Nn:
.1 — с газовым теплоносителем, 2 —
с жидкометаллическим теплоносителем.
Nn. Видно, что приАп > 104 кет
значение удельного веса реак¬
тора стабилизируется.
Для высокотемпературных
тепловых реактивных двигате¬
лей с реактором-теплообменни¬
ком вес последнего примерно пропорционален тяге двигателя
(2.21), что позволяет (как показано в § 1 этой главы) включить
его параметры в значения обобщенного удельного веса двига¬
тельной системы (см. выше табл. 2.1).
Выделение энергии в ядерном реакторе связано с некоторым
расходом массы делящихся веществ де. Рассмотрим соотношение
между расходом де и расходом массы через движитель в реак¬
тивную струю q. В случае использования ядерной энергии рас¬
ход расщепляющегося вещества де можно оценить из соотно¬
шения, связывающего массу с энергией. Если обозначить через к0
коэффициент превращения расхода qe в кинетическую энергию
реактивной струи, то связь между расходом рабочего вещества
через движитель и расходом расщепляющегося вещества запи¬
шется в виде
(2.64)
4~ ^ = Ио9ес2>
где с — скорость света. По данным работы [2.28] при х0 ^ 5-10 2
зависимость отношения qjq от скорости истечения струи V пред¬
ЭНЕРГОУСТАНОВКИ КОСМИЧЕСКИХ. АППАРАТОВ
81
ставлена в табл. 2.7. Данные табл. 2.7 показывают, что в харак¬
терном для обсуждаемого в литературе [2.32, 2.38] и др. уровня
скоростей струи V ^ 104ч-10в м/сек расход расщепляющегося
вещества qe пренебрежимо мал по сравнению с расходом через
движитель q.
Таблица 2.7
Отношение расхода расщепляющегося вещества
в реакторе qE к расходу через движитель q ядерной
двигательной системы в зависимости от скорости
реактивной струи V
V м/сек
104
105
К)6
Qj<l
10-8
10-6
10-4
Существенной весовой компонентой в двигательных системах
с ядерным реактором является вес защиты Gn от нейтронных
потоков и у-излучения. Так как интенсивность излучения падает
обратно пропорционально квадрату расстояния от реактора, то
для снижения веса защиты рассматривается теневая защита с
выносом полезной нагрузки на некоторое расстояние Г от реак¬
тора (рис. 2.48 [2.32]). С той же целью снижения веса защиты р.
Рис. 2.48. Схема теневой экранировки ядерного реактора
для космических летательных аппаратов:
1 — реактор, 2 — защита от т-излучения, з — защита от
потока нейтронов, 4 — полезная нагрузка.
работах [2.85, 2.86] и др. рассмотрены вариационные задачи об
оптимальном профилировании толщины защитного слоя х*.
В качестве примера по данным работы [2.86] на рис. 2.49 приве¬
дено изменение оптимального безразмерного веса Gn защиты от
у-излучения дискового источника в зависимости от безразмерной
допустимой дозы радиации в*
Gn =
2 л /*2р£
G =
2/слГ
(2.65)
Механика
82
ФИЗИЧЕСКИЕ ПРИНЦИПЫ ДВИГАТЕЛЬНЫХ СИСТЕМ
[ГЛ. 2
где [Г — коэффициент ослабления в защите, р — плотность мате¬
риала защиты, о* — допустимая доза радиации, Г — поверх¬
ностная интенсивность источника излучения, к — переводной
коэффициент интенсивности радиации; угол <р0 показан на рис. 2.48.
В целом вес защиты G*n зависит от полной мощности реактора
Nn. По данным [2.32] удельный вес за¬
щиты сохраняется примерно постоян¬
ным при Nn > 104 кет (рис. 2.50).
Рис. 2.49. Зависимость оптималь¬
ного безразмерного веса защиты
от безразмерной допустимой
дозы радиации а* для дискового
источника у-излучения.
Рис. 2.50. Зависимость удельного веса защи¬
ты от полной мощности реактора при выносе
полезной нагрузки I* = 25 м и мощности
дозы 100 мбэр/сут:
1 — реактор с газовым теплоносителем, 2 —
реактор с жидкометаллическим теилоноси-
телем.
Другим источником ядерной энергии является использование
энергии распада радиоактивных изотопов ([2.32, 2.38, 2.87] и др.).
Энергия распада радиоизотопов может использоваться в тепло¬
вых ракетных движителях и непосредственно в парусных движите¬
лях (см. § 1 настоящей главы), а также в тепловых энергетических
источниках энергоустановок.
В ядерной физике известно несколько сотен радиоактивных
изотопов, но только некоторые из них рассматриваются для
использования в источниках энергии космических двигательных
систем.
Первым критерием пригодности радиоизотопа является пери¬
од полураспада 1АТ (Кх — постоянная распада). Эффективными
считаются изотопы с периодом полураспада более — 100 суток,
так как изотопы с очень коротким периодом полураспада нельзя
экономично хранить или использовать в длительных полетах.
Вторым важным критерием является максимальная удельная мощ¬
ность и тип испускаемого излучения. В качестве иллюстрации по
данным [2.87] в табл. 2.8 приведены характерные параметры ряда
радиоактивных изотопов, рассматриваемых для использования в
космических двигательных системах. Отметим, что удельная
мощность радиоизотопного источника энергии уменьшается по
ЭНЕРГОУСТАНОВКИ КОСМИЧЕСКИХ АППАРАТОВ
83
времени в соответствии с периодом полураспада
15Г = (ir) •
Wi \ n /max
(2.66)
Из внешних потоков энергии наибольшую интенсивность в
межпланетном пространстве имеет поток солнечного светового
излучения, мощность которого на орбите Земли составляет 91а5 ~
^ 1400 вт/м2 (1.17). В литературе [2.39, 2.87, 2.88] и др. под¬
робно рассматривается устройство оптических концентраторов
солнечной энергии в виде параболических зеркал, отражателей
Таблица 2.8
Параметры радиоактивных изотопов, рассматриваемых в качестве
источников энергии космических энергоустановок
Изотоп
Тип излуче¬
ния
Период полу¬
распада 1 /Лт
Топливное
соединение
Плотность
Р кг/м3Л0~3
Максималь¬
ная удельная
МОЩНОСТЬ
(кет
\ /щах*
Ро2Ю
Альфа
138 суток
Ро
9,3
141
Cm242
»
162 »
Ст20з
11,8
100
рц238
»
86,4 года
РиС
12,5
0,55
Се144
Бета — гам¬
ма
285 суток
Се О 2
6,4
1,95
Pm147
То же
2,6 года
Рт203
6,6
0,12
Cs137
»
33 »
CsCl
3,9
0,33
Sr»o
»
28 лет
SrTiOg
4,8
0,11
Со«о
»
5,3 года
Со
9,0
0,30
Френеля и др. По данным [2.87] удельный вес концентраторов
солнечной энергии на орбите Земли составляет примерно
1,5 — 3,0 кГ/м2; (~3^) ~ 1—2 кГ/квт и изменяется со
Р. =
ответственно квадрату расстояния R до Солнца:
Gn __ (J±n_\ (R& \2
N.
Nn /6 \ R
(2.67)
Пример конструкции концентратора см. на рис. 2.51 [2.87].
2. Системы преобразования энергии. В тепловых реактивных
Двигателях преобразователем энергии является движитель (см.
§ 1), превращающий тепловую энергию нагретого источником
энергии газа в кинетическую энергию направленного движения
реактивной струи. В парусных двигательных системах (солнеч¬
ный и изотопный парус) движитель также является непосредст¬
венным преобразователем энергии. Специальных преобразова-
6*
84
ФИЗИЧЕСКИЕ ПРИНЦИПЫ ДВИГАТЕЛЬНЫХ СИСТЕМ
[ГЛ. 2
телей в основном тепловой энергии источников в электроэнергию
требуют рассмотренные выше (§ 1) электрореактивные движители.
В литературе [2.32, 2.36, 2.38, 2.87—2.115] и др. обсуждается
ряд типов преобразователей энергии и их элементов. На
рис. 2.52 указаны основные принципиальные схемы преобра¬
зователей энергии для электрореактивных движителей, исполь¬
зующих солнечную энергию, энергию радиоактивных изотопов
или ядерный реактор [2.47].
Рис. 2.51. Солнечный концентратор «Санфлауэр» (масштаб
модели 1:3); полная площадь Ь’0 = 08 м2, вес концен¬
тратора и конструкции Gn = 115 кг.
Схемы преобразователей энергии разделяются на использую¬
щие машинные и безмашинные циклы. Для преобразователей с
машинными циклами (см. [2.32, 2.36, 2.87, 2.92—2.94] и др.)
возможно использование газотурбокомпрессорного цикла Брай¬
тона и паротурбинного цикла Рэнкина. В газотурбокомпрессор-
ном цикле (рис. 2.53) нагретый в источнике энергии газ приводит
во вращение газовую турбину, на оси которой установлены га¬
зовый компрессор (компенсирующий перепад давления газа по
контуру) и электрогенератор; отвод неиспользованной в цикле
тепловой энергии осуществляется радиатором. В паротурбинном
цикле (рис. 2.54) испарившийся в источнике энергии теплоноси¬
тель приводит во вращение паровую турбину и электрогенератор;
в радиаторе осуществляется конденсация пара в жидкую фазу,
ЭНЕРГОУСТАНОВКИ КОСМИЧЕСКИХ АППАРАТОВ
85
о)
Роантиднал
струн
б)
Фото ила
термоэлемент
Яаробод
нотел
V
Движитель
"ч:
т
ю
'-источник
Ядерный
реантор
\ Г
—2vjjx/. /Л
Ч1-
Пар t|l
Злснтрогенератор
Жадность
Радиатор
Турбина
Злектрозенератор
Рис. 2.52. Принципиальные схемы преобразователей энергии космиче¬
ских энергоустановок: а) с использованием солнечной энергии, б) схема
с изотопным 0-источником, в) с ядерным реактором.
Рис. 2.53. Схема машинного
преобразователя тепловой энер¬
гии в электрическую, работаю¬
щего по циклу Брайтона: 1—ис¬
точник тепловой энергии, 2—
турбина, з — радиатор, 4 —
компрессор, 5 — электрогене¬
ратор.
Рис. 2.54. Схема преобразователя энергии, ис¬
пользующего паротурбинный цикл Рэнкина:
1 — источник тепловой энергии, 2 — влажный
пар, з — сепаратор, 4 — жидкий теплоноситель,
5 — насыщенный пар, 6 — турбина, 7 и 8 —
радиаторы, 9 и ю — дополнительные теплооб¬
менники, 11 — насос с эжектором, 12 — элек¬
трогенератор.
86
ФИЗИЧЕСКИЕ ПРИНЦИПЫ ДВИГАТЕЛЬНЫХ СИСТЕМ
[ГЛ. 2
Рис. 2.55. Термодинамические циклы машинных энергопреобразователей
в диаграммах температура — энтропия: а) газотурбокомпрессорный цикл
Брайтона, Т! — Т2 — сжатие газа в компрессоре, Т2 — Т3 — подвод тепла,
Т3 — Т4— расширение в турбине, Т4 — Т4 — отвод тепла в радиаторе;
б) паротурбинный цикл Рэнкина, Tt — Т2 — повышение давления жид¬
кого теплоносителя в насосе, Т2 — Т3 — подогрев до точки кипения и ис¬
парение, Т3 — Т4 — расширение пара в турбине, Т4 — Тх — конденсация
в радиаторе.
Рис. 2.58. Зависимость площади
радиатора от температуры перед
турбиной для машинного энерго¬
преобразователя с полезной мощ¬
ностью iVv = 1000 кет:
1 — паротурбинный цикл Рэнкина,
2 — газовый цикл Брайтона.
Рис 2.57. Изменение удельного веса турбо¬
агрегата Gx'/Nv в зависимости от полезной
мощности.
ЭНЕРГОУСТАНОВКИ КОСМИЧЕСКИХ АППАРАТОВ
87
давление которой повышается насосом. Диаграммы температура—
энтропия для указанных термодинамических циклов приведены
на рис. 2.55. Видно, что при одинаковых максимальных темпера¬
турах цикла Т3 (определяемых стойкостью материалов) и одина¬
ковом теплоперепаде на турбине Т3—Т4 в газовом цикле средняя
температура радиатора значительно ниже температуры радиатора —
конденсатора в паротурбинном цикле. Так как в космических
энергоустановках отвод тепла радиатором осуществляется излу¬
чением (подробнее см. ниже в § 3), то потребная площадь и вес
Рис. 2.58. Схема преобразователя
энергии, использующего жидкоме¬
таллический цикл с МГД-генерато-
ром:
1 — источник тепловой энергии,
2 — смеситель, з — сопло, 4 — се¬
паратор, 5 — МГД-генератор, 6 —
диффузор, 7 — радиатор, 8 — на¬
сос, 9 — теплообменник.
Рис. 2.59. Схема термоэлектриче¬
ского преобразователя энергии:
1 — источник тепловой энергии,
2 — насос контура жидкометалли¬
ческого теплоносителя, з — термо¬
элементы, 4 — канал теплоносителя,
5 — радиатор — холодный спай.
радиатора в газовом цикле значительно больше, чем в паротур¬
бинном цикле. В качестве иллюстрации на рис. 2.56 приведен
пример зависимости площади радиатора S^ от температуры перед
турбиной Т3 для газового и паротурбинного циклов при полезной
мощности преобразователя энергии Nv — 1000 кет [2.35].
Вследствие меньшей потребной площади радиатора в литера¬
туре [2.32, 2.36, 2.87, 2.93—2.94] и др. преимущественно обсуж¬
дается паротурбинная схема. Совершенство такой схемы во мно¬
гом определяется совершенством газогидродинамики турбоагре¬
гата (см., например, [2.95—2.98]) с учетом эрозии элементов в
двухфазном потоке [2.99]. Вес элементов машинных энергопре¬
образователей приблизительно пропорционален полезной мощ¬
ности 7Vv. Примерные значения удельного веса турбоагрегата при¬
ведены на рис. 2.57 [2.32]. Для электрогенератора по данным
[2.36] удельный вес составляет примерно GJN^ ^ 0,4 кПквт.
К энергопреобразователям с двухфазным потоком без турбо¬
агрегатов относятся преобразователи тепловой энергии в электри¬
ческую, использующие жидкометаллический цикл с магнито¬
88
ФИЗИЧЕСКИЕ ПРИНЦИПЫ ДВИГАТЕЛЬНЫХ СИСТЕМ [ГЛ. 2
гидродинамическим генератором [2.100, 2.101]. Такой преобра¬
зователь (рис. 2.58) содержит два контура: например, контур
жидкого лития и контур паров калия. Нагретый в источнике
энергии жидкий литий поступает в смеситель, где испаряет жид¬
кий калий. При расширении в газодинамическом сопле пары
калия ускоряют литиевый поток, а затем отделяются в сепара¬
торе. Ускоренный жидкий литий вырабатывает электроэнергию
в МГД-генераторе. В работах [2.100, 2.101] указывается, что
такие преобразователи энергии при мощности Nv > 500 кет
могут конкурировать по весовым показателям с турбогенератор¬
ными преобразователями.
Безмашинные преобразователи энергии используют также
термоэлектрические, солнечные и термоэмиссионные элементы
([2.32, 2.36, 2.87, 2.102—2.115] и др.). В термоэлектрических
преобразователях используется эффект Зеебека по прямому пере¬
ходу тепловой энергии в электрическую при разных температу¬
рах двух стыков различных материалов (рис. 2.59). К.п.д. тер¬
моэлектрического преобразователя равен [2.87, 2.102—2.104]
т. To s-e
Т)т = Т _ т , Z = . (2.68)
Т+ 2Тх—2—
где Тг — температура горячего спая (стыка), Т2 — температура
холодного спая, z — термоэлектрическая добротность материа¬
ла, s — коэффициент Зеебека, — проводимость, ^ — тепло¬
проводность.
Для полупроводниковых термоэлементов с z порядка 2 • 10_3
1/°К к.п.д. достигает — 10% при перепаде температур Tj — Т2 ^
^ 200° К [2.103]. Примерные значения удельного веса термоэлек¬
трического преобразователя SNAP-10A вместе с радиатором (ма¬
териал термоэлементов SiGe, z ~ 0,6-10"3 1/°К) по данным [2.103]
составляют
G g
——-^125 кГ/квтп. (2.69)
V
Другим видом полупроводниковых элементов, осуществляю¬
щих непосредственное преобразование энергии солнечного све¬
тового излучения в электроэнергию, являются кремниевые сол¬
нечные фотоэлементы (см. [2.32, 2.36, 2.87, 2.105—2.107] и др.).
Такой фотоэлемент состоит из тонкого, толщиною ~ 2,5 мкм
p-слоя кремния, нанесенного на /г-слой кремния (рис. 2.60).
Падающие на фотоэлемент фотоны солнечного излучения приво¬
дят к образованию пар электрон — «дырка», которые под дейст¬
вием электрического поля между п и p-слоями диффундируют
через контактную поверхность, создавая разность потенциалов
ЭНЕРГОУСТАНОВКИ КОСМИЧЕСКИХ АППАРАТОВ
89
0,3—0,5 в. Отдельные элементы собираются на панелях в батареи.
Удельный вес такого преобразователя энергии, естественно, по¬
вышается пропорционально квадрату расстояния до Солнца:
<2Л0)
По данным [2.32, 2.105] удельный вес преобразователя энер¬
гии с солнечными элементами на орбите Земли достигает пример¬
но G“/Nvx ^ 50 кГ/квт при .
к.п.д. до 10—14%. Кроме то- отояы
го, должны быть учтены ве¬
совые затраты на ориентацию
батарей солнечных элементов
на Солнце (см., например,
[2.107]).
В термоэмиссионных пре¬
образователях тепловой энер¬
гии в электрическую элект¬
роны эмитируются за счет
тепловой энергии из нагре¬
того катода и поглощаются более холодным анодом (см. [2.32,
2.36, 2.87, 2.108—2.115] и др.). Для обеспечения этого потока
электронов во внешнюю цепь (на полезную нагрузку) работа
выхода материала катода щ должна быть выше, чем у мате¬
риала анода фа. Данные о величине работы выхода электрона
для различных материалов приведены выше в табл. 2.4. Плот¬
ность тока эмиссии электронов с катода или анода по уравнению
Ричардсона—Дэшмана существенно зависит от температуры Т:
Л— г* ПП// iS/1 /Э AAU// О А
jU иУ/ии /ifjG/VfnCdsT
flap а зле/t
гтрон-
„дырна
л-слой яремная
Рис. 2.60. Схема кремниевого фотоэлемен¬
та — преобразователя энергии солнечного
светового излучения в электроэнергию.
i = АТ2 ехр
(2.71)
где А — универсальная постоянная, равная для чистых метал¬
лов 120 а/см2 -cpad2, к — постоянная Больцмана.
Для обеспечения тока электронов от катода к аноду при
Ф/с^>Фа необходимо, чтобы температура анода была существенно
ниже температуры катода. Схема распределения потенциальной
энергии в промежутке между электродами термоэмиссионного
преобразователя приведена на рис. 2.61. Величина выходного
напряжения, создаваемого термоэмиссионным элементом, опре¬
деляется соотношением
6^ = ф^ + фс — Фа-чу
(2.72)
где фс — кинетическая энергия электронов, фр — падение потен¬
циала в плазме разряда. Для типичных материалов, указанных
выше в табл. 2.4, величина напряжения % порядка — 1 в,
90
ФИЗИЧЕСКИЕ ПРИНЦИПЫ ДВИГАТЕЛЬНЫХ СИСТЕМ
[ГЛ. 2
Поэтому значительные удельные мощности в термоэмиссионном пре¬
образователе требуют большой плотности тока i, величина кото¬
рой ограничена пространственным зарядом (см. в § 1 соотноше¬
ния (2.41)—(2.43)). Согласно (2.43) осуществление большой плот¬
ности тока требует очень малых зазоров d между электродами
термоэмиссионного преобразователя; так, например, для плотно¬
сти тока — 1 а/см2 (мощность — 1 вт/см2) необходим зазор менее
10 мкм. Столь высокие требования к
меж электродному зазору существенно
упрощаются при заполнении термо¬
эмиссионного преобразователя парами
щелочных металлов (Cs, В а), которые
лехжо ионизуются и образуют в меж-
электродном пространстве плазменный
слой высокой проводимости. Эффектив¬
ный зазор как бы становится равным
пути пробега электрона до слоя плаз¬
мы, что много меньше геометрического
зазора. Кроме того, заполнение термо¬
эмиссионного преобразователя, напри¬
мер, парами Cs повышает эмиссионные
способности катода. В качестве иллю¬
страции на рис. 2.62 по данным работы
[2.115] приведены примерные характе¬
ристики термоэмиссионного преобразо¬
вателя, заполненного парами щелочных
Рис. 2.61. Схема термоэмисси- мртялттов
онного преобразователя энергии «iciajuxurj.
и распределение потенциальной КОНСТРУКТИВНО терМОЭМИССИОННЫв
энергии Е в межэлектродном ^ / го ос
зазоре преобразователя. Элементы В ряде работ (СМ. [А.оЬ,
2.87—2.114] и др.) рассматриваются
встроенными в ядерный реактор с жидкометаллическим охлажде¬
нием. На рис. 2.63 указаны примерные значения удельного веса
реактора с термоэмиссионным преобразователем в зависимости от
полезной мощности Nv [2.87] для схемы, изображенной на
рис. 2.64 [2.87].
В весовом балансе космической энергоустановки — источника
мощности, помимо указанных элементов существенное значение
имеет система теплоотвода неиспользованной в цикле энергии'
(см., например, [2.32] и др.). Поэтому общий весовой анализ ис¬
точников мощности приведен ниже в § 3 после рассмотрения харак¬
теристик систем теплоотвода от космических энергоустановок.
3. Аккумуляторы энергии. Как было указано выше, основ¬
ными видами энергии в космических энергоустановках являются
тепловая энергия и электроэнергия. Соответственно рассматри¬
ваются аккумуляторы тепловой и электрической энергии ([2.32,
2.87] и др.).
Ла/лод
ЛодЗод
/пелла
Вакуум
или
чуим
пары Cs
АноЗ
LJf
Л/лЗоЗ
/леЛлв
сЕЕРГОУСТ/ НОВКИ[ КССМИЕЕСКИХ АППАРАТОВ
91
Рис. 2.62. Характеристики термоэмис-
сиоиного преобразователя энергии, за¬
полненного парами Cs и Ва; анод W
Tt= 2000° К, катод Мо, зазор 0,25 мм,
давление паров соответствует кипению
при указанных температурах.
Рис. 2.63. Зависимость удельного веса
реактора с термоэмиссионным преобра¬
зователем от полезной мощности ЛГv:
1 — удельная мощность преобразовате¬
ля 10 вт/смгу 2 — то же 20 вт/см2.
Рис. 2.64. Ядерный реактор с термоэмиссионными преобразователями:
1 — клемма вывода электрической мощности, 2 — вывод продуктов деле¬
ния, 3—регулятор, 4 —опорная решетка, 5—ввод охлаждающего
теплоносителя, 6 — отражатель, '7 —термоэмиссионные элементы, 8 —
клемма вывода мощности для питания насоса, 9 — аварийная защита,
10 и 11 — резервуары с Cs, 12 — выход теплоносителя.
92 ФИЗИЧЕСКИЕ ПРИНЦИПЫ ДВИГАТЕЛЬНЫХ СИСТЕМ [ГЛ. 2
Аккумулирование тепловой энергии возможно за счет теплоем¬
кости материала аккумулятора или использования теплоты фа¬
зового перехода; второе предпочтительнее, так как позволяет
аккумулировать тепловую энергию при примерно постоянном
температурном уровне Тл. Из фазовых переходов рассматривает¬
ся плавление аккумулирующего тепло вещества, так как испаре¬
ние привело бы к соответствующему росту давления в контей¬
нере аккумулятора. В соответствии с физико-химическими свой¬
ствами меньший удельный вес аккумулятора тепловой энергии
Р — Ge/E0 имеет место при использовании хлоридов и гидридов
металлов [2.32, 2.87] (см. данные табл. 2.9). Использование чис¬
тых металлов (например, Pt [2.116], см. табл. 2.9) дает большее
значение удельного веса р.
Таблица 2.9
Удельный вес аккумулятора тепловой энергии
(без учета веса контейнера)
Аккумулиру¬
ющее вещес¬
тво
Температурили
уровень ТП°К
Удельнлй вес
°е кГ
Э ~~ Е дж
LiH
950
0,33*10-6
NaCl
1077
1,95-10-6
Pt
2042
8,8-10-6
Из аккумуляторов электроэнергии меньший удельный вес
имеют серебряно-цинковые щелочные аккумуляторы [2.32, 2.117],
примерные значения удельного веса которых по данным работы
[2.117] приведены на рис. 2.65. Удельный вес электроконденса¬
торов порядка р ^ 0,015 кГЮж [2.36].
Данные табл. 2.9 и рис. 2.65 показывают, что удельные веса
аккумуляторов тепловой и электроэнергии одного порядка
Р ^ 1 — 5 -10"в кГ/дж.
4. Системы подачи и хранения рабочего тела. Различают тур-
бонасосные и вытеснительные системы подачи жидкого рабочего
тела ([2.2, 2.30, 2.36, 2.118, 2.119] и др.)* Для тепловых реактив¬
ных двигателей с жидким рабочим телом, как было указано выше
(см. § 1 настоящей главы) вес системы подачи Gq примерно про¬
порционален максимальной тяге Ртах- Значения удельного веса
турбонасосных агрегатов поданным [2.2, 2.119] порядка Gq/Pmах ~
^ 0,005, и для анализа тепловых реактивных движителей с по¬
зиций механики полета удельный вес системы подачи целесо¬
образно включать в общий удельный вес двигателя (см. (2.16)).
В двигательных установках с энергопреобразователями теп¬
ловой энергии в электрическую, помимо системы подачи, необхо¬
ЭНЕРГОУСТАНОВКИ КОСМИЧЕСКИХ АППАРАТОВ
93
димо учитывать весовой вклад и других насосных систем, исполь¬
зуемых для прокачки теплоносителя по основному и вспомогатель¬
ным энергетическим контурам (см. рис. 2.54, 2.58 и 2.59). По
данным работы [2.94] удельный вес системы подачи и насосной
системы составляет примерно GqjNv ^ 0,35 кГ/квт при Nv —
= 415 кет.
Параметры баков для хранения рабочего тела (топлива) под¬
робно рассмотрены, например, в работе [2.30] и др. Вес баков
Рис. 2.65. Изменсг.ке удельного веса серебряно-
цкнкоесI о аккумулятора в зависимости от энергии,
ьвкаг ливасмсй в одном элементе (напряжение
да 1,5 в).
Gp пропорционален весу запасаемого рабочего тела (топлива)
GVi. Примерные значения удельного веса баков составляют:
для хранения жидкого кислорода + керосин Gp/G^ ^ 0,004
[2.120], для хранения Cs G?JG^ ^ 0,006 [2.94].
Следует отметить, что для твердотопливных тепловых реак¬
тивных двигателей (см. [2.11, 2.30] и др.) вес топливного контей¬
нера одного порядка с весом двигателя и пропорционален
полному импульсу движителя Pt; примерные значения удельного
веса контейнера твердотопливного РД по данным [2.11] состав¬
ляют Gfr/Pt ^ G-JPt ^ 0,8 *10“3 1 /сек.
5. Энергоустановки с забором рабочего тела из внешней среды.
Забор рабочего т,ела из внешней среды (атмосферы) используется
в воздушно-реактивных двигательных системах (см., например,
[2.2, 2.121—2.131] и др.). а также рассматривается в двигатель¬
ных системах с накоплением рабочего тела при орбитальном полете
в верхних слоях атмосферы ([2.134—2.137] и др.).
Начальным элементом таких двигательных систем является
воздухозаборник, основная задача которого осуществить забор
рабочего тела с минимальными потерями полного давления и с
минимальным внешним аэродинамическим сопротивлением. На
сверхзвуковых скоростях полета при торможении воздухозабор¬
94
ФИЗИЧЕСКИЕ ПРИНЦИПЫ ДВИГАТЕЛЬНЫХ СИСТЕМ [ГЛ. 2
ником набегающего потока могут иметь место значительные по¬
тери полного давления набегающего потока р0:
р.=р„(1+“-^1м;Г. <2-73>
где М0 = via — число Маха полета, а — скорость звука (см.
рис. 1.4). Эти потери полного давления р0/Ро дал,ёе вызывают
Рис. 2.66. Некоторые принципиальные схемы сверхзвуковых
диффузоров воздухозаборников,
а) Многоскачковый диффузор с внешним сжатием набегаю¬
щего сверхзвукового потока; б) диффузор, использующий
два конических течения: 1 — зона обтекания центрального
конуса, 2 — изоэнтропическое течение, з — расходящееся
коническое течение перед коническим скачком [2.132];
в) сжатие гиперзвукового потока в канале с параболической
ударной волной [2.133].
соответствующие потери тяги движителя (см. § 1 настоящей гла¬
вы). Для обеспечения малых потерь полного давления р0/р0 рас¬
сматриваются воздухозаборники — сверхзвуковые диффузоры,
примеры схем которых указаны на рис. 2.66 ([2.2, 2.132, 2.133]
и др.). На рис. 2.67 даны примерные значения относительного
полного давления на выходе из идеального воздухозаборника р0/р0
в зависимости от количества скачков уплотнения и числа Маха
полета М0. Такой воздухозаборник — сверхзвуковой диффузор —
не вызывает дополнительного внешнего аэродинамического со¬
противления при заборе из внешнего потока струи площадью,
равной площади входа f0 (см. рис. 2.66) и обеспечивает расход qv:
qv = — pvf0. (2.74)
ЭНЕРГОУСТАНОВКИ КОСМИЧЕСКИХ АППАРАТОВ
95
В прямоточном воздушно-реактивном двигателе (рие. 2.68) между
воздухозаборником и реактивным соплом-движителем располагает¬
ся камера сгорания или другой источник тепла; в турбореактивном
или турборакетном двигателях для обеспечения тяги на малых
скоростях полета перед камерой
сгорания осуществляется сжа¬
тие воздуха турбокомпрессором
([2.2, 2.121-2.131] и др.).
Использование газодинамиче¬
ской теории ([2.2, 2.4, 2.6] и др.)
позволяет определить характе¬
ристики воздушно-реактивных
двигателей.
При этом тяга воздушно-
реактивных двигателей Р при¬
мерно пропорциональна площа¬
ди входа в воздухозаборник £0
и атмосферному давлению на
данной высоте полета ph:
PxJcf0-ph. (2.75)
Удельная тяга Р/&0рн зави¬
сит от числа Маха М0. С уве¬
личением скорости полета удель¬
ная тяга сначала возрастает в
соответствии с увеличением сте¬
пени сжатия р0/Рл набегающего потока в воздухозаборнике.
Однако одновременно возрастает и температура торможения
набегающего потока Т0':
Т; = Th (1 + М0), (2.76)
Рис. 2.67. Изменение относительного пол¬
ного давления на выходе из идеального
воздухозаборника в зависимости от коли¬
чества скачков в системе п и числа Маха
полета.
что при заданной допустимой температуре Т0 за камерой сгорания
3
Рис. 2.68. Схема воздушно-реактивной двигательной установки:
1 — воздухозаборник, 2 — камера сгорания (источник тепла), 3 —
реактивное сопло-движитель.
(источником тепла) приводит к снижению возможного нагре¬
ва воздушного потока в двигателе ДТ0 = Т0 — Т0 и вызывает
падение удельной тяги при больших числах М0 полета.
В качестве иллюстрации на рис. 2.69 по данным [2.1271
96 ФИЗИЧЕСКИЕ ПРИНЦИПЫ ДВИГАТЕЛЬНЫХ СИСТЕМ [ГЛ. 2
приведено примерное изменение удельной тяги воздушно-реактив¬
ных двигателей в зависимости от числа Маха полета. Эффектив¬
ный удельный импульс воздушно-реактивных двигателей I° =
= Р/gqa также зависит от числа Маха полета (рис. 2.70) [2.127].
Вес воздушно-реактивных двигателей примерно пропорционален
площади входа в воздухозаборник Gp — f0; в табл. 2.10 по дан¬
ным [2.127] приведены ориентировочные значения удельных ве¬
сов воздушно-реактивных двигательных систем.
Таблица 2.10
Примерные значения удельного веса
воздушно-реактивных двигательных систем
Тип двигателя
Прямоточ¬
ный
Турбора¬
ке тный
Турбореак¬
тивный
Удельный вес
°р кГ
М2
1050
1350
2600
Характеристики воздушно-реактивных двигателей, исполь¬
зующих жидкий водород в качестве горючего, несколько улуч¬
шаются при дополнительном использовании теплоемкости жид¬
кого водорода для сжижения и накопления части воздушного
потока (кислорода), поступающего через воздухозаборник (под¬
робнее см. [2.127] и др.).
Другим типом двигательных систем, использующих забор
рабочего тела из внешней среды, являются системы с накопле¬
нием рабочего тела при орбитальном полете в верхних слоях ат¬
мосферы ([2.134—2.137] и др.)* Принципиальная схема такой
двигательной системы приведена на рис. 2.71 [2.136]. Поток воз¬
духа qv, поступающий в двигательную систему через воздухо¬
заборник, предварительно охлаждается системой теплообменни¬
ков с радиаторами, затем сжижается в детандерной установке
(см. [2.138]) и с возможным разделением компонент подается в баки
для рабочего тела. Лобовое сопротивление —qvv, как и аэроди¬
намическое сопротивление аппарата в целом компенсируется ре¬
активным движителем, потребляющим часть поступающего через
воздухозаборник расхода q<C\qv\- Разность указанных расходов
qa = q — qv накапливается в баках для рабочего тела. Так как
4<^\qv\i то Для компенсации аэродинамического сопротивления
скорость реактивной струи V должна быть существенно больше
орбитальной скорости полета v:
(2.77)
ЭНЕРГОУСТАНОВКИ КОСМИЧЕСКИХ АППАРАТОВ
97
Рис. 2.69. Зависимость удельной тяги воз¬
душно-реактивных двигателей от числа
Маха полета:
1 — турбореактивный двигатель, 2 — тур-
боракетпый, 3 — прямоточный с дозвуко¬
вым горением, 4 — прямоточный со сверх¬
звуковым горением.
Рис. 2.70. Изменение эффективного удель¬
ного импульса воздушно-реактивных дви¬
гателей в зависимости от числа Маха поле¬
та. Сплошная кривая — горючее водород,
пунктирная кривая — горючее керосин.
V
7
Рис. 2.71. Принципиальная схема двигательной системы с накоплением рабочего тела в
орбитальном полете в верхних слоях атмосферы:
1 — воздухозаборник, 2 — радиаторы, з — компрессоры, 4 — детандер, 5 — сжижающая
установка, 6 — бак для рабочего тела, 7 — движитель, 8 — энергоустановка, 9 — ядер-
ный реактор, 10— турбина, 11 — насос, 12 — электрогенератор; А — элементы, распо¬
ложенные по левую сторону черты, функционируют только в фазе накопления.
^ Механика полета
98
ФИЗИЧЕСКИЕ ПРИНЦИПЫ ДВИГАТЕЛЬНЫХ СИСТЕМ
[ГЛ. 2
Учитывая, что для полета в верхних слоях атмосферы Земли
v ^ 8 км/сек, необходимая скорость реактивной струи V в рас¬
сматриваемой двигательной установке с накоплением может быть
достигнута только в электроре-
активных движителях (см. § 1
данной главы).
Энергетические затраты на
работу электрореактивного дви¬
жителя Nr и сжижительной
установки накопителя Nv обес¬
печиваются энергоустановкой —
источником мощности (рис.2.71).
Оценим энергетические за¬
траты на работу сжижительной
установки. На рис. 2.72 по дан¬
ным [2.139] приведены значения
идеальных затрат мощности на
О 400 800 ТV°,K сжижение Nvo (при к.п.д., рав-
п _ч тт ном единице) в зависимости от
Рис. 2.72. Изменение удельных идеальных ^ ^ у
затрат мощности на сжижение воздуха температуры ВОЗДуха На ВХОДе
в зависимости от температуры воздуха на гжижитртттлпгю vPTaHORKv Т
входе в сжижительную установку Ту. й шижихельнуш уысшиычу ц.
Отметим, что эти значения удель¬
ной мощности Nv0Jqv более чем на два порядка меньше удельной
мощности реактивной струи движителя накопительной системы,
равной
-^-^2*105 квт/кг/сек при V ^ 2* 104 м/сек. (2.78)
Поэтому в работах [2.134—2.136] принимается, что удельный
вес двигательной системы с накоплением рабочего тела в орби¬
тальном полете в основном определяется весовыми параметрами
ее электрореактивной двигательной установки, элементы которой
были рассмотрены выше.
6. Внешнее сопротивление двигательной установки при по¬
лете в атмосфере. На этапе движения кисмического аппарата в
атмосфере планет аэродинамическое сопротивление может ока¬
зывать существенное влияние на механику полета, особенно в
случае двигательных систем с забором рабочего тела из внеш¬
него потока. Так как типичными компоновочными формами кос¬
мических двигательных систем являются тела вращения без
протока и с протоком, то рассмотрим основные закономерности
аэродинамического сопротивления тел такой формы. Аэродина¬
мическое сопротивление тела Fx (см. выше (2.2)) характеризует¬
ся коэффициентом сопротивления
- __ F* /О 70\
ЭНЕРГОУСТАНОВКИ КОСМИЧЕСКИХ АППАРАТОВ
99
где рг;2/2 — скоростной напор набегающего внешнего потока,
fm — характерная площадь, например, площадь миделевого сече¬
ния тела. Для заданной геометрии тела величина коэффициента
аэродинамического сопротивления сх в основном зависит от двух
безразмерных параметров [2.140]: числа Маха полета М0 = v/й и
числа Рейнольдса Re = vL/v (L — характерный линейный раз¬
мер, например, длина тела, v — кинематическая вязкость в потоке
0,4
0,3
0,3
0,1
По А
МОШОм
^/пМм
L П
п=и
~ и
Рис. 2.73. Зависимость коэффициента
аэродинамического сопротивления от
скорости и высоты полета для типич¬
ной компоновки ракетного аппарата;
нижняя пунктирная кривая — сопро¬
тивление трения при h = 0.
набегающего воздуха) или соответственно от скорости v и высоты
полета h, так как скорость звука а = г х— и кинематическая
г
вязкость v = / (Т) определяются высотой полета (см. рис. 1.4).
В качестве иллюстрации на рис. 2.73 приведен пример изменения
коэффициента сопротивления сх от скорости и высоты полета для
типичной компоновки ракетного аппарата [2.141].
Величина аэродинамического сопротивления определяется
двумя слагаемыми: суммой сил трения и давления внешнего
потока на тело (2.2)
Сх = схх + °хр- (2.80)
При дозвуковых скоростях движения (М0 1) основную часть
сопротивления тел обтекаемой формы определяют силы трения
(см. нижнюю пунктирную кривую на рис. 2.73). Величина со¬
противления трения может быть оценена по коэффициенту
7*
100
ФИЗИЧЕСКИЕ ПРИНЦИПЫ ДВИГАТЕЛЬНЫХ СИСТЕМ
[ГЛ. 2
трения для плоской пластины (S — площадь поверхности):
= г . <2-81>
который для турбулентного пограничного слоя на теплоизолиро¬
ванной поверхности определяется следующей формулой [2.1,
2.142-2.145]:
a8°.S^F<1+°-144M;>~"',i- (2-82)
Первый множитель этой формулы учитывает зависимость коэффи¬
циента трения от числа Рейнольдса при М0 = 0 (рис. 2.74, а)
0,0050
Шо
10,0030
'0,0020
> -п -
щ
-On.
©И
LJ
Рг
II
Ю7 1,5 2 2,53 4 5 6 8 /О8 1,5 2 2,53 4 6 8 Re
а)
Рис 2 74. а) Зависимость коэффициента турбулентного трения плоской пластины от
числа Рейнольдса при м0 = 0; сплошная кривая соответствует первому члену формулы
(2.82) точки — эксперимент; б) влияние числа Маха на коэффициент трения; сплошная
’ кривая соответствует второму члену формулы (2.82).
[2.143], второй множитель формулы (2.82) учитывает влияние
числа Маха (рис. 2.74, б) [2.145]. Следует отметить, что формула
(2.82) определяет значения коэффициента трения, отнесенные к
ЭНЕРГОУСТАНОВКИ КОСМИЧЕСКИХ АППАРАТОВ
101
«смоченной» поверхности S. Коэффициент трения схх, отнесенный к
площади мид ел ев ого сечения тела^т, определяется соотношением
S
Ср
(2.83)
При сверхзвуковых скоростях движения (рис. 2.73) коэффи¬
циент сопротивления резко растет и большую часть сопротивле¬
ния обусловливают силы давления, связанные с волновым обте¬
канием тела (см., например, [2.1,
2.146, 2.147] и др.)* Определение
о)
Рис. 2.75. Закон плоских сечений:
в плоскости А движение газа, как при
вытеснении эквивалентным поршнем;
1 — поршень, 2 — ударная волна.
Рис. 2.76. Зависимость коэффициента
волнового сопротивления тел кониче¬
ской формы сХр от угла конуса & и числа
Маха; кривая построена по закону пло¬
ских сечений и решению для цилиндри¬
ческого равномерно расширяющегося
поршня, точки — расчет для кониче¬
ских течений при & = 5°, 10° и 15°.
при сверхзвуковых скоростях движения величин коэффициента вол¬
нового сопротивления Схр рассматриваемых обтекаемых тел враще¬
ния возможно на основе общей теории сверхзвуковых течений [2.1,
2.5, 2.12,2.14,2.146—2.153]. При больших скоростях в связи с осо¬
бенностью гипзрзвукового обтекания тонких тел, которые вызы¬
вают в основном лишь поперечные смещения частиц газа, анало¬
гичные случаю расширения поршня, для анализа изменения схр
удобно использовать хорошо изученные автомодельные движения
газа, вытесняемого поршнем ([2.140, 2.145, 2.154—162] и др.).
По закону плоских сечений [2.163] задача об обтекании тонких
тел потоком газа с большой сверхзвуковой скоростью (рис. 2.75, а)
эквивалентна задаче о плоском неустановившемся движении газа,
вытесняемого подвижным поршнем, расширяющимся по соот¬
ветствующему закону (рис. 2.75, б).
В качестве примера приложения указанных принципов на
рис. 2.76 приведены результаты расчета изменения коэффициента
волнового сопротивления с*хр тел конической формы в зависимости
от угла наклона поверхности конуса Ф и числа Маха [2.162, 2.164];
Для сопоставления на рис. 2.76, помимо решения по расширяюще¬
муся поршню, приведены результаты точного расчета для кони¬
ческих течений. Данные рис. 2.76 показывают характер влияния
102
ФИЗИЧЕСКИЕ ПРИНЦИПЫ ДВИГАТЕЛЬНЫХ СИСТЕМ
[ГЛ. 2
скорости движения (числа Маха) и удлинения носовой части
L =Ь/г0 = ctg O' на величину лобового сопротивления.
Исследования автомодельных движений газа с ударными вол¬
нами, расширяющимися по степенному закону г = ctm [2.165—
2.167], позволили определить для больших чисел М0 влияние на
схр перехода от конической формы тела к степенной форме г —
= схт с большим объемом о (рис. 2.77). Данные рис. 2.77 пока¬
зывают, что при заданном удлинении носовой части тела сте¬
пенной формы минимум волнового сопротивления имеет место
при показателе степени т ^ 0,70; волновое сопротивление тела
такой формы примерно на 25% меньше, чем у конуса, при объеме
большем—на — 25 %. Отметим,что для тел степенной формы вследст¬
вие затупления носовой части (увеличивающегося для т<^ 1, при
пг-^0,5 — случай цилиндрического сильного взрыва) с увеличением
относительного затупления следует учитывать возрастающее влия¬
ние на параметры обтекания слоя потока с повышенной энтропией
у поверхности тела [2.168]. Однако по данным работы [2.168] в
рассматриваемом диапазоне 1 > т > 0,65 это влияние незна¬
чительно (рис. 2.78).
Тело вращения степенной формы г = схт при т ^ 0,75 ока¬
зывается оптимальным по волновому сопротивлению и при исполь¬
зовании известной приближенной зависимости для относитель¬
ного давления р на контуре тела (подробнее см. [2.165]):
__ _ sin2 О*
р = <2-84)
р — р^ __
где р — (схр равно среднему значению р по площади миделя),
ру2/2
й'г — местный наклон контура поверхности тела, рп и Фп — от¬
носительное давление и наклон в фиксированной точке, например
на носике.
Использование соотношения (2.84) позволило показать, что
учет сил трения [2.165] незначительно изменяет контур опти¬
мальной носовой части (рис. 2.79) (см. также [2.210]). Форма
оптимального контура тонкого тела вращения с учетом сил тре¬
ния при постоянном значении местного коэффициента трения
cF — const определяется соотношением [2.165]
/ с п \ 7з /с ™ \ 2/з
ЭНЕРГОУСТАНОВКИ КОСМИЧЕСКИХ АППАРАТОВ
103
т=/,0
0,90
0,80
0№^*^
4,0 1,08 1J6 1,24 2>
7 V*
Рис. 2.77. Изменение коэффициента волнового сопротивления тел
вращения степенной формы г = схт в зависимости от относительного
объема г/to*; объем ь и коэффициент сопротивления соотнесены
к соответствующим значениям ь* и с * для тела конической формы
(m = 1) с таким же удлинением.
Рис. 2.78. Влияние слоя потока с повышенной энтропией на пара¬
метры гиперзвукового обтекания тела вращения с ударной волной
степенной формы г = сх°>65- Сплошная кривая — точный контур
тела, пунктирная кривая — контур тела без учета энтропийного
слоя.
104
ФИЗИЧЕСКИЕ ПРИНЦИПЫ ДВИГАТЕЛЬНЫХ СИСТЕМ
[ГЛ. 2
Использование соотношения (2.84) позволило также определить
оптимальные формы носовой части тел вращения при заданном
объеме [2.165], которые оказались близкими к степенным фор¬
мам и определяются уравнением
Для тел вращения с протоком величина внешнего волно¬
вого сопротивления зависит от относительного радиуса входа
(2.85)
о о;г о,4 о,в о,s f
Рис. 2.79. Влияние сил*трения на фор¬
му оптимального контура [носовой ча¬
сти тела вращения при больших сверх¬
звуковых скоростях движения. Сплош¬
ная кривая — оптимальный контур с
учетом сил трения, пунктирная — без
учета трения [2.165].
Рис. 2.80. Зависимость коэффициента
волнового сопротивления тела с прото¬
ком от относительного радиуса входа
га/г0', с отнесено к кольцевой пло-
1 хр щади миделя.
rq = rq/r0, примерное изменение коэффициента сопротивления
cxv по rq показано на! рис. 2.80 [2.165].
ТЕПЛООТВОД ОТ КОСМИЧЕСКИХ ЭНЕРГОУСТАНОВОК
105
§ 3. ТЕПЛООТВОД ОТ КОСМИЧЕСКИХ ЭНЕРГОУСТАНОВОК
1. Радиационные системы отвода энергии. В тепловых реак¬
тивных двигательных системах с открытым циклом (см. выше
рис. 2.10) необходимый теплоотвод в основном достигается за
счет предварительного подогрева подаваемого рабочего тела.
Так, например, в построенном в 1930 г. тепловом реактивном
Рис. 2.81. Реактивный двигатель ОР-1: горючее — бензин, окисли¬
тель — сжатый воздух, тяга Р = 5,0 кг.
двигателе Ф. Цандера ОР-1 (рис. 2.81) охлаждение осуществ¬
лялось окислителем — сжатым воздухом, проходящим по
каналу вокруг камеры сгорания перед поступлением в каме¬
ру [2.71].
Для космических двигательных систем, включающих энерго¬
установку с замкнутым циклом (см. выше рис. 2.52), энергетиче¬
ский к.п.д. системы ре = NyJNn, равный отношению полной
мощности реактивной струи движителя N\ ^ 7Vv к мощности
энергоисточника Nn, как обычно, для энергоустановок порядка
десятка процентов. Поэтому для энергоустановок с замкну¬
тым циклом большая часть мощности, выделяемой источником
106
ФИЗИЧЕСКИЕ ПРИНЦИПЫ ДВИГАТЕЛЬНЫХ СИСТЕМ
[ГЛ. 2
энергии, равная
Nt = Nn — Ar). = -V, —- , (2.86)
По
должна быть отведена от космического аппарата примерно на
низшем температурном уровне энергетического цикла —Тшщ*).
Основным обсуждаемым в литературе (см. [2.32, 2.87] и др.)
методом отвода мощности N^ является лучистый теплоотвод с
помощью радиаторов различного вида. Величина потребной пло¬
щади поверхности радиатора S^ связана с мощностью N\ по за¬
кону Стефана—Больцмана
Nr N у 1 — Г)„
= X- = т • (2.87)
o«,T*lln ссоДп]п Ло
Соотношение (2.87) приведено для случая отсутствия сущест¬
венных внешних тепловых потоков и для радиаторов без само-
облучающихся поверхностей; примером такой системы может
служить плоская излучающая поверхность в космосе, располо¬
женная параллельно потоку солнечного излучения.
Как было указано выше, обсуждаемые в литературе типичные
космические энергоустановки работают по тепловому циклу. Энер¬
гетический к.п.д. г)о связан с максимальным и минимальным
температурными уровнями энергоустановки
Ло = ^ Ттах —Т1шп_ = ^ (1 _ Т), (2.88)
max
где Т = —111111 , коэффициент щ учитывает отличие от идеаль-
uiax
ного энергетического цикла.
Согласно (2.87), (2.88) величина потребной площади радиато¬
ра равна
N> II — ri (1 — Т)]
SK = —Ц 'Г _ 2- . (2.89)
* GcoTai;lx'i')^ (1 т) т
При заданных значениях мощности струи движителя 7V>., макси¬
мально допустимой температуре цикла энергоустановки Ттах
(а также со и р J величина площади радиатора достигает минимума
при следующем оптимальном значении Т:
in in Sr при T,pl = l-2K+ |/(l_AL)2 + _L._l. (2.90)
Зависимость T()1)L (pj приведена на рис. 2.82; видно, что при ри: =
*) Учет мощности Nqv, привносимой забираемым рабочим телом (см.
гл. 1, § 2), не изменяет принципиально дальнейшего анализа. Для простоты
рассматриваем случай Nqv = 0.
ТЕПЛООТВОД ОТ КОСМИЧЕСКИХ ЭНЕРГОУСТАНОВОК
107
= 1,0, Topt=3/4 и несколько повышается с уменьшением зна¬
чения щ. Соответствующие минимальные удельные значения
S^co/Nx приведены на рис. 2.83. Видно, что для обсуждаемого в
литературе диапазона допустимых значений Ттах ~ 1000ч- 2500° К
(см., например, [2.32, 2.87] и др.) удельная площадь радиатора
hpl
0,8
0,6
0,0
0,2
0,5 0,6 0,7 0,8 л. 0,0 у*
Рис. 2.82. Оптимальное соотношение темпе¬
ратурных уровней космической энергоуста¬
новки Topt = Tmin/Tmax, соответствующее
минимуму потребной площади радиатора.
Рис. 2.83. Зависимость удельных значе¬
ний площади радиатора от максимального
температурного уровня в энергоустановке.
Рис. 2.8V Плоской сребренный трубчатый радиатор.
составляет ~10_1—10"2 мУквт, т. с., например, уже для энер¬
гоустановки мощностью Arv ^ Nx ~ 20 000 кет (для движителя
с тягой порядка 10,0 кГ при удельном импульсе 7°^ 10 000 сек)
необходим радиатор площадью в сотни квадратных метров. В свя¬
зи с большими потребными площадями радиаторов существен¬
ными являются вопросы минимизации их веса; ниже эта пробле¬
ма рассматривается для двух типичных схем: оребронного труб¬
чатого и ленточного радиаторов.
2. Система отвода энергии с плоским оребренным трубчатым
радиатором. Принципиальная схема такой системы отвода энер¬
гии приведена на рис. 2.84 [2.32]. Отвод энергии, подводимой
108
ФИЗИЧЕСКИЕ ПРИНЦИПЫ ДВИГАТЕЛЬНЫХ СИСТЕМ
[ГЛ. 2
текущим внутри трубок теплоносителем, осуществляется излу¬
чением с поверхности оребренных трубок.
Задачу минимизации веса рассмотрим вначале для системы с
трубками очень малого диаметра, что эквивалентно плоской за¬
даче минимизации веса системы ребер, охлаждающих излучением
параллельно расположенные с некоторым шагом 2L линейчатые
источники тепла (рис. 2.85, а). Вследствие симметрии достаточно
рассмотреть участок ребра АВ (охлаждаемого излучением по АВ)
на полушаге!/ при одностороннем подводе тепла к ребру по осно¬
ванию ребра ОА (рис. 2.85, б) при заданной минимальной тол¬
щине ребра О'В [2.169]. Будем рассматривать тонкое ребро
жен обеспечить минимум площади сечения ребра f = —2\ydx
при заданных начальном тепловом потоке Q0, начальной темпе¬
ратуре Т? и минимальной толщине ребра у > ут[п.
Введем безразмерные переменные:
а)
с пологим контуром, для кото¬
рого уравнения теплопередачи
вдоль ребра и закон теплового
излучения справедливы в сле¬
дующей форме:
'I
(2.91)
L
где у — полутолщина ребра,
ось — х направлена вдоль ши¬
рины ребра, Q — тепловой по¬
ток по ребру на единицу длины
ребра, Х:;: — коэффициент теп¬
лопроводности, Т — температу¬
ра ребра.
Рис. 2.85. Схема плоского оребрения
радиатора.
Оптимальный контур сечения
ребра минимального веса дол-
L
0
X =
(2.92)
Тогда
о
(2.93)
ТЕПЛООТВОД ОТ КОСМИЧЕСКИХ ЭНЕРГОУСТАНОВОК
109
На краю ребра(при я = L) нам известно значение только пере¬
менной Q = Ql = 0. Поэтому удобнее искать остальные пере¬
менные как функции от Q:T (Q), х (Q), у (Q). Уравнения (2.93)
перепишем в виде
г/Т __ (J_
Г,т4 ’ * А т4
f = —2\4rdQ, (2.94)
dQ yTl J Т4 V V '
где при Q = 1 Т = 1, у = у0\ при Q = 0 Т = TL, у = ymin.
В такой постановке задача может быть решена на основании
принципа максимума [2.170]. Следуя [2.170], введем новую
Q —
переменную fi= —2\^-^dQ и будем рассматривать задачу об
i _
оптимизации конечного значения этой переменной при Q = 0.
Гамильтонова функция Н (см. [2.170]) запишется в виде
(2.95)
где
dll \ ( рхО 0 \ , ЭН п } ог
ЯГ-0- {1Щ
с граничными условиями: при Q = 0 р1 = 0, р2 = 1,0. Заметим,
что импульс р2 — постоянная величина, р2 = 1,0 (см. (2.96)).
Согласно [2.170] функция Н должна быть максимальной по у
при любых значениях Т и pv На краю ребра при Q = 0 и рг = 0
максимум//, естественно, достигается при уь = уШ[П, тогда IIL —
= — и {р[)ь = Отступая от края ребра, убеждаемся
Ч Т°
в том, что до тех пор, пока i / Pl(l_ ymin, максимум Н по у
I/ а
всюду имеет место при у = утт. Следовательно, на этом участке
оптимальный профиль ребра у = ymm = const.
В некоторой точке Q = величина достигает
значения ymjn; с этой точки и далее при Q^> Q** максимум функ¬
ции Н имеет место при у уш[п и р1 = — , что приводит
к следующему дифференциальному уравнению:
2^Т^- + 16Д( 4ГУ_ f4^- = 0. (2.97)
dQ2 v \ dQ I dQ v
110
ФИЗИЧЕСКИЕ ПРИНЦИПЫ ДВИГАТЕЛЬНЫХ СИСТЕМ [ГЛ. 2
В результате интегрирования уравнения (2.97) получаем
решение в виде
T = [(l -Tl)Q > + Ti]
(2.98)
а форма контура определяется интегрированием следующей сис¬
темы:
dx =
dQ
Ф 2 dQ
■1-т» dx '
(2.99)
где Tl соответствует температуре на краю ребра, если контур
(2.99) продолжить в область у X ут\а. На рис. 2.86 приведены
О 0,5 1,0 1,5 2,0 2,5 -х
Рис. 2.So. Оптимальные контуры плоского теплоотводнщего ребра, охлаждаемого
пзлучением.
результаты расчета оптимальных контуров (2.99) при ряде зна¬
чений параметра TL [2.169] (расчеты проведены Ю. В. Шалае¬
вым) .
Отметим, что контур с TL = 0, дающий абсолютный мини¬
мум площади ребра $f0pti соответствует рассмотренному в рабо¬
тах [2.171—2.174] частному случаю ребра с утщ = 0 (подробнее
§3]
ТЕПЛООТВОД ОТ КОСМИЧЕСКИХ ЭНЕРГОУСТАНОВОК
см. в [2.169]). Для этого контура
Т — 0':‘, <7 = (l + 4-f. Т = (1 + Д
У
Уо = 6>
7 ^
■'-'opt 9
^ = (1 + 4-)
V 3,5
■^opt
Qo
GO)T4
= -з,
, У
op г — 8»
Qo
(2.100)
О opt
X gcoT0
S opt
Qo
X gcoT9
6Г
К указанному значению f0pt удобно относить значения S
всех анализируемых контуров ребер.
При заданном значении ут[п по- ^
строение оптимального контура ребра <ropt
по параметру Тl на участке от нача-
ла ребра до //' /7.:и, (•?„, Q , ТД про- Л
водится по данным рис. 2.86; пара¬
метры участка с постоянной толщи¬
ной у = у mini примыкающего к краю
ребра, определяются по формулам 1,0
(при Q** > Q > 0)
для
2?/„
X — X =
**
Q
л
dQ
05
Q*
(Q2 — Q?) -i- Т1
11
^inin 1$
Утъп = 0
1
/
^У
о
0,5
1,0 т,
Рис. 2.87. Влияние относительной
температуры края ребра на площадь
сечения теплоотводящего ребра.
2^iuin
(2.101)
В качестве примера на рис. 2.86
указаны оптимальные контуры ребер
при ymin = 1,8. Значения относительной площади сечения
этих ребер S'/So^x по параметру TL приведены на рис. 2.87,
где пунктиром также указаны значения .fAfopt для случая ymin =
= 0. При ут[п = 1,8 утш/Уо =~- 0,31; минимум площади с поло¬
гим оптимумом имеет место при Tl ~ 0,70; минимальная пло¬
щадь составляет f/S' opt = 1,205, что существенно меньше, чем для
оптимального прямоугольного ребра, где f /f opt = 1,635 (см.
пунктирную кривую на рис. 2.86 [2.175—2.176]). Для сопостав¬
ления на рис. 2.86 пунктиром указан также контур оптимального
треугольного ребра [2.177], для которого f/Sopt = 1,103 (при
Vmin — 0).
112
ФИЗИЧЕСКИЕ ПРИНЦИПЫ ДВИГАТЕЛЬНЫХ СИСТЕМ
[ГЛ. 2
У реальных плоских оребренных трубчатых радиаторов с
трубками конечного диаметра (рис. 2.84) необходимо учитывать
излучение с поверхности трубок и взаимооблучение трубок и ребер.
Последний фактор для радиаторов с достаточно длинными ребрами
дает (по данным [2.175] и др.) относительно небольшой вклад, и
поэтому пренебрежем в первом приближении взаимным облуче¬
нием трубок и ребер. Рассмотрим оптимальное сочетание с ми¬
нимальным весом теплоотводящих ребер и трубки [2.169], нагре¬
ваемой изнутри теплоносителем, при заданных температуре стен¬
ки трубки Ту; = Т* и геометрии трубки (диаметр D, толщина
стенки б). Обозначим, как и ранее, через Q0 начальный тепловой
лоток по одному ребру; тогда полный отвод тепловой мощности
на единицу длины трубки z с ребрами составит
^ = 2Q0 + л(В + 6)ссоТ*. (2.102)
Пес единицы длины трубки с ребрами равен
9. ^ з
dG^ _ я(Р+б)-*Z>* ~ ^opt ,2 10os
dz ~ 4 Tl '
* *
где — удельный вес материала трубки, у2 — удельный вес
материала ребер.
Согласно (2.102) и (2.103) относительный вес радиатора
dG-JdN^ на единицу отводимой тепловой мощности составит ^
d G у сг'1/ -{- Q ^
где
Л = п (7J + 68)2~Z)'2 Гь 53 = У Г21 (в = я(Д+а) асоЦ.
° X 62co-TJ -
* *
Минимум относительного веса радиатора достигается при
() 2
Vo M(2Q 0 + 3<ё) ’
или
(1+Х)%2 = ^^|г, (2.105)
где
Y--A2!
1 " 3 <ё '
ТЕПЛООТВОД ОТ КОСМИЧЕСКИХ ЭНЕРГОУСТАНОВОК
ИЗ
При этом минимальный относительный вес составляет
( \ __
dNс * min 1 + X
(2.106)
т. е. в 1 + X раз меньше, чем для трубчатого радиатора без ребер.
В качестве иллюстрации на рис. 2.88 приведены значения
—^ при D = 10 мм, б = 0,25—0,75 мм, Т* = 1100° К, со =
= 0,9; трубка из стали, ребра из стали, меди или бериллия с
f/fopt — 1,205 (рассмотренный выше оптимальный контур с
2/miri/ у о = 0,31). Видно, что у оптимального оребренного плоско¬
го трубчатого радиатора относительный вес может быть примерно
вдвое меньше, чем у трубчатого радиатора без ребер.
Рис. 2.88. Влияние оребреиия па относительный вес плоского трубча¬
того радиатора.
Относительный вес трубчатого радиатора, естественно, суще¬
ственно зависит от допустимой толщины стенки трубки б, опре¬
деляемой из условий метеорной опасности (см. § 3 гл. 1). По
данным рис. 1.8 и формулы (2.104) для трубчатого радиатора без
ребер (при Q0 = 0) на рис. 2.89 приведена зависимость относи¬
тельного веса трубчатого радиатора от его температуры Т* при
различном допустимом числе метеорных пробоев радиатора ни
единицу излучаемой энергии [2.32]. При анализе данных рис. 2.89
следует подчеркнуть, что полезная мощность двигательной си¬
стемы (например, полная мощность реактивной струи движителя
Ni) значительно меньше излучаемой радиатором мощности 7V-;
даже для идеального цикла при ц = 1,0 (см. выше) полезная
о
Механика полета
114
ФИЗИЧЕСКИЕ ПРИНЦИПЫ ДВИГАТЕЛЬНЫХ СИСТЕМ
[ГЛ. 2
мощность втрое меньше излучаемой. Поэтому удельный вес труб¬
чатого радиатора, относимый к полезной мощности двигатель¬
ной системы, в несколько раз превышает приведенные на рис. 2.89
значения относительного веса радиатора (соответственно сдви¬
нется и шкала числа пробоев на 1 квт-ч полезн й энергии). Вид¬
но, что удельный вес трубчатого радиатора достигает заметной
величины по сравнению с ука¬
занными в §§ 1 и 2 настоящей
главы значениями удельных
весов энергоисточников, энер¬
гопреобразователей и движи¬
телей. Применение плоско¬
го оптимально оребренного
трубчатого радиатора соот¬
ветственно примерно вдвое
снижает удельный вес радиа¬
тора (см. рис. 2.88). Большее
снижение веса радиатора мо¬
жет быть достигнуто при
з в е з д о об ра з ном о реб ре ни п.
3. Система отвода энергии
со звездообразно оребренным
трубчатым радиатором. Выше
в п. 2 была рассмотрена пло¬
ская задача об оптимальном
контуре поперечного сечения
теплоотводящего ребра (ох¬
лаждаемого излучением) при
одностороннем подводе тепла
к ребру. Было показано, что
площадь поперечного сечения
оптимального ребра (мини¬
соотношением вида
Рис. 2.89. Огчосительпый вес трубчатого ра¬
диатора (мм единицу излучаемой мощности)
с учетом метеорной опасности для полетов
в'лизи Земли в зависимости от температуры
радиатора Т*.
мального веса) определяется
Ql
(2.107)
т. е. площадь сечения (вес) оптимального ребра пропорционален
кубу теплового потока Q0, отводимого ребром. Поэтому, если
заданный тепловой поток Qv будут отводить несколько (п) ребер
((?£ = nQo), то без учета их взаимного облучения суммарная
площадь сечения ребер $^ (и их вес) будет уменьшаться обратно
пропорционально п2:
при Qz = nQо = const.
(2.108)
ТЕПЛООТВОД ОТ КОСМИЧЕСКИХ ЭНЕРГОУСТАНОВОК
115
Тсплоотводящие ребра можно расположить, например, звез¬
дообразно у вершин охлаждаемого многогранника (трубки)
(рис. 2.90). При этом с п 2 существенно взаимное облучение
ребер, учет которого определит оптимальное количество ребер
ftopt и соответствующую оптимальную форму сечения ребер [2.178].
В указанной постановке задача об оптимальном звездообраз¬
ном оребрении была решена в работах [2.178—2.179]. На рис. 2.91
приведены результаты решения для формы контура оптимальных
звездообразных ребер при малых размерах центральной трубки
и со = 1,0. Отчетливо видно влияние взаимооблученности при
п 2, которое сказывается в увеличении относительных разме¬
ров ребра с возрастанием числа ребер. Однако с учетом зависимо¬
сти вида (2.108) абсолютная площадь сечения ребер (и соответ¬
ственно вес радиатора) при заданном значении суммарного
теплового потока имеет минимум при звездообразном располс
жении 4—5 ребер (см. сплошную кривую на рис. 2.92, где
отнесено к площади одиночного оптимального ребра f1 opt, отво¬
дящего тот же поток Qs). Для сопоставления на рис. 2.92 приве¬
дена пунктирная кривая, построенная по расчетным данным
работ [2.180—2.181 ] для выбранной системы наивыгоднейших звез¬
дообразно расположенных прямоугольных ребер. Площадь се¬
чения системы наивыгоднейших прямоугольных ребер в — 1,5
раза больше, чем у системы оптимальных ребер. Штрих-пунктир-
8*
116
ФИЗИЧЕСКИЕ ПРИНЦИПЫ ДВИГАТЕЛЬНЫХ СИСТЕМ
[ГЛ. 2
нал кривая на рис. 2.92 соответствует соотношению (2.108) без
учета взаимного облучения ребер. Подробные данные по плоско¬
му и звездообразному оребрению радиаторов см. в работах [2.178—
2.195] и др.
При сопоставлении звездообразно оребренного радиатора с
плоским оребренным трубчатым радиатором следует иметь в
виду, что у плоского оребренного радиатора п = 2. Соответ¬
ственно переход к оптимальному
звездообразно оребренному радиа¬
тору по данным рис. 2.92 снижает вес
ребер примерно на 40%.
4. Система отвода энергии с лен¬
точным радиатором. В связи с тем,
что большой удельный вес трубчатого
радиатора во многом определяется
'^fopt
1,5
1,0
0,5
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1\
\\
\\
\ \
\ \
\ \
V
X.
■—■/
/
Рис. 2.91. Влияние числа ребер п па форму
оптимального контура ребер звездообраз¬
ного оребренного радиатора.
12 3 4 5 6 7 8 п
Рис. 2.92. Влияние числа ребер п
на площадь сечения звездообразно
оребренного радиатора:
1 — ребра оптимальной формы,
2 — прямоугольные ребра.
требованиями защиты от метеорных пробоев, в работе
[2.196] был рассмотрен ленточный радиатор, вес основного
элемента которого — ленты, не зависит от метеорной опасности.
В этом радиаторе гибкая лента, прижимаемая валками [2.196]
(рис. 2.93, а) или центробежными силами [2.197—2.198] в слу¬
чае вращающейся ленты (рис. 2.93, б) к цилиндру с теплоноси¬
телем, отнимает от него тепло и излучает это тепло со своей поверх¬
ности. Пробои ленты микрометеоритами не должны нарушать
работу такого радиатора. Подробные данные о форме и устойчи¬
вости формы ленты в пространстве, влиянии взаимооблученности
элементов ленты и т. д. см. в работах [2.197—2.205]. Ниже рас¬
смотрены основные параметры ленточного радиатора [2.196].
§ 3]
ТЕПЛООТВОД ОТ КОСМИЧЕСКИХ ЭНЕРГОУСТАНОВОК
117
Пусть вес ленты С?^, теплоемкость длина ленты L, скорость
обкатки лентой барабана W, максимальная температура ленты
в точке схода с барабана Т#, температура в точке касания бара¬
бана Т2; тогда мощность, отводимая лентой (если пренебречь
участком, касающимся барабана), будет равна
Эту мощность лента должна излучить. Без учета взаимооблучения
элементов ленты, в первом приближении, следуя [2.196], мож¬
но записать соотношение
Средняя температура ленты Та определяется по закону паде¬
ния температуры вдоль ленты
Интегрированием уравнения (2.111) с использованием гранич¬
ных условий: при х = О Т = Т+; при х = L Т = Т2 определя¬
ется значение константы сх\
Ni = GKlc,{ Т. —Т2)^.
(2.109)
Рис. 2.93. Система отвода энергии с ленточным радиатором.
Nn = 2ЬЬошТ1,
L V.
(2.110)
где bt — ширина ленты,
о
(2.111)
Т-3 —Т~3
С1= -1Г-
и затем значение Т„:
(2.112)
118
ФИЗИЧЕСКИЕ ПРИНЦИПЫ ДВИГАТЕЛЬНЫХ СИСТЕМ
[ГЛ. 2
По соотношениям
ленты равен
(2.109), (2.110) и (2.112) потребный вес
Ni
6сД,Т7асоТ5 1
Та
т*
(2.113)
Минимум веса ленты достигается при (T2/TJ0pt = 0,69. Тогда
min i = 3,55
^opt = 0,31
^£1
n:
(2.114)
cj>jr<5 GOT® ^
В уравнениях (2.114) величина ТА примерно равна минималь¬
ной температуре цикла энергоустановки Tmin (тепловое контакт¬
ное сопротивление достаточно
мало [2.206—2.208]), скорость
ленты W ограничена ее механи¬
ческими свойствами; если счи¬
тать, что рациональная ширина
ленты Ъ+ (и барабана с тепло¬
носителем) пропорциональна от¬
водимой мощности Ь+ = kN^, то
первое уравнение (2.114) опре¬
делит относительный вес ленты
G^/Nn.
По данным работы [2.196]
при N\ = 20 000 кет, =
= 68 000 кет и использовании
стальной ленты с возможным
графитовым покрытием, при
1^=15,2—30,5 м/сек, 6^ = 11,6 л*,
Tmin = 1000° К полный вес лен¬
точного радиатора с теплоот¬
дающим цилиндром и необходи¬
мыми механизмами составит
~ = 3850 -г- 7250 кГ (G^/N^
^0,057 -к- 0,107 кГ/квт, GK/NX^
^ 0,19-4-0,36 кГ/квт), что суще¬
ственно меньше, чем для труб¬
чатого оребренного радиатора
на ту же мощность и темпера¬
туру, вес которого по данным
19 400 кГ (G^/N^ ^ 0,285 кГ/кет,
2Ш Т,
Рис. 2.94. Удельный вес радиационных
систем теплоотвода от космических энерго¬
установок (на единицу полезной мощно¬
сти):
I — плоский орсбреппый трубчатый радиа¬
тор, на кривых отмечено число пробоев
на 1 кет • ч; 2 — система отвода энергии
с ленточным радиатором.
G- =
[2.209] составит —
G^/Nx ж 0,97 кГ/квт).
На итоговом рис. 2.94 приведены примерные значения удель¬
ного веса для плоского оребренного трубчатого радиа-
N
ТЕПЛООТВОД ОТ КОСМИЧЕСКИХ ЭНЕРГОУСТАНОВОК
119
тора (сплошные кривые) и системы с ленточным радиатором (за¬
штрихованная область между пунктирными кривыми) в зависи¬
мости от максимального температурного уровня в энергоуста¬
новке Тшах. На кривых, соответствующих оребренному трубча¬
тому радиатору, отмечено число пробоев на 1 квт-ч полезной
энергии; эти кривые построены по данным рис. 2.89 в предпо¬
ложении, что выигрыш веса от оребрения трубчатого радиатора
примерно компенсирует переход от N* к N\ ^ Nv. Параметры
Вне. 2.у5. Области прейму11 шетвеч п юго использования различных видов космических
энергоустановок в зависимости от времени работы Т и полезной мощности .Vv.
систем отвода с ленточным радиатором приведены на основе рас¬
смотренного выше примера из работы [2.196], экстраполировав-
ного по формуле (2.114).
Данные рис. 2.94 показывают, что и с учетом возможной ми¬
нимизации удельные веса радиационных систем теплоотвода от
космических энергоустановок являются весьма значительными.
Поэтому вес системы теплоотвода является существенной частью
общего весового баланса космической энергоустановки.
5. Весовые характеристики космических энергоустановок —
источников мощности. Для рассмотренных в § 2 ряда видов ис¬
точников энергии и энергопреобразователей, а также для кратко¬
временно действующих энергоустановок, на рис. 2.95 по данным
работы [2.89] указаны области преимущественного использова¬
ния в зависимости от времени работы Т и полезной мощности Nv.
Приведенные в §§ 2 и 3 удельные веса элементов космических
К
/О
Юмин. 1час
1 сутки 1 неделя 1 месяц 1год Т
120
ФИЗИЧЕСКИЕ ПРИНЦИПЫ ДВИГАТЕЛЬНЫХ СИСТЕМ
[ГЛ. 2
энергоустановок определяют их весовые характеристики в целом
как источников мощности.
В соответствии с удельными весами элементов общий вес ис¬
точника мощности Gv зависит от величины максимальной мощно¬
сти вырабатываемой источником. В качестве иллюстрации в
Рис. 2.96. Примерные значения удельного веса источников мощ¬
ности — космических энергоустановок; кривая по данным [2.38],
точки по данным табл. 2.11.
табл. 2.11 по данным работ [2.90, 2.91, 2.104] приведены пример¬
ные параметры ряда рассматриваемых источников мощности. Из
данныхтабл.2.11,построенномупонейиработе [2.38] рисунку 2.96
Таблица 2.11
Примерные параметры космических энергоустановок
Энергоустановк а
Snap
1А
Snap
10А
Snap
2
Snap
8
Snap
59
ввс-
Krupp
в В С-1
ВВС-11
Полезная мощность
7Vv, кет
0,125
0,5
3,0
35
350
150
150
700
Максимальная тем-
пература Ттах, °К
810
925
980
1370
1180
Источник тепла и
Радио¬
Реак¬
Реак¬
Реак¬
Реак¬
Реак¬
Реак¬
Реак¬
цикл
изо¬
тор,
тор,
тор,
тор,
тор,
тор,
тор,
топ,
термо¬
цикл
цикл
цикл
цикл
тер¬
тер-
термо¬
эле¬
Рэн¬
Рэн¬
Рэн¬
Рэн¬
мо-
мо-
эле¬
менты
кина
кина
кина
кина
эм ис-
эмис-
Площадь радиатора
S, м2
менты
5,8
11,15
130
320
сия
сия
Вес Gv, кГ
79,3
295
544
1905
2270
1350
1200
1660
Удельный вес
кГ
а JV J кет
635
590
181
55
6,5
9,0
8,0
2,4
ТЕПЛООТВОД ОТ КОСМИЧЕСКИХ ЭНЕРГОУСТАНОВОК
121
следует, что удельный вес источника мощности а = Gv/Nv
для больших значений 102 ч- 103 кет почти постоянен,
несколько снижаясь с увеличением полезной мощности источ¬
ника Nv.
Сопоставление приведенных значений удельного веса источ¬
ников мощности а х 1 — 10 кГ/квт (при Nv 102 кет) с рас¬
смотренными выше удельными весами электрореактивных дви¬
жителей и другими элементами показывает, что в такой двига¬
тельной системе главные весовые свойства отражает удельный
вес источника мощности а ([2.48] и др.)* Поэтому с позиций ме¬
ханики космического полета двигательные системы с источником
мощности и электрореактивным движителем являются системами
ограниченной мощности, величина которой в основном опреде¬
ляет вес двигательной системы.
ГЛАВА 3
ОБОБЩЕННЫЕ ПАРАМЕТРЫ КОСМИЧЕСКИХ
ДВИГАТЕЛЬНЫХ СИСТЕМ
Обобщенные характеристики обсуждаемых в литературе основ¬
ных типов космических двигательных систем ниже приводятся
с позиций механики космического полета [3.1—3.3]. Эти обоб¬
щенные параметры следуют из рассмотренных выше во второй
главе физических принципов элементов космических двигатель¬
ных систем.
Введение обобщенных параметров, естественно, схематизи¬
рует проблему, сохраняя ее основные свойства. По изло¬
вленным принципам возможно дальнейшее более детальное иссле¬
дование.
Двигательные системы разбиты на три категории (см. §§1,2
и 3 данной главы) в зависимости от основных ограничений, накла¬
дываемых соответствующими физическими принципами на харак¬
теристики системы. Основное ограничение характеризуется тем,
что в механике полета, как правило, оптимальное движение со¬
ответствует выходу на это ограничение. Такими основными огра¬
ничениями являются ограничение скорости истечения реактив¬
ной струи, ограничение мощности и ограничение тяги двигатель¬
ной системы.
Рассматриваемые обобщенные характеристики относятся
к двигательным системам без забора рабочего тела из внеш¬
него потока; влияние забора рабочего тела было рассмотрено
в главе 2.
§ 1. ДВИГАТЕЛЬНЫЕ СИСТЕМЫ С ОГРАНИЧЕННОЙ СКОРОСТЬЮ
ИСТЕЧЕНИЯ РЕАКТИВНОЙ СТРУН
К этому типу относятся тепловые реактивные двигательные
системы, обобщенная схема которых приведена на рис. 3.1. Тягу
в таких двигательных системах создает реактивное сопло, пре¬
вращающее тепловую энергию рабочего тела в кинетическую энер-
I ию направленного движения реактивной струи.
На участке космического полета основные параметры тепловых
ракетных двигателей определяются площадью критического сече¬
ния реактивного сопла 1^, полным давлением р0 и температурой
5 lJ ДВИГАТЕЛИ О Г Р А ИIIЧ Г1 i IIОII СКОРОСТИ ИСТЕЧЕНИЯ
123
газа Т0 на входе в сопло:
Р = hf'Vo:
п /г ^*Ро
q-k2TTT’
Г = ^-=АзУТ0, N = ^ = ktf,p 0/Т0.
(3.1)
Для двигателя заданной геометрии = const) возможность ре¬
гулирования основными параметрами двигательной системы Р
и q определяется возможностью независимого управления полным
давлением р0 и температурой Т0.
Основным ограничением для теп¬
ловых двигателей является макси¬
мально допустимая конструкцией
температура Тотах, что ограничи¬
вает возможную скорость истече¬
ния реактивной струи (см. (3.1)):
h Ут,
отах*
(3.2)
Рис. 3.1. Обобщенная схема тепловой
реактивной двигательной системы:
1 — контейнер с рабочим телом, 2 —
реактивное сопло (движитель) с источ¬
ником, преобразователем энергии, си¬
стемами подачи рабочего тела и отво¬
да энергии.
Для заданной прочности конструкции вторым ограничением
является допустимое максимальное полное давление р0тах, ве¬
личина которого определяет удельные значения максимальной
тяги и мощности, отнесенные к площади сечения сопла
= h P°max’ Pomax V'• (3’3)
Вид регулировочных характеристик тепловой реактивной
двигательной системы на участке космического полета представлен
Рис. 3.2. Регулировочные характеристики тепловой реактивной двига¬
тельной системы.
на рис. 3.2. При движении в атмосфере тяга двигательно!
системы несколько снижается (см. рис. 2.12).
ОБОБЩЕННЫЕ ПАРАМЕТРЫ ДВИГАТЕЛЬНЫХ СИСТЕМ
[ГЛ. 3
Вес двигательной системы с ограниченной скоростью истече¬
ния реактивной струи в основном определяется весом контейнера
для запаса рабочего тела и максимальной тягой Ртах'
Gp ~ -\- Т^Рщах* (3*4:)
Значения весовых коэффициентов были приведены в главе 2.
§ 2. ДВИГАТЕЛЬНЫЕ СИСТЕМЫ ОГРАНИЧЕННОЙ МОЩНОСТИ
Двигательные системы ограниченной мощности состоят из
источника мощности (источник энергии, преобразователь энер¬
гии, система отвода энергии), реактивного движителя с системой
подачи и контейнера с рабочим
телом (рис. 3.3). Выработанная
источником энергия превращается
в движителе в кинетическую энер¬
гию направленного движения реак¬
тивной струи. Наличие отдель¬
ного источника ограниченной мощ¬
ности 7Vv 7Vv max определяет
основные свойства и название
рассматриваемой категории дви¬
гательных систем.
Характерным свойством двига¬
тельных систем ограниченной мощ¬
ности является их регулируемость
по параметрам q и V в широких пределах. Кроме того, можно
управлять величиной мощности Nv, подводимой к движителю.
В идеальном движителе вся подводимая мощность превраща¬
ется в мощность реактивной струи. Это определяет простую связь
между параметрами
= N, < ЛГ. m„, P = qV, (3.5)
где 7Vv max может зависеть от координат и времени.
Характеристики реальных движителей подробно рассмотрены
в главе 2. С учетом этих реальных свойств мощность реактивной
струи 1/2qV21 зависит от параметров движителя, например от ско¬
рости истечения струи V.
Максимальное значение мощности Nv max определяет величину
максимальной тяги, которая для случая идеального движителя
равна (см. (3.5))
Рис. 3.3. Обобщенная схема двига¬
тельной системы ограниченной мощ¬
ности:
1 — контейнер с рабочим телом, 2 —
источник мощности, з — реактивный
движитель.
2N
vmax
max — т/ •
(3.6)
ДВИГАТЕЛИ ОГРАНИЧЕННОЙ ТЯГИ
125
Вид регулировочных характеристик двигательных систем огра¬
ниченной мощности (с идеальным движителем) представлен на
рис. 3.4.
Вес двигательной системы ограниченной мощности в основном
■складывается из трех компонентов: веса контейнера для запаса
Рис. 3.4. Регулировочные характеристики двигательной системы
ограниченной мощности с идеальным движителем.
рабочего тела веса источника мощности Gv и веса движите¬
ля G{\
Gp = "Ь a^vmax ~\~ Т^шах- (3*7)
Возможно также использование аккумулятора энергии, вес
которого пропорционален максимальной запасаемой энергии
Ge = fiE0. Значения весовых коэффициентов были даны в главе 2.
§ 3. ДВИГАТЕЛЬНЫЕ СИСТЕМЫ С ОГРАНИЧЕННОЙ ТЯГОЙ
(ПАРУСНЫЕ СИСТЕМЫ)
К этому типу двигательных систем относятся парусные систе¬
мы (солнечный и изотопный парус), величина тяги которых ли¬
митируется максимальной площадью паруса 5шах:
Р ^max = ^тах* (3*8)
Расход массы у парусных систем отсутствует, величина тяги за¬
висит от координат или времени. Для идеального солнечного па¬
руса с зеркальными отражающими свойствами тяга направлена
по нормали к поверхности паруса, а величина тяги зависит от
угла установки паруса # и расстояния до Солнца R:
Р 7 cos й
(3.9)
126
ОБОБЩЕННЫЕ ПАРАМЕТРЫ ДВИГАТЕЛЬНЫХ СИСТЕМ
[ГЛ. 3
Для изотопного паруса величина тяги зависит от отношения вре¬
мени работы t к периоду полураспада 1АТ:
-£- = *6е~М. (3.10)
Вес двигательной системы ограниченной тяги определяется
ее максимальной тягой
Gp = r{Pm ах. (3.11)
Значения весовых коэффициентов и их зависимость от основ¬
ных параметров подробно рассмотрены в главе 2.
ПРОБЛЕМЫ
ОПТИМИЗАЦИИ
Когда сформулирована цель космического маневра, возни¬
кает проблема о наиболее экономичном ее достижении. Это озна¬
чает, что должен быть выбран оптимальный космический аппарат
и в том числе оптимальная двигательная система. Для последней
нужно указать наилучший для заданного маневра тип, опреде¬
лить наилучшие управляющие параметры и наилучшие програм¬
мы для управляющих функций.
Экономичность выполнения маневра характеризуется тем или
иным критерием оптимальности: максимум полезного веса, ми¬
нимум стоимости выполнения маневра и т. д. В нашем изложении
главное внимание уделяется критерию максимума полезного
веса. Дадим формулировку проблемы оптимизации для этого
случая.
Назовем динамическим маневром перелет из фиксированной
точки 0 фазового пространства координат — скоростей {r0, v0}
в фиксированную точку 1 {rlt vx} за фиксированное время Т.
Содержание изучаемой вариационной проблемы таково: тре¬
буется выполнить заданный динамический маневр с максималь¬
ным полезным весом GK при заданном стартовом весе G0.
Запишем дифференциальные связи вариационной проблемы
с соответствующими граничными условиями. Сюда относятся
уравнение расхода и уравнения, описывающие движение центра
масс аппарата:
Здесь г, у, G — набор фазовых координат (г и v — радиус-
вектор и скорость центра масс аппарата, G — текущий вес ап¬
парата); q, Р, е — набор управляющих функций и управляющих
параметров (q — массовый расход рабочего вещества, Р и | е | = 1 —
величина и направление вектора тяги). Остальные обозначения:
Н = Н (г, t) — вектор ускорения от гравитационных сил, g —
коэффициент пропорциональности между массой и весом, GK —
вес двигательной системы.
Сделаем несколько замечаний к записи (II.1).
^ Механика полета
G (0) = G0, G(T) = Gn + G„
г(0) = г0, г (Т) = гх,
v(0) = v0, v(7’)=v1.
(П.1)
130
ПРОБЛЕМЫ ОПТИМИЗАЦИИ
1°. Система (II.1) представлена в виде обыкновенных диффе¬
ренциальных уравнений первого порядка, разрешенных относи¬
тельно производных. Это позволит в дальнейшем" сформулировать
задачу Майера и свести вариационную проблему к краевой задаче
для системы обыкновенных дифференциальных уравнений с ко¬
нечными соотношениями для управляющих функций.
2°. В правой части третьего уравнения (II.1) выписаны уско¬
рения от реактивных и гравитационных сил. Помимо них могут
быть учтены и другие силы, например сила аэродинамического
сопротивления.
3°. В записи (II.1) аппарат считается состоящим из полезной
нагрузки G-, запаса рабочего вещества G[X и двигательной уста¬
новки G*. Весовая формула такого аппарата имеет вид
G = G, + G[X + Gx. (II.2)
Прочие весовые компоненты (например, вес конструктивных
элементов, вес баков для рабочего вещества) условно относятся
к полезной нагрузке. По мере необходимости эти компоненты могут
быть учтены в вариационной постановке.
4°. Размерность фазового пространства, описывающего состоя¬
ние аппарата, может увеличиваться при усложнении задачи.
К фазовым координатам г, v, G могут добавляться новые коорди¬
наты, например t[X — текущее время работы двигателя (для за¬
дачи с ограниченным ресурсом двигательной системы) или G* и
G$ — веса двигательной системы и баков (для задачи оптималь¬
ного сброса секций двигателя и баков). Тогда систему (II.1) нужно
дополнить дифференциальными уравнениями, описывающими
изменение этих фазовых координат; в отмеченных примерах эти
уравнения таковы:
в первом случае
^ = 6, (II.3)
во втором случае
Gy. = —gqх, 63 = — gq$. (П-4)
При этом могут появиться новые управляющие функции;
здесь б (t) = 1 или 0—функция включения—выключения двигателя,
qv. (t) 0, #з (t) 0 — функции, отвечающие за сброс секций
двигателя и баков.
Запишем теперь исходную систему (II.1) в виде, удобном для
формулировки вариационной задачи Майера. Для этого присо¬
единим к системе (II. 1) формальное уравнение неизменности по¬
лезного веса (тл = 0 и распишем полный вес аппарата в соответ¬
ствии с формулой (II.2). Тогда полная система уравнений и
ПРОБЛЕМЫ ОПТИМИЗАЦИИ
131
граничных условий представится следующим образом:
Ол — 0, gs(0) + Gx+ G* (Т) = max,
G^-gq, +Gv.(0) = G0, GV\T) = 0,
r = V, г (0) = r0, r (T) = l'b f (II>5)
V = g Cj + ^x'c7 + K| v(0) = v0, v(7’) = v1
и задача Maiiepa формулируется так: для системы (II.5) требу¬
ется определить управляющие функции и управляющие параметры
(е, q, Р, Ga или другие, через которые выражаются данные), обес¬
печивающие выполнение граничных условий и доставляющие мак¬
симум конечному значению фазовой координаты G-.
Вариационная постановка (II.5) может быть сведена в ряде
случаев к более простой. Опишем здесь один вариант перехода,
который может быть сделан при условии, что в весовой формуле
аппарата отсутствуют дополнительные компоненты, зависящие
от веса рабочего вещества.
Введем специальное обозначение для суммы полезного веса
G- и веса рабочего вещества Gv:
G0 = Gn + G,. (II.6)
Вес Ga в начальный момент выражается через стартовый вес и
вес двигателя, а в конечный момент совпадает с полезным весом
Go (0) = G0 - Gx, Go (T) = G-. (II.7)
При помощи новой фазовой координаты Ga (t) система (II.5)
трансформируется в следующую:
Go = ■— gq, Ca(0) + Gx = Go, GZ(T) = max,
r = v, r(0) = r0, г(Г) = г1,
V = g-T.-yV + R’ v (0) = v0, v(T) = Vi,
(II 8)
и задача Майера формулируется так же, как и для исходной си¬
стемы, только контрольным функционалом является конечное
значение веса Ga.
В описанных постановках задаются динамический маневр и
начальный вес, ищется максимум полезной нагрузки. Вместо
этого могут быть рассмотрены эквивалентные формулировки:
задаются динамический маневр и полезный вес, определяется
минимум начального веса; задаются полезный и начальный веса,
находится минимальное время выполнения маневра или экстре¬
мальное значение какой-либо фазовой координаты.
9*
132
ПРОБЛЕМЫ ОПТИМИЗАЦИИ
Последняя постановка может оказаться удобнее в тех слу¬
чаях, когда заранее известны располагаемые весовые затраты.
С другой стороны, эта постановка не является универсальной,
ибо в ряде задач время движения и часть фазовых координат
свободны и должны находиться из оптимальных соображений.
В дальнейшем для определенности будет рассматриваться задача
на максимум полезного веса при заданном начальном весе и
ваданном динамическом маневре.
Данная вариационная постановка должна быть конкрети¬
зирована для каждого типа двигательной системы.
Во-первых, нужно указать функциональные выражения тяги
Р и расхода q через независимые управления u = (uv . . ., ип)
и параметры w = . . ., wm) двигательной системы (регулиро¬
вочная характеристика двигателя):
Р = Р (u, w), q = q (и, w), umin < и (t) < umax, w = const. (II.9)
Во-вторых, нужно определить вес двигательной системы G*
как функцию параметров w и предельных значений управлений
и (весовая формула двигателя):
Gy. — Gy (Umin* umax7
w). (11.10)
Эти характеристики двигательной системы определим как ос¬
новные. Они не являются исчерпывающими; по мере усложнения
задачи могут потребоваться дополнительные сведения о свойст¬
вах двигательной системы. Эти сведения сообщаются в ходе из¬
ложения.
ГЛАВА 4
ИДЕАЛЬНЫЙ ДВИГАТЕЛЬ ОГРАНИЧЕННОЙ
МОЩНОСТИ —РАЗДЕЛЕНИЕ ВАРИАЦИОННОЙ
ЗАДАЧИ, ОПТИМАЛЬНЫЕ ВЕСОВЫЕ СООТНОШЕНИЯ
Рассмотрим задачу о доставке максимального полезного груза
для идеальной двигательной системы ограниченной мощности.
Изучение идеального случая интересно тем, что оно раскрывает
предельные возможности двигателей данного класса.
Регулировочная характеристика (II.9) и весовая формула (11.10)
для идеального двигателя ограниченной мощности выглядят
так (иг = N, и2 = q):
Р = Y2Nq, q = q, Gx = aNmax (4.1)
(0 < N (t) < N max» 0<g(K oo).
Запись (4.1) отражает следующие свойства идеального дви¬
гателя: во-первых, потери рабочего вещества и мощности отсут¬
ствуют х), во-вторых, регулирование подчиняется только огра¬
ничению на мощность (не считая требования неотрицательности
расхода q), в-третьих, вес двигателя линейно зависит от макси¬
мальной мощности.
Отметим, что в (4.1) характеристики даны через мощность N
и расход q. Можно выбрать и другие системы независимых управ¬
ляющих функций. Мощность N следует оставлять во всех вариан¬
тах, поскольку на нее наложены прямые ограничения. Вместо
расхода q могут фигурировать на равных основаниях скорость
истечения V или тяга Р, так как ни одна из этих величин в иде¬
альном случае не является ограниченной (требования неотрица¬
тельности тяги Р и скорости истечения V опять в расчет не при¬
нимаются); тогда (иг = N, и2 = V)
Р = 2N/V, q = 2N/V2, G.K = a#™* (4.2)
(0 ^ N (О Nmax » 0<F(0< oo),
*) Дальнейшая процедура не изменится, если считать потери в движи¬
теле ненулевыми, но коэффициент полезного действия движителя г\у пола¬
гать постоянным rjY = const < 1 (не зависящим от расхода и подводимой к
движителю мощности). В этом случае под а надо понимать удельный вес
двигателя на единицу максимальной мощности реактивной струи </Vmax или,
если вес Gy относится к максимальной мощности источника iVv0 = Nm t
нужно вместо а писать всюду а/т]г Данное замечание относится ко всем раз¬
делам, где обсуждаются идеальные двигатели ограниченной мощности.
134
ИДЕАЛЬНЫЙ ДВИГАТЕЛЬ ОГРАНИЧЕННОЙ МОЩНОСТИ [ГЛ. 4
или (uL = N, и2 = Р)
Р = Р, q = P42N, Gx = a7Vmax
(О < N (t) < Nmax, 0 < P (t) < сю).
max
(4.3)
Как будет ясно из дальнейшего, в идеальном случае удобно
представить тягу и расход через текущий вес аппарата G и ки¬
нематическую характеристику а — ускорение от тяги (и1 = N,
и2 = а)
Такое представление позволяет разделить проблему оптими¬
зации на две независимые:
1) весовую — нахождение оптимальных весовых соотношений и
оптимального управления мощностью;
2) динамическую — нахождение оптимальных программ уско¬
рения от реактивной тяги.
Наличие указанного разделения полной задачи существенно
упрощает исследование и в значительной степени оправдывает
идеализацию.
§ 1. ОПТИМАЛЬНЫЕ ВЕСОВЫЕ СООТНОШЕНИЯ ПРИ ПОСТОЯННОМ
И СТУПЕНЧАТО ИЗМЕНЯЕМОМ ВЕСЕ ДВИГАТЕЛЯ
1. Разделение задачи, управление мощностью. Запишем урав¬
нения (II. 1), когда характеристика двигателя задается в форме
(4.4) и вес двигателя не меняется вдоль траектории
(О N (t) <; G*/a, 0 а (t) < °°, | е (t) | = 1, const). J
Задача состоит в построении оптимальных программ N (t),
а (t), е (t) и выборе оптимального значения параметра Gx, обес¬
печивающих выполнение граничных условий для системы (4.5)
и доставляющих максимум полезной нагрузки Gry = G (Т) — Gx
при заданном начальном весе G0 (параметр а — удельный вес ис¬
точника мощности, задан).
Из физических соображений ясно, что мощность в процессе
полета выгодно поддерживать на максимальном уровне, так как
для создания одной и той же тяги при большей мощности потре¬
буется меньший расход рабочего вещества (см. (4.1)). Если выби-
Р = aG/g, q = a2G2/2Ng2, Gx = aNIimr
(0 < N (t) < ;Vmax, 0<a(*)<°c).
max?
(4.4)
G = — G'2a1j2Ng, G (0) = G0, G(T) - G-_ G'„
r=v, r(0) = r0, r (T) = 1'ь
v = ae + R, v(0) = vo, v(7’) = vi
(4.5)
ОПТИМАЛЬНЫЕ ВЕСОВЫЕ СООТНОШЕНИЯ
135
рать большие значения максимальной мощности, то расход ра¬
бочего вещества будет уменьшаться, но одновременно будет воз¬
растать вес двигательной системы. Начиная с некоторого значе¬
ния, увеличение веса двигателя превысит выигрыш от снижения
затрат рабочего вещества. Поэтому для каждого заданного маневра
должно существовать оптимальное соотношение между весом
запаса рабочего вещества и весом двигателя, обеспечивающее
максимум полезного груза.
Наличие оптимальных весовых соотношений для аппаратов
с двигателями ограниченной мощности было сначала установлено
на ряде модельных задач ([4.1—4.19] и др., см. обзор [4.20]).
Главное упрощение состояло в замене истинного гравитацион¬
ного поля на простейшее — бессиловое — поле и рассмотрении
одномерных движений. Кроме того, упрощение касалось и управ¬
ляющих функций: мощность и вес двигателя считались постоян¬
ными, а регулирование тяги отвечало либо случаю постоянного
реактивного ускорения, либо случаю постоянной тяги. Эти за¬
дачи даются в нашем изложении как иллюстрация общей проце¬
дуры.
Обратимся к анализу системы уравнений (4.5). Первое урав¬
нение из (4.5) может быть проинтегрировано в квадратурах [4.15,
4.21]
t
G(0 = G„(1 + (4.6)
0
Это соотношение дает закон изменения полного веса вдоль тра¬
ектории. При помощи него может быть записано выражение для
конечного веса = G (Г), а также для полезного веса Gn —
= G1 — Gy/.
т
G,= G/A + -Gx. (4.7)
0
Отсюда следует, что полезный вес при фиксированных 6?х и G0
возрастает с уменьшением интеграла
т
J (4.8)
0
Управляющая функция N (t) входит только в интеграл (4.8)
и не входит в уравнения движения (см. в (4.5) второе и третье
уравнения). Для постоянного верхнего предела мощности NmRX =
= const, имеющего место в рассматриваемом случае, оптималь¬
ный закон N (£), доставляющий минимум (4.8), устанавливается
136 ИДЕАЛЬНЫЙ ДВИГАТЕЛЬ ОГРАНИЧЕННОЙ МОЩНОСТИ [ГЛ. 4
независимо от остальных управляющих функций [4.15]:
N (0 = Nmax при 0 < t < Т. (4.9)
Тогда в (4.7) величина ах может быть вынесена из-под
интеграла
т
Go
G„ = G„ 1
Gy.
[j = \ a'dt) . (4.10)
Оставшийся в выражении (4.10) интеграл J не зависит от мощ¬
ности Nmax и весов GK, G0 и может быть подсчитан, если траектория
г (t) известна. Этот интеграл представляет в формуле для полез¬
ного веса динамическую часть задачи. Чем меньше его величина,
тем больше полезный вес при фиксированных G0, Nmax и Gx.
Таким образом, исходная задача разделилась на две незави¬
симые — динамическую и весовую.
Динамическая часть — это вариационная задача, которая со¬
стоит в построении оптимальных законов изменения величины
а (t) и направления е (t) вектора реактивного ускорения, обеспе¬
чивающих минимум интегрального функционала J для заданного
динамического маневра:
J = \ a°dt = min,
о
Г ■■= Y, г (0) = Го, г (Г) = 1 ь
v —_ ае + R, v(0) = v„, у(Т)=^\1
(0<а(0<ос, |е(0| = 1).
(4.11)
Весовая часть — это задача на максимум функции, состоящая
в определении оптимального значения веса двигательной системы
Gx или предельной мощности Nmax из условия максимума полез¬
ного веса (4.10):
шах Gn = max
v>o
[с.(
1
jV -Gx(iVmax) ; (4.12)
при этом значения интеграла J и начального веса G0 фиксированы
и зависимость Gx (А^тах) задана.
2. Оптимальные весовые соотношения. Если вес двигателя Gx
и мощность iVmax связаны линейно
Gx = ocNmах (а = const),
(4.13)
ОПТИМАЛЬНЫЕ ВЕСОВЫЕ СООТНОШЕНИЯ
137
то относительный полезный вес, согласно (4.10), может быть
представлен в виде
1 (Co/GJ (1) — (ф = 2^ S a4t) • (4-14)
Go
Правая часть (4.14) как функция (GJG0) имеет максимум
Рис. 4.1. Зависимость полезного веса Рис. 4.2. Оптимальные весовые соотно-
G- от веса двигателя Gy при фикси- шения G^, Gx, G^o в зависимости от
рованных значениях функционала Ф функционала Ф динамической задачи,
динамической задачи.
(рис. 4.1). При фиксированной величине функционала Ф полу¬
чаем решение задачи (4.12):
(4.15)
6'х/6’о = ]/Ф — Ф.
Максимальное значение полезной нагрузки (4.14), соответ¬
ствующее (4.15), равно
GJG0= (1-/Ф)2.
(4.16)
Оптимальная величина запаса рабочего вещества вычисляется^
как Gjj.0 = Gq — Gу. — G
gv.o/g0 = у ф.
(4.17)
Оптимальные весовые соотношения (4.15) —(4.17) [4.15, 4.21]
представлены на рис. 4.2. Функции (4.15), (4.16) теряют смысл
вне интервала Ф 1; отсюда следует, что при постоянном
весе источника мощности не может быть выполнен маневр, для
которого величина функционала J 2g/a (полезная нагрузка
(4.16) обращается в нуль при Ф = 1). Отметим, что оптимальное
значение веса двигательной системы не превосходит х/4 началь¬
ного веса.
138 ИДЕАЛЬНЫЙ ДВИГАТЕЛЬ ОГРАНИЧЕННОЙ МОЩНОСТИ [ГЛ. 4
Если вес двигателя и максимальное значение мощности свя¬
заны между собой нелинейно
Ga = G* (iVmax), (4.18)
то оптимальные весовые соотношения в общем случае не могут
быть выражены явно. Выпишем уравнение для определения опти¬
мального значения мощности Ninax [4.22].
При нелинейной зависимости (4.18) удельный вес двигателя
а = GJNm3iX будет функцией от iVmax. Выберем некоторое сред¬
нее значение удельного веса а* (не зависящее от Nm^) и запи¬
шем полезную нагрузку (4.10) через две безразмерные вел [чины
т
ф=1г$а*Л К = const). (4.19)
0
Первая из них — относительная мощность источника — явля¬
ется неизвестной, вторая — функционал (4.14) — задана; вес GK
в (4.10) можно считать зависящим от N, поскольку функция
Gy. C/Vmax) задана, a G0 и а* фиксированы.
Условие (4.12) в терминах параметров (4.19) записывается
следующим образом (dGJdN = 0):
Решив уравнение (4.20) относительно езразмерной мощности
N, можно определить размерную мощность iVmax и веса Gn
по формулам (4.19) и (4.18), (4.10) соответственно. Если решение
уравнения (4.20) окажется не единственным (что зависит от вида
функции (4.18)), то нужно выбрать такое, которое дает абсолютный
максимум (4.10).
Для линейной зависимости (4.13) полагаем а% = а = const,
после чего оказывается N = Gy. / G0 и уравнение (4.20), естест¬
венно, дает прежнее решение (4.15). Как нетрудно видеть, со¬
отношения (4.15)—(4.17) оказываются справедливыми и для об¬
щего вида линейной зависимости х)
б* = (0) -f- tfy/Vmax* (4.21)
если под GK и (?i в них понимать Gy. — Gy. (0) и G- — GK (0),
соответственно. При этом допустимый диапазон изменения функ¬
ционала Ф будет
0<Ф<1— YGx (0)/G„. (4.22)
х) Это же замечание относится и к следующим двум параграфам главы.
ОПТИМАЛЬНЫЕ ВЕСОВЫЕ СООТНОШЕНИЯ
139
Рассмотрим левую часть уравнения (4.20). Выражение в
круглых скобках — монотонно возрастающая функция N. В точ¬
ке N1= УФ — Ф, т. е. в точке, оптимальной для линейной
зависимости (4.13), оно равно единице. Поэтому оптимальная
точка будет смещаться от точки Nx = ]/Ф — Ф вправо при
d (GJG0)/dNx<^ 1 (большие значения мощности) и влево при
d (Gx/G0)/dN ^> 1 (меньшие значения мощности).
При параметрических расчетах по Ф в уравнении (4.20) мож¬
но Ф и N поменять ролями: N считать параметром (независимой
переменной), а Ф — неизвестной величиной. В этом случае ре¬
шение уравнения (4.20) записывается явно
"Г dN Y dN
(d (G.JGo) ~ 1 \
(123)
dN 4)
dN
Знак минус или плюс в (4.23) соответствует двум диапазонам
значений функционала Ф, разделяемым величиной
Ф. =
' d(GJG0)
4 —
dN
(4.24)
знак минус дает 0 ^ Ф Ф* (возрастающая ветвь оптимальной
зависимости Gx (Ф) (ср. рис. 4.2), знак плюс — Ф !> Ф* (убы¬
вающая ветвь Gх (Ф)).
Чтобы составить количественное представление о влиянии
нелинейности (4.18) на оптимальные весовые соотношения (4.15) —
(4.17), рассмотрим зависимость Gx (Л^тах), соответствующую кри¬
вой а (Nnmx) с рис. 2.96. Эта зависимость показана на рис. 4.3
(кривая i), там же для сравнения нанесены аппроксимирующие
зависимости: линейная (4.13) Gx [кГ] = 4 кПквт Nnmx Ывт] —
кривая 2 и общая линейная (4.21): Gx [кГ] = 1,5-103яГ +
+ 2,2 кПквт iVmax [кет] — кривая 3. Примеры оптимальных
соотношений Gx (Ф) и Gn (Ф), соответствующие трем этим кри¬
вым, показаны на рис. 4.4 для G0 = 105 кГ, а+ = 4 кГ/квт.
3. Ступенчатое изменение веса двигателя. Как показано в
предыдущем пункте, при неизменном весе двигателя не могут
быть выполнены маневры, энергетическая характеристика кото¬
рых превосходит определенный предел (J ^> 2g/a). Этот предел
можно отодвинуть, если в процессе движения сбрасывать секции
Двигательной установки [4.23].
140 ИДЕАЛЬНЫЙ ДВИГАТЕЛЬ ОГРАНИЧЕННОЙ МОЩНОСТИ [ГЛ. 4
Уменьшение веса двигателя сопровождается пропорциональ¬
ным уменьшением максимальной мощности, ибо iVmax = GJa
Рис. 4.3. Пример зависимости веса двигателя Gx от максималь¬
ной мощности Nmax:
1 — реальная зависимость с рис. 2.96, 2 —- линейная зависимость
(4.13), 3 — линейная зависимость (4.21).
О 02 0,0 0,6 0,8 / 1,2 Ф
Рис. 4.4. Примеры сравнения оптимальных весовых соотношений
при линейной и нелинейной зависимостях веса двигателя от макси¬
мальной мощности (обозначения кривых даны на рис. 4.3).
(рассматривается случай а = const; все несброшенные секции
двигателя работают параллельно). Аналогично первому пункту
§ 1] ОПТИМАЛЬНЫЕ ВЕСОВЫЕ СООТНОШЕНИЯ 141
можно показать, что мощность N всюду должна использоваться
максимально N (t) = Nmax (t).
Введем полезный вес i-й ступени G^ (i = 1, . . п), равный
сумме истинного полезного веса Gn и веса рабочего вещества,
оставшегося к моменту сброса i-й секции двигателя. Может быть
составлено рекуррентное соотношение
G(J^ = G(J} + AG(;\ (4.25)
где AGp* — количество рабочего вещества, израсходованного на
г-м участке (^-i <С * <С W-
Применим для вычисления AG^ соотношение (4.6), записан¬
ное для открытого промежутка t U:
Ч
G~ = %—^ (Фг = ^ { a*dt), (4.26)
1-ф jGJLj/gW \ г8 j 1 V
где G\ — вес аппарата до сброса i-й секции, G^—вес аппарата пос¬
ле сброса (i — 1)-й секции, С*г) —вес двигателя на i-м участке.
По определению AG^ = Gt-1 — G^. Подставив в (4.25) най¬
денное таким образом выражение для AG^ и заменив 6?t-i =
= + Gx\ получим отношение
1 + (1 + G^U/Gp) Ф1
(4.27)
Отношение истинного полезного веса Gn к начальному G0
можно представить как произведение отношений G*VG$_1):
G Cr^n) CS71'1') Ст^ G(1)
(Г(П) _ г , /Л 9£\
Go G{n~1} G(n_2) * * * G{1) * Go ' v1—'8)
7C 7C TC
Для последнего сомножителя этой цепочки справедлива форму¬
ла (4.14)
<#} _ 1 G?
°0 ~ 1 + (Go/GM) Ф1 ’ ^*29^
остальные сомножители определяются соотношением (4.27). Каж¬
дый сомножитель при фиксированных Ф| зависит только от GxVG„-1)
(при i = 2,..., 72) и от GW/G0 (при i = l). Последние незави¬
симы; поэтому максимум G^/G0 достигается при максимуме каж¬
дого из сомножителей по G^/G^_1). При фиксированных Ф* этот
142
ИДЕАЛЬНЫЙ ДВИГАТЕЛЬ ОГРАНИЧЕННОЙ МОЩНОСТИ [ГЛ. 4
максимум имеет место, когда
G< D
(i = 2, . . . , тг), /ф.-ф,. (4.30)
При этом полезная нагрузка С?л/6?0 равна
(4.31)
Все рассуждения проводились при фиксированной траектории
(неизменный закон а (t)); поэтому в (4.31) сумма
задана; оптимальные соотношения между Ф* должны определять¬
ся из условия максимума (4.31) при выполнении равенства (4.32).
Не проделывая этой процедуры в общем случае, можно опре¬
делить предельное значение функционала Ф, при котором ма¬
невр становится невыполним (Gn = 0). Положим в (4.31) и (4.32)
Фг = 1 — е* (0 < 8i << 1), тогда
Перейдя в (4.33) к пределу е* —> 0, получим Gn = 0 при Ф = тг.
Таким образом, в случае тг-ступенчатого уменьшения веса дви¬
гателя становятся выполнимыми маневры, для которых величина
функционала J лежит в диапазоне
т. е. допустимый интервал по J расширяется в п раз.
§ 2. ОПТИМАЛЬНАЯ ПРОГРАММА ИЗМЕНЕНИЯ
ВЕСА ДВИГАТЕЛЯ
1. Формулировка задачи. Как следует из результатов § 1,
вес двигательной системы ограниченной мощности может состав¬
лять в оптимальном случае до одной четверти начального веса
аппарата. На заключительном этапе движения, когда израсхо¬
дована большая часть рабочего вещества, вес двигателя стано¬
вится преобладающим (при условии, что величина полезной на¬
грузки мала). В такой ситуации может оказаться выгодным сброс
части двигателя; при этом уменьшится вес аппарата, но одно¬
временно уменьшится и мощность, идущая на ускорение рабо-
п
2 Фг = Ф
(4.32)
(4.33)
0 2ng/a,.
(4.34)
§ 2] ОПТИМАЛЬНАЯ ПРОГРАММА ИЗМЕНЕНИЯ ВЕСА ДВИГАТЕЛЯ
143
чего вещества. Чтобы выдержать заданную программу реактив¬
ного ускорения, после сброса потребуется меньшая тяга, и если
размер сбрасываемой секции выбран правильно, то и расход
рабочего вещества будет меньше.
Можно поставить задачу построения непрерывного закона из¬
менения веса двигательной системы, который является предель¬
ным для случая ступенчатого уменьшения веса [4.24, 4.25].
Наряду с этим в настоящем параграфе излагается второй подход
к решению задачи ступенчатого сброса [4.24, 4.25], отличный от
описанного в п. 3 § 1.
Как и в § 1, характеристика идеального двигателя берется в
виде (4.4). Вариационная задача формулируется, как задача
Майера (II.8). К управлениям здесь относятся: вектор ориента¬
ции тяги е (£), величина реактивного ускорения а (t), мощность
N (t) и вес двигателя Gх (t). Нахождение оптимальных законов
е (£), а (t) может быть проведено по известным правилам вариа¬
ционного анализа; аналогичная процедура для N (t) и Gx (t)
осложняется тем, что эти управления не являются независимыми.
Во-первых, верхний предел N (t) связан с Gx (t):
Ушах (t) = Gx (t)/a, (4.35)
и, во-вторых, Gy, входит в начальное условие (см. (II.7))
Ga (0) + Gy (0) = G0. (4.36)
Укажем замены, позволяющие выделить два независимых
управления вместо N (t), Gx (t) и применить в дальнейшем метод
JI. С. Понтрягина.
Сначала вместо управляющей функции N (0, изменяющейся
в диапазоне
0 < У (t) < Ушах (t) = Gy (0/а, (4.37)
введем безразмерную N (t):
N (0 = N (0/Ута* (0 = a N(t)!Gy (0, (4.38)
пределами которой будут
0<У (0 < 1. (4.39)
Новая управляющая функция Лг (t) независимая.
К системе (II.8) добавим дифференциальную связь, выражаю¬
щую изменение (уменьшение) веса двигателя (ср. (II.4)):
Gy = — gqy (4.40)
{Яу. — массовый расход двигателя, 0 ^ дх (0 < °о); будем счи¬
тать расход qx новой управляющей функцией, а вес Gx новой фазо¬
вой координатой. Управление qx (t) независимое.
144 ИДЕАЛЬНЫЙ ДВИГАТЕЛЬ ОГРАНИЧЕННОЙ МОЩНОСТИ [ГЛ. 4
Программы изменения веса двигателя G* (t) и мощности N (t)
находятся по известным N (t) и g* (t) следующим образом:
t
G* (t) = G* (0)-g[ qx (t) dt, N (t) = (t) N(t)/a. (4.41)
j
0
Описанные приемы носят общий характер и будут в дальней¬
шем применяться при подходящих ситуациях (например, в § 3
настоящей главы). Для нахождения оптимального закона G* (t)
в рассматриваемом случае можно обойтись без добавления диф¬
ференциального уравнения (4.40), имея в виду особые свойства
вариационной задачи.
Отнесем веса Ga, G*, G- к начальному весу G0, а также произ¬
ведем замену (4.38); для безразмерных весов и мощности будем
употреблять старые обозначения, опуская символы безразмер¬
ных величин.
Тогда система (II.8) преобразуется в такую:
G<s— — (Ga/VtGx)J ~ а~, GS(0) + GX(0) = 1, Ga(T) = max,
iVUx “О
i=v, г(0) = г„, г(Г) = Г1,
v = ae + R, v (0) = vn, v (T) — Vi
(Ie (01 = 1» 0<ЛГ(0<1, a(f)> 0, G*(*)< 0).
(4.42)
2. Разделение вариационной задачи. Исследуем оптимальные
управления N (f), е (t), a (£), G* (t). Следуя методу JI. С. Пон-
трягина, выпишем гамильтонову функцию Н и уравнения для
импульсов р:
тт ~ Gy? a ■-> | 1 / i
II = —p3 —щa- + pr-v + pB-(ae + K),
^ dll + Gy. <x
— — iVG.„ J a
дн э . ая
Pr — а. — a.. (Po'H), Рг; — —
(4.43)
ar ar '•l'° ™ — av
Импульсы pa, pr, pc пронормированы так, что
Pa (T) = -1. (4.44)
Функция P(j (г) отрицательна на интервале 0 t Т, ибо
дифференциальное уравнение (4.43) для импульса ра линей-
§ 2] Оптимальная программа изменения веса двигателя 145
ное однородное и в конечный момент импульс ра отрицателено:
Ра (t) < 0 при 0 < t < Т. (4.45)
Оптимальные управления N (£), е (£), а (t), Gx (t) должны до¬
ставлять абсолютный минимум гамильтоновой функции (4.43).
Множитель при 1 IN в гамильтоновой функции положителен
(см. (4.45)); поэтому оптимальное управление N (t) должно под¬
чиняться закону (ср. (4.9))
N (t) = 1 при 0 t ^ Т. (4.46)
Физически это означает, что вся располагаемая электриче¬
ская мощность должна идти на создание тяги.
Оптимальное вектор-управление е (t) выбирается так, чтобы
скалярное произведение р7. е было минимальным:
е = — Vv/Pv (Pv = | Pr |), (4.47)
т* e. вектор тяги должен быть антипараллелен вектору рг.
Оптимальный закон a (t) имеет вид (из условия dHlda = О,
поскольку а не ограничено)
—-wb*- (4-/i8)
Отметим, что оптимальное реактивное ускорение отлично от
нуля всюду, за исключением изолированных точек, где pv = 0;
иными словами, идеальный двигатель ограниченной мощности
включен во все время движения.
Обратимся к исследованию оптимального непрерывного за¬
кона изменения веса двигателя 1). Гамильтонова функция (4.43)
имеет относительный минимум по 6?х при
G* - Ga. (4.49)
К (4.49) присоединим границу управления Gx, отвечающую
знаку равенства в условии Gx 0 (см. (4,42)):
Gx = const (4.50)
(в дальнейшем будет показано, что граница (4.50) входит в со¬
став оптимального управления Gx (£)).
При функциональных зависимостях (4.49), (4.50) выражение,
являющееся коэффициентом при (а/2g) а2 в гамильтоновой функ¬
ции (4.43), не зависит от времени и имеет знак минус на всем
х) Непрерывная функция Gy (t) соответствует непрерывному сбросу бес¬
конечно малых элементов двигателя; этот случай является предельным
Для ступенчатого изменения веса Gy.
10 Механика полета
146
ИДЕАЛЬНЫЙ ДВИГАТЕЛЬ ОГРАНИЧЕННОЙ МОЩНОСТИ [ГЛ. 4
интервале [О, Т]:
pj ° +—— = const <0; (4.51)
^1/
это может быть проверено дифференцированием выражения с
учетом уравнений для ра из (4.43) и Ga из (4.42); знак константы
следует из (4.45).
Отсюда можно сделать вывод о разделении изучаемой вариа¬
ционной проблемы. Будем рассматривать комбинацию (4.51)
как новый импульс; тогда функция Н будет соответствовать ва¬
риационной задаче на максимум функционала
т
— / = — ^ a-dt, (4.52)
О
сформулированной для уравнений движения из (4.42). В каче¬
стве управляющих функций здесь будут фигурировать а (t) и
е (t). Заменим знак перед новым функционалом на обратный; при
этом вместо задачи на максимум — J будет рассматриваться за¬
дача на минимум /, т. е. полученная в § 1 вариационная проблема
(4.11).
После решения вариационной проблемы (4.11) следует опре¬
делить оптимальное управление GK (t), доставляющее максимум
величине Ga (Т) = Gn при известных законах .a (t), е (t) и изве¬
стном значении /.
Из уравнения расхода и краевых условий для весов (4.42)
вытекает интегральная связь
0 GdG а
1 3 (4.53)
} (Gx + Gq)* - 2g
1 -Gx (0)
Управление G* (t) должно быть построено из участков (4.49),
(4.50) так, чтобы достигался максимум Gn и при этом удовлетво¬
рялось условие (4.53).
Таким образом, как и для постоянного веса двигателя (§ 1),
рассматриваемая вариационная проблема (4.42) разделилась на
две части: динамическую (4.11) и весовую (4.53).
3. Решение весовой части вариационной п обломы. Требу¬
ется определить кусочно-непрерывную функцию Gx (Ga), состав¬
ленную из участков: Gx = Ga и GA = const, обеспечивающую
максимум G- при заданном значении J (см. (4.53)). Этой формули¬
ровке эквивалентна такая: определить функцию GK (Ga),
2]
ОПТИМАЛЬНАЯ ПРОГРАММА ИЗМЕНЕНИЯ ВЕСА ДВИГАТЕЛЯ
147
доставляющую максимум J при заданном значении Gn:
Gn
шах
iJ=Tx [“ S
(4.54)
~i-g;(o)
В дальнейшем будет использоваться как более удобная послед¬
няя формулировка.
Отметим прежде всего, что при Gn > 0,5 оптимальная програм¬
ма Gy, (Ga) не может содержать прямую (4.49), ибо в этом случае
нарушается начальное усло¬
вие Gx (0) + Ga (0) = 1. Сле¬
довательно, при Gn 0,5
оптимальный закон есть
Gy (G0) = Gx0 = const, (4.55)
'x0
— J-
2g ~ G„+Gx0
— Gy
(4.56)
Из условия максимума J
получаем экстремальное зна¬
чение
Gy.o = Y Gtz — G-\
при этом
ф = (1 - УК?,
\ /
(4.57)
(4.58)
Рис. 4.5. Состав оптимального закона изме¬
нения веса двигателя Gx в зависимости от
суммарного веса G0 (t) = Gn + G^ (t) полез¬
ной нагрузки Gn и рабочего вещества G^ (t).
что эквивалентно (4.15), (4.16).
Если Gn <С 0,5, то оптимальный закон Gх (G0) может состоять
не более чем из трех прямых (рис. 4.5):
Gy = Gy0
Gy = Ga
Gy, = Gxl
при 1 — Gx0 > Go > Gx0,
при Gy0 Go Gyi,
при GyX G0 Gn.
(4.59)
После вычисления интеграла (4.54) по участкам (4.59) по¬
лучаем
Gy 1 -f- In Gyo
(4.60)
где Gy.0 и GKl должны удовлетворять очевидным неравенствам
148
ИДЕАЛЬНЫЙ ДВИГАТЕЛЬ ОГРАНИЧЕННОЙ МОЩНОСТИ [ГЛ. 4
Из условия максимума Ф по Gxo, GX1 определяются оптималь¬
ные значения последних
<?х0 = 0,25, GK1 = Gn. (4.62)
Максимальное значение Ф равно
Ф = 0,25 (1 - 1п4б?я). (4.63)
Обращаясь к (4.59), находим, что ломаная экстремаль состоит
только из двух прямых
Gx = 0,25 при 0,75 > Ga ]> 0,25,
Gx = Gq при 0,25 ^ Ga Gn.
(4.64)
Полученное решение (4.63), (4.64) справедливо в диапазоне
0,25 > Gn > 0, так как при Gn > 0,25 и Gxo, Gxl из (4.62) нару¬
шаются неравенства (4.61). Если 1 > Gn > 0,25, то оптимальная
функция Gx (Ga) — прямая (4.55), оптимальное значение С?хо
и максимальная величина Ф даются формулами (4.57), (4.58).
Приведем сводку решения весовой части вариационной за¬
дачи в виде, разрешенном относительно Gn:
при 0 Ф 0,25
ся = (1_/ф)*, С,з/ф-ф,
при 0,25 ^Ф^оо
0,25 при 0,75 ;> G0 > 0,25,
G0 при 0,25 Ga Gn.
Gn =
Ga —
(4.65)
Зависимость Gn (Ф) из (4.65) показана на рис. 4.6—кривая,
обозначенная символом оо. Видно, что выигрыш в полезной на¬
грузке по сравнению со случаем постоянного веса двигателя (кри¬
вая п = 1) имеет место при малых значениях полезной нагрузки
и составляет 0,01—0,015 (0 Gn (сю) — Gn (1) ^ 0,017). Отно¬
сительный выигрыш весьма существенный: при Ф = 0,7 полез¬
ная нагрузка увеличивается в 1,5 раза, при Ф = 0,8—в 2,5 раза,
при Ф = 0,9 — в 6 раз и при Ф = 1 — в бесконечное число раз.
Допустимый диапазон значений функционала /, характеризу¬
ющего динамический маневр, расширяется до бесконечности
(0 < / < сю).
Отметим, что рассмотрение задачи оптимального програм¬
мирования веса двигателя при заданных законах реактивного
ускорения, например при a (t) = const [4.26], в силу доказан¬
ного свойства разделения (п.2), приводит к аналогичным резуль¬
татам.
§ 2] ОПТИМАЛЬНАЯ ПРОГРАММА ИЗМЕНЕНИЯ ВЕСА ДВИГАТЕЛЯ 149
4. Ступенчатая аппроксимация оптимального управления
весом двигателя. Пусть теперь управление Gx — кусочно-постоян¬
ная (ступенчатая) функция времени t (или веса рабочего веще¬
ства G0). Требуется определить оптимальные высоты уровней
(ступеней) управления и оп¬
тимальные моменты перехода
с одного уровня на другой,
если число уровней задано.
Для решения задачи сущест¬
венным оказывается то обсто¬
ятельство, что (?х — невоз¬
растающая функция времени
t (или неубывающая функ¬
ция веса Ga) и, следовательно,
высоты уровни ступен¬
чатого управления должны
убывать со временем t (или
возрастать с увеличением
веса G0).
Для рассматриваемого слу¬
чая интеграл (4.54) заменяет¬
ся суммой п интегралов по
участкам, вдоль которых
функция G* постоянна; после
интегрирования и подстанов¬
ке. 4 6. Сравнение полезной нагрузки Gn
для случаев непрерывного изменения веса
двигателя (п = оо), ступенчатого изменения
веса двигателя (п = 2) и постоянного веса
двигателя (n = 1).
ки соответствующих пределов получаем следующее выражение
Ф:
71—1
' +
+Gi%
+ G™ + с£*>
ej>) +
«) • «-«в)
Здесь n — заданное число уровней ступенчатого управления;
— высоты уровней; G$\ . . ., Gf~l) — моменты сме-
ны уровней.
Найдем (2п — 1) неизвестных: Gx1}, . . ., Gxn); Gi1}, . . м G*1 Х)
из условия обращения в максимум функции Ф; после дифферен¬
цирования выражения (4.66) получим
G^=YG^L)G^
q(Ud _ У£(i+1)
(i+l) ynr(i)
или Gx+1> = Gxl) (i — 1,
(i = 1, . . . , n — i),
n — 1),
= Vg™ - G(a].
(4.67)
150 ИДЕАЛЬНЫЙ ДВИГАТЕЛЬ ОГРАНИЧЕННОЙ МОЩНОСТИ [ГЛ. 4
В верхней строчке (4.67) выписаны две группы уравнений,
отвечающих условию максимума Ф по Gq\ Во втором случае
(Gk+1) = G(хг)) все п уровней ступенчатого управления Gx имеют
равную высоту; это соответствует аппроксимации оптимального
закона (4.55).
Укажем способ решения полученной системы алгебраических
уравнений. Величины G(al) и Ga+1) связаны следующим рекуррент¬
ным соотношением:
(£«)<г+1) = {GW)yGn (г = 2 п — 1). (4.68)
что легко проверяется методом полной индукции (см. (4.67)).
Величина Gопределяется из уравнения
(Gon))n+1 = (1 — V Gf)nGn. ;4.69)
Вычислив G(an) при заданном значении G- из (4.69) и найдя
последовательно все G(an_1) , . . ., G^\ а по ним и Gиз (4.67),
можно определить Ф по (4.66). Результат проведения такой про¬
цедуры представлен на рис. 4.6 для случая п = 2. Из сравнения
с предельной кривой непрерывного изменения веса двигателя
(п = ос) можно заключить, что уже однократный сброс части
двигателя (п = 2) позволяет реализовать большую часть выигры¬
ша от оптимального программирования веса двигателя.
Аналогичным образом может быть решена задача, когда тре¬
буется, чтобы двигатель состоял из равновеликих секций. Для
этого случая в (4.66) нужно выбирать оптимальным только один
уровень G£\ остальные уровни определяются по формуле
G® = G? (l — или GlP = G(x\ (4.70)
В заключение параграфа укажем, что предельная оптималь¬
ная программа (4.64), а также соответствующая ей ступенчатая
оптимальная программа, построенные по аргументу Ga, могут
быть записаны через аргумент t, если известен закон изменения
реактивного ускорения а (t). Связь между переменными Ga и t
имеет вид
t
GJGn а
“ S {G~+Gji= 2g\a>dt (4Л1)
1—Gx0 О
(в левый интеграл подставляется оптимальная] программа GK (Ga)).
СБРАСЫВАЕМЫЕ СЕКЦИИ КАК РАБОЧЕЕ ВЕЩЕСТВО
151
§ 3. ИСПОЛЬЗОВАНИЕ СБРАСЫВАЕМЫХ СЕКЦИЙ ДВИГАТЕЛЯ
В КАЧЕСТВЕ РАБОЧЕГО ВЕЩЕСТВА
1. Постановка задачи. При рассмотрении оптимальных зако¬
нов изменения веса двигателя в предыдущих двух параграфах
считалось, что сбрасываемые секции отделяются от аппарата с
нулевой скоростью и не сообщают дополнительного импульса
(пассивный сброс). Если предназначенные для сброса секции дви¬
гателя превращать в рабочее вещество и отбрасывать со скоро¬
стью реактивной струи (активный сброс), то можно получить
дополнительный выигрыш. Такая идея использования ненуж¬
ных элементов конструкции была высказана Цандером [4.27].
Поставим задачу об оптимальном использовании сбрасывае¬
мых секций двигателя [4.22, 4.28]. Будем считать, что не вся
масса сбрасываемых секций может превращаться в рабочее ве¬
щество, а только часть ее
(параметр хтах предполагается заданным). Таким образом, часть
расхода д* 0 (см. (4.40)), равная (1 —х) д*, не используется
и покидает аппарат с нулевой скоростью. Остальная часть хд*,
превращенная в рабочее вещество, направляется в движитель.
Суммарный расход через движитель q будет складываться из
расхода хд* и расхода запаса рабочего вещества д^ > 0:
Эта схема использования сбрасываемых секций двигателя от¬
носится к предельному случаю непрерывного сброса. Ступенча¬
тый сброс описывается в последнем пункте параграфа.
Выберем в качестве независимых управляющих функций без¬
размерную мощность (4.38), расходы g[JO g* и коэффициент прев¬
ращения массы двигателя в рабочее вещество х. Характеристики
двигательной системы, как и раньше, считаются идеальными и
записываются в форме (4.1). Вариационную задачу, аналогично
предыдущему параграфу, сформулируем как задачу Майеря
(II.8). Для этого присоединим к системе (II.8) уравнение (4.40)
и перепишем ее в терминах перечисленных выше управлений:
0 < х (t) < X]
-max
(0 %max — COIlSt 1)
(4.72
q = + Му,-
(4.73)
— — qv.,
Gi}(0) -j- (*a{T) — шах,
e + K, v(0) = v0, v(T) = Vi
+ Gy. (0) = 1, G*(n>0,
r(°) = r0. r{T) = r!,
• (4.74)
qv (0 > (t) > 0)-
152 ИДЕАЛЬНЫЙ ДВИГАТЕЛЬ ОГРАНИЧЕННОЙ МОЩНОСТИ
[ГЛ. 4
Здесь все веса отнесены к начальному весу аппарата, расхо¬
ды — к начальной массе, мощность — к максимально возможной
в данный момент; обозначения для отнесенных величин сохране¬
ны старые.
Нужно выбрать оптимальное начальное значение веса G* и
построить оптимальные программы для управлений е (t), N (t),
х (t), q^ (t), q* (t) (конструктивные параметры a, xmax и динами¬
ческий маневр {r0, v0, r1? v1? T} заданы). Максимизируемый
функционал — конечное значение фазовой координаты (?0, сов¬
падающее по определению (см. (II.6), (II.7)) с полезным весом.
2. Состав оптимального управления. Для отыскания
оптимальных программ управления воспользуемся методом
JI. С. Понтрягина. Согласно принципу максимума на оптималь¬
ной траектории гамильтонова функция
н = — paqv. — рхдк + ivv + iv к
4- р„ • е у (2g/a) GXN (q^ + %qx) (Ga + Gx)"1,
• dH • _ дН ■ _ _ 5Я • _ дН
~~ dG^ ’ Р* ~ dG~ ’ Р>* — fa I Рю — fa-
(4.75)
должна иметь абсолютный минимум по переменным е, N, х, q^ и
дх, подчиненным ограничениям из (4.74).
Программа для направления вектора тяги, как й в § 2, дается
соотношением (4.47), поскольку перед скалярным произведе¬
нием р^-е в функции Н стоит неотрицательный коэффициент.
Из анализа того же члена с учетом условия (4.47) следует
оптимальность полного использования мощности (4.46).
Аналогичным образом приходим к физически очевидному
выводу: доля расхода дх, превращаемая в рабочее вещество,
должна быть максимально возможной
х (/) = хтах при 0 t ^ Т. (4.76)
Для отыскания управлений и дх запишем с учетом полу¬
ченных оптимальных соотношений (4.46), (4.47), (4.76) часть
функции Н, зависящую от этих управлений г):
Ж = — РсЧ». — РхЯх-PvY (2£/a) g* iVv- + Ktfx) (G0 + Gx)'1 (4.77)
и уравнения для импульсов ра и рх:
Ра =,— Pv Y(2#/a) Gx (g^ + xgx) (Ga + Gx)“2,
\ (4*78)
px =ip0(l-G0/Gx).
*) Здесь и в дальнейшем под х без индекса подразумевается максималь¬
ное значение хтах.
СБРАСЫВАЕМЫЕ СЕКЦИИ КАК РАБОЧЕЕ ВЕЩЕСТВО
153
Из условия минимума (4.77) следует, что если один или оба
импульса ра, рх больше нуля либо равны нулю, то оптимальное
значение одного или обоих расходов обращается в бесконечность.
Рассмотрим теперь случай
Ра <0, рх < 0.
Перепишем функцию (4.77) через суммарный расход
и*расход qK:
(4.79)
(4.73)
(4.80)
Ж = — Poq — PvV(2ё/а) Gy.q (Ga+G*)-1—(рк—кра) qx
(q > 0, 0 < qx < q/%).
Отсюда видно, что оптимальное распределение суммарного
расхода g между составляющими дх
ется знаком комбинации
и q^ = q — xgx определя-
Д = Рк — хра. (4.81)
В самом деле, если А < 0, то минимум Ж по дх достигается
при дх = 0, т. е. при g^ = g, а если А >> 0, то при дх = д/х,
т. е. при д^ = 0. В случае А = 0 функция Ж не зависит от каж¬
дого из расходов q^ и дх по отдельности, а определяется суммар¬
ным расходом q. В этом смысле его можно считать особым.
Таким образом, в каждом из трех возможных случаев функция
Ж зависит только от одного из расходов ди дх или д, подчинен¬
ных лишь условию неотрицательности:
Ж\ = — ра?^ — Pv У (2^/a) Gxq^ (Ga -f Gy)'1
при A< 0 (gx = 0),
Ж2 = — pxgx — Pv У (2g/a) Gxxgx (Ga + Gx)'1
при A>0 (g^ = 0),
Жг = — Poq — pv У (2g/(x) Gyq (Ga + Gx)'1 при Д = 0.
(4.82)
Из условий стационарности дЖх/dq^ = 0 и дЖJдq^л = 0,
которые здесь соответствуют условию абсолютного минимума,
определяем оптимальные управления д^ и дх при А =/= 0:
в первом случае
(s/a) G*P2v
2 рЖ+G,
дх = 0 (А < 0),
во втором случае
q^ = 0,
и (g/Ц) gx^
2P1(C0+GX)«
(А>0).
(4.83)
(4.84)
154 ИДЕАЛЬНЫЙ ДВИГАТЕЛЬ ОГРАНИЧЕННОЙ МОЩНОСТИ [ГЛ. 4
При А = 0 из условия dffljdq = 0 следует
. (lf/^О / д /\\ / / ОС\
qи. Kq-K — —п (А = 0)» (4.85)
2pl(G0+Gx)* V К
Когда А обращается в нуль не в изолированных точках, а
на некотором конечном отрезке^времени (именно такой случай
будет особым), то производная А также равна нулю на этом от¬
резке
A = YPa(l — 2я — =0- (4.86)
{это уравнение получено из (4.81) и (4.78)).
Из (4.86) следует либо ра = 0, либо (1 — 2х — GJGX) = 0.
Рассмотрим первую возможность. Из (4.78) с помощью (4.84)
исключаем (^+и£х):
^ (g/a)Gx pi //( Qr?4
Р° - (Ge + Gx)3 рг • (4-87)
Правая часть (4.87), за исключением изолированных точек,
положительна. В самом деле, вес двигателя Gx может обратиться
в нуль только при t = Т; импульс р„, как это следует из уравне¬
ний (4.75)
Рг>= Pr> Pr = —С4.88)
может быть равен нулю или в изолированных точках, или тожде¬
ственно вдоль всей траектории. Последний случай вырожденный,
так как он соответствует пассивному движению q^ = = 0
(см. (4.83)—(4.85) при pv = 0).
Таким образом, первая возможность ра = 0 отпадает, оста¬
ется
1 _ 2% — GJGK = 0. (4.89)
Это выражение означает пропорциональное изменение весов
двигателя и запаса рабочего вещества (ср. (4.49)). Совместно с
соотношением (4.85) оно дает условие, определяющее оптималь¬
ные управления q^ и qA в особом случае:
,\ оч (1 — 2х) (g/a)
— (1 — 2к) qy. = г (Д = 0). (4.90)
* V 2 (1 — и) р% (Gg -г Gyf- к
Нетрудно видеть, что соотношения (4.89), (4.90) имеют смысл
при х < 0,5 и G* <С 0,5 (в противном случае 1—2 х < 0 или
Ga/Gx > 1).
СБРАСЫВАЕМЫЕ СЕКЦИИ КАК РАБОЧЕЕ ВЕЩЕСТВО
155
3. Чередование оптимальных программ для расходов. Выше
было установлено, что характер оптимальных законов изменения
расходов q^ и qx зависит от знаков импульсов ра, рх и комбина¬
ции А.
В начальный момент времени (t = 0), согласно условию транс¬
версальности, вектор импульсов (ра, рх) должен быть направлен
по нормали к прямой Ga (0) + Gx (0) = 1 (см. (4.74)), т. е.
Ра (0) = рх (0). (4.91)
В конечный момент времени (t = Т), согласно нормировке,
Рс (т) = -1 (4.92)
(поскольку импульс ра соответствует фазовой координате Gaj
конечное значение которой максимизируется).
Что касается конечного значения импульса рх, то тут возмож¬
ны два варианта. Первый: конечное значение фазовой координаты
Gy, в оптимальном случае выходит на границу Gx (Т) = 0 (см.
(4.74)), тогда значение ру, (Т) не определено. Второй: оптимальное
значение Gx (Т) > 0; тогда величину Gx (Т) можно считать не
заданной и по условию трансверсальности рх (Т) = 0. Таким
образом, получаем условие
Gx (Т) = 0 или Ру, (Т) = 0 (4.93)
(эти два равенства могут выполняться одновременно, если
dGa (T)!dGy (Т) = 0 при Gy (Т) = 0).
Начальное значение (4.91) импульсов р0, рх должно быть
строго меньше нуля. В противном случае, как следует из усло¬
вия минимума (4.77), qv, = оо и дх = оо. Это соответствует сбросу
конечной части запаса рабочего вещества и двигательной системы
с бесконечно малой скоростью (V = У 2N/{q^ + х#х)), т. е. слу¬
чаю, когда начальные весовые соотношения выбраны не опти¬
мально. Можно получить также ограничение на (4.91) снизу.
Производная (4.78) импульса ра всюду отрицательна, а конечное
его значение равно минус единице (4.92), поэтому
-1 < Ра (0) = рх (0) < 0. (4.94)
Таким образом,, импульс ра отрицателен во все время движе¬
ния {ра (0) <С 0, ра (t) < 0). То же самое можно сказать и об
импульсе рх (за исключением конечного момента времени, когда
Рх может обращаться в нуль (4.93)).В окрестности начальной точки
t = 0 импульс р.у отрицателен (4.94). Предположим, что через
некоторое время (0 ^ Т) он обращается в нуль; тогда про¬
изводная ру (^ — 0) > 0 и в силу (4.78) Ga (tm — 0) > Gx (tm — 0).
Справа от точки t = ^ последнее неравенство только усилится,
т*к как ga= 0, qx = ос при ра <Г 0, рх = 0. Значит, производная
156
ИДЕАЛЬНЫЙ ДВИГАТЕЛЬ ОГРАНИЧЕННОЙ МОЩНОСТИ [ГЛ. 4
рх будет оставаться положительной при переходе через точку
t = t и р* (0 > 0 при t Выполнение последнего неравен¬
ства на конечном интервале времени приведет к обращению в
нуль веса двигателя (дх = оо при р*^> 0). Последнее возможно
только при t = Т.
Итак, показано, что на всем интервале времени 0 t Т
выполняются неравенства (4.79). Остается исследовать поведе¬
ние комбинации (4.81), знак которой определяет в этом случае,
какой из оптимальных законов (4.83), (4.84), (4.90) управления
расходами будет иметь место.
Сначала рассмотрим случай 0<х<1. Из оптимального
граничного условия для импульсов (4.94) следует, что начальное
значение функции А отрицательно
А (0) = (1 - и) Ро (0) < 0. (4.95)
Конечное значение функции А должно быть положительным
А (Т) = рх (Т) - хра (Т) > 0,' (4.96)
поскольку, согласно условию (4.93), либо рх (Т) = 0, либо
Gx (71) = 0. В первом случае справедливость неравенства (4.96)
сразу следует из (4.92): А (Т) = — хрс (Т) = к. Во втором случае
это следует из (4.84), так как в окрестности конечного момента
времени вес GK должен убывать до нуля. Последнее возможно
только при одном оптимальном управлении .(4.84), которое реа¬
лизуется при А > 0 (Сг* (t) = const на (4.83) и G* (t) =
= G0 (0/(1 - 2х) на (4.89), (4.90)).
Исследуем функцию А внутри интервала [0, Г]. Ее произ¬
водная определяется выражением (4.86). Первый сомножитель
этого выражения 1/2р0 всюду отрицателен. Следовательно, харак¬
тер функции А будет определяться вторым сомножителем
% — 1 — 2х — GJGK. (4.97)
В начале движения функция А отрицательна (см. (4.95)),
поэтому изменение веса происходит по закону (4.83). Согласно
(4.83) вес G* остается постоянным, a Ga убывает, т. е. X вдоль (4.83)
возрастает. Если предположить, что А (0) 0, то конечное
значение А (Т) окажется отрицательным, ибо А (0) 0 и
A(t) ^ 0 (вследствие возрастания %). Отрицательность же А (Т)
противоречит условию (4.96).
Таким образом, производная функции А в начале движения
положительна. Рассмотрим все возможные комбинации, которые
могут иметь место внутри интервала [0, Т].
1°. Производная А (t) всюду остается положительной. Тогда
А (£) в некоторый момент времени i = пересечет ось t (так
СБРАСЫВАЕМЫЕ СЕКЦИИ КАК РАБОЧЕЕ ВЕЩЕСТВО
157
как А (0) < О, а А (Г) >0). На первом интервале 0 < t < tt
■будет иметь место управление (4.83), согласно которому Gx (t) —
— Gxо, а на втором £, < t < Т — управление (4.84), вдоль кото¬
рого Ga (t) = G0 (f.) (рис. 4.7), причем G0 (tj = G„, так как по
условию (II.7) G0 (Т) = G„.
Рис. 4.7. Первый возможный вариант
поведения функции А (0 и соответ¬
ствующий ей оптимальный закон изме¬
нения веса двигателя (0 < х < 1).
Рис. 4.8. Второй возможный вариант
поведения функции А (0 и соответ¬
ствующий ей оптимальный закон из¬
менения веса двигателя (0 < х <
П FS (] ^ 0.5V
2°. Производная А (£) сначала положительна, затем обраща¬
ется в нуль одновременно с самой функцией (A (tj = A (tj =
= 0). В интервале 0 ^ изменение веса происходит по
закону (4.83). При t = он сменяется на (4.89). Согласно (4.89)
веса Ga и GK меняются пропорционально, так что X и А остаются
равными нулю. В некоторый момент времени t = будет из¬
расходован весь запас рабочего вещества Gg (t^) = Gn. После
этого может меняться только вес G*. Комбинация X с умень¬
шением G* снова станет отрицательной, а производная А —
СБРАСЫВАЕМЫЕ СЕКЦИИ КАК РАБОЧЕЕ ВЕЩЕСТВО
159
положительной. Функция А перейдет в положительную об¬
ласть, и управление весом будет осуществляться по закону (4.84)
(рис. 4.8).
3°. Производная А (t) обращается в нуль при А (t) <^ 0.
В области А 0 веса Ga, GK меняются по закону (4.83), согласно
которому % возрастает. Поэтому после обращения в нуль произ¬
водная А станет отрицательной и функция А никогда не попадет
в область Д>0, что противоречит условию (4.96).
4°. Производная А (t) обращается в нуль при А (t) > 0. Эта
возможность также отпадает, так как в области А > 0 функция
X должна убывать согласно (4.84) и (4.97), а чтобы функция А
при некотором t = попала в положительную область, необ¬
ходимо Л (О > 0. Поэтому в области А^> 0 производная А остает¬
ся положительной, что опровергает начальное предположение.
Таким образом, последние два варианта, 3° и 4°, отпадают.
Изучим теперь поведение функции А для крайних значений
параметра х: х = 1 и к = 0. При х = 1 начальное значение
функции А равно нулю (см. (4.95)), а ее производная всюду по¬
ложительна (см. (4.86)). Поэтому все последующие значения А
лежат в положительной области, и в процессе движения меня¬
ется только вес двигателя Gx по закону (4.84). При этом вес
Ga (t) = Go (Т) = т. е. запас рабочего вещества отсутствует
(рис. 4.9).
В случае х = 0, рассмотренном в предыдущем параграфе,
функция А не может попасть в положительную область, так как
при х = 0 управление (4.84) не имеет смысла. Поэтому функция
А либо всюду отрицательна (за исключением, быть может, t = Т)
и тогда G* (t) = Gxq (рис. 4.10), либо сначала отрицательна, а
затем обращается в нуль при t = ^ Т. Тогда производная
A (£.) также обращается в нуль и до конца движения остается
равной нулю. На первом участке 0 t ^ изменение веса
происходит по закону (4.83), на втором ^ ^ t ^ Т — по за¬
кону (4.89) (рис. 4.11). Остальные возможности исключаются
аналогично тому, как было сделано при 0 х <* 1.
4. Разделение задачи на весовую и динамическую. Перейдем
от расходов q[X и qx к новой управляющей функции а — реак¬
тивному ускорению (см. (4.74)):
а = У (2g/a) GXN (q^ + щ-л) (Ga -f G*)'1- (4.98)
Тогда два векторных уравнения (4.74), определяющих траек¬
торию движения, не будут содержать весовых параметров:
г = v, у == ae + Н, а уравнения (4.74), описывающие изменение
весов Gx и С0,для каждого из оптимальных управлений (4.83),(4.90),
(4.84) будут выражаться через весовые параметры и квадрат
160 ИДЕАЛЬНЫЙ ДВИГАТЕЛЬ ОГРАНИЧЕННОЙ МОЩНОСТИ [ГЛ. 4
реактивного ускорения (безразмерная мощность N на опти¬
мальной траектории равна единице):
при A (t) 0
(Ge+<?*)*
2g
Ga = — a2, G/(*) = const; (4.99)
при A (t) 0
« (t)
,G5 = _4(l-x)Ga|ra2, Gx(r) = T-iyr (x<0,5; G„ < 0,5);
(4.100)
при Д (t) 0
Ga{t) = const, Су. = -{°°^у2--^а* (x>0). (4.101)
В предыдущем пункте было показано, что при 0 к 1 воз¬
можны два решения: первое состоит из последовательно состы¬
кованных участков (4.99) и (4.101), второе — из участков (4.99),
(4.100), (4.101). Переменные в каждом из дифференциальных
уравнений (4.99)—(4.101) разделяются. Квадратуры с учетом
непрерывности фазовых координат Ga и Gx, начального GO0 +
+ G*o = 1 и конечного Gai = Gn условий имеют вид:
для случая (4.99) + (4.101)
~Gx0 \ (G0+L)2 j («„ + <£)* =Ф’ ^Л02)
1-GxO Gx0
для случая (4.99) + (4.100) + (4.101)
(1—2х) Gx0 Gn
dGa i г» clG
r Г о 1 ?
*° J (G0 + Gx„)2 4(1-4) ) Ga
1 Gx0 (1—2x)Gxg
Gxl
K S (G.+ G*)* _ф* (4,103)
G„/( l-2x)
Здесь, как и в двух предыдущих параграфах,
т
Ф =^в2Л. (4.104)
После вычисления интегралов, содержащихся в левых частях
равенств (4.102) и (4.103), устанавливается конечная связь между
полезной нагрузкой G*, начальным и конечным значениями ве¬
са двигателя Gx, параметром х и величиной функционала Ф:
СНРАСЫНАЕМЫЕ СККД1Ш КАК раг.оч к к вкщю :т по
1(51
для случая (4.99) + (4.101)
(1 X) С л (i _ KG
1 - Gxo - V + * In 77— ут~ - —■ rr'-' - ф; (4Л05)
f,x0 i Gyl - (/_ &у1 -r Ол
для случая (4.99) -f- (4.100) + (4.101)
I -2Х г , 1 , ( I — СуЛ
— Gxn + тл -т- m
4 (I — х) Gr
(1. — 2Х) ((^xi ; ' (j'-r) Хбг_
X In гг—; -у 11 у ‘^—у = Ф. (4.106)
2(1—x)GL
Зависимости Ф от G-, определенные формулами (4.105) и
(4.106), монотонно убывающие (дФ/dGC <А 0). Это позволяет,
как и в §§ 1, 2, разделить задачу на независимые весовую и дина¬
мическую части. Динамическая часть задачи по-прежнему со¬
стоит в построении оптимальной программы вектора реактивного
ускорения и формулируется в виде (4.11). Весовая часть задачи
после проведенной процедуры сводится к определению началь¬
ного Gy.Q и конечного Gyl значений веса двигателя, обеспечиваю¬
щих максимум функции Ф (4.105), (4.106) при фиксированном
значении полезной нагрузки *), и к установлению границ реали¬
зации решений (4.105), (4.106).
Аналогичные рассуждения можно провести и для предель¬
ных значений параметра х. Только при х = 1 нужно брать один
участок (4.101), а при х = 0 — либо один участок (4.99), либо два
участка (4.99) и (4.100).
5. Решение весовой части задачи. Из рассмотрения частных
производных dO/dGy0 и dO/dGXJ находим оптимальные величины
Gx() и Gxli
для случая (4.99) + (4.101)
ОхП = 1/гХ — G-А- |Л/4х2 + (1 — х)G-, Gxt = 0; (4.107)
для случая (4.99) + (4.100) -|- (4.101)
С*п = 4 (Ах), ’ СуЛ = °* (4.108)
Сравнение выражений (4.105) и (4.106), в которые подставле¬
ны оптимальные значения (4.107) и (4.108) весов Gxo, Gxl, по¬
зволяет установить точные границы реализации каждого типа
решений. Решение (4.99) 4- (4.101) имеет место в диапазонах
(1 — 2х)/4 (1 — х) < G- < 1, 0<х<0,5
и 0<бя<1, 0,5<х<1, К ’
х) Зависимости (4.105), (4.106) разрешены относительно Ф, поэтому за¬
дачу о максимуме полезной нагрузки 64 при фиксированном Ф здесь удобно
заменить эквивалентной задачей о максимуме Ф при фиксированной вели¬
чине С_.
11 Механика полета
162
ИДЕАЛЬНЫЙ ДВИГАТЕЛЬ ОГРАНИЧЕННОЙ МОЩНОСТИ [ГЛ. 4
0,8
0,6
Ofi
0.2
V
ш
ж
\
о
0,2 Ofi '0,6 0.8 О,
'Л
Рис. 4.12. Области реализации различ¬
ных типов решений (пезаштриховаи-
ная область соответствует первому ти¬
пу — рис. 4.7, заштрихованная об¬
ласть — второму — рис. 4.8).
а решение (4.99) + (4.100) + (4.101) — в диапазоне
0 < G* < (1 - 2х)/4 (1 — х), 0 < х < 0,5. (4.110)
Области (4.109) и (4.110) показаны на рис. 4.12. Штриховкой
выделена область (4.110). Для х = 1
во всем диапазоне 0<^Gn*^l
изменение веса происходит по урав¬
нению (4.101), a Gx0 и 0УЛ опре¬
деляются формулами (4.107). При
х = 0 в интервале 0,25 £?- 1
реализуется решение (4.99):
Gy. (t) = Y G- — Gn,
а в интервале 0 Сгя<^0,25—
решение (4.99) +(4.100); при этом
G*,, = 0,25, GX1 = G-.
На рис. 4.13 представлены за¬
висимости оптимальной величины
начального веса двигателя Gxo от
полезной нагрузки 6С для раз¬
личных значений параметра %.
Кривые построены по формулам
(4.107), (4.108) с учетом границ
их реализации (4.109), (4.110).
Нижняя сплошная кривая соот¬
ветствует пассивному сбросу дви¬
гателя (х = 0, см. § 2). Пунктир¬
ный участок, продолжающий ниж¬
нюю кривую и правая ветвь этой
кривой относятся к случаю неиз¬
менного веса двигателя, рассмот¬
ренному в § 1. Видно, что опти¬
мальные весовые соотношения в
случае использования сбрасывае¬
мых секций двигателя в качестве
рабочего вещества (х + 0, актив¬
ный сброс) сдвигаются в сторо¬
ну увеличения начального веса
двигателя за счет запаса рабо¬
чего вещества.
Суммируем полученные резуль¬
таты. Оптимальный закон из¬
менения веса двигателя и запаса рабочего вещества описывается
следующими соотношениями:
для случаев 0 <Г х 0,5, (1 — 2х)/4 (1 — х) ^ G- 1 и
0,5 х < к о Gя 1 (рис. 4.7).
О 0,2 04 0,6 0,8
J7C
Рис. 4.13. Зависимость оптимальной
величины начального веса двигателя
Gxо от полезной нагрузки Gn при фик¬
сированных значениях коэффициента х
превращения материала двигателя в
рабочее вещество.
3]
СБРАСЫВАЕМЫЕ СЕКЦИИ КАК РАБОЧЕЕ ВЕЩЕСТВО
163
Gx(0 = Gx0 — Gn-Ь 'у/Г—b (1 — >0G^
(Ga + ^о)2 a
0 = — Г 9a
х0 &
(при 1 — Gx0 > G0 (О > Gn),
г — (G* + G*)2 « _2 п ,f\ г
Gx — xQ^ 2g a , Ga(t) — G„
a-
(4.111)
(при Gx,, > Gx (t) > 0);
для случая 0 < x < 0,5, 0 < G* < (1 — 2х)/4 (1 — х)
(рис. 4.8)
Gx (t) = Gx<| = , G0
(G,4-Gx0)s a
2?
G. (t)
С'М=Т=Ш’
(при 1 — Gx0 > G3 (0 > (1 — 2x) Gx0),
■4(1 — x) G3 JL a2
(при (1 — 2x) Gx0 > G3 (t) > G„),
GK
(G_ "Г Gx)4 $
^a2, G0(f) = G„
*G„ 2*
при t=i^ > G* (0 > °);
(4.112)
для случая и = 1, 0 < G„ < 1 (рис. 4.9)
г. _ (G* + G*)2 a ^ /J4 „
Gx vG^ 2g a"> Ga(t) — G„
(при 1 — G„ > Gx (t) > 0), (4.113
для случая x = 0, 0,25 < G„ < 1 (рис. 4.10)
Gx (t) = Gxo = ]/"G- — GT_, Ga =
(Ga GX0)S a
a-
-'xO 2S'
(при 1 —Gx0> Go(0>G„), (4.114)
для случая x =-. 0, 0 < Gn < 0,25 (рис. 4.11)
Gx (t) = Gxo = 0,25, G0 = — -(GgTG>to)- “ as
GXO
(при 1 — Gxo>Ga (t) > Gx0),
= -4G0^a2
(при GxO>Ga(0>G„).
Gx(0 = G3(0, G3 = — 4Ga a2
(4.115)
HI*
164
ИДЕАЛЬНЫЙ двигать:ЛЬ ОГРАНИЧЕННОЙ МОЩНОСТИ [ГЛ. 4
Окончательное выражение величины функционала
Gn имеет вид:
при 0<:х<^0,5, (1 — 2х)/4(1—x)<G,<l it при,
0,5<х<1, 0<GL<1
G, \ . G_
Ф
через
Ф = (1 — х) 1 —■
ТГ)
— х In -
К
G-
• К
Ф -
при 0 ^ х ^ О
I — 2х
О,
X 111
К. — -+ j/7*-j- + (1 — х) G-
0<СЯ<(1 — 2х)/4(1
In
1 — 2х
— х)
4(1 — х) От
(4.116)
4 (1 — х) 'v AJi 2(1 — х) 4 ( I — х) 1 - 2х
Зависимость максимальной полезной нагрузки G- от величины
функционала Ф для ряда фиксированных значений параметра х.
вычисленная по (4.116), пред¬
ставлена на рис. 4.14. Ниж¬
няя сплошная кривая, как
и на рис. 4.13, соответству¬
ет случаю х = 0, рассмот¬
ренному в § 2. Эта же кривая
(в диапазоне О Ф ^ 0,25)
и продолжающая ее пунктир¬
ная кривая (в диапазоне
0,25 < Ф 1) относятся к
случаю постоянного веса Gx,
рассмотренному в § 1,
Все кривые представлены
в интервале 0 ^ Ф 1. Од¬
нако если в случае постоян¬
ного веса двигателя, как от¬
мечалось в § 1, функция С?-(Ф)
теряет физический смысл вне
этого интервала, то здесь
функция G- (Ф) имеет смысл
на всей полуоси 0 Ф °о.
0 < Ф < 1 приближенно
0,8
0,6
0,4
0,2
V
/7= оо
%
%
/
0,2
0,4
0,6
0,8
Ф
Рис. 4. И. Максимальная полезная нагрузка
п зависимости от функционала динами¬
ческой части задачи Ф при фиксированных
значениях коэффициента превращении х.
Поведение G- (Ф) вне диапазона
(Gru 1) описывается следующими формулами:
1 — 2х
4(1-
ехр (-
х)
ехр [— 4 (1 — х) Ф]
■ Ф/х)
при 0 х 0,5,
при 0,5 х 1.
(4.117)
Зависимость полезной нагрузки от параметра х при малых
значениях функционала 0 Ф ^ 0,5 близка к линейной
(рис. 4.15), а при больших переходит в экспоненциальную (4.117).
СБРАСЫВАЕМЫЕ СЕКЦИИ КАК РАБОЧЕЕ ВЕЩЕСТВО
165
Выигрыш в полезной нагрузке от использования сбрасывае¬
мых секций двигателя в качестве рабочего вещества (х 0) по
сравнению с простым сбросом (х--0) может быть весьма существен¬
ным.Так например, в предельном случае % = 1 (полное превраще¬
ние) полезная нагрузка увеличивается при Ф = 0,05 — в 1,2 раза,
при Ф = 0,25 — в 1,8 раза, при Ф — 0,5 — более чем в 3 раза,
при Ф 0,75 — в 7 раз, при Ф — 1 — в 15 раз.
Однако сравнение полезной нагрузки при одних и тех же зна¬
чениях функционала Ф = (oc/2g) У дает завышенные результаты.
Превращение материала дви¬
гателя в рабочее вещество,
очевидно, потребует каких-то
в сп о мо га те л ьны х у с тр о й с тв,
которые увеличат удельный
вес двигателя на единицу
мощности, а значит, увели¬
чат и значение Ф (при фик¬
сированной величине интег¬
рала У). Для того чтобы стало
невыгодным полное превра¬
щение материала двигателя в
рабочее вещество (х 1),
удельный вес а должен воз¬
расти при Ф=0,05 в 2 раза,
при Ф = 0,25 в 2,5 раза, при
Ф = 0,5 примерно в 3 раза
и т. д. (здесь под Ф понимает¬
ся Ф = (ax,=.0/2g) J). Если будет существовать зависимость а (х),
то можно решать задачу о выборе оптимального значения х,
обеспечивающего максимум полезной нагрузки при заданной
величине интеграла У.
6. Ступенчатое уменьшение веса двигателя. Рассмотренный
выше случай непрерывного уменьшения веса двигателя соответ¬
ствует бесконечно большому числу п бесконечно малых секций
двигателя (w = ос на рис. 4.14). Сравним этот предельный слу¬
чай со случаем конечного числа секций конечного размера, как
это сделано в § 2 для х = 0.
Пусть в момент времени С сбрасывается /-я секция двигателя,
и х—часть веса этой секции — присоединяется к запасу рабочего
вещества, т. е.
^ т * ' (4.118)
(/ -= !>•••) "■■■ D-
где индекс j указывает на момент времени tj, а значок плюс
или минус относится к значению функции справа или слева от мо¬
мента t;.
О “ 0,2 0,4 0,6 0,8 х
Рис. Elf). Полезная нагрузка G- и зависимо¬
сти от коэффициента превращения к при фик¬
сированных значениях функционала Ф.
166
ИДЕАЛЬНЫЙ ДВИГАТЕЛЬ ОГРАНИЧЕННОЙ МОЩНОСТИ [ГЛ. 4
В интервале времени tj<^ t tj+i вес двигателя остается
постоянным
г о’)- __
Ljx — Сгх
(/ = 1, . . .,п).
(4.119)
Мощность N и параметр х, как и в случае непрерывного умень¬
шения веса двигателя, должны быть максимально возможными.
Изменение веса аппарата на
участках между сбросами опи¬
сывается уравнением (4.99).
Интегрируя это уравнение по
участкам от tj до tj+1 (j =
= 0, 1, . . ., п — 1; tn = Т) и
складывая, получаем
Ф = V G(l)+
2j л ло+ir
1
1
q(J)+ _u g{J)+
+ GiJ)+
(4.120)
Учтя соотношение на раз¬
рывах для запаса рабочего
вещества (4.118) и условие
Рис. 4.16. Сравнение полезной нагрузки Gn ПОСТОЯНСТВа веса ДВИГаТвЛЯ
при непрерывном (п = оо) и ступенчатом межДУ моментами сброса
(п = 2,4) уменьшении веса двигателя, а также МС"ЛМ.У
при пеменяющемся весе двигателя (п = 1) (4.119), перепишем ВЫраже-
для случая полного превращения материала
двигателя в рабочее вещество (х = 1).
п-1
ф _ /dO>
ние (4.120) в таком виде:
7=0
1
!. Gu>+ GU)~ _!_ xG0'-l)+ (1 _ x) Q(jb
(4.121)
Щ'Д' = ОТ = GyJ;, G'0)- = Ga0, Gp- = G3l = G-).
Вычислив частную производную дФ/dG-, можно убедиться,
что функция Ф (G-) монотонно убывающая. Задача снова разде¬
ляется, и весовая часть сводится к отысканию таких значений
/ДУН
G
(/>-
а = о, 1,..., п — 1),
(4.122)
которые обеспечивали бы максимум функции (4.121) при фикси¬
рованном значении G- и удовлетворяли бы условиям
Gan + GK0 = 1, G(K')+<G^
nr(j-l) +
(4.123)
(в дальнейшем для сокращения записи значки плюс у G-J)+ и
минус у G(aj)~ будут опускаться).
СБРАСЫВАЕМЫЕ СЕКЦИИ КАК РАБОЧЕЕ ВЕЩЕСТВО
167
Для определения 2п неизвестных величин (4.122) получаем
систему 2п алгебраических уравнений (при О < х < 1)
(G<y) + Gt1'1) Yg$ = {Gf + xGtl) + (1 - x) G^VW*’
_o\
3G<» “V
G«+1)
xC</+1)
(G0'+i) _j_ G^)- (G</+1) + xGf + (1 — x) С(/+1))2
G<« + xG^'-D
(G</> +- xG^ -f (1 — x) G^f
|^ = 0] или G?=G™,
Gil) xG<«
-| :Tr-^ — = 0
(C£> + G(x0))2 (G(al> + xGf> + (1 — x) G^)2
дФ
SG!,0)
(4.124)
Gf + Gf = 1 (/ = l,...,ra-l).
В предельном случае x = 1 соответствующая система уравне¬
ний имеет простое решение
■71/(71+1)
Ga0 = 1 - (G~‘
qU) __ ^-(n-;)/(n+1)
-l)Gni = re — 1),
1) Gr.
(/ = 0, 1, . . га — 1; X = 1).
(4.125)
Подставляя соотношения (4.125) в формулу (4.121), получим
связь между максимальной полезной нагрузкой Gл и функцио¬
налом Ф
ф = (и + 1) (1 — Gl/(n+1)) + Gr. — 1 при х = 1. (4.126)
При п > оо эта формула переходит в первое из соотношений
(4.116). Связь (4.126) представлена на рис. 4.16 в вида зависимости
G- (ф) для фиксированных значений п. Из рисунка видно, что
переход от п = 1 (постоянный вес двигателя) к п = 2 реализует
приблизительно V3 максимально возможного выигрыша в полез¬
ной нагрузке, а переход к п = 4 — приблизительно 2/3. Остальная
треть реализуется переходом оттг = 4ктг=ос.В случае х = 0
(см. § 2) при п = 2 реализуется подавляющая часть выигрыша.
Отсюда можно сделать вывод о том, что к предельным значениям
полезной нагрузки можно приблизиться при конечном, сравни¬
тельно небольшом числе секций двигателя и тем меньшем, чем
меньше коэффициент х. Отметим, что как и при х = 0, макси¬
мально допустимое значение функционала Ф здесь равно п.
ГЛАВА 5
ИДЕАЛЬНЫЙ ДВИГАТЕЛЬ ОГРАНИЧЕННОЙ
МОЩНОСТИ —ОПТИМАЛЬНЫЕ ПРОГРАММЫ
РЕАКТИВНОГО УСКОРЕНИЯ
В предыдущей главе было установлено, что для идеального
двигателя ограниченной мощности из общей проблемы оптими¬
зации выделяется независимая вариационная задача (4.11) о
построении оптимального закона реактивного ускорения (дина¬
мическая задача). После ее решения для каждого конкретного
динамического маневра, на основании формул главы 4 можно
рассчитать оптимальные параметры двигательной системы и ап¬
парата.
Динамическая задача (4.11) сформулирована как задача Лаг¬
ранжа с дифференциальными связями и краевыми условиями.
Реактивное ускорение а (t) в оптимальном режиме, как следует
из §§ 2, 3 главы 4, нигде не выходит на границу а — 0, за исклю¬
чением изолированных точек. Отсутствие граничных управлений
дает возможность применять для решения задачи (4.11) класси¬
ческие методы вариационного анализа..
В некоторых случаях удобно изменить формулировку (4.11),
избавившись от дифференциальных связей. Для этого нужно
исключить ускорение а из подынтегрального выражения функ¬
ционала при помощи уравнений движения (см. Приложение.
(П.47)):
Г
J --- \ [г-н (г, (.7.1 )
vl
('• (0) = !■„, г (0) = v0, V (Г) - I'lt ;• (Г) V,).
Задача сводится к построению min — экстремалей функцио¬
нала (5.1), проходящих через заданные начальную (r0, v0) и ко¬
нечную (гА , vT) точки пространства координат—скоростей при
фиксированных начальном и конечном моментах времени.
Будет использоваться также и другая формулировка вариа¬
ционной проблемы (4.11) — в виде задачи Майера
.7 - а2 (г/е)2, J (0) , О, J (Г) - min,'
г = у, г (0) - -- г0, v(T) ---- гь
v = ас -г Н, V (0) ^ V0, V (Г) ^ уг
(а(0>°. <М/) I).
§ 1J УРАВНЕНИЯ ЭКСТРЕМАЛЕЙ II ИХ СВОЙСТВА
§ 1. УРАВНЕНИЯ ЭКСТРЕМАЛЕЙ II ИХ СВОЙСТВА
169
1. Уравнения экстремалей, общий случай. Запишем функ¬
ционал (5.1) в прямоугольной инерциальной системе координат
г -/
/ = Ц Ik — X)- + (у — У)2 4 (z — zy-]dt =•» ^ F (I, х, х, у, у, г, z_)
dt
(5.3)
/г (0) --- х„, 1J (0) = 7/0, z (0)— 2,1, .<■' (0) = 7/0, г/ (0) — Vo, Z (0) = Wo, \
\х(Т) = хиу{Т) = уг, z(f)=zb ./(Г) = //ь y(T) = v1,z(T)=w1 /
где X =. X (t, х, //, z), Y = Y (t, x, y, z), Z = Z (t, x, y, z) —
компоненты вектора гравитационного ускорения В (г, £).
Первая вариация функционала (5.3) имеет вид
* г (пи dF dF •• г d dF .
6 J = [2t X I) — Z + —r. ~^T7. ./'
\ dx dij dz dt dx
. / dF A ■ , dF A • i ^/'
d dF
d dF .
dt dij У
г
о
d dF A 1
& d dF s d dF & \ .
di дх by + Zn~di 6zi\" +
Г 17 iP dF , Л/<’ \ s . / rf2 a/-’ , dF \ ,
+ } [(d? Ж f w)+ (rfT* Щ) + ai7)
Vk
(ALdJL AZ_
\ dt1 dz dz
6zJ dt.
(5.4)
При заданных начально!) (xQ, у0ч z0, w(), y0, w0) и конечной
(яд, г/19 zv ur, y1? M7j) точках вариации концов траектории в (5.4)
выпадают. Приравнивая нулю выражения при вариациях fix,
б г/, 6z под знаком интеграла, получим уравнения Эйлера рассма¬
триваемой вариационной задачи
ах
оХ
dx
, dY
a* + ^7
au
1
“Г
dZ
dx ~
аи
dX
, ()Y
a * f is7
av
i
dZ
~dy dz'
dz
dX
dz
+ Ж
au
i
~r
dZ
1STClz
(«.V -
r-X,
«и = a
—
y,
, az —
■Z),
(5.5)
или в векторной форме
R.
(5.6)
2. Первые интегралы уравнений экстремалей для простран¬
ственного движения в центральном поле. В указанном случае
(В = —/сг/г3) уравнения экстремалей (5.5) или (5.6) обладают
170 ИДЕАЛЬНЫЙ ДВИГАТЕЛЬ ОГРАНИЧЕННОЙ МОЩНОСТИ [ГЛ. 5
четырьмя первыми интегралами — одним скалярным и одним
векторным [5.1]
1/2(а-а)]— (а-у) — (a-Zcr/r3) — Н = const,
(ах v) — (ах г) = М = const
(скалярный интеграл обязан отсутствию в подынтегральной функ¬
ции (5.3) времени — dF/dt = 0 и имеет место для любого стацио¬
нарного поля dR/dt = 0; если полное время движения не задано,
то Н = 0).
В плоском случае остаются два интеграла [5.2]
lh {а% + а\) — (axii + avv) — к (ахх -f а„у) (х2 + г/2)-3 2 = const, |
(axv — avu) —(аху — аух) = const. J
(5.8)
3. Уравнения экстремалей — плоское движение в централь¬
ном поле. Исследуем подробно важный частный случай оптималь¬
ного движения, описываемого системой (5.5) — плоское движение
(z = az = 0) в центральном гравитационном поле (X = —кхг~3,
Y = —куг~3, г = Yхъ + у2) [5.3, 5.4].
В дальнейшем изложении будут использоваться безразмер¬
ные переменные. В качестве характерных величин берутся (II.2).
Характерная величина функционала J в этом случае равна
/с3/з г~5/г. Обозначения для безразмерных переменных сохраняют¬
ся прежние.
Перейдем в интеграле (5.3) к полярным координатам г, ф,
которые связаны с прямоугольными х, у формулами (П.4), где
0 = 0; тогда
т
J = \) — ГФ2 + 1/г2)2 + (фг + 2фг)2] dt (5.9)
о
(г(0) = г0, ф (0) = ф0, rj,0) = г0, ф (0) = ф0,
г (Т) = гг, ф (Т) = ф1? г (Т) = г19 ф (Т) = фг).
Под знаком интеграла (5.9) не содержатся аргумент t и функ¬
ция ф (£); этот факт может быть использован для понижения по¬
рядка дифференциального выражения под интегралом. Восполь¬
зуемся обозначениями (П.8) для первых производных г, ф:
г = vr, ф = уф/г и вместо аргумента t введем аргумент г:
dt = dr!vv.
(5.7)
§ 1] УРАВНЕНИЯ ЭКСТРЕМАЛЕЙ И ИХ СВОЙСТВА 171
После преобразований по указанной схеме интеграл (5.9)
принимает вид
ЩДч-4+Д + К+^Щ CS.10,
г
(здесь штрих обозначает дифференцирование по г). Экстремали
последнего интегрального функционала удовлетворяют началь¬
ным и конечным условиям, наложенным на уф, vr, г. По извест¬
ным зависимостям иг (г), уф (г) могут быть посчитаны время Т
и угловое перемещение — ф0:
г rlr г vm (г) dr
= (5Л1>
) о 1 П
Если величины Т ифх — ф0 заданы, то выражения (5.11) долж¬
ны фигурировать в качестве условий изопериметричности. Ва¬
риационная задача, эквивалентная (5.9), в новых переменных
записывается следующим образом:
' -11К-4+W+ (v*+(5.12)
1 о
vr (г0) = г;г0> гф (г0) — уф0, vr (щ) = игЪ гф (гг) = уф1
(параметры 2А,, 2v являются постоянными множителями Лагран¬
жа, отвечающими за выполнение условий (5.11); коэффициент 2
введен для удобства).
Приравнивая нулю первую вариацию функционала (5.12),
найдем два дифференциальных уравнения второго порядка от¬
носительно vr и Vcp. Если в них перейти обратно к аргументу t
и привлечь уравнения движения (П.8), то в результате получит¬
ся система уравнений первого порядка, описывающая оптималь¬
ные режимы плоского движения в центральном поле [5.3, 5.5]
г =vr, ф = гф/г, ur = ar -f v%/г — 1/г-, гф = аф — vrv~/r,
«г 2- [V-2 (а°; 4- а.|) + аг — -1-) — X — v Д] ,
^ф — ($Фгг 2&ггф -}- v).
(5.13)
Два последних уравнения системы определяют оптимальную
программу для компонент вектора реактивного ускорения.
4. Свойства уравнений (5.13). Система дифференциальных
Уравнений (5.13) имеет шестой порядок и содержит две константы
172 IIД К АЛЬПЫ Й ДВИГАТЕЛЬ ОГРАНИЧЕННОЙ мощности Ггл.
X и v (первые интегралы системы — ср. (5.8)), следовательно,
для ее решения должны быть заданы восемь краевых условий,
например (5.9). Если некоторые краевые значения не заданы,
то вместо них надо вычислить соответствующие оптимальные.
Они получаются приравниванием нулю внеинтегральной части
первой вариации функционала (5.12); последняя имеет вид
б J = 2 \аг8иг + яф6г;ф 4 (2 a^v^/r — аг) б г — v6cp — ХЬ Z]J. (5.14)
Когда угловое перемещение и время движения не заданы, то
постоянные v и X, как множители при соответствующих вариа¬
циях, должны быть приравнены нулю.
Уравнения (5.13) сохраняют вид, если произвести следующие
замены [5.4]:
r—>lr, t—>i~t, ср —> ф, V у —> /~ ^2v ,■, уф— >Г^ф,
аг —> 1~~аг, <7ф —> Х-> A'A, v —> Г’ J —> Г 2/
(инвариантность по отношению к преобразованию растяжения),
а также
t-> — t, г -> г, ф -> — ф, V,, -> — к,, уф -> уф, |
аг —> аг, уф —> — уф, А, —> Я, v —> v, J —> J J
(инвариантность по отношению к преобразованию замены знака).
Первое свойство (5.15) может быть использовано, например,
для получения оптимальных траекторий набора нулевой энергии,
начинающихся с круговой орбиты радиуса г (0) = Z, если име¬
ются таковые, начинающиеся с круговой орбиты радиуса г (0) = 1.
или для пересчета оптимальных траекторий перелета между кру¬
говыми орбитами: г (0) = 1, г (Т) = гх на траектории перелета
между орбитами: г (0) = Z, г (Т) = li\.
Согласно второму свойству (5.16) по прямому перелету
с одной круговой орбиты 1 на другую 2 может быть посчитан
обратный перелет, симметричный прямому, а по траектории на¬
бора энергии — траектория торможения.
5. Особая точка уравнений (5.13). Выражение для аг имеет
знаменателем vr, так что при приближении к точке vr — 0 про¬
изводная аг стремится к бесконечности, если только одновре¬
менно со знаменателем не стремится к нулю числитель. В послед¬
нем случае точка иг = 0 особая; ее тип может быть определен,
например, следующим образом [5.3].
Выделим из системы (5.13) два уравнения: третье и пятое,
которые будем изучать в окрестности точки иг — 0; входящие в
правые части функции г (t), (Z), (t) будут считаться извест¬
ными в окрестности этой точки. Запишем выделенные уравнения
(5.15)
УРАН I IE I ШИ ЭКСТРЕМАЛЕЙ II 111 СВОЙСТВА
173
в таком виде:
о,. аг 4- hu а, ~ ('I-,а* + a,.hx + h2) (5.17)
vr
(hx — v%!r — 1/r2, = 1Uja^ — A — vvjr).
Исключив ar из системы (5.17), придем к линейному уравне¬
нию относительно V2zy2, в котором аргументом является vr вместо
t; решение последнего записывается так:
1/2^г —: vr с + ^ (h\Vr — lhh\ + ho) vr2duj\, (5.18)
где с — постоянная интегрирования. Разложим подынтегральное
выражение в точке иг = 0 по степеням vr и вычислим интеграл:
xloVr - ЧЛ - h20 + сиг + . . . ; (5.19)
здесь нижний индекс 0 обозначает принадлежность к точке vr =
— 0; отброшенные члены разложения содержат vr в степенях
выше первой, коэффициенты при них не зависят от с.
Таким образом, на плоскости с координатами vr, V2^ инте¬
гральные кривые (5.19), пересекающие ось иг = 0, проходят
через одну и ту же точку независимо от значения постоянной с:
vr = 0, v2y? — V2A?o — h20. (5.20)
Эта точка является особой точкой типа «узел». Соотношение
(5.20), если в него подставить г;,, hx, Д2 из (5.17) оказывается
условием обращения в нуль числителя в выражении для произ¬
водной аг, так что
V2 (af + а\) -{- a, {v^ir — 1 //2) — А — vvjr = 0 при vr = 0.
(5.21)
6. Интегрирование в окрестности особой точки. Отметим одно
свойство дифференциальной системы (5.13), связанное с особой
точкой. Продифференцируем по времени t левую и правую части
предпоследнего уравнения из (5.13) и получившееся уравнение
вставим взамен исходного:
г •• иг, ср ^ 17ф/г, г,. а,. -4- i'll Г — 1 /г'2, ^ а. г — vrv^/r,
2
«Г ^ у (аф — Я -L* + 2-J-+V , а, = у (a^»v — 2а,.v* + v).
(5.22)
В новой системе отсутствует неопределенность в точке иг = 0,
затруднявшая проведение численного интегрирования; одновре¬
менно из уравнений выпал интеграл системы — параметр А,
174
ИДЕАЛЬНЫЙ ДВИГАТЕЛЬ ОГРАНИЧЕННОЙ МОЩНОСТИ
[ГЛ. 5
и при сохранении общего числа свобод увеличился дифферен¬
циальный порядок системы. Поэтому система (5.13) предпочтитель¬
нее (5.22) всюду, за исключением особых точек (они могут быть
в начале, в конце и в середине интервала интегрирования).
Пусть в начальный момент заданы координаты, компоненты
скорости, параметр v и компоненты ускорения:
' (0) = г0, ф (0) = ф0, vT (0) = vr0, vv (0) = vv0, v = v,
ar(0) = ar0, av (0) = аФ0. (5.23)
Если vr0 =4= 0, то в систему начальных условий вместе с (5.23)
входит параметр X; эта совокупность начальных значений опре¬
деляет задачу Коши для уравнений (5.13).
Если vr0 = 0, то начальная точка особая и в ней справедливо
соотношение (5.21), из которого находится значение параметра
X. В этом случае задача Коши формулируется для уравнений
(5.22), и она будет определена, если условия (5.23) дополнить
таким: аг (0) = аг0.
Описанная процедура интегрирования задачи Коши (5.13),
(5.23) может быть использована на каждом шаге решения какой-
либо краевой задачи для уравнений (5.13), если последняя реша¬
ется путем последовательного подбора недостающих начальных
условий.
7. Связь параметров начала и конца траектории. Если дина¬
мический маневр заключается в перелете между двумя круговыми
орбитами, то краевые точки траектории особые. Начальные и
конечные значения радиуса г и скоростей vr, г;ф в этом случае
следующие:
г (0) = 1, иг (0) = 0, v<p (0) = 1, г (Т) = rlt vr (Т) = 0,
v<t (Т) = Гг1*. (5.24)
Применяя условие в особой точке (5.21) к началу,/и концу
траектории, найдем две связи
1/2<Зо — X — v = 0, г12а\ — X — v /д3 2 = 0, (5.25)
где а0, ах — начальное и конечное значения реактивного уско¬
рения. Исключая X из (5.25), получим
а\ = «о - 2v (1 - >vv). (5.26)
Отсюда следует при rx 1
= а0, если v = 0, аг^> а0, если v << 0, а1<^ а0, если v > 0.
(5.27)
Чтобы выполнялось условие а\ > 0, параметр v должен удов¬
летворять неравенству
v < 42al (1 - г^Г1- (5.28)
§ 1]
УРАВНЕНИЯ ЭКСТРЕМАЛЕН И ИХ СВОЙСТВ,А
175
При г1<^1 неравенства (5.27), (5.28) заменяются на об¬
ратные.
8. Уравнения экстремалей — плоское движение в поле двух
центров. В виде, аналогичном (5.13), могут быть записаны урав¬
нения оптимальной программы реактивного ускорения для плос¬
кого движения в поле двух центров — Солнца i = 1 и планеты
Здесь v и X уже не являются постоянными, так как в систему
(П.49), (П.50) явно входят ф и t (переменные в (5.29) размерные).
Если движение происходит в малой окрестности одного из
и X малы по абсолютной величине; в пределе уравнения (5.29)
переходят в последние два уравнения (5.13).
В работе [5. 6] дана другая форма уравнений экстремалей, там
же проверено выполнение второго и третьего необходимых усло¬
вий минимума функционала.
9. Аналитические решения — плоскопараллельное поле1). За¬
дача построения экстремалей функционала J в общем случае тре¬
бует численного интегрирования, однако для модельных гравита¬
ционных полей она допускает простые аналитические решения.
К таким полям прежде всего относится плоскопараллельное
(R (v, t) ~ g = (0, —g, 0) — постоянный вектор, см. § 1 Прило¬
жения) и его частный случай — бессиловое поле (g = 0). Интег¬
рированием уравнений (5.5) определяем оптимальную програм¬
му вектора реактивного ускорения, а по ней — траекторию из
уравнений движения (П.53) и функционал:
i = 2 (см. (П.49), (П.50) и рис. П.6) [5.3]:
(5.29)
_ V0_ (v^/r0)) (v(i) — 2o,(.i)xF(i))
(y<*> = f(1), v? =■ (4l(i) + 0)) r(,\ i = 1, 2).
центров, т. e. в поле, близком к центральному, то производные v
(5.30)
176 11Д К ЛЛЬМ'ЫП. Д ВИГАТГЛЬ <) Г Г A I 111 4 1'' 11 11 () l"l МОЩНОСТИ [ГЛ. 5
Постоянные векторы b1? . . b4 находятся из граничных усло¬
вий; например, когда заданы координаты и скорость в начале
( *0. v0) и в конце (1Д, vx) траектории, то
1 ^ ( I о Г1 \ *“ I - •) - ‘J N
bi — -трг (vi 4- уо р j , b-2 — р- [Уг -j- ^vo 5 р j .
Ьц ^ v0, ь4 = гп. (5.31)
Представление о характере оптимальных программ реактив¬
ного ускорения можно получить, рассмотрев два простейших
Рис. 5.1. Оптимальная программа реак- Рис. 5.'1. Зависимость функционала днпа-
тивного ускорения для задачи набора мической задачи J (Т) / J (Т*) от полного
модуля скорости в бессиловом поле (а — времени движения T/T# для маневров в бес-
модуль ускорения, е = + 1 — паправле- силовом поле (кривая ut — набор скоро-
ние). сти — J (Т*) = иг/Т*. кривая I — пере¬
мещение между точками покоя — 1 (7Д) =
= 12 m\a).
маневра — одномерные движения в бессиловом поле ([5.1. 5.3,
5.5, 5.7] и др.).
1°. Набор заданного модуля скорости их за заданное время Т.
Начальные положение и скорость заданы, конечное положение
не фиксировано (см. (П.64)).
Граничные условия (П.64) совместно с условиями трансвер¬
сальности (5.4) дают следующие выражения для bv 62: Ьг = О,
Ь2 = иг/Т; отсюда
а (t) — uJT, е (t) = +1, J = щ)Т. (5.32)
Отметим, что в этом случае реактивное ускорение постоянно
и направлено по скорости (рис. 5.1), величина функционала об¬
ратно пропорциональна времени выполнения маневра (рис. 5.2,
кривая их). Такой же характер зависимости J (Т) получается для
маневров в центральном поле, когда реактивное ускорение много
меньше гравитационного.
2°. Перемещение между двумя точками покоя, отстоящими
одна от другой на расстоянии Z, за заданное время Т (см. (П. 65)).
УРАВНЕНИЯ ЭКСТРЕМАЛЕЙ И ИХ СВОЙСТВА
177
Подставляя граничные условия (П.65) этого маневра в (5.31),
находим
6/
J>2
6/
«(О =-у»
2 1) i e(t) = - 1
/ = I2l2/T3.
при О
при < £< Г,
(5.33)
<7
Здесь вектор реактивного ускорения — линейная функция
времени (рис. 5.3), а функционал обратно пропорционален кубу
времени выполнения маневра (см.
на рис. 5.2 кривую I). Этот ма¬
невр моделирует быстрый перелет
между орбитами в центральном
поле (реактивное ускорение много
больше гравитационного).
Определим выигрыш в функцио¬
нале, обязанный замене одной из
неоптимальных программ вектора
реактивного ускорения [5.8, 5.9]
на оптимальную. Рассмотрим по¬
стоянный по модулю (a(t) = AIIT2)
и однократно меняющий направ¬
ление (при t = 1/2Г) вектор реак¬
тивного ускорения (пунктир на
рис. 5.3). Такой программе уско¬
рения соответствует функционал
J = 16 12/Т3, т. е. по сравнению с
этим случаем выигрыш в функцио¬
нале при переходе к оптимальной
программе (5.33) составляет 25%.
10. Аналитические решения, однородное центральное поле.
Следующий пример точного решения уравнений вариационной
проблемы доставляет так называемое однородное центральное поле
[5.10]. Здесь вектор гравитационного ускорения представляется
в виде R = — Ar/jrjJ, г# = const (см. (П.54)). Взяв за характерное
расстояние а в качестве остальных характерных величин —
(П.2), перейдем к безразмерным переменным. Тогда Н = —г,
система (5.6) приводится к векторному линейному однородному
уравнению с постоянными коэффициентами
Рис. 5.3. Оптимальная программа ре¬
активного ускорения для задачи пере¬
мещения между точками покоя в бесси-
ловом поле (а — модуль ускорения,
е = + 1 — направление, пунктир —
программа ускорения, взятая для срав¬
нения).
d* г
dl*
+ 2*+г = 0.
Общее решение уравнения (5.34) имеет вид
г = (сг+ ог() cos t + (с3 + с4£) sin t,
12 Механика полета
(5.34)
(5.35)
178
ИДЕАЛЬНЫЙ ДВИГАТЕЛЬ ОГРАНИЧЕННОЙ МОЩНОСТИ [ГЛ. 5
где постоянные векторы с2, . . ., с4 определяются из граничных
условий, например, если г (0) = г0, г (0) = v0, v(T) =- г1У
г (Т) = уь то
Cl = Го.
с2 = sin„ [(sin т cos Т + Т) Го -г
+ v0 sin2 Т — (sin Т + Т cos Т) п + Tvx sin Г],
Сз = gill2 у [— (s*n Т COS Т + Т) Го Тг\о +
-'г (sin Т Т cos 71) гх — T\i sin Т\, \ (5.36)
с4 = ^.д., ,р [г0sin2 Т -f- (Т — sin Т cos T)vt)
— Ti'i sin T -f (sin T — T cos Т) Vi] *
при Т = 2ns (5 = 1, 2, . . .)х)
rt — Го
Cl = 1*0, Со =
/ji .Сз — Vo j, ,^4 j-i
Оптимальная программа реактивного ускорения и интеграл J
в соответствии с (5.35) таковы:
a (t) = 2 (с4 cos t — с2 sin t),
J = 2 (cl + cl) T + (c\ - ty sin 2T - 4 (c-2 • c4) sin2 T;
при T = 2л5(s = 1, 2, . . ,)1) ^ ^
a (0 = 2 cos t — T~T t° sin t),
J — -jr [(ri — Го)2 + (Vi Vo)2] •
11. Аналитическое решение, центральное поле. Частное реше¬
ние системы (5.6) для случая произвольного потенциального си¬
лового поля (К =- grad U) указано в работе [5.11]
ъ
14 — Го Vi — Vo
. с4 =
J
а (0 = г
+ 4ibi
(b = const).
(5.38)
Этот закон реактивного ускорения, как нетрудно проверить
прямой подстановкой, точно удовлетворяет уравнениям Эйлера.
Его можно использовать для построения траектории разгона,
но при этом не будут точно удовлетворены условия трансвер¬
сальности. Однако относительная погрешность в функционале
для величин реактивного ускорения, малых по сравнению с гра¬
витационным, оказывается небольшой — порядка а (где под а
понимается относительное ускорение).
Ч Время Ту кратное периоду движения по круговой орбите радиуса г*.
ОПТНМ А л Ь1 [ ЫII ME ЖИЛ А11Е ТЫ ЫII НЕ РЕ Л Е Т
179
2. ОПТИМАЛЬНЫЙ МЕЖПЛАНЕТНЫЙ ПЕРЕЛЕТ с идеальным
ДВИГАТЕЛЕМ ОГРАНИЧЕННОЙ МОЩНОСТИ
В настоящем параграфе дается решение вариационной зада-
чи (5.1) для межпланетных перелетов. Это в основном результаты
численных расчетов. Экстремальные значения и экстремали
исследуемого функционала определялись: по решению соответ¬
ствующих краевых задач для системы (5.13) методом организо¬
ванного подбора недостающих начальных значений в эквива¬
лентной задаче Коши [5.4, 5.5, 5.12—5.17] или прямыми метода¬
ми, примененными к функционалу (5.1) [5.18—5.21]. Получено
также два приближенных решения. Первое относится к участкам
движения вблизи планет [5.3, 5.11, 5.22—5.24, 5.37], второе — к
участкам движения между орбитами планет [5.1, 5.25].
Схема межпланетного перелета с двигателем малой тяги опи¬
сана в § 2 Приложения. Там указаны два качественно отличных
участка траектории такого перелета: участок движения в области
преобладающего влияния планет при возмущающем действии
Солнца и участок движения в области преобладающего влияния
Солнца при возмущающем действии планет. Отличия гравита¬
ционного поля от центрального на этих участках мало сказыва¬
ются на интегральных характеристиках траектории [5.4]. Ис¬
пользование приближенных граничных условий (П.55), (П.56) или
(П.57), (П.58) для каждого участка также оказывает небольшое
влияние. На этом основании вариационная задача решается не¬
зависимо для двух элементарных маневров: для набора нулевой
энергии в центральном поле планеты (или торможения с выходом;
на орбиту спутника планеты) и для межорбитального перелета
в центральном поле Солнца.
1. Набор нулевой энергии. Маневр начинается в заданной
точке начальной орбиты; за заданное время 71 требуется набрать
нулевую полную энергию Е (Т) = 0.
Угловое перемещение не фиксируется; между конечными зна¬
чениями радиуса г1? радиальной vrl и трансверсальной уФ1 про¬
екциями скорости имеется одна связь (см. (П.55)): Е (Т) =
= 1U (vn + vh) — 1/тд = 0. Из условия равенства нулю первой
вариации функционала (5.14) получаем следующие оптимальные
соотношения:
v = 0, аГ1/аФ1 = Vyjvm, аГ1 — 2ач>1иГ1г1 — arlvrlr\ = 0. (5.39)
Отметим, что, согласно двум последним соотношениям из
(5.39), в конце движения угол у между вектором тяги и вектором
скорости и производная у должны быть равны нулю [5.11].
Полная система дифференциальных уравнений и краевых
условий, определяющая оптимальный маневр набора нулевой
энергии, составляется из (5.13), (11.55), (5.39). Ниже будет
12*
180
ИДЕАЛЬНЫЙ ДВИГАТЕЛЬ ОГРАНИЧЕННОЙ МОЩНОСТИ [ГЛ. 5
исследоваться случай круговой начальной орбиты, для него пол¬
ная система может быть записана в виде (см. (5.22))
мещение ф, величина контрольного функционала /, определяются
после решения краевой задачи (5.40) интегрированием соответ¬
ствующих дифференциальных уравнений:
Ф = г;ф (t)!r (t), ф (0) = 0; J = ar (t) + а% (t), J (0) = 0. (5.41)
Уравнения оптимального разгона представлены в форме (5.22)
в связи с тем, что начальная точка траектории является особой
Vr (0) == 0. При отходе от особой точки предпоследнее уравнение
из (5.40) может быть заменено уравнением и ервого порядка с
первым интегралом % (см. (5.13)). Последний определяется ус¬
ловием
особую точку — в силу почти периодического характера движе¬
ния при малых ускорениях а особая точка может появляться на
каждом обороте.
Решение краевой задачи (5.40) может быть проведено путем
сведения к задаче Коши с подбором трех недостающих началь¬
ных значений аг0, аф(Ь аг0 [5.4, 5.5, 5.11, 5.12]. Другой путь —
применение прямых методов к минимизации функционала (5.9)
при краевых условиях (П.55), (5.39), [5.19].
Задача (5.40) содержит единственный параметр Т. Траектории
и законы управления задачи (5.40) пересчитываются для началь¬
ных круговых орбит произвольного радиуса и различных планет
по критериям подобия (5.15). Характерные значения величин, фи¬
гурирующих в задаче, для Венеры, Земли, Марса и Луны при-
.2
1
—■ -~ 2dyVfp'jp
К = ч214 (0) + а; (0)].
'(5-42)
Отметим, что траектория разгона может содержать не одну
§ 2] ОПТИМАЛЬНЫЙ МЕЖПЛАНЕТНЫЙ ПЕРЕЛЕТ 181
Таблица 5.1
Характерные значения величин в планетоцеитрнчсских (Венера, Земля,
Марс) и селеноцентрической системах координат для круговых орбит
с высотами 200, 250, 300 и 350 им]
Планета
Г *’ км
t , сек
vм/сек
8**
м/сек2
J*’ V
м2/сек*
*
м2/сек*
Воиера
6,361-103
6,411-103
6,461-Юз
6,511-103
879
889
900
910
7,233-Юз
7,210-103
7,182-Ю3
7,154-103
8,236
8,108
7,983
7,861
5,932-104
5,846-104
5,734•104
5,624-Ю4
67,84
65,75
63,74
61,80
Земля
6,571-103
6,621-Юз
6,671-103
6,721-103
844
854
864
873
7,783-Ю3
7,754-Юз
7,725•103
7,696-Ю3
9,219
9,08)
8,944
8,812
7,175•104
7,040-Ю4
6,909-1О4
6,781-Ю4
84,99
82,45
80,00
77,65
Марс
3,532-103
3,582-Юз
3,632-Ю3
3,682-103
1030
1052
1075
1097
3,427-Ю3
3,403-Юз
3,380-Юз
3,357-103
3,326
3,234
3,145
3,061
1,140-1О4
1,101-Ю4
1,063-Ю4
1,027-104
11,06
10,46
9,89
9,37
Луна
1,938-Юз
1,983-Юз
2,038-103
2,088-Юз
1239
1288
1336
1386
1,564-Юз
1,544-Юз
1,525-Ю3
1,507-103
1,262
1,199
1,141
1,087
0,197-Ю4
0,185-Ю4
0,174-Ю4
0,164-Ю4
1,59
1,44
1,30
1,18
ведены в табл. 5.1. Даются четыре значения каждой величины,
соответствующие круговым орбитам с высотами 200, 250, 300 и
350 км.
Вследствие свойства «обратимости» оптимальных траекторий
(5.16) все результаты, относящиеся к задаче набора нулевой энер¬
гии, можно использовать и для задачи торможения, причем в
соответствии с граничными условиями маневра набора нулевой
энергии здесь нужно считать, что в начале задано только условие
нулевой энергии (радиус и скорость по отдельности не фиксиру¬
ются), а в конце — условие выхода на круговую орбиту задан¬
ного радиуса (угловое перемещение не фиксируется).
2. Набор нулевой энергии — численные результаты. Числен¬
ное решение задачи (5.40) показывает, что для больших значений
времени Т 102 (малые величины ускорения а ^ 10"2) траек¬
тория выхода с круговой орбиты представляет собой пологую рас¬
кручивающуюся спираль (рис. 5.4).
Направление ускорения составляет малый угол с направле¬
нием скорости (заключено между касательной и трансверсалью),
совпадая с последним на заключительном этапе движения (см.
второе условие (5.39)). Модуль реактивного ускорения изменя¬
ется слабо вдоль траектории, увеличиваясь на конечном участке
182
Л САЛЬНЫЙ ДВИГАТЕЛЬ ОГРАНИЧЕННОЙ МОЩНОСТИ [ГЛ. 5
на 10—20°о. Характер изменения компонент реактивного уско¬
рения по времени иллюстрируется рис. 5.5 из [5.19]. Там же пред¬
ставлены соответствующие функции г (t) и иф (t) r(t). В табл. 5.2
проведено сравнение параметров трех траекторий набора нулевой
Рис. 5Л. Примеры оптимальных траектории набора пулевой энергии при старте
с круговой орбиты (первые витки спирали воображены условно, разметка траек¬
тории дана по времени, все параметры безразмерные).
энергии [5.19] (все параметры безразмерные). Время движения
для каждой траектории одинаково Т — 100. В первом столбце
таблицы даны результаты расчета оптимальной траектории вы¬
хода с начальной круговой орбиты, во втором — с эллиптической
ОПТИМАЛЬНЫЙ MEЖПЛАНЕТНЫЙ ПЕРЕЛЕТ
183
орбиты с эксцентриситетом е0 = 0,1. В третьем столбце приве¬
дены параметры траектории с постоянным трансверсальным уско¬
рением при старте с круговой орбиты.
Зависимость функционала задачи / от времени Т набора
нулевой энергии с круговой начальной орбиты дана на рис. 5.6
Рис. 5.5. Оптимальные законы изменения трансверсалыюй аф и радиальной аг компонент
реактивного ускорения, радиуса г и момента количества движения гфг для маневра набора
нулевой энергии (начальная орбита круговая, время выполнения маневра Г = 100, пара¬
метры безразмерные).
[5.4]. На рис. 5.7 показан выигрыш в функционале от програм¬
мирования вектора реактивного ускорения [5.4, 5.5, 5.11, 5.12,
5.26]. Видно, что разница между оптимальной программой реак¬
тивного ускорения и постоянным по модулю тангенциально
Т а б лица 5.2
Сравнение траектории набора нулевой энергии
с круговой и эллиптической орбит при оптимальной
программе реактивного ускорения и траектории
с постоянным трансверсальным ускорением
Парам ет-
ры траек¬
тории
е0 = п. ar (t) = opt, j
Оф ( t) = opt 1
!
so = 0,1, ar (f) = opt, j
o-cp (0 = opt j
So = o, ar (t) = 0,
аф {t) = const
So
—0,2257-10-3
—0,3068-Ю-з
0 j
So
0,6465*10"2
0,6891-10"2
0,7755-10-2
Si
0,4627-10"2
0,4481-10-2
0
Si
0,4521-10-2
0,4576.10-2
0,7755.10--
Г\
9,1.30
9,489
9,660
J
0,5531-lO"2
0,5620-10-2
0,6014-IQ"2
184
ИДЕАЛЬНЫЙ ДВИГАТЕЛЬ ОГРАНИЧЕННОЙ МОЩНОСТИ [ГЛ. 5
направленным ускорением невелика и уменьшается с увеличением
времени выполнения маневра.
Рис. 5.6. Функционал J динамической задачи для маневра набора нуле¬
вой энергии (сплошная кривая) в зависимости от времени движения Т (на¬
чальная орбита круговая, пунктирная кривая относится к маневру набора
скорости ut= 0,895 в бессиловом поле, параметры безразмерные).
Характер оптимального закона a (t), а также характер за¬
висимости J (Т) для маневра набора нулевой энергии в централь¬
ном поле близки к таковым для маневра набора модуля скорости в
бессиловом поле (см. (5.32) и
рис. 5.6). По этой причине
последний считается манев¬
ром, моделирующим набор
нулевой энергии в централь¬
ном поле.
Чтобы оценить влияние
третьего тела — Солнца — на
функционал /, были проде¬
ланы соответствующие рас¬
четы [5.4]. Они показали, что
относительная погрешность в
функционале от неучета этого
фактора для рассматривае¬
мого маневра в окрестности
Земли не превышает 10_3.
3. Набор нулевой энер¬
гии — аналитическое реше¬
ние. Обратимся к аналитическому представлению полученных ре¬
зультатов. Когда реактивное ускорение много меньше гравитацион¬
Рис. 5.7. Сравнение по функционалу J оп¬
тимально программируемого реактивного
ускорения (сплошная кривая) и постоянного
по модулю тангенциально направленного
ускорения (пунктирная кривая) для маневра
набора пулевой энергии с круговой орбиты
(параметры безразмерные).
ОПТИМАЛЬНЫЙ MEЖПЛАПЕТНЫ Й ПЕРЕЛЕТ
18&
ного (а^Ю'2), траектория разгона вначале представляет собой
пологую спираль, на которой приближенно выполняется условие
равенства гравитационного и центробежного ускорений: 1/г2 ^
^ v%/г. Найдем оптимальный закон a (t) на начальном участке
траектории выхода в предположении, что последнее условие
выполняется точно.
Уравнения движения и начальные условия при старте с кру¬
говой орбиты имеют вид
(здесь в уравнениях движения (П.8) учтено условие v%lr = 1/г2).
Исключив из последнего уравнения (5.43) уф = l/]/Y и vr =
= г, получим 1/2гг~3/2 = аф. Проинтегрировав это уравнение,
можно выразить радиус г и компоненты скорости уф, vr при по¬
мощи (5.43) в функции интеграла по времени от аф:
Начальные условия (5.43) выполняются для г и уф из (5.44)
и не выполняются для иг. Однако при малых значениях транс-
версального ускорения аФ0 1 радиальная скорость внача¬
ле также оказывается малой vr0 = 2яФ0 1, и в конечном
счете это нарушение начальных условий несильно влияет на
результат.
Характерное время задачи, согласно (5.44), порядка 1/аф
Поэтому при дифференцировании по времени порядок малости
относительно аф увеличивается приблизительно на единицу.
Так, в начале движения vr порядка аф, a ar = Ьг порядка яф.
Кинематические характеристики г, vr, иф определяются ве¬
личиной интеграла (5.44). Поэтому задача об оптимальном пере¬
ходе от заданного начального положения в заданное конечное
положение (например, Е (Т) = V2 (v*i + z^i) — 1 /гг = EJ за
заданное время формулируется как задача на минимум
(5.43)
о
о
о
т
т
(5.45)
о
о
Т
при заданном \ a^dt.
186
ИДЕАЛЬНЫЙ ДВИГАТЕЛЬ ОГРАНИЧЕННОЙ МОЩНОСТИ
[ГЛ. 5
После проведения обычной процедуры вариационного анализа
получаем оптимальную программу для проекции ускорения яф:
а.
(t) = const;
(5.46)
при этом
ar (t) = 6а% (1 - a^tyK (5.47)
Этот вывод получен при условии ат <§: аФ. В окрестности
точки выхода (Ег = 0) последнее неравенство не выполняется —
аг становится порядка яф. В этом можно убедиться, подставив
в (5.47) значение времени выхода, найденное из условия Е (Т) =
= 0 при помощи (5.44). Поэтому оптимальный закон (5.46) спра¬
ведлив только на начальном участке траектории набора нулевой
энергии. Отличными от изложенного способами приближенное ре¬
шение задачи получено в работах [5.11, 5.22—5.24,5.37].
4. Межорбитальный перелет. Маневр начинается в фиксиро¬
ванной точке орбиты одной планеты и заканчивается в фиксиро¬
ванной точке орбиты второй планеты; вектор скорости в начале
и в конце движения совпадает с соответствующими орбитальными
скоростями; время движения задано (см. (П.56)).
Оптимальный перелет между компланарными орбитами,
которые и будут в основном рассматриваться, описывается диф¬
ференциальными уравнениями (5.13) и граничными условиями
(П. 56)
г == гд,
гФ
ф = —•
= аг +
Г(Г> С1 (Г) '
ф
г
г (0) = 1, г(Т) = ги
ср(0) = ф0, ф(7’) = ф1,
vr (0) = vr0, vr(T) = vrl,
г>ф(0) = уфо, v<t(T) = v<pь
а,. =
Яр)
аг — —
— (<w — 2 arvv
v).
(5.48)
Система дифференциальных уравнений (5.48) имеет шестой
порядок и содержит две произвольные постоянные К и v, т. е.
число свобод в уравнениях равно числу краевых условий.
Если на траектории перелета встречаются особые точки vr =
= 0 (ими являются начальная и конечная точки, когда траек¬
тория соединяет круговые орбиты, см. (П.58)), то предпоследнее
уравнение из (5.48) заменяется уравнением второго порядка из
(5.22). Процедура взаимных переходов (5.48) <-> (5.22) анало¬
гична описанной в п. 1.
ОПТИМАЛЬНЫЙ’ ME ЖПЛАНЕТНЫЙ НЕ РЕ ЛЕТ
187
Параметрами задачи для круговых орбит являются г1? а0, v.
При фиксированном i\ каждой паре а0, v соответствует пара Г,
(или несколько пар 7\ ср15 если задача имеет не одно решение).
Перелеты могут классифицироваться как по параметрам а0, v,
так и по Г, фх. Первый способ классификации удобен при реше¬
нии краевой задачи путем сведения к задаче Коши, второй —
при нахождении экстремалей функционала прямыми методами
[5/18, 5.20, 5.21].
Если в расчетах учитывается реальное движение планет, то
в качестве параметров используются дата старта t0 и продолжи¬
тельность перелета Т или дата старта t0 и дата финиша tv Переход
/0, t1 t0, Т простейший: Т = tx — t0, t0 = t0. Связь между пара¬
метрами t0J tx и Г, ф1 определяется по таблицам эфемерид планет
из условия равенства угловых перемещений аппарата и планеты
назначения в конечный момент времени. В предположении, что
планеты движутся равномерно по средним круговым орбитам
и что даты старта t0 и финиша tl отсчитываются от момента
противостояния планет, можно записать формулы перехода t0,
t1 <-* Г, ф! следующим образом:
т = h — t0,
фх = ay1t1 — со2t0 ^ 2я5 (s = 0, 1, 2, . . .), (5.49)
где сох, со2 — средние угловые скорости движения планет старта
и финиша, s — целое положительное число (число дополнитель¬
ных оборотов планеты с большей угловой скоростью), знак плюс
берется для перелета на внешнюю орбиту, знак минус — на внут¬
реннюю.
Отметим, что перелет с орбиты 1 на орбиту 2 может быть пере¬
считан на обратный (зеркально отображен) по формулам (5.16).
Переход от безразмерных переменных, употребляемых в тексте,
осуществляется стандартным образом. Характерные значения ис¬
пользуемых величин для средних круговых орбит Венеры, Земли
и Марса приведены в табл. 5.3.
Таблица 5.3
Характерные значения величин в гелиоцентрическом системе координат
для средних круговых орбит Венеры, Земли и Марса
1
1
Планета
Г , 7Г.Л1
1 1
1
t * , v км!сек !
сут *’ j
I
1
g*, м.'сек2
J*, V* ,
м2/сек3
Х:,:, ль1'сек1
Венера
'Земли
jMapc
108,1-10е
149,5-106
227,8-10°
35,7 1 35,01
58,1 ! 29,76
109.3 ’ 24/11
i !
1.141■10"2
0,597-10-2
0,257-10-2
399.6
177.6
61,9
1,303-10-4
0,356-10-4
0,066-10-4
188
ИДЕАЛЬНЫЙ ДВИГАТЕЛЬ ОГРАНИЧЕННОЙ МОЩНОСТИ [ГЛ. 5
5. Решение краевой задачи (5.48) — метод транспортирую¬
щей траектории. Краевая задача (5.48) для оптимальных переле¬
тов между орбитами решалась либо путем подбора недостающих
начальных условий в эквивалентной задаче Коши [5.4, 5.5, 5.12—
5.17], либо методом «транспортирующей траектории» [5.1, 5.25].
Идея последнего метода состоит в следующем. Выбирается
кеплеровская траектория, проходящая через заданные точки
орбит 1 и 2. Искомое движение считается мало отличающимся
от кеплеровского, так что уравнения вариационной проблемы
допускают линеаризацию в его окрестности. Получается крае¬
вая задача для системы линейных дифференциальных уравнений.
Пусть х<°) (t), yW (t) — плоская кеплеровская траектория
(называемая транспортирующей), которая удовлетворяет задан¬
ным координатам г0 и г± в начале и в конце движения. Направим
ось z нормально к плоскости транспортирующей траектории и
представим истинную траекторию в виде
Считая функции £, г), £ малыми, линеаризуем уравнения (П. 1)
где через U = —1 !г обозначен потенциал поля: X = dUldx,
У = ди/ду, Z = du/dz (г = VУ + у2 + z2).
Вторые производные (d2U/dx2y°\ (d2U/dx дуУ°\ (d2U/dy2){^
являются функциями времени, вычисляемыми по известной транс¬
портирующей траектории х<0) (t), у^ (t). Представим кепле-
ровскую траекторию в терминах оскулирующих элементов: р —
фокальный параметр, в — эксцентриситет и со — долгота пери¬
гея, а также истинной аномалии (см. Приложение); тогда коэф¬
фициенты в линейных уравнениях (5.51) будут иметь вид
х = ж<°) + у = 1/(0) 4- Г), 2 = £.
(5.50)
(5.51)
I = — [(я(0))2 + (у(0))2] ‘/2 £ + az,
(dzU/dx*)i0) = — (rw)"3( 1 - 3 cos2 и),
(d2U/дх ду)(0) = (г(0) )"33 sin и cos и,
(5.52)
(.d*U/dy2)(0) = — (г(0) )"3 (1 — 3 sin2 и),
(г(0) = р(0) / (1 -f- B^COS Й1), и = ф + СО(0)).
Формулировка вариационной задачи при переходе к транс¬
портирующей системе координат сохраняется: как и раньше.
ОПТИМАЛЬНЫЙ МЕЖПЛАНЕТНЫЙ ПЕРЕЛЕТ
189
нужно искать минимум исходного функционала
т
J ^^(ai + al + a^dt. (5.53)
0
Это связано с тем, что в качестве транспортирующей была
выбрана кеплеровская траектория, т. е. траектория пассивного
движения. Поэтому в уравнениях (5.51) фигурируют не добавки
к реактивному ускорению, а полная величина ускорения.
Краевые условия для уравнений (5.51) записываются в виде
1 (0) = г, (0) = с (0) = I (Г) = л (Т) = Б (Г) = о, ч
f (0) = и0 — То°\ 'П(0) = ^о — Уо\ t(0)=Wo» 1 (5.54)
1(Т) = иг- 4(T)=Vl-y?\ Z(T) = Wl, )
где uQ1 v0, w0, ul7 vv wl задаются (компоненты орбитальных
скоростей планет), а z/q0), Хх\ уi0) вычисляются в начале и
в конце транспортирующей траектории.
Таким образом, в транспортирующей системе координат дви¬
жение начинается из нулевой точки с заданным вектором скорости
и через фиксированный промежуток времени заканчивается в
той же точке с другим заданным вектором скорости. Начальный
и конечный векторы скорости равны разностям между орбиталь¬
ными скоростями планет старта и финиша и скоростями в начале
и в конце транспортирующего эллипса.
Если реактивное ускорение намного превышает возмущения
гравитационного ускорения, то уравнение (5.51) могут быть
упрощены (первое приближение)
i = ахя г] = аи, £ = аг% (5.55)
Полученные уравнения совпадают с уравнениями движения
в бессиловом поле (П.53). Общее решение уравнений вариацион¬
ной задачи (5.53), (5.55) дается формулами (5.30). Постоянные
интегрирования определяются по соотношениям (5.31), где сог¬
ласно краевым условиям (5.54) нужно положить г0 = г± = 0,
v0 = (г (0), л (0), £ (0)), Vx = (| (Т), л (Г), I (Т)). В векторной
форме р = (£, т], Q искомое решение запишется следующим
образом:
а (0 = 6 (р0 + рх) ~ — (2р0 + рх) -jr,
Р (0 — (ро + pi) (2ро + Pi)~f + Ро*. (5.56)
J = ~f~ [?0 (Ро* pi) + pl]«
190 ИДЕАЛЬНЫЙ ДВИГАТЕЛЬ ОГРАНИЧЕННОЙ МОЩНОСТИ [ГЛ
На рис. 5.8 приведен пример оптимальной траектории пере¬
лета в транспортирующей системе координат [5.1]. Расчет про¬
веден по формулам (5.56) для межорбитального перелета Земля-
Марс: дата старта — 27 сентября 1960 г., время движения —
212 сут. Орбиты Земли и Марса
предполагались компланарными
(£ = 0). Краевые условия (5.54)
в этом случае таковы: £ (0) =
= р (0) = g (Г) = т) (Т) = 0,
|(0) =—0,0145, -п (0)= —0,1283,
| (Т) = 0,0769, ц (Т)= -0,1099
(скорости отнесены к орбиталь¬
ной скорости Земли в момент
старта). Из рисунка видно, что
максимальное удаление траек¬
тории от начала транспорти¬
рующей системы координат
(~ 8 млн. км) по сравнению
с радиусом орбиты Земли
(150 млн. км) невелико.
При более точных расчетах,
кроме ускорения от тяги в урав¬
нениях движения, учитываются
линейные члены гравитацион¬
ного ускорения от Солнца (вто¬
рое приближение), вызванные
удалением движущейся точки
от начала транспортирующей
системы координат (5.51).
Уравнения Эйлера для экст¬
ремалей функционала (5.53), выписанные по общим формулам
(5.5), в этом случае будут выглядеть так:
д'Щ ДО) /д*и
их^\дЩЦ “у* - \ШдЦ/ а* гДд
Рмс. 5.8. Вид оптимальной траектории
межорбитального перелета Земля — Марс
в транспортирующей системе координат
(стрелками показано направление движе¬
ния. точками дана разметка по времени
в сутках, полное время Т = 212 cijm).
(5.5 /)
(д*и ДО) , / d2U ДО)
ах+(^1 ау, а,
az = — [(я(0))'2 + (г/(0))2]_3/2
Полученная система линейных’ дифференциальных уравнений
(5.51), (5.57) с коэффициентами (5.52) интегрируется в квадра¬
турах (см. [5.1]).
Точность первого и второго приближений иллюстрируется
табл. 5.4, где приведены некоторые параметры оптимальных тра¬
екторий межорбитальных перелетов Земля — Марс и Земля — Ве¬
нера из [5.1]. В первом и втором столбцах выписаны величины
продолжительности и угловой дальности перелета, затем — зна¬
чения функционала динамической задачи /, начальные а0 и
§2]
ОПТИМАЛЬНЫЙ МЕЖПЛАНЕТНЫЙ ПЕРЕЛЕТ
191
а
ей Ч
К „
я й
VO л
ей &
н >3
С
>*
£
й
с
о
н
о
ч
ф ^
Л й
ф ф
К в
в
3 5
S8.
4 *4»
cd й
й Л
В В
н в
в о
о н
>1
л 3
® 8
£«
оЭ
н ф
а
as
о а
с к
о Я
Н Ф
sa
е о
5
2 а
С С
Ф g
2к
й ф
о й
Н О
a»g
о S
ю с
LO
"СО
ю ^
СЧ
СЧ
о
сч "Ч.
00 ^
о
"ОЭ
\о
, О"
05 ^
оо °
V®
О4'
05 ^
СЧ
СО
Ю
"С-
'гН ^
чг-1
со
СЧ
05
со
сч
Ю
О CN
\0
«■гЧ о\
•г—1
00
СЧ
со
~СО
СО
•>
"Г-1 г.
o'
05
о
тН
сч
о
4f
О
сч
LO
сч
_г
СО
t5-
'T-Н
05 ^
сч
''СО
05 ^
о
сГЧ
со
~05
^ О
00 ^
00
СО ^
СО
"СЧ
05 г.
05
о
05
00
сч
СЧ
СЧ
сч
СЧ
о
со
со
эйвэд — Bimeg
СЧ Я,
О
00 SO
05 ©х
ч 00
Ю
Ч'4 Г"-
сч
о
сч
сч
05^
_Г^
05 ^
СО
~ю
со
Ю
05
ю
СО
t"-
о
СО
ЧГ1
LO
СО
СО
ю
т—1
СЧ
сч
о
чГ
СЧ
BdoHog — Bimog
192 ИДЕАЛЬНЫЙ ДВИГАТЕЛЬ ОГРАНИЧЕННОЙ МОЩНОСТИ [ГЛ. 5
конечные ах величины реактивного ускорения. Для последних трех
параметров даны три значения, полученные соответственно в
первом и втором приближениях и при численном интегрировании
точных уравнений.
Сравнение параметров, собранных в таблице, свидетельствует
о высокой точности метода. Точность возрастает при сокращении
времени перелета, так как в этом случае увеличивается уровень
реактивного ускорения и оптимальная траектория приближается
к траектории импульсного пере¬
лета (которая берется в каче¬
стве транспортирующей). При
увеличении угловой дальности
точность метода падает (см.
рис. 5.9 из [5.1]), такимже обра¬
зом влияет увеличение радиаль¬
ных перемещений. В работе
[5.1] высказывается предполо¬
жение, что точность метода при
расчете траекторий с большими
угловыми дальностями может
быть увеличена, если состав¬
лять транспортирующую траек¬
торию не из одного, а из не¬
скольких эллипсов.
6. Решение краевой задачи
(5.48) — численные результаты.
На рис. 5.10—5.13 даны приме¬
ры перелетов между компланар¬
ными круговыми орбитами r0 = 1 и гг = 1,52 (орбита Земли —
средняя орбита Марса, рис. 5.10—5.12), r0 = 1 и гг = 1,38
(средняя орбита Венеры — орбита Земли, рис. 5.13) [5.4]. На
каждом из рисунков показаны траектория у (х), закон изменения
модуля реактивного ускорения a (t) и годограф аи (ах). На тра¬
ектории и годографе дана разметка по времени с шагом At =
= 0,2. В подписях к рисункам указаны интегральные характе¬
ристики перелетов, а также недостающие для решения задачи
Коши начальные значения аг0 и arctg (аг0/аФ0). Все параметры
безразмерные.
При больших значениях параметра а0 (рис. 5.10) закон a (t)
и годограф ау (ах) напоминают соответствующие зависимости,
имеющие место при плоском .движении в бессиловом поле (см.
(5.30)):
ах = b±xt -f- &2со dy ^2!/• (5.58)
Действительно, чем больше реактивное ускорение, тем мень¬
шую роль играют гравитационные члены в уравнениях движения
Рис. 5.9. Относительная погрешность
в функционале для второго приближения
метода транспортирующей траектории по
сравнению с точным решением в зависимо¬
сти от угловой дальности перелета (мсж-
орбитальные перелеты Земля — Марс
и Земля — Венера).
-]
ОПТИМАЛЬНЫЙ МЕЖПЛАНЕТНЫЙ ПЕРЕЛЕТ
193
Рис. 5.10. Оптимальные перелеты Земля — Марс с уровнем реактивного ускорения,
большим гравитационного (параметры безразмерные)
Кривые 1 Кривые 2
гt = 1,52, а0 = 4, V = о, П = 1,52, а0 = 4, v = — 7,
Tl= 0,880, Ф1 = 0,604, J = 4,561, . Т = 0,920, <р4 = 0,988, J — 5,920,
а о=—7,950, arctg (пг0/аф0) = 1,205, аг0=—0,100, arctg (аг0/аф0) = 0,3о0.
1 3 Механика полета
194 ИДЕАЛЬНЫЙ ДВИГАТЕЛЬ ОГРАНИЧЕННОЙ МОЩНОСТИ [ГЛ
Рис. 5Л1. Оптимальные перелеты Земля — Марс с уровнем реактивного ускорения
порядка гравитационного (параметры безразмерные)
Кривые 1 Кривые 2
гх = 1,52, а0 = 1, v = 0, г! = 1,52, а0 = 1, v = —1,3,
Т = 1,741, фх = 1,312, J = 0,538, ^ Т = 1,947, фх = 1,973, J = 1,053,
аго=— 0,670, arctg (аГ0/афО) = 0,898, аг0 = 1,326, arctg (аго/афо) = — 0,604.
ОПТИМАЛЬНЫЙ МЕЖПЛАНЕТНЫЙ ПЕРЕЛЕТ
195
Рис. 5 12. Оптимальные перелеты Земля — Марс с уровнем реактивного ускорена)
меньшим гравитационного (параметры безразмерные)
Кривые 1 Кривые 2
ri = 1 j 52, а0 = 0,2, v = 0, г, = 1 52 си = 0 О? v — о
Т = 3,478, Ф! = 2,636, J = 0,037, Т = 0,182, Ф1 = *6,9*87, J = 0,004,
( г) = о .о 1 о, arctg (аго/афо) = 0,420, аг0 — 0,001 arctg («го/сфо) = 0,044.
13*
196 ИДЕАЛЬНЫЙ ДВИГАТЕЛЬ ОГРАНИЧЕННОЙ МОЩНОСТИ [ГЛ. 5
Рис. 5.13. Примеры оптимальных перелетов Венера — Земля (параметры безразмерные»
Кривые 1 Кривые 2
тг = 1,38, а о = 1, v = 0, гх = 1,38, а0 = 1, v = 0,82,
Т = 1,492, ф, = 1,196, J = 0,465, Т — 2,140, <рх = 1,298, J = 0,446,
аго=— 0,908, arctg (аг0/афо) = 0,980, а*/’0 = —1,372, arctg (аг0/афо) = 1,588.
ОПТИМАЛЬНЫЙ МЕЖПЛАНЕТНЫЙ ПЕРЕЛЕТ
197
и тем лучше бессиловое поле аппроксимирует центральное. Сог¬
ласно формулам (5.58) график функции а (t) представляет собой
гиперболу, а годограф ау (ах) — прямую линию.
Упомянутое сходство сохраняется вплоть до а0 ~ 1 (рис. 5.11).
При дальнейшем уменьшении реактивного ускорения (рис. 5.12)
оптимальные программы a (t) и аи (ад.) уже существенно отлича¬
ются от (5.58). Траектория движения из кривой с точкой пере¬
гиба превращается в плавную кривую, стремясь в пределе к спи¬
рали. Годограф а,, (ах) переходит в окружность. Это предельное
решение аналогично описанному в пп. 2—3.
Отметим свойство траекторий оптимальных перелетов, свя¬
занное с параметром v. Случай v = 0, согласно (5.14), соответ¬
ствует перелету с незаданным угловым перемещением (см. кри¬
вые 1 на рис. 5.10, 5.11, 5.13 и кривые 7, 2 на рис. 5.12). Такие
перелеты возможны только при определенном (оптимальном)
расположении планет на орбитах; даты оптимальных стартов
повторяются через синодический период. Кроме упомянутой
работы [5.4], данные по перелетам с оптимальным угловым пере¬
мещением содержатся в [5.1, 5.5, 5.12—5.17, 5.25].
При v = 0 и = 1,52 отношение yJT (средняя угловая ско¬
рость перелета) приближенно равно 0,75—0,76 для всех а0 из
изученного диапазона (0,02 <; а0 4). С уменьшением пара¬
метра v средняя угловая скорость увеличивается (рис. 5.14) и
траектория заходит внутрь ближней к центру орбиты (см. тра¬
ектории 2 на рис. 5.10, 5.11), с увеличением v средняя угловая
скорость уменьшается и траектория выходит за внешнюю орбиту
(см. траекторию 2 на рис. 5.13).
Перейдем теперь к обсуждению зависимости функционала
задачи от параметров перелета. Для перелетов с оптимальным
угловым перемещением (v = 0) зависимость функционала J
от времени Г в диапазоне времени, представляющем практический
интерес, близка к зависимости (5.33) для маневра перемещения
между точками покоя в бессиловом поле (см. рис. 5.15 по данным
[5.4, 5.5, 5.12]). Это еще раз свидетельствует о том, что при до¬
статочно малых временах перелета (большой уровень реактивно¬
го ускорения) бессиловое поле является хорошим приближением
для центрального. На рис. 5.16 из [5.20] приведена зависимость
функционала J от параметров Г, фх, найденная при решении за¬
дачи методом функционального скорейшего спуска (см. часть III).
Параметрические расчеты, проведенные в [5.16] методом
Ньютона (см. часть III), выявили интересный тип неединствен¬
ности решения краевой задачи. На рис. 5.17 показан функционал
задачи для перелетов Земля — Марс (с учетом реального движе¬
ния планет) в зависимости от даты старта и продолжительности
перелета. На графике имеются два семейства кривых / и //,
соответствующих двум наиболее выгодным периодам старта
198 ИДЕАЛЬНЫЙ ДВИГАТЕЛЬ ОГРАНИЧЕННОЙ МОЩНОСТИ [ГЛ. 5
(семейство I — январь — апрель 1969 г., семейство II — март—
июль 1971 г.). Точки пересечения кривых двух семейств с рав¬
ными продолжительностями перелета (сентябрь—октябрь 1970 г.)
являются точками неединственности решения краевой задачи
для системы (5.5). В самом деле, в этих точках время Т, началь¬
ные и конечные значения координат и скоростей, а также вели¬
чины функционала совпадают. Пример двух перелетов, идентич¬
ных по этим интегральным характеристикам и отличающихся
Рис. 5.14. Влияние параметра v на среднюю Рис. 5.15. Зависимость функционала J для
угловую скорость ф!/Т и продолжитель- межорбитальных перелетов с оптимальным
ность Т межорбиталыюго перелета (пере- угловым перемещением (v = 0) от времени
лет с орбиты Земли на орбиту Марса — перелета Т. Сплошная кривая — перелет
гх = 1,52, начальное реактивное ускоре- Земля — Марс, орбиты круговые, комп-
ние а0 = 1, параметры безразмерные). лапарные; пунктирная кривая—перемеще¬
ние между точками покоя I = 0,487 в бес¬
силовом поле — нанесена для сравнения;
параметры безразмерные.
траекториями и законами изменения вектора реактивного уско¬
рения, дан на рис. 5.18. Еще один тип неединственности решения
краевой задачи для оптимальных перелетов будет отмечен в
следующем пункте.
Все описанные выше результаты получены при расчетах в
центральном поле. Неучет сил притяжения планет приводит к
относительной ошибке в вычислении функционала порядка
10_3—10"4 (см. [5.4)].
Большую ошибку доставляет пренебрежение эллиптичностью
орбит планет. Это иллюстрируется рис. 5.19 из [5.15, 5.16], где
приведены данные по перелетам между круговой орбитой Земли и
компланарной ей эллиптической орбитой Марса (сплошные кри¬
вые 1 ж 2). Нижняя кривая 1 соответствует достижению самой
выгодной точки эллиптической орбиты Марса, верхняя 2 — самой
невыгодной. Разница между соответствующими значениями функ¬
ционала получается значительной. Расчеты, проводимые для
§ 2]
' ОПТИМАЛЬНЫЙ МЕЖПЛАНЕТНЫЙ ПЕРЕЛЕТ
199
Рис. 5.1C. Зависимость функционала J для межорбитальных перелетов от времени пе-
рслета Т и углового перемещения (pt (перелет Земля — Марс, орбиты круговые компла¬
нарные, параметры безразмерные).
22 26 29 f 4
2 4 6 9 П
m
7 /2 15 /8 20 23 26 31 3 6 9 J2 14 19 22 25 28 31
1 3 5 7 9 1! 1 3 6 8 Ю 12 2 4 6 8 19 12
1969 1970 1971
день
месяц}*
Рне.^5.17. Зависимость функционала J для перелетов с орбиты Земли на орбиту Марса от
даты старта и продолжительности полета (орбиты планет реальные).
200 ИДЕАЛЬНЫЙ ДВИГАТЕЛЬ ОГРАНИЧЕННОЙ МОЩНОСТИ
[ГЛ. 5
средних круговых орбит, дают величины функционала, средние
по отношению к этим двум крайним (см. пунктирную кривую 3
на рис. 5.19).
Рис. 5.18. Пример двух оптимальных
траекторий Земля — Марс, различных
семейств (I и II — см. рис. 5.17), совпада¬
ющих по датам старта и финиша, по на¬
чальной и конечной точкам и по функцио¬
налу задачи. Стрелками показана опти¬
мальная программа вектора реактивного
ускорения, внизу дан масштаб для величи¬
ны ускорения.
300 Т,сут
Рис. 5.19. Влияние эллиптичности орбит
планет на функционал задачи межорбиталь-
ного перелета (перелет Земля — Марс):
1 — перелет в «лучшую» точку эллиптиче¬
ской орбиты Марса, 2 — перелет в «худ¬
шую» точку орбиты Марса, 3 — перелет ме¬
жду средними круговыми орбитами.
Учет некомпланарности орбит слабо влияет на интегральные
характеристики перелетов (см. табл. 5.5 из [5.16], а также данные
[5.14, 5.25]).
Таблица 5.5
Влияние некомпланарности орбит Земли и Марса на функционал задачи
межорбитального перелета (Т = 184 сут)
Дата стар¬
та (1971 г.)
J, м2/сек1
Погрешность
Ji J2 , qq 0/
Дата старта
(1971 г.)
J, м2/сек3
Погрешность
Jl—J? (О,) п/
прос-
тран-
ствен-
ная
траек¬
тория
J1
плос¬
кая
траек¬
тория
J2
прос¬
тран¬
стве н-
ная
траек¬
тория
Ji
плос¬
кая
траек¬
тория
J2
1UU /о
J1
1UU /о
J 1
14 февраля
37,373
37,230
0,38
21 мая
6,406
6,247
2,5
2 марта
27,733
27,597
0,49
6 июня
7,459
7,303
2,1
18 марта
19,931
19,796
0,68
22 июня
10,558
10,413
1,4
3 апреля
13,938
13,798
1,00
8 июля
16,046
15,918
0,80
19 апреля
9,703
9,555
1,5
24 июля
24,395
24,292
0,42
5 мая
7,187
7,032
2,2
9 августа
35,217
36,139
0,22
13 мая
6,576
6,418
2,4
17 августа
43,648
43,584
0,15
2]
ОПТИМАЛЬНЫЙ МЕЖПЛАНЕТНЫЙ ПЕРЕЛЕТ
201
Результаты систематических расчетов оптимальных траекто¬
рий межорбитальных перелетов для различных планет солнечной
системы (Земля — Меркурий, Земля — Венера, Земля — Марс,
Земля — Юпитер, Земля — Сатурн) можно найти в работах [5.13—
5.18, 5.25].
Приведенные в п. 2 и в настоящем пункте данные позволяют
определить параметры оптимального перелета «спутник Земли —
спутник Марса» (без возвращения). С этой целью воспользуемся
аппроксимациями зависимостей J (Т) для маневра набора ну¬
левой энергии с круговой орбиты r() = 1 (рис. 5.6): J (Т) ^
~ (0,895)2/Г и для перелета между круговыми компланарными
орбитами r0 = 1 и гх = 1,52 с незаданным угловым перемещением
(рис. 5.15): J (Т) ^ 12 (0,487)2/Г3 (переменные безразмерные).
Орбиты спутников Земли и Марса будем считать круговыми с
высотой 300 км над поверхностью планет, траекторию перелета —
плоской.
Подставляя в аппроксимационные формулы соответствующие
характерные значения функционала Jй и времени ^ из табл. 5.1
и 5.3, получим:
для разгона у Земли
Полное время перелета Та = Т+х + Тх + Г_2 задано, дата
старта не фиксирована; нужно найти распределение этого вре¬
мени между тремя участками перелета, обеспечивающее минимум
суммарного функционала Ja = J+x -f J\ + /_2. Проделав эту
процедуру, получим следующие выражения для оптимальных
времен Т+ъ Тх, Г_2 и минимального значения функционала Jn:
оптимальное угловое перемещение межорбитального перелета
при этом равно цх [рад] ^ 3,62т. В силу свойства «обратимости»
(5.16) полученные формулы оказываются справедливыми для пере¬
лета «спутник Марса — спутник Земли» (нужно только заменить
Т+1 на Т_х и Г_2 на Т+2).
J+х[м2/сек3] zz 5*102/Т+х[сут],
для межорбитального перелета Земля — Марс
Jx [м2!секъ] ^ 108/(7\ [суш])3,
для торможения у Марса
/_2 [м21секъ] ж 102/Г_2 [супь].
Т+х [суш] = 102т2, Тх [суш] = 2,783 • 102т, Т_2 [супь] =
= Та [cym] — 102 (т2 + 2,783т)
(т = ]/0,922 + 0,691 • 10^Та [суш] - 0,96),
202
ИДЕАЛЬНЫЙ ДВИГАТЕЛЬ ОГРАНИЧЕННОЙ МОЩНОСТИ [ГЛ. 5
7. Межпланетный перелет с возвращением. В задаче межпла¬
нетного перелета с возвращением задаются полное время перелета
Та и время пребывания у планеты назначения момент старта
с исходной орбиты не задается (см. § 2 Приложения). Кинемати¬
ческие параметры элементарных маневров, составляющих меж¬
планетный перелет, по отдельности не определены. Здесь необ¬
ходимо найти оптимальные значения времени движения для ма¬
невров набора нулевой энергии и торможения у планет, а также
времени движения и углового перемещения для прямого и об¬
ратного перелетов между орбитами планет. Выбор оптимальных
значений времен торможения и набора нулевой энергии у планеты
назначения в настоящем изложении не рассматривается (эти
времена входят в фиксированное время Тш), не учитываются также
энергетические затраты на выполнение этих двух маневров. Ор¬
биты планет предполагаются компланарными и круговыми.
Пусть времена набора нулевой энергии и торможения у пла¬
неты старта определены; тогда задача сводится к определению
оптимальных кинематических параметров межорбитального пере¬
лета с возвращением. Здесь заданы начальные и конечные ра¬
диусы и проекции скоростей для прямого и для обратного пере¬
летов; угловые перемещения и времена перелетов заданы не по от¬
дельности, а в сумме1) (см. (П.61),(П. 62)). Чтобы определить опти¬
мальное разбиение суммарного углового перемещения фх + ф2
и суммарного времени 1\ + Г2 между прямым (1) и обратным (2)
перелетами, воспользуемся условием обращения в нуль внеин-
тегральной части первой вариации функционала. Последний в
рассматриваемом случае представляет собой сумму двух инте¬
гралов (5.9), соответствующих прямому и обратному перелетам
Искомые члены первой вариации (5.59) в соответствии с (5.14)
записываются так [5.4]:
т
о
+ (<F + 2Ф7')2] dt
Г (0) =1, ф (0) = 0, г (0) = 0, Ф (0) = 1,
т (Т t) = ?’i, Ф(Т’1)=Ф1,'/' (Tj) = 0, Ф(Т1)= — г I '2
+
т,
(5.59)
о
~ (ф^ + 2фг)2] dt
Г (0) = ГЬ ф (0) = 0, г (0) = 0, ф (0) = гt 3' 2’
г (Г2) = 1, ф (Т2) = ф2> г(Т2) = 0, ф (Т2) = 1 .
б/х + б/2 = —2 (л^бф! + к16Т1 + v2бф2 + Я2бТ2). (5.60)
1) Если задать еще дату старта, то будут определены + Т2, — со2Тг
и ср2 — (о2Т2.
§ 2]
ОПТИМАЛЬНЫЙ МЕЖПЛАНЕТНЫЙ ПЕРЕЛЕТ
203
На заданных суммах (фх + ф2), (Т1 + Т2) условия обращения
в нуль выражения (5.60) будут х)
Равенства (5.61) заведомо соблюдаются, если в качестве об¬
ратного используется перелет, симметричный прямому (см. (5.16));
тогда cpi = ф2, = Т2, J х = /2. Однако, как показано рядом
авторов [5.2, 5.13, 5.15, 5.20, 5.21, 5. 36] при этом не всегда до¬
стигается абсолютный минимум суммы функционалов J\ + /2.
Условия (5.61) могут выполняться и в том случае, когда пря¬
мой и обратный перелеты не симметричны. При решении крае¬
вой задачи (см. (5.13))
с фиксированными параметрами A, v получаются два семейства
интегральных кривых vT (г), г>ф (г), аг (г), аф (г) и, следователь¬
но, две пары значений <рг, Г, т. е. краевая задача (5.62) не обла¬
дает свойством единственности решения. Чтобы проиллюстри¬
ровать этот факт, обратимся к графику v (А,). На рис. 5.20 в коор¬
динатах v, к нанесены линии равного углового перемещения фх
для перелетов между орбитами Земли и Марса [5.20] (зависи¬
мость J (Т) для тех же самых значений фх была показана на
рис. 5.16). Пересечение кривых на рис. 5.20 свидетельствует
о неединственности решения задачи (5.62), т. е. условия опти¬
мального сопряжения (5.61) могут выполняться и для несим¬
метричных траекторий.
Приведем пример несимметричного перелета с возвращением,
дающего выигрыш в функционале по сравнению с симметричным
перелетом на 16%; параметры симметричного перелета: =
= Т2 = 1,88, фх = ф2 2,14, + /2 = 3,80, параметры не¬
симметричного перелета: Тг — 2,41, Т2 = 1,35, фх = 3,14,
Ф2 = 1Д4, Jг + /2 = 3,20. Суммарное время и суммарное угло¬
вое перемещение для обоих перелетов одинаковы: Т1 + Т2 —
(5.61)
г = vr,
v% 1
Vr = <h + 7Г» vr (г<>) - vr0, ur (ri) = vru
VrvФ ч
V<$ — ^ , ^ф(%) — V<pQ, ^ф(?3.) — V(pi
(5.62)
— 3,76, Ф1 + ф2 — 4,28.
x) При заданной дате старта условия (5.61) заменяются на (vx — v2) со2 +
+ (кг — к2) = 0 (см. сноску на стр. 202).
204 ИДЕАЛЬНЫЙ ДВИГАТЕЛЬ ОГРАНИЧЕННОЙ МОЩНОСТИ [ГЛ. О
Оптимальное разбиение между прямым и обратным переле¬
тами заданных суммарных времени и углового перемещения на¬
ходится после решения задачи на минимум суммы J1 + J 2 по
аргументам фх, Тг при фх + ф2 = const, Т1 + Т2 = const. В ра¬
боте [5.17] это проделано для перелета Земля—Марс—Земля в
широком диапазоне параметров. Дальнейшее изложение пункта
будет базироваться на результатах [5.17].
Рис. 5.20. Линии равного углового перемещения ф! в координатах параметров v. к
для межорбитальиых перелетов Земля — Марс.
Процедура отыскания минимума J\ + J 2 проводится в тер¬
минах даты старта с орбиты Земли t0 (отсчитываемой от проти¬
востояния Земли и Марса) и времени перелета «туда» Тх (связь
между tQ и фх дается (5.49), где надо считать Т = Тг). Типичный
пример зависимости суммарного функционала )- /2 от t0 и Тг
при заданных суммарном времени Тх + Т2 = 496 сут и времени
пребывания у планеты назначения = 0 показан на рис. 5.21.
Минимум + /2 в этом примере достигается при t0 = —85 сут,
Тг = 184 суш (см. кривую 3), т. е. и здесь оптимальный перелет
оказывается несимметричным. Влияние распределения времени
Тх + Т2 между прямым 7\ и обратным Т2 перелетами на функцио¬
нал J\ + /2 иллюстрируется рис. 5.22 (время пребывания у Марса
фиксировано Т„ = 0, дата старта в каждой точке оптимальная).
Видно, что симметричные перелеты (771 = Т2 — пунктирная кри¬
вая на рис. 5.22) становятся оптимальными при сокращении сум¬
марного времени Т1 + Т2.
На рис. 5.23 дано оптимальное время прямого перелета
в функции Тг + Т2 при фиксированных значениях Тш. Отрица¬
§2]
ОПТИМАЛЬНЫЙ МЕЖПЛАНЕТНЫЙ ПЕРЕЛЕТ
205
тельные значения Тш введены условно для придания монотонности
соответствующим зависимостям. Чтобы получить действитель¬
ные значения Тш, нужно к Ты <С 0 прибавить синодический пе¬
риод (для Земли и Марса — 780 супь).
Минимизированный по Тг и t0 функционал Jx + /2 приведен
на рис. 5.24 в виде / (7\ + Г2, Тш). Эта зависимость вместе с
Рис. 5.21. Суммарный функционал Jt -f J2 для перелета между орбитами
Земли и Марса с возвращением в зависимости от даты старта t0 (от проти¬
востояния) для различных распределений заданного суммарного времени
Т, + Т2 = 496 сут между прямым г1\ и обратным Т2 перелетами: 1 —
Т! = 152 сут, Т2 = 344 сут; 2 — Т t = 168 cym, Т2 ~ 328 сутп; 3 —
= 184 cym, Т2 = 312 cym; i — Tt = 200 сут, Т2 = 296 сут; 5 —
Т i = 216 сут, То = 280 сут; 0 — Т t = 232 cym, Т2 = 264 сут; 7 — Т i =
=248 cym,T2 = 248 cym (время пребывания в окрестности Марса фикси¬
ровано = 0).
рис. 5.23 является результирующей для задачи оптимизации
межорбитального перелета с возвращением. Нижняя кривая —
огибающая, показанная на рис. 5.24 пунктиром, соответствует
перелетам с незаданным (оптимальным) временем пребывания в
окрестности планеты назначения (vx = v2 = 0).
Перейдем теперь к задаче определения оптимальных времен
набора нулевой энергии Т+1 и торможения у Земли. Прежде
всего можно заключить, что эти времена должны быть равны
между собой. В самом деле, исходная и конечная орбиты спут¬
ников Земли предполагаются идентичными, поэтому энергети¬
ческие затраты на маневр набора нулевой энергии /+1 и маневр
торможения /_г в силу (5.16) выражаются одной и той же
206
ИДЕАЛЬНЫЙ ДВИГАТЕЛЬ ОГРАНИЧЕННОЙ МОЩНОСТИ
[ГЛ. 5
м2/свп3
700
ООО
500
400
300
250
200
150
100
70
60
50
40
30
25
20
15
Ю30 40 5060 80 100 150 200250300 400 Т,,ср
Рис.'5.22. Минимизированные по дате старта значения сум¬
марного функционала Ji для межорбитального переле¬
та Земля — Марс — Земля в зависимости от продолжитель¬
ности прямого перелета 1\ при фиксированных значениях
суммарного времени 7VI- Т2. Интервал по 'Г х-\-Т 2 — 16 суш,
время пребывания у Марса Т^ = 0, пунктирная линия
соответствует симметричным перелетам Т1 = Т2-
Рис. 5.23. Оптимальное время 1\ перелета с орбиты Земли на орбиту Марса в зависи¬
мости от суммарного времени Тх + Т2 прямого и обратного межорбитальных перелетов:
при фиксированных значениях времени Тш пребывания у Марса (к Тш < о нужно прибав¬
лять 780 сут).
Рис. о.24. ^Минимальные значения суммарного функционала Jt 4- J2 (минимум по /0 и Тх)
для межорбиталыюго перелета Земля — Марс — Земля в зависимости от суммарного вре¬
мени т х i- То прямого и обратного перелетов при фиксированных значениях времени Tw
пребывания у Марса (пунктир соответствует перелетам с негаданными Tw, к < 0 нужно
прибавлять 780 сут).
208
ИДЕАЛЬНЫЙ ДВИГАТЕЛЬ ОГРАНИЧЕННОЙ МОЩНОСТИ [ГЛ. 5
функцией J (Т). Эта функция, вычисленная в п.2 (см. рис. 5.6),
монотонная с положительной второй производной. Для таких
функций можно показать, что минимум суммы двух значений
функции при заданной сумме аргументов (т. е. минимум J (7\ц)й-
, , +J(T-T+1) по Т,г)
J+f, М /CCff
достигается, когда аргу¬
менты равны (Г+1 =
= = Ч2Т).
Таким образом, сум¬
марное время, затрачи¬
ваемое на маневры на¬
бора нулевой энергии
и торможения у Земли,
равно 272.1, а суммар¬
ный функционал —2/+1.
Теперь нужно найти ми¬
нимум по Т+1 полного
функционала
Jа = 2J +1 -f- (J г -{- J 2)
(5.63)
при заданном полном
времени перелета
Та=2Т+1+(Т1+Т2)+Т„
(5.64)
(время Тш пребывания
в окрестности Марса
также задано).
Зависимость + /2
от 7\ + Т2 и Та дана
на рис. 5.24, а для
/+1 (7Vi) использована
аппроксимационная формула (в безразмерных переменных; пере¬
ход к размерным величинам осуществляется по табл. 5.1)
левой энергии и торможения у Земли и у Марса
виси мости от продолжительности маневра Т
+1’
в за-
под-
считанный по аппроксимационной формуле (5.65) (точ¬
ками показаны точные значения с рис. 5.6; орбита кру¬
говая с высотой 300 км).
/+1 = 0,3934271
0,9127
(5.65)
которая выведена для случая постоянного тангенциального уско¬
рения (ср. (6.48)). Результаты расчетов по (5.65) весьма близки
к точным, а значит, и к оптимальным (см. рис. 5.6). На рис. 5.25
проведено соответствующее сравнение для 300 км круговой ор¬
биты спутника Земли (эта орбита и используется в дальнейших
расчетах). Там же для оценок нанесена линия, соответствующая
300 км круговой орбите спутника Марса (напомним, что затраты
на маневры торможения и разгона у Марса не учитываются).
2]
ОПТИМАЛЬНЫЙ МЕЖПЛАНЕТНЫЙ ПЕРЕЛЕТ
T+f, сут
Рис. 5.2d. Оптимальное время набора нулевой энергии у Земли
Т+1 (равно времени торможения) в зависимости от су.ммар ого
времени Тх -\- Т2 прямого и обратного перелетов между орбитами
Земли и Марса при фиксированных значениях времени Тш пребы¬
вания у Марса (300 км круговая орбита; к Тш < 0 нужно прибав¬
лять 780 сут, пунктир соответствует незаданному 7'w).
14 Механика полета
210 ИДЕАЛЬНЫЙ ДВИГАТЕЛЬ ОГРАНИЧЕННОЙ МОЩНОСТИ [ТЛ
м2/секв
Рис. 5.27. Полный ! функционал Ja = 2J+j. — Jt -f J2 моьилаын^ы
перелета Земля — Марс — Земля в зависимости от полного времени
полета Та — Tw = 2 T+i -f- Tt + T2 (все время путешествия Тс, за выче¬
том времени пребывания у Марса Тш время Ты фиксировано; кТи<0
нужно прибавлять 780 суш, пунктир соответствует незаданному
ОПТИМАЛЬНЫЕ МАНЕВРЫ УПРАВЛЯЕМЫХ СПУТНИКОВ
211
В точке минимума (5.63) должно выполняться равенство
clj 1 cl (J j J •>) ^
dT\l~ cl{Tl 4- T2) = ’ (5.66)
полученное дифференцированием (5.63) при связи (5.64): 2dT+1 =
= —d (Тл + T2), Т0 — const, Ты = const.
Первый член (5.66) находился дифференцированием (5.65)
= - 370,8Г;ИШ (5.67)
си +1
([/+1] = м2/сек*. [Г+1] = сут, орбита спутника Земли с высотой
300 км). После этого для каждой пары значений Тг -f- и Т^
по уравнению (5.66) находилось оптимальное время Т+1:
Т+i = [-0,2697.10-2 cE^+^jj-°'622f. (5.68)
Здесь производная вычисляется по данным, на основании
которых построен рис. 5.24. Результаты соответствующих рас¬
четов представлены на рис. 5.26. На рис. 5.27 дан итоговый гра¬
фик — полный функционал JG — 2J+1 -j- Jх + /2 межпланет¬
ного перелета Земля — Марс с возвращением в функции време¬
ни Та — = 2Т+1 + Тг + Тг (полное время путешествия Т0
минус время цребывания у Марса Тш) для фиксированных зна¬
чений Тш.
§ 3. ОПТИМАЛЬНЫЕ МАНЕВРЫ УПРАВЛЯЕМЫХ СПУТНИКОВ
С ИДЕАЛЬНЫМ ДВИГАТЕЛЕМ ОГРАНИЧЕННОЙ
МОЩНОСТИ
Здесь собраны решения вариационной задачи (5.2) для сле¬
дующих маневров в окрестности планеты: поворот плоскости кру¬
говой орбиты (п.1), изменение радиуса круговой орбиты (п.2),
одновременное изменение радиуса и угла наклона круговой орби¬
ты (п. 3).
Общей чертой для всех маневров управляемых спутников с
двигателями ограниченной мощности является малость отноше¬
ния реактивного ускорения к гравитационному. Это открывает
возможности для аналитического решения при помощи различ¬
ного рода приближенных методов. Задачи параграфа подобраны
таким образом, чтобы дать представление о наиболее употребитель¬
ных из них.
1. Поворот плоскости круговой орбиты. Определим оптималь¬
ную программу реактивного ускорения для маневра изме¬
нения угла наклона плоскости круговой орбиты спутника (см.
§ 3 Приложения) [5.27]. Тяга направлена перпендикулярно мгно-
14*
212 ИДЕАЛЬНЫЙ ДВИГАТЕЛЬ ОГРАНИЧЕННОЙ МОЩНОСТИ [ГЛ. 5
венной плоскости орбиты (по нормали е = +1 или против нее
е = —1), угол i между исходной и конечной плоскостями (угол
поворота), конечное положение линии узлов и время движения
Т считаются заданными. Для простоты выкладок время Т пола¬
гается кратным целому числу оборотов: Т = 2ns, s = 1, 2, 3, . . .
(все параметры безразмерные — см. (П.2), где г# = г0). На¬
чальная орбита лежит в плоскости экватора (рис. 5.28).
Рассматриваемая вариационная проблема записывается в виде
задачи Майера
Вывод динамических уравнений (5.69) дан в Приложении (см.
(П.94)); последние получены из системы в оскулирующих пере¬
менных в предположении о малости угла поворота i.
Для решения задачи (5.69) используется метод JI. С. Понтря-
гина; следуя процедуре метода, выпишем гамильтонову функцию
и дифференциальные уравнения импульсов
Н = — (ае)2 -[- рхае sin (t — Qi) + р^ае cos (t — Qi),
В записи (5.70) учтено, что импульс, соответствующий миними¬
зируемой фазовой координате J, постоянен. Согласно общепри¬
нятой нормировке он положен равным минус единице.
Управления а же входят в дифференциальные уравнения
(5.69) и гамильтонову функцию (5.70) в виде произведения ае.
Оптимальная программа для этой комбинации управлений дается
выражением (из условия максимума Н)
По отдельности оптимальные управления а и е следующие *):
е = sgn [рх sin (< — Qi) + pm cos (t — Qt)], |
a = Vd/v.sin (f — Qx) + pacos(t — Qi)J. j J
После подстановки оптимального закона (5.71) в уравнения
движения (5.69) и интегрирования до конечного момента Т =
= 2ns получаются значения постоянных ру, рш, удовлетворяю¬
щих заданным граничным условиям из (5.69)
j = [ае)2, J( 0) = 0, /(2ns) = min,
X = ае sin (t — Qi), % (0) = 0, х (2я5) =
о — ае cos(t— Qx), (о(0) = 0, ю (2ns) — i
(a (t) >0, e(t) = Hh 1).
Px = — дН I д% = 0, рш = — дН/дсо = 0.
ае = V2 [рх sin (t — £>х) + рш cos (t — Qj)]. (5.71)
Px — 0, Pa = 2 i/sn.
(5.73)
l) Функция sgn x (знак x) определяется как sgn x = + 1 при x > 0,
sgn x = 0 при x = 0, sgn x = —1 при x 0.
! 3]
ОПТИМАЛЬНЫЕ МАНЕВРЫ УПРАВЛЯЕМЫХ СПУТНИКОВ
13
(5.74)
конечная
орбата
Начальная
орбита
Рис. 5.28. Схема маневра поворота плоскости
круговой орбиты; стрелками показала оптималь¬
ная программа вектора реактивного ускорения.
Тогда
ае = (i/sn) cos (t — Q±),
и величина контрольного функционала J равна
J (Т) = iVsn = 2i2/T (Т = 2ns). (5.75)
Оптимальный закон изменения реактивного ускорения (5.74)
в течение одного оборота
показан на рис. 5.28 и
5.29. Согласно (5.74) мо¬
дуль ускорения достигает
максимума при прохожде¬
нии конечного положения
линии узлов. Дважды за
оборот направление век¬
тора реактивного ускоре¬
ния меняется на обратное
в моменты обращения а (t)
в нуль. Эти точки сдви¬
нуты по углу от точек
максимума на я/2.
Величина контрольного
функционала J оказывает¬
ся не зависящей от поло¬
жения линии узлов конеч¬
ной орбиты (т. е. от угла £2Х). Зависимость функционала от вре¬
мени выполнения маневра такая же, как и для задачи набора мо¬
дуля скорости в бессиловом
поле (см. (5.30) и кривую и
на рис. 5.2). Если вместо
оптимальной программы
реактивного ускорения
(5.74) взять постоянное по
модулю ускорение с теми
же самыми моментами из¬
менения направления ае =
= (j/4s) sgn cos (t —
(пунктир на рис. 5.29, см.
§ 4 гл. 13), то величина
функционала увеличится в
1,23 раза: J = i2n/8s. На¬
помним, что результаты
этого пункта получены в
предположении, что время выполнения маневра кратно целому
числу оборотов Т = 2ns.
2. Переход между компланарными круговыми орбитами. Рас¬
сматриваемая задача является частным случаем задачи о межор-
Рис. 5.29. Оптимальная программа реактивного
ускорения для поворота плоскости круговой
орбиты в центральном поле (ускорение действует
нормально к мгновенной плоскости орбиты: е =
= ± 1, а — модуль ускорения, пунктир — про¬
грамма, взятая для сравнения).
214
ИДЕАЛЬНЫЙ ДВИГАТЕЛЬ ОГРАНИЧЕННОЙ МОЩНОСТИ
[ГЛ. 5
битальном перелете (§ 2, п.2). Здесь фиксированы время движе¬
ния, радиусы начальной и конечной орбит; начальная и конечная
скорости — круговые (см. (П.58)); угловое перемещение не за
дано (v = 0). Конечная орбита считается внешней по отношению
к начальной, заменой (5.16) все резулыаты могут быть пересчи¬
таны для обратного случая.
Если реактивное ускорение мало по сравнению с гравитаци¬
онным, то для этой задачи можно использовать приближенное
решение (5.44), (5.46), (5.47) из п.З предыдущего параграфа.
Согласно этому решению оптимальная программа вектора реак¬
тивного ускорения (5.46), (5.47) такова (при аф^<^1): модуль
ускорения почти постоянен, а направление близко к направле¬
нию скорости (вектор скорости здесь направлен практически по
трансверсали). Величина ускорения аф определяется при помощи
первого соотношения (5.44) из конечного условия г (Т) = гх:
<5-76)
здесь и ниже все параметры безразмерные (см. (П.2) при = г0).
Оптимальная траектория описывается формулами (5.44) с
аф из (5.76). Функционал J приближенно (см. (5.45)) равен
'“(‘-йгУК (5Л7)
Обратим внимание на то, что полученные здесь зависимость
J (Т) и оптимальная программа реактивного ускорения анало¬
гичны таковым для маневра набора модуля скорости в бессиловом
поле (5.32). Такой же вид имеет функция / (Т) для маневра пово¬
рота плоскости орбиты (5.75), хотя программа ускорения (5.74)
там существенно другая.
Несколько слов о точности приведенного решения. Неучтен¬
ная в (5.77) часть функционала J имеет величину (см. (5.45),
(5.47), (5.76))
с 2, 36 (ГгГ—I)3 (ri2 —1) /г 7Яч
J ardt = — да ; (D-78)
о 1
максимальное значение отброшенной компоненты реактивного
ускорения аг таково (см. (5.47), (5.76)):
max ar(t) = ar(T) = ■-Г,Г| (~1)3 ; (5.79)
0<ЦГ 1
невязки краевых условий по радиальной скорости (vr0 = иг1 =
= 0) следующие (см. (5.44), (5.76)):
vr(0)-vro = vr(T)-vr 1= 2Г| (У1г1-1>. (5.80)
1 V *
ОПТИМАЛЬНЫЕ МАНЕВРЫ УПРАВЛЯЕМЫХ СПУТНИКОВ
215
Формулы (5.78) —(5.80) позволяют определить пределы, где
решение (5.44), (5.76) дает нужную точность.
Рассмотрим приближенное решение задачи, основанное на
использовании модели однородного центрального поля (см. § 1
Приложения и (5.34)—(5.37)). Здесь уже не нужно делать пред¬
положения о малости реактивного ускорения, вместо этого тре¬
буется предположить малость радиального перемещения. Общее
решение уравнений вариационной проблемы в однородном цен¬
тральном поле было выписано в § 1 (см. (5.35)—(5.37)). Остается
только подставить соответствующие граничные условия.
До начала и после конца выполнения маневра движение долж¬
но происходить по круговым равновесным орбитам заданных
радиусов. В центральном поле уравнениями этого движения в
плоскости ху будут х (t) = г cos (г"3-2£), у (t) = г sin
?' = const (см. (П.З) при ах = ау = 0). Для модели однородного
центрального поля эти уравнения выглядят несколько иначе:
х (t) = г cos t, у (t) = г sin £, г = const (см. (П.54) при ах =
= а„ = 0). Таким образом, равновесная круговая скорость на
радиусе г в первом случае равна r~1/z, а во втором — г (перемен¬
ные безразмерные).
Согласно сказанному векторы r0, v0, r1? vx из (5.36) в прямо¬
угольной системе координат х, у (рис. П.4) будут иметь компо¬
ненты
1*0 = (г<„ 0), Vo = (0, г0),
1*1 = (/'xcosipi, rxsiiKjpi), 1 (5.81)
Vi = (—7*1 sinфх, ricosqh)..
Здесь считается, что начальная точка лежит на оси Ох. По¬
лярный угол фх по условию задачи не фиксирован, поэтому нужно
выбрать его оптимальное значение из условия минимума функ¬
ционала J.
Все переменные отнесены к своим значениям на круговой ор¬
бите некоторого радиуса i\ (см. (П.2)). На этом радиусе при¬
ближенная величина гравитационного ускорения полагается рав¬
ной истинной. В используемой модели поля гравитационное
ускорение с увеличением радиуса линейно возрастает, а в цен¬
тральном поле — убывает по квадрату радиуса. Некоторая ком¬
пенсация возникающих отсюда ошибок возможна за счет соот¬
ветствующего выбора 7’.: L).
J) При замене г* Г1/'* нужно изменить все безразмерные величины в
соответствии с (5.15); тогда соответствующие размерные величины останутся
без изменения. В работе [5.10] предлагается еще одни метод уточнения ре¬
шения, связанный с численным интегрированием: программа реактивного
ускорения (5.37) подставляется в точные уравнения движения, постоянные
векторы с2, подбираются по] точным краевым условиям.
216 ИДЕАЛЬНЫЙ ДВИГАТЕЛЬ ОГРАНИЧЕННОЙ МОЩНОСТИ [ГЛ. 5
Будем считать для простоты, что время выполнения маневра
кратно периоду обращения по круговой орбите радиуса г/, тогда
из последней формулы (5.37), подставляя в нее (5.81), находим
Отсюда видно, что минимум J по достигается при cos <рх = 1.
Используя это соотношение, запишем выражения для оптимальной
программы реактивного ускорения, оптимальной траектории и
функционала (см. (5.35) —(5.37), (5.81)):
Оптимальная программа реактивного ускорения получилась
такая же, как и в предыдущем решении рассматриваемой задачи:
модуль ускорения постоянен а = Vа1 + я* = 2(гх — г0)/Г, на¬
правление совпадает с трансверсалью ах/ау = —tg t = — tgcp.
Если же вместо граничных условий (5.81) здесь взять обычные
граничные условия для круговых орбит в центральном поле, то
программа реактивного ускорения получится далекой от опти¬
мальной
Сравним функционалы (5.77) и (5.83); первый обозначим через
JW, второй — через/(2). Перепишем/^) в тех же безразмерных
переменных, что и J^ (т. е. в качестве характерных возьмем
значения переменных на исходной орбите, а не на орбите радиу-
Считая гх — 1 = Дг 1, получим с точностью до о (Дг2)
J = ~^r(r\~2r[)rl cos cpi + Го) (Т = 2л5, 5 = 1,2,...). (5.82)
х (t) = j г0 + (гх — г0) cos t — 1l-Tr° sin t.
У (0 = ro + (ri — rn) ~pp~ sin t
- (5.83)
(0<*<Г = 2л5, s = l,2,...),
J (T) = -jr(rl — ro)3.
ax = — (rx — ;•„) sin t, au (t) = — cos t. (5.84)
j(2) = _4_ (n-1)8
т гз
(5.85)
ОПТИМАЛЬНЫЕ МАНЕВРЫ УПРАВЛЯЕМЫХ СПУТНИКОВ
21?
Функционалы при одинаковых r1? Т будут совпадать, если
принять = 2,52. При таком выборе естественно, совпадают
и величины реактивного ускорения (поскольку с№ (t) ^ const
и я(2)(£) = const, см. (5.76) и (5.83)). Формула (5.77) для функ¬
ционала подтверждается в следующем пункте, где она получена
отличным от использованных здесь методом — традиционным
методом линеаризации уравнений движения.
3. Переход между некомпланарными круговыми орбитами
разных радиусов. Заданы радиусы начальной г (0) = 1 и конеч¬
ной г (Т) = гг орбит и угол i между их плоскостями, время дви¬
жения фиксировано, положения линии узлов и точки выхода на
конечную орбиту свободны. Начальная и конечная орбиты счи¬
таются близкими: | i| 1, | гг— 1 | <^ 1 (переменные безразмер¬
ные, в качестве характерных взяты значения соответствующих
параметров на исходной орбите: = г0 в (П.2)).
Для решения задачи используется метод линеаризации в окре¬
стности начального движения [5.28, 5.29]. Выбирается система
координат £, г], £, начало которой движется с равновесной ско¬
ростью по исходной круговой орбите. Координаты £, ц, £ свя¬
заны со сферическими координатами г, ф, 0 (см. рис. П.1) соот¬
ношениями
i ^ — qp, л = г — 1, £ = 0. (5.87)
Используя формулы (П.4), (П.6) перехода к декартовым коор¬
динатам, можно выписать уравнения движения в координатах
£, г), £ и сформулировать соответствующие граничные условия.
Отклонения от начального движения и их производные во все
время движения предполагаются малыми, уравнения движения
линеаризируются, в граничных условиях также сохраняются
только главные члены.
Окончательно вариационная задача записывается следующим
образом (в виде (5.2)):
J ~= а\ -j- а% + а\у J (0) — 0, У (Г) — min,
i = 1(0) = 0, l(T) = opt,
>1 = V, Г] (0) = 0, ц (Т) Г1 — 1,
£=u', S(0) = 0, ?(T)+w*{T) = i\ } (5.88).
и = + 2у, и (0) = 0, г/ (Т) = 3/2 (п - 1),
v = ап Зг) — 2и, v (0) = 0, и (Т) — 0,
гс = — £, w (0) = 0.
Управляющие функции я; (t), а^ (t), ar (t) — компоненты
реактивного ускорения — не ограничены. Конечное значение
фазовой координаты £ свободно; конечные значения фазовых:
218 ИДЕАЛЬНЫЙ ДВИГАТЕЛЬ ОГРАНИЧЕННОЙ МОЩНОСТИ [ГЛ. 5
координат £ и w по отдельности также не заданы — они связаны
условием £2 (Г) + w2 (Т) = i2.
Отметим, что четвертое и последнее уравнения (5.88), описы¬
вающие движение в плоскости, перпендикулярной к исходной
орбите, не зависят от остальных уравнений движения (для дан¬
ного приближения). Обнаружив это обстоятельство, можно вос¬
пользоваться результатами двух предыдущих пунктов и соста¬
вить искомое решение как суперпозицию уже найденных. Однако
здесь изложение будет проведено независимо, с тем чтобы полу¬
чить подтверждение результатов п.2 и продемонстрировать про¬
цедуру метода.
Составим гамильтонову функцию:
Н = — (а| + а- -г ciV) + р%и — Pnv “г РхР + Pu(&i 2 у) +
+ Pv(dn + ЗГ) — 2и) + pw (ап — £) (5.89)
л выпишем дифференциальные; уравнения для импульсов (р\ =
= —дШдх{)\
Р'с* — Р п ~ ^Pi:» Pl, — Pw 1 n
\ (5.90)
Ри = — Р\ + 2А» Рх> ■-= —Ръ — 2Ри, Pw — — Рп- )
Оптимальная программа реактивного ускорения дается соот¬
ношениями (дН/дсц = 0)
= г/2Ри, а* = V2Pu, а; = г/2Рш- (5.91)
Уравнения для импульсов (5.90) интегрируются независимо
от основной системы (5.88), поскольку задача линейная:
р: = clf ри = ocit — 4с2 cos t + ^
+ 4c3sin£ -f Зс5, |
р,- = —6 (cLt —■ ~2 cos t -f- pv = 2 (ci -f c2 sin £ + c3 cos £), (5.92)
+ сз sin t +
p- = 2 (c4 cos t -j- c6 sin £), = — 2 (c4 sin £ — c6 cos £),
где'C1? . . ., сб — шесть неизвестных постоянных интегрирования,
кото])ые определяются из конечных условий (5.88) после реше¬
ния основной системы (5.88) с оптимальной программой ускоре¬
ния (5.91).
В (5.88), как уже отмечалось, часть фазовых координат в кон¬
це движения свободна: выпишем для них соответствующие усло¬
вия трансверсальности. Конечное значение координаты £ не за¬
дано, поэтому соответствующий ей импульс р = при t = Т должен
обращаться в нуль. Отсюда в силу первого уравнения (5.92) мож-
:НО заключить
сг = 0. (5.93)
S 3]
ОПТИМАЛЬНЫЕ МАНЕВРЫ УПРАВЛЯЕМЫХ СПУТНИКОВ
219
Конечные значения С и w лежат на окружности £2 (Г) + w2 (Т) =
= i2, из условия оптимальности вытекает, что вектор импульсов
(Рь Pw) Должен быть направлен по радиусу (нормально к окруж¬
ности), т. е. 1)
R {Т)Ц (Т) = pw (T)/w (Т). (5.94)
Выпишем теперь оптимальный закон изменения компонент
реактивного ускорения по времени, подставив (5.92) в (5.91) и
учтя (5.93):
а^ (t) = — 2со cos t + 2с3 sin* + 3/2 с5, ]
a.n (*) = Со sin t + с3 cos *,
а^ (t) = — с4 sin t + сь cos t.
(5.95)
Функции (5.95) подставляются в правые части уравнений (5.88),
после чего эта система неоднородных линейных уравнений с
постоянными коэффициентами интегрируется:
J (t) ■■— *-/2 (5с2 5с3 4~ 'V0C5 -р
+ 6с3с5 (1 — cos 0 4- V-2 (Зс2
- с\) t — 6с2съ sin t 4-
Зс3 — с\ + cl) sin t cos t —
— (3c*c3 + c4c6) sin21,
I (0 = £2 [8 (1 — cos t) —5* sin*] + c3(llsin *— 5*cos*— 6*)—
— c5 [%*” — 6 (1 — cos *)],
"П (0 = 5/2c2 (sin *— * cos *) — c3 [5/2*sin* — 4 (1 —cos*)] + (5.96)
+ 3c5(sin*— *),
Z (*) = 1/2c4 (* cos * — sin *) 1/2ciit sin *,
и (*) — c2 (3 sin * — 5* cos *) 4- Co [5* sin * — (> (I — cos *)] —
— Сь (''/2t — 6 sin *),
v (0 = ЬЫ c'2t sin * + V2C3 (5* cos * — 3 sin *) — 3c5 (1 — cos *),
w (*) = — 1!2c4t sin * 4- 1/2cQ (sin * 4- t cos *).
Здесь уже учтены нулевые начальные условия (5.88) для всех
фазовых координат. Третье, пятое и шестое конечные условия
(5.88) определяют постоянные с2, с3, съ (движение в плоскости
начальной орбиты), для них получается система линейных ал¬
гебраических уравнений. Четвертое конечное условие (5.88)
и условие трансверсальности (5.94) дают систему двух квадрат¬
ных уравнений относительно постоянных с4 и с6 (движение
в плоскости, перпендикулярной к плоскости начальной орбиты).
Выбираются такие корни этой системы, которые обеспечивают
J (Т) = min.
*).В работе [5.28] вместо условия (5.94) было ошибочно принято р^ (Т) =
— 0; исправленные формулы приведены в [5.29].
220 ИДЕАЛЬНЫЙ ДВИГАТЕЛЬ ОГРАНИЧЕННОЙ МОЩНОСТИ [1Л. ь
Окончательное выражение для постоянных с2, . . ., с6 через
параметры рассматриваемого динамического маневра таково;
2(74 — 1) sin Г — 2(г, —1)(1—cosT) )
Сг~ 16(1—cosjT) —r(5r + 3siiir)’ Сз~ 16 (1 — cos Т) — Т (5Т + 3sin Т)'
У 2 i (I — cos Т) Уз — 1) (ЪТ -|- 3 sin Т)
Ci~ Т -j-1 sin Т | ’ °5'~ 16(1—cos Г)— Т{ЪТ + 3sinZ')’ j
У 2 i sin Т f
Сб— (1 — cos Т) (Т | sin Т | ) !
(при Т = 2лх, s = 1, 2, . . . : с2 = с3 = с4 = 0. съ — (1 — }\)/ЗТ, \
св = 2ЦТ). {
(5.97)
Подставляя (5.97) в первое уравнение (5.96), находим функци¬
онал задачи
. (тд — I)2 (5Т -J- 3 sin Т) 2i*
' ’ 4[Т (5Т -i- 3 sin Т) — 16 (1 — cos Т)] Г| sin Г |
(5.98)
(/(2я5)=^^+-^).
Полученное выражение для функционала состоит из двух не¬
зависимых слагаемых, первое определяется радиусом конечной
орбиты г1? второе — углом наклона ее плоскости i. Эта аддитив¬
ность связана с тем, что в линейном приближении, как уже отме¬
чалось, уравнения движения в плоскости начальной орбиты не
связаны с уравнениями движения в перпендикулярной плоскости.
Сравним функционалы и оптимальные программы реактивного
ускорения, полученные здесь и в пп. 1 и 2. Время выполнения
маневра будем считать кратным периоду движения по начальной
орбите (Т — 2я5, 5=1,2,...). Первое слагаемое функциона¬
ла (5.98) совпадает с У(1) из (5.86), а второе — с (5.75). Оптималь¬
ная программа ускорения (5.95) с коэффициентами из круглых
скобок (5.97) имеет вид
ai(t) = 1Д" ' ari(t) = Q, ax,(t) = cost (5.99)
(Т = 2л5, 5 — 1,2,...).
Если вспомнить, что а; = —а¥, аГ( = аг* то первые два
соотношения (5.99) дадут оптимальную программу (5.76) для ма¬
невра изменения радиуса (с точностью до о (?\ — 1)), а последнее
соотношение — программу (5.74) для маневра изменения угла
наклона плоскости орбиты (при = 0). Таким образом, сложный
маневр изменения радиуса и угла наклона круговой орбиты в
ОПТИМАЛЬНЫЕ ПАРАМЕТРЫ АППАРАТА
221
линейной постановке представлен как суперпозиция двух про¬
стых: маневра изменения радиуса круговой орбиты и маневра
поворота плоскости круговой орбиты.
Помимо описанных выше, в литературе содержится еще ряд
решений для оптимальных маневров управляемых спутников с
идеальным двигателем ограниченной мощности. В работе [5.30]
выписаны дифференциальные уравнения и получены конечные
•соотношения нулевого приближения для оптимальной программы
реактивного ускорения при изменении всех элементов орбиты.
Маневры перехода между круговой и эллиптической компланар¬
ными орбитами разных радиусов, набора заданной энергии и пр.
рассматриваются в [5.31—5.33] на основе метода усреднения
Крылова — Боголюбова. Решение (5.95), (5.96) используется при
исследовании задач оптимальной встречи спутников [5.34] и
оптимальных межпланетных перелетов [5.35].
§ 4. ПАРАМаТРЫ АППАРАТА С ИДЕАЛЬНЫМ ДВИГАТЕЛЕМ
ОГРАНИЧЕННОЙ МОЩНОСТИ
1. Расчетные формулы. Оптимальный режим работы идеаль¬
ного двигателя ограниченной мощности и оптимальные пара¬
метры двигателя и аппарата в целом могут быть вычислены, как
только найдены функции
t
a (t), J{t) = ^a°-dt (5.100)
О
— закон изменения реактивного ускорения и интеграл от квад¬
рата ускорения по времени (см. гл. 4).
Для удобства пользования дадим сводку необходимых формул;
при этом ограничимся случаем одноступенчатого аппарата (без
сброса секций двигательной системы).
Весовые параметры аппарата (G- — полезная нагрузка, G^o —
вес запаса рабочего вещества, Gx — вес двигательной системы,
G (t) — текущий вес аппарата) определяются следующими соот¬
ношениями (см. (4.6), (4.15)—(4.17)):
0_ [>;Г] <7„п [кГ] r Gy [кГ] ,—
=(1 - >ф‘) ' тйат-»'*»- ияят
€ (/) \кГ]
Сп [кГ]
Си [кГ]
С, [Кг\
Ф (0
-1
(фх = Ф(Г). Ф(£) = 0,5-10“3а [к Г j кет] J (t) [м-jceK?]),
(5.101)
где Gq — начальный вес аппарата, а — вес двигательной системы
на единицу мощности реактивной струи.
222
ИД'-АЛЬНЫЙ ДВИГАТЕЛЬ ОГРАНИЧЕННОЙ МОЩНОСТИ [ГЛ. 5
Максимальная мощность двигателя Лгшах и программы тяги
Р (t), скорости истечения V (() и расхода д (t) рассчитываются по
формулам (см. (4.2), (4.4))
Nmax 1квт]
V (t) [м/сек]
q (t) [Г/сек]
(5.102)
Обратим внимание на то, что для вычисления GL, G^, G* до-
ста точно знать только конечное значение функционала J (Т)г
а для вычисления G (t), Р (t), V (t), q (Z) необходимы обе функции
(5.100).
Если маневр разбит на п последовательных этапов и на каж¬
дом этапе функции (5.100) известны: (т), J(i) (т) (0 ^ т Г(П,
/(й (0) = 0 — отсчет времени т и функционала J на каждом
этапе начинается с нуля), то в качестве функций a (t) и J (t).,
фигурирующих в (5.101) и (5.102), нужно брать
а (0 = аС) (t — Т] ти)), ./ (О = S JU) (Т(Л) + J(n (t — S ?’0))
' j=l 3=1 3=1
при У 710' < г < t Ти) (i = 1, . . п, у = 0, S Г(Л = т).
3=1 j=l j=l j=l J
(5.103)
2. Оптимальные параметры межпланетных аппаратов. Чтобы
составить представление о параметрах межпланетных аппаратов,
с идеальными двчгателями ограниченной мощности, воспользу¬
емся результатами решения вариационной задачи о перелете
Земля — Марс — Земля (§ 2, п. 7).
Для каждой пары значений полного времени путешествия Т&
и времени пребывания в окрестности Марса Тш по рис. 5.27 на¬
ходится конечная величина функционала /, после чего при помо¬
щи (5.101) вычисляются GJG0, G^0/G0J GJG0 (удельный вес
двигателя а задается). На рис. 5.30 из [5.17] показана зависимость
максимальной полезной нагрузки GJG0 от времени — Тш.
для различных значений удельного веса а и времени Т<*. Вели¬
чины G[xo/Gq и GyJG0 могут быть найдены из рис. 4.2 по известному
значению G-/G0.
Если задаться каким-либо уровнем полезной нагрузки, то
по рис. 5.30 можно найти соответствующие минимальные времена
путешествия. Такие данные приведены в табл. 5.6 для GJG0 =
= 0,3.
р (t) [*Г] _ я (t) [м/сек-] G (t) [кГ] )
а [кГ/квт] ’ G0 [кГ] ~~ 9,81 G0 [кГ] ’ I
204 Gx [кГ]/Со [кГ] [
а [кГ/квт] Р (/) [иГ]/С0 [кГ] ’ 1
9,81 ТО8 P(t) [кГ]
V (t) [м/сек] 9 )
ОПТИМАЛЬНЫЕ ПАРАМЕТРЫ АППАРАТА
223
Gjc/Gq
Git/Go
а)
6)
Grt/Go
&71>/
*)
Рис. 5.30. Максимальная полезная нагрузка Gn/G0 аппарата Земля — Марс — Земля G
идеальным двигателем ограниченной мсил сети в зависимссти от полного времени полету
Та — Tw при фиксированных значениях удельного веса двигателя а и времени пребыват.
ния у Марса
'224
ИДЕАЛЬНЫЙ ДВИГАТЕЛЬ ОГРАНИЧЕННОЙ МОЩНОСТИ [ГЛ. 5
Таблица 5.6
Минимальные вр?мена Та экспедиции Земля —
Марс — Земля при уровне полезной нагрузки
30 % для различных значений а — удельного
веса двигателя и — времени пребывания
у Марса.
ты,
Т а > c'Jm
сут
а = 0,1
кГ/квт
а - 0,4
кГ/кпт
а = 1
кГЧквт
а = 4
кГ/квт
а = 10
кГ/'квт
0
90
160
255
460
680
48
157
238
326
514
738
96
223
304
383
566
803
144
282
358
440
624
884
Приведем пример оптимальных зависимостей от времени t
■веса, аппарата G (t), тяги Р (t) и скорости истечения V (t). Выбе¬
рем следующие значения параметров перелета: полное время
Риз. 5.31. Траектории гелиоцентрических участков перелета Земля — Марс — Земля
>с параметрами: суммарное время Ta = G44 сут, время пребывания у Марса
Тш = 48 сут (траектории даны в проекции на плоскость эклиптики).
путешествия Та = 644 сут 1,76 года), время пребывания в
окрестности Марса Тш = 48 сут. Воспользуемся расчетами [5.14]
оптимальных гелиоцентрических траекторий, проведенных с
учетом эллиптичности и некомпланарности орбит Марса и Земли
для конкретных дат старта (рис. 5.31). Для большей точности
учтем также энергетические затраты на торможение /_2 и раз¬
гон/^ в окрестности Марса. Последние определяются по рис. 5.25,
причем считается Т_2 = Т+2 = 1/271С0. Сводка параметров эле¬
$ 4] ОПТИМАЛЬНЫЕ ПАРАМЕТРЫ АППАРАТА 225
ментарных маневров, составляющих перелет Земля — Марс —
Земля, дана в табл. 5.7.
Оптимальные весовые соотношения аппарата, предназначен¬
ного для выполнения этого маневра, находятся по формулам
(5.101), они указаны в табл. 5.8.
Таблица 5.7
Параметры оптимального перелета Земля — Марс — Земля
(Та — 044 cyni, = 48 суш) по участкам
Маневр
Дата начата
маневра
Дата
окончания
маневра
Время
выполнения
маневра, суш
Энергетиче¬
ские затраты
J, м2/сек3
(Разгон у Земли
24 марта
12 мая
50
12
1971
1971
Межорбитальный пере¬
13 мая
12 ноября
184
6,6
лет Земля — Марс
1971
1971
Торможение и разгон
13 ноября
30 декабря
48
8
у Марса
1971
1971
Межорбитальный пере¬
31 декабря
7 ноября
312
25
лет Марс — Земля
1971
1972
Торможение у Земли
8 ноября
27 декабря
50
12
1972
1972
Полный перелет Зем¬
24 марта
27 декабря
644
63,6
ля —Марс — Земля
1971
1972
Таблица 5.8
Оптимальное распределение веса аппарата
для перелета Земля — Марс — Земля
(Та = 044 суш, = 48 суш)
при двух значениях удельного веса
двигательной системы
Удельный
вес
двигателя а,
кГ/квт
Полезная
нагрузка
G_/G0
Вес дви¬
гателя
Gx/G0
Вес
рабочего
вещества
G\),b G0
5
10
0,36
0,19
0,24
0,24
0,4
0,57
Программа реактивного ускорения a (t) и зависимость функ¬
ционала от времени J (t) для рассматриваемого перелета приве¬
дены на верхнем графике рис. 5.32. Под ним представлены за¬
висимости G (t)/G0, P(t)/G0 и V (£), посчитанные по формулам
(5.101), (5.102).
Укажем две важные для дальнейшего особенности оптималь¬
ных режимов работы идеальных двигателей на межпланетных
^ 5 Механика полета
226 ИДЕАЛЬНЫЙ ДВИГАТЕЛЬ ОГРАНИЧЕННОЙ МОЩНОСТИ [ГЛ. 5
Рис. 5.32. Пример оптимальных зависимостей: а (1) — реактивное уско¬
рение, J (0 — функционал, G (<) — полный вес, Р (t) — тяга и V (t) —
скорость истечения для перелета Земля — Марс — Земля (Та =644 сут —
суммарное время, Гш = 48 сут = Т-2 + Т+2 — пребывание у Марса,
Т+! — разгон у Земли, Tt — перелет Земля — Марс, Т2 — перелет
Марс — Земля, Т-1 — торможение у Земли).
ОПТИМАЛЬНЫЕ ПАРАМЕТРЫ АППАРАТА
227
траекториях. Во-первых, идеальный двигатель включен на про¬
тяжении всего полета, что определяет потребный ресурс порядка
104 час. Во-вторых, по оптимальной программе необходимо регу¬
лировать тягу, скорость истечения и расход в очень широком
диапазоне (например, на рис. 5.32 Р и V изменяются на порядок).
3. Оптимальные параметры управляемых спутников. Запишем
в размерной форме оптимальные функции (5.100) для следующих
маневров в окрестности планеты (см. § 3).
JtM2/cen3
s-T.cym
Рис. 5.33. Максимальная полезная нагрузка Gn/G0 управляемых спутни
ков с идеальным двигателем ограниченной мощности для маневров изме
пения угла наклона г и радиуса Го-*?’,, круговой орбиты (оси с размет
кой по времени выполнения маневра Т нанесены для 24-часового спутник
Земли: г0 = 42,3 • 103 км, s = Т — число оборотов).
1°. Поворот плоскости круговой орбиты радиуса г0 на угол
i с заданным угловым положением линии узлов (см. (5.74),
(5.75)):
a (t) = йт,,2 -Е- cos (т — Ох),
JTS
J (t) = k3''-r0 —n2S2 It + sin t cos (т — 2Qi)]t (5.104)
2°. Переход между круговыми компланарными орбитами ра¬
диусов г0 и гг (см. (5.76), (5.77)):
а(<) = Ат,/— 1-|/ > J{t) = &'*/•„ (l — |/ ) т»
(5.105)
15*
228
ИДЕАЛЬНЫЙ ДВИГАТЕЛЬ ОГРАНИЧЕННОЙ МОЩНОСТИ
[ГЛ.
Рис. 5.34. Пример оптимальных зависимостей a (t), J (О, G (О» Р (О» V (О для
маневра поворота плоскости круговой орбиты на угол г = 10° с одновременным
изменение радиуса на I (rt /г„) — 11 = 23,6% (24-часовой спутник Земли:
г0 = 42,3-102 км, s = 10, Т = 10 crjm, промежуточные оборот;л 1 < S < 9
показаны условно).
ОПТИМАЛЬНЫЕ ПАРАМЕТРЫ АППАРАТА
229
Зэ. Переход между круговыми орбитами радиусов г0 и г19
плоскости которых составляют между собой угол i (см. (5.96) —
(5.99)):
*(*)=кго2 -k К11^)2+г'2 cos2 т ]'/2>
J (t) = /с3'2Го6/2 2^-г ( r\ir }°' f т + *2 (т + й*п т ^os т) J • (5.106)
В формулах (5.104)—(5.106) время выполнения маневра Т
считается кратным (5=1,2,...) периоду обращения по началь¬
ной орбите: 2яАг1/2Го2; время т безразмерное (0 т 2jts),
связь с размерным временем t такая: t — кг'^г^х. Размерности
остальных величин следующие: [а] = м/сек2, [J] = м2/сек3,
\к] = жъ1сек2 (для Земли к = 0,3986 1015 м*!сек2), [г0] = [гх] =
= м, i и — углы в радианах.
Относительная полезная нагрузка GJG0 снова вычисляется
по формуле (5.101), она показана на рис. 5.33 как функция J и
времени Т для маневров 1°—3°. Кривые посчитаны при фиксиро¬
ванных значениях удельного веса двигателя а. На графике даны
несколько временных масштабов для разных наборов параметров
маневра (г0, £, гг) 24-часового спутника Земли. Примеры зави¬
симостей G (t), Р (t), V (t), отвечающих (5.104)—(5.106), приве¬
дены на рис. 5.34.
По сравнению с рассмотренным выше случаем межпланетного
перелета режим работы идеального двигателя для управляемых
спутников несколько облегчается — для ряда маневров потреб¬
ный диапазон регулирования параметров двигателя получается
довольно узким.
ГЛАВА 6
НЕРЕГУЛИРУЕМЫЕ ДВИГАТЕЛИ — РАЗДЕЛЕНИЕ
ВАРИАЦИОННОЙ ЗАДАЧИ,
ОПТИМАЛЬНЫЕ ПРОГРАММЫ ВЕКТОРА ТЯГИ
Идеальные двигатели являются, в том числе, идеально регу¬
лируемыми; это означает, что их регулировка подчиняется только
главным для рассматриваемого типа двигателей ограничениям
(например, ограничению на мощность (гл. 4 и 5) или на скорость
истечения (гл. 8)).
Решение проблемы оптимизации в такой постановке обычно
приводит к трудно реализуемым законам изменения некоторых
параметров двигателя.
В настоящей главе изучается другая кратность в регулиров¬
ке — нерегулируемые двигатели.
Нерегулируемым называется двигатель, работающий по сле¬
дующей схеме: он может быть либо включен, и тогда тягаР и
расход q постоянны, либо выключен, и тогда тяга Р и расход q
нулевые. На изменение направления тяги ограничнеия не наклады¬
ваются.
Вариационная проблема для нерегулируемых двигателей, так
же как и для идеальных, разделяется на весовую и динамическую
части. Последняя, в отличие от идеального случая, содержит два
параметра двигателя Р и q, но зато является универсальной для
всех типов нерегулируемых двигателей (для ее решения не требу¬
ется знания характеристик (II.9), (11.10)). После установления
этого факта здесь вычисляется функционал динамической части
вариационной проблемы для ряда маневров; даются примеры ре¬
шения весовой части проблемы для нерегулируемых двигателей
ограниченной мощности.
§ 1. РАЗДЕЛЕНИЕ ВАРИАЦИОННОЙ ПРОБЛЕМЫ НА ВЕСОВУЮ
И ДИНАМИЧЕСКУЮ ЧАСТИ
1. Формулировка задачи. Введем релейную функцию б (t),
принимающую значение 1, когда двигатель включен, и значение
0, когда он выключен. Тягу Р (t) и расход q (t) нерегулируемого
двигателя запишем в виде РЬ (t) и qb (t). В этой записи Р, q —
постоянные управляющие параметры, а функция б (t) опре¬
деляет моменты включения и выключения двигателя.
РАЗДЕЛЕНИЕ ВАРИАЦИОННОЙ ПРОБЛЕМЫ
231
Вариационная проблема о доставке максимального полезного
груза записывается в виде (II.8)
Ga = — gq&i Ga (0) = Go — Gx, Ga(T) = шах,
r = v, r (0) = r0, v(T) = vu
v — G + G~ e + R» v(0) = v„, V(7’) = vi
а Л- x
(6.1)
(Pf q = const, 6 (t) = 1 или 0, | e (t) | = 1).
Здесь вес двигателя должен быть выражен через параметры
Р, q: Gx (Р, g). В вариационной задаче (6.1) требуется опреде¬
лить оптимальные программы е (£), б (г) и оптимальные значения
параметров Р, д. Вместо Р, д могут фигурировать другие пара¬
метры двигателя, через которые выражаются первые.
2. Выделение динамической части задачи. Индивидуальные
особенности двигателя, работающего в нерегулируемом режиме,
определяются только функциональной зависимостью Gy. (Р, д).
Для нахождения наилучшего двигателя из нерегулируемых
можно указать прием, позволяющий общую вариационную проб¬
лему разделить на две части: динамическую, в которой не нужно
знание функции Gx (Р, д) и которая вследствие этого является
универсальной, и весовую, в которой нужно знание функции
Gx (Р, д).
Введем новую фазовую координату t}. (t) — текущее время
работы двигателя, определив ее следующими дифференциальными
уравнениями и начальным значением [6.1, 6.2]
^ = б, ^ (0) = 0. (6.2)
Третье уравнение из (6.1) интегрируется
G (t) = G0-Gx (Р, g) - gqt, (0, (6.3)
и полезный вес выражается через параметры Р, g и конечное
время работы двигателя tv. (Т) = Т^ так:
Gn = G0 — Gx (Р, g) — gqTv. (6.4)
Если зафиксировать параметры Р и g, то максимум полезного
веса соответствует минимуму времени Т^.
Заменим в вариационной задаче функционал; пусть теперь
вместо максимума G- ищется минимум Т^ при фиксированных
Р, д. Выделенная вариационная проблема имеет вид (см. (6.3))
^ = 6* М0) = 0, ^(Г) = тт,
1' = v, Г (0) = Го, Г (Т) = п,
«об , ~ /Гкч /тч (Р*^/
Y = yi_fU e + R. v(0) = v0, v(f)=vi
(я0> (i = const, b(t) = i или 0, |е(£)| = 1).
232
ПК РЕГУЛИРУЕМЫЕ ДВИГАТЕЛИ
[ГЛ. 6
В этой записи а0 = gP/G0, ц = gq/G0 — параметры задачи
(начальное ускорение от тяги и относительный расход). Вместо
|ы часто используется скорость истечения V = aj\i. Формальным
предельным переходом ц —> О или V ос получается случай
постоянного реактивного ускорения a (t) = а0.
Вариационная проблема (6.5) представляет собой динамическую
часть общей проблемы; результат ее решения — функция
*V (sP/G0, gq/G0).
При известной функции Т^ (gP/G0, gq/G0) и известной зави¬
симости GK (Р, д) может быть решена заключительная — весо¬
вая — часть вариационной проблемы, найден максимум полез¬
ного веса по параметрам Р, q:
maxGx = max^Gn — Gx(P,q)-gqTv.(-^-, -|^)j. (6.6)
Сделаем несколько замечаний к изложенному.
1°. Можно по-другому выделить из общей вариационной проб¬
лемы часть, не связанную с видом функции G* (Р, д). Если вместо
t[X (t) ввести фазовую координату G (t) — текущий полный вес:
G (t) = GX + Ga (0, (6.7)
то будет достигнут тот же результат. Между функционалами
G (Т) = G1 и t[X (Т) = Т{Х существует очевидная связь:
Gt = G0 — gqT\), или GJGq = 1 — (6-8)
2°. Если из решения вариационной задачи (6.5) следует, что
6 (£) = 1 при 0 t Г, т. е. минимизируемое конечное время
работы двигателя Tv, равно заданному времени выполнения ма¬
невра Г, то постановка (6.5) теряет смысл. В этом случае нужно
либо, отказавшись от выделения динамической части проблемы,
вернуться к постановке (6.1), либо использовать постановку
взаимную (6.5): время Т[Х задано, ищется минимум Т.
Новая вариационная проблема является задачей на макси¬
мальное быстродействие:
4 = в. 4.(0) = О, tv.(T) = Tv., )
)• = v, г (0) = г,,, г (Т) = j'i, Т=min, I
v е + R’ v (°) = V|” v^Т) = Vl | (6-9)
(a0, \i = const, 6 (t) — 1 или 0, | e (£) = 1 |). J
В рамках этой постановки случай б (t) = 1 получается, когда
время Т[Х не фиксируется: (Т) = opt (см. п. 1 § 2).
3°. Если конечное время работы двигателя ограничено (за¬
дан ресурс двигательной системы (см. § 2 гл. 7)), то постановка
§ УРАВНЕНИЯ ОПТИМАЛЬНОЙ ПРОГРАММЫ ВЕКТОРА ТЯГИ 233
вариационной задачи (6.5) можно сохранить; в результате ее
решения получится функция Т[Х (gP/G0, gq/G{)), и дополнитель¬
ное условие выделит связь между gP/G0 и gq/G0:
где т — заданное значение конечного времени работы двигателя.
Решение весовой части проблемы теперь заключается в нахож¬
дении максимума (6.6) при дополнительной связи (6.10).
4°. Весовая компонента Gp — вес баков для рабочего веще¬
ства (см. § 1 гл. 7) может быть учтена в весовой части вариацион¬
ной проблемы, если вместо выражения (6.6) записать следующее:
§ 2. УРАВНЕНИЯ ДЛЯ ОПТИМАЛЬНОЙ ПРОГРАММЫ
ВЕКТОРА ТЯГИ. МОДЕЛЬНЫЕ ЗАДАЧИ
1. Произвольное гравитационное поле. Соотношения, опре¬
деляющие оптимальную программу тяги, выписываются на основе
принципа максимума. Все формулы, за исключением одного
граничного условия, для двух обсуждаемых постановок (6.5) и
(6.9) совпадают. При рассмотрении конкретных маневров в за¬
висимости от первоисточника будет использоваться тот или дру¬
гой вариант упомянутого граничного условия.
Функция Гамильтона динамической части задачи и уравнения
импульсов выглядят так:
Оптимальные соотношения для управляющих функций е (t) и
б (t) находятся из условия абсолютного максимума (6.12) по со¬
ответствующей переменной (так как в обеих задачах ищется мини¬
мум функционала: Т[Х — в (6.5) и Т — в (6.9)).
Оптимальная программа направления тяги получается сле¬
дующей (max Я по е, | е (t) | = 1):
т,, (gPIGn, gq/G0) < т,
(6.10)
шах Grz — max
Рл
)]. (6.11)
н = TV 6 + (lVOj^^ + OvR) + (Pr-v), (6.12)
где
Рг = — OvR), рг> ~ ' Pr- (6.13)
в = VrJPv (Pv = j Рг |)я
(6.14)
релейная управляющая функция б (t), отвечающая за включе¬
ние (б — 1) и выключение (б = 0) двигателя, с учетом (6.14)
234 НЕРЕГУЛИРУЕМЫЕ ДВИГАТЕЛИ [ГЛ. 6
определяется соотношением (max Н по б)
6 "II °р“д^' д-А-+/’»-=<-; <6-15>
[О при А <С0»
особый случай А = 0. А = 0 может иметь место только при pv = 0
(п. 3 настоящего параграфа, подробнее см. [6.3]).
Выпишем граничное условие, отвечающее за функционал
задачи. В постановке (6.5) функционалом является конечное зна¬
чение фазовой координаты t[X (Т); соответствующее граничное
условие есть р^ (Т) < 0 или после нормировки
р* (Т) = -1. (6-16)
В постановке (6.9) функционал — время Т, поэтому гранич¬
ным условием будет Н (Т) 0 или после нормировки
Н(Т) = (pv.(T) + pv(T) + МП-П(ПТ), Т) +
+ Рг (?)• v (Т) = 1. (6.17)
Таким образом, полная система уравнений оптимального дви¬
жения складывается в случае (6.5) из (6.5), (6.13)—(6.16), в слу¬
чае (6.9) - из (6.9), (6.13)—(6.15), (6.17).
Рассмотрим теперь, как в рамках постановки (6.9) получить
оптимальный режим б (t) = 1 (см. замечание 2° в § 1). Пусть
Jjj. (Т) не задано. Тогда по условию оптимальности (Т) = 0.
Производная импульса р,0., согласно (6.13), (6.14), всегда неполо¬
жительна:
^ = -л(т=^)5<0 ПРИ (6.18)
поэтому в данном случае р^ (t) > 0 при 0 t Т и по (6.15)
б (t) ее 1. Последнее условие означает отсутствие выключения
двигателя (Т[х = Т).
Если Т[х < Т, то из (6.15) следует р[Х (Т) < 0, в противном
случае было бы б (£) = 1 и Т[Х = Т.
2. Центральное поле. Уравнения оптимального движения в
центральном гравитационном поле получаются как частный слу¬
чай (6.5), (6.13)—(6.16) или (6.9), (6.13)—(6.15), (6.17) при
Н(г, t) — —/сг/г3.
Для плоского движения в полярных координатах (П.8) они
§ 21 УРАВНЕНИЯ ОПТИМАЛЬНОЙ ПРОГРАММЫ ВЕКТОРА ТЯГИ 235
имеют вид (без краевых условий)
ty, — б ,
г = уг,
<р = v,р/г,
aS
— Pv,
Ср г2 *
/>ср = 0,
Pv„
l’r
г г'1
аоб
р„г =—Рт + р% ,
Pvv — г (Pv^Vr 2pvV^ Р<р)
(б — 1 при Д 0, б = 0 при Д О,
А = г?. + а„ У plr + р\{ 1 — Ц.^)'1).
(6.19)
Здесь все величины безразмерные; в качестве характерных
берутся те же значения, что и в соответствующих разделах главы
5; характерное значение для параметра р — величина, обратная
характерному времени Краевые условия для г, ср, уг, и? за¬
писываются в соответствии с рассматриваемым динамическим ма¬
невром, к ним добавляются условия ^ (0) = 0 и (6.16) в поста¬
новке (6.5) или t[X (0) = 0 и (6.17) в постановке (6.9).
Система (6.19) обладает двумя первыми интегралами: (t) =
= const и Н (t) = const, поскольку угол ф и время t не входят явно
в правые части уравнений.
Укажем преобразования, аналогичные (5.15) и (5.16), которые
сохраняют уравнения (6.19):
преобразование растяжения
f8/*f Г —> 1г, ф—>Ф, Vr-+l-l!*Vr, Уф->/-Д/*Уф,
P^—^l Рг I 12 Pr, P(f>—>1 l2Pcpj Pvr~~> Pvri Pv^—* Pv^i
a{)->l~-a{), p->Z~3/2p;
(6.20)
236
11E PE Г У ЛII РУ Е М ЫЕ Д ЛIIГ АТЕ ЛИ
[ГЛ. 6
преобразование замены знака
tjj, > ^ ф ^ ф? V у> Vyi V(р Еф, 1
/V > /V’ Рт —> Ртч Pq>i Pv.r>Pvr, Ру^ ~> Pvi (6.21)
t —>— t, а()—>а(), р->— p. J
Использование замены (6.21) для пересчета «прямой» траек¬
тории на «обратную», в отличие от § 1 главы 5 здесь затрудни¬
тельно, хотя бы потому, что нужно иметь «прямые» траектории
с отрицательными значениями расхода (р —> — р).
3. Плоскопараллельное поле. Если ускорение от гравита¬
ционных сил положить постоянным (Н (г, t) = const, см. (П.52)),
то система уравнений оптимального движения упрощается. Им¬
пульсы рг и ри выражаются в конечном виде
pr = Ь1? pv = Ь2 — Ь^, (6.22)
где Ьх, Ь2 — постоянные векторы, определяемые из граничных
условий.
Отсюда в соответствии с (6.14) определяется направление тяги
е {t) = . (6.23)
Для одномерных движений (пп. 4, 5), когда тяга может быть
направлена либо по скорости, либо против скорости, последнее
соотношение преобразуется к следующему:
е (t) = sgn (b2 — bxt). (6.24)
Условие переключения (6.15) совместно с уравнением (6.22)
для импульса р7, позволяет сделать заключение о числе пассивных
участков. На пассивном участке выполняются соотношения б (t) =
= 0, рр = const, t[x = const (см. (6.13)), поэтому в начале (t = t±)
и в конце его (t = t2) должно быть pv (£х) = pv (t2) — из условия
Д (tj = А (t2) = 0. Поскольку для плоскопараллельного поля
функция, обратная pv (t), в общем случае двузначная, то на оп¬
тимальной траектории может быть не более одного пассивного
участка [6.1, 6.3].
4. Набор модуля скорости в бессиловом поле. Дифференциаль¬
ные уравнения и краевые условия (6.5) для маневра набора за¬
данного модуля скорости имеют вид (ср. (П.64))
их = б, (0) =■ 0, tlx (Т) = min,
и = е' 11 ^ = и ^ = щ
(а„, р ^ const, б (t) = 1 пли 0, е (t) —- ±1).
(6.25)
§ 2] УРАВНЕНИЯ ОПТИМАЛЬНОЙ ПРОГРАММЫ Ы'.КТО РА ТЯГИ 237
Функция II и уравнения для импульсов здесь таковы:
а^е \ х ^ ^
н = Р|
“ i-к,
рЛт) =
Pv-
(6.26)
Максимум Я по е достигается при е (t) = sgn ри = const,
считая uL О, получаем
e(t) = 1 (ри > 0).
(6.27)
Комбинация Д (см. (6.15)), стоящая множителем при б в функ¬
ции Я, в силу дифференциальных уравнений (6.25), (6.26) по¬
стоянна, поэтому
1 при Д(0)>>0,
А -- ри. "Г Ри Л f
0 при А (0) 0, ^ ^
а о
(6.28)
Второй вариант в (6.28) соответствует тривиальному случаю
их = 0. Остается рассмотреть еще А (0) = 0; здесь функция Я
не будет зависеть от управления б (поскольку А (t) = 0), распо¬
ложение моментов включения и выключения двигателя может
быть произвольно, определяется только суммарная протяженность
активных участков (из условия и (Т) = и1).
Интегрирование уравнения для и из (6.25) при условии (6.27)
дает конечную связь (формула Циолковского)
И1 = —-^-ln(l-iiTV), (6.29)
Г
отсюда можно выразить суммарное время работы двигателя Т^
через параметр маневра их и параметры двигателя а0, ц. Полное
время движения Т не влияет на функционал задачи Т[Х, оно сов¬
падает с Тр при А (0) > 0 и больше Т^ при А (0) = 0. Оконча¬
тельное выражение для функционала Т[Х записывается в виде
*v —И«(1 - V) < т- <*•*»
При отыскании максимума полезного веса по параметрам а0
и р, (что будет проделано в § 5) в оптимальном варианте оказыва¬
ется Т[Х = Т.
5. Перемещение между точками покоя в бессиловом поле.
Дифференциальные уравнения и краевые условия (6.5) для
238 НЕРЕГУЛИРУЕМЫЕ ДВИГАТЕЛИ [ГЛ. 6
перелета между двумя положениями покоя имеют вид (ср. (П.65))
*и = б, ^(0) = 0, (Т) miii, 1
х = и, ж(0) = 0, х(Т) = 1, I
«об \ (6.31);
“=Г=^и(°)=°. «(Г) = 0
(а,., [х = const, 6(f) = l или 0, е (t)=±l).
Уравнения для импульсов рх, ри интегрируются —см. (6.22)’для
^-компоненты. Оптимальное направление тяги (по скорости или
против скорости) определяется соот¬
ношением (6.24). Последнее позво¬
ляет определить знаки постоянных
Ь1? Ь2. В силу (6.24) направление
тяги может меняться на противопо¬
ложное не более одного раза. Гра¬
ничные условия (6.31) для х и и та¬
ковы, что тяга в начале движения
должна быть направлена по скоро¬
сти, а в конце — против скорости.
Отсюда следует, что Ъх > О, Ь2 < О
и что момент где ра обращается
в нуль (Ъ2 — b{t^= 0) лежит внутри
отрезка [0, Г]. На этом основании
соотношения (6.22), (6.24) можно
переписать так:
Рх = *1, Ри = ъ1 (tm — t),e = sgn (tt — t)
(^>0, 0<Ч<Г), (6.32)
т. e. на участке 0 t тяга на¬
правлена по скорости, и на участке
против скорости (рис. 6.1).
Функция Д, определяющая моменты
включения и выключения двигателя
(см. (6.15))} здесь равна
А — Р?. + М — * I Y—\Ht ' (®-33)
Чтобы выяснить характер поведения функции Д, выпишем ее
производную
А ^ — h (~t s£n (*. ~ *) (*=Н.) (6-34>
(при этом выражения для р^ и t[x берутся из соответствующих диф¬
ференциальных уравнений (6.18), (6.31)); отсюда
A (t) < о при о t А (0 > о при t т (6.35)
Рис. 0.1. Характер зависимости
импульса ри от времени и соответ¬
ствующий ему оптимальный закон
е (/) направления тяги (е = 1 — по
скорости, е = —1 — против скоро¬
сти) для задачи перемещения меж¬
ду точками покоя.
{2] УРАВНЕНИЯ ОПТИМАЛЬНОЙ ПРОГРАММЫ ВЕКТОРА ТЯГИ 239
(точка t = tA — угловая). Начальное значение Д (0) должно
быть строго больше нуля, в противном случае, согласно (6.35),
будет либо Д (0 < 0 при 0 < t < Т (целиком пассивное движе¬
ние), либо Д (t) < 0 при 0 < t < и Д (t) > 0 при < f < Г
(один активный участок с е (t) = —1, так как tj. Ив том
и в другом варианте не могут быть удовлетворены конечные усло¬
вия (6.31), следовательно,
Д (0) > 0. (6.36)
Из (6.36) и (6.35) можно зак¬
лючить, что возможны два случая:
первый JS
~ А (0 > 0 при_0j Г (6.37)
(пассивный участок [отсутствует) ги
второй
Д (t) 0 при 0 и ^ ^
Д (t) 0 при tx < t <[ t2 (6.38)
(0 < *1 < *. < *2 <
(пассивный участок в середине тра¬
ектории— при^^^^^ (рис. 6.2)).
Дальше будет рассматриваться
второй случай как более общий:
(6.37) получается из (6.38) при
= t* — ^2*
Отметим, что моменты t±, t2 вы¬
ключения и включения двигателя
расположены симметрично относи¬
тельно t = ^ [6.3]. В самом деле,
Ри. и на пассивном участке постоянны (см. (6.18), (6.31) при
б = 0) и
A (t) =■ pv. (<i) -f Ьх | tm — 11 j ^ при tx < t < to. (6.39)
Отсюда видно, что корни уравнения Д (t) = 0 равноудалены от
Проведенного исследования достаточно, чтобы довести задачу
до конца, не прибегая к интегрированию полной системы урав¬
нений (вместе с уравнениями для импульсов). Примем в качестве
неизвестных постоянных моменты £1? t2 вместо Ьг, tA. Оптималь¬
ные управления е (t), б (г) запишутся так [6.1, 6.3]:
е=-}-1, 6 = 1 при (участок разгона), j
6 = 0 при ti<^t<^t.2 (пассивный участок), I (6.40)
е = — 1, 6 = 1 при ?2<С (участок торможения), j
Рис. 6.2. Поведение функции Д (/)
и соответствующая ей оптимальная
программа Б (/) включения — вык¬
лючения двигателя (8=1 — вклю¬
чено, Б = 0 — выключено) для за¬
дачи перемещения между точ¬
ками покоя.
240
НЕ РЕГУЛИРУЕМЫЕ ДВИГАТЕЛИ
[ГЛ. 6
Соотношения (6.40) подставляются в правые части дифферен¬
циальных уравнений (6.31), последние интегрируются по участкам
с учетом соответствующих краевых условий
и /2 и to
i ^ - h) i Г=Дг +
0 0 о
dt
-о,
to 0 to
или после вычисления интегралов
— И*
^г)-
I
а0
- (6.41)
t\ -]- У — t2 ■— ТIn [1 — [X (^i -{- У — ^2)] — 21n (1 — p^i) = 0,
t\ + ^2 — 2 У1 j I11 (1 — рУх) —
— — ti t2 — Г)1п[1 — (i (t\ + T — to)] + t2 — T = — I.
[X / a 0
(6.42)
Первые два соотношения (6.42) позволяют выразить tx и
t2 через Г,,, Т, ц: t± = [Г1 (1 — ]/1 — p,TV), t2 = Т — Tv, + tv
Отсюда видно, что участок разго¬
на больше по времени, чем уча¬
сток торможения; с уменьшением
расхода ц их разность стремится
к нулю (см. на рис. 6.3 зависи¬
мость tJT^ от fiTV).
Исключив из третьего соотно¬
шения (6.42) t± и t2, получим ис-
. _г , комое выражение TV (ап, к) функ-
Рис. ().,!. Доля П/Гм полного врсме- г 1 и г ' ^
пн работы двигателя1!' приходящаяся ЦИОНала ДИНаМИЧвСКОИ ЧЭСТИ Зада-
на участок разгона, в задаче переме- чи в НвЯВНОМ ВИДв
щепия между точками покоя.
JV
а0
I = -^-(1 - У1 - ц'/V) - ?V — (Т - 2V) 1и У1 - (Д,- (6-43)
§ 3. ОПТИМАЛЬНЫЙ МЕЖПЛАНЕТНЫЙ ПЕРЕЛЕТ
С НЕРЕГУЛИРУЕМЫМИ ДВИГАТЕЛЯМИ
Рассмотрим вариационную задачу (6.5) для межпланетных
перелетов. Хотя формулировка (6.5) или (6.9) универсальна для
всех типов нерегулируемых двигателей, принятые здесь диапа¬
ОПТИМАЛЬНЫЙ МЕЖПЛАНЕТНЫЙ ПЕРЕЛЕТ
241
зоны изменения параметров а0, ц и схема перелета соответствуют
группе двигателей малой тяги. Сначала дается решение для каж¬
дого из элементарных маневров, составляющих межпланетный
перелет (см. §2 Приложениям § 2 гл. 5), а затем для полного ма¬
невра.
1. Набор нулевой энергии. По аналогии с модельной задачей
п. 4 § 2 предполагается, что двигатель включен на всей траекто¬
рии (задача (6.9) при ^ (Т) = opt на максимальное быстродей¬
ствие). Для этого случая уравнения оптимального движения (6.19)
примут вид (6 = 1, t[it = t)
Уравнение для полярного угла <р в (6.44) опущено, поскольку
Ф не входит в правые части уравнений движения и конечное зна¬
чение ф (Т) для рассматриваемого маневра не фиксировано. Дан¬
ное уравнение может быть проинтегрировано отдельно после ре¬
шения задачи.
Перечислим граничные условия для (6.44). Считая начальную
орбиту круговой, примем краевые условия (П.57) для кинемати¬
ческих параметров. Условие оптимальности конечной точки тра¬
ектории требует, чтобы вектор импульсов (pr, pVr, pvJ был кол-
линеарен вектору нормали к поверхности Е (Т) = 0:
Первое соотношение (6.45), как видно из (6.14), означает,
что вектор тяги в конце движения должен быть направлен по
вектору скорости, второе — соответствует равенству нулю про¬
изводной угла у между этими векторами (ср. (5.39)).
Последнее граничное условие исследуемой задачи (6.17) мож¬
но записать в виде (используя (6.45) и Е (Т) = 0)
Задача сводится к интегрированию системы дифференциальных
уравнений шестого порядка (6.44) с тремя начальными и четырьмя
(6.44)
рХт (T)/pVv(T) = IV (Г)Ч(Г), pVr (Т)/Рг(Т) = vr (Т) г2 (Т). (6.45)
Г
(6.46)
1 6 Мехаплка полета
242
IIЕ РЕ ГУЛИРУЕМЫЕ ДВИГАТЕЛИ
[ГЛ.
конечными условиями (П.57), (6.45), (6.46); «лишнее» гранич¬
ное условие служит для определения времени Т. Полученная крае¬
вая задача решается численно по методу Ньютона [6.4, 6.5] (см.
гл. 15). Расчеты проведены в широ¬
ком диапазоне параметров а0, и.
В области больших ускорений
а0 — 1 численное решение близко
к приближенному для а()^> 1,
данному в работе [6.6]. На рис. 6.4
приведен пример оптимального за¬
кона изменения угла у между
вектором тяги и вектором скоро¬
сти при а0 = 0,8, pt = 0; сплошная
кривая соответствует численному
решению [6.4], пунктирная —
приближенному [6.6]. Направлен
ние тяги здесь монотонно при¬
ближается к направлению ско¬
рости.
При малых ускорениях а0 ха¬
рактер оптимальной программы
направления тяги меняется: вектор тяги совершает малые колеба¬
ния относительно вектора скорости с периодом, приблизительно
равным времени одного оборота (рис. 6.5); в конечный момент
времени угол у и его производная у обращаются в нуль (см. (6.45)).
Рис. 6.5. Оптимальная программа 7(0 направления
тяги для маневра набора нулевой энергии с «малой»
тягой (а0 = И)-2, jLi = 0).
Зависимость минимального времени набора нулевой энергии
от ускорения а0 показана на рис. 6.6. Эти данные относятся к слу¬
чаю постоянного реактивного ускорения а (t) = а0, последний
получается формальным предельным переходом к р = 0 в форму¬
лах, записанных для движения с постоянной тягой. В логариф¬
мических координатах приведенная на рис. 6.6 кривая состоит
из двух линейных участков, соответствующих малым и большим
значениям ускорения, и переходного участка, сопрягающего
первые два.
Рис. 6.4. Оптимальная программа из¬
менения угла у (0 между тягой и ско¬
ростью для маневра набора нулевой
энергии с «большой» тягой (а0 = 0,8,
р = 0). Сплошная кривая — численное
решение, пунктирная — приближенное.
ОПТИМАЛЬНЫЙ Ml- жплапетный п КРЕЛЕТ
243
В результате обработки численных результатов найдено приб¬
лиженное аналитическое выражение для функционала зада¬
чи [6.5]
— (1 — 0,8209 ^Т„) Г-1 — ЛЬ (1 — 0,8209 {/7^,)
«О L -й0
= JL(1 - 0,8209 У a, [l - л_ (1 - 0,8209 fT„)] ; (6.47)
за основу бралась формула типа (13.37).
Аналогичные выражения получены в случае тангенциаль¬
ного *) и трансверсального направлений тяги:
для тангенциальной тяги
т = т* ~ w(1 — 0,8082 11—i(1 ~ 0,8082’ (6-48)
для трансверсальной тяги
Т = Ти
1
а0
/О*
I
ю
(1 — 0,7553 Yам) 1 — go" (1 — 0,7555 a0)"j. (6.49)
Формулы (6.47) —(6.49) справедливы для малых значений а0
иц (малая тяга), при а0 10“2 ир <Г 0,25-10-2 относительная
ошибка не превышает 1%,при
а0 <^10“2, р <^0,17-10"2 ошибка
меньше 0,5%, с уменьшением
а0 и р ошибка монотонно убы¬
вает.
Сравнение функционалов
(6.47)—(6.49) позволяет сделать
вывод о том, что для задачи на¬
бора нулевой энергии в цент¬
ральном поле тангенциальное и
трансверсальное направления
тяги дают результаты, близкие
к оптимальному. Относительный
проигрыш по времени при
а0 = 10-2, р = 0 в первом слу¬
чае составляет 0,5%, во втором
~2,5% (см. также [6.10]), с
уменьшением а0 и р проигрыш
уменьшается.
Соотношения (6.47)—(6.49) могут быть использованы и для
маневра торможения в центральном поле, начинающегося в точке
с нулевой энергией Е = 0 и заканчивающегося выходом на
Ю
Ю'2 НГ1 /
Рис. 6.6. Минимальное время набора
нулевой энергии Т = Т^ при постоянном
реактивном ускорении а0 (р = 0, вели¬
чины Т и а0 безразмерные).
2) В работах [6.7—6.9] содержатся подробные результаты расчетов ма¬
невра набора гиперболической скорости с постоянной тангенциально на¬
правленной тягой.
244
Н Е РЕ Г У ЛIIРУ Е М Ь1Е Д В И Г АТЕ ЛII
[ГЛ. 6
круговую орбиту заданного радиуса г0 (начальные значения коор¬
динат и компонент скорости по отдельности не заданы, так же как
и угловое перемещение). Параметры а0 и р при этом вычисляются
по весу аппарата G (Е0) в точке Е = 0: а0 = gk^r^P/G (Е0),
Такой расчет времени «обратного» маневра по формулам, по¬
лученным для «прямого», отличается от точного пересчета с ис¬
пользованием замены (6.21) двумя моментами. Первый: величины
а0 и р в (6.21) должны вычисляться по весу аппарата G (г0) на
конечной орбите: а' = gkrгг* Р/G (гоУ, j р/ | = gkrlf*r^q/G (г0),
второй: расчет «обратного» маневра по (6.21) должен произво¬
диться с отрицательными значениями параметра р/ =— | jut' | (возра¬
стающий вес аппарата).
Однако эти две ошибки компенсируют друг друга. В прибли¬
женном расчете программа реактивного ускорения а (t) =
= а0 (1 — pi)-1 получается симметричной точной программе
а' (t) = а0 [1 — р (Т — t)]"1 относительно середины интервала
[0, Г], поэтому интегральный эффект от обеих программ должен
быть примерно одинаковым (с точностью до гравитационных
потерь). Высказанные качественные соображения подтвержда¬
ются количественным сравнением, проведенным в работе [6.11].
Оказывается, что точность расчета времени «обратного» маневра
по формулам (6.47)—(6.49) такого же порядка, как и для «пря¬
мого» маневра; с уменьшением величин а0 и р точность увеличи¬
вается.
2. Межорбитальный перелет. Построение оптимальных тра¬
екторий перелетов между орбитами планет в центральном поле
Солнца будем производить* в рамках вариационной постановки
(6.9). Уравнения (6.9), (6.13) —(6.15) записываются в полярных
координатах, в качестве независимой переменной вместо времени
t принимается угол ф: dldt = (vjr) d/dy. Полная система уравне¬
ний оптимального движения принимает вид
dtjd^^rju\, t (0) = 0, t (фх) = min, '
V = gk-'l^qlG{E0).
dtv,jdq> = (rjv<p) 6,
dr/d(f = rvr/v ф,
dvr r a06
^ (°) = 0» h (<Pi) = Tp,
r( 0) = 1, r(q>i) = r,,
Ф
(6 = 1 при A 0, 6 = 0 при A 0,
A = p,, + a„ (1 — 1VPir + Plv). ^
ОПТИМАЛЬНЫЙ МЕЖПЛАНЕТНЫЙ ПЕРЕЛЕТ
245
с/ф
dpv
Г
с/ф
— ^ я^6.. лГг,г I n2
(! — "ф ' *Р
Гг „ "Ь
: — — б+
”<P %
* vr 1
Pr Pi) “ 1
г V
(1PV
б/ф
гД
' ^ Я r I * rvr
~ +iPr 1*'
— /V. (1 +
(6.50)
(импульс р/ = —1, так как t не входит в правые части уравнений
и ищется минимум t (фх); условие pt = —1 заменяет здесь (6.17)).
Система (6.50) имеет первый интеграл
Я (ф) = (гА/г;ф) 8 — г/г;ф + prrvr/vv + А,,. (уф — 1/гУф) — р^иг =
= А (0) 6 (0) — 1 = 7'/*А (фх) 8 (фх) — rx = const. (6.51)
Предельный случай — Т (отсутствие выключений двига¬
теля), как было установлено в п. 1 § 2, получается при р^ (фх) = 0;
в обычной ситуации (7\х Т) —
— Pv. (<Pi) < 0.
Результаты численного реше¬
ния краевой задачи (6.50) для
межорбитальных перелетов Зем¬
ля — Марс и Марс — Земля по¬
казаны на рис. 6.7—6.9. Эти дан¬
ные получены в работе [6.12] ме¬
тодом Ньютона (угловое переме¬
щение оптимальное — Я (фх) =
= 0, рис. 6.7).
В рассмотренном диапазоне па¬
раметров оптимальная траектория,
как и для задачи о перемещении
между точками покоя (6.40), состо¬
ит из начального активного участ¬
ка (протяженностью £х), промежу¬
точного пассивного участка (протя-
150
200
250 Тп оу/г?
Рис. 6.7. Оптимальное угловое переме¬
щение q>j межорбиталыюго перелета
Земля — Марс с нерегулируемым дви¬
гателем (сплошные линии а0 = 10-4 g,
V = 100 км/сек, 20 км/сек) и с идеаль¬
ным двигателем ограниченной мощно¬
сти (пунктирная линия).
женностыо Т — Т^) и конечного
активного участка (протяженностью Т^ — tx). Оптимальное рас¬
пределение времени между этими тремя участка mi показано на
рис. 6.8; области, охватываемые нижними и верхними ветвями
кривых, соответствуют времени пассивного полета. Из рисунка
видно, что при сокращении времени полета Т для фиксирован¬
ных значений параметров а0 и V время пассивного движения
246 НЕРЕГУЛИРУЕМЫЕ ДВИГАТЕЛИ [ГЛ. 6
Т — T[h уменьшается, обращаясь в нуль в крайних левых точках
кривых. Дальнейшее сокращение времени полета при этих зна¬
чениях а0 и V невозможно.
t,cym
а) Ту сут
£,сугр
б) Т’сУт
Рис. 6.8. Распределение полного времени
Т между пассивным и активными участ¬
ками для межорбитальных перелетов: it,
— tx — первый и второй активный уча¬
стки, т — Тjj, — пассивный участок.Сплош¬
ные кривые —V — 20 км/сек, пунктир¬
ные — V = 100 км/сек, ф! = opt. а) Зем¬
ля — Марс, б) Марс — Земля.
О 80 /60 240 320
а) Ту сут
Ти,сут
6) Т’сут
Рис. G.9. Минимальное время работы
двигателя 2’^в зависимости от началь¬
ного ускорения а„, скорости истечения
V и полного времени Т межорбиталь-
ного перелета: Фх = opt, сплошные
кривые —V = 20 км/сек, пунктирные—
у = 100 км/сек. а) Земля — Марс,
б) Марс — Земля.
Результирующая для динамической части задачи зависимость
(aoi V* Т) дана на рис. 6.9. Аналогичные данные получены в
работе [6.13]. Построение оптимальных траекторий межорбиталь¬
ных перелетов с нерегулируемыми двигателями производится
ОПТИМАЛЫ1ЫГ1 me жпланетный пе ре л ет
247
также и прямыми методами [6.14]. Данные по оптимальным тра¬
екториям с постоянным реактивным ускорением содержатся в ра¬
ботах [6.15—6.20]. В некоторых работах (например, [6.18—6.20])
при проведении расчетов с постоянной тягой функционалом зада¬
чи считался интеграл (4.11). Подобная замена при решении весо¬
вой части задачи приводит к существенным ошибкам (см. при¬
мечание к переводу [6.20]).
На основании результатов п. 1 и настоящего пункта можно
рассчитать оптимальные параметры перелета «спутник Земли —
спутник Марса» без возвращения (или перелета «спутник Марса —
спутник Земли»). Проделаем это для перелета с 300-ot круговой
орбиты спутника Земли на 300-км круговую орбиту спутника
Марса. Орбиты планет будем считать круговыми и компланар¬
ными, траекторию перелета — плоской.
Решение динамической части задачи для участков разгона у
Земли 7V>+1 = / (а^\ F, Тг1) и торможения у Марса Т{х>_2 =
= / (а&\ F, Т_2) дается формулой (6.47) или в размерном виде
(рис. 6.10):
т I [суш] = Т+х\ cym ] ^ (1 — 0,084 тЛ^1* [10-4g] ) X
V [1° %]
т 1 k'/'"l = T-i\cym\ х —(l —0,109 jV [10"4g|) X
а. ГЮ'"4^! v f !
1,688— ^ _ 0Д09 уago [10-4g])
[км/сек]
Для межорбитального участка перелета Земля — Марс Т^г =
= / (а^2), F, Тг) приведено на рис. 6.9, а.
Стыковка участков по начальному реактивному ускорению
&q2\ aW производится из условия постоянства тяги Р и
скорости истечения V и условия непрерывности массы
,Ч),4Л-4-, «Г’ЦО-^]
«Г |io-4g]
1 — 8,48.КггаО-1) [iQ-4„] r(*-D [Cym}/V [км/сек]
(.%? = а,, = Г= Т,л, Tf = ТхЛ, Tf = Т7,,.-2 = г_г).
Результаты соответствующих расчетов показаны на рис. 6.11, 6.12.
3. Межпланетный перелет с возвращением. Рассмотрим пере¬
лет Земля — Марс — Земля с нерегулируемым двигателем [6.11].
Так же как и в § 2 главы 5, орбиты планет считаются компланар¬
ными и круговыми; на каждом характерном участке учитывается
влияние только преобладающего гравитационного центра; сты¬
ковка участков по кинематическим параметрам траектории не
248
НЕРЕГУЛИРУЕМЫЕ ДВИГАТЕЛИ
[ГЛ. и
производится. Дополнительно к этому предполагается, что тор¬
можение в окрестности Земли осуществляется аэродинамическими
силами; время выполнения этого маневра и соответствующие ве¬
совые затраты в расчет не принимаются х). Затраты топлива и вре¬
мени на торможение (Г_2) и разгон (Т+2) у Марса, в отличие от
§ 2 главы 5, учитываются. Орбиты спутников Земли и Марса
взяты круговыми с высотой над поверхностью 300 км.
Т,сут
Рис. 6.10. Минимальное время разгона п торможе¬
ния у Земли (кривые 1) и у Марса (кривые 2) —
круговая орбита с высотой 300 км.
Задаются тяга, расход и суммарное время работы двигателя^
ищется минимум суммарного времени путешествия. Время пас¬
сивного движения по орбите спутника Марса (время ожидания
Т0) выбирается оптимальным; дата старта не фиксирована.
Участки разгона и торможения в окрестности планет рассчи¬
тывались по конечной формуле (6.47). На этих участках двига¬
тель работает без выключения. Соответствующие размерные
значения времени Т в функции а0 и V приведены на рис. 6.10.
На межорбитальных участках решалась краевая задача (6.50)
модифицированным методом Ньютона (см. гл. 15).
Безразмерные параметры р,(й и а(о) для i-то элементарного ма¬
невра определяются из условия постоянства физических
*) В заключение проведено сравнение со случаем, когда торможение у
Земли производится с помощью двигателя.
Рис. 6.11. Минимальное время работы двигателя Т^а для перелета с ЗОО-ял* орбиты
спутника Земли на ЗОО-kjvi орбиту спутника Марса в зависимости от времени движения
То при различных значениях начального ускорения от тяги а0 и скорости истечения У.
500 Тб, су/п
Рис. 6.12. Оптимальное распределение
полного времени движения Та (сплошные
кривые) и суммарного времени работы
Двигателя Г^0 (пунктирные кривые) между
участками разгона у Земли (Г-и=
межорбитального перелета Земля — Марс
(Ть Грд) и торможения у Марса (Т_2 =
= Тп
2).
250 НЕРЕГУЛИРУЕМЫЕ ДВИГАТЕЛИ [ГЛ. 6
параметров — тяги Р и расхода q и условия непрерывности массы:
1*(,) = L Г..Г- ' ’ ао = а;
(iyn
(6.52)
i-i ’ и 11 ’
1_ц(« 2 Д/ДЕЕ' 1 *
й=1
c^ = gPlG^\
Здесь для сокращения записи элементарные маневры, состав¬
ляющие межпланетный перелет, занумерованы (верхние индек¬
сы) в порядке их следования (соответствие между старыми ин¬
дексами и новыми таково: +1 <-»i = l,l«-»j = 2, —2 i = 3,
+ 2 i = 4, 2.<->?: = 5). Характерные значения времени ^г),
скорости г/г) и ускорения (размерные величины) берутся из
табл. 5.1 и 5.3 (причем v{*} = i/4)). Отсчет времени на
каждом участке начинается с нуля.
Расчет полного перелета производился по следующей схеме.
Задаются параметры а»К jx(L) и суммарное время работы двига¬
теля Т^а. По формуле (6.47) находится время набора нулевой
энергии у Земли
= Г,,+1 = Д (о£\ Е1')- (6.53)
Задаются угол <pL и время работы двигателя Т[П для перелета
Земля — Марс; решается краевая задача (6.50), в результате
чего определяется время перелета
T-i = Д (4г\ Е27 Ф1. Т.,г). (6.54)
По формуле (6.47) вычисляются времена торможения Г_2
и разгона Г+2 У Марса
7-а = Г*,-* = Д (а?\ Г+2 = ^,,.4-2 = Д («о\ И(4)). (6.55)
Задается угол ф2 перелета Марс — Земля; время работы двига¬
теля вычисляется как разность
Т|j.2 = ТlJiG — (Тр. +1 -j- Т-f- Тjj,t—2 + Т^,+2)5 (6.56)
в результате решения краевой задачи (6.50) находится время
т, = Д (а(?\ ф2, Д,2). (6.57)
Из условия (П.60) равенства угловых перемещений Земли
и аппарата в конце перелета Марс — Земля находится время
ожидания на орбите спутника Марса
=i(o1 (о2 0>l (^1 ~Ь ^2) (С°1 С°2) (^-:2+75 2) + 2Л5] 0
(6.58)
ОПТИМАЛЕН ЫЙ МЕЖПЛАНЕТНЫЙ ПЕРЕЛЕТ
251
(0)^0,19968 • 10_6 сек1, со2—-0,10615* 10'G сек 1 — средние угловые
скорости движения Земли и Марса, время размерное [Т] = сек,
углы ф1? ф2 — в радианах, s = 0, 1, 2 . . . выбирается таким,
чтобы Т0 было минимально возможным неотрицательным числом).
В заключение отыскиваются оптимальные значения углов
ф1? ф2 и времени Т,у1. обеспечивающие абсолютный минимум сум¬
мы времен Т1 + Г_2 + Т i + Т2 д- Т().
Для каждой пары значений а\}\ р(1) расчет начинается со
случая незаданного времени работы двигателя (б = 1). При этом
в задаче (6.50) условие С. (ф}) — Tv. заменяется на р{), (ф^ = 0,
минимум суммарного времени перелета ищется только по фх, ф2.
В результате определяется минимально возможное для данных
а\\] и fi(l) время движения Т- {а[}\ р/г)). После этого производит¬
ся расчет при заданном времени работы двигателя 7\ха Та.
Результаты расчетов представлены на рис. 6.13—6.16. На
рис. 6.13 показаны примеры оптимальных траекторий межорби-
тальных перелетов, (/грелки указывают направление вектора тяги,
пунктирными линиями показаны пассивные участки траектории.
Примеры а)—в) соответствуют минимальновозможному для данных
значений а , V времени перелета — траектории без пассивных
участков. На траекториях перелета большей продолжительности
при тех же значениях начального ускорения а0 и скорости исте¬
чения V появляются пассивные участки — пример г).
Межорбитальные траектории перелетов Земля — Марс и
Марс — Земля получаются несимметричными. Это иллюстриру¬
ется рис. 6.14, где даны оптимальные угловые перемещения
фх (а0, Т0) и ф2 (а0, ТС) перелетов в одну и в другую стороны без
выключения двигателя, оптимальное время ожидания получа¬
лось Г0 = 0.
Распределение полного времени Tz по всем участкам для дви¬
жения без выключений показано на рис. 6.15 (разгон у Земли
— Т х, межорбитальный перелет Земля —Марс — 7\, торможение
и разгон у Марса — Г_2 + ТС 2, межорбитальный перелет Марс —
Земля — Г2).
Зависимость минимального суммарного времени перелета 7\
от параметров а0, Г дана на рис. 6.16. Сплошные кривые отно¬
сятся к случаю аэродинамического торможения при возвраще¬
нии на Землю, пунктирные — к случаю торможения при помощи
двигателя. Последние получены следующим образом. После рас¬
чета оптимальной траектории с аэродинамическим торможением,
по формуле (6.47) вычислялось дополнительное время T_i =
— /С (а(06), р,(6)), потребное для торможения двигателем. Распре¬
деление времени между остальными участками не менялось, най¬
денное время Т-i прибавлялось к полному времени движения и
полному времени работы двигателя.
ОПТИМАЛЬНЫЙ МЕЖПЛАНЕТНЫЙ ПЕРЕЛЕТ
253
Рис. 6.14. Угловые перемещения «прямого»
<Р! и «обратного» ф2 перелетов между орби¬
тами Земли и Марса в зависимости от полного
времени движения Тв при фиксированных
значениях начального ускорения а0 (двигатель
работает без выключений Т^9 = Т0, торможе¬
ние у Земли аэродинамическое).
Тв,сут
600
600
400
200
/ J
/
,уа°
' \
=0,5-10'
1(Г%-
20
.— 2.
'‘501
-- --
Тд, cyrn
50 /ОО 150 V, км/сек
Рис. 6.15. Оптимальное распределение пол¬
ного времени Та перелета Земля — Марс —
Земля между участками: Т+разгон у Зем¬
ли, тх — межорбитальный перелет Земля —
Марс, T-г -f Т+2 — торможение и разгон
у Марса, То —межорбитальный перелет
Марс — Земля (двигатель на всех участках
работает без выключений T^j = Tj, тормо¬
жение у Земли аэродинамическое).
Рис. 6.16. Минимально возможное вре¬
мя Та перелета Земля — Марс — Зем¬
ля в зависимости от начального реак¬
тивного ускорения а0 и скорости [исте¬
чения V. Сплошные кривые — аэроди¬
намическое торможение у Земли, пунк¬
тирные — торможение двигателем (дви¬
гатель работает без выключений]
[
= та).
254
II10 PI О P У ЛIIР У Е МI >1Е Д В И ГА Т Г ЛII
[ГЛ.
§ 4. ОПТИМАЛЬНЫЕ МАНЕВРЫ УПРАВЛЯЕМЫХ СПУТНИКОВ
С НЕРЕГУЛИРУЕМЫМИ ДВИГАТЕЛЯМИ
В настоящем параграфе дается решение динамической задачи
для следующих маневров в окрестности планеты: удержание спут¬
ника в заданном шаровом слое (п. 1), поворот плоскости круговой
орбиты (п. 2). Последний маневр уже рассматривался для слу¬
чая идеального двигателя ограниченной мощности (§ 3 гл. 5).
1. Удержание спутника в заданном шаровом слое. В течение
s оборотов спутник не должен покидать шаровой слой, максималь¬
ный гшах и минимальный ririitl, радиусы которого заданы. Будем
считать, что в начальный момент спутник выводится на круговую
орбиту, лежащую посредине заданного слоя (см. § 3 Приложения):
1 + max (t) < тIiaix? 1 + min £<l> (t) > rmin, где max £(1)
min £Я) (г) — амплитуда колебаний радиуса на первом обороте.
Под действием силы сопротивления атмосферы спутник будет
снижаться и на п-ш обороте перейдет нижнюю границу слоя. Сле¬
довательно, не позже чем на п-м обороте должен включиться дви¬
гатель.
Потребуем, чтобы двигатель работал в периодическом режиме:
в течение (т — 1)-го оборота движение пассивное, на т-м обороте
(последнем обороте периода, 1 ^ т п) двигатель включается:
точки включения и выключения, продолжительность работы дви¬
гателя, закон ориентации вектора тяги на всех активных оборо¬
тах одинаковы.
Препятствием к построению периодического закона управле¬
ния двигателем является присутствие в уравнениях движения
(П.83), во-первых, монотонной функции времени G (t) и, во-вто¬
рых, долгопериодических осцилляционных членов в формуле
плотности р.
Можно построить желаемую периодическую программу управ¬
ления, считая вес G постоянным: G (t) = const и пренебрегая
долгопериодическими членами в выражении р (£), а затем прове¬
рить условия сохранения орбиты в заданном слое на протяжении
какого-то установленного времени. Невыполнение условий со¬
хранения орбиты будет указывать на необходимость введения
дополнительного активного оборота для коррекции. В пользу
такого подхода говорит еще один факт: закон плотности, прини¬
маемый в расчетах, не точен, движение в реальной атмосфере
может отличаться от идеализированного настолько, что потребу¬
ется коррекция орбиты. Эта коррекция заодно исправит отме¬
ченные вышезагрубления, тем более, что они весьма незначительны.
Периодический режим работы двигателя возможен лишь при
повторении через каждые т оборотов значений параметров 5,
5, Л, т. е.
Ъ,г = О, 1т = 0, rjTO = 0. (6.59)
оптимальный маневры управляемых спутников
Именно эти параметры отвечают за пребывание орбиты в за¬
данном слое, в частности, они определяют амплитуду колебания
радиуса на обороте: max (t) — min |('м) (t). На остальные пара¬
метры движения (г), 0, 0) пребывание в заданном слое не накла¬
дывает ограничений, поэтому условия повторяемости для них
отсутствуют.
Вариационная проблема для рассматриваемого маневра, вы¬
полняемого аппаратом с нерегулируемым двигателем, формули¬
руется в терминах интегральных выражений следующим обра¬
зом: требуется указать оптимальные законы е? (t), er (t), б (t)
(ео =+ У1 — ^ — е*), доставляющие минимум интегральному
функционалу:
— времени работы двигателя за период т оборотов (причем пер¬
вые т — 1 оборотов спутник движется пассивно, двигатель вклю¬
чается на т-м обороте) при соблюдении условий периодичности
(здесь параметры х, а0 и плотность р безразмерные — см. § 3
Приложения).
Плотность р есть известная функция времени t, радиуса г,}
и некоторых углов; поэтому интегралы
известны, если указаны радиус г0, эти углы и число оборотов т.
(6.60)
о
(см. (П.74), (6.59))
2х (1 — 2jz cos i) ^ pcos tdt — a(){2 ^ ejb cos t -j-
2x (1—2/2cosi) p sin tdt — a0 (2 ^ <?фб si ntdt— > (6.61)
<»
о
о
0
0
256
НЕРЕГУЛИРУЕМЫЕ ДВИГАТЕЛИ
[ГЛ. 13
Последнее равенство из (6.61) при учете дифференциальной
связи: tv. = б может быть записано так:
Правая часть выражения (6.63) — известная величина, в
нем пределе интеграла) и управляющая функция еф (t). Управле¬
ние еф (t) должно быть выбрано так, чтобы верхний предел №
был минимальным. Таким образом, задача о нахождении опти¬
мального закона еф (t) выделяется из вариационной проблемы
(6.60), (6.61); учитывая естественное ограничение | еф (t) | ^ 1,
получаем оптимальный закон:
(время работы двигателя не может превышать время движения);
отсюда следует ограничение снизу на ускорение а0
Как уже указывалось, закон изменения релейного управления
участков на обороте, момент начала и продолжительность каж¬
дого из них должны выбираться так, чтобы выполнялись три
интегральных условия (6.61) (последнее условие из (6.61) совпа¬
дает с (6.66)).
Первые два равенства (6.61) при учете (6.64), (6.65) и с обоз¬
начениями (6.62), (6.66) имеют вид
:(т)
!J*
(6.63)
О
левой части фигурируют контрольный функционал (в верх-
и, следовательно,
е<р (t) — 1
er (t) = 0, ее (t) = 0.
(6.64)
(6.65)
Минимальное значение функционала находится из (6.63);
оно не зависит от управления б (t):
^m) — х (1 — 2jz cos i) 2лтк0/а0. (6.66)
Отметим ограничение на время t^:
(6.66)
(6.67)
ао > х (1 — 2/z cos i) тк0.
(6.68)
5 (t) не влияет на функционал (см. (6.66)); число активных
о
(6.69)
О
О
§ 4] ОПТИМАЛЬНЫЕ МАНЕВРЫ УПРАВЛЯЕМЫХ СПУТНИКОВ 257
(интегрирование производится по активному обороту: 2л (т — 1)<;
t ^ 2пт\ так как подынтегральное выражение не зависит от
7/г, то можно интегрировать по промежутку 0 ^ t 2я).
Для простоты предположим, что на обороте имеются только
два активных участка
6 = 1 при t £2 и ПРИ h * <С ^4* (6.70)
Тогда для выполнения условий (6.69) должно быть
t'2 Т" ^1 * ^2 I ^4 + • ^4 ^3 1 1
COS jz Sin —73 h COS rr— Sin —= = -JT- J ,
Z Z Z Z Z lJj Ao I /p ryi v
i) -j- ^1 • ^2 — ^1 r • ^4 ~j~ ^3 • ^4 — ^3 1 /'771') Vi I
sm sin h sm sill ±"2-J = 4 ~yy J
и, кроме того, сумма продолжительностей активных участков на
обороте равна t^:
ti-h + h-t3 = t™. (6.72)
Итого для четырех неизвестных tv t2, t3, имеются три
уравнения: (6.71), (6.72); один из
неизвестных моментов времени не
определен.
Если р (t) == 1, то Х0 = 1,
= vx = 0 и уравнения (6.71),
(6.72) имеют простое решение:
оба активных участка равны по
продолжительности и их соответ¬
ственные точки сдвинуты на пол-
оборота, начало первого актив¬
ного участка произвольно в неко¬
торых пределах (рис. 6.17).
Полученное решение для одного периода работы двигателя
легко обобщается на [5/771] периодов1),^ е. на время существова¬
ния спутника в заданном слое не менее 5 оборотов:
Тц = [slrnlt^ = [slm] х (1 — 2jz cos i) 2лmX0/a0. (6.73)
Оптимальные законы еф, е,., ео, 6 сохраняются в виде (6.64),
(6.65), (6.70)—(6.72).
В рассматриваемой постановке задачи предполагалось, что
двигатель работает только на одном m обороте после m 1 пас¬
сивных оборотов спутника. Аналогичным образом может быть ис¬
следована постановка, в которой двигатель работает не на одно у,
а на нескольких оборотах в конце периода.
. •
х) Знак [slm] обозначает целую часть числа slm.
17 Механика полета
ИР
РШ
Lt(m'>
тС
1 + о
~2 %jul
Рис. 6.17. Одна из возможных опти¬
мальных программ включения двига¬
теля па активном обороте для маневра
удержания спутника.
258
НЕРЕГУЛИРУЕМЫЕ ДВИГАТЕЛИ
[ГЛ. &
2. Поворот плоскости круговой орбиты (см. § 3 Приложения и
§ 3 гл. 5). Задача (6.5) для данного маневра записывается следую¬
щим образом ([6.2], ср. (П.94) и (5.69)):
(а„, р = const, б (t) == 1 или 0, е (t) = +1).
Будем считать, что изменение веса аппарата за счет расхода
рабочего вещества намного меньше начального веса аппарата
(p7V<^l, Т^ = ^(Т)). Тогда модуль реактивного ускорения
a (t) = а0б (£) (1 — р^)'1 в правой части (6.74) можно заменить на
Для упрощения формул положим Т = 2ns, 5 = 1,2,...
(время выполнения маневра кратно периоду обращения по данной
орбите). Вариационная задача окончательно записывается в виде
(а0 = const, 6(t) = 1 или 0, e(t) = ± 1). j
Составим гамильтонову функцию и выпишем уравнения для
импульсов
Оптимальные законы е (t), б (t) даются такими выражениями:
Параметры рх, Рсо вычисляются из условий удовлетворения
граничным значениям для %, ш.
При времени движения, кратном периоду (что и рассматрива¬
ется в данном случае), оптимальные программы (6.78) периодич¬
ны с периодом 2я: активные участки равны по продолжительности,
С. (0) = 0, t^(T) = min,
х(0) = 0, х(Т) = о,
03 = ,| а°^, ecos(t — Q]),
1 ГС ij.
(6.74)
со (0) = 0, со (7') = i
а (t) = а08 (t).
(6.75)
^ (0) = 0, tv. (2ns) = min,
X (0) = 0, х(2я5) = 0,
,ач п ,оч. I <6-76)
со (0) = 0, со (2я5) = i
Я = — б + pyaQ8е sin (t — Qi) + paaQ8e cos (t — Qx),
p = const, p = const.
1 x * w
(6.77)
ОПТИМАЛЬНЫЕ МАНЕВРЫ УПРАВЛЯЕМЫХ СПУТНИКОВ
259
начала и концы двух соседних активных участков отличаются по
времени на я (за исключением, может быть, первого и последнего),
положительные и отрицательные направления вектора тяги после¬
довательно чередуются. Опираясь на это свойство, можно уста¬
новить явный вид зависимости управлений е, 8 от угла Qv
Пусть известны оптимальные управления е, б, реализующие
поворот плоскости орбиты на угол i за время 2ns при положе¬
нии линии узлов, характеризующемся углом
Оптимальные управления е', б', поворачивающие плоскость
орбиты на тот же угол i и за то же время 2ns, но при угле Qx,
отличном от йх, выражаются через е, б так:
е9 (t) = е (t + Q± - Q[), б' (t) =8 (t + Qx — Q^). (6.79)
Этот факт доказывается следующим образом. Управления
е, 8 и е', б' характеризуются двумя параметрами рх, рш и р'х,
которые определяются из условий
^ е8 sin (t — Qi) dt = О,
о
2ns
^ е'д' sin (t — Qi) dt = 0,
о
(в этих формулах е, е', б, б' даются выражениями (6.78)).
Два верхних равенства выполняются; требуется доказать,
что в этом случае и с законами е', б', взятыми в виде (6.79), вы¬
полняются два нижних равенства. Введем замену
t' = t Qx — Qi, (6.81)
интервал интегрирования после такой замены сдвинется на
Qi — Qi и выйдет за пределы промежутка [0, 2ns]. Доопределяя
периодические подынтегральные функции на участке [2ns,
2ns + | Qi — Qi|] (или [— | Qi — Qi' |, 0] в зависимости от знака
разности Qi — Qx), придем к требуемым равенствам.
Построим теперь оптимальные управления е, 8 для одного
избранного значения угла Q^; пусть это будет то значение, при
котором
б (+0) = 1, б (-0) - 0. (6.82)
При этом все активные участки без исключения равны по
продолжительности, начала и концы соседних участков сдвинуты
на л и функция е (t) на них имеет разные знаки. Найдем следующие
17*
2*.s
^ е8 cos (t — Qi) dt — i / a(),
э
;rcs
{ e'8' cos (t — Qi) dt — i/a{)
щ)
(6.80)
260
НЕРЕГУЛИРУЕМЫЕ ДВИГАТЕЛИ
[ГЛ. 6
законы 6 (t), е (t) (рис. 6.18):
е — -j-1,
8 = 1
при
0 < £ < / 2s,
е = -1,
8 = 1
при
я <С t < я + Гр, / 2s,
е = 1,
8 = 1
при
2я </ t </ 2я + Гр, / 2s,
е = —1,
6-1
при
(s — 1) я <Г t <С (s — 1) я + Гр. / 2s
(6.83)
где Ty.!2s — время работы двигателя на одном участке.
После вычисления интегралов (6.80) определяются связи
Q* = Tv/4s, i/a0 = 4s sin (T^/As). (6.84)
Для произвольного угла Qx, отличного от Qb законы е (tД
6 (t), согласно правилу (6.79), получаются такими:
для — T,JAs < < TvJAs
е (-1,
е = —1,
е = -j-1,
6 = 1 при
6=1 при
6=1 при
^2 ^ <С "i~
to “I- я t < 4“ 2я,
в = (—l)m_1,
6=1 при
^2 4~ (щ 2) я<7</ ^i4"(ni~"“l)я
(*1 =
Г,j. / 4s,
to = Qt — Гр,/4s + я);
для I,!J./4s<Q1< я —
Гр/4s
е = -j" 1»
е = — 1,
^ + 1,
6 = 1 при
6 = 1 при
6 = 1 при
tl<Ct<[to_,
ti —}— я t ^2 4- я,
/i 4- 2я < ^ < 4- 2я,
е = (-1)т-\
6 = 1 при
^1 4" (w — 1) я <C £<^2 + (/?i—1)я
(h
= ог _ rp./4s
, t-z = Qi 4- Гр,/4s).
(6.85)
(6.86;
В сумме два варианта (6.85), (6.86) охватывают промежуто:
изменения углов Q1? равный я:
-TvJAs < Qx < я - Ту4s. (6.87
Промежуток, дополняющий (6.87) до 2я, получается npi
смене знака управляющей функции е (t) на обратный.
ОПТИМАЛЬНЫЕ МАНЕВРЫ УПРАВЛЯЕМЫХ СПУТНИКОВ
261
После подстановки законов (6.85), (6.86) во второй интеграл
из (6.80) находится связь между i, s, aQ:
Ту, = 45 arcsin (i/4sa0) (Т = 2us, 5 = 1,2,...). (6.88)
Последнее есть требуемое выражение функционала задачи
через параметры маневра 5 и двигателя а0. Заметим, что, как и
для идеального двигателя ограни¬
ченной мощности, контрольный
функционал не зависит от конеч¬
ного положения линии узлов —
угла Q1? а середины активных
участков приходятся на это конеч¬
ное положение линии узлов (ср.
(6.88) и (5.75), (6.83) и (5.74),
рис. 6.18 и рис. 5.29). Маневр
поворота плоскости орбиты рас¬
сматривается также в [6.21].
В заключение настоящего пунк¬
та приведем приближенную фор¬
мулу для времени выполнения
маневра поворота плоскости круговой орбиты (на угол г) с одно¬
временным изменением радиуса (с 1 до гх) [6.5]:
ed
1
О
-1
9
ш
К Ш+К
1
7^
2s
ж
2тс t
Рис. 6.18. Оптимальная программа
ориентации тяги и включения двигате¬
ля на одном обороте для маневра пово¬
рота плоскости круговой орбиты.
г, =
_1_
и-
do
1 — exp
1 — exp
11 ,/ I 2 Л1 ,
■ — 1/ 1 -T= COS -T- +
do У у n 2 1
4-/i
V-
2 ni , 1
cos — +
. (6.89)
Здесь предполагалось, что двигатель включен на всей траек¬
тории. Радиальная компонента вектора тяги полагалась равной
нулю, имеются компоненты по вектору скорости и по (против)
нормали к мгновенной плоскости орбиты (смена знака нормальной
компоненты происходит на диаметре, перпендикулярном к линии
узлов). Абсолютные величины этих двух компонент вектора тяги
считаются медленно меняющимися функциями времени.
Это предположение позволяет провести усреднение уравнений
движения по обороту. Для усредненных уравнений найдена оп¬
тимальная программа ориентации тяги (от оборота к обороту),
обеспечивающая минимум времени выполнения маневра. Пред¬
положения о малости угла наклона i и радиального переме¬
щения | гх — 1 | не делается. Полученное соотношение (6.89)
дает хорошую точность для широкого диапазона параметров г, г*.
262
НЕРЕГУЛИРУЕМЫЕ ДВИГАТЕЛИ
[ГЛ. О
§ 5. ПАРАМЕТРЫ АППАРАТА С НЕРЕГУЛИРУЕМЫМ
ДВИГАТЕЛЕМ ОГРАНИЧЕННОЙ МОЩНОСТИ
Здесь приводятся примеры решения весовой части проблемы
оптимизации (задача на максимум (6.6)) для нерегулируемых
двигателей ограниченной мощности; при этом используются най¬
денные в предыдущих параграфах выражения функционала
Ту. (а0, ц). Значения полезного веса, соответствующие идеальному
двигателю ограниченной мощности (из § 4 гл. 5) сравниваются
с полученными, чтобы оценить выигрыш, даваемый регулиров¬
кой тяги.
1. Расчетные формулы. Если процесс ускорения в двигателе
ограниченной мощности происходит без потерь, то мощность N
связана с тягой Р и расходом q (или скоростью истечения V =
= P/q) идеальным соотношением (ср. (4.1)—(4.3))
N = PV2q = 4JPV
(N [кет] = 0,481 •10'"1Р2[кГ]/д [кГ/сек] = 0,49-10'2Р [кГ] V[м/сек]).
(6.90)
Вес двигательной системы (4.13) может быть представлен в
следующем виде х):
Gx = aP2/2q = VaaP7, GJG0 = {a!2g) a2J\x = (a/2g) a0V
(Gx [кГ] = 0,481 • 10_1a [кГ/квт] P2 [кГ]/д [кГ/сек] =
= 0,49• 10~2a [кГ/квт] P [кГ] V [м/сек]). (6.91)
Критерий (6.6) выбора оптимальных значений Р, q, V (или
а0, р, У) в этом случае записывается так:
max G„ = max (g0 — — gqTv] = maxfGu — фхРУ-g-X T'X'
P, q \ / pt у \ 6 V ' J
m‘*i = (‘ ~ i т ~= ?дх (‘ ~ i ■a‘v~ r- r’>
(ma xGn[nr\ =
= max(G0 [к/1] — 0,481 • 10-1 а [кГ/квт] P2 [кГ]/ q [кГ/сек] — 1
P, Q
— q [кГ/сек] T^ [сек]) = max (Gn [кГ] —
p, v
— 0,49 • 10~2 а [кГ/квт] P [кГ] V [м/сек] —
— 9,81 P [кГ] Tv, [сек] /V [м/сек])},
' (6.92)
1) Зависимости А и Gx для реальных двигателей ограниченной мощности
и соответствующие примеры решения весовой части вариационной проблемы
приведены в главе 7.
§ 5] ОПТИМАЛЬНЫЕ ПАРАМЕТРЫ АППАРАТА 263
где Tv, = Ту. (gP/G0, gq/G0) или Tv. = Tv, (а0, д) — решение ди-
намической части задачи; последний член в (6.92) представляет
собой начальный вес рабочего вещества
G,o = = gPTvJV, GJG0 = = a0T^IV (6.93)
(G,,0 [кГ] = г/[кГ/сек] Г,, [сея] = 9,81 Р [кГ] Tv, [сек] IV [,м/сек]).
Если в выражение для функционала T[}j не входит параметр
ц (или У), как это имеет место в задачах пп. 1 и 2 § 4 (см. (6.73)
и (6.88)), то максимум GJG0 по ц (или У) достигается при
Ц = «о / ]/ ^ или Т' = ^ Гр.
(q = 0,219Р/а/Т; или F = 0,447-102УТ^Та) (6.94)
(размерности величин в скобках здесь и ниже в настоящем пункте
те же, что и в формулах (6.90)—(6.93)).
Критерий (6.92) с учетом соотношения (6.94) имеет вид
max -^г- = max — 2я0 )/" тЛ
•“* А (6.95)
(шах G- = max (G0 — 0,439Р ]ЛхГн.)).
р
Заметим, что значение ц (или У), определяемое формулой
(6.94), соответствует равенству начального веса рабочего веще¬
ства и веса двигателя *)
У = У = «о Y^ ^ = G' = °’219р V«zV)* (6-96)
Если записать (6.96) через полезную нагрузку, получим оп¬
тимальные соотношения между весовыми компонентами (кривая 3
на рис. 6.19)
СдУ^о = GJ&0 = */2 (1 — GJG0), (6.97)
в то время как для идеального двигателя ограниченной мощности
мы имели (см. (4.15)—(4.17) и пунктирные кривые на рис. 6.19)
С,л!Go = 1 - Y~G7jGo, Gy./G0 = YGT/Щ- Gn /Go. (6.98)
2) Этот в;.иод для случая заданного времени работы двигателя при фик¬
сированной величине тягн сделан Штулингером [6.22], Мекелом [6.23] и
Престон-Томасом [6.24]. В работе [6.25] найдено соответствующее выра¬
жение для оптимальных весовых соотношений с учетом релятивистских
эффектов, вызванных большими скоростями истечения. Показано, что при
значениях параметра (77а) ~ 1 год-кетп1кГ релятивистские поправки к чле¬
нам порядка единицы в формулах для весовых соотношений составля¬
ют ~ 10_(\
204
НЕРЕГУЛИРУЕМЫЕ ДВИГАТЕЛИ
Соотношения (6.98) для идеального двигателя не зависят от
типа динамического маневра. Для нерегулируемого двигателя
такой инвариантности уже не существует — это мы проследим на
примерах маневров, рассмотренных в §§ 2—4 (рис. 6.19).
Рис. 6.19. Сравнение оптимальных весовых соотношений
для идеально регулируемых и нерегулируемых двигателей
ограниченной мощности. Пунктирные кривые — идеальный
двигатель (универсальны для всех маневров), сплошные
кривые — нерегулируемый двигатель (1 — набор скорости,
2 — перемещение между точками покоя, з — поворот пло¬
скости круговой орбиты, удержание спутника и другие манев¬
ры, где время работы двигателя не зависит от расхода).
Динамический маневр в случае идеального двигателя огра¬
ниченной мощности определяет величину полезной нагрузки
через функционал /. Значения J зависят от определенных ком¬
бинаций параметров маневра:
для маневра набора модуля скорости (см. (5.32))
Ju = и\Т-\ (6.99)
для маневра перемещения между точками покоя (см. (5.33))
/г = 12 VT-\ (6.100)
для маневра поворота плоскости круговой орбиты (см. (5.75) в
размерном варианте)
Ji = 2kro1PT-1 (Т = 2nsk-'hr’i\ s = 1, 2, . . .). (6.101)
Интересно отметить, что полезная нагрузка аппаратов с не¬
регулируемым двигателем ограниченной мощности для перечис¬
ленных маневров определяется теми же комбинациями (6.99)^
§ 5] ОПТИМАЛЬНЫЕ ПАРАМЕТРЫ АППАРАТА 265
(6.101): Ф = (a/2g) J (рис. 6.20). Это будет установлено ниже при
решении весовой части задачи.
Рис. 6.20. Сравнение полезной нагрузки аппаратов
с идеально регулируемыми и нерегулируемыми двигате¬
лями ограниченной мощности (обозначения те же, что и на
рис. 6.19, кроме кривой 3, которая здесь относится только
к повороту плоскости круговой орбиты).
2. Набор модуля скорости. Решение динамической задачи
для этого маневра, выполняемого нерегулируемым двигателем,
дается соотношением (6.30). Выберем в качестве параметров дви¬
гателя, по которым будем производить оптимизацию, aQ и V.
Тогда критерий (6.92) запишется в виде
max G- JGo = шах (e-Ui V— a0V) , а0 > Хр (1 — еу1^), (6.102)
[«о» У -8 /
Ограничение на а0 снизу следует из (6.30). Величина а0 вхо¬
дит в (6.102) линейно со знаком минус, поэтому максимум Gл
по а0 достигается при
Оо = ^г( (6.103)
г. е. в оптимальном случае выключение двигателя при наборе
модуля скорости невыгодно (см. (6.30)).
После проведения процедуры оптимизации полезной нагруз¬
ки GJG0 по скорости истечения V получим решение весовой части
266
НЕРЕГУЛИРУЕМЫЕ ДВИГАТЕЛИ
[ГЛ. С
задачи в параметрической форме (см. [6.26, 6.27] и др.):
°п __ 2(1-е-*) —£
G0 2(ег— 1) — %
Фи = и\Т~х = - ,
2S 2(eK — l) — Z
GP-0 л Gs. с
Oo Сто
I3
с*
Go ’
U1
V
(С.104)
Оптимальные весовые соотношения GK (G-) и G[x0 (G-) пока¬
заны на рис. 6.19 (кривые 2), зависимость максимальной полез¬
ной нагрузки Gn от Фи — на
рис. 6.20 (кривая 2), оптимальная
скорость истечения — на рис. 6.21
в виде зависимости £ (Ф^)* Пре¬
дельное значение функционала Ф
здесь равно — 0,65 (G- = 0 при
Фи ^ 0,65) вместо Ф = 1, как это
было для идеального двигате¬
ля. Оптимальная скорость исте¬
чения нигде не опускается ни¬
же половины приращения ско¬
рости аппарата (min V (Фи) ^
^0,63 ^i)1).
3. Перемещение между точками
покоя. Функционал динамической
задачи для нерегулируемого дви¬
гателя здесь определяется соотно¬
шением (6.43). Выразив из (6.43)
ускорение а0, запишем полезную
нагрузку (6.92) через запас ра-
G^q/Gq = 1 — fxT7^ и отношение времен T/T[L
О
0,2
0,4
0,6 Ф,
и
Рис. G.21. Оптимальная скорость исте¬
чения V в зависимости от комбинации
Фи = (a/2g)u2iTдля маневра набора
заданного модуля скорости щ.
бочего вещества
Gt
2^
Go
а /2
[2 (1 - Vl-G^/Go) - GVJ Go - V2 (GJGo) [(T/TJ-1] In (1-G^Go)}2-
(6.105)
при этом аналогично п. 2 выделилась комбинация параметров
маневра, входящая в функционал (6.100) для идеального дви¬
гателя.
1) Полученное решение справедливо и для маневра поворота плоскости
Круговой орбиты с одновременным изменением радиуса в случае, когда дви¬
гатель работает без выключений. Это следует из сравнения формул (6.89)
и (6.103). В качестве приращения скорости для такого маневра нужно взять
t(j = Vго8о [!—2 У cos (Уini) + г0/7,1)1/г-
ОПТИМАЛЬНЫЕ ПАРАМЕТРЫ АППАРАТА
267
Представим вес Gv.0 в виде G^Q = G0 (1 — е *>) (ср. (6.104)),
тогда задача сводится к отысканию максимума
тах-^- = шах
G° Z, Т/Тр ]
(1-
. (6.106)
1 + е ^2
Из условия равенства нулю частных производных по (Т/Т^) и
5 получаем решение весовой части задачи в параметрической
форме [6.1, 6.26] (ср. (6.104))
Gn £ [2 — (ё~^‘2 + е~")1 — 3 + 2 — Зе~* —11£1
“57 “ Е \(е-2 -4- еЧ — 21 — 3 •!- б*-2 — Зе* — '
ии,0
Go
= 1
V’)-2]-3
Go
= е~
0е!
G,
Go ’
ф, =£-i2PT-*=
7Л«
А - А
' ^ [(ве/2 + е5) _ 2] - 3 + 0/’/2 - Зе^ - i/£* ’
I
(6.107)
1 и- <Г’:3
По этим формулам посчитаны оптимальные весовые соотноше
ния G,;.0 (G^) и Gx (G-) — кривые
2 на рис. 6.19, зависимость
максимальной полезной нагрузки
GJG0 от функционала Фi — кри¬
вая 2 на рис. 6.20 и оптималь¬
ное время работы двигателя TVJT
в функции Ф/ — рис. 6.22. Пре¬
дельное значение функционала Ф
для нерегулируемого двигателя
оказывается меньше, чем при на¬
боре модуля скорости (G- = 0 при
Ф/ ^ 0,56, ср. кривые 1 и 2 на
рис. 6.20). Оптимальное время ра¬
боты двигателя слабо зависит от
Ф/ и составляет около 2/3 от пол¬
ного времени движения.
4. Межпланетный перелет Зем¬
ля— Марс. Результирующая для
динамической части задачи зави- т°^м“иси^
СИМОСТЬ i (^0, ) Д&На на рис. 6.11. Оииацпп = (a/2g)1212Т~3 для манев-
Значения а0ий, доставляющие мак- ра перемещения между точками покоя
симум (6.92), находятся численно иа Расстояние 1-
Для каждой пары величин Таиа с использованием данных рис. 6.11,
268
НЕРЕГУЛИРУЕМЫЕ ДВИГАТЕЛИ
[гл. а
V, км/сек
Qo/g
2W
J0~
%
I
7к8т
ЮкГ/кбт
150 200 250 ООО Ге,сут
Рис. 6.23. Оптимальное начальное ускоре- Рис. 6.24. Оптимальная скорость истече¬
ние от тяги а0 для перелета Земля—Марс ния V для перелета Земля —Марс,
в зависимости от времени перелета Т0
и удельного веса двигателя а. •
&
Рис. 6.2"'. Оптимальное время работы Рис. 6.26. Сравнение полезной нагрузки
двигателя !Г„0 для перелета Земля — Марс. аппаратов Земля — Марс с идеально ре¬
гулируемыми (пунктирные кривые) и нере¬
гулируемыми (сплошные кривые) двигате¬
лями ограниченной мощности.
ОПТИМАЛЬНЫЕ ПАРАМЕТРЫ АППАРАТА
269
Полученные оптимальные значения a0nV показаны на рис. 6.23
и 6.24, в зависимости от времени перелета при фиксирован¬
ных значениях удельного веса двигателя. На рис. 6.25 нанесены
отвечающие им величины времени работы двигателя.
Максимальная полезная нагрузка G-/G0 в функции Та и а по¬
казана на рис. 6.26. Там же для сравнения нанесены пунктирные
кривые, соответствующие идеальному двигателю ограниченной
мощности.
5. Удержание спутника в заданном шаровом слое. Функцио¬
нал динамической части задачи (6.73) для рассматриваемого
маневра зависит только от начального ускорения а0 и не зависит
от расхода ц или скорости ис¬
течения V. Поэтому здесь спра- Оро+О&кГ
ведливы оптимальные весовые W0
соотношения (6.97) (см. кривую
на рис. 6.19). Перейдем в (6.73) ^
от параметра % к сопротивле¬
нию х) F=yiG0/g и от ускорения
а0 к тяге P = a0G0/g. Поскольку 60
сила сопротивления F не связа¬
на прямо с начальным весом,
а определяется формой аппара- ^0
та, то весовую часть задачи
можно решить независимо от 20
начального веса.
Будем искать минимум сум¬
мы весов запаса рабочего вещест¬
ва и двигателя, т. е. минимум
удвоенного выражения (6.96).
После подстановки решения
(6.73) динамической задачи в
(6.96) получим
min (Gjj.0 + Gy.) =
Рис. G.27. Пример зависимости минималь¬
ного значения суммарного веса G^q -f- Gy
запаса рабочего вещества G1Ji0 и двигателя
G)C от времени Т удержания спутника в
шаровом слое, (а — удельный вес двигате¬
ля, G,1j0 = Gy, R = 0,5Г— сила сопротив¬
ления, двигатель работает па каждом
16-м обороте).
= min Y2gaTFР. (6.108)
Р
Отсюда видно, что тяга должна быть минимально возможной.
Ускорение а0, согласно (6.68), ограничено снизу, поэтому в
оптимальном варианте
Р = mJi, Gl* = GK = FV4»gamT (6.109)
(двигатель включается на каждом 7?г-м обороте, спутник удержи¬
вается в течение времени Т).
Это означает, что двигатель должен работать на протяжении
всего активного оборота
Тх, = Tim; (6.110)
х) Здесь принимается р — const, jz = 0 (см. (П.70)).
270
НЕРЕГУЛИРУЕМЫЕ ДВИГАТЕЛИ
[ГЛ. 6
скорость истечения и расход будут следующими (см. (6.94)):
1'=Г¥Г' <бли>
Для иллюстрации на рис. 6.27 дана зависимость (6.109) ми¬
нимального суммарного веса (G^0 + GK) от времени Т пребывания
спутника в пределах шарового слоя при различных значениях
удельного веса двигателя а (сила сопротивления F принята рав¬
ной F = 0,5 Г, m = 16).
6. Поворот плоскости круговой орбиты. Решение динамиче¬
ской части задачи дается формулой (6.88), для которой снова
имеем дТ^!д\1 = 0 (или dT^ldV = 0). Отсюда следует, что опти¬
мальные весовые соотношения определяются по (6.97)—кривая о
на рис. 6.19. Выразив а0 из (6.88) и подставив его в (6.95), по¬
лучим полезную нагрузку в функции относительного времени ра¬
боты двигателя T{JT (в (6.88) Т = 2ns, s = 1, 2, . . .):
Go Y2 sin (4^Tv / T) r
(<Dt = ~ 2kro1i2T~1 . T - 2nsK*!tr{'}. (6.112)
Оптимальное значение TXJT, максимизирующее (6.112), равно
T^/T = 0,7420; при этом полезная нагрузка GJG0, веса двигателя
GJG0 и рабочего вещества G^0/G0, скорость истечения V и на¬
чальное ускорение а0 получаются следующими:
GnjG0 = \ -2,0822 /ФГ, G^/G0 = Gx/G0 = 1,0411 /Ф~ J
V = 1,219 a0 = gP/G0 = 0,544kV'iT'1. j
(6.113)
Полезная нагрузка в функции Ф, = (oc/2g) J? дана на
рис. 6.20 — кривая 3. Напомним, что решение динамической
задачи (6.88) получено в предположении G (t) = const, поэтому
соотношения (6.112), (6.113) справедливы только при Ф,1
(при Ф; — 1 значения полезной нагрузки из (6.113) оказываются
заниженными). Кроме того, время выполнения маневра Т счи¬
талось кратным периоду обращения спутника (Т = 2nsk~'/zr30/z>
s = 1, 2, . . .).
ГЛАВА 7
РЕАЛЬНЫЕ ДВИГАТЕЛИ
ОГРАНИЧЕННОЙ МОЩНОСТИ
Основные отличия, реальных двигательных систем ограничен¬
ной мощности от идеальных состоят в следующем.
1°. В реальных движителях существуют потери рабочего ве¬
щества и мощности, связанные с фазовыми переходами (иониза¬
ция, нейтрализация), неоднородностью реактивной струи в вы¬
ходном сечении и др. Эти потери характеризуются коэффициен¬
тами использования рабочего вещества и мощности r)v; при
помощи их выражение для тяги реального движителя запишется
так (ср. (4.1)):
Р = У 2x]yNyq, (7.1)
где г]у — 'Hij'Hv — эффективный коэффициент полезного действия.
Последний зависит от мощности Ny и расхода д, подводимых к
движителю, а также от геометрических параметров и параме¬
тров электрической цепи:
у]у = т|у (Ny, g, м>1? . . ., wi).
2°. Регулирование движителя в полете может быть построено
так, что к нему подводятся переменные мощность Ny и расход
д, а геометрические параметры и параметры электрической цепи
wv . . .,Wi остаются постоянными.
Рассмотрим две вероятные схемы регулирования двигатель¬
ной установки, которые могут применяться в зависимости от
вида функции rjY (Ny, д).
Диапазон регулирования движителя с постоянными пара¬
метрами м?1т . . ,,W[ определяется областью jVY, g, в которой
T)Y (iV7, g) /> 0. Возможны два предельных случая. Первый:
поверхность г|7 Q) представляет собой всюду плоскость
г]т (2Vv, g) = 0, за исключением точки Ny, g*, в которой т]7 0;
этот случай соответствует нерегулируемому движителю, настроен¬
ному на один режим Ny, q*. Другой крайний случай — идеально
регулируемый движитель: г]7 Q) = const; здесь диапазон
регулирования не ограничен. В действительности о реальных
движителях можно говорить, что они обладают относительно
узким или относительно широким диапазоном регулирования, а
212
РЕАЛЬНЫЕ ДВИГАТЕЛИ ОГРАНИЧЕННОЙ МОЩНОСТИ
[ГЛ. 7
функция т|у (Лд, q) имеет острый или пологий максимум в точке
Ад, q*, положение которой определяется значениями параметров
wv . . ., wh
Изменение тяги двигательной установки с движителем, имею¬
щим широкий диапазон регулирования, может осуществляться
за счет изменения мощности Ny и расхода q, а также за счет изме¬
нения числа включенных элементарных движителей (когда дви¬
житель состоит из нескольких однотипных элементарных движи¬
телей).
Если диапазон регулирования движителя узкий, то изменение
тяги двигательной установки происходит при переключении с
одного движителя (или блока элементарных движителей) на дру¬
гой, настроенный на другие значения N*, q путем соответствую¬
щего выбора параметров wv . . .,Wj.
В последнем случае плавное регулирование двигательной уста¬
новки невозможно, тяга и расход — кусочно-постоянные (сту¬
пенчатые) функции времени 1).
3°. В идеальном двигателе веса источника мощности преобра¬
зователя и движителя зависят только от максимальной мощно¬
сти (см. (4.1)); вес Gv реальных источника мощности и преоб¬
разователя также определяется величиной максимальной
мощности
G, = / (Лгшах), (7.2)
а вес движителя G{ выражается для разных типов движителей
по-разному через предельные значения независимых управле¬
ний. Таким образом, вес реальной двигательной системы вклго- *
чает по крайней мере две компоненты:
Gx = Gv + Gy. (7.3)
4°. Идеальный двигатель ограниченной мощности не имеет
ограничения на время работы, тогда как ресурс реальных двига¬
телей ограничен, т. е. время работы не должно превышать наперед
заданного.
Отмеченные свойства реальных двигателей являются общими,
каждый конкретный тип движителя определяет выражение для
веса Gy и тяги Р.
В заключение этого вводного раздела заметим, что при решении
проблемы оптимизации для реальных двигательных систем в ве¬
совую формулу аппарата может быть включен вес баков для ра¬
1) Ограничения также могут быть наложены на регулирование направ¬
ления вектора тяги; рассматриваются, например, тангенциальное [7.1,
7.2] и неизменное или ступенчато изменяемое в пространстве [7.3] направ¬
ления.
ДОИОЛ 11ИТЕЛЫ1ЫЕ JНОСОВЫЕ KUMIIOHE1ITJ>L
273
бочего вещества. Последний обычно считается зависящим от на¬
чального веса рабочего вещества G^ = / (£;о.0); наиболее употре¬
бительна линейная зависимость [7.4—7.6]
§ 1. ДОПОЛНИТЕЛЬНЫЕ ВЕСОВЫЕ КОМПОНЕНТЫ
Идеальный космическрш аппарат с идеальным двигателем
ограниченной мощности считается состоящим из трех весовых
компонент: полезного веса G-, веса рабочего вещества веса
двигателя (?*, пропорционального максимальной мощности.
В данном параграфе приводятся формулировки вариационных
проблем, в которых учитываются дополнительные веса: вес баков
Gfi и вес движителя G(. Указанные весовые компоненты иссле¬
дуются по отдельности; даются особенности оптимальных управ¬
лений, появляющиеся из-за включения этих новых факторов в
проблему оптимизации.
1. Учет веса баков. Дополним весовую формулу исходной
вариационной постановки (II.2) компонентой G^ — весом баков;
для G?> примем выражение (7.4). Тогда вариационная проблема
в формулировке (II.5) примет вид
В том случае, когда в весовой формуле отсутствуют компоненты
типа Gy зависящие от начального веса рабочего вещества, изу¬
чаемая вариационная проблема может быть приведена к виду
(II.8), где роль функционала играет конечное значение суммы
весов:
Новая проблема имеет на одно краевое условие меньше,
чем исходная, и поэтому проще исходной.
Пусть проблема (7.5) редуцирована к краевой задаче для обык¬
новенных дифференциальных уравнений; тогда, несмотря на при¬
сутствие члена в уравнениях можно сделать некоторые за¬
мены, упрощающие краевую задачу наподобие того, как это имеет
место при отсутствии члена Gy
Для сведения проблемы Майера (7.5) к краевой задаче вос¬
пользуемся методом JI. С. Понтрягина; выпишем гамильтонову
Gfi = Р|хСг1Хо (Pjj. — const).
(V.4)
G-(0) -f Gx-\- G„(T) = max,
+ (l + Plk)G|i(0) = G0, Сц (T) — 0,
r (0) = i'n« r(7’) = i'i,
v =
Ga = G- + G
18 Механика no. .ста
274 РЕАЛЬНЫЕ ДВИГАТЕЛИ ОГРАНИЧЕННОЙ МОЩНОСТИ
функцию и уравнения импульсов:
[ГЛ. 7
н =ря-0 —D gg + pr-v + po.
g Ре
-г Д + Gj3 -I- G,
■2
+ R ,
Pn = Pf. = (P«'e) (Сл + + G(3 + G J ’
/’A7’) = — 1-p, = - -§f(p„-R)> p„ = — pr-
(7.6)
Заметим, что дифференциальные уравнения для импульсов
/?-, совпадают, и в начальный момент их значения удовлетво¬
ряют условию трансверсальности
(7.7)
Рр.О — (1 + $у)Рл О-
Последнее вытекает из того, что веса G,,, G- в начальный момент
заданы не по отдельности, а связаны соотношением из (7.5).
Учитывая эти факты, можно найти выражение импульса pv> (t)
через p-(t) и
Рц(0 = Ря (t) + KP-.o'
(7.8)
которое затем используется для исключения р^ (t) из уравнений
и гамильтоновой функции (7.6).
Введем новую фазовую координату Go (t):
Go = G^ -4 Gu. 4~ PulGjj.0 (7.9)
и заменим в дифференциальных уравнениях (7.5), (7.6) и в га¬
мильтоновой функции (7.6) G[}, на Go согласно соотношению (7.9).
Получившаяся в результате система дифференциальных уравне¬
ний и краевых условий, а также гамильтонова функция имеют вид
Go = — gq,
v = у,
у — ^2 !_ #
Gq-т Gx ' Н’
Рл = (Рв‘е) G0V Gy
G о (0) = Go — Gx,
v (0) = r0,
v(0) = y0,
* (T) = rb
v(T)=vb
pJT) = -i,
Pr =~ aF(Pc-H)’
P0 = —Pr
н = — (Рл + Р„рД sq + p.-v + p •
gPe
Gq + Gx
+ R
(7.10)
§ 1J ДОПОЛНИТЕЛЬНЫЕ ЬЕСОЬЫЕ КОМПОНЕНТЫ 275
Полезный вес определяется после решения задачи (7.10)
через Go (0), Go (Г) следующим образом (см. (7.9)): Gn =
= (1 + р,) Go (Т) - PpGo (0).
Входящие в (7.10) управления находятся из условия дости¬
жения функцией Я абсолютного минимума; для отыскания управ¬
лений двигателя необходимы характеристики последнего, т. е.
выражения типа (II.9), (11.10).
’/&£z>£/UbO>
V
08
0,6
ол
0,2
О 0,2 0,4 0,6 0,8 Ф
Рис. 7.1. Влияние веса баков на оптимальные весовые со¬
отношения аппарата с идеальным двигателем ограниченной
мощности (jS^—удельный вес баков, Ф— функционал дина¬
мического маневра).
В отличие от исходной краевой задачи, в (7.10) отсутствует
конечное условие для веса рабочего вещества G,M а также диффе¬
ренциальное уравнение для импульса поэтому новая задача
проще исходной.
Проиллюстрируем влияние веса баков на оптимальные весо¬
вые соотношения аппарата на примере задачи для идеального
двигателя ограниченной мощности [7.6]. Вес двигателя будем
считать неизменным. Задача, как и раньше, разделяется на весо¬
вую и динамическую части. Проделав выкладки, аналогичные § 1
главы 4, получим, что по сравнению со старыми оптимальными со¬
отношениями (4.15) —(4.17) оптимальный вес двигателя увели¬
чивается Gx = Y( 1 + PiO Ф — Ф, а вес запаса рабочего веще¬
ства уменьшается Gs,0 = УФ/(1 + P;Jl), полезная нагрузка, есте¬
ственно, падает G^ = 1 — 2 ]/(1 + рД Ф + Ф (рис. 7.1). Диа¬
пазон выполнимых маневров (Gn > 0) сужается до 0 Ф ^ 1 —
- 2 |/% (/Т+К - У%).
18*
276 РЕАЛЬНЫЕ ДВИГАТЕЛИ ОГРАНИЧЕННОЙ МОЩНОСТИ [ГЛ. 7
2. Учет веса движителя. Будем считать, что вес двигателя G*
составляется двумя компонентами: весом источника мощности
и преобразователя Gv и весом движителя G{ [7.7]:
G, = Gv + Gy. (7.11)
Первый зависит линейно от максимальной мощности Лгшах:
Gv = aiVmax (а = const), (7.12)
второй — в конечном счете от максимальной мощности Агтах и
максимальной тяги Ртах:
GY “ / (А^,пах? Ртах)» (^*13)
Рассмотрим случай, когда / — линейная функция своих аргу¬
ментов:
GY = а'Агшах + уРшах (а', у = const). (7.14)
В силу того, что веса Gv, G{ входят аддитивно в весовую фор¬
мулу (7.11), член a'iVnia4 из (7.14) может быть добавлен к Gv:
Gv + a'JVjnax = (а + а') NluiXX, (7.15)
так что составляющая веса движителя в (7.14), пропорциональ¬
ная iVmax, исключается из рассмотрения. Имея это в виду, будем
считать
Gy = 7Ршах. (7.16)
Регулировочную характеристику примем идеальную — (4.3),
будем только в соответствии с (7.16) накладывать еще ограниче¬
ние На ТЯГу Сверху 0 Р (t) Ртах-
Вариационная проблема о доставке максимального полезного
груза для двигателя ограниченной мощности, содержащего две
весовые компоненты Gv, GY, записывается следующим образом
(см. (II.6)—(II.8), (4.3)):
G0 = — gP2 / 2N, Ga (0) - G„ — Gv (0) - GY (0), Ga (T) = max,
1 = V, r(0)^=r0, r (T) = гг,
* pPq
v= Co + cv + cY +R> v(0) = Vo, v(T’) = Vi
(Gv = OCiVmax, Gy ■■=-- гЛnax, 0 < iV (<) < Amax,
0</5(£)<Pmax, | e (<) | = 1). i
(7.17)
К числу управляющих функций здесь относятся: е (t), N (t),
Р (t), Gv (£), Gy (£); последние четыре из них не являются неза-
Д О П О Л Н И Т Е Л ЬН Ы Е ] i К С О ВIЛ Е К О М ПОЛ 1511Т Ы
277
висимыми. Чтобы выделить независимые управляющие функции,
воспользуемся такими заменами (ср. § 2 гл. 4): отнесем мощность
N и тягу Р к их максимальным значениям
Nm-\x = G^/a, Рщл\ = G-(!y
и добавим к (7.17) две дифференциальные связи, выражающие
уменьшение весов Gv, G{\ Gv = — = — gq.{ (0 ^ oo,
0 < < °°)- Теперь Gv, GY — новые фазовые координаты, a
gy, — управляющие функции. Отнесем также все весовые
компоненты к начальному весу G0; для безразмерных тяги, мощ¬
ности, расходов gv, q{ и весов сохраним старые обозначения.
Тогда рассматриваемая вариационная проблема будет иметь вид
Ga =
2G.,iV ’
Gv = — gq„s
Gy = — gqy,
Ga (0)4-
H- Gv(0) +
Ga(T) — max,
G.,(T) = opt,
r = v,
v= g
+ GV(0) = 1, Gy (T) — opt,
r(T) =r„
PGye
+ R,
'• (0) = I'o,
v (0) = v0,
v (T) = Vi
t Ga + Gv+Gy
(0 < N (f) < 1, 0 < P (f) < 1, 0 < qv (t) < oc,
le(B| = В-
(7.18)
Для решения вариационной проблемы (7.18) по методу
JI. С. Понтрягина составим гамильтонову функцию и выпишем
дифференциальные уравнения импульсов:
р2
Н = — Ра ДГ 1TN ~ Р£Я — PygQy + Р, • v 4- рр •
К -(Р,‘е) *-(G0 + Gv + Gy)* ’
/?2 /32
* * ag у
Р* Р<з Ро 2у~ *
Py - IP. е' т (G0 + Gv + Gy)> + Ра ГГ СД ’
РС„е
tg3+cv+gy
-К ,
рг = —-gr(Pr-R)> Р0 = —Рг-
(7.19)
278
РЕАЛЬНЫЕ ДВИГАТЕЛИ ОГРАНИЧЕННОЙ МОЩНОСТИ
[ГЛ. 7
Граничные условия для импульсов таковы:
Рa (0)=Pv (0)=Ру (0), Pv (Т)=Р, (Т)=0, ра (Т) = -1. (7.20)
Оптимальные управления е (t), N (t), Р (t), qv (t), gY (t)
должны доставлять абсолютный минимум функции Н.
Из этого условия следует выражение для е (t)
е = —р Jpv (Р,. = |РГП- (7.21)
Функция UN входит в Н линейно, поэтому управление N (t)
принимает граничные значения: 0, 1 в зависимости от знака им¬
пульса ра (t). Покажем, что pG (t) 0 во всем промежутке
0<*< Т. Если ра (t) 0, то оптимальные N (t), Р (t) следую¬
щие: N (t) = 0, Р (t) = 1 (см. (7.19)). Это соответствует беско¬
нечному расходу рабочего вещества при нулевой скорости исте¬
чения. Такой режим явно не оптимален, поэтому предположение
Ро (t) > 0 неверно, и, следовательно, ра (t) <f 0 при 0 t Т.
Тогда
N (*) = 1. (7.22)
Уравнение Р (t) меняется в пределах замкнутого интервала
0.Х Р (*) < 1:
внутри интервала
р(1) = р„в1 ,7'23)
на верхней границе
P(t) = 1 при Р0 pt>l, (7.24)
на нижней границе
Р (t) = 0 при А > 0 (Д = р - Рп 4 СуаБ
а 2Т2 G.j т о,й + Gv + eY
(7.25)
При помощи выражения (7.23) для P„pt преобразуем комби¬
нацию Д
А = - Р3-if2 (l - 2 %-*) • (7.26)
Поскольку PovJP > 1, то всегда А <Г 0, и нижняя граница
(7.25) в состав оптимального управления Р (t) не входит — двига¬
тель включен на всей траектории.
Обратимся к исследованию оптимальных управлений qv (t),
gY (t). Если на управления gv, gY не наложены ограничения свер¬
ДОПОЛНИТЕЛЬНЫЕ ВЕСОВЫЕ КОМПОНЕНТЫ
279
ху, то импульсы pv, pY неположительны всюду на [О, Т]. Дока¬
зательство проведем для импульса pv. Предположим обратное.
Пусть в некоторый момент t = С импульс pv (tj > 0; тогда
управление gv принимает оптимальное значение qv (t) = оо
(см. (7.19)), что соответствует мгновенному сбросу конечной части
поэтому функция(t) не меняет знака на конечном интервале вре¬
мени в окрестности момента t = tr Следовательно, на конечном
интервале времени gv = оо; это означает сброс бесконечно боль¬
шого веса Gv, что невозможно. Поэтому исходное предположение
неверно и
В том случае, когда на управляющие функции qv, qy наложены
ограничения сверху и, в частности, предполагается gv (t) =
= gY (t) = 0, выводы (7.27) относительно знаков ру (t), pY (t)
становятся несправедливыми.
Анализ оптимальных управлений ду (0, Чч (0 Д^ет два типа
режимов: граничные управления gv = 0, gY = 0 при ру <С 0,
pY 0, соответствующие Gv = const, Gy = const, и особые управ¬
ления: pv (t) = 0, pY (£) = 0 при pv (0 = 0, pY (t) — 0, соответ¬
ствующие «внутреннему» минимуму функции Н по Gv, GY. Сле¬
дует заметить, что наличие двух указанных режимов является
общим свойством задач с граничными условиями типа (7.18),
наложенными на первоначальные управляющие функции (в рас¬
сматриваемом случае G,, (t), Gy (t)).
Выражения для ру, pY при помощи (7.23) можно преобразо¬
вать к виду
Если Р = ^opt* то второе условие (7.29) заведомо не выпол¬
няется и ру <СО. Следовательно, на участках траектории, на
которых вес Gy убывает (gY > 0), управление Р (t) граничное
веса Gv. Производпая ру остается конечной при qv = ос,
Pv (t) < 0, ру (t) < 0 при 0 < t < Т.
(7.27)
(7.28)
Особые режимы реализуются
для gv при -
для gv при р
Р
opt
р
opt
(7.29)
280
РЕАЛЬНЫЕ Д ПИТАТЕЛИ О Г Р A III 1Ч Е 11И 01' [ МОЩНОСТИ
[ГЛ. 7
Для выполнения граничного условия ру (Т) = 0 в случае,
когда отсутствует ограничение сверху и а управление qy (£), не¬
обходимо, чтобы траектория замыкалась участком Р (t) — 1.
В самом деле, импульс ру (t) неположителен всюду на 10, Т1
(см. (7.27)); поэтому для достижения верхней границы ру -- 0
производная ру в окрестности слева от точки достижения должна
быть неотрицательной, что, согласно (7.28), имеет место только
при Р (t) = 1.
Если Р (t) — Р0])t (t) и Gy = 0, то (7.29) переходит в соотно¬
шение (4.19), определяющее оптимальный закон убывания веса
идеального двигателя ограниченной мощности.
При gv (£)= qy (t) ~ 0 веса Gv, Gy неизменны, и решение
краевой задачи (7.18), (7.19), (7.20) даст оптимальные значения
управляющих параметров Gy. Примеры такого решения при¬
ведены в главе 8.
Отметим, что учет весовой компоненты, пропорциональной
максимальной тяге, изменяет состав оптимального управления
тягой по сравнению с идеальным: появляется верхняя граница
управления Р (t).
Коэффициент пропорциональности у, входящий в уравнения
вариационной проблемы, определяет важную характеристику
двигателя — максимально достижимое реактивное ускорение.
Действительно, реактивное ускорение а дается формулой (см.
(7.18))
а = (g/y) PGy (Ga + Gv + Gv)-\ (7.30)
из которой следует
а (0 < ^max; = g/y. (7.31)
При больших значениях параметра у (у ~ 102—105), харак¬
терных для двигателей ограниченной мощности, максимально
достижимое ускорение мало (а ~ 10-5—10-2 g) (см. [7.8]), что
оправдывает другие названия двигателей данного класса: двига¬
тели малого ускорения или двигатели малой тяги.
§ 2. ЗАДАННОЕ ВРЕМЯ РАБОТЫ ДВИГАТЕЛЯ
Согласно оптимальной программе идеальный двигатель огра¬
ниченной мощности включен во все время движения. Если это
время превосходит ресурс двигателя (что можно ожидать, напри¬
мер, для межпланетного перелета), то в вариационной постанов¬
ке должно фигурировать условие заданного времени работы
двигателя. Частично этот вопрос уже обсуждался в главе 6; здесь
дается общий метод решения вариационных задач с фиксирован¬
ным временем действия управления, который затем применяется
к изучаемой проблеме [7.9, 7.10].
ЗАДАННОЕ - ВРЕМЯ РАБОТЫ ДВИГАТЕЛЯ
281
1. Общая методика. Рассмотрим задачу Майера в применении
к динамической системе:
х{ = ик) (i, j = 0, 1, . . п\ к = 1, . . ., г). (7.32)
Величины х-п ик — фазовые координаты и управляющие
функции соответственно; граничные условия определены в задан¬
ные начальный t = 0 и конечный t = Т моменты времени; зна¬
чения фазовой координаты х0 (Т) — контрольный функционал.
Одна из управляющих функций ограничена снизу: и1 > 0.
Будем называть управление и1 включенным, если их 0, и вы¬
ключенным, если их = 0; сумму всех интервалов времени, на
которых управление иг включено, назовем временем действия
управления Т[х.
Решив вариационную задачу, найдем время Т[Х орт <7 Т, кото¬
рое определим как оптимальное время действия управления uv
Пусть в дополнение к сформулированной выше вариационной
проблеме задано время действия управления иг, меньшее оптималь¬
ного Т[Х <^Т[Х opt. Для сведенрш такой усложненной вариационной
постановки к стандартной постановке Майера воспользуемся
введенными в главе 6 текущим временем действия управления
и релейным управлением б (t), которые связаны дифференциаль¬
ным соотношением
£и. = 6. (7.33)
Управление б (t) — релейная функция, принимающая значение 1
в моменты включения и значение 0 в моменты выключения управ¬
ления uL. Используя это свойство функции б (t), заменим управ¬
ление их на и1 б; это произведение совпадает с иг в моменты вклю¬
чения и обращается в нуль в моменты выключения.
Запишем систему дифференциальных уравнений вариацион¬
ной проблемы в следующем виде:
Х\ /,- (Xj, ll1 б, Uji) ч t^ б /7 Q/S
(i, j = 0, 1, . . п; к = 2, . . г). ( •' ^
Если одновременно с упомянутыми выше краевыми условиями
для фазовых координат будут удовлетворены краевые условия
для вспомогательной координаты
т
V (0) = 0, t,,. (Т) = 5 6 (t) dt = Tv. < 7V opt, (7.35)
а релейное управление б (t) наряду с и1 (t), . . ur (t) будет
выбрано оптимальным в смысле контрольного функционала х0 (71),
то вариационная задача с дополнительным условием заданного
282
РЕАЛЬНЫЕ ДВИГАТЕЛИ ОГРАНИЧЕННОЙ МОЩНОСТИ
[ГЛ. 7
времени 7V<7VoPt будет решена. Иными словами, будут ука¬
заны оптимальное число включений и оптимальное время дей¬
ствия управления их для каждого активного участка.
При решении поставленной задачи методом JI. С. Понтрягина
составим, как обычно, гамильтонову функцию и выпишем уравне¬
ния для импульсов
Пусть для определенности ищется максимум контрольного
функционала х0 (Т), т. е. функция Н должна достигать абсолют¬
ного минимума на оптимальных управлениях uv щ, 6. Для
управления б абсолютный минимум Н достигается в том случае,
если выполняются условия
5 - 0 при Н1 — tf0 + > 0, б = 1 при Н± - Н0 + /V < 0. (7.38)
Разность Н1 — #0 неположительна. В самом деле, Нг = 7/0
при иг = 0, как это следует из определения (7.37) функций Н0.
Нр при других значениях иг разность Нх — Я0 должна быть отри¬
цательной, так как в противном случае гамильтонову функцию Н
можно уменьшить, положив и1 = 0, и тогда будет Н1 — Н0 = 0.
Отсюда определяется знак импульса pp.
Если бы p[it 0, то выражение Нх — Н0 + р{)1 никогда не
меняло бы знака, и б (t) == 1; при этом t[y (Т) = Т, что заведомо
нарушило бы краевое условие (7.35).
Заметим, что при и1 = 0 оптимальное значение релейной функ¬
ции б равно нулю, так как р^ > 0, Н1 — Н0. Если p[Jt = 0, то
получающееся при этом время Т[к совпадает с оптимальным:
Указанный метод применим также и для нескольких управле¬
ний с заданными временами действия, меньшими оптимальных;
при этом вместо одного вспомогательного управления б добавля¬
ется нужное число их.
п
Представим Я как функцию 6 следующим образом:
Я = Я0+ (#!-#« +Р,,) 6,
11
Но = Я5=п = У PifiiXj, 0, ик),
1=0
(7.37)
11
11
Hi = Я8=1 — рц = У p.fi (х , Uv Uk).
г= о
Pv- > °-
(7.39)
T'v ~ opt"
§ 2]
ЗАДАННОЕ ВРЕМЯ РАБОТЫ ДВИГАТЕЛЯ
283
2. Применение общей методики к изучаемой проблеме. В ис¬
ходных уравнениях (II.8) умножим расход q и тягу Р на функ¬
цию б (t) и добавим к системе дифференциальное уравнение для
текущего времени работы двигателя получим следующую
запись вариационной проблемы:
Ga =--—gq&,
f'n= 6,
•' - v,
gPb
Gc +
V =
G3(0) = G„ —Gx, G3 (T) = max,
*Д0) = 0, tv.(T) = Tv„
r (0) = I’m r(T)=ri,
e + R, v (0) = vr, y(7’) = v1.
(7.40)
Для двигателя ограниченной мощности без потерь, которому
посвящено дальнейшее изложение параграфа, вариационная
проблема (7.40) сводится к такой (ср. (5.2)):
(7.41)
./ = а°-Ь, J (0) = 0, J (Т) = min,
tv. = б, I,,. (0) :™ 0, tv. (Т) = Tv_,
Г = V, г (0) = г(1, г (Г) = 14,
v = a6e + R, v(0)=v«, v(7’) = v1
(а (t) ;> 0, б (t) — 1 или 0, | е (t) | = 1).
Чтобы найти оптимальные законы е (t), а (t), б (£), обратимся
к методу Л. С. Понтрягина и выпишем гамильтонову функцию
и дифференциальные уравнения импульсов
Я = — а-Ь + б + р(, • v + рк • (абе + R),
Р,, = °’ = — W (Рг’К). Р„ "= ~ Рг (Pv. < °)-
(7.42)
Управления е (t), a (t) в оптимальном режиме должны удов¬
летворять соотношениям
(7.43)
Оптимальные моменты включения (6 = 1) и выключения
(б = 0) двигателя связаны со сменой знака комбинации А
6 = 1 при А >> 0, 6 = 0 при А < 0 (А = г/4р1 + pv). (7.44)
Если Т[Х наперед не задано, то = 0 и A (t) 0 при
следовательно, пассивные участки на траектории
отсутствуют.
284
РТГЛЛЫ1ЫГ ДШ1ГЛТЕЛН oppai шчгп ПОЙ МОЩНОСТИ [ГЛ. 7
3. Маневры в бессиловом поле. Не обращаясь к конкретному
типу маневра, отметим прежде всего, что при движении в бесси¬
ловом поле х) может быть не более двух активных участков. Дей¬
ствительно, при В = 0 дифференциальные уравнения импульсов
рг, ру из (7.42) интегрируются:
Рг = 2ЬХ, Ру = 2bxt + 2Ь2, (7.45)
и входящая в (7.44) величина V4p- выражается так:
'Upl = bit2 + 2bj • b2i + bl. (7.46)
Уравнение A (t) = 0 — квадратичное относительно t и имеет
не более двух корней: tx (b4, Ь2) и t2 (b1? Ь2), определяющих на¬
чало и конец единственного пассивного участка, который разде¬
ляет два активных участка.
Оптимальная программа вектора реактивного ускорения ае
на активных участках — линейная функция времени. Для
нахождения постоянных векторов Ь1? Ь2, зависящих от заданных
начальных и конечных значений координат (г0, гх) и скоростей
(v0, v4), следует проинтегрировать уравнения движения из си¬
стемы (7.41) по активным и пассивному участкам; при этом
ае = + Ь2, 6 = 1 при и t2 <4 t Т;
6 = 0 при t± < t < t2. (7.47)
Сначала рассмотрим маневр набора заданного модуля скорости
иг в бессиловом поле при заданных времени маневра Т и времени
работы двигателя Т^.
Конечные значения координат г (Г) в этом маневре не фикси¬
рованы, поэтому имеет место следующее условие трансверсаль¬
ности:
рг (Т) = 2Ь, = 0. (7.48)
Согласно формулам (7.44), (7.46), (7.48) комбинация А не за¬
висит от времени, и знак, а также величина ее не определены.
Это означает, что расположение пассивного участка на траек¬
тории не определено и не влияет на контрольный функционал
J (Т); последний дается выражением (ср. (5.32))
J (Т) = u\iT^ (7.49)
Отметим, что в выражение (7.49) не входит время выполнения
маневра Т.
Вторым исследуем маневр перелета между двумя положениями
покоя в бессиловом поле, разделенными расстоянием Z, при за¬
данных временах выполнения маневра Т и работы двигателя 7V
х) Или в илоскопараллельном.
2]
ЗАДАННОЕ ВРЕМЯ РАБОТЫ ДВИГАТЕЛЯ
285
После интегрирования уравнений движения по активным и пас¬
сивному участкам получаем выражения постоянных hv b2 через
параметры маневра Z, Т и время Т.у. Подставляя эти выражения
в формулы для tv t2 находим
t — 1/ 71 t — Т Т
t'l — 1 ъ1 [J. э L 2 '2м |J-'
(7.50)
Программа вектора реактивного ускорения ае имеет вид (ср.
(5.33))
6/ 1—2/ / Т
ае =
Т1 1 — (1 -TJTf'
а выражение функционала J (Т) следующее (ср. (5.33)):
12/2 1
J(T)
т* 1 (1 Т / Т)3
(7.51)
(7.52)
Таким образом, пассивный участок в рассматриваемом слу¬
чае расположен посередине траектории. При заданном времени
Рис. 7.2. Зависимость функционала J от Рис. 7.3. Зависимость функционала J от
активного времени при заданном вре- времени маневра Т при заданном актив-
меяи маневра -J12 <7ГЧ -перелет иом времени Tv. (J*= 12 1*гф -перелет
в бессидовом поле между точками покоя.
в оессиловом поле между точками покоя.
движения Т и заданном расстоянии I функционал / монотонно
возрастает при уменьшении времени Т[у, (рис. 7.2). При задан¬
ном времени Т[У и заданном расстоянии I функционал J моно¬
тонно убывает при увеличении времени Т (рис. 7.3).
4. Поворот плоскости круговой орбиты. Аналогичное иссле¬
дование может быть выполнено и для маневра поворота плоскости
орбиты. Приведем конечные результаты; выберем следующие
286 РЕАЛЬНЫЕ ДВИГАТЕЛИ ОГРАНИЧЕННОЙ МОЩНОСТИ [ГЛ. 7
значения параметров (описание маневра см. в Приложении, § 3):
Т = 2 я, = 1/2я, (7.53)
наклонение i произвольно в допустимых пределах (i<^ 1), время
работы двигателя Tv_ — параметр задачи.
О ?/г к тс 3/ггс t
Рис. 7.4. Закон изменения модуля реактивного ускорения а (t) при раз¬
ных значениях активного времени = я, 3/2я, 2я — поворот [плоскости
орбиты на угол г за время Т = 2я.
рис. 7.5.J Зависимость функционала J от активного времени при
фиксированном времени маневра Т = 2л (J*= г2/л)— поворот плоскости
орбиты на угол i.
При отсутствии ограничения на время работы двигателя оп¬
тимальные законы а (£), е (t) и величина контрольного функцио¬
нала J (Т) таковы (см. (5.74), (5.75)):
ае = (с / л) sin t при 0 < t 2я, 1 п Ъ/\
J (Г) =--= i2 / л (Г- 2л). )
2]
ЗАДАННОЕ БРЕМЯ РАБОТЫ ДВИГАТЕЛЯ
287
Если время работы двигателя Т,х задано, то выражения (7.54)
заменяются на следующие:
а = О
ае =
при 0 t << 1/.2я — Vd^u.,
l/2Tu _|_ sin (1 fj\J ИРИ 1/2Я “ X/iT !'• < г < V-2n + 1/i Т ц,
i sin /
а — О
аг =
i sin t
7.7V + sin (Ч'Т,, )
a — О
при г/.2я + 1/4Т’ у < t < 3/2я —
при 3/2я — ’ДГи. ■< £ < 3/2я + 1/47’
при 3/2л + г/4?'|>. <Л ^ 2л.
(7.55)
На рис. 7.4 приведены законы а (г) при = 2я, 3/2я, я;
зависимость контрольного функционала от времени работы дви¬
гателя Т^ (0 Т[х ^ 2я) иллюстрируется рис. 7.5.
5. Межорбитальный перелет. Будем рассматривать плоское
движение в центральном поле в прямоугольных координатах
(см. Приложение, § 2).
Вариационная проблема (7.41) для маневра перелета между
круговыми орбитами записывается следующим образом [7.10]:
/== а2 б,
= б,
х — и,
У = v,
и = а6гт —
а z= абг,, —
J (0) =0, У (71) — min,
U°) = °> tv.{T) = T„,
х(0) = l, х(Т) --= ricos(pb
2/(0)= 0, у (Т) — i\ sin Ф1,
, и (0) = 0, и (Т) — — Гх'2 sin фх,
у
— v (0) = 1, v (Т) = тх'2 cos (pi
(7.56)
(*Ч-?/2) 2
(а (/) >0, 6 (/) — 1 или 0, е% (t) -j- ef, (t) — J).
Гамильтонова функция и дифференциальные уравнения им¬
пульсов (7.42) в данном случае имеют вид:
Я = — а26 + pix 6 + рхи + pv 4 ри [аЪех — х (хг + у2)-3'2] +
+ Pv 1а&е„ — У (х2 + у2)-*'*],
^. = 0, ри = —рх, pv = —p
Ру =
(** + i/2)'
Зж (рцж + Pvy)
(:X2 + f/2)S 2
Е,=
(** + !/Г/г
з?/ (у + л.-у) ’’
(я2 ~г У2)*72
(7.57)
288 РЕАЛЬНЫЕ ДВИГАТЕЛИ ОГРАТТНЧЕ HHOlf МОЩНОСТИ [ГЛ. 7
Из условия максимума функции Н следуют выражения для
оптимальных программ а, ех, е,п 6
"v = Ри(Pi + PIT А е„ = Pv(Pi + а -1/*у p2u + Pi’ j
6 = 1 при Д > 0, 6 = 0 при Д < 0 (А = хи {р\ + р\) +
(7.58)
Таким образом, вариационная проблема свелась к решению
следующей краевой задачи для дифференциальных уравнений:
А). = 6, tv. (0) = 0, tv. (Г) = Тм
£=«, ж(0) = 1, X (Т) = Гх СОЭф!,
у = V, у(0)=0, у (Т) = ?'i sin tpi,
и = — х (х2 -j- t/-)—’/г, и (0) =0, и (Т) = — Щ3 sin фь
V = — у (х- + г/'2)-72, v (0) = 1, V (Г) = riVscos Ф1
(6 = 1 при А > о, 6 = 0 при А < 0, А = г/4 (р2и + р\)
р,, = 0’ к =—рх> Я /V
Ри _ 3:с (Рцж + Р„?/)
(.г- + y-),J/2 (я2 + ?/-)7г
Ру _ 3?/ (/У7 "Г /У')
(.г2 t/2)3^2 (:к2 -j- J/2)"'2
(7.59)
Р„
После решения краевой задачи определятся функции х (t),
у (t), и (t), г; (t), p;j. (i), . . ., pu (i),pr (t) и может быть подсчитан
контрольный функционал
т т
/ (Г) = ^ п-6 dt = Щ ^ (р2 + р2) 6 Л. (7.60)
Задача (7.59) содержит четыре параметра: 7\ ф1? г1? 7^.. Если
параметр Т„, должен пробегать ряд значений, то удобно пара¬
метрический просчет вести по р ., а не по Т[}.. Тогда в краевой
задаче (7.59) исчезает необходимость удовлетворять условию
(Г) = Туравнение для можно интегрировать после опре¬
ЗАДАННО К ВРЕМЯ РАБОТЫ ДВИГАТЕЛЯ
289
деления функций х (t), . . б (t) одновременно с вычислением
контрольного функционала (7.60)
т
Tv. = ^ б (t) dt. (7.61)
О
При численном решении краевой задачи (7.59) применялся
метод последовательного подбора недостающих начальных значе¬
ний рх (0), ри (0), ри (0), рс (0). Расчеты проводились для пере¬
летов с круговой орбиты единичного радиуса на круговую орбиту
радиуса гг = 1,52 (Земля —
Марс); в большинстве слу¬
чаев средняя угловая ско¬
рость на перелете прини¬
малась равной угловой
скорости движения по на¬
чальной орбите: ф JT 1.
Результаты расчетов даны
на рис. 7.6—7.8.
На рис. 7.6 представ¬
лена зависимость функцио¬
нала J* = J (Т[х = Т)
от времени движения Т
при отсутствии пассивных
участков на траектории
(Т[Х = Т = фх). На рис. 7.7
дано семейство кривых
J (Г,,., T)/J* (Г), отличающихся одна от другой значениями
времени Т (по-прежнему фх = Т). При 0,5 Т 4,5 и
0,8 ^ TVJT <^1,0 относительное изменение функционала —
величина (//7*) — 1 — слабо зависит от времени перелета Т\
для TJT= 0,5 относительное изменение функционала при раз¬
личных Т составляет 12—13%, что хорошо согласуется с резуль¬
татами по бессиловому полю (см. рис. 7.2). В исследованном диа¬
пазоне параметров (0,5 ^ Т 4,5; 0,4 TJT <; 1) пассивный
участок на траектории один. На рис. 7.8 даны оптимальные про¬
граммы модуля реактивного ускорения a(t) при Т = 4,5 для
различных величин Tv,.
В заключение настоящего пункта сделаем два замечания.
1°. Движение в центральном поле может изучаться в прямо¬
угольных координатах или в полярных координатах. Последние
имеют то преимущество, что из системы дифференциальных
Уравнений для экстремалей, аналогичных (7.59), удается доста¬
точно просто выделить интегралы типа v, X (как в § 1 гл. 5) и
тем самым понизить дифференциальный порядок системы. На
19 Механика полета
Рис. 7.G. Функционал J* в зависимости от вре¬
мени движения — перелет между круговыми ор¬
битами (?’о =1, гх = 1,52, Тр, = Т = <pt).
290
РЕАЛЬНЫЕ ДВИГАТЕЛИ ОГРАНИЧЕННОЙ МОЩНОСТИ
[ГЛ. 7
пассивном участке траектории уравнения движения и уравне¬
ния импульсов интегрируются и их решения представляются в
конечном виде. Проведение процедуры интегрирования достав¬
ляет аналитические связи между параметрами в начале и в конце
пассивного участка. В п. 5 предпочтение было отдано прямоуголь¬
ным координатам потому, что разработанный численный метод
Рис. 7.7. Зависимость функционала J от доли
активного времени Т^/Г при фиксированном
времени движения Т — перелет между круговы¬
ми орбитами (J * = J (7'а = 7’), r0 = 1, тх= 1.52,
ср, .=*7’).
Рис. 7.8. Вид функции а (/)— реак¬
тивное ускорение при различных
значениях параметра Т^/Т — пере¬
лет между круговыми орбитами
(Т = Фх = 4.5, r0 = 1, = 1,52).
решения более удобно применять к уравнениям в этих коорди¬
натах.
2°. Укажем еще один способ получения оптимальных связей
между параметрами в начале и в конце пассивного участка; этот
способ не требует введения релейного управления б (t). Исход¬
ным здесь является представление рассматриваемой вариацион¬
ной проблемы в виде задачи Лагранжа (5.1) или (5.3).
Пусть на траектории имеются два активных участка. Сум¬
марный функционал равен сумме функционалов, соответствующих
первому и второму участкам. Начальные значения координат и
скоростей для первого функционала и конечные значения для
второго заданы; координаты и скорости в начале и в конце пас¬
сивного участка связаны конечными соотношениями, справед¬
ливыми для пассивного движения в центральном поле. Исполь¬
зуем для выбора недостающих параметров условие обращения
в нуль первой вариации суммы функционалов. В результате полу¬
чим отмеченные в первом замечании оптимальные связи между
параметрами в начале и в конце пассивного участка и в том числе
оптимальное расположение пассивного участка на траектории.
В отличие от метода с функцией б (t), этот подход не позволяет
указать оптимальное число пассивных участков.
ОПТИМАЛЬНАЯ СТУПЕНЧАТАЯ ПРОГРАММА ТЯГИ
291
§ 3. ОПТИМАЛЬНАЯ СТУПЕНЧАТАЯ ПРОГРАММА ТЯГИ
Изменение тяги и расхода двигательной системы с двигате¬
лями, обладающими узким диапазоном регулирования, осуще¬
ствляется за счет переключения расхода и мощности с одного
движителя на другой, настроенный на другие значения тяги и
расхода. Функции тяги и расхода при этом ступенчатые, харак¬
теризующиеся числом уровней (ступенек), высотой уровней и
моментами переключения с одного уровня на другой. Число уров¬
ней равняется числу разнонастроенных движителей, и добавле¬
ние нового уровня вызывает увеличение веса системы на вес дви¬
жителя, обеспечивающий этот уровень.
Решение вариационной проблемы о доставке максимального
полезного веса в данном случае должно определить, в том числе,
оптимальное число уровней (разнонастроенных движителей),
оптимальные высоты уровней и моменты переключения с одного
уровня на другой.
В данном параграфе сначала дается общий метод решения
вариационной задачи о ступенчатой аппроксимации оптималь¬
ного управления при заданном числе уровней [7.11], а затем
при помощи этого метода строятся оптимальные ступенчатые
программы реактивного ускорения и тяги для ряда маневров.
Предполагается, что процесс ускорения в движителе происходит
без потерь; поэтому тяга, расход и мощность, фигурирующие в
уравнениях вариационной проблемы, связаны идеальным соот¬
ношением (4.1).
1. Общая методика. Пусть динамическая система описыва¬
ется следующими дифференциальными уравнениями:
Х<= /г (*j. uu, t) (г, j = 0, 1, . . п; & = г). (7.62)
Здесь X) — фазовые координаты, ик — управляющие функции
(положения регуляторов); функционал задачи — х0 (71).
Решение вариационной задачи Майера (7.62) об экстремуме
функционала х0 (t) дает оптимальные управления Wioi>t(*)i • • •
. . ., ur()]){(t). Рассмотрим такое положение, когда программа
Для одной из управляющих функций, например и1, должна быть
ступенчатои с s уровнями, в отличие от Wiopt (t), которая явля¬
ется непрерывной вместе с первой производной. Высоты уровней
и точки переключения с одного уровня на другой ступенчатой
функции ил (t) должны быть выбраны так, чтобы иг (t) наилучшим
образом, в смысле контрольного функционала х0 (Т), аппрокси¬
мировала оптимальное управление иинл (О-
Введем релейные функции, принимающие значения 0 или
1: (t), . . ., 6,s_x(£), и параметры: л1? . . ., я8. Первые определят
точки переключения с одного уровня на другой, вторые — вы¬
соты уровней. Кусочно-постоянная функция ил (£}, принимающая
292 РЕ АЛЬ 11ЫК ДВИГАТЕЛИ ОГРАНИЧЕННОЙ МОЩНОСТИ [ГЛ. 7
s значений, может быть представлена через б1? . . ., б5_ь
я1? . . я8 следующим образом1):
и1 (0 “((••• (^1^1 "Ь Я2) б2 + . . . + Я8_2) Ss-2 Jts-i) 6S_! -f-
+ = щ (я, б), (7.63)
нри этом s значений управления ul (t) (высоты уровней) выража¬
ются так:
l/jS) = Я8, = Я,-! + Я8, . . = Ях + Я2 + . . . +
+ я^_х + я*. (7.64)
Определим времена действия параметров я1? . . ., я8. Пара¬
метр я8 включен в течение всего процесса (О t Т), параметр
я8_1 включен при 6s_x (t) = 1, . . параметр я2 включен тогда,
когда 62 (t) б3 (£)... 6S.-! (t) = 1, параметр ях включен тогда,
когда бх (t) . . . 6s_i (t) = 1. Текущие времена действия пара¬
метров t[)X , . . ., £1XS связаны дифференциальными соотношениями
с релейными функциями б (t)
ipS = 1, ^-11=1 • • • > М2. . . 6,_L. (7.65)
Полные времена действия даются интегралами
т т
T,m = Т, 7V-1 = 5 Л, . . ., Т1Л = 5 616, • • • 6Н_! dt. (7.66)
О о
Выбор параметров я1? . . ., я8 и точек переключения релейных
функций б1? . . ., 6s_i подчиним условию экстремума функцио¬
нала х0 (Т). Для этой цели воспользуемся методом JI. С. Понт-
рягина: составим гамильтонову функцию Н и выпишем
Н Представление (7.63) можно записать также в виде:
их (л, б) = лАб2 . . . б ._2бв^ +я2б2 . . . 63-26s_t + . . . + лч_2б^2бч_1 +
+ л8„А~г + n.s.
Отметим, что запись
и1 (Л1 б) = л А + л2б2 + . . . + я8-1б8-1 + я8,
которая с первого взгляда кажется наиболее естественной, не годится, так
как возможное число значений такой функции превышает s (кроме случая
s= 2); при 3 и Л| ф пj оно равно
с8Д + сД + . .. + сД + 1 = 1 + (* - 1) + ... + (* - 1) + 1 =
= 2« + . •
при 5=3 получается четыре значения.
§ я] ОПТИМАЛЬНАЯ СТУПЕНЧАТАЯ ПРОГРАММА ТЯГИ
дифференциальные уравнения импульсов
293
II = 2 pji (я, 6), Uk, t),
i=()
(О / = о, 1 п\ к — 2, . . . , г).
он
Pi ~ Ох.
(7.07)
Нахождение оптимальных управлений и2, . . ., мг производится
стандартным способом; для определения программ 8Х (£),.. .
. . 8s_i (t) следует вычислять функцию Н при следующих набо¬
рах значений этих управлений в каждый момент времени:
Пи
б,_г - О,
И 2,
бал — 1»
6,0 = 0.
п.-1,
бв-1=1,
6,-2 - 1.
б2= 1,
6i = О,
Яв>
6,-1 = 1,
6,-2 -1,
62 - 1,
б1 = 1.
(7.68)
Наибольшая (или наименьшая, судя по характеру экстре¬
мума х0 (Т)) величина Н из s вычисленных укажет оптимальный
набор значений релейных управлений в момент t.
Для отыскания оптимальных значений параметров лх, . . .
. . ns можно использовать следующий прием. Считая пара¬
метры Я], . . ., л8 новыми фазовыми координатами, дополним
систему (7.62) тривиальными дифференциальными уравнениями:
п1 = 0.
л8 0.
(7.69)
Гамильтонова функция при этом не изменится, а к уравнени¬
ям для импульсов (7.67) добавятся s дифференциальных уравне¬
ний вида
д/1 ОН - А
Pi 5— = ^— бг . . . 0,_1,
0 и| L
ОН. ,
р, л “ — л—6s_j,
1 (П1\
dll' &
Л бо . . . Og.!,
dui
ОН
Ощ
(7.70)
Начальные и конечные значения фазовых координат я1? . . .
. . ., л8 не фиксированы, поэтому импульсы /;х, . . ., р8 при t = О
и t — Т равны нулю. Отсюда следуют интегральные соотно¬
шения. определяющие оптимальные значения параметров
294
РЕАЛЬНЫЕ ДВИГАТЕЛИ ОГРАНИЧЕННОЙ МОЩНОСТИ
[ГЛ. 7
$ тЧг 61 ■ ' ' 6s_1 л ^ 5«, 62 • • • б*~1 dt ~ °’ • • •'
т
т
(7.71)
О
о
При помощи (7.65), (7.66) последние формулы могут быть
единообразно представлены в виде
В заключение настоящего пункта сделаем ряд замечаний.
1°. Может иметь место неединственность представления сту¬
пенчатой управляющей функции и1 (я, б) через параметры
я17 . . ., я8_! и релейные управления бх, . . ., 6s_i. Установим
этот факт для 5 = 2.
Допустим, что построено оптимальное двухступенчатое управ¬
ление
т. е. выбраны релейная функция бх (£) и параметры ях, я2. Заме-
Таким образом, получено второе представление управляю¬
щей функции и1 (я, б), не совпадающее с первым, но дающее оди¬
наковый закон их (t), и, следовательно, одинаковую величину
к он тр о л ьн о го ф у н к ц и он а л а.
т
т
.о
о
(7.72)
и1 (/) = Я j б j (t) Ч- я2,
(7.73)
ним функцию бх на 6L = 1 — 6j и найдем такие параметры яь я2,
которые вместе с составляют управление u^t):
ux(t) = ягбг (/) Ч- я2,
(7.74)
такое, что iiy(t) =1 и1 (t). При б, = 0 имеем: uL = я2, б]. = 1 и
Ну = яг Ч- я2? при бг = 1 имеем: ил = ях Ч~ я2, 6t = 0 и иу = я2.
Следовательно, для тождественного равенства ux(t) = (t) не¬
обходимо выполнение условий
я2 = я,. Ч я2, п1 Ч" я2 = я2 или = —ях, я2 = ях Ч- я2, (7.75)
ОПТИМАЛЬНАЯ СТУПЕНЧАТАЯ ПРОГРАММА ТЯГИ
295
2°. Если управляющая функция ограничена пределами:
О ui (0 ^ 1’ то на параметры я1? . . ., л8 накладываются огра¬
ничения:
min ui (я, 6) > 0. max щ (я, 6) <1. (7.76)
п. п.
% г
Граница может быть включена в состав оптимального ступенча¬
того управления и1 (t). Приведем пример записи трехступенчатого
управления их (я, б), включающего нижнюю (их = 0) и верхнюю
(их = 1) границы:
их - ((1 - я о) Ьх + я2) б2; (7.77)
при этом должно быть 0 я2 1 (предполагается, что оптималь¬
ное управление UiQVx(t) не граничное, т. е. принимает и промежу¬
точные значения). Если сумма времен включения нижней границы
их — 0 задана, то в вариационной проблеме появляется допол¬
нительное дифференциальное уравнение £;j.3 = 62 и дополни¬
тельное краевое условие tv,3 (Т) — Tv.3 в соответствии с мето¬
дом, описанным в предыдущем параграфе.
3°. Можно указать численный подход к решению задачи о
ступенчатой аппроксимации управления, не использующий пред¬
ставления с релейными функциями (7.63).
Зададимся искомыми s уровнями управлешш их : их\ и(21, ...
, . и будем решать задачу при помощи метода JI. С. Понтря-
гина. Моменты смены уровней определятся из условия экстре¬
мума гамильтоновой функции, а оптимальные высоты уровней —
из условия экстремума контрольного функционала. Последняя
процедура требует привлечения численного метода типа скорей¬
шего спуска.
Способ с релейными функциями дает аналитические соотноше¬
ния для выбора оптимальных высот уровней.
4°. Пример ступенчатой аппроксимации оптимального управ¬
ления уже рассматривался в главе 4. Там удалось построить оп¬
тимальную ступенчатую программу, не прибегая к предложен¬
ному методу, потому, что вариационная проблема обладает сле¬
дующим свойством: управление Gx (Ga) — неубывающая функ¬
ция своего аргумента, так что каждый уровень ступенчатого
управления может заниматься однократно. Это свойство позво¬
ляет вариационную проблему со ступенчатым управлением
GK (Ga) свести к задаче на максимум.
Еще один пример построения оптимальной ступенчатой про¬
граммы можно найти в работе [7.12]. В следующем пункте этот
пример рассмотрен как иллюстрация в общей методике. В упомя¬
нутой; работе решение найдено благодаря специальному виду оп¬
тимального непрерывного управления.
296
РЕАЛЫ IЫ К ДВИГАТЕЛИ ОГРАНИЧЕННОЙ МОЩНОСТИ [ГЛ.
2. Примеры ступенчатой аппроксимации программы реактив¬
ного ускорения. В этом пункте дается как иллюстрация предло¬
женного метода решение вариационной проблемы (4.11) при усло¬
вии, что управляющая функция a (/) выбирается из класса сту¬
пенчатых функций а (л, б) с заданным числом уровней. Рас¬
сматриваются два маневра: перелет в бессиловом поле между
двумя положениями покоя, разделенными расстоянием /, за
время Т и поворот плоскости круговой орбиты на угол i за один
оборот (Т = 2л) при = — л/2.
Вариационная проблема (4.11) с а = а (л, б) для первого из
рассматриваемых маневров за¬
писывается так:
У = а2, /(0) - 0, J(T) = min,'
х = и, я(0) = 0, х(Т) = /,
и = ае, и (0) = 0, и (Т) = 0
(а (/) =: а (л, 6), e(t) — zb 1). .
(7.78)
Если на управление a (t) не
наложены ограничения, то опти¬
мальные законы a (t), е (t) и
минимальное значение конт¬
рольного функционала J (Т) даются формулами (5.33) (криваяос
на рис. 7.9).
Ниже приведен ряд оптимальных ступенчатых программ
а (t) для задачи (7.78); на последнем примере подробно опи¬
сана процедура метода.
1°. При а (л, б) = п1 оптимальные законы a (t), е (t) таковы
(рис. 7.9, кривая 1):
а(/) = 4//Г2, e(t)= I при
a(t) = 4l/T2, e(t) = — 1 при 1/2Т
J (Т) - Ш2/Т\
2°. При а (л, б) = л181 оптимальные законы а (t), е (t) та¬
ковы (рис. 7.9, кривая 2):
a (t) = 4,5/ / Г2, е (/) ^ | при 0 t 1/:?7\
«(0 = 0 при V:,2r < ^ <
a (t) = 4,5* / 7’2, е(0 = —-1 при УЯТ < t < Т, 'С7-80)
/ (7’) =: 13,5/2 / Тя.
(7.79)
Рис. 7.9. Ступенчатая аппроксимация
управления а (i) — перелет в бессиловом
поле между точками покоя.
§ 3J
ОПТИМАЛЫ1АЯ СТУПЕНЧАТАЯ ПРОГРАММА ТЯГИ
297
г (*)
при 0 < t <4 1/i]T,
при 1//Т <” t <^1/.1Т,
при 1!оТ </<3/J\
при 3/4Г < /<; 7\
при 0< t<^xlbT,
при V5r </<2/57\
при 75Г </<3/57\
при 3/5Г < / < 4/57\
при 4/5Г < t < Г,
(7.82)
3°. При а (я, б) = я|бj + я2 оптимальные законы а (7,
таковы (рис. 7.9, кривая о):
а (£) — 4,8 I / Т-, e(t) -- 1
а (7 = 1,6/ / 72, г (7 = 1
a(t)-- \ ,Ы IТ-, е (/)—J при 1/2Т < t <Г 3/Л\ ■ (7.81)
а (t) = 4,8/ / Г2, г (/) ~ — 1
/(Г) = 12,8/2/7'3.
4°. При а (я, б) = (я^! + я2) б2 оптимальные законы а (/),
с (/) таковы (рис. 7.9, кривая 4):
a\t) = 5/ / Г2, с (/) = 1
я (/) = 2,5/ / 712, с (/) г- 1
а(*) = 0
а(0 - 2,5//Г2, <?(*) = —1
а (/) = 5/ / 71'2, с (/) —■ — 1
/ (71) = 12,5/2 / 7’3.
В примерах 2° и 4° в состав управления включены уровни с за¬
данной (нулевой) высотой; для участков с заданной величиной уп¬
равления остается определить только их оптимальное положение.
Опишем процедуру построения оптимального трехступенчато¬
го управления а (я, б) с нулевым нижним уровнем (пример 4°).
Дифференциальные уравнения для фазовых координат, крае¬
вые условия, гамильтонова функция, дифференциальные уравне¬
ния импульсов и уравнения для выбора оптимальных параметров
л1? я2 имеют вид (см. (7.78), (7.67), (7.71))
/ — Я16162 + 2я1Я2б1б.2 Ч- я262. J (0) — 0, / (Т) = min,
х = и, х (0) = 0, х (Т) = /,
и — (Я161 + я2) б2с, и (0) = 0, и (Т) = 0,
Н = — (я^бхбо. + 2яхя2.б1б2 + я*62) + рхи +
-у- Ри (Яхбх -[- я2) б2С,
Рх = °’ Ри ^ - Р,-
т т т
Ях ^ 6хб2 clt + я2\| бхб2dt — PueS\&2dt,
Ях
j. i 1
^ 62 clt + 60 dt — -Г ^ Pve&i dt.
(7.83)
298
РЕАЛЬНЫЕ ДВИГАТЕЛИ ОГРАНИЧЕННОЙ МОЩНОСТИ
[ГЛ. 7
Решение дифференциального уравнения для импульса ри
может быть представлено в следующем виде (см. (6.32)):
Ри = h (tt — t). (7.84)
Оптимальные управления е (/), 6 { (/), б2 (t) подчиняются тре-
бованиям
е 0) = sgn ри (t) (epv = \pj),
6i (/) = 1 при Дх^>0, 6i(i)—-0 при Ai О
(Ах = Л1 ( Я1 — 2я2 4- | ри |)), [ (7.85)
б2(^) = 1 при Д2>0, 62{t) = 0 при д2<0
(Д 2 ~J ^2 ( Jt-2 + I Ри |) 61Д1).
Параметр я2 может быть только положительным, гак как
a (t) 2^ 0. Параметр может быть положительным или отрица¬
тельным; в последнем слу¬
чае \л1\<Сл21 так как
a (t) 0. Рассмотрим сна¬
чала случай п1 0.
Пусть \ра\—2я2> О,
тогда Дг >0 при п1 0
(см. (7.85)) и б, = 1. При
этом выражение \ри \ — л2
заведомо положительно;
следовательно, Д2 ^>0 (см.
(7.85)) и 62 = 1. Пусть
|р,41—л2 0, тогда заве¬
домо Ах 0, и, следова¬
тельно, бх = 0. При этом
А2 < 0 и 62 = 0.
Эти рассуждения приводят к выводу: если бх = 1, то заведомо
62 = 1; если 6j = 0, то заведомо б2 = 0, т. е. участок 62 = 0
расположен внутри участка бх = 0, а участок бг = 1 не превос¬
ходит участка 62 = 1. Расположение участков показано на рис.
7.10. где ti, t2, 12, t! — корни уравнений
М (ti) = — я, — 2я2 + | Ъх j (tt — Ц) = 0, )
A. (ti) =-- I bx I (/, — ti) — я2 =з 0, !
Ai (ti) = — Я1 — 2я, J- j Ь, I (t'i — / ) = 0,
a, (ti) = 1 fri 1 (ti — tt) — я., = о.
Ич (7.86), в частности, следует
ti + tl = 2t„. ft + й = 21„,
Рис. 7.10. Расположение участков включении
уровней управления а (/) — перелет в бессило-
вом поле между точками покоя.
(7.86)
(7.87)
з] ОПТИМАЛЬНАЯ СТУПЕНЧАТАЯ ПРОГРАММА ТЯГИ 299
Оптимальные программы е (t), (t), б2 (t) могут быть записаны
при помощи параметров tL, t2, t2, i[ так (см. (7.85)):
6i(0 =
1,
fi2 (f) = 1,
e(t) = 1
при
о
fil(f) =
0,
62(0 = 1,
e(t) = 1
при
^1 <С t t 2 ?
6i(0 =
0,
bz (t) = 0
при
^2 <С ^ ^ ^2 »
61 (t) =
0,
62(f) = 1,
e(t) = -l
при
61(f) =
1,
62 (f) = 1,
e{t) = — i
при
После интегрирования уравнений движения и удовлетворения
краевых условий приходим к соотношениям
2^ - Т, л,*, (Г - Q + (Т - Q = I. (7.89)
Параметры л„ л2 выражаются через jfeA|, t~i, t2 так (см. две
последние строчки из (7.83)):
= V4 I&11 *2. ^2 = У4 \ЬЛ(Т — t~2 — t\). (7.90)
Из уравнений (7.86) при условиях (7.90) определяем
А = V57\ й = 2/5?\ (7.91)
из второго соотношения (7.89) находим
[6,1 = 251/Т2, (7.92)
тогда (см. (7.90))
л, - 2,5ИТ2, л2 = 2,Ы1Т2. (7.93)
Вид оптимальных управлений приведен в примере 4°.
Если считать параметр лА отрицательным, то по сравнению с
рассмотренным случаем изменяется оптимальный закон бА (£)
и параметры л ,, л2 (6А = 0 при 0 < 1/ьТ и при 4/5Г<^ t<^T,
8Х = 1 при VrST < t <2/.vr и при 3/5Г < t < 4/57\ б, — не
определено при 21ЬТ t 3/-Г; лА — —2,5; л2 = 5); при этом
оптимальные законы a (t), е (t), а также величина J (Т) остаются
неизменными (см. замечание 1° предыдущего пункта).
Рассмотрим маневр поворота плоскости круговой орбиты спут¬
ника. Если на управление а (I) не наложены ограничения, то
оптимальные программы а (/), е (t), а также минимальные зна¬
чения J (Т) даются формулами (5.74), (5.75) (кривая оо на рис.7.И)
Если управляющая функция a (t) выбирается из класса сту¬
пенчатых, то оптимальные программы a (I), e(t) и величина J (Т)
имеют следующий вид.
300 РЕАЛЬНЫЕ ДВИГАТЕЛИ ОГРАНИЧЕННОЙ МОЩНОСТИ [ГЛ.
1°. При а (л, б) = п1 (кривая 1 на рис. 7.11)
а(£) —0,25г\ e(t) = — 1 при 0 t <" 3,14,
а(£) = 0,25/, е (t) — \ при 3,1 4 t 6,28,
J(T) = 0,393 Г2.
(7.94)
О
f/27t
It
Ytlt
(7.95)
Рис. 7.11. Ступенчатая аппроксимация управления а (/) — поворот пло¬
скости круговой орбиты па угол г за время Т = 2л.
2°. При а (я, б) = я^ (кривая 2 на рис. 7.11)
a(t) = 0 при 0<^£ <^0,404,
a(t) — 0,273i, e(t) = — 1 при 0,404 t 2,74,
a(t) = 0 при 2,74<*<3,54,
a(t)=: 0,273г, е(7) = 1 при 3,54 t 5,88,
а(£) = 0 при 5,88 < t ^ 6,28,
/(Г) = 0,345г2.
3°. При а (я, б) = я^] + я.» (кривая 3 на рис. 7.11)
a (t) ОДОСн, e(t) = — 1 при 0 <С 0,664,
a(7) = 0,280j, e(t)■---= — 1 при 0,664 t 2,48,
a(t) = 0,1067, e(t) = — \ при 2,48 <7< 3,14,
a(t) = 0,1067, e(t) =-. 1 при 3,14<7<3,8Q, [(7.96)
а (0 = 0,280i, с (0 = 1 при 3,80 < г < 5,62,
a(t) = 0,106/, e(t) = l при 5,62 t 6,28,
J (Т) = 0,333/2.
ОПТИМАЛЫ ГАЯ СТУПЕНЧАТАЯ ПРОГРАММА ТЯГИ
301
4°. При а (я, 6) = (яА + я2) 62 (кривая 4 на рис. 7.11)
а (/
а (/
a(t
a (/
a (/
a (/
а (/
a(t
a (/
= 0
= 0,154/,
= 0,291/,
0,154/, (J (t)-
О
e(t) - I
e(t) = - 1
- 1
= 0,154i,
= 0,2911,
e{t) = 1
e{t) = 1
—- 0,154/, e (/) ---- 1
= 0
при
при
при
при
при
при
при
при
при
J (Т) =, 0,326/2.
0</<0,238,
0,238 </ <0,750,
0,750 </<2,39,
2,39 < / < 2,90,
2,90 < / < 3,38,
3,38 </<3,89,
3,89 </<5,53,
5,53 </<6,04,
6,04 < / < 6,28,
(7.97)
Как следует из приведенных примеров, величина контрольного
функционала J (Т) монотонно уменьшается при увеличении числа
уровней 5, приближаясь к идеальному значению при s ос.
В заключение этого пункта сделаем замечания, касающиеся
использования полученных результатов. В вводной части пара¬
графа было сказано, что движитель с узким диапазоном регули¬
рования характеризуется ступенчатым изменением тяги и расхода.
Здесь принята ступенчатая программа реактивного ускоре¬
ния. Такой переход возможен в том случае, когда затраты рабо¬
чего вещества на маневре малы и программы безразмерных тяги и
реактивного ускорения мало отличаются одна от другой.
Второе отступление от указанной в начале параграфа поста¬
новки заключается в том, что при добавлении нового уровня реак¬
тивного ускорения или тяги не учитывается дополнительный вес,
обеспечивающий этот уровень. Это отступление может быть оправ¬
дано, если дополнительный вес не зависит от величин, фигури¬
рующих в вариационной проблеме.
В следующих пунктах будет сформулирована вариационная
проблема, свободная от обоих принятых здесь допущений, и даны
примеры ее решения для маневра межорбитального перелета.
3. Формулировка задачи аппроксимации программы тяги с
учетом веса движителей. Назовем приращение веса двигателя от
добавления нового /-го уровня тяги и расхода весом i-то уровня
G{x. Если вес уровня не зависит от характеристик двигателя
вообще и уровня в частности, то процедуру построения оптималь¬
ного ступенчатого управления можно разделить на два этапа:
на первом этапе решается задача при фиксированном числе уров¬
ней тяги и расхода — здесь весовые характеристики уровней не
302
РЕАЛЬНЫЕ Д Ш1ГА1 ЕЛII ОП АГШЧЕШ1 ОЙ МОЩНОСТИ [ГЛ. 7
нужны, на втором этапе выбирается оптимальное число уровней
при известном их весе (ср. предыдущий пункт).
двигателя и уровня. Если изменение тяги и расхода осуществля¬
ется переключением с одного однорежимного движителя на дру¬
гой (этот способ и является здесь предметом изучения), то вес
нового уровня можно считать равным весу движителя, обеспечи¬
вающего этот уровень
Будем предполагать, что вес движителя зависит только от
максимальной тяги, создаваемой им; тогда
(все движители считаются однотипными, так что параметр у оди¬
наков для любого номера /).
Вариационная проблема о доставке максимального полезного
веса при ступенчатых законах изменения тяги и расхода имеет
следующий вид (ср. (7.17)):
(Р (£) = Р (л, 6), Gv = const, Gi =■- cons!, |e(£)| —1).
(7.100)
В записи (7.100) принято, что вес аппарата состоит из полез¬
ного веса G* = Ga (Т), запаса рабочего вещества G[y = Ga — G-y
веса источника мощности Gv и веса системы движителей G>. (веса
s уровней тяги и расхода Gk = у~Р•); процесс ускорения в дви¬
гателе считается идущим без потерь; величины G-, G0, G,, G\
безразмерные, тяга Р также безразмерная (все они отнесены к
начальному весу G0); вес источника мощности Gv — управляю¬
щий параметр.
Ступенчатая функция Р (л. 6). имеющая s уровней, может
быть записана при помощи релейных функций (/), . . ., б8_х (/)
и параметров л2, . . ., л, следующим образом:
В общем случае вес уровня — функция характеристик
G(p = G{.p.
(7.98)
С?’ = тТ;. G> = 2 G>" = r S pi (7.99)
|i=l !=1
6a = —g<x/»/2G„
G3( 0) = 1 — Gv — Gx,
Г (0) =: V, ,
G3(T) = max,
r(T) = iu
\(T) = уг
Г - V,
P (л, 6) = ((... (л^ + Л о) б2 + . . . + Л.,-2) 6s-2 + Л i) 6S_! + Л
■11 " S*
(7.101)
ОПТИМАЛЬНА}! (ЛГУ I НИТЧАТАЯ ПРОГРАММА ТЯГИ
303
Параметры лд определяют высоту уровней тяги Pj
Pi = Jli + Л2 “Г • • • 4“ лS, Р2 = л2 ~г л3 + . . . + Л8, . . .,
ps= Л„ (7.102)
а релейные функции 6*(/) — моменты смены уровней.
Сумма весов уровней 6Д, определяемая формулой (7.99),
запишется при учете (7.102) следующим образом:
G, = Т 2 (7.103)
В вариационной проблеме (7.100) с выражениями для Р (л, б)
и GK в виде (7.101), (7.103) требуется найти оптимальное число
уровней s. оптимальные управляющие функции е (t), б3 (2), . . .
. . ., б,—! (/) и оптимальные управляющие параметры
G,, д1? .... л,.
Сделаем несколько замечаний к сформулированной вариацион¬
ной проблеме.
1°. Число уровней s — целое число из натурального ряда
(s = 1,2,3,. . .); поэтому отыскание оптимального s связано с
перебором ряда значений 5 и многократным решением задачи.
Если бы у = 0, и соответственно G\ = 0, то оптимальное число
5 равнялось бы бесконечности.
2°. Если нижний уровень тяги нулевой (допускается выключе¬
ние двигателя), то Р* = л., = 0, и проблема оптимизации для
данного уровня состоит в определении оптимальных моментов
начала и конца участка, на котором используется этот уровень.
3°. В формулировке (7.100) вес источника мощности G* —
управляющий параметр; это значит, что он определяется из
условий выполнения заданного маневра и достижения максимума
полезного веса. Если рассматриваемый маневр является элемен¬
тарным, входящим частью в сложный маневр, то найденное по
первому оптимальное значение Gv не является оптимальным для
всего маневра. Поэтому при решении вариационной задачи для
элементарного маневра надо считать параметр х —aIGv — GJN
конструктивным, а не управляющим, имея в виду определение
его оптимального значения по полным результатам. Для этого
случая изменим вариационную формулировку (7.100) — введем
новое обозначение для суммы весов
6Ф = 62 -г Gv ся - Си, + Gv (7.104)
и будем считггь контрольным функционалом конечное значение
веса G.'j (Т) = G- -L G,: тогда запись (7.100) трансформируется
304
PU АЛЬПЫ К ДВИГАТЕЛИ ОГ Г АШ [ ЧЕ ILI К) 1"1 МОЩНОСТИ I ГЛ. 7
в следующую:
1* = Y,
(j,b (()) ^ 1 — G,*, (Т) : - max,
(0) = i-n, г (Г) = 14,1
v =
Glb
— + Н, v (0) Vi, V (Т) = Vi
I
р(t) -- р (л, б), с,-,, т 2 ijti- Iе(О! ^1 •
(7.105)
4°. В системах (7.100), (7.105) учтен тот факт, что оптимальное
управление мощностью — граничное. Поэтому в дальнейшем,
вместо того чтобы говорить о ступенчатых программах тяги и
расхода, будем говорить только о ступенчатой программе тяги,
имея в виду, что программа расхода при N (t) = 1 выражается
через Р (t) и параметр к.
4. Ступенчатая программа тяги с оптимальным числом уров¬
ней для межорбитального перелета. Нерегулируемый двигатель
обеспечивает простейшую ступенчатую программу тяги; он имеет
два уровня, один из которых нулевой. Обсудим следующий вопрос:
на каких маневрах добавление новых уровней тяги по сравнению
с двумя уровнями нерегулируемого двигателя ограниченной мощ¬
ности может дать выигрыш в полезной нагрузке, если учитывать
увеличение веса двигателя от добавления новых уровней?
Чтобы ответить на этот вопрос, будем каждый раз сравнивать
оптимальную программу тяги идеального двигателя с программой
тяги нерегулируемого двигателя.
Как отмечалось в главе 5, на маневре разгона с круговой ор¬
биты до параболической скорости идеальная программа модуля
реактивного ускорения представляет собой почти постоянную
функцрш времени. Если затраты рабочего вещества малы (что
соответствует большим временам разгона), то в смысле весовых
затрат закон постоянного ускорения близок к закону постоян¬
ной тяги. Поэтому для медленного разгона применение несколь¬
ких уровней тяги вместо одного, видимо, не даст выигрыша в
полезной нагрузке, если учитывать реальные значения весов
уровней.
Аналогичный вывод следует из анализа маневра набора за¬
данного модуля скорости в бессиловом поле; последний, как
известно, моделирует маневр медленного разгона в центральном
поле. Также нецелесообразно ступенчатое программирование
тяги и расхода на маневре удержания спутника в заданном ша¬
ровом слое.
ОПТИМАЛЬНАЯ СТУПЕНЧАТАЯ ПРОГРАММА ТЯГИ
305
Что касается маневра межорбитального перелета в централь¬
ном поле и моделирующего его маневра перелета между двумя
положениями покоя в бессиловом поле, а также маневра поворо¬
та плоскости орбиты спутника, то идеальные законы тяги на
них существенно отличаются от нерегулируемых; оптимальные
ступенчатые программы могут содержать, кроме нулевого, не
один уровень, а несколько.
Два последних маневра (перелет в бессиловом поле и пово¬
рот плоскости орбиты) были исследованы на предмет построения
ступенчатых программ при двух упрощающих допущениях в п. 2
настоящего параграфа. Здесь будет дано решение вариационной
проблемы (7.105) для маневра перелета между двумя круговыми
орбитами, свободное от этих допущений.
Рассматриваемая проблема записывается так (см. (7.105),
Здесь г1? ф1? Г, х, 5 — параметры задачи; коэффициенты Zx, 12
появились после перехода к безразмерным величинам t, х, у, и, v]
первый коэффициент 1г равен отношению гравитационного уско¬
рения на поверхности Земли (g) к гравитационному ускорению на
начальной орбите, второй коэффициент 12 равен произведе¬
нию Vog на период обращения по начальной орбите, деленный
на 2л; если за начальную принята средняя круговая орбита
Земли, то
Сведем вариационную проблему (7.106) к краевой задаче
для обыкновенных дифференциальных уравнений; выпишем
20 Механика полета
(7.56)):
6* = — ккР2,
Сф(0) = 1 — Gx, G±(T)-=max,
х (0) = 1, х (Т) = г, cos ф1,
у (0) — 0, у(Т) = г1 sin фь
и(Т)= —г^вщфъ
X — и,
У = v
V (0) = 1, V (Т) = 2 COS фх
| Р (Z) = Р(п, 6), еЩ) + e°-y(t) = 1 , = rS^;)-
(7.106)
li = 0,167 • 104, Z2 = 0,2448 -106 квтп/кГ.
(7.107)
306 РЕАЛЬНЫЕ ДВИГАТЕЛИ ОГРАНИЧЕННОЙ МОЩНОСТИ [ГЛ. 7
гамильтонову функцию и дифференциальные уравнения импульсов:
Н = - + ри + pv + ри +
llPev у
+ Pv
.чЗ ' / »
чСф + Сх (®г + у2у
Рф = ^1-Р (^ф + G\)~2 (риех + Pvey)> Рф (О = — Г
к = Ри (х2 + г/Т’/г — Зх (Рих + р„у) (х<1 + У') ~‘/г> к = — рх
к = р„ (** + рТ5/2—Зг/ (Риж+РьУ) (*' + рТ8/% к = — рУ
(7.108)
Формулы для оптимальных управлений ет, е(/ совпадают с
(7.58). Оптимальные релейные управления б1, . . ., 6s-i нахо¬
дятся после применения процедуры, описанной в п. 1 (см. (7.68)).
Чтобы определить оптимальные значения параметров л1? . . .
. . ., я5, входящие в данном случае в краевые условия (7.106),
воспользуемся тем же приемом, что и в п. 1: дополним исходную
систему (7.106) тривиальными уравнениями типа (7.69) и выпи¬
шем дифференциальные уравнения для новых импульсов рi, . . .
. . ., ps; последние имеют такой вид (ср. (7.70)):
(7.109)
дН я я * дН я я
Pi — -Qp-Oi . . . О,-!, Pi = op-02 . . . Owl,
di-i - dii
Ps~l ~ dP *~lJ dP
эн , YpI + pI , 07 _ D
- -dP = VfGT + 2l*P*P
Конечные значения импульсов px, . . . ,ps нулевые, как и в
п. 1, в начальный момент импульсы удовлетворяют условиям
трансв ерсальности
Pi (°) = ТРф (°) - Pi (0) = 2ТРф (0), • . ., Р5 (0) = вГРф (°) >)
Рг(Т) = 0, р2(Р)=0, р» (Т) = 0. j
(7 Л10)
Таким образом, вариационная проблема сведена к краевой
задаче (7.109), (7.108), (7.110). При численном решении последней
ОПТИМАЛЬНАЯ СТУПЕНЧАТАЯ ПРОГРАММА ТЯГИ
307
применялся метод последовательного подбора недостающих на¬
чальных значений рх (0), ру (0), ри (0), pv (0), р^ (0) и параме¬
тров я1? . . ., JTe.
Расчеты преследовали цель определить оптимальное число
уровней s в зависимости от конструктивных параметров у, х.
Конечный радиус rv угловая дальность перелета срх и время Т
были взяты следующими:
г1 = 1,52, фх = 1,57, Т = 1,57. (7.111)
Конструктивные параметры у, х выбирались из таких:
у = 0; 25; 50; 100; 200; 400 кГ/кГ, х = 5; 12,5; 25 кГ/квпъ. (7.112)
Число уровней тяги s принимало значения
^ - 1, 2, 3, 4, (7.113)
причем в каждом случае допускался нулевой уровень тяги. На
рис. 7.12 приведен характерный вид функции Р (t) при у ==
= 25 кГ/кГ, х = 25 кПквт, s = 4.
Интересно отметить, что для некоторых значений s, х, у +> 0
в оптимальном случае на траектории отсутствует пассивный учас¬
ток. Этот факт можно объяснить следующим образом. Появление
на траектории пассивного участка уменьшает время работы
двигателя и увеличивает в среднем высоты уровней тяги; при этом
потребный запас рабочего вещества Gуменьшается, а сумма
весов уровней Gx возрастает. Может оказаться, что в результате
вес Go (Т) уменьшится; тогда присутствие пассивного участка на
траектории невыгодно. Подобная ситуация не возникает при
у = 0 (невесомый движитель).
На рис. 7.13 приведены зависимости веса 6+ (Т) от параметра
У при различных значениях числа уровней s и фиксированном
параметре х: х = 25 кГ/квтп. Оптимальное значение числа уров¬
ней s при каждом данном значении параметра у определяется по
огибающей, выделенной жирной линией. Символом 5+0 обоз¬
начены варианты с выключением; точки на линиях постоянного
5 разграничивают варианты с выключениями и без него.
Влияние параметра х на максимальную величину Gф (Т)
видно из рис. 7.14, где для сравнения представлены огибающие
трех семейств х = 5; 12,5; 25 кГ/квш. На кривых отмечены точки,
соответствующие сменам числа уровней; например, обозначение
s = 2 относится к точке, начиная с которой вправо до точки
5 = 1 оптимальное число уровней равно двум.
20*
308
РЕАЛЬНЫЕ ДВИГАТЕЛИ ОГРАНИЧЕННОЙ МОЩНОСТИ
[ГЛ. 7
Р/03 Г
0,4
0,4
иг
0,8
Рис. 7.12. Ступенчатый закон изменения тяги Р (t) — пере¬
лет между круговыми орбитами (г0 =1, rt = 1,52, (pt =
= Т = 1,57, G0/N = к = 25 кГ/квт, G^)/P{ = y = 25 кГ/кГ).
Gf(T)
0,22
0,18
0,14
о,ю0
SЛ+О
7ч/
3+0
2+0
s=/+0
3
20
40
60
/00
/
Рис. 7.13. Зависимость веса G^(T) = Gn + Gv от удельного
веса движителей у при различных значениях числа уров¬
ней тяги s — перелет между круговыми орбитами (r0 = 1,
vj = 1,52, Ф1 = Т = 1,57, к = 25 кГ/квт).
Оу(Т)
0,4
0,2
о—
s=/
х =5нг)н5т
2^
s=f
s=2
х=/2,5пГ/п5т
X
=25пГ/п6т 8=/
20
40
60
80
Рис. 7.14. Зависимость веса Сф (Т) = Gn
70 у
от удель¬
ного веса движителей y при различных значениях параметра
х = G0/N и оптимальных числах уровней тяги s — перелет
между круговыми орбитами (?•<> =1, гх = 1,52, =
= Г = 1,57).
§ 4] РЕАЛЬНЫЕ РЕГУЛИРОВОЧНАЯ И ВЕСОВАЯ ХАРАКТЕРИСТИКИ 309
§ 4. РЕАЛЬНЫЕ РЕГУЛИРОВОЧНАЯ И ВЕСОВАЯ
ХАРАКТЕРИСТИКИ
Регулировочная и весовая характеристики (II.9), (11.10) двига¬
тельных систем ограниченной мощности зависят от типа движи¬
теля. Каждый конкретный тип движителя определяет выражения
веса Gy и тяги Р. Функция тяги Р от мощности Ny, расхода q
и параметров^!, . . wt может быть задана явно:
р = р (Ny, q, w) (7.114)
или параметрически при помощи одного общего параметра и:
Р = Р (Ny, u,w), q = q (Ny, и, w), (7.115)
или, наконец, при помощи двух общих параметров щ, и2:
Р = Р (щ, и2, w), q — q (uv u2, w), Ny = Ny (uv u2, w). (7.116)
Аналогичное положение имеет место и для функции Gyi
только при этом вес Gy зависит от предельных значений Nyt
q (или Ny, и, или и1ч и2).
В данном параграфе даны регулировочная и весовая харак¬
теристики двигателя ограниченной мощности с электростатическим
движителем; на примере его описаны процедуры выбора опти¬
мальных программ регулирования и оптимальных параметров.
Учету реальных регулировочных характеристик двигателей
ограниченной мощности в проблемах оптимизации посвящены
работы [7.13-7.19, 7.25].
1. Характеристики двигателя с электростатическим движи¬
телем. Схема процессов, протекающих в электростатическом дви¬
жителе, с поверхностной ионизацией описана в § 4 главы 2
([7.20-7.24] и др.).
Параметрические выражения тяги Р и расхода q движителя
этого типа записываются в соответствии с известной формулой
Чайльда—Ленгмюра (закон «3/2»), которая выводится для одно¬
мерного монохроматического пучка при условии неограниченной
обильности источника ионов
'-ты (7'117>
здесь d — расстояние между эмиттером и ускоряющим электро¬
дом, f — площадь поперечного сечения пучка, т п е — масса и
заряд иона, % — вытягивающий потенциал.
Мощность Ny, идущая на производство тяги, слагается из
мощности реактивной струи и мощности, излученной с горячей
310
РЕАЛЬНЫЕ ДВИГАТЕЛИ ОГРАНИЧЕННОЙ МОЩНОСТИ
[ГЛ. 7
поверхности эмиттера (главный источник потерь)
- ш&Т™у'+ fL' <7Л18>
где L — постоянные радиационные потери на единицу площади.
При выборе напряжения % и расстояния d следует учитывать
ограничения на область их изменения
< Emax, d>rfmin. (7.119)
Нарушение первого неравенства (средняя напряженность
электрического поля Е в ускоряющем промежутке превышает
Ешах) приводит к пробою, второе неравенство носит характер
к онст руктив ног о ог ранич ения.
На рис. 7.15, 7.16 приведен пример параметрических зави¬
симостей тяги Р и расхода q от площади f при различных значе¬
ниях мощности Ny (геометрический параметр d не меняется,
d = 0,3 см; Етах — 30 ООО в/см; L = 11 вт/см2 [7.22]); крайние
левые точки кривых отвечают условию %/d = Emax. На рис. 7.17
представлена функция Р (Ny, q); гам же для сравнения нанесены
пунктиром кривые тяги идеального движителя. Двузначность
функции тяги на рис. 7.17 (верхняя ветвь — сплошная линия,
нижняя — штрих-пуиктирная) комментируется в следующем
пункте.
Вес движителя рассматриваемого типа можно считать про¬
порциональным максимальной площади поперечного сечения
пучка:
Gy=--Tff max- (7.120)
Вместе с выражением (7.2) для веса источника мощности и пре¬
образователя соотношение (7.120) определяет весовую формулу
двигателя с движителем данного типа.
Изменение тяги, расхода и мощности электростатического
движителя с поверхностной ионизацией происходит при изме¬
нении потенциала % и площади Zf (последнее за счет подключения
различного числа элементарных движителей). В процессе регу¬
лирования должны выполняться условия (7.119), а также усло¬
вия (см. (7.2), (7,120)):
Nт (<) < Ытлх = GJa, $ (t) < f max = Gy/г/. (7.121)
2. Оптимальные программы регулирования реальных двига¬
телей. Вариационная проблема о доставке максимального полез¬
ного веса в общем виде (без конкретизации выражений Р, Gy)
описывается следующей системой дифференциальных уравнений
РЕАЛЬНЫЕ РЕГУЛИРОВОЧНАЯ И ВЕСОВАЯ ХАРАКТЕРИСТИКИ
Р,г
6
4
2
О
Рис. 7.15. Тяга Р двигателя с электростатическим движителем как функ¬
ция площади еГ и мощности Ny; крайние левые точки графика соответствуют
режиму максимальной напряженности электрического поля Е.
д,щ/сел
12
0.8
°' 2 4 6 810 20 40 6080100 200 gcu2
Рис. 7.16. Расход q двигателя с электростатическим движителем как
функция площади & и мощности Ny; крайние левые точки графика соответ¬
ствуют режиму максимальной напряженности электрического поля Е.
Р,г
6
4
2
О 0,4 0,8 1,2 ' 1,6 2,0 q, мг/сен
Рис. 7.17. Тяга Р двигателя с электростатическим движителем как
функция расхода q и мощности Ny; крайние левые точки графика соответ¬
ствуют режиму максимальной напряженности Е. Пунктирные линии—ана¬
логичные зависимости для идеального двигателя.
312 РЕАЛЬНЫЕ ДВИГАТЕЛИ ОГРАНИЧЕННОЙ МОЩНОСТИ [ГЛ. 7
и краевых условий (см. (II.8)):
Ga= — gq, Go(0) =G„ — Gv — Gv, G0 (Г) = max, }
1’ = v, r (0) = г„, Г (T) = ri,
v = G ^Тл-G + R’ V ^ = Vl'’ V ^ = Vl
(P (f) = P (.VY, q, w), | e (£) | = 1, G„ = aNmax ,
Gy = GT (Nmaxi <7mas, w)).
(7.122)
Чтобы найти условия выбора оптимальных управлений, выпи¬
шем гамильтонову функцию и дифференциальные уравнения
импульсов для задачи (7.122):
н = — Pagq + IVV + (р„-е)gP (Ga + Gv + Gy)-1 + p„.B,
Pa = (Pt>*e) SP (Ga + Gv + Gy)-, pa (T) = 1,
Pr = -i(p.,H)- pB = -Pr-
(7.123)
Оптимальная программа вектор-управления e (t) определя¬
ется выражением (7.21); управления, через которые выражается
тяга Р (см. (7.114)) или тяга Р и расход q (см. (7.115)), будут
оптимальными в том случае, когда они доставляют абсолютный
минимум функции Н или ее части, зависящей от Р и q
min [—(paq + PVP/G)] (pv = | pj, G = Ga + Gv + Gv).
(7.124)
Применим условие (7.124) для определения оптимальной
программы изменения мощности двигателя с электростатическим
движителем. Рассмотрим функцию тяги Р от мощности Ny и
расхода q в форме (7.114). Если зависимость тяги Р от мощности
Ny при любом q такова, что с возрастанием мощности тяга также
возрастает, т. е. dP/dNy 0, то оптимальное значение управле¬
ния Ny, согласно (7.124), следующее:
Ny (t) = Armax = Gv / a. (7.125)
Судя по рис. 7.17 (сплошные линии), это заключение справед¬
ливо для рассматриваемого типа двигателя. Напомним, что та¬
кой же факт имеет место для идеальных двигателей ограниченной
мощности.
§ 4] РЕАЛЬНЫЕ РЕГУЛИРОВОЧНАЯ PI ВЕСОВАЯ ХАРАКТЕРИСТИКИ 313
Обратимся к исследованию оптимальных программ регули¬
рования электростатического движителя. Расход q, тяга Р и
мощность Ny электростатического движителя с поверхностной
ионизацией определяются площадью £ и потенциалом % (см.
(7.117), (7.118)). Укажем состав оптимальных управлений q (t),
Р (t), применив критерий (7.124).
Вместо £, % введем безразмерные управления о, е:
б (t) — £ (t) / £ max — у Of (t) / Gy, e (t) — % (t)/Emaxd; (/. 126)
Выражения для расхода и тяги (7.117) через управления а, е
записываются следующим образом:
Оптимальное условие для мощности (7.125) определяет связь
между управлениями о, е; подставляя (7.125), (7.126) в (7,118),
находим
Выразим из (7.128) управление е через а и подставим в формулы
для тяги и расхода (7.117); ограничения, наложенные на управление
е, перенесем на а:
Вне указанного диапазона управление о (t) может принимать
значение о = 0, которое соответствует выключению движителя
Р = q = 0.
Функциональные зависимости (7.130) представлены на рис. 7.15
в координатах Р, f с параметром Ny и на рис. 7.16 в координатах
q, £ с тем же параметром; функции Р, q имеют максимум по £
(при £ —> 0 функции Р, q 0 и при £ —» Ny/L функции Р, q —> 0).
Это обстоятельство приводит к тому, что функция Р (q) и обрат¬
ная функция q (Р) двузначные (см. рис. 7.17) — одно и то же
значение тяги достигается при двух значениях расхода (большем
при этом
0<ст (0<1, 0<е(0<1.
(7.127)
Р = ciGyCe2, q = c2/GyC e3/z
2 К
2
'max
Cl 9it *(/
(7.128)
(7.129)
(7.130)
314 РЕАЛЬНЫЕ ДВИГАТЕЛИ ОГРАНИЧЕННОЙ МОЩНОСТИ [ГЛ. 7.
и меньшем), и, соответственно, двух значениях площади (большем
и меньшем). Второй вариант (меньший расход и меньшая площадь
при данном значении тяги) всегда выгоднее первого; поэтому
оптимальные режимы заведомо не реализуются на частях кривых
рис. 7.17, которые лежат правее точек максимума. Эти части
(и соответствующие им на рис. 7.15, 7.16) даны штрих-пунктиром.
Подставим выражения тяги и расхода (7.130) в формулу для
функции Н; оптимальный закон a (t) будет определяться из
условия
при GJGy(c3 + с4) а (t) 1 или а (t) = 0.
В состав оптимального управления а (t) входят участки пере¬
менного управления: о = aopt (0» определяемого из условия
минимума выражения (7.131) без ограничений на сг, участки гра¬
ничного управления сг = 1 при oopt (t) 1, участки граничного
управления а = GJGy (с3 + с4) при aopt (t) < GJGr (с3 + с4),
а также участки выключения движителя о = 0 в том случае, когда
выражение (7.131) положительно при сг = GJGy (с3 + с4).
3. Оптимальные параметры нерегулируемых реальных двига¬
телей. В данном пункте приводятся примеры определения опти¬
мальных параметров нерегулируемых реальных двигателей с
электростатическими движителями; рассматриваются два дина¬
мических маневра: поворот плоскости орбиты спутника и удер¬
жание спутника в заданном шаровом слое (компенсация лобового
сопротивления).
Решение динамической части вариационной проблемы для
обоих маневров дано в главе 6. Результат решения — функция
T.j. (gP/G0, gq/G0) для первого маневра имеет вид (ср. (6.88))
Расчеты проводятся для поворота плоскости круговой орбиты
24-часового спутника Земли, комбинация параметров iG0k/igrl
принята равной 1000 Г; число оборотов ,9 = 10—100. Формула
(7.132) при этих значениях такова:
Второй маневр (компенсация аэродинамического сопротив¬
ления) характеризуется следующей функцией (gP/G0, gq/G0)
min
a
(— gGy CiP
6 + сгр
(7.131)
(7.132)
Tv, [сек] = 5,5 -104s arcsin (103/sP LT]). (7.133)
(cp. (6.73)):
TV = V2cvp v^STiP.
(7.134)
§ 4] РЕАЛЬНЫЕ РЕГУЛИРОВОЧНАЯ И ВЕСОВАЯ ХАРАКТЕРИСТИКИ 315
Будем считать, что двигатель работает на каждом шестнад¬
цатом обороте; силу сопротивления V26^p^25 примем равной
Рис. 7.18. Весовые затраты G,ii0 -f Gv GY на реализацию
поворота плоскости орбиты спутника в зависимости от
времени маневра X; кривая т= 0 соответствует невесомому
движителю с идеальным процессом ускорения.
Рис. 7.19. Весовые затраты G^b Gv + GY на удержание
спутника в заданном шаровом слое в зависимости от времени
маневра X; кривая у = 0 соответствует невесомому движи¬
телю с идеальным процессом ускорения.
0,5 Г; при этом формула (7.134) запишется так:
Т^ = 0,5 TIP [Г] (Гр. < Г/16, Р > 8 Г). (7.135)
Для исследуемой двигательной системы необходимо опреде¬
лить оптимальные площадь f и напряженность Е; что касается
Межэлектродного расстояния d, то можно доказать оптимальность
требования
d = б/min* (7.136)
РЕАЛЬНЫЕ ДВИГАТЕЛИ ОГРАНИЧЕННОЙ МОЩНОСТИ
[ГЛ. 7
В расчетах взяты значения параметров L, Emax, е, т,
указанные в п. 1; в первой задаче (поворот плоскости орбиты)
удельный вес источника мощности и преобразователя считается
равным а = 20 кГ/квт, во второй задаче (компенсация сопротив¬
ления) а= 50 кГ/квт\ вычисления проведены при 7/ = 0,1 кГ/см2.
Результаты расчетов для двигателя с электростатическим
движителем в приложении к двум указанным маневрам даны
на рис. 7.18, 7.19. Там нанесены суммарные весовые затраты на
выполнение маневра 0 + Gv + в функции от времени вы¬
полнения маневра Т. Рис. 7.18 соответствует маневру поворота
плоскости орбиты, рис. 7.19 — маневру удержания спутника.
Для сравнения на рис. 7.18 и 7.19 нанесены кривые, соответст¬
вующие нерегулируемому двигателю ограниченной мощности
без потерь и с невесомым движителем; последние обозначены сим¬
волом у=0.
ГЛАВА 8
ДВИГАТЕЛИ ОГРАНИЧЕННОЙ СКОРОСТИ ИСТЕЧЕНИЯ.
ОПТИМАЛЬНОЕ СОЧЕТАНИЕ ДВИГАТЕЛЕЙ
ОГРАНИЧЕННОЙ СКОРОСТИ ИСТЕЧЕНИЯ
И ОГРАНИЧЕННОЙ МОЩНОСТИ
К двигателям ограниченной скорости истечения относятся
все тепловые реактивные двигатели, скорость истечения которых
не превышает предела, зависящего от максимальной температуры
стенок камеры сгорания или теплообменника (см. часть I). Дви¬
гатели этого класса характеризуются сравнительно малым удель¬
ным весом у А на единицу тяги (ух ~ 10"2). Такие двигатели могут
обеспечивать большие значения реактивного ускорения, отсюда—
другое название данного класса двигателей: двигатели боль¬
шой тяги.
На основании малости удельного веса ух для двигателей огра¬
ниченной скорости истечения весом двигателя Gx в задачах оп¬
тимизации обычно пренебрегается. Этого нельзя делать для тех
маневров, где потребная величина реактивного ускорения вели¬
ка (т. е. в тех случаях, когда нарушается условие GJGX =
= у* (uG)mRJgG1<^ 1).
Малый удельный вес двигателей ограниченной скорости исте¬
чения — положительное свойство двигателей данного класса, с дру¬
гой стороны, скорость истечения для таких двигателей по сравне¬
нию с двигателями ограниченной мощности существенно меньше —
это отрицательное свойство. Естественно, возникает вопрос, ка¬
кие двигатели «лучше»: двигатели ограниченной скорости исте¬
чения (двигатели большой тяги) или двигатели ограниченной мощ¬
ности (двигатели малой тяги). Стремление ответить на этот во¬
прос в формулировке, близкой к приведенной, было свойствен¬
но в основном начальной стадии исследования возможностей
Двигателей малой тяги (см., например, [8.1—8.6] и др.). Более
правомочна другая постановка: определить области преимущест¬
венного использования каждого типа двигательной системы и
целесообразность совместного применения двигателей различных
типов на одном аппарате.
Введем для каждого маневра пространство параметров ма¬
невра, параметров двигателя ограниченной скорости истечения
н параметров двигателя ограниченной мощности. Часть про¬
странства, в которой выгодно применение одного типа двига¬
теля, назовем областью применения данного двигателя. Простран¬
ство разделяется на область применения двигателя ограниченной
318
ОПТИМАЛЬНОЕ СОЧЕТАНИЕ ДВИГАТЕЛЕЙ
[ГЛ. 8
скорости истечения, область применения двигателя ограниченной
мощности и промежуточную область совместного применения
обоих двигателей.
В настоящей главе описываются особенности характеристик
и оптимальных режимов работы двигателей ограниченной ско¬
рости истечения, находятся оптимальные условия сочетаний дви¬
гателей ограниченной скорости истечения и ограниченной мощ¬
ности, дается критерий выделения областей применения двига¬
телей ограниченной мощности и для ряда маневров строятся гра¬
ницы этих областей.
§ 1. ОСОБЕННОСТИ ХАРАКТЕРИСТИК И ОПТИМАЛЬНЫХ РЕЖИМОВ
РАБОТЫ ДВИГАТЕЛЕЙ ОГРАНИЧЕННОЙ
СКОРОСТИ ИСТЕЧЕНИЯ
1. Характеристики двигателей ограниченной скорости исте¬
чения. Идеальный двигатель ограниченной скорости истечения
характеризуется следующими выражениями тяги Р, расхода
q и веса G* (ср. (II.9), (11.10) при их = Р, и2 = V):
Р=Р, q = P/V, Gx = 0 (0 < Р (0 < ос, о < V (t) < 7Шах), (8.1)
т. е. идеальный двигатель невесомый, скорость истечения ограни¬
чена сверху, на тягу ограничения сверху нет, и поэтому допуска¬
ется существование импульсных режимов работы (на бесконеч¬
но малом интервале времени тяга бесконечна, расход бесконеч¬
ный, выбрасывается конечное количество рабочего вещества).
Вес реальных двигателей ограниченной скорости истечения
зависит или от максимальной тяги (жидкостные реактивные дви¬
гатели), при этом выражения, аналогичные (8.1), имеют вид
Р = Р, q = PIV, Gx = rAnax (0 < Р (0< Ртах> 0 < V (() < Fmax),
(8.2)
или от начального веса рабочего вещества (двигатели на твердом
топливе), и тогда
Р = Р, q = P/V, GK= tG^o (0 < P (t) < ос, 0 < V (t) < 7ШД0 (8.3)
(значения удельных весов у приведены в главе 2, индекс у у
опускаем). Для реальных двигателей типа (8.3) на тягу ограниче¬
ния сверху нет и, подобно идеальному случаю, допускается суще¬
ствование импульсных режимов работы.
2. Особенности оптимальных режимов работы идеальных дви¬
гателей ограниченной скорости истечения. Запишем вариацион¬
ную проблему для идеальных двигателей ограниченной скорости
| 1] ДВИГАТЕЛИ ОГРАНИЧЕННОЙ СКОРОСТИ ИСТЕЧЕНИЯ
истечения в виде (II.8)
Gg = -gP/V, Go(0) = G0, Ge(2’) = max,
г = v, г (0) = г0> г (Т) = i'i,
v = gPe / Ga + К, v (0) = Vo, v(f) = Vi
(0<Р(^)<оо, 0<F(^<Fmax, j e (0 | = 1).
319
(8.4)
Здесь в весовой формуле фигурируют только две компоненты:
полезный вес Gn и вес рабочего вещества (£?„ + G^ = G„ = G),
вес двигателя Gx по определению идеального двигателя ограни¬
ченной скорости истечения равен нулю.
Введем в уравнения (8.4) вместо тяги Р реактивное ускорение
а = gP/G = gP/Gg и отнесем весовые компоненты Gx, Ga к на¬
чальному весу G0, оставив для них прежние обозначения:
Gg = — aGg/V, Gg( 0) = 1, G0(7’) = max,
г = v, г (0) = rn, г (Т) = ух,
v = ae + H, v(0) = v„, v(7’) = Vi
(0 а (t) оо, 0 ^ V (t) ^ V maxi | в (t) | = 1). .
(8.5)
Гамильтонова функция Н и уравнения для импульсов в рас¬
сматриваемом случае записываются так:
H = -panGg/V + pr-v +p0-(ae + R),
Р* = Р*1Г’ Р>- = —ir( Р,’К)-
Р„ = —Рг (рд(Т) = — 1).
(8.6)
Функция рв (t) отрицательна всюду на интервале 0 t Т
в силу того, что уравнение для ра линейное однородное, и в точке
t = Т функция ра отрицательна.
Множитель при HV в функции Н может быть либо положи¬
тельным (с учетом знака, стоящего перед всем членом), либо рав¬
ным нулю при а (t) = 0, поэтому вдоль активных участков тра¬
ектории (а (t) =f= 0) оптимальное управление V (t) (доставляющее
Минимум гамильтоновой функции Н) таково:
V (t) = F1T
управленж
е(0= —Р JPV (P„ = |PJ
Оптимальное вектор-управление c(t) выражается следующим
образом:
(8.7)
)ЩИМ
(8.8)
320
ОПТИМАЛЬНОЕ СОЧЕТАНИЕ ДВИГАТЕЛЕЙ
[ГЛ. 8
В состав оптимального управления а (t) могут входить три уча¬
стка: два граничных
a (t) = 0 при А 0
сi (£) — <2max ^ при А 0
и участок особого управления
а (t) = a0Pi(t) <С °о при А (t) = 0. (8.10)
Протяженности Х\ активных участков с а —* оо должны быть
равны нулю, иначе интегралы
^ a(t)dt (8.11)
t
не будут конечны (бесконечно большая затрата топлива), отсюда
следует, что комбинация А не может быть положительной на
конечном интервале времени.
Комбинация paGa/V в гамильтоновой функции (8.6) не за¬
висит от времени и отрицательна; первое свойство проверяется
дифференцированием по времени и подстановкой производных
ра и Ga из (8.5) и (8.6), второе обусловлено знаком ра.
Повторяя рассуждения главы 4, приходим к выводу, что ва¬
риационная проблема (8.5) на максимум Ga (Т) эквивалентна
вариационной проблеме на минимум характеристической скоро¬
сти I:
/=а, /(0) = 0, I(T)=m in,
г—у, г (0) = гп, г (Т) = 1Д,
у — ае -j- Н, у(0) = у0, у(Г)=У1
(a(t) >0 | е (^) | = 1).
Контрольный функционал (8.5) — полезный вес Ga (Т) =
= Gn — связан с характеристической скоростью / (Т) по формуле
г
<?я = «г* (¥=/(Г)/Гтах, I(T)=^adt). (8.13)
О
Таким образом, для идеального двигателя ограниченной ско¬
рости истечения общая вариационная проблема (8.4) приводится
к динамической части (8.12). Сравнивая (8.13) и (4.16), можно на
плоскости функционалов Т*, Ф выделить область 2 (рис. 8.1),
где полезная нагрузка для двигателя ограниченной мощности
больше, чем для двигателя ограниченной скорости истечения
(в области 1 полезная нагрузка для двигателя ограниченной ско¬
рости истечения больше, чем для двигателя ограниченной мощ¬
ности).
(8.12)
IJ
ДВИГАТЕЛИ ОГРАНИЧЕН llo l"l СКОРОСТИ ИСТЕЧЕНИИ
321
Заметим, что задача Майера (8.12) может быть заменена зада¬
чей Лагранжа аналогично тому, как это делается для идеального
двигателя ограниченной мощности:
т
/=$ J/V —R (■-, о и— R 0*> dt
(8.14)
(г (0) = г,-, г (0) л-„, г (Г) ^ 1Ь г (Т) ^ vj).
Однако применение классического метода вариационного ана¬
лиза — приравнивание нулю первой вариации — не дает полного
решения вариационной проб¬
лемы в этом случае; экстре¬
мали интегрального функцио¬
нала (8.14) соответствуют
только участку особого управ¬
ления (8.10).
Вариационная проблема
(8.12) о минимуме характе¬
ристической скорости I (соот¬
ветствующая задаче о мак¬
симуме полезного груза для
идеал ьного двигателя ограни¬
ченной скорости истечения)
решена для широкого класса
маневров в перечисленных во
введении работах [1.1 —1.49].
Ниже рассматривается влия¬
ние реальных характеристик
двигателя ограниченной ско¬
рости истечения на парамет¬
ры оптимального движения.
3. Учет веса двигателя. Рассмотрим реальный двигатель
ограниченной скорости истечения с характеристикой (8.2): тяга
ограничена, вес двигателя пропорционален максимальной тяге.
Отнесем тягу Р к максимальной Ршах, а все веса — к начальному
весу аппарата, сохранив за ними прежние обозначения; задача
о доставке максимального полезного груза в этом случае выгля¬
дит так (ср. (8.4)):
- — а„Р / V, Go (0) + у»» / g - 1,
О
V
Рис. 8.1. Граница областей применении
идеальных двигателей ограниченной скорости
истечения / и ограниченной мощности 2 на
плоскости гЕ, Ф функционалов динамических
тндач (lF — для двигателя 1, Ф —для дви¬
гателя 2).
а0Рс
()
: + Н,
. + У«о / g
(0 </->(*)<!, г (/) •'.
Ga (Т) = max,
г (0) = i*o, г (Г) = 1*г,
v (0) — v,*, v (Т) — Vi
: с (р ! = 1,
а., =■ g/Ji„ax/Go = const).
(8.15)
21 М
еханика полета
322
ОIГГПМАЛЫLOL-: со Ч I'ТА 11 ILK ;L inLFATEЛЕЙ
Здесь нужно построить оптимальные программы V (t)? Р (7),
е (t) и выбрать оптимальное значение параметра а0, обеспечиваю¬
щие максимум полезной нагрузки G- = Ga (Т) (удельный вес
двигателя у задан). Из этой задачи, аналогично случаю нерегу¬
лируемых двигателей (глава 6), можно выделить динамическую
часть, не зависящую от конструктивного параметра у.
Перейдем в (8.15) от веса Ga к полному весу G (t) = Ga (t) -r
H" Va0/g; в качестве функционала примем конечное значение
G (Т) = G- -f ya0/g. (8.16)
При фиксированных значениях а() максимум функционала
(8.16) совпадает с максимумом функционала (8.15), и задача (8.15)
редуцируется к стандартной задаче ракетодинамики о максимуме
конечного веса при ограниченных тяге и скорости истечения
С, = а„Р / V, G (0) = I. G (Т) = max, )
r=v, '■(") г (Г) = п, j (8 J7)
v = а()Ре /G + П, v (< >) vr. V (f) = Vi |
(0<p(t)<i,o<v(I)<гшах, ;e(o; • i). J
Решение задачи (8.17) определяет зависимость величины функ¬
ционала от параметра а0 : G (Т) G{ (а0). Имея в распоряжении
такую зависимость, можно найти оптимальное значение пара¬
метра а0 из условия максимума полезной нагрузки G- (см. (8.16))
max G- ~ max [Gi (я„) — yflo I g]. (8.18)
<G)
Динамическая задача (8.17) подробно исследовалась многими
авторами [8.7—8.54]. На основании сказанного их результаты
могут быть использованы для решения полной задачи (8.15).
Рассмотрим теперь двигатель ограниченной скорости исте¬
чения с характеристикой (8.3): тяга не ограничена, вес двигателя
пропорционален начальному запасу рабочего вещества. По¬
скольку на тягу нет ограничений, вариационная задача может
быть записана через реактивное ускорение (ср. (8.5)) в форме
(II.5), (7.5)
G, - 0, (Р (0) д- G- (Т) = max,
G- + GU + (0)
6V = 7 — «». + (1 -Г г) G, (0) = 1, G, (Т) = 0,
r — v> 1' (0) = г,.., 1 • (F) = и,
v = ае -j- R, v (0) = v(], v (Т) = Vi
(0<а(*)<оо, 0<F(f)<FIIinx> | е (<) | = 1). (8.19) J
g !] ДВИГАТЕЛИ ОГРАНИЧЕННОЙ СКОРОСТИ ИСТЕЧЕНИЯ 323
Как и в задаче (8.5), можно доказать оптимальность управле¬
ния V (t) = FmaK. Проинтегрировав второе уравнение (8.19) при
у = Fmax с учетом граничных условий, выразим функционал
задачи G- через характеристическую скорость I (ср. (8.13)):
т
Gr. = (1 + Т) гГ11У'"*' — г (I =- $ а(t)dt). (8.20)
'' О
Полезная нагрузка G- снова оказывается убывающей функ¬
цией характеристической скорости /, поэтому задача (8.19) сво¬
дится к описанной ранее динамической задаче (8.12) для идеаль¬
ного двигателя ограниченной скорости истечения.
Если к характеристике (8.3) добавить еще условие ограни¬
ченности тяги (0 Р (0 ^ Рпглх, гДе Лпах ~ конструктивный
параметр), то задача о максимальной полезной нагрузке сведется
к (8.17). В самом .деле, при — yG[yо полезная нагрузка равна
= Gx - Gy. = (1 Н- у) Gl - Y> (8.21)
т. е. условие максимума G- эквивалентно условию максимума
конечного веса Gv
Чтобы составить количественное представление о влиянии
веса двигателя, рассмотрим модельную задачу о вертикальном
подъеме ракеты в пустоте при постоянном гравитационном уско¬
рении (g = const) 18.45—8.54]. Начальная высота и начальная
скорость нулевые (у0 = v{) = 0), в конце требуется обеспечить
заданное значение полной энергии Е1 = + gyi при мак¬
симуме полезной нагрузки. Характеристика двигателя берется
в форме (8.2).
Введем безразмерные переменные
/ — ^ г (l // Е ~ v Б Р
|/ » с ’ " ' Д-2 ? v ' v ’ ^ — ~Т> ’
max и ^ шах max max
V , ап (8.22)
max 0
и заменим второе уравнение (8.15) на уравнение, описывающее
изменение энергии. Вариационная задача (8.15) запишется сле¬
дующим образом:
са == — а0Р /1 G, (0) + уаи 1, G, (Т) ==.- max, )
Ё = - , Е (0) = 0, Е (Г) = Еи
-I- Т"о ' 4
аПР
а ~ '
(0<Р(0 < 1, а0 const, Т = opt). ;
V = —^ 1, v(0) = 0, V (Т) = opt
-i Тао v 7
(8.23)
21*
324
ОПТИМАЛЬНОЕ СОЧЕТАНИЕ ДВИГАТЕЛЕЙ
[ГЛ. N
Здесь тяга направлена по скорости, черточки над безразмер¬
ными переменными опущены.
Отметим, что управляющий параметр а0 (отношение максималь¬
ной тяги к начальному весу) должен быть больше единицы из
условия взлета, наибольшее значение (1 <С я0 <С 1/у) ограничено
предельным случаем GK = уЛпах = G0. Выбор оптимального
значения этого управляющего параметра сводится к стандартной
процедуре, если присоединить к системе (8.23) формальное урав¬
нение а0 = 0. Оптимальные управления V (t) и Р (£), доставляю¬
щие максимум полезной нагрузке, определяются из условия абсо¬
лютного минимума гамильтоновой функции
Функция Н на оптимальной траектории тождественно равна
нулю, так как не содержит явно переменной t и конечный момент
времени Т не фиксирован. В точке t = Т для минимума II необ¬
ходимо V {Т) = 1.
Поскольку v{T) не задано, то pV/ (Т) = 0. Кроме того, v (Г) 0,
Р (t) > 0, так как иначе Е (Т) = 0 и траекторию можно было бы
оборвать при t < Т. Тогда из уравнения для Н (Т) =
= а0Р (Т) [pev (Т) (G- + уа0)-1 + 1] = 0 и второго уравнения
(8.24) следует, что импульс ре имеет постоянное отрицательное
значение ре = const <Г 0.
На основе (8.23), (8.24) можно определить импульс рг
Отметим, что импульс рс—неубывающая функция t, которая
достигает нулевого значения в конце интервала.
В точке t = 0 функция II (0) = рсо (а0Р (0) — 1) — а0Р(0) х
X ра (0)/V (0) = 0; из условия взлета а0Р /> 1; отсюда следует
Ра = (pev + pv)a•„ Р (Ga + г ап)-'2, ре = 0,
Pv = -- реа»р (Gg + уа,,)"1 (ра (Т) = — 1).
(8.24)
Pv = —Pe(l + V), Pv = Pvi) — Pet ~ Рс» <
где из условий в точке t — Т
Pro = рЛТ + V (Т)] < 0.
(8.25)
(8.26)
Ра (0) < 0, 7(0) = 1.
Согласно (8.25) и последнему уравнению (8.24)
(8.27)
ра = (Pv0 — Pet) а0р (G0 + уа0) 2.
(8.28)
§ 1] ДВИГАТЕЛИ ОГРАНИЧЕННОЙ СКОРОСТИ ИСТЕЧЕНИЯ 325
Из (8.26) —(8.28) и граничного условия pz (Т) = — 1 полу¬
чаем, что импульс pz монотонно изменяется по t. оставаясь всюду
отрицательным: pz (t) 0. Поэтому оптимальное управление
У (£), доставляющее минимум гамильтоновой функции //, всюду
граничное:
V (t) = 1 (0 <*<2"). (8.29)
Оптимальное управление Р (t) зависит от знака функции Д
Р (t) --- 1 при A (t) < 0 (д ^ Pr0 _ Pet
Р (t) 0 при A(t)^>0 I ^3 "Г
Возможность особого управления (при А = 0) отпадает, так
как производная функции А
всюду отлична от нуля:
А = — Ре (Gz + У^оУ1 =f=
Режим Р (t) -- 0 (при А 0)
внутри интервала 0<Г£ Т так¬
же не реализуется, так как на
нем, согласно (8.24), должно вы¬
полняться условие pr (t) — 0,
что имеет место лишь в конце
интервала (рг (Т) = 0).
Следовательно, оптимальное
управление Р (t) в рассматри¬
ваемой задаче также всюду
граничное
p(t) = 1
(0 < t < Т).
(8.31)
С учетом найденных оптималь¬
ных управлений (8.29), (8.31) :
V (t) 1, Р (t) — 1 система уравнений (8.23) интегрируется
111 (С- + уа0) ^ (О2- + ya0G- — Сх-) (Сх- + Г«0 — Г^Г1*
Ei :г= 1/Эп2 (6’- + г«и) + — [1 — G- — у а» + In (G- + уа,,)].
«0
Результаты решения представлены на рис. 8.2—8.4. На рис. 8.2
Дан типичный пример зависимости максимальной энергии Ех от
начального ускорения а0 при фиксированных значениях G- и у
(постановка взаимная к G- = max при Ел, у — const). Без учета
веса двигателя (у - 0) максимум энергии Ел достигается с дви¬
гателем бесконечно большой тяги (tf()0,,i —> ос). С учетом даже
малых значений удельного веса двигателя у = 0,01—0,02 (ве¬
личины у взяты с рис. 2.11) положение максимума смещается в
(8.32)
рау (8.30)
ОПТИМАЛЬНО!-: СОЧЕТАНИЕ ДВИГАТЕЛЕЙ
[ГЛ. 8
область конечных начальных ускорений (а0О,н = 2,5—4), а ве¬
личина максимума значительно уменьшается. Зависимость опти¬
мальной величины начального ускорения а0 от удельного веса
двигателя у для различных значений полезной нагрузки Gя при¬
ведена на рис. 8.3. Значения G- слабо влияют на оптимальную
величину а0 — все кривые а0 (у) для 0,1 GT, / 0,5 лежат в
узкой полосе (заштрихованная область на рис. 8.3). Полезная
нагрузка в функции энергии Ех при фиксированных значениях
удельного веса у показана на рис. 8.4.
*о/9
3,5
г,5п
Г" ■
ч
\
0,004 от 0,0/2 0,0/6 у
о 0,2 0,4 0,6 0,8 / Е/С
Рис. 8.:!. Область оптимальных, значе¬
ний ускорения а0/£ для величин полез¬
ной нагрузки из диапазона 0,1 < G- <
<0,5 — кортикальный подъем ракеты.
Рис. 8.4. Влияние удельного кеса двигателя у
на максимальную" полезную нагрузку G-
(в зависимости от конечной энергии
AV\'2 ) — вертикальный подъем ракеты,
шах
В качестве второго примера рассмотрим модельную задачу о
перемещении между двумя точками покоя на расстояние I за
время Т. Решение динамической части вариационной проблемы,
эквивалентной (8.17), для этого маневра описано в § 2 главы 6
(см. (6.43)). Вспоминая, что 1 — \iTv, = G± и р = Я(Дшах? разре¬
шим (6.43) относительно ajg:
«о (^так ' " ^ )
[(1 - У6\)2 + (1 - Gx) In УGi\. (8.33)
8 V/TViIULX)-\-inVG]
Эта функция а0 (GJ — обратная к G± (я0), безразмерные ком¬
бинации (Fmax/gT) и (l/TVmax) — параметры задачи. Подставив
выражение (8.33) в (8.18), получим полезную нагрузку G- в
функции конечного веса Gy.
(yV / аТ\
G- — Gi шах ' [(1 — У Gг)2 + (1 — GO In VGi].
V / TVmad + ln VGi LV ' V
(8.34)
Здесь G± — независимая переменная, по которой отыскивается
максимум G*. После этого по формуле (8.33) определяется соот¬
ветствующее значение а0. Результаты этой процедуры показаны
ДВИГАТЕЛИ ОГРАНИЧЕННОЙ СКОРОСТИ ИСТЕЧЕНИЯ
327
на рис. 8.5, 8.6: максимальная полезная нагрузка G- в функции
комбинации параметров (Z/TFjnax) при фиксированных значениях
(уИшах/#Г) — на рис. 8.5, пример
зависимости оптимального уско¬
рения (ajg) от (l/TVmax) при
(Vnmx/gT) = 0,5 для 7 = 0,01 и
у — 0,02 — на рис. 8.6.
Интересно сравн и т ь в л и я и и е
веса двигателя и влияние аэро-
Рлс. 8.5. Полезная нагрузка G_ в фупк-
ции параметра (*/'-ГГтах) при фиксиро¬
ванных значениях (yV}j1 ax/S'T) — пере-
мсчцение между точками покоя.
Рис. 8.6. Оптимальное ускоренно a0Fg в зави¬
симости от параметра (*/'ГУтах) при V'max
-= 0,5 для двух значении удельного веса двига¬
теля v— перемещение между точками покоя.
динамического сопротивления. Проделаем это на примере описан¬
ной выше задачи вертикального подъема ракеты. Сравнение прово¬
дится при одинаковых параметрах маневра; на рис. 8.7 даны
N.7. Влияние удельного веса двигателя у и коэффициента аэродинамического сопро-
вертпкалычып подъем ракеты (Сп = 0,5,
а) К j) = 0, 6) v — 0).
Рис.
тив.пения Ер на конечную oiu'pnno /;,/\’^1ах
зависимости конечного значения энергии от ускорения я0 при
одинаковых значениях полезной нагрузки G- - (3,5 (рис. 8.7, а —
328
ОI [Т11МАЛ Ь I I () К СО ЧЕТ A11 11 К ДВИГАТЕЛЕЙ
Г ГЛ.
движение в пустоте с учетом веса двигателя [8.45], рис. 8.7, 6 —-
движение в атмосфере с невесомым движителем [8.49], где К]} —
безразмерный коэффициент сопротивления: KD — cxf>()SXg,2G(].
р и X — параметры экспоненциального закона падения плотности
атмосферы по высоте: р р0ехр(— у/Х), S — площадь миделя
ракеты).
Вариационная проблема с одновременным учетом веса двига¬
теля и аэродинамического сопротивления для маневра вертикаль¬
ного подъема исследована А. И. Курьяновым.
§ 2. ОПТИМАЛЬНЫЕ УСЛОВИЯ СОЧЕТАНИЯ ДВИГАТЕЛЕЙ
ОГРАНИЧЕННОЙ СКОРОСТИ ИСТЕЧЕНИЯ И ОГРАНИЧЕННОЙ
МОЩНОСТИ
Здесь выводятся оптимальные условия сочетания для нерегу¬
лируемых и идеальных двигателем.
1. Общие оптимальные условия сочетания. Пусть на космиче¬
ском аппарате установлены два двигателя: двигатель ограничен¬
ной скорости истечения 1 и двигатель ограниченной мощности 2.
Введем обозначения: РЛщ Р., — реактивные тяги, е1, е2 —- еди¬
ничные векторы ориентации тяги, qx, <у2 — массовые расходы.
Сдь Gr>— веса рабочего вещества, Gyj, Gvi — веса двигателем.
Назовем режим работы двигателей 1 и 2 параллельным, если
двигатели могут быть включены одновременно. Последовательный
режим имеет место в том случае, когда в каждой точке траектории
может быть включен только один из двигателей1). Для определе¬
ния оптимального момента переключения при последовательном
режиме воспользуемся релейной функцией б (£), принимающей
значение 1 на части траектории, где двигатель 1 включен, а дви¬
гатель 2 выключен, и значение О на части траектории, где двига¬
тель 1 выключен, а двигатель 2 включен.
Суммарный массовый расход q и результирующий вектор тяги
V з а п и с ы в а то тся с л е д у ю щи м образом:
при па р а л л е л ь и о м р е > к и м е
q - qA -f q•>, P /V, • Ve2, (8.35)
при последовательном режиме
q - V -j- q2 (1 - б), P - I\ eT6 4- P2 e2 (1 - 6). (8.3(1)
г) При параллелг,пом режиме возможны такие варианты, включен пл —
выключении двигателем”! (знак «-;■» соответствует включенному двигателю,
знак «—» — выключенному): ; 1, —2: —1, ' 2; -■ 1, -:-2; —1, —2. После¬
довательный режим «беднее» параллельного, ]|бо в ]1ем отсутствует пред¬
последний вариант. Понятие' последовательного режима введено для тех слу¬
чаев, когда но техническим причинам двигатели не могут работать одно¬
временно.
01ITJ1МАЛЫ1ЫК УСЛ() HII я: СО Ч СТА I ШЯ ДВИГАТГЛК п
329
В ведем специальное обозначение для суммы трех весов:
Gn G- г Gl}'\ -f Ga2 (Ga ((.)) G{) — GyA (0) — Gy:i (0).
Ga (T) =-■ G-) (8..Ч7)
и сформулируем вариационную проблему о доставке максимально¬
го полезного веса двумя двигателями,
работающими в параллельном режиме:
(ra —g Gj\.-j- (pi), Gz (0) ^ Gn — Gyi(0) G (0), Ga (J ) |
- max.
г ^ V. r (0) v(). r (T) =r: 1Д.
V - g с + R v(0) " V»’ v(T) V| '
°0 1 (jy.\ ' ljy.2
(О с P\ (/), P->(£), (j\(t), ^ og , (*уЛ, (/y.2^0, | et (t) | —
I e2 (t) I = J),
(R.H8)
работающими в последовательном режиме:
с, = — 8 1?|б -|- <н (1 - б)], G3(<>) - о, - Gxl (0) — Gxi (0),
G3(T) = max,
>• = V, г (0)г(Т) = гг,
у= /VHl-б) к< v(0) v„, v(7*) = vi 1
('a O ' ^xl -r ox2
(0<^Pi(£), P2(0, ryt(0, (7*2(0^ 00 ’ ^V.2 0» ^ (0” 1 ИЛИ 0,
| Ci (0 | = \e2(t)\ - 1).
(8.39)
Сделаем ряд замечаний.
Г. Чтобы замкнуть вариационные постановки (8.38), (8.39),
необходимо, во-первых, указать функциональные выражения тяг
Pj, Р.2 и расходов q2 через независимые управления двига¬
тельных систем и, во-вторых, определить веса двигателей Gy,,
Gy2 как функции предельных значений зтих управлений (саг.
введение к части II).
2У Управления G/A (t), G>2 (t) могут непрерывно изменяться
вдоль траектории, подчиняясь оптимальным требованиям и огра¬
ничениям из (8.38), (8.39), и могут оставаться неизменными при
Движении (тогда GXJ, Gy2 — управляющие параметры). Следует
предусмотреть такую возможность: если один из двигателей прек¬
ращает работу и до конца движения работает только другой дви¬
гатель, то первый в момент окончания работы может быть либо
оставлен на аппарате, либо сброшен; в последнем случае его
330
ОПТИМАЛЬНОЕ СОЧЕТ АТГИЕ ДВИГАТЕЛЕЙ
[ГЛ. 8
весовая компонента исключается из уравнении после сброса (по
этому поводу см. примеры в работе [8.55], а также общие опти¬
мальные условия сброса в работе [8.56]). Ниже считается, что
веса Gxl, Gy.2 неизменны вдоль всей траектории.
3°. Чтобы определить оптимальные вектор-управления ег, е2,
выпишем гамильтоновы функции и дифференциальные уравнения
импульсов:
для задачи (8.38)
Вектор-управления (t),e2 (t) доставляют минимум функциям
И (8.40), (8.41) при выполнении условий
Применительно к задаче (8.38) условия (8.42) означают, что в
режиме параллельного включения направления векторов, тяги
двигателей 1 и 2 совпадают. Условие (8.42) позволяет считать в
задачах (8.38), (8.39)
2. Оптимальные условия сочетания нерегулируемых двига¬
телей. Примем следующие характеристики нерегулируемых
двигателей ограниченной скорости истечения и ограниченной
мощности:
Pi = Рю или 0, q1 = Pio / Ию или 0,
1 Г и — Рг»
P&i 4- р2е2
J
(8.40)
для задачи (8.39)
II = — pog [дг6 -f до (1 — 6)] у
Рк‘,б + Ле-2(1 -6)
Е : СХ1 -|- л
L
Рг = — §р(Р»-В), Р3(Т)=- — 1.
(8.41)
= е2 = — Pi-i'pv (pv = |P»D-
(8.42)
ei = e2 = e.
(8.43)
Pi =■ P20 или 0, q2 = P\d j 3iA 2o или 0,
ОПТИМАЛЬНЫ К УС Л OBJ I / I СОЧЕТАНИЯ ДВИГАТЕЛЕЙ
331
где ocN20 = Gv2, УоР'И) ^ ^7 2 — веса источника мощности и
движителя двигательной системы 2; далее подразумевается
Тд - V10.
Вариационная проблема о доставке максимального полезного
веса для двигателей с характеристиками (8.44) записывается так:
при параллельном режиме (ср. (8.38))
В уравнениях (8.45), (8.40) введены безразмерные тяги яь я2:
По определению нерегулируемых двигателей Р1 = 0 или
I\ = Gxi'Yi, Р2 = 0 или Р2 = Gy2/y2; поэтому я17 я2 = 0 или
л17 Яо — 1. Для решения вариационной проблемы (8.45) требуется
определить оптимальные управляющие функции е (t), п1 (t),
л2 (t) и параметры Gxl, Gv2, Gy2; в задаче (8.46) к перечисленным
Добавляется управление б (t).
Применим к задачам (8.45), (8.46) метод JI. С. Понтрягина;
требуемые для процедуры гамильтоновы функции и дифферен¬
циальные уравнения импульсов имеют вид (8.40), (8.41), если
там вместо тяг, расходов и весов двигателей подставить выраже¬
ния (8.44). Оптимальные управления е (t), n^t), я2 (t) (и б (t) для
при последовательном режиме (ср. (8.39))
— g
, G3(0) = Gz (71) = max,
= G*—GyA —
v,
г (0) — r(), r(7,) = i*i, \
V - : g
{яi(/), K2(t), 6(0 - 1 или 0, |e(0| —П GKl, Cv2? G-r3 = const).
(8.46)
ях - y^v'G*!, я2 - y2P2/Gy2.
(8.47)
332
С) Г1ТНМ АЛ Ь ТIО Е С О Ч Е Т А ТШ Е Д Ш [ Г АТ Е Л Е Й
последовательного включения) даются законами
l( } ~ I 0 при Д!>0
гг ( + \ - 1 F ^
Л ) I О при Д,>0
e(t) = — р J рг
| 1 при Дх О
1 при А2О
(D — Дх itx — Д2л2).
(8.48)
Отметим, что комбинация 2y2Gv2aG12. фигурирующая в
(8.48), есть скорость истечения V2 двигателя 2. Согласно оптималь¬
ным условиям (8.48) при V2 ^> Vx для случая параллельного вклю¬
чения активный участок двигателя 1 перекрывается активным
участком двигателя 2. В самом деле, при А1 0 заведомо Д2 0!
и при Д2 0 заведомо Дх 0.
Это означает, что если двигатель 1 включен, то двигатель 2
включен заведомо, и если двигатель 2 выключен, то двигатель
1 выключен заведомо. Таким образом, нерегулируемый двигатель
с большей скоростью истечения в режиме параллельного вклю¬
чения работает большее время.
Для иллюстрации общих положений дадим пример решения,
задачи (8.46) (нерегулируемые, последовательно включаемые дви¬
гатели) на маневре набора заданного модуля скорости в бессило¬
вом поле. Уравнения вариационной проблемы, краевые условия,
гамильтонова функция и дифференциальные уравнения импул ьсов
имеют вид (ср. (8.46), (8.41)):
^ххл'6/Т 1 -1- бт2Ло(1 — 6)/т>
((;п : • ^хх Т С,о -Ь бу2)-
е, и (0) = 0, и (Т) — иг, ри 0,
ОПТИМАЛЬНЫЕ УСЛОШШ СОЧЕТАНИЯ ДВИГАТЕЛЕЙ
333
Оптимальные законы е (t) = -J- 1, 6 (£), л^^ (t), я2 (t) = 1 или
О выражены формулами (8.48). Их анализ применительно к рас¬
сматриваемому случаю дает следующие результаты: е (t) ее +1
при О t Т; на траектории имеется единственная точка
переключения релейной функции 6 (£); если V2^>Vv то
8 (0) = 1; при 6 = 1 управление лг = 1, при 6 = 0 управле¬
ние л 2 = 1-
То обстоятельство, что функция е (t) не меняет знака, вытекает
нз условия ри = const (см. (8.49)); очевидно, при и1 0 должно
Лыть е (t) = +1 и ри 0 (см. (8.48)).
Последний факт (ях = 1 при 6 = 1, я2 = 1 при 6 = 0) сле¬
дует из рассмотрения гамильтоновой функции (заметим, что она
вдоль траектории остается постоянной). Представим Н в сле¬
дующем виде (обозначения см. в (8.48)):
Если 6 = 1, то А1л1 = с; если 6 = 0, то Д2я2 = с. Постоянная
с отрицательна; если бы с = 0, то должно быть ях = 0 при 6 = 1
и я2 - 0 при 6 = 0, т. е. оба двигателя выключены вдоль всей
траектории; случай с 0 исключается, ибо Д1я1 ^ Ои Д2я2 0.
Отсюда следует, что при 6 = 1 управление ях = 1 и при 6 = 0
управление л2 = 1. Так как я , и я2 входят во все уравнения в таких
комбинациях с управлением 6: я^, я2 (1 — 6), то можно было бы
положить л1 (t) ЕЕ 1, я2(£)ее1.
Оптимальный закон для релейного управления 6 (t) выписан
в (8.48). Вычислим производную функции/) (t):
D (t) может менять знак с минуса на плюс; поэтому, если на
траектории имеется участок 6 (t) = 1, то он расположен в начале
Этот анализ доказывает высказанные выше утверждения об
оптимальных законах е (t), 8 (£), ях (£), я2 (t).
Введем обозначение t:: для момента переключения функции
6 (t) и проинтегрируем уравнения движения и расхода вдоль
Двух участков:
Н = (Дхях — Д2я2) 6 + Д2я2 = с = const. (8.50)
(8.51)
при Vl V2 производная D (t) 0 (так как ри 0) и функция
6 (0) 1.
6 = 1 при 0 ^ <С I.,' 6 = 0 при t.: t ^ Т.
(8.52)
В результате получим выражения для полезного веса G- и
скорости ил через управляющие (^, Gxl, GV2,G72) и конструктивные
334
ОПТИМАЛЬНОЕ СОЧЕТАНИЕ ДВИГАТЕЛЕЙ
Г ГЛ. -S
(Vv у1? у2, а) параметры, а также время Т:
Gr. = Go — GyX — Gv2 — Gy2 — gtGyx !V\X\ —
-*aCr-OG?a/2rfcv2,
Задавшись значениями конструктивных параметров Fj.cc,.
71? 72 и скорости uv определим оптимальные величины GZ1,
Gy2, Gj2 и максимальный полезный вес как функции времени
маневра Т. На рис. 8.8 представлена функция G- (Г), значком 1
отмечена кривая, соответствующая выполнению маневра одним
двигателем 1 (£# = Г), значок 2 относится к одному двигателю 2
и значок 1 f 2 — к двум двигателям. На рис. 8.9, 8.10 даны
оптимальные управляющие параметры двигателя 2: F2/F1? Gv2/G(>
как функции Т. При расчетах принимались следующие значения
конструктивных параметров и скорости uL:
V1 — 4 -103 Mi сек, у1 — 0,02 кГ/кГ, у2 — 103 кГ/кГ,
а = 10 кГ/квш, Kj = 11,2*103 м/сек. (8.54)
Отметим для дальнейшего, что оптимальная величина скорости
истечения V2 при больших значениях времени Т превышает 2F]r.
а при малых — меньше 2Vv
3. Оптимальные условия сочетания идеальных двигателей.
Вариационную проблему об оптимальном сочетании идеальных
двигателей ограниченной скорости истечения 1 и ограниченной
мощности 2 удобно формулировать в терминах реактивных уско¬
рений
Уравнения расхода, записанные через ускорения а2, име¬
ют вид:
для режима параллельного включения (система (8.38))
(8.53)
ai = gPJG, а2 = gP2<G (аи а2 > 0).
(8.55)
(8.5(5)
для режима последовательного включения (система (8.39))
ОПТИМАЛЬНЫЕ УСЛОВИЯ СОЧЕТАНИЯ ДВИГАТЕЛЕЙ
335
Рио. 8.8. Зависимость относительного полезного веса
G-/C0 от времени Т набора заданного модуля скорости: 1 —
при выполнении маневра одним двигателем ограниченной
скорости истечения, г —одним нерегулируемым двигателем
ограниченной мощности. / - обоими нерегулируемыми
двигателями совместно, a (v2 = 0) — одним идеальным
двигателем ограниченной мощности, 1 ■-2 (тх= т2 = 0) —
обоими идеальными двигателями совместно (Ух = 4000 м/сек,
, — 0,02, у-, — 1000, а — 10 кГ/кеиг, иу = 1120 м/сек).
Рис. 8.0. Оптимальная относительная скорость истечения
VA/VA как функция времени выполнения маневра Т (обо¬
значения и величины параметров даны в подписи к рис. 8.8).
Рис. 8.10. Оптимальный относительный вес источника мощ¬
ности Gv/G0 как функция времени выполнения маневра
(обозначения и величины параметров даны в подписи
к рис. 8.8).
оптимально]-: сочktaiпи-: днигатклей
L I VI. N
В уравнениях (8.56), (8.57) величина N — безразмерная мощ¬
ность (0 N (t) ^ 1); вес G состоит из четырех компонент: по¬
лезного веса G-, весов рабочего вещества G,J/2 (G- + i
_r G[}_о — Ga) и веса двигателя ограниченной мощности
так что G —: Ga + Gv, причем вес двигателя Gv считается
пропорциональным максимальной мощности: G, ~ аД'пкж
(см. гл. 4).
Введем обозначения (ср. (8.13), (4.10)):
Решения уравнений (8.56), (8.57) при помощи этих обозначе¬
ний записываются в едином виде:
G (0 - G3 (0 + Gv - £07Г2 (0/(1 + G0L2 (t)/Gv). (8.60)
Величина относительного полезного веса GJG0 выражается
через К1 — К (Г), Lx= L (Т) так:
Максимум относительного полезного веса G-/G0 по управляю¬
щему параметру GJG0 может быть определен без решения дина¬
мической части вариационной проблемы (как и в случае одного
идеального двигателя ограниченной мощности); максимум имеет
место, если (ср. (4.15))
На основании формул (4.16), (8.13), (8.63) в пространстве
функционалов Ф, Чг, К + L можно построить области преимуще¬
ственного использования идеальных двигателей (рис. 8.11).
для (8.56)
и
о
о
о О О
(8.59)
GJG0 = К\!{ 1 -г L\GJG,) - GJG0.
(8.61s
GJG0 - -KlL1 - L
(8.62.)
при этом (ср. (4.16), (8.13))
GJG0 = (К, + L,f.
(8.63)
§ 21
ОПТИМАЛЬНЫЕ УСЛОВИЯ СОЧЕТАНИЯ ДВИГАТЕЛЕЙ
337
Вариационная проблема о доставке максимального полезного
веса свелась к задаче Лагранжа при дополнительных дифферен¬
циальных связях:
для параллельного режима
max(Ki -г £i) =
— max jexp
Г = V,
2 lvidt) i_2g5 ~N exp( SvI dt)dl\
r(0) = rn, r (T) = n,
V =-- (ax + a2) e + R, v (0) = v,,, v (T) =
/Г+Z
Рис. 8.11. Поверхности, разделяющие области применения
идеальных двигателей ограниченной скорости истечения (1),
ограниченной мощности (2) и комбинации двигателей (1-'г2),
в пространстве ХЕ, Ф, К + L функционалов динамических
задач (W — для двигателя 1, Ф — для двигателя 2, К -г
+ L—для комбинации двигателей 1-\ 2).
(8.64)
для последовательного режима
max (ifi + Li) =
т т
Г / 1 Г , \ Гг/.
= max*
:{ех',(-т$тгл)-й$
N
ехр
о о
г (0) = гП1 г (Т) == п,
г = V,
V = [^6 -f а2(1 — б)] е + R, v(0) = v0, v(71) = v1.
22 Механика полета
(8.65)
338
ОПТИМАЛЬНОЕ СОЧЕТАНИЕ ДВИГАТЕЛЕЙ
[ГЛ. я
Постановки (8.64), (8.65) могут быть записаны как задачи
Майера:
постановка (8.64)
к = - 7-2 Ка, / V!, К (0) = 1, К (Т) +
L = (а / 4 g) х2а! / LA, L (0) = 0, + L (Г) = max,
г = v, г (0) = Го, г (Г) = п,
у = (аа + а2)е + R, v(0) = vn, v(7’) = v1
МО» вг(0> 0, 0<iV(0<l,
1
I
\
I
КО 1 = 1); J
(8.66)
постановка (8.65)
jt = — 1/sKa16/V1, Л(0) = 1, К(Т) +
L = (а/ Ag) КЧ\ (1 — 6) /LiY, L (0) — 0, + L (Т) = max,
Г = У, v (0) = Го, г (Т) = 1 !,
v 1= [аг6 + а-i (1 — 6)] е +R , v (0) = vn, v (Т) = vt
(«i(0. a2(0>0, 6 (0 = 1 или 0<:Fi(<)<Fio, 0<Л'(<)^1,
|e(f)| = l).
(8.67)
Гамильтоновы функции и дифференциальные уравнения им¬
пульсов имеют вид:
для задачи (8.66)
К ах
н = —Рк Ж + Pirg4jT + Pr-v + P«>-[(ai+ а2)е + В],
31
Рк Рк 2у1 Pi ‘>а
а Ка*
'2 sLN ’
Pi = Pi
а КЧ\
Ag LlN ’
Рг == — gj(Po-H), Р» = —Рг. Рк(Т) = Pt (Т) = — 1;
(8.68)
для задачи (8.67)
К ах 6
н - — P*-WT + PiVg
а КЧ\{ 1-6)
LN
+
+ Pr-V + Pb-U®!5 “Ь а2 (1 ~ ^)] е + R}.
Рк — Рк 2у1 Р1
ах6 _ а Ка\(1-Ь) . _ аКЧ\{А-Ь)
!2 g
LN
' * Pi = PiVg
L>N
Vr — — ^ (Рв-R). Pt> = —Pr. Pk{T) = Pi{T) =— i.
(8.69)
g 2] ОПТИМАЛЬНЫЕ УСЛОВИЯ СОЧЕТАНИЯ ДВИГАТЕЛЕЙ 339
Дифференциальные уравнения для импульсов рк, р{ из систем
(8.68), (8.69) интегрируются в конечном виде; выражения полу¬
чаются одинаковыми в первом и во втором случаях:
Рк = (L2 - КгЬг - Ll)/KLV Pl = - L/Lv (8.70)
Оптимальные законы е (t), а2 (£), N (t), Vx (t) для задач (8.66),
(8.67) даются следующими формулами:
е (t) = — рv/pv, а2 (<) = —2gp0 Ьх/аК2,
N (t) (8.71)
Управление ах (t) входит линейно в уравнения вариационных
проблем и гамильтоновы функции; поэтому оптимальный закон
ах (t) в общем случае включает три участка: два «граничных»
(ах = 0, ах = а1тах = оо) и участок особого управления {ах = a10pt)
(ср. (8.9), (8.10)).
Выключение двигателя 1 (ах = 0) имеет место при (индекс 0
у Vx дальше опускается)
= —р]с KI2V1 — pv > 0, (8.72)
или (см. (8.70))
Дх = (L\ + - L2)i2VxLx - Pv > 0. (8.73)
Воспользовавшись выражением для скорости истечения дви¬
гателя ограниченной мощности
F2 (t) = 2gGJaGa, = (L1K1 + L\ - L2)/LlPv (8.74)
(последнее выражение получено при помощи (8.60), (8.62), (8.71)),
можно представить комбинацию А1 в таком виде:
Ai = Pv (У2/2Уг - 1). (8.75)
Если вдоль всей траектории выполняется неравенство
V2 (t) < 2V1, (8.76)
то двигатель 1 не включается ни в одной точке траектории и, сле¬
довательно, для выполнения данного маневра не нужен; этот
вывод дается в работе [8.56]. Условие (8.76) выше было получено
в предположении, что вес источника мощности Gv выбран опти¬
мальным по формуле (8.62). Однако это же условие сохраняется
и для произвольного неоптимального веса как это следует из
[8.56].
Оптимальный закон для релейной функции б (t), фигурирую¬
щей в задаче (8.67), имеет вид
6 = 0 при!) > о, 6 = 1 при!) < О (D = Axax — gplLJaK2).
(8.77)
22*
340
ОПТИМАЛЬНОЕ СОЧЕТАНИЕ ДВИГАТЕЛЕЙ
[ГЛ. .8
Если а1 = 0, то подавно 6 = 0. В самом деле, при аг = 0
оставшийся в комбинации D второй член всегда больше нуля;
поэтому в режиме последовательного включения двигатель 1
заведомо не будет включаться, если всюду выполняется неравен¬
ство (8.76).
Если а1так — °° (что имеет место в нашем случае), то условия
(8.76), (8.77) совпадают и режимы параллельного и последова¬
тельного включения не различаются.
Неравенство (8.76) позволяет для данного динамического ма¬
невра построить границу на плоскости a, V1 — параметров идеаль¬
ных двигателей 1 и 2, отделяющую область применения одного
двигателя 2 от области совместного применения двигателей 1 и 2.
Для этого достаточно иметь результаты решения вариационно]!
проблемы о выполнении данного маневра с одним двигателем 2.
Примеры построения границ содержатся в следующем параграфе.
В заключение этого пункта приведем результаты по задачам
оптимального сочетания идеальных двигателей 1 и 2 при наборе
заданного модуля скорости в бессиловом поле.
Уравнения вариационной проблемы, краевые условия, га¬
мильтонова функция и выражения импульсов имеют вид (см.
(8.66), (8.68), (8.70), (8.71))
k^-Ka.llW, К (0) = 1, Рк(Т) = - 1,
p^iV-KiU-LblKLu
L = (a/Ag)K*a*/L, L( 0) = 0, р,(Т) = - 1,
Pi — — L j Li, } (8.78)
и — (ai 4- a2) e, и (0) = 0, и (T) =
ри = const 0,
Н = — РкКах j 2Fi + р{ (а / 4g) К'2а\ / L + ри («1 + а*) е.
Оптимальные управления е (t), а1 (t), а2 (t) подчиняются сле¬
дующим законам:
е (t) = 1; аг (0) = oo, ах (t) = 0 (0 < t Т); а2 (t) = const.
(8.79)
Прокомментируем оптимальные законы ах (£), а2 (t). Оптималь¬
ное выражение для е (t) совпадает с полученным в п. 2 настоящего
параграфа. Комбинация Ax(cm. формулу (8.73)) может быть поло¬
жительной всюду на интервале 0 t ^ Т или в крайнем случае
обращаться в нуль в изолированных точках интервала; при
ри = const производная Д > 0, поэтому единственной точкой, где
Дх = 0 и нарушается условие (8.73) выключения двигателя 1,
является точка t = 0. Далее, так как К (Т) = const при 0 t ^ 7\
то а2 = const, что следует из (8.71).
§ я
ОПТИМАЛЬНЫЕ УСЛОВИЯ СОЧЕТАНИЯ ДВИГАТЕЛЕЙ 34^
Дифференциальные уравнения (8.78) интегрируются следую¬
щим образом!
дгх = ехр (— Д и / 2Ft), Lx = — Кг У (а / 2 g) а\Т, их = Д и + а2Г
(8.80)
(&U-— lim \ax(t)dt, >эс при t-* O').
V 0J >
Исключая w2 из второго и третьего уравнений (8.80), приходим
к следующему выражению для контрольного функционала:
Кх + Lx = ехр (— Ди 12Vx) [1 — Y(a/2g) (иг— Дм)2/ Г]. (8.81)
Здесь присутствует параметр А и — приращение скорости,
обязанное импульсу ускорения ах (O^A^^^j). Значение А и,
доставляющее максимум выражению (8.81), таково:
= mi 4- 2Fi — Y2gT /а при — wx < 2FX — /а<^ 0,
Aw = 0 при 2Уг — Y2gT I а ^ — mi, ’
Aw == wx при 2FX—"jAgT/а > 0.
(8.82)
Верхняя формула из (8.82) соответствует совместному приме¬
нению двух двигателей (1+2), средняя — одному двигателю 2 и
нижняя — одному двигателю 1.
На рис. 8.8 нанесены кривые относительного полезного веса
GJG0, отвечающие трем случаям (8 .82); значения параметров
взяты следующие (ср. (8.54)):
V1 = 4-103 м/сек, а = 10 кГ/квтп, их — 11,2 ИО3 м/сек. (8.83)
Эти кривые (в отличие от соответствующих кривых для нере¬
гулируемых двигателей) обозначены индексом 71 = 72— 0-
Графики минимальной на траектории скорости истечения дви¬
гателя 2 и веса источника мощности в зависимости от времени
маневра представлены на рис. 8.9, 8.10 (кривые 7Х = у2 — 0)-
Минимальная скорость истечения V2 достигается в данном слу¬
чае, судя по формуле (8.74), в начальной точке траектории.
В области времен Т, где оба двигателя работают совместно, началь¬
ная скорость истечения не зависит от времени маневра: V2 (0) =
= 2Vly что следует из условия включения двигателя 1.
Результаты проведенного анализа для задачи набора заданного
Модуля скорости могут быть представлены также в следующем виде
[8.55]. Из формул (8.63), (8.81), (8.82) следует, что относительный
342
ОПТИМАЛЬНОЕ СОЧЕТАНИЕ ДВИГАТЕЛЕЙ
[ГЛ. 8
полезный вес G~/G0 зависит от двух комбинаций параметров:
(u^Vi) и (gT/2aVl). На рис. 8.12 представлена эта зависимость:
линии 1 соответствуют одному двигателю ограниченной скорости
истечения, линии 2 — одному двигателю ограниченной мощности,
линии 1+2 — сочетанию двух двигателей; область совместного
использования двух двигателей выделена на рисунке штри¬
ховкой.
Помимо этой задачи, в работе [8.55] рассмотрены также сле¬
дующие маневры: перемещение между двумя положениями покоя
в бессиловом поле и набор
параболической и гипербо¬
лической скоростей в цент¬
ральном поле. В основу ана¬
лиза положено прямое срав¬
нение по полезной нагрузке
различных комбинаций из
участков движения с двига¬
телями одного и другого ти¬
пов. Некоторые результаты
по сочетанию двигателей огра¬
ниченной скорости истечения
и ограниченной мощности
содержатся в [8.57].
Анализируя представлен¬
ные здесь результаты, можно
заключить следующее. Дви¬
гатели ограниченной мощно¬
сти наиболее эффективны на
тех маневрах, где требуются
малые реактивные ускорения.
При увеличении ускорения
(что соответствует, напри¬
мер, уменьшению времени движения) доставляемый полезный
вес падает (см. рис. 8.8), в пределе обращаясь в нуль. В этой
области времен добавление двигателя ограниченной скорости
истечения повышает величину полезного веса. При дальнейшем
уменьшении времени двигатель ограниченной скорости истече¬
ния выполняет большую часть маневра, и, наконец, ниже неко¬
торого времени применение двигателя ограниченной мощности
не нужно — маневр выполняется одним двигателем ограничен¬
ной скорости истечения. Наибольший выигрыш от совместного
применения двух двигателей получается на тех маневрах, где
полезные нагрузки, доставляемые каждым двигателем по отдель¬
ности, близки.
Отмеченные закономерности одинаково справедливы для иде¬
альных и нерегулируемых двигателей.
Рис. 8.12. Зависимость относительного полез¬
ного веса G-JGq от комбинации параметров
двигателей и маневра (gT/'laY^) uitJYi (набор
заданного модуля скорости в бессиловом поле;
идеальные двигатели: / — двигатель ограни¬
ченной скорости истечения, 2 — двигатель
ограниченной мощности, 1 ■ 2 — сочетание
двигателей / и 2; штриховкой выделена об¬
ласть совместного использования двух дви¬
гателей).
ПРИМЕНЕНИЕ ДВИГАТЕЛЕЙ ОГРАНИЧЕННОЙ МОЩНОСТИ 343
§ з. ОБЛАСТИ применения ДВИГАТБЛей ОГРАНИЧеННОЙ
МОЩНОСТИ
Пусть для заданного динамического маневра решена вариа¬
ционная проблема, относящаяся к одному идеальному двигателю
ограниченной мощности (гл. 4 и 5); это означает, что определены
оптимальный закон реактивного ускорения а, (t) и функция J (t).
Изменение скорости истечения V2 (t) вдоль траектории подсчиты¬
вается по следующим формулам (ср. (5.102)):
V2 (t) = 2gNJG (t) a (*), G (t) = G0 (1 + G0J (t)/2gNoy\ (8.84)
Входящий в формулу (8.84) параметр G0/N0 может либо зада¬
ваться заранее
GJNо - х, (8.85)
либо определяться оптимальным, если задан конструктивный па¬
раметр a
G„ I Nn = a [ Y(a/2g)J(T) - (a / 2g) J (T)yK (8.86)
Минимальное значение V2 на траектории определяет по фор¬
муле (сл1. (8.76))
Fi = -^-min V2(t, к) (8.87)
- t
или по формуле
а) (8.88)
1 t
ту скорость истечения двигателя 1, ниже которой выгодно при¬
менять один двигатель 2 для выполнения заданного маневра.
Действуя подобным образом, можно рассчитать кривые на плос¬
костях параметров (а, Уг) или (х, FJ, отделяющие области приме¬
нения двигателя 2 от областей совместного применения двигате¬
лей 1+2, и, следовательно, указать предельные возможности
одного идеального двигателя ограниченной мощности. Не менее
интересна граница между областями 1+2 и 1, которая опреде¬
ляет предельные возможности одного двигателя ограниченной
скорости истечения; однако отсутствие во втором случае такого
простого критерия, как неравенство (8.76), не дает возможности
указать границу, не решая полностью вариационной проблемы
сочетания двигателей.
В настоящем параграфе вычисляются по формулам (8.87),
(8.88) границы применения идеального двигателя ограниченной
мощности на примере трех маневров: набора параболической
скорости с круговой орбиты, перелета между двумя круговыми
орбитами и межпланетного перелета. Необходимые для расчетов
оптимальные законы a2 (t) и функции / (t) взяты из главы 5.
344
ОПТИМАЛЬНОЕ СОЧЕТАНИЕ ДВИГАТЕЛЕЙ
[ГЛ. S
1. Набор параболической скорости. Космический аппарат
выводится на круговую орбиту и далее должен набрать парабо¬
лическую скорость при наличии двух двигателей.
ос,
©
ш
Шt
г=29,2сук
Bibi
а)
км/сек
кГ/кдт
24
16
0
9,2суm
®
&77р-гт-.
в
6
б)
у,.
км/сек
Рис. 8.13. Области применения идеального
двигателя ограниченной мощности 2 для
маневра набора параболической скорости
у Земли, а) Плоскость a, Yt (удельный
вес двигателя 2, скорость истечения дви¬
гателя 1); б) плоскость х, Vх (к = О0/Л'20—
параметр двигателя 2, параметр манев¬
ра— время движения Т).
s)
Рис. 8.14. Полезные веса G^/G0 для идеаль¬
ных двигателей ограниченной скорости
истечения 1 и ограниченной мощности
2 на маневре набора параболической скоро¬
сти у Земли как функции соответствующих
конструктивных параметров \\ и а; а) Т =
= (i,Seym; б) Т = 29,2 суш (см. рис. 8.13).
Традиционная схема выполнения этого маневра предполагает
применение одного двигателя ограниченной мощности. Оптималь¬
ная программа вектора реактивного ускорения для идеального
двигателя такова (см. гл. 5): модуль ускорения почти постоянен,
а направление вектора заключено между трансверсалью и каса¬
тельной к траектории, которые почти совпадают во все время
движения.
g 3] ПРИМЕНЕНИЕ ДВИГАТЕЛЕЙ ОГРАНИЧЕННОЙ МОЩНОСТИ
345
Из-за того, что модуль реактивного ускорения почти постоя¬
нен, минимальная скорость V 2 имеет место в начальной точке
траектории. Следовательно, условие (8.76) может нарушаться при
I = 0 и дополнительный двигатель ограниченной скорости исте¬
чения может включаться в начале траектории.
Предельные зависимости a (Fx) и к(Уг) представлены на рис. 8.13.
Б областях параметров a, VL (или х, Ух), лежащих ниже кривых,
целесообразно применение одного двигателя ограниченной мощ¬
ности (эти области выделены штриховкой). В качестве исходных
были приняты следующие характеристики маневров: высота на¬
чальной круговой орбиты над поверхностью Земли — 300 км;
Т = 6,8 сут, / (Т) = 80,8 мУсек3, а20 = 0,895 см/сек2 — первый
пример; Т = 29,2 сути, J (Т) = 17,95 мУсек3, а20 = 0,269 см/сек —
второй пример. Соответствующие зависимости относительных по¬
лезных весов от конструктивных параметров двигателей показаны
на рис. 8.14 (характеристическая скорость / = 3,167 • 103.м/сек,
значения функционала / см. выше).
2. Перелет между круговыми орбитами. Этот маневр характе¬
ризуется следующим оптимальным законом а2 (t) (см. гл. 5):
функция а2 (t) сначала убывает, а затем возрастает, так что мак¬
симальные значения а2 достигаются в начале и в конце траектории.
Соответственно этому скорость истечения V2 сначала возрастает,
а затем убывает либо вплоть до конечной точки, либо до неко¬
торой точки, близкой к конечной, где имеется относительный
минимум функции V2 (t). Таким образом, включение двигате¬
ля 1 может быть либо в начале, либо в окрестности конца тра¬
ектории в зависимости от того, где раньше нарушается усло¬
вие (8.76).
На рис. 8.15 даны границы областей применения двигателя
ограниченной мощности (области применения лежат ниже кривых)
на плоскостях параметров a, Fj и х, параметры маневров взяты
следующие (для времени Т функционала / указаны безразмерные
и размерные значения, соответствующие перелетам со средней
орбиты Земли на среднюю орбиту Марса):
а) г0 = 1, гг = 1,52, фг = 1,97,
Т = 1,94—> 113 cym, J(T) = 1,053 —> 187 м2 / сек\
б) г0 = 1, п = 1,52, ф! = 2,36,
Т = 2,55 —> 148 cym, J (Т) = 0,403 -> 71,4 м2 /сек3,
в) Г0 = 1, п = 1,52, ф! = 2,73,
Т = 3,70-^ 215 cym, J(T) = 0,0416 —> 7,38м2 / сек3
(8.89)
Относительные полезные веса для двигателей ограниченной
скорости истечения и ограниченной мощности в зависимости от
346
ОПТИМАЛЬНОЕ СОЧЕТАНИЕ ДВИГАТЕЛЕЙ
[ГЛ. 8
конструктивных параметров двигателей при фиксированных
параметрах маневра (8.89) показаны на рис. 8.16 (характеристи¬
ке ,
к//к 6 т
24
16
\vrl73
\Т=215сут
\
\2<
/ jjVo
з
7
v.-W
Т=ПЗсут
6
о)
км/сек
Gft/So
0,2
V
\
ЬсК
0,2
Ок/Go
0,6
0,4
02
8 Vf, км/сек
10
18
а)
26 сс,кГ/к6т
V
У
'I
6
Vf, к м/сек
2 10 18 26 сс, к Г/к 6 т
в)
\2
л
К
Vf,км/сек
Рис. 8.15. Границы областей применения
идеального двигателя ограниченной мощ¬
ности для маневра перелета между кру¬
говыми компланарными орбитами Земли
и Марса, а) Плоскость a, vt\ 6) плоскость
х, Vx; параметры маневра — угловое пере¬
мещение Фх и время движения Т.
2 10 18 26 сс, кГ/кбт
8)
Рис. 8.16. Полезные веса Gn/G0 для идеаль¬
ных двигателей ограниченной скорости
истечения 1 и ограниченной мощности
2 на маневре перелета между орбитами
Земли и Марса как функции соответствую¬
щих конструктивных параметров \\ и а:
я) = 1,97, Т = 113 сут] б) ср! = 2,30,
Т = 148 сут] в) срх = 2,73, Т = 215 сут
(см. рис. 8.15).
ческая скорость равна а) / = 13-103 м/сек; б) I = 9-103 м/сек;
в) I = 6,5-103 м/сек по данным [8.58], функционал J см. (8.89)).
g з] ПРИМЕНЕНИЕ ДВИГАТЕЛЕЙ ОГРАНИЧЕННОЙ МОЩНОСТИ 347
3. Межпланетный перелет с возвращением. Данный маневр
представляется как комбинация двух элементарных маневров, рас¬
смотренных выше (см. гл. 5).
ос.
лГ/лот
Zf, лм/сеп
я,
лГ/лот
V}, нм/сен
выше (см. гл.
В зависимости от параметров
элементарных маневров мини¬
мальная скорость истечения V2,
согласно предыдущему, дости¬
гается либо в начале одного из
участков движения в окрестно¬
сти планет, либо в начале или в
конце одного из гелиоцентриче¬
ских участков. По условию опти¬
мального сочетания элементар¬
ных маневров, составляющих
межпланетный перелет с возвра¬
щением (§ 3 гл. 5), величины
0,4
0,2
\
и
8 У;, пм/сеп
2
10
18
26 осглГ/лбт
Рис. 8.17. Область применения идеального
двигателя ограниченной мощности 2 для
маневра межпланетного перелета Земля —
Марс — Земля. а) Плоскость а, V t;
б) плоскость х, ТА; параметры маневра —
суммарное время Та = 044 cijm, время
пребывания в окрестности Марса
= 48 сут.
Рис. 8.18. Полезные веса G_/G0 для иде¬
альных двигателей ограниченной скорости
истечения 1 и ограниченной мощности
2 на маневре межпланетного перелета
Земля — Марс — Земля; Та = 644 сут,
Тw = 48 суш (см. рис. 8.17).
реактивного ускорения на участках разгона и торможения у одно¬
именной планеты равны. Поэтому начало разгона у планеты назна¬
чения и начало торможения у планеты старта выпадают из числа
«подозрительных» точек.
Для перелета Земля — Марс — Земля оптимальное реактив¬
ное ускорение в окрестности Марса обычно меньше, чем в
окрестности Земли, поэтому подлежащими сравнению остаются
следующие точки: начало разгона у Земли, начало и конец
межорбитальных перелетов Земля — Марс и Марс — Земля
(здесь раньше, чем в других точках, может оказаться выгодным
348
ОПТИМАЛЬНОЕ СОЧЕТАНИЕ ДВИГАТЕЛЕЙ
[ГЛ. 8
дополнительный импульс двигателя ограниченной скорости
истечения).
В качестве примера возьмем перелет Земля — Марс — Земля
с параметрами: суммарное время Та = 644 сут, время пребыва¬
ния в окрестности Марса Тш = 48 сут. Зависимости a (t), J (t) и
V (t) при а = 5 и 10 кГ/квт для этого перелета показаны на
рис. 5.32. Минимальная скорость истечения достигается: при
а <Г 5 кПквт в начале межорбитального перелета Марс — Земля
(а2= 0,215 см!сек2), а при а > 5 кГЫвт в начале разгона у Земли
(а2= 0,165 см!сек2). Область применения двигателя ограничен¬
ной мощности, определенная по критерию (8.76), показана на
рис. 8.17. Относительные полезные веса для двигателей ограни¬
ченной скорости истечения и ограниченной мощности в функции
конструктивных параметров двигателей даны на рис. 8.18 (ха¬
рактеристическая скорость 1а = 22,2 -103 м/сек — по данным
[8.58], функционал /а = 63,6 м2!секъ — табл. 5.7).
4. Замечания. 1°. Критерий (8.76) получен для идеального
двигателя ограниченной мощности. В применении к реальным
двигателям он дает неточный ответ — пример с нерегулируемыми
двигателями (см. рис. 8.8 § 2, пп. 2 и 3) подтверждает этот факт.
Поэтому для реальных двигателей критерий (8.76) позволяет
только оценить (а не вычислить точно) границу области приме¬
нения.
2°. Анализ примеров, посчитанных для маневров в централь¬
ном поле и для модельного маневра в бессиловом поле, дает осно¬
вание заключить, что необходимость в дополнительном двигателе
ограниченной скорости истечения возникает тем скорее, чем «на¬
пряженнее» динамический маневр (т. е. чем меньше полезной
нагрузки доставляет один двигатель ограниченной мощности).
3°. По результатам, представленным на рис. 8.13—8.18,.
можно судить о целесообразности применения двигателя ограни¬
ченной мощности одного или совместно с двигателем ограничен¬
ной скорости истечения на этапах межпланетного перелета.
г Л А В А 9
ДВИГАТЕЛЬНЫЕ СИСТЕМЫ С НАКОПЛЕНИЕМ
ЭНЕРГИИ И МАССЫ.
ДВИГАТЕЛИ, ТЯГА И МОЩНОСТЬ КОТОРЫХ ЗАВИСЯТ
ОТ КООРДИНАТ И ВРЕМЕНИ
В настоящей главе обсуждаются задачи оптимизации пара¬
метров и управлений следующих типов двигательных систем:
1°. Двигатели ограниченной мощности с аккумуляторами
энергии, тепловой или электрической (§ 1 и 2).
2°. Двигатели ограниченной мощности и ограниченной ско¬
рости истечения с накоплением атмосферного газа, используемого
в качестве рабочего вещества (§ 3).
3°. Солнечный парус (максимальная тяга зависит от расстояния
до Солнца и ориентации паруса (§ 4)).
4°. Изотопный парус (максимальная тяга зависит от време¬
ни (§ 5)).
5°. Двигатели с солнечным источником энергии (максимальная
мощность зависит от расстояния до Солнца (§ 6)).
6°. Двигатели с изотопным источником энергии (максималь¬
ная мощность зависит от времени (§ 7)).
§ 1. ДВИГАТЕЛИ ОГРАНИЧЕННОЙ МОЩНОСТИ С АККУМУЛЯТОРОМ
ЭНЕРГИИ — ИДЕАЛЬНЫЙ СЛУЧАЙ
Анализируя результаты решения динамической части проб¬
лемы оптимизации (гл. 5 и 6), можно сделать вывод о существо¬
вании участков траектории, где приложение тяги наиболее вы¬
годно. Для перелетов между орбитами в центральном поле и пере¬
мещения между положениями покоя в бессиловом поле — это
окрестности начальной и конечной точек траектории, для маневра
поворота плоскости круговой орбиты в центральном поле — окре¬
стность конечного положения линии узлов. В случае идеального
двигателя ограниченной мощности на этих участках уровень
реактивного ускорения, согласно оптимальной программе, много
больше, чем на остальной траектории; в случае нерегулируемых
двигателей здесь располагаются активные участки, в то время как
на остальных участках тяга выключена.
В исследованных выше схемах двигателей ограниченной мощ¬
ности энергия, вырабатываемая источником, подводится непосред¬
ственно к движителю. Поэтому на участках, где оптимальная вели¬
чина тяги мала или равна нулю, источник мощности фактически
350
ДРУГИЕ ТИПЫ ДВИГАТЕЛЬНЫХ СИСТЕМ
[ГЛ. 9
не используется. Показано, что эффективность работы источника
мощности можно повысить, если во время движения по участкам
с нулевой или почти нулевой тягой запасать энергию, вырабатывае¬
мую источником, а на участках, выгодных для приложения тяги,
направлять всю энергию (вместе с запасенной) в движитель
[9.1—9.3]. Накопление энергии может осуществляться при по¬
мощи тепловых [9.1] или электрических [9.2] аккумуляторов.
Описание их основных характеристик дано в § 2 главы 2. Предва¬
рительные оценки выигрыша в полезной нагрузке при исполь¬
зовании аккумуляторов сделаны в работах [9.1, 9.2].
Необходимость введения аккумуляторов энергии возникает
также в задачах движения спутника с солнечной энергоуста¬
новкой, если траектория
содержит затененные уча¬
стки.
1. Регулировочная и
весовая характеристики.
В состав двигательной ус¬
та нов ки ог р аниченно й мощ -
ности с накопителем энер¬
гии входят источник мощ¬
ности Л\,, накопитель энер¬
гии Е и движитель Р (рис. 9.1) [9.3]. Вырабатываемая источником
мощность 0 <; iVv Nvо может быть направлена в накопитель
7V3>0 и непосредственно в движитель N2 0 так, что Nx + N2=
= Nv. Накопитель энергии может отдавать мощность движителю
N3 = N± — Ё (N3 >0, 0 Е Е0), таким образом к движителю
подводится мощность Ny = N2 + iV3, которая используется для
создания тяги:
Р = qV, Ny = V2qV* (0 < Р < Р0). (9.1)
Здесь q — массовый расход рабочего вещества, V — скорость
истечения. Процесс ускорения рабочего вещества считается идеаль¬
ным. Тяга движителя в общем случае ограничена сверху. В слу¬
чае идеального движителя верхнее ограничение на тягу отсут¬
ствует (Р0 = ос). Для нерегулируемого движителя Р = Р0 или
0, предположение об отсутствии потерь в движителе при этом не
делается.
Исключив N2 = N„ — N± и заменив Ns — N± = Ne, можно
представить уравнение баланса мощности для рассматриваемой
системы в виде
Ё = -Ne, N,+Ne = 1/2qV-
(0<£<Я0, Ne>-Nv, о <iVv<iVvu). (9.2)
Отрицательные; значения мощности Ne соответствуют режиму
зарядки и ограничены величиной мощности 7Vv, вырабатываемой
Рис. 9.1. Принципиальная схема двигательной
установки ограниченной мощности с накоплением
энергии; IVvq — источник мощности, Ь’0 — акку¬
мулятор энергии, 1> — движитель.
§ 1] ИДЕАЛЬНЫЕ ДВИГАТЕЛИ С АККУМУЛЯТОРОМ ЭНЕРГИИ 351
источником. Положительные значения Ne соответствуют режиму
разрядки.
Вес двигателя ограниченной мощности с накопителем энергии
GX = GV + Ge + GY (9.3)
составляют следующие компоненты: вес источника мощности
(принимается пропорциональным максимальной мощности источ¬
ника Nv 0)
Gv = a7Vv0, (9.4)
вес накопителя энергии (принимается пропорциональным мак¬
симальной накапливаемой энергии Е0)
Ge= pi?0, (9.5>
вес движителя (принимается пропорциональным максимальной
тяге Р0)
G( = yPQ (9.6)
(в случае идеального движителя G ( = 0).
2. Формулировка вариационной проблемы. Состав оптималь¬
ного управления. Задача о максимуме полезной нагрузки для дви¬
гательной системы ограниченной мощности с накопителем энер¬
гии ставится так: заданы начальный вес G0, удельные веса а, |3, у
источника мощности, аккумулятора и движителя, фиксированы
граничные условия и время выполнения маневра Т\ требуется ука¬
зать оптимальные режимы работы источника мощности, накопи¬
теля энергии и движителя, а также оптимальные весовые пара¬
метры (9.4) — (9.6). обеспечивающие максимум полезного груза
GL [9.3].
Полная система дифференциальных уравнений, граничных
условий, ограничений на управляющие функции и фазовые коор¬
динаты этой вариационной проблемы в постановке Майера запи¬
сываются следующим образом (аналогично (II.8)):
Go — —7У уу ) > Go (0) + G* = 1, G0(7T) = max,
Ё = — k2N,Nel Е (0) = 1, Е (Т) = 0,
r=v, 1* (0) = г0, г(Т) = гъ
V = кЗ-7ГР? г + К, v(0)=y0, У (Т) = Vi
ua ~г у.
(0<P(0<1. 0<ЛД*)<Ь Ne(t)>- 1,
|e(«)| = U 0<£(<)<1,
2^0С„ ~2t2Gv’ 2 £0 aGe ’ 3 С» T
(9.7)
352
ДРУГИЕ ТИПЫ ДВИГАТЕЛЬНЫХ СИСТЕМ
[ГЛ.
Здесь первое уравнение — это уравнение расхода рабочего веще¬
ства (G0 (t) = G„ + G,j. (£) — суммарный вес полезной нагрузки
G- и запаса рабочего тела Gp,), второе — уравнение изменения энер¬
гии накопителя, третье и четвертое — векторные уравнения дви¬
жения центра масс аппарата в инерциальной системе координат.
Начальное условие для весов Ga и G* соответствует заданному
стартовому весу G0 (все веса отнесены к G0). В конце движения вес
Ga (Т) совпадает по определению с (!, и должен быть максималь¬
ным. Граничные условия для энергии Е (отнесены к Е0), радиуса-
вектора г и вектора скорости у могут меняться в зависимости от
типа маневра.
Управляющие функции P,N^,Ne, е безразмерные: тяга Р и
мощность источника Nv отнесены к своим максимальным значе¬
ниям Р0 и NQ, мощность Nе отнесена к текущей мощности источни¬
ка, е — единичный вектор направления тяги.
Управляющие параметры Gv, Ge, G{ — веса источника мощ¬
ности, накопителя энергии и движителя (отнесены к G0) — вхо¬
дят в правые части уравнений (9.7) и в начальное условие заданного
стартового веса. Выбор оптимальных значений этих параметров
можно свести к стандартной процедуре, если присоединить к
системе (9.7) формальные уравнения
(первое условие записывается вместо Ga (0) + Gx = 1). После
этого управляющие параметры Gv, Ge, GY превращаются в фазо¬
вые координаты, начальные значения которых связаны условием
трансверсальности, а конечные значения свободны.
Оптимальные управления е (£), Р (£), Ne (t), Nv (t) определя¬
ются по методу JI. С. Понтрягина из условия абсолютного мини¬
мума гамильтоновой функции Н:
При этом нужно различать участки траектории двух типов: ле¬
жащие внутри области 0 ^ 1 и лежащие на границах Е = 0
или Е = 1. Опуская промежуточные этапы отыскания минимума
функции 7/, приведем окончательные выражения для оптимальных
управлений.
Gv = 0, Ge = 0, Gy = 0
(9.8)
с граничными условиями
Ga (0) + G., (0) + Ge (0) + G, (0) = 1,
Gv (T) = opt, Ge (T) = opt, Gy (T) = opt
(9.9)
TT ~
= ~P° JVv (1 + Ne)
Pe =
ИДЕАЛЬНЫЕ ДВИГАТЕЛИ С АККУМУЛЯТОРОМ ЭНЕРГИИ
353
Законы изменения по времени направления тяги е и мощности
источника iVv одинаковы как для внутренних, так и для гранич¬
ных участков траектории
е = Рг / Pv » iVv — 1 (~ | Ри |) * (9.11)
т. е. вектор тяги антипараллелен вектору р*,, и мощность источ¬
ника максимальна (как и для двигательных систем ограниченной
мощности без накопителя — см. выше гл. 4).
Мощность Ne (управляющая энергией накопителя) и величина
тяги Р подчиняются следующим законам:
внутри области 0 Е <; 1
Ne = (ёг) ’ р = 1 приpi>^}
Ne = — 1, Р = 0 при pi < фх \ (9.12)
(ф1 = ЬроРв (Ро + G')2 ; j
на границах Е = 0 и Е = 1
Ns = О, Р = 1 при > фз, ^
w« = 0’ р = 21,.м^+ с,, j (9ЛЗ)
где импульсы ра и всюду отрицательны.
Таким образом, внутри области 0 Е 1 энергия накопи¬
теля либо расходуется с оптимально меняющейся скоростью (ре¬
жим разрядки), при этом тяга максимальна (см. первое соотно¬
шение (9.12)), либо запасается с максимальной скоростью (реяшм
зарядки), при этом тяга нулевая (см. второе соотношение (9.12)).
На границах Е = 0 и Е = 1 расход энергии накопителя, есте¬
ственно, нулевой, а тяга изменяется, как и при отсутствии нако¬
пителя: либо максимальна (первое соотношение (9.13)), либо
оптимально регулируется (второе соотношение (9.13)).
Чтобы установить чередование оптимальных законов (9.12),
(9.13), нужно знать поведение импульсов ра, ре, pv = | р*. | и фа¬
зовой координаты Ga. Импульсы р0, pv, рг и фазовые координаты
всюду непрерывны, а импульс ре при сходе с границ Е = 0 и Е = 1
в соответствии с «условием скачка» [9.4] имеет разрыв первого
Рода (вид функции Н и дифференциальные уравнения для импуль-
с°в (9.10) сохраняются).
23 Механика полета
354
ДРУГИЕ ТИПЫ ДВИГАТЕЛЬНЫХ СИСТЕМ
[гл
Из уравнений (9.10), (9.7) с учетом (9.11) имеем
А“0' г&<°- (9Л/"
Можно показать, что импульсы р0 и ре всюду отрицательны, функ¬
ции фх и ср2, входящие в условия (9.12), (9.13) смены режимов.
Рис. 9.2. Оптимальное изменение
по времени относительной энергии,
запасенной в аккумуляторе Е, и тя¬
ги движителя Р для случая, когда
функция Е не выходит на ограни¬
чения.
по времени относительной энергии
аккумулятора Е н тяги Р для
случая, когда функция Е выходит
на ограничения Е = 1 и Е = 0.
положительны. При помощи (9.14) можно заключить, что эти функ¬
ции неубывающие:
ф1 > о, ф2 > о при р\ > фь
ф1 = 0, ф2 = 0 при pi < фь
ф1>0, ф2>0 при р\ >ф2;
ф1 = 0, фо > 0 при pi < ф2.
Поведение импульса рц определяется в основном типом манев¬
ра. Для рассматриваемых в дальнейшем примеров характерно
немонотонное поведение р* (t) с минимумом внутри интервала [О,Т].
Если за все время движения энергия Е не выходит на границы
2? = Ои2?=1,то функции Е (t) и Р (t) будут иметь вид, показанный
на рис. 9.2. В общем случае между точками перехода с режима
разрядки на режим зарядки и обратно могут появляться участки
движения по границам Е = 0 и Е = 1 соответственно (рис. 9.3).
Момент схода с границы принципом максимума не определен и
должен находиться с помощью одного из достаточных принципов
§ П
ИДЕАЛЬНЫЕ ДВИГАТЕЛИ С АККУМУЛЯТОРОМ ЭНЕРГИИ
355
оптимальности или варьированием протяженности граничного
участка (п. 3).
В заключение настоящего пункта укажем на необходимость
рассмотрения двигательной системы с накопителем энергии, но
без источника мощности. Такая система будет целесообразной при
достаточно малых значениях (3 — удельного веса накопителя
энергии (9.5) — таких, что
fir/a < 1. (9.15)
Действительно, источник мощности весом Gv, вырабатываю¬
щий за время Т количество энергии Е* = (Gv/a) Т, при pTVa = 1
может быть заменен полностью заряженным к начальному мо¬
менту времени накопителем энергии емкостью Е* с тем же весом
G* = £>Е* = вфТ/а = Gv. При рг/a < 1 будет G* < Gv, по¬
этому применение источника мощности нецелесообразно.
Для случая двигательной системы с накопителем энергии без
источника мощности уравнения вариационной задачи (9.7) запи¬
сываются в виде (Gy = 0)
р3 Ga(0) + G* = l,
— к\ уу
Е = — k%Ne
г = V,
v = к3
Ре
К,
(0) = 1,
г (0) = Го,
v (0) = v0,
(0<Р(*)<1, Ne(t)> 0, j e(t)
Ga (Т) = max,
Е(Т) = О,
г(Г) =
v (Г) =
si,
i‘i,
VI
!■ (9.16)
h =
Здесь Ne,
gTPl gpTG*
к.
gPo _
Go т
2EqGo 2y-Ge
в отличие от (9.7), отнесено к EJT, ограничение на
фазовую координату Е отсутствует (оно автоматически выполня¬
ется, если удовлетворяются краевые условия для Е при Nе 0).
Оптимальные законы для управляющих функций следующие
(ср. (9.11), (9.12)):
£ ~ Ри I Pv-) 'I
Nt
Nt
= P = 1 npnp*>
==0,
P = 0 при pi■
Ф1,
9i
\
(9.17)
9i = pe (Go + Gyf
kjc-,
i-2
/l3
3. Идеально регулируемая двигательная система характери¬
зуется отсутствием ограничения на тягу сверху (Р 0) и нулевым
весом движителя (GY = 0). Рассмотрение этого случая позволяет
23*
356
ДРУГИЕ ТИПЫ ДВИГАТЕЛЬНЫХ СИСТЕМ
[ГЛ. 9
установить верхний предел возможностей системы и частично
разделить общую вариационную задачу на весовую и динамиче¬
скую части.
Отсутствие верхнего ограничения на тягу дает возможность
перейти в уравнениях (9.7) от тяги Р к реактивному ускорению а
а = kJP (G0 + Gy)~
(9.18)
Тогда первое из уравнений (9.7) может быть проинтегрировано
в квадратурах и разрешено относительно функционала задачи (ана¬
логично тому, как это делалось
выше для двигательной системы
ограниченной мощности без нако¬
пителя энергии):
a2clt
N, (l+Ne)
f-
Рис. 9.4. Зависимость максимальной
относительной величины полезного
груза и оптимального веса двига¬
тельной системы с аккумулятором
энергии GK от функционала задачи Фе
-Gv{ 1 + -^). (9.19)
Относительный вес источника мощ¬
ности Gv в остальные уравнения
вариационной проблемы (9.7) вхо¬
дит только в виде отношения GJGe.
Поэтому еще до решения полной
задачи, зафиксировав в (9.19) вели¬
чины интеграла и отношения Ge/Gv,
можно найти оптимальное значе¬
ние Gv, обеспечивающее максимум G*
(V Фе-Фе)
(9.20)
О
при этом
G- та, = (1 - Gx = G, + = ]/ Фв - Фе.
(9.21)
Последние соотношения (рис. 9.4) для максимальной полезной
нагрузки G* и оптимального полного веса двигательной системы
Gx совпадают с рассмотренными в § 1 главы 4 решениями (4.15),
(4.16) для двигательной системы без накопителя. Только вместо
Ф<, там фигурирует Ф из (4.14), и вес двигательной системы сос¬
тавляется только весом источника мощности Gx = Gv.
§ 1] ИДЕАЛЬНЫЕ ДВИГАТЕЛИ С АККУМУЛЯТОРОМ ЭНЕРГИИ 357
Отметим, что и в задаче с накопителем энергии оптимальный
полный вес двигательной системы не превышает 25% от начального
веса 6г0.
Полезная нагрузка (9.21) монотонно убывает с увеличением Фе,
поэтому вторая часть задачи сводится к отысканию минимума
функционала (параметра задан):
Je = (1 + I) дг^ (1 + Ne) (Фе = 2gJe)’ (9-22)
О
Эффективность использования накопителя энергии будет харак¬
теризоваться отношением величины функционала (9.22) к стан¬
дартному функционалу
J=\a4t\ (9.23)
если 0<^/е//<^1, то использование накопителя выгодно.
Уравнения вариационной задачи о минимуме Jе записываются
следующим образом:
Л = А(0) = 0, Jt(T)=min,
Д = -|ВД, E{ 0) = 1, E(T) = 0,
1- = v, 1- (0) = r„, r (T) = 1-1,
v = ae + H, v (0) — v„, v(f) = Ух
(a(f)> 0, 0<Wv(f)<l, Ne(t)>~ 1, | e (f) | •= 1, 0<£(f)<l).
(9.24)
Оптимальные управления таковы (ср. (9.11) — (9.13)):
е — Е« N — 1 а — Pv ^
Pv' Я'-1’ 2(1+5) ’
Ne = ОО при />2>4рл±^ Ре п 0<Я<1 (ре > 0),
Ne = — \1 при + ^ ре п 0<£<1,
уУе 0 при Е = 0 и Е -- 1,
(9.25)
т. е. режим разрядки оказывается импульсным.
Для оптимального выбора моментов схода фазовой координа¬
ты Е с границ Е = 0 (начало зарядки накопителя энергии) и
Е = 1 (начало разрядки) применим достаточные условия опти¬
мальности [9.5], так как принцип максимума [9.4] не определяет
конкретных значений константы ре на различных этапах движе-
358
ДРУГИЕ ТИПЫ ДВИГАТЕЛЬНЫХ СИСТЕМ
[ГЛ. О
нпя (см. (9.25)). Достаточное условие оптимальности [9.6] тре¬
бует максимизации по координатам и управлениям функции /?,
часть которой /?*, зависящая от координаты Е, имеет следую¬
щий вид:
Переход Е с граничного значения 1 на граничное значение О
(разрядка накопителя энергии) может быть произведен мгновен¬
но (Ё Ne = — ос, см. (9.25)). Согласно (9.26) момент этого
перехода совпадает с моментом смены знака произведения pvpv
с плюса на минус. Так как pv = |рг,| > 0, то такая смена знака
возможна лишь в точках максимума pv (t).
Обратный переход Е (с границы Е — 0 на границу Е = 1 —
зарядка накопителя) должен производиться, как видно из (9.26),
вблизи значений /, где произведение pvpv меняет знак с минуса
на плюс. Такими точками являются точки минимума pv (t).
Однако, в отличие от разрядки, зарядка не может быть осуществ¬
лена мгновенно, так как в этом случае (см. (9.25)) Е = |3/а£ 1.
Следовательно, соотношения (9.26) не могут быть выполнены точ¬
но в некоторой окрестности точки t3 (рис. 9.5). Ширина этой
окрестности зависит от соотношения мощности источника, пол¬
ностью идущей на зарядку накопителя (Ne = —1, Nv = 1),
и емкости накопителя. Значение постоянной/?,,, определяющей через
соотношение (9.25) момент т начала зарядки, должно быть как
можно более близким к значению ре, соответствующему мгновен¬
ной зарядке (ре3 на рис. 9.5), но таким, чтобы соотношение (9.26)
выполнялось за пределами интервала зарядки. Значение рп
на рис. 9.5 удовлетворяет указанным выше условиям, тогда
как ре2, хотя и меньше отличается от идеального значения рез,
чем ре1, но является неприемлемым, так как построение режима
зарядки по ре-2 (пунктирные линии на рис. 9.5) приводит к тому,
что граница Е = 1 не достигается. Так как значение импульса
ре может меняться лишь при выходе координаты Е на границу
или сходе с границы, то оно остается постоянным и сразу после
окончания зарядки (в момент ©2 происходит импульсная разрядка
накопителя согласно (9.25)). Таким образом, построение режима
зарядки по ре2 приводит к невыполнению соотношения (9.26):
Pv-Pv 0 для t ©2, а Е = 0 для тех же значений t. Вместо
оптимального значения ре1 можно непосредственно вычислять
величины т3 и 0Х — оптимальные границы интервала зарядки
R* = cpvpvE (0 <1 с = const).
Оптимальные значения Е получаются следующими:
(9.26)
ИДЕАЛЬНЫЕ ДВИГАТЕЛИ С АККУМУЛЯТОРОМ ЭНЕРГИИ
359
накопителя из следующих соотношении:
01
(9.27)
Первое соотношение — условие перехода Е с граничного значения
О на граничное значение 1, второе указывает на максимально воз¬
можное при выполнении первого
приближения выбранного зна¬
чения ре1 к «идеальному» рез.
Соотношение(9.25) для опре¬
деления оптимального значения
реактивного ускорения позво¬
ляет дать простое физическое
толкование полученным резуль¬
татам. Использование энергии,
з апас еннои в накопит ел е, яв л я ет -
ся оптимальным при значениях
ускорения, близких к макси¬
мальным, что в свою очередь
приводит к возрастанию уско¬
рения. Таким образом, энергия
накопителя расходуется тогда,
когда это может максимально
повлиять на выполнение кине¬
матических условии маневра.
3 а рядк а накопит еля, п рив одя-
щая к выключению движителя
(а = 0), производится вблизи
минимальных значении а (/), и
отрицательное влияние зарядки
на выполнение кинематических
условий становится наименьшим.
Для определения оптимального
(9.25)) получается соотношение
т
п
а
о
Рис. 9.5.
ментов
Определение оптимальных мо-
схода функции Е с границ.
значения параметра £ (см.
l/=/f a4t \-V.
+ Nt
(9.28)
Пока значения 3 из (9.28) удовлетворяют условию £ 0,
система с накопителем энергии имеет преимущество перед си¬
стемой без накопителя. Обозначим через фТ/а)° величину без¬
размерной комбинации удельных весов накопителя и источника
мощности, соответствующую обращению в нуль оптимального
значения Тогда применение накопителя энергии с удельным
360
ДРУГИЕ ТИПЫ ДВИГАТЕЛЬНЫХ СИСТЕМ
[ГЛ.
весом Р' в сочетании с идеально регулируемой двигательной систе¬
мой с удельным весом источника мощности а' целесообразно при
выполнении соотношения
?<(¥)'•
(9.29)
Для определения величины фТ/а)° соотношение (9.28) разре¬
шается относительно р/а:
4 = И^г^)($*да‘Г- <9-30>
Интегралы в правой части уравнения (9.30) могут быть вычис¬
лены по функции pv (t) [9.5].
Если исследуется предельный случай двигательной системы
без источника мощности, то соотношения (9.21) остаются в силе.
надо только положить
п о ф Р-^ С a~dt
v ~ ’ е “ 2g ) N е
Рис. 9.0. Оптимальные управления
относительной энергией аккумулятора
Е и ускорением от реактивной тяги
а в модельной задаче перелета между
двумя точками покоя с идеально регу¬
лируемой двигательной системой огра¬
ниченной мощности и накоплением
энергии.
(мощность Ne отнесена к Е0/Т).
Уравнения вариационной зада¬
чи (9.24) меняются аналогично то¬
му, как это делалось в конце пре¬
дыдущего пункта; функционалом
становится
4. Маневры перемещения меж¬
ду точками покоя и поворота пло¬
скости круговой орбиты. В качест¬
ве примеров решения общей задачи
рассматриваются два указанных
маневра, для которых уравнения вариационной задачи интегри¬
руются до конца [9.3].
Для задачи перемещения между точками покоя (и0 = иг = 0),
расположенными на расстоянии I (г0 = 0, ?\ = Z), за время Т
импульс pv — линейная функция времени, т. е. pi = (Ь2 — bj)'1.
При отсутствии накопителя энергии функционал (9.23) в этой
задаче равен (5.33)
Ji = 12 —
* уз >
ф, = 6 — —.
‘ gT3
(9.31)
g !] ИДЕАЛЬНЫЕ ДВИГАТЕЛИ С АККУМУЛЯТОРОМ ЭНЕРГИИ 361
Аналогично п. 2 по соотношениям (9.25) при известной функ¬
ции Pv(t) строятся оптимальные программы E(t), Ne(t) и a (t).
Они изображены на рис. 9.6, где t1>2 = V2 (Т -- £а/рГ). После
интегрирования уравнений (9.24) по участкам и удовлетворения
граничных условий находится функционал (9.22)
12/2 1 + у ( ^
J е — Тз ! + _ яЗ — рр S
Минимум этого выражения по £ = Ge/Gv достигается при
^<9-32>
и равен
JJJi = Фе/Ф, = (1 + 2 а:3)”1. (9.33)
На рис. 9.7 показана зависимость (9.32) оптимального отно¬
шения GJGv — веса накопителя к весу источника от безразмер¬
ного параметра РТ/а. Уменьшение функционала Ф при переходе
Рис. 0.7. Оптимальное отношение веса
аккумулятора энергии к весу источника
мощности Ge/Gv в задаче перелета между
точками покоя с идеально регулируемым
двигателем ограниченной мощности
Рис. 9.8. Относительное уменьшение (вслед¬
ствие использования аккумулятора) функ¬
ционала Ф в задаче перелета между точка¬
ми покоя с идеально регулируемым двига¬
телем ограниченной мощности.
к системе с накопителем показано на рис. 9 8. Выигрыш в полез¬
ной нагрузке определяется с помощью данных этого рисунка по
первой формуле (9.21) или по рис. 9.4. Видно, что в задаче пере¬
лета между точками покоя двигательная система ограниченной
мощности с накопителем энергии имеет преимущество перед си¬
стемой без накопителя в диапазоне 1 |ЗГ/а ^ 6. При 0 |37Уа<С
^ 1, как отмечалось выше, выгодна система с накопителем, но
362 ДРУГИЕ ТИПЫ ДВИГАТЕЛЬНЫХ СИСТЕМ [гл. 9
без источника мощности (Gv = 0 на рис. 9.7), для которой
Фс/Ф/ = 7з(Р?7а).
Для задачи поворота плоскости круговой орбиты радиуса
на угол i за s оборотов импульс pv меняется по косинусу, т.
pi = Ъ cos21
(время t отнесено к = ]/ r0/gQ — периоду оборота, деленному
на 2л; g0 — гравитационное ускорение на радиусе г0). В случае
идеальной двигательной систе¬
мы ограниченной мощности без
накопителя энергии функци¬
онал (9.23) здесь равен (5.75)
гп i2
т 0 t
(9.34)
Для задачи с накопителем
можно показать, что оптималь¬
ные законы изменения Е (*),
Ne(t), a (*) — периодические
функции времени, повторяющие¬
ся через полоборота. Характер
их изменения на одном обороте
показан на рис. 9.9, где
*1,2 = У2 (я + ^/677J,
*3,4 =z *1,2
Формулы для оптимального значения £ и минимального от¬
ношения Фе/Ф аналогичны (9.32) и (9.33)
РГ* 1 -j- cos х -j- 1/s
a
Рис. 9.9. Оптимальные управления отно¬
сительной энергией аккумулятора Е и ус¬
корением от реактивной тяги а в задаче
поворота плоскости круговой орбиты
с идеально регулируемой двигательной
системой ограниченной мощности и нако¬
пителем энергии.
л + sin х — х cos х
ф,-
л
л -г- sin х — х cos х
(9.35)
Зависимости Ge/Gv и Фе/Ф* от fiziTJa (пТл — время прохож¬
дения половины оборота, т. е. максимальное время зарядки)
для различных значений s даны на рис. 9.10 и 9.11. Видно, что в
диапазоне V2s finTJa ^2 + 1 Is оказывается выгодной дви¬
гательная система ограниченной мощности с накопителем энер¬
гии, в диапазоне 0 <7 (ЗлГДа V2s — двигательная система с
РЕАЛЬНЫЕ ;i Г> 11Г А ТЕ Л11 С АККУМУЛЯТОРОМ ЭНЕРГИИ
363
накопителем энергии без' источника мощности; при этом Фе/Ф*
^ s (finTJa) (см. линейные участки на рис. 9.11).
Рис. 9.10. Оптимальное отношение веса
аккумулятора энергии к весу источника
мощности Ge/Gv в задаче поворота плоско¬
сти круговой орбиты с идеально регулиру¬
емым двигателем; s—число оборотов по
орбите за время маневра.
Рис. 9.11. Относительное уменьшение
функционала Фе/Ф| вследствие использо¬
вания аккумулятора в задаче поворота
плоскости круговой орбиты с идеально
регулируемой двигательной установкой
ограниченной мощности.
Выигрыш в полезной нагрузке, как и в первом примере, опре¬
деляется с помощью данных рис. 9.11 по первой формуле (9.21)
или по рис. 9.4.
§ 2. ДВИГАТЕЛИ ОГРАНИЧЕННОЙ МОЩНОСТИ
С АККУМУЛЯТОРОМ ЭНЕРГИИ —ДОПОЛНИТЕЛЬНЫЕ
ОГРАНИЧЕНИЯ НА РЕГУЛИРОВОЧНУЮ
X АР АКТ Е РИСТНКУ Д ВIIЖ1 ГГ ЕЛ Я
В предыдущем параграфе движитель считался идеально регу¬
лируемым и невесомым. При отсутствии аккумулятора, в тех же
предположениях относительно характеристики движителя, опти¬
мальный режим его работы получался непрерывным (тяга конеч¬
ная), хотя прямых ограничений на тягу и не накладывалось. Это
связано с тем, что мощность, подводимая к движителю, конечная
и при увеличении тяги падает скорость истечения. Наличие ак¬
кумулятора приводит к появлению импульсных режимов (тяга
бесконечная), так как становится возможным подводить к дви¬
жителю бесконечную мощность. Помимо участков с импульсным
приложением тяги, в состав оптимального управления по-преж¬
нему входят участки с конечной тягой.
Предположение о невесомости движителя в таком случае ста¬
новится мало пригодным, поскольку удельный вес движителя
?елик, а оптимальная тяга в некоторые моменты бесконечна.
Кроме того, предъявляются тяжелые требования к регулируемости
364
ДРУГИЕ ТИПЫ ДВИГАТЕЛЬНЫХ СИСТЕМ
Пл. о
движителя: тяга должна меняться от конечных значений до бес-
конечности. Ниже исследуется влияние реальных свойств движщ
теля на параметры оптимального движения. Рассматриваются
следующие варианты.
1°. Тяга и мощность Ny, подводимая к движителю, постояниы
либо равны нулю; вес движителя пропорционален потребляемой
мощности (п. 1, [9.3]).
2°. Тяга не ограничена, мощность движителя ограничена свер~
ху; вес движителя пропорционален максимальной потребляемой
мощности (п. 2, [9.7]).
3°. Тяга не ограничена, мощность движителя постоянная (либо
нуль); вес движителя пропорционален потребляемой мощности
(п. 3, [9.7, 9.9]).
4°. Тяга ограничена сверху и снизу (либо нуль), мощность-
движителя постоянна (либо нуль); вес движителя пропорционален
потребляемой мощности (п. 4, [9.7]).
5°. Тяга и мощность движителя не ограничены, скорость исте¬
чения ограничена сверху; движитель невесомый (п. 5, [9.10]),
6°. Ограничено время работы движителя, тяга не ограничена,
мощность движителя постоянна (либо нуль); вес движителя про
порционален потребляемой мощности (п. 6, [9.7]).
В предположении малого изменения веса аппарата условия,
накладываемые на тягу (1°, 4е), заменяются соответствующими ус¬
ловиями на реактивное ускорение.
1. Нерегулируемый движитель. Нерегулируемая двигательная
система характеризуется постоянством величины тяги (при постоян¬
ной мощности реактивной струи). Допускается изменение направле¬
ния тяги и выключение движителя. Рассмотрение этого второго
предельного случая дает нижнюю границу возможностей системы.
Запись дифференциальных уравнений (9.7) здесь несколько
изменяется (для первых двух уравнений):
Ga = —k±P/Ny, Ё = к2 IN, (1 —Р) — (Ny - 1) Р]
(Р (t) = 1 или 0, Ny = const, 0 Arv (t) ^ 1). (9.36)
Управляющая функция Р (t) может принимать только два
значения: нуль и единица (при этом показатель степени при Р
в (9.7) можно опустить). Мощность Ny, потребляемая движителем,
постоянна, она является управляющим параметром (отнесена к
iVy0). На активных участках (Р = 1) происходит разрядка с по¬
стоянной мощностью Ny — 1: Ё = — &2 (Ny — 1), на пассивных
(Р = 0) — зарядка с мощностью 0 ^ Nv (t) 1: Ё = &2iVv.
Уравнения движения записываются по-прежнему, управляю¬
щая функция е (t) (направление вектора тяги) сохраняется.
Для упрощения условие постоянства тяги заменяется условием
постоянства реактивного ускорения (9.18). Это справедливо,
2] РЕАЛЬНЫЕ ДВИГАТЕЛИ С АККУМУЛЯТОРОМ ЭНЕРГИИ 365
если относительный вес рабочего вещества G^ значительно мень¬
ше единицы. Кроме того, вес движителя, в отличие от (9.6), при¬
нимается пропорциональным потребляемой мощности
= (у!а) GvNy. (9.37)
g таком приближении, аналогично предыдущему пункту, можно
до решения полной задачи найти оптимальный вес источника мощ¬
ности. Величина полезной нагрузки Gn и вес двигательной систе¬
мы G* = Gv + Ge -г Gy будут выражаться формулами (9.21), где
*-(* + » + **)*(*• <9-38>
Для системы без накопителя функционал Ф (с учетом веса
движителя (9.37)) будет равен
ф' = (1 + -г)-#Ьч< (8'39)
о
(в формулах (9.38) и (9.39) а2 (£) = a%P(t), а0 = const, Р (t) = 1
или 0). Вариационная задача записывается аналогично (9.24)
** = (iyA + -f)aoP’ Л(0) = 0, Je(T) = m in,
Ё= [,Уу(1_Р)_(/Ут _!)/>], Е (0) = 1, Е(Т) = 0,
Г = V, 1* (0) = Г0, Г (Т) = 1*1,
V = а0Рс + н, v (0) = У0, V (Т) = УХ
(Р (t) = 1 или 0, 0< JVv (t) <; 1, | е (0| = 1,
0<^2?(£)<;i; Ny, I, а{) = const).
(9.40)
Помимо управляющих функций Р (t), JVv (t), е (t), задача
содержит три постоянных управляющих параметра a0, iVY,
Для выбора оптимальных значений этих параметров можно полу¬
чить условия, воспользовавшись приемом, описанным в п. 2 пре¬
дыдущего параграфа.
Не выписывая состава оптимальных управлений, приведем
результаты решения для рассмотренных в § 1 модельных задач.
В задаче о перемещении между точками покоя отношение функ¬
ционалов (9.38) и (9.39) равно
Фе _ 4[g(l-4t, + 2il) — ]
ф* “ ml (i — 4^) (i — t*y- (i -f s)
T ' (9.41)
a
366
ДРУГИЕ ТИПЫ ДВИГАТЕЛЬНЫХ СИСТЕМ
[ГЛ. ,
где оптимальные параметры £ и £й, введенные вместо а0
= Ul(l — О-1» = (1 — tj Г\ находятся из соотношений
£ = 1Ел1_2П ^ = в(1 —/.) с1 — 3#.) —3/5
= а ^ а
/г (1—4М
(9./
При Р7 т/а +/ (РГ/а)* более выгодным оказывается применение
системы без источника мощности; тогда
Фр 2е / о .2 8Г
2г — — (1 — 3£ ) = 0). (9.43)
Ф1 27^(1 —(1 + е) \ * a v *' j \ ■ J
Зависимости отношений весов Ge/G,j и функционалов Фе /ф*
от Р 77а для различных значений е = у /а (отношение удельного
веса движителя и источника мощности) приведены на рис. 9.12,
9.13.
О
2
AL
ос
Рис. 0.12. Оптимально отношение веса
аккумулятора к весу источника мощности
Ge/Gv в задаче перелета между точками
покоя с нерегулируемой двигательной си¬
стемой ограниченной мощности (а = 0
либо (70); s — отношение удельного веса
движителя к удельному весу источника
мощности.
Рис. 9.13. Уменьшение функционала Ф
вследствие использования аккумулятора
в задаче перелета между точками покос
с нерегулируемым двигателем ограничен¬
ной мощности; пунктирная кривая — от¬
носительное уменьшение функционала
Фе / Ф/ по сравнению с идеально регули¬
руемым двигателем при е = 0.
В рассматриваемой задаче значение функционала J для по
стоянного реактивного ускорения с выключением равно (ср.
с (9.31))
Л- 13,5 ^-(l + X), ®; = 6,75-tp(l + X). (9.44)
Для сопоставления на рис. 9.13 пунктирной кривой показано
отношение Фе/Ф^ при у/а = 0 (вместо Фе/Фг). Иэ сравнения этой
g 2] РЕАЛЬНЫЕ ДВИГАТЕЛИ С АККУМУЛЯТОРОМ ЭНЕРГИИ 36?
пунктирной кривой и рис. 9.8 видно, что, как и в случае двига¬
теля ограниченной мощности без накопителя, переход от идеально
регулируемой двигательной системы к нерегулируемой требует
небольшого увеличения функционала Ф. С уменьшением пара¬
метра РГ/а различие стирается, так как обе системы переходят
в импульсный режим.
О
к
fin
оо
Рис. 0.14. Оптимальное отношение веса
аккумулятора к весу источника мощности
Ge/Gv в задаче поворота плоскости круго¬
вой орбиты с нерегулируемой двигательной
системой; s — число оборотов по орбите
за время маневра.
Рис. 9.15. Относительное уменьшение
функционала Ф вследствие использования
аккумулятора в задаче поворота плоско¬
сти круговой орбиты с нерегулируемым
двигателем ограниченной мощности; 1 —
.s = oо, 2 — s = 3, 3 — s = 1, 4 — s 7г
В задаче о повороте плоскости орбиты отношение функциона¬
лов равно
Фе 1,45 Vi t-g 7 ел7 tg 7 (7 — я/4)]
<l>!
377
а
л (1 -\- е) sin2 С, [7 (л — 27) — (л — J tg 7)
(7 -I- ]/4 ел) tg 7 — 7-j £я7 — О
(л 91 )
" * а /2(л—2/J —(л
at) =
As sin 7
IV — — J
v — 21 ’
■37)7 tg 7
2 -о
2,9л1?
(9.45)
Система без источника мощности имеет преимущество в диа¬
пазоне 0 РГ/а (рг/а)*:
Фе 0,3625Г::е
Ф,-* (1 -\- е) (sin К — 7 cos t.:.) sin ^ ^g^
а
(1 + e) (sin 7 — 7 cos 7) sin 7
27 cos 7 — sin 7
' Hst., (sin — 7 cos 7-.)/
По этим соотношениям построены рис. 9.14, 9.15. Выигрыш
в полезной нагрузке от примепения накопителя для рассмотрен-
368
ДРУГИЕ ТИПЫ ДВИГАТЕЛЬНЫХ СИСТЕМ
[ГЛ. 9
ных примеров определяется, как и выше, при помощи рис. 9.4 или
первой формулы (9.21).
2. Движитель ограниченной мощности. В рассмотренном выше
случае нерегулируемого движителя импульсные режимы прило¬
жения тяги были исключены как за счет прямого ограничения
тяги, так и косвенно за счет учета веса движителя. Рассмотрим
теперь раздельно влияние этих ограничений.
Пусть тяга движителя не ограничена, а мощность, подводи¬
мая к движителю, ограничена сверху. Как и в п. 1, вес движи¬
теля считается пропорциональным максимальной потребляемой
им мощности. Регулировочная характеристика и весовая формула
двигательной системы с накопителем энергии и движителем та¬
кого типа записывается следующим образом (ср. (9.1) —(9.6)):
P = qV, X, = y2qV* = Nv + Ne, Ё = — Ne j
(Р>0, 0<Л%<^0) (94?)
iV,0-iVvo>iVe>-M, 0<£<£0),
G-, = Gv = (xNvoi Ge = $Eo.
Аналогично предыдущему пункту задача о максимуме полез¬
ной нагрузки сводится к вариационной задаче на минимум функ¬
ционала
^ = (‘ + £ + «М ялн-*.) <9-48>
(О < Nv (t) <1, — 1 < Ne (t) < Ny0 — 1, a (t) > 0, Nyo отне¬
сено к Nvо)*
Оптимальные значения управляющих функций, полученные
по методу JI. С. Понтрягина [9.4], запишутся в виде
е = Ny, = I,
Pv
Pv (1 i
2(1 + !;+ 8ATy0) ’
pYY0—1 при Д>0 и 01,
М=] —1 при Д<0 и 0<£’<1,
0 при Е = 0 и Е = 1
Д =
Pv
Ре -J, Ре> 0
(9.49)
Процедура отыскания оптимального расположения интерва¬
лов зарядки и разрядки накопителя описана выше. В качестве
иллюстрации рассматривается задача о перемещении между двумя
точками покоя на расстояние I в бессиловом поле (R = 0) с сим-
2l
РЕАЛЬНЫЕ ДВИГАТЕЛИ С АККУМУЛЯТОРОМ ЭНЕРГИИ
369
Метричными граничными условиями для Е: Е (0) = Е (Т) = V2.
д-го исключает из рассмотрения двигательные системы с накопи¬
телем энергии, но без источника мощности.
Обозначив х = N,:0 — 1 и z = £а/рТ, можем записать вели¬
чину функционала Jе:
Т 12rg- [1 4~ (ftT/op z + (1 4~ х) 81 727^-3
е (1 -г 3z — z3) х2 — 3z-x + z3
(9.50)
Значения параметров х и z, при которых величина Jе достигает
минимума, могут быть определены из системы уравнений
г3 (1 - 2z3) е — 3xz- (1 + е) + 2z3 (1 + е) = 0, |
z2 (За;— 2z) — Зех [(х — z)2 — x2z2] = 0. J
Эффективность применения накопителя энергии характери¬
зуется отношением функционала /* к соответствующему функ¬
ционалу/,: для системы без нако¬
пителя (для данной задачи Jx =
= 12 (1 -4- е) /2Г“3). Это отно-
Рис. 9.16. Влияние относительного веса Рис. 9.17. Влияние относительного веса
движителя е на уменьшение функционала движителя е на оптимальное отношение
J в задаче перелета между двумя точками веса аккумулятора энергии к весу источ-
покоя (с симметричными граничными ника мощности,
условиями) при использовании аккумуля¬
тора энергии.
шение можно записать через х и z (решения системы (9.51)) в виде
5^! /О К9Л
Jx (1 -f8)(3a? — 2z)z* • W
На рис. 9.16 приведена зависимость Je/Jx от PTla для двух
значений отношения удельного веса движителя и источника мощ¬
ности: е = ОД и е = 0,001. Как и на данных рис. 9.13 и9.15,
нидно, что с увеличением относительного веса движителя е умень¬
шается выигрыш в функционале / (и соответственно в полезной
Нагрузке) от применения аккумулятора энергии. На рис. 9.17
Для рассмотренной задачи дана зависимость оптимального зна-
24 Механика полета
370
ДРУГИЕ ТИПЫ ДВИГАТЕЛЬНЫХ СИСТЕМ
[ гл
чения параметра g = GJGV от величины |}77а, и на рис. 9.18
зависимость от рГ/сс максимальной мощности движителя Avo,
отнесенной к мощности энергоисточника Nvo.
Рис. 9.18. Значения максимальной мощности движи¬
теля (отнесенной к мощности источника) в задаче
перелета между двумя точками покоя при исполь¬
зовании аккумулятора энергии.
3. Движитель постоянной мощности. Если относительно дви¬
жителя сделать единственное предположение, что его вес про¬
порционален максимальной мощности (п. 2), то в оптимальном
варианте мощность, потребляемая движителем на участках раз¬
рядки накопителя, может в 5—10 раз превосходить мощность
источника, при которой движитель работает в течение остального
активного времени движения (рис. 9.18). Аналогично п. 1 рас¬
смотрим двигательные системы с постоянным значением мощности
движителя AY (выбираемым из соображений оптимальности), но
без прямого ограничения на тягу. Вес движителя по-прежнему
будем считать пропорциональным мощности AY.
Дифференциальные уравнения типа (9.40) для такой системы
запишутся в виде
( 1 + 5. , „\ е = Ё_ (Дуб _ дд,
А =
г — у, у = аде + К
(9.53)
(TVY = const отнесено к Avo, б (£) = 1 или 0, 0<ЛГД9<1,
0 < Е (t) < 1, а (*) > 0), указанные в (9.40) граничные усло¬
вия не изменятся. Управляющая функция б принимает значения
1 на активных участках и 0 на пассивных. Можно показать,
что оптимальные законы изменения по времени a (t) и б (t) име¬
ют следующий вид:
, -1
1
а — ^ Pv
1
А.
■+ 8
1 при Л^>0,
0 при А 0
А = -г р2
4 ~ v
+ 8
Ре>0
(9.54)
2]
РЕАЛЬНЫЕ ДВИГАТЕЛИ С АККУМУЛЯТОРОМ ЭНЕРГИИ
371
Вид управлений е (t) и Arv (t) такой же, как и в рассмотренных
выше случаях. Для задачи перелета в бессиловом поле между
двумя точками покоя при симметричных граничных условиях
g (0) = Е (Т) = V2 величина функционала /е равна
(9.55)
,r-3 [1 + фТ/a) z] (1 - г) -I- е
1 — z3
и принимает свое наименьшее значение при z, удовлетворяющем
соотношению
pr (1 :-2z) (1 — г2) — 3z3e
“5" “ (1 - 22) (1 - д)2
(9.56)
На рис. 9.19 и 9.20 для этой задачи приведены зависимости от
рГ/а отношения функционалов JJJi (с использованием накопи¬
теля энергии и без него) и оп¬
тимального значения параметра
\ = Ge/Gv. Сравнение двигатель¬
ных систем с постоянной и
0,4 08
1,2 f,4
сс
Рис. 9.19. Уменьшение функционала J
в задаче перелета между двумя точками
покоя (с симметричными граничными ус¬
ловиями) при использовании аккумуля¬
тора энергии п движителя постоянной
мощности.
Рис. 9.20. Оптимальное отношение веса
аккумулятора энергии к весу источника
мощности в задаче перелета между двумя
точками покоя с движителем постоян¬
ной мощности.
неограниченной мощностью движителя произведено на рис. 9.21,
где приведена зависимость отношения соответствующих функ¬
ционалов (/e)tf=const/^0 от рГ/а(см. (9.50) и (9.55)). Видно, что тре¬
бование постоянства мощности движителя сказывается сильнее для
Двигательных систем с меньшим относительным весом движителя.
Рассмотрим движение по орбитам, близким к круговой. Урав¬
нения плоского движения в центральном гравитационном поле
могут быть записаны следующим образом (П.15):
г = v sin d, v a cos ф — г - sin д,
гф = v cos О, vh =-■ a sin у -f- (у2/г — 1/г2) cos й1.
(9.57)
24*
372
ДРУГИЕ ТИПЫ ДВИГАТЕЛЬНЫХ СИСТЕМ
[ГЛ.
Уравнения (9.57) безразмерные. Величина г — расстояние
центра масс аппарата от притягивающего центра, отнесенное
к начальному радиусу, v — скорость аппарата, отнесенная к
скорости свободного движения по орбите начального радиуса
N=Const
и
о
0,5
W
1,5
£1
сс
а — реактивное ускорение,
отнесенное к гравитацион¬
ному ускорению на рас¬
стояние начального радиу¬
са, время отнесено к пе¬
риоду обращения по кру¬
говой орбите начального
радиуса, деленному на 2л.
Углы ф, д и у показаны
на рис. П.2.
Ниже рассматриваются
маневры, для которых те¬
кущие значения координат
и скоростей центра масс
аппарата отличаются от соответствующих значений в свободном
движении по круговой орбите начального радиуса на величины,
много меньшие единицы:
r = l+Ti, ф = *+£, у = 1 + £
(л» л» Ь £> L ^
Рис. 9.21. Влияние ограничения — движитель
постоянной мощности — на увеличение функцио¬
нала J в задаче перелета между двумя точками
покоя при использовании аккумулятора энергии.
(9.58)
Подставляя соотношения (9.58) в уравнения (9.57) и ограничива¬
ясь членами первого порядка малости, запишем линеаризирован¬
ную систему уравнений движения
г| = Ф, £ = аб cos у — Ф,
£ = £ — г], й1 — аб sin у + Л + 2?
(9.59)
{^1(0 — релейная управляющая функция, равная 1 на активных
участках полета и 0 на пассивных).
Граничные условия для системы, составленной из (9.59) и
первых двух уравнений (9.53), при симметричных условиях для
Е следующие:
Je (0) = 0, Е (0) = J , if(0) = Tin. S (0) = So,
С(0) = Бо, 0(0)= Go,
Je(T) = min, E{T)=±, у] (T) = ль S (?) = Si,
(9.60)
e(7’) = Sx, G(r) = G!.
РЕАЛЬНЫЕ ДВИГАТЕЛИ С АККУМУЛЯТОРОМ ЭНЕРГИИ 373
Используя принцип максимума, получаем следующие выра¬
жения для оптимальных управляющих функций:
jvv = i, « =^Ур\ + р% (Чг7 + е)
[г = arcsin [ps (pi + Pl)-'h] = arceos [pr (p\ + р|)',/г],
(1 при A > О
^ — [О при A О
al
(9.61)
Уравнения для импульсов
pr\ “ Pi Р&Ч Pi — 0, р^ = Pi
Ра = — Р„ + Ра, Ре = 0 (9.62)
интегрируются независимо от основной системы
Pi = ^1» Р& = &2 sin t + Ъд cos £ — 26ь
р^ = 262 cos £ — 2&3 sin £ + Sbit + Ъ±,
р.п = ъ2 cos t — Ъъ sin t + 3bit -f- ^4-
Здесь Ь4, Ь2, 63, 64 — постоянные интегрирования.
Процедура отыскания оптимального расположения активных
и пассивных участков на траектории исследовалась выше.^По¬
стоянные интегрирования системы уравнений движения и по¬
стоянные Ьг, Ь2, Ь3, 64 определяются из граничных условий (9.60)
Для каждого конкретного маневра.
В качестве первого примера рассмотрим задачу об оптималь¬
ной встрече двух аппаратов, выведенных на одну и ту же круго¬
вую орбиту, вращающихся в одном направлении и находящихся
в момент времени t = 0 на угловом расстоянии ф0. Задача манев¬
ра — встреча аппаратов за время совершения одним из них,
который предполагается неуправляемым, половины ^оборота по
орбите (Т = л). Система граничных условий (9.60) в данном слу¬
чае имеет вид
/е (0) = О, Е (0) = 1/2, л (0) = 0, 1(0) = 0, I (0) = О, о (0) = 0,|
J«(л) = min, Е (я) = х/-2, Л (я) = 0, £ (л)=фп, £ (я) = 0, ft (л) =0. }
(9.64)
Оптимальные программы для управляющих функций записываются
(9.63)
374
ДРУГИЕ ТИПЫ ДВИГАТЕЛЬНЫХ СИСТЕМ
[ГЛ.
следующим образом:
а= У a\(t — я/2)2 + а\,
(1 при и я — т<^£<^я,
О при т<^£<^я — т,
. а 2
г = arcsm —
* а
arccos
ai (t — я/2)
(9.65)
Постоянные ах и а2 могут быть выражены через ф0 и длительность
активных участков т:
— 4ф0 (1 — cos т)
аг =
16т [2 (1 — cos т) + (я — 2т) sin т] — (1 — cos т) [я3 — (я — 2т)3] ’
4<ро [2 (1 — cos т) + (я — 2т) sinT]
16т [2 (1 — cos т) + (я — 2т) sin т] — (1 — cos т) [я3 — (я — 2т)3]
(9.66)
Величина функционала Jе для поставленной задачи выражается
через <р0 и т следующим образом:
4фд {24тU- (т) + (1 — cos т)2 [я3 — (л — 2т)3]} М (т)
Зя 16т V- (т) — (1 — cos т) [я3 — (я — 2т)3]2
(9.67)
где
L (т) = 2 (1 — cos т) -j- (я — 2т) sin т,
М (т) - |2т j4 + (я — 2т) + .
Значения параметров | и Ny связаны с т соотношениями
! = 2,),лг,= JL.
(9.68)
Значение функционала J
для рассматриваемого ма¬
невра при использовании
двигательной системы ог¬
раниченной мощности без
накопителя энергии вы¬
числяется по формуле
4ф*(48 + я2)(1 + е)
Рис. 9.22. Уменьшение функционала J в задаче
встречи аппаратов на круговой орбите при ис¬
пользовании накопления энергии и движителя
постоянной мощности.
Зя (16 — я2)2
(9.69)
На рис. 9.22 показано отношение функционалов, определяе¬
мых по (9.67) и (9.69), в функции отношения удельных весов ак¬
кумулятора энергии Р и источника мощности а для двух значе-
РЕАЛЬНЫЕ ДВИГАТЕЛИ С АККУМУЛЯТОРОМ ЭНЕРГИИ
375
з- -Z-
Ge
Муд Gy
15 4
2
яИй относительного веса движителя е = 0,1 и 0,01. Накопление
энергии целесообразно, пока указанное отношение функционалов
jJJ не превосходит единицы.
Выигрыш в полезной нагруз
ке при использовании аккуму¬
лятора энергии определяется, 20
как и выше, по уменьшению
функционала при помощи
данных рис. 9.4 или первой
формулы (9.21). Кривые на
рис. 9.23 определяют опти- /о
мальные значения параметров
I = Ge/Gv и Ny, £
доставляющих минимум фун¬
кционалу Je.
Вторым примером рас¬
смотрим задачу о переходе
на круговую орбиту радиуса
г = 1с близлежащей круго¬
вой орбиты радиуса г = 1 +
имеют вид
\
✓
/■
йг
0
0,8
1,6
PL*
ос
Рис. 9.23. Отношение веса аккумулятора энер¬
гии к весу источника мощности Ge/Gv (сплош¬
ные кривые) и относительная мощность дви¬
жителя (пунктирные кривые) в задаче встречи
аппаратов на круговой орбите с использова¬
нием накопления энергии.
г|0. Граничные условия (9.60) здесь
/е(0)=0, Е(0)=V2, Л(0)=т|о,
| (0) = 0, £(0) = —72ть О(0)= о,
Je (я) = min, Е (я) = 1/2, Ц (я) = 0,
£ (л) = opt, £ (я) =0, О (я) = 0.
(9.70)
Начальное условие для £ получается после линеаризации соот¬
ношения, связывающего радиусы г и угловые скорости со тел,
вращающихся по круговым орбитам около одного и того же цен¬
трального тела: г3со2 = const. Значение координаты £ (я) — угло¬
вое перемещение — заранее не фиксируется.
Вектор реактивного ускорения будем считать направленным по
касательной к траектории (у = 0 либо у = я). Введем в рассмо¬
трение вместо угла у управляющую функцию е = cos у, прини¬
мающую значения 1 при у = 0 и —1 при у = я, и запишем
Уравнения движения в виде
Г) = О, i = £ - Т|. £ = авб - О, <> = 2£ + Л* (9.71)
Система оптимальных управляющих функций (9.61) такова:
1 . . , /1 + 5 , N"1
76 ДРУГИЕ ТИПЫ ДВИГАТЕЛЬНЫХ СИСТЕМ [ГЛ. о
Как и в первом примере, траектория состоит из двух активных
участков протяженностью т, разделенных одним пассивным уча¬
стком. Оптимальная программа реактивного ускорения записы¬
вается в виде
ае = аг — а2 sin t, (9.78)
где
_ — 7г Ло (т — sin т cos т)
0/1 — 2т (т — sin т cos т) — 4(1 — cos т)- ’
_ — Т]0 (1 — cos т)
а2 2т (т — sin т cos т) — 4(1 — cos т)2 ’
Значение функционала Jе равно
J Ло (2т — sin 2Т) {2т [1 + (рг/а) (я — 2т)] + ле}
ё ~ 4я [2т (2т —sin 2т) —8(1—cost)'-] ’ (у-/4)
На рис. 9.24 показано уменьшение функционала J рассматри¬
ваемой задачи по сравнению с соответствующим функционалом J г
для двигательной системы
без накопителя энергии
ЯГ)“ (1 -V- £)
А=4§ЬГ8У'. (9.75)
Оптимальные значения g =
= Ge/Gv и Ny иллюстрируют¬
ся кривыми на рис. 9.25.
В качестве третьего при¬
мера рассмотрим задачу кор¬
ректировки направления век¬
тора скорости. Пусть в на¬
чальный момент времени
(t = 0) вектор скорости аппа¬
рата составляет с касатель¬
ной к расчетной орбите угол Фо. Задача маневра состоит в стаби¬
лизации движения аппарата на расчетной орбите за время, рав¬
ное половине расчетного периода вращения (Т = л); угловое
перемещение £ (л), как и в предыдущем примере, является про¬
извольным:
/е(0) = 0, Е(0) = 7*, г| (0) = о, ■
|(0) = О, £(0) = 0, ft(0) = ft.„
Je(n) = min, Е (л) = 1/2, г) (я) = 0, (9.76)
I (л) = opt, £ (л) = 0, ft (л) = 0.
Рис. 9.24. Уменьшение функционала J для
задачи перехода между близлежащими кру¬
говыми орбитами при использовании нако¬
пителя энергии и движителя постоянной мощ¬
ности.
§
РЕАЛЬНЫЕ ДВИГАТЕЛИ С АККУМУЛЯТОРОМ ЭНЕРГИИ
377
Вектор реактивного ускорения направляется по нормали к тра¬
ектории (у = V2я или у = —У2я), уравнения движения (9.59)
записываются в виде
Т] = i = t, — Г), С = —® = аеб + Т] + 2£
(е = sin у = 1). (9.77)
Оптимальные значения управляющих функций определяются
соотношениями
iVv= 1,
1
~
1 при Д>0,
О при Д О
1 + £
AL
Те)"1,
д =
-г е
_1 ^ PeNy),
ИЛИ
(9.78)
(9.79)
ае = а1 cos t (аг = — 2Ф0 (2т -j- sin 2т) *);
расположение активных и пассивных участков на траектории
совпадает с предыдущими примерами.
Величина функционала Jе равна
2Ф* {2т [1 + (рГ/а) (я - 2т)] + яе} /Q Qm
Je~' я (2т —sin 2т) ’ {У.ОЩ
а соответствующее значение функционала для двигательной
системы
энергии
виде
без накопления
записывается в
Ge
Mvo Gv
1,6 OJ
/, 5 0
II
8
II
II
II
l!
ь
шиш.
Of,5
7t
ОС
e). (9.81)
Отношение Je к /*>. и опти¬
мальные значения пара¬
метров \ = GJGv и Ny/Nv0
приведены на рис. 9.26.
Аналогично изложенно¬
му может быть также рас¬
смотрена задача поворота
плоскости орбиты; опти¬
мальные программы вели¬
чины и направления реактивного ускорения, величины функ¬
ционалов Jе и J совпадают с полученными для задачи корректиров¬
ки направления вектора скорости, если под углом ^ подразуме¬
вать заданный угол поворота плоскости орбиты и считать вектор
тяги направленным перпендикулярно к плоскости орбиты [9.9].
4. Движитель с ограниченной тягой. Рассмотрим промежу¬
точный случай между идеально регулируемым и нерегулируе¬
мым движителями. Пусть тяга движителя может принимать все
Рис. 9.25. Отношение веса аккумулятора энергии
к весу источника мощности (сплошные кривые)
и относительная мощность движителя (пунктир¬
ные кривые) для задачи перехода между близ¬
лежащими круговыми орбитами.
378
ДРУГИЕ ТИШ,I ДВИГАТЕЛЬНЫХ СИСТЕМ
[ГЛ. 9
/,0
а)
■ РА
значения из некоторого диапазона или обращаться в нуль, мощ¬
ность, потребляемая движителем постоянна либо нуль, вес дви¬
жителя пропорционален пот¬
ребляемой мощности.
Когда затраты рабочего
вещества на выполнение за¬
данного маневра малы по
сравнению с общим весом
аппарата, можно приближен¬
но считать реактивное уско¬
рение пропорциональным тя¬
ге, развиваемой движителем.
Обозначим через атах верх¬
нюю границу диапазона из¬
менения ускорения от тяги,
а через аШ1,г — нижнюю и вве¬
дем в рассмотрение параметр
регулируемости движителя
X = 1 — anVdJaw m, причем
О А, 1. Идеально регу¬
лируемой системе соответст¬
вует значение X = 1, нере¬
гулируемой — X = 0. Вели¬
чину X будем считать задан¬
ной, а значение атах выбирать
из соображений оптималь¬
ности. Исходные соотноше¬
ния вариационной задачи
о минимуме функционала Jе не отличаются от приведенных
выше (9.48), за исключением неравенства, ограничивающего а (t).
Соотношение а (£) > 0 в (9.48) заменяется на ашах (1 — X)
a (t) ^ ашах. Оптимальные выражения для управляющих функ¬
ций a (t) и б (t) следующие:
£ £е
Gv
15 5
уд--
<oj
*)
ТС
РА
ос
Рис. 9.26. Уменьшение функционала J в за¬
даче корректировки направления вектора
скорости при использовании накопителя энер¬
гии и движителя постоянной мощности — а)
и оптимальные параметры задачи: Ge/Gv —
сплошные кривые; Ny/]Vvq — пунктирные
кривые — б).
при
1 Pv
2 Pv
при
<
1 -!- £
ATy
1 Pv
2 a,
>
»\
N„
+ e
<
b =
(1 X)
при A^>0,
при A<^0
1
при — -
Pv
<
max
(L+L + e)(l-b),
(l-b)<
L+io.
AC 1
A = a
Pv —
AC
— СгРД-п Pe> 0).
(9.82)
§ 2] РЕАЛЬНЫЕ ДВИГАТЕЛИ С АККУМУЛЯТОРОМ ЭНЕРГИИ 379
Дктивный участок может закончиться на одном из трех интерва¬
лов регулирования ускорения: при а = а111ах, при (1 — К) ятах<
< а < атах и при а = атах (1 — К).
В модельной задаче перелета между двумя точками покоя
(с симметричными граничными условиями), если зарядка начина¬
ется на первом интервале, значение функционала /е не зави¬
сит от X
(l + z1 (1 — 2) + el
LV “ - 1 (9.83)
16
/„ =
',(1-0 (1+2)1
2 = ^-1
ргг
Оптимальное значение z определяется из соотношения
рт 2(1 — zf — e(3z — 1)
а (1 —zf
(9.84)
В случае, когда пассивный участок начинается при перемен¬
ном ускорении (amax (1 — к) <Т а (0 < Ятах)» функционал Jе за-
писывается иначе:
12 Г(.1 + ^- П (1 - z) + el (12ф* - 16ф3 - *3)
•'* = — ‘ (ЗФ-*„+■)■ • (9'85)
Здесь ф = V2 — т, где т определяется уравнением
Pv (т) = 2 + е) ашах. (9.86)
Из условия минимума JQ по ф (это соответствует минимуму /е
по ятах) получается:
Ф = z/2.
Подстановка этого результата в (9.85) приводит соотношение
для /е к виду (9.83). Таким образом, оптимальное значение атах
таково, что система и в этом случае работает как нерегулируемая
(а (£) = атах).
Наконец, если пассивный участок начинается при минималь¬
ном значении ускорения, функционал может быть записан в
следующем виде:
48 [(l + z) (1 — z) + е] [3 (1 — co2z) — 4ф (1 — со8)]
^е== = [3 (1 — coz2) — 4ф2 (1 — й8)]2 • (9-87)
Здесь со = 1 — Я. Величина Je достигает своего минимального
380 ДРУГИЕ ТИПЫ ДВИГАТЕЛЬНЫХ СИСТЕМ
значения, равного
'(l + t!I.z)(l-z) +ej (1 + оО2)-
12
/„ =
[1’Л.
(9.88)
(1 + zco'2)- [1 + 2or2 — zgT2 (2 + <в‘/г)]
при 2ф = (1 + zw'-) (1 + ш3А)-1. Абсолютный минимум величины
Рис. 9.27. Влияние ограниления диапазона регулирования
реактивного ускорения К на уменьшение функционала J
в задаче перзлзгя между двумя точками покоя с использо¬
ванием накопления энергии и движителя постоянной мощ¬
ности; сплошные кривые — относительный вес движителя
е = 0,1, пунктирные — е = 0,01.
Jei определяемой соотношением (9.88), достигается при значении
z, удовлетворяющем соотношению
,ЗГ (1 + zco /2) Q (со) -f 3 (1 — z е) а) [со — z (2 + со /2)]
а (1 — 2z) (1 + zo)1;2) Q (со) — 3 (1 - z) coz [со — z (2 -j- co3/z)]
, (9.89)
где Q (со) = 1 + 2со3/г _ £cof/2 (2 -f со3/*). Ha рис. 9.27 показана
зависимость отношения функционала Jе для системы с ограни¬
ченным диапазоном изменения ускорения и накоплением энергии
к соответствующему значению функционала J[ для системы без
накопителя:
J =12 ю'У (1 f е)
' " 4 + 4 со3 2
(9.90)
Данные рис. 9.27 иллюстрируют уменьшение функционала J
(и соответственно увеличение полезной нагрузки — см. рис. 9-4)
от применения накопителя энергии при наличии ограничения на
диапазон регулирования ускорения от реактивной тяги.
5. Движитель ограниченной скорости истечения. Накопле¬
ние энергии, как отмечалось в начале § 1, может осуществляться
21
РЕАЛЬНЫЕ ДВИГАТЕЛИ С АККУМУЛЯТОРОМ ЭНЕРГИИ
381
пловыми аккумуляторами. В этом случае используются тен-
т ые движители. Они характеризуются ограничением на ско¬
лов** А ^ ТТ ^ 17 /С Л 0\
рость
истечения реактивной струи 0 ^ V VmaK (§ 1 гл. 2).
Дополнительно примем следующие предположения: тяга и
мощность движителя не ограничены, движитель невесомый.
Полную систему дифференциальных уравнений, граничных
условий, ограничений на управляющие функции и фазовые коор¬
динаты вариационной проблемы о максимуме полезной нагрузки
в указанной постановке запишем следующим образом:
Gn —
(1 +Ne)
V2
Ё = — k2NvNe,
г = v,
(9.91)
Go(0) + Ge + Gv= 1,
Go (T) = шах,
Е( 0) = 1,
Е(Т) = 0,
V (0) = 1*о,
Г(П=ГЬ
v = А?1 у ) е + at, v(0) = Vn, v (Т) —■ Vi
(0< V (*)< V шах ч 0(f)<l, Nc(t) > — 1,
|e(f)| = l, 0<£’(i)<l;
/ci = 2gNv0JG() = 2gGvJ<x, /f2 = A'vo/^o = PGv/ocGe).
Здесь, как и в § 1, все весовые компоненты отнесены к стартово¬
му весу G0, мощность источника — к своему максимальному
значению Nv0, мощность 7Ve — к текущей мощности источника.
Закон изменения по времени направления тяги е (t) одинаков
Для участков 0 Е (t) I и Е = 0, Е = \ и совпадает с полу¬
ченным ранее
С = Vv/Pv
(9.92)
Скорость истечения реактивной струи V (t) зависит от импуль-
сов pv и ра:
V =
^opt при Vopt ^тах?
^шах при Fopt>V max
(^opt — — -■ (Go + Ge -[- Gy) Pa/Pv)
(9.93)
(импульсы p0 и pe в (9.93) всюду отрицательны).
Оптимальный закон мощности источника: Nv (t) = 1. Отметим,
То в случае двигателя ограниченной мощности и ограниченной
382 ДРУГИЕ ТИПЫ ДВИГАТЕЛЬНЫХ СИСТЕМ [ГЛ. г
скорости истечения без накопителя энергии появлялись участки
выключения источника мощности. Здесь они отсутствуют, так
как при выключенном движителе мощность источника направля¬
ется в аккумулятор.
Оптимальное значение мощности Ne, управляющей энергией
накопителя, определяется следующим соотношением:
pa
Pv
V
\ v
G
k\ I
( Po
Pv \
V
{ V
G 1
оо при
(9.94)
при — -17- ( Д- — Ц-) — к2ре > 0.
На границах Е — 0 и Е = 1 мощность Ne обращается в нуль.
Анализ соотношений (9.93) и (9.94) показывает, что в состав
оптимальной траектории могут входить участки движения с оп¬
тимально меняющейся скоростью истечения, участки, на которых
скорость истечения равна своему граничному значению, а также
пассивные участки. На последних движитель выключается (см.
правую часть четвертого уравнения системы (9.91) при Ne = —1)
и происходит зарядка накопителя энергии.
В случае достаточно большой величины Fmax, такой, что
Fmax^>[— 2 (Ga -\- Ge -j- Gv) Pa/jPrhnax nPir 9 ^ t ^ T , (9.95)
в состав оптимальной траектории не входят участки движения с
У — Fmax. В этом случае удается показать, что система уравне¬
ний движения (9.91) и дифференциальных уравнений для импуль¬
сов имеет (аналогично рассмотренному выше) интеграл
(Ga + Ge + Gv)2 pz = const. (9.96)
Отсутствие участков V = Fmax позволяет ввести в рассмотре¬
ние реактивное ускорение
и свести вариационную проблему о доставке максимального по¬
лезного груза к задаче минимизации функционала
J.
рассмотренной в § 1. Если величина Fmax удовлетворяет нера¬
венству
^шах <С [— 2 (G0 + Ge -f- Gv) Po/Pi’]min 1[РИ 0 ^ t ^ T, (9.99)
§ о] РЕАЛЬНЫЕ ДВИГАТЕЛИ С АККУМУЛЯТОРОМ ЭНЕРГИИ 383
то двигательная система на границах Е = 0 и Е = 1 работает
как нерегулируемая: Nv = 1, F = Fmax.
6. Движитель с ограниченным временем работы. Исследуем
случай, когда ресурс движителя меньше ресурса источника мощ¬
ности и меньше полного вре¬
мени движения. Для упро¬
щения выкладок предполо¬
жим, что ресурс источника
мощности больше полного
времени.
Кроме того, будем счи¬
тать тягу движителя неогра¬
ниченной, мощность, потреб¬
ляемую движителем, посто¬
янной, вес движителя пропор¬
циональным потребляемой
мощности.
Обозначим максимально
допустимую длительность ак¬
тивных участков через
Т и будем считать ее
заданной величиной. В этом
случае к рассмотренной выше
системе дифференциальных
уравнений (9.53) добавляется
соотношение [9.8]
К =
а выражение для величины А в (9.54) преобразуется к виду
(1жх+8Г1-^г^+^ (9Л00)
(величина = const <^0 — импульс, сопряженный t^).
В модельной задаче перелета между точками покоя выражение
Для функционала /е совпадает с (9.55)
/е = т2т-3 fl + *) +е f (9.101)
Значение z, доставляющее минимум /е, определяется соот¬
ношением (9.56) до тех пор, пока получаемые значения z удов¬
летворяют неравенству z > 1 — Т^/Т. В противном случае выби¬
рается z = 1 — Тр/Т. Зависимость от |377а; отношения функци-
°налов JJJi при накоплении энергии и без накопления при¬
едена на рис. 9.28. Величина функционала J\ для системы без;
О 2,5 5,0 7,5 £1
а) *
О 2,5 5,0 7,5 £1
Рис. 9.28. Влияние ограничения на время ра¬
боты движителя < Т в модельной задаче
перелета между точками покоя с движителем
постоянной мощности; — отношение
функционалов при полете с накоплением энер¬
гии и без накопления, а) относительный вес
движителя е = 0,1; б) е = 0,01.
384
ДРУГИЕ ТИПЫ ДВИГАТЕЛЬНЫХ СИСТЕМ
[ГЛ. :)
накопления энергии равна (7.52)
т 121-Т .у Ю9Ч
Результаты, приведенные на рис. 9.28, показывают, что при
ограничении на время работы движителя выгода от использования
накопителя энергии возрастает.
§ 3. ДВИГАТЕЛЬНЫЕ СИСТЕМЫ С НАКОПЛЕНИЕМ
АТМОСФЕРНОГО ГАЗА
Значительную (а во многих случаях и преобладающую) часть
веса космического летательного аппарата в оптимальном варианте
составляет рабочее вещество (топливо). В работах [9.11—9.17]
показано, что если выводить аппарат на орбиту «пустым» (или
с некоторой частью запаса рабочего вещества), а «заправку» про¬
изводить уже на орбите, то существенно снижается вес ракеты-
носителя.
Заправку предлагается осуществлять следующим образом
[9.11—9.17]. Аппарат снабжается воздухозаборником. Исход¬
ная орбита выбирается так, чтобы она проходила в верхних слоях
атмосферы. При движении по орбите аппарат захватывает атмо¬
сферный газ и сжижает его. Накопив нужное количество газа,
аппарат выполняет заданный маневр. Обсуждается и другой ва¬
риант заправки [9.17]: на орбиту предварительно выводится ап¬
парат-заправщик, который накапливает атмосферный газ; через
определенное время на орбиту выводится космический аппарат
с пустыми баками, аппарат-заправщик «переливает» накоплен¬
ный им газ в баки космического аппарата, после чего космический
аппарат выполняет требуемый маневр.
Сравнение этих двух схем заправки на орбите между собой и с
исходной схемой заправки на земле производится по отно¬
сительной полезной нагрузке космического аппарата. В первой
схеме полезная нагрузка относится к «сухому» весу космического
аппарата. По сравнению со случаем заправки на земле «сухой»
вес аппарата здесь увеличивается из-за дополнительных систем:
воздухозаборника, установки сжижения и пр. Если этот допол¬
нительный вес меньше, чем вес запаса рабочего вещества, потреб¬
ного для совершения маневра в случае заправки на земле, то
первая схема заправки на орбите дает выгоду. Во второй схеме
заправки на орбите собственный «сухой» вес космического ап¬
парата остается таким же, как и при заправке на Земле. Но зато
здесь выводится на орбиту дополнительный аппарат — заправ¬
щик. Его «сухой» вес при анализе распределяется между заправ¬
ляемыми космическими аппаратами, так что «сухой» вес космиче¬
ского аппарата, фигурирующий при вычислении относительной
ДВИГАТЕЛИ, НАКАПЛИВАЮЩИЕ АТМОСФЕРНЫЙ ГАЗ
385
полезной нагрузки, увеличивается на «сухой» вес аппарата-за-
правщика, деленный на максимальное число заправок. Если эта
добавка к весу меньше веса дополнительного оборудования,
необходимого в первой схеме, и меньше потребного запаса ра¬
бочего вещества при заправке на Земле, то вторая схема заправки
на орбите более выгодна. Ее преимущества, естественно, возрас¬
тают при увеличении максимального числа заправок.
1. Характеристики двигательной установки с накопителем
рабочего вещества. Принципиальная схема двигательной уста¬
новки, предназначенной для накопления рабочего вещества при
движении в верхних слоях атмосферы, показана на рис. 9.29 из
Рис. 9.20. Принципиальная схема двигательной установки с накоплением рабочего тела
при орбитальном полете в верхних слоях атмосферы:
1 — гиперзвуковой воздухозаборник, 2 — система сжижения, н — бак для накапливае¬
мого рабочего тела, 4 — реактивный движитель, 5 — энергоисточник, 0 — радиатор.
[9.17]. Такая установка содержит гиперзвуковой воздухозабор¬
ник, систему сжижения, бак для накапливаемого рабочего ве¬
щества. движитель для компенсации аэродинамического сопро¬
тивления и источник мощности, питающий движитель и систему
сжижения [9.11—9.17]. Если тот же самый аппарат предназна¬
чается для выполнения внеатмосферного маневра, то в состав
двигательной установки могут включаться дополнительный дви¬
житель и бак с дополнительным запасом рабочего вещества, не¬
обходимого для работы этого движителя (например, по условиям
химической реакции).
Секундный приход массы через воздухозаборник равен
qv = pvS, (9.103)
где р — плотность атмосферы, и — скорость движения аппарата
(предполагается равной скорости набегающего потока — не¬
подвижная атмосфера), S — площадь входа воздухозаборника.
Аэродинамическое сопротивление аппарата запишем в виде
F = 1/2cxpv2S = 1/2cxvqv, (9.104)
гДе сх — коэффициент аэродинамического сопротивления (отне¬
сено к площади S входа воздухозаборника). Если пренебречь
трением и считать, что весь аппарат находится в «тени» ВОЗДУХО-
25 Механика полета
386
Другие типы двигательных систем
[гл. <1
заборника (рис. 9.29), то аэродинамическое сопротивление будет
равно импульсу струи vqv, захватываемой воздухозаборником
(сх = 2). Эти предположения справедливы для разреженной
атмосферы при конфигурации аппарата типа обратного усечен¬
ного конуса. Более подробное обсуждение данного вопроса мож¬
но найти, например, в работе [9.17].
Захваченная масса газа или ее часть, используемая непо¬
средственно для накопления (за вычетом расхода через движи¬
тель) направляется в установку сжижения. Эта установка потреб¬
ляет мощность Nv, пропорциональную секундному приходу массы.
Далее предполагается, что сжижается вся масса, приходящая
через воздухозаборник, поэтому
Nv = kvqv (kv = const). (9.106)
Часть сжиженной массы воздуха потребляется движителем
(расход q), предназначенным для компенсации аэродинамиче¬
ского сопротивления. В стационарном режиме тяга движителя
р = qV должна быть равна сопротивлению (9.104). Чтобы при
этом осуществлялось накопление (qv — Q^> 0), скорость исте¬
чения движителя V должна быть больше скорости движения
аппарата v. Для круговой орбиты спутника Земли и — 8 км!сек.
поэтому в качестве движителя для аппарата-накопителя рас¬
сматриваются электрические движители. Таким образом, часть
Ny мощности 7Vv, вырабатываемой источником, должна тратиться
на питание движителя
Ny = P2l2v\yq (Ny 4-Nv = Ag, (9.106)
где t]y — коэффициент полезного действия движителя.
Уравнение для веса G^ накапливаемого рабочего вещества
с учетом расхода q через движитель запишется в виде
Gv. = g(qv-q). (9.107)
Полный вес двигательной установки аппарата-накопителя
составляют следующие компоненты [9.11—9.17]: вес воздухо¬
заборника и установки сжижения Gv, пропорциональный макси¬
мальному секундному приходу массы qvmах:
Gv = yvqv шах (Тг> — const), (9.1 OS)
вес источника мощности пропорциональный максима л ьной
вырабатываемой мощности Nvo:
G.j = aNv0 (ос = const), (9.109)
вес движителя пропорциональный максимальной тяге Р0
или максимальной потребляемой им мощности ЛД0:
Gy = уР0 или Gy = yNyо (у = const), (9.110)
ДВИГАТЕЛИ, НАКАПЛИВАЮЩИЕ АТМОСФЕРНЫЙ ГАЗ 387
вес бака G^, пропорциональный максимальньму весу рабочего
вещества G^x:
2. Накопление в стационарном режиме. Рассмотрим задачу
выбора оптимальных параметров и оптимального режима работы
двигательной установки аппарата-заправщика [9.11—9.18]. При
некоторых дополнительных ограничениях в пп. 4 и 5 аналогич¬
ная процедура будет проведена для фазы накопления в случае
аппарата, предназначенного для выполнения внеатмосферного
маневра.
Задача ставится следующим образом: при заданном стартовом
весе G0 за фиксированное время Tv накопить максимальное ко¬
личество рабочего вещества G,x. Можно использовать поста¬
новки, эквивалентные данной: накопить заданное количество
рабочего вещества за фиксированное время при минимальном
стартовом весе или за минимальное время накопить заданное
количество рабочего вещества при фиксированном стартовом
весе.
Будем считать, что орбита, на которой производится накоп¬
ление, круговая, плотность атмосферы вдоль орбиты постоянна,
тяга движителя в каждый момент времени равна сопротивлению
(стационарный режим).
Учитывая условие равенства тяги Р = qV и сопротивления
F = 1/2cxvqv, запишем выражения для веса накопленного за
время Tv рабочего вещества G^x = g (qv — q) Tv и начального
веса *■) Gq = Gu -j- Gv -j- Gy -j- G$ в виде
Начальный вес G0 и время Tv фиксированы; выразив qv из
второго соотношения (9.112), получим относительную скорость
накопления в функции скорости истечения V
*) Учитываются только те весовые компоненты, которые непосредствен¬
но связаны с накоплением.
G& = PpAa (Pp. = const).
(9.111)
G,i =gqv(i-1hcxv/V) Tv,
Gu = gqv
CxV
2V~
) •
(9.112)
_ G\i\ _ 1 — h/V
Go GqTv b2V -}- bs — b^/V
(9.113)
25*
388
ДРУГИЕ ТИПЫ ДВИГАТЕЛЬНЫХ СИСТЕМ
[ГЛ. 9
Будем считать к. п. д. движителя г\у не зависящим от скорости
истечения V и потребляемой движителем мощности Ny. Если
орбита накопления фиксирована (и, сх = const), то коэффици¬
енты bv b2, Ь3, Ь4 постоянные и задача сводится к отысканию мак¬
симума (9.113) по V. В результате получим
остальные параметры двигательной установки вычисляются по
формулам
qv = ~ (b2V + b3 — b4/V) \ q = г/2qvcxvjV, S = qv/pv. (9.115)
Если в весовой формуле учитывать только вес источника мощ¬
ности (G0 = Gv, = у = Р1Х = 0), пренебречь мощностью, по¬
требляемой установкой сжижения (kv = 0) и положить сх = 2,
то соотношения (9.114), (9.115) значительно упростятся (Ьх = и,
62 = avl2gy\y, Ъ3 = Ь4* = 0):
Сравнивая выражения (9.114) и (9.116) для оптимальной ско¬
рости истечения, видим, что при учете дополнительных весовых
компонент и доли мощности, расходуемой на сжижение, уровень
скорости повышается.
В рамках данной постановки параметры орбиты накопления
входят только через скорость полета v и коэффициент аэродина¬
мического сопротивления сх (если не считать соотношения для
площади воздухозаборника S, последняя определяется после
решения задачи). Величины и и сх для диапазона высот (100—
120 км для Земли), где рассматривается накопление, практиче¬
ски постоянны. Поэтому для выбора оптимальной высоты орбиты
нужно привлекать дополнительные соображения, связанные с
тепловыми режимами, соотношениями площадей воздухозабор¬
ника и миделя аппарата и пр.
Приведем численный пример для случая накопления у Земли
(v ^ 8 км/сек, сх = 2). На рис. 9.30 дана зависимость относитель¬
I
Yl + (bib3-h)/blb2
Go ' max
b$-\ - (b,b2i>i)/6i+ (2b1bi + b3) Yi _j_ (б^д— Ъ4)1Ъ\Ьг' J
(9.114)
(9.116)
ДВИГАТЕЛИ, НАКАПЛИВАЮЩИЕ АТМОСФЕРНЫЙ ГАЗ
389
ной скорости накопления (G^/Gq) из (9.116), где G0 = Gv, от удель¬
ного веса источника мощности а, отнесенного к к. п. д. движи¬
теля t]y« Отметим, что обратная величина GJG^ равна времени,
за которое накапливается количество газа, равное по весу источ¬
нику мощности. Оптимальная скорость истечения в рассматривае¬
мом случае равна 16 км/сек. На орбите высотой 100 км при пло¬
щади воздухозаборника 1 м2
накапливается ~ 200 кГ воз¬
духа в сутки.
3. Накопление в нестацио¬
нарном режиме. Пусть на¬
чальная и конечная точки
траектории накопления (или
только начальная) лежат вне
«пределов» атмосферы (т. е.
в области, где плотность
слишком мала для накопле¬
ния). Такая ситуация возни¬
кает, например, при заправ¬
ке, которая должна произ¬
водиться вне атмосферы, или
в случае неточного вывода
аппарата-накопителя на ста¬
ционарную орбиту накопле¬
ния. Требуется построить
такую программу управления
вектором тяги, которая обес¬
печивала бы в конце дви¬
жения выход на заданную
орбиту при максимуме на¬
копленной массы газа за фик¬
сированное время [9.19].
Как и в конце предыдущего пункта, учитывается только вес
источника мощности (G0 = Gv, yv = у = = 0), мощностью,
расходуемой на сжижение пренебрегается (kv = 0), коэффици¬
ент аэродинамического сопротивления полагается сх = 2 (т. е.
учитывается только импульс приходящей через воздухозаборник
массы газа). Рассматриваются два крайних с точки зрения регу¬
лировки движителя режима управления тягой. В первом случае
скорость истечения и тяга движителя вдоль траектории постоян¬
ны, управление происходит за счет включения и выключения
Движителя (нерегулируемый движитель). Во втором случае огра¬
ничений на скорость истечения и тягу, кроме условия постоян¬
на мощности, не накладывается (идеально регулируемый дви¬
житель). Потери в движителе для обоих случаев отсутствуют
01y = 1), По поводу направления вектора тяги делаются следую¬
Рис. 9.30. Вес накапливаемого в единицу вре¬
мени рабочего вещества G^ (отнесен к весу
энергоустановки) в зависимости от удельного
веса энергоустановки на единицу мощности
реактивной струп a/i\y — сплошная кривая;
пунктирная кривая 1/Gjj. —время накопления
количества рабо чего тела, равного весу
энергоисточника.
390
ДРУГИЕ ТИПЫ ДВИГАТЕЛЬНЫХ СИСТЕМ
[ГЛ. ц
щие предположения. Считается, что аппарат, совершающий на¬
копление, при полете в атмосфере обладает флюгерной устойчи¬
востью. Далее полагается, что направление тяги невозможно
менять относительно осей аппарата. Эти два предположения при¬
водят к тому, что вектор тяги будет коллинеарен вектору ско¬
рости (а значит, и силе аэродинамического сопротивления).
В случае идеально регулируемого движителя допускается реверс
тяги, в случае нерегулируемого движителя тяга направлена
строго по скорости.
Исследуется плоское движение в окрестности некоторой
круговой орбиты (базисная орбита), отклонения от которой
считаются малыми. Для описания движения используются линеа¬
ризированные уравненрш из (5.88): второе, третье, пятое и шестое:
1 = аг + 2г), т| = аТ{ + Зц — 2| (<р = t — g, г = 1 + ц).
(9.117)
Здесь все переменные безразмерные: в качестве характерного
расстояния взят радиус базисной орбиты, в качестве характер¬
ного времени — период оборота по базисной орбите, деленный на
2я. Координата £ = t — ф отвечает за сдвиг по фазе, а коорди¬
ната г] = г — 1 — з& радиальное отклонение относительно рав¬
номерно движущейся по базисной орбите точки.
Компоненты ускорения а^ и ап, фигурирующие в правой части
(9.117), представляют собой проекции разности векторов тяги и
сопротивления, деленной на текущую массу аппарата. Проек¬
цией ап на радиальное направление пренебрегается. Движение
рассматривается на протяжении нескольких оборотов, поэтому
изменение веса аппарата мало, так что
«5 = — (glgo)(p — F)!Go, ап = 0 (9.118)
(направление оси £ противоположно направлению возрастания
угла ф, g0 — гравитационное ускорение на базисной орбите).
Граничных условий на угол ф не накладывается. В этом слу¬
чае уравнения (9.117) сводятся к уравнению третьего порядка для
радиальной компоненты ц (с учетом (9.118))
Л + 1i = 2g (Р — F)!g»G0. (9.119)
Закон изменения плотности по высоте аппроксимируется ли-
нейной зависимостью
р = р0 (1 - ЬО, (9.120)
где р0 — плотность атмосферы на базисной орбите, коэффициент
% в диапазоне высот 100—150 км для атмосферы Земли порядка
К — 2 • 103.
Учитывая величину коэффициента А, можно записать прибли¬
женные выражения для силы сопротивления и для секундного
ДВИГАТЕЛИ, НАКАПЛИВАЮЩИЕ АТМОСФЕРНЫЙ ГАЗ
391
прихода массы (сх = 2)
F = F0(l — А/Г]), qv = qvо (1 — A/rj)
(9.121)
(F0- Qvo — сопротивление и приход массы на базисной орбите),
т. е. можно пренебречь изменением силы сопротивления и при¬
хода массы за счет изменения скорости по сравнению с влиянием
высоты полета.
Выразим тягу и расход движителя через скорость истечения,
воспользовавшись условием постоянства мощности Nv0 = G0/ol
(напомним, что Gv = G0, kv = 0, к. п. д. r|Y = 1):
2Gp
aV2
р =—° п =
aV ' 4
(9.122)
и «ведем функцию включения — выключения движителя: б (t) = 1
или 0. Вариационная задача в этих обозначениях записывается
следующим образом:
G,,. = /о (1 — Я.Т)) — а0б / V 2, С,,. (0) = 0,
Gv(Tv) - max,
Л = г,, п(0) = Дго,
11 (Tv) = A^i.
2!r = /r. vr (0) = vr0, j. (9123)
vr (Tv) = vn,
fr = 2a061 V — vr — 2/0 (1 — b]), fr (0) = Дг0 — 2Дг;Фо,
fr(Tv) = &r1-2Av(fl
(a0 = (2g / а) g-' °-r~'s /0 = gF0 j g0G0).
Здесь вес накапливаемого рабочего вещества G{ij отнесен к
начальному весу аппарата G0, скорость истечения V — к круго¬
вой скорости на базисной орбите v0 = Y£0г0. Параметр а0 пред¬
ставляет собой безразмерное ускорение от реактивной тяги при
скорости истечения, равной у0, параметр /0 — безразмерное
ускорение от силы сопротивления на исходной орбите. Для удоб¬
ства записи уравнений принципа максимума введены дополни¬
тельные обозначения для производных г) = vr — радиальная
скорость, т] = /,. — радиальное ускорение. Граничные условия
Для ц, vr, /,. записаны через относительные отклонения радиуса
А/\ радиальной vr и трансверсальной Дуф компонент скорости от
соответствующих значений на базисной круговой орбите.
Изложение будет иллюстрироваться численными результа¬
тами, которые получены для следующих значений параметров
задачи:
а0 = 1,33-10-3, /о = 1,67-КГ4, % = 1,94-10®, Т„ = 2я. (9.12-1)
граничные условия принимались такими:
т) (0) = т) (2я) = А г, vr (0) = иг (2я) = 0, /,. (0) = Д. (2л) = 0.
(9.125)
Исследуем сначала случай нерегулируемого движителя. Для
него скорость истечения постоянна V = V0, и задача сводится к
отысканию оптимального значения параметра F0 и построения
оптимальной программы б (t) включения — выключения двига¬
теля, обеспечивающих максимальное накопление G[X (Tv).
Запишем гамильтонову функцию
Н = — [(1 — V) /о — + Р,уг + Pvfr +
+ pf [2 a-f - г,, - 2 (1 - Ь|) /о] (9.126)
и дифференциальные уравнения для импульсов
К = ~ + 2/>/> /°’ Р9 = —Рг, + Pr Pf = —Pv (9-127)
Представим гамильтониан Н как функцию управления б:
И = Н0 + ^ Да, Д = 1 + 2pfV. (9.128)
Из условия минимума Н по б имеем
6 = 0 при Д > 0, б = 1 при Д 0. (9.129)
Корни уравнения Д (t) = 01 определяют моменты переключений
и их общее число на интервале [0, Tv].
Дифференциальные уравнения для импульсов (9.127) интегриру¬
ются независимо от основной системы, в частности, выражение
для импульса pf, определяющего поведение функции Д, выгля¬
дит так:
Pf = Cie~bit -f 2lht (с2 cos Ъ4 + c3 sin bd) — 1/2,
bx = (kf0 + Y(Vo)2 + х/27) 3 + (Vo — V (Vo)2 + V27) V
b-2 = (Vo + Y(Vo)2 + 1 /27) 3— (Vo — V (Vo)2 + V27) ,
(9/130)
Подставляя pf(t) из (9.130) в (9.128), получим выражение функции
Д (t), содержащее три неизвестных постоянных с1? с2, с3. Эти
постоянные должны определяться из граничных условий (9.123)
после интегрирования уравнений движения (9.123) по активным
§ 3] ДВИГАТЕЛИ, НАКАПЛИВАЮЩИЕ АТМОСФЕРНЫЙ ГАЗ 393
= 1) и пассивным = 0) участкам:
Y|(i) (t) = cWeblt + C-1/2bif (c(i) cos _[_ c{i) gjn bot) 1 )
(ti-\<t<tu i = 1, 2, . . n + 1, tn+1=Tv), (9.131)
где U = ti(cv c2, c3) — корни уравнения Д (t) = 0; c%\ cg\ —
постоянные интегрирования по участкам. Соседние участки сты¬
куются по г], т), г\:
т,(О(«0 = - >Гт1ЧО- п' ДО = тГ1^,). (9.132)
При помощи соотношения (9.131) и условий (9.132) можно выра¬
зить постоянные (i + 1)-го участка через постоянные i-то участка
и момент переключения t\ (из решения соответствующей системы
линейных алгебраических уравнений):
C(i+D _ c(i> I hl!bi a°
3 5 1 -!- 3b:
ci‘
X (2fcib.> cos b4{ + sin b2t{),
b\ an /Я(г)
(9.133)
i-*D = C(i) H u±- _?!L- (6W — ) x
X (2bфч sin boti — cos Mi)-
Постоянные первого участка (i = 1) определяются начальными
данными
ч(0) + X (1Сг_ 1) (1 + 6l2) + ^(0) bl + ^(0)} ’
ей) =
4
1 + 36* {
~ Г+зь| {
С<!) =
с<« =- 1—
6 1 -г- зь?
л (°) +
«пб
(I)
l-Vo
— 1
261 —Л (0)bi
Л (°) J
(I)
/А\ I ^ / ^пб
ч(°) + х -ПК
— 1
h.
Ьо
1- Л (°)
1 - г 3/ 2Ь\
- ч (0) I:
(9.134)
Последовательно подставляя в (9.133) выражения для постоян¬
ных последующего участка через постоянные предыдущего,
получим выражения c<i+1\ с. 11, через с£>, с<‘>, с*.11 и
394 ДРУГИЕ ТИПЫ ДВИГАТЕЛЬНЫХ СИСТЕМ [ГЛ. 9
моменты переключений t2, . . ., t{:
V = c(4l) -f- [sgn Д (0)] b3 [(— l)2 e~bili -f- (— l)3 e~bitz + • • •
h (—
c(i, i) __ c(i) _l jSgn д (0)] [(— l)2 (bb cos b2ti + sin b?ti) e 'Wi-f . . .
• • • -j- (— 1) (b-y cos b2t^ -f- sin b2t\j ^ ~ 1 * ] i
c(jti) c(i) — [sgn Д (0)] i>4 [(— l)2 (cos b2ti — b5 sin b2ti) e!*biti -f-
•••+(— l)1''1 {cos b2ti — b6sinb2ti) elWi],
j «0 i Г ^4 j Oq Ь] / b> у ryj j \
= Ti7T t , ■)!«>' ’ 4 “ ГР ) ' “ , OJ 2 1 ~ 12 I •
/wl'o./o 1-L Л»' о/о l .. 3&2 / J
(9.135)
Постоянные c2, c3, определяющие моменты переключения
tv t2, . . £n, подбираются так. чтобы посчитанные по (9.135)
постоянные с^ы1\ c^ntl\ c^nFl) соответствовали заданным конеч¬
ным условиям из (9.123) относительно т], f], rj.
Результаты проведения описанной процедуры для граничных
значений (9.125) с Дг = 0 и значений параметров задачи из
(9.124) представлены на рис. 9.31 —9.33 для различных скоростей
истечения V0. На рис. 9.31 показана функция Д (t), определяющая
моменты переключений (9.128), (9.129). Уравнение Д (t) — 0 имеет
три корня tv t2, t3. Они даны на рис. 9.32 в функции скорости
истечения. Движение начинается с пассивного участка: б (t) = 0
при 0 < t tv затем следуют активный участок: б (t) = 1 при
t1<C t 12 и пассивный участок б (t) 0 при t2<^t<^ t3; дви¬
жение заканчивается активным участком: б (t) = 1 при t3 t
<^ 2я. Оптимальная траектория i] (t) (рис. 9.33) сначала входит в
плотные слои атмосферы, а затем снова выходит на исходную
орбиту.
По известным траектории ц (t) и функции б (£) вычисляется
накопленная масса
Г, (Tv) = Тх)о — 2 [До ^ Л (t) dt -f а0 (tux— ti) 6wj . (9.136)
На рис. 9.34 показана зависимость относительной накоплен¬
ной массы G{). (2л) от скорости истечения F0 для различных зна¬
чений начального радиуса Дг. Видно, что для каждого Дг су¬
ществует своя оптимальная скорость истечения. Пунктиром
показана предельная кривая, соответствующая таким значениям
Рис. 9.31. Функция А (0, определяющая моменты вклю¬
чения — выключения нерегулируемого движителя на траек¬
тории накопления, при различных значениях скорости исто*
чения У о (отнесены к круговой скорости).
4
20 Ln я ±я 2я
Рис. 9.32. Распределение пассивных (5 = 0) и активных
(5 = 1) участков на траектории накопления с нерегули¬
руемым движителем.
Ik
^2 7/^/
ж
6=1
1
Рис. 9.33. Примеры оптимальных траекторий накопления
(и — радиальная компонента) для различных скоростей
истечения — нерегулируемый движитель.
396
ДРУГИЕ ТИПЫ ДВИГАТЕЛЬНЫХ СИСТЕМ
[ГЛ. о
скорости истечения, при которых движение происходит по началь¬
ной круговой орбите (тяга равна минимально возможной Р = F0).
Перейдем теперь к случаю идеально регулируемого движи¬
теля. Здесь ограничений на скорость истечения V не накладыва¬
ется, кроме того, допускается реверс тяги. Если под V в (9.123)
понимать — ос V (t) + 00, то функцию б в уравнениях
Рис. 0.34. Накопленная за один оборот масса (отнесена к на¬
чальной массе аппарата) в функции скорости истечения для
различных начальных радиусов — нерегулируемый дви¬
житель.
можно не писать. Выключению двигателя (нулевые тяга и рас¬
ход) будут соответствовать значения V = Ч- эо. Отрицательные
значения скорости истечения —ос V (t) 0 означают реверс
тяги.
Из условия минимума гамильтоновой функции (9.126), где
6 = 1, находим оптимальную программу скорости истечения
V (t) = -1 lpf. (9.137)
Уравнения для импульсов (9.127), (9.130) сохраняются пол¬
ностью. Таким образом, явное выражение для оптимального
закона V{t) будет
V (t) = — [с-^е-^1 + eV*bi< (с2 cos b2t + с3 sin b2t) — 1/2]~1, (9.138)
где постоянные Ь1ч Ьг определяются формулами (9.130).
ДВИГАТЕЛИ, НАКАПЛИВАЮЩИЕ АТМОСФЕРНЫЙ ГАЗ
397
Нули функции Pf(t) дают моменты выключения тяги V = ос;
если при переходе через нуль функция pf(t) меняет знак, то про¬
исходит «перекладка» тяги. Поскольку функция pj(t) непрерывна,
то перекладка тяги может иметь место, только когда тяга обра¬
щается в нуль.
Подставляя (9.138) в уравнение движения (9.123) и интегрируя,
получим закон изменения радиуса
’I W Cl 2>./о 6
-b,t
1ба0
hi -{- 30%j о
(c-i cos b2t + с3 sin b2t) 4-
С46
(съ cos b2t + cQ sin b2t) + -j- (1 — w')* (9-139)
(Iq
27o
Постоянные c1: . . ., cQ определяются из граничных условий (9.123)
для уравнений движения решением линейной системы алгебраи¬
ческих уравнений.
v
5
О
-/
W
\
j
л
з -
7
2ж
\|
t W(T
ч "Ч
/1
/ /
7
V"\
V"
/ /
/
7*
7 Л'
2л
Рис. 9.35. Оптимальная программа скоро¬
сти истечения идеального движителя на
траектории накопления (отрицательные
значения У соответствуют реверсу тяги).
Рис. 9.36. Примеры оптимальных траекто¬
рий накопления с идеальным движителем
(сплошная кривая) и нерегулируемым
движителем (пунктирная кривая).
Если параметры задачи выбраны так, что 2/0 — aQ = 0, и,
кроме того, г] (0) = у| (0) = ц (0) = г) (Tv) = т] (Тг) = ц (Г1?) =0*
то получается сх — с2 = . . . = с6 = 0. Это означает V (t) = 2
и г| (t) = 0, что соответствует результатам предыдущего пункта.
Численные результаты, относящиеся к идеально регулируе¬
мому движителю, даны на рис. 9.35—9.37. Пример оптимальной
программы V (t) изменения скорости истечения и соответствующей
траектории ц (t) при Аг = 0 показан на рис. 9.35 и 9.36. Для
сравнения нд рис. 9.36 нанесена пунктирная кривая ц (t), отве¬
чающая нерегулируемому двигателю с оптимальным значением
скорости F0 = 3,5. За счет реверса тяги (отрицательные значения
У на рис. 9.35) аппарат с идеальным движителем быстрее входит
н плотные слои атмосферы, к тому же возможность регулирова¬
ния (увеличения) тяги позволяет ему опуститься ниже, чем это
Может сделать аппарат с нерегулируемым движителем.
Величина накопленной массы для аппарата с идеальным дви¬
жителем подсчитывается по построенной траектории ц (t) и
398
ДРУГИЕ ТИПЫ ДВИГАТЕЛЬНЫХ СИСТЕМ
[ГЛ.
программе скорости истечения V (t)i
Tv Tv
Gv. (У„) = T,./о — Vo S Л (*) dt-a0 5 r2 (t) dt. (9.14<))
0 0
Зависимость относительной накопленной массы (9.140) от
радиуса Дг исходной орбиты при различных значениях /0 —-
ускорения от сопротивления на базисной орбите — показана на
рис. 9.37. Огибающей при¬
веденного семейства кривых
является горизонтальная пря¬
мая. Скорость истечения в
точках касания постоянна
вдоль траектории и равна 2.
Сравнение идеальных
(G>)v=Var и нерегулируемых
(G{))v~vо движителей по на¬
копленной массе представле
но в виде отношения
(Gy)v==vJ(G>)v=var на рис. 9.38 .
Кривые построены для раз¬
личных радиусов А г в функ¬
ции скорости истечения F()
нерегулируемого движителя.
Рис. 9.37. Накопленная за один оборот масса КраиНИб правые ТОЧКИ JKpH-
в функции начального радиуса для различ- ВЫХ (соединены ЛИНИвЙ СО
ных значений /0 (ускорения от аэродинамиче- шттшхт,ко*\ cootrptptrvtot
ского сопротивления на базисной орбите)— illiрилиычии; иии iBtsioibyiu 1
идеальный движитель. максимально ВОЗМОЖНОЙ СКО¬
РОСТИ V0 (минимальная тяга),
начиная с которой полет по орбите данного радиуса становится
невозможным. Из рисунка видно, что в области скоростей
2,5 < V0 < 5 проигрыш в накопленной массе для представлен¬
ного диапазона радиусов Дг будет минимальным и не превысит
15%.
4. Внеатмосферный маневр аппарата-накопителя с двигателем
ограниченной мощности. Рассмотрим теперь аппарат, который
после накопления на орбите должен совершить внеатмосферный
маневр. В фазе накопления и в фазе выполнения основного ма¬
невра используется двигатель ограниченной мощности. Его пара¬
метры уже нельзя выбирать исходя только из условия оптималь¬
ности одной из фаз маневра — они должны обеспечивать наи¬
лучшее выполнение маневра в целом [9.18]. Ниже определяются
оптимальные параметры двигательной системы и оптимальное
время накопления в зависимости от характеристики маневра и
удельных весовых характеристик системы. Находится область
преимущественного использования двигательной системы огра¬
§ зЗ ДВИГАТЕЛИ, НАКАПЛИВАЮЩИЕ АТМОСФЕРНЫЙ ГАЗ 399
ниченной мощности с накопителем рабочего вещества путем срав¬
нения по полезной нагрузке с системой без накопителя.
Задача ставится следующим образом. Фиксируется суммарное
время выполнения двух фаз маневра Г, а время выполнения ос¬
новного маневра определяет¬
ся как разность между этим
временем и временем накоп¬
ления Тv. Требуется при за¬
данном начальном весе G0
обеспечить максимум полез¬
ного груза GL. Орбита, на
которой происходит накопле¬
ние, считается круговой с не¬
изменной по всей ее длине
плотностью. Переходный уча¬
сток в атмосфере с орбиты
накопления на траекторию
выполнения основного манев¬
ра не рассматривается.
Двигательная система
ограниченной мощности пред¬
полагается идеально регули¬
руемой:
Р = qV, Ny = ±
0<F<oo, 0<iVY<‘iVv0).
(9.141)
При маневре вне атмосферы
определяться как
G = —gq, a = --%-V, (9.142)
где G — текущий вес аппарата.
Вес идеально регулируемой двигательной системы ограничен¬
ной мощности определяется весом источника мощности
Gx = Gv = a7Vv0. (9.143)
Исключив из (9.142) q и V на основании оптимального условия
Ny (t) = Nv0 = GJa, так же как и в § 1 главы 4, получим диф¬
ференциальное уравнение изменения веса аппарата
Рис. 9.38. Отношение накопленной массы
( G,}) у==у0 для нерегулируемого движителя к
накопленной массе (G^) у=Уаг для идеального,
движителя в зависимости от скорости истече¬
ния нерегулируемого движителя при фикси¬
рованных значениях начального радиуса.
расход и ускорение от тяги будут
400 ДРУГИЕ ТИПЫ ДВИГАТЕЛЬНЫХ СИСТЕМ [ГЛ. •'
Интеграл этого уравнения от момента начала внеатмосферного
маневра до конечного времени запишется в виде
-g-Г
Go -i-Gjj. ' Tv
(Gq — стартовый вес, состоящий из веса полезной нагрузки G-
и веса источника мощности Gv : G0 = G- + Gv).
Запас рабочего вещества, расходуемого при выполнении ос¬
новного маневра за время Т — Tv, должен быть предварительно
накоплен за время Tv. Для стационарного режима накопления
= *(?„- q) Тг. (9.146)
При площади миделя воздухозаборника S и массовой плотнострг
атмосферы р, забираемый воздухозаборником расход равен
qv = Spu. (9.147)
Соответственно условие для тяги движителя на режиме накоп¬
ления запишется в виде
Р = qV - ± сДогА (9.148)
Используя (9.147) и (9.148), уравнение (9.146) можно перепи¬
сать следующим образом:
G^gq^V -\yrv. (9.149)
Здесь скорость истечения V отнесена к скорости орбитального
полета v. Отнесем весовые компоненты G[JO Gv к стартовому весу
G0, сохранив для безразмерных величин прежние обозначения.
Тогда уравнение (9.145) примет вид
тТо;= ^ф’ ф = i I a*dt- (9Л50)
т
v
Представив расход через движитель как q = 2Gv/az;2F2, из (9.149)
и (9.150) можно определить его величину следующим образом:
q ^ +|/ 1 1 т ^ (9Ло1)
Уравнение (9.151) получено в предположении, что вес сжижи-
тельной установки равен нулю и мощность энергетической уста-
ДВИГАТЕЛИ, НАКАПЛИВАЮЩИЕ АТМОСФЕРНЫЙ ГАЗ
401
ловки на сжижение не расходуется (учет этих факторов произ¬
водится ниже). При этом можно определить полезный вес
в функции скорости истечения, времени накопления и величины
ф, характеризующей заданный маневр.
Найдем оптимальные значения Ти и F, дающие максимум
полезной нагрузки. Скорость истечения рабочего тела, макси¬
мизирующая С?*, равна (как и в п. 2)
Оптимальное время накопления определяется при конкрети¬
зации зависимости функционала Ф от времени маневра. В каче¬
стве примера, следуя [9.18], рассмотрим обратно пропорциональ¬
ную зависимость, что соответствует задаче выхода из гравита¬
ционного поля центра х)
где Дг; есть заданное приращение скорости, время Tv отнесе¬
но к Т.
При увеличении Tv растет Ф, и, следовательно, необходимо
увеличивать начальный запас рабочего тела G,м но одновремен¬
но увеличивается накопленная на орбите масса; поэтому сущест¬
вует оптимальное время накопления. В рассматриваемом случае
(9.154) оно равно
Отметим, что для рассмотренного в п. 2 случае, когда аэро¬
динамическое сопротивление равно импульсу струи, забираемой
воздухозаборником, коэффициент аэродинамического сопротив¬
ления равен сх = 2. Соответственно тогда связь параметра к с
Сд/Gq из (9.116) запишется в виде к = V^GJG{iT.
Подставив в уравнение (9.152) значения V0])t и (7\>)opt из
(9.153) и (9.155) соответственно, получим
х) Такая же зависимость функционала от времени выполнения маневра
имеет место для задачи перехода между двумя компланарными круговыми
орбитами и для задачи поворота плоскости круговой орбиты, когда реак¬
тивное ускорение много меньше гравитационного ускорения на исходной
G~ = 1 — Gv = 1 2~ (1 +
/
(9.152)
Fopt сх.
(9.153)
(9.154)
V
= У2a.v2c*l gT . (9.155)
G„ = 1 — к /Ф0 — Ф0.
(9.156)
орбите (§§ 2, 3 гл. 5).
26 Механика полета
/.02
ДРУГИЕ ТИПЫ ДВИГАТЕЛЬНЫХ СИСТЕМ
Область параметров, где накопление массы является выгодным,
можно определить, сравнивая полезную нагрузку (9.156) с по¬
лезной нагрузкой для двигательной установки ограниченноц
мощности без накопления (4.16):
Выигрыш (AGr, = G- — Gn^> 0) имеет место в следующем-
области параметров Ф0 и х:
Максимальный выигрыш AG- при заданной величине х будет,
когда Ф0 = (2 — х)2/16, причем
На рис. 9.39 приведена зависимость полезной нагрузки от
величины функционала Ф0 при различных значениях параметра
накопления. График для оптимального времени накопления
представлен на рис. 9.40. Ограничивающая кривая соответству¬
ет значениям параметров х и Ф0, для которых основной маневр
уже не может быть выполнен (точка пересечения с осью G- 0
на рис. 9.39).
Если учесть, что в данном случае вес установки сжижения
был принят равным нулю, то вес источника мощности опреде¬
лится как разность Gv = 1 — G- (х, Ф0). Таким образом, для
идеальной двигательной системы с накоплением оптимальны]'! вес
источника мощности Gv зависит не только от характеристики ма¬
невра Ф0 (как принималось в [9.17]), но и от параметра х.
В рассмотренном выше случае при наборе массы не учитыва¬
лись затраты на аккумулирование массы. Эти затраты сведем [9.18]
к расходованию дополнительной мощности источника и весу сжи-
жительной установки Gv. Тогда стартовый вес G0 будет определен
суммой трех слагаемых
G*. = 1 — 2 У Ф0 + Ф0.
(9.157)
0 < Ф0 < (1 - х/2х)2.
(9.158)
тах — -g- (2 х)2.
я max —
(9.159)
Относительный выигрыш в полезной нагрузке равен
q _ _ 1 — х YWp — (Dp
’ G* ~ 1 — 2 ГфО -f Ф0
(9.160)
и имеет максимум
G-
- шах
х. Пунктиром показана зависимость G- (Ф0) для случая без
G0 — G^ -Г Gv -f~ Gv,
(9.162)
ДВИГАТЕЛИ, НАКАПЛП ПАЮЩИЕ АТМОСФЕРНЫЙ ГАЗ
403
где Q0 = yvq„, коэффициент у„ далее принимается постоянным
(9.108). В режиме накопления массы мощность будет расходо¬
ваться на создание тяги и на сжижение. Последнюю будем счи¬
тать пропорциональной забираемому из внешнего потока расходу
qv (9.105). Тогда
fqV2
Т"
kvqv
(9.163)
где коэффициент пропорциональности кр полагается постоянным.
Используя уравнение (9.145) и проводя преобразования, анало¬
гичные проделанным выше, получим выражение для расхода
О
0,25 0,50 0,75
Рис. 9.39. Зависимость максимальной от¬
носительной величины полезного груза от
функционала задачи Ф0 при использовании
накопления рабочего тела в верхних слоях
атмосферы — двигатель ограниченной мощно¬
сти. Пунктирная кривая — значения полез¬
ного веса при полете без накопления рабо¬
чего тела.
Рис. 9.40. Оптимальное относитель¬
ное время накопления рабочего тела
Т V/T для полетов с двигательной
системой ограниченной мощности.
рабочего вещества через движитель д, необходимого для компен¬
сации аэродинамического сопротивления
Q
Ф
V- 1
сxv-V )
1
/
2av-
^ФГ7
4 к
JD-V
V — 1
(9.164)
Выражение для расхода рабочего тела через движитель полу¬
чено в предположении, что сжижается вся забираемая воздухо¬
заборником масса газа и в соответствии с этим расходуется мощ¬
ность, идущая на сжижение. Относительная полезная нагрузка
з функции скорости истечения, времени накопления и характе-
26*
404
ДРУГИЕ ТИПЫ ДВИГАТЕЛЬНЫХ СИСТЕМ
[IV1. я
ристики маневра Ф теперь будет записываться следующим
образом:
(
Г*
Gn
1
"r cxv- V
X
}
^ 1 -!- 9Т/
2av2 V 1 • cjo-V
Ф T,
i 2
. (9.165)
V — 1
Приуг = 0 и kVj = 0 уравнения (9.164) и (9.165), естественно,
переходят в (9.151) и (9.152). Аналогично предыдущему можно
показать наличие оптимальных времени накопления и скорости
истечения. Снова рассматривается маневр выхода из поля цен¬
тра, для которого величина Ф определяется формулой (9.154).
Оптимальное относительное время накопления, дающее макси¬
мум полезной нагрузки, равно
(^)opt ~
1 +
У
g-ФоТ
— V — 1
С
2av2
V'2
4Av
cv2V
-i
(9.166)
Оптимальная скорость истечения в этом случае не выражает¬
ся явно. Связь между оптимальной скоростью истечения и Ф0
дается выражением
2с, (с, — 1) |/
И + С 2
V [V — ■
Vs — (сх + С.,С3 — 2с2) V2 •—
j- схсЛ; -
с1сз
], (9.
167)
где
Cl — V
W' = Сз = 1 + 4 (9Л68)
— безразмерные величины.
Таким образом, в этом случае определяются оптимальные пара¬
метры двигательной системы, скорость истечения рабочего тела
в режиме накопления и относительный вес источника мощности.
На рис. 9.41 в качестве иллюстрации представлены резуль¬
таты расчета относительных весов полезной нагрузки Gn и ис¬
точника мощности Gv для двух наборов значений параметров:
§ 3]
ДВИГАТЕЛИ, НАКАПЛИВАЮЩИЕ АТМОСФЕРНЫЙ ГАЗ
1) а = 2,5 кГ/квт, с± = 0,15, с2 = 0,16, с3 = 9; 2) а =
= 5,0 кГЫвт, сг = 0,21, с2 = 0,16, с3 = 5.
0,25
ч)
и 0# 0,50 0,75 Ф0
Рис. 9.43. Оптимальное относительное вре¬
мя накопления рабочего тела Tv/T для
двигателей ограниченной мощности с уче¬
том весовых и энергетических затрат на¬
копительной системы. Случаи 1 и 2 соот¬
ветствуют данным рис. 9.41.
Рис. 9.41. Влияние на относительный по¬
лезный вес Gn и вес источника мощно¬
сти Gv весовых и энергетических затрат
на накопление рабочего тела в орбиталь¬
ном полете: 1 — а = 2,5 пГ/квт, 2 —
а = 5 кГ/квт. Штрих-пунктирная кривая
соответствует случаю 2 без учета ука¬
занных затрат.
Рис. 9.42. Оптимальные значения отно¬
сительной скорости истечения V/v на
режиме накопления с учетом весовых
и энергетических затрат накопительной
системы. Случаи 1 и 2 соответствуют
данным рис. 9.41.
Рис. 9.44. Выигрыш в полезной нагрузке
от применения накопления массы с двига¬
тельными системами ограниченной мощно¬
сти. Случаи 1 и 2 соответствуют данным
рис. 9.41. Штрих-пунктирная кривая —
случай 2 без учета весовых и энергети¬
ческих затрат на накопление рабочего тела.
Для тех же значений параметров на рис. 9.42 приведена опти¬
мальная относительная скорость истечения реактивной струи.
Зависимость от функционала Ф0 времени накопления, при котором
полезная нагрузка будет максимальной, дана на рис. 9.43. На
Рис. 9.44 показано относительное увеличение полезной нагрузки
406
ДРУГИЕ ТИПЫ ДПИТАТЕЛЬНЫХ СИСТЕМ
[ГЛ.
GL от использования накопления массы с двигательными уста¬
новками ограниченной мощности. Там же для сравнения штрих-
пунктиром нанесен относительный выигрыш в идеальном слу¬
чае при х = 0,401 (см. (9.160)), что соответствует значениям пара¬
метров на кривой 2.
5. Внеатмосферный маневр аппарата с двигателем ограничен¬
ной скорости истечения при использовании накопления. Рассмот¬
рим сочетание двигательной установки с накоплением рабочего
вещества и двигателя ограниченной мощности [9.20]. Установку
для накопления рабочего вещества на стационарной круговой
орбите будем считать идеальной (см. условия к формуле (9.116)),
движитель ограниченной скорости истечения V ^ Vmax, предназ¬
наченный для выполнения основного маневра,— невесомым,
идеально регулируемым.
В такой постановке начальный вес аппарата G0 на орбите
накопления будет состоять из полезного веса, веса источника
мощности Gv, веса топлива G^w и веса окислителя Gm (для хи¬
мического двигателя)
Go = Gn -|- Gv ~Ь G^m -|- G^oi. (9.169)
Исследуемая задача будет состоять в определении оптималь¬
ного соотношения весовых компонент в (9.169), обеспечивающих
максимум относительного полезного груза при выполнении ма¬
невра с заданным значением характеристической скорости Дщ
время накопления Tv фиксировано (параметр задачи).
Накапливаемое в орбитальном полете вещество весом GIJj02
будем считать окислителем (потребная сепарация, например, кис¬
лорода, может быть учтена соответствующим поправочным коэф¬
фициентом). Его величина за время накопления Tv в соответ¬
ствии с (9.116) будет равна (при pY = 1)
Gи» = £ т* или с'.-02 = (у, = ш) • (9Л7°)
Так как величина 2av2/g (рис. 9.30) характеризует время накоп¬
ления количества рабочего тела, равного весу энергоисточника
Gv, то т+ есть отношение времени накопления Tv к времени, пот¬
ребному для накопления веса рабочего тела, равного Gv.
Отношение веса топлива к общему весу окислителя задано
условиями химической реакции
G^m = к (Gij.01 “I- Gv,02). (9.171)
С учетом соотношений (9.170), (9.171) выражение (9.169) запишем
в виде
G0 = Gn + (1 + kxj + (1 + к) G,,01. (9.172)
ДВИГАТЕЛИ, НАКАПЛИВАЮЩИЕ АТМОСФЕРНЫЙ ГАВ
407
В конце фазы накопления вес аппарата составит
G (Tv) = G- + 6rv -j- + £^02 ~г Gym — Gq “I- (9.173)
а после совершения маневра (At>) с расходованием топлива и окис¬
лителя в двигателе ограниченной скорости конечный вес аппа¬
рата будет равен
G^G^ + Gv, (9.174)
где Av/Vm&x = ln[G{Tv)/G1].
При заданных значениях Gro а, и, Fmax и Tv максимум харак¬
теристической скорости Av соответствует минимуму отношения
GJG (Tv):
G] Ся4-Cv _ .... 44
G(Tv)
(9.175)
(здесь все весовые компоненты от¬
несены к начальному весу G0).
На рис. 9.45 дано изменение
GJG (Tv) по Gv для двух харак¬
терных режимов. При G^^ 1/т*
минимальное значение GJG (Tv)
достигается при Gv = 0; в этом
случае применение накопительной
установки нецелесообразно. При
G- > 1 /т:|с минимальное значение
СуС?(Гг) соответствует максималь¬
но возможному значению Gv, кото¬
рое, согласно (9.172), достигается
при G,li0l = 0; тогда
1 — G.
О
Gv
G j opt —
1 + hr*
(9.176)
Рис. 9.4 5. Характер изменения отно¬
шения конечного веса аппарата с дви¬
гателем ограниченной скорости О,
к весу в конце фазы накопления массы
G (Г ) в функции относительного
веса источника мощности Gv/G0: а) ре¬
шим G- < 1/т#; б) режим GK >1/т*.
В этом случае сочетание на
копительной установки и двига¬
теля ограниченной скорости истечения обеспечивает при задан¬
ных начальном весе и полезном весе достижение большей харак¬
теристической скорости, чем в случае использования одного
Двигателя ограниченной скорости истечения. Максимальная ве¬
личина характеристической скорости, достигаемая при указан¬
ном оптимальном сочетании систем, согласно (9.174)—(9.176),
равна
Av . 1 + тП- кх. — x»Gr_ /q.|77\
77—-—In т—~ . (9.17/)
max 1 + Лт.С^ '
В качестве примера на рис. 9.46 при к = 0, 2 для ряда зна¬
чений из (9.170) приведена зависимость относительного
408
ДРУГИЕ ТИПЫ ДВИГАТЕЛЬНЫХ СИСТЕМ
[ГЛ. о
полезного веса G- от параметра маневра Ay/Fmax. Там же для со¬
поставления приведена пунктирная кривая, соответствующая
О 1,0 2,0 A1L.
vmax
Рис. 9.4В. Максимальные значения относительного полезного
веса GK для полета с двигательной системой ограниченной
скорости струи и накоплением рабочего тела. Пунктирная
кривая — решение Циолковского для двигателя ограничен¬
ной скорости без накопления массы.
0,5
решению Циолковского для двигателя ограниченной скорости
без накопления массы.
Сравнение характеристик на¬
копительных систем с идеаль¬
ными двигателями ограничен¬
ной скорости истечения (настоя¬
щий пункт) и ограниченной мощ¬
ности (п. 4) для рассматривае¬
мого маневра набора модуля
скорости должно производиться
при одинаковых значениях
т+ = 4/х2 (см. (9.170) и (9.155)
при = 2). Это связано с тем,
что набор модуля скорости с
идеальным двигателем ограни¬
ченной скорости истечения про¬
исходит мгновенно, поэтому
время накопления Tv для него
совпадает с полным временем Т
выполнения обеих фаз маневра.
Полезная нагрузка аппарата
накопителя с идеальным двигателем ограниченной мощности,
посчитанная по формуле (9.156) при тех же значениях 4/х2 = т#,
что и на рис. 9.46, показана на рис. 9.47.
1 ....
О
0,5
Рис. 9.47. Максимальные значения относи¬
тельного полезного веса GK для полета с
идеально регулируемой двигательной си¬
стемой ограниченной мощности и накоп¬
лением рабочего тела.
ДВИГАТЕЛИ, НАКАПЛИВАЮЩИЕ АТМОСФЕРНЫЙ ГАЗ
409
В отличие от системы с двигателем ограниченной мощности,
накопительная система с двигателем ограниченной скорости в
фазе выполнения космического маневра может быть рассмотрена
О 1,0 2,0 Ли_
У/пах
Рис. 9.48. Максимальные значения относительного полез¬
ного веса для сочетания накопительной системы с двига¬
телем ограниченной скорости истечения, ускоряющим на фазе
космического маневра только полезный груз. Пунктирная
кривая — решение Циолковского.
без источника мощности. Этому случаю, естественно, соответ¬
ствует приращение характеристической скорости большее (9.177);
оно определяется минимумом отношения
Gl (9.178)
G' (Tv) 1 + (т. - 1) Gv
При т+ 1 минимальное значение (9.178) достигается при
Gv = 0; в этом случае применение накопительной установки не¬
целесообразно. При т* > 1 оптимальное значение относительного
веса источника мощности в фазе накопления определяется соот¬
ношением (9.176).
Максимальная величина характеристической скорости для
сочетания накопительной системы с двигателем ограниченной
скорости, ускоряющим на фазе космического маневра только
полезный груз (без источника мощности), равна
* (9Л79)
^тах £-И + /гС*)
Для этого случая на рис. 9.48 приведен пример зависимости
от Az;/Fmax при к = 0,2 для ряда значений т#.
410
ДРУГИЕ ТИПЫ ДВИГАТЕЛЬНЫХ СИСТЕМ
[ГЛ. !>
§ 4. СОЛНЕЧНЫЙ ПАРУС
1. Постановка задачи оптимизации полета с солнечным пару¬
сом. Рассматривается плоский парус с идеально отражающей зер¬
кальной поверхностью (§ 2 гл. 2). С учетом только гравитацион¬
ных сил и силы солнечного давления движение центра масс кос¬
мического аппарата с солнечным парусом описывается уравне¬
нием (1.1) при F = 0. Вектор е направления тяги, фигурирующий
в этом уравнении, совпадает с вектором нормали к теневой сто¬
роне паруса п, а величина тяги определяется из соотношения
Вес космического аппарата с солнечным парусом (если счи¬
тать площадь паруса постоянной S (t) = S0 и не принимать во вни¬
мание явления «износа» паруса) не меняется со временем G (t) =
= G0 и состоит из двух слагаемых: полезной нагрузки G- и веса
паруса Gs = gS0p& (2.54). Введя эти соотношения в уравнения
движения, получим
где п — единичный вектор нормали к теневой стороне паруса;
i — единичный вектор направления солнечных лучей; (n-i) —
косинус угла ni установки паруса по отношению к солнечным
лучам; pi — солнечное давление на единичную площадку, уста¬
новленную перпендикулярно к солнечным лучам, на орбите
Земли R$; R = R (г) — расстояние аппарата до Солнца (в ге¬
лиоцентрической системе координат R = г); р и б — плотность
и толщина материала паруса.
Таким образом, в уравнения движения вошли параметры па¬
руса 50, р, б и полезная нагрузка G-. Комбинацию этих пара¬
метров, содержащуюся в уравнении (9.180), можно заменить уско¬
рением, которое сообщает парус космическому аппарату на рас¬
стоянии от Солнца, будучи установленным перпендикулярно
к солнечным лучам (и = i):
Полезная нагрузка и потребная площадь паруса выражаются
через этот параметр
(2.53).
Г
(п • i)2 n + Н, (9.180)
а уравнение движения (9.180) записывается следующим образом:
СОЛ ILE 411 ЫЙ ПАРУС
411
Связь уравнения движения (9.183) с весовыми характеристи¬
ками G-, 50, р, б осуществляется через единственный параметр
а0, максимальная величина которого определяется массой еди¬
ницы площади паруса рб (9.181). Ускорение а0 для уравнения
движения (9.183) играет роль постоянного управляющего пара¬
метра. Единственная управляющая функция в этом уравнении —
угол установки паруса (направление нормали к теневой стороне
паруса), который может меняться в диапазоне (—я/2, я/2) по от¬
ношению к солнечным лучам:
| n (t) | = 1 (—я/2 n(t)i я/2).
Могут быть рассмотрены две эквивалентные формулировки
общей проблемы оптимизации: 1°. Задан полный вес аппарата
G0 и время выполнения маневра Т; требуется найти максимум
полезной нагрузки GL. 2°. Задан полный вес аппарата G0 и по¬
лезная нагрузка GC, требуется найти минимальное время выпол¬
нения маневра Т.
Для аппарата с солнечным парусом не обязательно опериро¬
вать с Gn и Gq по отдельности. Здесь можно использовать отно¬
шение G~/G0 из (9.182), т. е. считать его заданным и определять
минимум Т либо находить максимум GJG0 при заданном Т. От¬
носительная полезная нагрузка GJG0, согласно первому соот¬
ношению (9.182), определяет величину произведения а0рб. Масса
единицы площади паруса рб зависит от совершенства конструк¬
ции и должна быть минимально возможной. Таким образом, от¬
носительную полезную нагрузку можно считать однозначно
связанной с ускорением а0.
С другой стороны, величина а0 через уравнение движения
(9.183) определяет время выполнения маневра Г, и задача опти¬
мизации сводится к построению такого закона управления ори¬
ентацией паруса п (t), который обеспечивает при заданном а0
минимум Т или минимум а0 при заданном Т. Вторая формулиров¬
ка менее удобна вследствие того, что найденная в результате
решения величина ускорения а0 может оказаться больше, чем
«о шах = P^./ps из (9.181).
2. Перелет космического аппарата с солнечным парусом между
орбитами планет. На межорбитальном участке перелета, лежащем
вне сферы действия планет, орбиты которых считаются компла¬
нарными и круговыми, движение происходит в центральном гра¬
витационном поле Солнца под действием солнечного давления.
Поэтому, полагая в уравнениях (9.183) R = г, Н = — g0rlr~*r
и обозначая через б1 угол установки паруса, составляемый нор¬
малью к теневой стороне паруса и радиусом-вектором г (который
здесь совпадает с направлением солнечных лучей i = г/г, т. е.
(n-i) = cos б) (см. рис. 9.49), приходим к следующим уравнениям
412
ДРУГИЕ ТИПЫ ДПИТАТЕЛЬНЫХ СИСТЕМ
[гл. о
плоского движения:
г = vr,
Vr =
ф = —
V (Г)
Ц- + («0 cos3 ^ — So) (-у-)2,
+ ао cos2#sin О (~r) »
(9.184)
где g0 — гравитационное ускорение от Солнца на радиусе rQ.
В работах [9.21—9.27] рассматривалось движение космиче¬
ского аппарата с солнечным парусом между орбитами планет при
постоянном угле установки паруса
# = const. Получен ряд приближенных и
точных решений (§§ 1 и 2 гл. 13), найдено
оптимальное значение постоянного угла
установки паруса. Эта группа аналити¬
ческих решений помогла составить первые
представления о возможностях использо¬
вания солнечного паруса для перелетов
между орбитами планет. Однако указан¬
ные решения обладают существенным не¬
достатком: краевые условия по коорди¬
натам и компонентам скорости на обоих
концах траектории не могут быть удовле¬
творены.
Решения вариационной проблемы о перелете космического
аппарата с солнечным парусом между орбитами планет (минимум
времени перелета Т при заданном а0) получены в работах [9.28,
9.29]. Следуя [9.29], перейдем в уравнениях (9.184) к безразмер¬
ным переменным, отнеся линейные размеры к г0, скорости —
к Y8ого» ускорения — к g0 и время — к ]/V0/gn-
о
а0 cos3 О — 1
’
а0 sin ф cos2 d
Рис. 9.49. Схема межпланет¬
ного перелета с солнечным
парусом.
гд,
vr
ф .а
9-
-6
VV
/* ’
Г
(9.185)
Оптимальное управление тЭ1 (t) должно обеспечить переход из
точки (г = 1, vr ^ 0, уф = 1) в точку (г = тд, vr = 0, уф = 7Д~1/2)
за минимальное время (угловое перемещение не фиксируется).
Для этого в соответствии с принципом максимума [9.4] управ¬
ление (t) должно доставлять абсолютный максимум функции
и = р*.
ф
г
Я О COS3 д — 1
+ Pv
а0 sin О cos2 Ф
+
+ PTVT +
ф
Г
(9.186)
* 4J
СОЛНЕЧНЫЙ ПАРУС
413
где система уравнений для импульсов р0pv рГ1 рг> имеет вид
Pvr =
Zp v
г СС
— Рг' Рг= —
• +
Pvrvl 2PvT 2a°Pvr COS3 ф Pvj’vvr 2a°Pv Sin COS2 ft
Pv = -75 H ^ Д h
Pv = 0, рф(Г) = 0.
(9.187)
Оптимальная программа угла установки паруса *0- (t) опре¬
деляется из условия
,cf V*Ar + «A.-Sf,
4Ч
(9.188)
После подстановки этого выражения О в уравнения (9.185),
(9.187) получается система семи дифференциальных уравнений.
5
45'
О
-45'
h
о.о
0,'3
02
0,1
о
0 0,4 0,8 jr
Г
Г0
/ Л
\
1)<р
TJy^
V(L^
\
?
180°-
120°-
60'
О
г_
Го
1,6
tfi
12
0,2 0,0 0,6 0,8 4-
Рис. 9.50. Параметры оптимального перелета с солнечным
парусом между орбитами Земли и Марса при а0 =
=2 • 10-3 м/ськ-, продолжительность перелета Т — 322 сут.
Можно показать, что в начальный момент времени pv = +1 при
ri > ro> Pvy = — 1 при гг <^ г0 (единица получается в результате
нормировки). При указанных граничных условиях решение на¬
ходилось численно, по методу Ньютона. На рис. 9.50 и 9.51 даны
414
ДРУГИЕ ТИПЫ ДВИГАТЕЛЬНЫХ СИСТЕМ
[ГЛ. О
примеры решения [9.29] при а0 = 2 -10 3 м/сек2 для перелета
с орбиты Земли на орбиту Марса и с орбиты Земли на орбиту
Венеры.
На рис. 9.52 приведен пример решения задачи перелета на
Марс [9.28] при а0 = 10'3 м/сек?. Помимо закона управления па¬
русом 'fl‘Opt(0i соответствующего граничному условию vn = 0,
УФ1 = г\\ там показан также закон 0 (t) для случая, когда
45'
0
-45°
-90'
N
L
V 1
0
О,У
5,8 £
т
0,3 Р/,80 0,2 00 0,6 0,8 jr° 0,7
Рис. 9.51. Параметры оптимального перелета с солнечным
парусом между орбитами Земли и Неперы при а0 = 2-10“*
м/сек-, продолжительность перелета Т = 194 сут.
величина скорости аппарата на орбите Марса не задана и опре¬
деляется из оптимальных соображений. Естественно, что в таком
«облете» Марса время перелета соответственно сокращается с
Т = 420 суш до Z' = 170 сут.
Для сопоставления на рис. 9.52 приведен еще результат
решения [9.22] с постоянным оптимальным углом установки
солнечного паруса й = (начальные и конечные условия по
скорости на этом решении не выполнены).
На рис. 9.53 приведена зависимость минимального времени
перелета с солнечным парусом между орбитами Земли и Марса
от величины ускорения а0 (сплошная кривая) [9.29]. Сравнение
с решениями для й = const (пунктирные кривые) [9.23, 9.24]
указывает на сильное влияние граничных условий по скорости на
время перелета. Поэтому область применимости решений с
постоянным углом установки солнечного паруса, которые не
С С) Л Н Е Ч НЕТ Й ПА Р УС
415
могут удовлетворять всем граничным условиям по скорости,
весьма ограничена.
Результаты численных расчетов оптимальных перелетов с
солнечным парусом с орбиты Земли на орбиты всех планет Сол¬
нечной системы приведены в табл. 9.1 для начального ускоре¬
ния а0 = 2 -10'3 м/сек [9.29]. ,,
В заключение этого пункта рас- J,c^m
смотрим иллюстрирующий пример.
Пусть требуется перевезти 1 т 300-
полезного груза с орбиты Земли
на орбиту Марса за 420 сут при
200
400 tfii/m
200
Ю0
11
\
V
1
\
\
\
\N
\
\i-ff
\ч
Рис. 9.52. Оптимальные программы уп¬
равления углом установим солнечного
паруса для перелета между орбитами
Земли и Марса при «0 = 10-3 .и/сек-'.
Сплошная кривая — оптимальный пере¬
лет с выходом на орбитальную скорость
Марса, штрих-пунктирная кривая —
перелет с оптимальной конечной ско¬
ростью, пунктирная кривая — перелет
с постоянным углом установки паруса.
м
о /*/ / ш ~ОуСеп
Рис. 9.53. Зависимость от величины r/ft
времени перелета с солнечным парусом
с орбиты Земли на орбиту Марса.
Сплошная кривая — точное оптималь¬
ное решение, пунктирные кривые —
перелеты с постоянным углом установ¬
ки паруса (граничные условия по ско¬
рости не выполняются).
минимальной площади солнечного паруса, выполненного из пласт¬
массы (рб = 5-10'4 г/см2). Тогда согласно данным рис. 9.52, 9.53
а0 = 10м/сек2, по формуле (9.182) S0 = 0,26-104 м2, что экви¬
валентно кругу диаметром 575 м. Общий вес аппарата при этом
равен 2,3 т.
Т а б л и ц а 9.1
Минимальное время перелета с солнечным парусом при ао = 2-10_3 м/сек2
с орбиты Земли на орбиты планет Солнечной системы
Название
планеты
Мерку¬
рий
Венера
М аре
10 пптср
Сатурн
Уран
Нептун
Плутон]
Т, годы
0,53
0,45
1/12
0,6
17
49
96
145
416
ДРУГИЕ ТИПЫ Д В И Г АТЕ Л .Ь И Ы X СИСТЕМ
Г гл. о
3. Выход космического аппарата с солнечным парусом из
сферы притяжения планеты. Задача о выходе космического ап¬
парата с солнечным парусом из поля тяготения планеты рассма¬
тривается в работах [9.30, 9.31] при следующих предположениях:
аппарат выведен на начальную круговую орбиту; гравитацион¬
ное поле центральное; поток солнечного света плоскопараллель¬
ный, постоянной интенсивности и направления.
В работе [9.30] исследован выход аппарата с солнечным пару¬
сом из сферы притяжения планеты в случае, когда начальная орби¬
та и траектория выхода лежат в плоскости эклиптики. Парус,
обе поверхности которого считаются идеально отражающи¬
ми, вращается вокруг своей оси с угловой скоростью, равной по¬
ловине угловой скорости обращения аппарата вокруг планеты
(рис. 9.54).
Уравнения движения записываются следующим образом (тенью
планеты пренебрегается):
где R — радиус орбиты планеты, g0 — гравитационное ускорение
на начальной орбите спутника планеты.
После перехода к безразмерным переменным и замены неза¬
висимой переменной t на полярный угол ф система уравнений
(9.189) численно интегрировалась от точки, соответствующей
начальной круговой орбите, до момента обращения в нуль пол¬
ной энергии космического аппарата относительно планеты.
Характер траектории показан на рис. 9.54. По мере разгона
аппарата орбита становится эллиптической, причем перигейное
расстояние меняется слабо. Набор нулевой энергии («отрыв»)
происходит в окрестности перигея.
Зависимость времени выхода Т от величины начального ускоре¬
ния а0 представлена на рис. 9.55 (сплошная линия) в безразмерных
переменных. В этих переменных результаты всех расчетов, про¬
веденных для различных значений а0 и г0, приблизительно
укладываются в логарифмическом масштабе на одну прямую,
разброс по безразмерному времени указан на рисунке. Число
оборотов до момента отрыва примерно равно 0,1 g0R2/a0R2^. Для
наглядности в табл. 9.2 приводятся размерные параметры выхода
из поля притяжения Земли [9.30]. Следует отметить, что влияние
тени Земли на характеристики выхода с солнечным парусом не
оценивалось в работе [9.30]. Очевидно, что траектория с учетом
(9.189)
СОЛНЕЧНЫЙ ПАРУС
417
этого влияния будет существенно отличаться от изученной, в
особенности на начальном этапе движения.
II
^ _
!§■-
I.
Рис. 9.54. Схема выхода аппарата с солнеч¬
ным парусом из сферы притяжения планеты
по траектории, лежащей в плоскости
эклиптики.
Рис. 9.55. Изменение времени выхода Т
аппарата с солнечным парусом из сферы
притяжения планеты в зависимости от
начального ускорения а0. Сплошная кри¬
вая — выход в плоскости эклиптики,
пунктирная — выход с орбиты, перпенди¬
кулярной к плоскости эклиптики.
Таблица 9.2
Параметры космического аппарата с солнечным парусом на траектории
выхода из сферы притяжения Земли
Полезная на-
| грузка Gn, m
Масса единицы
площади паруса
р5, г/см'2
Размер]
ijQ
«
S-"
в ч
о
SCQ
ы паруса
, 3
® 2
& &
о к
S .
2 2
« 5
Суммарный вес
аппарата G0, ш
Начальное уско¬
рение от солнеч¬
ного давления
а0, м/сек2
Продолжитель¬
ность маневра
Т, суш
Радиус началь¬
ной круговой
орбиты Го, КМ
Максимальное
удаление траек¬
тории до момен¬
та отрыва, км
о о о о о
10-*
2*10-4
3 10-4
10-*
10-4
106
106
106
2,45*105
105
1.12-103
1.12-103
1.12-10з
0,56-Ю3
0,36-Юз
1,1
2,1
3,1
0,35
0,2
0,85-10-2
0,44-10-2
0,3-10-2
0,67-Ю-з
0,46-10-2
54
112
119
73
105
7,25*103
7,25*103
7,25*103
7,25*103
7,25*103
4,2*105
6,1*105
7,62-Ю5
4,78*105
5,87*105
Для того чтобы траектория выхода не попадала в затененные
области и на ней не было участков движения навстречу солнечным
лучам, движение должно происходить вне плоскости эклип¬
тики. В работе [9.31] рассмотрена следующая схема выхода ап¬
парата с солнечным парусом из поля тяготения планеты.
27 Механика полета
418
ДРУГИЕ ТИПЫ ДВИГАТЕЛЬНЫХ СИСТЕМ
[ГЛ. 9
Плоскость х^) начальной орбиты перпендикулярна к
плоскости (я(1), #(2)) эклиптики (рис. 9.56). Уравнения движе¬
ния записываются в декартовой системе координат (#(1\ я(2\
связанной с Землей, которая предполагается неподвижной:
IR \2 g г2#^
х(г) — а0(-£) cos «(*> cos2 «W + °° ^ =0 (i = 1,2,3).
Г 2 (*(i))2
L г =1 J
(9.190)
Здесь cosaO) —направляющие косинусы нормали к теневой
стороне паруса, которые выбираются из локально-оптимального
условия максимума скорости приращения энергии — max (n-v):
cos a(1) = (3 cos p(1) + У cos2 p(t) -f- 8 ) / k, cosa(2) =2cosP(l)/&
(9.191)
(&2 = 6 cos2 p(1) + 6 cos P(1) У cos2 p(1) + 8 + 12, p(i) =
= arccos (x(t) /1 v I), i = 1,2,3).
В начале движения смещение по оси х^ компенсируется гра¬
витационной силой, траектория близка к плоской и является
квазикруговой. На этом участке
используется приближенное реше¬
ние [9.32], которое стыкуется с
численным решением системы
(9.190), (9.191), записанной в без¬
размерных переменных из [9.32].
Время достижения точки от¬
рыва по этому решению показано
на рис. 9.55 пунктирной линией.
Видно, что время ухода по схеме
работы [9.31] меньше, чем в слу¬
чае плоской траектории, исследо¬
ванной в работе [9.30]. Однако
этот факт нельзя рассматривать
как окончательное свидетельство
преимущества разгона в перпенди¬
кулярной к эклиптике плоскости,
так как в обоих случаях исследо¬
вались неоптимальные программы
угла установки паруса. Сравнение с временем межорбитальных
перелетов показывает, что для аппарата с солнечным парусом
время выхода из поля притяжения планеты составляет значи¬
тельную часть общего времени межпланетного перелета.
Рис. 9.56. Схема выхода аппарата
с солнечным парусом из сферы притя¬
жения планеты с орбиты, перпендику¬
лярной к плоскости эклиптики.
ИЗОТОПНЫЙ ПАРУС
419
В заключение данного пункта отметим также исследование
локально-оптимального управления углом установки паруса для
задачи выхода из гравитационного поля Солнца [9.33]. На
рис. 9.57 показаны полученные зависимости оптимальной ориен¬
тации паруса, обеспечивающие
наибольшее приращение эксцен¬
триситета исходной орбиты
g0 = 0,5 за один оборот. В ра¬
боте [9.33] также анализируют¬
ся вопросы устойчивости полета
аппаратов с солнечным пару¬
сом.
§ б. ИЗОТОПНЫЙ ПАРУС
1. Основные характеристики
изотопного паруса и формули¬
ровка вариационной задачи.
Как было показано в главах 2
и 3, максимальная тяга изотоп¬
ного паруса экспоненциально
падает по времени, а вес паруса
практически постоянен и пропорционален максимальной площа¬
ди паруса (т. е. максимальной тяге)
0 Р (t) пах e~U, Gx = уРmax* (9.192)
Регулирование тяги может осуществляться за счет изме¬
нения площади паруса («свертывание» паруса). Ниже будет пока¬
зано, что площадь (тяга) паруса в оптимальном режиме должна
быть максимально возможной. На ориентацию тяги ограничений
не накладывается.
Вариационную задачу сформулируем как задачу на макси¬
мальное быстродействие: обеспечить минимальное время выпол¬
нения маневра при фиксированной величине относительной по¬
лезной нагрузки [9.20].
Полный вес аппарата с изотопным парусом в процессе полета
практически не меняется, он складывается из двух компонент:
G (£)■== Gq = Gn -|- GK = const. (9.193)
Из уравнений (9.192), (9.193) следует, что, как и для солнеч¬
ного паруса, динамическая часть задачи содержит единственный
постоянный параметр — максимальное ускорение от тяги дви¬
жителя а0, величина которого определяется удельным весом
Движителя у и заданным значением GJG0
(в-*94»
Рис. 9.57. Оптимальное направление тяги
солнечного паруса, обеспечивающее мак¬
симальное приращение эксцентриситета
исходной гелиоцентрической орбиты е„=0,5
за один оборот вокруг Солнца.
27*
420
ДРУГИЕ ТИПЫ ДВИГАТЕЛЬНЫХ СИСТЕМ
[ГЛ. 9
Соответственно текущая величина ускорения аппарата от тяги
движителя определится соотношением
а = aaQe'xt {а 1). (9.195)
Здесь управляющая функция а (t) определяет, какая часть воз¬
можной тяги движителя используется.
Полная система дифференциальных уравнений, граничных
условий и ограничений на управляющие функции рассматривае¬
мой вариационной проблемы записывается в виде
t — 1, t (0) = 0, Т = min, }
г = у, г(0) = г0, г (Т) = Pi, J
. ^ [ (9.196)
у = аа^ет™ е + R, v (0) = уС1 v(T) = Vi |
(0<а(*)<1, |е(<)| = 1). j
Задача сведена к определению оптимальных законов управле¬
ния величиной тяги а (t) и направлением тяги е (t), которые обес¬
печивают минимальное время Т выполнения заданного маневра
при фиксированной величине максимального ускорения а0.
2. Состав оптимального управления. Программы a (t) и е (t)
определяются из условия абсолютного максимума гамильтоно¬
вой функции
Н = аа0е->'г(йг>-е) + (рв-Н) + (pr-v) + ри
Рг> = Рг» Рг = jfp (Ро'К)»
Р( = А,(р„-е)аа0е-х', pt(T) = — 1.
(9.197)
Единичный вектор е (£), входящий в первый член функции
Я, должен быть выбран так, чтобы скалярное произведение
(Рг? • е), перед которым стоит неотрицательный коэффициент, было
максимально
(IVе) = pv или е = рv/pv, (9.198)
т. е. вектор тяги должен быть направлен по вектору р^. Из ана¬
лиза того же члена функции Я с учетом условия (9.198) следует,
что управляющая функция Ъ (t) всюду должна быть максималь-
но^возможной
a (t) == 1. (9.199)
3. Модельная задача. В качестве иллюстрирующего примера
рассмотрим модельную задачу перелета за минимальное время
с помощью изотопного паруса между двумя точками покоя на
расстояние I в бессиловом поле (Н =0, v0 =0, vx =0, | гх — г0| = /).
§ 6]
ДВИГАТЕЛЬ С СОЛНЕЧНЫМ ИСТОЧНИКОМ ЭНЕРГИИ
421
Так как для однородного гравитационного поля импульсру
является линейной функцией времени (см. (9.197) при й = 0), то
вектор тяги е направлен либо по скорости, либо против нее и может
только один раз изменить направление в некоторой промежуточной
точке ^ интервала [О, Т] (рис. 9.58). Интегрирование уравнений
(9.196) с учетом (9.198), (9.199) и указанного свойства опре¬
деляет связь отношения tJT и относительного расстояния
/Я2/а0 с характерным временем задачи т = ЯГ (рис. 9.59):
Отметим, что характерное время т является отношением вре¬
мени выполнения маневра Г к периоду полураспада изотопа
1/Я. Последнее соотношение (9.200) через формулу (9.194) опре¬
деляет минимальное время Г в зависимости от полезной нагрузки
GJG0 параметров паруса Я, у и маневра Z.
§ 6. ДВИГАТЕЛЬ (^СОЛНЕЧНЫМ ИСТОЧНИКОМ
ЭНЕРГИИ
Рассматривается задача о доставке максимального полез¬
ного груза с помощью идеального двигателя ограниченной мощ¬
ности, использующего солнечную энергию [9.34]. Отличитель¬
ная особенность такой двигательной системы состоит в том, что
ее максимальная мощность зависит от расстояния аппарата до
Солнца. Аналогично случаю постоянной максимальной мощно¬
сти определяются оптимальные весовые соотношения, выделя¬
Рис. 9.58. Оптимальное управ¬
ление тягой изотопного паруса
в задаче перелета между двумя
точками покоя в беосиловом
ноле.
Рис. 9.59. Момецт изменения направления
тяги tJT (пунктирная кривая) и относи¬
тельное расстояние 1№/а0 (сплошная кри¬
вая) в зависимости от характерного вре¬
мени г = А/Г —перелет между двумя точ¬
ками покоя с изотопным парусом.
(9.200)
422
ДРУГИЕ ТИПЫ ДВИГАТЕЛЬНЫХ СИСТЕМ
[ГЛ. о
ется вариационная задала о построении оптимальной програм¬
мы реактивного ускорения и выборе расчетного расстояния до
Солнца. Приводятся приближенные решения для бессилового и
центрального полей.
1. Формулировка задачи оптимизации. Вес двигательной
установки ограниченной мощности, использующей солнечную
энергию, можно представить в виде суммы двух составляющих (если
не считать веса движителя): веса кон¬
центратора солнечной энергии (зеркала,
линзы Френеля) или плоского преоб¬
разователя (фотоэлементы, термоэлект¬
рические генераторы) и веса преобразо¬
вателя тепловой энергии в электриче¬
скую. Первая составляющая пропор¬
циональна площади S захватываемого
потока солнечного излучения, вторая —
максимальной МОЩНОСТИ iVmax» которую
может перерабатывать преобразователь.
Таким образом, вес двигателя с сол¬
нечным источником энергии записы¬
вается в виде
Gx=a7Vmax+P^ (ос, Р = const). (9.201)
<v
'max
О
Rt я*
Рис. 9.60. Зависимость от рас¬
стояния до Солнца максималь¬
ной полезной мощности двига¬
тельной установки с солнеч¬
ным эиергоисточциком.
Плотность потока солнечной энергии убывает обратно пропор¬
ционально квадрату расстояния от СолнцаЗ}^ (.R) = 1,4 (R^/R)2
квт/м2. Максимальная мощность Nm3LX достигается при прибли¬
жении к Солнцу на некоторое расстояние которое будем на¬
зывать расчетным: Nmах = 91^(Д*) 8у\, где ц — коэффициент пре¬
образования солнечной энергии в электрическую. Если обозна¬
чить через N0 мощность силовой установки на орбите Земли, то,
пренебрегая изменением к.п.д., можно представить =
= (i?5/i?JW0. При дальнейшем приближении к Солнцу мощ¬
ность должна оставаться постоянной, так как преобразователь
тепловой энергии в электрическую не может работать при мощ¬
ности, превышающей максимальную расчетную, т. е. на расстоя¬
нии i?+ от Солнца должно быть введено ограничение на мощность
силовой установки (рис. 9.60):
N^<N(H) {{Bd/R)2No
((R6/RJ2 N0 = Nmax при R < Rt,
при R > Rt.
(9.202)
Выражение (9.201) можно представить в виде
Gx = о,[1 + (R6/R,)2 %\ N0, (9.203)
§ 6]
ДВИГАТЕЛЬ С СОЛНЕЧНЫМ ИСТОЧНИКОМ ЭНЕРГИИ
423
где as = Р/т]3?^ (R $) — вес концентратора или плоского преобра¬
зователя на единицу мощности, % = a/as. Следует отметить, что
в системах с плоскими преобразователями величина
поэтому можно считать GK = <xsN0 и = i?$.
Ставится задача отыскания максимальной полезной нагрузки
при выполнении заданного маневра; время выполнения маневра
Т, начальный вес аппарата G0, удельные веса as и % фиксирование
Предполагается, что движитель идеальный, т. е. вся мощность,
подводимая к движителю, превращается в мощность реактивной
струи, а параметры движителя — массовый расход рабочего
вещества и скорость истечения могут меняться в неограниченных
пределах. В этой задаче нужно указать оптимальные значения
весов G*, о и расчетного расстояния Д*, а также построить
оптимальные программы вектора реактивного ускорения а (t) и
мощности Nsj (t).
2. Оптимальные весовые соотношения и расчетное расстояние
до Солнца. Предварительно оценим величины сил, действующих
на аппарат. Покажем, что сила солнечного давления мала по
сравнению с тягой и гравитационными силами. На поверхность
преобразователя в единицу времени падает поток солнечной ра¬
диации с энергией 31^ S; при этом аппарату сообщается импульс,
не превосходящий величины 2Sl£S/c (здесь с = 3-108 м/сек —
скорость света). Импульс, сообщаемый аппарату двигателем,
использующим солнечную энергию, не меньше величины
29^5т|/УП1ах (здесь Fmax — 105 м/сек — максимальная ско¬
рость истечения реактивной струи). Сравнение показывает, что
последняя величина по крайней мере на два порядка больше
первой.
Для ускорения от солнечного давления справедлива оценка:
= 2Sl^S/cG 2<Sl^S/cGK. Воспользовавшись выражением
(9.201), последнее неравенство можно "представить в виде:
<С 2 [3l^(i?5)/cp](i?5/i?)2. При Р = 0,3 кГ/м2 ускорение от
солнечного давления 3 • 10-5 (R^/R)2 м/сек2, что по крайней
мере на два порядка меньше гравитационного ускорения от
Солнца, равного 5,92-10"3 (R^/R)2.
Исходя из полученных оценок, сила солнечного давления в
дальнейшем в расчет приниматься не будет.
Аналогично случаю движения с постоянной максимальной
мощностью можно независимо от уравнений движения проинтег¬
рировать уравнение, описывающее изменение веса аппарата,
и получить выражение для полезной нагрузки (§ 1 гл. 4)
(9.204)
424
ДРУГИЕ ТИПЫ ДВИГАТЕЛЬНЫХ СИСТЕМ
[ГЛ. о
Отсюда мощность iVv, как и раньше, должна быть макси¬
мально возможной
Воспользовавшись выражениями (9.202) и (9.203), находим,
что для фиксированного значения функционала
(N = (R&/R)2 при R < N = СД6/й)2 при Л > Л J
максимум Gn (Gy) имеет место при GyJG0 = "jAD — Ф и равен
Таким образом, задача определения оптимальных весовых
соотношений может быть решена, если известна величина функ¬
ционала /. Последний не зависит от весовых соотношений и
определяется, если известна траектория и параметр i?#. Для дви¬
жения с постоянной мощностью множитель перед интегралом
в выражении (9.206) и знаменатель подынтегрального выражения
были равны единице (4.10).
Задача сводится к нахождению такой величины параметра
и такой программы реактивного ускорения а (t), чтобы при
перемещении между начальной (r0, i*0) и конечной (гх, А) точками
за время Т функционал J был минимален. Далее рассмотрение
проводится в гелиоцентрической системе координат, поэтому
считается R = г, R^ ~ и R§ = г0.
Покажем, что оптимальная величина параметра г# заключена
внутри отрезка [r0, rj. Обозначим через J (г) минимальное
значение функционала /, которое зависит от параметра как
явным образом, так и через посредство функций а (t, г) и N (г, rj,
входящих в подынтегральное выражение. Пусть для определен¬
ности г0<^г.; тогда при изменении параметра вне отрезка
[r0, rj функция J (г) будет иметь вид
N,=N (R).
(9.205)
(9.206)
GJG0 = (1 - УФ)2, Ф = (as/2g)J. (9.207)
Г
Т
[1 + (г«/г.)2 X] /о при г < г0 (/„ = min ^ (т*//*п)а a-dt )
' п <i\ *
о = mm \
a(t) g
а (0 о
Т
[(r./r<>)2 + X) Л при г, > 7*1 (Л = min ^ a2d«)
' г/ m v 7
! — mm \
a (О о
(9.208)
ДВИГАТЕЛЬ С СОЛНЕЧНЫМ ИСТОЧНИКОМ ЭНЕРГИИ
425
(предполагается, что вся траектория г (t) лежит внутри интер¬
вала [r0, rj). Очевидно, при этом выражения /0 и Jx должны
оставаться постоянными; поэтому, как следует из приведенных
формул, J (rj с увеличением г# убывает при ^ г0 и возрастает
при г* > гх.
В точках г0 и гг функция J (гф) непрерывна и имеет односто¬
ронние производные
(■£L - - (£),.«. - £<9-209>
Можно показать, что производная функции J (гф) непрерывна
в указанных точках. В самом деле, пусть = г± — Агщ; тогда
справедливо неравенство
I (^^)! " < I ЛГ(г,Г-Аг.)' <9-210>
О о
Обозначим функции а (t), минимизирующие правую и левую
части неравенства, соответственно через al (t) и а2 (t)] тогда
S «<S AO<S * (9-211>
{.о 0 0
Нетрудно показать, что
a^clt
1
= jj(rri-Ar* )' a\dt + о (Ar.); (9.212)
J ^(r.rj—Дг.)
о о
тогда из неравенства (9.211) следует
т т
mint ггг—a-dt--r—г = rninC ( Г1~ А'« \ a^t _^0(ДГ ) (9.213)
а (О J ^(г.п-Дг.) Q(,)tH Гс / ^ \ .J \ )
w о о a
Воспользовавшись выражением (9.213), можно непосредствен¬
но вычислить производную dJ/drm в точке г± — 0. Сообщив
в точке г± приращение А г, и перейдя к пределу при А г, —► 0,
получим соответствующее выражение из (9.209). Аналогичным
образом можно показать непрерывность производной в точке
г. = ^0 + 0-
Таким образом, на отрезке [r0, rj функция J (rj, оставаясь
положительной, меняет знак производной с минуса на плюс.
Отсюда следует, что минимум функции J (rj достигается в не¬
которой точке r*opt <С ^1* Кроме того, зная производные
dJ/dr0 в точках г0 и гг, можно указать точку, близкую к r^opt>
426
ДРУГИЕ ТИПЫ ДВИГАТЕЛЬНЫХ СИСТЕМ
[ГЛ. 9
например абсциссу точки пересечения касательных к графику
J (rj в точках г0 и rv
3. Уравнения оптимальной траектории. Рассмотрим плоское
движение в центральном поле Солнца. Уравнения движения ап¬
парата, записанные в полярных координатах, имеют вид (П.8)
г = vr, гср = гф, vr = ar-\- vl/r — к/r2, гф = аф — гггф/г.
(9.214)
Требуется найти траекторию*, на которой достигается мини¬
мум функционала
J = I -vvh (tУ "р-r N «-• о =
О
= (?fj при r>r.) (9.215)
{здесь rt — фиксированная величина). Уравнения Эйлера для
задачи (9.214), (9.215) таковы (ср. (5.13)):
при г0 < г < г,
ат =
аф — —
у (а’ + а%) + ат (-2L - А) —— v-у-(-£*-) _
афгг — 2аггф + v j
при
ат =
<2Ф = —
ф г
1/2, 2ч, / & \
У (а-г + аф) + ат 1 — тг)
_2 arvr
a^vT — 2агг>ф + v (-у)
(9.216)
где к и v — интегралы системы (константы изопериметричности,
соответствующие заданному времени движения и заданному
угловому перемещению). При г = частная производная по г
подынтегрального выражения функционала (9.215) терпит раз¬
рыв. При этом для оптимальной траектории выполняются усло¬
вия Вейерштрасса — Эрдмана
aT (г. — 0) = аг (г. + 0), аг (у + 0) — аг (г, — 0) = — (2arvr/r),-m, j
«ф (г. — 0) = а9 (г. + 0), а<р (г, + 0) — аф (г, — 0) = — (2avvr/r r>. j
(9.217)
ДВИГАТЕЛЬ С СОЛНЕЧНЫМ ИСТОЧНИКОМ ЭНЕРГИИ
427
Уравнения (9.214), (9.216) вместе с двумя первыми интегра¬
лами X и v имеют в сумме 14 порядок. Краевые условия и усло¬
вия Вейерштрасса — Эрдмана дают 14 условий для определения
траектории.
Точка, в которой vr = 0, как и для системы (5.13), является
особой точкой типа «узел». Остается в силе и свойство инвариант¬
ности уравнений оптимальной траектории относительно пре¬
образований замены знака (5.16) и растяжения (5.15).
4. Приближенный метод построения оптимальной траектории.
Для решения задачи о минимуме функционала (9.215) можно
использовать итерационный процесс. Опишем его на примере
модельной задачи о перемещении между точками покоя в бес¬
силовом поле
х = и, и = а, х (0) = х0. и (0) = 0, х (Т) = I + х0,
и (Т) = 0. (9.218)
Определяется траектория, оптимальная в смысле минимума
функционала
J = <9-219>
о
(для простоты предполагается, что хш = х0). Уравнение Эйлера
в рассматриваемой задаче имеет вид
(ах2) + а2х = 0. (9.220)
Заменим функцию N = (х0/х)2 некоторой известной функцией
времени (£), принимающей на краях интервала те же значе¬
ния, что и N (х, х0): (0) = 1, £(°> (Т) = [xJ{xQ + 0^2*
Уравнение Эйлера для нового функционала примет вид
~~dt2 ( £<°)(*)') = (9.221)
Это уравнение легко интегрируется
t
з(0) (t) = Cl + c2t + 5 (т) (x— т) (c3 + c41) dt, (9.222)
0
где cx, . . . , c4 — постоянные интегрирования. По найденной
траектории определяется новая функция N (t), xQ\ = (t).
Повторяя описанную процедуру, найдем новое приближение
-£(1) (it) и т. д.
428
ДРУГИЕ ТИПЫ ДВИГАТЕЛЬНЫХ СИСТЕМ
[ГЛ. 9
В качестве нулевого приближения была использована ли¬
нейная функция £(0) (0 = 1 — bt, где Ъ = I (2х0 + 1)/(х0 + О2 Т.
Для дальнейших шагов функции (t) заменялись их прибли¬
женными выражениями с помощью интерполяционного многочле¬
на Ньютона, причем число узлов интерполяции увеличивалось
на каждом шаге процесса. Это дало возможность каждый раз
Оценим полученный резуль-
Рис. 9.G1. Последовательные приближения ТаТ СЛвДуЮЩИМ обраЗОМ. ИсКО-
равленис a (t) при постоянной мощности. ВуЮЩвЙ ОПТИМаЛЬНОМу ДВИЖв-
НИЮ С ПОСТОЯННОЙ МОЩНОСТЬЮ
'—-19,8 12Т~3. С другой стороны, зная производные минимального
значения функционала (9.215) по параметру в точках х0 и
х0 + I (см. п. 2) и значение его в точке х# = х0 + I, равное
2712Т'3, находим, что min / ^ 1812Т~3. Таким образом, опи¬
санный приближенный метод дает возможность построить тра¬
екторию, весьма близкую к оптимальной.
Рассмотренная простейшая модельная задача позволяет вы¬
явить особенности программы реактивного ускорения при полете
по оптимальной в смысле функционала (9.219) траектории.
Характер изменения ускорения в данном случае существенно
отличается от линейного закона (рис. 9.61), который соот¬
ветствует оптимальному движению с постоянной мощностью.
Получившийся закон изменения a (t) имеет простое физическое
а
доводить интегрирование до
конца.
На рис. 9.61 приведены гра¬
фики функций aS{)(t), соответ¬
ствующие последовательным
приближениям; для сравнения
пунктиром показан закон изме¬
нения а (t) для движения с по¬
стоянной мощностью (гранич¬
ные условия xQ и х0 + I при¬
мерно соответствуют средним
радиусам орбит Земли и Марса).
Значение функционала (9.219),
найденное описанным методом,
равно ~ 19 РТ'г.
Отметим, что для движения
с постоянной мощностью N=1
и N == [х0! (х0+1)]2 минималь¬
ные значения функционала рав¬
ны 12/2Г_3 и 27
ДВИГАТЕЛЬ С СОЛНЕЧНЫМ ИСТОЧНИКОМ ЭНЕРГИИ
429
толкование: высокий уровень ускорения выгодно поддерживать
там, где более высокая мощность силовой установки, т. е. в на¬
чале пути; торможение происходит при более низкой мощности,
и поэтому уровень ускорения в конце пути должен быть меньше,
чтобы не получить большого расхода рабочего вещесава.
5. Расчет межорбитального перелета с помощью транспорти¬
рующей траектории. Для приближенного построения оптималь¬
ной траектории в центральном поле воспользуемся методом
транспортирующей траектории (§ 2 гл. 5) в сочетании с изложен¬
ным в предыдущем разделе ингерационным процессом.
Запишем систему, описывающую движение центра масс ап¬
парата в виде
где U — потенциал гравитационного поля. Для нулевого при¬
ближения функционал (9.215) имеет вид
где ах, ау, az — компоненты вектора ускорения от тяги в декар¬
товой системе координат.
Уравнения Эйлера для задачи (9.223), (9.224) таковы:
Представим траекторию движения в виде: г (£) = ** (t) + р (£),
где г" (t) — известная траектория, удовлетворяющая части крае¬
вых условий, например по г (транспортирующая траектория),
а р г*. Транспортирующая траектория г* (t) описывается
уравнением
Подставляя г = г* + р в уравнение (9.225) и пренебрегая
малыми величинами второго порядка, получаем систему
г = а + grad U,
(9.223)
(9.224)
Y) — Afi = О, TJ = а/|<°> (t),
(9.225)
г* — grad Ф = 0.
(9.226)
"— А*р = а, V) —= 0 (а = Б<°>(0ч), (9-227)
где U* и А* — значения потенциала U и матицы А вдоль тран¬
спортирующей траектории.
430
ДРУГИЕ ТИПЫ ДВИГАТЕЛЬНЫХ СИСТЕМ
[гл. S'
Если в уравнениях (9.227) положить А = 0 (что соответствует
малым отклонениям траектории от транспортирующей, когда
можно пренебречь возмущениями гравитационных сил по срав¬
ЧУ/7
у10>т
г
/4/
1
( /
\ 1
/77V
N
и
/
1 W
\ \
\ \
\\
ч\
\>
т
9
/а
А \
\ \
\ \
L
щ
д10~Ъм
\!
~6
\Ю5
-4
~2 1
0
-2—
-4—
-6—
V57
\\
//
//
//
//
\ \
\ N
\
/ /
/ /
/
*0/ \
\М,4
~Г
/
нению с тягой), то уравнения¬
ми оптимального движения в
системе координат, поступатель¬
но перемещающейся вдоль транс¬
портирующей траектории, будут
р = 0, ч = °- (9.228)
В этом приближении опти-
Рис. 9.G2. Оптимальная траектория пере¬
лета орбита Земли — орбита Марса за
212 суток с двигательной установкой
ограниченной мощности и солнечным эцер-
гоисточцпком. Пунктирная кривая— с дви¬
гательной системой постоянной мощности
(транспортирующая система координат).
Рис. 9.G3. Оптимальная программа
управления ускорением от реактивной
тяги при перелете орбита Земли —
орбита Марса с двигательной установ¬
кой ограниченной мощности и солнеч¬
ным эпергоисточпиком (T = 212 сут.),.
мальный закон управления тягой имеет вид (на i-м шаге
процесса)
а«> (<) = £№ (<) (ef°f + 4) (9.229)
(с!г) и с— постоянные интегрирования). Отсюда р<0 (t) на-
ходится квадратурами или аналитически, если (t) имеет
удобный для интегрирования вид.
В качестве примера рассмотрим траекторию полета к Марсу,
оптимальную в смысле минимума функционала
т
/ = (г. = гп). (9.230)
о
Для простоты предполагается, что траектория плоская. В ка¬
честве краевых условий взяты условия, приведенные в § 2 главы 5
ДВИГАТЕЛЬ С ИЗОТОПНЫМ ИСТОЧНИКОМ ЭНЕРГИИ
431
(п.5)? для полета к Марсу продолжительностью Т = 212 суток в
плоскости ЭКЛИПТИКИ.
В качестве функции £(0) (t) берется приближенное выражении
N [г (t), rj, соответствующее траектории полета к Марсу с
двигателем постоянной мощности, приведенной на рис. 5.8. На
рис. 9.62 показана траектория полета в транспортирующей си¬
стеме координат, для сравнения пунктиром показана траектория
полета с двигателем постоянной мощности. Закон управления
а (0 представлен на рис. 9.63. Величина функционала J =
= 16,4 м2!секъ. Для движения с постоянной мощностью N ~ 1
и N ее (rjr-^)2 минимальные значения функционала соответственно
равны 9,25 мУсек* и 25,1 м2/сек3.
Зная величины минимальных значений функционала при
г, = г0 и при гл = гх, можем приближенно определить оптималь¬
ные значения параметра г# и функционала J (rj (п. 2): при
а = 1 кПквтп, (3 =1,5 кГ/м2, г\= 0,1 оптимальное расчетное
расстояние до Солнца r^pt ~ 175 -106 км (г0 = 150 -106 км, =
= 250-106 км), минимальное значение функционала J (r opt) =
= 17 м2!секъ (J (г0) = 18 мУсек*).
§ 7. ДВИГАТЕЛЬ С ИЗОТОПНЫМ ИСТОЧНИКОМ
ЭНЕРГИИ
1. Характеристики двигателя и формулировка вариационной
задачи. Максимальная мощность двигателя с изотопным источ¬
ником энергии, так же как максимальная тяга изотопного паруса
(§ 5), экспоненциально падает со временем:
0 < N < N0e~lt, (9.231)
где N о — максимальная мощность реактивной струи в началь¬
ный момент времени t — 0, X — параметр, характеризующий
падение мощности по времени (1/Х — период полураспада изотопа).
Как показано выше, для двигательных систем ограниченной мощ¬
ности при включенном движителе всегда выгодно максимальное
использование мощности. В этом случае основные параметры дви¬
гательной системы связаны соотношениями (ускорение рабочего-
вещества происходит без потерь)
| N = N0e~xt, Р = qV, N = V2gF2. (9.232)
Рассматривается движитель с ограниченным диапазоном регу¬
лирования скорости истечения
0<F(f)«Fmax, (9.233)
в предельном случае Fmax —* 00 > чт° соответствует идеальному
регулированию.
432
ДРУГИЕ ТИПЫ ДВИГАТЕЛЬНЫХ СИСТЕМ
[гл. о
Вес двигательной системы определяется начальным значением
мощности
G* = a N0. (9.234)
Задача о доставке максимального полезного груза записывается
в виде
G, = — Ga (0) + Gq (1) = max,
G, = 0, +йи(0) = 1, Gx(l) = opt,
r = V, r (0) = r„, r (1) = n,
W =Y^ 7C+Gjv e6 + R; v(°)=vo- v(l)=Vl
f/ci = ' ф = Yr* . 0 < F (<X 1,6 (i) = 1 или 0, |e (*)| = 1
^ max &
(9.235)
Здесь все величины безразмерные: веса G0, GK отнесены к на¬
чальному весу, время t и период полураспада 1/А к полному
времени движения, радиус-вектор г — к характерному рас¬
стоянию Z, скорость движения v — к ИТ, скорость истечения —
к l^raax-
Записанная вариационная задача соответствует стандартной
формулировке проблемы Майера: требуется определить управле¬
ния е (£), б (t), V (t) и параметр GK так, чтобы обеспечить макси¬
мум конечного значения фазовой координаты G0 (1) = GK. Далее
рассматривается решение этой задачи для двух модельных ма¬
невров в бессиловом поле.
2. Набор модуля скорости. В качестве характерного расстоя¬
ния возьмем ихТ, где их — заданное приращение модуля скорости.
Комбинация Ф запишется в виде Ф = (a/2g)u12T~1, граничные
условия будут х (0) = 0, х (0) = 0, х (1) = opt, х (1) = 1.
Согласно принципу максимума оптимальные управления
е (t) = +1, б (t), V (t) должны доставлять абсолютный минимум
гамильтоновой функции
(9.236)
где импульсы р определяются следующей системой дифференци¬
альных уравнений:
Рх = 0» Ри = Рх
JX1
ki PueY)GKe
Р°- W V{G' + Gxy
Aj Pue (0e X< . klPae U
P*- — Pa ф у (G , q j + y-2
(9.237)
ДВИГАТЕЛЬ С ИЗОТОП I И,I'M ИСТОЧН ИКОМ ЭНЕРГИИ 433
с граничными условиями
Pz (0) = Рл (0), рх (1) = 0, рх (1) = 0, /?0 (1)=—1. (9.238)
Оптимальные управления в рассматриваемой задаче определяют
ся следующими соотношениями:
Из анализа гамильтоновой функции Н и краевых условий сле¬
дует, что найденные управления е (t) и б (I) в задаче о наборе
заданного модуля скорости остаются такими же при любом режиме
регулирования двигателя.
В момент времени tx скорость истечения выходит на границу
Так как этот момент времени в зависимости от параметров мо¬
жет принимать различные значения, то при решении урав¬
нений (9.235), (9.237) получаются три вида выражений для функ¬
ционала G
В случае (9.241) управление V (t) граничное: V (t) е= 1; случай
(9.242) соответствует идеальному регулированию: V (t) = Fopt (05
в случае (9.243) V (t) = Fopt (0 при 0 < t < t± и V (t) = 1 при
с (/) = 1, б (0 = 1,
jyopt при F0J)t < 1
г<‘> = и
2 У/с,.Ф (С3 -|- GJ
при Troi,t > 1
(9.239)
J opt Cl) 1 •
. (9.24.0)
при ti^O: G- — е~л /с*ф — , (9.241)
1 — е д
при <1> 1: 6’, = (1 - У —^ ф)2, (9.242)
\ 6 /
при 0 < < 1: G* = -Г Г1 +
М 1 — е
+ У hФ — 1" fv4r + h 1 2{-) ]\ (9.243)
23 Механика полета
ДРУГИЕ ТИШ,I ДВИГАТЕЛЬНЫХ СИСТЕМ
[ГЛ
Оптимальное значение веса двигателя G* составит
2Х
М1- О
х { 1 Y
/а,ф — I — in;
\ -
1 — е-х
к
! 1 , кг 1-е-'
\.Т "и ~г
+ (|+*>iirLn- <02,"‘
Результаты полученного
решения приведены на рис.
9.64, где показана зависи¬
мость относительного полез¬
ного груза от XT при наборе
модуля скорости с идеально
регулируемым движителем
(0<F = Fopt<oc).
3. Перемещение между
точками покоя. Для второй
модельной задачи — перелег
между двумя точками покоя,
расположенными на расстоя¬
нии I.— аналитическое реше¬
ние получается только для
идеально регулируемого дви¬
жителя.
Полная система дифферен¬
циальных уравнений движе¬
ния, изменения веса и соп¬
ряженных импульсов в безразмерных переменных имеет вид
[‘но. 9. о Л. Влияние падения мощности реак¬
тивной струи по времени на величину отно¬
сительной полезной нагрузки Ол/О0 в задаче
набора заданного модуля скорости н, за
время Т (КГ — отношение времени выполнения
маневра к периоду полураспада изотопа).
X -- U,
12
с.
-'/Л
и =
Ф V (G -Г )
19 G
(‘3 •' е
(]у — 0,
п • • е-*-'
Р, = 0, Ра = - рх, р, - mv,n , • „ 6,
-и
Ру. Рз
12рир (1)К
ФУ(С0 -гг;х)
ФУ {Ga + Суу
-у л
/V
ФУ
^ (9.245)
§ 7] ДВИГАТЕЛЬ С ИЗОТОПНЫМ ИСТОЧНИКОМ ЭНЕРГИИ 435
функция Гамильтона следующая:
12G.Ae~Xi ( pue(l) Ра\А , /п 0/R,
н= фу [о^гдх~у-)ь + Р*и’ (9-246)
где Ф = (a/2g) 1212Т 3.
Граничные условия для импульсов и координат
Ро(°) = р*(0). Ро(1) = — г Рх. (1) = о, |
Ga (0) + Gx (0) =, 1, X (0) 0, и (0) = 0, Ж (1) = 1, и (1) = 0 J
(9.247)
полностью определяют задачу.
Минимум гамильтоновой функции достигается при следую¬
щих оптимальных управлениях:
e(t)=r_— sgn Ри, 6 (t) = 1,
v 2 fa(g, + Gx)
/>U
(9.248)
Максимальная полезная на¬
грузка определяется следующей
зависимостью от функционала Ф:
= (\ V У
\ Г 12 ((1 — е-*)2 — К2е~'‘ ])
(9.249)
На рис. 9.65 показана зави¬
симость от XT величины относи¬
тельного полезного груза в за¬
даче перелета между двумя точками покоя с идеально регули¬
руемым движителем. Данные рис. 9.64 и 9.65 показывают, что
падение мощности реактивной струи по времени заметно сказы¬
вается па величине полезной нагрузки при отношении времени
выполнения маневра к периоду полураспада порядка XT > ОД.
Рис. 9.Cj. Влияние падения мощности ре¬
активной струи по времени на величину
относительной полезной нагрузки Gn/G0
в задаче перелета между двумя точками
покоя па расстояние / за время Т.
28*
ГЛАВА 10
МОДИФИКАЦИИ КРИТЕРИЯ ОПТИМАЛЬНОСТИ
В предыдущем изложении при формулировке вариационных
задач использовался весовой критерий оптимальности — максимум
полезного веса при заданном стартовом; динамический маневр
фиксировался. Каждому набору параметров маневра отвечали
свои значения параметров двигательной системы, обеспечиваю¬
щие доставку максимального полезного веса.
Здесь формулировка проблемы оптимизации подвергается из¬
менениям в двух направлениях. Первое — весовой критерий за¬
меняется на критерий стоимости (§ 1, [10.1]). Второе — пара¬
метры двигательной системы выбираются не для одного маневра,
а для диапазона маневров (§§ 2 и 3). Распределение потребного
числа выполнений маневров по типам либо фиксируется (§ 2,
[10.2]), либо считается неизвестным, в последнем случае исполь¬
зуется игровой подход (§ 3, [10.3]). Для каждого конкретного ма¬
невра при выбранных универсальных параметрах двигательной
системы ищется оптимальный запас рабочего вещества (§ 4, [10.4]).
§ 1. МИНИМИЗАЦИЯ СТОИМОСТИ ВЫПОЛНЕНИЯ МАНЕВРА
Если один и тот же маневр предстоит выполнять многократно,
то весовой критерий целесообразно заменить критерием стоимо¬
сти. Стоимость выполнения маневра складывается из стоимостей
основных компонент аппарата; последние считаются пропор¬
циональными соответствующим весам.
1. Формула стоимости. Стоимость С выполнения маневра
слагается из следующих компонент:]
Здесь С0 — стоимость вывода на исходную орбиту (принимается
пропорциональной начальному весу G0 = GA + GtJ0 + GД:
Сх — стоимость двигательной системы (принимается пропорцио¬
нальной весу двигателя б?*):]
С = С0 + Сх + + Се.
(10.1)
(10.2)
Сх = c,Gx;
(10.3)
§ 1] МИНИМИЗАЦИЯ СТОИМОСТИ ВЫПОЛИ 1Н111Я МАНЕВРА 437
Cv. — стоимость запаса рабочего вещества вместе с баками (при-
нимается пропорциональной начальному весу рабочего веще¬
ства G,..ft):
С:, - c.uG,y); (10.4)
Се — прочие затраты, не зависящие от весовых параметров
аппарата. Коэффициенты с0, с[}, и стоимость Се считаются по¬
стоянными и заданными.
2. Критерий оптимальности. В качестве критерия оптималь¬
ности принимается стоимость доставки единицы полезного груза
(см. (10.1))
!с - C/Gn (10.5)
или с учетом соотношений (10.2) —(10.4) между стоимостью и весом
С -- —(С()С(, -j- CyGy -[- Cp.Gjj.o -р Се). (10.6)
Начальный вес G0 задан, поэтому вместо (10.6) вводится следую¬
щий функционал, характеризующий стоимость выполнения ма¬
невра:
1-1- А■ -f s„G„n
S = ~-c\ -l,Г • <10'7)
где веса Gx и G;J.() считаются отнесенными к начальному весу G0,
коэффициенты sx и — заданные величины:
** -= т-4тс-- > ^ - 7W > °- (10-8)
Функционал (10.7) отличается от функционала (10.6) фиксиро¬
ванным положител ьным множителем
с ^ (с0 + Се/ед (10.9)
поэтому задача на минимум S эквивалентна задаче на минимум с„
3. Формулировка вариационной задачи. В рамках принятых
предположений формулировка задачи оптимизации аналогична
изложенной во введении ко второй части, меняется только функ¬
ционал.
Введем дифференциальное уравнение, описывающее измене¬
ние функционала (10.7) по времени, и запишем рассматриваемую
438 МОДИФИКАЦИИ КРИТЕРИЯ ОПТИМАЛЬНОСТИ 1ГЛ. 1 и
вариационную задачу в постановке Майера (ср. (II.5)):
л 1 + V + (sx “ s[j) G'K о ^ + sxGx о/т\
S — q (1 — — Д^1Л.)2 ’ 1 —Gy ’ S(T) — \\\m,
AGyt=q, AG;J. (0) = 0, AG1Jr (Т) = opt,
г = v, г (0) = го, г(Г) = гь
у = Ре (1 — G* — АС;,)'1 + к, V (0) = у0, у (Т) = уг.
(10.10)
Здесь вместо G^ (текущий запас рабочего вещества) фигурирует
новая фазовая координата AG;;. = G;J.0 — G^ (£) — вес рабочего
вещества, израсходованного к моменту времени t. Это сделано
для того, чтобы минимизировать конечное (а не начальное) зна¬
чение S (Т) фазовой координаты S. Все веса в (10.10) отнесены
к начальному весу G0, тяга и расход — к GJg. Чтобы замкнуть
постановку (10.10), нужно конкретизировать характеристики
двигательной системы (II.9), (11.10).
При фиксированном весе двигателя G* задача о минимуме
стоимости S сводится к задаче о минимуме веса рабочего вещества
Gp.0. Из физических соображений это ясно, формально — следует
из положительности частной производной
dS _ V , 1 г *v.G* У ,
_ 1 - «X - <v, п (1 —Gx — > °* (10•11 >
так как slx и sx положительны (см. (10.8)) и G>. + G^o <С 1 •
Сделанное замечание позволяет использовать найденные ранее
оптимальные программы управления двигателем. Остается найти
новые оптимальные значения постоянных управляющих пара¬
метров.
4. Идеальный двигатель ограниченной мощности. Характе¬
ристики такого двигателя даются формулами (4.1)—(4.4). После
интегрирования уравнения расхода имеем (с учетом N (t) =
==^V'max см. (4.9))
т
G>о = ф ^ q (ф = a2 dt, а = const^. (10.12)
* О
Оптимальное значение веса двигателя Gx, как и прежде,
можно найти, не решая динамической части задачи о минимуме
функционала /. Подставив (10.12) в (10.7), найдем G* из условия
dS/dGx = 0:
Gx =У£Ф + £(£—1)Ф2— £Ф (£ - . (10.13)
V -*■ I У
Рис. 10.i. Оптимальные для критерия стоимости соотношения между
весом двигателя Gx (идеальный, ограниченной мощности) и запасом рабо¬
чего вещества G^q (С — отношение удельных стоимостей рабочего вещества
и двигателя, Ф — функционал динамической задачи).
б
Рис. 10.2. Стоимость а и полезная нагрузка G- для идеального двигателя
ограниченной мощности (весовые соотношения взяты с рис. 10.1, пункти¬
ром показана стоимость, когда весовые соотношения максимизируют по¬
лезную нагрузку).
440 МОДИФИКАЦИИ КРИТЕРИЯ ОГГТИМАЛЫЮСТИ [IVI.
Параметр £ характеризует отношение стоимости единицы веса
рабочего вещества к стоимости единицы веса двигателя (см.
(10.8)). При £ = 1 (равные стоимости) формула (10.13) дает старое
выражение (4.15) для веса двигателя, обеспечивающего максимум
полезной нагрузки. Оптимальное соотношение между весами рабо¬
чего вещества и двигателя сдвигается в сторону увеличения запаса
рабочего вещества при £ <С 1 или в сторону увеличения веса
двигателя при £ > 1 (рис. 10.1). Разница между оптимальными
весовыми соотношениями, как видно из рисунка, при переходе
от весового критерия к критерию стоимости может быть весьма
значительной в зависимости от того, насколько различаются
стоимости рабочего вещества и двигателя.
Посмотрим теперь, какой будет проигрыш в функционалах,
если при вычислении одного функционала пользоваться весовыми
соотношениями, оптимальными для другого. Выделим из функ¬
ционала стоимости (10.7) для уменьшения числа параметров
часть, зависящую только от £ и Ф:
а (£, Ф) = “ д ZTr~ - (1 Т 5к)(3 т 1). (10.14):
1 'Дао иу.
Величина а, так же как и S, характеризует стоимость выпол¬
нения маневра. На рис. 10.2 сплошными линиями показана зави¬
симость о (£, Ф), когда для G[X() и G* взяты оптимальные для
критерия стоимости значения (10.13), (10.12). Пунктирные линии
соответствуют случаю, когда для G;J.() и G* взяты значения, опти¬
мальные для весового критерия: G[)A) = |/ Ф, G* = |А0 — Ф
(см. (10.12), (10.13) при £ = 1 и (4.17), (4.15)). На этом же ри¬
сунке представлена зависимость полезной нагрузки G- ~ 1 —
— G* — G1J<0 от Ф для различных значений параметра £. Видно,
что проигрыш в полезной нагрузке при переходе от одних опти¬
мальных весовых соотношений к другим больше, чам проигрыш
в стоимости.
§ 2. ДВИГАТЕЛЬНАЯ СИСТЕМА, УНИВЕРСАЛЬНАЯ
ДЛЯ ЗАДАННОГО КЛАССА МАНЕВРОВ
Здесь рассматривается задача о выборе параметров двигатель¬
ной системы, обеспечивающей выполнение определенного диапа¬
зона маневров (а не одного маневра, как было в предыдущем
изложении). Определение такой универсальной системы позво¬
ляет сократить число неидентичных систем, а значит, и затраты
на разработку. Оптимизация проводится в рамках весового кри¬
терия.
1. Общая шнугановка задачи. Пусть имеется управляемый
объект (динамическая система), состояние которого описывается
§ 2] УНИВЕРСАЛЬНАЯ ДВИГАТЕЛЬНАЯ СИСТЕМА \/\ I
системой обыкновенных дифференциальных уравнений вида
•П = h (zj, (0) = Х;0, я* (Г) = Хц
{ик mi.i < W-k (t) < Ц/, max, = const; (10.15)
г, j = 0, 1, ..., /г; к = 1, . . . , г; I = 1, . . . . су),
где я* — фазовые координаты, ик (t) — управляющие функции,
wi — управляющие параметры.
«Маневр» характеризуется набором граничных значений фа¬
зовых координат х\ (i = 1, . . . , т п) и временем Т\ совокуп¬
ность этих величин обозначается вектором
Ь (я10, • • • , %?п0 ? Яц, • • • , ^) • (10.10)
Динамическая система характеризуется набором значении
управляющих параметров обозначается вектором
w = (wj, . . . , гггу) (10.17)
(к параметрам Wj могут относиться и предельные значения управ¬
ляющих функций ukJ nin, ukm ах).
Критерий «качества» выполнения маневра — конечное зна¬
чение фазовой координаты х0:
£0 (Г) = extr (х0 (0) = 0). (10.18)
В обычной формулировке задач оптимального управления
требуется построить такие функции ик (/) и выбрать такие значе¬
ния параметров wt из класса допустимых, которые обеспечивали
бы выполнение граничных условий (10.15) и доставляли экстре¬
мум функционалу (10.18).
Оптимальные управления ик (t) и оптимальные значения пара¬
метров wi, являющиеся решением сформулированной задачи,
будут в общем случае зависеть от параметров маневра Ь. Будем
считать динамические системы (10.15) различными, если значе¬
ния соответствующих параметров w не совпадают. Предпола¬
гается, что в одной и той же системе могут быть реализованы
различные управления ик (t).
Оптимальная в смысле функционала (10.18) реализация боль¬
шого числа маневров с различными наборами параметров
Ь(*> = (*й\ Г(8)), s Л’ (10.19)
потребует создания большого числа не идентичных систем.
Последнее может оказаться невыгодным с экономической точки
зрения.
Ставится задача реализации S различных маневров при
помощи заданного числа Q типов систем (10.15), меныпего
442
МОДИФИК АДИ IL К141TI-: PII Я 01ITIIMАЛЬП ости
[ГЛ. Ы
S: 1 Q <С S. В качестве критерия оптимальности принимается
осредненная по всем маневрам величина функционала (10.18).
Оптимальное число Q типов систем должно определяться из
критерия минимума стоимости. Для этого нужно знать стоимость
разработки системы (10.15) с отличными от прежних параметрами
и иметь соответствие между стоимостью и функционалом (10.18).
Здесь последняя задача не рассматривается — число Q типов
систем считается заданным.
Возможен второй вариант постановки задачи универсализа¬
ции оптимальных параметров систем. Если система (10.15) мо¬
жет быть собрана из элементарных секций, то ее параметры w
можно представить в виде
w = w (cr, Aw), а = 1,2,..., (10.20)
где Aw — параметры элементарных секций (в частном случае
зависимость (10.20) может быть линейной: w = a Aw). Ставится
задача о выборе оптимальных параметров Aw элементарных сек¬
ций, универсальных для всех S типов маневров и оптимального
числа секций о для каждого маневра.
2. Критерий оптимальности. При формулировке критерия оп¬
тимальности для двух поставленных выше задач используется
статистический подход. Задается распределение потребного числа
выполнения маневров по их параметрам (10.19). Если отнести
потребное число выполнения маневра каждого типа к суммарному
числу маневров всех типов, то это распределение можно тракто¬
вать как распределение вероятности ps маневров по типам
Л-МЬ(,)), = 1. (10.21)
1
Тогда в качестве критерия оптимальности будет фигурировать
математическое ожидание функционала (10.18)
<*„!> = 2 Р,хп (Ь(5)), (10.22)
os— I
т. е. осредненная по всем типам маневров (10.19) величина функ¬
ционала (10.18).
Параметры маневра могут быть заданы не дискретно, как
в (10.19), а непрерывно, например как функция одной переменной
b = b(s), 0<5<5, (10.23)
где s может принимать все значения из интервала [0, S] (не толь¬
ко целые). В этом случае распределение вероятностей (10.21)
УНИВЕРСАЛЬНАЯ ДВИГАТЕЛЬНАЯ СИСТЕМА
443
заменяется плотностью распределения вероятности
S
p = p(s), ^p(s)tfs=l,
(10.24)
О
а функционал (10.22) заменяется на
s
<£„!> = ^ р (s) x„i (b(s)) ds.
(10.25)
О
3. Формулировка задачи для заданного числа типов систем.
Пусть параметры w системы (10.15) могут принимать Q значений
w(co), (о=1, • • • , £5. Требуется реализовать S типов маневров
(10.19) с распределением вероятности (10.21), обеспечив максимум
(минимум) функционала (10.22).
Введем для каждого 5-го типа маневра вместо времени t новую
независимую переменную
с тем. чтобы отнести конечные условия (10.15) и функционал
(10.22) к одинаковой для всех маневров точке т = 1. После этого
задачу можно привести к стандартной формулировке (10.15) —
(10.18) для расширенной системы дифференциальных уравнений
Здесь, как и раньше, х(?'} — фазовые координаты (S (п + 1) штук),
— управляющие функции (Sг штук), w— постоянные упра¬
вляющие параметры (Qq штук).
т = t/T&
(10.26)
(0<т<1; 5 = ю = 1, . . . , Q <£; (10.27)
i, / = 0, 1, . . . , п; к = 1, . . . , г; Z = 1, . . . , </)
с граничными условиями
(10.28)
и функционалом
S
<ящ> = 2 =extr.
(10.29)
444
mo;{ИФПК АЦИII К РИТЕ рпя о ПТ 11 м алытости
г ГЛ. 1и
В случае непрерывного распределения (10.23) —(10.25) при¬
ходим к двумерной вариационной задаче для системы
дх •
= Т ($) /; (Xj, Uk, W„ Г (s) т)
(0<^т<0; i, j — 0, 1, . . п; (10.30)
к —- 1, . . . , г; I — 1, г/)
с граничными условиями
хй (0, s) = 0, Xi (0, s) = xi0 (s), Xj(i, s) = xik (s)
(0 О S, i = 1, . . . , /?) (10.31)
и функционалом
s
<я<ч> = ^ p {s) xt) (1, s) ds = extr. (10.32)
0
Здесь X\ = X\ (t, s), щ = щ (t, s) — фазовые координаты и управ¬
ляющие функции, зависящие от двух переменных, wt = w{ (s) —
кусочно-постоянные управляющие функции с заданным числом
уровней^', со = 1, . . . , £2, зависящие только от s {dwjdт = 0).
4. Формулировка задачи об универсальной секции. Данные
выше постановки вариационных задач (10.27) —(10.29) и (10.30) —
(10.32) переносятся на рассматриваемый случай с некоторыми
изменениями. Граничные условия (10.28), (10.31) и функционалы
(10.29), (10.32) сохраняются. Несколько меняется запись диффе¬
ренциальных уравнений (для простоты записи зависимость
(10.20) считается линейной):
для дискретного распределения (ср. (10.27))
-гг = J<s)/i(44)> ы£°’ °(">Агг'’г<8)т)
(0<т< 1; s=l S; i, j = 0, 1,... , п; (10.33)
/С 1 ,...,/ , I = 1 , . . . , С/) у
для непрерывного распределения (ср. (10.30))
дх.
—- = Т (s)fi (xj, 77/., <зДгг/, Т (s) т)
dt \ 3 и V t ; (10.34)
(0 т 1; 0^5^ S; 7, / = 0, 1, . . . , п; к = 1, . . ., г; 1 = 1, . . ., д).
В уравнениях (10.33) постоянные управляющие параметры
Awi одинаковы для всех s; = 1,2, ... — целые числа, для
каждого номера s могут быть свои (в отличие от (10.27), где число
Q параметров меньше, чем число S групп уравнений).
§
УНИВЕРСАЛЬНАЯ ДВИГАТЕЛЬНАЯ СИСТЕМА
445
И уравнениях (10.34) Awi — постоянные управляющие пара¬
метры (dAwi/дт = дАwilds = 0); а = о (s) — кусочно-постоянная
управляющая функция одной переменной .9, принимающая
любые целочисленные значения (в отличие от (10.30), где число Q
уровней, wкусочно-постоянного управления wi (.9) задано).
5. Идеальный двигатель ограниченной мощности. Единствен¬
ным параметром w в этом случае является вес двигателя G* или
максимальная мощность N}URX = GK /а, где в общем случае
а = а (i¥]nax) или а = а (Gy) (см. § 1 гл. 4). Функционал (10.18)
исходной задачи (10.15) — (10.17) — полезная нагрузка (4.5).
После решения динамической задачи (5.2) каждому набору
параметров маневра (10.19) b = (r0, v0, г1? у17 Т) отвечает значе¬
ние интеграла /, его и будем считать здесь параметром маневра Ь.
Полезная нагрузка выражается через G* и J (см. (4.10)):
Считаются заданными распределения маневров по типам в сле¬
дующем виде:
дискретное распределение (10.21)
s
Соответственно этому записывается функционал задачи:
для дискретного распределения (ср. (10.22))
(величина <(?-> представляет собой среднюю полезную нагрузку,
приходящуюся на один маневр из диапазона [/0, /J).
Таким образом, задача о реализации заданного класса манев¬
ров (10.36), (10.37) при помощи заданного числа Q < S типов
(10.35)
Ps = Ps(J(S), 2 Л = 1’
(10.36)
S— 1
непрерывное распределение (10.24)
(10.37)
для непрерывного распределения (ср. (10.25))
446 МОДИФИКАЦИИ КРИТЕРИЯ ОПТИМАЛЬНОСТИ [ГЛ. Г)
двигательной установки (см. п. 3) сводится к отысканию макси¬
мума суммы (10.38) при Gy, = со = 1, . . . , Q или макси¬
мума интеграла (10.39) при Gx (/) = со = 1, . . . , Q , где <>
задано, а уровни G^ должны быть выбраны оптимальными.
Если рассматривается задача о выборе оптимальных параме¬
тров универсальной секции (см. п. 4), то в (10.38), (10.39) вместо
Gy, нужно подставить a AGy и считать удельный вес а зависящим
не от Gy, а от A Gy. Тогда функционал (10.38) запишется в виде
<GL> = A Gy. у. psa 1 \ , (|П 40)
\ s^AGy -j- [a (^Gx)/2g] J j { ' '
а функционал (10.39) — в виде
«**> “ ('«.«)
Jo
В (10.40) a^s), .9=1,...,*?,— произвольные целые положи¬
тельные числа, в (10.41) a — кусочно-постоянная функция J
с произвольным числом целочисленных уровней.
Введем обозначения
Ф- У. = “ (0<ф<1, х>1), (10.42)
где аА — предельное значение удельного веса секции при беско¬
нечно большой мощности, и рассмотрим случай, когда маневры
распределены непрерывно в диапазоне [Ф0. ФД с равной вероят¬
ностью, т. е.
о (ф) = при Ф° < Ф < Ф| ’
р (Ф) = 0 при Ф < Ф0, Ф > Фх. (10.43)
Зависимость удельного веса двигателя а от его абсолютных
параметров Nm-л к или Gy, {da/dNnVlXX, da!dGy 0, см. рис. 2.96)
несущественна для методики решения. Для задачи с фиксиро¬
ванным числом уровней Сф введение этой зависимости не при¬
водит и к качественным особенностям. Однако в задаче об универ¬
сальной секции зависимость a (AGy) или у (AGy) важна с каче¬
ственной точки зрения. При у = ‘1 оптимальный размер секции
стремится к нулю (AGy —> 0), если же dyJdGy 0, то оптималь¬
ный размер секции конечен. Поэтому функционал (10.39) первой
задачи записывается в виде (у = 1)
<G„> _ Фо ^ Gx ( G^ ^ ф 1 ]<1Ф,
ф.
(10.44)
§ 2]
УНИВЕРСАЛЬНАЯ Д1Ш ГАТЕЛЫ IАЯ СИСТЕМА
447
а функционал (10.41) второй задачи — в виде (% = % (АС?*))
Ф1
ЛСх V
' s> = <I'i - Фо i
1
вД0х-1-Фх(ДСх)
lW<P. (10.45)
Интеграл (10.44) берется по отрезкам Фуа>) Ф Фх°\ где оп¬
тимален уровень (?£ы)
(G-д) =
Ф1
Фг
2 е
Ы=1
(«)
ф(“).
In 1
С(о.)
— (фГ — фг;
(“) 1
Ф<“> ■
о
G(со)
(10.40)
Моменты переключений с одного уровня на другой опреде¬
ляются из условия максимума подынтегрального выражения
(10.44). После этого задача
сводится к отысканию макси¬
мума функции Q переменных
<GK) = f(G*\ • • • , О при
условии неотрицательности
подынтегрального выражения
(10.44), что эквивалентно
условию
0 min {GхШ)} 1 — Ф] .
со
(10.47)
Эта процедура может быть
проделана численно методом
скорейшего спуска (см. гл. 14).
При Q = 1 оптимальное зна¬
чение единственного уровня
(^определяется из решения
уравнения
Риг. 10.3. Осредненная по маневрам полез¬
ная нагрузка <G_>, когда выполнение ма¬
невров из диапазона [Ф<ь ФоЧчДФ] обеспе¬
чивается фиксированным числом двигатель¬
ных систем Q = 1, 2. Пунктирные кривые
отвечают £2 -* оо.
1 jn
а>1 - ф« п ф0 сф (<i)„ б'Ф) (0), + сФ)
0>1
с<}>
гл1)
■ 1 = 0, (10.48)
если корень этого уравнения оказывается меньшим (1 — Ф3)»
в противном случае GW = 1 — Фг.
На рис. 10.3 представлен график осредненной полезной на¬
грузки <Gn> для интервалов различной длины АФ = Фх — Ф0 =
= 0; 0,2; 0,4; 0,8 в зависимости от начальной точки интервала Ф0.
Пунктирные кривые соответствуют непрерывному оптимально¬
му закону изменения (?х (Ф) = ]/фГ — ф (бесконечное число
типов двигательных систем, см. пунктир на рис. 10.4). Видно,
МОДИФИКАЦИИ КРИТЕ РИЯ ОПТИМАЛЬНОСТИ
[ГЛ. 10
что с помощью одного типа двигательной системы (кривые £2 = 1)
можно весьма близко подойти к максимально возможным значе¬
ниям полезной нагрузки. Переход к двум типам двигательной
0,2
OJ
О
22=2
АФ--0.8
Фо=0
22=/
0,2
ОА
0.6 Ф
Рис. 10.4. Пример ступенчатой аппрокси¬
мации (£2 = 1, 2) оптимального распреде¬
лении веса двигателя Gy по маневрам
в диапазоне [Ф0, Ф0 Н- АФ].
Рис. 10.5. Зависимость оптимального веса
G^ двигателя, универсального для диа¬
пазона маневров [Ф0, Ф0 г АФ].
0,2
о;
о
системы сводит проигрыш в полезной нагрузке практически до
нуля (пунктирные кривые и кривые £2=2, за исключением
случая АФ = 0,8, в масштабе
рисунка неразличимы).
На рис. 10.4 показан при¬
мер оптимального распределе¬
ния веса двигательной системы
по параметру маневра Ф
при £2 = 1, 2, оо. Зависимость
Grp (Ф0, АФ) для £2 = 1 пред¬
ставлена на рис. 10.5. Отрезки
прямых соответствуют выходу
на ограничение (10.47).
Во второй задаче требуется
построить кусочно-постоянную
функцию а (Ф) с целочисленны¬
ми уровнями и выбрать значение
параметра Aобеспечивающее максимум интеграла (10.45)
лри условии неотрицательности подынтегрального выражения.
Сделаем замену переменных х = %Ф и введем обозначение
!
II
^1
?
. /'
.-0,05
/
\
ч
ч
N
N
\
—i
0,2 Ofi 0,6 0,8
Рис. 10.6. Аппроксимация оптимального
распределения веса двигателя Gy по ма¬
неврам кусочно-постоянной кривой с рав¬
ной высотой ступенек AGx = 0,1; 0,05 (за¬
дача об универсальной секции).
о
— l)dar.
(10.49)
Тогда (10.45) перепишется в виде
<G"> = (ф1-?ф0)х Iх (хфь AG„) - Я (хФо, АСк)|. (10.50)
УНИВЕРСАЛЬНАЯ ДВИГАТЕЛЬНАЯ СИСТЕМА
449
Интеграл (10.49), как и (10.44), берется по отрезкам между
переключениями уровней Oj, а моменты переключений определя¬
ются из условия максимума подынтегрального выражения (10.49)
по целочисленным значениям а; = 1, 2, . . . , атах; сгшах =
■= [1/4ДGx] + 1 (где [...] обозначает целую часть числа) —
см. G* = а (Ф) ДСгх на рис. 10.6. На рис. 10.7 приведена зависи¬
мость К (х) для различных значений AGX. Видно, что при
Дбх 0,1 кривые практически совпадают с предельной
К (х, 0) = * (1 - 4/3 Ух + Va*) (АGx - 0). (10.51)
Заменим приближенно К (х, AGy) в (10.50) на К (х, 0), тогда
. ф3/г (Т)3/2 .
<G.) = 1 - 4 у X+ IX (Ф1 + Ф0) при AGX < 0,1, (10.52)
где 1 < % = х (ДСХ) < (1 — ДСХ)/Ф! (ограничение сверху полу¬
чено из условия неотрицательности подынтегрального выражения
(10.49)). Чтобы найти оптимальное значение ДGx, нужно задаться
зависимостью % (AGX), например
X (AGX) = ос (AGx)/a = AG*/(AG* - AGx), (10.53)
где AG* — предельный вес секции при мощности, стремящейся
29 Механика полета
450
МОДИФИКАЦИИ КРИТЕРИЯ ОПТИМАЛЬНОСТИ
[ГЛ. 10
к нулю. Характер этой зависимости совпадает с описанными в ли¬
тературе (ср. рис. 10.8 и рис. 2.96).
Из условия неотрицательно¬
сти полезной нагрузки для каж¬
дого маневра из диапазона [Ф0,
OJ определяется допустимый
интервал изменения %:
Xi<X<X2, Xlt2 =
i-до;
ф.
+
Рис. 10.8. Пример зависимости удельного
веса двигателя х = а/а* от размера секции
AGX/AG* (a*, AG* = const).
1 +
1 — A Gy
Фх
' 1_
Фх “
(10.54)
На этом интервале <£?„> из
(10.52) оказывается монотонно убывающей функцией %. Отсюда
оптимальные значения % и А£?*
равны
X=Xi, AGx=AG;Xi/(Xi-1). (10.55)
При ДGx 0,1 задача решается
численно по известной зависимо-
0,1
OS Фа
Рис. 10.9. Осредпегшая по маневрам полез¬
ная нагрузка <G_>, когда выполнение ма¬
невров из диапазона [Ф0, Ф0 + АФ] обес¬
печивается двигательными системами, соб¬
ранными из универсальных секций (ср.
рис. 10.3).
*1
лех-
I
—V \\
\ Q
Y
0
02
0,4
0,0
Фа
Рис. 10.10. Оптимальный размер универ¬
сальной секции AGX в зависимости от пара¬
метров диапазона маневров [Ф0, Ф0 + АФ]
(ср. i рис. 10.5).
сти К (х, AGy), представленной на рис. 10.7, и по формуле
(10.50). Результаты решения приведены на рис. 10.9 и 10.10
(AG* = 0,001), аналогичных рис. 10.3 и 10.5.
Когда выполнение маневров из данного диапазона обеспечи¬
вается одной двигательной системой (первая задача), то про¬
игрыш в полезной нагрузке заметно увеличивается с расшире-
ИГРОВОЙ ПОДХОД К ЗАДАЧЕ ОПТИМИЗАЦИИ
451
нием диапазона и при смещении его в область энергетически на¬
пряженных маневров (рис. 10.3). Использование универсальных
секций, из которых набирается двигатель для каждого конкрет¬
ного маневра (вторая задача), улучшает положение — проигрыш
в полезной нагрузке становится примерно одинаково малым для
любого диапазона маневров.
§ 3. ИГРОВОЙ ПОДХОД К ЗАДАЧЕ ВЫБОРА
ОПТИМАЛЬНЫХ ПАРАМЕТРОВ ДВИГАТЕЛЬНОЙ СИСТЕМЫ
Параметры двигателя, универсального для заданного класса
маневров, отыскивались выше в предположении, что известна
частота, с которой нужно выполнять каждый маневр. Здесь это
предположение отбрасывается, считаются известными только
границы диапазона возможных маневров. Требуется определить
параметры двигателя, оптимального в определенном смысле
для этого диапазона маневров.
Задача формулируется в терминах теории антагонистических
игр. Игровой подход позволяет гарантировать, что проигрыш,
обязанный требованию универсальности двигателя и отсутствию
полной информации о маневрах, при выбранных значениях пара¬
метров двигательной системы не будет превышать найденного
предела, какое бы распределение частоты выполнения маневров
ни задавалось.
1. Постановка задачи. Рассмотрим сначала, как и в предыду¬
щем параграфе, общий случай — динамическую систему (10.15)
с параметрами w и управляющими функциями щ (t). Маневр зада¬
ется вектором Ь (10.16), а качество выполнения маневра характе¬
ризуется функционалом х0 (Т) (10.18).
Управляющие функции щ (t) выбираются из класса допусти¬
мых так, чтобы1 выполнялись граничные^ условия (10.15) и до¬
стигался экстремум функционала (10.18)
extr £0 (Т) = х01 (b, w). (10.50)
ик (0
При фиксированном векторе w параметров системы управле¬
ния щ (t) могут браться различными в зависимости от вектора Ь,
параметров маневра. Вариационная задача о построении опти¬
мальных управлений щ (t) предполагается решенной и функция
(10.56) — известной.
Параметры маневра b могут с частотой v принимать любые
значения из фиксированной области В или фиксированного дис¬
кретного множества В. Частота v (Ь), с которой нужно выполнять
Маневр Ь, неизвестна. Частота v (b) записывается через функцию
распределения Fv (b) при помощи интеграла Стилтьеса (допу¬
скаются ступенчатые функции распределения). Частота v(bEEZ?')
29*
452
МОДИФИКАЦИИ КРИТЕРИЯ ОПТИМАЛЬНОСТИ
[ГЛ. 10
появления маневров, принадлежащих области В' cz В, равна
v(beB')= J dFv(b) ( J d^v(b) = l), (10.57)
be в'.; be в
где функция распределения Fv (b) в соответствии с предположен
нием относительно v (Ь) неизвестна.
Вектор w параметров (10.17) динамической системы для всех
значений b ЕЕ В может принимать только одно значение (требова¬
ние универсальности динамической системы для заданного класса
маневров). Если бы для каждого маневра b можно было выбирать
свою систему w (b), то можно было бы обеспечить наибольшее
(наименьшее) значение функционала (10.56), равное
extr х0 (Т) = #oi (Ь) (10.58)
ик (О, W
— идеальное решение. Универсальная же система будет обеспе¬
чивать значение функционала (10.56) меньшее (большее), чем
(10.58), за исключением того маневра Ь, для которого параметры
универсальной системы w оптимальны в смысле условия (10.18).
Проигрыш Л по сравнению с идеальным решением на каждом
маневре будем характеризовать относительным отклонением
М (b, w) = У01 (b’ w) . (10.59)
#oi (Ь)
Суммарный проигрыш для системы с параметрами w на серии
маневров b из множества В с распределением частоты Fv (b)
будет равен
М (Fv (Ь), w) = ^ Л (b, w) dFv (Ь). (10.60)
Возникает типичная игровая ситуация. В «игре» принимают
участие два «игрока». Одного игрока назовем «Природа», друго¬
го — «Конструктор». Природа задает распределение (10.57) ча¬
стоты выполнения маневров по параметрам маневра («ход» При¬
роды) так, чтобы увеличить проигрыш Конструктора (10.60).
Конструктор выбирает параметры динамической системы (10.17)
(«ход» Конструктора) так, чтобы уменьшить проигрыш. Первым
ход делает Конструктор; при этом ему известны лишь границы
диапазона, из которого Природа может назначать параметры
маневра. Затем играет Природа, информация о ходе Конструк¬
тора у нее отсутствует.
Если бы Конструктору разрешалось выбирать не одно значе¬
ние вектора w, а для каждого маневра b свое, и если бы он имел
полную информацию о маневрах, то его проигрыш был бы равен
ИГРОВОЙ ПОДХОД К ЗАДАЧЕ ОПТИМИЗАЦИИ
453
нулю. В описанной выше ситуации проигрыш Конструктора
всегда отличен от нуля г). Поставим задачу о вычислении величины
проигрыша, когда Природа играет так, чтобы максимизировать про¬
игрыш при любом ходе Конструктора, а Конструктор — так, чтобы
минимизировать проигрыш при любом ходе Природы. Решение
этой задачи определит параметры динамической системы, опти¬
мальные в следующем смысле: какое бы распределение частоты
выполнения маневра ни задавала Природа, проигрыш Конструк¬
тора не будет превосходить найденной минимальной величины
проигрыша (цена игры [10.5—10.8]).
В изложенной постановке Природа и Конструктор неравно¬
правны: Природа может назначать любое количество различных
маневров из допустимого множества В (ход Природы — задание
функции распределения частоты Fv (b) на множестве В), а Кон¬
структору разрешается выбирать только одну динамическую
систему (ход Конструктора — одно значение вектора w). Сделаем
обе стороны равноправными, как обычно в теории антагонисти¬
ческих игр. Разрешим Конструктору выбирать любое число раз¬
личных динамических систем из допустимого множества W7
т. е. ход Конструктора будет состоять в назначении функции рас¬
пределения Fx (w) частоты X, с которой нужно применять различ¬
ные системы. В терминах функции распределения частота при¬
менения систем с параметрами, лежащими в области W' a W,
равна (ср. (10.57))
Mwer)= jj dFx(w) ( jj dFx(w) = l). (10.61)
weW' wgW
Предположение об отсутствии информации у обеих сторон
о ходе противной стороны остается в силе, т. е. Конструктору
нужно указать, какая из выбранных динамических систем будет
применяться для выполнения очередного маневра, до того как
станут известными параметры маневра.
Проигрыш (10.60) при ходе Природы Fv (b) и ходе Конструк¬
тора F\ (w) в этом случае равен
М (Fv (Ь), Fx (w)) = Ц Л (Ь, w) 4FV (Ь) dFx (w). (10.62)
I) ЕВ
weVV
Если платежная функция Л (Ь, w) имеет во всей области опреде¬
ления положительные вторые производные d2dl!dwх2 ^>0, . . .
..., дгЖ!дю\ >0и если игра непрерывная (допустимые множества
В и W — области), то, как доказывается в теории игр [10.5—
л) За исключением маловероятного случая, когда требуется выполнять
только те маневры, для которых выбранная система w оптимальна в смысле
(10.18).
454
МОДИФИКАЦИИ КРИТЕРИЯ ОПТИМАЛЬНОСТИ
[ГЛ. 10
10.8], оптимальная стратегия Конструктора будет «чистой» стра¬
тегией:
т. е. Конструктору выгодно выбирать только одну динамическую
систему w*. Это означает, что в данном случае решение задачи
(10.62) совпадает с решением ранее поставленной задачи (10.60).
Далее исследование проводится в приложении к идеальному
двигателю ограниченной мощности (см. гл. 4). Для этого случая
маневр можно характеризовать одним параметром — величиной
функционала динамической задачи J или комбинацией Ф =
= (а/2 g)J, а двигатель — величиной максимальной мощности
/Vmax или весом Gx = аЛ/!11ах (удельный вес двигателя а = const
задан). Проигрыш Ж измеряется в единицах полезной нагрузки
G-. Параметры двигателя и маневра могут изменяться непрерывно
в ограниченных пределах (непрерывная игра).
2. Платежная функция. Полезная нагрузка (функционал (10.56))
для идеального двигателя ограниченной мощности с весом G* на
маневре с функционалом Ф равна (4.14)
(веса G- и G£ считаются отнесенными к начальному весу G0).
Для каждого значения Ф существует оптимальный вес дви¬
гателя (4.15), максимизирующий полезную нагрузку (10.64).
Это максимально достижимое значение (идеальное решение (10.58))
равно (4.16)
Платежная функция (10.59) составляется как относительный
проигрыш в полезной нагрузке (10.64) по сравнению с макси¬
мально возможной (10.65):
Область определения функции Ж (Ф, Gx) следующая (рис.
10.11):
0 < Ф < 1, 0 < Gx < min {V4, (1 - Ф)}. (10.67)
(10.63)
о
(10.64)
Gr. max (Ф) = (1 — УФ)2.
- шах
(10.65)
Л (Ф, Gx) -
Ограничение на Ф сверху соответствует условию неотрица¬
тельности максимальной полезной нагрузки (10.65). Альтерна¬
тивное ограничение на Gx появляется из-за того, что, во-первых,
ИГРОВОЙ ПОДХОД К ЗАДАЧЕ ОПТИМИЗАЦИИ
455
вес двигателя не имеет смысла делать больше 1/4 (см. (4.15)
и рис. 4.2), во-вторых, вес двигателя нельзя делать больше пре¬
дела, соответствующего нулевой полезной нагрузке (10.64).
Второе ограничение на Gy действует в диапазоне 3/4 Ф 1.
Рис. 10.11. Платежная функция Ж (Ф, Оу) игры «Приро¬
да — Конструктор» для случая идеального двигателя огра¬
ниченной мощности (относительный проигрыш в полезной
нагрузке в зависимости от параметров маневра Ф и двигателя
Gy. На плоскости Ф, Gy штрих-пунктиром показаны кривая
минимумов — нулей и след кривой внутренних максимумов).
Функция Ж (Ф, Gy) ограничена всюду в области (10.67):
0< Ж (ф, Gy) 1, непрерывна и дифференцируема по обеим
переменным во внутренних точках области. В граничных точках
(0, 0) и (1, 0) она имеет разрывы (см. рис. 10.11):
lim Ж (0, Gy) = 0 =j= lim Ж (Ф, 0) = 1,
G х-*0 Ф->0
lim Ж (Ф, /Ф —Ф) = 0 =j= lim Ж (Ф, 1 — Ф) = 1.
ф-*1 ф->1
В сечениях плоскостями Ф = const функция Ж с ростом Gy
сначала убывает, затем возрастает, вторая производная по Gy
(10.68)
456
МОДИФИКАЦИИ КРИТЕРИЯ ОПТИМАЛЬНОСТИ
[ГЛ. I.
всюду положительна (рис. 10.12):
дЛ 1
Ф
dGx (1— ГФ)-.
|#<0 при СхОАф — ф,
дЛ > 0 при Gx > /Ф — Ф,
1 2Ф
д-Л
*>0-
(10.(59)
dG\ (1 — V Ф)2(ф +
В сечениях плоскостями Gy = const функция Л имеет два
минимума и три максимума (два граничных и один внутренний)
cJf,
0,24 С*
рис. 10.12. Сечения платежной функции <M(0,Gy) плоскостями Ф = const
(кривая Ф = 0,3 практически совпадает с кривой (10.72) внутренних макси¬
мумов JH но Gy).
(рис. 10.13). Это устанавливается исследованием частных произ¬
водных Ж по Ф:
я //
1
dG_
dG
ИГРОВОЙ ПОДХОД К ЗАДАЧЕ ОПТИМИЗАЦИИ
457
Разрешая уравнение дЛ/дФ = 0 относительно 6>., получим
G, 1.2 = (У2 - Ф) ± (У2 - УЩ. (10.71)
Первое решение из (10.71) дает точки промежуточного мак¬
симума Л (рис. 10.13):
Сх = 1 —/Ф—Ф или ф = (|Л/4 — Gx— V*)2. )
= 1 —
дЖ ^
~дф = ’
(3А- Г5/4 -G,)3
&'-Л
= шах
(10.72)
мтг<°. 0<ф<.
След максимумов на плоскости Ф, С* показан на рис. 10.11 штрих-
пунктирной линией. Кривая Л (Gy) промежуточных максимумов
(10.72) практически совпадает с кривой Л (0,3, G*), последняя
изображена на рис. 10.12.
Второе решение (10.71) соответствует точкам
(нули функции Л—см. штрих-пунктирную кривую
— У Ф — Ф или Ф = (1/2 ± Vх 1ч
минимума Л
на рис. 10.11):
= 0 = min
М — о
эф ~ ’
дЛ1
ЭФ2
ех)2,
>0, 0<Ф<1).
(10.73)
Это решение дает оптимальный в обычном смысле вес двигателя
(4.15), изменяющийся в зависимости от параметра маневра Ф_
Проигрыш в полезной нагруз¬
ке на решении (10.73) равен
нулю (чтобы реализовать это
решение, нужно иметь пол¬
ную информацию о параметре
маневра Ф и для каждого
значения Ф выбирать свой
двигатель Gy).
3. Цена игры. Оптималь¬
ные стратегии Конструктора
и Природы. Пусть параметры
маневров, которые может на¬
значать Природа, лежат в
интервале Ф0 Ф Фх (гра¬
ницы 0 Ф0<С < 1 из¬
вестны Конструктору). Тог¬
да границы интервала, из
которого Конструктор может
выбирать параметр двигателя
Gy, будут (см. (10.67)):
0 < Gx < min {V4, (1 — Фа)}.
Шш {V4, (1 — Ф))}] платежная
Рис. 10.13. Сечения платежной функции М (Ф.,
Gy) ПЛОСКОСТЯМИ Gy = const (ПуИКТИрнОИ кри-
ooii соединены точки внутренних максимумов
функции Л).
в
этой области [Ф0, 0; Фх,
функция Л непрерывна (см..
458
МОДИФИКАЦИИ КРИТЕРИЯ ОПТИМАЛЬНОСТИ
[ГЛ. 10
(10.68)) и дифференцируема достаточное число раз. Вторая произ¬
водная d2Jt!dG\ здесь строго больше нуля (10.69), поэтому мини¬
мум проигрыша (10.62)
М (Fv (Ф), Fx (Gy)) = Ц Jt (Ф, Gy) dF.: (Ф) dF-,. (Gy) (10.74)
Ф, Gx
при любой стратегии F, (Ф) Природы достигается в классе
чистых стратегий F\ (Gy) Конструктора (10.63):
min М (F, (Ф), F) (Gx)) = min \ж (Ф, Gx) dF, (Ф). (10.75)
(Gx) Gx £
В этом случае цена игры М* равна [10.5—10.8]
М* = min max { Ж (Ф, Gx) dF, (Ф) =
Gx *\,(Ф) J
■= max [ [min Ж (Ф, Gy)] dF, (Ф) = min max Л (Ф, Gx). (10.76)
Fy (<&)<£ Gx Gx Ф
Максимум Ж по Ф при фиксированных значениях Gx дости¬
гается (в зависимости от Ф0, Фх, Gy) в одной из трех точек (см.
(10.70), (10.72) и рис. 10.13): Ф=Ф0,Ф=Ф1,Ф=Ф2=(/5/4-С)(-1/2)2;
случай Ф = Ф2 может иметь место, если Ф0 Ф2 Фх. Введя
обозначения Ж (Ф0, Gy) = /0 (Gx), Ж (Ф1? Gx) = Д (Gx) и Ж (Ф2,
'&*) = /2 (^х), результаты отыскания максимума Ж (Ф, Gx) по
Ф можно записать в виде
/ (Gx) = max Ж (Ф, Gx) = max {Д (Gx)}. (10.77)
Ф0<Ф<Ф! i=0, 1, 2
Найдем теперь минимум функции (10.77) по Gx. Нетрудно
показать, что минимум / (G*) может достигаться только в точках
пересечения функций Д (Gy) = Д (Gy), i Ф j. Предположим
противное, т. е. что минимум / (Gx) достигается в точке Gy],
в окрестности которой / (Gx) тождественно равна одной из функ¬
ций Д (Gx). Тогда min / (Gx) = min Д (Gy) = 0, поскольку
минимум функции Д (Gx) достигается только в одной точке и
равен нулю (см. (10.69) и рис. 10.12). Все функции Д (Gy) неот¬
рицательны, и их нули Gy] не совпадают: Gy] =j= Gy] при i =f= 7.
Значит, в точке Gy] найдется функция Д (Gx) такая, что
Д (Gy]) Д> Д (Gy]), т. е. функция / (Gy) в окрестности точки Gy]
не может быть тождественно равна Д (Gx), и наше предположение
неверно.
После установления этого факта отыскание минимума функ¬
ции Д (Gy) сводится к сравнению значений функций Д (Gy) в точках
ИГРОВОЙ ПОДХОД К ЗАДАЧЕ ОПТИМИЗАЦИИ
459
пересечения: /0 (Gx) = /, (Gx), /0 (Gx) = /2 (Gx), Д (Gx) = /2 (<?*),
причем подлежат сравнению только те точки пересечения, для
которых выполняется условие Д (G*) = /у (Gx) > Д (Gx), i=f=j ф I-
Из этих последних надо взять точку Gy с минимальным значением
функции, т. е.
min / (Gx) = min {/< (Gx) = /, (Gx) > /; (Gx)} = / (10.78)
(пару О*, Ф?, которая соответствует функциям Д (Gy) = Ж (Фь
Gy) и /у (Gx) = Ж (Фу, Gy), удовлетворяющим условию (10.78),
будем обозначать через Ф*, Ф**).
Уравнение /0 (Gx) = f1 (Gy) сводится к квадратному уравне¬
нию относительно Gy, а уравнения /0 (Gy) = /2 (Gy) и Д (Gy) =
— /2 (£*) — к уравнениям пятой степени относительно ]/Gy.
Последние могут быть заменены квадратными уравнениями от¬
носительно Gy, если функцию /2 (Gy) аппроксимировать функцией
Ж (0,3, Gy), что справедливо с точностью до третьего знака.
В этом приближении точки пересечения Gyi> у функций Д (Gy) =
= /у (Gy) для любой пары i, 7 определяются из однотипных урав¬
нений
М — фЛф.С . — (1 — ф.)ф.<2 .
- (1 - ф* - Ф^ gxU -( 3 =0
(10.79)
(G*, = (1 - /Ф^, Gn} = (1 -/Ф])2, i=hh i, 7 = 0,1, 2; Ф2 = 0,3).
Отбор корней G*i,y уравнений (10.79) по критерию (10.78)
определит единственное значение Gx параметра двигателя и два
значения Ф*, Ф** параметра маневров, для которых достигается
минимаксное значение платежной функции (совпадает с «макси-
мином»)
min max Ж (Ф, Gy) = Ж (Ф% Gy) = Ж (Ф**, Gy) =
Gy Ф
G*. (1 — Ф* — G*) G* (1 — Ф** — G*)
= 1 7=^ = 1 ^^ т=- = М\ (10.80)
(Ф + Gy) (1 - У Ф*)* (Ф + Gx) (1 - VФ*у
Найденное изложенным способом значение Gx есть единствен¬
ная оптимальная стратегия Конструктора, величины Ф*, Ф** —
параметры маневров, которые выгодно назначать Природе, а М*—
Цена игры. Если Конструктор выберет двигатель G* , то его про¬
игрыш будет не больше М* для любых распределений частоты ма¬
невров. В свою очередь, если Природа будет назначать маневры
Ф* и Ф**, то проигрыш Конструктора будет на меньше М*, какие
бы двигатели он ни выбирал.
460
МОДИФИКАЦИИ КРИТЕРИЯ ОПТИМАЛЬНОСТИ
[ГЛ. II
Оптимальный вес двигателя Gy и цена игры М* в функции
параметров Ф0 и АФ = Фх — Ф0 диапазона маневров показаны
сплошными кривыми на рис.
10.14 и 10.15. Видно, что цена
игры возрастает при расшире¬
нии диапазона маневров (уве¬
личение АФ) и при смещении
диапазона в область энергети¬
чески напряженных маневров
(увеличение Ф0). Для сравне¬
ния на рис. 10.14 пунктирными
кривыми показаны оптимальные
веса универсального двигателя
Gy, найденные в § 2 в предполо¬
жении, что распределение часто¬
ты маневров v (Ф) известно:
v (Ф) = 1/ДФ при Ф0 Ф ^
<Фх— равномерное распределе¬
ние маневров внутри допустимого
для такого распределения равен
Рис. 10.14. Оптимальный bccG^(O0,AO)
двигателя, универсального для маневров
Фо < ф < Фо -Г АФ. Сплошные кривые —
в случае отсутствия информации о распре¬
делении маневров, пунктирные — при из¬
вестном равномерном распределении.
диапазона. Проигрыш Mv=const
A/v=COnst (Фо» Фъ ^х) = *
Ф м
1
-®г-<■>.$“*
Ф1 __
‘ ■ Г‘1»о ,
= 2 A In
0,8
+ В
J- Y*j_
V Фд - V Фо
(1 — У Фд) (1 - i Фо)
С., -s- фд
+ С In
= + °,0
D
'УК
arctg
Gy -Г Фо ’
(Г^-ГФо)/^
А =
В =
С =
D =
V ФдФо
(10.81)
О.,
0,4
0,2
(I + Gjs’
а
[
Sb
/|{
11
1
hr
V
.2
1
:i 1
j
л
н
а
!
/
/ н
/ ft
7
ч ^
7
— 1,
■1-Gx
1 G.y
1 -Gy
(1 -'-GKY '
(1 - Gyf
02
0,4 06
0,8
Фп
Рис. 10.15^ Относительный проигрыш Ж* (Ф0, АФ)
в полезной нагрузке при выполнешш маневров
Фо < Ф < Ф0 + АФ универсальным двигателем.
Сплошные кривые соответствуют оптимальным
стратегиям Природы и Конструктора при отсут¬
ствии информации; пунктирные кривые — равно¬
мерному распределению маневров и параметрам
двигателя, оптимальным при отсутствии (!) и при
наличии(2) информации о распределении маневров.
(1 + G.yY
Этот проигрыш показан пунктирными кривыми 1 на рис. 10.15
§ з] ИГРОВОЙ ПОДХОД К ЗАДАЧЕ ОПТИМИЗАЦИИ 461
.для Gy = Gy. и кривыми 2 — для Gy. из §2. Переход Природы
с оптимального для нее распределения частоты v (Ф) на равно¬
мерное при Gy = Gy уменьшает проигрыш (ср. на рис. 10.15
сплошные кривые с пунктирными 1). Если Конструктору за¬
ранее известно, что Природа выберет равномерное распределение
v (Ф) = 1/ДФ, то оптимальным для него будет вес Gy, найденный
в § 2 (см. пунктирные кривые на рис. 10.14). При этом, как видно
из рис. 10.15, проигрыш по сравнению со случаем Gy = Gy умень¬
шится ненамного (ср. разность между пунктирными кривыми 1
и2с разностью между сплошными кривыми и пунктирными кри¬
выми 1).
Оптимальная стратегия Природы смешанная, ей выгодно назна¬
чать маневры Ф*, Ф** с частотами v*, v**, определяемыми из
уравнений dM'/dGy = 0, М* = v*М (Ф*, Gy) + v**J£ (Ф**, Gy)
[10.5-10.8]:
МЛ +(l — v*)(M\ =о, v”=l—v*
д0* )ф*,с* VaGx )ф",в»
(10.82)
/ дЖ 1 Г „ Ф
~ (1 — VW
1—
В качестве Ф*, Ф** в зависимости от параметров Ф0, Фх диа¬
пазона маневров могут фигурировать либо граничные точки диа¬
пазона: Ф* = Ф0, Ф** = Фх, либо одна из граничных точек
Ф0, Фх и точка промежуточного максимума Ф2 = (]/5/4 — G* —
— V2)2: Ф* = Ф<н Ф** — Ф2 или Ф* = Ф2» Ф** == Фр Это иллю¬
стрируется табл. 10.1, где для ряда значений Ф0, Фх приведены
оптимальные величины Ф* и Ф**; там же даны соответствующие
частоты v* и v**.
Таблица 10.1
Оптимальные значения Ф* , Ф ** параметра маневра и частоты v*, V**,
с которыми Природа должна назначать маневры Ф* и Ф**, для
различных допустимых диапазонов Ф0 Ф Ф1 (АФ = Ф* — Ф0)
ДФ
0,8
0,4
0,2
Фо
0,01
0,1
0,19
0,01
0,1
0,2
0,4
0,5
0,59
0,01
0,1
0,2
0,4
0,6
0,7
0,79
Фх
0,81
0,9
0,99
0,41
0,5
0,6
0,8
0,9
0,99
0,21
0,3
0,4
0,6
0,8
0,9
0,99
ф*
0,31
0,34
0,38
0,01
0,26
0,28
0,4
0,5
0,59
0,01
0,1
0,2
0,4
0,6
0,7
0,79
ф**
0,81
0,9
0,99
0,29
0,5
0,6
0,8
0,9
0,99
0,21
0,26
0,26
0,6
0,8
0,9
0,99
V*
0,84
0,82
0,98
0,63
0,55
0,6
0,7
0,8
0,97
0,62
0,65
0,6
0,59
0,64
0,78
0,99
V**
0,16
0,18
0,02
0,37
0,45
0,4
0,3
0,2
0,03
0,38
0,35
0,4
0,41
0,36
0,22
0,01
462
МОДИФИКАЦИИ КРИТЕРИЯ ОПТИМАЛЬНОСТИ
[ГЛ. 10
§ 4. ЗАПАС РАБОЧЕГО ВЕЩЕСТВА, ОПТИМАЛЬНЫЙ
ДЛЯ ЗАДАННОГО МАНЕВРА ПРИ ФИКСИРОВАННЫХ
ПАРАМЕТРАХ ДВИГАТЕЛЯ
Пусть по одному из критериев оптимальности выбраны парамет¬
ры двигателя. Эта процедура, как мы уже видели, может проде¬
лываться применительно к одному маневру или сразу к серии
маневров. Требуется с данным двигателем выполнить маневр,
отличный от расчетного, если двигатель предназначался для одного'
маневра, или какой-либо маневр из допустимого диапазона, если
двигатель предназначался для серии маневров.
Полезная нагрузка аппарата G- задана, вес двигателя GK
известен, запас рабочего вещества GlJ(0 ограничен объемом баков;
это ограничение записывается в виде 0 GlJf0 G0 — (GL + G>.),
где максимальный начальный вес аппарата G0 фиксирован. Можно
варьировать запас рабочего вещества Ср,0 в пределах, определяе¬
мых последним неравенством и управление двигателем в рамках
заданной регулировочной характеристики. Нужно обеспечить
минимальное время выполнения заданного маневра.
При уменьшении начального запаса рабочего вещества умень¬
шается стартовый вес аппарата, что при неизменной тяге двига¬
теля Р приводит к увеличению начального реактивного ускоре¬
ния и сокращению времени выполнения маневра. С другой сторо¬
ны, малого запаса рабочего вещества может не хватить для со¬
вершения заданного маневра. На основании качественных
соображений можно ожидать, что в ряде случаев оптимальный
запас рабочего вещества будет меньше максимально допустимого:
Gp,o<C Go — (G- + Gy). Пусть, например, дан двигатель с огра¬
ниченным расходом 0 q gmax-> предназначаемый для энер¬
гетически напряженного маневра. Если с этим двигателем
нужно выполнить ненапряженный маневр, то максимально до¬
пустимое количество' рабочего вещества может просто не успеть
израсходоваться за время совершения маневра. Такие рассуж¬
дения становятся несправедливыми в случае идеальных двига¬
телей, у которых нет ограничения на расход рабочего вещества.
1. Формулировка вариационной проблемы. Поставленная выше
задача относится к классу вариационных задач на максимальное
быстродействие и может быть записана следующим образом:
G = - gq, G (0) <Go, G(T) = Gn +
r = v, l* (0) = i*o, г (T) = i*!, T =Tnin,
V = gPe/G + В, V (0) = v0, V (T) = vT ^ (10.83)
(q = q (и), P = P (u), UIUi,i < U (*) < llmax, | e (t) \ = 1,
Gq-) Gr,, Gy — const).
§ П
ОПТИМАЛЬНЫЙ ЗАПАС РАБОЧЕГО ВЕЩЕСТВА
463-
Здесь G0, G„, Gy. — конструктивные параметры (заданы);
q = q (u), Р = Р (u), Umin- и (t) ишах — регулировочная ха¬
рактеристика двигателя (также задана), u (t) — независимые
управления двигателя (II.9). Требуется выбрать начальный вес
G (0) и построить программы u (£), отвечающие за расход q и
величину тяги Р, и программу е (t) направления тяги, которые
обеспечивали бы минимальное время Т выполнения заданного
маневра (кинематические параметры начала г0, v0 и конца гх,
ух траектории фиксированы).
Начальное условие (10.83), наложенное на вес аппарата, рас¬
щепляется на два: либо
G (0) = opt (при G (0) < G0), (10.84)
и тогда начальное значение импульса р, соответствующего фа¬
зовой координате G, равно нулю: р (0) = 0, либо
G (0) = G0, (10.85)
и тогда начальное значение импульса р неизвестно.
Заменив в (10.83) условие G (0) G0 условием (10.84) или
(10.85), получим стандартные задачи на максимальное быстродей¬
ствие. Если в (10.83) фиксировать вес G (0), то задача (10.83)
будет эквивалентна уже исследованной задаче о максимуме ко¬
нечного веса при фиксированном времени выполнения маневра
или соответствующей динамической задаче (см. гл. 4—8). Поэтому
здесь нет надобности снова разбирать вопрос об оптимальных
программах управления, остается только, опираясь на решение
упомянутых задач, найти оптимальное значение веса G (0), т. е.
оптимальный запас рабочего вещества. Эта процедура проделы¬
вается ниже для идеальных и нерегулируемых двигателей.
2. Идеальные двигатели ограниченной мощности и ограничен¬
ной скорости истечения. Динамический маневр для идеального
двигателя ограниченной мощности характеризуется функциона¬
лом / — интегралом от квадрата реактивного ускорения (гл. 4).
Чем меньше время выполнения маневра Г, тем больше величина J
(гл. 5). Конечный вес аппарата G (Т) выражается через функцио¬
нал / или Ф по формуле (4.6)
G (Т) = G„ + G, = eJIZm (ф = i J) <i0-S6>
(удельный вес двигателя а фиксирован). Разрешив это соотноше¬
ние относительно Ф, получим, что задача (10.83) сводится к оты¬
сканию максимума по G (0) функции Ф (G (0), Gx, Gr):
шах Ф = ■ - max ('1— Д(П 4 (10.87).
Gr. “Г GK G (0)<G„ \ Ь 0-0 /
МОДИФИКАЦИИ КРИТЕРИЯ ОПТИМАЛЬНОСТИ
[ГЛ. 10
при фиксированных значениях G0, G-, G*. Максимум (10.87)
достигается при G (0) = G0 (максимально возможный запас рабо¬
чего вещества) и равен
Ф,шх = ~gJ^Gk ^ (O)opt = <?о. (10.88)
По значению Фтах и удельному весу двигателя а вычисляется
максимальное значение функционала /тах — (2#/а)Фшах, а по
нему для каждого конкретного маневра — минимальное время
Т min*
Результаты такого расчета для маневров межпланетного пере¬
лета Земля — Марс — Земля, поворота плоскости орбиты и из¬
менения радиуса орбиты 24-часового спутника Земли приведены
в табл. 10.2.
Для ряда значений относительного полезного груза GJG0,
относительного веса двигателя G-JG0 и удельного веса двигателя
а (на единицу мощности) в таблице даны минимальные времена
выполнения перечисленных маневров. Зависимости J (Т) взяты
из главы 5: с рис. 5.27 — для перелета Земля — Марс — Земля
и с рис. 5.33 — для маневров 24-часового спутника Земли. При
этом брался перелет Земля — Марс — Земля со временем пре¬
бывания у Марса Тш = 48 суш и к величине J с рис. 5.27 добав¬
лялись затраты на торможение и разгон у Марса
/_2 + J+2 — 8 м2!сек3
(см. табл. 5.7). Для величин GJG0 и а в каждой клетке приведены
два значения, первое относится к межпланетному перелету,
второе — к маневрам управляемых спутников.
Аналогичная процедура проводится и для идеальных двига¬
телей ограниченной скорости истечения. В этом случае энергети¬
ческие затраты на выполнение маневра определяются характери¬
стической скоростью I — интегралом от реактивного ускорения
(гл. 8). При сокращении времени выполнения маневра Т вели¬
чина I увеличивается. Выразив / из формулы Циолковского
(8.13)
I = — Enax In [GJG (0)] (10.89)
(скорость истечения Fmax фиксирована, вес двигателя равен нулю,
так что G (Т) = бу, видим, что максимум / достигается при
G (0) = G0:
/max = - Finax In (GJG0), G (0)opt = G0. (10.90)
Таким образом, для обоих рассмотренных здесь типов идеаль¬
ных двигателей следует, что | минимальное время выполнения
§ '1]
ОПТИМАЛЬНЫЙ ЗАПАС РАБОЧЕГО БЕЩЕСТВА
465
В
Он
о
cd
и:
:В
о
g ■
г:
о
в
*
в
в
в
о
5
g
в £,
в Т
я 5
5 8
8 §
6 я
2 °
ф:В
н в
&§
в
§ §
& *
о
в
в
в
о
в
cd
В
со
о
3
в
л
cd
Он
В
о
& а
и л
I
g *
В
В
35 г
о О
В в
0 м
о н:
3 °
в о
ti 2
J3
* &
30
2 8 о
1 о в
g
О X g
3 ts g
8 s 1
2 в« S
л н
СО ф к
cd В
Q, В
в I
w О
Iв S
S vo н
В ^ 8
S ф В
Механика полета
§
в
в
п
м
о
о
СМ
545
гН
-
см
о
ю J
о
ю
тН
-
нН
см
о
о
03
545
(С1
см
о
о
ю
о
420
тН
-
тН
о
о
ю
о
см
550
см
см
о
ю
о
|435
-
ЧГ"1
о |
со
см
,585
чН
см
см
о
но
з
450
j
'гН
iO
см
о
о
см
665
i
со
со
о
ПО
о
495
тН
см
см
см
о
о
см
665
СО
03
1"
о
«
2
500
'Ч-Н
см
СМ
о
о
ю
о
о
см
675
-
со
со
о"
по
о
о
>4-1
LO
'чгН
тН
см
о
о
см
705
^гН
со
о
ПО
о
575
-гн
см
см
ю
см
о
о
см
820
1
1
1
о
1.0
о
о
00
ю
1
1
1
см
2
о
см
820
оо
оо
оо
со
оо
о
по
о
585
оо
1
оо
оо
о
о
UO
о
о
см
850
см
О'
см
■ч—1
о
по
12
о
о
со
LO
со
о
1 о
см
970
<С1
о*
00
о"
iO
о
о
00
СО
^гН
о
с|
5
£
~с
— Марс — Зем-
— 48 сут)
о
1!
<м
О*4
II
о
р
1!
о"
II
о
II
'С
сч
о"
Ч
ti'
о
«
в ^
5 к
<1°
<|я
<k !
1«
со
И1ШЭ£
МИНХ^ПЭ 'OMIx-^Z
сут
466
МОДИФИКАЦИИ^РИТЕРИЯ ОПТИМАЛЬНОСТИ
[ГЛ. 10
заданного маневра при фиксированных величинах полезной нагруз¬
ки и параметров двигателя достигается, когда запас рабочего
вещества берется максималь¬
но возможным.
3. Нерегулируемые двига¬
тели. Если тяга, расход и
скорость истечения двигателя
на активных участках посто¬
янны (Р (t) = Р0 или 0Т
q (f) = q0 или О, V (t) = V0
или 0), то независимо от типа
двигателя решается динами¬
ческая задача: найти мини¬
мум времени выполнения за¬
данного маневра Т при фик¬
сированных величинах вре¬
мени работы двигателя Tv, и
параметров а0 = gP0/G0, р =
= gq0/G (0) или минимум Tv,
при заданном Т (гл. 6).
Время работы двигателя Tv, выражается через заданные веса
Gn, G*, расход q0 и неизвестный вес G (0): gq0 Tv, = G (0)— Gr.— Gx.
Решение динамической задачи может быть записано в виде
Т = Т (-gP° gq° (10 91)
y \G(0) ’ G(0) ’ gqo Г
Будем считать зависимость (10.91) известной. Тогда задача
сведется к отысканию минимума (10.91) по G (0) G0. Ниже
дается решение этой задачи для трех маневров: (1°) набор модуля
скорости их в бессиловом поле, (2°) перемещение между точками
покоя, расположенными на расстоянии Z, в бессиловом поле,
(3°) поворот плоскости круговой орбиты в центральном поле.
1°. Набор модуля скорости. Решение динамической
задачи для данного маневра следующее (6.30):
т = 7V = (1 — е~г1,/у°). (10.92)
Вспоминая про связь Tv, = (G (0) — GK — Gx) V0/gP0, видим,
что начальный вес G (0) или запас рабочего вещества Gv$ =
= G (0) — G^ — Gx определяются формулой (10.92) однозначно
Рис. 10.16. Относительный начальный вес
G(0)/Go в зависимости от параметра щ/Vo при
фиксированных значениях суммарного веса
(G- + Gy)/G0 двигателя и полезной нагрузки —
набор скорости ut с нерегулируемым дви¬
гателем.
G (0) = (G* + Gx) eu'‘v° (о < Ul < F0 In -5^^). (Ю.93)
§ 4]
ОПТИМАЛЬНЫЙ ЗАПАС РАБОЧЕГО ВЕЩЕСТВА
467
В зависимости от комбинации uJV0 параметров маневра щ
и двигателя V0 изменяется потребный запас рабочего вещества
от нуля при
uJV* = О
до максимально возможного при
ujvо =ln IG0/(G„ + Cx)].
С большими значениями uJV0 при данных G0, Gn, G* маневр
становится невыполнимым. На рис. 10.16 показана зависимость
стартового веса G (0), отнесенного к максимальному G0, от ком¬
бинации uJVq при фиксированных значениях (Gn + G-A)/G0. От¬
личие G (0)/G0 от единицы дает разность между максимально
возможным и потребным запасом рабочего вещества.
2°. Перемещение между точками покоя. Решение
динамической задачи (6.43) здесь может быть представлено в виде
Т = с 1 {(g — 1) + 2 [с2 - (/I - 1)21 In'1 £} (10.94)
(Gji+GJFo gP0l t_ G (0)
Cl =
epo ’ (С„+сх)У*’ b g„ + gx
Из условия минимума T по | (дТ!д\ = 0) получаем неявное
£ = ■
Рис. 10.17. Оптимальный вес 1/5 = (Оте-|- Gx)/G (0) и мини¬
мальное время выполнения маневра T/ct в функции комби¬
нации с2 параметров маневра I и двигателя — перемещение
между точками покоя с нерегулируемым двигателем
(cj = (Gn Gy)\ojgpQ, с•> = gP0l (G- -L GX)-1V0-2).
выражение для оптимальной величины £ через комбинацию с2 пара¬
метров маневра и аппарата (рис. 10.17):
с2 = Va £ In2 g _ /1 (/I - 1) In I + (KI - I)2
(10.95)
30*
468
МОДИФИКАЦИИ КРИТЕРИЯ оптимлльности
[[VI. [П
Рассматривая теперь I как параметр, подставляем (10.95) в
(10.94) и получаем выражение для минимального времени
Тта = Cl [I In I - (VI - l)2]; (10.90)
по формуле (10.95) оно может быть представлено в функции ком¬
бинации с2 (рис. 10.17).
Соотношения (10.95), (10.96) дают полное решение задачи.
Посчитанная по ним зависимость оптимального начального веса
О 0,2 ф 0,6 0,8 / 9ро1
Фо
Рис. 10.18. Оптимальный цачальпый вес G(0)/Go в зависи¬
мости от параметра glJ0l/G]Vo при фиксированных значениях
суммарного веса (Gn -|- GX)JG0 двигателя и полезной на¬
грузки —• перемещение между точками покоя с иерегули-
руемым двигателем.
G (0) = s (Gn -j- Gy) от комбинации gP0l/GlVо при фиксирован¬
ных значениях (G- + Gy)/G0 показана на рис. 10.18.
3°. П о в о р о т плоскости круговой орбиты. Для ма¬
невра поворота плоскости круговой орбиты радиуса г0 на угол i
функционал динамической задачи (10.91) записывается в неявном
виде (6.88)
I — 1 = (Т/с) arcsin (10.97)
я; (Gn + GJVo iVkfa t_ G (0)
f| 2gP0 ’ Ca T0 ’ ~ GK + Gy
(здесь время T считается кратным периоду обращения по орбите,
равному 2я/с~1/2г0,/-).
Оптимальнее значение параметра £ (относительный началь¬
ный вес) и минимальное значение времени выполнения маневра Т
ОПТИМАЛЬНЫЙ ЗАПАС РАБОЧЕГО ВЕЩЕСТВА
469
равны (рис. 10.19)
G(0)
£opt —
'l min —
У 1-
+ Gy. J opt У \ — c\ — co arcsin У1 ■
CjC2
У1 — c\ — c-2 ar.csin Y1 —c\
(10.98)
Отношение начального веса G (0) к максимально возможному
G0 в функции комбинации с2 = ьУк/г^у^1 параметров дви¬
гателя и маневра приведено на рис. 10.20 для ряда значении
(Сг- -j- Gx)!Gq = const.
G(0)/Qo
Т/с,
8
6
4
г
О 0,2 0,0 0,6 0,8 с/
Рис. 10.19. Оптимальный вес 1/£ = (G- -J-
+ Gy)JG (0) и минимальное время выполне¬
ния маневра Т/сх в функции комбинации
с2 параметров маневра г, r0, к и двигате¬
ля — поворот плоскости орбиты нерегули¬
руемым двигателем (с!=л (G_ Gy,)Y0/2g],0,
с2 Vh/r0Vо-1).
Рис. 10.20. Оптимальный начальный вес
G (О)/G0 в зависимости от параметра
г Vk/roV'o-1 при фиксированных значениях
суммарного веса (G~ + Gx)/G0 двигателя
и полезной нагрузки — поворот плоскости
орбиты нерегулируемым двигателем.
Результаты настоящего пункта показывают, что в случае
нерегулируемых двигателей, в отличие от идеальных, для опреде¬
ленных значений параметров маневра и двигателя существует
оптимальный запас рабочего вещества, отличный от максимально
допустимого. Напомним, что эти результаты относятся ко всем
типам нерегулируемых двигателей.
ГЛАВА 11
ВОПРОСЫ НАДЕЖНОСТИ В ЗАДАЧАХ
ОПТИМИЗАЦИИ
Во время полета на двигательную систему могут действовать
случайные факторы, вызывающие отказы. Отказы двигателя
проистекают от внешних и внутренних причин; к первым можно
отнести, например, метеорные пробои, ко вторым — процессы
типа износа. В соответствии с характером этих воздействий веро¬
ятность отказов может зависеть от времени, координат, параме¬
тров двигателя и аппарата, от режима работы двигателя. Поэтому
учет фактора надежности приводит к изменению привычных
программ оптимального управления и оптимальных параметров
[11.1-11.4].
Под надежностью понимается вероятность бесперебойной
работы двигателя для данной реализации маневра. В случае отказа
двигателя (и только в этом случае) маневр считается невыполнен¬
ным, так что термины «вероятность безотказной работы двигателя»
и «вероятность успешного выполнения маневра» здесь совпадают
и могут употребляться равноправно. Вероятность выполнения
маневра либо задается (§§ 1—3), либо выбирается оптимальной
в некотором смысле (§ 4); рассматриваются случаи односекцион¬
ного (§ 1) и многосекционного (§§ 2 и 3) двигателей; для модельных
маневров даются примеры решения соответствующих вариацион¬
ных задач. В § 2 главы 7 была описана задача с фиксированным
временем работы двигателя. Если считать вероятность отказа
двигателя зависящей только от времени его работы, то эту задачу
можно трактовать как частный случай задачи о фиксированной
надежности.
§ 1. ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ ПРИ ЗАДАННОЙ ВЕРОЯТНОСТИ
УСПЕШНОГО ВЫПОЛНЕНИЯ МАНЕВРА
1. Формулировка вариационной проблемы. Рассмотрим общую
задачу оптимального управления. Пусть имеется динамическая
система, поведение которой описывается уравнениями вида
/i (^У» ^кч ^ 1ч 0* 1, . . . , 72, /i’ 1, . . . , 7 ,
1=1,..., q, (11.1)
§ i] ЗАДАННАЯ ВЕРОЯТНОСТЬ УСПЕШНОГО ВЫПОЛНЕНИЯ МАНЕВРА 471
где х, — фазовые координаты системы, ик (t) — управляющие
функции, ю, — постоянные управляющие параметры.
Заданы граничные условия относительно х в фиксированные
начальный t = 0 и конечный t = Т моменты времени. Нужно
обеспечить максимальное (минимальное) значение контрольного
функционала задачи х0 (Т). Эту вариационную задачу назовем
исходной.
Обратимся теперь к формулировке вариационной проблемы
о заданной надежности.
Динамическая система в отношении повреждений рассматри¬
вается как одно целое — повреждение одного элемента вызывает
прекращение работы всей системы. Считается, что при отказе
системы в любой момент времени задача не выполняется. После
отказа система не восстанавливается.
Требуется построить такую программу управления и выбрать
такие значения параметров, чтобы наряду с удовлетворением всех
условий, перечисленных выше, была обеспечена заданная ве¬
роятность безотказной работы системы (заданная надежность).
Предполагается, что повреждения образуют ординарный поток
без последействия [11.5—11.8]. Считается заданной интенсив¬
ность потока X (так называемое среднее число отказов в единицу
времени):
X = X (t, Xj, ик, Wi) (11.2)
в зависимости от времени, фазовых координат, управляющих
функций и управляющих параметров.
Тогда вероятность R отсутствия отказов на интервале [О, Т]
равна [11.5—11.8]
т
R= exp ^^ X dt'j , (11.3)
о
где X вычисляется вдоль траектории: X = X (t, Xj (t), ик (t), wx).
В соотношении (11.3) вероятность R фиксируется — условие
заданной надежности О R <С 1- Его надо присоединить к урав¬
нениям исходной вариационной задачи. Если используется по¬
становка Лагранжа, то это удобно сделать в виде условия изопе-
риметричности
т
V X (t, Xj (t), ик (t)f го,) dt = — In /?. (11.4)
V
О
В постановке Майера (11.3) нужно записать в виде дифферен¬
циального уравнения с граничными условиями
А = X (f, Xj, иъ юг), А (0) = 0, А (Т) = — In Д. (11.5)
472
ВОПРОСЫ НАДЕЖНОСТИ В ЗАДАЧАХ ОПТИМИЗАЦИИ [ГЛ. 11
Переменная Л будет фигурировать в качестве дополнительной
фазовой координаты системы (11.1). Значение AL — А (Т) назовем
условно допустимым средним числом отказов за все время дви¬
жения. Если задать надежность R = 1, то = 0, что невыпол¬
нимо. При уменьшении надежности допустимое число отказов
возрастает (так, например, изменению Я в диапазоне [1; 0,5] от¬
вечает изменение Лх в диапазоне [0; 0,7].
Обозначим через х} (t), щ(1), w\ решение исходной вариа¬
ционной задачи (без учета фактора надежности). Если на этом
решении окажется
т
А[ = X (£, х*. (£), u* (if), w*) dt < — In 1{, (11.(i)
0
то надежность R будет обеспечена. Отметим, что при Т
—In Л условие заданной надежности заведомо выполняется.
Считая, что условие (11.6) не имеет места, выпишем систему
уравнений задачи оптимального управления с заданной надеж¬
ностью (11.1) — (11.5)
= /г (С W/д Wl)i (0) — %i()i (J- ) — %ih ^ ext-T ^
Л = X (t, Xj, uk, wj), A (0) =.- 0, Л (T) = —ln /C I
(11.7)
В такой записи -- это обычная вариационная задача Майера.
Сделаем два замечания по обобщению (11.7).
1°. Пусть интенсивность потока отказов X зависит еще и от
текущего времени работы системы tv, С Тогда аналогично § 2
главы 7 нужно присоединить к (11.7) дифференциальное уравнение
с граничными условиями
С. = б, С. (0) = 0, tv, (Т) = opt, (11.8)
где б (С) - релейная управляющая функция, равная единице,
когда система включена, и нулю, когда система выключена.
Функцию б надо присоединить множителем к управлениям и
в (11.7), принимающим нулевые значения при выключении
системы г).
2°. Пусть управление и может принимать значения из диапа¬
зона [ищт, щпах! и обращаться в нуль при выключении. Интен¬
сивность потока отказов равна X (и), когда система включена, и
X (0), когда система выключена (рис. 11.1, а). Чтобы представить
в этом случае правую часть последнего уравнения (11.7) как
Ч Конечное значение t,x (Т), в отличие от основной задачи § 2 главы 7,
не задано и должно выбираться из соображений оптимальности траектории.
§ 1] ЗАДАННАЯ ВЕРОЯТНОСТЬ УСПЕШНОГО ВЫПОЛНЕНИЯ МАНЕВРА 473
функцию, не меняющую своего вида, можно снова воспользоваться
релейным управлением б:
А = Х(0) + IX (и) - Я (0)] б;
(11.У)
при этом в остальных уравнениях нужно заменить и на иб.
Этим же приемом можно воспользоваться, когда интенсив¬
ность потока отказов при выключенной системе X (0) (холодный
резерв) не равна пределу интенсивности X (+ 0) при и —> 0 (го¬
рячий резерв) (рис. 11.1, б).
ЯМ
Ш
О
е)
Рис. 11.1. Два случая, когда режим выключения (и = 0) является
выколотой точкой для зависимости интенсивности потока отказов
l от величины управления н.
Описанная постановка применяется ниже к задаче о доставке
максимального полезного груза. Рассматриваются два случая:
двигатели ограниченной мощности и ограниченной скорости ис¬
течения.
2. Двигатели ограниченной мощности. Для оптимальных без
учета надежности режимов работы двигательной системы ограни¬
ченной мощности характерно максимальное использование мощ¬
ности на активных участках. Кроме того, если двигательная си¬
стема идеальная, то оптимальная траектория не содержит пас¬
сивных участков.
Зададим теперь вероятность (11.3) успешного выполнения ма¬
невра. Интенсивность потока отказов (11.2) будем считать зави¬
сящей от мощности Ny отнесенной к максимальной iVmax, и кон¬
структивного параметра w:
X — X (t, Ny w)
(0<ЛГ(0<1, W = coast, ЗШУ> 0, dX/dw < 0). (11.Jo)
Влияние максимальной мощности здесь не учитывается; не¬
отрицательность производной dXIdN соответствует интуитивному
представлению о том, что при форсировании режима работы дви¬
гательной системы вероятность отказа увеличивается. Параметр w
отвечает за конструктивные мероприятия по увеличению надеж¬
ности: увеличение w соответствует уменьшению интенсивности
474 ВОПРОСЫ НАДЕЖНОСТИ В ЗАДАЧАХ ОПТИМИЗАЦИИ [ГЛ. 11
потока отказов X (dX/dw < 0), но при этом увеличивается удель¬
ный вес двигателя a (da/dw 0).
Ограничимся рассмотрением случая идеального двигателя
(см. гл. 4); задача о доставке максимального полезного груза при
заданной надежности R записывается в соответствии с общей
постановкой (11.7) аналогично (4.42)
(a(£)>0, 0<W(0<1, |е(01 = 1; £х, гг = const).
Здесь нужно выбрать оптимальные значения параметров G,.,
w и построить оптимальные программы а (£), N (t), е (t). До реше¬
ния полной задачи, так же как и в § 1 главы 4, можно найти опти¬
мальное соотношение для веса GK (он входит только в первое
уравнение и начальное условие из (11.11) для Ga). После про¬
ведения соответствующей процедуры (см. гл. 4, § 1, пп. 1 и 2)
получаем выражения для функционала Gc (Т) — Gn и оптималь¬
ного веса двпгателя Gx, совпадающие по виду с (4.15), (4.16):
После этого задача сводится к минимизации функционала Ф,
а при фиксированном параметре w — к минимизации функционала
У; за последней задачей (У = min) сохраним название динами¬
ческой.
Без учета надежности можно было до решения динамической
задачи делать вывод об оптимальности управления N (t) = 1.
В рассматриваемой постановке этого сделать нельзя. Более того,
качественные рассуждения свидетельствуют о возможности суще¬
ствования режима, отличного от идеального N (t) = 1. Дейст¬
вительно, при увеличении мощности N и неизменной программе
a (t) уменьшается функционал У (т. е. увеличивается полезная
нагрузка G~ (11.12)). Вместе с этим растет интенсивность потока
.отказов (11/10) (т. е. уменьшается надежность).
(G0+ GJ2 а (го) а2
~Gy l^'N
* Ga(0) + G* = 1, Ga(T) = max
г = v,
v = гге —(— К,
A — X (t, N, ?r),
r (0) = r0, г (T) = n,
у (0) = V0, V (T) == Vi, > (11.11)
A (0) = 0, A (T) —
= —In R
gt. = (i — уФ)2, Gy, = уФ — Ф,
где под Ф надо понимать (ср. (4.14))
(11.12)
т
Ф = '
(11.13)
и
I п ЗАДАННАЯ ВЕРОЯТНОСТЬ УСПЕШНОГО ВЫПОЛНЕНИЯ МАНЕВРА 475
Обсуждаемая вариационная проблема (о минимуме функци¬
онала J) в терминах задачи Майера записывается следующим
образом (ср. (5.2)):
Параметр w в (11.14) считается фиксированным, оптимальное
значение w определится после решения (11.14), т. е. после полу¬
чения зависимости Jmm(w), из условия минимума Ф (w) =
= [a(w)/2g] Jmin(w).
Оптимальные законы изменения реактивного ускорения a (Z),
мощности N (t) и направления вектора тяги е (Z), согласно прин¬
ципу максимума, должны обеспечивать в каждый момент вре¬
мени абсолютный максимум гамильтоновой функции Н (ищется
минимум /); последняя имеет вид
Н = -flW + а (Ри • е) + lpx + (pr*v) + (р®-Н), (11.15)
Часть функции Я, зависящая от N, с управлением а, взятым
из (11.17), записывается так:
Из рассмотрения (11.18) можно сделать вывод относительно
знака импульса рх. Предположим, что рх 0, тогда максимум
Н имеет место при N = 1 (так как по (11.10) dXldN > 0). Значит,
оптимальная траектория получится такой же, как и без учета
надежности. При формулировке общей задачи (11.7) предполага¬
лось, что условие (11.6) не выполняется и заданная надежность R
на такой траектории не может быть обеспечена. Следовательно,
J=a2/N, /(0)=0, J (Т) = min, '
г = V, г (0) = гп, г (Т) = 1Д,
v = ae + R, v(0)=vn, v(IT)=vi, ’ (11.14)
A=b(t,N,w), А (0) - 0, А (Т) = — In R
(a(Z)>0, 0<jV(Z)<l, | е (Z) | = 1).
где импульсы pr, p^, px, Pj удовлетворяют уравнениям
Г\ А
Рх -- 0, pj — 1.
1
\ (и.16)
J
Максимум Н по е и а достигается при
е = р,Jpv, а = 42pvN (pv = |р„|).
(11.17)
Ялг = 1/4p\N + к (t, N) р-К.
(11.18)
Рх = const <( 0.
(11.19)
476
ВОПРОСЫ НАДЕЖНОСТИ В ЗАДАЧАХ ОПТИМИЗАЦИИ [ГЛ. 11
Отметим два свойства оптимальных (с учетом надежности) тра¬
екторий, следующих из условия максимума (11.18) по N.
1°. Рассмотрим семейство характеристик надежности X (t, N),
имеющих две общие точки X (£, 0) = Х0 (t) и X (t, 1) = X, (t). Для
всех X (£, N) из (11.10), удовлетворяющих условиям (см. заштри-
зованную область на рис. 11.2)
X (t,N) > Я0 (0 + IX, (t) - Х0 (t)]N,
(11.20)
управление N (t) граничное, оптимальные траектории и значе¬
ния функционала / одинаковы.
В самом деле, если подставить
линейную функцию N из неравен¬
ства (11.20) в (11.18), то получен¬
ная функция
IIN maj ” Р\К -f- [V4pv -f-
+ Рх(К~К)Ж (11.21)
в силу (11.19) будет мажориро¬
вать все Ндг с функциямиX (£, N),
удовлетворяющими (11.20):
Рис. 11.2. Область па плоскости «ин¬
тенсивность потока отказов Я,—мощность
.V»(заштрихована), неразличимая в смы¬
сле функционала задачи J.
Ня (N) < HN
maj (N),Hn (0) =
= HN maj (0), HN (1) = HN maj (!)•
(11.22)
Следовательно, и max H^ max II ^ maj-, no HN maj — линей¬
ная функция N, и ее максимум достигается в граничных точках
N = 1 при pi > — 4рх (X1 — Х0), N = 0 при pl<C~ 4Рх (X, — Х(]).
(11.23)
В этих точках функции HN maj и II ^ совпадают, поэтому мак¬
симум Нм для всех X из (11.20) будет иметь место в этих же точ¬
ках. Таким образом, оптимальное управление N (t) оказывается
граничным (11.23), и промежуточные значения X не будут фигури¬
ровать в задаче. В точках N = 1 и N = 0 все X (*, N) из (11.20)
принимают одинаковые значения X, (t) и Х0 (t). Значит, оптималь¬
ные траектории и значения функционала J будут одни и те же
(т. е. заштрихованная часть области характеристик X (£, N) на
рис. (11.2) оказывается неразличимой в смысле функционала
задачи).
2°. Если dX/dN = 0 при N = 0, то оптимальная траектория
не содержит пассивных участков. В этом случае частная произ¬
водная (11.18) по N
0HN/dN = xUp%+ px()X/diV (11.24)
§ 1] ЗАДАННАЯ ВЕРОЯТНОСТЬ УСПЕШНОГО ВЫПОЛНЕНИЯ МАНЕВРА 477
в точке N = О всегда положительна (кроме изолированных мо¬
ментов времени, когда pv = 0). Следовательно, оптимальное
значение N, которое должно обеспечивать максимум (11.18),
всегда больше нуля, т. е. пассивные участки отсутствуют.
Рассмотрим теперь частный вид зависимости (11.10)
X = X(N, w) = (^max? W = Const > 0) (11.25)
(рис. 11.3). Для всех 0 <; и; 1 (заштрихованная область на
рис. 11.3) оптимальное управление N (t) определяется соотноше¬
нием (11.23), в котором следует положить Х0 = 0, \ = Хтах, и
справедливо свойство 1°. Для w 1 имеет место свойство 2°, а
оптимальное управление N (t) таково:
N = 1 При Pl> — 4
1
N = при —4^тахрх, (11.26)
т. е. здесь появляются участки с переменной мощностью, мень¬
шей максимальной.
Все полученные выше результаты не зависят от типа динами¬
ческого маневра (т. е. от r0, r1? v0, v3, Н (г, t)). Чтобы решить
вариационную задачу (11.14) до конца, зададим простейшие ма¬
невры: перемещение между двумя
точками покоя и набор заданной
скорости в бессиловом поле.
Если не задавать надежность
(Л (Т) = opt или р> = 0), то реше¬
ние задачи о перемещении между
точками покоя получается следую¬
щее (5.33):
N* (t) = 1,
a (t) е* (t) = 6 (l/T2) (1 - 2ИТ),
Г (Т) = 12 (12/Т3). (11.27)
При заданной надежности R
решение будет зависеть от пара¬
метра
* = - In R/lmxxT (0<х<1),
(11.28)
который представляет собой отношение допустимого числа отка¬
зов Л (Т) = — In R к максимально возможному Лтах = Хтах7’.
Рис. 11.3. Степснцо-показательная завив
симость интенсивности потока отказоо
Я от мощности N и конструктивнога
параметра w (штриховкой выделент
область, где функционал не зависит о-
вида функции Я (Аг)).
478 ВОПРОСЫ НАДЕЖНОСТИ В ЗАДАЧАХ ОПТИМИЗАЦИИ [ГЛ. 11
Окончательно решение записывается следующим образом *):
если 0 w <; 1, 0 х 1 (рис. 11.4, а, то
N(t) = l, a(t) = а0 (1—2t/T) при О <//h,
Отметим, что для значений конструктивного параметра
^ 1 величина к совпадает с отношением Т^/Т полного времени
работы двигателя ко времени маневра, а соответствующее решение
х) Функции N (t) и a (t) получаются{четными относительно середины ин¬
тервала t = V2T, функция е (t) = + 1 — нечетной: в (t) = + 1 при
О < t < V2T, е (t) = -1 при Ч2Т < t < Т.
N (t) = О, а (f) = 0 при hCt<: V2Г
(а„ = [1 - = У*хГ) ,
J (T) = 12 (/г/Г*) [1 — (1 — x)3]-1;
если w^> 1, (w — 1)/(Згг — 1) ^ x <; 1
(рис. 11.4, б), то
iV(0 = l,
а (£) = a{) (1—2t/T)
при
го-|-1
,ги—1
(1 — 2 h/T)™-1
при fi<«<V2r Г (11-29)
/ (Г) = 12 (^/IT3) I'l - (1 - X)3]"1
если гт^>1, 0 x (w — 1)/(Згг — 1)
(рис. 11.4, б), то
при 0< t < 7 >7\
/(Г) = 12(*7Пт(т^гг) " х
ги
§ 1] ЗАДАННАЯ ВЕРОЯТНОСТЬ УСПЕШНОГО ВЫПОЛНЕНИЯ МАНЕВРА 479
эквивалентно (7.50)—(7.52). Для сравнения с полученными
а)
(0<u/<J7 х,=0,6)
№ t
(их=2, х=0,6)
в)
(ш=2, z=0J5)
Рис. 11.4. Три возможных типа оптимальных программ мощности N (0 и реактивного
ускорения a (t) для задачи о перемещении между точками покоя:
а) 0 <гс < 1, х = 0,6; б) w = 2, х = 0,6; в) го = 2, х = 0,15 (w — параметр се¬
мейства кривых к (N), см. рис. 11.3; х—отношение допустимого числа отказов к макси¬
мально возможному; пунктир — программы, оптимальные без учета отказов).
N (t) и ре-
оптимальными законами (11.29) изменения мощности
активного ускорения a (t) на
рис. 11.4, а—11.4, в пунктир¬
ными линиями показаны ста¬
рые законы (11.27), оптималь¬
ные при отсутствии отказов.
На рис. 11.5 сплошными
линиями показана величина
функционала /, отнесенная
к J* из (11.27) в зависимо¬
сти от параметра надежности
х для различных значений
конструктивного параметра w
(показатель степени в (11.25)).
Увеличение надежности R
(уменьшение параметрах) при
прочих равных условиях при¬
водит к увеличению функ¬
ционала J. Разница между
кривыми, соответствующими
0 ^ w 1 и w = 2,3,4,
Дает представление о вы¬
игрыше от использования промежуточных значений мощность.
Ксли бы при w 1 условие заданной надежности удовлетворялось
Рис. 11.5. Функционал задачи J в зависи¬
мости от параметра w семейства кривых
к (N) (рис. 11.3) и отношения х допустимого-
числа отказов к максимальному. Сплошные
кривые — перемещение между точками по¬
коя — J* = 12/2/2'3, пунктирные — набор мо¬
дуля скорости — J* = иг2/Т.
480
ВОПРОСЫ НАДЕЖНОСТИ В ЗАДАЧАХ ОПТИМИЗАЦИИ
[ГЛ. 1
только за счет выключения двигателя (11.23), то функционал для
всех X(N,w) был бы одинаков (кривая 0^н;^1). Переход
на программу (11.26) позволяет существенно уменьшить значения
функционала.
Для задачи о наборе скорости без учета надежности (рх = 0)
пассивные участки на траектории отсутствуют, и получается сле¬
дующее решение (5.32):
N* (?) = 1, а* (0 е* (?) = uJT, J* (Т) = и\!Т.
(11.30;
Если показатель степени в формуле (11.25) для интенсивности
потока отказов взят из диапазона 0 ^ w 1, то появляются пас¬
сивные участки. Их число и расположение на влияют на функцио¬
нал задачи, а суммарная протяженность выбирается из условия
заданной надежности Л (Т) = —In/?. При w 1, согласно свой¬
ству 2°, пассивные участки отсутствуют, условие Л (Т) = — Ini?
удовлетворяется за счет уменьшения N. Проделав все выкладки,
получим (е (?) = 1):
если 0 1, 0 х 1 (рис. 11.6, а, то
N (?) = 1, a (?) = ui/ti при 0 ?i,
N (?) = 0, а (?) = 0 при ?i <( ? <. Г
J (Т) = (и1/Т) х"1;
если w^> 1, 0<х<^1 (рис. 11.6,6), то
(?i = хГ),
(11.31)
N (?) = хг", а (?) -- uxjT при 0 <; ?<; 7\
_ i_
J {Т) = iul/T) х w
(здесь, как и в (11.29), х = TXJT при 0 1).
Отношение функционалов (11.31) и (11.30) в зависимости от
х и w показано на рис. 11.5 пунктирными линиями. Видно, что
для задачи о перемещении между точками покоя (сплошные кри¬
вые) требование заданной надежности приводит к значительно
меньшему увеличению функционала, чем для задачи о наборе
скорости (при одинаковых значениях х и w).
Обратимся теперь к выбору оптимального значения конструк¬
тивного параметра w. От этого параметра зависят интенсивность
потока отказов (X убывает с увеличением w, см. (11.25)) и удельный
вес двигателя (а увеличивается при увеличении w, см. пояснения
к (11.10)). Зададимся простейшей зависимостью
a (w) = а* (1 + iv) (а* = const, w 0);
(11.32)
ЗАДАННАЯ ВЕРОЯТНОСТЬ УСПЕШНОГО ВЫПОЛНЕНИЯ МАНЕВРА 481
имея в распоряжении решения (11.29) и (11.31) динамической
fjfilf
1
1
1
1 -
1
Г
1
1
1
и
А/
Тр
S а)
(feuKf, z=0,6)
Т t
(ur=2, z=0,6)
Рис. 11.6. Два возможных типа оптимальных программ мощности N (О
реактивного ускорения а (0 для задачи набора модуля скорости:
а) о < w < 1,х — 0,6; б) w = 2,х = о.б (о ;рдль гые пояснения даны в под¬
писи к рис. 11.4).
задачи (11.14), найдем параметр w из условия минимума функции
(см. (11.12), (11.13)) Ф(и;,х) = [a(u>)/2g]J (и>, х):
для маневра перемещения между точками покоя
(1 + w) [1 — (1 — х)3]'1
при 0 w 1, 0 х 1,
при ю>1, («.-!)/(3«>—1)<х<1, (11.33)
гг—1 3_
, ч 1 /3w — 1 \ w w
(1 + w) -J ( w _ l ■) Я
при w 1, 0 x (w — l)/(3w — 1)
(Ф* = (a*/2g) 12Z2J-3),
mm
w
Ф (w, X )
Ф*
=■- min
w
для маневра набора модуля скорости
min ^ {w’ х)
Ф*
= mm
\\-*rw)yTx при 0 < 1, 0 <6 и <; 1,
_J_ (11.34)
(1 + w) я w при w > 1, 0<х<1
(ф* = (а’/2g) и\ТД.
31
Механика полета
482 ВОПРОСЫ НАДЕЖНОСТИ В ЗАДАЧАХ ОПТИМИЗАЦИИ [ГЛ. II
Результаты решения задач (11.33), (11.34) приведены на
рис. 11.7, 11.8. На рис. 11.7 показаны оптимальные значения
иг
ОД
00
Рис. 11.7. Оптимальные значения кон¬
структивного параметра го, определяющего
кривую надежности (рис. 11.3), в функции
ус — отношения допустимого числа отказов
Ai к максимальному Лтах. Сплошные ли¬
нии — перемещение между точками покоя,
пунктирные — набор модуля скорости.
Рис. 11.8. Минимизированные по го значе¬
ния функционала Ф (x) = inin [a(w)/2<?jx
xJ (ус, w), соответствующие зависимостям
a{w) = (1 + w)а* и J (ус, го) с рис. 11.5 (обо¬
значения те же, что и на рис. 11.5, 11.7;
Ф* = (а*/2 g)J*).
°*С
0,4
0,3
0,2
00
параметра w в функции к —отношения допустимого числа отказов
к максимально возможному, на рис. И-8 — соответствующие ми¬
нимальные значения функ¬
ционала Ф в зависимости
от того же параметра х.
Сплошные кривые относят¬
ся к задаче о перемеще¬
нии между точками покоя,
пунктирные — к задаче о
наборе модуля скорости.
После завершения этой
заключительной стадии за¬
дачи можно вычислить оп¬
тимальные весовые соотно¬
шения по формулам (11.12),
(11.13). Пример зависимо¬
сти полезной нагрузки от
вероятности успешного вы¬
полнения маневра R —■
= ехр (—хЛтах) дан на
рис. 11.9. Горизонтальные
участки кривых отвечают
таким значениям вероят¬
ности 7?, которые обеспе¬
чиваются на оптимальной
без учета надежности траектории (т. е. когда неравенство (11.6)
выполняется).
0,5
A max
0J
0,1
./
■ч —■
\
\
\ ^
ч \
X \
\ \
\ \
ч/
ч
\\
\\
\\
\ \
у \\ 1_
//
/
/
\
ч \
\\
\ \
\ ч1
\ Ч
\ ч
\ Щ-
>
max 0,5
V4
v\
ч\
/
/
/
\/ У
\\ Х
\ ч
, \ ч
V \ ч
\ Ш
5
N
\Ч
'O'v
чЧ.
\ \
Ч\ \
_ \
^—- ч
Л v\\
Л V
AVI
0,5
Ов
07 0,8
зависимости
0,9
Рис. 11.9. Пример зависимости максимальной
полезной нагрузки Gп от вероятности R успешного
выполнения маневра для различных значений Атах
— максимального числа отказов (Ф* = (а*/2£) J* =
= 0,1; величины го оптимальные, остальные обо¬
значения даны на рис. 11.7, 11.8).
§ 1] ЗАДАННАЯ ВЕРОЯТНОСТЬ УСПЕШНОГО ВЫПОЛНЕНИЯ МАНЕВРА 483
3. Двигатель ограниченной скорости истечения. Ранее, в
главе 8, было установлено, что оптимальный реяшм работы дви¬
гателя ограниченной скорости истечения достигается при V (t) =
= Ртах- Пусть теперь с увеличением скорости истечения (т. о.
с увеличением температуры) интенсивность потока отказов (11.2)
возрастает (ср. (11.10))
% = X{t,V,w) (OX/dV^O, 0<F<FmaXf dX/dw<: 0,
Как и в (11.10), здесь фигурирует конструктивный параметр
w; считается, что при увеличении w интенсивность потока отказов
падает (dXJdw <С 0), но это достигается ценой увеличения удель¬
ного веса двигателя (dy/dw^> 0, у = GyJPm3iX — см. (8.1), зави¬
симость у (w) предполагается известной).
Согласно общей постановке (11.7) задача о доставке макси¬
мального полезного груза для двигателя ограниченной скорости
истечения записывается в виде (см. (8.15), (11.11); тяга, скорость
истечения и веса отнесены к соответствующим максимальным
значениям)
у (Т) = уь
А = Х{) (С w) + [?C(£, F, w) — Х0 (С ?/;)] б, А (0) = 0,
А (Т) = — In li
(0 ^ р (t) < 1, 0<F(i)<l, б (t) = 1 или 0, | е (t) | = 1;
И» — ^Pmax/^oFmax? ао — gPmax/Go, w = Const).
Здесь считается, что при выключенном двигателе интен¬
сивность потока отказов становится равной (Я0 = Х0 (t, w) <С
<M*,F, М7), в частном случае Х0 = 0). Чтобы отразить этот факт
в уравнениях, был использован прием 2° из п. 1. Если было бы
известно, что тяга ни на какой оптимальной траектории не при¬
нимает промежуточных значений из интервала (0, 1) — особый
режим, то функцию б (t) можно было бы не вводить. В последнем
Уравнении вместо б тогда нужно было бы написать Р. Однако
отсутствие в составе оптимальной траектории участков с особым
управлением заранее не очевидно.
w = const).
(11.35)
G0 = — (яРб/F,
(°) + т Н ао/ё =1,
G0 (Т) = шах,
v
v (0) — v0, . (11>36)
484 ВОПРОСЫ НАДЕЖНОСТИ В В АДАНАХ ОПТИМИЗАЦИИ
[IV!. I!
В задаче (11.36), помимо оптимальных управлений Р (t),
V (t), 6 (t), е (/), нужно выбрать еще оптимальные значения пара¬
метров а0, (или Рщах, Bm;lx, w). Если а0, p,w зафиксировать,
то задача (11.36) сведется к следующей (ср. § 1 гл. 8):
Функционал G (Т) -- Gx после решения (11.37) будет функ¬
цией параметров а0, р, w. Оптимальные значения этих пара¬
метров определятся из условия максимума полезной нагрузки
G- = Ga (Г) = Gx (а0, — у (w)a0/g. Дальше будет рассматри¬
ваться задача (11.37).
Для анализа состава оптимального управления нужно иссле¬
довать па абсолютный минимум (ищется максимум Gx) по е, Р,
6, V функцию И (ср. (11.15)):
Импульсы рг, Ри и рх по-прежнему определяются уравнения¬
ми (11.16), а импульс pv. — уравнением
/V = -dHldG = (pv-e) «0G-2P6, Pv, (Т) = -1. (11.39)
Из минимума (11.38) по е следует (ср. (11.17))
Предположим, что в некоторый момент времени pv. (t) О,
тогда из минимума Н следует V = 0 (независимо от знака Р\) и
Р = б = 1. Режим Рб = 1 при V = 0 противоречит физическому
смыслу, поэтому всюду (t) 0. Если положить теперь Р\ 0,
то получим всюду V = 1 и более позднее выключение двигателя
(б = 0) по сравнению со случаем р\ = 0. При этом условие за¬
данной надежности не может быть выполнено, поскольку пред¬
полагается, что неравенство (11.6) не имеет места.
G (0) —- 1, G (Р) = шах,
Г (0) = го, Г (Р) — Г1,
v (aaP6/G) е + К, v (0) = v0, v (Р) = vb
A - К + [b (V) — %,] 6, Л (0) 0, Л (Р) = — In Л
(0р(г)<;1, о<'v(t)<; 1, б(t) = 1 или о,
Iе (01 = !)•
II = {[- Р, £ + -j- (Р„ • е) j Р + Р>. {X (F) - Ц б +
+ Х0р>. + (Pr-v) + (pv-H). (11.38)
е = — р Jpv.
Аналогично п. 2 (см. (11.19)) можно показать, что
Pv- (0 < 0. Рл = const > 0-
(11.40)
(11.41)
§ 1] ЗАДАННАЯ ВЕРОЯТНОСТЬ УСПЕШНОГО ВЫПОЛНЕНИЯ МАНЕВРА 485
Покажем теперь, что на оптимальной траектории управление
Р (/) не может принимать промежуточных значений О
Поскольку Р входит в (11.38) линейно, то промежуточные значе¬
ния Р в качестве оптимальных могут появиться, когда коэффи¬
циент при Р обращается в нуль на некотором отрезке времени
(особый режим). Но тогда 6 = 0, поскольку р\^> 0 (см. (11.41)),
т. е. тяга Р6 должна быть выключена. Это справедливо для любо¬
го маневра в произвольном гравитационном поле.
Установив отсутствие особого режима в составе оптимального
управления, исключим из (11.37) —(11.39) управляющую функцию
6 (t): там, где входит произведение Р8, нужно оставить просто Р,
а где функция 6 входит без Р, ее нужно заменить на Р. Тогда
часть функции II, зависящая от управлений V и Р, с учетом (11.40)
запишется в виде
V (t) == 1 при X (t, V) >X(t, 4) + Ш-i-l). (i 1.43)
* A
Если условие (11.43) не выполняется, то в каждый момент вре¬
мени существует оптимальное промежуточное значение 0
< V (0 <С определяемое из уравнения
Уравнение (11.44) может иметь несколько корней; тогда среди
них нужно выбрать такой, который дает абсолютный минимум
функции Ну из (11.42). Нулевые значения V не входят в состав
оптимального управления. Если
то условие (11.43) будет выполняться на всей траектории, так как
Pp. 0, /V < 0 (см. (11.39) —(11.41)). В этом случае скорость
истечения нигде не будет принимать промежуточных значении.
Оптимальное управление тягой, как было доказано выше,
может быть только граничное. Чередование активных и пассив¬
ных участков на траектории определяется соотношением
Яу, л = (#v — Pv — Кр>) р, Ну = - цр,,У + X (t, Г) рх.
Из условия минимума Ну но V следует
V2dX/dV = -[ipjpx (0 < V < 1).
(11.44)
X (t, V) > А (*, 1) + (mJpx) (V-1 - 1), (11.45)
Р
1 при Ну — pvdttG'1 — Х0р-,. <( 0,
0 при Ну — pva0G~x — Х0рх > О,
полученным из условия абсолютного минимума функции (11.42)
по Р.
486
ВОПРОСЫ НАДЕЖНОСТИ В ЗАДАЧАХ ОПТИМИЗАЦИИ [ГЛ. 11
Для полного решения задачи нужно проинтегрировать систе¬
му уравнений (11.37), (11.39) с конечными соотношениями (11.40),
(11.43) — (11.46) для управляющих функций.
Рассмотрим теперь случай ограниченной перегрузки а =
= a0P/G (вместо ограниченной тяги 0<JP<^1). Здесь задача
(11.37) о максимуме конечного веса Gx сводится к отысканию ми¬
нимума функционала
I =\y dt (Gt = 0 < V < 1, 0 < а < ап) (11.47)
(функционал (11.47) получается интегрированием в квадратурах
первого уравнения (11.37) и представляет собой обобщение ха¬
рактеристической скорости (8.13)).
Аналогично предыдущему можно доказать отсутствие проме¬
жуточных значений реактивного ускорения 0 < а а0 в составе
оптимального управления. Имея это в виду, можно использовать
запись (11.37) уравнений вариационной проблемы, заменив пер¬
вое и третье уравнения на
I = a08/V (1(0) = 0, I (Т) = min), ^ = а06е + К. (11.48)
Оптимальное направление тяги будет определяться первым
соотношением из (11.17). Управления V (t) и б (t) находятся из
условия максимума функции (ср. (11.42))
Оптимальная программа по скорости истечения будет опре¬
деляться соотношениями (11.43), (11.44), в которых надо поло¬
жить = — <70, причем, если дХJdt = 0, то оптимальное зна¬
чение скорости истечения вдоль траектории будет постоянно.
Моменты включения б = 1 и выключения 6 = 0 двигателя
находятся из соотношения, аналогичного (11.46)
§ 2. СЕКЦИОНИРОВАННЫЙ ДВИГАТЕЛЬ ОГРАНИЧЕННОЙ
МОЩНОСТИ — ФОРМУЛИРОВКА
И УРАВНЕНИЯ ВАРИАЦИОННОЙ ПРОБЛЕМЫ
Когда интенсивность потока отказов X и полное время движе¬
ния Т велики (так что максимальное число отказов Атах =
“ ^та\Т ^> 1), то односекционная двигательная система не может
обеспечить приемлемый уровень полезной нагрузки при доста-
т
о
Ну.ъ — (Ну + Pvdо — ^оР\)
Hv = - а0У~г ■ X (t, V) рх (рх < 0).
(11.49)
при Hv + pvaQ — Х0рх > 0,
при Ну -|- pva{) — ХьРх < 0.
(11.50)
§ 2\ СЕКЦИОНИРОВАННЫЙ ДВИГАТЕЛЬ ОГРАНИЧЕННОЙ мощности 487
точно высокой вероятности успешного выполнения маневра (см.
рис. 11.9). В этом случае двигательная система (или ее наиболее
ненадежные элементы) должна делиться на автономные секции.
Секции считаются равновеликими, повреждение каждой секции
приводит к ухудшению характеристик двигателя (например,
к уменьшению мощности для двигателей ограниченной мощности),
но не вызывает прекращения работы двигателя в целом, все сек¬
ции работают параллельно.
1. Ожидаемые моменты повреждений. Для прогнозирования
весовых характеристик аппарата нужно знать, как будет ме¬
няться число работающих секций по времени п (t). Аналогично
первому параграфу предполагается, что повреждения каждой
секции случайные и образуют ординарный пуассоновский поток
без последействия.
Известна интенсивность потока X (среднее число повреждений
одной секции в единицу времени)
Интенсивность потока здесь считается зависящей от времени
t и положения г аппарата в пространстве. Это соответствует, на¬
пример, повреждениям, вызываемым нестационарными неодно¬
родными потоками метеоров. Кроме того, X зависит еще и от кон¬
структивных параметров двигателя w. Например, в случае пробоя
метеорами холодильника-излучателя (радиатора) — это уязви¬
мая площадь секции радиатора и толщина стенок. В этом пара¬
графе рассматривается идеальный двигатель ограниченной мощ¬
ности и в качестве w принимается максимальная мощность N0/n0,
приходящаяся на одну секцию в начале движения (X — неубы¬
вающая функция N0/n0).
Если в момент времени tj выходит из строя /-я секция, то ве¬
роятность Rk (t — tj) того, что в интервале (tj, t) будет повреж¬
дено не более чем к секций для пуассоновского потока, определя¬
ется следующим соотношением [11.5—11.8]:
(п0 — общее число секций; повторные повреждения секции, если
таковые возможны, в расчет не принимаются).
Момент очередного повреждения будем определять из
условия, что вероятность отсутствия повреждений к = 0 в ин¬
тервале (tj, tjA1) равна заданной величине 7?. Положив в (11.52)
X = X (t, v, w).
(11.51)
к
("о — /)!
X 1 — exp ^^ A, exp —(n0 — j — i) ^ (11.52)
1.
t.
ВОПРОСЫ НАДЕЖНОСТИ В ЗАДАЧАХ ОПТИМИЗАЦИИ [ГЛ. 1
к = 0 и t = tj+1, получим (ср. (11.3))
ti+i
Я = ехр £— (п0 — /) ^ X dt J.
(11.53)
Будем считать, что в момент ^+1, определяемый соотношением
(11.53), происходит очередное повреждение. Тем самым мы вы¬
бираем наиболее неблагоприятный случай, так как с той же
самой вероятностью, согласью формуле (11.52), можно утверж¬
дать, что в интервале (tj, I) большем, чем (tj, tj+1), произойдет
не более одного повреждения. В следующем пункте будет дана
строгая оценка вероятности реализации найденных моментов
повреждений.
Окончательно принимается следующее соотношение для ожи¬
даемых моментов повреждений:
(т п0 — общее число повреждений за весь полет).
2. Вероятность реализации ожидаемых моментов поврежде¬
ний (11.54). Соотношения (11.54) определяют некоторый закон убы¬
вания числа неповрежденных секций по времени
п (t) = п0 — j при tj < *<*,•+1 (/' = 0, 1, . . п, tmil= Т). (11.55)
При каждой реализации маневра будет получаться свой закон
п (t) повреждения секций, отличный от ожидаемого п (t) [(11.54),
(11.55)]. Поставим задачу определения вероятности, с которой
для любой реализации маневра будет выполняться неравенство
п (t) ;> п (t) при 0 t Т. Выполнение этого неравенства га¬
рантирует, что фактический расход рабочего вещества на выпол
нение всего маневра не превысит вычисленного в соответствии с
законом п (t). Другими словами, это позволит доставить полез¬
ный груз, не меньший расчетного. В этом смысле можно говорить
о вероятности выполнения неравенства п (t) > п* (t) при 0 t Т
как о вероятности реализации решения.
Обозначим через А событие
т
jj л (г (t),t)dt = 1J±^ (Л, = • In И)
и о — m
тп
А: ii (t) п* (t) при 0 t Т
(11.56)
§ 2] СККЩЮНИРО^ЛИНЫЙ ДВИГАТЕЛЬ ОГРАШ[ЧКНПОЙ мощности 489
и через Р (А) — вероятность его реализации (искомая вероят¬
ность). Введем в рассмотрение следующую систему из (т + ^-го-
события:
А0: п (t) — 7?0 при 0
А\\ п (t) п0 — 1 при П <С' <С ^
А,: п (t) > /го — j при tj < t < *3-+1,
Ат: п (t) > ге0 — in при tm<^t Т.
Событие А есть пересечение (произведение) выписанных со-
бытий
А = А^ . . . Aj: . . . Am. (11.58)
Эго поясняется рис. 11.10, где реализация каждого из событии
Aj(j = 0,1,2) соответствует тому, что изображающая точка
попадает в определенным образом заштрихованную область. Пере¬
сечению событий А0, Av А 2 отвечает область, обладающая всеми
Рис. 11.10. Ступенчатый закон п* (I) уменьшения числа
работающих секции по времени и области, соответствующие
событиям А0, А1, А» и А из (11.57), (11.58).
типами штриховки (общая часть областей А0, Аг, А2), а это и полу¬
чается область, лежащая выше ступенчатой кривой п (t).
По теореме умножения (см., например, [11.6]) вероятность
реализации пересечения событий (11.58) равна
Р Й) = Р (Л 0 . . . AJ = Р (AJA0. . . Am^) Р (А 0. . . Am-г) = • • •
...=/> (Л„) Р (AJA,) . . . Р (AM, . . . А}М . . .
. . .Р (AJA, . . . АтМ, (И.59)
ЦЦе через Р (А,/А0 . . . Л3_х) обозначена вероятность реализации
события Aj при условии, что событие А0 . . . произошло
(условная вероятность).
490
ВОПРОСЫ НАДЕЖНОСТИ В ЗАДАЧАХ ОПТИМИЗАЦИИ [ГЛ. 1
Вычислим условную вероятность Р (Aj/A0 . . . Л;-_х). Пусть
событие А0 . . . произошло, тогда число неповрежденных
секций п (tj) в момент времени tj может быть равно одному из
7 значений:
п (tj) = п0 или п0 — 1, или /г0 — 2, . . или
Ло — (/ — 1)- (11-60)
В соответствии с этим событие Aj/A0 . . . Aj^ может быть ре¬
ализовано одним из следующих переходов:
(0)
(а)
(/-1)
.(0)
7?0 —> П0
п0 — а —> 7i0— а
П« —/
(1)
п0 -> п0—1
—и
1
«
1
0
?
1
о
«0—/ т 1 -* «о — /
(0
по П0 — *
/?0 — а —> 77о — а—i
</-
а) л0-»и0 —/-i-а
?
0
?
1
о
(/)
«о -* "о — /
(11.61)
{индекс столбца а = 0, 1, — 1 соответствует начальному со¬
стоянию п (tj) = п0 — а, индекс строки i = 0, 1, . . ., / — а —
конечному состоянию п (^+i) = п0 — а — г).
Переход
п (tj) — п0 — а > п (tj.л) = п0 — а — i
означает, что в интервале времени tj<^t<^ ^+1 из (п0 — а) непо¬
врежденных в начале интервала секций будет повреждено ровно
i секций (безразлично каких).
Число различных способов, которыми можно распределить
i повреждений между (п0 — а) секциями, равно Сг??.о_а — числу
сочетаний из (п0 — а) элементов по i, так как порядок выхода
секций из строя нас не интересует. Все эти способы равновероят¬
ны, вероятность каждого из них есть
бч-i , Ч-н .
expj^—(п0 — а — i) ^ X dt 1|Ч—exp ^ X dt j ; (11.62)
§ 2] СЕКЦИОНИРОВАННЫЙ ДВИГАТЕЛЬ ОГРАНИЧЕННОЙ МОЩНОСТИ 491
умножая (11.62) на число способов, получим вероятность пере¬
хода п (tj) = п0 — а —> п (tj+1) = п0 — а — i:
Р (п{) — а —> п0 — ос — i) =
4+1 4+1
= С^0_аехр —(п0— а—i) ^ X dt |l—exp ^ X dt\ . (11.63)
f ■ i •
J
Чтобы найти вероятность события А$/А0. . . А^ъ нужно
просуммировать (11.63) по i и по а (по строкам и столбцам таблицы
(11.61)):
j—1 а
Р (AjjAb. . . Лм) = 2 ^ р (п{)-а->п0 —a — i). (11.64)
а=0 г=0
Искомая вероятность Р (А) находится подстановкой (11.63),
(11.64) в (11.59):
р (А) = П {2 2 ехрх
j=о а=0г=0
*У+1 ^ 4+1 ■
X £— (гс() — а — i) ^ X d/j 1 — exp ^ X dtJ j
*У 4
(<Х-а = 1, «0 = 0, гт+1 = 71). (11.65)
Полученная формула позволяет вычислить вероятность реа¬
лизации любого закона п (t) повреждения секций (т. е. вероят¬
ность неравенства п (t) > п (t) при 0 ^ t Т). Применим ее
к закону (11.53)—(11.55). Подставляя выражения для интегралов
из (11.54) в (11.65), будем иметь
га У—1 j—а ?г0—а—i 1 .
Р (А) = П {2 2 Сп,-,П n°~j (1 - И • (11.66)
j= о а=0 1=0
С точностью до членов третьего порядка малости относитель¬
но (1 —R) формулу (11.66) можно переписать в виде (произведя
суммирование и умножение)
Р(А) = Я - 2 („0-1) (1 - ЛУ" + 0 [(1 - /?)*]■ (В .67)
Если добиваться высокой вероятности Р (А) реализации реше¬
ния, близкой к единице (именно этот случай и представляет прак¬
тический интерес), то, согласно (11.67), нужно брать (1 — R)<^ 1.
Тогда с точностью до членов второго порядка малости относительно
(1 — R) можно считать, что вероятность Р (А) реализации решения
492 НО 11 РОС 1)1 11 АДГ/Ж ПОСТИ Н ЗАДАЧАХ оптимизации [гл. I f
в целом для закона п (I) из (11.53) — (11.55) будет совпадать с
вероятностью R отсутствия повреждений у (л0 — /) секций на ин¬
тервале (tj, tj+i):
Р (Л) Р (п (t) 0 < * < Г) = 7* + о [(1 — /?)],
3. Весовые соотношения. Секция двигателя, поврежденная
в момент времени tj, отключается. Это приводит в общем случае к
изменению режима работы оставшихся секций и к уменьшению
максима л ьной мощноети
Здесь iVmax [п (£)] обозначает зависимость максимальной мощ¬
ности от числа работающих секций, N j — мощность, отнесенная к
начальной N0 (Nj <' Nj-± <^ ... <^ N0 = 1). В случае полно¬
стью автономных секции зависимость iVmax [п (£)] линейная:
Nmax (01 = (0/72о1 N, ИЛИ Nj = 1 — j/n0. (11.70)
Если поврежденные секции остаются на борту, то, интегри¬
руя уравнение изменения веса аппарата по участкам (tj, 6+1),
Под tj здесь будем понимать ожидаемые моменты повреждений
(11.54). Тогда (11.71) дает величину (GJG^f, которая с вероят¬
ностью, не меньшей R, ограничивает снизу все реализации:
(GJG0) (6г ] / 6г о) * j с отношением (GJG^)* и будем в дальнейшем
оперировать.
Вес двигателя Gx в процессе полета не меняется и связан с
начальным значением максимальной мощности Лг0:
Удельный вес а считается зависящим от мощности одной сек¬
ции N0/n0 (невозрастающая функция от N0/n0, рис. 2.96).
На основании (11.71) аналогично тому, как это делалось без
учета повреждений, можно записать выражение для суммарного
6+1
0 N (t) Nmах [п (01 или 0< У (t) ^ Nj
при tj<^t < ijn, / = 0,17..., т. (11.69)
получим
т 5'+1
Gx. = aNn.
(11.72)
3 2] СЕКЦИОНШ’ОПАШ! Ы П ДИН ГЛТК Л Ь ОГРА1 li! Ч К I П ЮЙ МОЩНОСТИ 49 О
относительного веса двигателя и осредненного запаса рабочего
вещества, потребного для осуществления маневра:
т
Gy. + Gv.о = i с /ф + Gy. (ф ^ dt\ (11.73)
Ч
(черточки над безразмерными величинами здесь и ниже опус¬
каются).
4. Формулировка задачи. В качестве критерия оптимальности
принимается условие минимума (11.73) — суммы весов двигателя
и осредненного запаса рабочего вещества. Это соответствует мак¬
симуму полезного груза, на доставку которого можно рассчиты¬
вать с вероятностью не меньшей R.
Суммарный вес (6>. -f Сч0Ь как видно из соотношения (11.73),
монотонно убывает с увеличением Ф. Поэтому задачу об отыска¬
нии минимума (Gx 4 67;,0) можно разбить на две: 1°. динамиче¬
скую и 2°. весовую.
1°. Для заданных величин А1? N0, п0 и при известной зави¬
симости X (г, С N0/n0) построить такие законы изменения мощ¬
ности N (t) и реактивного ускорения а (£), чтобы при выполне¬
нии заданного динамического маневра (с фиксированной вероят¬
ностью) достигался минимум суммы интегралов (ср. (4.11))
т Д'-fl
J ----- 2 ^ ;г min,
г — a -j- Н, г (0) — 1*п 9 г (0) — V0,
г (Т) = щ, г {Т) = \г
(0 < 7V (£)< при / = 0, 1, . . ., ггс),
(11.74)
где tj определяются условиями изопериметричности (11.54).
2°. Для заданных величин G0 и (N0/n0)m[n (минимально воз¬
можный размер секции) и при известных зависимостях
а = а (Л0//20), J — «/min {Nq, tiq, Аг) (11.75)
определить оптимальные значения мощности N0 и числа секций
п0, обращающие в минимум функцию (11.73).
Здесь в динамическую задачу 1° (вариационная задача) через
условия (11.54) для моментов повреждений tj входят параметры
двигателя — число секций п0 и мощность N0. Это отличает по¬
следнюю от задачи (4.11), когда повреждения не учитываются.
Весовая задача — задача на экстремум функции. Ее решение
494 ВОПРОСЫ НАДЕЖНОСТИ В ЗАДАЧАХ ОПТИМИЗАЦИИ [гл. 11
связано с конкретным видом зависимостей (11.75); в п. 1 § 3 будет
рассмотрен один из примеров.
5. Уравнения вариационной задачи (11.74). Для упрощения
предполагается, что интенсивность потока отказов не зависит от
режима работы секции, т. е. от промежуточных значений мощности.
Это влияние уже было выяснено в § 1 на примере односекцион¬
ного двигателя.
Относительная мощность N входит только в числитель подын¬
тегрального выражения минимизируемого функционала (11.74).
Ожидаемые моменты повреждений (11.54) и уравнения движения
(11.74) от N не зависят. Поэтому для минимума функционала
(11.74) необходимо, чтобы мощность N в каждый момент была мак¬
симально возможной
т. е. на участках между повреждениями мощность постоянна и
убывает в моменты повреждений в соответствии с уменьшением
числа работающих секций.
После этого задача сводится к минимизации функционала
(N (t) = Nj вынесено из-под знака интеграла) с дифференциаль¬
ными связями (11.74) и условиями изопериметричности (11.54).
Выразив, в (11.77) а = г — R, мы избавимся от дифферен¬
циальных связей. Условия изопериметричности (11.54) с постоян¬
ными множителями Vj/Nj по правилу Лагранжа присоединяются
к основному функционалу (11.77). Ищется минимум расширенного
функционала
. J . (11.78)
(г (0) = г0, г (0) = у0, г (Т) = Г1> г (Т) == Vl).
Для решения задачи необходимо построить экстремали этого
функционала и получить условия сопряжения экстремалей (то,
что экстремали г (t) будут иметь разрывы вторых производных при
t = tj, следует из наличия весовых коэффициентов v;- в подынтег¬
ральных выражениях).
N (t) = Nj при tj t tj+i, j = 0, 1, . . ., m, (11.76)
m
(;'+l
(11.77)
§ 2] СЕКЦИОНИРОВАННЫЙ ДВИГАТЕЛЬ ОГРАНИЧЕННОЙ мощности 495
Вдоль экстремалей должны выполняться уравнения Эйлера
(ср. (5.6))
* — i (* ■+v* If = 0 (и .79)
(а = г—К, tj < * < tj+х, / = 0, 1, . . пг, vm = 0).
Приравнивая нулю в моменты t = tj сумму коэффициентов
при вариациях6ги 6г в выражении для первой вариации функциона¬
ла J, получим следующие условия сопряжения экстремалей:
-ту— at = —ат, af-at = ^—а- (/ = 1, . . т), (11.80)
N,j з J ’ N. J Nj_± J w \ /
Здесь нижний индекс j указывает на момент времени tj, а
верхний значок плюс или минус относится к значениям функции
справа или слева от разрыва. Таким образом, реактивное уско¬
рение и его производная в моменты повреждений уменьшаются
пропорционально уменьшению мощности, т. е. скорость истече¬
ния V = 2gN/aG не терпит разрыва.
Когда среднее число повреждений X зависит от г, при состав¬
лении первой вариации J нужно еще варьировать моменты вре¬
мени tj. Это дает дополнительные условия
^ (*7 - -нц) + NhlN)Ni = ° (/ = !’ • • •’ т - !>•(11,81)
Задача свелась к решению системы дифференциальных урав¬
нений (11.79) с граничными условиями из (11.78) и условиями
(11.54), (11.80) и (11.81), причем неравенство в (11.54) служит
для определения суммарного числа т поврежденных за весь по¬
лет секций.
6. Непрерывная аппроксимация ступенчатого закона повреж¬
дений. При большом числе тг0 секций двигателя решение вариа¬
ционной задачи со ступенчатым законом п (t) уменьшения числа
неповрежденных секций затруднительно из-за наличия условий
(11.54), (11.80), (11.81). Но если число секций достаточно велико,
так что nQ — т^> 1, то ступенчатый закон (11.54), (11.55) мож¬
но заменить непрерывным и тем самым избавиться от этих условий.
Введем дифференциальное уравнение
п _ 7 0*>0 и (0) = тг0 (Ai = —In R = const). (11.82)
Решение n (t) этого уравнения будет аппроксимировать снизу
{п (t) п (t)) ступенчатый закон п (t), приближенно совпадая
496
ВОПРОСЫ НАД iB/К ПО С TIL Г» ЗАДАЧАХ О IIT11 ДНЮ АДПП 1 i\J. II
с ним в узлах аппроксимации t = tj. Чтобы убедиться в этом,
проинтегрируем уравнение (11.82) в пределах от tj до /дх:
Подставим сюда вместо п (t) ступенчатую функцию п (t)
из (11.55), а в правую часть — соответствующие выражения
Равенство будет выполняться с точностью до членов по¬
рядка Мп^. Отсюда можно сделать вывод, что уменьшение числа
неповрежденных секций от одного момента повреждения до дру¬
гого для непрерывного (11.82) и ступенчатого (11.55) законов по¬
вреждения при 720 -> сю одинаковы. Примеры решения, приве¬
денные в следующем параграфе, показывают, что интегральные
характеристики, соответствующие этим двум законам, становятся
близки, начиная с п0 ~ 10.
Для непрерывного закона повреждений (11.82) задача сводит¬
ся к отысканию экстремалей следующего функционала:
где v = v (£) — переменный множитель Лагранжа при дифферен¬
циальной связи (11.82), N (п) — зависимость максимальной мощ¬
ности Nmax/N0 от числа неповрежденных секций.
Уравнения экстремалей функционала (11.84) таковы (ср.
i •
(I 1.83)
(11.54).
о
(г (0) = Го, Г (0) == v0, г (Т) = гь Г (Т) =---- Vl),
(11.79)):
= a + г (0) = г0, г (0) =-- Vo, г (Т) = п, г (Т) = vb
(11.85)
п = — Kn/Ai, п (0) = щ.
Таким образом, вместо условий (11.54), (11.80), (11.81) здесь
появляются два дифференциальных уравнения первого порядка
(см. два последних уравнения (11.85)).
§ 3] СЕКЦИОНИРОВАННЫЙ ДВИГАТЕЛЬ ОГРАНИЧЕННОЙ мощности 497
§ 3. СЕКЦИОНИРОВАННЫЙ ДВИГАТЕЛЬ ОГРАНИЧЕННОЙ
МОЩНОСТИ — ПРИМЕРЫ РЕШЕНИЯ
ДЛЯ МОДЕЛЬНЫХ МАНЕВРОВ
Здесь даются примеры аналитических решений уравнений ва¬
риационной проблемы, полученных в предыдущем параграфе.
Упрощение уравнений достигается, во-первых, за счет отбра¬
сывания гравитационных сил (В = 0) — рассматривается одно¬
мерное движение (по оси Ох) между точками покоя в бессиловом
поле. Во-вторых, интенсивность X потока отказов одной секции
считается не зависящей от г и t: X (г, t) = Х0.
Всюду, кроме последнего пункта, предполагается, что секции
полностью автономны:
I. Ступенчатый закон повреждений. В рамках сделанных
предположений из формул (11.54) можно получить явное выра¬
жение для ожидаемых моментов повреждений
Интегрируя уравнения экстремалей (11.79) по участкам
C<C^<CCri с учетом условий (11.80) и (11.86), получаем
N (п) = п/п0.
п0 — пь
(11.86)
(/ ==0,1,..., т — 1, х == А,ДоТ).
(11.87)
' 1' 17
1 Y.T у1 1 М
6 "о . (1 — i/"o)' i.l
i =0
Величины а0 и а() определяются решением системы линейных
^ Механика полега
498
ВОПРОСЫ НАДЕЖНОСТИ В ЗАДАЧАХ ОПТИМИЗАЦИИ [ГЛ. И
алгебраических уравнений, полученных из граничных условий
X (0) = X (0) = i (Т) = О, X (Т) = I:
+
CL{)
m—1
L п0
j=1
m—1
j=0
111 \
П 0
+ (!■-«[», -f- + i (1 - -1) (T - <„))}
a0
m—1 j
%T \2 Г VI 1
'*0
771—1
1 иГ ^ 1
S-r^S<. + i£S
;'=i
i=i
771—1
,i0 iToC1-^0)2-
///?0 f
г
(Г — fm) (2 *7 + у *m) +
+
j=l
+ (T+2tm)
= I.
(11.88)
Суммарное число повреждений m за все время движения на¬
ходится, согласно второму условию (11.86), из неравенства
771—1 771
<“-S9)
«О 1 — //л О
j=о
Минимальное значение функционала / выражается через
(кТ/п0)у п0, т, а0, а0:
/ = 2 f(ao + d0tj)2 + (а0 -f- d0
771—1
а0 и Г
;=0
+
i/no по
3 (1 — /7«о);2
X [(во + во*™)2 + («о + в0*т) «о (Г - 7т) + Vs«S (Г ~ *»•)*]• С1-90)
Величина функционала (11.90), отнесенная к величине функ¬
ционала /* для этого маневра без учета повреждений
///*=//(»>!,
показана на рис. 11.11 в зависимости от параметра 1/х =
= (Х0Т)/{— In R) для различных значений п0 (сплошные кривые).
§ з] СЕКЦИОНИРОВАННЫЙ ДВИГАТЕЛЬ ОГРАНИЧЕННОЙ мощности 499
Пример оптимальной с учетом повреждений программы реак¬
тивного ускорения
a(t)/al = a(t) j (11.92)
приведен на рис. 11.12 (сплошная ломаная линия).
J/J*
20
10
8
6
4
2
10 1 2 3 4 1/я
Рис. 11.11. Функционал J/J* динамической задачи (11.74) в зависимости от
параметра 1/х — отношения максимального числа отказов одной сек¬
ции Amax=A0Т к допустимому Aj = —In R при фиксированном числе сек¬
ций п0 для маневра перемещения между точками покоя (J* = 12 l2JT*).
Сплошные кривые соответствуют оптимальной с учетом повреждений про¬
грамме ускорения, пунктирные — оптимальной без учета повреждений
программе.
Оптимальный без учета повреждений закон a* (t) (см. (5.33))
показан на рис. 11.12 пунктирной линией. Пунктирные кривые,
приведенные для сравнения на рис. 11.11, дают значения функ¬
ционала, которые соответствуют этому линейному закону а* (t)
при учете повреждений. Видно, что изменение программы реак¬
тивного ускорения позволяет существенно уменьшить функцио¬
нал задачи.
Обсудим влияние числа секций п0 на функционал /. При этом
нужно различать два случая: а) интенсивность Х0 потока отказов
одной секции не зависит от N0/n0 — энергетического размера
секции, б) интенсивность Х0 уменьшается с уменьшением
Случай а) имеет место, когда процессы, вызывающие повреждения,
не зависят от масштаба двигателя. Случай б) соответствует, на¬
пример, метеорной опасности, когда число пробоев прямо про¬
порционально площади радиатора секции (k0 ~ А,* =
6=5 const). Зафиксируем суммарную начальную мощность N0
32*
500 ВОПРОСЫ НАДЕЖНОСТИ В ЗАДАЧАХ ОПТИМИЗАЦИИ [ГЛ. II
и будем менять число секций п0. Сравнение будем проводить при
фиксированных параметрах маневра и потока отказов, которые
не зависят от щ. В случае а) этому соответствует х =
*= — \nR/(X0T) = const (рис. 11.13, а); в случае б) — х* =
= — In R/(VT) = const или х/п0 = const (рис. 11.13, б). В пер¬
вом случае (рис. 11.13, а) функционал J немного увеличивается
с ростом числа секций п0. но зато увеличение п0 позволяет выпол¬
нять более напряженные в смысле надежности маневры (т. е.
маневры с меньшим значением
х—см. на рис. 11.13, а ограни¬
чивающую кривую т = п0, где
т — суммарное число повреж¬
денных за весь полет секций).
Во втором случае (рис. 11.13, б)
увеличение п0 в обоих указанных
аспектах дает положительный эф¬
фект: функционал / и предельное
значение х/п0 уменьшаются.
Рассматривая влияние п0 на
функционал динамической части
задачи, нельзя забывать, что умень¬
шение мощности Nq/uq одной сек¬
ции приводит еще к увеличению
удельного веса а, это последнее
отрицательно сказывается на функ¬
ционале (11.73) полной задачи.
Окончательное заключение о наи¬
лучшем числе секций можно сделать только после того, как ре¬
шена весовая часть задачи (п. 4 § 2).
Дадим пример ее решения. В качестве зависимостей (11.75)
возьмем
а = а* (1 + n0AN*N0), а*, AN* = const и (11.90).
Фиксируем величины
Ф* = (а72g) Г = ОД и AG* - a*AN* = 0,001.
Снова рассмотрим два указанных выше случая: а) >и0 =
= const или х — — In R/(X0T) = const, б) h0 = Х*а*N0/(Gyn0)\
V, a*, G7 = const или х* = — In R/QCT) = const, GK = VФ*—
— Ф* = 0/216.
Результаты отыскания минимума суммарного веса (11.73)
двигателя и запаса рабочего вещества по G* = aN0 и п0 при¬
ведены на рис. 11.14, а и 11.14, б. Зависимости полезной
нагрузки от параметра х перестроены на рис. 11.15, а
Рис. 11.12. Пример оптимальной с уче¬
том повреждений программы аЧ)/а*
реактивного ускорения (сплошная ли¬
ния) для маневра перемещения между
точками покоя (?<0 = 2, х = 2/3, а* - -
= 61/Т2', пунктирная линия —оптималь¬
ная без учета повреждений программа).
§ 3] СЕКЦИОНИРОВАННЫЙ ДВИГАТЕЛЬ ОГРАНИЧЕННОЙ МОЩНОСТИ 501
и 11.15, б в виде функций Gn от вероятности R успешного выпол¬
нения маневра при Amax = const (R = exp [—хЛтах1)- Из этих
рисунков можно заключить, что дробление двигателя на авто¬
номные секции при параллельном режиме работы в случае а) мало
эффективно (интенсивность потока отказов секции не зависит от
d)
Рис И 13 Зависимость функционала J от числа п0 автономных.секции,
построенная по рис. 11.11 (суммарная мощность N0 фиксирована).
а) Интенсивность А0 потока отказов одной, секции не зависит от Л0/н,
б) интенсивность А0 ~ A*iY0/n, остальные пояснения даны в подписи
к рис. 11.11.
размера секции), а в случае б) дает хорошие результаты (интенсив¬
ность потока отказов линейно падает с уменьшением энергети¬
ческого размера секции).
502 ВОПРОСЫ НАДЕЖНОСТИ В ЗАДАЧАХ ОПТИМИЗАЦИИ [ГЛ. II
80
60
40
20
/
/ 1
V
h
—
0,2
0,4 0,6
0)
0,8
Ojt’Ox.
*и
0,4
80
0,3
60
0,2
40
OJ
20
0
0
Огс
L
е»
\
V
0,2
0,4 0,6
4)
0,8
0,4
0,3
0,2
0J
Рис. 11.14. Максимальная полезная нагрузка Gn, оптимальный вес двигателя Gx и опти¬
мальное число секций п0 для маневра перемещения между точками покоя (Ф* =
= (a*/2g) 1212Т~3 = 0,1— комбинация параметров маневра 1,Т и удельного веса а* секции
единичного размера, AG^ = 0,001—минимально возможный размер секции).
а) Интенсивность А0 потока отказов секции не зависит от мощности секции N0/n — х =
=— 1пД/А0Т; б) интенсивность А0 линейно падает с уменьшением мощности N0/n — х =
= —In R/h*T, где А* — интенсивность потока отказов секции единичного размера.
Рис. 11.15. Максимальная полезная нагрузка G^. в функции вероятности R успешного
выполнения маневра.
а) ^шах = V’; б) Лтах = 7*т (см. подпись к рис. 11.14).
§ з] СЕКЦИОНИРОВАННЫЙ ДВИГАТЕЛЬ ОГРАНИЧЕННОЙ мощности 503
2. Непрерывный закон повреждений. При постоянной ин¬
тенсивности потока отказов К (г, t) = К0 уравнение (11.82), опре¬
деляющее число неповрежденных секций п (£), интегрируется
гг (t)/n0 = erW (к = - Лг/К0Т). (11.93)
Тогда для рассматриваемого маневра функционал J может
быть записан в виде (секции полностью автономные)
г
J = J ^е"хТ dt (х (°) = х (°) = х{Т) = 0, г (Т) = I).
О
(11.94)
Оптимальная программа a (t) такова:
■«=(И-95>
Минимальное значение функционала задачи равно
<и-96>
Зависимость J (1/х) также показана на рис. 11.11 — кривая
п ос. Из рисунка видно, что, начиная с п = 10, точные и
предельные значения функционала достаточно близки.
3. Движение с возвращением. Пусть задано суммарное время
движения Г, за которое нужно попасть из одной точки покоя в
другую и вернуться обратно
х (0) = х (0) = 0, х (tj) = I, х (Jj) = 0, х (Т) = х (Т) = 0
(0 < t, < Т). (11.97)
Такой маневр моделирует «быстрый» межорбитальный перелет
с возвращением. Функционал задачи в случае непрерывного
закона повреждений (11.93) складывается из двух интегралов
и Т
J = J xV'-T dt + е*«/*г J x2e(l-^/xT dt, (И .98)
0 и
экстремали которых описываются соотношениями типа (11.95).
Из вариации момента времени tx получаем условие равенства
квадратов ускорения слева и справа от tx. Это условие позволяет
отыскать оптимальное значение tx\
Л'х!Г _ 1 _ _ (^/хГ) (Av-T — 1)_ etl!*T — еГк х-У‘/хГ
(1 — е“*|''хГ) (eti/xT — 1) — х-2
(e-fi/*r _ е~1!у-) (в1'* - Л'хГ) - и"2
(11.99)
504 ВОПРОСЫ НАДЕЖНОСТИ В ЗАДАЧАХ ОПТИМИЗАЦИИ [IV]. и
Решение этого уравнения tx (1/х) представлено на рис. 11.16
пунктирной кривой. Видно, что движение «туда» (0 < t < гл)
происходит быстрее, чем движение «обратно» \tx t Т). Эта
несимметрия возрастает с увеличением 1/х; причина ее состоит
в следующем.
На первом участке движения, пока мощность уменьшилась
еще незначительно, выгодно иметь большее ускорение, чем на
последующем участке.
Такая программа реактивного ускоренна обеспечивает всюду
достаточно большую скорость истечения, т. е. малый расход
рабочего вещества.
4. Движение с заданным активным временем. Введем условие
заданного времени работы двигателя < Т (§ 2 гл. 7). Можно
показать, что пассивный уча¬
сток для рассматриваемого ма¬
невра, как и без учета повреж¬
дений, единственный и располо¬
жен в середине траектории:
a (t) = 0 при 0<^ tX'
(11.100)
Рис. 11.16. Оптимальное распределение
времени между перелетами «туда» tt и «об¬
ратно» (пунктир) и между первым tx и вто¬
рым активным участками (сплошные кри¬
вые, где Тр,-- суммарное время работы дви¬
гателя) в функции 1/х — отношения мак¬
симального числа отказов одной секции
А шах = ^°т к Допустимому = — In Н.
вреждения равна нулю,
нуля
Как показано в § 2 главы?,
включение пассивного участка в
траекторию с идеальным дви¬
гателем ограниченной мощности
ухудшает характеристики. Если
при выключенном двигателе
вероятность повреждения оста¬
ется такой же, как и при рабо¬
тающем, то этот вывод, естест¬
венно, имеет силу и здесь.
Исследуем случай, когда на пас¬
сивном участке вероятность по-
на активных постоянна и отлична от
1о
— constat0 при a=f= 0,
при а = 0.
(11.101)
Функционал для непрерывного закона повреждений (11.93)
записывается аналогично (11.98)
ti т
J = ^ x2et y'Tdt + у'т ^ dt.
(11.102)
з 3] СЕКЦИОНИРОВАННЫЙ ДВИГАТЕЛЬ ОГРАНИЧЕННОЙ мощности 505
Внеинтегральные члены первой вариации (11.102) равны
6J = е^*т {[2^ [a.W -г -±г в®) - (а®)2] 6/1 + 2а®б/ -
- 2 (а® + ~ a® j bxt — [2/ (a® -r -^r а«) — (а®)2
1
bU
— 2aMbx, -2 a(2>+_La(2))ax2J. (11/103)
Здесь a^ и а(2) — оптимальные программы реактивного ускоре¬
ния на первом и втором участках, соответственно
а(1) (0 = (б£1} + b?t) e~tr'-T, fl(2) (0 = (bf + Ь?Н) е-«-т-т»),УЛ\
(11.104)
Скорости яд, я*2 и координаты яд, хг по берегам пассивного
участка связаны простыми соотношениями
^2 = ^1у %2 = ^1 (^2 ^l) *^1* (11.105)
Если и варьируются независимо с целью отыскания оп¬
тимальной протяженности пассивного участка, то из равенства
б/ = 0 следует
2x1 [(а/+4га/) - // “ 4г язг>)] - w2=°’ ]
а? = 0, а<» - а® - (f2 - f,) (а® + ~ а®) = 0, } (Ц.Ю6)
Три первых равенства с учетом последнего дают
а® в® = 0, (t2 - tj) а® = 0. (11.107)
Из последнего условия (11.106) имеем bli = Ь® = Ъи тогда
(11.107) дают
hh + ьУ = 0, ъхи -- ^'2) - О, (t2 - tj) bx = 0. (11.108)
Положить £д = 0 нельзя, так как отсюда последует б.,11 =
= bf] = 0, т. е. а (t) = 0. Следовательно, t2 = Это означает,
что на оптимальной траектории пассивный участок, если не зада¬
вать время работы двигателя, будет отсутствовать (напомним, что
при выключенном двигателе вероятность повреждения предпо¬
лагалась равной нулю — (11.101)). Если протяженность пассив¬
ного участка фиксирована U — t±= Т — Ти,, то бt2 = б^, а три со¬
отношения. аналогичные (11/106), дают
= ъ¥ = 6/ = б/ = bv 2b2 -f 2hh + W(T- Tv) = 0.
(11.109)
[)0G ВОПРОСЫ НАДЕЖНОСТИ В ЗАДАЧАХ ОПТИМИЗАЦИИ
[ГЛ. 11
Проинтегрировав по участкам уравнения движения с a (t), оп¬
ределяемым (11.104) и (11.109), найдем постоянные Ьг и Ъ2 из
граничных условий маневра:
Ъ,
1
+¥}-т-тУ1'”'т)=0’
г 1 Г / 1 л
1
+ Ьг
+
-T^V.T
— е ^
_■
Т,,/хГ
+
2 4- —
1
2)е~т^т +
(11.110)
J
Оптимальное расположение пассивного участка определяется
из третьего соотношения (11.109), где Ь21ЪХ подставляется из пер¬
вой формулы (11.110)
К —
(Т - TJ е
-Т,, у-Т
1 - е-1^т
= k-L-7^-
1 + е~Т^Т
(11.111)
2(1 —е )
Решение этого уравнения t^T / (1/х, T^JT) показано сплош¬
ными кривыми на рис. 11.16. Видно, что распределение времени
работы двигателя между первым и вторым активными участками,
аналогично движению с возвращением, несимметрично. На долю
первого участка приходится меньшая часть активного времени,
в то время как при 1/х = 0 было tx = 1/2 Т
5. Нелинейная зависимость мощности от числа работающих
секций. Рассмотрим источник мощности, работающий по циклу
Карно. Источник тепловой энергии (нагреватель) с температурой
Тп (максимальная температура цикла) обеспечивает мощность
Nn. Неиспользованная тепловая энергия излучается холодиль¬
ником (радиатором) со средней температурой Т (минимальная
температура цикла). Если метеорные пробои представляют
опасность для работоспособности радиатора, то он разбивается
на автономные секции. Повреждение каждой секции приводит к
уменьшению излучающей площади.
Как известно, коэффициент полезного действия цикла Карно
(коэффициент превращения тепловой энергии в электрическую)
равен
тр. 1 - Т/Т». (11.112)
По условию теплового равновесия радиатор должен излучать
мощность (1 — гр.) Nn, т. е.
еа£Т3Т„ - АГП, (11.113)
3] СЕКЦИОНИРОВАНЫ!! двигатель ограниченной мощности 507
где S — излучающая площадь радиатора, го — произведение
степени черноты на постоянную Стефана—Больцмана.
На основании (11.112) и (11.113) получаем выражение для элек¬
трической мощности (она же в идеальном случае и реактивная
мощность)
N = г|,Аг„ - eaST3 (Тп - Т). (11.114)
Предположим заданной максимальную тепловую мощность
нагревателя Nn> максимальную температуру в нем Тп и началь¬
ную площадь радиатора S0. Оптимальные значения температур
Тп и Т в каждый момент времени должны выбираться из условия
максимума мощности (11.114)
Тп(0= Т; при 0<*<7\
У Nn j eoS (t) Тп при eeS (t) Т *п > N*n
Т (t) =
при |^еа-5’(0Тп<Х;
(11.115)
при этом температура Т = 3/4ТП считается допустимой для ра¬
диатора.
Программа регулирования тепловой мощности определяется из
соотношений (11.113) и (11.115)
Nn (0 =
Nn
27
при ^есб^Тп > Nn,
NnS (t)/S() при seS (t) Tn4 < Nn.
(11.116)
Можно показать, что начальная площадь радиатора S0 при
заданных Тп и Nn должна удовлетворять неравенству
27
•jrjT F.eS0Тп ^>Nn.
(11.117)
Действительно, в противном случае, согласно (11.116), тепловая
мощность нагревателя никогда не будет использоваться пол¬
ностью, и его можно будет заменить на нагреватель меньшей мощ¬
ности, а значит и меньшего веса.
Таким образом, оптимальное регулирование термодинамиче¬
ского цикла источника мощности должно осуществляться по
следующей схеме (см. (11.115) —(11.117)). Температура нагрева¬
теля Тп поддерживается все время на максимальном уровне Тп.
Тепловая мощность в начале движения также максимальна. По
мере пробоя секций радиатора его излучающая площадь умень¬
шается, а температура Т увеличивается до тех пор, пока не до¬
стигнет уровня Т = 3/4 Тп. С этого момента температура радиа¬
508 ВОПРОСЫ НАДЕЖНОСТИ В ЗАДАЧАХ ОПТИМИЗАЦИИ [гл. и
тора остается постоянной, а тепловая мощность уменьшается
пропорционально излучающей площади.
Уменьшение площади радиатора в предположении большого
числа секций описывается уравнением (11.82), где п/щ нужно
заменить на S/S0. При постоянной вероятности пробоев получаем
5 (t)/S0 = е-^т, (11.118)
Условие минимума функционала J для рассматриваемого ма¬
невра перемещения между точками покоя определяет следую¬
щую оптимальную программу реактивного ускорения:
а (t) =
Здесь
1 — у уе‘ я'-г j (bo + bit) при 0 t <f С»
A- e_ixT (bo -f by) при t^<yt<^T.
(11.119)
v Л'" (64 ea6,0T„1j <1, | (11.120)
t:< = — kT ln v, x = — ОгД* (6) T/п() ln R I
(X* (б) — зависимость среднего числа пробоев в единицу времени
секции единичной площади от толщины стенок б; Q0 = kS0
(0<С k^i 1) — начальная уязвимая площадь радиатора).
Определив из граничных условий (11.94) постоянные Ь1 и Ь2,
можно построить зависимость J (v, х). После этого нужно из
условия минимума суммарного веса (11.73) найти оптимальные
значения начальной площади радиатора 50, толщины стенок б,
числа секций п0, максимальной тепловой мощности N*n и макси¬
мальной температуры Т?г. Для доведения этой процедуры до конца
нужно знать зависимость среднего числа пробоев секции еди¬
ничной площади от толщины стенок X* (б) и зависимость веса
двигательной системы от всех перечисленных выше параметров:
G, = G, (Nl Т;, 50, б, п0).
§ 4. ОПТИМАЛЬНАЯ ВЕРОЯТНОСТЬ ВЫПОЛНЕНИЯ МАНЕВРА
В предыдущих параграфах главы обсуждалась задача опти¬
мизации при фиксированной вероятности выполнения маневра.
Такая постановка гарантирует, что с вероятностью R каждая
реализация данного маневра будет успешной. Рассмотрим теперь
«транспортную» задачу. Пусть в конечную точку траектории
требуется доставить большое количество груза, такое, что ма¬
невр придется выполнять многократно, или поставлена задача
регулярного снабжения некоторого пункта.
§4] ОПТИМАЛЬНАЯ ВЕРОЯТНОСТЬ ВЫПОЛНЕНИЯ МАНЕВРА 509
Из примеров решения задач §§ 1—3 видно, что увеличение
вероятности успешного выполнения маневра для каждой попытки
достигается ценой уменьшения полезного груза, который можно
доставить за одну попытку. Значит, число успешных попыток,
потребное для выполнения транспортной задачи, при этом воз¬
растает. Если уменьшать вероятность успешного выполнения
маневра для каждой реализации, то потребное число удачных
попыток уменьшается, но зато увеличивается число неудачных
попыток, и суммарное число попыток, начиная с некоторого
момента снова будет возрастать. Эти рассуждения свидетельству¬
ют о наличии оптимальной вероятности R выполнения маневра, в
каждой попытке, причем оптимальное значение R всегда лежит
внутри интервала (0,1), поскольку при R= 0 равен нулю процент
удачных попыток, а при некотором значении 0 R <С 1 обра¬
щается в нуль полезная нагрузка.
1. Формулировка транспортной задачи. Рассмотрение про¬
водится в рамках схемы независимых испытаний: параметры ап¬
паратов при каждой реализаций манёвра считаются идентичны¬
ми, исход реализации не зависит от предыдущих исходов 1). Каж¬
дая i-я реализация может иметь два исхода: первый — груз
доставлен в конечную точку траектории, и второй — груз не
доставлен в конечную точку траектории. Это — два несовмест¬
ных элементарных события, они образуют полную систему воз¬
можных событий. Если обозначить через R вероятность первого,
то вероятность второго будет равна 1 —R.
Будем характеризовать исходы i-й реализации случайной ве¬
личиной Сг(г) — весом, доставляемым в конечную точку траек¬
тории при i-и реализации маневра. Если реализация успешная,
то вес (?(г) равен полезному весу G-, на доставку которого рас¬
считывается при каждой реализации; если реализация неудач¬
ная, то вес G(?) равен нулю. В этих обозначениях первое элемен¬
тарное событие будет G(z) — Gn, а второе — G{1) — 0; вероят¬
ности этих событий запишутся в виде
р (G{i) = Gn) =R, Р (G(i) = 0) = 1 - R. (11.121)
Напомним, что вероятность успешного исхода R и полезная
нагрузка Gn, согласно §§ 1—3, связаны между собой: G- умень¬
шается с увеличением R (см., например, рис. 11.9, 11.15).
Рассмотрим два варианта постановки транспортной задачи (в
обоих случаях начальный вес аппарата и параметры маневра
считаются фиксированными).
1) Это подразумевает, в частности, что аппараты повторно не исполь¬
зуются.
510 ВОПРОСЫ НАДЕЖНОСТИ В ЗАДАЧАХ ОПТИМИЗАЦИИ [ГЛ. П
1°. Обеспечить максимум математического ожидания вели¬
чины суммарного груза Gs, доставляемого в конечную точку за
фиксированное число попыток п^>\.
2°. С заданной вероятностью R0 за фиксированное число по¬
пыток п перевезти максимальный суммарный груз G£.
В постановке 1° фигурирует математическое ожидание груза
Gv, поэтому на реализацию соответствующего решения можно
рассчитывать только в среднем при очень большом числе попыток
(п 1 или Gs GK). Реализация же решения задачи 2° гаран¬
тируется с заданной вероятностью R0 при любом числе попыток.
Помимо приведенных могут быть использованы и взаимные фор¬
мулировки, они будут перечислены в пп. 2 и 3.
При обсуждении сформулированных задач 1°, 2° будет пред¬
полагаться известным результат решения GГк (R) задачи предыду¬
щих параграфов о максимуме полезного груза при фиксирован¬
ной вероятности выполнения маневра для каждой реализации.
В противном случае должна быть выписана вариацион¬
ная задача, отвечающая данному критерию оптимальности
(см. п. 2).
Рассмотрение транспортной задачи может быть проведено и в
рамках критерия стоимости аналогично § 1 главы 10. Стоимость
успешной попытки равняется стоимости аппарата без полезной
нагрузки (в предположении одноразового использования аппа¬
рата). В случае неудачной попытки сюда добавляется величина
ущерба, которая полагается равной стоимости полезного груза
(пропорциональна Gr). Стоимость аппарата связывается с веса¬
ми основных его компонент формулами (10.1)—(10.4).
Данные выше формулировки 1°, 2° легко перефразируются в
терминах стоимости.
1°. Обеспечить минимум математического ожидания стоимо¬
сти перевозки заданного груза GE.
2°. С заданной вероятностью R0 обеспечить минимум стои¬
мости перевозки заданного груза G^.
В дальнейшем изложении используется весовой критерий
оптимальности.
2. Максимум математического ожидания суммарного груза
(задача 1°). Запишем математическое ожидание х) величины сум¬
марного груза Ge, доставляемого за п попыток
п п п
<<^> =- \2 G{i)/ = 2 <G(°> = S lRG- A (1 — К) = nRGn
2=1 2 = 1 2=1
(11.122)
(математическое ожидание суммы случайных величин равно сумме
их математических ожиданий).
L) Обозначается символом < >.
§ ,1] ОПТИМАЛЬНАЯ ВЕРОЯТНОСТЬ ВЫПОЛНЕНИЯ МАНЕВРА 51).
Из (11.122) видно, что задача 1° фактически не зависит от п
и сводится к отысканию минимума математического ожидания
веса G{1\ доставляемого за одну попытку, по вероятности R по¬
ложительного исхода:
<G(i)> = _L<Gs>= таxRG-. (It). (11.123)
,l R
При известной зависимости G- (R) это — задача на максимум
функции одной переменной. В случае отсутствия готовой зави¬
симости Gn (R) нужно выписывать полную вариационную поста¬
новку. Для этого введем текущую величину (11.123), например,
для односекционного двигателя (§ 1)
<G(i)>( = e-vcoG0(f), (11.124)
t
где Gz(t) = G- + Gv.(t), A (t) = § kdt, А (Г) = — Ini?. В ко-
О
нечный момент времени <С(г)>/ совпадает с (11.123), и задача
сводится к отысканию максимума конечного значения (11.124).
Чтобы получить формулировку Майера, запишем (11.124) в виде
дифференциального уравнения
— <G(l)> — — A (Ga + Ga) e~lV, о = G0 (0), (G^)t==T = шах
(11.125)
и присоединим последнее к системе уравнений вариационной
задачи о максимуме полезного груза Gп = Ga (Т) при фиксиро¬
ванной вероятности R. Граничные условия G0 (Т) = шах и
А (Т) = — In R при этом нужно заменить на G0 (Т) = opt и
Л (Т) = opt. В случае идеального двигателя ограниченной мощ¬
ности (11.11) новая вариационная задача выглядит так:
i<Gii)>==e-A
(Ga + Gy)~ ОС (w) Or
Ga —
Gx 2g N]>
<Ga>},=о = Ga (0), <G(i)>i=r = max,
(G0 4" GXY a (w) a2
G, 2g N ’
Ga(0) + G-,= \, Ga (T) — opt,
r = v, r(0) = r0, г(Г) = г,,
V = ae -\- R, v (0) = v„, v (T) = vb
A = A, (t, N, w), A (0) = 0, A (T) - opt
(a (t) О 0, 0< N (?) О 1, I e (?) ] = 1, Gx, w = const).
(11.126);
512
ВОПРОСЫ НАДЕЖНОСТИ В ЗАДАЧАХ ОПТИМИЗАЦИИ
[ГЛ. 11
Процедура построения и все свойства оптимальных управле¬
ний (11.11) сохраняются и для (11.120). Поэтому ограничимся
примером отыскания максимума (11.123), воспользовавшись за¬
висимостью G- (R) из п. 2 § 1. На рис. 11.17 показано математи¬
ческое ожидание веса (Gv), приходящегося на одну попытку
(отнесено к G0), в функции вероятности R успешного выполнения
маневра. Приведенные данные соответствуют рис. 11.9. Кривые
различаются значениями па¬
раметра Amax ~ ^тах^1 — мак¬
симально возможного числа
отказов за время одного по¬
лета; сплошные кривые отно¬
сятся к задаче о перемещении
между точками покоя, пунк¬
тирные — к задаче о наборе
модуля скорости. Оптималь¬
ные значения вероятнос¬
ти R и максимальные значе¬
ния веса <G?S>, соответствую¬
щие точкам максимума на
рис. 11.17, приведены на
рис. 11.18 и 11.19 в зависи¬
мости от Лшахдля различных
значений параметра маневра
Ф* (см. (11.33), (11.34)). При
одних и тех же значениях
АШах п Ф* оптимальная веро¬
ятность R и максимальный
вес (GA) для задачи переле¬
та между точками покоя
(сплошные кривые) оказываются существенно выше, чем для
задачи набора модуля скорости (пунктирные кривые).
Рассмотрим теперь второй вариант формулировки задачи 1°:
найти минимум математического ожидания числа попыток, по¬
требного для перевозки заданного груза GA, и покажем эквива¬
лентность обеих формулировок.
Число успешных попыток пнеобходимое для доставки груза
Ge, равно Ч
/г. = [Gs/G.l-M; (11.127)
математическое ожидание суммарного числа затраченных попы¬
ток записывается так (по определению):
Рис. 11.17. Средняя величина груза, достав¬
ляемого в конечную точку траектории за
одну попытку, в зависимости от вероятности
R положительного исхода попытки при фик¬
сированном максимальном числе отказов
Лшах. Сплошные кривые — перемещение ме¬
жду точками покоя, пунктирные — набор
модуля скорости.
пР„
р 2 G >GZ, У! Gw<Gj
4=1 г=1
(11.128)
Ч Знак [G^/GL] обозначает целую часть числа G^/GL — ближайшее
целое число, меньшее G4/C-.
g 4] OJ [ТПМАЛЫ [АП ВЕРОЯТНОСТЬ ВЫПОЛНЕНИЯ МЕИЕ ВРА 513
где Рп — вероятность того, что необходимое число п0 удачных
попыток набирается ровно на га-й попытке (не раньше и не позже).
Это событие состоит в том, что из первых (га — 1) попыток
(п — raj неудачные, а последняя, га-я, попытка удачная. Такая
Рис. 11.18. Оптимальная для задачи 1°
вероятность успешного выполнения ма¬
невра в каждой попытке в зависимости от
максимального числа отказов Атах при
фиксированных значениях функционала
маневра Ф*. Сплошные кривые — переме¬
щение между точками покоя, пунктир¬
ные — набор модуля скорости.
Рис. 11.19. Максимальная величина мате¬
матического ожидания груза, доставляе¬
мого за одну попытку, в зависимости от
максимального числа отказов Атах при
фиксированных значениях [функционала
маневра Ф*. Сплошные кривые — переме¬
щение между точками покоя, пунктир¬
ные — набор модуля скорости.
ситуация может быть осуществлена Сп-i* равновероятными спо¬
собами (число сочетаний из га — 1 по га — raj, вероятность каж¬
дого из них (1 — R)n~n*Rn*.
Обозначив через i — га — га#, получим формулу для (11.128)
в виде
оо
<"> = Кп* 2 (щ|*£Гнг к + 0 (! -*f- (11Л29)
г=0 * ^ *
Заметим, что ряд, стоящий в правой части (11.129), представляет
собой разложение функции [1 — (1 —/?)]_(п*41), поэтому матема¬
тическое ожидание суммарного числа затраченных попыток будет
равно *)
<„> = nJR. (11.130)
Подставив в (11.130) выражение для п0 из (11.127) и отбросив
знак целой части, получим <га> = G^/RGn. Минимум <га> по R
*) Соотношение (11.130) можно было выписать сразу, исходя из стати¬
ческого определения вероятности.
33 Механика полета
514 ВОПРОСЫ НАДЕЖНОСТИ В ЗАДАЧАХ ОПТИМИЗАЦИИ [ГЛ. 11
при фиксированной величине Gs достигается, когда произве¬
дение RG-U максимально. Это означает, что решения задач на
минимум (п) и на максимум <GS> совпадают с точностью до от¬
личия дроби Gs/G- от целого числа (последнее в рассматриваемом
случае Gs G- несущественно).
3. Максимум суммарного груза при заданной вероятности
реализации решения (задача 2°). С вероятностью R0 будем гаран¬
тировать, что из п попыток неудачных будет не больше чем к /г.
Рис. 11.20. Максимальное число к неудачных попыток из п, вычисляемое с вероятностью
7?о, в зависимости от вероятности Щуекспнего выполнения маневра для одной попытки
Вероятность R0 складывается из вероятностей событий, состав¬
ляющих данное:
До = У Р« ’ рп = Р ( У G<i) = (и - 0 G=) , (! J •131)
1=0 ' j=l ’
где Р(п — вероятность того, что из п попыток неудачных будет £.
Последнее может реализоваться Сгп способами. Вероятность каж¬
дого из них одинакова и равна (1 — R)L Rn~\ поэтому Р{п =
= Сп (1 —R)lRn~l. Подставляя это выражение в (11.131), при¬
ходим к формуле
п к
Ro = Р ( 2 С(Л > (п - к) G-У = 3 iT-f^ (1 - (И .132)
i=i i=o
(биноминальное распределение для схемы независимых испыта¬
ний [11.6]).
§41
ОПТИМАЛЬНАЯ ВЕРОЯТНОСТЬ ВЫПОЛНЕНИЯ МАНЕВРА
515
При заданных R0 и п формула (11.132) определяет связь
между вероятностью R успешного выполнения маневра для одной
R,.
opt
0,9
0,8
0,7
0,6
0,6
Rr
II
%
ф =
1
¥
ч\
. Г/ V -г,.
0,7 ,0,9
\
V
и'
. ч
\ Vj
—.
JM99
/
/
'ч^Ч
М'
V.'
26,(Щ^
О 0,4 0,8 7,2 46 Лп
0,9
0,8
0,7
0,6
06
'
II
\\Ч
\
и*
\ х
\
N.
Я
%
чч
Ч
\
<Р*=4/Ч
ь
О
Ofi
08 7,2
■zmcx
ПЕд
0,4
0,3
0,2
0,7
к
п-6
VN
\Ч\ч
\^б,/,80=6
19
V4
ч ч
0,7,0,99
0,26,0,6
7
\ '
Ч
1У 1
//// /
I//11
0,4 0,8 7,2 7,6 Ал
Рис. 11.21. Оптимальная для задачи 2°
вероятность успешного выполнения манев¬
ра в каждой попытке в зависимости от
максимального числа отказов Атах при
фиксированных значениях функционала
маневра Ф*, вероятности Rо реализации
решения и числа попыток п. Сплошные
кривые — перемещение между точками
покоя, пунктирные — набор модуля ско¬
рости.
Рис. 11.22. Максимальная величина груза,
доставляемого за одну попытку, в зависи¬
мости от Лтах при фиксированных значе¬
ниях Ф*, н0 и п. Сплошные кривые — пе¬
ремещение между точками покоя, пунк¬
тирные — набор модуля скорости.
реализации и числом неудачных попыток к: к k(R, Д0»п)
(рис.И.20).
33*
516
ВОПРОСЫ НАДЕЖНОСТИ В ЗАДАЧАХ ОПТИМИЗАЦИИ
[ГЛ. И
Согласно (11.132) с вероятностью R0 суммарный груз
доставленный за п попыток, будет не меньше
f]G(i)> (п — k)Gn, (11.133)
г=1
поэтому задача 2° сводится к отысканию максимума правой части
неравенства (11.133)
= max [п — к (7?)] Gn (В) (11.134)
R
по вероятности R успешного однократного выполнения маневра.
Пример решения задачи (11.134) для зависимости Gn (.R) с
рис. 11.9 приведен на рис. 11.21, 11.22. Там показаны оптималь¬
ная вероятность R и максимальная величина суммарного груза
Gs, приходящаяся на одну попытку из п затраченных, в функции
Атак — максимально возможного числа отказов за время одного
полета*
При увеличении вероятности R0 реализации решения величи¬
на груза Gx/n падает; это влияние уменьшается с ростом общего
числа попыток п. При больших п решение задачи 2° (рис. 11.21
и 11.22 при п = 50) приближается к решению задачи 1° (рис. 11.18
и 11.19).
При исследовании задачи 2°, помимо использованной выше,
могут употребляться эквивалентные формулировки: с заданной ве¬
роятностью Д0 перевезти заданный груз за минимальное число
попыток п или обеспечить максимальную вероятность R0 пере¬
возки заданного грузаб^ за фиксированное число попыток п.
Дополнительные сведения по вопросам надежности примени¬
тельно к механике полета можно найти в работах [11.9—11.11].
ГЛАВА 12
ВЕСОВЫЕ ЗАТРАТЫ
НА КОРРЕКЦИЮ ТРАЕКТОРИИ
Круг вопросов, связанных с коррекцией траекторий, весьма
обширный. Вот примерный их перечень.
1°. Исследование возмущающих факторов, действующих на
аппарат в процессе полета, вычисление отклонений от расчетной
траектории.
2°. Выяснение потребной точности реализации расчетной тра¬
ектории, решение вопроса о необходимости коррекции.
3°. Измерение параметров действительной траектории, обра¬
ботка результатов измерений.
4°. Построение закона управления, обеспечивающего заданную
точность реализации расчетной траектории при минимуме весо¬
вых затрат.
Полное освещение этих вопросов выходит за рамки настоящей
книги. В качестве компенсации к главе приложен большой (но
отнюдь не исчерпывающий) список литературы [12.1 — 12.103],
где исследуются перечисленные проблемы.
Основное внимание в настоящей главе уделяется оценке до¬
полнительных затрат рабочего вещества, необходимых для осу¬
ществления коррекции траектории. Рассмотрение проводится в
приложении к идеальному двигателю ограниченной мощности.
В этом случае задача сводится к отысканию минимума математи¬
ческого ожидания приращения интеграла от квадрата реактив¬
ного ускорения. Учитываются ошибки реализации оптимальной
программы реактивного ускорения, ошибки измерений коорди¬
нат и скорости, отклонения от начальных условий. Считаются
известными вероятностные характеристики этих случайных вели¬
чин (математическоэ ожидание, корреляционная функция, дис¬
персия). Накладываются ограничения на дисперсию конечных
отклонений координат и скорости.
Принимается схема последовательных коррекций конечного
положения аппарата. Коррекция осуществляется основным дви¬
гателем, который работает непрерывно. На основании данных
измерений в некоторые моменты времени (моменты коррекции)
производится оптимальная поправка программы реактивного
518
ВЕСОВЫЕ ЗАТРАТЫ НА КОРРЕКЦИЮ ТРАЕКТОРИИ
[ГЛ. 12
ускорения. Из условия минимума математического ожидания
приращения функционала задачи выбираются оптимальное рас¬
пределение и оптимальное число моментов коррекции [12.62,
12.69].
§ 1. ОШИБКИ РЕАЛИЗАЦИИ ПРОГРАММЫ РЕАКТИВНОГО
УСКОРЕНИЯ И ОТКЛОНЕНИЯ ОТ РАСЧЕТНОЙ ТРАЕКТОРИИ
1. Ошибки в реактивном ускорении. Найденный в результате
решения вариационной задачи о минимуме функционала /, эк¬
стремальный закон а<0) (t) (гл. 4 и 5) будет реализоваться с не¬
которыми ошибками
6а — a (t) — ai,0) (t). (12.1)
Это приведет к отклонению действительной траектории г (г) от
расчетной г<0) (t):
t>av (t) = г (t) - rf (t), aor(f) = r (t)_,.<0)W> (12.2)
Предполагая эти отклонения малыми, можно записать для них
линеаризированную систему уравнений
6аг = 6а + (ЭЯ / 3r)(0) Av (12-3)
Для того чтобы получить аналитические результаты, вторым
членом в правой части уравнения (12.3) пренебрегается, т. е.
полагается
8аг = 6а. (12.4)
С этой же целью в качестве исходного невозмущенного дви¬
жения рассматривается перемещение в бессиловом поле между
двумя точками поля, расположенными на расстоянии Z, за время
Т (5.33):
Чтобы найти осредненные отклонения 8аг, 6аг, обусловлен¬
ные ошибками 8а, нужно знать вероятностные характеристики
последних: математическое ожидание и корреляционную функ¬
цию. Пусть эти характеристики заданы, например
М [6а (*)] = О,
К [8а (Z), 6а (f')I = alA (t) А (*') (12.6)
§ i] ОШИБКИ РЕАЛИЗАЦИИ ПРОГРАММЫ ТЯГИ 519
Здесь М и К — символы математического ожидания и корреля¬
ционной функции; оа и 8t можно интерпретировать как константы,
характеризующие точность и быстродействие системы регули¬
рования, которая обеспечивает выполнение программы ускоре¬
ния от тяги; A (t) — неслучайная известная функция, опреде¬
ляемая типом регулирования: A (t) = а (t) при регулировании
по относительному отклонению; A (t) ~ const при регулировании
по абсолютному отклонению (далее принимается A (t) = 1/Т2).
2. Среднеквадратичные величины отклонений от расчетной
траектории. Вычислим математические ожидания и дисперсии
отклонений 8ах и 8(1х. Операторы математического ожидания и
интегрирования перестановочны [12.4], поэтому
t t
М [6а.г (£)] = М ^ 8а dt = ^ М (8а) dt = О,
о
t
М [8ах (£)] — М ^ dt ^ 8а dt = ^ dt^M (8а) dt — 0.
(12.7)
0 0 0 0
Отличными от нуля будут дисперсии 8а:с и 8ах; здесь снова восполь¬
зуемся перестановочностью операторов математического ожида¬
ния и интегрирования:
i t
D [6n.r (t))=M [S.,г (/) 6a.t (OJ = M [(J Ьа (I) dt) (J 5a (£) dlj =
L 0 0 J
t t t t
= M J ^ 5 6a (t) 6 a (Q dl=\d%\ M [6a (£) ba (£)] (12.8)
0 0 0 0
Последнее подынтегральное выражение представляет собой, по
определению, корреляционную функцию (12.6), поэтому
i i
D 16,,./•(/)] = (12.9)
О О
Вычисляя этот интеграл и проделывая аналогичную процедуру
для 8ах. получаем окончательное выражение для дисперсий слу¬
чайных отклонений (12.2), обусловленных ошибками 8а типа
(12.6):
•°[6аа(т)] = 20^0 [т — 0 (1 — e~zie) ] (у= х = ~ , 0= у-),|
Л [6as (т)] = | б|0 {X3 - 30 [V, т2 + 6те-'° + 92 (1 - е~^)}} [
=4)- J
(12.10)
520
весовые затраты на коррекцию траектории [гл. 12
Отклонения от расчетной траектории обусловливаются не
только ошибками б а, но и неточной реализацией начальных ус¬
ловий:
60г — г (0) — г0, б0г = г (0) — г0. (12.11)
Ошибки 80v и 60v предполагаются независимыми случайными
векторами, компоненты которых не коррелированы между со¬
бой и распределены около нуля с известным среднеквадрагиче-
ским отклонением; для рассматриваемого одномерного движения
считается, что
М (б о г;) = М (б 0s) = 0, D (80v) = а0\„ D (80s) = а*8. (12.12)
Если к концу движения ожидаемые отклонения реальной тра¬
ектории от расчетной превосходят заданные допустимые откло¬
нения б г так и бгтпх? то в процессе движения необходима коррек¬
ция траектории. В рассматриваемом примере этому соответст¬
вует нарушение системы неравенств
2^0 + < б^ях1 |а|0 + а*, + 01 < б4ах, (12.13)
которая получена сложением дисперсий D (8av) и D (80v),
D (8as) и D (60s), так как отклонения ба и б0 независимы и
D (бrt + б0) — D (8а) -f D (б0). При этом членами порядка О2
и выше пренебрегалось, ибо по физическому смыслу 8t<^tT или
0 - бг/Г<1.
§ 2. ОПТИМАЛЬНА Я ПРОГРАММА КОРРЕКЦИИ
1. Измерения координат и скорости. Будем считать, что пера
венства (12.13) не выполняются, т. е. в процессе движения необ¬
ходима коррекция траектории. Для осуществления коррекции
нужно знать действительные значения координат и скорости.
Точность единичных измерений этих величин нельзя считать удов¬
летворительной, поэтому предполагается, что измерения произ¬
водятся регулярно с достаточно большой частотой, а результаты
измерений, произведенных между моментами времени и
t{ (i = 1,2,..., т), пересчитываются к моменту времени ^
и осредняются. Однако некоторая погрешность все же остается:
6„1Ч = р (ti) — г (ti), Ьп1\ = р (ti) — г (t;), (12.14)
где р (£*) и р (^) — радиус-вектор и вектор скорости, полученные
в результате пересчета и осреднения измерений. В рассматри¬
ваемом примере считается, что
М (5nVi)= М (6...V0 = 0, D (6nvd = (oiv)2, D (6(lSi) = (g«)2 (12.15)
ОПТИМАЛЬНАЯ ПРОГРАММА КОРРЕКЦИИ
521
и что ошибки = 1, . . ., т) не коррелированы между
собой.
сеть от продолжительности интервала осреднения — ^г-i)*
С ростом этого интервала они сначала будут уменьшаться в ре¬
зультате исключения случайных погрешностей, а затем будут
возрастать из-за того, что при пересчете на более отдаленный мо¬
мент начнут сказываться ошибки 6а, вносимые двигателем. В ре¬
зультате осреднения измерений в моменты времени tx (i = 1, . . .
. . т) с некоторой степенью точности известны отклонения
действительной траектории от (i — 1)-й расчетной траектории
2. Оптимальные поправки к программе реактивного ускоре-
из условия оптимальности «в большом»: оптимальная поправка
вычисляемая к моменту времени ti (момент i-ж коррекции),
должна обеспечивать минимум функционала
при перемещении между точками фазового] пространства {р(^)»
р (£*)} и {гх, гх} за время AU = Т — Ц.
мальными энергетическими затратами. Выходить на расчетную
траекторию до конца движения не требуется.
Считается, что погрешностей при вычислении поправки Да^ (t)
не вносится. Для одномерного движения в бессиловом поле поправ¬
ка к программе ускорения определяется следующим соотноше¬
нием:
В промежуток времени между моментами и ti+1 должна
реализоватып^ программа а^г) (t), которая в момент времени ti+x
сменяется на новую оптимальную программу а^г+1) (t) и т. д.
Среднеквадратичные ошибки измерений Gnh (?пз будут зави-
ния. Поправки к программе а^ (t) ускорения от тяги выбираются
Аа^ = а^ (t) — а<1_1) (£),
* * у *
(12.17)
г
(12.18)
Таким образом, от поправки Да^г) (t) требуется, чтобы она
свела к нулю отклонения Дг{ и Дг* в конце траектории с мини-
+ Д v
(12.19)
522 ВЕСОВЫЕ ЗАТРАТЫ НА КОРРЕКЦИЮ ТРАЕКТОРИИ [ГЛ. 12
3. Приращение функционала. Выражение для функционала
J в случае движения с ошибками и коррекцией можно записать
в следующем виде:
В бессиловом поле уравнения для оптимальных поправок
что позволяет преобразовать функционал (12.20) следующим
образом:
Предполагая, что А///0 1 и ограничиваясь членами линей¬
ными относительно Д///0, получаем приближенные выражения
для весовых компонент при движении с коррекцией (ср. (4.15) —
Для максимизации осредненной величины Gn нужно опреде¬
лить такое распределение моментов коррекции (i = 1, . . пг)
и такое их число т, чтобы при условии обеспечения в конце дви¬
жения заданной точности (в среднем) величина математического
ожидания ДJ была минимальна.
г=0 t.
т 1
1
т /V т }
+ 2 Г 23 5 .23 Мл) * + Д] Jj Aal^adT +
т. -I1- L J-
г г
где
1
(12.23)
о
(4.17))
1
| (12.24)
ОПТИМАЛЬНАЯ ПРОГРАММА КОРРЕКЦИИ
523
Чтобы вычислить М (А/), необходимо найти математическое
ожидание подынтегральных выражений в (12.22). Эти выражения
представляют собой поправки Да(Д, ошибки баи их произведения.
Поправки Аа^\ согласно (12.19), зависят от суммарных откло¬
нений A v{, As*. Последние складываются из отклонений, обуслов¬
ленных ошибками 6а, и из ошибок (i — 1)-го и i-то измерений.
При помощи соотношений (12.2), (12.4), (12.14) и (12.16) можно
показать, что
Tt
Т2 р
Avi = — \ 6 a dx + 6nVi -f 6nt>i_b
Математическое ожидание членов, содержащихся в первых
квадратных скобках выражения (12.22), равно нулю, так как
подынтегральные выражения этих членов линейны относительно
случайных величин А у*, As* и 6а, математические ожидания кото¬
рых равны нулю (12.6), (12.7.)
Считая, что случайные отклонения 6а (т) по разные стороны от
моментов времени т* перехода на новую программу а<Ш) не кор-
релированы между собой
получаем такой же результат и для второй квадратной скобки
формулы (12.22), так как индексы сомножителей в этих членах
отличаются больше чем на единицу. Это означает, на основании
(12.25), что сомножители не коррелированы между собой, а мате¬
матическое ожидание каждого из них равно нулю.
Два первых члена, содержащихся в последних квадратных
скобках формулы (12.22), выражаются через отклонения Д^-г,
Ai>i, Asi-i и A Si следующим образом:
т.
т.
(12.25)
тг-1 тг—1
К [6а (т), 8а (т')1 = О
при Ti_i < т < ть Ту_1 < т' < Ту, i =1= ), (12.26)
524 ВЕСОВЫЕ ЗАТРАТЫ НА КОРРЕКЦИЮ ТРАЕКТОРИИ [ГЛ. 12
Поэтому математическое ожидание приращения функционала,
с точностью до квадратичных относительно 0 членов, равно
т г
м{д/) = !^1{2 jaSe(2&?-3ii + 2£i-i) +
г—1 L
/б(г-1.)у2 (G(i_1))2 — (a(i))2 (g(*_1))2 — (G(i))2
, vunu / t /t 4 v | ' m > ' nx>) - ' ?гз / \ ПЗ/
+ 1 — ^ ~~ ' ^ 3(1—Ti) 1 (1 — Tj)3
G2 о (G(m))2 (G(m))2 I
• a | Z V-'nv / I 9 ' ns / ^ .
^ “12 ^ + (1 - Tm)8j ’
^ 6(0) = a0s, £, = . (12.28)
В конце движения (т = 1) траектория должна попасть в за¬
данную область конечных значений координат и скорости, т. е.
ожидаемые отклонения от расчетной траектории в конце движе¬
ния должны быть ограничены сверху. Это условие записывается
в виде системы двух неравенств, аналогичных (12.13):
2О*0(1 _Tm) + (o(->)’<6^naxI
§ с*0 (1 - тт)3 + (a<S>)» (1 - тт)2 + („£>)* <
(12.29)
4. Оптимальное распределение моментов коррекции. Выписан¬
ные неравенства накладывают ограничения на тт при отыскании
минимума М (AJ) по т*(£ = 1, . . т).
Если погрешности измерений не учитываются (а(й = =0
и если начальные условия предполагаются реализованными
точно (аПи = (Jos — 0), то для оптимального распределения мо¬
ментов коррекции получаем формулу геометрической прогрессии:
1г opt = (^f)opt = (1 (I- = 1..... m). (12.30)
Минимальная для заданного числа моментов коррекции вели¬
чина математического ожидания приращения функционала J
M(A/)min = ^a*(i09x + l),
ф1 = т [2 (1 _ тт)-3/т— 3 (1 - тт)-2 т + 2 (1 - Tm)-l m 1 ]
(12.31)
монотонно убывает с увеличением т, причем
lim фх = —ln(l — Tm) (12.32)
ОПТИМАЛЬНАЯ ПРОГРАММА КОРРЕКЦИИ
525
(см. log (1 + <Pi) на рис. 12.1, а в зависимости от т и (1 — тт)).
Видно также, что срх уменьшается с увеличением (1 — тт), поэ¬
тому оптимальное расположение момента последней коррекции
Рис. 12.1. Математическое ожидание приращения функционала «7, потребное для коррекции
траектории идеальным двигателем ограниченной мощности, в зависимости от числа момен¬
тов коррекции т и интервала (1 — тт) между последней коррекцией и концом траекто¬
рии — маневр перемещения между положениями покоя: <р4 — коэффициент при дисперсии
ошибок реализации программы реактивного ускорения, ср2 — коэффициент при дисперсии
ошибок измерений скорости (см. (12.31), (12.34)).
должно выбираться из неравенств (12.29) максимально удален¬
ным от конца траектории
/л ч ^max л/~~^ /49 00 \
(1 — tm)opt - min j-j —— . v 2 o20 j- (12.33)
В случае постоянной отличной от нуля дисперсии ошибок изме¬
рений (а^ = aw, <jW = о81 i = 0, 1, . . ., т) оптимальное рас¬
пределение моментов коррекции уже не выражается такой про¬
стой формулой, как (12.30), и должно определяться численно.
Если же воспользоваться формулой (12.30), то характер зависи¬
мости М (А/) от т и (1 — хт) сохранится (рис. 12.1, б):
М (А/) = — (у 0ф1 + + elф2 + (1 — 'tm)-3} » j
ф1 = т [2 (1 - тm)-3/m- 3(1- Tm)-2/m +2(1- xm)~Vm - 1 ], 1
<р, = (1 - Tm)-2m [(1 - Tmyl _ 1] + 1(1 - Tm)-4 I
(12.34)
526
ВЕСОВЫЕ ЗАТРАТЫ НА КОРРЕКЦИЮ ТРАЕКТОРИИ
[ГЛ. 12
Обсудим полученные результаты. Задача об оптимальной
коррекции была поставлена так, чтобы еще до реализации траек¬
тории выбрать оптимальные в среднем весовые соотношения и
оптимальные программы реактивного ускорения, которые обес¬
печат максимум полезного груза, на доставку которого можно
рассчитывать.
Найденное оптимальное распределение моментов коррекции
в случае точных измерений подчиняется формуле геометрической
прогрессии (12.30). Моменты коррекции сгущаются к концу
траектории. Момент последней коррекции должен быть макси¬
мально возможно удален от конца траектории при обеспечении
попадания в заданную область конечных значений координат и
скорости.
Сгущение моментов коррекции к концу траектории вполне
естественно. В начале движения для устранения отклонений от
расчетной траектории еще остается много времени, и можно до¬
пустить большую величину этих отклонений при достаточно малом
уровне поправок А(12.19), т. е. можно большее время двигаться
без коррекции, чем к концу движения. Такой же закон распре¬
деления моментов коррекции получен и в работе [12.14], в кото¬
рой рассматривается импульсная коррекция баллистических тра¬
екторий. В случае импульсной коррекции ошибка вносится только
в моменты приложения импульсов, в рассмотренном же случае
ошибка накапливается непрерывно независимо от того, произво¬
дится коррекция или нет. Поэтому при условии точных изме¬
рений здесь не существует оптимального числа т моментов кор¬
рекции.
Однако если дисперсия ошибок измерений отлична от нуля
и зависит от интервалов между моментами коррекции, то из фор¬
мулы (12.28) следует существование оптимального числа момен¬
тов коррекции, при котором М (А/) имеет минимум.
ЧАСТЬ III
ПОСТРОЕНИЕ ОПТИМАЛЬНЫХ
РЕШЕНИЙ
ГЛАВА 13
АНАЛИТИЧЕСКИЕ РЕШЕНИЯ УРАВНЕНИЙ
ДИНАМИКИ
Сформулированные в предыдущих разделах вариационные
задачи приводятся, как правило, к сложным системам дифферен¬
циальных уравнений. Нахождение оптимальных управлений и
оптимальных траекторий движения в аналитической форме для
истинных гравитационных полей всегда или почти всегда бывает
невозможным. Однако аналитические решения представляют
особый интерес в связи с их наглядностью и возможностью ши¬
рокого параметрического анализа.
Эти несомненные достоинства послужили основанием для раз¬
работки различного рода приемов и методов отыскания решений
в конечной форме. Разумеется, эти решения даются ценой за¬
мены истинного гравитационного поля на простое и отступления
от критерия оптимальности управлений.
Первое из этих упрощений сравнительно мало влияет на ре¬
зультат. В самом деле, движение космического аппарата в слож¬
ном поле нескольких гравитационных центров с достаточной сте¬
пенью точности можно разделить на этапы, ограничиваясь на
каждом этапе влиянием одного из центров. Например, перелет
аппарата с малой тягой с орбиты искусственного спутника одной
планеты на орбиту искусственного спутника другой в истинном
гравитационном поле может быть разделен на два характерных
участка: участок движения в области влияния планеты при на¬
личии возмущений от Солнца и других планет и участок межор-
битального перелета в поле тяготения Солнца при возмущающем
влиянии планет. На каждом из этих участков возмущениями
можно пренебречь и считать гравитационные поля центральными
(подробнее об этом см. в Приложении).
Это допущение принято и в данной главе: уравнения динамики
записываются для плоского или пространственного движения в
поле одного центра. В этом случае дифференциальные уравнения
упрощаются, однако не настолько, чтобы задача об оптимальных
управлениях и оптимальных траекториях могла быть доведена
До конечных выражений.
Чтобы достичь цели на этом пути, вместо оптимальных управ¬
лений рассматриваются, вообще говоря, неоптимальные, но поз¬
воляющие получить точные или приближенные формулы для
34 Механика полета
530 АНАЛИТИЧЕСКИЕ РЕШЕНИЯ УРАВНЕНИЙ ДИНАМИКИ [ГЛ. 13
параметров движения. Каждое такое решение описывает элемен¬
тарный космический маневр. Заданный маневр может быть состав¬
лен из элементарных. Управления и траектория движения полу¬
ченные таким способом будут неоптимальными, но в то же время
будут указывать главные особенности маневра.
Для аппаратов с двигателями малой тяги обычно рассматрива¬
ются следующие космические маневры: межпланетный перелет
с орбиты искусственного спутника одной планеты на орбиту
искусственного спутника другой (Земля—Марс, Земля — Ве¬
нера); изменение в пространстве орбиты спутника; поддержание
заданной орбиты, эволюция которой происходит под действием
возмущающих влияний, вызванных нецентральностью гравита¬
ционного поля планеты, атмосферой и пр.
Эти маневры назовем сложными. Они раскладываются на эле¬
ментарные: выход из гравитационного поля центра с круговой
начальной орбиты и обратный маневр — захват аппарата грави¬
тационным полем с выходом на круговую орбиту, перелет между
круговыми компланарными орбитами, поворот плоскости орбиты,
изменение положения спутника на орбите и элементов орбиты
(большой полуоси, эксцентриситета, наклонения, радиусов апогея
и перигея, фокального параметра) и др. Часть из упомянутых
здесь маневров описана в Приложении.
Наибольшее внимание уделяется элементарным маневрам с
заданной ориентацией постоянного по модулю вектора реактив¬
ного ускорения ос; как правило, вектор ускорения имеет какое-либо
выделенное направление: радиальное, трансверсальное, танген¬
циальное или нормальное к траектории, перпендикулярное к
мгновенной плоскости орбиты, постоянное в пространстве и др.
Целью настоящей главы является изложение решений урав¬
нений динамики для перечисленных случаев; предварительные
сведения о формах уравнений движения даны в § 1 Приложения.
§ 1. РАДИАЛЬНОЕ УСКОРЕНИЕ («Ф = 0в (П.9))
1. Уравнения и интегралы движения. При аф = 0 система
(П.9) Приложения имеет вид *)
Последнее уравнение выражает закон сохранения момента коли¬
чества движения (П. 12); отсюда
i) 13 настоящей главе используются уравнения в безразмерном виде;
процедура обезразмеривания описана в § 1 Приложения.
Vrv'r = ат + v\ / г — 1 / г\ |
= — vrv„ I г. j
(13.1)
уф = Ml г.
(13.2)
g 1] РАДИАЛЬНОЕ УСКОРЕНИЕ. 531
С учетом этого выражения для г;ф первое уравнение системы (13.1)
становится таким:
d,i ^ -1*'+^ (13-3)
clr \ 2 г) г3 г2
Для случая, когда реактивное ускорение постоянно (ат =
^ const), уравнение (13.3) интегрируется:
1 9 1 2 М2 t 1 . . М- 1
т vr -у = -ъ* + т + а'-г + ^
о
(13.4)
Здесь vr0, r0, М = г>Ф0г0 — параметры движения в начальный
момент. Если начальная орбита круговая, т. е. r0 = 1, vr0 = О,
v<p0 = 1, то уравнение (13.4) упрощается и формула для радиаль¬
ной скорости имеет вид
= ±уГ-FI+T+ 2аг(г-1)-1 =
где
= ±j/r^(r-l )(r-r1)(r-r2), (13.5)
zz ’ Гз = zz •
Эти выражения показывают, что в зависимости от величины
и знака ускорения аг могут быть различные режимы движения.
При аг 0 движение финитно (1 > г > г2 > 0); при х/8 ат >>0
движение также финитно (1 г <; гх <; 2); при ar > х/8 движе¬
ние инфинитно (г > 1).
Последний режим изучался в работе [13.1] для задачи о вы¬
ходе из гравитационного поля центра. В работе [13.2] рассмотре¬
но движение с малыми величинами радиального ускорения
(ar х/8). Общее исследование режимов было проведено в [13.3],
где даны формулы для угла ср и времени t через радиус г (см.
также [13.4, 13.5]). Эти формулы имеют вид:
при аг<^ 0
t = С d_L = У2
J vr V—ar({—ri)
nF ((В, к) + (1 — гг)Е (Р, к)
(1 — r2) sin 2(3
^ 2 У1 — /с2 sin2 р _
V2
VL=\r^n(p,-L\ k)-F®,k)],
n Y—ar{i — n) L 'J ’
Ф =
(13.7)
34*
532 АНАЛИТИЧЕСКИЕ РЕЩЕEIИЯ УРАВНЕНИЙ ДИНАМИКИ
[ГЛ. 13
где
1 — Го
1 — Г! ’
г —
— гт/ъ2 sin2 (3 -|- Го
— /с2 sin2 (3 -|- 1
при 0 < аг <1 У8
/2
t =
Ф =
V* (Г1 — 1)
где
/с2 =
[rtF (Р, /с) — (гх — 1) Е (р, /с)],
Л (Р> г2 — 1, /с),
г = (г 2 — 1) sin2 Р + 1;
при ат = V8
где
t == 4 [2 In tg (л / 4 + | / 2) — sin £],
Ф = 2 [со + V2 In tg (я/4 + со)],
sin2 £ = г — 1, tg2со = г — 1;
при ar > V8
* =yA|-[4^>/rzr^I^F-r(p, к) + Еф, к)
1
ф = arcsin (к sin (3) F ((3, к),
у 8аг
где
г =
1 — COS [3
/с2 -
(13.?
(13.9)
(13.10)
(13.11)
(13.12)
(13.13)
(13.14)
В формулах (13.7)—(13.14) использованы стандартные обо¬
значения для эллиптических интегралов первого F (|3, к), второго
Е (Р, к) и третьего л (|3, а, к) рода; при интегрировании постоян¬
ные выбирались так, что в начальный момент t = ф = 0; через
гх, г2 обозначены корни уравнения для радиальной скорости
(см. (13.6)).
2. Набор параболической скорости. При ar V8 движение
инфинитно, поэтому соответствующий режим может быть исполь¬
зован для анализа маневра набора параболической скорости с
круговой начальной орбиты [13.1].
Если в формулу (П. 11) для энергии Е подставить выражения
компонент вектора скорости vr, иф из (13.2), (13.5), то энергия
окажется функцией радиуса г:
Е
а-r (г — 1) — V2
(13.15)
§ 1]
РАДИАЛЬНОЕ УСКОРЕНИЕ
533
(начальное значение энергии в безразмерных единицах Е0 = —72
при Г0 = 1).
Из условия набора параболической скорости (Ег = 0) следует
связь между радиусом конечной точки гг и величиной радиального
ускорения
Максимальное значение конечного радиуса = 5 (ar = 78)
минимальное — = 1 (аг = оо). Время tx и угол срх в конце
маневра находятся из формул (13.13), (13.14), если в качестве
г принять гх. Радиальная и трансверсальная компоненты скорости
в конечный момент определяются следующими выражениями:
Полученные выражения (13.16), (13.17) для задачи набора
параболической скорости с постоянным радиальным ускорением
справедливы при ат > 78; меньшие значения ат соответствуют
финитным движениям. Инфинитное движение может быть орга¬
низовано и при малых значениях ускорения (ат <7 V8), если в
надлежащих точках траектории направление ускорения будет
изменяться на обратное.
Решение задачи о наборе параболической скорости с малым
попеременно положительным и отрицательным радиальным уско¬
рением содержится в [13.6] и [13.7]. Следуя [13.7], введем в рас¬
смотрение геометрическую диаграмму: квадрат эксцентриси¬
тета — радиус. При выводе формул не будем предполагать, что
начальная орбита круговая.
В приложении (см. П.21), (П.22)) дается выражение эксцентри¬
ситета е через радиус перигелия г-:
Последний при помощи уравнения энергии может быть свя¬
зан с текущим радиусом г и радиальной скоростью vr:
(13.16)
(13.18)
7 _i_ _ i _ Ml 1
2 2г2 г о г2 г-т
п 71
(13.19)
откуда
(13.20)
Полученная связь является основной для дальнейшего. На
рис. 13.1 сплошной линией представлена кривая нулевой ско-
534 АНАЛИТИЧЕСКИЕ РЕШЕНИЯ УРАВНЕНИЙ ДИНАМИКИ [ГЛ. 13
рости в координатах ?7М2, е2; при г —> оо кривая асимптотически
приближается к е2 = 1; пересечение кривой с горизонтальной ли¬
нией е2 = 1 происходит при г = 1/2М2. Движение в отсутствие
возмущающего ускорения соответствует на графике финитному
(при е2 1) или инфинитному (при е2 > 1) перемещению по
горизонтальной линии.
Вычислим производную tfe2/o?r, привлекая уравнение (13.3)
~ = 2 МЧГ, (13.21)
откуда при постоянном значении аг
82 = 82 + 2М2аг (г - г0). (13.22)
Движение при постоянно направленном возмущающем уско¬
рении соответствует финитному или инфинитному перемещению
вдоль прямой с угловым коэффициентом 2М2аг. На рис. 13.1
пример траектории с постоян¬
ным и постоянно направлен¬
ным радиальным ускорением
представлен прямой 1—2,
точка 1 — перигелий, точка
2 — афелий возмущенной ор¬
биты. Здесь движение проис¬
ходит вперед и назад по линии
1—2; максимальное значение
эксцентриситета достигается
в точке 2:
62 = 81 + 2М2а,. (г2 — Г]).
сила изменит знак (аг СО),
то значение эксцентриситета, достигнутое на такой орбите
(точка 3) будет превышать прежнее максимальное значение
(точка 2). Многократное повторение такого маневра 2—2, 2—3
обеспечивает набор заданного значения эксцентриситета при как
угодно малом значении возмущающего ускорения. Таким спо¬
собом может быть организовано управление в задаче набора пара¬
болической скорости (с2 = 1) с радиальным ускорением, мень¬
шим предельного (ar <7 V8).
Этого же эффекта можно добиться, если вместо реверсирова¬
ния ускорения ввести участки пассивного движения, как это
показано на рис. 13.1 (ломанная 1—2—2'—3').
Как уже было установлено, предельное значение постоянного
и постоянно направленного ускорения для набора нулевой энер¬
гии с круговой орбиты равно V8 в безразмерных единицах (ра¬
Рис. 13.1. Диаграмма: квадрат эксцентриси¬
тета е2 — относительный радиус г/м2.
Если в точке 2 возмущающая
§ 13
ДИАЛLI IО Е УСКОРЕИ НЕ
535
диус и момент на этой круговой орбите принимаются за единицы
измерения). При старте с эллиптической орбиты предельное зна¬
чение может оказаться выше. Из рис. 13.1 видно, что наихудшие
в этом смысле условия имеют место на правой ветви кривой нуле¬
вой радиальной скорости (в апогелии) в точке максимального
наклона этой кривой: г0/М2 = 1,5, г2 = У9 и при этом аг =
= 4/(27М4).
3. Межорбитальный перелет. Примеры перелета на орбиты
Марса и Венеры с постоянным и постоянно направленным ра¬
диальным ускорением можно найти в работах [13.3—13.5]. Что¬
бы траектория перелета имела на орбите Марса или Венеры ну¬
левую радиальную скорость, необходимы ускорения, меньше V8
(финитное движение). Трансверсальная составляющая скорости
в силу условия (13.2) не может быть сделана равной круговой на
орбите назначения никаким выбором величины или знака реак¬
тивного ускорения. Поэтому относительная скорость аппарата
и планеты назначения всегда отлична от нуля.
В работе [13.8] также изучается межорбитальный перелет на
орбиты Марса и Венеры с радиальным ускорением; однако модуль
ускорения здесь не постоянен, а пропорционален радиальному
расстоянию: аг = Ъг.
В упоминавшейся уже статье [13.7] вместе с постоянным рас¬
сматривается и переменное радиальное ускорение, обеспечиваю¬
щее постоянную радиальную скорость:
М2 А
vr = const, аг — —з (13.23)
В работах [13.9—13.10] исследовано движение с радиальным
ускорением, изменяющимся по закону
аг — ^ • (13.24)
Этот закон реактивного ускорения имеет место для аппара¬
тов с солнечным парусом, установленным перпендикулярно к
солнечным лучам (см. § 4 гл. 9).
Уравнения движения (13.1) с ускорением в виде (13.24) опи¬
сывают кеплеровскую траекторию с измененной гравитацион¬
ной постоянной (1 — а0 вместо 1).
Пусть в начальный момент аппарат выведен на круговую орбиту
единичного радиуса; выпишем выражения для эксцентриситета
е и большой полуоси А (ср. (П.21) — (П.23)):
е = Л = —тттл п- (13.25)
1 — я0 I 2 — 1 / (1 — а0)! }
Отсюда следует, что при а0 0,5 траектория полета — эллипс,
при а0 = 0,5 — парабола, при а0 > 0,5 — гипербола.
536 АНАЛИТИЧЕСКИЕ РЕШЕНИЯ УРАВНЕНИЙ ДИНАМИКИ
[ГЛ. 1 ;s
Для перелета между круговыми орбитами r0 = 1 и 1 по
эллипсу, касающемуся в апогее круговой орбиты назначения,
необходимо, чтобы
а0 = (г1 — 1)72?-!. (13.2G)
Время перелета при этом в Y+ 1) Раз больше времени
перелета по соответствующему эллипсу Хомана, а конечная
скорость в Yri раз больше круговой скорости на радиусе гг.
Зависимость времени перелета
с орбиты Земли на орбиту Марса
от ускорения ап показана на
рис. 13.2.
4. Изменения орбитальных
элементов. Момент количества
движения М, радиусы макси¬
мально га и минимально гп уда¬
ленных от центра точек оста¬
ются неизменными для траек¬
тории с постоянным по модулю
и постоянно направленным ради¬
альным ускорением. Эти свой¬
ства вытекают из пп. 1 и 2 на¬
стоящего параграфа.
Если невозмущенная орбита
круговая или близка к круго¬
вой (е0 1), а возмущающее
ускорение мало (ar V8), то
наибольшая разность между
радиусами равна
Рис. 13.2. Зависимость времени перелета
с орбиты Земли на орбиту‘Марса от вели¬
чины радиального ускорения а0
(аг = а0/г2).
максимальным и минимальным
Га , 1 2CLr,
(13.27)
а максимальное значение эксцентриситета, определяемого выра¬
жением (13.20), дается формулой
= 2 аг
(13.28)
(в (13.27) и (13.28) минимальное расстояние, равное радиусу
невозмущенной орбиты, принято за единицу длины).
Линия апсид, определяемая как линия, соединяющая точки,
максимально и минимально удаленные от центра, смещается
при наличии малого радиального ускорения на 2паг радиан за
оборот.
Изложенные здесь результаты были получены рядом авторов.
В работе [13.2] использовано разложение по малому параметру
аг в выражениях, определяющих изменения орбитальных эле¬
ментов. В [13.11] был применен метод Крылова—Боголюбова к
§ 2]
ТРАНСВЕРСАЛЫТОЕ УСКОРЕНИЕ
537
уравнениям (П.26). Результаты, полученные в [13.11], совпадают
с результатами [13.2], за исключением одного вывода относи¬
тельно регрессии линии апсид. Еще один метод — метод вариа¬
ции параметров применительно к анализу изменении орбиталь¬
ных параметров — описан в работах [13.12, 13.13]. Выводы
авторов этих работ также совпадают с изложенными выше.
§ 2. ТРАНСВЕРСАЛЬНОЕ УСКОРЕНИЕ (аг=0 в (П.7))
1. Уравнения движения. При сохранении одной трансвер-
сальной составляющей реактивного ускорения уравнения (П.7)
принимают вид
:, 1
г = г ср- — ,
ср г = — 2гф + аф.
(13.29)
Исключая из этих уравнений ф, приходим к одному уравнению
третьего порядка относительно г
Ш (гг3 + г),/' = ЯфГ- (13.30)
2. Набор параболической скорости. В упоминавшейся ранее
работе [13.1] рассмотрена задача о наборе параболической ско¬
рости с круговой орбиты под действием малого постоянного транс-
версального ускорения (аф 1). Начальные условия такого
движения выражаются следующим образом:
r0 = 1, /(0) = 0, ф0 = 1. (13.31).
Начальное значение второй производной г0, необходимое при
решении уравнения (13.30) вместо системы (13.29), находится из
первого уравнения (13.29)
г0 = 0. (13.32)
В работе [13.1] считается, что при малых аф член гг3 в (13.30)
значительно меньше г и им можно пренебречь. Тогда получается
простое дифференциальное уравнение, решение которого записыва¬
ется так:
г = (1 _ а^У2. (13.33).
I движения г (t), г (t), ф (t), ф
т при помощи (13.33):
г (t) = 2яф (1 — а4)~3, г (t) = 64 (1 — (V)-4, ( 34
Ф (0 = (4а,)-1 [1 - (1 - М)'1], ф (0 = (1 - М8- ‘
Остальные параметры движения г (t), г (t), ф (£), ф (t) выража
ются следующим образом при помощи (13.33):
538 АНАЛИТИЧЕСКИЕ РЕШЕНИЯ УРАВНЕНИЙ ДИНАМИКИ [ГЛ. 13
Уравнение орбиты в полярных координатах г (ф) имеет вид
г = (1 — 4афф)_1/% (13.35)
мри малых орбита — пологая спираль.
Согласно (13.34) начальные значения г0, г0 отличны от нуля:
Го = 2 яФ, Го = бяр, (13.36)
что противоречит начальным условиям (13.31), (13.32).
В точке набора параболической скорости (Ег = 0) параметры
движения равны
Т = а-i [1 - (2аф),/4], ф1 = (4аф)-1 - Ч2, ф1 = (2йф)'Ч] (13
1 \ = (2яр)~1/2, = (2яф)1/4, г 1 = Зяр. J
Член гг3, которым пренебрегается в уравнении (13.30), ока¬
зывается в конечной точке большим, чем г:
КЛ = (2аФ)-Ч /ч = (2аф)1/г. (13.38)
Это означает, что проведенное упрощение дифференциального
уравнения (13.30) неверно на заключительном участке траектории.
Для движения, описываемого соотношениями (13.34), харак¬
терным является равенство в каждой точке центробежного и гра¬
витационного ускорений (гф2 = 1/г2). Отличие второй производ-
••
ной г от нуля вдоль всей траектории свидетельствует о том, что
первое уравнение (13.29) не выполняется точно. Если наряду с
трансверсальной ввести радиальную составляющую ускорения,
равную аг = г = 6я2 (1 — яфг)-4, то полученное выше решение
станет точным решением уравнений (13.29) с компонентами яг,
яФ. На начальном этапе движения компонента яг, взятая в таком
виде, есть величина второго порядка малости по сравнению с
яф; на части траектории, где скорость приближается к местной
параболической, радиальная составляющая яг сравнивается с
трансверсальной яф (см. [13.14—13.16]).
3. Представление решения в виде рядов. Другой подход к
нахождению характеристик движения с трансверсальным уско¬
рением предложен в работе [13.17]. Используя метод вариации
параметров, можно найти выражения для функций г (£), г (£),
М (t) = г2 (t) ф (t) в виде рядов по степеням малой величины яф:
г (t) = 1 + яФ (2t — 2 sin t) -f я£ (312 + 3£2 cos t — "j
— t sin t — 4 sin21 -f 2 cos t — 2) -f . . ., [
r (t) = яф (2 — 2 cos t) + <4 (6£ + 5£ cos t — 3£2 sin t — [ (13.39)
— 3 sin t — 8 sin t cos t) + • • •, |
M (t) = 1 -f- яф£ -f- я2 (t~ -f- 2 cos t — 2) -j- . . . J
Т АНГКНЦПАЛЬП ОЕ У СКО РЕHUE
Эти функции точно удовлетворяют начальным условиям
(13.31) и приближенно, с; точностью до членов порядка а^, урав¬
нениям (13.29).
Аналогичный подход имеет место в работах [13.12, 13.13]; в
работе [13.18] получена поправка к решению (13.34).
4. Изменение орбитальных элементов. Эксцентриситет оску
лирующего эллипса при движении по спирали (13.34) есть мопо
тонная функция времени
при движении по траектории, описываемой выражениями (13.39),—
периодическая функция времени
Максимальная величина приращения радиального расстоя¬
ния Дг за один оборот при старте с круговой орбиты единичного
радиуса равна [13.11]
§ 3. ТАНГЕНЦИАЛЬНОЕ УСКОРЕНИЕ (\ = 0 в (П.16))
Для задачи набора параболической скорости с круговой ор¬
биты тангенциальное направление вектора реактивного ускоре¬
ния является наиболее близким к оптимальному из всех выделен¬
ных здесь законов. В [13.19, 13.20] показано, что вектор ускоре¬
ния в оптимальной программе набора с постоянным по модулю
ускорением в любой момент времени лежит между двумя направ¬
лениями: трансверсальным и тангенциальным, совпадая с по¬
следним в конечной точке маневра. Если ускорение постоянно и
направлено все время тангенциально, то отличие времени выхода
от оптимального не превышает 0,5% при значениях а из диапазона
О а 0, 1. В том же диапазоне значений модуля ускорения
разница между оптимальной и трансверсальной программами
меньше 8,5%. Эти результаты были получены в аналитической
форме; расчеты [13.31] подтвердили указанные числа (ср. § 3
гл. 6).
Аналогичные выводы сделаны в работе [13.22], посвящен¬
ной изучению трансверсальной и тангенциальной программы
направления тяги постоянной по модулю.
1. Уравнения и шгГеграл движения. Система (П. 16) при тан¬
генциальном (у = 0) направлении вектора ускорения имеет
е = 2аф (1 — a^t) 4;
(13.40)
(13.41)
Дг = 4ляф.
(13.42)
540 АНАЛИТИЧЕСКИЕ РЕШЕНИЯ УРАВНЕНИИ ДИНАМИКИ
[ГЛ. 13
следующий вид:
Здесь функции угла Ф заменены через производную dr/ds.
Сформулируем начальные условия для задачи набора пара¬
болической скорости с круговой орбиты:
г — 1, dr/ds = 0, v — 1 при s = 0. (13.44)
Первое уравнение (13.43) может быть проинтегрировано в
конечном виде для случая постоянного по модулю ускорения;
с учетом начальных условий (13.44) имеем
V2v2 = Hr + as- х/2. (13.45)
Это уравнение дает закон изменения энергии Е вдоль траектории:
Е = as- V2; (13.46)
длина траектории выхода равна
s1 = 1/(2 а). (13.47)
Заметим, что тангенциальное направление ускорения соот¬
ветствует максимальному темпу роста энергии: Е = av (см.
(П.14)).
Подставив выражение для v2 во второе уравнение (13.43), по¬
лучим дифференциальное уравнение второго порядка относи¬
тельно г (s) с начальными условиями из (13.44)
ёг-1+(£•)’] р+(£■)* -1-
(13.48)
К этому виду система (13.43) была приведена в работе [13.23].
2. Приближенные решения уравнения (13.48). Для малых
значений аргумента s(s<^!;l) решение уравнения (13.48) может
быть представлено в виде ряда по степеням а. Первые три члена
ряда имеют вид [13.23]
г — 1 + 2а (.s' — sin s) +
+ 4а2 (s2 + V2s2 cos s — l/2s sin 5+2 cos s — 2) + . . . (13.49)
Здесь уместно провести сравнение первых двух членов раз¬
ложений (13.39) и (13.49): трансверсальная (13.39) и танген¬
циальная программы ускорения дают одинаковые функциональ¬
ные выражения для г при малых значениях аргументов t или s
(в начале движения s ^ t, ибо ds/dt = v ^ 1).
(13.43)
ТАНГЕНЦИАЛЬНОЕ УСКОРЕНИЕ
541
Аналогичные выражения фигурируют в работах [13.24,
13.25], где определялись параметры движения в терминах пара¬
метра ф — углового перемещения.
При помощи (13.49) можно найти первые два члена разложе¬
ния для модуля скорости v:
Выражения (13.49), (13.50) указывают на колебательный ха¬
рактер изучаемого движения; на среднее движение (г = 1 + 2as,
v = 1 — as) накладываются колебания с периодом обращения
по исходной орбите 2я. Механизм этих колебаний связан со вза¬
имными переходами кинетической и потенциальной энергий.
Интересно отметить, что для среднего движения выполняется
с точностью до членов порядка а2 равенство вдоль траектории
центробежного и гравитационного ускорений: v2lr ^ 1/г2.
В работе [13.23] предложено простое аналитическое выраже¬
ние для г
Эта формула получается, если в дифференциальном уравнении
(13.48) исключить член (d2r/ds2) г, считая его малым по сравнению
с единицей. Аналогичный прием уже обсуждался в предыдущем
параграфе в связи с выражением (13.33), и высказанные там ком¬
ментарии могут быть перенесены сюда с несущественными изме¬
нениями.
3. Асимптотические решения задачи о разгоне. В работе
[13.26] дается решение задачи о разгоне с круговой орбиты под
действием тангенциального ускорения. Конечная точка движе¬
ния характеризуется заданной энергией, причем не обязательно
нулевой (разгон до гиперболических скоростей).
Здесь исходной для анализа является система в оскулирую-
щих переменных, описывающая плоское движение:
v = 1 — a (s — 2 sin s).
(13.50)
г = (1 — 2as) г.
(13.51)
8 -j- COS V
(13.52)
У p 2 sin v
7*'2 VG
где p — фокальный параметр, e — эксцентриситет, — уг¬
ловое положение перигелия, v — истинная аномалия, ско¬
рость v и радиус г, входящие в (13.52), определены формулами
542
АНАЛИТИЧЕСКИЕ РЕШЕНИЯ УРАВНЕН ИЙ ДИНАМИКИ [ГЛ. 13
невозмущенного движения
, , Р , v = л/' — (1 + е2 + 2е cos v)
1 -L е cos v V p v 1 1 '
r =
(13.53)
(все параметры в (13.52), (13.53) безразмерные). Уравнения (13.52),
(13.53) являются частным случаем системы в оскулирующих
переменных (П.37) при тангенциальном направлении вектора
реактивного ускорения.
Произведем замены, аналогичные [13.25]:
v = (2а)7% г - (2a)~1/2R, р = (2аГ’Ч t = (2a)J/4r. (13.54)
При этом система (13.52), (13.53) станет следующей:
8 + COS V
с/я
dx
с/ф,_
dx
я
~v
в =
я
1+8 COS V *
V&
V
d&
dx
dv
dx
V
V я
’ dx R2 Ve I
= j/'-i- (1 + e2 + 2e cos v)) • j
, (13.55)
Время t и угол cp- не фигурируют в правых частях (13.55), по¬
этому система может быть расщеплена на две части. Первая:
г/е 8 -|- cos v
с/я я
1
d cos v
с/я
= з~ К1 + е2 -f- 2е cos v (1 -f е cos v)2 Y1
- COS“ V -f
1 — COS2 V
Я8
; ]
(13.56)
вторая:
£; = V^1 + 8* + 2b cos v)
с/я
(13.57)
Решение второй системы определяется в квадратурах после
решения первой, которая является замкнутой системой уравне¬
ний для определения е и cos v в зависимости от я.
Преобразование (13.54) обладает тем свойством, что ускоре¬
ние а исключается из правых частей уравнений движения, но
зато, как легко убедиться, появляется в начальных условиях
задачи о разгоне с круговой орбиты. Так что два движения, на¬
чинающиеся с одной и той же круговой орбиты, но с разными зна¬
ТАНГЕНЦИАЛЬНОЕ УСКОРЕНИЕ
543
чениями параметра а, описываются одинаковыми уравнениями,
но разными начальными условиями.
Решение задачи о разгоне с малым по величине тангенциальным
ускорением обладает одной важной особенностью. Оказывается,
что все траектории с разными ускорениями в некотором смысле
мало отличаются одна от другой и мало отличаются от универсаль¬
ной траектории, идущей из гравитационного центра. Из этой
универсальной траектории можно вырезать по определенному
правилу куски, соответствующие конкретным граничным усло¬
виям. Правда, при этом граничные условия выполняются приб¬
лиженно: начальная орбита не круг, а эллипс с малым эксцен¬
триситетом (тем меньшем, чем меньше ускорение).
Факт существования универсальной траектории был подме¬
чен Перкинсом [13.25] при анализе результатов численных рас¬
четов. Построение универсальной траектории проведено в ра¬
боте [13.26], изложению которой мы следуем в настоящем пункте.
Приведем окончательные результаты из работы [13.26].
Искомую траекторию удобно разбить на три характерных уча¬
стка: первый участок, начало траектории, описывается асимпто¬
тическим решением при малых я (я <^: 1, а также 1, cos v<^l);
второй участок, середина траектории, определяется численными
расчетами, третий участок, конец траектории, описывается
асимптотическим решением при больших я (я 1, а также-
е 1).
При малых я асимптотические формулы для величин е, cosv,.
т, ср - имеют вид
8 = 2 ek7l4h>
к=о
CCS V = Я2 ^ V/^4fe,
к= о
Ф_ = — 3,40942 я-2 2
к=0
т = 1,34571 4 я-1'2 ^ Т/.ли‘.
к=о
Коэффициенты разложений ete, v/0 cpfci тц. собраны в табл. 13.1.
При больших я разложения е, cos v, т, ф- следующие:
8 = 0,76649л +
к=1
COSV= ^}v'kK~k>
1- (13.59)
cp_ = — 1,5708 4 я 1
k=о
T = — 1,611 + ’
k=о
[ (13.58)
>
544 АНАЛИТИЧЕСКИЕ РЕШЕНИЯ УРАВНЕНИЙ ДИНАМИКИ [ГЛ. 13
Коэффициенты рядов даны в табл. 13.2.
Таблица 13.1
Коэффициенты разложений в формулах (13.58)
к
£к
v/,-
*к
~к
0
1,0-100
1,0-lQo
—0,5-100
—2,0-100
1
-6,0-100
-3,0-101
2,75-100
—1,285714•101
2
3,53•102
3,177-Юз
—4,835417.101
—5,75-10°
3
—5,0216•104
—6,58080-105
4,292169-Ю3
3,604946-102
4
1,271935-1О7
2,162289-108
—8,098106-Юз
—5,110699-104
5
—5,007378•10°
—1,051549-101
2,555165-1О8
1,281759-1О7
0
2,829338-1012
7,073346-1013
— 1,204903-1011
—5,010652-1О9
7
—2,173519 -1015
—6,303206-1010
7,935154-1013
2,819974-1012
Таблица 13.2
Коэффициенты разложений в формулах (13.59)
к
£/с j
vfc
ф1-
~к
0
—1,30465-10°
1,53298-10°
1
—4,58000-10-1
9,16000-10-1
0
0
2
6,80189-10-1
—2,04057-Юо
—7,74093-10-2
-7,40216-10-1
3
—8,45172-10-^
3,38069-Юо
-3,20210-10-1
5,44150-10-1
4
8,85247-10-1
-4,42624-Юо
1,05876-10°
-3,77374-10-1
5
-4,86283-10-1
2,91770-Юо
—2,39421-10°
—1,23027-10"2
6
—9,64784-10-1
6,75349-10°
4,44336-100
8,58759-10-1
7
4,43942-Юо
-3,55154-101
—6,81926-10°
—2,41946-10°
8
—1,10624-101
9,95619-j.Oi
7,74454-Юо
4,80913-Юо
9
2,11182-101
—2,11182-1О2
—2,45367-Юо
—7,51512-10°
10
—3,13216.101
3,44538-102
—1,89947-101
8,33035-10°
11
2,90194-101
—3,4 8233-102
7,31602-101
—1,84542-10°
12
1,76253-101
—2,29129-Ю2
—1,79535•102
-2,32322-101
13
—1,71363-102
2,39908-103
3,41319-102
8,41939-101
14
5,27883 -10-
-7,91825-Ю3
—4,90991 - IQ2
-2,00519-102
Функции е (л), cos v (я), фл (я), т (я) для промежуточных
значений я определены табл. 13.3; наряду с перечисленными
функциями там фигурирует удвоенная полная энергия ц (я)
Поведение функций 8 (я), т (я), ц (я) показано на рис. 13.3,
функции cos v (я) — на рис. 13.4 и функции (я) — на рис. 13.5.
На рис. 13.6—13.8 даны зависимости безразмерных радиуса R,
§ з] ТАНГЕНЦИАЛЬНОЕ УСКОРЕНИЕ 545
Таблица 13.3
Параметры движения в промежуточной области
-
е
COS v
°р-
т
та
0,10
0,009994
0,009970
—53,3820
—4,97871
—9,99900
0,12
0,014382
0,014313
—38,0922
—4,42754
—8,33161
0,14
0,019556
0,019382
—28,8661
—3,99908
—7,14013
0,16
0,025503
0,025128
—22,8710
—3,65360
—6,24594
0,18
0,032207
0,031475
—18,7539
—3,36729
—5,54979
0,20
0,039646
0,038332
—15,8022
—3,12493
—4,99214
0,22
0,047793
0,045597
—13,6115
—2,91623
—4,53507
0,24
0,056615
0,053158
—11,9390
—2,73398
—4,15331
0,26
0,066076
0,060904
—10,6313
—2,57297
—3,82936
0,28
0,076137
0,068730
—9,58789
—2,42927
—3,55073
0,30
0,086757
0,076539
—8,74073
—2,29994
—3,30824
0,32
0,097896
0,084250
—8,04234
—2,18264
—3,09505
0,34
0,109512
0,091795
—7,45886
—2,07556
—2,90590
0,36
0,121566
0,099118
—6,96556
—1,97723
—2,73673
0,38
0,134020
0,106179
—6,54409
—1,88645
—2,58431
0,40
0,146838
0,112949
—6,18056
—1,80226
—2,44610
0,45
0,180027
0,110190
—5,39184
—1,61006
—2,15020
0,50
0,215315
0,142001
—4,93070
—1,45562
—1,90728
0,55
0,251470
0,153636
—4,50292
—1,31363
—1,70321
0,60
0,288902
0,163344
—4,20657
—1,19254
—1,52756
0,70
0,365541
0,178381
—3,73868
—0,98117
—1,23769
0,80
0,443994
0,188657
—3,41258
—0,80437
—1,00359
0,90
0,523513
0,195430
—3,17267
—0,65205
—0,80659
1,0
0,603641
0,199643
—2,98886
—0,51783
—0,63562
1,2
0,764699
0,202929
—2,72567
—0,28806
—0,34603
1,4
0,925942
0,202030
—2,54612
—0,09406
—0,10188
1,6
1,08688
0,198833
—2,41563
0,07546
0,11332
1,8
1,24734
0,194388
—2,31640
0,22720
0,30881
2,0
1,40726
0,189299
—2,23832
0,36543
0,49019
V 2
1 56666
0,183923
—2,17524
0,49306
0,61110
^4
1,72556
0,178472
—2,12318
0,61211
0,82398
2,6
1,88401
0,173075
—2,07947
0,72406
0,98058
2,8
2,04205
0,167807
—2,04223
0,83004
1,13213
3,0
2,19972
0,162713
—2,01012
0,93090
1,27959
3,5
2,59250
0,150857
—1,94631
1,16480
1,63459
4,0
2,98367
0,140292
—1,89878
1,37817
1,97558
4,о
3,37360
0,130929
—1,86198
1,57570
2,30692
5,0
3,76253
0,122627
—1,83263
1,76056
2,63133
6,0
4,53820
0,108656
—1,78875
2,10061
3,26588
8,0
6,08385
0,088240
—1,73408
2,6964.4
4,50165
10,0
7,62514
0,074166
—1,70136
3,21638
5,71428
12,0
9,16399
0,063919
—1,67957
3,68410
6,91490
14,0
10,7014
0,056140
—1,66402
4,11294
8,10847
16,0
12,2377
0,050040
—1,65236
4,51134
9,29756
15,0
13,7733
0,045130
—1,64329
4,88505
10,4836
20,0
15,3085
0,041095
—1,63604
5,23819
11,6675
35 Механика полета
Рис. 13.3. Вид функций £ (л), т(л),
ъ (Л).
Рис. 13.4. Вид функции cos v (л).
-20°
-40°
-60°
Рис. 13.5. Вид функции фя (я).
Рис. 13.7. Зависимость скорости V от
времени т.
Рис. 13.6. Зависимости радиуса R и
энергии я от времени *с. &
Рис. 13.8. Зависимость полярного угла от
времени т.
§ з]
ТАНГЕНЦИАЛЬНОЕ УСКОРЕНИЕ
547
удвоенной энергии г], скорости V и полярного угла <р от безраз¬
мерного времени т. Полярный угол ср (ср = срл + v) отсчитывается
от направления, которое отвечает бесконечно большому значе¬
нию я; значение т = 0 соответствует точке достижения парабо¬
лической скорости (г\ — 0).
Заметим, что скорость V сначала убывает, а затем в окрестно¬
сти параболической скорости начинает возрастать.
На рис. 13.9 изображена траектория движения в координатах х,у
(,x=R coscp, y=R sin ф) с раз¬
меткой по я. Точка, в которой
достигается параболическая
скорость, характеризуется
следующими значениями ра¬
диуса R и скорости V:
R = 1,24259, V
1,26846.
(13.61)
У
0,4
0,2
О
-0,2
-0,4
-0,6
-0,8
~f,0
Укажем правило, соглас¬
но которому можно по уни¬
версальной траектории по¬
строить траекторию разгона,
характеризующуюся задан¬
ными начальным радиусом г0,
ускорением а и конечной
энергией Е (г0, а, Е — раз¬
мерные величины).
Радиус начальной круго¬
вой орбиты г0 приравняем на¬
чальному значению большой
полуоси А0 для оскулирующего движения; выражение безраз¬
мерной величины А 0 имеет вид
-1,2
ч/
s'
\
I
(
In
1
\
щ
#
\
S7,3
X
Л,75
\
е
-0,6-0,4 -0,2 0 0,2 0,4 0,6 х
Рис. 13.9. Траектория разгона под действием
тангенциального ускорения; вдоль траектории
дана разметка по параметру л; е — точка, где
достигается параболическая скорость.
А{) — А{) У 2ajk = /*о У2а/к
(13.62)
(к — гравитационная постоянная центрального тела, к = /Ж).
По А0 находится удвоенная безразмерная энергия ц0:
Ло = -1М0- (13-63)
Конечное значение удвоенной безразмерной энергии тц вычис¬
ляется по формуле
Лх = 2 Ei/Y *2ка.
(13.64)
Данная траектория разгона, характеризующаяся размер¬
ными параметрами г0, а, Ех или безразмерными Ло> Лы состав-
35*
548
АНАЛИТИЧЕСКИЕ РЕШЕНИЯ УРАВНЕНИЙ ДИНАМИКИ
[ГЛ. 13
ляет часть универсальной траектории (см. (13.58), (13.59)), таб¬
лицы 13.1, 13.2, 13.3) от г) = т]0 до г] = гц.
Размерное время движения Т и приращение угла ф* опреде¬
ляются следующими соотношениями:
(13.65)
где т0, тх, фяо> ф-i — значения безразмерного времени и углово¬
го положения перигелия, посчитанные по асимптотическим фор¬
мулам (13.58), (13.59) или взятые из табл. 13.3 для значений г]0, тц.
В качестве иллюстрации приведем некоторые расчеты из
[13.26]. В табл. 13.4 даются времена разгона до параболической
точки Тх и расстояния параболической точки от центра гх для
траекторий, начинающихся с круговой орбиты, которая отстоит
от поверхности Земли на 500 км, размерное ускорение а — пара¬
метр таблицы.
ь Т а б л и ц а 13.4
Параметры траектории набора параболической скорости
с тангенциальным ускорением
а [мм се к2]
Гу [ТЫС. ?^н]
Т [сут]
а [.и*и сек2]
Гу [тыс. к.и]
Т [сут]
0,3
1012,8
275,7
30
101,3
2,365
1
554,7
80,80
100
55,47
0,649
3
320,3
26,16
300
32,03
0,192
10
175,4
7,508
1000
17,54
0,048
4. Движение по логарифмической спирали. Рассмотрим урав¬
нения движения в форме (П.17); частным решением этих урав¬
нений являются следующие функции:
т = о,
а — -^-sin Ф(| exp (— 2ср lg Ф„),
г (\ t / [> .м. i
(13.66)
v = v„ exp ^ «ptgtinj,
■О = = const,
r = exp (cptg fly),
t =
здесь в качестве начальных приняты значения
t = 0, ф (0) = 0, г (0) = 1, V (0) = Р0.
(13.67)
НОРМАЛЬНОЕ УСКОРЕНИЕ. БИНОРМАЛЬНОЕ УСКОРЕНИЕ
549
В исследуемом случае модуль реактивного ускорения изме¬
няется обратно пропорционально квадрату радиуса (см. (13.66)):
sin 'O'о / I о г»Q\
а= , (lo.bo)
начальное ускорение равно
а0 = у sin (13.69)
направление реактивного ускорения тангенциальное. Модуль
скорости v дается выражением
v = г;0г-,/2. (13.70)
Если =j= 0, то во все время движения радиальная составляю¬
щая скорости отлична от нуля, а трансверсальная — от круговой;
если = 0, то движение происходит по круговой орбите единич¬
ного радиуса и возмущающая сила отсутствует; при O0 —» V2rt
траектория вырождается в прямую, совпадающую с радиусом-
вектором. Описанные результаты содержатся в статьях [13.14,
13.27, 13.28].
В работе [13.28] приведены примеры решения задачи межпла¬
нетного перелета с орбиты спутника Земли на орбиту спутника
Марса; угол изменяется при переходе от одного этапа движения
к другому. В статье [13.29] логарифмическая спираль использу¬
ется в качестве опорной траектории для применения метода
вариации параметров. Аналитическое решение уравнений дви¬
жения, близкое к логарифмической спирали, дано в [13.30];
в отличие от последней это решение имеет число постоянных,
равное порядку системы дифференциальных уравнений. Здесь
ускорение направлено тангенциально и изменяется приблизи¬
тельно обратно пропорционально квадрату расстояния от цен¬
тра.
§ 4. НОРМАЛЬНОЕ УСКОРЕНИЕ (у = 1/2 я в (11.14)). БИНОРМАЛЬНОЕ
УСКОРЕНИЕ (aR = 0, аф = 0 в (П.37))
1. Уравнения и интегралы движения с нормальным ускоре¬
нием. Система (П. 14) при у = 1/2я (направление реактивного
ускорения перпендикулярно к скорости в плоскости орбиты)
существенно упрощается:
Е ~ const ~
М' - — — .
v
(13.71)
550
АНАЛИТИЧЕСКИЕ РЕШЕНИЯ УРАВНЕНИИ ДИНАМИКИ [ГЛ. 13
Поскольку v = У2£0 + 2/г (см. (П.И)), то уравнение для мо¬
мента М может быть приведено к квадратуре
'* 3/
М (г) — Мп )=\ rar:^dr. (13.72)
w У2 J Y Eor + 1 '
^0
При а = const интеграл берется в элементарных функциях [13.31].
2. Свойства траекторий движения с нормальным ускорением.
Так как полная энергия постоянна Е — Е0, то выход из грави¬
тационного поля невозможен — движение финитно. Расстояние
от центра г заключено в пределах гт[п г
Г так? ГД@ 7* min?
гтах — корни уравнения
М2 (г)/2г2 — 1 /г = Е0. (13.73)
Если начальная орбита круговая (r0 = 1, Е0 = —1/2, М0 = 1),
то при малых значениях а получаются следующие приближен¬
ные формулы для rmаХ. Afmin, emax [13.32]:
1
Гтах ~ 1 — 2а ’
Мтщ ж У1 —4а2,
Бщах 2а.
В точке траектории, где г = rmin = 1, момент М и эксцентри¬
ситет е возвращаются к исходным значениям:
rmin = 1 ? ^max — 1 ? Smin = 0. (13. /5)
Длина большой полуоси А оскулирующего эллипса (см. (П.23))
во все время движения остается без изменения в силу постоянства
энергии Е:
А = —1/(2Е0) = const. (13.76)
Если в точках траектории, максимально и минимально уда¬
ленных от центра, направление ускорения меняется на обратное
(у = V2ft ^ У = то эксцентриситет при таком движении
максимально возрастает [13.31]. В пределе орбита может тран¬
сформироваться в отрезок прямой линии длиной А с перигелием
в гравитационном центре.
3. Уравнения и интегралы движения с бинормальным ускоре¬
нием. При o,r = 0, аф = 0 вектор реактивного ускорения направ¬
лен перпендикулярно к плоскости мгновенной орбиты. Как
следует из системы (П.37), параметры, определяющие геоме¬
трию орбиты в плоскости: длина большой полуоси А, эксцентри¬
ситет е, время прохождения перигелия Тл в отсутствие сил ап,
(13.74)
| 4] НОРМАЛЬНОЕ УСКОРЕНИЕ. БИНОРМАЛЬНОЕ УСКОРЕНИЕ 551
а,ф остаются неизменными. Оставшиеся уравнения для накло¬
нения i, долготы восходящего узла Й, аргумента перигелия ср^
совместно с уравнением (П.38) описывают поворот плоскости
орбиты.
Задача о повороте плоскости орбиты под действием бинормаль¬
ного ускорения исследовалась в ряде работ [13.17, 13.32—13.36].
Авторы работ [13.17, 13.32, 13.34] использовали для анализа
систему уравнения в оскулирующих переменных типа (П.37),
В работе [13.33] выбрана система уравнений со смешанными
переменными (П.44), (П.45). Здесь рассматривались круговые
и эллиптические начальные орбиты, причем для последнего слу¬
чая был применен метод усреднения Крылова — Боголюбова.
В работе [13.35] уравнения движения представлены в сфериче¬
ских координатах (см. (П.5)). Наше изложение будет следовать
этой работе.
По определению орбитальная плоскость образуется радиусом-
вектором и вектором скорости точки. Поэтому для принятого
направления ускорения сразу можно установить два упрощаю¬
щих исследование факта: во-первых, радиальная составляющая
ускорения отсутствует (в сферических координатах аг = О,
так как бинормальное ускорение перпендикулярно к радиусу —
вектору) и, во-вторых, уравнения движения (П.5) обладают ин¬
тегралом энергии (работа бинормального ускорения равна нулю,
ибо вектор ускорения перпендикулярен к вектору скорости).
Из этих условий имеем
Е = V2 (г2 + г2Ф2 cos2 0 + г202) — 1/г = const, (13.77)
Последнее соотношение позволяет выразить компоненты аф, а9
через вектор бинормального ускорения ае (е = + 1 — ориен¬
тация вектора ускорения относительно мгновенной орбиты):
Система уравнений движения (П.5) при этом примет вид
а также
ЯфГф cos 0 + aQr0 = 0.
(13.78)
г — гф2 cos2 0 — г02 =
2гф -f npcos0— 2np0sin0 =
2r 0 -f- гф2 sin 0 cos 0 + r0 =
|f 02 + ф- cos2 0
552 АНАЛИТИЧЕСКИЕ РЕШЕНИЯ УРАВНЕНИЙ ДИНАМИКИ [ГЛ. 13
Пусть движение начинается с круговой орбиты, расположен¬
ной на экваторе:
г (0) - ф (0) ;= 1, г (0) = ф (0) = 0 (0) = 6 (0) = 0; (13.81)
тогда система (13.80) преобразуется в следующую:
г = 1,
Ф2 cos'2 0 + 0'2 = 1, (13.82)
0 + (1 — 02) tg 0 = ае V1 — 0 '2. .
Последние два уравнения интегрируются в конечном виде при
условии ае = const [13.35]:
0 = arcsin ^ — cos Y^ a~t)
У1 -г-a- sill У1 -{- аЧ
ф =■- arctg
(13.83)
а1 -'г cos У \ -{- а'Ч
При а 1 получается формула, данная JL А. Симоновым:
sin 0 = ае (1 — cos t). (13.84)
4. Свойства траекторий движения с бинормальным ускоре¬
нием. Из (13.83) следует, что угол 0 является периодической
функцией времени с периодом Та и амплитудой 0тах-
Та = ’ 9тах = arcsln i + а-2 • (13.85)
Траектория движения есть малый круг радиуса га:
1
V1 + а'2 ’
плоскость которого наклонена к исходной плоскости под углом ia:
in — 1 /2 ©max При а<1,
Vs Л — Vs 0max при
(13.86)
а<1,1
а>1;} (13-87)
по истечении периода Та траектория возмущенного движения
возвращается в начальную точку.
Если действие возмущающего ускорения прекращается по
достижении точки, где 0 = 0Шах » т° орбита оказывается поверну¬
той относительно исходной на угол in.
5]
ПОСТОЯННЫЙ ВЕКТОР УСКОРЕНИЯ
553
§ 5. ПОСТОЯННЫЙ ВЕКТОР УСКОРЕНИЯ
(ay==ciz= 0, asc=a = const в (П.З))
1. Уравнения и интегралы движения. Если реактивное уско¬
рение постоянно по модулю и направлено вдоль одной из коор¬
динатных осей, то уравнения движения интегрируются в квадра¬
турах [13.371.
Пусть вектор ускорения направлен вдоль оси Ох; тогда урав¬
нения (П.З) записываются следующим образом:
* = —7з-+а’ У =
(г = хг -f- if- -f- z-j a = const).
(13.88)
Система (13.88) имеет три первых интеграла: интеграл энергии
~ (х- + у2 + %2) — ctx = Е, (13.89)
интеграл момента количества движения (проекция на ось Ох)
ZU — yz = — Мх (13.90)
и третий интеграл
хг'г— у - — Yar°- — 2Ех = В. (13.91)
Введем новые переменные:
и = г — х, v = г - f х,
cos w = у/У у'2 + z-, sin гг7 = z/f у- ■
(13.92)
и заменим дифференцирование по времени t на дифференцирова¬
ние по переменной с:
dx = dtlr. (13.93)
Тогда исходная система приводится к квадратурам, в которых
фигурируют новые переменные и, v, w, т:
civ
VV(v)
cl и
УЩй)
о
(13.94)
554 АНАЛИТИЧЕСКИЕ РЕШЕНИЯ УРАВНЕНИЙ ДИНАМИКИ [ГЛ. 13
где
V (v) = аг;3 + 2Ev2 + 2(1+ Щ v — Af£,
U (и) = — аа3 + 2£а2 + 2 (1 — В) гг — Af£.
(13.95)
Соотношения (13.94) определяют функции v (т), и (т), w (т). Между
т и t существует связь, обязанная равенству (13.93):
== Х/2 ^ (U + V) dX»
(13.96)
которая дает возможность в конечном счете получить функции
г? (t)> u(t),w(t). Обращая формулы (13.92), получим выражения
х, у, z через v (t), и (t), w (t):
х = 1/ъ[и (t) — v(t)],
у = и (t) V (t) COS w (£),
z = u(t) v (t) sin гг; (t).
(13.97)
Таким образом, задача сведена к квадратурам. Заметим, что ин¬
тегралы в (13.94) эллиптические.
2. Классификация плоских траекторий. Если движение про¬
исходит в плоскости х, у (т. е. z = 0), то Мх = 0, w = = 0
и полиномы F (г;) и U (и) представимы в виде
V — av (v — г?2) (v — г;3),
U = — аи (и — и
V — Vz), |
2) (а — и3), J
(13.98)
причем
г;2 — — [— Е + ]/2?2 — 2а (1 + В)\,
г-’з =+[-£'- У#® —2а(1 + Я)],
щ = — [Е -\- |ГЕ1 -j- 2а (1 ■—•#)]>
из = т! E-YE*-2a (1 -В)].
(13.99)
На рис. 13.10 приведены четыре класса траекторий плоского
движения: а) неограниченные самопересекающиеся, не огибаю¬
щие центра притяжения, б) неограниченные самопересекающие¬
ся, огибающие центр притяжения, в) неограниченные несамо-
пересекающиеся, г) ограниченные.
§ 5]
ПОСТОЯННЫЙ ВЕКТОР УСКОРЕНИЯ
555
Области достижимости ограничены параболами на плоскос¬
ти у
Vх1 4- V2 — х — и — const, )
♦ (13Л00)
у у- X = V = const, j
Постоянные, характеризующие эти параболы, принимают зна¬
чения u2, v2, и3> v3, и\ Первые четыре значения даны формула¬
ми (13.99); последнее соответствует случаю v — оо.
ё)
г)
Рис. 13.10. Классификация траекторий плоского движения с постоянным
вектором ускорения.
Определим условия принадлежности к классам ограничен¬
ных и неограниченных траекторий для случая, когда начальная
орбита круговая. Обозначим через ср угол, который составляет
начальный радиус-вектор с вектором ускорения. Если выпол¬
нены совместно условия
а < V2, а2 - а (2 - cos ф) + 74 > 0, (13.101)
то движение ограничено. При а 72 движение неограничено для
любых значений >.
Если ф = 0, то движение ограничено при 0 <У а V2; макси¬
мальное значение радиуса в случае а = 0,5 равно rmax~l,4.
Если ф = я, то движение ограничено при 0 <С а <С % — У 2~
~ 0,086; максимальный радиус в случае а = 0,086 равен
^тах ~ 3,4.
Одно из возможных применений полученного решения —
расчет траектории спутника Земли, подверженного влиянию све¬
тового давления.
ГЛАВА 14
ФУНКЦИОНАЛЬНЫЕ ЧИСЛЕННЫЕ МЕТОДЫ
ПОСТРОЕНИЯ ОПТИМАЛЬНЫХ РЕШЕНИЙ
Изложенные в предыдущих разделах вариационные задачи
могут быть представлены в следующем общем виде.
Для динамической системы, описываемой дифференциальными
уравнениями относительно фазовых координат х\ (t)
Xi = fi{xh Uk, t),
(i, j = 0, 1, . . п; к = 1, . . т\ О < t < Г), (14.1)
требуется указать управляющие функции ик (t), обеспечивающие
экстремум функционала — конечного значения координаты х0(Т)
и переводящие систему из заданного начального
*i(0) = (ie/0) (14.2)
в заданное конечное состояние
xj(T) = xj 1 (/e/J. (14.3)
Это — формулировка классической вариационной задачи Майе-
ра. Другая классическая задача вариационного анализа, встре¬
чавшаяся выше,— задача Лагранжа. Она формулируется так:
для динамической системы, описываемой дифференциальными
уравнениями относительно фазовых координат
Xi = fi(Xj, uk, t) (i, 7 = 1,..., п\ к = 1, . . ., т), (14.4)
требуется указать управляющие функции ик1 обеспечивающие
экстремум интегрального функционала
т
J = ^ Ф (хи ukJ t) dt (14.5)
о
и переводящие систему из заданного начального
хг (0) = xi0 (i ZEE Iq) (14.6)
в заданное конечное состояние
*ЛТ) = (/еЛ). (14.7)
гл. *4
ФУНКЦИОНАЛЬНЫЕ ЧИСЛЕННЫЕ МЕТОДЫ
557
В ряде случаев задача Лагранжа (14.4) — (14.7) приводится к
виду, свободному от дифференциальных связей (14.4): тре¬
буется построить экстремали интегрального функционала
т
/ = ^ Ф Xh . . . , Xi1^) dt (i = 1, . . . , 72),
0
удовлетворяющие краевым условиям
Xi (0) = Xj,., Xi (0) = Xjo, . . . , (0) = xll‘i~l),
Xi (T) = XU, X; (T) = xn, x<?rl) (T) = ijjr»
(i == i, ... ,n)
(здесь выписана полная система разделенных и симметричных
краевых условии).
Указанные вариационные постановки могут быть сведены при
помощи формализма Лагранжа—Эйлера или Понтрягина к реше¬
нию краевых задач для обыкновенных дифференциальных урав¬
нений. Последние записываются в следующем общем виде:
Xi = fi (Xj, t) (/, / = 1, . . . , 72), ]
xi (0) — Xio (2 = 1,2,...,/), (14.10)
Xj (T) = Xj 1 (7 EE /1). j
Методы численного решения вариационных проблем (14.1)—.
(14.3), (14.4)—(14.7), (14.8)—(14.9) разделяются на прямые и не¬
прямые. Основу первых составляют различные итерационные
процессы последовательного уменьшения (увеличения) функ¬
ционала; для применения непрямых методов вариационная проб¬
лема предварительно сводится к краевой задаче типа (14.10).
В настоящей и следующей главах дается описание методов
решения сформулированных выше задач; глава 14 посвящена
функциональным методам, глава 15 — конечномерным методам.
Изложение общих идей иллюстрируется примерами из области
механики космического полета.
Наш список методов отнюдь не является исчерпывающим,
в изложение не вошли, например, методы, основанные на дина¬
мическом программировании [14.1 —14.5], метод, базирующийся
на принципе оптимальности [14.6] и др. Кроме того, здесь от¬
сутствуют методы решения линейных задач, ибо последние редко
встречаются в механике космического полета.
(14.8)
(14.9)
558
ФУНКЦИОНАЛЬНЫЕ ЧИСЛЕННЫЕ МЕТОДЫ
[ГЛ. 14
§ 1. ГРАДИЕНТНЫЙ СПУСК В ФАЗОВОМ ПРОСТРАНСТВЕ
Главной чертой градиентных функциональных методов явля¬
ется непосредственное исследование первой вариации функцио¬
нала на предмет определения условий скорейшего спуска (подъе¬
ма) к искомому значению функционала на каждом шаге итера¬
ционного процесса. Эти методы делятся на две группы: спуск в
пространстве управлений и спуск в фазовом пространстве. Метод
градиентного спуска в пространстве управлений применим к
задачам Майера (14.1)—(14.3) или Лагранжа (14.4) — (14.7);
первая вариация функционала 8х0 (Т) или б/ выражается через
вариации управляющих функций бuk(t). Метод градиентного
спуска в фазовом пространстве применим к задаче Лагранжа в
виде (14.8)—(14.9), свободном от дифференциальных связей и
управляющих функций; первая вариация функционала б/ вы¬
ражается через вариации фазовых координат бx\(t). Это разли¬
чие послужило основанием для раздельного изложения двух
идейно родственных методов: градиентному спуску в фазовом
пространстве посвящен настоящий параграф, градиентному спус¬
ку в пространстве управлений — следующий.
Метод функционального градиентного спуска был предложен в
1908 г. Адамаром для решения задачи о защемленной пластине,
позднее Курант [14.7] указал на возможность широкого приме¬
нения идеи градиентного спуска в функциональном пространстве.
Л. В. Канторовичем [14.8—14.10] в 1945—1948 гг. метод градиент¬
ного спуска был сформулирован в терминах функционального
анализа для квадратичных функционалов, была доказана схо¬
димость метода и установлена скорость сходимости. Предложен¬
ный Л. В. Канторовичем обобщенный метод для квадратичных
функционалов был исследован в более поздних работах [14.11],
[14.12]. Наконец, в [14.13] (см. также [14.14]) было предложено
применять метод градиентного спуска в фазовом пространстве
для произвольных, не только квадратичных функционалов. Там
же даны некоторые оценки сходимости метода, которые были
обобщены в [14.15] на многомерные функционалы.
Опыт применения метода для численного расчета вариацион¬
ных задач механики космического полета изложен в [14.16, 14.17].
Обсуждаемый метод иногда называется также методом функцио¬
нального скорейшего спуска или наискорейшего спуска.
1 Алгоритм метода. Изложим функциональный метод гра¬
диентного спуска в фазовом пространстве для следующего про¬
стого варианта задачи Лагранжа (14.8), (14.9).
Требуется найти экстремали функционала
т
(14.11)
о
g 1] ГРАДИЕНТНЫЙ СПУСК В ФАЗОВОМ ПРОСТРАНСТВЕ 559
если функция х {£) на границах интервала принимает значения
х (0) = *01 х (Т) = х±. (14.12)
Краевые условия этого типа называются разделенными и симме¬
тричными, общий вид разделенных и симметричных краевых
условий дается в записи (14.9).
Пусть известно некоторое нулевое приближение (t) для
экстремали функционала (14.11), удовлетворяющее краевым
условиям (14.12). Следующее приближение представим в виде
x<U (t) = ж<°> (t) + бх (t). (14.13)
Краевые значения функции Ьх (t) при этом нулевые:
бх (0) = бх (Т) = 0. (14.14)
Вариация функционала, вызванная малой вариацией бх (t)y
которая удовлетворяет условиям (14.14), имеет вид
г
6/ = 5 £(0> (t) Ьх (t) dt, (14.15)
(J
где Ew (t) — невязка уравнения Эйлера на траектории xw(t)
ЕФ)(0 = l*(0) W. *(0) (*).^~1й^ ^(0)(0. *(0) (*). Ф (14.16)
Интегрируя по частям (14.15) и опираясь на условия (14.14),
можно получить следующее выражение вариации интеграла
т t
6J — — ^ I \ (т) dr + cl бх (t) dt. (14.17)
о L о
Постоянная с под знаком внешнего интеграла произвольна
в том смысле, что от нее не зависит вариация б/. В этом можно
убедиться, вычислив такую производную:
т
= — jj бx{t)dt = —6x (Т) + Ьх (0) = 0 (14.18)
0
(последнее равенство в цепочке (14.18) вытекает из краевых
условий (14.14)).
Выберем производную вариации 8х (t) следующей:
560 ФУНКЦИОНАЛЬНЫЕ ЧИСЛЕННЫЕ МЕТОДЫ [ГЛ. Ц
Функция 6x(t) находится из дифференциального уравнения
(14.19) в виде
t t
дх (t) = сг + X К К EW (т) г/т dt ct\ . (14.20)
^оо
Определим постоянные с, сх так, чтобы выполнились задан¬
ные краевые условия (14.14); получим
т t
СХ = о, с = Ц ЕЮ (т) dr~\ dt (14.21)
(» О
И
( г т t
дх (f) = X Ц | ^ ЕЮ (т) dt] Л — 4- 5 [)Е(0) С) *] *} • (1-4.22)
0 0 ~ 0 0
При данном выборе вариации 8х (t) вариация функционала
б/ всегда будет иметь знак, обратный знаку параметра X или
обращаться в нуль независимо от величины X; действительно,
т t
6/ = — *4 Ц ЕЮ (г) dr + с]’ dt, (14.23)
о Lo
так что
6/<4 0 при ^^>0, 1
6/^>0 при X <4 0, i (14.24)
б/ = 0 при Я<°> (т) = 0. )
Если требуется уменьшить функционал /, то, приняв 8х (t)
в виде (14.22) и выбрав параметр X малым положительным (ма¬
лым для того, чтобы заведомо не выйти за пределы применимости
формулы для первой вариации), можно добиться желаемого изме¬
нения функционала /.
Выражение в фигурных скобках (14.22) есть функциональный
градиент, параметр X определяет длину вдоль градиента.
Запишем для удобства формулу (14.22) следующим образом:
8х (t) = А/г) (/), (14.25)
где
t t т t
т|(/) = EW (т) г/т! dt — ^(0) ^т] (14.26)
о и о и
Тогда первое приближение х(1) (t) можно переписать так:
х(1) (0 = я(0) (/) + Хг\ (/). (14.27)
ГРАДИЕНТНЫЙ СПУСК В ФАЗОВОМ ПРОСТРАНСТВЕ
561
Функция г) (t) полностью определяется нулевым приближением
xi0)(t) (см. (14.26)), остается свободным параметр X. Последний
можно назначать на каждом шаге равным малой величине так,
чтобы заведомо не выйти из пределов применимости линейного
представления функционала. Кроме этой существует другая
возможность — выбирать параметр X на каждом шаге процесса
из условия минимума функционала /.
Функционал (14.11) на семействе функций x(1\t) с функцией
г] (t), взятой в форме (14.26), зависит только от параметра X.
Условие минимума по X функционала /(,) = J Ы0)(£) + А/г)(£)]
выглядит следующим образом:
т
'ж \ Еа) ^ ^11W dt =
о
Т t t
= ^ ^ ДФ (т, X) dr ~j- с \ I ^ (т) dr + cl dt = 0. (14.28)
о L о о
Здесь
да) (t,X) = (х<0) 4- Хц, х^ + Хц, t) —
- 4г ^(^(0) + + Хц, t). (14.29)
Если X = 0, то ДФ = до» и производная (dJM/d X) 0.
Когда невязка уравнения Эйлера Д(°) тождественно равна нулю,
производная dJM/dX обращается в нуль при любом значении
параметра X.
Сформулируем окончательно алгоритм метода градиентного
спуска в фазовом пространстве:
На каждом шаге итерационного процесса, описываемого выра¬
жением (14.27), необходимо вычислять функцию ц (t) по невязке
уравнения Эйлера (14.26) и параметр X из условия обращения в нуль
производной (14.28).
2. Вычислительная процедура. Выражение (14.26) для функ¬
ции г) (t) может быть преобразовано к такому:
о о и
t Ггр} ЗФ(0) п 4 ? М>(0) ,Л ... олч
0 0 о
Формула (14.30) получена путем интегрирования по частям
(14.26); частные производные дФ^/дх, дФ^Удх входят в оператор
Эйлера согласно (14.16).
Механика полета
502
ФУНКЦИОНАЛЬНЫЕ ЧИСЛЕННЫЕ МЕТОДЫ
[ГЛ. 14
Вычисление функции ц (t) сводится к операции вычисления
интегралов по таблицам функции г(0)(£). Вместо того
чтобы хранить в памяти машины таблицу .т‘-0)(£), можно пользо¬
ваться операцией численного дифференцирования для нахож¬
дения по имеющейся таблице x^(t).
Согласно определению алгоритма на каждом шаге процесса
требуется, зная функцию r\ (t), определять минимизирующее зна¬
чение параметра X. Для вычисления минимума по % с задан¬
ной точностью необходим специальный итерационный процесс:
например, метод Ныотона или метод секущих применительно к
уравнению (14.28). В ряде случаев целесообразно отказаться от
такой трудоемкой процедуры и определять минимизирующее
значение параметра X, пользуясь каким-либо простейшим прие¬
мом. Например, таким. Значение функционала J при X = 0 из¬
вестно; это — результат предыдущего шага итерационного про¬
цесса. Вычислим функционал J при X = X' и X = X", где А/, X" —
пробные значения параметра. По трем точкам на плоскости
X, J: X = 0, / = /0; X = X', J = X = X", J = J" строится
парабола второй степени и по ней определяется минимизирующее
значение X.
Процесс можно считать закончившимся, если приращение
функционала А/ на последнем шаге не превышает установленной
точности
3. Обобщения алгоритма. Пусть значение функции х (t) не
задано в конце интервала t = Т и должно быть определено оп¬
тимальным в смысле функционала /. Опишем происходящее в
связи с этим изменение алгоритма.
Вариация функции 8х (t) в начале интервала по-прежнему
должна быть равной нулю, а в конце интервала отлична от нуля:
К вариации функционала 6/ добавляется новый член, отсут¬
ствующий в (14.15):
Интегрируя по частям в (14.33), получаем представление ва¬
риации б/, аналогичное (14.17):
| A J | ^ 8.
(14.31)
8х (0) - 0, 8х (Т) ф 0.
(14.32)
(14.33)
bJ = — \ I \£'W (г) ах -1- с I ох (t) at + i \ Е<°> (t) dt + ^ б^.
(14.34)
§ 1]
ГРАДИЕНТНЫЙ СПУСК В ФАЗОВОМ ПРОСТРАНСТВ В
563
Вариация 6/ не зависит от постоянной с, входящей в выраже¬
ние (14.34); в этом можно убедиться, вычислив производную
д&Лдс (ср. (14.18)),
Выберем производную вариации 8х по-прежнему в виде
(14.19), а конечное значение вариации 8хх следующим:
Выражение для вариации функции бx(t), как и ранее, дается
формулой (14.20); определим постоянные с, сг в этой формуле так,
чтобы выполнялись краевые условия (14.32), (14.35); получим:
При таком выборе вариации 8х (t) вариация функционала 8J
всегда будет иметь знак, обратный знаку параметра X, или обра¬
щаться в нуль независимо от величины X; в самом деле,
Последнее равенство в третьей строчке есть известное условие
для определения оптимального значения х (Т).
Параметр X, фигурирующий в формуле вариации (14.37),
находится из тех же соображений, которые были изложены в п. 1.
Описанный в п. 1 метод градиентного спуска обобщается на
тот случай, когда подынтегральная функция зависит от произ-
(14.35)
о
а = 0, с = ~1 J Е<0) (t) dt + 4- S [J m (T)ch] dt\ (1/j -36)
= ^E^ (r) dx~\dt ■ 4^ jj 2i(0) (t) dxj Л—
0 0 0 0
0
0 0 0
(14.38)
так что
б/<^ 0 при X О,
б/ О при X О,
б/ — 0 при Е(0) (т) еО и дФ^/дхг — 0.
(14.39)
564
Ф У JIК ЦIЮ11А Л L11Ы Е 411С Л Е11III > IЕ М Е Т О Д Ы
[ГЛ. 1\
водных выше первой, а краевые условия соответственно допол¬
нены условиями на все производные, кроме старшей. Метод может
быть распространен на функционалы, зависящие от нескольких
искомых функций.
4. Пример. В качестве примера рассмотрим задачу опреде¬
ления min-эксгремалей интегрального функционала следующего
вида:
т
j = $ {[я + z/(*2 + y-yh-]- + [у + у(х- -г уТЛ2} dt (14.40)
0
с краевыми условиями
я(0) = 1, у( 0) — 0, ж(0)—0, т/ (0) = 1,
х (71) = Т\ cos фь у (Т) = rx sin фх,
х (Т) = — 7д1/2 sin фх, у (71) = — i\hl cos фх.
(14.41)
Эта вариационная задача касается нахождения оптималь¬
ных траекторий и оптимальных режимов работы идеального
двигателя ограниченной мощности; она описана в главе 5. Рас¬
четы проведены для гх = 1,52; величины фх, Т — параметры
задачи.
Вариационная проблема (14.40)—(14.41) принадлежит к типу
задач Лагранжа без дифференциальных связей, краевые условия
являются разделенными и симметричными.
Опишем процедуру метода градиентного спуска в фазовом
пространстве для задачи (14.40)—(14.41).
По известному нулевому приближению (t), у(t), удов¬
летворяющему краевым условиям (14.41), определяются функ¬
ции г\х (t), т]?/ (t), обращающиеся вместе со своими первыми про¬
изводными в нуль на концах интервала; выражение, например,
для 'Цх имеет вид
£?)л* - 4Ш Е?л‘) -
0000 000 0 00 0
- iii^-т 111^’-“*) ■ <14'42>
где
сР д , д
Я-f = ф Г*(0) Уф) (*)• *(0) <*)• ^(0) (01.
Ф = [X + X + г/2)~Л2 + [у + у (г2 +
(14.43)
§ 1]
ГРАДиКИТПЫП СПУСК ]5 ФАСОНОМ ПРОСТРАНСТВЕ 565
Заменой х на у можно получить выражение для г]7.
Искомые функции на следующем шаге итерационного про¬
цесса записываются так:
x'V(t) = x<0)(t) + Vn.v (t), yM(t) = yin)(t) -f k,,r\v(t). (14.44)
Параметры спуска Xx, Xv находятся из условия минимума
функции д, А,,,) на данном шаге
Представим двукратные интегралы из (14.42) следующим
образом:
(аналогично для переменной у). В этой записи фигурируют функ¬
ции xW(t), г/(0)(0 и их вторые производные х(t), г/(0) (t), тре¬
тьи х (0)(0, £/{О)(0 и четвертые я(0)(г), y{0)(t) производные в пра¬
вой части (14.46) отсутствуют.
При определении функций r\x (t), r\v (t) по формулам (14.41),
(14.46) можно избежать численного дифференцирования, если на
каждом шаге вместе с функциями х (t), у (t) запоминать вторые
производные х (t), у (t)\ соответственно вместе с функциями т)д. (t),
ц?/ (t) следует запоминать их вторые производные г)т (/), ц,у (t)
(ср. рассуждения в п. 2). Выпишем выражения для у\х, т].т, выте¬
кающие из (14.42), (14.46) (выражения для %, тр, получатся
заменой х на у):
dJa)/dlx --■= 0, dJa)/dhy = 0.
(14.45)
о о
о о
(14.46)
цх = Mxdt — tMxdt ^ c0xxt3 — y Cixt2, (14.47)
о
0
где
дФ(0)
dx
о
0
T
(14.48)
0
T
6
0
566
ФУНКЦИОНАЛЬНЫЕ ЧИСЛЕННЫЕ МЕТОДЫ
[ГЛ. 14
В качестве функций нулевого приближения были взяты сле¬
дующие:
*(0) (/) = 1 + Г 3 (Г' С°1ф1 - 1)- 4- -^-1 *2 -
3 (rj cos ср] — 1) sin ф!
“ Г5 + Vr~T
2(r1cos91 —1) , sin cp]
т3 r YnT-
t\
Y'sYr2T
+
2r! sin cpi — T cos cpi ^
T3
Vr
(14.49)
Они являются решением вариационной проблемы (14.40)—(14.41)
для бессилового поля (см. гл. 5).
Применение описанного итерационного процесса к задаче
(14.40) — (14.41) оказалось весьма эффективным; время расчета
одного варианта (один вари¬
ант — это одна пара значе¬
ний ФЦ, Т) составляет 1—2мин
на ЭЦВМ М-20 при точности
4—5 знаков по функционалу.
Характер сходимости ме¬
тода иллюстрируется рис.
14.1, где по оси абсцисс от¬
ложен номер итерации, а по
оси ординат — соответствую¬
щая величина функционала;
дискретные точки соединены
непрерывной кривой; на кри¬
вой 1: фх = 1,017, Т 3,456;
на кривой 2: фх = 3,141,
Т = 3,456.
Для обоих примеров в ка¬
честве начального приближе¬
ния была выбрана оптималь¬
ная траектория в бессиловом
поле (14.49). Сравнение числа итераций в одном и другом слу¬
чаях позволяет судить о рациональности данного нулевого при¬
ближения: чем короче траектория и меньше время движения вдоль
нее, тем лучше бессиловое поле аппроксимирует центральное поле.
Диапазон изменения параметров фх, Т в расчетах был такой:
J
(0[
1,3
и -
0,9-
(2)
0,7-
3,765
- 0,5
3,760
- 0,3
3,755
2 3 4 5 к
Рис. 14.1. Убывание функционала J по шагам
итерационного процесса метода градиентного
спуска в фазовом пространстве. Кривая
1: ф4 = 1,047, Г = 3,456; кривая ^:ф1 = 3,141,
Г = 3,456.
О^фх^я,
(14.50)
Попытка применить в качестве нулевого приближения функ¬
ции (14.49) для углов фх > я наталкивалась на следующую труд¬
ность. Оказалось, что исследуемый функционал при этих углах
Г РА Д11Е L LTIIbl 1 [ СПУСК В ПРОСТРАНСТВ,Е УПРАВЛ EHIllI
567
перелета обладает не единственным минимумом, и использование
решения в бессиловом поле как нулевого элемента приводит к
значениям минимума, превышающим ожидаемые. Это означает
невозможность использования единого нулевого элемента для
всего диапазона изменения параметров.
Сказанное иллюстрируется рис. 14.2, где даны оптимальные
траектории бессилового и центрального полей для случая
Т = 2 и оптимальная траектория бессилового поля для случая
<рх == 5:23, Т = 4,92. Последняя
не огибает начала координат.
Видимо, это может служить
внешним признаком непригод¬
ности данной траектории в ка¬
честве нулевого элемента итера¬
ционного процесса.
Для нахождения начального
элемента в параметрических
расчетах можно рекомендовать
следующий прием. Пусть из¬
вестна оптимальная траектория
для некоторых значений пара¬
метров и требуется построить
новую оптимальную траекторию
для значений параметров, близ¬
ких к первым; краевые условия
на новой траектории отличаются
от старых краевых условий.
Трансформируем старую траек¬
торию, например, умножением на некоторую произвольную,
мало отличающуюся от единицы функцию, которая обеспечивает
выполнение на новой траектории заданных краевых условий. Эта
траектория и может быть использована в качестве нулевого
элемента.
§ 2. ГРАДИЕНТНЫЙ СПУСК В ПРОСТРАНСТВЕ УПРАВЛЕНИЙ
Основу градиентного спуска в пространстве управлений
[14.18—14.30] составляет вариационный подход, предложенный
в работе Д. Е. Охоцимского [14.31]. Первое приложение метода
для численных расчетов связано с выбором оптимальной про¬
граммы управления углом установки солнечного паруса [14.20].
В этой задаче на управляющую функцию (угол установки паруса)
не наложены ограничения. То же самое относится и к задачам
о выборе оптимального закона направления тяги при перелете
между орбитами в центральном поле [14.28], а также к задаче
о наборе параболической скорости [14.29].
Рис. 14.2. Оптимальные траектории в бес¬
силовом (1) и центральном (2) полях при
Ф! = 2, 2’ = 2 и оптимальная траектория
в бессиловом поле (з) при = 5,23,
Т = 4,92,
568
ФУНКЦИИ 1 [АЛЫ-IЬ1Е ЧИСЛЕННЫЕ МЕТОДЫ
[ГЛ. 14
В работах [14.19, 14.21, 14.30] содержится обобщение метода
на тот случаи, когда управляющие функции ограничены, а в
работах 114.25, 14.26, 14.32] дается развитие метода примени¬
тельно к задачам с фазовыми ограничениями.
1. Алгоритм метода для задач со свободным правым концом
траектории. Изложим алгоритм метода для задачи Майера (14.1) —
(14.3). В этом пункте правый конец траектории считается свобод¬
ным и для простоты рассматривается случай одной управляющей
функции.
Для динамической системы, описываемой дифференциальными
уравнениями и начальными условиями
требуется указать управляющую функцию и (£), доставляющую
минимум функционалу xQ (Т); конец временного интервала t = Т
задан.
Пусть известно нулевое приближение для управляющей
функции ц(0) (t) и по этой функции построена траектория ж(0)(£),
удовлетворяющая начальным условиям (14.51):
Представим первое приближение для управления в виде
где бu(t)—вариация управления.
Функции x{V (t), отвечающие управлению и(1) (t), могут быть
представлены в виде, аналогичном (14.53):
где 8xt (t) — вариации фазовых координат.
Исходная система (14.51), линеаризированная относительно
б и (t), 6xL (t), дает систему уравнений в вариациях:
= и, t), Xi (0) = xi0 (/, j = 0, 1, . . ., щ 0 < t < Т) (14.51)
z(i0)(0) = xi0.
(14.52)
= и(п) (t) + бu(t),
(14.53)
x^(t) = xf\t) + 6:Г£(0,
(14.54)
3=0
(14.55)
g 2] ГРЛДИЕ1ТТШ>[Й СПУСК К И РОСТРА! LCT 1VI" У11 РЛ Р,Л С 111 П"[ 569
Начальные условия для вариация 6х\ (t) нулевые (см. (14.52)):
8xi (0) = 0 (i =~ 0, 1, . . п). (14.56)
Введем линейную систему дифференциальных уравнений
п di(0)
Р> = — 2 Р; (7 = 0,1, ... , п), (14.57)
.7=0
сопряя^енную линейной системе (14.55). Основное свойство си¬
стем (14.55), (14.57) состоит в следующем:
п 71 д/(())
-К 2 P<bxi = 2 Pi-irbu. (14.58)
г=0 г=0
Учитывая начальные условия (14.56), это равенство можно
записать в интегральной форме:
Т » 5/(о)
2 Pi^ 2 Pi “щГ (14.59)
2=0 0 i=0
Если краевые значения функций сопряженных уравнений
задать в конце интервала (при t = Т) в виде
Ро (Т) = 1, Pi (Т) = 0 (i = 1, . . ., тг), (14.60)
то интегральная формула (14.59) дает значение приращения
функционала 8х0 (Г), отвечающее приращению управления б и (t)
? " df\o)
8хп(Т) = \ 2 Pi ди ^и dt. (14.61)
О 2=0
Выберем вариацию управления 8и следующей:
вв(0 = _Л2 (14.62)
2=0
При этом вариация функционала всегда будет иметь знак,
обратный знаку параметра А,, или обращаться в нуль независимо
от величины Я; в самом деле,
f / " dif \ 2
б*,,(7’) = -Л. J ( 2 Pi^r) dt, (14.63)
О 2=0
570
ФУНКЦИОНАЛЬНЫЕ ЧИСЛЕ ИНЫЕ МЕТОДЫ
[ГЛ. 14
так что
6я„ (Т) <' 0 при X 0,
бд:() (Г) 0 при ^<^0,
П д/(0)
dxlt (Т) = 0 при 2 Pi -Д- = °-
(14.64)
Структура выбранной формы (14.62) вариации управления б и
повторяет структуру вариации Ьх из метода спуска в фазовом
пространстве (ср. (14.19)): один множитель указывает направле¬
ние антиградиента в пространстве управлений, другой множитель
определяет длину шага вдоль антиградиента.
Выбор параметра X подчиним условию минимума функционала
х^ (Т) на данном шаге итерационного процесса. Функционал
(Т) на семействе управляющих функций (14.53) с вариацией
б и, взятой в виде (14.62), является функцией одного параметра X:
п
х{ = fi [Xj, и<0) -1 2 ft > 4 ■ xi (0) = *;» (г’> / =0,1,..., и).
i=0
(14.65)
Последний определяется из условия минимума £о1} (Т) каким-
либо численным приемом (см. § 1, п. 2).
Дадим формулировку алгоритма градиентного спуска в про¬
странстве управлений для задач со свободным правым концом
траектории.
По известной функции u^(t) решается задача Коши для ис¬
ходной системы (14.51). Результат этого решения — функции
%{i\t) используются для определения частных производных
df^/dxjy чтобы вычислить функции pi(t) сопряженной системы;
здесь решается задача Коши «назад» для системы (14.57) с крае¬
выми условиями (14.60). Затем составляется вариация б и (t) в
виде (14.62); параметр X определяется из условия минимума функ¬
ционала х^ (Т) на данном шаге процесса.
2. Ограничения на управляющую функцию. Если управляю¬
щая функция ограничена
ttmin (0 < U (t) < Mmax (0» (14.66)
то описанный выше алгоритм изменяется следующим образом.
Строим m(1}(£) по правилу, данному в предыдущем пункте
и затем на участках, где и{1) (t) ишin (t) полагаем u^(t) —
= Щит а на участках, где и{1) (t) > wmax (0 полагаем u(1)(t) =
= ^max (0- Иными словами, отсекаются выступающие за огра¬
ничения участки графика u^(t).
g 2l ГРАД LI E HT FI Ы l"[ СПУСК В ПРОСТРАНСТВЕ УПРАВЛЕНИИ:
571
3. Алгоритм метода для задач с фиксированными начальной
и конечной точками траектории. Обратимся теперь к изложению
метода градиентного спуска в пространстве управлений для
общей задачи (14.1) —(14.3); здесь х0 (Т) по-прежнему минимизи¬
руемый функционал; значения фазовых координат в конце дви¬
жения заданы:
хг = /г (xj> и, t) (i, j = О, 1, . . ., /г),
хг (0) = £;о (i ^ 0, 1 ??),
Х{(Т) = Хц, Хп (Г) — нп'п (i -- 1, . . 7?).
(11.67)
Опишем сначала метод штрафных слагаемых, идея которого
принадлежит Куранту [14.32].
Образуем следующую функцию конечных значений координат
[14.32, 14.18, 14.21, 14.27]:
п
Р [Х„(Т), Xi.iT). . . .,Хп(Т)] =■-■ ХП(Т) + 2 <lm[Xi(T) — X;ij2,
m=1
Ят > 0. (14.68)
При выполнении конечных условий xi (Т) = xi± и достиже¬
нии искомого минимума х0 (Т) выражение Р (Т) также имеет ми¬
нимум, совпадающий с минимумом х0 (Т).
Будем искать минимум Р (Т), подбирая одновременно значения
свободных параметров qm так, чтобы разности xi(T)—xil обра¬
тились в нуль. Для этого включим в процедуру метода процесс
последовательного увеличения параметров qm: пусть известно
начальное приближение для управляющей функции u^\t), за¬
дадимся «малыми» положительными значениями qf} и определим
в результате итерационного процесса для задачи со свободным
правым концом (см. п. 1) управление а(Г)(г), доставляющее мини¬
мум выражению (14.68).
Взяв за следующее приближение управление м(1) (t) и значе¬
ния параметров q\n , превышающее соответствующие значения
на первом шаге (qi} ^> £i0), . . ., q{a ^> q{n), повторим про¬
цедуру* Минимум Р (Т) даст решение задачи при qос [14.33].
Значения последовательности q(m, . . ., q(m} определя¬
ются конкретными условиями задачи. Этот прием позволяет
считать на каждом «большом» шаге процесса (0 К)
правый конец траектории свободным. В алгоритм метода, данного
в п. 1, необходимо внести изменение, касающееся граничных
условий для сопряженной системы:
Pi (Т) = дР("}/dXi (Л.
(14.69)
572 <1?У ПКЦПО] ГАЛ Ы1 ЫЕ ЧИСЛЕ! III ЫЕ МЕТОДУ)! [УVI. 14
Заметим, что если часть конечных значении фазовых коорди¬
нат по условию задачи оказывается свободной, то в выражении
для Р отсутствуют соответствующие члены.
Другой прием удовлетворения заданных краевых условий
состоит в следующем [14.19, 14.22—14.24].
Пусть известно нулевое приближение для управляющей функ¬
ции u([))(t) и по этой функции посчитана траектория #*0) (t), на¬
чальные условия на траектории выполняются точно, а отличия
конечных значений от заданных составляют малые величины Д*0):
х\н) (0) = х-,0 (i о, 1, . . п), 1 ^
4°> (Т) = ха + М0) (i = 1 ,7г). J
Порядок малости этих величин должен быть таков, чтобы из¬
менение в программе управления б и (t), необходимое для исправ¬
ления конечных условий, находилось в пределах справедливости
линейного представления.
Введем в рассмотрение п + 1 сопряженные системы типа
(14.57) с конечными условиями:
К(Т) = |0пР.(14?1)
( 1 при г — m (ь, ш — 0, 1, . . п)
(здесь верхний индекс без скобок m указывает номер системы).
При помощи этих систем могут быть получены п + 1 интеграль¬
ные соотношения, аналогичные (14.61):
г 71 д/(0)
&с„ (Т)= \ V p»^budt,
v г да
о i=o у
С п di(0) 1
bxm (Т) = ^ 2 P™-^--budt (m = 1,. . п).
(14.72)
J
Определим функцию б и (t), доставляющую знак минус вариа¬
ции б;г0 (Т) и обеспечивающую выполнение конечных условий
для вариаций фазовых координат
6*0 (Т) < 0, 6xm (Т) = — Am (т = 1, . . ., п). (14.73)
Составим следующую лагранжеву функцию:
7* / п д/10) п п <9/(°) п
х =) (s pint+а1» s ргпг6")л + з
[0 г=0 т=1 ti=0 т=1
(14.74)
3 2] ГРАДИЕНТНЫЙ СПУСК Б ПРОСТРАНСТВЕ УПРАВЛЕНИЙ 573
Если вариация управления 8и (t) подобрана так, что выполня¬
ются п конечных условии из (14.73), то лагранжева функция
X совпадает с вариацией контрольного функционала 8х0 (Т).
Выберем 8и (t) такого вида:
Пусть параметры X и v фиксированы; можно найти такие мно¬
жители Лагранжа Хъ . . ., Х1П входящие в выражение (14.75),
что конечные условия из (14.73) будут выполнены. Действительно,
множители Х1, . . ., Хп определяются из системы линейных урав¬
нений:
Эта система получается из (14.73), если под интегралом заме¬
нить 8и на выражение (14.75).
Определим теперь параметры X, v так, чтобы лагранжева
функция X была отрицательной при любых значениях невязок
вариация контрольного функционала 8xQ (Т) имеет знак минус.
Выражение (14.74) при выбранном 8и имеет вид
Следует выбрать X 0 и параметр v такой, чтобы второе
слагаемое (14.77) стало отрицательным. Определение v сопряжено
с трудностями многократного перебора, так как множители Хт
зависят от v согласно (14.76).
Если Ai0) = 0, . . ., Дп} = 0, то X 0 независимо от зна¬
чения параметра v. Решение задачи достигается при выполнении
следующей совокупности условий:
(& = !,..., п). (14.76)
в силу сделанного ранее замечания это будет означать, что
(14.78)
574
Ф УII 1л ЦП ОН А Л Ъ11Ы Е Ч11С Л Е ИНЫЕ М Е Т О ДI > I
[ГЛ. 1
Параметр X в отличие от прежнего выбирается не из условия
достижения минимума контрольного функционала Жо1’ (Т) на
данном шаге процесса, а из следующих соображений. Чем меньше
величина X, тем меньше длина шага и меньше приращения функ¬
ционала. С другой стороны, если параметр X слишком велик, то
длина шага велика и точность описания движения линейными
уравнениями (14.55) выходит из заданных пределов; к тому же
выполнение конечных условий (14.73) в линейной постановке
не гарантирует действительного выполнения конечных условий
с заданной точностью, что ограничивает сверху параметр X. По¬
этому целесообразно назначать параметр X равным своему верхне¬
му пределу, который, как правило, зависит от свойств конкрет¬
ной задачи.
4. Обобщения процедуры для произвольных краевых условий.
Описанные в предыдущем пункте приемы решения могут быть
обобщены на случай, когда в конце интервала задаются не сами
координаты, а связи между ними:
ф,- [хг (Т), . . ., хи (Г)] — 0 (£ = 1, . . ., I < п). (14.79
Изменения -касаются формул (14.68), (14.71)—(14.73). Выра¬
жение (14.68) заменяется следующим:
Р [ж„ (Т). Хг (71), . . ., ж„ (71)] = ж0 (Т) + 2 ЯтпФт- (14.80)
Вместо формулы (14.71) граничные условия для системы сопря¬
женных функций следует записать в виде
тогда выражения (14.72) для конечных значений координат заме¬
нятся на
а в качестве невязки конечных значений в (14.73) будут фигури-
А(0) , (И)
т = фт •
5. Алгоритм метода для задач со свободным правым концом и
свободным временем движения. В предыдущем изложении счи¬
талось, что начало п коней временного интервала заданы. Однако
о г=о
(14.82)
Т 77.
(/п — 1, . . ., п),
0 7=0
§ о] ГРАДИЕНТНЫЙ СПУСК К ПРОСТРАНСТВЕ УПРАВЛЕНИЙ
575
для ряда задач момент окончания движения Т не задается. Сюда
относится класс задач на максимальное быстродействие.
Рассмотрим обобщение полученных выше результатов на слу¬
чай свободного правого конца траектории и незаданного момента
окончания движения Т. Пусть минимизируемый функционал имеет
значения х0 (Т), хг (Г), . . хп (Т), Т являются свободными.
Определим значение Т на каждом шаге итерационного процесса
как точку t — Т, в которой функция Р (t), вычисляемая вдоль
траектории, достигает минимума (пусть такая точка на траекто
рии одна):
Приращение функционала бР (Г), вызванное приращением управ¬
ления б и (t), записывается следующим образом:
(верхний индекс 0, как обычно, указывает на то, что функции
посчитаны на основании нулевого приближения для управления
и{0) (t)). Поскольку в нулевом приближении момент Т<0) также
определяется из условия (14.84), то вариация функционала при¬
нимает вид
Краевые условия для сопряженной системы уравнений записыва¬
ются так (ср. (14.69)):
Особенность процедуры метода для задач со свободным пра¬
вым концом траектории и свободным моментом окончания дви¬
жения состоит в том, что последний определяется на основании
равенства (14.84) после нахождения закона управления на дан¬
ном шаге итерационного процесса.
Может оказаться, что равенство (14.84) не выполняется в об¬
ласти определения управляющей функции, т. е. протяженность
временного интервала на этом шаге превышает протяженность
вид (ср. (14.68))
Р[х0 (Т), хг (Г), . . ., х„ (Т), Т]
(14.83)
П
(14.86)
(14.87)
576
Ф У11К Ц110IIА ЛI) II ЫЕ ЧИСЛИ II1I ЫЕ МЕТОД Ь1
[ГЛ. 14
интервала на предыдущем шаге. Такое явление не будет иметь
места, если область определения управляющей функции на всех
шагах итерационного процесса будет не меньше максимальной
величины интервала. Для этого следует на каждом к-м шаге
доопределять вариацию управления и, следовательно, управление
на промежутке Гшах— Последнее может быть выполнено,
если сопряженную систему интегрировать не только «назад» от
t =z до t = 0, но и «вперед» от t = до t = Tmax.
Правда, значение TnvdX не может быть заранее установлено точно.
6. Примеры. Иллюстрацией метода градиентного спуска в
пространстве управлений могут служить два расчета, приведен¬
ные в работах [14.20, 14.26] (см. также [14.27]).
Первый из них [14.20] относится к перелету между круговыми
орбитами Земли и Марса при помощи солнечного паруса. Вариа¬
ционная проблема состоит в определении оптимальной программы
угла установки паруса ф(£), обеспечивающей минимальное время
перемещения Т между двумя круговыми орбитами. Уравнения
движения и краевые условия проблемы, записанные в безразмер¬
ном виде (ср. гл. 9), выглядят следующим образом:
Угловое перемещение аппарата не задано; примеры построе¬
ны для гх = 1,52; а0 = 0,17 ( = 0,1 см/сек2).
Второй расчет [14.28] проведен для межорбитального перелета
Земля — Марс с постоянной по модулю и постоянно включенной
тягой (ср. гл. 6). В вариационной проблеме требуется определить
оптимальный закон направления вектора тяги 6 (t), реализующий
минимальное время перемещения между двумя заданными точ¬
ками на круговых орбитах. Уравнения движения и краевые усло¬
вия имеют вид
г (0) = 1 > r(T) = ru 1
9.
а о .
sin г|) cos2 \]з , vv (0) — 1, vv (Т) = j
Т = min.
г(0) = 1, г(Т)^гг,
ф(0) = 0, ср(Г) = фь
1
с,,(0) = 0, и,.(Г) = 0,
(14.89)
а0 cos Q vrvф
М°) = г vv(T) = rl
Т = min;
ГРАДИЕНТНЫЙ СПУСК В ПРОСТРАНСТВЕ УПРАВЛЕНИЙ
577
здесь а0 — начальное реактивное ускорение (а0 = gP/G0), р0 —
приведенный массовый расход (ц0 = gcj/G^); в расчетах принято:
а0 = 0,846-10-^, p0 = 1,29-10-3 сущ-1.
Обе вариационные задачи (14.88), (14.89) принадлежит к клас¬
су задач на максимальное быстродействие; процедура решения
этих задач описана в п. 5 настоящего параграфа. Для удовлет¬
ворения заданных краевых условий могут быть использованы
оба приема, изложенные в п. 3.
В задаче (14.88) краевые условия удовлетворялись по методу,
родственному методу условного градиентного спуска (формулы
Рис. 14.3. Программы Ф (/) угла установки Рис. 14.4. Траектории перелета, соот-
паруса, соответствующие нулевому прибли- ветствующие нулевому приближению
жешио (0), первому (1) и второму (2) шагам (0), первому (i), второму (2) шагам
итерационного процесса и решению (оо), — итерационного процесса и решению
метод градиентного спуска в пространстве (оо), — метод градиентного спуска
управлении. в пространстве управлений.
(14.71), (14.75), (14.76)). Выполнение заданных краевых условий
в задаче (14.89) обеспечивалось по методу штрафных слагаемых
(формулы (14.68), (14.69)). В статье [14.28] есть указание на спо¬
соб подбора коэффициентов qm: в начале процесса величины qm
малы, затем после 25-го шага qm увеличиваются пропорционально
модулю разности | xfa) (Т) — хп | .
На рис. 14.3, 14.4 представлены программы ф (t) угла уста¬
новки паруса и траектории, соответствующие нулевому прибли¬
жению (0), первому (1) и второму (2) шагам итерационного про¬
цесса, а также окончательному (оо) решению задачи (14.88).
На рис. 14.5, 14.6 даны законы 0 (t) направления вектора тяги
и траектории в нулевом приближении (0), на втором (2) и седьмом
(7) шагах процесса, а также окончательное (оо) решение задачи
(14.89) со свободным угловым перемещением ср1.
37 Механика полота
578
ФУНКЦИОНАЛЬНЫЕ ЧИСЛЕННЫЕ МЕТОДЫ
[гл. I
Функционалы задач — время движения Г даны на горизон¬
тальных осях рис. 14.3, 14.5.
Несмотря на значительно большее число шагов в задаче (14.89),
необходимое для достижения заданной точности, полное время
счета методом штрафных слагаемых оказывается меньше, чем
методом условного градиента. Это связано с тем, что последний
метод требует весьма трудоемких операции при определении мно¬
жителей Лагранжа А,х, . . ., кп.
Рис. 14.5. Программы 0 (/) направления
вектора тяги, соответствующие нулевому
приближению (0), второму (2), седьмому
(7) шагам итерационного процесса и реше¬
нию (со),—метод градиентного спуска
в пространстве управлений.
Рис. 14.6. Траектории перелета, соответ¬
ствующие нулевому приближению (о), вто¬
рому (2), седьмому (7) шагам итерационного
процесса и решению (оо),— метод градиент¬
ного спуска в пространстве управлении.
7. Ограничения на фазовые координаты. Дополним задачу
Майера со свободным правым концом (14.51) условием ограничен¬
ности комбинации фазовых координат и управления.
Пусть в повой постановке требуется определить управление u(t),
доставляющее минимум контрольному функционалу х0 (Г), при
выполнении неравенства вдоль траектории:
фшт < ф (*y, U , t) < ф,
пах-
(14.90)
Аналитические результаты по решению вариационных задач
с фазовыми ограничениями содержатся, например, в монографии
[14.33] и статье [14.25], численные приемы решения описаны в
работах [14.18, 14.26, 14.32].
Следуя работе [14.26], дадим классификацию ограничений.
Назовем неравенство (14.90) фазовым ограничением нулевого
порядка, когда в функцию ср входит явно управление и: (дер/ди)ф
ф 0, фазовым ограничением первого порядка, когда управление
и входит явно в первую полную производную по времени функ¬
ции ср: (9ф/ди) ф 0 и т. д.
Фазовое ограничение нулевого порядка и только нулевого
порядка может трактоваться как ограничение на управляющую
ГРАДИЕНТНЫЙ СПУСК В ПРОСТРАНСТВЕ УПРАВЛЕНИЙ
579
функцию. Действительно, введем замену
V = ф (Xj, и, t)
(14.91)
и выразим, согласно этой замене, управление и через v, Xj, t
(пусть это удается сделать аналитически): и = ф {хп v, t);
в уравнениях движения (14.51) будет фигурировать вместо управ¬
ления и управление v, которое ограничено по (14.90).
Если управление и не ограничено, то такая замена приводит
к задаче Майера с ограничением на управляющую функцию v;
метод решения этой задачи дан в п. 2.
Пусть теперь и ограничено вместе с v. Разобьем интервал [0, Т]
на участки трех типов. На участках первого типа управление и
принимает одно из своих граничных значений, a v лежит внутри
своей области изменения, на участках второго типа v лежит на
границе, а и — внутри области изменения, на участках третьего
типа и и v находятся внутри области изменения; участки первого
и второго типа не перекрываются. Идея рассматриваемого ме¬
тода решения задачи Майера (14.51) с ограничением на управле¬
ние и и фазовым ограничением нулевого порядка на v состоит в
следующем.
На участках первого типа вариация контрольного функцио¬
нала выражается через вариацию управления и (t) и определя¬
ется оптимальный закон для этого управления, на участках вто¬
рого типа вариация контрольного функционала выражается через
вариацию управления v (t) и определяется оптимальный закон
для v (t), на участках третьего типа как управление и (t), так и
управление v (t) могут фигурировать в выражении для вариации
контрольного функционала. Метод решения задачи Майера с
ограничением на управление известен (см. п. 2), поэтому на каж¬
дом из участков можно указать свое оптимальное управление с
учетом существующего ограничения. Введем в отличие от (14.57)
следующую сопряженную систему:
Здесь б (t) — релейная функция, принимающая значение 1
на участках, где решение идет по ограничениям v = cpmin, v =
^ фтах и значение 0 на участках, где решение идет по ограниче¬
ниям и = Ыпяп, и = итах. На участках, где ни и, ни v не ограни¬
чены, функция б на равных основаниях может быть принятой
равной 0 или 1.
(14.92)
580
ФУНКЦИОНАЛЬНЫЕ ЧИСЛЕННЫЕ МЕТОДЫ
[ГЛ. 14
Вариация контрольного функционала 8х0 (Т) выражается сле¬
дующим образом:
п difi I Эф(о) I 3ф(о)^
О 7=0 3=0
<г> = ) 2 ■-ж- [ 3 (%■ Пг) 6*‘6+Н *• <14-93>
Принимая во внимание, что
б^ =
£ *р(0)в*,. + вф(0)
== V —1—
Zl dxj
'3 1 ди
Ьи,
(14.94)
3=0
выражение для вариации бж0 (Т) можно записать в виде
с 71 а/(0)
бхо (Т) = \ 2 Pi I6v6/(dq>(°)/du) + 8и (1 — б)] dt. (14.95)
Пусть управления и и v не ограничены; выберем тогда вариа-
ции управлений б и, 8v следующими:
при б (t) — 0
п дт
йв = - К 2 Pi ~ddT ’
i=0
при б (t) = 1
(0)
(0)
(14.96)
Параметры спуска KUJ Xv связаны между собой условием непре¬
рывности вариации 8и в точках смены значений функции б (£):
для точки t — t\ где функция б (t) меняет значение с 0 на 1, эта
связь запишется так:
б и (tf — 0) = Ьи (t' лг 0),
би (t' + 0) = бг; (*' -j- 0)/(dyWfdii)' — ^
г=0
(о)
дЩ
bxi (14.97)
2(SF)’*i
7=0
У » (9Л.\
2] pi [ ди )
1=0
(ОД
Kv — Кь
(штрихи обозначают принадлежность точке t = t').
(14.98)
ГРАДИЕНТНЫЙ СПУСК В ПРОСТРАНСТВЕ УПРАВЛЕНИЙ
581
Если бы управление v (t) было не ограничено, а и (t) ограни¬
чено, то следовало бы положить б (t) = 0; этот случай соответ¬
ствует рассмотренному в п. 2 ограничению на управляющую
функцию и (t).
Если бы управление и (t) было не ограничено, a v (t) ограни¬
чено, то следовало бы положить б (t) = 1. Дальнейшая проце¬
дура зависела бы от того, можно ли разрешить аналитическое
уравнение v — ср (ад, и, t) относительно и. Если можно, то за¬
дача свелась бы к предыдущей, если нельзя, то порядок действий
будет следующим (ср. п. 2).
Вариация б г; берется в виде (см. (14.96))
б v(t) =
d(D(0) П d/(0) d(Di0) n
~ ^ 2 Pi Тй~ ’ еСШ1 Фт«п<«(0)-^-|г 2 А —<фшак,
1 = 0 i = 0
~ (0) n 5/(0)
фтах — У(0), если l><°> — А, ^ Р'~ЩГ > ф|Па>; '
1=0
яш(°) " a/j0)
ф/nin — ^0), если Cp.ain > V(0) — К 2 Pi •
2=0
(14.99)
где параметр А, задается малым, так, чтобы линейное представле¬
ние задачи оставалось в силе. Соотношение (14.94) при известной
функции 8v (t) (см. (14.99)) определяет вариацию управления
б и через вариации координат бад. Это выражение подставляется
в систему (14.55) и решается задача Коши (14.55) — (14.56). Ре¬
зультат решения — функции б ад (t) используются для определе¬
ния вариации управления б и (t).
Заметим, что найденное таким способом управление и<l) (t)
удовлетворяет ограничению (14.90) только в линейном прибли¬
жении.
Вернемся к рассматриваемой задаче, в которой ограничены
управление и (t) и управление v (t).
Пусть в начале траектории (0 ^ t t') не ограничено управ¬
ление v (t). Положим на первом участке б (t) — 0 и будем для
каждого момента времени подсчитывать вариацию 8и (t) по форму¬
лам, аналогичным (14.99). Одновременно будем интегрировать
задачу Коши (14.51) с известным законом управления uiX)(t) и
проверять неравенства (14.90). Допустим, что момент времени
t = t' — первый момент, в который нарушилось одно из нера¬
венств (14.90). Тогда положим б (t) = 1 и по формулам (14.99)
будем определять вариацию бv (t). В точке t = t' вариация
б и (t) должна быть непрерывна (см. (14.98)). В каждый момент
582 ФУНКЦИОНАЛЬНЫЕ ЧИСЛЕННЫЕ МЕТОДЫ [ГЛ. 14
времени по известной функции 8v (t) будем подсчитывать б и (t)
согласно правилу, данному выше. Получаемая функция (t)
должна проверяться на выполнение неравенств (14.66). Таким
образом, искомое решение определяется путем чередования
градиентных спусков в пространстве и (t) и в пространстве v (t).
Описанный алгоритм решения пригоден для вариационных
задач с фазовыми ограничениями нулевого порядка.
Для численного построения оптимальных решений при нали¬
чии произвольных фазовых ограничений может использоваться
метод штрафной функции [14.18, 14.26, 14.32].
Исходная система дифференциальных уравнений (14.51) допол¬
няется уравнением для штрафной функции хп+1 следующего вида:
Хпл 1 — К (ф) (ф фтт) (фтах ф)* (14.100)
где К такая функция ф:
К (ф) Ki = const при ф<^ фтт, I
К (ф) = К1 = const при Ф> фтах» Г (14.101)
К (ф) — О при фтт < ф < фтах- J
Положим
хп+1 (0) = 0; (14.102)
тогда значение хп+\ (Т) ^ 0 будет характеризовать меру наруше¬
ния неравенств (14.90). Если xn+i {Т) = 0, то, согласно опре¬
делению функции К (ф), неравенства (14.90) выполняются всюду
на промежутке [0, Т].
Определим управление и (t), доставляющее минимум контроль¬
ному функционалу xQ (Т) и обеспечивающее нулевое конечное
значение штрафной функции xn+l (Т):
хп+1(Т) = 0. (14.103)
При выполнении условия (14.103) неравенства (14.90) будут
удовлетворены.
8. Численный метод, основанный на принципе максимума
Л. С. Понтрягина. В этом пункте будет описан метод, родствен¬
ный методам градиентного спуска в пространстве управлений и
основанный на применении принципа максимума [14.21, 14.35].
Рассмотрим задачу Майера со свободным правым концом
(14.51). Для решения по методу Л. С. Понтрягина составим
гамильтонову функцию Н и выпишем уравнения для импуль¬
сов р{:
ГРАДИЕНТНЫЙ СПУСК В ПРОСТРАНСТВЕ УПРАВЛЕНИЙ
583
Конечные значения импульсов pi(T) имеют вид
р0(Т) = -1 ,Pi(T) = 0 (i = 1 /г) (14.105)
(ср. конечные значения функций сопряженной системы (14.60);
в методе JI. С. Понтрягина система импульсов нормируется так,
что импульс, соответствующий контрольному функционалу, в
конечный момент отрицателен).
Чтобы функционал xQ (Т) достигал минимума, оптимальная
управляющая функция и (t) должна обеспечивать максимум
функции Н
н-opi (t)max Н (xh ph и, t). (14.106)
71(0
Предлагаемый в работах [14.21, 14.35] алгоритм решения
описанной задачи состоит в следующем.
По заданному нулевому приближению управления и<0) (t)
решается задача Коши «вперед» для системы фазовых перемен¬
ных (14.51). В результате вычисляются в каждой точке значения
фазовых координат х{У (t). По известным £(0) (t){ и<0) (t) решается
задача Коши «назад» для системы уравнений импульсов (14.104),
(14.105); в результате определяются функции pl0) (t). Управле¬
ние на следующем шаге н(1) (t) находится из условия максимума
гамильтоновой функции И в каждый момент времени:
max Я [а40)(£), рТ* (£)» м(1\ £]• (14.107)
гД1) (0
В работе [14.21] указана модификация этого алгоритма. Обоз¬
начим через и вместо н(1) (t) управление, максимизирующее
гамильтонову функцию (см. (14.107)) и следующее приближение
представим в виде
Ф) (t) = (t) + К [й (t) — и<°> (f)L (14.108)
Параметр А, здесь находится из условия минимума контрольного
функционала на каждом шаге процесса.
Приведем некоторые соображения по скорости сходимости
метода (см. [14.35]).
Приращение функционала kx0 (Т), вызванное вариацией
управляющей функции Ьи (t), дается следующей формулой:
т
A*0(2,) = -|J [Н(хТ\ pf, p?,u(°\t)\dt-L,
(14.109)
584 ФУНКЦИОНАЛЬНЫЕ ЧИСЛЕННЫЕ МЕТОДЫ [ГЛ. !
где L — остаточный член, оцениваемый следующим образом:
т
]L|< J \u^{t) — uW(t)\dtf (14.110!
О
(А — фиксированная константа, связанная с постоянными и
условиях Липшица для функций Д и дН/дх{). На каждом шаге
итерационного процесса управление (t) (или и (t) в модифи¬
цированном методе (14.108)) выбирается из условия максимума
Н по и\ поэтому рассматриваемый метод обеспечивает, с точностью
до малых высшего порядка по | и^х) (t) — и(0) (t) | наиболее быст¬
рое изменение функционала по сравнению с другими методами,
учитывающими лишь первую вариацию. Малость | u(1) (t) — и^0) (t)
понимается здесь в смысле интегральной нормы, фигурирующей
в оценке остаточного члена (14.110), т. е. величина | (t) —
— и^0) (t) | может быть конечной, но на малом отрезке времени.
Метод допускает применение для задач с ограниченным управ¬
лением, не нуждаясь в каких либо модификациях.
Заметим; что для правых частей системы (14.15) вида
п
fi ■■= 2 аи (*)*;• + h (и> t) (14.111)
j = 0
описанный итерационный процесс выражается в один шаг. Деи-
ствителыю, фазовые координаты Xj и управления и в дифферен¬
циальные уравнения для импульсов не входят (см. (14.104)):
71
Pi = — 2 аРР}’ (14.112)
поэтому функции p\(t) находятся однократным решением задачи
Коши «назад» для системы (14.112) с краевыми условиями (14.105).
Оптимальное управление и (t) определяется из условия макси¬
мума выражения
2 PiWhiu, t). (14.113)
7=0
Для задачи Майера (14.67) с фиксированными начальной и
конечной точками траектории описанный метод может найти при¬
менение, если воспользоваться приемом введения штрафных сла¬
гаемых (14.68). Конечные условия для импульсов (14.105) при
этом заменятся на такие:
Я р{0)
Po{T) = — i, Pi(T) = Е— (г = 1, . . ., ге) (14.114)
(выражение функции Р дано формулой (14.68)).
ФУНКЦИОНАЛЬНЫЙ МЕТОД НЫОТОНА
585*
В работе [14.35] описан пример применения метода; там же
даны рекомендации по вычислительной процедуре, связанные с
экономией машинной памяти.
§ з. ФУНКЦИОНАЛЬНЫЙ метод НЫОТОНА
Решения яд (£) краевой задачи (14.10), к которой редуцируются
вариационные проблемы, должны удовлетворять дифферен¬
циальным уравнениям, начальным и конечным условиям. Для
решения проблемы могут быть использованы итерационные про¬
цессы двух типов. Первый: на каждом шаге точно выполняются
начальные и конечные условия и неточно дифференциальные
уравнения; в ходе итерационного процесса происходит прибли¬
жение к решению, оцениваемое по расстоянию в функциональном
пространстве. Второй: на каждом шаге процесса точно удовлет¬
воряются дифференциальные уравнения и начальные условия;
от шага к шагу происходит приближение конечных значений
X] (Т) к требуемым x:il, оцениваемое по расстоянию в конечномер¬
ном пространстве.
В этом параграфе будет описан функциональный метод Нью¬
тона и его обобщение, относящиеся к итерационным процессам
первого типа. Вывод алгоритма дан для обобщенного функцио¬
нального метода Ньютона, традиционный метод Ньютона получа¬
ется из него как частный случай.
функциональный метод Ныотона изучался в работах [14.10,
14.13“ 14.36].
1. Алгоритм метода. Опишем алгоритм обобщенного функцнО'
нального метода Ныотона на примере краевой задачи первого
рода для дифференциального уравнения второго порядка:
х = / (х, э\ t)\ х (0) = х0, х (Т) = xv (14.115)
Введем функционал — расстояние до искомой точки в функ¬
циональном пространстве х (I)
т
J - [х — / (х, х, t)]2dt. (14.116)
о
Стремление функционала к нулю при выполнении граничных
условий (14.115) будет означать приближение к искомому эле¬
менту х* (t).
Пусть известно некоторое нулевое приближение к искомому
решению — функция х(0) (£), удовлетворяющая краевым усло¬
виям; следующее приближение представим в виде
#(1) (£) = я(0) (£) -j- §£ (t).
(14.117)
586 ФУНКЦИОНАЛЬНЫЕ ЧИСЛЕННЫЕ МЕТОДЫ [ГЛ. 14
Функция 8х (t) имеет норму, малую по сравнению с нормой
функции (t); краевые значения 8х (t) выберем следующими:
8х (0) - 8х (Т) = 0. (14.118)
Вариация функционала /, вызванная вариацией 8х (t), за¬
писывается так:
т
6/= 2 С'(£«» —/(0))(bx — dJ^_bx — ?flbx)dt\ (14.119)
" дх '
здесь /(0\ df&Vdx, df0)/dx — функции t, вычисленные при
х = х^ (£).
Среди всех вариаций 8х (£), удовлетворяющих краевым усло¬
виям (14.118), определим такую, которая уменьшала бы значение
функционала, вычисленное по нулевому приближению xW (£),
иными словами, искомая 8х (t) должна обеспечить первой вариа¬
ции 8J знак минус.
В частности, таковой может быть функция 8х (£), подчинен¬
ная условиям
дх — -Ц—дх — дх — — Я (х(® — /(0)), дх (0) = дх (Т) -- 0,
(14.120)
где Я — положительный параметр.
Введем функцию r\ (t) по формуле (ср. (14.25))
ц (t) = 8х (*)/Я; (14.121)
тогда соотношение (14.117) перепишется так:
*(1) (t) = ®(о) (t) + Хг\ (f), (14.122)
а дифференциальное уравнение и краевые условия (14.120) при¬
мут вид
Л — Л — ~g~ '•I — — i’(0) + /(0), л(0) = Л (?) = 0. (14.123)
Таким образом, процедура построения функции 8х (t) разде¬
лилась на две части: нахождение rj (t), удовлетворяющей усло¬
виям (14.123). и определение параметра Я. При решении краевой
задачи (14.123) для линейных дифференциальных уравнений может
быть привлечен метод прогонки или любой другой подходящий
метод (см., например, [14.37—14.39]). Определение параметра
Я связано с решением следующей задачи на минимум.
Пусть функция г) (t) найдена из (14.123); тогда зависимость
4Г(1) от t, Я известна, и функционал У является известной функ¬
ФУНКЦИОНАЛЬНЫЙ МЕТОД НЫОТОНА
587
цией параметра А. Будем искать то значение А, которое обращает
в минимум интеграл (14.116) на данном шаге процесса
/mill - min
л
jj [>) + %v\ — f + Я.Т], i(0) + Xii, t)fdt. (14.124)
Этот способ определения параметра А аналогичен тому, кото¬
рый используется в методе функционального градиентного спуска
применительно к параметру спуска (ср. (14.28), (14.65)).
Сформулируем окончательно содержание рассматриваемого
итерационного процесса:
На каждом шаге процесса, описываемого выражением шипа
(14.122), необходимо решать краевую задачу для линейного урав¬
нения (14.123) с коэффициентами и правой частью, определяемыми
по результатам предыдущего шага, и находить каким-либо чис¬
ленным методом значение параметра X из условия (14.124).
Если исходное дифференциальное уравнение (14.115) линей¬
ное, то итерационный процесс вырождается в один шаг, а миними¬
зирующее значение параметра X равно единице. Действительно,
когда функция / — линейная по аргументам х, х, то J (X) име¬
ет вид
J (X) = /(о) (1 - X)2, (14.125)
где /(0) — значение интеграла (14.116), вычисленное по нулевому
приближению (X = 0); минимум J (X) достигается при 1 = 1 и
равен нулю, что подтверждает высказанное выше суждение.
Для произвольного нелинейного уравнения (14.115) зависи¬
мость J (X) содержит помимо первого члена /<0) (1 — А,)2 еще
члены, зависящие от степеней X выше первой, причем коэффи¬
циенты при степенях тем меньше, чем лучше функция / описыва¬
ется линейными членами разложения по х — х*, х — х*. С ходом
итерационного процесса функция / (А) приближается к виду
(14.125), поэтому минимизирующее значение А стремится к 1.
Если для произвольного нелинейного уравнения параметр А
назначить равным единице] на всех итерациях, то предлагае¬
мый метод переходит в традиционный функциональный метод
Ныотона.
Метод обобщается на случай нелинейных дифференциальных
Уравнений произвольного порядка, а также систем уравнений.
Минимизируемым функционалом может служить соответственно
интеграл от квадрата невязки дифференциального уравнения или
интеграл от суммы квадратов невязок отдельных уравнений си¬
стемы.
2. Пример. Для иллюстрации скорости сходимости предлагае¬
мого метода, а также для сравнения с другими методами был про¬
считан пример с уравнениями движения в центральном поле.
588 ФУНКЦИОНАЛЬНЫЕ ЧИСЛЕННЫЕ МЕТОДЫ [гл. 14
Перелет между заданными координатами в центральном поле
описывается системой двух дифференциальных уравнений вто¬
рого порядка
х = — кх (х2 + у2У<\ х (0) = х0, X (Т) = хх, (U 12fi,
у = _ ку {х2 + у2)^, у (0) = у0, у (Т) — ух.
Здесь, в отличие от принятого (см. Приложение) за единицу
времени взяты 100 средних солнечных суток, а за единицу ли¬
нейного расстояния принята по-прежнему астрономическая еди¬
ница; при этом коэффициент к равен: к = 2,9591.
Следуя [14.17], выберем в качестве начальных и конечных
координат, а также времени следующие значения:
* (0) = 0,99850, х (2) = -1,3558, j
у (0) - 0,07107, у (2) - 0,96570, J
а в качестве нулевых приближений х(0) (t), г/(°) (I) такие функции:
(0) /,ч _ Sin /г (2 -t) , sin lit
sin 2/г 0 sin2ra ь
/Пх /.V sin п (2 — t) , sin nt
У (0 — 1—з У'■) ~~г ~—о— Vi
' ' sin 2/г J sin 2/г и
(14.128)
(п =. 1,0462).
Итерационный процесс обобщенного функционального метода
Ньютона в рассматриваемом случае описывается соотношениями
*(1) (f) = ж(о) (t) + Хцх (*), у( 1) (t) = у(0) (t) + %цу (*). (14.129)
Функции т]х (0, Цу (t) находятся из решения краевой задачи
= ~ ^<0) “ Х(0>’ ^ (0) = Ч* (2) =- 0 - ]
av(o) av(°) / \ I
Ли + -^-Л*+ — У(0) — Y(0\ % (0) = Лу (2) = 0, j
(X = кх (х2 + *2)Л Y =ку 0г2 + j/2)"72), J
(14.130)
а параметр А, — из условия минимума выражения
2
rn/n ii ^х ^ ^
+ [*/(0) + kr\y + Y (х^ + Arj*, z/(°) -!- ^цу)]2}Л. (14.131)
Для решения линейной краевой задачи (14.130) применялся
метод сопряя^енных уравнений [14.39]; определение минимизи¬
рующих значений параметров X производилось одновременно с
построением функций / (А,).
§ s'l
ФУНКЦИОНАЛЬНЫЙ МЕТОД НЫОТОНА
589
t-ис. 14.7. Пример измене- Рис. 14.8. Пример зависимости относительной величины
ния минимизирующего зпа- функционала J* от параметра X для первого, второго,
чения параметра А по шагам третьего шагов процесса — обобщенный функциопаль-
Л итерационного процесса— ный метод Ныотона.
.обобщенный функциональ¬
ный метод Ньютона.
Рис. 14.9. Траектории, соответствующие первому и второму шагам обоб¬
щенного метода Ныотона (1, 2), традиционного метода Ньютона (.?, 4),
функционального градиентного метода в фазовом пространстве (5, 6)\
значок 0 относится к начальной траектории, значок оо — к решению.
590
функциональный численные методы
[ГЛ. 11
Результаты применения метода следующие.
Представление о сходимости процесса дает табл. 14.1, в кото¬
рой выписаны значения интеграла / для каждого шага к (вторая
строка J\=opt). Для сравнения в третьей строке таблицы приво¬
дятся значения функционала / при использовании традицион¬
ного метода Ньютона (/x=i). Из данных таблицы следует, что за
счет выбора параметра X по критерию (14.131) число итераций,
сокращается на три.
Таблица 14.1
Убывание функционала по шагам итерационного процесса
обобщенного e/^opt и традиционного функциональных
методов Ньютона
Номер шага
к
0
1
2
3
т(Ю
J A=opt
12,346
7,0862
0,25858
0,46302-10-4
т(Ю
J X=i
12,346
460,12
29,233
4,0145
Номер шага
к
4
5
G
7
т(К)
J A=opt
0,565-10-8
0
0
0
j(k)
3,3005
0,030773
0,46178-IQ-1
0,52063-10-e
На рис. 14.7 показан характер изменения минимизирующего
значения X по шагам итерационного процесса (дискретные точки
соединены ломаной линией). В начале процесса Х<^1, в конце
X — 1, что подтверждает высказанное ранее суждение.
Зависимость интеграла (14.131) от параметра X представлена
на рис. 14.8 для трех шагов процесса. По вертикальной оси от¬
ложена величина интеграла, отнесенная к его значению на дан¬
ном шаге при X = 0 (эта величина обозначена J*).
На рис. 14.9 даются траектории, соответствующие первому и
второму шагам обобщенного метода Ньютона (линии 1,2), тра¬
диционного метода Ньютона (линии 3,4) и функционального гра¬
диентного метода в фазовом пространстве (линии 5,6). Началь¬
ная траектория, общая для всех трех методов, отмечена значком
0, решение — значком оо. Данные по градиентному методу взя¬
ты из работы [14.17]; в этой работе функциональный градиент¬
ный метод в фазовом пространстве (см. § 1 настоящей главы)
применен к минимизации интеграла действия.
КОНЕЧНОМЕРНЫЕ ЧИСЛЕННЫЕ МЕТОДЫ
ПОСТРОЕНИЯ ОПТИМАЛЬНЫХ РЕШЕНИЙ
В настоящей главе собраны конечномерные методы построе¬
ния оптимальных решений. Приведение вариационных задач
(14.1) — (14.9) к виду, пригодному для использования этой груп¬
пы методов, возможно двумя способами. В основе первого спо¬
соба лежит замена функционалов функциями конечного числа
переменных: метод Ритца, метод ломаных и другие. Второй спо¬
соб состоит в редукции вариационной задачи к краевой и нахож¬
дении конечного числа недостающих начальных условий (см.
начало гл. 14).
Глава содержит два параграфа. В первом описаны наиболее
употребительные конечномерные методы, во втором даны спо¬
собы приведения вариационных задач к требуемому виду.
§ 1. МИНИМИЗАЦИЯ ФУНКЦИИ ПРИ ДОПОЛНИТЕЛЬНЫХ
УСЛОВИЯХ
Требуется определить минимум функции п переменных:
J = J (х^ . . ., хп) (15.1)
при выполнении дополнительных условий
фу (хг, . . ., хп) = 0 (/ = 1, . . ., I < 72); (15.2)
переменные х1У . . ., хп изменяются в неограниченной области.
Будем заранее считать, что решение задачи (15.1), (15.2) су¬
ществует и единственно.
Для нахождения искомой точки х\ используют аналитический
прием с множителями Лагранжа составляется новая функция
i
I {хъ . . хп; . . . Д() = J (Xi) + 2 (ж0> (15-3)
3 = 1
и выписываются условия ее минимума по аргументам х\
592
КОНЕ ЧТТОМЕ Р1ГЫЕ ЧИСЛЕ ПIIЫЕ ME ТО ДЫ
[гл. 1 Г)
Система п уравнений (15.4) совместно с I уравнениями (15.2)
определяет неизвестные ад, . . хп\ . . ., Хг. Запишем эти
две группы уравнений в виде одной системы
f.(xj) = О, (С/ = 1,2, . . т), (15.5)
где
ОД = ОД, . • ., Хп = ХП1 Хц+Х — . . ., Xn+l := А-/,
г dl , 5/ , _ ,
' d#T ’ * * ’’ — dz~ ’ ^n+1 — * ’ *’ *nvl — ^
(/лг = 7г -f- Z).
Если / (ад, . . ., ад) — квадратичная функция своих аргумен¬
тов, а %(од, • хп) — линейные функции, то система (15.5) —
линейная относительно переменных ад, . . ., ад, . . ., xn+i; на¬
хождение минимума при дополнительных условиях сводится в
этом случае к решению системы линейных алгебраических урав¬
нений.
1. Градиентный метод. При отсутствии дополнительных усло¬
вий (15.2) процедура градиентного метода применительно к
нахождению минимума функции J (ад, . . ., хп) состоит в сле¬
дующем.
По известному нулевому приближению для аргументов xf]
вычисляются производные минимизируемой функции:
С=-ё (4“ ■ • • •• (15-6)
первое приближение представляется в виде
жр =--■ 40> — ^• (15.7)
Параметр X определяется из условия минимума функции
(15.8)
на данном шаге итерационного процесса.
Для решения исходной задачи (15.1) —(15.2) можно указать
две модификации описанной выше процедуры.
Первая модификация состоит в том, что задача на условный
минимум (15.1) — (15.2) заменяется задачей на безусловный мини¬
мум путем введения штрафных слагаемых (ср. § 2 гл. 14). Состав¬
ляется вспомогательная функция Y (ад, . . ., хп) с коэффициен¬
тами г/у > 0 (у = 1, . . ., I)
i
Y (хи . . хп) = / (жь . . хп) + ^ • • •> *п) (15.9)
/=1
п МИНИМИЗАЦИЯ ФУНКЦИИ 593
и ищется минимум новой функции Y (хг, . . ., хп) описанным выше
градиентным методом (15.7) — (15.8). В процедуру метода включа¬
ется процесс последовательного увеличения коэффициентов qj.
Другая модификация повторяет прием, также описанный в § 2
главы 14. Изложим процедуру для упрощенного случая, когда
начальное приближение точно удовлетворяет дополнитель¬
ным условиям:
% (х\0)) = # = о (/ = 1, . . I). (15.10)
Представим выражение для искомых х\ на первом шаге процес¬
са в виде
ж£1) = 40) + $Xi (i = 1, . • м п). (15.11)
Изменения функций J и фу, вызванные малыми приращениями
Ьх\, запишем, ограничиваясь линейными членами разложения
П д/(0)
i=l
” at(0)
У? — Ф;9' ~ Hi = 2 6xi (/ = 1, • • м I).
i=l
(15.12)
Определим вариации бх. из условия неположительности вариа¬
ции 6J при выполнении дополнительных связей
^ = 2 -g- в** = 0 (/ = 1 I). (15.13)
1=1 1
Аналогично § 2 главы 14 составим вспомогательную функцию с
множителями Лагранжа Ху:
г 6/ + 2 = 2 (iJ- + 2 (15.14)
3=1 1=1 г 3=1
Выберем в виде
te. — Ц!?+2^) (.' = < »>■ «5.«)
Х г 3=1
Если X > 0, то вспомогательная функция Г неположительна
при любых Ху:
Г--12 (^+ «5.16)
i=l г 3=1
38 Мех
ханина полета
594
КОНЕЧНОМЕРНЫЕ ЧИСЛЕННЫЕ МЕТОДЫ
[ГЛ. 15-
Множители Лагранжа Xj определяются из уравнений (15.13).
которые являются линейными уравнениями относительно L
(6xi в (15.13) берутся из (15.16)):
В силу такого определения параметров Xj сумма по j в выражении
для функции Г равна нулю:
i
= (15.18)
3=0
Отсюда вытекает, что Г совпадает с б/, и, следовательно, дан¬
ный выбор вариаций бх* обеспечивает неотрицательность вариа¬
ции б/.
Параметр X в формулах (15.15) определяет длину шага вдоль
условного градиента, последняя ограничена сверху требованием
малости ошибки линейного представления функций J и фу (ср.
§ 2 гл. 14).
В заключение этого пункта заметим, что в исходной постанов¬
ке (15.1) —(15.2) не фигурируют ограничения на область измене¬
ния параметров Это обстоятельство в значительной степени
упрощает вычислительную процедуру. Более общий случай опи¬
сан в монографии Зойтендейка [15.1] (там же имеется обширная
библиография). По поводу градиентного метода в конечномерном
пространстве и его модификаций применительно к задаче (15.1) —
(15.2) можно рекомендовать, например, работы [15.2—15.4].
2. Метод Ньютона. Для системы алгебраических уравнений
(15.5), к которой сводится задача на минимум (15.1) с дополни¬
тельными условиями (15.2), традиционный метод Ньютона со¬
стоит в следующем. По начальному приближению ху0) вычисля¬
ются производные djfVdxj, значения х^ на первом шаге процесса
Ньютона определяются из такой системы линейных уравнении:
71 а/<°)
2 (af -*Т) = ~ /i0’ (i = 1, •.., ») (15.19)
1 0
(чтобы сделать обозначения привычными в системе (15.5) х{ заме¬
нены на Х{, а порядок системы п + I заменен на п).
Опишем одно обобщение метода Ньютона [15.5—15.9], отли¬
чающееся от традиционного метода Ньютона введением некоторого
параметра, напоминающего параметр спуска X в градиентном
методе. Метод является конечномерным аналогом изложенного в
предыдущей главе обобщенного функционального метода Ньютона.
# ^ минимизация функции 595
Пусть задана система п алгебраических уравнении с п неиз¬
вестными:
fi(xj) — 0 (i, 7 = 1.* • *. п); (15.20)
требуется определить решения системы х* . Составим функцию
п
ф = 4- 2 /? (х}), (15.21)
i=l
которая в искомой точке х\ = х\ обращается в нуль вместе со
своими первыми производными
Ф- = 4-|/,-/;= о. ^=2/'||=о. (15.22,
2=1 J 2=1
Близость к решению в тг-мерном пространстве (хъ . . ., хп)
может быть оценена по величине функции Ф. Пусть в /г-мерном
пространстве дана точка Хх\ . . ., х£\ не являющаяся решением,
и в ней вычислены функции ф(°> и производные dffVdxj,
дФ^/dxj. Представим координаты Xj на следующем шаге итера¬
ционного процесса в виде
= ХТ + bXj (/ = 1,.. ., 72), (15.23)
где 8xj — малые приращения. Соответствующее приращение
функции Ф записывается следующим образом:
6®=S^«*f= 2 <15-24>
j=1 J 7,J=1
Чтобы итерационный процесс был сходящимся, необходимо
выполнение условия: Ф(1> ф(°), т. е. 6Ф 0. Из этого условия
можно выбрать приращения 8xj двумя способами: во-первых,
71 -/(0)
dfw.
6xj = - X 2 /10) -ё-. Л, >0 (/ = 1,.. П) (15.25)
и, во-вторых,
дх:
2=1 J
dfi>)
2 б Х>0 (i = l,...,n). (15.26)
j=1 ' 7
Выражение (15.25) определяет алгоритм градиентного метода
(ср. (15.7)). Если в формуле (15.26) положить К = 1, то она опре¬
делит алгоритм метода Ньютона.
38*
596
КОНЕЧНОМЕРНЫЕ ЧИСЛЕННЫЕ МЕТОДЫ
[ГЛ. 15
Произведем замену
SXj = А,г]у (/ = 1, . . п); (15.27)
тогда соотношения (15.26) будут иметь вид
п dfW
2-^г% = ~/'0) (*' = (15.28)
1 J
а выражения для координат xf* на первом шаге итерационного
процесса запишутся так:
х\х) = xf+ Ху(/ = 1, . . ., п). (15.29)
Определив г]у из линейной системы (15.28) и подставив их в (15.29),
обнаруживаем, что Ф становится функцией только параметра X
Ф (х?] + Хг\з) = ¥ (X). (15.30)
Этот параметр выбирается из условия минимума функции ¥ (X)
на каждом шаге итерационного процесса аналогично тому, как
это делается в градиентном методе:
min¥ (X). (15.31)
х
Разложим функцию ¥ (X) в ряд по степеням X
¥ (X) = ¥ (0) (1 - X)2 + аХ2 (1 - X) + ЪХ3 (1 - X) + сХ± + . . .
(15.32)
Здесь коэффициенты а, Ь, с выражаются через произведения ве¬
личин Т]у, }f\ d2ff)/dxidxk, d3jf)/dxidx]гдхг, 34/j°V dxidxkdxidxm, ...
Если fj — линейные функции своих аргументов, то
а = Ъ = с= ... = 0. (15.33)
В этом случае параметр X, доставляющий минимум функции
¥ (Я), равен единице и описанный итерационный процесс вырож¬
дается в один шаг. В близкой окрестности решения х\ функции
/у описываются линейными членами разложения; поэтому по
мере приближения к решению параметр X стремится к единице.
Таким образом, предлагаемый алгоритм решения системы
(15.20) заключается в следующем:
На каждом шаге итерационного процесса находятся гр из
линейной системы (15.28), затем по условию (15.31) определяется
параметр X; значения координат Xj на следующем шаге выража¬
ются в виде (15.29).
Как было указано выше, предлагаемый метод совпадает с ме¬
тодом Ньютона, если на всех итерациях X = 1. В близкой окре¬
g 2] СВЕДЕНИЕ ВАРИАЦИОННЫХ ЗАДАЧ К КОНЕЧНОМЕРНЫМ 597
стности решения минимизирующее значение X приближается к
единице, и метод не имеет никаких преимуществ перед традицион¬
ным методом Ньютона. Применение данного метода оказывается
рациональным в той области пространства Xj, где метод Ньютона
либо неэффективен, либо расходится; в этом случае минимизи¬
рующее значение X намного меньше единицы. Выбор параметра
X на каждом шаге процесса, в известном смысле, гарантирует
сходимость метода, как это имеет место в градиентном методе.
Сравним некоторые стороны двух методов: градиентного ме¬
тода и метода Ньютона. Известно, что минимизация квадратич¬
ных функционалов и решение линейных уравнений — взаимно
эквивалентные задачи. Методом Ньютона линейные уравнения
решаются за один шаг, минимум квадратичного функционала
определяется градиентным методом в ходе итерационного про¬
цесса. Таким образом, по числу потребных шагов для достижения
заданной точности (а зачастую и по времени счета) градиентный
метод уступает методу Ньютона; это положение справедливо в
близкой окрестности решения нелинейного уравнения (и соот¬
ветственно неквадратичного функционала).
С другой стороны, процесс Ньютона может оказаться расхо¬
дящимся в тех случаях, когда градиентный метод сходится. Это
объясняется, в частности, и тем, что в последнем фигурирует па¬
раметр спуска; на каждом шаге процесса он может быть определен
так, чтобы минимизируемый функционал не увеличивался.
По этим же соображениям введение параметра X в процессе
Ныотона в какой-то степени гарантирует сходимость; рациональ¬
ный выбор параметра может обеспечить выигрыш во времени
достижения результата.
В работах [15.8, 15.9] предлагается выбирать параметр X из
промежутка (0, 1) так, чтобы только выполнялось условие схо¬
димости процесса: Ф(0). Процедура выбора состоит в по¬
следовательном уменьшении X от единицы до того значения, когда
выполнится условие сходимости.
§ 2. СВЕДЕНИЕ ВАРИАЦИОННЫХ ЗАДАЧ
К КОНЕЧНОМЕРНЫМ
Здесь излагаются способы замены функционалов функциями
конечного числа переменных: метод Ритца с определением коэф¬
фициентов по градиентному методу, метод ломаных для задач
Лагранжа и Майера, кроме того, описываются методы органи¬
зованного подбора недостающих начальных условий в краевой
задаче.
1. Метод Ритца с определением коэффициентов по градиент¬
ному методу. Классический метод Ритца давно стал достоянием
учебников (см., например, [15.2, 15.10—15.12]); в настоящем
598 КОНЕЧНОМЕРНЫЕ ЧИСЛЕННЫЕ МЕТОДЫ [ГЛ. 15
пункте будет описан пример его применения [15.13] к отысканию
min-экстремалей интегрального функционала (14.40)—(14.41).
Алгоритм метода состоит в следующем.
Выбирается полная система п линейно независимых функций
{% (t)} таких, что
^ (0) = i (0) - % (Т) = % (Т) = 0, (15.34)
и выбираются функции (t), у(0) (t), удовлетворяющие крае¬
вым условиям (14.41). Решение ищется в виде линейной комби¬
нации
п п
Хп(0 = £(0) (0 + 2 «{%(*)» Уп(г) У{0) (0 + 2 (15.35)
i=0 i=0
После подстановки хп (£), уп (t) вместо х (t), у (t) в выражение для
интеграла (14.40) последний оказывается функцией коэффициен¬
тов а*, Ь{
J1 - /1 Ьг). (15.36)
Задача отыскания min-экстремалей функционала (14.40) свелась
к минимизации функции /х (ait
bi) по конечному числу перемен¬
ных.
Минимизация функции/!(сц,
bi) может быть проведена гра¬
диентным методом, алгоритм ко¬
торого изложен в § 1 настоящей
главы. Приведем формулы мето¬
да применительно к рассматри¬
ваемому случаю.
Пусть известно начальное
приближение для коэффициен¬
тов аь bi\ следующее приближе¬
ние представим в виде
af = af - % {dJffdai),
bP = bf -UdJ^/dbJ. (!5-37)
Параметр спуска X определяется из условия минимума функции
Ji М = Jx r«i0) - a, {dJf/ddi), bf - X (dJf/dbi)]. (15.38)
Таким образом, предлагаемая процедура минимизации состоит
из двух вложенных один в другой итерационных процессов:
1°. Итерационный процесс Ритца, заключающийся в увели¬
чении от шага к шагу чрюла п коэффициентов а\, Ъ\ в разложении
(15.35).
2°. Итерационный процесс градиентного метода, заключаю¬
щийся в отыскании минимума функции (15.36) на каждом шаге
итерационного процесса Ритца.
Рис. 15.1. Закон сходимости функционала
по номеру итерации к процесса Ритца
для примера перелета в центральном поле:
т! = 1,52, <рх = Т = 2.
СВЕДЕНИЕ ВАРИАЦИОННЫХ ЗАДАЧ К КОНЕЧНОМЕРНЫМ
599
Базисные функции %(£) в [15.13] были выбраны степенного
вида
фг(0 = {Ь/ту+* (1 - tlTf (i = 0, 1, . . /г), (15.39)
а в качестве нулевого приближения (£), г/<°> (t) были взяты
функции (14.49).
Применение описанного метода Ритца в сочетании с методом
скорейшего спуска оказалось гораздо менее эффективным для
изучаемой задачи, чем применение метода градиентного спуска
в фазовом пространстве (см. § 1 гл. 14); время, затрачиваемое на
расчет одного варианта с точностью по функционалу до 4—5 зна¬
ков, равнялось 100 мин (вместо 1—2 мин для градиентного ме¬
тода).
Закон сходимости функционала J1 по номеру итерации к
процесса Ритца (для параметров гг = 1,52, = Т = 2) пред¬
ставлен на рис. 15.1; там сплошной линией соединены дискретные
точки Ji \ jy\ . . J{y\ На первой итерации считается по пять
Рис. 15.2. Изменение коэффициентов сц, Ц разложения х (/), у (t) по базис¬
ным функциям (/) в зависимости от номера г при к = 8 (метод Ритца для
примера па рис. 15.1).
коэффициентов а*, Ь{ (п = 5); при переходе к каждой последующей
итерации число коэффициентов увеличивается на 10 (Д/г = 5),
причем начальные значения (для метода скорейшего спуска)
новых десяти коэффициентов нулевые, а в качестве начальных
значений старых коэффициентов берутся их значения на преды¬
дущей итерации.
Зависимости величин ai, hi при к = 8 от номера i условно
показаны непрерывными линиями на рис. 15.2.
2. Метод ломаных для задачи Лагранжа. Идея метода — заме¬
на интеграла суммой, а искомой функции — интерполяцион¬
ным многочленом.
600 КОНЕЧНОМЕРНЫЕ ЧИСЛЕННЫЕ МЕТОДЫ [ГЛ. 15
Для иллюстрации метода рассмотрим простую задачу (14.11),
(14.12). Обозначим в исходном функционале производную
х = и, (15.40)
так что
т
J — ^ ф (х, и, t) dt. (15.41)
о
Разобьем интервал изменения аргумента на m равных частей
т = Т/m; при этом tK = кх. Представим функцию и (t) на интер¬
вале (£ft, tft+x) в виде линейной функции:
и (t) = ик + (ик+1— uk)(t—\tk)lт 1, и(**)). (15.42)
Тогда искомая функция х (t) в силу (15.40) будет квадратичной)
функцией аргумента t на интервале (£ft, ^+i):
х (t) = а*+ uk (t — Mfc) (* — tk)2/2x (k = l,...,m),(15.43)
и значения в узлах интерполяции будут связаны следу¬
ющим образом:
= Ж/с + V2T (wR+i -г Wk) (А = 1, . . то). (15.44)
Если интеграл (15.41) записать в виде суммы т интегралов
по отрезкам протяженностью т и на каждом отрезке подынтег¬
ральную функцию Ф представить в виде, аналогичном (15.42), а
затем все интегралы вычислить, то получим выражение для /
в виде суммы
771—1
1 - Ф (х0, и0, 0) + Ф (хт, ит, Т) + 2 2 ф (**> Щ, h)
к=1
(15.45)
2Т
(здесь х0 = х (0), хт = х (Т) — заданные значения функции
на концах интервала).
Рекуррентная формула (15.44) дает возможность выразить
значение функции в любом узле интерполяции хх (I = 1, . . ., т)
через значения иг, щ-х, . . ., и0. Действительно, сложив правые и
левые части выражений (15.44), найдем
i—i
Xi = х0 4- ~Y% [пп + Ui + 2 2 ик) (1 = 1,..., т), (15.46)
>t=i
СВЕДЕНИЕ ВАРИАЦИОННЫХ ЗАДАЧ К КОНЕЧНОМЕРНЫМ
601
х(Т) — Xq -| X ^М0“Г um 4“ 2 • (15.4/)
Используя соотношения] (15.46), выражение для функционала
(15.45) можно сделать зависящим только от значений функции
и (t) в узлах интерполяции
Таким образом, первоначальная вариационная проблема (14.11),
(14.12) свелась к определению га -f 1 значений щ, дающих эк¬
стремум функции (15.48) при выполнении дополнительного усло¬
вия (15.47).
Изложенный метод был применен в работе [15.14] для расчета
экстремалей функционала (14.40), записанного в полярных ко¬
ординатах. Если на межорбитальный перелет в центральном поле
не наложено условие заданного углового перемещения, то пере¬
ход к полярным координатам в функционале (14.40) сокращает
на единицу порядок старшей производной одной из функций
(см. гл. 5): в подынтегральное выражение одна из функций входит
вместе с первой и второй производными по времени, а другая —
только вместе с первой производной.
Исходная задача была сведена в работе [15.14] к задаче об
отыскании минимума функции двух групп переменных с тремя
дополнительными условиями, соответствующими трем заданным
конечным значениям. По мнению авторов, удовлетворительные
результаты получались уже при числе интерполяционных узлов
га, равном 10—20 для времени перелета, не превышающих вре¬
мени одного оборота по начальной орбите.
3. Метод ломаных для задачи Майера. Идея метода — замена
дифференциальных уравнений разностными; его применение для
задач оптимизации описано в работе [15.15], где он назван мето¬
дом критического направления.
Опишем алгоритм метода для задачи Майера со свободным
правым концом.
Задана система дифференциальных уравнений и начальных
условий
/ = -Г- т Ф (х (0), к0, 0) + Ф (х (Т), Um. Т) +
+ 2 2 Ф (х (0)» Ко, ..., К*)] . (15.48)
ъ 1 -J
(15.49)
602 КОНЕЧНОМЕРНЫЕ ЧИСЛЕННЫЕ МЕТОДЫ [ГЛ. 15
минимизируемый функционал — функция конечных значений
фазовых координат
Р (хг (Г), . . хп (Т)), (15.50
требуется построить оптимальное управление и (t). Разобьем
опять интервал изменения аргумента на пг равных частей про¬
тяженностью т = Tim каждая. Дифференциальные уравнения
(15.49) дают связи между значениями координат в двух сосед¬
них точках £fc+1:
*£г, fc+l — к ~Г ^/г к> Щс» ^к)
(•£г,к *^г (J'k)> Щг ^ iPk)» ^к /t’T, t, / 1, . . ., 72,
к = 0, . . .,m - 1). (15.51)
Функционал (15.50), зависящий от конечных значений ко¬
ординат, при рассматриваемом подходе считается функцией зна¬
чений управляющей функции и (t) в дискретных точках интервала:
uQ, иг, . . ., ит_ъ Нахождение минимального значения функции
Р по и0, иъ . . ., ит_ 1 связано с вычислением частных производ¬
ных дР!ди]г. Приведем выражения для них:
j* т 2 дРдщ(Т)Э1^^ик, tk) m_
(15.52)
П
Произведение т2 [дР/дя* (Г)] [9^(Г)/Зд: ;ffc+1], как показано в
г=1
работе [15.15], совпадает с решением следующей системы диф¬
ференциальных уравнений в узлах интерполяции:
771
Pi = — 2 y^.PJ (г = 1,..., n) (15.53)
3=1 ‘г
с граничными условиями
= (15.54)
так что
= «<'*>• <15-55>
Последний факт легко усмотреть из связи описанного здесь ме¬
тода с функциональным методом градиентного спуска в про¬
странстве управлений. Выпишем, основываясь на результатах
§ 2 главы 14, вариацию функционала Р, вызванную вариацией
J о] СВЕДЕНИЕ ВАРИАЦИОННЫХ ЗАДАЧ К КОНЕЧНОМЕРНЫМ 603
управляющей функции 8и:
Т п
бр= $ 2*ФбиЛ; (15-56)
О 1=1
здесь р\ (t) — решение системы уравнений (15.53) с граничными
условиями (15.54). Заменим интеграл в последней формуле сум¬
мой
п 771
6Р = т 2 2 Pi (h) (h) (15.57)
fc=0 1=1
и выпишем частную производную:
m
<15-58>
Сравнение (15.52) и (15.58) обосновывает высказанное ранее
положение (15.55).
4. Подбор недостающих начальных значений в краевой задаче.
При помощи формализма Эйлера—Лагранжа или Понтрягина
вариационная проблема редуцируется к двухточечной краевой
задаче для системы обыкновенных дифференциальных уравнений
(см. начало гл. 14 и систему (14.10)). Решения x\(t) краевой зада¬
чи (14.10) должны удовлетворять дифференциальным уравнени¬
ям, начальным и конечным условиям. Для решения проблемы
можно привлечь следующий итерационный процесс: на каждом шаге
процесса точно удовлетворяются дифференциальные уравнения
и начальные условия и от шага к шагу происходит приближе¬
ние конечных значений xL(T) к требуемым хг1.
Основу этих процессов составляет сведение краевой задачи
к задаче Коши с последующим подбором недостающих начальных
условий по какому-либо алгоритму. В конечном счете проблема
приводится к решению системы алгебраических уравнений.
Каждому набору недостающих начальных значений xi+i (0), ...
- • ха (0) (см. (14.10)) соответствуют определенные конечные
значения Xj (Т) (2/= п — I). Будем подбирать недостающие на¬
чальные значения, чтобы удовлетворить конечным условиям.
Образуем разности — невязки между получающимися в конце
интервала значениями функций Xj (Т) и требуемыми я;1:
'Г; fen) = Xj (Т) — Xji (г = I + 1, ..п; 2/ = re — I). (15.59)
Решение проблемы состоит в подборе таких значений хг^ (0),..
• . . , хп (0), которые обращают в нуль все невязки Wj, т. о.
в решении системы алгебраических уравнений, заданных.
604
КОНЕЧНОМЕРНЫЕ ЧИСЛЕННЫЕ МЕТОДЫ
[ГЛ. 15
неявным образом:
= 0 (Z = Z + 1, . . ., тг; 2/ = n—l). (15.60)
Для применения того или иного численного метода решения
системы алгебраических уравнений необходимо вычислять произ¬
водные dWj/dXiо = dxj (T)/dxi0. Это можно сделать, во-первых,
применяя формулы численного дифференцирования и, во-вторых,
интегрируя систему уравнений в вариациях (см. (14.10))
совместно с дифференциальными уравнениями (14.10).
Краевые условия исходной задачи (14.10), данные в простей¬
шей форме, могут быть заменены на общие
Представленные в такой форме краевые условия не нарушают
подхода к краевой задаче как к системе алгебраических уравне¬
ний, ибо, добавив к п связям (15.63) еще п связей, получающихся
как следствие процесса интегрирования дифференциальных урав¬
нений (здесь каждому набору начальных значений xi0 отвечают
свои конечные х71), получим замкнутую алгебраическую систему
2п уравнений относительно 2п неизвестных. Если конец t = Т
интервала изменения аргумента неизвестен, то к связям (15.63)
добавляется условие, определяющее его.
Чтобы решить систему алгебраических уравнений, можно
воспользоваться, например, градиентным методом или методом
Ньютона (см. § 1 настоящей главы). Если задача содержит управ¬
ляющие параметры, которые надлежит определить из условия
экстремума функции конечных координат и этих параметров, то
уместно воспользоваться одной из модификаций градиентного
метода, представленных в § 1 настоящей главы.
Описанные в этом пункте приемы решения краевых задач
нашли применение в ряде работ по ракетодинамике [15.4, 15.8,
15.9, 15.16—15.23 и др.]. В этих работах вариационные проблемы:
сводились к решению краевых задач для систем уравнений, со¬
ставленных из уравнений для фазовых координат и уравнений
для импульсов (множителей Лагранжа); оптимальные управления
выражены через импульсы и фазовые координаты. Начальные и
п
п; к = 1, . .п) (15.61)
с начальными условиями
(15.62)
% (аЧо> ха) = 0 (i, j, к = I, . . и). (15.63)
§ 2] СВЕДЕНИЕ ВАРИАЦИОННЫХ ЗАДАЧ К КОНЕЧНОМЕРНЫМ 605
конечные значения фазовых координат (физические координаты и
скорости в задачах ракетодинамики), как правило, заданы и
требуется определить такие недостающие начальные значения
импульсов, которые обеспечивают попадание траектории в за¬
данную точку фазового пространства.
В работах [15.8, 15.16—15.19, 15.22, 15.23] подбор недостаю¬
щих начальных значений организован по методу Ньютона, в статье
[15.8] проведен сравнительный анализ методов Ньютона и гра¬
диентного; градиентный метод для нахождения оптимальных
управляющих параметров и одновременного удовлетворения крае¬
вых условий описан в [15.4].
ПРИЛОЖЕНИЕ
ОПИСАНИЕ ДИНАМИЧЕСКИХ МАНЕВРОВ
В приложении собраны системы 'дифференциальных уравне¬
ний и граничных условий, описывающие следующие основные
динамические маневры, характерные для двигателей малой тяги:
межпланетный перелет (§ 2), удержание спутника в заданном ша¬
ровом слое, поворот плоскости орбиты спутника (§ 3). Вместе
с указанными приведены соответствующие модельные маневры.
Описанию маневров предпослан параграф, в котором приведены
различные формы уравнений движения и даны соотношения для
перехода от одних переменных к другим.
§ 1. ФОРМЫ УРАВНЕНИЙ ДВИЖЕНИЯ
1. Уравнения движения в центральном поле. В прямоуголь¬
ной инерциальной системе координат х, у, z с началом в гравита¬
ционном центре уравнения движения имеют вид
х = ах — кх / г3,
у = ау— ку / г3,
z = az — kz / г3
(r=K^ + J/2 + z2))
(П.1)
где ах, Оу, az — проекции вектора реактивного ускорения на
оси системы, к = /Ж — гравитационная постоянная (произве¬
дение универсальной гравитационной постоянной / на массу
центрального тела Ж). Выберем характерное расстояние
за характерные время скорость ускорение g^ примем сле¬
дующие:
i, = rV!, р, = g. = K2- (п.;2>
Эти величины имеют такой физический смысл: 2я^ — период
обращения по круговой орбите радиуса г#, v# — модуль скоро¬
сти движения по орбите, — ускорение от гравитационного
центра на расстоянии г#. Если z^, g^ взять за едини¬
цы измерения линейного расстояния, времени, скорости и ус¬
корения, то уравнения (П.1), записанные в соответствующих
g !] ФОРМЫ УРАВНЕНИЙ ДВИЖЕНИЯ 607
безразмерных переменных, не будут содержать параметра к:
х=ах—х/г2, у = ау — у } г3, z= az — z/r3. (П.З)
Для безразмерных переменных сохранены прежние обозна¬
чения. Дальнейшее изложение в настоящем пункте будет прове¬
дено в принятых безразмерных переменных.
Рис. П.1. Прямоугольная и сферические Рис. П.2. Полярная система коор-
системы координат. динат.
Перейдем к сферическим координатам г, ср, 0; связь между
ними и декартовыми координатами дается формулами (см. также
рис. П.1)
х = г cos 0 cos ф, у = г cos 0 sin ф, z = г sin 0. (П.4)
Уравнения движения в сферических координатах имеют вид
г — гф2 cos20— r02 + 1 / г2 = аг, )
г соэ0ф + 2гфсоз0 — 2T4p0sin 0 = аф, ( (П. 5)
г0 + 2г 0 + гф2 sin 0 cos 0 = ав. '
Проекции реактивного ускорения ат, аф, а& выражаются череа
ах, ау, az следующим образом:
ат = ах cos 0 cos ф -)- а„ cos 0 sin ф -\- az sin 0, 1
аф = — ах sin ф + аУ c°s Ф, 1 (П. 6)
ае = ах sin 0 cos ф -f av sin 0 sin ф — az cos 0. I
608 ОПИСАНИЕ ДИНАМИЧЕСКИХ МАНЕВРОВ
Частным случаем системы (П.5) является система, описываю-
щая плоское движение (0 = 0, ае = 0):
1/Л1 (П. 7,
гср = аф — 2гф. J
Введем компоненты скоростей в полярных координатах г, ф
(рис. П.2): vr = г — радиальная скорость, уф = гф — транс-
версальная скорость. Тогда система (П.7) может быть записана
так:
г = Vr, )
ri=v j (П_8)
Vr = ar + Vv/r — 1 / г2, j
— аф — vrv<p /г. J
Если ускорения аг, аф не зависят от t и ф, то порядок послед¬
ней системы может быть понижен вдвое:
Vrv'r = ar + / г — 1 / г2, vrv'\= аф — urv9 /г; (П. 9)
здесь штрихи обозначают дифференцирование по г.
Функции t (г) и ф (г) находятся после интегрирования системы
(П.9) из дифференциальных уравнений
1 , V<? (Г) /ТТ .л,
t = —--в ф = . (II. 10)
vr (г) * Y rvr (г) 4 '
При отсутствии реактивных ускорений система (П.9), равно
как и (П.8), имеет два^ хорошо известных интеграла: интеграл
энергии
Я=4(^ + ^)-| (П. 11)
и интеграл момента количества движения
М = уф г. (П.12)
Последние могут быть использованы в качестве искомых функ¬
ций в уравнениях (П.9) вместо vr, vф:
Е’ = 1 (arvr + avvv), М'= °-f. (П. 13)
иг ит
Входящие в правые части уравнений (11.13) функции vr, ьф
должны быть выражены через г, Е, М из (II. 11), (П. 12).
Проекции скоростей vr, аф и ускорений аГ1 аф могут быть
записаны через модули скорости v и ускорения а и углы, опре-
§ и
ФОРМЫ УРАВНЕНИЙ ДВИЖЕНИЯ
609
деляющие направления векторов v, а (рис. 11.2): д — угол между
вектором скорости и перпендикуляром к радиусу-вектору точки
в сторону положительного вращения последнего, у — угол между
вектором возмущающего ускорения и вектором скорости. Пра¬
вые частя уравнений (П. 13) заменятся на следующие:
jj, a cos у
sin г)
М'
ar cos
v
' + т)
sin $
(Г1.14)
В этих переменных система (П.8) трансформируется в такую:
г = v sin Ф,
rep = v cos ft, (П. 15)
v = a cos у — sin Ф / г2,
vft = a sin у + (г;21 г — 1 / r2) cos
Если в последних уравнениях вместо независимого перемен¬
ного t ввести s — длину дуги траектории (ds2 = dr2 + r2diр2 =
= v2dt2), то получим следующую систему:
dr
ds
chр_
ds
dv 1
v ~r = a cosr г sim
as- * г2
= sin d,
= cos d,
\
(П. 16)
) . | / 272 1 \ о
._ = asinT + (7_-jcos#.
В терминах независимого переменного ф система (П.15) примет
вид
= г tg д,
с/ф & ’
dt
с/ф
27 COS Ф dv
(П.17)
— = a cos у
с/ф 1
— Sin ф,
272 COS Ф с/ф
Г с/ф
= a sin Т + (“ ~г) cos
Обратимся к исходной системе (П.7),* описывающей плоское
движение в полярных координатах, и выпишем дифференциаль¬
ное уравнение орбиты г (ф). С этой целью введем следующие
замены:
г = ±, = (П.18,
39 Механика полета
610
ОПИСАНИЕ ДИНАМИЧЕСКИХ МАНЕВРОВ
(здесь при замене аргумента t на аргумент ср, как и ранее, пред¬
полагается, что проекции возмущающего ускорения не зависят
от t). Система (П.7) станет следующей:
d-и 1 (* ar acp du
с/ф2 ' U М'1 V и- и- с/ф
Время t может быть найдено по известным функциям и (ср),
М (ср) из дифференциального уравнения:
dt _ 1
dcp ~ М (ф) и1 (ф)
(П. 20)
Если возмущающих ускорений нет (аг = 0, аф = 0), то ре¬
шение системы (П. 19) легко находится:
М = const,
и = А/2 ( и71
M*j
пли, возвращаясь к переменному г,
Р
г =
1 + В cos V *
)сов(ф — фя), (П. 21)
(П. 22)
обнаруживаем, что орбита г (v) — коническое сечение с параме¬
тром р и эксцентриситетом е.
В формулах (П.21) и
(П. 22) введены следующие
обозначения: р = М2 — фо¬
кальный параметр коническо¬
го сечения, е = М2ип— 1 =
= М2/гл—1 = УГ+1Ш*Ё —
эксцентриситет конического
сечения (е = 0 — окруж¬
ность, 1 е 0 — эллипс,
8 — 1 — парабола, е 1 —
гипербола), гя, ф* — радиаль¬
ное и угловое расстояния
перигелия, v = ф — ф^ —
истинная аномалия — угло¬
вое расстояние, отсчитывае¬
мое от направления F±n (ось
апсид).
На рис. П. 3 приведена ор¬
бита — эллипс, в одном из фо¬
кусов которого/7!находится начало координат — гравитационный
центр. Большая ось эллипса ал соединяет апсиды: а — афелий,
л — перигелий; длина большой полуоси А, длина малой полуоси
В, расстояние от фокуса до центра эллипса С связано следующими
Рис. П.З. Элементы, определяющие эллипти¬
ческую орбиту на плоскости.
§ 1] ФОРМЫ УРАВНЕНИЙ ДВИЖЕНИЯ
соотношениями с параметром р и эксцентриситетом е:
А =
1 — е-
В =
С =
ре
1 — е-'
611
(П. 23)
Таким образом, в отсутствие возмущающих ускорений система
(П.19) имеет в качестве постоянных интегрирования величины
гп, фя, М или произвольную их комбинацию. При аг ф 0, аф ф О
эти величины не являются постоянными. Выпишем дифферен¬
циальные уравнения, определяющие фя (ф), М (ф), S (ф) = ип—М~2
в зависимости от аг, аф.
Введем новые функции: w = duldy, р = М2\ после этого си¬
стема (П. 19) примет вид
da dw . 1 ат au>w dp 2а
= W, -j— = —м Н ^ -Цг , -у- = —(П. 24)
с/ф dq> Р ри- ри3 с/ф a3 v '
Представим функции и, м; следующим образом (ср. (Г1.21)):
и = — + s cos (ф — фя), w = —5 sin (ф — фя) (П. 25)
(по поводу представления функций и, w см. работы [П.1, П.2]);
тогда получим систему дифференциальных уравнений для 5,
Ф*. Р
+ •
ds ar sin v
dy pN-
<*Фя arcosv
с/ф spN2
dp _ 2аф
t/ф = W
2аф cos v
"^W2
2аф sin v
sp2Ns
a^s sin2 v
(П. 26)
(v = ф — фя, N= — + s cos (ф — cpj).
Если вместо представления (П.25) избрать такое [П.З, П.4]:
и> = -|, (П. 27)
то система уравнений примет вид
1 I Q
и — — -| ,
Р Р
612
ОПИСАНИЕ ДИНАМИЧЕСКИХ МАНЕВРОВ
При ат = 0, йф ее 0 из последней системы получаются урав¬
нения кеплерова невозмущенного движения в форме Гамильтона.
Системы (11.26), (11.28) называются системами в оскулирующих
переменных, т. е. таких переменных, которые в отсутствие воз¬
мущений (аг = 0, аф = 0) становятся постоянными, любая комби¬
нация параметров S, сря, р или Q,L,p также обладает этим
свойством. Выбор определенной системы оскулирующих пара¬
метров зависит от характера возмущающих ускорений.
Приведение уравнений движения в центральном ноле при
наличии возмущающих ускорений к уравнениям в оскулирую¬
щих переменных является стандартной операцией, давно применяе¬
мой в небесной механике. Для описания пространственных манев¬
ров нам понадобится система в оскулирующих переменных, опре¬
деляющая пространственное движение точки. Чтобы не прибегать
к громоздкому выводу, мы опишем эту операцию в общих чертах
и в заключение приведем окончательные формулы (см., например,
[П.5]). Вывод этих формул можно найти в учебниках и моногра¬
фиях [П.6—П.13].
За исходную примем систему (П.З) дифференциальных урав¬
нений движения в прямоугольных координатах. Три уравнения
второго порядка (П.З) могут быть преобразованы в систему
шести уравнений первого порядка:
Xi= Xi(xj) + d{ (i, / = 1,..., 6), (П.29)
где
Xi = X, Хо — Xj х3 = у, х4 = у, Хъ = Z, Х6 = Z,
хч = Х2( Хг = —£ , Хз = *4. *4 = - 7Т, *' = -%, ,
d 1 == 0, #2 —~ а3 —~ 9, CL^ — O']/> О5 — 0, CIq = &2
(г = Y*l+ xl + х\)-
(П. 30)
Если aL = 0 (i = 2, 4, 6), то уравнения (П.30) опреде¬
ляют движение в центральном поле и, как известно, могут
быть проинтегрированы в конечном виде. Пусть начальные усло¬
вия для системы (Г1.30) имеют вид
*t(0) = U (Pit • . Рб) (i = 1, . . 6), (П.31)
где pi — совокупность орбитальных параметров в задаче двух
тел. Решение уравнений (П.30) в отсутствие возмущающих уско¬
рений находится в виде
Xi= Fi (Pi, • • •. Ре. 0 (Fi (Pi. • • •> Ре. 0) = h (Pi, • • Ре). (П.32)
При наличии возмущающих сил орбитальные параметры
Ри . . ., р6 могут рассматриваться как новая совокупность пере-
ФОРМЫ УРАВНЕНИЙ ДВИЖЕНИЯ
613
менных, заменяющая старые переменные х-г по формулам (П.32).
Выпишем дифференциальные уравнения для рг, . . ., рв — оску-
лирующих переменных; с этой целью возьмем полные производ¬
ные от х\, представленных в виде (П.32):
*‘ = ‘ да-»»
3=1 п
В силу определения оскулирующих переменных
= Хй (П. 34)
поэтому
(П. 35)
Последняя система является системой в оскулирующих пере¬
менных; она определяет изменение орбитальных элементов при на¬
личии возмущающих ускорений. Отметим, что уравнения (П.35)
линейные относительно производных dpj/dt, это позволяет вы¬
разить dpjldt через возмущающие ускорения ах\
6
5 = 2 Ая (Pi рв, t)ai (/ = 1 6). (П. 36)
1=1
614
ОПИСАНИЕ ДИНАМИЧЕСКИХ МАНЕВРОВ
Рассмотрим в качестве орбитальных следующий набор пара¬
метров (рис. П.4): длина большой полуоси А и эксцентриситет е,
определяющие геометрию эллиптической орбиты; наклонение i
и долгота восходящего узла Q, определяющие ориентацию плос¬
кости орбиты; аргумент фл, отсчитываемый от линии узлов, и вре¬
мя прохождения Тп перигея, определяющие орбиту в ее плоскости.
Вектор возмущающего ускорения можно разложить по трем ор¬
тогональным направлениям: перпендикулярному к мгновенной
плоскости орбиты ан, радиальному яд, лежащему в плоскости
мгновенной орбиты, и перпендикулярному к радиусу-вектору
Яф. Дифференциальные уравнения для оскулирующих переменных
А, е, i, Q, фл, т = — пТп имеют вид:
dA 2е sin v . 2А У1 _ е2
&R Н —
dt. пyi _62
\f i — е2 si
7Га
di _ г cos (v -f- Ф-.)
dt
dz У1 — e2sinv . V" 1—e2 f Ap
dt = Va a« “Г ~r e®’
П
л2 у\ — E-
' UN,
dQ r sin (v -|- <p_)
aNi
dt
n A- Y1 — e“ An i
Y1—e2cosv ]4l
aR H ^— sin v 1 + Д ®Ф
dt //Ae nAz \ Pi
-YM i - e2) sin (v+
dt 1/2/* 1 — s2 \ 1 — 82 (. r \
cos v aB- —j— smv 1 + — аФ.
нД \ A 8 / яДв 1 \ p
(П. 37)
Здесь n = A~z‘2 — средняя угловая скорость движения (без¬
размерная), р = А (1 — е2) — фокальный параметр, г =
= р (1+е cos v)“l — уравнение оскулирующего эллипса, v —
истинная аномалия. Система уравнений (П. 37) должна быть
дополнена соотношением, определяющим скорость изменения
истинной аномалии,
dv (1 — е2) rf(Pя . dQ
V
dt ^ ~dr — COSi ft," Д-38)
Как видно из уравнений (11.37), (П.38), приведенная здесь
система орбитальных параметров теряет смысл при значениях
эксцентриситета и наклонения, равных нулю, и при значении
эксцентриситета, равном единице. В этих точках правые части
некоторых уравнений не определены или обращаются в бесконеч¬
ность. В самом деле, положение перигелия на круговой орбите
(е = 0) или положение линии узлов при совпадении фиксиро-
§ 1]
ФОРМЫ УРАВНЕНИЙ ДВИЖЕНИЯ
615
е cos — ком-
уравнения для
ванной и орбитальной плоскостей (i = 0) неопределенны. Это
обстоятельство ограничивает область применимости описанной
системы орбитальных параметров, например для численного
интегрирования, и является причиной поисков других, более
подходящих систем. В частности, чтобы исключить неприятности,
связанные с вырождением орбиты в круговую (е = 0), вводят
вместо параметров е, ср^ их комбинации с sin ср*
поненты вектора Лапласа. Дифференциальные
этих комбинаций не содержат
е в знаменателе (ср. (П.26).
(П.28)).
Также свободной от ука¬
занных особенностей являет¬
ся система орбитальных па¬
раметров, предложенная в
[П.14]. Систему составляют
два вектора: вектор момента
количества движения и век¬
тор Лапласа е, направленный
от центра к перигелию и по
модулю равный эксцентриси¬
тету в. Автор [П.13] исполь¬
зовал для исследования око-
локруговых орбит с малым
наклонением в качестве оску-
лирующих переменных на¬
чальные значения коорди¬
нат и скоростей. Эти переменные были применены в [П.16] для
произвольных орбит.
Для ряда пространственных задач оказывается целесообраз¬
ным использование системы смешанных переменных: часть пере¬
менных — полярные координаты, другая часть — оскулирую-
щие переменные. Удобная для анализа возмущенных движений
система пространственных переменных приведена в работах
1П.17, П.18]. Как и ранее, здесь выделяются три ортогональных
направления, берущих начало в гравитационном центре (рис. П.5):
1 r ~ орг вдоль радиуса-вектора движущейся точки, 1Ф — орт
вдоль перпендикуляра к радиусу-вектору в мгновенной плоско¬
сти орбиты, ljv — орт, направленный перпендикулярно к мгно¬
венной плоскости орбиты.
Обозначим через сод, соФ, соде проекции угловой скорости
системы координат R, Ф, N, связанной с точкой, которая движет¬
ся относительно инерциальной системы х, у, z. Если положение
системы У?, Ф, N в каждый момент времени; определять углами:
Й (до лгота восходящего узла), i (наклонение), ср (угловое расстоя¬
ние движущейся точки в плоскости орбиты, отсчитанное от линии
Рис. П.5. Смешанная система координат.
616 ОПИСАНИЕ ДИНАМИЧЕСКИХ МАНЕВРОВ
узлов (см. рис. П.5)), то угловые скорости сод, соф, a>N будут
Еыражаться следующим образом:
сод = Q sin ф sin i + i cos ф,
соф — Q cos ф sin ф — i sin ф,
wiv = Ф + Q cos i.
(П.39)
Согласно определению мгновенной орбиты вектор скорости
не должен содержать составляющих, перпендикулярных к мгно¬
венной орбите, т. е.
г • 1 jv — — ™>ф = 0. (П. 40)
С учетом этого условия векторное уравнение движения
г = а — v / г3 (П. 41)
в проекциях на оси 1д, 1ф, lN имеет вид
г — rah — 1 /г2 = aR, 1
2гсодг + raN = яф, \ (ГГ. 42)
ГОО^уСОд = Я]у. /
В последних уравнениях можно произвести замену перемен¬
ных по аналогии с плоским движением. Введем и = г-1, М =
= С0]уг2 и определим угол v дифференциальным уравнением
v = cdn = М/г2. (П.43)
Тогда система (П.42) станет следующей:
cl2u 1 (i aR афс1и\ dM аф aN /rr //v
dv1 1 U M'1 \ и- и3 dv) ’ dv Mu3 ’ Mu ’ * 1 ^
Первые два уравнения с точностью до обозначений совпадают
с уравнениями плоского движения (П.19). Если компоненты
ускорения ад, яф не зависят от переменных, кроме и и v, то си¬
стема расщепляется, и первые два уравнения могут быть проин¬
тегрированы независимо от остальных.
Добавив к (П.44) дифференциальные уравнения для ортов
1ф» 1JV
d^R _ 1 _ 1 „ aN d^N _ i aN /rr /<C;N
c/v ф’ dv AT-’w3 ’ dv ~~ M-u3 ’ l5i
получим замкнутую систему уравнений.
Вместо того чтобы определять орты 1 д, 1ф, 1^ из дифферен¬
циальных уравнений (П.45), а затем находить функции й (v),
ФОРМЫ УРАВНЕНИЙ ДВИЖЕНИЯ
617
i (v), Ф (v), можно сразу прибегнуть к дифференциальным урав¬
нениям для углов (П.39). Следуя [П. 17], введем в плоскости орбиты
координаты £, г\ (см. рис. П.5), вращающиеся относительно ор¬
тов In, 1ф с угловой скоростью (Ь = ф — V. Если в выражениях
(П.39) всюду заменить угол ф на v + со, то дифференциальные
уравнения для углов
dQ
dv
di
dv
г/со
dv
9
I, СО примут вид
л7 sin(o)+v)
MW
а
Sill i
N COS (о) -f-v),
W^sin (co +V) ctg i.
M2u?
a
(П.46)
J
Эти уравнения вместе с (П.42) также замыкают систему.
2. Уравнения движения в ноле двух центров. Векторное урав¬
нение движения в произвольном гравитационном поле записыва¬
ется следующим образом:
г = a -j- Н (г, t), (П. 4/)
где H(r, t) — ускорение от
гравитационных сил. В пре¬
дыдущем пункте рассматри¬
вались уравнения движения
в поле одного гравитацион¬
ного центра
Я (г,t) = —kr/r\ (П. 48)
Теперь дадим уравнения
плоского движения в поле
двух центров: 1 и 2. Будем
считать, что гравитационный
центр 1 неподвижен и, сле¬
довательно, связанная с ним
система координат инерци-
альная, а центр 2 вращается
вокруг центра 1 с постоянной
угловой скоростью со на постоянном удалении i?0, и, соответствен¬
но, связанная с ним система координат неинерциальная.
Движение может изучаться в инерциальной (1) или неинер-
циальной (2) системах координат. Приведем обе системы урав¬
нений, записанных в единой форме (обозначения и связь между
координатами одной и другой системы понятны из рис. П.6):
Рис.П. 0. Система координат для описания
движения в поле двух центров.
618
ОПИСАНИЕ ДИНАМИЧЕСКИХ МАНЕВРОВ
здесь — гравитационные постоянные центров 1 и 2, а
3. Уравнения движения в модельных полях. В качестве мо¬
дельных рассмотрим линеаризированное и однородное централь¬
ные поля, плоскопараллельное поле и бессиловое поле.
Пусть траектория укладывается в пределах малых угловых и
радиальных перемещений; тогда проекции ускорения, вызывае¬
мого гравитационным центром, могут быть разложены в ряд
Тейлора в окрестности некоторой характерной точки траектории,
например начальной: х0, у0, z0 [П.19, П.20]. Если система коор¬
динат ориентирована так, что начальная точка расположена на
оси Ox (xQ = г0, у0 — 0, z0 = 0), то уравнения пространствен¬
ного движения при сохранении первых членов разложения про¬
екций гравитационного ускорения имеют вид
В том случае, когда перемещения x(t) — г0, у (t), z (t) малы
по сравнению с начальным удалением от центра г0, так что
уместно ограничиться моделью плоскопараллельного поля:
Наконец, при условии, что величина реактивного ускорения
намного превышает величину гравитационного ускорения, мож¬
но исключить последнее из уравнений движения (модель бесси-
лового поля)
ф1 — ^1 (tit, ф2 — Х|)*2 + (tit у
а*1 = "х cos Сф2 —яЫ»
;,‘2
к >
Ti = -f-sin(ip2 —api),
ч
9*2 = jk COS ар, — ~ cos (op, — opx),
■0 I
(71.50)
•u 1
(IT. 51)
\&x — £ol 2?o 11 — dr0\, I av I >> £o | y/r01, az >> g01 z/r01,
x = ax — g0, у = a,„ z = az.
(П.52)
i = a.
(17.53)
Если при движении в центральном поле модуль радиуса-век¬
тора изменяется мало (траектория заключена в узком шаровом
ME >KJ.IJ1 АНЕ Til ЫЙ ПК РЕ Л Е Т
G19
слое), то справедлива модель однородного центрального поля
[П.21, П.22], векторное уравнение движения в этом случае
имеет вид
г = а — со2г, (П. 54)
где to2 - gjrt = к/rl .
§ 2. МЕЖПЛАНЕТНЫЙ ПЕРЕЛЕТ
1. Разбиение межпланетного перелета на элементарные ма¬
невры. Траектория межпланетного перелета с двигателем малой
тяги содержит следующие этапы (рис. П.7): разгон с начальной
орбиты в окрестности планеты старта (обозначается индексом
+ 1), межорбитальный перелет в поле Солнца (индекс 1), тор¬
можение в окрестности планеты назначения (индекс — 2), на
обратном перелете повторя¬
ются аналогичные же этапы
(обозначаются индексами 4-2,
2 и —1 соответственно).
Можно выделить два ха¬
рактерных участка траекто¬
рии межпланетного перелета:
участок движения в окрест¬
ности планеты и участок дви¬
жения в поле Солнца. Оста¬
ваясь в рамках задачи двух
тел, будем предполагать, что
гравитационное поле на каж¬
дом из характерных участков
образуется одним центром:
планетой или Солнцем соот¬
ветственно.
В этой постановке обычно
считается, что участок дви¬
жения в окрестности планеты
простирается от начальной
орбиты до точки, где дос¬
тигается нулевая полная энергия (параболическая скорость),
а участок межорбитального перелета начинается в фиксиро¬
ванной точке одной гелиоцентрической орбиты и заканчива¬
ется в фиксированной точке второй гелиоцентрической орби¬
ты; компоненты скорости в начальной точке первого маневра и в
начальной и конечной точках второго маневра совпадают с соот¬
ветствующими проекциями вектора орбитальной скорости.
Рис. П. 7.
Схема межпланетного
с возвращением.
перелета
620
ОПИСАНИЕ ДИНАМИЧЕСКИХ МАНЕВРОВ
В настоящем параграфе будем рассматривать только движение
в одной плоскости, игнорируя третью компоненту. Вопрос сты¬
ковки участков межпланетного перелета здесь также не рассма¬
тривается. Основанием для этого является оценка, указывающая
на то, что положение точки сопряжения участков слабо влияет на
энергетические затраты.
Согласно принятым упрощениям оба элементарных маневра,
составляющие межпланетный перелет: набор нулевой энергии
(или иначе разгон до параболической скорости) и межорбиталь¬
ный перелет описываются системой уравнений в центральном
поле (П.8) или (П.З) (последняя без третьего уравнения: z = (К
аг = 0).
Краевые условия к системе (П.З) имеют вид:
для первого элементарного маневра
г (0) = 1, ср (0) = 0, иг (0) = и пи уФ(0) = уф0,
Е (Т) =- i/а IvJ. (Т) + v% (Т)] — i / г (Т) — 0;
для второго элементарного маневра
7-(0) = 1, Ф(0) = 0, уг(0) = у,,„ уф (0) = yv0, 1 m 56)
r{T) = т-i, ф(Г) = фь vr (Т) — уг1, уФ (Т) = уф1. )
Здесь в обоих случаях за характерный линейный размер гш взят
начальный радиус (см. (П.2)); поэтому r(0) = 1; положение си-
стемы координат определено тем, что точка старта лежит на оси
абсцисс: ф (0) = 0.
Если начальная орбита первого маневра и начальная и конеч¬
ная орбиты второго маневра круговые, то условия (П.55), (П.56)
записываются следующим образом:
для набора нулевой энергии
г( 0)^1, ф(0) = 0, уг(0) = 0, уф(0)=1,
Е(Т) - Vs Ivf (Т) + уз (7’)] — [ I г (Т) — 0;
для межорбитального перелета
г(0) = 1, Ф(0) = 0, уг(0) = 0, Уф (0) = 1, ]
г(Т) = гь Ф (Т) = ф1, yr (Т) = 0, у, (Т) = { (П- 58)
Краевые условия для уравнений в прямоугольных коорди¬
натах (П.З) получаются по формулам перехода от полярной си¬
стемы к прямоугольной (ср. (П.4)):
х = г cos ф, у = г sin ф; и = vr cos ф — уф sin ф,
v = vr sin ф + Уф cos ф. (П.59)
j (П. 57)
(П. 55)
ME Ж J1ЛАНЕТ11:1,1 LI ПЕ PE ЛЕТ
021
2. Межпланетный перелет e возвращенном. Между кинема¬
тическими параметрами отдельных этапов перелета существует
связь, обязанная условию возвращения на планету старта.
Для простоты заменим области влияния планет точками на
их орбитах; тогда в системе координат, связанной с Солнцем,
траектории космического аппарата в окрестностях планет будут
неразличимы с орбитами планет.
Выделим из траектории межпланетного перелета с возвраще¬
нием ту часть, которая лежит вне орбиты старта; сюда входят:
перелет с орбиты 1 на орбиту 2, движение по орбите 2 вместе с
планетой и обратный перелет с орбиты 2 на орбиту 1. Обозначим
через 7\,ф1? Г2, ф2 времена и угловые перемещения межорбиталь-
ных перелетов (индекс 1—с орбиты 1 на орбиту 2, индекс 2 —
с орбиты 2 на орбиту 1 (рис. П.7), через Тш — время пребывания
на орбите 2 (оно складывается из времен торможения, разгона,
а также пассивного ожидания у планеты назначения).
Из равенства угловых перемещений планеты старта и косми¬
ческого аппарата следует связь между параметрами 7\, фX,7V Фз»
считая орбиты 1 и 2 круговыми, получаем
= I ф ! + ф2 — (Т3 + Т2) + 2шт]/(1 —со2)> (П.60)
где оз 2 — угловая скорость обращения планеты 2 по круговой
орбите вокруг Солнца (соi = 1), п — целое число оборотов пла¬
неты 1 (п = 0, 1, 2, . . .), знак плюс соответствует оз2 <Ccoi, знак
минус — со 2 > оз.
Если орбиты 1 и 2 не круговые, то в формуле (П. 60) появят¬
ся интегралы; для учета размеров областей влияния планет не¬
обходимо при составлении равенства угловых перемещений до¬
бавить угловые расстояния между точками входа в область
влияния и выхода из нее (см. [П.23]).
В краевой задаче, которая формулируется для выделенной
части межпланетного перелета, обычно считаются заданными
время То, пребывания на орбите 2 и время Тв пребывания вне
орбиты 1: Та = Г3 + Го + Т2. Они определяют угловые пере¬
мещения фг, ф2 и времена Тъ Т2 в сумме:
Фг + Ф2 — Та —аз2Лз + 2шт; -j~ Т2 — Та — То,,
а не по отдельности, как считается в краевых условиях (П.56).
При круговых орбитах 1 и 2 краевые условия для межорби-
тальных перелетов туда и обратно запишутся так:
перелет с орбиты 1 на орбиту 2
г (0) = 1 > ф (0) = 0, vr (0) = 0, уф(0)=т. 1, |
г(Т1) = г1, ф(7’1) = ф1, МГх) = 0, (74) = Д ч J ( Lbl)
622
ОПИСАНИЕ ДИНАМИЧЕСКИХ МАНЕВРОВ
перелет с орбиты 2 на орбиту 1
r {Тг 4- 7"^) = 7Д, ср (7Т -f- Ты) — cpi -j- J'coC02i 1
(Ti + Т») = о, Уф (Тг + T„) = г~'\ (П. 62)
г(Г0) = 1, <р(Та) = Тазр2пя, и г (Т q) — О, г;ф (Т а) = 1 J
(в этих формулах величины ф1? 7\ не определены).
Вместо параметров ф1? 7\ (угловое перемещение и продолжи¬
тельность перелета), фигурирующих здесь в краевых условиях
для межорбитального перелета, могут быть выбраны параметры
t0, 7\ (дата старта, продолжительность перелета). Связь между
этими двумя парами получается из условия равенства в момент
встречи угловых расстояний космического аппарата и планеты
назначения
Если орбиты 1 и 2 круговые, а дата старта t0 отсчитывается
от момента противостояния планет 1 и 2, то формула перехода
будет следующей:
Ф1 = “Ь Тi — со2^о i (п — 0, 1, 2, . . .). (П.63)
Параметры t0, 7Т оказываются более удобными для расчетов,
в которых учитываются реальные положения планет на их ор-
битах.
3. Модельные маневры. В настоящем пункте описываются два
примера одномерных движений в бессиловом поле: набор задан¬
ного модуля скорости иг за заданное время Т и перемещение между
двумя точками покоя, отстоящими одна от другой на расстоянии
Z, за время Т.
Эти маневры отражают характерные черты маневров в цент¬
ральном поле: первый моделирует маневр медленного набора
нулевой энергии с круговой начальной орбиты*- (см. (П.8),
(П.57)), второй — участок быстрого межорбитального перелета
(см. (П.8), (П.58)).
Уравнения движения и краевые условия для задачи набора
заданного модуля скорости имеют вид
й = ае; и (0) = 0, и (Т) = uv (П.64)
То же самое для задачи перелета между двумя положениями
покоя:
х = и, й = ае; х (0) = 0, и (0) = 0, х (Т) = I, и (Т) = 0. (П.65)
В формулах (П.64), (П.65) величина а — модуль реактивного
ускорения, е = + 1 — направление вектора тяги.
Э J Ю Л ЮIЦ J11 011 У TIII1К A
623
§ 3. ЭВОЛЮЦИИ СПУТНИКА
1. Удержание спутника в заданном шаровом слое. Спутник вы¬
водится на круговую орбиту, расположенную в верхних слоях
атмосферы. Гравитационные силы от притягивающего тела дают
периодическую составляющую движения, действие аэродинами¬
ческого сопротивления приводит к вековому уходу от начальной
орбиты. Возникает задача о такой компенсации силы сопротив¬
ления, чтобы спутник в течение заданного времени оставался в
пределах шарового слоя, максимальный и минимальный радиусы
которого заданы (см. работы [П.13, П.24, П.25]).
Движение в гравитационном поле при наличии сопротивления
описывается следующей системой дифференциальных уравнений
первого порядка:
г — v, v -- ае -|- К — gF / G; (П. 66)
здесь в отличие от предыдущего добавлен член gF/G, учитываю¬
щий аэродинамическое торможение; а — модуль реактивного
ускорения, е — единичный вектор ориентации тяги.
Выберем инерциальную прямоугольную систему координат
Oxyz: плоскость хОу совпадает с плоскостью экватора, ось Ох
направлена в точку весеннего равноденствия, ось Oz — к север¬
ному полюсу, а ось Оу дополняет их до правой тройки.
Составляющие гравитационного ускорения К определяются
потенциалом U притягивающего тела — Земли: К = dU/d г.
Принимая в расчет первые две гармоники потенциала сплющен¬
ного сфероида, имеем
и (х, у, Z) = ± [1 + 1(1_з£)] (г = Y*? + У2 + Z2); (П. 07)
величины к, 6 = -у Rl приведены в главе 1 (1.9).
Сила аэродинамического сопротивления F, которую испыты¬
вает аппарат в потоке, набегающем с относительной скоростью
В, равна
F = 1/2 с^рЭЗБ, (П. 68)
где сх — коэффициент аэродинамического сопротивления £ —
характерная площадь аппарата, р — плотность атмосферы.
Если атмосфера покоится, то скорость В совпадает со ско¬
ростью у аппарата в инерциальной системе Oxyz; при учете
вращения атмосферы с угловой скоростью j (0, 0, ;z), равной
скорости вращения Земли, к у добавляется векторное произве¬
дение г х /
В - у + г X j.
(П. 69)
624
ОПИСАНИЕ ДИНАМИЧЕСКИХ МАНЕВРОВ
Проекции силы сопротивления па оси инерциальной системы
координат выражаются следующим образом:
Величина jz считается положительной в формулах (П.70), если
вектор скорости аппарата v и вектор скорости потока гх j состав¬
ляют угол, меньший л/2 (спутник запущен по вращению Земли).
Плотность р, входящая в выражения (П.68), (П.70), является
функцией не только высоты над поверхностью Земли, но также
широты и времени года. Плотность как функция этих аргументов
дана, например, в [П.26].
Перейдем к сферической неинерциальной системе координат
г, ф, 0 (рис. П.8), экваториальная плоскость которой наклонена
на постоянный угол i к плоскости экватора и вращается с угловой
скоростью Q вокруг полярной оси Oz [П. 24]; в начальный мо¬
мент эта экваториальная плоскость совпадает с плоскостью орбиты
спутника, угол Q (t) — свободная функция, подлежащая опреде¬
лению в дальнейшем. Координаты х, у, z выражаются через г,
ф, 0, Й, i следующим образом:
х = г (cos ф cos 0 cos Q — sin ф cos 0 sin Q cos i + sin 0 sin Q sin i), \
у = r (cos ф cos 0 sin Q + sin Ф cos 9 cos Q cos i — sin 0 cos Q sin /), .
z = r (sin ф cos 0 sin i + sin 0 cos i). I
l\x — 1/2CT^pSS (x + IzU)'
ft a ~ {y 7z*^)’
Fz = 1/2 cx§p2J z
(23 = [(ж + ]zyf + (У — iz*? + z2]Vs). ■
(IT. 70)
г
Рис. 11.8. Система координат для задачи удержания спутника
в заданном шаровом слое.
(П. 71)
5 з] эволюции спутника 625
Опуская процедуру преобразования к новым переменным, при-
ведем окончательный результат:
г — г (0 -f- й cos ф sin i)~ — г [ф cos 0 + Q (cos 0 cos i —
— sin 0 sin ф sin г)]2 = — ^ [1 — 3 (sin 0 cos i +
-|- cos 0 sin гвтф)2] — x + aer,
^ {r2 cos 0 [ф cos 0 -f- Q (cos i cos 0 — sin 0 sin i sin ф)]} —
— r2Q sin i [0 sin ф — ф sin 0 cos 0 cos ф —
— Q cos ф cos 0 (sin0 cos i -j- cos 0 sin ф sin г)] =
= — ^ (sin 0 cos I -f cos 0 sin i sin ф) cos 0 sin i cos ф —
— x F’^~_cos cos ® (cos ®C( s * — s^n ® s*n Ф S*Q 01 +
+ cteф cos 0r,
ш f r~ ^ ^cos ф sin ^ 7'2^2 sin ®cos ® ^2 (sin ® cos * +
-f cos 0 sin ф sin i) (cos 0 cos i — sin 0 sin ф sin г)] +
-j- ф£2 [cos 0 (sin 0 cos i -f- cos 0 sin ф sin i) -f sin 0 (cos 0 cos i —
— sin 0 sin ф sin i)] = — ^ (sin 0 cos i + cos 0 sin ф sin i) X
X (cos 0 cos i — sin 0 sin ф sin i) —
— K 7Г~ ^ ^ 1z) cos ^ sin ^ aeQl'' I
(П.72)
Здесь даны три проекции уравнения Ньютона в безразмерной
форме: линейные расстояния отнесены к начальному радиусу г0,
время — к /г1''2, угловые скорости, в том числе /\ — к вели¬
чине /с1/2г^3/г, ускорения — к гравитационному ускорению /сг~2?
плотность — к максимальной на радиусе г0 плотности р0, коэф¬
фициент в разложении потенциала (3 — к квадрату начального ра¬
диуса г2, вес аппарата — к начальному весу G0; для безразмерных
величин сохранены старые обозначения (ср. переход от (П.1)
к (П.З)). Параметр сопротивления х выражается так:
х = gcx§ poV2Go- (П.73)
Через ег, е0 обозначаются проекции единичного вектора
направления тяги е (е2 + е2 + е\ = 1) на орты сферической
системы координат.
40 Механика полета
626
ОПИСАНИЕ ДИНАМИЧЕСКИХ МАНЕВРОВ
Начальные условия на круговой орбите в принятой системе
координат записываются следующим образом:
г (0) = 1, г (0) = 0, Ф (0) = Фо; ср (0) = 1, 0 (0) = 0 (0) =0. (П.74)
Конечные значения этих величин не определены, за исключе¬
нием радиуса г, который в конечный момент, равно как и во все
время движения, должен оставаться в пределах
J'min < г (0 < гтах (0 < t < Т). (П.75)
При дальнейшем анализе задачи ограничимся рассмотрением
больших высот, где параметр к мал; другие безразмерные пара¬
метры задачи /2, |3 имеют следующие численные значения:
U ~ 0,6 .10~\ [3 ж 0,5 Л0~3. (П.76)
Если силы от несферичности притягивающего тела, силы со¬
противления и тяги отсутствуют ((3 = к = 0, a (t) = 0) и свобод¬
ная функция Q (t) принята равной нулю: Q (t) = 0, то уравне¬
ния (П.72) описывают кеплеровскую орбиту, лежащую в эква¬
ториальной плоскости 0 = 0 системы координат г, ср, 0. В ре¬
альном движении кеплеровскую траекторию искажают малые
силы от несферичности и малые силы сопротивления.
По условиям задачи траектория движения должна быть за¬
ключена в узком шаровом слое Аг (Аг = г1Пах — rmill 1).
Поэтому функции г (£), г (t), ф (г) во все время движения должны
мало отличаться от соответствующих значений на невозмущен¬
ной круговой орбите: |г(*) — 1|<^1, |г |ф (t) —
Имея в виду этот случай, представим параметры траектории г (t)
и ф (t) следующим образом:
г (t) = 1 + g (*), ф (t) = ф0 - / + л (0, (П.77)
гДе |£(*)1^1»| 1(01^1» hi (0|<1. По величинам g, g, р
задача допускает линеаризацию.
Условие пребывания спутника в узком шаровом слое (гтач,
rmin) не накладывает физических ограничений на область изме¬
нения угла 0 (t). Однако из-за того, что в невозмущенном движе¬
нии 0 (t) = 0 и возмущающие силы реального движения малы,
можно считать на начальном этапе движения функции 0 (t) и
0 (t) малыми:
10 (t) I 1 - I о (0 I 1 при 0 < t < tv
Полагая производную свободной функции й (t) малой:
|Q(£)|^1, линеаризуем систему (П.72) по |, 1,11,0,0, й;
Э В О Л К') ЦI [ I I СII УТР [ ПК А
627
получим
I — 3g — 2т] = 2Q cos г — Зр [1 — 3 sin2 i sin2 (ф0 + £)] -j- aer, }
г| — 21 = — Q cos i — 6(3 sin2 i sin (ф0 + t) cos (ф0 + t) — [
— — /2cosi)+ ae^j 1.
0 Л- 0 = Q sin i cos (фо -f- t) — 2Q sin i sin (ф0 + 0 —
— 6(3 sin i cos i sin (ф0 -f t) — x/z ~ sin i cos (ф0 -f t) -j- ae0.
(П.78)
В этих переменных краевые условия (П.74), (П.75) запишут¬
ся так:
I (0) = £ (0) — г] (0) = т] (0) — 0 (0) = 0 (0) = 0,
Smin < l(t) < U (0 < t < T). (17.79)
В правых частях системы (П.78) сохранены члены только пер¬
вого порядка по /2; члены второго и высших порядков отброшены,
так как перед ними множителем стоит малая величина к. По
этой же причине следует оставлять только нулевой член в раз¬
ложении плотности по £, г], 0; входящая в (Г1.78) плотность р яв¬
ляется известной функцией времени, определяемой по начально]!
круговой орбите (g (t) = ц (t) = 0 (t) = 0).
Выберем свободную функцию Q (t) следующего вида (П.25]:
Q = —3(3 cos i = const (П.80)
(при этом упомянутое выше условие малости производной Q
выполняется).
Третье уравнение системы (П.78) преобразуется так:
0 -J- 0 = — х h sin i cos (фп + t) -f асв (0 (0) = 0 (0) = 0),
(П. 81)
Предположим, что составляющая тяги в направлении 0 от¬
сутствует (е{j = 0) и оценим максимальное значение угла 0, до¬
стигаемое к моменту времени t — для этого положим р (t) = 1,
G (0 =
0 (fi) = [sin Ф„ sin ti — ti sin (cp„ + fi)]. (П. 82)
Наличие смешанного члена в решении (П.82) указывает на
наличие колебаний с нарастающей амплитудой радиуса-вектора
относительно экваториальной плоскости. При £i<^1//2x угол
0! мал, и учет только линейного члена в разложении по 0 спра¬
ведлив.
Окончательно, дифференциальные уравнения и краевые ус¬
ловия, описывающие маневр удержания спутника в заданном
40*
628
ОПИСАНИЕ ДИНАМИЧЕСКИХ МАНЕВРОВ
шаровом слое, имеют вид
| _ 3£ _ 2т| = — 3(3 [1 + 2 cos'2 i - 3 sin2 i sin2 (<p0 -j- <)] + “n
ii‘ -f 2| = — 6(3 sin2 i sin (ф0 + t) cos (ф0 + t) —
— x E (1 — /zcos i) -f аеф,
ё + 0 = — x/* E sin i cos (ф0 + t) -j- aee,
1(0) = 4 (0) = -n (0) = ^ (0) = 0 (0) =0(O) = O,
Smin max
(П. 83)
Если движение спутника рассматривается в достаточно широ¬
ком диапазоне времени, то целесообразно изучать изменение
параметров g, ц, т], 0, 0 через целое число периодов 5. По про¬
шествии времени 2sn параметры |, г) станут равными:
|.= 2x(l-2/,cos0(- J ^ p_cos£2 J aejt_ ^
0 0 о
2 s- 2srt
— 2 ^ аеф cos tdt — ^ aer sin £ dt,
о о
23- ^ 2s-
|s —2/v (1 — 2/z cos i) ^ p s^n-- df — 2 ^ аеф sin tdt +
о о
2s jt
+ aer cos t dt,
о
Лз = И (1 — 2/z cos i) (3 jj — 4 ^ eft) —
0
2-s-. 2-s- 23- 2sr:
— 3 ^ cie^dt + 4 ^ 4 ^ ae? cos t dt 2
a^r sin t dt
V
0 0 0 6
(П.84)
(выражения для остальных параметров записываются аналогичным
образом; здесь они не даны, ибо в дальнейшем не понадобятся).
Члены в решении £ (£), g (£), ц (г), пропорциональные коэф¬
фициенту р, имеют осцилляционный характер и в усредненном
решении (П.84) отсутствуют. Их влияние сказывается на пове¬
дении траектории в интервале 0 ^ t ^ 2я. Если |3 5^>х, то ве¬
личины max min £ на обороте зависят в основном от (5, т. е.
толщина слоя, в пределах которого располагается траектория на
ЭВОЛЮЦИИ СПУТНИКА
629'
обороте, определяется силами от несферичности притягивающего
тела. Считается, что амплитуда колебаний радиуса на одном
обороте (п
пах тmin) укладывается в заданную толщину шаро¬
вого слоя.
2. Поворот плоскости круговой орбиты спутника поперечной
тягой. Дадим вывод дифференциальных уравнений и краевых
условий, описывающих рассматриваемый маневр, где в качестве
исходных используются уравнения в оску^лпрующих переменных.
Поперечной названа тяга, направленная перпендикулярно
к мгновенной плоскости орбиты (еще одно название — бинор¬
мальная тяга). В обозначениях, употребляемых для записи си¬
стемы (П.37), это проекция ау. Если в (П.37) аф = aR = 0, то
длина большой полуоси А, эксцентриситет е и момент прохожде¬
ния перигея Тп остаются неизменными при движении, так что
геометрия начальной орбиты сохраняется, причем, если началь¬
ная орбита круговая, то безразмерный радиус г, безразмерная
длина большой полуоси А и эксцентриситет е равны таким зна¬
чениям:
г (t) = 1, A (t) =1,е (t) = 0. (П.85)
Для описания движения остаются три уравнения:
cli dQ sin ф , . . . /л-r on\
-jj- — ае cos ф, _=а.рет, = 1 - aectg ism <р. (П. 86)
В уравнениях (П.86) приняты следующие обозначения:
aN = ае, а — модуль реактивного ускорения, е = 1 — ориен¬
тация вектора тяги относительно мгновенной орбиты (е = --1 —
по нормали, е = —1 — против нормали); <р = v — — аргу¬
мент широты, отсчитывается в мгновенной плоскости от линии
узлов.
Если начальная орбита лежит в плоскости экватора
i (0) = 0, (П.87)
то долгота восходящего узла (Q (0)) и аргумент широты (ср (0))
в начальный момент не определены по отдельности; их сумма —
широта точки старта в инерциальной системе координат задается
положением этой системы.
Примем
<р (0) + Q (0) - 0. (П.88)
В конечный момент задаются наклонение и долгота восхо¬
дящего узла
i (Т) = ils Q (Т) = Q,. (П.89)
630 ОПИСАНИЕ ДИНАМИЧЕСКИХ МАНЕВРОВ
Пусть тогда тригонометрические функции угла i
могут быть заменены в уравнениях (П.86) таким образом:
cli/dt = ае cos ф, Q — ае sin1 ф/£, ф = 1 — ае sin ф/£. (П.90)
Из (П.88), (П.90) следует:
Ф = t — Q. (П.91)
Подставляя последнее выражение в первые два уравнения
(П.90), получаем
di/dt = ае cos (t — Q), Q = ae sin (t — Q)/i. (П.92)
Введем следующие замены:
X = i sin (Q — Йх), о = i cos (Q — Qx). (П.93)
В терминах % со уравнения и краевые условия, описывающие
маневр поворота плоскости круговой орбиты, примут вид
X = ае sin (t — Qi), со = ае cos (t — Qi),
X(0) = 0, со (0) = 0, } (П. 94)
7С(Г) = 0, co(7’)=i1.
ОСНОВНЫЕ ОБОЗНАЧЕНИЯ
а — ускорение от тяги (реактивное ускорение).
А а — поправка к программе реактивного ускорения.
6а — ошибки реализации программы реактивного ускорения.
а — величина ускорения от тяги.
а'х| — компоненты вектора реактивного ускорения а в прямоугольной
системе координат {х, у, z).
яг1 — компоненты вектора реактивного ускорения а в полярной систе-
аср/ ме координат (г, ф).
%
а I — компоненты вектора реактивного ускорения в системе координат
а
«'О
П
а0 — начальное реактивное ускорение.
стоимость и удельная стоимость выполнения маневра (на единицу
полезного веса G__).
Се — затраты на выполнение маневра, не зависящие от весовых ком¬
понент аппарата.
СуД — стоимость и удельная стоимость двигателя (на едипицу веса
су (’ двигателя Gy).
С Л — стоимость и удельная стоимость запаса рабочего вещества (на
c,j J единицу начального веса рабочего вещества G^0).
Ср — коэффициент сопротивления трения, отнесенный к площади «смо¬
ченной» поверхности.
сх — коэффициент аэродинамического сопротивления.
с — коэффициент волнового сопротивления.
с* — коэффициент волнового сопротивления конуса.
с*- — коэффициент сопротивления трения,
с* — теплоемкость.
D — диаметр.
D0 — интенсивность метеорного потока.
d — расстояние между эмиттером и ускоряющим электродом ионного
движителя.
Е — энергия.
£ — полная энергия движения в гравитационном поле,
о — единичный вектор направления тяги.
в — электрический заряд частицы.
€х^ — компоненты единичного вектора направления тяги в прямоуголь-
е f ной системе координат на плоскости (е^. + еу = 1).
Сг л — компоненты единичного вектора направления тяги в сферической
системе координат (е^. + + с;} = 1).
F — вектор внешних сил, действующих на аппарат.
Fх у z — компоненты внешних сил, действующих на аппарат.
63- О СIIО В И Г Я Е О Б О 311А Ч Е ШIЯ
& — площадь сечения.
/ — универсальная гравитационная постоянная.
G — текущий вес аппарата.
G(, — вес аккумулятора энергии.
Or)
— вес аппарата до и после сброса i-и секции двигателя.
Gi \
Gn — вес энергоисточника.
Gp — вес двигательной системы.
Gq — вес системы подачи рабочего тела.
Gv — вес системы накопления рабочего тела с заборником,
— вес баков для рабочего тела.
Gy — вес реактивного движителя.
G^ — вес системы отвода энергии от аппарата.
G0 — суммарный вес полезного груза, рабочего вещества и баков
(G„ = С- + С,, (t) + Gf>
Gy — вес двигателя.
— вес двигателя на i-м участке < t < t{.
AGy — вес секции двигателя.
— суммарный вес s разно настроенных нерегулируемых движителей.
— приращение веса нерегулируемого двигателя от добавления i-ro
уровня тяги п расхода.
GtJ — текущий вес запаса рабочего тела.
G^0 — начальный вес рабочего вещества.
AGW — вес рабочего вещества, оставшегося к моменту сброса i-й секции
двигателя.
AG (t) — вес рабочего вещества, израсходованного к моменту времени t
(ДСи. (г) = с1л0 - G^ (<)>.
— вес источника мощности.
GL — полезный вес.
— полезный вес i-й ступени (сумма истинного полезного веса G2
и веса рабочего вещества AG^\ оставшегося к моменту сброса
i-й секции двигателя).
— суммарный груз, доставляемый в конечную точку траектории
за п попыток выполнения маневра.
Gg = G„ -j- G^ — суммарный вес полезной нагрузки п рабочего вещества.
G„ — вес преобразователя энергии.
G'b — суммарный вес полезного груза, запаса рабочего вещества и нс~
точника мощности (G^ = G_ + G^ (t) + Gv).
G0 — начальный вес аппарата.
— конечный вес аппарата.
g — коэффициент пропорциональности между весом и массой (грави¬
тационное ускорение на поверхности Земли).
go — гравитационное ускорение на радиусе г0.
Н — функция Гамильтона в процедуре принципа максимума.
/г — высота.
I — функционал динамической части задачи для идеального двига¬
теля ограниченной скорости истечения (интеграл по времени от
реактивного ускорения — характеристическая скорость).
/р— удельный импульс.
ОСНОВНЫЕ ОБОЗНАЧЕНИЯ
633
i — единичный вектор направления солнечного светового излучения.
i — плотность электрического тока, угол между начальным и конеч¬
ным положениями плоскости орбиты.
У — сила тока.
J — функционал динамической части задачи для идеального двига¬
теля ограниченной мощности (интеграл по времени от квадрата
реактивного ускорения).
Л/ — приращение функционала /, характеризующее затраты на кор¬
рекцию траектории.
Jа — полный функционал динамической задачи для межпланетного
перелета с возвращением (/0 = Jx + /2 + /+г + /_i + /+2 + /_2).
J-Л — величины функционала динамической задачи для перелетов между
Jo] орбитами планет туда (1) и обратно (2).
J+i)
J-А — величины функционала динамической задачи для маневров раз-
/+2| гона (+) и торможения (—) у планет старта (1) и финиша (2).
К (• • •) — корреляционная функция.
К ~т L — функционал маневра для комбинированного двигателя: идеаль¬
ный двигатель ограниченной скорости истечения + идеальный
двигатель ограниченной мощности.
к — гравитационная постоянная центрального тела (универсальная
гравитационная постоянная, умноженная на массу тела).
L — длина.
X — индуктивность.
I — расстояние между точками покоя в бессиловом поле.
М — момент количества движения.
М (. . .)—математическое ожидание (обозначается также <. . .>).
М0 — число Маха, соответствующее скорости полета.
m — масса.
N — мощность реактивной струи.
iVmax — максимальная мощность реактивной струи.
Ne — мощность, потребляемая от аккумулятора энергии.
JVj — мощность, соответствующая потерям в ионном движителе.
Nn — полная мощность, выделяемая источником энергии.
Nq — мощность системы подачи рабочего тела.
^Qv — мощность, передаваемая аппарату забираемым накопителем рабо¬
чим телом.
Nv — мощность, расходуемая накопителем рабочего вещества.
Ny — мощность, потребляемая движителем.
N£ — мощность, выделяемая системой отвода энергии.
N^ — полная мощность реактивной струи.
— полезная мощность энергоисточпика.
.V. — полезная мощность преобразователя энергии,
п — единичный вектор направления нормали к поверхности.
Р — вектор тяги.
Р — величина тяги.
Р (. . . ) — вероятность события ( . .).
р — фокальный параметр.
Pi — вспомогательная функция (импульс) в процедуре принципа мак¬
симума, соответствующая фазовой координате xi .
Q — тепловой поток.
q — массовый расход рабочего тела через движитель.
qv — расход, поступающий в накопитель (секундный приход массы
через воздухозаборник).
634
ОСНОВНЫЕ ОБОЗНАЧЕНИЯ
qр — расход массы баков.
qy — расход массы движителя.
qE — расход массы при выработке энергии.
qy. — расход массы двигателя.
gv — расход массы источника мощности.
qa — суммарный расход массы аппарата.
R — расстояние до Солнца, надежность (вероятность успешного выпол¬
нения маневра).
R* — вектор расстояния до гравитационного центра.
Ri — расстояние до гравитационного центра.
R s — радиус небесного тела.
/?Ф — средний радиус орбиты Земли.
Re — число Рейнольдса.
Ш — газовая постоянная,
г — радиус-вектор центра масс аппарата,
г — радиус в полярной системе координат.
Аг — измеренные отклонения траектории от расчетной.
6Qr — отклонения от расчетной траектории, вызванные ошибками да.
&7 т — ошибки измерений траектории.
гЛ — интенсивность солнечного светового излучения на орбите Земли.
S — площадь поверхности.
— площадь поверхности радиатора.
s — число оборотов по орбите.
s \ — безразмерные коэффициенты стоимости двигателя и запаса рабо-
чего вещества.
Т — полное время выполнения космического маневра.
Т — полное время работы двигателя.
Т„
полные времена действия соответствующих уровней
1x11 — П01
i 'J
Т I я1? . . ., Jts ступенчатого управления.
— суммарное время работы двигателя на межпланетном перелете
с возвращением (Т[х<3 = + Г[1>+1 + + Т^2 +
+ Тр.,-2).
Т — время работы двигателя на участках перелетов между орбитами
2 J планет «туда» (1) и «обратно» (2).
Т
Н', + 1
Т
1 ш-1.
т
1 Н ,+2
т
Та — суммарное время межпланетного перелета с возращением (Та
= Та -f 7^ + Г2 + Г+1 + г_х).
Тш — время пребывания в окрестности планеты назначения.
Т1\— времена перелетов между орбитами планет «туда» (1) и «обратно»
Т2) (2).
время работы двигателя на участках разгона (+) и торможения
(—) у планет старта (1) и финиша (2).
Т-1
г+2
Г-2.
времена разгона (+) и торможения (—) у планеты старта (1) и
финиша (2).
t — текущее время.
ОСНОВНЫЕ ОБОЗНАЧЕНИЯ 635
*а — текущее время работы двигателя.
Vil — текущие времена действия соответствующих уровней . . ., ns
• * Г ступенчатого управления.
t0 — дата старта, отсчитываемая от противостояния планет старта
и финиша.
U — потенциал поля тяготения.
% — напряжение (разность электрических потенциалов).
— компоненты вектора скорости v в прямоугольных системах коор¬
динат (х, у, z) и (I, ц, £).
иг — приращение модуля скорости в бессиловом поле.
V — скорость истечения реактивной струи,
v — вектор скорости центра масс аппарата.
г’Д — компоненты вектора скорости в полярный системе координат
— компоненты вектора гравитационного ускорения в прямоуголь¬
ной системе координат (х, у, z).
у I — прямоугольные координаты.
а — удельный вес источника мощности,
а* — соотношение состава топливной смеси.
Р — удельный вес аккумуляторов энергии.
— удельный вес контейнеров для рабочего тела (баков).
у — удельный вес движителя.
у. — удельный вес электростатического движителя (на единицу пло¬
щади ионного пучка).
yv — удельный вес системы накопления рабочего вещества (на [единицу
секундного прихода массы).
7х Удельный вес двигателя.
yL — удельный вес двигательной системы.
д — функция включения—выключения двигателя; обозначение пер¬
вой вариации; толщина стенок.
М — релейные функции, отвечающие за включение — выключение
* j соответствующего уровня ступенчатого управления.
Е — напряженность электрического поля.
г — отношение удельных весов движителя и энергоисточника; экс¬
центриситет.
£* — коэффициент отражения телом светового излучения.
II — напряженность магнитного поля.
г] — коэффициент полезного действия двигательной системы.
г)с — коэффициент полезного действия источника мощности, работаю-
— щего по циклу Карно.
— эффективный коэффициент полезного действия движителя
(•Пт =
r]Y — энергетический к. п. д. ионного движителя,
г) 0 — энергетический к. п. д.
г)^ — коэффициент использования рабочего вещества в движителе.
T|v — коэффициент использования мощности в движителе.
г]т — к. п. д. преобразователя энергии.
и j
л
W I
636
ОСНОВНЫЕ ОБОЗНАЧЕНИЯ
Ф — угол установки солнечного паруса, истинная аномалия.
к — коэффициент превращения материала сбрасываемых секций дви¬
гателя в рабочее вещество, отношение допустимого числа отка¬
зов А1 к максимально возможному Лтах, показатель адиабаты.
Лщах = ^тах^1 “ максимально возможное «число» отказов.
Ах = А (Т) — допустимое «число» отказов.
X — относительная скорость газового потока.
Хд — длина волны светового излучения.
Хт — постоянная распада радиоизотопов.
X* — коэффициент теплопроводности.
jll — масса элементарной частицы,
v — кинематическая вязкость.
£ — отношение веса накопителя энергии к весу энергоисточника, от¬
ношение удельных стоимостей запаса рабочего вещества и двига¬
теля.
q — радиус-вектор в транспортирующей системе координат,
р — плотность атмосферы.
— плотность распределения протонов в космическом пространстве-.
о — постоянная Стефана—Больцмана,
сг* — электропроводность.
Т — температура.
Тп — температура нагревателя.
Ts — температура поверхности небесного тела.
Ту — температура воздуха на входе в сжижительную установку.
Тт — эффективная температура.
Т0 — температура торможения газового потока.
Т* — температура радиатора.
Т0 — температура поверхности Солнца.
т — безразмерное время (отнесено к периоду обращения по начальной
орбите, деленному на 2я: т = k^r^'2 — глава 5, или к полному
времени).
т° — напряжение трения.
Ф — функционал маневра для идеального двигателя ограниченной
Фе — функционал маневра для идеального двигателя ограниченной
мощности с накопителем энергии.
Ф — полярный угол.
М — угловые перемещения перелетов между орбитами планет «туда» (1)
CP2j
и «обратно» (2).
Т — полный импульс газового потока.
Y — функционал маневра для идеального двигателя ограниченной
скорости истечения (Ч? = <Wmax).
Q — положение линии узлов.
Q0 — начальная уязвимая (в смысле матеорных пробоев) площадь
радиатора (Q0 = kS0l 0 < k ^ 1).
со — степень черноты поверхности, долгота перигея.
С0д — угол, под которым видно небесное тело.
г] > — координаты в транспортирующей системе.
• •} — уровни ступенчатого управления.
мощности ( Ф = (a/2g) J
ОСНОВНЫЕ ОБОЗНАЧЕНИЯ
637
0)2} — сРеДние угловые скорости обращения планет старта (1) и финиша
(2) вокруг Солнца.
'со0 — угол, под которым видно Солнце.
а — скорость звука,
4* — критическая скорость звука,
b — удельная потенциальная энергия.
3 — интенсивность корпускулярного излучения Солнца.
*$Ri — масса гравитационного центра,
m — масса метеорной частицы.
— удельная мощность солнечного светового излучения.
Щ — удельная мощность космического теплового излучения,
iftcj — удельная мощность корпускулярного потока от Солнца.
$ — вероятность пробоя стенки метеорными частицами,
р — давление.
Ра — световое давление.
РАб максимальное давление солнечного света на орбите Земли.
РЕ — электростатическое давление.
рн — магнитное давление.
Ph — атмосферное давление.
Рсу — давление корпускулярного потока от Солнца.
Ро — полное давление в потоке газа.
Н — вектор ускорения от гравитационных сил.
t> — объем.
4D — скорость солнечного ветра.
ЛИТЕРАТУРА
К введению и главе 1
1.1. Мещерский И. В., Работы по механике тел переменной массы.
Гостехиздат, М., 1949.
1.2. Циолковский К. Э., Исследование мировых пространств ре¬
активными приборами. Научное обозрение, № 5, М., 1903.
1.3. Циолковский К. Э., Собрание сочинений, Изд-во. АН СССР,
М., 1954.
1.4. Goddard R. Н., A method of reaching extreme altitudes. Smith¬
sonian Inst., Washington, 1919.
1.5. Цандер Ф. А., Проблема полета при помощи реактивных аппа¬
ратов. Межпланетные путешествия. Оборонгиз, М., 1961.
1.6. Oberth Н., Die rakete zu den planetenraiimen. R. Oldenbourg,
Miinchen, 1923. Русский перевод: О б e p т Г., Пути осуществления
космических полетов. Оборонгиз, М., 1947.
1.7. Hohmann W., Die erreichbarkeit der himmelskorper. R. Olden¬
bourg, Miinchen, 1925.
1.8. Esnault-Pelterie R., L’ Astronautique. Paris, 1930.
Русский перевод: Эыо Пельтри, Космические полеты (астро¬
навтика). Оборонгиз, М., 1950.
1.9. Королев С. П., Ракетный полет в стратосфере. Воениздат, М.,
1934.
1.10. Космодемьянский А. А:, Экстремальные задачи для точки
переменной массы. Докл. АН СССР, т. 53, № 1, 1946.
1.11. О х о ц и м с к и й Д. Е., К теории движения ракет. Прикл. матем.
и механ., т. 10, № 2, 1946.
1.12. Иш лин с кий А. Ю., Два замечания к теории движения ракет.
Докл. АН СССР, т. 53, № 7, 1946.
1.13. Космодемьянский А. А., Курс теоретической механики.
Учпедгиз, М., 1955.
1.14. Космодемьянский А. А., Основные теоремы механики те¬
ла переменной массы. Лекции по механике тел переменной массы.
Уч. зап. МГУ, Механика, вып. 152, 154, 1951.
1.15. TsienH., Evans R., Optimum thrust programming for a saun-
ding rocket. J. Amer. Rock. Soc., vol. 21, № 5, 1951.
1.16. L a w d e n D. F., Minimal rocket trajectories. J. Amer. Rock. Soc.,
vol. 23, № 11—12, 1953.
1.17. Кротов В. Ф., Расчет оптимальной траектории для перехода
ракеты на заданную круговую траекторию около Земли. Сб. «Меха¬
ника», МВТУ, Оборонгиз, М., 1955.
1.18. ОхоцимскийД. Е., Энеев Т. М., Некоторые вариацион¬
ные задачи, связанные с запуском искусственного спутника Земли.
УФН, т. 63, вып. 1а, 1957.
1.19. Егоров В. А., Некоторые проблемы динамики полета к Луне.
Докл. АН СССР, т. ИЗ, № 1, 1957.
1.20. Егоров В. А., Некоторые задачи динамики полета к Луне. УФН,
т. 63, вып. 1а, 1957.
ЛИТЕРАТУРА
639
1.21. В а г г е г е М., Jaumotte A., Veub еке В. F., Vanden-
kerckove J., La propulsion par fusees. Paris, 1957. Русский пере¬
вод: Б a p p e p М., ЖомоттА., ВебенеБ. Ф., В а н д е н-
керкхове Ж., Движение ракет. ИЛ, М., 1959.
1.22. М i е 1 е A., An extension of the theory of the optimum burning prog¬
ram for the level flight of a rocket-powered aircraft. J. Aeronaut. Sci.,
vol. 24, № 12, 1957.
1.23. Veubeke B. F., Le probleme du maximum derayon d’ action dans
un champ de gravitation uniforme. Astronaut. Acta, vol. 4, № 1, 1958.
1.24. Егоров В. А., О решении одной вырожденной вариационной за¬
дачи и оптимальном подъеме космической ракеты. Прикл. матем.
и механ., т. 22, № 1, 1958.
1.25. Исследование оптимальных режимов движения ракет. Сб. перев. под
ред. Садовского И. Н. Оборонгиз, М., 1959.
1.26. М i е 1 е A., General variational theory of the flight paths or rocket-
powered aircraft, missiles and satellite carriers. Astronaut. Acta, vol. 4,
№ 4, 1958.
1.27. Breakwell J. V., The optimization of trajectories. J. Soc. Indus*
trial and Appl. Math., vol. 7, № 2, 1959.
1.28. Гантмахер Ф. P., Левин Л. М., Теория полета неуправ¬
ляемых ракет. Физматгиз, М., 1959.
1.29. Herrick S., Astrodynamics. Princeton, N. Y., 1959.
1.30. L a w d e n D. F., Interplanetary rocket trajectories. Edvances in
Space Sci., Academic Press, N. Y.— London, 1959. Русский перевод:
Л о у д e и Д. Ф., Межпланетные траектории ракет. Сб. «Космиче¬
ские траектории», ИЛ, М., 1963.
1.31. Лурье А. И., Уравнения возмущенного движения в задаче Кеп¬
лера. Прикл. матем. и механ., т. 23, № 2, 1959, см. также сб. «Искус¬
ственные спутники Земли», вып. 4, 1960.
1.32. Горелов Ю. А., О двух классах плоских экстремальных движе¬
ний ракеты в пустоте. Прикл. матем. и механ., т. 24, № 2, 1960.
1.33. Исаев В. К., Принцип максимума Л. С. Понтрягина и оптималь¬
ное программирование тяги ракет. Автоматика и телемеханика, т. 22,
№ 8, 1961; т. 23, № 1, 1962.
1.34. Leitmann G., The optimization of rocket trajectories — a survey.
Progr. in Astronaut. Sci., vol. 1, Amsterdam, 1962.
1.35. Илларионов В. Ф., Ш к а д о в Л. М., Поворот плоскости
круговой орбиты спутника. Прикл. матем. и механ., т. 26, № 1, 1962.
1.36. Лурье А. И., Об одной форме уравнений движения материальной
точки. Применение к задаче о повороте плоскости орбиты искусствен¬
ного спутника Земли. Тр. Межвуз. конф. по прикл. теории устойчи¬
вости движения, Казань, 1962.
1.37. Optimization Techniques, ed. by G. Leitmann. Academic Press,
N. Y., 1962.
1.38. E h r i с k e K. A., Space flight. Princeton, N. Y., vol. 1, 1960; vol. 2,
1962. Русский перевод: Эрике К., Космический полет. Физматгиз,
М., 1963.
1.39. Lawden D. F., Optimal trajectories for space navigation. London,
1963.
1.40. КузмакГ. E., Исаев В. К., Давидсон Б. X., Оптималь¬
ные режимы движения точки переменной массы в однородном цент-
» ральном поле. Докл. АН СССР, т. 149, № 1, 1963.
1.41. Ильин В. А., Оптимальный переход космического аппарата, тор¬
мозящегося в атмосфере планеты, на орбиту искусственного спутника
Земли. Инж. журнал, т. 3, № 2, 1963.
1.42. Тарасов Е. В., Оптимальные режимы полета летательных ап¬
паратов. Оборонгиз, М., 1963.
640
ЛИТЕРАТУРА
1.43. Break w ell J. V., The optimum spacing of corrective thrusts in
interplanetary navigation. Math. Optimiz. Techn., California Press,
1963.
1.44. Miele A., Flight mechanics. Massach.— London, 1962. Русский
перевод: M и e л e А., Механика полета. «Наука», М., 1966.
1.45. Ильин В. А., К расчету траекторий перелета космических аппа¬
ратов между компланарными круговыми орбитами в ньютониан-
ском гравитационном поле. Космические исследования, т. 2, № 5.
1964.
1.46. Кузмак Г. Е., Копнин Ю. М., Новая форма уравнения дви¬
жения спутника и приложение ее к исследованию движений, близких
к кеплеровым. Ж. вычисл. матем. и матем. физ., т. 3, № 4, 1963.
1.47. Исаев В. К., Курьянов А. И., Сонин В. В., Примене¬
ние принципа максимума в ракетодинамике. Proc. XIV Internat. As¬
tronaut. Congr. 1963, Warszawa, 1964.
1.48. Алексеев К. Б., Бебенин Г. Г., Управление космическим
летательным аппаратом. «Машиностроение», М., 1964.
1.49. Коренев Г. В., Введение в механику управляемого тела. «Нау¬
ка», М., 1964.
1.50. Andreesen D. St., Nita М. М., Zborul rachetei. Editura
Militara, Bucuresti, 1964.
1.51. JI и д о в M. JI., Охоцимский Д. Е., Тесленко Н. М.,
Исследование одного класса траекторий ограниченной задачи трех
тел. Космич. исследования, т. 2, вып. 6, 1964.
1.52. Ross S., Optimal ascent into orbit — a new look at an old problem.
Proc. XV Internat. Astronaut. Congr., 1964, Warszawa, 1965.
1.53. Исследования по динамике полета. Сб. под ред. Остославского
И. В. «Машиностроение», М., 1965.
1.54. Пономарев В. М., Теория управления движением космических
аппаратов. «Наука», М., 1965.
1.55. Veubeke В. F., GeertsJ., Application du principe de maxi¬
mum a la syntese des transferts optimaux dans un champ de gravitation
planetare. Proc. XV Internat. Astronaut. Congr. 1964, Warszawa, 1965.
1.56. Кузмак Г. E., Линеаризированная теория оптимальных переле¬
тов. Космич. исследования, т. 3, № 1, 1965.
1.57. Егоров В. А., Пространственная задача достижения Луны.
«Наука», М., 1965.
1.58.^4 еботарев Г. А., Аналитические и численные методы небесной
механики. «Наука». М.— Л., 1965.
1.59. Аппазов Р. Ф., Л а в р о в С. С., М и ш и н В. П., Баллисти¬
ка управляемых ракет дальнего действия. «Наука», М., 1966.
1.60. Гродзовский Г. Л., Иванов 10. Н., Токарев В. В.,
Механика космического полета с малой тягой. Инж. журнал АН
СССР, т. 3, № 3 и 4, 1963; т. 43, № 1 и 2, 1964. См. также Тр. II Все-
союзн. съезда по теорет. и прикл. механике, вып. 1, «Наука», М.,
1965 и Proc. XV Internat. Astronaut. Congr. 1964, Warszawa, 1965.
1.61. Стечкин Б. С., Казанджан П. К., Алексеев Л. П.,
Говоров А. Н., Коновалов Н. Е., Нечаев Ю. Н.,
Федор о в Р. М., Теория реактивных двигателей. Оборонгиз, М., 1958.
1.62. Corliss W. R., Propulsion systems for space flight. N. Y.—
Toronto — London, 1960. Русский перевод: Корлисс У. P.,
Ракетные двигатели для космических полетов. ИЛ, М., 1962.
1.63. A u G. F., Entwicklungsstand zukunftiger raumfahrtantriebe. Luft-
fahrttechnik, vol. 7, № 1, 1961.
1.64. Sutton G., Rocket propulsion elements. N. Y.— London, 1949,
Toronto — London, 1958. Русский перевод: Саттон Д., Ракетные
двигатели. ИЛ, М., 1952.
ЛИТЕРАТУРА
641
1.65. Bussard R. W., Delauer R. D., Nuclear rocket propulsion,
N. Y.— Toronto — London, 1958. Русский перевод: Б а с с a p д P.,
Делауэр P., Ракета с атомным двигателем. ИЛ, М., 1960.
1.66. Квасников А. В., Теория жидкостных ракетных двигателей.
Судпромгиз, Л., 1959.
1.67. Space power systems. Ed. by S n у d e г N. W., Acad, press, N. Y.—
London, 1961. Русский перевод: Энергетические установки для кос¬
мических аппаратов. «Мир», М., 1964.
1.68. Белецкий В. В., Движение искусственного спутника относи¬
тельно центра масс. «Наука», М., 1965.
1.69. Дубошин Г. Н., Теория притяжения. Физматгиз, М., 1961.
1.70. Аллен К. У. (А 11 е п С. U.), Астрофизические величины. ИЛ, М.,
1960.
1.71. Дубошин Г. Н., Небесная механика. Физматгиз, М., 1963.
1.72. Субботин М. Ф., Курс небесной механики, т. 1. Гостехиздат,
1963, т. 2 и 3, ОНТИ, 1949.
1.73. С a m е г о n A. G. W., Physics of the planets. Space Physic, N. Y.—
London, 1964.
1.74. R e i f f e 1 L., Structural damage and other effects of solar plasmas.
J. Amer. Rock. Soc., vol. 30, № 3, 1960.
1.75. Ландсберг Г. С., Оптика. Гостехиздат, М.— Л., 1947.
1.76. Александров С. Г., Федоров Р. Е., Советские спутники
и космические корабли, изд. 2-е. Изд-во АН СССР, М., 1961.
1.77. Whipple F. L., The meteoritic risk to space vehicles. Vistas in
Astronautics, vol. 2, N. Y., 1958.
1.78. Gehring J. W., Cristman D. R., McMillan A. R.,
Experimental studies concerning the meteoroid hazard to aerospace
materials and structures. J. Spacecraft and Rock., vol. 2, № 5, 1965.
1.79. В j о r k R. L., Meteoroids vs space vehicles. J. Amer. Rock. Soc., vol.
31, № 6, 1961.
1.80. Станюкович К. П., Федынский В. В., О разрушитель¬
ном действии метеоритных ударов. Докл. АН СССР, т. 57, № 2, 1947.
1.81. В j о г k R. L., Effects of a meteoroid impact on steel and aluminum
in space. Proc. X Internat. Astronaut Congr., 1959, Vien., 1960.
1.82. Лаврентьев М. А., Проблема пробивания при космических
скоростях. Искусственные спутники Земли, вып. 3, 1959.
1.83. Kornhauser М., Satellite pressure losses caused by meteoroid
impacts. J. Amer. Rock. Soc., vol. 30, N° 5, 1960.
1.84. Зельдович Я. Б., Райзер Ю. П., Физика ударных волн
и высокотемпературных гидродинамических явлений. Физматгиз,
М., 1963.
1.85. Андрианкин Э. И., О пробивании преград метеоритами. Кос¬
мические исследования, т. 4, вып. 2, 1966.
1.86. Мухамеджанов А. К., О пробое тонкого экрана метеоритом.
Космические исследования, т. 4, вып. 2, 1966.
К главе 2
2.1. Prandtl L., Fiihrer durch die stromungslehre. Gettingen, 1944.
Русский перевод: Прандтль Л., Гидроаэромеханика. ИЛ, М.,
1949. .
2.2. Стечкин Б. С., Казанджан П. К., Алексеев А. П.,
Говоров А. Н., Коновалов Н. Е., Нечаев Ю. Н.,
Федоров Р. М., Теория реактивных двигателей. Оборонгиз,
М., 1958.
2.3. Зельдович Я. Б., Теория ударных волн и введение в газодина¬
мику. Изд-во АН СССР, М., 1946.
41 Механика полета
642
ЛИТЕРАТУРА
2.4. Христианович G. А., Гальперин В. Г., Миллион¬
щиков М. Д., Симонов JI. А., Прикладная газовая дина¬
мика. ЦАГИ, 1948.
2.5. Седов Л. И., Плоские задачи гидродинамики и аэродинамики.
Гостехиздат, М., 1950.
2.6. Абрамович Г. Н., Прикладная газовая динамика. Гостехиздат,
М., 1951.
2.7. Болгарский А. В., Щукин В. К., Рабочие процессы^в
жидкостнореактивных двигателях. Оборонгиз, М., 1953.
2.8. Мелькумов Т. М., Кузнецов Е. В., Мелик-Па-
шаев Н. И., Теория жидкостных реактивных двигателей. Изд.
ВВИА им. Н. Е. Жуковского, М., 1956.
2.9. В а г г е г е М., J aumotte A., Veubeke В. F., Vanden-
kerckove J., La propulsion parfrusees. Paris, 1957. Русский перевод:
Б a p p e p М., ЖомоттА., ВебекеБ. Ф., Ванденкерк-
х о в е Ж., Движение ракет. ИЛ, М., 1959.
2.10. Квасников А. В., Теория жидкостных ракетных двигателей
Судпромгиз, М., 1959.
2.11. Алемасов В. Е., Теория ракетных двигателей. Оборонгиз,
М., 1962.
2.12. Ландау Л. Д., Лифшиц Е. М., Механика сплошных сред.
Физматгиз, М., 1962.
2.13. Guderley G., Hantsch Е., Baste formen fur achsensymmet-
rische uberschallschubdusen. Zeitschrift fur Flugwissenschaften, Braun¬
schweig, № 9, 1955.
2.14. ДородницынА. А., Расчет распределения давлений по телам
вращения в сверхзвуковом потоке газа. Сб. теоретических работ по
аэродинамике, Оборонгиз, М., 1957.
2.15. Шмыглевский Ю. Д., Некоторые вариационные задачи га¬
зовой динамики осесимметричных сверхзвуковых течений. Прикл.
матем. и механ., т. 21, № 2, 1957.
2.16. R а о G. V., Exhaust nozzle control for optimum thrust. Jet Prop.,
vol. 28, № 6, 1958.
2.17. Стерни и Л. E., К расчету осесимметричного реактивного
сопла наименьшего веса. Изв. АН СССР, Механика и машинострое¬
ние, N° 1, 1959.
2.18. G u d е г 1 е у G., On Roo’s method for the computation of exhaust
nozzles. Zeitschrift fur Flugwissenschaften, Bd. 12, № 7, 1959.
2.19. Шмыглевский Ю. Д., Вариационные задачи для сверхзву¬
ковых тел вращения и сопел. ВЦ АН СССР, М., 1961.
2.20. Гродзовский Г. Л., Кузнецов Ю. Е., Токарев
М. В., Приближенный метод расчета осесимметричных сверхзвуковых
течений в условиях внутренней задачи. Промышленная аэродинами¬
ка, вып. 24. Оборонгиз, М., 1962.
2.21. Сергиенко А. А., Сандомирская И. Д., О профили¬
ровании сверхзвуковой части осесимметричного сопла наибольшей
тяги. Сб. работ Вычисл. центра Моск. ун-та, № 4, 1955.
2.22. Гродзовский Г. Л., Особенности односторонних оптических
установок для исследования газового потока и деформации плоских
поверхностей. Изв. АН СССР, ОТН, № 7, 1955.
2.23. Гродзовский Г. Л., Экспериментальное исследование взаимо¬
действия скачков уплотнения и пограничного слоя в диапазоне чисел
М=1,0-1,8. Изв. АН СССР, ОТН, Энергетика и автоматика, № 4, 1960.
2.24. Петров Г. И., Сообщение о докладе на сессии АН СССР. Изв.
АН СССР, ОТН, № 9, 1958.
2.25. MigdalD., Н organ J. J., ChamayA., An experimental
evaluation of plug cluster nozzles. AIAA J., vol. 2, № 7, 1964.
ЛИТЕРАТУРА
643
2.26. Bono P., Woodworth I. L., Ursini G. A., The reusable boos¬
ter for lunar logistics and planetary exploration. Proc. XV Internat.
Astronaut. Congr. 1964, Warszawa, 1965.
2.27. Stockel K., Chemische raumfahrttriebwerke. Jahrb. Wiss. Ges.
Luft-und Kaumfahrt, 1962.
2.28. Shepherd L. R., Cleaver A. V., The atomic rocket. J. Brit.
Interpl. Soc., vol. 7, № 5, 1948; vol 8, № 2, 1949; Realities of Space
Travel, London, 1957.
2.29. Bussard R. W., DeLauer R. D., Nuclear rocket propulsion.
N. Y., 1958. Русский перевод: Бассард P., Де-Лауэр P.,
Ракета с атомным двигателем. ИЛ, М., 1960.
2.30. Space technology. Ed. by S е i f е г t Н., N. Y., 1959. Русский пере¬
вод: Космическая техника. «Наука», М., 1964.
2.31. S u t t о n G. P., Rocket propulsion systems for interplanetary flight.
JASS, vol. 26, № 10, 1959.
2.32. Corliss W. R., Propulsion systems for space flight. N. Y., 1960.
Русский перевод: Корлисс У. Р., Ракетные двигатели для космиче¬
ских полетов. ИЛ, М., 1962.
2.33. С a m а с М., Plasma propulsion devices. Advances in Space Science,
vol. 2, N. Y., 1960. Русский перевод: Плазменные и электростатичес¬
кие ракетные двигатели. ИЛ, М., 1962.
2.34. Stenning А. Н., Rapid approximate method for analyzing nuc¬
lear rocket performance. J. Amer. Rock. Soc., vol. 30, № 2, 1960.
2.35. Cohen A. D., Beers L. S., Mars capabilities for electrical, nuc¬
lear and chemical propulsion systems. IAS Paper, № 120, 1962.
2.36. W i 1 1 i n s k i М. I., Orr E. C., A i 1 e n b e r d S. L., Hueb-
nerA.L., Kantrowitz A., Janes G. S., Camac M.T
KunenE., Mclllroy W. and others 1958—1959. Русский
перевод: Ионные, плазменные и дуговые ракетные двигатели. Сб.
переводов, Госатомиздат, М., 1961.
2.37. Meghreblian R. V., Gaseous propulsions reactors. Nucleonics,
vol. 19, № 4, 1961.
2.38. A u G. F., Entwicklungsstand zukunftiger raumfahrtantriebe. Luft-
fahrtechnik, vol. 7, № 1, 1961.
2.39. Linhardt H. D., Comparison of solar-thermal and solar-electric-
thermal propulsion methods. IAS Paper № 63—20, 1963.
2.40. W i 1 k s W. E., «Poodle» interests Saturn officials. Missiles and Ro¬
ckets, vol. 14, № 23, 1964. См. также: New YY)rk Times, l.VI, 1964.
2.41. Beckewith W. C., Johnson H. L., Advanced space mission
capabilities of nuclear rockets. J. Spacecraft and Rock., vol. 1, № 4, 1964.
2.42. Прайнинг С. (Preining О.), Получение высоких температур
(до 55 000° К) в лабораторных условиях. УФН, т. 55, № 4, 1955.
2.43. Даутов Г. Ю., Жуков М. Ф., С м о л я к о в Б. Я., Иссле¬
дование работы плазматрона с воздушной стабилизацией дуги. Прикл.
матем. и техн. физ., «N*2 6, 1961.
2.44. Герман В. О., Морозов М. Г., Плазматрон постоянного
тока и некоторые результаты исследования его работы. Теплофизи¬
ка высоких температур, АН СССР, т. 3, № 5, 1965.
2.45. Kantrowitz A., Horizons in plasma dynamics. Astronaut, and
Aeronaut., vol. 3, № 1, 1965.
2.46. В г о g a n T. R., Electric arcs gas heater for re-entry simulation
and space propulsion. Presented at the 13th Ann. Meeting, Amer. Rock.
Soc., N. Y., 1958.
2.47. Preston-Thomas H., International transport technique. J.
Brit. Interpl. Soc., vol. 11, № 4, 1952.
2.48. Stuhlinger E., Possibilities of electrical space ship propulsion..
Proc. V. Internat. Astronaut. Congr., 1954, Vien., 1955.
41*
644 ЛИТЕРАТУРА
2.49. Stuhlinger Е., Advanced propulsion systems for space vehicles.
Proc. IX Internat. Astronaut. Congr., 1958, Vien., 1959.
2.50. Стависский Ю. А., Бондаренко И. И., Кро¬
то в В. И., Лебедев С. Я., ПупкоВ. Я., Стумбур
Э. А., Опыт получения реактивной тяги в лабораторной модели
ионного движителя. Журнал техн. физ., т. 29, вып. 8, 1959.
2.51. В о d е n R. Н., Ion propulsion. Adv. Prop. Techn. 1960, Oxford, 1961.
2.52. Kaufman H. R., R e a d e r P. D., Experimental performance
of ion rockets employing electron — bombardment ion sources. Elec¬
trostatic Prop. Conf., Monterey, Calif., 1960.
2.53. Stuhlinger E., Seitz R. N., Electrostatik propulsion sys¬
tems for space vehicles. Advances in Space Science, vol. II, N. Y., 1960.
Русский перевод: Плазменные и электростатические ракетные двига¬
тели, ИЛ, М., 1962.
2.54. MickelsenW. R., Comparative performance of electrostatic ro¬
cket engines. IAS Paper, № 62—74, 1962.
2.55. Brown H., NicollH. E., Electrical propulsion capabilities
for Lunar exploration. AIAA J., vol. 1, № 2, 1963.
2.56. Kaufman H. R., The electron-bombardment ion rocket. Proc.
3rd Sympos. Advanced Propuls. Concepts, vol. 1, N. Y.— London,
1963.
2.57. Winicur D. H., Electric propulsion characteristics of a pulsed
plasma rail accelerator. AIAA J., vol. 2, № 9, 1964.
2.58. Kuskevics G., Thompson B. L., Comparison of commer¬
cial, spherical powder, and wire bundle tungsten ionizers. AIAA J.,
vol. 2, № 2, 1964.
2.59. Stuhlinger E., Ion propulsion. N. Y., 1964.
2.60. Davis J., A step towards nuclear electric propulsion. Astronaut,
and Aeronaut., vol. 3, № 1, 1965.
2.61. Mickelsen W. R., Reader P. D., Ion propulsion systems
for spacecraft. J. of Spacecraft and Rock., vol. 2, № 4, 1965.
2.62. В r e w e r G. R., Physical electronic phenomena in ion propulsion
engines. IEEE Spectrum, vol. 2, № 8, 1965.
2.63. T а м м И. E., Основы теории электричества. Гостехиздат, М., 1957.
2.64. Арцимович Л. А., Управляемые термоядерные реакции.
Физматгиз, М., 1961.
2.65. Арцимович Л. А., Лукьянов С. Ю., Подгорный
И. М., Чуватин С. А., Электродинамическое ускорение сгуст¬
ков плазмы. ЖЭТФ, т. 33, № 7, 1957.
2.66. Подгорный И. М., Чуватин С. А., Быков Г. А.,
Письменный В. Д., Исследование процесса электродинами¬
ческого ускорения сгустков плазмы. II. Физика плазмы и проблема
управляемых термоядерных реакций, т. IV, Изд. АН СССР, 1958.
2.67. Капцов Н. А., Электроника. Гостехиздат, М., 1956.
2.68. Добрецов Л. Н., Электронная и ионная эмиссия. Гостехиздат,
М., 1950.
2.69. Браун С., Элементарные процессы в плазме газового разряда.
Госатомиздат, М., 1961.
2.70. Lewis tests large ion engine. Aviation Week and Space Technol., vol.
81, № 4, 1964.
2.71. Цандер Ф. А., Проблема полета при помощи реактивных аппара¬
тов. Межпланетные путешествия. Оборонгиз. М., 1961.
2.72. Карымов А. А., Определение сил и моментов сил светового дав¬
ления, действующих на тело при движении в космическом простран¬
стве. Прикл. матем. и механ., т. 26, № 5, 1962.
2.73. JahsmanW. Е., Mass consideration in ring supported solar sails.
J. Amer. Rock. Soc., vol. 30, № 3, 1960.
ЛИТЕРАТУРА
645
2.74. Глушко В. П., Жидкое топливо для реактивных двигателей.
Изд. ВВИА, М., 1936.
2.75. Мельников М. В., Влияние формы камеры и сопла на тягу
ЖРД. Изд. БИТ, М., 1946.
2.76. Ваничев А. П., Термодинамический расчет горения и истечения
в области высоких температур. Изд. БНТ, М., 1947.
2.77. Зельдович Я. Б., Полярный А. И., Расчеты тепловых
процессов при высокой температуре. Изд. БНТ, М., 1947.
2.78. Варшавский Г. А., К вопросу о поведении быстродвижущегося
потока сжимаемого газа в прямой цилиндрической трубе при нали¬
чии охлаждения. Журнал техн. физ., вып. 4, 1946.
2.79. Романенко С. В. Течение вязкого газа в цилиндрической тру¬
бе при наличии конвективного теплообмена. Докл. АН СССР, т. 91,
№ 6, 1953.
2.80. Гродзовский Г. JL, Некоторые точные решения задачи о те¬
чении газа в трубе с учетом трения и конвективного теплообмена.
Изв. АН СССР, ОТН, № 8, 1958.
2.81. Межиров И. И., О течении газа в цилиндрической трубе при
наличии трения и теплообмена. Изв. АН СССР, ОТН, № 8, 1958.
2.82. Goldsmith W., Seban R. A., Pressure drop and heat trans¬
fer for subsonic air flow in a smooth pipe. Trans, of ASME, № 50-F-18,
1950.
2.83. Авдуевский В. С., Данилов Ю. И., Кошкин В. К.,
Кутырин И. Н., Михайлова М. М., Михеев Ю. С.,
Сергель О. С., Основы теплопередачи в авиационной и ракет¬
ной технике. Оборонгиз, М., 1960.
2.84. Гродзовский Г. JL, Кузнецов Ю. Е., Худяков
Г. Е., Газодинамическая теория течения двухфазной жидкости с из¬
менением агрегатного состояния. Труды ЦКТИ, Котлотурбострое-
ние, вып. 59, Л., 1965.
2.85. Киме ль JI. Р., Определение оптимальной формы защитного
барьера. Атомная энергия, т. 7, № 3, 1959.
2.86. Токарев В. В., Цветков В. И., Оптимальная форма защи¬
ты от гамма-излучения. Журнал прикл. мех. и техн. физ., № 1, 1964.
2.87. Energy conversion for space power. Space power systems. Ed. by S n y-
d e r N. W., Acad. Press, N. Y.— London, 1961. Русский перевод:
Преобразование тепла и химической энергии в электроэнергию
в ракетных системах. ИЛ, М., 1963. Энергетические установки для
космических аппаратов. «Мир», М., 1964.
2.88. Vernet-Lozet М., Les vehicules spatiaux a source d’energie
solaire. Le projet Platan. Ann. geofis., vol. 17, № 1, 1964.
2.89. Stafford G. B., Capabilities of power subsystems for space. Me¬
chanical Engineering, vol. 87, № 9, 1965.
2.90. О s m u n W. G., Space nuclear power: SNAP-50/SPUR. Space Aero¬
naut., vol. 42, № 7, 1964.
2.91. A u G. F., «Snapshot» ein electrostatisches ionentriebwerk mit nuclear
energie versorung. Luftfahrttechnik Raumfahrttechnik, № 7, 1965.
2.92. GlassmanA. J., Stewart W. L., Thermodynamic charac¬
teristics of Bray ton cycles for space power. J. Spacecraft and Rock.,
vol. 1, № 1, 1964.
2.93. Cochran D. L., Working fluids for dynamic APN systems. Space
Aeronaut., R&D Techn. Handbook, vol. 38, № 2, 1962—1963.
2.94. Beale R. J., Speiser E. W., Womack J. R., Electric
space cruiser for high-energy missions. J. Spacecraft and Rock., vol. 1,
№ i, 1964.
2.95. Дейч М. E., Техническая газодинамика. Госэнергоиздат, М.,
1953.
€46
ЛИТЕРАТУРА
2.96. ЛойцянскийЛ. Г., Механика жикости и газа. Гостехиздат
М., 1957.
2.97. Степанов Г. Ю., Гидродинамика решеток турбомашин. Физмат¬
гиз, М., 1962.
2.98. А б и а н ц В. X., Теория газовых турбин реактивных двигателей.
Машиностроение, М., 1965.
2.99. Дорогов Б. С., Эрозия лопаток в паровых турбинах. Энергия,
М., 1965.
2.100. Е 1 1 i о t t D. G., Two-fluid magnetohydrodynamic cycle for nuclear
electric power conversion. J. Amer. Rock. Soc., vol. 32, № 10, 1962.
2.101. MHD power converters for space. Nucleonics, vol. 21, № 7, 1963.
2.102. И о ф ф e А. И., Полупроводниковые термоэлементы. Изд. АН
СССР М. Л. 1956.
2.103. Dieckamp Н. М., В а 1 е n t R., W е t с h J. R., Reactor di-
.. rect-conversion units. Proc. 3rd Unit. Nat. Internat. Conf. on the Pea¬
ceful Uses of Atomic Energy, Geneva, 1964.
2.104. Stamm H., Radionuklid-batterien fiir die raumfahrt. Weltraum-
fahrt, № 4, 1963.
2.105. Mariner to Mars. Flight, vol. 86, № 2906, 19.XI 1964.
2.106. Hamilton R. C., Solar power system. Proc. XV Internat. Astro¬
naut. Congr. 1964, Warszawa, 1965.
2.107. TonkinS. W., Solar cell arrays for rigid earth-pointing satellites.
Proc. XV Internat. Astronaut. Congr. 1964, Warszawa, 1965.
2.108. Grover G. М., Los-Alamos plasma thermocouple. Nucleonics, vol.
17, № 2, 1959.
2.109. Добрецов Л. H., Термоэлектронные преобразователи тепло¬
вой энергии в электрическую. Журнал техн. физ., т. 30, № 4,
1960.
2.110. Harvey R. J., Propulsion and auxiliary power systems. Ballistic
Missile and Space Technology, vol. 2, N. Y., 1960.
2.111. Cobb J. E., Cutler W. E, DuganA. F, Olds R. H.,
Shook G. B., A nuclear-thermionic-ionic propulsion system. Proc.
XI Internat. Astronaut. Congr. 1960, Vien., 1961.
2.112. Моргулис H. Д., Термоэлектронный (плазменный) преобразо¬
ватель энергии. Госатомиздат, М., 1961.
2.113. Miller Н., Thermionic-nuclear space power systems. Proc. 3rd Sym-
pos. Advanced Propuls. Concepts, Cincinnati, 1962, vol. 1, N. Y.—
London, 1963.
2.114. Gronich A., H a 1 1 e t R. W.,MillerP. W.,A nuclear electric
propulsion system for manned interplanetary missions. Proc. XIV In¬
ternat. Astronaut. Congr. 1963, vol. 1, Warszawa, 1965.
2.115. Psarouthakis J., Thermionic conversion for electric propulsion
power. Proc. XVI Internat. Astronaut. Congr. 1965, Warszawa, 1966.
2.116. Краткий физико-технический справочник, т. I. Физматгиз, М., 1960.
2.117. Инженерно-технический справочник по электросвязи, электроуста¬
новки. Изд-во лит. по связи и радио, М., 1962.
2.118. СиняревГ. Б., Добровольский М. В., Жидкостные ра¬
кетные двигатели. Оборонгиз, М., 1957.
2.119. В ur la ge Н., Liquid engines for advanced launch vehicles. Astro¬
nautics and Aeronautics, vol. 2, № 7, 1964.
2.120. S-1B Tanks Missile and Space. Daily, vol. 10, № 26, 9.XII, 1964.
2.121. С т e ч к и н Б. С., Теория воздушного реактивного двигателя. Тех¬
ника воздушного флота, № 2, 1929.
2.122. Roy М., Recherches theoriques sur le rendement et les conditions de
realisation des systemes motopropulseurs a reaction. Paris, 1930.
Русский перевод: Pya М., О полезном действии и условиях при¬
менения ракетных аппаратов. ОНТИ, М.— Л., 1936.
ЛИТЕРАТУРА
647
2.123. Абрамович Г. Н., Газовая динамика воздушно-реактивных
двигателей. Изд. БНТ, М., 1947.
2.124. Иноземцев Н. В., Зуев В. С., Авиационные газотурбинные
двигатели. Оборонгиз, М., 1949.
2.125. Черкез А. Я., Применение метода малых отклонений в теории
и расчете авиационных ТРД. Оборонгиз, М., 1955.
2.126. Бондарюк М. М., Ильяшенко О. М., Прямоточные воз¬
душно-реактивные двигатели. Оборонгиз, М., 1958.
2.127. Lane R. J., Recoverable air-breathing boosters for space vehicles.
J. Roy. Aeronaut. Soc., vol. 66, № 618, 1962.
2.128. Ferri A., Review of problems in application of supersonic combus¬
tion. J. Roy. Aeronaut. Soc., vol. 68, № 645, 1964.
2.129. Gossick L. V., С о о k H. М., Trends in aerospace propulsion
development testing, their influence on future flight simulation faci¬
lity requirements. Proc. XVI Internat. Astronaut. Congr. 1965, War¬
szawa, 1966.
2.130. Скубачевский Г. С., Авиационные газотурбинные двигате¬
ли. Машиностроение, М., 1965.
2.131. Холщевников К. В., Согласование параметров компрессора
и турбины в авиационных газотурбинных двигателях. Машинострое¬
ние, М., 1965.
2.132. Гродзовский Г. JL, Сверхзвуковые осесимметричные кони¬
ческие течения с коническими скачками, граничащими с параллель¬
ным равномерным потоком. Прикл. матем. имехан., т. 23, № 2,
1959.
2.133. Гродзовский Г. JI., Автомодельное движение газа при силь¬
ном периферийном взрыве. Докл. АН СССР, т. 111, № 5, 1956.
2.134. DemetriadesS. Т., A noval sistem for space flight using a pro¬
pulsive fluid accumulator. J. Brit. Interpl. Soc., vol. 17, № 5, 1959.
2.135. CamacM., Berner F., An orbital air-scooping vechicle, Astro¬
nautics, vol. 6, № 8, 1961.
2.136. Reichel R. H., S m i t h T. L., Hanford D. R., Poten¬
tialities of airscooping electrical space propulsion systems. Progr. in
Astronaut, and Aeronaut., vol. 9, Electrical Prop. Devel., N. Y.,
1963.
2.137. Токарев В. В., Ф а т к и н Ю. М., Накопитель рабочего веще¬
ства в задачах оптимизации движения с ограниченной мощностью.
Инж. журнал АН СССР, т. 5, вып. 3, 1965.
2.138. Капица П. JL, Турбодетандер для получения низких температур
и его применение для сжижения воздуха. Техническая физика, вып. 2,
1939.
2.139. «Техника низких температур». Энергия, М.— Д., 1964.
2.140. Седов Л. И., Методы подобия и размерности в механике. «Наука»,
• М., 1965.
2.141. Alder R., Lecompte J., Etudes sur la propulsion nucleother-
mique. Estimation de performances d'un etage nucleaire pour lanceur
lourd europeen. Proc. XVI Internat. Astronaut. Congr., 1963, Warsza¬
wa, 1965.
2.142. Modern development in fluid dynamics, ed. by Goldstein S., vol.
2, London, 1943. Русский перевод: Современное состояние гидроаэро¬
динамики вязкой жидкости, под ред. Гольдштейна С., т.2, ИЛ,
М., 1948.
2.143. Гродзовский Г. Л., Турбулентный пограничный слой пло¬
ской пластины. Журнал прикл. мех. и техн. физ., № 4, 1962.
2.144. Liepmann Н. W., RoshkoA., Elements of gasdynamics.
N. Y., 1957. Русский перевод: Л и п м а н Г. В., Рошко А.,
Элементы газовой динамики. ИЛ, М., 1960.
648
ЛИТЕРАТУРА
2.145. Hayes W. D., Probstein R. F., Hypersonic flow theory.
Acad. Press., N. Y.— London, 1959. Русский перевод: Хейз У. Д.,
Пробст и н Р. Ф., Теория гиперзвуковых течений. ИЛ, М.
1962.
2.146. Karma п Т., Supersonic aerodynamics. J. Aeronaut. Sci., vol. 14,
№ 7, 1947. Русский перевод: Карман Т., Сверхзвуковая аэроди¬
намика. ИЛ, М., 1948.
2.147. КочинН. Е., Кибель И. А., РозеН. В., Теоретическая
гидромеханика. Физматгиз, 1963.
2.148. Мартынов А. К., Экспериментальная аэродинамика. Оборонгиз,
1958.
2.149. Т s i е n Н. S., Supersonic flow over an inclined body of revolution.
J. Aeronaut. Sci., vol. 5, № 12, 1938.
2.150. Франкль Ф. И., Карпович E. А., Газодинамика тонких
тел. Гостехиздат, М.— Л., 1948.
2.151. Ferri A., Elements of aerodynamics of supersonic flows. N. Y.,
1949. Русский перевод: Ферри А., Аэродинамика сверхзвуковых
течений. Гостехиздат, М.— JL, 1952.
2.152. Никольский А. А., О телах вращения с протоком, обладаю¬
щих наименьшим внешним волновым сопротивлением в сверхзвуко¬
вом потоке. Сборник теоретических работ по аэродинамике, Оборон-
гиз, М., 1957.
2.153. Краснов Н. Ф., Аэродинамика тел вращения. Оборонгиз, М.,
1958.
2.154. Седов Л. И., О некоторых неустановившихся движениях сжи¬
маемой жидкости. Прикл. матем. и механ., т. 9, № 4, 1945.
2.155. Т а у 1 о г G. J., The air wave surrounding an expanding sphere. Proc.
Roy. Soc., Ser. A., vol. 186, 1946.
2.156. Sakurai A., On the propagation and structure of the blast wave.
J. Phys. Soc. Japan, vol. 8, № 5, 1953; vol. 9, № 2, 1954.
2.157. Крашенинникова H. Л., О неустановившемся движении
газа, вытесняемого поршнем. Изв. АН СССР, ОТН, № 8,
1955.
2.158. Станюкович К. П., Неустановившиеся движения сплошной
среды. Гостехиздат, М., 1955.
2.159. Черный Г. Г., Одномерные неустановившиеся движения совер¬
шенного тока с сильными ударными волнами. Докл. АН СССР,
т. 107, № 5, 1956.
2.160. Григорян С. С., Задача Коши и задача о поршне для уравнений
одномерных неустановившихся движений газа (автомодельные дви¬
жения). Прикл. матем. и механ., т. 22, № 2, 1958.
2.161. К о ч и н а Н. Н., Мельникова Н. С., О неустановившемся
движении газа, вытесняемого поршнем. Прикл. матем. и механ.,
т. 22, № 4, 1958.
2.162. Черный Г. Г., Течения газа с большой сверхзвуковой скоростью.
Физматгиз, М., 1959.
2.163. Hayes W. D., On hypersonic simulitude. Quart. Appl. Math., vol. 5,
№ 1, 1947.
2.164. Бам-ЗеликовичГ. М., БунимовичА. И., Михай¬
лов а М. П., Движение тонких тел с большими сверхзвуковыми
скоростями. Теоретическая гидромеханика, Сб. № 4, Оборонгиз, М.,
1949.
2.165. Гродзовский Г. Л., Некоторые особенности обтекания тел
при больших сверхзвуковых скоростях. Изв. АН СССР, ОТН, № 6,
1957.
2.166. LeesL., Kubota Т., Inviscid hypersonic flow over blunt-nosed
slender bodies. J. Aeronaut. Sci., vol. 24, № 3, 1957.
ЛИТЕРАТУРА
649
2.167. Гродзовский Г. JI., Крашенинникова Н. Д., Автомо¬
дельные движения газа с ударными волнами, распространяющимися
по степенному закону по покоящемуся газу. Прикл. матем. и механ.,
т. 23, № 5, 1959.
2.168. Сычев В. В., К теории гиперзвуковых течений газа со скачками
уплотнения степенной формы. Прикл. матем. и механ., т. 24, № Зг
1960. Sychev V. V., On the theory of hypersonic flow over blunt-nosed
slender bodies. Adv. Aeronaut. Sci., 1960, vol. 3, N. Y., 1961.
2.169. Гродзовский Г. Д., Оптимальная форма теплоотводящих ре¬
бер, охлаждаемых излучением. Изв. АН СССР, ОТН, Энергетика и
автоматика, № 6, 1962, см. также Proc. XII Internat. Astronaut. Congr.
1961, Vien., 1962; Acta Astronautica, № 8, 1962.
2.170. ПонтрягинЛ. С., Болтянский В. Г., Мищенко
Е. Ф., Гамкрелидзе Р. В., Математическая теория опти¬
мальных процессов. Физматгиз, М., 1961.
2.171. Wilkins J. Е., Minimizing the mass of thin radiating fins. JASSr
vol. 27, № 2, 1960.
2.172. Wilkins J. E., Minimum mass thin fins witch transfer heat only
by radiation to surroundings at absolute zero. J. Soc. Ind. Appl. Math.,,
vol. 8, № 4, XII, 1960.
2.173. Wilkins J. E., Minimum mass thin fins for space radiators. Proc.
of 1960, Heat-Transfer and Mechanics Institute. Stanford University,.
1960.
2.174. Wilkins J. E., Minimum mass fins and constant temperature
gradient. J. Soc. Ind. Appl. Math., vol. 10, № 1, 1962.
2.175. BartasJ. G., Sellers W. H., Radiation fin effectiveness.
Trans. ASME. J. Heat Transfer, vol. 82, № 1, 1960.
2.176. С h e n Y. L., On mini mum-weight rectangular fins. JASS, vol. 27,
№ 11, 1960.
2.177. Nilson E. N., Curry R., The minimum-weight straight fin of
triangular profile radiating to space. JASS, vol. 27, № 2, 1960.
2.178. Гродзовский Г. Д., Фролов В. В., Оптимальные кон¬
туры теплоотводящих ребер, охлаждаемых излучением, ч. II. Ргос.
XIII Internat. Astronaut. Congr. 1962, Wien, 1963.
2.179. Фролов В. В., Оптимальная форма теплоотводящих ребер с уче¬
том взаимного облучения. Изв. АН СССР, ОТН, Энергетика и авто¬
матика, № 6, 1962.
2.180. Е с k е г t Е. R. G., Irvine Т. F. Jr., Sparrow М., Anali-
tical formulation for radiating fins with mutual irradiation. J. Amer.
Rock. Soc., vol. 30, № 7, 1960.
2.181. Sparrow М., E с к e r t E. R. G., I r v i n e T. F. Jr., The
effectiveness of radiating fins with mutual irradiation. JASS, vol. 28,
№ 10, 1961.
2.182. Kreith F., Radiation heat transfer for spacecraft and solar power
design. N. Y., 1962.
2.183. Sparrow E. М., E с к e r t E. R. G., Radiant interaction bet¬
ween fin and base surfaces. J. Heat Transfer, vol. 84, ser. С, № 1, 1962.
2.184. Plamondon J. A., Thermal efficiency of coated fins. J. Heat
Transfer, ser. C, vol. 84, № 4, 1962.
2.185. Karlekar В. V., Chao В. Т., Mass minimization of radiating
trapezoidal fins with negligible base cylinder interaction. Int. J. Heat
and Mase Transfer, vol. 6, № 1, 1963.
2.186. Haller H. C., Stockman N. O., A note on fin-tube view fac¬
tors. J. Heat Transfer, ser. C, vol. 85, № 4, 1963.
2.187. JohnssonV. K., Sparrow E. М., Angle factors for radiant
interchange between parallel-oriented tubes. J. Heat Transfer, ser. C,
vol. 85, № 4, 1963.
650 ЛИТЕРАТУРА
2.188. В а с а н о в Ю. А., Ж у л е в Ю. Г., Оптимальная форма треу¬
гольных теплоотводящих ребер с учетом взаимного облучения ребер
и охлаждаемой поверхности. Изв. АН СССР, Энергетика и транспорт,
№ 3, 1964, см. также Proc. XV Internat. Astronaut. Congr. 1964, War¬
szawa, 1965.
2.189. Соловьев Б. А., Графоаналитический метод определения пара¬
метров теплоносителя в холодильнике-излучателе на нерасчетных
режимах его работы. Изв. АН СССР, Энергетика и транспорт, № 4,
)65.
2.190. Васанов Ю. А., Характеристики теплового излучения системы
звездообразных излучателей. Изв. АН СССР, Энергетика и транспорт,
№ 5, 1964.
2.191. Васанов Ю. А., Влияние термического сопротивления покрытий
на характеристики теплового излучения звездообразных излучате¬
лей. Изв. АН СССР, Энергетика и транспорт, № 6, 1964.
2.192. Фролов В. В., Оптимальная система излучающих ребер. Изв.
АН СССР, Энергетика и транспорт, № 6, 1964.
2.193. Новоселецкий О. Ю., Уколов В. JL, Определение оп¬
тимальных размеров излучающих ребер. Инж.-физ. журнал, № 12,
1964.
2.194. Васанов Ю. А., Жулев Ю. Г., Исследование теплового из¬
лучения системы звездообразных излучателей. Теплофизика высоких
температур, № 6, 1965. См. также Proc. XVI Internat. Astronaut.
Congr. 1965, Warszawa, 1966.
2.195. Жулев Ю. Г., Косаренков В. А., Излучательная способ¬
ность трубчатого радиатора. Теплофизика высоких температур,
№ 3, 1966.
2.196. Weatherston R. С., Smitn W. Е., A method of heat rejec¬
tion from space powerplants. J. Amer. Soc., vol. 30, № 3, 1960.
2.197. С т а с e н к о A. JI., Форма гибкой нити в поле центробежных сил.
Изв. АН СССР, ОТН, Механика и машиностроение, № 6, 1962.
2.198. Гродзовский Г. JL, Стасенко A. Д., О форме теплоот¬
водящих элементов, охлаждаемых излучением, ч. III. Proc. XIV In¬
ternat. Astronaut. Congr. 1963, Warszawa, 1964.
2.199. Weatherston R. C., Smith W. S., A new type of thermal
radiator for space vehicles. Aeronaut. Eng., vol. 20, №. 1, 1961.
2.200. В u r g e H. L., Revolving belt space radiator. J. Amer. Rock. Soc.,
vol. 32, № 8, 1962.
2.201. Shipper L., Siegler R. C., Zwick E. B., Advanced
1-megawaft space power plant study. AIAA Paper, № 63-270, 1963.
2.202. Гродзовский Г. Д., Стасенко А. Д., Фролов В. В.,
О форме теплоотводящих элементов, охлаждаемых излучением, ч. IV.
Proc. XV Internat. Astronaut. Congr. 1964, Warszawa, 1965.
2.203. С т а с e н к о А. Д., Равновесные формы и малые колебания гибкой
нити, вращающейся в бессиловом поле. Изв. АН СССР, Механика
и машиностроение, № 1, 1964.
2.204. Стасенко А. Д., Предельные характеристики ленточного ра*
диатора с учетом самооблучения. Изв. АН СССР, Энергетика и тран"
спорт, № 1, 1965.
2.205. Стасенко А. Д., Влияние внешнего излучения на предельные
характеристики ленточного радиатора. Изв. АН СССР, Энергетика
и транспорт, № 5, 1965.
2.206. Шлыков Ю. П., Ганин Е. А., Контактный теплообмен. Энер-
гоиздат, М.— Д., 1963.
2.207. Fenech Н., Rohsenow W. Н., Prediction of thermal conduc¬
tance of metallic surfaces in contact. J. Heat Transfer, vol. 85, № 1,
1963.
ЛИТЕРАТУРА
651
2.208. Ста с ен к о A. JI., Двумерный периодический контакт. Контакт¬
ное сопротивление с учетом вторичных потоков в общем случае. Жур¬
нал нрикл. механ. и техн. физ., № 4, 1964.
2.209. English R. Е., Slone Н. О., Bernatowicz D. Т.,
Davison Е. Н., Lieblein S., А 20 000-kilowatt nuclear tur¬
boelectric power supply for manned space vehicles. NASA Memo
2-20-59 E, March 1959.
2.210. Гонор A. JL, Определение формы пространственного оптимального
тела с учетом силы трения, Изв. АН СССР, Механика, № 4, 1965.
К главе 3
3.1. Стечкин Б. С., Казанджан П. К., Алексеев А. П.,
Говоров А. Н., Коновалов Н. Е., Нечаев Ю. Н.,
Федоров Р. М., Теория реактивных двигателей. Оборонгиз, 1958.
3.2. Corliss W. R., Propulsion systems for space flight. N. Y., 1960.
Русский перевод: Корлисс У. Р., Ракетные двигатели для кос¬
мических полетов. ИЛ, М., 1962.
3.3. Г р о д з о в с к и й Г. Л., Иванов Ю. Н., Токарев В. В.,
Механика космического полета с малой тягой. Инж. журнал АН
СССР, т. 3, вып. 3 и 4, 1963; т. 4, вып. 1 и 2, 1964.
К главе 4
4.1. Preston-Thomas Н., Interorbital transport techniques. J.
Brit. Interpl. Soc., vol. 11, № 4, 1952.
4.2. Preston-Thomas H., Two aspects of the time element in in¬
terplanetary flight. Proc. V Internat. Astronaut. Congr. 1954, Vien., 1955.
4.3. Stuhlinger E., Possibilities of electrical space ship propulsion.
Proc. V Internat. Astronaut. Congr. 1954, Vien., 1955.
4.4. Bussurd R. W., A nuclear-electric propulsion system. J. Brit.
Interpl. Soc., vol. 15, № 6, 1956.
4.5. Preston-Thomas H., Interorbital transport techniques. Rea¬
lities of space travel, London, 1957.
4.6. Stuhlinger E., Design and performance data of space ships with
ionic propulsion systems. Proc. VIII Internat. Astronaut. Congr. 1957,
Vien., 1958.
4.7. Preston-Thomas H., A note on a nuclear electrical propul¬
sion system. J. Brit. Interpl. Soc., vol. 16, № 9, 1958.
4.8. Preston-Thomas H., Some design parameters of a simplified
ion rocket. J. Brit. Interpl. Soc., vol. 16, № 10, 1958.
4.9. Leitmann G., The nuclear-powered ion rocket. J. Brit. Interpl.
, Soc., vol. 16, № 10, 1958.
4.10. С or nog R., The optimum velocity of propellant ejection. Vistas
in Astronaut., vol. 1, N. Y., 1958.
4.11. Stuhlinger E., Advanced propulsion systems for space vehic¬
les. Proc. IX Internat. Astronaut. Congr., Madrid, 1958, Vien., 1959.
4.12. M о e с k e 1 W. E., Propulsion method in astronautics. Proc. IX
Internat. Astronaut. Congr., Madrid, 1958, Vien., 1959. Ш
4.13. Preston-Thomas H., The nuclear-powered ion rocket. J.
Brit. Interpl. Soc., vol. 17, № 3, 4, 1959.
4.14. Langmuir D. B., Optimization of rockets in which fuel is not
used as propellant. Space Technol., c. 9, N. Y., 1959.
4.15. Irving J. H., Low-thrust flight: variable exhaust velocity in gra¬
vitational fields. Space Technol., c. 10, N. Y., 1959.
4.16. Stuhlinger E., Seitz R. N., Electrostatik propulsion sys¬
tems for space vehicles. Adv. Space Sci., vol. 2, 1960.
652
ЛИТЕРАТУРА
4.17. С a m а с М., Use of energy storage in low-thrust spaceflight. J. Amer.
Rock. Soc., vol. 30, № 1, 1960.
4.18. С г о с с о L., Meccanica della propulsione spaziale. Proc. Seminar
Adv. on Astronaut. Prop. 1960, Milan, 1962.
4.19. Гродзовский Г. Д., О движении тела переменной массы с уче¬
том релятивистских эффектов, Изв. АН СССР, ОТН, Механика и ма¬
шиностроение, № 5, 1962.
4.20. Гродзовский Г. Д., Иванов Ю. Н., Токарев В. В.,
Механика космического полета с малой тягой. Инж. журнал АН
СССР, т. 3, № 3, 1963.
4.21. Irving J. Н., Blum Е. К., Comparative performance of bal¬
listic and low thrust vehicles for flight to Mars. Vistas in Astronaut. r
vol. 2, N. Y., 1959.
4.22. Гродзовский Г. Д., Иванов Ю. Н., Токарев В. В.>
О движении тела переменной массы с постоянной и убывающей зат¬
ратой мощности в гравитационном поле, ч. III. Proc. XIV Internat*
Astronaut. Congr., 1963.
4.23. Гродзовский Г. Д., Иванов Ю. Н., Токарев В. В.г
О движении тела переменной массы с постоянной затратой мощности
в гравитационном поле. Докл. АН СССР, т. 137, № 5, 1961; Proc. XII
Internat. Astronaut. Congr., Vashington, 1961, N. Y., 1963.
4.24. Иванов Ю. H., Оптимальное изменение мощности при движении
тела переменной массы в гравитационном поле. Прикл. матем. и ме-
хан., т. 26, № 4, 1962.
4.25. Гродзовский Г. Д., Иванов Ю. Н., Токарев В. В.г
О движении тела переменной массы с постоянной и убывающей зат¬
ратой мощности в гравитационном поле, ч. II, Proc. XIII Internat*
Astronaut. Congr., Varna, 1962, Vien. — N. Y., 1964.
4.26. Martelly J., Optimization of interplanetary propulsion systems*
IRE Trans, on Nuclear Sci., vol. № N S-9, № 1, 1962.
4.27. Цандер Ф. А., Применение металлического топлива в ракетных
двигателях. Сб. «Ракетная техника», № 1, 1936; см. Цандер Ф. А.,
Проблема полета при помощи реактивных аппаратов. Межпланетные,
путешествия. Оборонгиз, М., 1961.
4.28. Токарев В. В., Оптимальное управление источником мощно¬
сти при движении тела переменной массы в гравитационном поле с
активным сбросом мощности. Прикл. матем. и механ., т. 27, № 4„
1963.
К главе 5
5.1. Белецкий В. В., Егоров В. А., Межпланетные полеты с
двигателями постоянной мощности. Космические исследования, т. 2Т
№ 3, 1964.
5.2. Исаев В. К., Сонин В. В., Об одной нелинейной задаче опти¬
мального управления. Автоматика и телемеханика, т. 23, № 9, 1962.
5.3. Гродзовский Г. Д., Иванов Ю. Н., Токарев В. В.,.
О движении тела переменной массы с постоянной затратой мощности
в гравитационном поле. Докл. АН СССР, т. 137, № 5, 1961; Proc.
XII Internat. Astronaut. Congr., Washington, 1961, N. Y., 1963.
5.4. Иванов Ю. H., Токарев В. В., Шалаев Ю. В., Опти¬
мальные траектории и оптимальные параметры космических аппара¬
тов с двигателями ограниченной мощности. Космические исследова¬
ния, т. 2, № 3, 1964.
5.5. Irving J. Н., Low-thrust flight: variable exhaust velocity in gravi¬
tational fields. Space Technol., ch. 10, N. Y., 1959.
ЛИТЕРАТУРА
653
'5.6. Лебедев JI. А., ваковский С. А., О необходимых и доста¬
точных условиях экстремума функционала в задаче оптимального
перелета аппарата с двигателем малой тяги. Изв. вузов, сер. Авиац.
техн., № 4, 1964.
5.7. Leitmann G., Minimum transfer time for a power-limited rocket.
J. Appl. Meehan., vol. 28, № 2, 1961.
5.8. Preston-Thomas H., Interorbital transport techniques. Reali¬
ties of Space Travel., London, 1957.
5.9. Preston-Thomas H., Some design parameters of a simp¬
lified ion rocket. J. Brit. Interpl. Soc., vol. 16, № 10, 1958.
5.10. Исаев В. К., С о н и н В. В., Д а в и д с о н Б. X., Оптималь¬
ные режимы движения точки переменной массы с ограниченной мощ¬
ностью в однородном центральном поле. Космические исследования,
т. 2, № 4, 1964.
5.11. Белецкий В. В., Егоров В. А., Разгон космического ап¬
парата в сфере действия планеты. Космические исследования, т. 2,
№ 3, 1964.
5.12. I г v i n g J. Н., Blum Е. К., Comparative performance of bal¬
listic and low-thrust vehicles for flight to Mars. Vistas in Astronaut.,
vol. 2, N. Y., 1959.
5.13. Melbourne W. G., S a u e r C. G., R i с h a r d s о n D. E.,
Interplanetary trajectory optimization with power-limited systems.
Proc. IAS Symp. on Vehicle Syst. Optim., N. Y., 1961.
.5.14. M e 1 b о u r n e W. G., Three-dimensional optimum thrust trajec¬
tories for power-limited propulsion systems. J. Amer. Rock. Soc.,
vol. 31, № 12, 1961.
5.15. Melbourne W. G., Sauer C. G., Optimum thrust programs
for power-limited propulsion systems. Asntronaut. Acta, vol. 8, № 4,
1962.
5.16. Melbourne W. G., Sauer C. G., Optimum interplanetary
rendevous with power-limited vehicles. AIAA J., vol. 1, № 1, 1963.
5.17. Melbourne W. G., Sauer C. G., Optimum Earth-Mars
roundtrip trajectories utilizing a low-thrust power-limited propulsion
system. Adv. in-the Astronaut. Sci., vol. 13, 1963.
5.18. Saltzer C., Fetheroff C. W., A direct variational method
for the calculation of optimum thrust programm for power-limited in¬
terplanetary flight. Astronaut. Acta, vol. 7, № 1, 1961.
5.19. Sherman B., Low thrust escape trajectories. Proc. IAS Symp.
on Vehicle Syst. Optim., N. Y., 1961.
5.20. Иванов Ю. H., Шалаев Ю. В., Метод скорейшего спуска
в применении к расчету межорбитальных траекторий с двигателями
ограниченной мощности. Космические исследования, т. 2, № 3, 1964.
*5.21. Покровская С. А., О решении пространственной задачи ге¬
лиоцентрических перелетов с двигателем постоянной мощности мето¬
дом скорейшего спуска. Космические исследования, т. 2, № 6, 1964.
5.22. FauldersC. R., Optimum thrust programming of electrically
powered rocket vehicles in gravitational field. J. Amer. Rock. Soc.,
vol. 30, № 10, 1960.
5.23. FauldersC. R., Optimum thrust programming of electrically
powered rocket vehicles for earth escape. AIAA J., vol. 1, № 1, 1963.
5.24. Edelbaum T. N., The use of high and low thrust propulsion in
combination for space mission. Prepr. Amer. Astronaut. Soc., № 61 —
104, 1961.
5.25. Белецкий В. В., E г о p о в В. А., Е р ш о в В. Г., Анализ
траекторий межпланетных полетов с двигателем постоянной мощно¬
сти. Космические исследования, т. 3, № 4, 1965.
654
ЛИТЕРАТУРА
5.26. Лебедев В. Н., Вариационная задача о взлете космического
аппарата с круговой орбиты. Ж. выч. мат. и мат. физ., т. 3, № 6, 1963.
5.27.’ Иванов Ю. Н., Шалаев Ю. В., Оптимальный поворот пло¬
скости круговой орбиты поперечной силой. Косм, иссл., т. 3, № 5,1965.
5.28. G о b е t z F. W., Optimal variable-thrust transfer of a power-limited
rocket between neighboring circular orbits. AIAA J., vol. 2, № 2, 1964.
Русский перевод: Ракетная техника и космонавтика, № 2, 1964.
5.29. G о b е t z F. W., Errata: Optimal variable-thrust transfer of a power-
limited rocket between neighboring circular orbits. AIAA J., vol. 2,
№ 12, 1964. Русский перевод: Ракетн. техн. и космон., № 12, 1964.
5.30. Leitmann G., Ross S., Low acceleration trajectory optimiza¬
tion in a strong central force field. Proc. IAS Symp. on Vehicle Syst.
Optim., N. Y., 1961.
5.31. EdelbaumT. N., Theory of maxima and minima. Optimiz. Techn.,
ch. 1, G. Leitmann, Ed., Acad. Press, 1961.
5.32. EdelbaumT. N., Propulsion requirements for controllable satel¬
lites. J. Amer. Rock. Soc., vol. 31, № 8, 1961.
5.33. Edelbaum T. N., Optimum low-thrust transfer between circular
and elliptic orbits. Proc. 4th U. S. Nat. Congr. Appl. Mech., Berkeley,
Calif., 1962, vol. 1; Pergamon Press, 1962.
5.34. В i 1 1 i k В. H., Some optimal low-acceleration rendevous maneuvres
AIAA J., vol. 2, № 3, 1964.
5.35. GobetzF. W., A linear theory of optimum low-thrust rendevous
trajectories. J. Astronaut. Sci., vol. 12, № 13, 1965.
5.36. Исаев В. К., Курьянов А. И., Сонин В. В., Применение
принципа максимума в ракетодипамике. Proc. XIV Internat. Astro¬
naut. Congr. 1933, Warszawa, 1934.
5. 37. Ефимов Г. Б., Охоцимский Д. Е., 05 оптимальном разгоне
космического аппарата в центральном поле. Космические исследо¬
вания, т. 3, № 6, 1965.
К главе 6
6.1. Иванов 10. Н., О движении тела переменной массы с ограничен¬
ной мощностью и заданным активным временем. Прикл. матем. и
механ., т. 27, № 5, 1963.
6.2. Иванов Ю. Н., Шалаев Ю. В., Оптимальный поворот пло¬
скости круговой орбиты поперечной силой. Космические исследова¬
ния, т. 3, № 5, 1965.
6.3. Исаев В. К., Принцип максимума Л. С. Понтрягина и оптималь¬
ное программирование тяги ракет. Автоматика и телемеханика,
т. 22, № 8, 1961; т. 23, № 1, 1962.
6.4. Лебедев В. Н., Вариационная задача о взлете космического ап¬
парата с круговой орбиты. Ж. вычисл. матем. и матем. физ., т. 3,
№ 6, 1963.
6.5. Лебедев В. Н., Моисеев Н. Н., Задачи теории оптимальных
управлений космическими аппаратами. Proc. XVI Internat. Astronaut.
Congr. 1935, Warszawa, 1936.
6.6. L a w d e n D. F., Optimal escape from a circular orbit. Astronaut.
Acta, vol. 4, № 3, 1958.
6.7. MoeckelW. E., Trajectories with constant tangential thrust in
central gravitational fields. NASA Techn. Rep. R-53, Wash., 1959.
6.8. MoeckelW. E., Fast interplanetary mission with low-thrust pro¬
pulsion systems. NASA Techn. Rep. R-79, Wash., 1961.
6.9. MoeckelW. E., Interplanetary trajectories for electricaly-propel-
land space vehicles. Astronaut. Acta, vol. 7, № 5, 6, 1961.
ЛИТЕРАТУРА
655
6.10. Белецкий В.^ В., Егоров В. А., Разгон космического аппа¬
рата в сфере действия планеты. Космические исследования, т. 2,
№ 3, 1964.
6.11. Аврамченко Р. Ф., Безменов В. М., Винокуров В. А.,
Токарев В. В., Оптимальный перелет Земля — Марс — Земля
с нерегулируемым двигателем малой тяги. Космические исследова¬
ния, т. 5, № 2, 1967.
6.12. МасКау J. S., R о s s a L. G., Zimmerman А. V., Optimum
low-acceleration trajectories for Earth-Mars transfer. Proc. IAS Symp.
on Vehicle Syst. Optim., N. Y., 1961.
6.13. Z e h 1 e H., Zur optimalisierung interplanetarer iibergangsbahnen mit
kleiner schubbescbleunigung. Teil II und III. Raumfahrtforschung,
vol. 8, № 3, 1964.
6.14. Lindorfer W., Moyer H. G., Application of a low-thrust tra¬
jectory optimization scheme to planar Earth-Mars transfer. J. Amer.
Rock. Soc., vol. 32, № 2, 1962. Русский перевод: Ракетная техника,
№ 2, 1962.
6.15. Белецкий В. В., Егоров В. А., Межпланетные полеты с дви¬
гателем постоянной мощности. Космические исследования, т. 2,
№ 3, 1964.
6.16. Лебедев В. Н., Румянцев Б. Н., Вариационная задача о
перелете между двумя точками в центральном поле. Сб. «Искусствен¬
ные спутники Земли», вып. 16, 1963.
6.17. Faulders С. R., Minimum time steering programs for orbital trans¬
fer with low-thrust rocket. Astronaut. Acta, vol. 7, № 1, 1961.
6.18. Melbourne W. G., S a u e r C. G., R i с h a r d s о n D. E., In¬
terplanetary trajectory optimization with power-limited systems. Proc.
IAS Symp. on Vehicle Syst. Optim., N. Y., 1961.
6.19. Melbourne W. G., Sauer C. G., Optimum thrust programs
for power-limited propulsion systems. Astronaut. Acta, vol. 8, № 4,
1962.
6.20. Melbourne W. G., Sauer C. G., Payload optimization for po¬
wer-limited vehicles. Progr. in Astronaut, and Aeronaut., vol. 9, Elect¬
ric Prop. Devel., N. Y., 1963. Русский перевод: Вопросы ракетной
техники, № 8, 1964.
6.21. Копнин Ю. М., К задаче о повороте плоскости орбиты спутника.
Космические исследования, т. 3, № 4, 1965.
6.22. Stuhlinger Е., Design and performance data of space ships with
ionic propulsion systems. Proc. VIII Internat. Astronaut. Congr. 1957,
Vien., 1958.
6.23. M о e с k e 1 W. E., Propulsion method in astronautics. IX Internat.
Astronaut. Congr., 1958.
6.24. Preston-Thomas H., A note on a nuclear electrical propulsion
* system. J. Brit. Interpl. Soc., vol. 16, № 9, 1958.
6.25. Гродзовский Г. Л., О движении тела переменной массы с по¬
стоянной затратой мощности в гравитационном поле с учетом реля¬
тивистских эффектов. Изв. АН СССР, ОТН, Механика и машино¬
строение, № 5, 1962.
6.26. Preston-Thomas Н., Interorbital transport techniques. J. Brit.
Interpl. Soc., vol. 11, № 4, 1952.
6.27. Preston-Thomas H., Two aspects of the time element in inter"
planetary flight. Proc. V Internat. Astronaut. Congr. 1954, Vien, 1955*
К главе 75f
7.1. Faulders С. R., Optimum thrust programming of electrically po¬
wered rocket vehicles in a gravitational field. J. Amer. Rock. Soc.,
vol. 30, № 10, 1960.
656
ЛИТЕРАТУРА
7.2. FauldersC. R., Optimum thrust programming of electrically po¬
wered rocket vehicles for earth escape. AIAA J., vol. 1, № 1, 1963.
Русский перевод: Ракетная техника и космонавтика, № 1, 1963.
7.3. Melbourne W. G., Sauer С. G., Constant-attitude thrust prog¬
ram optimization. AIAA J., vol. 3, № 8, 1965. Русский перевод: Ра¬
кетная техника и космонавтика, № 8, 1965.
7.4. Bussurd R. W., A nuclear-electric propulsion system. J. Brit.
Interpl. Soc., vol. 15, № 6, 1956.
7.5. Preston-ThomasH., A note on a nuclear electrical propulsion
system. J. Brit. Interpl. Soc., vol. 16, № 9, 1958.
7.6. Ij v i n g J. H., Blum E. K., Comparative performance of ballistic
and low-thrust vehicles for flight to Mars. Vistas in Astronaut., vol. 2,
N. Y., 1959.
7.7. Иванов Ю. H., Дополнительные весовые компоненты в задачах
оптимизации движения с ограниченной мощностью. Прикл. матем.
и механ., т. 28, № 1, 1964.
7.8. Au G. F., Entwicklungsstang zukunftiger raumfahrtantriebe. Luftfahrt-
technik, vol. 7, № 1, 1961.
7.9. Иванов Ю. H., О движении тела переменной массы с ограничен¬
ной мощностью и заданным активным временем. Прикл. матем. и
механ., т. 27, № 5, 1963.
7.10. Винокуров В. А., Иванов 10. Н., Оптимальное движение в
центральном поле при заданном времени работы источника мощности.
Изв. АН СССР, Механика, № 5, 1965.
7.11. Иванов 10. Н., Ступенчатая аппроксимация оптимальных управ¬
лений. Прикл. матем. и механ., т. 28, № 3, 1964.
7.12. Белецкий В. В., Егоров В. А., Межпланетные полеты с
двигателем постоянной мощности. Космические исследования, т. 2,
№ 3, 1964.
7.13. Исаев В. К., Сонин В. В., Об одной нелинейной задаче опти¬
мального управления. Автоматика и телемеханика, т. 23, № 9, 1962.
7.14. Исаев В. К., С о н и н В. В., Д а в и д с о н Б. X., Оптимальные
режимы движения точки переменной массы с ограниченной мощно¬
стью в центральном однородном поле. Космические исследования,
т. 2, № 4, 1964.
7.15. Melbourne W. G., Sauer С. G., RichardsonD. Е., In¬
terplanetary trajectory optimization with power-limited systems. Proc.
IAS Symp. on Vehicle Syst. Optim., N. Y., 1961.
7.16. Melbourne W. G., Sauer C. G., Optimum thrust programms
for power-limited propulsion systems. Astronaut. Acta, vol. 8, № 4,
1962.
7.17. Melbourne W. G., Sauer C. G., Payload optimization for po¬
wer-limited vehicles. Progr. in Astronaut, and Aeronaut., vol. 9, Elec¬
tric. Prop. Devel., N. Y., 1963. Русский перевод: Вопросы ракетной
техники, № 8, 1964.
7.18. Shelton R. D., Р о t t е г R. A., L а с у L., S t u h 1 i n g e r E.,
Evaluation and analysis of thrust units for power-limited propulsion
systems. AIAA J., vol. 2, № 4, 1964. Русский перевод: Ракетная тех¬
ника и космонавтика, № 4, 1964.
7.19. Lawden J. Н., Trajectory optimization for a rocket with generalised
thrust characteristic. Astronaut. Acta, vol. 10, № 5, 6, 1964.
7.20. DulgeroffC. R., Speiser R. S., Forrester A. Т., Expe¬
rimental studies with small scale ion motors. ARS 14th Annual Meeting,
Wash., Nov. 16—20, 1959.
7.21. Fox R., Physics of the ion thrust system. ARS 14th Annual Meeting,
Wash., Nov. 16—20, 1959.
ЛИТЕРАТУРА
657
7.22. К a s li S. W., S t а г г W, L., Experimental results with a collinear
electrode plasma accelerator and a comparison with ion accelerators.
ARS 14th Annual Meeting, Wash., Nov. 16—20, 1959.
7.23. Moser W. A., Ion engine operation analysis. ARS Electrical Pro¬
pulsion Conference, Berkeley, March 14—16, 1961.
7.24. Brown H., N i с о 1 1 H. E., Electrical propulsion capabilities for
lunar exploration. ARS Electrical Propulsion Conference, Berkeley,
March 14—16, 1961.
7.25. Исаев В. К., Курьянов А. И., Сонин В. В., Применение
принципа максимума в ракетодинамике. Proc. XIV Internal. Astro*
naut. Congr. 1963, Warszawa, 1964.
К главе 8
8.1. Hunter M. W., Tschirgi I. М., The advantages of high thrust
space vehicles. Prepr. Amer. Rock. Soc., № 991, 1959.
8.2. Craig R., Fetheroff C. W., Saltzer C., Comparison of che¬
mical and electric propulsion systems for interplanetary travel. Proc.
IRE, vol. 48, № 4, 1960.
8.3. Stearns I. W., Electropropulsion system applications, Astro¬
nautics, vol. 7, № 3, 1962.
8.4. Beers L. S., Cohen A. D., Mars capabilities for electrical, nuclear
and chemical propulsion systems. IAS Paper, № 120, 1962.
8.5. Stuhlinger E., The rocket with electrical propulsion system.
Electrical Engineering, vol. 82, № 7, 1963.
8.6. Boucher R. A., Electrical propulsion for control of stationary
satellites., J. of Spacecraft and Rock., vol. 1, № 2, 1964.
8.7. Охоцимский Д. E., К теории движения ракет. Прикл. матем.
и механ., т. 10, № 2, 1946.
8.8. Охоцимский Д. Е., Энеев Т. М., Некоторые вариационные
задачи, связанные с запуском искусственного спутника Земли. УФН,
т. 63, вып. 1а, 1957.
8.9. Lawden D. F., Optimal rocket trajectories., Jet Prop., vol. 27,
№ 12, 1957.
8.10. M i e 1 e A., General variational theory of the flight paths of rocket-
powered aircraft, missiles and satellite carriers, Astronaut. Acta, vol. 4,
№ 4, 1958.
8.11. Miclc A., Gappellari I. O., Topics in dynamic programming
for rockets, Z. Flugwiss, vol. 7, № 1, 1959.
8.12. В r e a k w e 1 1 J. V., The optimization of trajectories, J. Soc. Indust.
Appl. Math., № 7, 1959. Русский перевод: Вопросы ракетной
техники, № 1, 1961.
8.13. Leitmann G., On a class of variation problems in rocket flight.
JASS, vol. 26, № 8, 1959.
8.14. Lei tm.ann G., Extremal rocket trajectories in position and time de¬
pendent force fields. VII Ann. Meet. Amer. Astronaut. Soc., №30,1961.
8.15. Лейтман Г. (Leitmann G.), Об оптимальных траекториях ракет.
Прикл. матем. и механ., т. 25, № 6, 1961.
8.16. Исаев В. К., Принцип максимума Л. С. Понтрягина и оптимальное
программирование тяги ракет. Автоматика и телемеханика, т. 22,
№ 8, 1961.
8.17. Исаев В. К., Дополнение к работе «Принцип максимума Л. С. Пон¬
трягина и оптимальное программирование тяги ракет». Автоматика
и телемеханика, т. 23, № 1, 1962.
8 18. Leitmann G., The optimization of rocket trajectories — a survey.
Progr. in Astronaut. Sci., vol. 1, Amsterdam, 1962.
8.19. Lawden D. F., Optimal intermediate — thrust arcs in a gravita¬
tional field., Astronaut. Acta, № 8, 1962.
42 Механика полета
658
ЛИТЕРАТУРА
8.20. Contensou P., Etude theoretique des trajectories optimale dans
un champ de gravitation., Astronaut. Acta, № 8, 1962.
8.21. Miele A., The calculus of variations in applied aerodynamics and
flight mechanics. Optimization techniques with applications to aero¬
space systems, ed. by Leitman G., Academic Press, N. Y.— London,
1962.
8.22. К у з м а к Г. Е., Исаев В. К., Давидсон Б. X., Оптималь¬
ные режимы движения точки переменной массы в однородном цент¬
ральном поле. Докл. АН СССР, т. 149, № 1, 1963.
8.23. Лурье А. И., Управление тягой в центральном поле тяготения.
Второй Всесоюзн. съезд по теорет. и прикл. механ. 1964. Аннот.
докл., М., 1964.
8.24. Диамандиев В., Тодоров К., Оптимални траектории при
реактивного движение. Годишник Софийск. ун-та. Матем. фак., 57,
1962—1963 (1964).
8.25. Keller J. L.f On minimum propellant paths for thrust limited
rockets. Astronaut. Acta, vol. 10, № 3—4, 1964.
8.26. Pines S., Constants of the motion for optimum thrust trajectories
in a central force field. AIAA J., vol. 2, № 11, 1964.
8.27. Veubeke B. F., Geerts J., Application du principe de maxi¬
mum a la syntese des transferts optimaux dans in champ de gravitation
planetaire. Proc. XV Internat. Astronaut. Congr. 1964, Warszawa, 1965.
8.28. Новоселов В. С., Теория приближенного решения вариацион¬
ных задач и ее приложение к исследованию движения точки перемен¬
ной массы. Вестн. Ленингр. ун-та, № 1, 1965.
8.29. Новоселов В. С., Аналитическая динамика и оптимальные пере¬
леты. Тр. II Всесоюзн. съезда по теорет. и прикл. механ., 1964.
Обзорн. докл., вып. 1, «Наука», М., 1965.
8.30. С a v о t i С. R., Optimization of multistage processes, J. Spacecraft
and Rock., vol. 2, № 1, 1965.
8.31. Lubowe A. G., Appication of dynamic programming to the opti¬
mum staging of rockets, J. Spacecraft and Rock., vol. 2, № 1, 1965.
8.32. Gurley I. G., Optimal-thrust trajectories in an arbitrary gravita¬
tional foeld., J. Soc. Industr. and Appl. Math., ser. A, vol. 2, № 3, 1965.
8.33. Robbins H. М., Optimality of intermediate thrust arcs of rocket
trajectories., AIAA J., vol. 3, № 6, 1965.
8.34. Cavoti C. R., Method of characteristic constants and retrothrust
optimality in a gravitational field-necessary and sufficient conditions,
J. Franklin Inst., vol. 279, № 3, 1965.
8.35. Bell D. I., Optimal trajectories and the accessory minimum problem.
Aeron. Quart., vol. 16, № 3, 1965.
8.36. Г у p м а н В. И., Об оптимальных траекториях реактивного аппара¬
та в центральном поле. Космические исследования, т. 3, № 3, 1965.
8.37. Горелов 10. А., К теории экстремальных движений точки пере¬
менной массы в центральном гравитационном поле. Инж. журнал,
т. 5, № 3, 1965.
8.38. Троицкий В. А., Оптимизация движения двухступенчатой раке¬
ты. Прикл. матем. и механ., т. 29, № 4, 1965.
8.39. Мил ьштейн Г. Н., Об оптимальном осуществлении траекторий.
Автоматика и телемеханика, т. 26, № 4, 1965.
8.40. Исаев В. К., О некоторых особенностях вариационной задачи
Майера в ракетодинамике. Автоматика и телемеханика, т. 26, № 7,
1965.
8.41. Литовченко И. А., Оптимизация систем при ступенчатых огра¬
ничениях на управление. Автоматика и телемеханика, т. 26. № 8,
1965.
ЛИТЕРАТУРА
659
8.42. Б о л о н к и н А. А., Оптимизация траектории многоступенчатых
летательных аппаратов. Сб. «Исследования по динамике полета»,
вып. 1, «Машиностроение», М., 1965.
8.43. KoppR. Е., МоуегН. G., Necessary conditions for singular
extremals, AIAA J., vol. 3, № 8, 1965.
8.44. Marec J. P., Transferts orbitaux economiques (orbites elliptiques,
coplanaires coaxiales). Rech. aerospatiale, № 105, 1965.
8.45. Гродзовский Г. JI., Некоторые вариационные задачи механи¬
ки космического полета. Механика твердого тела (Инж. журн.),
АН СССР, № 6, 1966.
8.46. М а П па F. I., S mi th А. М., Flight analysis of the sounding
rocket. IAS, vol. 5, № 5, 1938.
8.47. О x о ц и м с к и й Д. Е., О подъеме ракеты в воздухе на максималь¬
ную высоту. Прикл. матем. и механ., т. 10, № 6, 1946.
8.48. Белецкий В. В., О вертикальном подъеме точки переменной мас¬
сы в среде постоянной плотности. Прикл. матем. и механ., т. 20,
Я» 6, 1956.
8.49. М i е 1 е A., Generalized variational approach to the optimum thrust
programming for the vertical flight of a rocket. Z. Flugwiss., vol. 6,
№ 3, 1958.
8.50. LeitmannG., An elementary derivation of the optimal control
conditions. Proc. XII Internat. Astronaut. Congr. 1961, Vien., 1962.
8.51. В а г г e г e М., JaumotteA., VeubekeB. F., Vanden-
kerckhove J., Rocket propulsion, Amst.— London —N. Y., 1960.
Русский перевод: Баррер М., ЖомоттА., ВебекБ. Ф.г
В а н д е н к е р к х о в е Ж., Ракетные двигатели. Оборонгиз, М.г
1962.
8.52. Исаев В. К., К у р ь я н о в А. И., Сонин В. В., Применение
принципа максимума в ракетодштампке. Proc. XIV Internat. Astro¬
naut. Congr. 1963, Warszawa, 1964.
8.53. M i e 1 e A., Flight mechanics, vol. 1, Massachusetts — London, 1963.
Русский перевод: M и e л e А., Механика полета, т. 1, «Наука»,
М., 1965.
8.54. Munich Н., Goddard problem with bounded thrust. AIAA J.,
vol. 3, № 7, 1965.
8.55. EdelbaumT. N., The use of high- and low-thrust propulsion in
combination for space missions. Amer. Astron. Soc., prep. 61—104,
1961. Русский перевод: Вопросы ракетной техники, № 5, 1965.
8.56. Иванов 10. Н., Оптимальное сочетание двигательных систем. Изв.
АН СССР, Механика и машиностроение, № 2, 1964.
8.57. F i m р 1 е W.,R., An improved theory of the use of high and low-thrust
propulsion in combination. J. Astronaut. Sci., vol. 10, № 10, 1963.
Русский перевод: Вопросы ракетной техники, № 5, 1965.
8.58. Ильин В. А., К расчету траекторий перелета космических аппа¬
ратов между компланарными круговыми орбитами в ньютопианском
гравитационном поле. Космические исследования, т. 2, № 5, 1964.
К главе 9
9.1. LinhardtH. D., Comparison of solar-thermal and solar-electric-
thermal propulsion methods. IAS Paper, № 63—20, 1963.
9.2. С a m а с М., Use of energy storage in low-thrust spaceflight. J. Amer.
Rock. Soc., vol. 30, № 1, 1960.
9.3. Гродзовский Г. Л.,Кифоренко Б. H.,Токарев В. В.,
Накопитель энергии в задачах оптимизации движения с ограничен¬
ной мощностью. Изв. АН СССР, Механика, № 3, 1965; см. также
Proc. XVI Internat. Astronaut. Congr. 1965, Warszawa, 1966.
42*
660
ЛИТЕРАТУРА
9.4. Понтрягин JI. С., Болтянский В. Г., Гам к рели д-
зе Р. В., Мищенко Е. Ф., Математическая теория оптималь¬
ных процессов. Физматгиз, М., 1961.
9.5. К и ф о р е н к о Б. Н., К выбору оптимальных параметров дви¬
гательной установки в задачах оптимизации движения с ограничен¬
ной мощностью и накопителем энергии. Изв. АН СССР, Механика,
№ 3, 1966. тт .
9.6. Кротов В. Ф., Методы решения вариационных задач. 11. Авто¬
матика и телемеханика, т. 24, № 5, 1963.
9.7. Кифоренко Б. Н., Некоторые задачи оптимизации движения с
ограниченной мощностью и накопителем энергии. Механика твер¬
дого тела инж. журн.), № 5, 1966.
9.8. Иванов Ю. Н., О движении тела переменной массы с ограничен¬
ной мощностью и заданным активным временем. Прикл. матем. и
механ., т. 27, № 5, 1963.
9.9. Кифоренко Б. Н., О движении по орбитам, близким к круго¬
вым, при использовании двигательной системы с накоплением энергии
и движителем постоянной мощности. Механика тв. тела (Инж. журн.),
№ 2, 1967.
9.10. Гродзовский Г. JI., Кифоренко Б. Н., О движении тела
переменной массы с накоплением энергии и движителем с ограничен¬
ной скоростью истечения реактивной струи, ч. II. Proc. XVII
Internat. Astronaut. Congr. 1966, Warszawa, 1967.
9.11. Demetriades S. Т., A novel system for space flight using a
propulsive fluid accumulator. J. Brit. Interpl. Soc., vol. 17, № 5,
1959.
9.12. Berner F., С a m а с М., Air scooping vehicle. Air Force Ballistic
Missile Div., TR 59-17, 1959.
9.13. Demetriades S. Т., Orbital propulsion system for space ma-
neuvring (PROFAC). Astronaut. Sci. Rev., vol. 1, № 4, 1959.
9.14. D e m e t r i a d e s S. Т., Preliminary study of propulsive fluid accu¬
mulator systems. Proc. XI Internat. Astronaut. Congr. 1960, Vien.,
1961.
9.15. French E. P., Operation of an electric ramjet in a planetary atmos¬
phere. Prepr. Techn. Ses. Amer. Astronaut. Soc., № 90, 1960.
9.16. Camac М., Berner F., An orbital air-scooping vechicle. Astro¬
nautics, vol. 6, № 8, 1961.
9.17. Reichel R. H., Smith T. L., Hanford D. R., Potentiali¬
ties of airscooping electrical space propulsion systems. Progr. in Astro¬
naut. and Aeronaut., vol. 9, Electrical Prop. Devel., N. Y., 1963.
9.18. Токарев В. В., Фаткин Ю. М., Накопитель рабочего ве¬
щества в задачах оптимизации движения с ограниченной мощностью.
Инж. журн. АН СССР, т. 5, № 3, 1965.
9.19. Фаткин Ю. М., Выбор оптимального закона управления тягой
в задаче движения в режиме накопления массы. Механ. тв. тела
(Инж. журн.), № 1, 1967.
9.20. Гродзовский Г. JL, Некоторые вариационные задачи механи¬
ки космического полета. Механ. тв. тела (Инж. журн.), № 6,
1966.
9.21. Цандер Ф. А., Об использовании силы давления света для поле¬
тов в межпланетном пространстве, 1924—1925. См. Ф. А. Ц а н-
д е р. Проблема полета при помощи реактивных аппаратов. Межпла¬
нетные путешествия. Оборонгиз, М., 1961.
9.22. Tsu Т. С., Interplanetary travel by solar sail. J. Amer. Rock. Soc.,
vol. 29, № 6, 1959.
9.23. Tsu Т. C., Straight-line flight to Mars. Proc. VI Ann. Meet. Amer.
Astronaut. Soc., 1960, Adv. Astronaut. Sci., vol. 6, N. Y., 1961.
ЛИТЕРАТУРА
661
9.24. London Н. S., Some exact solution of the equation of motion of
solar sail with constant sail setting. J. Amer. Rock. Soc., vol. 30,
№ 2, 1960.
9.25. P о z z i A., Su un metodo di soluzionne del problema della vela solare.
Missile, vol. 3, № 6, 1961.
9.26. Pozzi A., Socio L., Some remarks on solar sail. J. Amer. Rock.
Soc., vol. 31, № 8, 1961.
9.27. Socio L., La navigazione con vela solare. Missili, vol. 3, № 3, 1961.
9.28. Kelley H. J., Gradient theory of optimal flight paths. J. Amer.
Rock. Soc., vol. 30, № 10, 1960.
9.29. Жуков A. H., Лебедев В. H., Вариационная задача о пере¬
лете между гелиоцентрическими круговыми орбитами с помощью
солнечного паруса. Космические исследования, т. 2, № 1, 1964.
9.30. Sands N., Escape from planetary gravitational fields by use of solar
sailes. J. Amer. Rock. Soc., vol. 31, № 4, 1961.
9.31. F i m p 1 e W. R., A generalized three-dimensional trajectory analysis of
planetary escape by solar-sail. J. Amer. Rock. Soc., vol. 32, №6, 1962.
9.32. Perkins F. М., Flight mechanics of low-thrust spacecraft. JASS,
vol. 26, № 5, 1959; Vistas in Astronaut., vol. 2, N. Y., 1959.
9.33. Валеев К. Г., Качественное исследование дифференциальных
уравнений полета при помощи солнечного паруса. Прикл. матем. и
техн. физ., № 2, 1964.
9.34. ИлютовичА. Е., Оптимальный перелет с двигателем, использу¬
ющим солнечную энергию. Космические исследования, т. 4, №6, 1966.
9.35. Овсянников Р. Н., Семенова Л. Н., О движении тела
переменной массы с экспоненциально убывающей мощностью реак¬
тивной струи. Механ. тв. тела (Ипж. журн.), № 4, 1966.
К главе Ю
10.1. Токарев В. В., Некоторые вопросы надежности в задачах опти¬
мального управления, Прикл. матем. и механ., т. 30, № 2, 1967.
10.2. Токарев В. В., К выбору параметров динамической системы,
универсальной для заданного класса маневров. Изв. АН СССР, Ме¬
ханика и машиностроение, № 5, 1964; proc. XVI Internat. Astronaut.
Congr. 1965, Warszawa, 1966.
10.3. Токарев В. В., Фаткин 10. М., Игровой подход к задаче
выбора оптимальных параметров динамической системы. Механика
тв. тела, (Инж. журн.), № 6, 1966.
10.4. Аврамченко Р. Ф., Токарев В. В., Запас рабочего веще¬
ства, оптимальный для выполнения заданного маневра при фиксиро¬
ванных параметрах двигательной системы. Космические исследова¬
ния, т. 5, № 1, 1967.
10.5. Вентцель Е. С., Элементы теории игр. Физматгиз, М., 1959.
10.6. Мак-Кинси Дж. (Me Kinsey J. С.), Введение в теорию игр.
Физматгиз, М., 1960.
10.7. Теория игр. Бесконечные антагонистические игры. Сб. под ред.
Н. Н. Воробьева. Физматгиз, М., 1963.
10.8. Дрешер М. (Dreshcr М.). Стратегические игры. Теория и при¬
ложения. «Сов. радио», М., 1964.
К главе И
11.1. Токарев В. В., Влияние случайных процессов уменьшения мощ¬
ности на движение тела переменной массы в гравитационном поле.
Прикл. матем. и мехаи., т. 26, № 4, 1962.
662
ЛИТЕРАТУРА
11.2. Гродзовский Г. JL, Иванов 10. Н., Токарев В. В.г
О движении тела переменной массы с постоянной и убывающей затра¬
той мощности в гравитационном поле, II. Proc. XIII Internat. Astro¬
naut. Congr. 1962, Vien. — N. Y., 1964.
11.3. Гродзовский Г. JI., Иванов Ю. Н., Токарев В. В.г
Механика космического полета с малой тягой, III. Инж. журнал,
т. 4, № 1, 1964.
11.4. Токарев В. В., Некоторые вопросы надежности в задачах опти¬
мального управления. Прикл. матем. и механ., т. 30, № 1, 1966.
11.5. X и н ч и н А. Я., Математические методы теории массового обслу¬
живания. Физматгиз, М., 1963.
11.6. Гнеденко Б. В., Курс теории вероятностей, «Наука», М., 1965.
11.7. П о л о в к о А. М., Основы теории надежности. «Наука», М., 1964.
11.8. Гнеденко Б. В., Беляев 10. К., С о л о в ь е в А. Д., Матема¬
тические методы в теории надежности. «Наука», М., 1965.
11.9. Edelbaum Т. N., Multi-engine reliability for electric propulsion
systems. ARS Prepr., 2338-62, 1962.
11.10. Pin kel B., Electrical propulsion for spaee: mission comparisons,
development cost, realiability, and their implications for planning.
The Rand Corp. Rep. RM-4056-NASA, 1933.
11.11. Ragsac R. V., Study of low-acceleration space transportation
systems. United Aircraft Corp. Research Labor. Rep. D-910262-3, 1965.
К главе 12
12.1. Л у p ь e А. И., Некоторые нелинейные задачи теорйи автоматиче¬
ского регулирования. Гостехиздат, М., 1951.
12.2. Каменков Г. В., Об устойчивости движения на конечном интер¬
вале времени. Прикл. матем. и механ., т. 17, № 5, 1953.
12.3. Галиуллин А. С., Об одной задаче устойчивости движения тя¬
желой точки переменной массы на конечном интервале времени. Тр.
Казанск. авиац. ин-та, вып. 28, 1953.
12.4. Пугачев В. С., Теория случайных функций и ее применение к
задачам автоматического управления. Гостехиздат, М., 1957.
12.5. Л э н и н г Д. (L a n i n g D.), Б э т т и н Р. (В a 11 i n R.), Случайные
процессы в задачах автоматического управления. ИЛ, М., 1958.
12.6. К р а с о в с к и й Н. Н., Некоторые задачи теории устойчивости
движения. Физматгиз, М., 1959.
12.7. Г а л и у л л и н А. С., Об устойчивости движения тяжелой точки
переменной массы. Тр. Казанск. авпац. ин-та, вып. 35, 1959.
12.8. Б а р б а ш и и Е. А., Об оценке среднеквадратичного значения от¬
клонения от заданной траектории. Автоматика и телемеханика,
т. 21, № 7, 1960.
12.9. Б а р б а ш и н Е. А., Об оценке максимума отклонения от заданной
траектории. Автоматика и телемеханика, т. 21, № 10, 1960.
12.10. К а ц И. Я., Красовский Н. Н., Об устойчивости систем со
случайными параметрами. Прикл. матем. и механ., т. 24, № 5, 1960.
12.11. Солодовников В. В., Статистическая динамика линейных си¬
стем автоматического управления. Физматгиз, М., 1960.
12.12. Breakwell J. V., Fuel requirements for crude interplanetary
guidance. Adv. in Astronaut. Sci., vol. 5, Plenum Press, N. Y., 1960.
12.13. Kalman R. E., A new aproach to linear filtering and prediction
problems. J. of Basic Eng., vol. 82, p. 35—45, 1960.
12.14. Lawden D. F., Optimal programme for correctional maneuvres..
Astronaut. Acta, vol. 6, № 1, 4, 1960.
ЛИТЕРАТУРА
663
12.15. Minneman М. J., Application of inertial techniques to interpla¬
netary navigation. Gonf. Proc. 4 Nat. Convention on Military Elect¬
ronics, Wash., 1960.
12.16. Renaudin D., Principes du guidance. Journees d’Information
Astronaut., vol. 1, 1960.
12.17. Stearns E. V., Guidance for interplanetary landings. Techn. Ses¬
sion prepr. AAS, № 11, 1960.
12.18. ZaborszkyJ., Diesel J. М., Investigation of the feasibility
of designing homing aircraft flight control systems for minimum pro¬
babilistic error. Applications and Industry, № 48, 1960.
12.19. Альбрехт Э. Г., Об оптимальной стабилизации нелинейных си¬
стем. Прикл. матем. и механ., т. 25, № 5, 1961.
12.20. Б а р б а ш и н Е. А., О приближенном осуществлении движения
по заданной траектории. Автоматика и телемеханика, т. 22, № 6,
1961.
12.21. Боднер В. А., Теория автоматического управления полетом.
Изд-во «Наука», 1964.
12.22. Кириллова Ф. М., К задаче об аналитическом конструирова¬
нии регуляторов. Прикл. матем. и механ., т. 25, № 3, 1961.
12.23. К р а с о в с к и й Н. Н., JI и д с к и й Э. А., Аналитическое конст¬
руирование регуляторов в стохастических системах при ограниче¬
ниях на скорость изменения управляющего воздействия. Прикл.
матем. и механ., т. 25, № 3, 1961.
12.24. Красовский Н. Н., О среднеквадратичной оптимальной стаби¬
лизации при случайных затухающих возмущениях. Прикл. матем.
и механ., т. 25, № 5, 1961.
12.25. Красовский Н. Н., JI и д с к и й Э. А., Аналитическое конст¬
руирование регуляторов в системах со случайными свойствами.
Автоматика и телемеханика, т. 22, № 9—11, 1961.
12.26. Курцвейль Я. (Kurzweil Ja),K аналитическому конструиро¬
ванию регуляторов. Автоматика и телемеханика, т. 22, № 6, 1961.
12.27. Летов А. М., Аналитическое конструирование регуляторов. Авто¬
матика и телемеханика, т. 21, № 4—6, 1960, т. 22, № 4, 1961, т. 23,
№ 11, 1962.
12.28. Л и д с к и й Э. А., О стабилизации стохастических систем. Прикл.
матем. и механ., т. 25, № 5, 1961.
12.29. ЛитовченкоИ. А., К изопериметрической задаче аналитиче¬
ского конструирования оптимального регулятора. Автоматика и те¬
лемеханика, т. 22, № 12, 1961.
12.30. П о п о в В. М., Об абсолютной устойчивости нелинейных систем
автоматического регулирования. Автоматика и телемеханика, т. 22,
№ 8, 1961.
12.31. СалуквадзеМ. Е., Аналитическое конструирование регуля¬
торов. Постоянно действующие возмущения. Автоматика и телеме¬
ханика, т. 22, № 10, 1961.
12.32. Bat tin R. Н., Laning J. H., A navigation theory for round-
trip reconnaissance missions to Venus and Mars. Proc. IV AFBMD/STL
Symp. Adv. in Ballistic Missile and Space Technol., vol. 3,
1961.
12.33. Breakwell J. V., The spacing of corrective thrusts in interpla¬
netary navigation. Techn. Session Prepr. Amer. Astronaut. Soc., № 76,
1960; Adv. in Astronaut. Sci., vol. 7, Plenum Press, N. Y., 1961.
12.34. Bryson A. E., Denham W., Multivariable terminal control for
minimum mean square deviation from a nominal path. Rept. BR-133,
Missile and Space Div., Raytheon Co., Bedford, Mass., 1961.
12.35. Винер H. (Viner N.), Нелинейные задачи в теории случайных
процессов. ИЛ, М., 1961.
664
ЛИТЕРАТУРА
12.36. FriedlanderA. L., Harry D. P., A study of statistical data-
adjustment and logic techniques as applied to the interplanetary mid¬
corse guidance problem. NASA TRR-113, Wash., 1961.
12.37. Kalman R. E., New methods and results in linear prediction and
filtering theory. RIAS, Techn. Rep., № 1, 1961.
12.38. Kalman R. E., В u с у R. S., New results in linear filtering and
prediction theory. J. of Basic Eng., vol. 83, p. 95—108, 1961.
12.39. К а л м а и P. E. (Kalman R. E.), Об общей теории систем управ¬
ления. Тр. I Междунар. конгр. ИФАК, Изд-во АН СССР, М.г
1961.
12.40. Pfeiffer С. G., Guidance for space missions. Current Research in
Astronaut. Sci., Oxford, 1961.
12.41. Scull J. R., Guidance of space vehicles. Navigation, vol. 8, № 1, 1961.
12.42. Костычев Г. И., Об оптимальном программировании в случае
различных условий реализации процесса. Изв. высш. учебных за¬
ведений, сер. Авиац. техника, № 2, 1962.
12.43. К р а с о в с к и й Н. Н., Об аналитическом конструировании опти¬
мального регулятора в системе с запаздыванием времени. Прикл.
матем. и механ., т. 26, № 1, 1962.
12.44. Красовский Н. Н., Об одной задаче преследования. Прикл.
матем. и механ., т. 26, № 2, 1962.
12.45. Красовский Н. Н., Летов А. М., К теории аналитического
конструирования регуляторов. Автоматика и телемеханика, т. 23,
№ 6, 1962.
12.46. Летов А. М., Устойчивость нелинейных регулируемых систем.
Физматгнз, М., 1962.
12.47. Л и д с к и й Э.1А., Об аналитическом конструировании регуляторов в
системах со случайными свойствами. Прикл. матем. и механ., т. 26,
№ 2, 1962.
12.48. Салуквадзе М. Е., К задаче синтеза оптимального регулятора
в линейных системах с запаздыванием, подверженных постоянно
действующим возмущениям. Автоматика и телемеханика, т. 23,
№ 12, 1962.
12.49. Салуквадзе М. Е., Об аналитическом конструировании регу¬
лятора при постоянно действующих возмущениях. Автоматика и
телемеханика, т. 23, № 6, 1962.
12.50. Чжан Ж е н ь - в е й, К задаче синтеза оптимального регулятора
в системах с запаздыванием. Автоматика и телемеханика, т. 22,
№ 10, 1962.
12.51. A study of interplanetary transportation systems, edited by S. E. Ross,
Lockheed Missiles and Space Comp. Rept., 3—17—62—1, 1962.
12.52. Б e л л м а н P. (Bellman 11.), Г л и к с б е р г И. (G 1 е е k s-
berg I.), Гросс О. (Gross О.), Некоторые вопросы матема¬
тической теории процессов управления, ИЛ, 1962.
12.53. В г е a k we 1 1 J. V., The optimum spacing of corrective thrusts in
interplanetary navigation. Optimization Techniques with Application
to Aerospace Systems, Acad. Press, N. Y., 1962.
12.54. Bryson A., Denham W., A guidance scheme for supercircular
re-entry of a lifting vehicle. ARS J., vol. 32, № 6, 1962.
12.55. Kalman R. E., Control of randomy varying linear dynamical sys¬
tems. Proc. of Symp. in Appl. Math., vol. 13, 1962.
12.56. Kelley H. J., Guidance theory and extremal fields. Inst. Radio
Engrs. Natl. Aero-Space Electronics Conf., Dayton—Ohio, 1962; Inst.
Radio Engrs. Trans, Auto. Control, AC-7, 75—81, 1962.
12.57. Leach R., Townsend G. E., Guidance and control requirements.
Design Guide to Orbital Flight, N. Y., 1962.
ЛИТЕРАТУРА
665
12.58. Peske A., Ward М., Techniques for error analysis of trajectories.
Guidance and Control, N. Y.— London, 1962.
12.59. Rosenbloom A., Orbital rendezvous systems. Navigation, vol. 9,
№ 4, 1962/63.
12.60. Аким Э. JI., Энеев Т. М., Определение параметров движения
космического летательного аппарата по данным траекторных изме¬
рений. Космические исследования, т. 1, № 1, 3, 1963.
12.61. Гальперин Е. А., КрасовскийН. Н., О стабилизации
установившихся движений нелинейных управляемых систем. Прикл.
матем. и механ., т. 27, № 6, 1963.
12.62. Гродзовский Г. Л., Иванов Ю. Н., Токарев В. В.,
О движении тела переменной массы с постоянной и убывающей за¬
тратой мощности в гравитационном поле, III. Proc. XIV Internat.
Astronaut. Congr. 1963, Warszawa, 1964.
12.63. Зайцев А. Г., Аналитическое конструирование оптимальных ре¬
гуляторов при случайных возмущениях. Автоматика и телемехани¬
ка, т. 24, № 4, 1963.
12.64. Кириллова Л. С., Задача об оптимизации конечного состояния
регулируемой системы. Автоматика и телемеханика, т. 23, № 12,
1962; т. 24, № 8, 9, 1963.
12.65. Красовский Н. Н., О стабилизации неустойчивых движений
дополнительными силами при неполной обратной связи. Прикл.
матем. и механ., т. 27, № 4, 1963.
12.66. Л и д с к и й Э. А., Оптимальное регулирование систем со случай¬
ными свойствами. Прикл. матем. и механ., т. 27, № 1, 1963.
12.67. Лурье А. И., Минимальный квадратичный критерий качества ре¬
гулируемой системы. Техническая кибернетика, JST° 4, 1963.
12.68. Ройтенберг Я. Н., Некоторые задачи управления движением.
Физматгиз, М., 1963.
12.69. Токарев В. В., Влияние случайных отклонений от оптимальной
программы по тяге на движение тела переменной с постоянной за¬
тратой мощности в гравитационном поле. Прикл. матем. и механ.,
т. 27, № 1, 1963.
12.70. Ф е л ь д б а у м А. А., Основы теории оптимальных автоматических
систем. Физматгиз, М., 1963.
12.71. Андерсон Т. (Anders о и Т.), Введение в многомерный статисти¬
ческий анализ. Физматгиз, 1963.
12.72. Berman L. J., SteinkerG. Е., Krupp R., Optimization of
stochastic trajectories. AIAA J., vol. 1, № 4, 1963.
12.73. Breakwell J. V., Striebel С. Т., Minimum effort control in
interplanetary guidance. IAS Prepr., 63—80, 1963.
12.74. Breakwell J. V., The optimum spacing of corrective thrusts in
interplanetary navigation. Math, optim. techn., Berkeley — Los An¬
geles, Univ. California Press, 1963.
12.75. Gurkendall D. W., Pfeiffer C. G.,A discussion of guidance
policies for multiple — impulse correction of the trajectory of a spa¬
cecraft. AIAA Paper, № 63—334, N. Y., 1963.
12.76. Kraft J. D., Guidance and control. Space Flight Handbook, vol. 1,
Wash., 1963.
12.77. Kraft J. D., Orbit computation. Space Flight Handbooks, vol. 1,
Wash., 1963.
12.78. Л о у д e н Дж. (Lawden D. F.), Межпланетные траектории ракет.
«Космические траектории». ИЛ, М., 1963.
12.79. Pfeiffer G. G., A technique for optimum final value control of
powered flight trajectories. N. Y., 1963.
12.80. Stearns E. V., Navigation and guidance in space, 1963.
43* Механика полета
666
ЛИТЕРАТУРА
12.81. SteinkerG. Е., Solutions for optimal stochastic trajectories. S. M.
thesis, Mass. Inst. Techn., 1963.
12.82. Townsend G. E., Maneuvers. Space Flight Handbook, vol. 1,
Wash., 1963.
12.83. Кожевников Ю. В., К оптимизации управляемых систем со
случайными параметрами. Прикл. матем. и механ., т. 28, № 3, 1964.
12.84. Лидов М. Л., К априорным оценкам точности определения пара¬
метров по методу наименьших квадратов. Космич. исслед., т. 2, № 5,
1964.
12.85. Breakwell J. V., Tung F., Smith R. R., Application of the
continuous and discrete strategies of minimum effort theory to inter¬
planetary guidance. AIAA J., vol. 2, № 5, 1964.
12.86. Duncan R. C.,GunnersenA. A., Inertial guidance navigation
and control systems. J. Spacecraft and Rock., vol. 1, № 6, 1964.
12.87. F u s с a J. A., Advanced guidance concepts. Space/Aeronautics, vol. 42,
№ 7, 1964.
12.88. Jazwinski A. H., Optimal trajectories and linear control of
non-linear systems. AIAA J., vol. 2, № 8, 1964.
12.89. T r a e n k 1 e C. A., Mittkurs navigation fur interplanetare raumtra-
jektorien. Ztschr. fur Flugwissenschaften, vol. 12, № 9, 1964.
12.90. Андреевский В. В., Об оптимальном уточнении программы
управления. Сб. «Исследования по динамике полета», вып. 1, «Ма¬
шиностроение», М., 1965.
12.91. Исследования по динамике полета, вып. 1, «Машиностроение», 1965.
12.92. Красовский Н. Н., Проблемы управляемости, наблюдаемости
и стабилизируемости динамических систем. Тр. II Всесоюзн. съезда
по теорет. и прикл. механ., вып. 1, «Наука», М., 1965.
12.93. Летов А. М., Оптимальное управление и устойчивость. Тр. II Все¬
союзн. съезда по теорет. и прикл. механ., вып. 1, «Наука», М., 1965.
12.94. Летов А. М., Теория оптимального управления. Тр. II Междуна¬
родного конгресса ИФАК, т. 2, «Наука», 1965.
12.95. Миль штейн Г. Н., Об оптимальном осуществлении траекто¬
рий. Автоматика и телемеханика, т. 26, № 4, 1965.
12.96. Оптимальные системы. Статистические методы. Тр. II Международн.
конгр. Международн. федерации по автоматическому управлению,
т. 2, «Наука», М., 1965.
12.97. Платонов А. К., Дашков А. А., Кубасов В. Н., Опти¬
мальное управление полетом космического аппарата. Тр. I симпо¬
зиума «Автоматическое управление в мирном использовании косми¬
ческого пространства», 1965.
12.98. Пономарев В. М., Теория управления движением космических
аппаратов. «Наука», М., 1965.
12.99. Кожевников Ю. В., Выбор программы движения и параметров
составных летательных аппаратов из условия наиболее вероятной
доставки полезного груза в заданную область. Прикл. матем. и
механ., т. 30, № 6, 1966.
12.100. Богуславский И. А,,Иващенко О.И.,Шепелев 10. Г.,
Об управлении космическим аппаратом с двигателями малой тяги
на участке разгона при отсутствии информации о текущем векторе
скорости. Космические исследования, т. 4, № 2, 1966.
12.101. Стратонов ич P. JI., Условные марковские процессы и их при¬
менение к теории оптимального управления. Изд-во МГУ, 1966.
12.102. Я рошевский В. А., Парышева Г. В., Оптимальное рас¬
пределение корректирующих импульсов при однопараметрической
коррекции. Космические исследования, т. 3, № 6, 1965; т. 4, № 1,
1966.
12.103. В г е a k w е 11 J. V., Rauch Н. Е., Optimum guidance for a low
thrust interplanetary vehicle. AIAA Journ., vol. 4, JV? 1966
ЛИТЕРАТУРА
667
К главе 13
13.1. Т si е n Н. S., Take-off from satellite orbit. J. Amer. Rock. Soc.f
vol. 23, № 4, 1953.
13.2. Dobrowolski A., Satellite orbit perturbation under a continuous
radial thrust of small magnitude. J. Amer. Rock. Soc.» vol. 28, № 7,
1958.
13.3. Copeland J., Interplanetary trajectories under low-thrust radial
acceleration. J. Amer. Rock. Soc., vol. 29, № 4, 1959.
13.4. Karrenberg H. K., Note on interplanetary trajectories under
low-thrust radial acceleration. J. Amer. Rock. Soc., vol. 30, N° 1, 1960.
13.5. Au G., Corrections for interplanetary trajectories under low-thrust
radial acceleration. J. Amer. Rock. Soc., vol. 30, № 7, 1960.
13.6. Paiewonsky B., The motion of an orbiting vehicle subjected to
continuous radial thrust, including a study of planetary encounters.
Proc. X Internat. Astronaut. Congr., London, 1959, Vien, 1960.
13.7. Petty С. М., Interplanetary maneuvres, using radial thrust. J. Amer.
Rock. Soc., vol. 33, № 9, 1961.
13.8. A u G.t Interplanetary Bahnen fur Raumfahrtzeuge mit kleiner Schub-
beschleunigung. Raketentechnik und Raumfahrtforschung, vol. 5, № 2.
13.9. Цандер Ф. А., Об использовании силы давления света для поле¬
тов в межпланетном пространстве, в сб. Ф. А. Цандер, Проблема
полета при помощи реактивных аппаратов. Межпланетные путешест¬
вия. Оборонгиз, М., 1961.
13.10. London Н. S., Some exact solution of the equation of motion of
solar sail with constant sail setting. J. Amer. Rock. Soc. vol. 30, № 2,
1961.
13.11. Lass H., Lorrel J., Low acceleration take-off from a satellite
orbit. J. Amer. Rock. Soc., vol. 31, № 1, 1961. Русский перевод:
Ракетная техника, № 1, 1961.
13.12. CitronS. J., Solution for satellite motion under low acceleration
using method of variation of parameters. J. Amer. Rock. Soc., vol. 31,
№ 12, 1961.
13.13. Arthur P. D., Karrenberg H. K., Stark H. М., Simple
method for approximation of the caracteristics of low thrust trajectories.
J. Amer. Rock. Soc., vol. 30, № 7, 1960.
13.14. F о r b e s G. F., The trajectory of a powered rocket in space. J. Brit.
Interpl. Soc., vol. 9, № 2, 1950.
13.15. Гродзовский Г. JI., Иванов Ю. Н., Токарев В. В.,
О движении тела переменной массы с постоянной затратой мощности
в гравитационном поле. Докл. АН СССР, т. 137, № 5, 1961.
13.16. Белецкий В. В., Егоров В. А., Межпланетные полеты с
двигателем постоянной мощности. Космические исследования, т. 2,
N° 3, 1964.
13.17. Levin Е., Low-thrust transfer between circular orbits. ASME prepr.,
59-AV-2, March, 1959.
13.18. Лурье А. И., Черемсин М. К., Движение материальной точ¬
ки в поле центральной силы тяготения при наличии малой трансвер-
сальной тяги. Сб. «Искусственные спутники Земли», № 16, Изд-во
АН СССР, 1963.
13.19. Lawden D. F., Optimal programming of thrust direction. Astro¬
naut. Acta, vol. 1, № 1, 1955.
13.20. Lawden D. F., Optimal escape from a circular orbit. Astronaut.
Acta, vol. 4, № 3, 1958.
13.21. Лебедев В. H., Вариационная задача о взлете космического аппа¬
рата с круговой орбиты. Ж. вычисл. матем. и матем. физ., т. 3, № 6,
1963.
43*
668
ЛИТЕРАТУРА
13.22. Moeckel W. E., Trajectories with constant tangential thrust in
central gravitational fields. NASA TRR-53, 1959.
13.23. В e n n e у D. J. Escape from a circular orbit using tangential thrust
J. Amer. Rock. Soc., vol. 28, № 3, 1958.
13.24. Anthony M. L.,Maday G. J., Motion of orbiting vehicles under
application of tangential microthrust. Prepr. Amer. Astronaut. Soc.,
№ 102, 21, 1961.
13.25. Perkins F. М., Flight mechanics of low-thrust space craft. JASS,
vol. 26, № 5, 1959.
13.26. Охоцимский Д. E., Исследование движения в центральном
поле под действием постоянного касательного ускорения. Космиче¬
ские исследования, т. 2, № 6, 1964.
13.27. Bacon R. Н.,Logarithmic spiral: an ideal trajectory for the inter¬
planetary vehicle with engines of low sustained thrust. Amer. J. Phys.,
vol. 27, p. 164—165, 1959.
13.28. Hughes J. V., Nomicas G. N., Trajectories for continuously
applied propulsive thrust. Planet Space Sci., № 7, p. 145—153, 1961.
13.29. Stark H. М., Arthur P. D., Simple approximate solutions for
tangential low-thrust trajectories. JASS, vol. 28, № 7, 1961.
13.30. Pinkham G., Reference solution for low-thrust trajectories. J.
Amer. Rock. Soc., vol. 32, № 5, 1962. Русский перевод: Ракетная
техника, № 5, 1962.
13.31. Rodriguez G., Method for determining steering programms for
low-thrust interplanetary vehicles. J. Amer. Rock. Soc., vol. 29, №10,
1959.
13.32. Levin E., Low acceleration transfer orbits. Handbook of Astronaut.
Eng., McGraw-Hill, N. Y., 1961.
13.33. Lass H., SollowayG. B., Motion of a satellite under the in¬
fluence of a constant normal thrust. J. Amer. Rock. Soc., vol. 32, № 1,
1962. Русский перевод: Ракетная техника, № 1, 1962.
13.34. Rider L., Low-thrust correction of orbital orientation. J. Amer.
Rock. Soc., vol. 30, № 7, 1960.
13.35. Илларионов В. Ф., Ill к а д о в JI. М., Поворот плоскости
круговой орбиты спутника. ПММ, т. 26, № 1, 1962.
13.36. Гуськов Ю. П., Метод управления поворотом плоскости круго¬
вой орбиты спутника. ПММ, т. 27, № 3, 1963.
13.37. Белецкий В. В., О траекториях космических полетов с постоян¬
ным вектором реактивного ускорения. Космические исследования,
т. 2, № 3, 1964.
К главе 14
14.1. Веллман Р., Динамическое программирование. ИЛ, М., 1960.
14.2. Веллман Р., Гликсберг И., Гросс О., Некоторые вопро¬
сы математической теории управления. ИЛ, М., 1962.
14.3. Веллман Р., Процессы регулирования с адаптацией. «Наука»,
М., 1964.
14.4. Веллман Р., Дрейфус С., Прикладные задачи динамического
программирования. «Наука», М., 1965.
14.5. М оисеев Н. Н., Методы динамического программирования в тео¬
рии оптимальных управлений. Ж. вычисл. матем и матем. физ.,
т. 4, № 3, 1964; т. 5, № 1, 1965.
14.6. Кротов В. Ф., Методы решения вариационных задач на основе
достаточных условий абсолютного минимума. Автоматика и телеме¬
ханика, т. 23, № 12, 1962; т. 24, № 5, 1963.
14.7. Курант Р., Принцип Дирихле, конформные отображения и мини¬
мальные поверхности. ИЛ, М., 1963.
ЛИТЕРАТУРА
669
14.8. Кантор ович JI. В., Об одном эффективном методе решении
экстремальных задач для квадратичного функционала. Докл АН
СССР, т. 48, № 7, 1945.
14.9. Канторович JI. В., О методе наискорейшего спуска. Док г
АН СССР, т. 56, № 3, 1947.
14.10. Канторович JI. В., Функциональный анализ и прикладная ма¬
тематика. Успехи матем. наук, т. 3, № 6, 1948.
14.11. Бирман М. Ш., Некоторые оценки для метода наискорейшего
спуска. Успехи матем. наук, т. 5, № 3 (37), 1950.
14.12. Самокиш Б. А., Исследование быстроты сходимости метода пан¬
скорейшего спуска. Успехи матем. наук, т. 12, № 1 (3), 1957.
14.13. S t е i n М. L., On Methods for obtaining solutions of fixed endpoint
problems in the calculus of variations. Nat. Bur. Standards, J. Res.,
vol. 50, № 5, 1953.
14.14. Томпкинс Ч. Б., Методы быстрого спуска. Сб. «Современная ма¬
тематика для инженеров» (под ред. Э. Ф. Беккенбаха), ИЛ, М., 1959.
14.15. Rosenblum Р. С., The method of steepest descent. Proc. of the
sixth Symp. in Appl. Math, of the Amer. Math. Soc., McGraw-Hill, 1956.
14.16. Иванов Ю. H., Шалаев 10. В., Метод скорейшего спуска в
применении к расчету межорбитальных траекторий с двигателями
ограниченной мощности. Космические исследования, т. 2, № 3, 1964.
14.17. Б р у м б е р г В. А., Численное решение краевых задач небесной
механики методом наискорейшего спуска. Бюл. ин-та теорет. астро¬
номии, т. 8, № 4, 1962.
14.18. ШатровскийЛ. И., Об одном численном методе решения задач
оптимального программирования. Ж. вычисл. матем. и матем. физ.,
т. 2, № 3, 1962.
14.19. Энеев Т. М., О применении градиентного метода в задачах теории
оптимального регулирования. Доклад на Всесоюзн. симпозиуме по
многоэкстремальным задачам. Вильнюс, 13—15 июня, 1963.
14.20. К е 1 1 е у Н. J., Gradient theory of optimal flight paths. J. Amer.
Rock. Soc., vol. 30, № 10, 1960.
14.21. К e 1 1 e у H. J., К о p p R. E., Moyer H. G., Successive appro¬
ximation techniques for trajectory optimization. Proc. of the Symp.
on Vehicle System Optimization, N. Y., 1961.
14.22. В г у s о n A. E., D e n h a m W. F., Multivariable terminal control
for minimum mean square deviation from a nominal path. Proc. of
the Symp. on Vehicle System Optimization, N. Y., 1961.
14.23. Bryson A. E., D e n h a m W. F., A steepest ascent method lor
solving optimum programming problem. Trans. ASME, № 2, 1962.
14.24. Bryson A. E., Denham W. F., С a г г о 1 1 F. J., M i k a-
m i K., Determination of lift or drag programms that minimize re-entry
heating. JASS, vol. 29, № 4, 1962.
14.25. Bryson A. E., Denham W. F., D rey f us S. E., Optimal
programming problems with inequality constraints I: necessary condi¬
tion for extremal solutions. AIAA J., vol. 1, № 11, 1963.
14.26. Denham W. F., Bryson A. E., Optimal programming problems
with inequality constraints II: solution by steepest-ascent. AIAA J.,
vol. 2, № 1, 1964.
14.27. Kelley H. J., Method of gradients. Optimization techniques, Ch. 6,
Ed. by G. Leitman, Acad. Press., N. Y., 1962.
14.28. Lindorfer W., Moyer H. G., Application of a low thrust tra¬
jectory optimization scheme to planar earth-mars transfer. J. Amer.
Rock. Soc., vol. 32, № 2, 1962.
14.29. Sherman B., Low thrust escape trajectories. Proc. of the Symp.
on Vehicle System Optimization., N. Y., 1961.
670
ЛИТЕРАТУРА
14.30. Lukes D. L., Steepest descent and maximum principle techniques
of system optimization. Proc. of the Symp. on Vehicle System Opti¬
mization., N. Y., 1961.
14.31. О x о ц и м с к и й Д. Е., К теории движения ракет. ПММ, т. 10,
№ 2, 1946.
14.32. Jazwinski А. Н., Inequality constraints in steepest-descent tra¬
jectory optimization. J. of Aerospace Sci., vol. 29, № 10, 1962.
14.33. Courant R., Calculus of variations and supplementary notes and
exercises. N. Y. Universitat, Institute of Mathematical Sciences, 1945—
1946, revised and amended by J. Moser, 1956—1957.
14.34. ПонтрягинЛ. С., Болтянский В. Г., Гамкрелид-
з е Р. В., Мищенко Е. Ф., Математическая теория оптимальных
процессов. Физматгиз., М., 1961.
14.35. Крылов И. А., Черноусько Ф. Л.,О методе последователь¬
ных приближений для решения задач оптимального управления.
Ж. вычисл. матем. и матем. физ., т. 2, № 6, 1962.
14.36. Акилов Г. П., О применении одного метода решения нелинейных
функциональных уравнений к исследованию систем дифференциаль¬
ных уравнений. Докл. АН СССР, т. 48, № 4, 1949.
14.37. Абрамов А. А., Вариант метода прогонки. Ж. вычисл. матем.
и матем. физ., т. 1, № 2, 1961.
14.38. Абрамов А. А.,О переносе граничных условий для систем линей¬
ных обыкновенных дифференциальных уравнений. Ж. вычисл. ма¬
тем. и матем. физ., т. 1, № 3, 1961.
14.39. Goodman Т. R., Lance G. N., The numerical integration of
two-point boundary value problems. Mathem. tables and other aids
to Comput. v. 10, № 4, 1956.
К главе 15
15.1. Зойтендейк Г., Методы возможных направлений. ИЛ, М., 1963.
15.2. Березин И. С., Жидков Н. П., Методы вычислений, т. 2.
Физматгиз, М., 1961.
15.3. В г у s о n А. Е., D е n h a m W. F., A steepest ascent method for
solving optimum programming problem. Trans. ASME, № 2, 1962.
15.4. LindorferW., Nathan A., Optimization of missile intercept
range. Proc. of the Symposium on Vehicle System Optimization,
N. Y., 1961.
15.5. Энеев Т. М., Платонов А. К., Казакова P. К., Опре¬
деление параметров орбиты искусственного спутника по данным
наземных измерений. Сб. «Искусственные спутники Земли», № 4,
Изд-во АН СССР, 1960.
15.6. Аким Э. Л., Энеев Т. М., Определение параметров движения
космического летательного аппарата по данным траекторных изме¬
рений. Космические исследования, т. 1, № 1, 1963.
15.7. Г а в у р и н М. К., Нелинейные функциональные уравнения и не¬
прерывные аналогии итеративных методов. Изв. высш. учеби. завед.,
№ 5, 1958.
15.8. Jurovics St. A., McIntyre J. Е., The adjoint method and
its application to trajectory optimization. J. Amer. Rock. Soc., vol. 32,
№ 9, 1962.
15.9. Исаев В. К., Сонин В. В., Об одной модификации метода Нью¬
тона численного решения краевых задач. Ж. вычисл. матем.* и матем.
физ., т. 3, № 6, 1963.
15.10. Гельфанд И. М., Фомин С. В., Вариационное исчисление.
Физматгиз, Москва, 1961.
ЛИТЕРАТУРА
671
15.11. Канторович JI. В., Крылов В. И., Приближенные методы
высшего анализа. Гостехиздат, Москва, 1941.
15.12. М и х л и н С. Р., Прямые методы математической физики. Гостех¬
издат, Москва, 1950.
15.13. Иванов Ю. Н., Шалаев Ю. В., Метод скорейшего спуска в
применении к расчету межорбитальных траекторий с двигателями
ограниченной мощности. Космические исследования, т. 2, № 3, 1964.
15.14. S а 1 t z е г С., F е t h е г о f f С. W., A direct variational method for
the calculation of optimum thrust programms for power-limited inter¬
planetary flight. Astronaut. Acta, vol. 7, № 1, 1961.
15.15. Pfeiffer C. G., Theory and application of the critical direction
method of trajectory optimization. Proc. of the Symposium on Vehicle
System Optimization, N. Y., 1961.
15.16. Лебедев В. H., Вариационная задача о взлете космического ап¬
парата с круговой орбиты. Ж. вычисл. матем. и матем. физ., т. 3,
№ 6, 1963.
15.17. Breakwell I. V., The optimization of trajectories. J. Soc. Indust¬
rial and Appl. Math., vol. 7, p. 215—247, 1959.
15.18. К u 1 a k о w s k i L. I., S t a n с i 1 R. Т., Rocket boost trajectories
for maximum burnout velocity. J. Amer. Rock. Soc., vol. 30, № 7,
1960.
15.19. Stancil R. Т., Kulakowski L. I., Rocket boost vehicle
mission optimizations. J. Amer. Rock. Soc., vol. 31, № 7, 1961. Рус¬
ский перевод: Ракетная техника, № 7, 1961.
15.20. J и г о v i с s St. A., Optimum steering programm for entry of multi¬
stage vehicle into a circular orbit. J. Amer. Rock. Soc., vol. 31, № 4,
1961.
15.21. Breakwell I. V., Optimum ascent into a circular orbit. Proc. of
the Symposium on Vehicle System Optimization, N. Y., 1961.
15.22. McIntyre I. E., JurovicsSt. A., G a r d i 1 1 W. P., John¬
son B., The application of optimum trajectory analysis to boost ve¬
hicle desing. Proc. of the Symposium on Vehicle System Optimization,
N. Y., 1361
15.23. Лебедев В. H., Румянцев Б. Н., Вариационная задача о
перелете между двумя точками в центральном поле. Сб. «Искусствен¬
ные спутники Земли», № 16, Изд-во АН СССР, 1963.
К Приложению
П.1. Lass Н., LorrelJ., Low acceleration take-off from a satellite
orbit. J. Amer. Rock. Soc., vol. 31, № 1, 1961.
П.2. Моисеев H. H., Методы нелинейной механики в задачах динами¬
ки спутников. Proc. XIII Internat. Astronaut. Congr. 1962, Vien, 1964.
П.З. Ларичева В. В., Р е й н М. В., Замечание об осреднении урав¬
нений возмущенного движения в оскулирующих элементах при изме¬
нении эксцентриситета в широких пределах. Космические исследова¬
ния, т. 3, № 3, 1965.
П.4. Ларичева В. В., Рейн М. В., Асимптотика уравнений небес¬
ной механики, пригодная при большом диапазоне изменения эксцент¬
риситета. Космические исследования, т. 3, № 1, 1965.
П. 5. Smith F. Т., Optimization of multistage orbit transfer processes
by dynamic programming. J. Amer. Rock. Soc., vol. 31, № 11, 1961.
Русский перевод: Ракетная техника, № 11, 1961.
П.6. Moulton F. R., An introduction to celestial mechanics. McMillan,
N. Y., 1914. Русский перевод: Мультон Ф., Введение в небесную
механику (под ред. Г. Н. Дубошина). ГТТИ, 1935.
П.7. Дубошин Г. Н., Небесная механика. Физматгиз, 1963.
672
ЛИТЕРАТУРА
П.8. С у б б о т и н М. Ф., Курс небесной механики, т. I. ГТТИ, 1933;
т. II, ОНТИ, 1937; т. III, ОНТИ, 1949.
П.9. Herrick S., Earth satellites an related orbit and perturbation
theory. Space Technol., ch. 5, ed. Seifert, N. Y., 1959. Русский перевод:
Космическая техника, под ред. Г. Сейферта, гл. 3, «Наука», 196 Y
П.10. Herrick S., Astrodynamics. Princeton, N. Y., 1959.
П.11. Ehricke K. A., Space flight, vol. 1. Environment and celestial
mechanics, ch. 6, Perturbation. Princeton, Van Nostrand, 1960. Рус¬
ский перевод: К. Эрике, Космический полет, т. I, гл. 6, Физмат-
гиз, 1963.
П. 12. Herrick S., Trajectory fundamentals. Handbook of Astronaut. Eng.,
c. 4. McGraw-Hill, N. Y., 1961.
П.13. Охоцимский Д. E., Энеев Т. М., Т а р а т ы н о в а Т. П.,
Определение времени существования искусственного спутника Земли
и исследование вековых возмущений его орбиты. УФН, т. 63, № 1а,
1957.
П.14. Newton R. R., Variables that are determined for any orbit. J.
Amer. Rock. Soc., vol. 31, № 3, 1961.
П.15. Pines S., Variation of parameters for near circular and low inclina¬
tion orbits. IAS Paper, № 61-7; 29th Ann. Meet IAS, N. Y., 1961.
П.16. Wong P., Nonsingular variation of parameter equation for computa¬
tion of space trajectories. J. Amer. Rock. Soc., vol. 32, № 2, 1962.
Русский перевод: Ракетная техника, № 2, 1962.
П.17. Кузмак Г. Е., Копнин Ю. М., Новая форма уравнений дви¬
жения спутника и приложение ее к исследованию движений, близких
к кеплеровым. Ж. вычисл. матем. и матем. физ., т. 3, № 4, 1963.
П. 18. Lass Н., Solloway G. В., Motion of a satellite under the influ¬
ence of a constant normal thrust. J. Amer. Rock. Soc., vol. 32, № 1,
1962. Русский перевод: Ракетная техника, № 1, 1962.
П.19. Охоцимский Д. Е., Энеев Т. М., Некоторые вариационные
задачи, связанные с запуском искусственного спутника Земли.
УФН, т. 63, № 1а, 1957.
П.20. Охоцимский Д. Е., Энеев Т. М., О выведении искусствен¬
ного спутника Земли на орбиту. Proc. VIHth Internat. Astronaut.
Congr. 1957, Vien, 1958.
П.21. Кузмак Г. E., Исаев В. К., Давидсон Б. X., Оптималь¬
ные режимы движения точки переменной массы в однородном цент¬
ральном поле. Докл. АН СССР, т. 149, № 1, 1963.
П.22. Исаев В. К., Сонин В. В., Д а в и д с о н Б. X., Оптималь¬
ные режимы движения точки переменной массы с ограниченной
мощностью в однородном центральном поле. Космические исследо¬
вания, т. 2, № 4, 1964.
П.23. Иванов 10. Н., Токарев В. В., Шалаев Ю. В., Опти¬
мальные траектории и оптимальные параметры космических аппара¬
тов с двигателями ограниченной мощности. Космические исследова¬
ния, т. 2, № 3, 1964.
П.24. Роберсон Р., Орбитальное движение спутников Земли. Сб.
«Научные проблемы искусственных спутников», ИЛ, М., 1959.
П.25. Citron S. J., Satellite lifetimes under the influence of continuons
thrust, atmospheric drag, and planet oblateness. AIAA J., vol. 1,
№ 6, 1963. Русский перевод: Ракетная техника и космонавтика,
№ 6, 1963.
П.26. Cospar International Reference Atmosphere (CIRA-64).
ИМЕННОЙ УКАЗАТЕЛЬ1)'
Абианц В. X. 84, 87, 646
Абрамов А. А. 586, 670
Абрамович Г. Н. 37, 38, 93, 95, 642
Авдуевский В. С. 79, 645
Аврамченко Р. Ф. 244, 247, 436,
655, 661
Аким Э. Л. 517, 594, 665, 670
Акилов Г. П. 585, 670
Александров С. Г. 32, 641
Алексеев А. П. 14, 21, 36, 37, 76—78,
92-95, 122, 640, 641, 651
Алемасов В. Е. 37, 39, 46, 76, 93,
642
Альбрехт Э. Г. 517, 663
Андреевский В. В. 517, 666
Андрианкин Э. И. 34, 641
Аппазов Р. Ф. 13, 640
Арцимович Л. А. 54—57, 67, 644
Бам-Зеликович Г. М. 101, 648
Барбашин Е. А. 517, 662
Бебенин Г. Г. 13, 640
Безменов В. М. 244, 655
Белецкий В. В. 17, 170, 176, 178—
180, 183, 186, 188, 190, 192, 197,
200, 201, 243, 247, 295, 322, 538,
553, 641, 652, 653, 655, 656
Беляев Ю. К. 471, 487, 662
Березин И. С. 594, 597, 670
Бирман М. Ш. 558, 669
Богуславский И. А. 517, 666
Боднер В. А. 517, 663
Болгарский А. В. 37, 39, 76, 642
Болтянский В. Г. 109, 353, 582,
649, 660, 670
Болонкин А. А. 322, 659
Валеев К. Г. 410, 419, 661
Ваничев А. П. 77, 645
Варшавский Г. А. 79, 645
Васанов Ю. А. 116, 650
Вентцель Е. С. 453, 458, 461, 661
Винокуров В. А. 287, 656
Воробьев Н. Н. 453, 458, 461, 661
Гавурин М. К. 670
Галиуллин А. С. 517, 662
Гальперин В. Г. 37, 38, 79, 95, 642
Гальперин Е. А. 517, 665
Гамкрелидзе Р. В. 109, 353, 582,.
649, 659, 660, 670
Ганин Е. А. 118, 650
Гантмахер Ф. Р. 13, 321, 639
Гельфанд И. М. 597, 670
Герман В. О. 52, 643
Глушко В. П. 76, 645
Гнеденко Б. В. 471, 487, 489, 662:
Говоров А. Н. 14, 21, 36, 37, 76—
78, 92—95, 122, 640, 641, 651
Гонор А. Л. 102, 651
Горелов Ю. А. 13, 321, 322, 639,
658
Григорян С. С. 101, 648
Гродзовский Г. Л. 14, 21, 39,
41—43, 79, 80,94, 100, 102, 104,
108, 110—112, 115, 116, 122,
135, 138, 139, 143, 151, 170-172,.
175, 176, 179, 263, 322, 328,
360, 364, 406, 419, 470, 517,
518, 538, 640, 642, 645, 648,.
649, 652, 655, 659, 660, 665, 667
Гурман В. И. 322, 658
Гуськов Ю. П. 551, 585, 668
Давидсон Б. X. 13,” 177, 309, 619,,
639, 653, 656, 672
Данилов Ю. И. 79, 645
Даутов Г. Ю. 52, 643
Дашков А. А. 517, 666
Дейч М. Е. 84, 87, 645
Диамандиев В. 322, 658
Добрецов Л. Н. 63, 66, 84, 89, 644,.
646
Добровольский М. В. 92, 646
Дорогов Б. С. 84, 87, 646
2) Цифры означают номера страниц, содержащих ссылки на] работы
указанных авторов.
674
ИМЕННОЙ УКАЗАТЕЛЬ
Дородницын А. А. 39, 101, 642
Дубошин Г. Н. 25, 612, 641, 671
Егоров В. А. 13, 170, 178—180,
183, 186, 188, 190, 197, 201,
243, 247, 295, 538, 638—640, 652,
653—656, 667
Ершов В. Г. 201, 653
Ефимов Г. Б. 186, 654
Жидков Н. П. 594, 670
Жуков А. Н. 410, 412, 413, 415,
661
Жуков М. Ф. 52, 643
Жулев 10. Г. 116, 650
Зайцев А. Г. 517, 518, 665
Зельдович А. Б. 34, 37, 77, 641,
645
Зуев В. С. 93, 95, 647
Иванов Ю. Н. 14, 21, 122, 143,
170, 172, 179, 180, 183, 184, 187,
188, 192, 197, 198, 202, 203, 209,
231, 236, 239, 258, 267, 276, 280,
291,328, 339, 383, 558, 598, 621, 640
652—656, 659, 660, 669, 671, 672
Иващенко О. И. 517, 666
Илларионов В. Ф. 13, 321, 551,
552, 585, 639, 668
Ильин В. А. 13, 321, 639, 640,
659
Идьяшенко О. М. 93, 95, 647
Илютович А. Е. 421, 661
Иноземцев Н. В. 93, 95, 647
Иоффе А. И. 84, 88, 646
Исаев В. К. 13, 170, 177, 203, 215,
234, 236, 239, 309, 321, 322,
594, 597, 604, 619, 639, 640, 652,
654, 656, 657, 659, 670, 672
Ишлинский А. Ю. 13, 321, 638
Казанджан П. К. 14, 21, 36, 37,
76-78, 92-95, 122, 640, 641, 651
Казакова Р. К. 594, 670
Каменков Г. В. 517, 662
Канторович JI. В. 558, 585, 597,
668, 671
Капица П. JI. 96, 647
Капцов Н. А. 60, 61, 63, 66, 68,
644
Карпович Е. А. 101, 648
Карымов А. А. 70, 644
Кац И. Я. 517, 662
Квасников А. В. 14, 21, 37, 39,
76, 77, 641, 642
Кибель И. А. 101, 648
Кимель JI. Р. 81, 645
Кириллова JI. С. 517, 518, 665
Кириллова Ф. М. 517, 663
Кифоренко Б. Н. 357, 360, 364,
377, 659, 660
Кожевников Ю. В. 517, 666
Коновалов Н. Е. 14, 21, 36, 37,
■ 76—78, 92—95, 122, 640 641, 651
Копнин Ю. М. 13, 261, 655
Коренев Г. В. 13, 321, 640
Королев С. П. 13, 321, 638
Косаренков В. А. 116, 650
Космодемьянский А. А. 13, 321,
638
Костычев Г. Н. 517, 664
Кочин Н. Е. 101, 648
Кочина Н. Н. 101, 648
Кошкин В. К. 79, 645
Краснов И. Ф. 101, 648
Красовский Н. Н. 517, 518, 662,
665
Крашенинникова Н. JI. 101, 102,
648
Кротов В. И. 54, 63, 644
Кротов В. Ф. 13, 321, 358, 557,
638, 660, 668
Крылов В. И. 597, 671
Крылов И. А. 582, 583, 670
Кубасов В. Н. 517, 666
Кузмак Г. Е. 13, 321, 322, 615,
617, 619, 639, 640, 658, 672
Кузнецов Е. В. 37, 39, 76, 642
Кузнецов ’Ю. Е. 39, 41, 43, 80,
642, 645
Курьянов А. И. 13, 203, 309, 322,
328, 640, 654, 657, 659,
Кутырин И. Н. 79, 645
Лаврентьев М. А. 34, 641
Лавров С. С. 13, 640
Ландау Л. Д. 37, 101, 642
Ландсберг Г. С. 31, 641
Ларичева В. В. 611, 671
Лебедев В. Н. 183, 242, 243, 247,
261, 604, 605, 654, ' 655, 667,
671
Лебедев Л. А. 175, 659
Лебедев С. Я. 54, 63, 644
Левин Л. М. 13, 639
Летов А. М. 517, 663, 664, 666
Лидов М. Л. 13, 640, 665
Лидский Э. А. 517, 663, 664
Литовченко И. А. 322, 517, 658, 663
Лифшиц Е. М. 37, 101, 642
Лойцянский Л. С. 84, 87, 646
Лукьянов С. Ю. 55, 56, 644
ИМЕННОЙ УКАЗАТЕЛЬ
675
Мартынов А. К. 101, 648
Межиров И. И. 79, 645
Мелик-Пашаев Н. И. 37, 39, 76,
642
Мелькумов Т. М. 37, 39, 76, 642
Мельников М. В. 77, 645
Мельникова Н. С. 101, 648
Мещерский И. В. 13, 321, 638
Миллионщиков М. Д. 37, 38, 79,
95, 642
Милыптейн Г. Н. 322, 517, 658,
666
Михайлова М. М. 79, 645
Михайлова М. П. 101, 648
Михеев Ю. С. 79, 645
Михлин С. Р. 597, 671
Мишин В. П. 13, 640
Мищенко Е. Ф. 109, 353, 582, 649,
660, 670
Моисеев Н. Н. 557, 611, 668, 671
Моргулис Н. Д. 84, 88, 89, 646
Морозов М. Г. 52, 643
Мухамеджанов А. К. 34, 641
Нечаев Ю. Н. 14, 21, 36, 37, 76—
78, 92—95, 122, 640, 641, 651
Никольский А. А. 101, 648
Новоселецкий О. Ю. 116, 650
Новоселов В. С. 322, 658
Овсянников Р. Н. 435, 661
Остославский И. В. 13, 640
Охоцимский Д. Е. 13, 186, 321,
322, 541, 543, 548, 567, 612, 615,
618, 623, 638, 654, 657, 659, 667,
669, 671, 672
Иарышева Г. В. 517, 666
Петров Г. И. 42, 642
Письменный В. Д. 55, 56, 644
Платонов А. К. 517, 666
Подгорный И. М. 55, 56, 644
Покровская С. А. 179, 187, 203, 653
Половко А. М. 471, 487, 662
Полярный А. И. 77, 645
Пономарев В. М. 13, 517, 640, 666
Понтрягин JI. С. 109, 353, 357, 368,
412, 649, 660, 670
Попов В. М. 517, 663
Пугачев В. С. 517, 519, 662
Пупко В. Я. 54, 63, 644
Райзер Ю. П. 34, 641
Рейн М. В. 606, 671
Розе Н. В. 101, 648
Ройтенберг Я. Н. 517, 518, 665
Романенко С. В. 79, 645
Румянцев Б. Н. 247, 605 655, 671
Садовский И. Н. 13, 639
Саковский С. А. 175, 652
Салуквадзе М. Е. 517, 663, 664
Самокиш Б. А. 558, 668
Сандомирская И. Д. 39, 642
Седов Л. И. 37, 99, 101, 642, 648
Семенова Л. Н. 435, 661
Сергель О. С. 79, 645
Сергиенко А. А. 39, 642
Симонов Л. А. 37, 38, 79, 95, 642
Синярев Г. Б. 92, 646
Скубачевский Г. С. 93, 95, 647
Смоляков Б. Я. 52, 643
Соловьев А. Д. 471, 487, 662
Соловьев Б. А. 116, 650
Солодовников В. В. 517, 662
Сонин В. В. 13, 170, 177, 203, 309,
594, 619, 640, 652—654, 656,
657, 659, 670, 672
Стависский Ю. А. 54, 63, 644
Станюкович К. П. 34, 101, 641,
648
Стасенко А. Л. 116, 118, 650
Степанов Г. 10. 84, 87, 646
Стернин Л. Е. 39, 642
Стечкин Б. С. 14, 21, 36, 76—78,
92—95, 122, 640, 641, 646, 651
Стратонович Р. Л. 517, 666
Стумбур Э. А. 54, 63, 644
Субботин М. Ф. 25, 612, 641, 671
Сычев В. В. 102, 649
Тамм И. Е. 54, 644
Тарасов Е. В. 13, 321, 639
Таратынова Г. П. 623, 671
Тесленко Н. М. 13, 640
Тодоров К. 322, 658
Токарев В. В. 14, 21, 81, 93, 96,
122, 151, 387, 398, 401, 402, 436,
470, 517, 518, 640, 645, 647, 652, 660,
661,665 667, 672
Токарев М. В. 39, 41, 43, 642
Троицкий В. А. 322, 658
Уколов В. Л. 116, 650
Фаткин Ю. М. 93, 96, 389, 647, 660
Федоров Р. Е. 32, 641
Федоров Р. М. 14, 21, 36, 37,
76-78, 92—95, 122, 640, 641, 651
Федынский В. В. 34, 641
Фельдбаум А. А. 517, 665
Фомин С. В. 597, 670
Франкль Ф. И. 101, 648
Фролов В. В. 115, 116, 649, 650
676
ИМЕННОЙ УКАЗАТЕЛЬ
Хинчин А. Я. 471, 487, 661
Холщевников К. В. 93, 95, 647
Христианович С. А. 37, 38, 79, 95,
642
Худяков Г. Е. 80, 645
Цандер Ф. А. 13, 70, 71, 104, 151,
321, 410, 412, 535, 638, 644, 652т
660, 667
Цветков В. И. 81, 645
Циолковский К. Э. 13, 321, 638
Цянь Сюэ-сэнь 13, 101, 321, 531,
532, 537, 638, 648, 666
Чеботарев Г. А. 13, 640
Черемсин М. К. 539, 667
Черкез А. Я. 93, 95, 647
Черноусько Ф. JI. 582, 583, 669
Черный Г. Г. 101, 648
Чжан Жень-вей 517, 664
Чу ватин С. А. 55, 56, 644
Шалаев Ю. В. 170, 192, 203, 209, 558,
598, 621, 652-654, 668, 670, 672
Шатровский JI. И. 567, 578, 582,
669
Шепелев Ю. Г. 517, 666
Шкадов Л. М. 13, 321, 551, 552,
585, 639, 668
Шлыков Ю. П. 118, 650
Щукин В. К. 37, 39, 76, 642
Энеев Т. М. 13, 567, 568, 572, 594,
669, 670
Ярошевский В. А. 517, 666
Ailenberd S. L. 48, 643
Alder К. 99, 647
Allen К. U. 25, 641
Anderson J. 517, 665
Andreescu D. St. 13, 640
Anthony M. L. 541, 663
Arthur P. D. 537, 539, 668
Au G. F. 14, 21, 48, 52, 54, 58, 74,
76, 78, 81, 82, 84, 120, 280, 531,
535, 640, 643, 645, 656, 667
Bacon R. H. 549, 668
Balent R. 84, 88, 646
Ваггеге M. 13, 37, 39, 76, 321, 322,
638, 642, 659
Bartas J. G. Ill, 112, 649
Battin R. H. 517, 662, 663
Beale R. J. 84, 87, 93, 645
Beckewith W. C. 48, 50, 643
Beers L. S. 48, 87, 317, 643, 657
Bell D. J. 322, 658
Bellman R. 517, 557, 664, 668
Benney D. J. 540, 541, 668
Berman L. J. 517, 665
Bernatowicz D. T. 118, 651
Berner F. 93, 96, 98, 384, 385, 386,
387, 647, 660
Billik В. H. 221, 654
Biork R. L. 34, 35, 641
Blum E. K. 135, 179, 180, 183,
188, 197, 272, 275, 651, 653,
656
Boden R. H. 54, 644
Bono P. 43, 642
Boucher R. A. 317, 657
Breakwell J. V. 13, 321, 322, 517,
604, 605, 639, 640, 657, 662, 666,
671
Brewer G. R. 54, 66, 644
Brogan T. R. 53, 643
Brown H. 54, 309, 644, 657
Brown S. C. 63, 66, 644
Bryson A. F. 517, 567, 568, 572,
578, 594, 663, 664, 669, 670
Bucy R. S. 517, 664
Burge H. L. 116, 650
Burlage H. 92, 646
Bussurd R. W. 14, 21, 48, 51, 76,
77, 135, 272, 640, 643, 651, 656
Camac M. 48, 52, 58, 76, 93, 96,
98, 135, 350, 384, 385, 386, 387,
643, 647, 652, 659, 660
Cameron A. G. W. 30. 641
Cappellari J. O. 322, 657
Carroll F. J. 567, 669
Cavoti C. R. 322, 658
Chamay A. 43, 642
Chao В. T. 116, 649
Chen J. L. Ill, 649
Citron S. J. 537, 539, 623, 627,
667, 672
Cleaver A. V. 48, 76, 77, 80, 643
Cobb J. E. 84, 88, 89, 646
Cochran D. L. 84, 87, 645
Cohen A. D. 48, 87, 643
Contensou P. 322, 658
Cook H. M. 93, 95, 647
Copeland T. 531, 535, 667
Corliss W. R. 14, 21, 33, 48, 51, 54,
59, 78, 80, 81, 82, 84, 87—90, 92,
106, 107, 113, 122, 640, 643, 651
Cornog R. 135, 651
Courant R. 558, 571, 578, 668, 670
Craig R. 317, 657
Cristman D. R. 34, 641
ИМЕННОЙ УКАЗАТЕЛЬ
677
Сгоссо L. 135, 652
Curkendall D. W. 517, 665
Curry R. Ill, 649
Cutler W. E. 84, 88, 89, 646
Davis J. 54, 644
Davison E. H. 118, 651
De Lauer R. D. 14, 21, 48, 51,
76, 77, 640, 643
Demetriades S. T. 93, 96, 98, 384,
402, 647, 660
Denham W. F. 567, 568, 576, 578,
582, 663, 664, 669, 670
Dieckamp H. M. 84, 88, 646
Diesel J; M. 517, 663
Dobrowolski A. 531, 537, 667
Dreyfus S. E. 557, 567, 668, 669
Drescher M. 453, 458, 461, 661
Dugan A. F. 84, 88, 89, 646
Dulgeroff C. R. 309, 656
Duncan R. C. 517, 666
Eckert E. R. G. 115, 116, 649
Edelbaum T. N. 179, 186, 221,
328, 341, 342, 516, 653, 654, 659,
662
Ehricke K. A. 13, 321, 612, 639, 672
Elliott D. G. 84, 88, 646
English R. E. 118, 651
Esnault-Pelterie R. 13, 321, 638
Evans R. 13, 321, 638
Faulders C. R. 179, 186, 247, 272,
653, 656
Fenech H. 118, 650
Ferri A. 93, 95, 101, 647, 648
Fetheroff C. W. 201, 317, 601, 653,
657, 671
Fimple W. R. 342, 410, 415, 418,
659, 661
Forbes G. F. 538, 549, 667
Fox R. 309, 656
French E. P. 384, 387, 660
Friedlander A. L. 517, 664
Fusca J. A. 517, 666
Gardill W. P. 605, 671
Geerts J. 13, 322, 640, 658
Gebring J. W. 34, 641
Glassman A. J. 84, 685
Glicksberg J. 517, 664
Gobetz F. W. 219, 221, 654
Goddard R. H. 13, 30, 321, 638
Goldsmith W. 79, 645
Goldstein S. 100, 647
Goodman T. R. 586, 670
Gossick L. V. 93, 95, 647
Gronich A. 84, 88, 89, 646
Gross O. 517, 557, 664, 668
Grover G. M. 84, 88, 89, 646
Guderley G. 39, 642
Gunnersen A. S. 517, 666
Gurley J. G. 322, 658
Haller H. C. 116, 649
Hallet R. W. 84, 88, 89, 646
Hamilton R. S. 84, 88, 646
Hanford D. R. 93, 96, 98, 384-387,
647, 660
Hantsch E. 39, 642
Harry D. P. 517, 664
Harvey R. J. 84, 88, 89, 646
Hayes W. D. 100, 101, 647, 648
Herrick S. 13, 321, 612, 639, 672
Hohmann W. 13, 321, 638
Horgan J. J. 43, 642
Huebner A. L. 48, 643
Hughes J. V. 549, 668
Hunter M. W. 317, 657
Irvine Т. E. 115, 116
Irving J. H. 135, 171, 176, 179,
180, 183, 188, 197, 272, 275, 651,
653, 656
Jabsman W. E. 72, 644
Janes G. S. 48, 643
Jaumotte A. 13, 37, 39, 76, 322,
323, 638, 642, 659
Jazwinski A. H. 517, 568, 578, 582,
666, 670
Johnson B. 605, 671
Johnson H. L. 48, 50, 643
Jonsson V. K. 116, 649
Jurovics St. A. 594, 597, 604, 605,
670, 671
Kalman R. E. 517, 662—664
Kantrowitz A. 48, 52, 643
Karlekar В. V. 116, 649
Karman T. 101, 648
Karrenberg H. K. 531, 535, 667
Kash S. W. 309, 310, 657
Kaufman H. R. 54, 66, 68, 644
Keller Jack L. 322, 658
Kelley H. J. 410, 412, 413, 517,
567, 568, 576, 582, 583, 661, 664,
669
Kopp R. E. 322, 567, 659, 669
Kornhauser M. 34, 641
Kraft J. D. 517, 665
Kreith F. 116, 649
Krupp R. 517, 665
Kubota T. 102, 648
678
ИМЕННОЙ УКАЗАТЕЛЬ
Kulakowski L. J. 604, 605, 671
Kunen E. 48, 643
Kurzweil Ja. 517, 663
Kuskevics G. 54, 644
Lacy L. 309, 656
Lance G. N. 586, 670
Lane R. J. 93, 95, 96, 647
Langmuir D. B. 135, 651
Laning D. 517, 662, 663
Lass H. 536, 537, 539, 551, 611,
615, 667, 668, 671, 672
Lawden D. F. 13, 242, 321, 322,
517, 526, 539, 638, 639, 654,
657, 662, 665, 667
Lawden J. H. 309, 656
Leach R. 517, 664
Lecompte J. 99, 647
Lees L. 102, 648
Leitmann G. 13, 135, 176, 221, 321.
322, 639, 651, 653, 654, 657, 659
Levin E. 538, 551, 667, 668
Lieblein S. 118, 651
Liepmann H. W. 100, 647,
Lindorfer W. 247, 567, 576, 577,
594, 604, 605, 655, 670
Linhardt H. D. 48, 50, 51, 83, 350,
643, 659
London H. S. 410, 412, 415, 535,
661, 667
Lorrel J. 536, 537, 611, 667, 671
Lubowe A. G. 322, 658
Lukes D. L. 567, 568, 670
Mackay J. S. 245, 655
Maday F. M. 541, 668
Malina F. J. 322, 659
Marec J. P. 322, 659
Martelly J. 148, 652
Mclllroy W. 48, 643
McIntyre I. E. 604, 605, 670, 671
McKinsey J. C. G. 453, 458, 461, 661
McMillan A. R. 34, 641
Meghreblian R. V. 48, 78, 643
Melbourne W. G. 179, 188, 197,
198, 200, 201, 203, 204, 222, 224,
247, 272, 309, 653, 655, 656
Mickelsen W. R. 54, 66, 69, 644
Miele A. 13, 321, 322, 328, 639,
640, 658, 659
Migdal D. 43, 642
Mikami K. 567, 669
Miller H. 84, 88, 89, 646
Miller P. W. 84, 88, 89, 646
Minneman M. J. 517, 663
Moeckel W. E. 135, 243, 263, 539,
651, 654, 655, 668
Moser W. A. 309, 657
Moulton F. R. 612, 671
Moyer H. G. 247, 322, 567, 655,
659, 669
Munick H. 322, 659
Nathan A. 594, 670
Newton R. R. 615, 672
Nicoll H. E. 54, 309, 644, 657
Nilson E. N. Ill, 649
Nita М. M. 13, 640
Oberth H. 13, 321, 638
Olds R. H. 84, 88, 89, 646
Orr E. G. 48, 84, 643
Osmun W. G. 84, 120, 645
Paicwonsky B. 533, 667
Perkins F. M. 410, 418, 541, 542,
543, 661, 668
Peske A. 517, 665
Petty С. M. 533, 535, 667
Pfeiffer C. J. 517, 601, 602, 664,
665, 671
Pines S. 322, 658, 672
Pinkel B. 516, 662
Pinkham G. 549, 668
Plamondon J. A. 116, 649
Potter R. A. 309, 656
Pozzi A. 410, 412, 661
Prandte L. 36, 37, 100, 101, 641
Preston-Thomas H. 54, 84, 135, 177,
263, 267, 272, 643, 651, 653, 655,
656
Preining O. 52, 643
Probstein R. F. 100, 101, 647
Psarouthakis J. 84, 88, 90, 646
Ragsac R. V. 516, 662
Rao G. V. 39, 642
Rauch H. E. 517, 666
Reader P. D. 54, 66, 68, 644
Reichcl R. H. 93, 96, 98, 384—387,
647, 660
Reiffel L. 30, 31, 641
Renaudin D. 517, 663
Richardson D. E. 179, 197, 201,
203, 247, 653, 655
Rider L. 551, 668
Robbins H. M. 322, 658
Roberson R. E. 623, 624, 672
Rodriguez G. 539, 550, 668
Rohsenow W. H. 118, 650
Rosenbloom A. 517, 661
Rosenblum P. C. 517, 558, 669
Roshko A. 100, 647
Ross S. E. 13, 221, 640, 654, 664
ИМЕННОЙ УКАЗАТЕЛЬ
679
Rossa L. G. 245, 655
Roy M. 93, 95, 646
Sakurai A. 101, 648
Saltzer C. 179, 187, 201, 601, 653,
671
Sands N. 410, 415, 416, 418, 661
Sauer C. G. 179, 188, 197, 198, 200,
201, 203, 204, 222, 224, 247, 272,
309, 653, 655, 656
Scull J. R. 517, 664
Seban R. A. 79, 645
Seifert H. 48, 76, 92, 93, 643
Seitz R. N. 54, 61, 63, 65, 644, 651
Sellers W. H. Ill, 112, 649
Shelton R: D. 309, 656
Shepherd L. R. 48, 76, 77, 80, 643
Sherman R. 179, 180, 182, 567, 653,
669
Shipper L. 116, 650
Shook G. B. 84, 88, 89, 646
Siegler R. C. 116, 650
Slone H. O. 118, 651
Smith A. M. 322, 659
Smith F. T. 612, 671
Smith R. R. 517, 666
Smith T. L. 93, 96, 98, 384—387,
647, 660
• Smith W. E. 116—119, 650
Snyder N. W. 14, 21, 82, 83, 84,
87—90, 92, 106, 107, 641, 645
Socio L. 410, 412, 661
Solloway G. B. 551, 615, 668, 672
Sparrow E. M. 115, 116, 649
Speiser E. W. 84, 87, 93, 645
Speiser R. S. 309, 656
Stafford G. B. 84, 119, 645
Stamm H. 84, 88, 120, 646
Stancil R. T. 604, 605, 671
Stark H. M. 549, 668
Starr W. L. 309, 657
Stearns E. У. 517, 663, 665
Stearns Y. W. 317, 657
Stein M. L. 558, 585, 669
Steinker G. E. 517, 666
Stenning A. H. 48, 643
Stewart W. L. 84, 645
Stockel K. 43, 46, 47, 76, 643
Stockman N. O. 116, 649
Striebel С. T. 517, 665
Stuhlinger E. 54, 59, 61, 63, 65,
121, 135, 263, 317, 643, 644, 651,
655, 657
Sutton G. P. 14, 21, 48, 76, 87, 88,
640, 643
Taylor G. J. 101, 648
Thompkins Ch. B. 558, 668
Thompson B. L. 54, 644
Tonkin S. W. 84, 88, 89, 646
Townsend G. E. 517, 664, 666
Traenkle C. A. 517, 666
Tschirgi J. M. 317, 657
Tsien H. S. 13, 101, 321, 531, 532,.
537, 638, 648, 667
Tsu Т. C. 410, 412, 413, 415, 660
Tung F. 517, 666
Ursini G. A. 43, 642
Yandenkerchove J. 13, 37, 39, 76,
321, 322, 638, 642, 659
Vernet-Lozet M. 83, 84, 645
Yeubeke B. F. 13, 37, 39, 76, 321_
322, 638—640, 642, 658, 659
Ward M. 517, 665
Weatherston R. C. 116—119, 650
Wetch J. R. 84, 646
Whipple F. L. 34, 641
Wiener N. 517, 663
Wilkins J. E. 110, 649
Wilks W. E. 48, 50, 51, 643
Willinski M. J. 48, 84, 643
Winicur D. H. 54, 644
Womack J. R. 84, 87, 93, 645
Wong P. 615, 672
Woodworth J. L. 43, 642
Zaborszky J. 517, 663
Zehle H. 246, 655
Zimmerman A. V. 245, 655
Zoutendejk G. 594, 670
Zwiek E. B. 116, 650
Георгий Львович Г родзовский
Юрий Николаевич Иванов
Владислав Васильевич Токарев
МЕХАНИКА КОСМИЧЕСКОГО ПОЛЕТА
С МАЛОЙ ТЯГОЙ
М., 1966 г., 630 стр. с илл.
Редактор JO. Е. Кузнецов
Теки, редактор С. Я. Шкллр
Корректор О. А. Сигал
Сдано в набор 22/VII 1966 г. Подписано к печати 23/XI 1966 г.
Бумага 60x90Vie- Физ. печ. л. 42,5-{-1 вкл.
Условн. печ. л. 42,625. Уч.-изд. л. 42,72.
Тираж 4000 экз. Т-15916
Цена книги 2 р. 83 к. Заказ № 1179.
Издательство «Наука»
Главная редакция физико-математической литературы
Москва, В-71, Ленинский проспект, 15.
2-я типография изд-ва «Наука». Москва, Шубинский пер., 10