Author: Боярчук А.К. Головач Г.П.
Tags: математика дифференциальные уравнения
ISBN: 5-8360-0213-4
Year: 2001
Similar
Text
А.К.Боярчук, Г.П.Головач
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ В ПРИМЕРАХ И ЗАДАЧАХ
Справочное пособие по высшей математике. Т. 5
М.: Эдиториал УРСС, 2001. - 384 с.
«Справочное пособие по высшей математике» выходит в пяти томах и
представляет собой новое, исправленное и существенно дополненное издание
«Справочного пособия по математическому анализу» тех же авторов. В новом
издании пособие охватывает три крупных раздела курса высшей математики —
математический анализ, теорию дифференциальных уравнений, теорию функций
комплексной переменной.
Том 5 охватывает все разделы учебных программ по дифференциальным
уравнениям для университетов и технических вузов с углубленным изучением
математики. Наряду с минимальными теоретическими сведениями в нем
содержится более семисот детально разобранных примеров. Среди вопросов,
нестандартных для такого рода пособий, следует отметить примеры по теории
продолжимости решения задачи Коши, нелинейным уравнениям в частных
производных первого порядка, некоторым численным методам решения
дифференциальных уравнений.
Пособие предназначено для студентов, преподавателей и работников физико-
математических, экономических и инженерно-технических специальностей,
специалистов по прикладной математике, а также лиц, самостоятельно
изучающих высшую математику.
Оглавление
Предисловие 3
Введение 4
Основные понятия. Составление дифференциальных уравнений 4
Основные определения D) Задача Коши D) Построение
дифференциального уравнения по заданному семейству кривых E)
Примеры E)
Упражнения для самостоятельной работы 10
Глава 1. Дифференциальные уравнения первого порядка 11
§ 1. Уравнения с разделяющимися переменными 11
Дифференциальное уравнение с разделяющимися переменными A1)
Разделение переменных линейной заменой аргумента A1) Примеры
(И)
§2. Геометрические и физические задачи, приводящие к уравнениям с 15
разделяющимися переменными
Использование геометрического смысла производной A5)
Использование физического смысла производной A5) Примеры A5)
§ 3. Однородные уравнения и уравнения, приводящиеся к ним 29
Однородное уравнение B9) Уравнение, сводимое к однородному C0)
Обобщенно-однородное уравнение C0) Примеры C0)
§ 4. Линейные уравнения и уравнения, приводящиеся к ним 39
Линейное уравнение первого порядка C9) Обмен ролями между
функцией и аргументом C9) Уравнения, приводимые к линейным
C9) Уравнение Миндинга — Дарбу D0) Примеры D0)
§ 5. Уравнения в полных дифференциалах. Интегрирующий множитель 53
Уравнение в полных дифференциалах E3) Интегрирующий
множитель E3) Дифференциальное уравнение для интегрирующего
множителя E4) Примеры E4)
§ 6. Уравнение Эйлера — Риккати 67
Уравнение Эйлера — Риккати. Специальное уравнение Риккати F7)
Каноническое уравнение Эйлера — Риккати F7) Примеры F7)
§ 7. Уравнения, не разрешенные относительно производной 73
Уравнение, не разрешенное относительно производной G3) Общий
интеграл уравнения F(y')=0 G3) Представление решения в
параметрической форме. Разрешение неполных уравнений G3)
Примеры G4)
§ 8. Существование и единственность решения 82
Теоремы Пикара, Пеано и Осгуда (82) Существование и
единственность решения задачи Коши для уравнения, не
разрешенного относительно производной (82) Продолжение решения
задачи Коши (82) Существование и единственность решения
векторной задачи Коши (83) Примеры (83)
§ 9. Особые решения 99
Особое решение. Дискриминантная кривая (99) Огибающая как особое
решение A00) Примеры A00)
§ 10. Задачи на траектории 106
Изогональные и ортогональные траектории A06) Эволюта и
эвольвента A06) Примеры A07)
Упражнения для самостоятельной работы 112
Глава 2. Дифференциальные уравнения высших порядков 114
§ 1. Виды интегрируемых нелинейных уравнений 114
Дифференциальное уравнение вида F(x,y(n)) = 0 A14)
Дифференциальное уравнение вида F(y{n~X),yw) = Q A14)
Дифференциальное уравнение вида F{y(n~2) ,у(п)) = 0 A14) Примеры
A15)
§ 2. Уравнения, допускающие понижение порядка 122
Дифференциальное уравнение вида F{x,y(k),y(k+v>,...,у(п)) = 0 A22)
Дифференциальное уравнение вида F(y,y},...,y^) = 0 A22)
Однородное дифференциальное уравнение вида F{x,y,y},...,у(п)) = 0
A22) Обобщенное однородное дифференциальное уравнение вида
F(x,y,y ,...,y{n)) = 0 A22) Уравнение, приводимое к виду
(ф,у,У,...,у(п-1))У= 0 A23) Примеры A23)
§ 3. Линейные дифференциальные уравнения с постоянными 135
коэффициентами
Линейное дифференциальное уравнение п -го порядка с постоянными
коэффициентами. Характеристическое уравнение. Общее решение
A35) Поиск частного решения линейного уравнения n-го порядка с
постоянными коэффициентами методом неопределенных
коэффициентов A36) Метод вариации произвольных постоянных
A36) Метод Коши нахождения частного решения неоднородного
линейного дифференциального уравнения n-го порядка с
постоянными коэффициентами A37) Примеры A37)
§ 4. Линейные дифференциальные уравнения с переменными 150
коэффициентами
Линейное дифференциальное уравнение n-го порядка с переменными
коэффициентами. Линейно зависимые функции. Определитель
Вронского A50) Критерий линейной независимости функций A51)
Фундаментальная система решений A51) Формула Остроградского
— Лиувилля A51) Общее решение неоднородного линейного
дифференциального уравнения с переменными коэффициентами
A51) Уравнение Эйлера. Уравнение Чебышева A52)
Дифференциальные уравнения второго порядка A52) Связь между
линейным дифференциальным уравнением второго порядка и
уравнением Эйлера — Риккати A52) Сведение линейного
дифференциального уравнения второго порядка с переменными
коэффициентами к уравнению с постоянными коэффициентами A53)
Об асимптотическом поведении решений дифференциальных
уравнений второго порядка A53) Примеры A53)
§ 5. Краевые задачи 169
Определение краевой задачи A69) Функция Грина краевой задачи
A70) Задача Штурма — Лиувилля A70) Условие эквивалентности
краевой задачи интегральному уравнению A70) Примеры A70)
Упражнения для самостоятельной работы 180
Глава 3. Системы дифференциальных уравнений 182
§ 1. Линейные системы 182
Неоднородная система линейных дифференциальных уравнений с
переменными коэффициентами. Фундаментальная матрица
уравнения. Определитель Вронского A82) Метод вариации
произвольного вектора A83) Матрицант A83) Неоднородные
линейные системы с постоянными коэффициентами. Метод Эйлера
A84) Примеры A84)
§ 2. Нелинейные системы 200
Нормальные системы дифференциальных уравнений. Метод
исключения B00) Подбор интегрируемых комбинаций B01)
Примеры B01)
Упражнения для самостоятельной работы 211
Глава 4. Уравнения в частных производных первого порядка 212
§ 1. Линейные и квазилинейные уравнения 212
Основные понятия B12) Решение квазилинейного уравнения в
частных производных первого порядка B12) Задача Коши B72)
Уравнение Пфаффа B13) Примеры B13)
§ 2. Нелинейные уравнения первого порядка 228
Нелинейные уравнения в частных производных первого порядка
B28) Решение задачи о нахождении интегральной поверхности,
проходящей через заданную кривую B28) Метод Коши B29)
Обобщение метода Коши B29) Примеры B29)
Упражнения для самостоятельной работы 239
Глава 5. Приближенные методы решения дифференциальных 240
уравнений
§ 1. Зависимость решения от начальных условий и параметров 240
Об оценке погрешности приближенного решения B40) Об отыскании
производных от решений по параметру B40) Примеры B41)
§2. Аналитические приближенные методы 246
Метод степенных рядов B46) Метод малого параметра B47)
Примеры B47)
§ 3. Численные методы решения дифференциальных уравнений 266
Метод Эйлера к-то порядка B66) Метод Рунге — Кутта 4-го порядка
B67) Метод Штермера B67) Примеры B67)
Упражнения для самостоятельной работы 273
Глава 6. Устойчивость и фазовые траектории 274
§ 1. Устойчивость 274
Устойчивость по Ляпунову. Асимптотическая устойчивость B74)
Исследование на устойчивость по первому приближению: первая
теорема Ляпунова B74) Исследование на устойчивость с помощью
функций Ляпунова: вторая теорема Ляпунова B75) Условия
отрицательности всех действительных частей корней уравнения
а0Х" + aft'1 +... + ап_^к + ап=0,а0>0,с действительными
коэффициентами B75) Примеры B76)
§ 2. Особые точки 292
Определение особых точек и их классификация B92) Практические
приемы исследования особых точек B93) Примеры B94)
§ 3. Фазовая плоскость 305
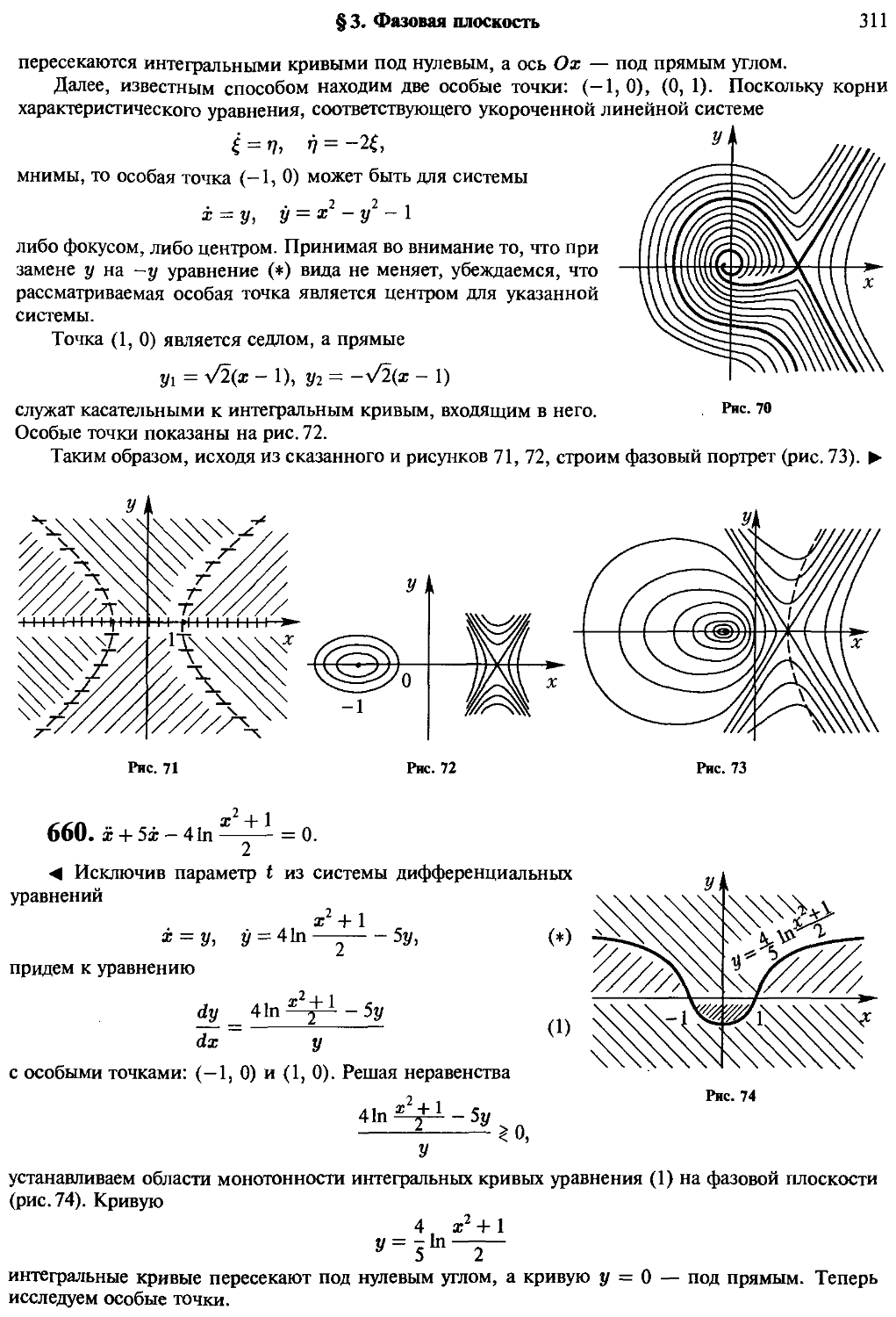
Основные понятия C05) Построение фазового портрета C05)
Предельные циклы C06) Признаки отсутствия предельных циклов
C06) Признаки наличия предельных циклов C06) Примеры C07)
Упражнения для самостоятельной работы 322
Глава 7. Метод интегральных преобразований Лапласа решения 323
линейных дифференциальных уравнений
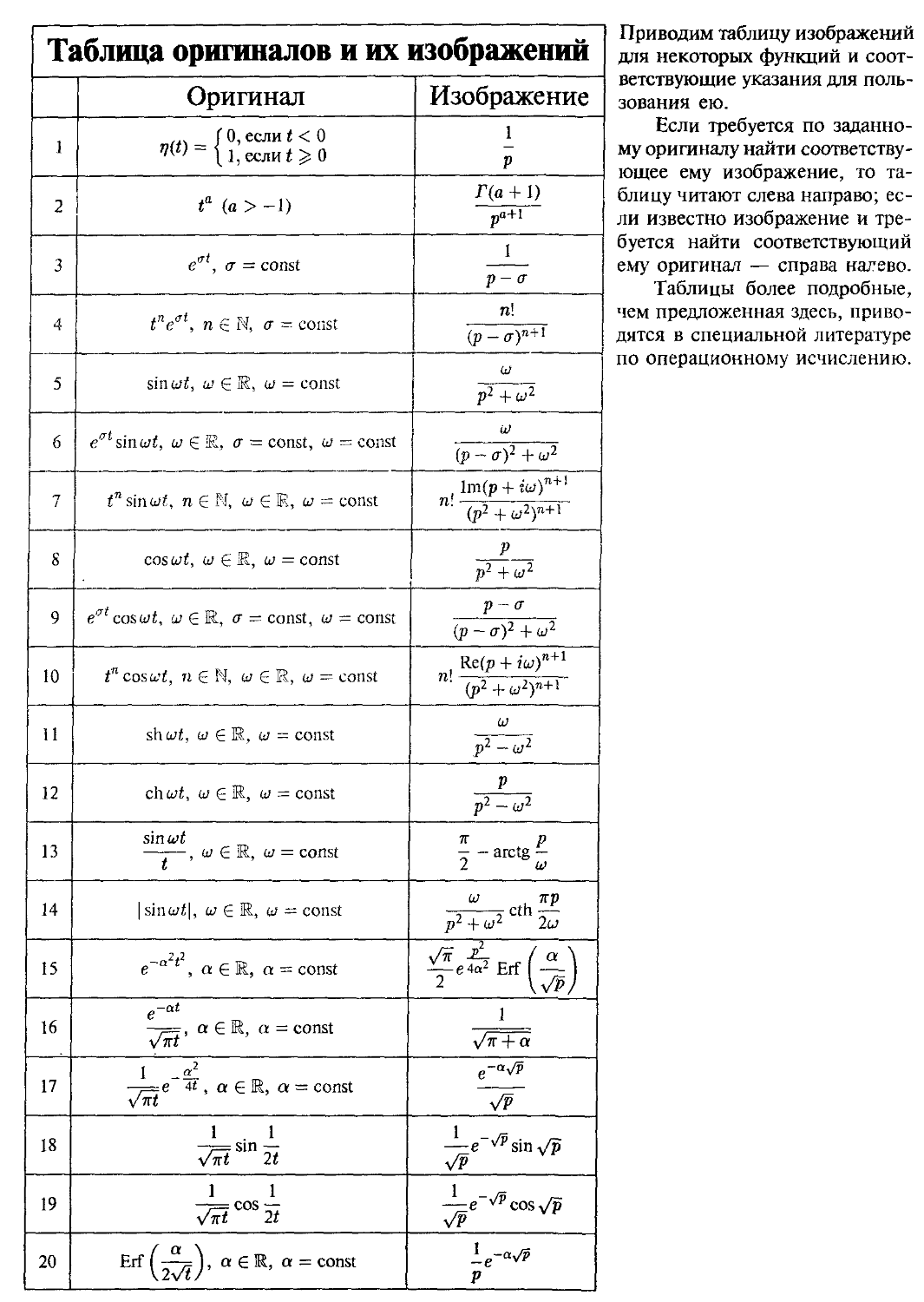
§ 1. Преобразование Лапласа. Основные понятия и свойства 323
Оригинал и изображение C23) Свойства преобразования Лапласа
C24) Примеры C25)
§ 2. Свертка функций. Теоремы разложения 336
Определение свертки C36) Теорема умножения (Э. Бореля) C36)
Обобщенная теорема умножения (А. М. Эфроса) C36) Формулы
Дюамеля C37) Примеры C37)
§3. Обратное преобразование Лапласа 339
Формула обращения Римана — Меллина C39) Сведения из теории
функций комплексного переменного C40) Теоремы разложения C41)
Примеры C42)
§ 4. Линейные дифференциальные уравнения и системы 346
Интегрирование уравнений с постоянными коэффициентами C46)
Решение систем линейных дифференциальных уравнений с
постоянными коэффициентами C47) Решение уравнений с нулевыми
начальными условиями при помощи интеграла Дюамеля C47)
Примеры C47)
§ 5. Интегральные уравнения типа свертки. Особые уравнения 357
Интегральные уравнения типа свертки C57) Интегральные уравнения
второго рода C58) Интегральные уравнения первого рода C59)
Особые интегральные уравнения. Интегральное уравнение Абеля
C59) Примеры C60)
§ 6. Применение операционного исчисления к решению уравнений с 366
частными производными
Примеры C67)
Упражнения для самостоятельной работы 370
Ответы 372
Предметный указатель 377
Предметный указатель
Настоящий предметный указатель призван облегчить поиск терминов по алфавитному
признаку. Для поиска терминов по тематическому признаку пользуйтесь подробно составленным
оглавлением.
В указателе, как правило, приводятся ссылки только на страницу, содержащую определение
термина; составитель указателя не ставил своей целью отследить все упоминания приведенных
терминов в тексте. Исключение составляют термины, описывающие методы, приемы,
практические результаты: для них в некоторых случаях после номеров страниц курсивом указаны
также задачи, в которых они используются существенным образом.
С целью уменьшения громоздкости указателя вместо термина "дифференциальное(ые)
уравнение(я)" применяется сокращение "д. у.".
А Бернулли уравнение, 39, 115, 97, 99,
Абеля 101, 103, 106, 168, 265, 447
— уравнение интегральное, 359 Бихари лемма, 83, 201, 202
формула, 159, 363, 364 Бореля теорема умножения, 336, 711-
астроида, 111 715, 719, 720, 740, 752, 753, 762
Б В
Бендиксона признак отсутствия вид канонический линейного д. у. 2-го
предельных циклов, 306, 672, 675 порядка, 152
Вольтерра уравнение интегральное
— 1-го рода, 358
— 2-го рода, 358
— особое, 359
Вронского
— матрица, 182
— определитель, 151, 183
вычет функции, 340
Г
Гессе
— прием, 208, 460-462
— система, 208
гипербола вырожденная, 18
Грина функция краевой задачи, 170,
393-406
Гурвица матрица, 275, 616-619, 621,
622, 624-627
Д
Дюамеля
— интегралы, 337
— формулы, 337, 347, 721, 742-744,
766
3
задача
— Коши, 4
векторная, 83
— краевая, 169
нестационарная, 367
— Штурма—Лиувилля, 170
, собственные значения, 170
, собственные функции, 170
значения собственные задачи
Штурма—Лиувилля, 170
И
инвариант линейного д. у. 2-го
порядка, 152
интеграл
— вероятности, 338, 715-718, 724, 733
— полный, 228
— системы д. у. первый, 201
интегралы
— Дюамеля, 337
— независимые, 201
интегрируемая комбинация, 201
интегрирующий множитель, 53
К
канонический вид линейного д. у. 2-го
порядка, 152
Клеро уравнение, 78, 191, 194
косинус-интеграл Френеля, 334, 707,
712,713,763
Коши
— задача,4
векторная, 83
— метод
отыскания интегральной
поверхности, 229, 519—521
, обобщение, 229, 522-524
— отыскания частного решения
неоднородного д. у., 137
— формула о вычетах, 341
краевая задача, 169
— нестационарная, 367
кривая дискриминантная, 99
критерий
— линейной независимости функций,
151
— Льенара—Шипара, 276, 618, 619,
626-628
— Михайлова, 276, 620, 621, 623
— Рауса—Гурвица, 276, 616, 617, 621,
625
Л
Лагранжа
— уравнение, 78, 192, 193
второго рода, 438-440, 629, 630,
750
— функция, 582, 629, 630
Лагранжа—Шарли метод, 228, 504, 517
Лапласа преобразование, 324
—, линейность, 324, 686, 688, 710, 734
—, однородность, 324
Левинсона—Смита теорема о наличии
предельных циклов, 306, 676
лемма Бихари, 83, 201, 202
Липшица условие, 82, 240
Лиувилля преобразование, 165, 381—
387
Лорана ряд, 340
—, главная часть, 340
—, правильная часть, 340
Льенара—Шипара критерий, 276, 618,
619, 626-628
Ляпунова
— теорема
вторая, 275, 606-609, 611, 615
первая (об устойчивости по
первому приближению), 274-275,
589-593, 595, 598-600, 602, 615,
630
— функция, 275, 606-615, 630
М
матрица
— векторного д. у.
интегральная, 182
фундаментальная, 182
— Вронского, 182
— Гурвица, 275, 616-619, 621, 622, 624-
627
матрицант, 183
метод
— вариации
произвольного вектора, 183,
429^31
произвольных постоянных, 39,
136, 151, 87-89, 91-93, 97, 108,
325,326,331,342,360,431
— исключения, 200, 408-420, 431, 435,
442,449-451,453,454
— Коши
отыскания интегральной
поверхности, 229, 519—521
, обобщение, 229, 522-524
отыскания частного решения
неоднородного д. у., 137
— Лагранжа—Шарпи, 228, 504, 517
— малого параметра, 247, 559—566,
568
— неопределенных коэффициентов,
136, 141, 315—324, 328, 329, 410,
432
— подбора интегрируемых
комбинаций, 201, 443-448
— последовательных приближений, Ш
— разбиения данного уравнения на две
части, 53, 149, 154-156, 15S-160
— Рунге—Кутта численного решения
д.у., 267, 572—575
— степенных рядов, 246-247, 537-555,
576, 577
— Штермера численного решения д.у.,
267, 575—577
— Эйлера
отыскания общего решения
неоднородной системы д.у., 184,
420-429, 433, 437, 439
численного решения д. у., 266,
569—571
Миндинга—Дарбу уравнение, 40, 106-
109
Михайлова критерий, 276, 620, 621,
623
множитель интегрирующий, 53
О
определитель Вронского, 151, 183
Осгуда теорема, 82
Остроградского—Лиувилля формула,
151, 362, 363
П
Пеано теорема, 82
Пикара теорема, 82,199-204, 207
плоскость фазовая, 305
показатель роста функции, 323
полюс, 340
порядок полюса, 340
преобразование
— Лапласа, 324
, линейность, 324, 686, 688, 710,
734
, однородность, 324
— Лиувилля, 165, 381-387
прием Гессе, 208, 460-462
признак отсутствия предельных циклов
— Бендиксона, 306, 672, 675
— Пуанкаре, 306, 673, 678
пространство фазовое, 305
Пуанкаре признак отсутствия
предельных циклов, 306, 673, 678
Пфаффа уравнение, 213, 233, 491-500,
503,505-508,511,517
Р
Рауса—Гурвица критерий, 276, 676,
6/7, 621, 625
Рейссига теорема о наличии
предельных циклов, 306—307,
677
решение
—дифференциального уравнения
изолированное, 105
особое, 99
— задачи Коши
общее, 4
частное, 4
— неустойчивое в смысле Ляпунова,
274
обыкновенного д. у. п -го
порядка, 4
— устойчивое
асимптотически, 274
по Ляпунову, 274
Риккати уравнение специальное, 67,
70—71, 164—167, 169-171
Романа—Мемина формула обращения,
339-340
Рунге—Кутта метод численного
решения д. у., 267, 572—575
ряд
— Лорана, 340
, главная часть, 340
, правильная часть, 340
— Фурье, 556-55S, 728
С
самосопряженная форма линейного д.
у. 2-го порядка, 152
седло,293 синус интегральный, 335
— гиперболический, 335
синус-интеграл Френеля, 334, 707, 712,
713,763
система
— Гессе, 208
— линейных д. у.
автономная, 305
неоднородная, 182, 184
нормальная, 200
однородная, 182
— решений однородного д. у.
фундаментальная, 151
скорость фазовая, 305
Т
теорема
— запаздывания, 324, 689, 739, 741,
768
— Левинсона—Смита о наличии
предельных циклов, 306, 676
— Ляпунова
вторая, 275, 606-609, 611, 615
первая (об устойчивости по
первому приближению), 274-275,
5*9-595, 595, 598-600, 602, 615,
630
— о дифференцировании
изображения преобразования
Лапласа, 325, 704—706, 723, 749
оригинала преобразования
Лапласа, 324, 700—702, 740
— о линейности преобразования
Лапласа, 324, 686, 688, 710, 734
— о предельных соотношениях, 325
— о существовании и единственности
решения задачи Коши, 82
— об интегрировании
изображения преобразования
Лапласа, 325, 708—710, 732
оригинала преобразования
Лапласа, 325, 707, 708, 718, 724,
733, 742
— об однородности преобразования
Лапласа, 324
— опережения, 324
— Осгуда, 82
— Пеано, 82
— Пикара, 82, 199-204, 207
— подобия, 324, 6*7, 6*9, 765
— разложения
вторая, 342, 725,727, 728, 736,
738, 739, 741, 743-745, 747, 750,
751, 767
первая, 341,729
— Рейссига о наличии предельных
циклов, 306—307, 677
— смещения, 324, 699, 7У5, 734
— умножения
обобщенная А. М. Эфроса, 336,
764
Э.Бореля, 336, 711-715, 719, 720,
740, 752, 753, 762
— Четаева о неустойчивости, 275,
612—614
точка
— разветвления многозначной
функции, 342
— системы двух д. у. первого порядка
особая, 293
— функции особая
однозначного характера, 340
устранимая, 340
— функции существенно особая, 340
траектории
— изогональные, 106
— на фазовой плоскости. 305
— ортогональные, 106
У
узел, 293
— вырожденный, 293
— дикритический, 293
уравнение
— Бернулли, 39, 115, 97, 99, 101, 103,
106,168,265,447
— в частных производных
гиперболического типа, 366
квазилинейное 1-го порядка, 212
нелинейное 1-го порядка, 228
параболического типа, 366
— дифференциальное
n-го порядка, 4
каноническое, 4
в полных дифференциалах, 53
для интегрирующего множителя,
54
линейное
1-го порядка, 39
2-го порядка, 152
, инвариант, 152
, канонический вид, 152
, самосопряженная форма,
152
n-го порядка, 135, 150
неоднородное, 135
однородное, 135
не разрешенное относительно
производной, 73
обобщенно-однородное, 30, 122
однородное, 29
однородное относительно
функции и ее производных, 122
с разделяющимися переменными,
11
— интегральное
Абеля, 359
Вольтерра линейное
1-го рода, 358
2-го рода, 358
особое, 359
Фредгольма
1-го рода, 357
2-го рода, 357
однородное, 357
особое, 359
— Клеро,78, 191, 194
— Лагранжа, 78, 192, 193
второго рода, 438-440, 629, 630,
750
— Миндинга—Дарбу, 40, 106-109
— Пфаффа, 213, 233, 491-500, 503, SOS-
SOS, 511,517
— Риккати специальное, 67, 70-71,
164-167, 169-171
— характеристическое, 136, 184
— Чебышева, 152
— Эйлера, 152, 371, 372, 39J
— Эйлера—Риккати, 67, 152, 163, 282
каноническое, 67, 172
условие Липшица, 82, 240
Ф
фокус, 293
форма
— векторная системы линейных д. у.,
182
— самосопряженная линейного д. у. 2-
го порядка, 152
— симметрическая нормальной
системы д. у., 201
формула
— Абеля, 159, 363, 364
— Коши о вычетах, 341
— обращения Римана—Меллина,
339—340
— Остроградского—Лиувилля, 151,
362, 363
— Циолковского, 29
формулы Дюамеля, 337, 347, 721, 742-
744, 766
Фредгольма уравнение интегральное
линейное
— 1-го рода, 357
— 2-го рода, 357
— однородное, 357
— особое, 359
Френеля
— косинус-интеграл, 334, 707, 712,
713,763
— синус-интеграл, 334, 707, 712, 713,
763
фундаментальная матрица векторного
Д. У-, 182
фундаментальная система решений
однородного д. у., 151
функции
— линейно зависимые, 151
— линейно независимые, 151
— собственные задачи Штурма—
Лиувилля, 170
функция
— аналитическая в области, 340
— влияния для задачи Коши, 137
— голоморфная, 340
— Грина краевой задачи, 170, 393-406
— дробная, 340
— Лагранжа, 582, 629, 630
— Ляпунова, 275, 606-615, 630
— мероморфная, 340
— моногенная в области, 340
— однородная степени т, 29
— регулярная в области, 340
— Хевисайда, 323, 679, 733
обобщенная, 329, 690-694, 728
— целая, 340
функция-изображение преобразования
Лапласа, 324
— обобщенная, 326
функция-оригинал преобразования
Лапласа, 323
— обобщенная, 326
Фурье ряд, S56-SSS, 728
X
характеристическое уравнение, 136,
184
Хевисайда функция, 323, 679, 733
— обобщенная, 329, 690-694, 728
Ц
центр, 293
цепная линия, 110
цикл предельный, 306
— неустойчивый, 306
— полуустойчивый, 306
— устойчивый, 306
циклоида, 111
Циолковского формула, 29
Ч
часть ряда Лорана
— главная, 340
— правильная, 340
Чебышева уравнение, 152
Четаева теорема о неустойчивости,
275, 612—614
Ш
Штермера метод численного решения
д. у., 267, 575—577
Штурма—Лиувилля задача, 170
—, собственные значения, 170
—, собственные фуншии, 170 569—571
Э — уравнение, 152, 371, 372, 391
эвольвента, 106 Эйлера—Риккати уравнение, 67,152,
эволюта, 106 163,282
Эйлера — каноническое, 67,172
— метод Эфроса теорема умножения
отыскания общего решения обобщенная, 336, 764
неоднородной системы д. у., 184, Я
420-429,433,437,439 ядро интегрального уравнения, 357
численного решения д. у., 266,
Предисловие
Предлагаемая вниманию читателей книга по замыслу авторов призвана способствовать глубокому
усвоению теории обыкновенных дифференциальных уравнений с помощью подробно решенных
нетривиальных примеров и задач.
Своеобразие предмета теории дифференциальных уравнений — его обширность и тесная
связь с теорией пределов, теорией функций, дифференциальным и интегральным исчисления-
исчислениями, теорией рядов и другими разделами математики — определяет соответствующую специфику
ее метода. Суть этой специфики состоит в том, что метод теории дифференциальных уравнений
есть метод математического анализа. В связи с этим теорию дифференциальных уравнений не без
оснований считают дальнейшим обобщением и развитием математического анализа на класс не-
неявных функций, заданных уравнениями, содержащими независимую переменную, функцию и ее
производные. Так, интегральное исчисление функции одной переменной фактически есть теория
интегрирования в элементарных функциях простейшего класса дифференциальных уравнений
вида у' = f(x).
Пособие охватывает все разделы учебных программ по дифференциальным уравнениям для
университетов и технических вузов с углубленным изучением математики.
Каждый параграф книги снабжен необходимым минимумом теоретических сведений, исполь-
используемых при решении соответствующих примеров. Кроме того, в книге разобраны нетрадиционные
для такого рода пособий примеры по теории продолжимости решения задачи Коши, нелинейным
уравнениям в частных производных первого порядка, некоторым численным методам решения
дифференциальных уравнений, на применение признаков существования предельных циклов на
фазовой плоскости. Каждая глава снабжена упражнениями для самостоятельной работы.
Книга содержит порядка семисот подробно решенных примеров и задач, взятых из следующих
учебников и сборников задач по дифференциальным уравнениям:
Степанов В. В. Курс дифференциальных уравнений. М., 1950;
Понтрягин Л. С. Обыкновенные дифференциальные уравнения. М., 1961;
Эльсгольц Л. Э. Дифференциальные уравнения и вариационное исчисление. М., 1998;
Гудименко Ф. С, Павлюк I.A., Волкова В. О. Зб1рник задач з диференщальних р1внянь. К.,
1972;
Гюнтер Н. М., Кузьмин Р. О. Сборник задач по высшей математике, т. II, 1958;
Филиппов А. Ф. Сборник задач по дифференциальным уравнениям. М., 1973;
Гречко Л. Г., Сугаков В. И., Томасевич О. Ф., Федорченко А. М. Сборник задач по теоретической
физике. М., 1972;
Мартыненко В. С. Операционное исчисление. К., 1968;
Краснов М.Л., Киселев А. И., Макаренко Г. И. Сборник задач по обыкновенным дифференци-
дифференциальным уравнениям. М., 1978;
Ляшко I.I., Боярчук O.K., Гай Я. Г., Капайда О. Ф. Диференциальш р1вняння. К., 1981;
Головач Г. П., Калайда О. Ф. Зб1рник задач з диференщальних та штегральних р1внянь. К.,
1997.
Введение
Основные понятия.
Составление дифференциальных уравнений
1. Основные определения.
Обыкновенным дифференциальным уравнением п-го порядка называется уравнение вида
F(x,y,y',y", ...,2/"')= 0, A)
где F — известная функция, заданная в некоторой области D координатного пространства пе-
переменных х, у, у', ..., t/<n), х € (хо, хО — аргумент, у, у', ..., t/(n) — неизвестная функция и ее
производные, п — порядок уравнения.
Под решением уравнения A) будем понимать любую функцию у = /(х), х € (х0, Xi), которая:
а) имеет п производных на интервале (хо, xi), причем
Vx € (х0, х,) (х, /(х), f(x), ..., /(n)(x)) € D;
б) удовлетворяет уравнению A), т.е. обращает его в тождество
F(x, /(х), /'(х), ..., /п)(х)) =0 Vie (хо, х,).
Уравнение A) называется проинтегрированным, если найдены все его решения.
Уравнение A), разрешенное относительно старшей производной t/(n), называется каноничес-
каноническим и имеет вид
-— Y \ X, У л У , • • - ) У ] • \~)
2. Задача Коши.
Пусть функция ip(x, у, у', ..., j/"') непрерывна в области D координатного пространства
переменных ат, у, у', ..., у( -1. Требуется найти интервал X, содержащий точку х0, и такую п-
кратно непрерывно дифференцируемую функцию у — /(х), что (х, /(х), /'(х),..., /<™~I)(x)J G D,
когда х € X, и выполняются условия:
1) Vx G X /<n)(x) s р(х, /(х), /'(х), ..., /"""(х));
где (х0, j/o, Уо, • • •, г/о""") € D.
Формально задача Коши для уравнения B) записывается в виде
у^^х.у',...,,/"-^, ^ j C)
где уо, уо,..., Уо"' — заданные числа. хе_
Каждое конкретное решение задачи C) называется частным решением задачи Коши• *?^*
ство частных решений, зависящее от параметров ха, уо, уо, ¦¦¦, У<? У > называется общим
задачи Коши.
Введение 5
3. Построение дифференциального уравнения по заданному семейству кривых.
Для того чтобы построить дифференциальное уравнение, которому удовлетворяют кривые
заданного семейства
Ф(х,у,С1,...,Сп) = 0, D)
где Cj (i = 1, п) — произвольные постоянные, принадлежащие некоторой области С, следует:
1) п раз продифференцировать равенство D), считая у п раз непрерывно дифференцируемой
функцией переменной х, т.е.
дФ _ дФ , _п д2Ф _ „ д2Ф , , 02Ф ,2 _ дФ „ _
E)
Зх" ду
2) Из соотношений D) и E) исключить произвольные постоянные Cit C-i, ¦ ¦ ¦, С„.
Составить дифференциальные уравнения данных семейств линий.
1. х2 + Су2-2у = 0.
¦4 Пусть у = у(х) — непрерывно дифференцируемое решение данного уравнения, где С —
параметр, не зависящий от х. Тогда должно выполняться тождество
F(x, С) = х2 + Су2(х) - 2у(х) = 0, A)
где х € X С R, X — некоторое множество. Функция F дифференцируема по х. Взяв производ-
производную, имеем
— = 2х + 2у(х)у'(х)С - 2«/'(х) = О,
дх
откуда
Подставив B) в A), получим дифференциальное уравнение
(х2 - «/)«/' - ху = 0. >
2. Cy-sinCx = 0.
•* Аналогично проделанному выше получим тождество
Cj/(x)-CcosCx = 0.
При С — 0 семейство кривых, для которых составляется дифференциальное уравнение, не опре-
определено, поэтому С ф 0. Из системы уравнений
у'2 = cos2 Сх, С2у2 = sin2 Cx A)
находим
С2 = Ц? у*0. B)
У
Подставив B) в A), имеем
/(^), „ли y'
3. (х-С,J + С2у2 = 1.
¦4 Дважды дифференцируя по х тождество (х - С{? + СгУ2(х) -1 = 0, получим:
2(х - С,) + 2С2у(х)у'(х) = 0, 1 + ((у'(х)? + у(х)у"(х)) С2 = 0.
Исключив из трех тождеств постоянные С\ и Сг, имеем
6 Введение
•* После дифференцирования по переменной х получим у'(х) = СеСх, откуда С = \ (У Ф 0)-
Таким образом, дифференциальное уравнение данного семейства имеет вид
= I,
5. х - dy2 - С2у - С3 = 0.
¦4 Трижды продифференцировав данное равенство по х, получаем:
1-2уу'С1-С2у' = 0, 2(у'2+уу")с1+С2у" = 0, 2(зУ'у" + t/t/'")c, + С2у'" = 0. A)
Из последнего равенства A) находим
Подставив B) во второе равенство A), получаем
/lT-3tf'/ = 0 или 3t/-t/V" = 0,
в силу того, что у' ф 0 (это следует из первого равенства A)). >
Примечание. Во всех рассмотренных выше примерах мы предполагали, что существует производная тре-
требуемого порядка неявно заданной функции. Это предположение существенно, поскольку уже простейшее
уравнение у2 - х1 - С = 0 определяет бесконечное множество разрывных неявных функций у = у(х, С),
-оо < х < +оо, например
( \JC + х2, xGQ,
(.-VC + z2, i6R\Q,
6. Написать дифференциальное уравнение всех окружностей на плоскости.
•< Из курса аналитической геометрии известно, что каноническое уравнение окружности с
центром в точке М(Сг, С2) и радиусом R = С} имеет вид:
Считая, что каждая окружность описывается двумя трижды непрерывно дифференцируемыми
функциями у = у(х), из A) находим".
х - С, + (у(х) - С2)у'(х) = 0, 1 + у'2(х) + (у(х) - С2)у"(х) = 0, Ъу\х)у"(х) + (у- С2)у'"(х) = 0.
Исключив из двух последних тождеств у(х) - С2, окончательно получим:
Примечание. Точнее говоря, мы получили дифференциальное уравнение всех окружностей, в каждой из
которых выколоты две точки, лежащие на концах горизонтального диаметра.
7. Составить дифференциальное уравнение окружностей радиуса 1, центры которых лежат
на прямой «/= 2х.
¦4 Согласно условию задачи, в предыдущем примере следует положить Съ = 1, С2 = 2С\.
Тогда уравнение A) из примера 6 примет вид
(x-C,J + (t/-2CIJ-l-0.
Получили однопараметрическое семейство окружностей. Дифференцируя тождество
(х - С,J + (t/(x) - 2С,J -1 = 0
по переменной х (считая при этом, что у — непрерывно дифференцируемые функции от х),
находим:
х - С, + (у(х) - 2С,)у'(х) = 0.
Из двух полученных тождеств путем исключения С\ имеем окончательно
Bх - уJ (у'2 + l) - Bt/ + IJ = 0. >
Введение *»
8. Составить дифференциальное уравнение парабол с осью, параллельной оси Оу, касаю-
касающихся одновременно прямых у = 0 и у = ж.
¦4 Семейство парабол с осью, параллельной оси Оу, имеет вид у = С]Х2 + С2х+С3, где Су —
произвольные параметры (j = 1, 2, 3). Из условия касания прямой у = 0 вытекает, что
х
С2хк + С3 = О,
где ж* — абсцисса точки касания. Отсюда следует, что
Сз = §г (Ci*0). A)
Из условия касания прямой у = х вытекает, что должно быть
С2
у' = 2С1хк+С2 = 1; хк = ук; ук = Схх\ + С2хк + -?-.
Отсюда находим, что С2 = -%¦ Подставив значение С2 в A), получим Съ = тгп~ ¦ Таким образом,
искомое семейство удовлетворяет уравнению
2 х 1
2 loCi
где С{ — произвольный параметр. Исключив его из тождеств
y' = 2ClX+-, C2 + +
2' у-^ ' 2 ' 16С,'
получим требуемое дифференциальное уравнение семейства
ху = уBу' - 1). >
9. Составить дифференциальное уравнение окружностей, касающихся одновременно пря-
прямых у = 0их = 0и расположенных в первой и третьей четвертях.
¦4 Ясно, что центры таких окружностей должны лежать на прямой у = х. Отсюда следует,
что С] = С2 (см. пример 6). А так как окружности касаются координатных осей, то С3 = |Cj|.
Таким образом, рассматриваемое семейство окружностей удовлетворяет уравнению
(х - С,J + («/ - С,J - С\ = 0.
Из тождеств относительно х:
(х - С,J + (у(х) - С,J - С2 = 0, x-d + (у(х) - Ci)y'(x) = 0
следует требуемое дифференциальное уравнение
«Да;2 - 2ху) - 1ху + у2 - 2ху = 0. >
10. Составить дифференциальное уравнение семейства циклоид
x = C(t-sint), y-C(l-cost).
¦4 Дифференцируя функции х и у по t и разделив y'(t) на x'(t), получим
1 — cos t tg I
Подставив значение t в равенство
(t - sin t)y - x(l - cos t) = 0,
после некоторых преобразований получим требуемое дифференциальное уравнение
, х + уу'
8 Введение
11. Показать* что дифференциальное уравнение кривых 2-го порядка имеет вид
•* Пусть в общем уравнении семейства кривых второго порядка ах2 -I- 2Ьху + су2 + 2dx +
+ 2еу+ / = 0 выполняется условие а Ф 0. Тогда, не умаляя общности, мЬжно считать, что а — 1.
Дифференцируя 5 раз, получим:
х + Ъ(у + ху) + суу'+ d + еу'= 0, A)
1 + ЬBу' + ху") + с(у'2 + «//) + еу" = 0, B)
ЦЗу" + ху'") + фу'у" + уу'") + еу'" = О, C)
bDy'" + X2/IV) + сC2/ + 42/У" + уу") + еу" = 0, D)
bEylv + X2/V) + с(Юу"у'" + 52/VV + yyV) + eyv = 0. E)
Из уравнений B), C), D) находим
3y"ylv-4y' 3yy + 4yf3yyy
Ь= , с- , F)
где Д = 32/'WV - 4у'2у' - 6у'уу'" + 9у"\
Исключив из уравнений B) и E) е и подставив в результат исключения значения Ь и с из F),
получим окончательно
что и требовалась показать. >
12. Показать, что дифференцируемое семейство кривых
X
удовлетворяет дифференциальному уравнению
(х + y)dx - (х - y)dy - 0.
¦4 Взяв полный дифференциал от тождества
arctg ^ - In y/x2 + 2/2(x) = In С,
получим
d(arctg ^ - In ^х2 + у2(х)) = О,
откуда
xdy-ydx xdx + ydy 2 2
х2 + 2/2 х^ + 2/2 -°' (Х +2/ ^0)'
или
(х + у) dx - (х - у) dy = 0. >
13. Составить дифференциальное уравнение всех окружностей, касающихся оси Ох.
¦4 Если в уравнении семейства окружностей (см. пример 6) положить С3 = \С2\, то получим
уравнение семейства окружностей с требуемыми свойствами:
(x-C,J + (j/-C2J-C22 = 0. A)
Определив С\ и С2 из тождеств
ж - С, + у'{у - С2) = 0, 1 + / + (у - С2)у" = О
и подставив их значения в A), получим дифференциальное уравнение
«/У2 + 2уA + у'2)у" - / A + /J = 0. >
Введение 9
Найти системы дифференциальных уравнений, которым удовлетворяют линии данных се-
семейств.
14. ax + z = b,y2 + z2 = Ь2.
Представив параметрические уравнения кривой в виде
х = х, у = у(х), z = z(x),
где у и z — непрерывно дифференцируемые функции, и подставив их в данные уравнения,
получим тождества относительно х
ах + z(x) = Ь, у2(х) + z2(x) = Ь2. A)
Продифференцировав эти тождества по х, получим
а + z'(x) = 0, у(х)у'(х) + z(x)z'(x) = О,
откуда а = —z'. Подставив значение а в первое из тождеств A), имеем Ь = z — xz'. Это соотно-
соотношение совместно со вторым тождеством из A) приводит к равенству у2 + Izz'x — xz' =0. Таким
образом, искомая система уравнений имеет вид
уу + zz =0, у2 + 2xzz' - xV = 0. >
15. х2 + у2 = z2 - 2bz, y = ax + b.
4 По аналогии с предыдущим примером имеем
2х + 2J/J/' = 2zz' - 2bz', у' = а,
откуда находим а = у', b = jr(zz' - х - уу'). Подставив значения а и Ь в исходные уравнения,
получим:
6 = 2/- ху, z'(y - ху) = zz' - х - 2/2/', х2 + у2 = z2 - 2z(y - ху).
Последние два соотношения и есть требуемые дифференциальные уравнения. >
16. Найти частное решение некоторого дифференциального уравнения, если его общее ре-
решение имеет вид
у = Сх cos ах + С2 sin ах и 2/@) = 1, у'@)=1.
¦4 Дважды дифференцируя у по х, легко находим соответствующее дифференциальное урав-
уравнение:
у" + агу = 0.
Для отыскания частного решения этого уравнения следует воспользоваться начальными услови-
условиями, чтобы найти постоянные С\ и С2. Имеем
у@) = (Cxcosax + C2sinax)\x=0 — Сх = 1, у'(О) = («(-C^sinax + C2cosax)|1=0 = «C2 = 0.
Итак, Ci = 1, С2 = 0, у = cos ax — частное решение. >
17. Найти частное решение дифференциального уравнения, если его общее решение имеет
вид
у = Сг + С2]пх + 3
и удовлетворяет следующим начальным условиям:
¦4 Исходя из условий примера, имеем
=0, у"A) = {-^ +6C3z) =2.
Отсюда находим, что Сх = -^, С2 = -1, Съ = у. Осталось записать частное решение:
2 2, 2 з
Составить соответствующее дифференциальное уравнение предоставляем читателю. >
10 Введение
18. Пусть некоторое частное решение удовлетворяет задаче Коши
у' = х + у2, «/(О) = 1.
Может ли оно удовлетворять другой задаче Коши
у" = 1 + 2ху + 2t/3, t/@) = 1, 2/'@) = 1?
¦4 Если частное решение дважды непрерывно дифференцируемо, то из первой задачи Коши
находим:
у" = 1 + 22/2/' =1 + 2у(х + у2) = 1 + 2ху+ 2у\
а также «/'(О) = 1. Следовательно, это возможно. >
19. Пусть общее решение некоторого дифференциального уравнения имеет вид
-оо<ж<+оо.
Может ли функция у = х + 1 быть частным решением этого уравнения?
¦4 Нет, не может, поскольку ни при каких значениях произвольных постоянных (в том числе
и ±оо) из формулы общего решения получить ее нельзя. >
Упражнения для самостоятельной работы
Путем исключения постоянных С;- найти дифференциальные уравнения следующих семейств
кривых:
1. y-tg(ClX) = 0. 2.y = de%. 3. ТТС7 W
X
4. у = С\ sinip(x) + С2 cos<р(х), <р(х) = [f(t)dt. 5.p =
о
6. р2 + ip2 - С[ = 0 (р, (р — полярные координаты).
7 f С1У2 - C2z2 + Сзх = 0, 8 Г С1У + С2г + С}х
' \ d sin у + 4C2ez - 2С3 = 0. ' { Cij/2 + C2z2 + Сгх2 + 2С4 = 0.
Глава 1
Дифференциальные уравнения
первого порядка
§ 1. Уравнения с разделяющимися переменными
1.1. Дифференциальное уравнение с разделяющимися переменными.
Уравнение вида
fi(x)f2(y) dx + gl(x)g2(y) dy = 0, A)
где /j, <7i (г = 1, 2) — заданные непрерывные функции, х € (а, Ь), у ? (с, d), называется диффе-
дифференциальным уравнением с разделяющимися переменными.
Для того, чтобы проинтегрировать уравнение A), следует сначала обе его части разделить на
произведение h(y)gi(x) (h(y)9i(x) Ф 0)> а затем, пользуясь формулой
d У f(x) dx + J g(y) dyj =f(x)dx + g(y) dy,
записать
/() gijy) J
аУ = c-
f /i(s) _, f gi
/ ~TT dx+ Т
При делении могли быть потеряны решения уравнений fi(y) = 0 и д\(х) = 0. Поэтому для по-
получения всех решений уравнения A) следует к семейству интегральных кривых B) присоединить
НуЛИ фуНКЦИЙ /jUj!.
1.2. Разделение переменных линейной заменой аргумента.
Уравнение вида
dy
— = f(ax 4- b) (a, b — постоянные), C)
dx
где / — непрерывная функция, посредством подстановки t = ах + b приводится к уравнению
с разделяющимися переменными
(a + bf(t))dx-dt = Q.
Решить следующие уравнения.
20. y/rf+idx = xydy.
•* Это уравнение вида A). Деля обе его части на произведение у/у2 + 1 -х, получаем
dx ydy
1
откуда
rdx=ry4y +
J X J y/v2 + 1
dx _ f ydy
или
Таким образом, все решения данного уравнения имеют вид
12 Гл. 1. Дифференциальные уравнения первого порядка
21. (х2 - 1)У' + 2хУ2 = о, гКО) = 1.
¦^ Сначала находим все решения этого уравнения. Имеем
(х2 - l)dy + 2ху2 dx = О,
откуда, разделив переменные хну, получаем
у2 х2-\
Интегрируя обе части полученного уравнения, находим
-- + 1п|х2-1| = С. A)
У
Для получения всех решений исходного уравнения к последнему семейству интегральных кривых
присоединим еще решение у ~ 0.
Далее, из совокупности всех интегральных кривых выделим ту кривую, которая проходит
через точку @, 1). Полагая вA)ж = 0иу=1, находим С — —\, Таким образом, функция
1
У~ 1 + 1п|ж2-1|
является решением поставленной задачи. >
22. ху' + у = у\ уA) = 0,5.
< Записывая уравнение в виде
xdy + (y-y2)dx = 0 A)
и разделяя переменные, имеем
dy dx
—У-г + — = 0.
у-У2 х
Интегрируя, получаем
ху{\ -у) = С. B)
Заметим, что несмотря на деление обеих частей уравнения на х(у - у2), его решения х = 0,
у = 0 и у = 1 не были потеряны. Наконец, подставив в B) х = 1, у = 0,5, находим С = ^.
Следовательно, дифференцируемая кривая
4хуA - у) - 1 = 0
— решение поставленной задачи. >
ds\
< Переписав уравнение в виде
разделяем переменные s и t:
е' -1
Проинтегрировав полученное уравнение, находим
In
или л =-l
24. у' = cos(y - х).
¦4 Полагая z = у ~ х, получим:
dx dx
Исходное уравнение приводится к виду
dz
COSZ — ]
§ 1. Уравнения с разделяющимися переменными 13
Интегрированием находим
z у - х
х - ctg - = С, или х - ctg = С.
К этим решениям следует присоединить потерянные решения z = 2&тг, к 6 Z. >
25. у' - у = 2х - 3.
•^ Записав уравнение в виде dy = (у + 2х — 3) dx и произведя замену z = у + 2х — 3, получим
уравнение с разделяющимися переменными
dz = (z + 2) dx.
Отсюда при z ф —2 следует, что
-^- = dx.
Интегрируя уравнение, имеем
ln|z + 2| = x + lnC,
или, окончательно,
у = 1 - 2х + Сех.
Очевидно, решение z = —2, т.е. у = 1 - 2х, принадлежит полученному семейству интегральных
кривых (его можно включить в семейство при С = 0). >
Найти решения уравнений, удовлетворяющие указанным условиям при х —» +оо.
26. zV - cos2j, = 1, u(+oo) = - тт.
4
¦4 Разделяя переменные, получим
dy dx
=
cosy
= C , или у = arctgBC- J-) + 2*тг, А € Z.
2 cos2 у х '
После интегрирования имеем
1 -Г--
-tgy-C--,
Используя дополнительное условие, находим
- тг = lim u = lim ( arctg BC - 1) + 2А?г) = arctg2C + 2Атг.
Поскольку | arctg 2С| < у, то отсюда следует, что к = 1, arctg 2C = ^-, С = -j. Таким образом,
окончательно получаем
у = arctg fl - |) +2тг. >
27. Зу2у' + 1бх = 2ху3; у(х) ограничено при х —» +оо.
¦4 Разделяем переменные х и у:
-^—dy = 2xdx, уф 2.
Интегрируя обе части уравнения, получим:
, 1п|г/3-8| = х2
Полагая С = inCi (Сх > 0), имеем
|t/3 - 8| =
Очевидно, что решение у = 2 можно включить в полученное семейство интегральных кривых,
если считать, что С( = 0. Таким образом, все решения исходного уравнения описываются фор-
формулой
|j,3-8| = C,e*2 <C,?0).
Из полученной формулы следует, что единственная кривая у = 2 удовлетворяет поставленному
в задаче условию. >
14 Гл. 1. Дифференциальные уравнения первого порядка
_ , з/ у2 + 1
. Показать, что каждая интегральная кривая уравнения у = \j —
имеет две горизон-
Х4+1
тальные асимптоты.
¦4 Разделяя в дифференциальном уравнении переменные х и у, а затем интегрируя, получим
где (хо, j/o) — произвольная точка на плоскости Оху.
+ 00
Пусть в A) х —> +оо. Тогда в силу сходимости несобственного интеграла / 3, ^ су-
J v t г 1
у(х) +оо
ществует lim / 3 = а. Поскольку несобственный интеграл / 3, " расходится, то
Х— + 00 J У у} -\-\ J yUl -f- 1
№ Уа
lim у(х) = у(+оо) существует и конечен, причем jK+oo) > уо, так как а > 0.
Далее, пусть в A) х —* -оо. Тогда
S(z) -сю
f du f dt
lim / j = Ь, где 6= / 3 4 < 0.
So *o
Следовательно, -оо < y(—оо) < y0- Таким образом, формула A) описывает семейство интеграль-
интегральных кривых, каждая из которых имеет две горизонтальные асимптоты у(-оо) и у(+оо). >
29. Исследовать поведение интегральных кривых уравнения
у sin ж
в окрестности начала координат. Показать, что из каждой точки границы первого координатного
угла выходит одна интегральная кривая, проходящая внутри этого угла.
¦^ Находим область D существования функции в правой части уравнения:
+ 00
D= (J Мк,
к=-оо
где
Мк = { (ж, у) € R212*тг < х < Bк + 1)тг, 0 < у < +оо} U
U { (х,у) € R2 BA + 1)тг < х < 2(А + 1)тг, -1< у < о} .
Пусть 0 ^ у < +оо, О<х<7г,О<хо<7г. Тогда разделяя переменные в уравнении
и интегрируя, получим
х у
/dt r du
-/=F= = / / A)
vsint J л/1пA + и)
Хо О
Поскольку при и —> 0 1пA+и) ~ и, то интеграл в правой части равенства A) сходится по признаку
у
сравнения. В силу положительности подынтегральной функции / ,. ." > 0. Следовательно,
о
X
/ J i ^ ®' ^тсюда находим, что х > х0. Такими образом, при х > х0 имеем у > 0 (и наоборот),
т. е. интегральная кривая, определяемая уравнением A) и выходящая из точки (х0, 0), находится
в первом квадранте. Из неравенства у' > 0 вытекает, что у = у(х) возрастает с возрастанием х.
Однако в силу расходимости интеграла в правой части A) при у -* +<» и сходимости интеграла
в его левой части при х -»тг - 0 следует, что у стремится к конечному пределу при х -+ тг - 0.
§ 2. Задачи, приводящие к уравнениям с разделяющимися переменными
15
Аналогичную ситуацию получим при рассмотрении равенства интегралов
du
f—=f-
О < у < +0°, 0<х<тг, 0<jfo< +оо.
о и
Пусть — 1 < у ^ 0, — тг < х < 0. Тогда, разделив переменные в исходном уравнении и проинте-
проинтегрировав полученное, имеем
dt } du
[ dt _ Г
J V— sini J J
щ о v
J- ln(l + и)
B)
Поскольку у < 0, то интеграл справа в B) отрицателен. Значит, ж < жо. Следовательно, инте-
интегральная кривая, выходящая из точки (жо, 0) (ж0 < 0) стремится вниз налево. Далее, как следует
из дифференциального уравнения, при ж —> — ж + 0 или при у —» —1+0 производная у' —» +оо.
Таким образом, интегральные кривые асимптотически приближаются к отрезкам прямых ж = - тг
или у = -1, причем к отрезку прямой х = -ж они приближаются по касательной, а к отрезку
прямой у = — 1 — по нормали. >
§ 2. Геометрические и физические задачи,
приводящие к уравнениям
с разделяющимися переменными
2.1. Использование геометрического смысла производной.
Для решения геометрических задач целесообразно использовать чертежи, а также геометри-
геометрический смысл производной и интеграла.
2.2. Использование физического смысла производной.
При составлении дифференциального уравнения, описывающего физический процесс, наря-
наряду с применением физических законов используем физический смысл производной, как скорости
изменения какой-либо величины.
30. Найти кривые, для которых площадь треугольника, образованного касательной, ордина-
ординатой точки касания и осью абсцисс, есть величина постоянная, равная а .
<4 Как видим из рис.1, площадь указанного треугольника равна 5 = -j\NK\y. Поскольку
2
tga = у' (это вытекает из геометрического смысла производной), то 5 = у-г, у' > 0. Таким
образом, имеем дифференциальное уравнение
У-=а2у'. У>
Считая у Ф 0 и разделяя переменные, получаем
2dy dx
Отсюда находим -^ = -^ +С,
или
У=-
2а2
\х,у)
N
Рис. 1
Если у' < 0 (см. рис.2), то 5 = —ifr = а2. Интегрируя это уравнение, получаем
2а2
У =
х-Са2'
Гл. 1. Дифференциальные уравнения первого порядка
Наконец, обозначив Са2 = —С, оба ответа объединяем в один:
2а2
Рис. 3
У ,
к
У\
о
1
1
/
М(х, у)
х
Рис.4
У ,
к
о
•у
1
х
У С±х
31. Найти кривые, обладающие следующим свойством: отрезок
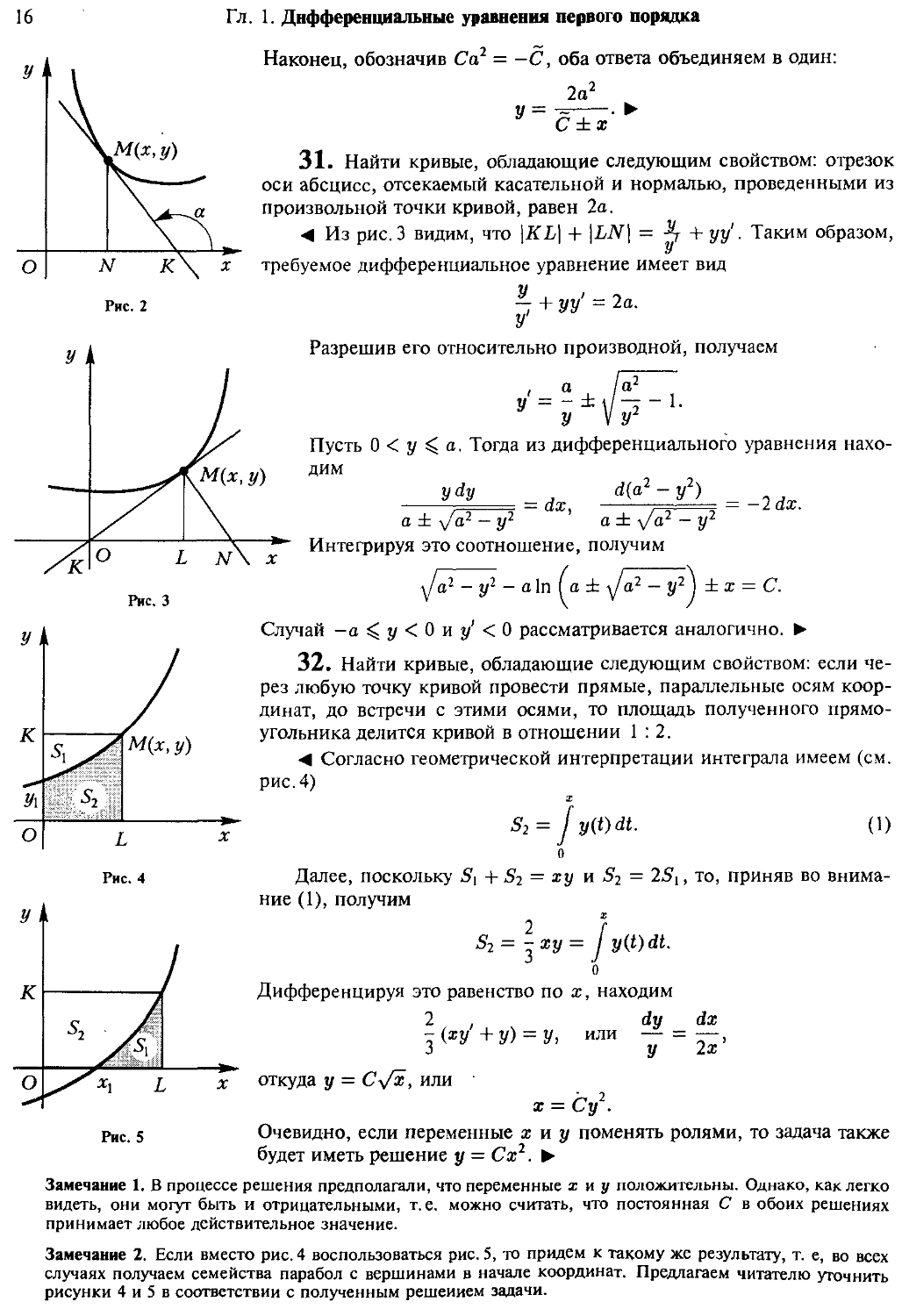
оси абсцисс, отсекаемый касательной и нормалью, проведенными из
произвольной точки кривой, равен 2а.
¦4 Из рис.3 видим, что \KL\ + |LiV| = -^ + уу'. Таким образом,
требуемое дифференциальное уравнение имеет вид
Разрешив его относительно производной, получаем
Пусть 0 < у
дим
а. Тогда из дифференциального уравнения нахо-
нахо= dx,
-у2)
а±
= -2dx.
Интефируя это соотношение, получим
±х = С.
Случай -а^у<0иу'<0 рассматривается аналогично. >
32. Найти кривые, обладающие следующим свойством: если че-
через любую точку кривой провести прямые, параллельные осям коор-
координат, до встречи с этими осями, то площадь полученного прямо-
прямоугольника делится кривой в отношении 1:2.
•^ Согласно геометрической интерпретации интеграла имеем (см.
рис.4)
= fy(t)dt.
A)
Далее, поскольку S\ + S2 = ху и S2 = 25[, то, приняв во внима-
внимание A), получим
S
= -xy
= Jy(t)dt.
Дифференцируя это равенство по ж, находим
- (ху' + у) = у, или
dy
У
dx
2х~'
откуда у = Су/х, или
х = Су2.
Рис. 5 Очевидно, если переменные х и у поменять ролями, то задача также
будет иметь решение у = Сх2. >
Замечание 1. В процессе решения предполагали, что переменные хну положительны. Однако, как легко
видеть, они могут быть и отрицательными, т.е. можно считать, что постоянная С в обоих решениях
принимает любое действительное значение.
Замечание 2. Если вместо рис. 4 воспользоваться рис. 5, то придем к такому же результату, т. е, во всех
случаях получаем семейства парабол с вершинами в начале координат. Предлагаем читателю уточнить
рисунки 4 и 5 в соответствии с полученным решением задачи.
§2. Задачи, приводящие к уравнениям с разделяющимися переменными
33. Найти кривые, касательные к которым в любой точке обра-
образуют равные углы с полярным радиусом и полярной осью.
¦4 Используя соотношения между углами а и <р (см. рис. 6), а так-
также геометрическую интерпретацию производной
dy y'(V) p' simp + pcosip 1
— = ,. . = — ;— = -tga, a= - (тг - <p),
dx tf(<p) p cos <p - p sin if 2
после несложных выкладок получим дифференциальное уравнение q
р' . v
/ X
Рис. «
N Р
интегрируя которое, находим
\ар — -21п
cos-
+ 1п2С,
или
р =
1 + cos <р
Замечание. Если вместо рис. 6 рассмотреть рис. 7, то получим диффе-
дифференциальное уравнение
р' v
= ctg
из которого следует, что
1 — cosip
Это семейство получим из семейства A) путем замены ip на
Таким образом, окончательный ответ записывается в виде
С
Q =
34. Найти уравнение кривой в полярных координатах, если ~/*^~ ~
известно, что тангенс угла 7. образованного радиусом-вектором, /К- О
проведенным в точку касания, и касательной к кривой в этой
же точке, равен полярному углу ip.
Рис.8
¦4 Используя условие tgy = ip и соотношение <р = а + у (см. рис. 8), можем записать
- tga
<p = tgy = 1ё(<р - о.) -
1 + tg ip tg a'
¦, поэтому из предыдущего уравнения после не-
несложных преобразований получаем
Решив это дифференциальное уравнение, найдем
Р=- (<р Ф 0). >
¦V
Замечание. Если вместо рис. 8 рассмотреть рис. 9, то аналогичным путем можно получить дифференци-
дифференциальное уравнение <р = -^-, из которого следует, что р = &р.
Рис.9
35. Нормаль MQ к некоторой кривой пересекает ось Ох в точке Q. Доказать, что если
абсцисса точки Q вдвое больше абсциссы точки М, то кривая — равнобочная гипербола
¦4 Из рис. 10 видим, что
18
Гл. 1. Дифференциальные уравнения первого порядка
У ,,
Используя условие жо = 2ж и соотношение j/' = tga, из A)
получаем дифференциальное уравнение
ж = уу'.
Разделяя переменные и интегрируя, имеем
2 2
ydy=^xdx, у —ж =С B).
Из курса аналитической геометрии известно, что каноничес-
каноническое уравнение гиперболы имеет один из видов:
х2 у2 х2 у2
~1 2 = ^ ИЛИ ~~2 2 = ~^'
причем, если a = Ь, то гипербола называется равнобочной.
Легко видеть, что второе соотношение в B) определяет два семейства равнобочных гипербол
(для О 0 и для С < 0). >
Примечание. При С = 0 из B) получаем пару прямых у = ±х — так называемые вырожденные гиперболы.
36. Доказать, что кривая, все нормали к которой проходят через одну и ту же фиксированную
точку, есть окружность.
< Пусть Мо(хо, уо) — точка, через которую проходят все нормали, и Мх(хх, yi) — точка,
расположенная на кривой. Тогда уравнение прямой, проходящей через эти точки, имеет вид
1
У = Г,—С (х ~~ жо) + Уо-
У\(х\)
Этому уравнению удовлетворяют также координаты точки Мх(хх, у\), поэтому должно быть
1
Разделяя переменные ж, и у\ и интегрируя, получим:
(У\ ~ Уо) d(yi - уо) + (xi
- х0) = 0,
Таким образом, если С Ф 0, то имеем уравнение окружности радиуса С с центром в точке Мо. >
37. Сосуд объемом в 20 л содержит воздух (80% азота и 20% кислорода). В сосуд при не-
непрерывном перемешивании каждую секунду втекает 0,1л азота и вытекает такое же количество
смеси. Через какое время в сосуде будет 99% азота?
•^ Пусть Q(t) — количество литров азота в сосуде в момент времени t после начала пере-
перемешивания. Тогда в 0,1 dt литрах смеси содержится ' ^— литров азота. Согласно условию
ОЛ-Qdt
задачи, в сосуд за время dt поступит 0,1 dt л азота, а вытечет ' ^ — л. Следовательно, количе-
количество dQ азота, котрое втекает в сосуд за время dt и остается в нем, равно 0,1 (\ — -l-fo) dt литров.
Получаем дифференциальное уравнение
-«)* или
20/
20 -Q 200'
интегрируя которое, находим
Q = 20 - Се'005'.
Для определения постоянной С используем условие Q(t)\t=o = 16 л. Получаем С = 4, вследствие
чего функция
<Э(О = 20-4е-°'0(Ш A)
есть решение поставленной задачи. Полагая в A) t = Т и Q = 19,8л (что составляет 99% от 20л),
находим
Т = 200 In 20 с = 599,2 с » 10 минут
— через такой промежуток времени после начала перемешивания в сосуде будет 99% азота. >
§2. Задачи, приводящие к уравнениям с разделяющимися переменными 19
38. В баке находится 100л раствора, содержащего 10 кг соли. В бак непрерывно подается
вода E л в минуту), которая перемешивается с имеющимся раствором. Смесь вытекает с той же
скоростью. Сколько останется соли в баке через час?
•41 Пусть Q(t) кг — количество соли в баке в момент времени t после начала истечения смеси
из бака. Тогда -^ есть ее концентрация в данном растворе, a jfo • 5dt — количество соли,
вытекающее из бака за время dt мин. Следовательно, имеем дифференциальное уравнение
dQ = -0,05 Qdt.
Здесь знак " - " указывает на то, что количество соли в баке уменьшается. Интегрируя уравнение,
получаем О = Ce~°'05t. Поскольку при t = 0 в баке имелось 10 кг соли, то С = 10. Таким образом,
Q = 10е~0' есть решение данной задачи. Полагая в последнем равенстве t = 60 мин, получаем,
что количество соли в баке через час равно 10е~3кг и 0,5 кг. >
39. В воздухе комнаты объемом 200м3 содержится 0,15% углекислого газа СО2. Вентилятор
подает в минуту 20 м3 воздуха, содержащего 0,04% СО2. Через какое время количество углеки-
углекислого газа в воздухе комнаты уменьшится втрое?
¦4 Пусть Q(t)Ml — количество углекислого газа в комнате в момент времени t после на-
начала работы вентилятора. Тогда Щ^- есть концентрация его в комнате в момент времени t.
Следовательно, 20 м3 воздуха, которые уходят из комнаты за минуту, содержат 0,1Q(<)m3 СО2.
Поэтому за время dt мин из комнаты уйдет 0,1@(<)<йм3 СО2. За это же время вентилятор подаст
j'qq^1 20 dt м3 = 0,008 dt м3 СО2 в комнату. Таким образом, приращение dQ газа СО2 за время dt
равно @,008 — O,lQ(t)) dt, и мы имеем дифференциальное уравнение
dQ = @,008 -O,\Q)dt.
Проинтегрировав, получим
<3(*) = @,08-Се~0>")м3.
Поскольку при t = 0 Q = 0,3м3 (т.е. 0,15% от 200м3), то С = -0,22. Таким образом, Q =
0,08 + 0,22е~0'". Момент времени Т, когда количество СО2 будет 0,1 м3, находим из равенства
0,1 = 0,08 + 0,22е~°'1т. Получаем
Г = 101п11к24мин. >
40. Скорость остывания (или нагревания) тела пропорциональна разности температур тела
и окружающей среды. Температура окружающего воздуха поддерживается равной 20°С. Когда
тело остынет до 25°С, если за 10 минут оно охладилось от 100°С до 60°С?
¦4 Согласно указанному закону, можем написать соотношение
dT
— =*(Г-Го), A)
at
где Т — температура тела, Го — температура окружающего воздуха, к — коэффициент пропор-
пропорциональности. В нашем случае Го = 20°С. Интегрируя уравнение A), получим
Г = 20+Се*'.
Из условия Г(^)|4=о = 100°С находим С = 80, а условие T(Olt=io = 60°C позволяет определить к.
Следовательно,
А = -0,1 In 2,
Полагая здесь Г = 25"С, находим требуемый момент времени
11 = 40 мин. >
41. В сосуд, содержащий 1 кг воды при температуре 20°С, опущен металлический предмет
с массой 0,5 кг, удельной теплоемкостью 0,2сн2о и температурой 75°С. Через минуту вода на-
нагрелась на 2"С. Когда температуры воды и предмета будут отличаться одна от другой на ГС?
Потерями тепла на нагревание сосуда и прочими пренебречь.
-4 По аналогии с предыдущим примером имеем
^ = *П(ТП - Г.), —- = кв(Тв - Г„),
20 Гл. 1. Дифференциальные уравнения первого порядка
где Г„ и Г, - температуры предмета и воды соответственно, кп и кв — постоянные коэффи-
коэффициенты. Вычитая почленно из первого соотношения второе и вводя обозначение R = Т„ - Тв,
можем записать
dR
—- = АД, к = кп + кв.
at
Отсюда находим R = Сем. Поскольку в начальный момент времени t — 0 разность R = 55°,
то С = 55. Поэтому R = 55ew. Для определения коэффициента к воспользуемся уравнением
теплового баланса. Имеем по общей формуле для теплоты Q = ст(Тк — Т„), где с — удельная
теплоемкость тела, m — его масса, 2» - Т„ — разность температур:
Q, = 2сН2о, Qi = 0,2 • 0,5G5 - Г)сн2о-
Здесь Q\ — количество тепла, поглощенное водой, Qi — количество тепла, выделенное пред-
предметом при остывании до температуры Т. Поскольку по условию Q, = Qi, то Т = 55°С. Таким
образом, через минуту R = 55°С - 22°С = 33°С. А тогда 33°С = 55°Се*, откуда к = In 0,6. По-
Поэтому R = 55 ¦ @,6)' есть закон сближения температур воды и тела. Из равенства 1 = 55 • @,6)''
находим
In 55
h = т—z——г и 8 мин
In 5 - In 3
— время, по истечении которого температура тела будет выше температуры воды на 1"С. >
42. Кусок металла с температурой а помещен в печь, температура которой в течение ча-
часа равномерно повышается от а до Ь. Скорость нагрева металла пропорциональна разности Т
температур печи и металла, коэффициент пропорциональности равен к. Найти температуру тела
через час.
< Согласно условию, имеем
~ = к(Тп - Гм), A)
at
где Г„ и Г, - температуры печи и металла соответственно. Далее, Т„ = а + щ(Ь - a)t в силу
равномерного повышения температуры печи, t — время, измеряемое в минутах. Таким образом,
дифференциальное уравнение A) можно записать в виде
( + 1(*-а)-Ги). B)
Введем замену а + -^ф — а) — Тш — z. Тогда уравнение B) преобразуется в уравнение с разделя-
разделяющимися переменными:
dz
t? ~ ~dt>
kz_ t?
KZ 60
интегрируя которое, находим
или
Так как TM(t)|t=0 = а, то С = ^? . Следовательно, окончательно имеем
Температура металла через час, очевидно, будет равна
§2. Задачи, приводящие к уравнениям с разделяющимися переменными 21
43. Лодка замедляет свое движение под действием сопротивления воды, которое пропорци-
пропорционально скорости лодки. Начальная скорость лодки 1,5м/с, а через 4с скорость ее 1 м/с. Когда
скорость лодки уменьшится до 1 см/с? Какой путь может пройти лодка до остановки?
•^ Пусть v(t) — скорость лодки в момент времени t от начала движения. Тогда -^ есть ее
ускорение. Согласно второму закону Ньютона
m^=F, A)
где F — сила сопротивления воды. По условию F = kv, поэтому A) принимает вид
dv к
— = — v = kov (fc0 = const).
at m
Интегрируя это уравнение, получим
v(t) = СеЧ B)
Используя условие v@) — 1,5, находим С = 1,5. Тогда B) имеет вид
v(t)= 1,5еЧ,
где t измеряется в секундах. Поскольку vD) = 1м/с, то из равенства 1 = 1,5е4А'0 следует, что
ко = 0,251пB/3). Поэтому скорость движения лодки выражается формулой
2- '
Подставляя сюда v = 1 см/с — 0,01 м/с, находим соответствующий момент времени
/ 1п0,01\
^ = 4 1 + ¦— и 50с.
\ 1пB/3);
Далее, поскольку v(t) = ^ ' , где s(t) — путь, из C) получаем
4 Н
где s0 — постоянная интегрирования. Пусть s@) = 0. Тогда «о = — [пп/з) (?) ' и закон
движения лодки имеет вид
Из C) видим, что lim v(t) = 0, поэтому из закона движения лодки получаем
где sj — путь, который проходит лодка до остановки. >
44. За 30 дней распалось 50% первоначального количества радиоактивного вещества. Через
сколько времени останется 1 % от первоначального количества?
•^ Воспользуемся законом радиоактивного распада: количество радиоактивного вещества,
распадающегося за единицу времени, пропорционально количеству этого вещества, имеющегося
в рассматриваемый момент. Пусть Q(t) — количество радиоактивного вещества в момент вре-
времени t после начала распада. Тогда, в соответствии с законом радиоактивного распада, имеем
q(t) = kQ(t), где к — коэффициент пропорциональности, q(t) — количество вещества, распада-
распадающегося за единицу времени. Следовательно, за промежуток времени от t до t + At распадется
kQ{txNd вещества, где t\ € (t, t + At), Q(t\) — некоторое промежуточное значение количества
вещества между Q(t) и Q(t + At). С другой стороны, это же количество равно Q(t + At) - Q(t),
поэтому окончательно имеем
At) - Q(t) = kQ(t,)At, или Q{t + ^9(t> =kQ(tl).
22 Гл. 1. Дифференциальные уравнения первого порядка
Считая функцию Q дифференцируемой и переходя к пределу в последнем соотношении при
At —> 0, получим дифференциальное уравнение
^ «**), О)
решением которого является функция Q(t) = Сеы. Очевидно, постоянная С здесь означает
первоначальное количество вещества. Далее, из условия 0,5С = Сеж находим к = -^ In 2, а из
-—1п2
условия 0,01 С = Се зо получаем
In 100
t{ = 30 « 200 (дней)
In 2
— время, по истечении которого останется лишь 1% первоначального количества вещества.
Общая же формула для оставшегося количества вещества имеет вид
где t — время, измеряемое в днях. >
45. Согласно опытам, в течение года из каждого грамма радия распадается 0,44мг. Через
сколько лет распадется половина имеющегося количества радия?
¦^ Пусть Q(t) — количество радия. Тогда оно удовлетворяет уравнению A) из предыдущей
задачи. Следовательно, функция Q(t) = Q@)ekt выражает закон его распада, где t — время,
измеряемое в годах. Для определения коэффициента к воспользуемся условием: через t = 1 год
Q = 999,56 мг, если Q@) = 1 г. Отсюда е* = 0,99956. Таким образом, Q(t) = Q@)@,99956)!
Положив здесь Q(tt) = 0,5Q@), определим время
In 2
<, = и 1600 лет. >
In 0,99956
46. В исследованном куске горной породы содержится 100 мг урана и 14 мг уранового свин-
свинца. Известно, что уран распадается наполовину за 4,5 • 109лет и что при полном распаде 238 г
урана образуется 206 г уранового свинца. Определить возраст горной породы, считая, что в мо-
момент образования горная порода не содержала свинца, и пренебрегая наличием промежуточных
радиоактивных продуктов между ураном и свинцом (так как они распадаются намного быстрее
урана).
¦4 Прежде всего, определим начальное количество урана в куске породы. Пусть у — коли-
количество полностью распавшегося урана в нем. Тогда, приняв во внимание условия задачи, можем
составить пропорцию
^ = 238
14 206'
из которой находим у = 14 • ^дг * 16,2 мг. Следовательно, первоначальное количество урана
составляет 116,2 мг.
Далее, исходя из общей формулы Q(t) = 11б,2е**, где Q(t) — количество нераспавшегося
урана, и периода его полураспада, находим к = — '".»$ • Принимая теперь во внимание, что по
истечении времени Т от начала распада в куске породы осталось 100 мг урана, определяем Т из
соотношения 100= 116,2е*т:
1 4 5-10'
Т = -~ In 1,162= ' ¦¦ In 1,162 «970- 106лет
к Ш2
— возраст горной породы. > /
§ 2. Задачи, приводящие к уравнениям с разделяющимися переменными
23
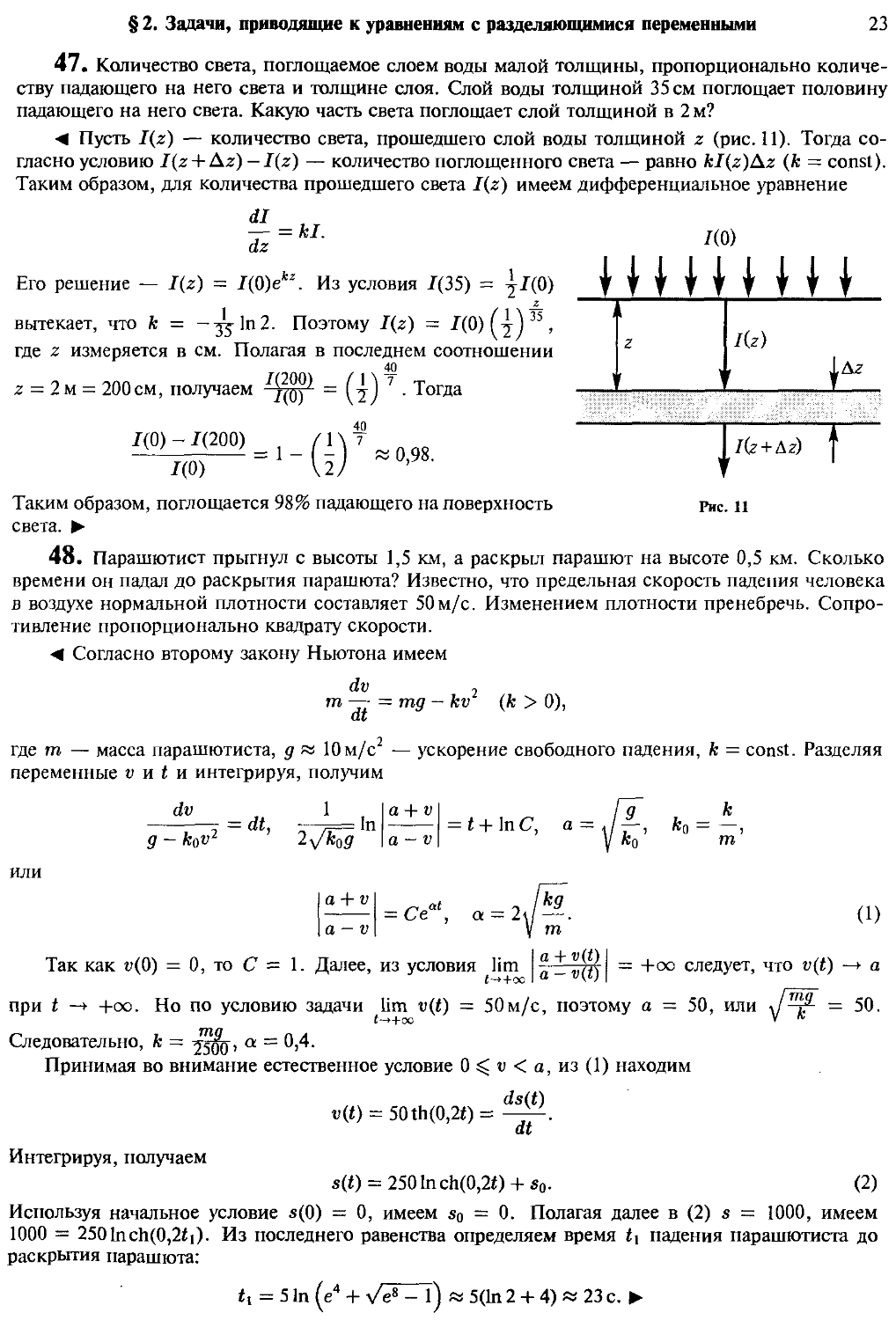
47. Количество света, поглощаемое слоем воды малой толщины, пропорционально количе-
количеству падающего на него света и толщине слоя. Слой воды толщиной 35 см поглощает половину
падающего на него света. Какую часть света поглощает слой толщиной в 2 м?
¦4 Пусть I(z) — количество света, прошедшего слой воды толщиной z (рис. 11). Тогда со-
согласно условию I(z + Az) -I(z) — количество поглощенного света — равно kI(z)Az (к = const).
Таким образом, для количества прошедшего света Дг) имеем дифференциальное уравнение
dl
— =hl.
dz
Его решение — I(z) = I@)ekz. Из условия 1C5) =
вытекает, что к = -^1п2. Поэтому Дг) = 1@)
где z измеряется в см. Полагая в последнем соотношении
40
= (!) ? ¦ Тогда
7@)
= 2 м — 200см, получаем
ДО) -1B00)
ДО)
-(
« 0,98.
падающего на поверхность
|/(г + Дг) f
Рис. 11
Таким образом, поглощается!
света. >
48. Парашютист прыгнул с высоты 1,5 км, а раскрыл парашют на высоте 0,5 км. Сколько
времени он падал до раскрытия парашюта? Известно, что предельная скорость падения человека
в воздухе нормальной плотности составляет 50 м/с. Изменением плотности пренебречь. Сопро-
Сопротивление пропорционально квадрату скорости.
•« Согласно второму закону Ньютона имеем
dv 2
т — = тд — kv
at
(к > 0),
где т — масса парашютиста, д « 10м/с2 — ускорение свободного падения, к = const. Разделяя
переменные v и t и интегрируя, получим
dv
д -
= dt,
1
In
a + v
а - v
= t+\nC, a =
или
a + v
а — v
Так как v@) = 0, то С — 1. Далее, из условия lim
а + v(t)
A)
+оо следует, что v(t) —* а
при t
+оо. Но по условию задачи lim v(t) = 50м/с, поэтому а = 50, или
Следовательно, к = -^qq, a = 0,4.
Принимая во внимание естественное условие 0^и<а,изA) находим
— 50.
v(t) = 50th@,2t) =
ds(t)
~dT'
Интегрируя, получаем
s(t) = 250 In ch@,2<) + s0. B)
Используя начальное условие s@) = 0, имеем so = 0. Полагая далее в B) s = 1000, имеем
1000 = 2501nch@,2<i). Из последнего равенства определяем время t\ падения парашютиста до
раскрытия парашюта:
= 5In (е4
5(ln2 + 4) « 23с. >
24 Гл. 1. Дифференциальные уравнения первого порядка
49. Футбольный мяч весом 0,4 кг1' брошен вверх со скоростью 20 м/с. Сопротивление
воздуха пропорционально квадрату скорости и равно 0,48 Г при скорости 1 м/с. Вычислить время
подъема мяча и наибольшую высоту подъема. Как изменятся эти результаты, если пренебречь
сопротивлением воздуха?
¦^ По второму закону Ньютона имеем
dv г
тп — = -тд - kv . A)
at
В нашем случае т = у = -fa, к = 0,00048 ;С , поэтому уравнение A) принимает вид
dv 1
— = -10- 0,012w2.
at
Разделив переменные и проинтегрировав, получим
10
,515lg((C-OV^12). B)
Так как v(fi) — 20, то из B) следует, что С = ,.* arctgf 2л/0^Т2). Из B) также следует, что v = 0
при t = С я 1,75 с (это, очевидно, соответствует наибольшей высоте). Принимая во внимание
равенство v(t) = —%(, после подстановки его в B) и интегрирования полученного дифференци-
дифференциального уравнения, имеем
250 / / и
s(t) — So H In cos [(С— t)J0,12 \\, s0 = const. C)
Формула C) выражает закон движения мяча. Полагая в C) s@) = 0, находим
Если же в C) положить t = С, то получим наибольшую высоту подъема мяча
«max = S0 И — In 1,48 И 16,3 М.
Случай к = 0 предоставляем разобрать читателю. >
50. Пусть жидкость вытекает из некоторого сосуда через отверстие в нем со скоростью,
равной 0,6,/2gh, где д = 10 м/с2, h — высота уровня жидкости над отверстием.
За какое время вся жидкость вытечет из цилиндрического бака с диаметром 2R = 1,8 м и вы-
высотой Н = 2,45 м через отверстие в дне диаметром 2г = 6 см? Ось цилиндра вертикальная.
•« Пусть h(t) — высота уровня жидкости в баке в момент времени t > 0. Через промежуток
времени At уровень жидкости понизится до значения h(t + At). Следовательно, из бака вытечет
количество жидкости, равное (h(t) - h(t + At))vR2. С другой стороны, через отверстие в баке
вытечет ¦Kr1v{tx)At жидкости, где tx 6 (t, t + At), v(tt) — некоторое промежуточное значение
скорости вытекания жидкости на интервале (?, t + At). В силу закона сохранения массы имеем
равенство:
Разделив обе части этого равенства на At и предположив, что функция h дифференцируема,
а функция v непрерывная, устремим At к нулю. Тогда получим дифференциальное уравнение
Решение этого уравнения имеет вид
/,(() = (С - 0,3^/2gk2tJ, С - const.
'> Через Г (грамм-сила) обозначается техническая единица силы, 1 Г = 1г • д as 0,0098 Н, где д = 9,8 Jy — ускорение
с
свободного падения; 1кГ = 1000 Г.
§ 2. Задачи, приводящие к уравнениям с разделяющимися переменными
Поскольку h@) = Я, то отсюда следует, что С = VH. Очевидно, h(t) = 0 при
lOv'ff R2
t = —-= -г и 1050с = 17,5мин. >
З/Т г2
25
51. Решить предьщущую задачу в предположении, что ось цилиндра расположена горизон-
горизонтально, а отверстие находится в самой нижней части цилиндра.
¦4 Как видим из рис. 12, при понижении уровня жидкости за время At на Ah через отвер-
отверстие Е вытечет 2H\/hBR - h)Ah + o(Ah) жидкости. Поэтому выпол-
выполняется равенство
- h)Ah + o(Ah) = nr2v(t{)At,
из которого, как и в предыдущем примере, получаем дифференциаль-
дифференциальное уравнение
Решением этого уравнения является функция
ft(<) =
\/2#
С = const.
A)
Рис. 12
Поскольку ft@) = 2R, то отсюда следует, что С - 0. Полагая в A) h = 0, находим время, за
которое вытечет вся жидкость:
1 9тг
40 R2H
1040 с. >
52. Воронка имеет форму кругового конуса радиуса R = 6 см и высоты Я = 10см, обра-
обращенного вершиной вниз. За какое время из воронки вытечет вся вода через круглое отверстие
диаметра 0,5 см, сделанное в вершине конуса?
¦4 Из рис. 13 видим, что количество воды AV, содержащееся в заштрихованном слое, с точ-
точностью до малых o(Ah) равно тгг2 Aft. С другой стороны, через отверстие О вытечет 7rr2t)(?i)A?
воды. Таким образом, имеем равенство ^ I ^
-тгг2 Ah = Kr]v(t\)At + o(Ah), C
где Г| = 0,25см, t\ G (t, t + At), из которого предельным пере-
переходом при At —> 0 получаем дифференциальное уравнение
г2 dh + r]v{t) dt = 0, v(t) = 0,6^2^. A)
Из подобия треугольников АМО и СОХО следует соотношение Н
г = -jif-. Поэтому уравнение A) записываем в виде
hi dh + к2 dt = 0, fc2 = 0,6 —
Интегрируя, получаем
-h?+k2t = C, С = const.
5 Рис. 13
Так как ft@) = Я, то отсюда следует, что С = ^Н2. Таким образом, решение поставленной
задачи имеет вид
5 5 5 ^
hi -HI = —кН.
Полагая здесь ft = 0, находим
5
— время, за которое вытечет вся вода из воронки. Вычисления дают t та 27 с. >
26
Гл. 1. Дифференциальные уравнения первого порядка
53. В прямоугольный бак размером 60 см х 75 см и высотой 80 см поступает 1,8 л воды в
секунду. В дне имеется отверстие площадью S = 2,5 см2. За какое время наполнится бак?
•« Пусть h(t) — высота уровня воды в баке. Тогда AVX = {hit + At) — h(t)) 60-75 — прира-
приращение ее объема за время от t до t + At. Это увеличение (или уменьшение) объема происходит за
счет поступления Д^ воды и ее утечки в количестве AVj через отверстие. Таким образом, имеем
уравнение Д7, = AV2-AV3. Поскольку AV2 = 1800Д«, AV3 = 2,5-0,6^/2дк~Щ)А1, t{ e (t, t+At),
то последнее уравнение можно представить в виде
4500(h(? + At) - h(t)) = 1800А* - 2,5 • 0,6J2gh(t{)At, g = 103 см/с2.
A)
Разделив в A) обе части на At и совершив предельный переход при At
циальное уравнение
30—= (n~0,0\j2gh)
0, получим дифферен-
дифференdt
проинтегрировав которое, найдем:
6000
1200
B)
Пусть h@) = 0, тогда из B) следует, что С = -3600In 12. Подставив в B) h — 80, найдем
время t\, за которое наполнится бак:
t, = 1200CIn-- Л «260с. >
54. Резиновый шнур длиной 1 м под действием силы / кГ удлиняется на kf метров. На
сколько удлинится такой же шнур длины / и веса Р под действием своего веса, если его подвесить
за один конец?
¦4 Пусть U(x) — удлинение шнура длиной х, a U(x + Ах) — удлинение шнура длиной
х + Ах. Тогда удлинение элемента длиной Да: равно разности U{x + Ах) — U(x) (рис. 14). На
элемент шнура Да: действует растягивающая сила /, равная весу шнура длиной 1-х — в Ах, т. е.
/ = у (J - х - в Ах),
и(х
где j- — удельный вес шнура, 0 < в < 1. Согласно условию, указанный
элемент должен удлиниться на kfAx метров. Таким образом, получаем
уравнение
Р
I '
где величина в введена с целью учета влияния силы, действующей на эле-
элемент Да:, обусловленной весом самого элемента. Далее, известным путем
из A) получаем дифференциальное уравнение
dU кР
из которого следует, что
Рис. 14
кР
Поскольку {7@) = 0, то С = 0. Следовательно,
кР
Щх) = — B1 - х)х.
Из последней формулы получаем удлинение шнура длиной I:
§ 2. Задачи, приводящие к уравнениям с разделяющимися переменными 27
55. Найти атмосферное давление на высоте h, если на поверхности Земли давление равно
1кГ/см2 и плотность воздуха 0,0012г/см3.
•« Пусть P(z) — давление воздуха на высоте z от поверхности Земли. Тогда разность давлений
P(z) — P(z + Az) равна весу столбика воздуха с площадью основания 1 см2 и высотой Az, т. е.
равна величине p(z + 6Az)g ¦ Az, где р — некоторая средняя плотность воздуха, 0 < в < 1.
Поэтому имеем
P(z) - P{z + Az) = p(z + 0Az)g ¦ Az,
откуда предельным переходом при Az —> 0 получаем дифференциальное уравнение
йР
Согласно закону Бойля—Мариотта, плотность воздуха при постоянной температуре пропорцио-
пропорциональна давлению, т. е.
р(г) = kP(z).
Используя это равенство, из A) находим
— = -kg, Р = PQe-k9Z кГ/см2.
Так как при г = 0?=1 кГ/см2, то Р = e~kgz, а поскольку
0,0012г/см3 = ЮООГ/см2 • к = ЮООг/см2^,
где д = 9,8м/с2 = -jy — ускорение свободного падения, то kg = 0,12 • 10см"' = 0,12(км)"'
Таким образом, на высоте h км давление воздуха
/> = е~°'12АкГ/см2. >
56. Для остановки речных судов у пристани с них бросают канат, который наматывают на
столб, стоящий на пристани. Какая сила будет тормозить судно, если канат делает три витка
вокруг столба, коэффициент трения каната о столб равен ^, и рабочий на пристани тянет за
свободный конец каната с силой ЮкГ?
•« Пусть Т(<р) — сила натяжения каната, соответствующая его углу наматывания <р на столб,
АР — нормальная реакция столба на участок каната длиной AS = RAip (рис. 15). Из условия
равновесия трех сил T(ip), АР и T(ip + Aip), с точностью до бесконечно малых величин угла Aip,
следуют равенства
T(ip + Aip)Aip + o(Aip) - АР,
T(ip + Aip) - T(ip) + o(Aip) = AF,
A)
где AF — сила трения, действующая на указанный элемент.
Согласно условию, AF = кАР, поэтому из A) получаем со-
соотношение
T(ip + Aip) - T(ip) = кТ(<р + Aip)Aip + o(Aip),
из которого известным читателю способом легко получить
дифференциальное уравнение
dT
dip
= кТ.
Его решение — Т = Тоек'р. Пусть при ip = 0 То = ЮкГ. Тогда
при ip = 6п (что соответствует трем виткам)
Т= 10е2х«5355кГ. >
Рис.15
57. На вращающийся в жидкости диск действует замедляющая его движение сила трения,
пропорциональная угловой скорости вращения. Найти зависимость угловой скорости от времени.
28 Гл. 1. Дифференциальные уравнения первого порядка
если вначале диск вращался со скоростью 100 оборотов в минуту, а по истечении одной минуты —
60 оборотов в минуту.
•* Пусть w(t) — угловая скорость движения диска. Тогда, согласно закону изменения момента
количества движения, имеем
ITt=M, A)
где J — момент инерции диска, М — момент сил, действующих на диск. По условию М = кцш
(fe0 = const), поэтому уравнение A) принимает вид
du> ь и к°
? = *"' к = Т
Его решение — ш = Шоеы. Пусть ш измеряется в оборотах за минуту, а время t — в минутах.
Тогда ш0 = 100, 60 = ЮОе*, откуда е* = 0,6. Таким образом, требуемая зависимость имеет вид
ш = 100@,6)'об/мин. >
58. В закрытом помещении объемом Ум3 находится открытый сосуд с водой. Скорость
испарения воды пропорциональна разности мезкду количеством q{ водяного пара, насыщающего
1 м3 воздуха при данной температуре, и количеством q водяного пара, имеющимся в 1 м3 воздуха
в рассматриваемый момент (считаем, что температура воздуха и воды, а также величина площа-
площади, с которой происходит испарение, остаются неизменными). В начальный момент в сосуде
было т0 г воды, а в 1 м3 воздуха qo г пара. Сколько воды останется в сосуде через промежуток
времени tl
¦^ Пусть Q(t) — количество испарившейся воды в граммах за время t. Тогда, согласно усло-
условию, скорость испарения -^- равна величине k(q{ -q), т.е. имеем дифференциальное уравнение
dQ
df=k(qi~~q)' U)
где к — коэффициент пропорциональности. Найдем значение q. Очевидно, что
(V-т0-КГ6) ?„ = <?!
есть количество пара в граммах, которое было в помещении, а
(V - т0 ¦ Ю-6) q0 + Q = Q2
— количество пара в граммах в помещении в момент времени t. Ясно, что количество Qi было
равномерно распределено в объеме
V2 = V - m0 • 10 + Q ¦ 10~6
(число 10~6 везде фигурирует вследствие того, что 1 г воды занимает 1см3 = 10~6м3 объема).
Поэтому
= Ог = (щ)д0 Я
4 V2 V-\0'6(m0+Q) "
Если V ^> 1О~6(то + Q), то из B) можно получить более простую формулу для q:
Подставив C) в A), получим окончательное дифференциальное уравнение
проинтегрировав которое, получим:
Поскольку Q@) = 0, то отсюда следует, что С = —V(q\ — qo). Таким образом, для оставшейся в
сосуде поды имеем формулу
= т0 - V(<?i - q0) (l -
§ 3. Однородные уравнения и уравнения, приводящиеся к ним 29
59. Масса ракеты с полным запасом топлива равна М, без топлива она равна т, скорость
истечения из ракеты продуктов горения равна с, начальная скорость ракеты равна нулю. Найти
скорость ракеты после сгорания топлива, пренебрегая силой тяжести и сопротивлением воздуха.
¦4 Пусть M(t), v(t) соответственно масса и скорость ракеты в момент времени t. Тогда
k(t) = M(t)v(t) есть количество движения ракеты. По закону сохранения количества движения
справедливо равенство
k(t + At) - k(t) = Ар, A)
где р — импульс внешних сил, действующих в течение времени At на промежутке времени
от t до t + At. В данном случае таким импульсом служат продукты сгорания ракеты, которые
отделяются от нее с абсолютной скоростью с - v(t) (с — относительная скорость отделения
продуктов сгорания). Поскольку отделяется (сгорает) масса M(t) - M(t + At), то
Ар = (с - v(t))(M(t) - M(t + At)). B)
Подставив B) в A), получим
M(t + At)v(t + At) - M(t)v(t) = (с - v(t))(M(t) - M(t + At)),
win
MAv + cAM + o(Av) = 0.
Разделив полученное на Av и устремив Av к нулю, имеем
Решение полученного дифференциального уравнения имеет вид
Постоянную Со определяем из начального условия: v(<)|(=0 = 0, т. е. в начальный момент времени
или, что то же самое, при M(t) = М скорость v равна нулю. Поэтому из C) имеем с0 = -с In -$¦.
Следовательно,
М М
v = cln—— = cln— ,
M(t) М - х
где х — сгоревшая масса топлива. Если, в частности, сгорит все топливо, т.е. х = М — т, то
ракета будет иметь скорость
М
v = с In — — формула Циолковского. >
т
§ 3. Однородные уравнения
и уравнения, приводящиеся к ним
3.1. Однородное уравнение.
Уравнение вида
M(x,y)dx + N(x,y)dy = 0, A)
где М, N — непрерывные в некоторой области D С R2 и однородные функции одной и той же
степени, называется однородным.
Напомним, что функция Ф называется однородной степени т (т — действительное число),
если V< 6 (а, Ь) t/>(tx, ty) = tmrj>(x, у), (х, yND.
С помощью замены у = х ¦ U(x) уравнение A) сводится к уравнению с разделяющимися
переменными х и U.
30 Гл. 1. Дифференциальные уравнения первого порядка
3.2. Уравнение, сводимое к однородному.
К однородному уравнению приводится следующее:
У = f(ZtbbwtCc2) («•• = const, Ь, = const, ,•= 1,2), B)
если a{b2 ~a2b\ ф 0. Для этого достаточно положить х = и+а, у = V+/3 и подобрать постоянные
a, J3 таким образом, чтобы правая часть уравнения B) приобрела вид /(а'ц + б'р)- ^сли же
а,\Ь2 — a2bt = 0, то ахх + bty = к(а2х + Ь2у), (к = const). В этом случае уравнение B) приводится
к уравнению с разделяющимися переменными заменой z = а2х + Ь2у.
3.3. Обобщенно-однородное уравнение.
Уравнение вида A) называется обобщенно-однородным, если существует такая постоянная а,
что после замены у = z" оно становится однородным.
Решить уравнения.
60. (у + \fx2 — у2) dx — xdy — §.
¦4 Здесь функции М(х,у) = у + \/х2 — у2 (\х\ ^ \у\), N(x, у) = —х однородные и имеют
степень т = 1, так как
M(tx, ty) = ty
для t ^ 0 (т. e. a = 0 и Ь = +oo), a
Nitx, ty) = -tx = tN(x, y)
для любого t. Следовательно, данное уравнение однородное. Применив замену у = хи, получаем
dy = xdu + udx, а уравнение преобразуется к виду
(хи + \x\Vl - u2) dx - х(х du + u dx) = 0. A)
Очевидно, что х = 0 является решением исходного уравнения, поэтому считая, что в A) х ф 0,
получим
sgn х v 1 — и2 dx — х du = 0.
Разделяя переменные и затем интегрируя, находим:
dx du у
sgnx In \x\ = arcsin —\-С.
\х\ VI -и1 х
Принимая еще во внимание, что и = ±1 (т.е. у = ±х) также есть решения, окончательно
записываем все решения данного уравнения:
sgn х In \x\ = arcsin — + С; у = ±х; х = 0. >
Замечание. Строго говоря, решение х =¦ 0 получается в результате допущения, что \]-у2 -0 = 0 для
произвольных значений у.
61. ху' = j/(l + lnj/ - 1пж).
Л Переписав уравнение в виде
xdy-y(\+\n~) dx = 0 (x>0,y>0),
\ X /
обнаруживаем, что функции М(х, у) = -у (\ + In &J и N(x> у) = х однородные одной и той же
степени т = 1. Поэтому, применив замену у = хи, dy = xdu + ndx, получим
х du — и In и dx = 0.
Разделяя переменные и интегрируя, находим
1пж-1п|1пи| = 1пС (« у^ 1),
§ 3. Однородные уравнения н уравнения, приводящиеся к ним 31
или
у = хес*.
Заметим, что решение у = х, которое соответствует значению и = 1, входит в формулу семейства
интегральных кривых при С = 0. >
62. xydx + (y2 -x2)dy = 0, M(l, 1).
4 В данном примере требуется найти кривую, которая удовлетворяла бы дифференциальному
уравнению и проходила через точку М.
Прежде всего, находим все решения этого уравнения. Полагая у = хи, получаем
иъ dx + x(u2 - \)du = 0.
Отсюда при и Ф 0 интегрированием находим
или
К полученному семейству присоединим еще кривую у = 0. Далее, подставив в A) х = 1, у = 1,
1
имеем С = е?. Поэтому требуемая кривая имеет уравнение
ж2 Ч-г/2{1пу2 - 1) = 0. >
63. (хуеУ + у2 ) dж - x2ev dy = 0.
¦4 Здесь удобно применить замену х = иу. Тогда dx = udy + ydu, udy Л-у (иеи + 1) du = 0,
dj/ (ue" + 1) du ,2
— + - =0, ln|as| +e» -C. >
t/ u
64. {2^/xy - y) dx- xdy = 0.
•^ Очевидно, жг/ ^ 0. Отбросив тривиальные решения ж = 0, j/ = 0, считаем, что жг/ > 0.
Полагая у = их (и > 0), имеем
dy = udx + xdu, 2 (\fusgnx - и) dx - xdu = 0. A)
Если х > 0, то отсюда находим (и Ф 1):
da; I f du
ИЛИ
а;
[ — =
J a;
2У у/п-и
Если же а; < 0, то полагая в A) ж = —а;!, получим
2(л/п + и) da;1+ж1du =
Разделяя переменные и интегрируя, имеем
7, или — х
Xi
Объединяя оба ответа (при х > 0 и при а; < 0) в один, окончательно можем записать
Заметим, что решение у = х (и = 1) входит в B) при х > 0 (С = 0), а решение г/ = 0 вообще
не входит. Поэтому все решения данного уравнения описываются формулой B) с присоединени-
присоединением у = 0. Решение же ж = 0 можно включить в B) лишь формально, поскольку дифференциал
d (ж - s/xy) при ж = 0 не существует. >
?Е I У
ОЭ. ху = j/cosln-.
4 Замена j/ = хи, (и > 0, ж ^ 0) приводит к уравнению
хи = u(coslnu— 1).
32 Гл. 1. Дифференциальные уравнения первого порядка
Считая, что lnu Ф 2кп (w Ф е2Ьг, к е Z), получаем
ж w(coslnw-l)'
или
«с
Наконец, легко проверить, что Vfc 6 Z функция у = же2*1, ж Ф 0, также является решением
исходного уравнения. >
66. Fх + у - l)dx + Dx + y- 2)dy = 0.
Ч Это уравнение вида B), п. 3.2. В данном случае
а, = 6, 6, = 1, а2 = 4, Ь2 = 1, сцЬ2 - а26, = 2 ф 0.
Следовательно, можно применить замену х = и + а, y = v + j3. При этом получим
dx = du, dy = dv, Fu + w + 6a +/?- l)du + Du + ю + 4а + /J- 2)dw = 0.
Полученное уравнение приводится к однородному, если положить
6а + р - 1 = 0, 4а + р - 2 = 0.
Решение этой системы имеет вид а = — -у, р = 4. Таким образом, после замены х = и - j,
у = v + 4 исходное уравнение приводится к однородному:
Fи + и) du + Du + t))dw = 0.
Теперь воспользуемся уже известной заменой и = «?, du = ю d? + ? dw. Следовательно,
F$ + 1)ю d? + F?2 + 5? + l)dv = 0.
Разделяя переменные и интегрируя, отсюда получаем {? Ф -? и ? ^ — j):
или
Возвращаясь к переменным ж и у, окончательно имеем
Решения 2а; + у — 3 = 0 (? = — ¦j) иЗж + у— -j = 0 К = ~7 ) можно включить в полученное
семейство кривых соответственно при С = 0иС = оо. >
67. Eж - 7у + \)dy + (ж + у - l)dx = 0.
¦* Поскольку прямые 5а:-7у+1 = 0иж + у-1 = 0не параллельны, то проводим замену
где постоянные аир удовлетворяют системе уравнений
5а - ip + 1 = 0, а + р - 1 = 0.
из которой находим а = р = ^. Таким образом, после замены ж = w + ^, y = w+^- получаем
дифференциальное уравнение
Ew — 7v) dv + (u + w) dw = 0.
Как и в предыдущем примере, пользуемся заменой w = ?v. Тогда du = v d? + ? dw, (?2 + 6? - 7) x
x dw +1»(? + l)d? = 0. Разделяя переменные и интегрируя, находим
« + D
откуда
«l)tf + 7)V = C или
§ 3. Однородные уравнения и уравнения, приводящиеся к ним 33
68. Bх + у + \)dx - Dж + 2у - 2)dy = 0.
•4 Так как прямые 2х + у+1 = 0и4ж + 2у-3 = 0 параллельны, то замену, которую произво-
производили в предыдущих примерах, здесь проводить нельзя. Однако, в силу того, что коэффициенты
при переменных ж и у пропорциональны, можем положить z = 2х + у. Тогда dy = dz - 2dx
и исходное уравнение принимает вид
5(z - 1) dx - Bz -2)dz= 0.
Интегрируя это уравнение и возвращаясь к переменной у, получаем
2х + у-1=Се1у-х. >
Посредством замены х = и+3, y = v — 2 приходим к однородному уравнению
dv . v1
du (« + vJ'
Применяя еще одну замену v = u?(u), получаем уравнение с разделяющимися переменными
du A+O2
Интегрируя это уравнение, находим
или (после возвращения к переменным х и у)
¦4 Замена ж = и - 3, у = и + 3 приведет к однородному уравнению
fdv \ u + v u + v
U + 1)ta—= —•
применение к которому замены v = u?(u) позволяет получить уравнение с разделяющимися
переменными
(«?' +? + 1IпA +0 = 1+?, «?'ln(l +0 = A +0A ~ 1пA +0)-
Разделяя в последнем уравнении переменные и интегрируя, находим:
/du Г 1пA + О d?
v~y a+o(i-in(i+o)= n '
или
In |u| + ln(l + 0 + In |1 - ln(l + 01 = In С
Отсюда, потенциируя и возвращаясь к старым переменным, окончательно имеем
, х + у С
In = i + . >
ж+3 х+у
Замечание. Для решения уравнения B), п. 3.2, применяют еще и замену
которая сразу приводит к уравнению с разделяющимися переменными. В данном случае можно восполь-
воспользоваться указанной заменой. Тогда получим уравнение
у + ж
z, где z =
——,
X ~г~ 3
откуда
+ ln|l-lnz|=lnC,
х+г
34 Гл. 1. Дифференциальные уравнения первого порядка
¦4 Уравнение приводится к однородному с помощью замены х = и — 1, у — v - 2:
dv _ и и - 2«
du « и
Далее, как и в предыдущих примерах, применяем замену v = u?(u). Тогда получим
< = tg« - 2).
Разделение переменных и интегрирование дает:
tg(/- 2) = ?' lnl«|-ln|sin(?-2)|=lnC.
Потенциируя и возвращаясь к прежним переменным, окончательно имеем
v — 2x
Заметим, что решения я + 1 = 0(и = 0)и у . t = ктт, к 6 Z (tg(? - 2) = 0) входят в полученное
семейство решений соответственно при С = 0иС = оо. >
•4 Уравнение не является однородным, однако, применив замену у = (z(a;))a, замечаем, что
уравнение
az°x:idz=[z2a+x4)dx A)
приводится к однородному, если выбрать а = 2. Полагая в A) z = xu, имеем
(и2 — IJ dx = 2uxdu.
Разделяя переменные и интегрируя, получаем
1
или
Замечание. В данном случае мы получили решение для у ^ 0, поскольку у = z2 Jj 0. Аналогично можно
установить, что и для у = — z $J 0 семейство решений описывается формулой B). Решение у = х2
входит в это семейство при С = оо.
73.2х2у' = у3 + ху.
•4 Положим у = za. Тогда получим
<¦! 2 а—1 / За а л 2 а—1 • / За а\ ¦ Л
2аг г 2 = г + xz , 2ax z dz - iz + xz ) dx = 0.
Отсюда следует, что функции 2ax2za~l и z3a + xza однородны лишь при одном условии: а+1 =
= За = а + 1, т. е.' при а = j. Таким образом, в случае у > 0 применяем замену у = s/z. Тогда
исходное уравнение примет вид
х2 dz-(z+ x)z dx = 0.
Замена z = хи(х) преобразует последнее уравнение в уравнение с разделяющимися переменными
хdu - и2 dx = 0. Интегрируя его, получаем ~ + In \x\ = С, или
~+]п\х\ = С.
Решение у — 0 входит в полученное семейство при С = оо. >
Замечание 1. В рассмотренном, и в некоторых других примерах мы включали "потерянные" решения
в семейство интегральных кривых при сингулярных значениях С. Однако,такое включение вызвано не
существом дела, а лишь формой записи решения. Покажем это на последнем примере. Имеем
^ n}x\)=:y2, С, = i.
Положив в последней формуле С\ = 0, получим у = 0.
§ 3. Однородные уравнения и уравнения, приводящиеся к ним 35
Замечание 2. Замена у = — yfz (для у 5$ 0) приводит к такому же результату.
74. у dx + хBху +\)dy = 0.
< Применив замену у = za, получим уравнение
za dx + xBxza + \)aza~x dz = 0.
Так как функции za и axza~lBxza + 1) однородны и имеют одну и ту же степень при а = — 1,
то данное уравнение приводится к однородному с помощью замены у = j. Однако его можно
привести к уравнению с разделяющимися переменными, если воспользоваться заменой у =
(в общем случае заменой у = хаи(х)).
Таким образом, получим уравнение
-2u2 dx + хBи + 1) du = 0,
откуда
In*
и
или
dx
X
du
и
Ti4i —
du
vbT2>
l
Заметим, что последняя форма записи решений исключает такие, как х = 0иу = 0, в то время
как ей предшествующая включает решение х = 0 (при С = оо). Легко показать, что никакие
преобразования формулы семейства интефальных кривых не позволяют включить в их состав
решение у = 0. >
75. 2у' + х = 4^/у.
¦4 Проверка на обобщенную однородность данного уравнения показывает, что показатель
однородности а = 2. Следовательно, замена у = хги(х) (« > 0) приводит к уравнению с разде-
разделяющимися переменными
Проинтегрировав его, получим:
1
' U=4'
или
Если же х < 0, то вместо уравнения A) получим уравнение
2xdu + (I + 4u + Vu) dx = 0,
интегрирование которого приводит к уже полученному результату для уравнения A). >
76. 2 (vVt/2 + 1 - хгу) dx-x*dy = 0.
4 Полагая у = za, получаем уравнение
2 (Vx4z2a + 1 - x2za) dx - aiV4 dz = 0.
Отсюда следует, что функции при дифференциалах однородны и имеют одинаковую степень толь-
только при a = -2. Поэтому замена у = ^§^ приводит к уравнению
X
откуда находим
х1 = С (м + Vv.2 + l) , или х2 = С (х2у + ^1 + х4у2).
36
Гл. 1. Дифференциальные уравнения первого порядка
77. Найти кривую, у которой точка пересечения любой касательной с осью абсцисс одина-
одинаково удалена от точки касания и от начала координат.
¦4 Согласно условию задачи, \ОК\ = \КМ\ (рис. 16). Поэтому а = 2/3 и tga = -—tg"_ . Но
l-tg'/З
tg/3 = &, следовательно, tga = г ху г.
х —у
Принимая во внимание геометрический смысл производной, окончательно получаем
О
М(х, у)
Это однородное уравнение и для его решения произведем замену
у = хи(х). При этом имеем
хи + и =
2«
dx 1-й2
du.
Интефируя, получаем
К
Рис.
N х
-(«+]) = С, или аг2+у =Су. >
78. Найти кривую, у которой расстояние до любой касательной от начала координат равно
абсциссе точки касания.
¦4 Из рис. 17 видим, что треугольники ONM и OML конгруэнтны, 2юскольку по условию
\ON\ = \OL\ и гипотенуза ОМ — общая. Следовательно, углы MOL и MON равны друг другу.
()
У
Но KON = f - а, поэтому MOL =
треугольника OLM имеем
f. Далее, из
1 + tgf
1-tgf
М{х,у) ь — х 2tg-
Отсюда tg у = ^-qr^ • Наконец, используя формулу tg a = -——fe
l - tg j
и соотношение tg a = у , получаем дифференциальное уравнение
Рис. 17
Применив замену у = iu(a:), имеем
dx 2u du
— +
= 0,
откуда следует, что хг + у1 = Сх. >
М(х,у) 79. Найти кривые, у которых поднормаль равна разности
между модулем радиуса-вектора кривой и абсциссой точки каса-
L х
Рис.18
ния.
ТО
По условию |JVX| = \ОМ| - |0ЛГ| (рис. 18). Поскольку
\ = ytga, \ОМ\ = -у/ж2 + у1, |0jV| = a:,
УУ = ух2 + у2-х.
Поскольку это дифференциальное уравнение однородное, то применяем замену у = хи(х).
Имеем (для х > 0): у
2 dx _ du r dx _ r
~х~ ~ Vu2 + 1 - 1 - и2' J х ~J
du2
+с,
/
'к
У
L
*—>
Р
О
N х
§ 3. Однородные уравнения и уравнения, приводящиеся к ним 37
Таким образом, искомое семейство кривых имеет вид
х - \]хг + у2 = С.
Случай х < 0 предоставляем разобрать читателю. >
80. Найти кривую, зная, что треугольник, образованный нормалью к ней и осями координат,
равновелик треугольнику, образованному осью Ох, касательной и нормалью к этой же кривой.
•4 По условию, треугольники KMN и OLN (рис. 19) равновелики, поэтому равновели-
равновелики также треугольники КОР и PML. Поскольку последние еще и подобны, то они конгру-
конгруэнтны. Следовательно, \ОР\ = \РМ\. Из уравнения касательной
Y - у = у'(Х — х), где X, Y — текущие координаты точки, лежащей
на касательной, следует, что
\РО\ = у- ух.
Длину отрезка РМ находим по формуле расстояния между точками
М(х, у) и Р@, \РО\):
\РМ\ = \/х2 + t/'V.
Таким образом, получаем дифференциальное уравнение
(у - y'xf = х2 + у' х1, или у2 - 2уу'х - х2 - 0.
Полученное уравнение однородное, поэтому воспользуемся заменой Рис'19
у = хи(х), которая после ее проведения дает возможность разделить переменные. Имеем
и2 + 2шх + 1 = 0,
откуда интегрированием находим:
хA+иг) = 2С, или (х-С)г + уг = Сг. >
81. При каких а и /3 уравнение у' = аха +Ьу^ приводится к однородному с помощью замены
У = 2™?
М Применив указанную замену, получим
mzm~lz' = ах" + bzmfs (m Ф 0). A)
Отсюда следует, что если а и Ъ отличны от нуля, то для однородности уравнения A) необходимо
и достаточно выполнения равенств
т — 1 = а = тр.
Из второго равенства имеем т = %, (/3 Ф 0, а Ф 0). Подставив m в первое равенство, получим
искомую связь:
1 1
82. Доказать, что интегральные кривые уравнения
(ах + by + c)dx + (ay -bx + C\)dy = 0 (a2 + b2 Ф 0)
являются логарифмическими спиралями.
¦4 С помощью формул параллельного переноса системы координат
х = и + а, у = v + /3
приводим данное уравнение к виду
(аи + bv)du + (av — bu)dv = 0.
Далее полагаем « = р cos уз, v — р sin уз, где р, tp — полярные координаты с полюсом в точке
(а, /3) относительно системы Оху. Имеем
ар = Ьр,
откуда находим
р = Сеа*.
Получили семейство логарифмических спиралей. >
38
Гл. 1. Дифференциальные уравнения первого порядка
Замечание. Если а = Ь = О, то получим семейство прямых. Если а = О, 6 Ф 0, то также получается
семейство прямых. Если Ь = 0, в Ф О, то получим семейство окружностей. Все эти случаи следуют
непосредственно из данного уравнения.
83. Найти форму зеркала, отражающего все лучи, которые выходят из одной и той же точки,
параллельно данному направлению.
¦4 На рис. 20 показано, что OMN = NMS (угол падения луча ОМ равен углу отражения
луча MS). Выберем направление отраженных лучей параллельно оси Ох. Тогда, исходя из ука-
указанного выше равенства углов и параллельности луча MS оси Ох, имеем
У
К
I
О
а+/?=-, КМО = а.
Следовательно, треугольник КМО —равнобедренный, т. е.
\КО\ = \ОМ\. Очевидно, |0Af| = у/хг + у2. Длину отрез-
отрезка КО можно найти, вычислив абсциссу точки пересечения
касательной с осью Ох. Из уравнения касательной к искомой
кривой
Y = y + y'(X-x),
где X,Y — текущие координаты касательной, находим тре-
требуемую абсциссу:
У
рис. 20 X = х -.
Тогда \КО\ = —X. Таким образом, имеем дифференциальное уравнение
Это уравнение однородное и с помощью замены у = хи(х), опуская простые выкладки, получаем
его решения
у2 - 2Сх - С2 = О,
геометрически представляющие собой семейство парабол (С Ф 0). >
84. Пусть ко — корень уравнения f(k) = к. Показать, что:
1) если f'(ko) < 1, то ни одно решение уравнения у' — fix), за исключением решения
у = кох, не касается прямой у = кох в начале координат;
2) если f'(ko) > 1, то этой прямой касается бесконечно много решений.
•4 Применим метод доказательства от противного. Пусть при выполнении условий f(k0) = ко,
f'(ko) < 1 существует решение уравнения у' = fix), касающееся прямой у = кох в начале
координат. Тогда в малой окрестности начала координат оно представляется в виде
у(х) = кох + х6(х),
где 6(х) —* 0 при х —> 0. Подставив A) в рассматриваемое уравнение, получаем
хб' + 6 = f(k0 + 6(х)) = f(k0) + f'(koN(x) + оF),
A)
или
откуда
Отбросив
находим 6
хб' =
xf_
6
оF),
где A =
(как величину, стремящуюся к нулю при х -+ 0), можем записать ^- я А, откуда
С|а:|А. Из полученной формулы следует, что если С Ф 0, то 6 к нулю не стремится
при х -+ 0 (в силу того, что А < 0). Полученное противоречие идоказывает утверждение 1).
2) В этом случае противоречия нет, поскольку А > 0 и &—К) при х -+ 0 для любых С. >
Замечание. Строго говоря, ни одно решение ни в одном из рассмотренных случаев не касается прямой
у = кох в начале координат, если молчаливо не допустить, что ' = llm *.
х 1ж=0 х-*0 *
§ 4. Линейные уравнения и уравнения, приводящиеся к ним 39
85. Две жидкости ж и у подвергают дистиллированию. Известно, что в любой момент
времени этого процесса отношение количеств жидкостей, которые превращаются в пар, про-
пропорционально отношению количеств, которые находятся еще в жидком состоянии. Определить
зависимость между х ч у.
•4 Пусть x(t) и y(t) — количество жидкостей, не превращенных в пар в момент времени t.
Тогда x(t + At) и y(t + At) — количества жидкостей, не превращенных в пар в момент времени
t + At. Следовательно, за время At в пар превратились следующие количества жидкостей:
x(t) - x(t + At) и y(t) - y(t + At).
Согласно условию, имеем
y(t + At)-y(t) =fey(<i) A)
(t)'
x(t + At) - x(t)
где к — коэффициент пропорциональности, t\ 6 (t, t + At). Если функции хну дифференци-
дифференцируемы, то из A) предельным переходом при At —> 0 получаем дифференциальное уравнение
dx x
проинтегрировав которое, находим требуемую зависимость
у = Схк. >
§ 4. Линейные уравнения
и уравнения, приводящиеся к ним
4.1. Линейное уравнение первого порядка.
Уравнение вида
^-+ Р(х)у = Q(x) A)
ах
называется линейным уравнением первого порядка. Наиболее употребительным способом его реше-
решения является метод вариации произвольной постоянной. Сущность метода состоит в следующем.
Сначала ищется решение однородного уравнения, соответствующего уравнению A):
dv
~+Р(х)у = 0. B)
ах
Затем в общем решении уравнения B) произвольную постоянную С считают некоторой диффе-
дифференцируемой функцией от х: С = С(х). Эту функцию находят из дифференциального уравнения
с разделяющимися переменными, которое получается в результате подстановки общего решения
уравнения B) в уравнение A).
4.2. Обмен ролями между функцией н аргументом.
Некоторые уравнения становятся линейными, если в них поменять ролями функцию и аргу-
аргумент.
4.3. Уравнения, приводимые к линейным.
К линейным уравнениям приводятся также уравнения вида:
f(y)~ + P(x)f(y) = Q(x), C)
ах
^-+P(x) = Q(x)en\ D)
ах
— + Р(х)у = Q(x)ym (уравнение Бернулли). E)
Полагая в C) /(у) = z(x), получаем /'(yV = z'(x) и z' + P(x)z = Q(x).
40 Гл. 1. Дифференциальные уравнения первого порядка
В уравнении D) целесообразно провести замену е~пу = z(x). Тогда получим
-пе'пуу =z, + P{x)z = Q{x) (n ф 0).
Уравнение Бернулли приводится к линейному с помощью замены z(x) = ух~т (тфО, тп Ф 1,
так как в этих случаях оно уже линейное).
4.4. Уравнение Мнндинга—Дарбу.
Уравнение Миндинга—Дарбу
М(х, у) dx + N(x, у) dy + Щх, у)(х dy-y dx) = 0, F)
где М и N — однородные функции степени m, a R — однородная функция степени п, по-
посредством замены у = их(и) приводится сначала к уравнению Бернулли, а последнее — уже
известным способом к линейному.
Решить уравнения.
86. у' + t/tga: = sec ж.
•4 Сначала находим все решения однородного уравнения, соответствующего данному:
t/+ t/tga: = 0.
Переменные разделяются, и после интегрирования находим
y=Ccosx. A)
Формула A) представляет общее решение однородного уравнения, где С — произвольная по-
постоянная. Для получения всех решений данного уравнения считаем С — С(х) и требуем, чтобы
функция у = С(х) cos х удовлетворяла ему, т. е.
С' cos х - С sin х + С cos x tg х = sec x,
или С' = —К—. Отсюда находим С(х) = tgx + Со, где Со — новая произвольная постоянная.
COS X
Подставив значение С(х) в A), окончательно получим
у = sin х + Со cos х. >
Примечание. В дальнейшем для новой произвольной постоянной будем использовать старое обозна-
обозначение С. Таким образом, в рассмотренном примере у = sinx + Ccosx есть общее решение, а С —
постоянная.
87. Bх + l)t/ = 4а: + 2у.
•4 Решаем соответствующее однородное уравнение
Bх + 1)у' = 2у.
Его общее решение имеет вид у = СBх + 1). Применим метод вариации произвольной постоян-
постоянной. Имеем
(С'Bа: + 1) + 2С)Bа: + 1) = 4а: + 2СBа: + 1),
или Bа: + lJ^ = 4а:. Отсюда находим
xdx 1
3 + Со = In \2х + 1| + + Со.
Таким образом, окончательно получаем
88. (ху + ех)dx — хdy = 0. ^—
Ч Считая dx Ф 0 (ж = 0 — тривиальное решение), записываем уравнение в виде
ху -ху = ех.
§4. Линейные уравнения и уравнения, приводящиеся к ним 41
Соответствующее однородное уравнение ху' - ху = 0 имеет общее решение у = Сех. Далее
применяем метод вариации произвольной постоянной. Имеем
х(С + С')ех - хСех = ех,
откуда С' = ^, С — In \х\ + Со. Получаем все решения неоднородного уравнения:
х = 0. > A)
89. (x + y2)dy = ydx, Af(l, 1).
•4 Уравнение не является линейным относительно переменной у, однако оно линейное от-
относительно х. Поэтому целесообразно считать х функцией у.
Считая dy Ф 0 (у = 0 — тривиальное решение), имеем
2 dx
dy
Соответствующее однородное уравнение х = ущ имеет общее решение х = Су. Применив
метод вариации произвольной постоянной, получим последовательно
Су + уг = у(С'у + С), С'*=1, С = у + С0.
Следовательно, все решения данного уравнения описываются формулами
х = Су + у2; у = 0. > A)
г-и2
Замечание. Переписав первую формулу в A) в виде у = g* и положив С = оо, получим реше-
решение у = 0. Таким образом, если допустить, что постоянная С может принимать сингулярное значение,
то решение у — 0 можно не выписывать отдельно.
Полагая в A) х = 1, у = 1, находим С = 0. Тогда из A) получим частное решение х = у2.
9О.Bеу-х)у' = 1.
¦4 Предложенное уравнение линейное относительно х. Так как -^ = -^-, то его можно
записать в виде
2еу-х = х. A)
Общим решением однородного уравнения х' + х = 0 является функция
х = Се~у. B)
Считая С — С(у) и подставив B) в уравнение A), получим последовательно
2еу - Се~у = С'е'у - Се~у, С' = 2е2у, С (у) = е2у + Со.
Окончательно имеем
х = Се-у + еу. >
91. (sin2 у + х ctg у)у' = 1.
Ч Уравнение линейное относительно переменной х, поэтому представляем в его в виде
х - х ctg у = sin2 у.
Применив метод вариации произвольной постоянной, получим
*(У) = С(у) sin у, где С(у) = - cos у + const. >
У ах
Л Это уравнение вида C), п. 4.3, поэтому применяем замену In у = z(x). Имеем
• = ig, У + B-,„-
42 Гл. 1. Дифференциальные уравнения первого порядка
Полученное уравнение линейное относительно z. Пользуясь методом вариации произвольной
постоянной, получаем
2x, где С(х) =
Таким образом, общее решение исходного уравнения имеет вид
¦4 Это также уравнение вида C) , п. 4.3. Следовательно, произведем замену z(x) = у/у2 + 1.
Тогда получим
Проделав всю необходимую процедуру, требуемую в методе вариации произвольной постоянной,
найдем:
г = С(х)е'г, где С(х) = ех (х2 - 2х + з) + Со.
Итак,
yV+1 = х2 - 2х + 3 + Се~х
— общее решение исходного уравнения. >
94.е-^-е-=в».
dx
¦4 Умножив обе части рассматриваемого уравнения на ех, получим уравнение вида D), п. 4.3.:
Следовательно, применяем замену z(x) = e'y. Тогда получим последовательно
z'(x) = -е-уу'(х), ~eyz' - 1 = eV, -г' - г = ех.
Полученное уравнение линейно относительно г. Его решение имеет вид:
* = Ce--ie*.
Осталось записать общее решение исходного уравнения:
95.
¦< Преобразовав уравнение к виду
замечаем, что оно относится к виду D), п. 4.3. Поэтому воспользуемся заменой z(x) = e~iy. Тогда
последовательно получим
*'(*) = -Зе~3У, -- + ! = --, z'-z = ex.
Z Z
Общее решение линейного уравнения находим известным способом, в результате чего имеем
z(x) = Се" + хех.
Осталось записать общее решение исходного уравнения: ~-—^
у=-~1(С + )
§ 4. Линейные уравнения н уравнения, приводящиеся к ним 43
у dx 3(х + 1)
¦4 Уравнение относится к виду C), п. 4.3, поскольку
dx\3y/K У)) у dx
Следовательно, произведя замену z(x) = j \/(\n уK, получим линейное уравнение
a;+l
общее решение которого имеет вид:
1 С
2х ' * + Г
Окончательно общий интеграл запишется в виде
97. (х + Щу1 + у2) = -у.
4 Считая, что а; Ф — 1, делим обе части уравнения на а; + 1 и записываем его в виде
Это есть уравнение Бернулли. Разделив обе его части на у2, затем производим замену у = z(x).
Тогда последовательно получаем
Полученное линейное уравнение решаем методом вариации произвольной постоянной. При этом
находим
z = С(х)(х + 1), где С(х) = In |а; + 1| + Со.
Окончательно решение исходного уравнения принимает вид
У= *
98. хуdx + (а;2 + у2 + 1) dy = 0.
¦4 Произведя замену а;2 = «(у), получим линейное уравнение первого порядка
1 du ,
-1уту+и=-{у+1)-
Его общее решение имеет вид « = —Щ*-, где С (у) = -у2(^ + 11+ const. Таким образом, имеем
все решения исходного уравнения:
у4 + 2* Y + 1у = С. >
99. (х3у - Зх2у + yi)dx + 2x3 dy = 0.
¦4 Разделив обе части уравнения на dx Ф 0 (а; = 0 — очевидное решение), получим уравнение
Бернулли
2х^
ах
Считая у Ф 0 (у = 0 — тривиальное решение), делим обе части последнего уравнения на —у3
и полагаем -\ = z(x). Тогда получим
-2jr = А*У. x3z' - (х3 - 3x2)z = 1.
44 Гл. 1. Дифференциальные уравнения первого порядка
Решая это линейное уравнение, находим
г = С(х)х~3ех, где С(х) = -е~х + Со.
Теперь запишем все решения исходного уравнения:
Су V - у2 - хъ = 0; х = 0; у = 0. >
, х ху
100. 2у - - =
у х2 - Г
Умножив обе части уравнения на у и положив у2 — и(х), получим линейное уравнение
Ищем решение в виде и = f(x)w(x). Подставив и и и' в A), имеем
Функции / и w находим из уравнений
Из первого уравнения получаем / = Су/\хг - 1|. Из второго уравнения следует, что
Следовательно, и = \х2 - 1|sgn(x2 - 1) + CV|x2 - 1| = х2 - 1 + С-^/|х2 - 1|, откуда
У2 = х2-1 + сУ|х2-1|. >
101. y'x3siny = xy'-2y.
¦< Разделив обе части уравнения на у' ф 0 (у = 0 — очевидное решение) и приняв х за
функцию от у, получим уравнение Бернулли
-, dx 3 .
7у х = —х smy.
dy
Используя замену х" = z(y), приходим к линейному уравнению
уг' + г = siny,
общее решение которого выражается формулой
С cosy
z~~ у у
Все решения исходного уравнения имеют вид:
1 С cosy , _ ,
у = 0; —г = , или у + х cosy-Cx =0. >
х2 у у
102. (x2 + y2 + 2x-2j0dx + 2(y-l)dy = 0.
¦4 Преобразовывая уравнение следующим образом:
((* + IJ + (у - IJ - 2) d(x + 1) + d(y - IJ = 0
и полагая х + 1 = и, (у— \J = v, приходим к линейному уравнению
dv ,2
— + v = 2 - ы2
и /
с его общим решением t/ = Се~" - и2 + 2и. Все решения исходного уравнения описываются
формулой
х2 + у2-2у = Се-х. >
§ 4. Линейные уравнения и уравнения, приводящиеся к ним 45
103. (е* - у')х = 2.
4 Полагая еу = г(х), получим уравнение Бернулли
X
Его общее решение имеет вид
г<ж>= nlr V
x(i -г и х)
Общее решение исходного уравнения запишется в виде
у = - 1п(х + Сх2). >
X
104. у(х) = / y(t)dt + x + \.
а
¦4 Взяв от обеих частей равенства производную, получим линейное уравнение
общее решение которого
у = Сех - 1.
Исходя из очевидного начального условия у@) = 1, находим С = 2. Следовательно,
105. (x-t)y(t)dt = 2x+ y(t)dt.
о о
¦4 Дважды дифференцируя левую и правую части равенства, имеем последовательно
X
fy(t)dt =
'о
откуда находим у@) = -2 и у(х) = Сех. Из начального условия следует, что С = 2. Итак,
функция
у(х) = ~2ех
есть решение поставленной задачи. >
106. у dx + х dy + y2(xdy - ydx) = 0.
¦4 Это уравнение Миндинга—Дарбу, поскольку функции М(х, у) = у и N(x, у) = х одно-
однородные и имеют степень 1, а функция R(x, у) = у2 однородная и имеет степень 2. Следовательно,
применима замена у = их(и). Имеем uxdx + x(udx + xdu) + u2x2(x(udx + xdu) - их dx) = 0,
или
2udx + x(l + x2u2)du = 0; x = 0. A)
Разделим обе части полученного дифференциального уравнения на du. Оно превратится в урав-
уравнение Бернулли
dx
du
Полагая х~2 — z, приходим к линейному уравнению
uz'-z = и2.
Легко проверить, что его общее решение представляется в виде г = и2 ¦+ Си. Последовательно
возвращаясь к старым переменным, окончательно имеем
у2 + Сху - 1 = 0.
Решения х = 0 и у = 0 входят, сюда при С = со. >
„ dx , ,
2и t-x = -их.
d
46 Гл. 1. Дифференциальные уравнения первого порядка
107. (х2у + у3 - ху) dx + x2dy = 0.
¦4 Записывая уравнение в виде
0 • у3 dy +¦ (х2у + y3)dx + x(xdy - ydx) = 0,
замечаем, что оно есть уравнение Миндинга—Дарбу. Поэтому, полагая у = их, получаем
хъ(и + и1) dx + x3du = 0,
или
du
0 d = 0; и = 0.
х = 0; +dx =
«A + и2)
Отсюда следует, что / У = Се. Возвращаясь к переменным х тл у, окончательно получаем
у2 = С2е~2х(х2 + у2); х = 0. >
108. у\х + a)dx + x(x2 -ay)dy = 0.
¦4 Это уравнение Миндинга—Дарбу, поскольку оно приводится к стандартному виду
у2х dx + xi dy + ау(у dx - х dy) = 0.
Произведя замену у = их(и), получим линейное дифференциальное уравнение
dx х а
du «(« + 1) и + 1'
для решения которого применим метод вариации произвольной постоянной. Решение соответ-
соответствующего однородного уравнения имеет вид
Считая С = С (и), получаем дифференциальное уравнение
решение которого имеет вид
С(и) = о1п(С0(«+ 1))+ -, Со = const.
Подставив значение С(«) в A) и принимая во внимание, что и = ?, запишем общее решение
исходного уравнения в виде
109. Bху - х2у - у3) dx - (х2 + у2 - хъ - ху2) dy = 0.
¦4 Это также уравнение Миндинга—Дарбу, поскольку
Bху - х2у - у3) dx - (х2 + у2-х3- ху2) dy = 2ху dx - (х2 + у2) dy - (х2 + у2)(у dx - х dy).
Полагая у = их(и), получим уравнение с разделяющимися переменными
(« - и3) dx + хA + и2)(х - 1) du = 0,
из которого следует, что
1
х
Следовательно, в старых переменных имеем
у(х - 1) = С(х2 - у2). >
Решить следующие задачи.
110. Найти кривую, которая имеет следующее свойство: отрезок оси Ох от начала координат
до пересечения с касательной к этой кривой в любой точке пропорционален ординате этой точки.
¦4 Из уравнения касательной к искомой кривой в точке М(х, у)
§ 4. Линейные уравнения н уравнения, приводящиеся к ним
47
где X, Y — текущие координаты касательной, следует, что абсцисса точки пересечения ее с
осью Ох равна а; — Л • Согласно условию, имеем уравнение
или
dx
-
Все решения полученного уравнения имеют вид
х = у(С - Ш\у\). >
111. Найти кривые, у которых площадь трапеции, ограниченной осями координат, каса-
касательной и ординатой точки касания, есть величина постоянная, равная За2.
¦4 Из уравнения касательной (см. предыдущий пример) находим длину отрезка ОК : \ОК\ =
= У ~ ху' (рис. 21). Пусть 5 — площадь трапеции KONM. Имеем
Согласно условию задачи, 5 = За2. Следовательно,
За2 = - (у - ху + у)х.
Полученное уравнение линейное относительно у:
, „ 6а2
•С
Его общее решение имеет вид
2о2 2
у = — + Сх . >
112. Найти кривую, в каждой точке которой поднормаль является средним арифметическим
квадратов координат этой точки.
¦4 Согласно условию, имеем (рис. 22.):
\NL\ = \ (\ОЩг + \MN\2) .
о 'к
N
Ряс. 22
Рассмотрим треугольник MNL и найдем длину катета NL.
Имеем |JVL| = yy'. Таким образом, дифференциальное урав-
уравнение искомых кривых имеет вид
2уу' = х2 + у2.
Полагая в нем у2 = «, получим линейное уравнение «'-« = х2.
Решая его, находим « = Сех -х2-2х-2. Окончательно имеем
у2 = Сех -х2-2х-2.+
113. В баке находится 100л раствора, содержащего 10кг соли. В бак втекает 5л воды в ми-
минуту, а смесь с той же скоростью переливается в другой 100-литровый бак, первоначально напол-
наполненный чистой водой. Избыток жидкости из него выливается. Когда количество соли во втором
баке будет наибольшим? Чему оно равно?
¦4 Пусть Qi(t) и Q2H) — количества соли в кг соответственно в первом и втором баке в мо-
момент времени t от начала переливания. Тогда }до количество соли, выливающееся из
первого бака во второй за время от t до t+At, a 5 jo'o^^* — количество соли, выливающееся из
второго бака за этот же промежуток времени, где tn 6 (t, t+At), tt2 6 (t, t+At). Следовательно,
+ At) =
100
At -
100
At
A)
48 Гл. 1. Дифференциальные уравнения первого порядка
есть количество соли во втором баке в момент времени t + At, a
t B)
есть количество соли в первом баке в этот же момент времени. Из B), переходя к пределу при
At —> 0, получаем дифференциальное уравнение
-f = -0,05Ql)
откуда Qi = Се °'05f, где время t измеряется в минутах. Поскольку Q]@) -= 10, то С = 10.
Следовательно,
<?, = 10е-°'05(. C)
Совершив предельный переход в A) при At —» 0, и принимая во внимание C), получим
dt
Решив линейное уравнение, имеем
Q2(t) = @,5*
Так как Q2@) — 0, то С = 0. Окончательно находим
Исследуя функцию Q2 на экстремум, получим, что max Q2 достигается при t = 20 мин и равен
Q2B0)= — « 3,68 кг. К
е
114. За время Д* (где At —» 0 и выражено в долях года) из каждого грамма радия распадается
0,00044 At грамма и образуется 0,00043 At грамма радона. Из каждого грамма радона за время
At распадается 70At грамма. В начале опыта имелось некоторое количество хо чистого радия.
Когда количество образовавшегося и еще не распавшегося радона будет наибольшим?
-4 Обозначим через P(t) и Q(t) количества нераспавшихся радия и радона соответственно
в момент времени t от начала распада (в годах). Тогда P(t) — P(t + At) есть количество распав-
распавшегося радия за время от i до t + At, a Q(t + At) - Q(t) — количество образовавшегося радона
за это же время. Согласно условию задачи, имеем уравнения:
P(t) - P(t + At) = P(tn) ¦ 0,00044Д«, A)
Q(t + At) - Q(t) = P(tn) ¦ 0,00043Д< - Q(tuO0At, B)
где tn 6 (t, t + At), ttf & (t, t + At). Совершив предельный переход при At —у 0 (предварительно
разделив на At левые и правые части уравнений A) и B)), получим дифференциальные уравнения
~ = -0,00044Р(<), C)
dt
dO
-? = 0,00043Р«) - 70Q(t). D)
Решение уравнения C) имеет вид
E)
Подставив E) в D), получим дифференциальное уравнение, проинтегрировав которое, найдем:
-0,00044*
0 00043жп
Принимая во внимание начальное условие Q@) = 0, определяем С: С = — б'д 99955 • Оконча-
Окончательно имеем '
0,00043ar0 / _о,ооо44* -7оА
Исследование на экстремум функции f(t) = е"'00044' — е~70( показывает, что max f(t) достигается
ПРИ 1 70 ¦—У
t ыи°'17годаи62дая- *
§ 4. Линейные уравнения н уравнения, приводящиеся к ним 49
115. Даны два различных решения j/i и у2 линейного уравнения первого порядка. Выразить
через них общее решение этого уравнения.
¦4 Линейное дифференциальное уравнение
у' + Р(х)у = Q(x)
имеет общее решение
у = (С + а(х))/3(х), A)
где а(х) = Q(x)/3~l(x)dx, C(х) = ехр ( — P(x)dxj. Согласно условию, из A) имеем
J/i (*) = (С, + а(х))р(х), у2(х) = (С2 + а(х))/3(х), B)
где С\ и С2 — постоянные, соответствующие решениям у\ и у2- Далее, исходя из равенств B),
выражаем функции а и /3 через решения yi и у2. Получим
».(«)*(») {С1ф С1У(х)С2У1(х)
Ci - С2 ydx) - уг(х)
Наконец, подставив значения а(х) и /3(ж) в A), найдем:
У = с с ((С! - С)у2(х) + (С - С2)у,(х)) = у2(х) + С(у2(х) -yd
где С = (ч2_ g произвольная постоянная. >
116. Найти то решение уравнения
у sin 2x = 2(j/ + cos x),
которое остается ограниченным при х —> —.
¦4 Из рассмотрения общего решения этого уравнения
y = Ctgx
cos а;
следует, что lim у(х) = lim [СЩх - 35ifz) существует лишь при С = 1 и равен нулю. Поэтому
у = tg х - sec x
является требуемым решением. >
117. Пусть в уравнении ху' + ау = f(x) имеем a = const > 0, непрерывная функция / —» 6
при i -+ 0. Показать, что только одно решение уравнения остается ограниченным при х —> 0, и
найти предел этого решения при а; —> 0.
¦4 Представляем общее решение уравнения в виде
(d(\t\) = sgntdt, <#0), или
о
где e(t) —> О при t —» О в силу условия. Вследствие оценки
; - sup \e(t)\ -> 0, х -> О,
а г' -
из A) следует, что lim у существует и ограничен только при С = 0 и равен |-. Решение уравнения,
о котором шла речь^в условии задачи, имеет вид
50 Гл. 1. Дифференциальные уравнения первого норядка
118. Пусть в дифференциальном уравнении в предыдущей задаче о = const < 0, f(x) —> b
при а; —» 0. Показать, что все решения этого уравнения имеют один и тот же конечный предел
при а; —» 0. Найти этот предел.
¦4 Очевидно, что общее решение рассматриваемого уравнения при соблюдении условия
f(x) —> b при а; —» 0 можно представить в виде
у = \хГ
Если интеграл e(x)\x["~l d(\x\) ограничен, то при любом С, очевидно, Iimy(a:) = ^. Если
J х—*0
указанный интеграл не ограничен при х —> 0, то применяем правило Лопиталя:
[е(х))хГ1 d(\x\) eWlxr1
lim - — = lim —г—;—г— = 0.
«-.о |а;|0 »-о а\х\а~1
Таким образом, lim y(x) = |- при всех значениях С. >
119. Показать, что уравнение ^ + а; = f(t), где функция / непрерывная и \f(t)\ ^ M при
-оо < t < +оо, имеет одно решение, ограниченное при —оо < t < +oo. Найти это решение.
Показать, что найденное решение периодическое, если функция / периодическая.
¦4 Общее решение данного уравнения можно представить в виде
x(t) = Се~' + еГ1 I f{r)e dr. A)
-00
Такое представление возможно в силу того, что несобственный интеграл
г
j №eTdr,
как показывает оценка
t
I f(r)eT
dr
Me', B)
i
сходится. Из неравенства B) также следует, что функция е~* / /(т)ег dr ограничена числом М
-00
для всех t e (-оо, +оо). Таким образом, необходимым (и достаточным) условием ограниченно-
ограниченности функции х является равенство С = 0. Упоминаемое в условии решение имеет вид
x(t) = в"' J f(r)er dr. C)
-00
Пусть, далее, Vt е (-оо, +оо) /(т + Т) = /(г), где Т > 0. Тогда из C) находим
*(*) = е"' I /(г + Т)ет dr = e'(UT) J /(r, )er' dr, = x(t + Г),
где г, = т + Т. Следовательно, а; — периодическая функция. > (
Замечание. Требование непрерывности функции / не является необходимым. Выделение класса функ-
функций /, для которого эта теорема верна, предоставляется читателю.
. 120. Показать, что только одно решение уравнения ху' — Bа;2 + \)у — х2 стремится к ко-
конечному пределу при а; —» +оо, и найти этот предел. Выразить это решение через интеграл.
¦4 Исходим из общего решения данного уравнения
у = хе*2 (с + J e~*2 dx) .
A)
§4. Линейные уравнения н уравнения, приводящиеся к ним 51
х
В силу сходимости несобственного интеграла / е~* dt, выражение в скобках в A) можно пред-
-00
ставить в виде
х
С + j e~xl dx = Ci+ f e"'2 dt, B)
-00
где С\ — некоторая постоянная. Равенство B) легко проверяется посредством дифференцирова-
дифференцирования. Таким образом, все решения изучаемого уравнения выражаются формулой
C)
-00 '
Пусть а; —> +00. Тогда из C) замечаем, что для ограниченности у при а; —> +оо необходимо
выполнение условия
= - j
+00
е"'2 А = -л
-00
Последнее равенство и достаточное для того, чтобы lim у был конечным. Действительно, по
х—»+оо
правилу Лопиталя имеем
lim : 5 = lim ^ г = -\.
х-,+00 а;-'е-1' «~+°° -(а; + 2)е~х2 2
Теперь запишем искомое решение:
у = are1'
dt — л/т! \ = х I ex dt. 1
/ +00
121. Найти периодическое решение уравнения
у' = 2у cos2 a; - sin a;.
4 В силу сходимости несобственного интеграла
+00
f c-***tmt tint А,
общее решение данного уравнения представляем в виде
+00
У
+00
= се**™*"** - f e~t+x~siat':ost+^':'axzsmtdt. A)
Поскольку функция ex+smxaxxj очевидно, не является периодической, а функция
+00 +00
е sin(a! + *) а*,
о
как следует из тождества,
+00
(а:)= J e-t>
х+2х
где 11 = t + 2к, является 2п-периодической, то функция у периодическая только при С = 0.
Полагая в A) С = 0, получим периодическое решение у = yi(.x). >
52 Гл. 1. Дифференциальные уравнения первого порядка
122. Пусть в уравнении
dx
— + a(t)x = f(t)
at
a(t) ^ С > 0, /(f) —> 0 при t —> +oo и функции a, f непрерывны при t > t0. Доказать, что
каждое решение этого уравнения стремится к нулю при t —> +оо.
¦* Исходя из общего решения данного уравнения
x(t) - (с+ I fit) exp (fa(t)dt) dt) exp (- I a(t)dtj ,
условий задачи, и применив правило Лопиталя, получим:
С + /"/(О exp ( la(t) dt) dt fit) exp ( I a(t) dt)
Jim x(t) = lim y-jM—r—'- = lim f~ (¦ = 0.
t^+x t^+x exp(/a(t)dt] '~+x a(t)exp( ait)dt
Заметим, что непрерывность функций аи/ здесь гарантирует дифференцируемость соответству-
соответствующих интегралов, а условие аЦ) ^ С > 0 используется дважды:
-+ 0 при t —> +оо. >
exp / аЦ) dt > e -> +oo и
a(t) ^ С
123. Пусть в уравнении из предыдущей задачи имеем a(t) ^С>0 и пусть Жо@ решение с
начальным условием жо(О) = Ь. Показать, что Уг > 0 3E > 0 такое, что если изменить функцию /
и число Ь меньше чем на <5 (т.е. заменить их такой функцией f\ и таким числом bt, что |/i(t) -
- f(t)\ < 6, |b| - b\ < 6), то решение xo(t) изменится при t ^ 0 меньше, чем на ?. Это свойство
решения называется устойчивостью по отношению к постоянно действующим возмущениям.
¦4 Пусть t0 = 0. Тогда общее решение рассматриваемого уравнения можно записать в виде
t , Т V V / t
x(t)= (с + I f(r)cxp( I aiOdAdrjexpl- I a(T)dr). A)
О ^0 ' ' х О
Исходя из формулы A) и условий задачи, имеем
*о@= (ь+ [ Пт)ехр([ a(OdCjdTJexp\- f a(T)dr\ B)
(} \ \ ( f ^
/f(r)exp / a(Qd? dr exp - / air)dr . C)
4 ) ) \ { i
Вычитая почленно из B) равенство C), получим оценку
|ar0(t)-a:i(Ol ^ \Ъ - Ь\\ ехр - J air)dr I + J |/(т) - /,(т)|ехр1 - j a(C)dC Ut. D)
^ о 'о V
Поскольку
¦ , , , ( Г \ а \ f Г \ at т)
\Ь — Ь\\ < 6, |/(т) — /i(t)| < б, ехр( — / ah-)dT ^ е , ехр/ — / a(f)d? ^ е ,
W ^ / W /
то из D) следуют оценки
|xo(t) — aij (t)) ^ б I е н— М—е J I <
Таким образом, если по заданному е > 0 выбрать число <5 = и еУр , то при t ^ 0 выполняется
неравенство
\xo(t) - x{(t)\ < е,
указывающее, согласно определению, на устойчивость решения xo(t) при постоянно действующих
возмущениях. >
§ 5. Уравнения в полных дифференциалах. Интегрирующий множитель S3
§ 5. Уравнения в полных дифференциалах.
Интегрирующий множитель
5.1. Уравнение в полных дифференциалах.
Уравнение вида
М(х, y)dx + N(x, y)dy = Q A)
называется уравнением в полных дифференциалах, если его левая часть является полным диффе-
дифференциалом некоторой функции Ф, т. е.
М(х, у) dx + N(x, у) dy = ёФ(х, у). B)
Теорема. Если функции М, N, ^г, ^г непрерывные некоторой односвязной области D С К.2,
то условие
dN дМ
дх ду
является необходимым и достаточным для того, чтобы выражение М dx + N dy было полным диф-
дифференциалом функции Ф.
При этом
х У
Ф(х, y) = J M(t, y)dt + J Щх0, t) dt. C)
ZQ УО
Точка (x0, y0) выбирается так, чтобы сегменты [х0, х], \у0, у] принадлежали области D. Функ-
Функцию Ф можно также представить в виде
у
, У) = j M(t, y0) dt + j N(x, t) dt.
Все решения уравнения A) содержатся в равенстве Ф(ж, у) = С, являющемся для этого урав-
уравнения общим интегралом.
5.2. Интегрирующий множитель.
Функция /х = /х(ж, у) ^ 0, после умножения на которую уравнение вида A) превращается
в уравнение в полных дифференциалах, называется интегрирующим множителем для этого урав-
уравнения.
Теорема 1. Если функции М и N непрерывны, имеют непрерывные частные производные, то
интегрирующий множитель существует, если М2 + N2 Ф 0 {достаточные условия).
Теорема 2. Если fio(x, у) — интегрирующий множитель уравнения вида A), а ио(х, у) —
соответствующий ему интеграл этого уравнения, т. е.
цй(Мdx + Ndy) = du0,
то jx = fio(x, y)<p{u0), где <р — произвольная дифференцируемая функция, также будет интегриру-
интегрирующим множителем указанного уравнения.
Это свойство интегрирующего множителя позволяет во многих случаях находить его методом
разбиения данного уравнения на две части.
Сущность метода заключается в следующем. Пусть щ{х, у) = Сь ^(ж, у); и2(х, у) = С2,
t*i(xi У) — общие интегралы и интегрир5тощие множители соответственно для уравнений
Mi dx + Nidy = 0, М2dx + N2dy = 0. D)
Тогда, в силу приведенной выше теоремы, функции ц\ = nif\{u{) и ц\ = Ц2<Р2(Щ) являются
интегрирующими множителями для первого и второго уравнений соответственно. Если удастся
подобрать функции <pi и <р2 так, чтобы выполнялось равенство Hi<pi(ui) = Ц2<р2(и2), то интегри-
интегрирующим множителем для уравнения
(Mi + М2) dx + (Ni + N2) dy = 0, E)
очевидно, является функция, /i = /iiy?i(ui) = ц2у>2(и2).
54 Гл. 1. Дифференциальные уравнения первого порядка
5.3. Дифференциальное уравнение для интегрирующего множителя.
Если известно, что р = ц(ш), где ш = ш(х, у) — известная дифференцируемая функция, то
интегрирующий множитель ц удовлетворяет дифференциальному уравнению
дх ду) du> \ду дх
Найти общие интегралы уравнений.
124. (ж In у- х2 + cosy)dy + (ж3 + ylny- у- 2xy)dx = 0.
-4 Так как на множестве D = |(ж, у) g R2 : -оо < ж < +оо, у > о| выполняется равенство
д з д 2
— (ж + у1пу-у-2жу) = — (ж1пу-ж +cosy) = 1пу-2ж,
ду дх
то левая часть рассматриваемого уравнения является полным дифференциалом некоторой функ-
функции Ф. По формуле C), п. 5.1, получаем
х У 4
/, Г X 2
(t +ylny-у-2ty)dt+ / cos<(ft = — +zy(lny- 1) - уж +siny-siny0.
0 »0
Общий интеграл уравнения записывается в виде
ж4 + 4жуAпу - 1) - 4ж2у + 4sin у = С. >
125. [х + . } . ) dx + | у -
V y/y2-x2j \ у у/у'
¦* Поскольку при |у| > |ж| выполняется тождество
д ( \ \ Э ( X \
— \Х+ -==%) = —[у = -
"У \ V У ~ ж / ох\ у у/у — ж2 ]
-х2Н,
то имеем уравнение в полных дифференциалах. Применив формулу C), п. 5.1, получим
? Ь 2 2 . Ж 1 2
-(ж + у ) + arcsin -уо.
о \ •" " ' № У
Общий интеграл уравнения имеет вид
ж2 + у2 + 2arcsin- = С. >
У
Решить дифференциальные уравнения методом интегрирующего множителя, зная, что ц =
= /(ж) или ^ = /(у).
¦< Полагая в F), п. 5.3, w = x,M = l + -^2-,JV=j + -^, получаем
/I 2у\ёц_ /2 4y\_2(ifl Щ
или
dx x '
Отсюда fi = х1 (С = 1). Видим, что выбор функции ш оказался удачным. Умножив почленно
данное уравнение на х2, получим уравнение в полных дифференциалах
(х2 + y)dx + (х + 2y)dy = 0.
Применив формулу C), п. 5.2, найдем общий интеграл:
х3 + Зху + Ъу2 = С. >
§ 5. Уравнения в полных дифференциалах. Интегрирующий множитель 55
127. у^ж - Зу) dx + A - 3xy2)dy = 0.
¦4 Положим в F), п. 5.3, ш = ж, М = у2(ж - Зу), N = 1 — Зжу2:
A-Зху2)^=2у(х-Зу)ц; lg = 2?*~™ ¦
Замечаем, что р не может зависеть только от ж, поскольку слева в последнем равенстве имеет-
имеется функция только от ж, а справа — функция отжиу(жиу — независимые переменные).
Испытаем теперь множитель ш = у.
Имеем
2 dp d/i
-у (ж - Зу) — = 2у(ж - Зу)/*; -у — = 2ц.
Интегрируя последнее уравнение, находим р = у'2 (С = 1).
Умножая обе части исходного уравнения на у~2, получаем уравнение в полных дифференци-
дифференциалах
(ж - Зу) dx + (у'2 - Зж) dy = 0.
По формуле C), п. 5.2, записываем общий интеграл этого уравнения
ж2у — бжу2 — 2 = Су (уф 0).
При почленном делении исходного уравнения на у2 мы потеряли решение у = 0, поэтому общий
его интеграл имеет вид
ж2у - бжу2 -2 = Су (у = 0 при С = оо). >
Проинтегрировать следующие уравнения с помощью множителя р = р(х+у) или р = р(х—у).
128. Bж3 + Зж2у + у2 - у3)<*ж + Bу3 + Зжу2 + ж2 - ж3)<*у = 0.
¦* Пусть р = р(х — у). Тогда, полагая в F), п. 5.3 ш = х - у, получим
Bу3 + Зжу2 + ж2 - ж3 + Bж3 + Зж2у + у2 - у3)) ^ = Fж2 - 6у2 + 2у - 2х)р,
или
(у3 - ж3 + ж2 + у2 + Зжу(ж + у)) -j- = 2Cж2 - Зу2 + у - х)ц.
Очевидно, что выражение -3—з I i+ У~х' не является функцией от (ж - у), поэтому
будем искать функцию р в виде р = р(х + у). Тогда, аналогично проделанному выше, имеем
Bу3 + Зжу2 + ж2 - ж3 - Bж3 + Зж2у + у2 - у3)) ^ = Fж2 - 6у2 + 2у - 2х)р,
или
(З(у - ж)(у2 + жу + ж2) - (у - ж)(ж + у) + Зжу(у - ж)) -? = (у - x){l - 6(ж + y))/i,
откуда окончательно находим
C(ж + уJ - (ж + у)) ^ = B - 6(ж + у))р,
или
Cw2 - ш)р = 2A - Зш)р; шр +2р = 0.
Решая последнее уравнение, получаем р = -\ = — ; (С = 1). Умножив исходное
уравнение на —-—т, будем иметь уравнение в полных дифференциалах. Его общий интеграл
(х + У)
имеет вид
2t +3*У + У 'У f
t2t +3*У + У 'У dt+ f
dt+ f2tdt = const
о i
или
ж3 + у3 + жу = С(ак+ у).
Отметим, что решение у = — ж содержится в общем интеграле при С = оо. >
56 Гл. 1. Дифференциальные уравиепня первого порядка
129. (у- — +х) dx + ady = Q.
¦4 Ищем интегрирующий множитель в виде ц = ц(х + у). Тогда из F), п. 5.3, получим
(ш = х + у):
( ay \dnf a
У+Х) = {1
или
((а-х)х - у(ж - а))/*'= (х - а)р; (х + у)р' + (х = 0; w/*'+/х = 0.
Таким образом, ц = ш~1 = (х + у)~1 (С = 1) и данное уравнение приводим к виду
/ ay \ a
1 - ——^— dx + dy = 0.
V х(х + у)/ х + у
Интегрируя его, получаем
X У
I dt + a I = const (ж„ Ф 0),
J J *с ~f~ t
= c. >
Решить следующие уравнения, считая, что интегрирующий множитель имеет вид: /х = /х(жу),
/* = /*(ж2 + у1) или /* = /*(ж2 - у2).
130. (ж2 + у) dy + жA - у) da: = 0.
Ч Испытаем множитель ц — /*(жу), т.е. в F), п.5.3, положим ш = ху. Тогда получим
((ж2 + у)у - A - у)ж2) -^ = (-ж - 2ж)/*,
или
BуЖЧу2-Ж2)? + 3Ж, = 0.
Замечаем, что отношение -—2 2 г через жу не выражается, следовательно, в рассмотренном
2ух + у — ж
виде интегрирующий множитель не существует.
Положим ш = х2 + у1. Тогда будем иметь
((ж2 + уJж - A - уJжг/) — = -Зхр,
или
i' +3/1 = 0.
3
Интегрируя полученное уравнение, находим /< = ш 2 (С = 1). Таким образом, исходное уравне-
уравнение преобразовьшается в уравнение в полных дифференциалах:
Г dV + г dx = °-
Проинтегрировав его, получим
" d(\y\)
или
п - »л I I = с- —
\У\ ' \У\
§ 5. Уравнения в полных дифференциалах. Интегрирующий мпожитель 57
131. BжУ - У) dx + BжУ -x)dy = 0.
¦4 Пусть ш = ху. Тогда из F), п. 5.3, получаем
(BжУ - х)у - Bх3у2 - у)х) ^ = 4ху(х2 - у2)ц,
или
{xyfn' + 2хуц = 0; шц' + 2р = 0.
Отсюда находим и = -К = -^-^ (С = 1). Исходное уравнение приводится к уравнению в полных
U! X У
дифференциалах:
dx
x'-y) \~ xy1
Применив формулу (З), п. 5.1, находим общий интеграл
у
Решить уравнения, найдя каким-либо способом интегрирующий множитель или сделав за-
замену переменных.
132. (ж2 + у2 + x)dx + ydy = 0.
А Записывая уравнение в виде
и полагая х2 + у2 = и, получаем
и dx + - du = 0.
Интегрируя это уравнение, находим
и = Се'2х, или (ж2 + у2) е21 = С.
>
133. (x2+y2 + y)dx-xdy = Q.
¦* Записав уравнение в виде
2 + 2
и приняв во внимание, что У i ,Xi^ = d (arctg f), получаем d (x + arctg i-) = О, откуда
x
x + arctg - = С
У
— общий интеграл уравнения. >
134. у dy = (ж dy + у dxWl + y2.
¦4 Представим уравнение в виде
2/i.i = а(хУ)>
откуда
y/l + y2 = ху + С. >
1j3i ху (ху + у) = 1.
А По аналогии с решением предыдущих примеров, имеем последовательно
(ху?(ху)' = ж; ху = и; «V = х; ^(«3)' = ж,
58 Гл. 1. Дифференциальные уравнения первого порядка
откуда
и3 = - х2 + С, или 2жУ - Зх2 = С. >
136. у2 dx - (ху + ж3) dy = 0.
¦4 Считая х ф 0, уф0(х = 0ну = 0 — тривиальные решения), преобразуем уравнение
к виду
у (у dx-x dy) -x3dy= 0,
откуда
ydx - xdy x
2 dy = Q.
x2 у
Полагая j = и, имеем
du+d-*=0.
и
Получили уравнение с разделяющимися переменными. Проинтегрировав его, получим и2 + 2у =
= С, или
у2 + 2х2у = Сх2.
Решение х = 0 входит сюда при С = оо, а решение у = 0 — при С = 0, поэтому можно
считать, что получили общий интеграл исходного уравнения. *¦
)
Преобразовываем последовательно уравнение следующим образом:
ydx+ d (in-) =0; xdx + - d An -~\ = 0; -d(x2) +-d(lnu) = 0,
где и = |.
Поэтому
Отсюда находим
х2 1 ,
= const, или х у - 2х = 2Су. >
2 и
138. (x2+3lny)ydx = xdy.
¦4 Вводя замену In у = и, получаем уравнение
(х2 + 3u)dx-xdu = 0, A)
интегрирующий множитель которого ищем в виде ц = р(х). Тогдабудем иметь
0, )
откуда следует, что 4/л + х/л' = 0. Интегрируя полученное уравнение, находим один из инте-
интегрирующих множителей // = аГ4. Разделив почленно уравнение A) на ж4 (ж Ф 0), приходим
к уравнению в полных дифференциалах
1 Ъи\ J du n
— + — )dx- — = 0,
х2 z4/ х3
общий интеграл которого имеет вид
}dt}dt 2 з
I ~л~ I Т~ъ= const> ига х + lny = Сх . >
§ 5. Уравнения в полных дифференциалах. Интегрирующий множитель 59
139. у2 dx + (ху + tg ху) dy = 0.
-4 Полагая ху = и, получаем у = %, dy = -\(xdu — udx).
Подставив у и dy в уравнение, имеем
u2 xdu — udx
— dx + (u +tgu) = 0,
X2 X2
откуда
и tg и dx — (u + tg u)x du.
Интегрируя, находим
x = Си sin и, или ysinxy = С. >
140. у(х + y)dx + (xy+l)dy = 0.
¦4 Разделив почленно обе части уравнения на у, получим уравнение в полных дифференци-
дифференциалах
С
Его общий интеграл имеет вид
x + y)dx+(x+-\ dy = 0.
х2 + 2xy + kiy2 = С.
При делении на у было потеряно решение исходного уравнения у = 0. >
Замечание. Полученный интеграл можно представить следующим образом:
= lnC-z2-2zj/,
откуда
где С — новая постоянная. Теперь легко видеть, что решение у = 0 содержится в последней формуле
общего решения при С = 0.
141. у(у2 + 1)dx + ж(у2 -x+l)dy = Q.
¦4 Цепочка преобразований над уравнением:
dy dixy) dy
=0; | = ;
du dy
V2=y4y4TY где u = ^'
приводит, как видно, к уравнению с разделяющимися переменными.
Общее решение этого уравнения имеет вид
г du г ( 1 1 \ х-у
/-т=/ -J--5—; МУ + С, т.е. f + arctg у = С. >
J и2 J \у2 уг + \) ху2
142. (ж2 + 2ж + у) dx - (ж - Зж2у) dy = 0.
¦* Проводим последовательно преобразования:
= 0; f 1 + -) dx - d f -) + - dy1 = 0 (ж ^ 0);
V x/ \xj 2
= 0.
V xi/
Интегрируя, находим
х ' 2'
Присоединим еще "потерянное" решение х = 0. >
143. у dx - х dy = 2х3 tg \ dx.
А Разделив обе части уравнения на х2 и произведя замену f- = «, получаем уравнение
du = 2xtgudx,
60 Гл. 1. Дифференциальные уравнения первого порядка
которое легко интегрируется. Имеем
d(sin и) _ „ /•__,_ , ,__ ^ _:_ у
г d(sin и) Г
I = 2 / х dx + In С, откуда
J sin и J
у
sin —
x
144. y2dx + (ex -y)dy = Q,
¦4 Замены ех = и и и = zy приводят к уравнениям
-du + (--I ) dy = Q; ydz + z2dy = 0.
и \y )
У
Последнее уравнение имеет общий интеграл
In |у| - уе'х = С; у = 0. >
14Э. xydx = (у + х у + х ) dy.
¦4 Проведем следующие преобразования уравнения:
2 2 у dx — xdy у ( У\ У
x(ydx-xdy) = y(x +y )dy; — — - - dy; -d arctg - ) = - dy.
xl + yl x \ x) x
Положим у = хи. Тогда
du
цA+ц2)
Интегрируя, получаем окончательно:
du
-d(arctg u) = u dy, - цA+ц2)- = dy.
¦и
и2 = A+ и2)Се'2у, или -~—-,еу = С.
\ ' х2 + у2
146. x2y(ydx +xdy) = 2ydx + xdy.
¦4 Действуем аналогично проделанному в предыдущем примере. Имеем
(x2y-l)d(xy) = ydx; (ж2у-1)^) = —.
ху х
Положим ху = и. Тогда получим
Пусть - j = »;, тогда
du dx ( \\ du dx
(xu-l)— = —, или [и —= —.
их V х) и х2
du
(и + »;) dv = 0, или и du + v du — и dv = 0.
Разделим обе части уравнения на и2 и проинтегрируем полученное уравнение:
du /v\ v
d-=0, In « - - = const.
и \u/ \u
Окончательно имеем ^^
x2y\nCxy — —I. >
147. (ж2 - y2 + y) dx + xBy -l)dy = 0.
¦4 Образуем уравнение для интегрирующего множителя и = и(ш):
дш 2 г дш\ du
дх дуS dw
Легко видеть, что оно допускает множитель вида и — и(х):
du
- 1) -f- = 2(-2y + \)и; хи' + 2и-0.
ах
§ 5. Уравпепия в полных дифференциалах. Интегрирующий множитель 61
, полу
дифференциалах
Интегрируя, получаем /л = х~2. Умножив обе части уравнения на /л, получаем уравнение в полных
Его общий интеграл имеет вид
+ у1 - у = Сх. >
148. BжУ + у) dx + (ж3у -x)dy = 0.
¦4 Из уравнения для интегрирующего множителя
видно, что оно допускает множитель вида /х = ц(ш), где w = жу:
ху(х2у - 1 - 2а:2у - 1) ^ = (а:2у + 2)/i,
aw
или w/x' + /x = 0. Из последнего уравнения находим fi = оГ1 = (жу). Разделив обе части
исходного уравнения на ху (х Ф 0, у Ф 0), получим уравнение в полных дифференциалах
проинтегрировав которое, находим:
2 =С.
Очевидно, что уравнение имеет также тривиальные решения х = 0, у = 0. >
149. у (ж + у2) dx + x\y -\)dy = 0.
А Применим метод разбиения на две части. Для этого рассмотрим два уравнения
ху dx — x2dy = 0, у3 dx + x2y dy = 0.
Легко убедиться в том, что для первого уравнения ^i = —5— и общий интеграл щ(х, у) = j- = С\,
х у
а для второго ц2 = -гг. и2(х, у) = -~^у = С2. Согласно методу разбиения на две части,
интегрирующий множитель ц для исходного уравнения удовлетворяет соотношению
откуда
Пусть <р2(г) = z2. Тогда
Следовательно,
Ж
и
Умножив обе части исходного уравнения на ц(х, у), получим уравнение в полных дифференци-
дифференциалах
62 Гл. 1. Дифференциальные уравнения первого породи
Выберем в формуле C), п. 5.1, х0 = 0, уо = 1- Получим общий интеграл в виде
*±1|-С.
*(*,У)=1^ф* = С, -f^+ta
Уравнение имеет также тривиальные решения х = О и у = 0, которые включаем в общий интеграл
соответственно при С = 0 и С = оо. >
150. (ж2 - sin2 у) dx + х sin 2y dy = 0.
¦* Составив дифференциальное уравнение для интегрирующего множителя
(дш 1 2 дш\ du
xsin2y- (х — sin у) — I —- = — 2sin2i/ • u, A)
ox oy J du)
видим, что оно допускает множитель вида у. = ц(х). Тогда из A) следует, что
ху! + 2ц = 0,
откуда fi = х~2. Разделив исходное уравнение на х2 (ж Ф 0) и проинтегрировав полученное,
имеем
- I sin2tdt + I dt = const, х0 ф 0,
или, окончательно,
sin2 у + х1 = Сх.
Решение ж = 0 включаем сюда при С = оо. >
151. жAпу + 2 In ж — \)dy = 2ydx.
< Из дифференциального уравнения для интегрирующего множителя
/ дш дш\ du
V дх ду) du)
следует, что оно допускает ш — 1пж + 21пу. Действительно, в этом случае р! + у. = 0, откуда
Разделив исходное уравнение на ху2 (ж Ф 0, у фО), получим уравнение в полных дифферен-
дифференциалах
2 1
— dx гAпу + 21пж- l)dy = 0.
ху у2
Общий интеграл уравнения имеет вид
ж, ч 2 fdt r In*-1 1пж2у
Ф(ж, у) = - / — - / —-— dt = const, или = С. >
у J t J t2 у
152. (ж2 + 1)Bжйж + cosydy) = 2xs\nydx. V_
¦^ Полагая х1 + \ = и, siny = v, приводим уравнение к виду
(u-v)du + udv = 0,
которое при и Ф 0 можно записать так:
du udv — vdu f v\
— + 2 = 0, т.е. rf(lnu+-)=0.
и и2 \ и/
Имеем hi и + % = const. Следовательно,
(ж2 + 1) ln(x2 + 1) + sin у = С(хг + 1).
§ 5. Уравнения в полных дифференциалах. Интегрирующий множитель 63
153. жУ + у + (*У - х)У' = о.
¦^ Из уравнения для интегрирующего множителя
(
(хУх)(х
усматривается возможность выбора ш = ху. Тогда будем иметь шу! + \i = 0, откуда
_1__J_
ш ху
Умножив исходное уравнение на /i(z, у), получим уравнение в полных дифференциалах:
(ху1 + - J dx + (х2у - - ) dy = 0.
Его общий интеграл имеет вид
ИЛИ -г I
X2
*(*, у) = j (t + j) dt + j (хЧ - j) * = const,
l l
Решение у = 0 следует из общего интеграла при С = 0. >
154. (ж2 - у) dx + x(y +l)dy = 0.
¦^ Применяем метод разбиения уравнения на два:
х1 dx + ху dy = 0 и z dy — у dx = 0,
Первое уравнение имеет интегрирующий множитель р\ = -^ и общий интеграл «i(a;, j)ei2 +
-f у2 = Ci, а второе уравнение — /i2 = -V, «гО^ у) = § — С2. Согласно указанному методу,
интегрирующий множитель для исходного уравнения имеет вид
где ipi, <р2 — произвольные дифференцируемые функции. Из A) следует, что z^i(z2 + у2) =
= f2Vx ) • Положим f\(z) = -д. Тогда получим
х - 1
Следовательно, <pi(a) = —т=^—у. Таким образом, ц(х, у) = —т—ь——- (х > 0). Умножив исход-
исходное уравнение на /i(z, у), получим уравнение в полных дифференциалах
Его общий интеграл имеет вид
или
х
Частное решение х = 0 получаем при С = 0. Непосредственно можно убедиться, что множитель
/i(z, у) пригоден и для х < 0. >
155. yHydx - 2х dy) = z3(z dy - 2у dx).
< Аналогично предыдущему напишем уравиения
y2(ydx-2xdy) = 0 и x3(xdy-2y*r) = 0.
64 Гл. 1. Дифференциальные уравнения первого порядка
Тогда ^| = —Ц-, и| = Щ- = С\\ ц2 = -J-, и2 = -j- = С2 — соответственно интегрирующие
множители и интегралы этих уравнений. Интегрирующий множитель исходного уравнения ищем
из соотношения
из которого следует, что
..2
Полагаем у2 = хи. Тогда
(х>0, и>0).
Замечаем, что правая часть последнего равенства будет функцией только от и, если взять <р2(а) =
4
= q з. Таким образом,
y?i(u) = Vu = »/3 ж з, fi(x,y) = x 3j/ з.
Умножив обе части исходного уравнения на [х(х, у), получим уравнение в полных дифференци-
дифференциалах
' -± 1 1 _4\ / _i I 8 _7\
х з у з + 2х з J/ з 1 dx - I 2ж з j/ з -f ж з у з J dy = 0.
Взяв в последней формуле п. 5.1 х0 = I, j/o = 1. получим общий интеграл уравнения
t 1 +№) dt- Bх Н г +хП 3J Л = const,
i i
1 4
J
х „
Частные решения х = 0, у = О получаем при С = 0. >
156. (бх - 2у — 2y2)dx + Eи2 - 8ху - ж )rfj/ = 0.
'Щ Для отыскания интегрирующего множителя воспользуемся методом разделения уравнения
на два:
Fх - 2у) dx-xdy = 0; Eу2 - 8xy) dy - 2y2 dx = 0.
Нетрудно установить, что интегрирующие множители этих уравнений, а также их интегралы име-
имеют вид:
Hi=x, ( = У2; и[=2хг-х2у = Си и2 = 2у4х - у5 = Сг.
Согласно указанному методу, интегрирующий множитель данного уравнения ищем из соотноше-
соотношения
ц - жу?,Bх3 - х2у) = у2(р2Bу4х - у5).
Отсюда
2
х
Полагая здесь у2 = их, получаем
или
6 у5
2 2у6 у5
>pi(a) = utp2(u а), где а = — -.
и' и1
Пусть fi(z) = -Tj- (z > 0). Тогда
, ¦> . 1 1
и' и1
-== - —=. (и > 0). .
Vu2a uva
§ 5. Уравнения в полных дифференциалах. Интегрирующий множитель 65
Следовательно,
1 х 1
ipi(a)=-=, ц(х, y)=-w =-=== Bх>у).
Va s/ix5 — х2у л/2х — у
Заметим, что для 2х < у аналогично можно найти ц(х, у) = —? г—.
л/у 2.x
В обоих случаях после интегрирования уравнения в полных дифференциалах и упрощений
получаем ответ
Bх - у)(х - у2J = С. >
157. х dx + (ху - у3) dy = 0.
¦^ Целесообразно записать уравнение в форме
и положить Щ- = и. Тогда получим
xdx + (х — 2и) du = 0.
Уравнение для интегрирующего множителя этого уравнения имеет вид:
/ дш дш\ du
(ж - 2и) х — ) -j- = -ц.
V дх ди) da/
Если взять о/ = ж — и, то отсюда получим уравнение 2шц'+ц = 0. Следовательно, /i = \ш\~* =
= (|z — u|)~2. Поэтому левая часть уравнения
xdx х — 2и
Н— du = 0
является полным дифференциалом некоторой функции Ф. Выбирая ж0 ф 0, и0 = 0, получим
общий интеграл уравнения в виде
} tdt } x-2t
Ф(ж, и)= —= + / dt = const.
После интегрирования и перехода к переменным хну, общий интеграл исходного уравнения
примет вид
Bх-у2)у/\2х-у*\(х + у1)=С, или Bх-у2)(х + у2J = С.
sgn (lx - у2) ,J\2x-y2\ (x + у2) = С, или Bх - у2) (х + y2f = С. >
158. у3 dx + 2(х2 - ху2) dy - 0.
¦^ Для каждого из уравнений
у3 dx - 2ху2 dy = 0; 2х2 dy = О
находим /ii = -Ц-, щ = 4-: fr = Л, «2 = У-
ху у х
Следовательно, интегрирующий множитель для исходного уравнения удовлетворяет соотно-
соотношению
Если взять у>2(У) = У, то получим, что <р\(а) = а. Таким образом, р(х, у) = -у- и
^ dx + 2 (- - ?) dy = 0
х2 \у х) *
66 Гл. 1. Дифференциальные уравнения первого порядка
— уравнение в полных дифференциалах. Записав его общий интеграл в виде
jfj(j^)t =const-
1 1
получим общее решение
2
159. (у - x)dy + у dx - x d (-J = 0.
Л Для уравнения (у — ж) dy + у dx = 0 интегрирующим множителем является функция [it =
= у~2, а интегралом — «i = yev. Для уравнения xd(jj-) = 0 интегрирующим множителем
1 X
является функция \ii = -^, а интегралом — и2 = -у . В соответствии с методом разбиения имеем
Если положим yi(a) = а, то отсюда получим, что ^е» = р2(? )¦ Следовательно, ц = jrev есть
интегрирующий множитель для данного уравнения, которое после умножения на ц принимает
вид
г/ х \ ( х х2\ х
ev 1 йж+1 + — \ еУ dy = 0.
V у2/ V У У )
Интегрируя, получаем:
} ч *\ }
/е» 1 j J dt-+ dt = const (у0 ф 0),
Ь !*)
2 -- У --
у + у - х = Суе у , или —. е » = С. >
у2 + у - ж
160. (бжу2 + ж2) dy - уCу2 - ж) dж = 0.
¦^ Поскольку уравнение бжу2 dy — Ъу2 dx = 0 имеет интегрирующий множитель fit = —Ц-
и интеграл Ui = Щ-, а уравнение ж2 dy -f xydx — 0 — интегрирующий множитель u2 = т~
х у
и интеграл U2 = жу, то, согласно методу разбиения на две части, интегрирующий множитель
исходного уравнения ищем в виде
1
откуда находим ~тТР\\х) = f2(xy). Полагая щ = \, получаем V'lf х ) ~ х • Следовательно,
\i = -j-. Умножив данное уравнение на ц(х, у), получим уравнение в полных дифференциалах
х у \~
)
ж2 ж/ \ ж у
Его общий интеграл запишем в виде
Вычислив интегралы, окончательно получим
е * ух = С. >
§6. Уравнение Эйлера—Риккати 67
§6. Уравнение Эйлера—Риккати
6.1. Уравнение Эйлера—Риккати. Специальное уравнение Риккати.
Уравнение вида
^ 2 A)
называется уравнением Эйлера—Риккати. Если положить Р(х) = Ьха, Q(x) = О, R(x) = —а, где
а,Ь,а — постоянные, то уравнение A) примет вид
^-+ауг^Ьха. B)
dx
Оно называется специальным уравнением Риккати. Уравнение Эйлера—Риккати, вообще говоря,
не интегрируется в квадратурах. Даже специальное уравнение Риккати приводится к квадратурам
ли 4?
только в том случае, когда а — ±l — 2k' где * — целое или оо. Если равенство а = j _^j.
выполняется при к > О, то в B) делаем замену у = ^ + -^, приводящую B) к виду
Полагая далее и = -^, имеем
dx
Наконец, после замены жа+3 = г приходим к уравнению
dv b , а а+4
— + V = Z «+3 .
dz а+3 а + 3
Эти преобразования проводим до тех пор, пока не получим уравнение с разделяющимися пере-
переменными.
Если равенство а = jzrjfc выполняется при к < О, то указанные преобразования следует
проводить в обратном порядке.
6.2. Каноническое уравнение Эйлера—Риккати.
Уравнение
и = ±иг + w(x) C)
называется каноническим уравнением Эйлера—Риккати. Если в A) функция R дважды дифферен-
дифференцируема, то с помощью замен
у = a(x)z, z = u + р(х) D)
уравнение A) приводится к каноническому виду. Иногда форма C) позволяет сравнительно легко
установить частное решение уравнения A).
Если »/i(z) — частное решение уравнения A), то заменой у = у\ + \ уравнение Эйлера—
Риккати приводится к линейному.
Путем подбора частного решения решить уравнения.
161. х2у' + ху + х2у2 - 4.
¦* Ищем частное решение в виде у\{х) — ?, где а = const. Подставив его в данное уравнение,
получаем
-а + а + а2 =4 откуда а = ±2.
Пусть а = 2. Тогда, произведя замену y=^ + j, имеем линейное уравнение
яУ - 5xz - х2 = 0.
Интегрируя его, находим z = Сх5 - f .'Следовательно,
_ 2 4
х Сх5 — х
68 Гл. 1. Дифференциальные уравнения первого порядка
есть общее решение исходного уравнения. Частное решение yi = -^ получается отсюда при
С = оо. >
162. ху' -Aх + \)у + у1 = -ж2.
А Частное решение У((ж) ищем в виде У\(х) = ах + 6. Подставив его в уравнение, получаем
тождество относительно х:
ах - Bх + Щах + Ь) + (ах + бJ = -ж2,
из которого следует, что 2аЬ — 26 = 0; а = 1; — 6 + Ь2 — 0. Возможны два решения последней
системы уравнений: а = Ь = I или а = 1, 6 = 0. Пусть а = ], 6 = 0. Тогда у\(х) = х есть частное
решение. Производя замену у = х + \, получаем линейное уравнение
-\ = -х2,
или
xz + z - 1 = 0.
Интегрируя его, находим z = I -f ~, вследствие чего
163. Выразить общее решение уравнения Эйлера—Риккати через три различных его реше-
решения.
¦^ Если известно одно частное решение уравнения Эйлера—Риккати у\(х), то его общее
решение имеет вид
где z(x) — общее решение соответствующего линейного уравнения первого порядка. Так как
общее решение последнего выражается через две функции, т.е. z(x) = а(х) + С/3(х), то общее
решение уравнения Эйлера—Риккати представляется в виде
Л) + A)
Пусть У2(х), уз(х) — частные решения рассматриваемого уравнения. Тогда из A) следует, что
1 1
Уг = У\+ , „-;, Уз = У1 + , п д, B)
а + Сф а + Ср
где С\, С2 — постоянные, соответствующие частным решениям уг(х) и уз(х) (Ci Ф С{). Разрешив
систему уравнений B) относительно а и /3 и подставив их значения в A), получим
y=--- - ><*-»?),
уз - У! + С(у3 - Уг)
где С = с~_<$ произвольная постоянная. >
Решить уравнения. V
164. у' + у2 = 2ж~4.
¦^ Это специальное уравнение Риккати, Так как а = —4, то ft = 1 — целое. Следовательно,
его можно привести к квадратурам. Произведем замену
и 1
Тогда получим уравнение
и'х2 + и2 = 2.
Разделяя переменные и интегрируя, находим:
1
in
-=1пС,
ж
§ 6. Уравнение Эйлера—Риккати 69
Окончательно имеем
V x(xy-\) Ш
е х — с >
л/2-f жA -ху)
165 v'-v2-2x~li
¦^ Это также специальное уравнение Риккати. Так как к = 3, то в данном случае придется
провести указанные в п. 6.1 преобразования трижды. Итак, полагая у = -\ — -% , получаем
du и2 _1
-, 2=2х S.
dx xl
j 3
Произведя замены и = -^, х s = z, снова имеем специальное уравнение Риккати
dv 10 2 5 _8
1- — v - -- z з.
dz 3 3
Выполняя эти же замены повторно, получаем:
I , ,
где Z\ = zi, v — —j + -mj. Применение проведенных преобразований еще раз приводит
к уравнению
dv2 2
dz2
где z2 = z\', V\ = —г — -?^. Решая последнее уравнение, находим
V2Zi 1
V2 = 4? tg EV2z2 + С) .
у А ^ '
Возвращаясь к переменным ж и у, окончательно получаем:
V2 \х 5 - 0,Зж 5 ctg 5\^ж 5 + С ) + 0,Зж 5-1,2
- „-> V / V / . ь.
0,3\/2а:5 ctg E\/2ж + с) - 0,06ж5 + 1
у = х
166. у' + у2 = х з.
¦^ Здесь а! = --у, следовательно, ft = -1. Рассматриваем данное уравнение как такое,
которое получено в результате проделанных в предьщущих примерах преобразований. Таким
образом, можем написать (см. п. 6.1):
Ь _ а а+4 4
а + 3 а + 3 а+3 3
Из этих равенств следует, что а = 0, а = 6 = 3. Теперь видим, что в уравнении
у +3у2 = 3 A)
были проведены замены по формулам
" 1 _ 1 з_
в результате чего получилось уравнение
dv 2 -4
т. е. исходное уравнение.
70 Гл. 1. Дифференциальные уравнения первого норядка
Решая уравнение A), получаем
«Cz3+z3)+3 ,_
= С.
Поскольку в исходном уравнении через у обозначена функция, а через х — аргумент, то его
общим интегралом будет
/1 ?\
+ 3
+ 3
¦^ В этом специальном уравнении Риккати к = — 2, следовательно, потребуется провести два
обратных преобразования над ним. Из уравнений
Ь а _ а + 4_ 8
а + 3~ ' а+3~ ' а + 3 ~ 5
следует, что данное уравнение получено в результате преобразования уравнения
' 12 2-_^ ^ (П
, 1 -
по формулам у[ = -У? + jqjt, и = Ь, х? = ж. В свою очередь, смотрим на уравнение A) как на
такое, которое получено в результате преобразования уравнения
~-5у\= 10 B)
2
посредством замен yi = -\ — -^-, v = jj-, x\ = xt.
Решив уравнение B), получаем
, = V5tg Ev^a;2 + С) .
Возвращаясь к переменным ж и у, окончательно имеем
yx's (бОжЗ — 3) — 10 , ,
= tgEV2a;5 +c) . >
168. жу' - 5у - у2 = ж2.
¦^ Сначала заметим, что специальное уравнение Риккати B), п. 6.1, после замен у — ?
и жа+2 = t переходит в следующее:
du и a j Ь
t Н и = t (аф-2) A)
dt а + 2 а + 2 а+2
ИЛИ
tu +lu + ти2 = nt. A')
В исходном уравнении заменим аргумент, полагая ж2 = t. Тогда получим (переобозначив у
через и):
У Л2Т2
Сравнивая A) и B), находим: а = -§, a = -\, b= j.
Таким образом, между исходным уравнением и специальным уравнением Риккати установле-
й АЪ>
на связь, причем, поскольку а = — j = i_ ц при к = —2, то первое интегрируется в квадратурах
и его общий интеграл можно получить методом преобразований, которые применялись выше. Од-
Однако мы применим иной подход к интегрированию уравнений A').
§6. Уравнение Эйлера—Риккати 71
Сущность метода состоит в следующем.
Если тп ФО к I Ф — ^, то уравнение A') можно преобразовать двумя путями:
1) применив подстановку и = p^.v , где р — -Щ1^-, получим
tv + (I + l)v + nv2 = mt;
2) подстановкой u = q+ |-, где 9 = -^-, приводим уравнение A') к виду
tv' + (I - l)v + nv2 = mt.
Если m = О или п = 0, то уравнение A') превращается в линейное уравнение или в уравнение
Бернулли соответственно.
Если I = - \, то его можно представить в виде
после чего оно интегрируется в квадратурах. Отсюда следует, что преобразования целесообразно
проводить тем из указанных выше способов, который приведет к уравнению C). В принципе это
возможно только в том случае, когда I = ш + \, где ш — целое число.
В данном примере I = — ^, т = — ^, п = X, ш = — 3, поэтому выбираем первый путь. Имеем
t , 3 v2 t
В полученном уравнении l = -j,m=^,n = -^. Применив замену v = w + j , получим
tw' --w- -!»2= -.
В последнем уравнении I = —X, поэтому оно приводится к уравнению вида C):
которое имеет общее решение w = Victg(—Vt + C). Возвращаясь к переменным ж и у, оконча-
окончательно имеем
х1 х2
у = ; v- ; w = х ctg(C - x). >
v - 3 w + 1
169. ху' + 3у + у2 = х2.
¦* По аналогии с решением предыдущего примера, посредством замены х2 = t приводим
уравнение к виду
Поскольку / = ^ > 0, то к полученному уравнению применяем второй путь преобразований,
указанный в примере 168. Имеем
t ,
и'
Еще раз применяем указанное преобразование:
t
и
L _j
Ь — 1
V
и2
h 2
v2
t
~ 2
t
Последнее уравнение запишем в виде
72 Гл. 1. Дифференциальные уравнения первого порядка
откуда находим v = Victh(Vi + С). Таким образом, общим решением исходного уравнения
является
х2
170. Зжу'-9у-у2 = жз.
2
¦4 Полагая х з = t, получаем
dy 9 у2 t
t v = —.
dt 2У 2 2
n
Поскольку I = --j, то применяем цепочку преобразовании:
t , 7 v2 t t . 5 w2 t
y= ; tv v H = —-г! v= •; tw w =-;
" v-7 2 2 2 w + S' 2 2 2
t , 3 x2 t t , ib tb2 t
W= **+ = : X = ; ** =
Из последнего уравнения получаем гр = v^ctg^C - \/?J. Совершить переход к переменным хну
предлагаем читателю. >
,_, dy 5 3 7
171. -f- + -y+-y2 = x.
dx x x
•^ Произведя замену х2 =t, получим:
dy 5 3 2 *
dt 2У 2У 2
Поскольку / = ^ > 0, то применяем второй путь преобразований, указанный в примере 168.
Имеем
t
t
X
Записав последнее уравнение в виде
3;
1
3'
dv
dw
dx
~dt
3
w
У
V
+
к
2
+
3
2
+
г;2
w2 =
X2
2 ~
3
Г
3
21'
и решив его, получаем х = \/3?сШ(\/зТ + С).
Обратный переход по цепочке вверх к переменным а; и у не составляет трудностей. >
т.у'+-у+хУ2=1-.
X X
•^ Приведем уравнение к каноническому виду. Сначала посредством замены у = a{x)z до-
добьемся того, чтобы коэффициент при z2 был равен единице. Имеем
/ / / 3 2 2 1
У za+az+ -az + xaz = -, A)
XX
откуда а(х) = i. Поэтому из A) следует, что z' + \z + z1 = 1. Далее, заменой z = и + /3(х)
последнее уравнение преобразуем так, чтобы в нем отсутствовала искомая функция и в первой
степени. Имеем
§ 7. Уравнения, не разрешенные относительно производной 73
Взяв /Э(х) = -¦?, получим каноническое уравнение Эйлера—Риккати
которое имеет общее решение и = th(a; + С).
Таким образом, общее решение исходного уравнения имеет вид
1 / 1\
у = - th(z + С) - - . >
а; V х)
§ 7. Уравнения, не разрешенные
относительно производной
7.1. Уравнение, не разрешенное относительно производной.
Уравнение вида F(x, у, у') = О, где F — известная функция, называется уравнением, не
разрешенным относительно производной.
Если функция F — многочлен степени п относительно производной, то уравнение F = О
называется уравнением первого порядка п -ой степени и имеет вид
п к
=0>
где р* — известные функции. Разрешив уравнение A) относительно у', получим:
/у) (* = ТГ^). B)
Пусть уравнения B) имеют общие интегралы
<Рк(х,у) = Ск (к = 1,п).
Тогда общим интегралом уравнения A) будет
(?>,(*, у) - С,) (<р2(х, у)-С2) ... (Vn(x, у) - с,) = 0. C)
7.2. Общий интеграл уравнения F(y') = 0.
Уравнение F(y') = 0 имеет общий интеграл F ( ^ х с j = 0, причем, если F(y') = 0 на неко-
некоторых частях области определения функции F, то отношение ^~с будем считать произвольной
функцией от х со значениями на этих же частях.
7.3. Представление решения в параметрической форме.
Разрешение неполных уравнений.
Пусть для уравнения F(x, у, у') = 0 существуют такие функции х = <р(и, v), у = \р(и, v),
у' = g(u, v), что F(<p(u, v), гр(и, v), g(u, v)) = 0 относительно параметров и и v из некоторой
области их задания. Тогда, используя соотношение dy — y'dx, получаем
dip , dip , /dip , dip
-^-du+^-dv= g(u, v)[^-du+^-
du dv \du dv
откуда
~ = /(«, v). D)
du
Если уравнение D) имеет общее решение v = a(u, С), то общее решение исходного уравнения
записывается в параметрической форме
х = <р (и, а(и, С)), у = V (и, а(и, С)). E)
Неполные уравнения F(x, у') = 0 и .F(y, у') = 0 приводятся к квадратурам, если их можно
разрешить относительно х или у соответственно. Если, например, х — (р(у'), то вводим пара-
параметр р по формуле у' = р. Тогда х = <р(р) и dy = pdx = pf'ip) dp, откуда у = Ip<p'(p) dp + С.
Аналогично поступаем в случае, когда уравнение F(y, у') = 0 можно разрешить относительно у.
74 Гл. 1. Дифференциальные уравнения первого норядка
Найти общие интегралы уравнений.
173. у* - C* - 2у)у' + 2х2 -ху- Зу2 = 0.
•^ Решая это квадратное уравнение относительно производной, получаем два дифференци-
дифференциальных уравнения первого порядка:
у =2х-3у и у -х + у.
Оба уравнения линейные, поэтому их общие решения находим без труда:
y=Cie~ix + -X-- и у = Сгех-х-\.
Общий интеграл исходного уравнения можно записать в виде C), п. 7.1:
174. у'3 - (ж2 + ху + у2)у' + ху(х + у) = 0.
•^ Уравнение допускает очевидное решение у' = х. Остальные решения находим из квадрат-
квадратного уравнения у1 + ху' - {х + у)у = 0:
У=У и у'=-х-у.
Общие решения полученных дифференциальных уравнений соответственно имеют вид
х2
у= — + Си У = С2ех, у = С3ег-х + 1.
Общим интегралом исходного уравнения будет
У-\- СЛ (Уе~Х - Ъ) ((У + х- 1)в* - С3) = 0. >
175. у' sin х - (у sin х — cos2 x)y' - (у cos2 x + sin x)y' + у sin x = 0.
•^ Очевидное решение у' = sin а; позволяет найти другие два решения кубического уравнения:
у' = у и у' = - jjj-тг. Решив полученные дифференциальные уравнения, имеем
у = —
х
ctg-
С2.
2
Следовательно, общий интеграл данного уравнения записывается в виде
(у + cosх - Ci)(ye~x - С2) (у - In
ctg ~
= 0. >
Найти решения уравнений.
176. х3/ +х2уу' + а = 0.
•^ Решив уравнение относительно у
вводим параметр р по формуле у1 = р. Тогда из A) следует, что
Для выражения х через р воспользуемся равенством dy = pdx. Дифференцируя B) и принимая
во внимание указанное равенство, получаем:
§ 7. Уравнения, не разрешенные относительно производной 75
откуда
Очевидно, последнее уравнение имеет решения х = з/-% и а; = ,. . . Подставив их в B),
находим у = -2^/ра и(/=-Л sgnp - СуДр\. Получили все решения в параметрической форме.
Исключив параметр р, получаем эти же решения в явном виде:
4а ас
ж=— и у= - + -. >
у2 с х
177. 9у/ 4 4*3у' - 4х2у = 0.
•^ Полагая у' = р и разрешая уравнение относительно у, получаем:
A)
Дифференцируя A) и принимая во внимание равенство dy = p da;, находим:
(l2a;4p - 27а;2р3 - 8ра;4) dx + Ux5 + 9pV) dp
pdx = 4 (^-эр2J '
или 9p3 dx = 4xidp (считаем, что 4х2+9р2 ф 0). Из последнего уравнения следует, что 4х2-9р2 —
= 4Сх2р2, поэтому из A) окончательно получаем:
у2 = Сх2+9-С2. >
178. / - *уУ -у5 = о.
•^ В данном случае уравнение удобно разрешить относительно х:
х=^-^. A)
У4 У'
Полагая в A) у' =р и продифференцировав полученное, имеем
dx_dl = 2pdp _ 4p2dy _ dy_ ydp
P ~ У4 У5 P P2 '
откуда
V p
Из этого уравнения находим:
= Су2 и р=-у№.
Подставим значения у' = р в A). Получим
Ж = С2* и ж=
Су
179. ж = у' sin у1.
¦4 Уравнение разрешено относительно х, поэтому можно ввести параметр р = у'. Тогда
х — psinp и остается'выразить у через р. Воспользовавшись связью dy — pdx, имеем
dy = pd(psinp) = p(sinp + p cos p) dp.
Отсюда интегрированием получаем
у = р2 sinp + p cosp - sinp + С.
Таким образом, имеем общее решение в параметрической форме:
z=psinp, i/ = p2sinp + pcosp-sinp + C. >
76 Гл. 1. Дифференциальные уравнения первого порядка
180. j, = B + yVb^F.
•^ Как и в предыдущем примере, вводим параметр у' — р. Тогда у = B + р)у/Т^~р. Так как
dx = ^ dy, a dy = d{(l+p)JT^p), то
p
Отсюда интегрированием находим х = З1/1 —p + С. Если исключим параметр р из выражений
для а; и у, то получим общее решение
I з
27
181. а;3 + у'3-За;у' = О.
•^ Полагая у' — tx(t), где t — параметр, находим
... 3* , 3t2
Из последнего равенства следует, что dy = ——г da;. Поскольку da; = 3——=rjdt, то
l+i (I +1 )
— 9-О1 ~зУ dt. Интегрируя, получаем
A +1 )
— общее решение исходного уравнения в параметрической форме. >
182. / - 8/ + 9/ - l/ + ву' + 1 = 0.
•^ Пусть ак (к = 1,5) — корни уравнения а5 - 8а4 + 9а3 - 7а2 + 6а + 1 = 0. Тогда у' = ак
v — С
и у = a,kX + С, или *—?— = а*. Поскольку а* — корни указанного уравнения, то должно быть
Это и есть общий интеграл данного уравнения. >
183. у'= lOsiny'.
•^ Поскольку j/ = а*, где ак — корни уравнения а = 10 sin а, то у = акх + С, и общий
интеграл дифференциального уравнения имеет вид:
у-с
у-С= lOxsin . >
184. у1 + }у'\ = 0.
•^ Это уравнение выполняется для всех у' ^ 0. Поэтому, полагая у' = fix), где <р — любая
неположительная функция, имеем:
у = J<p(x)dx + C=- J \ip(x)\dx + С.
Следовательно,
есть решение данного уравнения. >
185. а/^Л
•^ Уравнение имеет одно очевидное решение у1 — х; у = С + %%-. Кроме того, имеются и
другие решения, которые представим в параметрическом виде. Для этого положим у' = х*. Тогда
получим
§ 7. Уравнения, не разрешенные относительно производной 77
Отсюда
Интегрируя последнее соотношение, находим
186. у' = е^.
•^ Разрешив уравнение относительно а; и полагая у' = р, получим х = ^lnp. Так как
dy = pdx, то
/и \ у у / у \
dy = pd -lnp = - dp + lnpdy lnpdp, или A-lnp) dy dp)=0.
\p J p p \ p I
Из последнего уравнения находим р = е и р = Су. Таким образом, решения данного уравнения
имеют вид
х = - и Сж = In Су. >
е
187. Жу'3 - у/ + 1 = 0.
•^ Полагая здесь у' =р, разрешаем уравнение относительно х:
ур2 - 1 у 1
р3 р р3
Из равенства dy = pdx, а также A) следует, что
^)ypf B)
р рЧ р 3
Из B) находим р = С и у = -4-. Подставив эти значения в A), получим
.y'2 +2yy'ctex-y2 = 0.
•^ Разрешая уравнение относительно у', получаем два дифференциальных уравнения
y' = ytg| и y' = -yctg|.
Их соответствующие решения имеют вид
189. y(y-2xy'K = y' .
•^ Умножив обе части уравнения на у2 и обозначив у2 ~ и, получим
4(и - хи)ъ = и .
Полагая и' = р и разрешив последнее уравнение относительно и, будем иметь
2
A)
Поскольку du = pdx, то, дифференцируя обе части равенства A), найдем
dp, или
78 Гл. 1. Дифференциальные уравнения первого порядка
Отсюда имеем р = С, или р = — ~-т. Подставив значения р в A), окончательно получим:
27а;
2
И
190. (Ъх + 5)/ - (Ъу + х)у' +у = 0.
¦4 Положив у' = р и разрешив уравнение относительно у, имеем
Продифференцируем обе части равенства A), приняв во внимание, что dy = pdx. Получим
V \ 5pB-3p)dp
y 1з^ , или
Из этого уравнения находим
-Зр)
Подставив B) в A), получим решения исходного уравнения:
5С2 5рB - Зр) У
Последние два из них являются параметрическими уравнениями решения, не входящего в семей-
семейство интегральных кривых ни при каком С. >
191. у = ху'-у'\
•^ Полагая здесь у' = р и дифференцируя обе части равенства у = рх - р2, получаем
pdx = d(xp -pj = xdp+pdx - 2pdp,
или
(z-2p)dp = 0.
Отсюда находим р = С и р = §. Таким образом, решения исходного уравнения имеют вид
х
= Сх-С2 и у=~.р-
.у = 2ху'-4у'2.
¦4 Введение параметра у' = р с последующим дифференцированием обеих частей уравнения
приводит к следующему соотношению:
pdx = dBxp-4p2^ = 2xdp + 2pdx-Spdp, или 2xdp + pdx -%pdp-0.
Полученное уравнение можно рассматривать как линейное относительно х = х(р):
dx
р-
Его общее решение имеет вид:
С 8
х = 72 + зр-
Таким образом, общее решение исходного уравнения запишется в виде:
С 8 4 , 1С
J
Кроме того, имеется еще одно решение у — 0, не входящее в это общее решение ни при ка-
каком С. >
Примечание. Здесь и далее рассматриваем уравнения Лагранжа и Клеро, которые соответственно имеют
вид:
§ 7. Уравнения, ие разрешенные относительно производной 79
По аналогии с предыдущим примером имеем
У' = Pi У- хР2 ~ 2р3; pdx = d(xp2 - 2р3),
или
р((р - l)dx + 2(х - 3p)dp) = 0.
Отсюда следует, что р = 1, р — О, а также (р - 1)^ + 2х = Ър. Интегрируя линейное уравнение,
получаем
Таким образом, все решения данного уравнения описываются формулами:
194. 7yl\y-xyl)=\.
^+2р+1) y=
Разрешая уравнение относительно у и полагая у' = р, получаем
1
Используя равенство dy = pdx и дифференцируя обе части A), находим
pdx = d(xp+ — j =xdp + pdx j dp,
или
Отсюда следует, что р = С, а также х = -j. Подставив полученные значения в A), окончательно
—.
195. Найти кривую, каждая касательная к которой образует с осями координат треугольник
площадью 2а2.
¦Щ Из уравнения касательной к кривой в точке Mix, у)
Y = y + y'(x)(X-x),
где X, Y — текущие координаты касательной, следует, что абсцисса точки пересечения каса-
касательной с осью Ох равна жп = х — Л, а ордината точки пересечения ее с осью Оу уп = у — ху'.
If
Согласно условию \хпуп\ = 4а2, или хпуп = ±4а2. Таким образом, получаем дифференциальное
уравнение
(^) A)
или (жу' - уJ ± 4аV = 0. Полагая у' = р и дифференцируя, находим
2{хр - у)(х dp + pdx- pdx) dh 4o2 dip = 0,
или
(x2p -xy± 2a2) dp = 0.
Следовательно, р = С, а также р = ^ (у ± ~- j.
Подставляя значение р в уравнение (хр - уJ dh 4a2p = 0, получаем решения
= ±— и (Сх - уJ ± 4a2C = 0.
80
Гл. 1. Дифференциальные уравнения первого порядка
Легко проверить, что кривая у = ±^г является огибающей семейства прямых {Сх — у) ±
± 4а2С = 0, каждая из которых совместно с осями координат образует указанный в условии
треугольник. Исключая эти тривиальные возможности, получаем решение поставленной задачи
„2
196. Найти кривую, каждая касательная к которой отсекает на осях координат такие отрезки,
что сумма величин, обратных квадратам длин этих отрезков, равна единице.
•^ Если сохранить обозначения из предыдущего примера, то согласно условию получим
Разрешая уравнение относительно у и полагая у' = р, будем иметь
y = xp±yfl+p2. , A)
Продифференцируем обе части в A). Тогда, принимая во внимание равенство dy = pdx, получим
дифференциальное уравнение
х±
из которого следует, что р = С, а также х =
±1
. Подставив значения р и х в A), находим:
У =
и у = Сх ± Vl + C2.
Если исключим тривиальный случай у = Сх ± л/1 + С2, то получим решение данной задачи
197. Найти кривую, проходящую через начало координат и такую, что отрезок нормали
к ней, отсекаемый сторонами первого координатного угла, имеет
постоянную длину, равную двум.
•^ Из уравнения нормали
следует, что \ОР\ = у + 4, \OQ\ = х + уу' (рис.23). Согласно
условию,
У,
N
Р
О
\
'к
90°
/
(*.У)
о4 *
\PQ\ = yJ\OP\2 + \OQ\2 = 2,
поэтому
Рис.23
'J
-: +(х + уу')=4.
Положив в этом уравнении у' = р и разрешив его относительно у, получим
_ х
У = ~р
A)
Дифференцируя равенство A), имеем
.s'
xdp dx
или
§ 7. Уравнения, не разрешенные относительно производной
81
Последнее уравнение линейное относительно х и его общее решение имеет вид
^-О^-Л-^. B)
Параметрические уравнения общего решения исходного уравнения определяются равенства-
равенствами A) и B). Положив в A) х = у = 0, получаем р = оо. А тогда из B) следует, что С = 0. Таким
образом, кривая, параметрические уравнения которой имеют вид
р 2р2 + 1
Г. У= Г
+ 1J (р2 + 1J
C)
удовлетворяет поставленной задаче. Очевидно, что если в C) поменять местами а; и у, то получим
другую кривую
х = 2Р + \ , у = ^—j- (р>0), D)
(р2 + 1J (р* + 1M
которая также является решением поставленной задачи, поскольку с геометрической точки зрения
переменные хну равноправные. Ясно, что если в D) параметр р заменим на ^ (р > 0), то
получим ту же кривую, однако с другим параметрическим представлением
х=
РB+р2)
У=
(р > 0). >
198. Найти кривые, у которых произведение расстояний от каждой касательной до двух
данных точек является величиной постоянной.
•^ Согласно условию, \КА\ ¦ \LB\ = а2 (а = const) (см. рис.24). Пусть \АО\ = \ОВ\ = Ъ.
Тогда, подставив в нормальное уравнение касательной
Y-y'X-y + xy' n
вместо координат X и Y координаты точки А(-Ь, 0)., получим
\Ьу'-у + ху'\
У
\КА\ =
Аналогично получаем
\LB\ =
В
Рис. 24
Таким образом, имеем
\Ъу -у + ху'\ -\-Ьу'-у + ху'\ = a2(l + /), откуда (ху - уJ - by'2 = dha2(l + /).
Обозначив 62±a2 = m, dha2 = n и разрешив последнее уравнение относительно у, можем записать
у = ху' ± у ту'2 + п. A)
Полагая в A) у' = р и продифференцировав, получим
тр
х±-
откуда р = С и х =
dp = 0,
• Таким образом, отбросив тривиальный случай р = С, имеем
утр2 + п
параметрические уравнения искомого решения
тр т»
\Jrnp1 + п' у/тр2 + п'
Исключив параметр р, получим
пх1 + ту1 = тп.
Очевидно, что в зависимости от знаков тип, это могут быть как эллипсы, так и гиперболы. >
82 Гл. 1. Дифференциальные уравнения первого порядка
§ 8. Существование и единственность решения
8.1. Теоремы Пикара, Пеано и Осгуда.
Теорема (Пикара). Если в задаче Коши
dy
= /(* »)
= Уо A)
функция f непрерывна в прямоугольнике R = {(ж, у) ? К2 : |ж—хо\ ^ a, |j/-yo| ^ 6} и удовлетворяет
в нем условию Липшица по переменной у, т. е.
3L > 0 : V(yb у2 е [-6 + уо, 6 + у0]), V(z ? [-а + х0, а + ж0])
l/(«, yi) - /(^, Уг)| ^ Ь|У1 - Jfcl (Ь = const),
то на сегменте х0 - d ^ х ^ х0 + d, где d = minfa, jM, M = max |/(ж, у)|, существует
единственное решение задачи A), к которому равномерно сходятся при п —> сю приближения у„,
определяемые формулами
X
е
*\ с 17 11\
П с ^*0* \^/
Теорема (Пеано). ?1сли функция f непрерывна в R, то хотя бы одно решение у — ip(x)
задачи A) существует на указанном сегменте.
Теорема (Осгуда). Если:
1) функция ш = w(t) непрерывна при t~? 0, о;@) = 0 и w(t) > 0 при t>0;
гь
2) интеграл I -^щ = +оо;
о
3) \f(x, у() - f(x, j/2)| ^ ш(\у{ - j/2|) в Л,
то в R может существовать не более одного решения задачи A).
8.2. Существование и единственность решения задачи Коши
для уравнения, не разрешенного относительно производной.
Теорема. Если в замкнутой окрестности точки (х0, уо,уо) функция F = F(x, у, у') удовле-
удовлетворяет условиям:
1) F непрерывна по совокупности аргументов х, у, у';
2) существует частная производная Щ^ ф 0;
3) существует частная производная Щ-, причем Щ- ^ N (N = constA
то на сегменте [xq — е, xq + е], где е > 0 — достаточно малое число, существует единственное
решение у = у(х) уравнения F(x, у, у') = 0 с начальным условием у(хо) - уо, для которого у'(х0) =
= Уо и уо — действительный корень уравнения F(x0, у о, уо) = 0.
8.3. Продолжение решения задачи Коши.
Часто решение задачи Коши существует не только на сегменте, указанном в теоремах Пикара
и Пеано, но и на большем сегменте.
Если условия теоремы Пикара выполнены в замкнутой области, то решение задачи A) можно
продолжить вплоть до границы этой области.
. Если функция / непрерывна в полосе П = Ux, у) € R2 : а < х < f), -со < у < +оо} и удо-
удовлетворяет неравенству
где ip и ф — непрерывные функции, то всякое решение задачи A) можно продолжить на весь
интервал (а, /?).
Информация о величине интервала существования решения задачи Коши содержится в сле-
следующем утверждении.
§ 8. Существование и единственность решения 83
Лемма (Бихари). Если справедливо неравенство
у(х) ^C + J v(t)g(y(t)) ей, xo^x^a, E)
где С = const > 0, функции у = у(х), v = v(x) неотрицательные и непрерывные, а функция g = g(y)
непрерывная, неотрицательная и неубывающая, причем д(у) > 0 при у > 0, то
F)
где
G(u) = / —-, «о > 0, G)
J g(t)
«о
x
для всех тех х ? [х0, а), для которых функция G(С) + v(t)dt принадлежит области определения
функции G~l.
8.4. Существование и единственность решения векторной задачи Коши.
Если в задаче A) у и / векторы, т.е. у = (уь у2, ... ,у„), / = (/г, /2, ... ,/„), то вместо
задачи A) будем иметь задачу:
у'\ =f\(x, У1,у2, ... ,у„),
У7 = Ых,У\,Уъ ¦¦. ,у„),
(8)
Уп = /п(х, У1,У2, ¦¦¦ ,Уп),
У\(хо) = J/ioj Уг(^о) = У20) • • ¦ j Уп(хо) = упо-
При условиях, аналогичных изложенным в п. 8.1, существует единственное решение зада-
задачи (8). При этом под непрерывностью вектор-функции / понимается непрерывность ее коорди-
координат /i, /2, ... ,/„, а условие Липшица B) распространяется на каждую функцию /,• по каждой
переменной у*. Абсолютная величина \у\, |/| заменяется длиной соответствующего вектора.
К задаче (8) сводится следующая. Найти такую функцию у = у(ж) вместе с окрестностью
точки хо, которая удовлетворяет уравнению
и начальным условиям
Если в некоторой области D, содержащей точку (х0, у0, у'о, ...,Уо"""), функция / и ее част-
частные производные первого порядка по у, у',..., у<п~" непрерывны, то задача (9), A0) имеет един-
единственное решение в достаточно малой окрестности указанной точки, целиком лежащей в D. По-
Положив у = yi, у' = уг,... , у("~" = уп, вместо (9), A0) получим систему
У1=У2, У2 = УЗ, •••, Уп-1=Уп, У„ = f(x, уЬ у2) ... ,у„) A1)
с начальными условиями yi(x0) = у0, y2(xo) = уё,... ,уп{х0) = уо"'.
199. Построить последовательные приближения у0, yi, у2 к решению данного уравнения
с данными начальными условиями:
а) у1 = х - у2, у@) = 0; б) у1 = у + е", у@) = 1.
¦4 Воспользуемся формулами C), п. 8.1
а) В рассматриваемом случае хо = 0, уо = 0, уо(О = у0 = 0,
х
у„+1(х) = j(t - yl(t))dt, п € Zo. A)
84 Гл. 1. Дифференциальные уравнения первого порядка
Полагая здесь п = О, получаем первое приближение
х х 2
у,(а:) = J{t - yl{t))dt = Jtdt= у.
о о
Полагая в A) п = 1, находим
о о
б) Поскольку 1/@) = 1, то j/o@ = 1, ж0 = 0 и
yn+l(x)=l + J(yn(t) + ey"m-1) dt.
о
Отсюда при п = 0 получаем
х
Vl(x) = l+f(l+ е1)^ = 1 + 2х,
о
а при п = 1 находим
Ы*)= 1 + J(l+2t + e2t)dt= - + x + x2 + -e2x. >
о
200. Построить по два последовательных приближения (не считая исходного) к решениям
следующих уравнений и систем:
а) y' = 2x + z, z' = y; y(l)=l, г A) = О;
dx du i
б) — =!/, ^=*: *@)=l, У@) = 2;
в) y" + /-2y = 0, y@)=l, !/'@) = 0.
•4 а) Система интегральных уравнений, эквивалентная данной системе дифференциальных
уравнений с начальными условиями, имеет вид:
X X
у(х) = 1 + JBt + z(t))dt, z{x) = Jy(t)dt.
1 1
Последовательные приближения находим по рекуррентным формулам
X X
!/„+!(*) = 1 + J (а + zn(t)) dt, zn+l(x) = J yn(t) dt, A)
1 1
где za(t) = 0, yo(t) = 1, n ? Zo, вытекающим из формулы C), п. 8.1, если под у и / понимать
векторы с координатами (у, z) и Ы + z(t), y(t)\ соответственно.
Полагая вA)п = 0ип=1, получаем
X J X
ух(х) = 1 + j\2t + zo(t)) dt = x\ *,(*) = J yo{t) dt = x-\;
l l
X X
- jyi(t)dt =
§8. Существование и единственность решения 85
б) По аналогии с проделанным выше, имеем
t t
*»+!«) = 1 + / Уп(т) йт, yn+l(t) = 2 + У х1(т) dr.
о
Полагая здесь п = О и п = 1, последовательно находим:
t t
f f f 2 f
Xi(t) = 1 + / yo(T)dT — 1 + / 2dr = 1 + 2t, y{(t) = 2 + / xo(r)dT = 2 + / dr =
0 0 0 0
4 4 ,
x2(t)= 1+ / j/i(r)dr= 1+ /B +r)dr= l + 2t+-,
о о
4 4
/ 2 / 2
j/2(O = 2+ / »i(T)dT = 2+ / A + 2t) dr :
4 з
v-t.
о о
в) Как и в п. 8.4, данное уравнение второго порядка сведем к системе двух уравнений первого
порядка, полагая у = у, у' — z. Тогда получим
z' = 2y-z\ y' = z; j/@) =1, z@) = 0.
Из рекуррентных формул
X X
W*) = УBУп(«) - zl(t))dt, yn+l(x) = 1 + J zn(t)dt, n ? Zo,
о о
где zo(t) = 0, yo(t) = 1, находим
X X
z,(z) = УBу0(О - 4(t))dt = 2х, У1(х) = 1 + Jzo(t)dt = 1,
о о
Х Х А
z2(x) = J{2yl(t) - z\(t))dt = У B - At2) dt = 2x-- x\
о о
x x
y2(x)= 1+ f zi(t)dt= 1+ I2tdt= l + x2.
201. Указать какой-нибудь сегмент, на котором существует решение с данными начальными
условиями:
\ у@) = 0; б) у' = 2у2 - х,
¦^ а) Воспользуемся сначала теоремой существования, изложенной в п. 8.1. В данном слу-
случае х0 = у0 = 0, f(x, у) = х + уъ. Функция / непрерывна в любом прямоугольнике R =
= их, у) € R2 : |ж| ^ а, \у\ ^ b\ и удовлетворяет в нем условию Липшица, поскольку производ-
производная -gi = Зу2 ограничена числом ЗЬ2. Следовательно, на сегменте [-d, d], где d = min (a, -jyj,
М = max \f(x, y)\ = а + Ь3 существует единственное решение данной задачи. Найдем число
d — min I a, —2-т-). Ясно, что если на каком-то сегменте I существует единственное решение,
V а + ъ* J
то оно существует и на каждом меньшем сегменте, вложенном в /. Отсюда следует, что жела-
желательно найти как можно больший отрезок /, т. е. max min а, —ттт ) • Так как функция ip(a) = a
Гл. 1. Дифференциальные уравнения первого порядка
i функц
условии, что tp(a) = д(а), т.е.
возрастает при а ^ 0, а функция д(а) = —~х убывает, то maxmin ( a,
а + о '
достигается при
A)
Взяв производную по Ь от правой части A), найдем, что при Ь3 = § достигается максимум а,
который легко вычислить, подставив значение а = 263 в A). Тогда получим
1 2 = - уУзб» 0,66.
Таким образом, можно гарантировать существование и единственность решения данной за-
задачи на сегменте -0,66 ^ х ^ 0,66.
Если воспользоваться леммой Бихари (см. п. 8.3), то можно указать значительно больший
сегмент существования решения.
Действительно, в данном случае
х 2 х
у(х) = j{t + y\t))dt = у +Jy\t)dt
Ых)\
а
т
т.е. С = ^r, v(x) = 1, д(у) = уъ. Поэтому
Следовательно,
¦ jv(t)dt\ =
Из уравнения a = ~j находим max a = v^« 1,15.
Заменив в исходном уравнении ж на —ж (ж ^ 0) и проделав такие же выкладки, получим
неравенство
которое показывает, что решение задачи а) существует и при — у/2 ^ х ^ 0. Таким образом,
существование единственного решения задачи а) можно гарантировать на сегменте -1,15 ^ х ^
^ 1,15.
б) Применим теорему Пикара существования и единственности решения. Здесь х0 — уо = 1,
f(x, у) — 2у2 — х. Функция / непрерывна в любом прямоугольнике
^ R = {(х, у) е К2 : \х - 1К а, \у - 1| < ь)
и имеет ограниченную производную по у в Л:
§8. Существование и единственность решения 87
Поэтому на сегменте \х - 1| ^ d = min (a, -jg-j, где М = max |2у2 - х\ ^ 2A + бJ + 1 + а,
существует единственное решение. Как и в случае а), параметры а и 6 находим из условий:
Ь 8 /
бJ + а + 1 И дЪ V2
Ъ
2A
Следовательно, а = щ 1+ ц , 2Ъ2 - 3 = щ ^ ^ . Из последнего равенства следует, что Ь > у \ >
> 1,2. А тогда а < щ ^ щ =0,11.
Однако оценку для d можно улучшить, считая, что а < 1. Тогда М = 2A + ЬJ - 1 + а и из
равенств, аналогичных B), находим
262-1 = —1— <1 или
4A + 6)' 4A + 6) 4
Следовательно, а = ли \-h\ > ~~7— <-\ ~ 0,13. Итак, по меньшей мере, на сегменте 0,87 ^
4( +Ь) 4A + ^1)
^ х ^ 1,13 решение задачи существует и единственное.
Пользуясь леммой Бихари, можно указать еще больший сегмент существования и единствен-
единственности решения. Действительно, представляя данную задачу в виде
y(x)=-C-x2)+2Jy\t)dt
1
получаем оценку ее решения:
X
|y(z)| ^ С + 2 f \y(t)\2 dt, С = J • max |3 - х\
i
из которой, согласно лемме, следует неравенство
C)
где
J t2 «о «
«о
1 - uot
Таким образом, из C) получаем оценку
из которой следует, что решение задачи б) существует на сегменте 1 ^ х ^ -^ + 1. Величину X
находим из уравнения -^ + 1 = X, или
= max |3-ж2|. D)
Х-1 1<х<лг' ' v
Из D) получаем X = 1,5, т.е. существование единственного решения гарантируется на сегменте
1 ^ х ^ 1,5. Для выяснения вопроса о продолжимости решения левее точки х = 1 в задаче б)
произведем замену х — 1 — (((^0)и снова воспользуемся леммой Бихари. После аналогичных
выкладок приходим к оценке
Получаем уравнение
1
— = max
2 + 2t-t'
из которого следует, что 0,33 < Т < 0,41. Итак, можно гарантировать существование и един-
единственность решения задачи б) на сегменте 0,67 ^ х ^ 1,5.
88 Гл. 1. Дифференциальные уравнения первого порядка
в) Применим сначала теорему Пикара, все условия которой выполнены в прямоугольнике R,
а затем найдем
d = min I a, ] .
Из уравнений
д ( Ь \-о
(
°~ а + 1+е6' db \а+ 1 +
получаем а — е~ь, а — е~(а +а+1). Отсюда находим, что а ^ 0,2. Таким образом, на сегменте
0,8 ^ t ^ 1,2 решение существует и единственно.
Воспользуемся теперь леммой Бихари. Из интегрального уравнения данной задачи
1
следует оценка
x(t)= -(t2- 1)+ fexis)ds, <>1,
\x(t)\ ^C + J e|l(s)l ds, C=- raw, |<2 - 1| = - (Г2 - 1).
Поскольку
и
ds
G(u) = f — = е-"° - е-", и ^ щ > 0,
J es
«О
ТО
<?-'(«/) = -In (е-"°-у), (?(О = е" - е~с (О щ).
Согласно лемме, имеем оценку
\x(t)\ < - In (e""° - е""° + е"с -1 + l) = - In (e"c - < + l) ,
откуда 1 ^ t ^ е~с + 1. Следовательно, максимально возможный сегмент существования решения
справа от точки t — 1 найдем, решив уравнение
Г2-1 = -21п(Г-1) A<Г<2).
Из него следует, что Т > 1,5.
Для выяснения вопроса о продолжимости решения левее точки t = 1 произведем замену
г = 1-т@^т^то)и проделаем все выкладки согласно лемме Бихари. Тогда получим
~Т
|ж(т)|^-1п(е с - т), где С= max
Максимально возможное значение г0 находим из уравнения
Го = е~с или С = - In го @ < т0 < 1).
т2 т2
Так как С = т0 —j-, то -%— то = In го. Отсюда получаем ть > 0,6.
В результате делаем вывод о существовании и единственности решения на сегменте 0,4 ^
г) Применяем теорему Пикара для системы дифференциальных уравнений. Здесь @ = 0,
хо = 1, уо = 2. Функции fi(t, х, у) = у2, f2(t, х, у) = х2 непрерывны в области
и имеют в ней ограниченные частные производные -^ = 0, ^Й- = 2у, ^Ш- = 2х, Qfe- = 0.
Следовательно, на сегменте — h ^ t ^ Л, где h = min (о, -jrr), М = max Jft + Й, существует
4 lvl ' (t,x,y)€Sl v
единственное решение рассматриваемой задачи.
§ 8. Существование и единственность решения 89
Поскольку М = max Jx4 + у4 ^ J(\ + ЬL + B + ЬL ^ л/2B + ЬO, то из условий
Ь b д ( Ь \ _
"~М" л/2B + ЬJ' 96 1B+ ЬJ/ ~°
находим, что 6 = 2 и а ^ ~ЩТ> ~ ~ТТ—4 > 0,1. Следовательно, на сегменте -0,1 ^ t ^0,1
существует единственное решение.
Если применим лемму Бихари, то сможем указать сегмент существования и единственности
_ 1 <t< 1
Действительно, из интегральных уравнений рассматриваемой задачи следует, что
(s)\2ds, |j/(«)K2 +
о
откуда
N91 + \УФ\ < 3 + J(\x(s)\2 + \y(s)\2)ds s$ 3 + J(\x(s)\ + \y(S)\J ds,
о о
или
и ^ 3+ / u2(s)ds, где и = \х\ + \y\.
0
Согласно лемме Бихари имеем
1 _ 1 г "°
tH V' 1 - VOt
1-ЗГ
откуда 0 ^ t < -j. Аналогично получаем левый от точки t = 0 интервал продолжимости —\<
<t^0. >
202. Для уравнения у1 = х — у2 с начальным условием j/@) = 0 построить третье приближе-
приближение к решению и оценить его погрешность при 0 ^ х ^ 0,5.
< Согласно формуле C), п. 8.1, имеем
= 0; уЛх) = J(t-y20)dt=^; у2(х) = j it - *- J dt = у - ~;
е t5\2\ х2 х5
г/о
Оценим погрешность полученного приближения.
Легко установить, что решение данной задачи существует и единственно на сегменте - -4=
V4
х ^ -п=, так что последовательные приближения
V4
A)
равномерно сходятся на этом сегменте к решению интегрального уравнения
х
= yo+Jf(t,y(t))dt. B)
90
Гл. 1. Дифференциальные уравнения первого иорадка
Вычитая почленно из A) равенство B) при х ^ xq и оценивая соответствующие разности для
n ? Zo, получим
ш - уо
\y(x) - yi(z)| ^ j\f(t, y(t)) - f(t, yo)
dt
x
= LJ(x - и
\y(x)
J \f{t, y(t)) - f(t, 2/n_,(O)|<tt ^ ~f J (x - «)>(«) efti,
где L — постоянная Липшица функции / по переменной у в прямоугольнике
R = их, у) ? К2 : \х — хо\ ^ а, \у ¦
В рассматриваемом случае L ^ max |2«(ж)| = 2IMI,
(x,y)€R
хо=О, поэтому из C) получаем оценку
х 0,5
— |« - у2
\\y\\2, п = 3,
. D)
Остается оценить llwll на сегменте 0 < х ^ 0,5, который содержится в сегменте -тт=, -тт= ¦
[ V4 V4 J
2
Из леммы Бихари следует, что \у\
Г
г2
(см. пример 201), где С = max ^- = 0,125.
Поэтому ||i/|| ^ I -o'l^^-O 5 ^ 0,134. Принимая во внимание оценку D), окончательно имеем
||2/-2/з1КО,6-ПГ5. >
203. Пользуясь каким-либо достаточным условием единственности, выделить области на
плоскости хОу, в которых через каждую точку проходит единственное решение уравнения:
а)у' =
у2; б) у' = 2 + ^у - 2х; в) (х - 2)у = ^/у - х; г) «/'= 1 + tgу.
¦^ а) Функция /(ж, у) = 2жи + у2 непрерывна в любой части плоскости хОу, а ее произ-
водная Tji = 2(x + у) ограничена в любой конечной части D этой плоскости. Следовательно,
по теореме Пикара через каждую точку (ж0, j/o) ? D проходит единственная интегральная кривая
уравнения а).
б) Функция f(x, у) = 2 + у/у — 2х непрерывна V (х, у) ? R2, однако ее частная производная
Bf 1 -2
щ — \{у~ 2ж) 3 ограничена только при уф2х. Тогда, по теореме Пикара, через каждую точку
(хо, уо) 6 R2, где j/o ^ 2ж0, проходит единственная интегральная кривая.
в) Воспользуемся теоремой п. 8.2. Функция F(x, у, у') — {х - 2)у' - ^/у + х удовлетворяет
условиям: 1) она непрерывна при у ^ 0; 2) частная производная ^р- = х — 2 Ф 0 при х Ф 2;
3) частная производная %?т = —^цщ ограничена при у ^ е > 0; 4) у' = у_2 единственный
действительный корень уравнения F(x, у, у') = 0. Следовательно, через каждую точку (ж0) уо)
плоскости хОу, где ж0 Ф_%Л Уо ^ ? > 0, проходит единственная интегральная кривая уравне-
уравнения в).
г) Ясно, что при у ф y + кж, к ? Z, правая часть уравнения непрерывна и имеет огра-
ограниченную частную производную по у. Следовательно, по теореме Пикара, через каждую точку
плоскости хОу, за исключением прямых у = ^+кж, проходит единственная интегральная кривая
рассматриваемого уравнения. >
§8. Существование и единственность решения 91
Примечание. Если функция / в задаче Коши имеет в прямоугольнике В. ограниченную частную произ-
производную -тЛт, то она автоматически удовлетворяет условию Липшица.
204. При каких неотрицательных а нарушается единственность решений уравнения у' = \у\"
и в каких точках?
•4 При неотрицательных а функция f(x, у) = \у\а непрерывна, поэтому уравнение имеет
решения. Если у Ф 0, то частная производная -Jr = a\y\"~l sgny существует и ограничена в
каждой конечной части плоскости хОу. Следовательно, по теореме Пикара, если у ф 0, то
при любом а существует единственная интегральная кривая, проходящая через заданную точку.
Если у — 0, но а ^ 1, то функция / удовлетворяет условию Липшица:
М" = lyil'-'lVil ^ blVil (здесь у2 = 0).
Поэтому, согласно теореме Пикара, единственность решения и в этом случае гарантирована.
Остается проверить случай, когда 0 < а < 1 иу = 0.
Возьмем произвольную точку M(xq, 0) на оси Ох. Очевидно, что через эту точку проходит
интегральная кривая у = 0. Однако через эту точку проходит также кривая у_а sgn у = х — х0,
являющаяся решением рассматриваемого уравнения. Таким образом, при 0 < а < 1 в точках
(х, 0) € М2 нарушается единственность решений данного уравнения. >
205. С помощью необходимого и достаточного условия единственности для уравнений вида
у1 = f(y) исследовать дифференциальные уравнения:
а) у'= (у-1)^5 6)y'=arccosy; в) у' =
¦4 Согласно указанному критерию, если непрерывная функция / ф 0, то решение уравнения
существует и единственно. Если же f(y) = 0 при у = С = const, то вопрос о единственности
с
решается с помощью исследования на сходимость несобственного интеграла / ~тл ¦ Если этот
Уо
интеграл расходится, то у = С — частное решение, в противном случае через каждую точку
прямой у = С проходят другие интегральные кривые.
В случае а) имеем С = 1 и С = 0. Функция /(у) = (у - 1)\/у* непрерывна при у ^ 0.
Поскольку несобственные интегралы
1 о
/ ^ / ^ (о < уо < 1)
^тз (Уо > °; № ^ 1) и /
I (у - i)Vr I (у -
расходятся, то через каждую точку полуплоскости у ^ 0 проходит единственная интегральная
кривая данного дифференциального уравнения.
1
В случае б) С = 1 и несобственный интеграл / arcc^s (—1 ^ yQ < 1) сходится, так как
и
= ° [ J\- у ) при У ~* 1 ~ °' ПоэтомУ чеРез кажДУ10 точку (х, у), где -1 < у < 1,
1 б
проходит единственная интегральная кривая, а через каждую точку прямой у = 1 — любое число
интегральных кривых.
В случае в)С = 0иС=1. Так как несобственный интеграл
У2 = / тг" (° < Уо < 1)
Уо Inyo
сходится, а несобственный интеграл
1 П
dy_ =
v
In so
/аи г at
w~y = h ^>°^o#D
92 Гл. 1. Дифференциальные уравнения первого порядка
расходится, то через каждую точку верхней полуплоскости, за исключением прямой у = О, про-
проходит единственная интегральная кривая.
Предлагаем читателю выполнить геометрическую иллюстрацию рассмотренных случаев. >
206. При каких начальных условиях существует единственное решение следующих уравне-
уравнений и систем?
а) у" = tgy + \/х; б) (х + \)у" = у + -/у;
at
-4 Воспользуемся утверждениями п.8.4. В случае а) имеем f(x, у, у') = Xgy + Цх. Функ-
Функция / и ее частные производные -дтг — —т~> ~^гт — 0 непрерывны при уфЦ-+кж,к?71,
' оу cos у оу е " ±
поэтому в достаточно малой окрестности каждой точки (хй, уо, у'о), где у0 Ф ^ + ктт, существует
единственная интегральная кривая, проходящая через эту точку.
б) Функция f(x, у, у) = ~^f и ее частные производные Щ = ~j + ^^ + Д), |4 = 0
непрерывны при х Ф — 1 и у > 0. Следовательно, через каждую точку (ж0, у0, у'о), где Xq Ф — 1
и уо > 0, проходит единственная интегральная кривая.
в) Поскольку функция f(x, у, у', у") = -у (у" — \Jy' — х) вместе с частными производными
% ^ при у Ф 0 и у' ф х, то
через каждую точку (ж0, t/o, j/oi J/o), где уо Ф 0 и y'Q Ф х0, проходит единственная интегральная
кривая уравнения
y
г) Так как функции /,(?, х, у) = i/3+ln(t + l), /2(i, х, у) — ^ Jjy - I и их частные производные
Ъ = 0. Щ = V, Ш = -^Т1- Щ = 3xfo-tfi непрерывны при х ^ 0, i > -1, у Ф t,
то через каждую точку (i0, ж0, у0), где io > —1, J/o Ф to, х0 ф 0, проходит единственное решение
(x(t), y(t)). Заметим, что в случае системы уравнений -^ = /ь ~^ = /2 и т.д., ее решение
является вектор-функцией с координатами x(t), y(t) и т. д. >
207. Могут ли графики двух решений данного уравнения на плоскости хОу пересекаться
в некоторой точке (жо, j/o)
а) для уравнения у' = х + у2? б) для уравнения у" = х + у2!
Л а) Так как функция /(ж, у) = х + у2 непрерывна вместе со своей частной производной
-щ = 2у в любой конечной части плоскости хОу, то, согласно теореме Пикара, через каждую
точку (х0, уо) проходит единственная интегральная кривая уравнения у' = х+у2, т. е. пересечение
графиков двух его решений в этой точке невозможно.
б) В силу непрерывности функции /(ж, у) = х + у2 и ее частных производных -gr = 2j/,
— 0, через каждую точку (ж0, уо> Уо) проходит единственная интегральная кривая. Последнее,
однако, не исключает того, что через точку (ж0, уо) проходят две различные интегральные кривые
с различными угловыми коэффициентами касательных к ним, т.е. пересечение графиков двух
решений в некоторой точке (х0, у0) возможно. Этот факт можно установить и непосредственно,
дважды проинтегрировав данное уравнение и приняв во внимание, что у(х0) — уо- Тогда получим
3 2
X Х
3 2 3
X . ХоХ , Хп Г
У(х) = — + у'ах - -^- + уо - УоЖо + Т + /
о 2 ЗУ
Очевидно, что любая кривая у (ж) проходит через точку (ж0, уо), однако каждая из них имеет
в этой точке "свою" карательную с угловым коэффициентом у'о. >
§ 8. Существование и единственность решения 93
208. Могут ли графики двух решений данного уравнения на плоскости хОу касаться друг
друга в некоторой точке (жо, Уо)
а) для уравнения у' = ж + у2?
б) для уравнения у" = х + у2 ?
в) для уравнения у'" = х + у2?
¦^ а) Касание двух различных интегральных кривых в точке (жо, Уо) невозможно в силу тео-
теоремы существования и единственности (см. пример 207, а)).
б) Касание двух различных интегральных кривых означает, что через точку (ж0, уо, yd) про-
проходят две интегральные кривые уравнения у" = ж + у2. Последнее же невозможно в силу теоремы
существования и единственности решения, (см. пример 207, 6)).
в) Теорема единственности решения гарантирует существование в окрестности каждой точки
(го> Уо> УО)Уо) единственной интегральной кривой уравнения у'" = ж + у2. Она гарантирует также
существование единственного решения и в окрестности точки, (жо, Уо> Уо> yd'i)- Следовательно,
графики двух решений, проходящих через указанные точки, имеют общую касательную. >
209. Сколько существует решений уравнения у(л) = ж + у2, удовлетворяющих одновременно
двум условиям: у@) = 1, у'@) = 2? Рассмотреть отдельно случаи п = 1, 2, 3.
¦4 При п = 1 имеем у'@) = (ж + у2)|1=0 = у2@) = \ Ф 2. Следовательно, если п = 1, то
уравнение не имеет ни одного решения с указанными начальными условиями.
Так как функция /(ж, у, у') = ж + у2 непрерывна вместе со своими частными производными
-$У = 2у, J-*r = 0 в окрестности точки @, 1, 2), то согласно теореме существования (см. п. 8.4) за-
задача у" = ж+у2, у@) = 1, у'@) = 2 имеет единственное решение в достаточно малой окрестности
точки @, 1, 2).
В силу теоремы единственности (см. п. 8.4) задача у'" = ж + у2, у@) = 1, у'@) = 2, у"@) —
произвольное, имеет единственное решение в окрестности точки @, 1, 2, у"@)). Следовательно, в
достаточно малой окрестности точки @, 1, 2) имеется однопараметрическое множество решений
задачи
у'" = ж+у2, у@)=1, у'@) = 2. >
210. Сколько решений уравнения у'"' = /(ж, у) (/ и -? непрерывны на всей плоско-
плоскости жОу) проходит через точку (жо, уо) по заданному направлению, образующему угол а Ф -у
с осью Ох! Рассмотреть случаи п=1,п=2ип^3.
¦4 Пусть т» = 1. Тогда задача у' = /(ж, у), у(ж0) = уо в силу непрерывности функций /
и -fa имеет единственное решение в достаточно малой окрестности точки (жо,Уо). Если к тому
же у'(жо) = tga, т.е. tga = /(жо, уо), то поставленная задача имеет единственное решение. Если
же tga Ф /(ж0, уо), то эта задача решений не имеет.
Пусть п = 2. Тогда задача у" = /(ж,у), у(ж0) = Уо, у'(жо) = tga, в силу непрерывности
функций /, -fa, -д^г = 0, имеет единственное решение в достаточно малой окрестности точки
^0)y0,g)
Наконец, если п ^ 3, то задача у(п) = /(ж, у), у(ж0) = уо, у'(жо) = tga имеет бесчисленное
множество решений вследствие того, что задача у(п) = /(ж, у), у(ж0) = уо, у'(жо) = tg«. 2/"(ж0) =
= Уо> • • • i^""''(жо) = Уо""" имеет единственное решение в достаточно малой окрестности точки
(ж0, yo,tga, уо» ••• ,Уоп1))- Другими словами, в силу произвольности чисел yd', yd",... ,уоп~1} за-
задача у<п'= /(ж, у), у(ж0) = уо. у'(жо) = tga (n ^ 3) имеет (п - 2)-параметрическое множество
решений.
Последний вывод можно отнести и к предыдущему примеру для случая п > 3. >
211. При каких п уравнение ;/<п) = /(ж, у) (/ и -щ непрерывны на всей плоскости жОу)
может иметь среди своих решений две функции: у\ = х и yj = ж + ж4?
+ В точке @, 0) имеем «,@) = j/2@), yi(O) = tf@), у'{@) = y?@), !/i"@) = y?(Q), y!v@) = 0,
у\ @) = 24, т.е. у\ @) Ф yi @). Видим, что п не может быть равно единице, поскольку через
точку @, 0) проходит два различных решения, а теорема единственности (см. п. 8.4) утверждает,
94 Гл. 1. Дифференциальные уравнения первого иорядка
что через каждую точку плоскости хОу проходит только одно решение. Далее, п ф 2, так как
в противном случае, согласно указанной теореме, через точку @, у@), у'@)) проходила бы лишь
одна интегральная кривая. По этой же причине п ф 3, п ф 4.
Пусть п = 5. Тогда задача yv = /(ж, у), у@) = 0, у'@) = 1, у"@) = у'"@) = ylv@) = О
может иметь решение yt = х, а задача у = /(ж, у), у@) = 0, у'@) = 1, у"@) = у'"@) = О,
ylv@) = 24 — решение у2 = х + ж4. Это объясняется тем, что в пространстве переменных
(ж) J/i J/'i J/"у'"> yIV) кривые у, и у2 не совпадают ни в одной точке, т.е. могут быть решениями
одного и того же уравнения у = /(ж, у) (заметим, что функции /, -^, ^Л 4V i
здесь непрерывны). Указанные кривые не совпадают ни в одной точке и в пространстве пере-
переменных (х, у, у', у", у'", yJV, yv, ...), поэтому уравнение у(я) = /(ж, у) может иметь их в качестве
решений и при п > 5. Тривиальные примеры: yv = 0, у = 0. >
212. Пусть функция / непрерывна и при каждом х не возрастает при возрастании у. Дока-
Доказать, что если два решения уравнения у' = /(ж, у) удовлетворяют одному и тому же начальному
условию у(х0) = уо, то они совпадают при х ^ х0.
А Почленно вычитая из тождества у\ = /(ж, у](ж)) тождество у'2 = /(ж, у2(ж)) и вводя в рас-
рассмотрение функцию и, где и(х) = yi(x) - у2(ж) (ж ^ ж0), получаем задачу
- /(ж, у2(ж)), и(ж0) = 0, ж ^ ж0, A)
которая имеет очевидное решение и(х) = 0. Докажем, что других решений нет. Применим метод
доказательства от противоположного. Пусть существует такое ж > ж0, для которого и > 0. Тогда,
в силу непрерывности функции и, найдутся такие два числа Si ^ 0 и е2 > е\, что и(х) > 0 при
Жо ^ х0 + Si < х ^ хо + е2, причем, уменьшая е,, всегда можно иметь и(х0 + еО = 0. Интегрируя
в A), получаем
х
u(x)= j (f(t,y2(f) + u(t))-f(t,y2(t)))dt, xelxo + e^xo + ej. B)
xo+t,
Поскольку u(t) ^ 0 при t e [x0 + Si, ж], то, в силу невозрастания функции f(t, у) по у, справед-
справедливо неравенство
/ (*, »@ + «(*)) - /(*, »2(*)) < 0. C)
Принимая во внимание C), из B) находим, что и(х) ^ 0 при х 6 (жо + Si, х0 + s2]. Таким
образом, пришли к противоречию, из которого следует,что функция и не может быть положи-
положительной ни при каком х > х0. Аналогично устанавливаем, что и не может быть отрицательной.
Следовательно, и(х) = 0 при всех ж ^ ж0. >
213. Сколько производных имеют решения следующих уравнений и систем в окрестности
начала координат?
а)у' = ж + у?; б) у' = х\х\ - у2; в) у" = |ж3| + у!; г) /' = у - х&х~;
dx dy ¦, dx , ir- dy ,
¦4 Применяем теорему о дифференцируемости решений уравнения -^ = /(ж, у) в окрест-
окрестности точки (жо, уо), в которой утверждается, что если функция / имеет в этой окрестности
непрерывные частные производные до fc-ro порядка включительно, то решение указанного урав-
уравнения с начальным условием у(жо) = Уо имеет непрерывные производные до к + 1 -го порядка
включительно. Аналогичное утверждение справедливо и для случая, когда / — вектор-функция.
а) Имеем /(ж, у) = ж + уЗ, f? = 1, Ц = 'у!, 0 = 0, 0 = f y5, J^ = 0,
я~т = Щу'ъ'• Видим, что функция / дважды непрерывно дифференцируема в окрестности
начала координат. Следовательно, в силу приведенной выше теоремы, задача у' = х+у 3, у@) = 0
имеет в окрестности начала координат трижды непрерывно дифференцируемое решение у = у (ж).
§ 8. Существование и единственность решения 95
б) Так как функция /(ж, у) = ж|ж| — уг имеет непрерывные частные производные -jfe = 2\х\,
— — 2у и не дифференцируема дважды в окрестности начала координат (поскольку функция
-fit = 2\х\ не дифференцируема при х = 0), то решение у = у(ж) задачи у' - х\х\ - у2, у@) = 0
дважды непрерывно дифференцируемо.
в) Поскольку функция /(ж, у, у') = |ж3| + у з имеет непрерывные производные -gr = -jy з
= 0 в окрестности начала координат, то, согласно теореме существования п. 8.4, задача
у" = |ж3| + у 5, у@) = 0, имеет единственное непрерывное решение у = у (ж) в этой окрестности.
Подставляя у(х) в данное уравнение, получаем тождество
") \3\ Ц)
из которого следует, что функция у" непрерывна. Дифференцируя это тождество, находим:
у'"(ж) = 3xhgnx + -уЦх)у\х), A)
у'\ж) = 6\х\ + j у-Чх)у\х) + ^ уЦх)у"(х). B)
В силу того, что правая часть уравнения A) непрерывна в окрестности начала координат, а правая
часть уравнения B) разрывна при у = 0, то можно гарантировать существование непрерывной
третьей производной решения рассматриваемой задачи.
г) В силу того, что
iv / 4 i v „ 4 „а
У =У~2Х' У =У ~9Х '
задача у'" = у - xj/x, у@) = у'@) = у"@) = 0 имеет четырежды непрерывно дифференцируемое
решение у(х) в окрестности начала координат.
д) Функции fi(t, х, у) = t + у, f2(t, х, у) = х + t2\t\ непрерывны и имеют непрерывные
частные производные
«/ a/ «/ 9Л df2_ dh
It1' ^0) dyh дГзт' Ж1' ~ду~~ '
aV ^/^/ d2f 92f Э2/. =
ж
в окрестности точки (<0, »о, Уо), где t0 = ж0 = уо = 0, поэтому данная система уравнений имеет
трижды непрерывно дифференцируемое решение (ж(<), у(<)) в этой окрестности.
е) В этом случае функции /,(<, ж, у) = у + v^, /2^, ж, у) = у'ж непрерывны в окрестности
Я f 1 2
точки @, 0, 0), однако, поскольку производная -jg2- = ¦j*" разрывна в этой точке, то мож-
можно гарантировать только непрерывную дифференцируемость решений ж(<), y(t) данной системы
уравнений. >
214. При каких а каждое решение продолжается на бесконечный интервал —оо < ж < +оо
а) для уравнения у' = |у|а?
б) для уравнения у' = (у2 + е*)а?
в) для уравнения у' = \y\"~l + {{x^/yyj ?
г) для системы у' = (у2 + z2 + 2)"", z' = уA + z2)"?
1 1
¦^ а) Пусть a < 0. Тогда у ^ 0 и решение данного уравнения у = A — a) i-« ж i-« (sr > 0) не
1 1
продолжимо влево. Пусть а > 1. Тогда решение у = (a—I) i-« (С — ж) i-« не продолжимо правее
точки х — С, так как прямая х = С является асимптотой для этого решения. Если a = 0, то
уравнение у* = 1, где у # 0, также имеет непродолжимые решения вида у = ж + С (ж ^ —С).
96 Гл. 1. Дифференциальные уравнения первого порядка
При а = 1 все решения уравнения у = \у\ описываются с помощью формул у = \С\ех и у =
= -\С\е~х. Очевидно, что каждое из них продолжается на бесконечный интервал — оо < х < +оо.
Наконец, если 0 < а < 1, то все решения имеют вид
г/ = A-а)Т^(ж-С)Т^, (О О, 2/ = -A-а)Т^(С~ж)Т=г, (х^С), у = 0.
Легко видеть, что первое решение является продолжением второго. Таким образом, если 0 < а ^
= 1, то все решения рассмотренного уравнения продолжимы на всю ось Ох.
б) Так как функция f(x, у) — (у2 + ех)а вместе с частной производной -$- = 2ау(у2 + ех)"~'
непрерывна в любой окрестности начала координат, то согласно теореме существования через
каждую точку этой окрестности проходит одна интегральная кривая. Однако не при каждом а
все интегральные кривые имеют своей областью определения всю ось Ох. Так, если а > -j, то
в силу оценки у' = (у2 + ех)а > (у2)" = \у\2а (х > 0) и предыдущего примера заключаем, что ни
одно решение уравнения у' = (у2 + ех)п не продолжимо вправо (решения обязательно будут иметь
вертикальные асимптоты).
1 -i -
Пусть а ^ j и х ^ 0, тогда (у + ех)" ^ (у + ех)г ^ \у\ + е?. Таким образом, справедлива
формула D), п. 8.3. Значит, каждое решение данного уравнения продолжимо на полуинтервал
0 < х < +оо. Если 0 ^ а ^ -j, то они продолжимы и левее нуля, так как при х < 0
(у2 + ех)" ^ (у2 + If ^ (у2 + \)Х2 ^\у\ + \.
и применимо утверждение п. 8.3. При х ^ 0 и а ^ 0 имеем оценку
{у2 + еУ^е*\
из которой на основании указанного утверждения следует, что все решения уравнения продол-
продолжимы левее нуля и при а ^ 0. Таким образом, если а ^ -j, то каждое решение уравнения,
существующее в окрестности начала координат, непрерывно продолжимо как левее, так и правее
нуля на бесконечный интервал, т.е. оно продолжимо на всю ось Ох.
в) Очевидно, при а ^ 1 не каждое решение уравнения продолжимо на всю ось Ох, т. к.
у ф 0 (при а < 1 |j/|"~' + \{X\/y)j —* +оо при у —> 0, следовательно, интегральные кривые
приближаются к оси Ох под прямым углом и не определены при у = 0; при а = 1 правая часть
уравнения не определена в точке (х, 0)). Если а > 1, то правая часть уравнения непрерывна,
следовательно, уравнение имеет решения в окрестности любой точки плоскости хОу.
Очевидно, что каждое решение у{х), для которого \у(х)\ ^ 1, продолжимо на всю ось Ох,
поэтому будем считать, что существуют такие х, для которых справедливо неравенство \у{х)\ > 1.
Тогда при I < a ^ -j имеем оценку
м-1 + ((хш2)а - \уГ' + \х\2аФ = wa (м2а + м?-1) ^ Mhw2a + 1к м
В силу утверждения п. 8.3 и последнего неравенства заключаем, что если 1 < а ^ -j, то каждое
решение уравнения продолжимо на всю ось Ох.
Если а = -j + е (е > 0), то при |ж| > 1 имеем оценку
у' = \УГ2+'+1х?+2Ъ\1+2>С>\у\1+г>С-
Следовательно, при а > -j и |ж| > 1 решения данного уравнения растут быстрее решений урав-
уравнения у' = \у\ +5?, исследованного в примере а), т.е. не продолжимы.
г) Поскольку правые части системы уравнений непрерывны вместе со своими частными про-
производными по у и z при любом а во всем пространстве переменных (ж, у, z), то в окрестности
любой его точки существует единственное решение данной системы.
Пусть а ^ 0. Тогда для суммы квадратов правых частей уравнений при y2+z2 ^ 2 справедлива
оценка
§ 8. Существование и единственность решения 97
где г2 = у2 + z2, из которой при —4а - 2 ^ 0, т. е. при а ^ — \ следует, что
I/I = vV + 2)-2a + y\\ + z2Ja < гA + 4"a)i
Ha основании полученной оценки и утверждения п. 8.3 заключаем, что при — -j ^ а ^ 0 все
решения системы продолжимы на всю ось Ох.
Пусть а > 0. Тогда из первого уравнения системы можно получить оценку
\у\ ^ Ы +
7 dx
J (у2 + ^ -
+ 2)"
Ы +
dx
= Ы + \х - хо\,
где (жо, Уо) — произвольная точка. Как видим, решение у(ж) продолжимо на всю ось Ох. На
основании последней оценки правая часть второго уравнения при а < j оценивается следующим
образом:
у (l + z2)"\ «С \y\ (l + z2) Ч (Ы
I* -
+ D-
, то решения системы продолжимы
Отсюда в силу утверждения п. 8.3 следует, что если 0 < а j
на весь интервал —со < х < +оо.
Пусть а < - \, тогда у' > |у|~2а. Следовательно, решения уравнения у' = (у2 + z2 + 2)'" при
а < - \ не продолжимы, так как растут быстрее, чем решения уравнения у' = \у\~2а, имеющие
асимптоты (см. пример а)).
Пусть а > j. Тогда, как мы видели, все решения у (ж) продолжимы на всю ось Ох. Возьмем
кривую у = у(х) с начальным условием у@) = 0. В силу того, что у' > 0, функция у = у(ж)
возрастает (значит, она положительна при х > 0). Следовательно,
X
у(<) dt —> +00 При X —V +ОО.
Далее, интегрируя второе уравнение системы, получаем
A)
Поскольку
= у y(t)dt
о
сходится, то отсюда и из A) вытекает, что х —> ж, при z —> +оо (ж, < +оо),
т.е. прямая х — Х\ является асимптотой для решения z = z(x).
Итак, исходя из полученных результатов, заключаем, что лишь при \а\ ^ ^ все решения
системы продолжимы на интервал —оо < х < +оо. >
215. Для следующих уравнений доказать, что решение с произвольным начальным условием
у(жо) = уо существует при х0 ^ х < +оо и имеются решения, непродолжимые на полуинтервал
-оо <х ^ х0:
а) у' = ж3 - у3; б) у = ху + е~*.
¦4 Функции /,(ж, у) = ж3 - у3, /2(ж, у) = жу + е~у непрерьшны вместе с частными производ-
производными -jjfr- = —Зу2, -fy- = ж - е"*, поэтому согласно теореме существования п.8.1 через каждую
точку плоскости жОу проходит одна гладкая интегральная кривая, своя для каждого из уравнений
в а) и б). Покажем, что все кривые продолжимы на полуинтервал [жо, +оо).
а) Прямая у = ж делит плоскость жОу на две части, в левой из которых все решения у(х)
убывают, так как у'(ж) < 0, а в правой части — возрастают в силу того, что у'(х) > 0. При этом
ни одна интегральная кривая не может выйти из правой полуплоскости, поскольку для этого ей
пришлось бы пересечь прямую у = ж, на которой у' = 0. Следовательно, ни одна кривая в
полуплоскости ж > у асимптот не имеет, т.е. она продолжима на полуинтервал [Жо, +оо).
98 Гл. 1. Дифференциальные уравнения первого иорадка
Заменив в данном уравнении ж на —ж, получим уравнение
из которого интегрированием находим
} dt } dt
х~Ха = J ~хЦ^ъ ^ J х~Г^ (ж ^ ж°; у ^ Уо'' жо + Уо > 0).
» и °
Поскольку интеграл справа при у -+ +оо сходится, то х —> Ж[ при у —> +оо, где хх > х0. Значит,
каждое решение уравнения у' — ж3 - у3 не продолжимо на полуинтервал (—оо, Жо].
б) Поскольку у' = 0 при ху + е~у = 0, то кривая ж = —^у делит всю плоскость жОу на три
области, в каждой из которых решения или убывают, или возрастают. Исследуем эту ситуацию
подробнее.
Возьмем произвольную точку (ж0, уо) в области, определяемой неравенствами жу + е~у < 0,
х < 0. Поскольку в этой области у' < 0, то ордината кривой, проходящей через точку (х0, уо),
убывает и принимает минимальное значение на кривой жу + е~у — 0 (ж < 0). Перейдя через
кривую жу + е~у = 0, интегральная кривая попадает в область, где у' > 0. При этом ордината
интегральной кривой возрастает, однако в силу оценки
и утверждения п. 8.3 рассматриваемая интегральная кривая асимптоты не имеет, т. е. продолжима
вправо при х > 0.
Теперь возьмем произвольную точку (жо, уо) в области, где ху + е~у > 0. Так как у' > 0
в этой области, то решение у = у(х), у(ж0) = Уо, возрастает. Если кривая попадает в верхнюю
полуплоскость, то решение, как мы видели, продолжимо вправо. Если же она попадает в область
жу + е~у < 0, у < 0, то в силу отрицательности производной решение у = у (ж) будет убывать.
Благодаря конструкции этой области (любая вертикальная прямая пересекает границу области
в двух точках) ни одна интегральная кривая не сможет выйти из нее, а значит, не может быть
продолжена при х > 0.
Покажем теперь, что уравнение имеет непродолжимые на полуинтервал (—оо, Жо] решения.
Заменив в уравнении х на —х и у па —у , получим
у = ху + еу ^ еу.
Поскольку уравнение у' = еу имеет при ж > 0 непродолжимые решения, то полученное уравне-
уравнение, решения которого растут еще быстрее при ж > 0, также имеет непродолжимые решения. >
216. Пусть на всей плоскости жОу функции / и -*? непрерывны и * jf' ^ ^ -йГ(ж),
функция К непрерывная. Доказать, что решение уравнения у' — fix, у) с любым начальным
условием у(ж0) = Уо существует при ж0 ^ ж < +оо.
А Из двух дифференциальных задач
У = /(»> У), У(жо) = Уо; z = K(x)z, г(ж0) = у0,
вторая из которых является вспомогательной, почленным вычитанием получаем задачу
и = Q(x) + Р(х)и, и(ж0) = 0,
где и(ж) = у(ж) - z(x), Q(x) = /(ж, г(ж)) - K(x)z(x), а Р(х) = ^ '^{2{Ш{ " может быть
представлено в виде Р(х) — ' & ^
между графиками у (ж) и z(x).
Решение полученной задачи имеет вид
, где ?(ж) — некоторая функция, график которой лежит
X . X ¦.
"(я) = / <?(<) ехр I У P(s) ds J dt,
10 Ч '
§ 9. Особые решения 99
откуда в силу условия задачи следует, что
Ых)\ 4
X , X »
J\Q(t)\expUK(s)ds)dt = Ф(х).
Так как функция К непрерывна при х ^ Жо, то решение z = z(x) существует при ж ^ ж0 и
непрерывно. А тогда в силу непрерывности функции / и функция Q также непрерывна при ж ^
^ ж0. Следовательно, при ж ^ ж0 непрерывна и подынтегральная функция в последнем интеграле,
который также непрерывен. Таким образом, при всех ж ^ ж0 имеем
z(x) — Ф(ж) ^ у(ж) ^ z(x) + Ф(ж),
откуда на основании локальной непрерывности функции у = у(ж) следует ее существование
и непрерывность при ж ^ ж0. >
217. Дана система в векторной записи у' = /(ж, у), удовлетворяющая условиям теоремы
существования в окрестности каждой точки (ж, у). Пусть в области \у\ > 6 при всех ж
у/(ж, у) ^ К{х)\у\\
где у • / — скалярное произведение, а функция К непрерывна. Доказать, что решение с любым
начальным условием у(ж0) = уо существует при ж0 ^ х < +оо.
•4 Умножив скалярно обе части данного уравнения на вектор-функцию у = у(ж) и обозначив
|у|2 = и(ж), получим
и = 2у • / ^ 2К(х)и, и > Ь2,
откуда
..' / г \
K(t)dt),
или окончательно
w>.
Так как функция К непрерывна при х ^ х0, то функция Ф также непрерывна при х ^ х0,
следовательно, функция \у\ продолжима на полуинтервал [Хо, +оо). >
Примечание. Из неравенства \у\ ^ Ф(х) еще не следует продолжимость функции \у\ на полуинтервал
[х0, +оо), если при этом не будет гарантировано существование решения в окрестности каждой точки
полуплоскости х > Xq плоскости хОу.
§ 9. Особые решения
9.1. Особое решение. Дискриминантная кривая.
Решение у = у(ж) дифференциального уравнения F(x, у, у') = 0 называется особым, если в
любой окрестности каждой его точки проходит другое решение, имеющее в этой точке общую
с ним касательную.
Пусть функция F = F(x, у, у') непрерывна и имеет непрерывные частные производные пер-
первого порядка. Геометрическое место точек <р(х, у) = 0, получаемых путем исключения у' из
уравнений
F(x,y,y) = 0, — = 0, A)
называется дискриминантной кривой дифференциального уравнения F(x, у, у') = 0. Следует про-
проверить, является ли ветвь дискриминантной кривой, удовлетворяющая этому дифференциальному
уравнению, особым решением, т. е. касаются ли ее в каждой точке другие решения.
Аналогично поступаем с геометрическим местом ф(х, у) = 0, удовлетворяющим условиям
, У, у') = 0, — ' У> У — неограниченная.
ду
100 Гл. 1. Дифференциальные уравнения первого порядка
9.2. Огибающая как особое решение.
Семейство интегральных кривых Ф(ж, у, С) = 0 уравнения F(x, у, у') = 0 может иметь оги-
огибающую у = <р(х). В таком случае кривая у = <р(х) является особым решением указанного
уравнения. Если функция Ф = Ф(х, у, С) непрерывно дифференцируема, то огибающая удовле-
удовлетворяет системе уравнений
д^^=0. B)
Вообще говоря, системе B) удовлетворяет дискриминантная кривая семейства Ф(ж, у, С) = 0.
Для отделения от дискриминантной кривой некоторой ее части, состоящей из особых точек,
можно пользоваться условием:
2 2
на кривой, не состоящей из особых точек.
Оставшаяся часть дискриминантной кривой может оказаться огибающей. Если, в частности,
эта часть не принадлежит рассматриваемому семейству, то она заведомо будет огибающей.
В следующих задачах найти все решения данных уравнений и вьщелить особые решения, если
они есть.
218. у'2-у2 = 0.
А Функция F(x, у, у') = у' - у2 непрерывно дифференцируема, поэтому если данное урав-
уравнение имеет особое решение, то оно удовлетворяет системе A), п. 9.1: у' — у2 = 0, 2у' = 0, из
которой путем исключения у' получаем у = 0. Кривая у = 0 является решением рассматривае-
рассматриваемого уравнения, однако утверждать, что оно особое, мы пока что не можем.
Найдем остальные решения этого уравнения. Имеем у' = ±у, откуда интегрированием на-
находим у — C\tx, а также у = Cit~x. Теперь видим, что ни одна интегральная кривая из двух
полученных семейств не касается кривой у = 0 (за исключением, естественно, ее самой). Следо-
Следовательно, решение у = 0 не является особым. >
219. (у' + 1K = 27(х + у)\
¦4 Полагая х + у = и(х) и разрешая уравнение относительно производной, получаем
и = Зиз,
откуда и = (х + СK, или у = (х + СK - ж. Из системы уравнений
.(*, у, С) = х + у - (х + Cf = 0, -3(* + СJ = 0
следует, что кривая у = —х является дискриминантной кривой семейства интегральных кривых.
Так как на дискриминантной кривой
и эта кривая семейству не принадлежит, то решение у = — х является особым. >
22О.у'2=4у3A-у).
А Разрешаем уравнение относительно производной
у' = ±2^/у3A - у)
и интегрируем полученные уравнения:
sin'i
где положено y = sin<@<<< -j). Принимая во внимание и очевидное решение у = 1,
окончательно имеем
1
§ 9. Особые решения 101
Из уравнений
( 2) ^(( 2)l) =0
находим дискриминантную кривую у = 1. Поскольку на дискриминантной кривой
дФ\2
~дх)
и у = 1 семейству A) не принадлежит, то у = 1 — огибающая этого семейства. Следователь-
Следовательно, у = I — особое решение данного дифференциального уравнения.
Если для отыскания дискриминантной кривой воспользоваться системой уравнений A), п. 9.1,
то, кроме кривой у = 1, можно получить еще решение у = 0. Однако, как видно из A), ни одно
решение этого семейства (исключая, естественно, решение у = 0, получаемое из A) при С = со)
не касается решения у = 0. Таким образом, решение у = 0 не является особым. >
221. y'3 + y2 = yy'(y' + i).
¦^ Решив уравнение относительно производной, получим два дифференциальных уравнения:
у' = у; у' = ±W-
Проинтегрировав их, находим
_ 1 2
'4
Из уравнений
Ф = 4у - (ж + С2J = 0, -2(х + С2) = 0
следует, что у — 0 — дискриминантная кривая. В силу условия
дФ\2 /дФ\2
дх) \ду)
выполняющегося на дискриминантной кривой, и того, что кривая у = 0 семейству Ф(х, у, С) = 0
не принадлежит, заключаем, что у = 0 — огибающая семейства у = у(х + С2J, следователь-
следовательно, у = 0 — особое решение. >
222. 4A - у) = (Зу - 2Jу'\
А Имеем
у' = ±2^Щ (уф2-, y^lV
у |Зу-2| V 3' *^ /'
откуда
или
у2A-у)-(Ж + СJ = 0.
Кроме того, у = 1 — очевидное решение. Из уравнений
Ф = у2A-у)-(ж + СJ = 0, -2(х + С) = 0
следует, что у2A - у) = 0, или у = 0, а также у = 1. Так как у = 0 не является решением,
а на кривой у = 1, которая, очевидно, семейству Ф(х, у, С) = 0 не принадлежит, выполняется
условие
U
то у = 1 — особое решение. >
223. у' - ху + ^У = 0.
¦^ Полагая v/y = z, получим линейное дифференциальное уравнение
2z'-xz + l= 0,
102 Гл. 1. Дифференциальные уравнения первого порядка
проинтегрировав которое, находим
2=-(С-ж)е§.
Таким образом, общее решение исходного уравнения имеет вид
у=1-(С-хJех. A)
В процессе интегрирования было потеряно решение у = 0. В силу неограниченности произ-
производной -щ = х — Tjy ПРИ У = 0' где /(z> У) = ХУ ~ Vv — правая часть рассматриваемого
дифференциального уравнения у' = f(x, у), решение у = 0 может быть особым. Из уравнений
- У ;j , дс ~ 2 ~
также следует, что кривая у = 0 может быть особой. Так как
к\ 2
на этой кривой, а сама кривая семейству A) не принадлежит, то, согласно п. 9.2, решение у = 0
особое. >
224. у' = <р(х)\у\а @ < а < 1), где <р — непрерывная функция, отличная от тождественного
нуля.
•4 Пусть у > 0. Тогда, разделяя переменные и интегрируя, получим
у= (c + (\-a)Jv(x)dxy~a. A)
Так как производная щ(ч>(х)\у\а) не ограничена при у = 0, то, согласно теореме существования
единственного решения для уравнения у' = /(ж, у), решение у = 0 может быть особым. Из
уравнений
~а =0, ^ = -j±^ (с + (I - a) J <p(x)dxy~a =0
находим, что у = 0 — дискриминантная кривая семейства A). В силу условия
\
выполняющегося на дискриминантной кривой, и того, что кривая у = 0 не принадлежит семей-
семейству A), заключаем, что у — 0 — огибающая семейства A), т.е. у = 0 — особое решение.
При у < 0 аналогичным путем получаем другое семейство интегральных кривых, для которого
кривая у — 0 также является огибающей. >
225. Показать, что функция у — гр(а;) — особое решение уравнения
где <р — непрерывная, а гр — непрерывно дифференцируемая функции на интервале (а, Ь),
причем ^i Ф 0 на (а, V).
А Полагая у = z(x)tp(x), получим дифференциальное уравнение
где функция ™V непрерывная, поэтому (см. пример 224) решение z = 1 — особое, а тогда
и у = ф(х) — особой решение исходного уравнения. >
§ 9. Особые решения 103
226. Показать, что функции у = ±ip(x) — особые решения уравнения
где 0 < а < 1, tp, хр' — непрерывные на интервале (а, Ь) функции и Уж € (а, Ь) ip(x) ф 0.
¦4 В результате замены у — z(x)ip(x) получаем дифференциальное уравнение
z' = C(x)\z2-l\a,
где р = ^\гр\2а — непрерывная функция. Полагая в последнем уравнении z - 1 + е(х), где
/ It f s(t) \а \ 1-а
е(х) = \2a(\-a)jl3(t){\ + ~-J dt + CJ , x G (a, b), х0 е (a, b).
s(x) > 0, и интегрируя полученное уравнение, находим
A)
' " V 2 J )
Очевидно, дифференциальному уравнению е' = (ЗеаB + s)a удовлетворяет также функция е = О
на (а, Ь). Покажем, что в каждой точке х0 € (а, Ь) функции е и s = 0 имеют общую касательную.
Из A) имеем
В точке касания с абсциссой х0 должны выполняться условия
?(х0) = 0, s'(x0) = 0. C)
Из B) и C> следует, что С = 0. Таким образом, любая функция, определяемая уравнением
?(*)=B»A-а)//3(Ы1 + Ч?) dfl'a
4 ^0
тождественно равна нулю на (а, Ь). Это означает, что решение s — 0 — особое, т.е. решение
у = гр(х) — особое для данного дифференциального уравнения.
Аналогично доказывается, что решение у = —^(х) также является особым. >
Найти особые решения, не интегрируя самого уравнения.
227. у'\х2 - Ь) - 2*2/1/ - х2 = 0.
-< Разрешая уравнение относительно производной, получаем
, ^ xy±\xWy2+x2-b
У х2 - Ь
Если \х\ > Ь, то через каждую точку плоскости хОу проходит единственное решение каждого
из двух дифференциальных уравнений A), так как в этом случае их правые части непрерывные
и имеют непрерывные частные производные по у.
Пусть \х\ < Ь. Тогда условия непрерывности нарушаются на кривой х2+у2 = Ь. Однако в силу
лишь достаточности этих условий (достаточности для существования единственного решения), мы
не можем утверждать, что указанная кривая представляет собой особое решение.
Применим результат решения примера 226. Здесь функции <р(х) — ± \х' и гр'(х) — —-?=—у
X — О V О — X
непрерывны при \х\ < Ь, а = ^, следовательно, решения у = ±ф(х) — ±Vb — х2 — особые для
каждого из уравнений A), т. е. кривая х2 + у2 = Ъ действительно является особой. >
228. у-2ху' -у'2 =0.
¦^ Здесь F(x, у, у') = у- 2ху' - у' , частная производная щ- = 1 ограничена, а из уравнений
F — у - 2ху' -у1 =0, ^-т = —2х — 2у' = 0 следует, что особым решением может быть только
функция у = -х2. Однако, как легко проверить, у = —х2 не является решением уравнения,
следовательно, особых решений нет. >
104 Гл. 1. Дифференциальные уравнения первого порядка
229. /
•4 Разрешая уравнение относительно производной, получим
Полагая здесь и = у+ ~^(х4 + АхЛ , имеем
и = ±Vl + х2</п, и ^ 0.
Так как функции ±\/1 + х2 непрерывны, то, согласно примеру 224, решение и ~ 0 — особое.
А тогда у = - jg (х4 + 4х2) является особым решением исходного уравнения. >
230. уV2
х
¦^ Полагая у2 = 2и и разрешая полученное уравнение относительно и', находим
и = - ± -г-;\/и2 - а2х2, и > 0.
х \х\
Применим результат решения примера 226. В данном случае
ш = *' v{x) R
есть непрерывные при х ф 0 функции, а а = ^. Следовательно, и = ±ах (х Ф 0) — особые
решения. Тогда у2 = 2\ах\ является особым решением исходного уравнения при х ф 0. >
231. х + щ/-а/ = 0.
•4 Из уравнений
2 8F
F = x + yy -ay = 0, — = у - lay = 0
путем исключения у' находим кривую у2 + 4ах = 0, которая, как нетрудно непосредственно
проверить, не есть особая, поскольку функции у = ±2\/-ах не являются решениями данного
дифференциального уравнения. >
232. уу'1+у'(х-у)-х = 0.
¦^ Разрешим уравнение относительно у'. Получим
у'=\, уфО и у' = --, уфО.
У
Поскольку правые части полученных дифференциальных уравнений и их частные производные
по у разрывны только при у = 0, а функция у = 0 не является решением данного уравнения, то
особых решений нет. >
233.4y3-4y2=(l+a;2)/.
¦4 Записав уравнение в виде F(x, у, у') = 0, где F (х, у, у') = 4j/3-4j/2-N+a;2jj/' иисключив
у' из системы уравнений
ft P
F(x, у, у) - 0, — = 2у'(l + х2) = 0,
получаем уравнение у3 — у2 = 0, содержащее решения исходного дифференциального уравне-
уравнения у = 0 и у — 1, которые могут быть особыми.
Разрешив данное уравнение относительно производной, имеем
У ~
Поскольку правая часть уравнения A) существует при у ^ I и у = 0, то решение у = 0 является
изолированным. > (
§ 9. Особые решения 105
Примечание. Решение у = <р(х) называется изолированным, если в некоторой его Окрестности не проходят
другие интегральные кривые.
Полагая в A) у = 1 + е(х), где 0 ^ е(х) < 1, и пренебрегая функцией е 5 (х), можем записать
B)
+x2
Приближенное уравнение B) имеет решение е(х) = 0, которое, как следует из примера 224, есть особое.
А тогда для уравнения A) решение у = 1 также будет особым.
234. Найти особое решение дифференциального уравнения, если известно семейство реше-
решений этого уравнения.
а)у=Сх2-С2; 6)ху = Су-С2; в)у = С2(х-СJ.
¦^ а) Так как функция Ф(х, у, С) = у - Сх2 + С2 непрерывно дифференцируема, то согласно
п. 9.2 дискриминантная кривая семейства интегральных кривых у - Сх2 + С2 = 0 удовлетворяет
системе уравнений
^ = -х2 + 1С = 0, Ф = у - Сх2 + С2 = 0,
4
из которой путем исключения параметра С следует, что у = ^-. Получили явное выражение для
дискриминантной кривой.
В силу того, что || = -2Сх = -х\ || = 1, (Ц)'+ (ffJ = 1 + *6 Ф 0 на дискрими-
4
нантной кривой, и кривая у = ^- данному семейству не принадлежит, то последняя является
огибающей, т. е. у = ^- — особое решение соответствующего дифференциального уравнения,
б) Аналогично предыдущему имеем
дФ
откуда С = | и /- 4ху = 0 — дискриминантная кривая, распадающаяся на две: у = 4х
и у = 0. На первой кривой (Ц)' + (Ц)' = 17х2 ф 0, на второй - (ff)' + (||J = х2 ф 0.
Так как кривая j/ = 4ж ни при каком С не принадлежит семейству Ф(ж, у, С) = 0, то согласно
п. 9.2 она является особым решением соответствующего дифференциального уравнения. Вторая
кривая у = 0 (а; ф 0) принадлежит указанному семейству, поэтому вопрос о том, является ли она
особым решением, остается открытым. Для решения вопроса представляем кривые семейства при
х фС в виде
С2
A)
Поскольку у'(х0) ф 0 при С ф 0, то кривые семейства A) не касаются кривой у = 0 (а; Ф 0),
значит, последняя по определению не является особым решением,
в) Исключая параметр С из уравнений
Ф(х, у,С) = у- С2(х -СJ=0, ~= 2С(х - С)BС - х) = 0,
получаем две ветви дискриминантной кривой
16
Поскольку первая ветвь данному семейству не принадлежит и на ней
то она является огибающей. Вторая ветвь принадлежит семейству, поэтому несмотря на то, что
Ощ = 1 Ф 0, нельзя утверждать, что она также будет огибающей.
106 Гл. 1. Дифференциальные уравнения нервого порядка
Проверим условия касания кривой у=0к остальным кривым семейства. Пусть хо — про-
произвольная абсцисса. Тогда из условия касания следует, что должны выполняться равенства
у'(хо) = 2С2(хо-С) = 0, у(х0) = С2(*о - СJ = 0, С =ё 0.
Легко видеть, что они выполняются при С = х0. Следовательно, через каждую точку (х0, 0) про-
проходит по меньшей мере две кривые: у = 0 и у = х$(х — х^J, имеющие в ней общую касательную,
поэтому кривая у = 0 является огибающей. >
§ 10. Задачи на траектории
10.1. Изогональные и ортогональные траектории.
Линии, пересекающие все кривые данного семейства плоских кривых под одним и тем же
углом <р, называются изогональными траекториями этого семейства. В частности, если <р = ^, то
изогональные траектории называются ортогональными.
Д^я. отыскания изогональных траекторий семейства кривых Ф(х, у, С) = 0 следует сначала
составить дифференциальное уравнение указанного семейства. Пусть F(x, у, у') = 0 — диффе-
дифференциальное уравнение данного семейства. Тогда уравнение
где т = tg <р (<р Ф зг), является дифференциальным уравнением изогональных траекторий, а урав-
уравнение
*¦(*. »,-^г)=0 B)
есть уравнение ортогональных траекторий. Проинтегрировав затем уравнение A) или уравне-
уравнение B), получим семейство изогональных или семейство ортогональных траекторий.
Если имеем семейство кривых Ф(р,в, С) = 0, заданное в полярной системе координат р, в,
и F(p,e, р') = 0 — дифференциальное уравнение этого семейства, то изогональные траектории
((р ф ^) можем найти, проинтегрировав уравнение
Для отыскания ортогональных траекторий следует проинтегрировать уравнение
р(рА-^)=о. D)
10.2. Эволюта и эвольвента.
Геометрическое место центров кривизны, отвечающих возможным точкам некоторой кри-
кривой Г, называется эволютой К этой кривой. Кривая Г по отношению к своей эволюте К на-
называется эвольвентой. Основное свойство, связывающее кривые К и Г, состоит в том, что каса-
касательная к эволюте является одновременно нормалью к эвольвенте. Таким образом, если известна
эволюта, то семейство эвольвент можно найти, рассматривая их как ортогональные траектории
семейства касательных к данной эволюте.
Пусть ? = ?(t), rj = rj(t) — параметрические уравнения эволюты. Тогда, использовав ука-
указанное выше свойство, параметрические уравнения семейства эвольвент х = x(t, С), у = y(t, С)
можно определить из системы дифференциальных уравнений
I ,_ 1 _ «Ь
Решив первое уравнение этой системы и подставив найденное х во второе уравнение, получим
параметрические уравнения эвольвенты.
§ 10. Задачи на траектории 107
Найти ортогональные траектории семейств линий.
235. у = ах".
¦4 Согласно п. 10.1, сначала составляем дифференциальное уравнение данного семейства
Ф(х, у, а) = у - ах". Имеем
дФ
Ф(г, у, а) = 0, — = у' - аах" = 0.
ах
Отсюда путем исключения параметра а находим нужное уравнение ху' — ау = 0. Заменив в по-
последнем уравнении у' на —г, получим дифференциальное уравнение ортогональных траекторий
- + ау = 0. A)
У'
Общий интеграл уравнения A) имеет вид
х2 + ау2 = С.
Таким образом, если а < 0, то семейство гипербол ортогонально другому семейству гипербол;
если а > 0, то семейство парабол ортогонально семейству эллипсов; наконец, если а = 0, то
семейство горизонтальных прямых ортогонально семейству вертикальных прямых. >
aL50. Bа — *?)у -- *? -
¦^ Исключая параметр а из системы
Bа - х)у2 - хъ = 0, -у + 2Bа - х)уу - Зж2 = 0,
получаем дифференциальное уравнение данного семейства:
2у'хъ - Ъх2у - уъ = 0.
Ему соответствуют дифференциальное уравнение ортогональных траекторий
2а;3 + (За;2;/ + уъ)у' = 0.
Последнее уравнение однородное. Решая его известным способом, находим общий интеграл:
Зи + и3 г dx
г Зи + и г ах
/ -з ; du + / — = lnC,
J «4 + Зи2 + 2 J x '
или
л/J i л X ~т*У — 2.QX.
¦4 Аналогично проделанному выше, имеем
х2 + у2- 2ах = 0, 2х + 2уу - 2а = 0,
откуда 2хуу' + х2 - у2 = 0. После замены в последнем уравнении у' на —г получим дифферен-
дифференциальное уравнение ортогональных траекторий
(У2 ~ *2)У' + 2ху = 0.
Это однородное уравнение. Полагая у = хи(х), имеем
dx и2 - 1
+ -; du = 0.
х «¦• + «
Общий интеграл этого уравнения имеет вид
х(и2 + 1) = Си, или х2 + у2 = Су. >
238. у2 - 2р(х - а) = 0.
¦4 Исключение параметра а из уравнений
у2- 2р(х - а) = 0, 2уу' -2р = 0
108 Гл. 1. Дифференциальные уравнения первого порядка
с одновременной заменой у' на —г приводит к дифференциальному уравнению ортогональных
траекторий
у+ру' = 0.
Интегрируя его, находим
у = Се~т.
Таким образом, исходное семейство парабол ортогонально семейству экспонент. >
Найти семейства изогональных траекторий линий.
239.х-у = х2 + а2 (v = f).
•4 Дифференциальное уравнение данных линий имеет вид
1 - у - 2х = 0.
Отсюда, используя уравнение A), п. 10.1, (т = 1), получаем дифференциальное уравнение изо-
изогональных траекторий
1 ¦ 2х = 0, или 1 — х — ху = 0.
Интегрируя последнее уравнение, находим требуемые траектории
у = In Cx — х. >
240. х2 + У2 = 2а (
¦< Заменяя в дифференциальном уравнении х2 - у2 + 2хуу' = 0 данного семейства производ-
ную у' на i ,, , согласно A), п. 10.1, получаем
у'(х2 ~у2 + 2ху) + х2~у2- 2ху = 0.
Интегрируя это однородное дифференциальное уравнение, находим
г 1 - 2и - и2 f dx у
/ 5 i du+ — = In С, где и = -,
J 1 -и + а2 -и3 J х х
откуда
х2 + у2 = С(х - у). >
241. z2 + y2 = a2 (tp = a).
¦^ Если в дифференциальном уравнении данного семейства х + уу' = 0 вместо у' подставить
-У ~/ё" (а ф ^), то получим дифференциальное уравнение изогональных траекторий
, ут - х
У = , m = tga.
хт + у
Перейдя к полярным координатам х = р cos в, у = р sin в, получим уравнение р + тр = 0, откуда
si -тв
р-Сч . >
242. р = a(l + cos0) (<р = f).
¦^ Исключив параметр а из уравнений
/9' = -asin0, /э = a(l + cos0),
получим дифференциальное уравнение данного семейства:
,9sin0 + (l+cos0)p' = 0.
Отсюда, согласно D), п. 10.1, находим дифференциальное уравнение ортогональных траекторий
р sin 0 - A + cos в)р = 0,
которое можно записать в виде
1+COS0 р
, sin 0 ~ р '
§ 10. Задачи на траектории 109
Проинтегрировав полученное уравнение, находим искомое семейство
p = Csin -, или р = C(l -cos0). >
243. p2 = lntg0 + C (<Р=%)-
¦^ Заменив в дифференциальном уравнении семейства
1
РР=^2~в
производную р на-^т, согласно D), п. 10.1, имеем дифференциальное уравнение ортогональных
к данному семейству траекторий
р + р3 sin 20 = 0.
Разделяя в нем переменные и интегрируя, находим требуемые траектории:
Р ~ С-cos20' *
-< Действуем по той же схеме, что и в предыдущем примере. Сначала получаем дифферен-
дифференциальное уравнение данного семейства:
Заменив в этом уравнении р' на р- Р +mP) t где т = tga (а ф \), согласно C), п. 10.1, имеем
Р тР
дифференциальное уравнение изогональных траекторий р'A + mtg20) = p(tg20 — т), рфО, или
- = tgB0 - a).
Р
Интегрируя последнее уравнение, находим семейство изогональных траекторий
С
к v/| cosB0 - a)\
245. р = a(l +cos0) ((р = а; а Ф ЗА.
Дифференциальное уравнение данного семейства имеет вид
р\\ +cos0) + /9Sin0 = 0.
Заменив здесь р на р? _тР, (т = tga), получим дифференциальное уравнение изогональных
траекторий:
р'A + cos0 - msin0) + р(т + тcos0 + sin0) = 0,
или
в в
р т cos -j + sin ^
cos^ - msin j
Проинтегрировав это соотношение, получим
1п/э= 21njcos^-msin^ +1пСь или р = Ccos2 {% +а) . >
246. р = ecos0 ^у> = а; а ^
-4 Заменяя в дифференциальном уравнении этого семейства
р' cos 0 + р sin 0 = 0
ПО Гл. 1. Дифференциальные уравнения первого порядка
производную р на р? _m^i (m = tga), согласно C), п. 10.1, записываем дифференциальное
уравнение изогональных траекторий:
р' tg0 + tga
— = --=¦ = -tg@+a).
р 1-tgatge
интегрируя которое, получаем исходное семейство:
р~ Ccos@ + a).
Очевидно, если а = 0, то полученное семейство, естественно, совпадает с данным в условии
задачи. >
Найти эвольвенты линий.
247. у = а сп — (цепная линия).
а
¦4 Запишем сначала параметрические уравнения цепной линии:
? = at, г) — acht,
а затем, вычислив производную rfc = -Л = sht, воспользуемся первым уравнением в E), п. 10.2.
Тогда получим
dn dx
d? = adt, dr) = ashtdt, r)'( = — =sht = . A)
df dy
Второе уравнение в E) примет вид
y = acht + sht(x-at). B)
Дифференцируя обе части B) и подставив dy в A), получим:
dx
~~(x
или
dx
xsht + cht— = atsint.
dt
Решая линейное уравнение с помощью метода вариации произвольной постоянной, находим:
С
х = a(t - tilt) +-—- C)
cht
Подставив значение х в B), имеем
Csht + a
y=~i±r- D)
Параметрические уравнения семейства эвольвент цепной линии имеют вид C), D). >
248. ? = a(cos< + <sin<)) Ц — a(sini — tcost) (окружность).
¦4 Действуя по той же схеме, что и в предыдущем примере, получим:
d? = atcost, dtj = atsint, — = tg<,
a?
y = a(sint — tcost) + tgt(x — a(cost + tsint)j, dy = \%tdx-\ — fa; — a(cosi + ts\nty\ dt,
dx dx
tet = -. , t-xtgt = asint(l +ttgt).
\gtdx + ^rt(x-a(cost+tsint))dt dt
Интегрируя полученное линейное уравнение с помощью метода вариации произвольной по-
постоянной, находим:
at
х = С cost н Bsint — tcost).
Тогда
( at2\
у = —atcost + I С — I sint.
Получили параметрические уравнения искомого семейства эвольвент. >
§ 10. Задачи на траектории
249. ? = a(t — sint), t] — а(\ - cost) (циклоида).
А Аналогично с проделанным выше, имеем:
dn t
d? = аA - cost)d<, dn = a sint dt, — = ctg -,
dt, 2
у = a(\ — cost) + ctg - fa; — a(t - sin t)j =2a + ctg - (a; - at),
t (x — at) t dx
dy = (dx - a dt) ctg - - ^ ¦ f dt, ctg-=--
2 2sin2 j 2 (da;-ad0ctg2-
После несложных преобразований получим линейное дифференциальное уравнение
dx х t a t
общий интеграл которого имеет вид
t
х — С sin - + a(t + sin t).
Тогда
у = аA - cost) + ctg- (С sin- + a(t + sint) - a(t -sint) j = С cos- +aC + cos<)-
250. ^ = a cos31, tj = a sin31 (астроида).
Ч Поскольку d^ = —Заcos21sint dt, dr] = 3asin2< cost dt, то
dn з з xdt
— = - tg t, у = a sin t — tg t(x - a cos t), dy = a cos t d< r tg t da;,
d? cos-* <
da;
tgt=-
acostdt-^f-tgtdx'
cos t
Из последнего равенства получаем линейное дифференциальное уравнение
da; з
h x tg < = a cos < tg <.
dt
Его общее решение имеет вид
а 2
х = С cost + - cost sin t.
Осталось найти у. Находим:
у = asin3t — tgt ( Ccos< + -cos<sin2< — acos3t J = -Csin< + a cos2 < sint + -sin3<.
Получили параметрические уравнения требуемых эвольвент:
a , a 7
х = Ccost + -costsin t, y= -Сsint + -sintA4-cos t). >
Как и в предыдущих примерах,
2 *Ч
dl] 1
имеем:
1 у *
dx
2 1
t (ЖЧ
da;
з
).
X
(X
у~ \t2
2t2
+2 Л_ t(t2 + 1) ~ t2
112
Гл. 1. Дифференциальные уравнения первого порядка
Применив к полученному линейному дифференциальному уравнению метод вариации произволь-
произвольной постоянной, находим:
Для определения у подставим полученное значение х во второе уравнение системы E), п. 10.2.
Имеем
Таким образом, параметрические уравнения эвольвент данной кривой записываются в виде:
х = It +
Ct
= t2-2-
Tt2 + V ' " Vt2 + 1
Упражнения для самостоятельной работы
Найти решения следующих задач.
X
oo/l 1 \
1./=еИЙ ¦ X*Q- 2-у =
71=1 \ /
3. ydx + {^xy-y/xjdy = 0, уA) = 1. 4. х2у' - cos2y -1=0, у(+оо) = ?тг.
+ОО X
5. (ж2 + 1)у' = 2ху, I y(x)dx сходится. 6. ^ Jy(t)dt = ку(х), уA) = 1, к = const.
о
Проинтегрировать уравнения.
&Ь. 8.y'=f+sinxtgf. 9.Bx-
7.y'=f+e
10.
5. 11.
Найти решения следующих задач Коши.
12. sin Bж++\3) dy + е*+*У+5dx = 0, у@) = 2.
13. (ж2у3 - у) dx - (х4уг- 2ж3у2 + 6х) dy = 0, уA) = 1.
14. (x'-^dx + yt (ж! -»§) dy = O, y(l)=l. 15. xy' = ycoslnf, y(l) = ef.
Проинтегрировать следующие линейные уравнения и сводящиеся к ним.
16. у = х(у'-xcosx). П. у' +ysinx = sinx. 18. (ху + ex)dx - xdy = 0.
19. у' = т-^Ч-- 20. у' + 2у = ех ¦ у2. 21. ху' - 2х2^у = 4у.
jX у
Построить общее решение уравнений в форме Коши.
22. у' +Уу±^т = е1. 23. у' +y(l + ж2) sinx = cosz. 24. у' +ytgx = cosz. 25. у' + f = х.
Решить следующие дифференциальные задачи.
26.
-l), y(e) = 2-5i. 27. ж2у' + у = е« Л"*/.,
[X -\- I)
28. у' = (Зх4у2 + у5) (ху4 + 2х5у)"', уA) = 1.
Проинтегрировать следующие уравнения Риккати.
[y(x)dx
< 00.
29. 2у' = жу + у2 + Л- - 3. 30. у' = ? - \ +х. 31. у' - 2жу + у2 = 5 - х2,
X
2
32. ху' -у2 + Bх + 1)у = х2 + 2х, J(x -yJdx=l.
= 1.
§ 10. Задачи на траектории 113
Проинтегрировать уравнения в полных дифференциалах.
33. A + у2 sin 2х) dx - ly cos2 xdy = 0ч. 34. Зж2A + In у) dx = Bу - ^- J dy.
Проинтегрировать уравнения, подобрав интегрирующий множитель.
36. ху2(ху' + 1) = 1. 37. (ж2 + 3\ny)ydx = xdy.
38. (ж2 + 2х + у)dx - (ж - Зж2у)dy = 0. 39. (ж1 - у)dx + x(y +l)dy = O.
Найти возможные особые точки, кривые и особые решения.
40. у' = VP. 41. у' = уу- 42- У' = VV + 1- «. у' = 2^/ху. 44. у'=
Решить уравнения путем сведения их к дифференциальным.
хх х
45. у(х) = х+ fex~'y(t)dt. 46. f(x - t)t2^/ylf)dt + \ I'Ex - 6t)y(t)dt + 2х = 0.
Глава 2
Дифференциальные уравнения
высших порядков
§ 1. Виды интегрируемых нелинейных уравнений
1.1. Дифференциальное уравнение вида F(x, у<п)) = 0.
Дифференциальное уравнение вида F(х, у<п)) = 0 может быть проинтегрировано, если урав-
уравнение F(x, и) = 0 можно разрешить или относительно и = <р(х) или же относительно х = ^(и).
Действительно, в первом случае имеем
у(п) = <р(х), у = [ J(x - tf-l<p(t)dt + Cix-1 + C2x"-2 + ...+ С-цс + С„ A)
' ха
где Cj (j = 1, n) — произвольные постоянные.
Во втором случае полагаем у(п) = t. Тогда х = i/>(t) и d(yin~l)) = tdx = Up'(t)dt, откуда
Аналогично находим у("~2>, у("~3), ... ,у = g(t) + w(t, С\, С2, ... ,С„), где д и ш — известные
функции. Таким образом, общее решение находится в параметрической форме
х = W), у = g(t) + w(t, СиСг,..., С,). B)
Иногда уравнению F(x, y(n)) = 0 удовлетворяют параметрические уравнения х = a(t), y(n) =
= /3(t), т.е. F(a(f), /3(t)) = 0 при t € (to, 'i)- Тогда, действуя аналогично изложенному выше,
получаем параметрические уравнения общего решения, имеющего вид B).
1.2. Дифференциальное уравнение вида F (г/п-|\ t/™*) = 0.
Если уравнению -P(u, v) = 0 удовлетворяют параметрические уравнения u = a(t), v = /3(t),
t 6 (to, t\), то дифференциальное уравнение вида F(y(n~i), y(n)) = 0 можно проинтегрировать.
Действительно, тогда
у("-!) = а@, (п)
и d(yin-{)) = /3(t)dx, или a'(t)dt = /3(t)dx, откуда
a'(t)
-г-
Pit)
Функцию у находим из дифференциального уравнения у'"' = a(t) способом, указанным в п. 1.1.
1.3. Дифференциальное уравнение вида F (у(™~2\ у(п)) = 0.
Пусть u = a(t), v = P(t) — функции, удовлетворяющие уравнению, указанному в п. 1.2. Тогда
дифференциальное уравнение вида F (у(п~2\ y(n)j = 0 можно проинтегрировать. Действительно,
имеем,
y"-2) = a(t
или, если ввести обозначение у(я 2) = z(x), то
z"(x) =
+ C2.
§ 1. Виды интегрируемых нелинейных уравнений 115
Из первого уравнения находим
z< х - ? а t - - z" х - а"Х> " Х"а'
dx x'' а;'3
Используя второе уравнение, получаем
" J т"п — т ft C}
Если положить х' = к, то уравнение C) примет вид
а"х - к а = /Зх\ D)
Это уравнение Бернулли. Пусть к = х' = <р(С, t) — его общее решение. Тогда
х= f ip(C, t) dt ¦
Для получения функции у = y(t) интегрируем п — 2 раза уже известным нам способом урав-
уравнение y(n) = a(t). Таким образом, получаем общее решение дифференциального уравнения
рассматриваемого вида в параметрической форме.
Проинтегрировать дифференциальные уравнения и найти частные решения там, где заданы
начальные условия.
252. у"' = а; + cos x.
< Последовательно интегрируя обе части уравнения три раза, получаем
у" = (х + cos x)dx + C{ = V sin x + С\,
J ?
Г (х2 \ ж3
у = / —- + sins + СЛ dx + С2 = — - cosx + Схх + Съ
J \2 ) 6
г /ж3 \ ж4 ж2
у = / I —- - совж + С,ж + С2 J dx + С3 = sin ж + Ci — + С2х + С3. >
253. ylv = e'-l, при ж0 = 0, у0 = 2, у'о = 1, у? = 1, у?" = 1.
•^ Сначала находим общее решение:
~2
х3 х2 х4 хъ х2
+C+C + C х С + С
+C2x + C3, у = е + С1 + Сг
Затем подбираем значение пока произвольных постоянных таким образом, чтобы удовлетво-
удовлетворить заданным начальным условиям. Имеем
1 = 1+С,, 1 = 1 + С2, 1 = 1+С3, 2=1 + С4>
откуда находим Сх = Сг = С3 = О, С4 = 1. Частное решение имеет вид
254. у' + sin у'" - 1 = 0, при жо = 1, уо = у'о = у'о = 2.
•^ Легко показать графически, что уравнение а5 + sin а — 1 = 0 имеет единственный действи-
действительный корень ар Следовательно, у'" = а\, откуда, последовательно интегрируя, получаем
х2 „ „ хъ _х2
у =a1-j + Cix + C2, y=aij + Ci
Дяя определения постоянных интегрирования пользуемся начальными условиями. Имеем
2^ + !
откуда находим Ci=2-a1,C2=5|L,C'3 = l-^-.
116 Гл. 2. Дифференциальные уравнения высших порядков
В силу этого частное решение имеет вид
ж3 ж2 сц ai
у = а,—+B-а,)—+ —Ж + 1-—. >
о 11 о
255. у
•^ Разрешив уравнение относительно у", получим:
Поскольку уравнения относятся к виду у" = <р(х), то двукратным интегрированием можно полу-
получить их общие решения. Однако, полученные уравнения можно проинтегрировать также с помо-
помощью параметра, положив, например, х = t2 +1 (при этом радикал исчезает). Тогда получим
y"=e+t\ y" = -e-it7-t.
Далее имеем
d(y') = (t} + t2) dx = (t}+t2)Bt + l)dt,
откуда
у' = J(t3+t2)Bt + l) Л + С, = ^tb + 3-t* + у +С,
'4+
dy= (~5t5 + lt4 + J+Cl) dx= (l
Интегрируя еще раз, находим:
У= / (-t* + -t* + l- + сЛ Bt+ \)dt + Сг = ^-t1 + ^t" + ^t5 + ~ + Cdt2 +t) + C2.
J \5 4 3 ) 35 60 60 12
Аналогично интегрируем второе уравнение. >
256. у - 2у" - х = 0.
•^ Это уравнение вида F(ж, у(п)) = 0 при п = 2 и его можно разрешить относительно х.
Имеем
ж = у - 2у .
Положив у" = t, получаем х = t3 -2t. Далее, d(y') = tdx = tCt2 - 2)<W, откуда
В свою очередь, dy = (|t4 - f + d) dx = (|t4 - t2 + C,) Ct2 - 2) dt,
откуда
Таким образом, получили общее решение данного дифференциального уравнения в параметри-
параметрической форме:
257. у" + In у" - х = 0; при хв = 1, у0 = 1, у'о = 2.
•^ Аналогично изложенному выше, полагаем у" = t. Тогда
х = t + In t, d(y ) = t dx = t [ 1 + — ) dt = (t + 1) ей,
откуда
r t2
y'= (f + l)dt=-+t + Cu
J l
§ 1. Виды интегрируемых нелинейных уравнений 117
а также
6 4
Следовательно, общее решение имеет вид:
<3 3 ,
x = t + lnt, y=- + -r + (C1 + l)t + C,lnt + C2.
Очевидно, х0 = 1 при t — 1, поэтому
t1
3
t=l 2' Уо 1б + 4* + «71 + О* + С1Ы + С2)|
Из двух последних уравнений находим С\ = ^, С2 = - |j. Частное решение имеет вид
t2 t lt
z t + ln<, y + t + t + lnt .
258. у"'-е^"=0.
•^ Это уравнение вида ^(у*"', у(п)) = 0 при п = 3 и F(u, t) е в - е"* = 0. Согласно п. 1.2
имеем
откуда d(y") = е 'dx, или dt = е * dx. Интегрируя последнее уравнение, находим х = е* + С\.
Для получения функции у воспользуемся уравнением у" = t. Имеем d(y') = tdx = te' Л, откуда
у'= fte*dt + C2 = e'(t- 1) + С2.
Интегрируем еще раз:
Jdy = J(e\t - \) + С2) dx + Съ = J(e\t - \) + С2у dt + Съ,
или
е2' / 3\ ,
У = у И - j J + С2е + С3.
Окончательно имеем
У=у^--
259. у'"-у" = о.
•4 Уравнение относится к виду F(у'"', у<п)) = 0, однако, в отличие от предыдущего примера,
для его интегрирования применим другой способ. Полагая в нем у" — z(x), получим уравнение
первого порядка z' — z — 0, общее решение которого z = С[вх. Следовательно, у" = С\ех, откуда
у = Схех + С2х + С). >
260. у' + у-1 = 0.
•4 Как и в предыдущем примере, полагаем у" = г(ж). Тогда z + z2 - 1 = 0. В полученном
уравнении разделяются переменные:
dz
—, = dx.
Проинтегрировав, получаем
z = ± sin(x + Ci), или у" = ± sin(x + С\).
Интегрируя еще два раза последнее уравнение, окончательно находим
(у - Сгх - С3J = sin2(z + С,).
Кроме того, имеем еще очевидное решение
х2
У = ±у +С4х + С5. >
118 Гл. 2. Дифференциальные уравнения высших порядков
Примечание. Решение этого уравнения можно получить в параметрической форме, если воспользоваться
тождеством sin2 t + cos2t — 1=0. Действительно, полагая в данном уравнении у" = sint, у'" = cost,
можем записать d(y") = costdx, или d(sin<) = costdx, откуда х = t + C\ (cost Ф 0). Далее, d(y') =
= sintdx = sintdt, откуда
t/ = f sintdt+ C2 = -cost+C2.
В свою очередь, отсюда следует, что dy = (С2 — cost)dx = (С2 — cost)dt, поэтому
у= [(C2-cos,t)dt + C) = C2t-smt + C].
Кроме того, имеются еще решения уравнения у" = ±1, которые не принадлежат общему решению.
261.у+ЗуУ-/=о.
•^ Положим у" = ty'. Тогда из уравнения получим, что
у'=Г3-ЗГ2, у' = 0.
Таким образом, данному уравнению соответствует система уравнений
у' = Г3-ЗГ2, г/" = Г2-ЗГ' (t^O), у' = 0.
Поскольку d(y') = у" dx, то в силу первых двух уравнений системы находим
откуда
Из первого уравнения системы имеем
dy = (-ЗГ5 + 6Г4)Л, откуда у = - Г4 - 2Г3 + С2.
Кроме того, как следует из третьего уравнения системы, у = С есть также решение данного
уравнения. >
262.у+/-у'4 = о.
•^ Полагая в данном уравнении у' = ±cht, получаем
Отсюда следует, что d(± ch t) = ± ^ sh 2t dx, или
<te = ±—-.
cht
Интегрируя, находим х = ±2arctge( +Ct. Из уравнения у' = ±cht, принимая во внимание
выражение для dx, получаем у = t +С2. Таким образом, параметрические уравнения общего
решения имеют вид
х = ±2arctge' + Cb y = t + C2. >
263. у"+ 2у" In у'-1=0.
< Вводя параметр < по формуле у' = t, из уравнения получаем
" l+21nt
Так как d(y') = у" dx, го в силу параметрических представлений производных у' и у" имеем
уравнение
Интегрируя уравнение A), получаем
Функцию у находим из уравнения у' = t, пользуясь A):
,dy = tdx = t(l + 2int)dt, y =
§ 1. Виды интегрируемых нелинейных уравнений 119
Общее решение уравнения имеет вид
•4 Действуем по той же схеме, что и в предыдущем примере. Имеем
, , * е-'
y=t, у = —.
Отсюда, в силу соотношения d(y') = у" dx, получаем
Следовательно,
x = t
Из уравнения у' — t находим
у= ftdx + C2 = ft(l + t)
Итак, получили общее решение
x = te' + Cu y = (t2-t+ \)e + С2. >
265. у" - е» = 0.
¦4 Это уравнение вида F(у(п~7\ у(пЛ = 0 при п — 2. Согласно п. 1.3 имеем
у" = №, у = «(<), A)
где a(t) = hit, /3(t) = t. Уравнение C), п. 1.3, принимает вид
---^х' - -х" = tx , или 6/+K+tV = 0,
где х = х'. Решив последнее уравнение Бернулли (или, еще проще, уравнение (Ы)' + (tx)} = 0),
получаем
iv/27+TT
Отсюда находим:
Ш
W2t + С, + 2~^-/гг
л/2* + С,
+ С2, если Ci > 0;
— v 2t
2 Г 2t
W-1 - — +C2, если С] < 0;
С
/2
ж = -у - + С2> если С] = 0.
Присоединив сюда еще второе уравнение из A), будем иметь общее решение данного дифферен-
дифференциального уравнения в параметрической форме. >
Примечание. Рассмотренное уравнение допускает и другой способ решения. А именно, умножая обе
части уравнения на у', получаем: у"у1 = еуу , или
откуда интегрированием находим у' = 2еу + С\, или
Jy ^
120 Гл. 2. Дифференциальные уравнения высших порядков
Интегрируя еще раз, получаем общее решение в явном виде
= ±-=1п
C
+ С2, если С! > 0;
2 / 2
arctgW-1 - —ev + C2, если C\ < 0;
х = -\/2е~У + С2, если d = 0.
266. уУ" = 1.
•^ Умножив обе части уравнения на у', получаем уу"у' = у' (у' ф 0), или
)'
откуда интегрированием находим у' = In у2 + С\, или
Разделив переменные и опять проинтегрировав, окончательно имеем
dy
х + Сг = ±
J усГ
+ 1пу2
267. уу-у4 + 1 = о.
•^ По аналогии с проделанным выше, имеем
или
Отсюда следует, что у'2 = fу2 + уJ + С{, или
у' =
Разделяя переменные и интегрируя, получаем
268. у"Чу' = о.
< Умножив обе части уравнения на у", получаем
у'У" + у"у' =
Отсюда следует, что
а также
у+у'2 = с2. ^
Полагаем у' = Cisint, у" = Cicost. Из тождества d(y') = y"dx в силу последних уравнений
имеем d(sint) = costdx, или dx = dt, откуда
x = t + C2.
Из уравнения г/ = Ct sin t находим
у = Ci Isintdx + C3 = С] I smtdt + C3 = -Ci cost + C3.
Теперь окончательно можем записать:
ж = t + Ci, у = Ci cos t + Сз, или у = Ci cos(x + C2) + C3. >
§ 1. Виды интегрируемых нелинейных уравнений
269. у-4гу" + 4у' = 0.
Полагая у" = t, находим
у =xt--.
( t2\
Поскольку d(y') = у" dx, то из последних соотношений следует, что d Ixt - -^ \ =tdx, или
[х - - j dt = 0.
Решив полученное уравнение, имеем t = С{, а также х = j. Функцию у, которая соответствует
решению t = Си находим из уравнения
.2
4 '
С2
Получаем у' = хС\ —^-, откуда
1 2 4 ' 2'
Аналогично, для функции у, соответствующей решению х = -у, имеем
t2 t2 /t\ t2
Отсюда
.3
Интегрируя последнее уравнение, находим у = ^ + С3, или
х3
У=у+С3.
Таким образом, все решения данного уравнения описываются формулами:
С, / _С,
2
270. siny" + ylny"=l.
•^ Полагая в этом уравнении у" = t, получаем
Для получения функции х воспользуемся уравнением C), п. 1.3. Имеем
—2" 3 а = Р, где а = ,
Общее решение этого уравнения представляется в виде
а'
Следовательно,
Таким образом, A) и B) суть параметрические уравнения общего решения данного диффе-
дифференциального уравнения. >
122 Гл. 2. Дифференциальные уравнения высших порядков
§ 2. Уравнения, допускающие
понижение порядка
2.1. Дифференциальное уравнение вида F(x, у^к\ у^к+1\..., у(п)) = 0.
Если дифференциальное уравнение имеет вид
то его порядок можно понизить с помощью замены j/*' = z(x). Действительно, тогда получим
уравнение
порядок которого на к единиц меньше исходного.
2.2. Дифференциальное уравнение вида F(y, у', ... , t/n)) = 0.
Порядок дифференциального уравнения
можно понизить с помощью замены у' = р(у), где р = р(у) — новая неизвестная функция,
а переменная у является аргументом.
Имеем
и <* , dy' dy dp
У =^У)=^у1Х=Р1у'
y(/) (p)p(p)p((
у dx VdyJ dy VdyJ dx Fdy \pdy) P\\dy
и т.д., т.е. порядок дифференциального уравнения понижается на единицу.
2.3. Однородное дифференциальное уравнение вида F{x, у, у', у", ,У^) = 0.
Если дифференциальное уравнение F[x, у, у', у",... ,j/(n)J = 0 однородное относительно
функции и ее производных, т. е. справедливо тождество
F(x, ty, ty', ty", ... ,ty^) = t°F(x, y, y', y", ... ,2/<">),
то порядок уравнения можно понизить на единицу, положив у' = yz(x), где z = z{x) — новая
неизвестная функция. Действительно, последовательно дифференцируя соотношение у' = yz{x),
имеем:
у" = (yz(x))' = y'z + yz' = y{z2 + z\
у = (j/(z2 + z'))' = y'(z2 + z') + yBzz' + z") = y(z3 + 3zz' + z")
и т. д., j/(n) = yi>(z, z', ... , z1"'), где ip — известная функция. Подставив значения производных
в дифференциальное уравнение F(x, у, у', ... ,у(п)) = 0 и используя однородность функции F,
получаем:
F(x, у, yz,y(z2 + Д. ..,yi>(z, /,..., «<-«)) =y°F (x,l, z, z2 + z', ... ,ф(г, z',... ,z(n~li)) =0.
2.4. Обобщенно однородное дифференциальное уравнение вида
F(x,y, у', у", ...,2,<">)=0.
Дифференциальное уравнение F(x, у, у', у",... ,y(n)j = 0 называется обобщенно однородным,
если функция F удовлетворяет тождеству
F(tx, <-», «-У, «-У,... ,<—у<->) =t"F(x, у, у',... ,/"),
где m — некоторое действительное число.
§ 2. Уравнения, допускающие понижение порадка 123
Если уравнение F[x, у, у', ... ,у(п)) = О обобщенно однородное, то замена переменных
х = е(, у — emtz(t) приводит к уравнению, явно не содержащему независимую переменную t.
Следовательно, порядок такого уравнения можно понизить. Действительно, имеем
у' = ^?> = e-'i (e-z) = e-(+-(mz + Л
,,= dl= e-ttf = e-t± / (m-1)i(mz + gl)\ = e<»-*((m _ l)mz + Bm _ 1)z. +
dx dt at v ' v
и т.д., j/(n) = e(m"n)V(-z, z', ••• ,z(n)). где ф — известная функция. Подставляя значения произ-
производных в рассматриваемое уравнение и пользуясь обобщенной однородностью, получаем:
F(e\ emtz, e(m-l)\mz + z'), e(m-2)(((m - \)mz + Bm - l)z' + z"), ... ,e(m~n)txp{z, z',..., *<">)) =
= eatF(l,z,(mz + z'), ((m - l)mz + Bm - l)z' + z"), ... ,^>(z,z', ... ,2(n))) = 0.
2.5. Уравнение, приводимое к виду (<р(х, у, у', ... , у(п-1))) = 0.
Если путем алгебраических преобразований дифференциальное уравнение
F(x,y,y',...,y(n))=0
можно привести к виду
)'
то интегрированием его порядок можно понизить на единицу:
где <р — известная функция.
Решить уравнения.
-4 В это уравнение второго порядка явно не входит неизвестная функция. Следовательно,
согласно п. 2.1, полагая у = z(x), получим дифференциальное уравнение первого порядка
2 I 2
X Z = Z .
Разделяя переменные и интегрируя, имеем
dz [ dx
У-
Интегрируя еще раз, окончательно получаем
!-^х--^Ы\С{х~1\ + С2, если С15^0, С, ^ оо;
^ + С2, если С,=0;
С2, если С\ = оо. >
-4 Полагая »/" = г(ж), понижаем порядок уравнения на две единицы:
2' = z\
Разделяя переменные и интегрируя, получаем
dz I
C ^Q
f dz
—j—x —
J zL
или z=
, z^Q.
C\ — x
Остается дважды проинтегрировать уравнение у" = (С{ — х)~1. Имеем
у' = - In |С, - х\ + С2, y = (d- ar)ln |С, -х\ + С2х + Съ.
Кроме того, при разделении переменных мы потеряли решение z — у" = 0, или у = Сх + D. >
124 Гл. 2. Дифференциальные уравнения высших порядков
273. ху'"±у"-ху".
¦4 По аналогии с изложенным выше, имеем
у" = z(x), xz'(x) = A - x)z(x).
Разделяя переменные и интегрируя, находим
откуда
z = Cxxe~x, или у" = С]Хе~х.
Применяя двукратное интегрирование к последнему уравнению, получаем
у = Схе~х(х + 2) + С2х + С3. >
274. ху" = у'\пУ~.
¦Ч Так как ураинение не содержит яино функцию у, то, применив замену у = z(x), порядок
уравнения можно понизить на единицу. Имеем
, 2
xz = z !п —.
X
Полученное уравнение является однородным, поэтому воспользуемся заменой z = хи(х), где и —
новая неизвестная функция. При этом получим уравнение (и + хи1) = ulnu, в котором перемен-
переменные разделяются:
du dx
u(lnu - 1) х
Интегрируя, находим In | !nu - !| = !п \х\ + !пС,, откуда и = е1+с>х. Следовательно, требуется
проинтегрировать уравнение
y'=xel+c>x.
Имеем
Кроме того, разделяя переменные, мы потеряли решение и = е, или у = Ц- + С, которое, однако,
может быть получено из общего решения предельным переходом при С,—>0иС2 = С+-|у.
Действительно, пользуясь формулой Маклорена с остаточным членом в форме Пеано, можем
написать:
у= ^{х- ^{\ + С,х+^х2 + o(Cl)\+C + ~ = е-х2 + С + о(\) при
275. ху'у" + у'2 + 1 = ay''^/l + у'2.
•^ Произведя замену у' = -г(ж), получаем дифференциальное уравнение первого порядка
xzz + z2 + 1 = azVl + г2.
Положим г = tgi (|t| < j). Тогда
, _ dz _ dz 1 1
Z ~"dx~ ~dl"%- ~ x' cos21
и последнее уравнение примет вид
х cost + xsmt — a,
откуда легко находим ж:
х = Ci cos< + asin<. A)
Принимая во внимание A), из уравнения z = tgi = -^ получаем
у= [tgtdx + C2= /tgid(CiCOS< + asin<) + C2 = -Ciln|tg(| + f)| + Cismi-acosi + C2. B)
§2. Уравнения, допускающие понижение порядка 12S
Итак, уравнения A) и B) представляют общее решение исходного дифференциального урав-
уравнения в параметрической форме. >
216.х4у'" + 2х3у"-1=0.
•^ Замена у" = z{x) приводит к линейному уравнению первого порядка
arV + 2x\ -1 = 0,
общее решение которого имеет вид z = -К + Щ-. Следовательно,
X X
и 1 СХ
У = ^+ ^Т>
откуда двукратным интегрированием находим
у = — - С, In |ж| + С2х + Съ. >
2х
211.у'2+2уу" = 0.
•^ Уравнение не содержит явно переменную х, поэтому в соответствии с п. 2.2 полагаем
у' — Р(у)- Тогда у"' = р-? и уравнение запишется в виде
Отсюда находим р = 0 и р + 2у-? = 0. Из первого из двух последних уравнений получаем у = С,
а из второго имеем р2 — -^, или у' = -^, откуда
, или
у
Интегрируя, находим
Окончательно имеем
где С\ — новая произвольная постоянная. >
278.2// = /-/.
А Как и в предыдущем примере, полагаем у1 = р{у). Тогда у" = р-? и
dp _ 2_ з
Полученное уравнение распадается на два:
dp 2
р == 0 и у— — р — р .
dy
Из первого уравнения следует, что
у = С,
и из второго — что
Интегрируя последнее уравнение, имеем
х = С, In \y\ + у + С2. >
126 Гл. 2. Дифференциальные уравнения высших порядков
•4 Согласно п. 2.2, после замены у' = р(у) получаем
р-^ + р2 = 2е~у, или - -^ + z = 2е'у,
ау 2ау
где z = р2. Последнее уравнение линейное и его общее решение имеет вид
z = Cie-
2
Подставив сюда z = у , получаем уравнение
у'2 = Схе~2у + 4е~у, или у' = ±\[с1е~гУ + 4е-»,
а
г
/
J
интегрируя которое, находим
dy 1
а - - • " или ± -
откуда
где С[ — новая постоянная. ь>
280. / - 2у'у"' +1=0.
•^ Уравнение не содержит х, поэтому полагаем у' =р(у). Тогда
Отсюда следует, что
Р2
Так как полученное уравнение явно не содержит аргумента у, то производим замену р' = и(р).
Имеем
и du 2 , I ,1
р = и —, u + 2puu г = 0, или «) + pw = —z,
dp p2 г р2
где w = и2. Общее решение последнего уравнения имеет вид:
С{ 1 ,2 С, 1
U) = г, ИЛИ р = -,
р рг р р2'
откуда
' Г
Интегрируя уравнение A), получаем
f pdp 2
+- / , = = у + С2, или ± —j)
Воспользовавшись соотношением dx = -У- и уравнением A), имеем
/С,р - 1'
откуда интегрированием находим
x = ±—JclP-l + C3.
Наконец, исключив параметр р из выражений для хну, окончательно будем иметь:
где Ci и Сз — новые произвольные постоянные. >
Примечание. Данное уравнение не содержит явно переменной у, поэтому начать решать его можно
было бы с замены у' = z(x). Предлагаем читателю убедиться в том, что такой путь также приводит
к полученному ответу. /
§ 2. Уравнения, допускающие понижение норадка 127
Ши , i2 Уу'
.уу+у =
l +ar2
-4 Замечая, что левую часть уравнения можно записать в виде (уу')' и полагая уу' = z(x),
получим уравнение
переменные в котором разделяются. Проинтегрировав его, находим:
+ \/х2 +
Таким образом,
j/j/ = Ci(x+ Vx2 + l) ,
откуда следует, что
j/2 = Ci (ж2 + ж-/?2 + 1 + In (ж + \Лг2 + l)) + C2. >
282. х7уу"-2х2у'2+хуу' + у2 = 0.
¦4 Поскольку функция
F(x, У, У, у") = х2уу" - 2х2у + хуу + у2
вследствие тождества
xhyty" - 2x2(ty'J + xtyty' + {tyf = t2 (x2yy" - 2x2y'2 + xyy' + y2)
однородная относительно переменных j/, у', у", то данное дифференциальное уравнение одно-
однородное. Следовательно, согласно п. 2.3 порядок такого уравнения можно понизить, применив
подстановку у1 = yz(x). Тогда получим уравнение
x2z - x2z2 + xz + 1 = 0.
Это уравнение Эйлера—Риккати. Непосредственной проверкой можно убедиться, что z — -^
есть его частное решение. Поэтому посредством подстановки z = ^ + ^ приходим к линейному
уравнению
хи + и + х = 0,
из которого следует, что и = — ^ + -?¦. Отсюда, и из подстановки у' = yz, получаем уравнение
У' С1+х2
=
у ж(С,-ж2)'
где С{ — новая постоянная. Проинтегрировав его, окончательно находим
С2х
•4 Это также однородное уравнение. После замены у' = yz{x) получим уравнение
xz2
xz'-z+ п = О,
которое можно записать
откуда
Интегрируя уравнение
в виде
X
z
/«у
\z )
у1
У С
X
ИЛИ Z =
X
7| — л/1 — х2
128 Гл. 2. Дифференциальные уравнения высших норядков
окончательно имеем
\n\y\ = Vl - х2 + С, In С, - л/1 - ж
¦4 Полагая в уравнении у' — yz(x), получаем:
С2.
xBz2 + z) - 3z = 0.
Решив это дифференциальное уравнение, имеем z =
находим:
. Далее, интегрируя уравнение
285. у(ху" + у') = ху1 A- х).
Используя однородность уравнения, полагаем у' = yz(x). Тогда получим (xz)' + (xzJ = 0,
откуда
(**)'
(xzJ
1
Интегрируя, находим -^ = х + С\, откуда z = ,х ^_ ^ ч,
J/ Х(
Интегрируя еще раз, окончательно имеем
или
= С7
286. 4ж2-3-" - ~2 ¦¦*
у у =х - у .
•^ Проверим уравнение на обобщенную однородность. С этой целью вместо переменных
ж> У> у', у" подставим в выражение для функции F(x, у, у', у") = 4х2у*у" — х2 + у* соответствен-
соответственно tx, tmy, tm~ly', tm~2y" и, если это возможно, подберем значение т таким образом, чтобы
выполнялось тождество
Vy" - t2x2 + t4m = f Dх2уУ -х2 + у4).
Очевидно, что такое тождество выполняется лишь при условии 4т = 2, т.е. при т = i? (и при
этом а = 2). Следовательно, данное уравнение обобщенно однородное и, согласно п. 2.4, для
начала его интегрирования пользуемся заменой х = е(, у = e*u(t). Имеем
=«-*(;+4
4
Подставив значения производных, х и у в исходное уравнение, после некоторых преобразований
получаем:
4«V = 1.
Последнее уравнение явно не содержит переменную i, поэтому посредством замены «' = р(«)
понижаем его порядок на единицу:
§2. Уравнения, допускающие понижение порядка 129
Проинтегрировав последнее уравнение, находим
или p =
Далее, интегрируем уравнение и' = ±\/Cl — t
.udu I
±2 / , _ . . = t + С2, или ± —
/
откуда
Окончательно получаем решение уравнения в виде
х = е\ у2 = е (^Сф + С2J + ~У ^
287. — + у'= Ъху" н .
•^ Как и в предыдущем примере, проверяем уравнение на обобщенную однородность. Для
этого должны быть совместными следующие уравнения относительно т:
2т - 2 = 2(т - 1) = 1 + (т - 2) = т + (т - 1) - 1,
эквивалентные одному уравнению 2т - 2 = т - 1, имеющему решение т = 1. Следовательно,
данное уравнение действительно обобщенно однородное. Полагая х = е(, у = e'u(i). получаем:
Замена и' = г в последнем уравнении приводит к уравнению с разделяющимися переменными
Зг' = z1 — 3z, интегрируя которое, находим
In
z-3
или z =
3
1 - С,е« '
Интегрирование последнего уравнения приводит к следующему результату:
f d(e') _ f 3<-31n|l-C,e(| + C2, если С, конечное,
" ~ У е'A - С,е') I С2, если С, = оо.
Таким образом, общее решение исходного уравнения записывается в виде
_ Г Зж In ц_с,а;| + С2ж, если Ci конечное,
" ~ \ С2ж, если Ci = се. >
Примечание. В примерах 286, 287 мы нашли общие решения при х > 0. Для получения общего решения
при х < 0 следует применить замену ж = -е(, г/ = emtu(t) и провести аналогичные выкладки.
288. х4(/-2уу")=4х'уУ'+1.
•^ Проверяя уравнение на обобщенную однородность, получаем уравнения
4 + 2(т - 1) = 4 + m + (m - 2) = 3 + m + (m - 1) = 0,
совместные, эквивалентные одному уравнению 2тп+2 = 0. Следовательно, уравнение обобщенно
однородное. Решаем его для случая, когда х < 0, полагая х = —е', у = e~'u(t). Имеем
у' = е~2\и - и'), у" = е~3\2и - 3«' + и"), 2ии" - / - и2 + 1 = 0.
Полагая и' =р(и), получим уравнение
2ир^-р2-и2 + 1=0, или иУ?±-Р* = ^-1.
130 Гл. 2. Дифференциальные уравнения высших норядков
Это линейное уравнение относительно р2. Его общее решение имеет вид р2 = и2 +1 + С,и. Тогда
Разделяя переменные и интегрируя, находим:
[ du
± / , ,. : =t + C2, или ±In
J У u2 + C{u + 1
Подставляя в полученное соотношение значение и = — ху, t = Ln(—x) и произведя алгебраические
преобразования, будем иметь
2С2х2у = (с2х + у J - 1. A)
Кроме того, при замене и — р(и) мы потеряли решения « = ±1. Поэтому к интегралу A) следует
присоединить еще решения ху = ± 1. >
289. ху" - х2уу' -у' = 0.
¦4 Это уравнение также обобщенно однородное, поскольку уравнения
совместны и т = -2 — их решение. Однако, решение данного уравнения проще найти, поделив
обе его части на х2 (х ф 0). В результате получим:
-^- = Ю, или
Отсюда следует, что
Интегрируя это уравнение, находим:
arctg -JL; = у + С2, если Ct > 0;
t JL
1
л/—С
2
У
In
х2
- + съ
х1
2
если Ci
+ с2,
= 0. >
Понизив порядок данных уравнений, свести их к уравнениям первого порядка.
i\ 2
У \
- -
ж/
¦Ч Уравнение не содержит явно функцию у, поэтому произведя подстановку у' = z(x), по-
получим уравнение второго порядка
¦
Это уравнение однородно относительно переменных г, г', z", поэтому положив z' = г«(аг), будем
иметь уравнение первого порядка
«'+!¦= 0 и z = 0.>
2П.у2(уУ'-2у)=у'\
¦^ Поскольку независимая переменная явно не входит в уравнение, то произведя замену
У —Р(у)> получим уравнение второго порядка (см. п. 2.2):
§ 2. Уравнения, допускающие понижение порядка 131
Поделив обе части полученного уравнения на р2у2 (ру Ф 0), имеем
— = -z, откуда — = -—;
KPj У2 P У2
292.x2(y2y'"-y'})=2y2y'-3xyy'2.
•4 Уравнение однородное, поэтому замена у' = yz(x) приводит к уравнению второго порядка
(см. п. 2.3):
x2Czz + z") = 2z- 3xz2.
Так как уравнения 2 + m + (m-l) = 2-l-(m-2) = m = l-l- 2m совместны, то полученное
дифференциальное уравнение является обобщенно однородным. Следовательно, уместна замена
х = е( (ж > 0), z = e~'u(t), в результате которой приходим к уравнению (см. п. 2.4)
и" — Зии — Зи = 0.
Поскольку последнее уравнение явно не содержит независимой переменной t, то полагая и =
= р(и), получаем уравнения первого порядка
dp
— - Зи - 3 = 0 и и = 0. >
du
Решить уравнения, преобразовав их к такому виду, чтобы обе части уравнения являлись пол-
полными производными.
293.уу'" + Зу'у" = 0.
•^ Поделив обе части уравнения на уу"', получаем
— ч = 0, или
Интегрируя, находим
ln(l2/"IM3)=ln|CU или г/У = С,
(отбрасывая знак модуля, мы не теряем решений, поскольку постоянная С{ произвольная). Умно-
Умножив обе части последнего уравнения на \, снова получаем уравнение, обе части которого явля-
являются полными производными:
=Ci~^, или
/V2Y c{ 2,
Проинтегрировав его, имеем
,2
у +dy 2 = С2, или у' = ±у/с2 - Сху-2.
Еще раз интегрируя, окончательно находим
±7rJc2y1-Cl=x + C}, или у2 = С2(х + С,J + Си
О2
где Ci — новая постоянная. При делении на у" мы потеряли решение у" = 0, т. е. у = ах + р. >
294.5j/-3«,yv=o.
•^ Разделив обе части уравнения на у"у'", получим
-f=-f-, «ли
откуда находим
или
132 Гл. 2. Дифференциальные уравнения высших порядков
Интегрируя это соотношение, получаем
с}
или
= ±(Ci+C2x) 2,
где С[ и С2 — новые постоянные. Наконец, дважды интегрируя последнее уравнение, имеем
у = ±-=j (С, + С2х)Хг + С3х + С4.
С2
Присоединим сюда еще решение уравнения у'" = 0, потерянное при делении:
у = Сix2 + С2х + С,. >
295. у" = хУ' + у +1.
М Имеем
откуда следует, что
у' = ху + х + Си или (у + 1)'= х(у + 1) + Ci.
Это линейное уравнение первого порядка, и его общее решение имеет вид
у + 1 = е 2
ы
_1_
e 2 dx + Ci
296. xy"-у'= х2уу'.
•4 Поделив обе части уравнения на х2, имеем
VY_/VV
X
\
откуда
или
Интегрируя, получаем
или
7Г arctg
1
ln
= \-С2, если С, > 0;
х2
= \-С2, если С, < 0;
2 ж
= — + С2, если С, = 0.
При разделении переменных мы "потеряли" решения уравнения у2 + 2С\ = 0 (С\ < 0), или
t/ = ±y/-2Ci. Нетрудно, однако, показать, что они получаются в результате предельного перехода
при С2 —> =Foo из общего решения при С\ < 0. >.
В следующих задачах найти решения, удовлетворяющие заданным начальным условиям.
297. уу" = 2ху'2; t/B) = 2, у1 B) = 0,5.
-4 Поскольку уравнение однородное, то полагая у' = yz(x), получим
z' = z2Bx - 1).
§ 2. Уравнения, допускающие понижение порядка 133
Интегрируя, находим
Z~ С, + х - х1 = "у" *
Из начальных условий следует, что С\ = 6. Интегрируя уравнение A), получим
dx
откуда у = C2v/ji-|. Подставив сюда х = 2 и у = 2, определим С2 = ^8. Искомое решение
уравнения имеет вид
уу %
х1
¦^ Это обобщенно однородное уравнение и т = 2, поэтому производим замену х = е ,
у — e2tu(t). Получаем уравнение
и" - 6и2 = 0.
Умножая обе его части на и' и интегрируя, имеем
A)
Так как у = 1 при х = 1, то из формул замены следует, что и@) = 1. В силу того, что у' =
= е'(и' + 2и) и у'A) = 4, находим и'@) + 2и@) = 4, откуда и'@) = 2. Полагая в A) t = 0
и используя значения и@), «'@), определяем С\ = 0. Осталось проинтегрировать уравнение
Имеем и' = ±2иг, ±и 2 du = Idt, -±-щ =t + C2, или
1
Для определения постоянной С2 воспользуемся условием и@) = 1, в результате чего находим
С2 — ±1. Итак, и = —-—j, однако, в силу условия и'@) = 2, берем только решение и = ———у.
Окончательно можем записать
У =
AПЖ-1J'
2УУ. у cosy + у siny = у ; у(— 1) = —, у (-1) = 2.
¦4 Полагая у' = р(у), получаем уравнение
p'cosy+psiny = 1,
общее решение которого имеет вид:
р = sin у + С\ cos у, или у' = sin у + С\ cos у. A)
Для определения постоянной С\ воспользуемся условием, что у'(-1) = 2 при у = j. Находим
С\ = л/3. Далее, интегрируя уравнение A), получаем
Подставив сюда значения а: = -1, у = -g-, находим С2 = 1. Требуемое частное решение выража-
выражается формулой
Примечание. Знак | • | здесь отброшен в силу условия у'(-1) = 2 > 0.
134 Гл. 2. Дифференциальные уравнения высших порядков
300. Найти кривые, у которых радиус кривизны обратно пропорционален косинусу угла
между касательной и осью абсцисс.
¦4 Согласно условию задачи имеем уравнение R = ?„§<* > где -^ — радиус кривизны кри-
кривой, а — указанный в задаче угол, к — коэффициент пропорциональности. Поскольку R =
, а = arctg у', то написанное выше уравнение можно записать в виде
2, или ку"=\+у'\ ^р = \, (arctgj/)'=i.
Интегрируя последнее уравнение, находим
arctgy' = ^ + C,, или
Проинтефировав еще раз, окончательно получим
y=-feln|cos(f
301. Доказать, что уравнение движения маятника y"+siny = 0 имеет частное решение у(х),
стремящееся к ж при х —> +оо.
•4 Умножив обе части уравнения на у' и проинтегрировав полученное, будем иметь
y'2=2d+2cosy. A)
Выберем частное решение так, чтобы у'(х) —» 0 при х —» +оо. В силу того, что у(х) —> ж при
х —> +оо, из A) следует, что С\ = 1. Интегрируя теперь уравнение
получаем
Очевидно, что соотношение
z + lnCj @<у<тг) B)
также есть частное решение данного уравнения. Выполнив интегрирование в левой части B),
находим
или
у = arctg(C2e*) - ж, C)
где Сг > 0. Очевидно, что у(х) —* ж при х —> +оо. >
Замечание. Решение C) описывает физический процесс бесконечно долгого подъема математического
маятника в свое наивысшее положение (при этом переменная х играет роль времени, а переменная у —
роль угла поворота).
302. Определить форму равновесия нерастяжимой нити с закрепленными концами, на ко-
которую действует нагрузка так, что на каждую единицу длины горизонтальной проекции нагрузка
одинакова (цепи цепного моста). Весом самой нити пренебречь.
М Рассмотрим равновесие произвольного элемента нити длиной AS (рис. 25). Проектируя
силы, действующие на выделенный элемент, на оси Ох, Оу, получаем уравнения
-Т(х) cos а(х) + Т(х + Ах) cos а(х + Д х) = О,
-Т(х) sin а(х) + Т(х + Дх) sin а(х + Дх) - АР = О,
где Т(х) — величина натяжения нити в сечении х, а(х) — угол между касательной к нити
и осью Ох, АР — вес элемента AS (или величина какой-либо распределенной нагрузки).
§ 3. Линейные дифференциальные уравнения с постоянными коэффициентами
135
у
Из первого уравнения следует, что T(x)cosa(x) — Го = const, т.е. горизонтальная соста-
составляющая натяжения нити всегда имеет постоянную величину. Из второго уравнения находим,
что
d(T(x)sina(x)) = dP(x),
или
Tod(tga(x)) = dP(x), T<>dy' = dP(x). A)
В данной задаче dP(x) = kdx, где к — ко-
коэффициент пропорциональности. Тогда из A)
следует уравнение 2J>dy' = kdx, дважды инте-
интегрируя которое, получаем форму нити
к
y=—x2 + ClX + C2.>
303. Найти форму равновесия однородной нерастяжимой нити (с закрепленными концами)
под действием ее веса.
¦^ Пользуясь уравнением A) из предыдущей задачи и принимая во внимание соотношение
dP(x) = pgdS,
где рд — вес единицы длины нити, dS = у 1 + у' dx, получаем дифференциальное уравнение
формы этой нити:
тоу" =
или
У"
2 Р9
а =7F-
J-0
у"
Так как
то
откуда
Проинтегрировав еще раз, получим
1 - e'a2{x+Cl)).
§ 3. Линейные дифференциальные уравнения
с постоянными коэффициентами
3.1. Линейное дифференциальное уравнение та-го порядка
с постоянными коэффициентами.
Характеристическое уравнение. Общее решение.
Дифференциальное уравнение вида
у(п)
+ a,i/" + ... + а^у + апу = /(х),
аоу(п) + a,i/ + ... + а^у + апу = /(х), A)
где а,- = const (» = 0, п), / — известная функция, называется линейным дифференциальным урав-
уравнением п-го порядка с постоянными коэффициентами. Если /(х) = 0, то уравнение A) называется
однородным, в противном случае — неоднородным.
136 Гл. 2. Дифференциальные уравнения высших порядков
Если / — непрерывная на сегменте функция, то общее решение уравнения A) состоит из
суммы общего решения соответствующего однородного уравнения и частного решения неодно-
неоднородного уравнения A).
Алгебраическое уравнение
ао\п + аХ~1 + ¦¦¦ +ап^\ + ап = 0 B)
называется характеристическим, соответствующим однородному уравнению A). Пусть At, А2, ...,
Ап — корни уравнения B). Каждому простому корню Ад. соответствует частное решение однород-
однородного уравнения A), имеющее вид у& = еЛ*г, а каждому корню Аг кратности I (I Js 2) — решения
уТ = еЛгХ, уг+1 = хеХтХ, ... ,yr+i-i = х'~1еХтХ. Произвольная линейная комбинация всех частных
решений является общим решением однородного уравнения A), т. е.
3.2. Поиск частного решения
линейного уравнения n-го порядка с постоянными коэффициентами
методом неопределенных коэффициентов.
Если правая часть уравнения A) имеет вид f(x) = Pm(x)elx, где Pm(x) — многочлен степе-
степени т, то частное решение уравнения A) будет
у = xsQm(x)elx, D)
где s = 0, если число 7 не совпадает ни с одним из корней характеристического уравнения B),
и s равно кратности I корня уравнения B), если число j с ним совпадает, Qm(x) — многочлен
степени т. Для определения коэффициентов многочлена Qm(x) следует D) подставить в A)
и приравнять выражения при одинаковых функциях.
Если f(x) = fi(x) + f2(x) + ... + fv(x), то частное решение уравнения A) состоит из суммы
частных решений у, неоднородных уравнений
W /"" + ... + ап^у' + апу = /<(*) (г = ТТр).
3.3. Метод вариации произвольных постоянных.
Если / — непрерывная на сегменте функция, то частное решение уравнения A) можно найти,
применив метод вариации произвольных постоянных, заключающийся в следующем. Пусть постро-
построено общее решение однородного уравнения A), т.е. имеется выражение C). Тогда для отыскания
частного решения неоднородного уравнения A) поступают следующим образом:
а) предполагают, что С/. = С/.(х) — дифференцируемые функции;
б) частное решение ищут в виде
п
у (я) = ? с* (*)«/*; E)
в) функции C'k(x) определяют из системы алгебраических уравнений
« 1 = 0-^1
F)
где #я-и — символ Кронекера;
г) получив решения системы F) C'k(x) = <Pk(x), интегрируют эти уравнения:
Ск(х) = J<p(x)dx + ak, G)
) = J2yk( f(pk(x)
где oik — постоянные;
д) подставляют G) в E):
п . f
c)dx + ak). (8)
Заметим, что формула (8) определяет также общее решение неоднородного уравнения A).
§3. Линейные дифференциальные уравнения с постоянными коэффициентами 137
3.4. Метод Коши нахождения частного решения
неоднородного линейного дифференциального уравнения n-го порядка
с постоянными коэффициентами.
Пусть К(х, s) есть решение однородного уравнения A), удовлетворяющее начальным усло-
условиям:
К(х, 8)\х=. = К'х(х, 8)\х=. = ...= К?-2)(х, «)|х=, = О, Кхп-[\х, s)\x=s = 1. (9)
Тогда, если функция / непрерывна на сегменте [а, 6] и х<, 6 [а, Ь], х 6 [а, Ь], то
X
у(х) = j K{x,s)f(s)ds A0)
будет частным решением неоднородного уравнения A), удовлетворяющим начальным условиям
у(хо) = у'(хо) = ... = yl-l\x0) = 0.
Решение К(х, s) называется функцией влияния для задачи Коши.
Найти общие решения однородных уравнений, а также частные решения там, где указаны
начальные условия.
304. у" + у'-2у = 0.
¦4 Составляем характеристическое уравнение
А2 + А - 2 = 0.
Его корни — Ai = 1, А2 = —2. Корню Ai соответствует частное решение i/i = ех, а корню
Л2 — решение у2 = е~2х. Произвольная линейная комбинация этих решений есть общее решение
данного уравнения:
у = dex + С2е~2х. >
305. у" - 1у' = 0, у@) = 0, у'@) = 2.
¦4 Характеристическое уравнение А2-2А = 0, соответствующее данному дифференциальному,
имеет корни Ai = 0 и А2 = 2, поэтому общее решение исходного уравнения записывается в виде
Для нахождения частного решения, удовлетворяющего данным начальным условиям, про-
продифференцируем общее решение. Получим у1 = 2С2е2х. Затем в выражения для общего решения
и его производной вместо х, у, у' подставим их значения 0, 0, 2 соответственно. Имеем
Ct+C2 = 0, 2С2 = 2,
откуда Ci = — 1, С2 = 1. Искомое частное решение имеет вид
У = е2х - 1. >
306. у"' - 8у = 0.
¦4 Из характеристического уравнения А3 - 8 = 0 находим его корни А! = 2, А2 = -1 + »л/5,
Аз = -1 — *V3. Следовательно, общее решение есть произвольная линейная комбинация частных
решений:
у = С.е21 + (c2elVb + C3e-lV3*) e~\ A)
Поскольку коэффициенты данного дифференциального уравнения действительны, то решение A)
можно представить в действительной форме, воспользовавшись формулами Эйлера
cos V = Х- (eilp + в4*) , sin v = 1 (е" - е"'>) .
Подставляя значения e±lv/!l = cos-\/3x ± isin л/Зж в A), получаем
У = С,е2* + ((С2 + С3)cosу/Зх + i(C2 - С3) sin V5x) e~x. B)
138 Гл. 2. Дифференциальные уравнения высших порядков
Пусть С2 = С2 + гС3, С3 — С2 —163, где С2, Съ — действительные произвольные постоянные.
Тогда из B) следует, что
у = Суе2х + е х (сг cos V3x + С3 sin
где С2, С3 — новые действительные произвольные постоянные. Мы получили общее решение
в действительной форме. >
307. j/lv + 4t/ = o.
¦4 Корни характеристического уравнения А4+4 = 0 находим, пользуясь известной формулой,
которая, применительно к рассматриваемому случаю, имеет вид
\к = 4^4 = -Jletr-, к = 0, 3.
Отсюда следует, что Ai = 1 +1, А2 = 1 - i, А3 = -1 +»', А4 = -1 - г. Тогда линейная комбинация
у = (Cyeix + C2e~ix) ех + (с3е" + С*е'{*) е~х A)
является общим решением рассматриваемого дифференциального уравнения.
Так как коэффициенты дифференциального уравнения действительны, то решение A) можно
представить в действительной форме с помощью формул Эйлера ек"р = cos <p ± i sin <p и положив
Ci = Ci+ iC2,C2 = Cl-iC2,C}=C} + iC4,СА = Съ-гСА, где СиС2,Съ,СА — действительные
произвольные постоянные. Тогда получим
у = (Ci cos x + С2 sin x)ex + (Съ cosх + С4 sin x)e~x,
где С\, Сj, С'з, Сц — новые действительные произвольные постоянные. >
308. j/vl + 64t/ = o.
¦4 Находим корни характеристического уравнения А6 + 64 = 0:
6. i(x+ikx)
Хк = V-64 = 2е « , к = 0, 5.
После подстановки соответствующих значений к в формулу для А& имеем Ai = л/3 + i, Х2 = 2»,
А3 = —у/Ъ+%, А4 = —y/3 — i, А5 = —2», А6 = y/3—i. Следовательно, общее решение в комплексной
форме представится в виде
\e .+C2e + [Съе + C4e je + [Съв + C«e je .
Положив здесь Су = Су + iC2, C2 = Ci, C3 - С3 + iC4, C4 = С3, С5 = Съ + iC6, C6 = ~СЪ
и воспользовавшись формулами Эйлера, получаем общее решение в действительной форме
у = Су cos2a; + C2 sin2a; + (C3 cosa; + C4 sin x)e/ix + (C5 cos a; + C6 sin xje"^,
где Ci (i = 1,6) — новые действительные произвольные постоянные. >
309. у"-2у' + у = 0.
•4 Из характеристического уравнения А2 - 2А + 1 = 0 находим его корни Ai = А2 = 1. Так
как кратность корня равна двум, то согласно п. 3.1 частные решения данного дифференциального
уравнения имеют вид:
2/1 = ех, t/2 = хех.
Следовательно,
у = (Су + С2х)ех
— общее решение. >
310. y'v + 2y" + y = 0.
¦4 Решив характеристическое уравнение Л4 + 2А2 + 1 = (А2 + IJ = 0, получим А( = А2 = *,
А3 — А4 = —». Согласно п. 3.1 записываем частные решения
«Л = е'х, уг = же", t/3 = е~", 2/4 = хе~'х,
а затем и общее решение рассматриваемого дифференциального уравнения:
у = de" + C2e~ix + х (C3eix + CAe~ix) .
§ 3. Линейные дифференциальные уравнения с постоянными коэффициентами 139
Если положить С\ = С\ + %С2, С2 = С\, С3 = Съ + г'С4, С4 = С3, то придем к действительной
форме общего решения
у = С\ cosx + C2 sinx + х(С3 cosx + C4 sinx),
где С,- (t = 1, 4) — новые действительные произвольные постоянные. >
311. t/lv + 8у"' + 24t/" + 32t/' + 16t/ = 0.
¦^ Характеристическое уравнение А4 + 8А3 + 24А2 + 32А + 16 = (А + 2L = 0 имеет корень
А = -2 кратности 1 = 4. Согласно п. 3.1, этому корню соответствуют четыре частных решения
2/1 = е~2х, 2/2 = хе~2х, у} = хге~2х, у4 = х3е~2х.
Следовательно,
у = (С, + С2х + С3ж2 + САх3)е~и
— общее решение. >
312. yvl - 5t/v + 4t/v = 0; у@) = 2/@) = /@) = 2/'"@) = 2/'V@) = 0, t/v@) = 2.
¦^ Составив характеристическое уравнение A6 — 5A3 + 4A4 = 0 и решив его, получим А( = \2 =
= Аз = А4 = 0, А5 = 1, А6 = 4. Следовательно, общее решение представится в виде:
у = Су + С2х + Съх2 + САхг + С5ех + С6е41.
Для определения постоянных С± (» = 1, 6), соответствующих искомому частному решению, следу-
следует последовательно продифференцировать пять раз общее решение и воспользоваться начальными
условиями. Тогда получим систему уравнений относительно указанных постоянных:
Су + Съ + С6 = 0, 6С4 + Съ + 64С6 = 0,
С2 + С5+ 4С6 = 0, С5 + 256С6 = 0,
2С3 + С5 + 16С6 = 0, С5 + 1024Сб = 2.
2 1 85 21 S 1
Отсюда находим С5 = — -у, Сб = ^. Су = -^, С2 = ^, С3 = -fe, С4 = -^. Таким образом,
85 21 53132,. 1 ^
V = 1 хЧ х Н х е -\ е
У 128 32 16 12 3 384
— искомое частное решение. >
313. ущ + 3t/lv = 0; t/@) = 1, t/'@) = 2/"@) = 2/'"@) = t/lv@) = t/v@) = 0.
М Из характеристического уравнения А6 + ЗА4 = 0 находим его корни Ai = A2 = A3 = А4 = 0,
А5 = iV5, Аб = —i\/b. Согласно п. 3.1, записываем общее решение данного дифференциального
уравнения
у = Су + С2х + Съхг + С4г3 + С5 sin л/Зх + Сб cos Vix.
Аналогично проделанному в предыдущем примере составляем систему уравнений относительно
постоянных Ci (i = 1, 6) и решаем ее. Тогда получим: С\ = 1, С,- = 0 (i = 2, 6). Следовательно,
частное решение имеет вид:
У=1. >
Найти общие решения неоднородных уравнений, а также частные решения там, где указаны
начальные условия.
314. у" - 2у' -Зу = е4*; у@) = 1, у'@) = 0.
¦4 Сначала находим общее решение однородного уравнения, соответствующего данному не-
неоднородному, т. е. уравнения у" — 2у' — Зу = О. Так как корни его характеристического уравнения
А2 — 2А — 3 = 0 есть Ai = —1, \2 = 3, то указанное общее решение запишется в виде
2/ = С,е~* + С2е3х.
Поскольку правая часть уравнения /(х) = е4* и ^число у = 4 не совпадает ни с одним из
корней характеристического уравнения, то в соответствии с п. 3.2 частное решение данного не-
неоднородного уравнения ищем в виде:
' sooe41, A)
140 Гл. 2. Дифференциальные уравнения высших порядков
где ал — пока что неизвестная постоянная. Для определения ал подставим A) в исходное диф-
дифференциальное уравнение. Тогда получим тождество
5аое4*не4*,
из которого находим ал = j. Следовательно, у = -$е*х и общее решение неоднородного уравне-
уравнения запишется в виде
5 "
Подставив в общее решение, а также в производную от него, вместо х, у, у значения 0, 1, О
соответственно, получим систему уравнений относительно Ci, C2:
1 4
С,+С2 + - = 1, -С, + ЗС2 + - = 0.
Решив эту систему и подставив значения С1, С2 в общее решение, найдем искомое частное:
у = ~ е х + - ех. >
5 5
315. у"~у = 2ех-х2.
¦^ Легко находим общее решение соответствующего однородного уравнения
у = Ciex + С2е'х. A)
Так как правая часть данного дифференциального уравнения есть сумма функций /i + /2, име-
имеющих вид Рт(х)е1Х, то, согласно п. 3.2, частное решение также ищем в виде суммы частных
решений следующих неоднородных уравнений:
у"-у = 2ех, у"-у=-х2. B)
В силу того, что в первом уравнении 7 = 1 > а во втором 7 = 0, согласно формуле D), п. 3.2,
частные решения этих уравнений ищем соответственно в виде:
yl=aoxex, у2 = Ьлх2 + Ь{х + Ь2, C)
где ао, Ьо, Ьи Ь2 — пока что неизвестные коэффициенты. Для их определения подставим C) в B).
Тогда получим тождества
2аде = 2е , 26q — Ьлх — Ъ\х — Ь2 = —х ,
из которых, приравнивая коэффициенты при одинаковых функциях, находим:
ао=1, Ъл=\, -Ь\ = 0, 2Ь0-Ь2=0 или Ь2 = 2.
Следовательно, частное решение исходного неоднородного уравнения будет
У = Ш + h = хех + х2 + 2.
Наконец, принимая во внимание A), записываем и общее решение этого уравнения:
у = Схе* + С2е~х + хех + х2 + 2. >
316. у" - Зу' + 2у - sin х.
< Сначала запишем общее решение соответствующего однородного уравнения:
у = Схех + Сге2х.
Далее, представляя правую часть исходного уравнения в виде
замечаем, что 71 = «', Ъ — ~!- Поскольку *уф\, то, согласно п. 3.2, частное решение дифферен-
дифференциального уравнения ищем в виде:
У = У\ + Уъ
§3. Линейные дифференциальные уравнения с постоянными коэффициентами 141
где J/1 = аое11, у2 = Ьое~'х. Подставляя функцию у = аое'х + Ьое~'х в исходное уравнение и при-
приравнивая коэффициенты при е'х и е~'х, получаем
- — -^ h -~ -— —
Таким образом, частное решение запишется в виде
у = аое'х + аое~'х = (а0 + а0) cos х + г(а0 - а0) sin х = — cos x -I sin a;,
а общее — в виде
у = С\ех + С2е2х + — cosa; + — sina;. >
Примечание. Если коэффициенты левой части уравнения действительны, а его правая часть имеет вид
e7X(Pm(z)cosJ8a; + Cn(a;)sinJ3a;), A)
то частное решение неоднородного уравнения можно искать в виде
у = х" (Q$\x) cosjSa; + Qf(x) sin j3a;) е1Х, B)
где s = 0, если -у + pi не является корнем характеристического уравнения, и s равно кратности этого
корня в противном случае, р = max{m, n).
Так, в рассмотренном примере J = 0, Рт(х) = 0, Qn(x) = 1, р = 0, /3 = 1, Ai ^j + f3i, \2 Ф ¦у + pi.
Следовательно, s = 0 и частное решение имеет вид у = aocosa; + &osina;> где Оо, 6о — подлежащие
определению коэффициенты. Подставив у в исходное дифференциальное уравнение, находим оо = т?т,
317. у" +у = 4sina;.
¦^ Для нахождения частного решения данного неоднородного уравнения воспользуемся при-
примечанием к примеру 316. В нашем случае 7 = 0, Рт(х) = 0, Qn(x) = 4, р = 1, р = 0,
А[ = г = 7 + pi. Поэтому s = 1 и частное решение, согласно формуле B) предыдущего при-
примера, представится в виде
у = x(a<,cosx + b0sinx). C)
Подставив C) в исходное дифференциальное уравнение и приравняв коэффициенты при
функциях sina;, cosa;, находим ао = -2, Ьо = 0. Наконец, принимая во внимание общее решение
соответствующего однородного уравнения, записываем общее решение неоднородного уравнения:
у = С\ sin х + С2 cos х — 2х cos x. >
Для каждого из данных уравнений написать его частное решение с неопределенными коэф-
коэффициентами.
318. у" - 2у' + 2у = ех + хcosx.
М Находим корни характеристического уравнения: А[ = 1 + *, \2 = 1 — i. Далее, поскольку
правая часть рассматриваемого уравнения есть сумма двух функций, то частное решение у ищем
в виде суммы частных решений j/i и у2 соответствующих уравнений:
у" - 2у' + 2у = ех, у" -2у' + 2у = хcosx. A)
Для построения частных решений уи у2 воспользуемся примечанием к примеру 316. В случае
первого из уравнений A) имеем j = 1, р= 0, Рт(х) — 1, р = 0. Так как y+pi Ф А1( 7+/3* ф \2,
то s = 0. Следовательно, согласно формуле B) указанного примечания,
jfi = Соех.
В случае второго уравнения A) 7 = 0, р = 1, Рт(х) = х, Qn(x) = 0, р = 1. Поскольку -y+pi Ф \t,
7 + pi Ф \2, то s = 0. Таким образом, согласно формуле B) из примечания после примера 316,
у2 = (аох + a^cosx + (Ьох + b^sin x.
Итак, частное решение исходного дифференциального уравнения следует искать в виде
у = Сое1 + (аох + а{)cosх + (Ьох + bi) sinx. >
142 Гл. 2. Дифференциальные уравнения высших порядков
319. у" + 6у' + Юу = ЗакГ3* - 2e3*cosa?.
ч|Прежде всего находим корни характеристического уравнения А2+6А+10 = 0: Ai^=-3±«.
Далее, пользуясь примечанием к примеру 316, строим частные решения, соответствующие урав-
уравнениям
у" + 6у' + 10у = За?е~3*, у" + 6у' + Юу = -2е}х cos*. A)
В случае первого из уравнений A) имеем у = -3, /3 = 0, Рт(х) = За?, р = 1. Так как y+fii Ф А>>2,
то з = 0. В случае второго уравнения A) у = 3, /3 = 1, Рт(х) = -2, Qn(x) = 0, р = 0. Далее,
поскольку у + f3i = 3 + i ф \\l2, то а = 0.
Для первого из уравнений A) частное решение имеет вид
у, =(аоаЯ-а,)е~31,
а для второго —
у2 = (bo cos a; + Ь, sin a:)e3*.
Сумма этих частных решений и есть искомое частное решение данного уравнения:
у = (aox + ai)e~3x + (bo cosа? + bi sin x)e3x. >
320. у"' - 2y" + 4y' - 8y = e1* sin 2a? + 2a?2.
•< Находим корни характеристического уравнения А3 — 2А2 + 4А — 8 = 0: А! = 2, Aj,3 = ±2i.
По аналогии с проделанным в предыдущих примерах устанавливаем, что для каждого из двух
уравнений
у'" - 2у" + 4у' - 8у = еъ sin 2х, у'" - 2у" + 4у' - 8у = 2*2
имеем а — 0. Кроме того, для первого из этих уравнений у = 2, /3 = 2, Qn(x) = 1, Рт(а;) = 0,
р = 0, а для второго — 7 = 0> Д = 0> -Рт(*) = 2а? , р = 2. Следовательно,
j/j = (а0 sin 2a? + 60 cos 2x)elx, j/j = CQx2 + Ctx + C2,
У = til + Уг - ("о sin2a? + 60 cos2x)e2x + Cox2 + C,a? + Cj. >
321. y"-4y' + 5y = e2lsinJx.
•< Определив корни характеристического уравнения Aitj = 2 ± i и записав правую часть
уравнения в виде
elx sin2 х = - eJl - - е2х cos 2a?,
аналогично проделанному выше получим j/i = а0е2*, уг = F0 cos2a? + 6[ sin 2a?)e2*. Таким образом,
у == (о0 + Ьо cos2х + bi sin2x)e&. >
322. yw + 5y" + 4у = sin a? cos 2a?.
4 Так как sin a? cos 2х = j sin За? — j sin а? и АI2 = ±2», Аз,4 = ±«, то, согласно примечанию
к примеру 316, имеем yt = o0sin 3x+a{ cos3x, y2 = а;(Ьо sinx+bj cosx), где yi — частное решение
уравнения у'v + 5у" + 4у = \ sin За;, а у2 — частное решение уравнения ylv + 5у" + 4у = - -у sin x,
причем в этом последнем случае $ = 1 в силу того, что у + /3i'¦ = А3. Следовательно,
у = aQ sin За? + О| cos Зж + a?(bo sin a? + bi cos a?). >
323. у"-ЗуЧ2у = 2х.
ч| Поскольку 2х - ехШ и А( = 1 Ф In2, \г = 2 Ф 1п2, то, согласно п. 3.2,
у = аоехШ = aQ2*. >
324. ylv - 4у'" + 5у" = х2cos2s? + а?вх
¦4 Частное решение у ищем в виде суммы трех частных решений yIt у2, уз, соответствующих
дифференциальным уравнениям, левая часть которых совпадает с левой частью дифференциаль-
дифференциального уравнения в условии примера, а правые части — соответственно функции /i(a?) = a?2 cos 2a?,
§ 3. Линейные дифференциальные уравнения с постоянными коэффициентами 143
/2(х) = xeIsin2x, /3(x) = eJlsinx. Поскольку характеристическое уравнение имеет корни
Ai,2 = О, А3,4 = 2 ±«, то, согласно примечанию к примеру 316, имеем
yi = (uqx2 + aix + a2) cos2x +
Уг = ((сох + Ct)sin2x + (dox + dt)cos2x^ex,
уз = х(щ sin a; + a] cos x)eix.
Заметим, что только в последнем случае f + pi = А3, т. е. s = 1. >
Применяя метод вариации произвольных постоянных, решить уравнения.
325. у"-2У' + у=—.
X
¦4 Сначала находим общее решение соответствующего однородного уравнения:
у = Схех + С2хех.
Затем, предположив, что С\ = С\(х), С2 = Сг(а;), подбираем функции С\(х) и С2(х) так, чтобы
функция
у = Q(x)ex + С2(х)хех A)
была решением неоднородного уравнения. Эффективно такой подбор функций осуществляется
с помощью системы уравнений F), п. 3.3:
С[(х)ех + С'2(х)хех = 0, * С?х(х)ех + С'2(х)ех(х + 1) = —.
х
Отсюда находим С[(х) = — 1, С2(х) = ^. Интефируя полученные уравнения, имеем С\{х) =
= -х + С{, С2(х) = 1п\х\ -\- С2, где С\, С2 — новые произвольные постоянные. Подставив
найденные функции С\{х), С2(х) в A), окончательно получаем:
у = Схех + С2хех - хех + хех In \x\. >
\у"-у) = х2-2.
Легко находим общее решение соответствующего однородного уравнения:
Согласно п. 3.3, общее решение неоднородного уравнения записывается в виде у = Ci(x)ex +
+ С2(х)е~х, а производные функций Ci и С2 определяются из системы уравнений
Cfl(x)ex + С'2(х)е-Х = 0, С[{х)ех - С12{х)е~х = - - -|-
х х'
Решив эту алгебраическую систему, получим:
<*«-!(-?¦:)
Интефируя последние соотношения, находим
где С\,С2 — новые произвольные постоянные.
Дважды интефируя по частям, получим
Подставив значения С\{х) и С2(х) в формулу для общего решения неоднородного уравнения,
имеем:
1
х
144 Гл. 2. Дифференциальные уравнения высших порядков
Применяя различные методы, решить уравнения.
327. у" + 2у' + у = cosix.
¦4 Общее решение однородного уравнения имеет вид
y = Cie'z+Cixe'x.
Поскольку cosia; = ^-ex+je~x и корень характеристического уравнения А = -1 двукратный,
то, согласно п. 3.2, частное решение неоднородного уравнения ищем в виде
у = аех + Ьх2е~х.
Подставив у в данное уравнение, получаем тождество относительно х, из которого следует, что
а = -g, Ь = -^. Следовательно,
1 хг
у = - ех + — е~х + de-x + С2хе х
есть общее решение исходного уравнения. >
328.
-^ Характеристическое уравнение соответствующего однородного уравнения А2+2г = 0 имеет
корни
А(; = л/=2г = \/2е1лГ^ =\/2ei(-t+i!ir), к = 0,1,
т. е. Ао = л/2 (cos (— -J J + г sin (—^Y] = l~i,Xi = V2 (cos |-я- + »sin ^-яу = -1 +». Следователь-
Следовательно, общее решение однородного уравнения описывается формулой
Для получения частного решения воспользуемся методом неопределенных коэффициентов.
Поскольку 8ех sini = Zeii+')x — je(l'%)x, то, согласно п. 3.2, частное решение ищем в виде
y = ae<1+"e + teeA-°' A)
(заметим, что множитель х во втором слагаемом в A) появился в связи с тем, что корень Ао совпа-
совпадает с числом 1 — г). Подставляя A) в исходное уравнение, получаем тождество относительно х,
из которого определяем а = —1,Ь = —1+».
Таким образом,
у = (С, + (г - 1)х)еA-> + С2е(!М)* - еA+1)*
— общее решение неоднородного уравнения. >
329. y" + 2iy'-y = 8chix.
4 Общее решение однородного уравнения есть функция
Так как 8chix — 4е'х + 4е~'х, то для нахождения частного решения неоднородного уравнения
удобно воспользоваться методом неопределенных коэффициентов. В силу того, что А = — i —
двукратный корень характеристического уравнения, согласно п. 3.2 частное решение ищем в виде:
Подставив у в данное уравнение и приравняв коэффициенты при е'х и е~'х, получаем а = — 1,
6 = 2. Следовательно,
есть общее решение исходного уравнения. >
330. у" + ш2у = -!—; уA) = 2, у'A) = -3.
х + 1
<4 Решив известным способом соответствующее однородное уравнение, имеем у = С\ sinwa;+
+ С2 coswa;. Для получения частного решения неоднородного уравнения воспользуемся методом
Коши. Согласно п. 3.4 можем записать:
К(х, s) =
§ 3. Линейные дифференциальные уравнения с постоянными коэффициентами 145
причем К(х, s)\x=s = 0, К'х(х, s)\x=s = 1 (в данном случае п = 2). Следовательно,
Ci(s)sinws + C2(s)costus = 0, Ci(s)cosus — C2(s)sinws = — (ш Ф 0).
ш
Из последних двух уравнений находим Ci(s) = со^3 , Ci(s) = - sln^3 . Тогда
1
К(х, а) = — sinu;(x — s).
ш
Функция f(x) = х^ д непрерывна при х Ф -1, поэтому справедлива формула A0), п. 3.4:
1 f sinw(a; - s)
У(х) = - I — ds,
w J s+\
где х0 6 [a, b], x 6 [a, 6] и -1 $ [a, 6]; a, b — произвольные числа.
Приняв во внимание частное решение A), записываем общее решение:
A)
„ . „ 1 ? sinw(x - s) ,
у = Ci sin wi + С2 cos wi H— / as.
ш J s+\
B)
Теперь, исходя из общего решения, построим частное решение, удовлетворяющее заданным
начальном условиям.
Дифференцируя B), получаем
X
/ОЛС lilt'Т ^— в^
ds. C)
S + 1
Полагая в B) и C) х = Xq = 1 и принимая во внимание начальные условия, имеем
2 = Ci sinш + С2 cosш, -3 = w(Ci cosш — С2 sinш),
откуда Ci = 2sinw - ^cosw, C2 = 2zosw + ^sinw. Подставив значения Ci и С2 в B) и взяв
xq = 1, окончательно находим
3 1 /"
у = 2cosw(x - 1) sinw(x - 1) + - /
Ш Ш J
1 /" sinw(a; — s)
/
S + 1
1
ds. >
331. y" + y=f(x).
Какие условия достаточно наложить на функцию /, чтобы все решения этого уравнения
оставались ограниченными при х —¦ +оо?
¦4 Применив метод вариации произвольных постоянных С\(х) и Сг(х), входящих в общее
решение соответствующего однородного уравнения
у = CiSina; + C2COsa;, A)
получим систему
Cj(x)sina; + C^(a;)cosa; = 0, Ci(a;)cosa; -C^(a;)sina; = f(x),
из которой следует, что С[(х) = f(x)cosx, С'2(х) = —f(x) sina;. Интегрируя, будем иметь
Ci(х) = j f(x) cos xdx + Ci, C2(x) = - j f(x) sin x dx + C2. B)
Предположим, что имеют смысл выражения
= / /(«) cos s ds, C(х) = I /(s) sin s ds
146 Гл. 2. Дифференциальные уравнения высших порядков
при любых фиксированных х > х0. Тогда, как следует из B) и A), общее решение данного
уравнения можно представить в виде:
х
/ /(s)sin(a; - s)ds = C{ sin x + С2 cos x + a(a;)sina; + /3(a;)cosa: =
= (Ci + a(x)) sin x + (C2 + f3(x)) cos x = A(x) cos(at - <p(x)),
где
C\ + a(x) C-, + 0(x)
C2+P(x)J, sm<p(x)=- ' v , cos<p(x) = r" ', A(x)jtQ.
A(x) A(x)
Отсюда следует, что для ограниченности решений у(х) при х -+ +оо достаточно потребовать
ограниченности функции А (амплитуды) при х -» +оо, т.е. ограниченности функций а и /3 при
х -* +оо. >
Построить линейные однородные дифференциальные уравнения с постоянными коэффици-
коэффициентами (возможно более низкого порядка), имеющие данные частные решения.
32.j,, = zV.
Дифференцируя последовательно функцию у{, получаем:
у[ = х2ех + 2хех = у{ + 2хех;
у'! = у\ + 2ех + 2хех = у[ + 2ех + (у[ - у,) = 2у[ - у, + 2ех;
Исключив из последних двух соотношений 2ех, окончательно имеем
»i" - 3yi' + 3yi - у, = 0.
Заметим, что получить дифференциальное уравнение более низкого порядка нельзя, так как
частное решение yi=x2ex порождается корнем характеристического уравнения кратности / = 3. >
333. у, =хех, у2 -е~х.
А Частное решение у\ порождается двукратным корнем А! = 1 характеристического урав-
уравнения, а частное решение уг — корнем А2 = -1. Поскольку корни известны, то легко записать
и само уравнение:
(А - 1J(А + 1) = 0, или А3 - А2 - А + 1 = 0.
Ясно, что такому характеристическому уравнению соответствует дифференциальное уравнение
334. !/i = х, у2 = sini.
•< Так как х — хеОх, sin а: = -^(е'х—е~'х), то данные решения порождены корнями некоторого
характеристического уравнения: Ai = 0 (двукратный корень), А2 = г, Аз = —г соответственно.
Следовательно,
А2(А - г")(А + ») = А2(А2 + 1) = 0, или А4 + А2 = О
есть характеристическое уравнение, соответствующее дифференциальному
335. jfr =ieIcos2i.
¦4 Поскольку хех cos2i = ^ieA+2l)I + -jxe(ll)x, то данное частное решение порождено дву-
двукратными комплексно-сопряженными корнями Ai2 = 1 ± 2г некоторого характеристического
уравнения. Оно имеет вид
(А - 1 - 2гJ(А - 1 + 2г"J = 0, или А4 - 4А3 + 14А2 - 20А + 25 = 0.
Остается записать требуемое дифференциальное уравнение:
lv4'"O' O. >
§3. Линейные дифференциальные уравнения с постоянными коэффициентами 147
336. При каких а и Ь все решения уравнения у" + ay' + by = О ограничены на всей числовой
оси —оо < х < +оо?
•< Прежде всего находим корни характеристического уравнения А2 + а А + Ъ — 0. Имеем
А12 = -|±i/^— Ь. Далее рассмотрим различные случаи представления всех решений.
Если а2 = 4Ь, то общим решением будет
х. A)
Если же а2 Ф 4Ь, то общее решение принимает вид
хх. B)
Из A) следует, что каким бы ни было число а (действительным или комплексным), все реше-
решения у ограниченными быть не могут. Действительно, если Re а > 0, то функция у не ограничена
при х < 0; если Re а < 0, то функция у не ограничена при х > 0; если Re а = 0, то неограни-
неограниченность функции у также очевидна.
Теперь рассмотрим решения, представленные формулой B). Пусть Re А! < 0 или Re А2 < 0.
Тогда решения B) не все ограничены при х < 0. Пусть Re А! > 0 или ReA2 > 0. Тогда не все
решения B) ограничены при х > 0. Наконец, если Re А! = ReA2 = 0, т.е. если Ai = 171, А2 = ij2
G1 ^ 7г)> т0 все решения при всех х € (—оо, +оо) будут ограничены. Действительно, в этом
случае все решения представляются в виде произвольной линейной комбинации ограниченных
функций siri7i2:, COS712:, sir^z, COS72?-
Итак, для ограниченности всех решений имеем условия:
а а2 а а2
откуда находим
a = -«Gi+7г),
где 7i и 7г — любые отличные друг от друга действительные числа. В частности, если а —
действительный параметр, т. е. 71 = —7г> то все решения будут ограничены при 6 > 0 (а = 0). >•
337. При каких а и Ь все решения уравнения у" + ау' + Ьу = О стремятся к нулю при
х -+ +оо?
•< Воспользуемся представлениями A) и B) всех решений из предыдущего примера. В слу-
случае A) все решения стремятся к нулю при х -» +оо, если Re a > 0. В случае B) все решения
стремятся к нулю при х -* +оо, если ReAi < 0 и Re A2 < 0 одновременно.
В частности, если а и Ъ — действительные параметры, то в случае A) все решения стремятся
к нулю при х -» +оо, когда а > О (Ъ = ^- > 0). Эти же условия (а > О, Ъ > 0) пригодны
и в случае B). Действительно, если 6 < 0, то один из корней Ai или Х2 независимо от а будет
положительным, т.е. ех>х или еХгх —» +оо при х —» +оо. Если 6 = 0, то уравнение имеет
решение у — С Ф 0, которое не стремится к нулю. Таким образом, необходимо, чтобы Ъ было
положительным. Пусть 6 > 0 и а ^ 0. Тогда действительная часть одного из корней (А[ или А2)
обязательно будет неотрицательной, следовательно, eXlX или еХ2Х не будет стремиться к нулю при
х —* +оо. Остается рассмотреть случай, когда а > 0 и Ь > 0 одновременно. Если 0 < Ь ^ ^-,
то оба корня Ai и А2 отрицательны, поэтому у -» 0 при х -* +оо. Если 6 > ^-, то корни Аь
А2 комплексно сопряженные и имеют отрицательную действительную часть, поэтому у —¦ 0 при
х -» +оо. >
338. При каких действительных а и Ъ каждое решение уравнения у"+ау'+Ьу = 0 обращается
в нуль на бесконечном множестве точек х?
¦< Исходим из представления решений A) и B) уравнения из примера 336. Ясно, что фор-
формула A) не определяет колеблющихся решений, которые при некотором а обращались бы в нуль
на бесконечном множестве точек х.
Рассмотрим решения B). Если А! и А2 — действительные корни, то, как известно, сумма двух
экспоненциальных функций может обратиться в нуль только в конечном числе точек х. Пусть
Гл. 2. Дифференциальные уравнения высших порядков
Ai = -?+i\Jb- т- А2 = -f -«/б- (, т.е. 4Ь> а2. Тогда
= A cos I
Как видим, все решения (при произвольных значениях А и <р) в этом случае обращаются в нуль
на бесконечном множестве точек {ж*}, где
?*7Г -1- <П
(к € Z). >
Т
339. При каких а и ft все решения уравнения у" +ау' + Ъу = 0 удовлетворяют соотношению
у — о(е~х) при х —> +оо?
•< Мы должны найти такие значения параметров а и ft, чтобы при всех значениях С\ и С2
(произвольных постоянных в решениях A) или B) уравнения из примера 336) выполнялось усло-
условие:
xlimjy(x)ex) = 0. A)
Если а2 = 46, то согласно A) имеем
Jirn^ ((С, + С2х)е{1~$)х} - 0.
Ясно, что это соотношение может выполняться для произвольных С\ и С2 только при условии
Re(l - f) <0, или Rea>2.
В случае, когда Ai Ф А2, условие A) принимает вид:
lim \С\Е -Ь С2е
х->+х \
которое для произвольных С{ и С2 эквивалентно соотношениям
Дт^'+'^О и ilimoe<A2+I)I=0. B)
Отсюда следует, что последнее возможно лишь в случае, когда одновременно выполняются нера-
неравенства Re(At + 1)< 0 и Re(A2 + 1) < 0.
Если а и ft — действительные параметры, то последние неравенства можно записать более
конкретно.
2
Пусть b < ^-. Тогда А! и А2 — действительные корни и если Ai < 0, то и А2 < 0. Следова-
Следовательно, имеем два условия:
п п / /j2
C)
при которых выполняются соотношения B). Решив совместно неравенства C), получаем следу-
следующее условие выполнения соотношения A):
а2
а>2, а-] <Ь<—.
4
2 / 2~
Пусть 6 > ^-. Тогда AJ2 = — -j ± iyb— ^- и соотношения B) будут выполнены, если
-§ + 1 < 0, или а > 2.
Таким образом, если а и 6 действительные параметры, то указанное в условии задачи соот-
соотношение выполняется при а>2иЬ>а-1,т. е. при 2 < а < Ь + 1. >
340. Для заданного Ь > 0 подобрать такое а, при котором решение уравнения у"+ау'+Ьу = 0
с начальными условиями уф) = 1, у'@) = 0 возможно быстрее стремится к нулю при х —> +со.
2
¦4 Рассмотрим три случая. Пусть 6 = %-. Тогда решение задачи имеет вид:
Ь<-, -- + 1 + Д/— -Ь< О,
(ах\ "х
1 + у)е-Т. A)
§ 3. Линейные дифференциальные уравнения с постоянными коэффициентами
149
Ясно, что а должно быть положительным, иначе j/i не будет стремиться к нулю при х —> +оо.
Следовательно, а = 2л/5.
Далее, пусть а > 2л/5. Тогда задача имеет решение
e 2
Остается сравнить решения A), B), C) при достаточно боль-
больших х > 0. Пусть а; —» +оо. Тогда для решений A), B), C)
соответственно имеем асимптотические формулы
B)
Наконец, если 0 < а < 2\fb, то
= (— si
\2wi
D)
Так как
-xVb
то хе
lim
lim —;
= lim :
Z->+OC
=0 при а < 2л/Ь,
0 быстрее, чем е 2 . Далее, в силу того, что
= l'm
=0 при а > 2л/б,
-хт/Ъ
О также быстрее, чем е'" 2 Iх. Таким образом, из D)
то хе
следует, что решение A), полученное при а = 2\/b, стремится к нулю при х -» +оо быстрее
остальных решений. >
341. Найти периодическое решение уравнения х+х+4х = ewt и на комплексной плоскости
С начертить кривую, которую пробегает амплитудный множитель этого решения при изменении
Ш ОТ 0 ДО +00.
< Заметим, что обозначения х, х используются в механике и имеют смысл первой и второй
производной по времени.
Поскольку характеристическое уравнение А2+А+4 = 0 имеет корни
, то сре-
среди решений однородного уравнения нет периодического решения, отличного от тождественного
1 о. .• v 15 ^ то частное решение ищем в виде х = Ae'wt. Имеем:
jut
нуля. Далее, так как ш Ф — -^ ± »'—
А =
1
4 + гш — ш2' 4 + ш — ш2
Отделяя действительную и мнимую части, для множителя А получаем выражение
А= Ai +iA2,
где Ai -
4-w2
1
D-ш2J
-и,2)
,2ч2 .
., 0< ш < +сю.
Исследуя обычным способом функции А\, А2 и \А\ на экстремум, находим: A\msx = j при
_ 1
w, = V2 и Л1тш = -^ при ш2 = \/6; ^2min « -0,5 при w3 =
« 1,94; |Л|тах « 0,51 при
Вычисляя еще 42(wi) « -0,23, А2(ш2) и -0,22, АЛш-Л и 0,1, lim At = i, lim Л| = О,
ш-*+0 ^ ш-*+оо
lim А2 = 0, Um Л2 = 0, получаем необходимые данные для построения эскиза графика кривой
на плоскости С (рис.26). >
ISO Гл. 2. Дифференциальные уравнения высших порядков
342. Дано уравнение y" + ay' + by = f(x), причем |/(ж)| ^ я» (—оо < х < оо), а корни харак-
характеристического уравнения удовлетворяют неравенству \2 < Aj < 0. Найти решение, ограниченное
при -оо < х < +оо. Показать, что:
а) все остальные решения при х -* +оо неограниченно приближаются к этому решению;
б) если / периодическая функция, то решение также периодическое.
¦4 Исходя из общего решения однородного уравнения
и применяя метод вариации произвольных постоянных С\ и С2, для общего решения неоднород-
неоднородного уравнения получим выражение
у = С^х + С2ех>х + -^- [f(x)e-x'x dx - -^- f f(x)e~x>x dx. A)
Так как несобственные интегралы
f{s)e-x'3 ds,
сходятся абсолютно в силу оценки
X X
J \f(s)e'x"\ ds^m [ e'x"ds,
—00 —ОО
то решение A) можно записать более компактно:
у = QeXiX+C2ex>x+ I-^Ц- (еЛ|<1^ - eA2(I"s)) ds = Ciex>x + C2ehx+ f(x-t) — dt. B)
J \i — Л2 v ' J л\ — Л2
—оо
Далее, поскольку справедливо неравенство
+00
ел'< - e™ m m
о
то из B) следует, что частное решение данного уравнения, ограниченное при х е (—So, +oo),
имеет вид
7 еЛ'( - ех*
у= f(x-t) — — dt. C)
J A,-A2
Ясно, что CteXlX + C2eXlx -» 0 при х -* +оо, поэтому из B) вытекает, что все решения стремятся
к частному решению C) при х -» +оо. Наконец, полагая в C) х + Т вместо ж, где Г — период
функции /, получаем
7 еЛ''-еЛ^ 7 eAlf-eA2f
у(х + Т)= / /(ж + Г-О-г —Л= / f(x-t)— — dt = y(x).
J Ai — А2 J л! — А2
0 0
Следовательно, функция у также Т-периодическая. >
§ 4. Линейные дифференциальные уравнения
с переменными коэффициентами
4.1. Линейное дифференциальное уравнение n-го порядка
с переменными коэффициентами.
Линейно зависимые функции. Определитель Вронского.
Линейным дифференциальным уравнением п -го порядка с переменными коэффициентами называ-
называется уравнение вида
ао(х)у(п} + а|(а;)!/<п-1) + ... + ап^(х)у' + ап(х)у = <р(х), A)
§ 4. Линейные дифференциальные уравнения с переменными коэффициентамн
151
где ip, а,- (г = 0, п) — известные функции. Если у,(ят> — частное решение уравнения A) при
if> = 0, то посредством замены у = y\z{x), z'(x) = и(х) порядок уравнения A) при <р — О
можно понизить. Функции у,- (г = 1, п) называются линейно зависимыми на сегменте [а, Ь],
если существуют такие постоянные а,- (»' = 1, п), одновременно не равные нулю, что на [а, Ь]
выполняется тождество
«i!/i + а2у2 + ¦ • • + апуп - 0. B)
Если тождество B) справедливо лишь при а.\ = а2 = ... = а„ = 0, то указанные функции
называются линейно независимыми на сегменте [а, Ь].
Определитель
= W(yby2,...,yn) =
У!
У2
4
Уп
у'п
C)
называется определителем Вронского.
4.2. Критерий линейной независимости функций.
Если (п - 1) раз дифференцируемые функции j/i, у2,.. ¦, уп линейно зависимы на сегменте
[а, 6], то РГ(а;) = 0на [а, 6].
Если линейно независимые функции уи у2, ..., у„ являются решениями линейного однород-
однородного уравнения
у(п) + Pi (x)y(n~l) + ...+ Рп(х)у = 0, D)
где Pj (j = 1, п) непрерывные на сегменте [а, Ь] функции, то W(x) ф 0 на [а, 6].
п
Общее решение уравнения D) при х 6 [а, Ь] есть линейная комбинация у = 53 Qyi(x) ли-
1=1
нейно независимых частных решений «/, этого уравнения.
4.3. Фундаментальная система решений.
Совокупность п линейно независимых частных решений линейного однородного уравне-
уравнения n-го порядка называется его фундаментальной системой. Фундаментальная система решений
вполне определяет линейное однородное уравнение D). Такое уравнение имеет вид
Уг
У\
У,
Уп
уГ1)
у!,л)
„(п)
= 0.
E)
4.4. Формула Остроградского—Лиувилля.
Если в C) yi, у2, ..., у„ — фундаментальная система решений уравнения D), то для опреде-
определителя Вронского справедлива формула Остроградского—Лиувилля
F)
где xQ 6 [а, Ь], х 6 [а, 6].
4.5. Общее решение неоднородного линейного дифференциального уравнения
с переменными коэффициентами.
Если известно общее решение однородного уравнения, то общее решение неоднородного
уравнения с непрерывной на [а, Ь] правой частью можно найти, применяя метод вариации про-
произвольных постоянных (см. § 3).
152 Гл. 2. Дифференциальные уравнения высших порядков
4.6. Уравнение Эйлера. Уравнение Чебышева.
Дифференциальное уравнение вида
(ах + Ь)УП) + Мая + Ьу-У"-0 + ... + ап^(ах + Ъ)у' + апу =
называется уравнением Эйлера. С помощью замены ах+Ь = ±е' его можно привести к уравнению
с постоянными коэффициентами. При а = 1, 6 = 0 уравнение Эйлера переходит в уравнение
*У"> + „.аг-У"-1» + ... + а^ху' + апу = 0,
которое также называют уравнением Эйлера.
Уравнение
(\-х2)у"-ху' + п2у = 0
называется уравнением Чебышева. Заменив аргумент х по формуле х = cosi, получим уравнение
4.7. Дифференциальные уравнения второго порядка.
Среди уравнений высших порядков, часто встречающихся в приложениях, важное место за-
занимают дифференциальные уравнения второго порядка
у" + Р{(х)у' + Р2(х)у = 0, G)
где Р[ и Р2 — непрерывные на (а, Ь) функции. С помощью замены
его можно привести к каноническому виду
d2z
— + J(x)z = 0, (8)
где
J(x) = Р2(х) - l-P[(x) - l-Pf(x).
При этом считают, что Р| € С1 (а, Ь). Функция 3 называется инвариантом уравнения G).
Любое уравнение второго порядка
Ро(х)у" + Р{(х)у' + Р2(х)у = 0 (9)
с непрерывными на (а, Ь) коэффициентами можно привести к так называемой самосопряженной
форме
путем почленного умножения уравнения (9) на функцию а, где
4.8. Связь межоу линейным дифференциальным уравнением второго порядка
н уравнением Эйлера—Риккати.
Если в G) положим у' = yz(x), то получим уравнение Эйлера—Риккати
~ =-z2 - Px(x)z - Р2(х). A2)
ах
Обратно, уравнение Эйлера—Риккати
)y + R(x)y2
с помощью замены
можно привести к линейному уравнению второго порядка.
§4. Линейные дифференциальные уравнения с переменными коэффициентами 153
4.9. Сведение линейного дифференциального уравнения второго порядка
с переменными коэффициентами
к уравнению с постоянными коэффициентами.
Иногда уравнение G) сводится к уравнению с постоянными коэффициентами. Если такое
сведение возможно, то только с помощью замены
t = aJ-/P2&jdx, A4)
где t — новый аргумент.
4.10. Об асимптотическом поведении
решений дифференциальных уравнений второго порядка.
Если \f(t)\ ^ -ffc при t0 ^ * < +оо. С > О, а > 0 — постоянные, то дифференциальное
уравнение
у" + A + №)у = О
имеет два линейно независимых решения
yi(t) = cost + О (?¦) , у2(<) = sint + О (^г) при <-»+оо,
а уравнение
у" - 0 - /@)» = о
— решения
'( (^)) 1 ( + О (^г)) при t-*+оо.
Исследовать, являются ли данные функции линейно зависимыми.
343. у, =х + 2, у2 = х-2.
< Согласно определению линейной зависимости функций (см. п. 4.1) должны найтись такие
числа а, и а2. одновременно не равные нулю, что выполняется тождество относительно х:
а,(а; + 2) + а2(а:-2) = 0, х 6 (-оо, +оо).
Отсюда (если такое тождество выполняется) следуют равенства
а,+а2 = 0, 2(a,-a2) = 0,
или c«i = a2 = 0- Следовательно, функции t/i и уг линейно независимые. >
344. у, = 6х + 9, у2 = 8а;+12.
¦4 Пользуясь определением линейной зависимости функций, можем написать:
а,Fа; + 9) + а2(8а:+ 12) = 0, х 6 (-оо, +оо).
Отсюда 6ai + 8a2 = 0, 9at + 12аг = 0. Фактически получили одно уравнение с двумя неиз-
неизвестными. Поэтому, положив, например, он = -1, найдем с*2 = ^. Таким образом, согласно
определению, данная система функций линейно зависимая. >
345. у, = х2 - х + 3, у2 = 2х2 +х, уз = 2а; - 4.
М По аналогии с предыдущим составляем тождество по а; 6 (-оо, +оо):
а{(х7 -х + 3) + а2Bх2 + х) + а3Bх - 4) = О,
из которого следует, что должны выполняться равенства
с*1 + 2с*2 = 0, -см + а2 + 2а3 = 0, За, - 4а3 = 0.
Легко убедиться, что третье уравнение системы является следствием первых двух. Поэтому по-
положив, например, ац = 4, для с*2 и а3 получим а2 = —2, а3 = 3. По определению система
функций у\, у2, Уз линейно зависима на числовой прямой. >
346. ух =х, у7 = ех, уъ = хех.
< Положив в тождестве по х
^е" + ajxex = 0, а; € (—оо, +оо),
154
Гл. 2. Дифференциальные уравнения высших порядков
W(x) =
sin a; cos a;
cos a; -sin а:
- sin x - cos x
=3sin2x^0.
x = 0, получаем а2 = 0 и а\Х + а}хех = 0 или а, + а3ех = 0 (х Ф 0). Отсюда следует, что
е1 = -^ = const, если а3 ф 0. Но это, очевидно, невозможно. Если же а3 = 0, то и c*i = 0.
Таким образом, система функций уь у2, у3 при х ? (-оо, +оо) линейно независимая. >
347. In a:2, In За:, 7.
4 Из тождества по а; 6 @, +оо):
a. In х2 + а2 In Ъх + 1аъ = 0,
которое можно представить в виде
(lay + а2) In х + а2 In 3 + 7а3 = 0,
следует, что 2а! + а2 = 0, а2 In3 + 7а3 = 0. Положив, например, а3 = — In 3, из последних урав-
уравнений получаем а2 = 7, а, = -3,5. Следовательно, данная система функций линейно зависимая
при х > 0. >
348. sin a;, cos ж, sin 2а;.
4 Составим определитель Вронского для этой системы функций. Имеем
sin 2а;
2 cos 2а;
-4 sin 2а;
Следовательно, согласно п. 4.2, данные функции линейно независимые (если бы они были ли-
линейно зависимыми, то выполнялось бы тождество W(x) = 0,x? (—оо, +оо)). >
349. л/х, л/аГ+Т, Vx + 2.
4 Предположим, что выполняется тождество по х ^ 0:
а, л/х + a2Vx + 1 + azVx + 2 = 0
при некоторых а,, а2, а3, одновременно не равных нулю. Тогда, положив в нем последователь-
последовательно х = 0, х = 1, х = 2, получим систему
а2 + с*3\/2 = 0, «1 + V2a2 + \/За3 = 0, V^a, + \/За2 + 2а3 = 0.
Так как определитель этой однородной системы не равен нулю, то с*1 = а2 = а3 = 0. Полученное
противоречие показывает, что данная система функций линейно независимая при х ^ 0. >
jjU. a;, |z|, 2a; + v4a;2.
4 Из тождества
ахх + а2\х\ + а3Bа; + 2|а;|) = 0, а; € (-оо, +оо),
следует, что а, + 2а3 = 0, а2 + 2а3 = 0. Положив в полученных уравнениях, например, а3 = -^,
получим а, = а2 = 1. Это означает, что предложенная система функций линейно зависимая. >
351. Являются ли линейно зависимыми на сегменте [а, Ь] функции, графики которых изо-
изображены на рис. 27?
4 Предположим, что справедливо тождество по а; € [а, 6]:
где а] + а\ + а] ф 0. Полагая в этом тождестве по-
последовательно х = Xi, х = х2 и используя равенство
Уг(х\) = Уъ(х2), можем написать
t*i + a2y2(a;i) + а3у3(а;,) = 0,
в! + а2у2(х2) + а3у3(а;1) = 0.
Отсюда следует равенство а2(у2(х2) — y2(a;i)) = 0. Но
так как уг(а:2) ф y2(xi), то а2 = 0 и тождество A)
принимает вид
= °- Р-с.27
х2
§ 4. Линейные дифференциальные уравнения с переменными коэффициентами 155
Последнее, если принять во внимание рис.27, невозможно при а2 + с*з Ф 0- Получили про-
противоречие, источник которого в предположении, что функции yi, у2, Уз — линейно зависимые.
Следовательно, они линейно независимые. >
352. Если определитель Вронского для функций уь у2, ..., уп тождественно равен нулю, то
можно ли утверждать, что эти функции будут линейно зависимыми или линейно независимыми?
¦4 Примеры показывают, что если определитель Вронского равен нулю при всех х 6 (а, Ь),
то функции у,, у2, ..., уп могут быть как линейно зависимыми, так и линейно независимыми.
Пусть У|(ж) = х, уг(х) = 2х. Тогда W(x) = 0. Легко видеть, что функции у, и у2 линейно
зависимые.
Пусть
„М-{ О*-1L, если 0<аг<1, м /0, если 0< а: < 1,
yi(x) ~ \ 0, если 1 ^ х < 2, У2{х) = \ (х - IL, если 1 ^ х < 2.
Так как у[(х) = yi(x) = 0 при 1 ^ х < 2, то
W(x) =
у2(х)
= 0 при 1 $С х < 2.
!Й(*)
Аналогично W(x) = 0 при 0 < х ^ 1, так как у'2(х) = у2(х) = 0 при 0 < х ^ 1. Следовательно,
W(x) = 0 на @, 2).
Предположим теперь, что при некоторых ау и а2 (а? + ?*2 ф 0) выполняется тождество
aiyi(z) + а2У2(х) = 0, а; € @, 2). A)
Пусть 0 < х ^ 1. Тогда из A) следует, что aiyi(a:) = 0, т.е. at = 0. Аналогично, если 1 ^ х < 2,
то из A) получим а2 = 0- Следовательно, функции у, и у2 линейно независимые. >
353. Функции у\ = х, у2 = ж5, уз = |х|5 удовлетворяют дифференциальному уравнению
х2у" + 5ху' + 5у = 0. Являются ли они линейно зависимыми на интервале (—1, 1)?
М Из предположения, что
сцх + а2х* + а3\х\* = 0, а; 6 (-1,1), а? + а\ + а\ ф 0, A)
получаем совокупность тождеств
а{х + а2х5 + аъхъ = 0, х ^ 0,
5 5 _ г. ^ г.
oiix + а2х — а^х = U, а; ^ и,
или ахх + а2х5 + аз^5 = 0 и -ахх - а2хь + щхь = 0, х ^ 0. Складывая последние тождества,
получаем 2аза;5 = 0, откуда аз = 0. А тогда из A) следует, что О[ + а2х4 = 0 (ж ф 0), что при
а2 + а2фО невозможно. Таким образом, функции у,, у2, уз линейно независимые на интервале
(-1, 1).
С другой стороны, известно, что линейное однородное дифференциальное уравнение п-го
порядка с непрерывными на интервале (а, 6) коэффициентами (Л) (а;) = 1) имеет только п ли-
линейно независимых частных решений на (а, Ь). В данном случае имеем
Видим, что коэффициенты Р\(х) = - J-, Р2(х) — \ разрывны в точке хц = 0 и х0 6 (— 1, 1).
Следовательно, нет уверенности, что число линейно независимых частных решений совпадет с
порядком уравнения. Этот пример показывает, что требование непрерывности коэффициентов
уравнения D), п. 4.2, которое обеспечивает равенство числа независимых частных его решений
порядку уравнения, не является излишним. >
354. Доказать, что два решения уравнения у" + р(х)у' + q(x)y = 0 (р, q — непрерывные
на интервале (а, Ь) функции), имеющие максимум при одном и том же значении х0 6 (а, Ь),
линейно зависимые на (а,Ь).
¦4 Выберем числа О| и а2 так, чтобы в точке х0, где решения yt(x) и у2(х) имеют макси-
максимальное значение, выполнялось равенство
a2yi(x0) = 0. A)
156 Гл. 2. Дифференциальные уравнения высших порядков
Поскольку частные решения принимают максимальные значения в точке х0, то
aiyi(zo) + а2у'2(х0) = 0. B)
Из A) и B) следует, что решение
у(х) = atyi(x) + а2у2(х) ¦ C)
удовлетворяет начальным условиям у(х0) = у'(х0) = 0. Так как функции р и q непрерывные, то
задача Коши
[ У" = -Р(Х)У ~ Ч(Х)У>
г/Ы = у'Ы = 0
имеет единственное решение. Очевидно, что этим решением является у = 0 на (а, Ь). В силу
этого, из C) следует, что
а\У\(х) + а2у2(х) = 0 на (а, 6),
т.е. частные решения у, и у2 в связи с равенством A), где а\ + а\ ф 0, оказались линейно
зависимыми на интервале (а, Ь). >
355. Даны 4 решения уравнения у'" + ху = 0, графики которых касаются друг друга в одной
точке. Сколько среди этих решений имеется линейно независимых?
¦4 В силу условия, для частных решений у,, у2, у г, ул в точке х0 выполняются условия:
yi(x0) = Уг(хо) = Уз(ж0) = Уа(х0У, у[(х0) = у'2(.х0) = у'3(х0) = у'^х0). A)
Тогда для функций
«1 = «/1 ~ У2, «2 = 2/2- Уг, «3 = 2/3- 2/4,
являющихся решениями данного уравнения, выполняются начальные условия
щ(х0) = и2(ж0) = Щ(хо) = щ(х0) = и'2(х0) = щ(х0) = 0. B)
Для произвольных чисел а, и а2 можно выбрать число а3 так, чтобы
ai«i'(ar0) + (X2U2'(x0) + а3и"(х0) = 0, а? + а\ + а] ф 0. C)
В силу существования единственного решения задачи Коши
у" = ~ху, y(xQ) - y\xQ) = у"(х0) = 0,
где у(х) = a\Ui(x) + а2и2(х) + аъщ(х), имеем тождество:
а1и1(х) + а2и2(х) + аъщ(х) = 0, х g X, х0 € X, D)
где X — некоторый интервал. Определив а3 из C) и подставив в D), получим
<*\(Щ -р\Щ) + <*г(и2 -р2щ) = 0, E)
где /?! = и},,{, 02 = ^т^т (и'ъ(ха) Ф 0). Так как числа а, и а2 произвольные, то из E) следует,
что
щ(х) - piu3(x) = 0, и2(я) - р2щ(х) = 0, х?Х,
откуда t/i = уз + (Л + /ЗгХг/з - 2/4), 2/2 = 2/з + /Ыг/з - 2/4)- Следовательно, по меньшей мере два
решения линейно зависят от двух остальных, которые могут быть линейно независимыми. Если
же у4 = 7Уз G = const), то тогда имеется три линейно зависимых решения (уь у2, у4 выражаются
линейно через функцию у3). Предоставляем читателю разобрать случай, когда и"(х0) = и'2'(х0) =
= и'1(х0) = 0. >
356. Могут ли графики двух решений уравнения
с непрерывными коэффициентами на плоскости хОу: а) пересекаться; б) касаться друг друга?
¦4 Пусть у,, уг — два различных решения данного уравнения. Тогда и функция у = yi - у2
также есть решение этого уравнения, причем в случае а) у(х0) = 0, а в случае б) у(х0) = у'(х0) = 0,
где ха — абсцисса точки пересечения (касания) графиков решений у, и у2.
Если п = 1, то, в силу единственности решения задачи Коши, в случае а) имеется только
тривиальное решение у(х) = yi(x) — у2(ж) = 0. Следовательно, двух различных решений нет.
Этот вывод справедлив и в случае б).
§4. Линейные дифференциальные уравнения с переменными коэффициентами 157
Пусть п = 2. Тогда в случае а) имеем задачу
у" + Р,(х)у'+ Р2(х)у = 0;
У(хо) = О,
в которой у'(х0) произвольное, поскольку не задано. Следовательно, графики двух решений
задачи A) могут пересекаться при х = х0. Аналогичная ситуация и при п > 2.
В случае б) получается задача Коши (п = 2):
у(х0) = у'(х0) = 0,
имеющая, вследствие непрерывности коэффициентов, единственное решение, проходящее через
точку (х0, у(х0)).
Если же п > 2, то задача Коши
" + ... + Рп(х)у = о,
1 У(хо) = у'(х0) = 0
становится неопределенной, так как не заданы значения у"(х0), и'"(жо)> • ••> ^"''(^о). Следова-
Следовательно, в этом случае через точку (х0, у(х0)) проходит две (и более) кривых, касающихся друг
друга в этой точке. >
Составить линейное однородное дифференциальное уравнение (возможно меньшего поряд-
порядка), имеющее данные частные решения.
357. у, = 1, у2 = cosx.
¦4 Очевидно, функции у, и у2 линейно независимые, поэтому согласно E), п. 4.3, имеем
1 cos х у
0 — sin х у'
= 0,
О - cos х у"
или у" sinх — у' cos х = 0. >
358. у, = ех, у2 = shx, уз = спж.
¦4 Функции у2 и уз являются линейными комбинациями функций ех и е~х. Следовательно,
фактически имеется лишь два линейно независимых решения: ех и е~х. Их простейшее диффе-
дифференциальное уравнение имеет вид у" - у = 0. >
Решить уравнения.
359. A + х2)у" - 2ху' + 2у = 0, ух{х) = х.
¦4 Согласно п. 4.1, с помощью замен у = xz(x), z' = « понижаем порядок данного уравнения:
жA + х2)и + 2и-0.
Общее решение его имеет вид « = С\ A + -=j-). Интегрируя уравнение z' = сЛ\ + -\\, окон-
\ X J \ X J
чательно находим z = С\Х — ^- + С2, или
360. ху'" - у" -ху' + у = -2х\ у,(я) = ех, у2(х) = х.
¦4 Полагая у = xz(x), z' = u(x), соответствующее однородное уравнение приведем к виду
х2и" + 2xvl - B + х2)и = 0.
Поскольку частному решению yi соответствует частное решение z\, то zt = Щ- = ^-. Но z\ = и\,
поэтому и,(х) = (^-J = е1 (-i \) есть частное решение последнего уравнения. Согласно
158 Гл. 2. Дифференциальные уравнения высших порядков
п.4.1, производим замену и = е1 ( ^ —^ J W(x), W'(x) = w(x). Тогда получим уравнение
(х - 1)а/ + 2ш (- - 1+ х] = О,
\х )
общее решение которого
~~2х
Решая затем уравнение
_2
находим:
W(x) = С
Тогда
z(x) = С2 /ех (- - 4) dx - ^ /е-х (- + -1) йх + Сг = С2-
J \х х2J 2 J \х х2J х х
где Ci = ^-. Наконец, у = Cte~x + Сгех +С}х есть общее решение однородного уравнения. Для
получения общего решения неоднородного уравнения применим метод вариации произвольных
постоянных. Тогда получим систему уравнений
С\е~х + С'2е + С\х = О,
-С[е"х + С'2ех + С\ = О,
С'1е"х + С'2ех=~2х7,
из которой находим С[ = ех(х - х2), С2 = -е~х(х2 + х), С\ = 2х. Интегрируя последние
соотношения и подставив значения С\, С2, Cj в выражение для общего решения однородного
уравнения, после некоторых упрощений находим общее решение данного уравнения:
у = Схе~х + С2ех + Съх + х\ >
361. х\2х - 1)у" + (Ах - 3)ху" - 2ху +2у = 0; у,(х) = х, у2(х) = -.
х
М Полагая у = xz(x), z'(x) = u(x), получаем уравнение
х2Bх - 1)«" + 2жEа: - 3)« + 6(х - 1)« = 0. A)
Из соотношений у2(х) — xz2(x), z'2(x) = «2B) находим частное решение для последнего уравне-
уравнения и2(х) = —j. Применив еще раз указанную замену, можем записать:
W{x)
и = ——, W (ж) = ш(х).
х'
Тогда A) примет вид
A - 2х)ш' + 2ш - 0.
Интегрируя это уравнение, получаем ш = С\(\ — 2х), или
W{x) = Ci(\-2x).
§4. Линейные дифференциальные уравнения с переменными коэффициентами 159
Из последнего уравнения следует, что W(x) = С\{х — х2) + С2. Производя, далее, очевидные
подстановки, имеем уравнение
,'(*) = С, A-
\Х2
из которого находим
Остается записать общее решение данного уравнения:
С2
|)+
Съх.
х
362. ху" + 2у' + ху = 0; „,(*) = ~ (х ф 0).
= С, ехр - / Р,(ж) dx , где Р,(я) = - (х ф 0).
< Для нахождения второго частного решения у2 воспользуемся формулой Остроградского—
Лиувилля:
1/1 2/2
У\ 2/2
Тогда получим уравнение относительно у2:
B)
решив которое, имеем
2/2 = Ci 2/1
Тогда общим решением будет
si
у - аху\(х) + а2у2(х) - at —
/:
пх
X
2/1У 2
dx
-а2Сх
- 2/'i2/2
COSX
1
X
с,
~ хУ
«2^2
ctgx +
sinx
X
с2
с,
sinx
X
sin ж
ж
COSX
¦Ci , х ф О,
X
где d, С2 — новые произвольные постоянные. Отметим, что формула B) фактически описывает
общее решение. >
363. Bх + \)у" + 4ху' - 4у = 0.
< Попытаемся найти частное решение этого уравнения в виде у\ = ерх, где р = const.
Подставив t/i в уравнение и сократив обе части на ерх, получаем тождество
р2Bх+ 1) + 4рх-4 = 0,
возможное лишь тогда, когда одновременно выполняются равенства:
1 1
2р + 4р = 0 и р — 4 = 0.
Отсюда находим р = -2. Следовательно, yt = е~2х — частное решение. Исходя из дифференци-
дифференциального уравнения A) предыдущего примера, легко находим общее решение дифференциального
уравнения
по известному его частному решению t/i(x):
(с/:
ехр I -
у = У1(х) I С, / V J2/ ч '- dx + С2
(формула Абеля). Воспользовавшись формулой, сразу напишем общее решение данного уравнения
у = С{х + С2е~2х. >
160 Гл. 2. Дифференциальные уравнения высших порядков
364. х(х - 1)у" -ху' + у = 0.
¦4 Легко видеть, что у, = х — частное решение уравнения, поэтому воспользовавшись фор-
формулой Абеля (см. предыдущий пример), получаем
=Ci(xln\x\+l)
365. х(х2 + 6)у" + Цх2 + 3)у' + бху = 0.
¦4 Поскольку коэффициенты этого уравнения есть многочлены, то целесообразно (хотя и не
обязательно) искать частное решение в виде некоторого многочлена. Пусть у, = хп+ ... (пока не
найдено натуральное п, выписывать следующие слагаемые не будем). Число п найдем, если это
возможно, из условия равенства нулю коэффициента при старшей степени х многочлена, кото-
который получается в левой части дифференциального уравнения после подстановки в него частного
решения у\.
Имеем
х(хг + 6)(п(п - 1)х"~2 +...)- 4(х2 + 3)(пж"~' + ...) + 6х(хп +...) = 0.
Отсюда, согласно сказанному выше, получаем уравнение
п(п- 1)-4п + 6 = 0,
имеющее два решения Щ = 2, п2 = 3.
Ищем частное решение в виде у\ = х2 + ах + Ь (если в таком виде частое решение не су-
существует, то попытаемся найти его среди многочленов третьей степени; если же и в этом случае
потерпим неудачу, то данное уравнение вообще не имеет решений среди многочленов).
Подставив у\ в уравнение и приравнивая коэффициенты при одинаковых степенях х, нахо-
находим а = 0, Ь = 2. Следовательно, yt — х2 + 2 — частное решение. Аналогичные поиски частного
решения среди многочленов третьей степени дают другое частное решение у2 = хъ, которое,
очевидно, линейно не зависит от первого.
Таким образом, получаем общее решение данного уравнения
у = С1(х2 + 2) + С2х\ A)
Любопытно отметить, что данное уравнение допускает еще одно частное решение t/з = 1Ж|3>
линейно независимое от у1 и у2 при —оо < х < +оо.
Если исходить из общего решения A), то нельзя решить, например, следующую дифферен-
дифференциальную задачу:
х(х2 + 6)у" - 4(х2 + 3)г/ + бху = 0,
2/(-1)=1, 2/A) = 2, у'(-1) = -2.
Однако на самом деле существует ее единственное решение
1 , х3 15 ,,
( 2 + 2)+ + И3
2/(* + 2)+у + И,
дважды непрерывно дифференцируемое при всех х € (-оо, +оо), и его можно получить из более
общего решения данного уравнения
подчинив последнее заданным дополнительным условиям. >
Замечание. Рассмотренный пример показывает, что если коэффициент Pq(x) при старшей производной
обращается в нуль при х = Xq , то соответствующее дифференциальное уравнение п-го порядка может
иметь больше чем п линейно независимых частных решений. Последнее означает, что некоторые диф-
дифференциальные задачи, кажущиеся неразрешимыми с первого взгляда (т. е. переопределенными), вполне
могут иметь единственное решение.
§ 4. Линейные дифференциальные уравнения с переменными коэффициентами
161
366. Заменой независимой переменной t = <р(х) уничтожить член с первой производной в
уравнении х2{\ - ж2)у" + l(x - ж3)у' - 2у = 0.
< Сначала выразим производные -^, -р^ через производные
dy dy dt dip dy
dx dt dx dx dt'
d2y _ d /d<p(x) dy\ _ d2<p(x) dy d<p(x) d /dy\ _
dx2 ~ dx \ dx dt) ~ dx2 dt dx dx\dt)~
Подставив значения этих производных в уравнение, получим
, —$. Имеем
d2<p(x) dy /d<p(x)\2 d2y
dx2 dt \ dx )
dt2'
Замечаем, что если функцию <р выбрать из условия
dx dx1
то цель будет достигнута. Последнее уравнение легко решается, и мы имеем
V(x) = — +C2.
х
Поэтому исходное дифференциальное уравнение можно представить в виде:
dt2
- 2» = 0,
C\ Ci
или, если учесть, что х = и — с = t - С > в виде
Произвольными постоянными можно распорядиться в зависимости от дополнительных усло-
условий. >
367. Доказать, что в случае q(x) < 0 решения уравнения у" + р(х)у' + q(x)y = 0 не могут
иметь положительных максимумов.
М Предположим, что в точке х0 ? (а, Ь) имеется максимум решения у = у(х), равный
у(х0) > 0. Тогда, как известно, в силу дифференцируемое™ этого решения, обязательно у'(х0) =
= 0. Подставив в уравнение х = х0 и приняв во внимание последнее условие, имеем
у"(х0) = ~р(хо)у'(хо) - q(xo)y(xo) = -q(xo)y(xo) > 0.
Следовательно, в точке х0 имеется минимум функции у. Полученное противоречие и доказывает
предложенное утверждение. >
368. Могут ли графики двух реше-
ний уравнения y"+q(x)y = 0, где q — не-
непрерывная функция, располагаться так,
как на рис. 28, а)? так, как на рис. 28, б)?
¦4 В случае а), очевидно, выполня-
выполняются равенства
,
Так как задача Коши
f у" = -q(x)y
. I У(х<>) = у
о
р„с
в силу непрерывности функции q имеет единственное решение, то yi(x) = уг(х), что противоре-
противоречит рис.28,а). Следовательно, такое расположение графиков решений yi(x) и у2(х) невозможно.
162 Гл. 2. Дифференциальные уравнения высших порядков
В случае б), исходя из рисунка, можем написать:
у'/(х) = -д(х)у!(х) < 0, у2(х) = -д(х)у2(х) > 0 Vx е (х0, xt),
откуда следует, что q(x) < 0 и q(x) > 0 Vx G (хо, хх) одновременно. Значит, и в этом случае такое
расположение графиков решений yi(x) и yi(x) невозможно. >
369. Доказать, что в случае q{x) > 0 для любого решения уравнения у" + q(x)y — 0 отноше-
отношение \ убывает при возрастании х на интервале, где у(х) Ф 0.
Л Вводя в рассмотрение новую функцию и по формуле и(х) = ^-, получаем дифференци-
дифференциальное уравнение
«'(*) = -q(x) - U2(x),
из которого, вследствие условия q(x) > 0, следует, что и'(х) < 0, т.е. функция « = у убывает
на интервале, где у Ф 0. >
370. Доказать, что в случае q(x) ^ 0 все решения уравнения у" + q(x)y = 0c положитель-
положительными начальными условиями у(хо) > 0, у'(хо) > 0 остаются положительными при всех х > х<).
Л Дважды интегрируя данное уравнение и используя начальные условия, получаем:
X
у(х) = у(х0) + у\хо)(х - хо) + J(x - s)(-g(s))y(s) ds. A)
В силу положительности у(ж0) и непрерывности функции у, при достаточно малом х > Xq правая
часть уравнения A) положительная. Покажем, что она останется положительной при увеличении
х > хй. Предположим, что при некотором Х\ > х0 функция у все же обратится в нуль (первый
нуль справа от точки х0). Тогда из A) получим равенство
= 0 = у(х0) + у'^оХа:, - х0) + J (xi - s)(-g(s))y(s) ds. B)
Поскольку y(s) > 0 при Хо < s < хи то (а?! - s)(-g(s))y(s) > 0 Vs G (a;0, *i). Следователь-
Следовательно, выражение в правой части равенства B) строго положительно. Полученное противоречие
и доказывает, что Vx > х0 у(х) > 0. >
Решить следующие уравнения.
371. ху" + у' = 0
¦4 Так как это уравнение Эйлера, то частное решение ищем в виде у = хг, где г = const.
Тогда для г получаем уравнение
г(г - 1) + г = 0,
откуда находим п = 0, г2 = 0. Следовательно, частными решениями будут у( = х° = 1, у2 =
= In |х|, а общим решением —
у = Ct +C2ln|x|. >
372. (х + 1)У" - 3(х + 1Jу" + 4(х + 1)»' - 4у = 0.
•< Это уравнение Эйлера. Его частные решения ищем в виде
у = (х+1)г (х>-1). A)
Подставляя A) в уравнение, получаем
г, = г2 = 1, г3 = 4.
Поэтому частными решениями будут у\ = х+ 1, у2 = (х + 1Iп(х + 1), уз = (х + IL, а общим
решением —
у = С,(ж + 1) + С2(х + 1Iп(х + 1) + С3(х + IL. >
§4. Линейные дифференциальные уравнения с неременными коэффициентами 163
Положим t = arctg x. Тогда
_ _, wr rj 11 3 1 _f< w«* r | wx " », I i, ^Vl» V 1 VVJ V I COS F --• "™* Sill ^V I *
da; dt da;2 da;\dt / dt\dt J \ dt2 dt '
и уравнение примет вид
Решая его, получаем
у = С, cost + С2sini = ' . + -~=s. >
v 1 + a;2 VI + a;2
374. x4y" + 2хъу' + у = 0.
•4 Положим t = p(a;) и подберем функцию ip так, чтобы после замены отсутствовал член
с первой производной. Тогда получим
(*V + 2а;^')у' + У = 0-
В силу поставленного условия, имеем xtp" + lip' = 0, откуда t = <р(х) = Щ- + С2. Уравнение A)
принимает вид
С\у" + у = О
и легко решается. Окончательно можем написать, что
у = .4cos- +Bsin-. >
X X
Представить в канонической форме следующие уравнения второго порядка.
375. (а;2 + \)у" + 5ху' + Ау = 0.
¦4 Согласно п. 4.7, производим замену
_2 ( Sxdx\ _ z(x)
В результате получим уравнение
W
376. (l - х2)у" - 2ху' + п(п + \)у = 0.
¦4 Подберем функцию и так, чтобы после замены у = u(x)z(x) дифференциальное уравнение
относительно функции z не содержало производную z'. Имеем
- x2)z" + Bu'(l - а;2) - 2а;и)г' + ((l - х2)и" - 7xv! + n(n + l)u)z = 0. A)
В соответствии с поставленной целью, полагаем A - х2)и' — хи = 0, откуда u = i c
4 ' v'l1"*2!
v
Подставив полученное значение и(х) в дифференциальное уравнение A), после упрощений будем
иметь окончательно
(
164 Гл. 2. Дифференциальные уравнения высших порядков
Следующие уравнения привести к самосопряженной форме.
377. ху" - Bх + 1)у' + 2у = 0.
Сравнивая коэффициенты данного уравнения с коэффициентами самосопряженного урав-
уравнения
d I dy\
Tx (*•>I)+ q(x)y s
(
получаем соотношения
p'(x) = 2x + 1 g(*) = 2
p(x) x ' p(x) x (X* h
P~2x lp~2x
Из первого соотношения находим р(х) = ^~, а из второго — q(x) = 2 .
Таким образом, при х Ф 0 данное уравнение приводится к самосопряженной форме
d /е1 dy
, . + —
dx \ х dx) х
0. >
378. x{x2 + 6)у" - 4(x2 + 3)у' + бху = 0.
¦4 По аналогии с проделанным в предыдущем примере, имеем
р'(х) = Цх2 + 3) g(x) = 6
р(аг) х(х2 + 6)' р(#) х2 + 6'
откуда
Х^Т6) xW6)
Следовательно, при а; Ф 0 данное уравнение представимо в самосопряженной форме
d t \ dy\ 6y
dx V а? (х -(- 6) dx J х (х -(- 6)
379. Привести к линейному уравнение ху1 - 5у - у2 — х2 = 0.
Л Согласно замене A3), п. 4.8, можем написать
У—^ (ифО).
и
Тогда
, _ -(и' + *«")« + ги'
и данное уравнение преобразуется к виду
хи" - 4и' + хи = 0. >
380. Пусть у и г — решения уравнений у" + д(г)у = 0 и z" + Q(x)z = 0 с совпадающи-
совпадающими начальными условиями у(х0) = z(x0), у'(х0) = г'(х0), и на интервале (х0, х{) вьшолняются
неравенства Q(x) > q(x), y(x) > 0, z(x) > 0. Доказать, что на этом интервале отношение ^
убывает.
¦4 Умножая первое уравнение на z, а второе — на у и затем почленно вычитая их, получаем
(г'у - y'z)' = -{Q- q)yz.
Интегрируя полученное соотношение в пределах от Хо до х ? {xq, x() и принимая во внимание
начальные условия, будем иметь
z'y-y'z=- J{Q(s)-q(s))y(s)z(s)ds, или (-) =—j f (Q(s) - g(s))y(sJ(s)ds.
Так как y(s)z(s) > 0, Q(s) - q(s) > 0, то (|Л < 0 при x > x0. Следовательно, функция у
убывающая. >
§4. Линейные дифференциальные уравнения с неременными коэффициентами 165
381. Заменой независимого переменного t = <р(х) привести уравнение —\ ± т = О
dx (ip(x))
d2y dy
к виду —г- + b(t) —- ± у = 0, а затем избавиться от первой производной заменой у = a(t)u
dt' dt
(преобразование Лиувилля).
¦4 Имеем
», x<ty . >2, 4dV
d2y у ,2 d2y ., dy
Следовательно, должно быть
,.2 .
Тогда
Теперь подберем функцию о так, чтобы после замены у = о(<)« в полученном уравнении
отсутствовал член с первой производной. Произведя указанную подстановку, имеем
% = a'(t)u + a(t)u\ ^-| = а"и + 2а'и' + аи",
dt dt1
аи + Bа! + аЬ)и + (а" + а'Ь ± а)и = 0. A)
Следовательно, мы должны положить 2а! + аЬ = 0, откуда находим
B)
Поскольку dt = ^у, b(t) = -?(ip2(x)), то B) принимает вид
а = Сехр I —- / ——(ip2(x)) 2 J = Сехр I - / —-^- ) = Cip(x) (ip(x) > 0).
Полагая С = 1 и вычисляя требуемые производные, приводим уравнение A) к виду
В следующих задачах исследовать асимптотическое поведение при х —» +оо решений данных
уравнений, пользуясь преобразованием Лиувилля и утверждениями п. 4.10.
382. у" + х4у = 0.
•< Принимая во внимание решение предыдущего примера, имеем
Осюда х = \/М и дифференциальное уравнение для u(t) примет вид:
Далее, поскольку в обозначениях п. 4.10 f(t) = ^, то, согласно этому пункту, уравнение A)
имеет решения
({) (}) (a=l), t -»+оо.
166 Гл. 2. Дифференциальные уравнения высших порядков
Следовательно, общее решение уравнения A) будет
Переходя в этом решении отиигкуих, можем написать:
)(^) +оо. >
у=-(c,cos—
383. ху" + 2у' + у = 0.
¦4 Полагая у = a(x)yi(x), подбираем функцию о так, чтобы в уравнении относительно
отсутствовала первая производная у\. Тогда получим
1 » 1
а(х) = —, ух -\—t/i =0 (х -ф 0).
х х
Теперь воспользуемся примером 381. Имеем
Следовательно, х — ^- и
3
В силу п. 4.10, частные решения последнего уравнения имеют вид:
А тогда общим решением данного дифференциального уравнения будет
1 / j \
384. у" + (*4 + 1)у = 0.
¦4 Применив преобразование Лиувилля, получим (см. пример 381):
1 / х2Bх4 ~ Ъ
й(х) = (х + 1) 4 у = й(а;)и(<), u (t) + ( И J
У (ж4 + 1):
Так как t — /A + ж4) г da: = /(a;2 + O(-T-JJ da:= y + O f ^-J при а; —» +оо, то а; = О
при ( —» +оо. Следовательно,
2q 4 _ эч
А тогда, согласно п. 4.10, можем написать, что
Наконец, возвращаясь к старым переменным хну, получаем:
х3
| , X -» +ОО. >
J у \ л /
Примечание. Следует принять во внимание, что
sin ( — ¦
Аналогично,
cos I —
§ 4. Линейные дифференциальные уравнения с переменными коэффициентами 167
385. (x2 + iW-y = o.
Л Применив преобразование Лиувилля, получим уравнение
где
Полагая т = ^-t, приводим уравнение для функции и к виду:
хт ~ A ~ 77т~,—к)u = °> гда * -'
ат V 5A + аг2)/
Отсюда, согласно п. 4.10, имеем
Возвращаясь к переменным г и у и принимая во внимание асимптотическое равенство t =
= ОAп х), х -» +оо, окончательно получаем
у = <! + *')* C,e^ml + C2e 2Ш*+О -^ = с**^ +С2х~Т- +О
2 /
х —* +оо.
Здесь воспользовались тем, что A + я2)? = х? + О ( -V 1, х —» +оо. >
Примечание. Первые два члена полученного решения легко найти из уравнения х2у" — у = 0, являюще-
являющегося "грубым" приближением данного уравнения.
386. х у" + у In а; = 0.
Л Имея в виду преобразование Лиувилля, можем написать (см. пример 381):
)' где t=
т.е. <= ^^ ПРИ х^1-
Так как
3-1п2г
то непосредственно воспользоваться здесь результатом примера 381 нельзя, однако к уравне-
уравнению A) можно применить преобразование Лиувилля. Тогда получим:
= О,
где
f(t) = ^"(OV'iCO = 8:
+oo.
168 Гл. 2. Дифференциальные уравнения высших порядков
Поскольку f(t) = О 1-у\ — О (Xj ,t{ —> +tx>, то, согласно п. 4.10, общее решение послед-
последнего дифференциального уравнения представляем в виде:
где
«,;,(<,) = cos«, +О (|-), и22(и) = smtt + О (jrj , *,->+оо.
Далее, принимая во внимание соотношения
cos <i = cos 7B:) cos С - sin j(x) sin С, sin tt = sin 7C;) cos С + cos 7C:) sin C,
где 7(г) = -j In2 я - ^-lnlna;, C= ^у^ + О ( —\— j, а также то, что
In2 / , \ ^ 1п2 / , \
sinC = sin-— + O [А- ), cosC = cos-—+O -4~ ,
16 \inxj' 16 Vina;/
^,@= 1 + О (|) = l + O (?) при t,- +00,
и включая в произвольные постоянные sin ^Д, cos -j?-, окончательно получим:
= \j-~ (Ci cos7(x) + C2sin7(x) + О (^)) , x -» +00. >
387. Применяя преобразование Лиувилля два раза, получить более точное асимптотическое
представление решений уравнения у" — 4х2у = 0.
¦4 Применив указанное преобразование, получаем
«"(<) - (l - ув *) "(О = 0, у = ~x-lu(t), A)
ния
фЦх)
Так как j^x~4 = j$t~2 = О ( 4- J, то, согласно п. 4.10, для частных решений имеем выраже-
и,<9 = е' (l + О (})) , «2(9 = е-' (l + О ({)) ,
Теперь применим преобразование Лиувилля к уравнению
Имеем
¦ +00.
§ 5. Краевые задачи 169
Дифференциальное уравнение для щ(т) имеет вид:
Поскольку
то для частных решений уравнения B) получаем:
«н(т) - ет (l + О (^)) , Ui2(t) = e"r (l + О
Далее записываем асимптотические выражения для u(t), ет, еГт :
u(t) = (l + — + О (jf\\ (С,в„(т) + C2bI2(t)) , C)
Подставив D) и E) в C), находим:
Наконец, используя F), на основании A) имеем для частных решений данного уравнения
такие асимптотические представления:
§ 5. Краевые задачи
5.1. Определение краевой задачи.
Задача вида
ву'(а:о) + /Зу(*0) = «о, .
где q, f — известные непрерывные на интервале (аг0) *i) функции, р € С*(а;о) *i)> Р(«) ?* О, а,
/3, 7> *» wo. ^! — заданные числа, называется краевой задачей для функции у. В отличие от
задачи Коши она не всегда имеет решение.
Если ш0 = ш\ — о, то краевые условия задачи A) называются однородными.
170 Гл. 2. Дифференциальные уравнения высших порядков
5.2. Функция Грива краевой задачи.
Функция G = G(x, s), где х е [х0, Xi], s G (х0, я,), как функция переменной х, удовлетво-
удовлетворяет следующим условиям:
1) она непрерывная;
2) при х ф s она является решением дифференциального уравнения
а также удовлетворяет однородным краевым условиям задачи A);
3) ее производная при х = з имеет скачок, равный -rhj, т. е. справедливо равенство
С \ — с' 1 —
Если такая функция существует, то решение краевой задачи A) при шд = ш\ ~ 0 также
существует и имеет вид
у(х) = JG(x,s)f(s)ds.
В случае неоднородных краевых условий задачи A), т. е. при ш1 + ш\ ф О, следует ввести в
рассмотрение новую функцию z по формуле у{х) — z(x) + u(x), где вспомогательная функция и
выбирается таким образом, чтобы она удовлетворяла неоднородным краевым условиям задачи A)
(часто это линейная функция). Тогда относительно функции z получается краевая задачи вида A)
с однородными краевыми условиями.
5.3. Задача Штурма—Лиувилля.
Задача об отыскании тех значений А, при которых уравнение
где р G C1[Xq, xi], р(х) Ф 0, q G C[Xq,X\\, имеет ненулевые решения у, удовлетворяющие
краевым условиям
ау'(.х0) + Ру(хй) = 0, 7У'(*1> + ЫХ1) = 0,
где а2 + 01 Ф 0, у2 + б2 Ф 0, называется задачей Штурма—Лиувилля. При этом числа А назы-
называются собственными значениями, а соответствующие им функции у — собственными функциями
рассматриваемой задачи.
5.4. Условие эквивалентности краевой задачи интегральному уравнению.
Если А = 0 не является собственным значением задачи Штурма—Лиувилля и / G C(xq, X\) Л
П Li(xq, xi), То краевая задача для уравнения
равносильна интегральному уравнению
X
X X
у(х) = \J G(x, s)y(s) ds + J G(x, s)f(s) da. B)
Напомним читателю, что символом ?г(*0) *i) обозначается класс функций, интегрируемых
с квадратом на (хй, хх).
Решить следующие краевые задачи.
388. у"-у'= 0; у@) = -1, t/(l)-j/(l) = 2.
А Записываем общее решение данного уравнения
у = С, + Сгех.
§ 5. Краевые задачи
171
Подставляя общее решение в заданные краевые условия, получаем систему уравнений относи-
относительно постоянных Су и С%:
Ci+C2 = -1, С2е - С, - С2е = 2.
Отсюда находим C*i = —2, С2 = 1. Следовательно,
A)
389. у" - у' - 2у = 0; у'@) = 2, у(+оо) = 0.
¦4 Легко находим общее решение данного уравнения:
у = Се + С2ех.
Так как у(+оо) = lim у(г) = 0, то из A) следует, что С2 = 0. Из краевого условия у'@) = 2
следует, что Ct = —2. Окончательно имеем
у = -2е~х, 0^х< +00. >
390. у" - 2iy = 0; у@) = -1, у(+оо) = 0.
4 Известным способом находим:
у = C,e(l+I> + C2e"(l+1)I = Ciex(cosa; + isina:) + C2e"x(cosa; - isina:).
Поскольку lim у(z) = 0, то Сх =0. Далее, из условия у@) = — 1 получаем С2 = — 1. Поэтому
у = e~*(ismar -cosa;), 0 ^ х < +оо, >
391. х2у" - 2хх/ + 2у = 0; у(х) = о(х) при х -» 0, уA) = 3.
¦4 Это уравнение Эйлера. Его частные решения ищем в виде у = хх, где А удовлетворяет
характеристическому уравнению А2 - ЗА + 2 = 0, из которого находим Ai = 1, А2 = 2. Тогда
= 0. Поэтому Ct = 0. Из второго краевого
у =
есть общее решение данного уравнения.
Первое краевое условие означает, что lim ^
условия следует, что С2 = 3. Таким образом,
у = Зх2 @ < х < 1)
есть решение данной краевой задачи. >
392. При каких о краевая задача у" + ау = 1, у@) = 0, уA) = 0, не имеет решений?
•4 Записываем общее решение данного уравнения
| + Суе^* + Сге-^1, если о ф 0,
если а = 0.
Принимая во внимание краевые условия, имеем
0 Cv
~,
-=0 (о ф 0),
а
A)
= 0 (О =
Система A) неоднородная, поэтому, как известно, она не имеет решений в том и только в том
случае, когда определитель этой системы
1 1
и хотя бы один из определителей
-1/а е~
не равен нулю. Из B) следует, что
= 0.
или АС2 =
i = *V, fc e z.
1 -1/а
ef* -I/a
B)
C)
D)
172 Гл. 2. Дифференциальные уравнения высших поряокон
Принимая во внимание D), из C) следует, что cos kit Ф 1, т. е. число к не должно быть четным
и к Ф 0. Итак, если о = Bт + 1Jтг2, т € Ъ, то система A) решения не имеет. При этом же
условии не имеет решения и предложенная краевая задача. >
Для каждой из следующих краевых задач построить функцию Грина.
393. у" = f(x); г,@) = 0, г,A) = 0.
¦< Согласно п. 5.2, для функции Грина G имеем задачу:
С«=0, G@, s) = GA, s) = 0 (Q^x^l; хф$),
C*i I /'V I i
"*lz=j+0 "zla:=j-0 — *•
Интегрируя уравнение G"IX = 0 один раз, находим
G'(x s)~l Cu еСЛИ °<a:<s' m
G'lit' s) ~ \ C2, если s < x ^ 1. A)
Здесь С\ Ф Сг, так как по условию производная G'x терпит разрыв при х = s. Далее, интегри-
интегрируя G'x, получаем
С(х Л - / ClX + Сг' если ° ^ ж < s>
<х(я s) - |
х<1. B)
Поскольку функция G непрерывная, то должно выполняться условие
Из краевых условий для функции G следует, что
С3 = 0, С2 + С4 = 0. D)
Условие скачка производной G'x при х = s приобретает вид
C2-d = 1. E)
Решив систему уравнений C)—E) относительно постоянных Q (t = 1, 4), получим:
Подставив значения С,- в A), заканчиваем построение функции Грина для предложенной задачи:
с . _ f (s — 1)ж, если 0 ^ а; ^ s,
'Ж) s' ~ \ s(x - 1), если s ^ а; ^ 1.
394. у" + у = f(xy, 2/@) = г/(т), г/'@) = г/'(т)-
¦< Решая уравнение G'xx + G = 0, х Ф s, имеем
~ . _ f Ci sin а; + Сг cos ж, если 0 ^ а; < s,
' \ С3 sina; + C(COsa;, если s < а; ^ тс.
Из краевых условий для функции G получаем:
Из непрерывности G(x, s) при а; = s, а также скачка производной G'x при х = s следуют соот-
соотношения
Ci sin 5 + Сг cos s = C3SHI.S + C4COSS, C3COSS — C4SU15 — С\ cos* + C2sins = 1. B)
Из системы уравнений A), B) находим
= -Ci = -- coss, Сг = -С4 = - sin s.
Таким образом, имеем
{5 sin(s - ж), если 0 ^ а; ^ s,
| sin(x — s), если s ^ а; ^ ж,
или G(x, s) = A sin |ж — s| при 0 < х ^ ж. >
§5. Краевые задачи
395. s3t/" + ЗжУ + art/ = /(ж); г/A) = 0, t/B) + 2у'B) = О.
¦4 Из уравнения
x3Gxx + 3x2Gx + xG = O, 1 «$ х ^ 2, я
находим
f ^-Ь^5, если 1^ж<в,
G(x,s)={ х х ' " A)
I ? + ^Е, если в<ж^2.
Подчиняя функцию G по переменной а; краевым условиям, а также пользуясь ее свойствами,
перечисленными в п. 5.2, получаем систему уравнений относительно С,- (t = 1, 2, 3, 4):
С, =0, С4 = 0, C2lns = C3, -%-2(Ч
Решив систему и подставив значения С,- в A), окончательно имеем
-Ч?> если 1 < х <,,
G(a;, s) = i
396. j,"cos2 x - y'sin2ж = f(x); j,@) = j,'@), j, (f) + j,' (f) = 0.
¦< Поскольку
Gm cos2 я - G'x sin2a; = (G^ cos2 a;)^,
то из уравнения
(G'x cos2 x)'x = 0, 0 < я < -, я Ф s,
легко находим
{Сх tga; + С2, если 0 ^ я < s,
CVgx + C если «<ж^|.
Краевые условия приводят к равенствам
Из свойств функции Грина получаем
С 1
' COS2 S COS2 S COS2 S'
Решив систему уравнений A), B), имеем:
11 ч
4 ' 4 ч
Таким образом,
\(tgs- 3)(tga; + 1), если 0 ^ я ^ s,
G(x,s)=\
( %( l3) если 5^x^f. >
397. у" + 4t/ + 3t/ = /(ж); t/@) = 0, 2/(ж) = О(е 2г) при я -> +оо.
¦< В данном случае
^le + С2е~3х, если 0 ^ ж < s,
Ъе~х + C^e~ix, если s < ж < +оо.
Из условия задачи
={
о=цтСзе +^е =@' если ?=;-
i-.+oo е-2г ^ сю, если Сз т= 0,
следует, что Су = 0. Из первого краевого условия получаем, что С\ + С2 = 0. Непрерывность
функции Грина и условия скачка ее производной при ж = а соответственно дают:
Схе" + Cie* = С4е~3', -ЗСе* + Схе~' + ЗС2е~3' = 1.
174 Гл. 2. Дифференциальные уравнения высших порядков
Следовательно, С\ = -С2 = -уе', С4 = ^-A - е2*), и функция Грина рассмотренной задачи
имеет вид
\е'(е~гх - е~х), если 0 ^ х ^ 5,
G(x, s) =
-3»
если в
< +оо. >
398. При каких о существует функция Грина краевой задачи у" + ау = /(ж), t/@) = О,
2/A) = О?
А Пусть о Ф 0. В этом случае функция Грина имеет вид
+ С2е~л/=га:, если 0 ^ х < s,
G(x, s) =
ах + C4e~v=:Sx, если s < х ^ 1.
Из краевых условий и свойств 1)—3), п. 5.2, следует система уравнений относительно Q (» =
1, 2, 3, 4):
= О,
С, + С2 = 0,
Полученная система уравнений неоднородная, поэтому для существования ее решения необ-
необходимо и достаточно, чтобы для определителя системы выполнялось условие
0
0
е
-ev
ev
—ev
ФО, 0 < 5 < 1,
или shi/-o Ф 0. Очевидно, что если о < 0, то последнее условие выполняется. Если о > 0, то
в силу равенства sh(t у/а) = i sin у/а определитель системы не равен нулю при условии sin у/а ф 0.
Следовательно, у/а фкк (к € Z), или о ф к2ж2.
Пусть о = 0. Тогда
G(x, s) = I
Cia; + C2, если 0 ^ a; < 5,
С3Ж + C4, если s < a; ^ 1.
Относительно постоянных С,- (t = 1, 2, 3, 4) имеем систему уравнений
С2 = 0, С3 + Сб, = 0, Cis = C3s + С4) С3 - Ci = 1,
из которых находим
d=s-l, C3 = s, C4 = -s.
Следовательно,
Таким образом, если о Ф к2^2 (к 6 N), то функция Грина данной задачи существует и единствен-
единственна. >
Найти функцию Грина следующих краевых задач.
399. (ху')' - A + х)у = /(*); уA) = О, Ш\ < +°°-
•4 Для функции Грина имеем дифференциальное уравнение
xG"xx + Cix - A + x)G = 0, 0 < х < 1, х Ф s.
Применив подстановку G = <p(x)U(x), где <р(х) = ех, приводим уравнение к виду
хи" + Bж + 1)«' = 0.
§5. Краевые задачи
Последовательно интегрируя его, получаем
X J X
X
Если ввести в рассмотрение функцию Ф, где
1
-и
то функцию и можно представить также в виде и — С{Ф(х) + С2. Следовательно,
С{ехФ(х) + С2ех, если 0 < х < s,
G^X' *' ! С3ех9(х) + С4ех, если 5 < х ^ 1.
Запишем теперь систему уравнений относительно С,- (t — 1, 2, 3, 4):
С\ = 0 (так как lim Ф(ж) = +оо),
С4 = 0 (поскольку ФA) = 0),
С2е' = е'СзФ(в) (так как функция G непрерывная),
/ е~'\ 1
Сз | ФE)е' I - Cie' = - (скачок производной G'x).
\ s ) s
Решив систему и подставив значения Q в A), получим окончательно
1
~ех+' [^- dt, если 0 ^ а; ^ s,
G(x, s) =
i
~ех+а /^ dt, если « < z < 1.
( X2 \ ' X2
400. /е"Ту'I -e-fy = f(x); j/@) = j/(l) = 0.
¦< Функцию Грина G, удовлетворяющую дифференциальному уравнению
'A -e~TG = 0, 0 < z < 1, z ^ s,
ищем в виде G = e 2 и(ж), где функция и есть общее решение уравнения хи' +и" = 0. Последо-
Последовательно интегрируя его, получаем
о
Принимая во внимание, что производная G'x разрывная при х = s, имеем
X2 } t2 X2
Cxt г е~ 2 dt + C2e~T, если 0 ^ х < s,
G(x,s)={ «
C3e 1 e~ 2 dt + C4e 2 , если s < x ^ 1.
176
Гл. 2. Дифференциальные уравнения высших порядков
Воспользуемся теперь краевыми условиями и известными свойствами функции Грина. Тогда
получим следующую систему алгебраических уравнений относительно С,- (t = 1, 2, 3, 4):
1 2 ' 2 '
= 0, С3 /е"?еИ + С4 = 0, CX fe'i2dt = Ci fe'
О 0 0
T e~^dt\ +seTC4-Cil + seT / е"
о ' ^ о
C3l+seT
V
dt) =
из которой находим
- ih(l)
this)
Подставив найденные значения С,- в A), завершим этим самым процесс построения функции
Грина G. Она имеет вид
-ft* ft1
^ /e"T dt e~2 dt, 0 ^ я ^ s,
"г" dt, s ^ x ^ 1. >
401. ((х2 - 1)у')' - 2j/ = f(x); \уA)\ < +оо, уB) = 0.
¦< Очевидно, что функция G = х удовлетворяет уравнению
((я2 - 1)G')' - 2G = 0, х € A, 2), хфз.
Поэтому общее решение уравнения можно искать в виде
G = хи(х).
В этом случае функция и является решением уравнения
(Ах2 - 2)и 4- (х3 - х)и" = 0, х Ф s,
интегрируя которое, находим
я-11
« = Q (- + -In
\х 2
я + 1
+ С2, хф s.
Следовательно,
G(x, s) =
C,(l + f In
С3 (l + f In
X -
x +
X- 1
x+ 1
I ) + C2a;, если I < x < s,
П + С4ж, если s < я ^ 2.
Из условия ограниченности G(a;, s) при а; —» 1 вытекает, что Ct = 0. Определяя известным
способом оставшиеся Cj (t = 2, 3, 4), имеем
где ip(s) = 1 + j In
Таким образом,
в-1
7ТТ
G(a;, s) =
если
|AпЗ-1)), если в ^ я ^ 2. >
§5. Краевые задачи 177
402. Оценить сверху и снизу решение задачи х2у" + 2ху' — 2у = f(x) и его первую произ-
производную, если известно, что у ограничена при а; —» 0 и при х —> +оо, а функция / удовлетворяет
условию 0 ^ /(а;) ^ т.
А Предоставляем читателю возможность убедиться в том, что функция Грина данной задачи
имеет вид
(~тт> если 0 ^ а; ^ s,
—^7, если s < а; < +оо.
Зх
Согласно формуле из п. 5.2, записываем решение задачи в виде
+00
у(х)= J f(s)G(x, s)ds.
о
Теперь займемся требуемыми оценками. Поскольку
+00 +00 / X +00 \
sds г х \ т
ds =-
о о
//• I r sds r х
f(s)(-G(x, s))ds ^mj (-G(x, s))ds = m [ J -^ + J —
и у ^ 0, то для решения у имеем оценку
m
Далее,
+00
'(*) = Jf(s)G'x(x, s)ds + I f(s)G'x(x, s)ds = |/(s) ^ rfs - | ^ ds
Таким образом, производная у' удовлетворяет неравенствам
403. Свести к интегральному уравнению задачу Штурма—Лиувилля
-A + ех)у" - еху = Хх2у, 0 < х < 1, г/@) - 2у'@) = 0, г/'A) = 0.
¦< Прежде всего займемся построением функции Грина следующей краевой задачи:
f -A + ех)у" - еху' = f(x), 0< а? < 1,
\ у@) - 2у'@) = 0, у'A) = 0.
Согласно п. 5.2, искомая функция G удовлетворяет условиям:
-(l + ex)G'L-exG'x = 0, х е @, 1), х ф s, A)
G@, s) - 2G'x@, s) = 0, Cfx(\, s) = 0, G(s - 0, s) = G(s + 0, s),
Из уравнения A) получаем:
(Ci In -jrr-r + C2, если 0 ^ x < s,
x
если s<x^l.
Используя краевые условия и свойства функции Грина, вычислим величины С* (t = 1, 2, 3, 4).
Затем, подставив их в выражение для функции Грина, закончим процесс ее построения. Она
имеет вид
если 0 < х ^ s,
если * < х ^ 1.
г. . _ / ж-1п(е1 + 1)+И-1п2,
U(x'8}~\ s-in(e' + l)+l+ln2,
178 Гл. 2. Дифференциальные уравнения высших порядков
Теперь, в соответствии с п. 5.3, можем записать требуемое интегральное уравнение:
у(х) = A J s2y(s)G(x, s)ds. ».
о
404. Свести к интегральному уравнению нахождение решений уравнения —2ху" - у' =
= 2А\/жу, 0 < а; < 1, при граничных условиях
Mm(v%') = 0, г,A) = 0.
¦4 Записав дифференциальное уравнение задачи в форме
(-л/ж»')' = At/, 0 < х < 1,
функцию Грина определяем из условий:
(-у/х&У = 0, 0<х<1, хфа, lim (y/xG'z) = 0, G(l,s) = 0,
G(s - 0, в) = G(s + 0, в), G;|I=J+0 - G'x\x=s_0 = --=.
Vs
Имеем
_ Г 2A - v/г), если 0 ^ а: ^ s,
, s) = j
Следовательно,
у(х) = A j G(x, s)y(s)ds. >
о
С помощью функции Грина решить следующие задачи.
. _ ху" у'
405. — — = /(а:), 1 < х < е, 2/A) = 0, у(е) - еу (е) = 0, где е — основание
1 -I- Т I I -I- 1* 1^
1 + х A+ ж)
натуральных логарифмов.
А Из уравнения
1 + а; A + а;J ^14- ж/ '
ж ф s,
получаем:
жС^ _ Г Си если x<s, Г С!(ж + 1пх) + С2, если 1 ^ ж < s,
1 + х \ С3, если х > s, | Сз(а;+1пж) + С4, если s < а; ^ е.
Пользуясь заданными краевыми условиями и свойствами функции Грина, находим
Следовательно,
(s + In s)(x + In ж - 1), если 1 ^ ж ^ s,
(*> «) - < /_ , ,_ _ч/. . i_ . _ 1); если s ^ х ^ е
В соответствии с формулой B), п. 5.4, решение поставленной задачи записывается в виде
е
у(х) = J f(s)G(x, s)ds. >
406. -A + cos x)y" + sinx ¦ у' = /(ж), 0 < х < f, уф) - 2у'@) = 0, у (f) = 0.
-4 Из уравнения
-A + cosx)G"x + sins; • Gi = -(A + cosaOGi)' = 0 (ж Ф s)
§ 5.' Краевые задачи
голучаем
С1! tg | + С2, если 0 ^ я < s,
C3tg f + С4, если s < я ^ f.
Краевые условия и свойства функции Грина приводят к равенствам
последовательным интегрированием получаем
I >^1 IV
G(x, в) =
Таким образом,
/ H1+tg§) (J — tS3) * если
| ^(l+tgf)(l-tgf), если
а решение поставленной задачи имеет вид
г
у(х) = JG(x,s)f(s)ds.
407. Доказать, что краевая задача
- у" + q(x)y = /(ж), у (а) - hy(a) = С,, г/» + Нг/(Ь) = С2
эквивалентна трем задачам Коши:
1) -9+92 = q(x); g(a) = -h;
2) Y'- g(x)Y =-f(x); Y(a) = Cl;
C2 - Y(b)
3) y'+9(x)y = Y(x); у(Ь)= д
Дифференцируя уравнение З) и используя при этом 1) и 2), имеем
y"+9'(x)y+g(x)y' = Y'(x),
Отсюда получаем уравнение
-у"
Подставив в 3) г = а, находим: г/'(о) + д(а)у(а) = Y(a), или
у'(а) - hy(a) = Сх.
Подставив в 3) а; = Ь, имеем
Но у(Ь) = С2 + у(Ь)(д(Ь) - Н), поэтому из C) следует
Таким образом, исходя из трех указанных задач Коши, получили краевую задачу A), B), D).
С другой стороны, дифференциальное уравнение краевой задачи можно представить в виде
{у +9(*)г/)' -9(х){у' +д(х)у) = -/(ж),
где
-д'(х)+д =q(x).
Полагая в E)
получаем
У -g(x)Y = -/(«).
180 Гл. 2. Дифференциальные уравнения высших порядков
Далее, подставляя в G) х = а, х = Ь к пользуясь краевыми условиями, можем записать
С, - (h + д(а)) у (а) = Г (а), С2 - (я - $(Ь)) »(Ь) = Г (Ь).
Как видам, условий здесь два, а неизвестных три. Поэтому можно положить
<7(а) = -Л. (9)
Тогда
Г(о) = С„ У(Ь)=%—*^г- (Ю)
Н - дф)
Следовательно, получили три задачи Коши F)-A0). >
Примечание. Очевидно, что для справедливости проделанных операций необходимо, чтобы задача Ко-
Коши F), (9) имела решение на сегменте [о, Ь]-
408. Найти собственные значения и собственные функции задачи у" = At,; г/@) = 0,
»A) = 0.
¦< Общее решение данного уравнения имеет вид
j/ = C1shv/Aa; + C2Chv/Aa;. A)
Использовав краевые условия, находим Сг = 0, Ci sh л/А/ = 0.
Так как мы ищем те значения А, при которых существуют ненулевые решения, то из по-
последней системы уравнений следует, что sh-\/A/ = 0 (А Ф 0). Отсюда, в силу тождества sh%/A/ =
= tsinv^A/ получаем у/^\1 = кж, А* = — ¦=-?- (fc G N). Полагая в A) С\ = t, находим собствен-
собственные функции ук = sin ^ft (fc G N). >
Примечание. Собственные функции находятся, вообще говоря, с точностью до произвольного числово-
числового множителя. Однако для многих целей удобно записывать собственные функции в так называемом
нормированном виде, подбирая каким-либо способом произвольный множитель. В данном случае мно-
1
житель С\ был выбран из условий: у / \уь\2 dx = 1 и уь — действительная функция.
-I
Упражнения для самостоятельной работы
Построить решения следующих задач Коши.
I. У" = У + У'2, 2/@) = 1, »'(<>) = 0.2. у1" = sfi^, г,@) = 0, г,'@) = 0, j,"@) = 1.
3. j,lv = aTY'sin (*j?J , у(\) = 1, j,'(D = 1, 2/"(О = 2, J,'"(D = 1.
4. у"' = 6x~ly" + 16х-*у-16х-2у' + х~\ху'-уГ1(х2у"-4*У' + 4у)\ !Ю) = 1, у'О) =2, г,"A) = 3.
Произвести указанную замену переменных в линейных уравнениях:
5. у" + у = 0, х = t2. 6. ж3/" + у" = 0, х = Int. 7. 2у" - Ъу1 + х2у = 0, у = x2v(x) + х.
8. у'" - ху' + ху = 0, х = tf, у = tv(t).
Методом вариации произвольных постоянных проинтегрировать уравнения:
9. у" + Ъу' + 2у= ^rpi, t/i = е-21, г,2 = е-. 10. у" + 2у' + у = Эе-у/х + Т, г/i = е-, у2 = хе'х.
II. j,lv + г, = sina;, А,,2 = ^=A ±»), А3,4 = --^A ±»). 12. у"' - 8tj, = cos2a;.
Построить общее решение однородных и неоднородных уравнений, используя формулу Остро-
градского—Лиувилля.
13. у'" + х2у" - 2ху' + 2у = 0. 14. г,'" + х2у" - 4хг/ + 6у = х + 1, у, = х2, у2 = х3 - 1.
15. у" +y'thx-2y = shx. 16. у"' - \х2у" + ху1 - у = х2 + х, у{ = х, у2 = х2.
Методом Эйлера построить общие решения следующих уравнений:
17. j,v - Юг,'" + 9у' = 0. 18. j,v + 8г,'" + 16г,' = 0. 19. j,lv - j, = 0. 20. yv - 6j,IV + 9г,'" = 0.
Методом неопределенных коэффициентов построить частные решения следующих уравнений:
21. у" - У = 2ех - х2. 22. у" -Зу' + 2у = xcosx. 23. у" + у = \хех. 24. у" + У =
§5. Краевые задачи 181
Решить уравнения Эйлера:
25. ж у" + ху' + 4у= Юж. 26. х2у" - Зху' + 4у = Пх2. 27. Bж - 1)у" - 3Bж - 1)у' + у = х.
28. Bж + 3)г/"' + 3Bж + 3)у' -Зу = х.
Построить решения следующих краевых задач:
29. г," - г,' = 0, 2/@) = -1, г/(П - 2/A) = 2, 0 < х < 1.
30. у"+у = -жокж, 2t/@)-t/'@)+t/(l)+3t/'(D = -1, -t/@)+4t/'@)-2t/(l)+5t/'(l) = 0, 0 < х < 1.
31. г," -2у' + у = е~х, 2/@) + у'B) = 0, г,'@) + Зг/B) = 1, 0 < х < 2.
32. ylv+y = х2, г/@) + у'(я-) - 2, г,"@) - Зу(тт) = 3, г,'"@) - 5у\ж) = 1, уф) = 0, 0 < ж < ж.
Построить решения задач:
33. у" - у = 1, г/@) = 0, |г/| < +оо при х -> +оо. 34. у" - 2iy = 0, уф) = -1, у(+оо) = 0.
35. х2у" - 6у = 0, 2/A) = 2, |2/@)| < +оо. 36. жУ - 2ху' + 2у = 0, 2/A) = 3, 2/ = о(ж) при х -> 0.
37. (l-a;2J/"-2a:2/' + 22/=2a;sina;+(l+ar:!)cosa;, ж € [-1, 1], М <+оо, \у'\ < +оо, 2/'@) = 1.
Найти собственные числа и собственные функции задач:
38. 2/' + 2Ажи = 0, 2/@) - 2/A) = 0. 39. у' + 3\х2у = 0, 2у@) + ЗуB) = 0.
40. г/' + 6As52/ = 0, j/@) + 62/C) = 0. 41. у" + ЗАу' + 2А2у = 0, 2/@) = 0, »A) = 0.
42. у" + Ау = О, 2/'@) + 22/@) - 2/A) = 0, y'(l) + 3»(О) + 4»A) = 0.
43. у'" + Ау = 0, 2/@) = 0, 2/'A) = О, 2/'@) + 3»A) = 0.
44. у" + x'ly' + At/ = 0, 0 < х < 1, 2/A) = 0, |у| < +оо, \у'\ < +оо.
45. A - х2)у" - 2а;у' + Ау = О, -К х < 1, \у\ < +оо, \у'\ < +оо.
46. х2у" + Ху = 0, 0 < х < 1, 2/A) = 0, г/(+0) = 0.
Следующие уравнения свести к самосопряженному виду:
47. х2у" + ху' - ж32/ + \ху = 0. 48. у" + (х + 1)у' - х2у + Аж3у = 0.
49. (х* + 1J/" - (ж + 2J/' - ж42/ + А(ж + 5)у = 0.
Построить особые кривые и особые решения уравнений:
50. у'2 - у2 = 0. 51. у'2 - 4г/3 = 0. 52. уу + х - 1 = 0. 53. ху' - у" = 0.
Решить следующие дифференциальные задачи:
54. cos у" = 1, 2/@) = 0, г/'@) = 1, 2/"@) = 2*. 55. г/"B/ - 1) = 0, 2/@) = 0, 2/'@) = 1, у"ф) = 0.
56. (у" - 2)B/" - 3) = 0, у@) = 0, 2/'@) = 5, у"@) = 3.
Понизить порядок следующих уравнений:
57. 6г/ - 5y"ylv = 0. 58. Ж2/1У + у'" = с*. 59. 2/"'2/'2 - / = 0. 60. ху'" - у"A - х) = 0.
61. 2/2/" - / - 2/' = 0. 62. г/2/" + / = 1. 63. 2/У" - / - »V = 0. 64. г/'У - / = 0.
Проинтегрировать следующие уравнения:
65. г/'"" + 32/'" + 2 = 0. 66. 3(ж22/'"J + жУ" -4 = 0. 67. у" Ш ж sin(y" In x) + (г/" In жJ - 2 = 0.
68. (Ж2/'" - 1)(Ж2/'" - 5) = 0. 69. ж6 - у -1=0. 70. Vx-y'" -1 = 0. 71. г/' - / - 1 = 0.
72. г/" = е*1. 73. 2у'у" - у + 1=0. 74. е" - г/" = 0. 75. / - у4 - 1 = 0. 76. у = ху'- у'2.
77. г/ = 2ху - In г/'. 78. ж = ? + lfl?/'. 79. ж = y'\Jl + y'2.
Глава 3
Системы
дифференциальных уравнений
§ 1. Линейные системы
1.1. Неоднородная система линейных дифференциальных уравнений
с переменными коэффициентами.
Фундаментальная матрица уравнения. Определитель Вронского.
Система уравнений вида
a)
называется неоднородной системой линейных дифференциальных уравнений с переменными коэффици-
коэффициентами o,j(i). Будем считать, что коэффициенты и свободные члены fj(t) являются непрерыв-
непрерывными функциями на (о, Ь).
Система дифференциальных уравнений
-J^XXOZj, i=TTn, B)
3—'
называется однородной. Вводя в рассмотрение векторы
X = (*,(*), X2(t), ..., *„(*)), / = (/,(<), f2(t), ..., /»(*))
и матрицу
А = (оуЮ),
уравнения A), B) можно представить в векторной форме
Матрица
где Xij — координаты линейно независимых решений (векторов) Х\ = (хц, x2i, ... ,xni), х2 =
= (*12, «22, ¦•• , *пг). •••. 5„ = («!„, Ж2п, ••• ,ж„„).векторного уравнения B'), называется инте-
интегральной, или фундаментальной матрицей этого уравнения. Иногда ее называют матрицей Врон-
Вронского.
Определитель
xn(f) xl2(t) ... xln(t)
W(t) =
D)
§ 1. Линейные системы 183
составленный из частных решений системы B), называется определителем Вропского. Для того
чтобы матрица вида C), где x{j(t) — частные решения системы уравнений B), была интегральной,
необходимо и достаточно, чтобы detX(i) = W(t) Ф 0 при t 6 (а, Ь). При этом общее решение
векторного уравнения B') представляется в виде
x(t) = X(t)C, E)
где С — произвольный постоянный вектор. Общее же решение уравнения (!') будет
x{t) = X(t)C + x(t), F)
где г(?) — какой-нибудь вектор, являющийся частным решением уравнения (!').
1.2. Метод вариация произвольного вектора.
Если известна интегральная матрица уравнения B'), то частное решение x(t) уравнения (!')
можно найти, пользуясь методом вариации произвольного вектора С. Этот вектор удовлетворяет
уравнению
X(t)Cf(t) = /(<)• G)
Поскольку detX(t) = W(t) Ф О, то 3(X(i))~' и C(t) = Xtfr'/tf), откуда
C0, (8)
где Со — произвольный постоянный вектор. Подставляя (8) в E), имеем
x(t) = X(t)C0 +X(t)jX(t)-'f(t)dt. (9)
Сравнивая F) и (9), получаем
1.3. Матрицант.
Фундаментальная матрица У уравнения B'), удовлетворяющая начальному условию Y(ta) —
= Е, a <t0 <Ъ, Е — единичная матрица, называется матрицантом. В общем случае матрицант
находится из уравнения B') методом последовательных приближений:
t
Х0 = 0, п = 0,1,2,..., t0, t 6 (а, Ь), r=UmXn(<).
Случай Лаппо—Данилевского. Если справедливо тождество
A(t)JA(T)dr = J A(T)dr ¦ A(t), t0, t 6 (a, 6),
J J
то матрицант можно найти по формуле
yj A0)
где под ехр(Б) понимается матричный ряд:
exp(B) = Е + В+ — В +... + — Вп+
' 2! п!
Если матрицант известен, то решение начальной задачи
dx
— = A(t)x + /(О, x(t0) = х0, A1)
dt
находится с помощью формулы Коши:
t
x(t) = Y(t)x0 + J Y(t)Y-l(T)f(r) dr. A2)
184 Гл. 3. Системы дифференциальных уравнений
1.4. Неоднородные линейные системы с постоянными коэффициентами.
Метод Эйлера.
Если Uij = const, то система A) называется линейной неоднородной с постоянными коэффициен-
коэффициентами. Общее решение системы B) можно найти, пользуясь методом Эйлера, который заключается
в следующем. Ищем решение уравнения B') в виде
()
х = Be , где В = . — постоянный вектор, А — постоянная.
Тогда из B') получаем уравнение F(X)B = 0, где F(\) = А — \Е. Поскольку мы ищем нетриви-
нетривиальное решение, то
Это характеристическое уравнение. Пусть Л{, Л^, ... , Ап — его простые корни. Тогда соответ-
соответствующие им решения будут
Векторы Bk, к = 1, п, являются решениями уравнений
F(Xk)Bk = 0. A4)
Произвольная линейная комбинация векторов A3)
п
1» — \ ' П R р^ (л z\
X— 2_^,^i-Oie ) {.!¦>)
1=1
где С,- — постоянные, есть общее решение уравнения B')-
Далее, если среди корней характеристического уравнения имеется корень As кратности г ^ 2,
то соответствующее ему вектор-решение имеет вид
х3 = (е + F(K)t + jt F2(Xs)t2 + ...+ * -F*-1^,)?-1} Asex'\ A6)
где As — вектор, удовлетворяющий уравнению
Fr(X3)Aa = 0. A7)
В этом случае произвольная линейная комбинация векторов вида A3) и A6) составляет общее
решение уравнения B').
Применяя метод исключения, решить следующие системы дифференциальных уравнений:
409. х = 2х + у, у = Зх + 4у.
¦4 Разрешив первое уравнение относительно у и подставив во второе уравнение системы,
получаем
у = х-2х, (х- 2х)' = 3х + Цх - 2х),
или
х - 6х + 5х - 0.
Корни характеристического уравнения А2 — 6А + 5 = 0 суть Aj = 1, Аг = 5. Следовательно, общее
решение последнего уравнения будет
х = С\ег + С2ен.
Подставив значение х в первое уравнение системы, найдем
у = (С,е' + С2еьь) - 2(с,е' + С2еьь) = -Схе1
410.
¦4 Подставляя значение у = *2 + 6*+1 — А, найденное из первого уравнения системы, во
второе уравнение, имеем
х + х = 3<2 -1 + 5. A)
§ 1. Линейные системы 185
Интегрируя уравнение A), получаем общее решение х = Cisini + Cicost + x(t), где x(t) —
частное решение неоднородного уравнения, которое проще всего найти методом неопределенных
коэффициентов. В результате будем иметь
х = С\ sin* + С2cost + 3t2 -1 - 1.
Далее, подставив значение х в первое уравнение системы, найдем
у - С2sin* - Ci cosi +t2 + 2. >
411. x = -x + y + z, у = x — y + z, z = x + y — z.
M Дифференцируя первое равенство и используя затем все три уравнения данной системы,
имеем
х — — х + у + z = Зх — у - z — Зх — (х + х) = 2х — х,
или
х + х - 2х = 0.
Интегрируя полученное уравнение, находим
х = С,е+С2е~21.
Далее, вычитая почленно из первого уравнения второе и учитывая уже известное значение для
функции х, приходим к уравнению у + 2у = ЗС^е1. Решив его, получим
у = Съе-Ь + С,е'.
Наконец, подставляя х и у в первое уравнение системы, находим
z = х + х - у = [Схе + С2е-*)' + ((V + С2е() - С3е' - С,е' = Схе - (С2 + С3)еЛ >
412. х = -y+z + 2x, y = x + 2y-z, z = x-y + 2z.
М Продифференцировав третье равенство системы и воспользовавшись всеми уравнениями,
имеем:
z - х - у + 2z = 2х - у + z + 2(х - у + 2z) - (z + 2у - z) = Зх - 5у + 6z.
Дифференцируя полученное соотношение и пользуясь уравнениями системы еще раз, приходим
к уравнению
"z =3x-Sy+dz = lx- 19y + 20z.
Остается исключить переменные х и у из системы уравнений:
г = х - у + lz, z = 3x-5y + 6z, 'z =lx- \9y + 20z.
В результате исключения будем иметь одно уравнение относительно функции z:
"z -6z+ Hi — 6z = 0.
При этом
1 •¦ 5 • -, 1 .. 3 .
x = --z+-z-2z, y=--z+-z. A)
Корни характеристического уравнения A3 — 6A2 +11A — 6 = 0 суть А] = 1, \2 = 2, A3 = 3.
Следовательно, общее решение
z = Cie1 + C2e2t + C3e3'. B)
Подставляя B) в A), получаем
x = C2e2t + C3e3\ у = del + C2e2'. >
413. x = y — z, у — x + y, z = x + z.
¦4 Путем дифференцирования первого равенства системы и использования двух других по-
получаем уравнение: х = у — z, или х = х. Общее решение полученного уравнения имеет вид:
х - Сх + Сге1.
Подставляя значение х в третье уравнение и интегрируя его, будем иметь
z = (С3 + C2t)e' - d.
Наконец, из первого уравнения получаем
t(c (+l))-Cl. >
186 Гл. 3. Системы дифференциальных уравнений
414. х-Ъх-y + z, y = x + y + z, ? = 4x-y + 4z.
¦4 Аналогично проделанному в примере 412 имеем:
х = Зх-у + ? = 3Cж - у + z) - (х + у + z) + (Ах - у + Лг) = \2х - 5у + 6z;
х = \2х -Sy + 6z = ЩЗх -y + z)-S(x + y + z) + 6Dж - у + 4z) = 55ж - 23у + 3lz.
Исключив из системы
x = 3x-y + z, x = l2x-Sy + 6z, x = 55x-23y + 3\z
переменные у, z, получим дифференциальное уравнение относительно функции х:
х -8а: + \1х - \0х = 0. A)
При этом
у = х - 6х + 6ж, z = х - 5х + Зх. B)
Общее решение уравнения A) имеет вид
х = Сге' + С2еа + С3е5'. C)
Используя C), из B) находим
у = de - 2С2еп + С3е5', z = -С,е' - ЗСгеи + ЗС3е5'. >
415. х = Зх + 4у, у = —х — у.
¦4 Определив х из второго уравнения системы и подставив его в первое уравнение, получим
{-У - !/)"= Н-У ~У) + 4у, У™ - 2у + у = 0.
Решив последнее уравнение, будем иметь
у = (С, + C2t)eb + (С3 + С4)е~'.
Наконец, из второго уравнения находим
* = -У - У = 2(С4 - С3 - С4<)е"' - 2(С, + С2 + C2t)el. >
416. х = Зх — у — z, у = —х + Зу — z, z = —x — y + 3z.
¦4 Дифференцируя первое равенство дважды и учитывая все три уравнения системы, получаем
xw = 3x-y-z = 3Cx-y-z)-(-x+3y-z)-(-x-y + 3z)= Ux-5y-5z= 11ж + 5(ж- Зх),
или
Решив это уравнение известным способом, имеем
х = Qe1 + С2е'1 + Сгеи + С4е'. A)
Вычитая почленно из первого уравнения системы второе и пользуясь решением A), можем запи-
записать:
у - 4у = -3Cie' - ЗС2е~1,
откуда
у = С5еи + С6е' + С, е' + С2е"'. B)
Наконец, подставляя решения A), B) в первое уравнение системы, находим
z = Cie' + С2е~' - (С3 + С5)е2( - (С4 + С5)е-2(. >
417. х + х + у-2у = 0, х-у + х = 0.
¦4 Складывая почленно оба уравнения системы, имеем х + 2х + х = 2у, откуда находим
у = -(х + 2х + х). A)
Подставляя значение у из A) во второе уравнение системы, получаем дифференциальное урав-
уравнение относительно функции х:
х +22 - х - 2х = 0.
Решив его, будем иметь х = de1 + С2ег + С3е~г. Учитывая полученное решение, из A) находим
§ 1. Линейные системы 187
418. х - 2у + у + х - Зу = 0, Ау - 22 - х - 2х + 5у = О.
•^ Умножив почленно первое уравнение на 2 и сложив со вторым, приходим к равенству
2у - х - у = 0. A)
Дифференцируя A) и учитывая первое уравнение системы, получаем х = Зу. Подставляя значе-
значение х в A), имеем дифференциальное уравнение у + у = 0, из которого легко находим
У = Се"'.
А тогда
х = ЗСе~1. >
419. х + 4х - 2х - 2у - у = 0, х - 4х - у + 2у + 2у = 0.
•^ Сложив почленно эти уравнения, получим Bх — у)" = 2х - у, откуда 2х - у = C\el + Cie'1.
Подставив значение
у = 2х - Схе1 - С2е'1 A)
в первое уравнение системы, будем иметь дифференциальное уравнение для функции х:
х - 4х + ЗСхе - С2е"' = 0.
Общее решение этого уравнения
-^C2e't. B)
Наконец, подставив B) в A), имеем
у = 2С3е2' + 2С4е' + Схе* - j C2e'1. >
420. 2х + 2х + х + Зу + у + у = 0, х + 4х - х + Зу + 2у - у = 0.
М Разрешив систему уравнений относительно старших производных, имеем
х = 2х + у-2х-2у, у = -2х-у + х + у. A)
Дифференцируя последовательно два раза первое равенство системы A) и пользуясь при этом ее
уравнениями, можем записать:
х =-у-Ъх- Зу, х1У = -х-2у-х-у. B)
Разрешив систему B) относительно у и у и подставив их значения в первое уравнение системы A),
получим уравнение для функции х:
a;lv -x+x-x = 0.
При этом
y=-(a;lv-2ar4i-5i). C)
Интегрирование последнего уравнения дает
х = Сх + C2el + C3 cost + C4 sin*.
Наконец, подставив значение х в C), окончательно находим
y=-Ci- С2е' + - (-4С3 + 3C4)cos< - - DС4 + 3C3)sin<. >
Применяя метод Эйлера, решить следующие системы уравнений:
421. х = х- у, у = у-4х.
¦4 Согласно методу Эйлера частные решения системы ищем в виде
х = Аем, у = Веи, А, В,Х — постоянные. A)
Подставив A) в систему, имеем алгебраическую систему
АХ = А - В, ВХ = В-ЛА, B)
из которой в силу нетривиальности искомых решений следует, что определитель
А-1 1
4 А-1
188 Гл. 3. Системы дифференциальных уравнений
или (А — IJ — 4 = 0. Корни характеристического уравнения Ai = 3, Х2 — ~ 1 — простые.
Следовательно, частные решения, им соответствующие, имеют вид:
ж, =Л,е3', х2 = А2е~1, у{ = В,е3', у2=В2е'1.
Связь между постоянными Ак, Вк мы найдем, воспользовавшись системой уравнений B). Имеем
А\\\ = А{ — В[, Х2А2 = А2 — В2 (вторые уравнения являются следствием записанных), откуда
находим В\ = -2Aiy Bi = 2Ai- В силу произвольности Ах и А2 можем, например, положить,
что AY = А2 = 1. Тогда Bt = —2, В2 = 2. Таким образом, фундаментальная матрица запишется
в виде:
=(S ?)¦
Общее решение в векторной форме, согласно E) п. 1.1, будет
у
Отсюда следует, что
х = С,е3' + С2е-\ у = -2Cie3( + 2Сге~1.
422. х -х-уЛ-z, y = x + y-z, z=2x-y.
¦4 Ищем решения в виде
х = Аем, у=Вем, z = CeM. A)
Подставив A) в систему, имеем
Л(А - 1) + В - С = 0, -А + В(Х - 1) + С = 0, -2А + В + С\ = 0. B)
Поскольку мы ищем ненулевые решения, то должны положить
А-1 1 -1
-1 А-1 1 =0,
-2 1 А
откуда А3 - 2А2 - А+ 2 = 0. Корни этого уравнения Af = 1, А2 = 2, A3 = -1 — простые. Поэтому
частные решения представляются следующим образом:
z, = А{е1, х2 = А2еп, х3 = Аге~\
ух = Вхе\ у2 = B2e2t, уъ - В^е~\
zx = С,е', z2 = Сгеи, z3 = Сге~1.
Для установления связи между постоянными Ak, Bk, Ск пользуемся системой A). Имеем
Ак(Хк-1) + Вк-Ск = 0, -Ак + Вк(\к-1)+Ск = 0, -2Ак + Вк + Ск\к=0, к = 1, 2, 3.
Нетрудно получить решения последней системы:
В\ = А\ = С\\ А2 = С2, В2 = 0; Вз = — ЗАз, Сз = — 5 А}.
Поскольку часть из найденных постоянных произвольна, то можно положить С\ = 1, С2 = 1,
А?, — 1. Тогда В\ = А\ = 1; А2 = 1; Bj = —3, Сз = —5. Таким образом, фундаментальная
матрица рассматриваемой дифференциальной системы имеет вид:
(el e2t е~1
X(t) = е' 0 -Зе~{
\е1 e2t -5е~1
Общее решение будет
откуда
х = Cxel + C^e* + Съе~\ у = С,е' - ЪСъе~\ z = Cxel + С2ем -
§ 1. Линейные системы 189
423. х = 2х + у, y = x + 3y-z, z = -x + 2y + 3z.
•^ Действуя аналогично предыдущему примеру, имеем Ai = 2, А2 = 3 + *', A3 = 3 - 1. При
этом частные решения будут
Для определения постоянных Ak, Вк, Ск, к — 1, 2, 3, пользуемся системой алгебраических урав-
уравнений:
Ак(\к-2)-Вк=0, -Ак+Вк(Хк-3) + Ск = 0, Ак-2Вк + Ск(\к-3) = 0, к = 1, 2, 3.
Решив систему уравнений относительно Ак, Вк,Ск, получаем:
Bi-0, Ax-Cx = \; A2 = \, B2 = l + i, C2 = 2-i; A3 = l, B3 = \-i, C3 = 2 + i.
Следовательно, фундаментальную матрицу можно записать в виде:
leu e3((cos* + «sint) e3'(cosi - tsini)\
X(t) = О A+ *)e3((cos t + i sin t) A - i)e3'(cos t - i sin t) .
\e2t B-»)e3'(cos* + «sin<) B + i)eil{co&t - isint)/
А тогда согласно E), п. 1.1,
x = Cie2t + C2eu(cos.t + isint) + C3e3i(cost - isini),
у = C2(l + i)ell(cost + isint) + C3eu(\ - j)(cost - isini),
z = Cie2i + C2B - j)e3i(cos< + isint) + C3B + i)eil(cost - isint),
где Ci, C2, C3 — произвольные (вообще говоря, комплексные) постоянные. В частности, если
положить С2 = Ci + iC3, C3 = С2 - iC3, где С2, С3 — действительные постоянные, то из B),
считая что С\ — действительная постоянная, можно получить общее решение данной системы
дифференциальных уравнений уже в действительной форме:
x = Cxe2t + 2еъ\С2cost - C3 sint),
у = 2е3'((С2 - C3)cos< - (С2 + C3)sin*),
z = Схеи + 2e3((BC2 + C3)cos< + (C2 - 2C3)sin<). >
424. x = 2x + 2z - y, y = x + 2z, i = -2x + y-z.
¦4 Нетрудно найти корни характеристического уравнения
А-2 1-2
-1 А-2
2 -1 А+1
Они имеют вид: А, = 1, А2 = *', А3 = -». Поэтому, как и в предыдущих примерах, можно записать
частные решения данной системы:
Xi - Ахе1, х2 = А2еи, х3 = А3е~и,
У1 = Вхе1, у2 = В2еи, Уз=В3е~и, A)
zx = de', z2 = С2еа, z3 = С3е'н,
где постоянные Л», Вь, С», к = 1, 2, 3, связаны соотношениями
Ак(Хк - 2) + Вк - 2Ск = 0, -Ак + ВкХк - 2Ск = 0, 2Ак - Вк + Ск{\к + 1) = 0, к = 1, 2, 3.
Решив эти алгебраические системы уравнений, имеем:
Ах = 0, В, = 2С,; А2 = 52, С2 = - (-Л2 + *В2); Л3 = 53) С3 = i (-Л3 -
В частности,
С1 = 1,В,=2; А2=В2 = 2, C2=i-1; А3 = В3 = 2, С3 = -1 -i.
=0.
190 Гл. 3. Системы дифференциальных уравнений
А тогда из A) следует, что фундаментальную матрицу можно сформировать так:
0 2е" 2е~"
X{t) = 2e( 2е"
а общее решение данной системы будет
х = 2С2е" + 2С3е~", у = 2Схе + 2С2е" + 2С3е~", г ~ Схе + C2(i - 1)е" - С3A
Положив здесь С2 = С2 + «C3, С3 = С2 — «Сз, где С2> Сз — действительные постоянные, общее
решение можно получить в действительной форме:
х = 4(C2cos*-C3sini), у = 2Cie'+4(C2cos*-C3 sin0, z = C,e(-2(C2+C3)cos<-2(C2-C3)sint. >
425. х = -2x + y-2z, у = x-2y + 2z, z = 3x-3y+5z.
¦4 Поскольку среди корней характеристического уравнения имеются кратные (Af = 3, А2 =
= Аз = -1), то, согласно формуле A6), п. 1.4, частное вектор-решение, соответствующее этому
корню, ищем в виде:
где
/1 0 0\ /-2-А2 1 -2
Е = 0 1 0 , F(\2) = 1 -2 - А2 2
\0 0 1/ \ 3 -3 5-А2/
а вектор А2 = ( а2 | удовлетворяет уравнению:
t 4 -8\/а,\
= 0, или 4 -4 8 а2 = О,
12 -12 24/ \взУ
что соответствует одному скалярному уравнению ах — а2 + 2а3 = 0, или а{ = а2 - 2а3 (а2, а3 —
произвольные постоянные). Таким образом, приняв во внимание равенство F(X2)A2 = 0, соглас-
согласно A) имеем вектор-решение
/а2-2а3\
хг = а2 е '. B)
\ »з /
Вектор-решение, соответствующее корню Аь имеет вид xt = В^', где постоянный вектор Вх
удовлетворяет уравнению (см.A4), п. 1.4):
F(A,)B, = О
или
-5 1 -2\ /ЪЛ
1-5 2 Ь2 = 0.
3 -3 2/ V&3/
Легко получить одно из решений этой системы:
bi = -1, Ъ2 = 1, 63 = 3.
Произвольная линейная комбинация вектор-решений есть общее решение х данной системы
дифференциальных уравнений, поэтому
/ -С,е3' \ ( С2(а2-2а3)е-
х — C\Xi + С2х2 = С\еи
\ ЗС,е3'
Положив здесь С2а2 = С2, С2о3 = Cj и приняв во внимание, что а; = (ж, у, z), окончательно
имеем:
3' ' у = Се31 + С2е-', 2 = ЗС,е3(
§ 1. Линейные системы 191
426. i = 2x-y-z, y = 2x-y-2z, z = -x + y + 2z.
•^ Характеристическое уравнение данной системы имеет лишь один трехкратный корень А =
= — 1, поэтому, согласно формуле A6), п. 1.4, можем записать:
х = (е + F(X)t + - F2(X)t2} Ae\
где
/ 1 -1 -1\ /0 0 0
F(X) = 2 -2 -2 , F2(X) =000
\-1 11/ \0 0 0/
Вектор А удовлетворяет уравнению F2(X)A = 0 (см. A7), п. 1.4) и в силу тождества F2(X) = 0
является произвольным. Таким образом, общее решение в векторной форме имеет вид:
(\ + t -t -t \ (СЛ
х = (х, у, z)=[E + F(X)t)Ael = I 2t 1 - 2t -2t C2 el.
Отсюда находим
x = e((c,(l+*)-(C2 + C3)*), y = e{lClt + C1(\-2t)-2C3ty z = e{-
или
z = e'(c,+(Ci-C2-C3)<), y = et(c1 + 2(Cl-C2-C3)i), z = e (c3 + {-C{ + C,
427. x = 4x - у, у = 3х + у - z, z=x + z.
¦4 Нетрудно убедиться, что А = 2 — трехкратный корень характеристического уравнения,
поэтому, согласно формуле A6), п. 1.4, общее решение данной системы имеет вид:
х = (х, у, z)=(e + F(X)t + X- F2(X)t2) Aeu, A)
(СЛ
где А = I C*2 I —• произвольный постоянный вектор,
\С3)
/2-1 0\ /1 -1 1\
F(X)=[ 3 -1 -1 , F2(X)= 2 -2 2, i^3(A) = 0. B)
V 1 0-1/ \\ -1 1/
Из представления A) на основании B) следует общее решение в скалярной форме:
х = е2' (сх + BС, - C2)t + Х- (С, - С2
(ЗС, - <72 - С3)< + (С, - С2 + C3)t2) ,
= еи (сг + (С, - С3)< + i (С, - С2 + С3)<2) . >
428. х — хЛ-2у — 2у =: 0, х — х + у + у = 0.
¦4 Ищем частные решения в виде х = Aext, у = Вем. Подстановка их в систему дает
А(Х2 - 1) + 25(А2 - 1) = 0, А(Х - 1) + В(Х + 1) = 0. A)
Отсюда в силу условия А/ОиВ^О следует, что
А2 - 1 2(А2 - 1)
или (А2 - 1)C - А) = 0. Таким образом, Ai = 1, А2 = — 1, А3 = 3 — простые корни характеристи-
характеристического уравнения B). Им соответствуют следующие частные решения:
Ж] = Ахе1, х2 = А2е~1, х3 = А3еи, -,.
У\ = Вхе , у2 = В2е , у3 = В3е .
192 Гл. 3. Системы дифференциальных уравнений
Связь между коэффициентами Ак, Вк, к = 1, 2, 3, мы найдем, последовательно подставляя корни
А», к = 1, 2, 3, в систему A). Имеем
Ак(\\ - 1) + 2Вк(\\ - 1) = О, А*(А* - 1) + Вк(\к + 1) = 0.
Отсюда находим Bi = 0 (Ai — произвольно); Аг = 0 (В2 — произвольно); Вз = — 1, Ау = 2. Учи-
Учитывая эти соотношения и полагая, например, А\ = В2 = 1, из частных решений C) комбинируем
общее решение данной системы дифференциальных уравнений:
х = Сххх + С2х2 + С)Х3 = Cie1 + 2C3e3i, у = dyx + С2у2 + С3у3 = Сге~* - C3e3i. >
429. х + 5х + 2у + у = 0, Зх + 5х + у + Зу = 0.
¦4 Полагая х — Aext, у — Вем, как и в предыдущем примере, имеем
А(Х2 + 5А) + ВBА + 1) = 0, АC\2 + 5) + В(Х + 3) = 0, A)
откуда, учитывая условие А Ф 0 и В Ф 0, находим А1=Л2=:1, Аз = — 1. Частные решения,
соответствующие простому корню, имеют вид:
хъ = Аъа~\ г/з = Въе'\
Связь между Ay и В3 находим из системы A) известным способом: В3 = -443. Поэтому, по-
положив, например, Аз = —1, имеем В3 = 4. Следовательно, частные решения, соответствующие
корню А3 = -1, будут ху = —е~\ уу = 4е~*.
Далее, в силу того, что А = 1 — двукратный корень, мы должны искать частные решения,
соответствующие этому корню, в виде:
х = (а + Ы)е\ y = (c + dt)e, B)
где а, 6, с, d — пока неизвестные постоянные. Для их определения подставим B) в данную
систему уравнений. После некоторых упрощений, приравнивая коэффициенты при одинаковых
функциях, получаем систему уравнений:
6e+7b+3c+2d = 0, 2b+d = Q, 8a + 66+ 4с+ d = 0,
из которой находим d = —2b, с = -2а - Ь, где а,Ь — произвольные постоянные. Таким образом,
общее решение представляется следующим образом:
ж = (а + Ы)е* - Съе'\ у = (-2а -Ъ- 2Ы)е + 4Сге'\ >
Применяя метод вариации, решить следующие системы:
2 3
430. х = -Ах - 2у + -—-, у = 6х + Зу - -—-.
в* — 1 е* — 1
¦4 Прежде всего решаем однородную систему уравнений, соответствующую данной системе:
х = -Ах -2у, у = 6х + Зу.
Подставив значение у = —2х— ^х во второе уравнение, получаем х+х = 0, откуда х = Сх +С2е
А тогда у = -2С\ — ^С2е~*. Для определения общего решения неоднородной системы, согласно
методу вариации произвольных постоянных, считаем Су и С2 некоторыми дифференцируемыми
функциями. Эти функции мы найдем из системы уравнений, которая получается в результате
подстановки значений х и у ь неоднородную систему. Таким образом, мы имеем:
ft + fte--^, -20,-^е-—^.
Отсюда находим С2 = f , Ci = 0. Интегрируя последние уравнения, получаем
где Сю, С2о — произвольные постоянные. Наконец, подставляя значения Cj и С2 в общее
решение однородной системы, имеем общее решение данной системы:
ж = С, + С2е~* + 2е~( In |e* - 1|,
где C\,Ci — новые произвольные постоянные. >
§ 1. Линейные системы 193
431. х = х-у -, у = 2х-у.
cost
¦4 Легко найти (хотя бы методом исключения) общее решение соответствующей однородной
системы
x = dsmt + C2cost, y = (Ci+C2)smt+(C2-Ci)cost. A)
Считая (в согласии с методом вариации произвольных постоянных), что С\ и Сг — некоторые
дифференцируемые функции, и подставляя значения х и у из A) в данную систему, будем иметь
С1! cost - Cj sin* = , С\ sint + Со cost = ,
cost cost
откуда находим С\ = 1 + tgf, C2 = 1 — tgf. Интегрируя эти уравнения, имеем
Ci =t-ln|cost|+Cio, C2 = t + ln\cost\ + C20. B)
Наконец, подставляя B) в A), получаем общее решение предложенной системы:
х — f(sint + cost) + (cost - sint)In| cosf| + C\ sint + Cjcosi,
у = 2fsint + 2cosf + In | cosf| + (d +C2)sint + (C2 - C^cosf,
где C\, C2 — новые произвольные постоянные. >
Решить следующие системы:
432. tx + 2(х - у) = t, ty + x + 5y = t2.
¦4 Производя замену аргумента t по формуле г = ln|t|, t Ф 0, приходим к неоднородной
системе с постоянными коэффициентами:
~ + 2(х - у) = ±ет, ^+х + 5у = е2т.
Определив из второго уравнения системы
и подставив его в первое уравнение, получаем
у = 4е2ттет. A)
Характеристическое уравнение А2 + 7А + 12 = 0 имеет корни Ai = -4, А2 = -3, поэтому общее
решение однородного уравнения у + 7у+ 12у = 0 запишется в виде у = С\е~*т + С2е~Ът. Частное
решение у рассматриваемого неоднородного уравнения ищем, используя метод неопределенных
коэффициентов, в таком виде:
у = Ае2т+Вет.
Подставляя у в неоднородное уравнение и приравнивая в полученном тождестве коэффициенты
при одинаковых функциях слева и справа, будем иметь: А = j$, В = ±;jj. Таким образом,
у = j^e7r ± эдет- А тогда общее решение
у = С1в +С2е +-е ±-е.
Подставляя значение у в (*), получаем
3 10
Вернувшись к аргументу (, имеем окончательно
__А_ад f^ ад _^ с^ 2 2 1
433. tx + 6x - у - Ъг = 0, *ir + 23а; - 6у - 9г = 0, tz + х + у - 2z = 0.
•4 Аналогично предыдущему примеру имеем: г = In |(|, t Ф 0, и
+ 23x6y-9z = 0, -^- + x + y-2z = Q. A)
ат ' ат
194 Гл. 3. Системы дифференциальных уравнений
Полученную систему уравнений с постоянными коэффициентами будем решать методом Эйлера,
положив х = АеХт, у = ВеХт, z = СеХт. Тогда относительно постоянных А, В, С получим
линейную систему
АF + А) - В - ЗС = О, 23А + В(\ - 6) - 9С = О, А + В + С(\ - 2) = О,
из которой в силу условий А / О, В/О, С ФО следует, что определитель
6 + А -1 -3
23 А - 6 -9
= 0.
1 1 А-2
Легко найти корни этого уравнения: А! =2, А2 = — 1, А3 = 1. Следовательно, общее решение
системы A) имеет вид:
х = Схе2т + ЗС2ет - С3е"т, у = Схе7 + 2С2ет + Сге~т, z = Схег + 2Сге + Сге~т.
Возвращаясь к переменной t, общее решение данной системы записываем окончательно:
a i л dx dy
4.54. — = xip(t) + yi>(t), — = -xxj>(t) + yv>(t).
dt dt
< Полагая
получаем
a f + af' — af<p + fifty, 0 f + Pf' — —afxj) + fEf. B)
Пусть /' = ftp Ф 0. Тогда система B) примет вид:
а, /3 — неизвестные функции. Производя замену аргумента по формуле
т= [tfi(t)dt, D)
систему C) приводим к системе с постоянными коэффициентами:
da d/3
Решив систему E) и вернувшись к переменной t согласно D), а также приняв во внимание A)
и выбрав функцию / = ехр(/ ip(t)dt), окончательно имеем
х=(-С,cos(Ji>{t)dt\ + C2sin(JW)dtj J expU fit)dt\,
у ={Cism( fip(t)dt) +C2cos( fip(t)dt) ) exp( f ip{t)dt\. >
Примечание. В примерах 432—434 мы пользовались заменой аргумента т = / /(<) dt, которая применяется
в общем случае к системе уравнений вида
где А — постоянная матрица. Указанная замена преобразует приведенную систему к системе уравнений
с постоянными коэффициентами:
dx
-т- = Ах.
dr
435. В некоторой области пространства одновременно имеются однородные и стационар-
стационарные электрическое и магнитное поля с векторами напряженности Е и Н, угол между которыми
§ 1. Линейные системы 195
равен а. Частица с массой m и зарядом е, имеющая начальную скорость vo, попадает в это
пространство. Определить траекторию движения частицы.
¦4 На движущуюся в электромагнитном поле заряженную частицу действует сила Лоренца
f = eE + e[r,H],
где г = (х, у, z) — радиус-вектор частицы. Поэтому, согласно второму закону Ньютона, имеем
уравнение движения частицы:
mf = eE + e[r, H]. A)
Если векторы Е и Н расположить в плоскости zOy и направить вектор Н вдоль оси Oz, то
векторное уравнение A) можно представить в координатной форме:
тх = еуН, ту = еЕ sin а — exH, mi = eEcosa, B)
где Е = |Е|, Н = |Н|. Систему уравнений B), третье из которой интегрируется независимо,
решим методом исключения. Тогда получим
Е
х = A sin wt + В coso;f H t sin а + С,
Ы
y=Acoswt-Bsinwt + D, C)
еЕ 2 еН
z =—t cosa + Fit +F2, w=—,
2m m
A, B, C, D, Fx, F2 — произвольные постоянные. Для их определения воспользуемся начальными
условиями:
x\t=o = y\t=o = z\t=o = 0, x\t=0 = vox, y\t=t> = «о», *\t=o = 4z-
Тогда на основании C) получим:
Е
В + С = 0, А + D = 0, F2 = 0, Aw + —sina = vOx, -Bw = v^,, F{ = vOz. D)
H
Подставляя значения постоянных, найденных из D), в C), окончательно имеем:
1 / Е . \ . voy Et . voy
х = — [vOx sina smwt cosa;f + — sina H -,
ш \ H / w H w
1 ( E ¦ \ * % • , (E ¦ \ 1
У - - [Щх - Б7 Slna ) cosu;t + smwt + Б7 Slna ~ v°x I ^>
Ш \ It / W \U / W
еЕ 2
z — — t cos a + vOzt. >
2m
436. Пучок электронов влетает в пространство между двумя парами отклоняющих пластин,
на которые поданы напряжения: их — uisina;* — на вертикальные пластины ии,= u2coswt —
на горизонтальные. Определить траекторию электронного луча на экране, если все электроны
перед влетом имели начальную скорость г;0, параллельную всем пластинам; длина отклоняющих
пластин равна /, расстояние от отклоняющих пластин до экрана равно /, расстояние между пла-
пластинами равно d.
¦4 Направим ось Oz параллельно начальной скорости влета, ось Оу — вертикально вниз.
Тогда уравнения движения электрона с массой т запишутся в виде:
тх = еЕх = sinwt, ту = еЕу = coswt, mi = 0.
о о
Интегрируя их, получаем
х = т sinwt + A[t + А2, у= Tcoswt + B[t + B2, z = Cit + C2. A)
mdw' mdw*
Пусть x\t=h = y\t=to = z\t=h - 0. Согласно условию задачи, x|i=io = y\t=4 = 0, z\l=k = i;0; t0 —
начальный момент. Используя эти начальные условия, из A) получаем:
ещ
Л -
Ax =
coswto, At = I — sinwto — to coswto I,
mdw mdw \w )
2 sinwin, Вг=—г- I — coswto + to sinwto),
mdw \w )
mdw
= t;0, C2 = -
196 Гл. 3. Системы дифференциальных уравнений
Таким образом, формулы A) и B) определяют траекторию движения отдельного электрона, на-
находящегося в конденсаторе. Через время *i = щ от начала движения электрон вылетает из
конденсатора и далее летит по прямой до попадания на экран.
Легко найти координаты точки вылета из конденсатора, а также составляющие скорости элек-
электрона в этой точке. На основании A) имеем:
ещ
~ ° ' тёш2
У\ = V\t=to+t, = -рт coso;(fo + ti) + Bi(t0 + *i) + B2,
° тёш2
zi = г1(=г0+*1 — CiCo + 'i) + С21 ...
ещ <3>
таш
sina>(i0 + *i) + Bu
mdw
ii = По-
Последовательно, параметрические уравнения прямой, по которой будет лететь электрон до попа-
попадания на экран, запишутся в виде:
х = х\ +i\(f -t0 -*i), у = у\ + yi(t - t0 - t{), to + ti^t. D)
В момент t = t2 = ~ +10 электрон попадает на экран, поэтому из D) следует, что координаты
его на экране будут
'f0' 2 ' \о
Подставляя B) в C), а затем C) в E), окончательно получаем
х2= A cos ш1 о + В sin ш1о, у2 = С sin ш10 + D cos a>i0, F)
где
А = 2-
1 ещ /I ll I \
— I — sino; 1 cosw — I,
ЬоШаш таш \ш Vg vq vq/
ещ ещ /1 I I . 1\
В = г I — cosw sm ш — I,
таш1 таш \ш v0 vo vo/
С = -2
ещ ещ
ещ /1 / I I \
-\ —- I -srnii) 1 cosu; — I ,
таш \ш fo Vo Vq/
/1 I I . l\
I —cosu; sino; — I .
\Ш Vo Vo Vo/
тёш1 тёш \ш v0 vo v0/
Будем считать, что у каждого электрона есть свое начальное время и параметр to меняется не-
непрерывно. Тогда формулы F) описывают кривую встречи пучка с экраном. Нетрудно видеть, что
она представляет собой эллипс. >
437. Составить и проинтегрировать уравнение движения гармонического осциллятора, на-
находящегося в однородном стационарном магнитном поле Н и обладающего электрическим заря-
зарядом е (классический эффект Зеемана).
¦4 Уравнение движения гармонического осциллятора, не обладающего электрическим заря-
зарядом или не находящегося в магнитном поле, имеет вид:
где к > 0, г — радиус-вектор частицы с массой т. Если же такой осциллятор обладает элек-
электрическим зарядом е и помещен в магнитное поле В = /*оН, то на него будет действовать сила
Лоренца f = e[to\i, H]. Следовательно, по второму закону Ньютона, можем составить уравнение
движения:
тг + кг - /joe[r, H]. A)
§ 1. Линейные системы 197
Направляя ось Oz вдоль магнитного поля Н, векторному уравнению A) ставим в соответствие,
три скалярных:
тх + кх = е/ЛоуН, ту + ку = —е/л^хВ, mz + kz = 0.
Из последнего уравнения сразу находим
[к
z = C cos(a>0* + <р), щ = у — 1
С, ip — произвольные постоянные. Систему первых двух уравнений решаем методом Эйлера,
положив х = Аем, у = Bext. Тогда получим характеристическое уравнение
тХ2 + к -e(i0H\
ецйХН тХ2 + к
из которого следует, что (w2, — ш2J = шгшц, где ш2 = —А2, шя = е^ . Решив последнее
уравнение, получаем
Следовательно, частные решения имеют вид:
хк = Аке*', ук = Вке^, к = 1, 2, 3, 4.
Между коэффициентами Аъ, В/, существуют связи, определяющиеся уравнениями:
Ак(Х1+ш1) = ХкшнВк, A)
откуда
Хкш„
где St — произвольные постоянные.
Таким образом, общее решение системы будет
»«1«Я _ .Ш1( »«1«Я „ -&,,« ,
Ж — —j 2 -°1е 2 2 е т
у = Bxeiuii + Вге-^{ + Взв*' + В4е^2\ z = Ccos(o;0f + <p). >
438. Частица массы т движется по внутренней поверхности вертикального цилиндра ра-
радиуса г. Считая поверхность цилиндра абсолютно гладкой, найти закон изменения координат
частицы со временем, если в начальный момент времени частица находилась на оси Ох. Ее
начальная скорость и0 составляет угол а с горизонтом.
¦4 Кинетическая энергия частицы будет К — Щ- (х2 + у2 + z2), или, если учесть, что х =
= г cosip(t), у — г sin ?>(<), К — 5?- (г2ф2 + z2j. Потенциальная энергия определяется по формуле
Л = mgz. Поэтому функция Лагранжа L для данной частицы будет иметь вид
A)
Для составления уравнений движения частицы воспользуемся уравнением Лагранжа:
где L — функция Лагранжа, ?,- — обобщенные координаты, число которых равно количеству
степеней свободы физической системы; Fi — внешние силы. В данном случае Fi = 0, qi = <р,
Яг = z- Следовательно, на основании A) имеем:
dL dL г dL 8L dL dL
— = т— = mr ip, — = —г = mz, — = 0, — = -mg.
dqt dip r dq2 dz ' d<p dz *
Таким образом, на основании B) получаем два дифференциальных уравнения:
тггСр = 0, mz + та = 0.
198 Гл. 3. Системы дифференциальных уравнений
Интегрируя их, находим
at2
где С,- = const. Для определения С,- воспользуемся начальными условиями:
г|(=о = 0, <p\t=0 = ?>о = 0;
i\i=o = -rsin<po<i>\t=o = 0; V\i=o = rcos^oH^o = »vl<=o = v0cosa; z\t-0 =
Отсюда нетрудно найти, что С2 = 0, С\ = ^P-cosa, С4 = 0, С^ = i>osina. Наконец, подставляя
значения С; в выражения для ip и z и используя формулы х = г cos у, у = rsinip, приходим
к уравнениям движения:
/«о* \ . /«о* \ gt2
х = г cos I — cos a I, у = r sin I -— cos a I , z = — — + vot sm a. >
439. Два математических маятника одинаковой длины связаны между собой пружиной
с жесткостью к, укрепленной на расстоянии а от точки подвеса. Определить частоты малых
колебаний, а также проинтегрировать уравнение движения при условии, что в начальный момент
времени первый маятник был отклонен на угол у>о от вертикали.
¦4 Пусть <pi, <рг — углы, на которые отклоняются маятники от вертикали. Тогда кинетическая
энергия системы двух маятников (кинетической энергией пружины пренебрегаем) будет равна
К = ^j- up2 + ф\ 1. Потенциальная энергия системы состоит из суммы потенциальных энергий
трех тел: двух маятников и пружины. Потенциальная энергия маятников равна
Пх = mgl(l - cos^i) + mgl{\ —
а потенциальная энергия пружины Щ = ^a2(sin(pi -sin 1р2J. Таким образом, функция Лагранжа
всей системы
L = К - П = —г-(ф\ + Фг) ~ mglB - cos^i - cos^2) - т a2(siny>i - sin^2J-
Используя уравнение Лагранжа, имеем:
ml ipi + mglsimpt + ка (sin^i — sin <p2)C0StPi — 0,
ml2if2 + mgl sin ip2 ~ ka2(sinipi — siny>2)cosy>2 = 0.
Пусть углы <р\, <р2 малы, т.е. <p\, ip2, ipi<p2 пренебрежимо малы. Тогда из A) можно получить
так называемые линеаризованные уравнения:
д ка2 ка2
<Pi+ptpi-r<p2 = 0, ч>г+РЧ>г -ripi =0, Я = у Ч yj, »"=—тг- B)
Частные решения линеаризованной системы ищем по методу Эйлера, положив <р\ = A\exl,
<р2 = Агем. Тогда из B) получим частотное уравнение:
А2+р -г
-г \'+-р
= 0,
решая которое, находим А12 = ±ш\>г, где
2ka2
Здесь wi, ш2 — частоты малых колебаний системы маятников. Теперь строим систему частных
решений:
§ 1. Линейные системы 199
Между коэффициентами Aij, Bj;- существуют связи, определяемые равенствами:
A{j(p - ш2) - гАц = О, .7 = 1,2;
Ац(р-ш1)-гАу=0, j = 3,4.
Следовательно, Ац = — A2j, j = 1, 2 и .4у = -42;-, J = 3, 4. Тогда общее решение системы B)
будет иметь вид:
р, = -Се' - С2е-^1 + Съеш + С4е~^. C)
Так как, по условию, ^2|г=о = ФА=о = <Pi\t=t> = 0, <pi\t=o = <Ро, то С\ = С2 = Су = С4 = j^o-
Подставляя значения постоянных в C), окончательно получаем:
ipi — — (cos^it + coso;2f), ip2 = -^- (cosu2t — coso;,f). >
440. Тело массы М, соединенное с пружиной жесткости к, другой конец которой закреп-
закреплен неподвижно, может двигаться без трения по горизонтальной плоскости. К телу прикреплен
математический маятник массы т и длины /. Найти функцию Лагранжа системы и определить
частоты малых колебаний.
А Пусть хо — длина пружины в свободном состоянии, ж — абсцисса тела массы М,
(im, ут) — координаты тела массы т, <р — угол отклонения массы т от вертикали. Тогда
m М
K=j
есть кинетическая энергия рассматриваемой системы, а
Д=-(х- xof + lmg(l - cos <p)
потенциальная энергия. Поэтому функция Лагранжа
L = К - П = у (xl + Й) + у *2 - \ <* - ^оJ - lmg{\ - cos0. A)
Но хт = x + lsinf, ym = Icosip, поэтому
хт = х + ф1 cos <p, ym = -ipl sin (p. B)
Подставляя B) в A), находим
L = — [хг + 2хф1 cosip + 1гфг^ + — х2 - - (ж - ж0J - lmg(l - costp).
Составляем уравнения Лагранжа:
(М + т)х + ml{Cp cos ip—ф2 sin tp) + k(x — жо) = 0,
m(xl cos y? + I2<p) + mgl sin tp — 0.
Считая угол |yj| и разность |х — Жо| малыми, линеаризуем систему C):
(М + т)х + mlCp + к(х — хо) = 0, х + 1ф + gip = 0.
Частные решения этой системы ищем в виде: х = Хо + Ас1"*, <р = Веш*. Тогда относительно ш
получим частотное уравнение:
-(М + т)шг + к -т1ш2
= 0,
или
М I Af У Mi
Решение полученного уравнения и его анализ предоставляем читателю. >
200 Гл. 3. Системы дифференциальных уравнений
Согласно определению, имеем
I2 Ап
^^ . (I)
Далее, вычисляем
2 _ ( cos2t sin2f\ ап — ( cosn' sinn<\
~V-sin2t cos2i/' "•"' \-sinnf cos nt )¦
Подставляя B) в (l), имеем
A _ /l+cosi + |cos2i + ... sini + isin2t+ ... \
6 ~\ -sint-isin2t-... l + cost+icos2t+.../'
Так как eml = cosni + isinni, то cosnt = Reemi, sinnf = Ime'"'. Тогда
i2f R (l + il ^ Л R6" Recos'+istai = ecos'
l+cosi+iCos2f+ ... = Re (l + eil + ^-+ .Л = Ree6" = Reecos'+istai = ecos'cos(sin0,
sinf + - sin It + ... = Im (eil + — e2ii + ... j = Im (ee" - l) = ecosi sin(sint).
Используя эти соотношения, из C) получаем окончательно:
А _ ( COs(sinO Sir^sinf)^ cost
\-sin(sinf) cos(sinO/
§ 2. Нелинейные системы
2.1. Нормальные системы дифференциальных уравнений. Метод исключения.
Система дифференциальных уравнений вида
— = /i(t, хи хг, . ¦. , хп),
dx2
— = f2(t, xi, x2, ... ,xn),
dxn
— = fn(t, XUX2,... ,Xn),
где /j, i = 1, n, — известные функции (правая часть системы), называется нормальной системой
дифференциальных уравнений.
Существует два основных метода интегрирования системы A). Первый метод, который на-
называется методом исключения, состоит в сведении системы A) к одному уравнению n-го порядка
или к одному уравнению го-го (то < и) порядка и к системе го независимых уравнений. Такое
сведение достигается путем дифференцирования одного из равенств системы A) и последующего
использования всех уравнений этой же системы. Обычно приходится дифференцировать и — 1
раз, но бывают случаи, когда достаточно продифференцировать т (го < и — 1) раз. В резуль-
результате получаем некоторое число к тождеств, из которых, исключая к - 1 переменную, получаем
одно дифференциальное уравнение относительно одной неизвестной функции. Если это послед-
последнее уравнение удается проинтегрировать, то другие неизвестные функции можно найти путем
дифференцирования и простейших алгебраических операций.
§2. Нелинейные системы 201
2.2. Подбор интегрируемых комбинаций.
Второй метод заключается в подборе так называемых интегрируемых комбинаций. Инте-
Интегрируемой комбинацией называется дифференциальное уравнение, которое является следствием
системы уравнений A) и интегрируется в квадратурах; например, имеет вид:
<*Ф,(<, ari,*2, ...,*„) = 0, B)
где Xi = Xi(t) (i = 1, и) суть решения системы A). Функция Ф\A, х\, х2,... ,хп), которая то-
тождественно равна постоянной при подстановке в нее решений Х{ = #,(*) (i = 1, и) системы A),
называется первым интегралом системы A). Если имеется к первых независимых интегралов
$i(<, #i, «2, ••• ,аг„) = С\,
, хи х2, ... ,хп) = С2, .-
(интегралы называются независимыми, если между функциями Ф<, i = 1, &, не существует связи
вида Ф(Ф1, Ф2, ... ,Ф*) = 0), то из системы C) можно выразить к неизвестных функций через
остальные. Подставив их в систему A), придем к задаче об интегрировании системы уравнений
с меньшим числом неизвестных. В частности, если к = п, то все неизвестные функции опре-
определяются из системы интегралов C). Аналитическая форма проверки независимости интегралов
имеет вид
ff*"*'-'*'^0, D)
h,xh,...,xik)
где Xjt, Xj2, ... ,Xjt — какие-нибудь к функций из числа неизвестных.
Иногда нахождение интегрируемых комбинаций облегчается с помощью так называемой сим-
симметрической формы записи системы уравнений A):
<tii Лхг dXn dt
Vl(t, Xl, 12, ... ,Xn)~ ip2(t,Xi,X2, ...,Xn)~ <pn(t,XUX2, ...,Xn)~ <po(t,Xi,Xi In)'
где
4>i = <Pofi> » = 17«-
Заметим наконец, что все сказанное о нелинейных системах относится и к системам линей-
линейным, записанным в нормальной форме.
Проинтегрировать следующие системы дифференциальных уравнений:
dx аУ dz
х-у х+у z
¦4 Первый способ. Представляя данную систему в виде
dx dy dz
- = = — = atj
х-у х+у z
получаем
dx dy dz
*У) Ш* + У, dlz. A)
Третье уравнение системы A) интегрируется независимо от остальных, и его общее решение имеет
вид: z = Сзе'. К первым двум применяем метод исключения, в результате чего имеем:
—, x-2i + 2x = Q. B)
dt
Интегрируя последнее уравнение, находим
х = (С\ sin t + C2 cos t)e*.
Подставив х в первое соотношение B), получим
у = (С2 sin t - Cj cos t)e'.
202 Гл. 3. Системы дифференциальных уравнений
Если мы хотим получить решение без параметра t, то должны исключить его из выражений для
х, у, z. В результате имеем
— ) —, у = (C2sinln—-Cicosln —) —.
Сз/ Сз \ Сз Сз/ Сз
Отсюда, складывая квадраты левой и правой частей соотношений, получаем один первый инте-
интеграл:
^^. О)
А если взять их почленное отношение, то после некоторых преобразований будем иметь
С, С2
=, cosa =
или
ге^1=С2. D)
Очевидно, интегралы C), D) являются независимыми.
Второй способ. Сначала интегрируем уравнение
dx _ dy
х-у х + у'
Переход в нем к полярным координатам дает уравнение ^ = г, из которого следует, что г =
= Cxev. Используя это равенство, уравнение xfy = =§¦ приводим к виду:
dz
— = dip,
откуда интегрированием находим
х = С2е*.
Нетрудно проверить, что полученные интегралы являются следствием интегралов C), D). >
..~ dx _ dy dz _ du
'
у—и z — x и —у х — z'
¦4 Пользуясь свойством пропорции, имеем
dx + dy + dz + du du
-z) x-z'
xdx + ydy + zdz + udu du
A)
B)
x{y -u) + y(z -x) + z(u-y) + u{x- z) x-z'
dx + dz du
y) ~ xz'
Из соотношения A) получаем
d(x + у + z + и) = 0. D)
Из второго
2 у7 z2 и2
Соотношение C) дает еще одну интегрируемую комбинацию:
d{x + z) = 0. F)
Интегрируя в D), E), F), находим
Это первые интегралы рассматриваемой системы. Так как они независимы и число их совпадает
с числом уравнений данной системы, то мы получили все интегралы. ^
§2. Нелинейные системы 203
444. — = ^ = dz
х у xy + z
Из уравнения Щ- = -^ легко находим In|х| = In \y\ + inCj, или
У
Это первый интеграл. Далее, решаем уравнение
dy dz
У xy + z
с учетом того, что х = С\у. Таким образом, имеем -Н- — —т
" Ciy +
dz z
= dy.
dy У
Интегрируя линейное неоднородное уравнение первого порядка, получаем
z = Сху2 + Сгу или z = xy + C2y.
Итак, мы имеем два первых интеграла:
— = С], — х = CV
У У
Так как они независимы и число их равно числу уравнений рассматриваемой системы, то других
интегралов, которые были бы независимы от полученных (не являлись бы их следствием), нет. >
445 dx = dy = dz
' z2 - у2 z у '
¦4 Пользуясь свойством пропорции, имеем:
dx zdy + ydz
— г = —; 5~ или dx = d(zy),
г2 -у2 z2 - у2
откуда х - zy = Ci. Еще один первый интеграл мы получим из уравнения -%- = — =Ц-, или
ydy + zdz = 0.
Следовательно,
y2+z2 =
446. dx = dy dz
=
х(у + z) z(z - у) у(у - z) '
Из последнего уравнения системы находим
-d(y2 + z2) = O,
откуда следует у2 + z2 = С\ — первый интеграл. Полагая в нем у = Ciuntp, z = Cicostp, из
первого уравнения данной системы получаем
dx sinp + cosp
— = ; dip.
х cos <р — sin tp
Интегрируя это уравнение, имеем
ln|x| = -In | cosy — sintp\ +lnC2,
или _ _
x = C2^_ = C1C1 x{z_ c
cosip — smip z-y
204 Гл. 3. Системы дифференциальных уравнений
dx dy = dz
447.
= =
x(z - у) у(у - x) у1 - xz '
Имеем по свойству пропорции:
dx + dz dy
откуда находим первый интеграл
x-y + z = Ci.
Подставив значение z = Ci~х + у в первое уравнение, получим
dx dy , У у2
, или у +- = ——
x(d - х) у(у - х)
Это уравнение Бернулли. Его общее решение имеет вид
— х ~С\
У~ 1п\х\ + С2'
Исключив из него с помощью уже полученного интеграла постоянную С\, приходим к еще одному
первому интегралу
1- - — In |ж| = С2. >
У
448 dx = dy = dz
¦4 В силу свойства пропорции имеем:
xdx + ydy dz
x2(y2-z2)-y2(x2+z2) z(a
откуда
d(x2 + y2 + z2) = 0.
Интегрируя это уравнение, находим первый интеграл:
Используя его, последнее уравнение данной системы представляем в виде:
dy dz
V(Ci - у2) + z(Ci -z2)~ '
откуда интегрированием получаем еще один первый интеграл:
(здесь постоянная С\ была исключена с помощью ранее найденного первого интеграла).
Полученный интеграл можно упростить следующим образом:
где С2 — новая произвольная постоянная. >
Замечание. Последний интеграл можно получить сразу, если "увидеть", что
xydz + xzdy-yzdx dz
xyz(x2 + у2) - xyz(x2 + z2) - xyz{y2 - z2) ~ z(x2 + y2)'
Отсюда следует, что d [Щ-\ = 0, или Щ- = С2-
... dz , dy х
dt dt 2y
¦4 Значение х = 2y~$, найденное из второго уравнения системы, подставим в ее первое
уравнение. Тогда получим
§ 2. Нелинейные системы 205
Отсюда находим
у2 = С,е' + С2е"' sint.
А тогда
= —(у2) = С,е* - С2е-1 - - cost. >
at 2
450 — =
dt
dt у2 - ax' dt 2xy'
< Из второго уравнения следует, что -др- = ¦?. Деля почленно это уравнение на первое
уравнение системы, получаем линейное уравнение относительно функции t >-> у2:
d(y2) ^ у2
dx х
Общее решение
у2 = С\х - ая1п|ж|.
А тогда из первого уравнения системы получаем
dx 1
dt x(C\ -a- aln|z|)
откуда
t = [ х(с, - а - а\п\х\) dx + С-у = -(С\ - а)х2 - % ilx2 In |i| - х2) + С2 = — BС{ -a-2aln\x\) +C2- >
/\ / 2 4^ ' 4 *" '
; dt = x(Ci — a — a\n\x\)dx,
2х ' 4
dx I dy _ 1
dt ~ 2хъ + х2 - у2' dt ~ 2х2у'
¦4 Аналогично предыдущему примеру имеем:
d(y2) у2
dx x2
откуда
2 - - [ -- - 2
Подстановка у1 в первое уравнение системы дает:
dt= Bг -С,е^ 1 dx,
откуда интегрированием находим
t + Ci = —— C| / ег dz. >
dx
452. * X~l
•< Полагая и = ^, v = -^, приходим к системе
x = tu + /(и, v), y = tv + q(u, v).
Дифференцируя по t слева и справа последние равенства и учитывая, что и = х, v = у, получаем
Отсюда следует две возможности: либо й = ti = 0, либо определитель
«+.Л Л. =о.
206 Гл. 3. Системы дифференциальных уравнений
В первом случае имеем и = Су, v = С2. Следовательно,
x = Clt + f(CuC2), у = C2t + q{Cu C2)
— общее решение рассматриваемой системы. Во втором случае возможны другие решения. По-
Попытаться найти их предоставляем читателю. >
453 «'-- -'-
х
х х(у - 1)
< Применяя метод исключения, имеем
d^_ y + 2z-l__ 2
dl) У ~ 1 ~ У - 1
Отсюда z = С[(у - IJ - у + 1. Подставив значение z в первое уравнение системы и разделив
переменные, имеем:
dx dy
=
Интегрируя, получаем
In |х| = In |С,(у - 1) - 1| - In \у - 1| + 1пС2)
или _
Подставив A) в выражение для z, находим
454. 2zy' = у2 - z2 + 1, z' = z + у.
< Значение у = z' - z из второго уравнения подставим в первое:
2zz" - zn - 1 = 0.
Уравнение явно не содержит аргумента, поэтому порядок его можно понизить, положив z' = р.
Тогда z" = p-? и уравнение примет вид:
.24>g-J»2-1=0.
Разделив переменные и проинтегрировав, получим:
dz
Интегрируя последнее уравнение, после простых преобразований имеем
C (
А тогда
У = *' - * = -^Г (х + С,) - —¦ (х + С2? - С,. >
Для данных систем дифференциальных уравнений и данных функций ip проверить, являются
ли соотношения ip — С первыми интегралами этих систем:
455. х = ху, у = х2 + у2; у>! = ж In у - х2у; tp2= -j -21nx.
< Так как ipi = Cu то -^(ipi) = 0. Следовательно, ~^(х In у - х2у) = 0, или
ХЦ 2
х In у Ч 2хху — ху = 0.
Подставив сюда значения х, у, определяемые уравнениями системы, имеем
ху In у + - (х2 + у2) - Зх2у2 - х4 = 0.
§2. Нелинейные системы 207
Как видим, полученное тождество невозможно, поэтому равенство tpt = C\ не является интегра-
интегралом данного уравнения.
Проверяем второй интеграл. Имеем зу(Уг) = 0, или
dt \x*
Отсюда в силу уравнений системы получаем:
ху(х2 + у2) - ху3 - х3у = О, хф 0.
Последнее означает, что выражение <р2 = С2 является первым интегралом данной системы. >
л-с dx dy dz du
4Э0. — = = — = ; tp = yz — их.
у х и z
4 Поскольку tp = С, то должно быть
d(yz — их) = 0, или у dz + z dy — udx — x du = 0. (*)
Из уравнений системы находим
ух и
dx = — du; dy = — du; dz — du. A)
z z z
Подставляя A) в (*), имеем
Последнее тождество, очевидно, справедливо, поэтому соотношение tp = С действительно явля-
является первым интегралом рассматриваемой системы. >
457. Проверить, являются ли независимыми первые интегралы f-ijrf = Су,
системы ~ = -?¦ = -jr.
4 Сначала проверим, что указанные соотношения действительно являются интегралами.
Имеем
(z -y)dx + (x + z) dy-(x + y) dz
Подставив сюда значения dx = |- dz, dy = \dz, получаем
d\
(x + z)i
Аналогично устанавливаем, что гх~Л — С2 есть интеграл. Теперь проверяем их независимость.
Определив, например, у = С[(х + z) — x из первого соотношения, подставляем во второе:
или
l-Ci-CiC2 = 0 (x +
Видим, что между функциями <р{ = §ф^ и (р2 = |^-| существует зависимость
1 - (<з, - (р{<р2 = 0,
указывающая на то, что данные первые интегралы являются зависимыми. >
458. xdy-ydx = sds, dx1 + dy1 = ds2.
¦4 Положим dx = ds cos tp, dy = dssinip. Тогда второе уравнение превратится в тождество,
а из первого следует, что
s = х sin tp — у cos tp. A)
Отсюда дифференцированием по tp легко получить
ds /ds (dx
co + ^^
= xcosp + ysiny, ^^8mv-_c«^=0J. B)
208 Гл. 3. Системы дифференциальных уравнений
Из A) и B) находим
ds ds
х = s sin ip + — cos ip, у — -—smip — scosip. C)
dip dip
Остается найти s = s{ip). Для этого достаточно продифференцировать по ip равенство B) и учесть
выражения A), B) и равенства -gj = cos^p, -^ = smip. Тогда получим:
d2s dx dy ds /dx dy \ ds
—r = — cosip + —-smip — x sin ip +у costp = — I —-cosp + —- sin и I - zsinw + ucosw = s,
dip1 dip dip dip yds ds / dip
или
d2s ds
dip1 dip
Решив полученное уравнение и подставив значение s — s(ip, d, Cj) в C), найдем
х = x(ip, Сь С2), у = у(<р, Си С2). >
459. dx2 + dy2 = a2 dt2, (d2xf + (d2yJ = b2(dtf.
А Положив
dx = a cos ip dt, dy = a sin tp dt, A)
из второго уравнения получаем
Подставляя B) в A), имеем
а2
dx = ± — cos p d@, dj/ = ±-— sin v7 dip.
о о
Отсюда интегрированием легко находим
а2 а2
x + Ci=±—sintp, y + Ci = T—
о о
Интегрируя B) и подставляя в C), окончательно имеем
^ (
460. Доказать, что интегрирование системы Гессе:
где X, Y, Z,T — линейные формы от переменных х, у, z, подстановками х = QA, у = s
z = Q? сводится к интегрированию системы линейных однородных уравнений.
< Производя указанные подстановки, получаем
Отсюда находим
, т' , т' , т'
? = — ? + тХ + ?Т; п = —tj + tY + пТ; С = —
т т т
§2. Нелинейные системы 209
Так как функции X, У, Z линейны, то функции
также линейны, поэтому если в A) положить
то правая часть системы A) станет линейной относительно переменных ?, г], ?, т. Таким образом,
система уравнений
?' = тХ, г]' = tY, С,' = tZ, t = -тТ B)
является линейной и однородной. >
С помощью приема Гессе решить следующие системы:
лил dx dy dz 2
461. —=y + xz, — = x + yz, —=x + z.
dt dt dt
¦4 Так как в данном примере X = у, У = ж, Z = х, Т = г,то
XV't't)~t' yU'r'rJ"r' *{t't't)~t' \t't't)~t-
Следовательно, система B) из предыдущего примера представится в виде:
dt dt dt dt
Из первых двух уравнений этой системы находим
? = С,е( + С2е-\ г, = С,е( - С2е~\
С учетом последнего соотношения из третьего уравнения получаем
Интегрируя последнее уравнение, имеем:
Наконец, возвращаясь к переменным ж, у, z,
е1 + кхе~1 е1 - кхе~1 е1 - кхе~ь + к2
462. — = x + x(x + y), -^=z+y(x + y), —
< Аналогично предыдущему примеру имеем: X = х, У = z, Z = у, Т — х+у. Следовательно,
Согласно примеру 460, пишем:
f = t, i/ = C. <! = Ч,
Из первого уравнения получаем:
t = CV;
из системы второго и третьего уравнений следует, что
210 Гл. 3. Системы дифференциальных уравнений
Из четвертого уравнения находим
т = -(С, + С2)е( + С3е~' + С4.
Таким образом, общее решение данной системы имеет вид:
х = —-
+ С4
463. Пусть в пространстве Oxyz задано поле скоростей v течения жидкости
v = ((У2 - х2у)у, (х2 + ху2 + 1)у, (х2 + у2* + l)z).
Найти линии тока этой жидкости.
< Согласно определению линии тока, v || dr, dx = (dx, dy, dz). Следовательно,
dx _ dy _ dz
«* "y "z '
или с учетом значений vx, vy, vz,
dx dy dz
y(y2 - x2y) ~ y{x2+xy2 + 1) ~ z(x2 + y2x + 1)'
Поскольку выражение (уж2 - у2) dy + (z2 + гу2 + 1) dx является полным дифференциалом, то из
первого уравнения легко находим первый интеграл
Из второго уравнения следует, что ^ = С2. Таким образом, линии тока представляются в виде
пересечения двух однопараметрических семейств поверхностей в пространстве Oxyz:
3x2y2 + 6x = C1, y = C2z. >
464. Пусть плоское электростатическое поле
Найти его силовые линии.
¦< Исходим из того, что касательная к силовой линии коллинеарна вектору Е, т. е. Е || dr
(г — радиус-вектор силовой линии), или
dx dy dx dy
E^~Ey' ~x~~~y'
Интегрируя второе уравнение, имеем у = Схх. Таким образом, силовыми линиями являются
лучи, выходящие из начала координат (х2 + у2 Ф 0). >
465. Найти магнитные силовые линии, если напряженность поля В = (у, -2х).
< В каждой точке силовой линии должно вьшолняться условие: В || dr. Следовательно,
dx dy dx dy
WX~'BV' ~y~~~2x'
Интегрируя уравнение, имеем 2ж2 + у2 = С\. Таким образом, магнитные силовые линии пред-
представляют собой эллипсы. >
§ 2. Нелинейные системы 211
Упражнения для самостоятельной работы
Построить общее решение систем уравнений:
l.4*=x + 2y,$ = 2x-y.2.x = + y + ,y y + , y
3. х = х - Зу, у = 4ж + 5у. 4. х + у + х + Зу + х - 2у = 0, х - Зу + 5х + 8у + 6х - 4у = 0.
Методом неопределенных коэффициентов построить общее решение систем:
( ( ( (' ?)
/ 1 0 1\ / 3 0 1\
7.-1 1 о )у"+ -1 о 2 U = o, у ее3.
\ о о 1/ V 1 1 1/
/-1 0 -1\ /1 0 1\ /10 1\
8. 1 1 0 у"+ 0 1 1 у'+ -1 2 3 у = 0, у еС3.
V 0 1 0/ \2 3 1/ V О О 3/
Построить частные решения систем:
9. 3|| + 8y-6z = a;+sini, ||+6y-5z = ег + е2М0. 0 + y+z = xsinx, 0 -6y-8z = х+х2.
Построить общие решения систем:
/2 3 4\ / 1 2 3\ / 1 \
11. 0 1 0 \у' + х5 [-2 1 4 у= 0 ,уеС3.
\2 0 7/ V-1 0 1/ U6/
/1 0 0\ /1 0 0\ / 2 3 4\
12. A-х2) 0 1 0 \у"-х 0 1 0 у'+ -1 1 0 у = 0, уеС\
\0 11/ \0 1 1/ \-1 2 1/
Привести к системам с постоянными коэффициентами и построить общее решение следующих
уравнений:
(
-¦E
( 4 2)'-
1 -1 0\ /20 1\ / 1 3 4
15. г3 -1 1 0 у'" + ж2 -2 0 1 у" + -2 3 0 у = 0.
V 0 -1 1/ V 3 0 -\) \ 1 -1 \)
. 1 2 3\ / 1 2 3\ / 0 1 3\
17. D*+ 5K -1 2 3 у'" + Dг + 5J 0 -4 5 у" + Dа? + 5) -2 2 3 у'= 0.
\-2 3 1/ V—3 1 1/ V 0 1 47
Построить решения задач:
18. у'{ - у2 = ж, уЧ + 16у, = х\ 0 < х < +оо, ton (yi,2(x)e"f ) = 0, у,@) = 1, у2@) = 0.
19. х2у1' + жу2 + Зу, = 0, ж2у" + 4жу', + Зу2 = О, 1 < х < +оо, у,A) = 0, у2A) = 1, у,,2 =
¦ +00.
Проинтегрировать следующие нелинейные системы:
20. у' = f, z' = -f. 21. у' = у2г, х1 = f - уг2. 22. у' = z, z' = f (у + z).
Построить первые интегралы систем:
23 у' — — z' — ^— 24 ^g = dy_ _ _ rfz 25 _^з;_ dy = ^? 26 _ ^ = ^У = ^z
Построить общий интеграл систем:
27 — = ^ = — = — 28 dx _ dy _ dz _ du 20 _dx = dy _ dz_
Глава 4
Уравнения в частных производных
первого порядка
§ 1. Линейные и квазилинейные уравнения
1.1. Основные понятия.
Квазилинейным уравнением первого порядка в частных производных называется уравнение вида
" dz
^Х,(хь х2, ... , хп, z)— = R(xu х2, ... , хп, г), A)
i=i 0Xi
где Х{, R — известные функции, z = z(xt,X2, ... , хп) — функция, подлежащая определению.
Если функции Xt от z не зависят и R = 0, то уравнение A) называется линейным однородным
в частных производных.
1.2. Решение квазилинейного уравнения в частных производных первого порядка.
Для решения уравнения A) поступают следующим образом. Составляют систему уравнений
dx^ _ dx2 _ _ Ае„ _ rfz
Xi X2 Xn R
интегрируя которую находят п независимых первых интегралов:
Ф,(Х1,Х2, ... ,Xn,z)= Сь
92(хих2, ... ,xn,z)= C2,
Ф„(хь х2, ... , хп, г)= Сп.
Общий интеграл уравнения A) записывают так:
Ф(Ф„ Ф2, ...,Фп) = 0, D)
где Ф — произвольная дифференцируемая функция. При этом считается, что функции Х„ R —
непрерывно дифференцируемые, не обращающиеся в нуль одновременно в рассматриваемой
области изменения переменных X], х2, ... , х„, z.
1.3. Задача Коши.
В приложениях часто требуется найти решение уравнения A) при условии, что
Z = ЩХх, Х2, ... , Ж4_ь ХЫ, ... , Х„).
Схема решения задачи Коши такова. Фиксируя в C) переменную хк, получаем
Ф, (хи хь..., ж*_1, жм, ж*+1, ...,хп,<р)= Сь
Ф2(хи х2, ... , xk.u xk0, xM, ... , х„, <р) = С2, E)
~и хы, ж4+1, ... , х„, <р} - С„.
§ 1. Линейные и квазилинейные уравнения 213
Исключив, если это возможно, из E) переменные Xi,Xi, ... ,жЯг_1) ajt+1, ... ,хп, имеем зависи-
зависимость _ _ _
T{xk0,Cl,C2,...,Cn)=0. F)
Подставляя С,- = Ф,-, i = 1, п, взятые из C), в F) вместо С,-, имеем окончательно
Г(ж«ь Ф|,Ф2, ...,Ф„)=0. G)
Иногда начальное условие задается неявно:
0, ^{х^хг, ... ,хп, z) = 0. (8)
Тогда, исключив переменные хь х2, ... , хп, z из систем C), (8), получим уравнение
/¦(С„С2>...)СП)=О. (9)
Наконец, подставив в (9) значения интегралов из C), имеем:
Дф„Ф2,...,Фп)=0. A0)
1.4. Уравнение Пфаффа.
Уравнение вида
Р(х,у, 2) dx + Q(x, у, z) dy + R(x, y,z)dz=0 A1)
называется уравнением Пфаффа. К нему сводится задача о нахождении семейства поверхностей
и(х, у, z) = С, ортогональных векторным линиям поля F = [Р(х, у, z), Q(x, у, z), R(x, у, z)J.
При этом dx, dy, dz — координаты вектора, лежащего в касательной плоскости к искомым по-
поверхностям.
Если поле F потенциально, т.е. Р = 4^-r, Q = щ, R = ^, то искомая поверхность U
находится с помощью криволинейного интеграла:
u(x,y,z)= J Pdx + Qdy + Rdz. A2)
Если поле F не потенциально, то в некоторых случаях можно подобрать множитель ft = ц(х, у, z)
так, что потенциальным окажется поле /iF. Следовательно,
ди ди ди
"Р = ^' »Q=dy-' fiR=az-
Необходимым и достаточным условием существования семейства поверхностей, ортогональных
векторным линиям, является равенство (F, rotF) = 0. Если это условие выполнено, то урав-
уравнение A1) можно интегрировать как с помощью интегрирующего множителя, так и с помощью
следующего метода. Считают некоторую переменную в уравнении A1) постоянной и интегрируют
оставшуюся часть уравнения. В полученном интеграле постоянную интегрирования принимают
за неизвестную функцию от ранее зафиксированной переменной и подбирают ее таким образом,
чтобы интеграл удовлетворял уравнению A1).
Если (F, rotF) = 0, то говорят, что уравнение A1) интегрируется одним соотношением. Если
же (F, rotF) т^ 0, то уравнение Пфаффа интегрируют двумя соотношениями, т.е. ищут не по-
поверхности, ортогональные векторным линиям поля F, а линии, обладающие тем же свойством
и лежащие на заданной поверхности и(х, у, z) = 0. Исключив одну из переменных из уравне-
уравнений A1) и и(х, у, z) = 0, получают обыкновенное дифференциальное уравнение первого порядка.
Найти общее решение или общий интеграл для каждого из следующих уравнений:
dz dz
Согласно формуле B), п. 1.1, составляем систему уравнений:
dx _ dy _ dz
214 Гл. 4. Уравнения в частных производных первого порядка
Из второго уравнения получаем первый интеграл z = С\. Первое уравнение
является уравнением в полных дифференциалах, поэтому
о о
— его интеграл.
Общий интеграл данного уравнения имеет вид (см. D), п. 1.1):
ф(г, ху + у2^) =0.
Разрешив последнее уравнение относительно z, получим общее решение
где <р — произвольная дифференцируемая функция.
л^~ ди ди ди
467. (х - г) — + (у - z) — + 2z — = 0.
ox ay oz
•4 Составляем систему уравнений:
dx dy dz
A)
х - 2 у - z 2z
(и = C\ — первый интеграл — очевидно). Из системы A) получаем две интегрируемые комби-
комбинации:
d(x + z) _ dz d(y + z) _ dz
x + z ~ 2z' y + z ~2г'
откуда находим два первых независимых интеграла
(x + zJ =c (y + zJ ^c
Z Z '*
Таким образом, общий интеграл представляется в виде:
откуда следует общее решение
_ ((* + ^J (y+j)L\
U~V\ Z . 2 j.
где if — произвольная дифференцируемая функция. >
Составляем систему
dx dy dz
ех ~~ у2 ~ уех
Из первого уравнения находим один первый интеграл -к — е~х = Сх, а из второго с учетом
равенства ех = д _^.^ следует еще один первый интеграл
\a\y\-x
Z г — От-
е- - у~1
Таким образом, общий интеграл данного уравнения будет
' е х-у
Общее же решение его имеет вид
z =
§ 1. Линейные и квазилинейные уравнения 215
Из системы
dx dy dz
х2 + у2 2ху -z2
находим два первых независимых интеграла:
Следовательно,
¦* Система
общее решение
с ду
уравнений
х2
у у
имеет вид:
1 X
z У2-
dx
ху
X
' X2-
/
х2 'Н
dy
x-2z
У2
х2
1
Z
-U2>
а. '
dz
yz
= С2.
1- >
дает два независимых интеграла:
- = С,, 2x-y2-4z =
Следовательно, общий интеграл данного уравнения имеет вид:
ф(§,2х-у2-4г)=0. >
лпл ди ди ди
4/1. (y + z) h (z + ж) 1- (х + у) — = и.
дх ду dz
¦^ Находим первые интегралы системы:
dx dy dz du
y + z x + z x + y и
Из этой системы образуем три интегрируемые комбинации:
d(x — у) du d(x — z) du d(x + у + z) du
у — x и ' z — x и ' 2(x + y + z) и '
интегрируя которые получаем три независимых первых интеграла:
ы(ж — у) = Ci, и(х — z) — С2, z = С}.
А тогда общий интеграл данного уравнения представится в виде:
Ф(«(аг - у), и(х - z), а + У2+г) = 0. >
ди ди ди
U дх ду Z dz
¦4 Аналогично предыдущему примеру имеем:
dx dy dz du
u — x и- у —z x + y
На основании свойства пропорции получаем интегрируемую комбинацию
d(x -у) _dz
х-у z '
откуда следует первый интеграл
^^ = С,.
216 Гл. 4. Уравнения в частных производных первого порядка
Аналогично имеем еще одну комбинацию
d(x + y+2u) _ dz
2и - (ж + у) + 2(ж + у) ~ z '
или
d(x + у + 2и) _ dz
2и + х + у z '
откуда интегрированием находим (ж + у + 2u)z = Сг — первый интеграл. Остается найти еще
один первый интеграл. Для этого с помощью последнего интеграла исключим сумму х + у из
третьего уравнения системы. Тогда придем к уравнению
dz zdu
z 2uz - C2
Интегрируя это уравнение, имеем еще один первый интеграл:
Таким образом, общий интеграл имеет вид:
ф(—tL, (x + y+2u)z, и~!уУ-^ =0. >
Найти решения следующих уравнений, удовлетворяющие указанным условиям:
473. -^ + Bех - у) -^ = 0; z = у при х = 0.
ах ду
¦4 Согласно п. 1.2 сначала мы должны найти общее решение. Из уравнения
dx _ dy
Т~ 2е* -у
находим первый интеграл
уех-е2х =
Следовательно, общее решение будет
Теперь найдем функцию ip, пользуясь начальными условиями. Полагая здесь у- 1 = и, получаем
<р(и) = и + 1. Таким образом,
z = уех - е2х + 1
есть искомое решение. >
л-л ди ди ^ди
474. — + — + 2 — =0; u = yz при х = 1.
дх ду dz *
•4 Из системы уравнений
dx dy dz
Т~Т~ Т
легко находим два первых независимых интеграла:
х-у = Си 2x-z = C2.
Следовательно, общее решение
и = tp{x - у, 2х - z).
Начальные условия дают: yz = <р(\ - у, 2 — z). Полагая здесь 1 — у = ?, 2 - z = »/, получаем
выражение для функции <р(?, т;) = A — ^)B - т;). Таким образом,
u~(l-
есть решение задачи. >
§ 1. Линейные и квазилинейные уравнения 217
лп- ди ди ди , ,
475. х — +у—+ху—=0; и = х +у при z = 0.
дх ду dz
¦4 Аналогично предыдущему имеем
dx dy dz
х у ху'
Отсюда получаем первые интегралы
-=CU xy-2z = C2
У
и записываем общее решение
Вид функции <р, отвечающей начальным условиям, находим из уравнения:
а
Положив в нем ^ = ?, ху = т), имеем
Стало быть,
2z\
¦-(¦"+•¦)(¦—)•>
Найти поверхность, удовлетворяющую данному уравнению и проходящую через данную ли-
линию, если:
476. х -^ - 2у -^ = х2 + у2; у = 1, z = х2.
дх ду
¦* Прежде всего находим первые интегралы системы:
dx dy dz
х ~~ 2,у х ] у
Отсюда легко получаем:
Следовательно, общее решение имеет вид:
X2 У2 I 2\
* = у-j+ *>(»*)• A)
Функция <р, согласно начальным условиям, удовлетворяет уравнению:
х = — - - +<р\х J при
Следовательно,
¦)- 2 +4
А тогда из A) находим требуемое решение
_ х2 у2 ух2 1
M-*fx-ydiy=*2(x-3y),X=l,yz + l=0.
•^ Находим первые интегралы системы:
dx dy dz
х у z7(x — Зу)
Из первого уравнения получаем сразу
218 Гл. 4. Уравнения в частных производных первого порядка
Используя этот интеграл, решаем уравнение
dx dz
или
ЗС,
Отсюда находим еще один первый интеграл:
х + Зу + - = С2.
Далее можно было бы действовать так, как и в предыдущих примерах, однако на этот раз мы по-
поступим согласно формулам (8), (9), A0), п. 1.3, и исключим переменные х, у, z из соотношений:
1 _
' ' ' z
Этим самым мы получим связь между С\ и С2 на кривой х = 1, yz + 1 = 0. Имеем:
1 + 2С, - С2 = 0.
Наконец, подставляя в это соотношение значения Сх и С2, получаем интеграл данного уравнения:
1 + 2ху-х-Зу = 0. >
dz dz
'Za~~x~XVa~y = 1XZ' Х + У = 2> yz = L
¦4 Первые независимые интегралы системы
dx dy dz
z —xy 2x2
имеют вид
x2-z = Cu zy2 = C2.
Исключив переменные х, у, z из соотношений
x + у = 2, yz = \, x2 - z = Ci, zy2 = C2,
находим связь между интегралами на данной кривой:
B - С2J - С? - С, = 0.
Подставив сюда значения С\, С2, имеем уравнение искомой поверхности:
._» dz dz
47У. X — + Z-— =у; y=2z, x + 2y-z.
ox ay
¦* Легко находим два первых независимых интеграла:
y2-z2 =
Исключив переменные х, у, z из соотношений:
= Cu y2-z2 = C2, y-2z = Q, x + 2y-z=Q,
получаем связь между С\ и С2 на данной кривой:
С, = 0.
Таким образом, искомой поверхностью в данном случае оказалась плоскость
= 0. >
§ 1. Линейные и квазилинейные уравнения 219
xy3
X
z
dy
ySZ
''
dz
ЛОЛ Ч &^ ? 2 &% -i -1 j
480. ху3-— + x2z2-— = у\; х = -z3, у = z2.
ох ау
•4 Из уравнения
dx dz
находим первый интеграл
используя который из второго уравнения
находим еще один первый интеграл:
y4-*V = C2.
Исключая переменные х, у, z из системы
^ = Ci, y-x2z1 = C1, х + гъ=0, y-z2=0,
получаем С2 = 0. Таким образом, интеграл (поверхность)
является искомой. В силу начального условия х = —г3 переменные х, z не могут иметь одина-
одинаковых знаков. Следовательно, множитель у2 — xz ^ 0, и в уравнении
4 22,2, ч/2 чп
у - х z = (у + xz){y - xz) = 0
можно от него избавиться.
Итак, окончательно имеем
xz = -у2. >
лал dz dz г
481. х — + у — = 2ху; y = x,z = x.
ах ау
Ч Первые интегралы находим без труда:
- = С,, xy-z = C2.
X
Следовательно, общее решение данного уравнения будет
* = ату+ ?>(|), A)
где р — произвольная дифференцируемая функция. Для ее нахождения воспользуемся началь-
начальными условиями. Это дает ip(l) = 0. Следовательно, функция A) есть решение поставленной
задачи, если ^A) = 0. >
482. Среди функций, удовлетворяющих уравнению
dz dz
х — +у — = 0,
дх у ду
найти такую, которая удовлетворяет и уравнению
(dz\2 fdz\2 a2
) +UJ A)
( fdz\ _
\ai) +UJ ~хЧ^
¦4 Прежде всего, находим общее решение первого уравнения. Имеем
<?е _ dy
откуда
— — С[
х
— первый интеграл. Следовательно, имеем общее решение
220 Гл. 4. Уравнения в частных производных первого порядка
Подставляя его в A), получаем дифференциальное уравнение относительно функции р:
У >2/\ 1 2f\ a
v
откуда
,2 а2
Из последнего уравнения находим
Подставляя сюда значение ?, приходим к искомому решению:
z = ±|a|arctg- +C. >
х
Решить следующие системы уравнений:
^2 — z ®z — ^2
дх х ду у
¦Щ Сначала находим общее решение первого уравнения. Имеем:
dx dy xdz z
T = T = ~' y = c" x=C2'
Следовательно,
*(»' f) =0' ™ z = x<P(y)-
Затем, подставляя найденное z во второе уравнение, относительно функции <р получаем диффе-
дифференциальное уравнение:
х<р'(у) = ~х<р(у), или —— = - (хуф 0).
<Р(У) = Су2.
Интегрируя последнее уравнение, находим:
Таким образом, функция
2 = Сху (ху ф 0)
есть решение данной системы уравнений. >
лил dz dz
4о4. — — у — z, — = xz.
дх ду
•4 Покажем, что непрерывно дифференцируемых решений система не имеет. Предполагая
противное, на основании данных уравнений имеем:
dz
= 1 = 1 - xz;
д
1
дудх ду
d2z dz
= z + x-— = z + х(у - z).
дх ду дх
Отсюда в силу непрерывности смешанных производных следует тождество:
1 — xz = z + х(у — z), или z = 1 — ху.
Следовательно, функция z = 1 - ху должна быть решением обоих уравнений. Однако нетрудно
проверить, что это не так. Полученное противоречие и доказывает наше утверждение. >
ди ди ди ди 2
На основании первого уравнения составляем, а затем решаем систему:
§ 1. Линейные и квазилинейные уравнения 221
Следовательно, общее решение первого данного уравнения имеет вид:
и = <р(у, z - х).
Требуя, чтобы функция <р удовлетворяла второму уравнению, получаем
dtp д<р
1у + тг0' i = z~x-
Нетрудно получить общее решение последнего уравнения:
<р = *1>(у- О-
Таким образом,
« = Ф(у - z + x).
Остается найти вид функции гр, использовав начальные условия. Имеем:
22 = V(-Z), 1p(z) = Z2.
Итак, функция
и = (у - z + х)г
есть решение поставленной задачи. >
486. Найти поверхность, проходящую через прямую у = х, z = 1 и ортогональную к
поверхностям х2 + у2 + z2 = Сх.
¦* Пусть F{x, у, z) = 0 — уравнение искомой поверхности. Тогда, приняв во внимание,
^-, Щт, 7J5~J, из условия
ортогональности получаем:
dF dF 8F
BС)+2 Ъ°
Если исключим параметр С из полученного уравнения и уравнения данных поверхностей, то
будем иметь уравнение, которое определяет поверхности, ортогональные ко всем поверхностям
данного семейства:
* > дх
Из уравнений
dx dy dz
x2 — у2 — z2 2xy Ixz
находим первые интегралы:
-=Ci, x2 + y2 + z2 = C2-
Следовательно, общее решение уравнения A) имеет вид:
Но F = 0 на поверхности, поэтому должно быть
откуда следует, что
у = ztp(x2 + y2 + z2).
Для определения функции гр воспользуемся начальными условиями. Тогда получим х = фA +
а-1
+ 2ж2), откуда
iP(a) = :
Таким образом,
есть уравнение искомой поверхности.
222 Гл. 4. Уравнения в частных производных первого порядка
487. Найти уравнение цилиндрической поверхности с образующими, параллельными век-
ТОРУ A) —li 1). и направляющей х + у + z = 0, х2 + ху + у2 = 1.
¦4 Пусть
F(x,y,z) = 0
(ОЛ О Л ОГ1 \
Ж"' <5jT' <5z / и ^> ~*> ^ Должны
быть ортогональны; следовательно,
dF dF dF _
Jx~ ~ ~ду~ + ~dz~ ~~ °'
Первые интегралы системы da; = -dy = d2 суть
Исключив переменные х, у, z из соотношений
получаем уравнение, связывающее Ci и С2:
С2 + СХС2 + Cj = 1.
Подставив сюда значения Сх к С2, имеем окончательно
х2 + 3(у2 + ху + уг) + xz + z2 = 1. >
Примечание. Можно было бы провести решение, аналогичное предыдущему; однако, как нетрудно убе-
убедиться самому читателю, такой путь технически является более длинным, нежели предложенный в данном
примере.
488. Найти поверхности, у которых любая касательная плоскость пересекает ось Ох в точке
с абсциссой, вдвое меньшей абсциссы точки касания.
¦4 Если F(x, у, z) = 0 — уравнение искомой поверхности, то
dF dF dF
<*-*>^ + (г-|г>^ + (*-*>^=о (i)
есть уравнение касательной плоскости к этой поверхности в точке (ж, у, z)\ X,Y, Z — координа-
координаты произвольной точки на плоскости. Положив в A) Y = Z = 0, найдем абсциссу Х1 пересечения
касательной плоскости с осью Ох:
По условию, а; = 2Х\, поэтому из B) получаем уравнение
xFx + 2yFy + 2zFz = О,
интегрируя которое, находим общее решение:
Таким образом, искомые поверхности имеют вид:
489. Найти асимптотические линии поверхности, проходящей через кривую у = х, z = х3
и удовлетворяющую уравнению
dz dz
§ 1. Линейные и квазилинейные уравнения 223
зная, что асимптотические линии поверхности f(x, у, z) = 0 определяются уравнением:
d2z , d2z d2z ,
¦4 Прежде всего, ищем нужную поверхность, решая задачу
dz dz _ з
Общее решение этого уравнения
1
z = -<р(ху)
подчиняем начальным условиям:
откуда
ip(a) = a2.
Таким образом,
z = x2y
есть уравнение искомой поверхности.
Далее, подставляя значение z = x2y в уравнение асимптотических линий, получаем
у dx2 + 2x dx dy = О, или d(x2y) dx = 0.
Отсюда следуют решения:
х = Си х2у = С2.
Значит, на рассматриваемой поверхности имеется два семейства асимптотических линий:
z = х2у;
х2у = С2. >
490. Найти линии кривизны поверхности, проходящей через прямую z = 1, х = ул/2 и удо-
удовлетворяющей уравнению
1 dz I dz _ 1
х дх у dy z'
зная, что линии кривизны поверхности z = /(ж, у) определяются уравнением:
rdx + sdy sdx + tdy
где p, q, r, s,t — частные производные z'x, z'y, z'^x, z'^y, z'v'y.
¦4 Сначала находим поверхность. Интегрируя уравнение
]_dz_ idz _\_
х дх у ду z'
получаем
z2 = x2 + <p(x2-y2).
В силу начальных условий имеем 1 = 2у2 + <р(у ), откуда
<р(а) = 1 - 2а.
Таким образом, искомая поверхность описывается уравнением
pqdx+ ( g)y
j
Далее, для нахождения линий кривизны полученной поверхности вычисляем нужные производ-
производные и, подставляя их в уравнение A), получаем
((ж2 + z2) dx - 2ху dy)Cz2 + V - 4yz)dy = 0.
Отсюда находим два семейства решений:
» = С„ х2 = С2A + 2уг).
224 Гл. 4. Уравнения в частных производных первого порядка
Последнее совместно с уравнением поверхности дает:
2 = С3ж.
Легко видеть, что кривые у = Сь z = у/1 - х2 + 2у2 являются параллелями, а кривые z =
г = \/1 - х2 + 2у2 — меридианами. >
Примечание. Было бы неточностью считать, что поставленной задаче удовлетворяет поверхность z2 =
= 1 — х +2у , поскольку на плоскости z = 0 частные производные 9Л-, Ч?- не определены.
Проинтегрировать одним (если это возможно) соотношением следующие уравнения Пфаффа:
491. 3yz dx + 2xz dy + xydz = 0.
¦4 Согласно п. 1.4
F = Cyz, 2xz, xy).
Так как
rot F = -ix + 2jy - kz и (f, rot f) = 0,
то данное уравнение интегрируется одним соотношением. Следовательно, существует множитель
fi = fi(x, у, z) такой, что rot^F = 0, т.е. поле ^F потенциально. Таким образом, для множителя ц
имеем уравнения:
или
Интегрируя первое уравнение, получаем общее решение:
(г = у>р(х, О, ( = yz2-
Подставляя полученное значение fi во второе уравнение, имеем:
откуда находим
А тогда
fi = yx2xl>{rj), г) = x3y2z\
Остается найти функцию ip. Для этого воспользуемся третьим уравнением. Имеем
Отсюда
ip(r)) = С.
Таким образом,
(С полагаем равным единице). Умножая почленно данное уравнение на ух2, получаем уравнение
3x2y2z dx + 2x3yz dy + x3y2 dz = 0,
левая часть которого есть полный дифференциал функции и = и(ж, у, z), которую мы найдем,
вычислив криволинейный интеграл (см. A2), п. 1.4):
и(х, y,z)= ( 3x2y2z dx + 2x3yz dy + x3y2 dz =
(
= J 3x]yozo dxt + j 2x3y,z0 dyx + j x3y2 dzt = ylzo(x3 - x30"j + x3z0(y2 - yo) + x3y2(z - z0).
XQ У0 ZQ
Следовательно,
есть искомый интеграл данного уравнения. >
x3y2z = С
§ 1. Линейные и квазилинейные уравнения 22S
492. (z + xy)dx-(z + y2
¦4 Так как (F, rotF) = z + ж — у2 ф О, то данное уравнение не может быть проинтегрировано
одним соотношением. Значит, остается проверить, будет ли функция z = у2 — ху решением этого
уравнения. Вычислив dz = 2y dy - ж dy - у dx и подставив значения г и dz в уравнение, получаем
тождество. Следовательно, поверхность
z-y2 -ху
является единственной, которая ортогональна полю F = (z 4- ху, — z — у , у). >
493. Byz + Зж) dx + xz dy + ху dz = 0.
¦4 Здесь F = Byz + Зж, xz, xy). Поскольку (F, rotF) = 0, но rotF ф 0, то поле F не потенци-
потенциально, однако существует множитель [i такой, что rot^F = 0, т. е. потенциальным является поле
ц?. Из уравнения rot ц? = 0 следует три скалярных уравнения:
ди ди ди ди ди ди
Из первого уравнения находим
и = <р(х, ?), ? = yz.
Подставив значение и во второе уравнение, получим:
откуда
ip = x\j>(x2yz + ж);
поэтому
и = xip(x2yz + ж).
Наконец, подставив и в третье уравнение, имеем ¦ф' = 0, т.е. ¦ф = С. Таким образом,
и = х.
После умножения данного уравнения на и, получаем уравнение
Bxyz + Зж2) dx + x2z dy + х2у dz = 0,
интеграл которого имеет вид
ж3 + х2yz - С.
Решение ж = 0 входит в него при С = 0. >
494. (z2 -у2 + yz)dx + (xz - 2ху)dy + Bxz + 2z + xy)dz = 0.
¦4 Поскольку rotF = 0, где F = (z2-y2+yz, xz — 2xy, 2xz-Y2z-\-xy), то поле F потенциально.
Следовательно, левая часть данного уравнения является полным дифференциалом функции
и(ж, у, z) = J Fx dx + Fvdy + Fz dz = z2(x + 1) + xyz - xy2.
@,0,0)
Поэтому
Z2{x + 1) + xyz -xy2 = C
есть искомый интеграл. >
495. (Ах2уг2-2у2г*-3хуг) dx+Bxiyzi-3xyzi-2x2z) dy+Cx3yz3-4xy2z2-2x2y) dz = 0.
¦4 Поскольку rotF Ф 0, то поле F не потенциально; однако в силу того, что (F, rotF) = 0,
существует множитель ц = ц(х, у, z) такой, что потенциальным будет поле ц?. Легко найти, что
ц = xyz. Выполняя интегрирование
J
(fill, dr) = x2y2z2(x2z - yz2 - ж),
@,0,0)
получаем интеграл данного уравнения:
x2y2z2(x2z - yz2 - ж) = С. >
226 Гл. 4. Уравнения в частных производных первого порядка
496. 3xy2z dx + 3x2yz dy + 2ж2у2 dz = 0.
¦4 Поскольку rot F ф 0, но (F, rotF) = 0, то данное уравнение интегрируется одним соот-
соотношением. Найдем интеграл уравнения, используя метод, изложенный в конце п. 1.4. Считая
переменную z временно постоянной, интегрируем соотношение:
3xy2z0 dx + 3x2yz0 dy = 0, или d(xy) = 0.
Отсюда следует, что ху = С: Далее, принимая С = C(z), подбираем функцию С таким образом,
чтобы соотношение
ху = C(z) A)
стало интегралом данного уравнения. Вычислив
C'dz-xdy
dx =
У
и подставив в указанное уравнение значения ху = С и dx, после некоторых упрощений получим
уравнение:
3C'z + 1С = 0.
Интегрируя последнее уравнение, имеем
С-Сог'з.
Таким образом, из равенства A) следует, что
хъуъг2 = Со
есть интеграл исходного уравнения. >
497. A + x2y2z2 - yz)dx -xzdy- xydz = 0.
¦4 Непосредственно проверяем, что rotF Ф 0, но (F, rotF) = 0, поэтому уравнение интегриру-
интегрируется одним соотношением. Считая переменную х временно постоянной, интегрируем уравнение:
xoz dy + хоу dz = 0; или d(yz) = 0.
Следовательно,
yz = C(z). A)
Подберем функцию С так, чтобы данному уравнению удовлетворял интеграл yz = C(x). Из
последнего соотношения находим
C'dx Cdz
и подставляем в рассматриваемое уравнение значения у и dy. После упрощений имеем диффе-
дифференциальное уравнение:
1 - С - х2С2 - хС' = 0, или (хС)' = 1 + (хСJ,
интегрируя которое, получаем
arctg(xC) = x + Ci. B)
А тогда из равенства A) с учетом B) находим интеграл данного уравнения:
arctg(xyz) - х = С\. >
498. (ж - y)dx + zdy-xdz = Q.
¦4 Поскольку (F, rot F) = z — 2x + у и функция z = 2х — у не является решением данного
уравнения, то оно не может быть проинтегрировано одним соотношением. Проинтегрируем его
двумя соотношениями, положив, например, z = х + у. Тогда получим уравнение
dx — dy = 0,
откуда
у = х + С,.
Следовательно, однопараметрическое семейство прямых
x = t, y =
удовлетворяет данному уравнению. >
§ 1. Линейные и квазилинейные уравнения 227
499. (у + Зг2) dx + (х + у) dy + 6xz dz = 0.
¦4 Векторное поле F = (у + 3z2, x + у, 6xz) потенциально, поэтому
(z,»,z) 2
u(x,y,z) = j (F,dr) = xy+j + 3xz2.
@,0,0)
Следовательно,
у2 + 2ху + 6xz2 = С
есть интеграл данного уравнения. >
Найти поверхности, ортогональные векторным линиям векторного поля F, если:
500. F = Bху - 3yz)i + (ж2 - 3xz)j - Зхук.
¦4 Если dr = (dx, dy, dz) — вектор, лежащий в касательной плоскости к искомой поверхно-
поверхности, то согласно условию должно быть (F, dr) = 0, или
Bху - 3yz) dx + (x2 - 3xz) dy - Зху dz = 0.
Поскольку rotF = 0, то поле F потенциально. Следовательно,
и(х, y,z)= j (F, dr) = x2y - 3xyz.
@,0,0)
Таким образом,
x2y - 3xyz = С
— искомые поверхности. >
501. F = Bx - y)i + Cy - z)i + (x - 2y)k.
¦4 Поскольку (F, rot F) = z — x - 4y и функция z = x + 4y уравнению (F, dr) = 0 не удо-
удовлетворяет, то не существует ни одной гладкой поверхности, ортогональной данному векторному
полю F. >
502. Найти векторные линии, векторные поверхности и поверхности, ортогональные век-
векторным линиям поля
¦4 Векторные линии в каждой своей точке касаются вектора F. Следовательно, F || dr, где
dr — дифференциал радиуса-вектора линии.
В координатной форме условие касания в данном случае имеет вид:
da; = dy = dz
ж у -г'
Интегрируя уравнение A), получаем
а;
у~ '' yz~
Таким образом, пересечение семейств поверхностей ^ = С\, yz = Сг дает нам двухпараметричес-
кое семейство векторных линий. Поскольку векторные поверхности состоят из векторных линий,
то в каждой точке такой поверхности должно выполняться условие: (N, F) = 0, где N — вектор
нормали к поверхности. Пусть и(х, у, z) = О — уравнение поверхности; тогда указанное условие
в координатной форме приобретает вид:
ди „ди „
Подставив сюда значения координат вектора F, имеем
ди ди ди
228 Гл. 4. Уравнения в частных производных первого порядка
Используя интегралы системы A), получаем общий интеграл последнего уравнения:
«(*»*)= О,
откуда
где <р — произвольная функция. Итак, векторные поверхности найдены.
Поверхности, ортогональные данным векторным линиям, ищем из уравнения:
(F, dr) = О, или х dx + у dy — z dz = 0.
Интеграл этого уравнения усматривается непосредственно
X2 + у2 - Z2 = С. >
§ 2. Нелинейные уравнения первого порядка
2.1. Нелинейные уравнения в частных производных первого порядка.
Уравнение вида
,, х2, ... , xn,z,pi,p2, ... ,р„) = 0, A)
О
где pi = -jf^:, i = 1, п, называется нелинейным уравнением в частных производных первого порядка.
Для интегрирования уравнения
F(x,y,z,p,q) = 0, p=—,q=-~ B)
применяется метод Лагранжа и Шарпи, заключающийся в следующем. Соответственно уравне-
уравнению B) подбирают уравнение
и(ж, у, z, p,q) = a, a = const, C)
таким образом, чтобы оно удовлетворяло двум основным условиям: 1) систему уравнений B), C)
можно разрешить относительно переменных р, q; 2) уравнение Пфаффа
dz = р(х, у, z, a) dx + q(x, у, z, a) dy
интегрируется одним соотношением Ф(ж, у, z, а, Ь) = О, Ь = const. Тогда интеграл Ф = 0 будет
также интегралом уравнения B) (интеграл Ф = 0 носит название полного). Функция и удовлетво-
удовлетворяет уравнению
3F ди №9в / dF dF\ ди fdF dF\ ди (dF dF\ ди _
~др~Ъх~ + ~dq~ ду + V ~dp+q ~dq) dz~ ~ \дх~ +Р Jz~) ~др~~ \ду +Я ~dz~) dq ~ ' D)
2.2. Решение задачи о нахождении интегральной поверхности,
проходящей через заданную кривую.
Если известен полный интеграл Ф(ж, у, z, a,b) = 0 уравнения B), то можно решить задачу о
нахождении интегральной поверхности, проходящей через заданную кривую
* = *(*), » = »(*), * = *(*)• E)
Считая Ь = Ь(а), определяем функцию Ь из системы уравнений:
$(x(t),y(t),z(t), а, Ь(а))=0,
?,„
После того, как функция Ь будет найдена, искомую интегральную поверхность определяем, ис-
исключая параметр а из системы уравнений:
d
Ф(х, у, z, а, Ь(а)) = 0, — Ф(х, у, z, а, Ь(а)) = 0. G)
§ 2. Нелинейные уравнения первого порядка 22У
2.3. Метод Коши.
Предыдущую задачу можно решить по-другому. Сначала определяем функции р0 = Po(s),
<?о — <?o(s) из уравнений:
((«), Уо(«), zo(s), po(s), 5o(s)) = О,
pa(s)x'0(s) + 9o(s)yd(s) — ^o(s) = О,
где ж0 = xo(s), уо = Уо(«), ^о = го(«) — параметрические уравнения данной кривой. Затем
интегрируем систему с учетом найденных функций ро, q0:
J?,
(9)
с начальными условиями:
при t = О х = xo(s), у = уо(*), г = zo(s), p = po(s), q = qo(s). A0)
Тогда три функции х = x(t, s), у — y(t, s), z = z(t, s), являющиеся решением задачи (9), A0),
представляют собой параметрические уравнения искомой интегральной поверхности.
2.4. Обобщение метода Коши.
Метод Коши обобщается на уравнения вида A), когда требуется найти интегральную п-мер-
ную поверхность z = z(xh x2, ... , хп) уравнения A), проходящую через заданную (п- 1)-мерную
поверхность:
Хю = *io(«i, s2, ... , sn-i)> г = 1, n,
z0 = 20(«1, s2, ... , sn.i).
Схема решения задачи A), A1) следующая. Сначала определяем функции pl0 (sb s2, ... , sn-i) из
уравнений
)> Рю, Рго, ¦ ¦ ¦ > Рпо) - О,
= 0, j = T^=T. A2)
J 1—1 f<>7
Далее интегрируем вспомогательную систему уравнений
dx\ dx2 dxn dz dp\ dp2 dpn
= dt
с начальными условиями:
x,
z
Pi
(=0
(=0
FXl+PlFz FX2+p2Fz Fx,+pnFz
A3)
»i, s2, ... , sn-i),
l,*2, ...,*»-l), A4)
!l, S2, ... , Sn_l), t = 1, П.
В результате получаем параметрические уравнения искомой интегральной поверхности:
,;=Xi(t, SUS2, ... ,SB_l), t=l, «,
z = z(<, s,,s2, ... ,sn_,).
Найти полный интеграл в каждом из следующих уравнений:
¦ pq = х2у2
503. т = х2-2
Согласно п. 2.1, сначала составляем и решаем уравнение D) (F = pq — х2у2):
ди ди ди 7ди , ди dx dy dz dp dq
q+Pl+2M+2xy+2xy=0 = 7=^=^ =
230 Гл. 4. Уравнения в частных производных первого порядка
Используя равенство pq = х2у2, последние уравнения приводим к виду
х dp — у dq = dz = 2p dx — 2q dy.
Отсюда получаем два первых интеграла:
?яС" ? = Cj- A)
Но так как pq = х2у2, то С\С2 = 1. Следовательно, обозначив Ct = а, интеграл A) можно
представить так:
р = ах2, Я=-У2-
Далее, подставив значения р, q в уравнение Пфаффа dz.= pdx + qdy, имеем
dz — ах2 dx+ ~y2 dy.
а
Отсюда находим
а 1 V3
z-~xs + ^ + b = 0.
3 За
Таким образом, мы получили полный интеграл данного уравнения. >
504. z = рх + qy + p3q3.
¦4 Пользуемся методом Лагранжа и Шарпи. Вычислив производные -^-, -^-, ^|-, ^=-, %&-,
где F = z —рх — qy -piqi, и подставив их значения в уравнение D), п. 2.1, решаем уравнение:
ди
- + (у + зРу) + (рт + qy + 6РУ)
+ зРУ) - + (у + зРу) - + (рт + qy + 6РУ) - = о.
Из системы уравнений
dx dy _ dz dp
ж + 3p2qi ~ у + tyq2 ~ px + qy + 6piqi ~ 0 ~ 0
следуют интегралы: р = a, q = b. Из первого уравнения получаем:
dz = pdx + qdy, или dz = adx + bdy.
Следовательно,
z =
Ho z = px + qy + p3q3, поэтому
Съ = a3b\
a3b3. >
Итак, полный интеграл имеет вид:
5O5.pq = 9z2.
¦4 Вычислив необходимые производные от функции F = pq — 9z2, составляем и решаем
уравнение D):
ди ди „ ди ди ди „ dx dy dz dp dq
dx dy dz dp dq q p 2pq
Из последнего уравнения получаем один первый интеграл:
9 -гЛ
= 9z2
Из системы
-=С,2, pq
находим
р = Ъаг, q= - z
а
(мы ввели обозначение Ci = а). Подставив значения р, q в уравнение Пфаффа, получим
dz = 3az dx+ - z dy.
a
§ 2. Нелинейные уравнения первого норадка 231
Интегрируя это уравнение, находим полный интеграл:
ln|z|-3aa; у - Ь = 0. >
а
506. р = sinq.
¦4 В данном случае F = p — sinq, поэтому уравнение D), п. 2.1, принимает вид:
ди ди ди
__cos,_ + (p_,cosg)__=0.
Из системы уравнений
dx dy dz dp _ dq
1 - COS q p- q COS q 0 0
находим два первых интеграла:
р = Си q = C2.
В силу уравнения р = sin q имеем С\ = sin С2 ¦ А тогда соответствующее уравнение Пфаффа будет
иметь вид
dz = sin C2 dx + С2 dy;
интегрируя его, легко находим полный интеграл данного уравнения:
z = ж sin a + ay + b (a = Ci).>
507. Z=p2 + q2.
•4 Из системы уравнений
dx _ dy dz _ dp _ dq
которая соответствует уравнению D), п. 2.1,
ди ди , 2 2\ ди ди ди
находим один первый интеграл:
Р-=а.
q
Далее, решив систему:
V + Я2 = г, р = qa,
имеем
a\fz s/z
Р= i /, . 1' 9 =
±Vl + a2 ±Vl + a2
Подставив значения р и q в уравнение Пфаффа dz = pdx + qdy, можем записать:
dz _ adx + dy
откуда интегрированием находим ±2\/1 + a}^fz — ах — у — Ь = 0, или
4A + a2)z - (аж + у + ЬJ = 0.
Это есть полный интеграл данного уравнения. >
508. р2 + zpq = z2.
¦4 Уравнение D), п. 2.1, в данном случае имеет вид:
ди ди ди ди ди
q)Vx+zp-+2p(p + zq)--p(Pq-2z)--q(pq-2z)-
Далее решаем систему уравнений:
dx dy dz dp dq
2p+zq~ zp~ 2p(p + zq) ~ Bz - pq)p ~ Bz - pq)q'
Из последнего уравнения находим первый интеграл
232 Гл. 4. Уравнения в частных производных первого порядка
Из системы
рг + zpq = z2, р = qa
имеем:
Используя значения р, q, уравнение Пфаффа dz = pdx + qdy представляем в виде:
. dz
\/а(а + z)— = ±(а dx + dy) = ±d(ax + у).
z
Интегрируя уравнение Пфаффа, после некоторых преобразований получаем полный интеграл:
2
-(ах + у + bf = 0. >
^ 4
Р1 Ф
¦4 От переменных ж, у перейдем к переменным и, v, положив и — 4j-, v = ^-. Тогда
_ dz _ dz ди _ dz _ _ dz _ dz dv _ dz __
p"dx"d^a^'xd^ = xpi' q~d~y"d~vd^~vd~i = m
и данное уравнение примет вид:
Будем искать решение этого уравнения в виде: z = z(w), где w = аи + v, a = const. Тогда из A)
получим уравнение
интегрируя которое, находим
1
а1
z1 = ±2\1\ + — (au + v) + b (Ь = const).
Таким образом,
есть полный интеграл исходного уравнения. >
Примечание. Для интегрирования уравнения F(p, q, z) = 0 целесообразно применять следующий способ.
Ищем решение в виде г = z(w), где w = ах + у (а = const). Тогда
dz ,dw , dz ,
p = — = z — = z a, a — — = z .
F dx dz ' ч dy
Следовательно,
F(p, g, z) = F(z'a, z, z) = 0.
Интегрируя это уравнение, получаем его общий интеграл
Ф(л, w, а, Ь) = 0 (* = const),
который по отношению к исходному уравнению будет полным.
1O.pV + 9Y = *.
•^ Сначала переходим к новым переменным по формулам и = In \x\, v = In \y\:
>-"• -?¦
где
dz dz
Исходное уравнение принимает вид:
p] + q\ = z.
Далее, поскольку последнее уравнение не содержит явно независимых переменных, то к нему
применяют способ, лчсазанный в предыдущем примере. В результате получаем обыкновенное
§ 2. Нелинейные уравнения первого порядка 233
дифференциальное уравнение
процесс решения которого можно представить следующим образом:
, \fz dz dw f dz f dw
dz dw f dz
f' VZ = ±VT+P' J 7? =
2л/г =—===+b, BVz - bJ = *" , w = au + v =a\n\x\ + In|y|.
v 1 + a2
Итак, полный интеграл получен. >
у х х у
Л Перепишем уравнение в виде:
хр - х = yq + у (х ф 0, у ф 0).
Далее, полагая хр — х = a, yq + у = а, где а — произвольная постоянная, из последних двух
уравнений находим
а а
,= !+_, « = -1 + -.
Подставляя эти значения р и q в уравнение Пфаффа dz = p dx + q dy и интегрируя его, получаем
полный интеграл
z = х + а\п\х\ — у + aln\y\ + Ъ = х — у + а\п\ху\ + Ъ. >
Примечание. Если уравнение имеет вид
Fi(p, x) = F2(q, у),
то его полный интеграл можно найти, пользуясь следующей схемой. Из системы
Fi(p,x) = a, F2(q,y) = a
находим
подставляя которые в уравнение Пфаффа dz =pdx + qdy, имеем
dz = ip\(a, x)dx + ip2(a, y)dy.
Интегрирование этого уравнения и дает полный интеграл:
г- I <pi(a,x)dx— I <p2(a, y)dy — b = O.
J J
512. р2 + q2 - 2рх -2qy+l = Q.
Л Поскольку уравнение можно представить в виде
то вполне применим способ, указанный в выше приведенном примечании. Из уравнений
р2 - 2рх + 1 = a, 2qy - q2 = a
находим
р = х±л/а- 1+х2, q = y±Jy2-a, (\х\ ^ л/1 - а, \у\ ^ а).
Следовательно,
dz — (х ± \Лг2 + а — 1) dx+ (у ± у у2 — a)dy,
откуда следует, что
z- J (x± Vx2 + а - l) dx- I(у± у/у2 - aj dy-b = Q
есть полный интеграл. >
Olj,p -t- q -\- x + z = U.
•^ Вводя новую функцию ш = х + z и обозначения р\ = wi, qi = w'y, данное уравнение
представляем в виде:
234 Гл. 4. Уравйення в частных производных первого порядка
Поскольку это уравнение не содержит явно независимых переменных, то применяем способ,
изложенный в примере 509. Имеем
ш = ш(и), и = ах + у.
Тогда
Pi — w\u)a, <fi = w'(u), (pi — IJ + gi = ш = (w'a — IJ + w + w = 0.
Для решения последнего уравнения применяем метод введения параметра. Полагая ш' = t, имеем
, Аш dt 2(ta - Da ,
u) = -t-(ta-l) , du- — = ——— dt, « = Bo- l)ln|i| - 2a i + b.
Z t X
Таким образом, система уравнений
z+x = -t-(ta- IJ, ax + у = Ba - 1) In |*| - 2a2t + b
определяет полный интеграл. >
Примечание. В данном случае можно исключить параметр t и получить полный интеграл в вице
Ф(г, у, z, a, 6) = 0,
однако предоставляем это читателю.
В следующих задачах найти интегральную поверхность, проходящую через заданную кривую:
514. z — pq+ I, z — 2х+ 1 при у = 2.
¦4 Прежде всего находим полный интеграл данного уравнения, пользуясь примечанием к при-
примеру 509. Решение ищем в виде z = z(u), и = ах + у. Тогда р = z'a, q = z'uz — z'a + l.
Интегрируя это уравнение, получаем полный интеграл исходного уравнения:
Ф = 4a(z - 1) - (ах + у + ЪJ = 0.
Далее, для определения поверхности, которая проходит через указанную прямую, поступаем со-
согласно изложенному в п. 2.2. Именно, полагая х = х, у = 2, г = 2а;+1и считая 6 = 6(а),
относительно функции 6 = 6(а) записываем систему уравнений F), п. 2.2:
Sax -(ах + Ъ + 2J = 0, 8а - 2а(аж + 2 + 6) = 0.
Затем решение этой системы 6 = 0 подставляем в систему уравнений G), п. 2.2. Тогда получим
4a(z - 1) - (ах + уJ = 0, 4z - 2х(ах +y) = Q.
Отсюда, исключив параметр а, после упрощений окончательно находим уравнение искомой по-
поверхности
г = ху+ ). >
515. 2z = pq — Ъху, z = \Ъу при х = 5.
•* Предположим, что решение имеет вид z = <р(ху). Тогда относительно функции ц> получаем
уравнение:
2ip = ip и — 3«, и = ху,
которое среди прочих решений имеет и такое:
<р = аи,
где ai = -1, oti = 3. Следовательно,
z\ = -ху, гг = Зху.
В силу начальных условий имеем
г = Зху. >
516. 4z = р2 + q2, z =у2 при х = 0.
А Поскольку функция F = 4z — р2 — q2 явно от переменных х, у не зависит, то решение
уравнения ищем в виде z = ip(ax + у). Тогда относительно <р получим уравнение
интегрируя которое, находим:
§ 2. Нелинейные уравнения первого порядка 235
Далее в силу E), F), п. 2.2, имеем уравнения:
= О, У = У, z=y2,
a2 + 1 / Va2 + 1 \ v яг +
Отсюда, исключив переменную у, получаем Ь = 0. Используя теперь уравнение G), п. 2.2, и 6 = О,
имеем систему:
(ах + уJ _ 2(ах + у)(ау - х) _ п
2 а2 + 1 ~ ' (а2 + 1J
авнения нах
поверхности
Из второго уравнения находим а = | и подставляем в первое. В результате приходим к искомой
z = х2 + у2. >
Примечание. Равенство ах + J/ = 0 не подходит, так как из первого уравнения следовало бы, что z = 0.
517. pa; + ?у — /?<jr = 0, 2 = у при а; = 0.
4 Для нахождения полного интеграла воспользуемся методом Лагранжа и Шарпи. Из систе-
системы уравнений
dx dy dz dp dq
x-q~ У-Р ~ P(x - q) + q(y - p) ~ -p ~ -q'
соответствующей уравнению D), п. 2.1, находим один первый интеграл
p = qa.
Далее, решив систему уравнений р = qa, px + qy - pq = 0, получаем
у
р = ах + у, q = x+~.
а
Подставляя значения р и q в уравнение Пфаффа dz = pdx-Ь qdy и интегрируя его, будем иметь
z = - (ах1 + — | + ху + Ь.
2 \ а I
Это есть полный интеграл. Для нахождения поверхности, проходящей через указанную в условии
кривую, применяем схему, изложенную в п. 2.2. Записываем уравнение кривой в виде х = 0,
у = у, z = у, составляем систему вида F), п. 2.2:
U 2 У\ У
z - - [ах2 + — - ху - Ца) = 0, 1 - а; - - = 0.
2 \ а) а
Подставляя сюда х = 0, у = у, z ~ у и исключая параметр у, находим Ца) = -^а. Наконец,
исключая параметр а из системы уравнений, соответствующей системе G), п. 2.2:
а х2 у1 I
Таким образом,
518. z -px — qy — 3p2 + q2 = 0, z = у2 при х = 0.
Ф = z - ах - by - За2 + Ь2 = 0.
Аналогично проделанному в предыдущем примере имеем: ж = 0, у = у, z = у2 (параметрические
Нетрудно проверить, что полным интегралом данного уравнения будет
Ф = z
гично проделанному в предыдущ
уравнения данной в условии кривой),
z - ах - уЬ - Ъа2 + Ь1 = 0, 2у - Ъ = 0.
Подставляя сюда а; = 0, у = у, z = у2 и исключая переменную у, находим Ь = ±2а. Далее,
найденное значение Ь подставляем в систему G), п. 2.2:
z - ах =f lay - За2 + 4о2 = 0, -х =f 2у + 2а = 0.
236 Гл. 4. Уравнения it частных производных первого порядка
Исключив параметр а из этой системы, получаем окончательно:
Пользуясь методом Коши, найти интегральную поверхность, проходящую через заданную
кривую:
519. z -pq, х0 = s, yo = s2, z0 = s3.
•^ Применяем метод Коши, изложенный в п. 2.3. Согласно методу, сначала составляем и ре-
решаем систему уравнений (8), п. 2.2:
F
= 0, po(s) + 2sqo(s) - 3s2 = О,
Затем, учитывая найденные значения po(s), <fo(s), составляем и интегрируем систему уравне-
уравнений (9), п. 2.2,
dx _ dy __ dz dp _ dq
-q -p -2pq -p -q
с начальными условиями: х = s, у = s2, z = s3, p = s2, q = s при t = О, а также x = s, у = s2,
z = s3, p = 2s2, <jr = j при t = 0. Таким образом, возможны два варианта.
Из системы A) легко находим
/? = С]б , q = С2е , х = I (—q) dt + Сз = С2е + Сз,
у = Д-р)<й + С4 = Cie~' + С4, 2 = -2 fpqdt + Cs = CiC2e'2i + C5.
Исходя из начальных условий, определяем постоянные интегрирования:
С, = s2, С2 = s, С3 = 0, С4 = 0, С5 = 0
(для первого решения);
г 2 s г s г 2
1 - * , 2- 2> 3- 2> 4- -* , 5-
(для второго решения). Итак, имеем две интегральные поверхности:
х = se~', у = s2e~\ z = s3e~2t;
ж = |(е~* + 1), у = s2Be"' - 1), 2 = sV2'. >
520. р2 +q2 = 1; Яо = coss, jfo = sins, z0 = -.
•* Как и в предыдущем примере, сначала находим функции р0, qo из системы уравнений
(см. (8), п. 2.3):
pi + ql - 1 = 0, —ро sin s + q0 cos s = 0.
2
Имеем j>o = cosa, <jr0 = sina, где a = s + (—l)*y + Ая", Л 6 Z. Из системы уравнений (см. (9),
п. 2.3):
dx _ dy _ dz _ dp _ d<7 _
2p 2<jr г^ + з2) 0 0
следуют также решения:
Для определения постоянных интегрирования используем начальные условия:
s
х = cose, у = sins, z=~! p = cosa, <jr =
при t = 0.
§ 2. Нелинейные уравнения первого порядка 237
Тогда получим
s
Ct=cosa, C2=sina, C3=coss, C4 = sins, C5 = -.
Следовательно, три функции
s
х = 2tcosa+ coss, у = 2tsina + sins, z — 2t-\—
описывают искомую интегральную поверхность. >
521. z=px + qy+pq, х0- 1, yo = s, zo = s\
•* Из системы уравнений (см. (8), п. 2.3)
- Ро - Яо* ~ РМо = 0, qo-3s2 =
находим
Далее, составляем и решаем систему уравнений (см. (9), п. 2.3):
dx dy dz dp dq
x + q y + p z + pq 0 0
? ? ?
Исходя из начальных условий
2s3
а;
(=0
з
[=0
l+3s2'
определяем постоянные интегрирования:
Таким образом, параметрические уравнения поверхности имеют вид:
522. z = pj +pl +pl; ж10 = s, + s2, a;20 = st - s2, xM = 0, z0 = I - st + s2 (p,- = -щ,
i = 1, 2, 3).
•* Действуем по методу Коши, изложенному в п. 2.4. Именно, сначала определяем функции
¦Рю. Рю, -Рзо из системы уравнений (см. A2)):
2о - Pio - Р2о - Рз2о = 0, -1-Р10-Р2о = 0, 1-Рю + Р2о = 0-
Имеем:
Pl0 = 0, Р20 = -1, Рзо = ±у/82 - Si.
Затем интегрируем вспомогательную систему дифференциальных уравнений (см. A3), п. 2.4):
dxi _ dx2 _ dxi _ dz _ dp\ _ dp2 dp}
2pi ~ 2p~2~ 2p3 ~ liPi+pl+Pi) ~ -Pi~ -Pi~ -Рг~
Из последних трех уравнений этой системы получаем:
Pi = Схе\ р2 = С2е\ рг = С3еь.
Из первых трех уравнений с учетом полученных значений для р*, к = 1, 2, 3, находим
e' + С4, ж2 = 2С2е' + С5, ж3 = 2С3е' + С6,
238
Гл. 4. Уравнения в частных производных первого порядка
Для определения постоянных интегрирования воспользуемся начальными условиями (см. A4),
п. 2.4):
(=0
Х2
= Si- S2,
= 0,
Pi
В результате находим
C,=0, C2 = -l, C3 =±y/82-si, C4 = s1+s2, C5 = s,-s2+2, C6 = ^2y/s2-8h C7=Q.
Таким образом, параметрические уравнения искомой поверхности имеют вид (см. A5), п. 2.4):
«i = «1 + «2, х2 = —2е' + 2 + Si - s2,
ж3 = ±2л/*2 - «1 е' т 2>/«2 - *i = ±2\/s2 - «i (e' - 1). 2 = A + а2 - *i)e2'- >
523. z = xipi +х2р2+ХзРз +p\ +pl +pl\ xw = 1, x20 = a,, a;30 = s, +s2, 20 = 1 +s].
¦4 Как и в предыдущем примере, применяем метод Коши (см. п. 2.4). Составляем и решаем
систему уравнений относительно рю, Р20, Рзо'-
+ s2)p}0 + p2l0 + pj0
1 + S? =
Отсюда находим
Далее составляем и решаем систему дифференциальных уравнений:
dx\ dx2 dxj dz dp\ dp2
xx + 2px x2 + 2p2 x3 + 2ръ __.__,__, „ ^ .., 0 0
- p2Q - pw = Q, ръо = 0-
= dt.
Из последних трех уравнений следует, что р^ = С*, к = 1, 2, 3, а из первых трех —
Х\ — С4е — 2С|, х2 = С$€ — 2С2, я?з == С$е — 2Сз, z = [ С\С$ -^ С2С$ -\- С^Сь )е + CV*
Используя начальные условия
а;,
= 1,
= «1,
[=0
(=0
определяем постоянные Q, г — 1, 7:
, С2 = 2s,, С3 = 0, СА = 1 + 2Ci = ±v/5 - 20s?, C5 = s, + 2С2 = 5«,,
-3 ± л/5 - 20s?
07 — 1 Ч" Si — OiC'4 — О2С'5 — C^Og —
Итак, параметрические уравнения искомой поверхности имеют вид:
а;, = ±^5 - 20s?e' + 1 =f V'5 ~ 20si = ±\/5 ~ 20s?(e' - 1) + 1,
, , I/ 1 ч , , -3 ± л/5 - 20s?
a;2 = Ee'-4)s1, x} = (si + s2)e', z = -E =F V5 ~ 20e?)e' ¦¦ ~2 ' V
524. р]+р1+р2з+р1-1 = 0; a;10 = 1, жм = si, жю = Si+a2, xm = ei+s2+s3, z0 = s]+sl+sl.
-4 Поступаем аналогично проделанному в примерах 521—523, т.е. действуем по следующей
схеме.
а) Решаем систему уравнений:
\\ ]- 1 =0, 2s,-р2о-р30-Р40 = 0, 2а2 - fto - рт = 0, 2s3-p4o = 0.
§ 2. Нелинейные уравнения первого порядка 239
Отсюда имеем:
- «з), fto = 2(s, -s2), рю = ±y/l - 4(si - s2J - 4s2 - 4(s2 - s3J.
б) Интегрируем вспомогательную систему:
dx\ dx2 dXi dxi dz dpi dpi __ dp} _ dp^ _
2^ = 2^ = 2p7 = 2^ " 2(p? +^ +Яз +rf) ~ ~~0" ~ ~~0~ ~ ~~0~ ~ ~"«~ ~
Из последних четырех уравнений следует, что /jt = С», А: = 1, 4; а из первых четырех —
4
к = Т~4, z = 2
в) Исходя из начальных условий
хк
= хм, рк
= Рко, к =1,4»
(=0
определяем постоянные интегрирования Ск, Dk:
Ск = Ры, At = хк0, Ds = zo, к = 1, 4.
г) Записываем параметрические уравнения искомой поверхности:
«i = ±2т/1 - 4(«i - s2J - 4s] - 4(s2 -
x2 = 4(«! -s2)t + s,,
+ «2,
2 = It + s] + s\ + s\. >
Упражнения для самостоятельной работы
Построить общие решения следующих уравнений:
f Щ =0. 2. V5j|-»? =0- 3.хЦ+у||+х^ =0. 4.
Построить решения следующих задач Коши:
7-*Ш-ущ = °. «U =2г-8- у2II+*иЩ = х, «и
Построить решения следующих дифференциальных задач:
Ю. {у-и)^ + (и-х)Щ=х-у, и~у=~х. 11. (у + 2«2)||-2х2«|| = а;2, * = в,
12.(z-ti)?if+(y-«)fjf=2ti, z-y = 2, u + 2*=l. 13. tgx||+y|| = «, у = as,
Глава 5
Приближенные методы решения
дифференциальных уравнений
§ 1. Зависимость решения
от начальных условий и параметров
1.1. Об оценке погрешности приближенного решения.
Пусть у = y(t) — вектор-функция, являющаяся приближенным решением задачи Коши для
системы дифференциальных уравнений:
dx
— = f(t, х), x\t=0 = x(Q), A)
где x = (xi, X2, ¦ •. , xn), f = (/i, /2, ... , /„). Здесь и далее будем считать, что вектор-функция /
непрерывна по переменным t, x и удовлетворяет условию Липшица по переменной а;:
Н/(«, У) ~ /(*, яIК К\\у - х||, К = const, B)
где || • || обозначает какую-либо норму вектора:
1М1 = ?><1, Ы = max \x(\.
Пусть, далее, приближенное решение y(t) задачи A) удовлетворяет неравенствам:
||^-/(t,y)||^e, ||»@) - *@IК 6. C)
Тогда справедлива оценка погрешности:
\\x(,t)-y(t)\)^6em + ~(eKW-l). D)
1.2. Об отыскании производных от решений по параметру.
Пусть в задаче
dxi
—? - fi(t, xh x2,..., xn, (i), E)
хМ = ati/i), г = 177?, F)
(ц — параметр) функции ft, а< — непрерывны и имеют непрерывные производные. Тогда реше-
решение (xi, Xi, ... , хп) имеет непрерывную производную по параметру fi и его частные производные
^й- = «j, t = 1, я, являются решениями следующей задачи:
tn(O) = aJ-(p), i = ITS. (8)
Отметим, что частные производные -g^, -ф вычисляются при ж, = Xi(t), г = Т~п, где x,(t) —
решение задачи E), F).
§ 1. Зависимость решевия от начальных условий я параметров
241
В частности, если а*(р) = fi, а,(^) = const при i Ф к и функции /,-, » = 1, я от (i не зависимы,
то из G), (8) следует, что
(9)
;=1
В следующих задачах E25-528) оценить погрешность приближенного решения на указанном
отрезке (волной отмечено приближенное решение).
•* Действуем согласно изложенному в п. 1.1. Правая часть этого уравнения, очевидно, не-
непрерывна по совокупности переменных а;, у (|а;| ^ j, — оо < у < +оо) и имеет непрерывную же
по у производную
»Г = 2У
ду A + у2O'
причем
i 21у1 1 < 2|у|
ау 1 + Ы2' 1 + Ы2 " 1 + Ы2 "
Следовательно, в качестве постоянной Липшица К можем взять единицу. Далее, по формулам C),
п. 1.1, имеем оценки:
у---
1
1 а;
- 2)
1
—max
16
а;-2
8 - 4х + х2
4(8 - 4а; + х2)
|у@) - уф)\ = 0.
Поэтому ? = X, 6 = 0. Таким образом, согласно D), п. 1.1, получаем оценку погрешности:
1
64'
\\у(х) - у(г)|| = \у(х) - у(х)\
0,011. >
526. a;, =xi -x2, x2 =txt, а;,@)= 1, ж2@) = 0; г, = 1 +t+ -t1, ?2 = -t1, \t\ ^0,1.
•* Пусть ]|а;|| = |a;i| + ]а;2|. Тогда согласно C), п. 1.1, имеем
где
Следовательно,
—-— /2(t, Si, x2)
, *i, x2) = tii.
(t+ ^
| у < 0,0105;
= 0,0105, # = 0.
Так как
dxi ' дх2 ' dxi ' дх2 '
то постоянная Липшица К = 2. А тогда по формуле D), п. 1.1, имеем:
\\x(t) - x(t)\\ ^ 0,0053(e2|i| - 1) «? 0,0053(е0'2 - 1) < 0,0012. >
Примечание. Если в области определения правой части /(<, х), выпуклой по переменной х, выполняются
неравенства | -^-1 ^ с, то в качестве постоянной Липшица можно взять число К = пС
242
Гл. 5. Приближешше методы решевия дифференциальных уравнений
527. у" - х2у = 0, у@) = 1, у'@) = 0; у = еТг, |жК 0,5.
¦4 Переходя от уравнения второго порядка к системе уравнений первого порядка, имеем:
х = t, у = хи у' = х2, х\ = х2, х2 = t2xu
г,@) =1, ж2@) = 0; х, = еЬ, $2 = у = -t3eh, \t\ < 0,5.
Пусть ||ж|| = |ж,| + ]а?г|- Тогда согласно C), п. 1.1, имеем:
\dt
-/(*,*>
- №, xi, х2)
х2 - f2(t, хи х2)
A)
Поскольку
1 D
t3Ti
x2 - еТг
, f2(t,ih хг) =
то из A) следует, что
dx
-z - /(*. *>
Поэтому е = 0,0017; 6 = 0.
Далее, так как
^eii
max
t6 f @,5N (o,5L
- еИ = ^~ el?" = 0,0017 ...
дх\ дх2 дх\ дх2
то постоянная Липшица К = 2 max(l; 42) = 2 (см. примечание после примера 526). В силу
оценки D), п. 1.1, и имеющихся значений для е, 6, К справедливо неравенство
\\x(t) - x{t)\\ < ' (е2 - 1)< 0,009(е - 1)< 0,002.
Отсюда следует, что тем более |ж, - х,| < 0,002. >
528. у' = 2ху2 + 1, у@) = 1; у = ——, \х\^\.
Сначала находим числа е, 5. По формуле C), п. 1.1, имеем:
i |У(О) - у@)| = 0,
у' - 2ху2 - 1
A-Х) У
поэтому е = ^, 5 = 0.
Предположим, что решение у(ж) существует в прямоугольнике
(у(ж) 6 Л). Тогда для постоянной Липшица К имеем оценку
К^тгк- =,шх|4жу| = -.
Используя полученные оценки, по формуле D), п. 1.1, получаем
|у(ж) - у(*)| < 1
1 (е5 - l) = 0,034 ....
Остается проверить, действительно ли точное решение у(х) содержится в указанном прямоуголь-
прямоугольнике. Поскольку функции /(ж, у) = 2жу2 + 1 и f'y = 4жу непрерывны в любом прямоугольнике
Rx = {(ж, у): |ж| ^ а, \у - 1| ^ Ь], то, согласно теореме существования, на отрезке |ж| ^ h, где
h = min fa, ^g-J, M = maxBxy2 + 1), существует единственное решение рассматриваемой зада-
задачи. Найдем h. Для этого оцениваем М ^ 2а(Ь+ IJ + 1 и ищем max min fa, —;—-
v 2a(o +
уравнений
Ь t Ь V_o
a ~ 2а(Ь+1J + Г ^~^^^~~^ I ~
получаем
§ 1. Зависимость решения от начальных условий и пвраметров
= 0,308 ... , 6=1,617....
243
Следовательно, в Ri существует единственное решение у(х), где
-Ri = {(*, у): \х\ < 0,308, \у - 1К 1,617} .
Поскольку R < J?!, то оно существует и в R. >
Найти производные по параметру или по начальным условиям от решений следующих задач:
529. у' = у + р{х + у2), у@) = 1; найти ^
-* Дифференцируя по параметру fi тождества
имеем:
;, р)«, «@, р) = 0,
где « =
dU 2
— = « + x + у (ж,
dx
-. Полагая здесь и = 0, получаем задачу для функции 75^7 = «(*, 0):
"Р 1^=о
г, 0), «@, 0) = 0.
(D
Функция х и-» у(х, 0) является решением задачи:
у\х, 0) = у(ж, 0), у@,0) =1,
что непосредственно следует из данной задачи при ц = 0. Поскольку у(ж, 0) = ех, то, решая
задачу A), получаем окончательно
530. »' = у + у2 + хуъ, уB) = у0; найти
= е - а? - 1. >
и=0
-* Пусть у = у(ж, уо) — решение данной задачи. Тогда, дифференцируя тождества
yi(«, Уо) = У(ж, Уо) + У2(х, уо) + ху3(х, уо), уB, у0) = Уо
по параметру tfo, имеем:
ди(х, уо) _
«B, 0) = 1, «
Полагая здесь у0 = 0, получаем задачу для функции ж >
_ •
' 0) = «(*, 0) + 2у(х, ОЩх, 0) + Зху2(х, 0)и(х, 0),
«B, 0) = 1,
где у(х, 0) — решение следующей задачи:
Ух(х, 0) = У(ж, 0) + у\х, 0) + ху\х, 0), уB, 0) = 0.
Очевидно, у(х, 0) = 0, поэтому задача A) принимает вид:
ди(х, 0)
дх
Отсюда находим и(х, 0) = ег~2. Итак,
ду0
= и(х, 0), «B, 0) = 1.
и=о
= и(х, 0) = ех~2. >
244 Гл. 5. Приближенные методы решения дифференциальных уравнений
531. — = х2 + fttx3, ж@) = 1 + ft; найти —
at oft
_ dx(t,
Дифференцированием по ft из данной задачи получаем задачу для функции u(t, и) =
t )
du(t, ft) =
at
Положив здесь ft = О, имеем:
du(t, 0)
i, 0) + 2x(t, Q)u(t, 0), «@, 0) = 1,
где функция 11-> x(t, 0) является решением задачи:
^7— =: a;2(i, 0), s@, 0)=l,
A)
B)
получающейся из исходной при ft = 0. Из B) находим x(t, 0) = y^rj- Подставив x(t, 0) в A),
получаем задачу для искомой функции:
du(t, 0) t 2u(t, 0)
откуда
A - О3 1 - *
1 - t - ln(l - t)
, «(о, о) = 1,
«(*, 0) =
Таким образом,
О -1J
l-i-ln(l-f)
О ~ tJ '
2/A) = Уо;
найти
Дифференцируя по параметру у0 каждое равенство данной задачи, имеем:
( du(t, хо, Уо)
ift
«A, хо, уо) = 0,
= x(t, «о, VoMt, хо, у0) + u(t, xo, yo)y(t, х0, уо),
A)
2
v(l, хо, уо) - 1,
где введены обозначения:
«(*, «о, Уо) =
dx(t, хр, уд)
<i *о, Уо) =
dy(t, sp,
Функции х, у являются решениями исходной задачи. Полагая в ней х0 = 3, уо = 2 и интегрируя
соответствующие уравнения, получаем:
x(t, 3, 2) = <3 + 2t2, y(t, 3, 2) = -.
Подставляя в A) найденные функции, а также жо = 3, у0 = 2, имеем:
dUit'3'2) = (t3-,2t^<t,3,2)+2-u(t,3,2),
t
at
иA, 3, 2) = 0,
B)
§ 1. Зависимость решения от начальных условий н параметров
Из второго уравнения системы B) находим:
v(t, 3, 2) = 1.
Подставив v(t, 3, 2) в первое уравнение системы B), после интегрирования имеем:
245
u(t, 3, 2) = t2\nt-2t
Следовательно,
дх
дуо
= t2\nt-2t
найти *
/1=0
•^ С помощью дифференцирования каждого равенства данной задачи по параметру /J и по-
последующей подстановки р = 0 получаем:
**(*>0)
¦=ti(*,O) + »(*,_O), «@,0)=l,
= 2u(t, 0) + y\t, 0), v@, 0) = 0,
где u(t, fi) = f)l P , v(t, ц) = У()у ¦ Функцию y(t, 0) находим из задачи:
A)
*@, 0) = 1,
y(t, 0) = 2*(*, 0), t/@, 0) = -2,
которая получается из данной при ft = 0. Подставив x(f, 0) = \y(t, 0) в первое уравнение, имеем
задачу:
y(t, 0) - y(t, 0) - 2j/(i, 0) = 0, уф, 0) = -2, j/@, 0) = 2,
из которой находим y(t, 0) = — 2е~*. Используя этот результат, из системы A) методом исключе-
исключения получаем задачу:
C(f, 0)-v(t, 0)-2v(t, 0) = -12e', «@, 0) = 0, «@, 0) = 6,
решение которой имеет вид:
v(t, 0) = 2е"' + е2' - Зе'.
Это и есть искомое решение. >
534. х - х = (ж + IJ - fix2; х@) = -, х@) = -1; найти —
2 0/i M=1
-^ Дифференцируя равенства данной задачи и полагая затем в каждом из них ft = 1, получаем:
= 0,
аи2 <tt v' " v ' ' ' att
где u(f, /j) = "^' I1'. Функция t >-*¦ x(t, 1) является решением задачи:
d2x(t, I) dx(t, 1) 1
df2 ^ = 2ж(<, 1) + 1, г@, 1) = -, ±@, 1) = -1,
которую можно получить из данной при ft — 1. Решив последнюю задачу, имеем:
Учитывая это решение, задачу A) представляем в виде:
й«, 1) - u(t, 1) - 2«<«, 1) = - (е"( - 1) , «@, 1) = «@, 1) = 0.
Наконец, интегрируя последнее уравнение и используя начальные условия, получаем:
.. .. дх 1
246 Гл. 5. Приближевные методы решевия дифференциальных уравнений
535. Оценить, насколько может измениться при 0 ^ х ^ 1 решение уравнения у' = х + sin у
с начальным условием уф) = у0 — 0, если число у0 изменить меньше, чем на 0,01.
¦щ Пользуемся неравенством D), п. 1.1. В данном примере е = 0, так как сравниваются между
собой решения у(х) и г{х) одного и того же уравнения, т.е. у' = х + sin у, z' = х + sin г, где
решение у(х) удовлетворяет начальному условию у0 = 0, а решение z(x) —условию г@) = zo, для
которого, согласно условию, справедлива оценка \уо - го| ^ 0,01, или |«о| ^ 0,01. Следовательно,
по формуле C), п. 1.1, 6 = 0,01.
Далее, так как | sin у — sin г | ^ \у — г \, то постоянная Липшица К = 1, и, согласно оценке D),
п. 1.1, имеем окончательно:
\у(х) - z(x)\ < 0,01ew < 0,01e и 0,0271. >
536. Чтобы приближенно найти решение уравнения х + sin x = 0, его заменили уравнением
х + х -= 0. Оценить при 0 ^ t ^ 2 возникающую от этого погрешность в решении с начальными
условиями ж@) = 0,25, хф) = 0, если известно, что \х — sina;| < 0,003 при |г| ^ 0,25.
¦щ Пусть y(t) — решение задачи
y + siny = 0, уф) = 0,25, уф) = О, A)
a x(t) — решение задачи:
х + х = 0, хф) = 0,25, хф) = 0. B)
Тогда для погрешности u(t) = x(t) — y(t) путем почленного вычитания из равенств A) равенств B)
получаем задачу:
«(О + u(t) = siny- у, иф) = 0, «@) = 0,
решение которой имеет вид:
«(*) = У (sin у(т) - у(т)) sin(t - т) dr. C)
о
Умножив почленно уравнение A) на у и проинтегрировав, а также приняв во внимание
начальные условия, получим."
у2 = 2(cosy- cos 0,25).
Отсюда следует, что \у\ ^ 0,25. Поэтому | sin у - у\ ^ 0,003, и из C) находим нужную задачу:
( ( 2
1«(*Ж /1 sin у (г) - у (г )| | sin(t - т)\ dr < 0,003 f | sin(< - т)\ dr < 0,003 / dr = 0,006. >
0 0 0
§ 2. Аналитические приближенные методы
2.1. Метод степенных рядов.
Если коэффициенты ро(х), pi(x), рг(х) дифференциального уравнения
Po(x)y"+Pi(.x)y'+p2(x)y = O A)
в окрестности точки х = Хо являются аналитическими функциями, т. е. разлагающимися в ряд
по степеням х - х0, и ро(хо) Ф 0, то решения этого уравнения в некоторой окрестности ука-
указанной точки также аналитичны. Если же точка х = Хд является s-кратным нулем функции р0,
s - 1-кратным (или выше) нулем функции рх (если s > 1) и s — 2-кратным (или выше) нулем
функции рг (если s > 2), то существует по крайней мере одно нетривиальное решение уравне-
уравнения A) в виде суммы обобщенного степенного ряда
у(х) = (х- х0У Ylan(x - a*)",
n=0
где г — некоторое число.
Если функция / является аналитической в окрестности точки (ж0, Уо), то решение задачи
У = fix, у), у(жо) = Уо
§ 2. Аналитические приближенные методы 247
также является аналитической функцией в окрестности точки х = х0. Аналогично, если функция
/ = fix, у, у', ... , у{пЛ является аналитической в окрестности точки [х0, уо, у'о, ¦ ¦ ¦ , Уо""). то
существует решение задачи
в виде ряда по степеням (х—х0). Для отыскания коэффициентов ряда часто используется формула
Тейлора.
2.2. Метод малого параметра.
Если в задаче
~ = /.-(*, xltx2, ..., xn,fi), Xi(t0) = a,-(p), t = T7n, B)
at
функции /j, a; являются аналитическими по совокупности переменных х\, х2, ... ,хп, /1, то
вектор-решение ее x(t, /х) разлагается в сходящийся при малых значениях fi (малых по срав-
сравнению с единицей, т.е. \ц\ С 1) степенной ряд по ft:
x(t,n) = yo(t)+m(t) + (i2y2(t) + .... C)
Для того чтобы найти функции уц, j/i, ... , следует разложить правые части в задаче B) по степе-
степеням 11 и, подставив туда разложение C), приравнять коэффициенты при одинаковых степенях /л.
В результате получаем систему дифференциальных уравнений с соответствующими начальны-
начальными условиями, интегрируя которую последовательно определяем функции у0, у\, — При этом
произвольные постоянные находим, используя начальные условия:
y>(t0) = (aw, a2i, ... , ani), где аы = const.
Пользуясь методом малого параметра, можно приближенно находить периодические решения
уравнений вида
? + а2х = ftF(t, х, х, ft), D)
где F — известная периодическая функция по t. В этом случае постоянные интегрирования,
возникающие при решении дифференциальных уравнений относительно функций у0, уи ..., на-
находятся из условий периодичности функций, заключающихся в отсутствии резонирующих членов
в правых частях указанных дифференциальных уравнений.
Если правая часть уравнения D) явно от t не зависит, то период решения x(t, fi) заранее не
известен. В таком случае в уравнении D) следует сделать замену
г = t(l + blti + b2fi2 +...), E)
где г — новая независимая переменная, и искать решение ж(т, ц) периода ~. При этом коэф-
коэффициенты Ьь Ь2, ... определяются из условий периодичности решений Уо(т), j/i(r), ....
В каждой из задач 537-542 найти в виде степенного ряда решение, удовлетворяющее данным
начальным условиям. Вычислить несколько первых коэффициентов ряда.
537. у' = у2-х; у@) = 1.
¦4 Функция f(x, у) ~ у2 - х является аналитической по совокупности переменных х, у
в окрестности точки @, 1), поэтому существует аналитическое решение этой задачи
п=0
Подставив его в данное уравнение, получаем тождество по х:
а[ + 1а2х + ЗазХ2 + ...= (ао + а\Х + а2х2 + а^х3 + ... J — х.
Приравнивая коэффициенты при одинаковых степенях х, будем иметь систему уравнений отно-
относительно чисел a, (t = 0, 1, 2, ...):
ai = ао> 2аг = 2aoai — 1, За3 = а, + 2а0а2) 4а4 = 2aia2 + 2а0аз, —
Так как уф) = 1, то а0 = 1. А тогда из уравнений полученной системы последовательно находим:
1 2 7
«I = 1» «2=2' °3=5' а4=12' '¦¦¦
248 Гл. 5. Приближенные методы решения дифференциальных уравнений
Таким образом, приближенное решение имеет вид:
у(х) « 1 + х + - х2 + - х3 + — х4. >
Э.5О. у = у + хег\ у@) = 0.
<4 Функцию f{x, у) = у + хеу разложим в степенной ряд в окрестности точки @, 0) по
степеням х, у.
2 1 з !
6 24'
Далее, принимая во внимание начальное условие, ищем решение в виде ряда
2 3 4
Подставив его в уравнение
оо к
и приравняв коэффициенты при одинаковых степенях х, получим систему уравнений:
<ii = 0, 2а2 = 1, За3 = а2, 4а4 = аз + а2, ... ,
откуда находим
_ 1 _ 1 _ I
2' 3 6' 4 6'
Следовательно,
_ 1 2 1 з 1 4
2/(ж) - - х +-ж + - а? +....>
539. у" = ху' - у2; уф) = 1, у'@) = 2.
-^ Как и в предыдущих задачах, приближенное решение у(х) можно бьшо бы получить в виде
частичной суммы степенного ряда, находя коэффициенты его из некоторой системы рекуррент-
рекуррентных уравнений. Однако в данном случае мы поступим по-другому. Именно, зная, что искомый
степенной ряд является рядом Тейлора, путем последовательного дифференцирования правой
части данного уравнения по х вычисляем нужного порядка производные в точке х = 0. Таким
образом, учитывая начальные условия, имеем:
у"@) =-у2@) = -1,
у"\х) = ? (ху - у2) =у' + ху" - 2уу', /'@) = -2,
IV / \ -\ ft , Ш л '2 -% Ч IV ,ЛХ о
у (х) = 2у +ху -2у -2уу , у @) = -8, ....
Следовательно, по формуле Тейлора,
у(х) - 1 + 2х - - х2 - - х3 - - х4 -....>
540. *L = t 2 dy
^t + xy\ l + t+x + y; г@) 1
at at
¦щ Поскольку правые части уравнений являются аналитическими функциями переменных
х, у, t в совокупности, то решение ищем в виде
x(t) = ao+(nt + a2t2 + a3t3 + ...,
y(t) = Ьо + bit + bit2 + b3t3 + ... .
Подставив их в данные уравнения и приравняв коэффициенты при одинаковых степенях t, по-
получаем систему уравнений относительно чисел а,-, Ь,-,» = 1, 2, ...:
<»i = «о — Ьо, 2а2 = 1 + ai — 26obi, Заз = <»2 — Ь\ —
2Ъ2 = bi+ 2аоаь ЗЬ3 =
§ 2. Аналитические приближенные методы
Отсюда, принимая во внимание начальные условия, которые дают ад = 1, Ьо = —1, последова-
последовательно находим:
_ 1 _ 1 5.1
> 2 2' 2 2'
Следовательно,
= 0,
'—б' Ьз = -6' -•
t2 t3
1 , 5 , t
x(t)=l--t2--t'+ ..., y(t) = -\-t----+ ....*>
541 — =
'ей
= 0, 2/A) =1.
у2' dt l + (t + t$yJ
¦Щ Сначала, пользуясь формулой Тейлора, разложим правые части уравнений по степеням
1 8
ift
+ х
dx
ду
dy2
M
'dtdy
+ ... =
X, »)=(*"
2
м
+2ж(у -
4
дх м
St м
) dxdy
+ (
dy
м
+ 2x(t - 1)
dtdx
dtdy
id2h
м
dx2
где
a =
fdt,x,y) =
In 2
+ A + tg IJ'
¦+ (? - 1)
*, x, y) =
b =
¦+tgyJ '
In 2
In2+1
In 2
Таким образом, имеем задачу:
dx 1 t - 1 3(y -1) (i -1J 3(f - l)(y -1) x2 3
at
Далее, ищем решение задачи A) в виде:
Ж@ = а1(<-1) + о2(<-1
у(() = V+biit - 1) + Ь,(* - IJ + h(t - IK + ....
250 Гл. 5. Приближенные методы решения дифференциальных уравнений
Подставляя последние ряды в уравнения A) и приравнивая коэффициенты при одинаковых сте-
степенях t - 1, получаем систему уравнений, из которой находим
1 1 а 1-За 46-а
«,, = -, fci = 0, «,, = --, 62 = -, «3=-^-, *,= -?-, -.
Следовательно,
л -1 46 — а ,
-(* - IJ + -^- (У - D3
542. ^ = н
¦4 Поскольку
х"ф) , ж'"@) ,
—— <2 + —~t3+
то остается только найти значения производных в точке t = 0. Из уравнений системы имеем:
х'ф) = е2, x"(t) = 1 + е*+у(г' + у') = 1 + ег+у(ж' + 1 + sin жу), ж"@) = 1 + е2(е2 + 1+ sin 1),
уф) = 1+ sin 1, /(*) = cossy • (х'у + а?у'), у"@) = cos 1 - (е2 +1 + sin 1).
Далее,
z"' = e*+V + y'J + e*+V+y"),
ж"'@) = е2((е2 + 1 + sin IJ + 1 + е4 + е2 + e2sin 1 + е2 cos 1 + cos 1 + cos 1 • sin l);
y'"(t) = -sinxy ¦ (*'y + xy'J + cosxy ¦ (x"y + Ix'y' + xy"),
543. Оценить снизу радиус сходимости степенного ряда, представляющего решение уравне-
уравнения у' = у2 — х с начальным условием уф) — 1.
¦4 Используя уравнение и начальное условие, последовательно находим:
у'@)=1, у"(х) = 2уу' - 1, у"@) = 2у@)у'@)- 1 = 1,
п-2 п-2
*=0 *=0
у(п)@) = 2 J2 Сп-2У{к)Ф)у(п''!'1)Ф), » > 3.
*=0
Покажем, что |у<п)@)| ^ »!, » g N. С этой целью воспользуемся методом математической
индукции. Имеем |у'@)| ^ 1, |у"@)| < 1. Предположив, что |у(*'@)| < к\ для к = 3, 4,... , (»-1),
оценим
п-2 п-2
|г/п)@)| < 2?С*_2 \yik\0)\ \у{п~к-1)ф)\ < 2^Cn_2fe!(» - * - 1)! = 2<i» - 2)lf> - * - 1) = »!.
*=o *=o *=o
Следовательно, согласно указанному методу, |у(п)@)| < »! V» € N.
00
С учетом доказанного неравенства для коэффициентов степенного ряда J2 <h,xn, представля-
п=0
ющего решение в некоторой окрестности точки х = 0, справедлива оценка:
|а„| = ^|у(п)@)|^1. A)
§ 2. Аналитические приближенные методы 251
Наконец, используя формулы Коши—Адамара ^ = Шп v^Ja^, а также неравенство A), для
поо
радиуса R сходимости степенного ряда получаем требуемую оценку:
В задачах 544—549 найти линейно независимые решения каждого из данных уравнений в виде
степенных рядов.
544. у"-х2у = 0.
¦4 Поскольку функции р0 = ро(х) = 1, р, = р{(х) S 0, р2 - р2(х) = -ж2 аналитичны
Уж е (-оо, +оо) и ро(х) Ф О, то согласно п. 2.1 существует аналитическое решение у = у(х),
х 6 (—оо, +оо). Ищем его в виде ряда:
00
»(*> = 5] «.*"• A)
п=0
Подставив у(ж) в уравнение, получим тождество по х:
п=2 п=0
Заменив во второй сумме индекс суммирования по формуле » = »' — 4 (»' = 4, 5,...), имеем:
ИЛИ
оо
2а2 + 6а3* + ?("(" - 1)ап - а^)*" = 0.
п=4
Отсюда следует, что а2 = аз = 0, »(» - 1)ап — ап_4 = 0. Из рекуррентной формулы ап = п^п4
последовательно находим:
а0 а( а4 а0
а4=47з' а^ = ^, а6 = 0, а7 = 0, а, = — - j^^,
«5
Поскольку ао, а[ — произвольные постоянные, то можем положить а0 = 1, ах = 0 или
а0 = 0, а[ = 1. Тогда согласно A), B), имеем два частных решения:
хА Xs хп
1 + 4.з + 8.7.4.3+ 1211-8-7-4-3+ •'
ЪЫ * + ?а + 9ТТ4 + 13-12 9-8-5-4 + --
Очевидно, полученные степенные ряды сходятся Уж g (—оо, +оо). Решения Ух(х), у2(,х) линейно
независимы, так как тождество у\(х) = ку2(х), к = const, невозможно (например, t/i(O) = 0, что
противоречит определению yi(x)). Таким образом, решения yi(x), y2(x) образуют фундаменталь-
фундаментальную систему и общее решение данного уравнения представляется в виде:
у(ж) = С{у{(х) + С2у2(х), х € (-оо, +00). >
545. A - х2)у" - Лху' -2у = 0.
¦щ Поскольку функция
является аналитической по совокупности переменных х, у, у1 (х Ф ±1), то существуют анали-
аналитические решения данного уравнения при х Ф ±1. Найдем эти решения сначала в некоторой
окрестности нуля (ж = 0), т. е. будем искать их в виде
у(х) = a0 + aix + а2х2 + ... .
252 Гл. 5. Приближенные методы решения дифференциальных уравнений
Подставив написанный ряд в данное уравнение, получим тождество по х:
00 00 00 00
J2п(п - 1)апхп-2 -J2n(n- l)anxn - 4?папхп - 2?ап*п = 0.
n=2 n=2 n=I п=0
Заменив в первой сумме индекс суммирования п на п + 2, перепишем тождество в таком виде:
2> + 2)(n + l)an+2xn -J2n(n~ l)anxn - 4j^nanxn - 2?anzn = 0,
n=0 n=2 n^l n=0
ИЛИ
2o2 + 6аъх - 2a0 - 6a,x + Yl((n + 2)(" + 1)a«+2 ~ "(" ~ 1)a" ~ 4na" ~ 2an)a;n = 0.
Отсюда, приравнивая коэффициенты при одинаковых степенях х, имеем:
а2 = аа, «3 = 01, an+2 = an, n = 2, 3, ....
Пусть а0 =1H! = О, тогда а2* = 1> «2^+1 = О, Л = 0, оо. Следовательно,
12 4\\ 1
1+х + х+...= г, \х\ < 1.
I — аг
Аналогично, если во = 0, ai = 1, то получим аг* = 0, вгы-1 = 1- Поэтому
Нетрудно видеть, что функции у,, у2 являются решениями данного уравнения и при \х\ > 1. >
546. A-х)у"-2у' + у = 0.
•4 Как и в предыдущем примере, сначала ищем решения в некоторой окрестности точки
00
х = О, т.е. в виде ? апхп. Подставив ряд в уравнение, получаем тождество по х:
п=0
00 00 00
щп — 1)<1пх — 2__! "(я + 1)апа; — za, + 2_, "пж = U.
п=2 п=2 п=0
Заменив в первой сумме индекс суммирования п на п + 2, а во второй — п на ге + 1, имеем:
00 00 00
Y^{n + 2)(п + 1)ап+2хп - Yl(n + !)(« + 2)an+iarn - 2а, + J^ ana;n = О,
n=0 n= 1 n=0
откуда, приравняв коэффициенты при одинаковых степенях, получаем:
2а2 - 2ах +ай = 0, (п + 2)(п+1)(ап+2 - an+i) + an = 0, п€М A)
Пусть ai = 0, а0 = 1. Тогда из уравнений A) найдем:
-_I -_1 --11
Следовательно,
2 3 I 1
Положив а0 = 0, ai = 1, аналогично получаем:
1 5 3
а2 = I, аз=^, а4 = -, ...,
поэтому
2 5 з 3 4
г/2(х) =ж + а; + - ж + - ж +
6 4
Поскольку функция х >-* ^f^ аналитична при х Ф 1, то полученные ряды сходятся только
при \х\ < 1. Для получения частных решений при произвольных х Ф 1 произведем замену
х — t + хд, где хо ф 1, и будем искать частные решения в виде:
§2. Аналитические приближенные методы 253
После выкладок, аналогичных проделанным выше, приходим к таким частным решениям:
24A- хо)^
у2(х) = A - хо)(х - SB») + {х - хо? + — — (х - хвK + — ^-j (г - *0) + ... .
6A -х0) 4A -х0У
Поскольку радиус сходимости R полученных рядов определяется расстоянием от точки t = 0 до
особой точки функции 11-+ ^i~^l\, то R = 11 - хо\. Следовательно, функции yi, y2 определены
при всех х, удовлетворяющих неравенству \х — хо\ < |1 — acol- Из этого неравенства следует, что
функции уи уг описывают все частные решения данного уравнения при любых а: ф 1. >
Замечание. В предыдущем примере иам удалось просуммировать степенные ряды и, таким образом,
найти аналитические функции, являющиеся решениями дифференциального уравнения и при других
возможных х,
547. у" - ху' + ху = 0.
4 Поскольку ро(х) =1^0, функции pi = pi(x) - -х, рг = Рг(г) = х — аналитические,
то уравнение имеет частные решения, которые образуют фундаментальную систему и являются
аналитическими функциями при всех а; € (—оо, +оо). Степенной ряд
в виде которого мы будем искать частные решения, сходится при всех х. Подставляя в дан-
данное уравнение ряд и приравнивая коэффициенты при одинаковых степенях х, получаем систему
относительно чисел а„:
Отсюда, полагая в0 = 1, ol\ = 0, находим:
в3 = -1, «4 = 0, а, = -1, ....
Аналогично, полагая а0 = 0, а\ = 1, имеем:
1 1 1
вз = 6' в4 = ~Т2' в5=40' •••¦
Следовательно, частные решения представляются в виде:
1h + ^>
548. xy" + yln(l-x)=0.
4 Пользуемся разложением
( x2 xl \
и ищем частные решения н виде
2
у(х) = e0 + d\x + а2х2
Относительно коэффициентов известным путем получаем систему уравнений:
2в2-во = О, 6в3-в| --в0 = 0, 12в4--О|-а2--во = О,
из которой, полагая оо = 1, сц =0, получаем
1 1 5
72'
254 Гл. 5. Приближенные методы решения дифференциальных уравнений
Следовательно, первое частное решение имеет вид:
yi(x)=l+-x1 + —x3 + — х*+ ....
Для получения второго частного решения полагаем во = 0, а.\ = 1. Тогда из этой же системы
найдем
1 1
а2 = 0, аъ = -, ал = —, ....
Следовательно,
Радиус сходимости степенных рядов, представляющих «л(х), уг(х), равен единице. Для получения
частных решений, пригодных Vx € (—оо, 1), сделаем замену х = t — х0 (х0 > 0). Тогда данное
уравнение примет вид
„ „ / t \
(t - хо)у + м1пA + хо — t) = 0, или (t-xo)y + у 1пA + х0) + у In I 1 I = 0.
V 1 + Хо /
Подставляя в последнее уравнение разложения
и приравнивая коэффициенты при одинаковых степенях t, получаем:
2Ь2х0 - Ъо 1пA + х„) = 0, 2Ь2 - 6Ь3х0 + bi ln(l + х0) - —^— = 0,
1 +Х
6Ь3 + Ь21пA + х0) ~ у^ ~ 2A ^у = 0, .... A)
Пусть Ьв = 1, Ъ\ = 0. Тогда из полученной системы последовательно найдем
2х0 ' ' 6х0 \ хо 14-:
1 /1пA+х0) 1 1п2A+хр) 1
4 12х0 V 4 хоA+хо) 2х0 2A'-^'' *" * '
Пусть Ьо = 0, Ьх = 1. Тогда из системы A) получим:
1пA + х0)
Ь4
1 /1
=——
12х0 V
6х0 12х0 V х0 1 + х0
Заметим, что из выражений для Ь,-, i = 1, 2, 3, 4, предельным переходом х0 —» +0 можно получить
значения соответствующих at, i = 1, 2, 3, 4, вычисленных в случае х0 = 0.
Таким образом, частные решения при х0 > 0 можно записать так:
(х + х0J 1пA + х0) , (х + х0K /1пA + хр) 1 \
+ — — ) +
2 х0 6 V 1 +
2/i(x) = 1 + + — — )
2 х 6х0 V хо 1 + х0 /
ln(l + x0) 1 1п2A + х0)
+ 2
+ 12х0 V ХЪ x0(l+x0)
(X + Х0K |ПA + Х0) (Х + Х0L /1ПA + Хр)
+ —р51—(
о х0 12х0 V хо
549. у'" - ху" + (х - 2)г,' + у = 0.
^ Поскольку Ро(х) = 1 т^ 0 и функции pi = Pi(x) = —х, р2 = /^(^J = х — 2, р3 = Рз(я) = 1
являются аналитическими при всех х € (-оо, +оо), то фундаментальная система состоит из ана-
аналитических на всей числовой оси функций. Следовательно, соответствующие им степенные ряды
§ 2. Аналитические приближенные методы 255
00
сходятся при всех х. Подставляя в данное уравнение ряд ? а,,*" и приравнивая коэффициенты
п=о
при х°, х, х2, ..., получаем:
6а3 - 2сц + а0 = О, (п + 3)(п + 2)ап+3 - (n + 2)an+i +а„ = 0, п=1,2,....
Пусть а0 = 1, <*i = ^2 = 0. Тогда из последних уравнений найдем:
1 1 1
Следовательно,
; = --, в4 = 0, а5 = --, «6=Ш ••••
х3 х5 х6
Пусть а0 — а2 = 0, ai = 1. Тогда из указанных выше уравнений следует, что
1 1 1
вз=3' в4=~!2' в5=15' ••••
Поэтому второе частное решение имеет вид:
Наконец, если положим во = af = 0, вг = 1, то получим:
вз = 0, в4=^, es = -l ....
Следовательно,
2 х4 х5
В следующих задачах найти те решения данных уравнений, которые выражаются степенными
(или обобщенными степенными) рядами.
550. ху" + 2у' + ху=0.
-^ Поскольку функция рв = ро(х) = х имеет в точке х = 0 нуль 1-го порядка, функция
pi = Pi(x) = 2 нулей не имеет, а функция р2 = Рг(х) = х имеет в этой точке нуль 1-го порядка,
то, согласно п. 2.1, существует по крайней мере одно нетривиальное решение данного уравнения
в виде суммы обобщенного степенного ряда
п=0
Подставив ряд в данное уравнение и приравняв коэффициенты при х , х, ..., получим:
Ясно, что нетривиальное решение возможно только при условии ао+сц фО. Пусть оо = 1, а% = 0.
Тогда из первого уравнения A) следует, что г(г + 1) = 0. Взяв г = 0, из третьего уравнения A)
последовательно находим:
в2 = 2^' вз = °' =2- 3-4-5'
Следовательно,
х х siii х
Далее, положив г = — 1 (о0 = 1, а\ = 0), из A) получаем:
1 1
0
Поэтому второе частное решение имеет вид:
Т+4Г
256 Гл. 5. Приближенные методы решения дифференциальных уравнений
Пусть а0 = О, О) = 1. Тогда из второго уравнения A) следует, что (г + 1)(г + 2) = 0. Полагая,
например, г = — 1, из третьего уравнения A) последовательно находим:
1 _ 1
2 > з 2_3> 4 , 5 ~ 5!' '" '
Таким образом,
1 / х3 х5 \ sin а;
х \ 3! 5!
Если же положим г = — 2, то аналогично будем иметь
cos
Итак, если х Ф 0, то два линейно независимых частных решения представятся в виде:
sin х cos x
У!(а;) = , уг(х) = . >
X X
Примечание. Можно было бы обойтись рассмотрением случая ао — 1, ai = 0.
551. 9*У'-(*2-2)у = 0.
-^ Подставляя в уравнение ряд
п=0
и приравнивая коэффициенты при одинаковых степенях х, получаем:
an(9(n + r)(n + r-l) + 2)-a7l_2=0, n = 2,3,..., A)
ао(9г2 - 9г + 2) = 0, aj(9r2 + 9r + 2) = 0. B)
Пусть а0 = 1, О] = 0. Тогда из первого уравнения A) следует, что rt = j, гг = -|. Подставив
в B) сначала г = -j, а затем г = j, для каждого из этих двух случаев найдем:
Таким образом,
X1
Примечание. Рассмотрение случая ао = 0, а\ = 1 приводит к такому же результату.
552. х2у" + 2ху' - (х2 + 2х + 2)у = 0.
4 Аналогично предыдущему примеру имеем:
(г2 + г - 2)а0 = 0, r(r + 3)ai-2ao = O,
((n + r)(n + r+l)-2)an-an_2-2an_i=0, n = 2, 3,.... A)
Посколькумы ищем нетривиальные решения, то ao+ai # 0- Следовательно, определитель первых
двух однородных уравнений должен быть равен нулю, т. е.
(г-1)г(г + 2)(г + 3) = 0.
Отсюда находим возможные варианты:
г, = 1, г2 = 0, г3 = -2, г4 = -3.
§ 2. Аналитические приближенные методы 257
Пусть г = 1, по = 1, тогда из указанных уравнений получаем a t = ^, а из третьего уравнения A)
последовательно находим
-1 - ! 3
2 ~ 5' °г ~ 20' в4 ~ 280'
Соответственно этому запишем первое частное решение:
xl х3 х4 3^
Пусть г = -2, по = 1, тогда аналогичным образом можем получить
_ 1
Поскольку при отыскании а3 приходим к неопределенности {у, то поступаем следующим образом.
Считая, что г ф —2, из уравнений A) находим:
2 г2 + Зг + 4 4(г + 2)
Отсюда, устремив г —> -2, получим:
Коэффициенты а4, а5 и т.д. находим обычным способом. Таким образом, второе частное реше-
решение запишется в виде:
1 1 1 х1 хъ 7х4
xt-x + 2 + T + To + m + --
Рассмотрение случаев г = 0и г = -3 приводит к таким же результатам. >
553. ху"+у'-ху = О.
-^ Подставив ряд ?) опх в уравнение и приравняв коэффициенты при одинаковых степе-
нях х, получим:
a0r2 = 0, ai(l+rJ = 0, «n = ^
Пусть г = 0, тогда а\ = 0, а коэффициент во можем приравнять единице. Из третьего соотноше-
соотношения последовательно находим:
1 1
а2= 0
Следовательно,
Найти общее решение уравнений:
554. х2у" + ху' + A - х)у = 0.
00
4 Частное решение ищем в виде ряда X) а„а;п+г. Подставив ряд в уравнение, получим то-
ждество по х, из которого известным способом находим:
Поскольку аофЪ (при оо = 0 получается тривиальное решение), то из первого уравнения следует,
что г = ±t. Пусть г = t, во = 1> тогда из второго уравнения последовательно получаем:
1 1 1
а а
= ,. . Л.ч/, , .ч , аЗ —
1+2г' 2 A + 20A + 0' 12A+ 200+0C +2»-)'
258 Гл. 5. Приближенные методы решения дифференциальных уравнений
Таким образом, частные решения имеют вид:
yi(x) - х
х2
Общее же решение
У - Ciijiix) + С2уг(х) = C](w + iv) + C2(u - iv) = au + bv,
где a = C[ + C\, b = «(Ci - C2). Функции w, w легко получить из представления j/i(a;), если
воспользоваться формулами Эйлера. Имеем:
У1(х) = и(х) + iv(x) = еШх М + | A - 20 - ^ (
Зх* ( 2х Зх2 хг
^ + — +..
1040 \ 5 40 520
•3 ^ <2x Зх2 ~3
\ 12x Зх' х- \
4- ... cos(ln x)+ \ — + —r— 1- ... sin(ln x) ¦
I y 1С ЛП C1f\ I y
5 40 1040 •¦¦j"^—' • \S 40 520 ,
x x2 Зх3 \ Bх Зх2 хъ
Следовательно,
и(х) = a(x) cos(ln х) + /3(х) sin(ln х), v(x) — а(х) sin(ln х) - /3(х) cos(ln x),
х х2 Зхг 2х Зх2 х3
(I + «)+
555. х2у" + Cх-1)у' + у = о.
-^ Будем искать частное решение в виде
У(х) = ]Г)а„(а:-Хо)п.
Тогда для коэффициентов ап способом, изложенным в примере 539, получим:
(l-3xo)ai-ao 1 ( 1. о , ., 2\ ., -л
а2= —2 , аъ= ^j^ai^l-S^o+llxoJ - ao(l - 5х0)) , ...
Коэффициенты ао, о,\ произвольны, х0 ф 0. Если х0 = 0, то решение ищем в виде обобщенного
степенного ряда
у(х) - (а0 + а,х + агх2 + ...)ха.
Подставив ряд в уравнение и приравняв коэффициенты при соответствующих степенях х, найдем
(п + а)(п + а + 2) + 1
а + п+ 1
ап (п = 0, 1, 2,...). A)
В силу того, что мы ищем нетривиальное решение, следует положить a = 0. Пусть во = 1, тогда
из A) последовательно определяем
Следовательно,
Очевидно, что этот ряд.сходится лишь в точке х = 0. >
§ 2. Аналитические приближенные методы 259
В следующих задачах найти в виде тригонометрических рядов периодические решения данных
уравнений:
556. у" -Ъу = f(x), f(x) = \х\ при |*| < ж, fix + 2тг) = fix).
4 Поскольку функция / при |х| ^ ж непрерывна, дифференцируема при 0 < \х\ < ж,
/("¦) = /(—"¦)> то она разлагается в равномерно сходящийся к ней в каждой точке х € [—ж, ж]
тригонометрический ряд Фурье
ж 4™ cosBn - 1)*
2 ~*?f Bгс-1J
В силу равенства f(x + 2тг) = fix) Vx € (-оо, Ч-оо)
,. . т 4 ~ cosAnz
2 Т я=1 Л"
Далее, приняв во внимание 2тг-периодичность функции /, решение ищем также в виде 2тг-
периодической функции у:
а °°
yix) = —- + ^2 ак cos кх + bk sin fcx.
Подставляя этот ряд в уравнение и приравнивая коэффициенты при функциях х н-> sinfea;,
х ь-* coskx, имеем:
Следовательно,
--- „, , 2sin ж
557. у -у-у=
5-4cosx
Очевидно, функция
2 sin а;
х >-> f(x) =
5-4 cos x
2тг-периодическая, поэтому частное периодическое решение уравнения ищем в виде
п °°
yix) = 1- ^2 ак cos кх + Ьд. sin кх.
2 *=i
Подставив этот ряд в уравнение и приняв во внимание, что функция / нечетная, получим
ск = (fc3 + fc)a*-bfc, fc e N. A)
. _ I J 4 COS X
Умножив тождество на 5 — 4 cos а;, представим его в виде:
ОО ОО 00
5 ^2 с* sin fex — 2 ^ Cj_! sin кх — 2 ^ с,ь+| sin кх = 2 sin x.
t=! t=2 fc=O
Отсюда, приравнивая коэффициенты при одинаковых функциях, находим
5Cl-2c2 = 2, 5ск - 2ct_, - 2с*+, = 0, fc = 2, 3, ... B)
Из второго уравнения B) следует
ск = а2к+^, C)
где а, р — произвольные постоянные. Использовав первое уравнение B), получим а + E = 1.
Решив систему уравнений A), C), будем, иметь:
* * * *
260 Гл. 5. Приближенные методы решения дифференциальных уравнений
Поскольку а* -» 0, hi, -*• 0 при к -» +оо, то в последних соотношениях следует положить а = 0.
Итак, окончательно имеем:
2*
У
00
t=l
*3 + fc
A + (fc3 -i
00
sin 2 rex
fc2 '
cos 2kx
(fe3
6 - l
+ fe) cos kx -. sin fez
*(l+(*3 + fc)»)
558.
^ Поскольку правые части являются тг -периодическими функциями, то периодические ре-
решения у(х), z(x) ищем с тем же периодом в виде
у(х) = — + ^2 ак cos 2fex + Ък sin 2fex,
- —
Подставив написанные ряды в уравнения и приравняв коэффициенты при одинаковых функциях,
получаем:
Dfc3 + з)а* + 5ск = 0, -Dк2 + 3)bk - 5dk = -j,
4 ' re" * ^
откуда находим
_ 5 4 - 2к2
ft *Л??/О?Л 1/Л1? t 1\'
3 + 4fc2
* Л1.)/О1.Л 1Л1.0 , 14 > *
+ 3)' * fc2(8fc4 - 10fc2 + 3)'
Таким образом,
» 5 cos 2kx + 4 h, - к2) sin 2kx
У(-Х) = fri 2fe3(8fe4 - 10A2 + 3) '
cos 2fex + 6 sin 2kx
В задачах 559—562 найти 2—3 члена разложения решения по степеням малого параметра ц.
559.г/ = 4цх-у\ 2/A)= 1.
-^ Поскольку правая часть аналитична по у, ft, то, согласно п.2.2 решение ищем в виде
у(х, ц) = уо(х) + fiyi{x) + ц2уг(х) 4-....
Подставив ряд в уравнение и приравняв коэффициенты при одинаковых степенях \i, получаем
Уо = ~Ув, У\ =4х-2уоУь Уг =-у\ - 2уоуъ .... A)
Приняв во внимание начальное условие, имеем:
И>A) = 1, »i(D = 0, Ы1) = 0, .... B)
Теперь последовательно решаем рекуррентную систему A), используя начальные условия B):
2
~, »,(») = »
1 2 1 , х5 2х 1 32
() () + +
Итак,
§ 2. Аналитические приближенные методы
г5 2х 32 ,
261
есть решение поставленной задачи. >
560. ху' = ух2 + In 2/, 2/A) = 1 •
-^ Принимая во внимание аналитичность правой части как функции переменных у, у при
у > 0 и пользуясь методом малого параметра, решение задачи ищем в виде
у(х, ft) = ув(х) + уу^х) + у2у2(х) +
Далее, учитывая соотношения: у(х, 0) = уо(х),
A)
ду(х, у)
дгу(х, у)
ду
i?(*, 0) = №(*), ^«U*,
ду2
Л=о
д2
= 2у'2(х),
из данного уравнения дифференцированием по параметру /г находим:
/ 2,2/1 , Уг У\
хух=х+—, ху2= — -—1,
2/о 2/о 22/6*
B)
Исходя из начального условия 2/A) = 1, из A) получаем начальные условия для функций yt,
i = 0, оо:
2/оA) = 1, 2/i(l) = 2/гA) = ... = 0. C)
Последовательно интегрируя уравнения B) и пользуясь условиями C), находим:
2 •? 3
2/о=1, j/!=x-x, г/2 = -A -х) , ....
о
Наконец, подставляя D) в A), приходим к решению поставленной задачи:
D)
у(х, fi) =
- х)
* | A - xf
, 2/@) = -fi.
Как и в предыдущем примере, имеем:
у(х, у.) = уо(х
где
Уо(х) = 2/(», 0),
ду(х, (
2/о(а;) = у'х(х, 0), J/'i(a;) = — у'х(х, у)
fi=Q
Используя эти соотношения, из данного уравнения находим:
l
; + 2/1 + ~ <
A)
B)
Й = е"*, 2/i =e"u *2/.+2/о, 2/2 = е"
При этом начальные условия имеют вид:
2/о@) = »@) = ... =0,
Из первого уравнения A) следует, что е~у" = е~х + С\. В силу первого начального условия B)
С\ = 0, поэтому «/о = *• Далее, из второго уравнения A) нетрудно найти у\ = Сг^ — х — 1.
Постоянную С*2 определяем, пользуясь последним условием B), что дает С2 = 0. Следовательно,
ух = — х - 1. Аналогично решаем задачу:
.2
У2=У2~х-1+
у2@) = 0.
262 Гл. 5. Приближенные методы решения дифференциальных уравнений
Таким образом, окончательно имеем:
„2
у(х, ц) = х - ц(х + 1) + — (е* - х2 - 2х - 1) + ... . >
слч \х = х + ц(х-у\ ar(O)=l-/j,
562. {
), 2/@) = /Л
Подставляя в данные уравнения ряды
X(t, ft) = X0(t) + ftXX(t) + fl2X2(t) + ...,
y(t, ft) = yo(t) + fiy,(t) + р2у2(<) + •..
и приравнивая коэффициенты при одинаковых степенях ц, получаем:
хо-хо, aro(O)=l, Xi=xi+xj-yl, а;,@) = -1, х2 = х2 + 2х0х1 - 2уоуь х2@) = О,
2/о = 2/о, 2/о(°) = °, 2/1 = У1 - Х1 - I/O) 2/i@) = 0, j/2 = y2 - 2ж0Ж! - 2у0у!, у2@) = 1.
Отсюда интегрированием последовательно находим:
ж0 = е\ у0 = 0;
Xl = e2t-2e\ У1=е<-е*;
х2 = е3' - 4е2( + Зе', у2 = 4e2i - е3' - 2е'.
Таким образом, ряды A) можно записать в виде:
х = е1 + р(еЯ - 2е') + /,2(e3i - 4е2( + Зе') + ... ,
у = /.(e1-e2i)+p2De2i-e31-2e1) +....>
В задачах 563—566 с помощью малого параметра найти приближенно периодические решения
с периодом, равным периоду правой части уравнения.
563. x
•^ Согласно методу малого параметра, периодическое решение ищем в виде:
x(t, ft) = xa(t) + ftxiit) + f?x2(t) + ..., A)
где Xi (i = 0, oo) — 2к-периодические функции. Подставляя разложение A) в уравнение и при-
приравнивая коэффициенты при одинаковых степенях ft, получаем:
«о + Зато = 2 sin t, Xi+3x{=xl, x2 + Зх2 = 2х^хи .... B)
Первое уравнение имеет общее решение
xo(f) = Сю sin Vbt + C20 cos Vbt + sin t.
Поскольку требуется найти 2ж -периодическое решение, то в последнем равенстве следует поло-
положить do = do = 0 ¦ Следовательно,
xo(t) = sinf.
Принимая во внимание это значение, из второго уравнения системы B) находим
«1 @ = Си sin %/3< + di cos \/3< + cos 2t.
6 2
Отсюда в силу требования 2тг-периодичности функции х\ имеем:
6 2
Аналогичным образом из третьего уравнения системы B) получаем
ж2(<) = - 7 sin 3t + ^ sin *•
о 2
Подставляя х0, х\, х2,... в A), приходим к искомому решению:
x(t, р) = sint + ft (- - -cos2«J +ft2 f--sin3<+ jsintj +
§ 2. Аналитические приближенные методы 263
564. х + Зх + х* = 2ftcost.
4 Подставляя ряд
x(t, ft) = xo(t) + fixitf) + li2x2(t) + ...
в данное уравнение, известным способом получаем систему уравнений:
х0 + Заг0 + xl = О,
хх + 3xi + 3xjxt = 2 cos*,
х2 + Зх2 + Зхцх] + Зхоаг2 = О,
= 0, ... ,
из которой последовательно находим 2я-периодические решения:
= --cos< + — cos3<.
Следовательно,
ц3 /1 \
x(t, fj,) = ncost+ ^— 1 -cos3<— 3cost) + ....
8 \3 J
Примечание. Нетривиальные решения уравнения xq + 3zo + xj = 0 выражаются через эллиптические
функции, не являющиеся 2тг -периодическими.
565. x + sinx = fl%in2t.
¦* Как и в предыдущем примере, степенной ряд
x(jt, t) = xo(t) + fixi(t) + fi2x2(t) + ...
подставляем в данное уравнение и получаем тождество по параметру fj,, из которого следует си-
система уравнений:
хо + sina:o = 0,
ж, +Xi cosxq = sin2<,
x2 + x2cosx0——sina:o = O, A)
( x'\
#3 + I ХЪ 7" I COSXq — X\X2 Sill Жо = 0) ¦ ¦ ¦ ¦
V v
Первое уравнение в A) имеет серию ж -периодических решений:
х0к — кж, к € Z.
Второе уравнение дает
_ sin It
х'к = (
а третье —
Из четвертого, имеющего вид
следует ж -периодическое решение
(-
X2:
(-
¦1)*-
= 0.
6 A
sin6t
4'
sin3 2t
(_!)*_ 4K'
4+(-1)*
Таким образом,
Примечание. Для получения системы A) удобно пользоваться разложением
sin(z0 + u) = sin го cos u +sin u cos го,
264 Гл. 5. Приближенные методы решения дифференциальных уравнений
где и = fixt + /i2X2 + ..., а тахже
1 2 1 4 ! з
cosu = l--u +-u - ..., sinu = u- -u -f ... .
В результате имеем
sin(xo + и) = A sinx0 + В cos ж<>,
2 3
А=\-~-х\-цъх1х2 + ..., B = fiX1+/i2x2+ ... -~ х] + ....
I о
566. х + х = sin 3( — sin It + fix2.
¦* Представляя решение в виде ряда х = хо + цх{ + ... относительно функций х0, х{ ...,
известным способом получаем систему уравнений:
Жо + яо = sin 3< — sin It,
x\, A)
Из первого уравнения системы A) имеем:
хо = Acost + Bsint + -sin2< - - sin3?, ..., B)
3 8
где А, В — постоянные интегрирования. Эти постоянные мы определим, исходя из требования,
чтобы в правой части второго уравнения системы A) отсутствовали так называемые резонирую-
резонирующие члены. В данном случае резонирующими членами будут функции t >-* sinf, cos(, поэтому
в правой части
1 1 \ 2 л2 . тэ2 л2 тэ2
i2< i3t) cos2< +
sin2< jsin3t) =+
3 8/22
1 cos4t 1 cos6< , . A
+ ++AB2t +
A В 1 В
- — (sin At + sin 2t) - — (cos 2t - cos At) - — (cos t - cos 5t) н (cos t - cos 3<)
8 8 24 3
следует положить А = 0, В = -$. Тогда из B) получим
xo(t) = - (sint - sin3<) + - sin2f.
8 3
Аналогично находятся функции хх и т. д. >
В следующих задачах с помощью метода малого параметра приближенно найти периодические
решения данных уравнений.
567. х + х = fi(x - х3).
4 Поскольку правая часть от ( явно не зависит, то, согласно п. 2.2, сначала сделаем замену
т = t(\ + Ьф + Ъ2ц2 +...),
где &,-, г ? N — постоянные, подлежащие определению. Тогда получим уравнение
у) A)
Далее, приближенное решение уравнения A) ищем в виде
х(т, ц) = хо(т) + цхЛт) + ц2х2(т) + .... B)
Подставив B) в A) и приравняв коэффициенты при одинаковых степенях ц, получим:
= О,
=x0-xl- 2bix0, C)
= biio — 2b\Xi + ii — 36|Xo, — 3xo«i — b\xo — 2b2xo,
Решение первого уравнения
хо(т) = Acos(t + <p)
§ 2. Аналитические приближенные методы 265
(A, tp — произвольные постоянные) подставляем во второе уравнение C):
Xi + ж, = -Asin(r + <p) (l - A2 sin2(r + р)) + 2btAcos(r + v) =
= ( -Л3 - A j sin(r + <р) - — sin 3(r + <р) + 2b{Acos(r + p). D)
Поскольку мы ищем периодические нетривиальные решения, то в D) должны положить
-А3 - А = О, 2Ь{А = 0.
Отсюда следует, что bi = 0, А — -К*. А тогда из уравнения D) нетрудно найти, что
xi(t) = A\ cos(t + <pi) H т= sin3(r + <p), Ai, <pi — постоянные.
12v3
Учитывая найденное, третье уравнение системы C) представляем в виде:
х2 + х2 = х{ - 3xoii - 2Ь2*о =
= -Ai (l - 4sin2(r + у?)) sin(r + ^i) + -д b2 cos(r + <p) + --д (l - 4sin2(r + y>)) cos 3(r + v) =
= A{ (sin(r + ^i) + sinCr — Vi + 2y) - sinCr
+ (-J + —щ) cos(t + <p) + —ц (cos5(t + v?) - cos3(r + v?))
Отсюда видим, что условием отсутствия резонирующих членов является вьтолнение равенств:
* = о, 6, = -!.
Таким образом,
a?i(r)=
—^sin3
2 Р ,
аг(т, /i)=^=cos(T + 0+y^sin3(r + 0 + O(A т = t
Р2 \
- ^ + ... I .
568. ж + х = а:2.
¦^ Считая, что х мало, в качестве малого параметра возьмем амплитуду колебаний, являю-
являющихся решением уравнения х + х = 0. Полагая, для определенности, х = ft (ц — малый
параметр), периодическое решение данного уравнения ищем в виде:
х = цха(т) + /Л,(т) + цгх2(т) + ..., A)
где
т = t(\ + Ьф + Ь2ц2 + ...).
Подставив эти разложения в уравнение и приравняв коэффициенты при одинаковых степенях ц,
получаем:
%о + х0 = 0, #1 + Xi .= - + - cos 2т + 26t cos r, x2 + x2 = 2xx cos r + 2Ъ2 cos r, .... B)
Из первого уравнения с учетом начального условия находим
^о(т) = cosr.
Поскольку функция xi должна быть периодической, то в правой части второго уравнения систе-
системы B) следует положить i>i = 0. Тогда из этого уравнения нетрудно получить, что
Xi(t) = Acosr + - — - cos2т.
2 6
Учитывая условие ж^О) = 0, находим А = — |. Следовательно,
xi(r) = - - - cost - - cos2r.
2 3 О
266
Гл. 5. Приближенные методы решения дифференциальных уравнений
1 1 1 \
-- + -cos2r + -cos3rj + ...;
Подставив значение Х\(т) в правую часть третьего уравнения системы B) и потребовав, чтобы
она не содержала резонирующих членов, получаем
5 А 1
Ь\ = — —, хг = А — — cos 2т Н cos3r.
Так как х2@) = 0 , то А = — yj. Поэтому
Таким образом,
х = fj, cos r + [i2 ( - - - cos т — - cos 2т ) +
V2 3 6 /
Примечание. Такой же результат получится, если проделать аналогичные выкладки для уравнения х+х =
= цх , а затем в решении положить ft = 1.
§ 3. Численные методы решения
дифференциальных уравнений
3.1. Метод Эйлера fc-ro порядка.
Для численного решения дифференциальной задачи
У = /(я, у), у(х0) = 2/о, яо ^ х < Ь, A)
где
У = У(х) = (г/i(я), 2/2(а?), • •. , 2/т(а0), /(*, у) = (/i(a?, 2/1, 2/2, • ¦ • , Ут), /2(я, у,, у2, ... , ут), • • ¦)
— достаточное число раз непрерывно дифференцируемые функции, отрезок интегрирования
[ха, Ь] делят на равные части длиной h = ~~nXl} и по значению у(а:о + lh) = yt приближенно
вычисляют у(ха + (I + l)h) = j/(+i с помощью формулы
№+1 =
2! У'
—у}
B)
где
У1 = f(xi, уд, у" = т /(z>
, Уд
df
ду2
ЙУт
, ж, = ха + lh, 1 = 0,1,2,...,п-1.
3t/l 9t/2
Погрешность на шаге интегрирования [xh ж1+1] имеет порядок O(ft*+1).
§ 3. Численные методы решения дифференциальных уравнений
3.2. Метод Рунте—Кутта 4-го порядка.
Сначала определяются числа
( h hku hk2, hkn\
ki2 = /¦( x, + -,yn + —, y2, + -—, ..., ум + — ) .
ih Ун, ••• ,Утд,
h
-,
i
и t ( , h , hkn , hk22 .
кц = fi\xi + -, yu + —, У21 + —, ...,ум+
*.ч = /i (xi + ft, ук + hklh ya + hk2i, ...,у
hkn hk22 hkn \
а затем приближенные значения y,ii+i находятся по формуле
(fc,i + 2ki2 + 2ki3 + к„), i = 1, m.
Погрешность на шаге интегрирования [xi, аг;+1] имеет порядок О(Л5).
3.3. Метод Штермера.
Приближенное значение ylii+i в задаче A) ищется по одной из формул:
2/.\i+i = Уи + Яи + z д»,/-1.
№,(+i = У а + q« + j д9.,(-1 + у^ А2?., (-2,
+ + Д А2 д3
где
» = 1. п. №( = ydxi), xi=xo + lh, qu = у,'(аГ()Л,
Погрешность формул E), F), G) на одном шаге интегрирования составляет О(Л3), О(Л4), О(Л5)
соответственно. Для начала интегрирования по формулам E), F), G) требуется знать несколько
первых значений y,(a:i), которые предварительно можно найти, использовав либо метод Эйлера,
либо метод Рунге—Кутта, либо метод степенных рядов.
С помощью метода Эйлера к-то порядка найти приближенно на указанном отрезке решения
следующих дифференциальных задач:
569. у' = х + у2, O^x^l; уо = у@) = 0,3.
¦* Пусть к = 2, h = 0,2. Поскольку погрешность на каждом шаге имеет величину O(ft3) «
« 0,008, то вычисления по формуле B), п. 3.1, будем вести с тремя знаками после запятой. Имеем:
2
или
= у, + Л(ж, + у,2) + — (l + 2у,(ж, + у,2)) , / = 0, 1, 2, 3, 4,
Уш = У1 + 0,2@,2/ + у,2) + 0,02(l + 0,4Jy, + 2у,3).
268 Гл. 5. Приближенные методы решения дифференциальных уравнений
Полагая здесь последовательно 1 = 0, 1,... и принимая во внимание начальное условие, получа-
получаем:
t/j = 0,3 + 0,2 • 0,09 + 0,02A + 0,054) = 0,339;
t/2 = 0,339 + 0,2 @,2 + @,339J) + 0,02 (l + 0,4 • 0,339 + 2@,339K) = 0,426;
у} = 0,426 + 0,2 @,4 + @,426J) + 0,02 (l + 0,8 • 0,426 + 2@,426K) = 0,572;
2/4 = 0,572+0,2 @,6 + @,572J) + 0,02 (l + 1,2 • 0,572 + 2@,572K) = 0,799;
Уз = 0,799 + 0,2 @,8 + @,799J) + 0,02 (l + 1,6 ¦ 0,799 + 2@,799K) = 1,153. >
57О.у'=--у, 0<*<1;уь
¦* Пусть к = 1, h — 0,1. Погрешность на шаге интегрирования имеет величину О(Л2)« 0,01,
поэтому вьмисления будем вести с двумя знаками после запятой. Согласно формуле Эйлера 1-го
порядка имеем:
(xi \ /0,11
Ум = У1 + 0,1 I у; I , или 2/1+1 = 2Л + 0,1 1
\yi / \ yi
I = 0, 1, ..., 9, откуда находим:
yi = Уо - О,10о = О,92/о = 0,9; у2 = ух + 0,1 (— - у^ = 0,9 + 0,1 Q - 0,9^ = 0,82;
Уз = 0,902 + — = 0,76; j/4 = 0,92/з + — = 0,72; у5 = 0,9у4 + — = 0,70;
У2 УЗ У4
0,05 0,06
Уб = О,92/5 + — = 0,70; у7 = 0,9у6 + — = 0,72; у8 = 0,74; у, = 0,78; у1О = 0,81. >
У5 Уб
571. x=t + 2x-y, у = 1-х + 2у; 0^*^ 0,5; ж@) = t/@) = 0.
¦^ Возьмем h = 0,1; fc = 2 (метод Эйлера второго порядка). Вычисления ведем с тремя
знаками после запятой. Согласно формуле B), п. 3.1, имеем:
ari+1 = аг( + лж; + — Xt = Xj + ft(tj + 2xi — №) + ¦ — A + 2ж; — уЛ =
2! 2
= ж; + ft(i( + 2ж( - у;) + — (l + 2(<; + 2аг; - у() - A - :
= Л2«A + h)+(l+2h+- lA x,-(h + 2h2)y, = 0,011/ + 1,225a:, - 0,12№,
У1+1 =yi+hyi+ —yi = yi + ft(l -xi + 2yi) + — {-xi + 2yi) ~
= y, + ft(l - x, + 2y,) + — (-t, - 2ж, + у, + 2A - x,
= h A + ^ B - ft/)j - (ft + 2/»2)ж, + ^2ft + - ft2 + Л t/, =
= 0,110 - 0,0005/ - 0,12ж, + l,225t/,, / = 0, 1, 2, 3, 4.
Отсюда, учитывая начальные условия, находим:
х, = 0, 0, =0,110;
х2 = -0,002, у2 = 0,244;
жз = -0,009, 0з = 0,408;
х4= -0,027, 04 = 0,609;
х$ ^ —0H62, 1/5 == 0,857. >
§ 3. Численные методы решения дифференциальных уравнений 269
С помощью метода Рунге—Купа 4-го порядка вычислить приближенно решения следующих
дифференциальных задач (вычисления вести с тремя знаками после запятой):
572. у' = у2 - х, 0 < х ^ 0,5; у@) = 0,5.
¦* Пусть ft = 0,1. Тогда согласно п. 3.2 имеем:
ки = у2-х„ fc2i = (y,+0,05fc,,J-:c,-0,05,
*э( = (Si + 0,05fc2iJ - х, - 0,05, Аь« = (yi + 0,lfc3iJ - *i - 0,1,
№+i = 3ft + -г- (fcu + 2Ли + 2fc3i + *4i), a?, = 0,1/, y0 = 0,5, / = 0, 1, 2, 3, 4.
6 ч у
Отсюда, последовательно полагая / = 0, 1 ..., получаем:
fc,0 = 0,25; к2а = @,512J - 0,05 = 0,212;
3/1
fc30 = 0,210; few = @,521J - 0,1 = 0,171;
= 0,5 + у- @,25 + 0,424 + 0,420 + 0,17l) = 0,521;
*„ = @,521J - 0,1 = 0,171; к21 = @,53J - 0,150 = 0,131;
fc3, = @,528J - 0,150 = 0,129; кА1 = @,534J - 0,2 = 0,085;
j/2 = 0,521 + -у-(о,171 + 0,262 + 0,256 + 0,085) = 0,534;
6 v /
кп = @,534J - 0,2 = 0,085; к22 = @.538J - 0,25 = 0,039;
ki2 = @,536J - 0,25 = 0,037; кА2 = @,538J - 0,3 = -0,011;
j/з = 0,534 + ^- @,085 + 0,078 + 0,074 - 0,011) = 0,538;
кц = @,538J - 0,3 = -0,011; k2i = @,538J - 0,35 = -0,061;
к33 = @,535J - 0,35 = -0,064; к43 = @,532J - 0,4 = -0,117;
2/4
= 0,538 + -у (-0,011 - 0,122 - 0,128 - 0,1 п) = 0,532;
fc,4 = @,532J - 0,4 = -0,117; к2Л = @.526J - 0,45 = -0,173;
Лз4 = @,521J - 0,45 = -0,175; ки = @,515J - 0,5 = -0,235;
г/5 = 0,532 + -j- (-0,117 - 0,346 - 0,350 - 0,235) = 0,515. >
573. у' = х2-у2, \^х^2; уA) = 1.
¦^ Пусть h = 0,2. Тогда, как и в предыдущем примере, имеем:
*« = х] - у2, кг, = (х, + 0,1J - (у, + 0,lfc,,J,
*3i = ("i + 0,1J - (у, + 0,lk2lJ, *4i = (ж, + 0,2J - (у, + 0,2fc3,J;
Ум = И + -у- (*н + 2fc2i + 2Л31 + fe«), «1 = 1 + 0,2/.
Полагая в этих равенствах последовательно / = 0, 1, 2, 3, 4, получаем:
*ю = *о - Уо = 0; *м = A,1J.-1 = 0,21;
*зо = A,1J - A.021J = 0,168; ft*, = A,2J - A.034J = 0,371;
J/i = Уо + -у- (fcio + 2*20 + 2fc30 + Л«) = 1 + -у- @,42 + 0,336 + 0,371) = 1,037;
270 Гл. 5. Приближенные методы решения дифференциальных уравнений
*и = *? - у\ = A,2J - A,037J = 0,365; *21 = A,3J - A,073J = 0,538;
*3i = A,3J - A,091J = 0,500; *41 = 0,667;
У2=У\ + ~-(кп + 2к2, + 2кЪ1 + fcn) = 1,037 + -+- fo,365 + 1,076 + 1,0 + 0,667) = 1,141;
3 ^ ^ о ^ '
*12 = *г~ yl = d,4J - A,141J = 0,658; к22 = A,5J - A,207J = 0,793;
ki2 = A,5J - A,220J = 0,761; к42 = A,6J - A,293J = 0,888;
Уз = 1,141 + у- @,658 + 1,586 + 1,522 + 0,888) = 1,296;
*i3 = *з - У? = A,6J - A,296J = 0,880; к23 = A,7J - A,384J = 0,975;
*зз = A,7J - A,393J = 0,949; к43 = (],8J - A,486J = 1,032;
у4 = 1,296 + -~ @,880 + 1,950 + 1,898 + 1,032) = 1,488;
*м = *¦ - yl = A,8J - A,488J = 1,026; к24 = A,9J - A,591J = 1,079;
км = A,9J - A,536J = 1,063; км = 4 - A.701J = 1,109;
у5 = 1,488 + ^- (l,026 + 2,158 + 2,126 + 1,109) = 1,702. >
574. у" = ху, 0 < х < 0,6; у@) = 1, ;/'@) = 0.
¦* Вводя новую переменную z(x) = j/(x), переходим к системе дифференциальных уравне-
уравнений:
z' = xy, z@) = 0; y' = z, у@)=1; 0 < х < 1.
Пусть h = 0,2, тогда, согласно методу Рунге—Купа 4-го порядка, по формулам C), D), п. 3.2,
получаем:
кц = x,yh ри = 2,,
k2t = (xi + 0,1)(у, + 0,1ри), р-а = 2, + Q,\ku,
кц = (х, + 0,1)(у, + 0,1р2|), Рз, = 2, + 0,1Л2,,
к41 = (ж, + 0,2)(у, + 0,2й(), Ри = г, + 0,2fc3i,
2,+i = 2, + ~- (кц + 2к21 + 2к3, + k4ij, у,+, = у, + ~- \ри + 2р21 + 2рц ¦
х, = 0,2/, уо = 1, z0 = 0, / = 0, 1, 2.
Отсюда, полагая последовательно / = 0, 1, ... и учитывая начальные условия, находим:
*ю = 0, рю = 0, fc20 = 0,1, р2о = 0,
*зо = 0,1, рзо = 0,01, ^40 = 0,2, ^ = 0,02,
2, = ^@,2 + 0,2 + 0,2) = 0,02, у, = 1 + ~@,02 + 0,02) = 1,001,
*и = »il/i = 0,20, рп =z, = 0,02,
*2i = («1 + 0,l)(t/i + 0,1рц) = 0,3 • 1,003 = 0,30, p2l = z, + 0,l*u = 0,04,
*3i = 0,3 • 1,005 = 0,301, ри = г, + 0,1*21 = 0,02 + 0,1-0,3 = 0,05,
feu = (*i + 0,2)(t/! + 0,2р3() = 0,404, p41 = z, + 0^A3i = 0,080,
z2 = г, + -y (feu + 2*2i + 2*3i + *4i) = 0,02 + -— @,20 + 0,60 + 0,602 + 0,404) = 0,080,
= Уг + — (pi2 + 2р22 + 2рз2 +р4г) = 1,010 + -1- (о,О8О + 0,240 + 0,262 + 0,364) = 1,041.
§3. Численные методы решения дифференциальных уравнений 271
у2 = Ух + —(ри +2рп + 2рп+р41) = 1,001 + -^-@,02 + 0,08 + 0,10 + 0,08) = 1,010,
3 \ / з ч '
кп = х2у2 = 0,4 • 1,010 = 0,404, рп = z2 = 0,080,
*22 = (х2 + 0,1)(у2 + 0,1р12) = 0,5 • 1,018 = 0,509, р22 = z2 + 0,lfc,2 = 0,080 + 0,1 • 0,404 = 0,120,
*32 = (х2 + 0,1)(у2 + 0,1р22) = 0,5 • 1,022 = 0,511, рЪ2 = z2 + 0,1к22 = 0,080 + 0,1 ¦ 0,509 = 0,131,
к42 = (х2 + 0,2)(у2 + 0,2р32) = 0,6 • 1,036 = 0,622, р42 = z2 + 0,2к32 = 0,080 + 0,2 ¦ 0,511 = 0,182,
0I Л- ' "'- '¦ 2к32 + kv) = 0,080 + ~ @,404 + 1,018 + 1,022 + 0,622) = 0,182,
Г
В следующих задачах с помощью метода Штермера вычислить приближенно их решения. Вы-
Вычисления вести с тремя знаками после запятой. Для нахождения недостающих значений искомых
функций использовать метод степенных рядов или метод Рунге—Кутта 4-го порядка.
575. у'= у, 0<ж<0,5, у@)=1.
4 Применим формулу E), п 3.3, взяв h — 0,1. Тогда
№+i = .Уг + qi + j ЛФ-1 =У1+ hy'i + j (&' + &'->> = У1 + }1У' + 2 (№ ~ й-') = 1'15У ~ °,°5yi-i- ({)
Для вычисления значения t/i воспользуемся методом Рунге—Кутта. Имеем:
h h
ki=yo = l, *2-!/o +^*i = 1,05, A3 = Уо + -к2 = 1,052, кл = у0 + hk} = 1,105,
2/1 = 2/о + -~{ki + 2k2 + 2къ + fc4) = 1,105.
Поскольку погрешность на шаге составляет величину О(Л5) « 10 5, то все знаки в выражении
для у\ можно считать верными. Далее, полагая в A) последовательно / = 1, 2, ... и учитывая
найденное значение у,, а также начальное условие уо = 1, получаем:
У2 = l,15t/, - 0,05у0 = 1,15 • 1,105 - 0,05 = 1,221,
уз = 1.152Й - 0,05у! = 1,15 • 1,221 - 0,05 • 1,105 = 1,349,
у4 = 1,15у3 - 0,05у2 = 1,15 • 1,349 - 0,05 • 1,221 = 1,490, ( '
у5 = 1,152/4 - 0,05у3 = 1,15 • 1,490 - 0,05 • 1,349 = 1,649.
Погрешность этих результатов имеет величину О(Л3), т.е. можно считать, что в каждом из ра-
равенств B) два знака после запятой верны. >
х2
576. у = ——, 1 < * < 1,5, уA) = 0.
х + у
¦* Применяя формулу F), п. 3.3, выбрав шаг интегрирования ft = 0,1,
1 5 2
где
^' А 2
xi = 1 +0,1/, t/0 = 0, 1 = 2, 3, 4. Недостающие значения у, и у2 мы вычислим, использовав метод
степенных радов. С этой целью найдем t/'(l), t/"(l), y'"(l), ..., исходя из данного уравнения.
272 Гл. 5. Приближенные методы решения дифференциальных уравнений
Имеем:
- ж4
У'A) = 1,
„ = Bx + 2y - x2y")(x + y) - 2A + y')(x2 + Ixy - x2y') = ^
Поэтому по формуле Тейлора,
y(x) = x - 1 + \ (x - IK + О Ux - IL) . C)
3 ^ '
Отсюда находим
t/! = y(l,l) и 0,1 + -— = 0,100, y2 = 2/A,2) и 0,2 + 0,003 = 0,203.
Заметим, что погрешность формулы A) на шаге интегрирования составляет величину О(Л4), по-
поэтому в формуле Тейлора C) мы взяли только три первых члена разложения.
Далее, полагая в формулах B) 1 = 2, получаем:
0,1*2 2
9г = = 0,103, Aqi = 92 - 9i> Д 9о = Д91 ~ Д9о,
«2 + 2/2
где
_ _ <M*i _„,„, _ _ 0,1*2 -п,
ft ^ТТГ °'101' 9» Т70'1-
«1 + Vi «о + Уо
Следовательно, Д^ = 0,002, Дд0 = 0, Д2д0 = 0,002, а из A) находим j/з = 0,309. Аналогично
при / = 3 имеем
9з = -^р- = 0,105, Aq2 = q3 - q2 = 0,002, Д2?! = Д$Г2 - Д?1 = 0,
?з + Уз
Ул = Уз + 9з + j Д92 + -yi A^1 ~ °'415-
Наконец, при / = 4 из формул A), B) с учетом уже имеющихся величин получаем:
g4 = ' Ж" = 0,108, Д9з = 94 - 9з = 0,003, Д2д2 = Д<?з - Д<?2 = 0,001,
« + У
У5 = У4 + 94 + ^ Д9з + jj Д29з = °>525. >
577. ху" + у' + ху = 0, 0 < х ^ 1, у@) = 1, у'@) = 0.
< Вводя новую переменную z = у', приходим к задаче:
y' = z, y@)=l, z' = -y--, z@) = 0.
X
Применяем формулу E), п. 3.3, и выбираем шаг h = 0,1. Имеем:
Ум =У1 + 0,1р; + 0,05Дрг_ь z,+i =zt + 0,lq{ + 0,05Ддг_ь A)
где
Pi = *h 4i = -У» - —. Дрг-i =Pi~ Pi-ь Дф-i = * - ft-ь
*, = 0,Н, / = 079, уь=1, го = О. B)
Для начала счета нам нужно иметь значения у@,1) = у\, z@,l) = z\ = у'@,1), а также (в силу
неопределенности ^-) 9о- Все эти величины мы найдем, обратившись к методу степенных рядов.
Ищем решение данной задачи в виде
2 3.... C)
§ 3. Численные методы решения дифференциальных уравнений
273
Подставляя ряд C) в рассматриваемое уравнение и приравнивая коэффициенты при одинаковых
степенях х, получаем:
0
Следовательно,
х2
у(*)=1--+....
Отсюда находим
yi=y@,l) = 0,998, z, = у'@,1) = -0,05, qo = у"@) = -0,5.
Далее считаем по формулам A), B). Полагая в них I = 1, 2, ..., последовательно заполняем
следующую таблицу:
1
0
1
2
3
4
5
6
7
8
9
10
0,0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1,0
У!
1
0,998
0,991
0,983
0,966
0,944
0,918
0,889
0,854
0,815
0,772
0
-0,050
-0,100
-0,149
-0,197
-0,244
-0,289
-0,332
-0,373
-0,411
Pi
0
-0,050
-0,100
-0,149
-0,197
-0,244
-0,289
-0,332
-0,373
-0,411
4i
-0,500
-0,498
-0,491
-0,486
-0,476
-0,456
-0,438
-0,419
-0,394
-0,359
Дрг-i
-0,050
-0,050
-0,049
-0,048
-0,047
-0,045
-0,044
-0,041
-0,038
Дф-i
0,002
0,007
0,005
0,010
0,020
0,018
0,019
0,025
0,035
Упражнения дня самостоятельной работы
Построить решения следующих задач Коши, используя разложения в степенные ряды:
I. у' = х + у, у@)=1. 2. у' = ху, у@)=1. 3. у' = х - 2ху, у@) = 3.
4. у" = ху' - у, у@) = 1, у'@) = 0. 5. у'" = -х2у" + у'+ 2у, у@) = 1, у'@) = 0, у"@) = 0.
Построить приближенные решения в виде многочлена четвертой степени:
6. у' = у2 - х, у@) =1. 7.у' = хеУ + у, у@) = 0. 8. у' = х2 + у2, уA) = 1.
9. у" = х - у'\ уф) = 2, у'@) = 0. 10. у'" = у + у1 + у - х, у@) = 1, у'@) = у"@) = 0.
Построить приближенные решения следующих краевых задач:
II. г/ = х2-у2, уA) + уB)=1, 1<ж<2. 12. у' = х+±, у@)-4уA) = 5, 0<ж<1.
13. у" = ху' + у2, у@) = 0, у'A) = 2, 0 < х < 1. 14. у" = у'2 + у, уA) = 2, уB) = j, К х < 2.
Построить приближенные решения в виде многочлена третьей степени относительно малого па-
параметра /л для следующих задач Коши:
15. У' = f - 5/*е, уA) = 2. 16. у' = ^ + У2, УA) = 1 + 3/i. 17. у' = /*е3 + у2, уф) = е"".
18. у' = 1 + х + ру3, у@) = sinp. 19. у' = cosz + /jln(l + у), у@) = /х.
20. у' = sinx + /Je', y@) = 1 - ц.
Построить асимптоты интегральных кривых следующих уравнений (s — малый параметр,
х -* +оо):
21. еу' = 1 - у2. 22. еу' = х2 - у2. 23. еу' = у2 - A + хJ. 24. еу' = 1 - у3. 25. еу' = х3 - у3.
Глава 6
Устойчивость
и фазовые траектории
§ 1. Устойчивость
1.1. Устойчивость по Ляпунову. Асимптотическая устойчивость.
Пусть система дифференциальных уравнений
~П- =/.(<, Xi, х2, ... ,хп), i = T~n, A)
имеет при t 6 [<о, +ос) решения ж, = <Pt(t), г = 1, п, удовлетворяющие начальным условиям
Vi(*o) = xi0, i - l7n. B)
Определение 1. Решение tp(t) = (<pi(t), fid), ¦¦¦ iVn(t)) дифференциальной задачи A), B) на-
называется устойчивым по Ляпунову, если Ve > 0 36(е) > 0 такое, что для любого решения
х = x(t) = (xi(t), x2(t), ... ,xn{t)j этой же задачи, удовлетворяющего неравенству
Ык) - vKWII < б(е), C)
Vt > <o выполняется неравенство
\\x(f) - <p(t)\\ < e, D)
где через \\-\\ обозначена норма вектора.
Геометрически это определение означает, что близкие в начальный момент времени траекто-
траектории x(t) и <p(t) остаются близкими Vt^t0.
Чаще всего используются следующие нормы:
INOII = * Е 1ж-(«12' 11^I1 - max \xk(t)\, \\х(Щ = J2 \xk(t)l E)
Определение 2. Если Зе > 0: V6 > О Ш > tQ такое, что из неравенства C) не следует
неравенство {А), то решение tp(t) называется неустойчивым в смысле Ляпунова.
Определение 3. Если решение <p(t) устойчиво по Ляпунову и удовлетворяет условию
= 0, F)
то оно называется асимптотически устойчивым.
Исследование на устойчивость решения tp{t) может быть сведено к исследованию на устой-
устойчивость тривиального решения (точки покоя) с помощью замены у = х — <p(t).
1.2. Исследование на устойчивость по первому приближению:
первая теорема Ляпунова.
Первая теорема Ляпунова. Пусть система
dXi
— = auXi + а;2ж2 + • • • + «m*n + 9i(t, xux2,... ,xn), t = 1, п, aik = const, G)
где функции gt удовлетворяют условию
Ы < а,(х)||х||, (8)
§ 1. Устойчивость 275
а,(ж) —» 0 при ||ж|| —> 0, t = 1, п, имеет тривиальное решение. Тогда: если собственные значения А
матрицы А = (aik) имеют отрицательные действительные части (Re A < 0), то тривиальное
решение системы G) асимптотически устойчиво; если же хотя бы одно собственное значение имеет
положительную действительную часть (Re A > 0), то тривиальное решение неустойчиво.
1.3. Исследование на устойчивость с помощью функций Ляпунова:
вторая теорема Ляпунова.
Вторая теорема Ляпунова. Если существует дифференцируемая функция
v = v(t, хи х2, ... ,хп),
называемая функцией Ляпунова, удовлетворяющая в окрестности точки х = 0 следующим усло-
условиям:
1) v(t. хи х2, ... ,хп) ^ W(x{, х2, ... ,хп) > 0 при t ^ to, где непрерывная функция W имеет
строгий минимум в точке х = 0, причем v(t, 0, ... , 0) = W@, ... , 0) = 0;
2) полная производная
dv dv J^ dv
— = -^7 +2-,-^-fid, xux2, ... ,zn)s?0 при f?t0,
at at r^ axi
то тривиальное решение х = (xu x2, ... ,xn) = 0 устойчиво.
Если же вместо условия 2) выполняется неравенство
dv dv J^ dv
dt at r^ oXj
при t ^ <i > t0 и 0 < Si ^ 11ж11 ^ 62, где Si, S2, p — постоянные, то тривиальное решение
асимптотически устойчиво.
Теорема Четаева о неустойчивости. Пусть:
1) система A) обладает тривиальным решением;
2) в некоторой области V С JR" существует дифференцируемая функция v = v(xlt х2, ... ,хп);
3) точка х = (хь х2, ... , хп) = 0 принадлежит границе области V;
4) Зе0 > 0 такое, что v = 0 на той части границы области V, где \\x\\ ^ е0;
5) в области V выполняется неравенство v > 0, а при t > to также и неравенство
dv Л, dv
где функция w непрерывна.
Тогда тривиальное решение системы A) неустойчиво.
1.4. Условия отрицательности всех действительных частей корней уравнения
а0Лп + ajA"-1 + ... + an_jA + ап = 0, а0 > О,
с действительными коэффициентами.
Необходимым условием отрицательности всех действительных частей корней уравнения
1+ ... + an_,A + а„ = 0, а0 > 0 (9)
A0)
являются неравенства а,- > 0, i = О, п.
Матрица вида
/at а0 О О О О ... О\
з а2 а, а0 О О ... О
\0 0 0 0 0 0 ... ап/
получаемая заменой чисел а* с индексами i > п или « < 0 нулями, называется матрицей Гурвица.
276 Гл. 6. Устойчивость в фазовые траектории
Критерий Рауса—Гурвица. Для отрицательности всех действительных частей корней урав-
уравнения (9) необходимо и достаточно, чтобы были положительными все главные диагональные миноры
матрицы Гурвица:
а, а0 О
, Д? = «3 «2
«3 «2
«5 «4 «3
(И)
Критерий Льенара—Шинара. Необходимо и достаточно, чтобы все а,- > Ой чтобы Д„_1 > О,
Дл_з>0, Д„-5>0, ....
Критерий Михайлова. Необходимо и достаточно, чтобы anan_t > 0 й чтобы корни многочле-
многочленов
Р(О = ап- а„_2? + ап_4?2 - .. -,
2
удовлетворяли неравенствам:
0<?i<i7,<6<ife<.... A3)
Пользуясь определением устойчивости по Ляпунову, выяснить, устойчивы ли решения сле-
следующих дифференциальных задач:
578. х = 4х - t2x, ж@) = 0.
¦4 Очевидно, tp(t) = 0 является решением данной задачи. Разделяя переменные и интегрируя,
находим все другие решения:
x(t) = CexpUt- -
Далее, согласно определению 1 из п. 1.1, имеем:
Н*(*о) - *»(*о)|| = 1*@) - ?>@)| = |С|, \\x(t) - <p(t)\\ = \x(t) - <p(t)\ = \x(t)\ =
Пусть любое е > 0 задано. Тогда ясно, что из неравенства C) будет следовать неравенство D)
тах
(см. п. 1.1), если в данном случае в качестве числа 6(е) взять jj-, М = тахе з = е з , т.е.
6(е) = ее з . Таким образом, решение ip(t) = 0 устойчиво по Ляпунову. Кроме того, поскольку
lim ж(<) = lim Cexp [4t =0,
(-.+00 v' (-+00 у 3 I
то согласно определению 3, п. 1.1, заключаем, что это решение асимптотически устойчиво. >
579. 3(t - 1)ж = х, хB) = 0.
¦4 Здесь функция <р — <p(t) = 0 есть решение задачи, которое требуется исследовать на устой-
устойчивость. Все другие решения данного уравнения описываются формулой
x(t) = C{t - 1M.
Далее, пусть 6 > 0 задано. Возьмем е = 1. Тогда, несмотря на выполнение неравенства
И*«о) - *»«о)Н = Wo) ~ Ч*к)\ = Wo)l = \С\ < б,
все равно имеем неравенство
\\x(t) - <p(t)\\ = ||x@ll = |х«)| = \C\(t — l)i > 1
при t > 1 + —Jjj. Следовательно, нулевое решение неустойчиво. >
580. ж, = -ж,, х2 = -2ж2; ж,@) = х2@) = 0.
Ч Очевидно, нужно исследовать на устойчивость нулевое решение <pi(t) =¦ 0, <p2(t) = 0.
Интегрируя систему, получаем xi = С\е~г, х2 = С2е~™. Пусть е > 0 задано. Найдем в =
такое, что из неравенства
§ 1. Устойчивость 277
следует неравенство
/
> 0 одновременно. Поскольку из неравенства
следует
С\е-и + С\еГ* ^ С\ + С2 < б2,
то при t > 0 для произвольного е > 0, полагая 6(е) = е, получаем
\\x(t) -<pft)\\< е при ||г@) - *»@)||< Л
Поэтому согласно определению нулевое решение устойчиво. Более того, так как
= О,
то это решение устойчиво асимптотически. >
581. х = -у, у = 2х3; х@) = у@) = 0.
Ч Разделив второе уравнение на первое и проинтегрировав, получаем семейство траекторий
движения материальной точки на плоскости Оху:
где С — произвольный параметр. Для исследования на устойчивость материальной точки, нахо-
находящейся в покое в начале координат, с помощью произвольно малого возмущения переведем ее
из точки @, 0) в точку с координатами х = х0, у = Уо • Тогда из полученного семейства решений
следует, что материальная точка будет двигаться по траектории
хл + у2 = xt + yl
Поскольку эта траектория замкнута и при достаточно малых х0, у0 не выходит за пределы кру-
круга радиуса г0 = \Jxl + у2 (у2 + х* ^ у2 + xl при |жо| ^ 1), то точка покоя @, 0) устойчива
(асимптотической устойчивости нет). >
582. х = —ycosx, у = sina;; х@) = у@) = 0.
¦4 Аналогично проделанному в предыдущем примере имеем:
ехр (- — ) cos х = ехр (- у ) cos x0,
где |жо| < S < %, |уо| < 6. Составив функцию Лагранжа
/ 2
2 2 I / У \
L = х + у — А I ехр I —— I cos x — С
(А — постоянная, С = expf — Щ- J cos^o) и исследовав ее обьиным способом на экстремум, убе-
убеждаемся, что функция <р = <р(х, у) = х2 +у2 (квадрат расстояния от начала координат) принимает
экстремальные значения в точках @, yt) и (х\, 0) (заметим, что исследуемая кривая симметрична
относительно координатных осей, поэтому считаем, что а; ^ 0, у ^ 0). Легко найти, что
И = \Ы7ч> Xi= arccos C-
V ^
Так как С -* 1 при х1, + yl -* 0, то xt —» 0, у\ —» 0. Следовательно, точка покоя устойчива,
поскольку сколь угодно малым возмущениям соответствуют замкнутые траектории, вкладываю-
вкладывающиеся в круги сколь угодно малого радиуса). >
583. Траектории системы уравнений
f=P(*,y), * = <№,»>
278
Гл. 6. Устойчивость н фазовые траектории
изображены на фазовой плоскости (рис. 29). Что можно сказать о поведении решений при t —»
+оо? Является ли нулевое решение асимптотически устойчивым? Является ли оно устойчивым
по Ляпунову?
Ч Как видно из рис. 29, все решения стремятся к нулю при t —> +оо, так как все траектории
входят в начало координат. Далее, пусть выполняется неравенство |у(?оI < tf (в данном случае
if{t) = 0), где S > О может быть сколь угодно малым числом. Тогда, взяв момент времени t = t2,
имеем:
Ыг)\ > ltK*i)l = ?о > О,
где ?0 уменьшено быть не может. Следовательно, нулевое решение не является устойчивым по
Ляпунову. Наконец, поскольку оно неустойчиво по Ляпунову, то его нельзя считать и асимпто-
асимптотически устойчивым, хотя lim x(t) = 0. >
i>+oo
Рис. 29
В следующих задачах выяснить, является ли устойчивым нулевое решение системы, если
известно, что общее решение этой системы имеет указанный вид.
584. ж,(О = Сх cos21 - С2е~\ x2{t) = Cit4e~* + 2С2.
¦4 Пусть е > 0 задано, tQ — произвольный момент времени. По заданному ? найдем 6(е) > О
такое, что из неравенства
I Wo) - *»«о)|| = vWo) - ?>i(*o)J + (*2(*o) - ?>2(<o)J < б
вытекало бы неравенство
Mt)-<p(t)\\<e VO<o-
Положив для простоты to = O, имеем:
11*(<о) - *»('о)Н = Н*«о)|| = ((С, cos210 - С2е-'«J + (С^е^ + 2С2J) 2 =
+ \С2\J
: б; A)
cos21 -
+ 2C2f
-4 + 2\C2\)i
§ 1. Устойчивость 279
Но, как следует из A), \С\\ < б, \С2\ < 6, поэтому оценку B) можно продолжить следующим
образом:
1|я(ОН ^ \f№ + B56е~4 + 2Jtf2 = у4 + B56е~4 + 2J 6.
Отсюда следует, что если возьмем
л =
л/4 + B56е + 2J'
то получим неравенство ||ж(<I1 < ? V< > 0 одновременно. Таким образом, согласно определению,
нулевое решение устойчиво по Ляпунову. >
585. ал(*) = (С, - C2t)e'\ x2(t) = ^ф-^ + C2.
¦* Из равенства
следует, что если С2 + С\ —> 0, то ||ж(<0)[| -+ 0. Далее, так как
lim —— = +ос,
то, какими бы малыми ни взять \СХ\ Ф 0 и |С2|, найдется такое <, > 0, что для наперед заданного
е > 0 будет выполняться неравенство:
)
Поэтому, согласно определению, нулевое решение неустойчиво. >
586. Доказать, что если какое-нибудь одно решение линейной системы дифференциальных
уравнений устойчиво по Ляпунову, то устойчивы все решения этой системы.
¦4 Пусть решение f(t) = (y>i(.t), <p2(t), ... ,fn{t)j системы
где .4@ = (a,j(O) — их n-матрица, a x(t) и f(t) — вектор-функции со значениями в JR",
устойчиво по Ляпунову. Тогда, положив x(t) = (p(t) +e(t), из данной системы получаем
ds (dp \
A [iA f) A)
As
Так как решение tp(t) устойчиво, то нулевое решение системы A) также устойчиво. Далее, пусть
V40 — любое решение данной системы. Тогда аналогично проделанному выше относительно
малого возмущения S(t) (отклонения от решения V@) получаем систему
dS л,
нулевое решение которой устойчиво. Следовательно, все решения данной системы устойчивы по
Ляпунову. >
587. Доказать, что если каждое решение линейной однородной системы остается ограни-
ограниченным при ( —> +оо, то нулевое решение устойчиво по Ляпунову.
< Пусть У — интегральная матрица системы
dx
- = АХ (*)
т.е.
280 Гл. 6. Устойчивость н фазовые траектории
Тогда все решения системы (*) представляются в виде X — YC (С — произвольный постоянный
вектор). В силу ограниченности каждого решения системы (*) справедливо неравенство \\Y\\ ^ М
(М — постоянная, М ф 0). Следовательно,
Пусть е > 0 задано. Тогда, взяв <5 = -J^, из неравенства ||ж(<0)|| = ||С|| < «5 получаем
неравенство
\\x(f)\\ ^ М\\С\\ ^M6 = s V* > t0. >
588. Исследовать на устойчивость нулевое решение системы хх = an(t)xi +au(t)x2, х2 =
= a2l(t)xi + a22(t)x2 при условии, что au(t) + a22(t) -+ Ь > 0 при t —> +оо.
Ч Воспользовавшись формулой Остроградского, имеем:
A)
(считаем, что о,; — непрерывные на (t0, +00) функции). Из A) в силу условия ац(т) + а22(т) —>
Ь > О при т —» +оо следует, что [FF(?)| —* 00 при t —> +00. А тогда одно из решений хц(Ь),
xl2(t), x2l(t), x22(t), образующих фундаментальную систему, как вытекает из соотношения W(t) =
= xn(t)x22(t)-xi2(t)x2\(t), при t —> +00 не ограничено. Следовательно, решения данной системы
Xi(t) = хпС\ + xi2C2, x2(t) = х2\С\ + х22С2
при С\ + С\ ф 0 и t —> +00 будут также неограниченными, что указывает на неустойчивость
нулевого решения рассматриваемой системы. >
В задачах 589—593 с помощью теоремы Ляпунова об устойчивости по первому приближению
исследовать на устойчивость нулевое решение.
589. Xi = 2х\Х2 — х\ + х2, х2 = 2Ж( — Ъх2 + 5х\ + х2.
Ч Поскольку для нелинейных членов gi(t, хи х2) = 2ххх2, g2(t, хи х2) = 5х\ + х\ справед-
справедливы оценки:
\дх\ - 2\ххх2\ ^ х\ + х\ = ах(хъ ж2)||Х||, \д2\ = |5xf + х\\ ^ а2(хи ж2)||Х||,
где
ai(*ii хг) =
а,-0, а2-^0 при ||Х|| - О,
то согласно указанной теореме будем исследовать на устойчивость нулевое решение линейной
системы:
хх — -х\ + х2, х2 = 2х1 — Ъх2.
Составив и решив характеристическое уравнение
-1-А 1
2 -3-А
= А2 + 4А + 1; А! = -2 + л/3, А2 = -2 - \/3,
видим, что Re А! < 0, Re X2 < 0. Следовательно, нулевое решение данной системы асимптотиче-
асимптотически устойчиво. >
590. х, = In Dх2 + e'iXi) , х2 = 2х2 - 1 + A - 6х{)~ъ.
< Для выделения линейных членов разложим правые части данных уравнений, пользуясь
формулой Маклорена:
1пDж2 + е1') = In Ux2 + 1 - 3«i + - х, + o(x])\ = -3xt + 4x2 - 8x2 + 12xix2 + o(x\ + x\);
2x2 - 1 + A - 6ж,M = 2ж2 ~ 1+ (l ~ 2x, - 4ж?) + o(x\ + x\) = 2x2 - 2x, - 4x? + o(x\ + x\).
§ 1. Устойчивость
281
Поскольку
-8*24
+ о(х\ + х\)
16
ж2 + ж2 + о(х\ + ж2)
Ы = \-4х\ + о(х\ + хЦ ^ 4 |ж2 + ж2 + о(х\ + хЦ = а2(ж„ х2)\\Х\\,
где
хг)=
а2(хь х2) =
с*! —» 0, а2 —> 0 при \\X\\ —+ О,
то можно применять первую теорему Ляпунова, т. е. исследовать на устойчивость нулевое решение
линейной системы
Ж! = -Зж1 + 4ж2, х2 = -2Ж( + 2ж2.
Так как Re AiJ < 0, где Ai,2 — корни характеристического уравнения А2 + А + 2 = 0, то налицо
асимптотическая устойчивость. >
591. хх = tg(x2 - xi), x2 = 2Хг - 2cos (- - ж,).
¦4 Пользуясь формулой Маклорена, вьщеляем линейную часть в каждой из правых частей
данных уравнений:
- xi) = x2-xt + о(х\ + xj),
2I2-2cos(f-a;,) =
^ In22+o(x22)-l( cos f • (l-^-
+sin
f •
+ х2 In 2 + - [х\ + х\ In2 2) + о(х] + ж22).
Поэтому соответствующая линейная система запишется в виде:
Х\ = ж2 — Ж], х2 = х2 In 2 — \Ъх\.
Характеристическое уравнение полученной системы А2 + АA — In 2) + VI — In 2 = 0 имеет корни
АB, где ReAit2 < 0, т.о., нулевое решение асимптотически устойчиво. >
592. хх = еХ1 — е*3, х2 = 4ж3 - 351п(ж! + ж2), ж3 = 1пA + ж3 - 3xt).
¦4 Как и в предыдущих примерах, пользуясь формулой Маклорена, представляем правые
части в виде:
е — е = :
1 9
-x2--xl + о(х] + х\ + х]),
+ х2) -
+ х2) + о(х\
ж2),
= ж3 - Зж, - - (ж3 —
+ о(ж2 + х\ + х\).
Далее, исследуем на устойчивость нулевое решение системы:
Х\ = Ж] + Зж3, х2 = —3zi — Зж2 + 4ж3,
Корни А характеристического уравнения
1-А 0 3
-3 -3-А 4
= — 3xt + ж3.
1-А
= 0 суть А, =: -3, A2j3 = l±3t.
•3 0
Поскольку Re(A2,3) > 0, то по первой теореме Ляпунова нулевое решение данной системы не-
неустойчиво. >
593. ж, = Xi - х2 - ж3, ж2 = xi + хг - Зж3, хъ=х\- 5ж2 - Зж3.
< Поскольку один из корней характеристического уравнения
1-А -1 -1
1 1-А -3
1 -5 -3-А
удовлетворяет неравенствам 3 < А < 4 (FC) > 0, FD) < 0), то нулевое решение неустойчиво. >
= 0
282
Гл. 6. Устойчивость и фазовые траектории
a —
0
-1
A
-1
a —
0
A
_
a
0
1
_
594. При каких действительных значениях а точка покоя xi =0, х2 = 0, хз = 0 системы
Х\ = ах\ — Х2, х2 = ах2 ~ х^, Хз = axj — xi устойчива?
•^ Из характеристического уравнения
= (а - АK - 1 = 0
получаем А, = а—1, А2 = а+^-г^-, А3 = a+^+iX^-. Из условия а-1<0 Ла+^<0 находим
те значения а, при которых нулевое решение асимптотически устойчиво: а < — ^. Далее, если
а > --j, то ReA2,3 > 0. Следовательно, нулевое решение неустойчиво. Наконец, если а = — ^,
| \ = ±*^, и общее решение данной системы будет линейно выражаться через
л/3 л/3
t i
то А, = —-|, \2,з =
функции
exp
/ 3 \ л/3 л/3
I — 11, cos — t, sin — t.
Таким образом, мы имеем неасимптотическую устойчивость (вообще говоря, в некоторой окрест-
окрестности точки покоя будет наблюдаться колебательный процесс). >
В задачах 595—597 исследовать, при каких значениях параметров а и Ъ асимптотически устой-
устойчиво нулевое решение.
595. i\ = ахх - 2х2 + х\, х2 = Xi + х2 + ХуХ2.
¦4 Поскольку х\ < х\ + х\ = ai(ar,, x2)||X||, |аг,х2| < \(х\ + х\) = а2(хи аг2)||ЛГ||, ах(хи х2) =
= 2а2(х{, х2) = \Jxj + х\ = ||Х|| —> 0 при х\ + х\ —> 0, то пользуемся первой теоремой Ляпунова
(см. п. 1.2). Для асимптотической устойчивости, согласно указанной теореме, нужно потребовать,
чтобы Re A < 0, где А удовлетворяет характеристическому уравнению соответствующей линейной
системы:
Из выражения для корней видим, что Re A < 0 тогда и только тогда, когда выполняется условие:
= А2 - А(а + 1) + а + 2 = 0.
0, где D =
+ '
-a-2.
2 2 4
Отсюда следует, что —2 < a < — 1. >
596. x\ = X\ + ax2 + x2, x2 = bx\ ¦
M Легко видеть, что исследование на асимптотическую устойчивость нулевого решения дан-
данной системы сводится к выявлению условий, при которых Re А < 0, где А — корни характери-
характеристического уравнения
— х\.
1-А
Ь
-3-Х
= X2 + IX - 3 - аЬ = 0 =^ Ali2 = -1 ± V4 + аЬ.
Ясно, что при ab + 4 < 0 либо при аЬ + 4 ^ 0 и л/а6+ 4 < 1 будет Re А! < 0 и Re А2 < 0. Решив
последние неравенства, окончательно имеем: ab < -3. >
597. xi = 1п(е + ах\) - е*1, х2 = bx\ + tgx2.
М Предварительно разложив правые части уравнений в ряд Маклорена и отбросив нелиней-
нелинейные члены, будем исследовать на асимптотическую устойчивость линейную систему:
Ж2 = ЬХ\
Корни характеристического уравнения этой системы суть
= — Х\ — Х2,
\
§ 1. Устойчивость 283
Отсюда следует, что неравенства Re Ai < 0 и Re A2 < 0 будут выполняться, если
=>а<-еЛЬ>0>
598. Исследовать, устойчиво ли решение xi = cosf, х2 = 2sin? системы
хх = In ^ari + 2sin2 -jj ——, x2 = D - x\)cost - 2a;1sin2f -cos3i.
M Сделав замену Xi = cosf 4- ?i(f)> x2 = 2sin? 4- ?2(f), будем исследовать на устойчивость
нулевое решение системы:
ei =ln(l + ei)- -е2, е2 - -2ei -?2cosi. A)
Далее, имея в виду теорему Ляпунова об исследовании на устойчивость по первому приближению,
от системы A) переходим известным образом к соответствующей ей линейной системе:
?i=?,--e2, ё2 = -2е,.
Поскольку один из корней характеристического уравнения этой системы положителен (А12 =
= 2 )' то согласно первой теореме Ляпунова нулевое решение системы A) неустойчиво.
Следовательно, также неустойчивыми являются указанные решения данной системы. >
В задачах 599-604 для данных систем найти все положения равновесия и исследовать их на
устойчивость.
599. Х\ = Х2 - х\ - Xiy Х2 = ЗХ{ - х\ — Х2.
¦4 Сначала на плоскости Oxtx2 находим точки, в которых Х\ = хг = 0 (точки покоя или
положения равновесия), т. е. решаем систему уравнений
х2 - xi - х\ = 0, ixi - х2 - х2 = 0.
Имеем две точки равновесия: @, 0) и A, 2). Для исследования на устойчивость применяем пер-
первую теорему Ляпунова (см. п. 1.2). В случае точки @, 0) отбрасываем нелинейные члены в правых
частях данных уравнений и для полученной таким образом линейной системы составляем харак-
характеристическое уравнение, из которого находим корни: А! = -1 - л/3, \2 = -1 + л/3. Видим, что
точка равновесия @, 0) неустойчива.
Для исследования на устойчивость точки равновесия A, 2) сделаем замену переменных xi =
= 1 + ?1, х2 = 2 + ?2. Тогда получим систему
?l = ?2 - 3?i - ?2, ?2 = ?i - ?2 - ?2.
Далее, удерживая лишь линейные члены ?i и ?2, приходим к соответствующей линейной системе
i[ = ?2 - 3?i, ?2 = ?1 - ?2, характеристическое уравнение которой А2 + 4А + 2 = 0 имеет корни
А! 2 = —2 ± л/2, указывающие на асимптотическую устойчивость точки равновесия A, 2). >
600. Х\ = х2, х2 = sin(xi + X2).
•* Из системы уравнений х2 = 0, sin(xi + X2) = 0 находим точки равновесия: (кп, 0), к € Z.
Далее, полагая xi = кп + ?ь хг = ?г, получаем систему:
ei = ?2, ?2 = (-D* sin(?i + ?2),
которой ставим в соответствие линейную систему:
ё\=ег, ?2 = (-l)*(?i+e2).
Характеристическое уравнение
А2-(-1)*А + (-1)*+1 =0
*
(— IV* Л
этой системы имеет корни Ai>2 = ' 2 ^у? + (""!)*• Отсюда на основании первой теоремы Ля-
Ляпунова, п. 1.2, следует, что если к = In +1, то положение равновесия асимптотически устойчиво;
если же к = In, то положение равновесия неустойчиво. >
284 Гл. 6. Устойчивость и фазовые траектории
601. *i = 3 - yjA + x\+x2, х2 = Щх2 - 3).
•4 Решая систему уравнений
3 - ^4 + х\ + х2 = 0, 1п(х? - 3) = О,
находим точки равновесия: (-2, 1); B, 1). Сделав замену xt = 2(—1)* + е\, хг — 1 + е2, к — 1, 2,
приходим к системе уравнений с малыми возмущениями ei, е2:
ii=3- у/9 + е2 +4- (-i)*ei+eJ, ё2 = In (l + 4(-1)*е, + ej) .
Выделяя с помощью формулы Тейлора линейные члены в правых частях этих уравнений, получаем
соответствующую линейную систему:
ii = \(-l)Mei-\ei, ?2 = 4(-1)*?„
5 о
характеристическое уравнение которой
А2~<-1)*+1 + ^(-1)* = 0
имеет корни Alj2 = •*—5— ± у 5^ + f(-l)*+1- Отсюда следует, что ReAi?2 < 0 при к = 2;
а при ft = 1 один из корней положителен. Поэтому точка равновесия B, 1) устойчива, а точка
(-2, 1) — нет. >
602. ii = ln(l +x2 + sinxi), x2 = 2 + Csinx! -8M .
¦4 Система уравнений
ln(l +x2 +sinxi) = 0, 2 + Csinxi -8)з =0
имеет следующие пары действительных корней: (кп, 0), где ft € Z.
Далее, как и в предыдущих примерах, делаем замену xi = кп+еи х2 = е2, а затем уже извест-
известным способом получаем линейную относительно малых возмущений ei, e2 систему уравнений:
e1=e2 + (-l)*ei, ^2 = (-l)":-e1)
корни характеристического уравнения которой имеют вид:
Далее применяем первую теорему Ляпунова, п. 1.2. Именно, если ft = 2n + 1, то ReA1>2 < 0.
Следовательно, точки равновесия (Bя + 1)тг, 0) асимптотически устойчивы. Если же ft = 2n, то
ReAi > 0. Поэтому точки равновесия Bп7г, 0) неустойчивы. >
Исследовать на устойчивость решения следующих уравнений:
603. x + 9x = sinf.
•^ Пусть e(t) — малое возмущение общего решения
х = С\ sin 2t + C2 cos 2t + - sin t
8
данного уравнения. Тогда, произведя замену х = С\ sin 2t + C2 cos 2t + -g- sin t + e(t), относительно
функции е = e(t) известным путем получим уравнение
ё + 9е = 0,
общее решение которого
Отсюда следует, что если в начальный момент 20 возмущение мало (VA2 + В2 < 6), то в сил"
оценки \e(t)\ < VA2 + В2 < 6 = е оно останется малым W > t0. Таким образом, все решено-
данного уравнения устойчивы (асимптотической же устойчивости нет, поскольку e(f) ¦/* 0 при
t -* +00). >
1. Устойчивость 285
604. х +4х + 5i = t.
¦4 Для проверки устойчивости общего решения
x(t) = С, + е-*(Сг cost + С3 sint) + - - -t
предложенного уравнения введем функцию возмущения е = e(t), положив
? 4
x = Ci+e 2t(C2cost+Cisint) + — -—
Тогда относительно e(t) получим уравнение:
из которого следует
?(*) = Ах + e~2t (А2 cost + Аъ sin t).
Отсюда видим, что если \At | + \Ja\ + А\ < 6 (начальные возмущения малы), то и при t> tu будет
\e(t)\ ^ \Ai\+<\JaI + A\ < S = е, где е > 0 — наперед заданное число. Следовательно, все решения
исходного уравнения устойчивы (асимптотической устойчивости нет, так как lim x(t) Ф 0). >
605. Найти периодическое решение уравнения х+х = cos* и исследовать его на устойчи-
устойчивость.
•^ Из общего решения уравнения следует периодическое решение
x(t) = - (cost — sint).
Сделав замену х = x(t) + e(t), относительно функции е = e(t) получаем уравнение
ё'+е = 0,
общее решение которого
e(f) = Cie"' + eHc2 cos ^-t + С3 sin ^
неограничено в окрестности t = оо. Следовательно, найденное периодическое решение неустой-
неустойчиво. >
Построив функцию Ляпунова и применив теоремы Ляпунова или Четаева, исследовать устой-
устойчивость нулевого решения в следующих задачах.
606. Xi = Х2 — Xi + XiX2, Х2 — Xl - Х2 - х\ — х\.
Л Дифференцируемая функция v = «(хь хг) = х\ + х\ удовлетворяет условиям:
а) и(хь х2) > 0 при х, + х\ Ф 0, «@, 0) = 0;
б> Ж = ШТ^ + ък** = 2xi(x2-xl+xix2)+2x2(xl-x2-x]-xl) = -2 ((х, - х2J + xf) < 0.
Следовательно, согласно второй теореме Ляпунова (п. 1.3) можем утверждать, что нулевое
решение устойчиво. Более того, так как поверхность
z = 2(,(xi-x2f+x\)
имеет чашеобразный вид, то существует достаточно малая окрестность 0 < б1 < \\x\\ ^ 62 та-
такая, что -ffi ^ —р < 0, где р — число. Поэтому в данном случае нулевое решение устойчиво
асимптотически. >
607. ii = 2x2 - х\, хг = -xi -x\+x\.
¦4 Поскольку дифференцируемая функция v = v(xit x2) = х\ + х\ удовлетворяет условиям:
а) 1>(хь х2) > 0 при х\ + х2 Ф 0, «@, 0) = 0;
б) % = 2xiBxl - х?) + 4xi(-a:1 - х^ + х\) - -2(х? + х^ - 2х|) < 0 в некоторой малой
окрестности точки @, 0), то по второй теореме Ляпунова (п. 1.3) нулевое решение устойчиво. >
286 Гл. 6. Устойчивость и фазовые траектории
60о. Х\ = 2X2 ~ Xi — Х2, Х2 = X] — 2X2.
¦4 Функция v = v(xi, х2) = (xi+X2J+jX2 дифференцируема, неотрицательна при х2+х2 ф О
и «(О, 0) = 0. Ее полная производная jjf в силу уравнений данной системы имеет вид:
dv э 4
— = 2(х! + x2)(ii + х2) + 2х2х2 = —6х2 < 0.
dt
Следовательно, согласно второй теореме Ляпунова (п. 1.3), нулевое решение устойчиво. >
НПО л. — „ ~ ~ «Л а. — ~>~ ^.з
•^ Проверим, что дифференцируемая функция v = v(xi, х2) = х\ — х\х2 + ^Х2 удовлетворяет
условиям второй теоремы Ляпунова (п. 1.3). Действительно, v(xt, х2) > 0 при х\ + х\ Ф 0 B« =
= (ж,-ж2J+ж?>0)и «@, 0) = 0;
dv 2 I 2 7\
— = Bxi - x2)xi + (х2 - xi)x2 = -хг [(xi - х2) + xij < 0.
Таким образом, нулевое решение устойчиво. >
610. Xj = -sinx2, хг—х\.
А В данном случае можно подобрать функцию Ляпунова в виде:
v{x{, х2) = - ж2 + 1 - cosa^.
Очевидно, внекоторой малой окрестности точки @, 0), исключая саму эту точку, будет v(xt, x2) >
> 0. Далее, полная производная -^ в силу данной системы имеет вид:
dv
— = Х\Х\ + sin«2 ¦ ?2 = Xi(—smx2) + X\ sina^ = 0.
dt
Следовательно, нулевое решение устойчиво. >
611. ii = -/i(xi) - /2B:2), х2 = f3(xi) - /4(ж2), где sgn/i(^) = sgnz, i ~ 1, 2, 3, 4.
¦4 Возьмем функцию Ляпунова и в виде
X, Х2
ь х2) = J f3(z)dz + J f2(z) dz.
о о
Очевидно, «@, 0) = 0. Далее, в силу условия sgn/,(z) = sgnz, интегралы
xi х2
J Mz)dz, Jf2(z)dz
о о
положительны при Х[ ф 0 у х2 Ф 0 соответственно (считаем, что функции /: непрерывны).
Наконец, полная производная
~ = /з(х,)*1 + h(x2)x2 = -/3(xi)(/i(x,) + f2(x2)) + Д(х2)(/з(*,) - Л(х2)) =
= ~(/3(Xl)/l(Xi) + /2(Х2)/4(Х2)) ^ 0
(произведение функций, имеющих один и тот же знак, неотрицательно). Следовательно, нулевое
решение устойчиво. >
612. Х\=х\— Х2, Х2 = X! + х\.
¦4 Функция v = v(x\, x2) = х\ + х\ удовлетворяет условиям:
а) v(x\, хг) > 0 в области V: х\ + х\ Ф 0. На границе области V (в точке @, 0)) v@, 0) = 0.
б) |jr = 2Х1Х, + 2х2ж2 = 2xi(xJ - х2) + 2x2(a;i + х32) = 2(х\ + х$) > 0 при (хи х2) € V.
Следовательно, согласно теореме Четаева (см. п. 1.3) нулевое решение неустойчиво (заметим, что
в качестве функции w = w(x) здесь можно взять выражение w = 2(xf + X2)). >
613. i\ = х\х2 — х\ + х\, хг = х\ — х\.
Л В качестве функции Ляпунова возьмем функцию v(xit X2) = Х1Х2 в области V:
xi > 0 Л 0 < х2 < 1.
§ 1. Устойчивость
287
Очевидно, «(О, хг) = «(хь 0) = 0 и точка покоя @, 0) принадлежит границе области V. Далее,
v > 0 в области V (при всех t). Полная производная
— =Zl(l-Z2)(zl+zb + X2EEU)(Zl,X2)>0 В V.
Следовательно, по теореме Четаева, нулевое решение неустойчиво. >
614. Ац = ~Х[ — ХХХ2, Х2 — х\ — х\.
¦4 Рассмотрим функцию и = v(xi, х2) = х\ - х\ в области V: ал < 1 Л х2 > \xi\. На части
границы этой области (при ||ar|| ^ So = 1) v = 0, причем точка @, 0) принадлежит границе V.
Далее, в V функция v = v(xu x2) > 0. Полная производная в силу системы
at
в V.
Таким образом, поскольку все условия теоремы Четаева здесь выполнены, то нулевое решение
данной системы неустойчиво. >
615. При каких значениях а система уравнений ii = х2 + ах[ — х\, х2 = -zi - x\ имеет
устойчивую точку покоя ал = 0, х2 = О?
¦4 Отбросив нелинейные члены в правых частях уравнений, применим теорему Ляпунова об
исследовании на устойчивость по первому приближению. Характеристическое уравнение А2 -
- а\ + 1 = 0 линейной системы ал — х2 + ахь х2 = —ал имеет корни А, 2 = §¦ ± у j - 1.
Отсюда следует, что Re А < 0, если а < 0. При этом, согласно теореме Ляпунова, нулевое
решение устойчиво асимптотически. Если же а > 0, то по указанной теореме решение ал = 0,
х2 = 0 будет неустойчиво. Наконец, при а = 0 об устойчивости ничего сказать нельзя, если
пользоваться только этой теоремой.
Итак, пусть а = 0. Возьмем функцию v — v(x\, x2) = х\ + х\ в области V: х\ + х\ Ф 0.
Поскольку v(xu х2) > 0 в V, и@, 0) = 0 и ~% = -х\ - х\ < -/3 < 0 вне некоторой окрестности
начала координат, то, согласно второй теореме Ляпунова (п. 1.3), нулевое решение асимптотичес-
асимптотически устойчиво. Таким образом, при а ^ 0 тривиальное решение асимптотически устойчиво, а при
а > 0 оно будет неустойчивым. >
В задачах 616—623 исследовать устойчивость нулевого решения, пользуясь условиями отрица-
отрицательности действительных частей всех корней многочлена с действительными коэффициентами.
616. xiv + 2 х +4х + Ъх + 2х = 0.
М Для исследования устойчивости нулевого решения воспользуемся критерием Рауса—Гур-
Рауса—Гурвица. Матрица Гурвица в данном случае имеет вид:
2 10 0
3 4 2 1
Поскольку ее главные миноры
= о, = 2 > 0, Д2 =
= 5>0, Д3 =
2
3
0
1
4
2
0
2
3
= 7 > 0, Д4 =
2
3
0
0
1
4
2
0
0
2
3
0
0
1
4
2
= 14 > 0,
то, согласно указанному критерию, действительные части всех корней характеристического мно-
многочлена А4 + 2А3 + 4А2 + ЗА + 2 отрицательны. Следовательно, нулевое решение асимптотически
устойчиво. >
617. zv + 2zlv + 5z'" + 6z" + 5z' + 2x = 0.
¦4 Как и в предыдущем примере, применим критерий Рауса—Гурвица. Матрица Гурвица
2
6
2
0
0
1
5
5
0
0
0
2
6
2
0
0
1
5
5
0
0
0
2
6
2
288
Гл. 6. Устойчивость и фазовые траектории
имеет главные миноры
Д, = 2 > 0,
А4 =
д2
2
6
2
0
=
1
5
5
0
2
6
0
2
6
2
1
5
0
1
5
5
= 4>0,
= 8>0,
= 16 > 0, Д5 = 2Д4 = 32 > 0.
Поэтому согласно критерию действительные части всех корней многочлена Xs + 2А4 + 5А3 + 6А2 +
+ 5А + 2 отрицательны. Значит, нулевое решение асимптотически устойчиво. >
618. xv + 4хп + 16х'" + 25я" + Пх' + 9х = 0.
4 Применяем критерий Льенара—Шипара. Поскольку нужные нам главные диагональные
миноры матрицы Гурвица
все положительны:
/ 4
25
9
0
V о
4 I
25 16
— 5у > U,
1
16
13
0
0
0
4
25
9
0
0
1
16
13
0
4
25
9
0
0
0
4
25
9
1
16
13
0
\
/
0
4
25
9
0
1
16
13
= 5210 > 0,
и, кроме того, все коэффициенты характеристического уравнения
А5 + 4А4 + I6A3 + 25А2 + 13А + 9 = 0
положительны, то согласно указанному критерию действительные части всех корней отрицатель-
отрицательны. Следовательно, нулевое решение асимптотически устойчиво. >
619. xlv + 2х'" + 6х" + 5х' + 6х = 0.
•^ Матрица Гурвица
имеет положительные главные диагональные миноры
2 1
Д1 = 2 > 0, Д3 =
= 11 >0.
Поскольку, кроме того, все коэффициенты характеристического уравнения
А4 + 2А3 + 6А2 + 5А + 6 = 0
положительны, то по критерию Льенара—Шипара действительные части всех корней этого урав-
уравнения отрицательны. Таким образом, мы имеем асимптотическую устойчивость. >
620. xv + xlv + 4х'" + Зх" + — *' + 2х = 0.
4
•^ Для исследования на устойчивость воспользуемся критерием Михайлова. В данном случае
корни многочленов
4
имеют вид: ?iJ = 1, 2; щ,2 = \, 4- Следовательно, 0 < (х < щ < & < Чг- Как видим, здесь
выполнены условия критерия Михайлова (см. п. 1.4), поэтому нулевое решение асимптотически
устойчиво. >
§ 1.Устойчивость
289
621. х'" + х" + х' + 2х = 0.
•^ Испытаем здесь уже рассмотренные критерии. Так как а0 = 1, «и = 1, а2 = 1, а3 = 2,то
главные диагональные миноры матрицы Гурвица
= 1 > О, Д2 =
1 1
2 1
1 1 О
2 1 1
= -2 < 0.
0 0 2
Следовательно, по критерию Рауса—Гурвица, не все действительные части корней уравнения
/(А) = А3+А2 + А + 2 = 0
отрицательны. Значит, асимптотической устойчивости нулевого решения нет.
Далее, поскольку корни многочленов
не удовлетворяют неравенству 0 < ?i < 771, то по критерию Михайлова можем утверждать, что не
все корни уравнения /(А) = 0 имеют отрицательные действительные части.
Предположим теперь, что хотя бы один из корней уравнения /(А) = 0 чисто мнимый. Тогда,
очевидно, оба уравнения 2 — ш1 = 0 и w(l — ш1) = 0 должны иметь общие действительные корни.
Однако, поскольку общих корней нет, то мы пришли к противоречию.
Таким образом, уравнение /(А) = 0 обязательно имеет корень с положительной действитель-
действительной частью. Последнее означает, что нулевое решение неустойчиво. >
622. xlv + 2х'" + Зх" + 1х' + 2х = 0.
•^ Составляя и вычисляя первые главные диагональные миноры матрицы Гурвица
А. = 2,
замечаем, что не все корни уравнения
2 1
7 3
= -1,
/(А) = А4 + 2А3 + ЗА2 + 7А + 2 = 0
имеют отрицательные действительные части. Предположим, что один из корней имеет нуле-
нулевую действительную часть: А = гш. Тогда должно быть: «4 - 2шъ — 3w2 + Иш + 2 = 0, или
w4 - 3w2 + 2 = 0 Л -2шъ + 1ш = 0. Последнее соотношение показывает, что это невозмож-
невозможно. Следовательно, хотя бы один корень имеет положительную действительную часть. Значит,
нулевое решение неустойчиво. >
623. xv + 5xlv + 15х'" + 48х" + 44х' + 74х = 0.
¦4 Пользуемся критерием Михайлова. Здесь р(?) = 74 - 48? + 5?2, q(r]) = 44 - 15// + rf,
ап = 1А> 0, ая_! = 44 > 0. Кроме того, корни уравнений р(?) = 0, 17G7) = 0, имеющие вид:
1,9; 5,7;
М = 4; 11,
удовлетворяют неравенствам: 0 < d < 771 < ?2 < т]г- Следовательно, нулевое решение асимптоти-
асимптотически устойчиво. >
В следующих примерах F24—628) выяснить, при каких значениях параметров а и Ь нулевое
решение асимптотически устойчиво.
624. x"' + 3x" + ax' + bx = 0.
¦4 Составив матрицу Гурвица
3 1 0
Ъ а 3
0 0 Ь
видим, что все ее главные диагональные миноры положительны, если За — b > 0 и ЬCа — Ь)>0.
Следовательно, если За > Ь > 0,.то нулевое решение асимптотически устойчиво. >
290
Гл. 6. Устойчивость и фазовые траектории
625. axlv + х'" + х" + х' + Ьх = 0.
¦4 Как и в предыдущем примере, составляем матрицу Гурвица
и вычисляем ее главные диагональные миноры:
= 1 > 0; Д2 =
= 1 - а;
1
1
0
0
top
Аз
a
1
b
0
—
0
1
1
0
1
1
0
0
a
1
b
a
1
b
0
1
1
= 1 - a - 6; Д4 = ЬA - a - Ь).
Согласно критерию Рауса—Гурвица, для асимптотической устойчивости необходимо и достаточ-
достаточно, чтобы выполнялось соотношение:
1-а>0 Л 1-а-Ь>0 Л ЬA-а-Ь)>0 Л а>0.
Решив эту систему неравенств, получим требуемые условия: a>0, b>0, а + b < 1. >
626. xlv + ах'" + 4х" + 2х' + Ьх = 0.
¦4 Применяя критерий Льенара—Шипара, получаем:
= 8а - агЬ - 4 > 0.
Отсюда находим, что асимптотическая устойчивость наблюдается при выполнении неравенств:
al<a<a2, 0 < b < 4; aij2 = D=F 2%/4 - b) If1. >
627.xIV +
= a>
0,
b
>
o,
Дз =
a
2
0
1
4
b
0
a
2
'" + 4z" + 6x' + x = 0.
Аналогично предыдущему примеру имеем:
0, Ь > 0, Д3 =
0
= 4аЬ - а2 - б2 > 0.
Отсюда находим условия асимптотической устойчивости:
2 — л/3 < — < 2 + л/З (а > 0, b > 0). >
о
628. х'" + х" + а2х' + 5ах = 0. Найти область устойчивости.
М Применяем критерий Льенара—Шипара. Поскольку
a > 0, Д2 =
1 1
5а а2
= а(а - 5) > 0,
то нулевое решение асимптотически устойчиво, если a > 5.
Далее, пусть 0 < a < 5. Тогда, предположив, что один из корней уравнения
/(А) = А3 + А2 + а2А + 5а = 0
чисто мнимый, приходим к противоречию, так как
= -iw3 - w1 + %a2w + 5 = 0
ш2 = 5a Л w2 = a2.
Значит при a < 5 устойчивости нет. Если a = 5, из последних соотношений следует, что Ai?2 =
= ±5i. Нетрудно найти, что А3 = — 1. Таким образом, при a = 5 нулевое решение устойчиво
(асимптотической устойчивости нет, так как lim e(t) не существует, где e(t) — возмущенное
(-•+ОО
решение). >
1. Устойчивость
291
т
629. Маятник состоит из жесткого стержня длины / и массы т на конце
(рис. 30). К стержню прикреплены две пружины с жесткостью к на расстоя-
расстоянии а от точки крепления. Определить условие равновесия маятника в верх-
верхнем положении.
¦4 Пусть <р — угол отклонения стержня от вертикали. Тогда, считая угол <р
малым, легко составить функцию Лагранжа L = К - П, где К, П — кинети-
кинетическая и потенциальная энергия системы соответственно. Имеем
К=-т12ф2, П = ka2tp2 + mgl cos ip, L — -ml2ф2 - ka2ip2 — mgl cos <p
(кинетической энергией пружин пренебрегаем).
Далее, пользуясь уравнениями Лагранжа, составляем дифференциальное уравнение, описы-
описывающее малые колебания стержня около вертикального положения:
d (dL\ dL 2. 2
Jt (дф) ~ ¦^^^V + 2kaV
или (ввиду малости угла ц>):
Рис.30
где А = 2 ¦ Очевидно, при Л. sj 0 устойчивости не будет (угол <р увеличивается неогра-
неограниченно). При А > 0 стержень совершает малые колебания около вертикали. Следовательно,
если 2ka2 > mgl, то вертикальное положение стержня устойчиво. >
630. Механическая система, изображенная на рис. 31, вращается с постоянной угловой ско-
скоростью ш вокруг оси АВ. Тело массы М может двигаться вдоль вертикальной
оси АВ. Определить положение равновесия этой системы (массами стержней
пренебречь).
¦4 Для составления функции Лагранжа вычислим кинетическую и потен- т
циальную энергию системы. Имеем:
K 2e2 + +I2
где I = та2 sin2 0, х = \CD\ = 2а cos0. Поэтому
JiT = та2 в2 + 2Ма2в2 sin2 0 + та2ш2 sin2 0.
Потенциальную энергию системы рассматриваем относительно точки В (\СВ\ = 2а), поскольку
ниже точки В система расположиться не сможет. Легко видеть, что
П = 2тд\КВ\ + Mg\DB\ = 2тдBа - a cos0) + МдBа - 2a cos0).
Таким образом, функция Лагранжа
L = (m + 2M sin2 0)а202 +maW sin2 0 + 2да(т + М) cos 0 - 2адBт + М).
Составляем уравнение Лагранжа:
d
—
dt
2 sin
= 2a2e(m + 2Msin в) + 2а2Мв2 sin 20 + 2да(М + т) sin0- таи2 sin 20 = 0. A)
до
Поскольку в положении равновесия 0 = 0, 0 = 0, то из A) можно найти угол равновесия 0о,
удовлетворяющий соотношению
sin 6a{g(M + m) - таш2 cos во) = 0.
Отсюда следуют физически возможные значения угла ва:
таш*
Вводя обозначения х\ = 0, х2 = 0, уравнение A) представляем в виде системы:
(Xi = Х2,
х2 = f5^-sin2xi *- § (Af+ m) sinxi - Mx\ sin2xx j (m + 2ДГsin2xi)~'.
B)
292 Гл. 6. Устойчивость и фазовые траектории
Рассмотрим устойчивость точки равновесия @, 0). Ставя в соответствие системе B) линеаризо-
линеаризованную систему уравнений
д (М
и вычисляя корни ее характеристического уравнения
видим, что при условии таш2 > д(М + т), согласно первой теореме Ляпунова, точка равновесия
@, 0) неустойчива.
Пусть таш2 ^ д(М + т). Тогда, подобрав функцию Ляпунова
г 2 19 г г xl\
v = х2(т + 2Мsin X!) + 2(l -cosx() - (М + m) - тш cos — I,
\a 2 /
удовлетворяющую условиям:
v(Q,Q) = 0, v(xux2)>0 при 0<х2 + Х2<-,
4
i)(xu x2) = 0 (в силу теоремы B)),
заключаем, что точка равновесия @, 0) устойчива.
Рассмотрим теперь устойчивость равновесия точки @О) 0). Сделав замену переменных х{ =
= #о + У1 > хг = Уг выражении для функции Ляпунова из предыдущего случая, а также потребовав,
чтобы v@, 0) = 0, получаем
2/ 2 \ / \( If \ 2О
"(Ум Уг) = У2(т+2Мsin @o+yi)) + (cos@o+yi)-cos0o) mw (cos@o+3/i)+cos0o)
Поскольку производная
/'(у,) = тш2 (~~i (M + m)-cos@o + У\)\ sin@o
где
/(yi) = (cos@o + уi) - cos 0о) (тш2 (cos@o + yi) + cos 0o) (M + m) J ,
удовлетворяет условиям: /'@) = 0, /'(yi) > 0 при 6 > y1 > 0 и /'(yi) < 0 при -б < y1 < 0, то
функция / имеет строгий минимум в начале координат. Следовательно, функция v = v(yu y2)
также имеет строгий минимум в точке @, 0).
Далее, поскольку v(yu у2) = 0 в силу системы
2/1 = У2,
(тш2 д 2 \ 1
У2 = I ~1Г~ sin2@о + 2/i) (М + т)sin@o + у{) - My2 sin 2@O + у\)\
(M + m) sin@o + у,) My\ sin 2@O + уй\ О1|- . 2..
a J т + 2Мsin2(e0
то по теореме Ляпунова точка @, 0) на плоскости yiOy2 устойчива, т. е. устойчива точка @О, 0)
(на плоскости xiOx2). >
§ 2. Особые точки
2.1. Определение особых точек и их классификация.
Пусть в системе дифференциальных уравнений
Ах dv
— = М{х, у), -? = Щх, у) A)
функции М, N непрерывно дифференцируемы в некоторой окрестности точки (х0, у0), где они
одновременно обращаются в нуль, т.е. М(х0, уо) = 0, JV(x0, уо) = 0.
§2. Особые точки 293
Определение. Точка (х0, у0), в окрестности которой функции М, N непрерывно дифференцируе-
дифференцируемы и М(х0, уо) = N(x0, уо) = 0» назывоетсяособой точкой системы A) на плоскости Оху.
В простейшем случае, когда М, N линейны, т.е. М(х, у) — ах + by, N{x, y) = cx + dy, где
а, Ъ, с, d — постоянные, исследование особых точек проводится по следующей схеме. Сначала
находят корни Л12 характеристического уравнения
а-Л 6
с d-X
= 0. B)
Если корни действительные, А^ > 0 и А! Ф А2, то особая точка называется узлом (карти-
(картина интегральных кривых в окрестности начала координат напоминает собой семейство парабол,
вершины которых совпадают с точкой @, 0)). Если корни имеют разные знаки, то особая точка
называется седлом, а интегральные кривые представляют собой несколько деформированные ги-
гиперболы. Далее, если корни комплексные, но ReAli2 Ф 0, то особая точка называется фокусом,
а интегральные кривые имеют вид спиралей, закручивающихся вокруг начала координат. Если
же ReA12 = 0, но ImA12 Ф 0, то особая точка — центр. Интегральные кривые в этом случае
замкнуты и охватывают начало координат.
Кроме этих (основных) особых точек различают еще точки: вырожденный узел (А( = А2 Ф 0),
дикритический узел (имеет место лишь в случае, когда система имеет вид ^ = ах; -$¦ = ау,
афО).
В случае особых точек узла и седла система уравнений A) имеет решения, изображаемые пря-
прямыми, проходящими через начало координат. Направления прямых определяются собственными
векторами матрицы
С61
причем в случае узла интегральные кривые касаются собственного вектора, соответствующего
меньшему по абсолютной величине А.
Для выяснения направления движения по траектории достаточно построить в какой-нибудь
точке (ж, у) вектор скорости (ж, у).
2.2. Практические приемы исследованиа особых точек.
Предположим, что в некоторой окрестности особой точки (х0, у0) системы A), где введена
декартова система координат Оххух по формулам х = ж0 + хх, у = Уо + ух, правые части можно
представить в виде
М(х, у) = М(х0 +хх, уо + ух) = ахх + Ъух +а(хх, ух),
N(x, y) = N(xo + xx, yo + yi) = схх +dyx + Р(хх, ух),
где а, Ь, с, d — постоянные, а функции а, /3 таковы, что справедливы следующие оценки:
/Л В(х\. Vi) i ~
'1/ . п г~ \ п &I/ л п , Лч /„2 i -.2
Тогда, если Re А Ф 0, где А определяется из уравнения B), то особая точка (х0, уо) системы A)
будет того же типа, что особая точка @, 0) системы
—^=ахх+Ьуи ~= схх + dyx. C)
Если для системы C) особая точка — центр, то для системы
—± = ахх + 6yi + а(хи ух), ~ = схх + dyx + р(хх, у,) D)
она может быть центром или фокусом. Если траектории системы D) имеют ось симметрии,
проходящую через исследуемую особую точку, то последняя будет центром и для системы D).
Перейдя от системы D) к уравнению
dy = Nix, у)
dx М(х,уУ (>
294
Гл. 6. Устойчивость и фазовые траектории
легко обнаружить ось симметрии. Если уравнение E) не меняет своего вида при замене х на —х
или у на —у, то центр сиситемы C) будет центром системы D). Фокус имеется тогда и только
тогда, когда нулевое решение системы A) (после параллельного переноса системы координат
в особую точку) будет асимптотически устойчиво при t —» +оо или при t —» —оо.
В задачах 631—640 исследовать особые точки и изобразить графически семейство интеграль-
интегральных кривых в окрестности особой точки.
631. х = х + Зу, у = -6х - 5у.
•4 Составляем и решаем характеристическое уравнение
1-А 3
-6 -5 - А
У
Рис.32
= 0;
Поскольку ReAi,2 < 0, то точка @, 0) является устойчивым фокусом
A,-6) (рис.32).
Для выяснения направления закручивания интегральных кривых
(спиралей) построим вектор скорости в точке A,0):
х = 1, у = -6. >
632. х = -2х -5у, у = 2х + 2у.
< Характеристическое уравнение
-2-Л
2
—5
2-Л
= 0
Рис.33
имеет корни АB = ±iV6. Следовательно, особая точка — центр.
х Направление движения по траекториям определяем по вектору
скорости:
(*@, 1); 2/@, 1)) = (-5; 2)
(рис.33). Далее, для установления уравнений прямых у = кх, на
которых расположены оси эллипсов, найдем экстремумы функ-
функции / = fix, у) = х2 + у2 при условии, что ? = к и х = -2х — 5у, у = 2х + 2у. Из необходимого
условия экстремума получаем уравнение
df
-±=2хх + 2уу = 0,
at
подставив в которое значения ж, у, у — кх, после сокращения на х2 приходим к уравнению
2кг - 3fe - 2 = 0.
Следовательно, на прямых у = 2х, у = —^ расположены оси всех эллипсов. >
633. х = Зх — 4у, у = х — 2у.
¦4 Из уравнения
3-А
1
-4
-2-Л
= 0
= —2—
Рис.34
находим Л(_2 = —2—• Так как корни А^г действительны
и имеют разные знаки, то особая точка — седло. В этом случае
семейство интегральных кривых (гипербол) имеет две прямые,
проходящие через начало координат х = t, у = kt (t — пара-
параметр). Для нахождения углового коэффициента к подставим
параметрические уравнения прямых в систему дифференци-
дифференциальных уравнений.
После исключения параметра t получим уравнение для к:
4к2 - 5fe + 1 = 0,
§2. Особые точки 295
откуда &i = 1; к2 = \. Следовательно, среди интегральных кривых имеются две прямые: у = х,
у = %f (рис. 34). Наконец, построив четыре вектора скорости
»,@, -1) = D, 2); t>2@, 1) = (-4, -2); v3 (l, |) = A, 0); v4 (-1, - j) = (-1, 0),
устанавливаем направление движения по траекториям. >
634. х = 2х + Зу, у = х + 4у.
¦4 Решив характеристическое уравнение
B - Л)D - Л) - 3 = 0
(Л( = 5, А2 = 1), видим, что особая точка — узел. Далее, находим
интегральные прямые путем подстановки х = t, у = Ы в данную
систему. В результате получаем уравнение
3fe2 - 2k - 1 = 0,
корни которого суть fci = 1, к2 = —j. Следовательно, прямые
у = х, у — — ^ являются искомыми (рис. 35).
Подставляя в уравнение
0 I) И -СО
Рис.35
значение Л = Л2 = 1 (меньшего по абсолютной величине соб-
собственного значения матрицы К lj), для координат еп, е12 соб-
собственного вектора указанной матрицы, соответствующего значе-
значению Л2, получаем соотношение еп + Зе12 = 0. Отсюда, положив е12 = 1, находим еп = —3.
Следовательно, вектор е, = (-3, 1) направлен по прямой у = —| и все интегральные кривые,
имеющие вид парабол, своими вершинами с обеих сторон касаются указанной прямой.
Наконец, положив в данных уравнениях x1 = l;yi=2;x2 = -l, у2 = —2, найдем два
вектора скорости
»,A, 2) = (8, 9); t>2(-l, -2) = (-8, -8),
указывающие направления движения по траекториям. >
635. х = Зх + у, у = у — х.
¦4 Сначала находим корни характеристического уравнения
3-А 1
-1
1-Л
= 0; Л, = А2 = 2.
Следовательно, точка @, 0) — вырожденный узел. Из урав-
уравнения C - Л)еп + еп = 0, положив произвольно е12 = 1, при
Л = 2 получаем еп = —1. Таким образом, прямая у = -х являет-
является интегральной и ее касаются все интегральные кривые в начале
координат (рис. 36). Далее, пользуясь таблицей
Рис.36
X
У
X
У
-2
-4
-10
-2
-1
—2
-5
-1
0
0
0
0
1
2
5
1
2
4
10
2
-2
-2
-8
0
-1
-1
-4
0
1
1
4
0
2
2
8
0
-2
0
-6
2
-1
0
-3
1
1
0
3
1
2
0
6
-2
строим векторы скорости (поле направлений), а затем по ним чертим интегральны кривые. >
636. х = у - 2х, у = 2у- Ах.
А Из характеристического уравнения
-2-А 1
-4 2-Л
= 0
Гл. 6. Устойчивость и фазовые траектории
Рис.38
следует, что At = А2 = 0. Это значит, что коэффициенты данных
уравнений пропорциональны. Следовательно, прямая у = 2х состо-
состоит из особых точек. Семейство интегральных кривых легко найти из
уравнения
^ = 2 => у = 2х + С, СфО.
ах
Физически семейство кривых, изображенных на рис. 37, можно ин-
интерпретировать как картину ламинарного течения двух противопо-
противоположно направленных потоков жидкости, причем скорость течения
в обоих случаях растет по абсолютной величине по мере удаления от
линии их раздела (у = 2х), где она равна нулю. >
637. х = х, у = у.
•4 Составив и решив характеристическое уравнение, найдем его
корни
А, = Л2 = 1.
Значит, точка @, 0) — дикритический узел. Разделив почленно од-
одно уравнение на другое и проинтегрировав результат, получим се-
семейство прямых
у = кх, х = 0
(рис. 38). Поскольку Re А(>2 > 0, то узел неустойчив. >
638. х = 0, у = 0.
¦4 Очевидно, вся плоскость Оху состоит из особых точек. Се-
Семейство же интегральных кривых на плоскости Оху не существу-
существует. >
Примечание. В пространстве Oxyt интегральные кривые представляют
собой прямые, параллельные оси Ot.
в A,0)
= 0
Из характеристического уравнения
3-А -2
4 -1-А
находим корни
А1>2 = 1 ± 2i.
Следовательно, особая точка — фокус. Для выяснения вопроса о на-
направлении закручивания интегральных кривых (спиралей) положим
х = 1, у = 0 в системе уравнений:
х = 3х-2у, у~4х-у.
Тогда, приняв во внимание, что для этой системы фокус будет неустойчивым, а также направле-
направление вектора скорости »A, 0) = C, 4), заключаем, что при удалении от начала координат движение
по спирали осуществляется против хода часовой стрелки (рис. 39). >
Примечание. Об устойчивости особой точки исходного уравнения ничего сказать нельзя, так как при
замене t иа —t уравнение вида не меняет, траектории движения (интегральные кривые) не замкнуты и
устойчивость в данном случае зависит от направления движения по траекториям.
Рис.39
Составив и решив уравнение
3-А
2
4
1-А
= 0;
§2. Особые точки
297
видим, что особая точка — седло. Путем подстановки у = кх в диф-
дифференциальное уравнение находим интегральные прямые (асимпто-
(асимптоты семейства деформированных гипербол).
Имеем
к~ 3+lfe ^ *' ~ 2' к2 = ~1-
Таким образом, две прямые
— искомые. Далее, ясно, что особая точка неустойчива (в данном
случае, в отличие от предыдущего примера, характер тривиально-
тривиального решения не зависит от направления движения по траекториям).
Примерный вид семейства изображен на рис. 40. >
Рис.40
В задачах 641-647 найти и исследовать особые точки данных уравнений и систем.
641. у' =
2х + у
х-2у-5'
¦4 Из системы уравнений
2х + у = 0, ж - 2у - 5 = 0
находим координаты особой точки: х ~ 1, у = -2. Далее делаем
перенос начала координат в эту точку:
х=1+?, у = -2 + т).
В результате приходим к уравнению:
Поскольку корни уравнения
1-Л
2
:-2i»
1-Л
У
о-
-2-
I
Ж
ж
1
1
ш
Ш
I
вA,0)
X
= 0
Рис.41
имеют вид: Л12 = 1 ± 2г, то утверждаем, что особая точка — фокус. Положив в системе
I = Z - 2г), г) = 2? + г)
? = 1, г/ = 0, получим вектор скорости v(l, 0) = A, 2). Если принять еще во внимание, что
для этой системы точка @, 0) — неустойчивый фокус, то легко видеть, что при движении по
спиралям от начала координат O^rj будет происходить вращение против хода часовой стрелки
(рис.41).
Заметим, что, как в примере 639, об устойчивости фокуса ничего сказать нельзя. >
у^.
х2 - у2 - 1
< Из системы
2у = 0, х2-у2-1=0
находим координаты особых точек: (-1, 0); A, 0). Сделав замену х = -1 + ?, у = ц, приведем
данное уравнение к виду
Наряду с уравнением A) рассматриваем "укороченное" уравнение
298
Гл. 6. Устойчивость и фазовые траектории
полученное, очевидно, путем отбрасывания нелинейных членов из уравнения A). Поскольку дей-
действительные части корней характеристического уравнения, соответствующего последнему диффе-
дифференциальному, отличны от нуля (Ali2 = ±2), а также функция
при ?2 + гJ —> 0 (е > 0), то согласно п. 2.2 особая точка уравнения A) будет того же типа, что
особая точка укороченного уравнения. Более того, картины расположения интегральных кри-
кривых уравнения A) и укороченного уравнения в малой окрестности особой точки будут примерно
одинаковы (точнее, чем меньше окрестность, тем больше совпадение картин).
Таким образом, точка (-1, 0) — седло для исходного уравнения.
Далее, сделав замену ж = 1 + ?, у = г), приходим к уравнению
dr) ^ 2г)
и соответствующему ему укороченному
Укороченное уравнение имеет особую точку @, 0), которая, как следует из уравнения
2-Л 0
0
2-Л
= 0,
является дикритическим узлом. По причине, изложенной выше, точка A,0) будет дикритическим
узлом и для исходного уравнения. >
х + у+1
•4 Из системы уравнений
у + \Vl + 20ж2 =0, ж + у + 1 = 0
находим особые точки: @, —1); B, -3). Исследуем каждую из них. С помощью замены х = ?,
у = — 1 + г/ данное уравнение приводим к виду:
I ,, , ,
dr) rj - 1 + A + 20?L Ч + $? — у? + о(? )
Укороченное уравнение
dr)
как следует из соответствующего ему характеристического
1-Л 1
1-Л
= 0,
= о(гш), г = Ji2 + г,2, е > 0;
имеет седло (Л1]2 = 1 ± л/5). Далее, функция
>-» - —
поэтому, согласно п. 2.2, точка @, —1) является седлом и для исходного дифференциального урав-
уравнения.
Положив х = 2 + ?, у = — 3 + г/, из данного уравнения аналогично предыдущему получаем:
dr]
20
27'
Составив и решив характеристическое уравнение
1-Л 1
= 0;
убеждаемся в том, что @, 0) — узел. Учитывая еще соотношение О(?2) = о(г1+?), согласно п. 2.2
заключаем, что точка B, —3) является узлом и для данного дифференциального уравнения. >
§2. Особые точки 299
644. х = lnB - у2), у = ех-еу.
¦4 Сначала находим действительные решения системы уравнений 1пB - у2) = 0 и е1 - еу = 0.
Из первого уравнения получаем у = ±1; из второго — х = ±1. Следовательно, точки (-1, —1)
и A, 1) — особые.
Далее, исследуем каждую из этих точек. Полагая в данных дифференциальных уравнениях
х - ±1 + ?, у = ±1 +т), приводим их к виду:
? = ln(l ^2rj — rj
Отсюда, применяя формулу Маклорена, имеем:
i = ^2г) + 0{ц2), г}
Решив характеристическое уравнение
-А ^2
е^ -е±х-\
= 0; А, = -— + \1— Т2е±>, а2 = -т-а/т
соответствующее укороченной системе
видим, что первая особая точка (ей соответствует везде верхний знак) — устойчивый фокус, а
вторая — седло. В силу п. 2.2 утверждения относятся и к исследуемой системе. >
645. х = ^х2 -у + 2 - 2, у - arctg(i2 + ху).
< Система уравнений
^Jx2-y + 2 = 2, хг + ху = 0
имеет решения: хх = 0, хг = -2, х, = 1 и t/i = -2, у2 = 2, у3 = -1- Следовательно, точки
(О, -2); (-2, 2); A, -1) — особые.
Сделав замену х = {, у — —2 + q, приводим данную систему уравнений к виду:
Разлагая правые части этих уравнений по формуле Маклорена и удерживая лишь линейные члены,
получаем укороченную систему
Поскольку корни ее характеристического уравнения А^г = ±^^2, то особая точка — седло. А
тогда по п. 2.2 точка @, —2) является седлом и для исходной системы.
Теперь переносим начало координат в точку (—2, 2), положив х = -2 + ?,у = 2 + г]. Тогда
данная система принимает вид:
- О2 ~ 17, 7? = -a
Применяя к правым частям этой системы формулу Маклорена и отбрасывая нелинейные
члены, получаем укороченную систему:
i = -t-j, Ч = -2?-2г,-
Корни характеристического уравнения А^ = д действительны и имеют одинаковые знаки,
поэтому особая точка — узел. Следовательно, согласно п. 2.2, точка (—2, 2) является узлом и для
данной системы.
Наконец, полагая ж=1+?, у = -1 + г/, данные уравнения после аналогичных выкладок
приводим к укороченным:
$=2~4' '> = * + '>-
Поскольку корни характеристического уравнения (Alj2 = 4 ) комплексны и Re А^ ф 0, то
особая точка — фокус. Такой же она будет и для данной системы. >
300 Гл. 6. Устойчивость и фазовые траектории
646. х = In , у = х2 — у2.
3
•4 Из системы уравнений
находим координаты особых точек: (—1, -1); (-2, 2); A, —1); B, 2). Полагая х = ±1 +?, у
= -1 + т), приводим систему дифференциальных уравнений к укороченному виду:
Из характеристического уравнения
-А -I
±2 2-Л
= 0
на основании п.2.2 следует, что точка A, -1) — фокус (А, 2 = 1 ± г), а точка (—1, -1) — седло
(Ai>2 = 1 ± л/3). Аналогично, положив х = ±2 + ?, у = 2 + г) и удержав линейные члены, из
данной системы получаем укороченную:
Решив характеристическое уравнение
±4 -4-а|=°
и приняв во внимание п. 2.2, заключаем, что точка B, 2) — седло (А^г = —2 ± 2\/2), а точка
(-2, 2) — вырожденный узел (А12 = -2 Ф 0). >
647. х = ^Дх-уJ + 2- 2, у = еу2~х - е.
< Из системы уравнений
находим координаты четырех особых точек @, 1); @, -1); (—1, 0); C, 2). Сделав замену х = ?,
у = ±1 + »7, данные уравнения известным способом приводим к укороченным:
i = z$H- Фу V = еЫ ± 2Ф-
Корни характеристического уравнения для этой системы имеют вид:
4еA ± 1) + 4е2
Л( = 2+2' А2"^2¦
Поскольку А,А2 < 0 (А!, А2 — действительные корни), то на основании п. 2.2 точки @, 1); @, —1)
являются седлами. Аналогично, перенеся начало координат в точку (—1, 0) по формулам х =
= — 1 +{, у = г) и удержав в правых частях линейные члены, получаем укороченную систему:
Поскольку корни
комплексны, то согласно п. 2.2 особая точка (—1,0) — фокус. Наконец, полагая в данных урав-
уравнениях ж = 3+?, у = 2 +г) и используя формулу Маклорена, получаем укороченную систему:
{=2«-»»), *
характеристическое уравнение которой имеет корни А1;2 = 2е + ^ ± J[2е + тп ~Ц: ¦ Поскольку
корни действительные и одинаковые по знаку, то особая точка C, 2) — узел. >
В задачах 648—650 дать примерную картину расположения интегральных кривых в окрестно-
окрестности начала координат.
§ 2. Особые точки
301
648. у' =
ху
х + у
¦4 Сначала на плоскости Оху выделяем области знакопостоян-
ства производных у', у", а также кривые, на которых эти производ-
производные либо равны нулю, либо неограничены.
Решив неравенства
V (у>0 Л х + у<0),
V (у<0 Л х + у>0),
Рис.42
приходим к следующему результату. Если
(х>0 Л у>0) V (х > 0 Л х + у < 0)
то у' > 0, а если
(х<0 Л ж + у>0) V (ж < 0 Л у<0)
то »/' <0.
Поскольку у' = 0 при ж = 0 или у = 0, то интегральные кривые пересекают ось Оу под
прямым углом, а ось Ох является интегральной кривой. Далее, поскольку на прямой х + у = 0
производная у1 не ограничена (точнее было бы сказать, что
производная у' на прямой х + у = 0 не определена и у' —> оо
при х+у —> 0), то интегральные кривые подходят к этой пря-
прямой с обеих ее сторон под прямым углом к оси Ох. Таким
образом, если интегральную кривую с отрицательной произ-
производной изображать наклонной чертой \, а кривые с положи-
положительной производной — чертой вида /, то картину интеграль-
интегральных кривых в первом приближении можно представить так,
как показано на рис. 42. Для установления областей опре-
определенной выпуклости интегральных кривых решаем неравен-
неравенства
« _ У(У ~ У\)(У ~ Уг) . „
У ~ °
(х +
где
l-i-.— — I X
+ +^
+ + +^
+ + +
+ + + +
Рис.43
Решив эти неравенства и обозначив области, где у" > 0, знаком
"+", а области, где у" < 0 — знаком "—", получаем картину,
изображенную на рис. 43.
Таким образом, на кривых у = 0, у = yi(x), у = уг(х) вторая
производная обращается в нуль, а на прямой х + у = 0 она не
ограничена (вернее сказать, на прямой х + у = 0 она не опреде-
определена, а в окрестности ее не ограничена).
Теперь, имея такую информацию о поведении интегральных
кривых, можем представить их картину во втором приближении
(рис. 44). Остается выяснить некоторые детали в поведении ин-
интегральных кривых.
Поскольку функция (х, у) ь-> ХХУ вместе со своей частной
производной по у непрерывна при х + у Ф 0, то через каждую
точку плоскости (х + у Ф 0) проходит единственная интегральная
кривая. Далее, поскольку у = 0 (х Ф 0) есть решение данного дифференциального уравнения,
то ни одна интегральная кривая не может касаться оси Ох. Является очевидным факт, что все
интегральные кривые, заходящие в угол х + у>0 Л у<0, обязательно попадают в начало
координат (вернее было бы говорить об асимптотическом стремлении кривых в начало коорди-
координат, поскольку при х = у = 0 правая часть данного уравнения не определена). Отметим также,
что существует интегральная кривая, расположенная между семейством параболообразных и се-
семейством гаперболообразных интегральных кривых (см. второй квадрант) и входящая в начало
координат.
Рис. 44
302
Гл. 6. Устойчивость и фазовые траектории
Наконец, покажем, что ни одна интегральная кри-
кривая не входит в начало координат со стороны х > 0,
у > 0. Предполагая противное, записываем интеграль-
интегральное уравнение для кривой, входящей в точку @, 0) при
х>0, у>0:
Uy(t)dt
В силу неравенства
yd)
t + yit)
y(t)
1 (О 0, y(t) > 0)
из последнего уравнения получаем оценку:
В свою очередь,
t
' + Л- О ' '
о о
и т.д. Продолжая оценки, на n-ом шаге получаем
х™
"' ' ^ (п+1)!
Отсюда следует, что у(х) ^ 0 при п —> оо. Пришли к противоре-
противоречию. После этих замечаний строим третье приближение к истинной
картине интегральных кривых (рис. 45). >
2ху
Рис. 46
649. у'= 2
у + х2
•^ Из неравенств
1ху
у+х2
находим области знакопостоянства производной у'. Именно, если
(х>0Л у>0) V (у + х2<0Л х>0) V (х<0 Л у<0 Л
х2>0),
то у' > 0. На остальной части плоскости, исключая прямые у = 0, х = 0, где производная
равна нулю, а также параболу у = — х2, где производная не определена,
интегральные кривые имеют отрицательную производную. Таким обра-
образом, в первом приближении картина интегральных кривых имеет вид
(рис. 46). Далее, из выражения для второй производной
следует, что интегральные кривые при (у > 0) V (у < 0 Л х2 + у < 0)
выпуклы вниз, а при у<0 Лх2 + у>0 они выпуклы вверх. Поэтому
с учетом выпуклости картину, изображенную на рис. 46, можем уточнить
(второе приближение) (рис. 47).
Заметим еще, что при построении кривых на рис. 47 мы принимали во внимание соотношение
Ряс. 47
lim у' = lim -^rr = 0,
Х-*ОО X-+OG у -J- X
§ 2. Особые точки
303
геометрически означающее, что интегральные кривые при удалении от начала координат по лю-
любой горизонтали распрямляются. Кроме того, при замене х на —х уравнение вида не меняет,
поэтому все интегральные кривые симметричны относительно оси Ох.
Наконец, выясним вопрос о том, какие из интегральных кривых стремятся в начало коорди-
координат. Ясно, что любая интегральная кривая , выходящая из области у + х2 < 0, попадает в угол
(х > О Л у < 0) V (у + х2 > 0). С другой стороны, через каждую точку (х, у), где у + х2 Ф 0,
согласно теореме о существовании единственного решения, проходит единственная интегральная
кривая. Следовательно, ни одна интегральная кривая, вышедшая из области у + х2 < 0, не может
остановиться в указанном угле. В силу этой же теоремы ни одна из кривых не может пересечь
ось Ох, поскольку прямая у = 0 является интегральной. Далее, ни одна из интегральных кри-
кривых не может уйти вдоль оси Ох на бесконечность, поскольку в рассматриваемом угле у" < 0.
Итак, остается единственная возможность, когда все указанные интегральные кривые стремятся
попасть в точку @, 0).
Покажем теперь, что ни одна интегральная кривая не может попасть в начало координат со
стороны у > 0. Для этого, предполагая противное, для некоторой кривой у(х) > 0 при х > 0 от
дифференциального уравнения перейдем к интегральному
Х ty{t)dt l
Отсюда в силу оценки
1, находим
Аналогично,
у(х) ^ 2 / t max
2
i +y
и т.д. На п-ом шаге получаем неравенство у(х) ^ ^-. Следователь-
Следовательно, у(х) ^0 — противоречие.
Учитывая все замечания, строим картину интегральных кривых
в третьем приближении (рис. 48). >
У-я
¦4 Аналогично предыдущим примерам из неравенств
Рис.49
4*
y-xL
находим области монотонного возрастания и убывания интеграль-
интегральных кривых, а затем строим грубую картину поведения их на плос-
плоскости Оху (рис.49). Далее, из выражения для второй производ-
производной
„ _ у(у2 - 2х4)
У (у-хУ
видим, что на графиках функций у = ±</2х2 интегральные кри-
кривые меняют направление выпуклости. Области знакопостоянства
второй производной изображены на рис. 50.
Проследим за интегральной кривой, идущей из области
х <0 Л у > 0 Л у <хг.
+ +
+ +'
+ +
+ +
+ +
::
— —
- -
„ \_
«V-
+
+ -t
-
-
—
-
у\
-0?
~i
1 +
Й-
+
&
\
\
+
+
+
jil+
' + +
- -
if:
1" ~
+
+
+
+ »
- X
:
—
—
Рис. 50
304
Гл. 6. Устойчивость и фазовые траектории
Поскольку в этой области у' > О и у" > О, то ордината кривой растет при
увеличении х, а выпуклость кривой направлена вниз (рис. 51). Ясно, что
lim у' = +оо,
lim у
х->хк+0
- -оо,
Рис. 51
Рис. 52
поэтому кривая пойдет вверх и левее точки х = х*. В точке М пере-
перегиба нет, однако, как следует из рис.51, кривая поменяет направление
выпуклости. Далее, в точке N она должна иметь перегиб, поскольку эта
точка лежит на кривой перегибов интегральных кривых у = \/2х2. На-
Наконец, поменяв еще раз направление выпуклости, интегральная кривая
в силу отрицательности производной уйдет налево вверх (к +оо).
Теперь проследим за интегральной кривой, выходящей из точки
(О, у) и идущей в сторону х < 0. Поскольку у' < 0 при у > х , то
ордината кривой будет возрастать (рис. 52). Однако, в силу того, что па-
парабола у = ^х2 является решением данного дифференциального урав-
уравнения, наблюдаемая нами интегральная кривая не может ее пересечь,
а значит, и уйти из области у > \х2.
Следовательно, пространство между параболами
2
У
= V2x2
будет заполнено гиперболообразными кривыми, одна из ко-
которых рассмотрена выше. Парабола же у = -^х2 служит раз-
разделителем указанных кривых.
Далее, поскольку при фиксированном у < х2 будет
lim
ху
у - х2
= 0,
то все интегральные кривые в области у < х приближают-
приближаются к оси Ох и ее не пересекают (в силу того, что у = 0 есть
решение и при у = х2 выполняются условия теоремы о един-
единственности интегральной кривой). При у < —\/2х2 все ин-
интегральные кривые выпуклы вниз, поэтому попасть в точку
(О, 0) не могут. Таким образом, в начало координат заходит
только две интегральные кривые:
Рис.53
' = U И У =
У=\х2.
Итак, принимая во внимание проведенное исследование, строим окончательную картину ин-
интегральных кривых (рис. 53). >
651. Доказать, что если
1) уравнение
(ах + by) dx + (mx + ку) dy = О
не является уравнением в полных дифференциалах;
2) особая точка @, 0) этого уравнения — седло,
то оно имеет непрерывный в окрестности начала координат интегрирующий множитель.
М Интегрирующий множитель ц = ft(x, у), удовлетворяющий в данном случае уравнению
ди ди
(mx + пу) (ах + Ьу)-— = ц(Ъ - тп),
A)
будем искать в виде ц — ip(w), где ш = ах + /Зу, а, /3 — постоянные, подлежащие определению.
Подставив значение ц в A), получим
B)
<p'(w)((ma - а/3)х + (па - Ь/Э)у) =(Ь- тп)<р(ш).
§ 3. Фазовая плоскость 305
Положим (та - ар)х + (па — Ьр)у = А(ах + ру), где А — некоторая постоянная. Тогда из
последнего тождества найдем:
(т - Х)а - ар = 0, „
па-ф + Х)р = 0. к '
Поскольку а^0л/3^0,тов силу однородности системы C) приходим к условию:
т — А —а
п -6-А
= 0 =$> Ali2 = - Гm - 6 ± ^(т - ЬJ -
li2
ЬJ - 4(ап - Ьт) j .
Далее, так как особая точка @, 0) — седло, то корни Ai, Aj действительные. Следовательно,
числа а, /3 также действительны, и мы имеем, вообще говоря, два интегрирующих множителя,
получающихся путем интегрирования уравнения B):
Ь-т Ь-т
Mi^CJKI Al , М2 = С2|ш2| ^ , D)
где ш1 — <Х\Х + рху, ш2 = а2х + ргу, Clt С2 — постоянные интегрирования. Заметим, что так как
Ь фт (это следует из условия 1) теоремы), то множители D) отличны от постоянных.
Поскольку А1А2 < 0, то независимо от знака Ь-т один из показателей в D) является поло-
положительным. Последнее означает, что один из множителей непрерывен. >
§ 3. Фазовая плоскость
3.1. Основные понятия.
Система дифференциальных уравнений
dxi
dt (xi, X2, •¦¦ ,хп), i = l,n, A)
в которую переменная t (время) явно не входит, а функции /,¦ непрерывно дифференцируе-
дифференцируемы в некоторой области, называется автономной. Каждому решению х< = <fii(t), i = 1, п си-
системы A) поставим в соответствие движение точки в n-мерном пространстве (х[, х2, ... ,х„).
Кривая, описываемая точкой в процессе движения, называется траекторией. Таким образом,
х; = fi(t), г = 1, п суть параметрические уравнения этой траектории. Пространство размер-
размерности п, в котором решения системы A) изображаются в виде траекторий, называется фазовым
пространством. В частности, если п — 2, то фазовое пространство называется фазовой плоскостью.
Вектор / = (/i, /2, ... ,/п) называется фазовой скоростью. Положения равновесия автономной
системы находятся из условия / = 0, т.е. как решения системы конечных уравнений:
/,(xi, х2, ... ,х„) = 0, » = 17".
3.2. Построение фазового портрета.
Для того, чтобы начертить на фазовой плоскости картину траекторий автономной системы
* = fix, у), у = д(х, у), B)
нужно, во-первых, исследовать особые точки этой системы, а во-вторых, с помощью производных
Ух» Ух2 изучить поведение интегральных кривых уравнения
dy _ g(x, у)
dx fix, у)
(заметим, что иногда решения этого уравнения находятся в замкнутом виде).
В том случае, когда требуется построить траектории уравнения
х = д(х, ж),
нужно ввести переменную у = х и от этого уравнения перейти к системе
* = У. У = 9(х, у),
которая является частным случаем системы B).
306 Гл. 6. Устойчивость и фазовые траектории
3.3. Предельные циклы.
Предельным циклом системы A) называется замкнутая изолированная траектория этой систе-
системы, у которой существует окрестность, целиком заполненная траекториями, по которым фазовая
точка неограниченно приближается к этой замкнутой кривой при t —* +оо или при t —* -оо.
Если траектории системы A) приближаются к предельному циклу только при t —> +оо, то по-
последний называется устойчивым. Если же траектории системы A) приближаются к предельному
циклу только при t —* — оо, то он называется неустойчивым. В случае п = 2 (фазовая плоскость)
рассматривают так называемые полуустойчивые предельные циклы. Именно, предельный цикл
на фазовой плоскости называется полуустойчивым, если траектории системы B) с одной сторо-
стороны приближаются к нему при t —* +оо, а с другой — при t —* -оо. Следовательно, возможны
полуустойчивые циклы двух типов.
Теорема. Пусть К — предельный цикл системы B), правая часть которой непрерывна вместе
со своими частными производными по х и по у. Тогда все внутренние траектории, начинающиеся
вблизи К, наматываются на него, как спирали, либо при t —* +оо, либо при t —> -оо. Высказанное
утверждение справедливо и для внешних относительно предельного цикла траекторий.
3.4. Признаки отсутствия предельных циклов.
Признак Бендиксона. Если правые части уравнений B) имеют непрерывные частные производ-
производные первого порядка в односвязной области D и выражение
дх ду
нигде не меняет знак и не равно тождественному нулю, то в области В нет предельных циклов.
Признак Пуанкаре. Пусть v(x, у) = С — семейство гладких замкнутых кривых, покрывающих
плоскость Оху. Тогда если выражение
dv dv
П=^/+^Э D)
дх ду
в некоторой области D сохраняет постоянный знак, то в ней нет предельных циклов.
Односвязная область В на плоскости Оху не содержит предельных циклов, если в этой
области нет особых точек системы B).
3.5. Признаки наличия предельных циклов.
Теорема Левинсона— Смита. Пусть в дифференциальном уравнении
x + xf(x)+g(x) = 0, E)
функции fug непрерывны при всех х и обеспечивают единственное решение задачи Коши, непрерывно
зависящее от начальных условий. Пусть, кроме того, выполняются следующие условия:
1) хд(х) > 0 для хфО;
2) /, g —дифференцируемые функции;
3) /(х) < 0 на (—xi, х2), где х\, хг положительны, f(x) ^ 0 для всех остальных значений х,
причем F{<x>) = оо, где F(x) = I f(s) ds;
4) <?(±оо) = оо;
X
5) G(-xi) = G(x2), где G(x) = fg(s)ds.
Тогда уравнение E) имеет единственный устойчивый предельный цикл на фазовой плоскости (х, х).
Теорема Рейсе ига. Рассмотрим уравнение
x + f(x) + g(x) = O, F)
где f,g— непрерывные функции, /@) = 0, хд(х) > 0 при х Ф 0. Пусть функции /, д для всех их
аргументов непрерывны и обеспечивают существование единственного решения уравнения F), удовле-
удовлетворяющего заданным начальным условиям и непрерывно зависящего от этих условий. Пусть, кроме
того,
§ 3. Фазовая плоскость
307
0 при \у\
2) f(y) sgn у ^ ? > 0
3) max /(у) = М > 0;
г/2
4) g(x) sgn x ^ M + e при \x\ ^ 6 > 0.
Тогда на фазовой плоскости системы
существует по меньшей мере один устойчивый предельный цикл.
В задачах 652—666 для данных уравнений начертить траектории на фазовой плоскости.
652. х -х + х2 = 0.
¦4 Полагая х — у, переходим к системе
х = у, у = х - х2,
\У
из которой почленным делением ее уравнений получаем
dy х — х2
dx у
или (при у ф 0)
у dy — (х — х ) dx.
Общий интеграл уравнения (*) имеет вид:
С=0
(*)
Поскольку его характеристическое уравнение
= А2 - 1 = 0 имеет корни с отличными
3[у<-х<)+2х> = С.
Поскольку при замене у на -у интегральные кривые вида своих уравнений не меняют, то все
они симметричны относительно оси Ох. Давая параметру С конкретные значения и используя
обычные средства математического анализа, строим картину траекторий па фазовой плоскости
(рис.54).
Заметим, что кривым, охватывающим точку A, 0), соответствуют значения С, удовлетворя-
удовлетворяющие неравенству -1 ^ С < 0.
Далее, уравнение (*) имеет две особые точки: @, 0) и A,0). Отбрасывая х2 в указанном
уравнении, получаем укороченное уравнение
dy х
dx у'
-А 1
1 -А
от нуля действительными частями, то согласно п. 2.2, особая точка @, 0), являющаяся седлом для
укороченного уравнения, будет седлом и для уравнения (*).
Для исследования особой точки A, 0), как обычно, сначала перенесем начало системы ко-
координат в эту точку: х = 1 + ?, и = г]. Отбрасывая в полученном уравнении нелинейные члены,
приходим к укороченному уравнению
для которого особая точка @, 0) является центром. Таким образом, точка
A, 0) для исходной системы может быть фокусом или центром. В силу
симметрии интегральных кривых относительно оси Ох (см. п. 2.2), точка
A, 0) — центр. >
653. х + 2хъ = 0.
< Переходя к системе Оху, положив х = у, получаем
х = У, У= -2я3.
Отсюда почленным делением уравнений, а затем интегрированием находим Рис 55
семейство траекторий на фазовой плоскости: уг + хЛ = С. Каждая траектория представляет собой
деформированную окружность (рис. 55). Очевидно, точка @, 0) — центр. >
308 Гл. 6. Устойчивость и фазовые траектории
654. х + 2х3 -2х = 0.
¦4 Полагая х = у, приходим к уравнению
dy = 2(х - х3)
dx у
общее решение которого имеет вид:
У i
y = ±JC + x2B -х2).
х 0
A)
С>0
V?
Рис. 56
Рис. 57
Поскольку траектории симметричны относительно обеих координатных осей, то далее считаем
х ^ 0, у ^ 0. Если в A) положим х = у = 0, то получим С = 0. Следовательно, кривая
У,
проходит через начало координат (рис. 56).
При С > 0 все траектории проходят выше этой кривой
(рис. 57); причем в точке х = 0 производная у' = 0, а при у = 0
она не ограничена (точнее, у' —> — оо при у —> +0).
Далее, при С < 0 из неравенства
х2B - х2) ^ -С
Рис.59
следует, что
V 1 - %/1 + С ^ х ^ yi+ VI + С (С>-1).
Значит, при уменьшении С область существования семейства траекторий сужается и при С = — 1
траектории вырождаются в точку A, 0) (рис. 58). Наконец, зеркально отобразив кривые, изобра-
изображенные на рис.58, относительно оси Ох, а затем полученную картину — относительно оси Оу,
будем иметь полную картину траекторий (рис.59). Очевидно, точки A, 0) и (—1, 0) — центры,
а точка @, 0) — седло. >
655. х-2* + х+1 = 0.
In 2
Перейдя на фазовую плоскость, имеем
¦ - 2х - - dy _ 2х - х - 1
dx у
A)
Интегрируя уравнение A), получаем семейство траекто-
траекторий:
1п2
- х- - 2х + С.
B)
Далее, используя обычные методы математического ана-
анализа, строим картину интегральных кривых B) (рис. 60).
Отметим, что кривой, проходящей через точку A, 0), со-
соответствует значение
Рис. 60
§ 3. Фазовая плоскость
Замкнутым кривым, охватывающим начало коор- ^ д^
динат, соответствуют значения С, определяемые —в х—
М„
неравенством — ш
In 2 ~" In 2
Значения С для остальных кривых указаны на рис. 60. >
У ,
-f о f
Рис.61
Рис.62
Рис.63
Рис.64
656. х + 2cosx -1=0.
¦4 Из системы х = у, у = 1 — 2 cos x получаем
dy _ 1 - 2 cos х
dx у
у = 2х - 4 sin х + С.
—е-
Решив конечную систему у = 0, 1 — 2cosa; = 0, находим особые точки: Mt
Nic [ — -j + 2ft?r, О), где fc 6 Z. Далее, нетрудно установить, что М^ — седла, л
(рис.61). Для построения картины семейства A)
сначала строим кривую
<р{х) = 2х — 4sinx
(рис. 62), а затем картину семейства
¦ф(х) = 2х - 4 sin х + С
путем параллельного переноса графика функ-
функции <р (рис.63).
Теперь построим семейство кривых
ipi(x) = 2z-4sina: + C ^ 0
(рис. 64).
Далее строим семейство кривых
У = ±V^i(s)
(рис. 65) (точнее, на рис. 65 изображена только часть этого семейства в окрестности двух особых
точек (—у, 0J и (о, yj — центра и седла соответственно).
Для получения всей картины семейства траекторий на фазовой плоскости Оху следует карти-
картину, изображенную на рис. 65, периодически (с периодом 2зг) продолжить как влево, так и вправо
относительно ее первоначального положения. Тогда получим следующую картину (рис.66). >
-я/3
Рис.65
310
Гл. 6. Устойчивость и фазовые траектории
У
УI
Рис.67
Рис.68
Рис.66
657. х + 2х + 5х = 0.
< Сделав замену х = у, приходим к линейной системе
Х = У, У = ~2У - 5х
с особой точкой @, 0). Поскольку корни характеристического уравне-
уравнения этой системы равны — 1±2г", то особая точка — устойчивый фокус.
Положив в системе х = 1, у = 0, находим вектор фазовой скорости
v = @; — 5), с помощью которого мы, учитывая устойчивость фоку-
фокуса, устанавливаем направление закручивания траекторий на фазовой
плоскости (рис. 67). >
658. х + х+2х-х2 = 0.
¦4 Полагая в данном уравнении х = у, получаем систему диффе-
дифференциальных уравнений:
х = у, у = х2 - 2х - у,
из которой следует, что точки @, 0), B, 0) — особые. Обычное иссле-
исследование их показывает, что точка @, 0) — устойчивый фокус, а точка
B, 0) — седло, причем прямые
j/[ = х — 2, Уг — —2х + 4
являются касательными к интегральным кривым, входящим в него
(рис.68). Далее, судя по знаку производной
' „2
У =
-2х-у
У '
устанавливаем грубую картину интегральных кривых (рис. 69).
Заметим, что на параболе
у = х2 - 2х
интегральные кривые достигают экстремальных значений; ось
Ох они пересекают под прямым углом, а ось Оу — под уг-
углом 45°. Используя эти данные, строим картину интегральных
кривых (рис. 70). >
659. х + х2-х2+1 = 0.
•^ Из уравнения
dy
dx
х2-у2-1
У
(*)
находим области возрастания и убывания интегральных кривых на фазовой плоскости Оху
(рис.71). Кривые
х2-у2-1=0
§ 3. Фазовая плоскость
311
пересекаются интегральными кривыми под нулевым, а ось Ох — под прямым углом.
Далее, известным способом находим две особые точки: (—1, 0), @, 1). Поскольку корни
характеристического уравнения, соответствующего укороченной линейной системе
^ = г/) ^ = „ц, У i,
мнимы, то особая точка (—1, 0) может быть для системы
= У,
у = х2 -у2 -\
либо фокусом, либо центром. Принимая во внимание то, что при
замене у на -у уравнение (*) вида не меняет, убеждаемся, что
рассматриваемая особая точка является центром для указанной
системы.
Точка A, 0) является седлом, а прямые
у, = V2(x - 1), J/2 = -V2(x - 1)
служат касательными к интегральным кривым, входящим в него.
Особые точки показаны на рис. 72.
Таким образом, исходя из сказанного и рисунков 71, 72, строим фазовый портрет (рис. 73). >
660. х + 5х-41п:
= 0.
¦4 Исключив параметр t из системы дифференциальных
уравнений
придем к уравнению
dx у
с особыми точками: (—1, 0) и A, 0). Решая неравенства
(*)
A)
У
¦so,
устанавливаем области монотонности интегральных кривых уравнения A) на фазовой плоскости
(рис. 74). Кривую
интегральные кривые пересекают под нулевым углом, а кривую у = 0 — под прямым. Теперь
исследуем особые точки.
312
Гл. 6. Устойчивость и фазовые траектории
Рис. 75
Полагая в системе (*) х = 1 +?, у = т] и отбрасывая нелинейные
члены, получаем укороченную систему:
Поскольку корни характеристического уравнения
Ai,2 = ~5^ (Ai « 0,70; А2 и -5,7),
то особая точка A, 0) — седло. Прямые
у = А,(х - 1), у = \2(х - 1)
являются касательными к интегральным кривым, вхо-
входящим в эту точку. Аналогично, полагая в (*) х =
= —1+|, у = т), получаем укороченную систему:
? = Ч, 4 = -Ч ~ 57>
характеристический определитель которой имеет нули
Ai = -1, А2 = -4.
Следовательно, особая точка (—1, 0) — узел. Из уравне-
--} -Л) (г)-
находим, что все интегральные кривые, проходящие че-
через узел, касаются прямой у = -х — 1, а из уравнения
Рнс. 76
следует, что все указанные кривые пересекаются интегральной кривой,
проходящей через узел и имеющей в нем касательную у = — 4х — 4.
Окрестности особых точек изображены на рис. 75.
Наконец, учитывая все полученные данные, строим полную фазо-
фазовую картину (рис.76). >
661. х = 4 - 4х - 2у, у = ху.
¦^ Из системы
4 - 4х - 2у = 0, ху = 0
находим особые точки: A, 0), @, 2). Известным способом (см. выше)
устанавливаем, что A, 0) — седло, а точка @, 2) — вырожденный узел;
причем в седло входят интегральные кривые под углом а = - ^. Далее,
ось Оу интегральные кривые пересекают горизонтально, а прямую 4—4х — 2у = 0 — вертикально.
Решая неравенства
ху >()
4 — 4х — 2у
устанавливаем области монотонности интегральных кривых (рис. 77). Для более четкого предста-
представления о поведении интегральных кривых рассмотрим знак второй производной
/ =
Рнс. 77
D-4х-2уK '
3 3
где у, = 2 - х + х2, у2 = 2 - х - х2 (х ^ 0). Если х < 0, то
Решая неравенства
„ _ 4у (у2 + уBх - 4) + A - х)D + х2))
У ~ D - 4х - 2у? '
D — 4х — 2иK
§ 3. Фазовая плоскость
313
У
\ О при х < О,
D - 4x - 2yf
находим области выпуклости интегральных кривых
(рис.78). Заметим, что на прямой 4 — 4х - 2у = 0 и на
кривых у = уи у = у2 часть траекторий меняет напра-
направление выпуклости. Теперь проследим за интегральными
кривыми, проходящими через особые точки. Через седло О
проходит прямая у = 0 и кривая, пересекающая ось Ох
под углом а = - arctg |. Эта кривая на параболе у = у\
имеет точку перегиба и пересекает ось Оу горизонтально,
а прямую 4 - 4х — 2t/ = 0 — вертикально. Наконец, под
углом 135° к оси Ох она входит в узел. Нижняя часть ее
(при у < 0) проходит под параболой у = уг, поскольку:
1) у' ~ — y при у —+ —оо, a t/2 ~ ~7x!' ^ попасть в
область между кривыми 2/ = 2/2 и 4 - 4х - 2j/ = 0 при j/ < О
рассматриваемая кривая не может, ибо в противном случае, имея вы-
выпуклость, направленную вниз, ей бы пришлось либо пересечь прямую
4 — 4х — 2у = 0, что невозможно, либо остаться в этой области, что
в силу 1) также невозможно (рис. 79).
Рассмотрим узел. Выйдя из угловой точки по касательной к кри-
кривым у = 2/, и у = 2/2, траектория (а) может попасть лишь в область III,
поскольку в области I выпуклость направлена вверх, что для этой траек-
траектории невозможно, а в области И выпуклость направлена вниз и поэтому
траектория должна пересечь интегральную кривую (а), что также невоз-
невозможно. Таким образом, попав в область III, фазовая траектория пересе-
пересекает прямую 4 - 4х — 2j/ = 0 вертикально, затем ось Оу — горизонтально
и, имея выпуклость, направленную вниз, уйдет налево вверх. Теперь рас-
рассмотрим траектории, выходящие из узловой точки и идущие вверх нале-
налево. Здесь имеется две возможности. Первая состоит в том, что фазовая
траектория (/3) сначала попадает в область I, затем в области II, III и,
наконец, уходит налево вверх. Вторая возможность: фазовая траектория
G) попадает в область IV, затем пересекает прямую 4 — 4х —
— 2у = 0 вертикально, ось Оу — горизонтально, меняет на-
направление выпуклости на кривой у = j/, и, наконец, асим-
асимптотически стремится к оси Ох. Возможные выходы фазовых
траекторий из узловой точки представлены на рис. 80.
Покажем наконец, что все выходящие из узла интеграль-
интегральные кривые, за исключением кривой (а), асимптотически
стремятся к оси Ох при х —> +оо. Очевидно, для этого доста-
достаточно показать, что Ve > 0 Зх такое, что интегральная кривая
(/3) обязательно пересечет прямую 4 — 4х - 2у = 0. С этой
целью, заменив в дифференциальном уравнении
Рис. 78
Рис. 79
У ,:
У =
ху
4 - 4х - 2у
(*)
х на -х (ради удобства), перейдем к интегральному уравне-
уравнению кривой ф):
х
У(Х) = ? + J
ty(t)dt
4 + 4t-2y(t)
(х ^ 0).
A)
Очевидно, у(х) > е > 0 при х > 0. Пусть у(х) < 2A + х) при
314
Гл. 6. Устойчивость и фазовые траектории
х > 0. Тогда из A) следует оценка:
С учетом последнего неравенства из A) получаем более точную оценку:
+ t2-tln(l+t)
х 2 \ / х л. .2
yW>e\l + -f + ~ д( + dtUe U + -f-L-l
о / \ о
~2
+ 4
dt =
= е
32 16
, х^О.
Следовательно,
2A + x).
Отсюда уже нетрудно видеть, что Ve > 0 Зхо такое, что кривая ф) пересечет указанную прямую.
Действительное, такое xq удовлетворяет неравенству 0 < хо < х, где х есть решение уравнения:
=2A+х), х>0.
Далее, при х —> +оо и ограниченном у из диф-
дифференциального уравнения (*) следует, что
-| =»¦
т.е. при х -+ +оо все интегральные кривые
асимптотически стремятся к оси Ох. Поведе-
Поведение интегральных кривых при у < 0 не требует
детального исследования. Примерный вид фа-
фазовых траекторий изображен на рис.81. >
662. х = 2х + у2 - 1, у = 6х - у2 + 1.
¦^ Из неравенств
определяем области монотонности фазовых
траекторий (рис. 82). Отметим при этом, что за
исключением двух особых точек @, 1) и @, -1)
параболу 2х+у2 — 1 = 0 траектории пересекают
РиС- л вертикально, а параболу 6х — у2 + 1 = 0 гори-
горизонтально.
Далее, известным способом нетрудно установить, что точка @, —1) — неустойчивый фокус,
а точка @, 1) — седло, причем прямые у=1-3хиу=1+х являются касательными к ин-
интегральным кривым в этой точке (рис. 83). Покажем теперь, что любая траектория, проходящая
через точку (х0, 0), обязательно пересечет параболу 2х + у2 — 1 = 0 (х0 < 0). Поменяв, ради
удобства, в уравнении
, _ 6х - у2 + 1
§3. Фазовая плоскость
315
Рис. 82
х на —х, а у на —у, запишем интегральное уравнение ука-
указанной траектории:
- 1 + y\t)
dt.
A)
Поскольку y2(t) ^ 0, то из A) следует неравенство:
У(х)
х
J
а -1
= 3(х + х0) - 8 In
2х+1
1-2х0'
указывающее на возрастание ординаты исследуемой кривой.
Поскольку это возрастание происходит быстрее, чем по пря-
прямолинейному закону, то обязательно найдется такое х\, что
Далее, из выражения для второй производной
У =
Рис.83
Рис. 84
видно, что между параболами 6х-»/2 + 1 = 0и2х + у2 — 1 = 0 при у < 0 все траектории имеют
выпуклость, направленную вниз. Поэтому интегральные кривые пересекут параболу 6х—у2 + 1 = 0
и далее уйдут вверх направо.
Таким образом, учитывая все приведенное, строим семейство фазовых траекторий (рис. 84). >
663. х = 1 — х2 — у2, у = 2ху.
¦^ Поскольку дифференциальное уравнение
efy _ 2ху
dx" ~ 1 - х2 - у2
при замене х на — х, у на —у вида не меняет, то картина фазовых траекторий симметрична как
относительно оси Ох, так и оси Оу. Далее, легко найти, что особые точки @, ±1) — центры,
а точки (±1, 0) — седла, через которые проходит эллиптическая траектория
316
Гл. 6. Устойчивость и фазовые траектории
У ;,
Далее, решив неравенства
ху
находим участки монотонного убывания (воз-
(возрастания) фазовых траекторий (рис. 85). >
664. х = (х + уJ - 1, у = -у2 - х + 1.
¦< Как и в предыдущих примерах, снача-
сначала находим области монотонности интеграль-
интегральных кривых (рис. 86), а затем выявляем особые
точки и их характер: @, —1) — седло, A, 0) —
неустойчивый фокус, (-3, 2) — узел, @, 1) —
седло. Из укороченной системы дифференци-
дифференциальных уравнений следует, что в точку @, -1)
интегральные кривые входят, касаясь прямых
^1
У= 1-
- ж- 1 и у = ~
в точку @, 1) — прямых
Рис. 86
и y = -
\\\ В узловой точке траектории касаются прямой
^ 1-V5
У=~^Чх + 3) + 2.
Через эту точку проходит также интегральная кривая с каса-
касательной
_ 1 + л/З,
У — ~ \х
Особые точки и их малые окрестности представлены на
рис.87.
Наконец, представляется интересным выяснить поведе-
поведение интегральных кривых, проходящих через особые точки.
В частности, покажем, что кривая (а) перейдет в одну из
спиралей полюса A, 0), а кривая (б) обойдет полюс и в по-
полосе (х + уJ ^ 1 пройдет ниже кривой (а).
Записав интегральное уравнение кривой (б) при х > 0,
2/(х) = 1 +
¦ + 2/@)
2 -
¦dt
Рис. 87
и приняв во внимание неравенства 0
из A) имеем оценку:
y(t)
О)
lvtt+y(t)> 1,
1 - (* + y(t))
l-(t + y(t)J
dt
—/г
dt
> 1
-/*-!•
Отсюда следует, что кривая (б) пересечет ось Ох в точке х0 ^ 2. Далее, в полосе (х + уJ < 1
производная у' > 0, значит, ордината кривой (а) возрастает и поэтому последняя может пересечь
прямую х + у = 1 в точке (х,, yi), где х, < 2. Таким образом, траектории (а) и {б) "разминутся":
траектория (а), как видно из рис.88, превратится в спираль, а траектория (б), обогнув полюс
и совершив вертикальное пересечение прямых х+ у = 1 и х + у = — 1, станет асимптотически
сближаться с кривой (в).
§ 3. Фазовая плоскость
317
Изучить поведение других из ука-
указанных выше интегральных кривых,
примерный вид которых изображен
на рис. 88, предоставляем читателю.
Таким образом, исходя из про-
проведенных исследований, строим эс-
эскизный портрет фазовых траекторий
(рис. 89). >
Рис. 88 Рис. 89
665. х = Bх - уJ -%у=(х- 2уJ - 9.
¦4 Из неравенств
(х-2^-9
Bs - уJ - 9 <
находим области монотонности интегральных кривых (рис. 90). Заметим, что кривые
2х-у = ±3
интегральные кривые пересекают вертикально, а прямые
х - 2у = ±3
— горизонтально. Далее, легко обнаружить, что осо-
особые точки (-1, 1) и A, -1) — седла, а точки C, 3) и
(—3, -3) — узлы; причем интегральная прямая у = х про-
проходит через узловые точки, а две другие интегральные кри-
кривые проходят через них перпендикулярно указанной пря-
прямой. Угловые коэффициенты касательных к интегральным
кривым в точке (-1, 1) равны fci = 2+%/3, fc2 = 2—л/3- Пе-
Перейдя к переменным ы =
уравнение
dy =
dx
преобразуем к виду
, дифференциальное
(х - 2уJ - 9
Bх - уJ - 9
dv
dlt
Рис. 90
а + /3и2 + jv2'
Поскольку при замене « на —ы или v на -v последнее уравнение вида не меняет, то интегральные
кривые расположены симметрично как относительно прямой х + у = 0, так и прямой х - у = 0.
Таким образом, учитывая все сказанное, строим семейство фазовых траекторий (рис. 91)- >
318
Гл. 6. Устойчивость и фазовые траектории
666. х = х2 - у, у = (х-у)(х-
-V + 2).
¦4 Переходя к новой системе ко-
координат Ouv по формулам х = v,
у = 1-й, из данной системы полу-
получаем дифференциальное уравнение:
dv
dli
1 - и - u
(u + vJ - 1'
Рис. 91
Рис. 92
интегральные кривые которого уже изучены в примере 664. Следовательно, если изображенную на
рис. 89 систему координат сначала параллельно перенести вправо на единицу, а затем повернуть
ее на угол 90° против хода часовой стрелки, то мы получим портрет семейства фазовых траекторий
данной системы дифференциальных уравнений. >
Начертить на фазовой плоскости траектории систем 667-669, записанных в полярных коор-
координатах, и исследовать, имеются ли предельные циклы.
Шйг dip
¦ -^ = г(г-1)(г-2), -? = 1.
dt dt
•^ Почленно разделив одно уравнение на другое, получаем
dr _
dip
Отсюда, если 0 < г < 1, то -щ > 0, т. е. г = r(ip) монотонно возрастает при <р —> +оо (t —> +оо);
если 1 < г < 2, то ^~ < 0, т.е. г = r(ip) монотонно убывает при t —> +оо. Далее, очевидно,
что г = 1 есть решение уравнения A). Следовательно, согласно п. 3.3, окружность г = 1 есть
устойчивый предельный цикл.
Рассмотрим еще одну замкнутую траекторию г = 2. Поскольку при 1 < г < 2 производная
¦щ < 0, а при г > 2 будет -щ- > 0, то траектории г = г((р) при t —> +оо удаляются от окружно-
окружности г = 2. Следовательно, замкнутая кривая г = 2 — неустойчивый предельный цикл (рис. 92).
Других замкнутых траекторий данная система не имеет. >
A)
668. — = sin r,
dt
d^_
dt
¦^ Из уравнения sin г = 0 следует, что г = кк, к 6 Z, к ^ 0 есть изолированные замкнутые
траектории данной системы.
Если 0 < г < ж, то sin г > 0 =*> ^ > 0. Поэтому все траектории, выходящие из достаточно
малой окрестности начала координат, приближаются к окружности г = т при t —> +оо. Если же
§ 3. Фазовая плоскость
319
dr
+оо спирали удаляются от окружности
ж < г < 2тг, то -ffi < 0. Следовательно, г-иг + 0 при t —> +00, т. е. окружность г-= ж является
устойчивым предельным циклом.
Далее, пусть 2я- < г < Ъж. Тогда -gf > 0 и при
г = 2ж. Таким образом, цикл
г = 2тг У *
,—¦
является неустойчивым.
Аналогичным образом устанавливаем, что окружность
г = 3тг
— устойчивый цикл. Вообще, окружности
г = Bfc + 1)тг, к = 0,оо
представляют собой устойчивые, а окружности
г = 2fc;r, к G N
— неустойчивые циклы (рис. 93). >
Очевидно, окружности
Рис. 93
-1 * *-±1±2
являются изолированными траекториями данной системы. Исследуем их на устойчивость.
Пусть 0 < г < 1 - ^г. Тогда -щ > 0, значит, спирали приближаются к окружности г = 1 - -^
изнутри. Если 1 — ^г<г<1 — 2^г,то-д^<0. Следовательно, фазовые траектории навиваются
на эту окружность извне. Таким образом,
— устойчивый предельный цикл.
Аналогичные рассуждения показывают, что цикл
неустойчив. Вообще, циклы
— устойчивые, а циклы
г= 1
Bп +
1
(п = 0,1,2,...)
(п = 0,1,2,...)
Bп + 2)я-
— неустойчивые. Точно также находим, что циклы
r=l + f, 14, .... 1 + -^
2»г 47Г
устойчивы, а циклы
1 +
1
jr' ЗЯ-" • Bп+1)я-'
где п = 0, 1, 2, ..., неустойчивы. Начертить фазовые траектории предоставляем читателю. >
670. При каких условиях система
dp dip
где функция / непрерывна, имеет предельный цикл? При каких условиях этот цикл устойчив?
Неустойчив? Полуустойчив?
¦4 Пусть уравнение /(г) = 0 имеет изолированное положительное решение г = R, т. е. Зе > О
такое, что на сегменте [R — е, R + е] других решений нет. Пусть функция / определена на этом
320 Гл. 6. Устойчивость и фазовые траектории
отрезке. Интегрируя систему, получаем
f R~?<r<R>
R+e
^ R<r<R + e.
J
Отсюда видим, что если несобственные интегралы
R+e
+
dp г dp
расходятся к ±оо, то при i—> R + 0 или г —> R — О полярный угол у> стремится к бесконечности
определенного знака, т.е. окружность, уравнение которой г = R, является предельным циклом.
Далее, если fir) < 0 при Л<г<Л + еи /(г) > 0 при R - е < г < R, то все достаточно
близкие траектории при t —+ +00 приближаются как изнутри, так и извне к окружности г — R,
т.е. предельный цикл будет устойчивым. Очевидно, цикл г = R будет неустойчивым, если
функция / при переходе через нуль меняет знак с "-" на " + ". Наконец, полуустойчивость
наблюдается в том случае, когда с какой-либо стороны траектории приближаются к циклу при
t —> +00, а с другой — удаляются. Следовательно, должно выполняться равенство
dr dr
sgn — = sgn —,
(Д,д+е) dtp (Д-е,л) dtp
т. е. в окрестности г = R функция / знака не меняет.
Разбор вариантов, когда функция / существует только в одной из полуокрестностей точки г =
R или когда только один из интегралов A) является расходящимся, предоставляем читателю. >
671. При каких значениях постоянной а система
dr 2 dtp
- = (r-lX« + sinV), - = 1
имеет устойчивый предельный цикл? Неустойчивый?
А Разделив одно уравнение почленно на другое и проинтегрировав, получаем:
1\ sin2<?4
\г - 1\ = Cexp(Ja+ -) <p
Отсюда видим, что замкнутые кривые возможны только при С = 0 (любом а Ф ~\~)г а также
при а = — ^ (любом С). Однако в последнем случае мы имеем семейство замкнутых, но не
изолированных кривых, поскольку значение параметра С можно менять непрерывно. Таким
образом, окружность г — \ — единственное изолированное периодическое решение \а Ф ~\j-
Ясно, что г = r(ip) —> 1 при (р —> +оо только в случае, когда а < —-j, т.е. предельный цикл
устойчив лишь при а < — ^. >
В задачах 672-678 установить, имеются ли предельные циклы.
672. х = х5 + Зх3 + у2, у = х3 + у5 + t/3 + у.
-4 Поскольку функции / = /(х, у) = х5 + Зх3 + у2, д = д(х, у) = х3 + у5 + уъ + у имеют
непрерывные частные производные и выражение
У- + % = 5х4 + 9х2 + 5у4 + Зу2 + 1 > О,
ах ау
то согласно признаку Бендиксона на фазовой плоскости нет предельных циклов. >
673. х = х3 - 2j/3, jr = Зх + у.
< Возьмем семейство гладких замкнутых линий, покрывающих плоскость Оху, в виде
»(х, у) = Зх2 + у4 = С.
§3. Фазовая плоскость 321
Поскольку выражение
П=^/+!% = бх(х3 - 2уг) + 4у\3х + у) = 6х4 + 4у4 > О,
дх ду ч '
то согласно признаку Пуанкаре данная система дифференциальных уравнений предельных циклов
не имеет. >
674. х = х2 + у2 + 1, у = ху.
¦4 Поскольку система не имеет особых точек, то согласно п. 3.4 никакая односвязная область
на плоскости Оху предельных циклов не имеет. >
675. х + 2х + х3 + х - 0.
Л Переходим к системе
i = У, У = -2«/ - J/3 - х
и применяем признак Бендиксона:
ду д , -,
/х + -(-2у-у>-х) = -2-Зу1<0;
значит, предельных циклов нет. >
676. х + (х2 - \)х + х3 = 0.
М Пользуемся теоремой Левинсона—Смита. Здесь функции / = /(х) = х7 — 1, g = g(x) =
= ж3 непрерывны при всех х и обеспечивают, очевидно, единственность решения задачи Коши,
непрерывно зависящего от начальных условий. Кроме того, выполняются условия:
1) хд(х) - х4 > 0 Vx ф 0;
2) /, д — дифференцируемые функции;
3) х2 - К 0 на (-1, 1) и ж2 - 1 ^ 0 при \х\ ^ 1;
X
3
4) F(x) = I (s1 - \)ds - -т- - х и F(oo) = оо;
о
х
5) G(x) = /s3ds = \ и G(±oo) = оо;
Следовательно, согласно указанной теореме, на фазовой плоскости Оху имеется единствен-
единственный устойчивый предельный цикл. >
677 ж + ж3 — ж + ж = 0
¦Щ Применяем теорему Рейссига. Поскольку
1) /@) = 0, где f(y) = j/3 - у;
2) хр(х) > 0, где р(х) = ж при ж Ф 0;
3) у fly) = У4 -У2 = У2 (У2 - 1) < 0 при \у\ ^ 1;
4) /(y)sgny = Шу1 - 1) ^ е > 0 при \у\ >цг>\\
5) max \уъ - у\ = М = Д= > 0;
6) g(x)sgnx= |ж|^ ^Ят+е при \х\^ 6 = -Лт + е;
7) функции fug непрерывны и обеспечивают выполнение условий существования един-
единственного и локально устойчивого решения задачи Коши, то по указанной теореме на фазовой
плоскости (х, х) существует по меньшей мере один устойчивый предельный цикл. >
678. ж + -Р(ж) + х = 0, где F — непрерывная функция и F(y) > 0 при у > 0, F(y) < 0
при у < 0.
¦4 Возьмем семейство гладких замкнутых кривых v(x, у) = х2 + у2 = С и составим выражение
dv dv
322 Гл. 6. Устойчивость и фазовые траектории
где / = /(ж, у) = у, д = д(х, у) = —х — F(y) — правые части системы дифференциальных
уравнений
* = У, У = -х- F(y).
Тогда, поскольку п = —2yF(y) < 0, то согласно признаку Пуанкаре предельных циклов на
фазовой плоскости нет. >
Упражнения для самостоятельной работы
Исследовать на устойчивость решения уравнений и систем:
I. х2у" - 2ху' + у = 0. 2. Bх + 1Jу" + 3Bж + \)у' - Ау = 0.
3. хУ" + ху' - у = 0. 4. A + z V + ху' + 2у = 0.
f х - 2ty = 0, f ж' + tBx - у) = 0, j Г ж" + tx + ж - у = 0,
¦|у' + 2«х = 0. ' | у'- <(ж - у) = 0. * 1 *2у" + iy' - 2ж + у = 0. '
8. у" + 2г/ + 5у = 0. 9. гЛ + 2^lv + 5у'" = 0. 10. y!V + 2у'" + 4у" + Зу' + 2у = 0.
II. s/v + 2у'" + Зу" + 2у' +ау = 0, 12. х' + х + 5у = 0, у' - х - j/ = 0.
13. х' = х + z - у, у' = х + у - z, z' = 2х - у. 14. х' = 2х — z, у' = л - у, z' — Ъх - у - г.
15. ж' = Зх -Зу + z, у =3х- 2у + 2г, z' = -х + 2у.
Пользуясь первым методом Ляпунова, исследовать на устойчивость указанную точку покоя сле-
следующих систем:
16. х' = х1 + у2 - 2х, у' = Зх2 -х + Зу; @, 0).
17. х1 = ех+2у - cos3s, у' = V4 + Sx ~2ev; @. 0).
18. х' - 1пCеу - 2 cos ж), у' = 2ех - ^8Т12у; @, 0).
19. х' - tg(z - j/) - fx, у' = /9T2S - 3, z1 = ~?у; @, 0, 0).
Исследонать на устойчивость указанную точку покоя систем:
20. х" = 2х-3у + ху, у" = х - 2у + х2 + у1; @, 0). 21. х" = еу - 1, у" = ]пA + ж); @, 0).
22. х" + Зу" - ж + cosy = 0, ж' + Зу' - е2у + 1 = 0; A, 0).
23. х" - 2у" + е*' - 1 + sin(x - Зу) = 0, 4у" - 2х" - sin z' + г/Г^гжТЗу -2 = 0; @, 0).
24. ж" = -VI-2а: - sin у + 4, у" = 1пA + ж); @, 0). 25. ж" = ж - у, у' = е2х - еу; @, 0).
Используя второй метод Ляпунова, исследовать на устойчивость нулевую точку покоя следующих
систем:
26. ж' = у - Зх - ж3, у' = 6х - 2у. 27. ж' = -жу, у' = -г3. 28. ж' = -у - жу2, у' = 2ж - у - у3.
29. ж' = 2у - х3, у' = 2х~ у3. 30. ж' = Зу2 - ж5, у' = -Зж3 - у5. 31. ж" = -у\у" = ж'3.
32. ж" = у\у' = -ж'2. 33. ж' = -ж + Зу' + ж2, у" =-у'- у - Зх.
34. ж" = ж3 - у + ж' - х, у' = х' +у2 +у. 35. ж' = -у' - ж - жу3, у" = ж - у - у'.
36. ж' = -ж - жу, у" = -у3 + ж3. 37. ж" = -ж' - у - ж - жу2, у' = -у + х' - у3.
Глава 7
Метод интегральных
преобразований Лапласа
решения линейных
дифференциальных уравнений
При построении решения задачи Коши для определения соответствующих произвольных посто-
постоянных необходимо решать систему линейных алгебраических уравнений. Этого можно избежать,
если для построения решения указанной задачи применить метод интегральных преобразований
Лапласа. Тогда получим решение задачи, не используя общего решения уравнения. Этот метод,
который получил название операционного или символического исчисления, широко применяет-
применяется для решения многих классов линейных дифференциальных уравнений, как обыкновенных, так
и в частных производных, а также линейных интегро-дифференциальных уравнений типа сверт-
свертки. К этим классам уравнений приводят многие задачи электротехники, радиотехники, теории
автоматического регулирования и ряда других областей науки и техники.
§ 1. Преобразование Лапласа.
Основные понятия и свойства
1.1. Оригинал н изображение.
Функцией-оригиналом будем называть любую функцию / : R —+ С, определенную на всей
числовой прямой М и удовлетворяющую следующим условиям:
1) / — непрерывная или кусочно-непрерывная функция вместе со своими производными
n-го порядка на всей числовой прямой;
2) Ш < 0 f(t) = 0;
3) существуют такие постоянные М > 0 и а > 0, что Vt > 0 справедлива оценка
|/(*)| < Meai.
Показателем роста функции f называется число а = inf{a}. Для ограниченных функций
считаем, что a = 0.
Условия 1) и 3) выполняются для большинства функций /, описывающих физические про-
процессы. С физической точки зрения условие 2) вполне естественное, поскольку для физики безраз-
безразлично, как ведут себя искомые функции до начального момента времени, который всегда можно
принять за момент t = 0. Операционный метод приспособлен к решению дифференциальных
уравнений с начальными условиями, о чем упоминалось выше.
Простейшей функцией-оригиналом является функция Хевисайда т\, где
,«>={»¦
если t < О,
если t > 0.
324 Гл. 7. Метод интегральных преобразований Лапласа
Если функция <р удовлетворяет условиям 1) и 3) и не удовлетворяет условию 2), то произве-
произведение
t < 0,
удовлетворяет условию 2), т.е. будет оригиналом. В дальнейшем множитель т) будем опускать в
записи функций, считая их равными нулю при t < 0.
Определение. Изображением функции f по Лапласу называют функцию комплексного
переменного р = s + ia, определяемую соотношением
+ 00
F(P)= J f(t)e'vtdt. A)
о
Связь между функциями / и F символически обозначается знаком ==, т. е. / == F. Смысл
этого обозначения состоит в том, оригиналу / сопоставлено изображение F, а изображение F
имеет своим оригиналом /.
Если функция / — оригинал с показателем роста а, то функция F существует в полуплос-
полуплоскости Р = {р 6 С | Rep > а} и является в ней аналитической функцией.
1.2. Свойства преобразования Лапласа.
Теорема 1 (свойство однородности). Если / == F и а ? С, то а/ = aF.
Теорема 2 (свойство линейности). Если fj = Fj, Rep > а} (j = 1, п), то
п п
IT^j/j =F YtVjFj, Rep > max а,,
3 = 1 j = l '^"
где fij — заданные постоянные числа, действительные или комплексные, oij — показатели роста
функций fj.
Теорема 3 (свойство подобия). Пусть / = F, Rep > а. Тогда \/р > О
Теорема 4 (запаздывания). Если / = F и т > 0, то
f(t - т) = e-prF(p).
Смысл этого соотношения состоит в том, что смещению аргумента в классе оригиналов соответ-
соответствует операция умножения на экспоненту в классе изображений.
Теорема 5 (опережения). Если f = F и т > 0, то
fit + г) = epr (f(p) - J e-vtf(t) dt) .
Следствие. Если f — Т-периодическая функция, то
т
о
Теорема 6 (смещения). Если f == F, р0 6 С, то
Теорема 7(о дифференцировании оригинала). Если f = F и функции fk)ik = 1, п)
являются оригиналами, то
/(*)=pF(p)-/(O);
fmit)=p2Fip)-pf@)-f'i0);
= p~F(p) -/"'/(О) -pn'2fi0) - ... -
где /№)@) = Дщ /w@ (* = 0, » - 1) в общем случае.
§ 1. Преобразование Лапласа. Основные понятия и свойства 325
Теорема 8 (о дифференцировании изображения). Если F == /, Rep > а, то
F'(P) = -tf(t);
FB)(p) = t2f(t);
Теорема 9 (об интегрировании оригинала). Если f = F, Rep > а, то
. F(p)
4
Jf(T)dT =
О
Теорема 10 (об интегрировании изображения). Если f Ф F, Rep > а и интеграл
/ .F(<7) dq сходится в полуплоскости Р = {р 6 С j Rep > af > а}, то
7 ™ ***'-?¦
Теорема 11 (о предельных соотношениях). Если / является оригиналом вместе со
своей производной /' и F ф /, то MmpF(p) = /@), где р —> ос внутри угла |argp| < Ц- — 6 и
/@) = lim /(<)• Если, кроме того, существует Jim f(t) = f(+oo), то limpF(p) — f(+oo).
Найти изображения функций.
679. Функции Хевисайда t],
¦< Согласно формуле A), п. 1.1, имеем
+? ? е-р4 t=ti /j е~рз;\
Р(р)= n(t)e'ptdt= lim e~pt dt = lim = lim .
J X-+O.J х^+эо р t=x x-+o,yp p у
Если Rep > 0, то Jim e~TX = 0. Следовательно,
1 = -, Rep > 0.
P
680. f(t) = eat.
-^ Согласно определению, полунаем:
+0° +o° z -(p-a)
F(p)= f eate~pidt= j e""*""" dt = lim f e'^'^ dt = lim
(=0
P-
= lim j I = , если Rep > Re a.
z-+oo \p- a p - a J p - a
Таким образом,
eat = , Rep > Re a. >
p-a
681. f{t) = al (a > 0).
4 Представим функцию / в виде a' = e')na и воспользуемся решением предыдущего примера.
Получим
а' = , Rep > In a. to-
top-In a
326 Гл. 7. Метод интегральных преобразований Лапласа
682. f(t) = ta, а>-1.
^ По определению изображения имеем
+ 00
у^ F(p) = I tae-pt dt.
о
Полагая pt = т, получим
Рнс.94 Р"Л
где 7 — луч с направлением | argp| < у (рис. 94). Функция т i-+ е~тта аналитическая в полуплос-
полуплоскости Т = {т ё С | Rer > 0}. Рассмотрим замкнутый контур L, соста-
составленный из упорядоченного набора G1, 7д> 7~) ориентированных частей
(см. рис.95). По теореме Коши для аналитических функций имеем
О у,
Рис. 95
L
откуда
v dr = Je-rTa dr + j е'тта dr + /VV dr = 0,
/г
e~TTadT = — I e~TTadr и что т = t на 71). Поскольку ]im е~тта =
/ [г[^+ос;
= 0, то lim /e~TTadr = 0. Следовательно,
Л^+оо у
7Я
+ ОО
/ е~тта dr= I е~Ча dt = Г (а + 1), а + 1 > О,
7 О
где Г1 — гамма-функция Эйлера. Таким образом,
Р1^Г 0. A)
Полученный результат можно распространить и на случай, когда а < — 1 Л аф -п, п ? N,
п > 1. Для этого воспользуемся известным свойством Г'-функции, выраженным формулой:
Г(п + а) = (п + а- 1)(п + а - 2) ... аГ(а), а > О,
которая позволяет продолжить ее на отрицательную полуось с выброшенными точками хп — —п
(п 6 М), полагая
Г(п + а)
Г(а)= к ' -, -п<о<-п+1.
а(а + 1) ... (а + п- 1)
Для рассматриваемого случая а < -1 Л аф —n, n S N, n > 1, имеем
4
• (а + 1)(а + 2) ... (а
В последнем случае оригинал и изображение будем называть обобщенными.
683./(t) = «"+5.
¦4 В соответствии с формулой A) из примера 682, имеем
Воспользуемся известными свойствами Г-функции:
§ 1. Преобразование Лапласа. Основные понятия и свойства 327
Получаем
/ 1
= n+-
V 2
В частности, V? =
684./(t)=-
Применим формулу B) из примера 682. Получим
( ?)(|) (|) Bп - 1)!!
В частности, Д А|~
Г i, если 0 ^ t ^ а,
685. /(t) =| la - t, если a <t <2a,
{ 0, если t^2a,t <0.
< Применим формулу A), п. 1.1. Получим, интегрируя по частям:
F(p) = [ f(t)e~pt dt= [ tt'Tt dt+ I Ba - t)e'pt dt =
¦ +
(=0
e
P V1
Таким образом,
+
t=a
686. a) f(t) = sint; 6) /(?) = shi; в) f(t) = cost1; r) /(?) = cht.
•4 Воспользуемся решением примера 680: eat = „ 1 a , если Rep > Re a.
a)sini=Ife-'_e-^ > f >
2i ^ / ' 2i \p-i p + i/ p2 + I '
I / , a I / ] IN I
6) sht = - (e* - e~M =
2^ ) ' 2
2 Vp-1 p+i; p2- г
в)С0^Ч(е"+е"")Ц(р^^) = ?тт;
2 Vp- 1 Р+1У pL-Y
При решении примера применяли свойство линейности преобразования Лапласа.
687. a) f(t) = sin at; б) /(«) = sh at; в) /(*) = cosa«; г) f(t) = ch at.
Щ Воспользуемся теоремой подобия и предыдущим примером. Имеем
. . . . 1 1 а
а) sin at = j = — ;
a
iot a
б) i sh at = siniat = -r ;—r, shat = — -;
p2 + (iaJ p2 - a2
1 ^ p
в) cosa« = - -—e = ^^;
r) ch at = cos ia< =
— —т,
р2 + (iaJ
328 Гл. 7. Метод интегральных преобразований Лапласа
688. а) fit) = cos2 at; б) fit) = ch2 at; в) fit) = sin2 at; r) /(*) = sh2 at;
Д) /@ = sinatcos/?t; e) /(t) = sinat ch/й; ж) /(О = cosatsh/M.
¦4 а) Представим функцию / в виде f(t) = ^A + cos2at) и воспользуемся изображениями
функций fiit) = 1 (см. пример 679), функции /2(t) = cos2at (в примере 687, в) вместо а берем
2а), а также свойством линейности преобразования Лапласа. Получим:
2 + 2а2
2 /-'Г1 Р \ р2 + 2а
C0S а ~ 2 1 + )
б) Запишем функцию / в виде /(t) = cos2 tat и воспользуемся решением примера а). Находим
h2 at = P2+2('QJ = Р2 ~ 2«2
С п " р(р2 + 4(гаJ) pip2-4а1)'
в) Поскольку sin2 at = ^ A - cos 2at), то
1/1 р \ 2а2
sin at = - - -
2 Vp p2+4a2j p(p2 + 4a2)'
г) Воспользуемся равенством г2 sh2 at = sin2 iat и решением примера в). Имеем
'•^22а2 , 2а2 , 2а2
9 9 9 UJ iU ? iU 9
г2 sh2 at = sin2 iat == —-^ —-=г2-—5——5-, sh2 at =
• р(р2+4(гаJ) р(р2-4а2)' • p(p2 - 4a2)'
д) Представим функцию / в виде fit) = j (sin(a - /3}t + sin(a + /3)t) и воспользуемся реше-
решением примера 687, а). Получим
а-в а+/3
/ +
• 2 Vp2 + (а - РJ р2 + (а + /3JУ (р2 + (а-/3J)(р2 + (а+/3J)'
е) Запишем функцию / в виде sin at ch pt = sin at cos ipt. Тогда, согласно д), имеем
sin at ch pt = 7-
a (p2 + a2 + p2) a (p2 + a2 + /32
+ (a - i/3J) (p2 + (a + г/3J) (j,2 + a2 - /32J + 4a2/?2'
ж) Представим функцию / в виде cosatsh/ft = -isiniptcosat. Решение примера сводится
к случаю д). Получаем
г / t/3 - a if3 + a
cosatshpt = -- +
2 Vp2 + (г'/З - aJ p2 + (г/3 + аJ
\ ( в + ia p-ia \ _ pip1 -a1-
2 \р2 + а2-р2- i2ap р2 + а2 - р2 + i2ap) (р2 + аг _ /з2J + 4а2/32'
689. a) fit) = sinM - ?>о); б) f(t) = sh(wt - ip0); v) fit) = cosiwt - tp0);
r) fit) = ch(wt - ?>0); д) /<*) = (at - b)a.
¦4 Применим теоремы подобия и запаздывания для нахождения изображения оригинала вида
fiat - t0), где t0 > 0 и a — комплексное число. Пусть / == F, тогда по теореме подобия
fiat) == ^F (jj- j. По теореме запаздывания имеем
^. A)
а) Воспользуемся решением примера 687, а) и формулой A). Получим
§ 1. Преобразование Лапласа. Основные понятия и свойства
329
б) Аналогично, принимая во внимание решение примера 687, б), имеем
- ш1'
в) Согласно 687. в), coswt = -^—т. По формуле A) находим:
р + ш
_» р
cos(wt — <ра) = е <" — -.
г) Воспользуемся решением 687, г) и формулой A). Получим
ch(w< — ipa) = е~~ш — -.
д) Принимая во внимание формулу A) из примера 682, а также формулу A) из настоящего
примера, имеем
, ± гчв . 1 Г(а + 1) _рь ааГ(а + 1) _?»
— обобщенная единичная функция Хевисайда.
а/
690./(o = v(t-«o) = { j; JJ{001
¦4 Согласно решению примера 679 и формуле A) из примера 689, получаем:
e-pk
W -10) =
Р
691./(о = { S;
¦^ Представим функцию / в виде f(f) — (tj(t) - tj(t - т))а. Тогда
если 0 < t < т,
если t < 0 или ? > т.
\Р Р
Г t -2а, если 2а < ? < а + 6,
692. f(t) = I 26 -t, если а + Ъ < f < 26, (рис. 96).
[ 0, если ? > 26 или t < 2а
^ Поскольку функцию / можно представить в виде
Ь-а
А
0 2а
Рис.96
/(О = (« - 2o)v(t - 2а) - (f - 2а)»7(« - а - 6) + B6 - t)t](t - а - Ь) + (t - 2Ь)ф - 26) =
= (t- 2a)tj(t - 2а) - 2(t - а - 6)»/(« - а - 6) + (t - 26)?/(< - 26),
то
(е-р-е-*)'
f(t) =?
р' р^
(см. решение примера 689, д)). >
если t < О,
если n ^ t ¦
¦4 Записав функцию / в виде
f(t) = ф - 1) - ф - 2) + 2ф - 2) -
- 3) + Ъф - 3) -
4 *-
получаем
1 2 3
Ряс. 97
330
694. fit) = { J'_ е-ц(_0)]
Гл. 7. Метод интегральных преобразований Лапласа
если t < а,
если t > a
(рис.98).
¦4 Очевидно, что функцию / можно представить в виде
f(t)
Следовательно,
^ е
f{t) ^
О а
Найти изображения периодических оригиналов.
Рис.98
695.
2*) =
sint, если 2шг < t ^ Bп +
если (In + 1)тг < t ^ (.
^ Воспользуемся следствием из теоремы 5 п. 1.2: если /
является Т -периодической функцией, то
1 Т
В рассматриваемом случае получаем:
е
о
/ХО
7Г
лг 2я
Рис.99
ll/OO
1 + e1"
Таким образом,
A - e-2lr?)(p2 ¦
1
696. /@ = |sinot| (рис. 100).
< Функция / — \ -периодическая, следовательно
F(p)
1 1 -vt ¦ ... ! т / (-p+m)tj. !
= ^ / e p sin a? dt = =- Im / e r ' dt = s
1-е-»!/ l-e-'f / l-e-'г
Рис. 100
e ^(°cos at
D— — V —
a ep2a-fe2a
inf _ f 1, если 2n?r < t < Bn + l)?r,
in«| ~ I -1,
697. f(t)=< I sin*| 1-1, если Bn + 1)тг < f < Bn + 2)тг, „ e Zo (рис. 101).
( 0, если t < 0
¦* Сужение функции / на положительную полуось есть 2тг -периодическая функция, поэтому
1 *
| с-
Л 1 =
7 1-е*»
+ е-»1»)
> 2
§ 1. Преобразование Лапласа. Основные понятия н свойства
331
Следовательно,
sini 1 рж
#th
1
о
-1
л
2я
Зл:
4л:
t
7V7\
Ряс. 101
ц - 4п,
698. f(t) = f(t + 4а) =
О 2а 4д 6а 8а
Рис. 102
если 4па < t < Dn + 1)а,
если Dп + 1)а < t < Dп + 2)а, п 6 Zo
если Dп + 2)а < t < Dп + 4)а, t < О,
(рис. 102).
Щ Функция / 4а-периодическая, и ее изображение найдем по формуле
1
a(l - е-4"?)
Таким образом,
+
ар2A - ,
A -
1-.
thf
ap2(l
2(l - e-^
X + e-2"?) ap2(l +e-"J>)(l + e0?) ap2 A + e0?)'
thf
Пользуясь теоремой смещения, найти изображения функций.
699. а) f(t) = e~at sinut; б) f(t) = e~at shut; в) f(t) = e'at cosut;
r) f(t) = e~atchwt; д) f(t)=taepi; e) f (t) =ta sin/3t; ж) /(«) = ^
3)/(t) = ^shat; H)/(O = ^'shat; к) f(t) = ta cos/3t;
л) /(*) = D-e"'cosa«; м)/0) = |j-cha«; н) /(«) = ^e"'cha«.
•4 В случаях а)—д) можно непосредственно применять теорему смещения. В общем же случае,
если требуется найти изображение функции ip, следует, если это возможно, представить ее в виде
ip(t) — ePoiip(t), po = const и применить теорему смещения. Тогда
где Ф — изображение функции ip. Имеем:
a) sinut = -т-^—т (см. пример 687, а)). По теореме смещения
р +ш
е atsmwt =
б) shut = ¦, ш ¦, (см. пример 687, б)). Следовательно,
р — ш
" (р + аJ - ш2'
332
Гл. 7. Метод шгтегральных преобразований Лапласв
в) cosivt = -*-*¦—т (см. пример 687, в)). Тогда
р +ш
(р + аJ + ш1
г) chart = -j-2—j- (см. пример 687, г)). По теореме смещения
р —и
е-chart = +
д) fa = rfo+11) (см. пример 682). Тогда
д, ^ Г(а + 1)
6 ' (р)°+
В частности, tne^1 =
е) решение сводится к случаю д). Действительно, ta sin pt = -^(fV5' - tae-1/").
Если a = n, то
Если a = -1-, то
В частности,
sin /3t _ v^"
VI ~ ~2i
ж) Решение сводится к случаю е). Имеем
Г
з) Представим функцию / в виде f(t) — \ (^теа' - -д-е aiJ и воспользуемся случаем ж).
Получим
(р + а)п+{ - (р - a)"+1
n!Sha'4' 2 V(p -а)-+' (р + а)^1;" 2(р2-а2Г'
и) Воспользуемся решением з) и теоремой смещения. Имеем
— e^'shet =
к) Из представления функции f(t) = \ (fe'131 + tae~'^j, решения д) и теоремы смещения
находим:
C°SP ¦ 2 V (р - г/3)а+1 (р + г/3)а+1 У
+ /32)а+
л) Поскольку, согласно д), jjj- cos at, = &—tcy г +Уя+г —, то по теореме смещения имеем
(р - /3 + ia)n+l + (р - /3 - ia)n+l
§ 1. Преобразование Лапласа. Основные понятия и свойства 333
м) Так как ? chat = \ (^еа* + ще"") и, согласно д), tneat == _^ +| , то
tn ___ 1 / 1 1 \ _ (р + a)n+1 + (р - a)n+1
cha<^ + J
н) Воспользуемся решением м) и теоремой смещейия. Находим:
'" т , . (р- C + a)n+1 + ip- в- а)п+1
— ер chat = —— Л , —¦ >
п! ' 2((р - /ЗJ - a2)n+1
Найти изображения дифференциальных выражений.
700. ?у = yiv@ - 5у'"(<) - 4y"(t) + 2y'(t) - y(i) + 8 при условиях уф) = 5, у'ф) = 0,
«в Пусть у(О = Y(p). Тогда по теореме 7, п. 1.2, получаем, принимая во внимание начальные
условия:
y'(t)=pY(p)-5; y"(t)=p2Y(p)-5p; y'"(t) = p3Yip)- 5p2 + 1; yw(t) = p4Yip)-5p3+p-2.
Применим свойство линейности преобразования Лапласа. Имеем
+ 2(vY(v) -5)- Yip) +- =
Ly = P4Y(p) -5Р2+р-2-5(Р'?(р)-5Р2+\)-4 (P2Y(p) - 5р) + 2(pY(p) -5)-Y(
Q
= (p4 - 5ръ - Ар2 + 2p - l) Yip) - 5p3 + 25p2 + 21p - 17 + -.
V J p
701. Ly = y'"(t)-2y"(t) + 3y'(t)-y(t) при условиях у'@) = уф) = 0, y"@) = 1 и y(t) = У(р).
¦4 Действуем по той же схеме, что и при решении предыдущего примера. Получаем:
y'(t) = pYip) - уф) = PY(p); y"(t) = P2Y(p) - уф)р - у'ф) = P2Yip);
y'"(t) = P3Y(p) - уф)р2 - ру'ф) - у"ф) = p3Y(p) - 1.
Следовательно,
Ly = p'Yip) - 1 - 2P2Y(p) + 3PY(p) - Y(p) = (p1 - 2p2 + Ър - l)Y(p) - 1. >
702. Найти изображение производной функции f(t) = лД.
¦4 Имеем
з л з Г
Р2 1 р2 2р2
Функция f'(t) = у^/7 существует Ш > 0 и не существует при t = 0. Изображение таких функ-
функций находим по теореме дифференцирования оригинала, в которой предполагается, что fn)(t)
существует V< > 0, а при t = 0 f{n)(t) вообще может не существовать. Таким образом,
/'(О Ф Р ^-у - /(°) = -^Т <так как /(°) = °)- >
2рг 2р2
703. Ly = y" + 2yw + Ay, уф) = у'ф) = у"ф) = 0, у'"@) = ylv@) = -1.
•< Принимая во внимание начальные условия, получаем:
yv(t)=P5Y(p)+p+\, yw(t)=p4Yip)+\,
Ly = (р5 + 2р4 + 4) Yip) +p + 3.
>
334 Гл. 7. Метод интегральных преобразований Лапласа
С помощью теоремы о дифференцировании изображения найти изображения функций.
704. a) f(t) = t sinat; б) f(t) = tcosat; в) f(t) = tshat; г) f(t) = tchat.
¦4 а) Согласно теореме 8, п. 1.2, F'(p) = ~tf(t). Поскольку sinat = 3 Q ,, то
p + a
I a \i 2pa 2pa
—t sin at=[—z = —, t sinat = r—.
^p + a1' (p + a LY (p2 + a2J
б) Так как cos at = } P ¦, и -t cos at = I -r^—-?) = —s—%-у, то
p + a2 \ pl + a2 > (p2 + a1I
tcosat =- —2 j-y.
в) В примере 687, б) получили, что sh at = г а i. Тогда (- л а г) = т*"* i i >
р — а \р — а / (Р ~- ос )
2ра
tshat= , , .-.
(р2 - а2)-1
/ V 2 2
г) Поскольку chert = , У _, и -г^-т = —Л—ттт, то
(p)
705. f (t) - t sin at sh at.
¦4 Из представления /(<) = —i sin iat sin at = -^-(cos(l - i)at — cos(l + i)at) и решения
примера 687, в), получаем:
г / р р
= — -т т—т г = -— .
' 2 Vp2 + A - гJа2 р2 + A + гJа2 / р4 + 4а4
Согласно теореме 8, п. 1.2, имеем:
2а2Dа4-2р4) 2a2C/-4a4)
Таким Образом. 2a2Cp4 - 4a4)
=
== ——— . >
(p4 + 4a4J
706. f(t)-t2 cos2 at.
¦4 По теореме 8, п. 1.2, F"(p) = t2f(t), где F = /. При решении примера 688, а) получили,
что cos2 a< = Л fy-. Следовательно,
р(р' +4а')
,2 2 4 . ( Р + 2а2 \"
t2cos2at =
707. Найти изображения функций:
a) S(t) = / ^"ж- <*ж — синус-интеграл Френеля; б) C(t) = I c°sa: da; — косинус-интеграл Френеля.
j/ \/,TlX J \ J.TTX
о о
Произведя замену х = и2, получаем:
•Л
5@ = J- /sinu2du, C(t) = J- /cosu2du.
о о
Как известно из курса математического анализа,
+00 +00
/ sin u2 du = / cos u2 du = —= (интегралы Френеля).
§ 1. Преобразование Лапласа. Основные понятия и свойства 335
Следовательно, 5@) = С@) = 0, 5(+оо) = С(+оо) = \. Согласно теореме 9 об интегрировании
оригинала
где F = /. Поэтому 5@ = ^, C(t) = ^f-, где F(p) = -^L, Ф(р) = ^g. При решении
-^L,
v v р2 + 1 - Р JJp + P
примеров 699 е), к), получили: F(p) = -v , =—. Ф(р) = -*•—т=г—=—. Окончательно имеем
2У i I ' 2У + 1
708. Найти изображения функций:
/ sin г
a) Si(?) = / ат (интегральный синус);
о
/SH1 Г
dr (интефальный синус);
г
в) shi(f) = / dr (интегральный гиперболический синус).
о
¦4 Воспользуемся теоремой 10 об интегрировании изображения. Поскольку sinf = --,—-, то,
р + 1
согласно указанной теореме, получаем:
sint г dq
t
v
- Г dq
¦ J q2 + \~
arctgp
= - - arctg p = arctg -.
Применим теорему об интегрировании оригинала. Находим:
Г sin г 1 1
Щ) = / dr = - arctg -.
I г р Р
Далее, поскольку / ^р- dr = -j, то si(t) = S\(t) — -j. Следовательно
о
1 1 7Г 1 / 7Г 7Г 1\
si(t) = - arctg так как — • 1 = — .
р р 2р \ 2 2р/
Представив интегральный гиперболический синус в виде
получим, приняв во внимание решение в случае а):
1 it 1 1 р + 1
ishi(t) = - arctg - = - arth -, shi(t) = - In .
P P P P 2 p-1
Действительно, обозначив arctg ? = ia, получим:
i sin ia 1 e'(ia) - e-i(fa)
— = tg ia = = rr-T rr— = г th a,
p cos ia i e'<la> + e-<la>
откуда
1 11 г г г" , 1
tha=-, a = arth-, - arctg- = -a = -arth -. >
P P P P P P P
336 Гл. 7. Метод интегральных преобразований Лапласа
709. f(t) =eZ!p±.
¦4 Согласно решению примера 699, а), имеем e~ai sint = Ц • По теореме об инте-
(р + а) + 1
грировании изображения получаем:
t
e~Q(sin? . Г dq
"р
sin It sin Ж
= arctg(g + a)
q=p
= — - arctg(» + а) = arctg -
2 i
710. f(t)
Ч Сначала найдем изображение функции <p(t) = sin at sin/3t = -j fcos(a — /3)t — cos(a + /3)t
Согласно решению примера 685, в) и по свойству линейности изображения, имеем
*»(«)= ^ ' Р
В рассматриваемом случае sin It sin "it = —j ^ . Далее применяем теорему об интегри-
(р + 16)(р + 100)
ровании изображения. Из представления
1 1 /(р2+100)-(р2+16)\ 1/1
(р2+16)(р2+100) U\ (р2 + 100)(р2 + 16) у 84 Vp2 + 16
находим:
§ 2. Свертка функций. Теоремы разложения
2.1. Определение свертки.
Сверткой <р* f непрерывных функций <р и /, заданных на положительной полуоси числовой
прямой R, называется интеграл
J(t-T)f(T)dr. A)
Свертка коммутативна (т. е. <р * f = f * <р), ассоциативна (т. е. (<р * /) * ф = <р * (/ * г[>)),
дистрибутивна относительно операции сложения (т. е. <p*(f + ip) = <p*f + <p* ip).
2.2. Теорема умножения (Э. Бореля).
Если f == F, Rep > а0, <р = Ф, Rep > аь где а0 и at — показатели роста функций f и <р,
то f *<р = РФ.
2.3. Обобщенная теорема умножения (А. М. Эфроса).
Если f = F, <p(t, т) = Ф(р)е~т'(г>), где Ф и q — аналитические функции, то
+ОО
J f(r)<p(t, r)dr = 9(p)F(q(p)).
§ 2. Свертка функций. Теоремы разложения 337
2.4. Формулы Дюамеля.
Если f*<p = J f(r)<p(t -r)dT = .Р(р)Ф(р), то
о
или '
f(t)<p(O) + J f(T)<p't(t -r)dr = pF(p)*(p), B)
<p(r)ft(t -r)dr= pF(p)$(p). C)
о
Левые части соотношений B) и C) называют интегралами Дюамеля.
711. Найти ip * /, где <p(t) — t2, f(t) = cosotf.
¦4 Согласно определению, ,
ip * f = (t — t) cosojt dr.
о
Поскольку cosojf Ф —j-^—j, i2 = -^, то по теореме Бореля получаем
p -\- ш p
712. Найти изображение функции f(t) = CCOcosi + S^Jsint, где С(<) и 5@ соответственно
косинус-интеграл и синус-интеграл Френеля (см. пример 707).
¦4 Функция / имеет вид
t t . t
/cost г sin г /¦ 1
-7= dr + sin f / , dT = cos(t - t) . dr.
V2kt J V2ttt J у/2жт
о oo
Таким образом, / = <p* xf>, где ^@ = cos^, ip(t) = J-—. По теореме Бореля /(f) Ф ^(р)Ф(р), где
^~Т ^ cosi> ф(Р^ = ~7Т" ^ ~1Т1 ¦ Таким образом,
713. Найти изображение функции /(<) = C(?)sin< - S(t)cost.
¦4 Поскольку f(t) — J sin(t - t)^~ dr, то по теореме Бореля
, F(p) = ——-r=sint, Ф(р) =
Итак,
714. Найти свертку р * /, где <p(t) = ta, f(t) = tp, a > 0, /3 > 0, и ее изображение.
•< Согласно примеру 682 имеем
ta 1 «" 1
По теореме Бореля получаем
J1 ^
р"^^^^ Г(а + 1) * Г(/3 +
или
' Г(а + 1)Г(/3 +1)
338 Гл. 7. Метод интегральных преобразований Лапласа
Поскольку ^^г = TWTJT^, то Л.ТТДПУ = ТТа+ВГф + В1" *t • откуда
- _ Г
- _ Г(а+\)Гф+\)
Полученный результат позволяет установить связь между Г- и В-функциями Эйлера. Действи-
Действительно, согласно определению свертки, имеем
Полагая в интеграле г = tx, получаем dr = tdx, та = taxa, (t
f Q_, 0_, Г(а)Гф) def T>l
или уж A_ж/ da; = ___ = Bia, /3). >
v ' Г(а + р + 2) ' J ~ Г(а + Р)
о о
Функция erf i = -4= /е~т rfr называется интегралом вероятности. Ряд е"' = V (~1)™--г равномерно
сходящийся, поэтому его можно почленно интегрировать. Имеем
_2п ^ ш у2п+1
Очевидно, erf(-<) = -erfi, (erft)' = Д=е^'2 > 0, erf(O) = 0, erf(+oo) = Д= ^~ = l. Следовательно,
функция erf — нечетная, непрерывная, возрастающая.
При больших значениях аргумента t рассматривают функцию
J
Функция Erf — убывающая, непрерывная.
+ 00 t +00
Erf t = 1 - erfi = -= f е~т2 dr - —- /e"^ dr = -= f e'7' dr.
0Г J y/n ./ -У? У
715. Найти изображение функции f(t) — егГ(\Д).
Ч Воспользуемся соотношениями е( = j, -у- == —т- и теоремой Бореля. Получим:
t t t t -Л
= e erf
По теореме смещения имеем
erf (Vt) =
PVP+1
716. Найти изображение функции fit) = Erf (Vt).
¦4 Согласно определению, Erf (Vt) = 1 - erf ^V^J . Следовательно,
Erf(Vf) = - - ^== = p+l
P
717. Найти изображение функции f(t) = e~' .
¦4 Применим преобразование Лапласа. Получим:
-2 = Je-'-'e-'2 dt = et Je-MK dt = Л Je^ dr = ^ e^ Erf (f) . >
0 0 ?
§3. Обратное преобразование Лапласа 339
718. Найти изображение функции f(t) = erf?.
¦4 Воспользуемся решением примера 717 и теоремой об интегрировании оригинала: если
/ = F, то Jf(r)dT = Ш. находим:
о
1 е! /р\
erf<= -e4 Erf ^ . >
р V2/
719. Найти оригинал функции .F, где F(p) = — —j.
•< Разлагая функцию F на простые дроби, получаем:
p + 1 p + 2 (p + 2J'
Поскольку T^pj = e~\ y+j ^ e~2'> т0 решение примера сводится к отысканию оригинала
функции <р(р) = —*—-у = j_2 ' р + 2 ¦ По теореме Бореля
( t
<р(р) = J е'2A'т)е'2т dr = e'2t J dr = e'2tt.
о
Окончательно имеем
720. Найти оригинал функции F, где F(p) = —5
(Р
5^
(Р + 9)(pz + 4)
•< Записав Р(») в виде F(p) = —Л Л— и приняв во внимание, что —Л— = cos 3t,
р+9р+4 р + 9 ' '
= cos It, по теореме Бореля получаем:
t t
f(t) = j cos3(t - r)cos2r dr = - /(cosEr - 3t) + cosCi - т)) dr =
о о
1 /sinEr — 3t) \\T=t 1 /sin2f sin3< \ 1
= - sinCt-r) = - ——- + -— sin2< + sin3f = -Csin3t-2sin20- >
I \ 5 / [r=o 2 V 5 5 /5
721. Найти оригинал функции F, где F(p) = -ч—у .
р (Р +1)
Ч Запишем функцию F в виде F(p) = р- -у • -j = р<р(р)Ф(р), где w(p) = Л-, V(p) = ~г^— •
Р Р +1 Р Р +1
Л J.3 1
Из соотношений -у == -г = f(t), -^—- = sin< = g(t), по формуле B), п. 2.4, получаем (записав
ее в виде -% Jf(T)<p(t ~r)dr = F(p)*(p)):
} (t K 1
1 d } (t - гK 1 г 2 t2
JsiTdit)sid
§ 3. Обратное преобразование Лапласа
3.1. Формула обращения Римана—Меллина.
Теорема (формула обращения Римана—Меллина). Если функция f является ори-
оригиналом, т.е. удовлетворяет условиям 1), 2), 3) п. 1.1, a F служит ее изображением, то в любой
340 Гл. 7. Метод интегральных преобразований Лапласа
точке непрерывности функции f выполняется равенство
a+ioo
где интеграл берется вдоль любой прямой {р 6 С | Rep = а > а} и понимается в смысле главного
значения по Коши. В точках разрыва функции f вместо /(?) в левой части формулы A) следует
взять I (f(t + 0) + f(t - 0)).
3.2. Сведения из теории функций комплексного переменного.
Напомним читателю, что функция / : С —> С, дифференцируемая в каждой точке некоторой
области D, называется аналитической (иначе, регулярной или моногенной) в этой области.
Если функция / аналитическая в кольце К = {z 6 С | г < \г - zq\ < R}, то она может быть
представлена своим рядом Лорана
00
z0)\ A)
равномерно сходящимся в любой замкнутой области, принадлежащей кольцу К.
Ряд A) можно записать в виде
ОО 00
f{z) = ^cn(z~zor + Z7r~Tn- B)
При этом ряд ?с,(г — zo)" называется правильной частью ряда Лорана, а ряд X) т—~" \«- —
n=0 n=l \z~ z0)
главной его частью.
Если функция / дифференцируема в некоторой окрестности точки zo, за исключением, быть
может, самой точки z0, то za называется особой точкой однозначного характера.
Если главная часть ряда Лорана тождественно равна нулю, то z0 называется устранимой особой
точкой.
Если главная часть ряда Лорана содержит конечное число членов, то точка zo называется
полюсом. Число т называется порядком полюса, если с_т Ф 0, а с_т_; = 0 Vj 6 N.
Теорема 1. Точка z0 является полюсом т -го порядка тогда и только тогда, когда существует
такая непрерывно дифференцируемая функция <р, что
C)
Если с_„ Ф 0 для бесконечного множества значений п 6 N, то точка z0 называется су«<е-
- 1 1
ственно особой. Например, функции гне', z н-+ sin —, z ь+ cos ^ имеют в начале координат
существенно особую точку.
Функция / называется целой или голоморфной, если она вовсе не имеет особых точек. Напри-
Например, функции z *-* ez, z I-* sinz, ги cosz являются целыми.
Функция / называется дробной или мероморфной, если она не имеет других особенностей,
кроме полюсов.
Согласно определению, мероморфная функция есть частное двух аналитических на комплекс-
комплексной плоскости С функций, причем функция в знаменателе имеет хотя бы один изолированный
нуль на плоскости С, а если нулей бесконечное множество, то оно не имеет предельных точек.
Вычетом функции f в изолированной особой точке а называется число
7
где 7 — достаточно малая окружность 7 = {z 6 С : \z — а\ = 6}.
Если функцию / можно представить рядом Лорана B) в окрестности изолированной особой
точки а, то
res/= <:_,. E)
§ 3. Обратное преобразование Лапласа
341
В устранимой особой точке вычет всегда равен нулю. В полюсе порядка т вычет вычисляется
по формуле
Для полюсов первого порядка формула F) принимает вид
F)
G)
Если при этом в окрестности точки a f(z) = ±к?, где <р и t/> — аналитические функции в
точке а, причем <р(а) фО,а if>(z) имеет в точке а нуль первого порядка (т.е. ф(а) = 0 и ф'{а) Ф 0),
то вместо формулы G) можно пользоваться формулой
3.3. Теоремы разложения.
Непосредственное применение формулы A), п. 3.1, затруднительно. Мы рассмотрим здесь
так называемые первую и вторую теоремы разложения, которые значительно упрощают процесс
восстановления оригинала по его изображению.
Теорема 1. Если изображение F допускает в окрестности точки р0 = 0 разложение в сходя-
сходящийся ряд Лорана по степеням j
то ему соответствует функция-оригинал
4@/@ = '
A)
B)
*=о
Прежде чем формулировать вторую теорему разложения, приведем наводящие соображения.
Если / — аналитическая функция внутри области D всюду, кроме конечного числа особых
точек cij (j = 1, п) и непрерывна на границе С этой области, то справедлива формула Коши о
вычетах
f
C)
Подынтегральная функция F(p)epx в формуле A), п. 3.1, аналитическая и ее особые точки
находятся на плоскости р слева от прямой, уравнение которой s = а = а. Справа от этой прямой
функция F(p)epx аналитическая, поскольку оба сомножителя — аналитические функции. Если
применить теорему о вычетах к интегралу
a+6i
lepiF(p)dp= J eptF(p)dp +
C а-Ы CR
по контуру С = С, U CR (рис. 103) и перейти к пределу при 6 -+ оо,
то оказывается, что
а+Ы
<?lF(p) dp^O, I eptF(p) dp -* /@2тг1 = 2ni ]? KS^Fip)),
cR
т.е.
a
/v
P\
0
s
S = a
a — Ы
Рис. 103
Этот результат известен в теории операционного исчисления как вторая теорема разложения.
Сформулируем эту теорему.
342
Гл. 7. Метод интегральных преобразований Лапласа
Теорема 2. Если изображение F есть мероморфная функция на комплексной плоскости р и
аналитическая на полуплоскости Rep > а и если существует последовательность окружностей
Сп = {р 6 С : \р\ = Rn}, Ri < i?2 < • • •, Rn ~> +00» на которой F(p) стремится к нулю равномерно
fl+ioo
относительно argp, а также Va > а интеграл / F(p)dp абсолютно сходится, то оригиналом
a-ioo
изображения F(p) является функция
r\(t)f(t) = У] res(i
D)
Если для точки го можно указать такую 6 -окрестность, что при однократном обходе точки
г0 по любому замкнутому контуру, целиком лежащему в этой ^-окрестности, одна ветвь много-
многозначной функции переходит в другую, то точка z0 называется точкой разветвления данной мно-
многозначной функции.
Если среди особых точек функции eptF(p) кроме полюсов и су-
существенно особых точек рк (к = 1, п) имеются точки разветвления
f(t) =
1Ж1 ¦
Рис. 104
a,
где 7J — контуры, состоящие из окружностей C'j малого радиуса с цен-
центрами в точках разветвления, верхнего и нижнего края разрезов плос-
плоскости по лучам, проведенным из этих точек (рис. 104).
Найти оригиналы данных функций F.
111. Fip) =
——,
Vp
a > 0.
А Функция-J1 — аналитическая на плоскости р с разрезом по отри-
отрицательной полуоси. На верхнем крае разреза р = реш и у/р = iyfp, а на
нижнем его крае р = ре~п и у/р = -iyfp. Поскольку р = 0 — точка
разветвления функции F, то, согласно формуле E), имеем
Рис. 105 27
где 7о — контур, изображенный на рис. 105, ориентированный против хода
часовой стрелки, состоящий из двух лучей и окружности радиуса е > 0.
Оценим
е~
e*——dp
J>4
Се
Vp
Полагая р = ее1'', получим
-пуДих
\eFt\ \dp\ = / ectcosv —- • e dip sC e?tVe2n -» 0 при s -» 0.
VP j Vе
Cc v -ir
Поэтому
- e —— dp= - / e r —-
J y/p J -t.
VP
iVP
•-1<-Л~
m = l].
dp=- / e cosaudu
r ж J
§ 3. Обратное преобразование Лапласа 343
+ 00
(после подстановки ^/р — и). Обозначим Да) — I е~и ' cosaudu. Интегрируя по частям, нахо-
о
дим:
+ 00
sinaw _
Да) =
+0° U Т А 2tdl
2t f -Л
— /we s
a J
sin aw du = .
a da
о
Получили дифференциальное уравнение с разделяющимися переменными. Решая его, получаем
_°2
Да) = Се •*(¦.
Постоянную С находим из условия
Следовательно,
11Ъ. F(p) = е~а^, а > 0.
¦^ Пусть f(t) = е~а^. Тогда по теореме дифференцирования изображения получим
-tf(t) = (е-'<*)', или -tf(t) = -°~-.
a2
Согласно решению предыдущего примера ^tf(t) = ~т=те ^ ¦ Поэтому
724. J?(p) = , a > 0. '
p v/
А Воспользуемся решение^ предыдущего примера и теоремой интегрирования оригинала.
Получим
Произведя замену ^г = и2, находим:
и
Имеем
dr = ± 7е-2 du = Erf ( « ) .
725.
(p-2)(p2-p-20)'
¦^ Поскольку (p - 2)(p2 - p - 20) = (p - 2)(p + 4)(p — 5), то функция F имеет простые полюсы
в точках р! = 2, р2 = -4, рз = 5. Эти же полюсы имеет и функция eptF(p). Для нахождения
оригинала функции F воспользуемся формулой D), п. 3.3. Вычеты функции р t-> epl.F(p) найдем
с помощью формулы (8), п. 3.2. Имеем
= 3(р2-2р-6) „_, = ~l8~'
344
Гл. 7. Метод интегральных преобразований Лапласа
p=-4
p=5
27
Подставив полученное в формулу D), п. 3.3, находим:
/(<)=— (Не' + 58ея - 15еи). >
¦54
726. F(p) =
¦^ Функция epiF(p) имеет простые полюсы в точках р = ±2г и р = ±г. По формуле (8), п. 3.2,
находим
p=2i
1 -г
-e .
p=2i
В точках р= —г и р = — 2г' получим комплексно сопряженные выражения. Следовательно,
727. Fip) =
~^еы -е" ) = -(cos2< +sin2< -
6 6/3
1
- 2)"
¦4 Функция eptF(p) имеет простые полюсы в точках р = 2, р = ±г и полюс 3-го порядка в
точке р = 1. Согласно формуле D), п. 3.3, имеем
f(t) = res f?lF(p) + res eptF(p) + res ep'.F(p) + res eptF(p).
j>=2 y=i p=-i p=l
Вычислим вычеты по формулам F) и G), п. 3.2, получим:
(P-DV
р=2
" ••¦
res epiF(p) + res eptF(p) = 2 Re I res eptF(pI = 2 Re ( ) = — (cos t - 3 sin t),
t=* r=-t \p=' I \(p - lyip + i)(p - 2) /P=i 20
1
2 V (P2 + !K(P - 2K
Таким образом,
)с„ . 3p2-4p+l iM
728.
l
e2t 1 e' 2
fit) =-- + -- (cost - 3sin<) - - (Г + 1). >
5 20 4
pchp
¦4 Поскольку chp = cosip, то функция e^Fip) имеет бесконечное множество простых по-
полюсов ро = 0, р* = ±г (к — jj тг, fc 6 N. Согласно второй теореме разложения имеем
Vc
00 ,co%
(*-!)"
§ 3. Обратное преобразование Лапласа 345
Легко показать, что получено разложение в ряд Фурье на сегменте [0, 4] функции
.... /О, если 4fc-K<<4ft+l,
f(t) ~\2, если 4к + К t < Ah + 3,
по косинусам кратных дуг. Действительно, коэффициенты Фурье а* для функции / вычисляются
по формулам
2 '
а* = у У f (t) cos ~dt
о
В рассматриваемом случае I = 4, поэтому
} 1
I4, 1 } 1 / *ir
= 2 У /@<Й = 2 У 2* = 2' а* = 2 У C°S T tdt =
Так как cos ^ sin Щ = (-])* при n = 4fc - 2 (к € N), то at = 2,,(~',\-, и
4fc-K«<4fc + l,
2, если 4fc + 1 < « < 4fe + 3.
С помощью единичной функции г] можем представить функцию / в виде
оо
/(Q = 2?(-l)*.7(*-2fc-l).
Таким образом, *=о
1 °°
—т— = 2 53<- 1)*Ч« - 2* - 1). >
Найти изображения функций.
729. f(t) = sm2V't.
¦4 Воспользуемся теоремой 1, п. 3.3. Разлагая функцию / в степенной ряд, получаем
оо j2n+l j
E(l)"
Согласно решению примера 683, имеем
п]22п+1рп+1 '
Следовательно,
< Из разложения
cos^
s/t fa Bfc)!
и соотношения
p 2 2kp 2
находим
346 Гл. 7. Метод интегральных преобразований Лапласа
731. /(f) = t?JnBVt), где Jn(x) = J^(-l)* I - ) — — — цилиндрическая (бессе
лева) функция 1-го рода n-го порядка.
¦4 Подставляя в формулу для Jn(x) вместо х аргумент 2y/i, получим
ч п+2к ее / i \* *п+к
jit) = tbni2Vi) = t-2 V*J^(-1)f
Принимая во внимание решение примера 682, имеем
,
Следовательно,
732./«,
¦4 Воспользуемся решением предыдущего примера, полагая там п = 1. Получаем
1 г 1 -к
jB7)
По «^юрмуле интегрирования изображения (теорема 10, п. 1.2) находим
tU^Vt) __ f
1 ^J
-1
e 1 dq
— = e 9
= 1 - e
Таким образом, _i
Jit) = \-e p.»
§ 4. Линейные дифференциальные уравнения
и системы
4.1. Интегрирование уравнений с постоянными коэффициентами.
Пусть дано дифференциальное уравнение
~ly dy
++a^ + ay Jit)
?^^ y = Jit) A)
и начальные условия
У(""Ц@) = уГ". B)
Считаем, что ад Ф 0 и функция /, а также решение j/(?) вместе с его производными до п-го
порядка являются оригиналами. Обозначим У(р) = y(t), Fip) = Jit).
По правилу дифференцирования и свойству линейности вместо дифференциального уравне-
уравнения A) с начальными условиями B) получаем операторное уравнение
{аорп + alPn~l + ... +an)Y(p) =
= Fip) + уо(аорп~1 + alP"-2 + ...+ on_i) + у'0(а0рп'2 + а^" + ... + а„_2) + ... + у^п'1)а0,
или
A(p)Yip) = F(p) + B(p), C)
где Aip) и Bip) — известные многочлены. Решая это уравнение, найдем операторное решение
§4. Линейные дифференциальные уравнения и системы 347
Если уравнение A) при начальных условиях B) допускает решение y(t), удовлетворяющее
условиям, наложенным на оригиналы, то это решение является оригиналом для Y(p).
4.2. Решение систем линейных дифференциальных уравнений
с постоянными коэффициентами.
Аналогично применяется операционный метод к решению систем линейных дифференциаль-
дифференциальных уравнений с постоянными коэффициентами. Пусть требуется решить систему п дифферен-
дифференциальных уравнений второго порядка
с начальными условиями
^/3, B)
Если yk(t) и /„(i) — оригиналы, a Yk(p) и Fy(p) — их изображения, то система A) с начальными
условиями B) заменится операторной системой
vk) Yk(p) = Fv(p)
t=l k-l
Решая ее как алгебраическую линейную систему уравнений, найдем Yk(p), а потом и их оригиналы
УМ.
4.3. Решение уравнений с нулевыми начальными условиями
при помощи интеграла Дюамеля.
Пусть требуется найти частное решение дифференциального уравнения
Ly = «/"> + aly(n-l) + ... + «„_,!/' + апу = f(t) A)
с начальными условиями
У@)=у'@)= ... =2/(п)@) = 0. B)
Рассмофим задачу
Ly = 1; у@) = у'@) = ... = у^ф) = 0, C)
где Ly — левая часть уравнения A). Поскольку операторные уравнения, соответствующие задачам
A), B) и C), имеют вид
A(p)Y(p) = F(p), AipMfr) = -,
где F = f, то Y(p) = pYi(p)F(p). Таким образом, если известно решение задачи C), то, согласно
формуле Дюамеля, имеем
t
V(t) = J' f(T)y\(t-T)dr D)
о
(приняли во внимание, что ^@) = 0 согласно начальным условиям). Формула D) принимает вид
t
y{t) = »i(O/@) + jyl{t)f(t - т) dr. E)
о
Решить следующие дифференциальные задачи.
733. у" + а2у = 6sinai; уф) = у0, yJ(O) = у'й.
¦4 Операторное уравнение, соответствующее дифференциальной задаче, имеет вид
(р2 + a2)Y = -^—г + УоР + Уо.
Таблица оригиналов и их изображений
]
2
3
4
5
б
7
8
9
10
И
12
13
14
15
16
17
18
19
20
Оригинал
@, если t < 0
'7W~ \1,если* 3*0
f (а > -1)
е, G = const
<"е"(, п € N, о- = const
sinwi, ш 6 К, ш — const
e^'sinu/i, w?E, и = const, w = const
tn sino/i, n 6 N, иЯ|,и = const
coswi, ijj 6 K, w = const
e^'coswi, uj G R, и — const, w — const
i" coswi, n 6 N, w 6 R, w - const
shut, iiJ G R, w = const
chwi, ijj G R, oj — const
sin&><
—-—, iii ? R, w = const
sinwi|, w G R, a/ = const
e~° ' , a G R, a = const
e~at
—;=, a G R, a = const
i _«!
¦^=e 41 , a G I, a - const
1 1
A!sin27
l l
vTtC0STt
Erf (-Д= ), a 6 R, a = const
42vi/
Изображение
l
p
Г(a + 1)
pa+l
1
p-a
n\
(p-<r)»+i
p2 + w2
u)
(p - aJ + ш2
Aт(р + !ш)"+|
"' (р2+ш2)«+1
p2 +ш2
p-o-
(p~aJ + u2
| Re(p + iu)n+l
"' (р2+ш2)»+>
w
^2-а;2
P
p2-a;2
— - arctg —
2 w
ш np
p2 + ш2 2w
— ела2 Erf —- 1
1
VP
^e-^sinV?
—=e"^cosv?
vP
Приводим таблицу изображений
для некоторых функций и соот-
соответствующие указания для поль-
пользования ею.
Если требуется по заданно-
заданному оригиналу найти соответству-
соответствующее ему изображение, то та-
таблицу читают слева направо; ес-
если известно изображение и тре-
требуется найти соответствующий
ему оригинал — справа налево.
Таблицы более подробные,
чем предложенная здесь, приво-
приводятся в специальной литературе
по операционному исчислению.
§ 4. Линейные дифференциальные уравнения и системы 349
Решив его, находим:
ab р у'о
+
Из таблицы изображений функций находим:
Р . Уо . Уо . ,
Уо -г,—г = Уо cos at, — = — sin at.
p тй p + a a
Поскольку 7 -, i — л i a^ ¦> i Jr, то по формуле 7 таблицы и теореме об интегрировании
(р + я ) z (р +а) Р
оригинала имеем
ab Ь '
> Ь г Ь
—г-- = - т sinardr = —- (sin at — at cos at).
a2J 2 J 2a2
(р2 + а2)
и
Окончательно получаем:
/ , Ь\ sinat ( Ы\
y(t) = (Уо + г- ) + Уо - -г- cos at I»
V 2a / a \ 2a/
734. y" + Ay' + 4y = e~2'(cos< + 2sin?); y@) = —1, y'@)=l.
< Перейдем к изображениям:
y=:Y, y'=PY+l, y"=P7Y+p-l,
По теореме смещения получим
р + 4
Дифференциальной задаче соответствует операторное уравнение
решение которого имеет вид з „ г
Р Р
(р + 2J + 1'
Рапагая правую часть этого равенства на простые дроби, находим:
Перейдем к оригиналу, воспользовавшись свойством линейности, теоремой смещения и таблицей
изображений. Имеем
y(t) = e~2t(t - cost - 2sin<). >
735. у'" + Ъу" + Зу' + у = 1; )/@) = у'@) = /@) = 0.
¦< Пусть у(<) = У(р). Переходя д изображениям, получим операторное уравнение, соответ-
соответствующее дифференциальной задаче:
(р+1KУ=-.
Р
Его решение — 11111
Y(v) =
УУ> p(p+lf p
Оригинал изображения Y находим по формулам 1, 3 и 4 таблицы:
у(<) = 1 - е~' - te~l - \- е'1 = 1 - е'1 И + t + *- J . >
736. у'" + у = 1; »@) = у'@) = у"@) = 0.
¦^ Дифференциальной задаче соответствует операторное уравнение, решением которого явля-
является функция Y, где
1
350 Гл. 7. Метод интегральных преобразований Лапласа
Оригинал найдем с помощью второй теоремы разложения: y(t) = X)res(e?'y(p)). Функция К
имеет простые полюсы в точках pi = 0, рг = — 1 и рз = -^ — ^j-, р* = -j + Щ~ ¦ Вычисляя
вычеты функции р <-* eptY(p) в указанных точках, находим
r?seP - , , 1Ч = limep -—— = 1, resе" Г(р) = Jim.
V? ь р(рз + 1) ~ Го рз + ! - '. - — м" ~ —, р(р2 _ р + 1} ~ з '
'((! + ?» 2 « V^
z yp) f icse z tjy^ =iM - _ - -i лл.. —
Pt
Окончательно имеем
res eplY(p) + res e?IK(p) = 2 Re '-^-r-^-^- = - - e 2 cos V(
рз Р4 -3 3 2
2 1 v/3
3 3 2
737. yIV + 2y" + y = sint; y@) = y'@) = y"@) = y'"@) = 0.
¦4 Решение операторного уравнения, соответствующего дифференциальной задаче, находим
после перехода от функции, ее производных и правой части уравнения к изображениям. Оно
имеет вид
Y(p) = ——j~j.
Оригинал y(t) находим как вычет функции р ь-» eptY(p) в точке р — i:
1 , 3
= - C - t ) sin t - -t cos *. >
738. yv - y' = 8 sin<; y@) = y'@) = y"@) = y'"@) = 0, yIV@) = 1.
¦4 Поскольку y(t) = У(р), y'(t) = pK(p), yv(*) = Р5У(р) — 1, sin* == -y^—, то операторное
p + 1
уравнение, соответствующее дифференциальной задаче, имеет вид
откуда
Оригинал будем находить с помощью второй теоремы разложения. Функция У имеет простые
полюсы Pi = 0, р2,з = ±1 и комплексно сопряженные полюсы второго порядка р4,5 = ±»'.
Обозначим р2 + 9 = Pi(p), (р2 - 1)(р2 + IJ = F3(p). Тогда
Найдем вычеты функции eptY(p) в ее полюсах. Имеем
i 10е* 5 « ^ Pi(p3)eP3' 5 _г
V yr \r ¦ -'«д ~' / \tr \r -s\T • ~/ / p=i
= 2Re (— + -) e'f = — cos< + 2*sin«.
V 4 t/ 2
Окончательно находим:
y(t) = -9+ -cht+ — cost + 2tsint. >
§4. Линейные дифференциальные уравнения и системы 351
739. у" + ш2у = а (tjOt) -1?(< - Ъ)); уф) = у'@) = 0.
1 —Ьр
А Перейдем к изображениям. Имеем у = У, у" == р2У, /j(t) = j;, f](t — b) = ~— (по теореме
запаздывания). Дифференциальной задаче соответствует операторное уравнение
Р
решением которого является функция Y, где
а
Y=
По второй теореме разложения получаем
а о. а 2а yijit
= — - — coswf = -^sin --,
;= = гг coswf = г sin
р(р2 + иJ) • w2 ш2 и;2 2
а по теореме запаздывания находим:
ае~Ър 2а , шп - Ь)
± sin ^
± ~sin
2
p(p 2
Таким образом,
2а / -у uit 7 ш(? — 6)
sin2 пил sir2 v
sin —n(t) - sin r)(t - o) . >
2 2 /
740. y" + 4y = /(t); y@) = y'@) = 0, где
{i — 2п7г, если 2пя < t ^ Bn + l)?r,
-f + 2(n+lOr, если Bn+ 1 )тг < t < Bn + 2)тг, и 6 Zo.
0, если < < 0,
¦^ Сужение функции на положительную полуось является 2ж-периодической функцией. Име-
Имеем (см. следствие из теоремы 5, п. 1.2)
1 Г .... -*tdt= L ( [te'ptdt+ Ie-p\-t + 2v)dt\ =
_ e-2irp
0
e 2же
i_
p p2 p )\t=* I p2(l+e~*P) p
Функция / непрерывная V< 6 Ro. Ее производная
f 1, если 2пж < t < Bn + 1)тг,
f(t)= < -1, если Bn + 1)тг < < < Bга + 2)тг, n 6 Zo,
{ 0, если < < 0,
имеет разрывы 1-го рода в точках tn = пк (п ? N). Операторное уравнение, соответствующее
данной дифференциальной задаче, имеет вид
откуда
Оригинал изображения У (р) найдем по теореме умножения. Изображение функции /' по теореме
дифференцирования оригинала имеет вид
Имеем
1, если 2ягг < t < Bn + 1)тг, j j
-th^ = ^-l, если Bn + l)?r < t < Bn + 2)ж, n 6 Z0) -г—т = -(l-cos2<).
0, если «<0, P2(P2 + 4) 4
352 Гл. 7. Метод интегральных преобразований Лапласа
Оригинал функции У на различных интервалах изменения выражается следующими формулами:
Y(p) = I -A -cos2r)<fr + /-(-l + cos2r)dr = - (-< + ^— + 2тг j , если тг < « < 2п,
О т
(р)= /-(l-cos2r)dr + /-(-l + cos2r)dr + / - A - cos2r)dr = - fi
i 4 У4 \У4 4\
О 2
2
если 2тг < t < Зтг,
f i ff - 5in2< _ 2im) если 2rtt < « < (In + l)jr,
' | | ^_t + ana + Bn + l)»r) , если Br + 1)тг < t < (In + 2)»r.
Окончательно имеем
15 (* - ^^ ~ 2жп) ' если 2пж < * ^ B« + 1)я",
4(-«+^ + Bп+1)тг), если Bn+l)Tr<t^Bn + 2)ir, n € Zo. >
0. если t < 0,
741. у'" + 6у" + Ну' + 6у = f{t); уф) = 0, у'@) = у"@) = 1, где
0, если t < 1,
/(<)= < 1, если 1 <t <2,
1 «2 - 4« + 5, если « > 2.
¦4 Представим функцию / в виде
Тогда
fit) = tjit - 1) - tjit - 2) + Ц2 -4t + 5)f]it - 2) = tiit -l) + it- 2Jt]it - 2).
fit) = — +
P P3
(no теореме запаздывания). Далее,
y'it) = pY(p), y"it)=p2Y(p)-\, y'"it)=p3Y(p)-p-l,
3Y p 1 + 6p2Y 6+ UpY + 6Y = + ^
p3Y - p - 1 + 6p2Y - 6+ UpY + 6Y =
P
P P
откуда
J +e + 2J
Y(P) =
Для определения оригиналов функций Уь У2) 5з применим вторую теорему разложения. Функ-
Функция Yi имеет простые полюсы рх = —1, р2 = -2, р3 = -3, поэтому
§ 4. Линейные дифференциальные уравнения и снстемы 353
Функция Y2 имеет простые полюсы в точках р0 = 0, рх = — 1, рг = -2, р3 = -3. Имеем
з
2)(р+3)
р=о *=i V (р(р+ 1)(р + 2)(р + 3)O„=
Функция Уз имеет полюс 3-го порядка р0 = 0 и простые полюсы р{ = — 1, р2 = -2, Рз = -3,
следовательно,
(р + 1)(р + 2)(р + 3>у ^ \6р5 + ЗОр4 + 44р3 + 18р2
12р + 11J - 3(р + 1)(р + 2J(р + 3) p(t_2) (t
3 / p(t-2)
, у"' е
/85 11<* — 2)
-<t-2
\108 18 + 6 в + 4 27
Решением дифференциальной задачи является функция г/, где
6 2 2 6
/ 85 11 1 2 1
+ ( (t - 2) + - (t - 2) + - <
V108 18 6 4
742. г/" - a2j/ = be'12; уф) = у'ф) = 0.
•< Решать задачу будем с помощью интеграла Дюамеля, как указано в п. 4.3. Сначала решим
задачу
у"-а2у=1; уф) = у'ф) = 0, A)
а затем воспользуемся формулой D), п. 4.3. Обозначим через j/i решение задачи A), а через Yi —
его изображение. Тогда Yt = —т^—т-- Воспользуемся формулой 11 таблицы изображений и
р(р -а )
теоремой об интегрировании оригинала. Получим
Yi = - /shardT= —(chat- l) = yi(t).
a J a'
о
По формуле D), п. 4.3, находим:
г/@= - /е"т sh a(t -r) dr.
a J
Подставив в интеграл sha(t — т) = -j feaD~T) — е*''), после несложных преобразований, свя-
связанных с выделением полных квадратов, получим решение задачи в виде
354 Гл. 7. Метод интегральных преобразований Лапласа
743. t/lv + 2у" + у = cost; уф) = у'@) = у"@) = у'"@) = 0.
•4 Найдем решение у, задачи у1У + 2у" + у = 1, г/@) = у'@) = у"@) = у"'@) = 0. Имеем
^,(<) = У|(р), t/{v(f) = p4yj(p), y'!(p) = Р2!7!^), 1 Ф i • Получаем операторное уравнение
Р р'
решив которое, находим
Оригинал функции У| находим с помощью торой теоремы разложения. Функция Y{ имеет про-
простой полюс р = 0 и комплексно сопряженные полюсы 2-го порядка р = ±i. По второй теореме
разложения имеем
.2 е*
/«p3p+(<pl)i _Д i
2Re — ~—-~ -ept] = 1 - cosf - - sint.
Согласно формуле D), п. 4.3, решение исходной задачи имеет вид
г/@ = /cost ¦ - (sin(t — т) - (t — r)cos(t - t)J dr =
0
/ cos(«-2r) / sin(jt~2T)\ t2 cos(t - 2т)
~(tT)\TCOStЦCOS^+
2
/ sin(jt~2T)\ t2 cos(t - 2т)\
-(t-T)\TCOSt Ц- COS^+ ~
\ 2/2 4/
= -t (sint - tcost). >
8
744. у" + У + 2у = е'; уф) = y'@) = 0.
¦4 Действуем по той же схеме, что и при решении двух предыдущих примеров. Имеем
t
= JeTy[(t-r)dT,
где j/i — решение задачи
у" + 3у' + 2у=1, уф) = у'ф) = О. A)
Составим операторное уравнение, соответствующее задаче A). Получим:
»!<*) = *i(P), y"<t) = p2Yt{p), y[(t) = pYtip), 1 = 1,
P
Y= 1
1 p(p+l)(p + 2Y
Функция У) имеет простые полюсы в точках р0 = 0, рх — —1, р2 = —2. По второй теореме
разложения
»!<*) =
1
,=о PiP + 2)
^-е--
Поскольку y[(t - г) = е~D~т) - е~2('~т), то
р=-2
2
y(t) = Jer (e-D-T) - е-2('-т)) dr = j (e't+2T - е-а+3т) dr =
о о
§ 4. Линейные дифференциальные уравнения и системы 3SS
745. Точечная масса т совершает прямолинейные колебания, причем сопротивлением сре-
среды пренебрегаем, а восстанавливающая сила тш2х пропорциональна смещению. В моменты
времени <* = кт (к ? Zo) массе сообщаются импульсы величины а. Найти движение частицы,
если начальное отклонение и начальная скорость равны нулю.
¦4 Положение равновесия точки принимаем за начало координат. Согласно второму закону
Ньютона уравнение колебаний точки имеет вид
00
гпх + гпш2х = a J^ 6(t — кт),
*=о
где 6 — импульсная функция или функция Дирака.
Применив к этому уравнению интегральное преобразование Лапласа, получим уравнение от-
относительно изображения Х(р) == x(t)
;
m(p2 + w2)X(p) = aJ2 e~ptS(t - kr)dt.
t
Поскольку / S(s - kr)ds — t](t - кт), т.е. t]'(t - кт) = 6(t — кт), а по свойству оригинала
-00
е-ркт
6(t - кт) = r)'(t -кт) =
€
—ркт
= е~ркт.
"t-OG
Следовательно, / e~pt6(t - kr)dt = e~phT, ? е'ркт = A - e"pT)"', в силу чего окончательно
J к=0
находим
Совершив восстановление оригинала x(t) = X(p), получим решение задачи. Для восстано-
восстановления оригинала применим вторую теорему разложения. Функция х мероморфная, она имеет
полюсы в точках р1:2 = ±га> и рк = ~ (к ? Zo). Если т не является целым кратным т{ = ^ (что
и предполагается), то все полюсы простые, и, найдя вычеты, получим согласно второй теореме
разложения
... о (\ ш ( т\ ^ 2т г,
x(t)= г ^ . шт coso; t+ - - > -5—-r--cosfe — o)t
iw!\: 2sin^ V 2/ t^i т2 - к2тг т
Решить системы линейных дифференциальных уравнений с постоянными коэффициентами.
Г Bх" -х'+ 9х) - (у" +у' + Ъу) = О,
746. { Bх" + х' + 7х) - (у" -у' + 5у) = О,
[ х@) = х'@) = 1, 2/@) = 2/'@) = 0.
•4 Операторная система, соответствующая поставленной задаче, имеет вид
f Bр2 - р + 9)Х - (р2 + р + 3)У = 2р + 1,
\ Bр2 + р + 7)Х - (р2 - р + 5)У = 2р + 3,
где Х(р) = x(t), Y(p) = y(t). Взяв сумму и разность этих уравнений, получим
1
откуда
2р
, 2р 2
3(р2 + 4)' 3(р-1) 3(р2+4) 3(р2+4)'
Перейдем к оригиналам. Имеем
x(t)= -(е'+гсоза + япЭД, y(t) = -Be*-2cos2t-sin2t). >
356 Гл. 7. Метод интегральных преобразований Лапласа
!х" - х + у + г = О,
x + y"-y + z = 0,
x + y + z"-z = 0,
<в<0) = 1, 2/@) = *@) = х'ф) = у'ф) = z'@) = 0.
¦4 Пусть ж(?) == X(p), y(t) = Y(p), z(t) == Z(p). Операторная система, соответствующая
дифференциальной, имеет вид
(р2 - \)Х + Y + Z = р,
(p2-l)Z = 0.
Решая эту систему по формулам Крамера, получим
По второй теореме разложения находим оригиналы
x(t) = - ch(t\/2) + - cosi, y(t) = z(t) = -- ch(?\/2) + - cost. >
748. x'o = ~ax0, x'k - axk = axk-i (k = T7^);_jeo(O) = 1, xk@) = 0 (fc = T7S).
¦4 Пусть жо(О = X(p), xk(t) = X*(p) (ft = 1, n). Операторная система, соответствующая
дифференциальной, имеет вид
откуда
Оригиналы находим по формуле 4 таблицы:
Гх" + «' + »"-» = е',
749. { х' + 2ж - у' + у = е"',
[ х@) = 2/@) = г/'@) = 0, х'@) = 1.
•4 Пусть ж@ = Х(р), 2/@ Ф У(р). Поскольку выполняются соотношения
x\t)=pX, x"(t) = p2X-l, е' = -^, »'(<)= рУ, »"(<)= Л
то операторная система, соответствующая дифференциальной, имеет вид
P2X-l+pX+p2Y~Y=-±1,
решив которую, получим:
х<р)~ V -2 = -±-+ 3 1 — Зр
2(р-1)(р+1J 8(р — 1)
^ j = е' -^ =
Из соотношений _^_ j = е', -^ = sh f по теореме дифференцирования изображений находим
—y=-«sh«,
Окончательно получаем
§ 5. Интегральные уравнения типа свертки. Особые уравнения
357
750. Три одинаковые точечные массы m закреплены на струне так, что расстояния между
ними и расстояния от крайних масс до закрепленных концов струны равны /. В начальный
момент все массы находятся в положении равновесия, причем средней массе сообщается скорость
«о- Найти движение системы (рис. 106).
•< Дифференциальные уравнения движения системы
найдем с помощью уравнений Лагранжа, которые для ма-
малых свободных колебаний имеют вид
d /дТ\ дП _
It \di~J + i% ~~°'
кинетическая, Я — потенциальная энергия систе-
систегде Т
мы, qk — обобщенные координаты, а точка означает произ-
производную во времени. Если Xi(t), x2(t), X)(t) — отклонения
масс от положения равновесия, то
Т = — [х\ + х1 + x\j , nj
где Р — натяжение струны. Уравнения движения имеют вид:
M,(*,)
М2(х2)
М3(х3)
Рис. 106
- х2хъ
х2 + АBж2 - xi - Xi) = 0,
где А = ~j. Принимая во внимание начальные условия х{@) = ж2@) = Жз@) = *i@) = х^О) — 0,
?-2@) = v0, получаем операторные уравнения
(р2 + 2А№ - АХ2 = 0,
-АХ! + (р2 + 2А)Х2 - АХ, = «о,
-АХ2 + (р2 + 2А)Х3 = 0,
где Xi(p) == x{(t), X2(p) = x2(t), X3(p) = x3(t). Решив эту систему, имеем
X = ^ X=X = V
Применив вторую теорему разложения, находим:
[
V
x2(t)= — (
2 \
ш2
где щ = у/B + V2)\, шг = %]B - %/2)А.
§ 5. Интегральные уравнения типа свертки.
Особые уравнения
5.1. Интегральные уравнения типа свертки.
Уравнение вида
(t,T)f(T)dT, a <«</?, A)
где / — неизвестная функция, <р и К — заданные функции, о, А, а, /3 — постоянные, называется
линейным интегральным уравнением Фредгольма первого рода, если а = 0, или второго рода, если
афО.
Функция К, определенная в квадрате DK = {(?, т) € Ш2 | а < t < /3, а <т < /?}, называется
яфои интегрального уравнения. Если у>B) = 0, то уравнение называется однородным.
358 Гл. 7. Метод интегральных преобразований Лапласа
Уравнение t
«/(<) = fit) + A J K(t, r)/(r) dr B)
a
называется линейным интегральным уравнением Вольтерра первого рода, если a = 0, или второго
рода, если а Ф 0.
Если ядро уравнения К зависит только от разности t — т, т. е. Jif(?, т) = K(t — г), то интеграл
C)
J
о
является сверткой функций К и /. В этом случае уравнение Вольтерра
t
+ \
jK(t,T)f(T)dr D)
о
будет уравнением типа свертки, и его решение можно найти операционным методом, пользуясь
теоремой умножения Э. Бореля.
5.2. Интегральные уравнения второго рода.
Если интеграл
+00
J e-*K(t)*f(t)dt
о
абсолютно сходится, то преобразование Лапласа переводит свертку по теореме умножения Э. Бо-
Бореля в произведение изображений, т. е.
K{t) * f(t) = K(p)F(p),
где К(р) = K{t). Поэтому уравнение D), п. 5.1, после перехода к изображениям f(t) == F(p),
ip(t) = Ф(р), K(t) Ф К(р), перейдет в операторное уравнение
aF(p) = Ф(р) + XK(p)F(p),
откуда
Ф(р)
а - \К(р)'
или ^
1 Л К(р)
F(p) = - Ф(р) + - ¦ =— Ф(р).
^' а ^' а а-\К(р)
Обозначим rfe~T = Ф(р). и пусть Ф(р) = tb(t). Тогда равенству
а — лК (р)
Р(р)=-Ф(р)+-Щр)Ф(р)
а а
соответствует в классе оригиналов решение
В частности, если функция К есть многочлен K(f) = X) *М , то ее изображение К(р) при-
*=о
нимает вид
*(р)=- + -~
р р1 рп. .
Тогда _____
-^(Р) вор" + eip"~ + ... + г»!а„
ф(р) =
a - АА"(р) ap"+1 - AaOjP" - Aaip" - ... - Aann!'
Функция Ф является дробно-рациональной и ее оригинал t/> можно найти по второй теореме
разложения.
Таким образом, решение F(p) операторного уравнения, соответствующего интегральному
уравнению второго рода типа свертки, всегда можно преобразовать в пространство оригиналов.
§ 5. Интегральные уравнения типа свертки. Особые уравнения 359
5.3. Интегральные уравнения первого рода.
Интегральному уравнению первого рода
= \jK(t-r)f(T)dT A)
о
соответствует операторное уравнение
Ф(р) = \K(p)F{p),
решение которого
\J B)
нельзя перевести при помощи теоремы умножения в пространство оригиналов, так как функция
--: не является изображением, поскольку необходимым условием существования изображения
к
является выполнение соотношения lim (ЛГ(р)) = 0. Однако, в некоторых случаях решение
р-»оо
существует. Если функции К и <р дифференцируемы и К@) Ф 0, то, продифференцировав
уравнение A), получим интегральное уравнение 2-го рода
<p'{t) = A JK'(t - r)f(r) dr + K(O)f(t), C)
о
решение которого существует
Если К@) = К'ф) = ... = К{п~1}{0) = 0, а К(п)@) ф 0, то после (п + 1)-кратного дифферен-
дифференцирования уравнения A) получим интегральное уравнение второго рода
y>(n+1)(«) = A [Kln+l\t - r)f(T)dr + Kin\O)f(t). D)
о
5.4. Особые интегральные уравнения. Интегральное уравнение Абеля.
Интегральные уравнения A) и B), п. 5.1, называются особыми, если ядро K(t, т) обращается
в бесконечность в одной или нескольких точках сегмента [а, /3], либо один или оба предела
интегрирования а и /3 бесконечны. Примером особого интегрального уравнения Вольтерра 1-го
рода служит интегральное уравнение Абеля
f(r)
/
{t-TydT = ip{tx 0<a<1-
Уравнение получено Абелем для случая a = j при решении задачи о таутохроне: найти
кривую, скользя вдоль которой без трения, тяжелая частица достигает своего самого низкого
положения за одно и то же время, независимо от ее начального положения.
Пусть ядро К уравнения A), п. 5.3, при t = О обращается в бесконечность и не имеет произ-
t
водных. Рассмотрим свертку f(t) * 1 = I f{r)dr = g(t). По свойству интегрирования оригинала
о
имеем
g(t) = G(p) = - F(p)
Р
и равенство B), п. 5.3, принимает вид
ХрК(р)
A)
Согласно теореме 11, п. 1.2, lim рК(р) = iimK(t) = со, следовательно, lim -: = 0. Поэтому
р-*оо t~*0 p-»oo рК{р)
функция . является изображением. С помощью теоремы умножения равенство A) можно
перевести в пространство оригиналов.
360 Гл. 7. Метод интегральных преобразований Лапласа
Решить интегральные уравнения второго рода.
_-, 1 '
/Э1. fit) = sinf H—
о
< Перейдем к изображениям. Имеем
sin4=_i_ L _ тJ (Т)Л.=,> * т ± 1
f(t).F(p), an«^p2 + 1, y« r)/(r)dr ffV.f
Операторное уравнение, соответствующее интегральному, принимает вид
1 1 2
Р2 + 1 2 .
откуда
Представим функцию F как сумму простых дробей:
А Вр + С Dp + E
р - 1 р2 + 1 р2 + р + 1
Из тождества
р3 = Л(р2 + 1)(р2 + р + 1) + (Вр + С)(р3 - 1) + (Dp + Е)(р - 1)(р2 + 1)
получаем систему уравнений
A-C-E = 0,
решив которую, получим: A=-r,B=^,C=^,D = — ^, Е = — -j. Согласно второй теореме
разложения имеем
I < и I (Р + D^' I (P+De"' 1 Bр+1)е*" 1 Bр+ 1)е _
1A 2 _( \/ъ 1 / , _1 %/3 \
= -е + - (cos* + sint)- -e i cos—-t = - e + 3cost + 3sint - 4e 2 cos — t \ . >
62 326y 2/
о
Пусть J'Cp) = f(t). В правой части уравнения перейдем к изображениям. Получим
ф ^г,
р+2
о
(по теореме Э. Бореля). Тогда F(p) = ^ + 2)(р - 2) = 4(р + 2) + 4(р - 2)' откУда находим
§5. Интегральные уравнения типа свертки. Особые уравнения 361
8 г
753. f(t) = sin It - - I sh 3(i - r)f(r) dr.
¦* Пусть .F(p) = f(t). По таблице изображений sin2? = 2 , sh3f == 2 q > a п0 теореме
умножения Э. Бореля f
sh3(« - r)/(r)dr = F()
0 P
Интегральному уравнению соответствует операторное уравнение
р2 + 4 р2 — 9
решением которого является функция F, где
2{p2~9} =J +
Из тождества
A(p+ l)(p2 + 4) + B(p- l)(p2 + 4) + (Cp + D)(p2 - 1) = 2(p2 - 9)
о о л/г
находим А = -j, B= j, C = 0, D= -у-. Таким образом,
8 8 13 2
~5(р-1) + 5(р+ 1) + Т р2 + 4'
По таблице находим
8 , 8 , 13 1
/(«)= —е(+_е-(+_ Sin2«= - A3sin2f — 16sht). >
754. f(t) = f + |sin(« - T)f(r)dT.
о
•4 Для получения операторного уравнения перейдем к изображениям:
6 F(p) 6(p2 +1) 6 6
По таблице изображений находим:
Проинтегрировать уравнения Вольтерра первого рода.
t
755. 1 - cost = /sh(t - T)f(r)dr.
о
¦4 Здесь ядро K(t) = sht является дифференцируемой функцией и К'@) Ф 0, поэтому урав-
уравнение имеет решение. Перейдем к изображениям:
1 Р -
1 - cost = f— = ~3 > / shC ~ r)/(r)dT =
о
Операторное уравнение принимает вид
1 = F(P)
откуда
р2
362 Гл. 7. Метод интегральных преобразований Лапласа
Из таблицы изображений находим:
t
756. sin<= I cos(t - r)f(r)dr.
о
М Здесь К@) Ф 0, где K(t) = cost. Посредством формулы C), п. 5.3, получаем интегральное
уравнение второго рода t
cost = - Гsin(t - r)f(r)dr + f(t).
0
Перейдем к изображениям:
P f F(p)
f(t) = F(p), cost=^-j, I sm(t--^'-"J- ¦
о
Операторное уравнение принимает вид
Р F(p)
Отсюда F(p) = ~. Следовательно,
p2+l p2+l
757. 1 - cos* = /ch(* - r)f{r)dr.
0
<4 Поскольку ch 0 = 1, то, аналогично проделанному в предыдущем примере, сводим данное
интегральное уравнение первого рода к уравнению второго рода
sin t = f sh(t - r)f(r) dr + f(t).
о
Решение соответствующего операторного уравнения имеет вид
р2 - 1 2 1
F(p) = ^ТТТТ; = TTl - "Г-
Р (р +1) Р + 1 р
Следовательно,
f(t) = 2s\nt-t. >
758. t3= f(t~rJf(T)dT.
о
M Здесь K(t) = t2, Кф) = К'ф) = 0, К"ф) = 2. Применив формулу D), п. 5.3, находим:
6 = 2fit), f(t) = 3. >
Решить системы интегральных уравнений.
759.
x(t) = t2 + Jy(T)dr,
о
y(t)=t + jz(r)dr,
о
t
z(t)=l + Jx(r)dT.
J
о
Пусть x(t) = X(p), y(t) = Y(p), z(t) = Z(p). Тогда получим:
/ =
Р о
§ 5. Интегральные уравнения типа свертки. Особые уравнения
Система соответствующих операторных уравнений имеет вид
363
Решая эту систему, находим
4
Х(Р) =
4 p+\ _4 ^_
Перейдем в пространство оригиналов. Получим
4 , 4 _< л/3 4 _л . л/3
3 3 2 л/3 2
4 ( 4 _i л/3 4 _i л/3
= -2* + - е' - - е 2 cos — t + -^= е 2 sin — «,
4 ( 8 _i v^
= -3 + - e + - e 2 cos —- t. >
760.
y(t)=l + fx(T)dr.
0
¦« Пусть я(О ф Х(р), y(t) = Yip). Тогда
Yi)
f
x(r)dT=\*x(t)=
У
Xiv)
Решая эту систему, получим:
2
ТЯГОЙ ОV
Х(р)=
2р
1
Р'
I '00000' 1
Из таблицы изображений находим:
x(t) = 2sht, y(t) = 2cht - 1. >
107
761. В контур, состоящий из последовательно соединенных индуктивности L, емкости С
и сопротивления R (рис. 107) включается э.д.с. Е. Ток в контуре и заряд до конденсатора в
начальный момент времени равны нулю. Определить зависимость тока в контуре от времени.
•4 Как известно, ток i(t) и напряжение U(t) на концах элемента цепи, содержащего активное
сопротивление R, самоиндукцию L или емкость С, связаны соответственно соотношениями
364 Гл. 7. Метод интегральных преобразований Лапласа
где до — начальный заряд на обкладках конденсатора. На основании закона Кирхгофа имеем
уравнение
di
о
(принято во внимание, что до — 0).
Пусть i(t) = 1(р). Интегро-дифференциальному уравнению A) соответствует операторное
уравнение
1 \ Е
— Др) = -,
CpJ р
решение которого имеет вид
1(Р) = —т д рг- B>
Уравнение
2 R 1
P+LP+LC=°
имеет корни р,]2 = —^ ± V "^т ~ 3ZT- Обозначим ^ = а, уа2 - -^г = /3. Тогда р( =
= -а + р, р2 = -а - р. Тогда 1{р) из B) запишем в форме
L(p{-p2) \р-р\ р-
Перейдя к оригиналам, получим:
J -V - e""') = ? е-1 sh /К. C)
Если а2 > -?{-г, т. е. R > l\j jj , то корни р,, р2 действительные и формула C) пригодна для
вычислений. Если R < 2у^т, то корни р, и р2 комплексные. Обозначим ш = у хгг ~ а2-
Р = ш, и принимая во внимание, что sh(iwt) = isinwt, имеем
i(t) = — e'at smut.
wL
В этом случае в контуре происходит затухающий колебательный процесс с частотой ш. В
критическом случае, т. е. когда р — 0, значение i(t) можно получить из формулы C) с помощью
предельного перехода при р —> 0. Используя правила Лопиталя, находим:
Ee^jhpt _ Е г__а
р"о pi ~ L
Решить особые интегральные уравнения.
762.
Eeshpt E at
t(t) = Iim = — te . >
P-o pL L
о
•4 Поскольку K(t) = t~a, то K(t) = ' !_„"' = К(р) (см. пример 682). Ядро К в точке t = 0
Р
обращается в бесконечность, поэтому операторное уравнение, соответствующее интегральному,
определяем по формуле A), п. 5.4:
Оригинал изображения G(p) найдем по теореме умножения:
§ 5. Интегральные уравнения типа свертки. Особые уравнения 365
(воспользовались формулой дополнения Г(а)ГA - а) = ^ха' 0 < а < 1). Полагая, что функ-
функция д дифференцируемая, находим решение уравнения Абеля
fit) = fl'(O = —-^ I у t°->'(* - r) dr + tp№ \ ¦ *¦
763./^^L = sinf.
•Ц Полагая в предыдущем примере а = -j, ^(?) = sin?, находим:
/(*)= — [т~2 cos(t- т)dr= W-lcost [ ^=dr + smt /-^=== dr I = i/~ (C(t)cost+ 5(t)sint),
i J lit J V27rr 7 V27rr / V я-
0 \ 0 0 /
где C(t) и 5@ — интегралы Френеля (см. пример 707). >
764. m) = ta + x fsin2VF
о
Пусть / = F. Согласно решению примера 682, ta = \.ti '. При решении примера 727
Р
нашли, что sin2v^t = fJje~^ ¦ По теореме подобия имеем sin2^r ф l_-j Изображение
+00
интеграла / &'П/~^Т f<j)dr найдем с помощью теоремы Эфроса (см. п. 2.3), в которой следует
о
взять Ф(р) = ^гтщ, 9(р) = -р ¦ Следовательно,
+00 .
о
Операторное уравнение, соответствующее данному интегральному, имеет вид
A)
Заменим в A) р на ^. Получим
F (i) = Г(а + 1)ра+| + \py/pF(p). B)
Из A) и B) имеем
Г(а+1) Apa+1
¦F(P),
откуда
АГ(а + 1)
Перейдем от изображений к оригиналам. Получаем:
1 . 1 .... 1
366 Гл. 7. Метод интегральных преобразований Лапласа
(
765. <p(t) = j\a(t- T)f(r)dT.
о
•Ц Ядро Kit) = In ? имеет особенность в точке t = 0, поскольку lim K(t) = —оо. Следо-
Следовательно, интегральное уравнение особое. Найдем изображение функции t н-> \nt. Для этого
воспользуемся решением примера 682, где показано, что t" = '" J, ', а > -1. Дифференцируя
это соотношение по параметру а, получим
t" Ш = -Ij (г\а + 1) - Г(а + 1Iпр).
Полагая здесь а — 0 и принимая во внимание равенство ГA) = 1, имеем
1п^ГA)-^. A)
Р
Из курса математического анализа известно, что Г'A) = —С, где С = lim П + ^ + ... + -^ -
- Inn) = 0,577216... — постоянная Эйлера. Обозначим у = ес = 1,781072.... Тогда lnt =
= — J" = К(р). Воспользуемся полученным ранее равенством G(p) = ;;., Ф(р), являю-
щимся следствием из формулы B), п. 5.3. В рассматриваемом случае
Ц А=1.
1 t"
Найдем оригинал функции р н-> \n(~v\ ¦ Интегрируя по параметру а функцию а >-> р/а + j
пределах от 0 до +оо, получим:
о
По теореме подобия находим
J Г(а+ 1) ° ~ J pa+1
+00 . - О
pa+4np
plnp
Г
У
+ 00 t +0С
f tay~a f/f ra-y"a ^
Таким образом, g(t) = — I p^a'+ ^ da*<p(t), т.е. g(t) = - / I / ji(a'+ j) dajip(t-T)dT. Решение
0 0 0
уравнения имеет вид
( +оо . +оо
^(?) = g'(^) — ~ / I / da ]y'(? — r)dr — у@) / da
(см. формулу B), п. 2.4). >
§ 6. Применение операционного исчисления
к решению уравнений
с частными производными
Рассмотрим дифференциальное уравнение
д2и . 9и д2и . аи
где а, 6, с, a,i,bi — непрерывные функции, зависящие только от х, заданные на сегменте [О, I].
Считаем, что a > 0 и будем рассматривать два случая: 1) at < 0 (гиперболический случаи); 2) щ = О,
&i < 0 (параболический случай).
§ 6. Операционное исчисление н уравнения с частнымн пронзводными 367
Требуется найти решение и(х, t) дифференциального уравнения A) для 0 ^ i ( I и I ) О,
удовлетворяющее начальным условиям
и(х, 0) = <р(х) (для параболического случая),
ди(х, 0)
и(ж, 0) = <р(х), —д = 4>(х) (для гипероолического случая),
и краевым условиям
диA, t)
и@, 0 = /(*), а -^-2 +
ах
dt
где а, /3, 7 — постоянные.
Такие задачи называются нестационарными.
Предполагая, что и, -^,
оригиналами, обозначим через
Предполагая, что и, ^, и -^-у, рассматриваемые как функции переменной t, являются
U(p, x)= I u(x, t)e~ptdt
о
изображение функции и. Тогда, вследствие сделанных предположений, имеем
9и _^ +fdu _pt 8U_ д^и^_ +fd\ _pt d2U
дх ¦ J дхв дх' Эх1 ¦ J дхгв дх1'
о о
По правилу дифференцирования оригиналов получаем:
ди дги , ди(х, 0)
-=^-и(Ж,0), _ф^_в(г,0)р--^-,
или, принимая во внимание начальные условия,
ди д2и ,
—- =pU-tp(x), — = р U - р<р(х) - гр(х).
at at
Предполагаем также, что f(t) является оригиналом и F(p) = f(t). Тогда из граничных усло-
условий имеем
u\ =F(p), (а~ + p{pU - V))\
1х=0 \ dx J \x=i
Операционный метод приводит решение нестационарной задачи для уравнения A) с частны-
частными производными к решению обыкновенного дифференциального уравнения
d2U dU
a—-+b—-+AU + B = Q, B)
dx2 dx
где
A = с + а{рг + bip, В = -aipif - axip - Ъх<р,
p — комплексный параметр, при следующих граничных условиях:
U
= Fip), [а—- + (вр- f)U - /Зи>) I =0. C)
dx
Решить следующие задачи.
/66. Температура и(х, t) в тонком стержне удовлетворяет уравнению
ди гд2и 2
— =а —-, а = const. A)
Найти распределение температур в полупространстве х > 0, если известен закон изменения тем-
температуры его левого конца, а начальная температура стержня равна нулю:
«|(=0 = °> ttL, = /<*>• B)
368 Гл. 7. Метод интегральных преобразований Лапласа
•^ Перейдем к изображениям. Получим обыкновенное дифференциальное уравнение
pU = <?
Их1'
которое решаем при выполнении условия
17
= F(p).
C)
D)
Общее решение уравнения C) находим без труда:
Согласно условию задачи функции и п U должны быть ограниченными при х —> +оо, по-
поэтому С2 = 0 и общее решение уравнения C) записывается в виде
Из условия D) следует, что Сх = U@, p) = F(p). Следовательно,
_ 1
Для нахождения оригинала рассмотрим сначала частный случай f(t) = 1. Тогда F(p) = -р,
Ut(x, p) = ^е~ <¦ х. Воспользуемся решением примера 724. Получим:
щ(х, t) = '.
/е-2 dr.
E)
В случае произвольных граничных данных B) воспользуемся интегралом Дюамеля (см. фор-
формулу B), п. 2.4), полагая там <p(t) = Erf
U(p) =pF(p)U1(p) (см. п. 3.3), то
«(*, t) =
( 1^-п),
= 0, tp'(t) -
Поскольку
2а^/ж
О (*-ТJ
2aVi
(после замены переменной ? = 2 jt- ^' ^
767. Стержень длины I находится в состоянии покоя и его конец х — 0 закреплен, а к сво-
свободному концу х = I приложена сила Asinwt, направленная по оси стержня. Найти продольные
колебания стержня.
•Ц Уравнение колебаний стержня имеет вид
,д2и
A)
где « = и(ж, t) — продольное смещение, а — постоянный коэффициент, зависящий от матери-
материала стержня. Начальные и граничные условия следующие:
ди
(=о dt
-0, и
1=0
дх
Е
где Е — модуль упругости. Дифференциальной задаче соответствует операторная задача
U
1=0
6U
= 0, —
' dx
x=i E p2 + w2'
B)
C)
D)
Общее решение уравнения C) записывается в виде
U(x, р) = С1! ch - х + C2sh - х.
а а
§ 6. Операционное исчисление и уравнения с частными производными
Из условий D) находим:
Ъ
С, =0, С2 =
369
где Ъ =
pip2 + ш2) ch ^ /
. Получаем решение операторного уравнения в виде
E)
Для нахождения оригинала и(х, t) воспользуемся второй теоремой разложения. Функция U
имеет один действительный полюс р = 0 и бесконечное множество попарно сопряженных чисто
мнимых полюсов. Полюсы, лежащие в верхней полуплоскости р — ш, рк = i^f- (к - -jj = гшк
(к ? N) все первого порядка и различны, если шк Ф ш Vfc ? N (условие отсутствия резонанса). По
второй теореме разложения находим:
„ (X(x,iw) ш
и(х, t) = 2Re ——!—-е +
\Y;(i)
. ш
sin - х sin lotH—
a
, ш. а
' а
к
(-l)
t
•>
768. Два одинаковых стержня длины / с одинаковой скоростью va движутся найстречу друг
другу вдоль своих осей. Определить смещение точек стержней после удара.
М Пусть удар происходит при t = 0 в начале координат (отсчет времени начинаем с мо-
момента удара). В силу симметрии достаточно рассмотреть смещение u(a;, t) точек одного стержня,
например, правого. Задача сводится к решению уравнения
д2и _ 2д2и
Hi2 ~° Ъх1
при условиях
аи аи
= 0.
т
t=0
Дифференциальной задаче A), B) соответствует операторная задача
U =0, —
решение которой имеет вид
dx2
х=й
Ч
а2
4- -
dU
dx
>о е
а2'
х=1
X
" +
о,
е
_21-х
^ а
Поскольку
рядом
( -М\~1
< 1, то функция ри П+е а I
A + е-Г) =Y4-1)*
^ ' *=о
B)
C)
D)
ж E)
может быть представлена сходящимся
поэтому получаем:
С помощью теоремы запаздывания находим оригинал
Решение пригодно, пока стержни соприкасаются, т.е. пока
dul
370 Гл. 7. Метод интегральных преобразований Лапласа
Упражнения для самостоятельной работы
Найти изображения функций:
1. shatchpt. 2. cosatcosf3t. 3. chatchCt. 4. sinatsmfit. 5. shatsh/3t. 6. sh at - sin at.
T. chat - cosat. 8. sh at + sin at. 9. chat + cosat. 10. cosatchj3t. 11. sin at sh/3t.
{ {
(
0,
16.{f
5
IS.e'4' sin 3* cos It. 19. e3' cos 3« cos 4t. 20. sh t cos 2? sin 3*.
21. ch«sin2«sin3t. 22. ch3«sin2<. 23. 2
Найти изображения следующих дифференциальных выражений:
24. Ly = yw(t) + Ay'"(t) + 4/(t); j/@) = 1, j/'@) = 2, j/"@) = -2, /'@) = 3.
25. Ly = 3y"\t) - 2/@ + 5; y@) = -1, j/'@) = 2, /@) = -3.
IV / /
26. Ly = 4yw(t) + 3/@ + y(t); »/@) = 0, у'ф) = 3, /@) = 0, /'@) = -1.
27. Ly = /@ + 2y'v(t) + 4y(t); j/@) = y'@) = /@) = 0, /@) = yw@) = -1.
Применяя теорему дифференцирования изображения, найти изображения функций:
28. fcosat. 29.t2sinat. 30. tsinatshat. 31. tcosat chat.
Применяя теорему об интегрировании изображения, найти изображения функций:
shi
u cos bt — cos at
¦"• I
Пользуясь теоремой умножения Э. Бореля найти оригиналы функций F(p):
41.
Пользуясь теоремой умножения, найти оригиналы функций F.
^
Решить дифференциальные задачи:
55. 4/+12j/49j/=144e(; у@)=1, у'ф)= \. 56. у" - 2у'= е* (t2 +1 - 3); у@) = 2, у'@) = 2.
57. /+4j/'+3j/ = sh^sini; j/@) = 0, j/'@) = 1. 58. y"+2y'+y = e'^cost+t); y@) = 1, j/'@) = -1.
59. /' - 3»/' + 2y = Ste-'; уф) = j/@) = 0, /@) = 1.
60. j/IV - у = 2 cos3 «(sec21 - 1); уф) = у'ф) = /'@) = 0, /@) = 1.
61. / - 6/ + 9/ = 54* + 18; уф) = y'@) = 0, /@) = /'@) = j/lv@) = 1.
§6. Операционное исчисление и уравнения с частными производными 371
62. у" + 6у +%y = sint-r](t-%) cost; j/@) = «/(О) = 1.
63. у" + 4y' + 20y = r,(t- Щ-) cos (t - ?) ; y@) = 1, y\0) = 0.
Решить системы дифференциачьных уравнений:
64.
66.
Решить интегральные уравнения:
= о.
ж' 4- 2x 4- J/ = sin<,
x(=1 ж,@) = y-@) = ^ e г@) = г,@) = 0
67. f(t) = sin t + ff(r) dr. 68. fit) = t + f(t - T)f(r) dr. 69. f(t) = t+2 - 2 cos t - lit - r)f(r) dr.
0 0 0
70. f(t)=t2+ f}(r)dr. 71. f(t) = cost + Jf(r)dr. 72. f(t) = 1+ /'el~Tj'(т)dr.
о t t °
73. /(t) = e34 | / sh4(t -r)f(r)dr. 74. /(t) = e2t + cos3* + /sin(t -r)fir)dr.
75. sin2t = /sin(t - T)f(r)dr. 76. t4 = |Bt3 - 3t2r + т3)/(т)<1т.
о о
Решить системы интегральных уравнений:
t t
77.
x(t) = It - j(t - r)a;(r) dr + /j/(t) dr,
78.
= -2 -
- T)y(r)dr.
Jz(r)dr,
79.
x(t) = \- Jy(T)dT,
y(t) = cost-l + Jz(T)dr, 80.
i 0
jx(r)dT.
2@= 15+ lx(j)dr.
a
= t + Jy(T)dr,
= \-Ьъ + jz(j)dT,
t
/а:(т) d
Найти решение особых интегральных уравнений.
81.
u +00 2 « +°° 2
84. -4-у /e~^/(r)dr-In< = 0. 85. -4=/e"^/(r)dr = sin21.
о о
Решить следующие задачи.
86. g "(a:j г) = ij- g *^'f} ; и@, t) = u(l, t) = 0, m(x, 0) = 0, -g"(|(' 0) =
a2>0.
—tj и@, t) = j4, lim и(ж, t) = 0, и(ж, и) = 0, x ^ 0.
, о < х < г,
Ответы
Введение
1-2/
= 0. 2. у' = exp(f ). 3. (уу" + у'1)* - уу' = 0. 4. у" + yf - fy' = 0.
- *) = o, (/ + «") yf^j - ^j (/ + г/г/") + i = о.
Глава 1
1. 2y + x2-2x = С. 2. у = a; si (ж) + cos ж. 3.
10. у-х-30+у/3(х + П)\ = С x-y + 308 + V3(x + l7)
- In г/ = 4. 4. у = 2тг +arctg(l - |).
^- da: = С. 8. sin| = <7ея<г). 9. (у-2хK = С(у—х— IJ.
^ = ln(Ca:3),
1+чЛ
11.
15. In a: = ctg(|ln*) - 1. 16. у = a:(c+sina;). 17. у = 1 +Сеаях. 18. у = ^(C + lnx),
x = 0. 19. x = Су3 + у2, у = 0. 20. г/ (е* + Се2*) = 1, у = 0. 21. у = х4\п2Сх, у = 0.
22. у = г/ое°<1о)-и<1) + Г e"<"-«W+' Л> и(а.) = | in |1 + а:| + i In |х2 - х + 1| + ^ arctg ^. 23. у =
J Xq
= г/оехр(- J*u(t)dt) + ?«ф(- juiOd^J сое*Л, ti(t) = f^. 24. у = (Jl +г - as,,) cosa;.
25. г/ = f (to - i) + т • 26- У = exp(ilnlnz)B - 5« + j* exp(ilnlnt) (l - i) dt). 27. у =
' *-•*•».» = -*- «-1 + «"^ (С - I /Фчх)х-1. 30. у =
. 31. у = x + 2 + 4 (ce4x - l)"', c= -4^-. 32. г/i = ж + 1, y2 = x +
+2B-ЗжГ1. 33. х~у2со%гх = С. 34. а;3-г/2+а:31пМ = С- 35. 4ж+^ = С. 36. 2ж3у3-3ж2 =
= С. 37. (ж2 + 1пу)ж-3 = С, а? = 0. 38. ж + 21п|ж| + \? - \ = С, х = 0. 39. ^1+(|J +
(^ ч
| + у 1 + (f) I = С, ж = 0. 40. у = 0 — особое решение. 41. у = 0 — особое решение.
42. у = 0 — особая кривая. 43. @, 0) — особая точка. 44. @, 0) — особая точка. 45. у =
i
Ответы 373
Глава 2
1. х = Г (\ellf-l)-t- \Y~2 dt. 2. у = 1-cosa;. 3. а; = ехр( Г (i -
Г Гщ ( Гщ ( Г2 I ч -i \ \
y=\+ I (р(щ)%1>{щNщ, <р(щ) = 2 exp / u2exp(-/ (t-r+sint) dt)du2\g(ui)dui,
J0,5 J0,5 \ Jo,5 \ JO,5 V ' /
гр(щ) = exp( ? (t-t2 + sin*)"' d«) ^—, д(щ) = exp( /J (t - *2 + sint)"' <й) . 4. у =
= f (l + S2). 9. у = (в"* + e*) In (l + ex) + c{e'x + c2e~2x. 10. у = e (|(a; + 1I +c,
^пх. 12. у =
(c3 - f) e-2lI+ie2". 13. j/ = c2a;+c1a;2 f e~^x~2dx+c3x2. 14. г/ = Cla;2+c2 (a;3 - i)+a<p(x),
, c, = f x^a(
„(~\ - Bг3-212-:г)уч-*A-1У _ /* (»3+2)(V-2y)da! _ /" i(j+l)(i3+2)
"V ; ~ Dx42y-v"(x42x)-6x2V ' 2~ J (l3+2)(j>'-lj>")+3i2(Ij,'_2»,) "*"C20, <-3 - J Dxi_2)v>-6x2<f-(x
ii
J J
+c30. 17. г/ = Cx+c2eix+Cie~ix+сцех +c5e~x. 18. г/= C!+C2cos2a;+C3 sin 2a;+043; sin 2a;+c5a; cos 2a;.
9 * * 2 ж2 +e3l(c4 + с5ж) 21 a;eI + ж2
19. у = qe* +C2e~* +c3cosa; + c+sina;. 20. у = cx + сгх + с3ж2 +e3l(c4 + с5ж). 21. a;eI + ж2 + 2.
22. @, la; -0,12) -cos x -@,3a; + 0,34) sin x. 23. 2(ж- l)ex. 24. | sin a;- ^ cos a;. 25. dsinB1na;) +
+ c2 cosB In a;) + 2a;. 28. Ci+c2 cos (\/2 lnBa; + 3)) + c3 sin (\/2 lnBa; + 3)) + \ + e2x+3 lnBa; + 3).
( ^^
32. у = a;2 + e^(c1cosa; + c2sina;) + e"^(c3cosa;+C4sina;), с, = Ьтг~^, c2 = ""'Ato', Д =
, m, = 10 - 5e~^" +eV? +5е"Й, m2 = 10\/2ch^, m3 = e"Tv/2 + 4sh^ - 1,
,с3 = -с„ c4= Зе^1 ^ (Ь"»г - am4) - ^^ - ^. 33. y = e~x-h
34. г/ = -e"*(cosa! - isina;). 35. у = 2a;3. 36. у = "^f . 37. г/ = cosa; +Px(x). 38. г/к =
= cfce-W. 39. yfc = cke'Xtx\ \k = i (in | + B* + 1)тг) 41. у, = ск (е~Л** - ел'*), Afc =
= 2кш. 42. ^ = с, (е-** + '^ge^'), llshw» - 2w*chwt - Awk = 0. 43. у = g^*.
c2 = c3^f^, c, = c3^2f^, Д = г*» -z^, г, = /i + iw, z2 = -f/i + i (fp- f), z, =
= -f + f w+i (-1 - f /i), z2e^ (z, + 3eZ3) -г3егз (z2 + 3e2^) -z,ez' (z3 + 3e'3)+z3e'3 (z, + 3e2') +
+ Ziezi (z2 + ЗеГ2) - z2e22 B, + 3ezi) = 0. 44. jfc = ct Jo (xy/%), Jo (y/%) = 0, c* ^ 0. 45. y* =
= Pt(*), Ak = k(k + l). 46. у = С (а;7 - a;) 4^,2 = v/|Ta, |Rez| < |. 47. (xy')'-x2y+\y = 0.
eT+^'j + eT+I (да;3 - ж2) у = 0. 50. г/ = 0. 51. у = 0. 52. у = схх + с2. 53. у =
= С!а;2 + с2а; + с3. 54. у = {жх + 1)х. 55. у = х. 56. у = х(^х + 5}. 57. у" = г, 6/ - 5zz" = 0.
58. у'" = г, х*1 + z = е*. 59. г/' = г, 2"г2 - г3 = 0. 60. у" = г, хг' - z(l - х) = 0.
61. у + ? = г, г' = 0. 62. уу' = *,*' = 1. 63. у' = р, р = 0, р"-р'р = 0. 64. у' = р,
р = 0, (р"р+/)у2-р2 = 0. 65. (бУ-с'х2хТ'х^L + 48у-с'*2дТ2*-<* + 2 = 0. 66. Зг2 + z - 4 = 0,
68
. B - 1)B - 5) = 0, г = (у - c,a;2 - с2а; - с3) ( f f ln\x\(dxJJ . 69. а; = ±Vcos7, У =
374 Ответы
_ _ i Г ш,г_ш + 7q_ a. = ch4t j/ = c1ch8t + c2ch4t + c3+ / ( / (~ -3ch2t)ch3tshtdn x
2 J Vcosl » J \J У 4 I )
x ch'tshMt. 71. x = t + d, у = sh? + C2t + C3. 72. a; = C{ - e~*, у = e~\l - t) + c2.
2 Ш (ft Л-1
73. x = C, -ln|l-r|, ?/ = -2t + lnj^+C2. 74. ?/ = ?, a; = ± / f2e' + CiJ dt + C2. 75. г/ = t,
x = ± f \2 f (l+t4L dt + Ci) dt + C2. 76. у = Cx~C2, у = ~. 77. xp2 = p +С, у =
= 2+Cp"'-lnp. 78. x = kip+p~l, y = p-lnp+C. 79. a; = py/p2 + 1, г/= j Bp2 - l) л/р2 + 1+C.
Глава 3
-c3e"
= Cle2'
+ c2e-* + c3e~3'. 3. a; = E Лкел*', у = \Y, Ak(\ - \\) eXkt, Xk = V3±2</2i.
, At — корни уравнения 4A4 + 14A3 + 17A2 + 17A -
• 6.y =
П СгЪ сз7з
1 с-г Сз С4
О О Л3 Л4 Л5 Л6
О 0 С*з С*4 С*5 ^*б
' В«: = -АГ^РРС1*, * = 176. 9. у = Ц sina; + fcosa;+ |as - || - \ех -
- 2е2х, z = | sina; + --cosa; + \x - Ц - уе1 - уе21. 10. г/ = a;(asina; + bcosa;) + acosa; +
+ /Jsina; +mx + nx2 + k, z ~ x(ai sina; + &i cosa;) + a!Cosa; + /?[ sina; + mix + щх2 + ki. 14. у =
A2
SJ2
, Ak =
/ ±е* + 311197 2fx
_ П т — ,=' й — / V 107-27-540C \ < С „ _
-U, x - e , у - ( ^ , 916 a )¦ 13. г/ -
^ 54 е ' 214-27e У
A* + At - 4 -Ai + ЗА2. - 2Ai + 3
Al + Afc A^ - X2k + 2Xk + 3
Ai - 5At + 1 -Xl + 3X2k - 2At + 3
-Ai + 5X2k-2 Xl - Ai + 2Afc + 3
{ - 5X2k-i
-Xl + 5X1-2
-Xl + 3Xl - 2Xk + 3
; - A? + 2Afc + з
-Ai - A* + 4
-A2-.
2X1 - Afc + 2 -Xi + 4Xk + 3
-ЗА*-4 -5Ajfc + 4A,fc
M+^-4
-Xl+5X2k-2 X2k+Xk
= 0. 18. yi = fg
3Ai - ЗАк + 1 -At + 3Al - 2Ак - 1 A3. - 2Ai + 3Ak + 1
y2 = Ai (л3еЛз1 - Л4еА"*) - x + |, A3L = v^(-l ± i), Л3 = i + |, Л4 = \ - i. 19. y, =
6 - a,"' 6 j _i_, yj = x* ^ « -74a: 6 j ;_!_, 7, = ^^iL, fe = 3, 4;
, Л3 = aui
;_!_,
, B, = m|2"'""m"m" , A = т11(т22+тз2)+т3,т22-т12(т21+тз,)-тз2т21,
, z =
^ (), m21 ^ 1 -
m3, = ^f1, m32 = %1. 20. у = c^'1', г = (c^rV"*2. 21. у =
22. у = ^exp^ie"), z = y'. 23. у3 -23 = C1; | (d + г3)^5 dz -InИ = C2. 24. y2 + z2 = Cu
x-zy = C2. 25. xz = d, a;y + z2 = C2. 26. f = Cu x - 2y + z = C2. 27. x2 - z2 = Cu
у2-иг = С2: 28. i - ? = С,, ? - ? = C2, ? - ? = C3. 29. a;z = С, а;у+ z2 = C2.
Ответы 375
Глава 4
1. и = f(yex-e2x). 2. и = f(ye^). 3. и = f(-,xy-2z). 4. F (хе'", у2 - 2х(и - 1)) = 0.
§,
6. ^Чж2 -I- у2, —A=j arcsin , * 2 + е ") = 0. 7. u = f(xy), и = 2жг/. 8. .F (ж2 - у', и - In |
= 0 =>¦ и = In |г/| + /(ж2 - г/2), и = г/2 -ж2 + In /-у-?- 9. F (f, i^) = 0 =*- и = y^xy/ (^) - гг/,
и = Bx2/B - ж) + ж2 + 4г/2j Bх)"'. 10. 3(ж + г/ + иJ = ж2 + у2 + и2. 11. 2 (х2 - 4и3 - Зг/и) =
= 9 f 2/ + и2) ¦ 12. (ж — г/)Cж + у + Аи) — Аи. 13. , l\ sin ж = sin w ^.
Глава 5
у = 1+2+2 ЕД ¦ 2. у = Е (у)' i 3. у = 3+f E(-iyf. 4. у = 1-^-Е [т^^- 5. у =
= o0 + aix+..., а„ = 1, а, =0, а7 = 0, а, = |, а4 = 0, о;- = (B-(j-3)(j-4))a;-_3 + O'-2)aj_2) x
х (j(j~ 1H-2))"', j = 5, 6, .... 6. у= н-яг + ^ + ^ + ^ЧО (х5). 7. у = Ь2 A + ^) +
10. у=1 + у-^+О (ж5). 11. г/ = а0 + а,(ж - 1) + а2(х - IJ + О ((х - IK), а, = 1 - о2,
а2 = 1 - ао + ао3, а|> -а2 + а0 + 3 = 0 => а0 = -1, Oi = 0, а2 = 2. 12. у = ай-\-а{х + агх2 + 0 (ж3),
«з = т• 14. у = по + п\(х — 1) + а2(х — 1) + а3(г — 1) + О I (ж — 1) , а0 = 2, а, = -1, а2 = j,
Оз = —7.15. у = па + a\fi + О (fi ), at\ — х 2,а|=2(ж 2—ж \. ~\6. у = по + аф -I- О [ц ),
\ J \ ) \ /
а0 = х~\ а{ - 3. 17. о0 = A - ж)~2, а, = A - ж) (^ - |ж5 + ^ - l). 18. а0 = х + ^,
56 вЮ 4 'С/ "| V"/ \ J
о, = / 1пA + sins)ds + 1. 20. у = а0 + ^о, + О (^2), а0 = 2 - сскж, о, = / eao(s)ds - 1.
21. 2/ = 1. 22. 2/ = х. 23. г/ = -1- ж. 24. у = 1. 25. г/ = ж.
Глава 6
1. Неустойчивы. 2. Неустойчивы. 3. Неустойчивы. 4. Неустойчивы. 5. Устойчивы. 6. Асимпто-
Асимптотически устойчивы. 7. Неустойчивы. 8. Асимптотически устойчивы. 9. Неустойчивы. 10. Асим-
Асимптотически устойчивы. 11. 0<а<2. 12. Устойчивы. 13. Неустойчивы. 14. Асимптотически
устойчивы. 15. Асимптотически устойчивы. 16. Неустойчива. 17. Неустойчива. 18. Неустой-
Неустойчива. 19. Неустойчива. 20. Неустойчива. 21. Неустойчива. 22. Неустойчива. 23. Неустойчива;
25. Неустойчива. 26. Устойчива. 27. Неустойчива. 28. Устойчива. 29. Асимптотически устой-
устойчива. 30. Асимптотически устойчива. 31. Устойчива, v = х' + у4. 32. Неустойчива, v = х' — у.
33. Асимптотически устойчива, v = хг + у2 + у' . 34. Неустойчива, v = х2 + х' +у2- 35. Асим-
Асимптотически устойчива, v = х2 + у + у2. 36. Асимптотически устойчива, v = | (х2 + у' ) + \уА.
37. Асимптотически устойчива, v = х2 + х' +у2.
376
Ответы
Глава 7
2 Vp2-9 ~ ?-10? + ш)- ?а- *\р^
- Юр - 3. 25. (Зр3 - 2р2) Y{p) + Зр2 - :
+ 13+JJ. 26. Dр4 + Зр2 + l) У(р) - 12р2 - 5. 27. (р5 + 2р4 + 4) Y(p) +р + 3. 28. ^j^
29. "\ ~У. 30. 2" ; ^ ¦ 31. рд '°/ . 32. arctg^. 33. |ln-^. 34. ^In4
ОС I 1« Р ~~Ь ОС I 1« Р+1 О^ 1 1« Р +л ОО I 1« (Р+1) +1 on I p+I—в ja 1 1 (р+а)
35. ^lnfr-fr. 36. ^lnfrr. 37. ^ In 5га-. 38. =r In "Етт-г-. 39. \п^~-т-. 40. iln^^r-t:
. iCsin3*-2sin2*). 43. 5
. 44. ]e3'(
)
45. \e2t (t2 -4t + 6)- e~\t + 3). 46. \{cost + sin*)- 47. e' - * - 1. 48. ~\ - { +Ц-+ e-^-
49. i - e-4 ^ - ^. 50. I («2e2< - Ate2i + 6e2t - 2b* - 6e') .51. | ((й2 - 2t + l) e"' - e').
) ^ ^
( ) (( ) )
52. ^ -4< + 10-e-' (^ + ft2 +6* + IO). 53. ^(*- 1)+ ^ (<2 + ^ + §). 54. 1 -cose*- f sin a*.
55. e~i((m2 + 2*+l). 56. e'(e'-*2-*+l). 57. -^e' + О.Зе"' - ^e'cos* + ^e'sint +
+ 0,2е"'со5* + 0,1е"Eт*. 58. 2e~' + |е"'*3 - e"(cos*. 59, 2te~' + te( - e' + e'2t. 60. fchi-
- if cos* - Jg cos 3* - i* sin*. 61. *3 + 3t2 + %t + § + e~ B2* - f) . 62. f e-2' - ?е~4' - ^ cos* +
^ )- 63.
= |(e(+2cos2*
-f))). 64. *(*) =
, y(t) = | Be( - 2cos2* - sin2*). 65. x(t) = | cos* + |сИл/2*, г(*) =
= y(*) = j cost-i ch л/2*. 66. x(t) = 2sin*-3*, ?/(*) = 6*+3-2cos*-3sin*. 67. |(e' - cos* + sin*).
68. sh*. 69. (l+*)sin*. 70. 2 (e' -* - l). 71. \ (e* + cos * + sin *). 72. \ (l +e2'). 73. ^C5е3'+
+ 45ch5* + 27sh5*). 74. ^ D5e2' + 32cos3t- 18*- 5). 75. |(l+3cos2*). 76. |. 77. a:(*) =
= 2e~\l-t), y(t) = e"'(l-*). 78. x(t) = 2(l+6*2), ?/(*) = 24*, z(t) = 15+2*(l+2*2). 79. x(t) = cost,
y(t) = sin*, z(*) = sin* + cos*. 80. x(t) = It, y(t) = 1, z(t) = 3*2. 81. ^} • g^. 82. ^ +
= ^^kr «n =?, u(Z> *) = ? sin ss- Sm M5. 87.
«, p) = ±e
86>
, и(я!> 0 = A Erf
Предметный указатель
Настоящий предметный указатель призван облегчить поиск терминов по алфавитному признаку. Для
поиска терминов по тематическому признаку пользуйтесь подробно составленным оглавлением.
В указателе, как правило, приводятся ссылки только на страницу, содержащую определение термина;
составитель указателя не ставил своей целью отследить все упоминания приведенных терминов в тексте.
Исключение составляют термины, описывающие методы, приемы, практические результаты: для них в не-
некоторых случаях после номеров страниц курсивом указаны также задачи, в которых они используются суще-
существенным образом.
С целью уменьшения громоздкости указателя вместо термина "дифференциальное(ые) уравне-
ние(я)"применяется сокращение "д. у.".
А
Абеля
— уравнение интегральное, 359
формула, 159, 363, 364
астроида, 111
Б
Бендиксона признак отсутствия предельных циклов, 306,
672, 675
Бернулли уравнение, 39, 115, 97, 99, 101, 103, 106, 168,
265, 447
Бихари лемма, 83, 201, 202
Бореля теорема умножения, 336, 711-715, 719, 720, 740,
752, 753, 762
В
вид канонический линейного д. у. 2-го порядка, 152
Вольтерра уравнение интегральное
— 1-го рода, 358
— 2-го рода, 358
— особое, 359
Вронского
— матрица, 182
— определитель, 151, 183
вычет функции, 340
Г
Гессе
— прием, 208, 460-462
— система, 208
гипербола вырожденная, 18
Грина функция краевой задачи, 170, 393—406
Туреица матрица, 275, 616-619, 621, 622, 624-627
д
Дюамеля
— интегралы, 337
— формулы, 337, 347, 721, 142-744, 766
задача
— Коши, 4
— векторная, 83
— краевая, 169
нестационарная, 367
— Штурма—Лиувилш, 170
, собственные значения, 170
, собственные функции, 170
значения собственные задачи Штурма—Лиувилля, 170
И
инвариант линейного д. у. 2-го порядка, 152
интеграл
— вероятности, 338, 715-718, 724, 733
— полный, 228
— системы д. у. первый, 201
интегралы
— Дюамеля, 337
— независимые, 201
интегрируемая комбинация, 201
интегрирующий множитель, 53
К
канонический вид линейного д. у. 2-го порядка, 152
Клеро уравнение, 78, 191, 194
косинус-интеграл Френеля, 334, 707, 712, 713, 763
Коши
— задача, 4
векторная, 83
— метод
отыскания интегральной поверхности, 229, 519—
521
, обобщение, 229, 522-524
отыскания частного решения неоднородного д. у.,
137
— формула о вычетах, 341
краевая задача, 169
— нестационарная, 367
кривая дискриминантная, 99
критерий
— линейной независимости функций, 151
— Льенара—Шипара, 276, 618, 619, 626-628
— Михайлова, 276, 620, 621, 623
— Рауса—Гурвица, 276, 616, 617, 621, 625
Л
Лагранжа
— уравнение, 78, 192, 193
второго рода, 438-440, 629, 630, 750
— функция, 582, 629, 630
Лагранжа—Шарпи метод, 228, 504, 517
Лапласа преобразование, 324
— , линейность, 324, 686, 688, 710, 734
— , однородность, 324
Левинсона—Смита теорема о наличии предельных ци-
циклов, 306, 676
лемма Бихари, 83, 201, 202
Липшица условие, 82, 240
Лиувилля преобразование, 165, 381—387
Лорана ряд, 340
— , главная часть, 340
— , правильная часть, 340
Льенара—Шипара критерий, 276, 618, 619, 626-628
Ляпунова
— теорема
вторая, 275, 606-609, 611, 615
первая (об устойчивости по первому приближе-
приближению), 274-275, 589-593, 595, 598-600, 602,
615, 630
— функция, 275, 606-615, 630
м
матрица
378
Предметный указатель
— векторного д. у.
интегральная, 182
фундаментальная, 182
— Вронского, 182
— Гурвица, 275, 616-619, 621, 622, 624-621
матрицант, 183
метод
— вариации
произвольного вектора, 183, 429-431
произвольных постоянных, 39, 136, 151, 87—89,
91-93, 97, 108, 325, 326, 331, 342, 360, 431
— исключения, 200, 408-420, 431, 435, 442, 449-451,
453, 454
— Коши
отыскания интегральной поверхности, 229, 5/9-
521
, обобщение, 229, 522-524
— — отыскания частного решения неоднородного д. у.,
137
— Лагранжа—Шарпи, 228, 504, 517
— малого параметра, 247, 559—566, 568
— неопределенных коэффициентов, 136, 141, 315—324,
328, 329, 410, 432
— подбора интегрируемых комбинаций. 201, 443—448
— последовательных приближений, 1S3
— разбиения данного уравнения на две части, 53, 149,
154-156, 158-160
— Рунге—Кутта численного решения д.у., 267, 572—
575
— степенных рядов, 245-247, 537-555, 576, 577
— Штермера численного решения д. у., 267, 575—577
— Эйлера
отыскания общего решения неоднородной системы
д.у., 1S4, 420-429, 433, 437, 439
численного решения д. у., 266, 569-571
Миндинга—Дарбу уравнение, 40, 106-109
Михайлова критерий, 276, 620, 621, 623
множитель интегрирующий, 53
О
определитель Вронского, 151, 183
Осгуда теорема, 82
Остроградского—Яиувилля формула, 151, 362, 363
п
Пеано теорема, 82
Пикара теорема, 82, 199-204, 207
плоскость фазовая, 305
показатель роста функции, 323
полюс, 340
порядок полюса, 340
преобразование
— Лапласа, 324
, линейность, 324, 686, 688, 710, 734
, однородность, 324
— Лиувимя, 165, 381-387
прием Гессе, 208, 460-462
признак отсутствия предельных циклов
— Бендиксона, 306, 672, 675
— Пуанкаре, 306, 673, 678
пространство фазовое, 305
Пуанкаре признак отсутствия предельных циклов, 306,
673, 678
Пфаффа уравнение, 213, 233, 491-500, 503, 505-508,
511, 517
Рауса—Гурвица критерий, 276, 616, 617, 621, 625
Рейссига теорема о наличии предельных циклов, 306—
307, 677
решение
— дифференциального уравнения
изолированное, 105
особое, 99
— задачи Коши
общее, 4
частное, 4
— неустойчивое в смысле Ляпунова, 274
—¦ обыкновенного д. у. n-го порядка, 4
— устойчивое
асимптотически, 274
по Ляпунову, 274
Риккати уравнение специальное, 67, 70—71, 164—167,
169-171
Римана—Мелпина формула обращения, 339-340
Рунге—Кутта метод численного решения д. у., 267, 572—
575
Ряд
— Лорана, 340
, главная часть, 340
, правильная часть, 340
— Фурье, 556-558, 728
С
самосопряженная форма линейного д. у. 2-го порядка,
152
седло, 293
синус интегральный, 335
— гиперболический,335
синус-интеграл Френеля, 334. 707, 712, 713, 763
система
— Гессе, 208
— линейных д. у.
автономная, 305
неоднородная, 182, 184
нормальная, 200
однородная, 182
— решений однородного д. у. фундаменгальная, 151
скорость фазовая, 305
теорема
— запаздывания, 324, 689, 739, 741, 768
— Левинсона—Смита о наличии предельных циклов,
306, 676
— Ляпунова
вторая, 275, 606-609, 611, 615
первая (об устойчивости по первому приближе-
приближению), 274-275, 589-593, 595, 598-600, 602,
615, 630
— о дифференцировании
изображения преобразования Лапласа, 325, 704—
706, 723, 749
оригинала преобразования Лапласа, Ъ14, 700—702,
740
— о линейности преобразования Лапласа, 324, 686, 688,
710, 734
— о предельных соотношениях, 325
— о существовании и единственности решения задачи
Коши, 82
— об интегрировании
изображения преобразования Лапласа, 325, 708—
710, 732
оригинала преобразования Лапласа, 325, 707, 708,
718, 724, 733, 742
— об однородности преобразования Лапласа, 324
— опережения, 324
— Осгуда, 82
— Пеано, 82
— Пикара, 82, 199-204, 207
— подобия, 324, 687, 689, 765
— разложения
вторая, 342, 725, 727, 728, 736, 738, 739, 741,
743-745, 747, 750, 751, 767
первая, 341, 729
— Рейссига о наличии предельных циклов, 306—307, 677
— смещения, 324, 699, 715, 734
— умножения
обобщенная А. М. Эфроса, 336, 764
Э.Бореля, 336, 711-715, 719, 720, 740, 752, 753,
762
— Четаева о неустойчивости, 275, 612—614
точка
— разветвления многозначной функции, 342
Предметный указатель
379
— системы двух д. у. первого порядка особая, 293
— функции особая
однозначного характера, 340
устранимая, 340
— функции существенно особая, 340
траектории
— изогональные, 106
— на фазовой плоскости. 305
— ортогональные, 106
У
узел, 293
— вырожденный, 293
— дикритический, 293
уравнение
— Бернулли, 39, 115, 97, 99, 101, 103, 106, 168, 265, 447
— в частных производных
гиперболического типа, 366
квазилинейное 1-го порядка, 212
нелинейное 1-го порядка, 22S
параболического типа. 366
— дифференциальное
n-го порядка, 4
каноническое, 4
в полных дифференциалах, 53
для интегрирующего множителя, 54
линейное
— — — 1-го порядка, 39
2-го порядка, 152
, инвариант, 152
, канонический вид, 152
, самосопряженная форма, 152
гс-го порядка, 135, 150
неоднородное, 135
однородное, 135
не разрешенное относительно производной, 73
обобщенно-однородное, 30, 122
однородное, 29
однородное относительно функции и ее производ-
производных, 122
с разделяющимися переменными, 11
— интегральное
Абеля, 359
Вольтерра линейное
1-го рода, 358
2-го рода, 358
особое, 359
Фредгальма
1-го рода, 357
2-го рода, 357
однородное, 357
особое, 359
— Клеро, 78, 191, 194
— Лагранжа, 78, 192, 193
второго рода, 438-440, 629, 630, 750
— Миндиюа—Дарбу, 40, 106-109
— Пфаффа, 213, 233, 491-500, 503, 505-508, 511, 517
— Риккати специальное, 67, 70-71, 164-/67, 169-171
— характеристическое, 136, 184
— Чебышева, 152
— Эйлера, 152, 371, 372, 39}
— Эйлера—Риккати, 67, 152, 163, 282
каноническое, 67, 172
условие Липшица, 82, 240
Ф
фокус, 293
форма
— векторная системы линейных д. у., 182
— самосопряженная линейного д. у. 2-го порядка, 152
— симметрическая нормальной системы д. у., 201
формула
— Абеля, 159, 363, 364
— Коши о вычетах, 341
— обращения Римана—Меллина, 339—340
— Остроградского—Лиувилля, 151, 362, 363
— Циолковского, 29
формулы Дюамеля, 337, 347, 721, 742-744, 766
Фредголъма уравнение интегральное линейное
— 1-го рода, 357
— 2-го рода, 357
— однородное, 357
— особое, 359
Френеля
— косинус-интеграл, 334, 707, 712, 713, 763
— синус-интеграл, 334, 707, 712, 713, 763
фундаментальная матрица векторного д. у., 182
фундаментальная система решений однородного д. у., 151
функции
— линейно зависимые, 151
— линейно независимые, 151
— собственные задачи Штурма—Лиувилля, 170
функция
— аналитическая в области, 340
— влияния для задачи Коши, 137
— голоморфная, 340
— Грина краевой задачи, 170, 393-406
— дробная, 340
— Лагранжа, 582, 629, 630
— Ляпунова, 275, 606-615, 630
— мероморфная, 340
— моногенная в области, 340
— однородная степени m, 29
— регулярная в области, 340
— Хевисайда, 323, 679, 733
обобщенная, 329, 690-694, 728
— целая, 340
функция-изображение преобразования Лапласа, 324
— обобщенная, 326
функция-оригинал преобразования Лапласа, 323
— обобщенная, 326
Фурье ряд, 556-558, 728
X
характеристическое уравнение, 136, 184
Хевисайда функция, 323, 679, 733
— обобщенная, 329, 690-694, 728
ц
центр, 293
цепная линия, 110
цикл предельный, 306
— неустойчивый, 306
— полуустойчивый, 306
— устойчивый, 306
циклоида, 111
Циолковского формула, 29
ч
часть ряда Лорана
— главная, 340
— правильная, 340
Чебышева уравнение, 152
Четаева теорема о неустойчивости, 275, 612—614
ш
Штермера метод численного решения д. у., 267, 575—577
Штурма—-Лиувилля задача, 170
— , собственные значения, 170
— , собственные фунмиии, 170
э
эвольвента, 106
эволюта, 106
Эйлера
— метод
отыскания общего решения неоднородной системы
д.у., 184, 420-429, 433, 437, 439
численного решения д.у., 266, 569-571
— уравнение, 152, 371, 372, 391
Эйлера—Риккати уравнение, 67, 152, 163, 282
— каноническое, 67, 172
Эфроса теорема умножения обобщенная, 336, 764
Я
ядро интегрального уравнения, 357
Оглавление
Предисловие з
Введение . 4
Основные понятия. Составление дифференциальных уравнений 4
Основные определения D) Задача Коши D) Построение дифференциального уравнения по
заданному семейству кривых E) Примеры E)
Упражнения для самостоятельной работы . 10
Глава 1. Дифференциальные уравнения первого порядка и
§1. Уравнения с разделяющимися переменными 11
Дифференциальное уравнение с разделяющимися переменными (//) Разделение переменных
линейной заменой аргумента (//) Примеры A1)
§ 2. Геометрические и физические задачи,
приводящие к уравнениям с разделяющимися переменными 15
Использование геометрического смысла производной A5) Использование физического смысла
производной A5) Примеры A5)
§ 3. Однородные уравнения и уравнения, приводящиеся к ним 29
Однородное уравнение B9) Уравнение, сводимое к однородному C0) Обобщенно-однородное
уравнение C0) Примеры C0)
§4. Линейные уравнения и уравнения, приводящиеся к ним 39
Линейное уравнение первого порядка C9) Обмен ролями между функцией и аргументом C9)
Уравнения, приводимые к линейным E9) Уравнение Миндинга—Дарбу D0) Примеры D0)
§ S. Уравнения в полных дифференциалах. Интегрирующий множитель S3
Уравнение в полных дифференциалах E3) Интегрирующий множитель E3) Дифференциальное
уравнение для интегрирующего множителя E4) Примеры E4)
§ 6. Уравнение Эйлера—Риккати 67
Уравнение Эйлера—Риккати. Специальное уравнение Риккатн F7) Каноническое уравнение
Эйлера—Риккати F7) Примеры F7)
§ 7. Уравнения, ие разрешенные относительно производной 73
Уравнение, не разрешенное относительно производной G3) Общий интеграл уравнения F(у1) =
= 0 G3) Представление решения в параметрической форме. Разрешение неполных уравне-
уравнений G3) Примеры G4)
§ 8. Существование и единственность решения 82
Теоремы Пи кара, Пеано и Осгуда (82) Существование и единственность решения задачи Коши
для уравнения, не разрешенного относительно производной (82) Продолжение решения задачи
Коши (82) Существование и единственность решения векторной задачи Коши (83) Примеры (83)
Оглавление 381
§ 9. Особые решения 99
Особое решение. Дискриминантная кривая (99) Огибающая как особое решение A00) Приме-
Примеры A00)
§ 10. Задачи на траектории 106
Изогональные и ортогональные траектории A06) Эволюта и эвольвента A06) Примеры A07)
Упражнения для самостоятельной работы 112
Глава 2. Дифференциальные уравнения высших порядков 114
§ 1. Виды интегрируемых нелинейных уравнений 114
Дифференциальное уравнение вида F(x, j/"') = 0 A14) Дифференциальное уравнение вида
F (у(п~1), УМ) = О (U4) Дифференциальное уравнение вида F (у(п~2\ у(п)) = 0 A14) Приме-
Примеры A15)
§ 2. Уравнения, допускающие понижение порядка ¦ 122
Дифференциальное уравнение вида f(x, у^к\ у(*+1',... ,&|<п)) = 0 A22) Дифференциальное
уравнение вида F\y, у1,-... ,г/пЛ = 0 A22) Однородное дифференциальное уравнение вида
f(x, у, у', у",... ,?/<г1Л = 0 A22) Обобщенно однородное дифференциальное уравнение вида
Р{х, у, у1, у", ... ,!/<Г1)) = 0 A22) Уравнение, приводимое к виду [у(х, у, у',.,, ,у{п'']))' =
= 0 A23) Примеры A23)
§3. Линейные дифференциальные уравнения с постоянными коэффициентами 135
Линейное дифференциальное уравнение га-го порядка с постоянными коэффициентами. Харак-
Характеристическое уравнение. Общее решение A35) Поиск частного решения линейного уравнения
га-го порядка с постоянными коэффициентами методом неопределенных коэффициентов A36)
Метод вариации произвольных постоянных A36) Метод Коши нахождения частного решения
неоднородного линейного дифференциального уравнения га-го порядка с постоянными коэф-
коэффициентами A37) Примеры A37)
§4. Линейные дифференциальные уравнения с переменными коэффициентами ISO
Линейное дифференциальное уравнение га-го порядка с переменными коэффициентами. Ли-
Линейно зависимые функции. Определитель Вронского A50) Критерий линейной независимости
функций A51) Фундаментальная система решений A51) Формула Остроградского—Лиувил-
ля A51) Общее решение неоднородного линейного дифференциального уравнения с перемен-
переменными коэффициентами A51) Уравнение Эйлера. Уравнение Чебышева A52) Дифференциаль-
Дифференциальные уравнения второго порядка A52) Связь между линейным дифференциальным уравнением
второго порядка и уравнением Эйлера—Риккати A52) Сведение линейного дифференциального
уравнения второго порядка с переменными коэффициентами к уравнению с постоянными ко-
коэффициентами A53) Об асимптотическом поведении решений дифференциальных уравнений
второго порядка A53) Примеры A53)
§ 5. Краевые задачи 169
Определение краевой задачи A69) Функция Грина краевой задачи A70) Задача Штурма—Лиу-
вилля A70) Условие эквивалентности краевой задачи интегральному уравнению A70) Приме-
Примеры A70)
Упражнения для самостоятельной работы 180
Глава 3. Системы дифференциальных уравнений 182
§ 1. Линейные системы 182
Неоднородная система линейных дифференциальных уравнений с переменными коэффициен-
коэффициентами. Фундаментальная матрица уравнения. Определитель Вронского A82) Метод вариации
произвольного вектора A83) Матрицант A83) Неоднородные линейные системы с постоянны-
постоянными коэффициентами. Метод Эйлера A84) Примеры A84)
382 Оглавление
§ 2. Нелинейные системы 200
Нормальные системы дифференциальных уравнений. Метод исключения B00) Подбор инте-
интегрируемых комбинаций B01) Примеры B01)
Упражнения для самостоятельной работы 211
Глава 4. Уравнения в частных производных первого порядка 212
§ 1. Линейные и квазилинейные уравнения 212
Основные понятия B12) Решение квазилинейного уравнения в частных производных первого
порядка B12) Задача Коти B12) Уравнение Пфаффа B13) Примеры B13)
§ 2. Нелинейные уравнения первого порядка 228
Нелинейные уравнения в частных производных первого порядка B28) Решение задачи о на-
нахождении интегральной поверхности, проходящей через заданную кривую B28) Метод Ко-
ши B29) Обобщение метода Коши B29) Примеры B29)
Упражнения для самостоятельной работы 239
Глава 5. Приближенные методы решения
дифференциальных уравнений 240
§ 1. Зависимость решения от начальных условий н параметров 240
Об оценке погрешности приближенного решения B40) Об отыскании производных от решений
по параметру B40) Примеры B41)
§2. Аналитические приближенные методы 246
Метод степенных рядов B46) Метод малого параметра B47) Примеры B47)
§ 3. Численные методы решения дифференциальных уравнений 266
Метод Эйлера fc-ro порядка B66) Метод Рунге—Кутта 4-го порядка B67) Метод Штермс-
ра B67) Примеры B67)
Упражнения для самостоятельной работы 273
Глава 6. Устойчивость и фазовые траектории 274
§ 1. Устойчивость 274
Устойчивость по Ляпунову. Асимптотическая устойчивость B74) Исследование на устойчи-
устойчивость по первому приближению: первая теорема Ляпунова B74) Исследование на устойчивость
с помощью функций Ляпунова: вторая теорема Ляпунова B75) Условия отрицательности всех
действительных частей корней уравнения ацХ4 + ai\"~l + ... + an_iA + an = 0, uq > 0, с
действительными коэффициентами B75) Примеры B76)
§ 2. Особые точки 292
Определение особых точек и их классификация B92) Практические приемы исследования осо-
особых точек B93) Примеры B94)
§ 3. Фазовая плоскость 305
Основные понятия C05) Построение фазового портрета C05) Предельные циклы C06) При-
Признаки отсутствия предельных циклов C06) Признаки наличия предельных циклов C06) При-
Примеры C07)
Упражнения для самостоятельной работы 322
Оглавление 383
Глава 7. Метод интегральных преобразований Лапласа
решения линейных дифференциальных уравнений 323
§ 1. Преобразование Лапласа. Основные понятия н свойства 323
Оригинал и изображение C23) Свойства преобразования Лапласа C24) Примеры C25)
§ 2. Свертка функций. Теоремы разложения 336
Определение свертки C36) Теорема умножения (Э. Бореля) C36) Обобщенная теорема умно-
умножения (А. М. Эфроса) C36) Формулы Дюамеля C37) Примеры C37)
§3. Обратное преобразование Лапласа 339
Формула обращения Римана—Меллима C39) Сведения из теории функций комплексного пе-
переменного C40) Теоремы разложения C41) Примеры C42)
§ 4. Линейные дифференциальные уравнения и системы 346
Интегрирование уравнений с постоянными коэффициентами C46) Решение систем линейных
дифференциальных уравнений с постоянными коэффициентами C47) Решение уравнений с
нулевыми начальными условиями при помощи интеграла Дюамеля C47) Примеры C47)
§ 5. Интегральные уравнения типа свертки. Особые уравнения 357
Интегральные уравнения типа свертки C57) Интегральные уравнения второго рода C58) Ин-
Интегральные уравнения первого рода C59) Особые интегральные уравнения. Интегральное урав-
уравнение Абеля C59) Примеры C60)
§ 6. Применение операционного нечисления
к решению уравнений с частными производными 366
Примеры C67)
Упражнения для самостоятельной работы 370
Ответы 372
Предметный указатель 377
Список опечаток, замеченных в предыдущих томах "Справочного пособия по высшей математике''
Стр.
Строка*
Напечатано
Должно быть
Том 1
96
3-я снизу
120. lim
(l-sini)(cos2i+l)-isin2i
i^n •• (l-sini)(cos2i+l)-isin2i
12°- 4 2^T^
191
9-я снизу
lim ijexp<a;( tfracl2x2 + o(-~.
Um x exp < x [ =- + о I —^ I I H
E-+oo V v\ \x 2x2 \x2JJS)
198
8-я снизу
Область определения функции -\х\ > 1.
Область определения функции: \х
Том 4
23
25
36
50
53
54
56
86
91
92
93
347
98
186
231
237
278
339
2-я снизу
9-я сверху
13-я сверху
14-я снизу
4-я снизу
4-я сверху
5-я снизу
22-я снизу
1- и 22-я св.
7-я сверху
1-я сверху
17- и 18-я св.
17-я снизу
11-я сверху
13-я сверху
8-я сверху
1-я снизу
2-я колонка,
5-я снизу
уп —> xq при к —» оо
Х1т _ а1т 242се
приет на замкнутом ограниченном множестве D / С К
e"taA+?-) - 1
* = -!+«=[*
zn+\ — zn\ — \zn
1 + i\
V «п+1
проходящая че-их
w = yi
две ветки
Задаф2елась
трасцендентной
не зависит то выбора
получим формулу C).
одногFжества
х?Г\в')
Упк -» xq при к -> оо
х1т-а1т,все
принимает на замкнутом ограниченном множестве Df С R2
е,ь(,+ Ы)_1
\zn+l ~ zn — \zn\
/ ^
V ап+\
проходящая через них
z = tyw
две ветви
Задача свелась
трансцендентной
не зависит от выбора
получим формулу C). >
одного множества
' Первой строкой сверху считается строка колонтитула.
Боярчук Алексей Климентьевич, Головач Григорий Петрович
Справочное пособие по высшей математике. Т. 5: Дифференциальные уравнения в примерах
н задачах. — М.: Эдиторнал УРСС, 2001. - 384 с.
ISBN 5-8360-0213-4
«Справочное пособие по высшей математике» выходит в пяти томах и представляет собой новое,
исправленное и существенно дополненное издание «Справочного пособия по математическому анализу»
тех же авторов. В новом издании пособие охватывает три крупных раздела курса высшей математи-
математики — математический анализ, теорию дифференциальных уравнений, теорию функций комплексной
переменной.
Том 5 охватывает все разделы учебных программ по дифференциальным уравнениям для уни-
университетов и технических вузов с углубленным изучением математики. Наряду с минимальными
теоретическими сведениями в нем содержится более семисот детально разобранных примеров. Среди
вопросов, нестандартных для такого рода пособий, следует отметить примеры по теории продолжимости
решения задачи Коши, нелинейным уравнениям в частных производных первого порядка, некоторым
численным методам решения дифференциальных уравнений.
Пособие предназначено для студентов, преподавателей и работников физико-математических,
экономических и инженерно-технических специальностей, специалистов по прикладной математике, а
также лиц, самостоятельно изучающих высшую математику.