Клавдий Птолемей. II век н. э - Бронштен В.А.

Бронштэн В.А. Клавдий Птолемей: II век н. э. - 1988

Глава 2. Астрономия в Вавилоне и Греции до Гиппарха

Глава 3. Астрономические исследования Гиппарха

Глава 4. Краткое содержание «Альмагеста»

Глава 6. Небесная сфера: расчеты и измерения

Глава 11. «Преступление Клавдия Птолемея»

Глава 12. Работы Птолемея в области географии

Глава 13. Работы Птолемея в области оптики

Глава 17. От эпициклов Птолемея к законам Кеплера

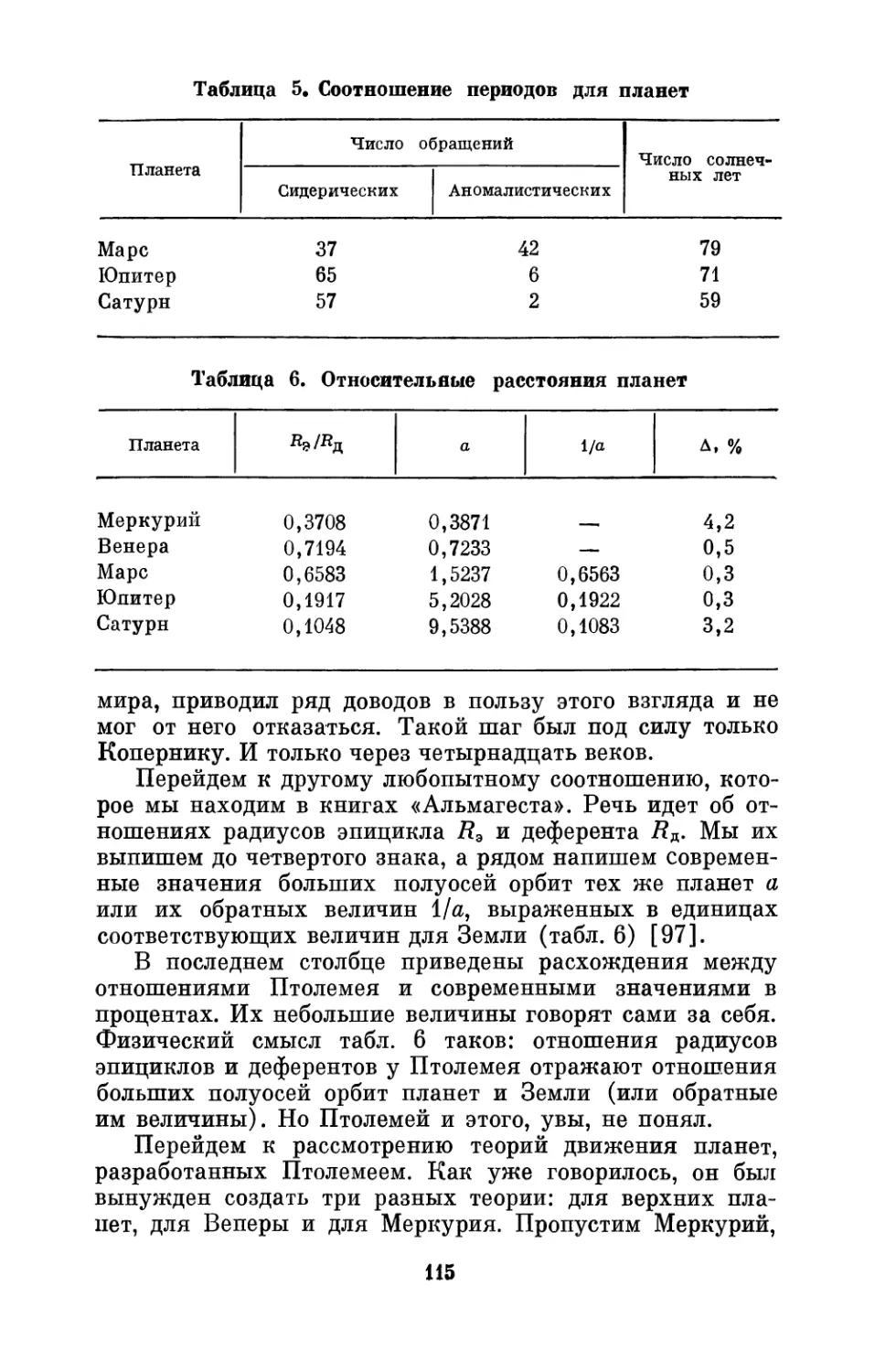
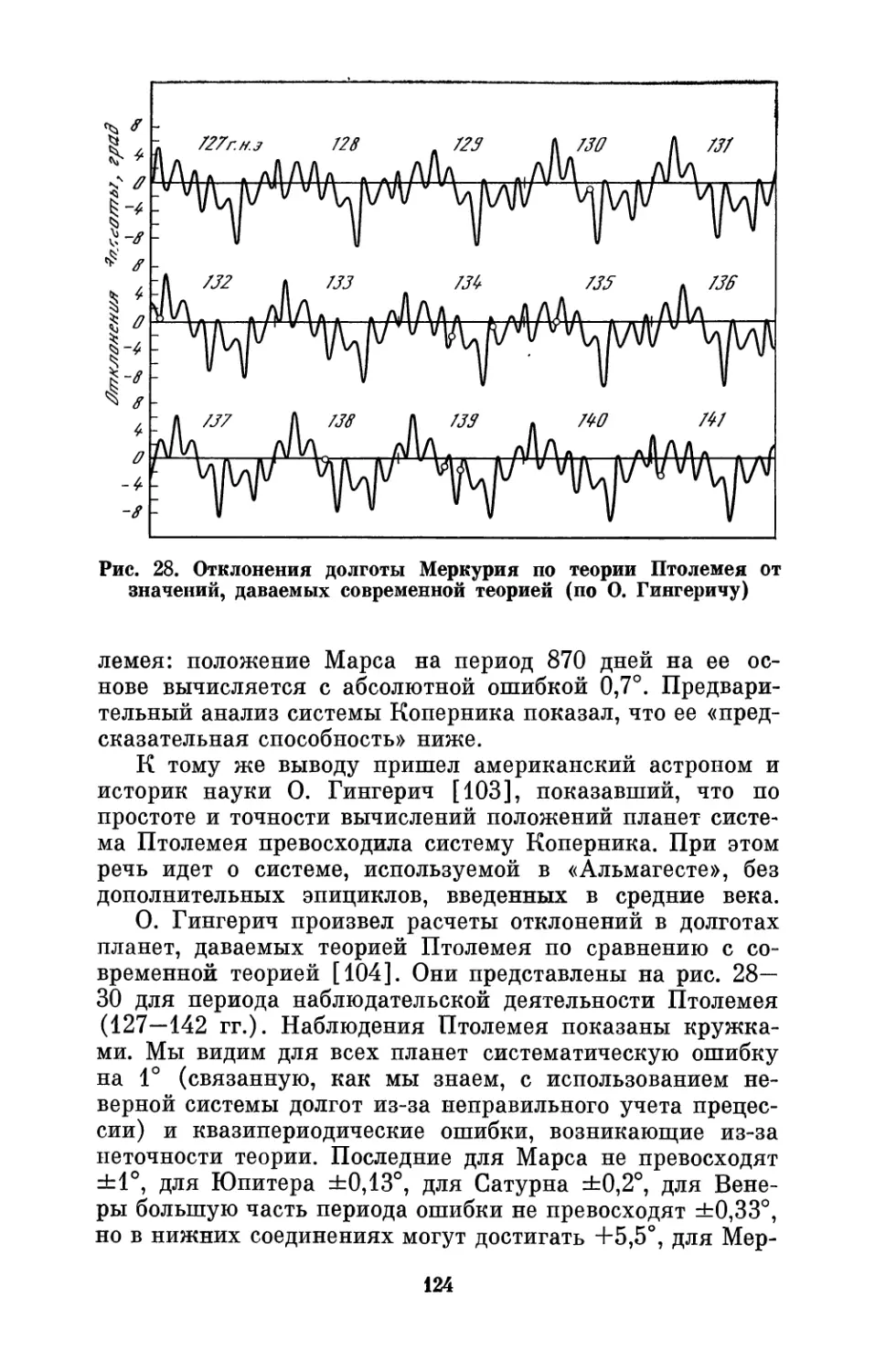
Автор: Бронштен В.А.

Теги: астрономия астрофизика исследование космического пространства геодезия история астрономии история науки биографии античная культура

ISBN: 5-02-001300-5

Год: 1988

Похожие

Изложение системы мира

М.В. Ломоносов - астроном и астрофизик

Извечные тайны неба

Расширяя границы Вселенной

Текст

АКАДЕМИЯ НАУК СССР
fll&Hfy-
ч

РЕДКОЛЛЕГИЯ СЕРИИ
«НАУЧНО-БИОГРАФИЧЕСКАЯ ЛИТЕРАТУРА»
И ИСТОРИКО-МЕТОДОЛОГИЧЕСКАЯ КОМИССИЯ
ИНСТИТУТА ИСТОРИИ ЕСТЕСТВОЗНАНИЯ И ТЕХНИКИ АН СССР
ПО РАЗРАБОТКЕ НАУЧНЫХ БИОГРАФИЙ ДЕЯТЕЛЕЙ
ЕСТЕСТВОЗНАНИЯ И ТЕХНИКИ
Л. Я. Бляхери А. Т. Григорьян, В. И. Кузнецов,
А. И. Купцов, В. В, Левшин, С. Р. Микулинский, Д. В, Ознобишин,
3. К. Соколовская (ученый секретарь), В. Н. Сокольский,
Ю. И. Соловьев, А. С. Федоров (зам. председателя),
И. А. Федосеев (зам. председателя),
Н. А. Фигуровскищ (зам. председателя),
А. П. Юшкевич, А. Л, Яншин (председатель),
М. Г. Ярошевский

В. А. Бронштэн
Клавдий
ПТОЛЕМЕЙ
II век Н. Э.
Ответственный редактор
доктор физико-математических наук
А. А. ГУРШТЕЙН
МОСКВА
«НАУКА»
1988

ББК 22.6г
Б 88
УДК 52(091)
Рецензенты:
член-корреспондент АН УзССР Г. П. МАТВИЕВСКАЯ,
доктор физико-математических наук Б. А. РОЗЕНФЕЛЬД
Бронштэн В. А.
Б 88 Клавдий Птолемей: II век н. э.— М.: Наука,
1988.— 240 с, ил.— (Серия
«Научно-биографическая литература»).
ISBN 5-02-001300-5
В книге освещается жизнь и научная деятельность
знаменитого ученого античности Клавдия Птолемея
(II век н. э.), известного своими трудами в области
астрономии, математики, географии, оптики, теории
музыки. Подробно анализируются труды Птолемея,
подчеркивается их научное значение не только для его эпохи, но
и для развития науки в целом. Изложена дальнейшая
история основных трудов Птолемея и их применения в
позднейшие времена — вплоть до наших дней.
Книга предназначена для всех, кто интересуется
историей науки.
-1402000000—125
054 (02)-88 32—88НПЛ ББК 22.6г
Бронштэн Виталий Александрович
Клавдий Птолемей
II век н. э.
Утверждено к печати редколлегией научно-биографической серии
Академии наук СССР
Редактор издательства М. А. Суханов. Художественный редактор
В. В. Алексеев. Технический редактор Т. С. Жарикова. Корректоры
Р. С. Алимова, Н. И. Казарина
ИБ № 37494
Сдано в набор 03.11.87. Подписано к печати 25.03.88. Т-07395.
Формат 84хЮ8'/з2. Бумага типографская № 1. Гарнитура обыкновенная.
Печать высокая. Усл. печ. л. 12,6. Усл. кр. отт. 12,81. Уч.-изд. л. 13,6.
Тираж 15 000 экз. Тип. зак. 1184. Цена 85 коп.
Ордена Трудового Красного Знамени издательство «Наука»
117864, ГСП-7, Москва, В-485, Профсоюзная ул., 90
2-я типография издательства «Наука»
121099, Москва, Г-99, Шубинский пер., 6
ISBN 5—02—001300—5 © Издательство «Наука», 1988

От редактора
Книга посвящена жизни и научной деятельности
'величайшего астронома древности Клавдия Птолемея (ок.
100—ок. 165), жившего и работавшего в Александрии —
научном центре эпохи позднего эллинизма.
Биографические данные о Птолемее почти неизвестны.
Автор пытается по весьма скудным сведениям
реконструировать его научную деятельность в хронологической
последовательности. Птолемей известен главным образом своим
капитальным трудом в области астрономии — «Великим
построением», обычно называемым «Альмагестом». В книге
дается тщательный анализ содержания «Альмагеста»,
раскрываются методы исследований и последовательность
изложения результатов Птолемея, его теории движения
Солнца, Луны и планет, работы по составлению звездного
каталога.
Автор не обходит молчанием спорные вопросы,
связанные с деятельностью Птолемея: кем был составлен
звездный каталог, почему Птолемей вносил поправки в свои
и чужие наблюдения для их лучшего согласования со
своей теорией. Автор приходит к выводу, что эти
поправки не снижают научного значения работы Птолемея,
которая на протяжении полутора тысячелетий служила
общепринятым руководством по астрономии.
Отдельные главы книги посвящены исследованиям
Птолемея в области географии, оптики, теории музыки,
его занятиям астрологией. В последних главах
прослеживается судьба «Альмагеста». Обсуждается значение
трудов Птолемея для пионерских работ Коперника и Кеплера.
А. А. Гурштейн
о

Предисловие
Знаменитый александрийский астроном, математик и
географ II века и. э. Клавдий Птолемей — одна из
крупнейших фигур в истории науки эпохи позднего эллинизма.
В истории же астрономии Птолемею не было равных на
протяжении целого тысячелетия — от Гиппарха (II в. до
н. э.) до Бируни (X—XI в. н. э.).
История довольно странным образом обошлась с
личностью и трудами Птолемея. О его жизни и деятельности
нет никаких упоминаний у историков той эпохи, когда он
жил. Если, например, о его современнике римском
естествоиспытателе и враче Галене известно, что он родился в
Пергаме в 129 г. н. э. и умер около 201 г., то даже
приблизительные даты рождения и смерти Птолемея неизвестны,
как неизвестны и какие-либо факты его биографии.
Птолемею повезло в другом. Почти все его основные
сочинения сохранились и были по достоинству оценены
потомками, начиная от его младших современников (Вет-
тий Валент и тот же Гален) и кончая астрономами наших
дней. Основной труд Птолемея, широко известный ныне
под названием «Альмагест», был переведен с греческого
на сирийский, средыеперсидский (пехлеви), арабский,
санскрит, латынь, а позднее — на французский, немецкий,
английский и русский языки. Вплоть до начала XVII в.
он был основным учебником астрономии.
Широкий круг читателей обычно связывает с именем
Птолемея так называемую «систему мира Птолемея», где
в центре расположена Земля, а вокруг нее по круговым
орбитам обращаются Луна, Меркурий, Венера, Солнце,
Марс, Юпитер и Сатурн. При этом пять планет движутся
не непосредственно вокруг Земли, а по малым кругам —
эпициклам, центры которых обращаются вокруг Земли по
другим кругам — деферентам.
Геоцентрическая система Птолемея
противопоставляется гелиоцентрической системе Коперника, который
совершил поистине революционный переворот, поставив в
центр нашей планетной системы Солнце и низведя Землю
до положения рядовой планеты, и якобы устранил
эпициклы, показав, что они были нужны лишь для представ-
6

ления движения Земли
вокруг Солнца.
Эта упрощенная схема,
глубоко укоренившаяся среди
многих лекторов, учителей,
студентов и даже научных
работников, на самом деле
в лучшем случае неточна,
а кое в чем ошибочна.
Те иллюстрации, которые
изображают в книгах
«систему Птолемея», это лишь
грубые эскизы, отражающие
только некоторые
признаки его системы:
центральное положение Земли и
наличие деферентов и
эпициклов. Но Земля у Птолемея
не совпадалас центрами Старинное изображение
деферентов, а положение эпи- Птолемея
циклов и самих планет на
них зависело от положения
Солнца; в теории планетных движений Птолемея
фигурировали и другие круги, о которых в учебниках и
популярных книгах обычно не пишут (эквант, эксцентр).
Из советских учебников по общей астрономии *
наиболее полное и обстоятельное изложение теории Птолемея
дает «Курс общей астрономии» С. Н. Блажко [31].
Нетривиальное математическое представление построений
Птолемея дает А. А. Иванов в «Курсе астрономии» [53].
В первом издании «Астрономии» П. И. Попова, К. Л. Ба-
ева, Б. А. Воронцова-Вельяминова и Р. В. Куницкого [81]
не только рассказывается о планетной теории Птолемея
и дается обзор содержания «Альмагеста», но говорится
и о звездном каталоге Птолемея. К сожалению, в
последующих изданиях этой книги указанные разделы были
сильно сокращены.
В современных учебниках системе Птолемея
уделяется не более двух страниц. Приходится констатировать,
что как в университетском «Курсе общей астрономии»
П. И. -Бакунина, Э. В. Кононовича и В. И. Мороза [25],
1 Здесь мы говорим только об учебниках. Прекрасный
обстоятельный анализ теории движения планет и Лупы Птолемея
содержится в работе Н. И. Идельсона «Этюды по истории планетных
теорий» [54].
7

так и в курсе для
педвузов «
Астрономия» М. М. Дагаева,
В. Г. Демина, И. А.
Климишина и В. М.
Чаругина [47]
система Птолемея
излагается неточно, а во
втором из них
положения Марса,
Юпитера и Сатурна на
эпициклах и вовсе
указаны ошибочно.
Неверно также,
что в системе
Коперника не было
эпициклов. Конечно,
эпициклы,
отражавшие движение Земли
Птолемей с угломерным вокруг Солнца, отпа-
инструментом ^ но ^ которые
были введены ради
представления обращений по эллипсам круговыми
движениями, остались. Из 79 кругов системы Птолемея
Коперник был вынужден сохранить 34 [63. С. 430].
В «Альмагесте» Птолемей широко использует
результаты наблюдений и построения своего великого
предшественника Гиппарха (И в. до н. э.). Надо сказать, что и о
жизни Гиппарха мы имеем не больше сведений, чем
о жизни Птолемея. Даты его рождения и смерти
неизвестны. Известно, что он родился в городе Никее 2, в Вифи-
нии, а большую часть своих наблюдений провел на
острове Родос.
За последние 200 лет не раз возникал вопрос, какие
наблюдения и результаты заимствованы Птолемеем у
Гиппарха, а какие принадлежат самому Птолемею. Дело
в том, что подлинные сочинения Гиппарха до нас не
дошли (за исключением небольшого «Комментария к Арату»),
и вопрос этот приходится решать косвенными путями.
Практически все, что нам известно о работах Гиппарха.
мы узнали благодаря их изложению в «Альмагесте»
Птолемея. То же можно сказать и о многих других
наблюдениях и математических исследованиях древнегреческих
2 Ныне город Изник в Турции.
8

и вавилонских астрономов. Благодаря этому «Альмагест»
стал своеобразной энциклопедией астрономии древности.
Не случайно «Альмагест» был переведен за полтора
тысячелетия на столько языков и служил учебником
астрономии во многих странах мира. Каждый уважающий
себя ученый Арабского Востока и Средней Азии считал
своим долгом составлять комментарии к «Альмагесту».
Некоторые из них подвергали те или иные положения
Птолемея критике. Среди этих ученых назовем аль-Фер-
гани (IX в.), Сабита ибн Корру (836—901), его внука
Ибрагима ибн Синана (908-946), аль-Баттани (850-929),
аль-Фараби (870-950), Абу-ль-Вафу (940-998), Ибн
аль-Хайсама, он же Альхазен (965—1039), Бируни
(973-1048), Насир ад-Дина ат-Туси (1201-1274). Этот
список можно было бы значительно расширить.
Коперник и Кеплер в своих работах также исходили
из построений Птолемея. Первый из них превратил
геоцентрическую систему Птолемея в гелиоцентрическую,
но сохранил принцип равномерного движения по кругам
и широко использовал математический аппарат Птолемея.
Второй, отказавшись от этого принципа, тем не менее
использовал построения Птолемея, чтобы найти истинную
форму планетных орбит. Обо ; всем этом мы расскажем
ниже.
Кроме «Альмагеста» Птолемей оставил ряд других
сочинений, причем не только по астрономии, но и по
математике, оптике, географии, музыке. Ему принадлежит
разработка основ математической картографии и
составление списка координат 8000 географических пунктов
(определенных, правда, весьма приближенно).
Задача настоящей книги — рассказать о научной
деятельности этого ученого, работавшего, в сущности говоря,
в одиночку. У него не было (насколько нам известно)
помощников и коллег 3. Нам неизвестно, был ли у него
учитель и оставил ли он сам после себя учеников.
Предшественник Птолемея Гиппарх жил и работал за 300 лет
до него, а ученые Арабского Востока приняли от Птоле-
3 Единственный человек, проводивший астрономические
наблюдения в Александрии почти одновременно с Птолемеем и
передававший их ему, как свидетельствует сам Птолемей, был
математик Теон. Он проводил наблюдения в 125-132 гг.
Отождествление его с Теоиом из Смирны хронологически возможно, но
вовсе не обязательно: тогда имя Теон было очень
распространено в эллинистическом Египте Г131].
9

мея своеобразную научную «эстафету» лишь семь веков
спустя.
По-видимому, своими успехами в области астрономии
Птолемей во многом обязан знаменитой Александрийской
библиотеке, которой он широко пользовался. Так стали
ему известны труды Гиппарха (не дошедшие, увы, до
нас), а также таких древнегреческих ученых, как Метон
(V в. до н. э.), Евклид, Аристотель, Каллипп (IV в. до
н. э.), Аристилл, Тимохарис, Архимед, Аристарх Самос-
ский, Эратосфен (III в. до н. э.), Аполлоний Пергский
(III—II вв. до н. э.). Птолемей широко использовал
также наблюдения астрономов Вавилона, не называя их,
правда, по именам. Это в основном наблюдения лунных и
солнечных затмений, а также некоторых других явлений
(покрытий звезд Луною, соединений планет),
проводившиеся вавилонскими астрономами начиная с VIII в. до
н. э. Эти наблюдения послужили Птолемею для создания
теории движения Луны, которой пользовались десятки
поколений астрономов, моряков, путешественников.
В этой книге мы рассмотрим историческую
обстановку, в которой пришлось жить и работать Птолемею, дадим
краткий очерк развития астрономии в Вавилоне и в
Древней Греции от Метона до Гиппарха (V—II вв. до н. э.),
познакомим читателей с содержанием «Альмагеста» и с
основными научными результатами, которые в нем
освещаются. Затем мы рассмотрим ряд спорных вопросов,
связанных с работами Птолемея. После этого мы
познакомим читателей с исследованиями Птолемея в области
географии, оптики и музыки, с его сочинением по
астрологии. Заключительные главы книги посвящены судьбе
«Альмагеста», его распространению по странам мира,
его использованию учеными этих стран, результатам
различных исследований нового времени, связанных с
«Альмагестом». По мере возможности мы постараемся
проследить судьбу и других сочинений Птолемея.
Основным текстом «Альмагеста», использованным
автором, был английский перевод Дж. Тумера [17], хотя
автор использовал в отдельных случаях и немецкий
перевод К. Манициуса [14], а также существующий пока в
рукописи русский перевод И. Н. Веселовского. За
разрешение пользоваться этим текстом автор благодарен
профессору А. Т. Григорьяну.
Автор пользуется случаем поблагодарить Г. П. Мат-
виевскую, Б. А. Розенфельда и А. А. Гурштейна за
ценные замечания и советы.

Глава 1
Место и время действия
Город Александрия, в котором протекала научная
деятельность Клавдия Птолемея, был основан Александром
Македонским в 332 г. до н. э. Вскоре он стал столицей
новой (последней) династии египетских царей, ведущих
свой род от диадоха i (полководца) Александра
Македонского — Птолемея Лага. Поэтому и основанную им
династию принято называть династией Птолемеев. Впрочем,
пятнадцать царей этой династии носили имя
Птолемей [30].
Последней правительницей Египта из этой династии
была известная царица Клеопатра. Потерпев поражение
в войне против римского полководца Гая Октавия
(ставшего вскоре императором под именем Октавиана
Августа) , Клеопатра в 30 г. до н. э. покончила с собой. Египет
был покорен Римом и получил статус римской провинции.
Династия царей Птолемеев пресеклась вместе с гибелью
Клеопатры.
Вопреки неоднократно высказывавшемуся мнению,
астроном Клавдий Птолемей не имеет никакого
отношения к царской династии Птолемеев. Начало версии о
царском происхождении Клавдия Птолемея положил,
вероятно, один из переписчиков сочинений Галена, который
написал после имени Птолемея, что он был «царем
Египта» [131. С. 2].
Очевидно, что сам Гален не мог этого написать. Он
прекрасно знал, кто такой Клавдий Птолемей, а кроме
того, будучи римлянином, не мог не знать, что никакого
царства в Египте нет, что это — римская провинция,
управляемая наместником, а, значит, там не может быть
никакого царя. Переписчик же, живший одним или
несколькими веками позже, легко мог спутать Клавдия Птолемея
с царями династии, правившей в Египте за несколько
веков до него. Он мог просто не знать истории и, делая свое
1 Буквальный перевод слова диадох - преемник.
И

«пояснение», был, вероятно, глубоко убежден, что этим
он поможет будущим читателям труда Галена.
С такими случаями — ошибками переписчиков древних
рукописей, сделанными иногда по небрежности, а
иногда намеренно (как в рассмотренном случае), — нам
придется сталкиваться не раз.
Клавдий Птолемей был просто тезкой египетских
царей 2. В этом нет ничего удивительного, потому что
обычай давать детям имена царей или полководцев был в те
времена довольно распространен.
Есть и другая версия, согласно которой Птолемей
родился в городе Птолемаиде Гермийской (Верхний Египет,
севернее Фив, на берегу Нила) и, как обычно делали в то
время, получил прозвище по месту рождения. Потом
Клавдий Птолемаидский превратился в Клавдия
Птолемея. По мнению известного историка науки П. Таынери
(1843—1904), Птолемей родом из Пелусия (у впадения
самого восточного рукава Нила в Средиземное море)
[130]. Однако все эти версии не имеют серьезного
исторического основания. К тому же городов под названием
Птолемаида было в Египте несколько.
К началу II в. н. э. Александрия была большим по тем
временам городом (в нем жило около 30 тыс. человек),
столицей провинции, крупным торговым центром,
связанным морскими путями с Римом, Афинами, Антиохией, со
многими другими центрами Средиземноморья, с Сирией,
Персией, Индией и другими странами Востока.
Гордостью Александрии была знаменитая библиотека.
Она была основана в правление Птолемея II Филадельфа
(282-246 гг. до н. э.) [17. С. 139]. Здесь были собраны,
все основные научные и литературные сочинения той
эпохи. Библиотекой руководили крупнейшие ученые. Так,
одним из первых ее хранителей был знаменитый астроном
и географ Эратосфен (276—194 г. до н. э.), занявший эту
должность в 225 г. до п. э. [78]. К I в. до н. э. в
библиотеке насчитывалось уже 700 тыс. папирусных свитков.
Слава об Александрийской библиотеке заставила пергамского
царя Евмена II основать аналогичную библиотеку в Пер-
гаме [55].
Постепенно центр научной мысли переместился из
Греции в Александрию. Здесь жили и работали такие
известные ученые древности, как математики Е'вклид
2 Даже такой известный историк науки, как Г. Хунгер [107],
говорит о происхождении Клавдия Птолемея от царской династии
Птолемеев.
12

(365—ок. 300 г. до н. э.), Аполлоний Пергский (ок. 260—
ок. 170 до н. э.), астрономы Аристилл и Тимохарис (III в.
до н. э.) и др.
Александрийская библиотека была частью Музея
(храма муз), при котором были зоологический и
ботанический сад, а также обсерватория. В помещениях Музея
жили приезжавшие в Александрию для научной работы
ученые.
Расцвет науки в этот период отражал расцвет
рабовладельческих государств, таких, как Рим, Карфаген, Пергам,
Египет, держава Селевкидов в Месопотамии, и др.
Впоследствии все остальные государства были поглощены
Римом и превратились в римские провинции.
Жизнь и деятельность Клавдия Птолемея протекала
в условиях начавшегося упадка рабовладельческого
общества. Античная наука тоже переживала упадок. На
горизонте уже не было таких фигур, как Платон, Аристотель,
Демокрит, Пифагор, Евдокс, Архимед, Гиппарх. Более
того, их не было уже давно — почти три столетия.
Клавдий Птолемей — «последний из могикан» античной науки.
Уже только поэтому его личность должна привлечь наше
внимание.
По свидетельству Олимпиодора (биографа Платона,
жившего в Александрии в середине VI в. н. э.), Птолемей
«в течение 40 лет жил в так называемых Крыльях Кано-
па, посвятив себя астрономии, о чем свидетельствуют
высеченные им на каменных табличках его астрономические
открытия» [132] 3. Этот текст Олимпиодора для нас очень
важен, поскольку Олимпиодор несомненно сам видел те
места, где жил и работал Птолемей. Поэтому остановимся
немного на содержании этого текста.
Каноп (ныне Абукир) — городок, расположенный в
западной части дельты Нила, на берегу Средиземного моря,
в 25 км к северо-востоку от Александрии. Там находился
храм Сераписа — бога природы \ а в боковых приделах
храма («крыльях») располагалась школа, основанная еще
царями Птолемеями. Там же жил и работал Клавдий
Птолемей. Некоторые результаты своих исследований он
действительно велел вырубить на каменной колонне, и
3 Здесь и далее цитаты из иностранных источников приводятся в
переводе автора, если это не оговорено особо.
4 Кстати, Каноп — это не только название пригорода Александрии,
но также и греческий эквивалент имени египетского бога
Сераписа. Храм Сераписа был разрушен фанатиками-христианами
в 391 г.
а

этот текст, получивший название «Канопской надписи»,
дошел до нас.
Как уже говорилось, точные даты жизни Птолемея
нам неизвестны. Упоминаемые в «Альмагесте»
астрономические наблюдения выполнены между 127 и 141 г. н. э.
Очень важно содержащееся в «Канопской надписи»
указание, что она исполнена на 10-й год правления римского
императора Антонина Пия, т. е. в 146 или 147 г. Как
доказал английский исследователь Н. Гамильтон, «Каноп-
ская надпись» по времени предшествует «Альмагесту»,
и можно полагать, что «Альмагест» был закончен около
150 г. н.э. [131].
Правомочно ли на основании подобных сведений
сделать какие-либо твердые выводы о годах жизни
Птолемея? Вспомним слова Олимпиодора о том, что Птолемей
прожил в Крыльях Канопа 40 лет, посвятив себя
астрономии. К сожалению, различные авторы по-разному
трактуют это важнейшее свидетельство. Так, Николай Коперник
в своем замечательном труде «О вращениях...» пишет, что
Птолемей в течение 40 лет проводил свои
астрономические наблюдения, хотя точные сведения имеются только
о 15 годах (127—141 гг.). А П. Таннери, ссылаясь на того
же Олимпиодора, пишет, что Птолемею было 40 лет, когда
он вел свои наблюдения. Другие авторы, начиная с
И. Л. Дрейера [97], восприняли это так, что Птолемей
начал свои наблюдения в возрасте 40 лет, откуда и
«вычислили» год его рождения — 87 г. н. э.
Посмотрим теперь, какие годы жизни приписывают
Птолемею различные авторы. Вот небольшая сводка:
Ф. Болл, 1894 [94] ок. 90 —ок. 160 г.
И. Л. Дрейер, 1907 [97] ок. 87 — 165 г.
М. Ф. Субботин, 1955 [88] ? — ок. 168 г.
Дж. Тумер, 1984 [131] 100 г. — 175 г.
Попробуем теперь оценить, какие из этих дат наиболее
вероятны. Если верить Дж. Тумеру, Птолемей приступил
к своим астрономическим наблюдениям в возрасте 27 лет,
если же верны даты его рождения, приводимые Ф. Бол-
лом и И. Л. Дрейером, то ему было тогда 37—40 лет.
Спрашивается, что же он делал до этого? Учился,
набирался знаний? Вообще говоря, несомненно, но нельзя же
только учиться до 40 лет. Поэтому, с нашей точки зрения,
более вероятен год рождения, приводимый Дж. Тумером.
Что касается года смерти Птолемея, то, конечно, он
мог прожить и 60 и 75 лет. Некоторые арабские источни-
14

ки указывают, что он прожил 78 лет. Но среди
приведенных выше предполагаемых дат смерти Птолемея одна
имеет намного большую вероятность, чем остальные.
Это — 165 г. В этот год по Египту прошла страшная
эпидемия чумы, захватившая также Малую Азию, Италию и
часть Средней Европы [30]. Весьма возможно, что эта
болезнь унесла и жизнь Клавдия Птолемея. Согласно [123],
Птолемей умер в Каноне.
Таким образом, вероятными годами жизни Птолемея
следует признать 100—165 гг. н. э. В 27 лет он приступил
к своим астрономическим наблюдениям и вел их в
течение 14 лет. Затем около девяти лет он работал над
главным трудом своей жизни — «Альмагестом». В ходе
подготовки «Альмагеста» он написал предварительное
изложение своих взглядов и теорий — «Канопскую надпись».
После окончания «Альмагеста» он написал еще одно
сочинение в четырех книгах, посвященное астрологии, но
не стал включать его в «Альмагест» и выпустил отдельно
под названием «Тетрабиблос», что означает «Четырехкни-
жие». Об этом сочинении Птолемея мы расскажем в гл. 15.
К моменту окончания работы над «Альмагестом»
Птолемею было уже около 50 лет. Но он был еще бодр и
продолжал работать: скорее всего, именно в этот период он
написал свои «Оптику» и «Географию», а также
несколько мелких сочинений, как дошедших, так и не дошедших
до нас. Эпидемия чумы прекратила его плодотворную
деятельность.
Конечно, все это не более чем гипотеза, но гипотеза
довольно вероятная. Мы будем придерживаться ее в
дальнейшем.
С точки зрения этой гипотезы получает простое
истолкование и число 40 лет, приводимое Олимпиодором. Это —
период с 127 г., когда Птолемей начал вести свои
астрономические наблюдения, до 165 г.— года его кончины.
Получается 38 лет, которые нетрудно округлить до сорока.
Впрочем, в «Альмагесте», как мы увидим дальше, есть
указание еще на одно наблюдение, дата которого не
приводится, но соответствующее расположение светил имело
место в 125 г. Если Птолемей действительно начал
наблюдать в 125 г., то и округлять ничего не нужно —
получается; что он занимался астрономией (и другими науками)
ровно 40 лет.
Несомненно, Птолемей был материально обеспеченным
человеком и мог целиком посвятить себя науке: сперва ее
изучению, а потом научным исследованиям. Мы ничего не
15

знаем об источниках его доходов. Был ли он владельцем
какого-то хозяйства, приносившего доход, или, как многие
ученые эпохи эллинизма, получал постоянное содержание
от властей?
Известные нам материалы не дают ответа на этот
вопрос. Но один любопытный факт заслуживает упоминания.
На восьмом году правления римского императора
Антонина Пия (144/145 г. н. э.) в Александрии была
выпущена серия из 12 медных монет с изображениями знаков
зодиака [48]. На всех монетах отчеканена восьмиконечная
звезда и мифологические изображения семи планет
(включая Солнце и Луну). Их расположение по знакам
зодиака соответствует гороскопу императора. Очевидно,
что эта серия была выпущена к 60-летию Антонина Пия.
Весьма вероятно, что Клавдий Птолемей принимал
участие в составлении императорского гороскопа (он ведь
занимался астрологией) и в выпуске этой серии монет.
Но золотые и серебряные монеты чеканили только в
Риме, поэтому в Александрии пришлось удовольствоваться
медными.
Глава 2
Астрономия в Вавилоне и Греции
до Гиппарха
Мы не предполагаем здесь давать обзор всей истории
астрономии в доптолемеевскую эпоху. Такие обзоры
имеются в ряде книг по истории астрономии [29, 78]. Наша
задача — рассказать лишь о тех работах, которые были
так или иначе использованы Птолемеем.
Наиболее старые из использованных им наблюдений
были произведены в Вавилоне в конце VIII в. до н. э.
В дальнейшем изложении мы будем для записи годов до
нашей эры использовать астрономический, а не
исторический счет годов. Их отличие состоит в следующем.
У историков первому году н. э. предшествует первый
год до н. э., нулевого года нет. Такой способ счета годов
неудобен для определения интервала между какими-либо
событиями до и после начала эры. Поэтому астрономы
ввели нулевой год (1 г. до н. э. у историков), а
предшествующие ему обозначают отрицательными числами.
16

Таким образом, год 0=1 г. до н. э., год —100=101 г. до н. э.,
год —720=721 г. до ы. э. и т. д. Теперь нетрудно
подсчитать интервал в годах, например от —720 до 125 г.: он
равен 845 годам.
Город Вавилон — один из древнейших городов на
Земле. Он основан в третьем тысячелетии до н. э. и
длительное время был столицей Вавилонского царства. Но к
VIII в. до н. э. Вавилон был покорен другой мощной
державой — Ассирией. Тем не менее город Вавилон
сохранил свое значение как богатый торговый и культурный
центр. Вавилонские жрецы, которые, собственно, и
занимались астрономией, вели и записывали наблюдения
редких небесных явлений: затмений Солнца и Луны,
появлений комет и некоторых других небесных тел. Эти
наблюдения они вели и в эпоху ассирийского владычества
(от —746 до —605 г.), и в эпоху Нововавилонского царства
(от —604 до —537 г.), и в эпоху, когда Вавилон стал
частью Персидской монархии (от —537 до —331 г.). Именно
в эти эпохи и были выполнены наблюдения лунных
затмений, использованные сперва Гиппархом, а затем
Птолемеем для построения теории движения Луны. Самое
первое из них произошло —720 марта 19, а последнее,
наблюдавшееся в Вавилоне, —381 декабря 12 [131.
С. 685].
Вавилонские астрономы записывали даты наблюдений
по годам царствования своих царей, например «второй
год Мардокемпада, месяц фаменот, 15-е число». Птолемей
был вынужден привести все эти даты к единой эре, в
качестве которой он выбрал эру от начала царствования
Набонассара (—746 г.), причем первым считался месяц
тот по египетскому календарю (вавилонские жрецы
использовали в то время египетские названия месяцев и
вообще египетский календарь). Для того чтобы
переводить все даты в единую эру, Птолемей составил
хронологическую таблицу царствований вавилонских царей
(начиная от Набонассара), персидских царей (от Кира до
Дария III), Александра Македонского и египетских
Птолемеев и, наконец, римских императоров от Октавиана
Августа (стал императором в —29 г.) до Антонина Пия,
при котором Птолемей жил и работал (начало
царствования 137 г. н. э.). Эта таблица была включена
Птолемеем в «Справочные таблицы», выпущенные им отдельно
[9]. В реконструированном виде она приводится в
английском издании «Альмагеста» под ред. Дж. Тумера, где
все даты даны в современном летоисчислении [131. С. И].
17

При датировке использованных им наблюдений,
выполненных в Греции и в самой Александрии, Птолемею
пришлось иметь дело с другими календарными системами.
Он сумел привести их к единой системе, так что
датировка всех наблюдений независимо от их времени и
места определяется однозначно.
От вавилонских математиков и астрономов Птолемей
позаимствовал шестидесятиричную систему счисления.
Евклид
Метон
Эвктемон каллипп ° Герон Александрийский
Аполлоний Пергский
Птолемей
Архимед Геминус
Аристарх Самосский ТеонСтарший
Аристотель Тимохарис Гиппарх д_ ^
111 Менелай Валент
Аристилл Гален
-J 1_ I ! I
-500 —400 —300 —200 —100 0 Ю0 200 г.
Рис. 1. Хронология жизни ученых древности (схема)
Эта система используется и в наши дни, правда в
ограниченном виде, при счете углов и интервалов времени.
Мы привыкли к тому, что час разделяется на 60 мин,
а минута — на 60 с. Точно так же один градус содержит
60 мин дуги, а минута — 60 с дуги. Но мы не используем
более мелких 60-х долей, а в работах Птолемея они
используются и довольно широко. Секунда (времени или
дуги) делится на 60 терций, терция — на 60 кварт и т. д.
Такой же принцип применяется не только к единицам
времени и дуги, но и к числам вообще.
Обратимся к астрономии древних греков (рис. 1).
Первые работы греческих астрономов относятся к
построению календаря. Около —433 г. астроном Метон ввел
19-летний цикл, получивший впоследствии название ме-
тонова цикла. Этот период содержит 6940 сут и почти в
точности равен длительности 235 лунных (синодических)
месяцев [78]. В самом деле, поделив 6940 на 235,
получаем среднюю длительность синодического месяца:
В цикле Метона 29,531914 сут
По современным данным 29,530588 сут
Иначе говоря, точность метонова лунного месяца
составляла 2 мин.
Средняя длительность года в метоновом цикле состав-
18

ляла 365,26316 сут, что на 19 мин длиннее введенного
четырьмя столетиями позднее юлианского года
(365,25 сут) и на 30 мин — действительной длительности
тропического года в эпоху Метона (365,2425 сут).
Нужно сказать, что календарная система в Вавилоне
и Греции была в ту эпоху очень сложной. Согласовать
солнечный тропический год с лунным синодическим
месяцем было очень трудно из-за их несоизмеримости.
Лунный год, состоявший из 12 лунных месяцев, содержал
(с округлением до целых суток) 354 сут, что было на И
с лишним суток меньше тропического года. Поэтому в
некоторые годы (примерно раз в три года) добавляли
тринадцатый месяц, так что такой год содержал уже
384 сут.
Метонов цикл значительно облегчал работу по
составлению календаря. Он давал простое соотношение между
годом и лунным месяцем. Кроме того, по номеру года в
цикле можно было легко узнать все даты в этом году,
поскольку по истечении цикла они повторялись.
Повторялись, как нетрудно сообразить, и лунные фазы.
Цикл Метона использовался еще в Вавилоне, так что
неизвестно, заимствовал ли его Метон у вавилонян или
определил независимо. Этот цикл использовался в
течение нескольких столетий.
Столетие спустя после Метона астроном Каллипп
улучшил метонов цикл, объединив 4 цикла по 19 лет и
отняв от итога одни сутки [78]. В каллипповом цикле
940 мес, равных в сумме 27 759 сут. Отсюда получаем
длину тропического года 365,25 сут (как в юлианском
календаре) и длину синодического месяца 29,530851 сут,
что всего лишь на 23 с продолжительнее истинного.
Циклы Метона и Каллиппа впоследствии критически
обсуждались Гиппархом, из сочинения которого «О
длительности года» сведения о них позаимствовал Птолемей,
в свою очередь подвергший этот вопрос критическому
анализу [17. С. 139].
Астроном Эвктемон, работавший вместе с Метоном,
из наблюдений равноденствий и солнцестояний
обнаружил неравенство четырех времен года. Согласно Эвктемо-
ну, длительность весны равнялась 93 сут, лета — 90,
осени — 90, зимы — 92. Каллипп спустя столетие уточнил их,
получив для весны, лета, осени и зимы соответственно
94, 92, 89 и 90 сут, тогда как их истинные длительности
были равны 94,1; 92,2; 88,6 и 90,4 сут [61]. Таким
образом, длительности времен года у Каллиппа были верны с
19

Аристотель Архимед
(384-322 до н. э.) (ок. 287-212 до н. э.)
точностью до полусуток (точнее, до ±0,35 сут), тогда как
точность этих величин у Эвктемона составляла ±1,88 сут.
Каллипп был учеником и помощником виднейшего
греческого философа IV в. до н. э. Аристотеля, автора
геоцентрической системы мира, где в центре мира
находится Земля, а орбиты Солнца, Луны и планет
изображаются кругами. Аристотель не был математиком и не
ставил себе задачей создание теории планетных
движений. Он резко разделял философию на теоретическую и
практическую части, отдавая преимущество первой, так
называемой «чистой» философии. Быть может, именно
поэтому Птолемей, астроном и математик,
позаимствовавший у Аристотеля геоцентрическое мировоззрение и
круговую форму орбит, упоминает его в «Альмагесте» только
однажды, в самом начале своего труда, там, где речь идет
о классификации наук [17. С. 35].
Много столетий спустя, когда христианская религия
стала господствующей в Европе, «отцы церкви», гневно
отметавшие все языческое, сделали своеобразное
исключение для геоцентризма Аристотеля и системы мира
Птолемея — они были официально признаны католической
церковью как правильные представления о строении
мира, не противоречащие Священному писанию. Но об
этом еще будет идти речь впереди.
20

Крупнейшим после Аристотеля греческим ученым
IV в. до н. э. был Евклид, чьи труды стали основой не
только греческой, но и мировой математики. Его
«Начала» содержат основные постулаты (аксиомы) и теоремы,
на которых в значительной мере базируется вся
элементарная математика вплоть до настоящего времени \
Птолемей в своих математических построениях постоянно
использует «Начала» Евклида, хотя не всегда на них
ссылается. По мнению Дж. Тумера, автора и редактора
новейшего английского перевода «Альмагеста», среди
сочинений древнегреческих авторов «Альмагест» занимает
второе место после «Начал» Евклида [131].
III в. до н. э. дал греческой науке целую плеяду
замечательных ученых — математиков и астрономов. Все они
жили и работали в Александрии, которая, как мы уже
говорили, стала к этому времени своеобразной «научной
столицей античного мира».
Астрономы-наблюдатели Аристилл и Тимохарис
производили, по-видимому, первые позиционные наблюдения
звезд, определяли их склонения и прямые восхождения,
т. е. координаты в экваториальной системе. Положения
звезд они определяли относительно некоторых
постоянных точек небесной сферы. Сам факт этих измерений
говорит о том, что в распоряжении Аристилла и Тимохари-
са были угломерные инструменты с градуированными
кругами, но их описания не сохранились. А. Берри
полагает, что Аристилла и Тимохариса можно считать
творцами первого в Европе звездного каталога в настоящем
смысле этого слова, в то время как их предшественники
пытались давать лишь словесные описания положений
звезд в созвездиях [12]. Кроме того, эти астрономы
произвели ряд наблюдений положений планет, Солнца и Луны.
Гиппарх и Птолемей использовали эти наблюдения
в первую очередь для исследования прецессии. В
частности, Гиппарх сравнивал положения звезды Спики (а
Девы) относительно точки осеннего равноденствия по
своим наблюдениям и по наблюдениям Тимохариса и его
школы. Тимохарис применял (по-видимому, впервые)
следующий способ [17. С. 329]. Он наблюдал положения
Спики относительно Луны во время полных лунных
затмений, происходивших в марте или апреле. Во время
полного лунного затмения Луна находится точно
напротив Солнца. Поэтому она в этот момент занимает такое
1 Доказано, что система аксиом Евклида неполна и содержит
излишние аксиомы. Однако многие из них используют и поныне.
21

положение относительно точки осеннего равноденствия,
которое симметрично положению Солнца относительно
точки весеннего равноденствия. Положения же Солнца
относительно равноденственных точек определялись Ти-
мохарисом и Аристиллом с помощью так называемого
экваториального кольца [17. С. 133]. Оно представляло
собой невысокий бронзовый цилиндр, верхний и нижний
края которого были ориентированы строго в плоскости
небесного экватора. Если Солнце было чуть севернее
небесного экватора, тень южной половины кольца оставляла
на внутренней стороне его северной половины узкую
полоску, освещенную Солнцем, близ верхнего края кольца.
Если же Солнце было южнее экватора, такая полоска
оставалась близ нижнего края. В дни равноденствия тень
южной половины кольца точно ложилась на внутреннюю
сторону северной половины, не оставляя светлой полоски.
Так, зная положения Солнца относительно
равноденственных точек на каждый день года, Тимохарис и Ари-
стилл могли определять и положения Луны во время
полных лунных затмений, а значит, и положения звезд
относительно этих точек.
Впоследствии Гиппарх соорудил такое же
экваториальное кольцо перед храмом Родоса2 и использовал его
для измерения положений Солнца [78]. Он применял
тот же метод определения положений звезд относительно
равноденственных точек, что и Аристилл и Тимохарис,
и из сравнения положений Спики в их время и в свою
эпоху (интервал около 150 лет) вывел значение
постоянной прецессии (см. ниже).
Птолемей приводит в «Альмагесте» таблицу
положений нескольких звезд по наблюдениям Аристилла и Ти-
мохариса, Гиппарха и своим собственным [17. С. 331—
332]. Из их сравнения он тоже нашел постоянную
прецессии, правда, с большой ошибкой.
Тимохарис и его школа наблюдали также покрытия
звезд Луною, определяли положения планет (его
наблюдения положений Венеры использованы Птолемеем в
«Альмагесте»).
В отличие от Аристилла и Тимохариса, которые были
лишь усердными наблюдателями, Аристарх Самосский
(310—230 г. до н. э.) не только производил те или иные
наблюдения (Птолемей использовал его наблюдения
моментов летних солнцестояний [17. С. 137—139]), но ста-
2 Главный город и порт на острове Родос.
22

рался глубже проникнуть в сущность мироздания.
Еще современник Аристотеля Гераклид Понтийский
(388—315 г. до н. э.) предполагал суточное вращение
Земли вокруг оси, заменяя им вращение вокруг Земли
всей небесной сферы. Более того, Гераклид пытался
объяснить характер видимого движения Меркурия и
Венеры, не отдалявшихся на небе от Солнца более чем на 29
и 48° соответственно. Гераклид полагал, что эти планеты
в действительности обращаются вокруг Солнца, а не
вокруг Земли. Однако в системе Гераклида Земля хотя и
вращается вокруг оси, но остается в центре мира: вокруг
нее движутся Луна, Солнце с Меркурием и Венерой,
Марс, Юпитер и Сатурн [78].
Аристарх Самосский пошел дальше своего
предшественника. Он был первым, кто предложил
гелиоцентрическую систему мира, поместив в центре планетной
системы Солнце, а Землю поставив в один ряд с другими
планетами3. За эту смелую идею Аристарх был обвинен
в безбожии и изгнан из Афин [80].
До нас дошло лишь одно сочинение Аристарха, в
котором он описывает свой способ определения отношения
расстояний до Солнца и до Луны (а значит, и их
размеров, поскольку видимые угловые размеры их почти равны).
Мы не станем описывать здесь хорошо известный способ
Аристарха (он описан во многих учебниках и книгах по
истории астрономии) [29]. Аристарх получил отношение
19:1 вместо правильного 390:1, что показывает неточность
его способа. Он доказал лишь, что Солнце во много раз
дальше и больше Луны.
Птолемей не ссылается на эту работу Аристарха.
Он использует лишь одно его наблюдение летнего
солнцестояния, а о геоцентрической системе упоминает, не
называя ее автора. Впрочем, Птолемей тут же подвергает
ее уничтожающей критике, о которой мы подробно
расскажем ниже.
Замечательный математик, механик и инженер,
Архимед (287—212 г. до н. э.), как и Аристарх,
производил наблюдения моментов летних солнцестояний,
использованных затем Гиппархом и Птолемеем. Он имел
также оригинальный взгляд на расположение планет,
полагая вместе с Платоном и Эратосфеном, что Мерку-
3 Об этих взглядах Аристарха мы узнали по рассказу его
младшего современника — Архимеда, изложенному в его сочинении
«Псаммит» («Исчисление песчинок»).
23

рий и Венера расположены дальше, а не ближе Солнца
[131. С. 419]. Аргументом в пользу такой точки зрения
он приводил то обстоятельство, что Меркурий и Венера
никогда не закрывали собой Солнце. Птолемей не
согласился с этим аргументом. Более того, его теория движения
Меркурия и Венеры позволяла предсказывать моменты
прохождений этих планет между Землей и Солнцем. Но
Птолемей понимал, что их диски весьма малы и заслонить
собой Солнце они не могут [131. С. 419].
Птолемей использовал в «Альмагесте» также
некоторые математические результаты Архимеда. Так, Архимед
вывел следующие приближенные пределы для числа п
(отношение окружности к диаметру) [17. С. 302]: от З1/?
до 310/т1, или, что то же самое, от 3,142857 до 3,140845. Сам
Птолемей выбирает число 3; 8,30, что следует читать так:
3 плюс 8- (Veo) плюс 30-(7бо)2. Это число равно 3,141667
и отличается от правильного значения (записанного с тем
же числом знаков) 3,141593 на 7,4-10~5.
Выводя свою теорему о хорде половины дуги
(понятие хорды будет подробно объяснено дальше, пока же
укажем, что это удвоенная линия синуса половины угла),
Птолемей не сообщает, что эта теорема была доказана
Архимедом за пять столетий до него. Вряд ли он не знал
об этом. Скорее он считал такие результаты настолько
общеизвестными, что полагал возможным не называть их
авторов. Мы уже приводили выше аналогичный пример
с использованием «Начал» Евклида. Впрочем, и в наше
время в учебниках далеко не всегда указывают, кто
впервые доказал ту или иную теорему из геометрии. Только
разве теоремы Пифагора и Аполлония носят имена их
авторов (из числа ученых древности).
Младший современник Архимеда, замечательный
геометр, астроном и первый в мире картограф Эратосфен
(276—194 г. до н. э.) впервые измерил дугу земного
меридиана между Александрией и Сиеной, получив длину
окружности меридиана с небывалой для того времени
точностью. Это был блестящий успех античной науки.
Впервые стали известны размеры земного шара [78].
Эратосфен считал, что Сиена и Александрия
находятся на одном меридиане, причем он проходит также через
Родос (имеется в виду город Родос, расположенный на
одноименном острове). Это обстоятельство использовали в
дальнейшем Гиппарх при сравнении своих наблюдений с
наблюдениями Аристилла, Тимохариса и других
александрийских астрономов и Птолемей, также сравнивав-
24

ший свои наблюдения в Александрии с наблюдениями
Гиппарха в г. Родосе [17. С. 225].
Заслугой Эратосфена в астрономии является одно из
первых определений угла наклона эклиптики к экватору.
Этот наклон он определял как половину разности
склонений точек летнего и зимнего солнцестояний. Эратосфен
нашел этот угол равным 11/83 окружности [17. С. 63],
т. е. 47° 42х 39 ", откуда половина этого угла, или наклон
эклиптики к экватору, равняется 23° 51'20". По
современным данным, наклон эклиптики к экватору в эпоху
Эратосфена был равен 23° 43' 34". Значение Эратосфена,
принятое также Гиппархом и Птолемеем, отличалось от
истинного значения лишь на 8 мин дуги. Впрочем, в
эпоху Птолемея наклон эклиптики к экватору уменьшился до
23° 40'36", т. е. ошибка значения Эратосфена возросла
до 11 мин дуги. Разумеется, Птолемей не мог знать о
вековом изменении наклона эклиптики к экватору
(в наше время этот угол составляет 23° 26' 28 " и
продолжает уменьшаться на 47 " в столетие) [86]. Он указал,
что по его собственным наблюдениям разность склонений
точек солнцестояний заключена в пределах от 47° 40' до
47° 45' и, следовательно, наклон эклиптики к экватору
должен быть заключен между 23° 50' и 23° 52' 30 ".
Значение Эратосфена хорошо укладывалось в эту «вилку»,
и Птолемей принял его в дальнейших расчетах, не зная,
что допускает при этом ошибку на 11' [17. С. 63].
На рубеже III и II вв. до н. э. жил и работал
известный математик Аполлоний Пергский, известный своим
капитальным трудом по теории конических сечений.
Разумеется, ни сам Аполлоний, ни Птолемей,
использовавший в своем «Альмагесте» некоторые леммы,
доказанные Аполлонием, не могли себе представить, что
конические сечения — эллипс, парабола и гипербола — это и
есть действительные формы планетных орбит.
Оторваться от предвзятого мнения, что небесные тела могут
двигаться лишь по самым «совершенным» орбитам —
окружностям, оказалось под силу только Иоганну Кеплеру
полтора тысячелетия спустя.
Пока же и Аполлоний, и Гиппарх, и Птолемей
использовали сложные комбинации окружностей, по
которым должны были двигаться планеты. Было два
варианта представления планетных движений для верхних
планет (Марса, Юпитера и Сатурна) : с помощью эксцен-
тра и с помощью эпицикла.
По-видимому, теория эпициклов возникла в III в. до
25

н. э. Первое упоминание о ней связано с именем
Аполлония, но об этом мы узнали опять же через Птолемея.
Аполлоний доказал теорему о том, что движение планеты
по эпициклу, жестко связанному с деферентом (т. е. так
поворачивающемуся по мере его обращения вокруг
центра деферента, словно он жестко скреплен с радиусом
последнего), если периоды обращения точки на эпицикле
(планеты) и центра эпицикла по деференту равны, а
движения направлены противоположно друг другу, можно
заменить обращением планеты по одной окружности,
эксцентричной относительно центра деферента, именно
по эксцентру [17. С. 555—558]. Подробное доказательство
этой теоремы и приводит Птолемей, не уточняя,
принадлежит ли оно Аполлонию или Гиппарху или разработано
им самим.
Аполлоний — последний по времени представитель
прошедшей перед нами блестящей вереницы греческих
и александрийских астрономов и математиков, труды
которых заложили фундамент работам Гиппарха. Конец
жизни и деятельности Аполлония примерно
соответствует по времени началу жизни и работы Гиппарха. Для
развития астрономии как науки Гиппарх сделал так
много, его деятельность настолько многообразна, что мы
посвятим ему здесь отдельную главу.
Глава 3
Астрономические исследования
Гиппарха
В отличие от всех античных ученых, с чьими трудами
мы познакомились в гл. 2, Гиппарх был, во-первых,
«чистый» астроном — он не занимался одновременно
вопросами математики, как Архимед или Аполлоний, или
философией, как Аристотель, не ограничивал свои исследования
узкими прикладными проблемами, как Метон, Эвктемон
и Каллипп, не был только лишь наблюдателем, как Ари-
стилл и Тимохарис. В то же время он не стремился ото-
рваться от привычных представлений о строении мира
подобно Гераклиду Понтийекому и Аристарху Самосскому.
Гиппарх был весьма разносторонним астрономом. Он
хорошо понимал основные задачи, стоявшие перед астроно-
26

мией в его эпоху, и
приложил все усилия, чтобы их
решить или хотя бы
способствовать их решению.
Гиппарх работал в не
очень благоприятных
условиях. У него не было на
Родосе коллег и сотрудников,
по крайней мере мы ничего
о них не знаем. Если Метон
и Эвктемон, Аристилл и Ти-
мохарис, Архимед и Эрато-
сфен могли так или иначе
общаться друг с другом, то
Гиппарх, казалось бы, был
лишен такой возможности.
Возможно, у него были
ученики и ближайшие
помощники, но они не оставили еле- Гиппарх
дов в истории науки. (ок- 180-125 до н. э.)
Работая на Родосе,
Гиппарх не имел в своем распоряжении и Александрийской
библиотеки. Правда, научная библиотека на Родосе была,
иначе откуда бы он узнал о работах Каллиппа, Тимоха-
риса, Аристилла, Аристарха, Эратосфена и других ученых,
чьи наблюдения он использовал. Более того, достоверно
известно, что Гиппарх поддерживал связи с
александрийскими астрономами того времени и знал об их
наблюдениях. Так, он сравнивал наблюдения с экваториальным
кольцом момента весеннего равноденствия — 145 марта 24
в Родосе и в Александрии и нашел между ними
расхождение на несколько часов [17. С. 134].
В то время не было почты в нашем понимании этого
слова. Но переписка была. Например, в 1906 г. было
обнаружено письмо Архимеда к Эратосфену, в котором
Архимед развивает метод нестрогого доказательства, имеющего
целью получение результата, который затем следует
доказать уже совершенно строго [87]. Вполне возможно, что
для обмена письмами с александрийцами Гиппарх
использовал купцов, чьи корабли регулярно поддерживали связь
между Родосом и Александрией.
Перейдем к обзору научных исследований Гиппарха в
области астрономии. При этом мы не будем вдаваться в
подробности, поскольку почти все работы Гиппарха были
так или иначе использованы и продолжены Птолемеем,
27

и мы к ним вернемся, когда будем описывать труды
последнего.
Работы Гиппарха можно сгруппировать по следующим
шести проблемам. Это — проблемы календаря,
исследования прецессии, составление звездного каталога, движение
Солнца, движение Луны, движение планет.
Проблема календаря имеет давнюю историю, и о
некоторых аспектах этой проблемы мы уже говорили: Гиппарх
посвятил этой проблеме два своих сочинения,
упоминаемых Птолемеем и, увы, не дошедших до нас: «О
длительности года» и «Об интеркаляционных месяцах и днях»
(так назывались «вставные» месяцы и дни в древних
календарях, например тринадцатый месяц, о котором мы уже
упоминали) [17. С. 139].
Гиппарх в своих работах использовал каллипповы
циклы для нумерации годов. Эти циклы начинались с летнего
солнцестояния. Так, первый год первого цикла начался
в летнее солнцестояние —329 г. Но для обозначения дат
Гиппарх использовал египетский календарь с
«плавающим» началом. Во времена Гиппарха египетский год
начинался в конце сентября. Это расхождение начал годов
каллиппова цикла и египетского календаря могло
привести к расхождению на 1 г. в датировке наблюдений,
выполненных между началами года по обеим календарным
системам. Такие случаи были и не раз обсуждались
историками науки. В случае солнечного или лунного затмения
такое расхождение разрешается однозначно с помощью
«Канонов затмений» или расчетов на ЭВМ, но другие
наблюдения могут пострадать от этой неоднозначности.
Одной из задач Гиппарха было определение точной
длительности тропического года, т. е. промежутка времени
от одного весеннего равноденствия до следующего. Этот
период — период смены времен года — играет основную
роль и в годовых ритмах живой природы, и в трудовой
деятельности человека, в первую очередь в земледелии и
скотоводстве. Из-за явления прецессии тропический год
на 20 мин короче сидерического года (периода обращения
Земли вокруг Солнца или, с точки зрения Гиппарха и
Птолемея, Солнца вокруг Земли).
В своем сочинении «О длительности года» Гиппарх
доказывает, что тропический год короче 36574 сут на очень
маленькую величину, которую можно определить лишь за
достаточно длительный промежуток времени. Эта разница
будет проявляться в систематическом смещении дат
равноденствий и солнцестояний относительно дат каллиппова
28

цикла (в котором, как мы помним, средняя длина года
составляет 36574 сут). В этом сочинении Гиппарх
утверждает, что за время, прошедшее от наблюдения
солнцестояния Аристархом в —279 г. до его собственного наблюдения
в — 134 г., т. е. за 145 лет, разница составила половину
суток, иначе говоря, одни сутки накапливались за 290 лет.
В другом сочинении («Об интеркаляционных месяцах и
днях») Гиппарх определяет, что разность в одни сутки
накапливается за 300 лет [17. С. 139]. В действительности
в эпоху Гиппарха сутки накапливались за 132 года
(сейчас—за 128 лет). Таким образом, в определении
длительности тропического года Гиппарх допускал ошибку в
6 мин. Его тропический год был короче юлианского
(36574 сут) почти на столько же, на сколько он был
длительнее действительного значения.
Открытие явления прецессии (предварения
равноденствий) является важной научной заслугой Гиппарха.
Он пришел к этой идее именно на основании различия
длительности сидерического и тропического годов. Это
различие было известно еще предшественникам Гиппарха,
которые, однако, не могли его объяснить. Гиппарх дал
этому явлению правильное объяснение, как видно из
заглавия его труда: «О смещении точек солнцестояний и
равноденствий» [17. С. 132—133, 327]. В этом он был
ближе к истине, чем Птолемей, который считал, что «сфера
неподвижных звезд» поворачивается относительно
равноденственных точек в прямом направлении, т. е. в сторону
возрастающих долгот [17. С. 321].
Гиппарх определил, что прецессия происходит вдоль
эклиптики, т. е. изменяются (возрастают) только долготы
звезд, а широты остаются неизменными [17. С. 329].
Величину постоянной прецессии Гиппарх мог
определить из сравнения положений Спики и других звезд
относительно точки осеннего равноденствия в эпоху Тимохари-
са и в, свое время. Вот что пишет об этом Птолемей в
«Альмагесте»: «В своем сочинении „О смещении точек
солнцестояний и равноденствий" Гиппарх при точном
сравнении наблюдений лунных затмений, выполненных в
его время, с теми, которые раньше наблюдал Тимохарис,
пришел к выводу, что в его время Спика опережала
осеннее равноденствие на 6°, а во времена Тимохариса — на 8°»
[17. С. 327]. Таким образом, за 169 лет прецессия по
долготе составила 2°, откуда следует, что постоянная
прецессии равна 43" в год.
В цитатах из Гиппарха, приводимых Птолемеем, это
29

значение не фигурирует. Птолемей приводит следующее
место из сочинения Гиппарха «О длительности года»:
«Если по этой причине солнцестояния и равноденствия за
один год отступают по меньшей мере на 1/100
градуса, то они должны отступать по крайней мере на 3°
за 300 лет» [17. С. 328] (разрядка наша.— В. Б.). Таким
образом, Гиппарх здесь приводит значение постоянной
прецессии 36" в год в качестве нижнего предела
этой величины. Это вполне согласуется с приведенным
выше значением 43", вытекающим из наблюдений Спики.
Ниже мы узнаем, что Птолемей, не придав значения
оговоркам Гиппарха (набранным в-разрядку), принял в
качестве постоянной прецессии именно 36" в год вместо
правильного значения 50" или хотя бы значения,
полученного Гиппархом, 43" в год. К каким последствиям это
привело, мы скоро узнаем.
Величайшей заслугой Гиппарха перед
астрономической наукой явилось составление звездного каталога —
первого звездного каталога, дошедшего до нас. Этот
каталог приводится Птолемеем в «Альмагесте». В нем 1022
звезды [17. С. 341—399]. Птолемей пишет, что он привел в этом
каталоге положения звезд по наблюдениям Гиппарха и по
своим собственным наблюдениям. Историков науки давно
уже беспокоит вопрос, какое количество звезд было в
каталоге Гиппарха, а сколько добавил к ним Птолемей. По
мнению одних специалистов (Ф. Болл, И. Л. Дрейер), Гиппарх
наблюдал положения 850 звезд [98], остальные 175
добавлены Птолемеем. С другой стороны, недавнее исследование
американского ученого Д. Роулинса [125] привело его
автора к твердому заключению, что все звезды каталога
наблюдались именно Гиппархом на широте Родоса (36°),
поскольку в нем нет ни одной звезды, которая могла быть
видна в более южной Александрии (31°), но не
наблюдалась на Родосе. К этому вопросу мы еще вернемся.
Важно лишь то, что большая часть звезд каталога наблюдалась
именно Гиппархом.
Как бы прелюдией к работе над звездным каталогом
явилось единственное сочинение Гиппарха, дошедшее до
нас,— «Комментарий к Арату» [114]. Напомним, что Арат —
греческий поэт, живший в III в. до н. э. при дворе
македонского царя Антигона Гоната и изложивший в одной из
своих поэм расположение на небе созвездий и звезд. В
«Комментарии к Арату» Гиппарх рассматривает положения на
небе около 350 звезд. Но тогда Гиппарх еще не применял
последовательно эклиптические координаты — долготу и
30

широту. Из 470 приводимых им координат звезд 64 —
склонения, 67 — прямые восхождения (экваториальные
координаты) , а остальные — дуги эклиптики от точки весеннего
равноденствия до пересечения с кругом склонения звезд,
а не с кругом широты, как при счете долгот. Там же
приведены моменты восходов, заходов и кульминаций звезд. Это
сочинение написано Гиппархом не только до составления
звездного каталога, но и до его работ по прецессии [75,
117].
Вот как оценил труд Гиппарха известный римский
историк и естествоиспытатель Плиний Старший (23—79 гг. н.
э.) : «Этот Гиппарх, который не может не заслужить
достаточной похвалы, так как он более чем кто-либо доказал
родство человека со звездами и то, что наши души
являются частью неба, исследовал новую звезду, появившуюся
в его время; ее движение в то время, когда она блистала,
навело его на мысль, не могут ли часто изменяться и
перемещаться те (светила), которые мы считаем
неподвижными; поэтому он решился на дело, смелое даже для
бога — перечислить для потомства звезды и пересчитать
светила, придумав приборы, которыми определил места и
яркость отдельных звезд, чтобы можно было легко
разобрать: исчезают ли они, появляются ли вновь, не движутся
ли или увеличиваются и уменьшаются (в яркости),
оставив потомкам небо в наследство, если нашелся кто-нибудь,
кто принял бы это наследство» [122].
Эти слова заимствованы из капитального труда Плиния
«Естественная история». Новая звезда, о которой идет
речь, вспыхнула в созвездии Скорпиона в —133 г.
(согласно китайским хроникам, обработанным французским
ученым Э. Био). Выражение «ее движение» некоторые
ученые переводят как «изменение» (блеска). Однако нет
ничего невозможного в том, что очевидцам казалось,
будто новая звезда перемещается относительно других.
Характеристика значения труда Гиппарха, данная
Плинием, жившим спустя 200 лет после него, вполне может
быть подтверждена и в наши дни.
Большое значение имело построение Гиппархом
теории движения Солнца. Обнаруженное еще Эвктемоном и
уточненное Каллиппом, а затем самим Гиппархом
неравенство длительностей сезонов позволило Гиппарху получить
все данные об орбите Солнца вокруг Земли. Гиппарх
считал, что Солнце движется по эксцентру, и принял так
называемую гипотезу простого эксцентриситета. Она
состоит в следующем [54].
31

Рис. 2. Эксцентр (к
определению длительности времен
года)
Представим себе (рис. 2)
круг, расположенный
эксцентрично по отношению к
эклиптике, но имеющий с
ней одинаковый радиус.
Отношение расстояния ОТ
между центрами обоих кругов
к радиусу назовем
эксцентриситетом.
Точка С на эксцентре,
ближайшая к Земле (т. е. к
центру эклиптики),
называется перигеем, самая
далекая А — апогеем.
Предполагается, что Солнце движется
по эксцентру равномерно.
Гиппарх сначала
определил среднее суточное
движение Солнца. Для этого он поделил 360° на
определенную им ранее длину тропического года — 365,24667 сут.
Получилась величина jx=3548,287", которая лишь на
0,042" меньше действительной [54].
Проведем через точку Т (Землю) две взаимно
перпендикулярные прямые, которые отсекут на эксцентре четыре
неравные дуги. Одна из этих прямых должна пройти через
точки равноденствий, другая — через точки солнцестояний.
Требуется так подобрать эксцентриситет и долготу
перигея, чтобы дуги AB, ВС, CD и DA были бы
пропорциональны длительностям соответствующих сезонов.
Гиппарх решил эту геометрическую задачу и получил
[17. С. 155, 157, 166] эксцентриситет 8=1/г4, долготу
перигея Солнца П=65°30' и наибольшее уравнение центра
Солнца #maa:=arcsine=2023'. Уравнением центра Гиппарх
называл отклонение положения центра Солнца от
среднего Солнца, движущегося по эклиптике со средним
суточным движением \i (равномерно) и выходящим из точки
весеннего равноденствия одновременно с центром
истинного Солнца. Это отклонение истинного Солнца от
среднего получило название первого неравенства.
Обратим здесь внимание читателя на то, что термины
«уравнение» и «неравенство» имели в те времена иные
значения, чем теперь. Ими обозначались не,
математические выражения типа ах=Ь или a<b, а отклонения от
равномерного движения, выраженные, как правило, в угловых
единицах. В астрономии до сих пор применяют такие тер-
32

мины, как «уравнение центра», «уравнение времени», хотя
это не уравнения, а величины, представляющие отклонения
от равномерного движения.
Значения, полученные Гиппархом, мало отличались от
точных значений, которые получились бы по его теории.
Известный советский астроном и историк науки
Н. И. Идельсон попробовал применить теорию Гиппарха
к современным положениям Солнца [54], сделав
соответствующие расчеты для 1942 г. (Эта работа выполнялась в
1943 г., накануне 400-летия со дня выхода в свет труда
Коперника «О вращениях небесных орбит».) Вот что
получилось:
П 8 xmax ^
По теории Гиппарха 102°06' 0,03348 1о55'10» 358°07'26
По современной теории 101°57' 0,03347 1°55'05" 358°07'30
Буквой L обозначена средняя долгота Солнца для
момента 1942 марта 21, 5 ч 50 мин. Как видим, согласие
теории Гиппарха, описывавшей видимое движение Солнца, с
современной теорией более чем хорошее. Как отмечает
Н. И. Идельсон, если бы мы построили таблицу долгот
Солнца по теории Гиппарха, то в течение нескольких
ближайших десятилетий погрешности не превысили бы 1—2 мин
дуги *.
Птолемей использовал теорию Гиппарха для Солнца,
но усложнил ее для планет, о чем мы расскажем дальше.
Однако, применяя теорию Гиппарха к Солнцу, Птолемей
допустил ошибку, приняв без всяких к тому оснований, что
долгота перигея Солнца постоянна. Между тем мы видели
выше, что значение П в 1942 г. отличается от П в эпоху
Гиппарха на 36°30'. Поделив эту величину на 21 (число
протекших столетий), мы найдем, что долгота перигея
Солнца увеличивается на 1°43' за столетие. Этот факт был
обнаружен уже в IX в. Сабитом ибн Коррой и аль-Бат-
тани [54].
От работ Гиппарха берет начало и теория движения
Луны. Луна среди других перемещающихся светил
занимает особое положение: она действительно
обращается вокруг Земли. Когда Коперник через 17 веков после
Гиппарха перенес центр планетной системы с Земли в
Солнце, теория движения Солнца Гиппарха—Птолемея была
1 Как можно видеть из приведенных выше значений, изменяется
не только долгота перигея Солнца, но и эксцентриситет его
орбиты (на самом деле - земной орбиты). Эти явления получили
физическое объяснение уже в рамках небесной механики,
основанной на теории тяготения Ньютона.
2 Клавдий Птолемей
33

им легко приспособлена для описания движения Земли
вокруг Солнца. Ведь Коперник сохранил равномерные
круговые движения, а с ними он был вынужден сохранить
и эксцентр, только по нему двигалась Земля, а не Солнце.
Вместо солнечного перигея был введен перигелий —
ближайшая к Солнцу точка орбиты Земли, вместо апогея —
афелий2.
Для Луны эта процедура была не нужна. Но движение
Луны было много сложнее, чем видимое движение Солнца.
Прежде всего ее путь был наклонен к эклиптике на угол
в 5°, что определил также Гиппарх с ошибкой всего в 8'.
Поэтому у Луны изменялась не тодько долгота, но и
широта.
Далее выяснилось, что период возвращения Луны к
перигею своей орбиты, так называемый аномалистический
месяц, не равен звездному (сидерическому) месяцу, т. е.
периоду обращения Луны вокруг Земли относительно звезд.
Аномалистический месяц (названный так потому, что
угол отстояния Луны от апогея назывался у древних
астрономов аномалией) был длиннее сидерического. Период
же возвращения Луны по широте, т. е. период между
двумя пересечениями ею эклиптики с юга на север (или с
севера на юг), был короче сидерического месяца[54].
Используя наблюдения вавилонских астрономов
(которых Птолемей называет «халдеями»)3, Гиппарх нашел
довольно точные соотношения между всеми периодами Луны
(месяцами). Как свидетельствует Птолемей, Гиппарх
показал, пользуясь наблюдениями «халдеев» и своими
собственными, что «наименьшее число дней, после которого
затмения повторяются через одинаковое число месяцев и при
одинаковых движениях, равно 126 007 дням и одному
равноденственному часу; он находит в нем 4267 полных
синодических месяцев, 4573 возвращения по аномалии,
4612 возвращений по долготе без 7У2°, которых недостает
Солнцу, чтобы закончить 345 оборотов по отношению к
неподвижным звездам»; он же нашел далее, что за
«5458 месяцев происходит 5923 возвращения Луны по
широте» [54. С. 206-209].
2 Это несколько странное слово происходит от греческих слов
аро - вдали и helios - Солнце; при их объединении в единое
слово буква «о» выпадает и вместо apohëlios пишут aphêïios —
афелий.
3 Слово «халдеи» происходит от ассирийского названия города
Вавилона - Халду. Таким образом, халдеи - это вавилоняне. В
современной исторической литературе термин «халдеи» не
употребляется [78. С. 566-5681.
34

Из этих соотношений, которые Н. И. Идельсон
справедливо называет циклами Гиппарха, можно получить
длительности всех месяцев с удивительной точностью.
Приведем их здесь.
Месяц (период) Гшшарх ^ggS^"
Синодический 29,530592 29,530588
Сидерический (возвращение по долготе) 27,321679 27,321661
Аномалистический 27,554568 27,554551
Драконический (возвращение по широте) 27,212218 27,212220
Термин «драконический месяц», введенный в средние
века, отражает легенду о том, что Солнце и Луна во время
затмений пожирались драконом. Даже современные
обозначения узлов (точек пересечения плоскостей орбиты с
плоскостью эклиптики) <Q и 13 напоминают
соответственно голову и хвост дракона.
Поражает точность, с которой Гиппарх сумел
определить длительность всех четырех месяцев. Расхождения с
современными значениями для синодического и дракони-
ческого месяцев не превосходят 0,35 с и лишь для
сидерического и аномалистического месяцев достигают 1,5 с.
Такой точности ему удалось достигнуть, использовав
наблюдения затмений и положений Луны за достаточно большой
срок — 345 лет. Это значит, что в распоряжении Гиппар-
ха были наблюдения вавилонских астрономов («халдеев»)
по крайней мере с V в. до н. э., а возможно, и более
ранние. Лунные затмения, упоминаемые в «Альмагесте»,
ведут счет с VIII в. до н. э. Несомненно, что и они были
использованы Гиппархом.
Однако это еще не все, что дали исследования Гип-
парха для развития лунной теории. Полученные им
соотношения для длин месяцев позволяли найти три
основных параметра, сыгравшие в дальнейшем важнейшую
роль при построении динамической теории движения
Луны на основании законов ньютоновой механики [54]
Пусть пи п2, п' — средние суточные движения перигея
и узла лунной орбиты и Солнца соответственно. Разделим
их на п — среднее суточное движение Луны по долготе.
Получим, используя данные Гиппарха,
üL. = m = 1 - 4612 Т1ыж = °'0748'
-£- = 1 - с = 1 - -|gf- (1 - m) = 0,008452,
35
2*

-^ = l_g = l_-g(l_m) = ~û,004Û23.
Теперь можно найти периоды обращения лунного
перигея (Ti) и узла (Т2):
Тг = ^b) = одаЙ = 3232 СУТ = 8'85 юлианского
года,
г- = tw^t = fsS = 6791 сут = 18,59 юлиан"
ского года.
Найденные Гинпархом значения Ti и Т2 лишь на 0,4 и
3,4 сут соответственно отличались от современных. Ясно,
что линия, соединяющая перигей и апогей (ось апсид),
поворачивается в ту же сторону, что и Луна, поэтому Луне
приходится как бы догонять свой перигей и
аномалистический месяц оказывается длиннее сидерического. Линия
узлов, напротив, движется навстречу Луне, поэтому дра-
конический месяц короче сидерического. Объяснение этих
движений дала только небесная механика, основанная на
законе всемирного тяготения Ньютона. Но величайшей
заслугой античной науки, и в первую очередь Гиппарха,
является обнаружение этих движений, а с ними — всей
сложности движения Луны вокруг Земли. Эта сложность
вступала в разительное противоречие с идеями Аристотеля о
наиболее совершенных — круговых и равномерных —
движениях небесных тел вокруг Земли.
Отмечая значение обнаружения всей этой сложной
картины лунного движения, Н. И. Идельсон говорит: «Еще
более поразительно, что, как "выяснилось через много
столетий, динамическая теория Луны не нуждается ни в каких
других равномерно нарастающих углах, кроме тех четырех,
которые с таким дивным искусством вавилонская и
греческая наука извлекла из наблюдений Луны» [54]. Эти
четыре угла следующие: 1) среднее угловое расстояние Луны
от Солнца (средняя элонгация4) Д суточное приращение
n—n'=n(l—m)', 2) среднее расстояние Луны от перигея
(средняя аномалия) Z; суточное приращение n—rii=crr,
3) среднее расстояние Луны от восходящего узла F,
приращение n—n2=gn; 4) средняя аномалия Солнца (его сред-
4 Элонгацией в астрономии обычно называют угловое расстояние
планеты или Луны от Солнца, хотя встречаются и другие
значения этого термина (момент наибольшей элонгации нижней
планеты, соответствующая конфигурация и др.).
36

нее угловое расстояние от перигея солнечной орбиты) 1\
приращение п=пт. Из общих теорем небесной механики
вытекает, что необходимо и достаточно иметь здесь именно
четыре независимых аргумента [54. С. 209, 477].
Гиппарх не разрабатывал теорий движений планет. Ов
лишь собрал наблюдения вавилонских астрономов и
добавил к ним свои собственные. Все это явилось впоследствии
материалом для планетной теории Птолемея.
Гиппарх ясно понимал, что прежние теории движений
планет неудовлетворительны. А ведь такие теории
существовали даже до Гиппарха, и по ним составлялись таблицы
положений планет, примером которых слуя^ат «Вечные
таблицы», на которые ссылается Птолемей в «Альмагесте»
[17. С. 421]. Эти таблицы были основаны на больших
циклах повторяемости положений планет как относительно
Солнца, так и относительно звезд и собственных перигеев
и апогеев. Подобные циклы подбирал и Гиппарх. Однако
построение более или менее точной теории движения
планет оказалось, как отмечает Птолемей, слишком трудной
задачей даже для Гиппарха.
Исследования Гиппарха явились необходимым этапом
для работ самого Птолемея. Вряд ли Птолемей сумел бы
поставить и решить многие задачи, если бы перед ним не
стоял пример Гиппарха.
Глава 4
Краткое содержание
«Альмагеста»
Название «Альмагест» принадлежит не самому
Птолемею, оно позднейшего, притом арабского происхождения.
Птолемей же писал по-гречески и назвал свое сочинение
так: Ме^оЛг) ouvrait («Мэгале синтаксис»), что
означает «Большое построение». Впрочем, слово «синтаксис»
имеет несколько значений. Его можно перевести и как
«трактат» и как «сочинение». В различных источниках
встречаются все эти варианты перевода [29, 31, 54].
Сам Птолемей в ссылках на свою книгу часто называет
ее МаЭгцыатахг] auvTa|iÇ, что означает «Математическое
построение» \ Арабские переводчики труда Птолемея —
1 О причинах выбора этого названия см. с. 43.
37

Первая страница «Альмагеста» (на греческом языке) (Виттен-
берг, 1549. Под ред. Э. Рейнгольта)
38

из уважения ли к его автору или просто по небрежности —
превратили [хг^аКц («большое») в [хе^хц
(«величайшее»), так что у арабов книга Птолемея стала называться
сокращенно Al Magisti, откуда и произошло название
«Альмагест» [29].
Что же собой представляет «Альмагест»? Это весьма
обширное сочинение, английский перевод его занимает
более 600 страниц большого формата. «Альмагест» был
разделен самим Птолемеем на 13 книг (в тексте встречаются
порой ссылки на ту или иную книгу). Впоследствии
переписчики, переводчики или комментаторы разделили
каждую книгу еще на главы (от 5 до 19 глав в каждой книге,
а всего 146 глав). В том, что деление на главы не
принадлежит Птолемею, нас убеждает отсутствие в тексте его
труда каких-либо ссылок на номера или названия глав
[131. С. 5, 27].
Книги «Альмагеста» не имеют заголовков, об их
содержании можно судить (если не читать весь текст) по
заголовкам глав.
Книга I является вводной. В ней утверждается, что
небесный свод движется как единая сфера, что Земля
шарообразна, находится в центре небесной сферы, имеет по
сравнению с ней ничтожно малые (точечные) размеры и
неподвижна. Во второй половине книги I приводятся
основы птолемеевой сферической тригонометрии и ряд
полезных таблиц, а также описание некоторых простых
угломерных приборов.
Надо сказать, что используемых в наше время
тригонометрических функций тогда еще не существовало.
Птолемей использует понятие «хорды угла» :
chord A=2R sin (4/2),
причем радиус принимается равным 60 единицам и в тех
же единицах выражаются хорды, а также другие отрезки
прямых и дуг, используемые в геометрии Птолемея. При
вычислении дробей Птолемей пользуется уже
упоминавшейся нами шестидесятиричной системой.
В книге II приводится решение ряда общих задач
сферической астрономии, в книге III рассматривается
движение Солнца по эклиптике и солнечная аномалия
(происходящая, как мы теперь знаем, от неравномерности
движения Земли вокруг Солнца по эллиптической орбите),
в книге IV —видимое движение Луны и его аномалии.
В книге V Птолемей строит свою теорию движения Луны,
39

основанную на комбинации нескольких круговых
движений, вводит понятия об эксцентре и эпицикле.
Книга VI посвящена теории солнечных и лунных
затмений, основой для которой служат расчеты моментов
сизигий (новолуний и полнолуний), а также движения Луны
по широте, связанного с тем, что ее орбита наклонена к
плоскости эклиптики на небольшой угол (5°00'). Здесь
же приведены таблицы затмений.
Книги VII и VIII посвящены неподвижным звездам.
В них приводятся описания созвездий, доступных
наблюдениям в Греции и в Александрии, и знаменитый каталог
звезд, составленный Птолемеем на основании наблюдений
Гиппарха и своих собственных. В этом каталоге
приведены положения 1025 звезд.
В книгах IX—XI строится теория движения планет, та
знаменитая «система мира Птолемея», которая
описывается (далеко не всегда правильно) во всех учебниках
астрономии и во многих популярных книгах.
В книге XII Птолемей рассматривает попятные
движения планет на небесной сфере и находит, что
охватываемые ими дуги находятся в согласии с его теорией. Здесь же
приводится таблица точек стояний планет (в которых
планета меняет прямое движение вдоль эклиптики на
попятное или наоборот). Книга XIII посвящена движению
планет по широте.
Это краткое перечисление, разумеется, не охватывает
всех вопросов, изложенных в труде Птолемея. Ему
приходится, развивая свои геометрические построения,
«попутно» доказывать ряд теорем, он приводит многочисленные'
примеры и расчеты, описывает применявшиеся приборы и
методы наблюдений, а также результаты наблюдений
обширного круга небесных явлений, как свои собственные,
так и своих предшественников: греческих и вавилонских
астрономов. В числе этих явлений солнечные и лунные
затмения, покрытия звезд Луною, положения планет
относительно звезд, солнцестояния, равноденствия, фазы
Луны и др.
В следующих главах мы познакомим читателя с
основными научными методами, применявшимися Птолемеем,
и с полученными им результатами. При этом мы не будем
углубляться в детали, а постараемся донести до читателя
идею метода или сущность того или иного результата.
Кое-где нам придется рассматривать и некоторые спорные
вопросы, относящиеся к творчеству Птолемея.
Наше изложение будет примерно (но не строго) следо-
40

вать порядку изложения материала в самом «Альмагесте».
После этого мы обратимся к работам Птолемея в других
областях знания.
Подробнейший критический анализ содержания
«Альмагеста» с весьма полезными комментариями содержится
в работах О. Нейгебауэра [116] и О. Педерсена [120],
которые мы постарались всемерно использовать. Однако мы
не будем дальше делать ссылки на эти работы (за
исключением отдельных случаев), иначе это пришлось бы делать
буквально на каждом шагу.
Глава 5
Мировоззрение Птолемея
«Истинные философы, Сирус \ были, я полагаю,
совершенно правы, отличая теоретическую часть философии от
ее практической части» — такими словами Птолемей
начинает «Альмагест» [17. С. 35]. И дальше он проводит ту
мысль, что, прежде чем приниматься за какую-либо
практическую задачу, надо ясно представить себе общий смысл
явлений, которые хочет анализировать и объяснять
исследователь.
«Даже практическая философия,— продолжает
Птолемей,— прежде чем стать практической, оказывается
теоретической, несмотря на то, что очевидно большое различие
между обеими; в первую очередь, для многих людей
возможно обладать некоторыми из моральных достоинств,
даже не обучаясь им; далее, в первом случае (практической
философии) извлекают большую прибыль из постоянной
практики в реальных делах, тогда как в другом случае
(теоретической философии) — путем совершенствования в
теории».
Деление философии на теоретическую и практическую
заимствовано Птолемеем у Аристотеля. Надо сказать, что
в ту эпоху (и много позднее тоже) философией называли
науку о природе вообще. Теоретическая философия дели-
Обращение к Сирусу встречается в книге Птолемея не один раз.
Такая форма - обращение к конкретному лицу - обычная для
книг древних авторов. Имя Сирус было в то время весьма
распространено в эллинистическом мире. Кто это, установить не
удалось, возможно, что Сирус-лицо вымышленное Г131. С. 35].
41

Птолемей с Астрономией и Уранией
Надписи означают: в центре — Астрономия, слева — Урания, небесная
муза, справа — Птолемей, принц в астрономии (гравюра из венецианского
издания 1490 г. книги Сакробоско «Сфера Вселенной», написанной в
первой половине XIII в.)
лась на три раздела: теологию, математику и физику. Это
деление принимает и Птолемей.
«Первопричину первого движения вселенной, попросту
говоря, можно рассматривать как некое невидимое и
неподвижное божество; раздел теоретической философии,
42

изучающий это, может быть назван теологией, поскольку
этот вид деятельности можно представить себе только где-
то высоко, вплоть до высочайших пределов вселенной, и он
полностью отделен от ощутимой реальности»,— пишет
Птолемей [17. С. 35-36].
Дальше он дает определения физики и математики.
Физика, по Птолемею, изучает материю и вечно
движущуюся природу, а также качества типа «белый», «влажный»,
«сухой», «теплый» и им подобные, относящиеся к
разложимым на составные части телам, находящимся под сферой
Луны (как принято говорить, «в подлунном мире»),
«Надлунный мир» — область приложения математики.
Математика, по Птолемею, изучает числа, а также
форму, размеры, место, время и другие свойства, выражаемые
числами. И не случайно свое сочинение он назвал
математическим построением.
В своем мировоззрении Птолемей почти точно следует
Аристотелю. И дело, разумеется, не столько в
геоцентризме обоих, сколько в их взгляде на основные категории
бытия. Вслед за Аристотелем Птолемей считает все сущее
состоящим из материи, формы и движения, причем ни одна
из этих категорий не может существовать без двух других.
Это значит, что материя не может существовать без
движения и движение нельзя себе представить без материи.
Классики марксизма высоко оценивали учение
Аристотеля о категориях бытия. Как отмечал Ф. Энгельс, в этом
учении нашла свое яркое выражение диалектическая
концепция развития. Он писал: «Два философских
направления: метафизическое с неподвижными категориями,
диалектическое (Аристотель и особенно Гегель) — с
текучими...» 2.
В своем конспекте «Метафизики» Аристотеля
В. И. Ленин отмечал его материалистический подход как
к вопросу о реальном существовании вещей, так и к
классификации наук. «Прелестно! Нет сомнений в реальности
внешнего мира»,—записывает В. И. Ленин3. Очевидно,
что этот отзыв может быть распространен и на взгляды
Птолемея.
Однако и Аристотель, и Птолемей не были ни
последовательными материалистами, ни последовательными
диалектиками. «Путается человек именно в диалектике
2 Энгельс Ф. Диалектика природы//Маркс К., Энгельс Ф. Соч.
2-е изд. Т. 20. С. 516.
3 Ленин В. И. Философские тетради//Поли. собр. соч. Т. 29.
С. 327.
43

общего и отдельного, понятия и ощущения etc., сущности
и явления etc.» — пишет об Аристотеле В. И. Ленин4.
Уже из приведенных выше выдержек из «Альмагеста»
ясно, что Птолемей допускал (вместе с Аристотелем)
«первый толчок», допускал существование божества. Но это
божество играет во взглядах Птолемея весьма
ограниченную роль: оно только создало и пустило в ход «небесный
механизм», управляющий движениями светил небесных.
Больше о боге и о его влиянии на процессы во Вселенной
в «Альмагесте» не говорится ничего.
Более того, приведя описанную выше схему
классификации наук, Птолемей отдает явное предпочтение
математике перед теологией и физикой. Вот как он это
аргументирует: «Из всего этого мы заключаем, что первые
два раздела теоретической философии должны быть
названы скорее предположениями, чем знанием: теология —
вследствие ее совершенно невидимой и неуловимой
природы, физика — вследствие непостоянной и неясной природы
материи ...только математика может обеспечить надежное
и нерушимое знание для ее энтузиастов при условии
строгого к ней подхода» [17. С. 36].
Не приходится удивляться столь критическому
суждению Птолемея о физике. Тогда физика переживала свое
детство, даже младенчество, а природа материи
действительно была неясна. О свойствах материи судили чисто
качественно. Было общепринято предложенное еще
Гераклитом (ок. 544—484 до н. э.) разделение всех веществ
на четыре элемента: землю, воду, воздух и огонь.
Аристотель изобразил даже четыре сферы, расположенные
концентрически снизу вверх: сфера земли, сфера воды,
сфера воздуха и сфера огня. Земля — холодная и сухая,
вода—холодная и влажная, воздух — теплый и влажный,
огонь — теплый и сухой. За сферой огня следует уже
сфера Луны, а затем — сферы других планет и сфера
звезд [21].
Несмотря на то что Птолемей и сам занимался
некоторыми вопросами физики (например, оптикой), он
отдает решительное предпочтение математике и
астрономии. В дальнейшем он применит эти точные науки для
нужд географии, точнее, геодезии, а математику — еще и
к теории музыки!
Не лучше, чем к физике, выглядит отношение
Птолемея и к теологии. Теология в его описании предстает пе-
4 Там же.
44

ред нами как нечто столь же возвышенное, сколь и
неясное. Правда, у Птолемея есть целый труд, посвященный
астрологии — «Четырехкнижие» [117], но не следует
отождествлять приверженность к астрологии с
отношением к религии. В «Четырехкнижии» Птолемей
пытается обосновать некие физические воздействия небесных
светил на земные явления, иначе говоря, он пытается
подвести некоторый физический «базис» под
астрологические представления. Этот вопрос мы рассмотрим
отдельно (в гл. 15), здесь же для нас важно то, что астрология
Птолемея не была основана на религиозных
представлениях.
Таким образом, по своим религиозным убеждениям
Птолемей был весьма умеренным деистом, иначе говоря,
он признавал существование бога, но не приписывал ему
никаких конкретных функций, за исключением создания
мира и «первого толчка».
С этой точки зрения историческим курьезом является
то обстоятельство, что спустя тысячу лет учепия
Аристотеля и Птолемея были официально признаны
христианской церковью как истинные. Правда, произошло это
далеко не сразу. Первые переводы трудов Аристотеля и
Птолемея на латинский язык появились в Европе в конце
XII в; это были переводы с арабского. Переводы работ
Аристотеля непосредственно с греческого были сделаны
(Вильгельмом Мербекским) уже в 60-х годах XIII в.
Вскоре после этого взгляды Аристотеля подверглись
жестоким нападкам со стороны доминиканцев, в первую
очередь Альберта Великого (1206—1280) и Фомы Аквинско-
го (1225—1274). Вместе с тем оба они приложили немало
усилий, чтобы с помощью хитроумно составленных
комментариев приспособить, адаптировать учение
Аристотеля к канонам христианской религии. Альберт Великий
положительно относился и к системе мира Птолемея [52].
В начале XIV в. она приобрела известное влияние в
христианском мире, а в середине XIV в. получила полное
признание сначала во Франции, а потом и в других
странах5.
Причин такого отношения христианской церкви к
сочинениям «язычников» Аристотеля и Птолемея было не-
5 Нелепейшим отголоском этого «христианизированного аоистоте-
лианства» является декрет парижского парламента, принятый в
1624 г., спустя 80 лет после издания книги Коперника,
грозивший изгнанием каждому, кто публично выступит против учепия
Аристотеля Г46].
45

сколько. Одна из них состояла в том, что учеыия обоих
ученых были основаны на геоцентрической системе мира,
полностью удовлетворявшей догмам христианства о том,
что человек создан богом по своему образу и подобию,
а потому он должен жить на неподвижной Земле, в
центре мира. О других причинах мы скажем ниже.
Рассмотрим геоцентризм Птолемея, опираясь на его
собственное изложение в I книге «Альмагеста». Доказав,
что небесный свод подобен сфере (что позволяет
использовать для определения видимых положений светил
сферические координаты), а также, что и Земля имеет
форму шара (что тоже позволяет применять сферические
координаты точек земной поверхности: долготу и широту),
Птолемей переходит к доказательству того, что Земля
находится в середине небесного свода, в центре небесной
сферы [17. С. 40-42].
Птолемей доказывает это утверждение от противного.
Если Земля не находится в центре небесной сферы, то
она должна быть либо смещена к одному из полюсов
мира, либо вообще не должна находиться на оси мира. В
первом случае горизонт делил бы небесную сферу на две
неравные части (та, что прилегает к ближайшему полюсу,
была бы меньше), во втором случае звезды при вращении
небесной сферы то приближались бы к Земле, то
удалялись бы, меняя свой блеск, а Солнце и Луна —видимые
размеры. Поскольку ни то, ни другое не наблюдается,
значит, Земля находится в центре небесной сферы. Дальше
Птолемей доказывает (совершенно правильно), что
размеры Земли ничтожно малы по сравнению хотя бы со
сферой «неподвижных звезд», что ее по сравнению-с этой
сферой можно принимать за точку. Доказательство
состоит в том, что из разных мест земного шара небесные
светила кажутся одинаковых размеров в любое время. Это
означает, что размеры Земли действительно ничтожно
малы по сравнению с расстояниями до небесных тел
[17. С. 43].
Доказательства центрального положения Земли,
которые мы только что привели, основаны на двух ошибочных
предположениях. Во-первых, это предположение о том, что
размеры небесной сферы, хотя и очень велики, но
конечны, а потому смещение Земли внутри небесной сферы к
одному из полюсов приведет к неравенству северного и
южного сегментов (здесь уже нельзя сказать «полусфер»).
Во-вторых, это предположение, что суточное вращение
небесной сферы происходит само по себе, независимо от
46

Земли. Но мы знаем, что это вращение является лишь
отражением реального вращения Земли вокруг оси, а
потому второе предположение Птолемея ошибочно в своей
основе. Что касается первого предположения, то
несомненно, что Птолемей обсуждал все возможные последствия
сдвига Земли из центра сферы, пользуясь моделью, где
маленький шарик (Земля) находился внутри большого
полого шара (небесной сферы). Мы знаем, что
расстояния до звезд настолько велики, что даже движение Земли
вокруг Солнца по орбите диаметром 300 миллионов
километров не приводит к заметным смещениям звезд. Эти
смещения (годичные параллаксы звезд) оказались столь
малы, что понадобилось 17 столетий после Птолемея и два
с лишним столетия после изобретения телескопа, чтобы
они смогли быть обнаружены6.
После доказательства центрального положения
Земли Птолемей доказывает ее неподвижность в
пространстве. В самом деле, утверя^дает он, если бы Земля имела
какое-либо движение, она бы смещалась со своего
центрального положения, и тогда имели бы место те же
эффекты, как и в случае нецентрального положения Земли
относительно небесной сферы. Но так как эти
эффекты не наблюдаются, значит, Земля неподвижна
[17. С. 43-45].
Вторым доказательством неподвижности Земли,
которое приводит Птолемей, является вертикальное свободное
падение тел во всех местах Земли. Все тела стремятся к
центру, и поскольку они падают вертикально вниз на
всех широтах Земли, значит, она и есть этот центр. И если
бы земная поверхность не преграждала путь падающим
телам, они падали бы дальше вниз, до самого центра
Земли. И хотя Земля велика и тяжела, не следует
удивляться тому, что она никуда не падает и не требует
опоры. Ведь Земля мала по сравнению с Вселенной, которая
оказывает на нее равномерное давление со всех сторон,
а потому Земля и не может никуда сдвинуться. Земля
тяжелее известных нам падающих тел, а потому, если бы
она тоже могла куда-нибудь падать, она падала бы
быстрее,7 и мы не могли бы этого не заметить.
Здесь я^е Птолемей объясняет понятия верха и низа:
Годичные параллаксы звезд, даже самых близких, измеряются
долями секунды дуги.
Обычная ошибка ученых древности и средневековья: тяжелые
тела считались падающими быстрее. Лишь Галилей доказал,
что скорость падающих тел не зависит от их веса.
47

низ — это направление к центру Земли, верх —
направление, ему противоположное. Тяжелые, плотные тела
стремятся вниз, легкие, разреженные — вверх. Направления
«вверх» и «вниз» различны в разных пунктах Земли
[17. С. 45].
Дальше Птолемей вступает в полемику со
сторонниками вращательного движения Земли, не называя их,
правда, по именам. Очевидно, он имеет в виду Гераклида
Понтийского и Аристарха Самосского, считавших, что
суточное вращение совершает Земля, а не небо.
Птолемей признает, что среди небесных явлений не* ничего,
противоречащего гипотезе о вращении Земли, но совсем
иначе обстоит дело с явлениями на земле и в воздухе.
«Они должны допустить,—пишет Птолемей,—что
вращательное движение Земли должно быть самым быстрым из
всех движений, связанных с ней, учитывая, что Земля
должна совершать одно обращение за столь короткое
время; в результате все предметы, не опирающиеся на
Землю, должны казаться совершающими такое же движение
в обратном направлении; ни облака, ни другие летающие
или парящие объекты никогда не будут видимы
движущимися на восток, поскольку движение Земли к востоку
будет всегда отбрасывать их, так что эти объекты будут
казаться двия^ущимися на запад, в обратном
направлении» [17. С. 45]. Даже если предположить, рассуждает
далее Птолемей, что и воздух движется в том же
направлении и с той же скоростью, что и Земля, плавающие и
парящие в воздухе тела не должны следовать его
движению. Если же они связаны с воздухом так, что следуют
его движению, то нам они казались бы неподвижными,
чего на самом деле нет.
Так Птолемей «опровергает» взгляды сторонников
вращения Земли. Некоторые его доводы сейчас могут
показаться наивными, но не надо забывать, что и полтора
тысячелетия спустя именно к таким доводам
прибегали противники Коперника и Галилея. Именно эти доводы
заставляет Галилей в своих «Диалогах» приводить
защитника системы Птолемея — Симпличио [ 42 ].
Птолемей не обсуждает предположения Аристарха о
движении Земли вокруг Солнца. По-видимому, покончив
с гипотезой о вращении Земли вокруг оси, он не счел
нужным даже упоминать о более сложном и
крупномасштабном движении Земли. Тем более, что приведенные
им аргументы говорили вообще против любого движения
Земли.
48

Но в приведенных выше рассуждениях Птолемея,
кроме тех наивных аргументов, о которых мы говорили,
есть и здравые мысли. Так, подчеркнем мысль Птолемея,
что ход небесных явлений не противоречит гипотезе о
вращении Земли. Птолемей прав и в том, что
вращательное движение Земли быстрее всех прочих известных в ту
эпоху движений. Если бы он попробовал вычислить ее
скорость (а у него были для этого все необходимые
данные: окружность Земли по Эратосфену и широта
Александрии), он нашел бы эту величину равной 385 м/с, что
в десять раз быстрее ураганного ветра. Но он не мог
понять, что воздух увлекается вращением Земли, а все
плавающие или летающие в воздухе тела тоже
участвуют во вращении Земли.
Таким образом, Птолемей предстает перед нами как
последовательный геоцентрист. Но свой геоцентризм он
старается обосновать соображениями, основанными на
физике явлений, а не схоластическими рассуждениями
или ссылками на авторитеты.
Геоцентризм Аристотеля и Птолемея был нужен
христианской церкви по трем причинам. Во-первых, на
геоцентрическом мировоззрении «держался» основной
догмат христианства — догмат искупления? а также ряд
других положений Библии, терявших смысл, если
признать Землю движущейся, а тем более рядовой планетой.
Во-вторых, система Птолемея как бы согласовывала
геоцентризм с математическим объяснением видимых
движений Солнца, Луны и планет. В-третьих, для
большинства людей неподвижность и центральное положение
Земли, движение небесных светил казались очевидными,
повседневно наблюдаемыми фактами —тут ничего не
надо было ни объяснять, ни доказывать.
Остановимся несколько подробнее на значении
второй из перечисленных причин. Математическое описание
движений планет, Солнца и Луны в системе мира
Птолемея достигло такой точности, что позволяло предвычислять
положения этих светил на небе, а также наступление
некоторых небесных явлений, связанных с их движением
(например, солнечных и лунных затмений), с весьма
высокой для того времени точностью. Таким образом, мате-
8 Согласно догмату искупления, бог-отец послал на Землю своего
сына Иисуса Христа, чтобы он своими страданиями искупил
грехи людей. Этот догмат еще раз подчеркивал единственность и
богоизбранность человечества, обитающего на Земле.
49

матическая модель Птолемея имела большую n р о г н о-
стическуюценность.
В то же время христианская церковь в странах
Европы в результате ряда объективных факторов взяла на себя
роль «хранителя учености». От периода заката
античной науки (совпавшего с развитием христианства) и до
начала эпохи Возрождения христианские богословы были
практически единственными носителями знания.
Конечно, отдавая первенствующее место среди наук того
времени богословию и подчеркивая его превосходство над
философией, эти деятели исходили из ошибочных
философских позиций. С этих же позиций они начиная с
XIII в. адаптировали, приспособили для своих целей идеи
Аристотеля и математические построения Птолемея.
Эти причины способствовали сохранению господства
системы Птолемея в науке на протяжении полутора
тысяч лет.
Глава 6
Небесная сфера:
расчеты и измерения
Установив, что небесный свод имеет форму сферы,
Птолемей формулирует некоторые ее свойства и
закономерности. Он вводит понятия полюсов мира, небесного экватора
и эклиптики. Далее он проводит через полюсы экватора и
эклиптики еще один большой круг {колюр солнцестояний),
перпендикулярный к обоим. Точки пересечения эклиптики
с экватором — это точки равноденствий, точки пересечения
эклиптики с колюром солнцестояний — это точки
солнцестояний.
Два основных движения небесной сферы — суточное и
годичное. Первое увлекает все светила, второе — Солнце
и планеты, но последние имеют еще свои, индивидуальные
движения [17. С. 45].
Затем Птолемей вводит понятие о хорде угла. Хотя мы
уже поясняли его в гл. 4, рассмотрим это понятие
подробнее. Проведем дугу окружности (рис. 3) с центром в О и
отложим некоторый центральный угол АОВ. Проведем
затем хорду AB. Введем шестидесятиричную систему
счисления и примем радиус (АО=ОВ) равным 60 единицам.
В этих же единицах будем считать и хорды. Будем
обозначать хорду угла а через chord а.
50

Рис. 3.
К понятию хорды
Рис. 4.
К доказательству теоремы
Птолемея
Нетрудно убедиться в том, что
chord a=2R sin (а/2),
где R — радиус окружности. Для доказательства проведем
ОС — биссектрису угла а. Она пересечет хорду AB в точке
D. Поскольку А А OB — равнобедренный, биссектриса
является в нем также и медианой и высотой. Поэтому AD-LOD
и AD=DB. В то же время AD : jR=sin (а/2), откуда
AB=2R sin (а/2). Справедливость формулы доказана.
Птолемей доказывает несколько теорем, которые
позволяют ему составить таблицу хорд всех углов от 0 до
180°. Чтобы показать метод доказательств Птолемея, мы
приведем здесь в качестве примера доказательство первой
из этих теорем [17. С. 48—49].
«Имеем (рис. 4) полукруг ABG, описанный около
центра D на диаметре ADG1. Проведем DB-i-AG в точке D.
Разделим отрезок DG пополам в точке Е, проведем
прямую ЕВ и отложим отрезок EZ=EB. Соединим Z с В
прямой ZB.
Я утверждаю, что ZD есть сторона правильного
десятиугольника, a BZ — сторона правильного пятиугольника.
Доказательство: Поскольку прямая DG делится
в точке Е пополам, а прямая DZ есть ее продолжение2,
GZ • ZD+ED2=EZ\
1 Разумеется, Птолемей обозначал точки на схемах греческими
буквами, в алфавитном порядке. Этим объясняется выбор букв.
В английском переводе Тумера и в нашем тексте греческие
буквы заменены латинскими: А, В, G, D, Е, Z и соответствуют
прописным греческим буквам А, В, Г, Д, Е, Z.
2 Нижеследующее равенство доказывается у Евклида («Начала»,
II, 6) [99]. Поскольку GZ.ZD=(EZ+EG)ZD={EZ+ED).(EZ-
-ED)=EZ2-ED\ GZ-ZD+ED*=EZ\
51

но
EZ2=BE2(EB=ZE)
и
EB2=ED2+DB2,
откуда следует GZZD+ED2=ED2+DB2. Вычитая из обеих
частей ED2, получим
GZ - ZD=DB2=DG2.
Таким образом, ZG разделено в крайнем и среднем
отношении 3 в точке D.
Но поскольку сторона шестиугольника и сторона
десятиугольника, вписанных в ту же окружность, образуют
крайнее и среднее отношения той же прямой линии и
поскольку GD, будучи радиусом, представляет собой сторону
правильного шестиугольника, DZ равна стороне
правильного десятиугольника.
Аналогично, поскольку квадрат стороны пятиугольника
равен сумме квадратов сторон шестиугольника и
десятиугольника, если все они вписаны в ту же самую
окружность, и в прямоугольном треугольнике BDZ квадрат BZ
равен сумме квадратов BD, которая есть сторона
шестиугольника и DZ, которая есть сторона десятиугольника,
отсюда следует, что BZ равно стороне пятиугольника».
Таково доказательство Птолемея. Почти на каждом
шагу он использует те или иные теоремы, доказательства
которых содержатся в «Началах» Евклида, хотя и не
делает ссылок, полагая, что этот классический труд известен
читателям (приводимые здесь ссылки принадлежат одному
из современных переводчиков «Альмагеста» Дж. Тумеру).
Как же использует Птолемей только что доказанную
теорему? Обозначая символом р (от английского слова
part — часть) те единицы, которыми пользуется Птолемей,
найдем вместе с ним, что DE=30P (DE — половина
радиуса). Dtf2=900p. #D=60p. SD2=3600P, EZ2=EB2=450()*
(EZ2=DE2+BD2), £Z=67;4,55P, DZ=£Z-Z)#=37;4,55P
(о способе записи в шестидесятиричной системе мы
говорили выше, с. 24). Но DZ — сторона десятиугольника,
которая стягивает центральный угол 36°. Япачит, хорда угла
36° равна 37;4,55р.
Аналогично Птолемей находит, что хорда центрального
3 Евклид («Начала», VI, определение 3): «Прямая разделяется в
крайнем и среднем отношении, если отношение всей прямой к
большему ее отрезку равно отношению большего отрезка к мень~
шему» [99].
52

угла пятиугольника, т. е. 72°, равна 70;32,3Р; хорда
центрального угла шестиугольника (60°) равна 60р (радиусу) ;
а поскольку квадраты хорд углов 90° и 120° равны
соответственно двум и трем квадратам радиуса, Птолемей
получает
chord 90°= (7200р) *=84;51,10р.
chord 120°= (10 800р),/2=103;55,23р.
Далее он использует известное свойство, что угол,
опирающийся на диаметр, — прямой. Поэтому квадрат хорды
Рис. 5.
Теорема о хорде разности
углов
л У>
угла, дополняющего данный угол до 180°, равен квадрату
диаметра минус квадрат хорды данного угла. Так он
находит
chord 144°=114;7,37*\ chord 108°=97;4,55р.
Имея хорды нескольких углов, Птолемей доказывает
теорему, что хорда разности двух углов может быть
найдена, если известны хорды этих двух углов. Для этого он
прежде доказывает другую теорему, которую можно
сформулировать так: произведение диагоналей произвольного
четырехугольника, вписанного в окружность, равно сумме
произведений его противоположных сторон4. Иначе говоря,
в четырехугольнике ABGD AG • BD=AB • DG+AD • BG.
Эта теорема получила название теоремы Птолемея [17.
С. 50-51].
Посмотрим теперь, как с помощью теоремы Птолемея
доказывается теорема о хорде разности углов. Пусть нам
даны хорды AB и AG (рис. 5) ; AD — диаметр окружности.
4 Для ясности мы здесь (и далее) приводим все теоремы и
доказательства в современных формулировках. Птолемей вместо
«произведение отрезков» писал «прямоугольник, построенный
на отрезках», имея в виду его площадь. Очевидно, что обе
формулировки равносильны.
£5к
53

Проведем хорду разности углов ADG и ADB — прямую BG.
По теореме Птолемея, поскольку ABGD — вписанный в
окружность четырехугольник,
AB • GD+AD - BG=AG • BD,
но AG • BD и AB • GD нам известны (4 G и Л В заданы, BG
и GZ) — хорды дополнительных углов), поэтому AD • 56?
находится путем вычитания. А так как AD=120р есть
диаметр, то, поделив AD • BG на 120, мы получим хорду BG.
Совершенно аналогично Птолемей доказывает далее
теорему о хорде суммы углов с заданными хордами. Она тоже
вычисляется без труда.
Теперь, составляя суммы и разности углов, хорды
которых известны, можно найти хорды этих сумм и
разностей, а затем использовать их, в свою очередь, для
составления новых сумм и разностей, и т. д. Поскольку хорда
180° тоже известна и равна 120р, мы можем так
постепенно найти хорды всех углов, кратных углу 6°. А дальше
Птолемей доказывает теорему о хорде половины угла.
Теорема эта была когда-то доказана Архимедом, и хотя она
является частным случаем теоремы о хорде разности углов,
Птолемей приводит ее доказательство отдельно. Не
повторяя его здесь, мы напишем лишь формулу хорды половины
угла:
chord y = Yr [2# — (4Д2 — chord2а)1/.].
С помощью этой формулы Птолемей смог составить
таблицу хорд всех углов от 0 до 180° через полтора градуса.
Но он поставил себе задачей вычислить хорды углов через
полградуса. А для этого надо было рассчитать хотя бы
chord 0,5° или chord 1°, чтобы затем найти остальные по
формулам сумм или разностей хорд.
Задача оказалась, как мы бы сказали теперь,
аналитически неразрешимой. Найти хорду трети угла по хорде
целого угла было невозможно. Это невозможно и в наши
дни, если использовать методы только евклидовой
геометрии5, подобно тому как неразрешима задача о трисекции
угла (т. е. о разделении угла на три равные части с
помощью только циркуля и линейки).
Птолемей нашел весьма остроумный выход из
положения. Он применил одну из теорем Евклида о том, что
отношение отрезков, отсекаемых прямой, проведенной из
5 Задача может быть разрешена с использованием кубических
уравнений, не известных Птолемею.
54

вершины треугольника, на противолежащей стороне,
меньше отношения самих углов. По формуле хорды половины
угла он вычислил chord (3/4)°=0;47,8Р и chord (11/2)°=1;
34,15р. Далее он составил отношения 1° : (зи)°=^/3 и
(Г/г)0: 1°=3/г. На основании теоремы Евклида он
утверждал, что
chord 1°<4/з0;47,8р=1;2,50р,
chord l°>Vs-l;34J5p=l; 2,50р.
Получив из этих двух соотношений одно и то же число
для нижнего и верхнего предела chord 1°, Птолемей
справедливо заключил, что chord 1°=1;2,50р. После этого для
него не представляло никаких затруднений вычислить по
формулам хорд сумм, разностей и половинных углов хорды
всех остальных углов через полградуса [17. С. 57—60].
Никаких затруднений... Кроме колоссальной затраты
времени. Ведь в распоряжении Птолемея не было никаких
счетных машин или облегчавших вычисления таблиц.
Неизвестно, были ли у него помощники, которым можно было
поручить эти расчеты. Ради интереса автор взял на себя
труд выполнить расчет хорды по формуле разностей,
пользуясь методикой Птолемея, т. е. без всяких
вычислительных средств, «на бумажке», как считают ученики
начальной школы, причем в шестидесятиричной системе.
Несмотря на известный опыт автора в такого рода вычислениях,
один расчет занял у нас полчаса6. Можно полагать, что
Птолемей был в таких расчетах опытнее автора и считал
быстрее, но вряд ли он мог делать один расчет менее чем
за 20 мин. Это значит, что расчет таблицы хорд (360 углов)
занял у него около 120 ч напряженного труда.
Вернемся к методу, примененному Птолемеем для
нахождения хорды угла в 1°. На первый взгляд кажется
странным, что оба предела, верхний и нижний, дали одно
и то же число. Но так получается, если ограничиться
точностью, до которой считал Птолемей. Если сосчитать на
один разряд шестидесятиричной системы точнее, то мы
получим
(4/з) chord (3Л)°=1;2,49,55,
(V,) chord (3/2)°=1;2,49,48.
Точное значение chord 1°=1;2,49,54.
6 Любопытно, что такой же расчет на микрокалькуляторе
«Электроника БЗ-36» занимает в десятичной системе 7-8 с, в
шестидесятиричной - 25 с.
55

Линейное интерполирование между значениями
верхнего и нижнего пределов (с учетом того, что угол 1° ближе к
0,75°, чем к 1,5°) дало бы: chord 1°=1; 2,49,53.
Есть указания, что таблица хорд, рассчитанная по
формуле хорд половинных углов (без формул хорд сумм и
разностей углов), была составлена еще Гиппархом. Но
в столь полном виде, да еще с первыми разностями
(приращениями хорды на один градус угла), она
несомненно была вычислена Птолемеем впервые.
Из этого примера мы видим, каким усердным
математиком и вычислителем был Птолемей. Стоит сравнить его
в этом отношении с Иоганном Кеплером, которому в
поисках истинной формы планетных орбит также приходилось
по многу раз производить одни и те же вычисления,
чтобы согласовать наблюдения Марса с теорией.
Рассказывая в «Новой астрономии» о ходе своей работы по
вычислениям (методом проб и ошибок) радиуса орбиты Марса,
долготы его афелия и расстояний от центра круговой
(тогда еще круговой!) орбиты Марса до Солнца и до центра
экванта, Кеплер писал: «Если этот обременительный
способ работы вам не нравится, вы можете справедливо
пожалеть меня, поскольку я вынужден был проделать это
по меньшей мере 70 раз с большой затратой времени».
Сохранившиеся до нашего времени черновики расчетов
Кеплера занимают 900 листов, исписанных мелким
почерком [26,92].
В книге Птолемея мы не найдем подобных жалоб. Он
спокойно и методично преподносит читателю
окончательные результаты своих расчетов. А ведь в дальнейшем,
при работе над теориями движения Луны и планет, ему
приходилось делать вычисления куда более трудные, чем
расчеты таблицы хорд. А главное, ему, как и впоследствии
Кеплеру, нужно было согласовать свою теорию с
наблюдениями, идти тем же методом проб и ошибок.
Об объеме математических вычислений и построений
Птолемея говорит количество чертежей,
иллюстрирующих его доказательства и выкладки: их в книге около
двухсот. Кроме того, Птолемей приводит двадцать пять
больших и малых таблиц, причем многие из них
занимают по несколько страниц. В числе таблиц — звездный
каталог, включающий положения 1025 звезд, таблицы
солнечных и лунных затмений, движений планет, Луны,
восходов и заходов светил и т. д.
Но вернемся к содержанию «Альмагеста». Покончив
с определением и табулированием хорд (напоминаем, что
56

хорды заменяют ему весь набор современных
тригонометрически« функций), Птолемей развивает основные
положения и теоремы сферической тригонометрии. Важное
место среди них занимают две теоремы Менелая о
соотношениях хорд дуг четырех больших кругов,
пересекающих друг друга, как показано на рис. 6. Птолемей
доказывает, что эти дуги связаны соотношениями
chord 2т chord 2r chord 2s2
chord 2mi chord 2гг chord 2s '
chord 2r2 chord 2m2 chord 2n
chord 2ri chord 2mt chord 2n2 '
которые в переводе на современные обозначения имеют
вид
sin m sin г sin s2
sin mi sin r± sin s »
sin r2 sin m2 sin n
sin ri sin mi sin n2
Здесь принято /тг=т1+т2, п=п^п2, r==ri+r2, s=Si+s2.
Эти теоремы были впервые доказаны александрийским
математиком и астрономом Менелаем, жившим и
работавшим во второй половине I в. н. э. Птолемей и здесь не
делает ссылки на приоритет Менелая (как не ссылается
он на Евклида и Архимеда), хотя он не мог не читать его
«Сферику», где изложены эти теоремы.7 В дальнейшем
он упоминает лишь о наблюдениях Менелая.
Далее Птолемей вводит понятия sphaera recta (прямая
сфера) и sphaera obliqua (наклонная сфера), которыми он
в дальнейшем неоднократно пользуется [17. С. 71—75].
Под «прямой сферой» он понимает такое положение
небесной сферы, когда небесный экватор перпендикулярен
горизонту (мы знаем, что такое расположение обоих
больших кругов наблюдается на экваторе). Под «наклонной
сферой» Птолемей понимает любое другое положение
небесной сферы, когда экватор наклонен к горизонту под
острым углом.
Для нас эти термины звучат немного странно, но
ведь именно от «прямой сферы» берет начало всем
известный термин прямое восхождение (одна из двух
сферических координат в экваториальной системе). В самом
7 Сочинение Менелая «Сферика» в обработке хорезмийского
ученого X-XI вв. Ибн Ирака (учителя Бируни) дошло до нас и в
1936 г. было издано М. Краузе [109] на арабском языке и в
немецком переводе.
57

деле, если наблюдатель расположен на экваторе, разность
времен восхода светила и точки весеннего
равноденствия, переведенная в единицы дуги (помня, что 1 ч
соответствует дуге в 15°), как раз и будет прямым
восхождением светила. Если точка весеннего равноденствия
находится на горизонте, то дуга, которую прошло светило
с момента его восхода, также будет равна прямому
восхождению.
Следующей задачей, которую решает Птолемей,
является вычисление «таблицы наклонений», как она
названа кем-то из переписчиков
или переводчиков «Альмагеста»,
а точнее, склонений точек на
эклиптике в функции дуг самой
эклиптики (т. е. небесных
долгот), отсчитываемых от точки
весеннего равноденствия через
градус [17, С. 72]. Именно для
этого расчета Птолемею и была
нужна первая теорема Ме-
нелая.
В наше время расчет
склонений центра диска Солнца
(который движется по эклиптике)
или интересующих нас точек на
эклиптике делается без громоздкой теоремы Менелая,
с помощью формул сферического треугольника,
образованного дугами эклиптики, экватора и круга склонения
данной точки. Птолемей не мог решать сферический
треугольник современным способом не только из-за отсутствия в
то время понятия косинуса, столь же нужного в формулах
сферической тригонометрии, как и синус (последний
можно было заменить хордой двойного угла), но и потому,
что в эти формулы входят функции двугранных углов
(например, между плоскостями экватора и эклиптики),
а Птолемей мог иметь дело только с дугами. И хотя он
использует угол наклона эклиптики к экватору, но, в
сущности говоря, он оперирует не с двугранным углом, а с
дугой колюра солнцестояний, равной наибольшему
расстоянию эклиптики от экватора. Этот угол, как мы
помним, Птолемей принял равным 23° 51'20".
От склонений Птолемей переходит к расчету прямых
восхождений точек эклиптики, выбранных через 10° по
долготе. На двух примерах он показывает, в каком
порядке следует вести вычисления, после чего дает небольшую
Рис. 6.
Теорема Менелая
58

табличку прямых восхождений девяти точек аклиптййй.
Собственно, Птолемей приводит не прямые
восхождения, а проекции на экватор десятиградусных и
тридцатиградусных дуг эклиптики — от точки весеннего
равноденствия до точки летнего солнцестояния (т. е. в
интервале долгот 0—90°). Но получить отсюда прямые
восхождения не составляет труда — это простая арифметика.
Равным образом нетрудно распространить расчет на всю
эклиптику: ввиду симметричного расположения обоих
кругов, те же десятиградусные дуги будут
фигурировать и в остальных трех квадрантах эклиптики, что
подчеркивает, заключая I книгу, Птолемей [17. С. 74].
Обратим внимание читателя на то, с какой
дотошностью подходит Птолемей к изложению своих
математических методов. Его доказательства теорем
безукоризненны с точки зрения математической логики и в то же
время просты и понятны. Свои построения он поясняет
чертежами. Так и кажется, что он писал свою книгу в расчете
не на таких же маститых астрономов, как он сам, а на
студентов. И действительно, «Альмагест» в течение
полутора тысяч лет был стандартным учебником астрономии:
по нему учились будущие ученые и студенты в первых
европейских университетах.
В этой связи интересно напомнить, что автор одного
из лучших переводов «Альмагеста» К. Манициус8,
выпуская это сочинение в Лейпциге в 1912 г. на немецком
языке, назвал его «Handbuch der Astronomie», что
буквально означало «Справочник по астрономии» или
«Руководство по астрономии». Конечно, «Альмагест» был
скорее руководством, чем справочником. Но когда спустя
полвека этот перевод был переиздан в ГДР (в том же
Лейпциге) под редакцией и с примечаниями крупнейшего
специалиста по истории античной науки О. Нейгебауэра
[14] и поступил в продажу в Москве в магазине
«Дружба», на карточке в картотеке наличия было написано
«Справочник по астрономии». Полагая, что в ГДР
выпущен новый современный справочник по астрономии,
автор попросил показать ему книгу. Велико же было его
удивление, когда выяснилось, что под этим вполне
современным названием продается древний «Альмагест» Пто-
8 Манициус Карл Генрих (1848-1922) - профессор высшей школы
в Дрездене, специалист по древним языкам и истории науки,
автор переводов на немецкий язык сочинений Гиппарха, Геми-
на, Птолемея, Прокла, «Малого астронома».
59

йемея! Автор пытался убедить работников магазина
«Дружба», что на карточке надо написать: «К. Птолемей.
„Альмагест4'», что это вовсе не справочник по
астрономии, а классический труд, написанный восемнадцать
веков назад и известный именно под этим названием, но
все было напрасно. «„Handbuch" по-немецки означает
„справочник", и мы обязаны название книги переводить
на русский язык точно»,—отвечали мне работники
магазина. Вносить исправления в картотеку они отказались.
Во второй книге своего труда Птолемей ставит и
решает ряд задач, как бы мы выразились теперь, практической
астрономии. Прежде всего он уточняет, что «наша часть
обитаемого мира» находится в северном полушарии и
занимает по долготе менее 180°. Неясно, какими данными
располагал Птолемей для последнего вывода. Долготы
были известны далеко не для всех стран, о которых мог
знать Птолемей. Так, он знал о существовании Британии
далеко на западе и, несомненно, Индии и Китая на
востоке (о них должны были рассказывать ему
александрийские и иностранные купцы). Но достоверное определение
разности долгот он имел лишь одно: лунное затмение—330
сентября 20 наблюдалось одновременно в Карфагене
(долгота ок. 10°) и в Арбеле, на реке Тигр (долгота ок. 46°).
Об этом факте сообщается в «Географии» Птолемея [116].
Тем не менее он был прав в своих представлениях о
расположении «нашей части обитаемого мира».
После этого введения Птолемей ставит и решает
следующие практические задачи [17. С. 75—76]:
1) определить угловое расстояние полюса от горизонта
или (равное ему) зенитное расстояние небесного экватора,
измеряемое вдоль небесного меридиана;
2) для тех мест, где Солнце достигает зенита,
определить, когда и как часто это происходит;
3) определить отношения полуденных теней от
гномона в дни равноденствий и солнцестояний;
4) определить разность между длительностью самого
длинного и самого короткого дня и длиной дня во время
равноденствий;
5) определить приращение и убывание длительности
дней и ночей в разные времена года;
6) определить дуги экватора, которые восходят и
заходят одновременно с заданными дугами эклиптики (эта
задача нужна для вычисления так называемых
гелиакических восходов и заходов) ;
7) определить величины углов между эклиптикой и
60

наиболее важными большими кругами: небесным
меридианом, горизонтом и кругом высоты (большим кругом,
проходящим4 через зенит и надир).
Методика решения этих задач Птолемеем нам уже
известна по примерам, рассмотренным выше. Результаты
своих расчетов Птолемей приводит в виде таблиц.
Представляет интерес описание Птолемеем 39
широтных поясов, которые он выбирает по аргументу
наибольшей длительности дня в день летнего солнцестояния [17.
С. 82—90]. Сначала он выбирает те широты, где
длительность дня нарастает с интервалом в *Д ч. Поэтому после
экватора (день 12 ч) он берет широту 4° 15', где
наибольшая длительность дня 1274 ч. Девятая по счету
параллель соответствует широте 30° 22' (что недалеко от
Александрии), где наибольшая длительность дня достигает
14 ч, одиннадцатая — проходит через остров Родос, где
наблюдал Гиппарх. В описаниях этих параллелей мы
находим целый ряд хорошо нам знакомых рек, морей, озер,
в том числе и находящихся теперь на территории нашей
страны. Так, перед нами проходят реки Дунай (тогда
Истр), Днепр (Борисфен), Дон (Танаис), Азовское море
(озеро Меотида), Черное море (Понт Евксинский). Из
других мест, представляющих интерес, Птолемей
называет город Массилию (нынешний Марсель), Британские
острова, и даже Гебридские и Шетландские острова. Но
о географических исследованиях Птолемея мы поговорим
ниже, в гл. 12. В своем описании параллелей Птолемей
приводит для каждой из них астрономические
характеристики. Кроме наибольшей длительности дня, он
указывает наибольшую высоту Солнца в полдень (или факт
прохождения Солнца через зенит), длину тени гномона
в это время и ряд других характеристик. Он правильно
определяет свойства тропиков и полярных кругов, условия
видимости светил на Северном полюсе.
Однако Птолемей не только доказывал теоремы и
производил вычисления, он еще и вел наблюдения. Это были
в основном позиционные наблюдения, сводившиеся к
определению астрономических координат небесных светил.
Птолемей использует две системы астрономических
координат, применяемые и в наше время: экваториальную
и эклиптическую. В экваториальной системе (рис. 7)
первая координата — уже известное нам прямое
восхождение а, отсчитываемое по дуге экватора EQ от точки
весеннего равноденствия Y до основания D круга склонения
светила, т. е. большого круга, проведенного через оба по-
61

Рис. 7. Экваториальная система координат
Рис. 8. Эклиптическая система координат
люса небесной сферы
(полюсы мира) PPi и светило S.
Вторая координата —
склонение ô — отсчитывается от не-
беспого экватора D до
светила S по кругу склонения PB.
Эти координаты в принципе
построены так же, как и
географические долгота и
широта, причем в обеих
системах есть и полюсы, и
экватор, и параллели (параллели
небесных светил называют
суточными параллелями,
поскольку светило описывает
свою параллель в течение
суток). Вот только вместо
географических меридианов,
сходящихся у полюсов Земли,
в экваториальной системе
фигурируют круги склонения,
также сходящиеся в полюсах
мира.
Совершенно аналогично
построена эклиптическая
система координат, только в ней основная плоскость —
плоскость эклиптики, основной большой круг — эклиптика eq.
У нее также есть два полюса, северный Pi и южный Р/,
располагавшиеся, как считал Птолемей, на расстоянии
Рис. 9.
Вертикальный круг
(по описанию Птолемея)
62

23°5Г20" от соответствующих полюсов мира (мы уже
указывали на с. 25 на ошибку, допущенную Птолемеем в
оценке этого угла). Первая координата — долгота % — от-
считывается вдоль эклиптики от точки весеннего
равноденствия Т против часовой стрелки до основания круга
широты светила К. Вторая координата — широта ß — отсчиты-
вается по кругу широты КР{ от эклиптики до светила S
(рис. 8). Эклиптические долготу и широту не надо путать
с одноименными географическими координатами.
Трудность определения астрономических координат из
наблюдений состоит в том, что ни точка весеннего
равноденствия (начало отсчета прямого восхождения и
долготы), ни экватор, ни эклиптика ничем на небе не
обозначены. Как выходил из этого затруднения Птолемей (а до
него Гиппарх), мы скоро узнаем.
Птолемей дает уже в конце первой книги описание
одного из своих приборов [17. С. 61—62]. Правда, он не
изобразил ни одного из них хотя бы схематически, но по
его подробным описаниям это сделали исследователи его
трудов.
Схемы приборов Птолемея, воспроизводимые в этой
книге, заимствованы у них.
Для измерения дуг в вертикальной плоскости
Птолемей использовал следующий прибор (рис. 9). На прочном
вертикальном столбе укреплено также в вертикальной
плоскости бронзовое кольцо, разделенное на градусы и
доли градуса. Внутри этого кольца и в одной с ним
плоскости поворачивается другое кольцо — с двумя стрелками-
указателями, лежащими точно на 180° одна от другой на
одной прямой. Бронзовое кольцо устанавливается строго
вертикально (что проверяется отвесом) и в плоскости
небесного меридиана. Как именно осуществляется
установка этого инструмента в плоскости меридиана, Птолемей не
сообщает, предполагая, что эта плоскость каким-то путем
проложена заранее. Как сообщает О. Нейгебауэр [116.
Т. 2. С. 841], остроумный способ прокладки направления
меридиана предложил Диодор Александрийский (I в. до
н. э.) в недошедшем до нас сочинении «Аналемма».
Плоскость меридиана устанавливалась по трем положениям
тени гномона. Несомненно, этот метод был известен
Птолемею, хотя возможно, что он использовал и какой-либо
другой метод, например метод равных высот. Этот метод
основан на том, что высоты светила в точках,
симметричных относительно небесного меридиана, равны. Но тогда
и длина тени гномона в моменты, когда Солнце находится
63

Рис. 10. Квадрант (по описанию Птолемея)
Рис. И. «Параллактический инструмент» (по Птолемею)
в таких точках, будет одинакова. Поэтому достаточно
начертить на горизонтальной площадке, где стоит гномон,
несколько концентрических дуг с северной стороны,
центром которых будет основание гномона, и отмечать
положения кончика тени, когда он будет касаться этих
окружностей. Если затем провести биссектрисы углов АОВ,
COD и т. д. (теоретически они должны совпасть), то мы
получим направление полуденной линии, а тем самым и
положение плоскости небесного меридиана.
Помимо описанного выше прибора, явившегося
прообразом целой серии инструментов, известных под
названием меридианного круга и используемых в наши дни для
наблюдений прохождений звезд и других светил через
меридиан, Птолемей приводит конструкцию другого, более
простого прибора [17. С. 62—63]. Он представляет собой
прочную доску из камня или дерева с гладко
отполированной боковой стороной (рис. 10). Доска устанавливается
вертикально в плоскости небесного меридиана. На ней из
некоторой точки вблизи верхнего южного угла проводятся
вертикальная и горизонтальная прямые и стягивающая их
дуга в 90°. Эта дуга делится на градусы и их доли. К
центру дуги крепится линейка, которая может поворачиваться
вокруг него. На линейке перпендикулярно доске
укрепляются два небольших цилиндрических шпенька, из которых
верхний должен проходить через центр дуги. Когда
Солнце проходит через меридиан, линейка устанавливается
так, чтобы тень верхнего шпенька падала точно на ниж-
64

ний. Тогда деление на дуге квадранта покажет нам высоту
Солнца.
Этот прибор послужил прообразом для измерительных
приборов, названных квадрантами и использовавшихся в
XV—XVI вв. такими наблюдателями, как Улугбек и Тихо
Браге. Ради повышения точности измерений им
придавали довольно большие размеры (десятки метров). Шпеньки
Птолемея были заменены диоптрами.
С помощью этих двух приборов Птолемей наблюдал
высоту Солнца в меридиане в дни равноденствий и
солнцестояний и из этих наблюдений вывел угол наклона
эклиптики к экватору, близкий к значениям, полученным ранее
Эратосфеном и Гиппархом (см. с. 25).
В пятой книге (гл. 12) Птолемей описывает третий
угломерный прибор, названный им параллактическим
инструментом. Такое название Птолемей дал этому прибору
потому, что он использовал его для определения
параллакса Луны [17. С. 244-247].
К установленному вертикально (с помощью отвеса dd)
деревянному столбу прямоугольного сечения 1 (рис. 11)
на шарнире крепится линейка 2 с укрепленными в ее
верхнем и нижнем концах диоптрами (визирами).
Отверстие нижнего диоптра а (в которое смотрит наблюдатель)
небольшое, у верхнего Ъ — побольше, чтобы в него была
видна вся Луна. Посередине столба 1 сверху вниз
проведена прямая с делениями, начинающимися от шарнира с.
Она разделена на 60 частей и их доли. Такая же прямая
длиной 60 частей проведена и на поворачивающейся
линейке 2. Линейка 2 укреплена на шарнире с так, чтобы
она не опускалась от собственного веса, но чтобы ее мог
повернуть наблюдатель. Она вращается в плоскости
меридиана.
В нижней части столба на другом шарнире е
укреплена еще одна планка 5, которая имеет также подвижное
соединение с линейкой 2 и при ее повороте тоже
поворачивается. Она также имеет деления, равные по длине
делениям на столбе 1 и на линейке 2.
Наблюдатель наводит линейку с диоптрами на Луну,
когда она проходит через меридиан, и закрепляет ее.
Поскольку в треугольнике ABC (рис. 12) стороны AB и АС
равны (и содержат по 60 делений каждая), сторона ВС
равна хорде угла z=BAC, т. е. зенитному расстоянию
Луны, в тех же единицах. Вертикальное положение
столба проверяется с помощью отвеса.
Почему же этот прибор назван параллактическим?
3 Клавдий Птолемей
65

Je//£//77
Рис. 12. К теории «параллактического инструмента» (трикветра)
Птолемея
Рис. 13. Суточный параллакс
Ведь с его помощью определяется лишь зенитное
расстояние Луны. Напомним, что суточным параллаксом
(рис. 13) называется угол, под которым в данный момент
из светила виден радиус Земли, на конце которого
находится наблюдатель. Если светило в зените, то
параллакс равен нулю, если на горизонте, параллакс достигает
своего максимального значения {горизонтальный
параллакс) . Вообще же параллакс р{ ^- ASC) равен
sin p=(R/d) sinz,
где R — радиус Земли, d — расстояние от центра Земли
до светила, z — его зенитное расстояние.
Казалось бы, в этой задаче два неизвестных аир
при одном уравнении. Но из рис. 13 видно, что явление
параллакса увеличивает зенитное расстояние светила
на величину самого параллакса. А поскольку Птолемей,
зная склонение Луны ö^ZEAS, мог вычислять ее
зенитные расстояния на моменты наблюдений, не
искаженные параллаксом, разность наблюденных и
вычисленных значений z сразу давала ему /?, а по
приведенной выше формуле (с заменой синуса на хорду
двойного угла) он мог определить и расстояние до Луны d в
долях радиуса Земли.
Поскольку Луна может иногда достигать склонения
б=+29°, на широте Александрии (ф=+31°) она
проходит в это время всего лишь в 2° от зенита. Для этого
нужно, однако, чтобы Луна была одновременно близ
точки летнего солнцестояния и в 90° к востоку от вос-
66

Коперник с трнкветром (картина Я. Матейки, 1873 г.)
ходящего узла своей орбиты. Поскольку линия узлов
лунной орбиты совершает полный оборот относительно
точки весеннего равноденствия за 182/з года, бочетание
обоих условий повторяется именно с этим периодом.
Птолемей утверждает, что он наблюдал Луну в
таком положении, но не сообщает даты наблюдения [17.
С. 246—247]. Поскольку, однако, известно, что 1
октября 135 г. Птолемей наблюдал Луну в 5° к северу от
точки зимнего солнцестояния, линия узлов должна была
сделать " полоборота, чтобы реализовалось положение,
описанное выше (Луна на 5° севернее точки летнего
солнцестояния). Это значит, что Птолемей мог
наблюдать Луну в этом положении либо в июне—июле 126 г.,
либо в начале января 145 г. [131. С. 247]. Обе даты вы-
67
3*

ходят за пределы периода, когда Птолемей проводил
астрономические наблюдения, упоминаемые в его книге
(26 марта 127 г.—2 февраля 141 г.). Конечно, нет
ничего невозможного в том, что Птолемей начал наблюдать
на 9 месяцев раньше, чем это зафиксировано
сообщаемыми им датами наблюдений, или провел
дополнительное наблюдение Луны в 145 г. Возможно также, что
наблюдение Луны в 126 г. провел и передал Птолемею
упоминаемый им не раз математик Теон (см. с. 9).
Параллактргческий прибор Птолемея, получивший
впоследствии название трикветр, применялся многими
астрономами после него. Его описание и чертеж мы
находим в классическом труде Коперника «О
вращениях...», а также в «Механике обновленной астрономии»
Тихо Браге. Именно он изображен на знаменитой
картине польского художника Яна Матейки «Коперник»
(1873 г.). Интересно, что подлинный трикветр
Коперника спустя 40 лет после его смерти попал в руки Тихо
Браге и был им подробно описан в вышеупомянутой
книге, вышедшей в 1598 г. [124].
Последний и самый сложный прибор, описанный
Птолемеем в той же пятой книге «Альмагеста» это —
армиллярная сфера с диоптрами для наблюдения. Впрочем,
Птолемей называет свой прибор астролябией (аотроАа-
ßov), что буквально означает «для определения
положений светил». Этот прибор стал «моделирующим» для
астролябий, получивших распространение на арабском
Востоке в IX—XIII вв., изображавших небесную сферу
в стереографической проекции (введенной Птолемеем в
«Планисферии»). Армиллярной сферой Птолемей
называл другой (демонстрационный) прибор.
Вот как устроен первый прибор (рис. 14). Основой его
является описанный нами ранее меридианный круг
(см. рис. 9). Но в диаметрально противоположных
точках, отмеченных на рисунке буквами dd, меридианного
кольца 6, соответствующих положениям полюсов мира
на данной широте9, просверлены отверстия и в них
укреплены два штифта, вокруг которых может
поворачиваться кольцо 4, изображающее колюр солнцестояний.
На расстоянии от точек dd, измеряемом углом наклона
эклиптики к экватору или равной ему дугой между
полюсами мира и эклиптики, через кольцо 4 пропущены
Напомним читателям, что угловая высота полюса мира над
горизонтом равна широте места.
68

Рис. 14.
Армилла Птолемея
два других штифта ее, образующих ось, вокруг которой
могут поворачиваться: с внутренней стороны кольцо 2,
разделенное на градусы и их доли, а с наружной
стороны кольцо 5. С кольцом 4 жестко скреплено
перпендикулярно ему кольцо 5, изображающее эклиптику и
также разделенное по наружной (внешней) поверхности
на градусы и их доли. Внутри кольца 5, в одной с ним
плоскости, укреплено кольцо 1 с двумя диаметрально
противоположными диоптрами 66, служащими для
наблюдений [17. С. 217-219].
С помощью этого прибора светило можно наблюдать
не только в меридиане, но в любом положении на небе.
По идее Птолемея после наведения диоптров ЪЪ на
светило можно было по делениям круга 2 отсчитать его
долготу, а по делениям круга 4 (отсчитываемым с
помощью круга 5, который для этого должен быть
установлен в одной плоскости с кругом 2) — широту.
Однако наблюдения с этим прибором требовали
известного навыка со стороны наблюдателя. В отличие от
современных астрономических приборов, в которых
наведение на светило осуществляется поворотом трубы
прибора вокруг двух взаимно перпендикулярных осей,
в астролябии Птолемея нужно было поворачивать
подвижные части прибора вокруг трех осей: вокруг
полярной оси dd, вокруг оси эклиптики ее и вокруг оси колец
1 и 2, лежащей в плоскости эклиптики (по аналогии с
осью склонений современных телескопов-экваториалов
ее можно назвать осью широт).
69

Впоследствии, в 1581 г., искусный наблюдатель Тихо
Браге воспроизвел по описанию Птолемея его прибор,
назвав его «зодиакальными армиллами» (слово «армил-
ла» означает «кольцо»; Тихо Браге употреблял это
слово во множественном числе). Видимо, этот прибор не
удовлетворил Тихо Браге, и спустя три года он заменил
его «экваториальными армиллами», где, кроме
меридиана, имеются лишь два кольца: небесный экватор и круг
склонения, а поворот осуществляется вокруг двух
взаимно перпендикулярных осей: полярной и оси
склонений [27].
С помощью описанных здесь приборов Птолемей и
производил все свои наблюдения положений небесных
светил. Естественно, все они велись невооруженным
глазом. Их точность зависела от точности наведения
шпеньков или диоптров, от правильности установки самого
инструмента, наконец, от точности делений и их
правильного считывания (большинство наблюдений
проводилось ночью). Точность наблюдений Птолемея не
превышала 10 мин дуги. Еще ниже была точность
наблюдений, связанных с регистрацией времени (моменты
затмений, покрытий звезд Луной, прохождений светил
через меридиан). Точных часов в те времена не было,
а существовавшие солнечные, песочные и водяные часы
давали точность не выше 15 мин времени, что в
переводе на единицы угла могло привести к ошибкам в
определении прямых восхождений и эклиптикальных долгот
в 3-4°.
Глава 7
Теория движения Солнца
В третьей книге «Альмагеста» Птолемей развивает
первую из своих теорий движения «блуждающих» светил —
теорию движения Солнца. Это — самая простая теория из
всех. Солнце движется точно по эклиптике, значит,
отсутствует смещение по широте. Солнце не описывает по
небу петель, как планеты, значит, у него нет так
называемого второго неравенства. Даже по сравнению с Луной
движение Солнца гораздо проще.
Но прежде чем строить теорию движения Солнца,
Птолемей рассматривает вопрос о длительности тропического
70

года. Здесь он приводит наблюдения солнцестояний на
протяжении нескольких веков, которые собрал до него
Гиппарх, и выводы, сделанные из них Гиппархом.
Птолемей принимает гиппархову длину года: 36574—7зоо сут,
не пытаясь уточнить ее на основании собственных
наблюдений. Мы уже рассматривали вопрос о погрешности этой
величины в гл. 3, посвященной Гиппарху.
На основании принятой им длины года Птолемей
вычисляет среднее суточное движение Солнца по эклиптике
(по долготе) и находит, что в шестидесятиричной записи
оно равно[17. С. 140]
0; 59, 8, 17, 13, 12, 31°,
что соответствует в привычных нам единицах
0,98563526°=0°59'8,28700238".
Умножая на 365 (число дней в египетском году), он
находит среднее годовое движение Солнца, или, что то
же самое, приращение его долготы за один египетский
год:
359; 45, 24, 45, 21, 8, 35°=359, 75687661°=
=359° 45/24,75587306".
Птолемей делает эти выкладки с потрясающей
точностью: одна единица последнего разряда
шестидесятиричной системы равна примерно 2-10-11 градуса или 7-10~8
угловой секунды. Разумеется, реальная точность его
результатов гораздо ниже. Даяш если бы принятая им
длина тропического года (365; 14,48) была точна до
последней единицы второго шестидесятиричного разряда, т. е.
до 7-Ю"7 длины года, все расчеты имело смысл вести
только с такой точностью. Но, как мы уже установили в гл. 3,
принятая Птолемеем (вслед за Гиппархом) длина года
была ошибочна на 0,0042 сут, или на 10~5 года.
Зачем же ему понадобилось вычислять таблицу
средних движений Солнца с высокой, но явно фиктивной
точностью? Птолемей не мог не понимать этого, даже если
он считал оценку Гиппарха верной. Делал он так, чтобы
избежать накопления погрешностей при
умножении. Ведь дальше он множит среднее годовое движение
Солнца на 18, отбрасывает 17 раз по 360° и находит
приращение долготы Солнца за 18-летний цикл:
355; 37, 25, 36, 20, 34, 30°.
71

Почему Птолемей выбрал именно 18-летний цикл? Не
потому ли, что он близок к саросу — периоду
повторяемости солнечных и лунных затмений, известному еще
вавилонским астрономам и равному 18 годам и 10 или 11
суткам? Возможно, что играло роль и это обстоятельство.
Но, по мнению Дж. Тумера, все объясняется гораздо
проще [131. С. 140].
Свитки папируса, на которых писал Птолемей, имели
стандартную ширину. Птолемей (как и другие ученые и
писатели той эпохи) писал так, что строки располагались
вдоль рулона, поэтому страницы его книги имеют
стандартную высоту. Этой высоте соответствуют 45 строк в
таблице с учетом места, отводимого заголовкам самой таблицы
и ее столбцов. Поэтому все большие таблицы Птолемея
(занимающие более одной страницы) имеют по 45 строчек.
В данном случае Птолемей расположил материал так.
Сперва идут приращения долготы за 18-летние циклы (от
первого до 45-го). Затем идут приращения за отдельные
годы в цикле (от первого до 18-го) и за часы суток (24
строки по числу часов в сутках). Вместе эти две таблички
занимают 42 строки плюс заголовки. Наконец, в третьей
части таблицы даны приращения долготы по месяцам
(12 месяцев — 12 строк) и по дням в месяце (30 строк), а
всего опять же 42 строки плюс заголовки.
Из-за такого ограничения на высоту таблиц Птолемей
смог охватить только период времени в 810 лет (45
циклов по 18 лет). Таким образом, от первого года эры Набо-
нассара (—746 г.) он не «дотянул» даже до эпохи своих
наблюдений, а лишь до 64 г. н. э.
Птолемей понимал неудобство такой формы
табулирования для своих современников и потомков, поэтому в
своих «Справочных таблицах», созданных позднее
«Альмагеста», он перешел к 25-летнему циклу, а за начало эры
принял начало правления Филиппа II (преемника
Александра Македонского) : —323 ноября 12.
После составления таблицы среднего движения
Солнца по долготе Птолемей обращается к теории
первого неравенства, т. е. отклонений движения истинного
Солнца от равномерного (среднего). В гл. 2, в рассказе
о работах Аполлония Пергского, мы уже приводили его
теорему, в которой доказывается эквивалентность
(равноправность) двух моделей движения планеты: по
неподвижному эксцентру и по комбинации
деферент—эпицикл, причем движение планеты по эпициклу
происходит с той же угловой скоростью, но в обратном направ-
72

Рис. 15.
Эквивалентность эксцентра
и эпицикла
лении по сравнению с
движением центра
эпицикла по деференту.
Приведем краткое
доказательство
эквивалентности этих двух моделей
(подробное
математическое доказательство этого
можно найти в
«Альмагесте» [17. С. 141, 144-
153], а также в работе
Н. И. Идельсона [54]).
Пусть наблюдатель
(рис. 15) находится в
точке Т7, которая является
центром деферента ABCD.
Представим себе
параллелограмм TOPN, одна из
сторон которого ТО
жестко закреплена на радиусе
деферента ТА, но ТО<ТА. Точка N всегда находится на
деференте. Допустим, что в вершинах параллелограмма
помещены шарниры, вокруг которых его стороны могут
поворачиваться, и будем вращать сторону TN вокруг точки
,]Т. Тогда параллелограмм будет изменять свою форму, но
всегда останется параллелограммом, иначе говоря, в любом
его положении NP\\TO и ТЩОР. Поскольку отрезок NP
сохранит при этом свое направление и величину, ясно,
что точка Р прочертит окружность, равную окружности
деферента ABCD, но смещенную относительно нее на
величину ТО. Эта окружность и называется эксцентром.
Если же отложить положения точки Р относительно
точки N, то нетрудно убедиться в том, что Р опишет
вокруг N небольшую окружность радиусом NP, причем угол
ее поворота на этой окружности P0NP равен углу ATN,
на который центр эпицикла сместился от своего
начального положения А. Окружность Р0Р и есть эпицикл.
Как уже говорилось в гл. 2, первым эту теорему
доказал Аполлоний Пергский, живший за 350 лет до Птолемея;
затем ее использовал Гиппарх при построении своей
теории движения Солнца. Оригинальные работы этих ученых
не дошли до нас, и мы узнали о них только через
«Альмагест» Птолемея. Приводя доказательство теоремы
Аполлония, Птолемей не сообщает, взято ли оно у Аполлония
73

или разработано им самим. Но, как и во всех других
местах, доказательство построено безукоризненно.
Основы своей солнечной теории Птолемей заимствовал
у Гиппарха. Он использовал и выведенную Гиппархом
среднюю длительность года, и найденный последним
эксцентриситет орбиты Солнца (фактически — орбиты
Земли) , и даже долготу перигея солнечной орбиты. В гл. 3 мы
приводили эти величины. Там же мы обратили внимание
читателя на то, что Птолемей не потрудился проверить
долготу перигея Солнца, найденную Гиппархом, и принял
ее постоянной, тогда как в действительности она
возрастает примерно на 1° 43' в столетие, и за 300 лет,
отделяющих эпоху Птолемея от эпохи Гиппарха, долгота перигея
должна была увеличиться на 5°.
Такой упрек уже не раз адресовали Птолемею
комментаторы «Альмагеста», например К. Манициус, автор
немецкого перевода этой книги [14. Т. 1. С. 428—429]. Но
этот упрек оказался незаслуженным. Вспомним, как
определял долготу перигея Солнца Гиппарх. Он сравнивал
длительность четырех времен года, причем измерять их
Гиппарх и Птолемей могли лишь с точностью до iU сут.
В эпоху Гиппарха Солнце проходило через перигей
27 ноября, в эпоху Птолемея — 2 декабря (на 5 сут позже),
в наше время Солнце ближе всего к Земле 3 января.
Перемещение перигея на 5° в прямом направлении должно
было привести к некоторому увеличению длительности
осени и лета и к сокращению длительности зимы и весны.
На сколько? Расчеты по точным формулам (они приведены
у Н. И. Идельсона [54] ) показывают, что длительности
сезонов между эпохами Гиппарха и Птолемея должны были
измениться... на 'Д сут. Но ведь именно такой (и даже
большей) была погрешность определений моментов
равноденствий и солнцестояний у обоих наблюдателей.
Чтобы выявить смещение перигея Солнца, Птолемей
должен был не только повысить точность своих
собственных определений моментов равноденствий и солнцестояний
хотя бы до ±2 ч (это в принципе было возможно), но
и иметь в распоряжении столь же точные наблюдения
Гиппарха (а это было вообще невозможно). Поэтому не
следует винить Птолемея в том, что он не заметил
смещения перигея — он и не мог его заметить. Напротив,
получив длины сезонов почти такими же, как и Гиппарх, он
с легким сердцем сделал вывод, что перигей Солнца не
смещается.
Только аль-Баттани (850—929), имея в распоряжении
74

наблюдения, сделанные на десять с лишним столетий после
Гиппарха, когда длительность сезонов заметно изменилась,
смог вычислить смещение перигея Солнца. К тому времени
оно достигло 16°.
Эти обстоятельства (недостаточная точность
наблюдений Гиппарха и Птолемея) были выяснены более 40 лет
назад бельгийским историком науки А. Ромом [126], затем
на него указали голландские исследователи В. Петерсен и
О. Шмидт [121]. (Однако наш расчет был выполнен
совершенно независимо и другим методом, чем у них).
Авторы указанных работ показали, что ошибка в определении
момента солнцестояния или равноденствия всего на 1 ч (!)
привела бы к погрешности в определении положения
перигея на 1°. Но точность в 1 ч была недоступна ни Гип-
парху, ни Птолемею.
Птолемей вычисляет из чисто геометрических
соображений, основанных на определениях длительности сезонов,
эксцентриситет орбиты Солнца [17. С. 155—157]. Он
получает в единицах, где радиус эксцентра равен 60р,
расстояние от Земли до центра эксцентра 2; 297гр. Этой величине
соответствует эксцентриситет орбиты 0,04153, что мало
отличается от величины, полученной Гиппархом, 0,04167.
Величину максимального уравнения центра хтах (см. с. 32)
Птолемей получил равной 2° 23' (как и Гиппарх).
Здесь нам надо отвлечься на время от расчетов
Птолемея и попробовать сравнить теорию движения Солнца
Гиппарха—Птолемея с современной теорией движения Земли
вокруг Солнца по эллиптической орбите [54]. На
основании последней уравнение центра х и расстояние Земли
от Солнца г можно следующим образом представить в виде
разложения в ряд по степеням эксцентриситета е:
х=2е sin М- (5/4) е2 sin 2М,
r/a=l+e2/2+e cos М-(е2/2) cos 2М.
Здесь мы берем отношение г/а, где а — большая полуось
эллипса, угол M есть средняя аномалия планеты, т. е. угол,
растущий пропорционально времени и принимающий
значения M=0° в афелии и Ж=180° в перигелии. В
разложении удержаны члены порядка е и е2 и отброшены члены с
высшими степенями е.
Запишем теперь те же величины по Птолемею, но
эксцентриситет обозначим (по причинам, которые вскоре
станут ясны) буквой г:
75

х=г sin М- {г212) sin 2M,
r/a=l+82/4+8cosM-(e2/4) cos2AT.
Здесь под а будем подразумевать радиус эксцентра, угол
М=0° в апогее и M=180° в перигее.
Сравнивая обе группы формул, мы найдем, что члены
порядка е в разложении для х совпадут, если положить
г=2е. Тогда мы будем иметь в гипотезе простого
эксцентриситета
х=2е$тМ-2е2$т2М,
r/a=l+e2+2e cos М-е2 cos 2 M.
Таким образом, в этой гипотезе разность выражений
для х по теориям Кеплера и Птолемея составит
3/4е2 sin 2ДТ, что при М=45° и е=б/2=0,02076 может дать
максимальную ошибкуi в долготе в 3,23 • 10~4 радиана
или 67".
Различие в оценке относительного радиуса окажется
больше, а именно
Д (г/а) =>е2/2+е cos М- (е2/2) cos2M.
При Д/=0° или М=180° А (г/а) =е=Ю,021.
Как известно, теория эллипса дает следующие
расстояния от Земли до Солнца в перигелии и афелии:
q=a(l-e), q'=a{i+e),
тогда как по теории Гиппарха—Птолемея получалось
q=a(l-2e), q'=a(l+2e).
Если бы Птолемей мог измерять видимый диаметр
солнечного диска, он заметил бы, что солнечный диаметр
изменяется от перигея до апогея на 4%, а не на 8%, как
должно было получаться по его теории2.
Но античные наблюдатели интересовались лишь
видимыми положениями светил на небесной сфере, а не их
расстояниями от Земли, поэтому теория Гиппарха для
Солнца вполне устраивала Птолемея, поскольку давала
более чем достаточную точность.
1 Здесь и далее у нас будут фигурировать иные оценки ошибок в
долготе и радиусе-векторе, чем у Н. И. Идельсона [54], потому
что он использовал современное значение е, а мы - его значение
в эпоху Птолемея.
2 В наше время это изменение составляет лишь 3,4% из-за
векового уменьшения эксцентриситета орбиты Земли.
76

Птолемей приводит таблицу аномалий движения
Солнца [17. С. 167], т. е. величины х в функции угла M при его
изменении от 0 до 360°. Максимальное значение этой
величины у него, как мы уже говорили, равно 2° 23' (по Гип-
парху).
Последний вопрос, который рассматривает Птолемей в
книге III «Альмагеста», это вопрос о неравенстве
длительности суток [17. С. 169—172].
Птолемей правильно указывает две причины, влияющие
на изменение длительности суток (считая от полудня до
полудня) в течение года. Одна из них — это только что
рассмотренное первое неравенство, вызываемое
эксцентриситетом круговой орбиты Солнца. Вторая причина —
изменение моментов прохождения Солнца через меридиан из-за
наклона эклиптики к экватору. Даже при равномерном
перемещении Солнца по эклиптике сутки были бы неравны
между собой, потому что вблизи равноденствий дуге
эклиптики в 1° соответствует дуга экватора в 1° cos е (где 8=
=23°51' — наклон эклиптики к экватору), равная 55',
тогда как вблизи солнцестояний той же дуге соответствует
дуга экватора в 66' (из-за расхождения кругов склонения
от полюса к экватору). Нетрудно подсчитать, что в первом
случае сутки будут на 44 с короче, чем во втором.
Накопление этих разностей приводит к смещению момента
истинного полудня относительно среднего. Их разность
называется уравнением времени.
Уравнение времени складывается из двух
составляющих (рис. 16) : уравнения от наклона эклиптики, график
которого имеет вид синусоиды с двумя максимумами и
двумя минимумами (в дни равноденствий и солнцестояний
оно равно нулю), и уравнения от эксцентриситета,
выражаемого синусоидой с одним максимумом и одним
минимумом (в дни прохождения Солнца через перигей и апогей
оно равно нулю). Суммарная кривая, отражающая оба
эффекта, имеет более сложный вид: с двумя неравными
максимумами и двумя минимумами. На рис. 16 изображен
современный график уравнения времени и обеих его
составляющих. В эпоху Птолемея этот график имел несколько
иной вид все из-за того же смещения солнечного
перигея и апогея. Как уже говорилось, Солнце тогда проходило
эти точки примерно на месяц раньше, чем в наши дни.
Поэтому кривую уравнения от эксцентриситета следует
сместить на один месяц влево.
Как видно из рис. 16, амплитуда уравнения от наклона
эклиптики составляет ±10 мин, уравнения от эксцентри-
77

Рис. 16. График уравнения времеии
ситета — _ю мин, она несимметрична относительно нуля
из-за особенностей движения по эллипсу. (Как известно,
в перигелии Земля движется быстрее и находится ближе
к Солнцу, ту же дугу в области перигелия она проходит
быстрее). Наибольшего значения—16 мин 23 с
—уравнение времени достигает 3 ноября.
Во времена Птолемея не умели чертить графиков,
подобных изображенному на рис. 16. В геометрических
построениях пользовались только циркулем и линейкой.
Птолемей мог вычислить таблицу уравнения времени на
каждый день года. Но он не сделал этого. Зато он дал
подробные указания к вычислению этой величины, а также
(с ее учетом) долготы истинного Солнца на любой день
любого года.
Птолемей ввел ряд важных понятий, используемых в
астрономии и поныне. К ним относятся и понятие среднего
Солнца, и среднего суточного движения, и понятие
средней долготы, и уравнение времени. Так что не следует с
его именем связывать одни эпициклы, как это делают
некоторые авторы популярных книг, преподаватели или
лекторы.

Глава 8
Теория движения Луны
Теория движения Луны — задача намного более
трудная, чем задача о видимом движении Солнца, в котором
как бы отражается реальное обращение Земли вокруг
Солнца. Мы уже приводили в гл. 3 ряд свидетельств в
пользу этого заключения. Но чтобы сразу понять, в чем
дело, посмотрим на обе задачи с современной точки
зрения.
Земля обращается вокруг Солнца под действием его
притяжения. Влияние других тел Солнечной системы —
планет — ничтожно по сравнению с притяжением Солнца.
Самая крупная из планет — Юпитер уступает Солнцу по
массе в 1000 раз, а кроме того, она находится от Земли в
среднем в 5 раз дальше, и из-за одного этого ее
притяжение еще в 25 раз слабее. Венера гораздо ближе, порой в
3,5 раза ближе Солнца, но ее масса уже в 400 тыс. раз
меньше солнечной, значит, ее притяжение слабее
солнечного в 35 тыс. раз. Действие других планет еще слабее:
Сатурн уступает Юпитеру втрое по массе и находится
вдвое дальше, Уран и Нептун — еще дальше и меньше,
Марс — дальше и меньше Венеры, о Меркурии и говорить
нечего.
И все же действие планет влияет на движение Земли.
На его долю приходится 18' из 1° 43' смещения перигелия
Земли (или перигея Солнца), остальное — следствие
прецессии. Сама прецессия частично вызывается действием
Луны, малая ее часть — действием планет, остальное —
опять-таки Солнцем. Под действием притяжения планет
происходит вековое изменение не только долготы
перигелия, но и других- элементов орбиты Земли, в частности
эксцентриситета. Сейчас эксцентриситет земной орбиты
медленно убывает. Примерно через 35 тыс. лет он
достигнет минимума — значения 0.002 (сейчас он равеп 0,017),
затем начнет расти, достигая в некоторые эпохи
величины 0,05 — почти как у орбиты Луны [79].
Луна — спутник Земли. И в этом вся трудность
построения" ее теории. Массивное Солнце теперь надо
рассматривать как возмущающее тело. Посмотрим, велико ли
возмущающее ускорение Солнца по сравнению с ускорением,
сообщаемым Луне Землей. Возмущающее ускорение
Солнца — это разность ускорений, сообщаемых им Луне
79

и Земле. В эпохи новолуний и полнолуний, когда Солнце,
Луна и Земля находятся на одной прямой, это ускорение
достигает своего максимального значения
ge=f(2MGr/R°),
где / — постоянная тяготения; MQ — масса Солнца; г
—расстояние от Земли до Луны, R— расстояние от Земли до
Солнца. Напишем теперь ускорение, сообщаемое Луне
Землей:
£е=/(Мф/г2),
где Ж© — масса Земли. Найдем отношение gJgQ:
gJge=2(MJM.)(r/R)*.
Подставив числовые значения Д/©/М©=332 000, i?/r=390,
получим £©/£©=1/90. Итак, действие Солнца может
достигать более чем одного процента действия центрального
тела — Земли. И вдобавок это действие все время меняется
в ходе обращения Луны вокруг Земли и Земли вокруг
Солнца.
Вот в этом и состоит причина необычайной трудности
теории движения Луны. Даже со времен Ньютона на
создание полной динамической теории Луны ушло почти три
столетия.
Но вернемся к Клавдию Птолемею. Что было в его
распоряжении для построения хотя бы кинематической
теории движения Луны? А такая теория была нужна,
потому что наблюдения Луны использовались для
определения долгот на земной поверхности, не говоря уже о
предсказании солнечных и лунных затмений. Ведь Птолемей
занимался и географией, и астрологией. Итак, что же у
него было?
Были наблюдения солнечных и лунных затмений,
выполненные в древнем Вавилоне, затем в Греции, на Родосе
(Гиппархом) и в Александрии (в том числе его
собственные наблюдения), почти за девять веков. Были
позиционные наблюдения Гиппарха и его, Птолемея. Были точные
определения длительности четырех лунных месяцев,
полученные Гиппархом из его знаменитых циклов. Были
основы теории, заложенные тем же Гиппархом. Дальше
надо было действовать самому.
И вот перед нами книга IV «Альмагеста». Птолемей
ни на минуту не забывает, что он пишет руководство
по астрономии, хотя, конечно, не имеет представления о
том, что пишет на века. И не на один-два века, а на целых
пятнадцать.
80

Какие наблюдения Луны можно использовать для
построения точной теории ее движения? Выбор большой:
наблюдения солнечных и лунных затмений, соединений
Луны с яркими звездами3, покрытий звезд Луной, просто
позиционные наблюдения с угломерным прибором. Но из
всей массы наблюдений Птолемей выбирает один их
вид — наблюдения лунных затмений. Они много точнее
всех остальных, потому что моменты начала и конца
лунного затмения не зависят от положения
наблюдателя на Земле. Моменты же солнечных затмений,
покрытий звезд Луной, соединений, положение Луны
относительно звезд от положения наблюдателя зависят.
Причина состоит в том, что орбита Луны не
располагается столь далеко от нас и имеет место параллактическое
смещение Луны в зависимости от положения
наблюдателя. (Позже Птолемей определит лунный параллакс и
приблизительно расстояние до Луны).
Александрийскому астроному было известно, что
солнечное затмение в разных местах Земли наступает
неодновременно (даже если учесть разность долгот) и имеет,
как говорят теперь, разную величину: Луна закрывает в
разных городах различные части солнечного диска. А то,
что Солнце во время затмения закрывается именно
Луной, это было известно еще Аристотелю [7]. Точно так же
именно Аристотель объяснил причину лунных затмений:
Луна попадает в тень, отбрасываемую Землей. Круглая
форма земной тени доказывала шарообразность Земли.
Но ведь момент вхождения и выхода Луны из земной
тени не зависит от положения наблюдателя. Где бы мы ни
находились, мы увидим эти явления в один и тот же
момент. Это важное соображение подсказало Птолемею
выбор: использовать в первую очередь лунные затмения.
В момент середины затмения Луна находится
диаметрально противоположно Солнцу. А теория движения
Солнца уже построена, его долготы на любой день и час
можно вычислить по таблицам книг II и III. Значит,
и положение Луны в момент середины затмения нам
точно известно4.
3 Соединением называется такое расположение двух светил,
когда они проходят через небесный меридиан одновременно или же
имеют одинаковую долготу (соединения по долготе).
4 Это рассуждение верно только для центрального лунного
затмения, когда ценр диска Луны проходит через центр земной
тени. Во всех остальных случаях Луна в середине полного
затмения может отклоняться от «антисолнца» до 40' по широте и
до 4' по долготе.
81

Приступая к построению своей теории, Птолемей
сначала вычисляет средние суточные движения Луны по
долготе (относительно точки весеннего равноденствия),
по аномалии (относительно перигея лунной орбиты),
по широте (относительно ее узла) и по элонгации
(относительно Солнца) [17. С. 179—180]. Затем он вычисляет
средние движения Луны за час, за месяц (30-суточный),
за год и за 18-летний цикл [17. С. 182—187]. Таким
образом, как и в случае Солнца, Птолемей начинает со
среднего движения Луны и строит таблицу, позволяющую
рассчитать четыре названных выше угла на любой день
и час любого года от начала эры Набонассара (—746 г.)
до 64 г. н. э. Причина такого ограничения — все те же
45 строк, которые можно было расположить на папирусе.
Впрочем, по данным Птолемея таблицу легко можно было
продолжить и на последующие годы и века.
Дальше Птолемей начинает вычислять первое, или
простое, неравенство в движении Луны, аналогичное
первому неравенству в движении Солнца. Еще раз доказав
эквивалентность моделей с эксцентром и с эпициклом,
он для дальнейших операций выбирает модель с
эпициклом (эксцентр ему еще понадобится). Первое
неравенство вызвано, по Птолемею, эксцентричным положением
орбиты Луны относительно Земли. Но ради удобства
геометрических построений и основанных на них расчетов
Птолемей строит такую модель [17. С. 181, 188—190].
Пусть мы имеем (рис. 17) деферент AG с центром в D,
совпадающий с эклиптикой (наклоном лунной орбиты
пока пренебрегаем). По нему движется центр эпицикла.
Пусть в момент прохождения Луны через апогей цеитр
эпицикла будет в точке А, а сама Луна — в точке Е. Пусть
далее за время, пока центр эпицикла опишет дугу AG,
Луна пройдет дугу E'Z<AG (в дуговой мере). Все
дальнейшие построения Птолемей строит только на эпицикле,
изображая на своих графиках лишь цеитр деферента D.
Он рассуждает так (рис. 18).
Рассмотрим движение Луны только по аномалии
(напомним, что под углом аномалии Птолемей подразумевает
угловое расстояние Луны от апогея ее орбиты; этот угол
он отсчитывает по эпициклу). Чтобы найти первое
неравенство, Птолемею нужно определить отношение радиусов
эпицикла и деферента. Тогда каждому значению угла
аномалии AKL (отсчитываемому по эпициклу) будет
соответствовать некоторый малый угол при точке D между
направлениями на Луну L и па центр эпицикла К
82

Рис. 17.
Деферент и эпицикл Луны
Рис. 18.
К определению первого
неравенства Луны
(AKDL). Соотношение между ними определяется из
треугольника DKL, в котором радиус деферента DK
считается известным и равным 60р, радиус эпицикла KL
определяется методом, который будет изложен ниже, а угол
AKL (а значит, и /.DKL в треугольнике DKL) служит
аргументом. Таким образом, в треугольнике DKL
известны две стороны и угол между ними, а этого достаточно,
чтобы решить треугольник и найти интересующий нас
^-KDL.
Но для этого требовалось определить радиус эпицикла,
точнее, его отношение к радиусу деферента. Эту задачу
Птолемей решает «методом трех затмений»,
предложенным еще Гиппархом. Метод этот состоит в следующем
[17. С. 190-204].
Выберем тройку лунных затмений так, чтобы
интервалы между соседними затмениями составляли от полугода
до полутора лет5. Эти интервалы^ очевидно, содержат
целое число синодических месяцев (напомним, что лунные
затмения происходят только в полнолуние), а за один
синодический мвбяц Луна проходит на небе больше одного
оборота как относительно звезд, так и относительно
апогея своей орбиты. Поэтому в моменты затмений на
эпицикле (полный оборот по которому в схеме Птолемея
* Минимальный интервал менаду двумя последовательными
лунными затмениями составляет 176 сут, максимальный — 680 сут.
83

Луна совершает за один аномалистический месяц) Луна
будет находиться в различных его точках.
Зная точные моменты затмений и интервалы между
ними, можно вычислить дуги эпицикла между этими
точками. Но как найти положение первой точки? Птолемей
поступает следующим образом. Он вычисляет разности
долгот Солнца в моменты затмений (по составленным
ранее таблицам Солнца). Очевидно, разности долгот Луны,
находящейся точно против Солнца, должны иметь точно
такие же значения. Но по таблицам среднего движения
Луны получаются несколько иные значения. Разности
между средними и истинными изменениями долготы
Луны должны быть отнесены за счет первого неравенства.
Искусно применяя далее некоторые геометрические
теоремы, доказанные в свое время Евклидом, Птолемей
определяет положение апогея Луны относительно трех точек
на эпицикле, выражающих положения Луны во время
затмений, и искомое отношение радиусов эпицикла и
деферента.
Для решения этой задачи Птолемей выбрал две
тройки лунных затмений: одну, наблюдавшуюся вавилонскими
астрономами в VIII в. до н. э., и другую —по своим
собственным наблюдениям. Приводим здесь данные об этих
затмениях (табл. 1).
Определения размеров эпицикла по обеим тройкам
затмений дали весьма близкие результаты: в единицах,
где радиус деферента равен 60р, радиус эпицикла
получился 5;13р и 5;14р соответственно. Отсюда наибольшее
значение первого неравенства, вычисляемое по формуле
sin а = r/R (г, R — радиусы эпицикла и референта
соответственно), составляет 5° 01х (правильное значение 4° 57').
Основываясь на полученном им значении
максимального первого неравенства, с помощью своей геометрии и
тригонометрии (по таблице хорд) Птолемей вычисляет
далее таблицу первого неравенства для всех значений
угла аномалии6.
Не случайно Птолемей взял свои две тройки затмений
с таким большим интервалом во времени. Он берет
средние затмения в каждой тройке и получает разность
долгот и аномалий Луны в моменты середины каждого из
6 Чтение труда Птолемея несколько затрудняется тем, что он
называет одним и тем же словом аномалия и угол положения
Луны относительно апогея, и неравенство (отклонение) лунной
долготы от ее средней долготы. Правда, вторую величину он
называет уравнением аномалии.
84

Таблица 1. Две триады лунных затмений, использованных
Птолемеем
Дата
—720 III 19/20
—719 III 8/9
—719 IX 1/2
133 V 6/7
134 X 20/21
136 III 5/6
Интервал,
сут, ч, мин
354, 02, 34
176, 20, 12
531,23,38
502, 05, 30
Разность долгот
истинных
349° 15'
169° 30'
161° 35'
138° 55'
средних
345° 51'
170° 07'
169° 37'
137° 34'
Первое

неравенство
+3° 24'
—0° 37'
-7° 42'
+ 1°21'
Разность
аномалий
306° 25'
150° 26'
110° 21'
81° 31'
затмений: по положению Луны в этот момент
(определяемому из условия, что Луна в это время находится точно
напротив Солнца) и по протекшему интервалу времени
и среднему движению Луны. По долготам получается
точное совпадение (с точностью до 1"), а по аномалии —
с расхождением на 17 мин (за 854 года с лишним).
Отсюда Птолемей находит поправку к ранее принятому
среднему суточному движению Луны по аномалии,
достигающему 12 единиц четвертого шестидесятиричного разряда
(1/300 угловых секунд в сутки) [17. С. 204].
Далее Птолемей обращается к движению Луны по
широте. Чтобы уточнить длину драконического месяца
(полного оборота Луны относительно узла ее орбиты), он
решает выбрать два лунных затмения, разделенные как
можно большим временным интервалом и
удовлетворяющие следующим четырем условиям [17. С. 206]:
1) величина затмения (его наибольшая фаза) должна
быть одинакова;
2) оба затмения должны происходить вблизи того же
узла (например, восходящего) ;
3) тень Земли должна закрывать ту же сторону Луны
(например, северную) ;
4) Луна должна быть примерно на том же расстоянии
от Земли.
При соблюдении этих условий Луна должна при обоих
затмепиях находиться в одинаковых положениях
относительно узла.
85

Птолемей выбирает для своего расчета следующие два
лунных затмения, удовлетворяющие всем четырем
условиям:
—490 апрель 25/26 6 ч (наблюдалось в Вавилоне),
125 апрель 5/6 20,4 ч (наблюдалось в Александрии).
Интервал времени между ними составляет 615 лет
133 сут 21 ч 50 мин. Здесь, как и в других расчетах, куда
входят большие промежутки времени, Птолемей
использует египетский год, равный точно 365 сут. Это должны
помнить те читатели, которые любят вычислять и уже
были готовы упрекнуть автора книги в неточности, а то
и в ошибке, поскольку простое вычитание дат дает
интервал 614 лет 345 сут 14 ч. Но эти даты и только что
полученный интервал выражены в юлианских годах
(365,25 сут). За 615 лет разница между юлианскими и
египетскими годами составит как раз 153 сут 18 ч.
Очевидно, что за этот период прошло целое число дра-
конических месяцев, по таблицам же средних движений
Пуна должна была пройти дугу, на 9°53f меньшую.
Из циклов Гиппарха следовала разность в 10° 02', так что
разность истинного и среднего движений по широте у
Птолемея отличалась от значения, вытекавшего из циклов
Гиппарха, всего лишь на 9'. Поправка к среднему
суточному движению по широте измерялась, таким образом,
восемью единицами четвертого шестидесятиричного
разряда (в долях градуса) или 1/450 угловой секунды [17.
С. 207].
Переводя исправленные Птолемеем значения средних
движений Луны по аномалии и широте в длины
аномалистического и драконического месяцев, получим для них
значения 27,554572 и 27,212221 сут соответственно.
Сравнивая их со значениями, приведенными на с. 35, мы
видим, что для драконического месяца поправка Птолемея
несколько улучшила результат (и без того прекрасно
согласующийся с современными данными), а для
аномалистического, напротив, несколько ухудшила его. Этому
не приходится удивляться, поскольку положение апогея
методом Птолемея определяется менее точно, чем
положение узлов орбиты Луны.
Эта часть приближенной теории видимого движения
Луны завершается вычислением долготы, аномалии и
аргумента широты Луны (ее положения относительно узла
орбиты) в начальную эпоху, за которую, как мы помним,
Птолемей принимает начало 1-го дня месяца тот (по
египетскому календарю) 1-го года эры Набонассара. Долго-
86

Рис. 19. Положения Луны относительно узлов ее орбиты
Рис. 20. Введение точки экванта для Луны
ту и аномалию Луны в начальную эпоху он вычисляет
без труда, отсчитав нужное число градусов и их долей
на 27 лет назад от момента лунного затмения—719 г.,
для которого эти величины ему были известны. Чтобы
найти аргумент широты, Птолемей прибегает к
следующему остроумному приему.
Он выбирает два лунных затмения, разделенных
большим промежутком времени и удовлетворяющих первому,
третьему и четвертому из условий, сформулированных
выше, но происходивших вблизи противоположных
узлов. Луна во время этих затмений была к северу от
узлов А и G (рис. 19), в точках D и Е проекции своей
орбиты на небесную сферу. Расстояния AD и GE в силу
первого и третьего условий равны. Рассчитываем поправки
на первое неравенство и находим точки Z и H положения
«средней Луны». По разности эпох определяем дугу ZBH
смещения «средней Луны» за интервал между
затмениями. Поскольку дуги ZBH, DZ и ЕЕ нам известны, а дуга
ABG равна 180°, не представляет труда найти удаление
Луны от узлов AD=GE в моменты затмений (это и есть
аргумент широты), а затем с помощью таблиц средних
движений найти значение этого узла в начальную эпоху.
Этим, собственно, и завершается приближенная теория
движения Луны.
В заключительной главе четвертой книги Птолемей
обсуждает некоторые расчеты Гиппарха, относящиеся к
движению Луны, и вносит в них уточнения.
Разработанная в четвертой книге «Альмагеста» тео-
87

рия, как указывает ее автор в начале пятой книги своего
труда, хорошо представляет положения Луны в сизигиях
(в полнолуниях и новолуниях), но при других
положениях Луны она требует уточнения. Это понимал еще Гип-
парх, и потому он начал наблюдать положения Луны вне
сизигий с помощью угломерного инструмента типа
описанной Птолемеем астролябии. Птолемей приводит и
использует три его наблюдения, выполненные 5 августа — 127 г.,
2 мая и 7 июля — 126 г. Интересно, что эти три
наблюдения — самые поздние наблюдения Гиппарха, дошедшие до
нас. Не означает ли это, что смерть помешала вскоре
замечательному родосскому астроному ' продолжить эти
наблюдения и определить предполагавшееся им второе
неравенство движения Луны?
Эту задачу, поставленную Гиппархом, решил Клавдий
Птолемей. Из наблюдений Гиппарха и своих собственных
Птолемей установил [17. С. 225], что в квадратурах (в
первой и последней четверти, когда Луна находится в 90°
от Солнца) амплитуда первого неравенства возрастает
примерно до 7° 40'. Геометрически он представил это
следующим образом (рис. 20). Центр эпицикла движется не
по эклиптике, а по эксцентру, так что Земля находится на
некотором расстоянии от его центра О. Поскольку обе
сизигии и обе квадратуры равноправны, Птолемей
совмещает их попарно, так что сизигии приходятся на апогей экс-
центра, а квадратуры — на перигей. Эта операция
равнозначна удвоению дуг на эксцентре, что компенсируется
удвоением скорости движения центра эпицикла по
эксцентру. Таким образом, угол ATOi между осью апсид эксцент-
ра АР и направлением на центр эпицикла TOi равен 2D,
где D — элонгация Луны от Солнца. В сизигиях D=0 или
0=180°, а значит, 2D=0 и точка Oi совпадает с апогеем
эксцентра А. В квадратурах D=±90°, 20=180° и Ot
совпадает с перигеем эксцентра Р.
Из соотношений амплитуд первого неравенства в
апогее и перигее эксцентра Птолемей получает значение
эксцентриситета ОТ. Поскольку радиус эпицикла
остается неизменным и известен из расчетов первого
неравенства (в долях расстояния ТА, принятого за 60р), нетрудно
по величине этого радиуса, равной 5;15р и по углу 7°40\
под которым виден эпицикл из Т, когда его центр
совпадает с Р, найти расстояние TP, диаметр эксцентра РА,
его радиус О А и эксцентриситет е=ОТ/ОА. Птолемей по-
88

лучает 0Г=1О;19Р, е=0,20765, относительный радиус
эпицикла (в долях радиуса эксцентра) г=0,10567.
Теперь и для сизигий, и для квадратур все обстоит
хорошо! Но наблюдения Луны в промежуточные моменты
требуют ввести в лунную теорию еще одно усложнение.
Именно, за начало отсчета обращения Луны по эпициклу
принимается так называемый средний апогей эпицикла,
лежащий на прямой, пересекающей ось апсид эксцентра
не в Т и не в его центре О, а в некоторой точке N,
отстоящей от Т на расстояние NT=TO (см. рис. 20). Птолемей
доказывает, основываясь на нескольких типичных
наблюдениях, что действительно NT=TO [17. С. 228-233].
Наряду со средним апогеем (и соответственно средним
перигеем) Птолемей рассматривает также истинные апогей и
перигей эпицикла, лежащие на прямой ТО\ и ее
продолжениях. Это точки аир. Угол z=aOiac называется у
Птолемея «уравнением апогея». Н. И. Идельсон в своем
превосходном обзоре развития лунпой теории [54] называет
этот угол «неравенством аномалии», что в общем-то
является тавтологией, ибо аномалия и неравенство —
синонимы. Мы будем применять терминологию Птолемея.
Уравнение апогея, как показывает Птолемей,
изменяется в пределах от 0° (в сизигиях и квадратурах) до
максимального значения 13° 09' при 2Z>=114° [17. С. 238].
Теперь все готово для построения полной теории
движения Луны. Птолемей вычисляет таблицу всех лунных
неравенств и объясняет, как с ее помощью найти для
любого момента долготу, широту, аномалию (угол,
отсчитываемый от апогея эксцентра) и элонгацию Луны от
Солнца.
Рассмотрим теперь эту теорию с современной точки
зрения. Вся сложная на первый взгляд кинематика
движения Луны по Птолемею может быть описана тремя
формулами элементарной математики, которые приводит
Н. И. Идельсон [54]:
р=е cos 2Z)+yi-e2sin22D,
tfr~— (Ф) sin 2D irr F— (r/P)gin(l + *)
lgZ— l + (*/p)cos2D ' bfe-a — 1 _ (r/p) cos (Z + z) •
Здесь p — переменный радиус-вектор центра эпицикла
OiT; I — средняя аномалия Луны (угол pcOiL) ; Е — общее
неравенство долготы, которое нужно прибавить к
средней долготе, растущей пропорционально времени. По
смыслу величина Е соответствует уравнению центра х для
Солнца (см. с. 32, 75), но по традиции обозначается бук-
89

вой Е. Точно так же угол 2D в данной теории равен 2М,
но только благодаря условию, что сизигии Луны
совпадают с апогеем эксцентра (с. 88).
Формулы для z и Е встречаются в теории
астрономического параллакса. Они допускают удобные разложения
в ряды [56] :
E=r sin l+r е sin (2Z)-Z)+72r2 sin 21+ ...,
где г,=г(1+3Дв2).
Подставляя в эти формулы г=0Д0567 и е=0,20765 по
Птолемею и переводя углы из радианов в градусы,
получаем
£=6° 15' sin Z+l° 18' sin (2D-Z) +19' sin 21.
Еще раз оговоримся, что синусов Птолемей не знал
(он пользовался хордами), и формул, приведенных выше,
в его сочинении мы не встретим. Но из его геометрии
следуют эти формулы. Коэффициенты, приводимые самим
Птолемеем, несколько отличаются от тех, что получились
по формулам при значениях гие, им выведенных. Именно,
с коэффициентами Птолемея получилось бы такое
выражение:
£=6° 20' sin Z+l° 19' sin (2D-1) +19' sin 21.
«К этой короткой формуле и сводится вся древняя
теория Луны в отношении ее долготы, — пишет Н. И. Идель-
сон, — но эта теория оказывается великолепной, так
как современное разложение для Е — сохраняя в нем,
разумеется, только члены с теми же аргументами — гласит:
2?=6°17,3' sinZ+l°16,4' sin(2D-Z)+13' sin2Z.
Согласие настолько замечательное, что его можно в
известной мере считать делом случая» [54].
Да, с Н. И. Идельсоном вполне можно согласиться.
Ведь кинематика, построенная Птолемеем для
объяснения второго лунного неравенства, ниоткуда не вытекала,
она построена, скорее всего, в результате ряда проб, о
которых Птолемей, правда, ничего не сообщает, но без
которых вряд ли он смог обойтись. В частности, равенство
расстояний NT=TO доказывается Птолемеем не в общем
виде, как многие его теоремы, а с помощью численных
примеров, основанных на наблюдениях. Вскоре мы убедимся,
что можно было использовать совсем иную кинематику.
А теперь рассмотрим физический смысл трех членов
выражения для неравенства долготы Е. Первый член назы-
90

ваётоя елаеным эллиптическим неравенством. Период его
аргумента I равен среднему аномалистическому месяцу
(27,55 сут). Этот член, как и третий, связан с
эллиптичностью лунной орбиты.
Второй член с аргументом 2D—I был впервые найден и
введен в лунную теорию Птолемеем. Птолемей назвал его
«покачиванием» лунного апогея. В 1634 г. французский
астроном И. Бульо, более известный под
латинизированным именем Буллиальд (1605—1694), предложил для
этого неравенства название эвекция, которое и стало с тех
пор общепринятым [95]. Период эвекции равен 31,81 сут.
Профессор Петербургского университета Н. П.
Долгоруков в своей монографии «Теория движения Луны» (1902)
[49] предложил называть этот период «птолемеевым
месяцем», о чем сообщает в своем обзоре Н. И. Идельсоы.
Но это предложешге не получило поддержки и, скорее
всего, прошло незамеченным.
Открытие Птолемеем эвекции получило весьма
высокую оценку астрономов нового времени. Французский
астроном и историк науки Ж. Деламбр (1749—1822) в своей
шеститомной истории астрономии [96] отмечает, что
одного этого открытия было бы достаточно, чтобы поставить
Птолемея в первые ряды астрономов. А ведь Деламбр
относился к работе Птолемея весьма критически, и с его
критикой мы еще познакомимся. Такой классик небесной
механики, как П. Лаплас, отметил громадный
вычислительный труд Птолемея при составлении таблицы лунных
неравенств [111], хотя итог этого труда —сама таблица —
занимает всего одну страницу.
Лишь полтора тысячелетия спустя Тихо Браге открыл
следующие два неравенства в движении Луны — вариацию
и годичное уравнение. И прошло еще сто лет, пока Исаак
Ньютон не объяснил физическую природу этих неравенств.
Оказалось, что причиной эвекции является изменение
положения Луны относительно Солнца: в новолуние Луна
ближе к Солнцу, чем Земля, и притяжение Солнца
стремится как бы отдалить Луну от Земли. Благодаря эвекции
орбита Луны стремится вытянуться по направлению к
Солнцу. Эвекция периодически изменяет эксцентриситет
лунного эллипса и влияет на положение перигея.
Вариация заключается в периодическом изменении
скорости движения Луны по орбите под действием Солнца.
Ее наибольшее значение составляет 39,5' и достигается в
октантах (точках, лежащих между квадратурами и
сизигиями). Годичное уравнение (доходящее до 11,2') объяс-
91

няется тем, что возмущающее действие Солнца Достигает
максимума в перигелии и минимума в афелии земной
орбиты.
Эти возмущения в движении Луны — лишь главнейшие.
Современная теория движения Луны представляет
долготу, широту и расстояние Луны рядами, состоящими из
нескольких тысяч членов. Составление этих рядов и
вычисление их членов и сумм производится теперь с помощью
ЭВМ.
Таких вычислительных средств и в помине не было у
Клавдия Птолемея. Он имел линейку, циркуль, угольник,
транспортир, да еще простейшие астрономические
угломерные инструменты, которые мы описывали. Он
располагал данными вавилонских и греческих наблюдателей,
работами Гиппарха, в совершенстве знал геометрию Евклида,
имел ясный ум и способности к математическому анализу.
И все это дало свои плоды.
Однако теория движения Луны, развитая Птолемеем,
давала лишь возможность определять ее положение на
небе — долготу и широту. Изменение расстояния Луны от
Земли эта теория представить не могла. Более того, она
приводила к серьезным противоречиям с наблюдениями.
В самом деле, согласно этой теории наибольшее расстояние
Луны от Земли в единицах радиуса эксцентра О А
составляло 1,31 (1+0,208+0,106), а наименьшее 0,69 (1-0,208-
—0,106). Их отношение равнялось 1,9, тогда как
действительное отношение наибольшего расстояния до Луны к
наименьшему составляет 1,14. Даже из наблюдений
невооруженным глазом ясно, что видимый угловой диаметр Луны
меняется в очень малых пределах (не более чем на 14%),
а никак не вдвое, как следовало из теории Птолемея.
Не надо думать, что Птолемей прошел мимо этого
обстоятельства. Нет, заключительные главы книги
посвящены именно определению лунных параллаксов и расстояний. |
Из своей схемы Птолемей находит, что среднее расстояние
до Луны в сизигиях равно 59 земным радиусам (с
возможными колебаниями от 54 до 64 радиусов Земли),
а в квадратурах — 38,7 радиуса (с разбросом от 33,6 до
43,8 радиуса Земли [17. С. 259]). Истинные пределы
расстояния до Луны в наше время составляют 55,9 и 63,8
земного радиуса. Иначе говоря, пределы расстояния для
сизигий у Птолемея почти равны действительным, а среднее
расстояние отличается от действительного (60 радиусов)
лишь на 2 %.
Почему же Птолемей не заметил столь разительного
92

Рис. 21. Схема двойного эпицикла (по Копернику)
противоречия между полученными им расстояниями и
видимыми размерами Луны в квадратурах? Ведь приводит
же он видимый диаметр Луны во время одного из лунных
затмений, наблюдавшихся в Вавилоне в —522 г., 31'20",
что вполне соответствует современным данным (видимый
диаметр Луны изменяется в пределах от 29' 23" до 33' 31").
Но видимых размеров Луны в квадратурах Птолемей не
приводит.
Это обстоятельство не раз служило темой для
дискуссий среди астрономов и историков науки. Пожалуй, одним
из первых обратил па него внимание Коперник. Великий
польский ученый нашел другое решение задачи о
движении Луны, по-прежнему основанное на концепции
равномерных круговых движений. Он убрал эксцентр, поместил
Землю в центре деферента, но добавил второй эпицикл,
центр которого движется по первому эпициклу7. В схеме
Коперника (рис. 21) центр первого эпицикла А движется
по деференту ВВ вокруг точки Т в прямом направлении с
равномерной скоростью, равной среднему движению Луны
по долготе. По этому эпициклу движется центр второго
эпицикла О в обратном направлении с угловой
скоростью, равной среднему движению Луны по аномалии I.
Началом счета угла аномалии при центре эпицикла А
является его перигей ри По второму эпициклу в прямом
направлении движется точка L, изображающая Луну. Ее
Коперник назвал второй эпицикл эпи-эпициклом.
93

угловая скорость равна удвоенной скорости движения
Луны по элонгации ее от Солнца, так что угол О A L всегда
равен 2D. В сизигиях точка L проходит через точку /?2,
лежащую на прямой ОА, а в квадратурах — через
противоположную ей точку а2. Таким образом, в течение
синодического месяца Луна дважды обходит второй эпицикл.
Коперник определил из наблюдений лунных затмений
радиусы обоих эпициклов в долях радиуса деферента и
нашел Г1=0,1097, г2=0,0237. Разложение в ряд выражения
для неравенства Луны по долготе в этой схеме дает:
Е=6°1Т sin 1+Г2Г sin (2D-1) +21' sin 2Z,
т. е. согласие с современными значениями коэффициентов
оказывается не хуже, чем у Птолемея. Зато наибольшее
и наименьшее расстояния до Луны в этой схеме составляют
(в тех же единицах) 1,13 и 0,87 соответственно, а их
отношение — 1,30, что уже гораздо ближе к реальному
значению 1,14.
Мы видим отсюда, что, действительно, схема Птолемея,
изображавшая движение Луны, была искусственной и во
многом уступала схеме Коперника. К этому надо добавить,
что в схеме Коперника нет двух перигеев и апогеев
(среднего и истинного), нет неравномерных движений (у
Птолемея центр эпицикла движется по эксцентру
неравномерно), нет «качания» перигея эпицикла. Такую схему вполне
мог бы придумать и сам Птолемей. Мог, но не придумал.
В шестой книге «Альмагеста» развивается теория
солнечных и лунных затмений. Прежде всего Птолемей
вычисляет таблицы новолуний и полнолуний на 1100 лет,
начиная от 1-го года эры Набоыассара, т. е. от —746 до
355 г. В этих таблицах он дает даты месяца тот (первый
месяц года по египетскому календарю), когда наступает
новолуние или полнолуние, с точностью до 24 с, угловое
расстояние Солнца от его апогея8, аномалию Луны и
аргумент ее широты. Птолемей использует то обстоятельство,
что 25 египетских лет (по 365 сут), т. е. 9125 сут, почти
равны 309 синодическим месяцам — разница составляет
лишь 0,05 сут, или 1 ч 07 мин. Поэтому в первой части
таблицы все данные приведены через 25-летние
интервалы, во второй —для каждого года такого интервала и в
третьей —для каждого месяца года. Вся таблица
умещается в трех страницах.
При этом Птолемей не учитывает смещение солнечного апогея,
о чем мы говорили в гл. 7.
94

Но, как известно, затмения Солнца и Луны происходят
не в каждое новолуние или полнолуние. Нужно, чтобы
Луна в сизигии была бы недалеко от одного из узлов
своей орбиты. Согласно А. А. Михайлову [73], для
наступления частного солнечного затмения на Земле вообще
разность долгот Луны и узла не должна превышать 18°, а если
этот угол меньше 16°, то затмение неизбежно наступит в
каком-то месте Земли (при промежуточных значениях
наступление затмения зависит от положения Солнца и
Луны относительно перигеев их орбит). Точно так же для
наступления частного лунного затмения удаление Луны
от узла не должно превышать 12°, а при разности долгот
меньше 10° затмение неизбежно.
Приведенные выше условия для солнечного затмения
выведены для всей Земли. Конкретный наблюдатель в
зависимости от места и времени суток может оказаться
севернее или южнее центра Земли, и для него Луна окажется
смещенной в результате параллакса соответственно к югу
или к северу. Птолемей пытается учесть это смещение.
Он выбирает крайние широты пунктов наблюдений — от
+16° 30' (в городе Мероэ при впадении реки Атбары в Нил,
современный Судан) до +48°30' (среднее течение Днепра,
тогда Борисфена). Крайние значения параллакса Луны
для этих пунктов составляют от 8' к северу до 58' к югу.
Поэтому условия наблюдений солнечных затмений будут
разными в зависимости от того, находится ли Луна
севернее или южнее узла. Если Луна севернее узла, то
параллакс, смещая ее к югу, улучшает условия наступления
солнечного затмения, расширяя область благоприятных
долгот Луны до расстояния 17° 41' от узла9. Если же Луна
южнее узла, ее смещение еще дальше к югу ухудшает
условия наступления солнечного затмения, сужая
допустимый интервал по долготе до 8° 22'. Мы видим, что
первое из приведенных двух значений близко к пределу,
указанному А. А. Михайловым, что неудивительно, так как
этот предел рассчитан для параллакса Луны (точнее, для
разности параллаксов Луны и Солнца) 61,3', что мало
отличается от 58' у Птолемея.
9 Птолемей в этом расчете всюду принимает наклон лунной
орбиты к" эклиптике г=5°, откуда вытекает используемое им
отношение дуг: (расстояние Луны от узла): (широта Луны) =11,5:1
(равное cosec i). Но из-за движения Солнца по эклиптике в
формулы войдет не *, a ï>i (5°17'<t'<5°52') [73]. Поэтому
используемое Птолемеем отношение может меняться от 9,8:1 до
10,9:1.
95

Птолемей в общем правильно представляет себе и
объясняет читателю геометрическую картину явлений,
приводящих к солнечному или лунному затмению. Для
условия наступления лунного затмения он находит предельное
расстояние Луны от узла 12° 12', т. е. близкое к
приведенному А. А. Михайловым.
Указанные выше расстояния от узла по долготе
относятся к истинной Луне. Учитывая неравенства в движении
Луны и Солнца по долготе, Птолемей находит, что
наибольшее отличие разности средних долгот обоих светил в
среднюю сизигию и разности их истинных долгот в истинную
сизигию может достигать 3°. Эту поправку он прибавляет
к найденным им предельным расстояниям Луны от узла,
расширяя их до 20° 41', 11° 22' и 15° 12' соответственно
(очевидно, такая операция нужна для тех, кто будет
пользоваться таблицами средних сизигий).
После обсуждения вопроса об интервалах времени
между затмениями Птолемей приступает к составлению своих
таблиц затмений. Он строит их по аргументу величины
затмения. Напомним, что величиной затмения называется
отношение закрываемой (Луной или тенью Земли) доли
диаметра закрываемого светила (соответственно Солнца
или Луны) к самому диаметру. Если величина затмения
превосходит единицу, затмение будет полным.
Птолемей измеряет величину затмения в двенадцатых
долях диаметра затмеваемого светила. Иначе говоря,
полному затмению (величина 1,00) соответствуют 12 единиц.
Но так как диск Луны может быть больше диска Солнца,
для наименьшего расстояния Луны от Земли величина
затмения у Птолемея может достигать 124/5 единиц, т. е.
1,067.
Это несколько больше современного значения 1,032,
что объясняется завышением Птолемеем наибольшего
видимого диаметра Луны (см. ниже). При наибольшем
расстоянии Луны, согласно Птолемею, величина затмения
может достигать точно 12 единиц (1,00 в современных
обозначениях). О кольцеобразных затмениях Птолемей даже
не упоминает. Очевидно, ему просто не была известна эта
форма затмений Солнца, хотя кольцеобразные затмения
столь же часты, как и полные (согласно А. А. Михайлову
[73], в течение сароса происходит 12 полных затмений,
14 кольцеобразных и два кольцеобразно-полных, когда в
разных частях полосы главной фазы наблюдается то
кольцеобразное, то полное затмение).
Другое, более важное обстоятельство, на которое мы
96

должны обратить внимание, состоит в том, что значения
наибольшего и наименьшего видимого диаметра получены
Птолемеем из наблюдений лунных затмений 16—17 июля
—540 г. в Вавилоне, когда Луна была близ апогея своей
орбиты, и 27—28 января —140 г. (Гиппарх, о-в Родос),
когда Луна была около перигея. Ее видимые диаметры
для этих эпох были определены Птолемеем в 31'20" и
35' 20" соответственно. На самом деле наименьший и
наибольший видимые диаметры Луны равны 29' 22" и 33' 30".
Видимый диаметр Солнца Птолемей принимает
постоянным и равным 31х 20", тогда как он может изменяться
в пределах от 31' 28" до 32' 32" [73].
Таким образом, Птолемей совершенно не использует
для этих определений свою же собственную теорию
движения Солнца и Луны, а опирается на давние, к тому же
весьма неточные наблюдения (в них отмечалось, например,
что в наибольшей фазе затмения была закрыта *Д
Диаметра Луны; эта оценка сделана, по-видимому, просто на
глаз).
Между тем из теории Птолемея следовало, что в
сизигиях отношение наибольшего расстояния до Луны к
наименьшему составляет
60 + 5,25 , ,„
60- 5,25 — МУ^'
тогда как использованные им наибольший и наименьший
видимые диаметры Луны относятся как 1,128 (в
действительности это отношение равно 1,141). Для Солнца теория
Птолемея дает аналогичное отношение 1,083, в
действительности тогда оно было равно 1,04 (см. с. 76).
Мы снова видим наличие противоречий между теорией
Птолемея и используемыми им (а значит, внушавшими
ему доверие) наблюдениями. На этот раз Птолемей отдает
предпочтение последним. Но он никак не обсуждает это
противоречие и даже не упоминает о нем.
Как же рекомендует вычислять условия видимости
солнечного затмения в данном пункте Клавдий Птолемей?
Прежде всего нужно вычислить время соединения Солнца
и Луны по долготе: это время приближенно равно
моменту середины затмения. На это время следует рассчитать
параллакс Луны по долготе и с учетом параллакса — ее
видимую долготу. Если разность долгот Луны и узла
окажется меньше 6° (когда Луна в апогее) или 6° 24" (когда
Луна в перигее), то затмение непременно произойдет. Его
величина (наибольшая фаза) определяется по таблице.
4 Клавдий Птолемей
97

Рис. 22.
График поверхностных фаз
солнечных и лунных
затмений
J — по Птолемею; 2 — по
современной теории (Дагаев)
4* /
Ф
Там же приведена величина дуги, которую проходит Луна
относительно Солнца от внешнего касания дисков
(первый контакт) до наибольшей фазы. Аналогичный метод
предлагается для лунного затмения, только здесь
параллакс уже не играет роли (вхождение Луны в тень Земли
не зависит от положения наблюдателя).
В приложении к своим таблицам Птолемей приводит
так называемые поверхностные фазы для солнечных и
лунных затмений, т. е. доли площади диска Солнца или
Луны, закрытой соответственно Луной или тенью Земли.
Интересно сравнить эти данные Птолемея с современными
таблицами, рассчитанными M. М. Дагаевым в
«Постоянной части Астрономического календаря» [24]. На рис. 22
мы приводим отношения поверхностной и линейной фаз
затмения в функции линейной фазы по данным Птолемея
и по современным данным. Нетрудно убедиться, что точки
Птолемея, кроме одной-двух при малых фазах прекрасно
ложатся на современную кривую.
Последний вопрос, который рассматривается в VI
книге «Альмагеста», это вопрос об углах положений точек
контактов (внешних и внутренних касаний) дисков
Солнца и Луны, Луны и земной тени во время затмений.
Птолемей дает решение и этой задачи.
Теория солнечных и лунных затмений — одно из
важнейших применений созданной Птолемеем теории
движения Луны. Мы уже убедились, что птолемеева теория
движения Луны была великолепной для уровня античной и
средневековой науки, когда наблюдения производились
98

невооруженным глазом, без оптических приборов. Но эта
теория давала лишь видим ы е положения Луны на
небесной сфере. Попытка Птолемея представить своей
теорией расстояния до Луны оказалась неудачной. Видимо,
Птолемей сам понимал это и в теории затмений
использовал не теоретические видимые диаметры Луны, а взятые
по данным наблюдений.
Кинематическая теория движения Луны, построенная
Птолемеем, явилась лишь моделью, схемой для вывода
формулы долготы Луны. Эту задачу Птолемей решил
успешно. Но он оказался бессилен перед решением задачи
о пространственном движении Луны. Эта задача
оказалась по силам только Ньютону.
Глава 9
Звездный каталог
Основу содержания седьмой и восьмой книг
«Альмагеста» составляет самый древний дошедший до нас
звездный каталог, в котором приведены координаты (долготы
и широты) более тысячи звезд.
В различных источниках можно встретить различные
числа, указывающие количество звезд в этом каталоге:
от 1022 до 1030. Если пересчитать все звезды,
содержащиеся в каталоге, то их окажется 1027, но в пяти случаях
имеют место повторения (одна и та же звезда отнесена к
двум созвездиям и записана дважды). Кроме того, из 1022
объектов следует исключить еще пять, обозначенных у
Птолемея как «туманные» и действительно
представляющие собой туманности (например, туманность Ориона),
звездные скопления (% и h Персея) или далекие
галактики. Таким образом, собственно звезд в каталоге 1017.
Эти звезды разделены на 48 созвездий, причем после
перечисления, так сказать, основных звезд созвездия
Птолемей приводит координаты ближайших звезд, не
входящих в созвездие. Напомним, что во времена Птолемея под
созвездиями понимали определенные конфигурации звезд,
которые связывались в воображении древних народов
(и на изображениях звездного неба) с фигурами людей,
животных, очертаниями предметов, по которым и
называли созвездие (рис. 23, а).
99
4*

a
Рис. 23. Изображение созвездия Персея и окружающих его звезд
в атласе Я. Гевелия (1690 г.) (а) и на современных звездных
картах (б)
В наше время применен другой принцип. Под
созвездием мы понимаем некоторый участок неба со строго
определенными границами (рис. 23, б). Все звезды,
попадающие внутрь этих границ, считаются принадлежащими к
данному созвездию, поэтому звезд «вне созвездий», как у
Птолемея, в наше время быть не может. На всем небе
теперь насчитывают 88 созвездий, из них звезды 50
созвездий присутствуют в каталоге Птолемея *.
Из 1017 звезд каталога 15 — звезды первой величины,
45 — второй, 208 — третьей, 474 — четвертой, 217 — пятой,
49 — шестой и еще 9, обозначенных как «слабые» (это не
значит, что они слабее шестой величины; составитель
каталога мог просто затрудняться в уточнении их блеска).
Мы видим из этих данных, что лишь немногие из звезд
пятой-шестой величин попали в каталог (звезд пятой ве-
1 Сам Птолемей указывает лишь 48 созвездий. Но большое
созвездие Корабль Арго было потом разделено на четыре: Корму,
Киль, Паруса и Компас. Звезды первых трех из них имеются в
каталоге.
100

личины —около 30% доступных наблюдению на широте
Родоса, звезд шестой величины и «слабых» — не более
2%). Очевидно, составитель каталога выбирал для
измерений координат не все слабые звезды, а лишь входившие
в определенные конфигурации. Скажем прямо: наблюдать,
а тем более измерять координаты этих звезд
невооруженным глазом было нелегко. Диоптры или иные визирные
устройства тех времен не облегчали, а затрудняли процесс
наблюдения, поскольку для измерения приходилось
постоянно менять аккомодацию хрусталика глаза (известно,
что при наблюдении ближних и дальних предметов
специальная мышца изменяет радиус кривизны нашей
естественной линзы —хрусталика; у близоруких и
дальнозорких людей возможности этой мышцы ограничены, что и
приводит к названным дефектам зрения).
Мы. намеренно использовали выше термин
«составитель каталога» вместо того, чтобы называть Птолемея.
Дело в том, что, как показывают многочисленные
исследования, Птолемей не является единственным автором этого
каталога, его бесспорная заслуга состоит лишь в его
публикации. Автор каталога, по крайней мере большей его
101

части,— Гиппарх, о чем мы уже говорили в гл. 3. Сейчас
мы рассмотрим вопрос об авторстве каталога подробнее.
В седьмой книге «Альмагеста» Птолемей неоднократно
говорит о том, что он сам проводил наблюдения
положений звезд и сравнивал свои измерения с теми, что
проводил Гиппарх, а также с более ранними (Тимохариса и
Аристилла). Он приводит примеры линейных
конфигураций звезд (т. е. расположений звезд по три в линию)
сперва по данным Гиппарха, а затем по своим
собственным наблюдениям. В главах о прецессии он пишет,
что промежуток времени между наблюдениями Гиппарха
и первым годом Антонина Пия, «в который мы также
наблюдали большую часть неподвижных звезд», равен 265 г.
[17. С. 328]. И далее: «...когда мы определяли широту
каждой звезды, мы нашли те же значения, что и во
времена Гиппарха, по крайней мере с небольшими
отклонениями, которые могли произойти от ошибок наблюдения;
но когда мы определяли расстояния от экватора по кругу
склонения, то мы нашли величины, значительно
отличающиеся от гиппарховых, тогда как эти последние
значительно отличаются от полученных астрономами школы
Тимохариса» [122. С. 329-330].
Описывая свой прибор — астролябию, о которой мы
уже говорили, и метод определения с его помощью широт
и долгот, Птолемей указывает: «Пользуясь опять тем же
инструментом, круги которого вращаются около полюса
эклиптики, мы пронаблюдали столько звезд до шестой
величины, сколько было возможно» [17. С. 339].
Итак, Птолемей, по его неоднократным заявлениям,
сам проводил наблюдения положений звезд с помощью
описанного им прибора и сравнивал свои измерения
долгот и широт звезд с более ранними измерениями
Гиппарха и школы Тимохариса. Из этого сравнения он сделал
правильный вывод о том, что на протяжении веков
широты звезд не меняются, а долготы возрастают в
результате прецессии пропорционально времени. Но насколько?
Мы знаем, что Птолемей допустил ошибку в определении
постоянной прецессии, получив для нее значение 36 " в
год вместо правильного значения 50" в год. Как это могло
произойти?
В качестве одного из предположений можно допустить,
что Птолемей не понял высказывания Гиппарха, который,
сравнивая свои наблюдения с проведенными Тимохари-
сом и Аристиллом, писал, что постоянная прецессии
составляет по меньшей мере 36" в год. Птолемей не
102

придал значения оговорке «по меньшей мере» и решил,
что 36" в год это и есть значение постоянной прецессии,
полученное Гиппархом.
А дальше сработал фактор, нередко определяющий
психологию ученых и в наше время. Если выдающийся
предшественник такого ученого получил некоторое
значение, скажем, постоянной прецессии, то и у него должно
получиться то же самое. Одним из наиболее ярких
примеров такого «подстраивания» под определение более или
менее авторитетного предшественника может служить
история безуспешных попыток определения периода
вращения Венеры вокруг оси из визуальных наблюдений.
В 1667 г. Доменико Кассини (1625—1712) определил
период вращения Венеры в 23 ч 21 мин. Перед ним стояли
примеры периодов вращения Земли (24 ч) и Марса (24 ч
40 мин по его определению). И чисто психологически, сам
того не сознавая, он «подгонял» данные своих наблюдений
под период, близкий к 24 ч. А его последователи
«подгоняли» свои наблюдения уже под его период (табл. 2).
Таблица 2. Определения периода вращения Венеры
учеными XVII—XX вв.
Год
Наблюдатель
Период вращения Венеры, ч, мин, с
1667
1732
1740
1789
1811
1841
1881
1895
1911
1928
1952
Д. Кассини
Ж. Кассини
Ж. Кассини
И. И. Шретер
И. И. Шретер
Ф. Де-Вико
В. Ф. Деннинг
Л. Бреннер
С. Болтон
Н. П. Шанин
Дж. Бартлетт
23 21
2315
23 20
23 21 19
23 2107,977
23 2121,934
23 21
23 57 36,2396
23 28 30
23 58
22 30
Этот список отнюдь не претендует на полноту.
Многие астрономы (Э. Л. Трувело, К. Фламмарион, А. С.
Васильев, X. Э. Лау, Р. Жарри-Делож, В. Шпангенберг
и др.) указывали просто, что этот период близок к 24 ч2.
2 Этот перечень и данные таблицы заимствованы из книги П.
Мура [74, 115], где приведены полный список всех определений
периода вращения Венеры и обширная литература.
103

Но период вращения твердого тела Венеры оказался
равным 243 сут, а период вращения ее облачного слоя — 4 сут
(из-за постоянных ветров, имеющих скорость до 100 м/с).
Направление вращения оказалось обратным по сравнению
с Землей. В свете этого как курьезны определения
периода Венеры с точностью до тысячных долей секунды
Шретером, Де-Вико и Бреннером!
Что же это было? Самовнушение, да еще в массовом
масштабе? Преклонение перед авторитетом
предшественников? Но если несколько десятков астрономов нового
времени на протяжении трех веков, вплоть до наших
современников, могли утверждать, что получили из
наблюдений абсолютно неверное (как мы теперь знаем) значение
периода вращения Венеры, то можно ли строго судить
Клавдия Птолемея за то, что он подтвердил, как ему
казалось, значение постоянной прецессии, приписываемое
им его великому предшественнику Гиппарху?
Рассмотрим подробнее, как Птолемей нашел это
значение. Он сравнил склонения 18 звезд, наблюдавшихся
Тимохарисом (или Аристиллом) в начале III в. до н. э.
(—282 г.), затем Гиппархом в —128 г. и им самим около
137 г. По изменениям склонения за интервалы времени
в 154 г. (от Тимохариса до Гиппарха) и 265 лет (от Гип-
парха до Птолемея) он вычислил постоянную прецессии.
Нужно заметить, что прецессия по склонению До
выражается через постоянную прецессии р формулой
А8=р sin 8 cos ocAt,
где Д^ —интервал между эпохами наблюдений в годах;
е — угол наклона эклиптики к экватору (Птолемей
принимал 8=23° 51х 20") ; а — прямое восхождение звезды.
Зная До и а, можно, наоборот, вычислить постоянную
прецессии р по формуле
р=До/(Д£ sin 8 cos а).
Мы повторили расчеты Птолемея для всех 18 звезд,
для которых он сам приводит значения склонений для
трех эпох3.
Результаты наших расчетов приведены в табл. 3.
О чем говорят данные этой таблицы? Прежде всего о
том, что средние значения р для обоих интервалов
времени совсем недалеки от правильного значения 50,2" (пер-
3 Авторы лучших переводов «Альмагеста» К. Манициус и Дж. Ту-
мер приводят эти данные в форме таблицы. У самого Птолемея
таблицы нет, а все данные приводятся в обычном контексте,
104

Таблица 3. Значения постоянной прецессии по наблюдениям
звезд, приведенным в «Альмагесте»
Звезда
Альтаир
* г] Тельца
Альдебаран
* Капелла
* Беллятрикс
Бетельгейзе
Сириус
Кастор
Поллукс
Регул
* Спика
*г) Б. Медведицы
Ç Б. Медведицы
8 Б. Медведицы
* Арктур
а Весов
ß Весов
Антарес
Среднее
Наблюдатели
Тимохарис—Гидпарх
43,0"
74,7
20,6
58,2
59,0
91,8
50,4
—
72,5
46,5
42,9
43,2
52,4
29,2
35,7
44,2
47,7
50,8+4,3
Гиппар х—Птолемей
62,1"
40,6
54,3
22,9
39,4
63,0
40,3
41,0
46,6
52,6
37,3
36,0
50,2
45,7
39,6
54,4
44,8
52,0
45,7±2,3
вое значение отличается от истинного лишь на 14%
средней квадратичной ошибки). Далее, мы видим, что оба
значения р, вытекающие из данных, приводимых самим
Птолемеем, вовсе не равны и не близки к используемому им
значению ^=36" в год. Это значение получено Птолемеем
по шести звездам, отмеченным в первом столбце таблицы
звездочками. Как, по какому принципу он их отбирал? По
три звезды из девяти в каждом из полушарий («летнем»
и «зимнем»)? Если это — случайная выборка, то
вероятность именно такого подбора (по три звезды из девяти в
каждой группе) равна 1,4 • 10 ~4 (один шанс из 7000).
Значит, Птолемей выбирал эти звезды не случайно. Он
выбирал их по признаку наименьших значений для интервала
эпох Гиппарх — Птолемей. И был очень рад, получив по
этим шести звездам р=36,0±2,7". Наблюдения же осталь-
105

ных 12 звезд Птолемей отбросил, посчитав полученные по
ним значения р завышенными.
Теперь становится ясной и точка зрения Гиппарха.
Два самых малых значения р (для Капеллы и Арктура)
он отбросил, сочтя их заниженными. Все остальные,
начиная от р для а Весов, были либо равны, либо превышали
значение р=1° в столетие (для а Весов значение р было
округлено). Гиппарх не стал выводить среднее, а так и
написал: «Годичное смещение точек солнцестояний и
равноденствий составляет по меньшей мере 1/100 градуса в
год, так что за 300 лет они сместятся не менее чем на 3°»
[17. С. 328].
Таким образом, Птолемей не понял оговорки
Гиппарха, упустил возможность найти близкое к истине
значение постоянной прецессии и на сотни лет закрепил эту
ошибку своим авторитетом.
Ошибка Птолемея имела роковые последствия. В
звездном каталоге «Альмагеста» ©ce долготы звезд оказались
меньше действительных (на эпоху Птолемея) почти
точно на один градус. Это обстоятельство заметил уже в
1817 г. французский астроном и историк науки Ж. Де-
ламбр. Отсюда он сделал вывод, что сам Птолемей вовсе
яе производил наблюдений звездных положений, а взял
долготы звезд из каталога Гиппарха и прибавил к ним
свою поправку за прецессию за 265 лет: 36" • 265=9540"=
=2° 40', тогда как надо было бы прибавить 50" • 265=
=13250//=3°40/. Получилась как раз разница в 1°.
«Наблюдал ли сам Птолемей? — такой ©опрос ставит
Ж. Деламбр в своей «Истории древней астрономии».—
Не называет ли он «наблюдениями» результаты
вычислений, выполненных им по своим таблицам, и примеры,
приводившиеся для лучшего понимания теории?» И
дальше Деламбр дает такой ответ на этот вопрос: «Что
касается основного вопроса, мы не знаем, как его решить.
Кажется затруднительным полное отрицание того, что
Птолемей сам проводил наблюдения... Если же, как он
говорит, он действительно имел в своем распоряжении
массу наблюдений, то мы можем упрекнуть его в том, что
он не приводит их и нигде не говорит о том, какой могла
быть вероятная ошибка его солнечных, лунных и
планетных таблиц. Астроном, который сегодня действовал бы
подобным образом, вызвал бы к себе полное недоверие. Но
Птолемей был один. У него не было ни судей, ни
соперников. Долгое время он восхищался своими собственными
словами» [96].
106

С этим выводом Деламбра трудно не согласиться. Но
основной вопрос — об авторстве звездного каталога —
требовал тщательного исследования. И такое исследование не
раз проводилось различными учеными с разных позиций.
В 1892 г. в одной астрологической рукописи XIV в.
был обнаружен неизвестный до того перечень созвездий
на греческом языке [98]. Автор рукописи (анонимный)
приписывал его Гиппарху. Вскоре было найдено еще
несколько рукописей, содержавших этот список. Сравнение
его с «Комментарием к Арату» подтвердило, что автором
списка действительно является Гиппарх. В 1901 г.
немецкий исследователь Франц Болл опубликовал список
Гиппарха [93]. В нем —46 созвездий против 48 в
«Альмагесте» (нет Малого Коня и Змеи), причем против 43
из них указано количество звезд, общим числом 653.
Интересно, что в 30 случаях из 43 число звезд в
каждом созвездии у Гиппарха в точности равно числу,
приводимому в «Катастеризмах» псевдо-Эратосфена \
Далее Ф. Болл рассуждал так. В 42 созвездиях по
списку Гиппарха насчитывается 640 звезд (он исключает
Корабль Арго), а в каталоге «Альмагеста» в тех же
созвездиях—770 звезд. Если учесть остальные шесть
созвездий и участки неба между созвездиями и принять, что
соотношение числа звезд в каталогах Гиппарха и
«Альмагеста» то же самое, то получается, что всего в каталоге
Гиппарха было около 850 звезд. Остальные 175 звезд
каталога «Альмагеста» наблюдал или сам Птолемей, или
другой астроном, живший после Гиппарха, но до Птолемея.
Исследование этой версии провел в 1917 г. известный
историк науки Й. Л. Дрейер [98]. Он показал, что таким
астрономом не мог быть Менелай, наблюдавший в самом
конце I в. н. э. Других известных астрономов,
проводивших наблюдения, в рассматриваемый период не было.
Но если координаты 175 звезд наблюдал Птолемей, то
откуда взялась ошибка в их долготах на один градус?
Й. Л. Дрейер полагает, что эта ошибка возникла при
измерении долготы опорной звезды (Регула или Спики),
к которой потом уже «привязывались» долготы
остальных звезд. Вызывает удивление, однако, что Птолемей
не перепроверил свое определение новыми наблюдения-
4 Компилятивное сочинение конца II или III в. н. э.,
первоначально приписывавшееся Эратосфену [111]. Его название (от
«ката» — о, «астер» — светило, звезда) можно перевести: «О
созвездиях».
107

ми, как поступил бы любой современный астроном.
Конечно, можно полагать, что Птолемей, допустив
случайную ошибку в определении долготы опорной звезды и
сравнив ее с долготой по Гиппарху, нашел, что смещение
как раз соответствует принятой им постоянной прецессии
36" в год и не стал перепроверять свое измерение, сочтя
его точным и правильным. Но совпадение получается
довольно странное, хотя взаимная компенсация двух
ошибок — событие не столь уж редкое в научной практике.
Й. Л. Дрейер отмечает еще один факт. Большинство
отсчетов сделано через 7в градуса, но для 145 звезд
широты имеют дробные части: 4Д и 3Д. градуса. Отсюда он
делает вывод, что наблюдения велись двумя
наблюдателями или на двух инструментах с различной
градуировкой кругов. Интересно, что в 42 созвездиях, указанных
в списке Гиппарха, по каталогу «Альмагеста» значится
106 звезд из 772, имеющих дробные части градуса *Д и
3Д, следовательно, без них получается 666 звезд, что
близко к действительному числу звезд в этих 42
созвездиях списка Гиппарха — 640. Надо учесть при этом, что
отсчеты в 7г градуса и в целый градус можно было
делать при обеих градуировках кругов (и через 7в и через
74 градуса), поэтому точного совпадения может не быть.
Работы Болла и Дрейера казались настолько
убедительными, что вопрос о том, наблюдал ли сам Птолемей
звездные положения, был отложен более чем на
полвека—до середины 70-х годов. Но за последнее
десятилетие появились новые исследования, сильно поколебавшие
изложенную точку зрения.
Так, американский исследователь Р. Ньютон [77,119]
подсчитал распределение координат в каталоге
«Альмагеста» по дробным частям градуса. Распределение широт
дало максимум, как и следовало ожидать, на отсчете 0',
на втором месте идет отсчет 30' (известный в научной
практике «эффект округления»). Но долготы дали
максимумы на отсчетах 40' и 10'. Это показывало, что
составитель каталога прибавил к отсчетам наблюдателя целое
число градусов и 40', скорее всего, 2° 40' — поправку за
прецессию, о которой мы уже говорили. Отсюда Р.
Ньютон делает вывод, что Птолемей не наблюдал положения
звезд, а просто взял их координаты у Гиппарха и
прибавил к долготам поправку за прецессию, вычисленную
с ошибкой в 1°.
В 1982 г. другой американский астроном, Д. Роулинс
[125], применил к звездам каталога два теста. Первый со-
108

стоит в проверке предположения, будто у прибора
Птолемея был неверно установлен круг, по которому велся
отсчет долгот, откуда и получилась ошибка в один градус во
всех долготах. Д. Роулинс показал, что этого не могло быть,
так как в армиллярной сфере поворот кругов
осуществляется вокруг оси мира, а не вокруг оси эклиптики, и,
значит, неверная установка кругов затронула бы не только
долготы, но и широты, а ошибка изменялась бы с долготой.
Второй тест состоял в том, что на разных широтах
(Родос—36°, Александрия —31°) и в различные эпохи (из-за
прецессии, изменяющей координаты звезд) вероятность
наблюдать звезды с южными склонениями зависит от
звездной величины. Дело в том, что слабые звезды у
горизонта наблюдать практически нельзя из-за поглощения
света атмосферой, а яркие — можно.
Этот тест привел Д. Роулинса к количественно
обоснованному выводу: вероятность того, что наблюдатель
работал на Родосе в эпоху Гиппарха, в 5 раз больше, чем в
предположении, что он работал в Александрии в эпоху
Птолемея. Проще говоря, в каталоге нет ни одной звезды,
невидимой на Родосе (из-за ее южного склонения), но
наблюдаемой в Александрии.
Еще один тест применили московские астрономы
Ю. Н. Ефремов и Е. Д. Павловская [50]. Они выбрали ряд
звезд с большими собственными движениями и, сравнив их
положения в каталоге «Альмагеста» с современными,
вычислили эпоху каталога 5. Получился II в. до н. э., т. е.
эпоха Гиппарха. Советские астрономы проверили свой
метод на других ранних звездных каталогах, эпоха которых
была точно известна (Улугбека, Тихо Браге, Ауверса).
Метод действовал безукоризненно.
Можно ли после всех этих работ утверждать, что
Птолемей не наблюдал положений звезд и не определял их
координат, а взял их у Гиппарха, придав долготам
неверную поправку за прецессию? Оказывается, окончательный
вывод пока еще сделать нельзя, и вот почему.
Взглянем на результаты описанных выше работ
критически. Вот что мы получим.
Тест Р. Ньютона (распределение дробных долей
градуса) говорит лишь о том, что большинство отсчетов
долгот взято Птолемеем у Гиппарха. Но в этом никто и не
сомневался. Если верить подсчетам Ф. Болла и Й. Л. Дрей-
5 Идея этого метода была предложена в 1983 г. Е, С, Голубцовой
и Ю. А. Завенягиным [43].
109

ера, то таких звезд — 83% всех звезд каталога, и
описанный Р. Ньютоном эффект будет проявляться в полной мере.
Первый тест Д. Роулинса (неверная установка
кругов) доказывает лишь, что исходное предположение автора
теста неверно и дело не в установке кругов прибора
Птолемея. Источник ошибки в один градус другой, только и
всего.
Второй тест Д. Роулинса (видимость звезд в Родосе и
Александрии) вновь говорит о том, что большинство
звезд наблюдалось Гиппархом на Родосе (но необязательно
все). Что касается отсутствия в каталоге звезд, невидимых
на Родосе, то Птолемей мог ограничить свои наблюдения
теми же созвездиями, которые наблюдал Гиппарх, но
расширить число звезд за счет более слабых.
Тест Ю. Н. Ефремова и Е. Д. Павловской
подтверждает, что избранные ими звезды с большим
собственным движением наблюдал именно Гиппарх. Вероятность
того, что избранные ими звезды попадут в число 850 звезд
Гиппарха, намного больше, чем того, что они попадут в
число 175 звезд, приписываемых Боллом и Дрейером
Птолемею.
Впрочем, с аргументацией Болла и Дрейера дело
обстоит не лучше. Все подсчеты Болла рушатся, если мы
предположим, что Гиппарх после составления своего списка
653 звезд продолжал наблюдения и довел число звезд в
каталоге до 1022.
Какие же выводы можно сделать? Предлагаем
следующие выводы на суд читателей6.
1. Можно считать твердо установленным, что
подавляющее большинство звезд каталога, приведенного в
«Альмагесте», наблюдал Гиппарх. Его и следует считать
основным автором каталога.
2. Нельзя пока исключить возможность того, что
положения некоторой части звезд (около 15—17%) определял
Птолемей. Но при этом он допустил роковую ошибку при
определении долготы опорной звезды (или звезд).
3. К долготам звезд Гиппарха Птолемей придал
неверную поправку за прецессию с ошибкой на 1°.
Тщательный анализ ряда вопросов, связанных со звездным
каталогом «Альмагеста», и критика выводов Р. Ньютона даны в
работе: Шевченко М. Ю. Звездный каталог Клавдия Птолемея:
специфика астрометрических наблюдений древности//Истори-
ко-астроном. исслед. 1988. Вып 20. G. 167-186.

Глава 10
Теория движения планет
Вот мы и подошли к планетной теории Птолемея, к его
знаменитой «системе мира». Теория движения планет
охватывает книги IX—XIII «Альмагеста». Излагать ее в
полном объеме мы здесь не будем, ибо это заняло бы
слишком много места. К тому же Птолемей для объяснения
движения пяти планет вынужден был разработать три
разные теории: одну для Меркурия, другую для Венеры
и третью для внешних планет — Марса, Юпитера и
Сатурна.
Основные свойства планетных движений, деферентов
и эпициклов в системе Птолемея таковы (рис. 24).
1. Земля, центры эпициклов Меркурия и Венеры и
Солнце всегда лежат на одной прямой. Следовательно,
период обращения центров эпициклов Меркурия и Венеры
вокруг Земли равен в точности одному году.
2. Периоды обращения Меркурия и Венеры по
эпициклам различны; они меньше года и составляют
соответственно для Меркурия 88 сут, для Венеры 225 сут.
3. Центры эпициклов Марса, Юпитера и Сатурна
обращаются по своим деферентам за различные промежутки
времени: от 687 сут для Марса до почти 30 лет у Сатурна.
4. Марс, Юпитер и Сатурн обращаются по эпициклам
ровно за один год.
5. Плоскости деферентов Меркурия и Венеры
совпадают с плоскостью эклиптики; плоскости эпициклов
Марса, Юпитера и Сатурна параллельны плоскости эклиптики.
6. Плоскости эпициклов Меркурия и Венеры,
деферентов Марса, Юпитера и Сатурна наклонены к плоскости
эклиптики на малые углы (не более 7° в случае Меркурия).
7. Радиусы эпициклов Марса, Юпитера и Сатурна,
соединяющие центр эпицикла с планетой, всегда
параллельны направлению Земля — Солнце.
Эти свойства ясно показывают, что, во-первых, условия
движения нижних и верхних планет существенно
различны. Во-вторых, определяющую роль в движении и тех и
других планет играет Солнце. Периоды обращения
планет либо по деферентам (у нижних планет), либо по
эпициклам (у верхних) равны периоду обращения Солнца,
т. е. году. Ориентация деферентов нижних планет и
эпициклов верхних связана с плоскостью эклиптики.
ill

/ff/7l//77e/7a
Тщательный анализ
этих свойств планетных
движений привел бы
Птолемея к простому
выводу, что Солнце, а
не Земля — центр
планетной системы. К
тому же еще Аристарх
Самосский доказал, что
Солнце в несколько раз
больше Земли. Было бы
естественнее, если бы
меньшее тело двигалось
вокруг большего, а не
наоборот. Из других тел
Луна была еще меньше,
чем Земля, и подавно
меньше Солнца.
Размеры планет определить
прямым путем было
невозможно, но было
ясно, что они гораздо
меньше Солнца. В
самом деле, Меркурий и
Венера считались более
близкими к Земле, чем
Солнце, но не имели видимых дисков. Не имели их и
другие планеты.
И все же Птолемей нашел способ выяснить, хотя бы
приблизительно, размеры планет в сравнении в Землей.
Еще Гиппарх, согласно свидетельству Птолемея, говорил,
что видимый диаметр Солнца в 30 раз больше, чем у
наименьшей (т. е. самой слабой) звезды. В этом рассуждении
есть доля истины. Ведь угол в одну минуту дуги (7зо
видимого диаметра Солнца) — это как раз предел
разрешающей способности человеческого глаза. Источники света
с меньшими угловыми диаметрами представляются
нашему глазу точками. В то же время известно, что более
яркие звезды кажутся крупнее. Вот почему Птолемей в
своем сочинении «Планетные гипотезы», написанном после
«Альмагеста», оценивает видимый диаметр Венеры в 1/10
солнечного, Юпитера — в 1/12, Марса — в 1/20,
Меркурия — в 1/15, Сатурна — в 1/18. Эти видимые размеры
отнесены к средним расстояниям планет от Земли [106].
Расстояния Птолемей оценил по своей модели с деферента-
Рис. 24.
Система мира Птолемея
112

Таблица 4. Радиусы плайетных сфер (по Птолемею)
Планета
Расстояние от Земли (в земных радиусах)
наименьшее
наибольшее
Луна
Меркурий
Венера
Солнце
Марс
Юпитер
Сатурн
33
64
166
1160
1260
8 820
14 187
64
166
1079*
1260
8 820
14187
19 865
* Между внешней сферой Венеры и внутренней сферой Солнца в модели
Птолемея имеется небольшой вазор.
ми и эпициклами, исходя из условия, что кратчайшее
расстояние более дальней планеты (радиус ее «внутренней
сферы») равно наибольшему расстоянию более близкой
планеты (радиусу ее «внешней сферы»). Эти расстояния
(табл. 4), вычисленные Птолемеем по своей модели,
приведены в «Планетных гипотезах» (в «Альмагесте» их нет).
Табл. 4 дает богатую пищу для размышлений.
Птолемей знал величину земного радиуса в линейных единицах
(стадиях) хотя бы по измерениям Эратосфена.
Полученное им среднее расстояние до Луны лишь на 20% меньше
действительного. Но среднее расстояние до Солнца
занижено уже в 20 раз (а с ним и линейные размеры Солнца),
расстояние до Юпитера —в 9 раз, до Сатурна —в 12 раз.
Таким образом, масштабы нашей планетной системы были
занижены Птолемеем примерно на порядок. Но даже эти
оценки были большим достижением, ибо они показывали,
что межпланетные расстояния намного больше любых
земных масштабов.
Видимые угловые размеры планет были Птолемеем
завышены в несколько раз. Так, угловой диаметр Венеры
у него получался 3", тогда как на среднем от Земли
расстоянии он равен 17" ~ 0,3' (в десять раз меньше). Для
Юпитера имеем соответственно 2,5' и 0,6х (различие в
четыре раза), для Сатурна— 1,7' и 0,3х (разница в шесть
раз). Это преувеличение угловых размеров
скомпенсировало до некоторой степени занижение расстояний, так что
размеры планет у Птолемея близки к реальным. Он, так же
113

как и мы, считал самой большой планетой (после
Солнца) Юпитер, потом шел Сатуры, но они превосходили
Землю по диаметру в 4,4—4,3 раза, тогда как на самом деле
они больше Земли в 11 и 9 раз. Марс, по Птолемею, был
чуть больше Земли (в действительности он вдвое меньше).
Для Луны получилось почти правильное соотношение, но
Венеру Птолемей считал чуть меньше Луны, а
Меркурий — почти в 8 раз меньше (его размеры преуменьшены
в 10 раз). Тем не менее и размеры планет по порядку
величины Птолемей представлял себе правильно.
Согласно его расчетам это были тела, сравнимые с Землей, а
некоторые даже превосходили Землю *.<
Отсюда был один шаг до признания Земли рядовой
планетой, но и этого шага Птолемей не решился сделать.
В девятой книге «Альмагеста» (гл. 3) есть
любопытное указание на то, что число возвращений верхней
планеты к той же точке зодиака (число ее сидерических
обращений) и число ее обращений по эпициклу
(аномалистических) в сумме равно числу солнечных лет.
Эти числа приведены в табл. 5 [17. С. 424].
С позиций гелиоцентрической системы это
соотношение можно строго доказать [35]. Пусть угловая скорость
планеты на орбите за год равна cûi, а угловая скорость
Земли — о)2. Тогда (поскольку для верхних планет ol>i<
<(û2) за год Земля обгонит планету на угол ю2—оз±.
Число обращений планеты вокруг Солнца за время Т
равно rû)i/360°, число обращений Земли за то же время (т. е.
число солнечных лет) равно Гсо2/360°, число обращений
планеты относительно звезд для земного наблюдателя
равно Т((д2—cûi)/360°. Сокращая на 27360°, мы видим, что
соотношение Птолемея тождественно выполняется. Увы,
сам Птолемей не дал никакого объяснения этому
соотношению. А ведь правильное понимание его значения
открывало путь к гелиоцентрической системе мира.
Но переход к гелиоцентрической системе был
невозможен для Птолемея. Мы уже говорили в гл. 5 о его
мировоззрении. Он считал Землю находящейся в центре
1 Метод определения размеров планет Птолемея, несмотря на все
его недостатки, имеет рациональное зерно. В сущности говоря,
это определение размеров планет по их блеску при известном
расстоянии и заданном альбедо. Такой метод еще недавно
применялся для определения размеров астероидов и малых
(далеких) спутников планет. Другое дело, что Птолемей не знал
истинных расстояний до планет и не умел сравнивать их блеск.
Трудно сказать, понимал ли он, что планеты, как и Луна,
светят отраженным светом Солнца.
114

Таблица 5. Соотношение периодов для планет
Планета
Число обращений
Сидерических
Аномалистических
Число
солнечных лет
Марс
Юпитер
Сатурн
37
65
57
42
6
2
79
71
59
Таблица 6. Относительные расстояния планет
Планета
Щ/R
Э/Лд
1/а
А, %
Меркурий
Венера
Марс
Юпитер
Сатурн
0,3708
0,7194
0,6583
0,1917
0,1048
0,3871
0,7233
1,5237
5,2028
9,5388
—
—
0,6563
0,1922
0,1083
4,2
0,5
0,3
0,3
3,2
мира, приводил ряд доводов в пользу этого взгляда и не
мог от него отказаться. Такой шаг был под силу только
Копернику. И только через четырнадцать веков.
Перейдем к другому любопытному соотношению,
которое мы находим в книгах «Альмагеста». Речь идет об
отношениях радиусов эпицикла Дэ и деферента Лд. Мы их
выпишем до четвертого знака, а рядом напишем
современные значения больших полуосей орбит тех же планет а
или их обратных величин 1/а, выраженных в единицах
соответствующих величин для Земли (табл. 6) [97].
В последнем столбце приведены расхождения между
отношениями Птолемея и современными значениями в
процентах. Их небольшие величины говорят сами за себя.
Физический смысл табл. 6 таков: отношения радиусов
эпициклов и деферентов у Птолемея отражают отношения
больших полуосей орбит планет и Земли (или обратные
им величины). Но Птолемей и этого, увы, не понял.
Перейдем к рассмотрению теорий движения планет,
разработанных Птолемеем. Как уже говорилось, он был
вынужден создать три разных теории: для верхних
планет, для Веперы и для Меркурия. Пропустим Меркурий,
115

теория которого наиболее сложна и содержит к тому же
существенную ошибку, и рассмотрим схему движения
Венеры.
Сначала Птолемей из наблюдений наибольших
элонгации Венеры к востоку и к западу от Солнца определяет
направление линии апсид ее эксцентра (являющегося
одновременно деферентом). Он получил долготу апогея
Венеры 55° и долготу ее перигея 235°. Затем из сравнения
углов наибольших элонгации Венеры в апогее и перигее
простым геометрическим построением Птолемей находит
радиус эпицикла (в долях радиуса эксцентра, он же
деферент) и расстояние между центрами деферента и
эклиптики.
Ввиду простоты этого расчета приведем его здесь
[17. С. 471—472]. Пусть окружность ABG (рис. 25) есть
эксцентр (деферент) с центром в D. Земля находится в Е,
центр эпицикла в апогее находится в точке А, а в
перигее — в точке G. Проведем касательные из Е к эпициклу в
обоих положениях EZ и ЕН. Треугольники AEZ и GEH —
прямоугольные, так как касательные (EZ, ЕН)
перпендикулярны к радиусам (AZ, GH) в точке касания. Углы при
точке Е нам известны из наблюдений и равны: /.GEH=
=444/5°, Z4£,Z=471/3°. Но радиусы эпицикла равны друг
другу (AZ=GH), а кроме того, AE+EG=2AD, причем
принимается, что радиус деферента AD=60P. Из
прямоугольных треугольников AEZ и GEH по известному острому
углу находим 42?=1,42 Re и i?C?=l,36 /?е, где Re — радиус
эпицикла2. Таким образом, AE/EG=1404:4 и AE+EG=
=120р, откуда расстояние между центрами ED^VU*,
ED/AD=0,02, радиус эпицикла (в долях радиуса
деферента) уже был приведен выше, в табл. 6.
Но для представления движения центра эпицикла
Венеры по деференту Птолемей вынужден ввести на оси
апсид еще одну точку —центр равномерного движения,
или точку экванта F, так что обращение центра эпицикла
кажется равномерным именно из этой точки. Это можно
представить себе так (рис. 26). Пусть вокруг точки
экванта F описана окружность (круг экванта, или для краткости
просто эквант), по которой в прямом направлении
равномерно движется точка А0, последовательно занимая
положения Ai, А2, Л3,... Им соответствуют точки на
деференте А), Di, D2, A*,..., по которому, однако, центр
Здесь мы несколько отошли от подлинных расчетов Птолемея,
что почти не влияет на результат.
116

Рис. 25. Расчет радиуса эпицикла и эксцентриситета
Рис. 26. Введение экванта для планет
эпицикла движется неравномерно. Это
физическое неравенство усиливается оптическим
неравенством, связанным с тем, что Земля Е не совпадает ни с F,
ни с центром деферента D. Птолемей из сравнения
наибольших элонгации Венеры к западу и к востоку от
Солнца с помощью расчета, аналогичного предыдущему,
находит расстояние EF=2^UV=2ED. Называя Z?F простым,
или полным, эксцентриситетом, Птолемей приходит,
таким образом, к важному заключению о том, что
эксцентриситет ED (расстояние Земля—центр деферента) равен
половине полного эксцентриситета. Это заключение
получило название правила биссещии эксцентриситета.
Оно было применено Птолемеем не только к Венере, но и
к трем верхним планетам и сыграло важную роль в
дальнейшем. Его использовали в своих работах Коперник и
Кеплер.
Рассмотрим, следуя Н. И. Идельсону [54], смысл этого
правила с позиций современной астрономии. Мы уже
сравнивали в гл. 7 формулы уравнения центра х и радиуса-
вектора планеты г в долях большой полуоси а в гипотезе
простого эксцентриситета. Напомним эти формулы, чтобы
можно было сравнить их с теми, что соответствуют
гипотезе биссекции. Итак, имеем первые члены разложения
по современной теории:
х=2е sin М- (5/4) е2 sin IM,
r/a=l+e2/2+e cos M- (e2/2) cos 2АГ,
117

в гипотезе простого эксцентриситета:
x=2esmM-2e2sin2M,
r/a=l+e2+2e cos M - e2 cos 2M,
в гипотезе биссекции эксцентриситета:
x=2esmM-e2siii2M,
г/а=1+ (3/4) е2+е cos М- (3/4) е2 cos 2М.
Ошибки в гипотезе простого эксцентриситета:
8х= (3/4) е2 sin 2М; Ô (г/а) =-е cos М- (е2/2) (1- cos 2М),
ошибки в гипотезе биссекции:
оя=_ (е2/4) sin 2М; Ô {гla) =- (в2/4) (1- cos 2М).
Таким образом, по сравнению с гипотезой простого
эксцентриситета ох уменьшилась втрое, в величине ö(r/a)
исчез член ecosM, а член второго порядка относительно
е уменьшился вдвое.
Птолемей применил правило биссекции и в теории
движения верхних планет: Марса, Юпитера и Сатурна.
Интересно, какова точность этой теории? Для оценки
выберем планету Марс, у которой наибольший (среди этих
четырех планет) эксцентриситет орбиты — 0,093. Для
Марса оказалось ô^=±7,5/, ô (г/а) =+0,00435.
Как мы знаем, точность измерений положений звезд в
то время была ±10' (одна шестая доля градуса). Очевидно,
что и для планет точность была не лучше. Поэтому
точность теории Птолемея устраивала и его, и многих его
последователей. Но именно из этих предельных уклонений
в долготах и радиус-векторах Марса выросла
впоследствии, как справедливо указывает Н. И. Идельсон, теория
истинного эллиптического движения планет,
разработанная Кеплером.
В одиннадцатой книге Птолемей приводит таблицы, по
которым следует рассчитывать положения всех пяти
планет. По аргументу средней аномалии M дается уравнение
центра х0 в гипотезе простого эксцентриситета и поправка
к нему х—х0 для перехода к гипотезе биссекции. Сравним
несколько значений этих углов, вычисленных самим
Птолемеем и по точным формулам (но по теории и с
параметрами Птолемея), для планеты Марс (табл. 7).
Согласие результатов говорит само за себя. А ведь для
этих расчетов Птолемей не имел ничего, кроме своей таб-
118

Таблица 7. Уравнение центра и поправка к нему
M
х0
Точная
формула
По Птолемею
х-х0
Точная
формула
По Птолемею
30° 4°52' 4°52' +0°24' +0°24'
60 8 57 8 57 +° 27 +° 27
90 11 19 11 19 +0 03 +0 04
120 10 54 10 53 —0 32 —0 31
150 6 54 6 54 —0 39 —0 38
лицы хорд. Он делал расчеты шести величин (четыре
остальные определяют движение планеты по эпициклу) для
пяти планет, для 45 значений аргумента. Это значит, что
всего для составления таблиц движения планет ему
пришлось выполнить 1350 расчетов. Колоссальный труд!
А ведь это еще не все: как и в книгах, посвященных
теории видимого движения Солнца и Луны, Птолемей
начинает изложение теории движения планет в книге IX с
таблиц средних движений, приводя для каждой
планеты средние смещения по долготе за год, за месяц, за сутки,
за час, а затем дает таблицы на 45 18-летних циклов, на
18 лет в цикле, на 12 мес, на 30 сут. месяца и на 24 ч,
а всего по 129 числам для пяти планет, т. е. 645 чисел до
шестого шестидесятиричного разряда долей градуса (13—
15 цифр, в зависимости от того, будет ли число целых
градусов однозначным, двузначным или трехзначным).
Обратимся теперь к Меркурию. В отличие от других
планет для Меркурия Птолемей вводит второй, подвижный
эксцентр, центр которого обращается вокруг центра экван-
та по малому кругу с радиусом, равным расстоянию Земли
от центра первого, неподвижного эксцентра, т. е. половине
полного эксцентриситета. Это обращение происходит в
направлении, обратном движению эпицикла. При такой
комбинации центр эпицикла обращается относительно Земли
и центра неподвижного эксцентра уже не по окружности,
а по иной замкнутой кривой, имеющей две точки
наибольшего сближения с Землей (два перигея). Птолемей не
объясняет причин этого. Американский исследователь Р.
Ньютон [77, 119] показал, что такое предположение вовсе не
обязательно следует из наблюдений Меркурия,
приводимых Птолемеем. Р. Ньютон построил обычную модель с
одним неподвижным эксцентром и эпициклом, которая да-
119

Вала fié худшее согласие с наблюдениями, Чей модель
Птолемея. Но у Р. Ньютона была в распоряжении ЭВМ,
которой у Птолемея, увы, не было.
Как же пришел Птолемей к этой странной модели?
Ведь он выполнил 16 наблюдений элонгации Меркурия,
тогда как другие планеты наблюдал не более пяти раз.
Сначала Птолемей определяет направление на апогей
деферента Меркурия [17. С. 449—457]. Для этого он
использует наблюдения его наибольших элонгации,
приведенные в табл. 8.
Здесь первые четыре наблюдения выбраны таким
образом, чтобы наибольшие восточная и западная
элонгации Меркурия были попарно равны. Тогда, заключает
Птолемей, средние положения планеты на эпицикле (их
долготы равны долготам среднего Солнца) должны быть
расположены симметрично относительно апогея. Первая
пара (наблюдения 1 и 2) дает среднюю точку с долготой
9°52' (созвездие Овна), вторая пара (наблюдения 3 и
4) —с долготой 190° 15х (созвездие Весов).
Чтобы разрешить неопределенность (Овен или Весы),
Птолемей прибегает к старым наблюдениям. К
наблюдению 5 подходящей пары нет, но он берет два
наблюдения (6 и 7), такие, что наибольшая западная элонгация
в наблюдении 5 имеет промежуточное значение между
наибольшими восточными элонгациями в наблюдениях
6 и 7. Интерполируя между ними, он находит, что
наибольшей элонгации 25° 5(У соответствовала бы долгота
среднего Солнца 53° 3(У. Средняя точка между этой
долготой и долготой Солнца в наблюдении 5 дает долготу
направления на апогей (или ему противоположное) 5°50'
(Овен).
Точно так же, не подобрав симметричного положения
Меркурия наблюдению 8, Птолемей комбинирует
наблюдения 9 и 10 и получает направление на апогей 186°
(Весы).
То, что старые наблюдения дали долготы, на 4°
меньшие, чем его собственные наблюдения, Птолемей
объясняет прецессией, которая, по его мнению, составила бы
за 400 лет как раз 4°. Но неопределенность (Овен или
Весы?) старые наблюдения не устраняют.
Тогда Птолемей берет еще два своих наблюдения
(11 и 12), сделанных как раз тогда, когда Солнце было в
созвездии Весов (наблюдение 11) и в созвездии Овна
(наблюдение 12). Поскольку наибольшая элонгация в первом
случае значительно меньше, чем во втором, Птолемей де-
120

Таблица 8. Наблюдения элонгации Меркурия
Номер

наблюдения
Дата
Долгота
Меркурия
Долгота
среднего
Солнца
Наибольшая
элонгация
1
2
3
4
5
6
7
8
9
10
11
12
132
134
138
141
—261
—261
—256
—261
—236
—244
134
135
II 2
VI 4
VI 4
И 2
II 12
IV 25
V 28
VIII 23
X 30
XI 19
X 3
IV 5
331°00'
48 45
97 00
283 30
292 20
53 40
89 20
169 30
194 10
212 20
170 12
34 20
309°45'
70 00
70 30
310 00
318 10
29 30
62 50
147 50
215 10
234 50
189 15
11 05
21°15'
21 15
26 30
26 30
25 50
24 10
2Q 30
21 40
21 00
22 30
19 03
23 15
Е
W
Е
W
W
Е
Е
Е
W
W
W
Е
лает окончательное заключение, что апогей Меркурия
находится в созвездии Весов на долготе 190°.
Казалось бы, отсюда следует, что перигей должен
быть расположен в диаметрально противоположном
направлении, в созвездии Овна. Но Птолемей находит, что
это не так, что есть два «перигея», в Близнецах и в
Водолее. Действительно, комбинируя наблюдения 1 и 4 с
почти одинаковой долготой среднего Солнца (в созвездии
Водолея), Птолемей находит сумму обеих элонгации
(видимый диаметр эпицикла) 47° 45'. Такая же сумма
получается для наблюдений 2 и 3, для которых в среднем
долгота Солнца равна 70° 15х (созвездие Близнецов). Для
созвездия же Овна (наблюдение 12) он получает сумму
элонгации только 46° 30', считая (без достаточных
оснований), что наибольшая западная элонгация при таком
положении Солнца (которую он не наблюдал) равна
наблюдавшейся им восточной.
На таких-то довольно шатких основаниях и была
построена Птолемеем модель с двумя перигеями. В
принципе можно представить себе форму орбиты, у
которой было бы два перигея. Возьмем для примера эллипс
(рис. 27), а Землю поместим не в фокусе F, ав центре
эллипса О. Тогда «перигеями» для нее будут точки на
концах малой оси эллипса С, D, а «апогеями» — точки на
концах большой оси А, В. Будем смещать Землю от цент-
121

Рис. 27. Схема орбиты с двумя перигеями
ра О к одному из фокусов эллипса F. «Перигеи» будут
смещаться вдоль эллипса в ту же сторону, занимая
положения Ci, öi, С2ч D2 и т. д., пока не сольются в точке
истинного перигея В на конце большой оси, ближайшем
к фокусу F, в который придет Земля. Разумеется, такая
схема с двумя перигеями возможна только на бумаге —
динамически она нереальна. Но Птолемей не мог
использовать эллипс, в его распоряжении были только круговые
движения. Вот он и ввел второй эксцентр, комбинация
которого с первым (неподвижным) эксцентром и дала
ему два «перигея».
Кстати, взятие этого слова в кавычки вполне
соответствует терминологии Птолемея. Он называет эти
точки не перигеями ^eptyeiov )? а использует для них
термин jtepfyeioTaxov, превосходную степень от слова
«перигей», что-то вроде «перигеища» или «суперперигея».
Это звучит немного забавно, поскольку, если уж
перигеев два, опи не могут быть оба «главными».
Описанную модель Птолемея не раз критиковали,
причем не только резко отрицательно относящийся к
этому ученому Р. Ньютон, но и симпатизирующий
Птолемею О. Гингерич Г102]. Последний, в частности,
упрекает Птолемея за то, что он не производил наблюдений
Меркурия в месяцы, промежуточные между февралем и
апрелем, апрелем и июлем, июлем и октябрем. Упрек
справедливый: ведь благодаря краткости периода
обращения Меркурия вокруг Солнца его синодический период
(относительно Земли) равен всего 116 сут и за год можно
наблюдать шесть элонгации Меркурия (по две за каждый
синодический период). Конечно, не все они
благоприятны для наблюдений. Особенно неудобны те из них, при
которых склонение Меркурия южнее склонения Солнца,
122

т. e, восточные (вечерние) элонгации конца лета и осени
и западные (утренние) элонгации второй половины зимы
и весны. В это время Меркурий заходит (восходит) почти
одновременно с Солнцем и наблюдать его очень трудно.
Но Птолемей наблюдал Меркурий и в этих элонга-
циях (наблюдения 4, 5, 8 в табл. 8).
В связи с этим нелишне здесь разоблачить
получившую широкое распространение легенду о том, будто
Коперник ни разу не видел Меркурий. Коперник никогда
не утверждал ничего подобного. Он писал лишь, что
очень трудно наблюдать и измерять
положения Меркурия [63], что совершенно справедливо для
широты Фромборка или Олыптыня (52—54°) в значительно
большей степени, чем для широты Александрии (31°).
В двенадцатой книге «Альмагеста» исследуются
попятные движения и точки стояния планет. Как показал
недавно американский астроном Дж. Эванс [100],
удовлетворительное описание попятных движений планет
(в течение полного периода обращения планеты) как
набора дуг обратного движения с определенными
промежутками между ними потребовало усовершенствования
теории и сыграло важную роль в ее завершении
Птолемеем.
Интересно, что в случае Марса величины этих дуг
близ перигея и апогея планеты различались вдвое, что
и привело Птолемея к идее экванта и биссекции полного
эксцентриситета. Таким образом, Марс сыграл
решающую роль в построении теории Птолемея, как и спустя
полтора тысячелетия в построении теории Кеплера. Но
у Кеплера были в распоряжении точнейшие наблюдения
Тихо Браге и его собственные за 12 противостояний
Марса (24 года!), а у Птолемея таких наблюдений не было.
Рассмотрев в тринадцатой книге движения планет по
широте, Птолемей заканчивает на этом изложение своей
теории движения планет. Заканчивает, чтобы она еще
пятнадцать веков служила человечеству.
В последнее время некоторые ученые предприняли
любопытную проверку точности ряда исторических
теорий движения планет. Так, еще в 1975 г. трое
американских ученых с помощью ЭВМ провели математический
анализ нескольких систем, в том числе Птолемея и
Коперника [108]. Эти системы использовались для
предсказания положений Марса и Венеры на определенную дату,
предвычисления квадратур, соединений и противостояний
верхних планет. Наилучшей оказалась система Пто-
123

Рис. 28. Отклонения долготы Меркурия по теории Птолемея от
значений, даваемых современной теорией (по О. Гингеричу)
лемея: положение Марса на период 870 дней на ее
основе вычисляется с абсолютной ошибкой 0,7°.
Предварительный анализ системы Коперника показал, что ее
«предсказательная способность» ниже.
К тому же выводу пришел американский астроном и
историк науки О. Гингерич [103], показавший, что по
простоте и точности вычислений положений планет
система Птолемея превосходила систему Коперника. При этом
речь идет о системе, используемой в «Альмагесте», без
дополнительных эпициклов, введенных в средние века.
О. Гингерич произвел расчеты отклонений в долготах
планет, даваемых теорией Птолемея по сравнению с
современной теорией [104]. Они представлены на рис. 28—
30 для периода наблюдательской деятельности Птолемея
(127—142 гг.). Наблюдения Птолемея показаны
кружками. Мы видим для всех планет систематическую ошибку
на 1° (связанную, как мы знаем, с использованием
неверной системы долгот из-за неправильного учета
прецессии) и квазипериодические ошибки, возникающие из-за
неточности теории. Последние для Марса не превосходят
±1°, для Юпитера ±0,13°, для Сатурна ±0,2°, для
Венеры большую часть периода ошибки не превосходят ±0,33°,
но в нижних соединениях могут достигать +5,5°, для Мер-
124

Рис. 29. Отклонения долготы Венеры по теории Птолемея от
значений, даваемых современной теорией (по О. Гингеричу)
Наблюдения Птолемея показаны кружками
г
г
Af/Z/7C
ц_/У\.гь/Ч^
/ûnt/mep
fami/prt
m /so /J2 /s*
/Jâ US №0 г.н.з.
Рис. 30. Отклонения долгот Марса, Юпитера и Сатурна по теории
Птолемея от значений, даваемых современной теорией
(но О. Гингеричу)
Наблюдения Птолемея показаны кружками
125

курия ошибки достигают ±7°. Наблюдения Птолемея
хорошо ложатся на кривые, показывая, что между ними и
его теорией существенных расхождений не было. Но
число этих наблюдений было слишком мало, чтобы судить
(по современным меркам) о достоинствах и недостатках
теории.
Теперь мы имеем все необходимые данные, чтобы
судить о планетной теории Птолемея. Для своего времени
(и многих последующих столетий) она удовлетворяла
предъявляемым к такой теории требованиям. Методика
ее разработки, подробно изложенная в «Альмагесте», сама
по себе имела большое научное значение. Основные
положения этой теории использовали впоследствии
Коперник и Кеплер для построения своих теорий, которые
положили начало современной астрономии.
Глава И
«Преступление
Клавдия Птолемея»
Вот мы и подошли к самому драматическому
моменту нашего повествования о Клавдии Птолемее. Спустя
1800 лет после его смерти великий античный астроном
был обвинен в преступлении, а именно в сознательной
подделке своих собственных и приводимых им в
«Альмагесте» чужих наблюдений. Причем подделаны не одно-
два, а десятки наблюдений. А те, о которых нельзя
прямо сказать, что они подделаны, во всяком случае, могут
быть подделкой.
В качестве заголовка этой главы мы выбрали название
книги уже не раз упоминавшегося выше американского
геофизика, занявшегося историей астрономии, Роберта
Ньютона [77, 119]. После ряда статей в научных
журналах с «разоблачениями» Птолемея он выпустил эту книгу
на английском языке в 1977 г., а недавно она вышла и в
русском переводе. Название «Альмагест» в ней
фигурирует только один раз: с целью объяснить, почему автор
от него отказывается и предпочитает именовать труд
Птолемея «Синтаксисом» >в соответствии с тем названием,
которое дал ему сам Птолемей. Это — безусловное право
126

Р. Ньютона, как и любого другого ученого. Но, как
говорится, дело не в названии.
Метод, которым пользуется Р. Ньютон для выявления
«подделок» Птолемея, прост до крайности. Он выбирает
из «Синтаксиса» некоторую наблюдавшуюся Птолемеем
(или другим древним астрономом) величину (координаты
светила, момент какого-либо явления и т. п.), вычисляет
по современным теориям ее истинное значение, затем
делает аналогичный расчет по теории Птолемея и находит
результат: наблюдение хорошо сходится с теорией
Птолемея и плохо — с современной теорией. Затем Р. Ньютон
делает предположение, что отклонение от современной
теории — результат случайной ошибки наблюдения. Зная
точность наблюдений той эпохи, он подсчитывает вероятность
такой ошибки и получает, как правило, что эта
вероятность крайне мала (особенно, если речь идет не об одном,
а о нескольких однотипных наблюдениях). Значит,
заключает он, наблюдение подделано.
Далее Р. Ньютон прибегает еще к такому приему.
Стараясь показать свою объективность, он ставит вопрос:
быть может, Птолемей ни в чем не виноват, а его
постоянно обманывал проводивший наблюдения по его заданию
помощник. Отличаясь ленью (или желая провести время
иным образом), он ничего не наблюдал, а вычислял по
теории Птолемея предполагаемый результат наблюдения
и выдавал его за таковой. Не говоря уже о том, что
трудно так морочить голову своему руководителю в течение
15 лет, далеко не во всех случаях вину можно возложить
на помощника. К тому же Птолемей во многих местах
«Синтаксиса» прямо пишет, что наблюдения проводил он
сам. Анализируя эту »версию, Р. Ньютон приходит к
вполне обоснованному выводу: гипотетическим помощником
мог быть только... сам Птолемей.
Оставим версию с помощником и поставим вопрос
прямо: почему наблюдения Птолемея часто хорошо
согласуются с его же теорией и в то же время
противоречат результатам расчетов по современным теориям?
Некоторые примеры мы приводили в гл. 9,
посвященной звездному каталогу. Мы видели, как Птолемей,
стремясь подтвердить значение постоянной прецессии,
полученное, по его мнению, Гиппархом (и, как мы теттерь
зиаем, ошибочное), выбрал из наблюдений склонений
18 звезд как раз те шесть, которые в среднем давали
гиппархово значение (36" в год), а остальные 12 звезд
(которые дали бы ему верное значение) отбросил. Там
127

же мы постарались дать этому факту объяснение с
учетом психологии исследователя, не только древнего, но и
современного, стремящегося подтвердить результат
предшественника, для него авторитетного. Вспомните
приведенный там же пример с периодом вращения Венеры.
Еще один пример был приведен в гл. 10 при описании
того, как Птолемей искал положение апогея Меркурия.
Его собственные наблюдения давали ему долготу апогея
10° или 190° (из этих наблюдений он находил,
собственно говоря, направление оси апсид как линии симметрии
между двумя положениями центра эпицикла), а
наблюдения середины III в. до н. э. давали долготы 6 или 186°
(на 4° меньше). Но между эпохой этих и его
собственных наблюдений прошло четыре столетия, а прецессия
давала (по Гиппарху и Птолемею) как раз 1° в
столетие — вот и получается разница в 4°, и все сходится. Но
действительная прецессия за 400 лет составляет 5,5°. Ее
прибавление к долготам, полученным из древних
наблюдений, мало изменит общий результат — получится 191,5°
вместо 190°, а при усреднении с результатом по его
собственным наблюдениям —190,75°, на 3/4 градуса больше,
чем он получил вначале. Но Птолемею хотелось, чтобы
все сошлось точно, и он усмотрел здесь подтверждение
найденной им и Гиппархом постоянной прецессии.
А посмотрите, как хорошо согласуются с неточной
теорией Птолемея его наблюдения долгот планет,
показанные кружочками на рис. 28—30. И как они расходятся с
современной теорией! Что же здесь к чему подгонялось:
теория к наблюдениям или наблюдения к теории? Р.
Ньютон дает ответ однозначно: наблюдения подделаны,
подогнаны к теории.
В том, что такие случаи (согласие наблюдений с менее
точной теорией и расхождения с более точной) имели
место не раз и даже в новое время, нас убеждает табл. 9,
приводимая О. Гингеричем [104]. В ней даны
расхождения четырех наблюдений положения Марса, выполненных
Коперником, с данными его собственной теории, той же
теории, улучшенной Э. Рейнгольдом, и современной теории.
Мы видим здесь ту же картину: согласие с
несовершенной теорией хорошее, а с точной — плохое. Как же
объяснить наблюдения 1518 и 1523 гг., давшие отклонения от
действительных положений в 1—2° при точности
наблюдений Коперника ±10' (некоторые авторы, например А. Бер-
ри [29], оценивают их точность гораздо ниже: ±40')?
Между прочим, и сам Коперник это понимал. В одной из
128

Таблица 9. Расхождение наблюдений Коперника с теориями
Дата наблюдения
Расхождения наблюдений с теориями
Коперника
Рейнгольда
современной
1512 VI 5
1518 XII 12
1523 II 22
1512 I 1
-9'
—9
—2
+4
-2'
—3
—5
+4
—0°20'
+1 17
+2 16
+0 02
своих черновых тетрадей, найденной потом в Упсале и
изданной уже в наше время под названием «Упсальская
запись», Коперник пишет о своих наблюдениях Марса и
Сатурна 1512—1514 гг.: «Марс превышает расчет более чем
на 2 градуса, Сатурн расчет превышает на 17г градуса»
[63].
О том, что у Птолемея имеются неточности, ошибки
в наблюдениях и даже некоторые противоречия, знали еще
арабские и среднеазиатские ученые. Так, Абу Али ибн
аль-Хайсам (965—1039), известный также под
латинизированным именем Альхазен, опубликовал «Книгу о
сомнениях по поводу Птолемея» [83]. За столетие до него
Сабит ибн Корра (836-901) и Аль-Баттани (850-929)
обнаружили движение солнечного перигея, который
Птолемей считал неподвижным. Аль-Баттани нашел постоянную
прецессии равной 54,5" против 36" у Птолемея. Он же
уточнил наклон эклиптики к экватору, для которого
Птолемей вслед за Эратосфеном принимал завышенное
значение 23° 51'20". Сам Аль-Баттапи получил 23° 35' 41",
что гораздо ближе к действительному значению в его эпо-
ху [84].
Астрономы нового времени обратили внимание на
ошибки у Птолемея еще более 200 лет назад. Так, в 1753 г.
Тобиас Майер [104] в письме к Леонарду Эйлеру писал:
«Вполне возможно, что Птолемей понимал, что его
солнечные таблицы содержат ошибки, происходящие от его
наблюдений равноденствий, последних в ряду его обширных
наблюдений; но, поскольку он уже построил на их
основе всю свою систему, он предпочел, вероятно,
пожертвовать своими наблюдениями, чем начинать все сначала.
Поскольку, однако, никто не мог ему возразить, он сделал
вид, что ошибочные равноденствия в его таблицах были
истинными и наблюдались. Мы имеем множество приме-
5 Клавдий Птолемей
129

ров современных астрономов (речь идет о середине
XVIII в.— В. Б.), которые настолько обожают свои
построения, что фальсифицируют наблюдения (например,
Лансберг и Риччиоли) *. Птолемей, который,
по-видимому, не мог и представить себе, чтобы кто-нибудь был
способен уличить его в обмане, легко мог впасть здесь в
ошибку».
На ошибки Птолемея, в частности в его наблюдениях
моментов равноденствий, не раз указывал астроном и
историк науки Ж. Б. Деламбр (1749—1822).
Как мы помним, основную роль в построении теории
движения Луны у Птолемея играли наблюдения лунных
затмений, причем он использовал наблюдения вавилонских
астрономов начиная с VIII в. до н. э., наблюдения
греческих астрономов (И в. до н. э.) и свои собственные.
Анализитзуя эти наблюдения, Р. Ньютон объявил почти все
их «сфабрикованными», хотя все затмения, о которых идет
речь, содержатся в «Каноне затмений» Т. Оппольцера.
Впрочем, для рассматриваемых эпох канон Оппольцера
сам содержит значительные ошибки во времени и долготе
(для солнечных затмений). Ошибки канона Оппольцера
для начала нашей эры достигают 20 мин, для —500 г.
40 мин, для —1000 г. 60 мин [73]. Поэтому мы решили
сравнить наблюдения лунных затмений, приводимые в
«Альмагесте», со «Специальным каноном затмений»
Ф. Гинцеля [ 105], не содержащим подобных ошибок
(табл. 10). При переводе времен принята разность долгот
Рим—Александрия 1 ч 10 мин, Рим—Вавилон — 2 ч 10 мин.
В табл. 10 даны: местное время середины затмения,
наибольшая фаза затмения в дюймах, т. е. двенадцатых
долях диаметра Луны. В графе «город» В означает
Вавилон, А — Александрия.
Буквой А мы обозначили разность моментов по Гинце-
лю и Птолемею. Подсчитав среднее квадратичное
значение этой величины, получим Ä=±28 мин. Иначе говоря,
в среднем ошибка в моменте середины затмения
составляет полчаса. Этому не приходится удивляться, поскольку
древние наблюдатели фиксировали не момент середины
затмения, а момент его начала, и к тому же весьма
приблизительно. Для примера воспроизведем одно из сообщений
1 Филипс фон-Лансберг (1561-1632) - немецкий астроном,
составитель планетных таблиц, предсказал прохождение Венеры по
диску Солнца в 1639 г.; Джованни Батиста Риччиоли (1598—
1671) -итальянский астроном, автор современной системы
названий лунных объектов.
130

Таблица 10. Сравнение параметров лунных затмений
Дата
—720 Ш 19
—719 Ш 8
—719 IX 1
—620 IV 22
-522 VII16
—501 XI19
-490 IV 25
—382 XII23
-381 VI18
-381 XII12
—200 1X22
—199 HI 19
—199 1X12
—173 V 1
—140 127
125 IV 5
133 V 6
134 X 20
136 Ш 6
Время середины
Гинцель
21
23
19
4
23
23
22
7
21
22
18
0
2
1
22
20
22
22
3
27
40
51
52
24
44
39
53
00
59
37
54
21
42
00
51
51
48
45
ч, мин
затмения
Птолемей
21
0
20
5
23
23
23
7
21
23
19
1
2
2
22
20
23
23
4
30
00
30
50
00
36
30
20
06
00
00
20
15
20
10
24
15
00
00
А,
мин
—3
—20
—39
-58
+24
+8
—51
+33
-6
—1
—23
-26
+6
-38
—10
+27
—24
—12
-15
Величина
затмения

Гинцель
18,7
1,8
6,4
1,6
6,2
2,1
1,0
2,4
5,7
17,6
8,6
16,9
19,4
7,6
3,3
1,8
12,9
10,2
5,3
Птолемей
Полное
3
>6
3
6
3
2
Малая
доля
—
Полное
—.
Полное
Полное
7
3
2
>12
10
6
Город
В
В
в
в
в
в
в
в
в
в
А
А
А
А
А
А
А
А
А
о наблюдениях лунного затмения в Вавилоне, а также все
операции, проделанные Птолемеем для получения
момента его середины. Цитируем из «Альмагеста»: «Первое
(из этих затмений,— В. Б.) наступило в первый год Мар-
докемпада, в месяце тот, 29/30 числа по египетскому
календарю 2. Затмение началось, как говорят, более часа
спустя после восхода Луны и было полным. Поскольку
Солнце было в это время в конце созвездия Рыб3 и ночь
длилась около 12 равноденственных часов, начало
затмения наступило, очевидно, за 47г равноденственных часа
до полуночи, а середина затмения (поскольку оно было
полным) —за 27г часа до полуночи» [17. С. 191]. Вот ка-
2 19/20 марта -720 г.
3 В той его части, которая прилегает к созвездию Овна.
13J
5*

кая цепочка оценок и расчетов стоит за числом 21 ч 30 мин
первой строки табл. 10.
Разобьем эту цепочку на отдельные звенья. t Луна в
полнолуние восходит одновременно с заходом Солнца.
8 дни, близкие к равноденствию, это происходит около
18 ч на всех широтах. «Более часа спустя» Птолемей
понимает как 17г ч, т. е. затмение началось в 19 ч 30 мин.
Поскольку затмение было полным, Птолемей принимает
его длительность равной 4 ч, отсчитывает половину этого
интервала и считает, что середина затмения наступила в
21 ч 30 мин.
Как видим, здесь два источника ошибок. Весьма
приблизительное сообщение наблюдателя, что затмение
началось «более часа спустя» после восхода Луны, можно
понять и как через 1 ч 10 мин, и как через 1 ч 40 мин.
Далее, не всякое полное лунное затмение длится ровно
4 ч. Так, длительность затмения 4 мая 1985 г. (величина
14,9 дюйма) составила 3 ч 20 мин [23], в случае затмения
9 января 1982 г. (16,0 дюйма) — 3 ч 25 мин, и только
затмение 6 июля 1982 г. (20,7 дюйма) продолжалось 3 ч
56 мин [22].
Так что не приходится удивляться тем
ошибкам в моментах середины затмений, которые были
допущены Птолемеем, а тем более утверждать на основе этих
ошибок, что все эти наблюдения «сфабрикованы».
Удивляться приходится другому. Как сумел
Птолемей, опираясь на такие наблюдения, построить свою
теорию движения Луны, которая, по уже приведенной в гл. 8
оценке Н. И. Идельсона, является великолепной,
а открытие Птолемеем эвекции — тоже на основе этих
наблюдений — замечательным фактом в истории
астрономии.
Если Птолемей, как считает Р. Ньютон, подделывал
свои и чужие наблюдения, подгоняя их под свою теорию,
то, спрашивается, на основании чего же он ее построил?
Ведь не взял же он ее с потолка?! А что эта теория
работала полтора тысячелетия и даже потом, как показали
расчеты на ЭВМ, способна была выдержать «состязание»
с позднейшими теориями — это факт. Мы отнюдь не
отрицаем, что Птолемей допускал и ошибки (не случайные,
а полусознательные, как в случае с прецессией) и вполне
мог вводить в свои и чужие наблюдения некоторые
поправки, отдавая теории приоритет перед наблюдениями.
Но это ни на йоту не уменьшило значения его трудов в
астрономии. Птолемей первый (или один из первых) со-
132

Ставил учебник по астрономии 4, служивший
одновременно справочником. Ни один учебник, пи один справочник
в истории науки (за исключением «Начал» Евклида) не
служил так долго и плодотворно.
А вот что говорит о соотношении между теорией и
наблюдениями сам Птолемей. В «Четырехкнижии»
(книга I, гл. 2) он обсуждает вопрос о сопоставлении древних
наблюдений с новыми и об ошибках, проистекающих из
неумелого пользования ими. Птолемей указывает, что
обнаруживающееся в большинстве случаев несовпадение
между ними объясняется тем, что обработка их в целом
носит лишь приблизительный, а не вполне достоверный
характер. Наблюдения не могут совпасть и потому, что
полного возвращения небесных светил в прежнее
состояние нельзя ожидать либо вообще, либо в срок, обозримый
человеческим умом [34].
Итак, Птолемей ясно понимал, что полного
совпадения результатов старых и новых наблюдений добиться
практически невозможно из-за отсутствия простой
периодичности в небесных явлениях, а также из-за неточности
методов обработки. Но дело не в причинах, которые
приводит Птолемей, а в том, что он прекрасно сознает:
полного согласования наблюдений разных эпох между собой
и с теорией достичь на уровне науки его времени
невозможно.
Как же отнеслись современные ученые к
«разоблачениям» Р. Ньютона? Сам Р. Ньютон в своей книге горько
жалуется на то, что крупнейшие специалисты по
Птолемею О. Педерсен и О. Нейгебауэр даже не упоминают в
своих монографиях о его работах [77, 119]. Можно
привести также высказывание автора новейшего перевода
«Альмагеста» на английский язык Дж. Тумера (Лондон) :
«Задача (о манипуляциях Птолемея с данными
наблюдений и вычислений.— В, Б.) представляет интерес и
заслуживает содержательного и критического обсуждения.
4 Астроном первой половины I в. до н. э. Гемин из Родоса
написал книгу «Элементы астрономии», где излагаются основы
сферической астрономии. В ней Гемин сообщает, что планетные
теории он изложит в другой книге, но она не дошла до нас.
Современник Гемина Клеомед написал «Теорию небесных тел»,
в которой приводятся синодические периоды планет и
рассматриваются их отходы от эклиптики. Кроме того, в этой книге
содержатся важные сведения об измерении Земли Эратосфеном
и Посидонием. Современник Птолемея Теон из Смирны написал
«Изложение математических вопросов, могущих быть полезными
при изучении Платона», в котором есть и астрономический
раздел [97]. Все эти книги по своей полноте намного уступают
«Альмагесту».
133

К сожалению, недавняя книга Р. Ньютона на эту тему не
содержит ничего подобного, а скорее стремится
дискредитировать весь труд» [131. С. VIII].
С горячими возражениями Р. Ньютону выступил
американский историк науки О. Гингерич. Некоторые из них
мы использовали в этой главе. В конце своей острой
полемической статьи Гингерич привел два случая из жизни
Исаака Ньютона и Альберта Эйнштейна [104].
Когда известный наблюдатель, королевский астроном
Джон Флемстид прислал Ньютону выполненные им
наблюдения положений Луны, чтобы Ньютон сравнил их со
своей теорией лунного движения, Исаак Ньютон ответил:
«Пусть лучше ваши наблюдения разошлись бы с моей
теорией — это говорило бы больше в пользу Вашей
репутации как наблюдателя, чем если бы Вы держали их в
тайне до Вашей смерти или опубликовали бы вне связи
с теорией. Потому что теория служит мерой их точности
и позволяет признать Вас точнейшим наблюдателем,
когда-либо жившим на свете».
Альберт Эйнштейн, получив от А. Эддингтона
телеграмму о том, что наблюдения, сделанные во время
полного солнечного затмения, подтверждают предсказанное
общей теорией относительности гравитационное
отклонение лучей звезд, на вопрос студента, что бы он стал
делать, если бы подтверждения не получилось, ответил:
«Я послал бы дорогому лорду Эддингтону мои
сожаления — теория должна быть верна».
Приведя эти высказывания двух великих ученых в
пользу примата теории перед наблюдениями, Гингерич
заявляет: «Когда Ньютон и Эйнштейн будут признаны
обманщиками, я готов и Птолемея отнести к их числу.
Пока же я предпочту считать его величайшим астрономом
античности».
Соглашаясь с Гингеричем в его оценке Птолемея как
ученого, мы все же не можем отдать безусловное
предпочтение теории перед наблюдениями (или результатами
эксперимента). Все зависит от того, какова теория и
каковы наблюдения. К сожалению, наблюдения прошлого
невоспроизводимы. Можно провести много новых
наблюдений с самыми совершенными приборами современности,
но нельзя воспроизвести наблюдений далекого прошлого.
И то, что в труде Птолемея они доведены до нас, что мы
можем ими пользоваться для изучения различных
вековых изменений в Солнечной системе и за ее пределами,
в этом состоит еще одна заслуга Клавдия Птолемея.
134

Правда, Р. Ньютон предупреждает нас: ради своей
теории Птолемей подправлял и старые наблюдения, они
дошли до нас в искаженном виде. На примере с лунными
затмениями мы видим, что серьезных искажений в
наблюдениях, приводимых Птолемеем, нет. В других
случаях «поправки» Птолемея легко выявляются, как,
например, в координатах звезд каталога, и могут быть
исключены.
На развитие астрономии как науки эти мелкие
поправки не повлияли и не могли повлиять. Поэтому
совершенно неправильно мнение Р. Ньютона о том, что для
науки было бы лучше, если бы «Альмагест» не дошел ни
до нас, ни до арабских и среднеазиатских ученых.
А давайте попробуем представить себе, читатель, что
бы произошло, если бы рукопись «Альмагеста» погибла
бы в огне пожара, уничтожившего Александрийскую
библиотеку. Страшно подумать, но все-таки попробуем. Мы
не узнали бы ничего (или почти ничего) о наблюдениях
вавилонян, о работах Гиппарха и самого Птолемея. Не
было бы звездного каталога —до самого Улугбека! Не
было бы теории движения Солнца, Луны, планет. Впрочем,
быть может кто-то из ученых последующих поколений
взял бы на себя этот тяжкий труд. Но кто именно? Сабит
ибн Корра? Аль-Баттани? Бируни? Ат-Туси? Но даже
если бы они сделали это, то почти с тысячелетним
опозданием!
Этот вопрос — часть более общего вопроса: что бы
было, если бы такой-то великий ученый вообще не
существовал? Например, если бы Исаак Ньютон умер в
детстве или погиб на дуэли в юности, как Эварист Галуа?
Конечно, теория всемирного тяготения была бы
разработана другим ученым. Ведь к идее всемирного тяготения
независимо от Ньютона пришел Роберт Гук, многие
другие его открытия независимо сделали Декарт и Лейбниц.
Но наука безусловно пострадала бы.
История науки показывает нам немало примеров
иного рода. Ученые жили, работали, но некоторые их труды
до нас не дошли. Мы уже приводили множество подобных
примеров. А также фактов недавнего обнаружения работ
классиков науки, считавшихся неизвестными или
утерянными. Рукопись «Малого комментария» Коперника была
обнаружена только в 1878 г. в Вене. Лишь в 1967 г. была
найдена заключительная часть первой книги «Планетных
гипотез» Птолемея. В 1906 г. было обнаружено письмо
Архимеда к Эратосфену.
135

Значит, надо искать. Большие перспективы сулит
исследование рукописей на арабском и персидском языках,
хранящихся в библиотеках Ташкента, Душанбе,
Ленинграда. Оно уже начато, но отнюдь не закончено.
Интересные находки могут быть сделаны в хранилищах других
стран. Пожелаем же успеха тем, кто ищет.
Глава 12
Работы Птолемея
в области географии
Мы подробно познакомились с Птолемеем-астрономом.
Конечно, работы в области астрономии — основные в его
научном творчестве. Основные, но не единственные.
Большой вклад внес Птолемей в математическую картографию,
оптику, теорию музыки (гармонию). Об этом мы
постараемся рассказать в трех следующих главах.
До Птолемея география в античном мире носила
чисто описательный, страноведческий характер. Обширные
описания различных стран и народов, их быта, обычаев,
верований оставил нам замечательный историк и географ
древности Геродот (ок. 480—425 до н. э.). Но если страны,
относящиеся к Средиземноморью и к берегам Черного
моря, описаны им достаточно подробно и с весьма
ценной информацией, то об Индии, Аравии и странах,
находившихся на севере от Причерноморья, Геродот сообщает
множество сказочных небылиц.
Военные походы (Ксенофонта в V в. до н. э.,
Александра Македонского в 332—322 гг. до н. э.)
использовались для изучения и описания тех стран, по которым
пролегал путь завоевателей. Ксенофонт в своем «Анабазисе»
дал описание Малой Азии и Армении. Полководцы
Александра Македонского и ученые, сопровождавшие его
армию, составили описание Индии. Армию Александра
сопровождали специальные «счетчики шагов», которые
должны были измерять расстояния между населенными
пунктами, считая шаги. По описаниям и подсчетам
участников походов карту известной области Земли, Ойкумены,
составил Дикеарх из Мессины (ученик Аристотеля).
Это направление в географии античного периода
заключает «География» Страбона (65 г. до п. э.—2 г. н. э.)
136

в семнадцати книгах. Хотя Страбон в течение своей
долгой жизни совершил несколько далеких путешествий,
большая часть его описаний основана не столько на его
собственных наблюдениях, сколько на обобщении
описаний других авторов. Первые две книги его «Географии»
носят вводный характер, в книгах III—X описывается
Европа, в книгах XI—XVI — Азия, в книге XVII —
Африка. Страбон много описывал такие явления, как
землетрясения, извержения вулканов, работа рек, а также
климат различных поясов земного шара. То, что Земля имеет
шарообразную форму, Страбон знал, опираясь на данные
Эратосфена, но он предпочитал собирать сведения о тех
или иных странах у путешественников и моряков, а не
использовать методы математической картографии.
Основы второго направления в географии —
математической картографии — заложил Эратосфен, весьма точно
определивший размеры земного шара.
Правда, еще в IV в. до н. э. мореплаватель Пифей из
Массилии (современный Марсель) определял широты
городов по формуле -ср=о+^о, где о —склопение светила,
z0 — его зенитное расстояние в меридиане. Так, широта
Массилии, по определению Пифея, равна 43° 12', а в
действительности — 43° 17'. Пифей определил этим
способом широты ряда городов Атлантического побережья
Европы и Великобритании и сумел даже определить длину
дуги в 1°, получив один раз 105 км, а другой—112 км
(верное значение — 111,11 км). Более точно эту величину
определил Эратосфен.
Как известно, метод Эратосфена заключался в
определении дуги меридиана между Александрией и Сиеной
в день летнего солнцестояния. В этот день, по рассказам
лиц, посещавших Сиену, Солнце в полдень освещало дно
самых глубоких колодцев и, значит, проходило через
зенит. Следовательно, широта Сиены равнялась углу
наклона эклиптики к экватору, который Эратосфен
определил в 23° 51' 20". В тот же день и час в Александрии тень
от вертикального столбика гномона закрывала 1/50 часть
окружности, центром которой служил кончик гномона. Это
значит, что Солнце отстояло в полдень от зенита на 1/50
часть окружности, или на 7° 12'. Приняв расстояние между
Александрией и Сиеной равным 5000 стадиев, Эратосфен
нашел, что окружность земного шара равна 250 000
стадиев. Вопрос о точной длине стадия, принятого Эратосфеном,
долгое время служил предметом дискуссий, поскольку
существовали стадии длиной от 148 до 210 м [60]. Боль-
137

шинство исследователей принимали длину стадия 157,5 м
(«египетский» стадий). Тогда окружность Земли равна,
по Эратосфену, 250 000 • 0,1575 = 39 375 км, что очень
близко к действительному значению 40 008 км. Если же
Эратосфен пользовался греческим («олимпийским»)
стадием длиной 185,2 м, то получалась окружность Земли
уже 46 300 км.
По современным измерениям [97] широта Музея в
Александрии 31° 11,7х, широта Асуана (Сиены) 24° 5,0',
разница широт 7° 6,7', чему соответствует расстояние
между этими городами 788 км. Деля это расстояние на 5000,
получим длину стадия, использованного Эратосфеном,
157,6 м. Значит ли это, что он использовал египетский
стадий?
Этот вопрос сложнее, чем может показаться. Уже одно
то, что Эратосфен привел явно округленное число — 5000
стадиев (а, скажем, не 5150 или 4890) не внушает к нему
доверия. А если оценка Эратосфена была завышена хотя
бы на 15%, получим, что он использовал египетский
стадий в 185 м. Решить этот вопрос пока нельзя.
Эратосфен написал большой труд под названием
«География» в трех книгах, к сожалению не сохранившийся.
Однако о его содержании мы знаем по довольно
подробному изложению Страбона. В первой книге Эратосфен
приводит географические описания своих
предшественников начиная с древнейших времен. Он рассказывает о
первых географических картах, построенных Анаксиманд-
ром и Гекатеем. Во второй книге изложены
доказательства шарообразности Земли и описанный выше метод
измерения ее размеров. Эратосфен (как и многие другие)
считал Ойкумену островом, окруженным со всех сторон
океаном. Он впервые высказал мнение, что можно достичь
Индии морским путем, плывя на запад. В третьей книге
Эратосфен давал подробные комментарии к составленной
им карте Ойкумены.
С резкой критикой «Географии» Эратосфена выступил
Гиппарх, посвятивший этому вопросу отдельную книгу,
также до нас не дошедшую. О ней мы, как и о труде
Эратосфена, знаем из «Географии» Страбона. Гиппарх считал
недопустимым использовать для построения карт земной
поверхности свидетельства путешественников и моряков
о той или иной удаленности географических пунктов друг
от друга.
Для построения карт Гиппарх признавал лишь
точные определения широт и долгот. В те времена это было
138

не так просто. Широты можно было измерять, как это
делал Пифей, по высоте звезд в меридиане или по высоте
Солнца в полдень (определяемой, например, с помощью
гномона). Делать это можно было в любой ясный день или
ночь. Хуже обстояло дело с долготами. Для определения
разности долгот двух пунктов в то время существовал
только один способ: одновременные наблюдения лунных
затмений, которые происходят нечасто (см. с. 88), да и
пасмурная погода может помешать.
Гиппарх ввел в употребление сетку меридианов и
параллелей в качестве математической основы для
составления карт земной поверхности. Наряду с Эратосфеном
его по праву можно считать одним из основоположников
математической картографии [82].
Определенный вклад в измерение размеров Земли внес
Посидоний (ок. 135—50 гг. до н. э.), работавший, как и
Гиппарх, на Родосе, а позже — в Риме. Он был
философом-стоиком, но много занимался и математикой. Его
метод измерения размеров Земли был хотя и оригинален, но
уступал по точности методу Эратосфена. Посидоний
заметил, что яркая звезда Канопус в созвездии Корабль
Арго (теперь в созвездии Киля) даже в верхней
кульминации видна на Родосе у самого горизонта. В
Александрии же, согласно Посидонию, она может подниматься над
горизонтом «приблизительно на четвертую часть одного
знака», т. е. на 7°30' (один знак зодиака
соответствует 30°).
Следовательно, разность широт Родоса и
Александрии, по Посидонию, равнялась 7° 30', тогда как в
действительности она равна 5° 14'. Дальше можно не продолжать,
хотя против надежности метода Посидония можно
привести еще ряд аргументов (неучет рефракции, невозможность
точно определить расстояние по морю и др.). Посидоний
получил окружность Земли равной 240 000 стадиев, но
здесь уже нет смысла обсуждать, какой именно стадий
использовал Посидоний '.
Таковы были работы предшественников Птолемея.
Впрочем, в своей «Географии» он ссылается еще на одного
своего предшественника — географа Марина Тирского
(т. е. родом из города Тира), который, как й Птолемей,
развивал методы математической картографии. К
сожалению, время жизни Марина Тирского нам точно не известно
1 Обсуждение старинных методов определения размеров Земли
имеется в работах А. В. Клименко [60, 61].
Д39

(ориентировочно I в. н. э.). Именно Марин предложил
отсчитывать долготы от одного из Канарских островов,
чтобы все долготы Ойкумены имели один знак [82]. Этот
способ отсчета долгот Птолемей у него и позаимствовал. Для
построения карт Птолемей использовал прямоугольную
проекцию, предложенную Марином. Марин, по-видимому, тоже
определял размеры земного шара. По свидетельству
Птолемея, он нашел, что 1/360 окружности земного меридиана
равна 500 стадиям, так что вся окружность составляет
180 000 стадиев. Птолемей неоднократно подчеркивает,
однако, что эта величина получена Марином в результате
вычислений (а не измерений). Академик И. Ю. Крачков-
ский [64], ссылаясь на средневекового арабского географа
Йакута2, пишет, что Птолемей выполнил определение дуги
одного градуса меридиана в 66 2/з мили на основе
измерений в Верхней Месопотамии.
Действительно, такое измерение было выполнено еще
до Птолемея (но не им самим) и именно в Верхней
Месопотамии между городами Ракка (на реке Евфрат) и Тад-
мор (Пальмира) 3. Подробное исследование обстоятельств
этого измерения сделал А. В. Клименко [60]. Это
измерение не следует путать с другим измерением того же типа,
выполненным группой из четырех арабских астрономов в
827 г. в долине Синджара, на 250 км восточнее Ракки.
Разность широт Ракки и Тадмора была определена в
1°21/ (фактически 1°22'), а расстояние между ними —
в 90 вавилонских миль (1 миля = 1975,5 м). Измерители
не учли, что Ракка и Тадмор имеют разность долгот в 45'.
Расстояние между городами было завышено на 7%. В
результате длина градуса была получена равной 66 2/з мили=
=131,7 км вместо 111 км, а окружность Земли —24 000
миль, или 47 413 км. Вавилонская миля равнялась 77г
ионийских стадиев, иначе говоря 24000 миль
соответствовали 180 000 стадиев. Вот откуда произошло число,
приводимое Птолемеем.
Заметим тут же, что измерение, проведенное в 827 г.
в долине Синджара, оказалось намного точнее. Для
длины градуса было получено 562/з мили = 111,9 км, а для
окружности земного шара — 40 300 км.
«География» Птолемея —это громадный том (ненамно-
2 Имеется в виду ученый XIII в. Йакут ар-Руми аль-Хамави,
автор так называемого «Словаря стран».
3 Об этом же измерении (с указанием, что оно выполнено
«древними учеными») свидетельствует Бируни.
140

го уступающий «Альмагесту»). В этой книге приводятся
долготы и широты примерно 8 000 населенных пунктов.
Книга иллюстрируется 27 картами: одной общей и 26 по
регионам (Птолемей их называет греческим словом
«епархия», в латинских переводах фигурируют «провинции»).
Общая карта мира приписывается александрийскому
географу Агатодемону.
К сожалению, подлинные карты Птолемея до нас не
дошли, так что мы можем судить о них только по копиям
и реконструкциям.
«География» Птолемея, называемая также
«Географическим руководством», состоит из восьми книг. В I книге
Птолемей излагает свои представления о земном шаре и
дает понятие о географических координатах: широте и
долготе.
В основе его взглядов на географическую науку лежит
математический подход к составлению карт и
определению положений городов и иных пунктов. Птолемей резко
критикует страноведческий подход, основанный лишь на
использовании качественных описаний
путешественников, без математической основы.
Книги II—VII посвящены описанию отдельных
регионов. Согласно представлениям Птолемея, Ойкумена
расположена в интервале долгот (в принятой им системе) от 0
до 180° и в интервале широт от 20° ю. ш. до 63° 30' с. ш.
За начальный меридиан, как уже говорилось, принят
меридиан, проходящий на 0,5° западнее Островов
Блаженных, т. е. Канарских островов. Поскольку самый западный
из них, о-в Пальма, имеет долготу 17°45' з. д., получаем,
что начальный меридиан у Птолемея имеет долготу
18°15' з. д.
Это не значит, однако, что все долготы у Птолемея
смещены на эту величину против современных долгот.
Сравнение координат городов, существовавших в эпоху
Птолемея и существующих до сих пор, показывает, что
сетка долгот у Птолемея как бы растягивается на восток.
Поэтому долготы Лондона (Лондиниума) и Парижа
(Лютеции) отличаются от современных на 20° и 21°
соответственно, долгота Херсона — на 2il/2°, долгота Феодосии —
на 28°, долгота Ростова-на-Дону (Навариса) — на 30°,
долгота Самарканда — на 45°.
Представляет интерес сравнить широты таких городов.
Сравнение сделано в табл. И, откуда видно, что для этих
восьми городов средняя квадратичная ошибка в
определении широты у Птолемея составляет ±90' (1 7а граду-
141

Титульный лист «Географии» Птолемея (базельское издание
1540 г. Под ред. С. Мюнстера)
са). Для трех городов ошибки превосходят 2°, но для пяти
остальных они меньше градуса.
Перейдем к изложению содержания II—VII книг
«Географии» Птолемея4. В шестнадцати главах книги II
описаны страны Западной Европы. Среди них (если
двигаться с запада на восток) Гиберния (Ирландия), Альбион
(Великобритания), Испания (сюда входят современные
Испания и Португалия), Галлия Аквитания (Франция),
4 В этом изложении мы будем следовать описанию труда
Птолемея, приведенному в книге П. Г. Булгакова, Б. А. Розенфельда
и А. А. Ахмедова [34], в которой даны и современные названия
географических объектов, упоминаемых Птолемеем.
142

Таблица 11. Сравнение широт городов по Птолемею
и по современным данным
Название города
современное
Птолемей
Широта
современная Птолемей
Лф
Лондон
Париж
Неаполь
Херсон
Кабул
Дамаск
Тегеран
Анкара
Лондиниум
Лютеция
Неаполис
Борисфен
Ортоспана
Дамаскос
Рагая
Анкира
+51°40'
48 40
40 50
46 40
34 30
33 20
35 15
40 00
+ 54°00'
48 30
40 30
49 00
35 00
33 00
34 20
42 00
+ 2°20'
—0 10
-0 20
+2 20
+0 30
—0 20
—0 55
+2 00
Галлия Бельгика (северо-восточная Франция, Бельгия и
Нидерланды), Великая Германия (ФРГ, ГДР и часть
Польши до Вислы), Реция, Винделиция и Норик (Бавария и
Австрия), Паннония (Венгрия). В книге III
рассматриваются в основном страны Восточной Европы. Среди
них — Иллирия (адриатическое побережье Хорватии),
Далмация (побережье Боснии и Албании), Италия,
острова Корсика, Сардиния и Сицилия, Европейская Сар-
матия (Восточная Европа от Вислы до Дона), Херсо-
нес Таврический (Крым), Дакия (Румыния), Верхняя
и Нижняя Мезия (Сербия и Болгария), Фракия (южная
Болгария и европейская часть Турции), Македония, Эпир,
Ахейя (Греция), Пелопоннес, острова Эвбея и Крит.
Азиатскую Сарматию, т. е. Восточную Европу от Дона до
Волги, Птолемей относит к Азии и описывает в книге V.
Восточной границей Европы он считает р. Танаис (Дон).
Птолемей неправильно представлял себе северные
страны и моря Европейского материка. Полуостров
Скандинавию он считал небольшим островом Скандия. Балтийское
море он считал частью Северного моря, объединяя эти
моря в Сарматский океан. Британские острова на его
картах сильно искажены, особенно в их северной части.
Интересно, что у Птолемея уже имеются названия
некоторых славянских племен. Так, он упоминает венедов
и даже называет по их имени часть Балтийского моря Ве-
недским заливом. Он называет сербов, а упоминаемые им
ставаны и свовены — это славяне и словены, буланы —
поляне. Таким образом, уже в птолемеевскую эпоху сла-
143

вяиские народы существовали й населяли часть Восточной
Европы.
Из гор Птолемей упоминает Альпы, Судеты, Карпаты
и Сарматские горы. Трудно сказать, что подразумевал
Птолемей под Сарматскими горами. Они, по Птолемею,
расположены севернее Карпат. Возможно, что он
предполагал существование каких-то северных отрогов Карпат.
Азовское море Птолемей называет Меотидой, по
наименованию племени меотов (адыгов). Он упоминает
несколько рек, впадающих в него. Кроме Танаиса (Дона),
перечислены Вардан, или Гипанис (нынешняя Кубань), Порит
(ныне Миус), Лик (Кальмиус), Марубий (Кагальник),
а всего 13 рек, из которых семь рек впадают с востока,
а шесть — с запада.
Волгу Птолемей называет Ра. Такое название
существовало у древних народов Поволжья; ведь до сих пор на
мордовском языке Волга называется Рав.
В IV книге своей «Географии» Птолемей описывает
Африку. Он делит ее на следующие 12 «епархий»:
Мавритания Тиигитанская, Мавритания Цезарейская, Нумидия,
собственно Африка, Киренаика, Мармарика, Ливия
внешняя, Нижний Египет, Средний Египет, Фиваида, Ливия
внутренняя, Эфиопия, Верхний Египет, области южнее
Эфиопии. Крайним южным пунктом, который он
упоминает, является гора Бардит (16° ю. ш.), хотя южной
границей Ойкумены Птолемей считает параллель 20° ю. ш.
Часть Африки, входящая в Ойкумену, изображена
Птолемеем на четырех картах. Ее очертания искажены по
сравнению с современными, прежде всего за счет
растягивания в долготном направлении. Так, Средиземноморское
побережье Африки от Тингина (ныне Танжер) до Кассиу-
ма (Порт-Саид) охватывает у Птолемея более 57° по
долготе вместо 38° в действительности. Южнее экватора
Африка у Птолемея расширяется к востоку и западу. Кроме
того, налицо ряд других отклонений формы побережья
(как Атлантического, так и Средиземноморского) от
правильной.
Описывая (и притом довольно подробно) реку Нил и
города бассейна Нила, Птолемей смещает его исток к югу
на 9°30/ в сторону Лунных гор. Страну в Восточной
Африке, расположенную на месте нынешних Сомали и Кении,
Птолемей называет Барбарией5. Самый южный город в
5 По-видимому, это название имеет следующий источник. Есть
сведения, что племена берберов, ныне населяющие Алжир и
144

Восточной Африке, упоминаемый Птолемеем, — Рапта на
7° ю. ш. (ныне Дар-эс-Салам в Танзании), древний порт
и торговый центр Африки.
В «Географии» Птолемея в Африке указаны 40 гор,
в том числе Лунные горы, Ливийские горы, Большой и
Малый Атлас, Солнечная гора и др. Из рек, кроме Нила,
указаны р. Дарадус (ныне Сенегал), Нигейр (Нигер) и
многие другие.
В той же IV книге Птолемей описывает острова
Красного моря (перечислено 29 островов), а также острова
Средиземного моря, прилегающие к африканскому
материку.
Более половины «Географии» (книги V—VII)
посвящено описанию Азии (рис. 31). При этом если страны
Передней Азии, Ближнего и Среднего Востока описаны
довольно правильно, то по мере перехода к более
восточным странам сведения Птолемея становятся все менее и
менее точными.
Вот какие «епархии» Птолемей относит к Азии: Понт,
Вифииия, собственно Азия, Ликия, Галатия, Пафлагония
и Писидия, Памфилия и Исаврия, Каппадокия, Армения
малая, Киликия, Азиатская Сарматия, Колхида, Иверия,
Албания, Армения великая, о-в Кипр, Сирия дольная,
Сирия Финикия, Сирия Палестина и Иудея, Аравия
Каменистая, Месопотамия, Аравия Пустынная, Вавилония,
Ассирия, Мидия, Сузиана, Персида, Парфия, Кармания
Пустынная, Аравия Счастливая, другая Кармания, Гирка-
ния, Маркиана, Бактриана, Согдиана, страна саков,
Скифия, Серика, Ария, Паропамис, Дрангиана, Арахосия,
Гедросия, Индия, страна синов, о-в Тапробана.
Большинство из этих названий требуют пояснений (см.
карту на рис. 32) [55]. Понт и Вифиния —это части
черноморского побережья нынешней Турции, прилегающие к
Босфору. Галатия расположена южнее. Каппадокия
находится восточнее, также на территории современной
Турции. Южная часть Турции вдоль побережья Средиземного
моря называлась тогда Киликией. Остальные части
современной Турции Птолемей называет «собственно Азией».
Колхида и Иверия — черноморское побережье и горные
районы Грузии соответственно, Албания — это теперь
Азербайджанская ССР (не путать с Албанией на Балка-
Марокко, раньше заселяли Восточную Африку. Об этом говорит
название г. Бербера в Сомали. Птолемей же превратил Бербершо
в Барбарию (от слова «варвары» - так тогда греки и римляне
называли другие народы).
145

146

пах). Армения в эпоху Птолемея занимала не только
нынешнюю территорию Армянской ССР, но и значительную
часть Восточной Турции. Западная ее часть называлась
Малой Арменией. Гиркания прилегала к южному берегу
Каспийского моря (часть современного Ирана), Мидия
была расположена к юго-западу от нее, дальше на юг
простиралась Сузиана, а у побережья Персидского залива —
Персида. Все эти «епархии» тоже находились на
территории современного Ирана. Восточнее Мидии находилась,
Парфия (Восточный Иран), а восточнее Персиды —Кар-
мания. Еще дальше на восток от Кармании, вдоль
северного берега Аравийского моря, располагалась Гедросия,
захватывающая юго-восточную часть Ирана и западную
часть Пакистана. Арахосия располагалась к северу от нее,
на территории современного Афганистана. Еще севернее
находилась Бактриана (северный Афганистан), а затем
Согдиана (на территории нынешней Узбекской ССР). На
северо-восток от нее простиралась страна саков (юг
Казахстана, по берегам Сырдарьи). Под Скифией
подразумевалась часть территории РСФСР от Волги до озера Балхаш,
Маркиана — часть Туркменской ССР. Азиатской Сарматией
назывался тогда Северный Кавказ. Тапробана — это остров
Шри-Ланка.
Птолемей считал Индийский океан замкнутым морем,
ограниченным с запада и с юга берегами Африки, с
севера — Счастливой Аравией, Персидой, Гедросией и Индией,
с востока — страной синов. Юг Малаккского полуострова
Птолемей называл Золотым Херсонесом. Серика — это
Китай («страна шелка»), а страна синов — Индокитай.
Несмотря на многочисленные ошибки в изображении тех
или иных географических регионов, труд Птолемея
сохранил свое значение почти до XVII в. Хотя в работах
арабских и среднеазиатских ученых (особенно Мухаммеда
аль-Хорезми и Абу-Райхана Бируни) многие ошибки
Птолемея были исправлены и координаты ряда азиатских
городов определены заново, «География» Птолемея
продолжала использоваться, а в XII в., как и «Альмагест»,
попала в Европу. С началом книгопечатания, в период
между 1475 г. и 1600 г., было выпущено 42 издания этой
книги [71]. С шестью из них, хранящимися в отделе редких
книг Научной библиотеки им. А. М. Горького при МГУ
и в Музее книги Государственной библиотеки им. В. И.
Ленина, автору удалось познакомиться. Большинство из
них были изданы на латинском языке, в разных
переводах [1, 4, 6, 7, И].
147

148

История изданий «Географии» Птолемея в XV—
XVII вв. (в буквальном смысле — история с
«Географией»!) сама по себе представляет немалый интерес,
потому что до некоторой степени отражает развитие в ту
эпоху географических познаний, техники книгопечатания,
общей культуры и отношения к культурному наследию
античности. В нашем обзоре мы будем следовать
изложению этого вопроса в подробном очерке Р. А. Скелтона
[129].
Первое издание «Географии» (без карт) было
выпущено в 1475 г. в Виченце (Италия) в латинском переводе
Джакопо д'Анджело, выполненном еще в 1406 г. Спустя
два года, в 1477 г., в Болонье было выпущено первое
издание с картами. В 1482 и 1486 гг. Николай Герман
выпустил два издания «Географии» в Ульме (Германия). Эти
издания были подготовлены весьма тщательно и по
точности воспроизведения названий и координат населенных
пунктов превосходят многие последующие издания6. Во
всех изданиях «Географии», вплоть до венецианского
издания 1511 г., используется перевод Джакопо д'Анджело.
Лишь в римском издании 1478 г. текст был сверен с
греческим оригиналом его издателем Домицио Кальдерино,
внесшим в текст некоторые поправки.
В 1514 г. Иоганн Вернер7 издал в Нюрнберге книгу I
«Географии» без карт, сделав попытку внести в текст
Птолемея новые сведения, в частности некоторые таблицы.
Эти дополнения Вернера были более чем произвольными
и лишь запутывали понимание текста Птолемея.
Важным этапом явилось страсбургское издание 1513 г.,
подготовленное Мартином Вальдзеемюллером и Маттиасом
Рингманом на совершенно новой основе. Прежде всего они
разыскали в Базеле и в Италии греческие рукописи
«Географии», по которым внесли ряд исправлений в ее текст.
При подготовке издания они поставили целью показать
6 Экземпляр ульмского издания 1482 г. имеется в отделе редких
книг Научной библиотеки им. А. М. Горького МГУ.
7 Вернер Иоганн (1468-1528) — нюрнбергский священник,
принадлежавший к кругу гуманиста Вилибальда Пиркхаймера,
занимался и некоторыми вопросами астрономии.
Опровержению его гипотезы о переменности скорости прецессии
посвящено сочинение Коперника «Послание против Вернера» (1522).
Рис. 32. Современная карта части Ойкумены эпохи позднего
эллинизма (от Греции до Индии), описанной Птолемеем,
с названиями государств той эпохи
149

различия между древней и новой географией и для этого
включили 20 новых карт, которые известный географ,
путешественник и полярный исследователь Адольф Эрик
Норденшельд (1832—1901) назвал «первым новым
атласом мира».
Картографическая традиция страсбургского издания
1513 г. (повторенного в 1520 г.) была продолжена Лорен-
цом Фризом, который проиллюстрировал четыре издания
«Географии» с 1522 по 1541 г. Начиная с издания 1525 г.
текст труда Птолемея был дан в новом латинском
переводе, осуществленном известным гуманистом историком Ви-
либальдом Пиркхаймером (1470—1530), а два последних
издания были исправлены замечательным испанским
философом, математиком и медиком Мигелем Серветом
(1509/1511—1553). Этот ученый вошел в историю науки
и как деятель Реформации, и как открыватель малого
круга кровообращения (сердце—легкие—сердце), и как
мученик науки — один из вождей Реформации Жан
Кальвин сжег его на костре якобы за отрицание троичности
бога, а фактически — за его научные исследования. Это
случилось почти за полвека до сожжения Джордано
Бруно.
Вернемся, однако, к «Географии» Птолемея. В своей
работе по редактированию перевода Пиркхаймера Сервет
использовал новое издание греческого текста «Географии»,
осуществленное в 1533 г. в Базеле одним из крупнейших
философов эпохи Возрождения Эразмом Роттердамским
(1469—1536). Эразм был не только философ, но и
филолог, он превосходно знал греческий язык и ясно понимал
значение труда Птолемея в эпоху развития торговли и
мореплавания. Эразм явился вдохновителем издания в
Базеле целой серии научных работ ученых древности, в
частности географов. Для этого имелись все условия: хорошие
типографии и опытные издатели-типографы, такие, как
Иоганн Амербах, Иоганн Фробен и его сын Иероним,
Адам Петри и его сын Генрих, Христофор Фрошауер. Уже
после смерти Эразма Роттердамского, в 1538 г. были
изданы описательные географии Помпония Мелы (I в. н. э.),
Кая Юлия Солина (III в. н. э.), а в 1540 г. было
выпущено собрание сочинений самого Эразма в десяти томах.
Продолжателем этого начинания Эразма явился
Себастьян Мюнстер (1489—1552), немецкий филолог,
математик и географ. Он был учеником известного астронома е
математика Иоганна Штеффлера (1452—1531), автора
комментариев к «Географии» Птолемея. Помогая Штефф-
150

леру, Мюнстер принял участие в транскрибировании
географических названий и терминов, использованных
Птолемеем, на латинский язык. Мюнстер и другие ученики
Штеффлера завели Kollegienbuch — нечто вроде
коллективной записи лекций своего учителя. Этот документ,
дошедший до нас, содержит много интересных фактических
сведений о ранних географических исследованиях Мюнстера.
При подготовке базельского издания «Географии»
Птолемея Мюнстер взял за основу страсбургское издание
1513 г., но намного улучшил его. При подготовке карт он
использовал в качестве исходного материала карты ульм-
ского издания 1486 г., греческий текст «Географии»,
подготовленный Эразмом, и ее лионское издание 1535 г.,
содержавшее поправки Сервета. Таким образом, он
постарался наилучшим образом использовать труды своих
предшественников. В предисловии он замечает, что Джакопо
д'Анджело хорошо знал греческий язык, но был несведущ
в математике. Иоганн Вернер, напротив, знал математику,
но недостаточно хорошо знал греческий язык, а Вилибальд
Пиркхаймер, хотя в равной степени был подготовлен и в
том и в другом, но делал перевод с греческого оригинала,
содержавшего ошибки (впоследствии исправленные Сер-
ветом и самим Мюнстером).
В комментариях к книге I при обсуждении
картографических проекций, использованных Птолемеем, Мюнстер
во многом соглашается с Вернером. В книгах II и III он
дает современные эквиваленты (или варианты) старых
названий пунктов, приводимых Птолемеем. Координаты
он дает в градусах, минутах и секундах дуги (вместо
долей градуса в прежних изданиях).
Из 27 карт Птолемея общая карта мира построена
во второй, или гомеотерической, проекции Птолемея8,
как и карты Азии под номерами VII и VIII. Остальные
региональные карты построены в трапецеидальной
проекции Николая Германа (редактора ульмских изданий
1482 и 1486 гг.). Исключение составляет картаXII Азии,
составленная в прямоугольной проекции Марина Тир-
ского. По конструкции и по рисунку карты Птолемея в
базельском издании 1540 г. близки к ульмским, но по
географическому содержанию сильно отличаются от них
8 Считается, что Птолемей ввел в практику две картографические
проекции: равнопромежуточную коническую (на касательном
конусе) и равновеликую псевдоконическую, которую он назвал
гомеотерической, т. е. «более подобной».
151

и от последних страсбургских и лионского издания
(1522-1535).
Мюнстер применил новый способ печатания
географических названий, отливая целые слова и строки и
внедряя отливку в деревянные доски, на которых
гравировалось изображение. Это позволяло применять
однократное, а не двукратное печатание каждого листа.
К 27 картам Птолемея Мюнстер добавил 21 новую
карту: одну общую карту мира (уже с Америкой!) и
20 региональных. Общая карта выполнена в
эллиптической проекции, региональные — в прямоугольной
проекции, но без координат и с различной ориентировкой
(вверху — то север, то юг, то восток).
Кроме первого издания 1540 г., Мюнстер выпустил
еще три, все в типографии Генриха Петри. У того же
Петри в 1541 г. был издан «Альмагест» и другие
астрономические работы Птолемея. Поэтому на титульном
листе издания «Географир!» 1545 г. изображен Птолемей-
астроном и подчеркивается его тождество с автором
«Географии» 9.
Вместо стоявшего в издании 1540 г. посвящения ба-
зельскому епископу (который к тому времени умер)
издание 1545 г. содержит посвящение «искусным
исследователям в астрономии и небесной философии». В конце
предисловия говорится о систематических ошибках при
наблюдениях затмений, отраженных в астрономических
таблицах, находившихся в обращении, и в координатах
городов, приводимых Птолемеем, о чем мы уже говорили
выше. Кроме того, в этом и в последнем издании 1552 г.
заменены и добавлены некоторые «новые» карты.
Кроме «Географии» Птолемея Мюнстер издал в 1544 г.
свой собственный труд — «Космографию»,
замечательный свод историко-географических и биологических
сведений об известных тогда странах. Этот труд выдержал
24 издания на немецком языке и еще много — в
переводах на латинский, французский, итальянский,
английский и чешский языки. Там есть и описание Московии по
Случаи, когда замечательных деятелей науки и культуры,
прославившихся в совершенно различных сферах, считали
разными людьми (однофамильцами), бывали и в новое время. Так,
академик П. Л. Капица приводит выдержку из работы
французского историка науки Ф. Гефера, написанной в 1860 г.: «Среди
русских химиков, которые стали известными химиками, мы
упомянем Михаила Ломоносова, которого не надо смешивать с
поэтом того же имени». Комментарии тут, как говорится,
излишни!
152

данным Антония Вида и Матвея Михова с картой.
Переиздания «Космографии» Мюнстера (в которой он продолжал
использовать несколько карт Птолемея) Генрих Петри и
его сын Себастьян продолжали выпускать до 1628 г.
После 1552 г. центр изданий «Географии» Птолемея
переместился в Венецию, где до 1578 г. вышло не менее
девяти изданий на итальянском языке. Все они, за
исключением двух, основаны на переводе Пьетро Андреа
Маттиоли из Сиены, сделанном с издания Мюнстера,
с комментариями переводчика и с 34 новыми картами,
построенными Джакомо Гастальди па базе карт
Мюнстера.
В 1561 г. Джироламо Ручелли сделал новый перевод
«Географии» на итальянский язык непосредственно с
греческого. Этот перевод использовался во всех
остальных венецианских изданиях вплоть до 1600 г., но
основой для карт по-прежнему служили карты Гастальди.
В 1842—1845 гг. «География» Птолемея была издана
в Лейпциге в новом переводе на немецкий язык под
редакцией К. Ф. Ноббе [11]. И уже в 1966 г. в Амстердаме
было осуществлено факсимильное переиздание базель-
ского издания 1540 г. Себастьяна Мюнстера с очень
интересной вводной статьей Р. А. Скелтона [129].
Глава 13
Работы Птолемея
в области оптики
Клавдий Птолемей оставил после себя не только
выдающиеся труды по астрономии и географии — ему
принадлежит также монография по оптике, прочно
вошедшая в историю мировой науки.
Термин «оптика» происходит от греческого опсис
(зрение) и в античную эпоху означал собственно науку
о зрении. Кроме того, существовала катоптрика — наука
об отражении лучей света от зеркальных поверхностей и
диоптрика — наука об оптических измерениях [52].
Примерно в V в. до н. э. сложились два
противоположных представления о свете и его восприятии зрением
человека. Согласно одному из них, развитому древпими
атомистами, свет и цвета — это материальные истечения,
153

выходящие из предмета и достигающие глаза.
Переносчиками изображения служат мельчайшие частицы
(«атомы света»). Известный римский поэт Лукреций Кар (I в.
до н. э.) в поэме «О природе вещей» так излагает эту
точку зрения [71]. На поверхности предметов находится
Множество крохотных тел, что способны от них отрываться
В точном порядке, всегда сохраняя их облик и форму.
Другое представление (которого придерживался,
например, Евклид) основано на том, что лучи исходят из
наших глаз и как бы «ощупывают» предмет. Такая
точка зрения лучше соответствовала представлениям
геометрической (лучевой) оптики. Угловые размеры и
расстояния между объектами также легко истолковывались
с этих позиций. В качестве обоснования сторонники этого
взгляда приводили тот факт, что у кошек и некоторых
других животных глаза ночью светятся, как бы испуская
«лучи зрения» *.
Независимым от этих двух представлений было
учение о свете Аристотеля. В нем подчеркивалось значение
промежуточной прозрачной среды в передаче света и
цветовых ощущений. Этой средой может быть воздух,
вода и даже некоторые твердые вещества (например,
стекло). Цветовые свойства предметов Аристотель
связывал с изменением свойств промежуточной среды и ее
воздействием на наш глаз.
Наиболее старой, дошедшей до нас работой в этой
области является «Оптика» Евклида. Как уже говорилось,
Евклид придерживался взглядов о том, что лучи исходят
из наших глаз. Он развил основные положения
геометрической оптики и теории перспективы. Евклид
выводит законы перспективы из четырнадцати положений,
основанных на данных наблюдений. Евклид использует
закон отражения как нечто уже известное, указывая,
что он доказывается в другой его книге, «Катоптрике».
К сожалению, «Катоптрика» Евклида до нас не дошла.
Сочинение с таким названием, некоторое время
приписывавшееся Евклиду, оказалось компиляцией IV в. н. э.,
автором которой является, возможно, Теон
Александрийский. Подлинная «Катоптрика» Евклида вскоре была
оттеснена на второй план «Катоптрикой» Архимеда (также
1 Несмотря на очевидную для пас нелепость этого представления,
оно просуществовало в пауке два тысячелетия. Еще в начале
XVII в. подобное представление высказывал и защищал
итальянский оптик Дж. Б. Порта (1535-1615) [59].
154

не дошедшей до нас). Известно, однако, что книга
Архимеда содержала строгое изложение достижений
геометрической оптики того времени. Архимед был не только
теоретиком в области оптики, но и экспериментатором.
Однако версия о том, что Архимед якобы сжег
вражеский флот, направив на него лучи Солнца с помощью
вогнутых зеркал,— всего лишь красивая легенда, хотя и
основанная на том, что Архимед, возможно, проводил
какие-то опыты с вогнутыми зеркалами.
По сравнению с оптическими трактатами Евклида и
Архимеда «Катоптрика» Герона Александрийского
(ок. 150 — ок. 250 г. н. э.) содержала ряд новых элементов.
В ней Герон обосновывал прямолинейность световых
лучей бесконечной скоростью их распространения. Далее
он доказывал справедливость закона отражения
(равенство углов падения и отражения), исходя из принципа,
что путь, проходимый светом, должен быть наименьшим
из всех возможных. Это — частный случай принципа
Ферма, доказанного известным французским физиком и
математиком через полторы тысячи лет. Впрочем,
в VI в. н. э. александрийский ученый Олимпиодор,
известный своими комментариями к Аристотелю и Птолемею,
в доказательстве прямолинейного распространения лучей
исходил из принципа целесообразности: природа не
терпит никаких излишеств и потому выбирает для световых
лучей самый короткий путь.
В своем трактате Герон рассматривает различные
формы зеркал (в частности, цилиндрические) и
вызываемые ими искажения изображений. Любопытно, что
«Катоптрика» Герона первоначально приписывалась...
Птолемею.
Кроме «Катоптрики» Герон написал трактат «О
диоптре», в котором описывается визирное устройство для
угловых измерений.
В уже упоминавшейся «Катоптрике» псевдо-Евклида
рассматривается отражение света как от плоских, так и
от вогнутых и выпуклых зеркал и доказывается, что
пучок лучей, отраженный от вогнутого зеркала, может быть
сходящимся или расходящимся, а от выпуклого зеркала —
только расходящимся. Но положение фокуса вогнутого
зеркала* определяется в этом трактате неверно.
Как видим, большинство античных авторов уделяли
основное внимание отражению света. Вопрос о
преломлении света находился в менее ясном положении.
Аристотель писал о «переламывании» луча (называя это
155

явление термином анакласис), но включал в это понятие
и отражение, и преломление. Позднейшие авторы
называли преломление термином диакласис или, как Клеомед
(середина I в. н. э.), катакласис. Клеомед считал, что при
насыщенном влагой воздухе Солнце можно видеть даже
тогда, когда оно находится ниже горизонта. Это
явление — астрономическая рефракция. Клеомед основывался
на представлении о лучах, исходящих из глаза. По его
мнению, проходя через влажный воздух, лучи тяжелеют
от проникающей в них влаги и потому искривляют свой
путь [52].
Той же концепции лучей, испускаемых глазом,
придерживался и Птолемей. В вопросах отражения света и
природы зрения он не пошел дальше своих
предшественников. С проблемой рефракции дело обстояло иначе.
В «Альмагесте» явление рефракции только
упоминается (в книге IX, гл. 2). Кроме того, в книге I, гл. 3
Птолемей обсуждает вопрос о кажущемся увеличении
видимых диаметров Солнца и Луны у горизонта. Там он
объясняет это явление «увеличением влажности в
атмосфере» на пути горизонтального луча. В «Оптике» этому
явлению дается совершенно правильное объяснение —
как чисто психологическому эффекту. В сочетании с тем,
что в «Оптике» подробно рассматривается явление
рефракции, это дает все основания считать, что «Оптика» —
более позднее произведение Птолемея, чем «Альмагест».
История дальнейшей судьбы этого произведения
Птолемея не менее интересна, чем история судьбы
«Альмагеста». По-видимому, в IX в. «Оптика» была переведена
с греческого на арабский язык. В XII в. эмир Евгений
Сицилийский (ок. 1125—ок. 1195) выполнил ее перевод
с арабского языка па латынь [16]. Личность этого
человека заслуживает более подробного освещения. Грек по
национальности, дворянин по происхождению, он жил
при дворе норманнских королей Сицилии во второй
половине XII в. Титул эмира (столь редкий для
европейцев) еще в XI в. был пожалован его деду, по-видимому,
одним из арабских правителей в ознаменование каких-то
его заслуг. (До 1091 г. Сицилия принадлежала арабам.)
Евгений Сицилийский был поэтом (до нас дошли два
десятка его поэм), он был весьма эрудирован в науках и в
совершенстве знал три языка: родной греческий,
арабский и латинский, что и позволяло ему делать переводы.
Он участвовал в самом первом переводе «Альмагеста» с
арабского языка на латынь, осуществленного на Сици-
156

лии в 1160 г. (анонимный основной переводчик
благодарит его в предисловии за сотрудничество).
Об «Оптике» Птолемея сообщали в своих
произведениях Дамиан (IV в.), Симпликий (VI в.), Олимпиодор
(VI в.) и Симеон Сет (XI в.). Приводимые ими отрывки
из «Оптики» на греческом языке хорошо согласуются с
текстом Евгения Сицилийского.
Латинский перевод «Оптики» (тогда еще
рукописный) использовали в своих трудах по оптике Роджер
Бэкон (ок. 1214-1292) и Вителло (ок. 1225-ок. 1280).
Но если Бэкон прямо ссылается на труд Птолемея и
высоко оценивает его, то у Вителло ссылок на Птолемея
нет, но в его сочинении «Перспектива» много общего с
рассмотрением тех же вопросов у Птолемея [16].
В XII в. была переведена на латинский язык
«Оптика» арабского ученого Ибн аль-Хайсама, известного под
латинизированным именем Альхазен. Она сыграла
большую роль в творчестве и Бэкона, и Вителло. В наше
время многие специалисты считали, что Бэкон и Вителло
пользовались лишь трудом Альхазена, так как «Оптика»
Птолемея считалась утраченной. В действительности она
продолжала распространяться в копиях (впоследствии
были обнаружены копии XIV—XVII вв.). В XVII в.
о ней говорили еще как об общеизвестной книге. Затем
она исчезла из обращения, и только в 1800 г. ее
обнаружил в Парижской библиотеке известный французский
астроном Пьер Симон Лаплас, живо интересовавшийся
историей науки [83]. После этого в разных хранилищах
мира было обнаружено до 15 рукописей этой работы.
Но издана «Оптика» Птолемея была только в 1885 г.
итальянским физиком Дж. Джови [12]. До 1956 г. это
издание было единственным, пока бельгийский историк
науки А. Л ежен не выпустил новое издание «Оптики» со
своими комментариями, основанное на скрупулезном
анализе 12 ее списков.
«Оптика» Птолемея состоит из пяти книг. Первая
книга (увы, до нас не дошедшая) была посвящена общим
рассуждениям о свете и зрении. Во второй книге
рассматриваются условия зрительного восприятия, а также
обманы и ошибки зрения. Третья книга содержит общие
законы " отражения, теорию плоских и выпуклых зеркал,
четвертая — теорию вогнутых, конических и
пирамидальных зеркал. Пятая книга, наиболее интересная и
оригинальная, посвящена диоптрике. Здесь же, в главах 23—
30, подробно обсуждается проблема рефракции.
157

Этим она отличается от
который начинает свою
Рис. 33.
Прибор Птолемея
для измерения
преломления света
(схема)
Как уже говорилось, «Оптика» Птолемея была
основана на идее зрительных лучей (выходящих из глаза).
концепции Ибн аль-Хайсама,
«Книгу оптики» с разделения
ученых, занимавшихся
оптикой, на «математиков»
(пифагорейцы, Евклид,
Птолемей) и «физиков»
(атомисты). К последним
принадлежит и он сам.
Для экспериментального
исследования преломления
света на границе двух сред
Птолемей построил прибор,
схематически изображенный
на рис. 33 [16]. Медная
пластинка BCD, согнутая в
виде полукольца, разделена
на градусы и их доли. Диск
с этой пластиной
погружается либо наполовину в воду
(в вертикальном
положении), либо его нижняя
половина загораживается стеклом. С помощью скользящего
по дуге DC стерженька H и двух небольших
окрашенных шариков Z и Е определяется угол преломления
СЕН=$ как функция известного угла падения AEZ=a.
В табл. 12 приведены углы преломления по
Птолемею и по современным данным при переходах луча из
воздуха в воду и в стекло, а также из воды в стекло [52].
Дж. Джови, А. Лежен, В. П. Зубов и другие авторы
обратили внимание на одну особенность этой таблицы,
свидетельствующую о том, что Птолемей измерял лишь
часть углов преломления, а остальные вычислял. В самом
деле, во всех трех случаях углы преломления ß для угла
падения а = 60° получились точно, тогда как для
меньших и больших углов налицо расхождения, доходящие
ДО 2°.
Далее мы видим, что разности углов ß,
соответствующие Да = 10°, убывают с переходом к следующему
интервалу ровно на 30'. Так, для перехода «воздух—вода»
имеем следующую последовательность разностей:
а° 0-10 10-20 20-30 30-40 40-50 50-60 60-70 70-80
Aß 8°00' 7°30' 7°00' 6°30' 6°00' 5°30' 5°00' 4°30'
158

Таблица 12. Углы преломления по Птолемею и современным
данным
s
H«
g Si
Воздух — вода
»ой
аа $
S £ «в
о о» ш
Воздух — стекло
2
I « S
а № tu
« И со
О СО Щ
us«
Вода — стекло
со
• £ H
§|g
USB
10°
20
30
40
50
60
70
80
8°00'
15 30
22 30
29 00
35 00
40 30
45 30
50 00
7°29'
14 52
22 01
28 49
35 04
40 30
44 48
47 36
+31'
+38
+29
+11
-4
0
+42
+144
7°00'
13 30
19 30
25 00
30 00
34 30
38 30
42 00
6°31'
12 56
19 05
24 52
30 04
34 30
37 55
40 06
+ 29'
+34
+25
+8
-4
0
+35
+114
9°30'
18 30
27 00
35 00
42 30
49 30
56 00
62 00
8°46'
17 29
26 02
34 22
42 16
49 30
55 35
59 52
+44'
+61
+58
+38
+14
0
+25
+128
Такая же картина, с той же второй разностью, равной
30', наблюдается для двух других переходов. Полученная
Птолемеем закономерность может быть выражена
следующей формулой:
Р = [т + ж) а - а2/400' т = (ß/a)«=*>°,
если углы а и ß выражены в градусах. Величина m равна
для перехода воздух—вода 0,8; для перехода воздух-
стекло — 0,7; для перехода вода—стекло — 0,95.
Между тем, если бы Птолемей аккуратнее измерял
углы ß, он не только получил бы более верные (хотя и
округленные) их значения, но вполне смог бы после
нескольких проб найти следующее соотношение между а и ß:
chord 2а : chord 2ß = const,
или, переходя к современным обозначениям,
sin а : sin ß = const,
т. е. закон преломления света (закон Декарта—Снеллиу-
са). Постоянная величина справа равна отношению
показателей преломления обоих веществ: того, куда входит
луч, пересекая границу двух сред, и того, откуда он
выходит. Как мы теперь знаем, показатель преломления
воздуха (при комнатных условиях) равен 1,0003;
показатель преломления воды — 1,333; для обычного стекла он
равен 1,529. Таким образом, их отношения для трех рас-
159

гсмотренных Птолемеем переходов равны соответственно
:1,333, 1,529 и 1,147. Читатель может проверить
справедливость формулы преломления, вычислив на
микрокалькуляторе отношения2 синусов углов а и ß.
Итак, мы вновь встретились с фактом замены
Птолемеем истинных (экспериментальных) значений — в
данном случае углов ß — вычисленными по некоторой
принятой им теории. И снова он отдает предпочтение теории
перед экспериментом, теории, которая к тому же весьма
трубо представляет результаты экспериментов (даже с
учетом точности измерений углов в те времена). Видимо,
этот недостаток был ему свойствен и проявлялся не
только в астрономии. Можно также согласиться с теми
авторами, которые считают, что Птолемей был хорошим
теоретиком, но довольно посредственным
экспериментатором и наблюдателем.
Углы преломления при переходе из более плотной
гсреды в менее плотную (например, из воды или стекла в
воздух) Птолемей не приводит, полагая, что пути лучей
остаются теми же, но проходятся в обратном
направлении. По вопросу же о знании Птолемеем явления полно-
то внутреннего отражения в литературе существуют
прямо противоположные утверждения. Вот два из них.
В. П. Зубов [52]: «Полное внутреннее отражение
осталось ему (Птолемею. — В. Б.) неизвестным».
И. Д. Рожанский [82]: «Птолемей обнаружил также
явление полного внутреннего отражения».
Кроме того, в «Оптике» Г. С. Лаыдсберга [68]
говорится: «Птолемей учитывал уже влияние преломления
в атмосфере на видимое положение светил (атмосферная
рефракция) и даже составил таблицы рефракции».
Изучение подлинника — «Оптики» Птолемея —
показывает, что ни таблиц атмосферной рефракции, ни
упоминаний о полпом внутреннем отражении в нем нет3.
«Таблицы рефракции», упоминаемые Г. С. Лапдсбергом,
это уже приведенные выше таблицы углов преломления
при переходах из одной среды в другую. Что касается
атмосферной рефракции, то о ней Птолемей говорит
довольно много, но чисто качественно. Он знает, что реф-
2 В последнем случае налицо небольшое расхождение (табличные
данные соответствуют отношению 1,139). Это объясняется тем,
что для разных сортов стекла и разных длин волн показатели
преломления заметно различаются.
3 Это обстоятельство специально подчеркивает редактор
последнего издания «Оптики» А. Лежен [16].
160

ракция возрастает по мере перехода от зенита к
горизонту, где достигает измеримых (даже в его время)
значений. Но построить теорию астрономической рефракции
Птолемей затрудняется. Он полагает, что рефракция
возникает на границе раздела эфир—воздух. Но где
расположена эта граница? Очевидно, где-то между внутренней
сферой Луны и верхней границей атмосферы [113]. Но
ему неизвестна ни высота этой границы, ни, самое
главное, то, что плотность атмосферы убывает с высотой и
что именно это явление и порождает атмосферную
рефракцию. Свет звезд и иных небесных тел, переходя из
менее плотных слоев воздуха в более плотные, испытывает
преломление, как при переходе из воздуха в воду, но не
одноразовое, а постепенное, так что луч света
представляется не ломаной, а плавной кривой. Увы, этого
Птолемей не знал.
Обнаружение и исследование «Оптики» Птолемея
позволило современным ученым понять, до какого уровня
дошла древнегреческая наука в этой области знания. Ряд
открытий в оптике, ранее приписывавшихся арабским
ученым (в частности, Альхазену), в действительности
принадлежат Птолемею и некоторым его
предшественникам.
Конечно, «Оптика» Птолемея не имела такого
влияния на развитие науки, как «Альмагест» и «География»,
но свою роль она сыграла. Птолемей прочно поставил эту
науку па математический фундамент, введя в нее
результаты измерепий и экспериментов.
Глава 14
Математика и музыка
Еще один трактат Птолемей посвятил... теории
музыки, точнее, гармонии. Он называется «Гармоники», что
означает гармонические соотношения, представляющие
собой фактическое выявление принципа или идеи,
называемой гармонией.
Что же заставило Клавдия Птолемея заняться вдруг
столь, казалось бы, далекой от его основных интересов
областью знания — музыкальной гармонией? Для того
чтобы яснее понять это, обратимся мысленно в глубь
веков, к взглядам Пифагора и пифагорейцев.
$ Клавдий Птолемей 161

Титульный лист «Гармоник» Птолемея (параллельное издание
на греческом и латинском языках, Оксфорд, 1682. Под ред.
Дж. Вал лиса)
По представлениям Пифагора и его школы, в мире
должна царить гармония, проявляющаяся во всем: в
строгости математических соотношений, в совершенстве
движений небесных тел, а в музыке — в гармонических
соотношениях частот (тонов) звучаний музыкальных
инструментов. Именно Пифагор заложил основы
математической теории музыки [91].
Согласно этой теории, благозвучные сочетания или
чередования звуков должны соответствовать отношениям
162

частот 2: 1 (этот частотный интервал называется
октавой), или 3:2 (чистая квинта), или 4:3 {кварта),
короче говоря, отношению двух соседних целых чисел
натурального ряда [44]. Такой музыкальный строй
называется точным в отличие от принятого в настоящее время
темперированного строя (иначе говоря, выровненного,
сглаженного). В темперированном строе октава делится
на 12 полутонов, так что частотному интервалу в один
полутон соответствует отношение частот -j/2~^ 1,06 •
В пифагоровом строе каждый звук может быть
получен от заданного (основного) звука путем целого числа
квинтовых и октавных шагов (октавные шаги
применяются для возвращения звуков, полученных квинтовыми
шагами, в пределы нужной октавы). Рассмотрим этот
порядок на примере. Пусть основной звук имеет частоту 1.
Первый квинтовый шаг дает нам частоту 3/2.
Следующий—дает нам 9/4, но так как это число больше двух,
возвращаемся на один октавиый шаг вниз и получаем
частоту 9/8 (большая секунда). Делаем третий квинтовый
шаг и получаем 27/16. Четвертый квинтовый шаг дает
нам 81/32, откуда вторым октавным шагом приходим к
частоте 81/64 (большая терция). Мы получили пятизву-
чие (пентатонику), которая и сейчас проявляется в
музыке некоторых восточных народов. Она выражается
следующим числовым рядом:
1, 9/8, 81/64, 3/2, 27/16,
в котором первый, второй и четвертый интервалы равны
секунде (9/8) и только третий интервал равен 32/27.
Будем называть интервал в одну секунду тоном, тогда
интервал 32/27 близок к полутора тонам.
В пифагоровом строе интервал в одну большую
терцию не считался благозвучным, так как он не выражался
отношением двух соседних чисел натурального ряда [52].
Тон делился на два неравных полутона: большой
(2187/2048) и малый (256/243). (Перемножив эти числа,
в которых числители и знаменатели — степени двух и трех,
получим 9/8.)
Против такой излишней математизации
музыкального строя выступил один из учеников Аристотеля — Ари-
стоксен из Тарента (середина IV в. до н. э.). Философ,
историк и музыкант, он внес в пифагорейское учение
много нового, так что эта форма пифагорейства стала
называться неопифагорейством. В частности, в музыке Ари-
163
6*

Ноты в «Гармониках» Птолемея
(оксфордское издание 1682 г.)
стоксен настаивал на приближении ее к запросам
публики. Музыка должна быть приятной для слуха, и тогда
она благозвучна. Аристоксен ввел так называемый
чистый строй, отличающийся от пифагорова тем, что он
основан на использовании трех интервалов: октавы,
чистой квинты и большой терции, которую Аристоксен
«подправил», заменив в числителе 81 на 80 и получив
после сокращения 5/4, что и с формально-пифагорейских
позиций делало ее благозвучным интервалом.
Нелишне будет привести здесь следующее
высказывание Цицерона об Аристоксене: «Аристоксен, музыкант
и философ, утверждал, что душа есть некоторое (внутрен-
164

нее) напряжение, подобное тому, что называют гармонией
в пении и игре на струнных инструментах...». Таким
образом, Аристоксен утверждал не только то, что душа
есть гармония, но он считал ее телесной гармонией. «Кто
таков этот Аристоксен, который отрицает какую бы то ни
было душу вообще, даже в живом теле? — восклицает
христианский писатель конца ЛИ—начала IV в. н. э. Лактан-
ций. — Но как в струнном инструменте от натяжения струн
возникает согласное звучание, так в телах по причине
соединения тканей и жизненной силы членов существует
способность чувствовать» [33].
Мы остановились так подробно на некоторых
воззрениях Аристоксена потому, что он был прямым
предшественником Птолемея в его взглядах на гармонию и на ее
связь с математикой.
«Гармоники» Птолемея состоят из трех книг. Первые
две из них посвящены теоретическим соображениям о
чисто музыкальных явлениях, о законах консонирующих
тональных сочетаний и о звучании музыкальных
инструментов. Третья книга излагает учение о гармонии, причем
не только в музыке. Птолемей переносит принципы
гармонии на небесные тела, полагая, что в расположении
небесных тел, в закономерности их расстояний от Земли
проявляются те же гармонические соотношения, что и в музыке.
Птолемей жил и творил в атмосфере, насыщенной
неопифагорейскими идеями. Вместе с тем он поставил себе
целью преодолеть противоположность между взглядами
тех, кто доверяет «только ушам» (т. е. слуху), и тех, кто
основывается «только на разуме» (т. е. на математических
соотношениях). Если в «Альмагесте» Птолемей
последовательно придерживался философии Аристотеля, то в
«Гармониках» он становится все более эклектичным.
Напомним читателям, что эклектизм — направление в
философии, возникшее в I в. до н. э., стремившееся объединить
элементы различных философских учений [33]. Время
жизни и деятельности Птолемея совпадает с эпохой
наивысшего развития эклектизма. Неудивительно поэтому,
что Птолемей, подпав под его влияние, стремился в своих
«Гармониках» объединить разнородные взгляды на
музыку и гармонию.
Не следует удивляться и тому обстоятельству, что
философские учения столь глубоко проникали в, казалось
бы, такое практическое занятие, как музыка. Музыка — это
вид искусства, а философские идеи находили свое
отражение в любом виде искусства или науки. Теория музыки в
165

Птолемей — теоретик гармонии
(с гравюры Ж. Саважа)
те времена вообще относилась к области чистой философии.
«Музыкант — это тот, кто совершенен в рассуждении»,—
писал известный римский философ Боэций (480—524),
последователь и продолжатель идей Птолемея в области
гармонии [65].
Идея о связи между гармонией музыкальной и
гармонией мироздания ярко выражена в следующих словах
выдающегося византийского философа Григория Нисского
(ок. 335—394): «...порядок мироздания есть некая
музыкальная гармония, в великом многообразии своих прояв-
166

лений подчиненная некоторому строю и ритму,
приведенная в согласие сама с собой, себе самой созвучная и
никогда не выходящая из этой созвучности, нимало не
нарушаемой многообразными различиями между
отдельными частями мироздания» [65].
Эта «музыка сфер» (термин, приписываемый самому
Пифагору) проходит в истории науки длинный путь,
в 23 столетия — от первых пифагорейцев, Аристоксена, Ар-
хита к Птолемею, и далее к его продолжателю Боэцию и к
ученым нового времени вплоть до Кеплера, который в своем
известном труде «Мировая гармония» (1619) продолжил
идеи Птолемея о соответствии расположения планет по их
расстояниям от Солнца (уже на основе гелиоцентрической
системы мира) музыкальным интервалам.
Кеплер еще с молодых лет интересовался трудом
Птолемея. К этому времени латинский перевод «Гармоник» уже
был издан в Венеции (в 1562 г.), но, по-видимому,
полностью разошелся, так что покровитель Кеплера баварский
меценат Иоганн Герварт прислал ему в 1600 г. рукопись
на< греческом языке [92]. Зимой 1617 г., приступая к
работе над «Мировой гармонией», Кеплер писал своему другу
Вакгеру фон Ваксенфельсу: «Когда, возвратясь домой из
поездки в Регенсбург... я оставил ,,Таблицыи, которым и
следовало подождать *, и все свое внимание обратил на
«Гармонию»: я перевел на латинский язык третью книгу
«Гармоник» Птолемея и написал к ней примечания, где
сравниваю свои открытия в области небесных гармоний
со взглядами на этот предмет упомянутого автора» [92].
Перевод книг о гармонии Птолемея и Аристоксена,
выполненный Кеплером, вместе с его примечаниями к первой
из них вошел в четвертый том рукописей Кеплера,
приобретенных Российской академией наук в 1773 г. Они и
сейчас хранятся в Ленинградском отделении Архива АН СССР
[62].
Спустя полвека после смерти Кеплера, в 1682 г.,
английский математик и механик Джон Валлис2 предпринял в
Оксфорде издание «Гармоник» Птолемея на греческом и
латинском языках с соблюдением всех научных требова-
1 Имеются в виду так называемые «Рудольфовы таблицы»,
изданные в 1627 г. и заменившие «Прусские таблицы», вычисленные
и опубликованные в 1551 г. Э. Рейнгольдом и основанные на
теории Коперника.
2 Валлис — это традиционная транскрипция фамилии ученого
(правильнее - Уоллис).
167

ний к такой публикации. В приложении приведен список
всех известных автору публикаций рукописей труда
Птолемея и их местонахождения, а также ранее вышедших
изданий [8]. Оксфордское издание «Гармоник» было
повторено в 1699 г. Как это ни странно, но за последовавшие
два с лишним столетия этот трактат, сыгравший столь
значительную роль в истории музыки, больше не
переиздавался, пока в 1934 г. И. Дюринг не выпустил в Гетебор-
ге его новое издание на немецком языке.
Глава 15
Птолемей и астрология
Во времена Птолемея астрология — искусство
предсказания судьбы по расположению небесных светил —
пользовалась всеобщим признанием и считалась наукой.
Астрология уходит своими корнями в глубокую
древность. В древнем Египте эпохи фараонов, в Вавилоне и
Ассирии жрецы поддерживали свое могущество,
укрепляя в народе веру в то, что им одним доступна
возможность читать на небе судьбы целых народов и их
властителей. В рабовладельческой Греции, в древнем Риме
влияние астрологии упало, астрологов не раз высмеивали,
особенно за неудачные, неоправдавшиеся предсказания.
Известный римский ученый, писатель и оратор Цицерон
(I в. до н. э.) указал на такой факт. Видным римским
полководцам той эпохи Помпею, Крассу и Цезарю было
предсказано, что они умрут в своем доме в глубокой
старости, окруженные всеобщим почетом [45]. В
действительности все трое были убиты, и притом в среднем
возрасте.
Несмотря на многочисленные ошибки астрологов,
некоторые римские императоры держали их при своих
дворах и пользовались их советами, а иные (как,
например, Тиберий), не доверяя даже придворным астрологам
(а вдруг они кем-нибудь подкуплены), пытались
осваивать астрологическую «науку» сами. В то время в
Римской империи было неспокойно. После смерти Октавиана
Августа (14 г. н. э.) императоры сменяли друг друга
быстрее, чем в наши дни чемпионы мира по боксу. Как
правило, они умирали насильственной смертью, в резуль-
168

тате заговоров среди императорской гвардии —
преторианцев. Немудрено, что каждый новоиспеченный император
желал узнать свою судьбу.
Ко II в. н. э. обстановка стабилизировалась.
Положение императоров упрочилось. Но услугами астрологов
власть имущие продолжали пользоваться не столько из
боязни за свою собственную судьбу, сколько для
«небесного» подкрепления своей политики, внешней и
внутренней. Надо ли говорить, что для простого народа прямой
контакт с астрологией был недоступен — ведь услуги
астролога стоили дорого. Конечно, были и среди народа
свои ведуны и гадатели, но их деятельность имела мало
общего с «официальной» астрологией.
В то время астрология считалась «наукой». У нее
были основные положения, что-то вроде «астрологических
правил» и методов. Предсказываемые судьбы делились
по значимости на четыре категории:
1) судьба Земли и мира в целом;
2) судьба отдельной страны или группы стран;
3) судьба того или иного человека;
4) судьба некоторого предприятия или начинания.
Основой для предсказания служило расположение
движущихся светил (Солнца, Луны и пяти планет) по
знакам зодиака. Так как знаков зодиака было 12, а
планет — семь (Солнце и Луна тоже считались планетами),
то нетрудно подсчитать, что различных расположений
планет по знакам зодиака могло быть 4-6-125«6-106
(6 миллионов) 4. Для того чтобы рассчитать расположение
■планет на определенную дату, надо было уметь это
делать. Таким образом, разработка теорий движения
Солнца, Луны и планет нужна была не только в чисто
практических целях (календарь, предсказание затмений,
определение долгот по положению Луны и т. д.), но еще
и для нужд астрологии.
Каждый знак зодиака имел свое значение и смысл,
каждая планета — тоже, из их сочетания "выводились те
или иные прогнозы на судьбы и характеры людей, на
результаты войн и походов, торговых сделок, браков,
политических союзов, на урожайность и даже на
превратности погоды.
Чтобы уметь составлять эти прогнозы (получившие
1 Здесь учтено, что Меркурий при данном положении Солнца
может находиться лишь в четырех, а Венера в шести знаках
зодиака.
169

Немецкий астролог
(гравюра на дереве XVI в.)
название гороскопов), надо было обладать определенной
суммой знаний по астрономии и математике. Поскольку
астрологи были нужны (не только властителям, но и
просто богатым людям), их надо было готовить, обучать.
А для этого нужны были не только учителя, но и учебники.
Вот такой учебник по астрологии и написал Клавдий
Птолемей сразу после окончания работы над
«Альмагестом».
Этот трактат из четырех книг, названный поэтому
«Тетрабиблос», что означает «Четырехкнижие», в
дошедших до нас копиях не был подписан, что породило
некоторые сомнения в принадлежности его Птолемею. Однако
170

известный историк науки И. Л. Гейберг, составитель
«канонического» греческого текста «Альмагеста», на основе
анализа дошедших до нас его копий доказал, что автором
«Четырехкнижия» действительно является Птолемей [45].
Что же утверждает Птолемей в этом трактате? Вот
какие доводы он приводит, чтобы обосновать идею о
влиянии небесных светил на земные явления: «Мы имеем
здесь, во-первых, тезис, который вполне очевиден и не
требует длинной аргументации: сила, которая исходит от
вечных частей эфира, распространяется на всякий
предмет, окружающий Землю, и подвержена непрерывным
изменениям. Первые элементы под Луной — огонь и
воздух — приходят в расстройство от движения окружающего
эфира; в своем беспокойстве они увлекают за собой
более низкие элементы — воду, землю, а также растения
и животных, которые из них происходят. Солнце, вместе
с небом окружающее все земные предметы, налагает на
них установленный порядок... Луна, которая ближе
всего к Земле, влияет на весь земной мир очевидным
образом; одушевленные и неодушевленные предметы следуют
ее изменениям; реки подымаются и опускаются вместе с
Луной; когда она восходит и заходит, моря приводятся
в движение противоположными потоками, а растения и
животные чувствуют в некоторой части или целиком
влияние роста и убывания Луны. Кроме того, движение звезд
есть предзнаменование ко многим явлениям в воздухе,
как жара, холод или ветер. Относительное положение
звезд является причиной различных изменений, так как
при своих комбинациях небесные тела смешивают свое
действие. Сила Солнца превосходит, согласно строению
мира, другие светила, но последние могут увеличить или
уменьшить его действие. Луна показывает это наиболее
ясно в своих фазах, для других светил мы можем
проверять это так же часто и ясно» [45].
Итак, Птолемей пытается подвести под
астрологические воззрения своеобразную «научную базу». Он
отталкивается от всем известных фактов о влиянии Солнца на
погоду, на развитие растительности, на обеспечение своим
теплом и светом жизни животных и людей, о влиянии
Луны на приливы и отливы в океанах и морях. К этим
несомненным проявлениям физических влияний Солнца и Луны
на земные процессы «пристегивается» представление о
влиянии Луны на течение рек, на растения и животных,
о влиянии небесных светил на погоду. Кстати, это
последнее представдение — о влиянии Луны, планет и звезд н$
17*

Гороскоп Людовика XIV, доставленный на основе системы
Коперника
Расположение планет показано на день рождения короля, 8 сентября
1638 г.
погоду — оказалось необычайно устойчивым и живучим.
Именно под его влиянием уже в XVII в. астроном Джо-
ванни Риччиоли присвоил темным пятнам на диске Луны
такие названия, как Море Дождей, Море Холода, Море
Ясности, Море Облаков и др. Даже в наши дни приходится
172

слышать в народе приметы о влиянии Луны (в частности,
ее фаз) на погоду.
А вот как распределял Птолемей «роли» между
отдельными светилами в их влиянии на Землю: «Солнце
вследствие своей природы производит действие теплоты,
в меньшей степени также сухости; относительно Солнца
мы замечаем это гораздо легче своими чувствами, чем
относительно других планет, вследствие его величины и
вследствие явственности, с какой в течение времени
изменяется его действие. Луна имеет влажное действие
потому, что она ближе всего к Земле, из которой
подымаются влажные пары; она размягчает вещи, подверженные
ее влиянию, и способствует их гниению, а благодаря
своему сходству с Солнцем она обладает способностью
согревать. Сатурн есть светило, преимущественно
приносящее холод; он также сушит, но в незначительной степени,
и это вполне естественно, так как он находится всего
дальше и от теплоты Солнца и от влажности Земли. Впрочем,
его силы, как и всех остальных светил, находятся в
зависимости от их положений относительно Солнца и Луны.
Юпитер — умеренная, благосклонная планета. Он
расположен посередине между холодным Сатурном и жарким,
удушливым Марсом. Он дает теплоту и влажность,
но так как сила теплоты преобладает, то от него исходят
ветры, производящие плодородие. Марс сушит и сжигает;
его цвет огня согласуется с его свойствами, он находится
вблизи Солнца, круг которого лежит внутри его сферы.
Венера по своей умеренности имеет сходство с Юпитером,
но причина для этого совершенно иная: так как она
находится вблизи Солнца, то несколько согревает, но при этом,
подобно Луне, возбуждает гораздо больше влажности, ибо
при содействии этого большого светила (Луны.— В. Б.)
она притягивает 'влажность из ближайших к ней мест
Земли. Меркурий сушит и в довольно значительной
степени всасывает влажность, так как он лежит недалеко от
Солнца; но иногда он немного и увлажняет, ибо находится
вблизи Земли, ближе всех остальных планет, за
исключением Луны» [45].
Все это поражает сегодня своей нелепостью, связанной
с полным непониманием физической природы планет и
возможности их влияния на Землю. Но чтобы внушить
доверие к этим заключениям о влияниях планет на тепло и
холод, на влажность и на сухость, Птолемей начинает с
неоспоримого и для всех очевидного действия Солнца: «Солнце
производит действие теплоты, в меньшей степени также су-
173

хости». «Да, конечно, это понятно каждому,— подумает
читающий трактат Птолемея.— Что касается Луны и
других планет, то их влияние прямо не ощущается, но ученые
знают больше нас, и раз они так пишут, значит, это
так и есть».
Взгляды на влияние различных светил на погоду
прослеживаются и в «Альмагесте». Так, в конце восьмой
книги, говоря о гелиакических (одновременных с
Солнцем) восходах и заходах звезд, он отмечает, что их
влияние на погоду не постоянно, а зависит от
противостояний с Солнцем и от положения Луны [17. С. 416—417].
В «Четырехкнижии» Птолемей дает детальное
изложение вопроса о тех или иных влияниях планет
(включая Солнце и Луну) в зависимости от их расположения
относительно знаков зодиака и друг друга.
Расположение планет по-разному должно было влиять на природу
и человека, если они находятся в соединении или в
противостоянии друг с другом, в квадратуре или в триго-
нальной конфигурации (в 120° друг от друга). От
влияния планет и их расположений на погоду Птолемей
переходит к их влиянию на судьбы людей, прокламирует
связь между жизнью человека и расположением планет
в момент его рождения [78].
Этот нелепейший тезис приводит (как давно уже
заявляли критики астрологии, еще в античную эпоху) к
парадоксальным следствиям. Выходит, что у всех людей,
родившихся в один и тот же день, должна быть одна
судьба. Что это не так, можно проследить, изучая,
например, судьбы близнецов, родившихся не только в один
день, но и почти в один час. Как порой различны бывают
их судьбы!
Птолемей пытался навести некоторый порядок в хаосе
различных астрологических систем и методов, основанный
на рациональных принципах, стремясь избежать
мистических комбинаций. Мы уже видели, что Птолемей хотел
подвести под астрологию некую «физическую базу». Этот
подход имел целью пополнить запасы аргументов,
направленных против критиков астрологии. Оправдывая
случаи ошибок в предсказаниях астрологов, Птолемей
защищал ее основные принципы и сводил дело к их
неправильному применению.
Хотя «Четырехкнижие» по своему значению не идет ни
в какое сравнение с «Альмагестом», эта книга сыграла
определенную роль в дальнейшем развитии астрологии.
В развитии, которое все затруднялось перед лицом ра-
174

стущей точности астрономических наблюдений и
строгости теоретических построений.
Ряд позднейших авторов составляли комментарии к
«Четырехкнижию». Среди них назовем неоплатоника
Порфирия (234—303), ученика Плотина, и другого
неоплатоника, жившего двумя столетиями позже, Прокла
Диадоха (412-485).
Неоплатонизм как философское течение возник и
оформился в III в. н. э. Это — идеалистическое и к тому
же эклектическое направление в философии,
стремившееся объединить платонизм с взглядами Аристотеля,
ставившее во главу угла абстрактные категории, такие,
как Единое, Ум, Душа, не чуждое мистике [33].
Поэтому не случайно, что именно неоплатоники
интересовались астрологией, комментировали «Четырехкнижие»
Птолемея и издавали собственные сочинения по этому
предмету. Так, Порфирий написал трактат «Введение
в астрологию Птолемея», хотя и в других своих
сочинениях он излагал астрологические вопросы. Прокл Диа-
дох, основатель Афинской школы неоплатонизма,
переработал «Четырехкнижие» с намерением дать
объяснение птолемеевской астрологии. Увлечение астрологией
в Византии стало развиваться все сильнее [65].
В конце V—начале VI в. н. э. философ Павел
Александрийский написал книгу «Введение в астрологию»,
которая вскоре вытеснила «Четырехкнижие» Птолемея
и заняла место основного учебника по астрологии.
Профессор Александрийской школы Олимпиодор в 564 г.
вел преподавание этого предмета уже по книге Павла
и написал к ней толкование [65]. Олимпиодор соотнес
семь известных в древности металлов семи планетам
и ввел обозначения этих металлов символами планет
(используемыми и сейчас). Солнцу соответствовало
золото, Луне — серебро, Венере — медь, Марсу — железо,
Юпитеру — олово, Сатурну — свинец, Меркурию — ртуть2.
На протяжении V—VI вв. христианская церковь
вела ожесточенную борьбу против астрологии, утверждая,
что будущее — в руках божьих и надо не пытаться
узнать божью волю наперед, а молиться богу и просить
его о ниспослании счастливой судьбы. Несколько
церковных соборов осудили астрологию. Были сожжены
сочинения Порфирия, был казнен философ Боэций, также
2 Отсюда - название ртути на многих языках (например,
по-английски — mercury, по-французски - mercure и т. д.).
175

тяготевший к неоплатонизму и не чуждавшийся
астрологии.
И все же астрология не исчезла. Те же самые
римские папы, проклинавшие астрологию на вселенских
соборах, дома тайно содержали своих астрологов и
руководствовались их предсказаниями. Не чурались их и
светские правители.
В IX в. «Четырехкнижие» Птолемея было переведено
на арабский язык. В середине XIII в. благодаря
стараниям короля Кастилии Альфонса X это сочинение было
переведено на латинский язык, а в 1484 г. в Венеции
Ратдольт выпустил его первое печатное издание. На
греческом языке оно было издано в 1525 г. в Нюрнберге,
после чего не раз переиздавалось [130]. В 1551 г. в
Базеле было издано своеобразное «собрание избранных
сочинений» Птолемея [6], куда вошли «Альмагест» в
переводе Георгия Трапезундского, «Четырехкнижие» в
переводе Иоахима Камерария, «Центилоквиум» («Книга
плодов») и более мелкие сочинения, а также комментарии
к «Альмагесту» Прокла Диадоха (в переводе Джорджио
Валла Плацентино) и комментарии редактора
издания — профессора Тюбингенского университета Эразма
Освальда Шреккенфукса (1511—1579), известного
своими переводами и комментариями к сочинениям
астрономов древности и средневековья.
«Четырехкнижие» — сравнительно небольшое
сочинение, оно занимает около 600 страниц in folio. Сейчас
для нас это лишь страница в истории развития культуры
эпохи позднего эллинизма, или, выражаясь словами
Г. А. Гурева, страница «истории одного
заблуждения» [45].
Глава 16
Судьба «Альмагеста»
Мы уже не раз рассказывали читателям о судьбе тех
или иных сочинений Клавдия Птолемея. Но самая
интересная судьба — у главного труда Птолемея, у его
«Альмагеста». От завершения этого труда до последнего известного
нам его издания прошло ни много ни мало 1834 года !
Первые читатели «Альмагеста», известные науке, это
176

Младшие современники Птолемея: римский
естествоиспытатель и врач Гален и сирийский астролог Веттий Валент.
Последний, хотя и был современником Птолемея,
работал независимо от него, используя труды Гиппарха и
вавилонских астрономов. От него осталась «Антология»
в девяти книгах и более мелкие сочинения [107].
Поскольку Гален жил и работал в Риме, а Веттий
Валент — в Антиохии, очевидно, что «Альмагест» еще при
жизни Птолемея попал в эти города (рис. 34).
В самой Александрии первые известные нам
комментарии к «Альмагесту» написал астроном (или группа
астрономов), присвоивший себе псевдоним «Малого
астронома» (в отличие от Птолемея, считавшегося «Великим
астрономом»). Сочинения «Малого астронома» были
направлены к облегчению понимания «Альмагеста». О них
сообщает и следующий комментатор Птолемея — Папп
Александрийский (между 300 и 320 гг.), спустя
полстолетия комментарии к «Альмагесту» составил Теон
Александрийский (ок. 370 г.). Комментарии к некоторым
книгам «Альмагеста» написала и женщина-математик, дочь
Теона Гипатия, трагически погибшая в 415 г. от рук
фанатиков-христиан.
Ученик Гипатии Синесий Киренский, ставший затем
епископом Птолемаиды, руководствуясь указаниями,
содержащимися в «Альмагесте», усовершенствовал
астролябию. Он же спроецировал небесную сферу на конус,
который, как известно, развертывается на плоскость
[65]. Таким образом, с помощью конической проекции
можно изобразить небесную сферу на плоской карте. Этой
задаче — проецирования сферы на плоскость — были
посвящены два небольших сочинения Птолемея: его «Плани-
сферий» и «Аналемма». Задача эта имеет и другое
практическое применение — для построения географических карт.
На примере Синесия Киренского мы видим, как
некоторые ученые, работавшие в Египте, а также в Сирии и
в Византии, принимали христианство, но продолжали
дело своих учителей-язычников. Впрочем, послептолемеев-
ская эпоха не блещет именами, которые можно было бы
поставить на одну доску с именами Евклида, Аристотеля,
Гиппарха, Птолемея. Были добросовестные комментаторы,
роль которых заключалась прежде всего в том, что они
переносили культурное и научное наследие своих
выдающихся предшественников следующим поколениям, не
давали науке, и в частности астрономии, угаснуть.
Одним из таких комментаторов был и Прокл Диадох
177

§
л
е-
о
о
&
ев
H
&
СО
со
&4
178

(ок. 412—485), представитель Афинской школы
неоплатонизма, убежденный язычник. Прокл оставил много
комментариев к трудам античных ученых (Платона,
Аристотеля и др.). В них Прокл часто выражал свое несогласие
с ученым, чей труд он комментировал, и противопоставлял
его мнению свое. Не повезло и Птолемею. Прокл Диадох
обвинял его в непоследовательности, в отходе от
принципа равномерных круговых движений, закрепленного
авторитетом Евдокса и Аристотеля [65].
Мы уже знаем, что комментарий Прокла Диадоха
нередко присоединялся к тексту «Альмагеста», так что даже
в XVI в. их издавали вместе. Критика Прокла в
дальнейшем получила развитие в трудах арабских и
среднеазиатских ученых, о чем речь пойдет дальше.
В первой и начале второй половины VI в. в
Александрии жил и работал философ Иоанн Филопон, в начале
своей деятельности — аристотелианец, впоследствии
порвавший с учением Аристотеля и принявший
христианство. Он, как и Синесий Киренский, занимался, между
прочим, усовершенствованием астролябии. Однако осталось
неизвестным, производил ли кто-нибудь из них
астрономические наблюдения.
Иоанн Филопон был широко эрудированным
философом, он был знаком не только с воззрениями Платона
и Аристотеля, но также Гиппарха и Птолемея. Однако
его интересовали не математические построения
Птолемея, а его представления о наличии над сферой
неподвижных звезд еще одной — верхней сферы, лишенной
каких-либо светил. И тут Иоанн Филопон выступил с
заявлением, что приоритет в этом воззрении принадлежит
не Гиппарху и не Птолемею, а ... Библии. Филопон
считал, что пространство между двумя сферами заполнено
водой, которая, впрочем, непохожа на земную воду. С
другой стороны, Филопон признавал шарообразность Земли,
наличие описанных Птолемеем климатических поясов,
пытался объяснить природу землетрясений [65].
Ученик уже известного нам астролога Олимпиодора
(который, будучи язычником, много дискутировал с
Иоанном Филопоном по космогоническим вопросам), Стефан
Александрийский был в 618 г. приглашен в
Константинополь,. столицу Византии, для преподавания философии.
Император Ираклий, серьезно интересовавшийся
астрономией, предложил Стефану написать совместный
комментарий к одному из астрономических трактатов Теона
Александрийского, что и было сделано. Деятельность Стефана
179

в Константинополе оказала большое влияние на
творчество одного из крупнейших философов (и поэтов) Византии
первой половины VII в. Георгия Писиды.
Писида был хорошо знаком с творчеством античных
и византийских философов и астрономов, в частности
с трудами Клавдия Птолемея. Подобно Лукрецию, он
изложил свои взгляды в стихотворной форме в поэме «Гек-
самерон». В основу своих воззрений он берет идеи
Платона, Аристотеля и Птолемея о небесных сферах, признает
шарообразность Земли. Ссылки на Священное писание
он сочетает с защитой античных философов от нападок,
которым они подвергались в те времена со стороны
деятелей христианской церкви и чересчур воинственных
философов-христиан.
Эта эпоха — VI и VII вв. — ознаменовалась рядом
событий, оказавших существенное отрицательное влияние
на дальнейшее развитие науки. Эти события были связаны
с наступлением двух религий, претендовавших на
безраздельное влияние на умы и души людей,— христианства на
Западе и ислама на Востоке. В 529 г . христианский
император Юстиниан закрыл Афинскую школу, где еще
преподавали ученики Прокла Диадоха. В 640 г. войска
халифа Омара взяли штурмом Александрию, уничтожив при
этом все, что осталось от Александрийской библиотеки.
Ислам оказался еще более нетерпимым к сочинениям
античных ученых, чем христианство. Если в этих книгах
говорится то же, что и в Коране, — заявляли
приверженцы ислама,— то они не нужны. А если в них говорится то,
чего нет в Коране, то они вредны. В обоих случаях эти
сочинения следует уничтожить.
К счастью, такое крайнее, нетерпимое отношение к
сочинениям классиков античной науки проявлялось в
мусульманском мире не всегда. Уже в конце VIII в.
отношение к этим творениям резко меняется, благодаря чему
именно на мусульманском Востоке были сохранены для
мировой цивилизации многие труды ученых древнего
мира.
Но вернемся к судьбам «Альмагеста». Как мы знаем,
уже во II в. по крайней мере одна из его копий попала
в Антиохию. Есть сведения, что в III в. «Альмагест» был
доставлен в Персию, где при дворе сасанидского царя
Шапура I (241—272) был сделан его перевод на средне-
персидский язык (пехлеви). К сожалению, этот перевод
не сохранился, да и сведения о нем не очень
определенные [17. С. 2]. От середины VII в. дошел до нас «Зидж-и-
180

Шах» на языке пехлеви, * один из первых зиджей, как
называли на Востоке книги астрономического
содержания с таблицами, позволявшими предвычислять те или
иные астрономические явления. «Зидж-и-Шах» означает
«Царский зидж». В иранских зиджах как бы
законсервированы данные вавилонской астрономии
(алгебраические, иногда тригонометрические методы, различные
таблицы). Во многих описываемых там методах
проявляется не только птолемеевская, но и доптолемеевская
астрономия. К сожалению, по степени изученности иранские
зиджи далеко уступают арабским и среднеазиатским.
Гораздо больше данных, мы имеем о развитии
астрономической науки в Индии. Много интересных сведений об
индийской астрономии читатель сможет почерпнуть в
работах А. И. Володарского [38, 39]. Нас здесь интересует
лишь один вопрос: какое влияние на ее развитие оказали
работы Птолемея, в частности «Альмагест».
Основные сведения по астрономии были изложены в
пяти сочинениях, получивших название сиддхант. Это
слово имеет примерно такое же значение, что и слово
«зидж». Все пять сиддхант были написаны в III—IV вв.
н. э. В названиях некоторых из них прослеживается
влияние греко-римской культуры. Так, «Ромака-сиддханта»,
вероятно, получила название от Рома — Рим, «Явана-
сиддханта» — от Ионии (название одной из частей
Греции). Происхождение «Паулисы-сиддханты» связывают
с именем Павла Александрийского, астролога, жившего
в IV в. н. э.2
Первый из известных нам индийских астрономов и
математиков — Ариабхата I (476 — сер»едина VI в.)
использовал в своих работах все сиддханты, особенно
самую содержательную из них — «Сурью-сиддханту».
Его дошедший до нас труд называется «Ариабхаттия».
Он был написан в 499 г., когда его автору
исполнилось 23 года.
А. И. Володарский считает, что индийцы были
знакомы как с доптолемеевскими методами, так и с теориями
движения Солнца, Луны и планет, изложенными в
«Альмагесте». Действительно, в сиддхантах и в «Ариабхат-
1 Собственно на пехлеви он называется «Зиг-и-Шатроаяр». От
пехлевийского «зиг» произошло арабское и новоперсидское
«зидж».
2 Некоторые авторы полагают, что Павел Александрийский бежал
от преследования христиан в Индию и там написал эту сиддхан-
ту. Но прямых исторических доказательств этого мы не имеем.
181

тии» мы найдем эксцентры и эпициклы, сложные
построения с этими кругами и выводы формул, определяющих
движение планет. Все это так напоминает построения и
выводы «Альмагеста»!
Но надо быть осторожным в выводах. Прежде всего
ни в одной из сиддхант, а также в «Ариабхаттии» и
трудах последователей Ариабхаты — Варахамихиры (VI в.),
Брахмагупты (VII в.) и Бхаскары I (VII в.) — мы не
найдем имени Птолемея. Конечно, сам по себе этот факт
еще ни о чем не говорит. Использовал же Птолемей
«Начала» Евклида, не ссылаясь на него.
Но вот перед нами другие факты, приведенные
известным историком науки Отто Нейгебауэром в его лекции,
прочитанной в Обществе друзей прикладной математики
в Колумбийском университете (США) в апреле 1956 г.
[118]. О. Нейгебауэр подчеркивает, что планетные
теории в сиддхаытах и в «Ариабхаттии» отличаются от
теорий «Альмагеста». Сам факт применения эпициклов и
эксцентров ничего не говорит нам об их заимствовании
у Птолемея, так как эти понятия были известны еще до
Птолемея. В индийских построениях не используется
эквант, а вместо него вводится двойной эпицикл: по
одному эпициклу движется другой, а по нему уже —
планета. Впоследствии такое построение независимо применил
Коперник.
В теориях индийских астрономов вместо хорд
применяются синусы, в теории движения Луны нет члена,
учитывающего эвекцию. Если переход от экванта к
двойному эпициклу можно объяснить стремлением сохранить
принцип равномерных круговых двиясений (от которого
отошел Птолемей, введя эквант), то отсутствие в лунной
теории члена, учитывающего эвекцию, объяснить трудно.
Поэтому, по мнению О. Нейгебауэра, факт знакомства
индийских астрономов III—VII вв. с «Альмагестом» не
может считаться доказанным, хотя влияние греческой
астрономии на развитие астрономии в Индии в ту эпоху
несомненно.
К сожалению, исследование О. Нейгебауэра осталось
неизвестным А. И. Володарскому, который, по-видимому,
усмотрел влияние идей и методов Птолемея на работы
индийских астрономов именно в применении ими
эпициклов.
«Альмагест» уже в XI в. доставил в Индию Бируни
и сам перевел его на санскрит. Но об этом мы расскажем
ниже, А пока вернемся в V в.
Щ

Как полагал в 30-е годы советский астроном Р. В. Ку-
ницкий [66], несравненно большее влияние по
сравнению с Индией на развитие астрономии у арабов оказала
христианская секта несториан, последователей
константинопольского патриарха Нестория, осужденного за ересь
на Эфесском соборе в 431 г. Несториане образовали в
Эдессе (Малая Азия, ныне г. Урфа в Турции)
философскую школу, где изучалась греческая наука. После того
как византийский император Зиной в 489 г. закрыл школу,
несториапе бежали в Персию, в Нисибис (ныне г. Мардитт
в Турции), где основали Нисибисскую академию. Они
действительно сыграли известную роль в переводе сочинений
Аристотеля, Евклида, Галена, Птолемея сперва на родной
сирийский, а затем и на арабский язык [76]. Однако по
некоторым сведениям перевод «Альмагеста» на сирийский
язык был выполнен уже в конце VIII в. (этот перевод не
сохранился) [111].
После арабских завоеваний середины VII в. научный
центр из Александрии переместился в Византию. Отсюда
сочинения Птолемея и его александрийских
последователей попали, между прочим, в Трапезунд — город на
южном берегу Черного моря (ныне турецкий город
Трабзон), где в это время учился армянский математик,
астроном и географ Анания Ширакаци (умер в 685 г.).
Вернувшись на родину, Анания написал ряд книг, в том числе
«Космографию» — своеобразный учебник по астрономии
и космогонии, в значительной степени основанный на
данных «Альмагеста» [65]. В то же время видно, что
Анания Ширакаци был знаком и с «Планетными
гипотезами» Птолемея, потому что в его сочинении фигурируют
небесные сферы, связанные с планетами, равно как и две
внешние сферы, разделенные воздухом или водой
(эта концепция заимствована, вероятно, у Иоанна
Филопона).
Византийский философ, теолог и историк Иоанн Да-
маскин (675—754) в числе многочисленных сочинений
философского и теологического содержания написал
книгу «Источник знания», где приводилась, между прочим,
последовательность сфер планет по Птолемею [35]. Этот
отрывок из сочинения Дамаскина спустя полтораста лет
после его смерти был переведен на болгарский язык
Иоанном Экзархом, ученым, находившимся при ,тгворе
болгарского царя Симеона (893—927). Спустя еще
170 лет болгарский протограф попал в Киев, где был
переведен на древнерусский язык и включен в «Изборник»
183

Рис. 35. Знаки зодиака из «Изборника» великого князя Святослава
Ярославича (1073 г.)
великого князя Святослава Ярославича — замечательный
памятник культуры Киевской Руси [69]. В «Изборнике»,
кроме перевода отрывка из Иоанна Дамаскина, можно
найти изображения всех 12 знаков зодиака (рис. 35),
заимствованные из того же источника [40]. Так
мировоззрение Птолемея проникло и на Русь — гораздо раньше,
чем в Западную Европу.
Одновременно, в XI в., то же самое сочинение Иоанна
Дамаскина попало в Грузию, где было переведено на
грузинский язык Ефремом Мцыре. Этот перевод, как
указывают Е. К. Харадзе и Т. А. Кочлашвили [90], был
хорошо встречен в Грузии, так как излагавшиеся в нем фило-
184

софия Аристотеля и система мира Птолемея проникли в
Грузию задолго до этого. Когда же именно ? И каким
путем? На эти вопросы авторы работы [90] не дают ответа.
Однако все перечисленные нами направления
«миграции» «Альмагеста» и других сочинений Птолемея (или
отрывков из них) — это не главные пути. Основной путь,
который и привел в конце концов к широкому
распространению «Альмагеста» по странам мусульманского
Востока, а затем к проникновению его в Европу, лежал через
Багдад.
Город Багдад был построен в 762 г.3 Халифы из
династии Аббасидов перенесли туда столицу халифата из
Дамаска. Уже при дворе второго халифа этой династии
аль-Мансура (754—775) работал автор одного из первых
арабских зиджей Ибрахим аль-Фазари (умер в 777 г.),
известный также своими конструкциями первых в
странах ислама астролябий. Там же работал Йакуб ибн Та-
рик (умер ок. 796 г.), написавший «Зидж, извлеченный
из Синдхинда» [84].
Что же такое Синдхинд? Как сообщает Бируни,
в 771 г. (по другим данным — в 773 г.) в Багдад прибыл
индийский астроном Канака, привезший два сочинения
индийского математика и астронома Брахмагупты
(598—позже 665). В этих сочинениях описывалась
принятая теперь у нас позиционная десятичная система
записи чисел, понятие синуса угла, различные способы
вычисления движения планет, восхода и захода светил,
солнечных и лунных затмений. Халиф приказал
перевести индийский трактат на арабский язык. Этот перевод,
выполненный сыном Ибрахима аль-Фазари Мухаммедом,
и получил название «Большой Синдхинд» [39]. Так было
положено начало передаче достижений индийской
астрономии и математики арабам.
Но это было только начало. От несториан правители
халифата узнали о существовании богатейшего научного
наследия античной греческой и эллинистической науки.
При аль-Мансуре и его внуке Харун ар-Рашиде (правил
в 786—809 гг.) был осуществлен сбор и перевод многих
сочинений античных ученых. В Багдаде был основан
«Дом мудрости» с обширной библиотекой, обсерваторией
и школой. Около 800 г. был переведен с сирийского на
арабский язык и «Альмагест» [111]. К сожалению, этот
перевод не сохранился и имя переводчика нам неизвестно.
3 Ранее на этом месте существовал персидский город,
разрушенный арабами. Название Багдад тоже персидское.
185

В 823 г. халиф аль-Мамун потребовал от
побежденного им византийского царя Михаила II передачи ряда
греческих рукописей или их копий. В их числе был
получен и «Альмагест».
В 828 г. Хаджадж ибн Йусуф ибн Маттар выполнил
первый перевод «Альмагеста» непосредственно с
греческого оригинала. Спустя полвека, в 879—890 гг., был
осуществлен новый перевод, выполненный Исхаком ибн
Хунайном ан-Насрани (умер ок. 910 г.), придворным
врачом халифа. Этот перевод был отредактирован
выдающимся ученым IX в. Сабитом ибн Коррой (836—901)
[84,131].
К настоящему времени сохранились три греческих
текста «Альмагеста» в копиях IX—X вв. Они хранятся
в Париже и в Ватикане. Единственная рукопись
арабского перевода Хаджаджа (в копии XI в.) находится в
Лейдене. Переводы Исхака ибн Хунайна (в копиях)
имеются в Национальной библиотеке Туниса (копия 1085 г.),
в Париже (копии 1221 г. и XV в.) и Эскориале (Мадрид)
(копия 1276 г.). Парижский текст и текст Эскориала
неполны, но удачно дополняют друг друга [131].
Появление в арабоязычном мире переводов
«Альмагеста» оттеснило влияние индийской астрономии как бы
на второй план, хотя некоторые авторы (например, аль-
Хорезми) широко пользовались и индийскими сиддхан-
тами. В Багдад «Альмагест» попал из Александрии через
Антиохию и Харран, где одно время жил и работал
Сабит ибн Корра. Дальнейшее знакомство с трудами
арабских ученых облегчит составленная нами
хронологическая схема (рис. 36).
Ахмад ибн Мухаммад ибн Касир аль-Фергани (ок.
800—861), уроженец Ферганы, много лет работавший в
Багдаде, в своей «Книге об элементах науки о звездах»,
написанной в 836 г., дает довольно подробное изложение
основных положений «Альмагеста» [84]. По замыслу
автора, его книга должна была служить учебником для
изучающих астрономию, но аль-Фергани старался не
перегружать изложение сложными математическими
выкладками, изобилующими в труде Птолемея, а сделать
это изложение по возможности доступным и понятным4.
Аль-Фергани много занимался и конструированием
астролябий.
В это же время арабские астрономы начали сами про-
4 Расстояния и размеры планет аль-Фергани приводит согласно
«Планетным гипотезам» Птолемея.
186

изводить астрономические наблюдения. Вируни в своих
работах приводит определения наклона эклиптики к
экватору, наблюдения моментов равноденствий и другие,
выполненные астрономами Багдада, Дамаска, Ракки,
Самарры и других городов в 828—889 гг. (у Бируни
приводятся и более поздние наблюдения). Их методика во
многом напоминает методику наблюдений, описанную
Птолемеем [89].
Мы уже упоминали не раз о работах Мухаммеда ибн
Мусы аль-Хорезми (783—ок. 850). К моменту начала
его научной деятельности при дворе халифа аль-Мамуна
аль-Баттани аль-Маджрити
' — Омар ланям
„ аль-Хурагзни „, ,. ^ Инб Афлах
аль-Хорезми —— Ион Ирак т" ат-Тусй
Гчбит Ибн KYmna Ии» Синаи Ибн БаДЖ
Саоит ИОн Корра аль-Хайсам „g т л „
аль-Фараби Бируни И6н1уфаИЛ
аль-Фергаки Ае^афа аль.Ш^труджи
""""""~"~""~— ас-Су фи аз-Заркали
J L
800 900 1000 1100 1200 1300г.
Рис. 36. Хронология жизни ученых Востока (схема)
(813—833) в его распоряжении были и «Большой Синд-
хинд», и перевод «Альмагеста». Как свидетельствует
историк XIII в. ибп аль-Кифти, «большинство людей
пользовались этой книгой («Большим Синдхиндом».—
В. Б.) до дней халифа аль-Мамуна. Абу Джафар
Мухаммед ибн Муса аль-Хорезми сократил это для него и
сделал из этого свой зидж, известный в странах ислама.
В нем он доверился в средних движениях «Синдхинду»,
но отступил от него в неравенствах и склонениях: он
сделал неравенства согласно мнению персов, а склонения
Солнца — согласно мнению Птолемея» [34].
Итак, аль-Хорезми в работе над своим зиджем прибег
к своего рода компиляции. Он использовал для каждой
величины (или группы величин) тот источник, который
считал наиболее надежным. Под «мнением персов» ибн
аль-Кифти подразумевает, скорее всего, «Шахский зидж»
VII в., о котором мы уже упоминали и который сам по
себе содержит заимствования из «Альмагеста». Следуя
индийцам, аль-Хорезми ввел вместо хорд синусы,
использовал тангенсы.
В предисловии к своему «Зиджу» аль-Хорезми пишет
о некоторых требованиях, предъявляемых к читателю:
«В том же случае, если он окажется хорошо обученным
187

этим наукам (арифметике и геометрии.— В. Б.) и имеет
практику изучения «Альмагеста» Птолемея, он не будет
сомневаться во всем том, что имеет здесь место по
необходимости, и во всем, что относится к этому» [84].
В изложении теории движения планет аль-Хорезми в
основном следует геоцентрической системе Птолемея и
постоянно на него ссылается.
Другой труд аль-Хорезми посвящен работе с
астролябиями. Этот прибор несомненно был самым
употребительным у арабских астрономов.
Выше, в главе о «Географии» Птолемея, мы уже
упоминали, что и в этой области знания аль-Хорезми
использовал «Географию» Птолемея, во многом дополнив и
расширив ее.
Уже упоминавшийся Сабит ибн Корра был не только
редактором арабского перевода «Альмагеста». В отличие
от Птолемея, считавшего солнечный апогей
неподвижным, ибн Корра учитывал его движение и связывал его
с изменением наклона эклиптики к экватору. Внук ибн
Корры Ибрахим ибн Синан (908—946) написал «Книгу
о целях «Альмагеста». Мухаммед ибн Синан аль-Батта-
ни, известный в истории астрономии под
латинизированным именем Альбатегний (850—929), провел много
наблюдений, получив иные результаты, чем Птолемей.
Он тоже использовал синусы вместо хорд, разработал
методы вычисления сферических треугольников. Наряду
с Сабитом ибн Коррой ему принадлежит открытие
движения апогея орбиты Солнца. Аль-Баттани составил
звездный каталог на основе каталога Птолемея, но с
учетом прецессии. Поправка к долготам звезд за
прецессию на эпоху каталога аль-Баттани (880 г.) составила
11° 10'. Поскольку разность эпох обоих каталогов
равнялась 745 годам, получаем отсюда постоянную прецессии
54 " в год. Однако целесообразнее сравнить долготы
каталога Баттани с долготами Гиппарха. Поскольку, как
мы видели в гл. 11, они отличались па 2° 40' от долгот
Птолемея (из-за принятия последним неверного
значения постоянной прецессии), разность долгот Баттани—
Гиппарх составит 13°50'. Деля это число на разность
эпох (1010 лет), получим постоянную прецессии 49,3"
в год, что очень близко к правильному значению 50,2" в
год. Таким образом, аль-Баттани не только правильно
учел прецессию, но и исправил ошибку Птолемея.
Он получил также правильное значение наклона
эклиптики к экватору 23°35', всего на 6" меньшее точного
значения для той эпохи.
188

Младший современник аль-Баттани, Мухаммед аль-
Фараби (870—950), написал «Книгу приложений к
„Альмагесту4'», в которой изложена тригонометрия аль-Фара-
би, включающая хорду, синус, косинус, тангенс и
котангенс [84], а также «Комментарии к „Альмагесту4'
Птолемея».
Абд-ар-Рахман ас-Суфи (903—988), работавший в
Ширазе, в своей «Книге созвездий неподвижных звезд»
приводит результаты проверки звездного каталога Гип-
парха—Птолемея по своим наблюдениям. Ас-Суфи
исследовал положения всех звезд каталога, исправил
ошибки и учел поправку за прецессию, которая для
эпохи 964 г. составила 12°42\ Ас-Суфи исходил из
постоянной прецессии 1° за 66 лет (т. е. 54,5" в год),
вычисленной группой багдадских астрономов под руководством
Йахьи ибн Аби Мансура в 830 г. Эта величина несколько
завышена, и причиной этого является все та же ошибка
Птолемея на один градус. (Поскольку долготы в
каталоге «Альмагеста» занижены на эту величину, поправка за
прецессию неизбежно получится завышенной). Если же
считать от эпохи Гиппарха, то поправка на 15° 22' за
1094 года даст постоянную прецессии 50,6'' в год —
почти правильное значение. В книге ас-Суфи приведены
также изображения 48 созвездий. Ас-Суфи сравнил
греческие созвездия со староарабскими и привел
названия всех звезд по Птолемею и по староарабским
источникам [84].
Багдадский астроном Абу-ль-Вафа аль-Бузджани
(940—988) написал «Книгу Альмагеста», содержавшую
ревизию ряда положений Птолемея. Комментарии к
«Альмагесту» написал также Мухаммед аль-Казин ибн аль-Ху-
расани (умер в 965 г.), работавший в Рее (близ
современного Тегерана). Абу Али ибн аль-Хайсам, известный под
латинизированным именем Альхазен (965—1039), о
котором мы уже рассказывали в гл. 13, оставил целый ряд
сочинений, в том числе «Книгу о сомнениях по поводу
Птолемея», «Книгу о движении Лупы», «Книгу о форме
движений каждой из семи планет». Как видим, ибн аль-
Хайсам, живший и работавший в Каире, в новой столице
Фатимидского Египта, не стеснялся выражать свои
сомнения по поводу тех или иных результатов Птолемея.
В частности, он подвергал критике его теорию движения
планет. Интересно, что «Книга о форме движения планет»
ибн аль-Хайсама была лишь в 1974 г. случайно
обнаружена в Куйбышеве [84].
189

Хорезмийский
астроном Абу Наср Мансур
ибн Ирак (умер в 1036 г.)
был автором «Шахского
Альмагеста», названного
так потому, что книга
была посвящена хорезмша-
ху. Она представляла
собой обработку
«Альмагеста» Птолемея. Ибн Ирак
написал много
астрономических и математических
сочинений, дошедших до
нас. Он работал в
тогдашней столице Хорезма Кяте
(ныне г. Бируни Кара-
Калпакской АССР).
Ибн Ирак был
учителем крупнейшего
астролог „ „ - нома мусульманского сред-
Абу-р-Раихан аль Бируни J J r ^
(973-1048) невековья,
ученого-энциклопедиста Абу-р-Рай-
хана аль-Бируни (973—
1048). Бируни оставил нам много сочинений по
астрономии, геодезии, географии и другим наукам [58]. Значение
этих книг состоит не только в собственном вкладе
Бируни в эти науки, но еще и в том, что он собрал и обобщил
результаты своих предшественников, начиная от Гиппар-
ха, а также в том, что он постарался передать
астрономические и географические знания другим народам. Так,
оказавшись в 1021—1024 гг. в Индии, куда он прибыл с
войсками газневидского султана Махмуда, Бируни
изучает санскрит и переводит на этот язык «Начала» Евклида
и «Альмагест» Птолемея, сделав, таким образом,
«Альмагест» доступным индийским ученым. Некоторые
сочинения индийцев Бируни перевел с санскрита на арабский
язык.
В своем главном астрономическом произведении
«Канон Масуда» Бируни следует общему плану «Альмагеста»,
но использует и другие сочинения Птолемея —его
«Географию», «Четырехкнижие», «Канон царей». В «Каноне
Масуда» Бируни приводит результаты своих наблюдений,
сравнивая их с наблюдениями своих предшественников.
Среди них сводка определений наклона эклиптики к
экватору по данным примерно десяти арабских и средне-
190

азиатских астрономов, определения моментов
равноденствий и солнцестояний и основанные на них определения
долготы солнечного перигея, наблюдения солнечных и
лунных затмений, определения широт и долгот звезд из
каталога Гиппарха—Птолемея. В звездном каталоге Би-
руни 1029 звезд. Помимо их координат, Бируни приводит
звездные величины по Птолемею и по ас-Суфи. В
предисловии к этому каталогу Бируни пишет: «В этих
таблицах установлены те же положения звезд, что и в книге
„Альмагести, но к ним прибавлены 13° по долготе, о чем
было упомянуто раньше. Это было сделано после весьма
тщательного исправления их по нескольким
экземплярам в разных переводах и с добавлением того, что
следовало добавить, после того как они стали похожими на
оригинал. Мы усердно исправляли и то, что нашел Абу-л-
Хусейн ас-Суфи5, так как, хотя он и видел
несоответствия, достойные изумления и порицания, это не
произвело на него впечатления и он не взял на себя
ответственности, чтобы исправить все это» [58].
Таким образом, и ас-Суфи, и Бируни видели ошибки
и несоответствия в имевшихся в их распоряжении
переводах «Альмагеста» (бывших, как правило, на совести
переводчиков и переписчиков), но ас-Суфи не решился
внести исправления, а Бируни сделал это после
тщательного сличения различных копий с различных
переводов, как и следовало поступать в подобных случаях.
Работа, проделанная Бируни, — образец научного подхода
к исследованию текста сочинения, представляющего не
только чисто научный, но и исторический интерес.
Для сравнения скажем, что канонический греческий
текст «Альмагеста», составленный И. Л. Гейбергом
в 1898 г. на основе анализа всех имевшихся копий, все
же потребовал внесения многочисленных поправок, что
и было сделано авторами новейших переводов на
немецкий и английский языки К. Манициусом и Дж. Тумером.
Список этих исправлений приложен к переводу Туме-
ра [131].
Вернемся к использованию «Альмагеста» в работах
мусульманских астрономов. Еще в середине VIII в. арабы
завоевали Испанию и основали там Кордовский халифат
во главе с халифами династии Омейядов. Во второй
половине X в. в трудах одного из испано-арабских ученых, Мас-
5 Читателя не должпо смущать, что Бируни называет Абд-ар-Рах-
мана ас-Суфи Абу-л-Хусейном. Это— так называемая кунья по
сыну, означающая «отец Хусейна» и ставящаяся впереди имени.
191

лама аль-Маджрити (ок. 940—1008), уроженца Мадрида,
мы находим «Примечания к книге Птолемея о
проецировании поверхности сферы на плоскость» (речь идет о его
«Планисферии») [84].
Но на территорию Кордовского халифата попал и
«Альмагест». Это произошло уже в XI в. Целый ряд испано-
арабских ученых занялись усовершенствованием труда
Птолемея. Работавший в Толедо Ибрахим аз-Заркали,
получивший латинизированное имя Арзахель (1029—1087),
опубликовал в 1080 г. «Толедские таблицы», содержавшие
сведения о положениях планет, восходах и заходах светил,
затмениях и т. д. Они были вычислены на основе теории
Птолемея. Джабир ибн Афлах (XII в.) озаглавил свое
сочинение «Усовершенствование Альмагеста». Мухаммад ибн
Баджа (умер в 1138 г.), Мухаммад ибн Туфейль (1100—
1185) и его ученик Hyp ад-Дин аль-Битруджи (умер в
1185 г.) критиковали планетные теории Птолемея с
позиций физики Аристотеля [84].
Испано-арабские ученые, можно сказать, открыли
«Альмагесту» и другим произведениям классиков
античной науки «окно в Европу», поскольку именно там, в
Испании, а точнее, в Толедо, в конце XII в. собралась
большая группа западных ученых, поставивших целью
перевести сочинения классиков античной науки на латинский
язык — основной язык европейских ученых, остававшийся
таковым до начала XIX в.
До этого положение европейских ученых было
сложным. Многие сочинения классиков античной науки в их
греческих оригиналах или хотя бы в копиях погибли.
Французский математик Герберт Орийякский, живший во
второй половине X в. и ставший в конце жизни римским
папой под именем Сильвестра II (930—1003), был вынужден
пользоваться арабским переводом «Альмагеста» [32, 78].
В XII в. начались работы по переводу основных трудов
классиков науки на латинский язык. Апгличанин Аделяр
Батский в 1124—1141 гг. перевел «Начала» Евклида и
астрономические таблицы Аль-Хорезми (включая таблицы
синусов), Герман из Каринтии в 1143 г. — «Планисферии»
Птолемея, Роберт из Честера в 1145 г.— «Алгебру» аль-
Хорезми, Иоанн Севильский в это же время — «Физику»
Абу Али ибн Сины [52, 78].
Но особенно крупный вклад в это дело внес врач и
астролог Герардо Кремонский (1114—1187), который в
1175 г. и перевел «Альмагест» на латинский язык. Кроме
того, он перевел на латынь сочинения Евклида, Аристо-
192

теля, Архимеда, Гиппократа, Галена, аль-Фараби и Абу
Али ибн Сины (Авиценны) [52, 78].
Другая группа переводчиков, как мы уже знаем,
сформировалась на Сицилии. Здесь Евгений Сицилийский
перевел «Оптику» Птолемея, а другой, неизвестный нам
переводчик при содействии Евгения сделал перевод
«Альмагеста». Дальше в течение трех веков, т. е. до начала
книгопечатания, «Альмагест» и другие сочинения
Птолемея получили хождение в странах Европы в рукописях на
латинском языке. В середине XIII в. по указанию короля
Альфонса X Кастильского большая группа астрономов
подготовила так называемые «Альфонсрвы таблицы» [29],
которые должны были заменить «Толедские таблицы»
1080 г. В них, кроме положений планет, восходов и заходов
светил и моментов затмений, вошел и звездный каталог
Птолемея, приведенный к эпохе 1252 г.
Так обстояло дело в Западной Европе. А в Восточной
Европе, в Византии, продолжали распространяться
рукописи сочинений античных ученых на греческом языке.
Несколько византийских списков сочинений Птолемея,
Евклида, Диоскорида и других античных ученых
относятся к IX в. Герберту Орийякскому не нужно было ездить
в Барселону в поисках копий этих сочинений на арабском
языке. Ему следовало отправиться в Константинополь,
и он получил бы их на греческом языке.
В XI в. в Византии трудились два замечательных
человека: писатель и философ Михаил Пселл (1018—1097) и
ученый-энциклопедист Симеон Сет, расцвет творчества
которого пришелся на 1071—1078 гг. [41, 107]. В области
космологических представлений они оба продолжали
линию неоплатоников, Иоанна Филопона и Георгия Пи-
сиды.
Михаил Пселл многое позаимствовал из учений
Платона и Аристотеля, а конкретные астрономические данные
заимствовал у Птолемея. Рассматривая периоды
обращения планет, он устанавливает соотношения между ними
по образцу «Гармоник» Птолемея. Пселл пытался
вычислить период, за который все планеты возвращаются к
исходным местам, и получил 1 753 200 лет. Но, как
указывает П. Таннери [129], это не общее наименьшее кратное
всех периодов, а кратное сотическому периоду Сириуса
(1461 год): 1461-1200=1753 200.
Оба автора неоднократно ссылаются на Птолемея.
Симеон Сет объясняет лунные и солнечные затмения
согласно «мудрейшему Птолемею». У Птолемея заимствованы
7 Клавдий Птолемей
193

порядок сфер планет, относительные размеры Солнца,
Земли и Луны, определения небесного экватора, небесного
меридиана и горизонта, наклона оси мира к горизонту,
объяснение смены времен года наклоном плоскостей
эклиптики и экватора на угол около 24°.
Большой интерес представляют космологические
воззрения упомянутых византийских ученых 6. Будучи
христианами, они все же занимают достаточно независимую
позицию в этих вопросах. Отрицая множественность
обитаемых миров, Симеон Сет пишет, что «вне мира не
пустота, не занебесное пространство, но умный духовный
космос». Солнце Пселл, следуя Аристотелю, считает не
раскаленным телом, а лишь окруженным «огненными
воспарениями». Из подобных же воспарений образуются и
кометы. Звезды не получают свет от Солнца, а подобно
ему имеют «по преимуществу огненную» природу.
В дальнейшем эти научные традиции были
продолжены. В середине XII в. Иоанн Каматир, следуя примеру
Лукреция и Георгия Писиды, пишет астрономическую
поэму, и в ней многократно упоминается имя Птолемея,
которого автор называет «премудрым и прекрасным». Феодор
Метохит написал «Комментарий к Альмагесту» [41].
В этот период на Востоке происходили бурные события.
Кочевники-сельджуки, разгромив в 1040 г. империю Газ-
невидов (при которых жил и работал Бируни), завоевали
Иран, взяли в 1055 г. Багдад и захватили Ирак. К концу
XI в. под их властью оказалась огромная территория от
Китая до Средиземного моря. Замечательный таджикский
астроном, философ и поэт Омар Хайям (1048—1131) так
пишет об этих событиях, мешавших ему заниматься
наукой: «Но я был лишен возможности систематически
заняться этим делом и даже не мог сосредоточиться на
размышлении о нем из-за мешавших мне превратностей
судьбы. Мы были свидетелями гибели ученых, от которых
осталась малочисленная, но многострадальная кучка
людей» [84]. Так было в первые годы нашествия сельджуков.
Но уже в 1074 г. по приказанию султана Малик-шаха в
Исфахане была построена обсерватория, оснащенная
хорошими по тем временам приборами, были приглашены
лучшие астрономы во главе с Омаром Хайямом. Там он
создал свой знаменитый календарь. Обсерватория работала
6 В основном они изложены в трактате Пселла «О
всеобъемлющей доктрине» и в сочинении Сета «О природе», хотя у них есть
и другие астрономические сочинения.
194

до 1092 г., после чего астрономам пришлось перебираться
в Мерв — новую столицу султана.
Внешние потрясения не раз, как мы видели, оказывали
отрицательные воздействия на развитие науки. Еще одним
таким потрясением явилось в начале XIII в. нашествие
монголов, сокрушивших Хорезм и покоривших русские
княжества. В этот период астрономия продолжала развиваться
лишь в Мараге, на территории Иранского Азербайджана,
где астроном Насир ад-Дин ат-Туси (1201—1274),
пользовавшийся покровительством внука Чингиз-хана Хула-
гу, построил обсерваторию [72]. Он написал книгу
«Изложение Альмагеста», в предисловии к которой пояснял, что
книгу Птолемея, принимаемую астрономами как готовую
формулу, он изложил для учеников так, чтобы
содержащиеся в ней теоретические мысли, а также порядок глав,
распределение вычислений и чертежи не были бы
сокращены или искажены. Свои замечания и дополнения к книге
Птолемея ат-Туси вписал другими чернилами, чтобы
можно было сразу отличить его собственные мысли от идей и
выводов Птолемея [18]. В «Альмагест» ат-Туси включил
ряд дополнений, из которых важнейшим является
сомнение в справедливости планетной теории Птолемея. Он
разработал свою собственную теорию движения Луны и
планет, пожалуй, еще более сложную, чем у Птолемея. Ат-
Туси доказал также возможность представить
прямолинейное движение комбинацией двух круговых движений. Ат-
Туси перевел на арабский язык «Центилоквиум» («Книгу
плодов») Птолемея. Ученик ат-Туси Кутб ад-Дин аш-Ши-
рази (1236—1311) в 1292—1306 гг. написал книгу под
названием «Жемчужина короны для украшения Дубаджа»,
где он рассматривает «Альмагест» в обработке ат-Туси, но
со своими дополнениями. В этой же книге
рассматривается теория музыки Птолемея [84].
При Марагинской обсерватории была создана большая
библиотека. Обсерватория просуществовала до середины
XIV в. Ее развалины сохранились до сих пор.
Среднеазиатская астрономия испытала новый подъем
в первой половине XV в., когда в Самарканде была
построена обсерватория Улугбека (1394—1449), внука
известного завоевателя Тимура. Вместе с Улугбеком там
работали астрономы Казы-заде ар-Руми и Гиясаддин Джемпгид.
Громадной заслугой Улугбека было составление заново, по
собственным наблюдениям, звездного каталога,
включавшего положения 1018 звезд. Благодаря высокой точности
его приборов, особенно большого стенного квадранта, ради-
195
7*

ус дуги которого
составлял 40 м, Улугбек смог
получить координаты звезд
своего каталога с большой
точностью [57, 70, 84].
Первоначальной целью
Улугбека была проверка
каталогов Птолемея и ас-
Суфи. Вот что он пишет
по этому поводу: «Мы
наблюдали все звезды,
видимые у нас. Мы
вынуждены были пропустить 27
звезд, которые не
восходят над горизонтом в
Самарканде... Мы
заимствовали их у Абд-ар-Рахмана
(ас-Суфи.— В, £.),
соблюдая расчет, связанный с
Мухаммед Тарагай Улугбек различием эпох». И далее:
(1394-1449) «Прежде чем установить
с помощью собственных
наблюдений положение этих звезд, мы расположили их
согласно этому трактату (ас-Суфи. — 5. Б.), и мы
нашли их в большинстве случаев расположенными иначе,
как об этом можно судить на основании тщательного
изучения неба... Это заставило нас наблюдать самих» [57].
Улугбек уточнил наклон эклиптики к экватору (ошибка
его результата не превосходит 30", тогда как у Птолемея
она больше 10', а у ат-Туси — 2'), длину звездного года
(с ошибкой в 1 мин), постоянную прецессии (с ошибкой
в Г).
Из приведенных выше выдержек мы видим, что
Улугбек нашел ряд ошибок в каталогах Птолемея и ас-Суфи и
решил получить независимые координаты звезд, что и
было выполнено. Каталог Улугбека -^это первый
независимо составленный звездный каталог после Птолемея.
После трагической гибели Улугбека в 1449 г. звездный
каталог Улугбека и его таблицы (среди них — таблицы
тригонометрических функций через 1') были спасены его
учеником и сотрудником Али Кушчи, уехавшим в Герат
[84].
Астрономические традиции Самаркандской школы и
труды ее предшественников — астрономов Средней Азии и
Арабского Востока, впитавшие в себя опыт античной
196

науки, в том числе и исследований Птолемея, продолжали
распространяться дальше — в Иран, Индию, а также в
Турцию. Представитель школы Улугбека аль-Бирджанди
(умер в 1525 г.) написал очередной «Комментарий к
изложению Альмагеста» (по его обработке Насир ад-Дином
ат-Туси) [84]. Но в это время Николай Коперник уже
работал над своей рукописью «О вращениях небесных сфер»,
которой было суждено произвести полный переворот в
представлениях о положении Земли и планет во
Вселенной и об их движениях.
Глава 17
От эпициклов Птолемея
к законам Кеплера
В 1453 г. под ударами турок-османов пал
Константинополь. Прекратила свое существование Византийская
империя. Многие греческие ученые и деятели культуры бежали
в Италию и в другие страны Европы, перевозя с собой те
сочинения античных авторов, которые им удалось спасти.
По времени конец Византии почти совпал с
разрушением Самаркандской обсерватории и с гибелью "Улугбека.
Эти события наряду с наступлением эпохи Возрождения
определили роль Западной Европы в дальнейшем
развитии науки вообще и астрономии в частности.
На протяжении трех предшествовавших веков в
астрономии шла борьба между сторонниками представлений
Аристотеля о небесных сферах и системы мира
Птолемея с ее сложной комбинацией кругов: деферентов,
эпициклов, эксцентров и эквантов. Представления Аристотеля
достигли Европы в обработке ученика Ибн Туфейля Му-
хаммада ибн Рушда, более известного в Европе под именем
Аверроэс (1126—1198). Согласно концепции Аристотеля—
Аверроэса, существуют лишь идеальные хрустальные
сферы, по одной для каждой планеты, плюс еще три сферы,
необходимые для размещения неподвижных звезд, для
объяснения прецессии и трепидации — предполагаемого
периодического изменения постоянной прецессии, якобы
открытого Сабитом ибн Коррой. (В действительности это
была одна из ошибок средневековой науки, ибо никакой
трепидации не существует [29] *.)
1 Как показал Г. Е. Куртик [67], впервые трепидацию ввел еще
197

Система Аристотеля—Аверроэса привлекала своей
стройностью и простотой, хотя она не позволяла вычислять
точные положения планет, как система Птолемея.
Последнее обстоятельство склоняло чашу весов все более на
сторону системы Птолемея. К середине XV в. ее торжество
стало полным, тем более, что появились греческие тексты
«Альмагеста».
Папа римский Николай V (1447—1455), оказавший
гостеприимство греческим ученым, бежавшим от турок,
стремился собрать в Ватиканской библиотеке как можно
больше рукописей античных ученых, чтобы организовать
их перевод на латынь. Перевод «Альмагеста» он поручил
своему секретарю Георгию Трапезундскому (1396—1484),
греку по национальности2. Однако Георгий не был сведущ
в астрономии, да и латынь знал неважно. За перевод он
взялся из чисто карьеристских соображений. К декабрю
1451 г. перевод был завершен, причем Георгий добавил к
нему комментарии к «не совсем правильным местам».
Этот перевод архиепископ Никколо Перотто назвал «не
латинским, а варварским, со многими ошибками». Вскоре
выяснилось, что комментарии к «Альмагесту», которые
Георгий выдал за свои, принадлежат Теону
Александрийскому. Эта литературная кража стоила Георгию его
выгодной должности. Он бежал в Неаполь3, но потом, видимо,
вымолил у папы прощение, ибо в 1461 г. мы вновь
находим его в Риме.
Между тем «Альмагестом» заинтересовался кардинал
Иоанн Виссарион (1403—1472), человек весьма
образованный. Он хорошо знал древнегреческий, сам занимался
литературной деятельностью и способствовал в этом другим.
Три рукописи «Альмагеста» из Ватиканской библиотеки
содержат его пометки на полях, а одна из них переписана
большей частью его рукой.
Убедившись в низком качестве перевода Георгия Тра-
пезундского, Виссарион решил было сам сделать перевод
«Альмагеста», но его многочисленные обязанности,
связанные с кардинальской должностью, мешали этому.
В 1460 г. Виссарион как папский легат прибыл в Вену,
Теон Александрийский, задолго до Сабита ибн Корры. Ее
краткое изложение есть и в «Квадривиуме» аль-Хорезми Г 34].
2 Отец Георгия происходил из Трапезундского государства,
отделившегося от Византии в 1204 г. после захвата
Константинополя крестоносцами и просуществовавшего до его завоевания
турками в 1461 г.
3 Неаполитанское королевство в то время было независимым
государством, где правила Арагонская династия.
198

где познакомился с профессором математики Венского
университета Георгом Пурбахом.
Астроном Георг Пурбах (1423—1461) еще до приезда
Виссариона начал работать над «Сокращенным
изложением астрономии», основанным на «Альмагесте» Птолемея
[78]. При этом он столкнулся с многочисленными
неточностями и ошибками латинского перевода Герардо Кре-
монского, сделанного с арабского текста, который тоже
возможно был не прямым переводом с греческого, а
переводом с сирийского языка. Пурбах решил поехать в Италию
и там найти и перевести на латинский язык греческий
текст «Альмагеста». К этой работе он привлек своего
ученика, Иоганна Мюллера (1436—1476) родом из
Кенигсберга (во Франконии), более известного под латинским
именем Региомонтан4. Оба ученых уже собрались
выехать в Италию, как вдруг Пурбах неожиданно скончался.
Региомонтан поехал один, изучил греческий и сделал если
не полный перевод, то, во всяком случае, достаточно
подробное изложение «Альмагеста». Его учителями в
греческом языке оказались... Георгий Трапезундский и Теодор
из Газы. Региомонтан оказался способным учеником,
не побоявшимся вскоре выступить против своего учителя.
Он не только завершил работу Пурбаха, но и перевел
комментарий Теона. Перевод Георгия Трапезундского он
назвал «тяжелым и неприятным, так что, если бы Птолемей
вдруг ожил, он не узнал бы самого себя». И Региомонтан
написал специальное сочинение «Защита Теона против
Трапезундского», заслужив глубокую ненависть и самого
Георгия и его сыновей. В Италии он пробыл семь лет,
после чего еще около трех лет проработал в Венгрии.
В 1476 г. Региомонтан приехал в Рим, где внезапно
скончался. Первые шесть книг «Альмагеста» в переводе
Пурбаха с примечаниями и дополнениями Региомонтана
были изданы в Венеции лишь через 20 лет после смерти
последнего — в 1496 г. Это было первое издание
«Альмагеста», с которым познакомился прибывший в те годы в
Италию для изучения наук молодой Коперник.
Только в 1515 г. в Венеции был напечатан полный
латинский вариант «Альмагеста» в переводе Герардо Кре-
монского, а в начале 1484 г. старший сын Георгия
Трапезундского Андреас представил «Альмагест» в переводе
своего отца со своим предисловием и с посвящением папе
4 Кенигсберг по-немецки означает «королевская гора».
Региомонтан по-латыни означает «житель королевской горы».
199

Фронтиспис «Географии» Птолемея (Лейден, 1618. Под ред.
П. Бертиуса)
Изображены фигуры Птолемея (слева) и Марина Тирского (справа)
Сиксту IV. Но Сикст IV умер в августе 1484 г. Из-за
постоянных франко-итальянских войн издание задержалось
на целых 45 лет. Лишь в конце 1528 г. его осуществил в
Венеции Лука Гаурик, профессор математики из Неаполя
(производивший и некоторые астрономические
наблюдения). Это издание было затем повторено дважды: в 1541 г.
200

в Базеле Иеронимом Гемузеусом и в 1551 г. там же
Освальдом Шреккенфуксом, который напечатал не только*
«Альмагест», но также «Четырехкнижие», «Центилокви-
ум», «Географию» Птолемея и «Гипотипозис» Прокла
Диадоха. В 1538 г. в Базеле Симон Гринеус осуществил«
первое издание греческого текста «Альмагеста» [14].
В 1549 г. в Виттенберге — известном центре протестантской
науки — была издана на греческом и латинском языках
первая книга «Альмагеста» с предисловием известного
деятеля Реформации Филиппа Меланхтона (1497—1560}
[5]. Интересно, что это издание было выпущено спустя
всего шесть лет после выхода первого издания труда
Коперника «О вращениях...», причем издателем был
астроном и математик, профессор Виттенбергского
университета Эразм Рейнгольд (1511—1553), автор первых
астрономических таблиц, вычисленных по теории Коперника
(эти так называемые «Прусские таблицы» вышли в свет
в 1551 г.).
Достоверно известно, что Коперник начинал свое
знакомство с «Альмагестом» по переводу и изложению Пур-
баха и Региомонтана, а в дальнейшем получил
венецианское издание 1515 г. (на латинском языке) и базельское
издание 1538 г. (на греческом языке), которое привез ему
его ученик и последователь Георг Иоахим Ретик (1514—
1576). С этими датами связаны и определенные этапы в-
работе Коперника над его основным трудом «О
вращениях небесных сфер»: в 1515 г. был написан «Малый
комментарий» — краткое изложение гелиоцентрической
системы Коперника и начата работа над первой книгой «О
вращениях...»; в 1538 г., после почти восьмилетнего
перерыва, Коперник по настоянию Ретика возвращается к
прерванному труду, пишет шестую книгу (последнюю)
и делает ряд добавлений к пятой книге. Профессор«
И. Н. Веселовский на основе глубокого анализа текстов
Коперника и Птолемея установил примерную датировку
всех этапов работы Коперника5. Этими данными мы здесь
и пользуемся [63].
Первые идеи, связанные с концепцией
гелиоцентризма, возникли у Коперника еще в начале 1500-х годов, в
период его пребывания в Италии. В это время на полях
принадлежавшей ему книги астронома Сакробоско (ла-
5 И. Н. Веселовский является автором переводов на русский язык
обоих бессмертных сочинений: труда Коперника «О
вращениях...» [46] (изданного в 1964 г.) и «Альмагеста» (пока не
изданного) .
201

тинизированная форма фамилии Джона Галифакса,
жившего в первой половине XIII в.) Коперник записал ряд
вопросов, среди них следующие: «Находится ли Земля по
своей природе в центре мира?» «Движется ли небо?
Будет ли движение неба равномерным и регулярным?»
Экземпляр этой книги, изданной в 1499 г. и много лет
служившей учебником для студентов университетов, с
пометками Коперника и сейчас хранится в библиотеке Упсаль-
•ского университета [37].
Коперник не знал о гелиоцентрической системе мира
Аристарха Самосского, поскольку сочинение Архимеда
«Об исчислении песчинок», из которого мы узнали об
идеях Аристарха, было опубликовано уже после смерти
Коперника. Однако он знал о взглядах пифагорейца Фи-
лолая (V в. до н. э.) и Гераклида Понтийского,
допускавших вращение Земли вокруг оси (Филолай считал, что
Земля и «противоземля» вращаются вокруг
«центрального огня») [37].
План основного труда Коперника «О вращениях...»
близок к плану «Альмагеста». Может вызвать удивление,
что Коперник, ставя себе целью показать ошибочность
системы мира Птолемея, в то же время заимствует у
своего великого предшественника не только план его
сочинения, но и целые фрагменты. Примеры таких
заимствований мы приведем ниже. Мнение Коперника о Птолемее
выражено во вступлении к первой книге «О
вращениях...»: «Действительно, хотя Клавдий Птолемей
Александрийский, стоящий впереди других по своему
удивительному хитроумию и тщательности, после более чем
сорокалетних наблюдений завершил созидание всей этой науки
почти до такой степени, что, как кажется, ничего не
осталось, чего он не достиг бы, мы все-таки видим, что
многое не согласуется с тем, что должно было бы вытекать
из его положений; кроме того, открыты некоторые иные
движения, ему неизвестные» [63].
Мы видим, что Коперник давал достаточно высокую
оценку заслуг Птолемея, который, по его мнению, стоит
«впереди других по своему удивительному хитроумию и
тщательности». Более того, он «завершил созидание всей
этой науки почти до такой степени, что, как кажется,
ничего не осталось, чего он не достиг бы...». И все-таки
Коперник заявляет, что не согласен с Птолемеем и притом
во многом.
Обратим внимание на одну деталь. Коперник
указывает, что Птолемей завершил построение своей системы
202

мира «после более чем сорокалетних наблюдений».
Откуда такой срок? Ведь мы знаем, что Птолемей вел свои
наблюдения с 127 по 141 г., т. е. в течение 15 лет. Не мог
не знать этого и Коперник, тщательно и не один раз
прочитавший и изучивший «Альмагест». Очевидно, это
роковое число «сорок» исходит от Олимпиодора, который писал,
что Птолемей в течение 40 лет работал в Каноне (с. 15).
Быть может, Коперник не имел под рукой текста
Олимпиодора, но помнил, что «сорок лет» как-то
относится к наблюдениям Птолемея, и сделал ошибочный
(или по крайней мере необоснованный) вывод, что труд
Птолемея основан на сорокалетних наблюдениях.
Что касается движений, неизвестных Птолемею, то
под ними Коперник мог подразумевать изменение
наклона эклиптики к экватору и трепидацию. Но возможно,
что он имел в виду гораздо более существенные
движения, а именно — вращение Земли и ее обращение вокруг
Солнца, а также движение планет.
Уже в первой книге своего труда Коперник старается
обосновать возможность движений Земли, центральное
положение Солнца в планетной системе. Он сперва
приводит известные нам аргументы Птолемея в пользу
центрального и неподвижного положения Земли, а затем
опровергает их. Этим опровержениям посвящена восьмая
глава первой книги труда Коперника.
Почему, спрашивает Коперник, древние астрономы
считают, будто Земля не может вращаться? Потому что
в этом случае она имела бы слишком большую скорость
вращения? Но ведь они допускают вращение неба,
которое во много раз больше Земли и должно иметь во
столько же раз большую скорость. Движение Земли, по
Копернику, является естественным. «Поэтому напрасно боится
Птолемей, что Земля и все земное рассеется в результате
вращения, происходящего по действию природы»,— говорит
Коперник. И далее: «...вращается не только Земля с
соединенной с ней водной стихией, но также и немалая часть
воздуха и все, что каким-либо образом сродно с Землей,
или уже ближайший к Земле воздух, пропитанный
земной и водной материей ...имеет приобретенное движение,
которое сообщается ему прилегающей Землей в
постоянном вращении и без всякого сопротивления» [63].
В этих словах заключено интуитивное понимание
Коперником двух из трех законов Ньютона, которые будут
четко сформулированы спустя 150 лет: закона инерции
и закона переноса импульса. Это не единственный пример
203

такого рода. Вот как понимал Коперник явление
тяготения: «Что касается меня, то я полагаю, что тяготение
есть не что иное, как некоторое природное стремление,,
сообщенное частям божественным провидением творца
Вселенной, чтобы они стремились к целостности и
единству, сходясь в форму шара. Вполне вероятно, что эта
свойство присуще также Солнцу, Луне и остальным
блуждающим светилам, чтобы при его действии они
продолжали пребывать в своей шарообразной форме, совершая
тем не менее различные круговые движения» [63].
Итак, Коперник понимал, что тяготение (или, точнее,,
тяжесть) есть «некоторое природное стремление»; он
распространял это «стремление» и за пределы Земли,
приписывая такое же явление Солнцу, Луне и планетам, но
он не дошел еще до завершающей идеи о том, что все тела
притягивают друг друга, а не только частицы
своего вещества. Земная тяжесть, солнечная тяжесть,
лунная тяжесть, планетные тяжести не объединились у него-
во всемирное тяготение. Это сумел сделать, как мы
знаем, только Ньютон. Но Коперник, а затем Галилей, и
Кеплер проложили своими трудами ему дорогу. А дорогу
Копернику проложил Птолемей. В этом мы еще не раз
сможем убедиться.
Обосновав логически возможность вращения Земли
вокруг оси6, Коперник как бы развязал себе руки: если
Земля способна совершать одно движение, то она может
совершать и другие движения, в частности вокруг Солнца.
Между тем особенности видимого движения нижних и
верхних планет, хорошо известные еще Птолемею (и его
предшественникам), но не использованные им хотя бы
для попытки построения гелиоцентрической системы (см.
с. 111), прямо указывали на то, что Земля движется
вокруг Солнца, как и все планеты, будучи третьей по
расстоянию от центрального светила после Меркурия и
Венеры. Обоснование этого Коперник дает в главах 9, 10
книги I своего труда.
Далее Коперник вводит третье движение Земли,
которое он называет деклинационным, или движением по
склонению [63]. Упоминания о таком движении читатель не
найдет ни в одном учебнике астрономии — просто потому г
что его не существует. Коперник не знал и не мог знать
Коперник не имел физических доказательств вращения
Земли, о которых теперь знает каждый школьник (отклонение
падающих тел к востоку, маятник Фуко, подмыв реками в
Северном полушарии правого берега, а в Южном - левого,
пассаты и др.).
204

закона сохранения момента количества движения,
согласно которому ось вращения Земли (и любого тела)
сохраняет постоянное направление в пространстве (если на
тело не действуют посторонние силы; действие Солнца и
Луны на экваториальный «горб» Земли приводит к
прецессии). Чтобы объяснить это наблюдаемое явление
(неизменность положения полюса мира в течение года), он
ж был вынужден приписать земной оси третье движение.
По мнению Коперника, если бы его не было, ось Земли
должна была бы в течение года поворачиваться вокруг
нормали к плоскости эклиптики, занимая в то же время
одинаковое положение относительно Солнца. Так было бы,
-если бы ось Земли была бы жестко связана с
радиусом-вектором Земли (иначе говоря, с прямой Солнце—Земля).
Сообщая земной оси противоположное движение с тем
же периодом в один год, Коперник компенсирует это
предполагаемое «увеличение» земной оси ее орбитальным
движением и «устанавливает» ее в нужном направлении.
Изложив основные принципы своей системы мира,
Коперник переходит к математической части своей
теории. В книгах I, II рассматриваются общие положения
(известные и до Коперника), в книгах III—V излагается
-сущность его теории движения Солнца, Луны и планет,
в книге VI — движения планет по широте. Представляет
интерес сравнить содержания обоих сочинений:
«Альмагеста» и «О вращениях...»
«Альмагест>> «О вращениях...»
Книга I. Форма и движение Книга I. Форма и движение
Земли и неба. Введение в сфе- Земли и неба. Плоские и
сферическую астрономию рические треугольники
Книга И. Основы сфериче- Книга II. Основы сферической
■ской астрономии астрономии. Восход и заход
звезд. Звездный каталог
Книга III. Теория движения Книга III. Теория движения
Солнца Солнца.
Книга IV. Теория движения Книга IV. Теория движения
Луны Луны, солнечных и лунных
затмений
Книга V. Теория лунных
неравенств
Книга VI. Теория солнечных
и лунных затмений
Книга VII. Сфера
неподвижных звезд. Звездный каталог
Книга VIII. Звездный каталог
{продолжение). Созвездия,
восход и заход звезд
205

Книга IX. Теория движения Книга V. Теория движения
планет (общая часть). Теория планет
движения Меркурия
Книга X. Теория движения
Взнеры и Марса
Книга XI. Теория движения
Юпитера и Сатурна
Книга XII. Попятные
движения и стояния планет
Книга XIII. Движение планет Книга VI. Движение планет
по широте. Их элонгации и по широте
условия видимости
Оговоримся сразу же, что ни в том, ни в другом
сочинении названия книг не приводятся. В обоих сочинениях
имеются лишь названия глав, на которые
подразделяются книги, причем если Коперник сам давал названия
своим главам, то названия глав у Птолемея, как уже
говорилось, придуманы не им самим, а кем-то из
переписчиков или комментаторов его труда (но не
переводчиками, так как эти названия имеются и в греческих
рукописях). Мы последовали примеру этих лиц и придумали
названия книгам обоих сочинений для удобства их
сравнения.
Как видим, в общем Коперник следует порядку
изложения, принятому Птолемеем. Однако он
объединяет вопросы, относящиеся к той или иной проблеме, в
одной книге. Так, если у Птолемея теория движения
Луны занимает три книги (IV—VI), то Коперник
излагает ее в одной (IV). Теория движения планет занимает
у Птолемея тоже три книги (IX—XI), а у Коперника —
одну (V). (Отдельная книга для описания попятных
движений и стояний Копернику не понадобилась).
С другой стороны, деление на главы у Коперника
более дробное, чем у Птолемея. Если в книгах Птолемея
от 5 до 19 глав, то в книгах Коперника — от 9 до 36 глав.
Интересно сравнить общее число глав в обоих
произведениях. У Птолемея их 146, у Коперника — 131, причем
звездный каталог не входит в число глав.
Основной математической задачей Коперника былог
выражаясь современным языком, перенесение начала
отсчета в принимаемой системе координат с Земли на
Солнце. С этой задачей он справился мастерски. На
первый взгляд может показаться, что система планетных
движений при этом резко упростится. С переходом к
гелиоцентрическим орбитам отпадут эпициклы планет,
отображавшие в системе Птолемея орбитальное движе-
206

ние Земли вокруг Солнца (которое Птолемей в принципе
отрицал), и общее число кругов сократится. Но дела
обстояло сложнее.
Коперник считал, что планеты могут двигаться
только по окружности и только равномерно. Поэтому он на
принял введенный Птолемеем эквант, а с ним и
гипотезу биссекции полного эксцентриситета. Но отказавшись
от экванта, Коперник был вынужден ввести... второй
эпицикл. Рассмотрим кинематическую модель
Коперника на примере Луны.
Как уже говорилось, Луна — единственное небесное
тело, в отношении которого у астрономов никогда не
возникало разногласий по вопросу, вокруг какого тела
она движется. Все в один голос считали (и обоснованно
продолжают считать), что Луна обращается вокруг
Земли. Поэтому при построении теории движения Луны
Копернику не пришлось переносить начало отсчета, как он
это сделал в отношении Солнца и планет. Надо было
только заменить чем-нибудь так беспокоивший его
эквант.
Причиной отказа Коперника от экванта было не простое
неудовольствие неудачной, по его мнению, моделью.
Так может быть причиной было противоречие этой
модели наблюдениям? И да, и нет. Мы знаем, что
положения Луны на небесном своде теория Птолемея
представляла хорошо. Но расстояния от Луны до Земли она
представляла из рук вон плохо: в квадратурах Луна
должна была находиться к Земле ближе, чем в сизигиях,,
и притом на одну треть расстояния. Значит, на столько
же должен был измениться видимый диаметр Луныг
что полностью расходилось с данными наблюдений.
Коперник прямо на это указывает. Однако если бы Луна
была столь мала, что не имела бы видимого диаметра
(для этого она должна была бы быть примерно 100 км r
диаметре), этот вопрос не возник бы, как не мог он
возникнуть для планет. А ведь Коперник освобождает и
планеты от эквантов, вводя, если нужно, добавочные
эпициклы.
Отказ Коперника от экванта был связан с
приверженностью великого ученого к принципу равномерных
движений, провозглашенному еще Аристотелем. Мы знаемг
что за отход от этого принципа критиковали Птолемея
многие арабские ученые, в частности аль-Битруджи (Аль-
петрагий) и ибн Рушд (Аверроэс), о которых мы писали
в предыдущей главе и которых упоминает в своем труде
2Ö7

Коперник. Правда, он ссылается на них по другим пово*
дам, но эти ссылки доказывают, что Копернику были
известны их труды и их взгляды.
Разрабатывая теорию движения Луны, Коперник
перепробовал несколько кинематических схем,
удовлетворявших принципу равномерного движения. Одну из них —
схему эпи-эпицикла — он применил к Луне (см. рис. 21).
Мы уже излагали ее на с. 93—94. Там же мы сравнили
выражения для неравенства долготы Луны по теориям
Птолемея и Коперника и пришли к выводу об их
равноценности для 2? и о преимуществах схемы Коперника для
радиуса-вектора Луны г.
Что касается планет, то для них Коперник принял
модель с эксцентром и одним эпициклом [54]. Но он
предварительно доказал, что эта модель кинематически
совершенно эквивалентна предыдущей. Расстояние от
центра земной орбиты до центра эксцентра планеты
Коперник принял равным zUae, а радиус эпицикла — iUae,
где а — радиус деферента, е — эксцентриситет. Схема
Коперника, как указывает Н. И. Идельсон [54], может
быть представлена следующей группой формул (у самого
Коперника, как и у Птолемея, никаких формул нет, все
соотношения выводятся чисто геометрически) :
х=2е sinM—e2 sin 2ЛТ,
r/a=l-\re2+e cos M—e2 cos 2M.
Сравнивая эти формулы (в которых мы, как и
раньше, сохранили только члены порядка не выше е2) с
приведенными ранее формулами гипотезы биссекции
полного эксцентриситета и формулами точной теории
эллиптического движения (с. 118), найдем, что уравнение центра
в обеих схемах (эксцентр-эпицикла и биссекции)
выражается совершенно одинаково, но ошибка в
радиусе-векторе у Коперника равна
ô(r/a)=~(e2/2)(l-cos2M)
и, таким образом, вдвое превышает ошибку в гипотезе
биссекции эксцентриситета. Таким образом, модель
Коперника дает даже несколько худшее представление
реального движения планет, чем модель Птолемея (что
подтвердили недавние расчеты О. Гингерича [101],
выполненные на ЭВМ). Но самое интересное состоит не в этом.
Читатель, очевидно, охотно простит Копернику
неточность его модели, как и приверженность к окружностям
208

Тихо Браге
(1546-1601)
и к равномерному движению. Ведь Коперник совершил
поистине научный подвиг, отказавшись от центрального
положения Земли, допустив возможность ее движения и
низведя Землю до положения рядовой планеты. На фоне
этих революционных актов весьма скромным покажется
сделанный Коперником вывод о том, что орбиты планет
не являются точными окружностями: «Таким образом,
планета в результате равномерного движения центра
эпицикла по эксцентру и ее собственного равномерного
движения в эпицикле описывает окружность не
в точности, но только приближенно»
(разрядка наша. -В. Б.) [63].
Концепцию о центральном положении Земли в
планетной системе попытался спасти Тихо Браге (1546—
8 Клавдий Птолемей
209

1601), предложивший «компромиссную» систему мира,
в которой все планеты движутся вокруг Солнца, а Солнце
с планетами и Луна — вокруг Земли. Конечно, эта модель
кинематически равноправна с моделью Коперника, но она
необъяснима не только динамически (до «Начал»
Ньютона оставалось еще сто лет), но и логически — ведь еще
Аристарх Самосский знал, что Солнце больше Земли. Быть
может, именно поэтому научный мир не принял систему
Тихо Браге, несмотря на все уважение к ее автору и к
его заслугам.
Были, однако, для этого и другие причины. Тихо
изложил свою систему в книге о комете 1577 г. под названием
«Вторая книга о недавних явлениях в небесном мире»
[27]. Эта книга была набрана и отпечатана в Ураниборге
(на острове Вен в Зундском проливе, принадлежавшем
тогда Дании) в 1588 г. и разослана самим Тихо
нескольким друзьям и знакомым. Основной тираж этой книги был
отпечатан усилиями Кеплера в Праге в 1603 г., спустя
два года после смерти Тихо. Но лишь через шесть лет,
в 1609 г., там же была издана книга Кеплера «Новая
астрономия», в которой содержался вывод его первых двух
законов движения планет по эллиптическим орбитам.
Несмотря на предсмертную просьбу Тихо обработать его
наблюдения Марса в соответствии с его гипотезой, Кеплер
обработал их на основе гелиоцентрической системы
Коперника. Видимо, он действовал по известному принципу
Аристотеля: «Платон мне друг, а истина дороже». Зато
Кеплер, как уже было сказано, издал оставшиеся
неизданными труды Тихо. Прекрасным памятником Тихо явился
эпиграф-посвящение Кеплера в его книге «Новая
астрономия» [92]:
Если бы в звездные сферы
Ты не взирал чрез диоптры,
С неба не мог бы я зреть
Круговращенье Земли.
Тихо Браге был замечательным наблюдателем. На
основе своих наблюдений, намного превосходивших по
точности наблюдения его предшественников, он составил
звездный каталог, содержавший положения около 1000
звезд с непостижимой для дотелескопического периода
точностью ±0,5' [27]. Его наблюдения положений Марса
за 20 лет оказались неоценимым материалом для расчетов
Кеплера. Обрабатывая наблюдения Луны, Тихо Браге
открыл два следующих (после эвекции) неравенства
движения Луны: вариацию и годичное уравнение. Звездный
210

каталог Тихо Браге и
открытые им лунные
неравенства — словно эстафетные
палочки, переданные из
второго века в шестнадцатый, от
Птолемея — в верные руки
Тихо Браге.
И Иоганн Кеплер,
пристукал к выводу законов
планетных движений, начал с
анализа системы Птолемея и
на протяжении всей своей
работы над «Новой
астрономией» (продолжавшейся
более восьми лет) исходил из
основных построений
Птолемея. Конечно, Кеплер был
убежденным коперниканцем.
Но, по меткому
выражению пулковского астронома И?157?-1б5)ТР
П. И. Яшнова, автора
превосходного очерка о жизни и
научной деятельности Кеплера, «он все время пользуется
геометрическими образами птолемеевской гипотезы и
самое построение Коперника транспонирует, так сказать, на
тональность птолемеева Альмагеста» [92].
В первой части своего труда Кеплер сравнивает
системы Птолемея, Коперника и Тихо Браге. Он показывает,
что сложная и неизящная комбинация Коперника с эпи-
эпициклом или с эксцентр-эпициклом почти равноценна
схеме первого неравенства, используемой Птолемеем, и не
вносит ничего существенно нового. Такой же «приговор»
Кеплер выносит системе Тихо Браге. Поэтому в
дальнейших своих построениях Кеплер пользуется схемой
Птолемея, но ...видоизмененной согласно гелиоцентрической
теории [92].
Как мы уже говорили, центром планетной системы у
Коперника является не само Солнце, а центр земной
орбиты. Через эту фиктивную точку и проводил
Коперник все линии апсид планетных орбит. Кеплер сразу
же отказывается от этого варианта. По его мнению,
высказываемому чисто интуитивно, причиной планетных
движений является некая физическая сила, исходящая
от Солнца и ослабевающая с расстоянием. Правда, до
открытия третьего закона Кеплеру еще далеко, но свою,
211
8*

как он ее называет, физическую гипотезу он
проводит красной нитью через всю свою работу.
Во второй части «Новой астрономии», опираясь на
наблюдения Марса за 20 лет, выполненные Тихо Браге
(к которым он по ходу работы добавил свои собственные
наблюдения противостояний 1602 и 1604 гг.), Кеплер
доказывает, что орбиты планет — плоские кривые, причем
плоскости их орбит проходят через Солнце. Переход к
реальному Солнцу дает первый важный результат,
которого не могли получить ни Коперник, ни Тихо.
Но главной задачей Кеплер ставит себе исследование
первого неравенства Марса, т. е. неравномерности его
видимого (а может быть, и истинного) движения,
происходящей от эксцентричности его орбиты. Вторая часть
его труда так и называется: «О первом неравенстве
Марса по примеру древних». Под «древними» Кеплер
подразумевает в основном Птолемея. Смысл выражения «по
примеру древних» означает, что Кеплер пока ищет
параметры круговой эксцентричной по отношению к Солнцу
орбиты Марса, используя птолемеев эквант и стремясь
проверить правило биссекции полного
эксцентриситета.
Для вывода элементов первого неравенства орбит
планет Птолемей использовал их наблюдения в трех
противостояниях (такие наблюдения называются акрони-
стическими) и принимал правило биссекции,
которое им, однако, в общем виде доказано не было (см. с. 89).
Кеплер вводит четвертое противостояние и определяет
независимо полный эксцентриситет, эксцентриситет
деферента и долготу афелия орбиты Марса. После долгих
и утомительных вычислений методом последовательных
приближений (именно к ним относилась жалоба Кеплера,
которую мы приводили на с. 56) Кеплер находит:
е=0,18567 (полный эксцентриситет), е=0,11332
(эксцентриситет деферента) и долготу афелия Àa=148° 48' 55" [92]
(по современным данным на эпоху наблюдений Тихо
Àa=148°41'48//, т. е. Кеплер ошибся здесь лишь на 7').
Правило биссекции этим расчетом не подтверждается.
Зато сравнение найденных элементов с акронистическими
наблюдениями для всех 12 противостояний дает
поразительный результат: при точности наблюдений Тихо ±2'7
1 Для отдельных положений планеты Марс эта точность ниже, чем
для мест неподвижных звезд в каталоге, поскольку звезды Тихо
наблюдал неоднократно, а планету в данном положении можно
наблюдать только один раз.
212

восемь наблюдений нз двенадцати разошлись с теорией
меньше чем на 1' и лишь одно — на 2х. Кеплер был
наверху блаженства. «Теперь ты видишь,— обращается он
к читателю,— что перенесение акронистических
наблюдений со среднего Солнца на истинное позволило мне не
только достигнуть точности наблюдений Тихо, но даже
превзойти их в этом отношении» [92].
Закончив этими словами восемнадцатую главу
второй части своего сочинения, Кеплер так начинает
следующую главу: «Кто бы мог подумать! Эта гипотеза,
так прекрасно представляющая акронистические
наблюдения, оказалась совершенно ложной». Что же произош-
ло?Для проверки своей гипотезы Кеплер определил
эксцентриситет деферента из наблюдений Марса в
перигелии и афелии, учтя также и изменения его широты.
Он получил 8=0,0900, что близко к е/2=0,0928 и вроде
бы подтверждает гипотезу биссекции, но приводит к
расхождениям с наблюдениями Тихо, достигающим 8'.
И все же гипотеза, построенная «по примеру древних»,
хорошо представляет акронистические долготы, и
Кеплер использует ее в дальнейшем под названием
«замещающая гипотеза» до тех пор, пока он не получит
окончательное решение задачи.
Замечательной чертой Кеплера (о чем мы уже
говорили) является то, что он в отличие от Птолемея и
Коперника раскрывает перед читателем весь нелегкий путь
своих поисков, достижений и неудач, а не представляет
лишь готовое решение. Поэтому историки науки, с
трудом реконструирующие ход работы Птолемея и
Коперника по их сочинениям (с привлечением иногда других
источников, например писем), не испытывают таких
затруднений, изучая работы Кеплера.
Мы не можем столь же подробно освещать здесь
дальнейший ход работы Кеплера. Используя наблюдения
Марса, он исследует в третьей части своего труда
движение Земли вокруг Солнца. Для этого он выбирает
положения Марса, разделенные промежутками в один
сидерический период его обращения вокруг Солнца (687 сут),
когда Марс приходит в одну и ту же точку своей орбиты.
Но Земля из-за несоизмеримости периодов оказывается
при этом в разных точках орбиты. В треугольнике STM
(Солнце—Земля—Марс) все углы известны из наблюдений,
расстояние SM (Солнце—Марс) — одно и то же во всех
положениях, отсюда можно было найти расстояния ST
(Солнце—Земля) в разных точках земной орбиты (рис. 37).
213

Рис. 37.
Солнце, Земля и Марс
(к методу Кеплера
определения орбиты Земли
из наблюдений Марса)
Здесь Кеплер получил
важный результат: Земля также
следует принципу биссекции
полного эксцентриситета.
Эксцентриситет ее деферента
оказывается равным 0,016, что
очень близко к половине
полного эксцентриситета, найденного
Птолемеем (0,033) и Тихо
Браге (0,036). По современным
данным эксцентриситет земной
орбиты равен 0,0167.
Убедившись в
справедливости гипотезы биссекции,
Кеплер получает из нее строгое
доказательство, что скорости
планеты в перигелии и афелии
обратно пропорциональны ее
расстояниям от Солнца в этих
точках. Затем по известным ему
радиусам-векторам Земли
Кеплер вычисляет их через
каждый градус от перигелия до
афелия и нелегким путем геометрических построений и
рассуждений приходит в конце концов к закону площадей,
ныне известному как второй закон Кеплера: площади,
описываемые радиусом-вектором планеты,
пропорциональны временам.
После такого успеха Кеплер приступает к четвертой
части «Новой астрономии», которую он называет так:
«Нахождение истинной меры для первого неравенства на
основе физических причин и по моей собственной теории».
Теперь в его распоряжении — точная форма орбиты
Земли, закон площадей и доказанное правило биссекции
полного эксцентриситета. Но Кеплер хочет еще раз проверить
его. Он объединяет пять наблюдений Марса вблизи
перигелия и три вблизи афелия, находит наибольшее,
наименьшее и среднее расстояния Марса от Солнца и
эксцентриситет его орбиты. Они приведены в табл. 13 в сравнении с
современными данными (все расстояния выражены в
астрономических единицах).
Это сравнение говорит нам и о точности расчетов
Кеплера, и о точности наблюдений Тихо, на которых они
основаны. Мы видим также, насколько подтверждается
гипотеза биссекции.
214

Таблица 13. Параметры орбиты Марса
Параметр
По Кеплеру
По
современным данным
Расстояние в афелии, а.е. 1,66780 1,66597
Расстояние в перигелии, а.е. 1,38500 1,38141
Среднее расстояние, а.е, 1,52640 1,52369
Эксцентриситет 0,09264 0,09338
Дальше Кеплер сравнивает теоретически
вычисленные на основании закона площадей расстояния от Солнца
до Марса с расстояниями, полученными из обработки
наблюдений Тихо, и приходит к важнейшему выводу:
орбита Марса между перигелием и афелием лежит
внутри окружности, она овальна! Но долго еще он ищет
истинную форму орбиты Марса. Яйцеобразная кривая (ойо-
ида) не подходит — истинный путь Марса лежит между
ней и окружностью. Кеплер в последний раз вводит
движение планеты по эпициклу. С третьей попытки Кеплер
находит, наконец, истинную форму орбиты Марса —
эллипс, причем Солнце находится в одном из его фокусов.
Открыт первый закон Кеплера. Сравнение с
наблюдениями Тихо показывает их полное совпадение с теорией.
Громадная работа завершена!
Так эпициклы, деференты и экванты теории Птолемея
в соединении с гелиоцентрической системой Коперника
проложили путь к законам Кеплера. Проложили — чтобы
навсегда уйти в историю. Законы Кеплера ознаменовали
начало подлинно новой астрономии. Впереди
было открытие Кеплером своего третьего закона,
связывающего расстояния и периоды обращений планет, а
затем — гениальный труд Исаака Ньютона, который на
основании этих законов вывел закон всемирного тяготения.
В свете истории развития астрономической науки мы
можем теперь глубже понять роль и место в ней Клавдия
Птолемея. С одной стороны, он собрал и обобщил всю
сумму знаний своих предшественников, создал поистине
великое построение астрономической картины
мира, отвечающее представлениям своей эпохи. С другой
стороны, он как бы предоставил это построение в руки
исследователей позднейших эпох, которые смогли так его
переделать, что получилось величественное здание, имя
которому — научное представление о Вселенной.
215

Птолемей и Коперник
(послесловие редактора)
Птолемей создал естественнонаучную теорию, которая
более тысячелетия претендовала на абсолютную
истинность. Коперник открыл человечеству глаза на то, что
научная истина еще отнюдь не составляет истины
абсолютной. На базе давно известного, давно устоявшегося
эмпирического материала Коперник предложил великую
теорию, в корне отличную от великой теории Птолемея.
Отсюда берет истоки традиция недооценивать значение
творчества Птолемея, противопоставлять «ненаучности»
Птолемея подлинно научные взгляды Коперника. Но кто
и как способен удостоверить подлинную научность в ходе
рождения и становления новых смелых идей?
Нам хотелось бы заявить в полный голос, что Птолемей
и Коперник — две личности, не уступающие друг другу по
значению в реальном историческом процессе развития
естествознания. Их имена не должны противопоставляться,
они должны стоять рядом как символы двух величайших
достижений естественнонаучной мысли. Нам хотелось бы
одновременно подчеркнуть, что не только Птолемей, но
даже и Коперник отнюдь не были единоличными творцами
общенаучных революций. Оба они стали авторами научных
представлений, переживших многие столетия, оба активно
способствовали выработке нового стиля мышления, однако
общенаучные революции — относительно краткосрочные
этапы перехода науки на новые рельсы, определяющие
формирование иных исторических типов науки, —
происходили не только благодаря деятельности гениальных
ученых, но и в силу вызревания необходимых условий,
наступающих в связи со всем ходом социально-экономического
развития человечества.
Особенно непросто обстоит дело с анализом творчества
Птолемея.
«Альмагест» Клавдия Птолемея — научное
произведение, значение которого нельзя по достоинству оценить в
прокрустовом ложе одной лишь истории астрономии. Роль
216

Шесть крупнейших астрономов мира вокруг музы астрономии
Урании
Слева направо: Ян Гевелий, Вильгельм IV Гессенский, Улугбек,
Птолемей, Тихо Браге, Риччиоли (из «Предвестника астрономии» Я. Гевелия,
посмертное издание 1690 г.)
Птолемея в процессе становления естествознания
уникальна. Она не знает себе равных. Какие бы новые
обстоятельства его работы ни были извлечены на суд общественности,
какие бы аспекты его деятельности ни подвергались
сегодня критике, место Птолемея в истории мировой науки
навечно останется столь же незыблемым, как место
Менделеева, Ньютона, Коперника или Евклида.
Дело, разумеется, не только в той счастливой
случайности, что труд Птолемея не затерялся в раннем
средневековье и полностью дошел до наших дней в византийских
списках и арабских переводах. Сравнительный анализ
различных источников дает известное представление и о
многих других крупных сочинениях древности как до, так и
после Птолемея. Суть заключается в самом характере
этого уникального сочинения.
Сколь бы древними ни были пласты человеческой
культуры, которые лопата археолога вырывает время от
времени из пучины забвения, следы пытливости человеческого
217

Ян Гевелий преподносит свой труд десяти крупнейшим
астрономам мира
Слева направо: Вальтер, Тихо Браге, Улугбек, Тимохарис, Гиппарх,
Птолемей, аль-Баттани, Вильгельм Гессенский, Региомонтан, Коперник; в
центре — Урания (из «Уранографии» Я. Гевелия, посмертное издание
d690 г.)
разума предстают перед нашим взором всегда и
повсеместно. В палеолите и в неолите, на заре эры рабовладения и
в античности, в гротах скованной ледниковым панцирем
Европы и в африканском ущелье Олдовей, на территории
Индии и Китая, в Междуречье и в Мезоамерике, на всем
протяжении изначально освоенного человечеством
экваториального пояса Земли в пределах между широтами ±45°
наши далекие предки оттачивали на оселке практики
научный метод познания окружающей природы: наблюдали,
систематизировали объекты и явления,
экспериментировали, добивались теоретических обобщений, которые волей-
неволей проходили дальнейшую проверку жизнью.
Древние народы Армянского нагорья были,
по-видимому, среди первых, кто не только заметил взаимосвязь
между движением Солнца по эклиптике и временами года, но
и закрепил положение эклиптики среди звезд путем
выделения «круга зверей» — зодиакальных созвездий. С точки
218

зрения рождения научных понятий в высшей степени
поучительно, что в Мезоамерике, подле экватора Земли,
практика наблюдений за небесными светилами была
совершенно иной, и там вообще не возникло понятия эклиптики:
времена года фиксировались по уклонению в полдень
Солнца от зенита. В разных концах мира древние люди
возводили шедевры научно-технической мысли: Стоун-
хендж, египетские пирамиды, Храм надписей в Паленке,
акведук Эвпалина и много, много иных.
Вырвавшаяся несколько вперед в своем развитии
греко-римская цивилизация на стыке Европы, Азии и
Африки впервые взяла на себя на рубеже нашей эры труд в
письменном виде подвести предварительные итоги
развития Ойкумены. Античность стала эпохой гигантских по
размаху обобщающих трудов. К ним можно отнести
философские сочинения Аристотеля, «Начала» Евклида,
«Географию» Страбона, «Естественную историю» Плиния
Старшего, медицинские труды Галена и, наконец, «Синтаксис»
Птолемея, который чаще известен под арабским названием
«Альмагест».
Мы характеризуем то или иное историческое лицо
эпитетом великий лишь в том случае, если в своей сфере
деятельности ему удалось наиболее полно выразить
сущность эпохи. Великий Птолемей с успехом свел воедино и
изложил на языке математики астрономические
представления поздней античности. При этом сам он как человек
остается для нас почти совершенно безликим. Его
биография, как могли убедиться читатели настоящей книги, —
сплошное белое пятно.
О. Нейгебауэр пишет в книге «Точные науки в
древности»: «Как однажды сказал Гильберт, значение научной
работы можно измерить числом публикаций, чтение
которых становится ненужным после этой работы»1. Он делает
свое замечание именно в той связи, что после «Начал»
Евклида и «Альмагеста» Птолемея для исследователей (не
беря в расчет, конечно, историков науки) отпала
необходимость в чтении вообще всех предшествующих книг по
математике и астрономии.
1 Нейгебауер О. Точные науки в древности. М.: Наука. 1968. С. 147.
219

Идеал естествознания
Ни у кого не вызывает возражений, что Птолемей в
«Альмагесте» впервые изложил в связной форме
астрономическую картину мира. Однако значение
«Альмагеста», как мы уже подчеркнули раньше, несравненно
глубже. Если Плиний Старший остановился на уровне
систематизированных описаний, т. е. на относительно низком,
предварительном этапе естественнонаучной деятельности,
и если Евклид ограничивался собственно математикой,
т. е. аппаратом, формализованным языком научного
анализа, поскольку математика сама по себе не принадлежит
к естествознанию, то Птолемей впервые в истории
человечества дал бросающийся в глаза образец развернутой,
математизированной, полнокровной естественнонаучной
теории. Она охватила широкий круг проблем и обобщила
громадный эмпирический наблюдательный материал. Она
имела очевидную прогностическую ценность и широко
использовалась на практике. В сущности, теория Птолемея
для своего времени отвечала самым строгим критериям
научности, выработанным наукой XX в. Она заняла место
своего рода эталона для всего естествознания. А Птолемей
в качестве автора этой теории по справедливости может
быть причислен к сонму классиков
естествознания. Именно после труда Птолемея астрономия приобрела
то «поистине уникальное положение, которое она занимает
среди других наук»2.
Характерно, что ни упомяпутые нами Евклид, Страбон,
Плиний, ни многие другие античные мыслители никак не
повлияли на мировоззренческие установки раннего
христианства. И в то же самое время христианская церковь
принуждена была считаться со взглядами язычника
Птолемея. Разумеется, после многовековых диспутов они были
деформированы, адаптированы, тщательно подогнаны к
приемлемой для религии форме. Однако факт остается
фактом: религия использовала убедительно обоснованную
естественнонаучную теорию Птолемея в собственных
целях и в конечном счете пе рискнула пойти, как требовали
некоторые, на открытую конфронтацию с идеями этого
язычника.
Таким образом, Клавдий Птолемей и в его лице
античная астрономия преподнесли всему естествознанию пред-
2 Алексеев И. С. Проблема существования в астрономии //
Философские проблемы астрономии XX века. М.: Наука, 1976. С. 2§9Т
?2Q

метпый урок. Птолемей первым в исполинском масштабе
продемонстрировал великое искусство полноценно
описывать природные явления на языке математики — на кине-
матико-геометрической модели.
К сожалению, всякая медаль имеет обратную сторону.
Вследствие существования теории Птолемея стала
окончательно узаконенной появившаяся задолго до него
убежденность в реальности разделения Космоса на два мира:
надлунный и подлунный. В надлунном мире царил Логос,
божественный порядок, птолемеева гармония. Его
изучение составляло предмет великой и рано обособившейся
научной дисциплины — астрономии. Подлунный же мир
отличался аморфностью, беспорядком и изменчивостью.
Он достался в удел прозябающей физике, точнее говоря,
еще слабо расчлененной «натуральной философии».
А. Койре3 задается вопросом: почему греческая наука
не создала физики? И дает на него ясный ответ: она к
этому не стремилась, поскольку была уверена в
невозможности добиться успеха.
«Действительно, — пишет А. Койре, — создать физику
в нашем смысле слова, а не в том, как ее понимал
Аристотель, означает применить к действительности строгие,
однозначные, точные математические, и прежде всего
геометрические, понятия. Предприятие, прямо скажем,
парадоксальное, так как повседневная действительность, в
которой мы живем и действуем, не является ни
математической, ни математизируемой. Это область подвижного,
неточного, где царят «более или менее», «почти», «около того»
и «приблизительно»... Отсюда следует, что желание
применить математику к изучению природы является
ошибочным и противоречит здравому смыслу... Верное на
небесах — неверно на Земле. И поэтому математическая
астрономия возможна, а математическая физика — нет» \
Таким образом, величие теории Птолемея как
недостижимого эталона естественнонаучного знания подмяло
под себя остальные области естествознания. Эта теория
подавляла, сдерживала развитие тех научных дисциплин,
которые на первых порах никак не могли тягаться с ней в
изощренности математического аппарата. Недосягаемой
вершиной высилась она среди остальных наук, адепты
3 Койре Александр Владимирович (1892-1964) — выдающийся
историк науки. Родился в Таганроге, с 1908 г. учился в Гёттинге-
не, впоследствии работал преимущественно во Франции и США.
* Койре А. Очерки истории философской мысли, Ц.: Црогресс,
1985. С. 109-110.
m

которых еще не успели освоить ни эксперимента со
строгим количественным исчислением его результатов, ни
математических методов представления сводных данных.
Крушение
Теория Птолемея отнюдь не напоминала карточный
домик. Скорее ее можно уподобить величественному
замку. Обветшание этого замка происходило мучительно
медленно, оно затянулось на многие века. Замок приходил
в упадок, стены давали трещины, башни кренились, но
трещины замазывали, башни ставили на капитальный
ремонт, и никому не приходило на ум, что выправить
положение уже невозможно: замок держался на насквозь
прогнившем фундаменте.
Среди ранних критиков теории Птолемея обычно
выделяют нескольких корифеев арабоязычного мира: Ибн
аль-Хайсама (известного в Европе под именем «отца
оптики» Альхазена), Ибн Рушда (философа, более
известного под именем Аверроэса), аль-Битруджи
(переводившегося под латинизированным именем Альпетрагия), На-
сир ад-Дина ат-Туси, аш-Шатира и ряд других5. Занятые
определением фундаментальных астрономических
постоянных, составлением звездных каталогов и эфемерид
планет, эти в большинстве своем астрономы-наблюдатели, как
никто другой, не раз наталкивались на вопиющие
разночтения между теорией Птолемея и данными наблюдений.
Они брались за доработку теории, не меняя ее основ.
Были у некоторых из названных ученых возражения и
философского характера, однако с ними были
дополнительные трудности.
Математические построения Птолемея в «Альмагесте»
носили исключительно кинематико-геометрический
характер и не касались неясных вопросов реального
воплощения небесных сфер, эпициклов, деферентов и т. п.
В действительности Птолемей писал на эту тему в
небольшой работе «Планетные гипотезы», однако основная
«физическая» суть концепции небесных сфер была
разработана задолго до Птолемея Аристотелем. В этой связи
количественная кинематико-геометрическая картина
Птолемея с течением времени была пополнена гораздо более
ранней качественной картиной мира Аристотеля. Вот
5 Гингерич О. Средневековая астрономия в странах ислама//
В мире науки. 1986. № 4. С. 16-26.
222

этот-то птолемеево-аристотелевский конгломерат уже
отнюдь не отвечал критериям научности не только
современным, но даже весьма древним, поскольку содержал в
себе явные противоречия: аристотелевские сферы никак
не должны были пересекаться в пространстве, а потому не
могли приходить в движение так, как того требовала все
более усложнявшаяся с течением времени кинематика
Птолемея. Особые неприятности со временем стали
создавать кометы, и, как едко высказался журналист Н. Кол-
дер, «на протяжении столетий кометы обладали
определенным философским значением, как ручные гранаты
космической революции. Далеко улетевшая комета 1577 г.
разбила вдребезги прозрачные хрустальные сферы,
которые якобы несли на себе всю компанию планет...» 6.
Остановил Солнце, двинул Землю
«Современное исследование природы... как и вся
новая история, ведет свое летоисчисление с той великой
эпохи, которую мы, немцы, называем, по приключившемуся
с нами тогда национальному несчастью, Реформацией,
французы — Ренессансом, а итальянцы — Чинквеченто и
содержание которой не исчерпывается ни одним из этих
наименований... Это был величайший прогрессивный
переворот из всех пережитых до того времени
человечеством, эпоха, которая нуждалась в титанах и которая
породила титанов по силе мысли, страсти и характеру, по
многосторонности и учености»,—так писал Ф. Энгельс в
«Диалектике природы» 7.
Жизнь Коперника и гений Коперника целиком
принадлежат этой великой эпохе. Его современниками были
Леонардо да Винчи, Колумб, Магеллан, Васко да Гама,
Микеланджело Буонаротти и Рафаэль.
Коперник был свидетелем яростных столкновений и
раскола в рядах католиков. На его памяти профессор
Виттенбергского университета Мартин Лютер прибил к
дверям собора «95 тезисов» и сжег папскую буллу.
Каноник Коперник был свидетелем и ответной реакции
католической церкви — рождения Ордена иезуитов с их
беспримерным девизом «цель оправдывает средства».
События этого бурного времени наложили отпечаток
6 Колдер Н. Комета надвигается! М.: Мир, 1984. С. 42.
7 Энгельс Ф. Диалектика природы//Маркс К., Энгельс Ф. Соч.,
2-изд. Т. 20. С. 345-346.
223

на личность Коперника, научная деятельность которого
сама стала едва ли не самой высокой из вершин эпохи
Возрождения. Имя Коперника — объект особой гордости
зсего человечества, и нам приятно добавить — объект
особой гордости славянской науки.
В отличие от биографии Птолемея жизнь и
творческая деятельность Николая Коперника из Торуня
известны ныне вдоль и поперек. Мы не будем освещать их
здесь, ограничившись констатацией общего факта. Если
в лице Птолемея астрономия как созидательница
впервые в истории человечества выработала великую
научную теорию, то в лице Коперника именно астрономии
пришлось впервые в истории сокрушать великую
научную теорию.
Впоследствии всем без исключения научным
дисциплинам доводилось повергать в прах своих идолов.
Химики похоронили флогистон. Теория относительности
ограничила безбрежность концепции Ньютона. Открытие
Гарвеем кровообращения поставило крест на
предшествующих взглядах в биологии. Но ни одна смена
основополагающих научных представлений не протекала столь
же драматично, как крушение астрономической
картины мира Птолемея, безраздельно
господствовавшей более тысячелетия.
Как мы уже отмечали, астрономия намного раньше
других естественнонаучных дисциплин, как минимум со
времени Птолемея, четко определила и объект, и метод
своих исследований. Она занималась, казалось бы,
наиболее общей из всех возможных сущностей — космосом,
Вселенной. Не случайно, что с глубокой древности и на
протяжении всего долгого средневековья именно
астрономическая деятельность в наибольшей степени отвечала
идеалам научности, а астрономия справедливо слыла
царицей естественных наук. Это обстоятельство
отразилось в бесчисленном количестве фактов: от существования
музы астрономии Урании до официального положения
астрономии в квадривиуме средневекового университета.
И крушение великой астрономической теории Птолемея
радикально отозвалось на всем естествознании.
Через несколько десятилетий после смерти автора
труд Коперника оказался в центре водоворота событий
общенаучной революции. Само собой разумеется, что
спор шел и о проблемах астрономии тоже. Но это отнюдь
не исчерпывает основных результатов общенаучной
революции. Более того, мы склонны видеть главный ре-
224

зультат совсем в ином. Он нашел выражение в так
называемой доктрине «двух книг», которую разделяли Том-
мазо Кампанелла, Галилео Галилей и ряд других
современных им мыслителей. Согласно этой доктрине
Священное писание представляет собой книгу божественного
откровения, в то время как природа, хотя и является
«книгой» божественного творения, сочинена на языке
математики. Она может быть прочитана человеком вне
божественного откровения и составляет, по Галилею,
«настоящий предмет философии» 8.
Такая кардинальная перемена в понимании места
науки в обществе, еще скованном средневековыми
религиозными традициями, сочеталась с мыслью о важности
прагматической направленности науки, провозглашенной
Ф. Бэконом: «Зпание — сила». Соображения о
практической пользе науки звучат рефреном буквально у всех
авторов этого периода, особенно четко в Британии.
«...Эти знания приобретаются не просто ради самих себя,
а для того, чтобы дать возможность человеку... вызывать
и совершать такие эффекты, которые могут наиболее
способствовать его благополучию в мире»,— слова,
принадлежащие Р. Гуку9. Р. Бойль прямо называет один из
своих памфлетов «Да будут блага человечества
приумножены проникновением естествоиспытателя в ремесло».
Вовсе не случайно XVII в. заслужил в литературе имя
«века опытной науки».
Экспериментально-количественный подход в сочетании с прагматической нацеленностью
науки на решение задач, приумножающих блага
человека (т. е., строго говоря, господствующего класса),
открыли в новое время дорогу для невиданного ранее
прогресса науки.
Коперник и общенаучная революция
Из исследований последних лет, посвященных копер-
никовской теме, нам хотелось бы специально отметить
хорошо взаимно дополняющие друг друга работы
американских историков астрономии О. Гингерича и Б. Райт-
смена. На конкретном документальном материале они
убедительно показали специфику восприятия труда
Коперника его современниками, отсутствие революционного
подъема мысли у читателей Коперника еще на протяже-
8 Галилей Г. Избранные труды. М.: Наука, 1964. Т. 1. С. 99.
9 Espinasse M. Robert Hooke. London, 1956. P. 19.
225

ний полустолетий после смерти автора. Есть основания
полагать, что в подлинном значении гелиоцентризма для
естествознания поначалу отдавали себе отчет лишь сам
Коперник да его юный друг Ретик. К остальному
научному миру осознание этого пришло гораздо позднее 10.
Было бы полной наивностью полагать, что Коперник
на все сто процентов согласовал свою теорию с
существовавшими наблюдениями. Это, конечно, далеко не так,
и трудности, стоявшие перед сторонниками нового учения,
были на самом деле исключительно велики, а позиция
консерваторов отнюдь не сокрушена. Широко известно,
что теория Коперника в ее «чистом» виде не могла
приблизиться по прогностической точности к модели
Птолемея. Чтобы не превзойти, а всего-навсего сравняться по
точности с Птолемеем, Коперник принужден был
сохранить многие архаические элементы: несколько малых
эпициклов и эксцентры. «Система Коперника была ни более
простой, ни более точной, чем система Птолемея, и с
прагматической точки зрения ей трудно было отдать
предпочтение»,—справедливо заключает И. С. Алексеев11.
Критический ум известного современного западного
философа П. Фейерабенда, апологета анархистской
теории познания, беспощадного бичевателя всех слабостей
науковедческих конструкций, не оставил без внимания
того, что Коперник предумышленно обходил молчанием
неразрешимую для него проблему изменения блеска
планет в связи с изменениями их расстояния до Земли —
кардинальное научное возражение XVI в. против
реальности гелиоцентризма 12. Коперник сосредоточился на
кинематике движения планет и не желал реагировать на
явные противоречия в возникающей физической картине.
Фейерабенд выделяет отрывок из «зловредного» введения
А. Осиандера: «Ибо кто же не знает, что такое допущение
необходимо влечет, что диаметр планеты, когда она ближе
всего к Земле, должен быть в четыре раза больше по
сравнению с тем, который она имеет, будучи в самой
отдаленной точке, а ее тело — в шестьдесят раз больше, что
противоречит опыту всех времен». Таким
образом, заключает Фейерабенд, «в реалистической интер-
10 Райтсмен Б. Проблема коперниканской революции и
распространения коперниковских идей//Историко-астрономические
исследования. М.: Наука, 1987. Вып. 19. С. 295-310.
11 Алексеев И. С. Указ. соч. С. 274.
12 Фейерабенд П. Избранные труды по методологии науки. М.:
Прогресс, 1986. С. 248-251.
226

претации учение Коперника было несовместимо с
очевидными фактами».
Нам хотелось бы наконец подчеркнуть, что в новых
исследованиях обращено серьезное внимание на роль
Реформации в формировании социальных условий,
сопутствовавших созданию гелиоцентрической системы мира.
Все эти исследования как нельзя лучше подкрепляют
взгляд на Коперника как на предтечу грядущей
общенаучной революции, происшедшей на рубеже XVI и
XVII вв.
История науки наглядно свидетельствует о
неравномерном характере ее прогресса: эпохи сравнительно
спокойного развития сменяются периодами стремительных
взлетов научного творчества. Некоторые из этих периодов
«бури и натиска», которым, в частности, свойственно
коллективное освоение сообществом ученых принципиально
новых фундаментальных взглядов, получили название
научных революций. Интерес к проблеме научных
революций как важнейших переломных моментов развития
науки традиционен и характерен для марксистско-ленинской
философии. Вспомним высказывание Ф. Энгельса из
«Диалектики природы», что «Революционным актом,
которым исследование природы заявило о своей независимости
и как бы повторило лютеровское сожжение папской
буллы, было издание бессмертного творения, в котором
Коперник бросил — хотя и робко и, так сказать, лишь на
смертном одре — вызов церковному авторитету в вопросах
природы» 13.
Проблемы научных революций исследовались во
многих широко известных работах. В последние десятилетия
на Западе интерес к проблеме научных революций был
подогрет концепцией Т. Куна 14. Большое внимание
анализу этой проблемы уделялось рядом советских
исследователей. Эта тема не сходит со страниц научной
периодической печати. Например, в № 7—8 журнала «Вопросы
философии» за 1985 г. были помещены очень интересные
материалы «Круглого стола» по проблеме «Сущность и
социокультурные предпосылки революций в естественных
и технических науках».
Важный шаг на пути к корректной постановке
проблемы был сделан Н. И. Родным, который различал науч-
13 Энгельс Ф. Диалектика природы//Маркс К., Энгельс Ф. Соч.,
2-е изд. Т. 20, С. 347.
14 Кун Т. Структура научных революций. 2-е изд. М.: Прогресс,
1977. 300 с.
227

ные революции трех масштабов: глобальные научные
революции, революции в отдельных фундаментальных
науках и «микрореволюции» 15. Если использовать для
анализа науки кибернетическое понятие сложной системы,
приведенному членению соответствует исследование
состояний собственно системы, ее подсистем и отдельных
элементов.
Придерживаясь в дальнейшем этой же классификации,
мы считаем целесообразным уточнить терминологию,
выделяя:
а) революции в науке, т. е. общенаучные революции,
захватывающие все без исключения ее области —
естественные, общественные и технические;
б) революции в отдельных областях знаний (цикл
физико-математических наук, химические науки,
медико-биологические науки, общественные науки и т. д.) ;
в) локальные революции в отдельных научных
направлениях, которые как таковые не влияют на состояние
системы в целом.
Анализ трех уровней научных революций позволяет
прийти к выводу, что революции в отдельных научных
дисциплинах и локальные революции происходят в
результате прогресса собственно науки и свидетельствуют
об относительной самостоятельности и активности
научного познания. Эти революции второго и третьего уровня
не сопряжены с коренной ломкой общей
социально-философской картины бытия, а отражаются только на
специальных (частных) картинах исследуемой реальности. Что
же касается научных революций высшего уровня —
общенаучных революций, то, будучи многомерными явлениями
с рядом обратных связей, они тем не менее
стимулируются и определяются преимущественно социокультурными
факторами, причем в ходе этих революций меняется сам
исторический тип науки. В ходе этих революций меняется
весь комплекс ценностей науки. Сопоставление
рассмотренных обстоятельств приводит к выводу о
приуроченности общенаучных революций к периодам
социально-экономического переустройства общества.
Исключительно плохую услугу в решении проблем
научных революций оказывает пагубная традиция их
«персонификации», и соображения по этому поводу
отнюдь не новы. «Мы почти всегда стараемся упростить
Родный Н. И. Очерки по истории и методологии естествознания.
М.: Наука, 1975. С. 197.
m

историю, прибегая к системе эпонимов 16, иными словами,
приписываем важные события отдельным личностям и
даем названия этим событиям и эрам по именам этих
личностей, — так начал один из своих докладов в поездке по
СССР в 1977 г. известный американский исследователь
Дж. Г. Симпсон.— Более внимательный взгляд на
историю, однако, наводит на мысль, что один человек никогда
не совершал великих открытий и ни разу не положил
начало новой эре. Обычно эпоним, герой,— это личность,
связавшая воедино туманные и разрозненные мысли и
превратившая их в единое прочное целое... Это относится,
например, к Н. Копернику. Должно было пройти более
двух с половиной веков, прежде чем теория Коперника
получила всеобщее признание. И хотя мы можем сказать,
что Коперник положил начало революции, названной его
именем, эта революция шла постепенно, в течение
длительного времени, благодаря работам многих ученых,
имена которых в большинстве своем забыты... В более
широком смысле эта революция была столь медленной, что
вернее считать ее интеллектуальной эволюцией...» 17
Занимаясь проблемами научных революций,
непростительно упускать из виду, что наука отнюдь не сводится к
совокупности научных знаний. Наука — это в первую
очередь специфический вид духовной деятельности,
неразрывно связанной с социально-историческими
условиями. Хотя наука имеет своей задачей постижение
объективной истины, которая не зависит ни от конкретного
человека, ни от всего человечества, носитель науки —
человек — не может существовать вне общества. Историческая
ограниченность науки прямо связана с ограниченностью
общественной практики человечества на данном этапе его
социально-экономического развития. Рассматривая науку
в социально-историческом аспекте, мы обязаны
констатировать, что в общенаучных революциях большую роль
играют их глубокие социальные корни. И лишь
революции в отдельных научных дисциплинах, которые
выделяются по изменению содержания научного знания,
связаны, как правило, с деятельностью определенного
выдающегося ученого.
Великий польский астроном Н. Коперник был пред
вестником грядущей общенаучной револю-
16 Эпоним - должностное лицо, с началом деятельности которого
в данном греческом полисе начинался новый счет времени.
17 Симпсон Дж. Г. Новое небо, новая Земля, новый человек //
Природа. 1979. № 5. С. 37.
229

ц и и, социальные условия для которой в середине XVI в.
еще не созрели. Радикально преобразовав практическую
астрономию, Коперник совершил революцию в этой
фундаментальной науке. В дальнейшем его
гелиоцентрическая картина мира стала краеугольным камнем
общенаучной революции начала XVII в., символами ее по праву
служит подвижническая деятельность Дж. Бруно, И.
Кеплера, Г. Галилея.
Сводить, однако, научный подвиг Коперника
единственно к преобразованию частной науки астрономии было
бы неоправданным и незаслуженным принижением
значения гелиоцентризма. С другой стороны, придавать
«революционному акту» Коперника значение общенаучной
революции неправомерно из-за отсутствия в его эпоху
надлежащих социальных условий для восприятия
революционной стороны учения Коперника.
Нам представляется единственно корректным выходом
(точно так давно поступают историки применительно к
революциям социальным) отказаться от попыток
персонификации общенаучных революций. Этот отказ, кстати
сказать, вполне соответствует марксистско-ленинской
точке зрения на роль личности в истории. Таким образом,
можно согласиться с позицией Б. Райтсмена, что
общенаучная революция конца XVI —начала XVII столетия
имела среди своих гениальных предвестников великого
Коперника и нашла ярких выразителей в лице таких
ученых, как Дж. Бруно, И. Кеплер, Г. Галилей.
Следует обратить внимание на то, что в марксистской
исторической литературе последних лет выполнено
углубленное исследование противоречивого и исключительно
важного периода религиозной Реформации. Не случайно
в 1984 г. издательство «Молодая гвардия» массовым
тиражом выпустило биографическую книгу Э. Соловьева
«Непобежденный еретик» о Мартине Лютере. В предисловии
к ней академик Т. И. Ойзерман подчеркивает, что
сущность Реформации «не исчерпывается тем, что
непосредственно подразумевается самим словом, т. е. реформой,
переустройством тогдашней церкви. Реформация, как
массовое народное движение, подорвала духовную
диктатуру папства, нанесла внушительный удар по церковному
феодализму и активизировала повсеместное недовольство
светским феодальным господством. Она проложила путь
новым этическим, юридическим и практико-экономиче-
ским воззрениям, которые соответствовали
формирующимся капиталистическим отношениям.
230

Возрождение и Реформация различны по СйоеМу КулЬ^
турному облику: их деятели подчас относятся друг к
другу с непримиримой враждебностью. И все-таки это лишь
различные исторические выражения одного и того же
социально-экономического процесса: революционного
рождения буржуазного общества. Оба они образуют пролог
к великим классовым битвам XVII—XVIII столетий» 18.
Реформация и представляет собой тот важный
социокультурный фон, на котором совершено великое
интеллектуальное достижение Коперника. Аналогичные мысли
его предшественников Аристарха Самосского и Николая
Кузанского не были восприняты и подхвачены.
Астрономия еще несколько столетий после Коперника
играла роль лидера естествознания. Она, как и прежде,
вырабатывала для других дисциплин эталоны научности.
Еще один выдающийся астроном, Лаплас, в XIX в. взял
на себя труд методолога и сформулировал ясную
концепцию механицизма. Пожалуй, «лапласов детерминизм»
стал последним крупным вкладом астрономии в
методологию естествознания. К концу XIX в. на мощном стволе
экспериментальной физики взросла теоретическая
физика, которая в конечном счете перечеркнула как
«лапласов детерминизм», так и все другие классические
представления о природе. На пороге стояла эра
неклассического естествознания.
Развенчанный Птолемей
Гелиоцентризм трудно внедрялся в научную жизнь,
однако в конечном счете одержал всеобъемлющую
победу. С теорией Птолемея происходило обратное: она
господствовала более тысячелетия и потерпела
сокрушительное фиаско. Подобный прецедент имел место впервые,
и в сознании научного общества еще безраздельно
господствовала кумулятивная модель научного прогресса.
Значительно позже — скажем, при смене взглядов Ньютона
теорией относительности — никому не могло даже прийти
в голову упрекать Ньютона в заблуждениях. Было
очевидно, что на смену одним научным представлениям
приходят другие, более глубокие. Но, не имея подобного
опыта, некоторые критики сплошь да рядом упрекали Птоле-
Ойзерман Т. И. Антифеодальная религиозная революция и ее
зачипатель//Соловьев Э. Непобежденный еретик. М.: Молодая
гвардия. 1984. С. 3.
231

мея именно в научной некомпетентности, писали, что он
грубо заблуждался и повел науку по ложному пути.
Рецидивы резко отрицательного отношения к деятельности
Птолемея не новы.
Как всякий ниспровергнутый с пьедестала деятель,
будь то рвавшийся к власти Лжедимитрий или
развенчанный Наполеон, Птолемей тоже стал привлекать к себе
пристальное внимание историков. Ныне широко
цитируются критические высказывания в его адрес со стороны
Деламбра, который упрекал Птолемея за то, что он нигде
не приводит ясных данных о своих наблюдениях и «не
говорит о том, какой могла быть вероятная ошибка его
солнечных, лунных и планетных таблиц. Астроном, который
сегодня действовал бы подобным образом, вызвал бы к
себе полное недоверие» 19.
Впрочем, Деламбр понимает и отчасти оправдывает
Птолемея. И уж, конечно, он не опускается до
спекуляций, пытаясь стяжать геростратову славу на уличении
маститого естествоиспытателя далекого прошлого в
мошенничестве. Мы, разумеется, имеем в виду недавно
переведенную на русский язык работу Р. Ньютона
«Преступление Клавдия Птолемея» с ее воинствующим апофеозом:
«Я не знаю, что могут подумать другие, но для меня
существует лишь одна окончательная оценка: „Синтаксис"
нанес астрономии больше вреда, чем любая другая
когда-либо написанная работа, и было бы намного лучше для
астрономии, если бы этой книги вообще не существовало.
Таким образом, величайшим астрономом античности
Птолемей не является, но он является еще более необычной
фигурой: он самый удачливый обманщик в истории
науки» 20.
К сожалению, в русском издании, вышедшем в 1985 г.
с использованием английского оригинала 1978 г.,
оказался обойденным молчанием тот факт, что под давлением
взрыва всеобщего негодования западных коллег Р.
Ньютон принужден был отказаться от некоторых своих
положений 21. Но он продолжает настаивать на том, что
большинство приводимых Птолемеем наблюдений является на
самом деле результатом вычислительной подгонки, и это,
19 Паннекук А. История астрономии. М.: Наука, 1966. С. 163.
20 Ньютон Р. Преступление Клавдия Птолемея. М.: Наука, 1985.
С. 368.
21 Newton R. R. The Origin of Ptolemy's astronomical parameters.
N. Y.: Center of Archeoastronomy, University Maryland, 1982.
228 p.
232

по всей вероятности, действительно так. Факты, как
говорят, упрямы. Но в чем же суть проблемы?
Птолемей, создатель первой крупной
математизированной естественнонаучной теории, впервые столкнулся с
колоссальной противоречивостью реальных наблюдений.
Напомним для наглядности, что диск Луны имеет на
небесной сфере поперечник в 0,5°, т. е. 30 угловых минут.
Принято считать — и это впоследствии блестяще
продемонстрировал Тихо Браге, — что точность угловых наблюде-
вий невооруженным глазом составляет несколько
угловых минут и большим ошибкам взяться неоткуда. Однако
это глубокое заблуждение.
Птолемей использовал наблюдения, в которых
регистрировались не только угловые положения, но и время,
а это могло выполняться — особенно при определении
характерных точек в движениях Солнца, Луны и планет —
очень грубо. Скорость же собственного движения Луны
по небесной сфере среди звезд составляет около 0,5° в час.
Среди использованных Птолемеем шумерских и
вавилонских наблюдений многовековой давности наверняка
попадались такие, которые имели ошибки регистрации
времени в несколько часов — вот явный источник ошибок в
положениях, достигающих нескольких градусов дуги!
Птолемей создал геоцентрическую систему мира, но
он не брал на себя задачу создать теорию ошибок
измерений. Он не знал способа наименьших квадратов и
вообще всего того математического аппарата, который мы
называем сегодня теорией уравнительных вычислений. Он
стоял перед лицом грубо противоречащих друг другу
наблюдений, и он каким-то образом привел их в порядок,
к единой системе, поскольку в «Альмагесте» не осталось
никаких следов противоречий: все данные тщательно
согласованы друг с другом. Имеются ли основания
квалифицировать действия Птолемея как подгонку
экспериментальных данных, за которую сегодня научного работника
могут уволить с работы? Конечно, нет.
Возьмем для наглядного примера современную
систему фундаментальных астрономических постоянных. Все
постоянные идеально согласованы друг с другом. И
незнакомый с современной методикой критик через тысячу
лет, подобно Р. Ньютону, тоже может поднять крик о
вычислительной подгонке этой системы. Конечно, некоторая
разница со случаем Птолемея существует. Эмпирический
материал к системе фундаментальных постоянных
опубликован, равно как опубликована и методика согласова-
233

ния системы. Птолемей же скрыл «кухню» своих
уравнительных вычислений. Из неразберихи противоречивых
данных он извлек в общем и целом вполне
удовлетворительные осредненные результаты, однако нигде не привел
самих исходных измерений.
Наш анализ не будет полным, если пройти мимо того,
что новейшие достижения физики, как это ни
парадоксально, вновь всколыхнули вопрос о приоритетах между
системами Птолемея и Коперника. Теория
относительности с отсутствием в ней привилегированных систем
координат ставит их сегодня как бы на одну доску.
И выделенность гелиоцентрической системы Коперника
нуждается в наши дни в специальном философско-мето-
дологическом обосновании. «Несмотря на принципиальное
равноправие способов существования в любых системах
отсчета (в одних системах отсчета существуют одни
характеристики реальности, в других — другие), для ряда
конкретных задач проще выбирать определенный вид
системы отсчета и тем самым определенную картину
существования. Система Коперника является именно такой
«относительно привилегированной» системой по
сравнению с системой Птолемея, ибо подавляющая часть массы
системы Солнца и планет (99,86%) сосредоточена в
Солнце...» 22.
Кстати сказать, все астрономические ежегодники мира,
как и во времена Птолемея, приводят эфемериды
небесных тел не в гелиоцентрической, а в геоцентрической
системе координат.
Наука не открывает вечных истин, и все
исследователи постоянно в пути. Заблуждение думать, что, не будь
Птолемея, сразу мог бы на ровном месте расцвести гений
Коперника. Кстати, уже после Коперника астрономия
совершила ряд следующих шагов, передвинув центр
мироздания из центра Солнца в центр Галактики, а
впоследствии признав множественность «островных вселенных»
и всякое отсутствие какого бы то ни было центра. Эти
принципиально важные шаги астрономии уже не
отличались драматизмом, поскольку их возможность была
понята в процессе драмы перехода от геоцентризма к
гелиоцентризму.
Честь и хвала первопроходцам — великому Птолемею
и великому Копернику!
А. А. Гурштейп
22 Алексеев И. С. Указ. соч. С. 280.

Литература
Публикации трудов Клавдия Птолемея
(в хронологическом порядке)
1. Glaudii Ptolomei viri Alexandrini Cosmographie octavuset ulti-
mus liber explicit. Opus donni Nicolai Germani secundum Ptolo-
meum finit. Anno MGGGGXXXII Augusti vero kalendas XVII.
Impressum Ulme per Ingerosum virum Leonardum hoi prefati
oppidi Givis. (Ульмское издание «Географии» 1482 г.)
2. Almagestum Gl. Ptolemaei Pheludiensis Alexandrini, astronomo-
rum principis. Opus ingens ac nobile, omnes celorum motus
continens. Felicibus astris eat in lucem: Dictu Petri
Liechtenstein Coloniensis Germani, anno Virginei Patrus 1515. die 10 Jan.
Venetiis ex officina eiusdem litteraria fol. (Первое венецианское
издание «Альмагеста».)
3. Cl. Ptolemaei Pheludiensis Alexandrini Almagestum seu Magnae
constructionis mathematicae opus plane divinum latina donatum
lingua ab Georgio Trapezuntio usquequaque doctissimo, per Lu-
cam Gauricum, Neap, divinae matheseos prof, egregium im alma
urbe Veneta orbia regina recognitum 1528. (Первое издание
«Альмагеста» в переводе с греческого Георгия Трапезунд-
ского.)
4. Geographia universalis vêtus et nova, complectens Clavdii
Ptolemaei Alexandrini enarrationis libros VIII. Basilaea Apud
Henricum Petrum mense Martio anno MDXL. Quorum primus
nova translatione Pirckheimeri... Succedunt tabulae Ptolemaice,
opera Sebastiani Munsteri novo paratae modo. (Базельское изд.
«Географии» 1540 г.)
5. Ptolemaei Mathematicae constructionis Liber primus graece et
latine editus. Additae explicationes aliquot locorum ab. Erasmo
Rheinholt salueldensi. Wittenbergae, Ex officina Iohannis Luft.
Anno 1549. (Книга I «Альмагеста» с предисловием Ф. Меланх-
тона под ред. Э. Рейнгольта.)
6. Claudii Ptolemaei Pelusiensis Alexandrini omnia quae extant
opera, praeter Geographiam, quam non dissimile forma... Erasmo
Osualdo Schreckenfuchsio. Basilea, febr. 1551. (Первое собрание
сочинений Птолемея, включающее «Альмагест», комментарий
к нему Прокла Диадоха, «Четырехкнижие», «Центилоквиум»,
«Обозначения неподвижных звезд», «Географию».)
7. Geographiae Glaudii Ptolemaei Alexandrini, Philosophi ас Mathe-
matici praestatissimi, Libri VIII, partim a Bilibaldo Pirkheimero
translati ac commentario illustrati, partim etiam Graecorum...
Marte 1552, Gonradi Lycostensis ac Sebastianum Munsterum.
Paris.
8. Claudii Ptolemaei Harmonicorum Libri très. Ex codd. mss. un-
decim nunc primum graece editus. Johannes Wallis, Th. D., geo-
metriae professor, Savilianus, Oxoniae, Regiae souclafis Londi-
ni... Oxonii, Theatro Scheldoniano, An. Dom. 1682. (Издание
«Гармоник» на греческом и латинском языках.)
235

9. Halma N. (ed.). Tables manuelles astronomiques de Ptolomée et
de Theon. 3 parts. Paris, 1822-1825.
10. Halma N. (ed., transi.). Composition Mathématique de Claude Pto-
lemée. 2 vols. Paris, 1813, 1816.
11. Claudii Ptolemée Geographia, ed. C. F. A. Nobhe, 2 vols.,
Leipzig: Teubner, 1843, 1845.
12. L'Ottica di Claudio Tolomeo da Eugenio di Sicilia... publ. G. Go-
vi, Turin, 1885.
13. Heiberg J. L. (ed.). Claudii Ptolemaei Opera quae extant omnia.
Syntaxis Mathematica. 2 vols. Leipzig: Teubner, 1898, 1903.
14. Ptolemäus. Handbuch der Astronomie. Deutsche Übersetzung von
K. Manitius, 2 Vols. Leipzig: Teubner, 1912, 1913. Zweite
Ausgabe, herausgegeben bei 0. Neugebauer. Leipzig: Teubner, 1963.
15. The Almagest, by Ptolemy. Ed. Hutchins R. Transi. Great Books
of the Western World, v. 16. Encycl. Brit. Chicago, 1952, 478 p.
16. Lejeune A. (ed.). L'Optique de Claude Ptolemée dans la
versification latine d'après l'arabe de l'émir Eugène de Sicile//Univ.
Louvain, Recueil de travaux d'histoire et de philologie, 4e sér.,
fasc. 8. Louvain, 1956.
17. Toomer G. J. (ed., transi.). Ptolemy's Almagest. London:
Duckworth, 1984, 694 p.4
Работы других авторов
18. Абдулькасумова H. А., Усейнова 3. Э. «Альмагест» Птолемея в
обработке Насирэддина Туей//XIII Междунар. конгресс по
истории науки: Материалы по истории физ.-матем. наук. М.:
Наука, 1971. С. 1.
19. Абрамян Р. А., Туманян Б. Е. Об астрономических работах
Анания Ширакаци // ИАИ2. 1956. Вып. 2. С. 239-246.
20. Амбарцумян В. А. Философские вопросы науки о Вселенной.
Ереван: Изд-во АН АрмССР, 1973. 428 с.
21. Аристотель. О небе. Соч. Т. 3. М.: Мысль, 1981. С. 329.
22. Астрономический календарь на 1982 г. М.: Наука, 1981. 336 с.
23. Астрономический календарь на 1985 г. М.: Наука, 1984. 320 с.
24. Астрономический календарь. Постоянная часть. 7-е изд. М.:
Наука, 1981. 704 с.
25. Бакулин П. И., Кононович Э. В., Мороз В. И. Курс общей
астрономии. М.: Наука, 1970. 536 с.
26. Белый Ю. А. Иоганн Кеплер. М.: Наука, 1971. 296 с.
27. Белый Ю. А. Тихо Браге. М.: Наука, 1982. 230 с.
28. Белый Ю. А. Иоганн Мюллер (Региомонтан). М.: Наука, 1985.
128 с.
29. Берри А. Краткая история астрономии. М., Л.: Гостехиздат,
1946. 364 с.
30. Бикерман Э. Хронология древнего мира: Пер. с англ.М.:
Наука, 1975. 336 с.
31. Блажко С. Н. Курс общей астрономии. М.: Гостехиздат, 1947.
500 с.
32. Боголюбов А. Н. Математики, механики. Киев: Наук, думка,
1983. 640 с.
1 Все ссылки на «Альмагест» даются по этому изданию. Ссылки
на текст самого Птолемея даются на [17], а на комментарии
Дж. Тумера-на [131], хотя это одна и та же книга.
2 Историко-астрономические исследования. М.: Наука.
236

33. Богомолов А, С. Античная философия. М.: Изд-во МГУ, 1985.
368 с.
34. Булгаков П. Г., Розенфелъд Б. А., Ахмедов А. А. Мухаммед ал-
Хорезми. М.: Наука, 1983. 240 с.
35. Веселовский И. Н. Аристарх Самосский — Коперник античного
мира // ИАИ. 1961. Вып. 7. G. 63.
36. Веселовский И. Н. Комментарии к книге: Коперник Н. О
вращении небесных сфер. М.: Наука, 1964. G. 556-558.
37. Веселовский И. Н., Белый Ю. А. Николай Коперник. М.:
Наука, 1974. 456 с.
38. Володарский А. И. Астрономия в древней Индии//ИАИ. 1975.
Вын. 12. С. 237-252.
39. Володарский А. И. Ариабхата. М.: Наука, 1977. 112 с.
40. Воронцов-Вельяминов Б. А. Очерки истории астрономии в
России. М.: Гостехиздат, 1956. 372 с.
41. Гаврюшин Н. К. Византийская космология в XI веке//ИАИ.
1983. Вып. 16. С. 327-338.
42. Галилей Галилео. Диалог о двух главнейших системах мира,
птолемеевой и коперниковой: Пер. с итал. М., Л.: Гостехиздат,
1948. 380 с.
43. Голубцова Е. С, Завенягин Ю. А. Еще раз о «новых
методиках» и о хронологии древнего мира//Вопр. истории. 1983.
№ 12. С. 68-83.
44. Голъдберг Г. А. Музыкальный строй//Физический
энциклопедический словарь. М.: Сов. энциклопедия, 1963. Т. 3. С. 335-
336.
45. Гурев Г. А. История одного заблуждения. Л.: Наука, 1970.
192 с.
46. Гурев Г. А. Коперниковская ересь в прошлом и настоящем.
М.: ОГИЗ, 1933. 140 с.
47. Дагаев М. М., Демин В. Г., Климишин И. А., Чаругин В. М.
Астрономия. М.: Просвещение, 1983. 384 с.
48. Добровольский И. Г., Брабич В. М. Александрийские монеты
Антонина Пия с изображением созвездий Зодиака//ИАИ.
1959. Вып. 5. С. 223-230.
49. Долгоруков II, П. Теория движения Луны. СПб: Росс. АН,
1902. XV+351 с.
50. Ефремов Ю. IL, Павловская Е. Д. Датировка «Альмагеста» по
собственным движениям звезд//Докл. АН СССР. 1987. Т. 294,
№ 2. С. 310-313.
51. Зубов В. П. Примечания к трактату Н. Орема «О
соизмеримости или несоизмеримости движений неба» // ИАИ. 1960. Вып. 6.
С. 301-400.
52. Зубов В. П. Физические идеи древности, средневековья,
Ренессанса//Очерки развития основных физический идей. М.: Изд-
во АН СССР, 1959. С. 11-155.
53. Иванов А. А. Курс астрономии. Л., М.: Главсевморпуть, 1940.
304 с.
54. Идельсон Н. И. Этюды по истории планетных теорий//Этюды
по истории небесной механики. М.: Наука, 1975. С. 124-
204.
55. История древнего мира. Кн. 2. Расцвет древних обществ. М.:
Наука, 1982. 576 с.
56. Казаков С, А. Курс сферической астрономии. М., Л.:
Гостехиздат, 1940. 284 с.
237

57. Кары-Ниязов T. H. Астрономическая школа Улугбека. M., Л.:
Изд-во АН СССР, 1950. 332 с.
58. Кедров Б. М., Розенфельд Б, А. Лбу Райхан Бирули. М.:
Наука, 1973. 56 с.
59. Кеплер И. О шестиугольных снежинках. М.: Наука, 1983. 192 с.
60. Клименко А. В. Древнейшие определения размеров Земли//
Развитие методов астрономических исследований. М., Л.: ВА-
ГО-ГАО-ИТА, 1979. С. 70-83.
61. Клименко А. В. О происхождении упоминаемых Аристотелем
и Архимедом результатов определения размеров Земли//МАИ.
1980. Вып. 15. С. 189-197.
62. Копелевич 10. X. К истории приобретения Россией рукописей
Кеплера//ИАИ. 1972. Вып. 11. С. 131-146.
63. Коперник Н. О вращениях небесных сфер. Малый
комментарий. Послание против Вернера. Упсальская запись/Пер.
И. Н. Веселовского под ред. А. А. Михайлова. М.: Наука, 1964.
654 с.
64. Крачковский И. Ю. Избранные сочинения. М., Л.: Наука, 1967.
Т. 4. С. 84.
65. Культура Византии. IV-первая половина VII в./Под ред.
3. В. Удальцовой. М.: Наука, 1984. 726 с.
66. Куницкий Р. В. История развития взглядов на строение
солнечной системы. М.: Гостехиздат, 1951. 80 с.
67. Куртик Г. Е. Теория прецессии в античной и средневековой
науке: Дис. ... канд. физ.-мат. наук. М., 1984. 214 с.
68. Ландсберг Г. С. Оптика. М., Л.: Гостехиздат, 1947. 632 с.
69. Левочкин И. В. О естественнонаучном и философском
содержании Изборника Святослава 1073 года//Памятники науки и
техники 1982-1983. М.: Наука, 1984. С. 114-119.
70. Леонов Н. И. Улугбек - великий астроном XV века. 2-изд. М.:
Гостехиздат, 1950. 68 с.
71. Лукреций. О природе вещей. М.: Изд-во АН СССР, 1945. 451 с.
72. Мамедбейли Г. Д. Основатель Марагинской обсерватории
Мухаммед Насйрэддин Туей. Баку: Изд-во АН АзССР, 1961. 316 с.
73. Михайлов А. А. Теория затмений. М.: Гостехиздат, 1954. 272 с.
74. Шур П. Планета Венера: Пер. с англ. М.: Изд-во иностр. лит.,
1961. 146 с.
75. Нейгебауэр О. Точные науки в древности. М.: Наука, 1968.
224 с.
76. Несторианство//БСЭ. 2-е изд. 1954. Т. 29. С. 497.
77. Ньютон Р. Р. Преступление Клавдия Птолемея: Пер. с англ.
М.: Наука, 1985. 384 с.
78. Паннекук А. История астрономии. М.: Наука, 1966. 592 с.
79. Планеты и спутники: Пер. с англ./Ред. Дж. П. Койпер.
Б. Миддлхерст. М.: Изд-во иностр. лит., 1963. 520 с.
80. Плутарх. Соч. М.: Худож. лит., 1983. 704 с.
81. Попов П. И., Баев К. Л., Воронцов-Вельяминов Б. А.,
Куницкий Р. В. Астрономия. М.: Учпедгиз, 1940. 572 с.
82. Рожанский И. Д. Античная наука. М.: Наука, 1980. 200 с.
83. Розенбергер Ф. История физики: Пер. с нем. М.; Л.: ОНТИ,
1937. Ч. 1. 185 с.
84. Розенфельд Б. А. Астрономия стран ислама//ИАН. 1984.
Вып. 17. С. 67-122.
85. Розенфельд Б. А., Рожанская M. М. Астрономический труд Ал-
Бируни «Канон Масуда»//Там же. 1969. Вып. 10. С. 63-95.
238

86. Справочное руководство по небесной механике и
астродинамике/Под ред. Г. Н. Дубошина. М.: Наука, 1971. 584 с.
87. Стройк Д. Я. Краткий очерк истории математики. М.: Наука,
1984. 285 с.
88. Субботин М. Ф. Птолемей Клавдий//БСЭ. 2-е изд. 1955. Т. 35.
С. 271-272.
89. Умаров Г. Я. Беруни, Коперник и современная наука. Ташкент:
ФАН, 1973. 120 с.
90. Харадзе Е. К., Кочлашвили Т. А. К изучению истории развития
астрономических знаний в Грузии // ИАИ. 1958. Вып. 4. С. 499-
505.
91. Шевченко В. В. Небесная музыка//Земля и Вселенная. 1973.
№ 4. С. 56-58.
92. Яшнов П. И. Иоганн Кеплер//Русск. астрон. календарь на
1930 г. Н.-Новгород, 1930. С. 125-145.
93. Boll F. Die Sternkataloge des Hipparch und des Ptolemaios//
Bibl. Math. 1901. Ser. 3. Bd. 2. S. 185-195.
94. Boll F. Studien über Claudius Ptolemäus//Jb. Klass. Philol.
1894. Suppl.-Bd. 21. S. 51-244.
95. Bouillaud I. Astronomia Philolaica. P., 1634.
96. Delambre J. B. J. Histoire de l'astronomie ancienne. P., 1817.
Vol. 2.
97. Dreyer J. L. E. A history of astronomy from Thaïes to Kepler.
Cambridge: Dover, 1953. X+438 p.
98. Dreyer J. L. E. On the origin of Ptolemy's Catalogue of stars//
Mon. Not. of the RAS. 1917. Vol. 77, N 7. P. 528-539.
99. Euclides Alexandrinus. Die Elemente // Dt. Übersetz. Leipzig,
1933-1937. Bd. 1-3.
100. Evans J. On the function and the probable origin of Ptolemy's
equant//Amer. J. Phys. 1984. Vol. 52, N 12. P. 1080-1089.
101. Gingerich O. «Crisis» versus aesthetic in the Copernican
revolution//Copernicus. Oxford, 1975. P. 85-95. (Vistas Astron. Vol. 17).
102. Gingerich O. Ptolemy and the maverick motion of Mercury // Sky
and Telescope. 1983. Vol, 66, N 1. P. 11-13.
103. Gingerich O. The astronomy and cosmology of Copernicus //
Highlights Astron. Vol. 3. 15th Gen. Assemb. and Extraordinary Gen.
Assemb. IAU 1973. Dordrecht; Boston, 1974. P. 67-85.
104. Gingerich O. Was Ptolemy a fraud? // Quart. J. Roy. Astron. Soc.
1980.Vol. 21, N 3. P. 253-266.
105. Ginzel F. Spezieller Kanon der Sonnen- und Mondfinsternisse für
das Ländergebiete der klassischen Alterumswissenschaften von
900 v. Chr. bis 600 n. Chr. В., 1899.
106. Goldstein B. R. The Arabic version of Ptolemy's «Planetary
Hypotheses»//Trans. Amer. Phil. Soc. 1967. Vol. 57, pt 4. P. 3-55.
107. Hunger H. Die hochsprachliche profane Literatur der Bysantiner.
München, 1978. Bd. 2. XX+528 S.
108. Knupp P., Gaughlan G., Mullen P. Ptolemaic astronomy: a modern
approach//Proc. Montana Acad. Sei. 1975. Vol, 34. P. 132-133.
109. Krause M. Die Sphärik von Menelaus aus Alexandrien in der
Verbesserung von Abu Nassr Mansur b. Ali b. Iraq//Abb. Ges.
Wiss. Göttingen, Phil.-hist. KL, 3 F. В., 1936. VII+364 S.
HO. Kunitsch P. Der Almagest. Die Syntaxis Mathematica des
Claudius Ptolemäus in arabisch-lateinischer Überlieferung.
Wiesbaden, 1974. XVI+384 S.
111. Laplace P. S. Oeuvres. P., 1884. Vol. 6.XI+509 p.
239

112. Larousse P. Grand dictionnaire universel du XIX siècle. P.:
Larousse, s. a. T. 3. P. 560.
113. Lejeune A. Les tables de réfraction de Ptolemée//Ann. Soc. Sei.
Bruxelles. Sér. 1. 1946. Vol. 60. P. 93-101.
114. Manitius C. (ed.). Hipparchi in Arati et Eudoxi Phaenomena
Commentariorum Libri Très. Leipzig: Teubner, 1894.
115. Moore P. The planet Venus. N. Y.: Macmillan, 1959. 152 p.
116. Neugebauer 0. History of Ancient mathematical astronomy.
Berlin; Heidelberg. N. Y.: Springer, 1975. Vol. 1. 1456 p.
117. Neugebauer 0. The exact sciences in Antiquity. Copenhagen:
Munksgaard, 1951. 192 p.+14 PI.
118. Neugebauer 0. The transmission of planetary theories in Ancient
and Medieval astronomy. N. Y.: Yeshiva Univ., 1956. 30 p.
119. Newton R. R. The crime of Claudius Ptolemy. Baltimore. L.:
J. Hopkins Univ. press, 1978. XIV+412 p.
120. Pedersen O. A survey of the Almagest//Acta hist. sei. Natur.
Medic. 1974. Vol. 30. P. 1-428.
121. Petersen V. M., Schmidt O. The determination of the longitude
of the apogee of the orbit of the Sun according to Hipparchus
and Ptolemy//Centaurus. 1967. Vol. 12. P. 73-96.
122. Pline VAncient. Histoire naturelle. Livre IL P.: Collection Budé,
1950. XXI+282 p.
123. Ptolemée. Claude//Larousse de XX siècle. P.: Larousse, 1932.
T. 5. P. 839.
124. Raeder H., Strömgren E., Strömgren Б. Tycho Brahe's description
of his instruments and scientific work. Köbenhavn, 1946. 144 p.
125. Rawlins D. An investigation of the Ancient Star Catalogue //
Publ. Astron. Soc. Pacif. 1982. Vol. 94, N 558. P. 359-373.
126. Rome A. Les observations d'équinoxes de Ptolemée. Ptolemée et
le mouvement de l'apogée solaire // Ciel et Terre. 1943. Vol. 59.
P. 1-15.
127. Sagazan, de. Les observations et les calculs de Pythéas le Mas-
siliote//Rév. maritime. 1955. N 111. P. 930-936.
128. Skelton R. A. Introduction. Amsterdam: Theatrum Orbis Terra-
rum, 19663. P. V-XXI.
129. Tannery P. Psellos sur la Grande Année // Revue des Études Gré-
ques. P., 1892. T. 5. P. 206-211.
130. Tannery P. Ptolemée Claude//La Grande Encyclopédie. P.: Ar-
rault, s. a. T. 27. P. 905-906.
131. Toomer G. J. Ptolemey's Almagest. L: Duckworth. 1984. 694 p.
132. The Greek commentaries on Plato's Phaedo. Vol. 1. Olympiodo-
rus/Ed. L. G. Westerlink. Amsterdam: North-Holland Publ. Co,
1876. P. 142-143.
3 Факсим. изд. Г4].

Оглавление
От редактора . 5
Предисловие 6
Глава 1
Место и время действия . . , И
Глава 2
Астрономия в Вавилоне и Греции до Гиппарха ... 16
Глава 3
Астрономические исследования Гиппарха 26
Глава 4
Краткое содержание «Альмагеста» 37
Глава 5
Мировоззрение Птолемея 41
Глава 6
Небесная сфера: расчеты и измерения 50
Глава 7
Теория движения Солнца 70
Глава 8
Теория движения Луны 79
Глава 9
Звездный каталог У9
Глава 10
Теория движения планет 111
Глава 11
«Преступление Клавдия Птолемея» 126
Глава 12
Работы Птолемея в области географии 136
Глава 13
Работы Птолемея в области оптики 153
Глава 14
Математика и музыка 161
Глава 15
Птолемей и астрология 168
Глава 16
Судьба «Альмагеста» 176
Глава 17
От эпициклов Птолемея к законам Кеплера .... 197
Птолемей и Коперник (послесловие редактора) . . 216
Литература 235