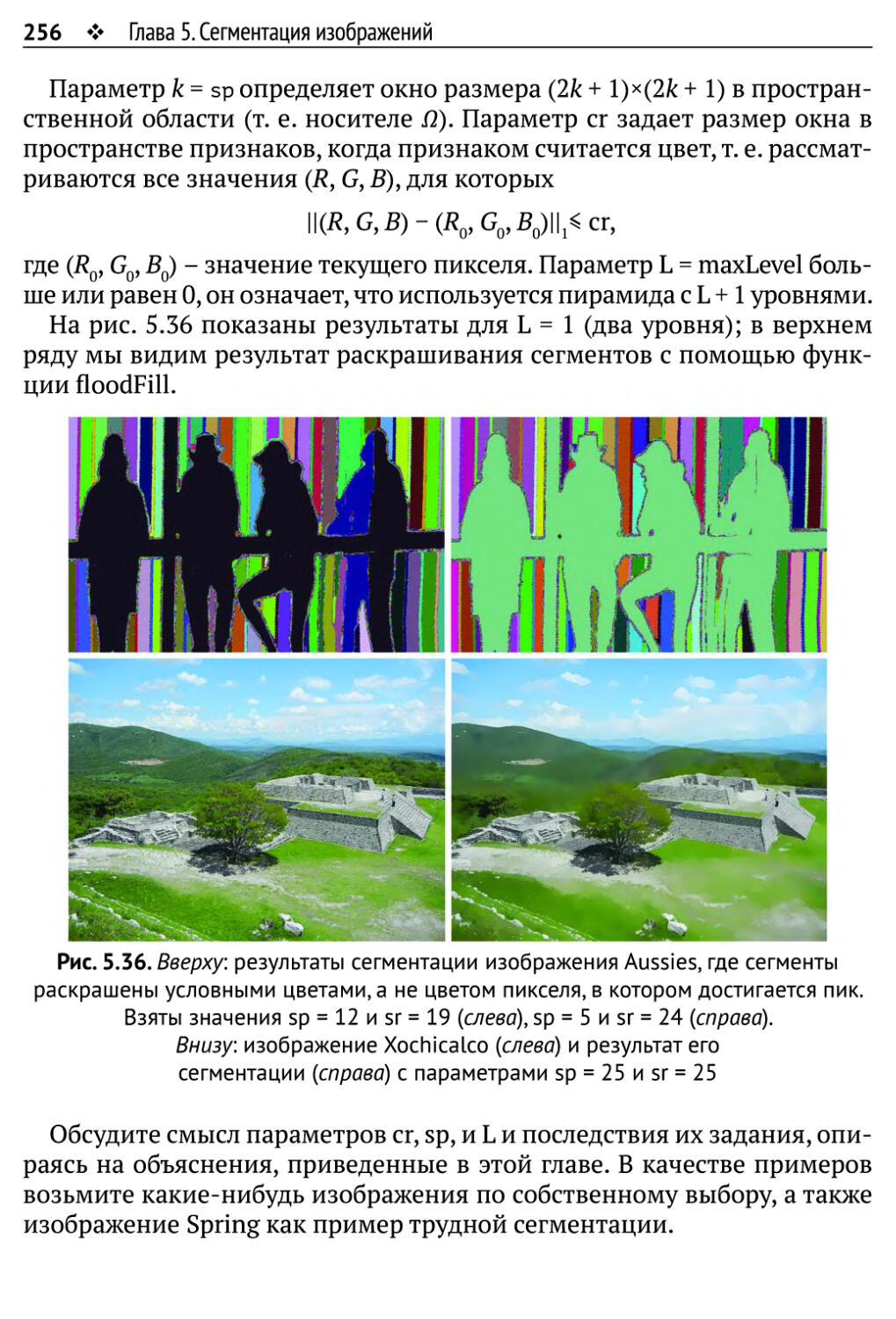
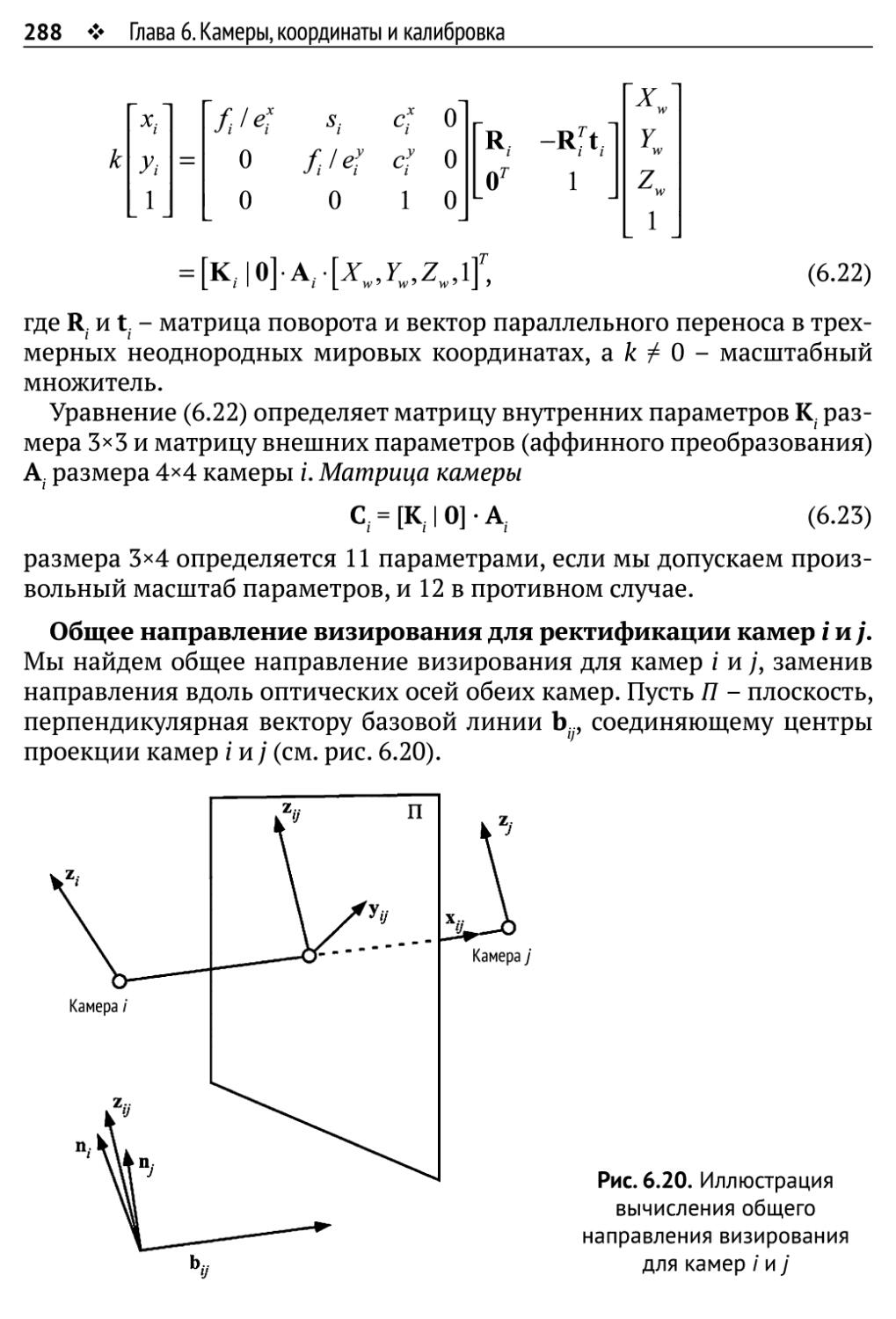
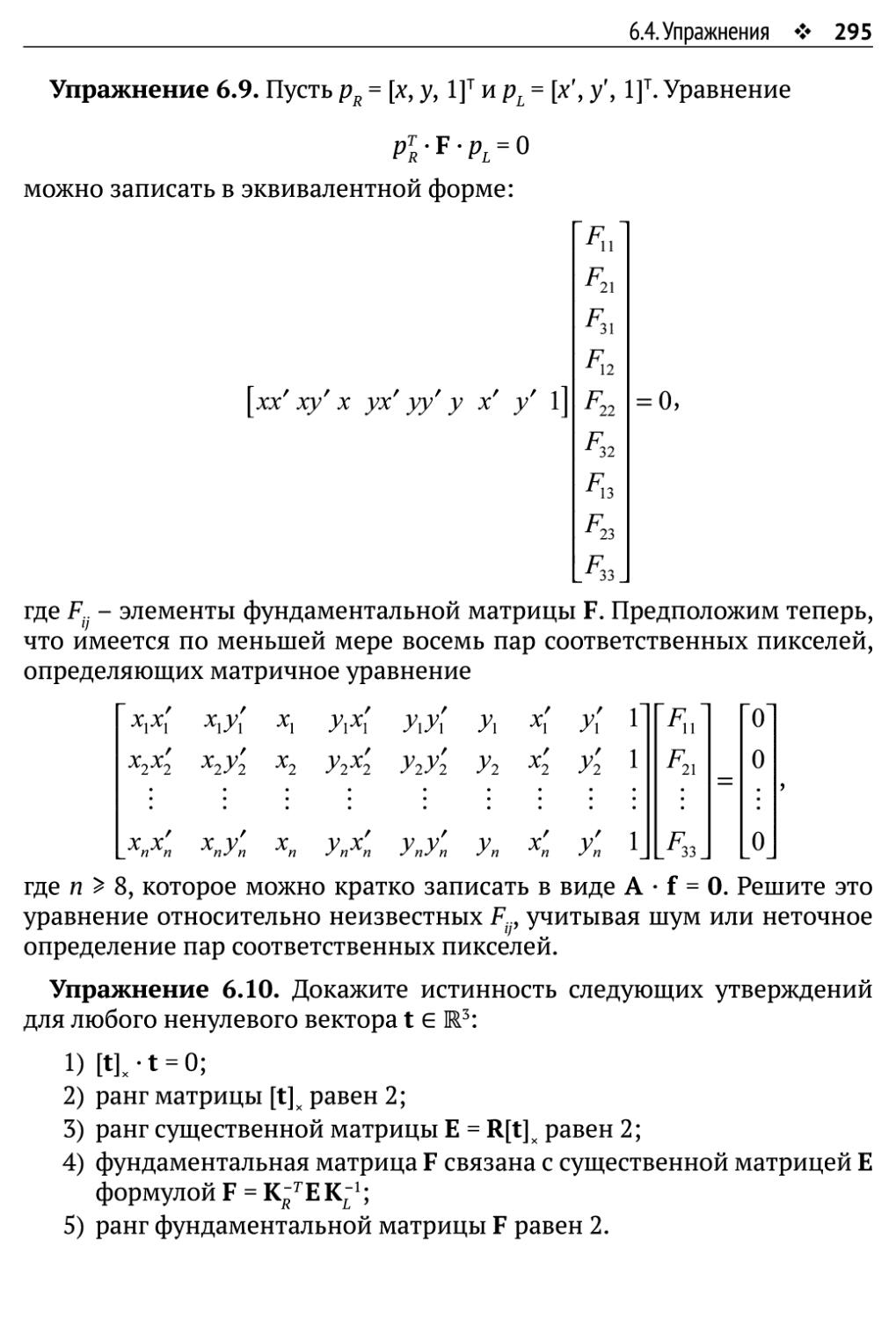
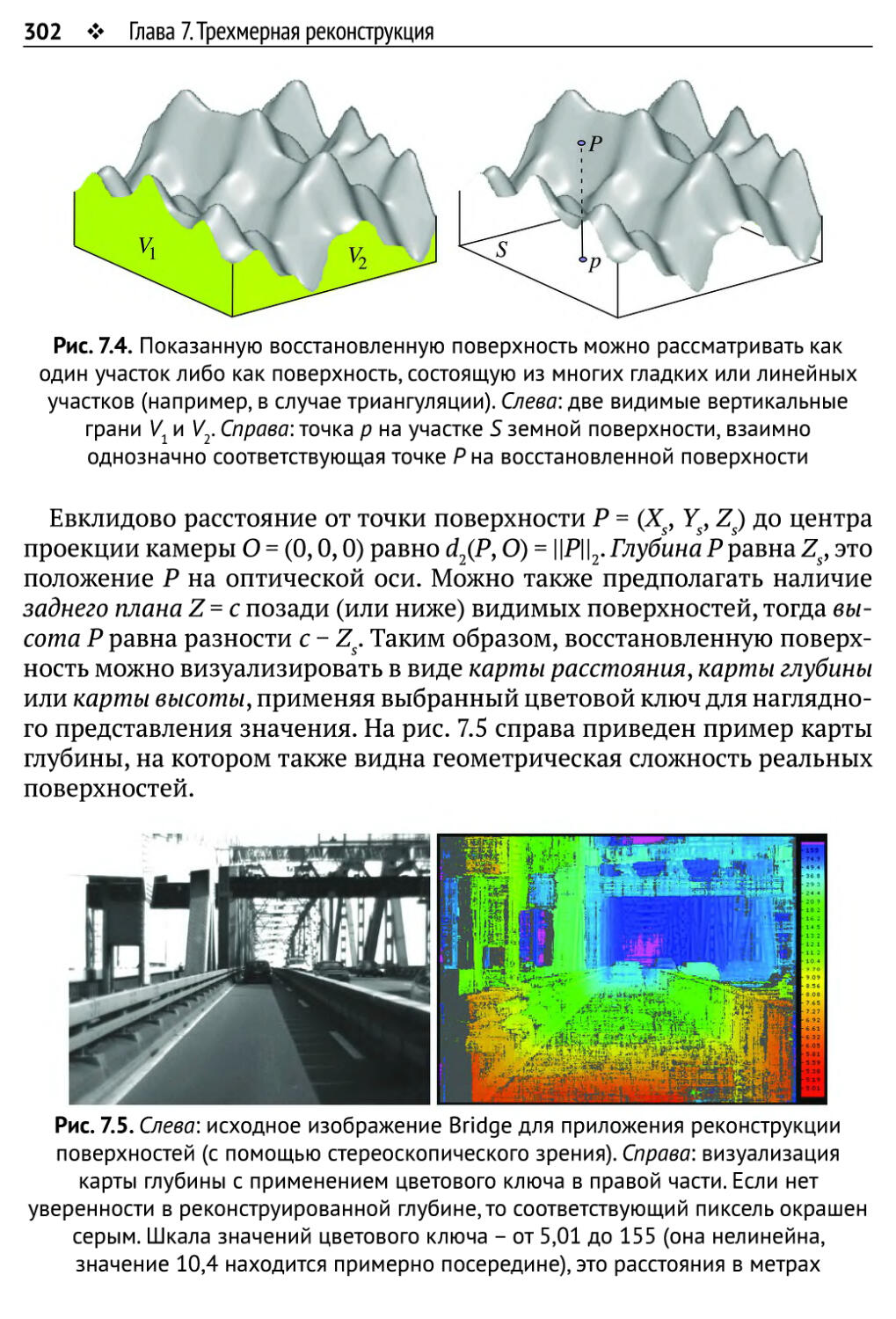
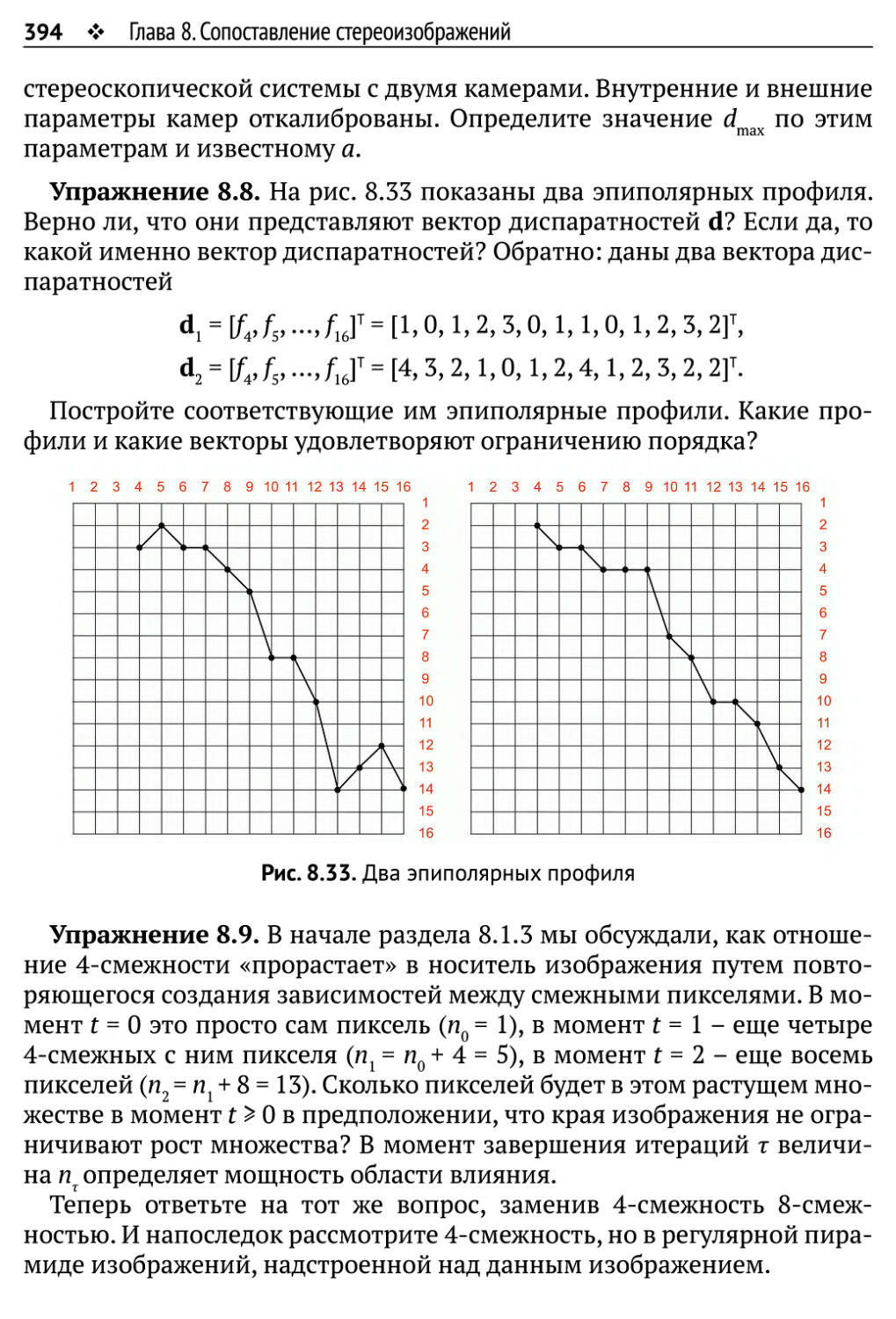
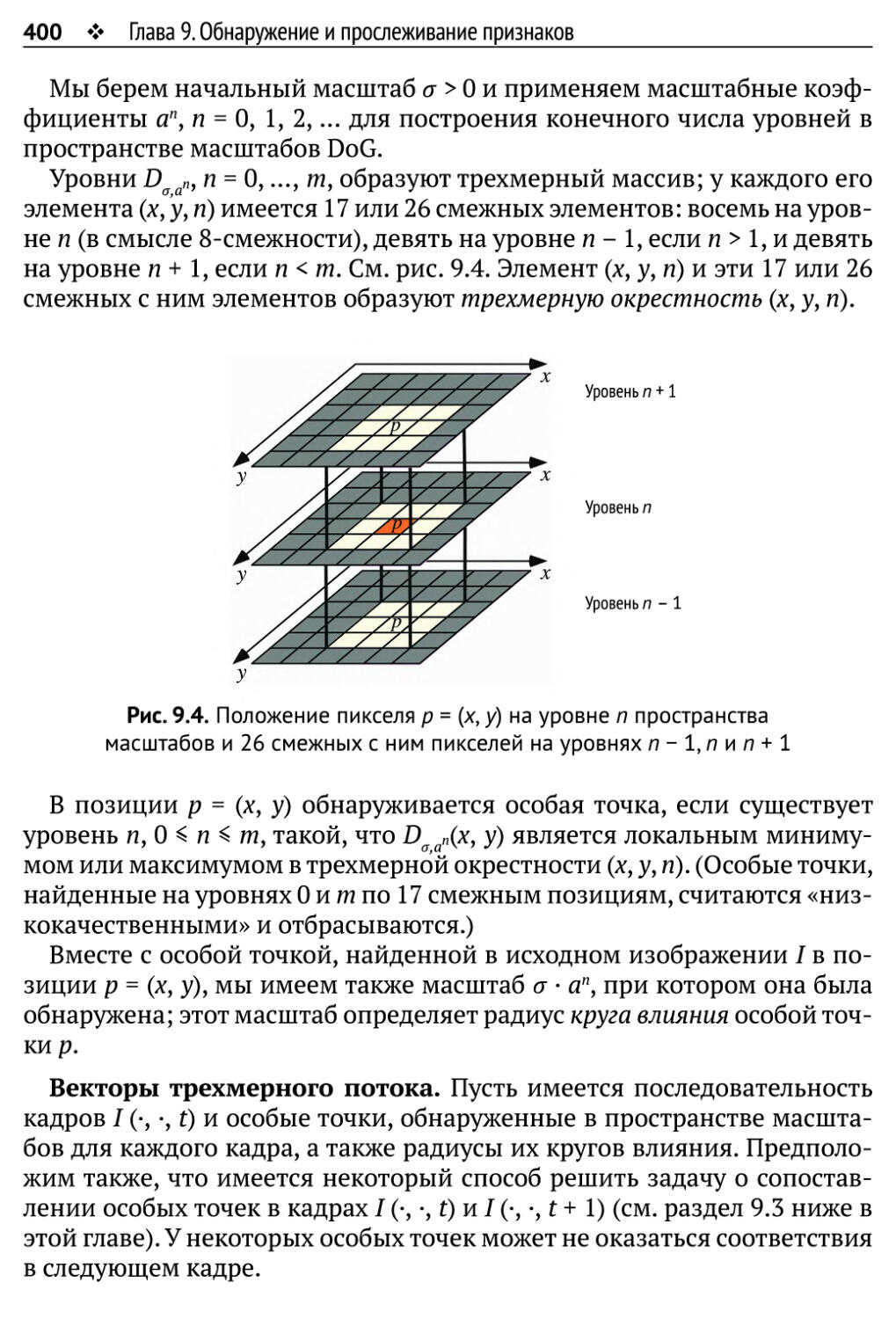
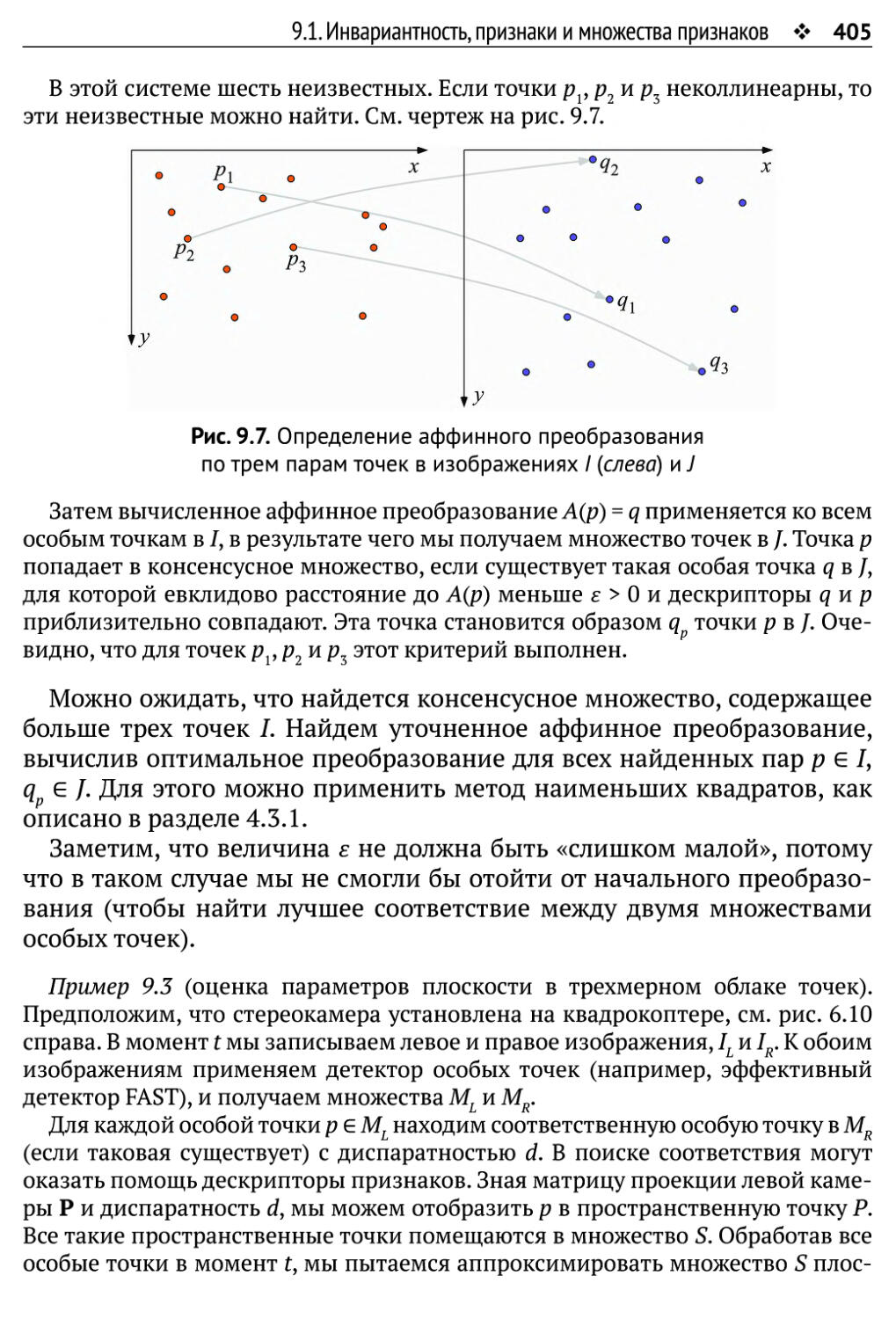
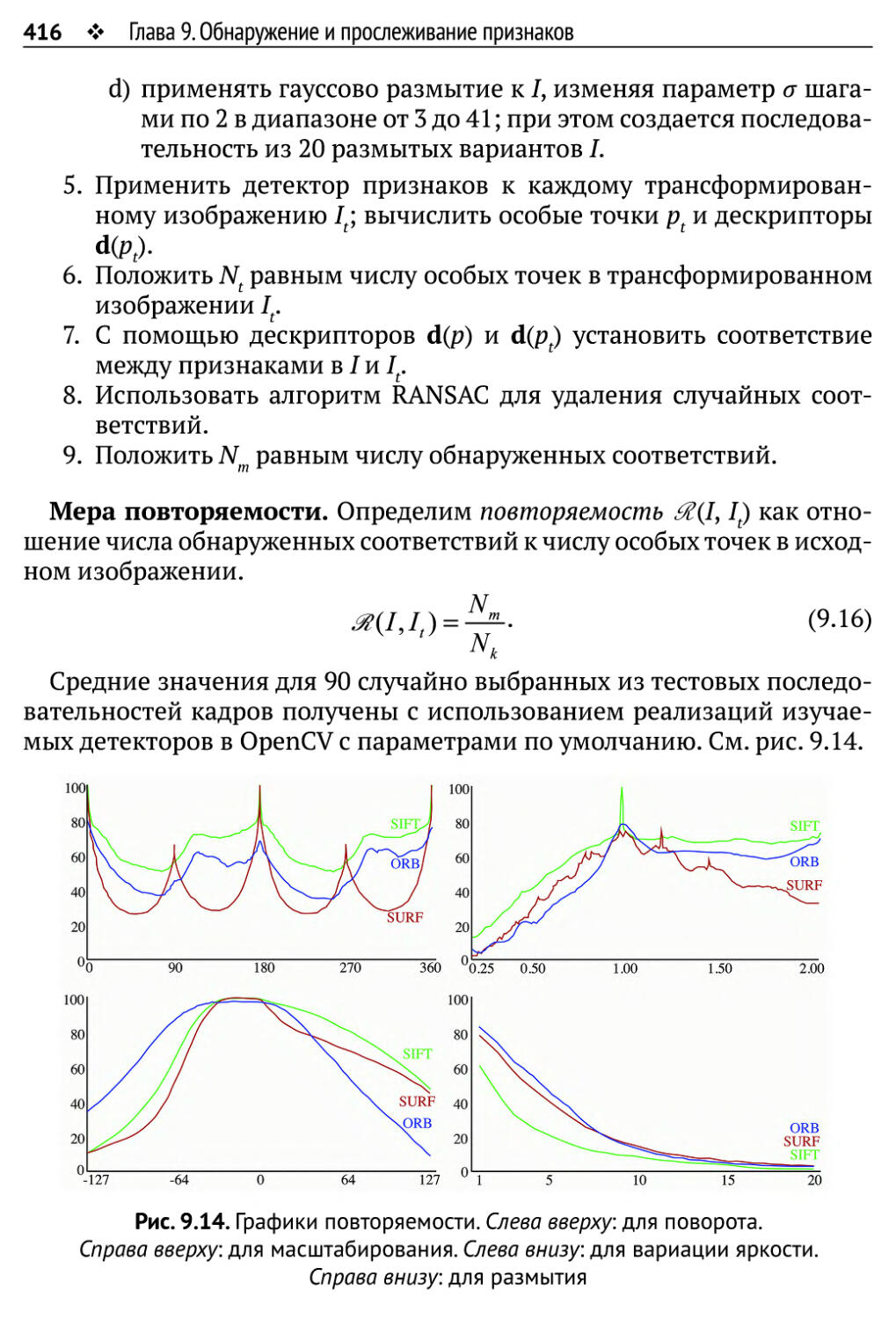
Автор: Рейнхард Клетте
Теги: искусственный интеллект кибернетика алгоритмы цифровая обработка изображений компьютерное зрение
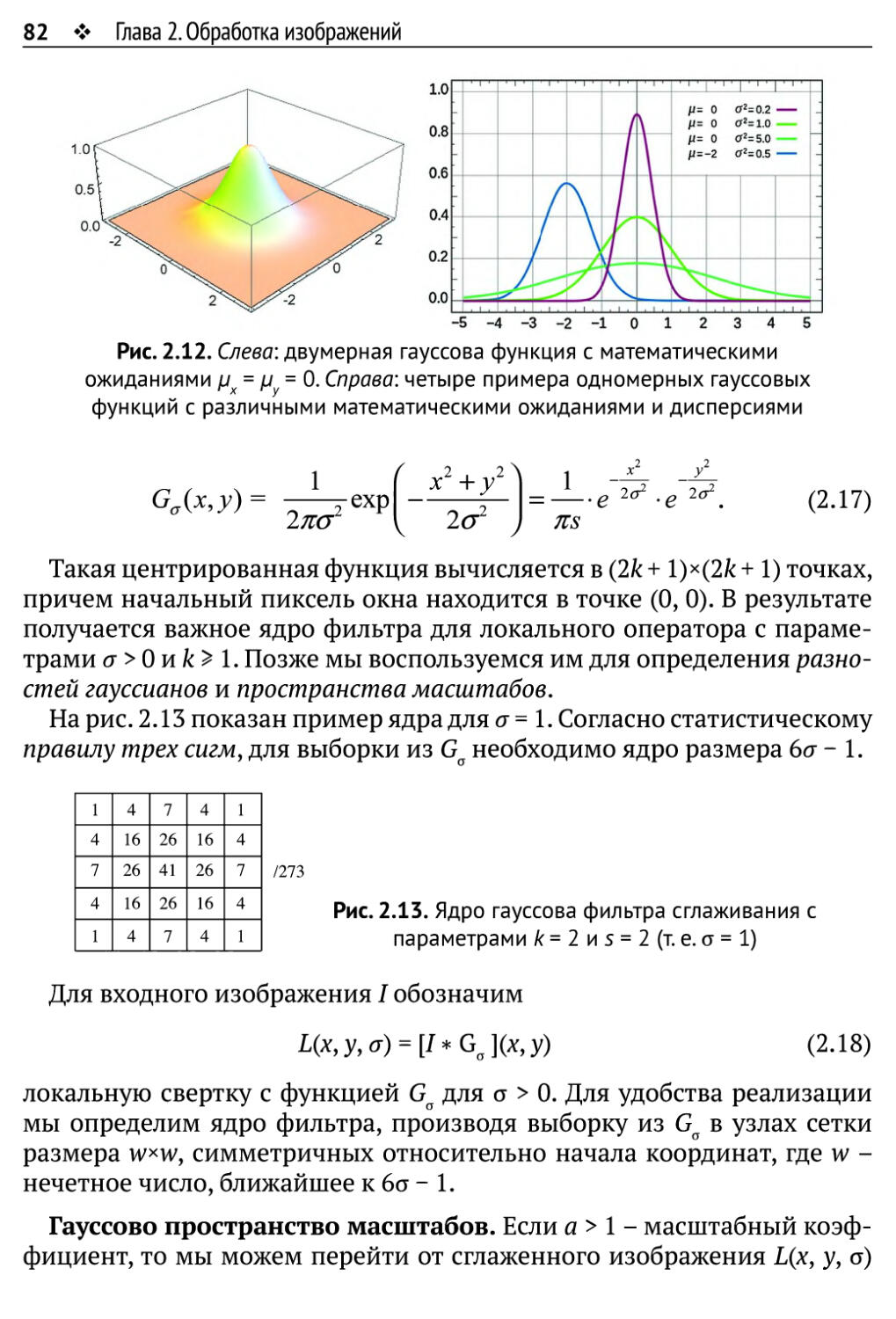
ISBN: 978-5-97060-702-2
Год: 2019
Текст
омпьютерное
ЗРЕНИЕ
Теория и алгоритмы
Springer
Рейнхард Клетте
к
Рейнхард Клетте
Компьютерное зрение
Теория и алгоритмы
Reinhard Klette
Concise Computer Vision
An Introduction into Theory and Algorithms
Springer
Рейнхард Клетте
Компьютерное зрение
Теория и алгоритмы
УДК 004.8
ББК 32.81
К48
К48 Рейнхард Клетте
Компьютерное зрение. Теория и алгоритмы / пер. с англ. А. А. Слин-
кин. - М.: ДМК Пресс, 2019. - 506 с: ил.
ISBN 978-5-97060-702-2
В этой книге рассмотрены основные аспекты компьютерного зрения:
обработка и анализ изображений, анализ плотного движения, сегментация
изображений, работа с камерами, трехмерная реконструкция, сопоставление
стереоизображений, обнаружение объектов и др. Материал дополняется
историческими справками, рекомендациями по дальнейшему чтению и
сведениями о рассматриваемых математических понятиях. В конце каждой
главы имеются проверенные на практике упражнения и вопросы на
понимание материала.
Издание предназначено широкому кругу специалистов по анализу
данных и изображений, а также может использоваться в качестве учебника для
студентов старших курсов и для самообразования.
УДК 004.8
ББК 32.81
First published in English under the title Concise Computer Vision; Copyright
© Springer-Verlag London, 2014. This edition has been translated and published under
licence from Springer-Verlag London Ltd., part of Springer Nature. Springer-Verlag
London Ltd., part of Springer Nature takes no responsibility and shall not be made liable
for the accuracy of the translation. © 2019 by DMK Press. All rights reserved.
Все права защищены. Любая часть этой книги не может быть воспроизведена
в какой бы то ни было форме и какими бы то ни было средствами без письменного
разрешения владельцев авторских прав.
Материал, изложенный в данной книге, многократно проверен. Но, поскольку
вероятность технических ошибок все равно существует, издательство не может
гарантировать абсолютную точность и правильность приводимых сведений. В связи
с этим издательство не несет ответственности за возможные ошибки, связанные с
использованием книги.
ISBN 978-1-4471-6319-0 (англ.) © Springer-Verlag London, 2014
ISBN 978-5-97060-702-2 (рус.) © Оформление, перевод на русский язык, издание,
ДМК Пресс, 2019
Всем, кто любит мечтать
С помощью компьютерного зрения можно посчитать деревья,
оценить расстояние до островов, но нельзя понять, что грезится людям,
заглянувшим в эту бухточку.
Оглавление
Предисловие 11
Предмет книги 11
Характер изложения 11
Целевая аудитория 12
Использование материала на практике 12
Замечания для преподавателя и рекомендуемый порядок использования
книги 13
Дополнительные ресурсы 13
Благодарности (в алфавитном порядке по фамилии) 13
Обозначения 16
Глава 1. Данные изображения 18
1.1. Изображения в пространственной области 18
1.1.1. Пиксели и окна 19
1.1.2. Значения и основные статистики изображения 21
1.1.3. Пространственные и временные меры данных 26
1.1.4. Ступенчато-граничная модель 29
1.2. Изображения в частотной области 34
1.2.1. Дискретное преобразование Фурье 34
1.2.2. Обратное дискретное преобразование Фурье 35
1.2.3. Комплексная плоскость 37
1.2.4. Данные изображения в частотной области 39
1.2.5. Фазово-конгруэнтная модель признаков изображения 44
1.3. Цвет и цветные изображения 47
1.3.1. Определения цвета 49
1.3.2. Цветовое восприятие, дефекты зрения и уровни серого 51
1.3.3. Представления цвета 56
1.4. Упражнения 61
1.4.1. Упражнения по программированию 61
1.4.2. Упражнения, не требующие программирования 64
Глава 2. Обработка изображений 65
2.1.Точечные, локальные и глобальные операторы 65
2.1.1. Градационные функции 65
2.1.2. Локальные операторы 68
2.1.3. Фильтрация Фурье 71
2.2.Три процедурных компонента 75
2.2.1. Интегральные изображения 75
2.2.2. Регулярные пирамиды изображений 76
2.2.3. Порядок обхода 78
Оглавление ♦ 7
2.3. Классы локальных операторов 80
2.3.1. Сглаживание 80
2.3.2. Повышение резкости 85
2.3.3. Простые детекторы границ 86
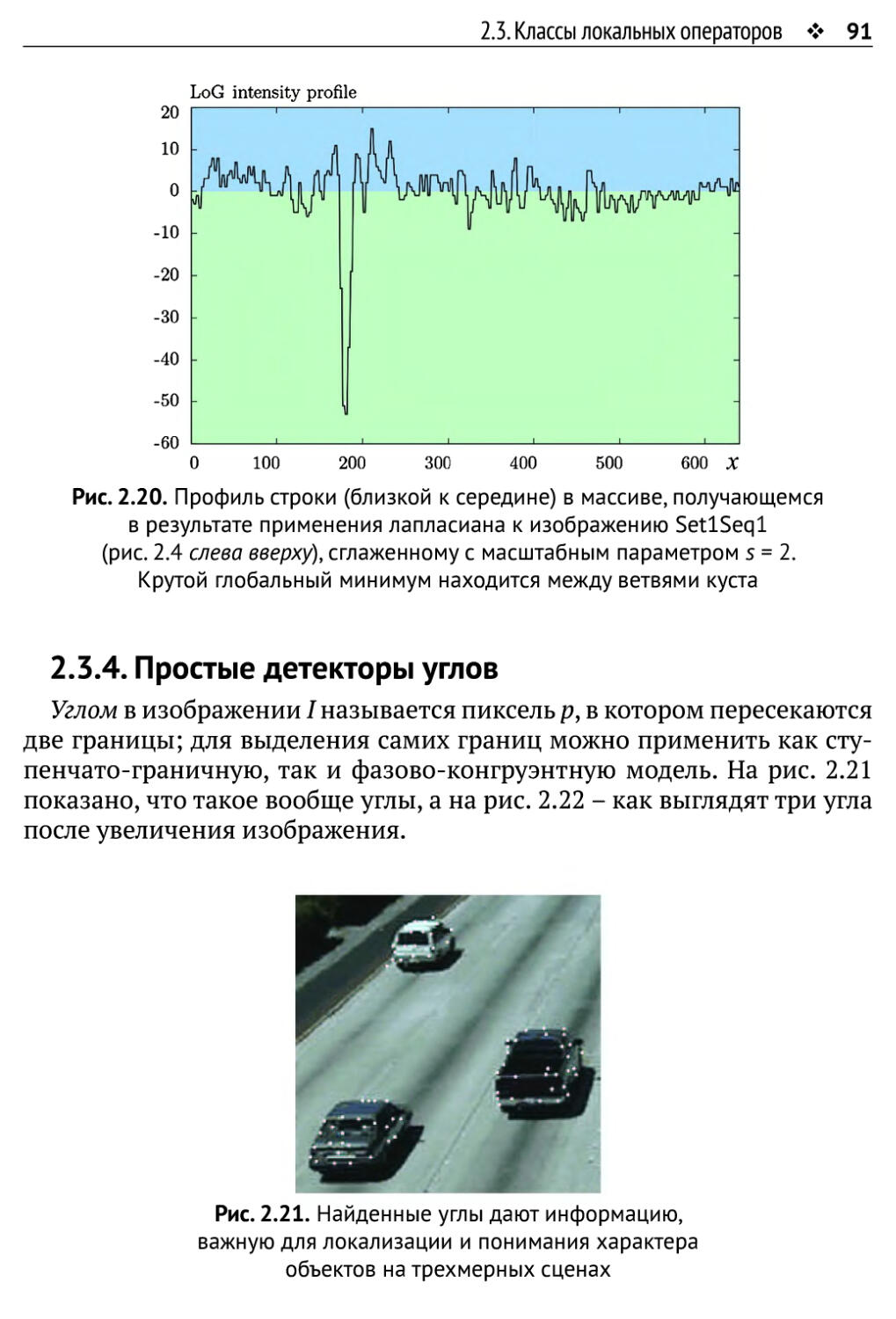
2.3.4. Простые детекторы углов 91
2.3.5.Удаление артефактов освещения 95
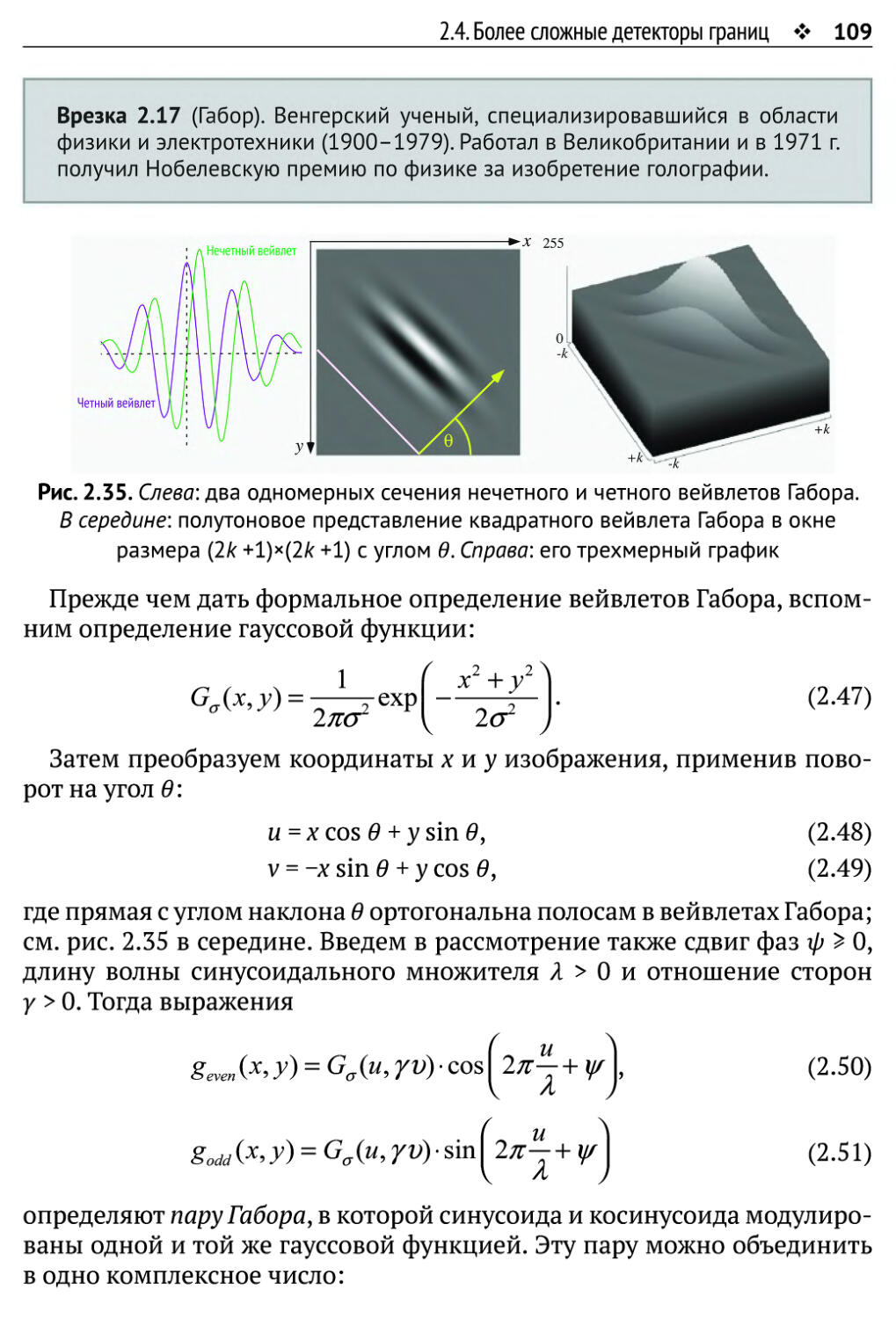
2.4. Более сложные детекторы границ 98
2.4.1. LoG и DoG и их пространства масштабов 98
2.4.2. Встроенная уверенность 103
2.4.3. Алгоритм Ковеси 107
2.5. Упражнения 113
2.5.1. Упражнения по программированию 113
2.5.2. Упражнения, не требующие программирования 115
Глава 3. Анализ изображений 117
3.1. Основы топологии изображений 117
3.1.1.4- и 8-смежность в бинарных изображениях 118
3.1.2. Топологически непротиворечивая смежность пикселей 123
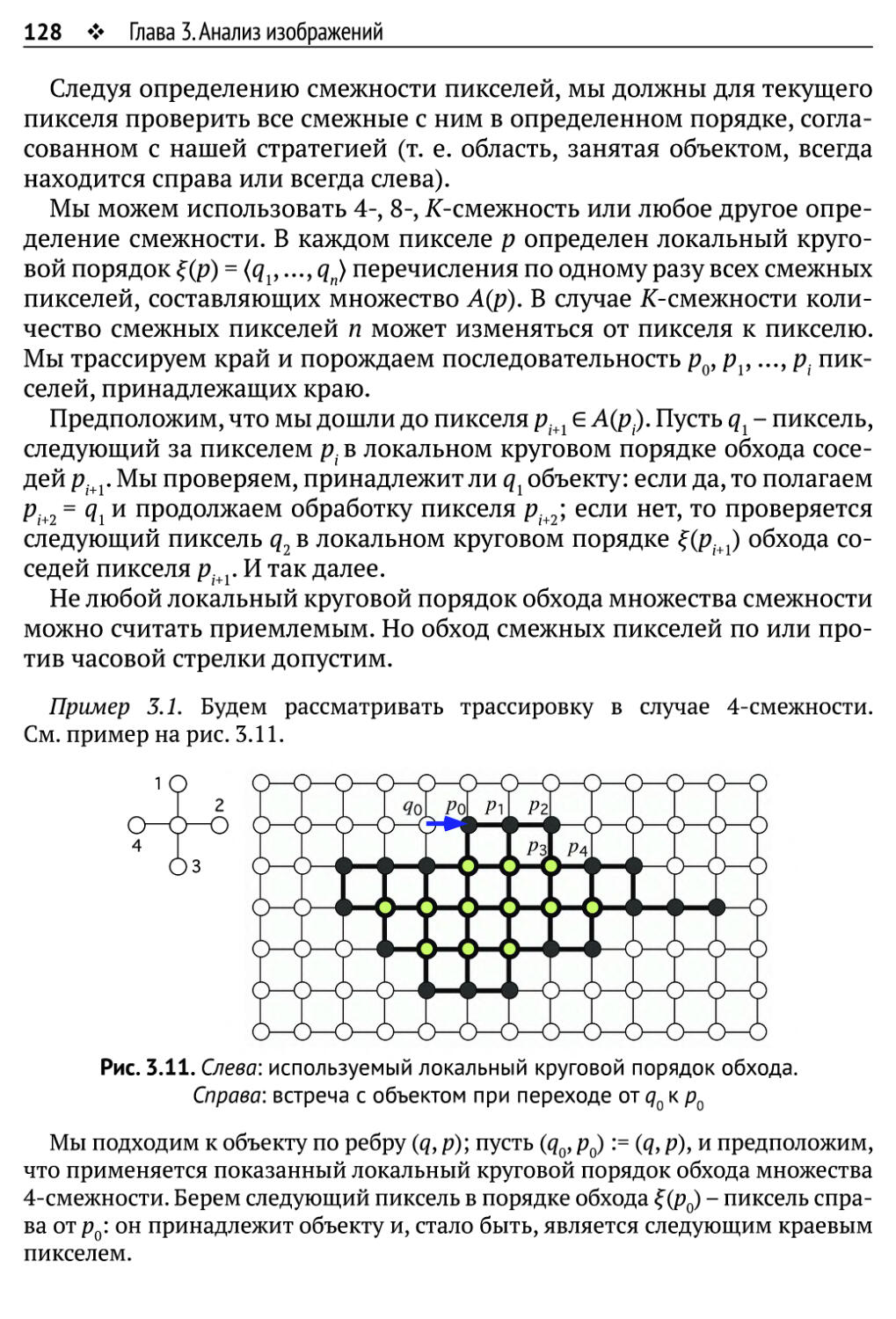
3.1.3. Трассировка краев 126
3.2. Анализ двумерных геометрических фигур 130
3.2.1. Площадь 130
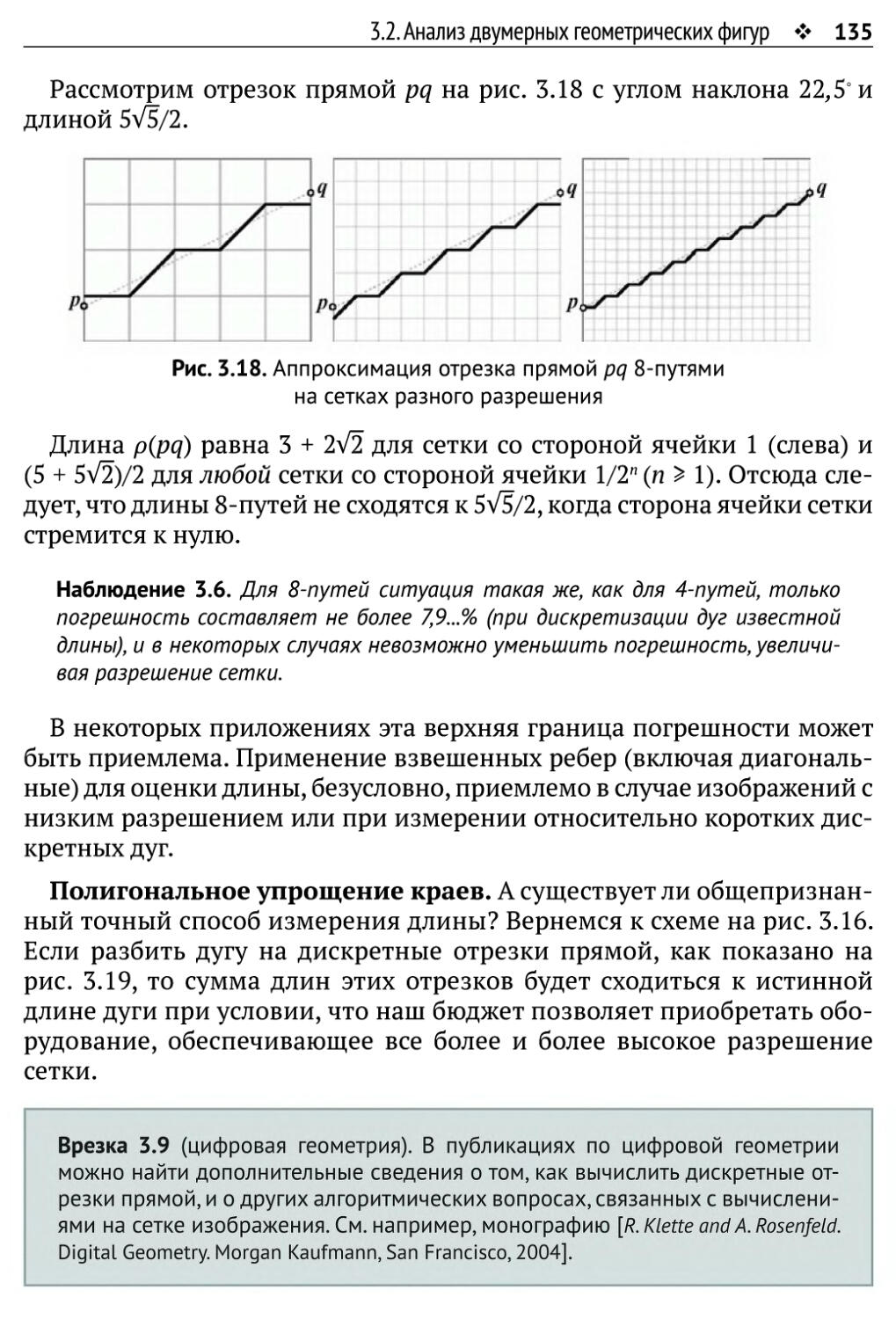
3.2.2. Длина 133
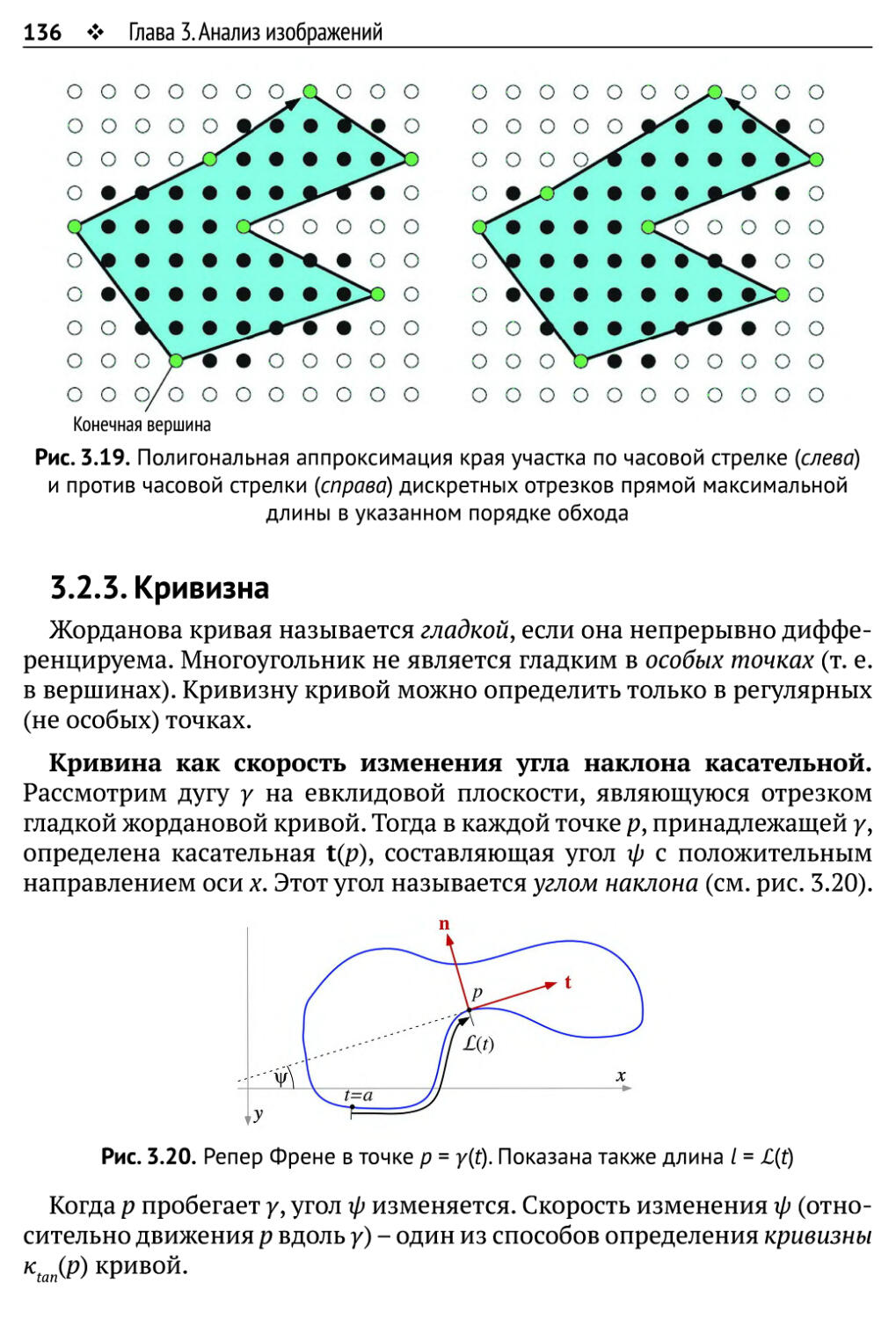
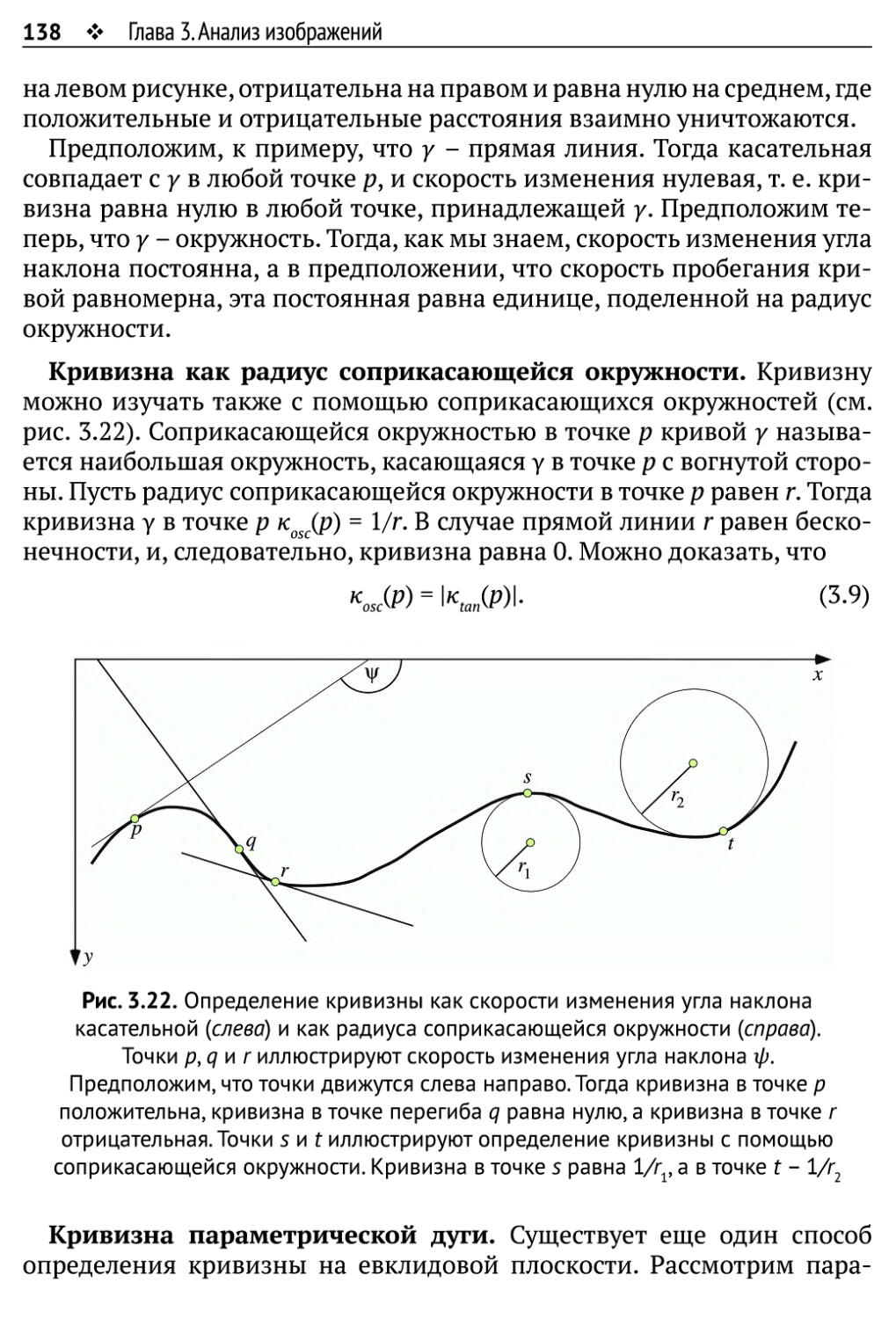
3.2.3. Кривизна 136
3.2.4. Дистанционное преобразование 140
3.3. Анализ значений изображения 147
3.3.1. Матрицы совместной встречаемости и метрики 148
3.3.2. Анализ участков с привлечением моментов 151
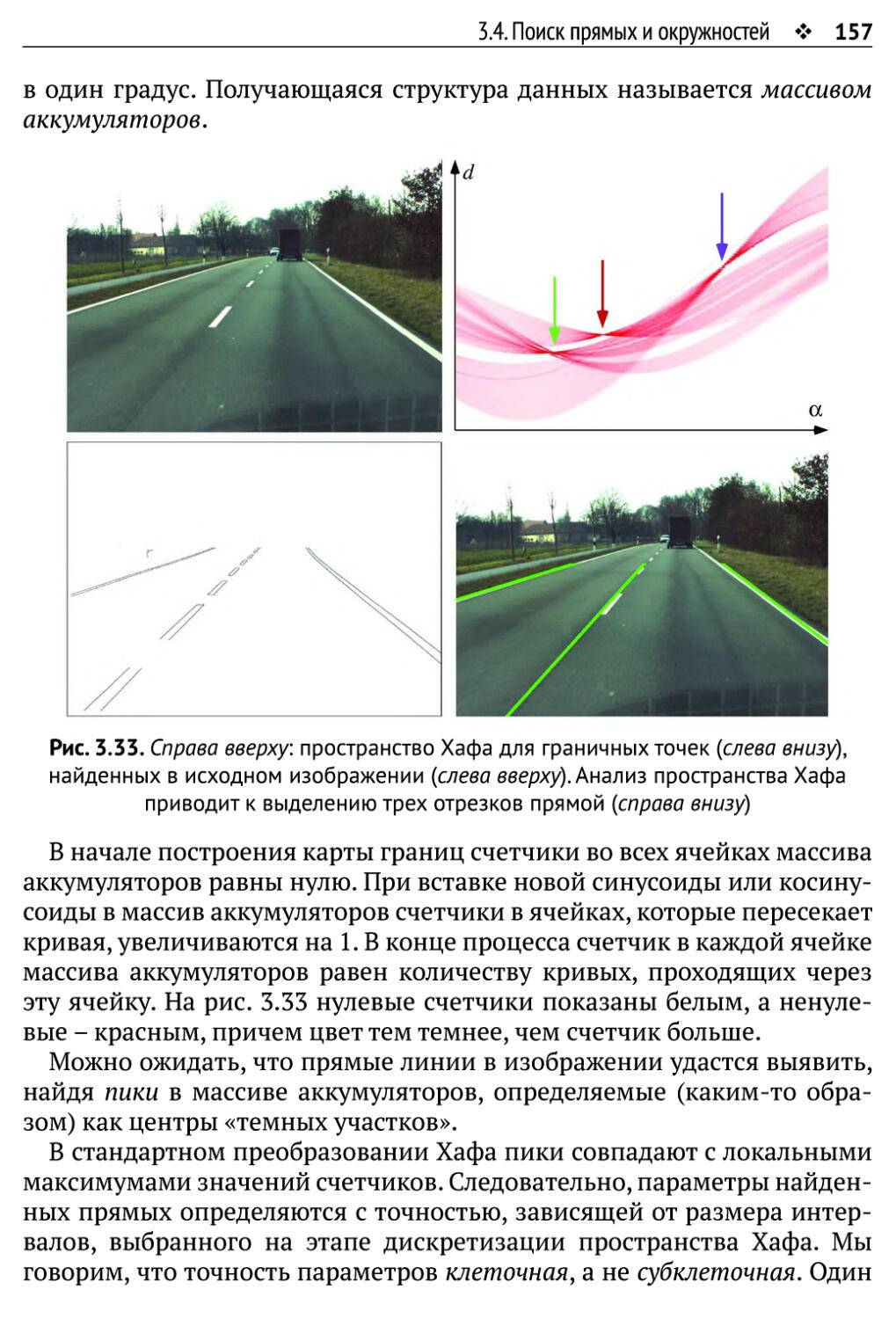
3.4. Поиск прямых и окружностей 153
3.4.1. Прямые 153
3.4.2. Окружности 160
3.5. Упражнения 162
3.5.1. Упражнения по программированию 162
3.5.2. Упражнения, не требующие программирования 167
Глава 4. Анализ плотного движения 169
4.1. ЗР-движение и двумерный оптический поток 169
4.1.1. Локальное смещение и оптический поток 169
4.1.2. Проблема апертуры и градиентный поток 173
4.2. Алгоритм Хорна-Шанка 175
4.2.1. Подготовительная часть 175
4.2.2. Алгоритм 183
4.3. Алгоритм Лукаса-Канаде 187
4.3.1. Линейное решение методом наименьших квадратов 188
4.3.2. Оригинальный алгоритм и алгоритм с весами 191
8 ♦ Оглавление
4.4. Алгоритм BBPW 193
4.4.1. Исходные предположения и функция энергии 193
4.4.2. Краткое описание алгоритма 195
4.5. Оценка качества алгоритмов вычисления оптического потока 197
4.5.1. Стратеги и тестирования 197
4.5.2. Меры ошибки для сравнения с контрольными данными 200
4.6. Упражнения 202
4.6.1. Упражнения по программированию 202
4.6.2. Упражнения, не требующие программирования 204
Глава 5. Сегментация изображений 206
5.1. Простые примеры сегментации изображений 207
5.1.1. Бинаризация изображения 209
5.1.2. Сегментация путем выращивания семян 212
5.2. Сегментация методом сдвига среднего 218
5.2.1. Примеры и подготовка 218
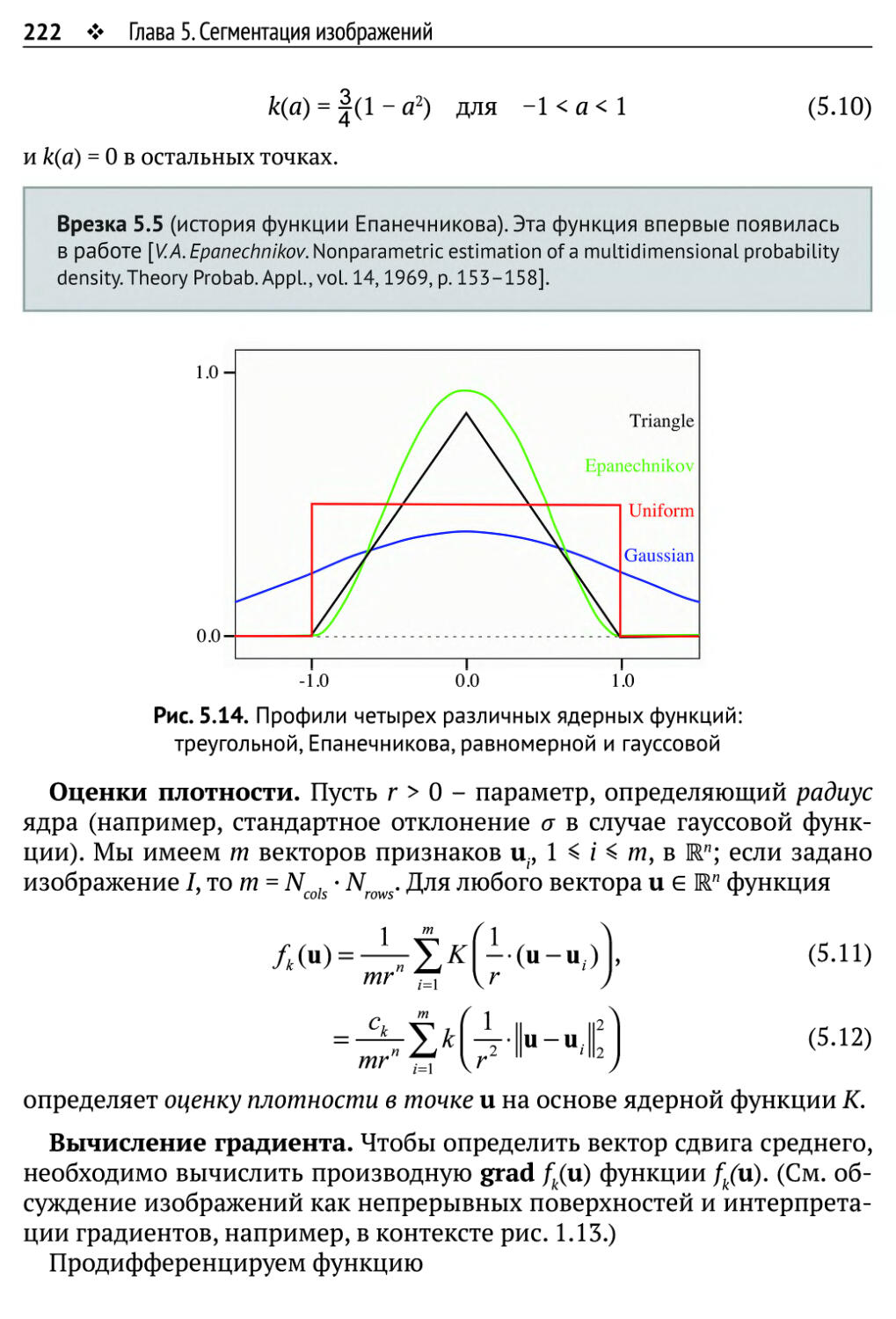
5.2.2. Модель сдвига среднего 221
5.2.3. Алгоритмы и оптимизация по времени 224
5.3. Сегментация изображений как задача оптимизации 230
5.3.1. Метки, пометка и минимизация энергии 231
5.3.2. Примеры членов данных и гладкости 234
5.3.3. Передача сообщений 237
5.3.4. Алгоритм распространения доверия 239
5.3.5. Распространение доверия в задаче о сегментации изображений 245
5.4. Сегментация видео и прослеживание сегментов 247
5.4.1. Использование согласованности признаков изображений 248
5.4.2. Использование временной согласованности 249
5.5. Упражнения 254
5.5.1.Упражнения по программированию 254
5.5.2.Упражнения, не требующие программирования 257
Глава 6. Камеры, координаты и калибровка 262
6.1. Камеры 263
6.1.1. Свойства цифровой камеры 263
6.1.2. Центральная проекция 268
6.1.3. Система с двумя камерами 271
6.1.4. Системы панорамных камер 273
6.2. Координаты 276
6.2.1. Мировые координаты 276
6.2.2. Однородные координаты 279
6.3. Калибровка камеры 281
6.3.1. Калибровка камеры сточки зрения пользователя 282
6.3.2. Ректификация пар стереоизображений 286
6.4. Упражнения 292
Оглавление ♦ 9
6.4.1.Упражнения по программированию 292
6.4.2. Упражнения, не требующие программирования 294
Глава 7.Трехмерная реконструкция 296
7.1. Поверхности 296
7.1.1.Топология поверхности 297
7.1.2. Локальные параметризации поверхности 301
7.1.3. Кривизна поверхности 304
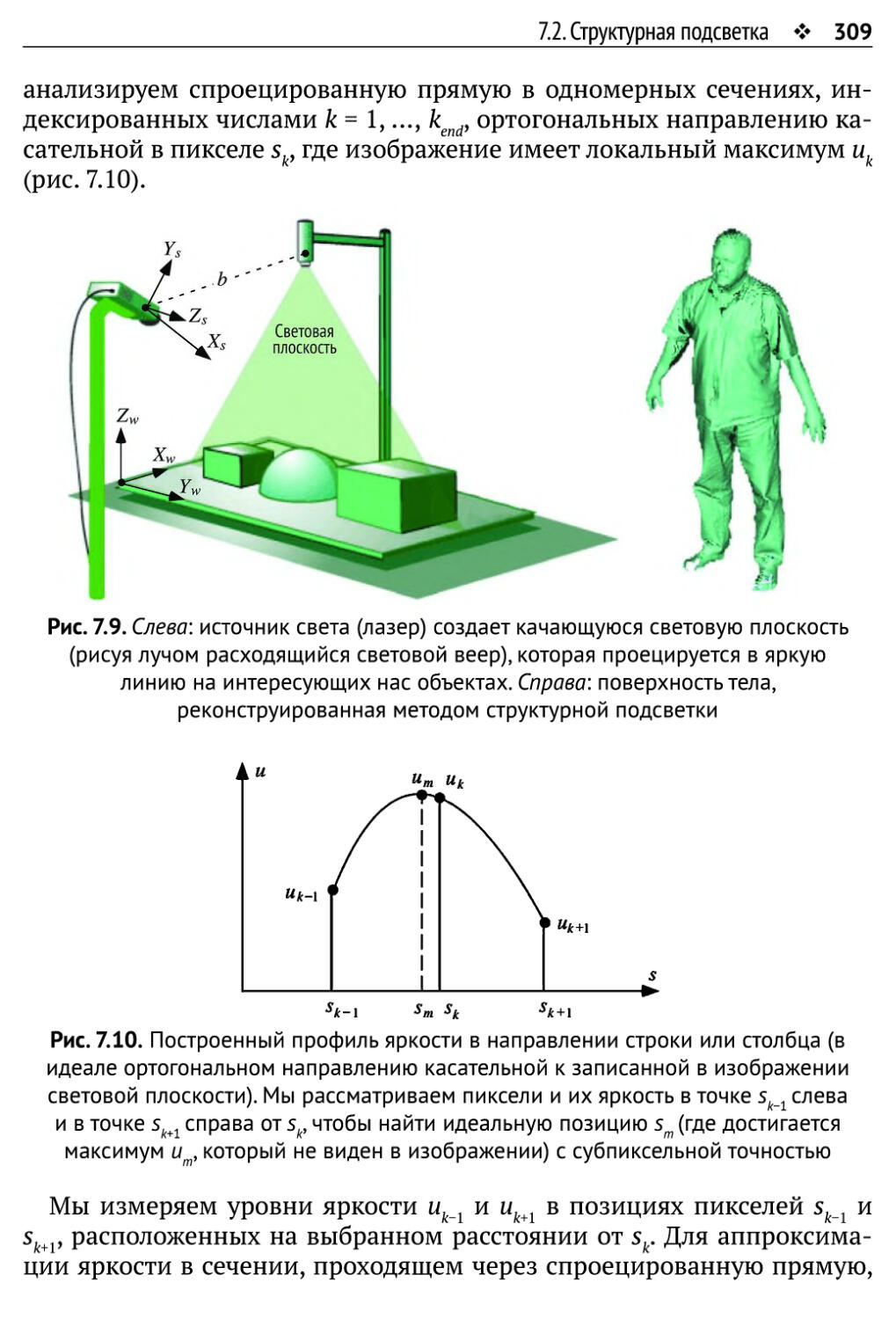
7.2. Структурная подсветка 308
7.2.1. Проекция световой плоскости 308
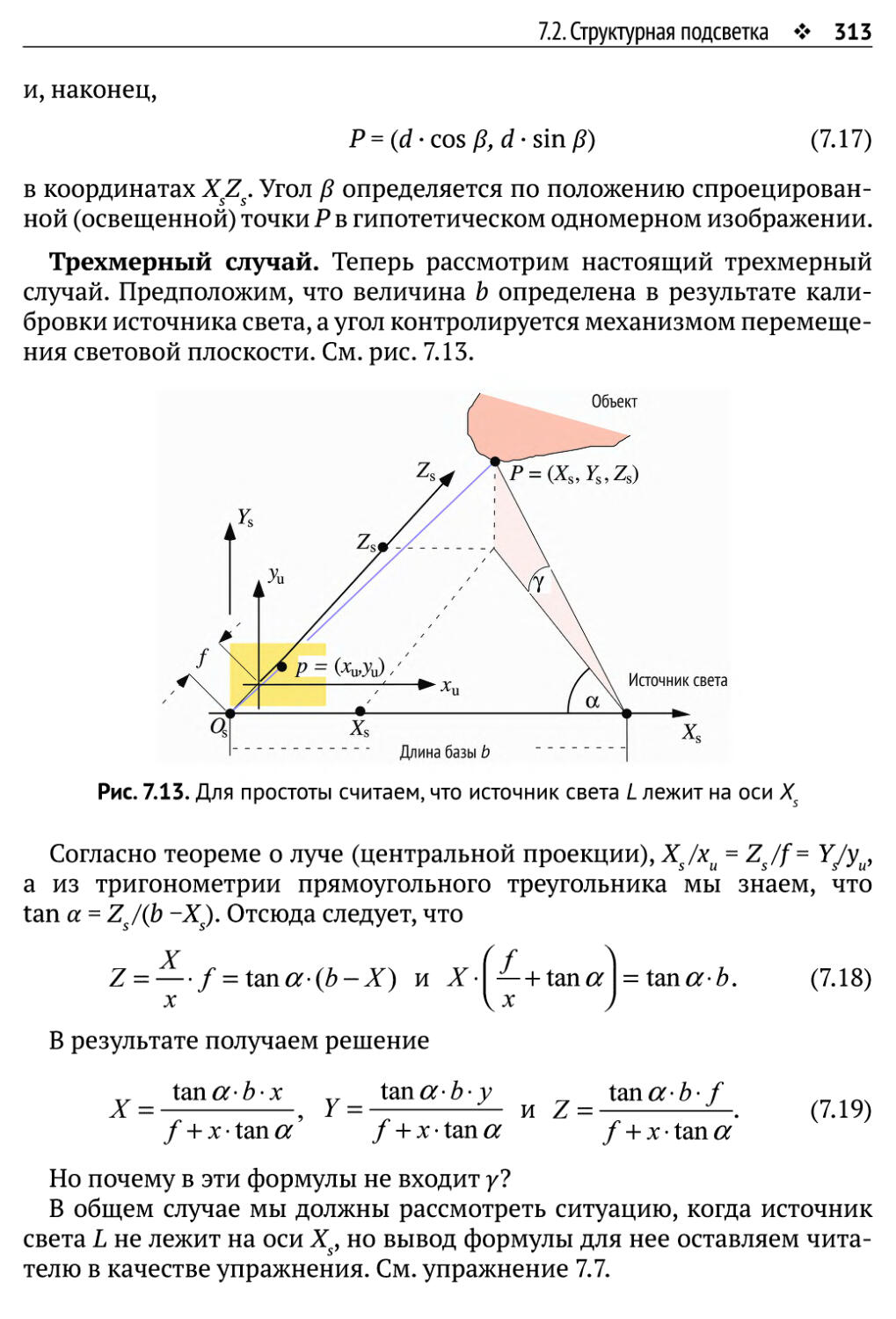
7.2.2. Анализ световой плоскости 311
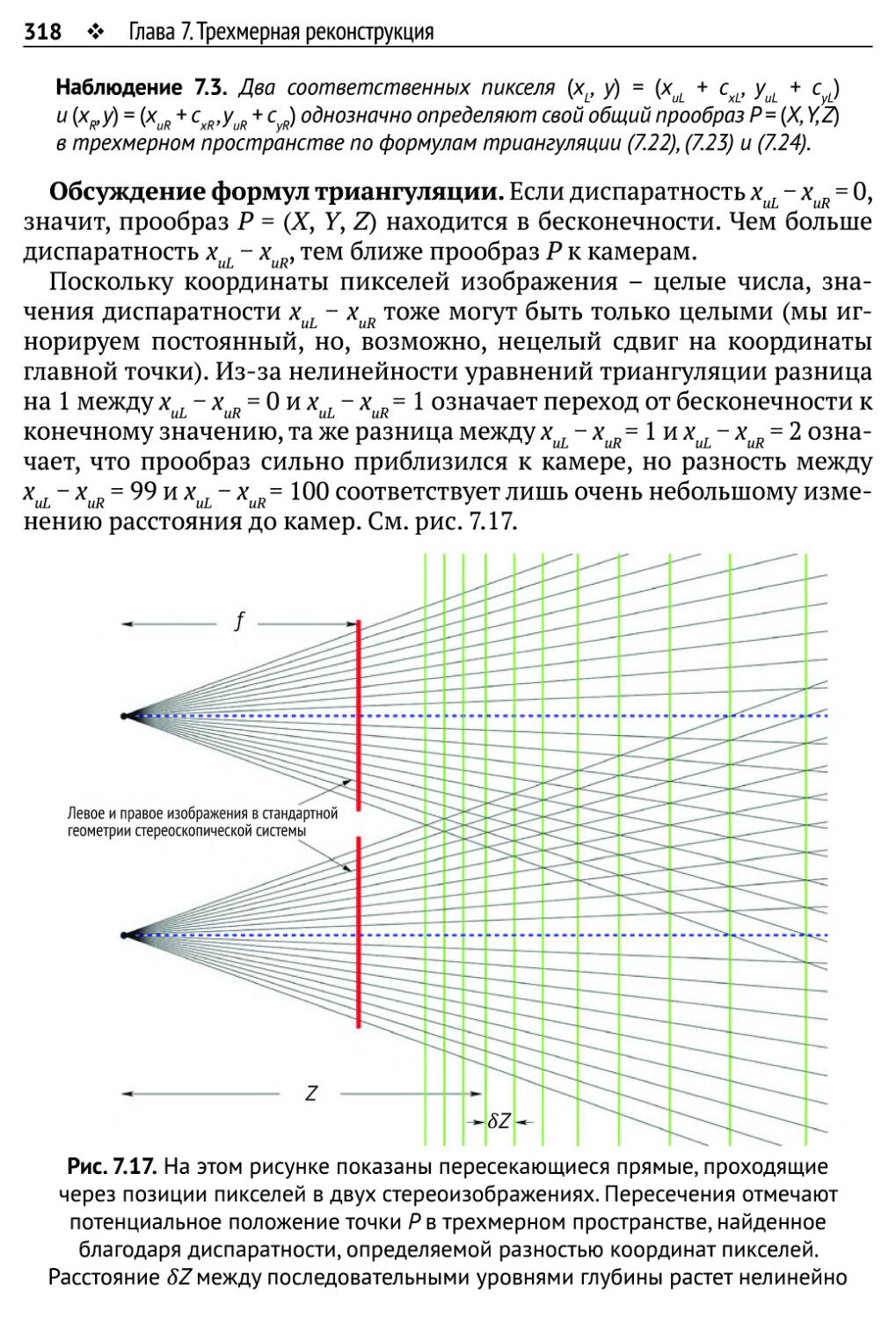
7.3. Стереоскопическое зрение 314
7.3.1. Эпиполярная геометрия 314
7.3.2. Бинокулярное зрение в канонической геометрии стереоскопической
системы 316
7.3.3. Бинокулярное зрение в конвергентной системе 319
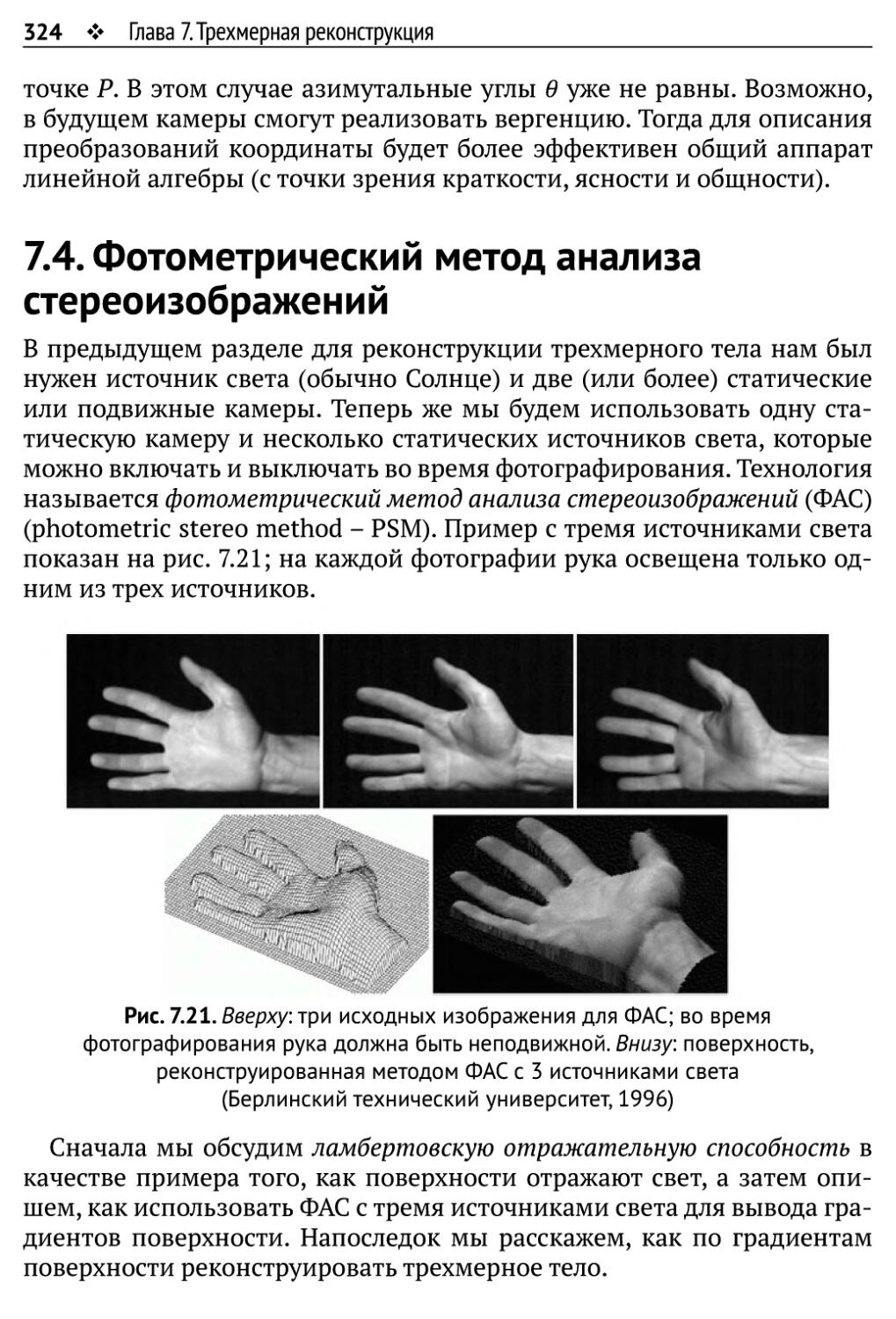
7.4. Фотометрический метод анализа стереоизображений 324
7.4.1. Ламбертовская отражательная способность 325
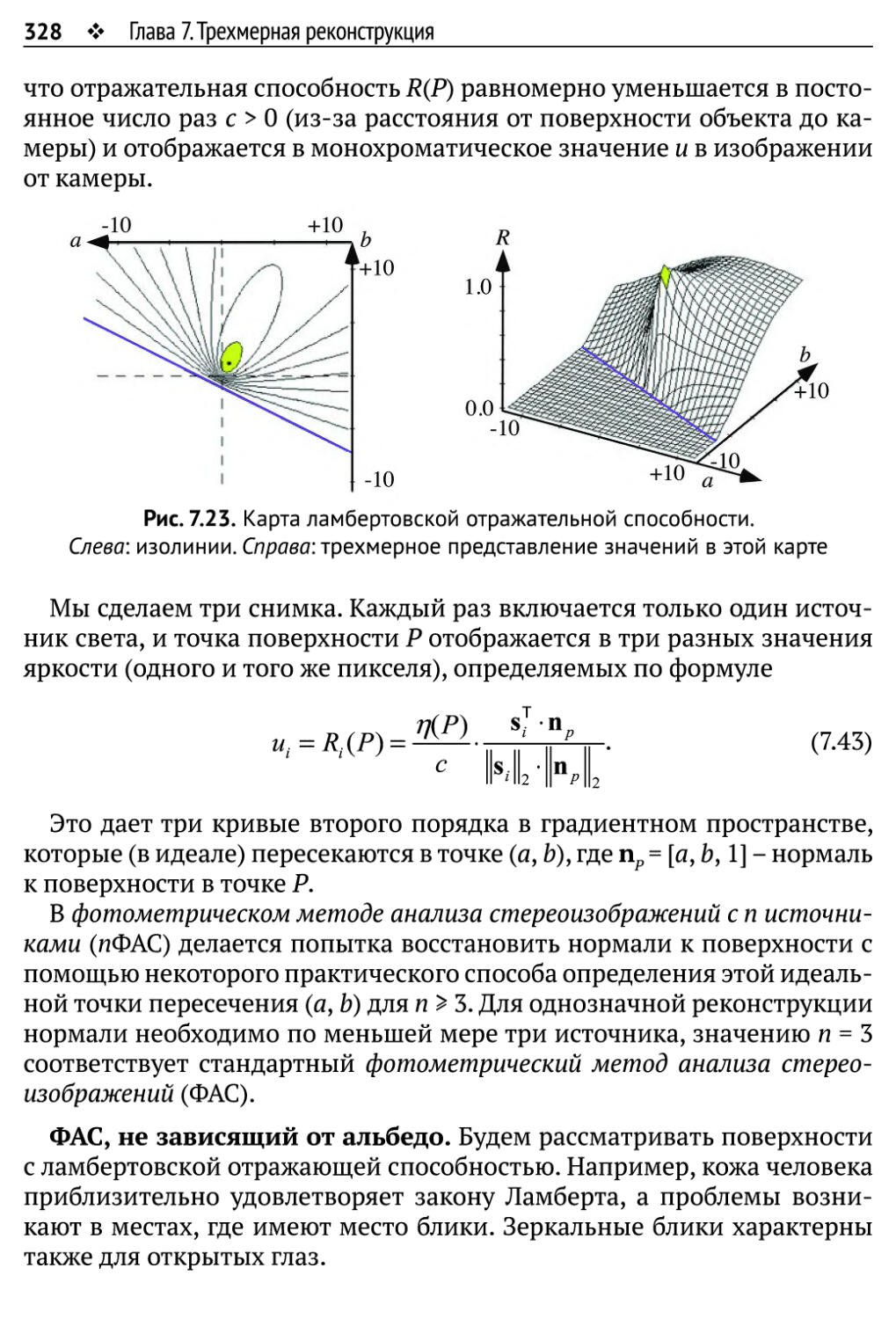
7.4.2. Восстановление градиентов поверхности 327
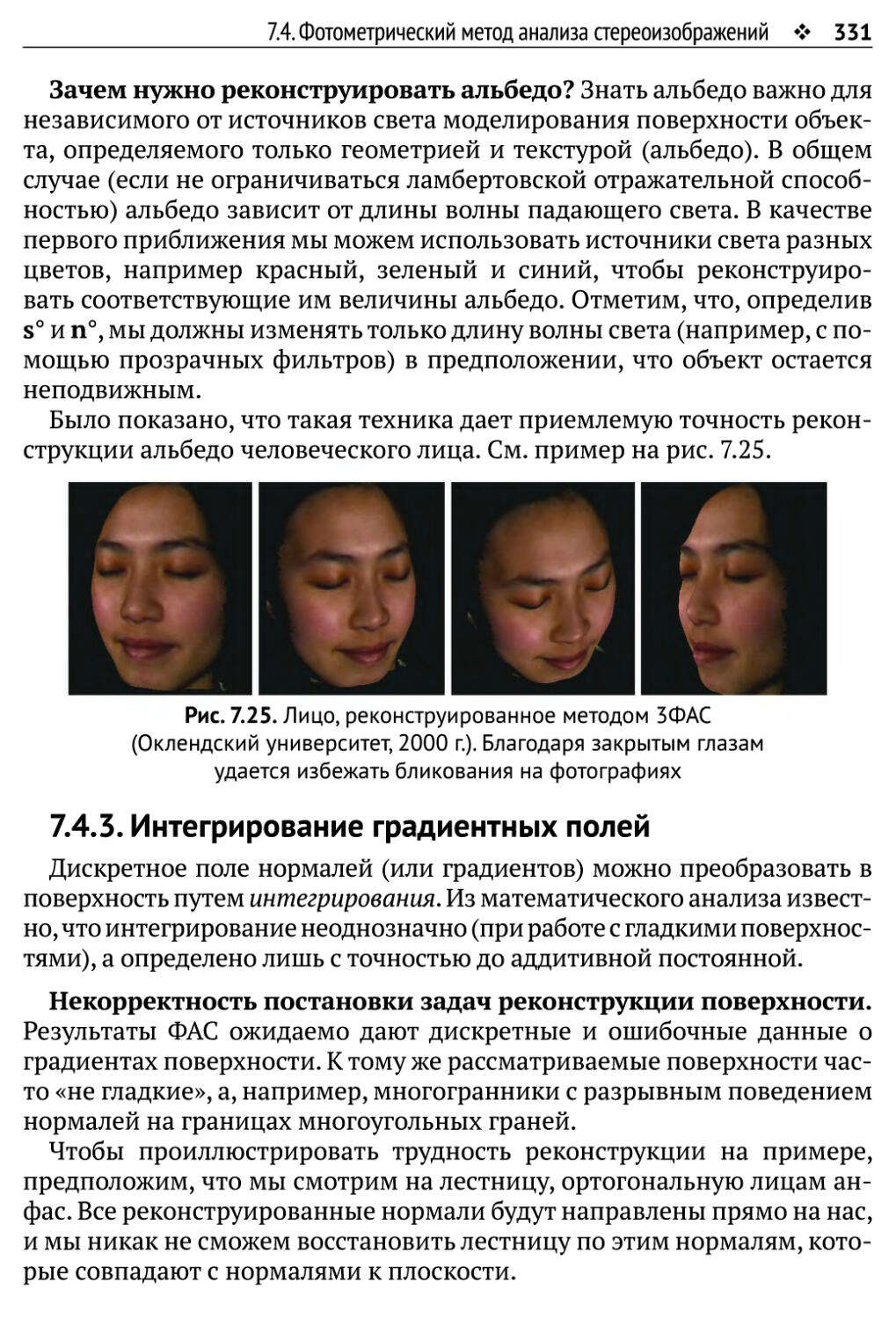
7.4.3. Интегрирование градиентных полей 331
7.5. Упражнения 340
7.5.1.Упражнения по программированию 340
7.5.2. Упражнения, не требующие программирования 343
Глава 8. Сопоставление стереоизображений 345
8.1. Сопоставление, стоимость данных и уверенность 346
8.1.1. Общая модель сопоставления 347
8.1.2. Функции стоимости данных 351
8.1.3. От глобального сопоставления к локальному 354
8.1.4.Тестирование функций стоимости данных 358
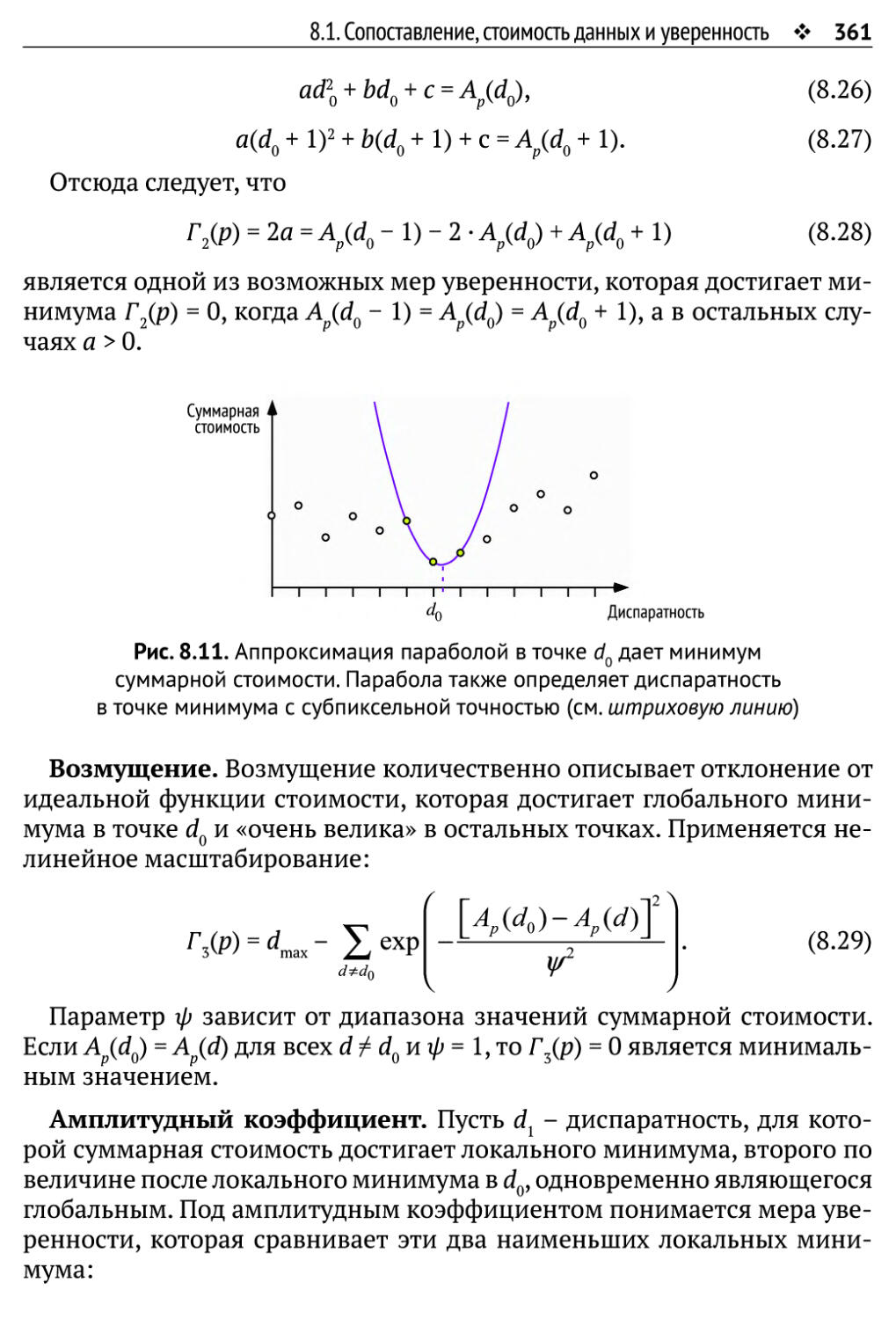
8.1.5. Меры уверенности 360
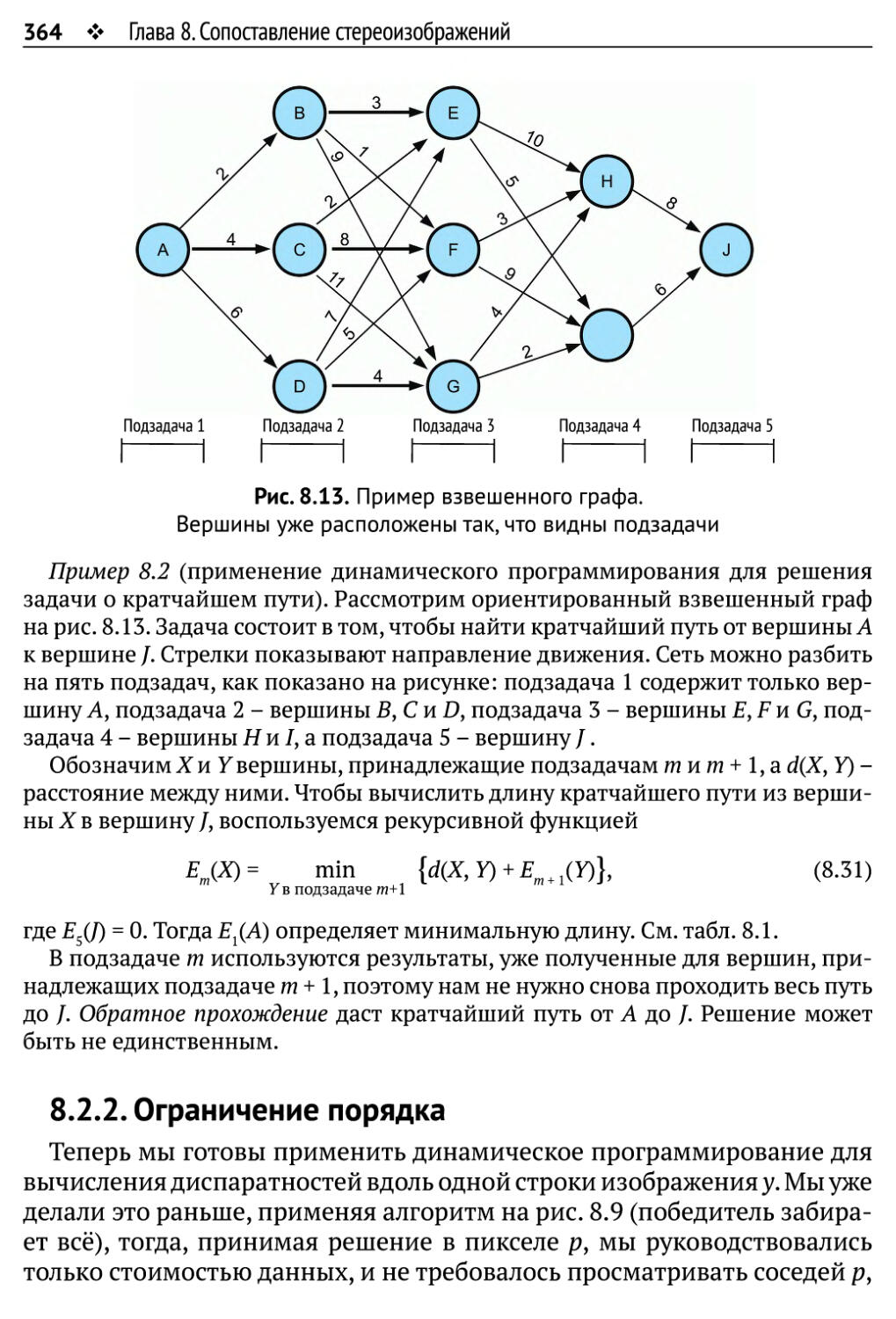
8.2. Сопоставление методом динамического программирования 362
8.2.1. Динамическое программирование 363
8.2.2. Ограничение порядка 364
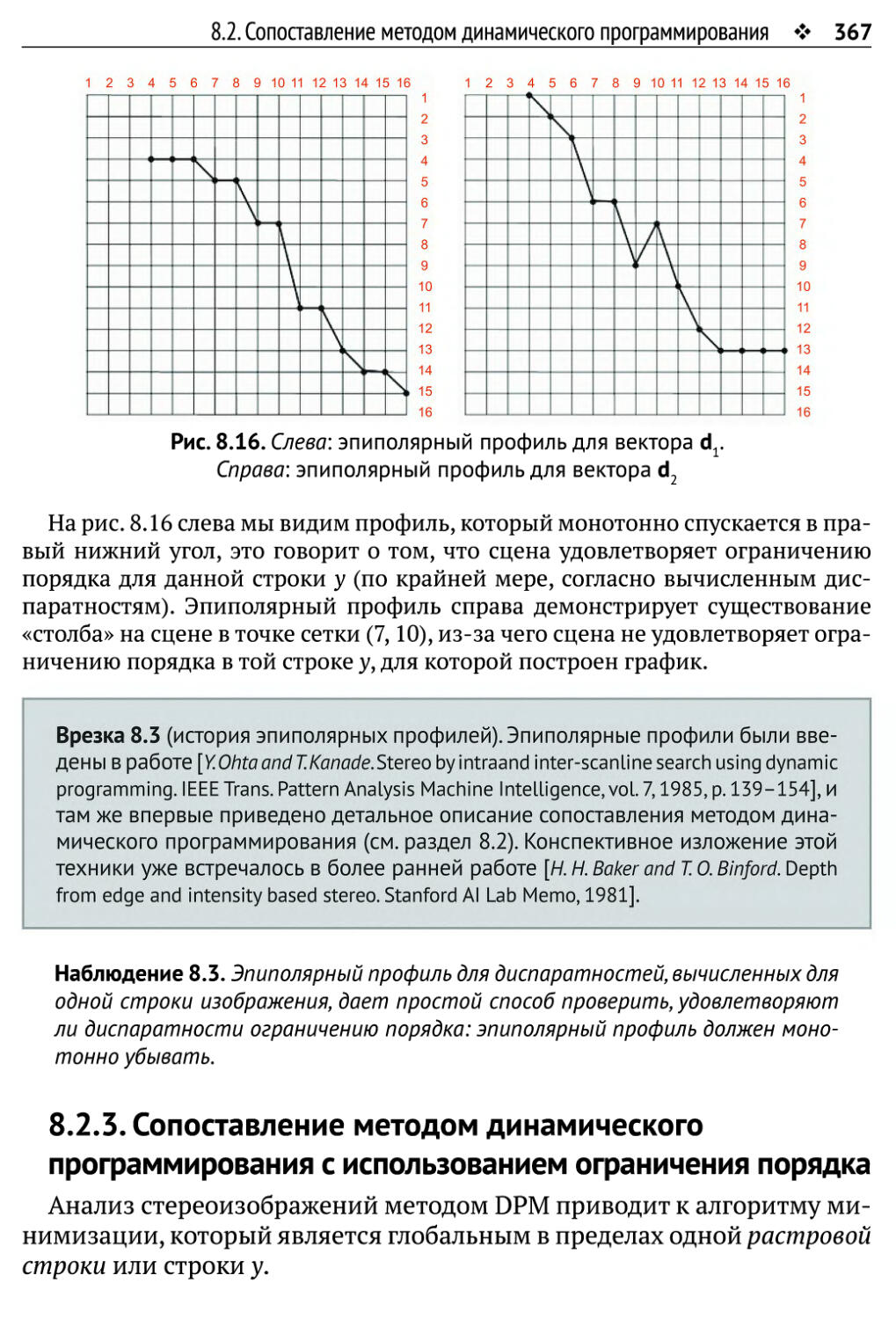
8.2.3. Сопоставление методом динамического программирования
с использованием ограничения порядка 367
8.2.4. Алгоритм DPM с ограничением гладкости 373
8.3. Сопоставление методом распространения доверия 379
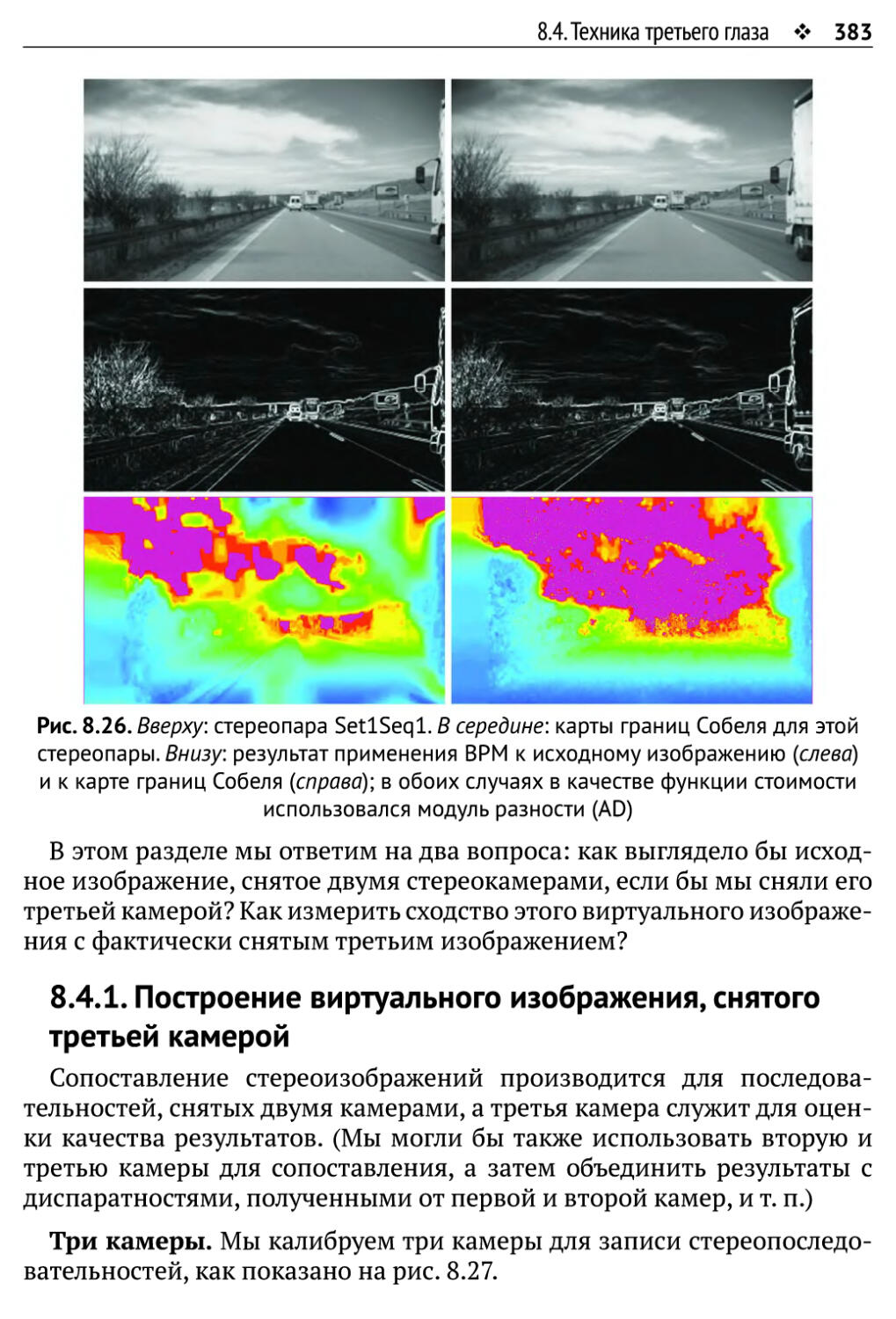
8.4.Техника третьего глаза 382
8.4.1. Построение виртуального изображения, снятого третьей камерой 383
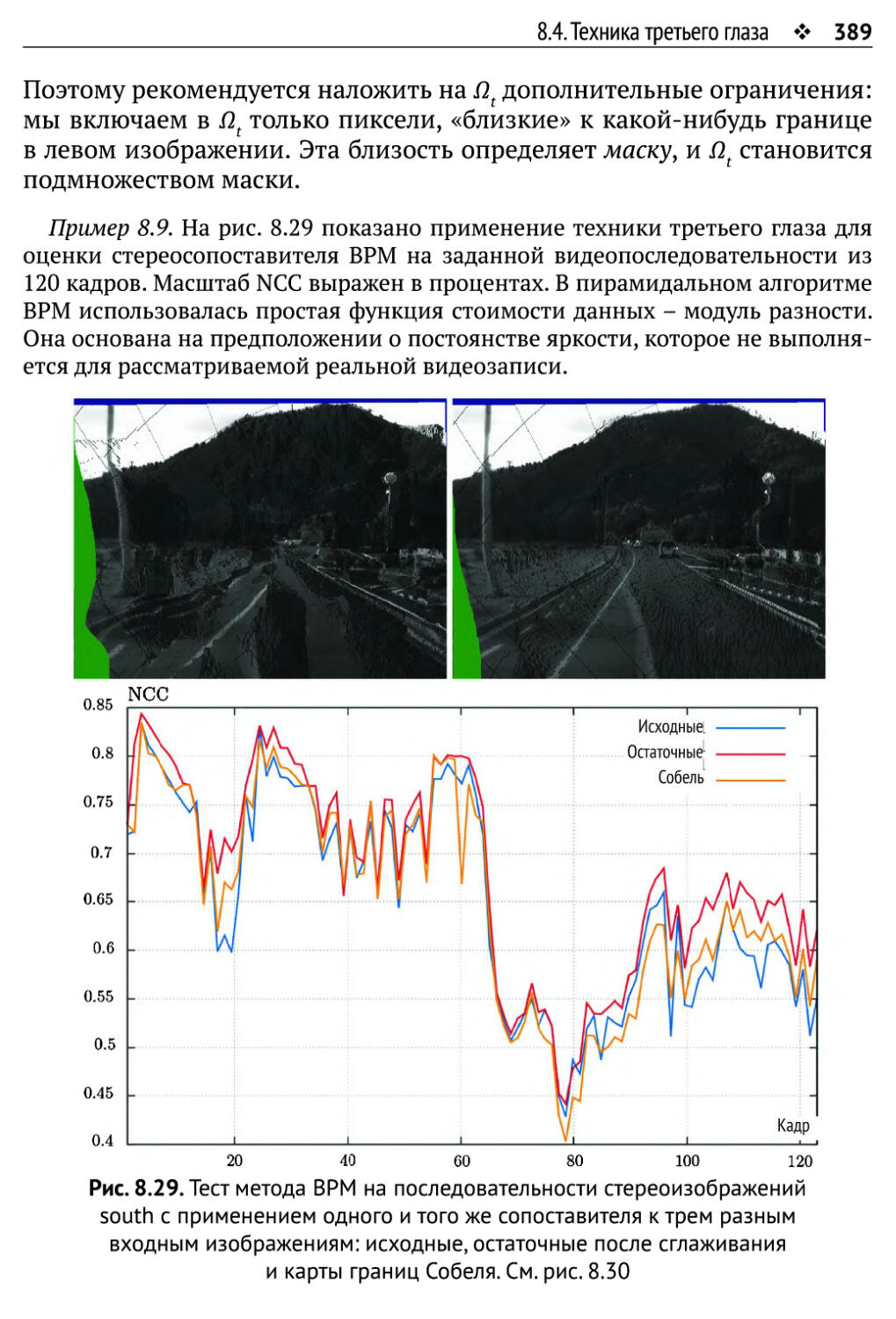
8.4.2. Сходство между виртуальным и третьим изображениями 388
8.5. Упражнения 391
8.5.1. Упражнения по программированию 391
8.5.2.Упражнения, не требующие программирования 393
10 ♦ Оглавление
Глава 9. Обнаружение и прослеживание признаков 396
9.1. Инвариантность, признаки и множества признаков 396
9.1.1. Инвариантность 396
9.1.2. Особые точки и векторы трехмерного потока 398
9.1.3. Множества особых точек в соседних кадрах 402
9.2. Примеры признаков 407
9.2.1. SIFT-признаки 407
9.2.2. SURF-признаки 410
9.2.3. ORB-признаки 411
9.2.4. Оценка признаков 414
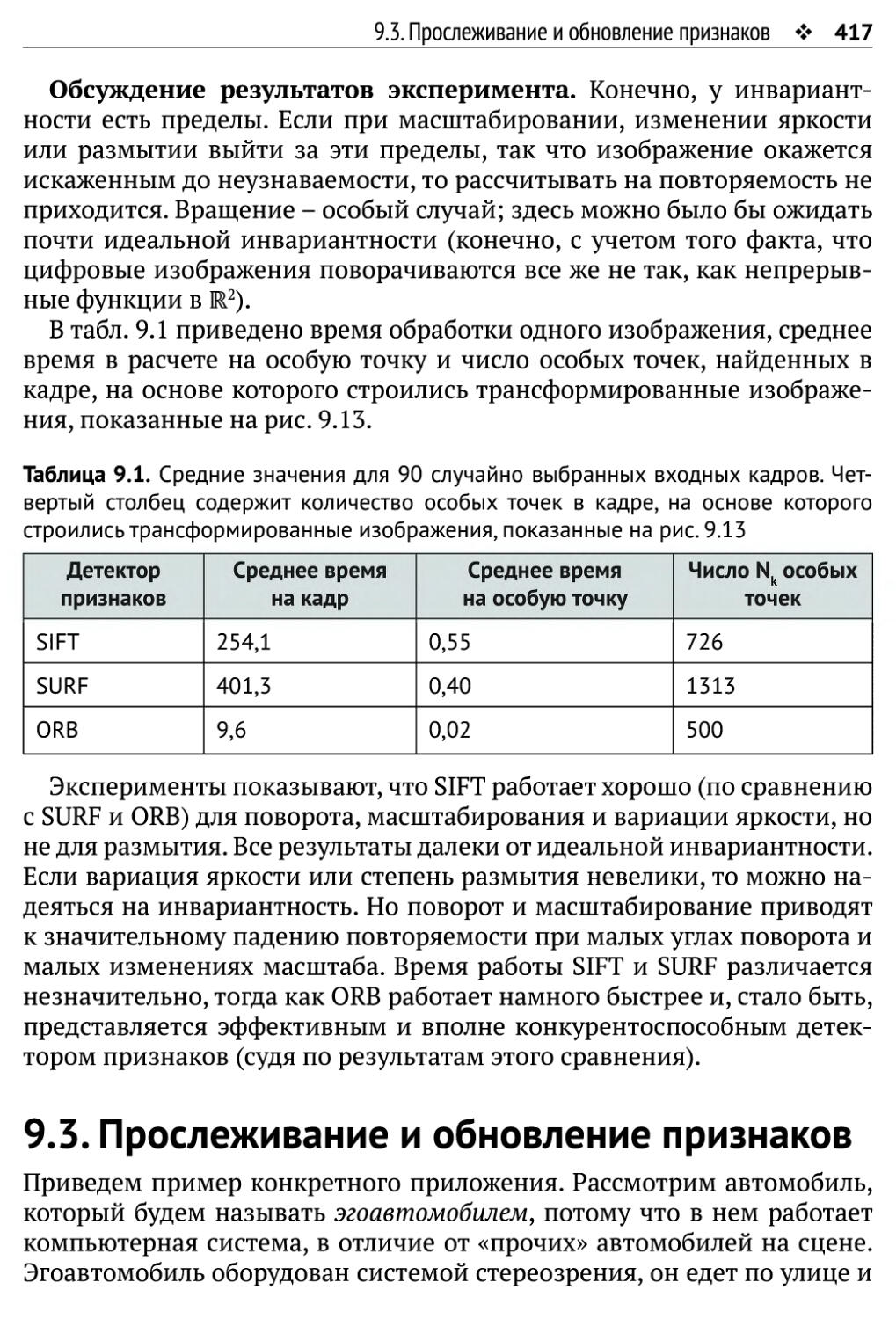
9.3. Прослеживание и обновление признаков 417
9.3.1. Прослеживание - задача разреженного соответствия 419
9.3.2. Проел ежи ватель Лукаса -Канаде 420
9.3.3. Фильтр частиц 426
9.3.4. Фильтр Калмана 435
9.4. Упражнения 442
9.4.1. Упражнения по программированию 442
9.4.2. Упражнения, не требующие программирования 447
Глава 10. Обнаружение объектов 449
10.1. Локализация, классификация и оценка 449
10.1.1. Дескрипторы, классификаторы и обучение 450
10.1.2. Качество детекторов объектов 456
10.1.3. Гистограмма ориентированных градиентов 458
10.1.4. Вейвлеты и признаки Хаара 460
10.1.5. Метод Виолы-Джонса 464
10.2.AdaBoost 467
10.2.1. Алгоритм 468
10.2.2. Параметры 470
10.2.3. Почему именно такие параметры? 474
10.3. Случайные решающие леса 476
10.3.1. Энтропия и информационный выигрыш 476
10.3.2. Применение леса 479
10.3.3. Обучение леса 481
10.3.4. Леса Хафа 486
10.4. Обнаружение пешеходов 488
10.5. Упражнения 491
10.5.1. Упражнения по программированию 491
10.5.2.Упражнения, не требующие программирования 493
Предметный указатель 495
Предисловие
Это учебник для студентов третьего и четвертого года обучения,
посещающих курс компьютерного зрения - одной из научно-технических
дисциплин.
Предмет книги
Задача компьютерного зрения - применение фото- и видеокамер для
анализа или понимания реальных сцен. Эта дисциплина изучает
методологические и алгоритмические проблемы, а также вопросы,
относящиеся к реализации предложенных решений.
В компьютерном зрении нас может интересовать, на каком
расстоянии от камеры находится здание, движется ли автомобиль посередине
своей полосы, сколько человек присутствует на изображении и даже
присутствует ли на нем конкретный человек. На все эти вопросы нужно
дать ответ, имея лишь сохраненные фотографии или видео. Благодаря
недавним достижениям область применимости компьютерного зрения
значительно расширилась. Прогресс затронул как технологии
изготовления камер и методы вычислений, так и теоретические основания
компьютерного зрения.
За последние годы компьютерное зрение стало ключевой
технологией во многих областях. Если речь идет о потребительской электронике,
то достаточно упомянуть мобильные телефоны, помощь водителям или
взаимодействие пользователя с компьютерными играми. В
автоматизации промышленности компьютерное зрение повсеместно
применяется для контроля качества и технологических процессов.
Существенный вклад компьютерное зрение внесло в киноиндустрию (вспомним,
например, аватары или создание виртуальных миров на основе
отснятых изображений, дополнение исторических видеоданных или
высококачественные презентации фильмов). И это лишь малая часть областей
применения, связанных с обработкой и анализом фотографий и видео.
Характер изложения
В книге дается общее введение в основы компьютерного зрения,
которые находят применения в самых разных прикладных областях.
Математика играет важную роль в изложении, обсуждаются также
алгоритмы. Конкретные приложения в книге не рассматриваются.
12 ♦ Предисловие
На врезках представлены историческая информация, ссылки на
источники излагаемого материала и сведения о математических объектах в
том месте, где они впервые встречаются. Врезки следует рассматривать
как дополнения к основному тексту.
Книга не является справочником по текущим исследованиям в
области компьютерного зрения, и объем библиографических ссылок очень
ограничен; читатель легко найдет интересующий его материал в сети.
Компьютерное зрение - активно развивающаяся дисциплина,
количество ссылок огромно, поэтому любая попытка втиснуть полную
библиографию в ограниченное пространство книги обречена на провал.
Но мы, по крайней мере, дадим совет: на странице homepages.inf.ed.ас.
uk/rbf/CVonline/ вы найдете онлайновое введение в различные проблемы
компьютерного зрения.
Целевая аудитория
Книга задумывалась как вводный курс для студентов третьего-четвертого
курсаов, специализирующихся в научных или технических дисциплинах.
Предварительные знания в области обработки и анализа изображений
или компьютерной графики были бы полезны, но первые две главы
содержат начальные сведения о компьютерной обработке изображений.
Использование материала на практике
Материалы, представленные в книге, частично использовались в моих
лекциях по мехатронике и информатике в Оклендском университете
(Новая Зеландия), в Центре исследований и математики (CIMAT) в Гуа-
нахуато (Мексика), в университете Фрайбурга и Гёттингена (Германия),
в Кордобском техническом университете (Аргентина), в Тайваньском
национальном нормальном университете (Тайвань) и в Уханьском
университете (Китай).
В книге использовались также материалы из предыдущих
публикаций автора: [R. Klette and P. Zamperoni. Handbook of Image Processing Operators.
Wiley, Chichester, 1996], [R. Klette, K. Schluns and A. Koschan. Computer Vision.
Springer, Singapore, 1998], [R. Klette and A. Rosenfeld. Digital Geometry. Morgan
Kaufmann, San Francisco, 2004] и [F. Huang, R. Klette and К Scheibe. Panoramic
Imaging. Wiley, West Sussex, 2008].
Первые две из перечисленных выше книг использовались как
дополнение к лекциям автора по компьютерному зрению в Германии и
Новой Зеландии в 1990-х и в начале 2000-х г., а третья - в лекциях,
прочитанных в более поздний период.
Предисловие ♦ 15
Замечания для преподавателя
и рекомендуемый порядок использования
книги
Книга содержит больше материала, чем можно охватить в односемест-
ровом курсе. Преподавателю следует отбирать материал, сообразуясь с
контекстом: предварительными знаниями студентов и
направленностью последующих курсов.
Каждая глава заканчивается упражнениями, в том числе
предполагающими программирование. В книге не отдается предпочтение какой-либо
конкретной среде. Но обычно применение функций, имеющихся в таких
библиотеках, как OpenCV, упрощает решение. Упражнения по
программированию намеренно сформулированы так, чтобы у студентов было
несколько вариантов ответа. Например, в упражнении 2.5 к главе 2 можно
визуализировать результаты с помощью Java-аплетов (хотя в тексте этого
не требуется), использовать изображения большого или малого размера
(в тексте размер не указан) и ограничить движение курсора
центральной частью входного изображения, например квадратом 11 х 11 с
центром в точке р, который всегда целиком содержится в изображении (или
рассмотреть также особые случаи, когда курсор может приближаться к
границе изображения). Поэтому каждый студент может дать свое
решение упражнений, и творческий подход следует всячески приветствовать.
Дополнительные ресурсы
На сопроводительном сайте книги имеются дополнительные
материалы (данные, исходный код, примеры, презентации). См. www.cs.auckland.
ас. nz/~rklette/Books/K2014/.
Благодарности (в алфавитном порядке
по фамилии)
Я благодарен перечисленным ниже коллегам, бывшим и нынешним
студентам и друзьям (если упоминается только рисунок, то я выражаю
признательность за совместную работу или контакты, относящиеся к
теме рисунка).
• А-Кп
АН Al-Sarraf (рис. 2.32), Hernan Badino (рис. 9.25), Anko Borner
(различные комментарии по черновым вариантам книги и вклад в
14 ♦ Предисловие
раздел 5.4.2), Hugo Carlos (помощь во время работы над книгой в
CIMAT),Diego Caudillo (рис. 1.9,5.28,5.29), Gilberto Chavez (рис. 3.39
и 5.36, верхний ряд), Chia-Yen Chen (рис. 6.21 и 7.25), Kaihua Chen
(рис. 3.33), Ting-Yen Chen (рис. 5.35, вклад в раздел 2.4, в главу 5,
предоставление исходного кода), Eduardo Destefanis (вклад в
пример 9.1 и рис. 9.5), Uwe Franke (рис. 3.36, 6.3 и 9.23, правый
нижний), Stefan Gehrig (замечания по вопросу анализа
стереоизображений и рис. 9.25), Roberto Guzman (рис. 5.36, нижний ряд),
Wang Han (привлечение студентов к проверке черновика книги),
Ralf Haeusler (вклад в раздел 8.1.5), Gabriel Hartmann (рис. 9.24),
Simon Hermann (вклад в разделы 5.4.2 и 8.1.2, рис. 4.16 и 7.5),
Vaclav Hlavac (предложения по улучшению состава глав 1 и 2),
Heiko Hirschmuller (рис. 7.1), Wolfgang Huber (рис. 4.12, правый
нижний), Fay Huang (вклад в главу 6, особенно в раздел 6.1.4), Ruyi
Jiang (вклад в раздел 9.3.3), Waqar Khan (рис. 7.17), Ron Kimmel
(предложения о способе изложения локальных операторов и
оптического потока - они вынужденно запланированы в основном
для следующего издания книги), Karsten Knoeppel (вклад в
раздел 9.3.4).
• Ko-Sc
Andreas Koschan (замечания к различным частям книги и рис.
7.18, справа), Vladimir Kovalevsky (рис. 2.15), Peter Kovesi (вклад в
главы 1 и 2, касающийся фазовой конгруэнтности, включая
разрешение на публикацию рисунков), Walter Kropatsch
(предложения по главам 2 и 3), Richard Lewis-Shell (рис. 4.12, левый нижний),
Fajie Li (упражнение 5.9), Juan Lin (вклад в раздел 10.3), Yizhe Lin
(рис. 6.19), Dongwei Liu (рис. 2.16), Yan Liu (разрешение на
публикацию рис. 1.6), Rocio Lizarraga (разрешение на публикацию рис.
5.2, нижний ряд), Peter Meer (замечания к разделу 2.4.2), James
Milburn (замечания к разделу Sect. 4.4). Pedro Real (замечания на
темы геометрии и топологии), Mahdi Rezaei (вклад в материал о
распознавании лиц в главе 10, включая текст, рисунки и
упражнение 10.2), Bodo Rosenhahn (рис. 7.9 справа), John Rugis
(определение кривизны подобия и упражнения 7.2 и 7.6), James Russell
(вклад в раздел 5.1.1), Jorge Sanchez (вклад в пример 9.1, рис. 9.1
справа и 9.5), Konstantin Schauwecker (замечания о детекторах
признаков и обнаружении плоскостей методом RANSAC, рис. 6.10
справа, 7.19,9.9 и 2.23), Karsten Scheibe (вклад в главу 6, особенно
в раздел 6.1.4, и рис. 7.1), Karsten Schliins (вклад в раздел 7.4).
Предисловие ♦ 15
• Sh-Z
Bok-Suk Shin (предложения по редактированию в Latex,
замечания к различным частям книги, вклад в разделы 3.4.1 и 5.1.1 и рис.
9.23 с относящимися к нему комментариями), Eric Song (рис. 5.6
слева), Zijiang Song (вклад в главу 9, особенно в раздел 9.2.4),
Kathrin Spiller (вклад в изложение трехмерного случая в
разделе 7.2.2), Junli Tao (вклад в материал об обнаружении пешеходов
в главе 10, включая текст, рисунки, упражнение 10.1 и
замечания о структуре этой главы), Akihiko Torii (вклад в раздел 6.1.4),
Johan Van Horebeek (замечания к главе 10), Tobi Vaudrey (вклад
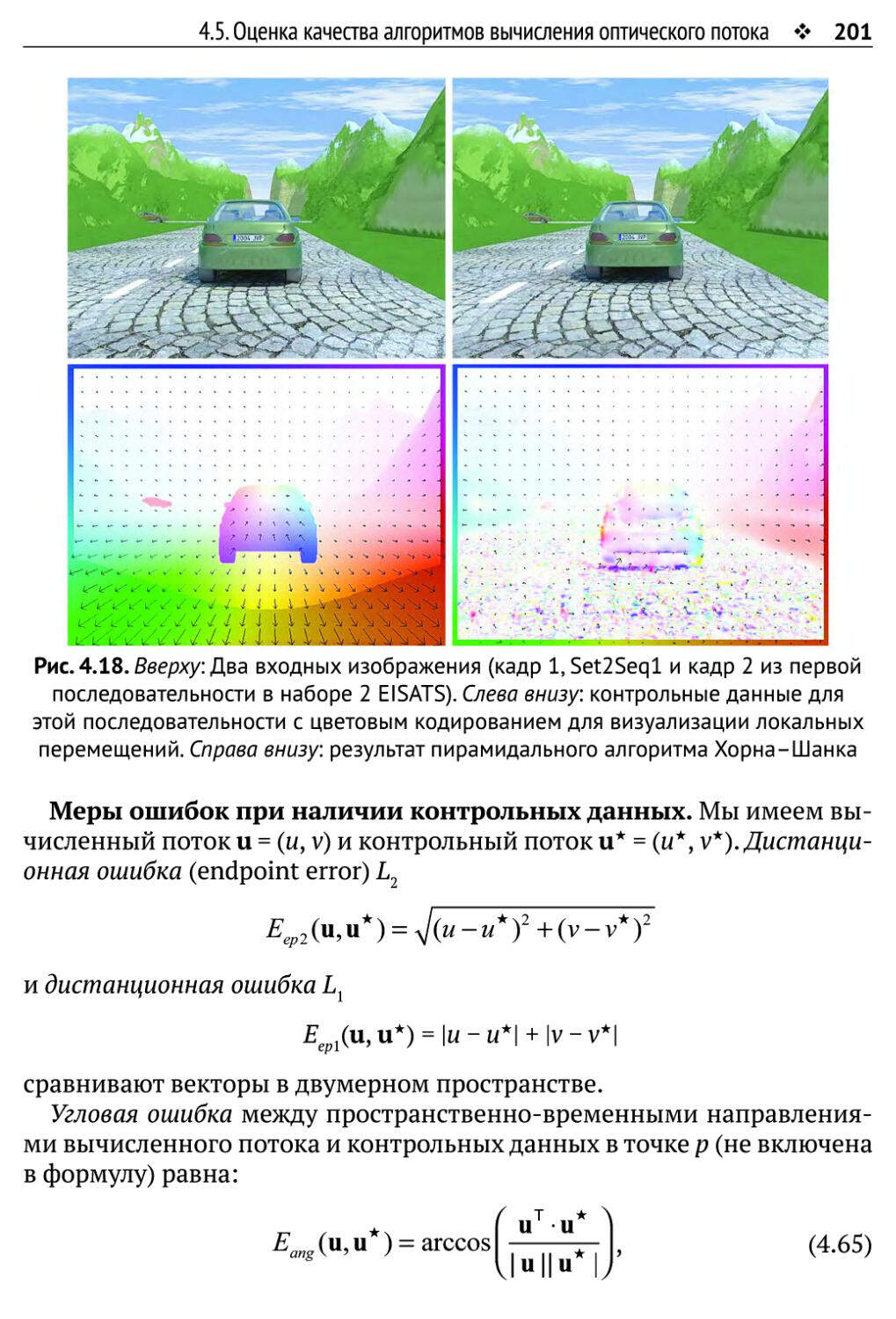
в раздел 2.3.2 и рис. 4.18, вклад в раздел 9.3.4, упражнение 9.6),
Мои Wei (замечания к главе 4), Shou-Kang Wei (совместная
работа над вопросами, относящимися к разделу 6.1.4), Tiangong Wei
(вклад в раздел 7.4.3), Jiirgen Wiest (рис. 9.1 слева), Yihui Zheng
(вклад в раздел 5.1.1), ZezhongXu (вклад в раздел 3.4.1 и рис. 3.40),
Shenghai Yuan (замечания к разделам 3.3.1 и 3.3.2), Qi Zang
(упражнение 5.5, рис. 2.21, 5.37 и 10.1), Yi Zeng (рис. 9.15), Jovisa Zunic
(вклад в раздел 3.3.2).
Автор особенно признателен Саидино Моралесу (Sandino Morales)
(федеральный округ Мехико) за реализацию и тестирование алгоритмов,
предоставление многих рисунков, вклад в главы 4 и 8 и многочисленные
замечания, касающиеся различных частей книги, Владиславу Скарбеку
(Wladyslaw Skarbek) (Варшава, Польша) за разнообразные предложения
по улучшению содержания книги и за предложенные упражнения 1.9,
2.10, 2.11, 3.12, 4.11, 5.7, 5.8, 6.10 и Гарри Ти (Garry Tee) (Окленд, Новая
Зеландия) за тщательную редактуру, замечания, части врезки 5.9,
сноску на стр. 480 и еще много ценных советов.
Я благодарю свою жену, ГизелуКлетте (Gisela Klette), за написание
раздела 3.2.4 о дистанционном евклидовом преобразовании и за
критические замечания о структуре и деталях книги во время работы над ней в
Центре исследований и математики (CIMAT) в Гуанахуато в период
между серединой июля и началом ноября 2013 г. в период творческого
отпуска, предоставленного Оклендским университетом (Новая Зеландия).
Рейнхард Клетте
Гуанахуато, Мексика
3 ноября 2013 г.
Обозначения
|S| мощность множества S
\\а\\г норма Lx
||а||2 норма L2
л логическое «И»
V логическое «ИЛИ»
п пересечение множеств
и объединение множеств
□ конец доказательства
а, Ь, с вещественные числа
А множество смежности
Л(-) площадь измеримого множества (как функция)
а, Ь, с векторы
А, В, С матрицы
а, /?, у углы
Ъ длина базы в системе стереокамер
(С множество комплексных чисел вида a + / • Ь, где i = V^T, a, b e R
d диспаратность
dx метрика L1
d2 метрика Lv известная также как евклидова
е постоянная е = ехр(1) * 2,7182818284
£ вещественное число, большее О
/ фокусное расстояние
/, g, h функции
Gmax максимальная яркость в полутоновом изображении
у кривая в евклидовом пространстве (например, прямая линия,
ломаная или гладкая кривая)
Н матрица Гессе (гессиан)
z, /, к,1,т,п натуральные числа; координаты пикселей (/, /) в окне
7, /(.,., t) изображение, один из последовательных кадров, кадр в момент
времени t
L длина (вещественное число)
Обозначения ♦ 17
$(-) длина спрямляемой кривой (функция)
Л вещественное число; значение по умолчанию от 0 до 1
п натуральное число
N окрестность (в сетке, наложенной на изображение)
Ncolsy Nrows количество столбцов, количество строк
N множество натуральных чисел {0,1,2,...}
0(-) асимптотическая верхняя граница
П носитель изображения (image carrier), множество всех позиций
пикселей N . хЛГ
cols rows
р, q точки в R2 с координатами л: и у
Р, О, R точки в R3 с координатами X, У, Z
л вещественная постоянная я = 4х arctan(l) * 3,14159265358979
П многогранник
г радиус окружности или сферы; точка в R2 или R3
Ж множество вещественных чисел
R матрица поворота
Р путь с конечным числом вершин
s точка в R2 или R3
S множество
t момент времени; точка в R2 или R3
t вектор параллельного переноса
Ту г пороговое значение (вещественное число)
и, v компоненты оптического потока; вершины или узлы;
точки в R2 или R3
и вектор оптического потока и = (и, v)
W, W окно внутри изображения, окно с начальным пикселем р
х,у вещественные переменные; координаты пикселя
изображения (х, у)
Х9 У, Z координаты в R3
Ж множество целых чисел
Глава
1
Данные изображения
В этой главе мы познакомимся с базовыми обозначениями и
математическими понятиями для описания изображения на регулярной сетке в
пространственной или частотной области. Здесь же мы опишем
способы задания цвета и познакомимся с цветными изображениями.
1.1. Изображения в пространственной
области
Цифровое изображение определяется посредством дискретизации
непрерывных аналоговых данных в пространственной области. Оно
состоит из прямоугольного массива пикселей (х, у, и), каждый из которых
является комбинацией местоположения (х, у) е 1? и значения и,
представляющего отсчет в точке {х, у). Здесь 1 - множество всех целых
чисел. Точки (а:, у) 6 1? образуют регулярную сетку. Формально
изображение / определено на прямоугольном множестве Q, которое называется
носителем (carrier) /;
n = {{xyy):l^x^NcolsM^y^NxoJczl? (l.l)
и содержит узлы сетки, или местоположения пикселей для Ncols > 1 и
N >1.
rows
Мы предполагаем левостороннюю систему координат,
показанную на рис. 1.1. Строка у содержит узлы сетки {(1, у), (2, у),..., (Ncols, у)}
для 1 ^ у ^ iVrows, а столбец х - узлы сетки {(*, 1), (х, 2),..., (х, АГ^Удля
cols
В этом разделе мы начнем знакомство с предметом обработки
цифровых изображений с обсуждения способов представления и описания
данных изображения в пространственной области, определяемой
носителем П.
1.1. Изображения в пространавенной облааи ♦ 19
Рис. 1.1. Левосторонняя система координат. Большой палец указывает
положительное направление оси х, указательный палец - положительное
направление оси у, если смотреть с внутренней стороны ладони.
(На левом рисунке видна также барочная церковь в городке Валенсиана,
которая всегда была перед глазами автора, когда он писал эту книгу
в Центре исследований и математики в Гуанахуато)
1.1.1. Пиксели и окна
На рис. 1.2 показаны два способа геометрической интерпретации
пикселей, т. е. отборов изображения на регулярной сетке.
Рис. 1.2. Слева. На увеличенном изображении видны ячейки сетки;
разными оттенками серого представлены значения пикселей изображения.
Справа. Можно также считать, что значения изображения - это метки
в узлах сетки, являющихся центрами ячеек сетки
Ячейки сетки, узлы сетки и смежность. Изображения, которые мы
видим на экране, состоят из ячеек, закрашенных одним цветом. Исходя
из такого представления, мы можем считать пиксель крохотным
закрашенным квадратиком. Это так называемая модель ячеек сетки. Но
можно также рассматривать пиксель как узел сетки, помеченный
значением изображения. Эта модель узлов сетки уже была показана на рис. 1.1.
20 ♦ Глава 1. Данные изображения
Врезка 1.1 (происхождение термина «пиксель»). Термин «пиксель» -
сокращение от «picture element» (элемент изображения). Он был введен в оборот в
конце 1960-х гг. группой исследователей из Лаборатории реактивного движения
в Пасадене, штат Калифорния, которая занималась обработкой изображений,
снятых космическими аппаратами. См. [/?. В. Leighton, N. Н. Horowitz.A. G. Herriman,A.
Т. Young, В. A. Smith, M. E. Domes and С. В. Leovy. Mariner 6 television pictures: First report.
Science, 165:684-690,1969].
Пиксели - «атомарные элементы» изображения. Сами по себе они не
определяют никаких отношений смежности. В модели ячеек сетки мы
можем предполагать, что пиксели являются смежными тогда и
только тогда, когда соответствующие им закрашенные квадратики имеют
общую сторону. Но можно также считать пиксели смежными, если они
различны и их закрашенные квадратики имеют хотя бы одну общую
точку (сторону или вершину).
Окна изображения. Окном W™y"{I) называется часть изображения I,
имеющая размер т*п и позиционированная относительно начальной
точки р (т. е. некоторого пикселя). По умолчанию подразумевается, что
т = п - нечетное число, ар- центр окна. На рис. 1.3 показано окно
^(453!l34)(SanM'9Uel)-
1 100 200 300 400 500 600 700 800
Рис. 1.3. Окно 73*77 изображения SanMiguel. На изображении главной
пирамиды музея Каньяда-де-ла-Вирген в Мексике помечен начальный
пиксель с координатами р = (453,134)
Обычно мы упрощаем нотацию и пишем просто W, поскольку само
изображение и размер окна известны из контекста.
1.1. Изображения в пространавенной облааи ♦ 21
1.1.2. Значения и основные статистики изображения
Значения изображения и берутся из дискретного множества
возможных значений. В компьютерном зрении часто рассматривают отрезок
вещественной оси [0, 1]сЦ как область значений скалярного
изображения. Это особенно полезно, если значения изображения
интерполируются выполняемыми процедурами и представляются типом данных
real. В этой книге мы по умолчанию считаем, что значениями
изображения являются целые числа.
Скалярные и бинарные изображения. Значениями скалярного
изображения являются целые числа: и £ {0,1,..., 2а - 1}. Принято
интерпретировать такие скалярные значения как уровни яркости, когда 0
соответствует черному цвету, 2я - 1 - белому, а остальные уровни линейно
интерполируются между черным и белым. В таком случае мы говорим,
что изображение полутоновое. На протяжении многих лет было
принято использовать а = 8, но недавно техническим стандартом стало а = 16.
Чтобы не зависеть от таких деталей, мы будем обозначать Gmax = 2а - 1.
В бинарном изображении пиксели могут принимать только два
значения, традиционно обозначаемые 0 = белый и 1 = черный, т. е. черные
объекты размещены на белом фоне.
Векторные и RGB-изображения. В векторном изображении, в
отличие от скалярного, имеется более одного канала или полосы.
Значениями изображения являются векторы {uv ..., uNchamels) длины
^channels- Например, цветные изображения в широко распространенной
цветовой модели RGB имеют три канала, по одному для красной,
зеленой и синей компоненты. Значения ui в каждом канале принадлежат
множеству {0, 1,..., Gmax}, т. е. каждый канал - это просто полутоновое
изображение. См. рис. 1.4.
Среднее. Пусть имеется скалярное изображение / размера Ncols*Nrom.
Вслед за математической статистикой мы называем средним (средним
уровнем яркости) изображения I величину
1 N , N
| cols rows
М,= N -N ХХ/(*'^ =
1УсоЬ lyrows jc=1 У=\ f (1.2)
где \П\ = Ncols • Nrows - мощность носителя О,, содержащего все пиксели. Мы
предпочитаем второй способ записи. В этой формуле мы используем /,
22 ♦ Глава 1. Данные изображения
а не и; I - это отображение, определенное на П, а и мы оставляем для
значений отдельных пикселей.
Рис. 1.4. Исходное цветное RGB-изображение Fountain (слева вверху),
на котором запечатлена площадь в Гуанахуато, и его разложение на три канала:
красный {справа вверху), зеленый {слева внизу) и синий (справа внизу).
Красному цвету соответствует высокая яркость красного канала
и одновременно низкая яркость зеленого и синего каналов
Дисперсия и стандартное отклонение. Дисперсией изображения I
называется величина
(1.3)
Квадратный корень из нее <т7 называется стандартным отклонением
изображения /.
Применимы такие хорошо известные формулы статистики, как
С72 =
/
"| (x,y)eQ
-t.
(1.4)
Формула (1.4) позволяет вычислять среднее и дисперсию путем
однократного прохода по изображению. Если бы мы использовали
определения (1.2) и (1.3), то понадобилось бы два прохода: один для
вычисления среднего и второй для вычисления дисперсии.
1.1. Изображения в пространавенной облааи
23
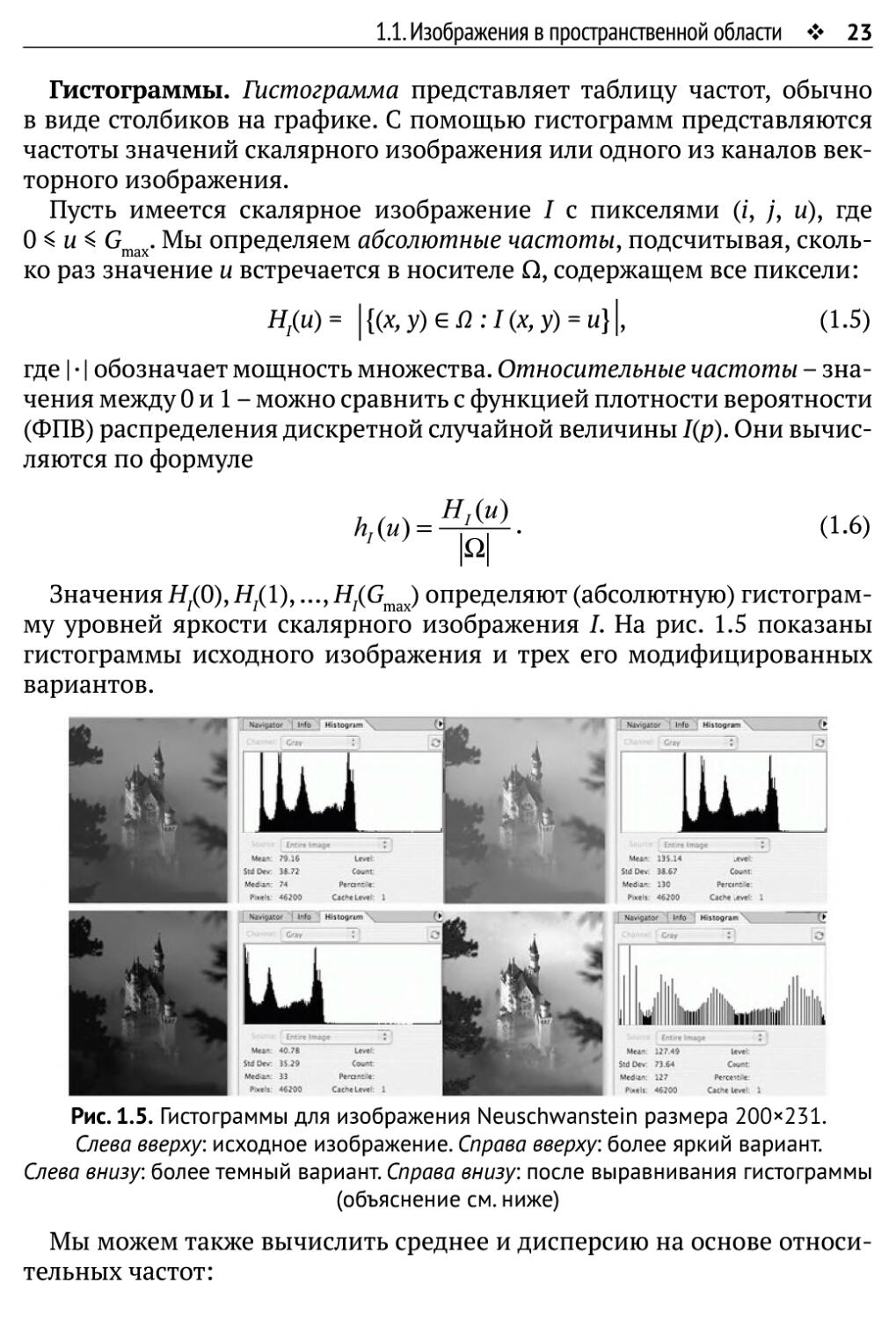
Гистограммы. Гистограмма представляет таблицу частот, обычно
в виде столбиков на графике. С помощью гистограмм представляются
частоты значений скалярного изображения или одного из каналов
векторного изображения.
Пусть имеется скалярное изображение / с пикселями (/, /, и), где
0<и< Gmax. Мы определяем абсолютные частоты, подсчитывая,
сколько раз значение и встречается в носителе Q, содержащем все пиксели:
Щи)= \{(х,у)ЕП:1(х,у) = и}
(1.5)
где | • | обозначает мощность множества. Относительные частоты -
значения между 0 и 1 - можно сравнить с функцией плотности вероятности
(ФПВ) распределения дискретной случайной величины 1(р). Они
вычисляются по формуле
hj (и) =
(1.6)
Значения Я/0), Я.(1),..., НЮ ) определяют (абсолютную) гистограм-
11 1 IllctX
му уровней яркости скалярного изображения /. На рис. 1.5 показаны
гистограммы исходного изображения и трех его модифицированных
вариантов.
PMW ОД»
Рис. 1.5. Гистограммы для изображения Neuschwanstein размера 200><231.
Слева вверху: исходное изображение. Справа вверху: более яркий вариант.
Слева внизу: более темный вариант. Справа внизу: после выравнивания гистограммы
(объяснение см. ниже)
Мы можем также вычислить среднее и дисперсию на основе
относительных частот:
24 ♦ Глава 1. Данные изображения
'"дл —max
jUI=^u-hI(u) или с^ =^[u-jUi] ЛОХ (1.7)
Так получается быстрее, если гистограмма уже вычислена.
Абсолютная и относительная кумулятивная частота определяются
следующим образом:
и и
СДи) =£#/(*>) и с»=£/г70). (1.8)
у=0 ъ>=0
Эти значения показываются на кумулятивных гистограммах.
Относительные частоты можно сравнить с функцией вероятности Рг[/(р) < и]
дискретной случайной величины 1(р).
Статистики значений в окне. Рассмотрим окно по умолчанию
W = W"'"{I)t где п = 2к + 1 и р = (х, у). Тогда в координатах окна имеем
+к +к
1 +К +К
Yl i-_Jr i-_lr
(1.9)
i=-k j=-k
См. рис. 1.6. Формулы для дисперсии и других показателей можно
модифицировать аналогично.
256
Count 10192 Min: 9
Mean: 133.711 Max: 255
StdOev: 55.391 Mode: 178 (180)
256
Count: 10192 Min: 11
Mean: 104.637 Max: 254
StdDev: 89.862 Mod»: 23 (440)
Рис. 1.6. Пример двух окон размера 104*98 в изображении Yan
и соответствующих им гистограмм.
Верхнее окно: /jWi = 133,7, oWl = 55,4. Нижнее окно: ущ = 104,6, ащ = 89,9
Пример 1.1 (примеры окон и гистограмм). В изображении Yan размера
489*480, показанном на рис. 1.6, мы видим два выделенных рамкой окна раз-
1.1. Изображения в пространственной области
25
мера 104x98: Wv содержащее лицо, и W2, содержащее части скамьи и платья.
Там же приведены гистограммы для обоих окон.
Трехмерное представление уровней яркости (которые в таком случае
интерпретируются как возвышения) иллюстрирует различные «степени
однородности» изображения. Пример см. на рис. 1.7. Крутой подъем с нижнего плато на
верхнее на левом рисунке - типичная иллюстрация «границы» внутри
изображения.
255
кселя
Рис. 1.7. Слева: «крутой переход от темного к яркому».
Справа: «незначительное» изменение. Обратите внимание
на разные масштабы трехмерных представлений обоих окон на рис. 1.6
В процессе анализа изображения мы должны классифицировать окна
по категориям, например: «внутри однородной области», «низкая
контрастность», «содержит границу между двумя разными областями» или
«высокая контрастность». Мы определяем контрастность С(1)
изображения / как среднюю абсолютную величину разности между значением
пикселя и средним значением соседних пикселей.
А(х,у)
(1.10)
где ц - среднее значение, вычисленное по пикселям, соседним с
находящимся в позиции (х, у).
Еще один пример использования низкоуровневых статистик для
простой интерпретации изображений показан на рис. 1.4. Средние
значения, посчитанные по красному, зеленому и синему каналам,
показывают, что в изображении больше красного цвета (правый верхний
рисунок, среднее значение равно 154) и меньше зеленого (левый нижний
26 ♦ Глава 1. Данные изображения
рисунок, среднее значение равно 140) и синего (правый нижний
рисунок, среднее значение равно 134). Это можно проверить более точно,
взглянув на гистограммы всех трех каналов. На них видно, что «более
ярким» является красный канал, особенно в области, занятой домом
в центре, а зеленый и синий каналы в той же области «более темные».
1.1.3. Пространственные и временные меры данных
Уже приведенных выше базовых понятий из математической
статистики достаточно, чтобы определить функции, описывающие
изображения: построчно в случае одного изображения или покадрово в случае
последовательности изображений.
Статистики значений в профиле яркости. При первоначальном
анализе изображений в новой предметной области можно получить
весьма полезную информацию, если визуализировать профили
яркости, определяемые одномерными сечениями скалярных массивов
данных.
На рис. 1.8 показаны два профиля яркости по оси х, построенных для
заданного полутонового изображения. Как и раньше, мы можем
использовать среднее, дисперсию и гистограммы «узких» окон размера
Ncols*\, чтобы получить общее представление о распределении
значений изображения.
Рис. 1.8. Слева: выделены две строки изображения для представления в канале
яркости (т. е. значения (/? + 6 + В)/Ъ) для изображения SanMiguel на рис. 1.3.
Справа: профили яркости обеих выбранных строк
Пространственные и временные статистики значений.
Гистограммы и профили яркости - примеры пространственных статистик
значений. Так, профили яркости для строк с номерами от 1 до Nrom одного
изображения / определяют последовательность дискретных функций,
1.1. Изображения в пространственной области
27
которую можно сравнить с соответствующей последовательностью для
другого изображения /.
Рассмотрим еще один пример - последовательность изображений,
состоящую из кадров It,t= 1,2,..., Г, определенных на одном и том же
носителе П. Для лучшего понимания распределения значений
полезно определить скалярную меру данных (£), которая сопоставляет одному
кадру It одно число, и сравнить различные меры данных для заданного
дискретного временного интервала [1,2,..., 7], получив тем самым
временные статистики данных.
Например, определение контрастности (1.10) индуцирует меру
данных T(t) = C(It), определение среднего (1.2) - меру данных M(t) = ^ ,
а определение дисперсии (1.3) - меру данных V(t) = а\.
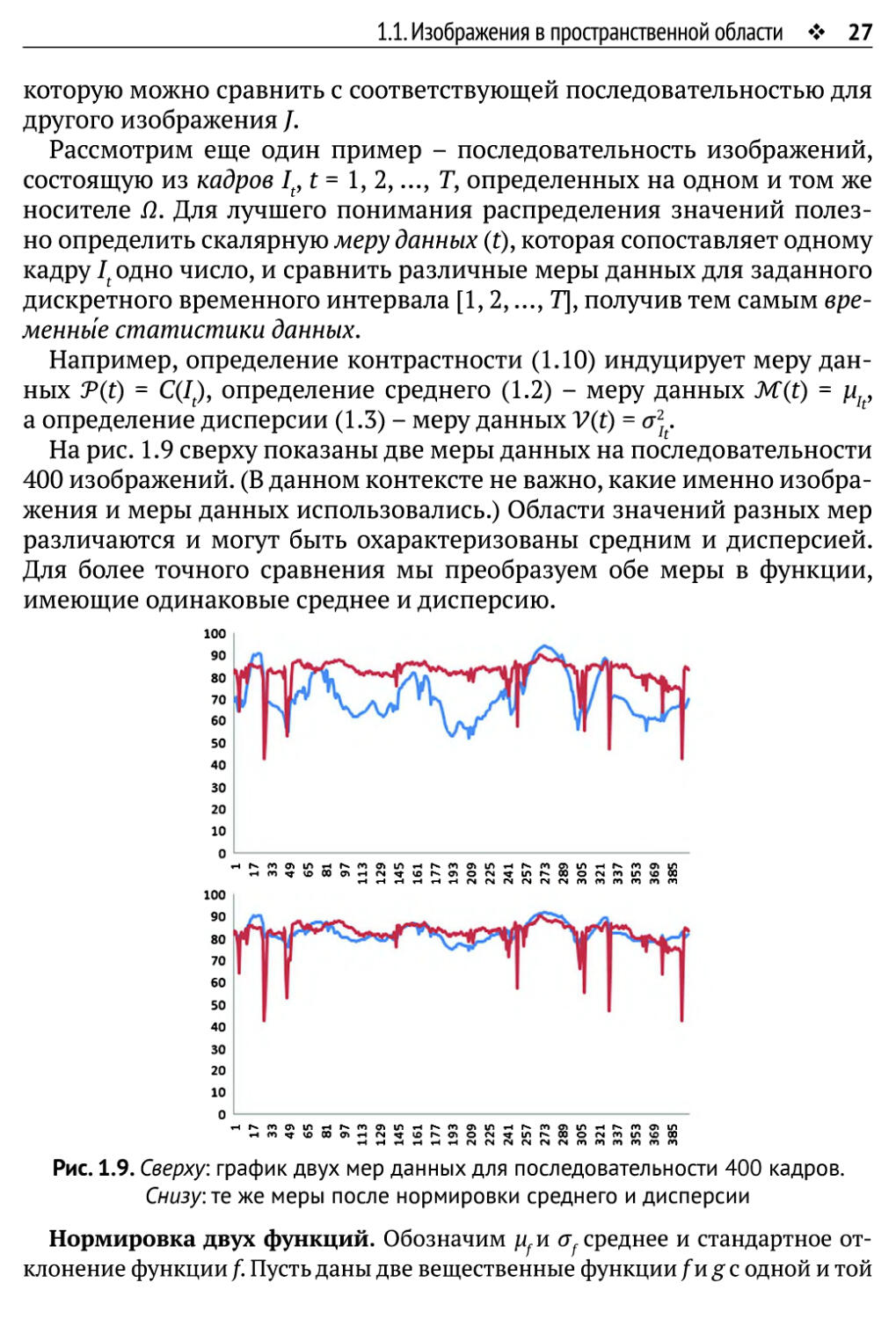
На рис. 1.9 сверху показаны две меры данных на последовательности
400 изображений. (В данном контексте не важно, какие именно
изображения и меры данных использовались.) Области значений разных мер
различаются и могут быть охарактеризованы средним и дисперсией.
Для более точного сравнения мы преобразуем обе меры в функции,
имеющие одинаковые среднее и дисперсию.
100
90
80
70
60
50
40
30
20
10
0
100
90
80
70
60
50
40
30
20
10
0
tops^vOto
L^^-r^pY'Yf^
Рис. 1.9. Сверху: график двух мер данных для последовательности 400 кадров.
Снизу: те же меры после нормировки среднего и дисперсии
Нормировка двух функций. Обозначим pifn oy среднее и стандартное
отклонение функции /. Пусть даны две вещественные функции /и g с одной и той
28 ♦ Глава 1. Данные изображения
же дискретной областью определения, скажем 1,2,..., Т, и ненулевыми
дисперсиями. Положим
gMW(x) = fi(g(x)+a). (1.12)
Тогда функция gnew будет иметь такие же среднее и дисперсию, как
функция /.
Расстояние между двумя функциями. Теперь определим
расстояние между двумя вещественными функциями с одной и той же
областью определения, например 1,2,..., Т:
-* х=1
di(f,g)= ^J2(/W-^W)2. (1.14)
Оба расстояния являются метриками, т. е. для них выполняются
следующие аксиомы:
1) /= 5" тогда и только тогда, когда d(f, #) = 0;
2) d(f,g) = d(g>/) (симметричность);
3) d(/jg) < d(f, h) + d(ft,g) для произвольной третьей функции h
(неравенство треугольника).
Структурное подобие мер данных. Пусть заданы две разные
пространственные или временные меры данных 7 и Q с одной и той же
областью определения 1, 2,..., Г. Сначала отобразим Q в Qnew, так чтобы
у обеих мер были одинаковые среднее и дисперсия, а затем вычислим
расстояние между 7 и Qnew, применяя любую из метрик Ьг или L2.
Две меры 7 и Q называются структурно подобными, если расстояние
между 7 и Qnew близко к нулю. Структурно подобные меры принимают
локальные максимумы и минимумы приблизительно в одних и тех же
точках.
1.1. Изображения в проаранственной области ♦ 29
1.1.4. Ступенчато-граничная модель
Изломы в изображениях - это признаки, которые часто бывают
полезны на начальной стадии процедуры анализа. Границы представляют
собой важную информацию, позволяющую лучше понять изображение
(например, устранить влияние переменного освещения). Удалив все
данные, кроме границ, мы сможем упростить данные. На рис. 1.10
понятие «границы» иллюстрируется тремя примерами.
Рис. 1.10. Границы, или визуальные силуэты, уже много тысяч лет используются,
чтобы показать «существенную информацию», например в пещерных рисунках.
Слева: изображение Taroko, на котором показаны древние рисунки коренного
населения Тайваня. В середине: фрагмент изображения Aussies с силуэтами,
спроецированными на стену здания 01 в городе Голд-Кост, Австралия.
Справа: торговый центр в Шанхае, изображение OldStreet
Изломы в изображениях могут быть локализованы в небольших
окнах (например, зашумленные пиксели) или определять границы между
областями с разными характеристиками сигнала.
Что такое граница? На рис. 1.11 показано разнообразие границ в
изображениях. Для этого мы двигаемся слева направо по профилю
яркости в соответствии со ступенчато-граничной моделью (step-edge
model). В этой модели предполагается, что границы определяются
изменениями локальных производных. Альтернативную фазово-конгру-
энтную модель мы обсудим в разделе 1.2.5.
После удаления шума предположим, что изображение
представляет отсчеты непрерывной функции 1{х, у), определенной на евклидовой
плоскости Е2, для которой можно взять первую и вторую частные
производные по а: и у. На рис. 1.12 иллюстрируются свойства таких
производных.
50 ♦ Глава 1. Данные изображения
I -v
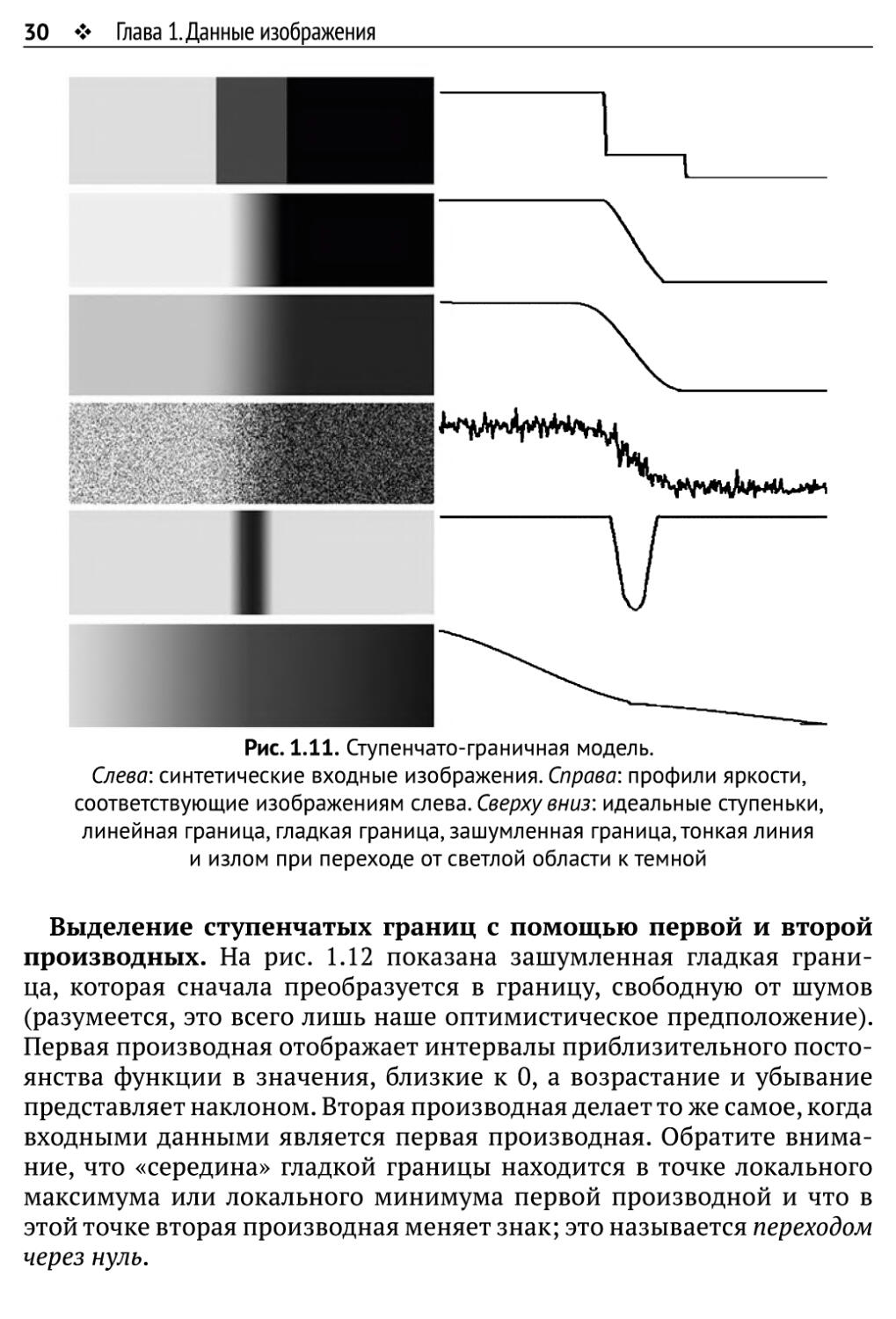
Рис. 1.11. Ступенчато-граничная модель.
Слева: синтетические входные изображения. Справа: профили яркости,
соответствующие изображениям слева. Сверху вниз: идеальные ступеньки,
линейная граница, гладкая граница, зашумленная граница,тонкая линия
и излом при переходе от светлой области к темной
Выделение ступенчатых границ с помощью первой и второй
производных. На рис. 1.12 показана зашумленная гладкая
граница, которая сначала преобразуется в границу, свободную от шумов
(разумеется, это всего лишь наше оптимистическое предположение).
Первая производная отображает интервалы приблизительного
постоянства функции в значения, близкие к 0, а возрастание и убывание
представляет наклоном. Вторая производная делает то же самое, когда
входными данными является первая производная. Обратите
внимание, что «середина» гладкой границы находится в точке локального
максимума или локального минимума первой производной и что в
этой точке вторая производная меняет знак; это называется переходом
через нуль.
1.1. Изображения в пространавенной облааи
31
Профиль яркости входного изображения
После устранения шума
Первая производная
Вторая производная
Рис. 1.12. Входной сигнал, сигнал после устранения шума,
первая производная, вторая производная
Изображение как непрерывная поверхность. Значение
изображения / можно интерпретировать как аппликату некоторой поверхности
в точке расположения пикселя. См. рис. 1.13. При такой интерпретации
изображение I определяет долины, плато, плавные или крутые склоны
и т. д. Значения частных производных по а: и по у соответствуют
убыванию или возрастанию высоты либо пребыванию на одном уровне.
Напомним некоторые основанные на производных понятия,
применяемые в математическом анализе для описания поверхностей.
Рис. 1.13. Слева: синтетическое входное изображение с пикселем в точке (х,у).
Справа: касательная плоскость (зеленая) к поверхности в точке (х,у, /(х,у)),
нормаль п = [а, Ь, 1]т, ортогональная этой плоскости, и частные производные
а (по х) и b (по у) в левосторонней декартовой системе координат, определенной
координатами изображения х и у и осью значения изображения и
32
Глава 1. Данные изображения
Первые производные. Нормаль п ортогональна касательной
плоскости в точке, соответствующей пикселю (х, у, 1{х, у)); касательная
плоскость аппроксимирует поверхность, определяемую значениями
изображения 1(х, у) на плоскости лгу. Нормаль составляет угол у с осью
значений изображения.
Градиент
-|Т
Э/ Э/
V/ = grad / =
Эх ду
(1.15)
объединяет обе частные производные в точке р = (х, у). Символ
V/читается «набла /». Правильнее было бы писать [grad/)(p) и т. д., но мы будем
опускать позицию пикселя р, чтобы формулы было проще читать.
Направление нормали
п =
— — +1
Эх Эу
-|Т
(1.16)
может совпадать с положительным или отрицательным направлением
оси и; мы выбрали положительное направление, поэтому в
формальном определении фигурирует +1. Углом наклона
^=arccos
1
п
(1.17)
называется угол между осью и и нормалью п. Первые производные
позволяют вычислить длину (или модуль) градиента и нормали:
1/ЗтЛ2
Э/
l|grad/||2 = A —
Эх
+
\ОЛ J
(-Т
и
(1.18)
п
(-Т
+1
Из рис. 1.12 и следующего за ним обсуждения мы делаем вывод:
Наблюдение 1.1. Похоже, имеет смысл искать границы в точках, где модули
Hgrad /||2 или ||п||2 достигают локального максимума.
Вторые производные. Вторые производные объединяются в
лапласиан I, определяемый как
1.1. Изображения в пространавенной облааи
33
А/ = V2/ =
д21 д21
+
.2 '
дх2 ду2
или квадратичную вариацию I, определяемую как1
(1.19)
'э2/^2
дх2
+ 2
Э2/
дхду
\
+
'э2/л2
ду2
(1.20)
Отметим, что лапласиан и квадратичная вариация - скаляры, а не
векторы, как градиент и нормаль. Таким образом, мы приходим к
следующему выводу.
Наблюдение 1.2. Похоже, имеет смысл искать границы в точках, где лапласиан
Д/ или квадратичная вариация переходят через ноль.
Карты границ и способы выделения границ. Операторы
выделения границ преобразуют изображения в граничные изображения, или
карты границ; пример см. на рис. 1.14. Не существует «общего
определения границы», а стало быть, и «общего детектора границ».
I J4b
Рис. 1.14. Полутоновое изображение WuhanU (слева)
преобразовано в граничное изображение (или карту границ) (в середине)
и раскрашенную карту границ (справа). Цвет можно использовать для иллюстрации
направлений или силы границ. Изображено главное административное здание
Уханьского университета в Китае
В пространственной области границы можно обнаружить, следуя
ступенчато-граничной модели (см. разделы 2.3.3 и 2.4) или с помощью
остаточного изображения относительно сглаживания (см. разделы 2.3.2
и 2.3.5).
Разрывы можно обнаружить и в частотной области, например с
помощью фильтра верхних частот, как описано в разделе 2.1.3, или путем
применения фазово-конгруэнтной модели; см. описание этой модели в
разделе 1.2.5 и алгоритм ее использования в разделе 2.4.3.
1 Точнее, функция I удовлетворяет условию дважды дифференцируемости, если I -°-L I = I -°-L
В (1.20) мы предположили, что это условие выполнено.
у дхду ) ydydxj
54 ♦ Глава 1. Данные изображения
1.2. Изображения в частотной области
Преобразование Фурье относится к традиционным способам обработки
сигналов. В этом разделе мы приведем основные сведения о
преобразовании Фурье и о фильтрации Фурье, а заодно объясним смысл фраз
«высокочастотная информация» и «низкочастотная информация»
применительно к изображениям. Двумерное преобразование Фурье
переводит изображение из пространственной в частотную область,
полностью меняя его представление (хотя математически оба представления
эквивалентны).
1.2.1. Дискретное преобразование Фурье
Двумерное дискретное преобразование Фурье (ДПФ) отображает скалярное
изображение / размера NcoIsxNrom в комплексное преобразование Фурье I.
Таким образом, это отображение пространственной области изображения в
частотную область преобразования Фурье.
Врезка 1.2 (преобразование Фурье и интегральные преобразования).
Жан-Батист Жозеф Фурье (1768-1830) - французский математик. Он изучал
функциональные ряды и интегралы, ныне носящие его имя.
Преобразование Фурье - наиболее известный пример интегрального
преобразования. С ним связано вычислительно более простое косинусное
преобразование, которое используется в базовой версии алгоритма кодирования
изображений JPEG.
Преобразование Фурье и фильтрация Фурье - общие сведения.
Анализ или изменение данных в частотной области дает полезную
информацию об изображении I. В частотной области к изображению
применяются операции фильтрации Фурье. Затем двумерное обратное ДПФ
переводит модифицированное преобразование Фурье в
модифицированное изображение.
Весь этот процесс называется фильтрацией Фурье и позволяет,
например, усилить контрастность, убрать шумы или сгладить изображение.
Одномерная фильтрация Фурье часто применяется в теории обработки
сигналов (например, при обработке звуковых сигналов в мобильном
телефоне), а двумерная фильтрация изображений построена на тех же
принципах, только не на прямой, а на плоскости.
В контексте преобразования Фурье мы будем предполагать, что
координата а: изображения изменяется от 0 до iVco/s - 1, а координата у -
от 0 до N - 1; иначе во всех формулах пришлось бы писать а: - 1 и у - 1.
1.2. Изображения в чааотной облааи
35
Двумерное преобразование Фурье. Формально двумерное
дискретное преобразование Фурье определяется следующим образом:
I(u,v) =
1
Ncols-Nri
N i -\ N -1
1 v cols l 1 v rows l
x=0
y=0
f
-iln
xu
yv
. N
V cols
N,
rows J
(1.21)
для частот u = 0,1,..., Ncols - 1 и v = 0,1,..., iVrow5 - 1. Буква i = V^l
обозначает (в этой книге только в контексте преобразований Фурье) мнимую
единицу2. Для любого вещественного а формула Эйлера
ехр(/а) = eia = cos а + / • sin а (1.22)
показывает, что преобразование Фурье на самом деле является
взвешенной суммой синуса и косинуса, только в комплексной плоскости.
Если угол а не принадлежит интервалу [0, 2я), то в этой формуле его
значение берется по модулю 2тт. Число Эйлера е = 2,71828... = ехр(1).
Врезка 1.3 (Декарт, Эйлер и комплексные числа). Рене Декарт (1596-1650),
французский ученый, оказавший огромное влияние на современную
математику (например, он изобрел декартовы координаты), называл отрицательные
решения квадратного уравнения а-х2 + Ь-х + с = 0 «ложными», a комплексные
решения «мнимыми». Швейцарский математик Леонард Эйлер (1707-1783)
понял,что
е'а = cos а + / • sin а,
где е= limn^oo(l + 1/п)п = 2,71828....Это внесло важный вклад в принятие
комплексных чисел научным сообществом в конце XVIII века.
Комплексное число имеет действительную и мнимую части, это понятие
позволило упростить математику. Например, благодаря им стало возможно
сформулировать основную теорему алгебры, утверждающую, что любой полином
имеет хотя бы один корень. Многие задачи математического анализа, физики,
техники и других научных дисциплин удобнее всего решать в терминах
комплексных чисел, даже тогда, когда мнимая часть решения не используется.
1.2.2. Обратное дискретное преобразование Фурье
Двумерное обратное ДПФ переводит преобразование Фурье I назад в
пространственную область:
^ cols ~1 ^rows ~*
1(х,у)= ]£ ^ I(w,v)exp \Пл
и=0 v=0
/ Л
xu yv
\
. N
V cols
N,
rows J
(1.23)
В физике и электротехнике используют букву/ вместо z, чтобы отличить ее от силы тока.
56 ♦ Глава 1. Данные изображения
Отметим, что показатели степени в экспоненте противоположны
степеням в формуле (1.21) (т. е. знак минус заменен на плюс).
Варианты формул преобразования. Определения ДПФ и
обратного ДПФ могут варьироваться. Можно поставить знак плюс в ДПФ и знак
минус в обратном ДПФ. Можно включить масштабный коэффициент
^■/(Ncols • Nrom) в ДПФ и коэффициент 1 в обратное преобразование.
Важно, чтобы произведение коэффициентов в ДПФ и в обратном ДПФ было
равно 1/(JV , • N ). Можно было бы представить величину 1/(N , • N )
г I \ cols rows' f 1-^ j i v co/s rows'
в виде произведения двух одинаковых масштабных коэффициентов,
равных 1/ViV , -JV .
с ' cols rows
Базисные функции. Формула (1.23) показывает, что изображение /
представлено в виде взвешенной суммы базисных функций ехр(гос) =
cos a + i sin а, являющихся линейными комбинациями синуса и
косинуса на комплексной плоскости. На рис. 1.15 показано пять таких
базисных функций sin(u + nv), соответствующих мнимым частям Ъ
комплексных чисел а + ib в комплексной плоскости uv; для вещественной части а
надо было бы взять косинусы вместо синусов.
Рис. 1.15. Слева вверху: волны на воде. Остальные рисунки: длина волн,
описываемых функциями sin(u + nv) для п = 1,..., 5, убывает
(а стало быть, частота возрастает) с ростом п
Значения I(u, v) преобразования Фурье изображения / в формуле
(1.23) называются коэффициентами Фурье; это веса при базисных функ-
1.2. Изображения в частотной области
37
циях ехр(гсс). Например, в представлении точечного шума или границ
такой взвешенной суммой коэффициенты при высокочастотных (с
малой длиной волны) компонентах должны быть достаточно велики.
1.2.3. Комплексная плоскость
Мы кратко обсудим элементы, участвующие в определении ДПФ
(1.21), чтобы читатель лучше понимал это фундаментальное для
обработки сигналов преобразование.
Очень часто комплексное число а + i • Ъ наглядно представляют
точкой (а, Ъ) или вектором [а, Ъ] на комплексной плоскости (см. рис. 1.16).
Мнимая часть
Действительная часть
Рис. 1.16. Единичная окружность на комплексной плоскости.
Обозначены все степени числа W= /2л/24. На рисунке также показано
одно комплексное число z = а + ib и его полярные координаты (г, ос)
Операции с комплексными числами. Пусть z1 = ах + i • bl и z2 =
a2+i-b2- два комплексных числа. Здесь / = V11!, a1 и а2 - действительные
части, а Ъх и Ъ2 - мнимые части. По определению
z1 + z2=(fl1 + fl2) + i-(b1 + b2) (1.24)
и
z\'zi= (а\аг~ ^А) + z' (flA + aPi- (1.25)
Сумма и произведение двух комплексных чисел снова являются
комплексным числом, и обе операции обратимы (т. е. определены
вычитание и деление комплексных чисел; см. определение z~l ниже).
58 ♦ Глава 1. Данные изображения
Модулем (или нормой) комплексного числа z = a + i-b называется
длина вектора [а, Ь]т (с началом в начале координат [О, 0]Т) в смысле
нормы L2, т. е. ||z||2 = Vfl2 + b2.
Число z* = a- i-b называется сопряженным к числу z = a + i-b. Имеет
место тождество (z*)* = z. Кроме того, (zl • z2)* = z*- z* и в предположении,
4toz^0,z-1 = ||z||2_2-z*.
Комплексные числа в полярных координатах. Комплексное
число z можно также записать в виде z = г • е'а, где г = ||z||2, а а (аргумент
числа z) определен с точностью до кратного 2л, если z Ф 0. Тем самым
мы получаем представление комплексных чисел в полярных
координатах (г, а).
Результатом поворота вектора [с, d]T (с началом в начале координат
[0, 0]т) на угол а является такой вектор [а, Ь]т, что
a + i-b = eia-(c + i-d). (1.26)
Корни из единицы. Комплексное число WM = ехр[/2я/М]
называется М-м корнем из единицы. Имеем W*j = W™ = W^= ... = 1.
Предположим, что М кратно 4. Тогда WJ = 1 + i • 0, W™/4 = 0 + i • 1, W™/2 = -1 + / • 0
Врезка 1.4 (быстрое преобразование Фурье). Свойства М-х корней из единицы,
когда М - степень двойки, лежат в основе оригинального алгоритма быстрого
преобразования Фурье (БПФ) - эффективной реализации ДПФ.
У проектирования БПФ интересная история, см. [J. M. Cootey, P. A. Lewis, P. D. Welch.
History of the fast Fourier transform. Proc. IEEE 55,1967, p. 1675-1677]. Его истоки
восходят еще к Карлу-Фридриху Гауссу (см. врезку 2.4). Но популярность алгоритм
приобрел благодаря работе [J. M. Cooley, J. W. Tukey. An algorithm for the machine
calculation of complex Fourier series. Math. Сотр. 19,1965, p. 297-301].
Алгоритм БПФ обычно выполняется «на месте»: исходное изображение
используется для инициализации матрицы Ncol5xNrows действительных частей, а
матрица мнимых частей инициализируется нулями. Затем производится
двумерное ДПФ, и все элементы обеих матриц заменяются его результатами.
На рис. 1.16 показаны все степени корня из единицы 24-й
степени, W24 = ei2n/24. В этом случае W£4= е°= 1, Щ4= cos л/12 + i sin л/12,
Щ4= cos л/2 + / sin л/2 = /, WH = cos л + / sin л = -1, a W™ = cos Зл/2 +
/ sin Зл/2 = -L
Формулу (1.21) можно упростить, воспользовавшись корнями из
единицы. Легко видеть, что
1.2. Изображения в чааотной облааи ♦ 59
■»' rnlv * ** ты)? *■
1 ^cols * ^rows 1
«»>*>= л, », I s я^)-^--^:,. а.27)
cols rows х=0 у=0
Для любого корня из единицы Wn = i2n/n, n > 1, и для любой степени
m G Z имеет место тождество
FT.
Икт/п
= ^cos(2;rm / и)2 + sm(27rm I nf = 1. (1.28)
Поэтому все степени корня из единицы расположены на единичной
окружности, как показано на рис. 1.16.
1.2.4. Данные изображения в частотной области
Комплексные значения двумерного преобразования Фурье
находятся в частотной области uv. Значения для низких частот и или v (близких
к 0) соответствуют компонентам синуса и косинуса с большой длиной
волны, а значения для высоких частот и или v (удаленных от нуля)
соответствуют коротким волнам. Примеры синусоидальных волн
приведены на рис. 1.15.
Интерпретация матрицы I. Низкие частоты соответствуют
длинным волнам и, стало быть, однородным аддитивным вкладам в
исходное изображение /. Высокие частоты соответствуют коротким волнам
и, следовательно, локальным изломам в /, например границам или
аномальным выбросам яркости.
Направленные структуры в /, например прямые линии под углом /?
или /? + я, создают распределения значения в I в ортогональном
направлении (в нашем примере - в направлении /? + я/2).
В изображениях начало координат расположено в левом верхнем
углу (поскольку мы предполагаем левостороннюю систему координат,
см. рис. 1.1). Значения матрицы I можно периодически повторить на
плоскости с периодами Ncols и Nrows. Такое бесконечное количество копий
матрицы I образует замощение плоскости прямоугольным орнаментом
(см. рис. 1.17).
Если мы захотим поместить начало координат (т. е. область низких
частот) в центр преобразования Фурье, то сможем сделать это путем
перестановки всех четырех квадрантов матрицы. Также (и это нетрудно
проверить математически) такой сдвиг I в центр можно реализовать,
сначала умножив все значения Дат, у) на (-1)х+у, а затем выполнив
двумерное ДПФ.
Три свойства ДПФ. Мы рассматриваем двумерное преобразование
Фурье изображения /. Оно состоит из двух массивов размера Ncols*NroM/s,
40
Глава 1. Данные изображения
представляющих действительные (т. е. величины а) и мнимые (т. е.
величины Ъ) части полученных комплексных чисел а + / • Ъ. Таким
образом, реальные данные входного изображения / - один массив размера
NcolsxNrows - теперь «удвоились». Но имеет место важное свойство
симметричности:
l(Nh - и, iV - v) = I(-u, -v) = I(u, v)*
rows
(1.29)
(напомним, что в правой части находится комплексно-сопряженное
число). Следовательно, одну половину данных в обоих массивах,
составляющих I, можно получить из другой. Второе свойство выглядит
так:
1(0,0) =
1
,-i
N -N
cols rows
^ cols 1 ^rows
y=0
(1.30)
x=0
В правой части находится среднее значение /. Поскольку / содержит
только действительные значения, отсюда следует, что мнимая часть
1(0, 0) всегда равна нулю. Благодаря приложениям преобразования
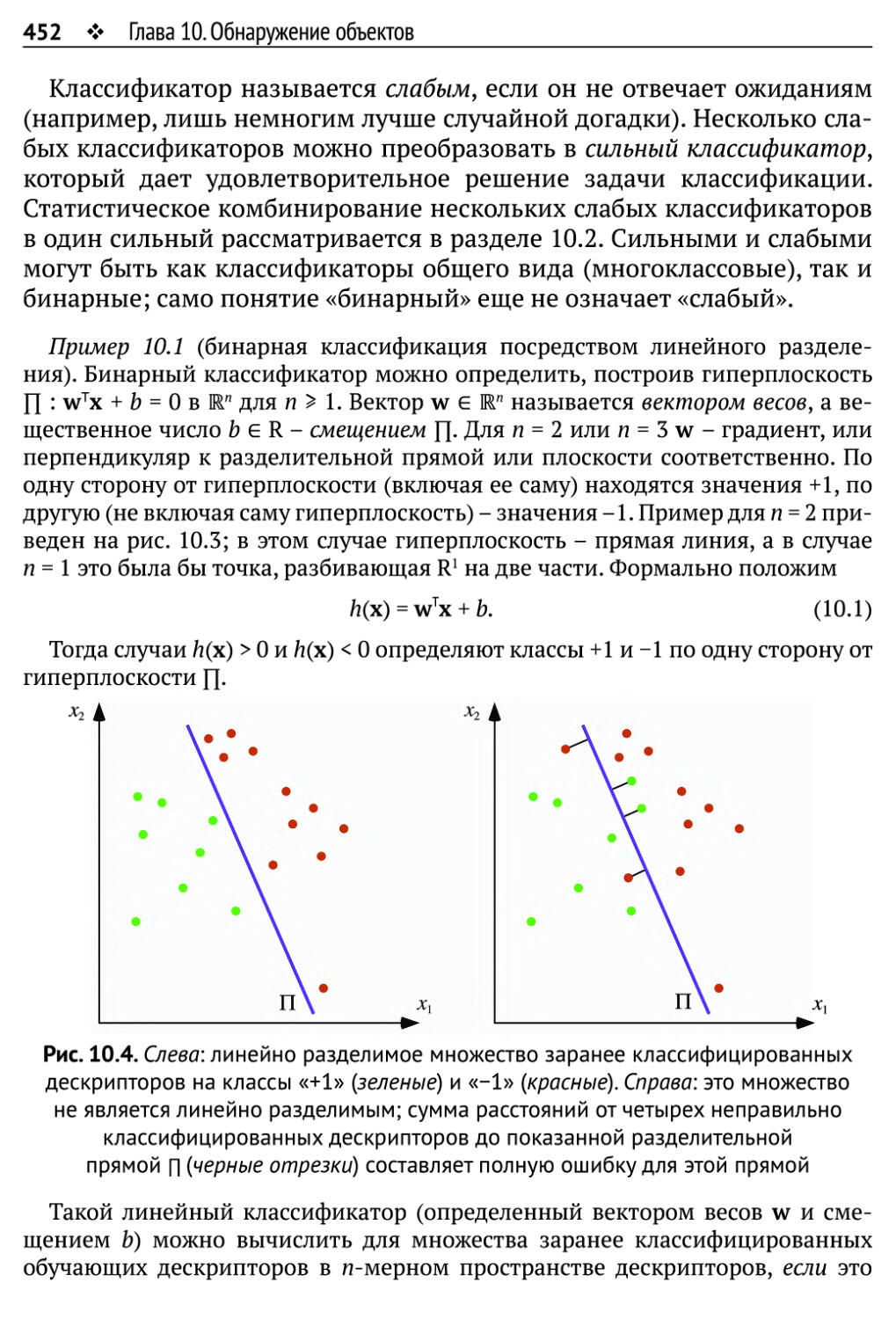
Фурье в электротехнике средняя величина сигнала 1(0, 0) называется
постоянной составляющей / (имеется в виду постоянный ток). Для
любой другой частоты (и, v) ф (0, 0), I(u, v) называется переменной
составляющей / (имеется в виду переменный ток).
} Низкие
Низкие /\
—с^'^Высокие ^^»
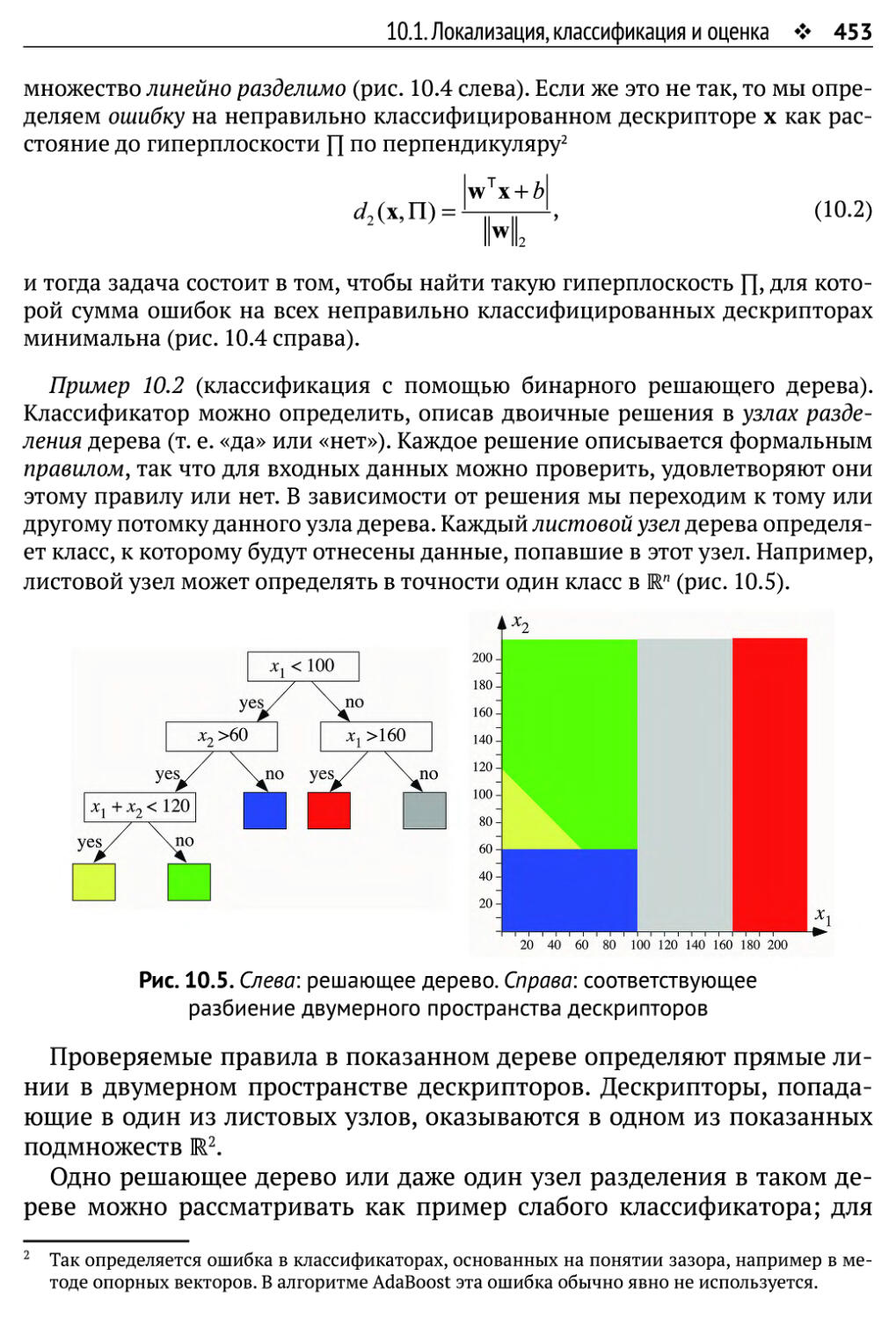
Низкие у Низкие
•
•
•
Рис. 1.17. Закрашенная область соответствует матрице I размера Ncol*Nrows.
Она окружена во всех сторон еще восемью копиями I. Начала координат
всегда находятся в левом верхнем углу. Благодаря периодичности
область низких частот располагается внутри эллипсов, т. е. в четырех углах
матрицы 1,а самые высокие частоты находятся в центре I
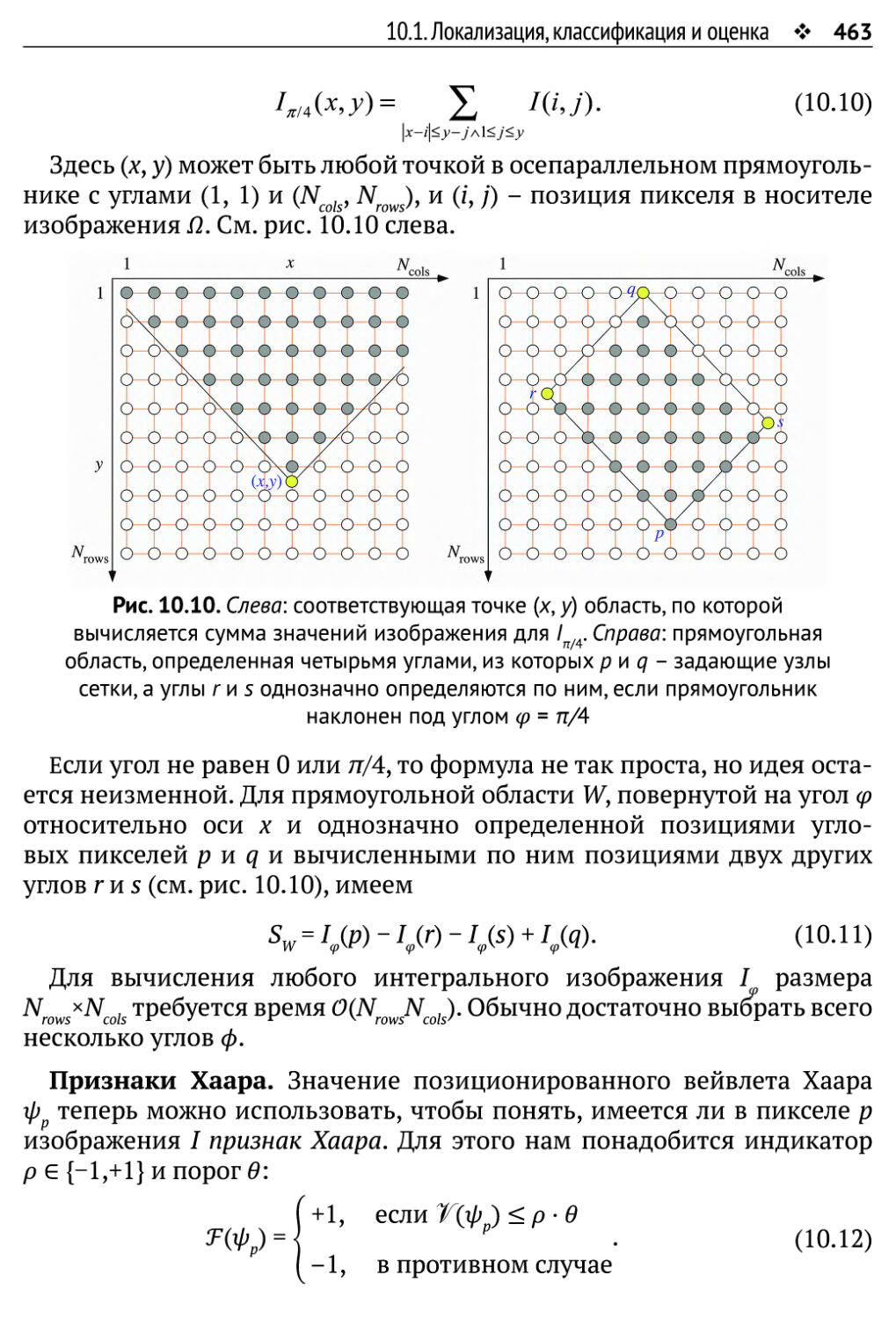
1.2. Изображения в чааотной облааи ♦ 41
Третье свойство выражается теоремой Парсеваля
ЛЦ/(х^)Г=1|К«,у)|2, (1.31)
которая утверждает, что суммы квадратов модулей значений пикселей
исходного изображения / и элементов матрицы его преобразования
Фурье I совпадают; масштабный коэффициент 1/|Q| присутствует лишь
потому, что мы решили включать этот коэффициент только в прямое
преобразование.
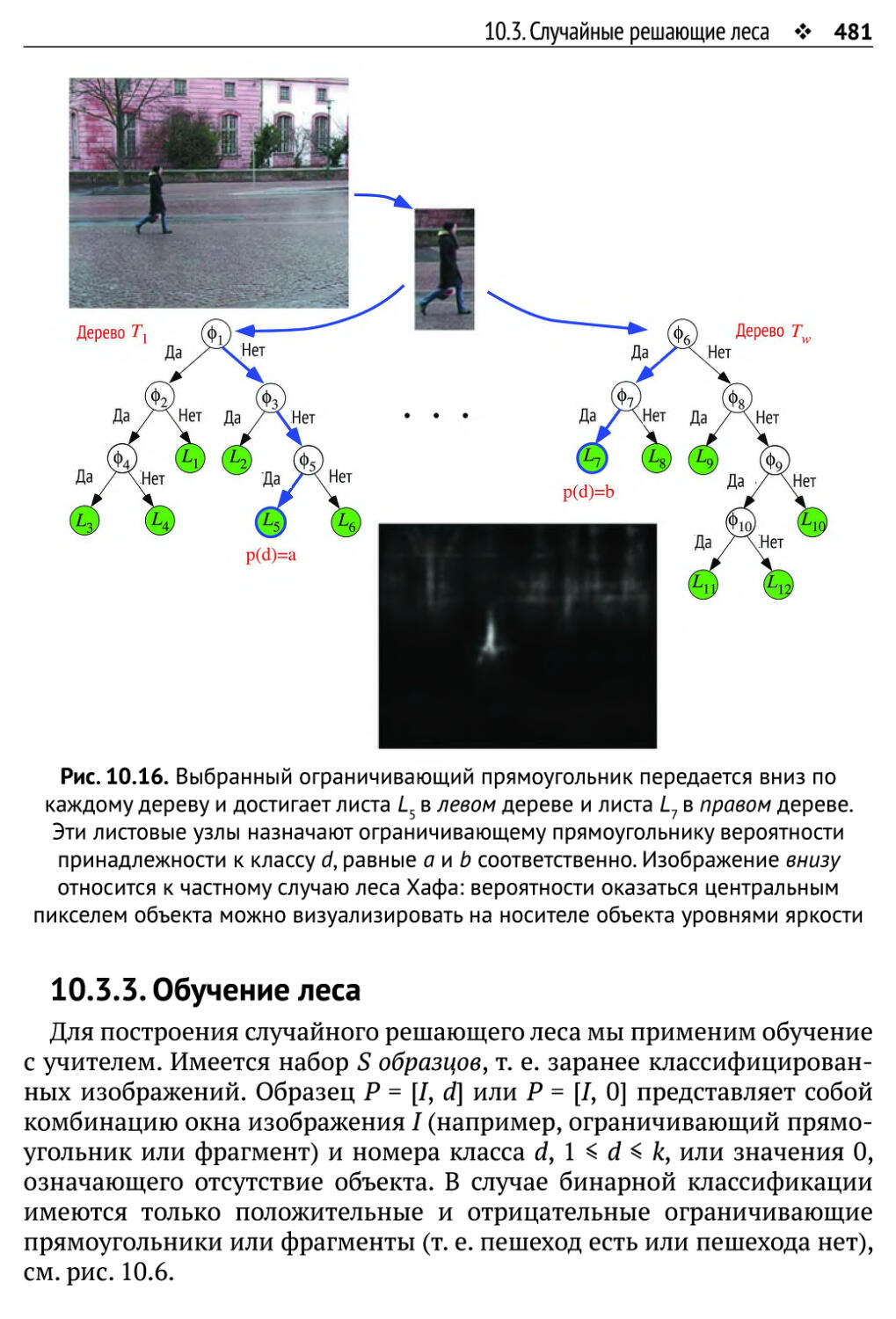
Врезка 1.5 (Парсеваль и теорема Парсеваля). Французский математик Марк-Ан-
туан Парсеваль (1755-1836) известен теоремой о том, что интеграл квадрата
функции равен интегралу квадрата ее преобразования Фурье.Тождество (1.31)
представляет собой дискретный вариант этой теоремы, в котором интегралы
заменены суммами.
Спектр и фаза. Норма L2, называемая также модулем или
амплитудой \\z\\2 = г = Va2 + Ь2, и аргумент, или фаза а = atan2(b, а), образуют
представление комплексного числа z = а + i • Ъ в полярных
координатах (г, а)3. Норма заслуживает внимания, потому что дает удобный
способ представить комплексную матрицу I в форме спектра ||1||. (Точнее,
||I||(u, v) = ||I(u, v)||2 для всех Ncols • Nrows частот (ы, v).)
Если представить типичный спектр ||1|| в виде полутонового
изображения, то получится черный прямоугольник с яркой точкой в начале
координат (представляющей среднее). Все дело в том, что значения I, как правило,
довольно малы. Чтобы повысить наглядность, спектр обычно подвергают
логарифмическому преобразованию log10(l + ||I(i/, v)||2). См рис. 1.18.
Визуализация фазовых компонент I применяется не так часто, но это
не значит, что фаза не важна для представления содержащейся в
изображении информации.
Изображение на нижнем рис. 1.18 характеризуется наличием
направленной структуры, в спектре она повернута на угол я/2. В примере на
верхнем рисунке нет преобладающего направления, поэтому нет его и
в спектре.
На рис. 1.19 видно, что однородное преобразование входного
изображения, например прибавление константы к значению каждого пикселя,
выравнивание гистограммы или инверсия значений, не изменяет
характер распределения значений в спектре.
Функция atan2(b, а) с двумя аргументами возвращает арктангенс величины b/а, т. е. угол в
диапазоне [0,2л), вычисленный с учетом знаков аргументов.
42
Глава 1. Данные изображения
Рис. 1.18. Слева: Исходные изображения Fibers и Straw.
Справа: спектры этих изображений после центрирования
и логарифмического преобразования
Пары Фурье. Исходное изображение и его преобразование Фурье
определяют пару Фурье. Приведем несколько примеров пар Фурье,
лаконично выражающих некоторые свойства преобразования Фурье:
функция I^ee преобразование Фурье I
1(х, у) ^ 1(ы, v)
/ * G(x, у) <^> I о G(u, v)
/
1(х,у)-(-1ГУ <*1
N
и
cols
N..
,V +
2 2
а • I(x, y) + b- J{x, у) **а- l(u, v) + Ъ • ](и, v).
1.2. Изображения в частотной области ♦ 45
Рис. 1.19. Левый столбец, сверху вниз: исходное низкокачественное изображение
Donkey в формате jpg (взято из открытых источников), оно же после выравнивания
гистограммы (проявились артефакты jpg) и после инвертирования уровней яркости.
Справа: на соответствующих спектрах нет существенных изменений, потому что
«структура изображения» осталась той же
44 ♦ Глава 1. Данные изображения
Первая строка выражает просто общее соответствие. Вторая строка
говорит, что преобразование Фурье свертки / с ядром (фильтром) G
совпадает с поэлементным произведением преобразований Фурье J и G;
ниже мы обсудим это важное свойство, известное под названием теоремы
о свертке, оно составляет теоретическую основу фильтрации Фурье.
Третья строка выражает уже упоминавшееся выше свойство сдвига
преобразования Фурье в центр, если пиксели исходного изображения в
шахматном порядке умножаются на +1 и -1.
Наконец, четвертая строка - это краткое выражение линейности
преобразования Фурье. Поворот основных направлений показан на рис. 1.20,
аддитивное поведение - в правом верхнем примере на рис. 1.21.
Рис. 1.20. Простые геометрические фигуры, показывающие,
что основные направления, присутствующие в изображении, в спектре
поворачиваются на 90° (например, вертикальная полоса порождает
дополнительную горизонтальную полосу в спектре)
1.2.5. Фазово-конгруэнтная модель признаков
изображения
С помощью фазовой конгруэнтности мы количественно описываем
соответствие фаз, вычисленных в окне изображения с начальной
точкой р; ниже оно выражено мерой Т Dhase(p).
1.2. Изображения в частотной области ♦ 45
Рис. 1.21. Слева вверху: идеальная волновая структура порождает неотрицательные
значения только при v= 0. Слева внизу: диагональная волновая структура
подвержена влиянию «эффекта конечного массива». Справа вверху: наложенная
диагональная волновая структура, сравните со спектром ДПФ на рис. 1.19.
Справа внизу: мы наложили очень простую маску в частотной области,
блокирующую все значения, расположенные на черной диагонали;
обратное ДПФ порождает отфильтрованное изображение, показанное
справа, диагональная структура почти убрана
Локальное преобразование Фурье в особых точках изображения.
Формула (1.23) описывает входной сигнал в частотной области как сумму
синусоидальных и косинусоидальных волн. На рис. 1.22 это показано
для одномерного сигнала: ступенчатая кривая - это входной сигнал,
который в частотной области разложен в набор синусоид и косинусоид,
сумма которых приближенно совпадает с входным сигналом. В точке,
где имеет место ступенька, все кривые находятся в одной фазе.
Обсуждая преобразование Фурье, мы заметили, что вещественно-
значные изображения отображаются в комплекснозначные
преобразования Фурье и что каждое комплексное число z = а + У-ТЬ люжно
представить в полярных координатах амплитудой ||z||2 = г = Va2 + b2 и фазой
а = arctan(b/a). Здесь мы не употребляем букву i для обозначения
мнимой единицы, потому что ниже она используется как индекс
суммирования. Согласно формуле (1.30), в начале координат частотной области
Ъ = 0, т. е. фаза постоянной составляющей а = 0.
Рассмотрим локальное преобразование Фурье с центром в пикселе
р = (х, у) изображения /. В нем используется ядро фильтра размера
(2k + l)x(2fc + 1), состоящее из базисных функций Фурье:
J(w'v)=т^Гг^ £ X/(*+и y+jy w^ •w™ - (1 -32)
yAK + I) i=_k J=_k
46
Глава 1. Данные изображения
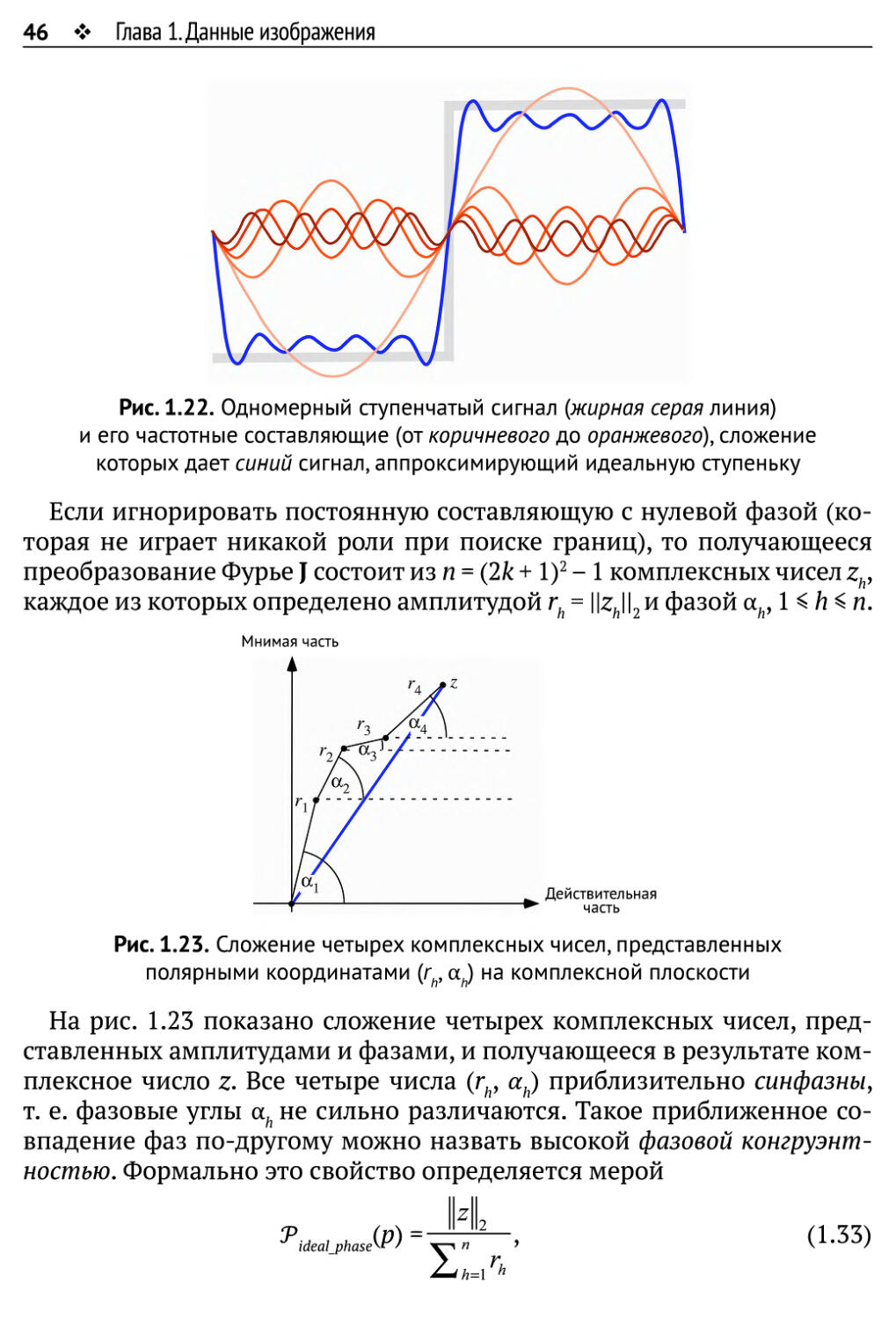
Рис. 1.22. Одномерный ступенчатый сигнал (жирная серая линия)
и его частотные составляющие (от коричневого до оранжевого), сложение
которых дает синий сигнал, аппроксимирующий идеальную ступеньку
Если игнорировать постоянную составляющую с нулевой фазой
(которая не играет никакой роли при поиске границ), то получающееся
преобразование Фурье J состоит из п = (2к + I)2 - 1 комплексных чисел zh,
каждое из которых определено амплитудой rh = |^Л||2и фазой ай, 1 < h < п.
Мнимая часть
А
Действительная
часть
Рис. 1.23. Сложение четырех комплексных чисел, представленных
полярными координатами (rh, ah) на комплексной плоскости
На рис. 1.23 показано сложение четырех комплексных чисел,
представленных амплитудами и фазами, и получающееся в результате
комплексное число z. Все четыре числа (гй, ah) приблизительно синфазны,
т. е. фазовые углы ah не сильно различаются. Такое приближенное
совпадение фаз по-другому можно назвать высокой фазовой
конгруэнтностью. Формально это свойство определяется мерой
idealphase
(Р) =
(1.33)
1.5. Цвет и цветные изображения ♦ 47
где z - сумма всех п комплексных векторов, представленных
координатами (rh, ah). Если Tideal hase(p) = 1, то фазовая конгруэнтность идеальна, а
если Tideal hase(p) = 0, тофазовые углы в точности противоположны.
Наблюдение 1.3. Локальная фазовая конгруэнтность свидетельствует о
наличии особой точки (признака) в изображении. В рамках модели фазовой
конгруэнтности ступенчатые границы представляют лишь один узкий класс
бесконечно разнообразных признаков. Фазовая конгруэнтность позволяет
выделить прямые линии, углы, «коньки крыш» и непрерывный диапазон гибридных
признаков, промежуточных между прямыми и ступеньками.
Врезка 1.6 (история фазовой конгруэнтности). Фазовая конгруэнтность
была предложена в качестве меры в работе [M.CMorroneJ. R.Ross, D. С. Burr and
R.A. Owens. Mach bands are phase dependent. Nature, vol. 324, November, 1986, p. 250-
253], где были подведены итоги исследования связей между признаками в
изображении и коэффициентами Фурье.
На рис. 1.24 приведен пример применения алгоритма Ковеси
(описывается ниже в разделе 2.4.3), реализующего модель фазовой
конгруэнтности.
Рис. 1.24. Слева: исходное изображение AnnieYukiTim.
Справа: карта границ, получающаяся в результате применения алгоритма Ковеси
1.3. Цвет и цветные изображения
Воспринимаемый цвет не имеет объективного определения. Разные
люди воспринимают цвета по-разному, да и освещение играет
немаловажную роль. В отсутствие света нет цвета, как, например, внутри
непрозрачного тела. Цвет может быть важной составной частью данных
изображения, а условные цвета ценны для визуализации данных (см.,
например, рис. 7.5). Человек может различить лишь несколько десятков
48 ♦ Глава 1. Данные изображения
оттенков серого на экране, но при этом различает от нескольких сотен
до нескольких тысяч цветов.
В этом разделе мы расскажем о различных интересных вопросах,
связанных с понятием цвета, и объясним, как устроены цветовые модели
RGB и HSI, которые часто применяются в ходе анализа цветных
изображений и для визуализации данных с помощью цвета.
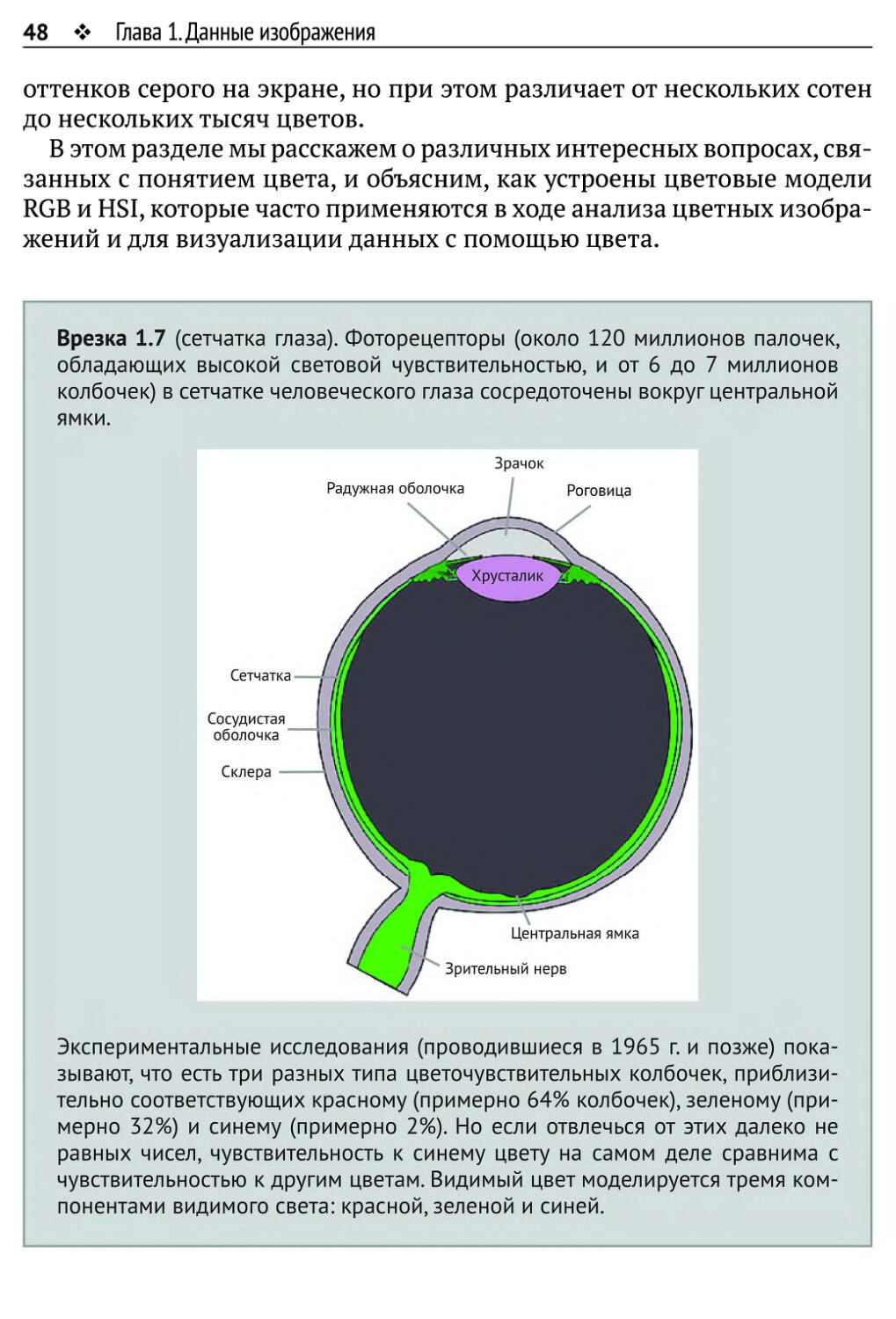
1.5. Цвет и цветные изображения
49
1.3.1. Определения цвета
«Средний человек» воспринимает цвета видимого спектра
следующим образом (напомним, что 1 нм = 1 нанометр = 10~9 м):
1) красный (приблизительно от 625 до 780 нм) и оранжевый
(приблизительно от 590 до 625 нм) соответствуют длинноволновой
части видимого спектра (за которой следует инфракрасная
область);
2) желтый (приблизительно от 565 до 590 нм), зеленый
(приблизительно от 500 до 565 нм) и голубой (приблизительно от 485 до
500 нм) занимают среднюю часть видимого спектра;
3) синий (приблизительно от 440 до 485 нм) соответствует короткой
длине волны, например так выглядит небо в ясный день, когда
солнце стоит высоко и нет ни облаков, ни загрязнения воздуха
(но длина световой волны короткая из-за влияния многослойной
атмосферы);
4) фиолетовый (приблизительно от 380 до 440 нм) - соответствует
самой коротковолновой части видимого спектра, за которой
следует ультрафиолетовая область.
Цветовые компоненты. Международная комиссия по освещению
(CIE - Commission Internationale de l'Eclairage) начиная с 1930-х гг.
определила несколько цветовых стандартов.
380
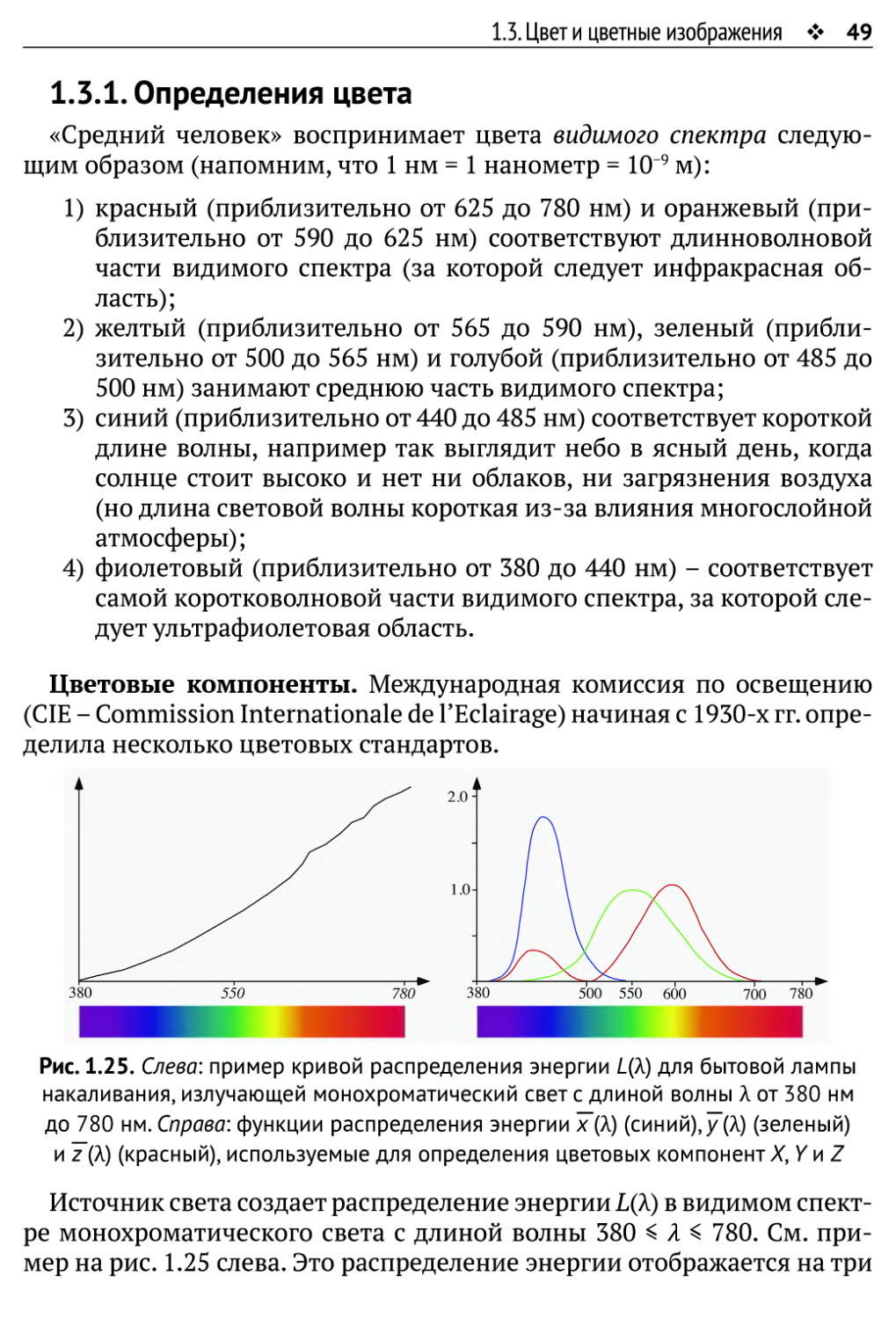
Рис. 1.25. Слева: пример кривой распределения энергии ЦХ) для бытовой лампы
накаливания, излучающей монохроматический свет с длиной волны Л от 380 нм
до 780 нм. Справа: функции распределения энергии х(Я) (синий), у (Я) (зеленый)
и z (Я) (красный), используемые для определения цветовых компонент X, Yv\Z
Источник света создает распределение энергии L(X) в видимом
спектре монохроматического света с длиной волны 380 < Я < 780. См.
пример на рис. 1.25 слева. Это распределение энергии отображается на три
50 ♦ Глава 1. Данные изображения
цветовые компоненты X, У и Z посредством интегрирования заданной
функции распределения энергии L, умноженной на весовые функции
распределения энергии х, у и z:
/•700
Х=\ ЦЛ)х(Л)йЛ, (1.34)
J400
•700
л/ии
Y = ] ЦЛ)у(Л)йЛ, (1.35)
/•700
Z = j Ь(ЛЩЛ)<1Л. (1.36)
Весовые функции х, у и z определены CIE в пределах видимого
спектра. Границы их областей определения не точно соответствуют
способности человека воспринимать более короткие (до 380 нм) или более
длинные (до 810 нм) длины волн. Все три кривые нормированы, так
чтобы их интегралы были равны:
/•700 л 700 л 700
\ х{Л)&Л = Г у(Л)&Л = Г 2(Л)6Л. (1.37)
J 400 «MOO J 400
Например, значение У моделирует яркость, или приближенно
зеленую компоненту заданного распределения L. Соответствующая кривая
распределения энергии у была построена путем моделирования
реакции «среднего человеческого глаза» на количество света. См. пример на
рис. 1.25 справа.
По цветовым компонентам X, У и Z определяются нормированные
параметры ху:
х = и у = . (1.38)
X+Y+Z X+Y+Z
Если У задано, то по известным а: и у мы можем вычислить X и Z. Если
еще определить z = Z/(X + Y+ Z), то будем иметь а: + у + z = 1, поэтому
третье значение z на самом деле лишнее.
Цветовое пространство ху, определенное CIE. Параметры х и у
определяют двумерное цветовое пространство СШ, в котором
представлены «только» цвета, но не яркость. Обычно цветовое пространство ху
представляется диаграммой цветности, изображенной на рис. 1.26. Она
занимает область 0 < х, у < 1. Эта диаграмма показывает только
цветовую гамму человеческого зрения, т. е. цвета, которые различает средний
человек; оставленные белыми части квадрата находятся в невидимой
части спектра.
1.5. Цвет и цветные изображения ♦ 51
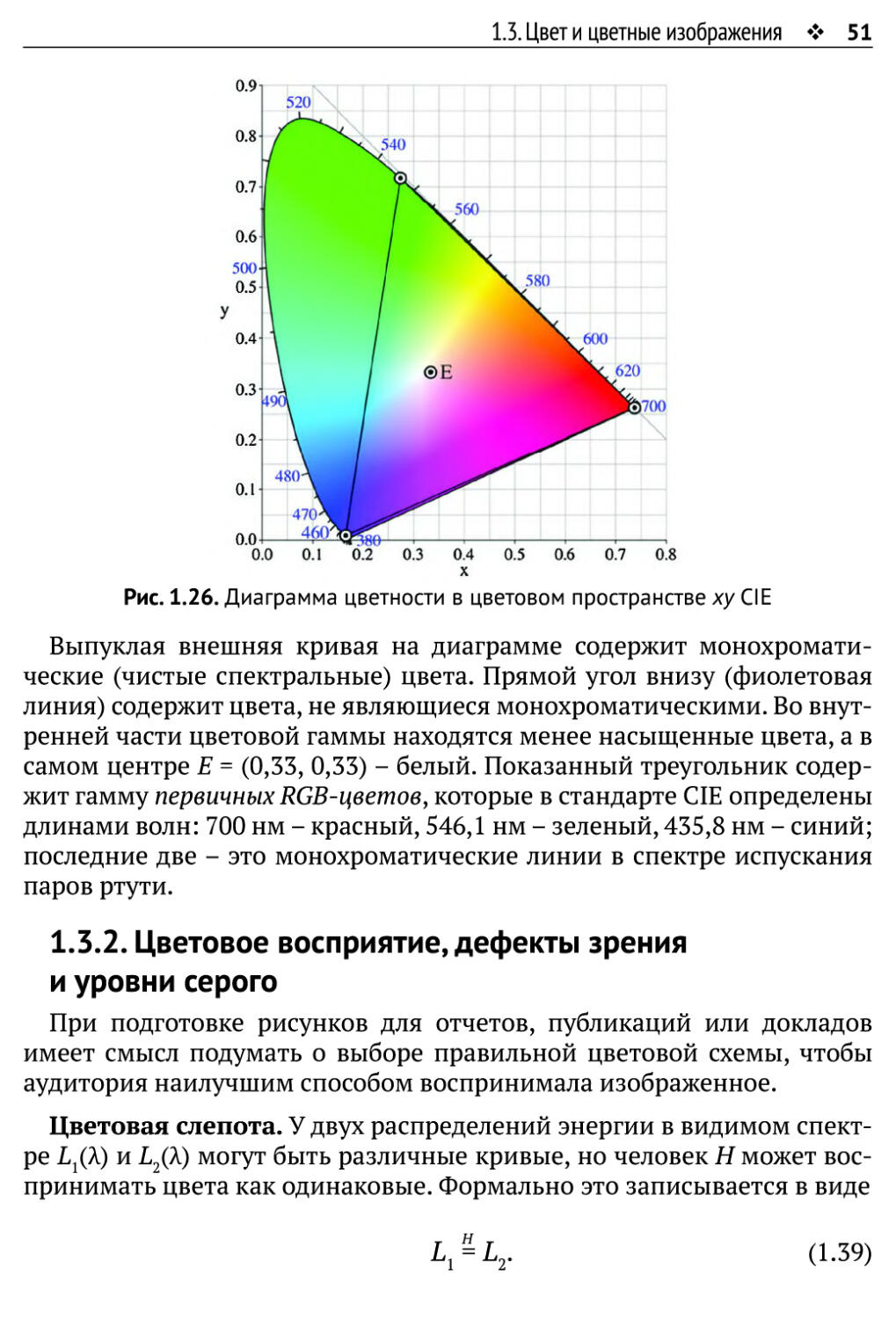
Рис. 1.26. Диаграмма цветности в цветовом пространстве xyCIE
Выпуклая внешняя кривая на диаграмме содержит
монохроматические (чистые спектральные) цвета. Прямой угол внизу (фиолетовая
линия) содержит цвета, не являющиеся монохроматическими. Во
внутренней части цветовой гаммы находятся менее насыщенные цвета, а в
самом центре Е = (0,33, 0,33) - белый. Показанный треугольник
содержит гамму первичных RGB-цветов, которые в стандарте CIE определены
длинами волн: 700 нм - красный, 546,1 нм - зеленый, 435,8 нм - синий;
последние две - это монохроматические линии в спектре испускания
паров ртути.
1.3.2. Цветовое восприятие, дефекты зрения
и уровни серого
При подготовке рисунков для отчетов, публикаций или докладов
имеет смысл подумать о выборе правильной цветовой схемы, чтобы
аудитория наилучшим способом воспринимала изображенное.
Цветовая слепота. У двух распределений энергии в видимом
спектре Lj(X) и L2(X) могут быть различные кривые, но человек Я может
воспринимать цвета как одинаковые. Формально это записывается в виде
Lx=Lr (1.39)
52 ♦ Глава 1.Данные изображения
Врезка 1.8 (различные цветовые гаммы носителей информации). Цветовая
гамма - это диапазон доступных цветов (например, «воспринимаемая»,
«печатная» или «отображаемая»). Она зависит от используемого носителя.
Изображение на экране может выглядеть совсем не так, как то же изображение,
напечатанное на бумаге, потому что у экрана и принтера разные цветовые
гаммы. Возможно, вы встречали подобное предупреждение в своем
графическом редакторе.
j Cancel
'Лг'п ~g о-: of garrut fcr or ^tmg I
Как правило, у прозрачных носителей (телевизор, экран компьютера или
слайды) цветовая гамма значительно шире, чем у печатных материалов. Это
показано на следующем (очень приблизительном!) наброске. К числу
наиболее распространенных цветовых гамм (они также называются цветовыми
пространствами) относятся, например, DCI-P3, Rec709 и sRGB.
Преобразование цветов из одной гаммы в другую - важная тема в обработке цветных
изображений.
Под цветовой слепотой понимается неспособность различить
некоторые цвета. Приблизительно в 99% случаев не отличают красный цвет
от зеленого. Полная цветовая слепота (когда человек видит только
оттенки серого) встречается крайне редко. Согласно оценкам, среди
представителей европейской расы красно-зеленой цветовой слепотой
страдают приблизительно 8-12% мужчин и 0,5% женщин.
Человек с нормальным цветовым зрением видит среди точек на
рис. 1.27 цифру 5, а люди с красно-зеленой цветовой слепотой - цифру 2.
Наблюдение 1.4. Если для презентации используются красные и зеленые
цвета, то в европейской аудитории указанный выше процент людей может
увидеть не то, что вы хотели показать.
Врезка 1.9 (Дальтон, Ишихара и цветовой тест Ишихары). Красно-зеленая
цветовая слепота была открыта химиком Дж.Дальтоном (1766-1844), обычно
ее называют дальтонизмом. Японский офтальмолог С. Ишихара (1879-1963)
со своим ассистентом (врачом, страдавшим дальтонизмом) разработал серию
тестов для диагностики цветовой слепоты.
п
1.3. Цвет и цветные изображения ♦ 55
Рис. 1.27. Тест Ишихары. Большинство людей видят цифру 5,
но некоторые - цифру 2
Алгебра цветового зрения. Под сложением двух цветов L и С
понимают суперпозицию световых спектров L(X) и С(А). Экспериментально
установлено (Р. П. Фейнман, 1963 г.), что
Lj + С = L2 + С, если Lx = L2; (1.40)
aLx = aL2, если Ьг=Ь2 и 0 < а < 1. (1-41)
Эти уравнения определяют (для испытуемого Я) алгебру цветового
восприятия посредством линейных комбинаций общего вида aL + ЪС.
Если вы захотите поставить подобные эксперименты, то имейте в
виду, что в компьютерных мониторах применяется гамма-коррекция
с некоторым у > 0. При задании значения цветового канала и = к/2а
(например, для каналов R, G, В) на экране на самом деле отображается
значение иу, где у < 1 означает гамма-сжатие, ау >1 - гамма-расширение.
На восприятие изменений цвета влияет значение y-
Основные типы цветового восприятия. Люди воспринимают
цвета по-разному; «цвет» - это физиологическое явление. Но принято
считать, что желтый (верхний ряд в цветовой пирамиде на рис 1.28),
красный (правый столбец), зеленый (левый столбец) и синий (нижний ряд)
определяют четыре основных типа цветового восприятия.
54 ♦ Глава 1. Данные изображения
Чтобы избежать недопонимания, связанного с зеленым и красным
цветами, можно, например, использовать для презентации желтый,
красный и синий в качестве основных цветов.
Уровни серого. Уровни серого (или уровни яркости) - это не цвета,
они описываются светимостью (физической интенсивностью) или
яркостью (воспринимаемой интенсивностью). Обычно используется
равномерная шкала уровней яркости, например:
uk=k/2a для 0<к<2а, (1.42)
1.5. Цвет и цветные изображения ♦ 55
где и0 = 0 соответствует черному, а ы2<м ~ 1 - белому. В главе 1 мы приняли
решение представлять такие уровни яркости целыми числами 0, 1,...,
G =2а- 1, а не дробями от 0 до 1.
Щ-Ц-
~ J п ' I. Пищ» innmii^^^^^M
1 -4-4- —■
ТТТТТТТД
Н5в1
Рис. 1.28. Четыре основных типа цветового восприятия
Оба квадрата на верхнем рис. 1.29 имеют одну и ту же постоянную
яркость. Но человек воспринимает отношение яркостей. На нижнем
рис. 1.29 во всех трех случаях отношение яркостей внутреннего и
внешнего прямоугольников составляет 5:6. Визуально очень трудно
различить немного различающиеся, но очень темные оттенки серого.
Человеческий глаз гораздо лучше замечает очень яркие оттенки серого.
Рис. 1.29. Вверху: два квадрата одинаковой яркости.
Внизу: три примера отношения уровней яркости 5:6
56 ♦ Глава 1. Данные изображения
1.3.3. Представления цвета
На рис. 1.4 показано цветное RGB-изображение и его представление в
трех скалярных каналах, по одному для красной, зеленой и синей
компонент. Цветовая модель RGB аддитивна: добавление цвета, т. е.
увеличение значений в скалярном представлении, приближает цвет к белому.
Это стандартный способ представления цветов на экране. Но для печати
используются субтрактивные цветовые модели: добавление цвета
означает увеличение количества краски, а значит, приближает цвет к черному.
Цветовое пространство RGB. Предположим, что 0 < R, G, В < Gmax,
и рассмотрим многоканальное изображение / со значениями пикселей
u = (R, G, В). Если Gmax = 255, то имеется 16777216 различных цветов,
например: и = (255,0,0) - красный, и = (255,255,0) - желтый и т. д.
Множество всех возможных значений RGB определяет RGB-куб -
стандартное представление цветового пространства RGB. См. рис. 1.30.
1.5. Цвет и цветные изображения
57
Сиреневый
Красный
R
Черный
Голубой
Зеленый
G
Желтый
Рис. 1.30. RGB-куб, построенный
на осях Красный, Зеленый, Синий.
Показан один цвет q, определенный
значением тройки (/?, 6, В)
Диагональ куба, соединяющая вершины Белый (255, 255, 255) и
Черный (0,0,0), - это геометрическое место всех уровней серого (и, и, и), не
являющихся цветами. В общем случае точка q = (R, G, В) внутри или на
границе RGB-куба определяет либо цвет, либо уровень серого, а среднее
R + G + B
М =
(1.43)
равно интенсивности цвета или уровня серого q.
Цветовое пространство HSI. Рассмотрим секущую плоскость RGB-
куба, перпендикулярную диагонали уровней серого, и пусть точка
q = (R, G, В) лежит на этой плоскости, но не принадлежит диагонали
(см. также рис. 1.33). Получившееся сечение мы можем представить
абстрактным кругом, игнорируя тот факт, что на самом деле сечение куба
плоскостью является многоугольником. См. рис. 1.31.
Рис. 1.31. Ось интенсивности направлена вдоль диагонали уровней серого
в RGB-кубе. В сечении куба плоскостью выделим один цвет (в данном случае
красный) в качестве опорного.Точку q можно описать интенсивностью (средним
значением), оттенком - углом относительно опорного цвета (в данном случае
красного, угол отсчитывается, скажем, против часовой стрелки) и насыщенностью,
которая измеряется расстоянием до оси интенсивности
58 ♦ Глава 1. Данные изображения
В этом круге мы зафиксируем один опорный цвет, на рис. 1.31 это
красный. Положение точки q внутри круга однозначно определяется
углом Н (оттенок) и приведенным расстоянием S (насыщенность) до
точки пересечения с диагональю уровней серого. Формально
Н =
S если B<G (144)
2п-8 если B<G
где
(/? — СЛ -\- ( R — ИЛ
S= arccos—, в диапазоне [0, л), (1.45)
2^(R-G)2+(R-B)(G-B)
mm\R,G,B\ /i Ar.
S= 1-3 l » » К (1.46)
R + B + G
Таким образом, мы определили цветовую модель HSL Мы будем
обозначать интенсивность буквой М, а букву I оставим для обозначения
изображений.
Пример 1.2 (примеры RGB и HSI). Для уровней серого (и, и, и) при и ф 0
интенсивность М= и, а насыщенность S = 0, но оттенок Я остается неопределенным,
поскольку не определен угол б (из-за деления на 0). Для черного цвета (0, 0, 0)
интенсивность М = 0, а насыщенность и оттенок не определены.
Если не считать этих случаев, которые в RGB-кубе соответствуют не цветам,
то преобразование из RGB в HSI взаимно однозначно, т. е. значения HSI можно
преобразовать обратно в RGB. Оттенок и насыщенность могут представлять
векторы RGB относительно предполагаемой фиксированной интенсивности.
Для красного цвета (Gmax, 0,0) интенсивность М= Gmax/3, оттенок Н = 0°
(примечание: красный цвет был выбран в качестве опорного), а насыщенность
S = 1. Насыщенность 5 всегда равна 1, если R = 0, или G = 0, или В = 0.
Для зеленого цвета (0, Gmax, 0) интенсивность М = Gmax/3 и насыщенность
5=1; имеем S = arccos(-0,5), т. е. 6 = 2л/Ъ иН= 2я/3, поскольку В = 0 ^ G = Gmax.
Для синего цвета (0, 0, Gmax) также получаем 8 = 2я/3, но Н = 4я/3, поскольку
В = G > G = 0.
max
Предположим, что мы линейно отобразили 5 и Я в множество
уровней серого {0, 1,..., Gmax} и визуализировали получившиеся
изображения. Тогда, например, оттенок точки (Gmax, ev s2) может быть близок к
черному или к белому в зависимости от небольшого изменения ех и е2.
Почему? Этот эффект показан на левом нижнем рис. 1.32.
На левом верхнем рис. 1.32 показана одна из цветовых таблиц,
используемых для проверки камеры, которую предполагается
использовать в приложениях компьютерного зрения. Она содержит три строки
1.5. Цвет и цветные изображения ♦ 59
очень точно (одинаково) окрашенных квадратиков, пронумерованных
от 1 до 18, и одну строку квадратиков с уровнями серого. Если сделать
фотографию этой таблицы, то результат будет зависеть от освещения.
В предположении, что свет монохроматический, все серые квадратики
должны выглядеть абсолютно одинаково в каналах красного (не
показан), зеленого, синего и интенсивности. Канал насыщенности на
рисунке справа внизу показывает, что для уровней серого насыщенность
имеет нулевое значение, присвоенное программой. Конечно, в
программе не может быть «неопределенных» случаев. Отметим, что
оттенок опорного красного цвета (квадратик 15) «прыгает» между белым и
черным, как и следовало ожидать.
Рис. 1.32. Вверху: цветовая испытательная таблица, предложенная
компанией Macbeth™, и канал зеленого. В середине: каналы синего
и интенсивности. Внизу: каналы для визуализации оттенка
и насыщенности с помощью уровней серого
60 ♦ Глава 1. Данные изображения
Врезка 1.12 (Иттен и цветовое восприятие). Иоганнес Иттен (1888-1967,
Швейцария) написал оказавшую большое влияние книгу «Искусство цвета»,
в которой рассматривал контрастность, насыщенность, оттенок и цвет с точки
зрения человеческой психологии. Вкратце, он придавал цветам следующие
смысловые значения:
• красный: материя в состоянии покоя, цветторжественности и укрывистости;
• синий: вечно мятущийся ум, расслабление и непрерывное движение;
• желтый: свирепый и агрессивный, размышления, невесомый;
• оранжевый: ярко светящийся, легкий и порывистый, энергия и развлечения,
непопулярный цвет (впрочем, не стоит так говорить о нем в Нидерландах);
• фиолетовый: античная пурпурная краска делалась из морских улиток и
ценилась дороже золота,лишь царям дозволялось носить пурпурные одежды;
цвет власти, религии и могущества или смерти и тьмы, цвет одиночества, но
также преданности и духовной любви;
• зеленый: покоящийся в центре, не активный и не пассивный, естественный,
жизнь и весна, надежда и доверие, тишина и расслабленность, здоровый,
но также отравленный.
Иттен также ассоциировал с цветами геометрические фигуры, на рисунке
выше приведено несколько примеров.
Мы завершим этот краткий раздел о цвете замечанием, сделанным
Леонардо да Винчи (1452-1519); см. [Записные книжки / Леонардо да
Винчи. - М.: Эксмо, 2006]:
Замечание 273: эффект цвета в камере-обскуре.
Края окрашенного предмета, рассматриваемые через маленькую дырочку
выглядят более отчетливо, чем центральные области.
Края изображений любого цвета, рассматриваемые через небольшое
отверстие в темной камере, всегда выглядят резче, чем средняя часть.
В своих записных книжках Леонардо да Винчи оставил много
интересных замечаний о цвете.
1.4. Упражнения ♦ 61
1.4. Упражнения
1.4.1. Упражнения по программированию
Упражнение 1.1 (первое знакомство с программированием
обработки изображений). Напишите (например, на Java, C++ или Matlab)
программу, выполняющую следующие действия:
1) загрузить цветное (RGB) изображение / в формате без потери
информации, например bmp, png или tiff, и показать его на
экране;
2) отобразить гистограммы всех трех цветовых каналов /;
3) двигая мышь внутри изображения, для текущего пикселя р
вычислить и отобразить
a) внешнюю рамку (см. пояснение ниже) квадратного окна W
размера 11 * 11 вокруг пикселя р (т. е. р будет центральной
точкой этого окна);
b) (над этим окном или в отдельном окне команд) координаты
пикселя р под курсором мыши и значения компонентов RGB
изображения в этой точке;
c) (под этим окном или в отдельном окне команд)
интенсивность [R(p) + G(p) + В(р)]/Ъ в точке р;
d) среднее piw и стандартное отклонение aw ;
4) рассмотрите примеры окон изображения W (для выбранных
вами изображений), в которых вы видите «однородные
распределения значений изображения», и окон, в которых присутствуют
«неоднородные области». Попытайтесь дать определение
«однородного» и «неоднородного» в терминах гистограмм, среднего и
дисперсии.
Внешней рамкой квадратного окна 11 х 11 является квадрат 13><13
(который можно нарисовать, например, белым цветом) с центром в точке
нахождения курсора. Вы должны динамически перерисовывать
внешнюю рамку окна 11х 11 при перемещении курсора.
Вместо этого можно было бы показать окно Их 11 в отдельном
фрейме на экране. Подходите к задаче творчески: ваше решение может быть
даже более элегантным, чем предложено в книге. Также приветствуется
поиск функционально эквивалентных решений (пользователю
предлагается одна и та же информация, время работы примерно одинаково и
т. д.).
62 ♦ Глава 1. Данные изображения
Врезка 1.13 (почемуне форматjpg?).JPG -формате потерей информации,т.е.
сжатое изображение отличается от исходного, поэтому он, вообще говоря,
непригоден для анализа изображений. При использовании форматов bmp, raw
или tiff механизм сжатия не изменяет значения пикселей. В изображениях в
формате jpg часто наблюдается блочная структура с блоками 8*8 (при
увеличении), это следствие низкокачественного сжатия.
Упражнение 1.2 (мера данных на последовательности
изображений). Определите три меры данных 2).(t), i = 1,2, 3 для анализа
последовательности изображений. Ваша программа должна выполнять
следующие действия:
1) прочитать входную последовательность изображений (например,
в формате VGA), содержащую не менее 50 кадров;
2) вычислить определенные вами меры £>(.(t), i = 1, 2, 3 для каждого
кадра;
3) нормировать полученные функции, так чтобы у всех них были
одинаковые средние и дисперсии;
4) сравнить нормированные функции, пользуясь нормой Lv
Обсудите степень структурного подобия между мерами в
зависимости от выбранной последовательности изображений.
Упражнение 1.3 (различное влияние амплитуды и фазы в частотном
пространстве на результаты фильтрации изображений).
Предполагается, что у вас есть доступ к программе БПФ для прямого и обратного
двумерного ДПФ. Задача состоит в том, чтобы исследовать проблему
оценки информации, содержащейся в амплитуде и фазе
преобразования Фурье.
1. Переведите изображения одинакового размера в частотную
область. Отобразите получившиеся комплексные числа в
амплитуды и фазы. Возьмите амплитуды одного изображения и фазы
другого изображения и переведите получившийся массив
комплексных чисел назад в пространственную область. Кто
«победил», т. е. какое изображение вы можете различить: источник
амплитуд или источник фаз?
2. Возьмите скалярные изображения какой-нибудь однородной
текстуры; переведите их в частотную область и модифицируйте
амплитуду или фазу преобразования Фурье неким
единообразным способом (одинаковым для всех частот), перед тем как пере-
1.4. Упражнения ♦ 63
ходить обратно в пространственную область. Какая модификация
приводит к более значительному изменению изображения?
3. Проделайте те же операции и тесты для набора изображений
человеческих лиц.
Обсудите полученные результаты. Каким образом единообразные
изменения (разной степени) амплитуды или фазы изменяют
содержащуюся в изображении информацию?
Упражнение 1.4 (аппроксимация цветового пространства HSI
плоскостями сечения). Пусть G = 255. Рассечем RGB-куб плоскостью П ,
' J max ' ц'
перпендикулярной диагонали уровней серого и проходящей через
точку (и, и, и) на этой диагонали, где 0 < и < 255. Любое сечение (т. е.
пересечение Пи с RGB-кубом) представляется одним изображением 1и размера
N*N, где значение u = (R, G, В) пикселя с координатами (х, у) либо
определено ближайшей целочисленной точкой в RGB-кубе (или средним по
всем ближайшим точкам, если их несколько), если расстояние до
ближайшей точки меньше V2, либо равно некоторому значению по
умолчанию (скажем, черное). Решите следующие задачи:
1) напишите программу, которая показывает RGB-изображения 1и
для ы = 0, м = 1,...,и = 255 (можете задать значение и в диалоговом
окне или запустить непрерывную анимацию);
2) также покажите (скалярные) значения насыщенности вместо
RGB-значений. На рис. 1.33 показаны результаты для и = 131;
Рис. 1.33. Сечение RGB-куба, проходящее через точку и = 131. Показано RGB-
изображение /ш и значения насыщенности для одной и той же секущей плоскости
3) можете взять фиксированное значение N > 30 (размер
изображения) или попросить пользователя выбрать N из заданного
диапазона.
64 ♦ Глава 1. Данные изображения
1.4.2. Упражнения, не требующие программирования
Упражнение 1.5. Докажите тождество (1.4).
Упражнение 1.6. Кем был Фурье? Когда было придумано быстрое
преобразование Фурье? Какое отношение преобразование Фурье имеет
к оптической системе линз?
Упражнение 1.7. Рассмотрим изображение размера N*N. Докажите,
что умножение на (-1)х+у в пространственной области приводит к сдвигу
на N/2 (в обоих направлениях) в частотной области.
Упражнение 1.8. В развитие примера 1.2 вручную преобразуйте еще
несколько (простых) RGB-значений в соответствующие HSI-значения.
Упражнение 1.9. Пусть (8, S, М) - представление цвета в
пространстве HSI. Обоснуйте следующие шаги восстановления компонент RGB в
описанных ниже частных случаях:
• если5е[0,2я/3],тоВ = (1-5)М;
• если 8 е [2я/3,4я/3], то R = (1 - S)M;
• если 8 £ [4я/3, 2я], то G = (1 - S)M.
Как вычислить остальные компоненты в каждом из этих случаев?
Упражнение 1.10. В цветовом пространстве RGB, предложенном CIE
(которое моделирует восприятие цветов человеком), скаляры R, G и В
могут быть отрицательными. Предложите физическую интерпретацию
(разумеется, мы не можем вычесть свет из заданного спектра).
Глава
Обработка изображений
В этой главе вводятся основные понятия, связанные с
преобразованием одного изображения в другое, обычно с целью повышения качества
или для других надобностей, определяемых более сложным контекстом
компьютерного зрения.
2.1. Точечные, локальные и глобальные
операторы
Когда изображения записываются вне помещения (типичный для
компьютерного зрения случай), возникают специфические трудности по
сравнению со съемкой в помещении: качество освещения, размытость
из-за движения или внезапные изменения на сцене. На рис. 2.1
показаны изображения, снятые из автомобиля (для системы помощи водителю,
основанной на компьютерном зрении). Нежелательные данные
называются шумом. Мы видим три примера таких «нежелательных данных».
В первом случае наша цель - преобразовать изображения, так чтобы в
результате получились изображения, «как будто сделанные при
равномерном освещении». Во втором случае мы хотели бы повысить резкость
и устранить размытие. В третьем случае требуется устранить шум.
В этом разделе мы предложим эффективные методы
предварительной обработки данных для подготовки к последующему анализу
изображения.
2.1.1. Градационные функции
Мы преобразуем изображение / в изображение Inew того же размера,
отображая с помощью градационной функции g уровень яркости и в
пикселе р изображения / в уровень яркости v = g(u) в точно так же
расположенном пикселе изображения Inew. Поскольку это изменение зависит
только от значения и в точке р, говорят также о точечном операторе,
66
Глава 2. Обработка изображений
определенном градационной функцией g. Если наша цель заключается в
том, чтобы Inew обладала некоторыми свойствами, определенными в
терминах ее гистограммы, то мы говорим о преобразовании гистограммы.
Рис. 2.1. Вверху: два изображения SouthLeft и SouthRight, снятые в один и тот же
момент времени, но с разной яркостью; см. сопровождающие гистограммы
уровней яркости. Слева внизу: размытие из-за дождя на изображении Wiper.
Справа внизу: шум на сцене Uphill, снятой ночью
Выравнивание гистограммы. Мы преобразуем скалярное
изображение /, так чтобы в новом изображении Inew все уровни яркости
встречались с одинаковой частотой. Цель заключается в том, чтобы добиться
выполнения условия
N -N
Н, (и) = const = cols '
G-x+1
(2.1)
для всех и G {0,1,..., Gmax}.
К сожалению, в общем случае это невозможно, т. к. одинаковые
значения в /должны отображаться в одинаковые значения в Inew. Например,
бинарное изображение / нельзя преобразовать в полутоновое
изображение Inew с выровненной гистограммой (даже если бы мы имели
непрерывное аналоговое бинарное изображение, к тому же ограничения
2.1.Точечные,локальные и глобальные операторы
67
цифровой техники вносят свой вклад в невозможность идеального
выравнивания). Описанное ниже преобразование - лишь приближение к
недостижимому идеалу.
Пусть дано скалярное изображение /размера Ncols><Nrows с абсолютными
частотами Н^и) для 0 < и ^ Gmax. Мы преобразуем / в изображение J
такого же размера, применяя следующую градационную функцию
g(u) = с, (и) • Gmax, (2.2)
где Cj - интегральная функция распределения. На рис. 2.2
иллюстрируется такое выравнивание гистограммы.
new
Рис. 2.2. Слева: Входное изображение RagingBuLl (взято из открытого источника)
и его гистограмма. Справа: То же изображение после выравнивания гистограммы
Нетрудно доказать свойство выравнивания для преобразования
гистограммы (2.2), воспользовавшись тем фактом, что интегральная
функция распределения ^монотонно возрастает. Относительная
гистограмма hl (и) соответствует оценке функции плотности распределения,
Cj (и) - оценке функции распределения вероятностей, a hInew(u) - оценке
плотности равномерного распределения.
Линейное масштабирование. Предположим, что в гистограмме
изображения / положительные значения сосредоточены в
ограниченном интервале. Наша цель - сделать так, чтобы все значения,
встречающиеся в I, были линейно распределены во всем интервале от 0 до Gmax.
Положим и. = min{/ (х, у): (х, у) £ Q}, ытах = тах{/ (х, у): (х, у) е О} и
а = -и
и Ъ =
и —и ■
max mm
g(u) = b(u + a).
(2.3)
(2.4)
в но-
B результате пиксели, имевшие в изображении / значение ип
вом изображении / будут иметь значение 0, а пиксели, имевшие в изо
68
Глава 2. Обработка изображений
бражении / значение итах, в новом изображении будут иметь значение
Gmax. Это показано на рис. 2.3, который послужит также иллюстрацией
к обсуждению корректности преобразования гистограммы,
определенного функцией (2.4).
Рис. 2.3. График градационной
функции линейного
масштабирования, определенной
двумя точками (и . , 0) и (и ,G )
" ' х mm' ' v max' max'
Условное масштабирование. Приведем еще один пример
градационной функции - мы хотим отобразить изображение / в изображение
/ , сохранив среднее и дисперсию. Для такого условного масштабиро-
new
вания положим
a = jUj
Mi и
b = ^
°J Oj
(2.5)
g(u) = b(u + a). (2.6)
Теперь отобразим уровень яркости и в пикселе р изображения / в
новый уровень v = g(u) того же пикселя р в Jnm. Нетрудно показать, что
Vj„ew = Viи aJnew = аг ^т0 та же ноРмиРовка>чт0 в формуле (1.12), где мы
нормировали меры данных.
2.1.2. Локальные операторы
Для заданного изображения / размера Ncols*Nrows рассмотрим
скользящие окна W размера (2к + 1)х(2к + 1) с центром в качестве начальной
точки р. Начальная точка обегает все возможные позиции пикселей в /
и таким образом перемещает окно по изображению. В каждой позиции
окна мы выполняем локальную операцию, ее результат определяет новое
значение в точке р. В итоге исходное изображение / преобразуется в
новое изображение /.
Два примера: локальное среднее и локальный максимум. В
качестве первого примера локальной операции возьмем вычисление
локального среднего J(p) = piw :
2.1.Точечные, локальные и глобальные операторы ♦ 69
+к +к
^(7)=р^55/(х+^+л
(2.7)
для р = (х, у).
Другой пример - вычисление локального максимума
J(p) = max{/ (х + i,y + j):-k<i<kA-k<j< k]
для р = (х, у). См. рис. 2.4.
(2.8)
... В ...с
/
Рис. 2.4. Слева вверху: исходное изображение SetlSeql с Ncols = 640.
Справа вверху: локальный максимум для к = 3. Слева внизу: локальный минимум
для к= 5. Справа внизу: локальный оператор с ядром фильтра Зх3,
показанным в средней части рис. 2.5
Окна с центром в точке р, которые не целиком находятся внутри /,
нуждаются в специальной «стратегии обработки краевых пикселей».
Общего согласия относительно такой стратегии не существует. Один из
вариантов - выполнить ту же самую локальную операцию, но в
меньшем окне - применим к обеим рассмотренным выше операциям.
Линейные операторы и свертка. Линейный локальный оператор
определяется сверткой изображения / в точке р = (х, у) с ядром
фильтра ^следующим образом:
+к +к
I +К +К
J(j>) = l*W{p) = -YdY<wi.j-I(x+i>y + fi>
(2.9)
i=-k j=
70
Глава 2. Обработка изображений
где веса w.. е Е и масштабный коэффициент S > 0. Аргументы в
формуле (2.9) выходят за пределы /2, если р близка к краю носителя
изображения. Существует теорема, утверждающая, что применение правила по
модулю концептуально эквивалентно периодическому продолжению
изображения / с П на всю сетку Ж2.
Ядро фильтра W полностью определено массивом весов размера
(2k + l)x(2fc + 1) и масштабным коэффициентом S. Обычно ядра
линейных локальных операторов представляют, как показано на рис. 2.5.
wu
w2l
w31
wl2
w22
W32
w13
W23
w33
/s
1
2
1
0
0
0
-1
-2
-1
/9
1
1
1
1
1
1
1
1
1
/9
Рис. 2.5. Слева: общее представление ядра фильтра 3*3.
В середине: ядро фильтра, примененного на рис. 2.4 справа внизу,
аппроксимирующее частную производную по х.
Справа: ядро прямоугольного фильтра 3*3
Выражение (2.7) - пример линейного локального оператора,
известного под названием прямоугольный фильтр (box filter). В нем все веса
равны 1, a S = (2к + I)2 - сумма всех весов.
Общие сведения о локальных операторах. Приведем сводку
свойств локальных операторов.
1. Операции ограничены окнами, обычно квадратными и
нечетного размера (2fc + l)x(2k + 1). Конечно, с точки зрения изотропности
(т. е. инвариантности относительно вращения) предпочтительнее
было бы использовать приблизительно круглые окна, но с
прямоугольными проще работать.
2. Окно перемещается по изображению в выбранном порядке
сканирования (обычно стремятся к полному сканированию, так
чтобы каждый пиксель рано или поздно оказался начальным
пикселем окна).
3. Не существует общего правила, как обращаться с пикселями,
расположенными близко к краю изображения (когда окно не
помещается в области изображения целиком), однако их тоже надо
как-то обрабатывать.
4. Выполняемая над пикселями окна операция должна быть
одинаковой при любом положении окна, она определяет назначение
локального оператора.
2.1.Точечные, локальные и глобальные операторы ♦ 71
5. Результат операции может заменять значение пикселя исходного
изображения /, совпадающего с начальной точкой окна, и тогда
мы имеем последовательный локальный оператор, который
«волной смывает» исходные значения (в этом случае окна локального
оператора содержат как исходные, так и уже обработанные
значения пикселей). Альтернативно результаты могут
записываться в другой массив, а исходный остается неизменным - тогда мы
имеем параллельный локальный оператор, название говорит о
том, что такой оператор теоретически можно реализовать с
помощью специализированного оборудования, обеспечивающего
распараллеливание.
Если к = 0 (т. е. окно состоит всего из одного пикселя), то говорят о
точечном операторе. Если к настолько велико, что все изображение
покрывается одним окном, то оператор называется глобальным.
Двумерное преобразование Фурье изображения - пример глобального
оператора.
Врезка 2.1 (Замперони). Количество предложенных в литературе операторов
обработки изображений огромно, что объясняется разнообразием данных и
конкретных приложений. В книге [R. Klette and P. Zamperoni. Handbook of Image
Processing Operators. Wiley, Chichester, 1996] подробно описаны многие
распространенные точечные, локальные и глобальные операторы.
В память о Пьеро Замперони (1939-1998), выдающегося просветителя в
области распознавания образов, Международная ассоциация по
распознаванию образов (IAPR) учредила награду его имени за лучшую студенческую
работу, доложенную на Международной конференции по распознаванию
образов (ICPR), которая проводится раз в два года под ее эгидой.
2.1.3. Фильтрация Фурье
Обратное двумерное ДПФ (см. (1.23)) переводит преобразование
Фурье I из частотной области назад в пространственную. Его
результатом является вещественная функция / при условии, что I удовлетворяет
свойству симметричности (1.29). Следовательно, на любое изменение в
частотной области налагается такое ограничение.
Фильтрация Фурье. Обратное двумерное ДПФ можно прочитать
следующим образом: комплексные числа \(и, v) - это коэффициенты Фурье
функции I, определенные для различных частот и и v. Каждый
коэффициент Фурье умножается на комбинацию синуса и косинуса (см. фор-
72 ♦ Глава 2. Обработка изображений
мулу Эйлера (1.22)), и сумма этих комбинаций образует изображение I.
Короче говоря, изображение / представляется линейной комбинацией
базисных функций - корней из единицы в комплексной плоскости, -
а коэффициенты Фурье определяют форму этого представления.
Это означает, что если мы модифицируем один из коэффициентов
Фурье (и симметричный ему коэффициент в силу ограничения
симметричности) до применения обратного двумерного ДПФ, то получим
модифицированную функцию /.
Чтобы выполнить линейное преобразование изображения /, у нас
есть две возможности.
1. Модифицировать данные изображения с помощью линейной
свертки
J(x,y) = (I*G)(x,y) = X £ I(iJ)-G(x-i,y-j) (2.10)
i=0 j=0
в пространственной области, где G - ядро фильтра (называемое
также функцией свертки, или просто сверткой). Функция
/является профильтрованным изображением.
2. Модифицировать двумерное ДПФ I изображения /, поэлементно
умножив значения I на соответствующие комплексные
элементы G [т. е. выполнив операцию I(u, v) • G(u, v)]. Мы обозначаем
эту операцию I ° G (не путайте с умножением матриц).
Получающийся комплексный массив преобразуется с помощью обратного
двумерного ДПФ в модифицированное изображение /.
Интересно, что в обоих случаях мы получаем одинаковые результаты
при условии, что G - двумерное ДПФ G. Этот факт составляет
содержание теоремы о свертке:
I* G равно обратному двумерному ДПФ I ° G. (2.11)
Таким образом, свертка в пространственной области и поэлементное
умножение в частотной области дают одинаковые профильтрованные
изображения. Однако в случае свертки мы лишаем себя возможности
применить зависящие от частоты функции фильтрации в частотной области.
Шаги фильтрации Фурье. Пусть дано изображение / и комплексная
функция фильтрации G (обладающая свойством симметричности (1.29))
в частотной области. Применить программу БПФ для выполнения
описанных ниже действий (если программа БПФ того требует,
предварительно преобразовать изображение J в больший массив размера 2"*2"):
2.1.Точечные, локальные и глобальные операторы
73
1) с помощью программы БПФ перевести изображение / в
частотную область, получив комплексную матрицу I;
2) поэлементно умножить I на комплексную функцию
фильтрации G;
3) с помощью программы БПФ для обратного ДПФ перевести
результаты назад в пространственную область.
Функцию фильтрации G можно получить как результат применения
преобразования Фурье к ядру фильтра G в пространственной области.
Но обычно функции фильтрации проектируют прямо в частотной
области.
Пример 2.1. Прямоугольный фильтр - это линейная свертка в
пространственной области. Его ядро определяется весами G(x, у) = \/а для (х, у) в окне размера
(2к + 1)х(2к + 1) с центром в начале координат, при этом а = (2к + I)2. Вне этого
окна G(x, у) = 0.
Двумерное ДПФ этой функции G характеризуется амплитудами, близкими
к 1, при низких частотах и резким убыванием амплитуды почти до нуля при
высоких частотах.
Преобразование Фурье G функции из примера 2.1 -типичный фильтр
нижних частот: низкие частоты «пропускаются» (поскольку
умножаются на амплитуды, близкие к 1), а высокие - «значительно уменьшаются»
(поскольку умножаются на амплитуды, близкие к 0).
X
а
к
а
к
L
а
к
Г\ 1 Г\
Рис. 2.6. Одномерные профили функции фильтрации с вращательной симметрией.
Вверху: линейный фильтр верхних частот и идеальный фильтр нижних частот.
Внизу: экспоненциальный фильтр высокочастотных предыскажений и линейный
полосовой фильтр
Проектирование функций фильтрации. Частотная область
хорошо подходит для проектирования функций фильтрации (см. рис. 2.6).
Мы можем остановиться на фильтре верхних частот (например, для
выделения границ или для визуализации деталей и подавления
нижних частот), фильтре высокочастотного предыскажения (например, для
74 ♦ Глава 2. Обработка изображений
повышения контрастности), полосовом фильтре (который пропускает
только частоты из определенного диапазона) или фильтре, который
подавляет либо усиливает выбранные частоты (при соблюдении
ограничения симметричности). Фильтр нижних частот убирает выбросы и
снижает контрастность, т. е. оказывает сглаживающее действие.
Прилагательные «линейная», «экспоненциальная» или «идеальная» в
применении к функции фильтрации описывают характер перехода от
больших амплитуд к малым. Примеры переходов показаны на рис. 2.6.
На рис. 2.7 показаны результаты применения фильтра нижних частот и
полосового фильтра к изображению.
Рис. 2.7. Верхний ряд, слева: канал интенсивности изображения Emma,
показанного в цвете на рис. 2.9. Верхний ряд, справа: его спектр,
центрированный и подвергнутый логарифмическому преобразованию.
Нижний ряд, слева: результат применения к Emma идеального фильтра
нижних частот, демонстрация типичного эффекта сглаживания.
Нижний ряд, справа: результат применения к Emma экспоненциального
полосового фильтра, который показывает больше высоких частот, чем низких
2.2.Три процедурных компонента
75
Помимо гибкости в плане проектирования функций фильтрации,
важным аргументом в пользу использования фильтров на основе ДПФ,
а не глобальной свертки, является наличие эффективных алгоритмов
двумерного БПФ. Локальные свертки обычно более эффективно
выполняются в пространственной области локальным оператором.
2.2. Три процедурных компонента
В этом разделе мы опишем три процедурных компонента, которые
часто используются в программах обработки изображений, в частности в
локальных операторах, а также при реализации отдельных процедур
анализа изображений или компьютерного зрения.
2.2.1. Интегральные изображения
Вычисление интегрального изображения 1т для заданного
изображения / - часто применяемый шаг предобработки, цель которого -
ускорить операции, в которых участвуют прямоугольные окна I (например,
обнаружение признаков). Под «интегрированием» понимается
сложение малых величин. В данном случае малыми величинами являются
значения пикселей. Для пикселя р = (х, у) интегральным значением
1*(Р)= X WJ) (2.12)
является сумма значений /(/,;') в позициях q = (/, /), расположенных не
ниже и не правее р (см. рис. 2.8 слева).
К
cols
1
к
AL
О О
ооооооооооо
AL
cols
ооооооооо
ооооооооо
ооооооооо
ооооооооооо
Рис. 2.8. Слева: значением ljnt(x,y) является сумма значений всех выделенных
пикселей. Справа: если в алгоритме требуется использовать сумму значений
всех пикселей в показанном прямоугольном окне, то нам нужно будет только
воспользоваться значениями интегрального изображения в четырех
углах р, g, r и £; соответствующая формула приведена в тексте
76 ♦ Глава 2. Обработка изображений
Врезка 2.2 (появление интегральных изображений в компьютерном зрении).
В литературе по компьютерному зрению интегральные изображения впервые
упоминаются в работе [F. С. Crow. Summed-area tables for texture mapping. Computer
Graphics,vol. 18,1984, p. 207-212]. Затем они получили дальнейшее освещение в
работах [J. P. Lewis. Fast template matching. In Proc. Vision Interface, 1995, p. 120-123]
и [P. Viola and M.Jones. Robust real-time object detection. Int. J. Computer Vision, 2001,
p. 137-154].
Теперь рассмотрим прямоугольное окно W, определяемое четырьмя
пикселями р, q, r, s (рис. 2.8 справа), так что q,rws отстоят от границы
W на один пиксель. Тогда сумма Sw значений всех пикселей внутри W
равна
Sw-IJP)-IJ»-IJis)*IJq). (2.13)
Независимо от размера окна W мы должны выполнить только одно
сложение и два вычитания. Ниже это очень пригодится нам для
классификации объектов, присутствующих в изображении.
Пример 2.2 (количество операций при наличии интегрального изображения
и без него). Пусть требуется вычислить сумму значений пикселей в окне п*т по
формуле (2.13). Каковы бы ни были тип, нам придется выполнить всего три
арифметические операции.
Не будь у нас интегрального изображения, для сложения всех т • п чисел в
окне потребовалось бы т • п - 1 операций.
Если учитывать еще операции адресации для последовательного
скользящего окна в интегральном изображении, то понадобится всего четыре
операции инкремента ++, если хранить адреса пикселей р, q, r, s в регистрах.
Наблюдение 2.1. После того как выполнен один шаг предобработки -
вычисление интегрального изображения, - чтобы узнать сумму пикселей в любом
прямоугольном окне, нужно постоянное время, не зависящее от размера окна.
2.2.2. Регулярные пирамиды изображений
Пирамида - стандартная структура данных для представления одного
изображения / в разных размерах (см. рис. 2.9). Исходное изображение
находится в основании пирамиды, а изображения меньших размеров -
на последующих уровнях.
Использование масштабного коэффициента 2. Если каждый раз
уменьшать размеры вдвое, как показано на рис. 2.9, то все дополни-
12.Три процедурных компонента
77
тельные слои пирамиды занимают менее трети памяти, отведенной
под исходное изображение, что следует из формулы геометрического
ряда
1 +
1
+
1
+
1
+
2-2 2 -2L Т-Т
4
< —
3
(2.14)
При переходе к следующему уровню снизу вверх среднее значение
2x2 пикселей становится значением пикселя следующего уровня. Во
избежание пространственных искажений в виде ступенек рекомендуется
перед вычислением средних произвести гауссово сглаживание
(объясняется в следующем разделе).
Изображение /
ЕЬ.
Рис. 2.9. Пирамиды изображений. Слева: регулярная пирамида лежит в основе
уменьшения размера изображений. Справа вверху: попарно непересекающиеся
массивы. Справа внизу: пример уровней для изображения Emma
Создав на уровне п + 1 пирамиды новый пиксель г, определенный
четырьмя пикселями pv р2, ръ, р4 на уровне п, мы породили новые
пары соседей (pv г), (р2, г), (р3, г) и (р4, г) в дополнение к четырем
соседям на уровне п, как показано на рис. 2.9 справа. Чтобы перейти
по соседним пикселям от пикселя р к пикселю q в изображении /, мы
теперь можем подняться по пирамиде до некоторого уровня, сделать
несколько шагов вбок на этом уровне, а затем спуститься к q. Вообще
говоря, при этом образуются более короткие соединительные пути,
чем если бы мы пользовались только четырьмя соседями в исходном
изображении.
78 ♦ Глава 2. Обработка изображений
Пример 2.3 (самый длинный путь в регулярной пирамиде с масштабным
коэффициентом 2). Пусть имеется изображение / размера 2"*2П и построенная
для него регулярная пирамида с масштабным коэффициентом 2.
Чтобы найти самый длинный путь между двумя пикселями, рассмотрим
пиксели р и q в противоположных углах /. Если переходить от пикселя к одному
из его четырех соседей в /, то для перехода к другому концу диагонали
понадобится 2" - 1 шагов вдоль одной стороны и 2" - 1 шагов вдоль другой стороны,
причем не важно, в каком порядке мы будем эти шаги делать. Поэтому самый
длинный путь в / без использования пирамиды имеет длину
2"+1-2. (2.15)
Если же использовать также соседей из других уровней пирамиды, то длина
пути составляет всего 2п.
Наблюдение 2.2. Соседство в пирамиде значительно сокращает расстояния
между пикселями, и этим можно воспользоваться, чтобы послать «сообщение»
от одного пикселя другому.
Пирамиды можно также использовать, когда нужно начать некоторую
процедуру компьютерного зрения на одном уровне, а затем уточнить
результаты, распространяя их на уровни с более высоким разрешением.
Примеры такого рода встретятся нам в нескольких местах.
2.2.3. Порядок обхода
В основной управляющей структуре программы анализа
изображений (не только для локальных операторов, но и, к примеру, для пометки
компонент) обычно задается порядок обхода, т. е. посещения всех или
только некоторых пикселей.
Стандартный порядок обхода и его варианты. На рис. 2.10 показан
не только стандартный порядок обхода, но и другие, которые могут
оказаться интересны при определенных условиях. Спиральный и меанд-
ровый обход дают возможность использовать результаты предыдущих
вычислений в новой позиции скользящего окна, поскольку в окно
попадает только 2к+ 1 новых пикселей, замещая 2к + 1 «выбывших».
Обход в порядке магического квадрата (рис. 2.10, нижний ряд в
середине, показан простой пример 4*4) приводит к псевдослучайному
доступу кпикселям.В магическом квадрате суммычисел в каждой строке,
в каждом столбце и на обеих главных диагоналях одинаковы. Гильбертов
обход - еще один способ посещения пикселей в псевдослучайном
порядке (например, он может применяться для вывода картинки на
экран). См. рис. 2.11.
2.2.Три процедурных компонента ♦ 79
__-i--p"'-
■■
*
13
8
12
1
3
10
6
15
2
11
7
14
~1б]
5
9
4
^^^^^^^^^^^^^^^
1
-+ 1
...--"""
--Г
.-f-j
J i— 1—f
- * * р
Рис. 2.10. Порядки обхода: стандартный (верхний ряд, слева), закручивающаяся
спираль (верхний ряд, в середине), меандр (верхний ряд, справа), стандартный
инвертированный (нижний ряд, слева), магический квадрат (нижний ряд, в середине)
и стандартный избирательный (как при чересстрочной развертке),
например каждая вторая строка (нижний ряд, справа)
Гильбертов обход. На рис. 2.11 показан гильбертов обход, который
начинается с северо-западного угла изображения и заканчивается в
северо-восточном. Обозначим а, Ь, с, d четыре угла изображения размера
2"*2", начиная с северо-западного в порядке по часовой стрелке.
Гильбертов обход Нп(а, d, с, Ь) начинается в угле а, продолжается в углах d и
с и завершается в угле Ъ.
1 1 1 1 1 1
V\S L_T\
~] 1 1 Г1
1 1 1 1 ; 1 \
1 1 1 1
^и ^^
I \ _L
Рис. 2.11. Гильбертовы обходы изображений 2*2,4*4 и 8*8, иллюстрирующие
рекурсивное продолжение на изображение большего размера
Нх(а, Ъ, с, d) - обход изображения 2*2, при котором мы просто
посещаем углы а, Ь, с, d, как показано на рисунке.
80 ♦ Глава 2. Обработка изображений
Обход Нп+1(а, d, с, Ъ) строится следующим образом. Мы начинаем
обход в северо-западном угле, выполняем обход Нп(а> Ь, с, d), затем делаем
один шаг вниз, потом выполняем обход Нп(а, d, с, Ь), делаем один шаг
вправо, вновь выполняем обход Нп(а, d, с, Ь), делаем шаг вверх и
наконец выполняем обход Нп(с, d, а, Ь), который приводит нас в
северо-восточный угол изображения размера 2П+1><2П+1.
Врезка 2.3 (Гильберт, Пеано и Евклид). В 1891 г. Давид Гильберт (1862-1943),
великий немецкий математик, построил кривую, целиком заполняющую
единичный квадрат и удовлетворяющую определению кривых, данному Жорда-
ном.На рис. 2.11 показаны начальные этапы построения. На каждой итерации
производится гильбертов обход сетки размера 2А7*2'7, который не следует
путать с оригинальной кривой, определенной Гильбертом в евклидовом
пространстве. Кривая Гильберта-это вариант кривой, описанной в 1890 г.
итальянским математиком Дж. Пеано (1858-1932) с той же целью.
Евклид из Александрии (приблизительно 300 г. до н. э.) - древнегреческий
математик, знаменитый своими «Началами», которые оставались
стандартным учебником геометрии до XIX века.
2.3. Классы локальных операторов
Паттерны локальной интенсивности в одном изображении можно
считать «относительно» независимыми, если они находятся на некотором
расстоянии друг от друга внутри носителя П. Локальные операторы
пользуются этим и к тому же легко и эффективно реализуются как на
обычном последовательном, так и на параллельном оборудовании.
Поэтому неудивительно, что предложено много локальных операторов
для разных целей. В этом разделе мы рассмотрим лишь несколько
«популярных» представителей четырех классов локальных операторов.
2.3.1. Сглаживание
Цель сглаживания изображения - устранение «выбросов», которые в
данном контексте считаются шумом.
Прямоугольный фильтр размера (2к+ 1)*(2к+ 1) вычисляет
локальное среднее по формуле (2.7). Это простой пример оператора
сглаживания, он устраняет выбросы, но заметно уменьшает контрастность С(Г)
изображения I. Часто бывает достаточно использовать ядро размера 3x3
или 5x5. Локальное среднее для ядер большего размера удобно вычислять
с помощью интегрального изображения /. исходного изображения /.
2.3. Классы локальных операторов ♦ 81
Медианный оператор. Медианой 2п + 1 значений называется
значение, которое оказалось бы в позиции п + 1 после сортировки. Например,
медианой последовательности {4, 7, 3,1, 8, 7,4, 5, 2, 3, 8} является 4,
поскольку этот элемент занимает позицию 6 в отсортированной
последовательности 1, 2, 3, 3,4,4, 5, 7, 7, 8, 8.
Медианный оператор (2к+ 1)*(2к+ 1) отображает медиану окна
размера (2к + 1)х(2/с + 1) в начальный пиксель р. Он устраняет выбросы,
лишь немного изменяя контрастность изображения С(1).
Врезка 2.4 (Карл-Фридрих Гаусс (1777-1855), блистательный немецкий
математик, работавший в Гёттингенском университете, очень хорошо описан в
романе «Измеряя мир» Даниэля Кельмана (М.: ACT, 2016).
Фильтр Гаусса. Фильтр Гаусса представляет собой локальную
свертку с ядром, определенным выборками из двумерной гауссовой
функции. Эта функция является произведением двух одномерных гауссовых
функций:
<W>><) = ^гехр
(х-цх)2+(у-а)
V 2^
^ {х-цх? (у-ЦуУ
2
2nd1
е 2о2 е 2о2 , (2.16)
где (jUx, ц) - математические ожидания по осям хиу, а - стандартное
отклонение (а2 - дисперсия), которое также называют радиусом этой
функции, а е - число Эйлера.
Гауссова функция названа по имени Карла-Фридриха Гаусса (см.
врезку 2.4), а число Эйлера - по имени Леонарда Эйлера (см. врезку 1.3
и формулу Эйлера 1.22). На рис. 2.12 приведены примеры гауссовых
функций. Стандартное отклонение о называется также масштабом.
Наблюдение 2.3. Вторая строчка в формуле (2.16) показывает, что двумерный
фильтр Гаусса можно реализовать с помощью последовательного применения
двух одномерных фильтров, в горизонтальном и в вертикальном направлении.
Центрированная гауссова функция. Если предположить, что
гауссова функция центрированная (т. е. средние цх= ц =0, как на рис. 2.12
слева), то формула (2.16) упрощается:
82
Глава 2. Обработка изображений
1.0
0.8
0.6
0.4
0.2
0,0
'
■
-
1 1 '
. 1 .
■ 1 •
1
—г4-
, 1 .
■ 1 '
1 i '
.1.1.1.
1 i '
• |.|. |.,Ч'|М> |
р= 0 tfz=0,2 J
р= 0 <72=5.0
ц=-2 С72=0.5
. i ■ ,_1_.
!
1
]
-
J
._i_._L_l
-5-4-3-2-1012345
Рис. 2.12. Слева: двумерная гауссова функция с математическими
ожиданиями /jx = /j =0. Справа: четыре примера одномерных гауссовых
функций с различными математическими ожиданиями и дисперсиями
&ЛХ>У)
2коА
ехр
2 2 Л
дг+Г
2а2
7TS
2а2 . Л 2С72
(2.17)
Такая центрированная функция вычисляется в (2k + l)x(2fc + 1) точках,
причем начальный пиксель окна находится в точке (0, 0). В результате
получается важное ядро фильтра для локального оператора с
параметрами а > 0 и к > 1. Позже мы воспользуемся им для определения
разностей гауссианов и пространства масштабов.
На рис. 2.13 показан пример ядра для а = 1. Согласно статистическому
правилу трех сигм, для выборки из Ga необходимо ядро размера 6а - 1.
1
4
7
4
1
4
16
26
16
4
7
26
41
26
7
4
16
26
16
4
1
4
7
4
1
/273
Рис. 2.13. Ядро гауссова фильтра сглаживания с
параметрами к = 2 и s = 2 (т. е. а = 1)
Для входного изображения / обозначим
L(x,y,<7) = [/*Ge](x,y)
(2.18)
локальную свертку с функцией Ga для о > 0. Для удобства реализации
мы определим ядро фильтра, производя выборку из Ga в узлах сетки
размера w*w, симметричных относительно начала координат, где w -
нечетное число, ближайшее к во - 1.
Гауссово пространство масштабов. Если а > 1 - масштабный
коэффициент, то мы можем перейти от сглаженного изображения L(x, у, о)
2.3. Классы локальных операторов ♦ 85
к L(x, у, аа). Используя масштабы а" • а, где а - начальный масштаб, а
п = О, 1,..., т, мы можем создать последовательность уровней гауссова
пространства масштабов. Пример показан на рис. 2.14.
Рис. 2.14. Сглаженные варианты изображения SetlSeql (показанного
на рис. 2.4 слева вверху) при значениях параметра а = 0,5, с = 1, а = 2, а = 4,
а = 8 и <т = 16, определяющих шесть уровней гауссова пространства масштабов
В этой книге все уровни пространства масштабов имеют одинаковый
размер Ncols><Nrows. Для более эффективной реализации некоторые
авторы предлагали уменьшать размер изображения вдвое одновременно с
удвоением масштаба а, создавая тем самым октавы размытых
изображений. Размытые изображения в одной октаве сохраняют постоянный
размер до следующего удвоения а, после чего размер снова
уменьшается вдвое. Но это деталь реализации, и мы не будем использовать октавы
при обсуждении пространства масштабов.
Сигма-фильтр. Это еще один пример простого, но зачастую
оказывающегося полезным локального оператора для удаления шума. Ре-
84 ♦ Глава 2. Обработка изображений
зультат показан на рис. 2.15. Этот локальный оператор также определен
для окон W (I) размера (2к + 1)*(2к + 1) при к > 1. Параметр о > 0
интерпретируется как аппроксимация шума, сопутствующего получению
изображения I (например, о приблизительно равно 50, если Gmax = 255).
В предположении, что локальный оператор вычисляется параллельно,
новое изображение / формируется следующим образом:
1) вычислить гистограмму окна W (7);
2) вычислить среднее pi всех значений в интервале [1(р) - <т, 1(р) + а];
3) положить J{p) = pi.
Рис. 2.15. Удаление шума. Слева вверху: исходное изображение 128><128
с наложенным равномерным шумом (±15). Справа вверху: прямоугольный
фильтр 3*3. Слева внизу: сигма-фильтр 3*3 с параметром а = 30.
Справа внизу: медианный фильтр 3*3
2.3. Классы локальных операторов ♦ 85
В некоторых случаях производитель камеры публикует параметры
ожидаемого шума сенсорных ПЗС- или КМОП-элементов. Тогда
параметр о можно положить равным амплитуде шума, умноженной на 1,5.
Заметим, что
I 1{р)+<У
ju = -- X и Щи), (2.19)
Ь U=I{p)-G
где Щи) - гистограмма значений и для окна W (I), а масштабный
коэффициент S = Щ1(р) -&) + ... + Щ1(р) + с).
На рис. 2.15 показаны результаты работы прямоугольного фильтра,
медианного фильтра и сигма-фильтра для одного и того же небольшого
изображения.
2.3.2. Повышение резкости
Смысл повышения резкости заключается в том, чтобы получить
улучшенное изображение /, увеличив контрастность исходного
изображения / вдоль границ, не добавляя шума в однородные участки.
Нерезкое маскирование. Этот локальный оператор вычисляет
разность R(p) = I(p) - S(p) между исходным и сглаженным изображениями.
Затем разность прибавляется к исходному изображению I:
Jip) = 1(р) + Щр) - S(p)] = [1 + А] 1{р) - Щр), (2.20)
где Я > 0 - масштабный коэффициент. В принципе, для получения
сглаженного изображения S(p) годится любой оператор из раздела 2.3.1. На
рис. 2.16 приведено три примера.
Размерный параметр к («радиус») этих операторов управляет
пространственным распределением эффекта сглаживания, а параметр Я -
влиянием корректирующего сигнала [I(p) - S(p)] на окончательный
результат. Таким образом, к и Я - обычные интерактивные управляющие
параметры нерезкого маскирования.
Согласно второму из выражений в формуле (2.20), процесс можно
также количественно описать уравнением
J{p) = I{p)-X'S(p) (2.21)
(для некоторого Я' > 0), которое сокращает время вычислений. Вместо
того чтобы применять нерезкое маскирование единообразно ко всему
изображению /, мы также можем ввести некоторую локальную
адаптивность, например подавить изменения в однородных участках.
86 ♦ Глава 2. Обработка изображений
Рис. 2.16. Нерезкое маскирование с параметрами к = 3 и Я = 1.5 формулы (2.20).
Слева вверху: размытое входное изображение Altar размера 512*512
(алтарь барочной церкви в городке Валенсиана, штат Гуанахуато).
Справа вверху: результат применения медианного оператора.
Слева внизу: результат применения фильтра Гаусса с параметром а = 1.
Справа внизу: результат применения сигма-фильтра с параметром а = 25
2.3.3. Простые детекторы границ
Мы описываем простые детекторы границ, отвечающие
ступенчато-граничной модели, аппроксимируя первые или вторые
производные.
Дискретные производные. Производная непрерывной функции
одного аргумента/определяется сходимостью отношений разностей, в
которых ненулевое приращение аргумента е стремится к 0:
2.3. Классы локальных операторов ♦ 87
У(х) = Г(х) = ШДх + е)-Дх). (2.22)
Ck e-*0 £
Функция /дифференцируема в точке х, если это отношение
стремится к некоторому пределу. Для функций двух аргументов определяются
частные производные, например производная по у:
?(^у) = Л(х>7) = ИшЛ£^±£ЬЛм). (2.23)
бу £^° е
Производная по а: определяется аналогично.
Однако на дискретной сетке наименьшее расстояние равно
расстоянию между соседними пикселями г = 1. Вместо того чтобы сводить
определение производной (2.23) к отношению разностей при е = 1, мы
можем взять симметричное представление, в котором г = 1 в обоих
направлениях. Простейшее симметричное представление отношения
разностей для производной по у имеет вид:
г , ч = 1(х,у + £)-1(х,у-£)
= 1(х,у + 1)-1(х,у-1) (2 24)
2
где мы взяли симметричную разность для лучшего баланса. Чтобы
использовать меньшее значение е, необходима какая-то субпиксельная
интерполяция.
Выражение (2.24) дает аппроксимацию первой производной, крайне
чувствительную к шуму. Обозначим 1х{х, у) соответствующую простую
аппроксимацию —(х, >>). Тогда итоговая аппроксимация модуля гради-
дх
ента имеет вид
^Ix(x,yf+Iy(x,y)2 - |gradI(x,y)\\2. (2.25)
Здесь мы видим комбинацию двух линейных локальных операторов,
ядро одного представляет /, а ядро другого - / (см. рис. 2.17). В этом
случае масштабный коэффициент 2 не равен сумме весов в ядре.
Сумма весов равна нулю, и это соответствует тому факту, что производная
постоянной функции равна 0.
Результат свертки с одним из этих ядер может оказаться
отрицательным. Поэтому 1хи1 - не настоящие изображения в том смысле, что
значениями пикселей могут быть отрицательные и рациональные числа, а
88
Глава 2. Обработка изображений
не только целые в диапазоне {0,1,..., Gmax}. При визуализации
дискретных производных, таких как 1х и /, принято показывать округленные
целые значения |J | и |/1.
0
-1
0
0
0
0
0
1
0
/2
0
0
0
-1
0
1
0
0
0
/2
Рис. 2.17. Ядра разностных фильтров,
определенных формулой (2.24)
Врезка 2.5 (история оператора Собеля). Описание оператора Собеля впервые
было опубликовано в работе [/. Е. Sobel. Camera models and machine perception.
Stanford, Stanford Univ. Press, 1970, p. 277-284].
Оператор Собеля. Оператор Собеля аппроксимирует обе частные
производные изображения /, применяя ядра, показанные на рис. 2.18.
На рис. 2.4 справа вверху показан результат свертки с ядром фильтра,
аппроксимирующим производную по х.
-1
-2
-1
0
0
0
1
2
1
/1
-1
0
1
-2
0
2
-1
0
1
/1
Рис. 2.18. Ядра фильтров
для оператора Собеля
Эти две маски - дискретные варианты простых гауссовых сверток
по строкам или по столбцам, за которыми следует вычисление оценок
производных с помощью масок на рис. 2.17. Например:
■1 0 1]
■2 0 2
■1 0 lj
—
"ll
2
lj
= 2 [-1 0 1].
(2.26)
Обе маски на рис. 2.18 определяют локальные свертки для
вычисления аппроксимаций Sx и 5 частных производных. Значение оператора
Собеля в точке (х, у) равно
\Sx(x,y)\ + |Sy(x,y)| * Hgrad Jfry)!^. (2.27)
Это значение показывается в виде уровней яркости на карте границ,
определяемой оператором Собеля. Конечно, затем можно найти
локальные максимумы оператора Собеля; этим объясняется, почему
оператор Собеля называют также детектором границ.
2.3. Классы локальных операторов ♦ 89
Врезка 2.6 (история оператора Кэнни). Описание этого оператора впервые
было опубликовано в работе [J. Canny. A computational approach to edge detection.
IEEE Trans. Pattern Analysis Machine Intelligence, vol. 8,1986, p. 679-698].
Оператор Кэнни. Оператор Кэнни отображает скалярное
изображение в бинарную карту границ, состоящую из «тонких» (шириной всего в
один пиксель) отрезков. Результат зависит от двух пороговых значений,
Т. и Т... таких, что 0 < Т. < Г,., < G , а также от фиксированного мас-
low high ' low high max' Y c
штаба, используемого при гауссовом сглаживании.
Обозначим / уже сглаженное исходное изображение, получающееся
после применения свертки с гауссовой функцией Ga с масштабным
параметром а > 0, например, 1 < о < 2.
Теперь применим простую оценку градиента, например оператор
Собеля, который для любого пикселя р £ П дает оценки частных
производных 1х и /, что позволяет оценить величину g(p) модуля градиента
Hgrad I(p)\\2 и его направление в(р) в виде atan2(/, /). Оценки в(р)
округляются до кратного я/4, для чего вычисляется (0(р) + я/8) по модулю я/4.
На шаге подавления немаксимумов проверяется, является ли величина
g(p) максимальной в направлении (уже округленном) в{р). Например,
если 6(р) = я/2, т. е. градиент в точке р = (х, у) направлен вниз, то g(p)
сравнивается с g(x, у - 1) и g{x, у + 1) - значениями в точках выше и
ниже р. Если g(p) не больше значений в обоих соседних пикселях, то g(p)
сбрасывается в 0.
На последнем шаге прослеживания границ ищутся траектории
пикселей р, на которых g(p) > Tlow, и все принадлежащие им пиксели
помечаются как граничные. Поиск таких траекторий начинается в точках, для
которых £(р) >Тт.
Если в процессе обхода П, например стандартного, слева направо и
сверху вниз, мы нашли еще не помеченный пиксель р, для которого
g(p) > Тм й, то выполняются следующие действия:
1) пометить р как граничный пиксель;
2) пока в 8-окрестности р существует пиксель q, для которого
g(q) > Tlow, пометить q как граничный пиксель;
3) положить р равным q и перейти к шагу 2;
4) искать следующий начальный пиксель р, пока не будет
просмотрен весь носитель П.
Благодаря использованию двух порогов в алгоритм вносится
гистерезис: значение следующего пикселя q, возможно, и меньше Th h, но на
90
Глава 2. Обработка изображений
той же траектории ему предшествует хотя бы один пиксель со
значением, большим Ты й, и эта «положительная» история поддерживает
рассмотрение q в качестве кандидата, поэтому мы соглашаемся
продолжить траекторию, если выполнено условие g(q) > Tlow.
Врезка 2.7 (Лаплас). Пьер-Симон, маркиз де Лаплас (1749-1827) -
французский ученый, занимавшийся прикладной математикой и теоретической
физикой.
Лапласиан. Согласно ступенчато-граничной модели, границы
идентифицируются также переходом вторых производных через ноль.
Стандартные (простые) аппроксимации лапласиана изображения I
определяются ядрами фильтров, показанными на рис. 2.19.
0
1
0
1
-4
1
0
1
0
1
1
1
1
-8
1
1
1
1
-1
2
-1
2
-4
2
-1
2
-1
Рис 2.19. Три маски для приближенного вычисления лапласиана
Ниже мы выведем показанное на левом рисунке ядро фильтра как
пример дискретизации оператора.
Пример 2.4. Для вывода первой маски на рис. 2.19 сначала отобразим /в
матрицу отношений разностей первого порядка
1Лх,У)
I(x,y + 0.5)-I(x,y-0.5)
1
= I(x,y + 0.5)-I(x,y-0.5),
а затем в матрицу отношений разностей второго порядка
Iyy(x,y)=Iy(x,y + 0.5)-Iy(x,y-0.5)
= [I(x,y+l)-I(x,y)]-[I(x,y)-I(x,y-l)]
= I(x,y+l)+I(x,y-l)-2-I(x,y).
Проделаем то же самое для аппроксимации I и сложим результаты. Тем
самым мы определили аппроксимацию V2/ = Д/, которая совпадает с первой
маской на рис. 2.19. На рис. 2.20 показан профиль строки изображения после
применения этого приближенного лапласиана.
2.5. Классы локальных операторов ♦ 91
LoG intensity profile
Рис. 2.20. Профиль строки (близкой к середине) в массиве, получающемся
в результате применения лапласиана к изображению SetlSeql
(рис. 2.4 слева вверху), сглаженному с масштабным параметром 5 = 2.
Крутой глобальный минимум находится между ветвями куста
2.3.4. Простые детекторы углов
Углом в изображении /называется пиксель р, в котором пересекаются
две границы; для выделения самих границ можно применить как
ступенчато-граничную, так и фазово-конгруэнтную модель. На рис. 2.21
показано, что такое вообще углы, а на рис. 2.22 - как выглядят три угла
после увеличения изображения.
Рис. 2.21. Найденные углы дают информацию,
важную для локализации и понимания характера
объектов на трехмерных сценах
92 ♦ Глава 2. Обработка изображений
III
1 1
L _кь=рЬ
и, -44
| Z |
г II 1 1
rt+V'H "ttttl
ffff^ U_11_LLM_U_U_UJ
1 I 0 I
1 Z 1 1
Г~Г INI ГП III
1 Г г Г Г
——————————i— i——————————————————————————шИ——————
——————————————————————————————————————н————————
1 1 1 1 1 1 1 1 1 1 1 Н 1
Рис. 2.22. Пиксели p,q и г - точки пересечения границ, направления
этих границ обозначены синими линиями. Дискретные окружности
(состоящие из 16 пикселей) встретятся при обсуждении детектора углов FAST.
Небольшое окно изображения SetlSeql
Врезка 2.8 (Гессе и гессиан). Гессиан (также матрица Гессе) назван по имени
немецкого математика Л. О. Гессе (1811-1874).
Нахождение углов с помощью матрицы Гессе. В соответствии с
данным выше определением угол характеризуется большой кривизной
графика интенсивности. Следовательно, для его нахождения нужно
вычислить собственные значения Ях и Я2 (см. врезку 2.9) матрицы Гессе
в точке р. Если оба собственных значения «велики» по модулю, то мы
нашли угол; если одно значение велико, а другое мало, то имеет место
ступенчатая граница, а если оба собственных значения малы, то мы
находимся в области с низкой контрастностью.
Щр) =
JXX(P) LyiP)
IxyiP) IyyiP)
(2.28)
2.5. Классы локальных операторов ♦ 95
Врезка 2.9 (след, определитель и собственные значения матрицы). Следом
Тг(А) матрицы А = (а.) размера п*п называется сумма > а„ элементов на
главной диагонали. Определитель матрицы А = (а.) размера 2*2 вычисляется
по формуле
det(A) = апа22 - а12а21.
Определитель матрицы А= (а.) размера 3*3 вычисляется по формуле
det(A) = апа22аъъ + о12а2ЪаЪ1 + о1Ъо21оЪ2 - а1ЪапаЪ1 - а12а21аъъ - апа2ЪаЪ2.
Собственными значениями матрицы А размера п*п называются п корней ее
характеристического полинома,т. е. решений уравнения det(A - Л1) = 0, где I -
единичная матрица размера п*п, a det обозначает определитель.
Для вещественной матрицы А собственные значения - вещественные числа.
Они применяются для моделирования устойчивости решений системы
линейных уравнений, определяемой матрицей А.
Определитель квадратной матрицы равен произведению ее собственных
значений, а ее след - сумме собственных значений.
Детектор углов Харриса и Стивенса. Этот метод обнаружения углов
называется детектором Харриса. Вместо рассмотрения гессиана
исходного изображения /(т. е. вторых производных) мы пользуемся первыми
производными сглаженного изображения L(.,., а), определенного
формулой (2.18) при некотором о > 0. Обозначим
G(j>,&) =
г2
LUp,a) Lx(p,G)L(p,G)
Lx(p,a)L(p,a) LUp,a)
У
(2.29)
Собственные значения Лх и Я2 матрицы G представляют изменения
интенсивностей изображения / в ортогональных направлениях. Но
вместо вычисления этих значений мы рассмотрим меру угловатости
(cornerness measure)
К (р, а, а) = det(G) - а • Tr(G) (2.30)
при небольшом значении параметра а > 0 (скажем, а = 1/25). В силу
общих свойств собственных значений имеем
Н(р,а,Л) = Л1Л2-а-(Л1 + Л2). (2.31)
Если одно собственное значение мало, а другое велико (как,
например, на ступенчатой границе), то благодаря включению следа в выраже-
94 ♦ Глава 2. Обработка изображений
ние (2.30) результирующее значение "Н (р, а, а) останется относительно
малым.
Мера угловатости К была предложена в 1988 г. как более
эффективный способ расчета по сравнению с вычислением и анализом
собственных значений. Результаты показаны на рис. 2.23 слева.
Врезка 2.10 (история детектора Харриса). Этот метод был опубликован в
работе [C.Harris and M.Stephens. A combined corner and edge detector. In Proc.Alvey Vision
Conference, 1988, p. 147-151].
FAST. Временные ограничения, характерные для современных
встраиваемых систем технического зрения (т. е. «небольших» независимых
систем, таких как микророботы или камеры в миниатюрных мультикоп-
терах), диктуют постоянное стремление к повышению эффективности
вычислений. Критерий FAST (Features from an Accelerated Segment Test)
определяет наличие угла путем рассмотрения значений изображения
на дискретной окружности с центром в данном пикселе р; на рис. 2.22
показаны 16 значений на окружности радиуса р = 3.
Критерий наличия угла: значение в центральном пикселе должно
быть темнее (или ярче), чем значения в 8 (или в 11, если требуется
определить настоящий угол, а не просто нерегулярный пиксель на в целом
прямой границе) соседних пикселях на окружности, и «похоже» на
значения в остальных пикселях на окружности.
Результаты показаны на рис. 2.23 справа.
Рис. 2.23. Окно изображения SetlSeql. Слева: углы, найденные детектором
Харриса. Справа: углы, найденные детектором FAST
Эффективность вычислений. Чтобы обеспечить эффективность,
мы сначала сравниваем значение в центральном пикселе со
значениями в точках 1, 2, 3 и 4 в указанном порядке (см. рис. 2.22), и лишь в
2.5. Классы локальных операторов ♦ 95
том случае, когда шансы на выполнение критерия наличия угла кажутся
высокими, мы продолжаем проверять пиксели, расположенные между
точками 1, 2, 3 и 4. В оригинальной работе, посвященной FAST, для
оптимизации времени работы предлагается обучить решающее дерево.
В библиотеке OpenCV (а также в HbCVD) детектор FAST реализован с
помощью SIMD-команд параллельного сравнения, так получается
быстрее, чем при использовании решающего дерева.
Подавление немаксимумов. В алгоритме FAST также применяется
подавление немаксимумов, чтобы количество найденных углов было не
слишком велико. Например, для найденного кандидата на роль угла мы
можем вычислить максимальную разность Т между значением в
среднем пикселе и значениями на дискретной окружности,
классифицированными как «более темные» или «более яркие», при которой кандидат
считается углом. Затем механизм подавления немаксимумов удаляет
кандидатов в порядке убывания Т.
Врезка 2.11 (история детектора FAST). Алгоритм FAST как детектор углов был
опубликован в работе [Е. Rosten and T. Drummond. Machine Learning for high-speed
corner detection. In Proc. European Conf. Computer Vision, vol. 1,2006, p. 430-443].
2.3.5. Удаление артефактов освещения
Артефакты освещения, вызванные различиями в экспозиции,
тенями, отражениями или виньетированием, представляют проблемы для
алгоритмов компьютерного зрения. Примеры показаны на рис. 2.24.
Невыполнение предположения о постоянстве яркости.
Алгоритмы компьютерного зрения часто опираются на предположение о
постоянстве яркости (intensity constancy assumption - ICA), согласно которому
внешний вид объектов не изменяется из-за различий в освещении на
текущем и следующем кадре или в двух кадрах, синхронизированных
по времени. Для реальных изображений это предположение на самом
деле нарушается из-за таких эффектов, как тени, отражения, различие
во времени экспозиции, шум в сенсорных элементах и т. д.
Существует по меньшей мере три подхода к этой проблеме. (1) Мы
можем преобразовать входные изображения, уменьшив артефакты
освещения (например, перейти к модели равномерного освещения
путем удаления теней); в этом направлении есть ряд предложений, но
пока успехи невелики. (2) Мы можем попытаться улучшить алгоритмы
96 ♦ Глава 2. Обработка изображений
компьютерного зрения, сделав их независимыми от ICA, и примеры
такого рода ниже будут рассмотрены. (3) Мы можем преобразовать
входные изображения, сохранив «релевантную» информацию, но ставя
целью не добиться визуальной эквивалентности с исходными данными,
а устранить эффекты переменного освещения.
Рис. 2.24. Примеры реальных сцен (черные пиксели по краям - результат
ректификации изображения, мы обсудим ее ниже). Два изображения NorthLeft
и NorthRight в верхнем ряду демонстрируют разницу в освещении между кадрами,
снятыми двумя синхронизированными камерами при плохо выставленной
экспозиции. На левом нижнем изображении LightAndTrees виден эффект плохой
тени от деревьев. На правом нижнем изображении MainRoad показана снятая ночью
сцена, на которой передние фары выглядят как большие яркие пятна
Мы обсудим два метода, относящихся к третьему подходу. Один из
них - воспользоваться выравниванием гистограмм или условным
масштабированием, определенными выше. При этом все изображение
равномерно отображается в изображение, нормализованное относительно
гистограммы с равномерными градациями серого, либо в изображение
с постоянными средним и стандартным отклонением. Но эти
равномерные преобразования не способны справиться с неглобальной
природой артефактов освещения.
2.3. Классы локальных операторов ♦ 97
Например, системы содействия водителю, основанные на
техническом зрении, должны учитывать «танцующий свет» от лучей солнца,
пробивающихся сквозь деревья, который создает локальные артефакты
освещения. См. изображение на левом нижнем рис. 2.24.
Карты границ. Локальные производные не изменяются, когда к
значениям изображения прибавляется константа. Для вывода
представлений изображений, менее чувствительных к вариациям освещения,
можно использовать локальные производные, градиенты или карты
границ.
Например, мы можем просто подать на вход последующих
алгоритмов компьютерного зрения карты границ Собеля вместо исходного
изображения. См. рис. 2.5 справа. Карта границ Собеля - это не
бинарное изображение, и она не модифицирована путем применения
подходящей эвристики (как во многих других граничных операторах), это
просто «первичные данные о границах».
Рис. 2.25. Исходное изображение Set2Seql (слева), его остаточное изображение
(в середине), вычисленное методом TV-L2 (в этой книге не рассматривается)
с целью сглаживания, и карта границ Собеля (справа)
Врезка 2.12 (видеоданные для тестирования компьютерного зрения в сети).
На рис. 2.25 показано синтетическое изображение, взятое из набора 2 EISATS,
доступного по адресу www,mi.auckland.ac.nz/EISATS. В сети имеется несколько
тестовых наборов данных для сравнения алгоритмов компьютерного зрения,
применяемых к записанным последовательностям изображений, в
частности KITTI Vision Benchmark Suite по адресу www.cvlibs.net/datasets/kitti/. См.
также конкурс Heidelberg Robust Vision Challenge на Европейской
конференции по компьютерному зрению ECCV 2012. hci.iwr.uni-heidelberg.de/Static/
challenge2012/.
Еще одно применение остаточных изображений относительно
сглаживания. Пусть / - исходное изображение, и предположим, что
оно допускает аддитивное разложение
98 ♦ Глава 2. Обработка изображений
I(p) = S(p) + R(p) (2.32)
для всех пикселей р. Здесь 5 обозначает гладкую компоненту /
(определенную выше при обсуждении вопроса о повышении резкости), a R -
остаточное изображение, получающееся после применения операции
сглаживания, породившей S. Разложение (2.32) называют также
структурно-текстурным разложением (structure-texture decomposition), где
под структурой понимается гладкая компонента, а под текстурой -
остаточное изображение.
Остаточное изображение - это разность между входным
изображением и его сглаженной версией. Значения остаточного изображения могут
оказаться отрицательными, иногда полезно перемасштабировать его в
стандартный диапазон {0, 1,..., Gmax}, например для визуализации. На
рис. 2.25 показан пример остаточного изображения R относительно
сглаживания оператором TV-L2 (в этой книге не рассматривается).
Сглаживающий фильтр можно применять итеративно по следующей
схеме:
5(0) = /,
S(«) = S(S(«-D) дЛЯ п>о, (2.33)
R(ri) = J _ £(л)_
Номер итерации п определяет применяемый остаточный фильтр.
Если п раз применить прямоугольный фильтр 3x3, то результат будет
приблизительно такой же, как после применения фильтра Гаусса
радиуса п + 1.
Какие методы подходят для данного класса входных изображений,
надо проверять экспериментально. Для таких тестов полезна
итеративная схема (2.33).
2.4. Более сложные детекторы границ
В этом разделе мы обсудим ступенчато-граничные детекторы,
объединяющие несколько идей в одном алгоритме, например
комбинирование выделения границ с пред- или постобработкой. Мы также
рассмотрим фазово-конгруэнтную модель выделения границ на примере
оператора Ковеси.
2.4.1. LoG и DoG и их пространства масштабов
Лапласиан гауссиана (LoG) и разность гауссианов (DoG) -
чрезвычайно важные преобразования изображений, с которыми мы еще не раз
встретимся.
2.4. Более сложные детекторы границ ♦ 99
Врезка 2.13 (история детектора границ LoG). Детектор границ LoG впервые
описан в публикации [D. Marr and E. Hildreth. Theory of edge detection. Proc. Royal
Society London, Series B, Biological Sciences, vol. 207,1980, p. 187-217]. Поэтому его
также называют алгоритмом Марра-Хилдрет [Эллен Кэтрин Хилдрет - женщина,
поэтому правильное написание «алгоритм Марра-Хилдрет». - Прим. перев.].
Детектор границ LoG. Применение лапласиана к изображению,
пропущенному через фильтр Гаусса, может быть выполнено в виде
одной операции свертки, что следует из тождества
V2(Ga*7) = J*V2Ga, (2.34)
где * обозначает свертку двух функций, а / предполагается (для
доказательства тождества) дважды дифференцируемой. Тождество сразу
следует из двукратного применения общих правил сворачивания:
D(F * Н) = D(F) * Н = F * D(H), (2.35)
где D обозначает производную, а F и Н - дифференцируемые функции.
Справедливо следующее наблюдение.
Наблюдение 2.4. Для вычисления лапласиана изображения, пропущенного
через фильтр Гаусса, нужно выполнить только одну свертку с V26a.
Ядро фильтра для V2Ga необязательно должно иметь размер 3x3, как
показано на рис. 2.19. Поскольку гауссова функция непрерывна, мы
можем точно вычислить ее лапласиан. Вот выражение первой частной
производной по х:
Щ^(^У) = -Т^е^г^, (2.36)
и аналогичная формула имеет место для первой частной производной
по у. Повторяя дифференцирование по а: и по у, получаем следующее
выражение для LoG:
V2Ga{x9y)= X
2ш4
Гх2+у2_2о2\
а2
e-(*V)/2<^ (237)
LoG еще называют функцией сомбреро. На самом деле это
«перевернутое сомбреро». Точки, где она обращается в ноль, определяют границы.
См. рис. 2.26.
100 ♦ Глава 2. Обработка изображений
1
0.8
0.6
0.4
0.2
О
-0.2
-0.4
-6-4-2 0 2 4 6
Рис. 2.26. Двумерная гауссова функция симметрична относительно начала
координат (0,0); достаточно показать сечения графиков функции 6
и двух ее производных
Замечание о дискретизации ядра LoG. Теперь мы должны дис-
кретизировать этот лапласиан, получив ядро фильтра размера
(2к + \)*(2к + 1) при подходящем значении к. Но каково это
подходящее значение? Начнем с оценки стандартного отклонения о для
данного класса входных изображений.
Параметр w определяется нулями функции V2Go(a:, у); см рис. 2.26.
Положим V2Gct(x, у) = 0, и пусть, например, у = 0. Тогда оба нуля являются
корнями уравнения х2 = 2а2, т. е. хг = -V2a, x2 = +V2a. Таким образом,
имеем
w = \хг - х2\ = 2V2a. (2.38)
Для правильного представления функции сомбреро дискретной
выборкой предлагается использовать окно размера 3w*3w = 6V2<r><6V2a.
И напоследок получаем:
2к + U2k + 1 = ceil(6V2a)xceil(6V2<r), (2.39)
где функция ceil равна наименьшему целому числу, большему или
равному аргументу.
Мы должны оценить значение о для заданного класса
изображений. Сглаживать изображение очень «узким» фильтром Гаусса (<т < 1)
не имеет особого смысла. Поэтому будем рассматривать только о > 1.
Наименьшее ядро (при о = 1, т. е. 3w = 8,485...) будет иметь размер 9x9
(т. е. к = 4). Для заданных изображений интересно сравнить результаты,
получаемые при к = 4, 5,6,....
Гауссова функция
Первая производная
Вторая производная
2.4. Более сложные детекторы границ ♦ 101
Пространство масштабов LoG. На рис. 2.13 показано шесть
уровней гауссова пространства масштабов для изображения SetlSeql. Мы
вычислили лапласианы этих шести уровней и на рис. 2.27 показали
получившиеся изображения (по абсолютной величине); ко всем
изображениям было применено линейное масштабирование, чтобы
наглядно проявились закономерности распределения яркости. Это пример
пространства масштабов LoG. Как и в случае гауссова пространства
масштабов, каждый уровень определяется масштабом о - стандартным
отклонением гауссовой функции, и мы можем сгенерировать
последовательность уровней с масштабными коэффициентами ап • а для а >1
и п = 0,1,..., т.
■■'
Рис. 2.27. Лапласианы изображений на рис. 2.13, представляющие шесть
уровней пространства масштабов LoG для изображения SetlSeql
Разность гауссианов (DoG). Оператор разности гауссианов (DoG) -
часто применяемая аппроксимация оператора LoG, характеризуемая
меньшим временем вычислений. В формуле (2.17) определена
центрированная (с нулевым средним) гауссова функция Ga.
102 ♦ Глава 2. Обработка изображений
Оператор DoG определяется начальным масштабом о и масштабным
коэффициентом а > 1:
Daa(x, у) = Цх, у, а) - L(x, у, ао). (2.40)
Это разность между результатом размытия изображения / и
результатом еще большего его размытия. Как и в случае LoG, границы (в
соответствии со ступенчато-граничной моделью) определяются как точки,
где эта функция обращается в ноль.
Между операторами LoG и DoG имеется следующее соотношение:
^вЛх,у)^(Х'У)-^У\ (2.41)
где а = 1,6 - рекомендуемый параметр аппроксимации. Благодаря
этому приближенному равенству разность гауссианов используется в
качестве эффективной аппроксимации лапласиана гауссианов.
Пространство масштабов DoG. Различные масштабы о
порождают уровни Doa в пространстве масштабов DoG. На рис. 2.28 приведено
сравнение трех уровней пространства масштабов LoG и DoG при
масштабном коэффициенте а = 1,6.
Врезка 2.14 (история исследований пространств масштабов).
Многомасштабные представления - хорошо разработанная область компьютерного зрения
с многообразными применениями (см. врезку 2.13). П.Дж. Бэрт (P.J. Burt) ввел
в рассмотрение гауссовы пирамиды, когда работал в группе А. Розенфельда
(A. RosenfeLd) в College Park; см. [P. J. Burt, Fast filter transform for image processing.
Computer Graphics Image Processing, vol. 16,1981, p. 20-51].
Также см.ранние публикации о гауссовых пирамидах [J.LCrowley.krepresentation
for visual information. Carnegie-Mellon University, Robotics Institute, CMU-RI-TR-82-07,
1981] и [А Р Witkin. Scale-space filtering. In Proc. Int. Joint Conf. Artificial Intelligence,
1983, p. 1019-1022]. Тогда каждый последующий уровень создавался из
предыдущего путем умножения на коэффициента = 2,а получающиеся размытые
изображения переменного размера назывались октавами.
Позже в теории пространств масштабов стали рассматривать произвольные
масштабные коэффициенты а>1; см., например, [T.Lindeberg. Scale-Space Theory
in Computer Vision. Kluwer Academic Publishers, 1994] и [J. L Crowley and А. С Sanderson.
Multiple resolution representation and probabilistic matching of 2-D gray-scale shape.
IEEE Trans. Pattern Analysis Machine Intelligence, vol. 9,1987, p. 113-121].
2.4. Более сложные детекторы границ ♦ 105
Рис. 2.28. Уровни пирамиды изображений, построенные операторами
LoG (слева) и DoG (справа) при о = 0,5 и ап= 1,6"для п = 0,..., 5.
Показаны только результаты для п = 1,п = Ъип = 5
2.4.2. Встроенная уверенность
Мера уверенности (confidence measure) - это количественная
информация, полученная в результате обсчета данных и позволяющая решить,
существует ли некоторый признак; если обсчитанные данные
достаточно хорошо согласуются с моделью, принятой в детекторе признаков, то
значение этой меры должно быть велико.
Врезка 2.15 (история алгоритма Меера-Георгеску). Этот алгоритм был
опубликован в работе [P.Meerand B.Georgescu. Edge detection with embedded confidence.
IEEE Trans. Pattern Analysis Machine Intelligence, vol. 23,2001, p. 1351-1365].
Алгоритм Меера-Георгеску выделяет границы, применяя меру
уверенности, основанную на предположении о достоверности
ступенчато-граничной модели.
104 ♦ Глава 2. Обработка изображений
В этом методе имеется четыре параметра. Результат оценки вектора
градиента g(p) = V/(x, у) в точке р = (х, у) определяется оценкой модуля
градиентаg(p) = llg(p)ll2, оценкой направления градиента в(р),
уверенностью в наличии границы т)(р) и процентилем рк интегрального
распределения абсолютных величин градиента. Ниже мы зададим значения,
используемые в алгоритме Меера-Георгеску, показанном на рис. 2.29.
1: for каждого пикселя р изображения / do
2: оценить модуль градиента д(р) и направление границы в(р);
3: вычислить меру уверенности q(p);
4: end for
5: for каждого пикселя р изображения / do
б: определить значение р(р) интегральной функции распределения
абсолютных величин градиента;
7: end for
8: построить диаграмму pq для изображения /;
9: выполнить подавление немаксимумов;
10: выполнить гистерезисную бинаризацию (hysteresis thresholding);
Рис. 2.29. Алгоритм выделения границ Меера-Георгеску
Врезка 2.16 (транспонированная матрица). Транспонированной матрицей W1
называется результат отражения элементов матрицы W относительно
главной диагонали. Если матрица симметрична относительно главной диагонали,
то WT = W.
Пусть А - матричное представление окна размера (2к + 1)х(2/с + 1) с
центром в пикселе р входного изображения /. Обозначим
W= sdT (2.42)
матрицу весов размера (2к + 1)х(2& + 1), полученную перемножением
векторов d = [dv..., d2k+l] и s = [sv..., s2k+l], где:
1) оба вектора имеют единичную Lj-норму, т. е. \dx\ + ... + \d2k+1\ = 1
M|sl| + ... + |s2jtfl| = l;
2) d - антисимметричный вектор, т. е. dx = ~d2k+v d2 = -d2k,..., dk+l = 0,
представляющий результат дифференцирования одной строки
матрицы А;
3) s - симметричный вектор, т. е. s1 = s2k+1 ^s2 = s2k<..A sfe+1,
представляющий результат сглаживания одного столбца матрицы А.
Например, антисимметричный вектор d = [-0.125, -0.25,0,0.25,0.125]т
и симметричный вектор s = [0.0625,0.25,0.375,0.25,0.0625]7 определяют
матрицу W размера 5 х 5.
2.4. Более сложные детекторы границ
105
Обозначим а. /-ю строку матрицы А. Полагая
dx = Tr(WA) = Tr(scTA),
2k+\
(2.43)
(2.44)
i=\
получаем первые два параметра алгоритма:
g(p) = -yjdf + d\ и 6{р) = arctan
\d2j
(2.45)
Обозначим A.deal матрицу размера (2к + l)x(2fc + 1), представляющую
шаблон идеальной ступенчатой границы с направлением градиента
9(р). Величина г](р) = |Tr(AT.dea/A)| определяет меру уверенности. Элементы
матриц А и АШеа1 нормированы, так что 0 ^ t](p) < 1и г](р) = 1 в случае
точного совпадения с идеальной ступенчатой границей.
Пусть g <... < gk <... < g - упорядоченный список различных
(округленных) модулей градиента, встречающихся в изображении /, с
интегральной функцией распределения вероятностей
Pk = Vrob[g<g[k]] (2.46)
для l^k^N. Предположим, что для заданного пикселя Igk - ближайшее
число к модулю g(p); тогда процентиль р(р) = рк.
В итоге для каждого пикселя р мы имеем процентиль р(р) и
уверенность г\{р) в диапазоне от 0 до 1. Эти значения определяют двумерную
диаграмму рл для изображения / (см. рис. 2.30 слева).
/
• °q2 '
<7l
0 Р 1
Рис. 2.30. Слева: кривые L и Н на диаграмме ртц каждая из них делит квадрат
на области знакопостоянства L или Н. Если точка (р, г]) лежит на кривой,
то либо L(p, т]) = 0, либо Н(р, г)) = 0. Справа: окрестность пикселя р размера 3*3
и виртуальные соседи дхи q2B направлении оценки градиента
Мы рассматриваем кривые в пространстве рв, заданные в неявной
форме L(p, в) = 0. Например, это может быть вертикальная прямая,
пересекающая квадрат, или дуга эллипса. На рис. 2.30 слева изображены
две кривые L и Я. Каждая такая кривая разбивает квадрат на три
части: в одной находятся точки, для которых L(p, 9) > 0, в другой - точки,
106 ♦ Глава 2. Обработка изображений
для которых L(p, в) < О, в третьей - точки самой кривой, для которых
L(p, в) = 0. Вот теперь у нас есть всё необходимое для описания процесса
принятия решений.
Подавление немаксимумов. Для текущего пикселя р определим
виртуальных соседей q1nq2B направлении оценки градиента (рис. 2.30
справа) и соответствующие им значения р и л, полученные интерполяцией по
соседним пикселям.
Точка р определяет максимум относительно кривой X в
пространстве рв, если знаки обоих виртуальных соседей ql и q2 относительно X
отрицательны. На шаге 9 алгоритма мы подавляем немаксимумы,
применяя некоторую выбранную кривую X; оставшиеся пиксели являются
кандидатами на включение в карту границ.
Гистерезисная бинаризация (hysteresis thresholding) - это общая
техника принятия решений на основе ранее полученных в процессе
результатов. В рассматриваемом алгоритме гистерезисная бинаризация
применяется на шаге 10 и основана на двух кривых L и Я в
пространстве рв, которые называются порогами гистерезиса (рис. 2.30 слева). В
общем случае эти кривые могут пересекаться.
Мы передаем все пиксели /, оставленные на шаге 9. Каждому
пикселю р соответствуют значения р и в. Пиксель остается в карте границ,
если (a) L(p, л) > 0 и Н(р, л) > 0 или (Ь) он является соседом пикселя,
принадлежащего карте границ, и удовлетворяет условию Цр, л) • Н(р, л) < 0.
Условие ф) описывает процесс гистерезисной бинаризации, оно
применяется рекурсивно.
Этот метод выделения границ вырождается в оператор Кэнни, если
оба порога гистерезиса - вертикальные прямые, и в детектор,
основанный только на уверенности, если оба они - горизонтальные прямые. На
рис. 2.31 показаны результаты применения алгоритма Меера-Георгеску.
Рис. 2.31. Изображения, получающиеся в результате применения алгоритма
Меера-Георгеску с большим (слева) и меньшим (справа) ядром фильтра,
определяемым параметром к. Сравните с рис. 2.32, на котором использовано
то же самое входное изображение SetlSeql (показанное на рис. 2.4 слева вверху)
2.4. Более сложные детекторы границ ♦ 107
2.4.3. Алгоритм Ковеси
На рис. 2.32 показаны результаты применения четырех детекторов
границ к одному изображению, снятому в ночное время системой
содействия водителю. Две верхние карты границ получены на основе фа-
зово-конгруэнтной модели, а две нижние - на основе
ступенчато-граничной модели.
■
\-±j»
■ i...
Рис 2.32. Сравнение фазово-конгруэнтной и ступенчато-граничной моделей
для изображения SetlSeql, показанного на рис. 2.4 слева вверху.
Верхний ряд: слева - результат применения оператора Ковеси, основанного
на фазово-конгруэнтной модели и реализованного в программе phasecongmono.m
(см. ссылку во врезке 2.18), а справа - результат применения того же оператора,
но реализованного более современной программой phasecong3.m, параметры
в обоих случаях одинаковы. Слева внизу: оператор Собеля, основанный
на ступенчато-граничной модели и реализованный функцией Sobel()
из библиотеки OpenCV с параметрами dx =l,dy= 0, ksize = 3.
Справа внизу: оператор Кэнни - еще одна реализация ступенчато-граничной
модели; изображение построено функцией СаппуО с минимальным
порогом 150 и максимальным порогом 200
Различия между операторами, основанными на той и другой модели,
еще нагляднее проявляются для простого синтетического изображения
на рис. 2.33. В соответствии со своей моделью оператор, основанный
на градиенте, например оператор Кэнни, находит граничные
пиксели, ориентируясь на максимумы модулей градиентов, что приводит к
двойному отклику вокруг сферы и искажению границы тора на рис. 2.34
108 ♦ Глава 2. Обработка изображений
слева. Мы опишем алгоритм, использованный для генерации
результата, показанного на рис. 2.34 справа.
Рис. 2.33. Слева: синтетическое входное изображение. Справа: профили
яркости вдоль сечения А-А (сверху) и сечения В-В (снизу)
Рис. 2.34. Слева: границы, выделенные оператором Кэнни.
Справа: границы, выделенные алгоритмом Ковеси
Вейвлеты Габора. Для локального анализа частотных компонент
удобнее использовать не волновые формы, равномерно
распространяющиеся во всем окне размера (2к + 1)*(2к + 1) (как на рис. 1.15), а
вейвлеты, например вейвлеты Габора, т. е. синусоидальные и косину-
соидальные волны, модулированные гауссовой функцией с некоторым
масштабом а, амплитуды которых убывают по мере удаления от
центральной точки (см. рис. 2.35). На среднем рисунке видны полосы,
ортогональные прямой с углом наклона в.
Существуют нечетные и четные вейвлеты Габора. Нечетный вейвлет
порождается синусоидальной волной и потому равен нулю в начале
координат. Четный вейвлет порождается косинусоидальной волной и
потому достигает максимума в начале координат.
2.4. Более сложные детекторы границ ♦ 109
Врезка 2.17 (Габор). Венгерский ученый, специализировавшийся в области
физики и электротехники (1900-1979). Работал в Великобритании и в 1971 г.
получил Нобелевскую премию по физике за изобретение голографии.
X 255
Четный вейвлет
Рис. 2.35. Слева: два одномерных сечения нечетного и четного вейвлетов Габора.
В середине: полутоновое представление квадратного вейвлета Габора в окне
размера (2/с +1)*(2/г +1) с углом в. Справа: его трехмерный график
Прежде чем дать формальное определение вейвлетов Габора,
вспомним определение гауссовой функции:
.2 Л
GtT(x,y) = -
1
ехр
х + у
(2.47)
2ЖС72 *\ 2СГ2
Затем преобразуем координаты а: и у изображения, применив
поворот на угол в:
u=xcos9 + ysm9, (2.48)
v = -х sin в + у cos в, (2.49)
где прямая с углом наклона в ортогональна полосам в вейвлетах Габора;
см. рис. 2.35 в середине. Введем в рассмотрение также сдвиг фаз гр > 0,
длину волны синусоидального множителя Я > 0 и отношение сторон
у > 0. Тогда выражения
/
2ет,(*>У) = GAU>yi>)-cosl 2яг-+ уг |,
и
( и \
godd(x>y) = G*(u>rv>*ib\ 2л-+у/\
V А )
(2.50)
(2.51)
определяют пару Габора, в которой синусоида и косинусоида
модулированы одной и той же гауссовой функцией. Эту пару можно объединить
в одно комплексное число:
110
Глава 2. Обработка изображений
8раЛХ>У) = geven(X>y) + ^-l-godd(X>y)
( и \
= Ga(u,yv)exp\ 27T-+ у/ [
у л j
(2.52)
Подготовка к применению алгоритма. Алгоритм Ковеси
применяет набор п квадратных пар Габора с центром в текущем пикселе р = (х, у).
На рис. 2.36 иллюстрируется такой набор для п = 40, но из каждой пары
показана только одна функция (скажем, нечетный вейвлет). По
умолчанию в алгоритме Ковеси используется 24 пары.
II II
Шт Ш
DDD
О о ~> |
■■
в
в
= 1
^
**
ч
в
Рис. 2.36. Набор функций Габора, используемый для обнаружения
фазовой конгруэнтности в пикселе
Врезка 2.18 (история алгоритма Ковеси). Этот алгоритм впервые
опубликован в работе [P. D. Kovesi. A dimensionless measure of edge significance from phase
congruency calculated via wavelets. In Proc. New Zealand Conf. Image Vision Computing,
1993, p. 87-94]. См. также исходный код, приведенный на странице www.csse.
uwa.eduMu/-pk/Research/MatlabFns/index.htmWphasecong. Программа работает
очень быстро и стандартно применяется к изображениям размера 20002000
и более; на самом деле в ней используются Log-вейвлеты Габора, а не
оригинальные вейвлеты, чтобы улучшить отклик оператора и повысить
эффективность.
Свертка с каждой парой Габора определяет одно комплексное
число. У каждого из полученных таким образом п комплексных чисел есть
амплитуда rh и фаза ah.
Формула (1.33) определяет идеальную меру фазовой конгруэнтности.
Для случаев, когда сумма 2^н=\Гк становится слишком малой,
удобно прибавить к знаменателю небольшое положительное число г,
например е = 0,01. В изображении также присутствует шум, обычно
2.4. Более сложные детекторы границ ♦ 111
равномерный. Обозначим Г > О сумму всех шумов по всем
переменным составляющим (для заданных изображений ее можно оценить).
В предположении, что шум постоянный, мы просто вычитаем
составляющую шума и получаем
pos(||z|L -Г)
P+JP)-*^* -. (2-53)
2-м 1 + г
где функция pos возвращает свой аргумент, если он положителен, и 0 в
противном случае. Имеем
Случайно выберем т1 равномерно распределенных направлений
в.,..., в и т„ масштабов s,,..., s (например, т = 6 и т = 4). Чтобы
X III -1 Л X III гу X Л
задать набор т1- т2 вейвлетов Габора, выберем наименьший масштаб
(например, 3) и масштабный коэффициент между двумя
последовательными масштабами (например, 2.1). Свертку с этими вейлетами Га-
бора эффективнее производить в частотной, а не в пространственной
области. Если все же она производится в пространственной области, то
размер ядра свертки (2к + 1)*(2к + 1) должен быть таким, чтобы 2к + 1
было примерно в три раза больше длины волны фильтра.
Обработка в одном пикселе. Теперь у нас есть всё необходимое для
анализа фазовой конгруэнтности в точке р = (х, у):
1) применить в точке р набор сверточных масок, состоящий из п =
тх- т2 пар Габора. В результате получится п комплексных чисел
(гн> ан)>
2) вычислить меры фазовой конгруэнтности Т^р), 1 ^ i < ml по
формуле (2.53), но использовать при этом только т2 комплексных
чисел (rh, cch), определенных для направления в1 и каждого из т2
масштабов;
3) вычислить компоненты направления X и Y. для 1 < / < т1 по
формуле
[X, У. ]т = Tfp) • [sin(0), cos(0.)]T; (2.55)
4) для получившейся ковариационной матрицы компонент
направления
У"'х2 У"1 хх
^i=\ i ^Ji=\ l l
(2.56)
112 ♦ Глава 2. Обработка изображений
вычислить собственные значения Ях и Я2; предположим, что Ях > Я2.
(Эта матрица соответствует матрице Гессе вторых производных
размера 2*2; о том, кто такой Л. О. Гессе, см. врезку 2.8.)
Абсолютная величина Ях показывает важность локального признака
(граница, угол или какой-то другой признак). Если абсолютная
величина Я2 также велика, то мы имеем угол; главная ось соответствует
направлению локального признака.
Нахождение граничных пикселей. После применения описанной
выше процедуры ко всем точкам реП мы получаем массив значений Ях,
который называется первичным результатом алгоритма. Все значения,
оказавшиеся ниже заранее выбранного порога отсечения (скажем, 0,5),
можно игнорировать.
В этом массиве производится подавление немаксимумов (возможно,
в сочетании с гистерезисной бинаризацией, как в алгоритме Меера-Ге-
оргеску), т. е. все значения, которые не определяют локального
максимума в своей 8-окрестности (например), обнуляются.
Все пиксели, сохранившие ненулевые значения после подавления
немаксимумов, считаются граничными.
Помимо технических параметров, которые могут быть постоянными
для всех обрабатываемых изображений (например, выбранные пары
Габора, параметр е для устранения неустойчивости знаменателя или
порог отсечения), алгоритм зависит только от параметра Г в формуле
(2.53), и даже этот параметр можно оценить по математическому
ожиданию шума в обрабатываемых изображениях.
Формула (2.53) определяет меру Т(р), пропорциональную косинусу
угла отклонения фазы, т. е. «мягкий» отклик.
Учитывая, что Т(р) представляет взвешенную сумму косинусов углов
отклонения фазы, взятие арккосинуса даст взвешенную сумму углов
отклонения фазы. Поэтому предлагается модифицированная мера
отклонения фазы:
TJp) = pos(l - arccos(:P(p))), (2.57)
где функция pos определена, как и раньше.
Классификация пикселей как граничных или линейных. Имея
для каждого пикселя два собственных значения, мы можем
использовать их для классификации найденных признаков. Пример приведен
на рис. 2.37.
2.5. Упражнения ♦ 115
Рис. 2.37. Цветокодированные результаты классификации локальных
признаков от «ступенька» до «линия». Цветовой ключ показан справа.
Исходное изображение приведено на рис. 2.33 слева
2.5. Упражнения
2.5.1. Упражнения по программированию
Упражнение 2.1 (вариации на тему выравнивания гистограмм).
В книге [R. Klette and P. Zamperoni. Handbook of Image Processing Operators.
Wiley, Chichester, 1996] обсуждаются различные способы преобразования
гистограмм, в частности варианты их выравнивания
Г1 и Gmax
Возьмите зашумленные (скалярные) изображения по своему выбору
и примените сигма-фильтр до выравнивания гистограммы.
Экспериментально проверьте следующие утверждения.
Изменяя показатель степени г > О, можно добиться более сильного
или более слабого выравнивания. При г = 1 результирующая
гистограмма имеет равномерное распределение (насколько это возможно). При
г > 1 редкие значения яркости будут встречаться в исходном
изображении чаще, чем в выравненном. При г = 0 получается почти (но не в
точности!) тождественное преобразование. При г < 1 получается более
слабое выравнивание, чем при г = 1.
Наглядно представьте результаты, воспользовавшись двумерными
гистограммами, когда по одной оси откладывается г, а по другой, как
обычно, уровни яркости. Отобразите эти гистограммы либо в виде дву-
I
Ступенька
Линия
114 ♦ Глава 2. Обработка изображений
мерного полутонового изображения, либо в виде графика трехмерной
поверхности.
Упражнение 2.2 (разработка детектора границ путем
комбинирования различных стратегий). В детекторе границ мы можем применить
одну или несколько из перечисленных ниже стратегий.
1. Граничному пикселю должен соответствовать локальный
максимум, когда применяется оператор (например, оператор Собеля),
который аппроксимирует градиент V/.
2. После применения фильтра LoG следует проанализировать
получившиеся массивы положительных и отрицательных значений
на предмет перехода через ноль (т. е. найти такие пиксели р, для
которых LoG дает результат, близкий к нулю, и в точках, соседних
с р, имеются как положительные, так и отрицательные значения
LoG).
3. Рассмотренные выше операторы вычисляют только производные
в направлениях л: и у. Но можно также рассмотреть производные
в других направлениях, например под углами, кратными 45°.
4. Для выделения границ можно применить дополнительные
эвристические соображения, например: граничный пиксель должен
соседствовать с другими граничными пикселями.
5. Наконец, получив последовательность граничных пикселей, мы
хотели бы выделить из нее «тонкие дуги», а не «жирные границы».
В этом упражнении ваша задача - спроектировать свой собственный
детектор границ, в котором комбинируются по меньшей мере две из
описанных выше стратегий. Например, проверьте наличие граничных
пикселей, вычислив как первые, так и вторые производные. Или
примените оператор, основанный только на первых производных, в
сочетании с проверкой на соседство с граничными пикселями. Наконец,
можно обобщить оператор, основанный на первых производных, так
чтобы вычислялись производные в более чем двух направлениях.
Выберите один из предложенных вариантов или придумайте свою
комбинацию.
Упражнение 2.3 (амплитуды и фазы локального
преобразования Фурье). Определите два локальных оператора с ядром размера
(2к + 1)х(2к + 1), один для амплитуд, другой для фаз, которые будут
отображать исходное изображение / в амплитудное изображение Ж и
фазовое изображение Т, определенные следующим образом.
2.5. Упражнения ♦ 115
Выполним двумерное ДПФ для текущего входного окна
размера (2к + 1)*(2к + 1) с центром в пикселе р. На основе получившихся
(2к + I)2 - 1 комплексных коэффициентов переменной составляющей
вычислим значение М(р), представляющее процент амплитуд в
высокочастотных пикселях относительно общей суммы всех (2к + I)2 - 1
амплитуд, а также меру фазовой конгруэнтности Т(р), определенную
формулой (2.53).
Визуализируйте М(р) и Tip) в виде полутоновых изображений и
сравните с границами во входном изображении /. Для этого выберите
какой-нибудь оператор выделения границ, величины порогов для карты
границы, амплитудное и фазовое изображения и сравните количество
пикселей в бинаризованной карте границ и амплитудном изображении
с количеством пикселей в бинаризованной карте границ и фазовом
изображении.
Упражнение 2.4 (остаточные изображения относительно
сглаживания). Рекурсивно примените прямоугольный фильтр 3x3 (не более
30 итераций) для генерации остаточных изображений
относительно сглаживания. Сравните с остаточными изображениями,
полученными при сглаживании фильтром Гаусса размера (2/с + 1)х(2/с + 1) при
к= 1,..., 15. Обсудите общую связь между рекурсивным применением
прямоугольного фильтра и фильтрами Гаусса соответствующего
радиуса. И кстати, что такое «соответствующий радиус»?
2.5.2. Упражнения, не требующие программирования
Упражнение 2.5. Линейными локальными операторами называются
операторы, которые можно определить с помощью свертки. Какие из
следующих операторов являются линейными: прямоугольный фильтр,
медианный фильтр, выравнивание гистограммы, сигма-фильтр, фильтр
Гаусса, оператор LoG?
Упражнение 2.6. Выравнивание цветных изображений - интересная
область исследований. Обсудите, почему следующий подход
неидеален: выполнить выравнивание гистограмм всех трех цветовых каналов
(например, RGB) по отдельности, а затем использовать получившиеся
скалярные изображения как цветовые каналы результирующего
изображения.
Упражнение 2.7. Докажите, что условное масштабирование
порождает изображение /, среднее и дисперсия которого совпадают с
соответствующими характеристиками исходного изображения /.
116 ♦ Глава 2. Обработка изображений
Упражнение 2.8. Опишите, как именно можно использовать
интегральное изображение для минимизации времени работы
прямоугольного фильтра с ядром большого размера.
Упражнение 2.9. Рассуждая так же, как в примере 2.4, объясните,
каким могло бы быть ядро фильтра для квадратичной вариации (вместо
того, что было выведено для оператора Лапласа).
Упражнение 2.10. Докажите, что маски Собеля имеют вид dsT и sdT,
где s и d - трехмерные векторы, удовлетворяющие предположениям
алгоритма выделения границ Меера-Георгеску.
Упражнение 2.11. Сигма-фильтр заменяет 1(р) значением Др) в
соответствии с формулой (2.19). В этой процедуре используется
гистограмма Н(и), вычисленная для значений и в окне W (Г), принадлежащих
интервалу [1(р) - о, 1(р) + а]. Но можно вместо этого произвести прямое
вычисление:
Ар) =
qeZe>° " (2.58)
\ZP*
где Zpa = {qE W(I): I(p) -a< I(q) < I(p) + о). Проанализируйте возможные
преимущества этого подхода для небольших окон.
Упражнение 2.12. Нарисуйте (по аналогии с рис. 2.6), как примерно
выглядят в частотной области кривые фильтров, которые можно было
бы назвать «экспоненциальный фильтр с низким предыскажением» и
«идеальный полосовой фильтр».
Глава
Анализ изображений
В этой главе мы познакомимся с топологическими и геометрическими
основами анализа участков изображений, а также с двумя стандартными
способами анализа распределения значения изображения. Мы обсудим также методы
нахождения прямых и окружностей как примеры распознавания конкретных
образов в изображении.
3.1. Основы топологии изображений
В разделе 1.1.1 было сказано, что между пикселями как таковыми не
определено внутренне присущее отношение смежности. Лишь
принятая нами модель определяет, что считать смежными пикселями. Выбор
отношения смежности оказывает существенное влияние на то, какие
участки изображения используются для вывода его свойств в процессе
анализа. См. рис. 3.1.
Рис. 3.1. Слева: количество черных участков не зависит
от выбранного отношения смежности. Справа: на евклидовой
плоскости количество черных участков зависит оттого,
считать ли клетки, имеющие общий угол, соединенными или нет
В этом разделе приводится краткое введение в цифровую топологию
в объеме, необходимом для понимания таких терминов, как «участок
изображения» или «край участка изображения». Мы также отметим ряд
аспектов, отличающих цифровое изображение от евклидовой плоскости.
118 ♦ Глава 5. Анализ изображений
Врезка 3.1 (топология и Листинг). Неформально топологию можно описать как
«геометрию листа резины». Нас интересует количество компонент связности
множества, отношения соседства между такими компонентами, количество
дыр в множестве и другие подобные свойства, не зависящие от результатов
измерения в пространстве, наделенном системой координат.
Часто началом топологии считают теорему Декарта-Эйлера, согласно которой
ccQ - ах + сс2 = 2, где сс2, ах\л а0- соответственно количество граней, ребер и
вершин выпуклого многогранника. (Выпуклый многогранник - это непустое
ограниченное множество, являющееся пересечением конечного числа
полупространств.) О личностях Эйлера и Декарта см. врезку 1.3.
И. Б. Листинг (1802-1882) впервые употребил слово «топология» в частной
переписке в 1837 г. Он дал такое определение: «Топологическими
называются свойства, зависящие не от мер или величин, а от взаимного положения и
следования в пространстве».
3.1.1.4- и 8-смежность в бинарных изображениях
Принятое понятие смежности (или соседства) пикселей определяет
связность изображения и, следовательно, участки попарно связанных
пикселей.
Смежность пикселей. Понятие 4-смежности означает, что каждый
пиксель р = (х, у) является смежным со всеми пикселями из множества
AJp) = p+A4 = {(x+l,y),(x-l,y),(x,y+l),(?c,y-l)}, (3.1)
где А4 = {(1,0), (-1,0), (0,1), (0, -1)} - множество 4-смежности.
Иллюстрация 4-смежности приведена на рис. 1.1 и 1.2. Этому типу смежности
соответствует реберная смежность, когда каждый пиксель
рассматривается как небольшой закрашенный квадратик (т. е. принимается модель
узлов сетки). В предположении 8-смежности каждый пиксель р = (х, у)
является смежным со всеми пикселями из множества
Ai(p) = p+Ai = {(x+l,y+l),(x+l,y-l),(x-l,y+l),(x-l,y-l),
(х + 1, у), (х - 1, у), (х, у + 1), (х, у - 1)}, (3.2)
где Ag = {(1, 1), (1, -1), (-1, 1), (-1, -1)} и А4 - множество 8-смежности.
В это множество включены также пиксели, расположенные на
диагоналях, которые не показаны на рис. 1.1 и 1.2. Этому типу смежности
соответствует реберная и вершинная смежность в модели узлов сетки.
5.1. Основы топологии изображений ♦ 119
Врезка 3.2 (смежность, связность и планарность в теории графов).
Неориентированный граф G= [А/, £] определяется множеством вершин N и множеством
ребер Е; каждое ребро соединяет две вершины. Граф G называется конечным,
если N - конечное множество.
Две вершины называются смежными, если они соединены ребром. Путем
называется последовательность вершин, в которой каждая следующая вершина
смежна с предыдущей.
Множество вершин S Q N называется связным, если между любыми двумя
вершинами S существует путь, проходящий только по вершинам,
принадлежащим S. Максимальные связные подмножества графа называются
компонентами связности.
Планарный граф можно нарисовать на плоскости таким образом, что ребра
будут пересекаться только в концевых точках (т. е. вершинах). Обозначим ах
количество ребер, а0 - количество вершин графа.Для любого планарного
графа с а0 Z Ъ справедливо неравенство аг $ Ъа0 - 6; если в графе нет циклов
длины 3,то справедливо более сильное неравенство аг $ 2а0 - 4.
Формула Эйлера утверждает, что для конечного планарного связного графа
aQ - аг + а2 = 2, где а2 - количество граней графа.
Окрестности пикселей. Окрестность пикселя р содержит сам
пиксель р и смежные с ним пиксели. Так, 4-окрестностъ р равна А4(р) и {р},
а 8-окрестность р равна А8(р) и {р}. См. рис. 3.2.
о • о ••• о • о •••
• Ор • • Ор • • Фр • • Фр •
о • о ••• о • о •••
Рис. 3.2. Слева: множество 4-смежности и множество 8-смежности
для пикселя р. Справа: 4-окрестность и 8-окрестность р
Пиксельная связность. Описанное ниже транзитивное замыкание
отношения смежности определяет связность. Пусть SQH:
1) каждый пиксель связан с самим собой;
2) смежные пиксели S связаны;
3) если пиксель р £ S связан с пикселем q £ 5, а пиксель q £ S связан
с пикселем г £ S, то р также связан с г (в 5).
В зависимости от выбранного определения смежности мы получаем
4-связность или 8-связность подмножеств П.
120
Глава 5. Анализ изображений
Участки. Максимальные множества связанных пикселей определяют
участки (region), называемые также компонентами связности. Черные
пиксели на рис. 3.3 слева образуют один 8-участок и восемь 4-участ-
ков (изолированных пикселей); на том же рисунке имеется два белых
4-участка и только один белый 8-участок.
о о о о о о о
о о
о
о о
о о о
о о
о
чо о
о о о
Рис. 3.3. Слева: В предположении 4-смежности: несвязные черные пиксели
отделяют связный «внутренний участок» от связного «внешнего участка».
В предположении 8-смежности: черные пиксели связаны (на что указывают
проведенные ребра), но все белые пиксели по-прежнему связаны (см., например,
ребро, изображенное пунктирной линией). Справа: простая кривая на евклидовой
плоскости всегда разделяет внутреннюю (закрашенную) и внешнюю области
На рис. 3.4 слева приведен более общий пример. Предположим, что
наша задача - подсчитать «частицы», представленные в изображении
(после предварительной обработки) черными пикселями. Результат
будет зависеть от выбранного отношения смежности, а не от входного
изображения!
о
о
о
о
о
о
о
о
о
о
о
о
о
•
•
о
о
о
о
о
о
о
о
•
•
•
•
о
о
о
о
о
о
о
о
•
•
•
о
о
•
о
о
о
о
о
о
•
•
о
•
•
•
о
о
о
о
о
о
о
•
•
•
•
о
о
о
о
о
о
о
о
•
•
•
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
•
•
о
о
о
о
о
о
о
о
•
•
•
•
•
о
о
о
о
о
о
о
•
•
•
•
о
о
о
о
о
•
•
о
о
о
о
о
о
о
о
•
•
•
о
о
•
о
о
о
о
•
•
•
•
о
•
•
•
о
о
о
о
•
•
о
о
•
•
•
•
о
о
о
о
о
о
о
о
•
•
•
о
о
о
о
о
о
о
о
о
•
•
о
о
о
о
о
о
о
о
о
о
о
о
Рис. 3.4. Слева: в предположении 4-смежности черных пикселей мы насчитаем
в этом бинарном изображении пять «частиц», в предположении 8-смежности -
только три частицы. Справа: пример приложения, в котором такой подсчет важен
5.1. Основы топологии изображений ♦ 121
Врезка 3.3 (Жордан). Камиль Жордан (1838-1922) - французский ученый,
внесший вклад во многие отрасли математики. Например, он показал, что
центром дерева является либо единственная вершина, либо пара смежных
вершин. Широкую известность ему принесли определения и характеристики
кривых на плоскости.
Двойственные смежности в бинарных изображениях. На рис. 3.3
показано, к каким последствиям приводит выбор конкретного типа
смежности, путем сравнения с геометрией евклидовой плоскости М2, где
R обозначает множество вещественных чисел. Простая, или жорданова,
кривая всегда разделяет плоскость на внутреннюю область
(внутренность) и внешнюю область (внешность). Это кажется очевидным и
согласующимся с интуицией, но строгое доказательство этого факта,
известного как теорема Жордана-Брауэра, весьма трудное. А как выглядит
соответствующая теорема для изображений с их понятием связности?
Врезка 3.4 (Розенфельд и история двойственных смежностей). Рисунок 3.3
слева был использован в работе [A Rosenfeld and J, L Pfaltz. Sequential operations
in digital picture processing. J. ACM, 13:471-494, 1966], чтобы показать, что одно
единообразно применяемое отношение смежности ведет к топологическим
«проблемам». Авторы пишут:
«Парадокс», изображенный на рис. 3.3 слева, можно выразить следующим
образом: если «кривая» связная (не имеет разрывов), то она не
разделяет свою внешность и внутренность; если же кривая вполне несвязная, то
она разделяет их. Разумеется, это не является математическим
парадоксом, но неудовлетворительно с интуитивной точки зрения. Тем не менее
связность остается полезным понятием. Следует отметить, что если
оцифрованное изображение определить как массив шестиугольных, а не
квадратных элементов, то парадокс исчезает.
Комментируя эту публикацию, Р. О. Дуда (R. О. Duda), П. Э. Харт (P. E. Hart) и
Дж. X. Мансон (J. H. Munson) предложили (в неопубликованном техническом
отчете 1967 г.) двойственное использование 4- и 8-связности для черных и
белых пикселей.
А. Розенфельд (1931-2004) известен многочисленными пионерскими
исследованиями в области компьютерного зрения. На конференции ICCV 2007 в
Рио-де-Жанейро была учреждена премия имени Азриэля Розенфельда за
выдающиеся достижения, присуждаемая ученым, которые, по общему
признанию, внесли значительный вклад в компьютерное зрение на протяжении всей
своей научной карьеры.
122 ♦ Глава З.Анализ изображений
На рис. 3.3 слева показан один 8-участок, образующий простую
цифровую кривую. Но эта кривая не разделяет два 8-участка. С другой
стороны, в предположении 4-смежности мы имеем изолированные пиксели,
не образующие простую кривую, поэтому никакого разделения быть не
должно. Однако же налицо два разделенных 4-участка. Следовательно,
применение одного и того же отношения смежности к белым и черным
пикселям при попытке найти простые кривые в изображении приводит
к топологическому результату, не соответствующему теореме Жорда-
на-Брауэра на евклидовой плоскости, и, стало быть, противоречащему
интуиции. Прямолинейное решение таково.
Наблюдение 3.1. При двойственном использовании разных типов смежности
для черных и белых пикселей, например 4-смежности для белых и 8-смежности
для черных, гарантируется, что простые цифровые кривые разделяют свою
внутренность и внешность. Такое двойственное использование приводит к
планарному графу смежности для заданного бинарного изображения.
Врезка 3.5 (две теоремы разделения). Пусть ф - параметрический
непрерывный путь ф : [а, Ь] -> Ж2 такой, что а * Ь, ф(а) = 0(b), и пусть 0(s) * ф(Г) для
всех s,t (a$ s <t< b). Следуя К. Жордану (1893), будем называть жордановой
кривой на плоскости множество
7 = {(х,у):ф(Г) = (х,у)ла^Г^Ь}.
Открытое множество М называется топологически связным, если оно не
является объединением двух непересекающихся непустых открытых подмножеств М.
Теорема 3.1 (К. Жордан, 1887; О. Веблен, 1905). Пусть у - жорданова кривая
на евклидовой плоскости. Открытое множество Е2 \ у состоит из двух
непересекающихся топологически связных открытых множеств с общей границей у.
Эту теорему впервые сформулировал К. Жордан в 1887 г., но его
доказательство оказалось некорректным. Первое правильное доказательство дал
Освальд Веблен в 1905 г.
Два множества Sv S2 Q Rn называются гомеоморфными, если существует
непрерывное взаимно однозначное отображение Ф такое, что 0{S±) = S2 и
отображение Ф'1 также непрерывно [при этом 0~\S2) = 5J.
В 1912 г. Л. Э. Я. Брауэр обобщил определение жордановой кривой. Жорда-
новым многообразием в пространстве Rn (n Z 2) называется гомеоморфный
образ границы /7-мерного единичного шара.
Теорема 3.2 (Л. Э. Я. Брауэр, 1911). Жорданово многообразие разделяет Жп на
два связных подмножества и совпадает с границей каждого из этих
подмножеств.
3.1. Основы топологии изображений
123
3.1.2. Топологически непротиворечивая смежность
пикселей
Двойственное использование 4- и 8-смежности позволяет избежать
топологических проблем в бинарных изображениях. Для
многоуровневых изображений (содержащих более двух различных значений) мы
можем либо решить, что будем игнорировать топологические
проблемы, показанные на рис. 3.3 (и просто предполагать 4- или 8-связность
для всех пикселей, понимая, что иногда это будет приводить к
топологическим проблемам), либо применить какой-нибудь топологически
непротиворечивый подход, смирившись с дополнительными
вычислительными затратами.
Если ваше приложение должно быть топологически
непротиворечивым на уровне смежности пикселей или если вас интересует
возникающая математическая задача, то этот раздел для вас. На рис. 3.5
представлена математическая проблема: как построить математически
непротиворечивую модель, учитывающую топологию многоуровневых
изображений?
(КМИ)
(ХуО-
оЧ>
ттттттт
6-6-
Рис. 3.5. Проходит ли черная линия «поверх» серой?
Сколько существует серых компонент?
Сколько черных? Сколько белых?
Что касается структуры шахматной доски, показанной на рис. 3.1
справа, то мы предполагаем, что она определена на евклидовой
(непрерывной) плоскости и требуется решить, какого цвета должны быть
вершины квадратов: черного или белого. Топология - это именно та
математическая теория, которая дает ответы на такие вопросы.
124 ♦ Глава З.Анализ изображений
Врезка 3.6 (топология евклидова пространства). Кратко перечислим
некоторые факты из топологии евклидова пространства. Рассмотрим евклидову
метрику d2 в л-мерном евклидовом пространстве Rn (для наших целей
достаточно п = 1,2, 3). Пусть г > 0. Множество
U£(p) = [q : q e Rn Л d2(p,q) < а]
называется (открытой) £-окрестностью точки р е Rn, или (открытым) г-шаром
с центром в точке р, а в случае, когда е = 1, - единичным шаром.
Пусть S ^ MP. Множество S называется открытым, если для любой точки р е S
существует такое положительное £, что UJp) Q S. Множество Set"
называется замкнутым, если его дополнение 5 = Rn\S открыто. Класс всех открытых
подмножеств Rn определяет топологию /7-мерного евклидова пространства.
Пусть S Q Rn. Максимальное открытое множество 5°, целиком содержащееся
в S, называется внутренностью S, а минимальное замкнутое множество S#,
содержащее S внутри себя, называется замыканием S.
Из этих определений следует, что множество открыто тогда и только тогда,
когда оно совпадает со своей внутренностью, и множество замкнуто тогда и
только тогда, когда оно совпадает со своим замыканием. Разность множеств
SS = S* \ S° называется границей S.
Примеры. Рассмотрим случай п = 1. Для двух вещественных чисел a < b
отрезок [а, Ь] = {х : a $ х$ Ь} замкнут, а интервал (а, Ь) = {х : a < х < Ь} открыт.
Границей каждого из множеств [а, Ь], (а, Ь], [а, Ь) и (а, Ь) является множество {а, Ь].
Прямая линия у = Ах + В в двумерном пространстве также содержит открытые
и закрытые сегменты. Например, множество {(х, у) : а < х < Ь Л у = А* + 6} -
открытый сегмент. Одноточечное множество {р}, где р е R2, замкнуто. Границу
квадрата можно разбить на четыре (замкнутые) вершины и четыре открытые
отрезка прямой.
Множество в Rn называется компактным, если оно замкнуто и ограничено; у
него есть внутренность и граница. После удаления границы множество
становится открытым. Иллюстрация множеств на плоскости показана на рис. 3.6.
Мы можем считать, что все черные квадраты на шахматной доске
замкнуты, тогда будет существовать всего один связный черный участок.
Можно вместо этого считать, что все черные квадраты открыты, тогда
будет один связный белый участок. Возникает важный вопрос: какой
пиксель «владеет» вершиной, общей для всех четырех пикселей?
Наблюдение 3.2. Мы должны решить, какие полутоновые пиксели должны
быть замкнуты или открыты относительно другого уровня яркости; если
считать замкнутые пиксели «более важными», то нужно определить, что
более, а что менее важно.
3.1. Основы топологии изображений
125
Рассмотрим пример на рис. 3.5 и предположим следующий порядок
важности: «черный > серый > белый». Если четыре пикселя сходятся в
одной вершине (как показано на рис. 3.6) и среди них имеется черный
пиксель, то вершина тоже будет черной. Если среди четырех пикселей
нет ни одного черного, то серый пиксель «выигрывает» у белых. При
таком порядке важности мы будем иметь две черные, три серые и семь
белых компонент. См. рис. 3.7.
*г *
♦г •
♦ г ■
«г ■
•Г •
Т
T ■
г *
1
'Г *
I
♦ г ■
; i
и
U
♦ И
А* ,
U
-Г
■ I*
U
■Г •
|Ы
I*
I*
\*
I*
Рис 3.6. Пунктирной линией обозначены открытые внутренности,
сплошной линией - границы. Конечно, на непрерывной плоскости нет разрывов
между внутренностью и границей, это всего лишь грубый набросок
Рис. 3.7. Компоненты связности в случае «черный > серый > белый»
С другой стороны, в предположении, что «белый > серый > черный»,
мы будем иметь одну белую, две серые и пять черных компонент.
126 ♦ Глава 5. Анализ изображений
Порядок важности задает ключ (key) к такому определению
смежности, поэтому мы называем ее К-смежностью. Для скалярного
отображения действует простое общее правило: порядок важности должен либо
совпадать с порядком уровней яркости, либо быть противоположным.
Для векторного изображения можно взять порядок модулей векторов,
а в случае равенства использовать лексикографический порядок.
Определение iC-смежности на основе подобных порядков важности решает
возникающую математическую проблему (благодаря разбиению
плоскости в смысле евклидовой топологии), и последующий анализ
изображения согласуется с ожидаемыми топологическими правилами.
Но прибегать к этому порядку необходимо лишь в том случае,
когда два пикселя в противоположных углах массива 2*2 пикселей имеют
одинаковые значения, отличающиеся от значений двух других
пикселей в том же массиве. Будем называть такую ситуацию косым крестом
(flip-flop case). На рис. 3.8 показаны три косых креста.
Рис. 3.8. Три массива 2*2 пикселя,
определяющих возможные косые кресты
Количество косых крестов в реальных изображениях невелико;
см. четыре примера полутоновых изображений на рис. 3.9. Но,
несмотря на небольшое количество, они оказывают весьма заметное влияние
на форму или число связных участков (определяемых одинаковыми
значениями пикселей).
Наблюдение 3.3. Отношение К-смежности порождает планарный граф
смежности для заданного изображения и гарантирует, что простые цифровые
кривые разделяют внутренний и внешний участки.
Но вернемся к бинарным изображениям. Если предположить, что
«белый > черный», то iC-смежность будет означать, что для белых
пикселей применяется 8-смежность, а для черных - 4-смежность. Если же
«черный > белый», то все обстоит наоборот.
3.1.3. Трассировка краев
Встречая объект при построчном сканировании изображения, мы
часто хотим определить его край, т. е. такую линию, что весь объект
находится целиком слева или справа от нее. См. рис. 3.10.
5.1. Основы топологии изображений
127
Рис. 3.9. Размер этих изображений 2014x1426 (каждое содержит 2 872 964
пикселей), а 6тах = 255. Для изображения Tomte слева вверху косой крест имеет
место в 0,38% от общего числа пикселей. В изображениях PobleEspanyol справа
вверху, Rangitoto слева внизу и Kiri справа внизу процент косых крестов равен
соответственно 0,22%, 0,5% и 0,38%
Рис. 3.10. Две растровые строки, в первый раз наткнувшиеся на объекты,
представляющие интерес,-лампы (предполагается стандартный порядок
просмотра: сверху вниз, слева направо). В этот момент начинается процедура
трассировки для обхода края объекта
128 ♦ Глава З.Анализ изображений
Следуя определению смежности пикселей, мы должны для текущего
пикселя проверить все смежные с ним в определенном порядке,
согласованном с нашей стратегией (т. е. область, занятая объектом, всегда
находится справа или всегда слева).
Мы можем использовать 4-, 8-, К-смежность или любое другое
определение смежности. В каждом пикселе р определен локальный
круговой порядок f (р) = (qv ...,qn) перечисления по одному разу всех смежных
пикселей, составляющих множество А(р). В случае К-смежности
количество смежных пикселей п может изменяться от пикселя к пикселю.
Мы трассируем край и порождаем последовательность р0, pv ..., р.
пикселей, принадлежащих краю.
Предположим, что мы дошли до пикселя р.+1 б А(р.). Пусть qx - пиксель,
следующий за пикселем р. в локальном круговом порядке обхода
соседей р.+1. Мы проверяем, принадлежит ли qx объекту: если да, то полагаем
pi+2 = qx и продолжаем обработку пикселя pi+2; если нет, то проверяется
следующий пиксель q2 в локальном круговом порядке f (p/+1) обхода
соседей пикселя р.+1. И так далее.
Не любой локальный круговой порядок обхода множества смежности
можно считать приемлемым. Но обход смежных пикселей по или
против часовой стрелки допустим.
Пример 3.1. Будем рассматривать трассировку в случае 4-смежности.
См. пример на рис. 3.11.
Рис. 3.11. Слева: используемый локальный круговой порядок обхода.
Справа: встреча с объектом при переходе от q0 к р0
Мы подходим к объекту по ребру (q, p); пусть (q0, p0) := (q, p), и предположим,
что применяется показанный локальный круговой порядок обхода множества
4-смежности. Берем следующий пиксель в порядке обхода f (p0) - пиксель
справа от р0: он принадлежит объекту и, стало быть, является следующим краевым
пикселем.
5.1. Основы топологии изображений ♦ 129
Мы останавливаемся, если оказывается, что снова проверяем начальное
ребро, но в направлении (р, q), противоположном направлению подхода (q, р).
Сам факт повторного попадания в уже посещенный пиксель еще не является
причиной для остановки алгоритма.
Общий алгоритм трассировки краев Босса. Дано изображение с
определенным отношением смежности и начальное ребро (q, p), по
которому мы впервые подходим к пикселю р на еще не
протрассированном крае объекта. Примечание: мы не говорим «впервые подходим к
объекту», поскольку у одного объекта может быть один внешний и
несколько внутренних краев. Алгоритм приведен на рис. 3.12.
1: Положить (qQ, р0) = (q, р), / = 0, к = 1 ;
2: Пусть q1 - пиксель, следующий за q0 в порядке обхода £(р0);
3: while (qkfp.)^(qofp0) do
4: while qk принадлежит объекту do
5: Положить /;= / +1 и р. := qk;
6: Положить g1 равным пикселю, следующему за р в порядке обхода £(р.), а к = 1;
7: end while
8: Положить к = к +1 и перейти к пикселю qk в порядке обхода £(р.);
9: end while
10: Вычисленная последовательность краевых пикселей - (p0,pv ...# Р-);
Рис. 3.12. Алгоритм Восса
Объект О может содержать дырки, которые сами выступают в роли
объектов (и, в свою очередь, могут содержать дырки). Дырки
порождают циклы обхода внутренних краев объекта О, см. пример ниже.
Представленный алгоритм трассировки годится и для вычисления
внутренних краев. Локальный круговой порядок обхода всегда остается тем же
самым, разница лишь в том, какие смежные пиксели обходятся:
принадлежащие или не принадлежащие объекту.
Врезка 3.7 (Восс). Клаус Восс (1937-2008) описал приведенный выше общий
алгоритм трассировки краев в своей книге [К, Voss. Discrete Images, Objects, and
Functions in Zn. Springer, Berlin, 1993]. Он внес вклад во многие теоретические
вопросы анализа изображений и компьютерного зрения.
Пример 3.2. Проиллюстрируем все случаи трассировки краев для бинарного
изображения. См. рис. 3.13. Здесь мы применяем двойственную смежность для
бинарных изображений, определенную ключом «белый < черный». На рисунке
изображен один объект с тремя дырками. Обратите внимание на
непротиворечивость топологической двойственности связности и разделения. Множество
130
Глава З.Анализ изображений
всех циклов обхода краевых пикселей, не принадлежащих объекту, разбивает
плоскость и множество всех циклов обхода краевых пикселей, принадлежащих
объекту. Оба разбиения топологически эквивалентны и описывают одно
множество с тремя дырками.
Цикл обхода внешнего края
L'
□
Здикла обхода внутренних
краев
Рис. 3.13. Слева: Объект в предположении «белый < черный».
В середине: все циклы обхода краевых пикселей, не принадлежащих объекту.
Справа: все циклы обхода краевых пикселей, принадлежащих объекту
3.2. Анализ двумерных геометрических фигур
В этом разделе обсуждается измерение трех базовых характеристик
двумерных изображений: длина, площадь и кривизна. Переходя к
измерениям, мы покидаем область топологии и вступаем в область
геометрии. В этом разделе описано также дистанционное преобразование на
евклидовой плоскости.
У каждого изображения имеется геометрическое разрешение,
задаваемое в виде размера Ncols*Nrows. Чем выше разрешение, тем выше
точность измерения геометрических характеристик. Например,
измерение периметра объекта в изображении размера 1000x600
должно (теоретически) давать более точное значение, чем измерение
периметра того же объекта в изображении размера 500*300. Затраты
на более качественное оборудование должны окупиться улучшением
результатов.
3.2.1. Площадь
Площадь треугольника П = (р, q, г), где р = (xv yt), q = (х2, у2), г = (xv y3),
равна
«4(7) = ! • VXp, q, r)
(3.3)
где D(p, q, r) - определитель
3.2. Анализ двумерных геометрических фигур ♦ 151
.Л/1
Л"->
J\"l
Ух
Уг
Уз
~~ ^\У2 ^ъУ\ ^2Уз ^зУ2 ^2У\ ^\Уъ*
(3.4)
Значение Dip, q, r) может быть как положительным, так и
отрицательным, его знак определяет ориентацию упорядоченной тройки (р, q, r).
Площадь простого многоугольника П = (pv р2,..., рп) на евклидовой
плоскости, где р.= (х., у.) для / = 1,2,..., п, равна
Л{П) = |
^Zxi(yM-yi-i)
1=1
(3.5)
в предположении, что у0 = уп и уп+1 = уг В общем случае площадь
компактного множества R в Ж2 равна
Я(Т)= J dxdy. (3.6)
Спрашивается: как измерить площадь участка изображения?
На рис. 3.14 приведена иллюстрация эксперимента. Мы генерируем
простой многоугольник на сетке размера 512*512 и субдискретизируем
его на сетках меньшего разрешения. Площадь исходного
многоугольника П равна 102 742,5, а его периметр равен 4040,7966....
Рис. 3.14. Простой многоугольник Я на сетках с разрешением от 8*8 до 128><128.
Исходный многоугольник был нарисован на сетке с разрешением 512*512.
Все изображения показаны в модели ячеек сетки
152 ♦ Глава З.Анализ изображений
Чтобы вычислить периметр многоугольника общего вида, мы
подсчитываем количество сторон ячеек на границе многоугольника и
умножаем его на длину стороны при данном разрешении. Для
изображения с разрешением 512><512 предполагается, что длина стороны равна 1,
с разрешением 128x128 - 4 и т. д.
Чтобы вычислить площадь многоугольника, мы подсчитываем
количество пикселей (т. е. ячеек сетки) внутри него и умножаем эту
величину на квадрат длины стороны.
Относительным отклонением называется абсолютная величина
разности между значением некоторой характеристики для субдискрети-
зированного и исходного многоугольника П, поделенная на значение
этой характеристики для П.
На рис. 3.15 показаны ошибки измерения в форме графика
относительных отклонений. Очевидно, что периметр, измеренный для суб-
дискретизированных многоугольников, не сходится к истинному
значению - относительное отклонение даже возрастает!
Относительное отклонение
(в процентах)
25
20
15
10
5
i
'Отношение периметра субдискретизированного
многоугольника к периметру исходного
Отношение площади субдискретизированного
^многоугольника к площади исходного
О *- * ° °—■ о «-Разрешение изображения
8 16 32 64 128 (количество узлов сетки)
Рис. 3.15. Отклонения площади и периметра субдискретизированных
многоугольников относительно истинного значения на сетке 512*512
Что касается измерения площади участка изображения, то еще со
времен Гаусса известно, что количество ячеек сетки в выпуклом
множестве S дает точную оценку площади 5. Поэтому неудивительно, что
измеренная площадь сходится к истинной по мере увеличения
разрешения.
Наблюдение 3.4. Количество ячеек сетки внутри участка - надежная оценка
площади объекта.
Экспериментальные данные показывают, что при оценке периметра
предложенным методом неизбежны «сюрпризы».
5.2. Анализ двумерных геометрических фигур ♦ 155
3.2.2. Длина
Начнем с определения длины на евклидовой плоскости. Длина
измеряется для дуг (например, отрезков прямой или дуг окружности).
Предположим, что имеется параметрическое взаимно однозначное
представление 0(г) дуги у, начинающейся в точке ф(с) и
заканчивающейся в точке ф{й), где с < d. Значения в точках t0 = с < tx < ... < tn = d
определяют полигональную аппроксимацию этой дуги (рис. 3.16).
Рис. 5.16. Полигональная аппроксимация дуги,
определенной последовательностью лежащих на ней точек ф(^
Врезка 5.7 (жордановы дуги). Приведем общее математическое определение
дуги.Жорданова дуга у определяется как отрезок [с, d] жордановой (простой)
кривой
{(х,у):0(Г) = (х,у)ло^Г^Ь},
гдео^с<с/^Ьи ф(^) ф 0(t2) для tx * t2, за исключением точек tt = а и t2 = b.
У спрямляемой жордановой дуги у длина ограничена:
п
Цу) = sup £ de (0ft ), фЦ(_х ))<«,.
n>\/\c=t§<-'<tn=d i—i
См. рис. 3.16. В 1883 г. Жордан предложил следующее определение кривой:
у = {(х,у) :x=a(t)Ay= P(t)Aa$t$ b].
В 1890 г. Джузеппе Пеано показал, что такое определение допускает кривые,
целиком заполняющие единичный квадрат. Кривая Пеано не
дифференцируема ни в одной точке отрезка [0, 1]. Для вычисления длин дуг используется
определение Жордана 1883 г.:
(в предположении, что функции а и /? дифференцируемые).
134
Глава 5. Анализ изображений
Длина полигональной аппроксимации корректно определена (она
равна сумме длин всех отрезков, составляющих эту ломаную). Предел
длины полигональной аппроксимации при п, стремящемся к
бесконечности (когда отрезки становятся все короче и короче), по определению,
равен длине у.
Зубчатость. Рассмотрим диагональ pq квадрата со стороной а. Длина
диагонали равна aV2. Рассмотрим 4-путь, аппроксимирующий
диагональ, как показано на рис. 3.17 вверху (для разных разрешений сетки).
Длина этих 4-путей при любом разрешении равна 2а.
В качестве второго примера рассмотрим границы дискретизирован-
ных кругов, показанные на рис. 3.17 внизу. При любом разрешении
сетки длина границы равна 4.
pi
У
<
Г
Р'
к-
—*
Г
и
-И
1 Гч 1
И
N
РШ
тт?#
И
и
и
► X
► X
► X
У
1 I ГТ
o-l—^Ш
III -►х
Рис. 3.17. Вверху: аппроксимации диагонали квадрата 4-путями для сеток разного
разрешения. Внизу: дискретизация единичного круга на сетках разного разрешения
Наблюдение 3.5. Использование длины 4-пути для оценки длины дискретной
дуги может приводить к погрешности 41,4% (относительно длины исходной
дуги на непрерывном изображении до его оцифровки). Этот метод не
рекомендуется применять для измерения длин в процессе анализа изображений.
Использование взвешенных ребер. Предположим, что для
измерения длины используются 8-пути. Будем назначать вес V2 диагональным
ребрам и вес 1 ребрам, параллельным осям координат. (Прямая или
отрезок на евклидовой плоскости называется осепараллельной, если она
параллельна одной из двух осей декартовой системы координат.)
5.2. Анализ двумерных геометрических фигур ♦ 155
Рассмотрим отрезок прямой pq на рис. 3.18 с углом наклона 22,5° и
длиной 5V5/2.
..
н
/
о
Рис. 3.18. Аппроксимация отрезка прямой pq 8-путями
на сетках разного разрешения
Длина pipq) равна 3 + 2V2 для сетки со стороной ячейки 1 (слева) и
(5 + 5V2)/2 для любой сетки со стороной ячейки 1/2" (п > 1). Отсюда
следует, что длины 8-путей не сходятся к 5V5/2, когда сторона ячейки сетки
стремится к нулю.
Наблюдение 3.6. Для 8-путей ситуация такая же, как для 4-путей, только
погрешность составляет не более 7,9...% (при дискретизации дуг известной
длины), и в некоторых случаях невозможно уменьшить погрешность,
увеличивая разрешение сетки.
В некоторых приложениях эта верхняя граница погрешности может
быть приемлема. Применение взвешенных ребер (включая
диагональные) для оценки длины, безусловно, приемлемо в случае изображений с
низким разрешением или при измерении относительно коротких
дискретных дуг.
Полигональное упрощение краев. А существует ли
общепризнанный точный способ измерения длины? Вернемся к схеме на рис. 3.16.
Если разбить дугу на дискретные отрезки прямой, как показано на
рис. 3.19, то сумма длин этих отрезков будет сходиться к истинной
длине дуги при условии, что наш бюджет позволяет приобретать
оборудование, обеспечивающее все более и более высокое разрешение
сетки.
Врезка 3.9 (цифровая геометрия). В публикациях по цифровой геометрии
можно найти дополнительные сведения о том, как вычислить дискретные
отрезки прямой, и о других алгоритмических вопросах, связанных с
вычислениями на сетке изображения. См. например, монографию [R. Kiette and A. Rosenfetd.
Digital Geometry. Morgan Kaufmann, San Francisco, 2004].
156 ♦ Глава З.Анализ изображений
Конечная вершина
Рис. 3.19. Полигональная аппроксимация края участка по часовой стрелке (слева)
и против часовой стрелки (справа) дискретных отрезков прямой максимальной
длины в указанном порядке обхода
3.2.3. Кривизна
Жорданова кривая называется гладкой, если она непрерывно
дифференцируема. Многоугольник не является гладким в особых точках (т. е.
в вершинах). Кривизну кривой можно определить только в регулярных
(не особых) точках.
Кривина как скорость изменения угла наклона касательной.
Рассмотрим дугу у на евклидовой плоскости, являющуюся отрезком
гладкой жордановой кривой. Тогда в каждой точке р, принадлежащей у,
определена касательная t(p), составляющая угол гр с положительным
направлением оси х. Этот угол называется углом наклона (см. рис. 3.20).
Рис. 3.20. Репер Френе в точке р = y(t). Показана также длина / = £(t)
Когда р пробегает у, угол гр изменяется. Скорость изменения гр
(относительно движения р вдоль у) - один из способов определения кривизны
Ktan(P) кривой.
5.2. Анализ двумерных геометрических фигур ♦ 157
Врезка 3.10 (Френе и репер Френе). Для определения кривизны удобно
использовать репер Френе, представляющий собой пару взаимно
перпендикулярных осей координат (см. рис. 3.20) с началом в точке р = y(t) на кривой.
Свое название он получил в честь французского математика Жана Фредерика
Френе (1816-1900). Одна ось определена касательным вектором
t(f) = [cos^(t),sin t/;(t)]T,
где ф- угол наклона, образованный касательной и положительным
направлением оси х. Другая ось определена нормальным вектором
n(t) = [-sim/>(t),cosi/;(f)[T.
Обозначим / = L(t) длину дуги между начальной точкой у (а) и текущей
точкой р = y(t). Определение кривизны не должно зависеть от скорости
V(t) = —^ (3.7)
at
параметризации у. Формально кривизна в точке y(t) = (x(t), y(t)) гладкой
жордановой кривой у определяется следующим образом:
Скорость изменения может быть положительной, отрицательной или
равной нулю в точках перегиба. Если кривизна в точке р
положительна, то эта точка называется точкой выпуклости, а если отрицательна, то
точкой вогнутости. См. рис. 3.21.
Рис. 3.21. Три касательные (пунктирные линии). Кривизна положительна
на левом рисунке, переходит через ноль на среднем и отрицательна на правом
Как видно из рис. 3.21, ситуацию в точке р можно аппроксимировать
путем измерения расстояния между у и касательной к у в р вдоль
равноотстоящих прямых, перпендикулярных касательной. На рис. 3.21
положительные расстояния представлены жирными отрезками, а
отрицательные - «полыми» отрезками. Площадь между кривой и касательной
можно аппроксимировать суммой этих расстояний; она положительна
158 ♦ Глава 5.Анализ изображений
на левом рисунке, отрицательна на правом и равна нулю на среднем, где
положительные и отрицательные расстояния взаимно уничтожаются.
Предположим, к примеру, что у - прямая линия. Тогда касательная
совпадает с у в любой точке р, и скорость изменения нулевая, т. е.
кривизна равна нулю в любой точке, принадлежащей у. Предположим
теперь, что у - окружность. Тогда, как мы знаем, скорость изменения угла
наклона постоянна, а в предположении, что скорость пробегания
кривой равномерна, эта постоянная равна единице, поделенной на радиус
окружности.
Кривизна как радиус соприкасающейся окружности. Кривизну
можно изучать также с помощью соприкасающихся окружностей (см.
рис. 3.22). Соприкасающейся окружностью в точке р кривой у
называется наибольшая окружность, касающаяся у в точке р с вогнутой
стороны. Пусть радиус соприкасающейся окружности в точке р равен г. Тогда
кривизна у в точке р козс(р) = 1/г. В случае прямой линии г равен
бесконечности, и, следовательно, кривизна равна 0. Можно доказать, что
Рис. 3.22. Определение кривизны как скорости изменения угла наклона
касательной (слева) и как радиуса соприкасающейся окружности (справа).
Точки р, q и г иллюстрируют скорость изменения угла наклона \р.
Предположим, что точки движутся слева направо. Тогда кривизна в точке р
положительна, кривизна в точке перегиба q равна нулю, а кривизна в точке г
отрицательная. Точки s и г иллюстрируют определение кривизны с помощью
соприкасающейся окружности. Кривизна в точке s равна l/rv а в точке г - 1/г2
Кривизна параметрической дуги. Существует еще один способ
определения кривизны на евклидовой плоскости. Рассмотрим пара-
3.2. Анализ двумерных геометрических фигур ♦ 159
метрическое представление y(t) = (x(t), y(t)), изначально предложенное
Жорданом для определения кривой. Из него следует, что
„ ГЛ_*(0-Я0-Я0-*(0 mm
[m2+m2]
где
i(0=M), яо=м), ад=<Що, m=*m. (З.П)
df d/ dr dr
Алгоритмы оценивания кривизны дискретных кривых в
изображениях - предмет цифровой геометрии. Как правило, для этого
используется скорость изменения угла наклона, а не соприкасающаяся
окружность, и лишь в нескольких алгоритмах делается попытка представить
в дискретном виде уравнение (ЗЛО).
Пример 3.3 (один из вариантов оценивания кривизны дискретной кривой).
На самом деле воспользоваться уравнением (ЗЛО) очень просто. Пусть дана
дискретная кривая (pv..., pm), где точки р. = (*., у), l^j^m, получены
дискретизацией параметрической кривой y(t) = (x(t), у(£)), t e [0, m]. Предполагается, что
y(i) = pr Функции x(t) и у(£) локально аппроксимируются многочленами второй
степени:
x(t) = a0 + a1t + a2t\ (3.12)
y(t) = b0 + b1t + b2t\ (3.13)
а кривизна вычисляется по формуле (ЗЛО). Положим х(0) = х., х(1) = х._к, х(2) = х.+к,
где к > 1 - целочисленный параметр, и аналогично для y(t). См рис. 3.23. Тогда
кривизна в точке рх определяется по формуле
2(аД —ЪлаЛ
*•/= г 2T--S • (ЗЛ4)
Вместо константы к > 1 можно использовать локально-адаптивные решения.
ооооооооо
о
о
о--
Р; i
О
о
m
-•-
о
•-
у
о
--•-
о
--•-■
Pi
о
--•
о
--•-
о
о
m
--•
о
о
о
'Рм:
О
о
о
•
•
v-
о
0
О
о
S
•
о
о
Рис. 3.23. Использование к = Ъ
О О О О О Ш---Ф О О
при оценке кривизны в точке р.
140 ♦ Глава 5. Анализ изображений
3.2.4. Дистанционное преобразование
Дистанционное преобразование (distance transform) помечает
каждый пиксель объекта (например, пиксели, определенные неравенством
1{р) > 0) евклидовым расстоянием от его местоположения до
ближайшего пикселя, не принадлежащего объекту (например, определенного
равенством 1(р) = 0). Для простоты можно сказать, что дистанционное
преобразование сопоставляет всем пикселям р ЕП значение
D(p) = min{ d2{p,q): I(q) = О}, (3.15)
qeQ,
где d2(p> qk) - евклидово расстояние. Отсюда следует, что D(p) = 0 для всех
пикселей, не принадлежащих объекту.
Врезка 3.11 (история дистанционного преобразования). Статья [A Rosenfeld and
IL Pfaltz. Distance functions on digital pictures. Pattern Recognition, vol. 1, p. 33-61] -
пионерская работа, в которой не только определено дистанционное
преобразование изображений, но и представлен эффективный двухпроходный
алгоритм. А. Розенфельд и Й. Пфальц использовали сеточные метрики, а не
евклидову метрику и предложили два варианта аппроксимации евклидовых
расстояний: с помощью 4-путей и 8-путей. Эту аппроксимацию можно
улучшить с помощью фальцевания (chamfering), как описано в работе [G. Borgefors,
Chamfering - a fast method for obtaining approximations of the Euclidean distance in
N dimensions. In Proc. Scand. Conf. Image Analysis, 1983, p. 250-255].
В работах [T.Saito and J. Toriwaki. New algorithms for Euclidean distance transformation
of an n-dimensional digitized picture with applications. Pattern Recognition, vol. 27,1994,
p. 1551-1565] и [T.Hirata.A unified linear-time algorithm for computing distance maps.
Information Processing Letters, vol. 58,1996, p. 129-133] использована евклидова
метрика и предложен новый алгоритм на основе нижних огибающих
семейства парабол.
Максимальные окружности на сетке изображения. Пусть S с П -
множество всех пикселей, принадлежащих объекту, аВ = П\Б-
множество всех пикселей, не принадлежащих объекту. Дистанционное
преобразование обладает следующими свойствами:
1) D(p) равно радиусу наибольшего круга с центром в р, который
целиком содержится в S;
2) если существует всего один пиксель q e В, не принадлежащий
объекту, для которого D(p) = d2(p, q), то возможно два случая:
а) существует пиксель р' е S такой, что круг с центром в рг
содержит внутри себя круг с центром в р; или
5.2. Анализ двумерных геометрических фигур ♦ 141
Ь) существуют пиксели p'eSnq'eB такие, что d2(p, q) = d2(p', q^n
p является 4-смежным с р';
3) если существует два (или более) пикселей q, q' e В, не
принадлежащих объекту и таких, что D(p) = d2(p, q) = d2(p, q*), то круг с
центром р является максимальным кругом в 5; в таком случае точка р
называется симметричной.
В случае 2(b) оба пикселя pup' являются центрами максимальных
кругов и 4-смежны друг с другом.
На рис. 3.24 вверху показан прямоугольник с подмножеством
максимальных кругов. По меньшей мере два пикселя, не принадлежащих
объекту, находятся на одинаковом расстоянии от центра одного из этих
кругов. В среднем ряду показаны максимальные круги, центры которых
являются 4-смежными, и для каждого круга существует только один не
принадлежащий объекту пиксель на расстоянии г (радиус круга). На
нижнем рисунке показан круг В, для которого существует только один
не принадлежащий объекту пиксель на расстоянии г от его центра и
который содержится в максимальном круге А.
Рис. 3.24. Вверху: множество максимальных кругов. В середине: симметричные
точки, определенные в случае 2(b). Внизу: иллюстрация случая 2(a)
142 ♦ Глава 5. Анализ изображений
Карта расстояний и карта строковых и столбцовых компонент.
Карта расстояний - это двумерный массив такого же размера, как
исходное изображение, в котором хранятся величины D(p) для каждого
пикселя р еП.
Пусть кратчайшее расстояние D(p) равно расстоянию d2(p, q) между
точками р = (хр, ур) и q = (xqJ yq). Тогда
D(p) = yl(xp-xq)2+(yp-yg)2. (3.16)
ЗнаяДл: = л: -х иДу = у -у, мы также знаем D(p), но знание D(p)
ничего не говорит о строковой компоненте Ах со знаком и столбцовой
компоненте Лу со знаком. Поэтому вместо карты расстояний нам может быть
более интересна карта строковых и столбцовых компонент: для каждой
точки р Е П мы храним пару (Ах, Ау), по которой можно вычислить D(p).
Квадратичное евклидово дистанционное преобразование
(SEDT). Для экономии времени обычно вычисляют квадрат D(p)2
евклидова расстояния. Мы объясним принцип работы одного алгоритма,
который строит точную карту SEDT за линейное время. Многие авторы
добились успеха в уменьшении времени его работы.
В самом начале алгоритм выполняет ряд целочисленных операций
для вычисления SEDT до ближайшей не принадлежащей объекту
точки по одному измерению, выполняя два прохода по строкам. Затем он
переходит к работе на непрерывной плоскости Ш.2 и вычисляет нижнюю
огибающую семейства парабол для каждого столбца. Алгоритм находит
параболы, отрезки которых являются частями нижней огибающей, и
вычисляет конечные точки этих отрезков. Квадраты евклидовых
расстояний вычисляются в процессе дополнительного прохода по
столбцам с помощью уравнений парабол, найденных на предыдущем шаге.
Мы подробно рассмотрим этот алгоритм в двумерном случае и
отметим, что все вычисления можно производить независимо для каждого
измерения, поэтому описанный подход легко обобщается на
произвольное число измерений.
Расстояния по строке. Первый шаг алгоритма - вычисление
расстояния от каждого пикселя, принадлежащего объекту, до ближайшего
пикселя, не принадлежащего объекту и находящегося в той же строке:
№, У) = fx(x - 1, у) + 1, если 1(х, у) >0, (3.17)
f1(x,y) = 0, если 1(х,у) = 0, (3.18)
f2(x,y) = mm{f1(x,y),f2(x+l,y) + l}, если fx(xyу) ф 0, (3.19)
/2(х,у) = 0, если/;(х,у) = 0. (3.20)
3.2. Анализ двумерных геометрических фигур ♦ 145
Здесь /j(а:, у) определяет расстояние между пикселем р(х, у) и
ближайшим не принадлежащим объекту пикселем q слева, а/2 заменяет/^, если
расстояние до ближайшего не принадлежащего объекту пикселя справа
короче.
В результате получается матрица, в которой хранятся целые
значения (f2{x, у))2 в каждом пикселе. См. пример на рис. 3.25 слева.
Выражение f2(x, у) для фиксированной строки у выглядит так:
/2(x,>0=._min {\x-i]:I(i,y) = 0}. (3.21)
l—i9...9Iycols
На рис. 3.25 слева показаны результаты одномерного SEDT после
вычисления \f2(x, у)]2 для каждой строки с номером 1 ^ у < N
С
0
0
0
с
0
0
0
0
0
1
0
0
4
4
9
1
0
4
9
16
4
0
1
16
16
9
Э
0
9
S
4
0
0
4
4
1
0
0
1
1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
1
0
0
1
1
0
0
1
4
2
1
0
1
4
4
1
0
1
2
4
1
rows
0
0
1
4
1
0
0
1
2
1
0
0
1
1
0
0
0
0
0
с
00 0000000000
Рис. S.25. Нулями обозначены пиксели, не принадлежащие объекту.
Числа равны квадрату евклидова расстояния. Слева: промежуточные результаты
после начальных проходов по строкам. Справа: окончательные результаты
после прохода по столбцам
Расстояния по столбцу. Если существует всего два пикселя, не
принадлежащих объекту, то для данного пикселя р = (х, у) нам нужно знать
только, какой из пикселей (х, уг) и (х, у2) ближе. Для этого нужно сравнить
[(№, У,))2 + (У " У,)2] < Ш*,У2))2 + (У " У2)2]. (3.22)
Функция f3(x, у) определяет значения двумерного SEDT для каждого
столбца, считая х фиксированным, а у изменяющимся от 1 до Nrom:
f3(x,y)= min \(f2{x,y))2+{y-jf\ (3.23)
Обсудим геометрическую интерпретацию, иллюстрирующую
основную идею эффективного решения.
Нижние огибающие. Для фиксированного столбца (например, для
а: = 5 обозначим /"2(5, у) = g(y)) и для фиксированной строки (например,
у = 3) рассмотрим уравнение
144 ♦ Глава 5. Анализ изображений
Уз</) = (#(3))2 + (3-;-)2, (3.24)
где / = 1,..., Nrows. Мы по-прежнему обращаемся к рис. 3.25; значения,
вычисляемые по этой формуле, расположены на третьей параболе на
рис. 3.26.
30 т
Рис. 3.26. Семейство парабол для столбца [0,4,9,16,4,0] на рис. 3.25 слева
Для Ky<N мы рассматриваем семейство N парабол (рис. 3.26).
" ■' rows r r rows f \tr /
Для каждой строки существует одна парабола, а для каждого столбца -
Nrows парабол. По горизонтальной оси откладывается номер строки у,
а по вертикальной оси - у (/), локальный минимум достигается в точке
у = /иравенуу(/)=£(у).
Нижняя огибающая семейства парабол соответствует вычислению
минимума по формуле (3.23). Эффективные алгоритмы SEDT
вычисляют нижнюю огибающую семейства парабол, а затем сопоставляют
высоту (т. е. расстояние по вертикали до оси абсцисс) нижней огибающей
точке с координатами (х, у). Вычисление нижней огибающей - главная
часть алгоритма SEDT.
Наблюдение 3.7. Вычисление нижней огибающей сокращает квадратичную
сложность наивного алгоритма EDT до линейной, поскольку огибающие можно
вычислять инкрементно.
Пример 3.4 (вычисление секций). На рис. 3.26 показано семейство,
состоящее из шести парабол. Нижняя огибающая состоит из двух
криволинейных отрезков. Первый отрезок начинается в точке (1, 0) и
заканчивается в точке пересечения первой и последней парабол. Второй
отрезок начинается в этой точке пересечения и заканчивается в
точке (6, 0). Проекции этих отрезков на горизонтальную ось называются
секциями.
3.2. Анализ двумерных геометрических фигур ♦ 145
В этом простом примере отрезок [1,6] разбит на две секции. Только
две из шести парабол вносят вклад в нижнюю огибающую. Для
вычисления/^) (при фиксированном х) нам нужно знать начало и конец
каждой секции и индекс соответствующей ей параболы.
Это можно сделать, выполнив два прохода по столбцам. На
проходе сверху вниз мы определяем отрезки парабол, входящие в нижнюю
огибающую, и ассоциированные с ними секции, а на втором проходе
вычисляем значения/3(у).
Подготовка к вычислению нижней огибающей. Для вычисления
нижней огибающей мы последовательно вычисляем нижние
огибающие первых к парабол. Вычисляется точка пересечения двух парабол.
Пусть ys - абсцисса точки пересечения? и пусть yt < y2. Уравнение точки
пересечения ys = ys(yv у2) любых двух парабол у1 и у2 имеет вид
[g(y1)]2 + (ys-yi)2 = [s(y2)]2 + (ys-y2)2'
Отсюда находим
(3.25)
(3.26)
2(У2-^)
Выражение (3.26) применяется на первом проходе по столбцам в
алгоритме SEDT, когда вычисляется нижняя огибающая парабол в каждом
столбце. Эта информация хранится в стеке.
В стеке остаются только параболы, дающие вклад в нижнюю
огибающую, а все остальные из стека удаляются. В результате получается
довольно простой алгоритм, см. также эскиз на рис. 3.27.
k \
к \ ^-—■
\\/з
Рис. 3.27. Слева: эскиз для ys{y2, уъ) > ys(yv y2). Справа: эскиз для ys(y2, уъ) < yjyv y2)
Вычисление нижней огибающей. В каждом стеке хранится пара
вещественных чисел (Ь, е), описывающих начало и конец секции
параболы, являющейся частью нижней огибающей. Пара (bt, et) относится к
146 ♦ Глава 5.Анализ изображений
параболе на вершине стека, а ф„ е.) - пара, ассоциированная со
следующей параболой в последовательном процессе просмотра.
В первом элементе хранится начало и конец секции первой
параболы. Он инициализируется значениями (l,iVrows); нижняя огибающая
состояла бы из одного отрезка между точками 1 и Nrows, если бы все
последующие параболы не пересекались с первой.
Параболы упорядочены в соответствии со значениями координаты у
в изображении. На каждом шаге вычисляется пересечение элемента на
вершине стека, представляющего yt, со следующей параболой у~
Возможны три случая:
1) ys(yt, yj) > Nrows. Тогда у. не дает вклада в нижнюю огибающую, стек
не изменяется, и мы переходим к следующей параболе;
2) ys(yt, у) < bt. Тогда удаляем yt из стека и вычисляем пересечение
нового элемента на вершине стека с у,(см. рис. 3.27 справа); если
стек пуст, то добавляем в него элемент, соответствующий у;
3) ys(yt, у.) > bt: корректируем yt, заменяя et на ys(yt, у.), добавляем
в стек элемент, соответствующий у„ в котором b = et, e=n (см.
рис. 3.27 слева).
Этот процесс продолжается, пока не будет вычислено пересечение
последней параболы с элементом на вершине стека. В конце работы в
стеке останутся только секции, вошедшие в состав нижней огибающей,
и они будут использованы для вычисления значений f3(x, у) на
следующем проходе.
Пример 3.5 (нижняя огибающая). В нашем простом примере (см. рис. 3.26)
нижняя огибающая состоит из секции yv начинающейся в точке Ьх = 1 и
заканчивающейся в точке ех = 3,5, и секции у6, начинающейся в точке Ь2 = 3,5 и
заканчивающейся в точке е2 = 6. Теперь вычислим значения
¥>(}) = W))2 +(1-J)2 Для/=1,2,3 (3.27)
и
Y6(j) = (£(6))2 + (6 - /)2 для j = 4,5,6. (3.28)
У описанного базового подхода есть вариации, позволяющие уменьшить
объем вычислений.
Предобработка и временная сложность. На шаге предобработки
можно исключить все параболы, для которых g(y) > (Nrows - 1)/2,
поскольку никакой их отрезок не является частью нижней огибающей. В нашем
простом примере (см. рис. 3.26) параболы у3(/), для которойg(3) = 3 > 2,5,
и у4(/), для которой g(4) = 4 > 2,5, будут исключены еще до начала
вычисления пересечений.
З.З.Анализ значений изображения ♦ 147
Время работы алгоритма SEDT линейно. Вычисления для
каждого измерения производятся независимо. Получающийся в результате
квадрат минимального расстояния по одному измерению будет целым
числом в каждой ячейке сетки, и это целое число используется для
обсчета следующего измерения.
Произвольное число измерений. Двумерный алгоритм SEDT
можно записать следующим образом:
D(x,y) = min {(х-О2 +(y-j?\ (3-29)
l l,--;NcolSAj=\^ ,.,Nrows
Поскольку i не зависит от/, мы можем переписать это в виде
D(x,y)= min ( min Ux-if + (y-jf}\ (3.30)
j=\,...,Nrows \J-\,-,Ncois JJ
Вычисление минимума min {(x - i)2)=g(j)2 в формуле (3.30)
соответствует проходу по строкам в первой части алгоритма SEDT. Мы можем
переписать это выражение, зафиксировав х, и вывести формулу для
второго измерения
D(x,y) = min {g(if+(y-j)2}. (3.31)
j—\,...,Nrows
Вычисление минимума в (3.31) соответствует проходам по
столбцам.
Пусть р - точка трехмерного пространства с координатами (а:, у, к), где
к = 1,..., Nla er, a h(k)2 - результат вычисления минимума в формуле (3.31)
для фиксированных х, у. Тогда можно записать выражение для третьего
измерения:
D(x,y,z)= min {h{kf+{z-kf}. (3.32)
k=\,...,Niayer
Эту процедуру можно распространить и на большее число
измерений.
З.З.Анализ значений изображения
Помимо геометрического анализа содержимого изображения, нас также
интересует описание сигнала, т. е. распределение значений изображения.
Мы и далее будем предполагать, что задано скалярное изображение /.
В этом разделе описываются матрицы совместной встречаемости,
метрики, определенные на этих матрицах, а также моменты участков
или окон изображений.
148
Глава З.Анализ изображений
3.3.1. Матрицы совместной встречаемости и метрики
Базовые статистики (среднее, дисперсия, гистограмма уровней
яркости) представляют собой метрики, основанные на обобщении
значений отдельных пикселей. Совместная встречаемость предназначена
для изучения распределения значений с учетом значений смежных
пикселей. Эта информация представляется в виде матрицы совместной
встречаемости С.
Предположим, что дано входное изображение /и множество
смежности А. Например, в случае 4-смежности А4 = {(О, 1), (1, 0), (0, -1), (-1, 0)},
так что для любого пикселя р А4(р) = А4+ р. Как и раньше, будем
обозначать П множество всех N , *N координат пикселей. Определим
cols rows гг^ г гп
матрицу совместной встречаемости С; размера (Gmax+ l)x(Gmax+ 1) для
изображения / и значений пикселей и и v из множества {0, 1,..., Gmax}
следующим образом:
CI(u,v) = J, X
pe.Q. qe.A/\p+q&Q.
1 если 1{р) = и и I(p + q) = v
0 в противном случае
(3.33)
Множество смежности может быть несимметричным, например:
А = {(0,1), (1, 0)}. На рис. 3.28 предполагается, что множество
смежности А = {(0,1)}. Показаны три примера увеличения счетчика значений в
матрице совместной встречаемости. Так, в точке (х, у) = (3,2) находится
значение и = 2, а строкой ниже - значение 1. Поэтому счетчик в
элементе (u, v) = (2,1) увеличивается на 1.
-►х
2
3
3
ф-
т
3
3
3
3
3
1
о
0
^2~~
2
1
■
~0|
0
0
0
1
0 1
-►и
1
* +1
Рис. 3.28. Слева показано небольшое изображение 5х5,
для которого Gmax= 3,a справа - его матрица совместной встречаемости
размера 4x4. Множество смежности А = {(0,1)} содержит только одно смещение,
т.е. мы должны просматривать лишь пиксель, расположенный строкой ниже.
В точке (х, у) = (5,1) значение пикселя и = 0, а значение пикселя строкой ниже v = 0.
Следовательно, счетчик в элементе матрицы (и, v) = (0,0) увеличивается на 1
5.5. Анализ значений изображения
149
Пример 3.6 (примеры матриц совместной встречаемости). Мы
рассматриваем небольшое изображение / размера 5х5 (рис. 3.29 слева), для которого
Gmax = 3, и четыре разных множества смежности: Аг = {(О,1)}, А2 = {(О,1), (1, 0)},
Аъ = {(0,1), (1,0), (0, -1)} и обычное множество смежности А4. На таких простых
данных легко проследить за вычислениями.
На среднем и правом рис. 3.29 показаны соответствующие матрицы
совместной встречаемости.
-►х
2
3
3
2
3
1
3
3
3
3
1
2
1
1
2
0
2
2
1
1
0
0
0
0
1
-► и
у
3
1
1
0
0
2
2
1
0
2
1
2
0
0
1
4
► и
f
4
1
1
0
2
5
3
1
2
4
2
3
0
2
3
7
7
1
1
0
3
7
5
1
3
6
3
4
0
3
5
11
► и
8
3
3
0
3
10
7
3
3
7
4
6
0
3
6
14
Рис 3.29. Слева вверху, входное изображение 1,х изменяется от 1 до Nco[s= 5,
а у - от 1 до Nrows= 5. б середине вверху: матрица совместной встречаемости Сг
для множества смежности А • и и v изменяются от 0 до G =3.
м 1' " max
Справа вверху: матрица совместной встречаемости С2 для множества смежности А2.
В середине внизу: матрица совместной встречаемости С3 для множества
смежности Ау Справа внизу: матрица совместной встречаемости С4
для множества смежности А4
Приведем несколько примеров вычислений. Начнем с Аг. Вначале имеем
(u, v) = (0, 0). Мы должны подсчитать, сколько раз встречается ситуация, когда
1(х, у) = 0 и 1(х, у + 1) = 0, т. е. под нулевым пикселем также находится нулевой
пиксель. Это имеет место в трех случаях. Поэтому для множества смежности Аг
Сх(0, 0) = 3. Рассмотрим еще один пример: (м, v) = (3, 1). Нет ни одного случая,
когда значение 3 расположено непосредственно над значением 1, поэтому
Сх(3,1) = 0.
Далее рассмотрим два примера для А2. Аг - подмножество Av поэтому
Сх(и, v) < С2(м, v) для любой пары значений пикселей (и, v). В случае (и, v) = (0,0),
помимо ситуации «1(ху у) = 0 и 1(ху у + 1) = 0», мы должны подсчитать, сколько
раз встречается ситуация, когда оба пикселя в точках (х, у) и (л: + 1, у) равны 0.
Такое имеет место всего один раз. Поэтому С2(0,0) = 3 + 1 = 4. Последний при-
150 ♦ Глава 5. Анализ изображений
мер: (и, v) = (2,1). Для q = (О,1) мы насчитали два случая, и для q = (1,0) тоже два
случая, поэтому С2(2,1) = 2 + 2 = 4.
Суммы всех элементов в любой из этих матриц совместной встречаемости в
20 раз больше количества элементов в множестве смежности. Последняя
матрица (для А4) симметрична, потому что симметрично само множество А4.
Этот пример иллюстрирует два важных свойства матриц совместной
встречаемости.
1. Каждый элемент q множества смежности добавляет Ncols • (Nrows - 1)
или (N , - 1) • N к общей сумме элементов матрицы совместной
v cols ' rows ' * tr —\
встречаемости в зависимости от своего направления: вдоль
строки или вдоль столбца.
2. Если множество смежности симметрично, то и матрица
совместной встречаемости тоже симметрична.
Матрицы совместной встречаемости используются для
определения метрик, основанных на совместной встречаемости, позволяющих
количественно представить информацию в изображении /. Заметим,
что присутствующий в изображении шум при использовании этих
метрик также считается информацией. Мы рассмотрим две такие
метрики:
Mhom(I)= X 7| 1 | (мера однородности), (3.34)
Mmi(I)= ^ Cj(u,vf (мера равномерности). (3.35)
«,ue{0,l,...,Gmax}
Неформально можно сказать, что высокая однородность или
равномерность свидетельствует о наличии большого количества
«бестекстурных» областей в изображении /.
Можно также определить метрики, сравнивая суммы всех элементов
на главной диагонали матрицы совместной встречаемости или близко
к ней с суммой всех остальных элементов этой матрицы.
Врезка 3.12 (метрики совместной встречаемости). В книге [/?. М. Haratick and
L G. Shapiro. Computer and Robot Vision, vol. 1, Reading, MA, Addison-Wesley, 1992]
приведены дополнительные метрики совместной встречаемости и подробно
обсуждается их роль в анализе изображений.
З.З.Анализ значений изображения ♦ 151
3.3.2. Анализ участков с привлечением моментов
Рассмотрим участок пикселей S с П в изображении /. Этот участок
может представлять «объект», как показано на рис. 3.30.
Рис. 3.30. Главные оси и центроиды обнаруженных участков,
где имеются рыбные косяки
По-прежнему предполагаем, что изображение I скалярное. Моменты
участка S изображения I определяются следующим образом:
/ил
\ь($)= X хауЬ'1{х,У), (3.36)
(x,y}eS
где аиЬ- неотрицательные целые числа. Сумма а + Ь называется
порядком момента. Существует всего один момент
т,
0,0
(S) = X 1{х,У)
(3.37)
(x,y)eS
нулевого порядка. Если 1{х, у) = 1 в каждой точке 5, то m00(S) = <A(S),
площади S. Моменты первого порядка
*MS)= X xl(x,y) и m0l(S)= X yl(x,y)
(3.38)
(x,y)eS
(x,y)eS
определяют центроид (xs, ys) участка S:
х? —
™0,о(5)
и
Л =
m0JS)
(3.39)
Отметим, что центроид зависит от значений / в S, а не только от
формы S.
Центральные моменты участка 5 изображения / определяются по
формуле
152 ♦ Глава З.Анализ изображений
Ma,b(S)= X (x-xsy(y-ys)b-I(x,y), (3.40)
(x,y)cS
где аиЬ- неотрицательные целые числа. Центральные моменты
позволяют охарактеризовать участок S с помощью признаков, инвариантных
относительно линейных преобразований.
Мы приведем только два примера таких признаков. Главные оси,
показанные на рис. 3.30, определены углом 6(S) (по модулю я) между
прямой, проходящей через центроид, и положительным направлением
оси а:. Имеет место тождество
tan(2fl(S)) = ,У^,СЧ- (3-41)
ju20(S)-ju02(S)
Эксцентриситет s(S) участка 5 определяется по формуле
^[W-^WT-y' (з.42)
и характеризует отношение главной оси к ортогональной ей оси S.
Эксцентриситет равен нулю, если S - круг, обладающий вращательной
симметрией, тогда ц2 0(5) = ц0 2(S). Эксцентриситет отрезка прямой равен 1 в
идеальном случае (и близок к 1 при измерении изображения). Для
множеств, обладающих вращательной симметрией с центроидом в начале
координат, также имеет место равенство тг г(Б) = 0.
Пример 3.7 (точность записанных отметок). В компьютерном зрении бывают
случаи, когда специальную отметку на поверхности (например, в виде
нарисованного крестика или кружочка) необходимо точно локализовать на
записанном изображении /. Для этого существует стандартная двухшаговая процедура:
1) найти участок S пикселей, считающийся изображением отметки;
2) вычислить по формуле (3.39) центроид участка S, используя значения I
в 5.
Это позволяет определить позицию отметки в 7с субпиксельной точностью.
Пример 3.8 (достижение инвариантности относительно вращения для
анализа участка). Часто желательно, чтобы признаки участка изображения были
изотропными (т. е. инвариантными относительно вращения). С помощью
моментов можно спроектировать четырехшаговую процедуру для решения этой
задачи.
1. Выделить участок пикселей 5, подлежащий анализу.
5.4. Поиск прямых и окружностей ♦ 155
2. Вычислить главную ось по формуле (3.41).
3. Повернуть 5, так чтобы его главная ось совпала с осью х (или любой
другой заранее выбранной фиксированной осью). Если цх X(S) = 0 или
pi20 = pi02 (т. е. фигура обладает вращательной симметрией), поворот не
нужен.
4. Вычислить изотропные признаки нормализованного относительно
вращения множества, полученного после поворота.
Отметим, что поворот на сетке вносит небольшие искажения в участок 5,
и его форма может немного измениться из-за ограничений, налагаемых
сеткой.
Врезка 3.13 (моменты и классификация объектов). Работа [М.К.Ни.Visual pattern
recognition by moment invariants. IRE Trans. Info. Theory, vol. IT-8, 1962, p. 179-187]
заложила основы инвариантной относительно линейных преобразований ха-
рактеризации объектов с помощью моментов. Набор моментов Ху во время
публикации статьи был практически бесполезен вследствие существовавших
в то время ограничений мощности компьютеров, но сегодня это стандартные
признаки для классификации объектов. Поищите в сети «моменты Ху» - и вы
узнаете, что это такое.
ЗА Поиск прямых и окружностей
Прямые и окружности предстают в изображении как «зашумленные
объекты», и их обнаружение - пример распознавания образов.
В этом разделе мы приведем подробное руководство по поиску
отрезков прямых и краткие сведения о поиске окружностей.
3.4.1. Прямые
В реальных изображениях прямые линии встречаются часто,
например границы зданий, края дорог (см. рис. 3.31) или опоры линий
электропередачи. Точная локализация таких прямых помогает
интерпретировать изображение.
Прежде всего мы с помощью детектора границ преобразуем заданное
изображение в бинарную карту границ. Затем выделенные граничные
пиксели необходимо проанализировать и понять, есть ли среди них
подмножества, образующие что-то похожее на отрезок прямой. При
этом детектор прямых должен быть устойчив к шуму, который
неизбежно имеет место.
154 ♦ Глава 3. Анализ изображений
Рис. 3.31. Края дорог и их аппроксимации найденными отрезками прямых
Как описать прямую, присутствующую в изображении размера
NcolsxNrows? Очевидный ответ - с помощью уравнения
у = ах + Ь. (3.43)
Отрезок прямой, описываемой этим уравнением, показан синим
цветом на рис. 3.32 слева.
Оригинальное преобразование Хафа было предложено для
описания отрезков прямой в пространстве параметров ab; см. рис. 3.32
справа. Позиции пикселей p,q,rB изображении отображаются в три прямые
в пространстве параметров. Три прямые, показанные красным,
зеленым и синим цветами в изображении, соответствуют трем точкам
соответственных цветов в пространстве параметров.
Если синяя прямая описывается уравнением у = ахх + Ьр то она
пересекает ось у в точке bv Точки p = (x,y)nq = (x,y)Ha синей прямой
описывают соответственно прямые Ъ = -х а + у иЬ = -х а + у в
пространстве параметров. Например, точки на прямой b = -х а + у описывают все
прямые в изображении, проходящие через точку р в любом направле-
5.4. Поиск прямых и окружностей ♦ 155
нии (кроме вертикальной прямой, для которой а = °°). Таким образом,
прямые Ъ = -х а + у иЬ = -х а + у пересекаются в пространстве
параметров аЪ в точке (ар Ь^, определенной параметрами ах и Ьх синей прямой.
1 Ncols Ъ
Рис. 3.32. Слева: три отрезка прямых в изображении. Синяя прямая пересекается
с осью у в точке bv проходит на расстоянии d от начала координат и составляет
угол а с положительным направлением оси х. Каковы значения b,d и а для красной
и зеленой прямых? Справа: пространство параметров ab
На рисунке представлены и другие примеры. Красная, синяя и
зеленая точки в пространстве аЪ соответствуют красной, синей и зеленой
прямым на плоскости изображения. Если бы п точек располагались в
точности на одной прямой у, то соответствующие им п прямых в
пространстве параметров пересекались бы в одной точке (а , Ь ),
соответствующей прямой у.
Но в изображениях прямые неидеальны из-за шума. Множество п
пикселей изображения, лежащих «почти» на одной прямой у,
определяет множество п прямых в пространстве аЪ, которые пересекаются
«почти» в одной точке {а , Ъ ), соответствующей у. Идея в том, чтобы найти
такие кластеры точек пересечения прямых в пространстве параметров
и соответствующую им прямую у в изображении.
Идея-то хороша, только не работает. Почему? Потому что параметры
а и Ъ не ограничены изображением N *N . Для обнаружения класте-
r c cols rows " CJ
ров нам пришлось бы анализировать бесконечное пространство
параметров.
Врезка 3.14 (история преобразования Хафа). Оригинальное преобразование
Хафа было опубликовано в работе [RV.C.Hough.Methodsand means for recognizing
complex patterns. U.S. Patent 3.069.654,1962].
156 ♦ Глава З.Анализ изображений
Пространство параметров, предложенное Дуда и Хартом. Вместо
того чтобы представлять прямые линии в стандартной форме (3.43), мы
будем описывать их параметрами d и а, также показанными на рис. 3.32
слева для синей линии:
d = х • cos а + у • sin а. (3.44)
А в остальном будем следовать идеям оригинального преобразования
Хафа. При этом пространство параметров будет ограничено. Угловой
параметр а принадлежит интервалу [0, 2л), а параметр расстояния d -
интервалу [0, dmJ, где
4-х = JKIS+KWS- (3.45)
Этот способ известен под названием стандартное преобразование
Хафа. Теперь точке изображения соответствует синусоида или
косинусоида в пространстве параметров da, которое называется
пространством Хафа.
Врезка 3.15 (Радон). Представление прямой в виде (3.44) было впервые
предложено в работе [/.flacfon.Uberdie Bestimmung von Funktionendurch ihre Integralwerte
Langs gewisser Mannigfaltigkeiten. Berichte Sachsische Akademie der Wissenschaften.
Math.-Phys. KL, 69:262-267,1917], где использовалось для определения
преобразования в непрерывном пространстве, которое сегодня известно как
преобразование Радона. Это преобразование составляет теоретическое
основание методов, применяемых в компьютерной томографии. Исторически более
раннее преобразование Радона является обобщением преобразования Хафа.
На рис. 3.33 показано применение стандартного преобразования
Хафа. Исходное изображение (из последовательности в наборе EISATS)
показано слева вверху. Карта границ (слева внизу) построена с
помощью оператора Кэнни (см. раздел 2.3.3). Справа вверху показано
представление этой карты в пространстве Хафа da после вставки синусоид
и косинусоид для всех найденных граничных пикселей. Отчетливо
видны три кластера (область в пространстве Хафа, где пересекается
много кривых). Соответственно, во входном изображении выделяются три
прямые.
Пространство Хафа как дискретный массив аккумуляторов. При
реализации пространства Хафа создается массив последовательных
интервалов d и а для определения конечного числа ячеек. Например,
множество значений d можно дискретизировать, разбив на интервалы
[0,1), [1, 2), [2, 3),..., а множество значений а - на интервалы шириной
3.4. Поиск прямых и окружностей ♦ 157
в один градус. Получающаяся структура данных называется массивом
аккумуляторов.
Рис. 3.33. Справа вверху: пространство Хафа для граничных точек (слева внизу),
найденных в исходном изображении (слева вверху). Анализ пространства Хафа
приводит к выделению трех отрезков прямой (справа внизу)
В начале построения карты границ счетчики во всех ячейках массива
аккумуляторов равны нулю. При вставке новой синусоиды или
косинусоиды в массив аккумуляторов счетчики в ячейках, которые пересекает
кривая, увеличиваются на 1. В конце процесса счетчик в каждой ячейке
массива аккумуляторов равен количеству кривых, проходящих через
эту ячейку. На рис. 3.33 нулевые счетчики показаны белым, а
ненулевые - красным, причем цвет тем темнее, чем счетчик больше.
Можно ожидать, что прямые линии в изображении удастся выявить,
найдя пики в массиве аккумуляторов, определяемые (каким-то
образом) как центры «темных участков».
В стандартном преобразовании Хафа пики совпадают с локальными
максимумами значений счетчиков. Следовательно, параметры
найденных прямых определяются с точностью, зависящей от размера
интервалов, выбранного на этапе дискретизации пространства Хафа. Мы
говорим, что точность параметров клеточная, а не субклеточная. Один
158
Глава З.Анализ изображений
из способов улучшить клеточную точность (ценой увеличения
времени вычислений) - выбрать меньшие интервалы. Добиться
субклеточной точности можно также посредством вычисления центроида в окне
с максимальной суммой счетчиков. См. рис. 3.34 справа вверху и слева
внизу.
н
12
9
12
12
13
14
9
13
12
б
5
4
12
9
12
12
13
14
9
13
12
6
5
3
h
15
13
17
13
17
16
lit
6
4
0
3
щ
15
13
17
13
17
16
14
6
4
у
0
2
6
20
17
21
26
15
12
у
9
9
9
2
б
20
17
21
26
15
12
0
9
0
0
0
?
13
20
39
2S
15
У
0
0
3
0
0
2
13
20
39
28 I
15
0
0
0
3
в
0
0
и
19
59
32
4
и
У
0
2
0
в
0
к
Г
59
^
4
в
0
0
2
2
0
2
0
12
52
48
2
2
У
0
0
2
У
2
J^
12
5?
48
2
2
У
У
У
0
3
0
3
16
39
35
29
Ь
9
9
9
9
3
9
3
1Й
39
_2*
20
5
9
9
9
0
2
Л
12
19
20
25
22
16
5
0
0
0
2
0
12
19
20
I 25
22
16
5
О
0
6
0
7
13
15
14
19
14
16
15
6
0
0
0
7
13
15
14
19
14
16
15
8
0
4
12
9
12
12
13
14
9
13
12
6
5
4
9
12
12
13
14
9
13
А2^
5
3
4
15
13
17
13
Af
16
14
6
4
0
3
4
АВ*
17
13
17
16
Jj^
^г
4
0
е
2
б
26
17
21
26
15
12
с
е
в
0
2
6
1Г*
21
26
*Л2
0
9
О
й
0
2
13
20
39
•га
15
0
0
0
3
0
0
2
13
3?*
^15
О
0
0
3
0
0
0
4
А
©
ТЙГ
4
б
0
0
2
В
6
В
4
19
""32
4
в
В
в
2
?
0
2
0
12
52
4«
2
2
0
0
0
2
0
2
В
12
2
2
0
е
0
0
3
0
3
16
39
35
29
5
0
0
0
0
3
0
3^
"*39
2(К
5
У
У
0
0
2
О
12
19
2в
25
22
16
5
0
0
0
2
19
20
25
\22
5^
9
9
0
0
7
13
15
14
If
14
16
15
8
0
0
^7
13
15
14
19
14
16
^5
0
Рис. 3.34. Слева вверху: счетчики в пространстве da.
Справа вверху: пик в локальном максимуме. Слева внизу: окно счетчиков
с максимальной суммой размера 3*3; пик может быть определен
как центроид этого окна. Справа внизу: бабочка пика
Повышение точности и уменьшение времени вычислений.
Распределение значений счетчиков в окрестности пика напоминает по
форме бабочку, см. рис. 3.34 справа внизу. Бабочку пика можно
аппроксимировать кривыми второго порядка, описывающими ее нижнюю и
верхнюю части. Это позволяет определить пик с субклеточной
точностью.
В стандартном преобразовании Хафа, показанном на рис. 3.32,
прямые линии описываются относительно начала системы координат
изображения. Посмотрим, что будет, если перенести начало координат в
центр изображения (рис. 3.35). Уравнение прямой принимает вид:
/
d =
N
\
х-
cols
COSOT +
N.
\
у-
sin a.
(3.46)
Значение d в пространстве da упрощается:
3.4. Поиск прямых и окружноаей
159
=ffi
cols
+n:
(3.47)
Это не только наполовину уменьшает размер массива аккумуляторов,
а значит, и объем вычислений, но еще и улучшает форму бабочек, как
показывают эксперименты. Бабочки оказываются «менее
вытянутыми», поэтому находить пики становится проще.
AL
—г->
2л
Рис. 3.35. Слева: система координат с началом в центре для представления
прямых в изображении. Справа: показано максимально возможное
значение d (c/max) и эскиз бабочки для одной прямой
Результат, показанный на рис. 3.33, был вычислен с помощью
стандартного преобразования Хафа. А результаты на рис. 3.31 получены
путем применения системы координат с началом в центре и
аппроксимации бабочек кривыми второго порядка с целью определения пиков с
субклеточной точностью.
Несколько отрезков прямой в одном изображении. Бабочка
определяется с использованием окна поиска размера т*п в пространстве
Хафа, например т = п = 11. Если пики далеко друг от друга, то никаких
проблем не возникает. Но при наличии нескольких прямых в
изображении / может возникнуть наложение бабочек в пространстве Хафа.
Обычно в таком случае только одно крыло бабочки пересекается с
другой бабочкой. Это нарушает симметрию бабочки.
После обнаружения пика в точке {d, а) мы, чтобы не мешать
обнаружению следующих пиков, выбираем некоторые пиксели изображения
(близкие к найденной прямой) и инвертируем процесс вставки этих
пикселей в массив аккумуляторов: теперь, когда синусоида или коси-
160 ♦ Глава 5. Анализ изображений
нусоида пересекает ячейки, мы не увеличиваем, а уменьшаем
счетчики.
После устранения эффектов пика, найденного в пространстве Хафа,
для нахождения следующего пика нужно просто продолжить поиск в
окнах размера т*п.
Конечные точки отрезков. До сих пор мы говорили об
определении прямой, а не отрезка прямой, имеющего два конца. Принятый в
настоящее время метод нахождения концов отрезка был
опубликован М. Атикуззаманом (М. Atiquzzaman) и М. У. Ахтаром (М. W. Akhtar)
в 1994 г. В общем случае конечные точки можно найти, протрассировав
найденную в изображении прямую и проанализировав потенциально
принадлежащие ей граничные пиксели в близкой окрестности.
Альтернативно конечные точки можно искать в пространстве Хафа.
3.4.2. Окружности
Идею преобразования Хафа можно обобщить: рассмотреть для
представляющих интерес геометрических объектов такую параметризацию,
для которой возможен ограниченный массив аккумуляторов. Затем в
этот массив вставляются пиксели и находятся пики. Проиллюстрируем
это обобщение на примере окружностей. Так, на рис. 3.36 показано
приложение, в котором очень важно умение находить окружности - ведь
знаки «Стоп» почти круглые.
Рис. 3.36. Входное изображение для обнаружения знаков «Стоп».
Их края представляют собой окружности, диаметры которых
попадают в ожидаемый диапазон
В данном случае для получения ограниченного массива
аккумуляторов достаточно очевидной параметризации окружностей. Будем опи-
3.4. Поиск прямых и окружноаей ♦ 161
сывать окружность центром (хс, ус) и радиусом г. Тем самым мы
определяем трехмерное пространство Хафа.
Рассмотрим пиксель р = (х, у) изображения /. Во-первых, он лежит на
окружности радиуса г = О, совпадающей с самим пикселем. Это
определяет точку (х, у, 0) в пространстве Хафа - вершину прямого кругового
конуса. Теперь предположим, что пиксель р = (х, у) лежит на
окружностях радиуса г0 > 0. Центры этих окружностей образуют окружность
радиуса г0 с центром в точке р = (х, у). См. рис. 3.37 слева. Эта окружность
принадлежит поверхности прямого кругового конуса с вершиной в
точке (а:, у) в пространстве Хафа. Точнее, это пересечение поверхности
конуса с плоскостью г = г0 в пространстве хуг.
Рис. 3.37. Слева: пиксель (х,у) и геометрическое место центров всех окружностей
радиуса rQ > 0 с центром в (х, у). Справа: пиксель (х, у) определяет поверхность
прямого кругового конуса в пространстве Хафа
Возможные радиусы окружностей в изображении принадлежат
диапазону г0 < г < rv Верхняя граница определяется размером самого
изображения. Таким образом, трехмерное пространство Хафа для
поиска окружностей сводится к «бруску» толщиной гх - rQ над П, т. е.
пространство Хафа ограничено.
Это пространство Хафа можно дискретизировать, разбив на
трехмерные ячейки, образующие трехмерный массив аккумуляторов. В начале
процесса поиска все счетчики в массиве инициализируются нулями.
При вставке пикселя (х, у) в массив аккумуляторов счетчики во всех
ячейках, которые пересекает поверхность конуса с вершиной в точке
(х, у), увеличиваются на 1.
Например, при вставке трех неколлинеарных пикселей в трехмерное
пространство Хафа порождаются поверхности трех прямых круговых
конусов. Мы знаем, что через любые три неколлинеарные точки на
162 ♦ Глава 5.Анализ изображений
плоскости можно провести единственную окружность. Поэтому все три
поверхности пересекаются только в одной точке, которая однозначно
определяет параметры некоторой окружности.
Далее мы, как и при поиске прямых, должны найти пики в
трехмерном массиве аккумуляторов. Наличие нескольких окружностей обычно
не создает существенной интерференции в этом массиве, и, в отличие
от задачи поиска прямых, не существует «проблемы конечных точек».
3.5. Упражнения
3.5.1. Упражнения по программированию
Упражнение 3.1 (идентификация и анализ компонент бинарного
изображения). Рассмотрите произвольное скалярное изображение /.
Примените следующую операцию бинаризации с выбранным
порогом Г, 1 < Т< G , для порождения бинарного изображения:
J(x,y) = {
0 если/(*,у)<Г
1 в противном случае
В диалоговом окне пользователь может задать для получающегося
бинарного изображения / два режима:
1) подсчет компонент: если пользователь выбирает этот режим, то
можно использовать ключ «черный < белый» или «белый <
черный» для подсчета черных компонент бинарного изображения /;
2) геометрические характеристики выбранной компоненты: если
пользователь выбирает этот режим и щелкает по какой-то
черной компоненте, то вычисляются площадь, периметр и диаметр
этой компоненты. В данном упражнении достаточно вычислять
периметр как длину 8-пути, описывающего край компоненты
(т. е. результат трассировки края в предположении 8-смежности).
Диаметром компоненты называется максимальное расстояние
между двумя принадлежащими ей пикселями (следовательно,
диаметр определяется двумя пикселями, принадлежащими краю
компоненты).
Факультативно можно перед выполнением операций 1 и 2 удалить
малые компоненты, площадь которых меньше заданного порога, а в
режиме 2 перекрашивать выбранные компоненты, чтобы избежать
повторного выбора.
3.5.Упражнения ♦ 165
Упражнение 3.2 (удаление компонент, диаметр которых меньше
заданного порога, и гистограммы признаков). Сгенерируйте бинарное
изображение, как описано в упражнении 3.1. Перед тем как приступать
к последующей обработке, удалите все черные компоненты, диаметр
которых меньше заданного порога Т.
Для этого примените процедуру, показанную на рис. 3.38.
Рассмотрите окно размера Т*Т внутри окна (Т + 2)х(Г + 2). Если количество
черных пикселей в меньшем окне равно количеству черных пикселей
в большем окне (т. е. внутри множества, являющего их разностью, нет
черных пикселей), то обнулите все пиксели в меньшем окне (сделайте
белыми).
|« т
Рис. 3.38. Удаление артефактов
диаметра, не меньшего Т
Для каждой из оставшихся компонент S сгенерированного бинарного
изображения вычислите площадь <Л(5), периметр T(S) и коэффициент
формы
T(S) =
&(sy
2л-Я{$)
(3.49)
Постройте гистограммы распределения этих трех признаков для
оставшихся в бинарном изображении компонент.
Упражнение 3.3 (вычисление метрик совместной встречаемости).
Возьмите скалярные изображения / разумного размера (не менее
256x256). Рекурсивно примените прямоугольный фильтр 3x3 или
локальный медианный оператор 3x3 к входному изображению и получите
сглаженное и остаточное изображение S(n) и R(n) относительно этих двух
операций сглаживания и удаления шума для п = 0,..., 30. См. (2.33).
Вычислите матрицы совместной встречаемости для / и
изображений 5(п) и R(n). Обозначим Т сумму всех элементов матрицы совместной
встречаемости /.
164 ♦ Глава 5.Анализ изображений
Врезка 3.16 (коэффициент формы и изопериметрическое неравенство). Изо-
периметрическое неравенство на плоскости, известное со времен античности,
утверждает, что для любого множества на плоскости, для которого корректно
определены площадь Л и периметр, имеет место неравенство
тг>1. (3.50)
4лг-Я
Отсюда следует, что из всех таких множеств, имеющих одинаковый периметр,
наибольшая площадь у круга. Выражение в левой части неравенства (3.50)
называют также изопериметрическим дефицитом множества; он измеряет
степень отличия множества от круга. Первое доказательство античной изопе-
риметрической задачи было опубликовано в 1882 г.
Цитируется по изданию [R.KtetteandA.Rosenfeld. Digital Geometry. Morgan Kaufmann,
San Francisco, 2004].
Вычислите меры однородности и равномерности для
изображений S(n) и R(n) и масштабируйте полученные значения, разделив их на Г.
Тем самым вы получите нормированные значения в диапазоне [0,1].
Нанесите полученные результаты на график в виде функций от
п = 0,..., 30 для обоих операторов сглаживания.
Обсудите сходство и различие результатов для входных
изображений с разными распределениями яркости, например для равномерно
освещенных изображений, снятых в помещении, или для изображений,
снятых под открытым небом, с артефактами освещения.
Упражнение 3.4 (признаки компонент на основе моментов).
Сгенерируйте бинарные изображения, как описано в упражнении 3.1. Прежде
чем приступать к последующей обработке, удалите все черные
артефакты, например все компоненты, диаметр которых меньше
заданного порога Г, или все компоненты, площадь которых меньше заданного
порога.
Реализуйте пользовательский интерфейс для выбора оставшихся
компонент (щелчком мыши) по одной. Для выбранной компоненты
вычислите центроид, главную ось и эксцентриситет и каким-либо
образом визуализируйте результаты. Для визуализации эксцентриситета
можно, например, нарисовать эллипс с таким эксцентриситетом или
просто вывести поверх выбранной компоненты полосу, высота которой
равна эксцентриситету. Что касается центроида и главной оси,
поступите примерно так, как показано на рис. 3.30.
5.5. Упражнения ♦ 165
Упражнение 3.5 (нормализация изображения по направлению).
Сделайте снимки сцены, где много вертикальных и горизонтальных
границ, держа камеру в руке (т. е. без применения треножника и других
средств установки по уровню).
Найдите «почти вертикальные» и «почти горизонтальные»
прямолинейные границы, применяя преобразования Хафа и критерий
отбрасывания прямых, угол наклона которых не подходит под
определение «почти вертикальности» или «почти горизонтальности». Зная все
найденные вертикальные и горизонтальные прямые, вычислите угол
поворота изображения, при котором эти прямые станут действительно
осепараллельными. Пример см. на рис. 3.39.
Рис. 3.39. Снятое (слева) и нормализованное (справа) изображение
Это один из способов (безусловно, не самый простой) нормализации
изображений относительно условий съемки.
Упражнение 3.6 (генерация зашумленных отрезков прямых и
преобразование Хафа). Напишите программу, которая будет генерировать
зашумленные отрезки прямых, как показано на рис. 3.40. Программа
должна поддерживать задание плотности сгенерированных точек, а
также задание количества, длин и направлений сгенерированных
отрезков.
Примените свою программу поиска прямых (почему бы не написать
ее самостоятельно?), основанную на преобразовании Хафа, для
отыскания этих отрезков, включая их концы. Сравните полученные
результаты с истинными данными, использованными при генерации отрезков.
Увеличьте уровень шума и обсудите устойчивость своей программы
поиска прямых.
Упражнение 3.7 (нахождение краев дороги). Посадите в машину
второго человека (кроме водителя), который будет записывать видео при
166 ♦ Глава 5. Анализ изображений
движении по хорошо размеченной автотрассе. Найдите края дороги на
всех кадрах записанного видео (их должно быть не менее 200).
1. Найдите граничные пиксели в каждом кадре с помощью своего
любимого детектора границ.
2. Найдите прямые линии на картах границ. Просто продлите
найденные границы, начав с нижней строки, примерно на две
трети высоты изображения вверх, как сделано на рис. 3.31 и 3.33
справа внизу. Искать концы отрезков не нужно.
3. Сгенерируйте видео (например, с помощью avi или другого
кодека) по сгенерированным краям дороги.
Факультативно можете подумать о прослеживании прямых, чтобы
сделать процесс поиска более эффективным.
Рис. 3.40. Зашумленные отрезки прямых
3.5. Упражнения ♦ 167
3.5.2. Упражнения, не требующие программирования
Упражнение 3.8. Рассмотрим следующее отношение 6-смежности в
изображениях для пикселя р = (х, у): в четной строке (когда у четно)
используется множество
Лбстя, = А4и{(х+1,у+1),(х+1,у-1)},
а в нечетной строке - множество
^ = А4и{(х-1,у+1),(х-1,у-1)}.
Теперь рассмотрите рис. 3.3 слева и обсудите результат. Далее
рассмотрите входное бинарное изображение в виде шахматной доски.
Какой получается результат?
Упражнение 3.9. Для вычисления iC-смежности в некоторых
случаях требуется проверять, кто владеет центральным пикселем окна 2*2.
Сформулируйте условие, при котором такая проверка необходима.
Например, если значения всех четырех пикселей одинаковы, то проверка
не нужна. И если значения трех пикселей одинаковы, проверка тоже не
нужна.
Упражнение 3.10. Что произойдет, если использовать в алгоритме
Босса изображенный ниже локальный порядок обхода, а не локальный
круговой порядок, показанный на рис. 3.11?
Упражнение 3.11. Обсудите сходство и различие эксцентриситета и
коэффициента формы. При обсуждении привлекайте примеры
двоичных изображений.
Упражнение 3.12. Объясните, как можно воспользоваться
информацией о градиенте изображения, чтобы повысить точность и скорость
нахождения окружностей, используя идею преобразования Хафа.
Упражнение 3.13. Спроектируйте основанный на идеях
преобразования Хафа метод нахождения парабол, например в изображении на
рис. 3.41.
168
Глава 5. Анализ изображений
Рис. 3.41. Фотография первой велогонки «Тур де Франс» в 1903 г.
(срок действия авторского права истек)
Глава
Анализ плотного движения
В этой главе мы обсудим оптический поток - стандартное
представление плотного движения в компьютерном зрении. Каждый пиксель
помечается вектором движения, показывающим, как изменяются данные
изображения между моментами t и t + 1. Анализ разреженного
движения (называемый также прослеживанием движения) - тема главы 9.
4.1. Зй-движение и двумерный оптический
поток
Рассмотрим последовательность изображений (или кадров видео),
снятых с интервалом St. Например, при записи видео с частотой 30 Гц (герц)
6t = 1/30, что часто записывают как 30 кадров/с (англ. fps). Обозначим
/(•, •, t) кадр, записанный в момент £, в котором значения пикселя с
координатами (х, у) равны 1{х, у, t).
Врезка 4.1 (Герц). Генрих Рудольф Герц (1857-1894) - немецкий физик,
изучавший электромагнетизм.
В этом разделе описываются основы анализа движения в
последовательностях изображений.
4.1.1. Локальное смещение и оптический поток
Точка трехмерного пространства Р = (X, Y, Z) в момент t • 6t
проецируется в пиксель р = (х, у) изображения /(•, •, £); см. рис. 4.1. Камера
характеризуется фокусным расстоянием /", центром проекции О и смотрит
в направлении оптической оси, представленной осью Z. В такой
идеальной модели камеры определена центральная проекция на плоскость
изображения ху; более подробно мы обсудим модели камеры в главе 6.
170 ♦ Глава 4. Анализ плотного движения
Рис. 4.1. Проекция скорости v на плоскость изображения определяет смещение d
Двумерное движение. Предположим, что точка Р в промежутке
между моментами t • St и (t + 1) • St совершает в трехмерном
пространстве линейное перемещение со скоростью (имеющей величину
и направление) v = (vx, Vy, vz). Это определяет трехмерное движение
v • St, начинающееся в точке Р = (X, У, Z) и заканчивающееся в точке
(X + vx-St, Y+ vY-St,Z + vz• St).
Вектор d = (f, гру - проекция этого трехмерного перемещения точки
Р между изображениями /(•, •, t) и /(•, •, t + 1). Геометрически это
перемещение на плоскости определяет локальное смещение пикселя,
первоначально расположенного в точке р, в предположении, что нам
известно трехмерное движение.
Видимое смещение на плоскости - это оптический поток и = (и, v)T;
он начинается в точке р = (х, у) и заканчивается в точке р = (х + и, у + v),
зачастую он не совпадает с фактическим локальным смещением.
Вычисление оптического потока преследует цель оценить движение на
плоскости.
На рис. 4.2 показано различие между движением на плоскости и
оптическим потоком. Алгоритм анализа плотного движения должен
преобразовать направленный вверх оптический поток и в реальное
двумерное движение d.
В качестве еще одного примера рассмотрим фиксированный
(относительно Земли, далее мы будем называть его статическим) «текстури-
4.1. ЗР-движение и двумерный оптический поток ♦ 171
рованный» объект и движущийся источник света (например, Солнце).
При этом генерируется оптический поток. Заметьте: объект не
двигается, т. е. никакого двумерного движения нет, а оптический поток есть.
Рис. 4.2. Слева: в случае вращающегося столба со спиральной раскраской
(реклама парикмахера) мы имеем двумерное движение слева направо.
В середине: эскиз двумерного движения (без масштабирования векторов).
Справа: эскиз оптического потока, который «почему-то» направлен снизу вверх
Векторные поля. Чтобы понять движение трехмерных объектов, мы
хотим анализировать поведение проекций большого количества
точек, расположенных на их поверхности P=(X,Y,Z). Результаты должны
быть согласованы с перемещениями объекта или с формой движущихся
твердых тел.
Векторы двумерного движения образуют векторное поле. На рис. 4.3
приведен пример, иллюстрирующий вращение прямоугольника
(вокруг неподвижной точки) в плоскости, параллельной плоскости
изображения.
Предположение о твердости тела упрощает анализ двумерных
векторных полей движения, но даже в этом случае интерпретировать их
нелегко. В качестве графического упражнения можете построить
визуализации двумерных векторных полей для движения простых
трехмерных тел, например куба или другого простого многогранника.
Сделать выводы о форме многогранника, глядя на поле движения, очень
трудно.
Вычисленное векторное поле движения называется плотным, если
оно содержит векторы движения (почти) во всех пикселях. В противном
случае оно называется разреженным.
172 ♦ Глава 4. Анализ плотного движения
Рис. 4.3. Векторное поле вращения прямоугольника. Векторы движения
начинаются в точках, соответствующих моменту времени f, и заканчиваются
в точках, соответствующих моменту времени t + 1, в которые начальные точки
перешли в результате вращения
На рис. 4.4 представлен цветовой ключ для визуализации векторов
оптического потока. Оттенок цвета представляет направление
движения, а насыщенность - его абсолютную величину.
Рис. 4.4. Цветовой ключ для визуализации оптического потока.
Оттенок цвета представляет направление вектора (с началом в центре круга),
а насыщенность соответствует абсолютной величине этого вектора.
Белый цвет означает отсутствие движения
4.1. ЗР-движение и двумерный оптический поток ♦ 175
На рис. 4.5 приведен пример - два входных кадра и цветокодирован-
ные результаты. По цветам движения можно четко идентифицировать
велосипедиста - пиксели в этой области явно отличаются от соседних.
Результат можно улучшить, обогатив базовый алгоритм Хорна-Шанка
дополнительными идеями.
Рис. 4.5. Верхний ряд, слева и в середине: два последовательных кадра видео
bicyclist, снятого с частотой 25 кадров/с. Верхний ряд справа: цветокодированное
поле движения, вычисленное с помощью базового алгоритма Хорна-Шанка.
Помимо цветового кодирования, имеется несколько разреженных (увеличенных)
векторов, это избыточная информация, помогающая, однако, в интерпретации
поля потока. Нижний ряд, слева и в середине: два последовательных кадра видео
tennisball. Нижний ряд справа: цветокодированное поле движения, вычисленное
с помощью базового алгоритма Хорна-Шанка
4.1.2. Проблема апертуры и градиентный поток
Анализируя спроецированные изображения, мы наблюдаем
ограниченную область видимого движения, определяемую кадровым окном
(апертурой) камеры. Такой алгоритм в общем случае делает выводы
только на основе ограниченной окрестности пикселя.
Проблема апертуры. Представьте себе, что вы сидите в поезде,
который вот-вот должен тронуться, и смотрите в окно. Вам кажется, что
ваш поезд начал движение, хотя на самом деле это движется поезд на
соседнем пути. Проблема апертуры связана с ограниченным обзором
динамической сцены. Она вносит дополнительную неуверенность в
оценку движения.
На рис. 4.6 показана ситуация, когда алгоритм обрабатывает
изображение и «видит» лишь круговую область вокруг пикселя и ничего более.
174 ♦ Глава 4. Анализ плотного движения
Мы можем предположить, что движение направлено вверх, ведь
диагональной компоненты в круговом окне не видно.
Рис. 4.6. Видя только два круговых окна в моменты t (слева) и t + 1 (справа),
мы приходим к выводу, что движение направлено вверх, и упускаем
движение по диагонали в сторону правого верхнего угла
А на рис. 4.7 показан реальный пример. Автомобиль движется по
кругу, удаляясь от камеры влево. Мы наблюдаем его через ограниченную
апертуру. Видя только внутренние прямоугольники, можно заключить,
что имеет место смещение вверх.
Рис. 4.7. Три изображения, снятых в моменты t, t + 1 и t + 2. Видя только
внутренние прямоугольники, мы можем предположить, что имеет место сдвиг
вверх с небольшим вращением, но анализ полных изображений ясно показывает,
что автомобиль движется влево
Но, возможно, происходит нечто совершенно иное, например
машина движется не самостоятельно, а погружена на прицеп, а быть может,
изображения получены с помощью подвижной камеры,
перемещающейся вокруг грузовика. Увеличение апертуры поможет, но все равно
информация может оказаться неполной.
Градиентный поток. Из-за проблемы апертуры локальный метод
обычно определяет градиентный поток - проекцию истинного
двумерного движения на вектор градиента в данном пикселе. Двумерный
градиент по координатам а: и у записывается в виде
4.2.АлгоритмХорна-Шанка ♦ 175
VxyI=[Ix(x,y,t),Iy(x,y,t)]\ (4.1)
Он ортогонален прямой линии излома в изображении (границе), как
показано на рис. 4.8 в предположении, что яркость изображения
убывает слева направо. Напомним, что 1хи I в формуле (4.1) обозначают
частные производные кадра /(•, •, t) соответственно по а: и по у.
Результат можно улучшить (т. е. приблизиться к истинному
пониманию движения), приняв во внимание значения смежных пикселей.
Например, учет угла объекта может помочь в вычислении правильного
двумерного движения.
\ Двумерное
\ движение
Градиентный поток ^\ / У^ \
\1/\ Градиент {1Х ,1У)Т
Излом в изображении
Рис. 4.8. Градиентный поток. Истинное двумерное движение
происходит вверх по диагонали в направлении вектора d,
но идентифицируемое движение - проекция d на вектор градиента
4.2. Алгоритм Хорна-Шанка
Мы хотели бы установить связь между значениями в кадрах /(-, •, г) и
/(•, •, t + 1). Прямолинейный подход - рассмотреть разложение функции
/(•, •, t + 1) в ряд Тейлора до членов первого порядка.
В этом разделе подробно описывается оригинальный алгоритм
Хорна-Шанка. Обсуждаемая здесь математическая техника до сих пор
является основой проектирования алгоритмов вычисления оптического
потока. Мы также расскажем о том, как оценивать качество алгоритмов
оптического потока в общем случае.
4.2.1. Подготовительная часть
В нашем случае имеется функция трех аргументов /(•, •, •), и мы
применяем разложение в трехмерный ряд Тейлора до членов первого
порядка:
176 ♦ Глава 4. Анализ плотного движения
Врезка 4.2 (Тейлор и разложение функции в ряд Тейлора до членов первого
порядка). Брук Тейлор (1685-1731) - английский математик. Разложение в
ряд Тейлора часто применяется в прикладной физике и технике. Напомним,
что отношение разностей
ф(х)- ф(х0) _ ф(х0 - дх)- ф(х0)
Л/ Лл
дх
функции ф сходится (в предположении, что ф непрерывно дифференцируема)
к производной
dx
когда Sx -> 0. Для малых значений Sx имеем разложение в ряд Тейлора до
членов первого порядка
ф(х0 + Sx) = ф(х0) + Sx • ° + е,
dx
где погрешность е равна нулю, если функция ф линейна на отрезке [х0,х0 + 5х].
См. рисунок ниже.
Обобщением этой формулы служит разложение в бесконечный ряд Тейлора:
ф(х0 + 3х)= £ - ^х-
d>(x0)
&х
где 0! = 1, /! = 1 • 2 • 3 • ... • / для / £ 1, d' - /-я производная. Эта формула
справедлива при условии, что ф имеет непрерывные производные всех требуемых
порядков.
4.2.АлгоритмХорна-Шанка ♦ 177
I(x + Sx, у + Sy, t + St)
= I(x,y,t) + Sx-—(x,y,t) + Sy-—(x,y,t) + St-—(x,y,t) + e, (4.2)
dx ay ot
где член е представляет производные второго и более высоких
порядков в ряде Тейлора. Как обычно в физике и технике, мы предполагаем,
что е = 0, т. е. функция /(•, •, •) ведет себя почти как линейная при малых
Sx, Sy и St.
В качестве St мы берем разность между моментами съемки двух
последовательных кадров /(•, •, t) и /(•, •, t + 1). С помощью 8х и 8у мы хотели
бы смоделировать перемещение одного пикселя в промежутке времени
от t до t + 1. В предположении о постоянстве яркости (intensity constancy
assumption - ICA)
/(* + 8x,y + фу, t + St) = I(x,y, t) (4.3)
до, и после перемещения имеем
0 = Sx—(x,y,t) + Sy—(x,y,t) + St-—(x,y,t). (4.4)
ox oy ot
Поделив на St, получаем
Sx dl, ч Sy dl, ч dl,
~st'^x,y,t)+st'Y^x,y,t)+Tt^x,y,t)' (4'5)
Изменение координат л: и у за время St представляет оптический
поток u(x, у, t) = (и{х, у, t), v(x, у, t))J, который мы и хотим вычислить:
0 = u(x,y,t)-—(x,y,t)+v(x,y,t)—(x,y,t) +—(x,y,t). (4.6)
ox oy ot
Уравнение (4.6) называется уравнением оптического потока, или
ограничением Хорна-Шанка.
Врезка 4.3 (история алгоритма Хорна-Шанка). Этот алгоритм впервые был
опубликован в работе [В. К. P. Horn and В. G. Schunck. Determining optic flow. Artificial
Intelligence, vol. 17,1981, p. 185-203], которая и заложила основы оценивания
оптического потока.
Вывод алгоритма сопряжен с применением довольно длинных
формул и вычислений. Но вы удивитесь тому, как просто выглядит
конечный результат и как легко реализовать алгоритм, если не пытаться
178 ♦ Глава 4.Анализ плотного движения
добавить различные стратегии оптимизации. Если вам не очень
интересны детали вывода, можете перейти сразу к разделу 4.2.2.
Наблюдение 4.1. Уравнение (4.6) выведено путем рассмотрения малых
шагов в предположении постоянства яркости. Логично, что эти предположения
определяют ограничения на область применения окончательного алгоритма.
Пространство скоростей uv. Запишем уравнение (4.6) короче,
опустив координаты (а:, у, г):
-J=u-I+v/=u-V /. (4.7)
t х у х,у v '
Здесь 1хи1 обозначают частные производные по л: и у соответственно
и It - частную производную по г. Скаляр и • Vx I - это скалярное
произведение вектора оптического потока на вектор градиента (состоящего
только из производных по а: и у, без г).
Врезка 4.4 (скалярное произведение векторов). Рассмотрим два вектора
а = (av а2,..., ап) и b = (М, Ы,..., Ьп) в евклидовом пространстве W. Скалярным
(или внутренним) произведением векторов называется величина
a b = аД + а2Ь2 + ... + abn
Оно обладает свойством
где ||а||2 и ||Ь||2 - модули векторов, например:
а Ь = ||а||2 • ||Ы|2 • cos a,
ца
а а - угол между векторами в диапазоне 0 ^ а ^ п.
= Ja2x + a
2 , ,2
2+"- + ЯИ,
1х, I и It играют роль параметров в уравнении (4.7). Для их оценки в
заданных кадрах используются дискретные аппроксимации
производных (например, значения оператора Собеля Sxu S вместо /хи /).
Компоненты оптического потока - неизвестные в уравнении (4.7). Таким
образом, это уравнение описывает прямую линию в пространстве
скоростей uv. См. рис. 4.9.
Из (4.7) мы знаем, что оптический поток (u, v) для рассматриваемого
пикселя (х, у, t) - точка на этой прямой, но пока еще не знаем, какая
именно.
Вычисление оптического потока как задача о пометке.
Низкоуровневые задачи компьютерного зрения часто сводятся к
сопоставлению каждому пикселю метки /, выбираемой из множества допустимых
меток L. Например, L может быть дискретным множеством идентифи-
4.2.АлгоритмХорна-Шанка ♦ 179
каторов сегментов изображения (см. главу 5) или дискретным
множеством значений диспаратности в задаче о сопоставлении
стереоизображений (см. главу 8). В данном случае мы имеем дело с метками (и, v) £ Ш?
из двумерного вещественного пространства.
Рис. 4.9. Прямая линия -lt= и • lx+ v • I в пространстве скоростей uv.
Точка О обсуждается в примере 4.1
Метки сопоставляются всем пикселям /2 с помощью функции пометки
f'.n^L. (4.8)
Решить задачу о пометке значит найти такую функцию пометки /",
которая каким-то образом находит приближенный оптимум.
Первое ограничение. Пусть/- функция пометки, которая
сопоставляет метку {и, v) каждому пикселю р £ П изображения /(•, •, t). В силу
уравнения (4.7) нас интересует решение/, которое минимизирует
ошибку данных, по-другому именуемую энергией данных:
где u-I +V-I +1{=0в идеальном случае для пикселей р Е П изображения
Второе ограничение - постоянство пространственного
движения. Помимо (4.7), мы сформулируем второе ограничение на
решения (и, v) в надежде получить единственное решение на прямой
-It= и • Ix+v • I. Сформулировать его можно многими разными
способами.
180 ♦ Глава 4.Анализ плотного движения
Мы будем предполагать постоянство движения в окрестности
пикселей в момент t; это означает, что для смежных пикселей изображения
/(-, •, t) векторы оптического потока почти одинаковы. Чтобы функция
была почти постоянной в локальной окрестности, ее первые
производные должны быть близки к нулю. Следовательно, условие постоянства
движения можно выразить в виде ограничения гладкости, согласно
которому сумма квадратов первых производных должна достигать
минимума для всех пикселей р е D. изображения /(•, •, г). И на этот раз для
краткости опустим аргументы (х, у, г).
Пусть / - функция пометки, сопоставляющая метку (и, v) каждому
пикселю р Е П изображения /(•, •, г). Ошибка гладкости, или энергия
гладкости, определяется формулой
Jsmooth
(/)=!
а
удх )
+
\дУ;
/
+
dv
дх
+
dv
\дУ;
(4.10)
Задача оптимизации. Мы хотим вычислить функцию пометки f,
доставляющую минимум комбинации энергии данных и гладкости
EuJfi-EtJfi + X-EMjm, (4.11)
где Я > 0 - весовой коэффициент. В общем случае мы берем Я < 1, чтобы
избежать слишком сильного сглаживания. Точное значение параметра
зависит от приложения и релевантных данных изображения.
Мы ищем оптимум /на множестве всех возможных функций
пометки, для чего применяется полная вариация (total variation - TV).
Энергия гладкости описывает квадратичный штраф (по норме L2). В итоге
получаем задачу оптимизации TV-L2. При Я > 1 гладкость получила бы
больший вес, чем ограничение Хорна-Шанка (т. е. член данных), а это
не рекомендуется. В качестве первого приближения часто выбирают
Я = 0,1, отводя гладкости сравнительно небольшую роль.
Врезка 4.5 (оптимизация среднеквадратической ошибки, СКО). Метод
оптимизации среднеквадратической ошибки в общем случае выглядит так:
1) определить ошибку, или функцию энергии;
2) вычислить производные этой функции по всем неизвестным параметрам;
3) приравнять производные нулю и решить получившуюся систему
уравнений относительно неизвестных. В результате мы получаем стационарную
точку, которая может быть локальным минимумом, седловой точкой или
локальным максимумом.
4.2.АлгоритмХорна-Шанка ♦ 181
Выполним оптимизацию среднеквадратической ошибки. Функция
ошибки определена выражением (4.11). Единственно возможная
стационарная точка - это минимум функции ошибки.
Неизвестными являются значения и и v во всех N , XN пикселях, а
cols rows '
это значит, что нужно задать 2NcolsNrows частных производных функции
СКО. Произведем формальное упрощение, исключив t из следующих
далее формул. Кадр /(•, •, t) и соседние с ним кадры /(•, •, t - 1) и /(•, •, t + 1)
в последующих рассуждениях фиксированы. Вместо 1(х, у, £) будем
далее писать просто 1(ху у).
Для простоты будем предполагать, что для каждого пикселя все
4-смежных с ним пикселя также принадлежат изображению.
Аппроксимировав производные в члене энергии гладкости простыми
асимметричными разностями, получим
Esmooth(f) = X^x+l,, -Uxy)2+(Ux,y+l -Uxyf
х,У
v2 , ,лх лч \2
+ (*W ~ vxy) +(vx,y+l - vv) . (4.12)
Асимметричные разности дают некоторую систематическую ошибку,
симметричные (т. е. их+1 - их_х и т. д.) были бы лучше, но мы продолжим
излагать оригинальный алгоритм Хорна-Шанка.
Имеем следующие выражения для частных производных Edata(u, v):
data
ди
xy
и
ЪЕ.
data
Эй.
{u,v) = 2[lx(x,y)uxy+Iy(x,y)vxy+It(x,y)]lx(x,y) (4.13)
(u,v) = 2[lx(x,y)uxy+Iy(x,y)vxy+It(x,y)]ly(x,y). (4.14)
xy
А вот выражение для частной производной Esmooth(u, v):
smooth
(и, v) = -2[(ux+ly -u^ + iu,^ -uxy)\
x,y
+ 2 [(«v - ux_Xy) + (uxy - uxy_x)]
= 2 [(UXy ~ UX+ly ) + (UXy - UX,y+l )]
+ 2[K -ux-i,y) + (Uxy -ux,y-iJ]. (4.15)
Это единственные члены, содержащие неизвестное и . После
упрощения получаем
182 ♦ Глава 4. Анализ плотного движения
1 дЕ
4 Эй
и —
ху
л \ l+l,J Х,у+\ 1—1,J X,y—\ -
х,у
Обозначим ы среднее 4-смежных пикселей, тогда
(4.16)
ху
1 дЕ.
smooth
4 ди ■(M'U) = 2[^"^} (4Л7)
(u,v) = 2[vxy-vxy]. (4.18)
х,у
1 дЕ.
smooth
4 э^,,
Уравнение (4.18) выводится аналогично.
Заменив Я/4 на Я и приравняв производные нулю, получаем такую
систему уравнений:
° = Л[иху-йху]
+ [1х(х>У)ич,+1у(х>У)1>ч+1Ах>У)]1х(х>У)> (4Л9>
0 = A\v -v 1
\_ ху ху_\
+ [lx{x,y)uxy+Iy(x,y)vxy+IXx,y)\ly(x,y). (4.20)
Это дискретная разностная схема для минимизации функции (4.11).
Мы имеем систему линейных уравнений для нахождения 2NcohNrows
неизвестных их и vx. Значения 1х, I и /(оцениваются по данным входного
изображения.
Итеративная схема решения. Эта система уравнений содержит
также средние й и v , которые вычисляются по значениям неизвестных.
Зависимость между неизвестными и и v и средними й и v на самом
деле оказывается очень полезной. Она позволяет определить
итеративную схему (пример метода Якоби; о К. Г. Я. Якоби см. врезку 5.9) с
начальными значениями.
1. Инициализация. Инициализируем значения и0^ и v^.
2. Итерация 0. Вычисляем средние й0^ и v °, используя начальные
значения. Затем вычисляем и1 и vl .
3. Итерация п. Зная и" и v" вычисляем средние u"nv",a затем
значения w"*1 и v^J1.
Продолжаем, пока не будет выполнен критерий остановки.
4.2.Алгоритм Хорна-Шанка
183
Мы опускаем детали решения системы уравнений (4.19) и (4.20),
поскольку это стандартная линейная алгебра. Решение выглядит так:
К (*» У)К + 7у (*> УЖ + h (*> У)
и„
п+\ —п
ху
= К-1х(х>У>
ху
_ху
Ji+l т^п
vn+l = v" -I (х,у)
XV XV V\ 9 У /
Л2+12х(х,у) + 12(х,у)
h(х,У)й" +1 (х,y)v" + /,(х,у)
ху
ху
ху
(4.21)
(4.22)
Л2+12х(х,у) + 12(х,у)
Теперь мы готовы обсудить сам алгоритм.
4.2.2. Алгоритм
Описанная выше итерационная схема и найденные решения
позволяют вычислить значения и" и v" на n-й итерации для всех пикселей
Л J/ ^у
(х, у) изображения /(•, •, £). Для оценки значений It необходимо хотя бы
одно соседнее изображение, /(•, •, t - 1) или /(•, •, t + 1).
Положим
К (х, У)К + Jy (*» У)% + h (x, У)
а(х,у,п) =
Я2+12х(х,у) + 12(х,у)
(4.23)
Алгоритм показан на рис. 4.10, где й и v обозначают средние,
вычисленные по 4-смежным пикселям. Мы используем «нечетные» и «четные»
массивы для хранения значений и и v; в самом начале (на итерации 0)
инициализируются четные массивы. На итерации п = 1 мы вычисляем
значения в нечетных массивах и т. д. с обязательным чередованием.
Порог Т, максимальное число итераций, определяет критерий остановки.
1
2
з
4
5
6
7
8
9
10
11
12
13
14
15
16
17
for у- 1 to Nrows do
forx= 1 to Ncols do
Вычислить /х(х,у), /у(х,у) и /f(x,y);
Инициализировать и{х,у) и v(x,y) (в четных массивах);
end for
end for
Выбрать весовой коэффициенте; выбрать Г>1; положить п - 1;
while n< Tdo
fory= 1 до Л/ do
' " rows
forx= 1 до Ncols {чередуя четные и нечетные массивы} do
Вычислить а(х,у, п);
Вычислить и(х,у) = й- а{х,у, п) ■ lx{x,y, t);
Вычислить v(x,y) = v-a{x,y, n) ■ I (x,y, t);
end for
end for
n:=n+1;
end while
Рис.4.10. Алгоритм Хорна-Шанка
184 ♦ Глава 4. Анализ плотного движения
В оригинальном алгоритме Хорна-Шанка предлагалось
инициализировать все элементы их и vx нулями. При этом значения и1 и vl будут
не равны 0 при условии, что 1х{х, у) • It(x, у) и / (х, у) • It(x, у) не равны 0 на
всех пикселях. (Разумеется, в таком случае никакого оптического
потока не было бы вообще, так что инициализация нулями была бы
правильной.)
В оригинальном алгоритме Хорна-Шанка использовались
следующие асимметричные аппроксимации 1х, I и It:
Ix(x,y,t) = -[l(x + l,y,t) + I(x + l,y,t + \)
+I(x + l,y + l,t) + I(x + \,y + \,t + \)]
- - [1(х, у, t) + I(x, y,t + l) + I(x, у +1,0 + I(x, y + l,t + Y), (4.24)
Iy(x,y,t) = -[l(x,y + l,t) + I(x,y + l,t + l)
+I(x + l,y + l,t) + I(x + l,y + l,t + \)]
--[l(x,y,t) + I(x,y,t + l) + I(x + l,y,t) + I(x + l,y,t + l), (4.25)
It(x,y,t) = -[l(x,y,t + l) + I(x,y + l,t + l)
+I(x +1, y, t +1) + I(x +1, у +1, t +1)]
- - [I(x, y, t) + I(x, y + l,t) + I(x +1, y, t) + I(x +1, у +1,0. (4.26)
На рис. 4.11 эти локальные аппроксимации показаны в виде
соответствующих сверточных масок. Заметим, что эти маски сильно помогают
в понимании того, как именно аппроксимируются 1х, I и It.
X
-1
-1
1
1
У
-1
-1
N
1
1
-/
-1
1
-1
1
-1
1
-1
1
t+l
X
-1
-1
-1
-1
У
1
1
гл
1
1
-/
Рис. 4.11. Маски для аппроксимации частных
производных 1х, I и Цслево направо), предложенные Хорном и Шанком
Для работы алгоритма нужны только два последовательных
изображения. Существует много модификаций этого алгоритма. На рис. 4.12
4.2. Алгоритм Хорна-Шанка ♦ 185
показаны результаты, полученные оригинальным алгоритмом Хорна-
Шанка.
Рис 4.12. Вверху: два соседних кадра из последовательности «Гамбургское такси»,
опубликованной в 1983 г. для тестирования алгоритмов вычисления оптического
потока. Слева внизу: использование цветового кодирования (1995 г., университет
Отаго, Данидин) для представления направления и модуля вычисленных векторов
оптического потока (цветовой ключ отличается от показанного на рис. 4.4: здесь
черный означает отсутствие движения). Справа внизу: иллюстрация векторов потока
(так называемая игольчатая карта) в увеличенной части изображения
Пример 4.1 (градиентный поток). Неизвестный оптический поток и = [и, v]
в пикселе р = (х, у) изображения /(-, •, t) относительно изображения /(-, •, t + 1)
может быть любым вектором, исходящим из начала координат О на рис. 4.9 и
заканчивающимся в какой-то точке на содержащей этот вектор прямой. Эта
неоднозначность с очевидностью проявляется в проблеме апертуры.
186 ♦ Глава 4. Анализ плотного движения
Для инициализации можно выбрать произвольную точку на прямой,
определенной уравнением оптического потока в пространстве
скоростей uv, а не только 0. Например, можно взять точку О, ближайшую к
началу координат (см. рис. 4.9).
Прямая It = и • Ix + v • I пересекает оси и и v в точках (-It / Ix, 0) и
(0, -IJI) соответственно. Следовательно, вектор
[-It I /, 0] - [0, -ItI / ] = [-/,/ /, ItI Iy] (4.27)
параллелен этой прямой.
Пусть а - вектор, соединяющий О с О; скалярное произведение равно
(о скалярном произведении см. врезку 4.4 и вспомните, что cos я/2 = 0):
a-[-/t//,/f//y] = 0. (4.28)
Памятуя, что а = [ах, а ], из этого уравнения получаем
ax-(-It/Ix) + ay(It/Iy) = 0 (4.29)
и
/f(V/y) = /t(V/). (4.30)
В предположении, что в рассматриваемом пикселе р = (х, у) имеет
место изменение (т. е. It f 0), отсюда следует, что al =а/и
a-c-g° (4.31)
для некоторой константы с f 0, где g° - единичный вектор в
направлении градиента g = [Ix, IY. Следовательно, вектор а коллинеарен
градиенту, как показано на рис. 4.91.
Врезка 4.6 (единичный вектор). Рассмотрим вектор а = [av a2,..., ап]т. Модуль
этого вектора равен ||а|| = Jax +a2 H \- ап. Модуль единичного вектора
а =
а
равен 1,а направление совпадаете направлением вектора а.Скалярное
произведение а° • а° равно ||а°||2 • ||а°||2 • cos 0 = 1.
Вектор а удовлетворяет уравнению оптического потока и • g = -It.
Отсюда следует, что
1 Мы могли бы опустить вывод (4.28)-(4.30), поскольку вектор а перпендикулярен прямой по
определению: он соединяет начало координат с его ортогональной проекцией напрямую
(свойство, определяющее ближайшую точку). Но раз он перпендикулярен прямой, то должен быть
параллелен вектору градиента.
4.3. Алгоритм Лукаса-Канаде ♦ 187
c-ge-g = c-|lgll2 = -/t- (4-32)
Таким образом, мы получили значение сив итоге имеем
I.
а =
g
Ы- (4-33)
Мы можем использовать точку О, определенную вектором а, для
инициализации массивов и и v до начала итераций. Это значит, что мы
начинаем с градиентного потока, представленного вектором а. На
последующих итерациях алгоритм может отклониться от градиентного потока
из-за влияния значений в окрестности рассматриваемого пикселя.
Для аппроксимации 1х, I и I можно также попробовать очень простую
(например, по двум пикселям) аппроксимацию. Алгоритм устойчивый,
но часто дает ошибочные результаты, в основном из-за предположения
о постоянстве яркости, но также из-за проблематичности ограничения
гладкости (например, в случае разрыва непрерывности движения в
рассматриваемых кадрах) и, конечно, из-за проблемы апертуры.
Количество итераций Гможно брать довольно малым (скажем, Т= 7), потому
что его увеличение не дает реального улучшения.
В пирамидальном алгоритме Хорна-Шанка используются пирамиды
изображений, обсуждавшиеся в разделе 2.2.2. Обработка начинается на
выбранном уровне изображений (с низким разрешением). Полученные
результаты служат для инициализации оптического потока на более
низком уровне (с более высоким разрешением). Эта процедура
продолжается до достижения истинного разрешения оригинальных кадров.
4.3. Алгоритм Лукаса-Канаде
Уравнение оптического потока определяет прямую и- Ix + v • I + Jt = 0 в
пространстве скоростей uv для каждого пикселя р £ П. Рассмотрим все
прямые для всех пикселей в локальной окрестности. В предположении,
что они не параллельны, но определены приблизительно одинаковым
двумерным движением, эти прямые должны пересекаться где-то
вблизи истинного двумерного движения. См. рис. 4.13.
Врезка 4.7 (история алгоритма вычисления оптического потока
Лукаса-Канаде). Этот алгоритм был опубликован в работе [В. D. Lucas and T. Kanade. An
iterative image registration technique with an application to stereo vision. Proc. Imaging
Understanding Workshop, 1981, p. 121-130], вскоре после публикации алгоритма
Хорна-Шанка.
188 ♦ Глава 4. Анализ плотного движения
В этом разделе мы опишем новаторский алгоритм вычисления
оптического потока, математические основы которого объяснить гораздо
проще, чем для алгоритма Хорна-Шанка. Он послужит иллюстрацией
альтернативного способа определения движения.
Рис. 4.13. Включение в рассмотрение все большего и большего количества
пикселей в локальной окрестности путем анализа точек пересечения прямых,
определенных уравнением оптического потока для этих пикселей
4.3.1. Линейное решение методом наименьших
квадратов
В алгоритме Лукаса-Канаде применяется метод наименьших
квадратов для анализа пересечений нескольких прямых (больше двух).
Врезка 4.8 (метод наименьших квадратов). Этот метод применяется для
решения переопределенных систем уравнений. Задача состоит в том, чтобы найти
решение, доставляющее минимум сумме квадратов ошибок (называемых
невязками) решения каждого уравнения.
Например, если имеется п неизвестных и т > п линейных уравнений, то
используется метод наименьших квадратов.
Начнем со случая двух прямых (т. е. пикселя р1 и смежного с ним
пикселя р2). Предположим, что двумерное движение в обоих смежных пик-
4.5. Алгоритм Лукаса-Канаде ♦ 189
селях одинаково и его вектор равен и. Также предположим, что
единичные градиенты g° и g° в этих пикселях различны.
Рассмотрим уравнение оптического потока ит • g° = -/f/||g||2 в
обоих пикселях (в формулировке, предложенной в примере 4.1). Имеем
два уравнения с двумя неизвестными и и v - компонентами вектора
u = (u, v)T:
uT-g°(p1) =
uT-g°(p2)
g
L
g
(Pj,
■<P,).
(4.34)
(4.35)
Обозначая правые части Ьг., мы можем переписать эту систему в виде
двух линейных уравнений с двумя неизвестными и и v:
Щп + V8V2 = К
У2
(4.37)
где g° = [gxl,gyl] и g°2 = [gx2,gy2] - единичные векторы. Запишем эти
уравнения в матричной форме:
£х2
Syl
Syl
и
v
(4.38)
Эта система разрешима, если матрица в левой части обратима (т. е. не
является сингулярной):
и
v
Sx\
Sx2
Sy\
Syl
(4.39)
В этом случае система не является переопределенной. Мы имеем
пересечение двух прямых, определяемых уравнениями оптического
потока для рх и р2; см. рис. 4.14.
Но при оценивании Ix, I nlt всегда бывают ошибки, а данные
изображения в любом случае зашумленные, так что лучше искать решение и
в смысле метода наименьших квадратов, рассматривая окрестность,
содержащую к > 2 пикселей, и тогда мы получаем переопределенную
систему уравнений. Окрестность не должна быть слишком большой,
потому что мы предполагаем, что для всех пикселей в этой окрестности
вектор двумерного движения и одинаковый. Таким образом, мы
приходим к переопределенной системе линейных уравнений
190 ♦ Глава 4. Анализ плотного движения
u= (u,v)
Рис. 4.14. Простой случай, когда рассматривается всего два пикселя
ёх\
£х2
•
с>хк
Syl
Syl
•
Syk ]
\и
IV
"*il
К\
•
k J
(4.40)
которую будем записывать в виде
кх2 2x1 кх\
(4.41)
Эту систему можно решить при к > 2 методом наименьших квадратов.
Сначала приведем систему к квадратному виду:
GTGu = GTB. (4.42)
Затем найдем решение с наименьшей квадратичной ошибкой:
u = (GTG)-1GTB. (4.43)
Вот и все. GTG - матрица размера 2><2, a GTB - матрица размера 2*1.
Например, если
GTG =
то
а Ъ
с d
(G^)-^
1
ad —be
d -b
—с а
(4.44)
(4.45)
Остальное - обычное перемножение матриц.
4.3.Алгоритм Лукаса-Канаде ♦ 191
4.3.2. Оригинальный алгоритм и алгоритм с весами
По сравнению с алгоритмом Хорна-Шанка математика оказалась
довольно простой. Мы обсудим оригинальный алгоритм и его
модификацию.
Оригинальный алгоритм вычисления оптического потока
Лукаса-Канаде. Базовый алгоритм выглядит следующим образом:
1) принять решение о размере локальной окрестности - к
пикселей - и придерживаться его во всех кадрах;
2) в кадре с номером t оценить 1х> I и It;
3) для каждого пикселя р в кадре t построить систему уравнений
(4.40) и решить ее методом наименьших квадратов, применяя
формулу (4.43).
Иногда полезно оценивать используемые производные на
изображениях, сглаженных, к примеру, фильтром Гаусса с небольшим
стандартным отклонением, скажем, а = 1,5.
Веса участвующих пикселей. Мы можем назначить всем к
участвующим пикселям положительные веса w., i = 1,..., к. В общем случае
текущему пикселю назначается максимальный вес, а смежным с ним
(и входящим в состав этих к пикселей) - меньшие веса. Обозначим
W = diagfWj,..., wk] - диагональную матрицу весов к*к. Любая
диагональная матрица удовлетворяет тождествам
WTW = WW = W2. (4.46)
Теперь наша задача - решить уравнение
WGu = WB (4.47)
вместо (4.41); правые части нужно взвесить так же, как и левые. Для
решения необходимо проделать ряд манипуляций с матрицами:
(WG)TWGu = (WG)TWB, (4.48)
GTWTWGu = GTWTWB, (4.49)
GTWWGu = GTWWB, (4.50)
GTW2Gu = GTW2B, (4.51)
и, следовательно,
u = [GTW2G]_1 GTW2B. (4.52)
192 ♦ Глава 4. Анализ плотного движения
Смысл этих преобразований заключается в том, чтобы снова
получить матрицу 2x2 GT W2 G, которую можно обратить для вычисления и в
текущем пикселе.
По сравнению с оригинальным алгоритмом нужно только внести
следующее изменение в шаг 3:
3) для каждого пикселя р в кадре t построить систему уравнений
(4.47) и решить ее методом наименьших квадратов, применяя
формулу (4.52).
На рис. 4.15 показаны результаты оригинального алгоритма Лукаса-
Канаде для окрестности размера 5*5. Применяя для решения
формулу (4.43), мы принимаем только те решения, для которых собственные
значения (см. врезку 2.9) матрицы GTG больше выбранного порога. Тем
самым отфильтровываются «зашумленные» результаты.
Рис. 4.15. Рассматриваются те же два соседних кадра из записанной
последовательности, что и на рис. 4.5. Оптический поток,
вычисленный оригинальным алгоритмом Лукаса-Канаде;
к =25 для окрестности размера 5*5
Матрица GTG имеет размер 2*2 и является симметричной и
положительно определенной; у нее есть два собственных значения Ях и Я2. Пусть
О < Ях ^ Я2. Выберем порог Т > 0. Мы «принимаем» решение,
полученное по формуле (4.43), если Ях > Т. Это приводит к разреженному полю
оптического потока, показанному на рис. 4.15. Заметим, что немногие
показанные векторы в общем случае близки к истинному смещению.
4.4.Алгоритм BBPW ♦ 195
4.4. Алгоритм BBPW
Алгоритм BBPW является обобщением алгоритма Хорна-Шанка. Его
цель - улучшить результаты, особенно для больших смещений, и
попытаться преодолеть ограничения, налагаемые предположением о
постоянстве яркости. Кроме того, из-за применения квадратичной нормы
для оптимизации выбросы оказывают большое влияние на результаты,
поэтому в алгоритме BBPW используется норма Lv а не L2, как в
алгоритме Хорна-Шанка.
Врезка 4.9 (история алгоритма BBPW). Этот алгоритм был опубликован в
работе [Т. Brox,A. Bruhn, N. Papenberg and J. Weickert. High accuracy optical flow estimation
based on a theory for warping. In Proc. European Conf. Computer Vision, vol. 4, 2004,
p. 25-36].
В этом разделе формулируются исходные предположения,
объясняется, какая функция энергии используется, и приводятся краткие
сведения о теоретических основах алгоритма; подробное его изложение
выходит за рамки этой книги. Мы покажем, каких успехов удалось
добиться в области вычисления оптического потока с момента
публикации алгоритмов Хорна-Шанка и Лукаса-Канаде.
4.4.1. Исходные предположения и функция энергии
В рассматриваемом контексте предположение о постоянстве
яркости (ICA) формально записывается в виде 1(х, у, t) = 1(х + и, у + v, t + 1),
где и и v - перемещения в направлениях х и у соответственно за
время St. После линеаризации мы получаем ограничение Хорна-Шанка
Ixu + Iu + It = 0. Предположение о постоянстве яркости не выполняется
для съемки под открытым небом, поэтому алгоритмы Хорна-Шанка и
Лукаса-Канаде зачастую дают неудовлетворительные результаты,
когда рассматриваются изменения на расстоянии от 5 до 10 пикселей (т. е.
векторы двумерного движения не являются «короткими» в смысле
разложения в ряд Тейлора до членов первого порядка).
Постоянство градиента. Предположение о постоянстве градиентов
яркости по смещениям (constancy of intensity gradients over
displacements - GCA) записывается в виде
Vxy/(x, у, t) = VxyI(x + и, у + v, t + 1), (4.53)
где Vx , как и раньше, ограничивается только производными по а: и у,
производная по времени не включается. Как было сказано в главе 1,
194 ♦ Глава 4. Анализ плотного движения
градиенты считаются более-менее устойчивыми относительно
изменения яркости.
Предположение о гладкости. Одни лишь предположения ICA и GCA
еще не дают достаточной информации для однозначного определения
оптического потока, нам необходимо привлечь смежные пиксели и
сделать некоторые допущения о регулярности векторного поля потока.
Необходима осторожность на краях объектов. Нельзя полностью
исключить разрывы непрерывности движения; кусочное сглаживание
представляется эффективным средством избежать влияния векторов
потока вне объекта на поле потока внутри объекта и наоборот.
Первая попытка вывести формулу функции энергии. В
описываемом ниже варианте функции ошибки или энергии мы все еще
опираемся на предположение ICA (но не прибегаем к ограничению Хорна-
Шанка и тем самым избегаем аппроксимации первыми членами ряда
Тейлора), но в сочетании с предположением GCA. Мы рассматриваем
позиции пикселей (х, у, t) в кадре /(•, •, t), векторы оптического потока
w = (и, v, 1), содержащие третью компоненту для перехода от плоскости
изображения в момент t к плоскости в момент t + 1, и используем
градиент V = (дх, д , dt) в трехмерном пространстве. Уравнение (4.9)
приобретает вид:
Edata if) = X {U(X + U,y + Vj + \)~ /(*, у, tjf
+ Al{WxJ(x + u,y + v,t + l)-WxyI(x,y,t)]2]j, (4.54)
где Aj > 0 - вес, который еще нужно задать. Что касается члена
гладкости, то мы в основном сохранили выражение (4.10), но теперь
используем пространственно-временные градиенты в формуле
*— (/)=X[lNM|vt|} <4-55>
а
Таким образом, задача заключается в том, чтобы найти функцию
пометки /", которая сопоставляет оптический поток u, v каждому пикселю
изображения /(-, •, £), так чтобы доставить минимум сумме
£„„,(/) = £*,„(/)+ Л2 •*—,<» (4-56)
при некотором значении веса Я2 > 0. Как и в (4.11), в выражении (4.56)
по-прежнему используется квадратичный штраф по норме L2, т. е. мы
имеем задачу оптимизации TV-L2. При такой схеме выбросы играют
слишком большую роль в оценке оптического потока.
4.4. Алгоритм BBPW ♦ 195
Регуляризированная полная вариация по норме Lv Для перехода
от 12-оптимизации к Ь1 -оптимизации мы используем функцию
iKs2) = VFTi*|s|, (4.57)
а не просто \s\. Это приводит к более устойчивой функции энергии, не
лишая нас возможности рассматривать непрерывные производные при
s = 0 даже для небольшой положительной константы s. В качестве е
можно взять, например, 10~6 (т. е. очень маленькую величину). У функции
|s| нет непрерывной производной в точке s = 0, а она нам нужна, чтобы
можно было применить схему минимизации ошибки.
Монотонно возрастающая и выпуклая функция ip(s2) = Vs2 + e
применяется к членам функции энергии в формулах (4.54) и (4.55), чтобы
уменьшить влияние выбросов. Таким образом, мы определяем член
полной вариации, регуляризированной по норме Lv Члены функции
энергии имеют вид
Edata{f) = ^W^I{x + u,y + v,t + \)-I(x,yJ)f
О.
+ К ■ [ V*,/(* + u,y + v,t + l)- VxJ(x, у, О]') (4.58)
и
£„-(/)=2>((v»>2+<Vv)2)- <4-59)
Формула же полной энергии остается такой же, как (4.56).
4.4.2. Краткое описание алгоритма
Мы должны найти функцию пометки /", которая минимизирует
функцию ошибки Ета1, определенную формулой (4.56) и состоящую из двух
членов (4.58) и°(4.59).
Минимизация нелинейной функции такой, как ЕшаР - трудная задача.
В процессе поиска глобального минимума алгоритм может застрять в
локальном минимуме.
Врезка 4.10 (Лагранж и уравнения Эйлера-Лагранжа). Жозеф Луи Лагранж
(1736-1813) - французский математик итальянского происхождения. Эйлер
(см. врезку 1.3) и Лагранж разработали общий способ нахождения функции/,
минимизирующей функционал энергии £(/). В предположении, что/- не
просто функция с одним аргументом, предлагаемое решение выражено в виде
системы дифференциальных уравнений.
196 ♦ Глава 4.Анализ плотного движения
Уравнения Эйлера-Лагранжа. Обозначим гр' производную \р по ее
единственному аргументу. Дивергенцией div называется сумма
производных, в нашем случае это сумма трех частных производных,
являющихся компонентами вектора
Vu =
ди ди ди
дх ду dt
(4.60)
Функция пометки /", минимизирующая функционал Etotal(f), должна
удовлетворять приведенным ниже уравнениям Эйлера-Лагранжа. Мы
не станем выводить эти уравнения средствами вариационного
исчисления, а просто сформулируем конечный результат:
гр'(Р + ЛАР+Ру(П+ЛЛ I+I /,),
т V t 1V ATt yU V X t 1V XX Xt Xy ytn
-A2 • divO'(IIVu||2 + ||W||2)Vu) = 0 (4.61)
ip'(P + AAPt + Ру(П+АЛ I+I I,),
* V t 1V ATt yU V у t 1V yy yt Xy Xtn
-A2 • div(i/;'(IIVu||2 + ||Vv||2)Vv) = 0. (4.62)
Как и раньше, Ix, I nlt- производные /(•, •, t) по координатам пикселей
и по времени, а 1хх, I и т. д. - вторые производные. Все эти производные
можно рассматривать как константы, которые приближенно
вычисляются по последовательности кадров. Таким образом, оба уравнения
имеют вид
сг-А2- divO'(IIV"ll2 + ||Vv||2)Vw) = 0, (4.63)
с2-А2- divO'fllVull2 + ||Vv||2)Vv) = 0. (4.64)
Решение этих уравнений для и и v в любом пикселе р £ П можно
найти, применив пирамидальный подход.
Пирамидальный алгоритм. Для эффективной оценки векторов
потоков можно сначала использовать передискретизированные с
понижением копии обрабатываемых кадров, образующие пирамиду (см.
раздел 2.2.2), а затем уточнить полученные результаты на копиях с
более высоким разрешением. При таком подходе можно также найти
длинные векторы потока. Пример пирамидальной реализации
алгоритма BBPW приведен на рис. 4.16, где для визуализации используется
тот же цветовой ключ, что был описан на рис. 4.4.
4.5. Оценка качества алгоритмов вычисления оптического потока ♦ 197
Рис. 4.16. Визуализация оптического потока, вычисленного с помощью
пирамидального алгоритма BBPW. Вверху: для кадров, показанных на рис. 4.5.
Внизу: для кадра из последовательности queenStreet
4.5. Оценка качества алгоритмов вычисления
оптического потока
Первым для вычисления оптического потока был предложен алгоритм
Хорна-Шанка, с тех пор появилось много других алгоритмов. Анализ
движения и по сей день остается весьма трудной проблемой
компьютерного зрения.
В этом разделе мы коротко расскажем о методах сравнительного
анализа качества алгоритмов вычисления оптического потока.
4.5.1. Стратегии тестирования
Алгоритм Хорна-Шанка в общем случае отклоняется от потока
градиента. Следующий простой пример (который можно просчитать даже
вручную) показывает, что этого не происходит, если окрестности
пикселей не позволяют вычислить правильное движение.
198 ♦ Глава 4. Анализ плотного движения
Пример 4.2 (простой пример входных данных). Рассмотрим 1Х изображение
размера 16х 16, показанное на рис. 4.17, для которого Gmax = 7. Оно содержит
вертикальную прямолинейную границу; градиент в граничных пикселях
направлен влево.
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 х
1 I I I I I I I I I I I I I I I »
Го
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
4
4
4
4
4
4
4
4
4
4
4
4
4
4
4
5
5
5
5
5
5
5
5
5
5
5
5
5
5
5
6
6
6
6
6
6
6
6
6
6
6
6
6
6
6
7
7
7
7
7
7
7
7
7
7
7
7
7
7
7
7
7
7
7
7
7
7
7
7
7
7
7
7
7
7
7
7
7
7
7
7
7
7
7
7
7
7
7
7
7
7
7
7
7
7
7
7
7
7
7
7
7
7
7
7
Т]
7
7
7
7
7
7
7
7
7
7
7
7
7
7
Рис. 4.17. Простые входные данные для ручного просчета
алгоритма Хорна-Шанка
Изображение 12 сгенерировано в результате одного из трех движений,
показанных слева: (А) сдвиг на один пиксель (ОД) вправо, (В) сдвиг по диагонали
(1,1), (С) сдвиг на один пиксель (-1,0) вверх. Для простоты будем предполагать,
что новые «вдвигаемые» слева пиксели равны нулю, а снизу - такие же, как в
строке над ними.
В этом простом примере значения, порождаемые алгоритмом
Хорна-Шанка, можно вычислить вручную. Ограничимся только первыми тремя
итерациями [(4.22) и (4.22)], применив инициализацию нулями и простые схемы
аппроксимации по двум пикселям для 1х91 и It.
Оценка качества алгоритмов вычисления оптического потока.
Для оценки алгоритма вычисления оптического потока на реальной
последовательности изображений существует три возможности.
1. В предположении, что последовательность изображений
записана с высокой частотой (скажем, больше 100 Гц), можно
попытаться использовать чередующиеся кадры для анализа ошибки
прогнозирования: оценить оптический поток для кадров t и t + 2,
вычислить виртуальное изображение в момент £ + 1 путем интер-
4.5. Оценка качеава алгоритмов вычисления оптического потока ♦ 199
поляции вычисленных векторов потока и сравнить это
виртуальное изображение (например, методом нормированной взаимной
корреляции, см. врезку 4.11) с кадром t + 1.
Врезка 4.11 (нормированная взаимная корреляция). Рассмотрим два
изображения / и J одинакового размера. Нормированная взаимная корреляция
(normalized cross-correlation - NCC) служит для сравнения двух изображений.
Это скалярная величина, вычисляемая по формуле
м (т n- -L V [l(*>y)-Mi][Ax,y)-Mj]
IVINCC\I>J)~ |0| 2^ ,- ^ '
где jL/; и jl/7 - средние, a af и а} - стандартные отклонения / и J соответственно.
Чем больше Ммсс(/,7),тем более похожи изображения.
Благодаря нормировке - вычитанию среднего и делению на стандартное
отклонение - изображения / и J с различными значениями этих характеристик
могуттем не менее быть похожи. Это особенно интересно, когда сравниваются
изображения, не удовлетворяющие предположению о постоянстве яркости,
что иногда случается для двух соседних кадров в последовательности
изображений.
Нормированную взаимную корреляцию можно также использовать для
сравнения небольшого изображения (шаблона) с окнами того же размера
большего изображения. Библиотека OpenCV предлагает несколько способов такого
рода сравнения с шаблоном, и среди них варианты нормированной взаимной
корреляции.
2. Если существует контрольная информация о фактическом
двумерном движении (как, например, данные для коротких
последовательностей на сайте Миддлбери-колледж vision.middlebury.
edu/ или в наборе 2 EISATS для последовательностей длиной 100
и более кадров), то оценить результаты вычисления оптического
потока можно на основе мер ошибки (см. ниже), сравнивая
истинные (конечно, с точностью до ошибок измерения при генерации
контрольных данных) и вычисленные векторы.
3. Можно также сравнить результаты, полученные разными
методами, чтобы понять, какие методы дают похожие результаты, а
какие - совсем разные.
4. Метод можно оценить на реальных данных, постепенно вводя во
входные данные различные виды шума разной интенсивности,
чтобы понять, насколько метод устойчив. В качестве шума можно
использовать вариации яркости, гауссов шум или размытие.
200 ♦ Глава 4.Анализ плотного движения
5. Зная геометрию сцены и приблизительное движение камеры,
можно сравнить результаты с ожидаемым полем потока.
Например, камера может прямолинейно и равномерно приближаться к
стене.
4.5.2. Меры ошибки для сравнения с контрольными
данными
Получить контрольные данные для анализа движения трудно,
особенно если речь идет о реальных последовательностях изображений.
Альтернативой являются синтезированные последовательности.
Рендеринг изображений с учетом физических законов может порождать
«достаточно реалистичные» синтетические последовательности
изображений, даже с возможностью изучать поведение алгоритмов
вычисления оптического потока в зависимости от меняющихся
параметров (что для последовательностей реально записанных изображений,
конечно, невозможно).
Врезка 4.12 (контрольные данные). По-английски контрольные данные
называются «ground truth» (буквально «наземная истина»). Изображения,
снятые с летательного аппарата, часто используются для оценивания
расстояний на земле и даже для реконструкции целых ландшафтов или городов.
Для проверки результатов широко применялась практика идентификации
заметных объектов на местности, например углов зданий, и прямого
измерения их координат или расстояний между ними. Это и была «наземная
истина» - контрольные данные для сравнения с вычисленными на основе
аэрофотосъемки.
В настоящее время термин используется для обозначения данных прямых
измерений, которые считаются относительно точными и, стало быть,
полезными для оценивания алгоритмов, которые должны давать такие же
результаты.
На рис. 4.18 показаны контрольные данные для синтетической
последовательности изображений (из 100 кадров) и результаты
пирамидального алгоритма Хорна-Шанка. Помимо цветового кодирования, мы
включили также разреженные векторы в контрольное и вычисленное
изображение. Это избыточная информация (похожая на игольчатую
карту на рис. 4.12), но она помогает зрителю понять происходящее
движение. Кроме того, цвет вокруг нарисованных векторов потока
подсказывает, какие цвета соответствуют разным направлениям.
4.5. Оценка качества алгоритмов вычисления оптического потока ♦ 201
4-~ ** 1е* У ** V Г У ."
t^V'".' / J -l i i i V \ \ \
wV^^^
.'l., л.
Рис. 4.18. Вверху: Два входных изображения (кадр l,Set2Seql и кадр 2 из первой
последовательности в наборе 2 EISATS). Слева внизу: контрольные данные для
этой последовательности с цветовым кодированием для визуализации локальных
перемещений. Справа внизу: результат пирамидального алгоритма Хорна-Шанка
Меры ошибок при наличии контрольных данных. Мы имеем
вычисленный поток и = (ы, v) и контрольный поток и* = (и*, v*).
Дистанционная ошибка (endpoint error) L2
Еер2(иУ) = J(u-u*)2+(v-v*)2
и дистанционная ошибка L1
Eepl(u,u*) = \u-u*\ + \v-v*\
сравнивают векторы в двумерном пространстве.
Угловая ошибка между пространственно-временными
направлениями вычисленного потока и контрольных данных в точке р (не включена
в формулу) равна:
Е^„(и,и*) = arccos
апя v ' /
ang
( Т •
u -и
u llu*
(4.65)
202 ♦ Глава 4. Анализ плотного движения
где и = (и, v, 1) - вычисленный оптический поток, к которому добавлена
еще одна координата (1 соответствует расстоянию между
изображениями, записанными в моменты времени t и t + 1), a u* = (ut, vt, l) -
контрольный поток, также продолженный на трехмерное пространство.
Эта мера ошибки позволяет оценить точность направления и
абсолютной величины потока.
Такие меры ошибок применяются ко всем пикселям кадра, что
позволяет вычислить среднюю угловую ошибку, среднюю дистанционную
ошибку L2 и т. д., а также их стандартные отклонения.
4.6. Упражнения
4.6.1. Упражнения по программированию
Упражнение 4.1 (вариации на тему алгоритма Хорна-Шанка).
Реализуйте алгоритм Хорна-Шанка для вычисления оптического потока.
Разумеется, уже есть программы, доступные для свободного
использования, но от вас требуется реализовать свой вариант.
Протестируйте алгоритм на парах изображений одной и той же
сцены с небольшими различиями, перемещения должны быть ограничены
расстоянием 5-6 пикселей, не больше.
Используйте обе рассмотренные в тексте стратегии инициализации
значений и и v (т. е. просто нулями или точкой О, ближайшей к
началу координат в пространстве скоростей, см. пример 4.1). Используйте
также две разные схемы аппроксимации 1х, I и It. Обсудите, как все это
влияет на результат.
После каждой итерации п + 1 вычислите среднее значение всех
изменений и и v по сравнению с предыдущей итерацией п. Постройте
график этих изменений в зависимости от номера итерации.
Получилась ли у вас монотонно убывающая функция? Можно ли использовать
пороговую величину таких изменений в качестве критерия остановки
алгоритма?
Обсудите, какое число итераций можно считать достаточным для
ваших входных последовательностей и как это зависит от выбранных
схем инициализации и аппроксимации /,, / и It.
Наконец, сравните с результатами, полученными, когда просто
используется уравнение (4.33), которое вычисляет градиентный поток, не
используя ограничение гладкости, позволяющее учесть смежные
пиксели.
4.6. Упражнения ♦ 205
Упражнение 4.2 (вариации на тему алгоритма Лукаса-Канаде).
Разумеется, уже есть программы, доступные для свободного использования,
но от вас требуется реализовать свой вариант.
Протестируйте алгоритм на парах изображений одной и той же
сцены с небольшими различиями, перемещения должны быть ограничены
расстоянием 5-6 пикселей, не больше.
Выберите схему аппроксимации 1х, I и /t и реализуйте следующие
варианты:
1) окрестность 3*3 без весов;
2) окрестность 5*5 без весов;
3) окрестность 5x5 с весами, имеющими нормальное распределение.
Обсудите, что получилось (точность, различие в результатах, время
вычислений) на реальных тестовых данных.
Упражнение 4.3 (оценка качества алгоритмов вычисления
оптического потока, имеющихся в библиотеке OpenCV). Воспользуйтесь
угловой и дистанционной мерами ошибки для оценки качества алгоритмов
вычисления оптического потока, имеющихся в библиотеке OpenCV, на
последовательностях изображений (не менее 100 кадров), для которых
доступны контрольные данные.
1. Используйте синтетические последовательности, например из
набора 2 EISATS.
2. Используйте реальные последовательности, например из
тестового набора KITTI Benchmark Suite.
Для сравнения прогоните алгоритмы на конкурсных входных
последовательностях (без контрольных данных, только с визуальной
оценкой), например тех, что предлагались на соревновании по устойчивым
алгоритмам компьютерного зрения на конференции ECCV 2012 в Гей-
дельберге (Heidelberg Robust Vision Challenge). Обобщите полученные
результаты в отчете.
Упражнение 4.4 (алгоритмы вычисления оптического потока на
остаточных изображениях после сглаживания). Прогоните алгоритмы
вычисления оптического потока, имеющиеся в библиотеке OpenCV, на реальных
последовательностях изображений (не менее 100 кадров) и сравните:
• результаты, полученные для исходных последовательностей, с
• результатами, полученными для последовательностей
остаточных изображений после сглаживания исходных
последовательностей.
204 ♦ Глава 4.Анализ плотного движения
Для создания остаточных изображений применяйте различные
итеративные схемы. Например, используйте для сглаживания
прямоугольный фильтр 3x3 и рекурсию с числом шагов не более п = 30. Какое
число итераций вы рекомендовали бы для тестовых последовательностей,
с которыми работаете?
Упражнение 4.5 (тесты при известной геометрии движения).
Выберите какой-нибудь алгоритм вычисления оптического потока и
протестируйте его на изображениях, записанных следующими способами:
1) перемещайте камеру перпендикулярно статической сцене, так
чтобы вычисленные поля движения можно было сравнить с
движением камеры;
2) перемещайте камеру, обращенную к текстурированной стене,
например снимая из автомобиля или смонтировав камеру на
роботе, так чтобы вычисленные поля движения можно было сравнить
с ожидаемым круговым двумерным движением;
3) запишите движение метронома с качающимся маятником
(можно использовать последовательности из набора 8 EISATS).
Записанные последовательности должны содержать не менее 100
кадров.
Попытайтесь оптимизировать параметры алгоритма для таких
последовательностей.
4.6.2. Упражнения, не требующие программирования
Упражнение 4.6. Вычислите коэффициенты разложения в ряд
Тейлора функции
1(х, у, t) = 2х2 + ху2 + xyt + 5t3
до членов третьего порядка.
Упражнение 4.7. Проверьте правильность формул (4.13), (4.14) и
(4.15).
Упражнение 4.8. Инициализация нулями в алгоритме Хорна-Шанка
была бы невозможна, если бы получающиеся в результате начальные
значения и и v также были бы равны нулю. Убедитесь, что в общем
случае так не может быть на первой итерации алгоритма (если движение
действительно имеет место).
Упражнение 4.9. Для данных из примера 4.3 вручную просчитайте
первые три итерации алгоритма Хорна-Шанка, применив
инициализацию нулями и простую схему аппроксимации 1х, I и /tno двум пикселям.
4.6. Упражнения ♦ 205
Упражнение 4.10. Проверьте правильность формулы (4.45).
Упражнение 4.11. Для алгоритма Лукаса-Канаде покажите, что
обращение матрицы в (4.43) завершается неудачно, если градиенты
изображения в выбранной окрестности параллельны. Возможно ли такое
для реальных изображений? Возьмите какой-нибудь учебник линейной
алгебры и прочитайте, как при наличии таких сингулярностей получить
решение методом наименьших квадратов.
Глава
5
Сегментация изображений
В этой главе мы опишем специальные подходы к бинаризации и
сегментации статических изображений или кадров видео. В последнем
случае мы уделим особое внимание обеспечению временной
согласованности. Мы подробно обсудим сегментацию методом сдвига
среднего. Мы также предложим общий взгляд на сегментацию изображения
как на еще один пример пометки пикселей в компьютерном зрении,
дадим введение в сегментацию с этой абстрактной точки зрения и
обсудим в этом контексте решения, основанные на алгоритме
распространения доверия.
В процессе сегментации изображение разбивается на участки,
называемые сегментами, с целью дальнейшего анализа, повышения
эффективности сжатия или просто для визуализации (см. рис. 5.1). С точки
зрения математики, мы разбиваем носитель П на конечное число
сегментов S{, i = 1,..., и, так что
1) S-Ф 0 для всех / G {1,..., п};
2) \Jni=lSi = Q;
3) S.nSf=0 для всех /,;' 6 {1,..
п} таких, что / Ф ').
ismttttg
^F
;ш:гт'"oil
i 1
"
Щ Сегмент 1 Сегмент 4
Щ Сегмент 3
Сегмент 2 Сегмент 5
т
Сегмент 6
Рис. 5.1. Слева: изображение Yan, разбитое на сегменты.
Справа: шесть сегментов этого разбиения
5.1. Простые примеры сегментации изображений ♦ 207
В процессе сегментации создаются связные сегменты пикселей,
схожих относительно некоторого критерия, возможно, дополненного
обнаружением пикселей, чем-то непохожих на смежные с ними. Несхожесть
определяет края сегментов, см. раздел 2.4.1. В идеале оба подхода
должны дополнять друг друга. К сожалению, границы редко бывают
простыми кривыми, очерчивающими сегмент; как правило, это просто дуги.
Преобразовать эти дуги в простые кривые - нетривиальная задача.
Цель сегментации - выделить «осмысленные» сегменты, которые
можно было бы использовать для описания содержимого изображения,
например: сегмент «фона», сегменты «объектов» вообще или объектов
определенных категорий (глаз, рот, волосы, как показано на рис. 5.2 в
нижнем ряду, в середине и справа; приближение позволяет разглядеть
на этом рисунке различные степени сегментации).
Рис. 5.2. Верхний ряд: изображение AnnieYukiTim (слева) и результат его стилизации
Виннемёллера (почти бинарный). Связные темные и светлые участки - это
сегменты. Нижний ряд: сегментация изображения Rocio (слева) методом сдвига
среднего с радиусами г= 12 (в середине) и г = 24 (справа), объяснения см. в тексте
5.1. Простые примеры сегментации
изображений
На рис. 5.3 показано приложение анализа изображения, в котором
первый шаг - сегментацию - можно свести к бинаризации, т. е. созданию
208 ♦ Глава 5. Сегментация изображений
черных участков, определяющих объекты (в данном приложении это
следы), и белых участков, определяющих сегменты фона1.
Монохромные изображения следов мелких животных фиксируются на покрытых
специальной краской карточках, различать уровни яркости в темных
участках (кляксах) нет необходимости. Цель процедуры анализа -
автоматически определить, какое животное оставило данный след.
Рис. 5.3. Изображение RattusRattus, сделанное в Новой Зеландии для контроля
состояния окружающей среды. Его требуется сегментировать, выделив пиксели,
принадлежащие и не принадлежащие объектам. Слева: пример следов на
следоулавливающей карточке. Справа вверху: туннель для сбора следов.
Справа внизу: след черной крысы (Rattus rattus)
В этом разделе объясняются базовые процедуры сегментации
изображений: один метод адаптивной бинаризации, один метод стилизации,
в котором простая постобработка также ведет к получению
бинаризованного изображения, и идеи выращивания сегментов из выбранных
начальных пикселей.
1 Рисунок взят из публикации [B.-S. Shin, /. Russell, Y. Zheng and R. Klette. Improved segmentation for
footprint recognition of small mammals. In Proc. IVCNZ, an ACM publication, Nov., 2012].
5.1. Простые примеры сегментации изображений ♦ 209
5.1.1. Бинаризация изображения
В процессе бинаризации к скалярному изображению применяется
один глобальный порог Г для преобразования его в бинарное
изображение:
Ах,у) = \
0 если 1(х, у)<Т
к'л • (5.1)
1 в противном случае
Величину глобального порога можно определить, применив
стратегию оптимизации, нацеленную на создание «больших» связных
участков и уменьшение количества малых участков, называемых
артефактами.
Врезка 5.1 (история бинаризации Оцу). Этот алгоритм бинаризации был
опубликован в работе [N. Otsu. A threshold selection method from grey-level histograms.
IEEE Trans. Systems Man Cybernetics, vol. 9,1979, p. 62-66].
Бинаризация Оцу. В этом методе используется гистограмма
уровней яркости для заданного изображения /, а цель - найти
оптимальный порог в том смысле, что «перекрытие» двух классов - объектов
и фоновых пикселей - минимально (путем отыскания «наилучшего
баланса»).
В алгоритме Оцу выбирается порог, который доставляет максимум
межклассовой дисперсии а2ь, определяемой как обычная дисперсия,
вычисленная для средних значений классов. В случае двух классов
формула особенно проста:
а\ = Рх(цх - uf + Р2{ц2 - Uf = PxP2{Ul - ц2)\ (5.2)
гдеРгиР2- вероятности классов.
Выбранный порог и, 0 < и < Gmax, определяет «темные» пиксели
объектов, для которых 1(р) < ы, и «светлые» пиксели фона, для которых и < 1(р).
Обозначим ц{и), i = 1, 2, средние по классам объектов и фона. Пусть с7-
гистограмма относительных кумулятивных частот изображения /,
определенная формулой (1.8). Вероятности Р1 и Р2 аппроксимируются
значениями с {и) и 1 - с7(ы) соответственно; это общее число пикселей в
каждом классе, поделенное на мощность множества |/2|.
Алгоритм Оцу показан на рис. 5.4; он просто проверяет всех
возможных кандидатов на роль оптимального порога Т.
210 ♦ Глава 5. Сегментация изображений
1: Вычислить гистограмму Н, для и - 0,..., Gmax;
2: Обозначить Т0 приращение для вычисления потенциальных порогов
3
4:
5
б:
7
8:
9:
10:
и положить и - Т-, T-u;S - 0;
0' ' max '
while u<G do
max
Вычислить с:{и) и ju.(u) для / = 1,2;
Вычислить о\{и) = c,(u)[1 - c,(u)][/u.(u) - jU2(u)]2;
if о2Ли) > S then
6х ' max
S = o2Au) и 7"= u;
end if
Положить и = и + T0
end while
Рис. 5.4. Алгоритм Оцу. Значения гистограммы используются
для обновления на шаге 4. Шаг 5 производится на основе формулы (5.2)
На рис. 5.5 показаны результаты бинаризации окна изображения
следов (рис. 5.3). Если порог слишком мал, то в участках объектов есть
дырки, а если слишком велик, то участки сливаются. Порог, вычисленный
методом Оцу, равен Т= 162.
* 0
7=63
t
i
Г=92
''*♦
• •
Г=187
» 9
Г =141
**?*
Г =230
9
Г=162
Рис. 5.5. Примеры для различных порогов 7~е {0, ...,255}
Стилизация Виннемёллера. В разделе 2.4 рассматривался детектор
границ на основе разности гауссианов (DoG). Здесь мы опишем
обобщение этого детектора для нефотореалистичного рендеринга (NPR)
отснятых фотографий. Стилизация Виннемёллера, по существу, определяет
бинаризацию изображения.
5.1.Проаые примеры сегментации изображений ♦ 211
Врезка 5.2 (история стилизации Виннемёллера). Этот алгоритм бинаризации
был опубликован в работе [Н. Winnemoller. XDoG: Advanced image stylization with
extended difference-of-Gaussians. In Proc. ACM Symp. Non-Photorealistic Animation
Rendering, 2011, p. 147-155].
Повторим определение DoG (2.40), только перенесем L(x, у, а) в левую
часть:
Цх, у, а) = Цх, у, аа) + Daa(x, у). (5.3)
Здесь а - масштаб, а а > 1 - масштабный коэффициент. Таким образом,
Daa{x, у) дает высокочастотные компоненты, которые нужно прибавить
к Цх, у, аа) для получения менее сглаженного изображения Цх, у, а).
Сделаем еще один шаг в том же направлении и рассмотрим тождество
°аЛт (*' У) = L(x> У>°)-т' Д*> У> аст)
= (1 - т) • Цх, у, а) + т • Daa{xy у). (5.4)
Параметр т управляет чувствительностью детектора границ. При
малых значениях т границы становятся «менее важными», преимущество
в том, что при этом обнаруживается меньше шума. Этот
модифицированный детектор затем используется для определения функции
е£Л*,у) = \
0 если D (х,у)> е
аАт i > уу . (5.5)
tanh(^- (DaaT(x, у) - ё)) в противном случае
Вещественные значения линейно отображаются в диапазон {0,1,...,
Gmax}, так что в итоге получается изображение Е£^фат. Это изображение и
есть результат алгоритма стилизации Виннемёллера. Функция tanh
монотонно возрастает, когда аргумент изменяется от 0 до 1, а ее значения
принадлежат диапазону [0,1).
Параметр е определяет разделение по порогу. Благодаря функциям
tanh и ф изображение становится менее контрастным; увеличивая ф,
мы делаем его более резким.
Пример стилизации Виннемёллера приведен на рис. 5.2 справа
вверху. Еще один пример приведен на рис. 5.6 справа.
Значения Е%фа т обычно близки либо к 0 (черный цвет), либо к G
(белый цвет), и лишь небольшое количество пикселей имеет промежу
точные цвета. Следовательно, порог Г, приблизительно равный Gmax/2,
и применение формулы (3.48) порождают бинарное изображение
(которое визуально почти не отличается от стилизованных изображений
max
212 ♦ Глава 5. Сегментация изображений
на рис. 5.2 сверху или на рис. 5.6 справа), если это нужно для анализа
изображения или для визуализации.
Рис. 5.6. Слева: входное изображение MissionBay.
Справа: результат его бинаризации методом Виннемёллера
5.1.2. Сегментация путем выращивания семян
Для сегментации полутонового или цветного изображения мы
можем взять начальный пиксель (х, у, 1{х, у)) (семя) и рекурсивно добавлять
к нему соседние пиксели, удовлетворяющие «критерию похожести» на
пиксели, составляющие уже выращенный участок вокруг начального
пикселя. Этот процесс можно повторять, пока каждый пиксель
изображения не окажется в одном из сегментов.
Возникает важный вопрос: как сделать, чтобы этот процесс не
зависел от выбора начальных пикселей, т. е. чтобы результирующая
сегментация определялась данными изображения, а не тем, как выбрана
последовательность начальных пикселей?
Отношение эквивалентности на признаках пикселей. Для
изображения / мы уже имеем или можем вычислить вектор признаков и(р)
в позиции пикселя р. Например, для цветного изображения / мы уже
имеем вектор RGB. Для полутонового изображения мы можем
вычислить векторы градиента V/ в точке р и локальное среднее или
дисперсию в р для формирования вектора и(р). Один лишь уровень яркости
пикселя р образует одномерный вектор признаков.
Обозначим = отношение эквивалентности на множестве векторов
признаков и, которое разбивает все это множество на классы
эквивалентности.
Сегменты, определяемые отношением эквивалентности на
признаках. Две позиции пикселей р и q называются 1-эквивалентными,
если и(р) = u(q). Тем самым определено отношение эквивалентности
на носителе П, зависящее от изображения /. Классы /-эквивалентности
5.1. Простые примеры сегментации изображений ♦ 215
С Q П по этому отношению еще не являются сегментами /относительно
отношения =. Одинаковость признаков в точках pnq еще не означает,
что р и q принадлежат одному и тому же сегменту.
Врезка 5.3 (отношение эквивалентности и классы эквивалентности). Пусть
R - бинарное отношение, определенное на множестве 5. Способы записи aRb,
(a, b) E R и а е R(b) эквивалентны, все они означают, что элементы а 6 S и
b E S связаны отношением /?. Например, рассмотрим отношение 4-смежности
А4 на П; тогда запись р е A4(q) означает, что позиция пикселя р е П является
4-смежной с позицией пикселя q e П, и то же самое можно выразить, написав
pA4qw\v\{p,q)EA4.
Отношение R называется отношением эквивалентности на S, если оно
обладает следующими свойствами:
1) для любого а е 5 имеет место aRa (т. е. отношение R рефлексивно на 5);
2) для любых a,b е S,если aRb,то Ь/?а (т.е./? симметрично на 5);
3) для любых а, Ь, с £ S, если а/?Ь и Ь/?с,то а/?с (т. е. /? транзитивно на 5).
Например, >44 не является отношением эквивалентности на П; оно
симметрично, но не рефлексивно и не транзитивно: из того, что pA4q и qA$, не
следует, что рА^р. Отношение N4 = A4(p) и {р} также не является отношением
эквивалентности; имеют место рефлексивность pN^ и симметричность, но
транзитивность отсутствует.
Отношение С4 4-связности в бинарном изображении /, определенное
следующим образом: pC4q тогда и только тогда, когда существует путь р = р0, pv ...,
pn = gтакой, что р. 6 N4(p._J и 1{р) = /(р,..^ для / = 1,...,л является отношением
эквивалентности, оно обладает также свойством транзитивности.
Пусть R - отношение эквивалентности на S.Тогда для любого а е S множество
R(a) определяет класс эквивалентности на S. Если b e /?(а),то R(b) = /?(а).
Множество всех классов эквивалентности на S определяет разбиение S на
попарно непересекающиеся непустые множества.
Обозначим Си множество всех р е П таких, что 1(р) = и. Каждый
класс /-эквивалентности Си является объединением (скажем, 4-, 8- или
iC-связных) участков, и вот эти участки являются сегментами.
Наблюдение 5.1. Результат сегментации путем выращивания семян не
зависит от начальных пикселей при условии, что выращивание согласовано с
отношением эквивалентности, определенным отношением эквивалентности на
признаках изображения.
Пример 5.1 (пометка сегментов). Мы хотим пометить каждый из
получившихся сегментов (т. е. все пиксели, принадлежащие этому сегменту) одной и
той же уникальной меткой. В качестве меток можно выбрать, например, числа
214 ♦ Глава 5. Сегментация изображений
или (для визуализации) цвета. Чтобы не изменять входное изображение /, мы
запишем метки в массив такого же размера, что и /.
На рис. 5.7 слева показано бинарное изображение. В качестве
признаков мы берем значения пикселей 0 и 1, и совпадение значений
определяет отношение эквивалентности на множестве признаков {0, 1}.
Существует всего два класса /-эквивалентности.
В бинарном изображении Monastry не важно, используется ли 4-, 8-
или /С-смежность; в любом случае оба класса /-эквивалентности Сг и С0
разбиваются на одни и те же сегменты, помеченные разными цветами
или уровнями яркости соответственно (см. рис. 5.7 справа).
Рис. 5.7. Слева: архитектурный план Monastry монастыря Бебенхаузен
(Тюбинген, Германия). Сколько здесь черных и сколько белых сегментов?
Справа: черные сегменты помечены различными цветами,
а белые сегменты - уровнями яркости
Рекурсивная пометка сегментов. Мы опишем алгоритм
сопоставления общей метки всем пикселям одного сегмента. Пусть А -
выбранное отношение смежности пикселей.
Предположим, что мы находимся в позиции пикселя р, который еще
не помечен как член какого-то сегмента. Сделаем р следующим
начальным пикселем для инициализации нового сегмента.
5.1. Простые примеры сегментации изображений
215
Обозначим 1к метку, принадлежащую множеству возможных меток и
еще не использованную для пометки сегментов /. Рекурсивная
процедура пометка показана на рис. 5.8.
пометить р меткой /^
поместить р в стек;
while стек не пуст do
извлечь г из стека;
for тех q E А{г), для которых u{q) = u и q еще не помечен do
пометить q меткой 1к;
поместить q в стек;
end for
end while
Рис. 5.8. Рекурсивная процедура пометки, которая начинается
в начальном пикселе р с вектором признаков и = и(р) и назначает
пикселям входного изображения /еще не использованную ранее метку/
В этом рекурсивном алгоритме пометки может случиться так, что в
стеке окажется примерно половина всех пикселей изображения. Но,
конечно, такие случаи крайне маловероятны.
Пометив сегмент, содержащий р, мы можем продолжить поиск
непомеченных пикселей и поступать так до тех пор, пока не будут помечены
все пиксели.
Пример 5.2 (обход пикселей в глубину). Рассмотрим бинарные изображения
с ключом «белый < черный» для iC-смежности (т. е. для белых пикселей
предполагается 4-смежность, а для черных - 8-смежность). На рис. 5.9 слева показаны
первые посещенные пиксели в этом белом сегменте в количестве 21.
—
18
19
20
15
16
17
■
21
6
7
12
13
14
1
2
3 4 1
5 8
9|
101
|
■
4
t
Р
J
2
■ 1
4
t
\
2
Рис. 5.9. Слева: числа обозначают порядок, в котором помечались пиксели,
в предположении стандартного обхода сетки (слева направо, сверху вниз).
Справа: каким будет порядок, если стек в алгоритме заливки
на рис. 5.8 заменить FIFO-очередью?
Показанный на рисунке справа порядок используется для посещения
смежных пикселей, когда алгоритм применяется для пометки сегмента белых
216 ♦ Глава 5. Сегментация изображений
пикселей. При пометке сегмента черных пикселей был бы применен обход
8-смежных пикселей по или против часовой стрелки.
Пример 5.3 (зависимость от начальной точки в случае, когда отношение
эквивалентности не используется). Рассмотрим следующую процедуру
выращивания семян, определяемую параметром т > 0:
1) собираем в полутоновом или цветном изображении начальную точку
pseed, имеющую яркость B(pseed). Вначале текущий сегмент содержит толь-
2) в процессе выполнения итераций присоединяем к текущему сегменту
пиксель q, являющийся 8-смежным с каким-либо пикселем текущего
сегмента, при условии что он еще не помечен и его яркость B(q)
удовлетворяет неравенству \B(q) -B(pseed)\ < т;
3) останавливаемся, когда не осталось непомеченных пикселей q,
8-смежных с текущим сегментом, которые можно было бы к нему
присоединить.
Критерий присоединения в этой процедуре не основан на отношении
эквивалентности на множестве значений яркости. Поэтому построенные сегменты
зависят от выбора начального пикселя. Пример приведен на рис. 5.10.
в результате работы алгоритма выращивания семян, основанного на разности
яркостей т с начальным пикселем. Слева: выращивание участка, начиная
с показанной точки, при т = 15. Справа: снова т = 15, но начальная
точка выбрана по-другому- в ранее построенном сегменте
Чтобы объяснить этот эффект, рассмотрим изображение [0, 1, 2, 3, 4, 5, 6, 7]
размера 1х8 и предположим, что т = 2, pseed = 3, а В(Ъ) = 2. При таком выборе
начального пикселя получается участок [0, 1, 2, 3,4]. Пиксель р = 4 принадлежит
этому участку, его яркость Б(4) = 3, и если взять его в качестве начального, то
будет порожден участок [1,2, 3,4, 5].
5.1. Простые примеры сегментации изображений ♦ 217
Зависимость от выбора начального пикселя можно устранить, разбив
диапазон {0,..., Gmax} на интервалы V0 = {0,..., т}, VI = {т + 1,..., 2т},..., Vm = {тт + 1,...,
Gmax}. Теперь при выборе начального пикселя р яркость В(р) определяет
интервал Vk, для которого В(р) е Vk. И мы присоединяем к сегменту только те
пиксели q, для которых яркость B(q) принадлежит тому же интервалу Vk. Тем
самым определяется отношение эквивалентности на множестве значений
яркости. Получающаяся сегментация не зависит от выбора начального пикселя
сегмента.
Предложенную схему разбиения (на непересекающиеся интервалы)
диапазона значений признака можно обобщить и на многомерные векторы
признаков и.
Сегментация посредством кластеризации. Мы кратко упомянем
этот метод, альтернативный выращиванию семян и заключающийся
в том, что вначале выбирается несколько пикселей и все они
объединяются в кластеры параллельно (т. е. все начальные пиксели
рассматриваются одновременно) путем отнесения непомеченных пикселей к
«самому похожему» начальному. В ходе этого процесса выбранные
начальные пиксели можно заменять, делая новым начальным пикселем
центроид уже построенного к этому моменту сегмента. Обычно
результат таких методов зависит от выбора начальных пикселей. См. также
упражнение 5.9.
Врезка 5.4 (история алгоритма сдвига среднего). Анализ функций плотности
распределения методом сдвига среднего был описан в работе [К. Fukunaga and
L D. Hosteller. The estimation of the gradient of a density function, with applications
in pattern recognition. IEEE Trans. Information Theory, vol. 21, 1975, p. 32-40]. Было
показано, что алгоритм сдвига среднего сходится к локальному максимуму
функции плотности (что соответствует локальным максимумам
распределения значений в каналах изображения).
Процедуры, основанные на сдвиге среднего, приобрели популярность в
компьютерном зрении благодаря следующим двум работам: [У. Cheng. Mean shift,
mode seeking, and clustering. IEEE Trans. Pattern Analysis Machine Intelligence, vol. 17,
1995, p. 790-799] и [D. Comaniciu and R Meer. Mean shift: A robust approach toward
feature space analysis. IEEE Trans. Pattern Analysis Machine Intelligence, vol. 24, 2002,
p. 603-619]. После их появления было опубликовано много вариантов
алгоритма сдвига среднего как для компьютерного зрения,так и для анализа
данных вообще.
Реализация алгоритма сдвига среднего имеется в библиотеке OpenCV (метод
meanShift).
218
Глава 5. Сегментация изображений
5.2. Сегментация методом сдвига среднего
Сдвиг среднего - вариант итеративного метода наискорейшего
подъема, применяемого для поиска стационарных точек (пиков) функции
плотности распределения, который используется во многих вопросах
многомерного анализа данных, а не только в компьютерном зрении.
В этом разделе будут представлены варианты алгоритма сдвига
среднего для сегментации изображений. В данном случае под
«распределением» понимается распределение значений в изображении.
5.2.1. Примеры и подготовка
Для полутонового изображения с его скалярными значениями
пикселей пространство признаков одномерно. Чтобы лучше понять идеи
алгоритма сдвига среднего, предположим, что требуется
сегментировать л-канальное изображение, где п > 1. Например, для цветного
изображения имеется п = Ъ канала. А для скалярного изображения / можно
определить п = 2 градиентных канала
Т-(Р)>¥-(Р)\ • <5-6>
ох ду J
или п = 2 канала (среднее, стандартное отклонение) (см. рис. 5.11), или
п = 4 канала, если объединить градиентные каналы с каналами среднего
и стандартного отклонения. В общем случае мы можем добавлять
каналы, представляющие локальные свойства в позиции пикселя р.
Vl(p) = grad I(p) =
Рис. 5.11. Слева: Полутоновое изображение Odense, для которого Gmax = 255.
Справа: визуализация двумерного пространства признаков (в виде двумерной
гистограммы) изображения, определенного средним и стандартным отклонением
в окрестностях пикселей размера Зх3. Полоса справа - цветовой ключ
для показанных на рисунке частот
5.2. Сегментация методом сдвига среднего ♦ 219
Средние для «-мерных пространств признаков. Формула (3.39)
для вычисления среднего, или центроида, (xs, ys) множества S
обобщается на векторы признаков и = (ир ...,ип) следующим образом:
т,
Ui,S =
0,...,0,1,0,...,0
(S)
ДЛЯ/б{1,...,П},
(5.7)
^оо...о(£)
где моменты /Wo,...,o,i,o,...,o(^) О- в г_и позиции) и т00 0(S) (n нулей)
определены формулой (3.36), в которой в качестве весов используются не
значения изображения, а кратности векторов признаков.
Основные идеи алгоритма сдвига среднего. Пусть имеется
изображение /размера 5*5 (здесь не показано) с двумя каналами,
значения а и Ь которых принадлежат диапазону 0 < а, Ъ ^ 7. На рис. 5.12
показан пример распределения 25 пар признаков в пространстве аЪ (не
на плоскости изображения, а в двумерной гистограмме значений
пикселей). Числа 1,2 и 3 - это кратности встречающихся пар признаков.
f
|0 0
0 0
0 0
1/2
( 1
0\0
0 0
"о"
0
J^
0
ш
0
^г
0
0 0 0
0 11
1 1
1\3 1
о )о о
0/1 2
1 2
0 0 0
0 0
0 0
0 0
1 0
0 0
0 0
0 0
—^
а
0 0 0 0 0 0 0
00000000
?
loooooooo
0 0 0 110 0
/^ ^Ч 1
И1 О 4 3 11
у 1 г J
1 2
11 2
| 0 0 0 0 0 0 0
а
Рис. 5.12. Распределение 25 вычисленных локальных свойств изображения
и = (а, Ь) в пространстве признаков ob, начальная позиция окна {слева)
и два последующих перемещения в результате сдвига среднего {слева направо)
В качестве начального значения мы выбираем пару (2,4) с
кратностью 2 (т. е. в двух пикселях изображения 5x5 признак принимает
значение (2,4)).
Мы вычисляем среднее по множеству S радиуса г = 1.6 (к примеру)
с центром в точке (2, 4). Это новое среднее смещено немного влево и
вверх от предыдущего.
Мы сдвигаем круговое окно, определяющее текущее множество 5, так
чтобы его центр совпал с новым средним. Среднее us= (u1 s, u2S) по
этому новому множеству S снова немного сместилось вверх относительно
предыдущего.
Итерации прекращаются, если расстояние между текущим и
следующим средним оказывается меньше заранее заданного положительного
порога т (например, т = 0.1); среднее установится финальным средним.
220 ♦ Глава 5. Сегментация изображений
В результате все пиксели изображения с признаком (2,4) отнесены к
этому финальному среднему us.
Эта процедура повторяется для других начальных пар признаков.
Все они определяют какое-то финальное среднее. Финальные средние,
расположенные очень близко друг к другу, можно объединить в один
кластер. Пиксели, отнесенные к финальным средним, оказавшимся в
одном кластере, эквивалентны по значениям; этот класс
эквивалентности распадается на несколько участков (сегментов).
Сдвиг среднего как метод наискорейшего подъема. Будем
рассматривать кратности в пространстве признаков как высоты. Сдвиг
окна означает подъем в гору (следование за средним), и конечный
ориентир приблизительно совпадает с локальным пиком,
определяющим финальное среднее. Рисунок 5.12 слишком мал, чтобы отразить
это должным образом; на рис. 5.13 показана трехмерная визуализация
наискорейшего подъема.
Рис. 5.13. При сдвиге среднего мы поднимаемся вверх в направлении
наибольшего градиента. Здесь это перемещение показано на примере пяти
начальных точек - движение, начатое из каждой, стремится к одному и тому же
пику (вообще говоря, это локальный максимум, но в данном случае глобальный)
Метод зависит от двух параметров гит, определяющих
соответственно «область влияния» и критерий остановки.
Наблюдение 5.2. При последовательных операциях сдвига среднего окно
движется к локальному пику распределения векторов признаков, и тем самым
реализуется метод наискорейшего подъема в направлении наиболее быстрого
изменения локального градиента.
5.2. Сегментация методом сдвига среднего ♦ 221
Локальный пик и глобальная мода. Глобальной модой множества
данных называется значение, встречающееся чаще всего. Например,
мода множества {12,15,12,11,13,15,11,15} равна 15. У множества
может быть несколько мод. Так, множество {12, 15, 12, 11, 13, 10, 11, 14}
бимодальное, т. к. в нем есть две моды, 12 и 11. У множества {16,15, 12,
17,13,10,11,14} вообще нет мод, поскольку все значения встречаются с
одинаковой частотой. Для определения моды множество не
обязательно должно состоять из чисел, его элементами могут быть цвета, имена
и вообще все, что угодно.
Локальный пик (т. е. локальный максимум плотности), вообще
говоря, не является глобальной модой. Моды множества векторов
признаков определяют глобальные пики.
В некоторых публикациях локальные пики функций плотности
также называются «модами», но мы избегаем такой практики, чтобы не
возникало путаницы с более распространенным определением моды,
приведенным выше.
5.2.2. Модель сдвига среднего
В этом подразделе излагаются математические основы алгоритма
сдвига среднего. Если вас интересует только сам алгоритм, то можете
сразу перейти к разделу 5.2.3.
«-мерная ядерная функция и одномерный профиль. На рис. 5.12
иллюстрируется использование кругового окна для равномерного
включения всех векторов признаков, оказавшихся в этом окне, в
вычисление нового среднего. В этом случае вычисление среднего
производится по формуле (5.7).
Чтобы обобщить вычисление локального среднего, рассмотрим
симметричную относительно вращения п-мерную ядерную функцию
K(u) = cfe-/c(||u||22), (5.8)
определенную в точках и n-мерного пространства признаков.
Одномерный профиль к и константа ск подбираются так, что
JR„^(u)du = l. (5.9)
Константа ^обеспечивает нормировку интеграла на 1.
Ядро JC определяет веса по аналогии с локальными свертками
изображений (см. раздел 2.1.2). Но теперь ядро применяется в пространстве
признаков. На рис. 5.14 приведено четыре примера профилей к(а) для
аеШ. Функция Епанечникова определяется следующим образом:
222 ♦ Глава 5. Сегментация изображений
fc(a) = |(l-a2) для
-\<а< 1
(5.10)
и к(а) = 0 в остальных точках.
Врезка 5.5 (история функции Епанечникова). Эта функция впервые появилась
в работе [KAEpanecftn/'fov. Nonparametric estimation of a multidimensional probability
density. Theory Probab. Appl., vol. 14,1969, p. 153-158].
Рис. 5.14. Профили четырех различных ядерных функций:
треугольной, Епанечникова, равномерной и гауссовой
Оценки плотности. Пусть г > 0 - параметр, определяющий радиус
ядра (например, стандартное отклонение а в случае гауссовой
функции). Мы имеем т векторов признаков и., 1 < i < т, в Ш"; если задано
. . N .
cols rows
изображение 1,тот= Nc
1 т I \
/*(■>=—L* -<■-■<>
Для любого вектора uel" функция
/1 Л
тг
тг
,-=1 \г
)
S*
i=\
\r
u-u,
Л
(5.11)
(5.12)
определяет оценку плотности в точке и на основе ядерной функции К.
Вычисление градиента. Чтобы определить вектор сдвига среднего,
необходимо вычислить производную grad fk(u) функции fk(u). (См.
обсуждение изображений как непрерывных поверхностей и
интерпретации градиентов, например, в контексте рис. 1.13.)
Продифференцируем функцию
5.2. Сегментация методом сдвига среднего ♦ 225
М „ .,2Л
\г
u-u,
взяв производную
(5.13)
— (u-u.)
г
внутренней функции и умножив ее на производную
*'
<\ ■■ „2^
\Х
u-u;
(5.14)
(5.15)
внешней функции; к'- это производная профиля к.
Локальные пики в пространстве признаков находятся в тех точках и,
где
2с ^. . ./ 1 „ „2Л
0 = gradfk(u) = ^1^(u-ui)k'
wr
;=1
^г
u-u,
2с, -
wrw+2 /=1
5>-«/)*'(#Г)):
(5.16)
где для краткости мы обозначили
^(г)=4-
u-u,
(5.17)
Мы хотим преобразовать градиент (5.16), так чтобы выделить
вектор сдвига среднего при перемещении из любой точки и к следующему
среднему в направлении локального пика.
Сначала введем функцию g(a) = -k'(a). Знак минус позволяет
заменить (и - и.) на (и.- и). Из (5.16) получаем:
2с т
grad/4 (и) = —& X (»,-«)■ * (^)
тг
i=i
2с, »
/W
_ 2ск
п+2
г2с„
g L
= АВС
E[oi^(^r))]-»-S^(^)
1=1 1=1
i:,yg(^')
>о га
mr 77
и
(5.18)
224 ♦ Глава 5. Сегментация изображений
Множитель А в (5.18)2 - константа. Множитель В - оценка плотности
f в пространстве признаков для функции g, поскольку формула (5.12)
определяла оценку плотности fk для функции к. Константа с нормирует
интеграл в пространстве признаков на 1, если/ применяется в качестве
веса.
Вектор сдвига среднего как масштабированный вектор
градиента. Множитель С в формуле (5.18) - это вектор сдвига среднего,
который ведет из точки и в новое положение среднего в пространстве
признаков. Мы обозначаем его
ш,(а)=&-' ' М ' ;-и. (5.19)
В итоге имеем
или
ffTRdfk(u) = -^-fg(uymg(u) (5.20)
г cg
rng(u) = —^—-g^dfk(u). (5.21)
2v/*00
Таким образом, мы доказали наблюдение 5.2: сдвиг среднего
происходит в направлении градиента grad fk(u). Действуя таким образом, мы
приближаемся к вектору признаков и0, в котором grad /fc(u0) = 0, как и
утверждается в (5.16).
5.2.3. Алгоритмы и оптимизация по времени
Метод сдвига среднего дает неплохие результаты с точки зрения
качества сегментации, но объем вычислений при буквальной реализации
весьма велик. Мы проиллюстрируем его на простом примере, в
котором используется линейная алгебра (точнее, операции над матрицами).
В этом варианте нет никакой оптимизации времени работы, мы
приводим его только для объяснения общего алгоритма.
Пример 5.4 (сдвиг среднего с применением линейной алгебры). В качестве
входа будем использовать двумерное пространство признаков, показанное на
рис. 5.12. Оно представляет данные
См. графическую иллюстрацию этого уравнения на рис. 10.11 в книге [G. Bradski and A. Kaehler.
Learning OpenCV. O'Reilly, Beijing, 2008] (Брэдски Г., Келер А. Изучаем OpenCV. M.: ДМК Пресс,
2017). В ней сдвиг среднего обсуждается не как средство кластеризации в пространстве
признаков, а как средство прослеживания в области пикселей.
5.2. Сегментация методом сдвига среднего
225
[(5, 2), (6, 2), (3, 3), (3, 3), (4, 3),
(5,3), (1,4), (2,4), (2,4), (4,4),
(5,4), (5,4), (5,4), (6,4), (7,4),
(2, 5), (3, 5), (3, 5), (5,6), (6,6),
(6, 6), (3, 7), (4, 7), (6, 7), (6, 7)]
в предположении, что а и Ъ - целые числа, начинающиеся с 1. Представим эти
данные в матричной форме:
D =
563345 1224555672335663466
2233334444444445556667777
Процедура сдвига среднего начинается с выбора пары признаков в качестве
начального значения среднего. Возьмем одну из двух пар (3, 5), как показано
на рис. 5.12, и создадим матрицу средних М, в которой в каждом столбце
находится пара (3, 5):
М =
3333333333333333333333333
5555555555555555555555555
Вычислим квадраты евклидовых расстояний между столбцами матриц М
и D, возведя в квадрат значения разностей соответственных элементов D - М.
Получим матрицу (квадратов) евклидовых расстояний:
Е =
"4 9001441114449 16 100499019 9
9944441111111110001114444
Просуммировав значения в каждом столбце, получим
[13 18 4 4 5 8 5 2 2 2 5 5 5 10 17 1 0 0 5 10 10 4 5 13 13 ].
Теперь мы готовы применить ядерную функцию. Для простоты
предположим, что профиль равномерный с некоторым радиусом г > 0; простая
ступенчатая функция, определяющая равномерный профиль, показана на рис. 5.14.
Вычисленные суммы необходимо сравнить с г2. Для генерации рис. 5.12
было взято значение г = 1,6, поэтому г2 = 2,56. Шесть квадратов евклидовых
расстояний меньше 2,56. Это шесть точек в пространстве признаков, которые
находятся внутри окружности на левом рис. 5.12 и определяют активное
множество признаков
S = {(2,4), (2,4), (4,4), (2, 5), (3, 5), (3, 5)}
на этой итерации сдвига среднего.
Среднее по множеству 5 равно us = (2,67,4,5) (поскольку профиль
равномерный). Сравниваем (2,67,4,5) с предыдущим средним (3,5) и выясняем, что
расстояние все еще больше порога т = 0,1.
Продолжаем итерации - генерируем новую матрицу средних М, все столбцы
которой равны (2,67,4,5), снова вычисляем вектор квадратов евклидовых рас-
226 ♦ Глава 5. Сегментация изображений
стояний до этого среднего (с помощью матрицы Е), вычисляем текущее
множество S активных признаков, находящихся на расстоянии меньше г от точки
(2,67,4,5), и новое среднее по этому множеству. Сравниваем расстояние от
нового среднего до точки (2,67,4,5) с порогом т = ОД.
Процедура останавливается, когда расстояние между двумя
последовательными средними будет меньше т. В этот момент мы получили финальное
среднее, к которому относим начальный признак и = (3,5).
Обработав все точки в пространстве признаков, мы объединяем в
кластеры те точки, для которых финальные средние равны или «близки». Тем самым
определяются классы эквивалентности в пространстве признаков.
В рассмотренном примере мы взяли равномерный профиль, но
могли бы взять другие профили, показанные на рис. 5.14. При этом
изменился бы способ аппроксимации локальных средних (использовались
бы взвешенные суммы значений признаков).
Описанный только что алгоритм можно оптимизировать.
Использовать матрицу М для сравнения со всеми имеющимися признаками
и неэффективно. Организовать многократный поиск точек, близких к
текущему среднему, можно эффективнее, например с помощью
хеширования. Далее мы обсудим вопрос о временной сложности.
Разбиение пространства признаков на окна. Рассмотрим
алгоритм, который начинается с разбиения пространства признаков на
«небольшие» окна, по возможности равномерно. См. результат
сегментации на рис. 5.15 и пример простого двумерного пространства
признаков на рис. 5.16 слева.
о mi а х
Рис. 5.15. Слева: эскиз разбитого пространства признаков для изображения
Odense на рис. 5.11. Справа: результат сегментации этого изображения с
применением разбиения пространства признаков на окна размера 39*39;
всего получилось 33 метки
5.2. Сегментация методом сдвига среднего
227
1 1
□
||о 0 2
111 2
2 [Т] 2
6 6 3
||7 7 7
И 7 И 6
3 2 2
1 3 1
3 Щ 6
4 5 2
6 5 4
7 0 6
ц
1
1 2 1
7 0
5 6
6 4
4 0
1
1 1
О+О.
) 2
2
||2 1 2
6 Й 3
Р 0 7
f
||7 4 6
3
1 11
1*1 2
1 3 1
щ
| 1 2
3 ■ 6 7|
4 5 2 5 6
6 5 4 6 4 |
7
■ б
«■
1 1
Q 1 1
2 3 | 2
13 1
3 | 6
4 5 2
6 5 4
-■«
1 2
2 1 2
6 ■ 3
7 ■ 7
7 4 6
5 6
6 4
4В
2
1 2
2 1 2
6 ■ 3
7 ■ 7
7 4 6
0 0 0 0 0
1 1
3|2
13 1
3 ■ б
4 5 2
6 5 4
1
1 2
Й
5 6
6 4
4В
1 1
2
1 2
2 1 2
6 6 3
||7 7 7
Ь 4 6
1 1
3 2 2
13 1
3 1 6
4 5 2
6 5 4
7 5 6
1
1 2
7 7
5 6
6 4|
4 jl
Рис. 5.16. Центры девяти начальных окон, показанных слева, считаются
начальными средними. В результате последовательных операций сдвига среднего
они перемещаются в новые позиции. Перемещение прекратится, когда будут
достигнуты синие или красные клетки, являющиеся финальными средними.
Красная клетка соответствует единственному случаю, когда центры двух начальных
окон переместились в одно и то же финальное среднее,так что оба окна
объединились в один класс эквивалентности 2*6, показанный справа
Мы выполняем несколько раундов операции сдвига среднего для
каждого окна, пока окна не перестанут сдвигаться в новую позицию.
Средние округляются до ближайшего целого, поэтому центры окон
всегда совпадают с какой-то точкой в пространстве признаков. Векторы
исходных окон, центры которых сместились в одну и ту же позицию
финального среднего, мы относим к одному классу эквивалентности (т. е.
сегменту в пространстве признаков).
Пример 5.5 (попарно непересекающиеся квадратные окна в пространстве
признаков). Рассмотрим двумерное пространство признаков,
представленное массивом 8х8 на рис. 5.16 слева, в котором показаны кратности векторов
признаков. Применим равномерный профиль в квадратных (а не в круговых)
окнах.
После первого раунда сдвига средних этих девяти начальных окон мы
обнаруживаем, что четыре вообще не изменили положения, их центры выделены
синим цветом. Пять окон стали предметом рассмотрения на втором раунде.
Далее мы замечаем, что четыре из этих пяти больше не двигаются, так что у
нас появилось еще четыре синие клетки. На третьем раунде сдвига средних
осталось рассмотреть всего одно окно, его среднее переместилось в позицию,
которая уже была помечена синим цветом, так что эти два окна должны быть
объединены, что и показано на рисунке справа.
На рис. 5.17 мы разбиваем то же самое пространство признаков 8х8 на окна
размера 2*2. В правом верхнем окне все значения равны нулю, т. е. в нем нет
ни одного признака, поэтому дальше с ним делать нечего. Синие клетки снова
отмечают конец перемещения, а красные - объединение двух синих клеток. На
этот раз мы имеем ситуацию, когда с двумя уже объединенными окнами
объединяется еще и третье, их общий центр закрашен черным цветом. Кроме того,
мы замечаем, что желтая клетка уже рассматривалась, поэтому в этой точке
можно остановиться и просто воспользоваться уже инициализированным для
228
Глава 5. Сегментация изображений
нее путем вычисления. Это тот случай, когда открывается потенциальная
возможность сократить время сегментации больших изображений.
Гц
1гЩ
2 ll
II6 Й
7 7
\2Ш
1 Р
|2 3|
Щ
2 3|
7 6
ш
ы
|2 2|
зга
|1 б|
5 41
|s [б]
□
1
1Ш
17 7
I5 И
6 4J
^ гп
СЕМ
2 на 2
1 ■ 1 З4!
2 1 2 3 1 [б]
ГО-6 3|5 2
171 7 \Т\ 6 5 4
7 4 6 7 [i}-6
U
1
1 ■
7 Щ
5 б]
6 4
LM
Рис. 5.17. Опорные точки 16 начальных окон, показанных слева, алгоритм сдвига
среднего перемещает в новые позиции. Серый: окно не представляет интереса.
Синий: больше не двигается. Красный: объединена с синей клеткой. Черный:
объединена с красной клеткой.Желтый: самый интересный случай, когда мы
заходим в клетку, уже рассмотренную ранее
Ну и наконец, финальные средние (в нашем примере синие, красные или
черные клетки) можно объединить в кластеры, ориентируясь, например, на 4-
или 8-смежность. Кластеры определяют классы эквивалентности. См. рис. 5.18.
Г]
1 П
ищ
2 ll
6 Щ
7 7
fl
1 П
2 3
Щ
|2 3
7 6
km
id
]2 2|
|з[Т]
ll 6|
Is Щ
5 4|
5 [б]
□
1
1Й
7 7J
5 [б]
6 4|
ш
I 1 с
2 ■ 2 2
1 | 13
2 12 3 1
86 3 ■ 5 2 5 6
7 7 6 5 4 6 4
74675641
1 1
I1 2
2 1
6 6
2 3
1
2 3
3 4
I1 1\
2 2
3 1
1 6
5 2
7 7 7 6 5 4
7 4 6 7 5 6
1
I1 2 1
7 7
I5 6
6 4
|4 1\
1 1
I1 A
2 1
6 6
7 7
| 7 4
2 3
1
|2 3
3 4
7 6
6 7
I1 *1
2 2
3 l|
1 6
5 2
5 4
5 6
1
1 2|
7 7
5 6|
|б 4
|4 1\
1 1
1 1 21
|2 1
6 6
7 7
| 7 4
|2 3
1
2 3
3 4
10 01
1 1
2 2
3 1
1 6
5 2
7 6 5 4
6 7 5 6
^1
1 2
7 7
5 6
6 4
|4 1\
Рис. 5.18. Слева направо: исходное разбиение на окна 2х2 такое же, как
на рис. 5.17, позиции финальных средних с обозначенной 4- или 8-смежностью,
результирующие классы эквивалентности, определяемые объединенными окнами,
результирующие классы эквивалентности, если объединяются только 4-смежные
финальные средние, и результирующие классы эквивалентности, если при
объединении учитывается также 8-смежность
Алгоритм сдвига среднего при разбиении пространства
признаков на окна. Мы используем n-канальное представление заданного
изображения / и тем самым определяем п-мерное пространство
признаков для п> 1. Все \П\ признаков изображения вставляются в
равномерно дискретизированное пространство признаков, представленное
в виде сетки (по аналогии со счетчиками в пространстве
аккумуляторов для преобразования Хафа), при необходимости округляя значения.
В результате получается n-мерная гистограмма.
Мы объявляем активными начальные n-мерные окна в пространстве
признаков, если они содержат хотя бы один вектор признаков; тем
самым определяется разбиение этого пространства. В момент инициа-
5.2. Сегментация методом сдвига среднего ♦ 229
лизации класс эквивалентности такого окна состоит только из самого
окна. Затем начинается процедура сдвига средних.
На каждой итерации все активные окна перемещаются в позицию,
определяемую новым средним (округленным до позиции клетки в
пространстве признаков). Возможно три случая:
1) если новое вычисленное среднее совпадает с предыдущим, то
имеет место остановка: среднее является финальным. Это окно
удаляется из списка активных;
2) если на текущей итерации средние по двум окнам совпадают, то
имеет место объединение: классы эквивалентности обоих окон
объединяются, и второе окно удаляется из списка активных;
3) если среднее перемещается в точку пространства признаков, уже
занятую на предыдущей итерации средним другого окна, то
имеет место повторение: классы эквивалентности обоих окон
объединяются, и только что сдвинутое окно удаляется из списка
активных.
Итерации повторяются, пока список активных окон не опустеет.
Пример результата показан на рис. 5.19: трехмерные окна размера 91х91х91
привели к 10 различным средним (меткам).
Рис. 5.19. Слева: цветное изображение HowMany. Справа: результат сегментации
этого изображения с применением трехмерного пространства признаков RGB,
разбитого на окна 91х91><91 с помощью описанного выше алгоритма
без кластеризации финальных средних
Конечный результат можно подвергнуть постобработке, например
путем кластеризации 4- или 8-связных финальных средних и объединения
классов эквивалентности окон, отнесенных к этим средним. Алгоритм
можно упростить, объединив случаи 2 и 3; в обоих случаях новое среднее
оказывается в уже занятой позиции - с одинаковыми последствиями.
Временная сложность этого алгоритма уменьшается благодаря
«блочной структуре» классов эквивалентности в пространстве признаков и
250 ♦ Глава 5. Сегментация изображений
аппроксимацией допустимых перемещений: возможными позициями
средних считаются только узлы сетки.
Алгоритм сдвига среднего при рассмотрении отдельных
векторов в пространстве признаков. Теперь будем рассматривать сдвиги
отдельных векторов в пространстве признаков, но по-прежнему будем
считать, что вектор и вычисленное среднее может располагаться только
в узлах регулярной сетки.
Для этого выберем какую-нибудь ядерную функцию радиуса г > 0;
в силу дискретной аппроксимации пространства признаков г должно
быть больше 1, и чем больше значение г, тем дальше может
перемещаться среднее, но при этом возрастает временная сложность.
Мы объявляем все ненулевые векторы в пространстве признаков
активными средними; начальный класс эквивалентности каждого вектора
содержит только его собственную начальную позицию. Далее
начинается итеративная процедура сдвига средних.
На каждой итерации мы перемещаем каждое активное среднее и в
позицию нового среднего, используя кратности векторов признаков в
окрестности и, взвешенные с помощью выбранной ядерной функции.
Эта операция соответствует сдвигу среднего в формуле (5.19).
Полученное значение округляется до ближайшего узла сетки в пространстве
признаков. Возможно два случая:
1) вновь вычисленное среднее совпадает с предыдущим. Имеет
место остановка. Это среднее является финальным, оно удаляется из
списка активных средних;
2) вновь вычисленное среднее совпадает с одним из вычисленных
ранее. Имеет место объединение (см. упражнение 5.7). Классы
эквивалентности обоих средних объединяются, вновь вычисленное
среднее удаляется из списка активных средних.
Итерации прекращаются, когда список активных средних
становится пустым. Полученный результат, как и раньше, можно подвергнуть
постобработке, объединив финальные средние в кластеры. Результаты
показаны на рис. 5.20.
5.3. Сегментация изображений как задача
оптимизации
В этом разделе мы опишем сегментацию как частный случай задачи
пометки и решим ее методом распространения доверия. Задача
пометки описывается членами ошибки (штрафами за расхождение данных
5.5. Сегментация изображений как задача оптимизации
231
и негладкость), и мы в общих чертах объясним, как можно подойти к
решению этой задачи оптимизации.
Рис. 5.20. Слева: результат сегментации (26 меток) изображения HowMany
на рис. 5.19 с применением трехмерного пространства признаков RGB, алгоритма
сдвига среднего для отдельных векторов признаков и гауссова ядра радиуса г= 25.
Справа: все то же самое, но с объединением финальных средних, находящихся
на расстоянии ^ 50 друг от друга. Количество меток сократилось с 26 до 18
5.3.1. Метки, пометка и минимизация энергии
В процессе подготовки к применению алгоритма Хорна-Шанка в
разделе 4.2.1 (см. (4.9) и следующий далее текст) мы использовали функции
пометки для сопоставления векторов оптического потока (и, v) (т. е.
меток) позициям пикселей (х, у). Нахождение попарно непересекающихся
сегментов, т. е. сегментация всего множества пикселей П, также
является задачей пометки. На рис. 5.2 приведено два примера.
Четырех меток достаточно. Когда мы преобразуем заданное
изображение в бинарное, мы сопоставляем каждому пикселю метку
«белый» или «черный». Для определения участков изображения можно
воспользоваться 4-, 8- или К-связностью (см. раздел 3.1); участки
созданного бинарного изображения и есть сегменты.
Врезка 5.6 (теорема о четырех красках). Примерно в середине XIX века была
выдвинута гипотеза о том, что любое разбиение плоскости на связные
области, называемое картой, можно раскрасить четырьмя разными цветами,так что
любые две области с общим участком границы (т. е. имеющие более одной
общей точки) будут раскрашены в разные цвета. В 1976 г. эта гипотеза,
получившая название «теорема о четырех красках», была доказана
математиком из США К.Аппелем (1932-2013) и уроженцем Германии В.Хакеном (род.
в 1928 г.).
252 ♦ Глава 5. Сегментация изображений
Преобразуя заданное изображение в карту цветов, мы сопоставляем
каждому пикселю его цвет в качестве метки. И снова 4-, 8- или iC-связные
участки созданной карты цветов определяют сегменты. Согласно
теореме о четырех красках, для визуализации любой сегментации
изображения достаточно всего четырех цветов.
Общий подход к пометке. Пометка - часто применяемый способ
моделирования различных задач компьютерного зрения (например,
оптический поток в главе 4, сегментация изображений в этой главе,
интегрирование векторных полей в разделе 7.4.3 и сопоставление
стереоизображений в главе 8). Множество меток может быть дискретным:
L = {/1,Z2,...,U» r*e lLl = m> (5-22)
или непрерывным:
LcM" для п>1. (5.23)
Сегментация изображений или сопоставление стереоизображений -
примеры дискретных множеств меток, при вычислении оптического
потока используются метки из множества L с I2, а в процессе
интегрирования векторного поля - из множества Lcl.
В этом разделе мы будем предполагать, что множество меток
дискретно и его мощность равна т = \Ь\. Кроме того, мы будем пользоваться
нотацией
h=fp=f(p) или l=fq=f(q). (5.24)
Метки назначаются местам (site), а местами в этой книге могут
быть только позиции пикселей. В заданном изображении имеется
\П\ = Ncols • Nrows мест, это много, поэтому так важна эффективность
вычисления функции пометки
f:H^L, (5.25)
или, в других обозначениях,
/={(р,й):р€ДлДр) = й}. (5.26)
Наша цель - вычислить такую функцию пометки /", которая
минимизирует (полную) ошибку, или энергию
~ (5.27)
реО.
^data \Р<> Jр)~*~ 2ша smooth \Jр > Jq )
qeA(p)
где А - отношение смежности между пикселями (см. раздел 3.1):
q E А(р)у если позиции пикселей q и р смежные. (5.28)
5.5. Сегментация изображений как задача оптимизации ♦ 255
Если явно не оговорено противное, то мы будем использовать
4-смежность, определение см. в (3.1). Функция ошибки Edata назначает
неотрицательный штраф позиции пикселя р, когда сопоставляет ей метку/" £ L.
Функция ошибки Esmooth назначает неотрицательный штраф, сравнивая
метки / и f, сопоставленные смежным позициям пикселей р и q.
Уравнение (5.27) описывает модель для задачи оптимизации,
характеризуемой локальными взаимодействиями вдоль границ между
соседними пикселями. Это пример модели марковского случайного поля
(МСП). В этом разделе мы применим метод распространения доверия
для приближенного решения этой задачи.
Врезка 5.7 (Марков, Байес, Гиббс и случайные поля). Русский математик
А. А. Марков (1856-1922) изучал случайные процессы, в которых
взаимодействие нескольких случайных величин может быть смоделировано
неориентированным графом. Сейчас такие модели называют марковскими
случайными полями. Если граф модели ориентированный и ациклический,
то мы имеем байесовскую сеть, названную в честь английского математика
Т. Байеса (1701-1761). Если допустимы только строго положительные
случайные величины, то МСП называется гиббсовским случайным полем в честь
американского ученого Дж.У. Гиббса (1839-1903).
Функция Edata - это член данных, а функция Esmooth - член гладкости,
непрерывности, или соседства полной энергии Е.
Говоря неформально, Edata(p, f) = 0 означает, что метка f «идеальна»
для позиции пикселя р. Функция Esmoo[h определяет решение, в
котором предпочтение априорно отдается одинаковым меткам в смежных
пикселях. Это критически важный аспект проектирования: сегменты
разделены краями (где метки просто необходимо изменить), и мы не
можем штрафовать такие изменения слишком сильно, если хотим
сохранить их возможность.
Чтобы решить задачу пометки, мы должны сопоставить каждому
месту в П метку из множества L. Если множество меток дискретно и \Ь\ = т,
то всего имеется т1а{ возможных функций пометки. Руководствуясь
теоремой о четырех красках, мы можем сократить их количество до 4|П|. Но
и это число очень велико.
Выбрать пометку, которая доставляла бы (точный) минимум
функции ошибки (5.27), - трудная задача. В качестве компромисса мы
можем задаться целью получить приблизительно минимальное решение.
Экстремальный выбор члена данных или гладкости дает тривиальные
оптимальные решения уравнения (5.27). Например, если штраф за не-
254 ♦ Глава 5. Сегментация изображений
гладкость очень велик, то оптимальной будет постоянная функция
пометки. С другой стороны, если взять член гладкости близким к нулю, то
в результате получится член данных, определенный отдельно в каждом
пикселе, и этот случай оптимизировать тоже несложно. Если член
данных или гладкости доминирует, то задача оптимизации упрощается.
Наблюдение 5.3. Вычислительная сложность нахождения оптимального
решения уравнения МСП (5.27) зависит от выбранных членов функции ошибки.
5.3.2. Примеры членов данных и гладкости
В контексте вычисления оптического потока мы рассматривали
примеры членов данных (4.9) и (4.58) и членов гладкости (4.10) и (4.59).
Примеры членов данных. Сначала определимся с количеством т > 2
меток для пометки различных сегментов. Сегментов может быть и
больше т, потому что одну и ту же метку /. можно использовать для пометки
нескольких сегментов, не имеющих общей границы. Сегменты,
помечаемые одной и той же меткой, можно определить с помощью некоторого
отношения похожести данных, например сходимости алгоритма сдвига
средних к одному и тому же пику в пространстве признаков.
Пример 5.6 (член данных, основанный на случайных начальных пикселях).
Мы случайным образом выбираем т пикселей заданного скалярного
изображения/и вычисляем среднее и стандартное отклонение в их окрестностях
размера 5Х5 (к примеру). В результате получаются трехмерные векторы
признаков и. = [/(*., у), ц., ст.] для 1 < / < т. Эти пиксели рассматриваются как начальные
значения в т классах признаков, которые должны быть помечены т метками
от /, до / .
1 " т
Рассмотрим функцию f =1в позиции пикселя р. Определим
EjataiPJi) = \\и>-ир\\2 = ХК* -Up,k)\ (5.29)
если используется норма L2,
п
EdataiP^) = \^i-^P\=^\UUk-UpX (5-30)
к=\
если используется норма Lx (менее чувствительная к выбросам, чем L2), или
\2
E<hlAP,li) = x4»i,»r) = i(U'J' "М> , (5.31)
к=\ UUk + Up,k
если используется критерий х2 (в общем случае еще менее чувствительный к
выбросам; х2 не является метрикой, т. к. не удовлетворяет неравенству тре-
5.5. Сегментация изображений как задача оптимизации ♦ 255
угольника). Здесь и - вектор признаков, определяемый средним и
стандартным отклонением в окрестности пикселя р размера 5х5.
Начальные значения можно сначала проверить на дисперсию, несколько раз
произведя случайную выборку, а затем остановиться на том множестве, для
которого дисперсия максимальна. Размер окрестности и состав признаков также
можно варьировать.
Пример 5.7 (член данных, основанный на пиках в пространстве признаков).
Пространство признаков изображения представляет собой п-мерную
гистограмму, определенную значениями п-мерных признаков и во всех пикселях,
принадлежащих П. Уровни яркости определяют только обычную одномерную
гистограмму, обсуждавшуюся в разделе 1.1.2. Двумерные признаки (например,
локальные среднее и стандартное отклонение) определяют двумерные
гистограммы типа той, что показана на рис. 5.12.
Мы выбираем т локальных пиков в пространстве признаков. Чтобы найти
их, мы можем начать с т случайных векторов признаков и применить к ним
алгоритм сдвига среднего, тогда будет найдено < т пиков и. в пространстве
признаков, каждому из которых сопоставляется метка /.. Затем член данных
Edata определяется, как в примере 5.6.
Подход к выбору начальных значений, предложенный в примере 5.7,
дает более осмысленную сегментацию, чем в примере 5.6, но занимает
больше времени. Можно даже сначала выполнить сегментацию
методом сдвига среднего целиком, а затем использовать те т из найденных
пиков, к которым отнесено больше пикселей, чем к остальным. См.
упражнение 5.8.
Примеры членов гладкости. Будем рассматривать член гладкости,
определяемый симметричной функцией с одним аргументом:
smooth^ ' smooth^ ' smooth^ '', \ ' /
где /, h G L - метки. Члены гладкости с двумя аргументами Esmooth(l, h) -
более общий случай, а включение зависимостей от позиции пикселя
Esmooth(P> <?; h h) - еще более общий.
Врезка 5.8 (истории модели Поттса). Эта модель была предложена
австралийским математиком Р. Б. Поттсом (1925-2005) в докторской диссертации
1951 г., посвященной изучению моделей Изинга.
Пример 5.8 (модель Поттса). В этой модели отсутствие непрерывности между
метками штрафуется равномерно, в расчет принимается только равенство или
неравенство меток:
256 ♦ Глава 5. Сегментация изображений
Го если а = О
[с в противном случае
где с > 0 - константа. Эта простая модель особенно хороша, если векторы
признаков действительно имеют небольшую дисперсию внутри участков
изображения, а значительные разрывы встречаются только на краях участков.
Пример 5.9 (линейная функция стоимости). Линейная функция стоимости
определяется следующим образом:
*—О - Ъ = ^00» = Ь -1/ - Л| = Ь -14, (5.34)
где Ъ > О определяет скорость возрастания стоимости.
В случае усеченной линейной функции задается еще константа усечения
с>0и
Esmooth(l ~ k) = Esmoot№ = ™п{Ь ' l/ " К С) = т1П(Ь ' М, <} (5.35)
(т. е. стоимость перестает возрастать, если разность оказывается больше с). Оба
случая - линейный и усеченный линейный - показаны на рис. 5.21.
Рис. 5.21. Слева: линейная функция стоимости.
Справа: усеченная линейная функция стоимости
В общем случае усечение представляет баланс между корректным переходом
к другой метке (путем усечения штрафующей функции) и шумом или
незначительными вариациями, недостаточными для изменения метки (в линейной
части графика). Изредка встречающиеся различия в метках, не превышающие
константы усечения с, считаются шумом и штрафуются (тем больше, чем
больше разность меток).
Пример 5.10 (квадратичная функция стоимости). Возможна квадратичная
(без ограничений, формула опущена) или усеченная квадратичная функция
стоимости
*,*»«*(' - Л) - Esmooth(a) = mm{b • (/ - h)\ с] = mm{b • а\ с). (5.36)
Положительные вещественные константы Ъ и с определяют коэффициент
наклона и усечение соответственно.
Наблюдение 5.4. Члены данных специально проектируются под задачу,
например вычисление оптического потока или сегментация изображения, тогда как
члены гладкости (обычно) имеют общий характер.
5.3. Сегментация изображений как задача оптимизации ♦ 257
5.3.3. Передача сообщений
Алгоритм распространения доверия (РД) передает сообщения
(доверие) в локальной окрестности, определяемой неориентированным
графом соответствующего МСП. Мы предполагаем отношение 4-смеж-
ности на сетке изображения. Обновления в результате передачи
сообщения производятся итеративно (возможно, вы уже знакомы с такой
стратегией передачи сообщений по теории клеточных автоматов);
сообщения передаются параллельно от помеченного пикселя к четырем
4-смежным с ним пикселям. См. рис. 5.22.
Рис. 5.22. Центральный пиксель получает сообщения от смежных пикселей,
например р, и этот процесс одинаков для всех пикселей изображения.
На следующей итерации центральный пиксель g получает от смежных пикселей
сообщения, включающие все сообщения, которые пиксели (в частности, р)
получили на предыдущей итерации
Неформальное описание. Тонкие черные стрелки на рис. 5.22
обозначают направления передачи сообщений. Например (слева),
пиксель р находится слева от пикселя q, и пиксель р посылает сообщение
пикселю q на первой итерации. Сообщение от пикселя р уже содержит
сообщения, полученные от его соседей (справа), на всех последующих
итерациях. В пикселе q передача сообщений производится
одновременно всем четырем 4-смежным пикселям. На одной итерации
каждый помеченный пиксель графа смежности вычисляет свое сообщение,
основываясь на информации, которой он располагал в конце
предыдущей итерации, и посылает это новое сообщение всем смежным с ним
пикселям одновременно.
Неформально говоря, чем больше штраф Edata(p, l), тем «труднее»
уменьшить стоимость метки / в пикселе р с помощью сообщений,
посланных смежными пикселями. «Влияние» смежных пикселей убывает
при возрастании стоимости конкретной метки в данном пикселе.
Формальное описание. Каждое сообщение - это функция, которая
отображает упорядоченное дискретное множество меток L в
одномерный массив длины т = \Ь\ неотрицательных вещественных чисел,
называемых значениями сообщения.
258 ♦ Глава 5. Сегментация изображений
Обозначим т1 ^ такое сообщение, т. е. массив длины т, содержащий
значения для меток / 6 L, который посылается из узла р в смежный
узел q на итерации t. Для / е L введем в рассмотрение уравнение
обновления сообщения
( \
и«о=™
Я*.(Р.Л)+ *„«.(*-/)+ I <ХЩ (5.37)
s<=A(p)\q J
где / обозначает одну из возможных меток в q, a h пробегает L и
представляет возможные метки в р.
Мы собираем в q все сообщения от смежных пикселей р и
комбинируем их со стоимостью данных для метки / в q. Тем самым в пикселе q
определен одномерный массив стоимостей
E^(qJ)+ I m'p^(.l), (S.38)
peA(q)
ассоциированных с назначением метки / пикселю q в момент t. В
стоимость входит независимый от времени член данных Edata(q, l) и сумма
всех \А\ полученных значений сообщений для / 6 L в момент t.
Неформальная интерпретация. Понимание формул (5.37) и (5.38) -
ключ к пониманию алгоритма распространения доверия. Мы дадим их
неформальную интерпретацию.
Мы находимся в узле q. Узел q запрашивает у смежных узлов,
например, р, их мнение об уместности выбора метки / в q. В ответ на такой
запрос узел р просматривает все метки h и сообщает q наименьшую
возможную стоимость в случае, если q решит выбрать /.
Член гладкости определяет штраф в случае, когда q выбирает /, а р
выбирает h. С меткой h ассоциирована также стоимость Edata(p, h) в узле р.
Наконец, р располагает информацией, полученной в момент t - 1 от
всех смежных с ним узлов, кроме q, поскольку q не может повлиять на
мнение р о метке /.
Таким же образом узел q собирает в момент t мнения обо всех
возможных метках /. Для каждой метки / он опрашивает все смежные узлы.
В выражении (5.38) мы суммируем мнение всех смежных узлов об
уместности выбора метки / в узле q. В этот момент мы также должны
принять во внимание стоимость данных, ассоциированную с выбором
/ в q. Стоимость гладкости уже была учтена в сообщениях,
передаваемых от р к q.
Доски сообщений. Вместо передачи одномерных массивов длины
т = \Ц удобнее использовать т досок сообщений размера Ncols*Nrows, по
5.5. Сегментация изображений как задача оптимизации ♦ 259
одной доске для каждой метки (см. рис. 5.23). Обновление сообщений
в этих досках производится так же, как было описано выше и показано
на рис. 5.22. Одномерные векторы длины т во всех позициях пикселей
просто рассматриваются как стек т скалярных массивов, по одному для
каждой метки / б L.
/,/2/3/4 • • • 1т Изображение
Рис. 5.23. т досок сообщений, по одной для каждой метки, и пиксель входного
изображения. Стоимость с. находится в /*-й доске сообщений для метки /.;
метка /в конечном итоге определяет значение, вычисленное
в данном пикселе, равное минимуму значений с. по всем с(. для 1$ i $ т
5.3.4. Алгоритм распространения доверия
Мы опишем общий алгоритм распространения доверия в случае,
когда множество пикселей П и есть множество мест (или узлов),
подлежащих пометке. Итеративный процесс состоит из следующих частей:
инициализация, процедура обновления (при переходе от (t - 1)-й итерации
к t-й) и критерий остановки.
Инициализация. Мы инициализируем все т досок сообщений во
всех \П\ позициях, отправляя начальные сообщения
ml^(l) = mm{Edaa(p,h) + E_oolh(h-l)), (5.39)
что дает начальные стоимости
E*.(q,D+ I Кч(0 (5-4°)
peA(q)
в пикселе q £ П на доске сообщений /.
240 ♦ Глава 5. Сегментация изображений
Итерации алгоритма РД. На итерации t > 1 по формуле (5.37)
вычисляются сообщения т1 ^ (/), которые затем объединяются, чтобы
обновить стоимость во всех пикселях q е П и для любой из т досок
сообщений / по формуле (5.38).
Прежде чем обсуждать эти итерации, перепишем уравнение
обновления сообщений (5.37) следующим образом:
^Uq(0 = rmn{Esmooth(h-l) + HpJh)}, (5.41)
где
Hp,q{h) = Edata(p,h)+ X KUQ- <5-42)
seA(p)\{q}
Прямолинейное вычисление Н (для всех h £ L) занимает время 0(т2)
в предположении, что вычисление Edata(p, h) занимает постоянное
время.
Если использовать модель Поттса для члена гладкости, то уравнение
(5.41) упрощается:
<-(/)=чй1{я«^адя«(*>+с}- (5-43)
Мы вычисляем минимум по всем h и сравниваем его с Я (/).
Если использовать неусеченную линейную модель для члена
гладкости, то уравнение (5.41) принимает вид
<^0 = ™?{b-\h-l\ + Hp,q(h)), (5.44)
где Ъ - параметр, определяющий линейную стоимость. Рассмотрим
пример.
Пример 5.11 (неусеченная линейная модель члена гладкости). Пусть
L = {0,1,2,3},Ь = 1,и
ЯР,Я = 2>5> HJV = 1>
HJ2) = l,5, Ям(3) = 0
для заданной комбинации смежных пикселей р и q. Эти данные
показаны на рис. 5.24 для неусеченного линейного случая. Значение Н (/)
определяет вертикальный сдвиг линейной функции стоимости (уголка)
в метке /.
5.5. Сегментация изображений как задача оптимизации ♦ 241
Рис. 5.24. Пример четырех кусочно-линейных функций.
Минимумы берутся в красных точках. На зеленых линиях нет минимумов.
Синие линии образуют нижнюю огибающую
Выполним вычисления по формуле (5.44):
/и^(0) = min{0 + 2.5,1 + 1,2 + 1.5, 3 + 0}
= min{2.5,2,3.5,3} = 2;
m^(l) = min{l + 2.5,0+1,1 + 1.5,2 + 0}
= min{3.5,1,2.5,2} = 1;
/n^(2) = min{2 + 2.5,1 + 1,0+ 1.5,1 + 0}
= min{4.5,2,1.5,1}=1;
m^(3) = min{3 + 2.5,2 + 1,1 + 1.5,0 + 0}
= min{5.5, 3,2.5,0} = 0.
Вычисленные минимумы показаны на рис. 5.24 красными точками.
Заметим, что на зеленых линиях нет ни одного минимума. Все
минимумы расположены на нижней огибающей, нарисованной синим
цветом.
Задачу минимизации (5.44) (в неусеченном линейном случае)
можно сформулировать следующим образом: вычислить нижнюю
огибающую т раскрывающихся вверх уголков с одинаковым коэффициентом
наклона, определяемым параметром Ъ. Вершины уголков расположены
в точках (Л, Hpq{h)). См. рис. 5.25. Тогда минимум для метки h просто
лежит на нижней огибающей, что и показано красными точками.
В усеченной линейной модели схема аналогична. Обновления
сообщений можно вычислить за время 0(т); вычисление нижней
огибающей семейства парабол мы обсуждали в разделе 3.2.4 в контексте
общего дистанционного преобразования на евклидовой плоскости.
242 ♦ Глава 5. Сегментация изображений
npqih) 4
V
О 1 2 3 ... тЛ
Рис. 5.25. Общий случай: т меток, одним из которых соответствуют
минимумы (черные линии), а другим - нет (зеленые линии)
Если использовать для члена гладкости квадратичную модель, то
уравнение (5.41) принимает вид
т'р^(1) = гтп(Ь(И-1)2+Нрд(к)).
(5.45)
И в этот раз минимумы располагаются на нижней огибающей парабол,
определенных квадратичными штрафными функциями (см. рис. 5.26).
Hpq(h)
т-\
Рис. 5.26. Нижняя огибающая семейства парабол
Вершины парабол находятся в точках (h, H (/?)), и это в точности
соответствует входным данным для евклидова дистанционного
преобразования (EDT); вычисление нижних огибающих является частью
алгоритма EDT. Для их вычисления необходимо время 0(т), см. раздел 3.2.4.
Прекращение итераций и результаты алгоритма. Критерий
остановки говорит алгоритму РД, что необходимо остановиться после
заранее заданного количества итераций. Другие варианты, например
дождаться, когда среднее значение всех изменений на всех досках со-
5.3. Сегментация изображений как задача оптимизации ♦ 245
общений при переходе от итерации t - 1 к итерации t станет меньше
заранее заданного порога т, на практике не слишком полезны, поскольку
не гарантируют сходимости.
В момент остановки t0 в каждой позиции пикселя р имеется т
значений стоимости (с{°,..., с'°) в точке р на т досках сообщений, где с? -
стоимость для метки /гдля 1 < i < т. Возвращаемое алгоритмом значение
в позиции р равно /* = /., где
j = arg min cj° (5.46)
\<i<m
в предположении, что минимум единственный. Если для нескольких
меток минимальная стоимость одинакова, то мы принимаем решение
с учетом метки в пикселе, 4-смежном с р.
Как улучшить временную сложность? Первый способ - так
называемый метод красного и черного. Множество позиций пикселей П
разбивается на черные и красные. На t-й итерации посылаются только
сообщения от черных пикселей смежным с ними красным; исходя из
полученных сообщений, на (t + 1)-й итерации красные пиксели
посылают сообщения черным. На рис. 5.27 показано одно из возможных
разбиений П.
Рис. 5.27. Шахматное разбиение П на красные и черные позиции пикселей
Второй способ ускорить работу - воспользоваться измельчаемым
(coarse-to-fine), или пирамидальным, алгоритмом РД. Измельчаемый РД
не только позволяет сократить время вычислений, но и дает более
надежные результаты.
Обратимся к регулярной пирамиде изображений, описанной в
разделе 2.2.2. Пиксели, принадлежащие окну 2x2 на одном уровне пирамиды,
являются смежными с одним пикселем на следующем уровне (тем,
который порождается на основе этого окна). Таким образом, отношение
смежности А, используемое в алгоритме РД, распространяется на всю
244 ♦ Глава 5. Сегментация изображений
пирамиду. Мы ограничим количество уровней пирамиды (скажем,
пятью).
При использовании такого отношения смежности в пирамиде
расстояния между пикселями нижнего уровня уменьшаются, что ускоряет
распространение сообщений.
Врезка 5.9 (Якоби и метод релаксации Гаусса-Зейделя). Рассмотрим систему
N линейных уравнений Ах = Ь, в которой все диагональные элементы А
отличны от нуля. Без ограничения общности можно считать, что каждое уравнение
нормировано, так что соответствующий ему диагональный элемент равен 1.
Представим А в виде А = I - L - U, где квадратные матрицы L и U состоят из
элементов А, расположенных соответственно ниже и выше главной диагонали
и взятых со знаком минус. Тогда систему N уравнений можно записать в виде
х = (L + U)x + b.
К. Г. Я. Якоби (1804-1851) предложил итеративный метод решения этих
линейных уравнений относительно х, идея которого заключается в следующем:
берем произвольную начальную оценку х0 и вычисляем последовательность
векторов
*** = (L + "К + Ь.
При определенных условиях последовательность векторов х^ сходится к
решению х при любой начальной оценке х0. Например, если Sw \a.\ < 1 для всех
/ = 1,..., А/, то метод Якоби сходится. Для применения метода Якоби
необходимо выделить память для хранения двух последовательных приближений к
решению.
В 1823 г.Гаусс (см. врезку 2.4) в частном письме к своему ученику К. Л. Герлин-
гу (1788-1864) описал модификацию метода Якоби, а доказательство было
опубликовано в 1874 г. П. Л. Фон Зейделем (1821-1896). В методе Гаусса-
Зейделя требуется хранить только один вектор х - всякий раз как элемент
обновляется, новое значение замещает предыдущее. Этот алгоритм можно
представить в виде
х = Lx + Ux + b
В первой строке L находятся только нули, поэтому можно вычислить первый
элементхк+1,а за ним последовательно элементы 2, 3,..., А/.
Теперь рассмотрим матрицы А с ненулевыми элементами такие, что х можно
разбить на красный и черный подвекторы,так что каждый красный элемент
соединен (посредством А) только с черными элементами, а каждый черный
элемент - только с красными (как на рис. 5.27). В работе ([D. W. Young, Iterative
methods for solving partial difference equations of elliptic type. Trans. American Math.
Society, vol. 76,1954, p. 92-111] доказано, что для таких матриц А метод Гаус-
са-Зейделя сходится тогда и только тогда, когда сходится метод Якоби, и его
асимптотическая скорость сходимости в два раза выше, чем у метода Якоби.
5.5. Сегментация изображений как задача оптимизации ♦ 245
Что необходимо задать в алгоритме РД? Мы должны выбрать член
гладкости, например, из трех вариантов: модель Поттса, усеченная
линейная или усеченная квадратичная) - и задать несколько параметров.
Необходимо задать отношение смежности; чаще всего используется
4-смежность или ее распространение на пирамиду.
Наконец, конкретное приложение (вычисление оптического потока,
сегментация изображений и т. п.) диктует выбор члена данных.
Задав все параметры, мы можем начать итерации, решив
предварительно, по какому условию останавливать работу.
5.3.5. Распространение доверия в задаче о сегментации
изображений
В примерах 5.6 и 5.7 мы предложили два вида членов данных. В
обоих случаях выбирались начальные векторы признаков и. для т меток
сегментов и затем вычислялись как минимум т связных участков
(сегментов); на самом деле каждой метке может соответствовать несколько
участков. Существует много других способов инициализировать
векторы признаков и.
На рис. 5.28 показано применение пирамидального метода РД (пять
уровней пирамиды, самый нижний имеет разрешение 1296х866) без
обновления начальных значений в процессе работы алгоритма.
Если начальные векторы и., выбранные, например, как в примерах 5.6
и 5.7, не изменяются в ходе итеративного процесса, то гибкость этого
подхода оказывается ограниченной.
Наблюдение 5.5. Полезно обновлять начальные значения и\ на каждой
итерации алгоритма РД.
Чтобы выполнить обновление, мы рассматриваем результаты в
конце t-й итерации алгоритма РД. В этот момент в точке р алгоритм
вырабатывает значение f =/.для
j = arg min c\ • (5.47)
\<i<m
Одинаковые метки определяют связные участки изображения -
сегменты в момент t. Опуская технические детали, скажем лишь, что
основная идея состоит в том, чтобы выбрать т наибольших сегментов (по
площади, т. е. по количеству пикселей), переназначить т меток этим т
сегментам и взять их центроиды в качестве новых значений Щ на
следующей итерации. См. рис. 5.29.
246 ♦ Глава 5. Сегментация изображений
Рис. 5.28. Слева вверху: исходное цветное изображение Spring, на котором
запечатлен праздник весны в Миннесотском университете, Миннеаполис.
Справа вверху: результат сегментации после пяти итераций пирамидального
метода РД с членом гладкости Поттса с с= 5 и членом данных,описанным
в примере 5.6, с нормой /_2. Слева внизу: после 10 итераций,также с= 5.
Справа внизу: после 10 итераций с с = 10
Рис. 5.29. Результаты для изображения Spring на рис. 5.28. Слева: результат
сегментации после пяти итераций пирамидального алгоритма РД с членом
гладкости Поттса с с = 5 и членом данных из примера 5.6. Но на этот раз
используется критерий х2 и обновление центроидов и*,. Справа: результат
применения того же алгоритма после 10 итераций с с = 10
Поскольку метки сегментов нужны только для идентификации и
никак не характеризуют свойства сегментов, для этого конкретного
применения алгоритма РД разумным кажется только член гладкости
5.4. Сегментация видео и прослеживание сегментов ♦ 247
Поттса. В качестве альтернативы можно было бы взять член гладкости,
который штрафует за сходство данных, представленных смежными
метками. Это означает, что разные метки должны действительно
отражать различие в данных изображения.
Наблюдение 5.6. Заменять член гладкости Поттса чем-то другим в
сегментации методом РД, похоже, имеет смысл, только если в член гладкости
включаются характеристики данных.
Это наблюдение сформулировано как приглашение к исследованию.
См. также упражнение 5.10.
5.4. Сегментация видео и прослеживание
сегментов
При сегментации видео можно воспользоваться схожестью
последовательных кадров. Схожесть можно определять с помощью:
1) согласованности признаков изображения. Это означает, что у
соответственных сегментов должны быть схожие статистики
признаков;
2) согласованности формы. Это означает, что у соответственных
сегментов должна быть приблизительно одинаковая форма (тут
возможны уточнения: требования инвариантности относительно
масштаба, вращения и т. д.);
3) пространственной согласованности. Это означает, что
соответственные сегменты расположены приблизительно в одном месте
(вследствие медленного перемещения, обычно это
сопровождается также приблизительно одинаковым размером и даже формой);
4) временной согласованности. Это означает, что соответственные
сегменты можно проследить благодаря моделированию
движения камеры и (или) объектов на сцене (возможно, в
предположении сходства размера или формы).
В этом разделе мы обсудим согласованность признаков и временную
согласованность. Мы поговорим об алгоритме сдвига среднего, в
котором используется согласованность признаков в видеоданных. Что
касается согласованности формы, то могут оказаться полезны признаки
формы, о которых шла речь в разделе 3.2. К пространственной
согласованности имеют отношение моменты и, в особенности, центроиды (см.
раздел 3.3.2).
248 ♦ Глава 5. Сегментация изображений
5.4.1. Использование согласованности признаков
изображений
Сегменты должны оставаться устойчивыми на протяжении
времени и не должны спонтанно появляться и исчезать. Рассмотренный
ранее метод сдвига среднего для сегментации статических изображений
можно обобщить на видео.
Если для пометки сегментов используются цвета, то они должны
оставаться примерно одинаковыми, а не изменяться, как на рис. 5.30.
Рис. 5.30. Слева: кадр из последовательности tennisball.
В середине и справа: пометка сегментов цветами в качестве меток;
видна несогласованность пометки в кадрах t и f + 1. К обоим кадрам алгоритм
сдвига среднего применялся по отдельности
Сопоставление локальных пиков. Мы будем рассматривать
л-мерные векторы признаков изображения и в \П\ пикселях каждого
кадра. Например, для цветных изображений п = Ъ и u = (R,G, В).
Мы предполагаем, что локальные пики векторов признаков и в
сегментах на последовательных кадрах располагаются примерно в одних
и тех же точках изображения. Следовательно, мы можем расширить
п-мерное пространство признаков до (п + 2)-мерного, включив в состав
признаков координаты а: и у, но рассматривая пространственные
координаты и значения как разные компоненты: us = (а:, у) и uv = u
соответственно. Комбинированные векторы uc(t) = [us(t), uv(t)] теперь являются
элементами (п + 2)-мерного пространства признаков для кадра L Для
краткости снова воспользуемся обозначениями
^i,s ~ 2 '
иД'+1)-М0|[ и ^>v=4-|ttv(/+i)-u/>v(o|'» (5-48)
V
предполагая, что профиль ядра ks для пространственной компоненты
имеет радиус rs > 0, а профиль ядра kv для компоненты значения имеет
радиус г, > 0.
Вначале кадр 1 сегментируется методом сдвига среднего как
статическое изображение. Далее нужно сегментировать кадр t + 1, основываясь
на результатах сегментации кадра t. Кадр t уже обработан, мы имеем
5.4. Сегментация видео и прослеживание сегментов ♦ 249
значения u.(t) для i = 1,..., т, являющиеся комбинированными
векторами признаков кадра t
Формулу (5.19) сдвига среднего для статических изображений можно
обобщить на случай следующего кадра:
w,M'+1) =^Ь ис^+1)- (5-49)
Работа алгоритма сдвига среднего продолжается, пока uc(t + 1) не
сойдется к локальному пику, соответствующему значениям признаков
в предыдущем кадре, и не будут обработаны все подмножества
признаков. Локальный пик в кадре t + 1 сопоставляется с ближайшим
локальным пиком в кадре t в предположении, что расстояние между ними
действительно мало. В противном случае локальный пик в кадре t + 1
создает новый класс сегментов.
Теперь реализуем уравнение (5.49) по аналогии с тем, как мы
поступали с уравнением (5.19) для статических изображений. Мы
обнаруживаем новый локальный пик, когда процесс сдвига среднего
сошелся, т. е. модуль вектора сдвига т (uc(t +1)) оказался ниже порога
(например, меньше 100 в случае цветных RGB-изображений).
Признаки пикселя заменяются признаками сопоставленного ему локального
пика. На рис. 5.31 это показано для кадров последовательности tennis-
ball, в которых признаками являются трехмерные цветовые значения.
Соответствующим локальным пикам можно сопоставить условные
цвета, чтобы повысить наглядность помеченных цветами сегментов
(см. рис. 5.32).
5.4.2. Использование временной согласованности
В этом разделе описывается более простая процедура, в которой
используется только пространственная информация, а не распределение
значений в сегментах. На рис. 5.33 показана временная
согласованность (в системе содействия водителю, основанной на компьютерном
зрении), где прослеживание сегментов упрощается благодаря тому, что
соответственные сегменты в последовательных кадрах существенно
перекрываются по позициям пикселей. Сегменты были выделены в
результате анализа стереоизображений (обсуждается ниже в этой книге),
что заодно позволяет пометить сегменты расстоянием (в метрах) до
записывающей камеры.
Мы выбираем в последовательных кадрах видеопоследовательности
сегменты, представляющие интерес для данного приложения (т. е. иг-
250 ♦ Глава 5. Сегментация изображений
норируем сегменты, которые, скорее всего, являются частью фона). Для
каждого выбранного сегмента в кадре t мы хотели бы знать,
продолжается ли он в кадре t + 1. Мы предполагаем, что между соответственными
сегментами в соседних кадрах должно быть существенное перекрытие.
Рис. 5.31. Верхний ряд: два соседних кадра из последовательности tennisball.
Средний ряд: черные пиксели (внутри мяча) -те, для которых
не нашлось соответствующих пиков в предыдущем кадре.
Нижний ряд: результирующие сегменты
Набросок программы прослеживания. Пусть {Af0, A\,..., А[} -
семейство сегментов, выбранных в кадре t. Наша цель - сопоставить
сегменты А] и At+1 в кадрах t и t + 1; если проделать это для всей
видеопоследовательности, то получится прослеживание (tracking).
Выбранное в начальный момент семейство [А*0,А\,..., а' } определяет
активный список сегментов. Мы ищем соответственные "сегменты
такие, что каждый А\ соответствует не более чем одному А"1 и каждый
А'*1 не более чем одному А\. Для некоторых А1, или At+X может не
найтись соответствия. Не прибегая к моделированию движения камеры
или объектов, мы просто устанавливаем соответствие на основе
перекрытия между сегментами А\ и At+1, принимая во внимание перемеще-
5.4. Сегментация видео и прослеживание сегментов ♦ 251
ние сегмента А\, оцененное по результатам анализа плотного движения
(см. главу 4).
Рис. 5.32. Сегменты, раскрашенные в условные цвета. Соответственные пики
отображаются в один и тот же цвет на четырех последовательных кадрах видео
Рис. 5.33. Ограничивающие прямоугольники прослеженных сегментов
на видеопоследовательностях bicyclist и motorway
Если мы не смогли найти соответственный сегмент (опять-таки без
применения метода цифровых отпечатков, описанного ниже), то
удаляем сегмент из списка активных. Должен также существовать
периодически выполняемый процесс добавления предположительно новых
активных сегментов в список.
252 ♦ Глава 5.Сегментация изображений
Мера несходства. Для измерения несходства сегментов А и В,
каждый из которых определен как множество позиций пикселей в одной и
той же области изображения П на плоскости ху, мы применяем метрику,
основанную на отношении мощности симметрической разности
множеств АиВ (см. рис. 5.34), к мощности их объединения:
Ъ(А, В) = * j-^-j \ (5.50)
\A\jB\
Эта метрика равна 0 тогда и только тогда, когда множества совпадают,
и равна 1, когда они не имеют ни одного общего пикселя.
Рис. 5.34. Симметрическая разность множеств А и В
Соответствие двух кадров. Поскольку положение сегмента А может
измениться при переходе от кадра t к кадру t + 1, мы будем
использовать относительное движение, полученное в результате применения
алгоритма вычисления плотного оптического потока (например, Хор-
на-Шанка, Лукаса-Канаде, BBPW или иного), чтобы компенсировать
параллельный перенос. Пусть (и , v) - оптический поток в пикселе р.
Вычислим средний поток в области, занятой сегментом А в кадре V.
UA,t=(U>V) = TT\^(U
А^Р'ТрУ (5'51)
II РеА
Произведем параллельный перенос пикселей множества А на вектор
\хА t и получим новое множество А = иА t[A].
Для сегмента А\, \^i^nt найдем такой индекс ;0, для которого
величина Т>{А\, At+1) для всех/ = 1,..., nt+1:
y0=aigmin©(A;, A'/1). (5.52)
j=l,...,nt+l
Чтобы исключить несущественные соответствия, выберем
некоторый порог Г, 0 < Т < 1, и будем учитывать только те соответствия, для
которых
ЩА], А%) < Г. (5.53)
5.4. Сегментация видео и прослеживание сегментов ♦ 255
В результате мы нашли сегмент А? в кадре t + 1, который
соответствует сегменту А*, в кадре t Введем формальное обозначение
А=>иБ (5.54)
для ситуации А = А1., В = А'^ и u = иА t. Поскольку теоретически в кадре t
может быть несколько сегментов А,' для которых установлено
соответствие с одним и тем же сегментом В в кадре t + 1, мы преобразуем (5.54)
во взаимно однозначное соответствие, считая, что В - образ множества
А кандидатов, доставляющих минимум метрике V(А, В).
История длины т. Чтобы прослеживать соответственные сегменты в
нескольких кадрах, мы повторно применяем процедуру сопоставления
двух кадров и пытаемся также обрабатывать случаи, когда сегменты
изменяются или даже на короткое время пропадают. Для этого мы
применяем простой статистический фильтр.
Для каждого прослеженного сегмента фильтр хранит историю, т. е.
т соответствующих ему сегментов в предыдущие временные
интервалы. Например, если частота записи составляет 25 Гц, то можно взять
т = 6, т. е. меньше одной четверти секунды.
История длины г сегмента В в кадре t определяется
последовательностью
А1 =>UjA2=>u2... =>ut_jAt=>utJB, (5.55)
если при обратном переходе от кадра (£ - /) к кадру (t - [/ + 1]) для всех
i = 0,..., т - 1 всегда найдется соответствующий В сегмент.
Отображение исторических сегментов в кадре L При поиске
наилучшего соответствия сегменту В в кадре t сегмент Ат в кадре t - 1
был сдвинут на вектор ит и занял положение ut[AJ. При поиске
наилучшего соответствия сегменту Ат в кадре t - 1 сегмент Ат_1 в кадре t - 2
был сдвинут на вектор ит1 и занял положение u^fA^J. Таким образом,
определено множество u^u^^A^J] в кадре t, образующееся в результате
применения следующего перемещения ит, хранящегося в истории.
Продолжая этот процесс, мы получаем, что сегмент А1 переходит в сегмент
uT[uT_![... uj... [AJ ...]]] в кадре t.
Итак, мы отобразили все т предыдущих сегментов, которые были
поставлены в соответствие сегменту В в кадре t, на их нормализованные
позиции в кадре t; сегмент А1 был параллельно перенесен т раз, сегмент
А2-т-1 раз и т. д.
Временная релевантность и временной отпечаток. Мы
сопоставляем вес т. каждой позиции пикселя в сегменте А. для 1 < i < т таким
254 ♦ Глава 5. Сегментация изображений
образом, что о)1 < а)2< ... ^ ыт< 1. Тем самым мы взвешиваем временную
релевантность сегмента А. его появлению в кадре t.
Например, для т = 6 можно было бы использовать веса 0.1, 0.1, 0.15,
0.15,0.2,0.3 в указанном порядке.
Эти веса аккумулируются (путем сложения) в позициях пикселей,
являющихся результатами параллельных переносов сегментов А. в кадр t,
и таким образом определяется временной отпечаток множества Ат на
протяжении его истории длины т - множество всех позиций пикселей,
в которых аккумулированный вес превышает порог 0,5.
Пересмотр алгоритма сопоставления двух кадров. Теперь при
поиске соответствий между кадрами t - 1 и t мы можем использовать
сгенерированный временной отпечаток в кадре t. Если в кадре t не нашлось
соответственного сегмента В, то мы используем в качестве В временной
отпечаток множества Ат и тем самым определяем новое множество Ат
путем сдвига всех исторических параметров вперед с целью
определения цифрового отпечатка в кадре t + 1, применяя средний оптический
поток uBt. Такой способ распространения (когда в кадре t нет
настоящего соответственного сегмента) можно применять на протяжении
ограниченного времени, например т кадров, в предположении, что
временное пропадание сегмента объясняется его разделением на другие
сегменты, объединением с другими сегментами и другими подобными
операциями, но он снова появится в более позднем кадре. Если сегмент
так и не появился, то он удаляется из списка активных сегментов, на
основе которого производится прослеживание.
5.5. Упражнения
5.5.1. Упражнения по программированию
Упражнение 5.1 (уменьшение количества сегментов после
сглаживания). В качестве входных данных возьмите какие-нибудь
полутоновые изображения / или сгенерируйте такие изображения, случайным
образом выбрав уровни яркости в диапазоне от 0 до Gmax (указание: для
каждого посещенного пикселя вызовите функцию RANDOM). Размер
входных изображений должен быть не менее 500><500. Обработайте
изображения, как описано ниже.
1. Примените к / прямоугольный фильтр 5x5 для сглаживания
значений.
2. Реализуйте алгоритм пометки, показанный на рис. 5.8, и
посчитайте, сколько получилось сегментов.
5.5. Упражнения ♦ 255
3. Повторите эти шаги несколько раз (для одного и того же
изображения). Постройте диаграмму, показывающую, как число
сегментов зависит от количества применений прямоугольного фильтра.
Сравните результаты своей реализации с результатами функции
floodFill из библиотеки OpenCV.
Упражнение 5.2 (стилизация Виннемёллера, сегментация методом
сдвига среднего и упрощение). Это небольшой проект, цель
которого - художественный рендеринг отснятых фотографий. Объедините
следующие три процедуры в одну программу нефотореалистичного
рендеринга.
1. Выделите в заданном цветном изображении бинарные границы,
воспользовавшись стилизацией Виннемёллера.
2. Выполните сегментацию методом сдвига среднего с целью
создать участки постоянного цвета.
3. Примените альфа-смешение к полученным на предыдущем шаге
результатам и еще упростите результирующее цветное
изображение, так чтобы участки, обведенные границами, как правило,
были одного цвета (т. е. усильте эффект постеризации -
огрубления цветовых переходов внутри этих участков).
На рис. 5.35 приведены примеры двух изображений, полученных
применением описанных приемов.
Рис. 5.35. Слева: нефотореалистичный рендеринг изображения MissionBay;
оригинал и стилизация показаны на рис. 5.6. Справа: нефотореалистичный
рендеринг изображения AnnieYukiTim; оригинал и стилизация показаны на рис. 5.2
Упражнение 5.3 (сегментация методом сдвига среднего в OpenCV).
В функции meanShift из библиотеки OpenCV задаются следующие
параметры: пространственный радиус (sp), цветовой радиус (сг) и
количество уровней пирамиды изображений (L).
256 ♦ Глава 5. Сегментация изображений
Параметр к = sp определяет окно размера (2к + 1)х(2/с + 1) в
пространственной области (т. е. носителе П). Параметр сг задает размер окна в
пространстве признаков, когда признаком считается цвет, т. е.
рассматриваются все значения (R, G, В), для которых
\\(R,G,B)-(R0>G0)B0)\\l<cr,
где (R0, G0, B0) - значение текущего пикселя. Параметр L = maxLevel
больше или равен 0, он означает, что используется пирамида с L + 1 уровнями.
На рис. 5.36 показаны результаты для L = 1 (два уровня); в верхнем
ряду мы видим результат раскрашивания сегментов с помощью
функции floodFill.
Рис. 5.36. Вверху: результаты сегментации изображения Aussies, где сегменты
раскрашены условными цветами, а не цветом пикселя, в котором достигается пик.
Взяты значения sp = 12 и sr = 19 (слева), sp = 5 и sr = 24 (справа).
Внизу: изображение Xochicalco (слева) и результат его
сегментации (справа) с параметрами sp = 25 и sr = 25
Обсудите смысл параметров cr, sp, и L и последствия их задания,
опираясь на объяснения, приведенные в этой главе. В качестве примеров
возьмите какие-нибудь изображения по собственному выбору, а также
изображение Spring как пример трудной сегментации.
5.5. Упражнения ♦ 257
Упражнение 5.4 (сегментация методом распространения доверия).
Реализуйте сегментацию методом распространения доверия с
параметрами, описанными в подписях к рис. 5.28 и 5.29 (например, используйте
простую модель Поттса). Включите в состав тестового набора
изображение Spring. Сравните полученные результаты сегментации с
показанными на этих рисунках. Попробуйте подобрать другие параметры
алгоритма, например чтобы уменьшить число сегментов или улучшить
сегментацию, оставив «всего одного человека» или несколько
«объединенных» человек.
Упражнение 5.5 (моделирование фона). Изображения (например,
в системах видеонаблюдения) часто сегментируются на объекты и фон,
т. е. множество П разбивается на пиксели всего двух типов.
Моделирование фона смесью гауссианов (от трех до пяти) многие годы было
стандартным подходом к решению этой задачи. На рис. 5.37
показаны результаты применения этой техники, которая в настоящей книге
не описывается. Оригинальное описание метода было опубликовано в
работе [С. Stauffer and W. E. L. Grimson. Adaptive background mixture models for
real-time tracking. In Proc. Computer Vision Pattern Recognition, 1998], а в сети
имеется много материалов на эту тему, включая исходный код.
Сами снимите видео в помещении или под открытым небом,
разберитесь в этом методе и смоделируйте фон смесью гауссианов, как
предлагали Штауффер и Гримсон.
Упражнение 5.6 (вычисление коэффициента восстановления).
Выберите «простые» изображения, на которых сегментов мало - меньше 10.
Подготовьте контрольные данные для этих изображений, например
вручную выделив края сегментов. Выберите какой-нибудь алгоритм
сегментации и сравните полученные сегменты с контрольными
данными, воспользовавшись в качестве меры коэффициентом
восстановления, определенным в упражнении 5.9.
5.5.2. Упражнения, не требующие программирования
Упражнение 5.7. Предположим, что в алгоритме сдвига среднего
для кластеризации признаков (описан на стр. 230) используется окно,
содержащее К ячеек сетки, таблица гистограммы содержит С непустых
клеток и в результате всех вычислений среднего посещено ровно М> С
различных ячеек сетки.
258 ♦ Глава 5. Сегментация изображений
Рис. 5.37. Вверху: оригинальные сцены. В середине: фон и объекты.
Внизу: устранение теней в результате постобработки
Покажите, что асимптотическая временная сложность3
алгоритма сдвига среднего равна 0(МК + М2), где степень 2 объясняется
несколькими проходами по одному и тому же пути из заданной
ячейки сетки в устойчивое положение среднего.
Чтобы избежать нескольких проходов, примените идеи
алгоритма UNION-FIND (R. Tarjan, 1975 г.): если ячейка сетки v = и + т (и)
о
Рассмотрим возрастающие функции /и^, отображающие множество натуральных чисел N в
множество положительных вещественных чисел Е+. Говорят, что f(n) e 0(g(n)), если существуют
константы с > 0 и п0 > 0 такие, что f(n) < с - g(n) для всех п > п0.
5.5. Упражнения ♦ 259
посещается в результате сдвига среднего в ячейку сетки и, то
записывать в q следующий сегмент:
SEG(v) = UNION(SEG(u), FIND(q)),
где v округляется до ближайшей ячейки сетки, a FIND(<?)
возвращает сегмент, которому принадлежит q.
Покажите, что благодаря использованию структуры данных
UNION-FIND (системы непересекающихся множеств) временная
сложность кластеризации методом сдвига среднего уменьшается
с 0(Л4ХЧ А/2) до 0(МК).
Упражнение 5.8. Если мы захотим использовать идею сдвига
среднего для нахождения локальных максимумов в гистограмме в
пространстве признаков, то должны будем искать все ячейки сетки в
пространстве признаков, для которых сдвиг т (и) достаточно мал:
M={u:\\mg(u)\\2<Au},
где Аи - шаг сетки.
Покажите, что если использовать окно, содержащее К ячеек сетки для
гистограммы признаков с С непустыми клетками, то для нахождения
множества ячеек М, аппроксимирующего локальные максимумы,
потребуется время 0(СК).
Упражнение 5.9. Определим коэффициент восстановления - меру,
полезную для сравнения различных алгоритмов сегментации или
кластеризации.
Рассмотрим кластеризацию векторов х £ Ш^для d > 0. Например,
рассмотрим векторы х = [х, у, R, G, B]J (d = 5), применяемые для сегментации
цветного изображения.
Дадим общее определение: алгоритм кластеризации А отображает
конечное множество S точек Rd в семейство попарно
непересекающихся кластеров. Алгоритм сегментации - частный случай этого более
общего определения.
Предположим, что имеется алгоритм А, который отображает S в т > 0
попарно непересекающихся кластеров С. (т. е. сегментов), i = 1, 2,..., т,
каждый из которых содержит т;.= |С.| векторов х.. £ Rd. В случае
сегментации изображения сумма всех т.равна мощности множества \П\. Будем
называть Ci старыми кластерами.
Теперь рассмотрим другой алгоритм кластеризации В, который
отображает то же самое множество S в п > 0 попарно непересекающихся
кластеров Gk, k = 1,2,..., п. Будем называть Gk новыми кластерами. Новый
260 ♦ Глава 5. Сегментация изображений
кластер Gk содержит векторы х, которые были отнесены алгоритмом А к
старым кластерам. Положим
где каждое Gk.- непустое подмножество в точности одного старого
кластера С.,/ = 1,2,..., sk. Индексы, или имена i и к, старых и новых кластеров
не связаны друг с другом, и в общем случае можно ожидать, что пф т.
Предположим, что п ^ т (т. е. число новых кластеров ограничено сверху
числом старых).
Идеальное восстановление имело бы место, если бы каждый старый
кластер совпадал с одним из новых кластеров, т. е. два множества
кластеров отличались бы только перестановкой имен ип = т. Например, оба
алгоритма АиВ могли бы порождать одну и ту же сегментацию
изображения, а единственное различие было бы в цветах меток.
Теперь выберем по одному представителю Gv , G2.,..., Gn. для каждого
нового кластера, так чтобы оптимизировать следующие два свойства:
1) для любой пары а. и Ь. различных индексов из множества
{1., 2.,..., п.} существуют два разных старых кластера Са и Съ
такие, что G .'tC и Gh. с С •
2) пусть Ск- старый кластер, соотнесенный с подмножеством Gk
нового кластера Gk в смысле предыдущего пункта. Тогда сумма
к=\ \Gk
максимальна, и максимум достигается для всех возможных
множеств индексов {1,2.,..., п.}.
'1 '2 >п
Таким образом, выбранные представители Gv , G2 ,..., Gn. соотносят
каждый новый кластер Gk ровно с одним старым кластером Ск путем
максимизации указанной суммы. В частности, мощность выбранного
подмножества G, необязательно наибольшая из всех подмножеств, со-
ставляющих разбиение Gk; представители выбирались так, чтобы
максимизировать общую сумму. Величина
%(£) = I
kjk
100%
х
*=i \Gk\ n
называется коэффициентом восстановления алгоритма В относительно
алгоритма А на входном множестве S.
5.5. Упражнения ♦ 261
Отметим, что сам алгоритм А для сравнения и не нужен; чтобы
вычислить коэффициент восстановления, достаточно знать множество
старых кластеров (так сказать, контрольные данные).
Обсудите асимптотическую временную сложность предложенного
способа измерения коэффициента восстановления для кластеризации
(и, в частности, сегментации).
Упражнение 5.10. В наблюдении 5.6 предлагается заменить простой
член гладкости Поттса в алгоритме сегментации РД каким-нибудь
другим членом. Например, если цх и ц2 - средние яркости смежных
сегментов, то константу с в (5.33) можно заменить членом, в котором с
масштабируется в зависимости от разности \цх - ц2\. Задайте на основе
формулы (5.33) модифицированные функции гладкости, включающие
характеристики данных.
Упражнение 5.11. Покажите, что мера несходства D, определенная
в формуле (5.50), является метрикой на семействе множеств пикселей,
т. е. обладает тремя свойствами, описанными в разделе 1.1.3. Для
каждого множества пикселей определена мощность (количество пикселей
в этом множестве).
Глава
6
Камеры, координаты
и калибровка
В этой главе описаны три основных компонента системы
компьютерного зрения. Необходимо (до некоторой степени) понимать
геометрические и фотометрические свойства используемых камер. Для
моделирования проективного отображения трехмерного мира на двумерные
изображения и выполнения действий по калибровке камеры
приходится иметь дело с несколькими системами координат. В результате
калибровки мы преобразуем записанные изображения в нормализованные
(например, геометрически ректифицированные) представления, что
упрощает последующие процедуры обработки.
Врезка 6.1 (Ньепс и первая фотография). Первая в мире фотография (доступная
для широкой публики) была сделана Н. Ньепсом (1765-1833) во Франции в
1826 г. На ней изображен вид из окна его рабочего кабинета на ферме в Ле Гра.
Экспозиция длилась восемь часов (обратите внимание, что строения освещены
солнцем справа и слева),фотография была зафиксирована на пластинке
размера 20х25 см, покрытой тонким слоем битума, растворенного в животном масле.
6.1. Камеры ♦ 263
6.1. Камеры
На рис. 6.1 показан принцип работы камеры-обскуры. Через небольшое
отверстие на стену затемненной комнаты проецируется внешний мир,
при этом изображение получается перевернутым. Эта идея известна
тысячи лет (например, она использовалась 2500 лет назад в Китае), но
лишь в начале XIX века удалось записать проецируемое изображение
на носитель, т. е. «заморозить во времени». В XVI веке знали, что если
вставить в отверстие линзу, то яркость и четкость изображения
повысятся.
Рис. 6.1. Рисунок (в общественном владении) камеры-обскуры, взятый из «Книги
эскизов о военном искусстве, включая геометрию, фортификацию, артиллерию,
механику и пиротехнику» XVII в. Внешние объекты через небольшое отверстие
проецируются на стену затемненной комнаты в перевернутом виде
В этом разделе мы обсудим свойства камер, это поможет принимать
решение о том, какую камеру (или камеры) использовать в конкретном
исследовании или приложении. Мы также опишем базовые модели
одной камеры и системы стереокамер, поскольку они понадобятся в
последующих главах.
6.1.1. Свойства цифровой камеры
В цифровой камере используется один или несколько матричных
датчиков (сенсоров) для записи проецируемого изображения (см.
264 ♦ Глава 6. Усовершенствование функциональных тестов
рис. 6.2 слева). Матрица датчиков представляет собой массив
сенсорных элементов (фототранзисторов) размера NcolsxNrows, изготовленный
по технологии приборов с зарядовой связью (ПЗС) или комплементарных
металло-оксидных полупроводников (КМОП). Первую цифровую камеру
Mavica изготовила компания Sony в 1981 г., а за ней стали появляться и
другие.
Рис. 6.2. Слева: матрица датчиков. Отдельные ячейки настолько малы,
что их невозможно разглядеть даже на увеличенном изображении.
Справа: эскиз фильтра Байера
Камеры для компьютерного зрения. Для компьютерного зрения
лучше использовать высококачественные камеры. Особенно важны
такие свойства, как точность цветопередачи, пониженная дисторсия
объектива, идеальное соотношение сторон, высокое пространственное
разрешение (называемое также высокой четкостью), большая глубина
цвета, широкий динамический диапазон (т. е. точность значений в
темных и ярких участках одного и того же изображения) и высокая
скорость кадрового переноса. На рис. 6.3 приведен пример приложения,
требующего высококачественных камер (например, для ответа на
вопрос «Ударилась ли голова манекена о руль?»).
Камеры для компьютерного зрения обычно постоянно подключены
к компьютеру (через видеопорт или плату видеозахвата) и нуждаются
в специальном программном обеспечении для захвата кадров и
управления камерой (временной синхронизации, панорамирования,
изменения масштаба или угла наклона).
Цифровое видео. Цифровые камеры обычно имеют два режима:
для съемки статических фотографий и видео. Для конкретной камеры
произведение временного и пространственного разрешения обычно
постоянно. Например, камера, способная захватывать изображения
размера 7680х4320 (т. е. 33 мегапикселя, Мп) с частотой 60 кадров/с,
записывает 1,99 Гп (гигапикселя) в секунду. Та же самая камера может
6.1. Камеры ♦ 265
поддерживать запись изображений размера 2560x1440 (3,7 Мп) с
частотой 540 кадров/с, что дает те же 1,99 Гп в секунду.
Рис. 6.3. Анализ результатов краш-теста (компания Daimler А.6.,3индельфинген,
Германия) в 2006 г. был основан на изображениях высокого разрешения,
снятых с частотой 1000 импульсов/с
При съемке цифрового видео с чересстрочной разверткой в
последовательных кадрах сканируются нечетные или четные строки матрицы
датчиков (см. рис. 6.4). В аналоговом видео эта техника применялась
для уменьшения полосы частот, необходимой для передачи. Для
современных технологий обработки изображения эта причина уже не
актуальна.
Рис. 6.4. Полукадры с нечетными (слева) и четными (справа) номерами строк
Чересстрочная развертка особенно мешает, когда нужно произвести
автоматизированный анализ видео. Для объединения обоих
полукадров в один полный применяется, например, линейная интерполяция
или простое удвоение строк в полукадре.
В случае прогрессивной развертки каждый кадр содержит полное
изображение. Это не только повышает визуально воспринимаемое
качество видео, но и порождает данные, пригодные для анализа.
266 ♦ Глава 6.Усовершенствование функциональных тестов
Разрешающая способность и глубина цвета. Фототранзистор
представляет собой прямоугольный элемент размера а*Ь (порядок а и
Ъ обычно составляет 2 мкм). В идеале соотношение сторон а/b должно
быть равно 1 (квадратные элементы).
Разрешающая способность, или разрешение изображения N , *N
г ' 7 Г Г f cols rows
(количество сенсорных элементов), обычно указывается в мегапикселях
(Мп). Например, в 4-мегапиксельной камере приблизительно 4 000 000
пикселей, образующих изображение формата 3 : 4 или 9:16. Далее мы
не будем специально оговаривать, что под пикселями понимаются
«цветные пиксели». Например, компания Kodak в 1991 предложила
камеру DCS-100, в которой матрица датчиков имела разрешение 1,3 Мп.
Но одно лишь количество пикселей еще не гарантирует высокого
качества изображения. Например, чем больше пикселей, тем обычно
меньше площадь одного датчика, а значит, на него падает меньше
света и ухудшается отношение «сигнал-шум» (ОСШ, англ. SNR).
Используемая в оптике функция рассеяния точки призвана гарантировать, что
увеличение количества пикселей не приводит к привнесению
дополнительного шума в изображение. В приложениях компьютерного зрения
часто требуется, чтобы значение пикселя в одном канале было
представлено более чем 8 битами (например, для анализа движения или
стереоизображений предпочтительнее иметь полутоновое изображение с
16-битовыми пикселями).
Фильтр Байера и разделение лучей. Фильтр Байера (названный
в честь Б. Байера из компании Eastman Kodak) обычно применяется
в бытовых цифровых камерах. Один цветной пиксель захватывается
четырьмя датчиками, два для зеленого цвета и по одному для
красного и синего (см. рис. 6.2 справа). Поэтому матрица датчиков размера
NcolsxNrows на самом деле записывает цветные изображения с
разрешением (Ncols 12)x(JVrows / 2). Значения R, G и В в одном записанном пикселе
относятся к точкам, отстоящим друг от друга на один датчик.
С другой стороны, в высококачественных цветных цифровых
камерах применяется светоделитель (например, состоящий из двух дихро-
идных призм), который разделяет световой пучок на три луча с разной
длиной волны, по одному для красной, зеленой и синей компонент.
В этом случае используются три матрицы датчиков размера Ncols*Nrows, a
значения R,G,Bb одном пикселе действительно соответствуют этому и
только этому пикселю.
Точность цветопередачи. Мишень для проверки цветов
представляет собой карточку с цветными и серыми квадратными полями. На
рис. 1.32 и 6.5 показана такая мишень от компании Macbeth™.
6.1. Камеры ♦ 267
Рис. 6.5. Окно, расположенное в красном поле, и гистограммы
для каналов R, G и В
Пример 6.1 (определение точности цветопередачи путем анализа
гистограммы). Для оценки точности цветопередачи сделайте снимок такой
карточки, предпочтительно при рассеянном освещении (чтобы уменьшить влияние
освещения на видимый цвет). Расположите окно в пределах одного
квадратного поля отснятого изображения. Гистограмма для такого окна (если речь идет
о цветном поле, то три гистограммы для каналов R, G и В) должна иметь
«тонкий пик», если фотография сделана камерой с качественной цветопередачей.
См. рис. 6.5.
Средние по окнам в разных полях должны относиться друг к другу
(мы говорим об относительных, а не абсолютных величинах из-за
эффектов освещения) как нормативные значения RGB этих полей,
указанные в технической спецификации изготовителя мишени.
Дисторсия объектива. Оптические линзы привносят радиальную
дисторсию в процесс проецирования. Этот эффект известен также под
названием бочкообразность или подушкообразность (см. рис. 6.6).
Рис. 6.6. Слева направо: сетка изображения с бочкообразной дисторсией, идеальное
прямоугольное изображение, сетка изображения с подушкообразной дисторсией,
перспективные искажения и дисторсия объектива в одном изображении
268 ♦ Глава 6.Усовершенствование функциональных тестов
Если делается фотография плоской прямоугольной области таким
образом, что центр проекции расположен на прямой, проходящей через
центр области перпендикулярно к ее плоскости, то в идеале на
фотографии должен получиться прямоугольник.
Пример 6.2 (количественное измерение дисторсии объектива). Отклонение
прямых линий от идеала на фотографии регулярной сетки (например,
шахматной доски) можно использовать для количественной характеристики
дисторсии камеры. Эффект дисторсии зависит от расстояния до контрольной сетки и
часто сочетается с перспективными искажениями (см. рис. 6.6 справа).
Линейность камеры. Камеры часто конструируются так, чтобы
соответствовать воспринимаемой человеческим глазом яркости, которая
изменяется нелинейно. При анализе изображений мы стараемся
выключить нелинейность записанных значений. Если же это невозможно,
то хотелось бы знать функцию коррекции, которая приводит
записанные яркости к линейному распределению.
Серые поля, как, например, в нижнем ряду на контрольной мишени
Macbeth™ или на полоске с линейным градиентом яркости на рис. 6.7,
можно использовать для проверки линейности измеренных значений
яркости M=(R + G + В)/Ъ.
Рис. 6.7. Полутоновая полоска, в которой уровень яркости линейно
изменяется от черного (значение 0) до белого (значение Gmax)
Предположим, что для черного поля получается средняя яркость umin
(в идеальном случае 0), а для белого -и (в идеальном случае G ). Те-
IllctX IllctX
перь рассмотрим поле, в котором а % белого (соответственно (100 - а) %
черного). Если измеренная яркость изменяется линейно, то для него
должно получиться значение
а
Umin + Too ax ~Umin ^'^
находящееся между umin и ытах. По отклонению от ожидаемого значения
можно вычислить величину коррекции.
6.1.2. Центральная проекция
Если забыть о радиальной дисторсии оптической линзы, то
проекцию через небольшое отверстие можно описать теоретической моделью
камеры с точечной диафрагмой, или стенопа.
6.1. Камеры
269
Модель камеры-стенопа. В модели предполагается, что диаметр
отверстия «очень близок» к нулю. В реальных стенопах, иногда
называемых «обувными коробками» (shoebox camera) (для получения
изображения используется либо пленка, либо матрица датчиков,
фотографии можно найти в интернете), диафрагма действительно очень мала,
а время экспозиции велико.
На рис. 6.8 справа показана модель камеры-стенопа. Отверстие
называется центром проекции. Чтобы избежать переворачивания, в модели
центр проекции помещен позади плоскости изображения.
^,
\—f-+
Zs
р
Центр проекции
Рис. 6.8. Слева: принцип работы реальной камеры-стенопа; точка Р проецируется
через отверстие (центр проекции) на плоскость изображения, расположенную на
расстоянии/от отверстия; спроецированное изображение перевернуто.
Справа: модель стенопа для изображения ширины И/ и угла визирования а;
в модели предполагается, что плоскость изображения расположена
между сценой и центром проекции
Мы предполагаем правостороннюю систему координат камеры
ХУД1. Ось Zs направлена в сторону сцены и называется оптической
осью. Поскольку мы не учитываем радиальную дисторсию, на
плоскости изображения получаются спроецированные без искажения точки с
координатами хи и уи. Расстояние /"между плоскостью изображения ху/и и
центром проекции называется фокусным расстоянием.
В случаях, когда величина /"не определяется (даже в некотором
абстрактном смысле) фокусным расстоянием камеры, ее можно также
назвать параметром проекции.
У идеального стенопа угол визирования (см. рис. 6.8 справа) равен
W
Gf=2arctan-
2/'
Подстрочный индекс «s» происходит от слова «sensor» (датчик). Камера - это своего рода датчик
для измерения данных в реальном трехмерном мире. Другие примеры датчиков - лазерный
дальномер и радар.
270
Глава 6.Усовершенствование функциональных тестов
Фокусное расстояние /обычно начинается от 14 мм и может
достигать величин, кратных 100 мм. Например, при W = 36 мм и /= 14 мм
горизонтальный угол визирования равен приблизительно а = 104,25°2.
В этой модели стенопа понятия оптики абстрагированы - волновая
природа света не принимается во внимание, т. е. предполагается, что
лучи света - идеально прямые линии. Также предполагается, что
объекты всегда находятся в фокусе, каким бы ни было расстояние от них
до камеры. При проецировании видимой точки поверхности с близкого
расстояния мы на практике должны были бы сфокусировать камеру на
это расстояние (тогда параметр f камеры увеличился бы до
некоторого f+z).
Уравнения центральной проекции. Для представления любой
точки в трехмерном пространстве можно использовать декартову
систему координат камеры XYZs. Видимая точка Р = (X, У, Z) в результате
центрального проецирования отображается в позицию пикселя р = (хи, уи)
в плоскости неискаженного изображения (рис. 6.9 слева). Согласно
теореме о луче из элементарной геометрии, / относится к Zs (координате
точки Р) так же, как хи (координата пикселя р) относится кХ
(координате точки Р), и аналогичное соотношение имеет место в плоскости УД
Таким образом, имеем
S S
Хи =
&s
И
Уи =
Л
Z " Z
S S
Мы еще не раз будем пользоваться этими уравнениями.
(6.2)
р=&*уА ...-■■-
V-f—
1
к
'Хи
P=(X,Y,Z)
4 S' S' SJ j
---""*
*"'-.__
1
Т
и
х
^s
1
/
г
Zs
Рис. 6.9. Слева: центральная проекция в плоскости XZsc фокусным расстоянием/.
Справа: иллюстрация теоремы о луче, хи относится к X так же, как/относится к Zs
Главная точка. На рис. 6.8 справа показано, что оптическая ось
пересекает изображение в точке, близкой к его центру. В принятой нами
2 Для читателей, предпочитающих точное определение широкого угла: будем так называть любой
угол а от 104,25° до 360°.
6.1. Камеры ♦ 271
системе координат изображения ху (рис. 1.1) начало координат
расположено в левом верхнем углу, а не близко к центру, как в системе
координат хиуи.
Обозначим (сх, с) точку пересечения оптической оси с плоскостью
изображения в системе координат ху. Эта точка называется главной
точкой в плоскости ху и должна определяться в процессе калибровки
камеры. Имеем
(х,у) = (хи+сх,уи+с) =
+ Сх> +Cv
Z Z у
(6.3)
У позиции пикселя (а:, у) в двумерной системе координат
изображения ху имеются также трехмерные координаты (х - сх, у - с, /) в системе
координат камеры XYZs.
6.1.3. Система с двумя камерами
Чтобы понять трехмерную геометрию сцены, удобно использовать несколько
камер. Для стереоскопического зрения необходимо по меньшей мере две
камеры.
Система стереокамер. Если в приложении компьютерного зрения
используется две или более камер, то они должны быть по возможности
идентичны, чтобы избежать ненужных сложностей. Тогда калибровка
позволит получить две практически одинаковые копии одной и той же
камеры. Длиной базы Ъ называется расстояние между центрами
проекции двух камер (рис. 6.10 слева). На рис. 6.10 справа показан квадро-
коптер, на котором смонтирована система стереокамер с фронтальным
обзором с базой ПО мм (база второй системы стереокамер с нижним
обзором, установленной на том же квадрокоптере, равна 60 мм).
Рис. 6.10. Слева: стереокамера на вакуумной присоске с базой Ь.
Справа: система стереокамер с фронтальным обзором, интегрированная
с квадрокоптером
272
Глава 6.Усовершенствование функциональных тестов
После калибровки двух «почти параллельных» камер длина базы Ъ
остается единственным параметром, определяющим положение одной
камеры относительно другой.
Каноническая геометрия системы стереокамер. Можно считать,
что в результате калибровки (описывается ниже) мы получаем две
практически идентичные идеально соосные камеры, как показано на
рис. 6.11. Каждую камеру будем описывать с помощью модели стенопа.
Каноническая (или стандартная) геометрия системы двух стереокамер
характеризуется тем, что правая камера является точной копией левой
и отстоит от нее на расстояние Ъ вдоль оси Xs системы координат левой
камеры XYZs. Центр проекции левой камеры находится в точке (0,0,0),
а центр проекции правой - в точке (Ь, 0,0). Иными словами, мы имеем:
1) два компланарных изображения одинакового размера Ncols*Nrows;
2) параллельные оптические оси;
3) одинаковое эффективное фокусное расстояние f;
4) коллинеарные строки изображения (т. е. строка у одного
изображения расположена на одной прямой со строкой у второго
изображения).
Оптическая ось левой камеры
У P=(X,Y,Z)
Оптическая ось правой камеры
Правое
изображение
Строка у
Рис. 6.11. Каноническая геометрия системы стереокамер
Применив уравнения центральной проекции (6.2) к обеим камерам,
мы отобразим точку Р = {X ,Y, Z) в системе координат левой камеры
XYZ в точки
S S S
S7 S' S'
PuL ~ \XuL ' УиЬ ) ~
'f-x. f-У,^
v Z, ' Z, j
(6.4)
PuR ~ \XuR •> УиЯ ) ~
rf\Xs-b) f-Y^
v
(6.5)
Js J
6.1. Камеры ♦ 273
на плоскостях левого и правого неискаженного изображения
соответственно. Калибровка должна дать точные значения Ь и f, чтобы мы могли
использовать эти уравнения в системах стереоскопического зрения.
6.1.4. Системы панорамных камер
Технология получения панорамных изображений дополняет
компьютерное зрение, компьютерную графику, техническое зрение роботов и
изобразительные искусства. Система панорамных камер может либо
сразу записать одно широкоугольное изображение, либо несколько
изображений, которые потом сшиваются в широкоугольное.
Система всенаправленных камер способна снимать окружающее
пространство с углом обзора 360 градусов, на рис. 6.12 показаны две
такие камеры. Всенаправленные системы можно разделить на два
класса: катадиоптрические и диоптрические3. Катадиоптрическая система
состоит из зеркала в форме поверхности второго порядка и обычной
камеры; в диоптрической системе имеется специально
сконструированный рефрактор, управляющий углами лучей, проходящих через
объектив камеры.
Рис. 6.12. Всенаправленные камеры. Слева: камера «рыбий глаз».
Справа: цифровая камера с зеркалом в форме гиперболоида
На рис. 6.13 показаны примеры отснятых изображений.
Отображение захваченного широкоугольного поля зрения на цилиндрическую
панораму упрощает последующий анализ изображения. Цилиндрическая
панорама с одним центром выглядит как перспективное изображение,
при этом подавляется круговая дисторсия, присутствующая в
изображениях, снятых катадиоптрической или диоптрической системой.
3 Катадиоптрический - отражающий и преломляющий свет; диоптрический - преломляющий
свет.
274
Глава 6. Камеры, координаты и калибровка
Рис. 6.13. Верхний ряд: исходные изображения, снятые камерой «рыбий глаз»
(Пражский Град и группа людей, снятые с углом обзора 180 градусов).
Нижний ряд: полученные в результате обработки панорамные изображения
Вращающаяся система на основе линейной камеры в составе
установки, показанной на рис. 6.14, создает цилиндрические
панорамы. Основными параметрами установки являются радиус R и угол
зрения а). Линейная камера за один раз записывает lxNrows пикселей. За
один оборот она записывает несколько изображений (скажем, Ncols), и
эти Ncols столбцов шириной 1 пиксель можно затем объединить в одно
изображение размера Ncols*Nrows.
^^ Линейная камера
Выдвигающаяся
направляющая
Малая поворотная платформа
Большая поворотная
платформа
Рис. 6.14. Экспериментальная
установка, состоящая из линейной
камеры, смонтированной на
малой поворотной платформе (для
выбора фиксированного угла со с
нормалью к окружности вращения,
определенной большой поворотной
платформой), которая может
скользить вдоль выдвигающейся
направляющей, что позволяет
выбрать расстояние R до центра
большой поворотной платформы
6.1. Камеры ♦ 275
Преимущество состоит в том, что длина линейки датчиков Nrows
может составлять тысячи пикселей. Вращающаяся линейная камера
может записывать панорамные изображения с обзором 360° за время
одного полного оборота, на котором создается NcoIs отдельных снимков.
На рис. 6.15 показан пример панорамы 56 580 10 200, снятой в 2001 г.
вращающейся линейной камерой. Технология подразумевает запись
динамических изменений в последовательных однострочных
изображениях - желательно это или нет, зависит от задачи, которую ставит
перед собой фотограф.
Рис. 6.15. Панорама Оклендского центрального делового района,
снятая в 2001 г. с верхней точки Оклендского моста через гавань с помощью
линейной камеры, изображенной на рис. 6.14
Реализация стереоскопического зрения с помощью
вращающейся линейной камеры. Вращающаяся линейная камера может
записать стереопанораму - для этого она должна совершить один
оборот с углом визирования со и второй оборот с углом визирования -со. В
результате будут записаны два цилиндрических изображения,
составляющих стереопару (см. рис. 6.16). Если используется матричная
камера (стандартный стеноп), то достаточно сделать один полный оборот
камеры и составить панорамные изображения для симметричной пары
углов со и -со из пары столбцов, симметричных относительно главной
точки камеры.
276 ♦ Глава 6. Камеры, координаты и калибровка
Рис. 6.16. Слева: вид сверху на линейную камеру с фокусным расстоянием/,
движущуюся по окружности радиуса R и ориентированную так,
что оптическая ось составляет угол ш с нормалью к окружности вращения.
Справа: все то же самое, но угол визирования равен -ш
Врезка 6.2 (панорамное зрение). Это очень активная область исследований
и прикладных разработок, здесь мы приведем только две ссылки для
самостоятельного чтения: книги [К. Daniilidis and R. Klette, eds. Imaging Beyond the Pinhole
Camera.Springer, Dordrecht, 2007] и [F.Huang,R.KLette and K.Scheibe. Panoramic Imaging.
Wiley, West Sussex, England, 2008].
6.2. Координаты
В этом разделе мы обсудим мировые координаты, используемые как
система отсчета для камер или объектов на сцене. Мы рассмотрим
также однородные координаты, позволяющие единообразно выражать
геометрические преобразования как умножение на матрицу (после
добавления к трехмерной системе мировых координат еще одной оси).
6.2.1. Мировые координаты
Имеются камеры и трехмерные объекты на сцене, а система
компьютерного зрения должна все это проанализировать. Удобно ввести
систему мировых координат XwYwZw, не связанную с конкретной камерой или
объектом. Затем нужно будет описать преобразование между системой
координат камеры XYZs и выбранной системой мировых координат
(см. рис. 6.17). На рис. 6.18 показана система мировых координат в
момент выполнения процедуры калибровки камеры.
6.2. Координаты ♦ 277
Система координат
камеры
Х„
w Мировая сиаема
А координат
Xw J^ 9 ""' w * w ^w^
Рис. 6.17. Система координат камеры и мировая система координат
Рис. 6.18. Слева: шахматная доска часто используется для калибровки камеры.
Справа: передвижная калибровочная установка; видимое отражение света
на поверхности узора помешало бы анализу записанных изображений
калибровочной установки. Какова здесь мировая система координат?
Аффинное преобразование трехмерного пространства переводит
прямые линии в прямые линии и не изменяет отношение расстояний
между тремя коллинеарными точками. В математике аффинное
преобразование представляется линейным преобразованием, которое
описывается умножением на матрицу и параллельным переносом.
Например, мы можем сначала применить параллельный перенос на вектор
Т = [tv tv £JT, а затем поворот
R =
rn
r21
r31
r12
r22
'32
r13
r23
r33
= Rl(ayR2(fi)-R3(r\
(6.6)
где матрицы
278
Глава 6. Камеры, координаты и калибровка
R,(a) =
R2 (Л =
R3(r) =
1 О О
О cos a sin a
О - sin a cos a
cos/? О -sin/?
О 1 О
sin/? О cos/?
cos у sin у О
- sin у cos 7 О
О 0 1
(6.7)
(6.8)
(6.9)
описывают повороты вокруг осей на углы а, /? и у соответственно (эти
углы называются эйлеровыми). Если бы параллельный перенос
выполнялся раньше поворота, то в общем случае и вектор переноса, и
матрица поворота были бы другими.
Наблюдение 6.1. Поворот и параллельный перенос в трехмерном
пространстве однозначно определяются шестью параметрами: а, /?, у, tv t2, ty
Координаты камеры и мировые координаты. Переход от
координат камеры к мировым координатам и наоборот описывается линейным
(или аффинным) преобразованием. Рассмотрим аффинное
преобразование точки Pw с мировыми координатами (Xw, Yw, Zw) в ее
представление в системе координат камеры Ps = (Xs, У, Z). Помимо
координатной нотации, которой мы пользовались до сих пор, будем применять
для обозначения точки Р также векторную нотацию Р = \Х , Y, Z ]Т.
Имеем:
(X„YS,ZJ =R[(XW,YW,ZJ +T] =
'11
r21
'31
'12
'22
'32
'13
'23
'33
X+t
Yw+t2
zw+t3
(6.10)
где матрица поворота R и вектор параллельного переноса Т
определяются в процессе калибровки. Отметим, что Pw = (Xw, Yw, Zw) и Ps = (Xs, У, Z) -
представления одной и той же точки в трехмерном евклидовом
пространстве, только в разных системах координат. Умножение матрицы
на вектор в формуле (6.10) дает три скалярных уравнения:
6.2. Координаты ♦ 279
ys = ГА + fi)+ r22(^ + У + rjzw + g,
(6.П)
(6.12)
(6.13)
Проекция из мировой системы координат на плоскость
изображения. Пусть точка трехмерной сцены с мировыми координатами
Pw = (Xw, Yw, ZJ проецируется камерой в точку изображения (х, у) в
системе координат лгу. Аффинное преобразование между мировой системой
координат и системой координат камеры описывается уравнениями
(6.11)—(6.13). Применяя формулу (6.3), получаем уравнение в
координатах камеры:
х~сх
У-су
f
—
Хи
Уи
L/J
=/
x.iz.
Ys/Zs
1
=/
r21(^+/1) + r22(rw + /2) + r23(Zw+r3)
rn(Xw+ti) + rn(Yw+t2) + r33(Zw+t3)
1
, (6.14)
в котором также смоделирован сдвиг в плоскости изображения на
вектор (сх, с , 0) в главную точку в координатах неискаженного
изображения.
6.2.2. Однородные координаты
В общем случае удобнее работать с однородными координатами, а не
с неоднородными, как мы делали до сих пор. Из всех преимуществ
отметим одно: в однородных координатах два шага аффинного
преобразования: умножение на матрицу и сложение с вектором, как в формуле
(6.10), сводятся к единственному умножению на матрицу.
Однородные координаты на плоскости. Прежде чем переходить
к трехмерному пространству, познакомимся с однородными
координатами на плоскости. К двум координатам хиу добавим третью
координату w. В предположении, что w ф 0, запись (хг, у', w) представляет
точку (x'/w, y'/w) в обычных неоднородных координатах; масштабный
коэффициент w несуществен, поэтому мы называем (х', yr, w)
однородными координатами точки (x'/w, y'/w) на плоскости. Очевидно, что для
представления точек на плоскости можно взять w = 1, тогда х = х' и у = у'.
280 ♦ Глава 6. Камеры, координаты и калибровка
Вы, конечно, заметили, что w может быть также равно 0. Однородные
координаты вида (х, у, 1) соответствуют существующим точкам, а
координаты (х, у, 0) - бесконечно удаленным точкам.
Прямые на плоскости. Прямую линию на плоскости теперь можно
представить уравнением
а • х + Ъ • у + 1 • с = [а, Ъ, с]т • [х, у, 1] = 0. (6.15)
Рассмотрим две прямые на плоскости: ух = (av bv сх) иу2 = (а2, Ь2, с2),
записанные в однородных координатах. Они пересекаются в точке с
однородными координатами
Ух х У г = (bic2" b2ci> fl2ci " aic2> аА " a2bi)- (6Л6)
Формула (6.16) называется векторным (или перекрестным)
произведением двух векторов. Если прямые параллельны, то alb2 = а2Ьх;
параллельные прямые пересекаются в бесконечности. В однородных координатах
реальные и бесконечно удаленные точки трактуются единообразно.
Рассмотрим две разные точки рх = (хх, ух, wx) и р2 = (х2, у2, w2); они
определят прямую рххр2 (инцидентны этой прямой). Пусть одна из точек
бесконечно удаленная, скажем, рх = (хх, yv 0). Тогда рх х р2 = (yxw2, xxw2,
хху2 - х2ух) определяет некоторую прямую. Точка рх = (xv ух, 0) является
бесконечно удаленной в направлении [хх, ух]Т.
Если обе точки бесконечно удаленные, т. е. wx = w2 = 0, то мы получаем
бесконечно удаленную прямую рххр2 = (0, 0, хху2 - х2ух); заметим, что в
этом случае хху2 ф х2ух, если рх ф р2.
Пример 6.3. Рассмотрим точку р = (х, у) и параллельный перенос на вектор
t = [tv t2]T в неоднородных координатах на плоскости. Умножение
[1
0
L0
0
1
0
'll
*2\
\\
[х,у,\]Т =[x + tlty + t29lf (6.17)
дает точку (х + tx, у + t2) в неоднородных координатах.
Наблюдение 6.2. Однородные координаты позволяют производить
однозначно определенные вычисления на плоскости, включая и такие, которые было бы
невозможно выразить в неоднородных координатах ху.
Однородные координаты в трехмерном пространстве.
Точка (X, У, Z) G Ш? представляется в однородных координатах в виде
(X', Y, Z', w), где (X, Y, Z) = (X'/w, T/w, Z'/w). Теперь аффинные
преобразования можно представить умножением матриц размера 4*4.
6.5. Калибровка камеры ♦ 281
Пример 6.4. Рассмотрим точку Р = (X, Y, Z) и вектор параллельного переноса
t = [tj, t2, t3]TB неоднородных координатах. Умножение
10 0t
О 1 0 t2
0 0 1/3
0 0 0 1
■[X,Y,Z,l]T =[X + tltY + t2,Z+t3,lf
(6.18)
дает точку (X +tvY+ t2, Z + t3) в неоднородных координатах.
Теперь рассмотрим аффинное преобразование, включающее поворот и
параллельный перенос и описываемое уравнением (6.10). Умножение на
матрицу 4x4
'и
о
'12
Г22
Г32
о
'13
Г23
гзз
0
U
1
[X,Y,Z,\f =
R
0Г
[X,Y,Z,l]T =[Xs,Ys,Zs,lf (6.19)
дает точку (Xs, У, Zs) в неоднородных координатах.
В формуле (6.19) мы ввели в рассмотрение матрицу 4x4, содержащую
подматрицу R размера 3x3, вектор t с тремя столбцами и
вектор-строку 0гс тремя элементами. Мы иногда будем пользоваться этой нотацией
в дальнейшем.
6.3. Калибровка камеры
Калибровка характеризуется внутренними (зависящими от камеры) и
внешними параметрами заданной конфигурации из одной или
нескольких камер.
К внутренним параметрам относятся (эффективное) фокусное
расстояние, размеры матрицы датчиков, размер одного элемента
матрицы или отношение высоты датчика к ширине, параметры радиальной
дисторсии, координаты главной точки или масштабный коэффициент.
Внешние параметры - это параметры аффинных преобразований,
описывающих положения (т. е. местонахождение и ориентацию) камер в
мировой системе координат.
В этом разделе мы дадим обзор калибровки в объеме, достаточном
для того, чтобы вы могли самостоятельно откалибровать камеру с
помощью имеющихся в сети программ и понимали, что при этом
происходит в принципе. Мы не приводим детали какого-то конкретного
метода калибровки, поскольку это выходит за рамки книги.
282 ♦ Глава 6. Камеры, координаты и калибровка
6.3.1. Калибровка камеры сточки зрения пользователя
Производитель камеры обычно сообщает некоторые внутренние
параметры (например, физический размер сенсорных элементов). Но эти
данные зачастую недостаточно точны для использования в
приложениях компьютерного зрения.
Краткое руководство. Для калибровки камеры используются
геометрические фигуры на плоской или трехмерной поверхности,
допускающие очень точное измерение. Например, можно использовать
калибровочную установку, жестко прикрепленную к стене или движущуюся
перед системой камер, которая делает несколько снимков (см. рис. 6.18
6.5. Калибровка камеры ♦ 285
справа). Геометрическая фигура фотографируется, затем мы
локализуем ее в отснятых изображениях и сравниваем с известными данными о
реальной геометрии фигуры.
Калибровку камер можно производить поочередно (если речь идет о
системе из нескольких камер) в предположении, что положение камер
неизменно или что мы калибруем только внутренние параметры.
Обычно в компьютерном зрении имеется подвижная система
нескольких камер, которые калибруются совместно с целью определить
внутренние и внешние параметры. Начинать запись можно после того,
как принято решение, какие параметры калибровать, и в нашем
распоряжении имеется калибровочная установка и необходимое
программное обеспечение. Время от времени калибровку необходимо повторять.
При калибровке системы нескольких камер все камеры должны быть
точно синхронизированы по времени, особенно если калибровочная
установка перемещается во время процедуры.
Релевантные преобразования. С каждой камерой связана своя
система координат, начало которой находится в центре проекции, как
показано на рис. 6.8 справа. Калибровочная установка обычно
используется для определения мировых координат в момент фотографирования
(см. рис. 6.18 справа). Мы должны рассмотреть следующие
преобразования:
1) преобразование из мировой системы координат (Xw, Yw, ZJ в
систему координат камеры (Xs, У, Zs);
2) центральную проекцию (Xs, У, Z) в координаты неискаженного
изображения (хи, уи);
3) дисторсию объектива, которая отображает (хи, уи) в реальные (т. е.
искаженные) координаты (xd, yd); см. рис. 6.17;
4) сдвиг координат xdyd, определяемый главной точкой (хс, ус),
который дает координаты датчика (xs, ys);
5) отображение координат датчика (xs, ys) в координаты
изображения в памяти (х, у) (т. е. фактический адрес пикселя), как показано
на рис. 1.1.
Дисторсия объектива. Отображение трехмерной сцены в точки
двумерного изображения складывается из перспективной проекции и
отклонения от модели камеры-стенопа, вызванного радиальной дистор-
сией объектива (см. раздел 6.1.1).
Правило (упрощенное): если дана точка искаженного объективом
изображения pd = (xd, yd), то мы можем следующим образом получить
соответственную точку неискаженного изображения ри = (хи, уи):
284 ♦ Глава 6. Камеры, координаты и калибровка
хи = сх + (** - ОС1 + Ч\+ Ч\ + е)> (6-20)
Уи = су+ <Уа ~ SX1 + КЛ + Ч\ + еУ)> (6-21)
где (сх, с) - главная точка, a rd = ^(х, -cxf +(yd -cyf.
Ошибки е^ие незначительны, можно считать их равными нулю.
Имеются экспериментальные свидетельства в пользу того, что
аппроксимация посредством разложения в ряд с точностью до двух членов кх и
к2 корректирует более 90% радиальной дисторсии. Если оставить
только член kv то точность позиционирования в массиве датчиков составит
примерно 0,1 пикселя.
Дисторсию объектива необходимо откалибровать для каждой
камеры, и этот процесс можно отделить от всего остального. После того как
дисторсия объектива будет скорректирована, камеру можно
рассматривать как реализацию модели стенопа.
Проектирование метода калибровки. Прежде всего мы должны
определить, какие параметры будем калибровать, и выбрать
соответствующую этим параметрам модель камеры. Например, если требуется
откалибровать параметры радиальной дисторсии кх и к2, то модель
камеры должна включать уравнения (6.20) и (6.21).
Если мы уже знаем параметры радиальной дисторсии и применили
их для преобразования записанных искаженных изображений в
неискаженные, то можем использовать уравнения вида (6.14). Точки (Xw, Yw, Zw)
на калибровочной установке (например, углы квадратов) или
калибровочные маркеры (специальные отметки на трехмерной сцене, на
которой производится калибровка) известны, т. е. мы знаем их измеренные
физические координаты. Для каждой точки (Xw, Yw, Zw) мы должны найти
соответственную ей точку (х, у) (если возможно, то с субпиксельной
точностью), являющуюся проекцией (Xw, Yw, Zw) на плоскость изображения.
Если имеется, например, 100 различных точек (Xw, Yw, ZJ, то мы
получаем 100 уравнений вида (6.14) относительно неизвестных сх, с, /", гп-гъъ,
tv t2 и tr Таким образом, имеется переопределенная система уравнений,
и требуется найти разумную процедуру оптимизации для ее решения.
Мы можем уточнить модель камеры. Например, хорошо бы различать
фокусное расстояние fx в направлении оси х и фокусное расстояние f
в направлении оси у; хорошо бы также включить длины сторон
сенсорных элементов матрицы ех и е в уравнения перехода от координат
камеры в мировых единицах измерения к однородным координатам
камеры в пикселях или учесть коэффициент скоса (shearing factor) s при
вычислении ортогональности записанного изображения.
6.5. Калибровка камеры ♦ 285
Все эти параметры можно включить в базовое уравнение (6.14). Тогда
получающаяся система уравнений станет более сложной и в ней будет
больше неизвестных.
Итак, мы вкратце описали общую процедуру: известные позиции
точек (Xw, Yw, ZJ в мировых координатах сопоставляются с найденными
в записанных изображениях позициями (х, у). Тогда уравнения модели
камеры будут содержать известные величины Xw, Yw, Zw, x, у и
неизвестные внутренние или внешние параметры камеры. Эту систему
уравнений (нелинейных из-за наличия центральной проекции и радиальной
дисторсии) нужно решить относительно всех неизвестных. Поскольку
система переопределена, можно надеяться на устойчивость
применяемой численной схемы решения.
В этой книге мы не будем далее обсуждать эту систему уравнений и
методы ее решения.
Изготовление калибровочной доски. Часто для калибровки
применяется твердая доска с черными и белыми квадратными клетками в
шахматном порядке размера не менее 7*7. Квадраты должны быть
достаточно большими, чтобы их размер на плоскости изображения был не
менее 10х 10 пикселей (зная эффективное фокусное расстояние камеры
/"и расстояние Ъ метров между камерой и доской, мы сможем оценить
размер каждого квадрата а*а в сантиметрах).
Чтобы получить требуемую калибровочную сетку, мы можем
напечатать на листе бумаги черные квадраты одинакового размера и
приклеить его к твердой доске. Метод дешевый и надежный.
Подготовить такую сетку можно в любой графической программе,
главное - чтобы все квадраты были в точности одинаковыми.
Локализация углов на шахматной доске. В случае шахматной
доски калибровочными маркерами являются углы квадратов, а их можно
найти, аппроксимировав точки пересечения линий сетки.
Потенциально мы таким образом можем определить углы квадратов с
субпиксельной точностью.
Предположим, к примеру, что на доску нанесено 10 вертикальных
и 10 горизонтальных линий сетки, как на рис. 6.18 справа. Тогда в
пространстве Хафа da должно получиться 10 + 10 пиков, соответствующих
отрезкам прямых. Каждый пик определяет одну линию сетки, а их точки
пересечения определяют углы клеток шахматной доски в записанном
изображении.
Для применения этого метода нужно предварительно устранить
эффект дисторсии объектива из изображения, иначе вместо идеально
прямых линий сетки мы получим искривленные.
286 ♦ Глава 6. Камеры, координаты и калибровка
Локализация калибровочных маркеров. Калибровочная фигура
может содержать и другие маркеры, например круглые или
квадратные точки. Такие фигуры часто применяются, когда калибруются
камеры, занимающие неизменное положение, так что маркеры можно
раз и навсегда нарисовать на стенах или других неподвижных
поверхностях.
Предположим, что мы нашли участок изображения S (допустим,
полутонового), содержащий калибровочный маркер. Его положение
можно затем определить с субпиксельной точностью, вычислив центроид
этого участка, как обсуждалось в примере 3.7.
6.3.2. Ректификация пар стереоизображений
Рассмотрим записывающую систему с двумя камерами, описанную в
разделе 6.1.3. Это стандартная конфигурация стереоскопического
зрения - базовой процедуры, позволяющей получить данные о
расстоянии, располагая только визуальной информацией.
Сложность стереоскопического зрения связана главным образом с
задачей нахождения соответственных точек в парах входных
изображений, записанных двумя камерами. Эта задача - предмет главы 8.
Чтобы упростить ее, удобно трансформировать пары записанных
изображений так, чтобы казалось, будто они созданы в канонической
конфигурации системы стереоскопического зрения (двумя идентичными
камерами). Этот процесс называется геометрической ректификацией,
без упоминания о стереоскопическом зрении (поскольку
ректификация применяется и в других контекстах).
Система с несколькими камерами. Часто для применения
компьютерного зрения в сложных окружающих условиях или процессах двух
камер недостаточно. Например, в помещении для испытания
автомобилей на безопасность при столкновении (краш-тестов)
устанавливается много высокоскоростных камер высокой четкости, записывающих
несколько секунд испытания под разными углами. На рис. 6.19
показано два геометрически ректифицированных изображения. Как это
можно сделать?
Мы дадим ответ на данный вопрос в этом подразделе. Не будем
ограничиваться только левой и правой камерами, а рассмотрим общий
случай камеры i и камеры /, где / и / - номера различных камер в системе с
несколькими камерами.
6.3. Калибровка камеры ♦ 287
Рис. 6.19. Вверху: изображения, записанные двумя камерами с существенно
различными внешними параметрами и (незначительно) различающимися
внутренними параметрами. Внизу: два геометрически ректифицированных
изображения, снятых с разных точек двумя камерами, установленными в
помещении для краш-тестов
Матрица камеры. В качестве примеров внутренних параметров
камеры i будем рассматривать:
1) длины сторон е] и е\ сенсорных элементов;
2) параметр скоса s.;
3) координаты главной точки с. = (с*, ср, в которой оптическая ось
камеры / пересекает плоскость изображения; и
4) фокусное расстояние f..
Предполагается, что дисторсия объектива уже откалибрована и
включать ее в состав внутренних параметров больше не нужно.
Вместо простого уравнения (6.14), описывающего модель камеры
только на основе внутренних параметров f, сх и с, мы теперь имеем
уточненное уравнение проекции в 4-мерных однородных координатах,
которое отображает точку Р = (Xw, Yw, Zw) в точку изображения р. = (х.у у.)
в координатах /-й камеры (см. рис. 1.1):
288
Глава 6. Камеры, координаты и калибровка
1
О file!
О О
о
о
о
тл
I I
-R;t
1
Yw
1
= [KJO].Ar[Xw,Fw,Zw,lf,
(6.22)
где R. и t. - матрица поворота и вектор параллельного переноса в
трехмерных неоднородных мировых координатах, а к f 0 - масштабный
множитель.
Уравнение (6.22) определяет матрицу внутренних параметров К.
размера 3x3 и матрицу внешних параметров (аффинного преобразования)
А. размера 4*4 камеры /. Матрица камеры
С. = [К. | 0] • А. (6.23)
размера 3*4 определяется 11 параметрами, если мы допускаем
произвольный масштаб параметров, и 12 в противном случае.
Общее направление визирования для ректификации камер i и/.
Мы найдем общее направление визирования для камер i и /, заменив
направления вдоль оптических осей обеих камер. Пусть П - плоскость,
перпендикулярная вектору базовой линии Ьг, соединяющему центры
проекции камер /и/(см.рис. 6.20).
Камера j
Рис. 6.20. Иллюстрация
вычисления общего
направления визирования
для камер /' и у
6.5. Калибровка камеры ♦ 289
Спроецировав единичные векторы г°и г°обеих оптических осей на Я,
получим векторы п. и п. соответственно. Алгебраические соотношения
выглядят так:
п. = (Ь х z°) х Ъ.. и п = (Ь х z°) х b . (6.24)
Можно было бы использовать в обоих уравнения b., но только во всех
четырех местах сразу.
Стремясь к «балансированию» обеих камер, мы используем биссек-
тор векторов п. и п. для определения единичного вектора общего
направления
п. + п.
h+nji
Рассмотрим единичный вектор х°, направленный так же, как Ьг, и
единичный вектор у°, который однозначно определен условием
левостороннее™ (к примеру) трехмерной декартовой системы координат.
Формально имеем
b
'if ~ "
х, =й-Л- и у° = z х х° = -х° х z... (6.26)
ь«
Вообще, для любых двух векторов а и b (a, b, a * Ь) является
левосторонней координатной тройкой, показывающей ориентацию осей х, у, z.
Тройка (х°., z°. х х°, z°.) левосторонняя, потому что
ц> ц
Х° х (z° х х°) = Z°(X0 • Х°) - Х0(Х° • Z°) = Z°, (6.27)
i) v i] ц' ip ij ly yv ;/ ly ly v '
а тройка (x°, x° x z°, z°) была бы правосторонней.
Оба изображения - с камер /и/- необходимо модифицировать так,
будто оба сняты с направления R.. = (х.. у., z Jr, а не с направлений R. и R.,
как на самом деле.
Создание ректифицированной пары изображений. Матрицы
поворота, приводящие обе камеры к новому (виртуальному)
направлению визирования, имеют вид
R*. = R..Rr и R*. = R.RT. (6.28)
Вообще, при повороте камеры вокруг ее центра проекции,
описываемого матрицей R, изображение подвергается преобразованию
поворотной гомографии (проективному преобразованию)
Н = К R К"1, (6.29)
290 ♦ Глава 6. Камеры, координаты и калибровка
где К - матрица внутренних параметров камеры размера 3*3. Матрица
К1 преобразует координаты пикселей в систему координат камеры в
мировых единицах измерения, матрица R поворачивает их в
плоскости, после чего матрица К возвращает координаты пикселей.
Ректифицированное изображение вычисляется попиксельно по
формуле
р = Н!р, (6.30)
так что новое значение в позиции пикселя р вычисляется по значениям
исходного изображения в окрестности точки р (которая в общем случае
не совпадает с позицией пикселя) с применением, например,
билинейной интерполяции.
Создание идентичного близнеца. Допустим, мы хотим получить
изображение с камеры / после преобразования поворотной
томографии относительно параметров камеры /, т. е. создать копию камеры / в
положении, занимаемом камерой /. Для этого нужно просто применить
поворотную томографию
Н^КГК:1, (6.31)
т. е. сначала с помощью умножения на матрицу К:1 преобразуем точки
в плоскости изображения с камеры / в «нормализованную» систему
координат, затем производим поворот R* в нужное положение и, наконец,
умножаем на матрицу К., чтобы преобразовать результат поворота в
соответствии с параметрами матрицы /.
Врезка 6.4 (фундаментальная и существенная матрица в системах
стереоскопического зрения). Опираясь на публикацию X. К.Логе-Хиггинса (Н. С. Longuet-
Higgins) 1981 г.,К.Т.Луонг(О.Т.1_иопд) в своей докторской диссертации 1992 г.
определил две матрицы, фундаментальную и существенную, которые
описывают геометрию бинокулярной стереоскопической системы - с учетом и без
учета характеристик используемых камер соответственно.
Фундаментальная и существенная матрица. Вернемся к случаю,
когда есть только левая и правая камеры. Обозначим pL и pR
соответственные стереоточки, т. е. проекции точки трехмерного пространства Р
на плоскости левого и правого изображений. Предположим, что pL и pR
заданы в однородных координатах. Тогда имеем
pI-*-pl = o
(6.32)
6.5. Калибровка камеры
291
для некоторой матрицы F размера 3x3, определенной конфигурацией
(внутренними и внешними параметрами) обеих камер, и это
справедливо для любой пары соответственных стереоточек pL и pR.
Матрица F называется фундаментальной матрицей, а также эпипо-
лярной матрицей или бифокальным тензором. Например, произведение
F • pL определяет прямую на плоскости изображения с правой камеры, и
любая стереоточка, соответствующая pL, должна лежать на этой прямой.
(Это так называемая эпиполярная прямая, о которой мы еще
поговорим ниже.)
Матрица F имеет ранг 2 и определена однозначно (левой и правой
камерами) с точностью до масштабного коэффициента. В общем случае
для нахождения матрицы F достаточно семи пар соответственных
точек (находящихся в общем положении). Существует связь
F = Кт
ВД,
к,"1
(6.33)
между матрицами KR и Кг Мы переходим от координат пикселей к
координатам камеры в мировых единицах измерения. Здесь [t]x
обозначает матрицу векторного произведения вектора t: [t]x • а = t * а, или
Мх =
О -U
h
-и
Матрица
О
Е = R[t],
-ч
о
(6.34)
(6.35)
называется существенной матрицей, у нее имеется пять степеней
свободы, и она определена однозначно (левой и правой камерами) с
точностью до масштабного коэффициента.
Врезка 6.5 (геометрия системы с несколькими камерами). В этой главе были
приведены основные сведения, относящиеся к геометрии систем с одной и
несколькими камерами. Стандартными справочными руководствами по
геометрической проблематике компьютерного зрения считаются, например,
книги [R. Hartley and A.Zisserman.Mu[t\p[eV\e\N Geometry in Computer Vision, Second Edition.
Cambridge University Press, Cambridge, 2004] и [К. Kanatani. Geometric Computation for
Machine Vision. Oxford University Press, Oxford, 1993].
292 ♦ Глава 6. Камеры, координаты и калибровка
6.4. Упражнения
6.4.1. Упражнения по программированию
Упражнение 6.1 (вычисление характеристик камер). Возьмите по
крайней мере две разные цифровые камеры и вычислите для них
следующие характеристики:
1) точность цветопередачи;
2) линейность;
3) дисторсию объектива.
Интерес могут представлять даже две камеры одной модели, скорее
всего, их характеристики будут немного различаться.
Спроектируйте, обсчитайте и распечатайте по меньшей мере одно
тестовое изображение (испытательную таблицу) для каждой
характеристики. Попробуйте обосновать свой выбор тестовых изображений.
Очевидно, что на результаты тестов влияет качество принтера.
Проведите измерения несколько раз при изменяющихся условиях
(например, устанавливайте тестовые изображения или другие
тестовые объекты на разных расстояниях от камеры при разном освещении).
Далее необходимо будет выполнить статистический анализ (вычислить
средние и стандартные отклонения в серии испытаний).
Отметим, что сравнение характеристик обычно не приводит к
простому выводу типа «эта камера лучше той». Результат формулируется не
так однозначно, например: «по такому-то критерию эта камера лучше
при таких-то условиях».
Упражнение 6.2 (сшивка изображений). Используя стандартную
цифровую камеру (матричную или стеноп), установленную на
треножнике, сделайте серию фотографий, поворачивая камеру.
Последовательные изображения сцены должны немного перекрываться.
Самостоятельно напишите простую и бесхитростную программу
сшивки изображений на поверхности цилиндра или в прямоугольную
панораму. Первым шагом должна быть регистрация изображений, т. е.
их пространственное выравнивание и определение мест разреза. На
рис. 6.21 показаны шаги регистрации и сшивки.
(Сшивка изображений - область, в которой уже опубликовано много
решений, поищите идеи в сети.)
Для сравнения возьмите какую-нибудь коммерческую или свободно
доступную программу сшивки (зачастую они входят в комплект
поставки камеры или их можно скачать с сайта производителя), которая умеет
6.4. Упражнения ♦ 293
создавать из изображений панораму с обзором 360°. Сравните
полученные результаты с результатами вашей программы.
Рис. 6.21. Вверху: зарегистрированные изображения. Внизу: сшитые изображения.
Результаты проекта, выполненного в 1998 г. в Оклендском университете
Упражнение 6.3 (стереопанорама). Поворачивая видеокамеру на
треножнике, создайте стереопанорамы, как описано в конце раздела 6.1.4.
Выбирать столбцы для генерации видов с углами визирования со и -со
следует аккуратно; они должны быть симметричны относительно
главной точки видеокамеры. В противном случае сгенерированная из двух
видов панорама не будет иметь правильной геометрии, необходимой
для стереоскопического просмотра.
Что касается выбора радиуса R и угла визирования со, существует два
рекомендуемых значения, которые максимизируют количество
уровней диспаратности между ближайшим интересным объектом,
расположенным на расстоянии Dv и самым отдаленным, расположенным на
расстоянии Dr Эти два (однозначно определенных) значения можно
найти во второй из книг, упомянутых во врезке 6.2. Можете также
поэкспериментировать с другими значениями R и со.
Чтобы сгенерированные стереопанорамы можно было
просматривать с помощью стереоскопических очков, используются анаглифы.
Анаглифические изображения генерируются путем объединения
красного канала из одного изображения с синим и зелеными каналами из
другого изображения. Порядок фильтров в имеющихся анаглифных
стереоскопических очках определяет, какой канал берется из какого
изображения. Продемонстрируйте созданные вами стереопанорамы с
помощью анаглифных очков.
Упражнение 6.4 (нахождение калибровочных маркеров). Запишите
изображения для калибровки камеры, используя шахматную доску, как
294
Глава 6. Камеры, координаты и калибровка
описано во врезке 6.3. Напишите сами или возьмите готовую
программу для выделения прямых линий (см. раздел 3.4.1) и найдите в
записанных изображениях углы с субпиксельной точностью. Обсудите влияние
радиальной дисторсии на правильность определения углов.
Упражнение 6.5 (конструирование камеры-стенопа). Это не
упражнение по программированию, а практическая задача для тех, кто хотел
бы поэкспериментировать с простейшей из возможных камер, которую
можно изготовить самостоятельно, имея лишь коробку из-под обуви и
фоточувствительную бумагу. Поищите в сети «pinhole cameras» (стеноп,
пинхол, камера с точечной диафрагмой) - и вы получите как
практические советы, так и интересную подборку фотографий, снятых такими
камерами.
6.4.2. Упражнения, не требующие программирования
Упражнение 6.6. Найдите в этой главе уравнения, записанные в
неоднородных координатах, и перепишите их в однородных.
Упражнение 6.7. Опишите бесконечно удаленную точку на прямой
31а: + 5у -12 = 0. Запишите уравнение этой прямой в однородных
координатах. В какой бесконечно удаленной точке эта прямая пересекается
с прямой 31а: + 5у - 14 = 0?
Обобщите результат, изучив прямые ах + by + сх = 0 и ах + by + с2 = 0
при сх ф с2.
Упражнение 6.8. Рассмотрим камеру, описываемую следующей
матрицей камеры 3x4:
С =
Вычислите проекции следующих точек (в мировых координатах) при
фотографировании такой камерой:
р,=
1
0
0
0
1
0
0
0
1
0
0
1
1
1
1
1
> р2 =
1
1
-1
1
> Рз =
3
2
1
1
. Р4 =
0
0
0
1
6.4. Упражнения ♦ 295
Упражнение 6.9. Пусть р = [х, у, 1]т и р = [х', у', 1]т. Уравнение
можно записать в эквивалентной форме:
[хх' ху' х ух' уу' у х' у' 1]
К
11
К
21
К
31
К
12
К
22
К
32
Я
13
F
I 23
■ F .
L зз J
= 0,
где F.. - элементы фундаментальной матрицы F. Предположим теперь,
что имеется по меньшей мере восемь пар соответственных пикселей,
определяющих матричное уравнение
Л/1 «Л/1
Jv"-yJv"-y
ЗД ^1 Уххх УхУх Ух хх
^гУг Х2 У 2х г У2У2 У 2 Х2
х х' х у' х ух' у у' у
п п ns п п sn п у ns п уп
X.,
Ух
У2
Уп
1]
1
lj
\¥Л
\?2Х
F
L зз _
=
"°1
0
_oJ
где п > 8, которое можно кратко записать в виде А • f = 0. Решите это
уравнение относительно неизвестных F.., учитывая шум или неточное
определение пар соответственных пикселей.
Упражнение 6.10. Докажите истинность следующих утверждений
для любого ненулевого вектора t е Жъ:
1) Мх • t = 0;
2) ранг матрицы [t]x равен 2;
3) ранг существенной матрицы Е = R[t]x равен 2;
4) фундаментальная матрица F связана с существенной матрицей Е
формулой F = К^ЕК^1;
5) ранг фундаментальной матрицы F равен 2.
Глава
Трехмерная реконструкция
В этой главе описаны три разных метода реконструкции трехмерных
тел с помощью компьютерного зрения. Применение
структурированной подсветки - сравнительно простой и при этом точный метод.
Стереоскопическое зрение тоже можно назвать методом трехмерной
реконструкции - возникающие при этом проблемы сопоставления
стереоизображений рассматриваются в следующей главе, а здесь мы только
обсудим, как результаты такого сопоставления можно использовать для
реконструкции трехмерного тела. Наконец, мы кратко опишем, как
составить представление о форме трехмерного тела на основе затенения.
7.1. Поверхности
Цель компьютерного зрения - реконструкция и анализ видимого мира,
как правило, состоящего из текстурированных поверхностей (мы не
рассматриваем полностью или частично прозрачные объекты).
В этом разделе дается введение в топологию поверхностей,
параметрическое описание участков поверхностей и градиентное
пространство - модель для анализа соотношений между нормалями к
поверхностям. Мы также определим кривизну поверхности.
Врезка 7.1 (трехмерная визуализация города или ландшафта). Начиная
примерно с 2000 г. для создания крупномасштабных и очень детальных
трехмерных визуализаций города или ландшафта (см. пример на рис. 7.1) применяются
фотографические или лазерные дальномеры. Такие трехмерные
визуализации - шаг вперед по сравнению с двумерным представлением земной
поверхности (с помощью аэрофотосъемки) или с объединением изображений
улиц, на которых отсутствуют трехмерные здания и геометрические
особенности улиц. Соответствующие технологии компьютерного зрения описаны в
книге [F. Huang, R. Klette and К. Scheibe. Panoramic Imaging. Wiley, West Sussex, 2008].
7.1. Поверхности ♦ 297
Рис. 7.1. Слева: поверхности, реконструированные по данным аэрофотосъемки.
Справо:те же поверхности после наложения текстуры на записанные изображения.
Показан центр Sony в Берлине, Германия
7.1.1. Топология поверхности
Поверхность S (также край или границу) трехмерного тела можно
описать следующим образом:
1) гладкая поверхность, в каждой точке которой Р е S (а) существует
непрерывная производная в любом направлении вдоль S и (Ь)
существует принадлежащая 5 окрестность, топологически
эквивалентная1 кругу; или
2) поверхность многогранника, состоящая из плоских
многоугольников (например, треугольников). На ребрах многогранника
имеются разрывы, но по-прежнему для каждой точки Р е S
существует принадлежащая 5 окрестность, топологически эквивалентная
кругу.
Существование для любой точки Р б S окрестности, которая целиком
принадлежит S и топологически эквивалентна кругу, означает, что
поверхность 5 не имеет дырок, через которые «можно было бы заглянуть
внутрь тела». См. рис. 7.2 в середине и справа.
В первом случае мы говорим о гладкой поверхности без дырок.
Например, таковыми являются поверхности сферы и тора. Во втором случае
мы говорим о поверхности многогранника без дырок, см. рис. 7.2 слева.
Поверхность, изображенная на рис. 7.1 слева, построена методом
триангуляции; одной из граней является земная поверхность, на которой
возведены здания, а также все вертикальные поверхности строений (см.
1 Два множества в евклидовом пространстве называются топологически эквивалентными, если
существует гомеоморфное преобразование (гомеоморфизм) одного на другое;
гомеоморфизмом называется непрерывное взаимно однозначное преобразование, обратное к которому
также непрерывно.
298 ♦ Глава 7. Трехмерная реконарукция
также рис. 7.4). Мы можем рассматривать ее как поверхность без дырок
при условии отсутствия дырок в вычисленной триангуляции.
Рис. 7.2. Слева: поверхность многогранника без дырок. В середине и справа: две
гладкие поверхности с дырками; поверхность сферы с несколькими вырезанными
круговыми участками и поверхность тора с одним вырезанным круговым участком
С точки зрения топологии поверхности, не имеет значения,
является участок поверхности многогранным или гладким. Под поверхностью
без дырок может пониматься как первая, так и вторая в зависимости от
контекста. Топологически оба случая эквивалентны.
Ориентируемые поверхности. Ориентированным треугольником
называется треугольник с заданным направлением границы - по
часовой стрелке или против часовой стрелки, - которое называется
ориентацией. Ориентация треугольника индуцирует ориентации его сторон.
Два треугольника, входящие в триангуляцию, называются когерентно
ориентированными, если они индуцируют противоположные
ориентации на общей стороне.
Триангуляция поверхности называется ориентируемой, если
возможно ориентировать все составляющие ее треугольники так, что любые
два треугольника, имеющих общую сторону, будут ориентированы
когерентно. В противном случае триангуляция называется неориентируе-
мой.
Триангуляция ориентируемой поверхности может иметь только
одну из двух возможных ориентации; выбрав ориентацию одного
треугольника, мы однозначно определяем ориентацию всей триангуляции
(рис. 7.3). Если Zj и Z2 - триангуляции одной и той же поверхности, то Zx
ориентируема тогда и только тогда, когда Z2 ориентируема.
Наблюдение 7.1. Поскольку ориентируемость не зависит от триангуляции,
мы можем ввести определение: поверхность называется ориентируемой, если
для нее существует ориентируемая триангуляция. Отметим также, что
7.1. Поверхности ♦ 299
«ориентация» (поверхности) и «направление» (вектора) - это разные
математические понятия.
Рис. 7.3. Слева: выбрав ориентацию синего треугольника, мы тем самым
определили ориентации всех прочих треугольников, составляющих триангуляцию
поверхности без дырок. Добавьте отсутствующие ориентации на верхней
грани куба. Справа: лист Мёбиуса - пример неориентируемой поверхности.
Показанную на рисунке синюю линию можно продолжить, так
что получится петля, проходящая по всем граням поверхности
Эйлерова характеристика поверхности. Обозначим а0, av a2 -
число вершин, ребер и треугольных граней в триангуляции Z поверхности.
Эйлерова характеристика Z равна
Х(г) = а0-аг + а2. (7.1)
См. врезки 3.1 и 7.2. У любых двух триангуляции одной и той же
поверхности эйлерова характеристика одинакова. Этот факт позволяет
говорить об эйлеровой характеристике самой поверхности. Эйлерова
характеристика - топологический инвариант, т. е. топологически
эквивалентные поверхности имеют одинаковые эйлеровы характеристики.
Эйлерова характеристика уменьшается с ростом топологической
сложности поверхности; для одиночной (т. е. связной) поверхности
максимальное значение равно 2. Какова эйлерова характеристика
поверхности на левом рис. 7.3?
Пример 7.1 (эйлерова характеристика поверхности куба и сферы).
Поверхности куба и сферы топологически эквивалентны. Каждую грань куба можно
разбить на два треугольника. Получается 8 вершин, 18 ребер и 12 треугольников,
поэтому эйлерова характеристика такой триангуляции равна 2. Поверхность
сферы можно разбить на четыре криволинейных треугольника (рассмотрим
вписанный в сферу тетраэдр, его вершины и будут вершинами этих четырех
треугольников); получается 4 вершины и 6 простых дуг, так что эйлерова
характеристика снова равна 2.
500 ♦ Глава 7. Трехмерная реконструкция
Врезка 7.2 (эйлерова характеристика, числа Бетти и жордановы поверхности).
О топологии евклидова пространства уже заходила речь во врезке 3.6.
Рассмотрим связное компактное множество S в Шъ. Его край называется
поверхностью. Множество может иметь полости, не связанные с неограниченным
дополнением к множеству, а также ручки.
Родом g(S) поверхности S называется максимальное число разрезов, при
котором поверхность еще не теряет связность. Например, род сферы равен О,
а род тора - 1.
Для связного компактного множества 5 в Шъ (например, сферы с п ручками)
самым простым комбинаторным топологическим инвариантом является
эйлерова характеристика j. Если поверхность связная (T.e.SHe имеет полостей),то
X(S) = 2 - 2 • g(5).
Эйлерова характеристика поверхности сферы (или результата ее
топологической деформации, например поверхности куба) % = 2. Для поверхности тора
эйлерова характеристика j = 0. Если поверхность S несвязная и имеет b Z 2
краевых компонент (т. е. b - 1 полостей),то
X(S) = 2-2-g(S)-(b-l).
Теперь рассмотрим поверхность 5 ограниченного многогранника общего
вида в Е3 (т. е. ограниченное множество, край которого состоит из конечного
множества плоских многоугольников). Тогда
X(S) = a2(S) - at(S) + a0(S) - (b - 1),
где b - число компонент связности S; о смысле а0, ах и а2 см. врезку 3.1.
С другой стороны, в случае b = 1 справедлива также формула
X(S) = /?2(S) - /^(S) + /?0(S),
где /?0, (Зг\л Р2- числа Бетти множества S, названные так в честь итальянского
математика Э. Бетти (1823-1892); /?0 - число компонент связности, j51 - число
«туннелей» («туннель» - это интуитивное понятие, строгое определение рг;
см., например, в главе 6 книги [/?. KLette and A. RosenfeLd. Digital Geometry. Morgan
Kaufmann,San Francisco, 2004]), a /?2 - число полостей. Например, для
поверхности тора Р0 = 1 (она связная), (31-2 (один туннель внутри поверхности,
проходящий через «дырку бублика»), /?2 = 1 (внутренность поверхности).
Жорданова поверхность (К. Жордан, 1887) определяется как параметризация,
описывающая топологическое отображение на поверхность единичной
сферы. В компьютерном зрении нас обычно не интересует глобальная
параметризация поверхностей (важно только поведение в локальной окрестности).
Как правило, общего топологического определения поверхности достаточно.
Согласно теореме Гавейна (I. Gawehn), доказанной в 1927 г., любая гладкая
поверхность без дырок топологически эквивалентна поверхности
многогранника без дырок.
7.1. Поверхноаи ♦ 501
Разделение трехмерного пространства жордановой
поверхностью. В разделе 3.1.1 мы обсуждали разделения в двумерном
евклидовом пространстве 12ив дискретном изображении. Жорданова кривая
топологически эквивалентна окружности, а жорданова поверхность -
поверхности сферы. В 1911 г. Л. Э. Я. Брауэр доказал, что любая
жорданова поверхность разделяет пространство Ш3 с евклидовой топологией
на два связных подмножества, при этом сама жорданова поверхность
является краем (или границей) обоих подмножеств.
7.1.2. Локальные параметризации поверхности
В компьютерном зрении мы обычно не интересуемся глобальными
параметрическими представлениями видимых поверхностей. Для
обсуждения методов реконструкции полезны локальные
параметризации.
Представление участков поверхности. Гладкую поверхность или
многогранник можно разбить на (связные) участки. Линейные участки
поверхности (называемые также гранями, например треугольные грани
триангулированной поверхности) лежат в плоскости Z=aX+bY+c
(инцидентны этой плоскости).
Рельефной картой (elevation map) называется восстановленная
поверхность на прямоугольном участке S земной поверхности такая, что
каждой точке Р = (X, Y, Z) восстановленной поверхности взаимно
однозначно соответствует точка р = (X, У) е S (см. рис. 7.4). Локальный
участок рельефной карты может быть задан в виде явного представления
Z = Fe(X, У), где плоскость XY соответствует земной поверхности, или
неявного представления FfX, У, Z) = 0. В случае участка гладкой
поверхности мы предполагаем, что функции в явном или неявном
представлении непрерывно дифференцируемы (до нужного порядка).
Пример 7.2 (поверхность сферы). Видимая поверхность сферы в координатах
камеры XYZs записывается в виде
*, =Fe&, У) = а~ ^2-X2s-Y2 (7.2)
в предположении, что сфера расположена перед плоскостью изображения
Zs = fy а в неявном виде поверхность той же сферы представляется в виде
F.(X,y,Z)=X2s + Y2s + (Z-fl)2-r2 = 0, где a-r>f. (7.3)
502 ♦ Глава 7. Трехмерная реконарукция
\^ I \ ^^ ^\ р I ^ ^3^
Рис. 7.4. Показанную восстановленную поверхность можно рассматривать как
один участок либо как поверхность, состоящую из многих гладких или линейных
участков (например, в случае триангуляции). Слева: две видимые вертикальные
грани V1 и Vr Справа: точка р на участке S земной поверхности, взаимно
однозначно соответствующая точке Рна восстановленной поверхности
Евклидово расстояние от точки поверхности Р = (Xs, У, Zs) до центра
проекции камеры О = (0,0,0) равно d2(P, О) = | |Р| |2. Глубина Р равна Zs, это
положение Р на оптической оси. Можно также предполагать наличие
заднего плана Z=c позади (или ниже) видимых поверхностей, тогда
высота Р равна разности с - Zs. Таким образом, восстановленную
поверхность можно визуализировать в виде карты расстояния, карты глубины
или карты высоты, применяя выбранный цветовой ключ для
наглядного представления значения. На рис. 7.5 справа приведен пример карты
глубины, на котором также видна геометрическая сложность реальных
поверхностей.
Рис. 7.5. Слева: исходное изображение Bridge для приложения реконструкции
поверхностей (с помощью стереоскопического зрения). Справа: визуализация
карты глубины с применением цветового ключа в правой части. Если нет
уверенности в реконструированной глубине,то соответствующий пиксель окрашен
серым. Шкала значений цветового ключа - от 5,01 до 155 (она нелинейна,
значение 10,4 находится примерно посередине), это расстояния в метрах
7.1. Поверхности ♦ 505
Нормали к поверхности. Градиентом поверхности Z = Fe(X, Y)
называется вектор
-|Т
VZ = grad Z =
dz az
эх'эг
(7.4)
Для плоскости aX+bY+ Z=c градиент равен [а, Ь].Нормаль
описывается уравнением
-|Т
п =
dz az
эх'эг
1
= [яА1] •
(7.5)
Как и в формуле (1.16), мы приняли соглашение о том, что нормаль
направлена в сторону от плоскости изображения, поэтому третья
компонента равна+1.
Единичная нормаль (длины 1) описывается уравнением
о Г 1Т П
п = и,, и,, и, = -п—п- =
nl
[аД1]
п—i— (7-6)
В формулах (7.5) и (7.6) мы также использовали параметры а и Ъ для
обозначения компонент нормали.
Рассмотрим сферу радиуса 1 с центром в начале координат О (ее
еще называют гауссовой сферой), показанную на рис. 7.6. Угол между
вектором п° и осью Z называется полярным углом и обозначается а. Угол
между вектором, исходящим из О и заканчивающимся в точке Р = (X, Y, 0),
и осью X называется азимутальным углом и обозначается в. Точка Р
удалена от О на расстояние sin а. Единичная нормаль п° пересекает
поверхность гауссовой сферы в точке, однозначно определяемой углами
(а, в), которые называются сферическими координатами точки.
Рис. 7.6. Гауссова сфера с радиусом 1
Градиентное пространство. Определим пространство аЪ (рис. 7.7
справа), в котором каждая точка {а, Ъ) представляет градиент (а, Ъ) в
504 ♦ Глава 7. Трехмерная реконарукция
пространстве XYZ (например, с мировыми координатами) объектов
сцены. Это так называемое градиентное пространство.
<АА)'
(я >ь)
4V 2' 2/
/Р^
а
о
Рис. 7.7. Слева: Две ортогональные нормали к поверхности в пространстве
сцены XYZ. Справа: градиентное пространство ab, иллюстрирующее
значения р и q нормалей п1 и п2
Например, рассмотрим плоскость Z = аХ + bY + с. Тогда точка (а, Ъ)
представляет в градиентном пространстве все плоскости,
параллельные данной (т. е. с любыми значениями с £ Ж).
Рассмотрим нормаль iij = [av bv 1]T в пространстве XYZ, которая
отображается в точку (flj, b2) в градиентном пространстве, и нормаль п2 =
[а2, Ь2, 1]т, ортогональную nr См. рис. 7.7 слева. Согласно определению
скалярного произведения векторов:
nrn2 = flia2 + foA+1 = Hnill2
П
2И2
cos — = 0.
2
(7.7)
Предположим, что вектор пг задан и мы хотим охарактеризовать
направление ортогонального вектора п2. Для заданных ах и Ьх мы
имеем прямую у в градиентном пространстве, определенную уравнением
аха2 + Ьр2 + 1 = 0, в котором а2 и Ъ2 - неизвестные. Геометрически ее
можно описать следующим образом:
1) прямая, проходящая через начало координат о = (0, 0) и точку р,
ортогональна прямой у;
2) Ja? + Ъ] = d2((av Ъх), о) = Щ(р, о);
3) точки р и (ар Ьх) находятся в противоположных квадрантах.
Прямая у определяется этими условиями однозначно. Она
называется двойственной прямой к нормали пх или к точке (аг, Ъх). Любое
направление п2, ортогональное п^ сонаправлено прямой у.
7.1.3. Кривизна поверхности
Этот подраздел адресован читателям, интересующимся
математикой. В нем вы найдете руководство по анализу кривизны поверхностей,
7.1. Поверхности ♦ 505
реконструированных методами компьютерного зрения.
Приведенные здесь определения кривизны не используются далее нигде, кроме
упражнений 7.2 и 7.6. Существует несколько способов определить
кривизну в точке поверхности.
Гауссова кривизна. К. Ф. Гаусс определил кривизну поверхности в
точке Р, введя в рассмотрение «малые» участки поверхности Se радиуса
е > 0 с центром в Р. Для выбранного S£ обозначим Re множество концов
единичных нормалей к поверхности в точках О е Se; множество R£
образует участок на поверхности единичной сферы. Теперь положим
(7.8)
где <А обозначает площадь. Этот предел называется гауссовой кривизной
в точке поверхности Р.
Нормальная кривизна. Мы определим также две часто
используемые главные кривизны Хх и А2 в точке Р на гладкой поверхности. Но
прежде определим, что такое нормальная кривизна.
Пусть Aj и Л2 - две различные дуги на данной поверхности, которые
пересекаются в точке Р, и пусть tx и t2 - касательные векторы к Лх и Я2
в точке Р. На эти векторы натянута касательная плоскость Пр в точке Р.
Будем рассматривать углы 0^г]<ттвПр (полуокружность с центром в Р).
Нормаль к поверхности пр в точке Р ортогональна плоскости Пр и кол-
линеарна векторному произведению t^l^. Пусть П - плоскость,
содержащая пр и расположенная под углом г\ (рис. 7.8).
Рис. 7.8. Сечение поверхности плоскостью |~|
П образует двугранный угол rj с Пр и пересекает поверхность по
дуге у . (П может пересекать поверхность по нескольким дугам, но мы
506 ♦ Глава 7. Трехмерная реконарукция
рассматриваем только ту, которая содержит точку Р.) Обозначим t, n и
к касательную, нормаль и кривизну у в точке Р.
Кривизна к любой дуги у с Г п П , проходящей через Р, называется
нормальной кривизной в точке Р.
Пример 7.3 (два примера нормальной кривизны). Рассмотрим
горизонтальную плоскость в Ш?, проходящую через точку Р = (О,0,0). Любая дуга у является
отрезком прямой в этой плоскости, проходящим через (0,0,0); имеем Я = 0 и
t =у .
Рассмотрим «колпачок» сферы с центром в северном полюсе Р, тогда у -
отрезок большого круга на сфере, п лежит на прямой, проходящей через Р и
центр сферы, ак = 1/г, где г - радиус сферы.
Главные кривизны. Напомним, что характеристический
полином р матрицы А размере п*п определен формулой р(Я) = det(A - Я1) =
(-Я)" + ... + det(A), где I - единичная матрица п*п. Собственные
значения Я. матрицы А - это п корней ее характеристического полинома, т. е.
уравнения det(A - Я1) = 0.
Пусть v - единичный вектор на плоскости Пр. Взятая с обратным
знаком производная -Dvii векторного поля п единичных нормалей к
поверхности, рассматриваемая как линейное отображение Пр в себя,
называется оператором формы (также отображением Вейнгартена или
вторым фундаментальным тензором) поверхности.
Обозначим Мр матричное представление отображения
Вейнгартена в точке Р (в произвольном ортонормированном базисе Пр), и пусть
Я1 и Я2 собственные значения матрицы Мр размера 2*2. Заметим, что
собственные значения не зависят от выбора ортонормированного
базиса Пр.
Тогда Я1 и Я2 называются главными кривизнами заданной поверхности
в точке Р.
Формула Эйлера. Пусть wt и w2 - два ортогональных вектора,
принадлежащих касательной плоскости Пр в точке Р, т. е. это касательные
векторы, которые определяют нормальные кривизны в направлениях л
и г) + л/2. Тогда формула Эйлера
к (р) = Я1 • cos(r})2 + Я2 • sin(77)2 (7.9)
позволяет вычислить нормальную кривизну к (р) в любом направлении
г] в точке Р, зная главные кривизны Хх и Я2 и угол г].
Средняя кривизна. Среднее арифметическое (Ях + Я2)/2
называется средней кривизной поверхности в точке Р. Средняя кривизна равна
(к(Р) + к (Р))/2 для любого л G [0, я).
7.1. Поверхности ♦ 507
Можно показать, что абсолютная величина произведения ХХХ2 равна
гауссовой кривизне кс(Р), определенной формулой (7.8).
Теорема Мёнье. Мы можем рассечь поверхность в точке Р
произвольной плоскостью Пс, идущей в каком-то направлении. Пересечение Пс
с поверхностью определяет дугу ус в окрестности Р, и одномерную
кривизну кс дуги ус в точке Р можно оценить. Однако нельзя предполагать,
что Пс проходит через нормаль к поверхности пр в точке Р.
Пусть пс - главная нормаль к ус в точке Р. Теорема Мёнье утверждает,
что нормальная кривизна к в любом направлении г] связана с
кривизной кс и нормалями пр и пс соотношением
к^ = кс • cos(np, nc). (7.10)
Следовательно, оценив две нормальные кривизны кик , мы
сможем оценить среднюю кривизну.
Врезка 7.3 (Мёнье). Ж. Б. М. Мёнье (1754-1793) - французский дивизионный
генерал, занимался теорией воздухоплавания, считается изобретателем
дирижабля.
Кривизна подобия. Пусть кхик2- две главные кривизны заданной
поверхности в точке Р (выше мы обозначали их Я1 и Я2). Определим
коэффициент кривизны къ следующим образом:
тт(Ы,|к*2|)
**з= 'i к- (7.П)
тахф^ , лг2)
Если и кх, и к2 равны нулю, то къ по определению равно нулю. Из
определения следует, что 0 ^ къ < 1.
Кривизна подобия (similarity curvature) J(P) определяется следующим
образом:
(kv 0), если к1 и к2 положительны
„т. ) (~к*> 0)» если к1 и Ki отрицательны
(0, къ), если знаки кх и к2 различны и \к2\ > \к^ v * '
(0,-к3), если знаки кх и к2 различны и \кг\ > \к2\
Отметим, что J(P) G Е2.
508 ♦ Глава 7. Трехмерная реконструкция
Врезка 7.4 (30-сканеры). На рынке имеется немало продуктов для
реконструкции трехмерных поверхностей, обычно они называются «ЗР-сканеры»,
или «ЗР-дигитайзеры». В этой главе рассматриваются сканеры со структурной
подсветкой (например, Kinect 1), а также системы, основанные на
стереоскопическом зрении и на отражающей способности поверхности. Так, сканеры
со структурной подсветкой часто применяются для моделирования
человеческого тела (например, сканеры всего тела в киноиндустрии), а
стереоскопическое зрение широко используется в аэрофотосъемке, для трехмерной
реконструкции зданий и даже для обработки в режиме реального времени, когда
необходимо составить представление о трехмерной окружающей среде.
В этой книге не обсуждаются технологии, которые пока слабо интегрированы
с компьютерным зрением, как то:
• лазерные сканеры, работающие на основе принципа «времени
прохождения сигнала» и дополненные модуляцией длины волны для очень
точного измерения расстояния (в новой модели Kinect 2 структурная
подсветка заменена временем прохождения сигнала, так что этот принцип
стал ближе к компьютерному зрению);
• голография все еще нечасто используется для 30-измерений, но
популярна как средство трехмерной визуализации;
• в контактных датчиках, лазерных приборах сопровождения, оптических
и магнитных устройствах слежения за местоположением практически
никогда не применяются технологии обработки изображений.
7.2. Структурная подсветка
Структурная подсветка - это проекция при калиброванных
геометрических условиях некоторой световой конфигурации (например, луча,
световой плоскости, решетки или кодированного света в форме
сменяющих друг друга двоичных световых комбинаций) на объект, форму
которого нужно реконструировать. Обычно используется одна камера и
один источник света, а с помощью калибровки мы должны определить
положение источника относительно камеры. На рис. 7.9 слева показана
одна из возможных установок.
В этом разделе описывается математика, необходимая для
реконструкции поверхностей методом структурной подсветки.
7.2.1. Проекция световой плоскости
Нахождение проекции световой плоскости. Освещенная прямая
на трехмерной сцене прослеживается в пикселях изображения. Мы
7.2. Структурная подсветка ♦ 509
анализируем спроецированную прямую в одномерных сечениях,
индексированных числами к = 1,..., кепйУ ортогональных направлению
касательной в пикселе sk, где изображение имеет локальный максимум ик
(рис. 7.10).
Рис. 7.9. Слева: источник света (лазер) создает качающуюся световую плоскость
(рисуя лучом расходящийся световой веер), которая проецируется в яркую
линию на интересующих нас объектах. Справа: поверхность тела,
реконструированная методом структурной подсветки
А и
Sk-\ sm sk Sk + \
Рис. 7.10. Построенный профиль яркости в направлении строки или столбца (в
идеале ортогональном направлению касательной к записанной в изображении
световой плоскости). Мы рассматриваем пиксели и их яркость в точке sk_t слева
и в точке sk+1 справа от sk, чтобы найти идеальную позицию sm (где достигается
максимум ит, который не виден в изображении) с субпиксельной точностью
Мы измеряем уровни яркости ик_г и ик+1 в позициях пикселей sk_x и
sk+v расположенных на выбранном расстоянии от sk. Для
аппроксимации яркости в сечении, проходящем через спроецированную прямую,
510 ♦ Глава 7. Трехмерная реконструкция
используется квадратичный полином u = a-s2+b-s + c. Коэффициенты
полинома а, Ъ и с находятся из системы уравнений
а
Ъ
2
'jfc+1
h
Sk+l
1
1
lj
-11
r -.
w*-l
Щ
.Mt+lJ
(7.13)
(На самом деле с не нужно для определения sm.) Затем мы находим
положение sm спроецированной прямой с субпиксельной точностью;
полином достигает максимума в точке sm = -b/2a. Почему?
Генерирование световых плоскостей с помощью
кодированного света. Вместо того чтобы генерировать за один раз одну световую
плоскость, мы можем с тем же успехом использовать п проецируемых
двоичных комбинаций для генерирования 2" световых плоскостей,
закодированных в п отснятых изображениях.
Рассмотрим диапроектор для проецирования п слайдов, каждый
из которых содержит двоичную комбинацию с разрешением 2"* 2"
(рис. 7.11). На каждом слайде столбец либо черный (не пропускает свет),
либо белый. Следовательно, один столбец во всех слайдах генерирует
на протяжении времени некую световую плоскость, описываемую
двоичной последовательностью «освещена» / «не освещена». Зная такую
последовательность для конкретной точки поверхности, мы можем
понять, какая световая плоскость отображалась на эту точку.
Объект
Диапроектор „
1°
Рис. 7.11. Диапроектор проецирует по одной двоичной комбинации, так что
в каждый момент освещены точки поверхности, попавшие в белые столбцы
(черные столбцы не пропускают свет). Таким образом, последовательность
слайдов генерирует в точке поверхности двоичный код (1 = освещена этим
слайдом, 0 = не освещена). На рисунке показана одна световая плоскость,
определенная последовательными двоичными комбинациями
7.2. Структурная подсветка ♦ 511
Спроецировав п слайдов в моменты £ = 1,..., л, мы записали л
изображений и сгенерировали 2" световых плоскостей. (Можно уменьшить число
слайдов до п - 1, предположив, что световые плоскости в левой части
отснятой сцены нельзя спутать со световыми плоскостями в правой части.)
Чтобы уменьшить количество ошибок, рекомендуется использовать в
проецируемых слайдах код Грэя, а не обычный двоичный код.
Врезка 7.5 (Грэй и код Грэя). Этот двоичный код был предложен американским
физиком Ф. Грэем (1887-1969). Последовательные целые числа
представляются двоичными числами, различающимися только в одном разряде. В
приведенной ниже таблице код Грэя иллюстрируется на примерах чисел от 0 до 7:
Целые
Обычный
Код Грэя
код
0
000
000
1
001
001
2
010
011
3
011
010
4
100
110
5
101
100
6
110
101
7
111
111
7.2.2. Анализ световой плоскости
Вспомните системы координат камеры и мира, изображенные на
рис. 6.17 и 7.9. Кроме того, теперь у нас есть еще и источник света.
Системы координат камеры, источника света и мировая. Камера
расположена в трехмерном пространстве, и с ней связана
левосторонняя (для определенности) система координат XYZs. Центр проекции
находится в начале координат Os. Оптическая ось камеры совпадает
с осью Zs. Плоскость изображения параллельна плоскости XYs и
находится от нее на (эффективном) фокусном расстоянии Zs = /". С
изображением связана либо левосторонняя (с направлением визирования в
сторону О), либо правосторонняя (точка съемки совпадает с Os) система
координат ху.
Из-за дисторсии объектива пространственная точка Р проецируется
в точку pd = (xd, yd) на плоскости изображения, где индекс d означает
«distorted» (искаженная). В предположении модели камеры-стенопа
(т. е. центральной проекции) позиция pd корректируется и
преобразуется в ри = (хи, уы), где индекс и означает «undistorted» (неискаженная).
Применяя теорему о луче, получаем уравнения центральной проекции
*и=Щ*- и Уи=^Г- (7-14)
512 ♦ Глава 7. Трехмерная реконструкция
Точки трехмерного пространства представлены в мировой системе
координат XwYJZw. Координаты камеры можно преобразовать в
мировые с помощью поворота и последующего параллельного переноса, что
удобно описывается в 4-мерных однородных мировых координатах.
Для структурной подсветки требуется (в общем случае) также откалиб-
ровать используемые источники света. Необходимо знать положение
(т. е. позицию и направление) источника света в мировой системе
координат. Например, мы должны определить длину базы Ь, т. е. расстояние
между центром проекции камеры и точкой, из которой исходят
световые лучи (рис. 7.9).
Двумерный случай. Сначала обсудим гипотетический случай
камеры на плоскости, а затем перейдем к расположению камеры в
трехмерном пространстве. Предположим, что в результате калибровки
определены углы а и /? и длина базы Ъ. Нам нужно вычислить положение Р.
См. рис. 7.12.
Рис. 7.12. Простой гипотетический случай: камера, источник света
и неизвестная точка на поверхности Р принадлежат одной плоскости;
предполагается, что L лежит на оси X
Центры проекции О и L вместе с неизвестной точкой Р образуют
треугольник. Мы определим положение Р с помощью триангуляции,
применив хорошо известные геометрические факты, в т. ч. теорему синусов:
d
Ъ
Отсюда следует, что
Ъ • sin a
d =
sin a sin у
bsma
(7.15)
bsma
sin у sm{n-a-p) sin(a+j3)
(7.16)
7.2. Структурная подсветка ♦ 515
и, наконец,
P = (d- cos p, d • sin /?)
(7.17)
в координатах XZ$. Угол /? определяется по положению
спроецированной (освещенной) точки Р в гипотетическом одномерном изображении.
Трехмерный случай. Теперь рассмотрим настоящий трехмерный
случай. Предположим, что величина Ъ определена в результате
калибровки источника света, а угол контролируется механизмом
перемещения световой плоскости. См. рис. 7.13.
Объект
Источник света
Длина базы b
Рис. 7.15. Для простоты считаем, что источник света L лежит на оси X
Согласно теореме о луче (центральной проекции), XJxu = Zs/f= YJyu,
а из тригонометрии прямоугольного треугольника мы знаем, что
tan a = Z /ф -X). Отсюда следует, что
Z = —f = tma(b-X) и X
х
В результате получаем решение
/
/
+ tan а \ = tmab.
ух
Х =
tmabx
f + x- tan a
tanaby ^ tmab-f
Y = — и Z =
f + x- tan a
f + x- tan a
(7.18)
(7.19)
Но почему в эти формулы не входит yl
В общем случае мы должны рассмотреть ситуацию, когда источник
света L не лежит на оси Xs, но вывод формулы для нее оставляем
читателю в качестве упражнения. См. упражнение 7.7.
514 ♦ Глава 7. Трехмерная реконарукция
7.3. Стереоскопическое зрение
Бинокулярное зрение - реальность, и зрение человека - тому
доказательство. Трудная часть задачи - определить соответственные точки на
левом и правом видах сцены (пример см. на рис. 7.14), т. е. точки,
являющиеся проекцией одной и той же точки на поверхности. (Этой задаче
мы посвятим целую главу 8.) В предположении, что она уже решена и у
нас имеется пара откалиброванных камер (известны их внутренние и
внешние параметры), не составляет труда вычислить глубину, т. е.
расстояние до видимой точки поверхности.
Рис. 7.14. Входная пара для системы стереоскопического зрения, идея которой -
обеспечить каноническую геометрию системы за счет использования камер,
точно смонтированных на оптической скамье (Берлинский технический
университет, лаборатория компьютерного зрения, 1994 г.). В наши дни более
эффективна калибровка камеры с последующей ректификацией изображений
на этапе подготовки исходных данных (см. раздел 6.3.2)
В этом разделе объясняется геометрическая модель
стереоскопического зрения, в центре которой находятся понятия эпиполярной
геометрии и диспаратности. Описано также, как использовать диспаратность
для вычисления глубины сцены.
7.3.1. Эпиполярная геометрия
Мы имеем две камеры, находящиеся в общем положении, а не просто
«правую» и «левую». Будем считать, что к камерам применима модель
стенопа, и обозначим центры проекции Ох и 02 (рис. 7.15). Мы
рассматриваем евклидову геометрию в Е3, игнорируя на время ограничения,
налагаемые дискретностью изображений.
7.3. Стереоскопическое зрение ♦ 515
Эпиполярная плоскость
Плоскопь изображения 2
Плоскость
изображения 1
Базовая линия
Эпиполюс
Эпиполярная прямая 1 -
Рис. 7.15. Эпиполярная геометрия двух камер в общем положении
Точка Р с мировыми координатами XwYwZw проецируется в точку рг
изображения 1 (точно, а не в позицию пикселя) и в соответственную
точку р2 изображения 2. Задача сопоставления стереоизображений
(предмет следующей главы) - найти точку р2, зная ру
Как известно, три неколлинеарные точки в трехмерном пространстве
однозначно определяют плоскость. Точки Ov 02 и неизвестная точка Р
определяют эпиполярную плоскость. Точки Ор 02 и точка рх определяют
ту же самую плоскость.
Пересечение плоскости изображения с эпиполярной плоскостью
определяет эпиполярную прямую. При поиске соответственной точки р2
можно ограничиться только эпиполярной прямой в изображении 2.
Наблюдение 7.2. Если в результате калибровки камер стало известно
положение центров проекции 01и01в мировой системе координат, то, зная точку
рх в изображении 1, мы уже можем сказать, на какой прямой искать
соответственную точку р2 во втором изображении; необязательно искать ее «всюду».
Это ограничение на геометрическое место возможных точек очень
важно для сопоставления стереоизображений.
Каноническая эпиполярная геометрия. В разделе 6.1.3 мы
познакомились с канонической геометрией стереоскопической системы,
которую теперь можем описать в терминах канонической эпиполярной
геометрии. См. рис. 6.11, на котором имеются левая и правая камеры.
Там точка Р определяет эпиполярную плоскость, которая пересекает
плоскости обоих изображений по одной и той же строке. Если начать с
точки рг = (хи, уи) от левой камеры, то соответственная точка (если Р
видна правой камере) находится в строке у изображения с правой камеры.
516 ♦ Глава 7. Трехмерная реконарукция
Где находятся эпиполюсы в канонической эпиполярной геометрии?
Их можно точно описать в 4-мерных однородных координатах. Это
бесконечно удаленные точки.
7.3.2. Бинокулярное зрение в канонической геометрии
стереоскопической системы
После геометрической ректификации две соответственные точки в
левом и правом изображениях оказываются в строках с одним и тем же
номером. Если начать, к примеру, с пикселя pL = (xL, у) в левом
изображении, то соответственный пиксель pR = (xRt у) в правом изображении
удовлетворяет условию xR < xv т. е. пиксель pR находится слева от пикселя pL в
массиве всех пикселей размера Ncols*Nrows. Иллюстрация такого порядка
показана на рис. 6.11. Если быть совсем точным, то координаты cxL и cxR
главных точек левой и правой камер могут оказывать влияние на этот
порядок в местах, где xL и xR почти совпадают, см. (6.3). Но для простоты
мы будем предполагать, что неравенства xR < xL и xuR < xuL справедливы
для неискаженных координат.
Диспаратность в общем случае. Пусть имеются два прямоугольных
изображения /. и I. одинакового размера Ncols*Nrows, поданных на вход
системы стереозрения; как и в разделе 6.3.2, мы используем в общем
случае индексы / и /, а не слова «левая» и «правая». Рассмотрим
наложение изображений друг на друга в системе координат изображения ху,
показанное на рис. 7.16.
Рис. 7.16. В продолжение рис. 6.19: два ректифицированных
изображения наложены друг на друга в одном массиве Ncols*Nrows пикселей.
Диспаратность показана на примере двух соответственных точек
7.5. Стереоскопическое зрение ♦ 517
Точка Р = (X, Y, Z) проецируется в точку р. /-го и в точку р./-го
изображения. Тем самым определены векторы дыспаратности (виртуального
сдвига)
di=pi-p. или d.. = p.-pr (7.20)
Скалярная диспаратность d.. = d..t по определению, равна модулю
lld..||2 = d2(p., р) вектора d... Имеем ||d..||2 = ||d..||2.
Диспаратность в канонической геометрии стереоскопической
системы. В этом случае мы имеем левое и правое изображения.
Пиксель pL = (xL, у) левого изображения соответствует пикселю pR = (xRt у)
правого изображения. Поскольку xR < xL, диспаратность равна xL - xR.
Триангуляция в канонической геометрии стереоскопической
системы. Теперь у нас есть все необходимое, чтобы перейти от входных
стереоизображений к результатам, т. е. восстановить пространственные
точки Р = (X, Y, Z) в координатах камеры или в мировых координатах.
Применив (6.4) и (6.5), мы восстановим неизвестные видимые
точки Р в системе координат левой камеры Р = (Xs, У, Zs) по неискаженным
координатам пикселей изображения {xuL, yuL) и (xuR, yuR) на входе,
которые удовлетворяют условиям yuL = yuR и xuR $ х^.
Длина базы обозначена Ь > 0, и, как всегда,/"- унифицированное
фокусное расстояние. Прежде всего мы можем исключить Zs из уравнений
(6.4) и (6.5):
~e=LL_=f <*.-». (7.21)
XuL XuR
Из (7.21) находим Xs
(7.22)
Подставив это значение X в (7.21), получаем
Zs= b'f . (7.23)
XuL ~ XuR
Наконец, подставляя Zs в (6.4) или (6.5), получаем
Y= Ь'Уи , (7.24)
XuL
xs
XuR
= Ь'ХиЬ
XuL "" XuR
s
XuL ~ XuR
Taeyu = yuL = y,
uR*
518 ♦ Глава 7. Трехмерная реконарукция
Наблюдение 7.3. Два соответственных пикселя (xL, у) = (xuL + cxL, yuL + cyl)
и (ХрУ) = (xuR + cxR,yuR + с R) однозначно определяют свой общий прообраз Р=(Х, Y,Z)
в трехмерном пространстве по формулам триангуляции (7.22), (7.23) и (7.24).
Обсуждение формул триангуляции. Если диспаратность xuL -xuR = 0,
значит, прообраз Р = (X, Y, Z) находится в бесконечности. Чем больше
диспаратность xuL - xuR, тем ближе прообраз Р к камерам.
Поскольку координаты пикселей изображения - целые числа,
значения диспаратности xuL - xuR тоже могут быть только целыми (мы
игнорируем постоянный, но, возможно, нецелый сдвиг на координаты
главной точки). Из-за нелинейности уравнений триангуляции разница
на 1 между xuL - xuR = 0 и xuL -xuR=l означает переход от бесконечности к
конечному значению, та же разница между xuL - xuR = 1 и xuL -xuR = 2
означает, что прообраз сильно приблизился к камере, но разность между
xul ~ xur = 99 и xuL - xuR =100 соответствует лишь очень небольшому
изменению расстояния до камер. См. рис. 7.17.
Рис. 7.17. На этом рисунке показаны пересекающиеся прямые, проходящие
через позиции пикселей в двух стереоизображениях. Пересечения отмечают
потенциальное положение точки Р в трехмерном пространстве, найденное
благодаря диспаратности, определяемой разностью координат пикселей.
Расстояние 8Z между последовательными уровнями глубины растет нелинейно
7.3. Стереоскопическое зрение ♦ 519
Наблюдение 7.4. Если не пытаться уточнить измерения, то количество
доступных значений диспаратности между dmax и 0 определяет количество
уровней глубины. Эти уровни распределены нелинейно: чем ближе к камерам, тем
плотнее, а чем дальше, тем реже.
Если увеличить длину базы Ъ и фокусное расстояние /", то можно
будет получить больше уровней глубины, но при этом уменьшится
количество пикселей, которым есть соответствие во втором изображении.
Увеличение разрешения изображения - обычный способ повышения
точности уровней глубины, но за это приходится расплачиваться
увеличением времени вычислений.
Реконструкция разреженных и плотных данных о глубине. Одна
пара соответственных точек дает одну реконструированную точку в
пространстве. Методы поиска соответствий иногда дают много
соответственных точек в паре стереоизображений, а иногда очень мало. На
рис. 7.18 слева несколько разреженных соответствий найдено близко к
границам внутри изображения с применением локального
(неиерархического) сопоставителя стереоизображений на основе корреляции.
Такая стратегия сопоставления использовалась на заре компьютерного
зрения. На рис. 7.18 справа показано плотное соответствие,
демонстрирующее, что иерархическое сопоставление на основе корреляции уже
дает разумные результаты.
В процессе сопоставления стереоизображений возможны ошибки.
Так что даже если найдено всего несколько соответствий, их качество
все равно нужно тщательно проверить.
Реконструкция разреженных данных о глубине во
встраиваемых системах технического зрения. Разреженное сопоставление
стереоизображений даже в наши дни представляет интерес в
«небольших» встраиваемых системах технического зрения, где время расчетов
и точность результатов имеют первостепенное значение. На рис. 7.19
показаны результаты сопоставителя стереоизображений, основанного
на модифицированном детекторе признаков FAST. Сами изображения
сняты с квадрокоптера.
7.3.3. Бинокулярное зрение в конвергентной системе
Чтобы максимально увеличить пространство, видимое обеими
камерами, полезно отойти от канонической геометрии стереоскопической
системы и воспользоваться конвергентной конфигурацией со
сходящимися направлениями визирования, показанной на рис. 7.20.
320
Глава 7. Трехмерная реконструкция
Рис. 7.18. Слева: разреженные соответственные пиксели, найденные методом
сопоставления стереоизображений, показаны цветными точками, причем цвета
кодируют глубину (это продолжение рис. 7.16). Справа: входная стереопара
Andreas (вверху), плотная карта глубины, на которой глубина кодируется уровнем
яркости, а также триангулированное и текстурированное представление
поверхности, полученное на основе сопоставления (Берлинский технический
университет, лаборатория компьютерного зрения, 1994)
Рис. 7.19. Слева: разреженные соответствия, найденные алгоритмом
сопоставления на основе анализа признаков, встроенного в ПО квадрокоптера
(Тюбингенский университет, 2013). Справа: стереокамеры смонтированы
на этом квадрокоптере
7.3. Стереоскопическое зрение ♦ 521
Наклоненные камеры с соответственными строками
изображений. Будем предполагать декартову систему координатXYZ. На рис. 7.20
показаны оси XuZ,a ось Y направлена в сторону зрителя. Оптические
оси левой и правой камер пересекаются в точке С на оси Z. Координаты
левой камеры обозначаются XLYLZL, а координаты правой - XRY^ZR.
Центры проекций находятся в точках 0L и 0R, оба лежат на оси X. Отрезок
0L0R называется базой определенной таким образом конвергентной
системы бинокулярного зрения, а величина Ъ - длиной базы.
Рис. 7.20.Левая и правая камеры симметричны относительно оси Z;
их оптические оси пересекаются в точке схождения Сна оси Z
Расстояние между точками 0L и 0R равно Ъ, а угол между оптическими
осями ZL и ZR и осью Z одинаков и равен в. Пространственная точка Р
проецируется в точки изображений с абсциссами xuL и xuR и
одинаковыми ординатами уи = yuL = yuR (это вариант ректификации, достигаемый
калибровкой камер). Фокусное расстояние обеих камер /"также
одинаково.
Преобразования координат. Система XYZ преобразуется в XLYLZL
поворотом
cos(-0) 0 -sin(-<9)
0 1 0
sin(-0) 0 cos(-<9)
cos(<9) 0 sin(<9)
0 1 0
-sin(0) 0 cos(0)
(7.25)
на угол -в вокруг оси Ус последующим параллельным переносом
ь ^
X-,Y,Z
(7.26)
522 ♦ Глава 7. Трехмерная реконарукция
т. е. на величину Ь/2 влево. Тем самым определяется аффинное
преобразование
Аналогично
xL
Yl
Л.
=
cos(0) 0 sin(0)
0 1 0
-sin(<9) 0 cos(<9)
x-b-
2
Y
Z
(7.27)
YD
L R J L
cos(0) 0
0 1
sin(0) 0
-sin(0)
0
cos(<9)
x+b-
2
Y
Z
(7.28)
Рассмотрим точку Р = (X, У, Z) в системе координат XYZ,
спроецированную в точки хи1уи и xuRyu в левой и правой системах координат
соответственно. Согласно общим уравнениям центральной проекции:
XuL ~
L2L. v f-YL fY«
Z9 У U rj rj
J ^7 ^ D
И XuR =
f-xb
(7.29)
Отсюда получаем
*ul=/-
( Ъ
cos(<9) \Х—| + sin(0)Z
V 2
-sin(<9)| X--| + cos(<9)Z
(7.30)
Л=/"
7
-sin(0)
/
Л
X-
(7.31)
+ cos(0)Z
XuR ~ J
cos(<9) X + -|-sin(0)Z
X + -| + cos(<9)Z
(7.32)
sin(<9)
Таким образом, получается следующая система уравнений:
7.3. Стереоскопическое зрение ♦ 525
[-*,. • sin(0) - /•• сов(в)]Х + [xiiL • cos(9) - f- sin(0)]Z
uL
-xuL-sm(0) + -f
[-yu • sin(0)]X + [-f]Y+ [yu • cos(0)]Z
-jVsin(<9)
KR • sin(0) -/• cos(0)]X + [хия • cos(0) +/• sin(0)]Z
(7.33)
(7.34)
-xuRsm(6)--f
(7.35)
Решение относительно неизвестной точки в трехмерном
пространстве. Может показаться трудным проделывать все эти
вычисления для одной лишь проецируемой точки Р = (X, У, Z). (Неужели люди
делают «это» для всех соответственных точек, видимых левым и правом
глазом, чтобы свести изображения и оценить расстояния до объектов?)
На самом деле эта система уравнений позволяет точно вычислить
координаты XYZ проецируемой точки Р. (Биологическая система зрения
не измеряет расстояния точно, а лишь дает оценки.)
Обозначим al = [-xuL • sin(0) - f- cos(0)],..., с0 = -[(b/2) xuR • sin(0) - (b/2) f\
коэффициенты в показанной выше системе уравнений, все их можно
найти в предположении, что азимутальный угол 0 фиксирован,
фокусное расстояние /известно и идентифицирована пара соответственных
точек изображений с координатами (xuL, yu) и (xuR, yu), являющихся
проекциями одной и той же точки Р= (X,Y,Z):
(7.36)
(7.37)
ахХ + azZ = а0,
ЪХХ+Ъ?+ЪЪ2=\,
cxX+czZ = cQ.
(7.38)
Из этой системы легко найти X, Y и Z.
Наблюдение 7.5. Конвергентная система вычислительно не намного сложнее
канонической стереоскопической системы.
Вергенция. Если точка Р особенно интересна человеку, то его
зрительная система фокусируется на этой точке (это называется вергенци-
ей). Геометрически это означает, что оба глаза движутся в
противоположных направлениях, так что оси ZL и ZR пересекаются в точности в
524 ♦ Глава 7.Трехмерная реконструкция
точке Р. В этом случае азимутальные углы 9 уже не равны. Возможно,
в будущем камеры смогут реализовать вергенцию. Тогда для описания
преобразований координаты будет более эффективен общий аппарат
линейной алгебры (с точки зрения краткости, ясности и общности).
7.4. Фотометрический метод анализа
стереоизображений
В предыдущем разделе для реконструкции трехмерного тела нам был
нужен источник света (обычно Солнце) и две (или более) статические
или подвижные камеры. Теперь же мы будем использовать одну
статическую камеру и несколько статических источников света, которые
можно включать и выключать во время фотографирования. Технология
называется фотометрический метод анализа стереоизображений (ФАС)
(photometric stereo method - PSM). Пример с тремя источниками света
показан на рис. 7.21; на каждой фотографии рука освещена только
одним из трех источников.
Рис. 7.21. Вверху: три исходных изображения для ФАС; во время
фотографирования рука должна быть неподвижной. Внизу: поверхность,
реконструированная методом ФАС с 3 источниками света
(Берлинский технический университет, 1996)
Сначала мы обсудим ламбертовскую отражательную способность в
качестве примера того, как поверхности отражают свет, а затем
опишем, как использовать ФАС с тремя источниками света для вывода
градиентов поверхности. Напоследок мы расскажем, как по градиентам
поверхности реконструировать трехмерное тело.
7.4. Фотометрический метод анализа аереоизображений ♦ 525
7.4.1. Ламбертовская отражательная способность
Предположение о точечном источнике света. Чтобы упростить
математическое описание, будем предполагать, что каждый источник
света можно представить единственной точкой в пространстве Ш?; этот
источник излучает свет равномерно во всех направлениях. Конечно,
реальный источник света имеет ограниченную дальность,
характеризуется конкретной кривой распределения энергии 1(A) (см. пример на
рис. 1.25 слева) и имеет геометрическую форму. Но мы предполагаем,
что источники «не слишком близки» к интересующим нас объектам,
поэтому предположение о точечном источнике света правомерно.
Предполагается, что источник света L находится в направлении
sL = [aL, bL, 1]T по отношению к освещаемой поверхности
(интересующим нас объектам) и излучает свет интенсивности EL. Постоянную EL
можно рассматривать как интеграл по кривой распределения энергии
источника L в видимой части спектра.
Врезка 7.6 (Ламберт и его закон косинуса). Швейцарский физик и математик
И. Г. Ламберт (1728-1777) внес вклад во многие дисциплины, в т. ч.
геометрическую оптику, цветовые модели и теорию отражательной способности
поверхностей. Он также первым доказал, что число л иррационально.
Ламбертовская отражательная способность характеризуется законом косинусов
(закон Ламберта), опубликованным в 1760 г.
Закон косинуса Ламберта. Наблюдаемая интенсивность излучения
от идеально рассеивающей отражающей поверхности (известной также
под названием ламбертовский отражатель) прямо пропорциональна
косинусу угла а между нормалью к поверхности п и направлением s
на источник света (рис. 7.22). Каково бы ни было направление вектора
визирования v., камера получит одно и то же количество отраженного
света.
Обозначим пр = [а, Ъ, 1]т нормаль к поверхности в видимой и
освещенной точке Р. Чтобы формально записать закон Ламберта, заметим
сначала, что
sT-np=||s||2-||np||2-cosa, (7.39)
откуда
IN
2 '
К
\2
526 ♦ Глава 7. Трехмерная реконструкция
Источник света
Центр проекции камеры
Ламбертовский отражатель
Рис. 7.22. Источник света, расположенный в направлении s, плоский
ламбертовский отражатель и нормаль п к его поверхности, а также камера
с направлением визирования vr Ламбертовский отражатель излучает свет
равномерно во всех направлениях vi,..., V4 при условии, что направление
принадлежит полусфере возможных направлений визирования,
которая находится с освещенной стороны отражателя
Далее интенсивность излучаемого в точке Р света умножается на
коэффициент
ij(P) = р(Р) • ^, (7.41)
п
где EL - энергия источника света, отражаемая в точке Р равномерно во
всех направлениях полусферы (потому-то мы и делим на я, величину
телесного угла полусферы), р(Р) - постоянная характеристика
отражающей способности поверхности, которая называется альбедо2 и
находится в диапазоне 0 < р(Р) < 1.
Врезка 7.7 (альбедо). Мы определили альбедо как скаляр, равный отношению
отраженного излучения к падающему, разность между тем и другим
поглощается поверхностью в данной точке. Это соответствует упрощенному
использованию EL для вычисления падающего излучения.
И. Г. Ламберт дал более общее определение альбедо для отражательной
способности поверхности любого типа в виде функции от длины волны Я в
видимой части спектра. Поскольку здесь мы обсуждаем только ламбертовскую
отражательную способность, определения альбедо как скаляра достаточно:
отраженный свет не зависит от функции распределения энергии падающего
излучения.
Таким образом, наблюдаемый в точке поверхности Р излученный свет,
называемый отражательной способностью, вычисляется по формуле
«Альбедо» по-латыни означает «белизна».
7.4. Фотометрический метод анализа стереоизображений ♦ 527
R{P)=t](P)
*1-ПР
SL
ПР
aLa + bLb + \ плп\
= Л{Р)• i 2 2L I 2 2 2' (7<42)
^Ja2L+b2L+l-Ja2+b2+l2
Отражательная способность R(P) > 0 будет функцией второго порядка
от неизвестных а и Ъ, если предположить, что комбинированная
отражательная способность поверхности rj(P) постоянна (т. е. мы
продолжаем освещать и наблюдать одну и ту же точку, но рассматриваем разные
углы визирования). Направление на источник света считается
постоянным (т. е. объекты малы по сравнению с расстоянием до источника).
Карта отражательной способности определяется в градиентном
пространстве ab нормалей (а, Ь, 1), см. рис. 7.7; она сопоставляет
величину отражательной способности каждому градиенту (а, Ъ) в
предположении, что отражательная способность поверхности однозначно
определяется градиентом (как в случае ламбертовской отражательной
способности).
Пример 7.4 (карта ламбертовской отражательной способности). Рассмотрим
точку Р с альбедо р(Р) и градиентом (а, Ь).
Если np = sL, то а = О и cos а = 1; формула (7.42) вырождается в R(P) = rj(P), и это
максимальное возможное значение. Мы получаем значение г](Р) в точке (aL, bL)
градиентного пространства.
Если пр перпендикулярна sL, то точка Р «просто» не освещена, пр лежит на
двойственной к sL прямой (показана на рис. 7.7 справа). Поскольку а = л/2 и
cos а = 0, формула (7.42) вырождается в R(P) = 0, и это минимальное
возможное значение. Следовательно, на двойственной к (aL, bL) прямой в
градиентном пространстве значение R(P) равно 0, и мы продолжаем нулевое значение
на полуплоскость, которая определяется этой прямой и не содержит точку
(aL, bL) (т. е. градиенты тех точек поверхности, которые не могут быть
освещены источником света L).
Для значений R(P) между 0 и г}(Р) формула (7.42) описывает параболу или
гиперболу. Множество всех таких кривых определяет карту ламбертовской
отражательной способности в градиентном пространстве, показанную на
рис. 7.23.
7.4.2. Восстановление градиентов поверхности
Предположим, что имеется одна неподвижная камера (на
треножнике) и три источника света в направлениях s., i = 1, 2, 3. Предположим,
528 ♦ Глава 7.Трехмерная реконструкция
что отражательная способность R(P) равномерно уменьшается в
постоянное число раз с > 0 (из-за расстояния от поверхности объекта до
камеры) и отображается в монохроматическое значение и в изображении
от камеры.
а^
-10
—i—\Ь
+10
+10
-10
Рис. 7.23. Карта ламбертовской отражательной способности.
Слева: изолинии. Справа: трехмерное представление значений в этой карте
Мы сделаем три снимка. Каждый раз включается только один
источник света, и точка поверхности Р отображается в три разных значения
яркости (одного и того же пикселя), определяемых по формуле
щ = ЧР) =
тКР)
sin,
п
(7.43)
Это дает три кривые второго порядка в градиентном пространстве,
которые (в идеале) пересекаются в точке (а, Ь), где пр = [а, Ь, 1] - нормаль
к поверхности в точке Р.
В фотометрическом методе анализа стереоизображений с п
источниками (пФАС) делается попытка восстановить нормали к поверхности с
помощью некоторого практического способа определения этой
идеальной точки пересечения (а, Ъ) для п > 3. Для однозначной реконструкции
нормали необходимо по меньшей мере три источника, значению п = 3
соответствует стандартный фотометрический метод анализа
стереоизображений (ФАС).
ФАС, не зависящий от альбедо. Будем рассматривать поверхности
с ламбертовской отражающей способностью. Например, кожа человека
приблизительно удовлетворяет закону Ламберта, а проблемы
возникают в местах, где имеют место блики. Зеркальные блики характерны
также для открытых глаз.
7.4. Фотометрический метод анализа аереоизображений ♦ 529
Мы не можем предполагать, что альбедо р(Р) постоянно на всей лам-
бертовской поверхности. Изменяются цвета точек, а вместе с ними
альбедо. Нужно ввести в рассмотрение ФАС, не зависящий от альбедо. Еще
раз запишем формулу (7.43) но вместо г](Р) подставим его определение:
en s • п
II '112 || Р\\2
где Е. (/ = 1,2,3) - энергия источников света. Умножая первое уравнение
(в котором / = 1) на и2 • l|s2||2, а второе на -их • \\sx\\2 и складывая
результаты, получаем:
р(Р) • пр • (b'1w2||s2||2 • sl - E^fis^ • s2) = 0. (7.45)
Это означает, что вектор пр ортогонален указанной взвешенной
разности векторов Sj и s2 в предположении, что р(Р) > 0. В этом
предположении разделим обе части на р(Р). Для первого и третьего изображений
получаем аналогично
пр • (ВДад ' sl - VjIIsJI, • S3) = 0. (7.46)
В итоге получается, что вектор пр коллинеарен векторному
произведению
(EjMjIsJ^ • sx - UjUJIsJIj • s2) x (E^WsJi^ - Sj - ^ujlsjlj • s3). (7.47)
Отсюда мы однозначно определяем искомую единичную нормаль к
поверхности п°.
Заметим, что в этом методе нам нужны только относительные
интенсивности источников света и никаких абсолютных результатов
измерений.
Направление на источники и обратный ФАС. Для калибровки
направлений на три источника света s. применяется обратный
фотометрический метод анализа стереоизображений. Используется
калибровочная сфера, обладающая (приблизительно) ламбертовской отражающей
способностью и равномерным альбедо (рис. 7.24). Сфера располагается
примерно в том же месте, где впоследствии нужно будет
реконструировать нормали к поверхности объекта. Точность калибровки будет тем
выше, чем больше сфера, т. е. желательно, чтобы она заполняла все
изображение, снятое неподвижной камерой.
Мы выделяем в изображении круговую границу сферы. Это позволит
вычислить нормали к поверхности сферы во всех точках Р,
проецируемых в позиции пикселей внутри этой окружности. В силу ожидаемой
550 ♦ Глава 7. Трехмерная реконструкция
неточности по отношению к ламбертовской отражающей
способности (см. приближенные изолинии интенсивности на рис. 7.24 справа)
понадобится больше трех точек Р (скажем, примерно 100 равномерно
распределенных точек с нормалями внутри круговой области, занятой
сферой в изображении, которое было снято при освещении источником
света /), чтобы определить направление s. методом наименьших
квадратов с использованием уравнения (7.44): нам известны значения ui и
нормали пр, а требуется найти направление s.. Таким же образом мы
измерим отношение интенсивностей Е. всех трех источников света.
Рис. 7.24. Слева: изображение калибровочной сферы, которая в идеале должна
обладать равномерным альбедо и ламбертовской отражательной способностью.
Справа: обнаруженные изолинии яркости, показывающие наличие зашумленности
Что касается расположения источников света относительно объектов
(или калибровочной сферы), то, согласно некоторым оценкам, для
получения оптимальных результатов методом ФАС угол между
направлениями на два источника (установленных симметрично относительно
направления визирования камеры) должен составлять примерно 56°.
Реконструкция альбедо. Рассмотрим уравнение (7.44) для i = 1, 2, 3.
Мы знаем все три значения и. в позиции пикселя р, являющейся
проекцией пространственной точки Р. Мы также знаем приближенные
значения единичных векторов s° и п°. Мы измерили относительные
интенсивности трех источников света.
Осталось одно неизвестное - р(Р). В описанном выше методе ФАС,
не зависящем от альбедо, мы комбинировали первое и второе
изображения, а затем первое и третье. Можно еще скомбинировать второе
изображение с третьим. Благодаря этим действия мы можем получить
надежную оценку р(Р).
7.4. Фотометрический метод анализа стереоизображений ♦ 551
Зачем нужно реконструировать альбедо? Знать альбедо важно для
независимого от источников света моделирования поверхности
объекта, определяемого только геометрией и текстурой (альбедо). В общем
случае (если не ограничиваться ламбертовской отражательной
способностью) альбедо зависит от длины волны падающего света. В качестве
первого приближения мы можем использовать источники света разных
цветов, например красный, зеленый и синий, чтобы
реконструировать соответствующие им величины альбедо. Отметим, что, определив
s° и п°, мы должны изменять только длину волны света (например, с
помощью прозрачных фильтров) в предположении, что объект остается
неподвижным.
Было показано, что такая техника дает приемлемую точность
реконструкции альбедо человеческого лица. См. пример на рис. 7.25.
Рис. 7.25. Лицо, реконструированное методом ЗФАС
(Оклендский университет, 2000 г.). Благодаря закрытым глазам
удается избежать бликования на фотографиях
7.4.3. Интегрирование градиентных полей
Дискретное поле нормалей (или градиентов) можно преобразовать в
поверхность путем интегрирования. Из математического анализа
известно, что интегрирование неоднозначно (при работе с гладкими
поверхностями), а определено лишь с точностью до аддитивной постоянной.
Некорректность постановки задач реконструкции поверхности.
Результаты ФАС ожидаемо дают дискретные и ошибочные данные о
градиентах поверхности. К тому же рассматриваемые поверхности
часто «не гладкие», а, например, многогранники с разрывным поведением
нормалей на границах многоугольных граней.
Чтобы проиллюстрировать трудность реконструкции на примере,
предположим, что мы смотрим на лестницу, ортогональную лицам
анфас. Все реконструированные нормали будут направлены прямо на нас,
и мы никак не сможем восстановить лестницу по этим нормалям,
которые совпадают с нормалями к плоскости.
552 ♦ Глава 7.Трехмерная реконструкция
В общем случае плотность реконструированных нормалей к
поверхности изменяется не так же, как локальный наклон поверхности.
Методы локального интегрирования. В непрерывном случае
значения функции глубины Z = Z(x, у), определенной на односвязном
множестве, можно реконструировать, начав с одной точки (х0, у0) с
начальным значением Z(x0, y0) и проинтегрировав градиенты вдоль пути у,
целиком проходящим внутри этого множества. Оказывается, что
интегрирование по различным путям дает одинаковое значение в точке
(xv уг). Если быть точным, глубина Z должна еще удовлетворять условию
интегрируемости
— = — (748)
дхду дудх
во всех точках (х, у) рассматриваемого односвязного множества, но это
условие представляет больше теоретический интерес. На рис. 7.26
показаны два пути.
Рис. 7.26. В предположении, что участок поверхности определен на односвязном
множестве и функция в явном уравнении поверхности удовлетворяет условию
интегрируемости, локальное интегрирование вдоль разных путей, начинающихся
в точке (х0, у0), приводит (в непрерывном случае) к одинаковым значениям
возвышения в точке (х^ уг)
Методы локального интегрирования реализуют интегрирование вдоль
выбранных путей (например, один или несколько проходов по
изображению, как показано на рис. 2.10). Для инкрементного обновления
значений Z используются начальные значения и локальные окрестности
пикселя.
Двухпроходный метод. Опишем локальный метод реконструкции
глубины по градиентам. Мы хотим восстановить функцию глубины Z
такую, что
7.4. Фотометрический метод анализа аереоизображений ♦ 555
(х>У) = ах,у, (7.49)
Эх
3Z
ду
(*,У) = К,У (7.50)
для всех значений градиента ах иЬх в позициях пикселей (х, у) £ /2.
Рассмотрим узлы сетки (х, у + 1) и (х + 1, у + 1); поскольку прямая,
соединяющая точки (х, у + 1, Z(x, у + 1)) и (х + 1, у + 1, Z(x + 1, у + 1)),
приблизительно перпендикулярна средней нормали на отрезке между
этими точками, скалярное произведение направляющего вектора этой
прямой и средней нормали равно нулю. Отсюда получаем рекурсивное
соотношение
Z(x+l,y+l) = Z(x,y+l) + i(flXty+1 + flx+lty+1). (7.51)
Аналогично получаем рекурсивное соотношение для пикселей
(*+1,у)и(х+1,у+1):
Z(x+l,y+l) = Z(x+l,y) + i(bx+1>y + bx+lty+1). (7.52)
Сложив оба равенства и поделив результат на 2, получим
Z(*+l,y+l) = J(Z(x,y+l) + Z(x+l,y))
+ 1(я .1 + 0,, ,1+Ь+1 +ЬФ1 Л. (7.53)
4Ч х,у+1 х+1,у+1 х+1,у x+l.y+l' v '
Предположим далее, что общее число точек на поверхности объекта
равно N *N . Пусть в точках (1,1) и (JV ,, iV ) заданы произвольные
с cols rows J \ ■> / \ coiS7 rows' " c
начальные значения высоты. Тогда двухпроходный алгоритм состоит из
двух этапов. На первом этапе мы начинаем с левого верхнего угла (1,1)
заданного градиентного поля и определяем значения высоты вдоль
осей а: и у, для чего аппроксимируем уравнения (7.49) правыми
разностями:
Z(x,l) = Z(x-l,l) + flx_u, (7.54)
Z(l,y) = Z(l,y-l) + bly_1, (7.55)
где х = 2,..., Ncols и / = 2,..., Nrom. Затем выполним вертикальный проход
по изображению, применяя формулу (7.53). Второй этап начинается в
правом нижнем углу (Ncols, Nrows) заданного градиентного поля
установкой такими значениями высоты:
554 ♦ Глава 7. Трехмерная реконарукция
Z(* ~ 1, KoJ = Z(x, NrmJ - a4JW (7.56)
Z(AU, У - 1) = Z(Ncols, y) - bNcohy. (7.57)
Затем выполняется горизонтальный проход по изображению с
применением рекуррентного соотношения:
Z{x- 1,у- 1) = \(Z{x- 1,у) + Z(x,y- l))
-{{а , +a +Ь , + b ). (7.58)
4V х-1,у х,у х,у- \ х,у' v '
Поскольку на оценку высоты может влиять выбор начальных
значений, в качестве окончательных значений мы берем среднее
арифметическое значений, полученных на обоих проходах.
На рис. 7.27 показаны результаты двухпроходного метода.
Синтетическое изображение вазы сгенерировано с помощью следующего
явного уравнения поверхности:
Z(x, у) = jf\y) + x2, (7.59)
где Ду) = 0.15-0.1-у(6у+1)2(у-1)2(Зу-2)2
при -0.5^х< 0.5 и 0.0<у^ 1.0.
Это синтетическое изображение вазы показано на рис. 7.27 слева
внизу, а реконструированная поверхность, полученная описанным
двухпроходным алгоритмом, - на рис. 7.27 справа внизу.
Глобальное интегрирование. Предположим, что мы оценили
векторы градиентов во всех точках р е П. Наша цель - сопоставить этому
равномерному и плотному градиентному полю трехмерную
поверхность, которая и является вероятным источником этого поля. Значения
глубины Z(x, у) можно интерпретировать как метки в позициях
пикселей (х, у), так что мы снова сталкиваемся с задачей нахождения пометки
с минимальной ошибкой (или энергией).
По аналогии с полными вариациями, рассмотренными в главе 4, мы
снова сложим член данных
*ЛМ(2) = Ж " a)2 + (Z, ~ Ъ? ] + Л0]Г[(2„ - «д» + (Zyy - byf] (7.60)
о. а
с членом гладкости
7.4. Фотометрический метод анализа стереоизображений
335
где Zx и Z - первые частные производные Z, ахиЬ - первые частные
производные аиЬ, a Z , Z = Z и Z - вторые частные производные.
Г г-| ' XX' ЛГУ ух уу г Г" г-1
С помощью параметра Я0 > 0 мы управляем согласованностью между
кривизной поверхности и изменениями известных градиентов, с
помощью параметра At> 0 - гладкостью поверхности, а параметр Я2 > О
позволяет сделать еще один шаг - управлять гладкостью кривизны
поверхности. В итоге мы хотим найти такую поверхность Z (т. е. функцию
пометки), для которой полная ошибка (или полная энергия)
достигает минимума, зная градиенты (а, Ъ) в точках (а:, у).
(7.62)
Рис. 7.27. Результаты двухпроходного метода для синтетического объекта «ваза».
Сверху: исходное изображение. Слева внизу: трехмерный график вазы.
Справа внизу: результат реконструкции двухпроходным методом
Методы на основе преобразования Фурье. Для решения задачи
минимизации (7.62) можно применить преобразование Фурье.
Двумерное преобразование Фурье (см. раздел 1.2) функции поверхности Z(x, у)
определяется следующим образом:
556 ♦ Глава 7.Трехмерная реконструкция
Z(w, v) = 7-7 ^ Z(x, у) • exp
а обратное преобразование Фурье:
—г!к
хи yv
. N N
\ cols rows J
(7.63)
Z(x,j>) = ]TZ(M,v)-exp
a
iln
xu yv
+^—
г N N
\ cols rows J
(7.64)
где / = V^T - мнимая единица, а и и v - частоты в двумерной области
Фурье.
Врезка 7.8 (методы на основе преобразования Фурье). Задачу оптимизации
(7.62) можно решить, применив теорию проекций на выпуклое множество.
Заданное градиентное поле (ох , Ьх ) проецируется на ближайшее в смысле
среднеквадратичной погрешности интегрируемое градиентное поле, причем
оптимизация производится в частотной области с помощью преобразования
Фурье. См. работу [/?. Т. Frankot and R. Chellappa.A method for enforcing integrability in
shape from shading algorithms. IEEE Trans. Pattern Analysis Machine Intelligence, vol. 10,
1988, p. 439-451] для случая, когда вторая часть ограничения на данные не
используется, а ограничения на гладкость отсутствуют вовсе.
Чтобы улучшить точность и устойчивость алгоритма, а также усилить связь
между функцией поверхности Z и заданным градиентным полем, в уравнение
(7.62) можно включить дополнительные ограничения, как описано в работе
[Т. Wei and R. Klette. Depth recovery from noisy gradient vector fields using regularization.
In Proc. Computer Analysis Images Patterns, LNCS 2756, Springer, 2003, p. 116-123].
Помимо пар Фурье, перечисленных в разделе 1.2, имеют место также
следующие:
Zx(x,y) <^> /mZ(u,v);
Zy(x,y) ^ /vZ(m,v);
ZJx,y) фф -u2Z(u,v);
ZyjLw) *> -v2Z(u,v);
ZJx,y) о -uvZ(m,v).
xy4
Эти пары Фурье определяют внешний вид интересующих нас
производных функции Z в частотной области.
Обозначим A(u, v) и В(ы, v) - преобразования Фурье заданных
градиентов А(х, у) = ах и В(х, у) = Ъх соответственно. Нам понадобится также
теорема Парсеваля, см. (1.31)!
7.4. Фотометрический метод анализа стереоизображений ♦ 557
Алгоритмы Франкота-Челлаппа и Вэя-Клетте. Имеет место
эквивалентность между задачей оптимизации (7.62) в пространственной
области и задачей оптимизации в частотной области, заключающейся
в минимизации выражения
X [(iuZ - А)2 + (zVZ - В)2]
Q
+ Я0Х [(-«2Z - шА)2 + (-v2Z - zVB)2]
+ A1X[(/uZ)2 + (/vZ)2]
+ Я2Х [-u2Z2 + 2(-m/Z)2 + (-v2ZF)2]. (7.65)
Q
Раскрывая скобки в этом выражении, получаем:
£ [«2ZZ* - zuZA* + zuZ*A + АА* + v2ZZ* - zvZB* + zvZ*B + BB*]
й
+ Я0Х ["4ZZ* - zu5ZA* + zu3Z*A + u2AA* + v*ZZ* - zv3ZB* + zv3Z*B + v2BB]
+ ЯХХ (w2 + v2)ZZ* + Я2Х (w4 + 2u2v2 + v*)ZZ*, (7.66)
a a
где * обозначает комплексное сопряжение.
Дифференцируя по Z* и приравнивая производную к нулю, мы
выведем необходимо условие минимума функции стоимости (7.62) в виде:
(u2Z + ША + v2Z + /vB) + A0(u4Z + ш3А + HZ + z*v3B)
+ Aj(u2 + v2)Z + Л2(и4 + 2u2v2 + HZ) = 0. (7.67)
После перегруппировки членов получаем:
[Я0(и4 + v4) + (1 + AjXu2 + v2) + Я2(ы2 + v2)2] Z(u, v)
+ z"(u + Я0ы3) А(ы, v) + z"(v + Я0у3) В(ы, v) = 0. (7.68)
Решаем это уравнение при условии (u, v) 7^ (0,0):
—i(u + Я0и3)А(и, v) — /(v + A0v3 )B(w, v)
Я0(и4 +v4) + (l + Xx)(u2 +v2) + Я2(и2 +v2)
tyu-rxi^u )r*yu,v, ^ут/^у J**\", V)
Z(m,v)= „ , 4 . 4ч . „ . . w 9 . ,,ч.„,7. 2ч2- С'-69)
Это преобразование Фурье неизвестной поверхности Z(x, у),
выраженное в виде функции от преобразований Фурье заданных градиентов
558 ♦ Глава 7. Трехмерная реконарукция
А(х, у) = ах и В(х, у) = Ьх . Получающийся в результате алгоритм
представлен на рис. 7.28.
1
2
з
4:
5
6:
7
8
9:
10:
11
12
13
14:
15
16:
17
18:
19:
20:
21
22
23
24:
25
вход градиенты а{х,у), Ь{х,у); параметры Х0, Xv X2
for (x, у) G О do
■f(N^y)l<^ax&|b(x-y)|<cmax;then
А1(х,у) = а(х,у);А2(х,у) = 0;
В1(х,у) = Ь(х,у);В2(х,у) = 0;
else
А1(х,у) = 0;А2(х,у) = 0;
В1(х,у) = 0;В2(х,у) = 0;
end if
end for
Вычислить преобразование Фурье на месте: А1 (и, v), A2(u, v);
Вычислить преобразование Фурье на месте: В1 (и, v), B2(u, v);
for(u,v)eDdo
if(u^0&v^ 0)then
Л = Л0(и4 + И) + (1 + Л,)(и2 + v2) + Х2(и2 + v2)2;
Н1 (и, v) = [(и + V3)A2(u, v) + (v+Ху)В2(и, v)VA;
Н2(и, v) = [-(и + /\0и3)А1 (и, v)-(v + V3)B1 (и, v)]/A;
else
Н1 (0,0) = средняя глубина; Н2(0,0) = 0;
end if
end for
Вычислить преобразование Фурье Н1 (и, v) и Н2(и, v) на месте: Н1 (х,у), Н2(х,у);
for(x,y)GDdo
Z(x,y) = H1(x,y);
end for
Рис. 7.28. Алгоритм Вэя-Клетте на основе преобразования Фурье (обобщение
алгоритма Франкота-Челлаппа, в котором Я0 = Хх = Л2= 0, и потому вторая
часть ограничения на данные, а также ограничение на гладкость целиком
не используются) для вычисления оптимальной поверхности по заданному
плотному градиентному полю
Постоянная стах позволяет отбросить оценки градиентов, в которых
углы с плоскостью изображения близки к я/2, подходящим значением
является с =12. Вещественные части хранятся в массивах Al, B1 и
max ' с '
HI, а мнимые - в массивах А2, В2 и Н2. В строке 19 для
инициализации используется оценка средней глубины видимой сцены. Параметры
Я0, Яр Я2 следует выбирать, исходя из экспериментальных данных для
заданной сцены.
На рис. 7.29 показано три фотографии гипсового бюста Бетховена,
снятые неподвижной камерой с тремя источниками света. Градиенты
вычислялись с помощью независимого от альбедо метода ЗФАС. На
рисунке ниже показаны реконструированные поверхности при одном и
7.4. Фотометрический метод анализа аереоизображений ♦ 559
том же плотном градиентном поле на входе, но с Я0 = 0 (как в алгоритме
Франкота-Челлаппа) и с Я0 = 0,5 (как в алгоритме Вэя-Клетте); для
уточнения реконструированной поверхности можно попробовать
положительные значения Хх и Я2.
Рис. 7.29. Вверху: три изображения бюста Бетховена, использованные
в качестве входных данных для метода ЗФАС. Слева внизу: поверхность,
реконструированная с помощью алгоритма Франкота-Челлаппа.
Справа внизу: поверхность, реконструированная с помощью
алгоритма Вэя-Клетте с параметрами Я0 = 0.5,Я1 = Я2 = 0
Тест на зашумленные градиенты. Вообще говоря, локальные
методы дают ненадежную реконструкцию, если на вход подаются
зашумленные градиенты, поскольку ошибки распространяются вдоль пути
обхода. Мы проиллюстрируем глобальное интегрирование для показанного
на рис. 7.27 синтетического изображения вазы. Сгенерируем для него
дискретное градиентное векторное поле и прибавим к нему гауссов-
ский шум (с нулевым средним и стандартным отклонением 0,01).
Результаты показаны на рис. 7.30.
540 ♦ Глава 7. Трехмерная реконструкция
Рис. 7.30. Результаты реконструкции синтетической вазы (рис. 7.27)
при зашумленном градиентном поле. Слева: поверхность,
реконструированная с помощью алгоритма Франкота-Челлаппа.
Справа: поверхность, реконструированная с помощью алгоритма
Вэя-Клетте с параметрами Я0= 0,Л1 = 0.1, А2 = 1
7.5. Упражнения
7.5.1. Упражнения по программированию
Упражнение 7.1. (отображение поверхности цилиндрического тела
на плоскость). Решите следующую задачу. Дан набор изображений
одного цилиндрического объекта, например банки или бутылки (см.
рис. 7.31). Разрешается построить загораживающий контур объекта
вручную, а не автоматически.
Рис. 7.31. Слева: пример входного изображения цилиндрического тела
с наклеенной этикеткой, б середине: приближенное положение загораживающих
контуров цилиндра, построенное вручную. Справа: плоская метка, выделенная
из нескольких входных изображений
Сделайте несколько фотографий цилиндрического объекта, на
которых присутствует какая-нибудь «интересная» часть (на рис. 7.31 это
этикетка). Ваша программа должна выполнить следующие действия:
7.5. Упражнения ♦ 541
1) отобразить каждое изображение на один и тот же цилиндр
фиксированного радиуса;
2) воспользоваться сшивкой изображений, чтобы объединить
сегменты изображений на поверхности этого цилиндра;
3) отобразить сшитое изображение на плоскость.
Тем самым вы должны получить плоское представление некоторых
частей заданного цилиндрического объекта, как показано в примере на
рис. 7.31.
Упражнение 7.2 (визуализация кривизны подобия). Визуализируйте
кривизну подобия для трехмерных поверхностей. Значением кривизны
подобия является вектор в Ж2. На рис. 7.32 показаны два возможных
цветовых ключа для первого (горизонтальная ось) и второго (вертикальная
ось) элементов пары, определяющей кривизну подобия, а также
применение этой цветовой схемы к нескольким простым фигурам.
Выберите по своему усмотрению несколько трехмерных тел, каждое
со своим масштабом, и визуализируйте их кривизну подобия, нанеся
значения цветовых ключей на их поверхности.
Обобщите результаты своих экспериментов по визуализации
кривизны подобия одного и того же тела в разных масштабах.
(ОД)
(-1,0)
(1,0)
(0,-1)
Рис. 7.32. Слева: возможный цветовой ключ для визуализации кривизны подобия.
Справа: применение этого ключа к сфере, цилиндру, эллипсоиду и тору
Упражнение 7.3 (построение простого ЗБ-сканера). В этом проекте
рассматривается «очень простой» способ построить ЗБ-сканер.
Предполагается, что имеется цифровая камера и плоский источник света
(например, потолочный проектор или источник типа того, что
используется для просмотра рентгеновских снимков; впрочем, обе технологии
уже устарели).
Вырежите из картона круг, на котором помещались бы объекты
размером от 20 до 50 см (например, деревянная статуэтка), нанесите по
542 ♦ Глава 7. Трехмерная реконструкция
краям шкалу в градусах (скажем, с шагом 5 градусов), положите круг
на стол, обведите его контур и пометьте на этой окружности место, где
в начальный момент находилась нулевая отметка шкалы. После этого
можно будет поворачивать круг внутри окружности на указанные вдоль
его края углы.
Теперь создайте фиксированную световую плоскость, проходящую
через ось вращения круга, для чего закройте свой плоский источник
света двумя листами бумаги, оставив между ними очень узкую щель.
(Конечно, для создания световой плоскости лучше было бы
использовать свет лазера и оптический клин.)
Расположите камеру так, чтобы она «видела» вращающийся круг, и
откалибруйте расстояния следующим образом: перемещая
какой-нибудь предмет, например книгу, внутри круга точно измеренными
шагами, определите столбец (или столбцы) изображения, в которых
световая плоскость видна на предмете при данном расстоянии. Тем самым
вы создадите таблицу соответствия между освещенными столбцами
изображения от камеры и расстояниями.
Теперь всё готово к нахождению точек на поверхности объекта,
помещенного на вращающийся круг. Составьте отчет об эксперименте и
приложите к нему входные изображения и реконструированный набор
точек на трехмерной поверхности.
Упражнение 7.4 (недостоверность стереореконструкции). На рис. 7.17
иллюстрируется недостоверность вычисленных значений диспаратно-
сти. Точки пересечения прямых отмечают потенциальные положения в
трехмерном пространстве, которые определяются вычисленными дис-
паратностями, но на самом деле точка поверхности, которой
соответствует диспаратность, может находиться внутри трапеции вокруг точки
пересечения. Площади таких трапеций (т. е. недостоверность)
возрастают с увеличением расстояния до камер.
В действительности на рисунке показана только одна плоскость,
определенная общей строкой в левом и правом изображениях.
Области недостоверности являются трехмерными многогранниками, а
трапеции - это всего лишь их плоские сечения.
В этом упражнении необходимо провести геометрический анализ
объема этих многогранников (в качестве упрощения можно
ограничиться площадью трапеций) и графически представить
недостоверность в виде функции от расстояния до камер.
Считайте, что имеется две камеры с фиксированным разрешением
NrowsxNcols в канонической конфигурации стереоскопической системы с
фокусным расстоянием f и длиной базы Ъ. Постройте график зависи-
7.5. Упражнения ♦ 545
мости недостоверности от расстояния до камер; изменяйте только /и
покажите, как при этом изменяется недостоверность. Затем изменяйте
только Ъ и снова покажите, как при этом изменяется недостоверность.
В идеале интерфейс программы должен допускать интерактивное
изменение /и Ъ.
Упражнение 7.5 (удаление небольших бликов). Описанный метод
ФАС работает, только если отражательная способность поверхности
близка к ламбертовской. Однако если текстура поверхности «не
слишком детальная», то небольшие блики можно «удалить»,
воспользовавшись дихроматической моделью отражения для цветных поверхностей.
Возьмите объект, поверхность которого состоит лишь из участков
приблизительно постоянного цвета, на которых есть небольшие блики.
Сфотографируйте этот объект и отобразите значения пикселей внутри
одного участка постоянного цвета и цветовой куб RGB. Эти значения
должны образовать Т- или L-образную линию в кубе RGB,
определяемую базовой линией (диффузной компонентой) и более яркими
значениями вдали от базовой линии (блики).
Аппроксимируйте базовую линию и ортогонально спроецируйте на
нее RGB-значения. Замените в изображении спроецированные
значения их проекциями на базовую линию.
Таким образом можно удалить небольшие блики.
Продемонстрируйте это на нескольких изображениях выбранного объекта под разными
углами зрения и при разных условиях освещения.
7.5.2. Упражнения, не требующие программирования
Упражнение 7.6. Гладкое компактное множество в трехмерном
пространстве является компактным (т. е. связным, ограниченным и
топологически замкнутым) и таким, что кривизна определена в любой
точке края (т. е. поверхность дифференцируема в любой точке).
Докажите, что кривизна подобия 5, определенная в (7.12), является
(положительным) инвариантом относительно масштабирования для
любого гладкого трехмерного множества.
Упражнение 7.7. Вместо того чтобы применять тригонометрический
подход в рассуждениях на стр. 313, специфицируйте детали для
реализации линейно-алгебраического подхода к структурной подсветке,
руководствуясь следующими указаниями.
1. В результате калибровки мы знаем неявное уравнение каждой
световой плоскости в мировых координатах.
544 ♦ Глава 7. Трехмерная реконструкция
2. В результате калибровки мы также знаем параметрические
уравнения (в мировых координатах) лучей, соединяющих центр
проекции камеры с центрами каждого квадратного пикселя.
3. Анализ изображения дает нам идентификатор световой
плоскости, видимой в позиции данного пикселя.
4. Пересечение луча со световой плоскостью дает координаты точки
на поверхности.
Упражнение 7.8. Определите фундаментальную матрицу F для
канонической геометрии стереоскопической системы. Рассмотрите
также пару наклоненных камер, показанных на рис. 7.20, и определите для
нее фундаментальную матрицу.
Упражнение 7.9. Опишите карту ламбертовской отражательной
способности в сферических координатах на гауссовой сфере (указание: в
этом случае линиями равной интенсивности будут окружности).
Воспользуйтесь этой моделью, чтобы ответить на вопрос о том, почему
двух источников света недостаточно для однозначного определения
нормали к поверхности.
Упражнение 7.10. К чему на стр. 336 предложение «Нам понадобится
также теорема Парсеваля...»?
Глава \J
Сопоставление
стереоизображений
В этой главе обсуждается поиск соответственных пикселей в паре
стереоизображений. Сначала мы рассмотрим поиск соответствий как
задачу пометки, определенную двумя функциями ошибок - данных и
гладкости - и управляющей структурой. Мы опишем сопоставление
методом распространения доверия и полуглобальное сопоставление. А в
конце главы обсудим, как оценить точность результатов сопоставления
на реальных данных, в особенности для стереоскопического видео.
На рис. 8.1 показаны два геометрически ректифицированных
входных изображения, составляющих стереопару. Мы рассматривали
системы двух камер в разделе 6.1.3, их калибровку и геометрическую
ректификацию в разделе 6.3, геометрию стереоскопического зрения в
разделе 7.3.1 и использование найденных соответственных пикселей
для реконструкции трехмерных поверхностей в предположении о
канонической геометрии системы - в разделе 7.3.2. Остается ответить на
вопрос: «Как найти пары соответственных пикселей в стереопаре?»
Рис. 8.1. Стереопара Crossing. Начав с пикселя р в левом изображении,
мы ищем на эпиполярной прямой соответственный пиксель д. Как найти q
(например, в области с однородной текстурой, как на этом рисунке)?
Правильное положение q должно быть правее показанного q
346
Глава 8. Сопоаавление стереоизображений
В этой главе мы всюду предполагаем, что стереопары уже
геометрически ректифицированы и, возможно, подвергнуты предварительной
обработке для устранения проблем с яркостью (см. раздел 2.3.5).
Поэтому мы ожидаем, что соответственные пиксели находятся в одной и той
же строке левого и правого изображений, как показано на рис. 6.11 для
стандартной конфигурации стереоскопической системы. На рис. 8.2
показана вычисленная карта диспаратности.
Рис. 8.2. Визуализация карты диспаратности, вычисленной для стереопары Crossing.
Для визуализации различных значений диспаратности применяется цветовое
кодирование. Черным цветом обозначены пиксели, в которых степень
уверенности в правильности вычисленного значения низкая
8.1. Сопоставление, стоимость данных
и уверенность
Сопоставление стереоизображений - пример подхода на основе
пометки, описанного в разделе 5.3.1. Функция пометки/назначает метку
f E L, диспаратность, каждой точке р е П, вычисляя функции ошибок
Edata и Esmooth, как описано для общего случая формулой (5.30), которую
мы для удобства повторим ниже:
реО.
^data \Р<> Jр)^~ 2ша smooth Uр > Jq )
qeA(p)
(8.1)
Суммарная стоимость метки f в точке р складывается из ошибок
данных и гладкости в окрестности р:
Л-data \Р-> Jp)~ ^data \Р> Jр) + 2-1 ^smooth \J р > Jq Г
qeA(p)
(8.2)
8.1. Сопоставление, аоимость данных и уверенность
347
Примеры члена ошибки, или энергии гладкости Esmooth (который также
называется членом непрерывности), были приведены в разделе 5.3.2,
начиная с простой модели Поттса и заканчивая линейной (усеченной)
и квадратичной (усеченной) функциями стоимости.
В этом разделе задача сопоставления стереоизображений
описывается на абстрактном уровне; мы представим применяемые в этой
задаче функции стоимости данных Edata, а также расскажем, как выбирать
наиболее подходящую функцию стоимости для конкретных стереодан-
ных. И закончим раздел перечислением мер уверенности в
правильности вычисленных значений диспаратности.
8.1.1. Общая модель сопоставления
Имеется левое и правое изображения, обозначаемые соответственно
L и R. Одно из них считается базовым, а другое - сопоставляемым; они
обозначаются соответственно ВиМ. Взяв пиксель (х, у, В{х, у)) базового
изображения, мы ищем соответственный пиксель (х + d, у, М(х + rf, у)) в
сопоставляемом изображении; он должен находиться на эпиполярной
прямой, т. е. в строке у. Соответственные пиксели являются проекциями
одной точки сцены Р = (X, Y, Z), как показано на рис. 6.11 (на этом рисун-
ке В = L, М = R, х = xuLn х + d = xuR).
Базовое и сопоставляемое изображения и интервалы поиска. На
рис. 8.3 показан случай, когда В = L (и, стало быть, М = К). Мы начинаем
поиск с пикселя р = (х, у) изображения В. При этом задается интервал
поиска, содержащий точки q = (х + d, у) изображения М, для которых тах-
[х - dmax, 1}^х + d^x. Иными словами,
О <-d<imn{d ,*-!}. (8.3)
\в
Щ
р
\м
Щ
ч
%
р
Рис 8.3. Предположим, что левое изображение базовое (т. е. В = /.),
а правое - сопоставляемое (т. е. М = /?). Начиная с пикселя р базового
изображения, мы рассматриваем его квадратную окрестность
и сравниваем ее с окрестностями пикселей q на эпиполярной прямой
(т. е. в той же самой строке - поскольку предполагается каноническая
геометрия системы) сопоставляемого изображения
348
Глава 8. Сопоаавление стереоизображений
(В разделе 7.3.2 объяснялось, почему достаточно искать только слева
от а:.) Например, если начать с пикселя р = (1, у) в Б, то можно
рассматривать лишь d = 0, поэтому, чтобы для точки Р нашлись соответственные
пиксели, она должна быть бесконечно удаленной. Если начать с пикселя
Р = (N ,, у) и при этом N , > d , то будем иметь -d ^ d , и интервал
» v cols7 J' * cols max7 *rn max7 ~
поиска заканчивается в точке N , - d слева от р.
-- max ~
cols
Если переменить изображения, положив В = R (и, следовательно,
M = L), то знак d сменится с минуса на плюс, и мы будем иметь
0<d<min{d ,N , -х\
l max7 cols J
(8.4)
Мы снова начинаем поиск с выбора р = (х, у) в В = R, а
интервал поиска состоит из таких точек q = (х + d, у) в М = L, для которых
х^х + d<: minfiV ,,х + d }. См. рис. 8.4.
i cols' maxJ r
\м
wP
р
wq
q
\в
%
p
Рис. 8.4. Здесь в качестве базового выбрано правое изображение (т. е. В = R),
а в качестве сопоставляемого - левое (т. е. М = L)
Множество меток для сопоставления стереоизображений. Чтобы
в последующем изложении не приходилось проводить различие между
положительными и отрицательными величинами, будем считать, что
сопоставление производится справа налево, а множество меток таково:
L = {-1,0, l,...,d },
I 7 7 7 7 maxJ7
(8.5)
где -1 означает «диспаратность не назначена», а неотрицательные
числа - это возможные значения диспаратности, причем dmax > 0.
При сопоставлении слева направо множество меток было бы таким:
L = {+1,0, -l,...,-d }.
1 ' ' ' ' max-1
Зная внутренние и внешние параметры камеры, мы можем оценить
величину dmax по ближайшим объектам на сцене, которые «все еще
представляют интерес». Например, если речь идет об анализе сцены
впереди движущегося автомобиля, то всё, что ближе, скажем, 2 м, нам
неинтересно, поэтому в качестве dmax можно взять порог 2 м. См.
упражнение 8.7.
8.1. Сопоставление, стоимость данных и уверенность ♦ 349
Окрестности для поиска соответствий. При поиске
соответственных точек первое, что приходит на ум, - сравнить окрестности (для
простоты - прямоугольные окна) пикселя р в изображении /. Мы будем
рассматривать окна Wl'k(I) размера (2/ + 1)*(2к + 1). Окно W°'k(I) целиком
расположено в одной строке изображения1. Мы рассматриваем только
полутоновые изображения, в которых яркость изменяется от 0 до Gmax.
В каждый момент рассматривается только одна строка
изображения у. Будем писать Вх вместо В(х, у), W'k(B) вместо Wl>%B), Mx+d вместо
М(х + d, у) и wlx*d (M) вместо Wl>\M). Мы говорим «позиция пикселя а: в В»
и «позиция пикселя а: + d в М», не упоминая индекс текущей строки у.
Центры окон расположены в рассматриваемых пикселях. Данные в
окнах вокруг начальной позиции пикселя р = (х, у) и вокруг
пикселя-кандидата q = (х + d, у) считаются совпадающими, если мера стоимости
/ к
Essd(P> <0 = IX [В(* + U У + /) -M(x + d + i,y + /)]2 (8.6)
/=-/ j--k
равна 0, где SSD означает sum of squared differences (сумма квадратов
разностей). С тем же успехом можно было бы взять меру стоимости на
основе суммы модулей разностей (SAD - sum of absolute differences):
/ к
ESAD(p,d)=JJ1£\B(x + i,y + j)-M(x + d + i,y + j)\. (8.7)
В обеих формулах значение каждого пикселя в окне Щк(В)
сравнивается со значением пикселя в окне Wlxfd (В), занимающего то же
относительное положение (/,;'). В граничном случае / = к = 0 сравнивается
просто значение пикселя со значением пикселя. Например, модуль
разности (AD), равный
EJp, d) = \В(х, у) - М(х + d, y)|, (8.8)
может рассматриваться как простейшая из возможных функций
стоимости данных.
Пять причин, по которым SSD и SAD сами по себе не работают.
Перечислим пять трудностей, мешающих успешному применению SSD
и SAD для поиска соответственных пикселей:
1) не выполняется предположение о постоянстве яркости.
Стереопары не удовлетворяют предположению о постоянстве яркости; на
яркость в соответственных пикселях и их окрестностях обычно
1 Эта нотация является сокращенным вариантом нотации W2,+1'2k*1(I), употреблявшейся в
разделе 1.1.1.
550 ♦ Глава 8. Сопоставление аереоизображений
влияют небольшие изменения в условиях освещения или просто
шум камеры;
2) различия в локальной отражательной способности. Из-за
разных углов визирования поверхность в точке Р и ее окрестности
по-разному отражают свет в камеры, снимающие изображения
В и М (за исключением случая, когда отражательная способность
в точке Р ламбертовская);
3) различия камер. Различия в коэффициентах усиления и
смещении камер приводят к большим ошибкам SAD и SSD;
4) искажение перспективы. Пространственная точка Р = {X, Y, Z),
спроецированная в две соответственные точки, расположена на
изогнутой поверхности. Локальная окрестность Р на этой
поверхности по-разному проецируется на изображения ВиМ, поскольку
она видна под (немного) разными углами (т. е. форма окон W и W
в идеале должна была бы повторять форму спроецированной
локальной окрестности);
5) минимум не единственный. Может существовать несколько
позиций пикселя q с одним и тем же минимумом, например в случае,
когда большой участок равномерно затенен или когда имеет
место периодически повторяющийся узор.
В следующем подразделе мы опишем более подходящие меры.
Трехмерная матрица стоимости данных. Рассмотрим базовое
изображение В и сопоставляемое изображение М. Мера стоимости
данных Edata(p, /) для р е О (т. е. определенная на носителе изображения В)
и метка / £ L \ {-1} определяют трехмерную матрицу стоимости данных
С, , размера N *N x(d + 1) со следующими элементами (в предпо-
data с с cols rows ч max ' "•' ' v r i~i
ложении, что B = R):
С<1Ша(Х>У><1) =
Edata (*, У, d) если 0 <d < min{dmax, Ncols - x} (g ^
-1 в противном случае
Так, меры SSD и SAD определяют матрицы стоимости CSSD и CSAD.
Трехмерная матрица стоимости данных дает полное представление
о всех стоимостях данных, и ее можно использовать для последующей
оптимизации (например, с применением функции стоимости
гладкости) в управляющей структуре стереосопоставителя (т. е.
алгоритма сопоставления стереоизображений). На рис. 8.5 показаны матрицы
данных. Каждая диспаратность определяет один слой трехмерной
матрицы. Если В = R, то во всех элементах столбцов, показанных
темно-серым цветом, находится значение -1. Светло-серым цветом показаны те
8.1. Сопоставление, стоимость данных и уверенность
351
координаты х, в которых диапазон возможных диспаратностей
ограничен, т. е. они не могут достигать максимального значения dmax.
Если мы рассматриваем только по одной строке изображения у за раз,
а функция стоимости данных фиксирована, то нотацию можно
упростить и писать С(х, d), опуская текущую строку у и функцию стоимости.
хк
Диапазон
ограниченных
диспаратностей
0 12 3 ...
Рис. 8.5. Слева: трехмерная матрица стоимости данных для функции Edata.
Каждый элемент содержит либо значение Edata(x, у, а), либо -1.
Справа: вид на эту матрицу сверху в предположении, что Ncois > dmax и В = R;
темно-серым цветом показаны все столбцы (в направлении у), содержащие
значение -1, светло-серым цветом обозначен диапазон ограниченных
диспаратностей, потому что существует хотя бы один столбец
(в направлении у), помеченный значением -1
8.1.2. Функции стоимости данных
Стереосопоставитель часто определяется членами стоимости
данных и гладкости и управляющей структурой, которая показывает, как
эти члены применяются для минимизации полной ошибки функции
пометки f. Член гладкости определен в очень общем виде, а об
управляющих структурах мы поговорим позже. Главным элементом стерео-
сопоставителя является вычисление стоимости данных. Мы определим
несколько функций стоимости данных, уделив особое внимание
обеспечению некоторой инвариантности относительно артефактов
освещения и различий в яркости левого и правого изображений.
Вариант с нулевым средним. Вместо того чтобы вычислять
функцию стоимости данных, например ESSD(x, /) или ESAD(x, /), для исходного
изображения, мы сначала вычислим среднее Вх по окну W*(B) и среднее
Mx+d по окну Wlxfd (M), вычтем Вх из всех значений яркости в окне Wf(B) и
Mx+d из всех значений в окне wlx*d (M), а затем вычислим функцию
стоимости данных - получится вариант с нулевым средним. Это один из спо-
552 ♦ Глава 8. Сопоставление аереоизображений
собов уменьшить влияние артефактов освещения (т. е. устранить
зависимость от предположения о постоянстве яркости).
Мы будем обозначать этот способ обработки начальной буквой Z в
подстрочном индексе функции стоимости данных. Так, EZSSD и EZSAD -
функции стоимости SSD SAD в варианте с нулевым средним.
Формально они определяются следующим образом:
/ к
EZSSDC,d)= 1Х[(В,н,+ГВ;(М,,1Ы,.гад; (8.10)
i=-lj=-k
I к
E7qAn(x,d)= У У \[В+. + .-В][М+/|+. +.-M.J\2. (8.11)
ZSADK ' ' i-U Ш |L x + i,y+; xJL x + d + i,y+) i+dJl v '
i=-lj=-k
Функция стоимости данных NCC. Нормированная взаимная
корреляция (normalized cross correlation - NCC) для сравнения двух
изображений была определена во врезке 4.11. В нее уже входит приведение к
нулевому среднему, но для единообразия мы все же будем добавлять Z в
подстрочный индекс. Стоимость данных NCC определяется следующим
образом:
EZNCC(x,d) = \ J- . ^ 2 , (8.12)
V^S.* '^M,x+d
где
<x=II[Bx+i,y+j-Bx]2> (8.13)
i=-ij=-k
l к
<,,<t=ll[M^>,y4-Kj- (8-14)
i=-lj=-k
Стоимость ZNCC также позволяет отказаться от предположения о
постоянстве яркости.
Переписная функция стоимости данных. Нормированная
переписная функция стоимости с нулевым средним {zero-mean normalized census
cost function) определена следующим образом:
/ k
Ezcm(x, d) = XI P(* + h У + Л Ф, (8.15)
i=-ij=-k
где
8.1. Сопоставление, стоимость данных и уверенность
353
p(u,v,d) =
0 В IB иМ _ 1М.
" uv х u + d,v x+d
1 в противном случае
(8.16)
где 1 означает либо <,_либо > в обоих случаях. Если использовать Вх
вместо Вх и Mx+d вместо Mx+rf, то получится переписная функция
стоимости Ест (без нормировки на нулевое среднее).
Пример 8.1 (пример переписной функции стоимости данных). Рассмотрим
следующие окна Wx(B) и Wx+d(M) размера 3х3:
2
1
2
1
2
1
6
4
3
5
7
5
5
6
4
9
7
6
иМ
Имеем В * 2.44, АГ * 6.11.
Положим i = ) = -1, тогда u = x-lnv = y-l. Имеем Вх_х _х = 2 < 2.44
x-1+d,
f _x = 5 < 6.11, следовательно, р(х - 1, у - 1, d) = 0.
М
В качестве второго примера рассмотрим i =j = +1. Имеем Бх+1 = 3 > 2.44, но
x+l+d,y+l
= 6 < 6.11, следовательно, р(х + 1, у + 1, d) = 1
В случае / =/ = -1 значения находятся по одну сторону от среднего, а в случае
i = j = +1 - по разные стороны. В нашем примере отсюда следует, что Е = 2.
Пространственное распределение значений р показано в матрице ниже:
0
1
0
0
0
0
0
0
1
В следующем векторе cxd эти значения р перечислены в порядке слева
направо, сверху вниз: [0, 0, 0,1, 0, 0, 0, 0, 1]т.
Обозначим Ъх вектор, в котором значения sgn(Bx+j . - Вх) выписаны в
порядке слева направо, сверху вниз (sgn обозначает функцию сигнум).
Аналогично вектор mx+d содержит значения sgn(Mx+j+d - Mx+d). Для
данных из примера 8.1 имеем:
m
Ъх=[-1,-1,+1,-1,-1,+1,-1,-1,+1]т,
= [-1,-1,+1, +1,-1, +1,-1, -1,-1],
cxd=[0,0,0,l,0,0,0,0,l]T.
(8.17)
(8.18)
(8.19)
Вектор cxd показывает, в каких позициях различаются векторы Ъх и
mx+d; количество позиций, в которых два вектора различаются,
называется расстоянием Хэмминга между этими векторами.
554 ♦ Глава 8. Сопоставление аереоизображений
Наблюдение 8.1. Нормированная переписная функция стоимости данных с
нулевым средним EZCEN(x, d) равна расстоянию Хэмминга между векторами Ьх и тх+сГ
Адаптировав определения векторов Ъх и mx+d к переписной функции
данных ECEN, мы также сможем представить ее в виде расстояния
Хэмминга.
Врезка 8.1 (Хэмминг). Американский математик Р. У. Хэмминг (1915-1998)
внес большой вклад в информатику и телекоммуникации. Его имя носят код
Хэмминга, окно Хэмминга, числа Хэмминга и расстояние Хэмминга.
Заменив в векторах Ьхи mx+d значения -1 на 0, мы сможем очень
эффективно вычислять расстояние Хэмминга между получившимися
двоичными векторами2.
8.1.3. От глобального сопоставления к локальному
В совокупности функции стоимости данных и гладкости определяют
задачу минимизации полной ошибки (8.1). В члене гладкости
используется множество смежности А(р), обычно подразумевается 4-смежность
или еще большее множество.
Распространение 4-смежности на носитель изображения.
Предположим, что множество А определено отношением 4-смежности.
Метка / (т. е. диспаратность, если мы говорим о сопоставлении
стереоизображений) в пикселе р через член гладкости зависит от меток,
назначенных четырем 4-смежным с ней пикселям q Е АА(р), см. рис. 8.6
слева.
г
г
q
г
q
г
q
г
q
г
q
q
р
q
q\
Рис. 8.6. Слева: зависимость от 4-смежных пикселей.
Справа: зависимость 4-смежных пикселей от 4-смежных с ними пикселей
Метки в пикселях q также зависят - благодаря ограничению
гладкости - от меток 4-смежных с ними пикселей г, см. рис. 8.6 справа.
Метки в пикселях г опять-таки зависят от 4-смежных с ними
пикселей. Продолжая этот процесс, мы приходим к выводу, что метка в пик-
2 См. [Я. S. Warren. Hacker's Delight, Addison-Wesley Longman, New York, 2002, p. 65-72].
8.1. Сопоставление, стоимость данных и уверенность ♦ 355
селе р зависит от всех пикселей носителя П. Если множество А больше
множества 4-смежности, то зависимости данных распространяются
по П еще быстрее.
Член данных определяет локальную зависимость значения от
пикселей изображения, а член гладкости - глобальную зависимость от всех
назначенных значений диспаратности, что гарантирует точность
решения задачи минимизации (8.1).
Глобальное сопоставление и его временная сложность.
Глобальное сопоставление (ГС) аппроксимируется благодаря использованию
менее накладных управляющих структур стереосопоставителя. Кратко
опишем временные характеристики ГС.
Рассмотрим очень высокий штраф за негладкость, скажем, Esmooth(f,/") =
G -N -N , если f' ff (или даже еще выше). В таком случае складыва-
max cols rows' ' р > q v rn ' ' j r-\
ется ситуация, когда (обычный) член данных уже не играет роли; любая
карта диспаратности с одинаковыми значениями для всех пикселей В
дает решение задачи оптимизации, и сложность такого решения
определяется временем, необходимым для записи одного и того же
значения во все пиксели В. С другой стороны, предположим, что штраф за
негладкость пренебрежимо мал и решение определяется только
стоимостью данных. Тогда (согласно принципу «победитель забирает всё»,
см. об этом ниже) мы также можем получить эффективное и точное
решение задачи минимизации.
Наблюдение 8.2. Член данных, множество смежности и член гладкости в
задаче минимизации (8.1) влияют на время, требуемое для нахождения ее точного
решения.
Рассмотрим изображения В и Мразмера Ncols*Nrows. Для реализации ГС
каждый пиксель Б должен взаимодействовать со всеми остальными
пикселями Ву скажем, посредством отношения 4-смежности; самый
длинный путь распространения информации имеет длину Ncols + Nrows (если
пиксель находится в углу П), а средняя длина пути равна (Ncols + JVrows)/2.
Каждый из N , -JV пикселей должен взаимодействовать с остальными
^" cols rows " "
Ncois' Nrows ~ 1 пикселями. В результате получаем асимптотическое время
вычисления одной глобальной пометки /":
t =0((N , +N )N2; -JV2 ) (8.20)
one \v cols rows' cols rows/ v '
(т. е. время порядка ^(iV5), eamN=Ncols = Nrows). Мощность множества всех
возможных пометок равна
Call ~
fle&(d^sN™s). (8.21)
356
Глава 8. Сопоаавление стереоизображений
Для полной проверки всех возможных пометок понадобится время
caii' 1опе- Конечно, так обстоит дело в худшем случае, которого можно
избежать; существуют ограничения на возможные пометки, и объем
взаимодействия между пикселями можно сократить, если не распространять
одну и ту же информацию по изображению В многократно или построить
пирамиду изображений (см. раздел 2.2.2) для уменьшения длины путей
между пикселями. Но все равно не известно ни одной серьезной попытки
реализовать ГС (например, на параллельном оборудовании).
Область влияния. Решая, какую метку/- назначить пикселю р,
управляющая структура стереосопоставителя просматривает пиксели в
множестве p + S, применяя ограничение гладкости, чтобы получить обратную
связь на выбор данной /. Мы называем множество 5 областью влияния.
На рис. 8.7 слева показана такая область, определенная пересечением
дискретных лучей с Q; в данном случае в направлении пикселя р идут
16 лучей. Область влияния теперь не совпадает со всем носителем П, как
в случае ГС, но и не является локально ограниченной, поскольку лучи
простираются до границ изображения. Мы получили область влияния
для полуглобального сопоставления (СГС) (лучевого).
На рис. 8.7 справа показана область влияния, полученная многократным
расширением путем добавления пикселей, 4-смежных с предыдущей
областью влияния. Количество расширений определяет радиус созданного
4-круга. Такая область влияния используется в методе сопоставления на
основе распространения доверия (belief-propagation matching - ВРМ).
р
/^Л
^\\J
7D
т
L
> 1
J~^
Рис. 8.7. Слева: пространство поиска, определенное 16 лучами, идущими
от границы изображения к пикселю р. Справа: пространство поиска,
получающееся в результате восьмикратного включения 4-смежных пикселей
ГС - это один из крайних случаев определения области влияния. Другой
крайний случай - S = {(0,0)}, когда область влияния р + S=р не содержит
никаких других пикселей; в таком случае мы не учитываем ограничение глад-
8.1. Сопоставление, стоимость данных и уверенноаь ♦ 557
кости путем анализа меток в смежных пикселях, и функция стоимости
данных принимает во внимание только значение в р (например, функция Е^).
Локальное сопоставление. Если область влияния ограничена
некоторой фиксированной константой, то алгоритм сопоставления является
локальным. Разумеется, при 5= {(0,0)} сопоставление будет локальным.
Если количество расширений 4-смежными пикселями (как на рис. 8.7
справа) фиксировано, то сопоставитель также локальный. Если же это
количество растет с увеличением размера N , *N изображений В и М,
г J г г cois rows f ■>
то мы имеем полуглобальный сопоставитель (круговой).
На рис. 8.8 приведен пример использования локального и
полуглобального стереосопоставителя для одной и той же сцены.
Рис. 8.8. Вверху: входное изображение из стереопоследовательности, записанной
в Оклендском университете. В середине: карта диспаратности, построенная
с помощью локального сопоставителя (блочный сопоставитель, который был
включен в библиотеку OpenCV по состоянию на начало 2013 г.). Внизу: карта
диспаратности, построенная с помощью полуглобального сопоставителя iSGM
558 ♦ Глава 8. Сопоставление аереоизображений
8.1.4. Тестирование функций стоимости данных
Чтобы проверить, насколько точно различные функции стоимости
данных определяют соответственный пиксель в М, мы можем
применить стереосопоставитель, который не зависит ни от управляющей
структуры, ни от выбранного члена гладкости, а кроме того, понадобятся
стереопары с контрольными данными, для которых мы точно знаем,
какие пиксели соответствуют друг другу.
Победитель забирает всё. Мы сведем задачу минимизации полной
ошибки функции пометки /к задаче минимизации выражения
E(f)=lEdata(p,fp). (8.22)
рей
Поскольку соответственный пиксель М должен находиться в той же
строке изображения (на эпиполярной прямой), то для оптимизации
нужно просто вычислить для любой точки р = (х, у) и любой возможной
диспаратности f [см. (8.3) и (8.4)] все значения Edata(p, f) и точно найти
минимум (8.22), взяв для каждого р диспаратность /, которая
доставляет минимум функции Eda[a(p, f). Для этого мы построим трехмерную
матрицу стоимости данных Cdata, выберем позицию пикселя р = (х, у),
пробежимся по всем слоям d = 0, d = 1 и т. д. до d = dmax (см. рис. 8.5) и
сравним все значения Cdata(x, у, d) > 0, чтобы найти диспаратность
fp = argmm{Cdata(x,y,d) > 0}, (8.23)
0<d<dmax
доставляющую минимум. Иными словами, для любой точки р = (х, у) е Q
мы применяем управляющую структуру, показанную на рис. 8.9.
Положить d-d . -0,Е. -Е. Ар, 0);
mm ' mm data*r' "
while d <x do
Положить d = d+ 1;
Вычислить Е - Edata{p, d);
if£<£ then
mm
E . =Ev\d =d;
mm mm '
end if
end while
Рис. 8.9. Победитель забирает всё в точке р = (х, у) е П,
производится сопоставление слева направо
Этот стереосопоставитель порождает артефакты глубины. Мы не
считаем его пригодным, нам просто любопытно понять, как ведут себя
различные функции стоимости данных при попытке найти соответствен-
8.1. Сопоставление, аоимоаь данных и уверенность ♦ 559
ные пиксели. Этот тест не зависит ни от ограничений гладкости, ни от
сложной управляющей структуры.
Контрольные данные для измерения точности сопоставления
стереоизображений. Во врезке 4.12 был определен термин
«контрольные данные». Предположим, что метод измерения дает
(относительно) точные значения диспаратности в пикселях изображений, взятых
из множества или последовательности стереопар В и М. Метод может
основываться на синтетических стереопарах, сгенерированных для
некоторой трехмерной модели, и программе трехмерного рендеринга,
которая вычисляет стереопары. Или же на использовании лазерного
дальномера для измерения расстояний на реальной трехмерной сцене.
См. врезку 2.12, где приведены примеры наборов данных в сети; еще
один возможный источник онлайновых тестовых данных - сайт vision.
middlebury.edu/ Миддлбери-колледжа.
Точка р е П определяет плохой пиксель В, если вычисленная в р диспа-
ратность отличается от контрольного значения больше, чем на 1 (к
примеру). Процент пикселей, не являющихся плохими, - широко
распространенная мера точности сопоставления стереоизображений.
Эксперимент можно поставить следующим образом. Выберем
тестовый набор данных, для которых имеются контрольные данные.
Выберем интересующие нас функции стоимости данных. Произведем
статистический анализ процента плохих пикселей в результате
применения управляющей структуры, описанной на рис. 8.9, к выбранным
функциям стоимости на выбранном тестовом наборе. На рис. 8.10
приведен пример тестовых данных (длинные стереопоследовательности),
для которых имеются контрольные данные.
Рис. 8.10. Слева: исходное изображение Set2SeqlFramel из набора EISATS.
Справа: визуализация карты диспаратности с помощью цветового ключа,
используемого всюду в этой книге
560 ♦ Глава 8. Сопоставление аереоизображений
8.1.5. Меры уверенности
В начале раздела 2.4.2 мы определили меры уверенности, которые
можно использовать, если контрольных данных нет. В данном
контексте меру уверенности Г(р) в точке р £ П (базового изображения В)
следует формировать на основе моделей сопоставления стереоизображений
или правдоподобного предположения о процессе сопоставления.
Согласованность слева направо. Проверка согласованности слева
направо определяется следующим образом. Положим В = Яи выполним
сопоставление правого изображения с левым, в результате получится
диспаратность f{R) в точке р. Затем положим В = L и выполним
сопоставление левого изображения с правым, получится диспаратность f{L)
в точке р. В обоих случаях берутся абсолютные величины вычисленных
диспаратностей. Для сравнения f{R) с f{L) положим
Г,(Р) ■ lw« ,ш1.,- <8-24)
MR) _ HL)
J p J p
+ 1
Как видим Гх(р) = 1, если f(R} = f(L) и 0 < ГДр) < 1 в противном случае.
Например, если Гх(р) < 0,5, то вычисленные диспаратности следует
отбросить как несогласованные.
В основе этой меры уверенности лежит ожидание того, что два
согласованных результата поддерживают друг друга. Однако наш
повседневный опыт свидетельствует совсем о другом (вспомните-ка о газетах,
которые врут, но по-разному).
Аппроксимация параболой. Более подходящими представляются
меры уверенности, основанные на использованных функциях
стоимости данных, их значениях или моделях сопоставления.
Для точки р рассмотрим параболу ах2 + Ъх + с, которая
аппроксимирует суммарную стоимость (см. формулу (8.2)) в окрестности
диспаратности dQ, в которой значение A (d) = Ada[a(p, d) достигает глобального
минимума (рис. 8.11). В точке минимума этой параболы диспаратность
определяется с субпиксельной точностью] единичное расстояние между
двумя соседними диспаратностями определяется как единичное
расстояние между двумя 4-смежными пикселями.
Параметр а определяет кривизну параболы, и это значение можно
принять в качестве меры уверенности. Для нахождения а нужно решить
следующую систему уравнений:
a(d0 - I)2 + b(d0 - 1) + с = A(d0 - 1), (8.25)
8.1. Сопоставление, стоимость данных и уверенность
361
ad\ + bd0 + c = Ap{dQ),
a(dQ+iy + b(d0+l) + c=Ap(d0+l).
Отсюда следует, что
Г2(р) = 2а = Ap(d0 - 1) - 2 • Ap(d0) + Ap(d0 + 1)
(8.26)
(8.27)
(8.28)
является одной из возможных мер уверенности, которая достигает
минимума Г2(р) = 0, когда Ap(d0 - 1) = Ap(d0) = Ap(d0 + 1), а в остальных
случаях а > 0.
Суммарная f
стоимость
т—г
~Г~1 Г
1 Г
Диспаратность
Рис. 8.11. Аппроксимация параболой в точке d0 дает минимум
суммарной стоимости. Парабола также определяет диспаратность
в точке минимума с субпиксельной точностью (см. штриховую линию)
Возмущение. Возмущение количественно описывает отклонение от
идеальной функции стоимости, которая достигает глобального
минимума в точке dQ и «очень велика» в остальных точках. Применяется
нелинейное масштабирование:
Гъ(Р) = rfmax " X еХР
d*dn
[Ap(d0)-Ap(d)]
w2
(8.29)
Параметр \р зависит от диапазона значений суммарной стоимости.
Если A (d0) = A (d) для всех d ф d0 и гр = 1, то Гъ(р) = 0 является
минимальным значением.
Амплитудный коэффициент. Пусть dx - диспаратность, для
которой суммарная стоимость достигает локального минимума, второго по
величине после локального минимума в dQt одновременно являющегося
глобальным. Под амплитудным коэффициентом понимается мера
уверенности, которая сравнивает эти два наименьших локальных
минимума:
362
Глава 8. Сопоаавление стереоизображений
Г Ар) = 1 -
(8.30)
Значение dx не определяется вторым снизу значением суммарной
стоимости, оно может оказаться соседним с d0. Как и раньше, если все
значения A (d) равны, то Г4(р) принимает минимальное значение 0.
Использование мер уверенности. При плотном (в каждом пикселе
р G П) сопоставлении стереоизображений иногда имеет смысл заменить
вычисленные диспаратности с низкой степенью уверенности
специальной меткой -1. Последующие процессы могут подставить «разумные»
значения диспаратности в этих пикселях, например применив
интерполяцию диспаратностей в ближайших точках, где степень уверенности
в результатах высока. На рис. 8.12 показаны примеры пикселей, для
которых метка свидетельствует о низкой степени уверенности.
Рис. 8.12. Слева: изображение из стереопары Bridge.
Справа: карта диспаратности, в которой диспаратности с низкой степенью
уверенности заменены серым цветом. Мелкие числа в цветовом ключе справа
изменяются от 5,01 до 155 (шкала нелинейна, число 10,4 находится примерно
посередине) и обозначают расстояние в метрах
8.2. Сопоставление методом динамического
программирования
Динамическое программирование - метод эффективного решения
задач оптимизации путем кэширования решений подзадач вместо их
повторного вычисления.
В этом разделе мы кратко напомним, в чем состоит идея
динамического программирования, и затем применим его к анализу стереоизо-
8.2. Сопоставление методом динамического программирования ♦ 563
бражений, описав сопоставление методом динамического
программирования (dynamic-programming matching - DPM).
Врезка 8.2 (динамическое программирование, Беллман и компьютерное
зрение). Динамическое программирование вошло в обиход проектирования
алгоритмов в 1953 г. благодаря американскому специалисту по прикладной
математике Р. Беллману (1920-1984), который занимался вопросами
планирования, принятия решений и теории оптимального управления.
В 1960-е гг. динамическое программирование стало популярным способом
решения задач, связанных с компьютерами (например, разбор
контекстно-свободных языков, оптимизация умножения матриц).
Ранние примеры применения методов оптимизации пути к выделению
границ см. в работах [V.A. Kovatevsky. Sequential optimization in pattern recognition and
pattern description. In Proc. IFIP, 1968, p. 1603-1607], [U. Montanori. On the optimal
detection of curves in noisy pictures. Comm. ACM, vol. 14,1971, p. 335-345] и [A.Martetti.
Edge detection using heuristic search methods. CGIP, vol. 1,1972, p. 169-182].
8.2.1. Динамическое программирование
Чтобы задачу можно было решить методом динамического
программирования, она должна удовлетворять следующим условиям.
1. Задачу можно разбить на несколько подзадач, каждая из которых
решается по отдельности.
2. Эти подзадачи можно упорядочить по времени, так что все
подзадачи, результаты которых необходимы для решения
последующей подзадачи, уже решены ранее.
3. Существует рекурсивное соотношение между подзадачами.
4. Решение любой подзадачи не зависит от истории решения
предыдущих подзадач.
5. Решение последней подзадачи должно быть замкнутым.
Задача о нахождении кратчайшего пути во взвешенном
графе. Рассмотрим нахождение кратчайшего пути во взвешенном графе.
О графах см. врезку 3.2. Во взвешенном графе каждому ребру
сопоставлен положительный вес. Пример приведен на рис. 8.13.
Взвешенный граф можно рассматривать как дорожную сеть, тогда
наша цель - найти кратчайший путь от одной вершины до другой,
считая, что вес ребра равен длине соответствующего участка дороги.
564 ♦ Глава 8. Сопоставление стереоизображений
Подзадача 1 Подзадача 2 Подзадача 3 Подзадача 4 Подзадача 5
Рис. 8.13. Пример взвешенного графа.
Вершины уже расположены так, что видны подзадачи
Пример 8.2 (применение динамического программирования для решения
задачи о кратчайшем пути). Рассмотрим ориентированный взвешенный граф
на рис. 8.13. Задача состоит в том, чтобы найти кратчайший путь от вершины А
к вершине /. Стрелки показывают направление движения. Сеть можно разбить
на пять подзадач, как показано на рисунке: подзадача 1 содержит только
вершину А, подзадача 2 - вершины В, С и Д подзадача 3 - вершины Е, F и G,
подзадача 4 - вершины Н и /, а подзадача 5 - вершину /.
Обозначим X и У вершины, принадлежащие подзадачам т и т + 1, a d(X, У) -
расстояние между ними. Чтобы вычислить длину кратчайшего пути из
вершины X в вершину /, воспользуемся рекурсивной функцией
Ет(Х)= min {d(X,Y) + Em + l(Y)}, (8.31)
У в подзадаче т+\
где ES(J) = 0. Тогда Е^А) определяет минимальную длину. См. табл. 8.1.
В подзадаче т используются результаты, уже полученные для вершин,
принадлежащих подзадаче т + 1, поэтому нам не нужно снова проходить весь путь
до /. Обратное прохождение даст кратчайший путь от А до /. Решение может
быть не единственным.
8.2.2. Ограничение порядка
Теперь мы готовы применить динамическое программирование для
вычисления диспаратностей вдоль одной строки изображения у. Мы уже
делали это раньше, применяя алгоритм на рис. 8.9 (победитель
забирает всё), тогда, принимая решение в пикселе р, мы руководствовались
только стоимостью данных, и не требовалось просматривать соседей р,
8.2. Сопоставление методом динамического программирования ♦ 565
чтобы подтвердить решение. Поэтому не было также возможности (да
и необходимости) применить динамическое программирование. Такая
необходимость возникает, если мы включаем в задачу оптимизации
зависимости между смежными пикселями. Один из вариантов -
применить ограничение гладкости, и мы это сделаем в следующем разделе.
Другой вариант - применить ограничение порядка, которое также
вводит зависимости между диспаратностями в смежных пикселях.
Таблица 8.1. Длины Е (X) кратчайших путей до вершины У
Подзадача
5
4
3
2
1
Кратчайшая длина
£5(7) = 0
Е4(Н) = d(H,J) + ES(J) = 8
E4(l) = d(l,J) + Es(J) = 6
£,(£) = d(E, 1) + E4(l) = 11
El(F) = d(F,H) + E4(H) = 11
£3(G) = d(G, 1) + £4(/) = 8
E2(B) = d(B,F) + El(F) = 12
E2(Q = </(C, £) + £,(£) = 13
E2(D) = d(D, G) + £3(G) = 12
E1(A) = d(A,B) + E2(B) = 14
Путь
J
H,J
U
EJJ
F.H.J
GJJ
B.F.HJ
C,E,I,J
D.GJJ
A,B,F,H,J
Ограничение порядка для геометрии сцены. Когда производится
стереоскопическая аэрофотосъемка и расстояние до камер велико по
сравнению с высотой видимых объектов на поверхности Земли, можно
предполагать, что соответствия упорядочены на эпиполярной прямой.
Предположим, что точка (х + at, у) изображения В соответствует точке
(а: + Ь;, у) изображения М при / = 1, 2, 3. Заданная геометрия
стереоскопической системы удовлетворяет ограничению порядка, если
из того, что 0 < а1 <а2 <аъ, вытекает, что x + b1<x + b2<x + br (8.32)
Если В = L, то может случиться, что Ьх < 0, но 0 < Ъ2 < Ъъ. Если В = R, то
может случиться, что 0< bv но ЬЪ<Ь2< 0. См. рис. 8.14.
\в
х+ах х+а2 х+а3
х+ах х+а2 х+а3
\м
x+bx x+b2 x+b3
x+Z?1 i+b3 x+b2
Рис. 8.14. Верхняя строка удовлетворяет ограничению порядка, нижняя - нет
566 ♦ Глава 8. Сопоставление аереоизображений
На рис. 8.15 показана геометрия сцены, для которой ограничение
порядка не выполнено. Вообще говоря, это возможно всегда, когда
имеются значительные различия в глубине по сравнению с расстоянием от
камер до объектов на сцене.
Рис. 8.15.Левая камера видиттри пространственные точки
в порядке Р, R, О, а правая камера - в порядке Р, О, R
Эпиполярные профили. Эпиполярный профиль можно использовать
для иллюстрации результатов сопоставления строки у изображения В
со строкой у изображениия М; ссылаться на у нет необходимости.
Профиль представляет собой дискретную дугу, «общее направление»
которой - из левого верхнего в правый нижний угол квадрата размера
NcolsxNcols; координаты а: изображения В соответствуют столбцам, а
координаты а: изображения М - строкам. Диспаратности f в точке р = (х, у)
соответствует точка квадратной сетки (х - f, х); соседние точки такого
вида соединяются отрезками прямых, так что образуется ломаная дуга.
Эта дуга и называется эпиполярным профилем.
Профиль - это сечение трехмерной сцены, видимое обеим камерам в
(ректифицированных) строках у в северо-восточном направлении, т. е.
по диагонали, идущей вниз из правого верхнего угла квадрата.
Пример 8.3 (два эпиполярных профиля). Пусть Ncols = 16, dmax = 3 и В = L. При
поиске соответствий мы рассматриваем только пиксели левого изображения,
для которых а: = 4,5,..., 16; для х = 1,2,3 не набирается dmax значений. Для строки
у вычисляем 13 меток (диспаратностей) f4,f5,..., /16. Предположим, что
получились два таких вектора:
d2 = [f4,/s,...,/16]T=[3,3,3,l,2,0,3,l,0,0,l,2,3]T.
На рис. 8.16 показаны эпиполярные профили для обоих векторов.
8.2. Сопоставление методом динамического программирования ♦ 567
12 3 4 5
9 10 11 12 13 14 15 1С
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
N
S
я;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
шш
шш
i 1 —> 9 ■ •
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Рис. 8.16. Слева: эпиполярный профиль для вектора dr
Справа: эпиполярный профиль для вектора d2
На рис. 8.16 слева мы видим профиль, который монотонно спускается в
правый нижний угол, это говорит о том, что сцена удовлетворяет ограничению
порядка для данной строки у (по крайней мере, согласно вычисленным дис-
паратностям). Эпиполярный профиль справа демонстрирует существование
«столба» на сцене в точке сетки (7,10), из-за чего сцена не удовлетворяет
ограничению порядка в той строке у, для которой построен график.
Врезка 8.3 (история эпиполярных профилей). Эпиполярные профили были
введены в работе [Y.OhtaandT.Kanade.Stereo by intraand inter-scanLine search using dynamic
programming. IEEE Trans. Pattern Analysis Machine Intelligence, vol. 7,1985, p. 139-154], и
там же впервые приведено детальное описание сопоставления методом
динамического программирования (см. раздел 8.2). Конспективное изложение этой
техники уже встречалось в более ранней работе [Н.Н. Baker and Т. О. Binford. Depth
from edge and intensity based stereo. Stanford Al Lab Memo, 1981].
Наблюдение 8.З. Эпиполярный профиль для диспаратностей, вычисленных для
одной строки изображения, дает простой способ проверить, удовлетворяют
ли диспаратности ограничению порядка: эпиполярный профиль должен
монотонно убывать.
8.2.3. Сопоставление методом динамического
программирования с использованием ограничения порядка
Анализ стереоизображений методом DPM приводит к алгоритму
минимизации, который является глобальным в пределах одной растровой
строки или строки у.
568 ♦ Глава 8. Сопоаавление стереоизображений
По точности он часто (в зависимости от конкретного приложения)
уступает многим лучшим современным стереосопоставителям. Но в
некоторых частных случаях (например, при обработке фотографий,
снятых приборами ночного зрения, или изображений со сравнительно
низким разрешением), а также в определенных контекстах (например,
когда требуется обработка в реальном масштабе времени, во
всепогодных устройствах и т. д.) динамическое программирование все еще
является достойным кандидатом.
Задача оптимизации. Дана пара ректифицированных
стереоизображений и функция стоимости данных Ех; для краткости положим
Ex(fx) = Edata(p, f) для р = (х, у). Будем предполагать, что L = В. Требуется
вычислить оптимальную функцию пометки f, которая:
1) минимизирует ошибку
"cols
£(/)=£ Ш); (8.зз)
х=\
2) удовлетворяет ограничению порядка;
3) любому пикселю L можно сопоставить пиксель R (ограничение
уникальности).
Несмотря на то что процесс производится слева направо, мы
предполагаем, что значения fx принадлежат множеству {0,1,..., dmax}. Таким
образом, пикселю (х, у) левого изображения соответствует пиксель вида
(xr,y) = (x-fx,y)-
Вывод верхней и нижней границ. Соответственный пиксель
(xr, y) = (x- fx, у) должен быть виден в правом изображении (т. е. ничем
не загорожен и И х < -Wco/s), и это условие выражается неравенствами
(8.3). Перепишем их здесь в виде:
О < fx < min {x - 1, dmJ. (8.34)
Если а: < dmax, то fx может принимать только значения из множества
{О, 1,..., а: - 1}. Если fx = х - 1, то хг = х - (х - 1) = 1, так что неравенства
1 < х < N , удовлетворяются. Если f = d и d < х- 1,то х = х- d >
г cols ■'" " >х max max ' r max
х-(х-1) = 1. Например, если <imax = 5 и х = 3, то fx может принимать только
значения {0,1,2}. Следовательно, мы с большой вероятностью
сопоставим неправильные точки (хг, у) пикселям (х, у), близким к левому краю
левого изображения.
Теперь изучим влияние ограничения порядка. Если точке (х, у) в L
сопоставлена точка (xr, y) = (x- fx, у) в R, то точка (хг- 1, у) может соответ-
8.2. Сопоставление методом динамического программирования ♦ 569
ствовать только точке (х - а, у) левого изображения, для которой а > 1
(если вообще существует соответственный пиксель). Поэтому хг - 1 =
(х ~а)-La-
Случай 1. Предположим, что (л:, у) в L - первый (слева) пиксель в
строке у, сопоставленный пикселю (хг, у) в R. Значение а может определять
первый пиксель в L (в строке у, слева), сопоставленный пикселю (хг - 1, у)
в Д, при этом все пиксели (а: - а, у), (х - а + 1, у),..., (х - 1, у) в L тоже
сопоставлены пикселю (хг - 1, у) в 7?. Отсюда следует, что
х =*-£>*-l^x-1)-/^. (8.35)
Следовательно,
*"£>*-£!-! (8-36)
или эквивалентно
/.-£.<!. С8-37)
где (х, у) первый пиксель в L, считая с левого конца, который
сопоставлен пикселю (хг, у) в R.
Случай 2. Теперь предположим, что пикселю (х, у) в L сопоставлен тот
же пиксель {хг,у) вR,что и пикселю (х- 1,у) вL.Тогдаxr = x-fx = (x-l)-fx_1
Vlfx = fx-i + 1- При этом неравенство (8.37) также удовлетворяется.
В совокупности неравенства (8.34) и оба рассмотренных случая
приводят к выводу, что
max{0, fx - 1} < fx_x < min{x - 2, dmax}. (8.38)
Этим определяется зависимость между диспаратностями fx и fx_v
которую можно использовать в алгоритме динамического
программирования.
Наблюдение 8.4. Выполнение неравенств (8.38) для меток (диспаратностей) -
необходимое и достаточное условие того, что вычисленное решение будет
удовлетворять ограничениям порядка и уникальности.
Подзадачи. Так как же определить подзадачи, чтобы можно было
применить динамическое программирование? Мы будем
использовать частичную функцию ошибки Em(f), равную сумме значений Ex(fx) для
Кх^т:
т
к(л=1ча (8.39)
х=1
570 ♦ Глава 8. Сопоставление аереоизображений
В подзадаче т мы должны присвоить значения меткам fx для всех а: в
диапазоне 1<х< т; меткам сх> т значения еще не присвоены.
Результаты подзадач. Стремясь минимизировать полную энергию
E(f) = EM(f), мы в подзадаче т вычисляем ошибки следующим образом:
В-(»-.<Ж,^.(й)+ *..,(»}, (8.40)
где функция /уже назначила метки всем пикселям с индексами, не
превышающими номер подзадачи (т. е. для £т1(/)/должна сопоставить
значения т - 1 пикселям, считая слева направо), а Em(d) относится только к
ошибке при выборе диспаратности d для л: = т.
Мы начинаем с т = 1 в изображении В; инициализируем Eml(f) =
E0(j) = 0 и вычисляем /j = 0 и значение £^(0).
Для т = 2 мы уже выбрали d = 0 или d = 1 и так далее. Должны
удовлетворяться неравенства (8.38).
Добравшись до подзадачи х = М, мы имеем оптимальное значение
E(f) и, выполнив обратное прохождение ота, = Мка, = М- 1, от а: = М - 1
кл: = М-2ит. д., можем найти метки, позволившие получить этот
оптимум.
Пример 8.4 (простой пример). Рассмотрим соответственные строки у в левом
и правом изображениях, как показано на рис. 8.17. Имеем dmax = 3, Ncols = 7. В
качестве функции стоимости данных возьмем модуль разности (AD); см. (8.8).
| г а
1 ? 3 3
il
Рис. 8.17. Пример строки у в левом и правом изображениях
Начинаем с Ex(f) = Et(0) = |2 - 1| = 1 для /j = 0. Других возможностей
нет. Далее вычисляем E2(j). Рассмотрев варианты Е2(0) = |3 - 2| = 1 и
Е2(1) = |3 - 1| = 2, мы можем предпочесть f2 = 0, и, следовательно,
E2(f) = E2(0) + E1(f) = 1 + 1 = 2.
Заметим, что f2 = /j, так что неравенства (8.38) удовлетворяются. Эти
неравенства позволяют также взять f2 = 1, и тогда E2(f) = 1 + 2 = 3.
Запомним, какие значения функция Е принимает для выбранных начальных
последовательностей /: ДО, 0) = 2, ДО, 1) = 3.
Для E3(f) мы можем рассмотреть диспаратности 0, 1 или 2 (в
случае Еъ(0, 0, •) только 0 и 1 с D3(0) = 2 и D3(l) = 1). Таким образом,
£3(0,0,0) = 2 + 2=4и £3(0,0,1) = 2 + 1 = 3. Для £3(0,1, •) можно рассмотреть
диспаратности 0,1 или 2, в результате чего получим £3(0,1,0) = 3 + 2 = 5,
£3(0, 1, 1) = 3 + 1 = 4, £3(0, 1, 2) = 3 + 0 = 3.
8.2. Сопоставление методом динамического программирования ♦ 571
Для т = 4 имеем:
£4(0,0,0,0) = 4+1 = 5,
£4(0,0,1,0) = 3 + 1=4,
£4(0,0,1,2) = 3 + 0 = 3,
£4(0,1,0,0) = 5 + 1 = 6,
Е4(0,1,1,1) = 4+1 = 5,
£4(0,1,2,0) = 3 + 1=4,
£4(0,1,2,2) = 3 + 0 = 3,
£4(0,0,0,1) = 4+1 = 5,
£4(0,0,1,1) = 3 + 1=4,
£4(0,1,0,0) = 5 + 1 = 6,
£4(0,1,1,0) = 4+1 = 5,
Е4(0,1,1,2) = 4 + 0 = 4,
£4(0,1,2,1) = 3 + 1=4,
£4(0,1,2,3) = 3 + 1=4.
В этот момент может показаться, что в подзадаче т - 1 нам
придется запомнить все частичные пометки (т. е. последовательности длины
т - 1), чтобы можно было решить подзадачу т. Но это не так!
Неравенства (8.38) выражают тот факт, что нужно рассматривать
только соотношение между fm_x и/т,ав (8.40) мы выбираем d на основе
одной лишь метки fm_x (и условия минимизации суммы).
Поэтому из всех значений E4(fv fv fv f4) нам нужно запомнить только
минимальные значенияЕ4(..., 0) = 4,JS4(..., 1) = 4,£4(..., 2) = 3 и£4(..., 3) = 4,
и вместе с каждым из них мы храним метку, для которой в подзадаче 3
был достигнут этот минимум:
backtrack(4, 0) = 1 (см. £4(0, 0,1, 0) = 3 + 1 = 4),
backtrack(4, 1) = 1 (см. £4(0, 0,1, 1) = 3 + 1 = 4),
backtrack(4, 2) = 1 (см. £4(0, 0,1, 2) = 3 + 0 = 3),
backtrack(4, 3) = 2 (см. £4(0,1, 2, 3) = 3 + 1 = 4).
Сравним с примером нахождения кратчайшего пути в разделе 8.2.1:
в подзадаче т мы имеем от одной до dmax + 1 вершин, каждая
вершина fm является возможной меткой (диспаратностью) в подзадаче ш,
а функция backtrack соединяет эту вершину с меткой fm_x (примечание:
в общем случае таких меток может быть несколько), что позволило нам
найти минимум Ет(..., fm_v fj.
Граф на рис. 8.18 схематично иллюстрирует наш пример вплоть до
подзадачи 4. Каждая вершина дополнительно помечена минимальной
суммарной стоимостью пути к ней от подзадачи 1.
Для единственной возможной вершины в подзадаче 1 начальная
стоимость равна 1. Стрелки, ведущие из вершины fn в подзадаче п к
вершине fn+1 в подзадаче п + 1, помечены дополнительной стоимостью
вследствие использования диспаратности fn+1 в подзадаче п + 1.
В подзадаче М мы имеем одну вершину, определяющую минимум
E(f) = EM(f), это означает, что нужно принимать решение только для
одной возможной диспаратности/^. После этого диспаратности fM_vfM_2, •••
определяются обратным прохождением.
572 ♦ Глава 8. Сопоставление аереоизображений
1£^1^У
Подзадача 1 Подзадача 2 Подзадача 3 Подзадача 4 Подзадача 5
I—:—i I—:—i I—:—i I—:—i I—:—i
Рис. 8.18. На этом графе иллюстрируется рассмотренный
пример сопоставления вплоть до подзадачи 4
Алгоритм. В подзадаче М мы имеем вершину с минимальной
стоимостью и можем пройти обратно по стрелкам, которые привели к этой
вершине.
Вновь вернемся к развернутой нотации: Е(х, у, d) = Ex{d) для строки у, а
backtrack^, d) возвращает массив размера Ncols*(dmax + 1). Emin - минимум
частичной энергии, которая выше обозначалась EJf). Мы вычисляем
/м»/мч» —»f\ в этом порядке. См. алгоритм на рис. 8.19.
fory=1,2, ...,Л/ do
' / / / rows
вычислить £(1, у, 0) {только d = 0 для х = 1}
forx = 2to/V . do
cols
for d = 0 to min{x -1, d } do
E . =+oo
mm
for cT = max{0, d - 1} to min{x - 2, dmJ do
ifE(x-1,y,cf)<Fminthen
E . =£(x-1,y,cf);d =d
mm v ''' " mm
end if
EOc, y,d) = Emjn + f (x, y, d); backtrack(x, d) = dmjn
end for
end for
end for
fmjn = +00 {подготовка к обратному прохождению при х = М}
forc/ = 0tomin{/V ,-1,g( }do
t cols ' maxJ
if£(/V ,,y,d)<E . then
v cols'' ' ' mm
E =E{N ,,y,d);d . =d
mm v cols''' " mm
end if
end for
fN = c/mjn {Fmin - минимум энергии для строки у}
for$x = N . to 2 do
cols
/^ = backtrack(x, f )
end for
end for
Рис. 8.19. Алгоритм DPM с использованием ограничения порядка при В = L
8.2. Сопоставление методом динамического программирования ♦ 575
В роли функции стоимости данных £ может выступать любая из
функций, рассмотренных в разделе 8.1.2.
Распространение ошибки. При динамическом программировании
ошибки имеют тенденцию распространяться вдоль растровой строки
(в рассмотренном алгоритме с В = L - слева направо), что приводит к
горизонтальным полоскам в вычисленной карте диспаратности или
глубины (см. рис. 8.20). На рисунке также видно, что «лучшая» функция
стоимости данных заметно улучшает результаты. См. также рис. 8.28.
Рис. 8.20. Карты диспаратности, построенные методом DPM для стереопары
Crossing, показанной на рис. 8.1. Значения с низкой степенью уверенности
обозначены черным цветом, применялась проверка согласованности слева
направо с порогом 1. Слева вверху: модуль разности в качестве функции
стоимости данных. Справа вверху: переписная функция 5*5.
Слева внизу: переписная функция 5*5 с нулевым средним.
Справа внизу: переписная функция 3*9 с нулевым средним
8.2.4. Алгоритм DPM с ограничением гладкости
Ограничение порядка применимо не ко всем сценам, о чем
свидетельствует рис. 8.15. Сейчас мы заменим ограничение порядка
ограничением гладкости вдоль растровой строки. В предыдущем разделе
574 ♦ Глава 8. Сопоаавление стереоизображений
растровая строка обязана была совпадать с эпиполярной прямой (т. е.
строкой изображения), потому что ограничение порядка
формулируется именно для эпиполярной прямой.
Если вместо ограничения порядка вдоль растровой строки
применяется ограничение гладкости, то мы уже не ограничены эпиполярной
прямой. И тут преимущества не исчерпываются возможностью
применения к сценам, не удовлетворяющим ограничению порядка; теперь
мы можем использовать более одной растровой строки. Возможные
растровые строки показаны на рис. 8.7 слева.
Двухшаговая модель Поттса для функции стоимости гладкости.
Мы выделим в функции гладкости, применяемой вдоль растровой
строки, два члена:
^00Д> Q = Xtfp> Q + X2(fp, fq), (8.41)
где pnq- смежные пиксели на одной растровой строке, а
Л1 \J р •> Jq )
%2 \J р > Jа)' —1
сх
0
С2
0
если
vP-fy
= 1
в противном случае
(р>я)
если
\f -Л>1
в противном случае
(8.42)
(8.43)
Cj > 0 и с2(р, q) > cv xtfp, fq) + X2(fp> fq) = ° Т0ГДа и только тогда, когда fp = fq.
Константа сх задает штраф за малую разность диспаратностей в
смежных пикселях. Функция с2 привносит больший штраф, чем сх, в случаях,
когда разность диспаратностей велика.
Уменьшение штрафа на ступенчатых границах. Полагая
c?(p,q) = -. г (8.44)
2KF,4) \B(p)-B(q)\
для некоторой константы с > 0, мы определяем масштабирование
(посредством очень простой аппроксимации градиента изображения В
между пикселями р и q). В этом случае штраф за разность
диспаратностей на ступенчатой границе в стереопаре уменьшается.
Минимизация ошибки вдоль одной растровой строки. На рис. 8.21
показаны вычисленные карты диспаратности при выполнении DPM
вдоль одной растровой строки. Для заданной растровой строки
рассмотрим сегмент р0, pv ..., рт = р, где р0 находится на краю базового
изображения В,ар = (а:, у) - текущий пиксель, т. е. тот, для которого мы ищем
соответственный пиксель р = (х + d, у) в сопоставляемом изображении М.
8.2. Сопоставление методом динамического программирования
375
Рис. 8.21. Карты диспаратности для стереопары KITTI, полученные
при использовании всего одной растровой строки в методе DPM
с рассмотренным ограничением гладкости и переписной функцией стоимости
данных Зх9 с нулевым средним. Сверху вниз: горизонтальная растровая
строка (слева направо), диагональная растровая строка (из левого верхнего
угла в правый нижний), вертикальная растровая строка (сверху вниз)
и диагональная растровая строка (из левого нижнего угла в правый верхний).
Розовым цветом обозначены пиксели с низкой степенью уверенности
576 ♦ Глава 8. Сопоаавление стереоизображений
По аналогии с (8.40) выпишем уравнения динамического
программирования (т. е. результат подзадачи i в зависимости от результатов
подзадачи i - 1):
Е<РР d) = E*JP? d) + Esmooth P, - l) - ™П Щ - V А)> (8.45)
0 < А < dmax
где
E{q,fq) если fp = fq
E(q, fq) + c, если \fp -fq\ = l (8.46)
mino<A<rfmax E(<1>A) + c2 (P> Ч) если \fp - fq\ > 1
и Edata(p., d) - стоимость данных в пикселе pi для диспаратности d, a c1
и с2 -штрафы в члене гладкости, определенные в (8.43). Член гладкости
(8.46) имеет вид (8.41) и определен таким образом, что нужно
рассматривать только гладкость изменения диспаратности между пикселем pi
в растровой строке и предыдущим пикселем p. v В (8.45) мы вычитаем
miri(KMd E(p._v А), чтобы ограничить диапазон результирующих
значений, не затрагивая саму процедуру минимизации.
Матрица стоимости данных и интегрирующая матрица. Мы
вычисляем трехмерную матрицу стоимости данных по формуле (8.9) и
интегрирующую матрицу для указанной растровой строки. Мы начинаем
со значения Е(р0, d) = Edata(p0, d) на краю изображения и выполняем
динамическое программирование, применяя уравнение (8.45). Минимум,
найденный по достижении противоположного края, определяет
(посредством обратного прохождения) оптимальные диспаратности вдоль
растровой строки.
Пример 8.5 (эффективность различных растровых строк для простых и
трудных данных). Рассмотрим автомобильную систему записи стереоскопических
видеоданных (например, для содействия водителю). Сложность записанных
сцен может сильно различаться, например из-за артефактов освещенности,
ночного времени, дождя, снега, плотности движения, формы видимых
поверхностей (скажем, при обгоне грузовика), среднего расстояния до объектов и т. д.
Все это можно классифицировать, выделив различные ситуации, или
сценарии. Имеются простые сценарии (скажем, ровная, хорошо размеченная дорога,
однородное освещение, неплотный поток машин) и трудные сценарии вроде
показанного на рис. 8.22.
На этом рисунке мы видим стереопару, снятую во время дождя. На правое
изображение повлиял стеклоочиститель, и дорога бликует. На рис. 8.23 показа-
Еsmooth \Р-> Я.) —
8.2. Сопоставление методом динамического программирования ♦ 577
ны реконструкции этой стереопары по одной растровой строке
(горизонтальной и вертикальной), а также реконструкции в простой ситуации.
Рис. 8.22. Стереопара изображений во время дождя из набора HCI.
Показаны также гистограммы
Рис. 8.23. Слева: трудные стереоданные (дождь), показанные на рис. 8.22.
Справа: простые данные для автотрассы. Вверху: диспаратность, вычисленная
для горизонтальной растровой строки, бшзу: диспаратность, вычисленная
для вертикальной растровой строки
В простой ситуации вертикальный обход также дает «разумную»
оценку диспаратностей, тогда как попытка сопоставления вдоль
вертикальной растровой строки в трудной ситуации терпит неудачу.
578 ♦ Глава 8. Сопоставление аереоизображений
Наблюдение 8.5. Метод DPM с ограничением гладкости применим сразу к
нескольким растровым строкам. От выбранных растровых строк зависит
точность карт диспаратности. Горизонтальные строки особенно полезны, когда
предполагается анализировать земную поверхность (например, дорогу).
Врезка 8.4 (история DPM с несколькими растровыми строками). Метод DPM с
несколькими растровыми строками, названный полуглобальным
сопоставлением (semi-global matching - SGM),впервые был описан в работе [H.Hirschmuller.
Accurate and efficient stereo processing by semi-global matching and mutual information.
In Proc. Conf. Computer Vision Pattern Recognition, vol. 2, 2005, p. 807-814]. Этот сте-
реосопоставитель проектировался для построения трехмерных карт города
вроде показанной на рис. 7.1. В настоящее время он применяется во многих
областях, в т. ч. в автомобильных камерах, которые устанавливаются в составе
системы содействия водителю или беспилотной системы.
Базовое и итеративное полуглобальное сопоставление. В
результате применения DPM с ограничением гладкости вдоль одной
растровой строки а мы имеем значения стоимости EJf) в каждом пикселе В.
Складывая эти стоимости для нескольких растровых строк и выбирая
диспаратность, которая дает минимум, мы получаем простой способ
агрегирования результатов вычислений вдоль нескольких растровых
строк в одну диспаратность в каждом пикселе. Этот метод называется
алгоритмом базового полуглобального сопоставления (bSGM).
С момента публикации оригинальной статьи в 2005 г. было
предложено несколько вариантов SGM. Это может быть, например,
пирамидальная обработка стоимостей, включение в процесс нескольких итераций,
различные веса при объединении результатов обработки нескольких
растровых строк, а также использование априорной информации,
гарантирующей распознавание, к примеру, «тонких вертикальных»
фигур на сцене, если приоритет отдается результатам, полученным на
горизонтальных растровых строках. Все перечисленные выше
дополнения - отличительные особенности итеративного полуглобального
сопоставления (iSGM)3.
На рис. 8.24 даны результаты обработки стереопары rain (рис. 8.22)
алгоритмами bSGM и iSGM. Отдавать приоритет результатам,
полученным при обработке горизонтальных растровых строк, разумно для сцен
дороги, в которых преобладает ровная земная поверхность.
3 Опубликовано в работе [S. Hermann and R. Klette. Iterative semi-global matching for robust driver
assistance systems. In Proc. Asian Conf. Computer Vision 2012, LNCS 7726, 2012, p. 465-478]; этот
стереосопоставитель получил награду на конкурсе Robust Vision Challenge на Европейской
конференции по компьютерному зрению 2012 г.
8.5. Сопоставление методом распространения доверия ♦ 579
.Д.~»ч
Рис. 8.24. Карты диспаратности для стереопары rain; см. рис. 8.22.
Слева: после применения bSGM. Справа: после применения iSGM
8.3. Сопоставление методом распространения
доверия
В разделе 5.3 мы рассмотрели распространение доверия как общую
схему оптимизации, которая позволяет назначать метки всем пикселям на
основе заданных членов данных и гладкости и процесса передачи
сообщений, определяющего пространство поиска (рис. 8.7 справа). В этом
коротком разделе мы опишем сопоставление методом
распространения доверия (belief-propagation matching - ВРМ).
Врезка 8.5 (история ВРМ). В работе [J.Sun, N.-N.Zheng and H.-Y.Shum. Stereo matching
using belief propagation. IEEE Trans. Pattern Analysis Machine Intelligence, vol. 25,2003,
p. 1-14] описано, как применить общую стратегию оптимизации методом
распространения доверия к сопоставлению стереоизображений. Этот
подход приобрел широкую известность благодаря работе [P. F. Felzenszwalb and
D. P. Huttenlocher. Efficient belief propagation for early vision. Int. J. Computer Vision,
vol. 70, 2006, p. 41-54].
ВРМ решает задачу сопоставления стереоизображений путем
пометки пикселей, рассматривая носитель П (базового изображения В)
как совокупность мест, которые должны получить метку из множества
L = {0,1,..., d }. Это делается путем оптимизации функции ошибки
peQ
^data\P>Jp)+ 2ша ^smooth\Jp Jq)
(p,q)eA
(8.47)
580 ♦ Глава 8. Сопоставление аереоизображений
где член гладкости можно считать функцией одной переменной, в роли
которой выступает разность между метками смежных пикселей. ВРМ
применяет механизм передачи сообщений, описанный в разделе 5.3.
Варианты функций гладкости описаны в разделе 5.3.2. О
функциях стоимости данных для сопоставления стереоизображений см.
раздел 8.1.2.
Пример 8.6 (применение ВРМ). На рис. 8.25 показан простой пример двух
изображений 5 х 7, образующих стереопару. Предполагается, что левое
изображение базовое. Мы ищем пиксель, соответствующий пикселю (х, у).
Левое изображение Правое изображение
х-3 х х-Ъ х
У
Начальные доски сообщений
•А- .Л/ т\ ~\r
D
В
d=0 d=l d=2 d=3
x
Итерации передачи
сообщений
Конечные доски сообщений
•Л/ «Л' .А- .Л-
В'
D'
d=0 d=l d=2 d=3
Рис. 8.25. Простой пример для обсуждения ВРМ
Будем предполагать, что dmax = 3. Следовательно, мы имеем четыре доски
сообщений, размером 5х7 каждая, но для экономии места на рис. 8.25 не
показаны d столбцов слева от х.
max ^
Каждому пикселю левого изображения потенциально может
соответствовать d +1 пикселей правого изображения. Пикселю (х, у) левого изображения
8.5. Сопоставление методом распространения доверия ♦ 581
могли бы соответствовать пиксели (х, у), (а: - 1, у), (х - 2, у) и (х - 3, у) правого
изображения.
Мы имеем dmax + 1 досок сообщений. Диспаратность между
пикселями (а:, у) и (х, у) равна 0, поэтому стоимость назначения диспаратности О
пикселю (х, у) находится в позиции (х, у) доски 0. Диспаратность
между пикселями (х, у) и (х - 1, у) равна 1, поэтому стоимость назначения
диспаратности 1 пикселю (х, у) находится в позиции (х, у) доски 1. И так
далее.
В начальный момент мы помещаем значения стоимости данных в
позицию (х, у) на всех dmax + 1 досках сообщений: А = Edata((x, у), 0) и
аналогично B,CnD. Так определяется инициализация досок.
Теперь мы начинаем с t = 1 и рассылаем сообщения между смежными
пикселями. Каждый пиксель р отправляет в сообщении смежному
пикселю q вектор длины dmax + 1, содержащий значения для всех deb. Пусть
т1 ^ - такое векторное сообщение, отправленное пикселем р смежному
с ним пикселю q на итерации t. Для d e L выражение [см. (5.40)]
m'(d) = mm
р^ ' ' hcL
(8.48)
Edata(p,h) + Esmooth(h-d)+ X О)
V ssA(p)\q J
определяет обновление в сообщении. Мы собираем в q все сообщения
от смежных пикселей р, складываем их с не зависящей от времени
стоимостью данных и получаем полную стоимость
E^(g,d)+ X m'p^(d) (8.49)
peA(q)
в пикселе q для назначения диспаратности d этому пикселю в момент t.
Вернемся к нашему примеру. После некоторого количества итераций
процесс прекращается, и определяются новые стоимости A', Br, C'hD'b
позиции (х, у) досок сообщений.
Минимум этих стоимостей принимается за диспаратность (метку),
которая будет назначена пикселю в позиции (х, у) в результате алгоритма
ВРМ. Например, если В' = min{A', В', С, D'}, то диспаратность для пикселя
(х, у) левого изображения будет равна 1.
Пирамидальный ВРМ. Воспользовавшись регулярной
пирамидальной структурой данных для каждого изображения (левого и правого),
как описано в разделе 2.2.2, мы сможем сократить длины путей, по
которым передаются сообщения между пикселями. Возьмем к > 1 уровней
в обеих пирамидах, расположив исходное изображение в первом
(нижнем) уровне.
582 ♦ Глава 8. Сопоаавление стереоизображений
Доски сообщений также преобразуются в fc-уровневые структуры
данных. Мы инициализируем стоимости данных на первом уровне, а
также на к - 1 уровнях выше него.
Множество смежности пикселя теперь содержит пиксели из соседних
уровней, а связи между ними определяются регулярной процедурой
построения пирамиды.
Процесс передачи сообщений выполняется точно также, как описано
в разделе 5.3 для общей схемы распространения доверия и
проиллюстрировано на конкретном примере 8.6.
Два свойства передачи сообщений. «Сила» передачи сообщений
из слабоконтрастных областей изображения В в контрастные меньше,
чем «сила» передачи сообщений из высококонтрастных областей в
слабоконтрастные. Об этой асимметрии следует помнить.
Соответственно алгоритм «хорошо справляется» с вычислением согласованных
меток (диспаратностей) в бестекстурных участках, но может испытывать
трудности, если текстура меняется.
В зависимости от выбранных функций стоимости данных и
гладкости передачу сообщений могут в какой-то мере «заблокировать»
ступенчатые границы. Разрывы в изображении часто дают положительный
эффект, поскольку способствуют сохранению разрывов глубины в
местах разрыва яркости.
На рис. 8.26 приведен пример применения ВРМ к реальным
последовательностям слабоконтрастных изображений. Стереопара SetlSeql
из последовательности 1 в наборе EISATS создает проблемы для ВРМ,
если выбор функции стоимости данных основывается на
предположении о постоянстве яркости. Проблему можно решить, подвергнув
входные данные предварительной обработке (например, построив карты
границ Собеля или остаточное изображение относительно
сглаживания) или взяв варианты функций стоимости с нулевым средним.
8.4. Техника третьего глаза
При выполнении стереоскопического анализа видеоданных
желательно иметь механизм управления, который принимает решения о
качестве вычисленных диспаратностей на основе одного обобщенного
показателя, скажем, числа в диапазоне от 0 до 1. При обсуждении
точности (путем сравнения с контрольными данными) или уверенности в
найденных значениях диспаратностей нас интересовали вычисления в
каждом пикселе. А сейчас мы опишем эффективный метод обобщенной
(по стереопаре в целом) оценки качества стереосопоставителя.
8.4.Техника третьего глаза ♦ 583
Рис. 8.26. Вверху: стереопара SetlSeql. В середине: карты границ Собеля для этой
стереопары. Внизу: результат применения ВРМ к исходному изображению (слева)
и к карте границ Собеля (справа); в обоих случаях в качестве функции стоимости
использовался модуль разности (AD)
В этом разделе мы ответим на два вопроса: как выглядело бы
исходное изображение, снятое двумя стереокамерами, если бы мы сняли его
третьей камерой? Как измерить сходство этого виртуального
изображения с фактически снятым третьим изображением?
8.4.1. Построение виртуального изображения, снятого
третьей камерой
Сопоставление стереоизображений производится для
последовательностей, снятых двумя камерами, а третья камера служит для
оценки качества результатов. (Мы могли бы также использовать вторую и
третью камеры для сопоставления, а затем объединить результаты с
диспаратностями, полученными от первой и второй камер, и т. п.)
Три камеры. Мы калибруем три камеры для записи стереопоследо-
вательностей, как показано на рис. 8.27.
584 ♦ Глава 8. Сопоаавление стереоизображений
Рис. 8.27. Вверху: системы координат трех камер.
Внизу: примеры трех снятых изображений - слева направо: третье, левое, правое
Например, при записи сцен дорожного движения из автомобиля
(рис. 8.27 внизу) расстояние между левой и правой камерами может
быть примерно 30 см, а третья камера отстоит от левой примерно на
40 см влево (для лучшей идентификации ошибок сопоставления: если
бы третья камера находилась посередине между левой и правой, то
выявить «проблемы» было бы труднее). В приведенном примере все три
камеры монтировались на одной планке за лобовым стеклом, чтобы
аппроксимировать каноническую конфигурацию стереоскопической
системы. Изображения с левой и правой камер геометрически
ректифицированы перед сопоставлением.
Техника третьего глаза. В общих чертах техника третьего глаза
выглядит так.
1. Записать стереоизображения двумя камерами и вычислить дис-
паратности.
2. Установить третью откалиброванную камеру, снимающую ту же
сцену, что и остальные две.
3. Использовать вычисленные диспаратности для отображения
записанного изображения (скажем, левой камерой) на плоскость
изображения от третьей камеры. Тем самым создается
виртуальное изображение.
8.4.Техника третьего глаза ♦ 385
4. Сравнить виртуальное изображение с тем, что в
действительности записано третьей камерой.
Если виртуальное изображение «в основном совпадает» с третьим, то
стереосопоставитель вычислил «полезные» диспаратности.
Как сгенерировать виртуальное изображение? Деформирование
изображения (image warping) отображает окна входного изображения /
в конечное изображение / с помощью преобразования координат Ку так
чтобы значения пикселей остались по возможности неизменными (из-
за дискретной природы изображений это, вообще говоря, невозможно,
если не ослабить требования). Примерами преобразования К являются
поворот, параллельный перенос и зеркальное отражение.
Поскольку в общем случае узлы сетки не переходят в точности в узлы
сетки, для рендеринга (согласующегося с обратным
преобразованием К'1) максимально возможного количества пикселей в изображении /
обычно применяется какая-то интерполяция. Но в данном случае нас
интересует не создание «красивых изображений», а выявление
«проблем». Например, черные параболические дуги, заметные в виртуальном
изображении на рис. 8.28 справа, в нормальных обстоятельствах были
бы замещены интерполированными значениями; их появление
объясняется неполнотой геометрического преобразования К, а не ошибками
использованного стереосопоставителя.
Рис. 8.28. Слева: третье изображение. Справа: виртуальное изображение, которое
предстоит сравнить с третьим. Виртуальное изображение вычислено путем
применения DPM с ограничением порядка и простой функции стоимости AD
в предположении, что L = В; видны полосы - обычное явление для DPM
с единственной растровой строкой. Синие пиксели (в верхней части) различаются
из-за геометрической ректификации левого изображения. Зеленые пиксели вообще
не заполнены из-за «отсутствующих» диспаратностей стереосопоставителя.
Параболические черные дуги вызваны деформированием изображения,
эта проблема не связана с используемым стереосопоставителем
386
Глава 8. Сопоаавление стереоизображений
Все три камеры откалиброваны, и третье изображение можно
получить в плоскости изображения базовой камеры (в качестве которой мы
выбрали левую). Мы рассматриваем пиксели в изображении с левой
камеры, для которых левая и правая камеры (с помощью стересопостави-
теля) позволили получить значения диспаратности, а значит, и
глубины, поскольку камеры откалиброваны. Пусть d - диспаратность между
парой соответственных пикселей (от левого изображения в пару входит
пиксель р = (х, у)). Согласно (7.22), (7.24) и (7.23), координаты
спроецированной точки Р = (X, Y, Z) равны:
Х =
Ъ-х
Y =
d
J d
(8.50)
Пример 8.7 (только параллельный перенос). В этом примере мы
предполагаем, что система координат третьей камеры получена из системы координат
левой камеры одним лишь параллельным переносом.
Шаг 1. Записываем координаты пространственной точки в системе
координат третьей камеры, начало которой имеет координаты (£х, ty, tz) в системе
координат левой камеры. Получаем такую связь между системами координат:
\г*"Г> *т
(8.51)
Шаг 2. Центральная проекция отображает точку Р в пиксель на плоскости
изображения от третьей камеры, имеющий координаты
ухт ,yT) — JT
* Z
yZT
(8.52)
т J
где fT - фокусное расстояние, найденное в результате калибровки третьей
камеры.
Шаг 3. Согласно шагу 1 и формуле (8.50), мы можем переписать правую часть
(8.52) в виде:
уХт, у j ) JT
Отсюда получаем:
JC — t v Y — tv
/~i l ry £j I
= fr
z J
( ь
x—
d
h
} —
\ d
-tx
~tz
b
yT
' b
J —
J d
-tY
~tz
(8.53)
_ bx-dtx
fb-dtz
и
Ут=/т
by - dtY
fb-dtz
(8.54)
Таким образом, точка Р = (X, Y, Z), которая была отображена в пиксель (х, у)
левого изображения, отображается также в точку (хг, уг) третьего изображения,
8 А Техника третьего глаза
387
а (хТУ ут) теперь можно выразить через (х, у), а не через (X, У, Z),
воспользовавшись откалиброванным вектором параллельного переноса (£х, tv tz), длиной
базы Ьу фокусным расстоянием fT и диспаратностью d, вычисленной стереосо-
поставителем.
Шаг 4. Теперь отобразим яркость в пикселе (ху у) базовой (т. е. левой)
плоскости в плоскость третьего изображения. Для этого мы просто ищем ближайшую
точку сетки. Если несколько разных пикселей базового изображения
отображаются в один и тот же пиксель на плоскости третьего изображения, то мы можем
применить какую-нибудь меру уверенности и выбрать из всех кандидатов то
значение, которое определяется диспаратностью с максимальной степенью
уверенности.
Пример 8.8 (поворот вокруг одной оси). Модифицируем пример 8.7:
предположим, что система координат третьей камеры получается поворотом на
угол в вокруг горизонтальной оси X системы координат левой камеры.
Имеем:
ОгЛ
\^т J
О
о
0
COS0
sin#
0 ^
- sin в\
cos в J
(Х)
Y
UJ
(
=
V
X ^
YcosO-ZsmO
7sin#+Zcos#y
(8.55)
в качестве промежуточного результата получаем:
Xj — J j
и окончательно
X _ 7cosfl-Zsin#
7sin0+Zcos0 И ^"^Fsintf+Zcostf'
х
хт j j
b_
d
= fr
x
b ■ a . r b a V sin 6+f cos в
y—sme+f—cosv J J
d d
y — cosO-f — sine a r • n
* d d * ycosO-fsme
b • /э ■ r b /э У sin 0+f cos 0
y—sm0+f—cos0 * J
d d
(8.56)
(8.57)
(8.58)
Это снова проекция Р на плоскость третьего изображения (не обязательно
узел сетки).
Оставляем разбор общего случая аффинного преобразования
системы координат левой камеры в систему координат третьей камеры в
качестве упражнения для читателя.
588 ♦ Глава 8. Сопоставление аереоизображений
8.4.2. Сходство между виртуальным и третьим
изображениями
Из-за артефактов освещения или изменения яркости в записанном
несколькими камерами видео прямое сравнение путем вычисления
суммы квадратов разностей и суммы модулей разностей невозможно.
Как сравнить виртуальное изображение с третьим. Мы хотим
сравнить виртуальное изображение У (построенное в момент t) с
третьим изображением Т (записанным в момент t). Подходящим средством
выглядит нормированная взаимная корреляция NCC (см. врезку 4.11).
Обозначим Ht множество пикселей, используемых для сравнения
кадров в момент t. Мы не будем включать пиксели, значения которых в
виртуальном изображении остались черными и потому отличаются от
пикселей третьего изображения вследствие (см. рис. 8.28):
1) геометрической ректификации левого изображения;
2) «отсутствия» диспаратностей (т. е. пиксель не является образом
какого-либо отображенного значения); или
3) отсутствия пикселей для примененного преобразования
координат К (т. е. принадлежности параболическим дугам).
Таким образом, в соответствии с этими правилами D.t - это просто
множество всех пикселей, которые оказались прорисованы в образе
левого изображения.
Среднее и стандартное отклонение вычисляются на множестве /2f,
они обозначаются р.^ av для виртуального изображения V и цт, ат для
третьего изображения Г в момент t Тогда NCC имеет вид:
мжс(У,т)-^[Т{Р)-"ЛПР)-^ <**>
где 0 < Мжс{1, J) < 1, а точное совпадение достигается, когда MNCC{I, J) = 1.
Правила определения множества flt влияют на оценку качества. Если
для некоторого стереосопоставителя Пг оказывается относительно
малым, но в этих разреженных пикселях яркости прорисовываются
правильно, то сопоставитель получит высокую оценку. Следовательно,
в состав меры качества имеет смысл включить мощность \nt\.
Более существенную проблему представляют участки изображения с
однородной текстурой. Если яркость пикселя из такого участка левого
изображения неправильно отображается в другую позицию
виртуального изображения, находящуюся, однако, в пределах того же участка, то
NCC, вычисленная для Qt, не заметит таких некорректных деформаций.
8 А Техника третьего глаза ♦ 589
Поэтому рекомендуется наложить на Ht дополнительные ограничения:
мы включаем в Пг только пиксели, «близкие» к какой-нибудь границе
в левом изображении. Эта близость определяет маскуу и Qt становится
подмножеством маски.
Пример 8.9. На рис. 8.29 показано применение техники третьего глаза для
оценки стереосопоставителя ВРМ на заданной видеопоследовательности из
120 кадров. Масштаб NCC выражен в процентах. В пирамидальном алгоритме
ВРМ использовалась простая функция стоимости данных - модуль разности.
Она основана на предположении о постоянстве яркости, которое не
выполняется для рассматриваемой реальной видеозаписи.
20 40 60 80 100 120
Рис. 8.29. Тест метода ВРМ на последовательности стереоизображений
south с применением одного и того же сопоставителя к трем разным
входным изображениям: исходные, остаточные после сглаживания
и карты границ Собеля. См. рис. 8.30
590 ♦ Глава 8. Сопоаавление стереоизображений
Для предварительной обработки данных было применено два
метода: карты границ Собеля и остаточные изображения после
сглаживания. На рис. 8.30 показаны примеры предобработанных изображений,
которые подавались на вход стереосопоставителя вместо исходных. Оба
метода улучшают результаты, если судить по NCC, вычисленной для
замаскированного множества flt, когда в роли маски выступали пиксели,
находящиеся на расстоянии не более 10 от ближайщей границы Кэнни.
Рис. 8.30. Предобработка последовательности стереоизображений south.
Вверху: карты границ Собеля. Внизу: остаточные изображения после сглаживания
Анализ графиков NCC. На рис. 8.29 мы видим резкий спад качества
стереосопоставителя в районе 60-го кадра. Это одно из важных
преимуществ техники третьего глаза - возможность находить ситуации, когда
записанное видео не может быть правильно обработано выбранным
стереосопоставителем. В этом случае нужно поискать пути решения
возникшей проблемы. Можно ли обобщить геометрическую или
фотометрическую модель на данную ситуацию? Как адаптировать стереосо-
поставитель к возникшей ситуации?
Вычисленные значения NCC можно использовать также для
сравнения качества стереосопоставителей на очень длинных последователь-
8.5. Упражнения ♦ 591
ностях, например сравнивать их покадрово, а затем посчитать общую
сумму разностей NCC с учетом знака или просто количество кадров, на
которых один сопоставитель оказался лучше другого.
8.5. Упражнения
8.5.1. Упражнения по программированию
Упражнение 8.1. (сегментация карт диспаратности и вычисление
средних расстояний). Используйте входные стереоизображения,
записанные из движущегося автомобиля (см., например, наборы KITTI, HCI
или EISATS). Примените алгоритм сегментации к картам
диспаратности, вычисленным каким-нибудь стереосопоставителем (например,
имеющимся в OpenCV), чтобы идентифицировать сегменты объектов,
«значимые» в контексте дорожного движения. Подумайте о
применении к сегментам временной согласованности, как описано в
разделе 5.4.2.
Вычислите средние расстояния до выделенных сегментов и
визуализируйте их в сгенерированном видео, которое подытоживает
полученные вами результаты. См. пример на рис. 8.31.
Рис. 8.31. Средние расстояния до сегментированных объектов. Слева: расстояния
только до объектов на дороге. Справа: расстояния до всех найденных объектов
Упражнение 8.2 (меры уверенности для трудных стереоданных).
Выберите или напишите сами два разных стереосопоставителя и
примените их к трудным последовательностям стереоизображений из набора
HCI. Примеры см. на рис. 8.32.
Выберите три разные меры уверенности в вычисленных диспаратно-
стях и визуализируйте результаты их применения в виде графического
наложения на входные последовательности, например, от левой камеры.
592 ♦ Глава 8. Сопоставление аереоизображений
Рис. 8.32. Трудные последовательности стереоизображений из набора HCI
и примеры вычисленных картдиспаратности (методом iSGM)
Обсудите «видимую корреляцию» между значениями с низкой
степенью уверенности и показанными на рисунках ситуациями во
входных последовательностях.
Упражнение 8.3 (метод DPM с ограничением порядка и различными
функциями стоимости данных). Реализуйте алгоритм DPM, как
показано на рис. 8.19, используя ограничение порядка и по меньшей мере три
разные функции стоимости данных, включая AD и ZCEN (окно
выберите по своему усмотрению).
Визуализируйте полученные карты диспаратности, как на рис. 8.20,
выбрав цветовой ключ и исключив значения диспаратности с низкой
степенью уверенности.
На вход подайте:
1) простые стереоскопические изображения (например, снятые в
помещении);
2) трудные стереоскопические изображения, снятые под открытым
небом в условиях, не удовлетворяющих предположению о
постоянстве яркости;и
3) стереограммы из случайных точек, описанные в книге [D. Man.
Vision: A Computational Investigation into the Human Representation and
Processing of Visual Information. The MIT Press, Cambridge, Massachusetts,
1982].
Обсудите видимые различия в полученных цветных картах
диспаратности.
Упражнение 8.4 (метод DPM с несколькими растровыми строками
и членом гладкости). Реализуйте алгоритм DPM с несколькими растро-
8.5.Упражнения ♦ 595
выми строками (известный также под названием SGM), взяв в качестве
члена гладкости двухуровневую модель Поттса (см. раздел 8.2.4). В
качестве функции стоимости данных возьмите ZCEN или ZSAD.
Визуально сравните результаты (цветные карты диспаратности) для
случаев, когда использовались:
1) только горизонтальные растровые строки;
2) только горизонтальные и вертикальные растровые строки;
3) также диагональные растровые строки.
Выберите какую-нибудь меру уверенности и вычислите процентную
долю пикселей с «высокой степенью уверенности» при разном выборе
растровых строк.
Используйте те же входные данные, что в упражнении 8.3.
Упражнение 8.5 (ВРМ, точность и временная сложность). Реализуйте
пирамидальный алгоритм ВРМ. Отметим, что в сети можно найти
исходный код ВРМ. Используйте функцию стоимости данных ZCEN и член
гладкости по собственному усмотрению.
Проанализируйте влияние количества уровней пирамиды на время
работы и видимую точность построенных карт глубины
(воспользуйтесь цветовым кодированием, чтобы сделать представление более
наглядным).
В качестве входных данных используйте те же, что в упражнении 8.3.
Упражнение 8.6 (оценка стереосопоставителей с помощью техники
третьего глаза). Реализуйте технику третьего глаза для оценки
стереосопоставителей. Например, возьмите в качестве входных данных три-
нокулярные последовательности из набора 9 EISATS. Оцените на этих
данных свой любимый стереосопоставитель.
Для сопоставления либо используйте исходные
видеопоследовательности, либо предварительно обработайте их оператором Собеля и
примените сопоставитель к полученным картам границ.
Примените в качестве меры качества NCC с маской (только
пиксели, близкие к границам) или без маски. В итоге получится два варианта
стереосопоставителя и два варианта анализа результатов.
Обсудите графики NCC, получившиеся для всех четырех вариантов
сопоставления тринокулярных видеопоследовательностей.
8.5.2. Упражнения, не требующие программирования
Упражнение 8.7. Предположим, что наша стереосистема должна
анализировать объекты, удаленные по меньшей мере на а метров от
394
Глава 8. Сопоставление стереоизображений
стереоскопической системы с двумя камерами. Внутренние и внешние
параметры камер откалиброваны. Определите значение dmax по этим
параметрам и известному а.
Упражнение 8.8. На рис. 8.33 показаны два эпиполярных профиля.
Верно ли, что они представляют вектор диспаратностей d? Если да, то
какой именно вектор диспаратностей? Обратно: даны два вектора
диспаратностей
di = K*»fs» —»/iJT = [!»О» L 2, 3,0,1,1, 0,1, 2, 3, 2]т,
d2 = \f4,f5, ...JJ = [4,3,2,1,0,1,2,4,1,2, 3,2,2]т.
Постройте соответствующие им эпиполярные профили. Какие
профили и какие векторы удовлетворяют ограничению порядка?
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
/
\
2
3
4
5
6
7
8
9
10
11
12
13
» 14
15
16
\
\
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Рис. 8.33. Два эпиполярных профиля
Упражнение 8.9. В начале раздела 8.1.3 мы обсуждали, как
отношение 4-смежности «прорастает» в носитель изображения путем
повторяющегося создания зависимостей между смежными пикселями. В
момент t = 0 это просто сам пиксель (п0 = 1), в момент t = 1 - еще четыре
4-смежных с ним пикселя (пг = п0 + 4 = 5), в момент t = 2 - еще восемь
пикселей (п2 = пх + 8 = 13). Сколько пикселей будет в этом растущем
множестве в момент t > 0 в предположении, что края изображения не
ограничивают рост множества? В момент завершения итераций т
величина пт определяет мощность области влияния.
Теперь ответьте на тот же вопрос, заменив 4-смежность 8-смеж-
ностью. И напоследок рассмотрите 4-смежность, но в регулярной
пирамиде изображений, надстроенной над данным изображением.
8.5. Упражнения ♦ 595
Упражнение 8.10. Вы считаете, что сопоставители должны
работать для любой входной стереопары? Отлично, вот вам пример -
рис. 8.34. Возьмите простую функцию стоимости данных - модуль
разности (AD) - и обсудите (в качестве «умозрительного
эксперимента»), что получится в результате применения к этой паре алгоритмов
«победитель забирает всё», DPM с ограничением порядка, DPM с
несколькими растровыми строками и ограничением гладкости и ВРМ.
Рис. 8.34. Стереопара
Глава У
Обнаружение
и прослеживание признаков
В этой главе описывается обнаружение особых точек и дается
определение их дескрипторов; особая точка в сочетании с дескриптором
составляет признак. В качестве примеров мы рассмотрим признаки
SIFT, SURF и ORB, а при рассмотрении последнего кратко
остановимся на признаках BRIEF и FAST. Мы обсудим инвариантность признаков
в общем случае и приведем конкретные примеры. В этой главе также
рассматриваются три способа прослеживания признаков: KLT, фильтр
частиц и фильтр Калмана.
9.1. Инвариантность, признаки и множества
признаков
На рис. 9.1 слева показаны обнаруженные особые точки, а справа - их
круговые окрестности, которые можно использовать для вывода дескриптора.
В этом разделе определены свойства инвариантности, которые
представляют интерес, когда нужно охарактеризовать (или спроектировать)
признак. Для обнаружения особых точек в пространстве масштабов мы
рассматриваем круг влияния, радиус этого круга используется также для
определения векторов трехмерного потока, обобщающих векторы
двумерного оптического потока. Множества признаков в
последовательных кадрах видео необходимо коррелировать, и в этой связи мы дадим
введение в алгоритм RANSAC (random sample consensus - консенсус на
случайной выборке) как один из методов решения этой задачи.
9.1.1. Инвариантность
Фотографии снимаются при разном освещении и погодных
условиях, под разными углами, в разное время суток и т. д. Во время аэро-
9.1. Инвариантность, признаки и множества признаков ♦ 597
фотосъемки имеет место поворот объектов на случайный угол, так что
становится важна изотропность (инвариантность относительно
вращения), которая уже упоминалась ранее в разделе 2.1.2.
Рис. 9.1. Особые точки в пространстве масштабов DoG. Слева: особые точки
на сцене дорожного движения. Справа: особые точки и их круги влияния;
радиус круга зависит от масштаба, при котором особая точка обнаружена
При анализе изображений, снятых под открытым небом, часто
требуется инвариантность относительно таких операций, как изменение
освещения или расстояния до фотографируемого объекта.
Процедура 9С Пусть имеется входное изображение / сцены S е 3 и
камера (т. е. процесс формирования и записи изображений) С. Для
изображения 1= C(S) процедура анализа 9С отображает /в некоторый,
допустим, векторный результат R(I) = г. Например, это может быть список
обнаруженных признаков. Таким образом,
R(I)=R(C(S)) = r. (9.1)
Инвариантность относительно изменения сцены. Теперь
предположим, что в снимаемой сцене S происходят изменения вследствие
перемещения объектов, изменения условий освещения, движения
камеры и т. д. В результате определяется новая сцена Snew = N(S) и Inew = C(Snew).
Процедура 9С называется инвариантной относительно изменения N
(в идеальном случае), если
R(InJ=R(C(N(S))) = r, (9.2)
т. е. для Inew получается такой же результат г, как и для /.
Например, если изменение N ограничено только изменением
условий освещения в заранее определенном диапазоне, то % инвариантна к
изменению освещения в этом диапазоне. Если изменение N ограничено
поворотом сцены, как в случае самолета, летящего по другой траекто-
598 ♦ Глава 9. Обнаружение и прослеживание признаков
рии, но на той же высоте и при тех же погодных условиях, то процедура
9С изотропна. См. рис. 9.2.
Рис. 9.2. Сама снятая сцена может обладать инвариантностью
(как, например, изотропная сцена на левом рисунке)
Инвариантность относительно камеры. Теперь предположим, что
имеет место модификация М способа формирования и записи
изображения I (т. е. используется другая камера или только другой объектив),
обозначим Cmod=M(C), a Imod= Cmod(S). Процедура 9Синвариантна
относительно модификации М, если
R(ImJ=R(M(C(I))) = r, (9.3)
т. е. для Imod получается такой же результат г, как и для /.
9.1.2. Особые точки и векторы трехмерного потока
Особая точка определяется характерным изменением яркости
окружающих пикселей, как, например, в угле (см. раздел 2.3.4). На рис. 9.3
показаны особые точки, найденные четырьмя разными программами.
Особую точку можно использовать для вывода дескриптора. Не с
каждым детектором особых точек ассоциирован отдельный дескриптор.
Дескриптором называется конечный вектор, обобщающий свойства
особой точки. Дескриптор применяется для классификации особых
точек. Вместе особая точка и дескриптор образуют признак (в понимании
данной главы).
Особые точки, определенные методом фазовой конгруэнтности.
Фазовая конгруэнтность - один из возможных способов обнаружения
признаков (см. раздел 1.2.5). Локальный максимум меры Tideal hase(p),
определенный в (1.33), идентифицирует особую точку р. Дескриптор
d(p) можно вывести из некоторых свойств в окрестности точки р в
заданном изображении /; например, вектор D(p) = [Лр Я2]т, состоящий из
собственных значений матрицы (2.56).
9.1. Инвариантность, признаки и множества признаков ♦ 599
Рис. 9.3. Четыре детектора особых точек в библиотеке OpenCV.
Слева вверху: особые точки, обнаруженные детектором FAST.
Справа вверху: особые точки, обнаруженные детектором ORB.
Слева внизу: особые точки, обнаруженные детектором SIFT.
Справа внизу: особые точки, обнаруженные детектором SURF
Врезка 9.1 (история обнаружения особых точек в пространстве масштабов).
В работе [Т. Lindeberg. Feature detection with automatic scale selection. Int.J. Computer
Vision, vol. 30,1998, p. 79-116] пространство масштабов впервые было
использовано для нахождения особых точек.
Особые точки в пространствах масштабов LoG и DoG. Оба этих
пространства масштабов определены в разделе 2.4.1. Мы объясним
определение особых точек в обозначениях пространства масштабов
DoG; в LoG подход аналогичен. Напомним, что разность гауссианов
(DoG) с масштабом о и масштабным коэффициентом а > 1 используется
для объединения соседних уровней гауссова пространства масштабов в
один уровень пространства масштабов DoG:
Я,Д*> У) = L(*> У>а)" L(x> У>аа)- (9-4)
400 ♦ Глава 9. Обнаружение и прослеживание признаков
Мы берем начальный масштаб о > 0 и применяем масштабные
коэффициенты а", п = 0, 1, 2,... для построения конечного числа уровней в
пространстве масштабов DoG.
Уровни Daan, n = 0,..., т, образуют трехмерный массив; у каждого его
элемента (х, у, п) имеется 17 или 26 смежных элементов: восемь на
уровне п (в смысле 8-смежности), девять на уровне п - 1, если п > 1, и девять
на уровне п + 1, если л < т. См. рис. 9.4. Элемент (х, у, п) и эти 17 или 26
смежных с ним элементов образуют трехмерную окрестность (х, у, п).
уУУУУ'УУ
X
Уровень п +1
Уровень п
Уровень /?-1
Рис. 9.4. Положение пикселя р = (х, у) на уровне п пространства
масштабов и 26 смежных с ним пикселей на уровнях п-1,пип + 1
В позиции р = (х, у) обнаруживается особая точка, если существует
уровень п, 0 ^ п < т, такой, что Daan{x, у) является локальным
минимумом или максимумом в трехмерной окрестности (х, у, п). (Особые точки,
найденные на уровнях 0 и т по 17 смежным позициям, считаются
«низкокачественными» и отбрасываются.)
Вместе с особой точкой, найденной в исходном изображении / в
позиции р = (х, у), мы имеем также масштаб а • а", при котором она была
обнаружена; этот масштаб определяет радиус круга влияния особой
точки р.
Векторы трехмерного потока. Пусть имеется последовательность
кадров / (•, •, t) и особые точки, обнаруженные в пространстве
масштабов для каждого кадра, а также радиусы их кругов влияния.
Предположим также, что имеется некоторый способ решить задачу о
сопоставлении особых точек в кадрах / (•, •, г) и / (•, •, t + 1) (см. раздел 9.3 ниже в
этой главе). У некоторых особых точек может не оказаться соответствия
в следующем кадре.
9.1. Инвариантность, признаки и множества признаков ♦ 401
Теперь рассмотрим особую точку pt = (xt, yt) в кадре /(-,-, t) с радиусом
круга влияния rt > 0 и предположим, что она переходит в особую точку
P»i = (xt+v yt+i) в кадре / (•, •, t + 1) с радиусом круга влияния rt+l > 0.
Предположим также, что оба круга влияния - проекции локальной «круговой
ситуации» на сцене, см. рис. 9.5 слева.
Увеличение радиуса от rt до rt+1 (в приведенном примере)
обратно пропорционально скорости приближения центральной точки этой
«круговой ситуации» к камере (см. пример 9.1). Если бы центральная
точка удалялась от камеры, то радиус проекции увеличивался бы.
Таким образом, изменение радиуса круга влияния определяет трехмерное
движение центральной точки спроецированной локальной «круговой
ситуации». На рис. 9.5 справа показаны выведенные векторы
трехмерного потока1.
Рис. 9.5. Слева: круг в трехмерном пространстве, движущийся по направлению
к плоскости изображения, порождает круги влияния разного радиуса.
Справа: двумерные проекции обнаруженных векторов трехмерного потока;
цвета представляют различные направления и модули векторов движения
в трехмерном пространстве
Пример 9.1 (приближающиеся к камере круги в трехмерном пространстве).
На рис. 9.5 показан круг радиуса р, приближающийся к камере. Пусть f-
фокусное расстояние камеры, а круг движется параллельно плоскости XY в системе
координат камеры XYZ. Для простоты предположим, что радиус параллелен
оси У и соединяет центр Рс с точкой на граничной окружности Ре.
Точка Р=(X, Y, Z) в системе координат камеры проецируется в точку р = (х, у, f)
в плоскости изображения, где а: = f(X/Z), у = f(Y/Z). Точка Рс проецируется
в Рс = (хс, ус, /), а Ре - в ре = (хе, уе, /).
1 Описанное построение векторов трехмерного потока опубликовано в работе [/. A. Sanchez,
R. Klette, and E. Destefanis. Estimating 3D flow for driver assistance applications. Pacific-Rim
Symposium Image Video Technology, LNCS 5414,2009, p. 237-248].
402 ♦ Глава 9. Обнаружение и прослеживание признаков
Движущийся круг в момент времени t находится на расстоянии Zt и
проецируется на плоскость изображения / (•, •, t) в круг радиуса rt площадью
Лг = т\ = п(ус - у/ = & (у - у )2 = яГВ-. (9.5)
Радиуса круга р не изменяется со временем, поэтому не изменяется и
произведение <AtZ2t = nfp2. Отсюда следует, что
bit-
что дает устойчивую оценку этого отношения расстояний.
Особые точки с субпиксельной точностью. Особые точки,
обнаруженные в пространстве масштабов на уровне с масштабом о • ап,
находятся в позициях пикселей (т. е. имеют целочисленные координаты).
Мы интерполируем полином второй степени от двух переменных g(x, у)
по найденной особой точке и четырем ее 4-смежным соседям,
используя в качестве функции g значения в слое с масштабом о • а",
приравняем к нулю производные^, у) по а: и по у и из полученной системы
уравнений найдем минимум или максимум с субпиксельной точностью.
9.1.3. Множества особых точек в соседних кадрах
Сравним множества особых точек, обнаруженных в двух соседних
кадрах последовательности изображений. Наша цель - найти
соответственные особые точки. Вполне возможны выбросы, т. е. особые точки,
которым нет соответствия в другом изображении. Здесь мы обсуждаем
сопоставление как глобальную задачу на всем множестве, а не как
локальную задачу в одной точке (поточечное сопоставление показано на
рис. 9.24).
Рассматривая сопоставление как задачу на множестве, мы
предполагаем, что существует некая глобальная закономерность в
распределении особых точек - паттерн, и требуется поставить в соответствие этому
паттерну другой глобальный паттерн. Пример показан на рис. 9.6. Если
два изображения различаются только размером, то такой глобальный
подход к сопоставлению оправдан.
Консенсус на случайной выборке. Алгоритм RANSAC (random
sample consensus - консенсус на случайной выборке) - это
итеративный метод оценивания параметров предполагаемой математической
модели. Дано множество регулярных точек (inlier), согласующихся с этой
моделью, а также множество выбросов (outlier), не согласующихся с мо-
9.1. Инвариантность, признаки и множества признаков ♦ 403
делью и рассматриваемых как шум. Для применимости RANSAC
вероятность выбрать регулярную точку должна быть достаточно высока.
Рис. 9.6. Слева: множество особых точек SIFT. Справа: множество особых точек
SIFT в уменьшенном изображении. Цветными линиями показано соответствие
между особыми точками, представленное одним глобальным аффинным
преобразованием, которое находит RANSAC
Например, все данные, включая регулярные точки и выбросы, могут
быть зашумленным представлением прямой линии у = ах + Ъ, а задача
состоит в том, чтобы оценить а и Ь. В нашем случае данные - это
множества особых точек в двух изображениях, а модель описывается
геометрическим преобразованием, которое устанавливает соответствие
особых точек. Это пример задачи сопоставления. Мы будем
рассматривать аффинные преобразования, считая этот класс достаточно общим:
в него входят повороты, параллельные переносы и масштабирование.
На рис. 9.6 показан пример соответствий, вычисленных путем
оценивания одного аффинного преобразования.
Врезка 9.2 (история RANSAC). Метод впервые был опубликован в работе
[М. A. Fischier and R.C. Bolles. Random sample consensus: A paradigm for model fitting
with applications to image analysis and automated cartography. Comm.ACM.vol. 24,1981,
p. 381-395].
Алгоритм RANSAC. Нам нужен критерий, который позволил бы
судить, удовлетворяют ли некоторые данные параметрической
модели (или аппроксимируются моделью). В нашем случае особая точка
р одного изображения / отображается параметрическим аффинным
преобразованием в точку q другого изображения /. Критерий можно
сформулировать следующим образом: если существует особая точка г
404
Глава 9. Обнаружение и прослеживание признаков
изображения / на расстоянии d2(q, г) < £, то говорят, что р удовлетворяет
данному параметрическому аффинному преобразованию. Порог е > О
определяет, аппроксимируются ли данные моделью.
Чтобы инициализировать процесс, выберем случайное
подмножество S данных (в нашем случае особых точек изображения /), считая их
регулярными точками, и попробуем оценить параметры модели, которой
они аппроксимируются.
Проверим модель с этими параметрами на других данных; все
данные, удовлетворяющие модели, попадают в консенсусное множество
(это значит, что консенсусное множество содержит S).
Сравним мощность консенсусного множества с мощностью множества
всех данных. Если отношение достаточно велико, то итеративная
процедура прекращается. В противном случае оцениваем параметры
обновленной модели, основанной на консенсусном множестве и называемой
уточненной моделью. Повторяем описанные действия для уточненной
модели, если мощность нового консенсусного множества больше
мощности предыдущего. Если же мощность не увеличилась, то можно вернуться
к шагу инициализации и выбрать другое случайное подмножество S.
Применение RANSAC для сопоставления признаков. Признак
определяется особой точкой и дескриптором. Для оценки параметров
аффинного преобразования мы используем дескрипторы
соответственных признаков в другом изображении. В начальное множество S могут
войти три случайно выбранные особые точки изображения /. Для этих
трех точек мы можем поискать в изображении /три особые точки с
приблизительно совпадающими дескрипторами. Что касается начального
множества 5, то можно заменить случайную выборку систематической
оценкой «силы» признака, основанной на определении и измерении
свойств дескрипторов.
Пример 9.2 (оценка аффинного преобразования). Точка р = (х, у, 1)
изображения /, записанная в однородных координатах, отображается в точку q = (и, v, 1)
изображения / с помощью аффинного преобразования
'и
>21
о
'12
Г22
о
1
х
У
1
(9.7)
представляющего систему линейных уравнении
u = rnx + rny + t1,
v = r2i* + r22y + t2-
(9.8)
(9.9)
9.1. Инвариантность, признаки и множеава признаков
405
В этой системе шесть неизвестных. Если точки рх, р2 и ръ неколлинеарны, то
эти неизвестные можно найти. См. чертеж на рис. 9.7.
Р\
Pi
Ръ
1У
•q2
•<?1
.ь
\У
Рис. 9.7. Определение аффинного преобразования
по трем парам точек в изображениях / {слева) и J
Затем вычисленное аффинное преобразование А{р) = q применяется ко всем
особым точкам в /, в результате чего мы получаем множество точек в /. Точка р
попадает в консенсусное множество, если существует такая особая точка q в /,
для которой евклидово расстояние до А(р) меньше s > 0 и дескрипторы q и р
приблизительно совпадают. Эта точка становится образом q точки р в /.
Очевидно, что для точек pv p2 и ръ этот критерий выполнен.
Можно ожидать, что найдется консенсусное множество, содержащее
больше трех точек I. Найдем уточненное аффинное преобразование,
вычислив оптимальное преобразование для всех найденных пар р е J,
q E /. Для этого можно применить метод наименьших квадратов, как
описано в разделе 4.3.1.
Заметим, что величина е не должна быть «слишком малой», потому
что в таком случае мы не смогли бы отойти от начального
преобразования (чтобы найти лучшее соответствие между двумя множествами
особых точек).
Пример 9.3 (оценка параметров плоскости в трехмерном облаке точек).
Предположим, что стереокамера установлена на квадрокоптере, см. рис. 6.10
справа. В момент t мы записываем левое и правое изображения, IL и IR. К обоим
изображениям применяем детектор особых точек (например, эффективный
детектор FAST), и получаем множества ML и MR.
Для каждой особой точки peML находим соответственную особую точку в MR
(если таковая существует) с диспаратностью d. В поиске соответствия могут
оказать помощь дескрипторы признаков. Зная матрицу проекции левой
камеры Р и диспаратность d, мы можем отобразить р в пространственную точку Р.
Все такие пространственные точки помещаются в множество 5. Обработав все
особые точки в момент £, мы пытаемся аппроксимировать множество S плос-
406
Глава 9. Обнаружение и прослеживание признаков
костью с помощью метода RANSAC (см. упражнение 9.8). Псевдокод этой
процедуры приведен на рис. 9.8.
1: ML = match Feat ures(/L) {особые точки в левом изображении};
2: MR = matchFeatures^) {особые точки в правом изображении};
3: S = [] {пустой список; в нем будут храниться пространственные точки};
4: forp in ML do
5: d = findDisparity(p, MR);
6: P= (p.x, p.y, d) • P {спроецировать найденную точку в трехмерное пространство,
умножив на матрицу проекции};
7: append(S, Р) {добавить спроецированную точку Р в множество S};
8: end for
9: Пу = ransacFitPlane(S);
10: П2 = ransacRefinePlaneModeKS, П,);
Рис. 9.8. Аппроксимация разреженного множества
найденных пространственных точек плоскостью
Вычисленную плоскость квадрокоптер может использовать для
управления посадкой на плоскую поверхность. На рис. 9.9 показана
ситуация, когда квадрокоптер готовится к посадке.
Рис. 9.9. Плоскость, аппроксимирующая множество точек в трехмерном
пространстве.Точки вычислены с помощью сопоставителя разреженных
стереоизображений на основе модифицированного детектора признаков
FAST (реализованного в ПО квадрокоптера).Желтые точки - выбросы.
Аппроксимирующая плоскость спроецирована обратно в неректифицированное
изображение, в результате чего получилось криволинейное многообразие
(из-за дисторсии объектива). Пространственные точки были обнаружены
направленной вниз системой стереокамер, интегрированной
с квадрокоптером (см. рис. 6.10 справа)
9.2. Примеры признаков ♦ 407
9.2. Примеры признаков
В этом разделе описываются три популярных типа признаков: SIFT,
SURF и ORB, а также сравнивается их качество с точки зрения
инвариантности.
9.2.1. SIFT-признаки
Предположим, что мы обнаружили особые точки в пространстве
масштабов DoG или LoG. Для особой точки р Е П нам известен также
масштаб о • ап, который определяет радиус г = а • а" круга влияния этой
точки. Поместив этот круг с центром в р на все уровни пространства
масштабов, мы определим цилиндр влияния особой точки.
Пересечение этого цилиндра с входным изображением также является кругом
радиуса г с центром в точке р.
Исключение слабоконтрастных и лежащих на границах особых
точек. Обычно нас не интересуют особые точки, находящиеся в
слабоконтрастных участках или на границах. Особые точки в
слабоконтрастных участках легко удалить, следуя модели (1.10). Например, если на
нижнем уровне пространства масштабов DoG значение в точке р мало,
то у данного изображения контрастность в р низкая.
Чтобы понять, принадлежит ли какая-то из оставшихся особых
точек р границе, мы можем рассмотреть градиент AI(p) = [Ix(p), I (p)f. Если
его компоненты существенно различаются по модулю, то мы
заключаем, что р лежит на границе, которая приблизительно перпендикулярна
оси координат, соответствующей большей компоненте.
Другой подход - брать только особые точки, расположенные в углах,
см. раздел 2.3.4. Угол можно идентифицировать по собственным
значениям Aj и Я2 гессиана в точке р (см. врезку 2.8). Если оба собственных
значения «велики» по абсолютной величине, то имеет место угол; если
одно собственное значение мало, а другое велико - то ступенчатая
граница, а если оба малы - то слабоконтрастный участок.
Таким образом, после исключения всех слабоконтрастных особых
точек для оставшихся нас интересует отношение
Л, {'*, +1„ f + *К \К +{'» -*» f ^ (910)
K (/„ +1„f -4/w,/<+(/„ -IJ
позволяющее различить особые точки в углах и на границах.
408 ♦ Глава 9. Обнаружение и прослеживание признаков
Сопоставим оставшимся особым точкам р дескрипторы d(p). Цель
масштабно-инвариантного преобразования признаков (scale-invariant
feature transform - SIFT) - добиться инвариантности относительно
вращения, относительно масштабирования (на самом деле
«инвариантность относительно размера», а не относительно масштаба а) и
относительно вариаций яркости.
Врезка 9.3 (история SIFT).Дескриптор SIFT впервые описан в работе [D.G.Lowe.
Object recognition from local scale-invariant features. In Proc. Int. Conf. Computer Vision,
vol. 2,1999, p. 1150-1157].
Дескриптор, инвариантный относительно вращения. Круг
влияния радиуса г = о • а" на уровне Da a„(x, у) используемого пространства
масштабов DoG можно проанализировать на предмет главного
направления вдоль главной оси и повернуть так, чтобы главное направление
совпало с фиксированным заранее заданным направлением.
Например, для определения главной оси в круге влияния на уровне Daan(x, у)
можно применить уравнение (3.41).
В дескрипторе SIFT применен эвристический подход. Для пикселей
(х, у) в круге влияния на уровне L(x, у) = Da an(x, у) с центром в особой
точке р модуль и направление локального градиента
аппроксимируются выражениями
т(х, у) = У[Цх, у + 1) - Цх, у - I)]2 + [Цх + 1, у) - Цх - 1, у)]2, (9.11)
в(х,у) = а1ап2([Цх,у+1)-Цх,у-1)],[Цх+1,у)-Цх-1,у)]) (9.12)
(о функции atan2 см. сноску на стр. 41). Направление отображается
в один из 36 счетчиков, каждый из которых представляет интервал
10 градусов. Начальные значения счетчиков равны 0. Если направление
отличается от направления счетчика не более чем на 10 градусов, то
к счетчику прибавляется соответствующий модуль. В итоге получается
гистограмма градиентов.
Локальные максимумы счетчиков величиной не меньше 80% от
глобального максимума определяют доминантные направления. Если
доминантных направлений больше одного, то особая точка используется
в связке с каждым из них.
По аналогии с обработкой главного направления круг влияния
поворачивается так, чтобы найденное доминантное направление совпало с
фиксированным предопределенным направлением.
9.2. Примеры признаков ♦ 409
Инвариантность относительно яркости. Для определения
признаков, инвариантных относительно яркости, нам нужно описать круг
влияния во входном изображении (а не в том слое, где была
обнаружена особая точка). Для устранения артефактов освещения можно
применить любое из преобразований, рассмотренных в разделе 2.3.5.
SIFT вычисляет признаки для градиентов в круге влияния, разбивая
его на квадратные окна. Для каждого квадратного окна (о его размере
см. ниже) входного изображения мы строим гистограмму градиентов,
как описано выше при обсуждении доминантных направлений, но на
этот раз с интервалами 45 градусов, так что всего получается восемь
счетчиков, в которых аккумулируются модули градиентов.
Инвариантность относительно масштабирования. Мы
разбиваем повернутый (см. «Инвариантность относительно вращения») круг
влияния во входном изображении на квадраты 4*4 (геометрически
«настолько близко, насколько возможно»). Для каждого из 16 квадратов
мы имеем вектор длины 8, представляющий значения счетчиков в
гистограмме градиентов для этого квадрата. Объединяя все 16 векторов
длины 8, мы получаем вектор длины 128. Это и есть SIFT-дескриптор
cL (р) рассматриваемой особой точки р. См. рис. 9.10.
Рис. 9.10. Слева вверху: квадрат, содержащий круг влияния.
Справа вверху: карта градиентов для построения гистограмм
градиентов в 16 квадратах. Слева внизу: схема найденных градиентов.
Справа внизу: эскиз гистограмм градиентов
410 ♦ Глава 9. Обнаружение и прослеживание признаков
9.2.2. SURF-признаки
Детектор SURF (speeded-up robust features - ускоренные устойчивые
признаки) основан на тех же идеях, что и SIFT. При его
проектировании ставилась цель повысить эффективность работы. В нем
используются интегральные изображения Ijm, рассмотренные в разделе 2.2.1, и
упрощенные ядра фильтров вместо сверток с производными гауссовой
функции.
Маски SURF и применение интегральных изображений. На
рис. 9.11 показаны две из четырех использованных масок (или ядер
фильтров); маски SURF в направлении л: и другой диагонали
определяются аналогично. Размер масок соответствует выбранному масштабу.
Помимо масок 9*9, в SURF используются маски размера 15х15, 21x21,
27x27 и т. д. (они разбиваются на октавы, но, как уже было сказано, мы
не собираемся обсуждать детали реализации) с соответственно
увеличенными прямоугольными подокнами.
III
sfTTTd
ттг
Рис. 9.11. Иллюстрация для наименьшего масштаба а = 1.2 и обрезанных вторых
частных производных гауссовой функции на дискретной сетке 9*9, а также
соответствующих ядер фильтров в SURF. Пара слева: производная по у и ее
упрощенная аппроксимация в SURF. Пара справа: производная по диагонали
(из левого нижнего в правый верхний угол) и соответствующее ядро фильтра в SURF
Элементы этих ядер могут принимать значения 0, -1, +1, -2. В каждом
из прямоугольных подокон W маски значения одинаковы и равны -1,
+1 или -2. Это позволяет воспользоваться формулой (2.13) для
эффективного вычисления суммы Sw значений яркости в W. Затем останется
только умножить сумму Sw на соответствующий коэффициент (-1, +1
или -2). Сумма этих трех или четырех произведений считается
результатом свертки в заданном начальном пикселе с одной из четырех масок.
Врезка 9.4 (история SURF). Признаки SURF определены в статье [Н. Bay, A. Ess,
Т. Tuytelaars and L Van Gooi SURF: Speeded up robust features. Computer Vision Image
Understanding, voL. 110,2008, p. 346-359].
0
i
I
zm Ш1Ш
1 mz
i
1
9.2. Примеры признаков ♦ 411
Масштабы и обнаружение особых точек. На рис. 9.11
иллюстрируется значение а = 1.2, это наименьший масштаб (т. е. наибольшее
пространственное разрешение) в SURF. Свертки в пикселе р входного
изображения / с четырьмя масками аппроксимируют четыре
коэффициента матрицы Гессе [см. (2.28) и (2.29)]. Четыре сверточные маски
дают значения Dx х(р, а) и Dx (р, <т), и предполагается, что они равны
D х{р, о) и D (р, о). Затем приближенное значение определителя
матрицы Гессе при масштабе о вычисляется по формуле
S(p, a) = Dxx(p, a) • Dyy(p, a) - (с, • Dxy(p, а))\ (9.13)
где са (0 < са < 1) - весовой множитель, который в принципе можно
оптимизировать для каждого масштаба в отдельности. Однако в SURF для
всех масштабов используется константа са = 0.9, потому что
оптимизация весов не оказывает заметного влияния на результаты.
Затем особая точка р ищется как локальный минимум S(p, а) в
массиве размера Зх3><3, по аналогии с обнаружением особой точки в
пространстве масштабов LoG или DoG.
Дескриптор SURF. Дескриптор SURF (вектор чисел с плавающей
точкой длины 64) включает информацию о локальных градиентах, как
дескриптор SIFT, но в нем используются взвешенные суммы по
прямоугольным подокнам (так называемые хаароподобные признаки, см. их
обсуждение в историческом контексте в разделе 10.1.4), окружающим
особую точку, чтобы упростить и ускорить аппроксимацию значений
градиентов.
9.2.3. ORB-признаки
Прежде чем знакомиться с ориентированными устойчивыми
бинарными признаками (oriented robust binary features - ORB), необходимо
определить бинарные устойчивые независимые элементарные признаки
(binary robust independent elementary features - BRIEF), поскольку этот
дескриптор в сочетании с детектором признаков FAST (см. раздел 2.3.4)
и составляют ORB.
Бинарные паттерны. В BRIEF в качестве дескриптора особых точек
выступает не вектор длины 128 (как, в SIFT), а всего 128 бит. В
результате бинаризации представление в виде чисел с плавающей точкой
значительно упрощается. Эта идея нашла применение при
проектировании переписного преобразования (census transform) (см. раздел 8.1.2)
с помощью локальных бинарных паттернов (local binary pattern - LBP;
412
Глава 9. Обнаружение и прослеживание признаков
см. определение на рис. 9.12 слева) и простого критерия для обучения
набора классифицирующих деревьев (см. следующую главу).
%
р
%
%
%
%
V
ч
\Рз
4} 1 \
г
РГ
[\
0
L^
^г
V
\
л
S
ч
\
%
%
Ч*
ч
Рг
Рис. 9.12. Слева: на рисунке показан один пиксель р изображения /
и 16 пикселей q, расположенных на дискретной окружности с центром в р.
Положим s(p, q) = 1, если 1{р) - l(q) > 0, и 0 в противном случае.
Тогда s(p, q0) • 2° + s(p, qj • 21 + ... + s(p, (?15) • 215 определяет LBP-код в пикселе р,
т. е. двоичное число, содержащее 16 бит. Справа: в BRIEF предлагается использовать
случайный порядок пар пикселей в выбранной квадратной окрестности.
Для иллюстрации взято четыре пары (р., д.), определяющие
число s{p09 q0) • 2° + s{pv qj • 21 + s{pv q2) ' 22 + s{pv q} • 23
Врезка 9.5 (история LBP). Идея локальных бинарных паттернов была впервые
изложена в статье [D. С Не and L Wang. Texture unit, texture spectrum, and texture
analysis. IEEE Trans. Geoscience Remote Sensing, vol. 28, 1990, p. 509-512], а затем
популяризирована в работе [Т. Ojala, M. Pietikainen and D. Harwood. Performance
evaluation of texture measures with classification based on Kullback discrimination of
distributions. In Proc. Int. Conf. Pattern Recognition,vol. 1,1994, p. 582-585] и
последующих публикациях об использовании расхождения Кульбака-Лейблера в
распознавании образов (названо в честь американских математиков С. Кульбака
(1907-1994) и Р.Лейблера (1914-2003)).
BRIEF. В случае BRIEF паттерн LBP определен на множестве п пар
пикселей (р, q), окружающих текущий пиксель и выбранных в
определенном порядке из окрестности размера (2к + 1)х(2/с + 1) (например, к =
4 или к = 7) после выполнения гауссова сглаживания изображения / с
заданным параметром а > 0. Таким образом, конкретный вариант
дескриптора BRIEF определен порядком пар, а также параметрами к и о.
В общем случае сглаживание может быть слабым (т. е. значение о мало),
а в оригинальной статье предлагалось выбирать пиксели в случайном
порядке. См. рис. 9.12 справа. Как видим, инвариантность относительно
9.2. Примеры признаков ♦ 415
масштаба или вращения авторами оригинального дескриптора BRIEF
не закладывалась.
Врезка 9.6 (история BRIEF и ORB). BRIEF определен в работе [М. Catonder,
V. Lepetit, С. Strecho and P. Fuo. BRIEF: Binary robust independent elementary features. In
Proc. European Conf. Computer Vision, 2010, p. 778-792], a ORB - в работе [E. Rubtee,
V. Rabaud, K. Konotige and G. Bradskl. ORB: An efficient alternative to SIFT or SURF. In Proc.
Int. Conf. Computer Vision, 2011, p. 2564-2571].
ORB. Дескриптор ORB, акроним которого можно также
расшифровать как oriented FAST and rotated BRIEF, объединяет особые точки,
найденные обобщенным детектором углом FAST (см. раздел 2.3.4), с
обобщением дескриптора признаков BRIEF:
1) ORB сначала выполняет FAST (для обеспечения инвариантности
относительно масштаба), а затем производит обнаружение
особых точек в пространстве масштабов, вычисляет доминантное
направление и
2) применяет вычисленное направление для преобразования
дескриптора BRIEF в ориентированный дескриптор BRIEF (для
обеспечения инвариантности относительно вращения).
Авторы ORB предлагают также способы анализа дисперсии и
корреляции компонент ориентированного дескриптора BRIEF. Можно
воспользоваться тестовой базой данных для определения множества пар
BRIEF (p(., q), которые устраняют корреляцию компонент
ориентированного дескриптора BRIEF с целью улучшить различительную
способность вычисленных признаков.
Пирамида изображений, фильтр Харриса и направление.
Авторы ORB предлагали использовать алгоритм FAST для определения
дискретной окружности радиуса р = 9; на рис. 2.22 показан FAST для
дискретной окружности радиуса р = 3. (Конечно, выбор радиуса зависит
от разрешения и структуры сигнала в изображениях.) Построенная по
входному изображению пирамида используется для нахождения
особых точек FAST при разных масштабах. Затем применяется мера
угловатости (2.30) (заимствованная у детектора Харриса), чтобы выбрать Т
«наиболее угловатых» особых точек при этих масштабах, где Т > 0 -
заранее заданное количество особых точек. Этот алгоритм называется
фильтром Харриса.
Моменты тю и тя01 [см. (3.36)] используемого круга S радиуса р
определяют направление
414
Глава 9. Обнаружение и прослеживание признаков
9 = atan 2(m
т
ю' '"oi
).
(9.14)
По определению FAST, можно ожидать, что т10 Ф т01. Обозначим R0
матрицу поворота плоскости вокруг этого направления на угол в.
Дескриптор с направлением. Пары (p., q) для BRIEF (0 < i ^ 255)
выбираются из гауссова распределения внутри используемого круга
(радиуса р). Они образуют матрицу S, которая после поворота
преобразуется в
$в - R#S - R^
Ро
Piss
#255
Ро,в
Яо,в
Piss,e
QlSSti
(9.15)
Теперь вычисляется ориентированный дескриптор BRIEF, равный
сумме s(p0t9, qOt0) • 2° + ... + s(p2SS>e, q255e) • 2255, где s определено в подписи
к рис. 9.12. Благодаря переходу от оригинального дескриптора BRIEF к
ориентированному удается повысить корреляцию составляющих его
значений.
По соображениям эффективности комбинация 256 пар BRIEF
(выбранных из гауссова распределения) поворачивается на углы, кратные
2я/30, и все получившиеся комбинации сохраняются в справочной
таблице. Это избавляет от необходимости каждый раз вычислять
повороты, угол в просто заменяется ближайшим кратным 2я/30, и результат
выбирается из таблицы.
9.2.4. Оценка признаков
Оценим описанные детекторы признаков с точки зрения свойств
инвариантности. Будем систематически изменять кадры записанных
последовательностей, как показано на рис. 9.13. Например, уменьшим
размер изображения. Если детектор признаков инвариантен
относительно масштабирования, то он должен обнаружить (в идеале) те же
самые признаки, что и в исходном изображении.
Процедура оценки признаков. Мы обсудим четыре типа
систематического изменения кадров: поворот, масштабирование (увеличение
и уменьшение), варьирование яркости и размытие2. Для заданной
последовательности кадров выберем какой-нибудь один детектор
признаков и выполним следующие действия.
1. Прочитать следующий кадр /, представляющий собой
полутоновое изображение.
2 См. [Z. Song and R. Klette. Robustness of point feature detection. In Proc. Computer Analysis Images
Patterns, LNCS 8048,2013, p. 91-99].
9.2. Примеры признаков ♦ 415
Рис. 9.13. Слева вверху: повернутое изображение; исходный кадр
из видеопоследовательности bicyclist имеет размер 640*480 и записан
с глубиной 10 бит/пиксель. Справа вверху: уменьшенное изображение.
Слева внизу: равномерное изменение яркости.
Справа внизу: размытое изображение
2. Найти особые точки ръ1и вычислить их дескрипторы d(p).
3. Положить Nk равным числу особых точек в /.
4. Для данного кадра построить четыре последовательности
изображений:
a) поворачивать / вокруг центра на углы, кратные 1 градусу; при
этом создается последовательность из 360 повернутых
изображений;
b) изменять размер / шагами по 0,01 от 0,25 до удвоенного
размера исходного изображения; при этом создается
последовательность из 175 масштабированных изображений;
c) изменять яркость /, добавляя скалярную величину к значению
каждого пикселя, значение скаляра изменяется на 1 в
диапазоне от-127 до 127; при этом создается последовательность
из 255 изображений с модифицированной яркостью;
416
Глава 9. Обнаружение и прослеживание признаков
d) применять гауссово размытие к /, изменяя параметр о
шагами по 2 в диапазоне от 3 до 41; при этом создается
последовательность из 20 размытых вариантов /.
5. Применить детектор признаков к каждому
трансформированному изображению It; вычислить особые точки pt и дескрипторы
d(pt).
6. Положить Nt равным числу особых точек в трансформированном
изображении 1{.
7. С помощью дескрипторов d(p) и d(pt) установить соответствие
между признаками в I и It.
8. Использовать алгоритм RANSAC для удаления случайных
соответствий.
9. Положить Nm равным числу обнаруженных соответствий.
Мера повторяемости. Определим повторяемость £(I, It) как
отношение числа обнаруженных соответствий к числу особых точек в
исходном изображении.
N
0(1,1,) = -*-
(9.16)
Средние значения для 90 случайно выбранных из тестовых
последовательностей кадров получены с использованием реализаций
изучаемых детекторов в OpenCV с параметрами по умолчанию. См. рис. 9.14.
Рис. 9.14. Графики повторяемости. Слева вверху: для поворота.
Справа вверху, для масштабирования. Слева внизу: для вариации яркости.
Справа внизу: для размытия
9.5. Прослеживание и обновление признаков ♦ 417
Обсуждение результатов эксперимента. Конечно, у
инвариантности есть пределы. Если при масштабировании, изменении яркости
или размытии выйти за эти пределы, так что изображение окажется
искаженным до неузнаваемости, то рассчитывать на повторяемость не
приходится. Вращение - особый случай; здесь можно было бы ожидать
почти идеальной инвариантности (конечно, с учетом того факта, что
цифровые изображения поворачиваются все же не так, как
непрерывные функции в Е2).
В табл. 9.1 приведено время обработки одного изображения, среднее
время в расчете на особую точку и число особых точек, найденных в
кадре, на основе которого строились трансформированные
изображения, показанные на рис. 9.13.
Таблица 9.1. Средние значения для 90 случайно выбранных входных кадров.
Четвертый столбец содержит количество особых точек в кадре, на основе которого
строились трансформированные изображения, показанные на рис. 9.13
Детектор
признаков
SIFT
SURF
ORB
Среднее время
на кадр
254,1
401,3
9,6
Среднее время
на особую точку
0,55
0,40
0,02
Число Nk особых
точек
726
1313
500
Эксперименты показывают, что SIFT работает хорошо (по сравнению
с SURF и ORB) для поворота, масштабирования и вариации яркости, но
не для размытия. Все результаты далеки от идеальной инвариантности.
Если вариация яркости или степень размытия невелики, то можно
надеяться на инвариантность. Но поворот и масштабирование приводят
к значительному падению повторяемости при малых углах поворота и
малых изменениях масштаба. Время работы SIFT и SURF различается
незначительно, тогда как ORB работает намного быстрее и, стало быть,
представляется эффективным и вполне конкурентоспособным
детектором признаков (судя по результатам этого сравнения).
9.3. Прослеживание и обновление признаков
Приведем пример конкретного приложения. Рассмотрим автомобиль,
который будем называть эгоавтомобилем, потому что в нем работает
компьютерная система, в отличие от «прочих» автомобилей на сцене.
Эгоавтомобиль оборудован системой стереозрения, он едет по улице и
418 ♦ Глава 9. Обнаружение и прослеживание признаков
порождает трехмерные реконструированные облака точек для каждого
кадра стерео в момент t. Поняв движение эгоавтомобиля, мы сможем
привязать эти облака точек к единой системе мировых координат и
поддержать трехмерное моделирование краев дороги. На рис. 9.15
показано такое применение стереозрения3.
Рис. 9.15. Сверху, прослеженные признаки в кадре стереоскопической
видеопоследовательности, записанной из автомобиля. В середине: прослеженные
признаки используются для вычисления движения автомобиля; это позволяет
привязать точки, полученные от системы стереозрения, к единой трехмерной
системе мировых координат. Внизу: в данном примере использовался
стереосопоставитель iSGM (пример карты диспаратности для записанной
последовательности)
3 См. [Y. Zeng and R. Klette. Multi-run 3D streetside reconstruction from a vehicle. In Proc. Computer
Analysis Images Patterns, LNCS 8047,2013, p. 580-588].
9.3. Прослеживание и обновление признаков ♦ 419
Чтобы понять движение эгоавтомобиля, мы должны проследить
обнаруженные признаки между кадрами t и t + 1, которые подаются на
вход программы вычисления эгодвижения автомобиля. Такая
программа представляет интерес и сама по себе; в этом разделе мы лишь
опишем технику прослеживания признаков между соседними кадрами.
9.3.1. Прослеживание - задача разреженного
соответствия
В бинокулярном стереозрении вычисляется соответствие между
точками или признаками двух изображений, снятых в один и тот же
момент времени; соответственная точка всегда лежит на эпиполярной
прямой, поэтому мы имеем задачу одномерного соответствия.
В случае анализа плотного движения (т. е. оптического потока)
вычисляется соответствие между точками или признаками изображений,
снятых в последовательные моменты времени. Пиксели могут
перемещаться в разных направлениях, а не только вдоль одной прямой.
Поэтому анализ плотного движения - задача двумерного соответствия.
Прослеживание признаков в последовательности изображений - это
задача разреженного двумерного соответствия. Теоретически ее
решение можно было бы использовать и для анализа бинокулярного зрения
или плотного движения, но стратегии решения задач плотного и
разреженного соответствия различны. В случае разреженного соответствия
мы не можем воспользоваться членом гладкости и сначала должны
заняться обеспечением точности на основе одного лишь члена данных,
однако потом сможем использовать глобальное соответствие
паттернов прослеженных признаков для стабилизации результата.
Прослеживание посредством понимания изменений в
пространстве. Для пары точек Pt = (Xt, Yt, Z) и Pt+1 = (Xt+1, Yt+V Zt+1),
спроецированных в моменты t и t + 1 записи видеопоследовательности в точки
Pt= (xt* y?f) и Ptn = (xt+v yt+i>/) соответственно, определим Z-отношение:
Wz=^ (9.17)
На основе Z-отношения можно определить также Х- и У-отношения:
I//- — М-1 — t+\ Xt+\ _ ,., Xt+\ /Q 1 0\
¥x-—^-— ~¥z > (9Л8)
¥y=^- = ^.^-=¥z^±. (9.19)
Yt zt Уг Уг
420
Глава 9. Обнаружение и прослеживание признаков
В результате получаем следующее уравнение обновления:
X.
Н-1
L/+l
'Н-1
¥х
0
0
0
y/Y
0
0 1
0 •
¥z\
\хЛ
U
Ы
(9.20)
Иными словами, зная ipz и отношения х х/х и ym/yt, мы можем
перейти от точки Pt к точке Pt+1. В предположении, что Pt и Рт - позиции
одной и той же пространственной точки Р в моменты времени t и t + 1,
мы должны решить только две задачи:
1) придумать способ прослеживания точек между моментами t и t + 1;
2) оценить^.
Если начальная позиция Р0 прослеживаемой точки Р известна, то мы
можем найти ее пространственное положение в последующие моменты.
Не зная начальной позиции, мы имеем только направление от Pt к Pt+1,
но не положение точки в пространстве.
Стереозрение - общий способ оценивания значений Z или просто
отношений грг Выражение (9.17) дает альтернативный способ
оценивания xpz в монокулярной последовательности. В следующих подразделах
мы обсудим прослеживание точек между моментами t и t + 1 тремя
разными способами.
Врезка 9.7 (история прослеживателя Лукаса-Канаде). Метод был
опубликован в работе [В. D. Lucas and T. Kanade.kw iterative image registration technique with
an application to stereo vision. In Proc. Int.Joint Conf. Artificial Intelligence, 1981, p. 674-
679]. Выбор «хороших признаков» для сопоставления (или прослеживания)
впоследствии изучал К.Томаси, сначала вместе с Т. Канаде, а затем с другими
соавторами. С учетом этого п росл ежи ватель Лукаса-Канаде иногда называют
прослеживателем Лукаса-Канаде-Томаси, или KLT-прослеживателем.
9.3.2. Проел ежи ватель Лукаса-Канаде
Мы сравниваем шаблон W, окно размера (2к + 1)*(2к + 1) с центром в
особой точке р = (х, у) базового изображения /, с окнами W[ja
сопоставляемого изображения /, причем метод сравнения должен быть достаточно
общим - учитывающим параллельный перенос, масштабирование,
поворот и другие преобразования между W и W а. Вектор а
параметризует преобразование р в новый центральный пиксель, а также
трансформацию формы окна W. См. рис. 9.16.
9.3. Прослеживание и обновление признаков ♦ 421
Изображение /
р
Изображение J
УТ УТ
Рис. 9.16. Шаблон, или базовое окно W базового изображения /, сравнивается
с окном И/ а сопоставляемого изображения J. В данном случае вектор расхождения
а определен параллельным переносом t и уменьшением высоты h. На рисунке
также видно, что круг влияния содержится внутри И/. Позиция пикселя р в7такая
же, как в /, он определяет начало параллельного переноса
Врезка 9.8 (Ньютон, Рафсон и метод Ньютона-Рафсона). Исаак Ньютон (1642-
1727 по юлианскому календарю, который в то время использовался в Англии)
и Дж. Рафсон (ок. 1648 - ок. 1715). Метод Ньютона-Рафсона вычисляет нули
функции одного переменного / и является обобщением метода, которым
древние вавилоняне находили приближенное значение квадратного корня.
Мы вычисляем ноль гладкой функции ф(х) для х Е [а, Ь] при условии, что
ф(а)ф(Ь) < 0. Входами алгоритма являются вещественные числа а и Ь. У нас
также имеется способ вычислить ф(х) и производную ф'(х)
(например,аппроксимировать отношением разностей) для любого х е [а, Ь]. Мы следующим
образом находим точку с е [а, Ь], являющуюся приближением к нулю ф:
1: Выбрать какое-нибудь с Е [а, Ь] в качестве начального приближения;
2: while STOP CRITERION = false do
3: Заменить с на с - ф(с)/ф'(с);
4: end while
Предполагается, что производная ф'(с) отлична от нуля. Если знак
производной ф постоянен на отрезке [а, Ь],то на этом отрезке есть только один ноль.
Начальное значение с можно выбрать, например, в результате небольшого
числа шагов двоичного поиска, чтобы уменьшить время работы
итерационного алгоритма Ньютона-Рафсона. Условие остановки STOP CRITERION задается
в виде \ф{с)\ $ е при небольшом е > 0.
В общем случае метод сходится, только если с «достаточно близко» к нулю z.
Однако если знак ф"(х) постоянен на отрезке [а, Ь],то справедливо
следующее утверждение: если знак ф(Ь) совпадает со знаком ф"(х),то сходимость к z
имеет место при выборе начального значения с = Ь, в противном случае - при
выборе начального значения с = а.
422
Глава 9. Обнаружение и прослеживание признаков
На рисунке ниже показаны гладкая функция ф(х) и интервал [а, Ь] такой, что
ф(а)ф(Ь) < 0. Предположим, что начальное значение с = хг Касательная в точке
(xv ф(хг)) пересекает ось х в точке х2, для которой
х2 хх -
ф'(хх)
Мы знаем, что ф'(х^) * 0. Продолжим, положив с = хт При этом определяется
новая касательная и новая точка пересечения ху И так далее.
При выборе начального значения хх последовательность х2, хъ,... сходится к
нулю z. Если бы мы начали со значения с = х0,то алгоритм не сошелся бы.
Заметим, что знак ф"(х) на отрезке [а, Ь] изменяется. Мы должны начать именно
в той «долине», где находится z. Нуль ищется в направлении наискорейшего
спуска. Если начать «не в той долине», то мы не сможем пересечь
разделяющий долины «гребень».
По следам Ньютона-Рафсона. В прослеживателе Лукаса-Канаде
используются приближенные градиенты (т. е. аппроксимации
производных в направлениях л: и у), устойчивые относительно вариации
яркости4. Для сравнения окон определяется функция ошибки Е, основанная
на критерии оптимизации среднеквадратичной ошибки.
Параллельный перенос. В простейшем случае мы вычисляем
только вектор параллельного переноса t = [tx, t.y] такой, что ]{х + t.x + i,
y + t.y + j) ~ I(x + i>y + j) для всех /,;, удовлетворяющих условию -к < i, j < k.
Этот вектор определяет относительные позиции в шаблоне W.
Чтобы упростить обозначения, предположим, что р = (х, у) = (0, 0) и
будем писать W и Wa вместо W и W а. Тогда в случае одного лишь
параллельного переноса задача состоит в том, чтобы найти приближение
к нулю (т. е. минимум) функции ошибки
Наше изложение следует введению в метод Лукаса-Канаде в лекциях Т. Свободы, см. cmp.felk.
cvut.cz/cmp/coiirses/Y33ROV/Y33ROV_ZS20082009/Lectures/Motion/klt.pdf.
9.5. Прослеживание и обновление признаков ♦ 425
к к
ВД = 11 [J(tx + i, t.y + /) - /(W(i, ;))]2, (9.21)
где t = [t.*, t,y] и W(/,/) = (/,/).
Цель для деформаций общего вида. Мы опишем прослеживатель,
пригодный не только для параллельных переносов, но и для
произвольной деформации, которая описывается аффинным преобразованием,
параметризованным вектором а.
Пусть J(Wa(q)) - значение в точке Wa(q) б /, которая является
результатом деформации в пикселе q = (/,/), -к < i,j < к, с параметрическим
вектором а. Деформация не переводит позицию пикселя в позицию пикселя,
поэтому для нахождения /(Wa(q)) необходима интерполяция.
Например, в случае переноса на вектор а = [Lx, t.y] имеем
Wa(q) = (Lx, t.y) + qu J(Wa(q)) = J(t.x + i, t.y + j) дляq = (i,/).
Но вернемся к общему случаю. Наша цель - вычислить вектор
расхождения а, доставляющий минимум функции ошибки
Да) = £ [j(Wa(q)) - I(W(q))]\ (9.22)
я
Итеративный алгоритм наискорейшего подъема. Предположим,
что мы уже нашли вектор параметров а = [ах,..., ап]Т. По аналогии с
алгоритмом сдвига среднего для сегментации изображений вычисляем
сдвиг та = [тх,..., тп]Т, при котором функция
Е(а + та) = X U(Wa + m(q)) - I(W(q))f (9.23)
ч
достигает минимума; это шаг на пути к нахождению минимума
функции (9.22). Чтобы решить эту задачу оптимизации среднеквадратичес-
кой ошибки (СКО), рассмотрим разложение f(Wa(q)) в ряд Тейлора по
вектору расхождения а с небольшим сдвигом та:
КК + т (q)) = J(Wa(qj) + т[ ■ grad J.^ + e. (9.24)
a da
Напомним, что аналогичную операцию мы производили при
выводе ограничения Хорна-Шанка; здесь мы дополнительно предполагаем,
что е = 0 и, следовательно, значения пикселей / изменяются линейно в
окрестности позиции пикселя Wa(q).
В выражении (9.24) второй член в правой части является
произведением транспонированного вектора сдвига т , производной grad /
424
Глава 9. Обнаружение и прослеживание признаков
внешней функции (т. е. обычного градиента изображения) и
производной внутренней функции, что в итоге дает скаляр - как и в левой части.
Оконная функция W возвращает точку с координатами а: и у. Ее
производная по вектору параметров а имеет вид
dW.
Эа
Чч) =
Э^а (<?).* dWu(q)jc'
дх ду
dWa(q).y dWa(q).y
дх
ду
(9.25)
и называется матрицей Якоби, или якобианом деформации. О К. Г. Я. Яко-
би см. врезку 5.9.
Подставляем разложение (9.24) в выражение (9.23). Теперь задача
минимизации принимает вид:
bW.
1 КЩФ) + ml ■ grad J —^ - I(W(q))
Эа
(9.26)
Для вычисления оптимального сдвига ma применяем стандартную
процедуру оптимизации СКО (см. врезку 4.5).
Процедура оптимизации СКО. Вычисляем производную суммы
(9.26) по сдвигу та, приравниваем ее к нулю и получаем уравнение:
21
grad J
d_W^
Эа
j(Wa(q)) + mTa • grad J~~I(W(q))
= 0, (9.27)
где в правой части находится нулевой вектор-столбец 0. Здесь
я"?[
grad J
q ■- Эа
grad J
Эа
(9.28)
- матрица Гессе размера 2x2, содержащая вторые производные.
(О Л. О. Гессе см. врезку 2.8). Решение уравнения (9.27) вида
^н-1^
grad J
Эа
[l(W(q)) - J(Wa(q))]
(9.29)
дает оптимальный вектор сдвига та заданного вектора параметров а, а
значит, и обновленный вектор параметров а + та.
Аналогия с методом Ньютона-Рафсона. Отправляясь от
начального вектора расхождения а, мы итеративно вычисляем новые векторы
а + т , применяя метод наискорейшего подъема. Алгоритм останав-
9.3. Прослеживание и обновление признаков ♦ 425
ливается, когда величина ошибки (9.22) или длина вектора сдвига та
окажется меньше г > О или будет выполнено заранее заданное число
итераций.
Пример 9.4 (случай параллельного переноса). Предположим, что мы ищем
только вектор параллельного переноса а, для которого Wa(q) = [t.x + i, t.y + j] для
q = (z, /). Матрица Якоби имеет вид
dWa{q).x dWa(q).x
Эа
(?,Ю =
Эх Эу
dWa{q).y dWa(q).y
Эх
ду
1 О
О 1
А матрица Гессе равна5
«-?[
grad J——t
q ■- Эа
grad J
dwa
Эа J
=1
\(dJ1
UxJ
a/2
дхду
dJ2
дхду
[dy)
;
2
Направление наискорейшего подъема равно просто
ЭЖ
grad/
Эа
grad/,
и
I(W(q)) - J(Wa(q)) = I(W(q)) - J{q + a).
Соберем всё вместе:
Э^„
^н-1^
grad J
(dJ}2
[дх
dJ2
дхду
Эа
dJ2
дхду
а/
/Л т\2
[l(W(q)) - I(Wa(q))]
X[grad/]T[J(W(0)-/(<? +a)].
(9.30)
(9.31)
(9.32)
(9.33)
После того как производные изображения / в окрестности текущего пикселя
(окне W) аппроксимированы, т. е. гессиан и вектор градиента вычислены, для
вычисления вектора сдвига танам осталось только посчитать сумму разностей.
5 Мы используем практически пригодную аппроксимацию матрицы Гессе. Вместо смешанных
производных мы берем произведение первых производных.
426 ♦ Глава 9. Обнаружение и прослеживание признаков
Алгоритм Лукаса-Канаде. Пусть дано изображение /, его
градиентное изображение grad / и локальный шаблон W(okho), содержащий
(к примеру) круг влияния особой точки. Псевдокод алгоритма приведен
на рис. 9.17.
1: Положить а равным начальному значению вектора расхождения;
2: while STOP CRITERION = false do
3: Для данного вектора а вычислить оптимальный сдвиг та по формуле (9.29);
4: Положить а = а + т ;
а'
5: end while
Рис.9.17. Алгоритм Лукаса-Канаде
В строке 3 производятся вычисления для всех пикселей q,
определенных шаблоном W. По существу, эти вычисления состоят из трех шагов:
1) деформировать окно W, принадлежащее /, в окно Wa(q),
принадлежащее /;
2) вычислить матрицу Якоби и ее произведение с grad /;
3) вычислить матрицу Гессе.
Алгоритм работает на несколько порядков быстрее, чем
исчерпывающий поиск оптимального вектора а. Реализация алгоритма Лукаса-
Канаде имеется в библиотеке OpenCV.
Холмы и впадины. Предположим, что вектор а двумерный
(например, описывает только параллельный перенос). Тогда величина ошибки
(9.22) определена на плоскости и при различных значениях а описывает
«холмистый ландшафт» с локальными минимумами и максимумами и,
возможно, единственными глобальным минимумом и максимумом (см.
рис. 9.18). Для иллюстрации поменяем местами минимумы и максимумы,
т. е. будем искать глобальный минимум методом наискорейшего спуска.
Итерации могут привести к единственному глобальному минимуму
(методом наискорейшего спуска), только если начальный вектор
параметров выбран так, что последующие сдвиги способны достичь этого
глобального минимума.
Существует также возможность дрейфа. Хотя каждое локальное
вычисление по отдельности точно, в результате последовательного
выполнения нескольких шагов могут накапливаться заметные ошибки, в
основном в силу дискретной природы данных.
9.3.3. Фильтр частиц
Теперь рассмотрим другой способ прослеживания. Признаки
(каждый из которых определен особой точкой и дескриптором) прослежи-
9.5. Прослеживание и обновление признаков ♦ 427
ваются согласно некоторой общей («нечеткой») модели, описывающей
их перемещение. Прослеживать можно как от кадра к кадру, так и
внутри одного изображения. См. рис. 9.19.
Рис. 9.18. Голубая точка «не может подняться» по самому крутому склону
к глобальному максимуму, поскольку находится в долине, окруженной одними
лишь локальными максимумами. То же самое относится к розовой точке, которая
уже находится в локальном максимуме.Желтая точка в «центральной долине»
(глобальный минимум) может подняться на глобальный пик (в середине рисунка),
совершая итерации, предписанные алгоритмом наискорейшего подъема
Изображение / х
i ►
Т
i
\
Г
Строка у -1
Строка у
Рис. 9.19. Две точки прослеживаются между строками у и у - 1.
Обе точки включены в один признак, содержащий координаты / и г
и другие параметры, которые составляют зависящий от модели дескриптор а.
Следующий признак в строке у- 1 должен быть выбран посредством
оптимизированного сопоставления с моделью признаков
428
Глава 9. Обнаружение и прослеживание признаков
Частицы, веса и итеративный подход. Предположим, что
признаки определены конкретной, зависящей от приложения моделью, а не
обобщенной моделью, включающей (только) круг влияния. Это
позволит с большим основанием назначить веса в зависимости от
согласованности позиций признаков с моделью.
Фильтр частиц пригоден в следующей ситуации: частица
представляет признак в многомерном пространстве, координатами в нем
являются позиция пикселя изображения (а:, у) или просто позиция л: в
определенной строке изображения, а также значения дескриптора в векторе
параметров а = (av a2,..., ат). См. рис. 9.20.
Итерация t
х
Иитерация t +1
о° о
о
о
о
о
X?
о°-о"
о
о
•
о
Рис. 9.20. Трехмерное пространство частиц, в котором координатами служат
одна пространственная компонента х и две дескрипторные компоненты аг и о2.
Алгоритм конденсации определяет отображение взвешенных частиц с итерации г
на итерацию г + 1. Серым цветом обозначены веса; на каждой итерации веса
изменяются в соответствии с выбранным алгоритмом конденсации
Фильтр частиц может прослеживать векторы параметров во
времени или в пространстве, оценивая согласованность с определенной
моделью. По результатам оценки согласованности с моделью частице
присваивается вес (неотрицательное вещественное число).
Затем алгоритм конденсации анализирует кластер взвешенных
частиц и находит в нем «частицу-победитель». Существует много разных
стратегий конденсации. Как правило, веса частиц в кластере
итеративно пересчитываются. По завершении процесса в качестве
частицы-победителя берется некоторое среднее или локальный максимум.
В примере на рис. 9.20 частицы неподвижны, а меняются только веса.
В общем случае алгоритм конденсации может сливать частицы,
изменять их позиции или создавать новые частицы.
Пример. Мы рассмотрим простой случай. Имеется признак,
включающий левую и правую точки в одной строке изображения. Требуется
9.3. Прослеживание и обновление признаков ♦ 429
проследить его в пределах изображения. Будем считать, что переход от
следующей строки к предыдущей происходит снизу вверх. Смещения
обеих точек, входящих в состав признака, могут (немного) различаться.
Ситуация показана на рис. 9.19.
Рис. 9.21. Верхний ряд, слева направо: входной кадр, вид сверху, обнаруженные
вертикальные границы. Нижний ряд, слева направо: строковые компоненты
евклидова дистанционного преобразования, показанные в виде абсолютных
величин; обнаруженные середина и края полосы; края полосы,
спроецированные обратно в перспективный вид на записанных кадрах
На этом простом примере мы сможем продемонстрировать
основные идеи фильтра частиц в применении к конкретному приложению
(обнаружение дорожной разметки в видеозаписи, сделанной
движущимся эгоавтомобилем)6. Мы лишь кратко перечислим шаги этого
приложения, см. рис. 9.21.
Преобразовать записанные видеокадры в вид сверху, т. е.
ортогональную проекцию сверху вниз.
Выделить доминантные вертикальные границы на виде сверху,
удалить артефакты границ.
Выполнить евклидово дистанционное преобразование (Euclidean
distance transform - EDT) для вычисления минимальных
расстояний от пикселей р = (х, у) до граничных пикселей. Использовать
строковые компоненты со знаком х - х , вычисленных расстояний
г edge г
у1(х-х . )2 + (у-у А )2 для идентификации середин полос в местах,
1.
edge'
у edge-
где знак меняется, а величина расстояния составляет примерно
половину ожидаемой ширины полосы.
Применение фильтра частиц для распознавания дорожной разметки предложено в работе
[S. Sehestedt, S. Kodagoda, A Alempijevic and G. Dissanayake. Efficient lane detection and tracking in
urban environments. In Proc. European Conf. Mobile Robots, 2007, p. 126-131].
450 ♦ Глава 9. Обнаружение и прослеживание признаков
4. Применить фильтр частиц для продолжения найденных на
краях полос пикселей снизу вверх, строка за строкой, с целью найти
наиболее вероятные краевые пиксели в следующей строке.
Шаг 2 можно выполнять в предположении ступенчатости границ,
используя только аппроксимацию частной производной 1х. О том, как
удалять граничные артефакты, см. упражнение 3.2.0 преобразовании EDT
на шаге 3 см. раздел 3.2.4.
Построение вида сверху. Шаг 1 можно выполнить с помощью
преобразования обратной перспективы с использованием откалиброван-
ных параметров камеры или просто пометить четыре пикселя
изображения, которые должны находиться в углах прямоугольника на
плоскости дороги (т. е. образовывать трапецию в перспективном
изображении), и применить гомографию, которая переводит эти точки в
вершины прямоугольника, а заодно преобразует перспективный вид
в вид сверху.
Частицы на основе модели. Модель дорожной разметки показана
на рис. 9.21. Обнаружив середину полосы, где сходятся положительная
и отрицательная строковые компоненты EDT (абсолютные величины
различаются не более чем на 1) на виде сверху, мы берем
фиксированную высоту h и находим (воспользовавшись положительной и
отрицательной строковыми компонентами) угол а, определяющий
координаты а: точек / и г. Локальные аппроксимации касательных в точках / и г к
обнаруженным краям полос определяют углы /? и у. Все эти параметры
показаны на рис. 9.22.
X X
1 /
1
[/
Левый
край
)
Lj
у
V
Правый
край
Рис. 9.22. Слева: визуализация модели для перспективного изображения.
Точка, расположенная над средней точкой с на фиксированной высоте h,
определяет угол а с точками / и г на левом и правом краях полосы соответственно.
Справа: вид сверху. На этом виде показаны параметры модели. Касательные
в обнаруженных точках / и г образуют углы /? и у с левым и правым краями,
которые определяются как доминантные вертикальные границы
9.3. Прослеживание и обновление признаков ♦ 451
Высота h и угол а показаны на перспективном виде с целью
иллюстрации модели. Координаты / и г в действительности определены на
виде сверху.
Признак, включающий две точки (/, у) и (г, у) в строке у на левом и
правом краях полосы (или одну особую точку (с, у)), определен одним
вектором а = [с, а, /?, у]т. Следовательно, мы имеем 4-мерное
пространство частиц.
Инициализация процесса прослеживания. Имея
последовательность кадров, мы можем использовать результаты обработки
предыдущего кадра для инициализации признака в строке, близкой к
нижнему краю текущего кадра. Предположим, что обрабатывается самый
первый кадр последовательности или кадр, следующий за тем, где мы
потеряли разметку.
Начальная строка у0 выбирается близко к нижнему краю первого
кадра.
• Вариант 1: ищем пиксель (с, у) с положительной строковой
компонентой расстояния такой, что строковая компонента
расстояния в смежном пикселе в той же строке отрицательна. Возможно,
придется подняться на несколько строк, прежде чем будет
найдено подходящее начальное значение с.
• Вариант 2: запускаем специальные детекторы для нахождения
точек (/, у) и (г, у).
Эти начальные значения определяют вектор первого признака:
а0 = [с0, а0, £0, у0]т (9.34)
для начальной строки. Углы /?0 и у0 можно положить равными 0 и задать
более точно на следующем шаге продолжения.
Обновление вектора признака в фильтре частиц. Мы
прослеживаем вектор признака а = [с, а, /?, у]т от начальной строки вверх до
строки, которая определяет верхний предел ожидаемых краев полосы.
Номер строки у на виде сверху вычисляется путем прибавления
фиксированного приращения А, начиная с у0; на шаге п он равен
уп = (у0 + п • А). В процессе обновления фильтра частиц применяются
следующие две модели.
Динамическая модель. Матрица динамической модели А
определяет движение по умолчанию частиц в изображении. Обозначим рп
особую точку на шаге п, выраженную в виде вектора. Предсказанное
значение рп вычисляется по формуле рп = А • pnV Самый общий и простой
452 ♦ Глава 9. Обнаружение и прослеживание признаков
выбор А - единичная матрица I (в данном приложении это выражает
предположение о гладкости краев полос).
Модель наблюдения. В этой модели вес частицы определяется в
процессе передискретизации. Предполагается, что точки (сп, уп) имеют
большие по абсолютной величине строковые компоненты расстояния.
Пусть Ln и Rn - короткие отрезки дискретных прямых с центрами в
точках (1п, уп) и (гп, уп), представляющие касательные в этих точках на виде
сверху. Предполагается, что эти отрезки образованы пикселями, для
которых абсолютные значения строковой компоненты расстояния близки
к 0. Мы предполагаем, что Ln и Rn - это 8-пути длины 2к + 1 с центрами
в точках (1п, уп) и (гп, уп) соответственно.
Порождение случайных частиц. На каждом шаге при переходе к
следующей строке мы порождаем N ап > 0 частиц, случайно
распределенных вокруг предсказанного (согласно динамической модели)
вектора параметров в т-мерном пространстве частиц. Результаты
получаются лучше, если число порожденных частиц велико (например,
N т = 500). На рис. 9.20 показано 43 частицы в 3-мерном пространстве
частиц. Обозначим
4 = 14%. &г!Г <9-35>
z-ю частицу, порожденную на шаге п, 1 < К N ап.
Пример 9.5 (порождение частиц с равномерным распределением). Мы
можем порождать равномерно распределенные частицы в m-мерном
пространстве частиц. В рассматриваемом примере это реализуется следующим
образом.
Для первой компоненты вектора возьмем интервал [с - 10, с + 10] и
случайным образом с равномерным распределением выберем значения с в этом
интервале. Этот процесс не зависит от других компонент вектора аЧ Для второй
компоненты возьмем, к примеру, интервал [а - 0.1, а + 0.1], для третьей
компоненты - интервал [/? - 0.5, (3 + 0.5] и аналогично для у.
Пример 9.6 (порождение частиц с нормальным распределением). Мы
можем вместо этого выбрать нормальное распределение порождаемых частиц в
ш-мерном пространстве. В рассматриваемом примере это делается так.
Распределение с нулевым средним порождает значения вокруг
предсказанного. Для отдельных компонент возьмем такое стандартное отклонение о > 0,
чтобы порожденные значения находились примерно в таких же интервалах,
как при равномерном распределении в примере 9.5. Например, для
компоненты с берем а= 10.
9.5. Прослеживание и обновление признаков ♦ 455
Веса частиц. Определим вес г-й частицы а|. Левая позиция равна
/'=<;'-/?• tan а'. (9.36)
Сумма абсолютных величин строковых компонент расстояния
dr{x, у) = \х - xed J, определяемых EDT на виде сверху, вдоль отрезка L
(который, как мы предполагаем, является 8-путем длины 2к + 1) равна
s[=l№+r*™ft>yn+rcosP«)\-
(9.37)
j=-k
Сумма S'R для второго отрезка вычисляется аналогично, и мы
получаем вес
G)dist =
1
2<т/сг.;г
ехр
/ &-и)2 №-/ОгЛ
2Gl
2сг
(9.38)
относительно значений расстояния на L и R, где цр цг, ох\\.ог- оценки
констант (скажем, в идеальном случае средние равны нулю: цг = цг = 0),
выведенные на основе экспериментов с конкретным приложением.
Вес сгенерированной средней точки (d, yn) равен
/
со'
centre
or4bt
ехр
/
1
d (с1 .у
\
-Мс
2\
2<7
(9.39)
v )
где цс и ас - также оценки констант.
Наконец, полный вес z-й частицы а'п в начале итеративного процесса
конденсации равен
О). = (О1,. • (х)1 „ .
i dist centre
(9.40)
Эти веса отвечают за «влияние» частиц в процессе конденсации.
Обычно перед применением стандартных программ конденсации
необходимо нормировать все N весов. Результаты показаны на рис. 9.23.
В общем случае использование нескольких строк для определения
частицы позволяет улучшить результаты. Но просмотр на три строки
вперед представляется более разумным, чем, скажем, на восемь.
Количество строк можно изменять динамически в зависимости от характера
построенных краев полос, например прямые они или кривые.
Конденсация. Итеративный процесс конденсации решает, какие из
случайно сгенерированных («рядом» с предсказанными) частиц
следует взять в качестве результата для следующей строки изображения.
454 ♦ Глава 9. Обнаружение и прослеживание признаков
Рис. 9.23. Слева вверху: точки (1п, уп) и (гп, уп), построенные описанным методом
(показаны желтым цветом) и обобщенным методом, когда частицы определяются
в ходе просмотра на две строки назад и на восемь строк вперед (показаны
голубым цветом). Справа вверху: построенные точки обратно спроецированы
в соответствующий исходный кадр. Внизу: здесь голубые точки соответствуют
просмотру на две строки назад и только на три строки вперед
Одна итерация алгоритма конденсации называется
передискретизацией (resampling). На шаге передискретизации возможно также
слияние, удаление или создание новых частиц; цель - улучшить «качество»
частиц.
У частицы с высоким весом гораздо больше шансов «пережить»
процесс передискретизации. На вход передискретизации подаются все
текущие взвешенные частицы, а на выходе получается новое множество
взвешенных частиц. Зачастую частицы «дрейфуют» в сторону входных
частиц с более высоким весом. В библиотеке OpenCV имеется
реализация фильтра частиц, см. CvConDensation.
Достаточно небольшого числа итераций или передискретизаций
(скажем, от 2 до 5). По завершении итераций в качестве результата берется
частица с наибольшим весом или взвешенное среднее всех частиц.
9.3. Прослеживание и обновление признаков ♦ 455
9.3.4. Фильтр Калмана
Фильтр Калмана - весьма эффективное средство контроля зашумлен-
ных систем. Главная его идея такова: «зашумленные данные на входе и,
предположительно, менее зашумленные данные на выходе».
У фильтра Калмана множество приложений, например:
прослеживание объектов (мячей, лиц, голов, рук и т. д.), аппроксимация данных
кривыми Безье, экономика, навигация, а также различные приложения
компьютерного зрения (стабилизация измерения глубины,
прослеживание признаков, прослеживание кластеров, синтез данных от радара,
лазерное сканирование и применение стереокамер для измерения
глубины и скорости). В этом разделе мы изложим основные идеи с
прицелом на применение к прослеживанию признаков.
Непрерывное уравнение линейной динамической системы. Мы
рассматриваем линейную динамическую систему, описываемую
уравнением вида
х = Ах. (9.41)
n-мерный вектор х е Ж" описывает состояние процесса, а А -
постоянная матрица системы размера п*п. Символ х обозначает
производную х по времени t.
Знаки и модули собственных значений А (т. е. корней
характеристического полинома det(A - XI) = 0) определяют устойчивость
динамической системы. Другими ее свойствами являются наблюдаемость и
управляемость.
Пример 9.7 (объект, движущийся с постоянным ускорением). Видеокамера
захватывает объект, движущийся по прямой. Его центроид (т. е. положение)
описывается координатой х на этой прямой, а движение характеризуется
скоростью v и постоянным ускорением а. Мы не рассматриваем ни начало, ни
конец этого движения.
Состояние процесса описывается вектором х = [х, v, а]Т, и х = [v, а, 0]т, потому
что
х = v, v = а, а=0. (9.42)
Отсюда следует, что
[v
а
[_0_
=
"0 1 0"
0 0 1
0 0 0
•
х|
V
aj
456 ♦ Глава 9. Обнаружение и прослеживание признаков
Тем самым определена матрица системы А размера 3*3. Для этой матрицы
det(A - Л) = -Х\ (9.44)
Следовательно, все три собственных значения одинаковы и равны нулю, т. е.
система «очень устойчива».
Дискретные уравнения линейной динамической системы.
Преобразуем непрерывную линейную систему, описываемую матрицей А
в уравнении (9.41), в дискретно зависящую от времени. Обозначим At -
разность между моментами времени t и t + 1. Вспомним разложение
экспоненты в степенной ряд
00 х1
^ = 1 + 1- (9.45)
для любого х. Обозначим
F„=e-*=I+X^A
,1 (9.46)
матрицу перехода состояний для At. Мы предполагаем, что интервал At
определен раз и навсегда, поэтому далее не будем указывать его в
подстрочном индексе.
Заметим, что обычно существует такое /0 > 0, что матрица А. содержит
нули во всех столбцах с номерами / > /0. В таком случае ряд (9.46)
сводится к конечной сумме, определяющей матрицу F дискретной системы
xt = Fx^ (9.47)
с начальным состоянием х0 в момент t = 0. Иногда для краткости мы
будем говорить «момент t» вместо tQ + t- At.
Матрица перехода состояния F преобразует внутреннее состояние
(непрерывной линейной системы, описываемой матрицей А) в момент
t во внутреннее состояние в момент t + 1.
Дискретная линейная система с управлением и шумом. На
практике системы обычно зашумлены и зачастую управляются извне.
Поэтому уравнение (9.47) заменяется более детальными уравнениями
дискретной системы:
xt = FxM + But + wt,
yt = Hxt + vt.
Здесь мы дополнительно имеем управляющую матрицу В, которая
применяется к вектору управления ut, вектор шума системы wt, матрицу
9.5. Прослеживание и обновление признаков ♦ 457
наблюдения Н, зашумленные наблюдения у£ и вектор шума наблюдения vt.
Предполагается, что векторы шума системы и шума наблюдения в
различные моменты времени независимы. Управление описывает некое
воздействие на систему в момент t, не являющееся внутренне
присущим самому процессу.
Пример 9.8 (продолжение: объект, движущийся с постоянным ускорением).
Продолжим пример 9.7. Мы имеем векторы системы xt = [xt, vt, at], где at = a.
Имеем матрицу перехода состояний F (проверьте, что она связана с заданной
матрицей А формулой (9.46)), определенную следующим образом:
/
x?+i
1 At
О
О
1
О
1д/
2
At
1
/
Л =
1АЛ
х,+A/-V, +—At a
t t 2
v. + At ■ а
а
(9.48)
Рассмотрим наблюдение yt = [xt, 0, 0] ; мы наблюдаем только текущее
положение. Тогда матрица наблюдения Н имеет вид:
У/ =
1 0 0
0 0 0
0 0 0
(9.49)
Векторов шума wf и vt в примере 9.7 не было, при идеальных условиях они
были бы нулевыми. Вектор управления и управляющая матрица в этом
примере не используются.
Дискретные предсказания. Пусть дана последовательность
у0, ур..., ytl зашумленных наблюдений линейной динамической
системы. Наша цель - оценить внутреннее состояние системы в момент t,
xt = [хг t,x2t,...,xn JT. Ошибку оценки следует минимизировать (т. е. мы
хотим заглянуть «на один шаг вперед»).
Обозначим х оценку состояния х , основанную на перечисленной
'11*2
tl'
ниже информации, имеющейся в момент tr
Обозначим Pt |t матрицу дисперсий ошибки предсказания х( - х
tll'2*
Наша цель - минимизировать Pflf в некотором математически строгом
смысле.
tit
Информация, доступная в момент предсказания. Подступаясь к
задаче предсказания в момент t, мы сначала инвентаризуем все, что
нам известно в этот момент.
458 ♦ Глава 9. Обнаружение и прослеживание признаков
1. Матрица перехода состояний F, которая применяется к («хорошо
известному») предыдущему состоянию xtl.
2. Управляющая матрица В, которая применяется к вектору
управления ut, если в данную систему вообще встроен механизм
управления.
3. Понимание характера шума системы wt (например,
моделируемого многомерным нормальным распределением),
выраженное в виде матрицы дисперсий Ot и математических ожиданий
Uit = E[wit] = 0 для z = 1, 2,..., п.
4. Вектор наблюдений yt состояния xt.
5. Матрица наблюдения Н («Как наблюдать yt»?).
6. Понимание характера шума наблюдения vt (например,
моделируемого многомерным нормальным распределением),
выраженное в виде матрицы дисперсий Rt и математических ожиданий
ht= Щ,А = ° для ' = *> 2' -» "•
Предсказание и фильтр. Ключевая идея состоит в том, что мы не
просто стремимся получить предсказания одно за другим, применяя
описанную выше доступную информацию. Вместо этого мы
определяем фильтр, цель которого - уточнить наши знания о шуме системы на
основе прошлых ошибок предсказания и наблюдений, и этой
уточненной информацией о шуме системы мы хотим воспользоваться, чтобы
уменьшить ошибку предсказания в будущем.
Фильтр не решает такие фундаментальные проблемы, свойственные
этому подходу, как выбор неправильной матрицы перехода состояний
или управляющей матрицы. Чтобы понять, образуют ли эти матрицы
корректную модель системы, необходим более общий анализ.
Фаза экстраполяции (предсказания) фильтра. На первой фазе
фильтра мы вычисляем предсказание матрицы дисперсий, зная
матрицу перехода состояний F и управляющую матрицу В. Также
применяется матрица дисперсий шума системы Qt:
V." •*.-.«-.+ ВИн (9-50)
Vi-pp.-«-.Fr + Q>- С-51)
Фаза коррекции фильтра. На второй фазе вычисляется вектор
невязки измерений zt и матрица невязки дисперсий St, для чего
используется входящая в модель матрица наблюдения Н. Мы также применяем
матрицу дисперсий шума наблюдения Rt и ставим целью улучшить
матрицы шума:
9.3. Прослеживание и обновление признаков ♦ 459
zt = yt-Hxtlt_p (9.52)
St = HPf|(1HT + Rt. (9.53)
Чтобы вычислить скорректированный вектор оценки состояния (т. е.
предсказание решения в момент t), мы рассматриваем также шаг
коррекции фильтра в момент t:
Можно ли определить матрицу Kt, так чтобы этот шаг коррекции имел
смысл? И существует ли оптимальная матрица Kt? Утвердительный
ответ был дан Р. Э. Калманом.
Врезка 9.9 (Калман, Сверлинг, Тиле, линейный фильтр Калмана и Аполлон-8).
Р. Э. Калман (родился в Венгрии в 1930 г.) нашел и опубликовал [R. E. Kalman.
A new approach to Linear filtering and prediction problems. J. Basic Engineering, vol. 82,
1960, p. 35-45] рекурсивное решение задачи линейной фильтрации
дискретных сигналов, которое сегодня известно под названием линейный фильтр
Калмана. Над родственными задачами в то же время работал американский
специалист в области теории радиолокации П. Сверлинг (1929-2000).
Датского астронома Т. Н.Тиле (1838-1910) также упоминают в связи с истоками
этих идей. Аполлон-8 (декабрь, 1968 г.), первый пилотируемый космический
корабль, запущенный с Земли на орбиту Луны, безусловно, был бы
невозможен без линейного фильтра Калмана.
Оптимальная матрица коэффициентов усиления Калмана.
Матрица
Kt = PmlHTS^ (9.55)
минимизирует среднеквадратичную ошибку E[(xt - х )2], что
эквивалентно минимизации следа (суммы элементов на главной диагонали)
матрицы Р . Эта теорема была доказана Р. Э. Калманом.
Матрица Kt называется оптимальной матрицей коэффициентов
усиления Калмана и определяет линейный фильтр Калмана. Для этого
фильтра нужна также скорректированная оценка матрицы дисперсий шума
системы
Pt|1 = (I-KtHt)Pt|t_, (9.56)
для подготовки к фазе экстраполяции в момент t + 1. Матрицу
дисперсий Р0|0 необходимо инициализировать в начала процесса
фильтрации.
440
Глава 9. Обнаружение и прослеживание признаков
Пример 9.9 (объект, движущийся со случайным ускорением). Продолжим
примеры 9.7 и 9.8. Мы по-прежнему предполагаем, что объект (например,
автомобиль) движется (например, впереди камеры) по прямой, но теперь его
ускорение at случайным образом изменяется в промежуток времени между t - 1
и t. Случайность будем моделировать нормальным распределением с нулевым
средним и дисперсией а2а. Результаты измерения положения объекта
предполагаются зашумленными, и шум также моделируется нормальным
распределением с нулевым средним и дисперсией а2.
Вектор состояния этого процесса имеет вид xt = [xt, *JT, где
производная xt равна скорости vf. Как и раньше, мы не предполагаем, что процесс
управляемый (т. е. ut - нулевой вектор).
Имеем (заметим, что случайное ускорение больше не может быть
частью состояния; что такое матрица А в непрерывной модели?):
х, =
[1
|_°
АЛ
1J
|Vi
v, ,
+ a,
l
L t-\ J
\At2]
?,
[At \
= Fx,_1+w/,
(9.57)
где матрица дисперсий Qt = var(wt). Обозначим Gt = [At2/2, At]T. Тогда
Q, = E[wrf] = GtE[af]Gj = a2^ = <£
At4 At3
4
A^3
At'
(9.58)
Это означает, что не только F, но также Qt и Gt не зависят от t. Поэтому
будем обозначать их просто О и G. (Вообще, Ot часто задают в форме
диагональной матрицы.)
В нашем примере мы измеряем положение объекта в момент t (но не
его скорость), т. е. имеем
t
\\ 0]
0 0
х,+
V/l
_°J
= Нх. + v.
(9.59)
где vt - шум наблюдения с такой матрицей дисперсий
R = £[v,vJ] =
^ 0
о о
(9.60)
Начальное положение х0|0 = [0,0]. Если это положение известно точно,
то матрица дисперсий нулевая:
9.5. Прослеживание и обновление признаков ♦ 441
В противном случае
р =
г0|0
р =
*0|0
0
0
с
0
0
0
0
с
(9.61)
(9.62)
где с > 0 - достаточно большое вещественное число.
Теперь мы готовы рассмотреть момент t = 1. Сначала предскажем х1|0
и вычислим его матрицу дисперсий Р , применяя уравнения
экстраполяции
х =Fx
tit—i t—i it — i»
P = FP FT + О.
tit—i t— nt— i ^t
(9.63)
(9.64)
Затем вычислим вспомогательные данные ъх и Sv пользуясь
уравнениями коррекции
z^-Hx^, (9.65)
St = HPt|t jHT + R. (9.66)
Это позволяет вычислить оптимальную матрицу коэффициентов
усиления Калмана Кг и обновить хщ:
(9.67)
*t = Pt,t -Рф,
х
tu
Хт-1 + КЛ
(9.68)
Наконец, вычисляем Р , чтобы подготовиться к моменту t = 2:
Рт = (1-К{Н)Рт_г (9.69)
Заметим, что все эти вычисления - элементарные операции
матричной алгебры, хотя выглядят они довольно сложно. С другой стороны,
реализация вполне прямолинейна.
Настройка фильтра Калмана. От задания матриц дисперсии Ot и
Rt или константы с > 0 в Р0|0 зависит, сколько временных интервалов
фильтра Калмана понадобится, чтобы предсказанные состояния
сошлись к истинным.
Вообще говоря, чем выше недостоверность (т. е. чем больше число
с > 0 или чем больше элементы Of и Rt), тем больше значения в матрицах
Pt|t_j и St; из-за операции обращения S^1 в определении оптимальной
матрицы коэффициентов усиления Калмана это приводит к умень-
442 ♦ Глава 9. Обнаружение и прослеживание признаков
шению значений в Kt и вклада вектора невязки измерений в уравнение
коррекции (9.54).
Например, в предельном случае, когда мы абсолютно уверены в
правильности начального состояния z0|0 (т. е. с = 0) и не обязаны
предполагать наличие шума в системе и в процессах измерения (как в
примере 9.7), матрицы Р и St вырождаются в нулевые; обратная матрица S"1
не существует (примечание: этот случай нужно специально
рассматривать в программе) и Kt оказывается неопределенной. Предсказанное
состояние совпадает с обновленным; это случай самой быстрой
сходимости фильтра.
Альтернативная модель для фазы экстраполяции. Если имеется
матрица непрерывной модели А данного линейного динамического
процесса х = А • х, то проще воспользоваться уравнениями
K-i=Akt-№-i + *,n,> (9-7°)
а не уравнениями с дискретными матрицами F. (Разумеется, при этом
нужно также модифицировать определение матрицы В, учтя влияние
управления на производные векторов состояния.) Формально такая
модификация фазы экстраполяции никак не отражается на фазе
коррекции.
9.4. Упражнения
9.4.1. Упражнения по программированию
Упражнение 9.1 (сравнение RANSAC и преобразования Хафа).
Найдите прямые линии в изображениях на рис. 3.40; напишите генератор
зашумленных отрезков прямых, если еще не сделали этого раньше.
Сравните качество детекторов прямых, основанных на преобразовании
Хафа и на алгоритме RANSAC, используя контрольные данные,
доступные генератору зашумленных отрезков.
Спроектируйте и реализуйте детекторы на основе преобразования
Хафа и алгоритма RANSAC, если не сможете найти их по-другому. В
любом случае опишите детали работы метода на основе RANSAC.
Упражнение 9.2 (пространство масштабов прямоугольного
фильтра). Выбрав п > 0, п раз подряд примените прямоугольный фильтр 3x3,
определенный в формуле (2.7), к заданному изображению /. В результа-
9.4. Упражнения ♦ 445
те получится размытое изображение В"(1). При п = 0 это будет исходное
изображение: / = В°(1).
Постройте пространство масштабов прямоугольного фильтра,
выбрав конечное множество уровней с номерами п = 0 < п1 <... < пт. Из него
мы получаем остаточное пространство масштабов соответствующих
т + 1 уровней:
Rn(I) = I - &(Г).
Определим особые точки как локальные максимумы и минимумы в
этом пространстве, точно так же, как в пространствах масштабов LoG и
DoG. Радиус круга влияния определяется номером уровня п, на котором
была обнаружена особая точка.
Сравните качество этого детектора особых точек и детектора на
основе DoG, применяя идеи, изложенные в разделе 9.2.4.
Упражнение 9.3 (поиск изображения - запрос по образцу).
Найдите «похожее» изображение (имеется в виду сходство по визуальному
содержанию, а не по текстовому описанию) в базе изображений. База
должна содержать не менее 300 изображений. Пользователь подает на
вход программы изображение (необязательно присутствующее в базе),
а на выходе получает подмножество базы (скажем, 10 изображений),
отсортированное по степени сходства.
Понятие «сходства» определите на основе расстояния между
дескрипторами признаков изображений. Количество пар «почти
идентичных» дескрипторов, поделенное на общее количество обнаруженных
особых точек, будет считаться мерой сходства.
На рис. 9.24 показано несколько лучших соответствий особых точек с
«почти идентичными» SURF-дескрипторами. Обратите внимание, что
для этих соответственных точек нет единого аффинного (или
перспективного) преобразования, как на рис. 9.6, где предполагалось сходство
между глобальными паттернами особых точек.
Включите в дескриптор используемого детектора признаков еще
«типичный цвет» в особой точке (например, цвет, усредненный по
небольшой окрестности). Сгенерируйте эти расширенные дескрипторы
для изображений в своей базе.
Особый алгоритмический интерес представляет следующая задача:
для поданного на вход изображения («запрос по образцу») вычислить
его расширенные дескрипторы и постараться найти в базе «самые
похожие» изображения в смысле данного выше определения сходства.
Иными словами, требуется спроектировать специальный
классификатор для решения этой задачи. Сравнение многомерных векторов мож-
444 ♦ Глава 9. Обнаружение и прослеживание признаков
но ускорить с помощью KD-деревьев (в этой книге они не описаны,
обратитесь к другим источникам).
Рис. 9.24. Сопоставление SURF-признаков в двух изображениях,
имеющих похожие дескрипторы
Если базу данных можно разбить на классы «различных»
изображений, то первым шагом может стать вычисление расстояния Махалано-
биса (в этой книге не описано, обратитесь к другим источникам) между
входным изображением и этими классами, чтобы найти класс, для
которого это расстояние минимально. А затем уже можно искать похожие
изображения в этом классе.
Упражнение 9.4 (применение фильтра частиц для обнаружения
дорожной разметки). Реализуйте фильтр частиц, описанный в
разделе 9.3.3 для модели с одной строкой. Можете использовать реализации
дистанционного преобразования (EDT) и процедуры конденсации (на
каждой итерации фильтра), имеющиеся в библиотеке OpenCV. В
качестве входной последовательности можете взять набор 3 EISATS, где
имеются простые изображения, снятые в дневное время, на которых
отчетливо видны края полос движения.
Упражнение 9.5 (линейный фильтр Калмана). Реализуйте фильтр
Калмана, описанный в примере 9.8.
Случайную последовательность приращений Axt = xt+l - xt можно
получить, например, с помощью системной функции RANDOM,
моделирующей равномерное распределение.
Измените (увеличьте или уменьшите) параметр с > 0 и параметры
шума в матрицах дисперсий О и R.
Обсудите, как это влияет на сходимость фильтра (т. е. на соотношение
между экстраполированным и скорректированным состояниями
процесса).
9.4. Упражнения ♦ 445
Не забудьте применить принятую модель шума измерения для
генерации располагаемых данных yt в момент L
Упражнение 9.6 (интеграция с измерениями диспаратности).
Реализуйте на основе фильтра Калмана способ улучшить диспаратности,
вычисленные системой стереозрения в автомобиле, движущемся в
статическом окружении.
1. Описание ситуации. Рассмотрим эгоавтомобиль, движущийся в
статическом окружении. В процессе движения диспаратность
немного изменяется. Если предположить еще, что каждый пиксель
независим от остальных, то можно настроить иконические фильтры
Калмана (по одному фильтру на каждый пиксель изображения).
2. Модель состояния процесса. В абсолютно статическом мире
диспаратность была бы постоянной (если нет даже эгодвижения, то
xt = dt = dt_x и ¥At = 1).
Однако мы имеем движущуюся платформу, поэтому диспаратность
изменяется при движении автомобиля. Позиция пикселя (х, у) также
изменяется. В процессе движения автомобиля все пиксели расходятся
из фокуса расхождения (focus of expansion)7. Именно здесь мы можем
воспользоваться переменными Вии, описывающими управляющее
воздействие.
Состояние (диспаратность) в момент t определяется диспаратностью
в момент t - 1 (вообще говоря, в другом пикселе) и управляющими
переменными.
Предполагается, что информацию об эгодвижении можно получить
от инерциальных датчиков, потому что большинство современных
автомобилей сообщают скорость v и угол поворота вокруг вертикальной
оси ф за период времени. Это поможет нам определить, куда сместятся
пиксели в следующем интервале.
Математически вывести управляющие переменные трудно, т. к.
получающиеся уравнения нелинейны. Но попробуем рассуждать логически.
Поскольку мы знаем движение автомобиля в мировых координатах, то
могли бы точно так же использовать наши управляющие переменные.
Это нельзя выразить линейно (с помощью В и и).
Процесс подразумевает триангуляцию и обратное проецирование
координат пикселей плюс диспаратность, т. е. пикселей карты
диспаратности р = (х, у, d), зная мировые координаты Р = [X, Y, Z\J (в
векторном формате) относительно эгоавтомобиля.
7 Это точка на сетчатке, в которой сходятся линии, параллельные направлению поступательного
движения, в предположении соответствующего направления взгляда.
446
Глава 9. Обнаружение и прослеживание признаков
Для каждого измерения мы выполняем следующие действия.
1. Преобразовать пиксельные координаты (xt_v yfl) в момент t - 1
в мировые координаты Ptl, как обычно делается в стереозрении.
2. Предсказать новую позицию Рм в мировых координатах,
пользуясь данными о движении; зная скорость v и угол поворота вокруг
вертикальной оси гр, можно вычислить:
r,=
cos(^) 0 -sin(^)
О
1
О
[sin(^) 0 cos(^) J
и
Т,=
v-At
¥
l-cos(^)
О
-sin(^
3. Преобразовать новые мировые координаты Pt = RtPtl + Tt в
пиксельные координаты (xt, yt) с помощью обратного
проецирования.
Здесь Rc - матрица поворота в плоскости XZ вследствие
изменения угла поворота относительно вертикальной оси, aTt- вектор
параллельного переноса между моментами t и t -1; гр - угол
поворота вокруг вертикальной оси, a v - скорость автомобиля в
промежуток времени At.
Если известны координаты пикселя (х, у) и диспаратность d в момент
t - 1, то эти уравнения дают оценку диспаратности d' в пикселе (х', у')
в момент t, которая равна значению FAtxM|M + Btut в точке (Y, у'), где ut
определяется скоростью изменения угла поворота вокруг вертикальной
оси гр (t) и скоростью движения vt.
3. Модель процесса измерения. В нашей модели фильтрация
измерений производится непосредственно (т. е. вычисляется
диспаратность). Поэтому для отдельного пикселя у = у и Н = 1.
4. Модель шума. Для измерений диспаратности шум имеет
нормальное распределение в направлении глубины (т. е. для
субпиксельных измерений), поэтому возможны флуктуации измерений в
обе стороны. Основная ошибка состояния приходится на глубину,
следовательно, мы можем предположить, что Р = Р = о\.
В нашей модели шум процесса и шум измерений (в одном пикселе) -
скаляры. Поэтому О = qd и R = rd. Можно было бы предположить, что
эти значения изменяются на каждой итерации, но мы будем считать их
постоянными.
5. Тестирование фильтра. В одном пикселе уравнения
упрощаются:
9.4. Упражнения ♦ 447
• экстраполяция:
хт_г = как выведено выше с использованием ut;
Р =Р + а'
• коррекция:
хт = xm-i +Kt (yt ~ xtit-i)'
«;=Vi(p«-.+^':
В этом случае матрица В определяется путем проецирования в
момент t - 1, аффинного преобразования и обратного проецирования в
момент t. Это можно реализовать попиксельно или сразу для всего
изображения.
Идея здесь в том, чтобы логичным образом выбрать параметры шума.
Для шума измерения логично положить rd = 1, считая, что в нашем
процессе измерения он не превосходит 1 пикселя.
Если мы хотим отфильтровать все движущиеся объекты, то логично
положить qd = 0,0001 (т. е. взять небольшое значение, отражающее наше
предположение о том, что модель хорошая).
На этом заканчивается описание иконического фильтра Калмана.
Для тестирования понадобится стереоскопическое видео, записанное
из движущегося автомобиля с известными параметрами эгодвижения.
Такие данные есть в наборах KITTI и EISATS. На рис. 9.25 показаны
результаты применения описанного метода. Посмотрите, удастся ли вам
добиться аналогичного улучшения по сравнению с обработкой тех же
данных без использования иконических фильтров Калмана.
Поскольку мы предполагали, что окружение статично, следует ожидать ошибок
для движущихся объектов, например велосипедиста на рис. 9.25.
Врезка 9.10 (иконические фильтры Калмана). Об иконических фильтрах
Калмана см. работу [Т. Vaudrey, H. Badino and S. Gehrig. Integrating disparity images by
incorporating disparity rate. In Proc. Robot Vision, 2008, p. 29-42].
9.4.2. Упражнения, не требующие программирования
Упражнение 9.7. В конце раздела 9.1.2 было предложено, как
находить особые точки с субпиксельной точностью. Выберите значения aN,
аЕ, as, aw (позиции 4-смежных пикселей) и а (в пикселе, где обнаружена
особая точка) для функции g и дайте общее решение с субпиксельной
точностью.
448 ♦ Глава 9. Обнаружение и прослеживание признаков
Рис. 9.25. Слева показана стереопара с изображением велосипедиста,
движущегося по дороге впереди эгоавтомобиля. Справа показан вид сверху
на карту глубины (т. е. проекция диспаратности в трехмерное пространство):
левая сетка содержит результаты без интеграции с фильтром Калмана,
а правая - результаты с использованием иконических фильтров
Упражнение 9.8. В алгоритме на рис. 9.8 встречаются две
процедуры: ransacFitPlane и ransacRefinePlaneModel. Детализируйте эти
процедуры для аппроксимации начальной и уточненной плоскостью,
следуя общей идее метода RANSAC.
Упражнение 9.9. На стр. 429 предлагалось строить вид сверху с
применением преобразования томографии, которое определяется
четырьмя углами трапеции (в изображении), являющейся образом
прямоугольника (на дороге). Определите эту томографию.
Упражнение 9.10. Объясните, какие соображения положены в
основу определения весов частиц в формулах (9.36)-(9.40).
Упражнение 9.11. Покажите, что для матрицы А из примера 9.7
F =I + AtA + (At2/2)A2.
Глава
Обнаружение объектов
Последняя глава содержит введение в вопросы классификации и
обучения с подробным описанием базового алгоритма AdaBoost и
случайных лесов. Эти методы иллюстрируются на примерах обнаружения лиц
и пешеходов соответственно.
10.1. Локализация, классификация и оценка
В названии этого раздела перечислены три главных шага любой
системы обнаружения объектов. Объекты-кандидаты локализуются внутри
ограничивающих прямоугольников. Ограничивающий прямоугольник -
это частный случай интересующей области (region of interest - Rol).
См. рис. 10.1.
Рис. 10.1. Локализованные ограничивающие прямоугольники
в задаче обнаружения транспортных средств и людей
Локализованные объекты-кандидаты передаются классификатору,
который различает обнаруженные объекты и отклоненные кандидаты.
Результаты классификации должны быть оценены самой системой или
в ходе последующего анализа качества системы. На рис. 10.2
иллюстрируется обнаружение лиц.
450 ♦ Глава 10. Обнаружение объектов
Рис. 10.2. Обнаружение лиц с одним ложноположительным и двумя
ложноотрицательными результатами (лицо в профиль не считается)
Истинно положительный результат, попадание или обнаружение
имеют место, когда объект обнаружен правильно. Если же мы обнаружили
объект там, где его на самом деле нет, то имеет место ложноположитель-
ный результат, промах или ложное обнаружение. Ложноотрицательный
результат имеет место в случае пропуска объекта, а истинно
отрицательный - в случае, когда участки, не содержащие объектов, именно так
и классифицированы. На рис. 10.2 мы видим один ложноположитель-
ный результат (самый большой квадрат) и два ложноотрицательных
(мужчина в центре и девочка справа). Голова с правой стороны снимка
повернута так, что лица не видно (такой случай всего один).
10.1.1. Дескрипторы, классификаторы и обучение
Классификация - это установление принадлежности к одному из
попарно непересекающихся классов, т. е подмножеств Жп при некотором
п > 0. Иными словами, классы определяют разбиение пространства Ш".
При выполнении классификации очень важна эффективность. В этом
подразделе мы дадим лишь краткий обзор обширной дисциплины,
изучающей алгоритмы классификации.
10.1. Локализация, классификация и оценка ♦ 451
Дескрипторы. Дескриптором х = (х1,...,хп) называется точка в
пространстве Ш" (которое в данном контексте называется пространством
дескрипторов), представляющая измеренные или вычисленные значения
свойств в определенном порядке (например, SIFT-дескриптор имеет
длину п = 128)1. На рис. 10.3 приведена иллюстрация для случая п = 2.
Например, в этом пространстве дескрипторов с двумя свойствами -
«периметр» и «площадь» - имеется дескриптор хх = (621.605, 10 940),
соответствующий сегменту 1.
3
200 600 1,000 1,400 1,800 2,200 2,600
Рис. 10.3. Слева: шесть участков в изображении. Справа: соответствующие
дескрипторы в двумерном пространстве дескрипторов, состоящие из двух свойств:
«периметр» и «площадь» участка изображения. Синяя линия определяет бинарный
классификатор, она разбивает пространство дескрипторов на две полуплоскости
и сопоставляет дескрипторам в одной полуплоскости значение +1,
а дескрипторам в другой полуплоскости - значение -1
Классификаторы. Классификатор сопоставляет дескрипторам
номера классов. Обычно сначала это делается для заранее
классифицированных дескрипторов из множества {хр..., хт}, называемого обучающим
набором, а затем обученный классификатор применяется к
дескрипторам, сгенерированным для изображений или видео.
1. В общем случае классификатор назначает номер 1, 2,...,к одного
из к> 1 классов и 0, если дескриптор «не классифицирован».
2. В случае бинарного классификатора номерами классов являются
числа -1 и +1. Он применяется, когда нам интересно только,
произошло некоторое событие (например, «водитель закрыл глаза»)
или нет.
1 В теории классификации дескриптор называют также признаком. Но в анализе изображений
признаком называется комбинация особой точки и дескриптора. Поэтому во избежание
путаницы мы и дальше будем употреблять термин «дескриптор», а не «признак».
i
80,000-
70,000-
60,000-
50,000-
40,000-
30,000-
20,000-
ю,ооо-
' Площадь
+1
5--6
•4
-1
•Г2
•3
^\ Периметр
452
Глава 10. Обнаружение объектов
Классификатор называется слабым, если он не отвечает ожиданиям
(например, лишь немногим лучше случайной догадки). Несколько
слабых классификаторов можно преобразовать в сильный классификатор,
который дает удовлетворительное решение задачи классификации.
Статистическое комбинирование нескольких слабых классификаторов
в один сильный рассматривается в разделе 10.2. Сильными и слабыми
могут быть как классификаторы общего вида (многоклассовые), так и
бинарные; само понятие «бинарный» еще не означает «слабый».
Пример ЮЛ (бинарная классификация посредством линейного
разделения). Бинарный классификатор можно определить, построив гиперплоскость
П : wTx + Ъ = 0 в W1 для п > 1. Вектор w 6 Ш" называется вектором весов, а
вещественное число Ъ е R - смещением П- Для п = 2 или п = Ъ w - градиент, или
перпендикуляр к разделительной прямой или плоскости соответственно. По
одну сторону от гиперплоскости (включая ее саму) находятся значения +1, по
другую (не включая саму гиперплоскость) - значения -1. Пример для п = 2
приведен на рис. 10.3; в этом случае гиперплоскость - прямая линия, а в случае
п = 1 это была бы точка, разбивающая R1 на две части. Формально положим
/](x) = wTx + b. (10.1)
Тогда случаи h(x) > 0 и h(x) < 0 определяют классы +1 и -1 по одну сторону от
гиперплоскости П-
х2
Рис. 10.4. Слева: линейно разделимое множество заранее классифицированных
дескрипторов на классы «+1» (зеленые) и «-1» (красные). Справа: это множество
не является линейно разделимым; сумма расстояний от четырех неправильно
классифицированных дескрипторов до показанной разделительной
прямой п (черные отрезки) составляет полную ошибку для этой прямой
Такой линейный классификатор (определенный вектором весов w и
смещением Ъ) можно вычислить для множества заранее классифицированных
обучающих дескрипторов в п-мерном пространстве дескрипторов, если это
10.1. Локализация, классификация и оценка ♦ 455
множество линейно разделимо (рис. 10.4 слева). Если же это не так, то мы
определяем ошибку на неправильно классифицированном дескрипторе х как
расстояние до гиперплоскости П по перпендикуляру2
d2 (х, П) =
wTx + Z>
(10.2)
w
и тогда задача состоит в том, чтобы найти такую гиперплоскость Ц, для
которой сумма ошибок на всех неправильно классифицированных дескрипторах
минимальна (рис. 10.4 справа).
Пример 10.2 (классификация с помощью бинарного решающего дерева).
Классификатор можно определить, описав двоичные решения в узлах
разделения дерева (т. е. «да» или «нет»). Каждое решение описывается формальным
правилом, так что для входных данных можно проверить, удовлетворяют они
этому правилу или нет. В зависимости от решения мы переходим к тому или
другому потомку данного узла дерева. Каждый листовой узел дерева
определяет класс, к которому будут отнесены данные, попавшие в этот узел. Например,
листовой узел может определять в точности один класс в Rn (рис. 10.5).
Л<л т Л/г
уеу
х.
уеу
»<120|
\по
хх < 100
усУ \по
,>60 Xj >160
\no yes\/ \^по
1 1
20 40 60
100 120 140 160 180 200
Рис. 10.5. Слева: решающее дерево. Справа: соответствующее
разбиение двумерного пространства дескрипторов
Проверяемые правила в показанном дереве определяют прямые
линии в двумерном пространстве дескрипторов. Дескрипторы,
попадающие в один из листовых узлов, оказываются в одном из показанных
подмножеств Ж2.
Одно решающее дерево или даже один узел разделения в таком
дереве можно рассматривать как пример слабого классификатора; для
Так определяется ошибка в классификаторах, основанных на понятии зазора, например в
методе опорных векторов. В алгоритме AdaBoost эта ошибка обычно явно не используется.
454 ♦ Глава 10. Обнаружение объектов
определения сильного классификатора нужно множество решающих
деревьев (оно называется лесом).
Наблюдение 10.1. Одно решающее дерево позволяет разбить пространство
дескрипторов на несколько областей (классов). Чтобы создать аналогичное
разбиение, нам понадобится несколько бинарных классификаторов, каждый из
которых определяет линейное разделение.
Обучение. Обучение - это процесс определения классификатора с
помощью множества дескрипторов; обученный классификатор затем
применяется для классификации. В процессе классификации может
выявиться неправильное поведение (некорректная классификация),
и тогда потребуется новый раунд обучения. Дескрипторы, на которых
производится обучение, могут быть или не быть заранее
классифицированы.
Обучение с учителем. При обучении с учителем мы сопоставляем
номера классов дескрипторам «вручную», опираясь на собственный опыт
(например, «да, на этом изображении у водителя действительно
закрыты глаза»). В результате мы можем определить классификатор, выделив
в Ш" оптимизированные разделительные многообразия для обучения
на множестве дескрипторов. Гиперплоскость П ~ простейший случай
оптимизированного разделительного многообразия, см. пример 10.1.
Другой способ использования экспертных знаний - задание правил в
узлах решающего дерева, см. пример 10.2. Для этого нужно знать
возможные последовательности решений.
Обучение без учителя. При обучении без учителя у нас нет
априорной информации о принадлежности дескрипторов классам. Поставив
целью разбить пространство дескрипторов Ш" на классы (как в
примере 10.1), мы можем применить к заданному множеству дескрипторов
какой-нибудь алгоритм кластеризации. Например, можно
проанализировать плотность распределения дескрипторов в Ш"; участок с
высокой плотностью определяет начальную точку одного класса, а затем мы
относим дескрипторы к найденным начальным точкам, ориентируясь,
например, на ближайшего соседа.
Пытаясь определить решающее дерево для разбиения
пространства дескрипторов (как в примере 10.2), мы можем обучиться
решениям в узлах дерева, опираясь на общие правила анализа данных.
(Позже мы расскажем об этом подробнее для случайных решающих
лесов.) Тогда сгенерированные правила будут зависеть от
распределения данных.
10.1. Локализация, классификация и оценка ♦ 455
Комбинированные подходы к обучению. Бывает также, что мы
хотим объединить стратегии обучения с учителем и без учителя.
Например, мы можем указать, что в заданном окне изображения, которое
называется также ограничивающим прямоугольником, показан пешеход; это
часть обучения, в которой присутствует учитель (см. рис. 10.6). Мы
можем также указать фрагмент - часть ограничивающего
прямоугольника, - который, возможно, принадлежит пешеходу. Так, на рис. 10.6 голова
велосипедиста тоже трактуется как возможный фрагмент пешехода.
Рис. 10.6. Слева вверху: два положительных примера ограничивающих
прямоугольников для пешеходов. Справа вверху: два отрицательных примера
ограничивающих прямоугольников для пешеходов. Слева внизу: положительные
примеры фрагментов, вероятно, принадлежащих пешеходам.
Справа внизу: отрицательные примеры фрагментов пешеходов
При генерации дескрипторов ограничивающих прямоугольников
или фрагментов (например, измеренная яркость в выбранных пикселях
456 ♦ Глава 10. Обнаружение объектов
изображения) мы уже не можем вручную решить для каждого
отдельного дескриптора, принадлежит он пешеходу или нет.
Например, для заданного множества окон изображения мы знаем,
что все они - части пешеходов, и в какой-то момент алгоритм
построения классификатора решает использовать определенный признак этих
окон для дальнейшей их обработки. Но этот признак может не быть
достаточно общим в том смысле, что не отличает окно, содержащее часть
пешехода, от окна, в котором таких частей нет.
Этот «внутренний» механизм программы построения
классификатора характерен для обучения без учителя. Общая задача состоит в том,
чтобы сочетать анализ данных с учителем и без него при построении
классификатора.
10.1.2. Качество детекторов объектов
Детектор объектов применяет классификатор для обнаружения
объектов в изображении. Мы предполагаем, что любое принятое решение
можно оценить на предмет его правильности. См. например, рис. 10.2.
Спроектированные детекторы объектов необходимо оценивать для
сравнения их качества при определенных условиях. Для оценки
качества классификаторов в распознавании образов и информационном
поиске применяются общие меры.
Обозначим tpnfp- количество истинно положительных и ложнопо-
ложительных результатов соответственно. Аналогично определим
величины tn wfn для отрицательных результатов. На рис. 10.2 tp = 12,/р = 1,
fh = 2. Глядя на одно лишь изображение, невозможно сказать, сколько
было проанализировано участков, не содержащих объекты (и
правильно идентифицированных как «не лица»), поэтому мы ничего не можем
сказать о значении tn. Чтобы узнать, чему равно tn, нужно
проанализировать примененный классификатор. Поэтому tn обычно не участвует
в мерах качества.
Точность (PR) и полнота (RC). Точностью (precision) называется
отношение числа истинно положительных результатов к числу всех
результатов. Полнотой (recall), или чувствительностью (sensitivity),
называется отношение числа истинно положительных результатов к числу
всех потенциально возможных результатов (т. е. к числу видимых
объектов). Формально говоря,
PR= tp и RC = Ф . (10.3)
tp + fp tp + fn
10.1. Локализация, классификация и оценка ♦ 457
PR = 1 (точность 1) означает, что не зафиксировано ни одного лож-
ноположительного результата. RC = 1 означает, что обнаружены все
видимые объекты в изображении и нет ни одного ложноотрицательного
результата.
Частота промахов (MR) и коэффициент ложноположительности
изображения (FPPI). Частотой промахов (miss rate) называется
отношение числа ложноотрицательных результатов к числу всех объектов в
изображении. Коэффициентом ложноположительности изображения (False-
Positives per Image) называется отношение числа ложноположительных
результатов к числу всех обнаруженных объектов. Формально говоря,
MR= fn и FPPI = fp . (10.4)
tp + fn tp + fp
MR = 0 означает, что обнаружены все видимые в изображении
объекты, что эквивалентно условию RC = 1. FPPI = 0 означает, что все
обнаруженные объекты правильно классифицированы.
Коэффициент истинно отрицательных (TNR) и верность (АС).
В этих мерах используется величина tn. Коэффициент истинно
отрицательных (true-negative rate), или специфичность - это отношение числа
истинно отрицательных результатов к числу всех решений «не объект».
Верностью (accuracy) называется отношение числа правильных
решений к числу всех решений. Формально говоря,
tnr=^- и АС = £±* . (10.5)
tn + fp tp + tn + fp + fn
Поскольку обычно число истинно отрицательных результатов нас не
интересует, эти две меры не так важны для оценки качества.
Обнаружен? Как решить, является ли обнаруженный объект
истинно положительным? Предположим, что объекты в изображении были
вручную обведены ограничивающими прямоугольниками, и
результаты этой работы выступают в роли контрольных данных. Для сравнения
каждого обнаруженного объекта с контрольными прямоугольниками
мы вычисляем отношение площадей перекрывающихся участков
Я(РпТ)
ап=— -> (10.6)
0 лфиГ)
где Л - площадь участка изображения (см. раздел 3.2.1), D -
обнаруженный ограничивающий прямоугольник объекта, а Г- контрольный
ограничивающий прямоугольник. Если ао больше некоторого порога, например
458 ♦ Глава 10. Обнаружение объектов
Т = 0,5, то считается, что обнаруженный объект истинно положительный.
Но при таком подходе мы можем сопоставить обнаруженный
ограничивающий прямоугольник с несколькими контрольными. В таком случае для
принятия решения берется тот, для которого значение ао максимально,
а все остальные совпадения считаются ложноположительными.
10.1.3. Гистограмма ориентированных градиентов
Гистограмма ориентированных градиентов (histogram of oriented
gradients - HoG) - распространенный способ представления дескриптора
ограничивающего прямоугольника объекта-кандидата. Например, мы
можем перемещать по изображению окно, размер которого совпадает с
размером ожидаемого ограничивающего прямоугольника, и
останавливать просмотр на потенциальных объектах-кандидатах. В этом
процессе могут учитываться результаты, полученные от системы стереозрения
(например, ожидаемый размер объекта на данном расстоянии) или от
детектора признаков. После того как потенциальный ограничивающий
прямоугольник найден, начинается процесс вычисления дескриптора,
который мы объясним для случая HoG-дескрипторов.
На рис. 10.7 показано разбиение ограничивающего прямоугольника
(пешехода) на крупные блоки и более мелкие ячейки с целью
вычисления HoG.
Рис. 10.7. Блоки и ячейки при вычислении HoG-дескриптора ограничивающего
прямоугольника (синего цвета).Желтые сплошные и пунктирные прямоугольники
обозначают блоки, которые делятся на красные прямоугольники (ячейки).
В трех окнах слева показано, как блок перемещается слева направо и сверху
вниз для вычисления дескриптора. В окне справа показаны модули вычисленных
векторов градиента
10.1. Локализация, классификация и оценка ♦ 459
Алгоритм вычисления HoG-дескриптора. Мы вкратце опишем
один из возможных алгоритмов вычисления HoG-дескрипторов
выделенного ограничивающего прямоугольника.
1. Предобработка. Применить к данному окну изображения I
нормировку яркости (например, условное масштабирование,
описанное в разделе 2.1.1) и фильтр сглаживания.
2. Вычислить карту границ. Оценить производные по
направлениям а: и у и вычислить модули и углы градиентов в каждом пикселе,
построив карту модулей 1т (см. рис. 10.7 справа) и карту углов 1а.
3. Распределение по пространственным интервалам. Выполнить
следующие два шага:
a) нанести на окно изображения сетку из непересекающихся
ячеек (например, размера 8x8), см. рис. 10.7 слева;
b) с помощью карт 1т и 1а распределить значения модулей по
интервалам направления (например, 9 интервалов шириной 20°,
покрывающих весь диапазон 180°). В результате получаются
векторы голосования (например, длины 9) для каждой ячейки,
см. рис. 10.8. Для эффективного вычисления сумм можно
воспользоваться интегральными изображениями.
шщтщ. .1 i i
Щ^:
■ ■*« ЗУмц
_—^_
|Айн
_
.% • AJJ
• *+ +Tlt ¥
****FT Г
.4 J.
%*
-4 i
—
5k
*
I
*
1^1
■ь —4=
*tj
# * * $
3HF
i *H
U-
1
*1
-.
;
1
\
!•
HI-—-
kg
■#"4*h
fr * *
S* % +
|* Г* ■ *
■ ***!
TiT ^
1 U%
» <
11
«Jfc"#
!!
4 1 j 1
+ 11 1
# *
* if 1
< i
t \
Рис. 10.8. Длины векторов в девяти направлениях в каждой клетке представляют
обобщенные модули векторов градиента в каждом из этих направлений
4. Нормировать векторы голосования для построения дескриптора.
Выполнить два шага:
a) сгруппировать ячейки в один блок (например, размера 2x2);
b) нормировать векторы голосования в каждом блоке и
объединить их в один блочный вектор (т. е. векторы четырех ячеек
объединяются в блочный вектор длины 36).
460 ♦ Глава 10. Обнаружение объектов
5. Конкатенировать все блочные векторы для получения
окончательного HoG-дескриптора. Например, если блок состоит из
четырех ячеек, а размер ограничивающего прямоугольника равен
64x128, то в HoG-дескрипторе будет 3780 элементов; этот де-
скрипторный вектор удобно представить в виде дескрипторной
матрицы В (например, размера 420х9).
Ограничивающие прямоугольники можно использовать для обучения
классификатора или применения его в задаче обнаружения пешеходов.
Обычно для классификации используются прямоугольники
одинакового размера (например, 64x192, обе стороны кратны 32 - просто чтобы
вы понимали порядок чисел). Для построения HoG-дескрипторов
можно брать блоки разного размера (например, 8х8,16х 16 или 32х32).
Врезка 10.1 (история HoG-дескрипторов). Гистограммы ориентированных
градиентов были предложены в работе [N. Dalai and В. Triggs. Histograms of oriented
gradients for human detection. In Proc. Computer Vision Pattern Recognition, 2005,
p. 886-893] для обнаружения пешеходов в статических изображениях.
10.1.4. Вей влеты и признаки Хаара
Мы опишем общий подход к обнаружению объектов, в котором для
повышения эффективности используются интегральные изображения
(см. раздел 2.2.1).
Вейвлеты Хаара. Рассмотрим простые бинарные паттерны,
показанные на рис. 10.9 слева и в середине. Они называются вейвлетами
Хаара (об истории, связанной с этим именем, см. врезку 10.2). Белому
пикселю в таком вейвлете соответствует вес +1, а черному - вес -1.
Вейвлеты применяются для установления «приблизительного сходства
яркости» участка изображения с таким паттерном.
На рис. 10.9 справа показано, как располагаются в изображении
отдельные вейвлеты Хаара. Рассмотрим, к примеру, вейвлет яр = [Wv W2, В]
с двумя белыми участками ^и^2и одним черным участком В.
Предположим, что у каждого вейвлета Хаара есть начальная точка, скажем,
левый нижний угол. Параллельно перенесем вейвлет в изображение /
и совместим его начальную точку с позицией пикселя р. При этом мы
определили положение вейвлета гр (мы считаем изображение /
фиксированным и не включаем его в обозначение вейвлета): W1 занимает
прямоугольный участок Wx(p) <= П, W2 - участок W2(p) с /2, а В -
участок В(р) с П. Обозначим
10.1. Локализация, классификация и оценка ♦ 461
sw= £/(р) (10-7)
peW
сумму значений всех пикселей в множестве Wc /3.
Рис. 10.9. Слева: одномерный профиль вейвлета Хаара, сам вейвлет показан
справа от профиля, б середине: несколько примеров осепараллельных
вейвлетов Хаара. Справа: места на лицах людей, где показанные
вейвлеты Хаара «приблизительно» совпадают с распределением яркости;
«черный» соответствует более темным участкам, а «белый» - более светлым.
Исходное изображение AnnieYukiTim см. на рис. 5.2
Значение вейвлета Хаара. гр в начальном пикселе р можно
определить как сумму
Шр) = SWi + Бщ - SB. (10.8)
На рис. 10.9 справа показано, что яркость изображения в области лба,
глаз и под глазами на левом лице соответствует (немного повернутому)
паттерну. Также показаны распределения яркости в области глаз,
поперек носа и в уголке рта (среднее лицо) и паттерны яркости обоих глаз
на правом лице. Во всех случаях черные участки вейвлетов Хаара
находятся поверх более темных участков изображения, а белые участки -
поверх более ярких участков изображения. Поэтому в формуле (10.8)
мы прибавляем большие значения (близкие к Gmax) в членах S и SW2,
а вычитаем только малые значения (близкие к 0) в члене SB.
Размер белых и черных участков в вейвлете Хаара гр также следует
принимать во внимание для уравновешивания значений у\\р )
(например, возможное влияние значений в двух больших белых участках или в
одном маленьком черном участке одного вейвлета следует
«справедливо» распределить, увеличив вес маленького черного участка). Таким
образом, было бы уместно применить к этим значениям веса сог. > 0. Вместо
суммы (10.8) мы будем использовать взвешенные суммы вида
ПФР) = (о, • SWi + <о2 • SW2 - о)ъ • SB. (10.9)
Веса а), необходимо задавать при определении вейвлета Хаара.
462 ♦ Глава 10. Обнаружение объектов
Врезка 10.2 (Хаар,Адамар, Радемахер,Уолш и история метода
Виолы-Джонса). Венгерский математик А. Хаар (1885-1933) ввел в работе [A Hoax. Zur
Theorie der orthogonalen Funktionensysteme, Mathematische AnnaLen, 69:331-371,
1910] очень простое вейвлет-преобразование. Его простота объясняется
использованными базисными функциями. Как и двумерное преобразование
Фурье, двумерное преобразование Хаара вычисляет представление
заданной матрицы (в контексте изображений) в базисе, состоящем из двумерных
функций, которые являются волновыми формами с различной длиной волны
и направлением. Преобразование Хаара «остается в вещественной области»,
т. е. в нем не используются и не порождаются комплексные числа.
В случае двумерных дискретных данных мы можем применить дискретное
преобразование Хаара, в котором базисные функции описываются рекурсивно
определенными матрицами, содержащими лишь несколько различных
значений, например: 0,1, -1, V2 или 2. Поскольку значения изображения
целочисленные, дискретное преобразование Хаара можно даже реализовать, применяя
только целочисленную арифметику. Если преобразуются изображения размера
А/хД/, где N- 2", двумерные волновые формы являются матрицами А/*А/.
Преобразование Адамара-Радемахера-Уолша также отличается простотой
в силе используемых базисных функций. Оно названо в честь французского
математика Ж. Адамара (1865-1963), немецкого математика Г. Радемахера
(1892-1969) и американского математика Дж. Л.Уолша (1895-1973).
Для вывода вейвлетов Хаара двумерные волновые формы, используемые в
дискретном преобразовании Хаара или преобразовании
Адамара-Радемахера-Уолша, упрощаются: допускаются только значения «+1»
(представленное «белым» цветом) и «-1» (представленное «черным» цветом). Вейвлеты
Хаара можно рассматривать как прямоугольные подокна общих волновых
форм Хаара или Адамара-Радемахера-Уолша.
Применение вейвлетов Хаара к обнаружению объектов было предложено в
работе [P. Viola and MJones. Rapid object detection using a boosted cascade of simple
features. In Proc. Conf. Computer Vision Pattern Recognition, 2001, 8 p.], вместе с
полным описанием метода обнаружения объектов. Эта работа стала ориентиром
для современных точных и эффективных алгоритмов обнаружения лиц.
Вычисление значений с помощью интегральных изображений.
В разделе 2.2.1 мы говорили, что сумму Sw можно эффективно
вычислить, построив предварительно интегральное изображение Iint для
заданного изображения I (см. (2.12)). В формуле (2.13) используются
только суммы по осепараллельным прямоугольным областям.
Эту идею можно обобщить на повернутые прямоугольные области.
Для некоторых углов поворота ср относительно оси х можно построить
повернутые интегральные изображения. Например, для ср = л/А
интегральное изображение I вычисляется по формуле
10.1. Локализация, классификация и оценка ♦ 465
\x-i\<y-JA\<j<y
(10.10)
Здесь (х, у) может быть любой точкой в осепараллельном
прямоугольнике с углами (1, 1) и (Ncols, Nrows), и (/, /) - позиция пикселя в носителе
изображения П. См. рис. 10.10 слева.
N.
1
У
г
rows
1
1
о
о
о
о
о
о
о
о
!ГГ
О4
о
о
о
о
о
о
о
\°
№
о
о
о
о
о
\°
б4
о
о
о
о
о
о
\°
д4
о
о
о
о
о
\°
X
#
о
о
о
о
о
^cols .
гш
о о
о о
о о
о/6
о д\о/6 о
ШУЯ
о о о о о
о
о
о
о
о
о
о о
о о
о о
о/6
/О О
о о
о о
о о
о о
О О i
к
1
1
1
о
о
о
о
о
о
о
о
о
о
1
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
ояа
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
^cols ^
о о
о о
о о
о о
Vo
щ
о о
о о
о о
о о
Рис. 10.10. Слева: соответствующая точке (х, у) область, по которой
вычисляется сумма значений изображения для / . Справа: прямоугольная
область, определенная четырьмя углами, из которых р и q - задающие узлы
сетки, а углы г и s однозначно определяются по ним, если прямоугольник
наклонен под углом ц> = л/4
Если угол не равен 0 или я/4, то формула не так проста, но идея
остается неизменной. Для прямоугольной области W, повернутой на угол ср
относительно оси х и однозначно определенной позициями
угловых пикселей р и q и вычисленными по ним позициями двух других
углов г и s (см. рис. 10.10), имеем
Sw = I9(P)-I9(r)-I9(s) + I9(q). (10.11)
Для вычисления любого интегрального изображения / размера
N XN , требуется время 0(N N ,). Обычно достаточно выбрать всего
rows cols tr J r v rows cols' " r
несколько углов ф.
Признаки Хаара. Значение позиционированного вейвлета Хаара
гр теперь можно использовать, чтобы понять, имеется ли в пикселе р
изображения / признак Хаара. Для этого нам понадобится индикатор
р G {-1,+1} и порог 0:
(+1, еслиТ(Ф)<р-в
П%) = \ Р • (10.12)
( -1, в противном случае
464 ♦ Глава 10. Обнаружение объектов
Если Т{\р ) = 1, то в точке р обнаружен признак Хаара. Если
предполагается, что черные участки вейвлета Хаара соответствуют темным
пикселям (а белые, стало быть, ярким пикселям), то берется индикатор р = -1.
10.1.5. Метод Виолы-Джонса
Маской называется окно, содержащее небольшое число вейвлетов
Хаара, скажем, два или три. На рис. 10.11 показано размещение трех
разных (в данном случае неквадратных) масок одного размера в одном
месте изображения.
Рис. 10.11. Три неквадратные маски одинакового размера размещены в одном
месте изображения, каждая маска содержит два или три вейвлета Хаара.
Дескриптор Хаара, вычисленный для одной маски, дает слабый классификатор;
набор таких масок (т. е. набор слабых классификаторов) используется для того,
чтобы решить, присутствует ли лицо в окне, занимаемом масками.
Деталь изображения Michoacan; изображение целиком см. на рис. 10.12
Дескрипторы Хаара. Рассмотрим маску М= [\pv ip2, i/>3], содержащую
три вейвлета Хаара. Допустим, что начальная точка этой маски
расположена в левом нижнем углу. Поместим маску в изображение /,
совместив начальную точку с пикселем р, и для простоты будем считать, что
р также является начальной точкой всех трех вейвлетов Хаара. Таким
образом, мы определили дескриптор Хаара
Ъ{Мр) = TOP J + Т0Р2р) + Т(грър) (10.13)
- целое число (т. е. одномерный дескриптор).
Слабый классификатор. Наконец, порог т > 0 используется для
сопоставления изображению бинарного значения
+1, если2)(М)>т
Р . (10.14)
-1, в противном случае
h(M) =
10.1. Локализация, классификация и оценка ♦ 465
Так, на рис. 10.11 показан случай, когда три разные маски Мх ,М2 и
М3 (одного размера) с одним и тем же начальным пикселем р
определяют три слабых классификатора ЫМ. ,), h(M„ ,) и h(Mz ,) для одного и
того же окна W:
hrh(Mjp),j=l,2,3. (10.15)
Для получения окончательного решения о существовании объекта
необходимо объединить эти три слабых классификатора в один
сильный.
Скользящие маски. Цель скользящего поиска - найти в скользящем
окне объект, который определит размер применяемых масок. В нашем
распоряжении два варианта:
1) сначала построить пирамиду изображений (см. раздел 2.2.2), а
затем перемещать по разным уровням пирамиды маски одного
размера;
2) работать с одним лишь входным изображением, но применять
скользящие маски разного размера.
Для разнообразия выберем второй вариант. Будем использовать
маски разного размера для обнаружения крупных и мелких объектов. См.
рис. 10.12. Как правило, у нас имеется оценка размера самого большого
и самого маленького объекта из числа представляющих интерес.
Сначала для одного размера окна определяется набор масок. Для
каждого размера окна мы обходим изображение целиком, сверху вниз
и слева направо, вычисляем дескрипторы Хаара для каждого
местоположения маски, получая тем самым слабый классификатор, затем
объединяем слабые классификаторы в один сильный, который и сообщает,
обнаружен объект или нет. Затем мы применяем те же маски в
следующей позиции окна. Добравшись до правого нижнего угла изображения,
мы изменяем размер окна поиска (и соответственно масштаб масок)
и начинаем заново с левого верхнего угла. Так продолжается, пока не
будут рассмотрены все релевантные размеры окон.
На рис. 10.13 показано, как увеличивается размер прямоугольного
скользящего окна, если выбран коэффициент Az =1,1.
Чтобы алгоритм работал эффективно, высота и ширина
скользящего окна на каждой итерации должны увеличиться по меньшей мере на
10%. При большом коэффициенте увеличения падает точность
обнаружения, поэтому следует искать компромисс.
Порядки обхода. Задача скользящего поиска - обнаружить все
видимые объекты. Один из вариантов - исчерпывающий поиск (начина-
466 ♦ Глава 10. Обнаружение объектов
ющийся, как описано выше, в левом верхнем углу и заканчивающийся в
правом нижнем) с коэффициентом масштабирования Az в
направлениях а: и у. При этом размер масок, содержащих вейвлеты Хаара,
изменяется от заранее заданного минимума до заранее заданного максимума.
Рис. 10.12. Лица разного размера в изображении Michoacan. Детектор лиц
обнаруживает более крупные лица с помощью масок большего размера
(два лица справа), а более мелкие - с помощью тех же самых масок, но меньшего
размера. Имеется два ложноотрицательных результата - похоже, использованный
сильный классификатор был обучен на изображениях, где «лоб виден»
Рис. 10.13. Увеличение размера прямоугольного окна в bz = 1,1 раза по обоим
направлениям (обычно маски квадратные, а не вытянутые)
Метод обнаружения объектов Виолы-Джонса. Этот
предложенный в 2001 г. метод (см. врезку 10.2) был рассчитан прежде всего на
обнаружение лиц, но он применим и к другим классам объектов, для
которых характерно наличие «типичных закономерностей распределения
теней». Метод состоит из следующих этапов:
10.2.AdaBoost ♦ 467
1) построение w слабых классификаторов h., 1 < ; < w, каждый из
которых определен одной из w масок; каждая маска содержит к.
(обычно от 2 до 4) вейвлетов Хаара. Маски перемещаются по
входному изображению, а их размеры систематически
изменяются;
2) использование алгоритма статистического усиления для
объединения w слабых классификаторов hi,..., hw в один сильный
классификатор Я (это тема следующего раздела);
3) применение каскада слабых классификаторов для обнаружения
объектов.
У этого процесса есть несколько параметров.
Во-первых, на «микроуровне», для каждого вейвлета Хаара, осепа-
раллельного или повернутого на некоторый угол (р, определены веса
o)i > 0, корректирующие влияние черных и белых прямоугольников;
индикатор р G {-1,+1}, определяющий соответствие между парами
«черный-белый» и «темный-светлый» или «светлый-темный», и порог
в > 0, который задает чувствительность вейвлета Хаара к обнаружению
признака Хаара.
Во-вторых, на «макроуровне» для каждой маски М., 1 ^ / < w, задается
порог т., который определяет, когда дескриптор Хаара Ъ{М. )
свидетельствует о том, что h. = +1; в этом случае слабый классификатор h.
указывает, что в этом месте может быть объект (например, лицо).
Обнаружение лиц и постобработка, w результатов слабых
классификаторов hi, ..., hw для размещенного окна передаются обученному
сильному классификатору с целью обнаружения лица или его
отсутствия. Если лицо обнаружено, то мы находим его позицию в текущем
прямоугольном окне.
После классификации обычно остается несколько пересекающихся
окон разных размеров, расположенных вокруг видимого объекта.
Постобработка призвана вернуть единственное положение объекта. Для
постобработки обычно применяются разного рода эвристики (например,
берется какое-то среднее по всем обнаруженным прямоугольникам).
На рис. 10.14 показан пример финального шага постобработки.
10.2.AdaBoost
AdaBoost - адаптивный метаалгоритм машинного обучения. Его
название - сокращение от adaptive boosting (адаптивное усиление). Слово
метаалгоритм означает, что в нем участвуют подпроцедуры, называе-
468 ♦ Глава 10. Обнаружение объектов
мые слабыми классификаторами, которые можно задавать по-разному
(в предыдущем разделе мы строили бинарные классификаторы из
слабых). В начале работы AdaBoost имеется w > 1 слабых классификаторов,
описываемых функциями h. (см., например, определение
гиперплоскости (10.1)), которые отображают пространство дескрипторов Еи в {-1,+1}.
AdaBoost является адаптивным, потому что он итеративно уменьшает
частоту неправильных классификаций: веса ошибающихся
дескрипторов корректируются, с тем чтобы в конечном итоге построить
наилучшую взвешенную комбинацию исходных w слабых классификаторов.
Врезка 10.3 (история AdaBoost). Работа [Y. Freud and R.Schapire. A decision-theoretic
generalization of on-line Learning and an application to boosting. J. Computer System
Sciences, vol. 55,1995, p. 119-139] положила начало многочисленным
исследованиям по алгоритмам типа AdaBoost. В настоящее время существует много
вариантов, мы в этой главе обсудим только базовую стратегию AdaBoost.
Рис. 10.14. Слева: несколько окон, в которых обнаружен объект.
Справа: результат после финальной постобработки нескольких окон
10.2.1. Алгоритм
Рассматривается обучение с учителем. Имеется множество т > 1
заранее классифицированных дескрипторов xv..., хт в Ш", которым
сопоставлены значения у. е {-1,+1}, i = 1,..., т.
Например, чтобы использовать AdaBoost для обучения сильного
классификатора, умеющего обнаруживать лица, мы возьмем большой
набор данных, содержащий изображения с лицами и без них. Предполо-
10.2.AdaBoost ♦ 469
жим, что в окне изображения, в котором присутствует лицо, проведено
п > 0 измерений, например вычислены значения у{$ ) для множества
размещенных вейвлетов Хаара \р . Эти п значений определяют точку
в Е". Присутствующее лицо можно «вручную» классифицировать как
«смотрящее вперед» (+1) или «не смотрящее вперед» (-1), если
требуется не просто обнаружить объект, а сделать что-то более специфическое.
Пример 10.3 (пять дескрипторов и два слабых классификатора). Рассмотрим
пять дескрипторов хр ..., х5 в двумерном пространстве (см. рис. 10.15). Здесь
т = 5. Каждая точка показана кругом с весом 1/5, одинаковым для всех пяти
точек. В начале работы AdaBoost всем дескрипторам xz. назначаются одинаковые
веса o)(i) = l/m, i = 1,..., т.
Рис. 10.15. Пять примеров дескрипторов
в двумерном пространстве дескрипторов
Соответствующие этим дескрипторам образцы (т. е. изображения, на
которых присутствует лицо) были классифицированы. Жирная синяя окружность
означает, что образцу сопоставлен класс +1, а тонкая красная - что сопоставлен
класс -1.
Мы рассматриваем два слабых классификатора (т. е. w = 2), обозначенных
hx и hr Классификатор hx сопоставляет класс +1 любому из пяти дескрипторов,
а классификатор h2 - только дескрипторам хг и х5, а остальным сопоставляет
класс -1. Положим:
т
и^Х^о-Цу,.*^.)], (10.16)
где рЦ равно 1, если Ж истинно, и 0 в противном случае.
В соответствии с определением Wx = 0,4 и W2 = 0,2. Классификатор h2 лучше
согласован с данной классификацией и W2 < 0,5. В итоге мы отдаем h2 контроль
над модификацией весов данных. Вес a)(i) можно интерпретировать как
стоимость неправильной классификации наблюдения. Таким образом, W. -
средняя стоимость неправильной классификации для классификатора /?.,
поскольку сумма всех весов равна 1. Мы продолжим рассмотрение в примере 10.4.
470 ♦ Глава 10. Обнаружение объектов
Итерации в AdaBoost. Вычисления в примере 10.3 - это только
начало итеративной процедуры. Веса <o(i) модифицируются на
итерациях / = 1,..., т. В результате получаются новые суммарные веса W. для
/ = 1,..., w. Зная веса W.t мы снова ищем классификатор hp для которого
достигается минимум. Если минимум больше или равен 0,5, то мы
останавливаемся.
Номер итерации. Итерации нумеруются от£=1доГ=Ги
продолжаются до тех пор, пока минимум суммарных весов не станет больше или
равен 0,5.
Инициализация итерации. Выбираем начальные веса co^i) = o)(i) = \/m
для i= \,...,m.
Шаг итерации. Для t > 1 вычисляем суммарные веса W. для; = 1,..., w:
т
WrJJcot(i)-{yi*hj(x)l (10.17)
где обозначение J...J объяснено в примере 10.3. Положим a(t) = arg min
{Wv..., Ww} (в примере 10.3 имеем я(1) = 2). Производим обновление
(oM(i) = ct(i) • u>t(0, (10.18)
где ct(i), i=l,...,m, выбраны так, что X м^СО = 1-
Конец итерации. Когда окажется, что W > 0,5, результатом
окончательного классификатора будет
H(x) = signftat-/ifl(0(x)J. (10.19)
Это и есть сильный классификатор, построенный AdaBoost. Он может
содержать один и тот же слабый классификатор в различных позициях t
с разными весами at.
10.2.2. Параметры
В предыдущем подразделе мы описали метаалгоритм AdaBoost, для
которого слабые классификаторы являются свободными
переменными. Но нужно еще объяснить, что означают параметры at и ct(i), где
t= 1,..., Ги /= 1,..., т.
Параметры at и ct(i). На t-й итерации W - это минимальный
суммарный вес; h - классификатор с наименьшей средней стоимостью
или ошибкой для данного образца из т заранее классифицированных.
10.2.AdaBoost ♦ 471
Таким образом, мы разрешаем h внести вклад в решение при условии,
что W < 0,5, т. е. классификатор лучше, чем случайная догадка.
Выбранному на t-й итерации слабому классификатору разрешено
внести в общее решение вклад at • h . При t = 1 мы выбираем самого
сильного сторонника правильной классификации. Следовательно, ах
должен быть большим. На всех последующих итерациях t = 2, 3,... мы
также выбираем сильнейшего сторонника правильной классификации
для модифицированного набора весов, наша цель при этом - улучшить
определение окончательного классификатора Н.
Величина at - это качество классификатора h (или доверие к нему).
Значения at имеют тенденцию уменьшаться с ростом t (с
вероятностью 1), но в общем случае их последовательность не является
убывающей, поскольку мы на каждом шаге изменяем веса, а стало быть, и
задачу. Но ничего плохого в том, что ctt не убывают монотонно, нет.
Параметр at используется на t-й итерации для определения
масштабных коэффициентов ct(i); они зависят от at.
Эти параметры необходимо выбирать таким образом, чтобы
гарантировать прекращение итераций, и так, чтобы они повышали качество
окончательного классификатора Н.
Типичные параметры AdaBoost. a(t) дает нам «победителя» на t-й
итерации, имеющего минимальный суммарный вес W . Обычно
параметры at выбираются следующим образом (ниже мы объясним,
почему):
^ = 2 g
где логарифм берется по основанию е = ехр(1), в технической литературе
часто встречается обозначение In = loge. Параметр at определяет
влияние h на окончательный классификатор.
Например, если имеет место «полная согласованность» между заранее
заданными классами у(. и результатами h М) (т. е. у. = h (i) для всех
/ = 1,..., т), как может случиться при t = 1, то мы можем использовать
уже h в качестве окончательного классификатора, и никакой
дополнительной обработки не нужно (т. е. AdaBoost останавливается).
В противном случае, если 0 < W < 0,5, at > 0 увеличивается при
уменьшении W .
Значения ct(i) обычно выбираются следующим образом:
ct(i) = \/st • ехр(-ед/2 (Х/)), (10.21)
1 YYa(t)
(10.20)
472 ♦ Глава 10. Обнаружение объектов
st = Iexp(-aty./2a(f)(x.)) • o)f(/), (10.22)
и таким образом Ц ^6)^(0 = 1, если cot+1(i) = ct(i) • a)t(i) для i = 1,..., т.
Это простые формулы. Формулы для вычисления ct(i) и st в
действительности очень просты. Заметим, что y;./i (х.) равно +1 или -1.
Оба значения у. и h (х) принадлежат множеству {-1,+1}. Их
произведение равно +1 тогда и только тогда, когда у. = h (х), и -1 в противном
случае. Таким образом, имеем
ф = Щ • (е-<% = hjp)] + е<% * fta(t)(X/)]) (10.23)
И
+ (Ё[у^^)(хЛ-^(0]А (10-24)
где
1) е~а* < 1 (т. е. вес уменьшается) для элементов данных, с которыми
«всё уже ясно»; и
2) еа* > 1 (т. е. вес увеличивается) для элементов данных, которые
«нуждаются в пристальном внимании на следующей итерации».
Пример 10.4 (продолжение примера 10.3). У нас имеются образцы xv ..., xs,
которым назначены классы у1 = +1,у2 = -1,у3 = -1,у4 = +1,у5 = +1. Классификатор
/it назначает класс +1 всем пяти дескрипторам, а классификатор h2 - только
дескрипторам Xj и х5, а остальным - класс -1.
При t =1 имеем ы^Г) = 1/т для i = 1,..., т, W1 = 0,4, W2 = 0,2 < 0,5, поэтому
я(1) = 2. Отсюда
1
f 1-0.2^
2
0.2
1
ai = т1о§е ^г^~ = T!oge 4 = loge 2 - 0.693 (10.25)
2
и
5
st=L= exp(-a1y!7i2(x.)) • -
«•=i 5
= _ (e~al + e~al + e~al + eal + e~al)
5
* - (0.500 + 0.500 + 0.500 +2.000 + 0.500) * 0.800. (10.26)
10.2.AdaBoost ♦ 473
При этом получается: cx(l) = 5/8, с,(2) = 5/8, сх(3) = 5/8, сх(4) = 5/2, сх(5) = 5/8 и,
следовательно, о>2(1) = ОД 25, ш2(2) = ОД 25, о>2(3) = 0,125, а>2(4) = 0,5, <о2(5) = 0,125.
Сумма весов равна 1, как и должно быть.
Теперь можно перейти к итерации t = 2. Классификатор h1 по-прежнему
продолжает ошибаться для i = 2 и i = 3. Поэтому Wx = 0,25. Классификатор h2 неверен
для / = 4. Поэтому W2 = 0,5. Стало быть, теперь hx - победитель. Имеем а(2) = 1.
Поскольку Wl<0,5, мы продолжаем. Вычисления дают
1. Л-0.25 "\ 1
а2 = 21о8е
о.25 ; 2
= -loge 3-0.549 (10.27)
и
s2 = Z = ехр(-а2у./г2(х.)) • <u2(i)
= 0.125 (е_а2 + еа2 + еа2 + е~а2) + 0.5 • е~а2
* 0.125(0.578 + 1.731 + 1.731 + 0.578) + 0.5 • 0.578 * 0.866. (10.28)
При этом с2(1) * 0,667, с2(2) * 1,999, с2(3) * 1,999, с2(4) * 0,667, с2(5) * 0,667 и,
следовательно, й)3(1) * 0,083, ш3(2) * 0,250, <ы3(3) * 0,250, <и3(4) * 0,334, шъ(5) * 0,083.
Сумма этих приблизительных весов вновь равна 1.
Переходим к итерации t-Ъ. Для классификатора hx (который по-прежнему
ошибается для / = 2 и i = 3) имеем Wx ~ 0,5. Для классификатора h2 получаем W2 =
0,334. При t = 3 побеждает классификатор h2, следовательно, а(Ъ) = 2. Поскольку
W2 < 0,5, процесс продолжается, и мы получаем
1,
А-0.334^1
= -loge 1.994 «0.345. (10.29)
0.334
Продолжите вычисления самостоятельно.
п независимых слабых классификаторов. Рассмотрим
дескрипторы в R". Для каждого / = 1,..., п мы имеем слабый классификатор h.(x),
результат которого зависит только от х., где х = (xv..., х.,..., хп). (Здесь п =
w, где w раньше обозначало количество слабых классификаторов.)
Например, мы можем остановиться на простом пороговом решении:
если а:. > т.
' ' (10.30)
если а:. > т.
для п вещественных порогов тх,..., тл. Если п = 1, то мы просто разбиваем
все множество вещественных чисел на две половины, в одной из
которых «все» h. равны +1, а в другой «по крайней мере» один не равен +1.
Если п = 2, то геометрическое место точек, в которых оба
классификатора равны +1, - прямоугольник.
474
Глава 10. Обнаружение объектов
Каково геометрическое место точек трехмерного пространства (при
п = 3), в которых все три слабых классификатора равны +1?
Например, каждый из этих п классификаторов может быть определен
с помощью одного скалярного измерения в цифровом изображении. То
есть у нас имеются различные функционалы Ф., каждый из которых
ставит в соответствие изображениям вещественные числа, т. е. Ф.(7) £ R.
Для п таких функционалов пространство дескрипторов состоит из
кортежей длины п (Ф^Г), Ф2(0, •••■> Фп(1))- Обнаружение лиц - пример
приложения, в котором применяется такой подход.
10.2.3. Почему именно такие параметры?
Почему at выбираются именно таким образом? Этот раздел
адресован любителям математики.
Наша цель - минимизировать количество случаев, когда Я(х.) ф у. для
i = 1,..., т. Рассмотрим последовательность обновлений весов k>t(z),
начиная с £ = 1. Имеем:
(o^i) = 1/т,
б)2(0 = Cj(D ' ^(0 = cx{i)/m,
шъ(1) = c2(i) • o)2(i) = [сгф • с2(0//л],
(10.31)
(10.32)
(10.33)
coT+l(i) =
Гксо
t=\
т
п
1т
ехр
-yi'Y,atKtMi)
t=\
t=\
(10.34)
Положим /(х.) = £[=1at/?a(t)(x.). Тогда
0)Т+Х (/) = — • ехр {-yt ■ f(xt)).
m-11 st
(10.35)
Если Н(х) = sign(/"(x(.)) ф у., то у. • f(x) < 0. Таким образом, ехр(-у. • f(x)) > 1:
1) если [Я(х.) ф у] = 1, то ехр(-у. • f(x)) > 1;
2) если [Я(х.) Ф у.] = 0, то 0 < ехр(-у. • /(х.)).
В обоих случаях [Я(х.) ф у.] < ехр(-у;. • /"(х(.)). Взяв среднее по всем х. для
i = 1,..., m, получаем:
10.2.AdaBoost ♦ 475
л т л т
-1Их,)^^,]<-Хехр(-7,-Лхг.))
ехр(-^,-Дх.))
1=1
m
m f
m
т \
^r+i(oTl^
1=1 V t=\ J
f m \ Т
[см. (10.35)]
T
J t=\
=1'1Ь=1Ъ-
(10.36)
t=\
t=\
Наблюдение 10.2. Этот результат означает, что среднее число
неправильных классификаций ограничено сверху произведением масштабных
коэффициентов, и, следовательно, ошибка сильного классификатора непосредственно
связана с ошибками слабых классификаторов, из которых он построен.
Таким образом, мы можем сократить количество неправильных
классификаций, уменьшив это произведение. Один из способов -
попытаться минимизировать каждый масштабный коэффициент st, t = 1,..., Г,
поодиночке.
Последний шаг минимизации СКО. Вспомним выражение (10.22)
для st. Приравняем его первую производную по at к нулю и решим
получившееся уравнение относительно at - это и будет точка экстремума.
В данном конкретном случае имеет место однозначно определенный
минимум:
ds
da,
'- = -1уА«}(х) • ехР(-«дЛ(Е)(х,)) • *>,(0
=- L e~af(ot(i)+ L eafcot(i)
yi=ba(t)(*i) yi*ha(t)(*i)
=-e_at- X cot(i) + eaf £ wf(0
=-e-a<l - W J + eatW,ft
v a(ty a(t)
= 0.
[в силу (10.16)]
(10.37)
476 ♦ Глава 10. Обнаружение объектов
Отсюда следует, что
(1-W }
е2а<= a{t)\ (10.38)
W
a=-log^~Wait)\ (10.39)
2 W
Этим и объясняется выбор параметра обновления в AdaBoost.
и, значит,
10.3. Случайные решающие леса
В примере 10.2 были введены решающие деревья как еще один
способ разбиения пространства дескрипторов, альтернативный бинарным
классификаторам. Конечное множество случайно построенных
решающих деревьев образует лес, который называется случайным решающим
лесом (СРЛ). В этом разделе описывается два способа использования
таких лесов для обнаружения объектов. Общий подход иллюстрируется
примерами на тему обнаружения пешеходов.
10.3.1. Энтропия и информационный выигрыш
При построении деревьев мы будем использовать аппарат теории
информации, чтобы оптимизировать распределение входных данных
по путям в построенных деревьях.
Энтропия. Рассмотрим конечный алфавит S = {av..., ат} с заданным
распределением вероятностей символов р = Р(Х = а), / = 1, ..., т, где
X - случайная величина, принимающая значения из S. Нас интересует
нижняя граница среднего числа бит, необходимых для представления
символов из 5, относительно моделируемого случайного процесса.
Энтропия
т
H(S) = -Xp/'log2Py (10.40)
как раз и определяет такую нижнюю границу; если т - степень 2, то эта
величина в точности равна среднему числу бит.
Для данного множества S максимум энтропии достигается, если
распределение равномерно (т. е. р. = \/т цпя.} = 1,..., т), так что
H(S) = log2m - log21 = log2m. (10.41)
10.5. Случайные решающие леса ♦ 477
Врезка 10.4 (Шеннон и энтропия). К. Э. Шеннон (1916-2001), американский
инженер, математик и криптоаналитик, который в 1937 г. заложил основы
теории информации в своей магистерской диссертации «Символический
анализ релейных и переключательных схем» (МТИ). Фактически эта работа
никогда не публиковалась, но считается, что из всех магистерских
диссертаций эта оказала наибольшее влияние на развитие науки. Заложенные в ней
идеи получили развитие в знаменитой статье [С. E.Shannon A mathematical theory
of communication. The Bell System Technical Journal, vol. 27,1948, p. 623-656],
центральными темами которой являются энтропия и условная энтропия. В этом
разделе то и другое используется в очень специфичном контексте.
Если распределение вероятностей неравномерно, это энтропия
уменьшается.
Пример10.5 (вычисление энтропии). Пусть X - случайная величина,
принимающая каждое из значений А, В, С, D, Е с одинаковой вероятностью 1/5.
Алфавитом является множество S = [А, В, С, D, Е}. В силу (10.41) в этом случае
H(S) = log2 5 * 2.32, и в коде Хаффмана (см. упражнение 10.8) для этого примера
на один символ в среднем приходится 2,4 бита.
Теперь рассмотрим тот же алфавит 5 = {А, В, С, Д £}, но с вероятностями
Р(Х = А) = 1/2, Р(Х = В) = 1/4, Р(Х = Q = 1/8, Р(Х = D) = 1/16 и Р(Х = £) = 1/16. Имеем
Я(5) = -0,5(-1) - 0,25(-2) - 0,125(-3) - 2 • 0,0625(-4) = 1,875. (10.42)
При таком распределении вероятностей в коде Хаффмана на каждый
символ приходится в среднем 1,875 бита.
Наблюдение 10.3. Максимум энтропии достигается, когда все события
происходят с одинаковой частотой.
Разделив энтропию H(S), определенную некоторым распределением
вероятностей на S, на максимальную энтропию из формулы (10.41), мы
получим нормированную энтропию
H„m(S) = ^-- (10.43)
log2 m
Эта величина принадлежит интервалу (0,1], если \S\ = m.
Условная энтропия. Условной энтропией H(Y\X) называется нижняя
граница ожидаемого числа бит, необходимых для передачи У, если
значение X (предусловие) известно. Иными словами, Y - дополнительная
информация, которую нужно передать в предположении, что Хуже
известно.
478 ♦ Глава 10. Обнаружение объектов
Заглавными буквами X и У обозначаются классы событий, а
строчными буквами а: и у - отдельные события, принадлежащие множествам S и
Т соответственно. Для дискретных случайных величин X и У обозначим
p(x,y) = P(X = x,Y=y), (10.44)
p(y\x) = P(X = x\Y=y) (10.45)
совместную и условную вероятность соответственно. Величина
H(Y\X) = -XX р(х, у) log2 p(y\x) (10.46)
xeS yeT
равна условной энтропии величины Y, принимающей значения из
множества Т, при условии величины X, принимающей значения из
множества S. Аналогично
H(X\Y) = -XX Р(*> У) 1о§2 Р(*1У) (10-47)
xeS yeT
- условная энтропия X при условии У3.
Пример 10.6 (иллюстрация условной энтропии). Рассмотрим гипотетический
пример: мы снимаем стереоскопическое видео из автомобиля, и существует
адаптивный процесс, который решает, какой алгоритм - iSGM или ВРМ -
использовать для сопоставления стереоизображений.
Имеется вход X (заданная вручную краткая характеристика дорожной
обстановки), и мы хотим предсказать событие У (отдать предпочтение iSGM или
нет).
Пусть S = {с, /2, г}, где с означает съемку в центральном деловом районе (ЦДР),
h - съемку на автомагистрали, а г - съемку на проселочной дороге.
Пусть Т = {у, п}, где у означает событие «использовать iSGM», an- событие
«использовать ВРМ».
Все наблюдаемые случаи сведены в табл. 10.1. Из нее мы знаем, что
Р(Х= г) = S/U,P(X= c) = 4/U,P(X=h) = 5/14, Р(У= у) = 9/14, Р(У= п) = 5/14 и
H(Y) = -(9/14) • log2(9/14) - (5/14) • log2(5/14) - 0,940. (10.48)
Эта энтропия H(Y) выражает тот факт, что для передачи информации
нужно как минимум 0,940 бит вне зависимости от того, каким
алгоритмом производится анализ: iSGM или ВРМ.
Мы хотим предсказать, какой алгоритм решит использовать система,
зная только приблизительную характеристику сцены. Например:
p(y\r)=P(Y=y\X= r) = 3/5, (10.49)
Энтропия Шеннона и энтропия, используемая в термодинамике, различаются знаком.
10.5. Случайные решающие леса ♦ 479
p(n\r)=P(Y= п\Х= г) = 2/5, (10.50)
Я(У|г) = -(3/5) • log2(3/5) - (2/5) • log2(2/5) - 0,971. (10.51)
Таким образом, условная энтропия для «проселочной дороги» равна
H(Y\X = г) = 0,971. Условная энтропия использования iSGM при условии
характеристики сцены X равна
H(Y=y\X) = 5/14 • 0.971 + 4/14 • 0 + 5/14 • 0.971 * 0.694 (10.52)
(см. упражнение 10.9). Зная характеристику сцены, мы можем
сэкономить приблизительно 0,940 - 0,694 = 0,246 бита на каждом сообщении
при передаче информации о том, что был использован iSGM.
Таблица 10.1. Таблица адаптивных решений об использовании алгоритма iSGM или
ВРМ для сопоставления стереоизображений в 14 записанных последовательностях.
Дорожная обстановка в каждой последовательности кратко охарактеризована
вручную, чтобы лучше понимать контекст адаптивного принятия решений
Последовательность
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Ситуация
Автомагистраль
Автомагистраль
ЦДР
Проселочная дорога
Проселочная дорога
Проселочная дорога
ЦДР
Автомагистраль
Автомагистраль
Проселочная дорога
Автомагистраль
ЦДР
ЦДР
Проселочная дорога
Решение, использовать ли iSGM
Нет
Нет
Да
Да
Да
Нет
Да
Нет
Да
Да
Да
Да
Да
Нет
Информационный выигрыш. Информационный выигрыш G(Y\X) =
H(Y) - H(Y\X) - это количество бит, сэкономленных в среднем благодаря
тому, что мы использовали условную энтропию вместо безусловной.
10.3.2. Применение леса
Предположим, что для решения задачи классификации мы обучили
случайный лес, состоящий из w деревьев Tv ..., Т . В заданном изобра-
480 ♦ Глава 10. Обнаружение объектов
жении мы выделили прямоугольное окно W (например,
ограничивающий прямоугольник или фрагмент) и хотим подать его на вход каждому
из w деревьев.
Передача окна лесу. Будем использовать окно W как входные
данные для дерева Т.. В каждом внутреннем узле дерева мы применяем
функцию разделения h (I) с параметрами <р, которая на основе
векторного дескриптора x(i) принимает решение «да» или «нет». В результате
окно Жпередаетсялевомуилиправомудочернемуузлу(см.рис. 10.16)4.
Изображение взято из базы данных TUD Multiview Pedestrians5.
Классификация окна одним деревом. Наконец, окно W достигает
листового узла L дерева Т.. В этом узле хранятся вероятности
принадлежности к различным классам. Например, мы назначаем окну W
вероятность p(d) = а принадлежности к классу d, 1 < d < к, если в листе L
хранится значение а для класса d.
Сильный классификатор, порожденный лесом. Окно W
достигает какого-то листового узла в каждом из w деревьев, образующих
случайный лес. И в каждом из этих узлов ему назначается вероятность ad
принадлежности к классу d. В итоге окну W сопоставлена сумма w
значений ad, по одному от каждого дерева.
Порожденный лесом сильный классификатор сравнивает суммы для
различных классов d = 1,...,к и сумму для класса 0 (отсутствие объекта)
и относит W к тому классу d или к классу 0, для которого сумма
максимальна.
Врезка 10.5 (Брейман и случайные решающие леса). На становление
случайных решающих лесов в качестве метода ансамблевого обучения решающее
влияние оказали работы американского статистика Л. Бреймана (1928-2005),
в частности статья [L Breiman. Random forests. Machine Learning, vol. 45, 2001,
p. 5-32]. Своими корнями эта техника уходит в методы построения деревьев и
связанные с ними классификаторы - область, в которую внесли вклад многие
исследователи, начиная с начала 1980-х гг.
Дерево рисуется корнем вверх (в соответствии с общепринятой традицией). Тем, кто считает,
что дерево с корнем наверху выглядит противоестественно, приведем в назидание два
примера. В большой пещере Рикорико на островах Пур-Найтс в Новой Зеландии деревья растут вниз
от корня, а на севере Новой Зеландии немало крупных деревьев похутукава укоренилось на
вершинах прибрежных скал, тогда как ствол с ветвями распростерся по скале ниже корня.
База данных TUD Multiview Pedestrians находится в свободном доступе по адресу www.d2.mpi-inf.
mpg.de/node/428.
10.5. Случайные решающие леса ♦ 481
Рис. 10.16. Выбранный ограничивающий прямоугольник передается вниз по
каждому дереву и достигает листа Ls в левом дереве и листа L7 в правом дереве.
Эти листовые узлы назначают ограничивающему прямоугольнику вероятности
принадлежности к классу d, равные а и b соответственно. Изображение внизу
относится к частному случаю леса Хафа: вероятности оказаться центральным
пикселем объекта можно визуализировать на носителе объекта уровнями яркости
10.3.3. Обучение леса
Для построения случайного решающего леса мы применим обучение
с учителем. Имеется набор S образцов, т. е. заранее
классифицированных изображений. Образец Р = [I, d\ или Р = [I, 0] представляет собой
комбинацию окна изображения / (например, ограничивающий
прямоугольник или фрагмент) и номера класса d, 1 < d < к, или значения 0,
означающего отсутствие объекта. В случае бинарной классификации
имеются только положительные и отрицательные ограничивающие
прямоугольники или фрагменты (т. е. пешеход есть или пешехода нет),
см. рис. 10.6.
482 ♦ Глава 10. Обнаружение объектов
Случай более двух классов. В общем случае классов больше двух; см.
раздел 10.1.1, где имеются классы 1, 2,..., к и значение 0 - «не
классифицирован». На рис. 10.17 показаны пешеходы в четырех ракурсах (т. е.
к = 4 и 0 - «нет пешехода»). Такие заранее классифицированные данные
имеются, например, в базе данных TUD Multiview Pedestrians; см. также
пример на рис. 10.16. Обозначим
S = S0Kj(jSd (10.53)
набор образцов, т. е. заранее классифицированных данных, где S0 -
содержит все образцы, не являющиеся объектами, a Sd - все образцы,
отнесенные к классу d, 1 ^ d < к. Для описываемого подхода на основе
случайных решающих лесов набор должен быть достаточно велик,
например \S\ = 50 000.
Рис. 10.17. Образцы ограничивающих прямоугольников с изображением
пешеходов (здесь они еще и отсортированы по направлению движения - С, В, Ю, 3)
Случайно обученные деревья. В процессе обучения с учителем мы
строим несколько решающих деревьев, образующих случайный лес.
Для каждого дерева необходимо определить правила разделения во
внутренних узлах. Наша цель - сформулировать правило так, чтобы в
результате разделения обучающего набора данных S информационный
выигрыш был максимален. Согласно наблюдению 10.3, нам хотелось
бы (игнорируя реальный условный контекст), чтобы на каждый из двух
10.3. Случайные решающие леса ♦ 485
возможных путей приходилась примерно половина входящих в узел
данных. Если это удается, то построенные деревья сбалансированы, т. е.
имеют минимальную глубину, и, стало быть, обеспечивается
эффективность процесса классификации.
Мы предполагаем, что случайный решающий лес состоит из w
случайно обученных решающих деревьев Т., 1 < / < w. Каждое дерево
считается слабым классификатором, а лес служит для определения сильного
классификатора. В качестве w имеет смысл выбирать число порядка 100.
Функции разделения. Правило, применяемое во внутреннем узле v,
называют также функцией разделения. Функция разделения с одним
аргументом h решает, какой узел - левый или правый - будет следующим:
SL(cp) = {lESv:h(p(I) = 0}, (10.54)
SR(<p) = {IeSv :/2ф(7) = 1}, (10.55)
где Sv - множество образцов, поступающих в узел v. (Точнее, образцом
является пара [/, d] или [/, 0], но мы упростили обозначения, оставив
только заранее классифицированное окно /.) Ниже приводятся
примеры функций разделения h и наборов параметров (р.
О выращивании деревьев. В процессе обучения случайно
выбранное подмножество
к
Sj = Sj,o^[JSj,^S (Ю.56)
всех заранее классифицированных образцов используется для
выращивания дерева Г., входящего в состав леса (1 ^ / < w). Каждое дерево растет
случайно и независимо от остальных. Случайность - важный элемент
обучения дерева. Она гарантирует разнообразие леса, т. е. уменьшение
взаимной корреляции деревьев. Было бы бессмысленно собирать лес из
«похожих» деревьев. В каждом S. должно быть где-то от 5000 до 10 000
образцов.
Идея процедуры выращивания дерева. Вначале имеется всего один
корневой узел, он же единственный активный. Далее мы рекурсивно для
каждого активного узла решаем, должен ли он стать узлом разделения
(внутренним) с соответствующей функцией разделения h или остаться
листовым (это определяется критерием остановки). Будучи обработан,
активный узел становится пассивным, а вновь созданные узлы
разделения - активными.
Идея процедуры определения листа. В созданном решающем дереве
образцы I E S. спустились по внутренним узлам к листовым. В общем
484
Глава 10. Обнаружение объектов
случае мы не просто сопоставляем один класс одному листовому узлу
(как было в упрощенном примере 10.2). Для приходящих в узел
образцов мы должны проанализировать распределение этих образцов по
классам.
В листовом узле L мы оцениваем вероятность классификации р(с =
0\Ь) (т. е. вероятность, что поступающим образцам сопоставлен номер
класса 0) и вероятности классов
р(с f 0, d\L) = [1 - р(с = OIL)] • p(d\L)
(10.57)
для d G {1,..., к}. Например, на рис. 10.17 образцы распределяются по
классам С, В, Ю, 3 (т. е. к = 4), кроме того, ограничивающий
прямоугольник может быть классифицирован как «нет пешехода» (значение 0).
Компенсация смещения образцов. В множестве S.cS будет иметь
место смещение, вызванное тем, что для построения разных
деревьев Г., 1 < j <w, выбирается разное количество случайных образцов.
Вероятности классификации р(с\Ь) и p(d\L) оцениваются на основе
количества образцов из множеств S.0 и S.rf, 1 < d < к, поступающих в узел L.
Обозначим
SL=SL u
j j,o
■IK
d=\
(10.58)
множество всех обучающих образцов, поступающих в узел L. Без
компенсации мы использовали бы значения
p(c = 0\L) =
jfi
(10.59)
P(d | L) =
j,d
U s
L
j,d
(10.60)
которые удовлетворяют условию р(с = 0\L) + £ J=1 p(c f 0, d\L) = 1.
Использование этих оценок вероятности подразумевает, что отношения
0,0 =
'у,о
Sj
и
rj,d ~
SU
(10.61)
где 1 < d<k, для случайно сгенерированного обучающего множества Sj
приблизительно совпадают с отношениями
10.3. Случайные решающие леса
485
го =
и г,
(10.62)
для всего обучающего множества S. Чтобы компенсировать ожидаемое
смещение, мы можем использовать в качестве оценок вероятностей
величины
p(c = 0\L) =
jfi
ГУ,0
(10.63)
p{d | L) =
j,d
M* sL
^Jd=\ j,d
'j,d
(10.64)
Например, если r.0 < r0, то коэффициент rJr.Q > 1 соответственно
увеличивает оценку вероятности.
Признаки и функции разделения. Определение функций
разделения в общем случае основано на признаках изображения (их позициях
и дескрипторах). Из соображений эффективности функции разделения
должны быть простыми, но при этом обеспечивать максимальный
информационный выигрыш.
Поскольку дочерних узлов два, функция разделения h должна
возвращать бинарный результат, например значение из множества {0, 1}.
Поэтому часто сравнивают значения признаков, которые легко
вычислить для любого входного изображения / (например, / может быть
представлено ограничивающим прямоугольником или фрагментом). Так,
очень простая функция определяется следующим образом:
K(D =
(10.65)
0, если IJp) - IJq) > т
^ 1, в противном случае
где 11ос(р) - значение заданного локального оператора в пикселе р
изображения /. Параметры ф = {р, q, т} представляют две разные позиции
пикселя и порог т > 0. Если параметров больше, то возрастает опасность
переобучения. Есть даже более простой вариант:
w{l
0, если 11ос(р) > т
в противном случае
(10.66)
486 ♦ Глава 10. Обнаружение объектов
Параметры, например ф = {р, q, т} или ф = {р, т}, обучаются, так чтобы
максимизировать информационный выигрыш. Могут существовать и
другие цели для обучения «хорошей» функции разделения.
Обучение узла разделения. Начиная с первого узла разделения
(корня), образцы распределяются между левым и правым дочерними узлами
в соответствии со значением функции разделения. Поскольку
предполагается, что функция разделения должна разделять различные классы,
необходимо обучить ее параметры ф на предъявляемых образцах.
Чтобы гарантировать разнообразие деревьев и эффективность
работы, параметры ф выбираются случайно. Например, если речь идет о
параметрах ритв формуле (10.66), то можно случайно выбрать
множество пикселей входного изображения J и интервал [rmin, rmax], скажем,
1000 пар [р, т]. После этого мы выбираем такую пару параметров [р, т],
которая максимизирует информационный выигрыш на множестве,
содержащем 1000 пар.
Прекращение выращивания. Если в текущем узле выполнен
критерий остановки, то этот узел больше не разделяется. Примерами
критериев могут служить глубина узла в дереве (т. е. максимальная глубина
ограничена) или тот факт, что количество образцов, достигших узла,
оказалось меньше пороговой величины. Слишком глубокие деревья
склонны к переобучению, а если в листовой узел попало всего
несколько образцов, то возможно смещение при классификации.
Алгоритм. Обучение случайного решающего леса осуществляет
алгоритм 10.1 (рис. 10.18). Этот алгоритм генерирует одно дерево леса.
Для генерации всего леса алгоритм нужно вызвать несколько раз.
Случайный выбор 5. и вектора параметров ф5 гарантирует независимость
деревьев. Определение функции разделения h фиксировано, т. е. не
меняется в процессе работы алгоритма.
10.3.4. Леса Хафа
Вместо крупных ограничивающих прямоугольников мы можем
предпочесть небольшие прямоугольные фрагменты (patch) внутри
ограничивающего прямоугольника. Тогда и на стадии применения
классификатора можно будет использовать только «небольшие» фрагменты.
Положительные фрагменты должны «как-то сотрудничать» в деле
обнаружения объекта. Леса Хафа не укладываются в общую схему из трех
последовательных шагов: локализация, классификация, оценка, -
описанную в начале главы. В них локализация и классификация
объединены в одном процессе.
10.5. Случайные решающие леса ♦ 487
Алгоритм 10.1 (обучение дерева из случайного решающего леса)
Вход: индексу создаваемого дерева, случайно выбранное множество S. с S, содержащее тысячи
образцов вида Р= [/, d], 1 <d< к, или Р= [1,0] с соответствующими дескрипторами х.
Выход: обученное дерево Г..
1: Положить Т.= 0,1 = S., пит = |/|, dep = 0, пороги в критерии остановки равными (например)
f =20 и Г =15;
пит аер '
2: if пит <t II dep > t. then
пит и ~ аер
3: Вычислить p(0|L) и р{с* 0, d\L) на данном / в соответствии с формулами (10.63), (10.64) и (10.57);
4: Добавить лист L в дерево Т.;
5: return T;
6: else
7: dep - dep + 1 ;
8: for s = 1,..., 1000 {1000 взято просто для примера} do
9: Случайно выбрать вектор параметров ф$ в заранее определенном диапазоне;
10: Применить функцию разделения h ;
11: Разделить / на lL и lR, например, согласно формуле (10.66);
12: Выбрать функцию ф*=ф$, которая оптимизирует разделение;
13: end for
14: Включить в дерево Tj новый узел разделения, определенный функцией h ;
15: Разделить / на lL и /R, как того требует h ;
16: Случай 1: пит = |/J, / = lL; перейти к строке 2;
17: Случай 2: пит - \IR\, I - /R; перейти к строке 2;
18: end if
Рис. 10.18. Алгоритм обучения для генерирования
дерева из случайного решающего леса
Основная идея преобразования Хафа (см. раздел 3.4.1) состоит в том,
что объекты описываются параметрами и повторно встречающиеся
параметры (кластеры) свидетельствуют о существовании
параметризованного объекта.
Центроидная параметризация. Например, мы можем взять
центроид объекта (о том, что такое центроид, см. раздел 3.3.2) в
качестве его параметрического описания и соединить центральные точки
фрагментов с центроидом объекта (определив тем самым вектор). См.
рис. 10.19.
Теперь образцами в обучающем наборе S являются тройки Р = [I, d, a]
или пары р = [/, 0], где / - «небольшой» фрагмент, d - номер класса,
1 < d < к, иа- вектор, соединяющий центр фрагмента с центроидом
объекта класса d, которому принадлежит фрагмент. В случае отсутствия
объекта (когда d = 0) векторов не будет.
Далее случайный решающий лес обучается на таких фрагментах, и в
листовых узлах хранятся вероятности двумерных классов,
определенные значениями вероятностей в точках, на которые указывают векто-
488 ♦ Глава 10. Обнаружение объектов
ры а. Если обучающие фрагменты, достигшие одного и того же листа,
выбраны из одного ограничивающего прямоугольника, то все они
указывают на один и тот же центроид, так что все вероятности вносят вклад
в одну и ту же точку на двумерной диаграмме вероятностей.
Рис. 10.19. Центры фрагментов (показанных на рис. 10.6) соединены
с центроидом объекта (в двух случаях это пешеход, в одном велосипедист).
В окне без объекта центроид объекта отсутствует
Врезка 10.6 (история неявных моделей форм и лесов Хафа). Категоризация
объектов на основе сегментов, содержащих только детали объекта, впервые
была описана в работе [В. Leibe and В. Schiele. Interleaved object categorization and
segmentation. In Proc. British Machine Vision Conference, 2003, p. 759-768]. Такое
использование неявных моделей форм (implicit shape model - IMS) было в
дальнейшем развито в работе [J. Gall and V. Lempitsky. Class-specific Hough forests for
object detection. In Proc. Computer Vision Pattern Recognition, 2009,8 p.], где
определены леса Хафа на основе центроидов объектов.
Леса Хафа объединяют в рамках одной схемы классификацию с
помощью случайных решающих лесов и локализацию объектов на основе
центроидов.
10.4. Обнаружение пешеходов
К локализованному ограничивающему прямоугольнику, который,
возможно, содержит пешехода, мы применяем HoG-дескрипторы, опреде-
10.4. Обнаружение пешеходов ♦ 489
ленные в разделе 10.1.3. В этом разделе мы опишем, как локализовать
такой объект-кандидат (т. е. прямоугольную интересующую область,
которую следует проверить с помощью случайного решающего леса),
приведем конкретные функции разделения, которые в общем виде
обсуждались в предыдущем разделе, и расскажем о шаге постобработки
(на котором оцениваются результаты, полученные от леса).
Локализация интересующих областей. Для применения
классификатора, основанного на случайных решающих лесах, мы сначала
должны найти потенциальные ограничивающие прямоугольники, а
затем прогнать их через деревья леса. (У лесов Хафа, основанных на
фрагментах, есть то преимущество, что мы можем заменить поиск
ограничивающих прямоугольников случайным выбором фрагментов в тех
участках изображения, где вероятно появление пешеходов.)
Использование результатов анализа стереоизображений.
Исчерпывающий поиск, т. е. перемещение окон ожидаемого размера по
всему изображению, отнимает много времени. Вместо этого мы можем
воспользоваться картами диспаратности, построенными стереосопо-
ставителем (как описано в главе 8).
Например, можно предположить, что рост человека составляет
примерно 2 м, и оценить по картам диспаратности (которые зависят от
параметров камеры, в частности длины базы Ъ и фокусного
расстояния/) соотношения между расстоянием от камеры до человека, высотой
в изображении (в пикселях) и соответствующим диапазоном диспарат-
ностей. Пример приведен в табл. 10.2, где высота человека, отстоящего
от камеры на 10 м, в плоскости изображения равна примерно 260
пикселей.
Таблица 10.2. Соотношения между расстоянием, высотой в отснятом изображении
и диапазоном диспаратностей для записанных стереоизображений, на которых
предполагается присутствие человека ростом 2 м
Расстояние (м)
Высота (пиксели)
Диспаратность
10-17
260-153
26-15
15-22
173-118
17-12
20-32
130-81
13-8
30-42
97-62
9-6
40-52
65-50
7-5
Чтобы выбрать интересующую область, вычисленная карта
диспаратности используется для построения серии карт, на которых показаны
только значения для выявленных диапазонов глубины. Эти частичные
карты диспаратности (которые еще называют слоями) анализируются
490 ♦ Глава 10. Обнаружение объектов
на предмет наличия объектов примерно такой же высоты, как
предполагаемый рост человека в этом диапазоне диспаратностей: нужно
пройтись по одному слою карты диспаратности окнами
соответствующего размера и затем обработать только те окна, внутри которых
находится достаточное число подходящих диспаратностей.
Диапазоны глубины для определения слоев должны
перекрываться; мы хотим гарантировать, что человек появляется целиком в одном
слое, а не так, что разные части тела разбросаны между двумя
соседними слоями.
Функции разделения. Вместо того чтобы использовать на
этапах обучения и применения классификатора сгенерированные (очень
длинные) векторы целиком, для определения функции разделения
берется всего несколько элементов (быть может, даже один случайно
выбранный элемент) векторного дескриптора. Исходя из
постулированного подразбиения ограничивающих прямоугольников и вычисленных
HoG-дескрипторов, функции разделения можно было бы определить,
например, так:
0, если В(а, /) - Вф, /) > т
(10.67)
1, в противном случае
где параметрами ф = {а, Ъ, /, /, т} являются два номера блоков а и Ь,
номера интервалов / и/ и порог т; В(а, /) и Вф,;') - это суммы модулей
векторов в указанных интервалах направлений.
Подавление немаксимумов. Часто в процессе классификации
обнаруживается более одного окна вокруг изображенного человека. Для
последующего прослеживания или оценки позы разумно объединить
эти окна в одно. См. рис. 10.20.
Сильный классификатор, построенный случайным лесом,
сопоставляет каждому истинно положительному окну некоторую вероятность.
Выбирается окно с наибольшей вероятностью в определенной
окрестности. Есть и альтернатива: зная центры окон и вероятности,
применить процедуру поиска в режиме сдвига среднего для определения
окончательного положения объекта.
Что касается отбрасывания всех ложноположительных результатов,
то можно проанализировать записанную последовательность
изображений и считать основанием для отбрасывания неудачную попытку
прослеживания или повторного обнаружения.
K(i) =
10.5. Упражнения ♦ 491
Рис. 10.20. Красными прямоугольниками представлены комбинированные
результаты; голубые окружности - это центры прямоугольников, в которых
классификатор обнаружил пешехода. Несколько окружностей в середине
изображения (на отдаленной машине) не объединены
10.5. Упражнения
10.5.1. Упражнения по программированию
Упражнение 10.1 (HoG-дескрипторы, обнаружение пешеходов
и обучение случайного решающего леса). Реализуйте вычисление
HoG-дескрипторов для ограничивающих прямоугольников. Разрешите
задавать разные параметры (размер прямоугольников или ячеек,
количество интервалов направлений).
Для обучения и применения случайного решающего леса можно
пользоваться исходным кодом, выложенным Дж. Тао на сопроводительном
сайте книги (или напишите программу самостоятельно, например на
основе OpenCV).
Примените свои HoG-дескрипторы к заранее классифицированным
изображениям пешеходов, обучите свой случайный решающий лес и
примените этот лес к классификации заданных вручную
(положительных и отрицательных) ограничивающих прямоугольников. Обсудите
последствия изменения параметров программы вычисления
HoG-дескрипторов.
Охарактеризуйте качество своего детектора пешеходов с помощью
мер из раздела 10.1.2.
492 ♦ Глава 10. Обнаружение объектов
Упражнение 10.2 (обнаружение глаз). Напишите программу
обнаружения глаз в изображениях лиц анфас. Можете выбрать любой из
описанных ниже подходов.
Обнаружение глаз можно выполнять уже после обнаружения лица
или путем анализа заданного изображения без предварительного
обнаружения лица.
В первом случае, зная область лица, обнаружить глаза проще и
быстрее. Частота ложноположительных результатов уменьшается, однако
детектор лиц играет решающую роль. Если лицо по какой-то причине
не обнаружено, то не будут обнаружены и глаза.
Во втором случае мы ищем глаза во всем изображении, не
ориентируясь на положение лица. Процент истинно положительных обнаружений
при этом может оказаться выше, чем в первом методе, но процедура
занимает больше времени и частота ложноположительных результатов,
скорее всего, возрастет.
При любом подходе существуют различные способы обработки
изображений для обнаружения глаз.
Как и при обнаружении лиц, можно спроектировать слабые
классификаторы на основе вейвлетов Хаара и затем построить сильный
классификатор, собрав из них каскад. Основное отличие от обнаружения
лиц заключается в диапазоне размера скользящих масок и выборе
параметров обучения.
Возможны и принципиально иные методы; например, глаза можно
моделировать вертикально ориентированными эллипсами, а для их
обнаружения использовать преобразование Хафа для эллипсов
(например, после выравнивания гистограммы, выделения границ или
какой-то бинаризации изображения).
Охарактеризуйте качество своего детектора глаз с помощью мер из
раздела 10.1.2.
Упражнение 10.3 (обучение и применение леса Хафа). Напишите
программу, которая позволит интерактивно собрать обучающий набор
данных для обнаружения пешеходов с помощью леса Хафа,
определенного центроидами ограничивающих прямоугольников пешеходов. См.
иллюстрацию на рис. 10.19.
Для данного изображения программа в интерактивном режиме
определяет ограничивающие прямоугольники (пешеходов) и фрагменты.
Если фрагмент находится внутри ограничивающего прямоугольника,
то программа идентифицирует его как «объект» и сохраняет вектор,
соединяющий центр фрагмента с центроидом ограничивающего
прямоугольника. Если фрагмент не принадлежит никакому ограничивающе-
10.5.Упражнения ♦ 495
му прямоугольнику (т. е. не является частью пешехода), то программа
идентифицирует его как «не объект» и больше ничего не делает.
Сгенерировав таким образом несколько сотен положительных и
отрицательных образцов (т. е. фрагментов), вы можете написать вторую
программу для обучения леса Хафа. Чтобы обучить одно дерево,
выберите случайным образом подмножество сгенерированных образцов
и начните строить дерево с корня. Узлы разделения, листовые узлы и
функции разделения определяйте, как описано в разделе 10.3.3.
Наконец, напишите третью программу, которая будет применять
сгенерированные деревья. Входной фрагмент, выбранный из
изображения /, спускается по каждому дереву, где к нему применяются
обученные функции разделения, и попадает в листовой узел, где хранится
распределение позиций центроидов для фрагментов объектов и
вероятность того, что фрагмент не принадлежит никакому объекту. Все
листовые узлы, по одному из каждого дерева, определяют окончательное
распределение для данного фрагмента. Во входном изображении
/указывается это распределение в месте выбранного фрагмента. После
обработки большого числа фрагментов вы получите суммарные
распределения, как показано на нижнем изображении на рис. 10.16. На этом
упражнение можно считать выполненным.
10.5.2.Упражнения, не требующие программирования
Упражнение 10.4. Продолжите вычисления (еще хотя бы одну
итерацию), как предложено в конце примера 10.4.
Упражнение 10.5. Вручную выполните итерации AdaBoost для
шести дескрипторов хх, ..., х6 при наличии трех слабых классификаторов
(т. е. w = 3) hv h2 и /?3, где hx назначает класс +1 всем шести дескрипторам,
h2 назначает класс -1 всем шести дескрипторам, a hz назначает класс +1
дескрипторам х1... хЗ и класс -1 - дескрипторам х4... х6.
Упражнение 10.6. Пусть 5= {1, 2, 3,4, 5, 6}, аХи Y- случайные
величины, определенные на S : X = 1, если число четное, a Y = 1, если число
простое (т. е. равно 2, 3 или 5). Пусть выражения р{х, у) и р(у\х)
определены, как в формулах (10.44) и (10.45). Вычислите их значения для всех
возможных комбинаций а: и у, например р(0, 0) или р(0|1).
Упражнение 10.7. Рассмотрим конечный алфавит S = {av..., ат} и две
случайные величины 1и7, принимающие значения из S. Обозначим
р. = Р(Х = a), q. = P(Y = а). Относительной энтропией дискретного рас-
494 ♦ Глава 10. Обнаружение объектов
пределения вероятностей р относительно дискретного распределения
вероятностей q называется величина
т р
я(/?к) = -5>,-1о§2—•
Покажите, что
1) H(p\q) > 0;
2) существуют случаи, когда H(p\q) ф H(q\p);
3) H(p\q) = 0 тогда и только тогда, когда р = q (т. е. р. = q. для всех
/=1,...,тл).
Упражнение 10.8. Вычислите код Хаффмана (в этой книге не
рассматривается, обратитесь к другим источникам) для обоих распределений
вероятности из примера 10.5.
Упражнение 10.9. Убедитесь, что в примере 10.6 Н(У|с) = 0.
Предметный
Символы
Зй-сканер 308
Q 18, 21
А
AdaBoost 467
Altar 86
AnnieYukiTim 47, 255
atan2 41, 89
Aussies 29, 256
В
bicyclist 173, 251, 415
BRIEF 411
С
CIE 49
Crossing 345, 373
D
Donkey 43, 45
E
ECCV конференция 203
EISATS 97, 156, 199, 201, 203, 359
Emma 74, 77
F
FAST 94, 411
Fibers 42
Fountain 22
G
Gmax 21
указатель
H
HCI набор данных 377
Heidelberg Robust Vision Challenge 97, 203
HoG-дескриптор 459
HSI цветовое пространство 57, 63
I
IAPR (Международная ассоциация по
распознаванию образов) 71
ICCV конференция 121
iSGM алгоритм 478
J
JPG графический формат 62
К
Kinectl 308
Kinect 2 308
Kiri 127
KITTI набор данных 97, 203, 375
К-смежность 126
L
LightAndTrees 96
LoG (лапласиан гауссиана) 98, 100
М
MainRoad 96
Michoacan 466
MissionBay 255
motorway 251
N
Neuschwanstein 23
496 ♦ Предметный указатель
NorthLeft 96
NorthRight 96
О
OldStreet 29
ORB-признаки 411
Р
PobLeEspanyoL 127
Q
queenStreet 197
R
RagingBull 67
Rangitoto 127
RANSAC 396, 402
RGB 21, 25, 57
RGB-куб 57
Rocio 468
S
SanMiguel 20, 26
SetlSeql 69, 83, 91, 94, 101, 106, 107
Set2Seql 97, 201
SIFT 408
SouthLeft 66
SouthRight 66
Spring 256
Straw 42
SURF 410
T
Taroko 29
tennisbaLL 173, 248
Tomte 127
TV-L2 97
U
Uphill 66
W
Wiper 66
WuhanU 33
X
Xochicalco 256
Y
Yan 24
A
адаптивное усиление 467
алгоритм
BBPW 193
Bocca 129
вычисления оптического потока
Лукаса-Канаде 187
Вэя-Клетте 338, 339
двухпроходный 333
Ковеси 107
конденсации 428
Марра-Хилдрет 99
Меера-Георгеску 103, 252
мета 467
пирамидальный 196
сдвига среднего 249
Франкота-Челлаппа 338, 339
Хорна-Шанка 173, 183
альбедо 326
амплитуда 41
анаглифическое изображение 293
апертуры проблема 173
артефакты освещения 95
асимптотическая временная сложность 258
аффинное преобразование 277
Б
бабочка 159
база 321
Предметный указатель ♦ 497
базисные функции 36, 72
Байера фильтр 266
Бенхемадиск 54
бинарные устойчивые независимые элементарные
признаки 411
быстрое преобразование Фурье 38
В
вейвлеты 108
Вейнгартена отображение 306
вектор невязки измерений 438
векторное поле 171
плотное 171
разреженное 171
векторное произведение 280
вектор расхождения 423
векторы трехмерного потока 396
вергенция 323
вероятность 24
условная 478
веса 191, 428, 452, 461
взвешенный граф 363
видеонаблюдение 257
вид сверху 430
внутренность 124
Восса алгоритм 129, 167
вращающаяся змея 56
временной отпечаток 254
выброс 402
выравнивание гистограммы 67
высота 302
Г
Габора вейвлеты 108
гамма-сжатие 53
гауссова сфера 303
Гессе матрица 92, 112
гильбертов обход 79
гистерезис 89, 106
гистограмма 23, 163
выравнивание 66
градиентов 408
двумерная ИЗ
кумулятивная 24
ориентированных градиентов 458
уровней яркости 23
главная ось 151, 152
главная точка 271
глобальное интегрирование 334
глобальное сопоставление 355
глубина 302
голография 308
гомеоморфизм 122
томография 289, 430
градиент 32
пространственно-временной 194
градиентное пространство 304
градиентный поток 174, 185
граница 25, 29, 98
граница топологическая 124
Грэя код 311
д
движение
двумерное 170
трехмерное 169
двойственная прямая 304
Декарта-Эйлера теорема 118
дескриптор 398, 451
детектор объектов 456
деформация 423
дивергенция 196
диоптрическая система 273
дискретизация 18, 100
дискретное преобразование Фурье (ДПФ) 34
обратное 35
дискретный отрезок прямой 135
диспаратность 314, 317
дисперсия 22, 81
дистанционная ошибка 201
дистанционное преобразование 140
дисторсия объектива 267
498 ♦ Предметный указатель
дихроматическая модель отражения 343
длина базы 272, 321
доска сообщений 381
дрейф 426
дуга
жорданова 133
дырки 129, 297
Е
единичный вектор 186
Ж
Жордана-Брауэратеорема 121
жорданова поверхность 301
3
задача о пометке 178, 334
задача сопоставления 403
задний план 302
замыкание 124
запрос по образцу 443
земная поверхность 297
зубчатость 134
И
идеально рассеивающая отражающая
поверхность 325
изображение 18
анаглифическое 293
базовое 347
бинарное 21, 162
векторное 21
виртуальное 384
интегральное 75
как поверхность 31
остаточное 98, 204
поиск 443
полутоновое 21
скалярное 21
сопоставляемое 347
сходство 443
сшивка 292
изопериметрический дефицит 164
изопериметрическое неравенство 164
изотропность 152, 397
инвариантность 397
относительно вращения 152
интегрирование 331
глобальное 334
локальное 332
интенсивность 54, 57
интервал поиска 347
интересующая область 449
информационный выигрыш 479
истинно отрицательный результат 450
истинно положительный результат 450
итеративная схема решения 182
Ишихарытест 53
К
кадр 27
калибровочная отметка 152, 284
Калмана фильтр 435, 444
иконический 445
камера
вращающаяся линейная 275
всенаправленная 273
обскура 60, 263
панорамная 273
рыбий глаз 274
канал 21
яркость 26
каноническая геометрия стереоскопической
системы 272
карта
высоты 302
глубины 302
границ 33
игольчатая 185
ламбертовской отражательной способности 327
отражательной способности 327
Предметный указатель ♦ 499
расстояния 302
рельефная 301
катадиоптрическая система 273
квадратичная вариация 33
квадратичное евклидово дистанционное
преобразование(SEDT) 142
класс 450
классификатор 451
сильный 452, 465
слабый 452, 468
классификация 454
кластеризация 259
КМОП 264
консенсусное множество 404
контрастность 25, 27
контрольные данные 200, 261
координаты
однородные 279, 404
сферические 303
корень из единицы 38
коррекции шаг 439
косинусов закон 325
коэффициент восстановления 259
коэффициент усиления Калмана 439
коэффициент формы 163
коэффициенты Фурье 36
край 297
внешний 129
внутренний 129
кривая
гладкая 136
жорданова 121
простая 121
кривизна 136
гауссова 305, 307
главная 306
кривой 137
нормальная 306
подобия 307, 343
средняя 306
круг влияния 396
кумулятивная частота 24
Кэнни оператор 89
Л
Лаборатория реактивного движения 20
лазерный сканер 308
ламбертовская отражательная способность 324
ламбертовский отражатель 325
лапласиан 32, 90, 98
лес 454, 476
линейная динамическая система 435
линейная разделимость 453
л истовый узел 453
ложноотрицательный результат 450
ложноположительный результат 450
локальная операция 68
локальный бинарный паттерн (LBP) 411
локальный максимум 68
Лукаса-Канаде алгоритм вычисления оптического
потока 187, 191
Лукаса-Канаде прослеживатель 422
М
магический квадрат 78
маска 389, 464
масштаб 81, 89
масштабирование
линейное 67, 101
условное 68
масштабно-инвариантное преобразование
признаков (SIFT) 408
матрица
векторного произведения 291
Гессе 92, 112, 424
дескрипторная 460
диагональная 191
интегрирующая 376
камеры 288
наблюдения 437
невязки дисперсий 438
перехода состояний 436
системы 435
500 ♦ Предметный указатель
совместной встречаемости 147
стоимости данных 350
существенная 291
управляющая 436
фундаментальная 291
Якоби 424
матричный датчик 263
Махаланобиса расстояние 444
меандр 78
Мёбиуса лист 299
Международная конференция по распознаванию
образов (ICPR) 71
мера
данных 27
качества классификатора 456
несходства 252
ошибки 200
совместной встречаемости 163
точности 359
уверенности 360
угловатости 93
меры совместной встречаемости 150
метод
наименьших квадратов 188
метрика 28, 252
мнимая единица 35
многогранник 118
многоугольник 131
множество
замкнутое 124
компактное 124, 343
открытое 124
модель
HSI 57
RGB 21
ступенчато-граничная 29
узлов сетки 19, 118
фазово-конгруэнтная 29
цветовая аддитивная 56
цветовая субтрактивная 56
ячеек сетки 19
модуль разности 349, 370, 373
моменты 151
центральные 151
мощность 21
Н
наблюдаемость 435
насыщенность 58
начальная точка 20
недостоверность стереореконструкции 342
нерезкое маскирование 85
нефотореалистичный рендеринг 255
норма
L2 38
нормализация по направлению 165
нормаль 32
единичная 303
нормированная взаимная корреляция 199
нормировка функций 27
носитель 18, 21
О
область
пространственная 34
частотная 34
обнаружение
краев дороги 165
лиц 467, 474
пешеходов 476, 488, 491
образец 481
обратное прохождение 364, 376
обучение 454
без учителя 454
с учителем 454
объект-кандидат 449
огибающая
нижняя 145
ограничение порядка 364
ограничение уникальности 368
ограничивающий прямоугольник 449, 455, 457
однородность 150, 164
окно 20
по умолчанию 24
окрестность 119
трехмерная 400
окружность 160
соприкасающаяся 158
октава 83
оператор
глобальный 71
Кэнни 89
линейный локальный 69
локальный 71
медианный 81
прямоугольный 80
Собеля 88
точечный 65, 71
определитель 93, 130
оптимальная матрица коэффициентов усиления
Калмана 439
оптимизация
TV-L1 195
TVL2 180, 194
среднеквадратической ошибки 180
оптическая ось 269
оптический поток 170
алгоритм вычисления 252
уравнение 177
ориентация 131
когерентная 298
треугольника 298
осепараллельность 134, 165
основная теорема алгебры 35
основные типы цветового восприятия 53
особая точка 398
относительное отклонение 132
отношение разностей 176
отражательная способность 326
карта 327
ламбертовская 324
оттенок 58
ошибка 179, 453
дистанционная 201
предсказания 437
Предметный указатель ♦ 501
угловая 201
ошибка гладкости 180
ошибка данных 179
П
панорама
стерео 275
цилиндрическая 273
парабола 140, 145
параметры
внешние 281
внутренние 281
Парсеваля теорема 41, 336
переменный ток 40
переписная функция стоимости 352
переход через ноль 30, 114
периметр 132, 163
ПЗС (прибор с зарядовой связью) 264
пик 157
локальный 248
пиксель 18
плохой 359
позиция 19
соответственный 347
пирамида 76
планарный граф 119
плоскость
касательная 32
комплексная 37
плотность вероятности 23
плохой пиксель 359
площадь 130
поверхность 297
гладкая 297
жорданова 300
многогранника 297
неориентируемая 298
ориентируемая 298
участок 301
повторяемость 416
повышение резкости 85
подавление немаксимумов 89, 95, 106, 112
502
Предметный указатель
полная вариация 180
полоса 21
полуглобальное сопоставление 356
базовое 378
итеративное 378
пометка 180
попадание 450
порядок
момента 151
обхода круговой 128, 167
порядок важности 125
порядок обхода 78
постеризации эффект 255
постоянный ток 40
Поттса модель 261
предположение о постоянстве градиента
(GCA) 193
предположение о постоянстве яркости
(ICA) 95, 178, 187, 193, 349, 389
представление
неявное 301
передискретизация 434
явное 301
преобразование
аффинное 277
бочкообразность 267
гистограммы 66
дистанционное 140
интегральное 34
косинусное 34
линейное 277
подушкообразное^ 267
Фурье 34
преобразование обратной перспективы 430
признак 398
прогрессивная развертка 265
производная
дискретная 86
промах 450
прослеживание 250
пространство
градиентное 304
дескрипторов 451
скоростей 178
Хафа 156
пространство масштабов 82
DoG 102
LoG 101
гауссово 83
прямоугольного фильтра 442
профиль
яркости 26
прямоугольный фильтр 73, 80
путь
в пирамиде 78
равномерность 150, 164
разность гауссианов (DoG) 82, 98
расстояние
Махаланобиса 444
между функциями 28
Хэмминга 354
растровая строка 367
регулярная сетка 18
регулярная точка 402
ректификация геометрическая 286
свертка 44, 69, 72, 81
светимость 54
светоделитель 266
связность 119
сглаживание 80
гауссово 77
сегмент
соответственный 250
сегментация
видео 248
методом сдвига среднего 255
сигма-фильтр 83
симметрическая разность 252
симметричность, свойство ДПФ 40
Предметный указатель ♦ 505
система координат
левосторонняя 18
мировая 276
ситуация 376, 390
скалярное произведение 178, 304
скорость 170
след 93
случайный решающий лес 476
смежность
4- 118
6- 167
8- 118
К- 126, 167
Собеля оператор 88, 116
собственные значения 92, 192, 306
согласованность
временная 247, 249
согласованность слева направо 360
соотношение сторон 266
сопоставление методом динамического
программирования (DPM) 363, 375
сопоставление методом распространения
доверия (ВРМ) 379, 389, 478
сопряженное комплексное число 38
состояние 435
спектр 41
видимый 49
спрямляемая жорданова дуга 133
среднее 21
локальное 68
стандартное отклонение 22, 81
статистики
временные 27
пространственные 26
стеноп, модель камеры 268
стереопара 345
стереосопоставитель 350
стереоточки соответственные 290
стоимость
суммарная 346
структурная подсветка 308
структурное подобие 28
структурно-текстурное разложение 98
субпиксельная
точность 152, 360
сумма квадратов разностей 349
сумма модулей разностей 349
суммарная стоимость 346
сценарий 376
сшивка 292
Т
Тейлора ряд 175, 193, 423
теорема
Жордана-Брауэра 121
Мёнье 307
о свертке 44, 72
Парсеваля 41
техника третьего глаза 384
топология
евклидова пространства 124
цифровая 117
точка
бесконечно удаленная 280
вогнутости 137
выпуклости 137
особая (сингулярная) 136
соответственная 315
точность
субклеточная 158
субпиксельная 152
транспонирование 104
трассировка краев 126
триангуляция 312
У
уверенность 104
угловая ошибка 201
углы поворота
эйлеровы 278
угол
азимутальный 303
в изображении 91
504 ♦ Предметный указатель
наклона 32, 136
полярный 303
узел разделения 453
узел сетки 19
управление 437
управляемость 435
уровень 83
уровни яркости 54
условие интегрируемости 332
устойчивость 435
участок 120
Ф
фаза 41
синфазность 46
фазовая конгруэнтность 44, 46
фильтрация Фурье 34
фильтр верхних частот 73
фильтр нижних частот 74
фильтр частиц 428
фокусное расстояние 169, 269
фокус расхождения 445
фотометрический метод анализа
стереоизображений 324
не зависящий от альбедо 328
обратный 329
фрагмент 455
Френе репер 137
функция
ceil 100
гауссова 81
градационная 65
пометки 179, 196
разделения 483
сомбреро 99
среднеквадратической ошибки 180
Фурье коэффициенты 71
Фурье пара 42
Фурье преобразование 34
локальное 45
X
Хаара вейвлет 460
Хаара дескриптор 464
Хаара дискретное преобразование 462
Хаара признак 463
хаароподобные признаки 411
Харриса детектор 93
Харриса фильтр 413
Хафа преобразование
оригинальное 154
пространство параметров Дуды и Харта 156
стандартное 157
Хорна-Шанка ограничение 177, 193
Хэмминга расстояние 353
ц
цвет 47
цветовая гамма 50
цветовая испытательная таблица 59, 266
цветовая слепота 51
цветовое пространство CIE 50
цветовой ключ 172, 185
центральная проекция 270
центроид 151
центр проекции 169, 269
цикл обхода краев 129
цифровая геометрия 135
Ч
частичная функция ошибки 369
частота 34
абсолютная 23
кумулятивная 24
относительная 23
Ш
широкий угол 270
шум 65, 435
наблюдения 437
системы 436
Предметный указатель
505
эгоавтомобиль 417
эгодвижение 419
Эйлера-Лагранжа уравнения 196
Эйлера формула 55, 119, 306
Эйлера число 81
эйлерова характеристика 299
эксцентриситет 152
энергия гладкости 180
энергия данных 179
энтропия 476
нормированная 477
условная 477
эпиполярная геометрия 314
каноническая 315
эпиполярная плоскость 315
эпиполярная прямая 291, 315
эпиполярный профиль 366
ядро фильтра 69
якобиан 424
Якоби матрица 424
Якоби метод 182
яркость 54
ячейка сетки 19
Книги издательства «ДМК Пресс» можно заказать в торгово-издательском холдинге
«Планета Альянс» наложенным платежом, выслав открытку или письмо по почтовому
адресу: 115487, г. Москва, 2-й Нагатинский пр-д, д. 6А.
При оформлении заказа следует указать адрес (полностью), по которому должны
быть высланы книги; фамилию, имя и отчество получателя. Желательно также указать
свой телефон и электронный адрес.
Эти книги вы можете заказать и в интернет-магазине: www.a-planeta.ru.
Оптовые закупки: тел. +7(499) 782-38-89.
Электронный адрес: books@alians-kniga.ru.
Рейнхард Клетте
Компьютерное зрение
Теория и алгоритмы
Главный редактор Мовчан Д. А.
dmkpress@gmaiL.com
Перевод с английского Слинкин А. А.
Корректоры Светлова О. Ю., Синяева Г. В.
Верстка Паранская К В.
Дизайн обложки Мовчан А. Г.
Формат 70х100У16. Печать цифровая.
Усл. печ. л. 41,11. Тираж 200 экз.
Веб-сайт издательства: www.dmkpress.com
В этой книге вы найдете доступное введение в основные аспекты компьютерного
зрения. При этом подчеркивается важная роль алгоритмов и математики.
Материал дополняется историческими справками, рекомендациями по дальнейшему
чтению и сведениями о рассматриваемых математических понятиях.
В конце каждой главы имеются проверенные на практике упражнения и вопросы
на понимание материала, сформулированные так, чтобы читатель мог предложить
различные варианты решения.
Рассматриваемые темы:
• введение в систему обозначений и математический аппарат, необходимый для описания
изображений, а также основные сведения об отображении одного изображения в другое;
• топологические и геометрические основы анализа участков изображений и
распределения значений в них, а также нахождение паттернов в изображениях;
• введение в оптический поток как средство представления плотного движения, а также
вопросы анализа разреженного движения: обнаружение особых точек, определение
дескрипторов и прослеживание признаков с помощью фильтра Калмана;
• описание некоторых подходов к бинаризации изображений и сегментации фотографий
и видео;
• три основных компонента системы компьютерного зрения: геометрические и
фотометрические характеристики камеры, системы координат и калибровка камеры;
• обзор методов трехмерной реконструкции на основе компьютерного зрения,
в частности: структурная подсветка, стереозрение и оценка формы с помощью анализа
отраженного света;
• стереосопоставители и фазово-конгруэнтная модель для построения признаков
изображения;
• введение в методы классификации и обучения с подробным описанием алгоритма
AdaBoost и случайных лесов.
Интернет-магазин:
www.dmkpress.com
Springer
'JSSs
www. дм к. рф
ISBN 978-5-97060-702-2