Принцип относительности Галилея и неевклидова геометрия - Яглом И.М.

Автор: Яглом И.М.

Теги: математика геометрия

Год: 1969

Похожие

Неевклидова геометрия

От проективной геометрии - к неевклидовой

Введение в неевклидову геометрию Римана

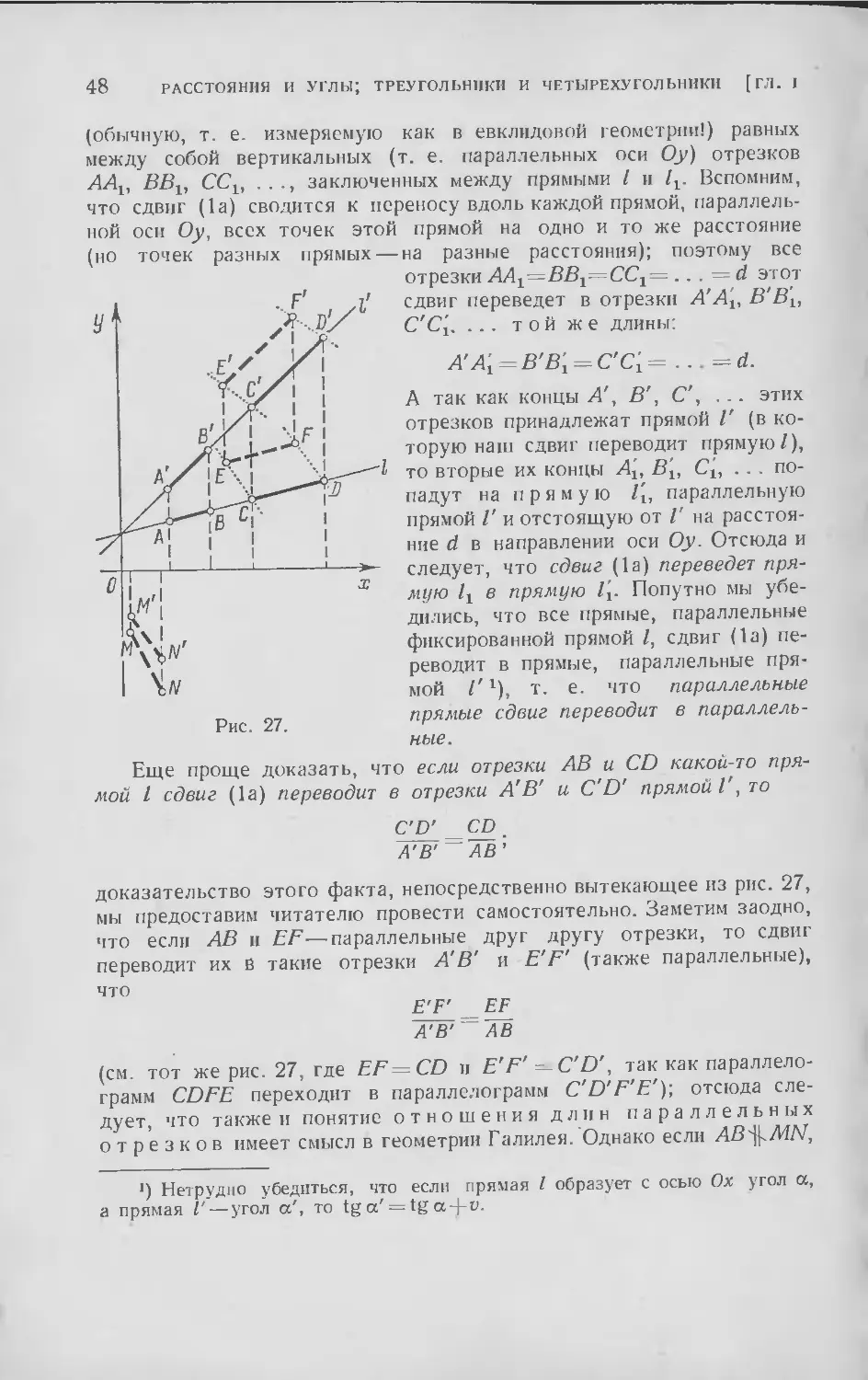
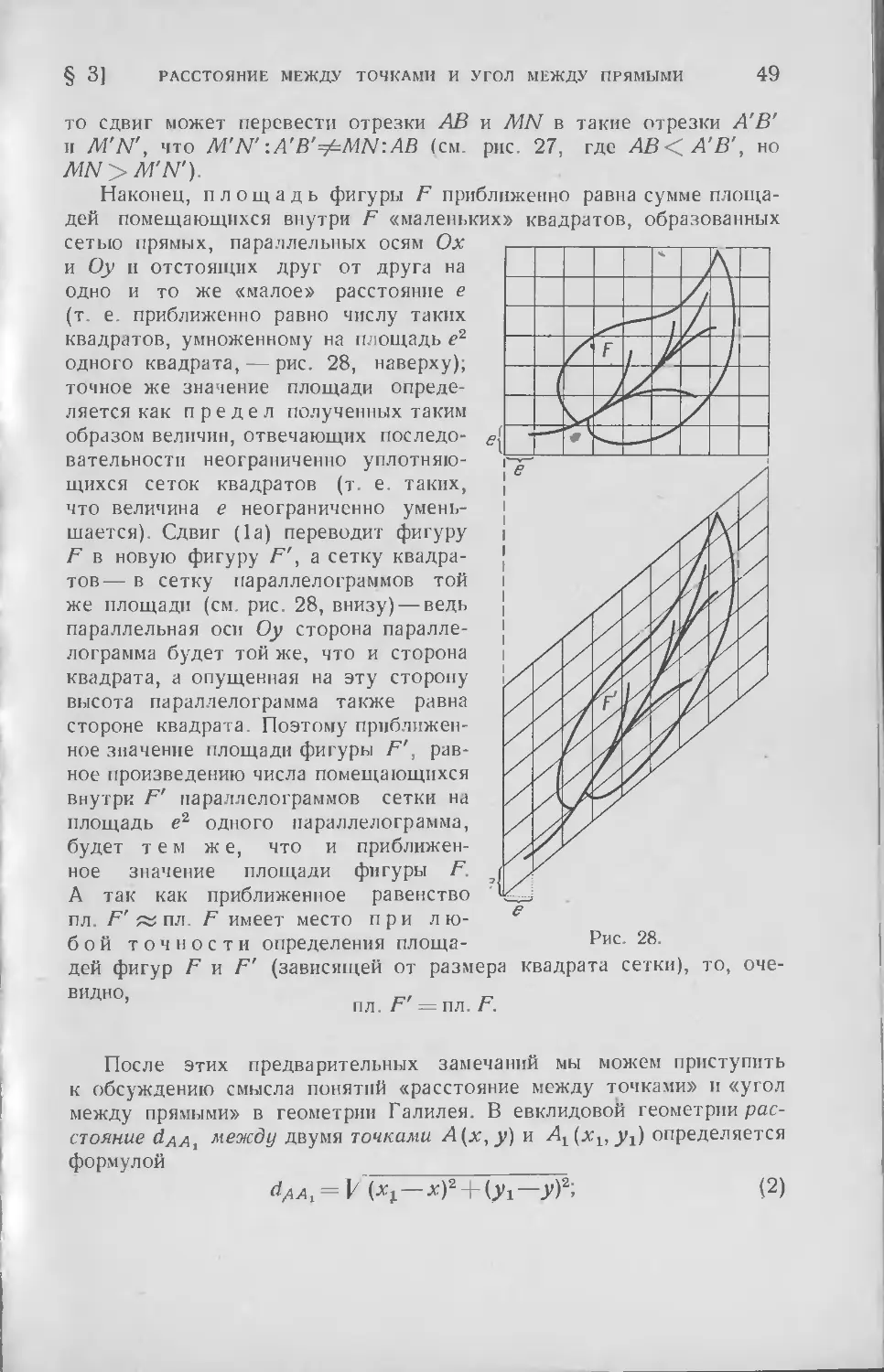
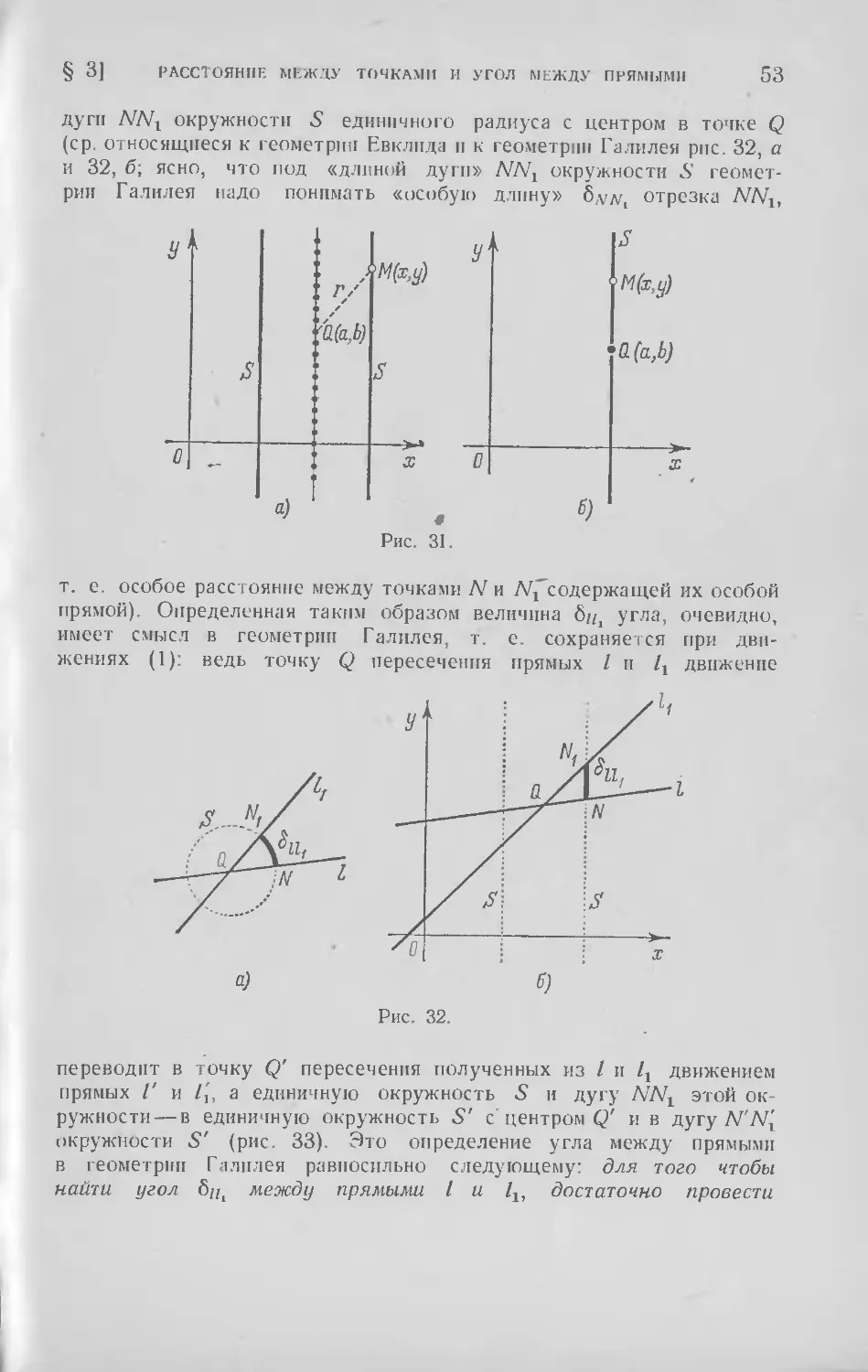
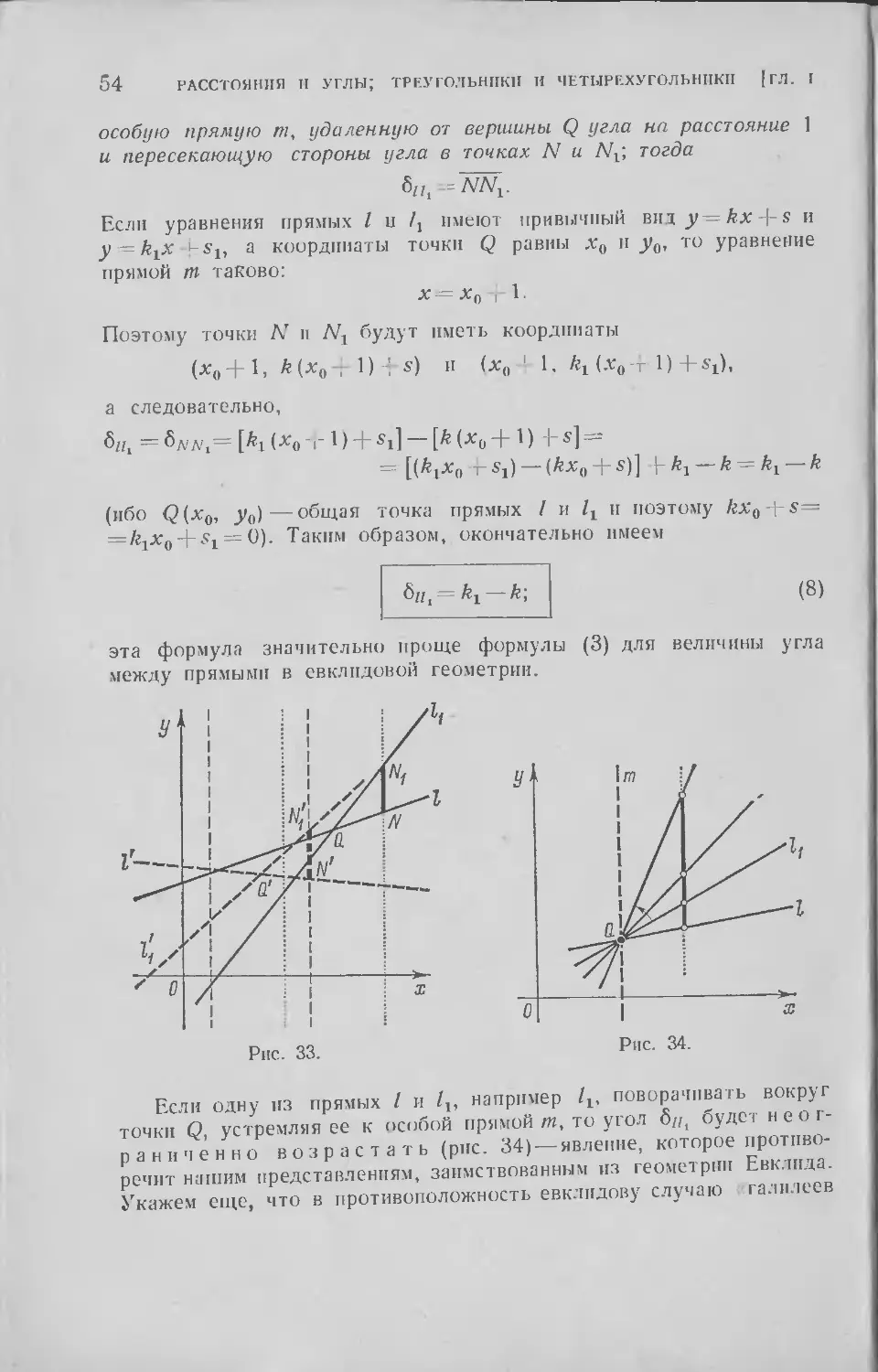
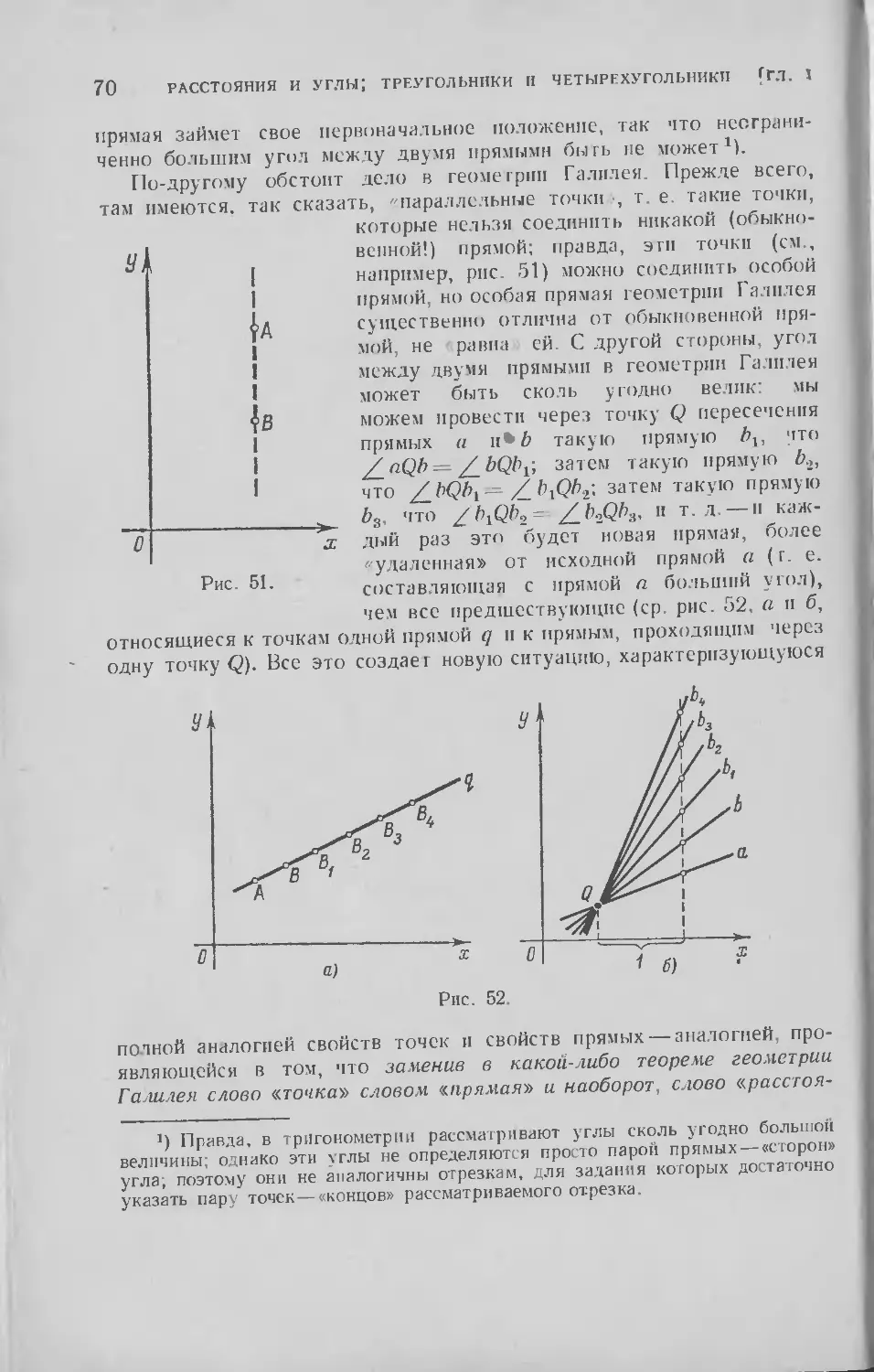
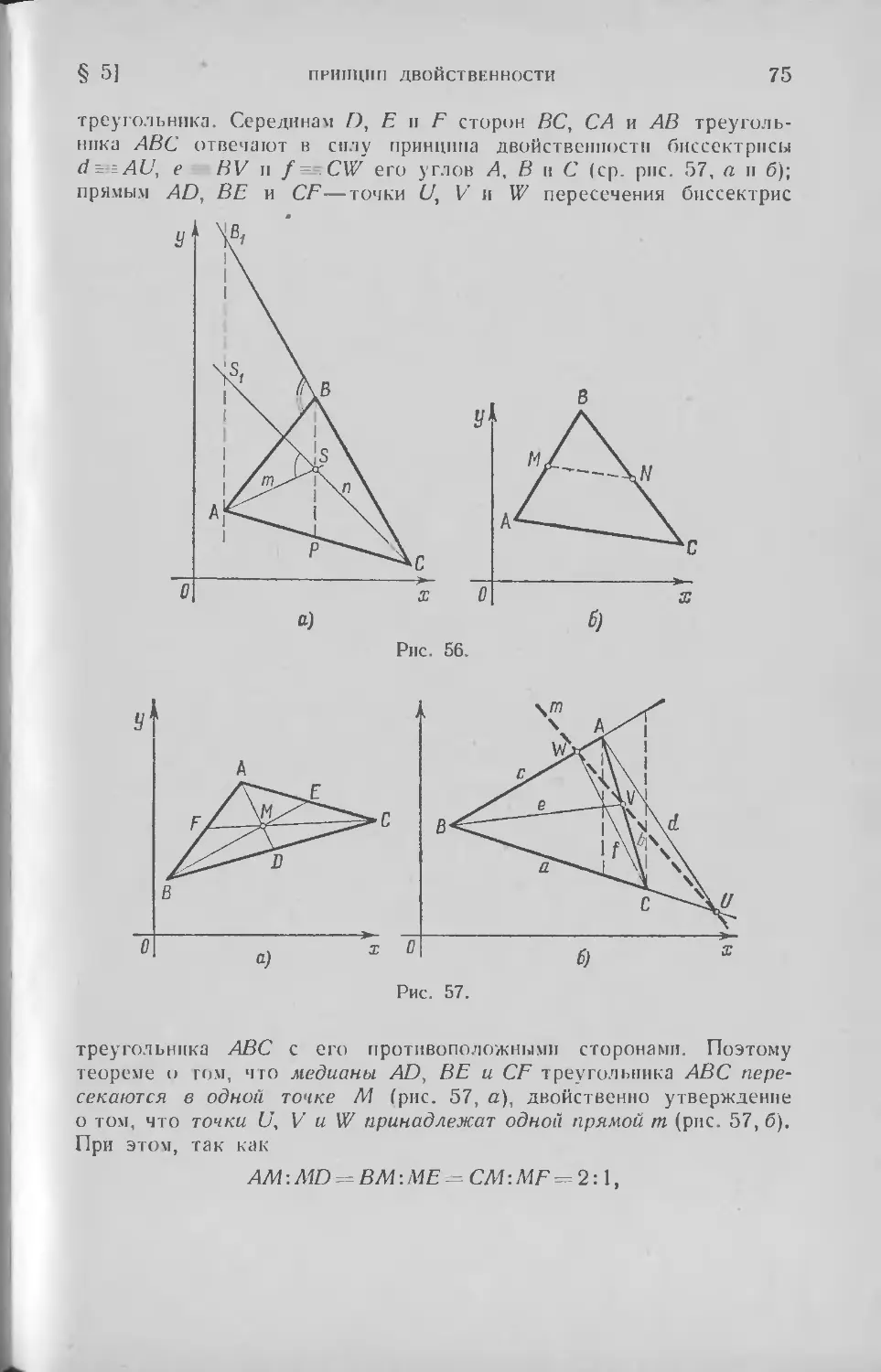
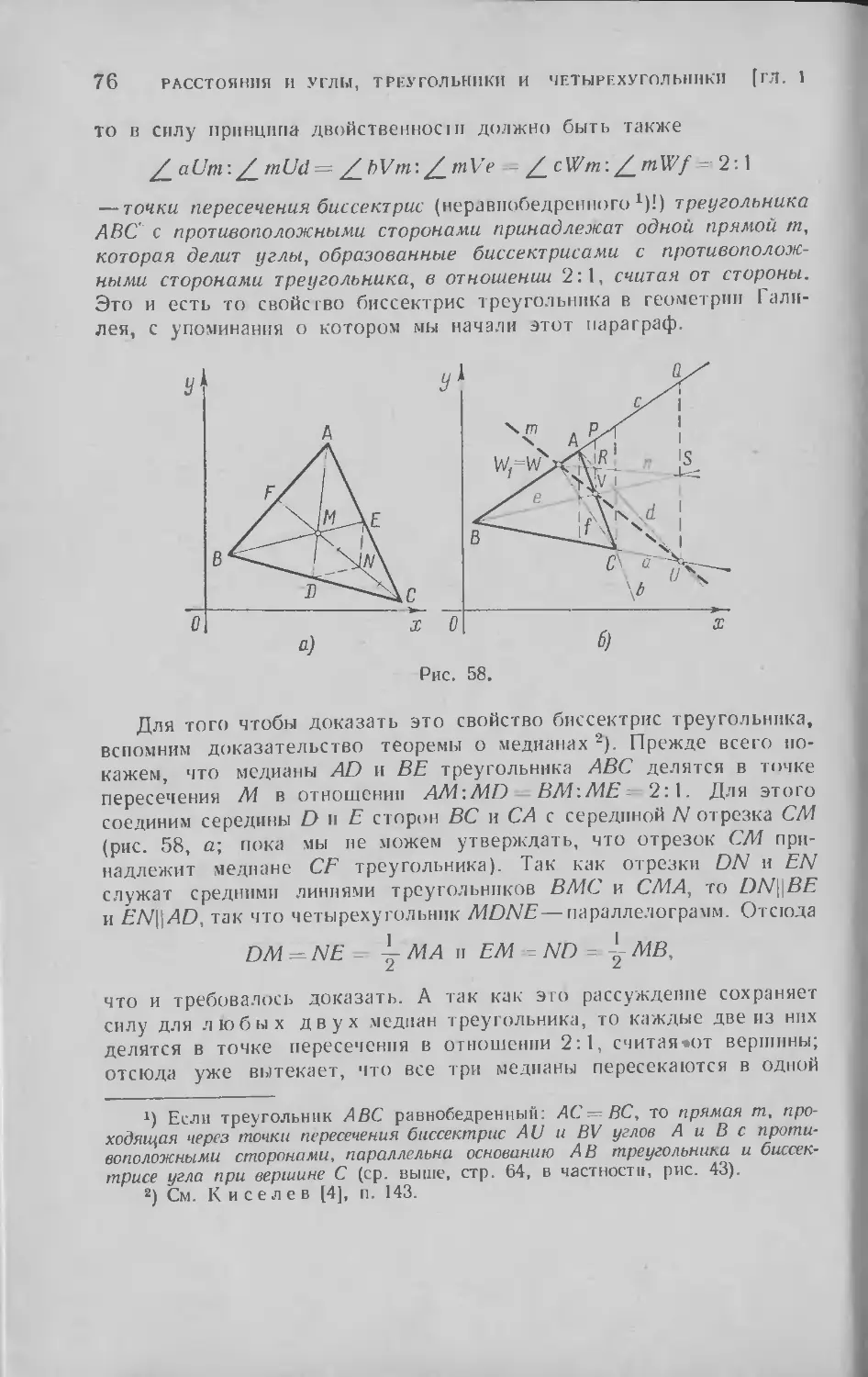
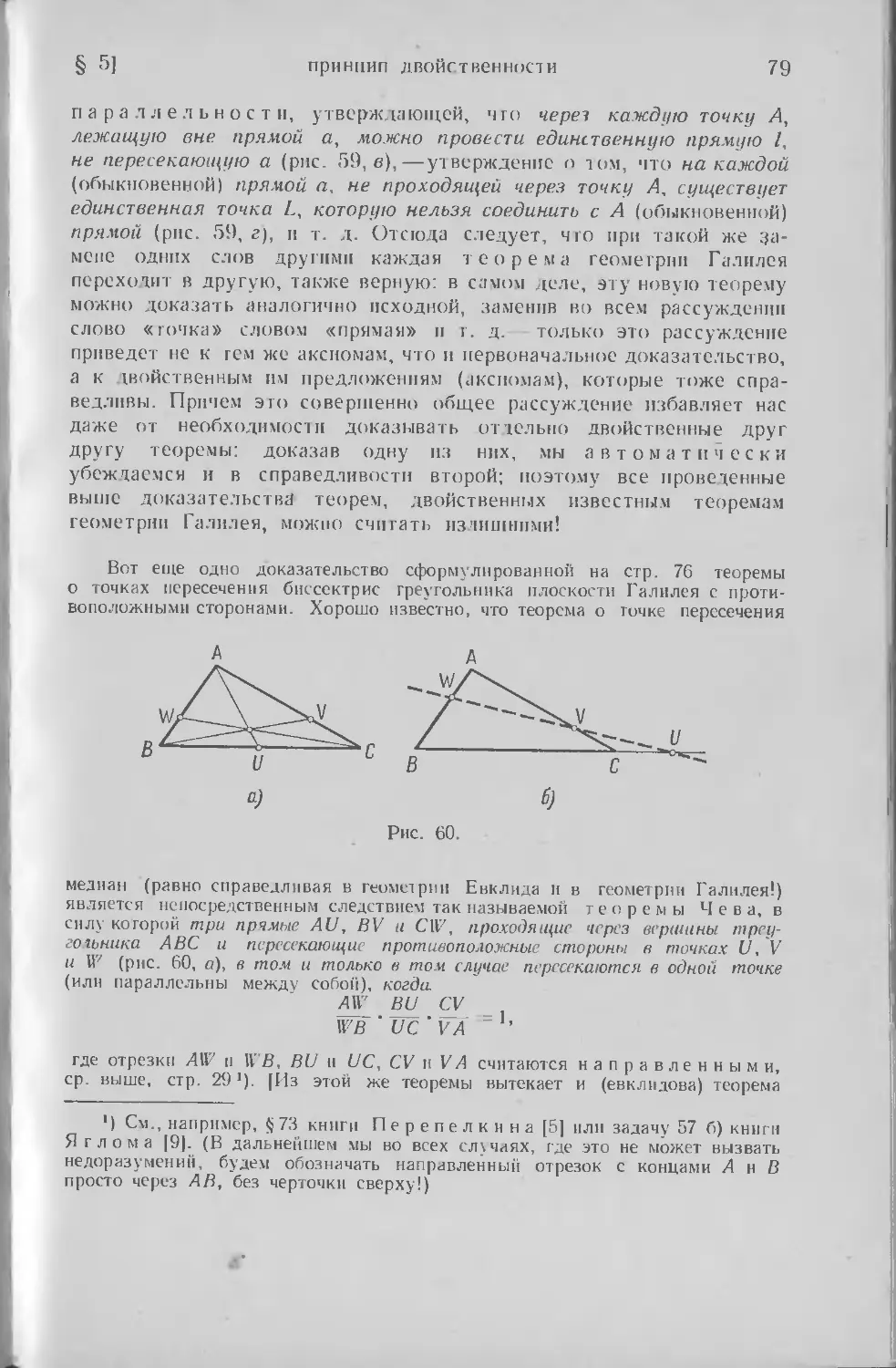
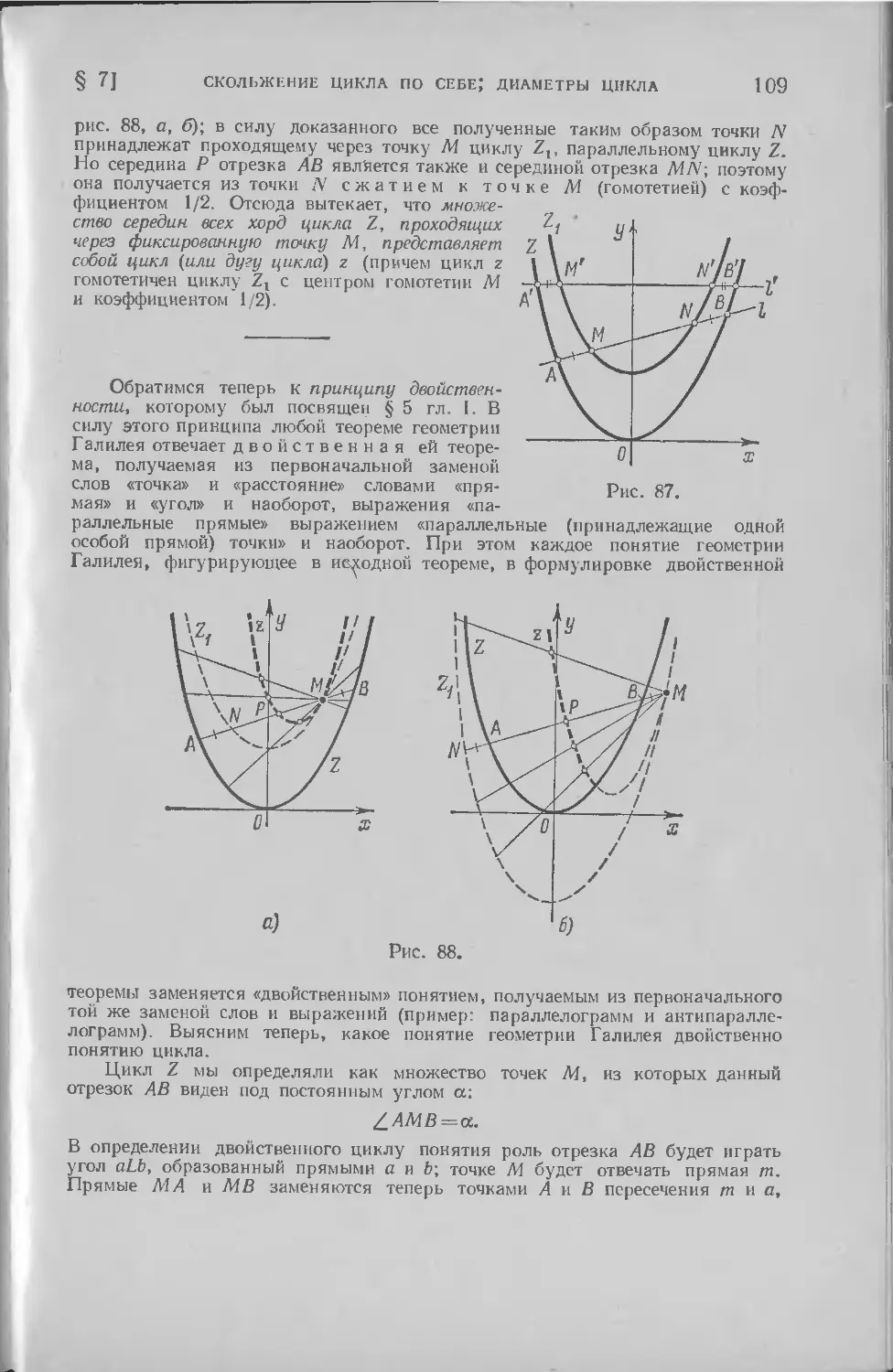
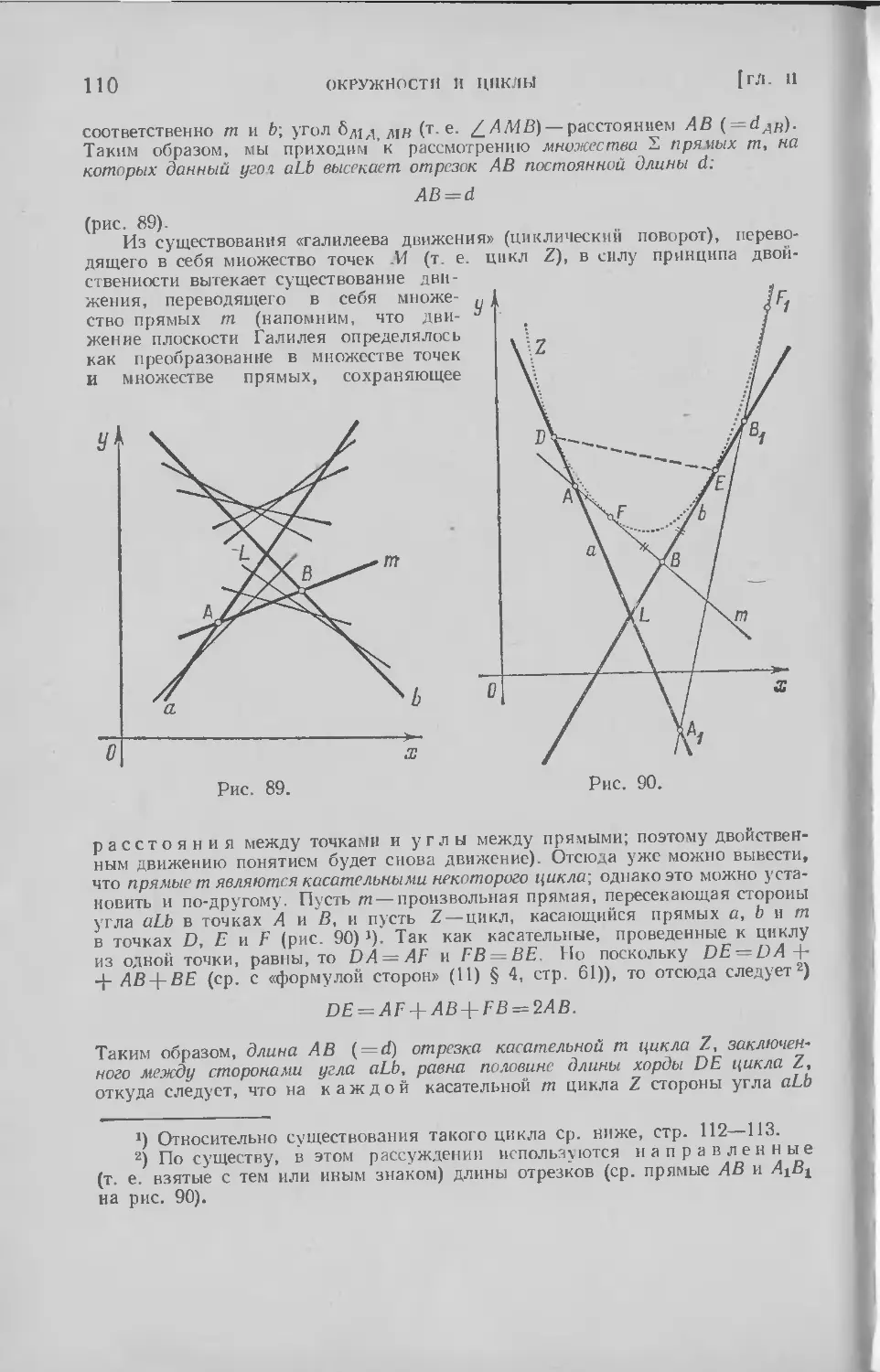
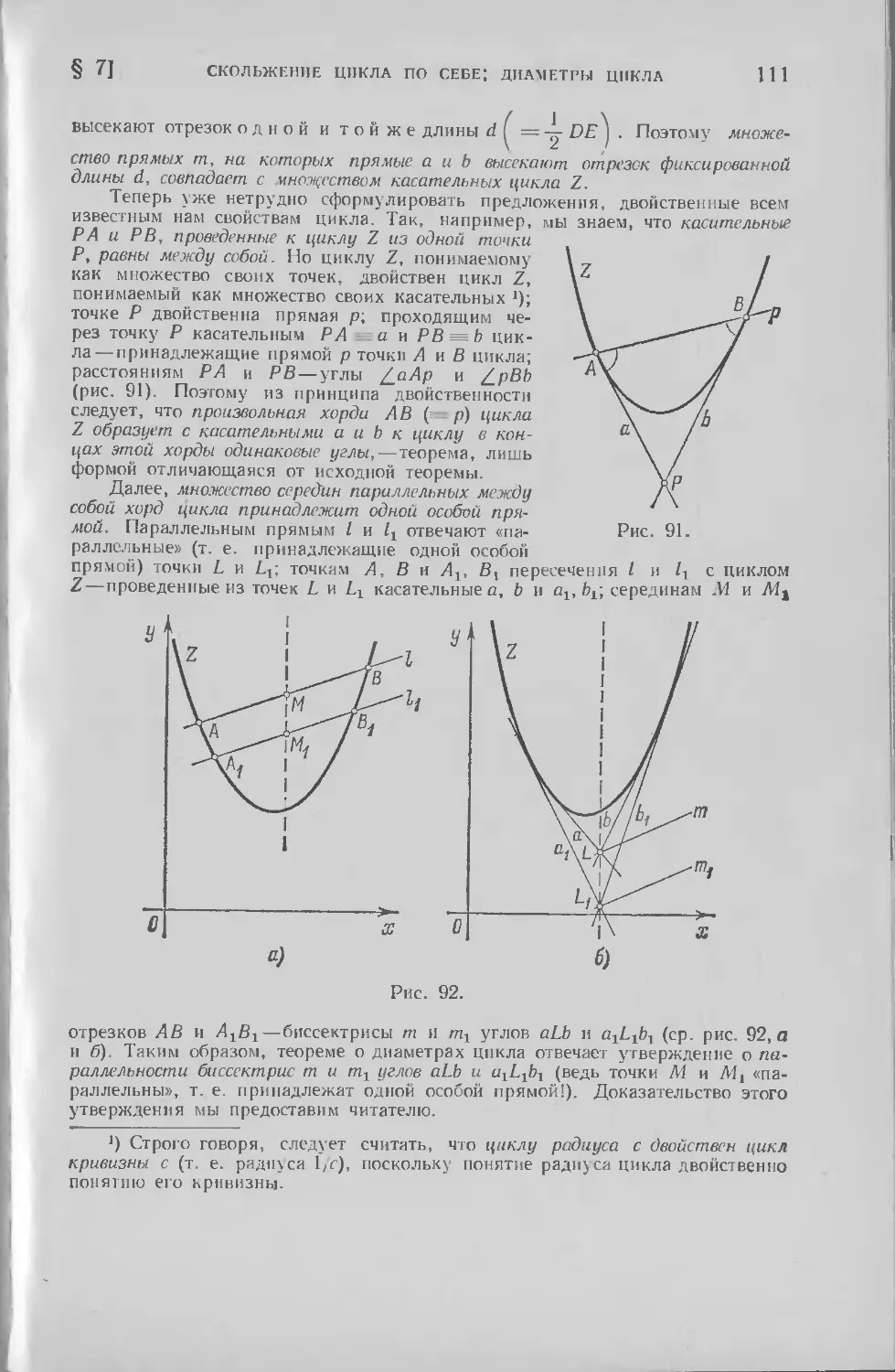
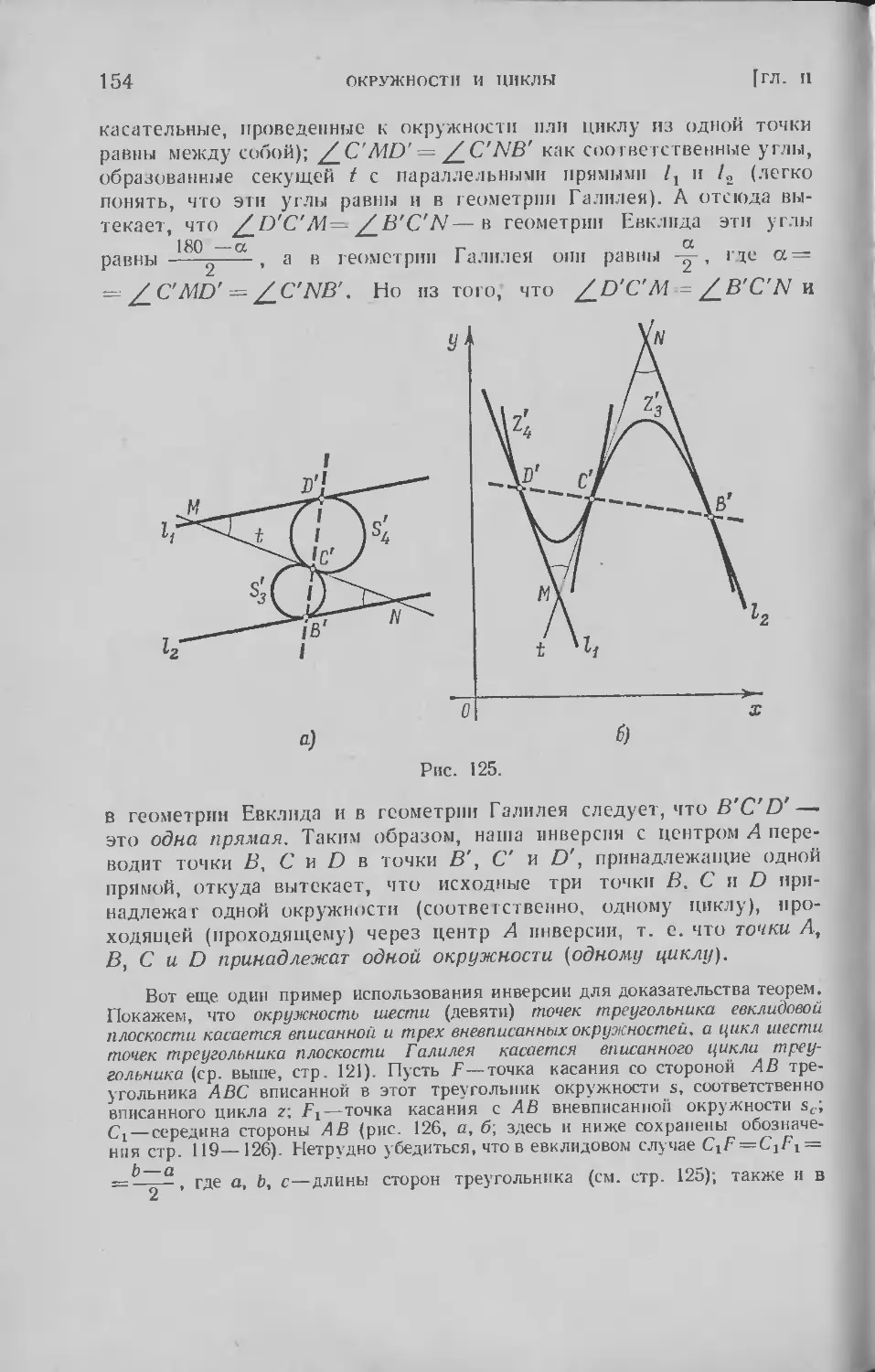
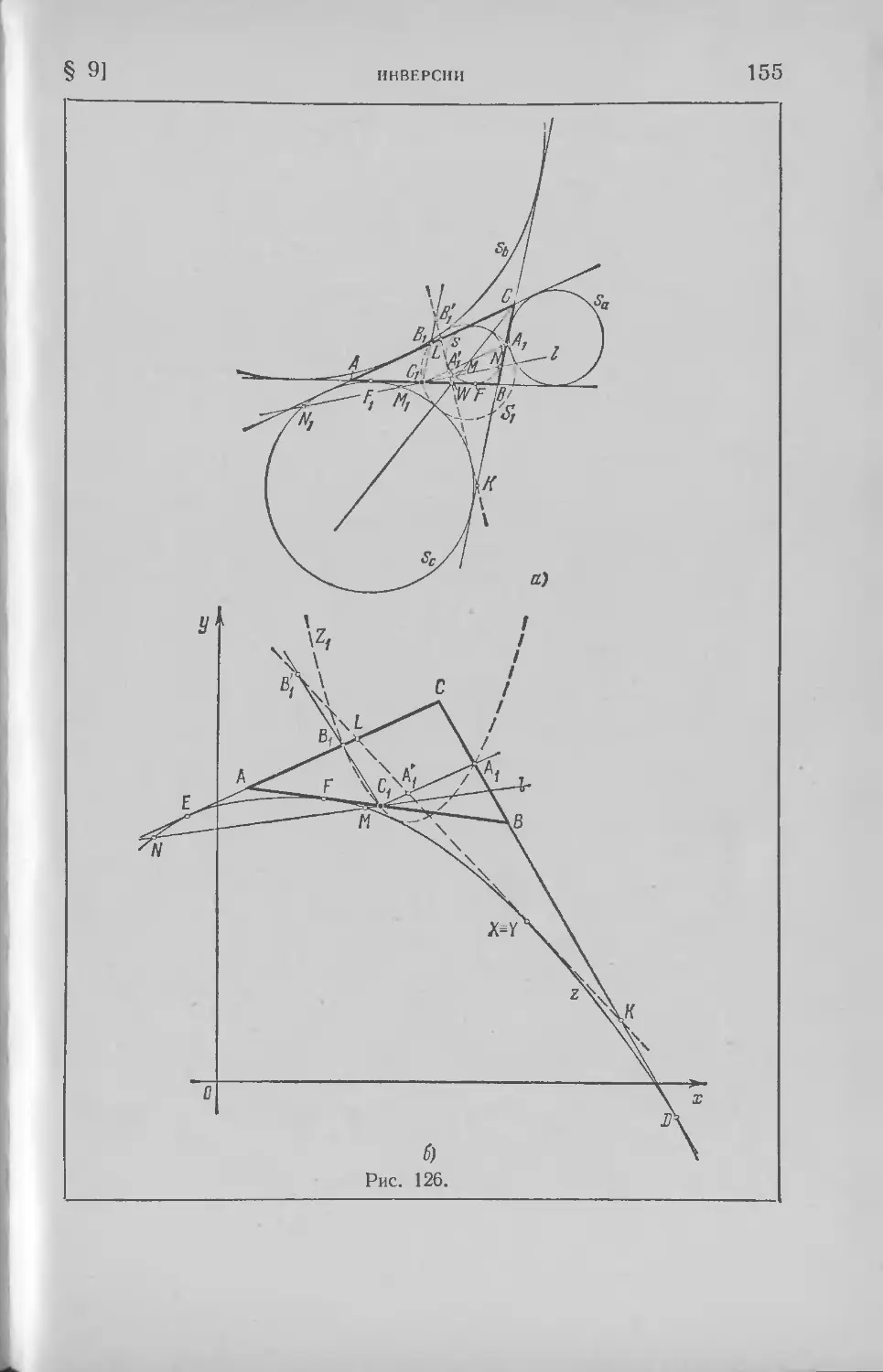
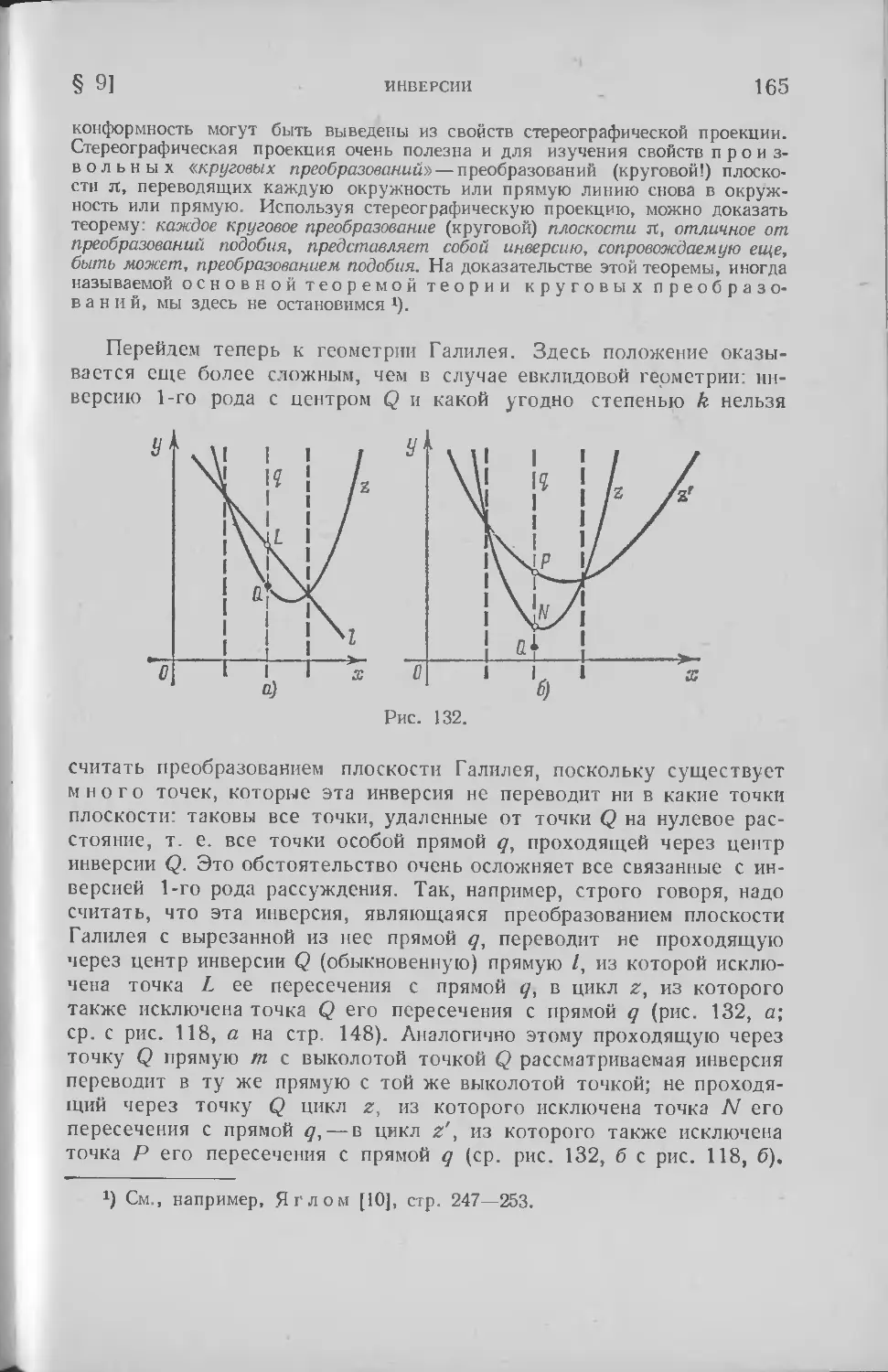
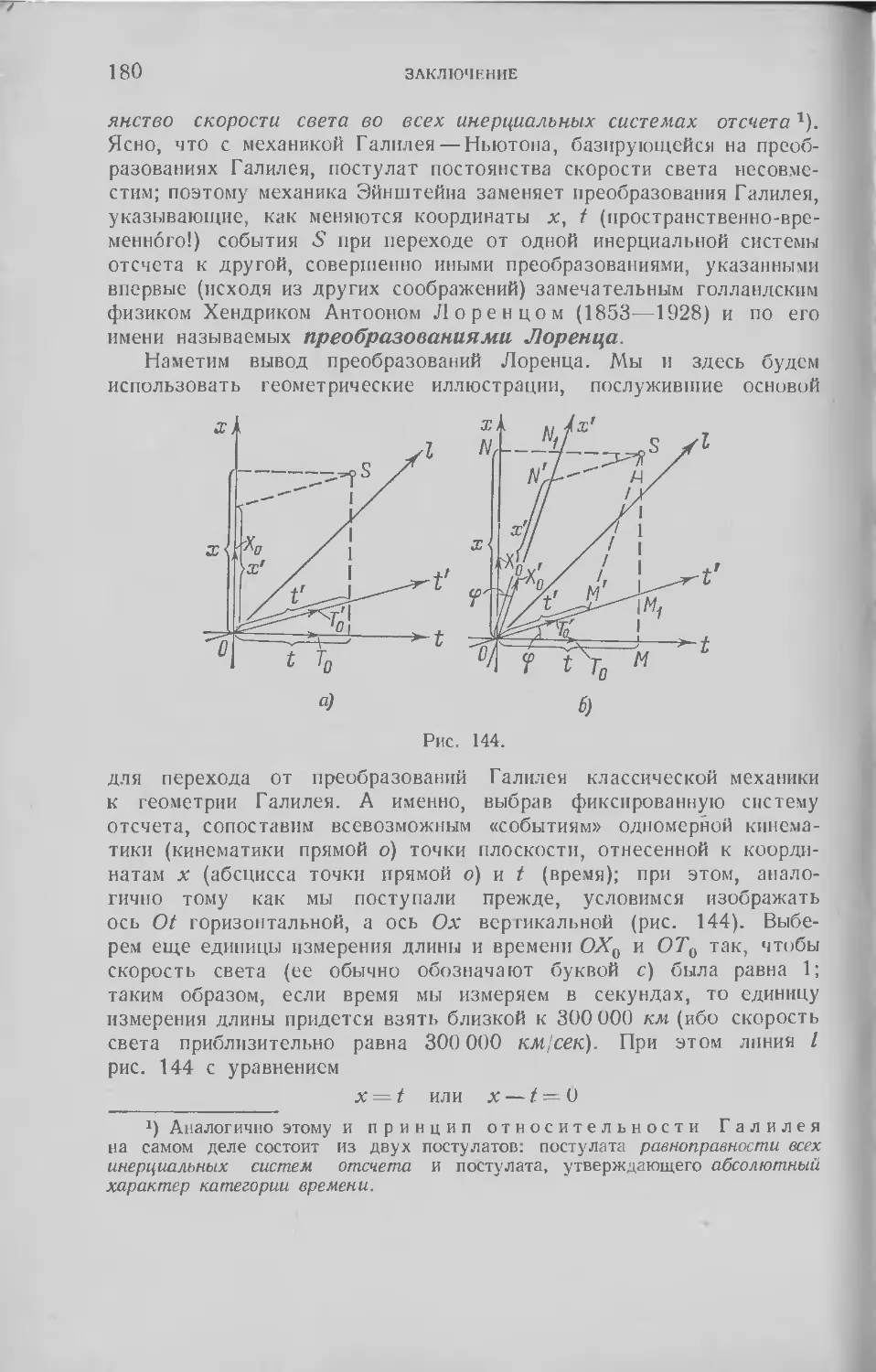
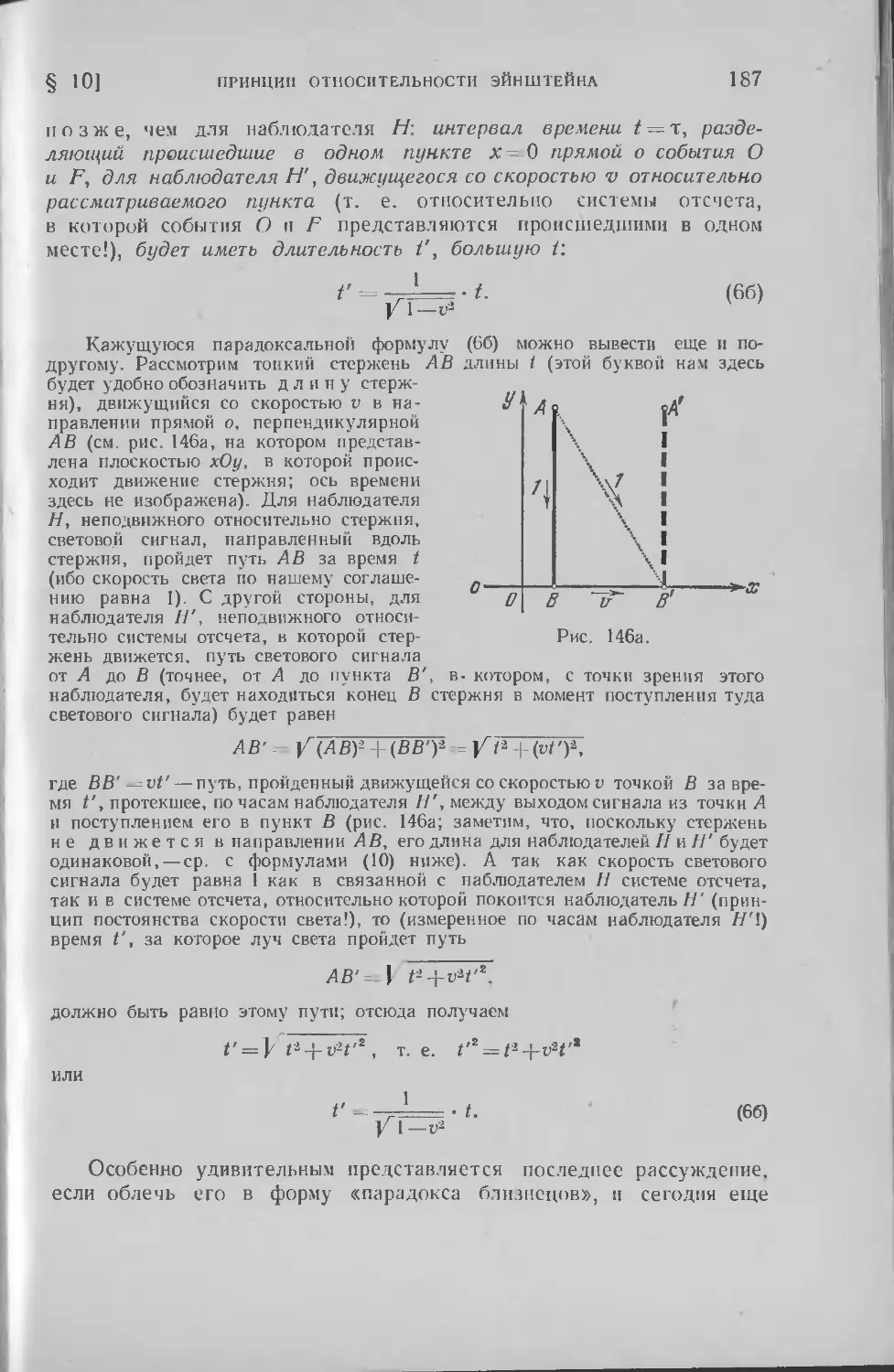
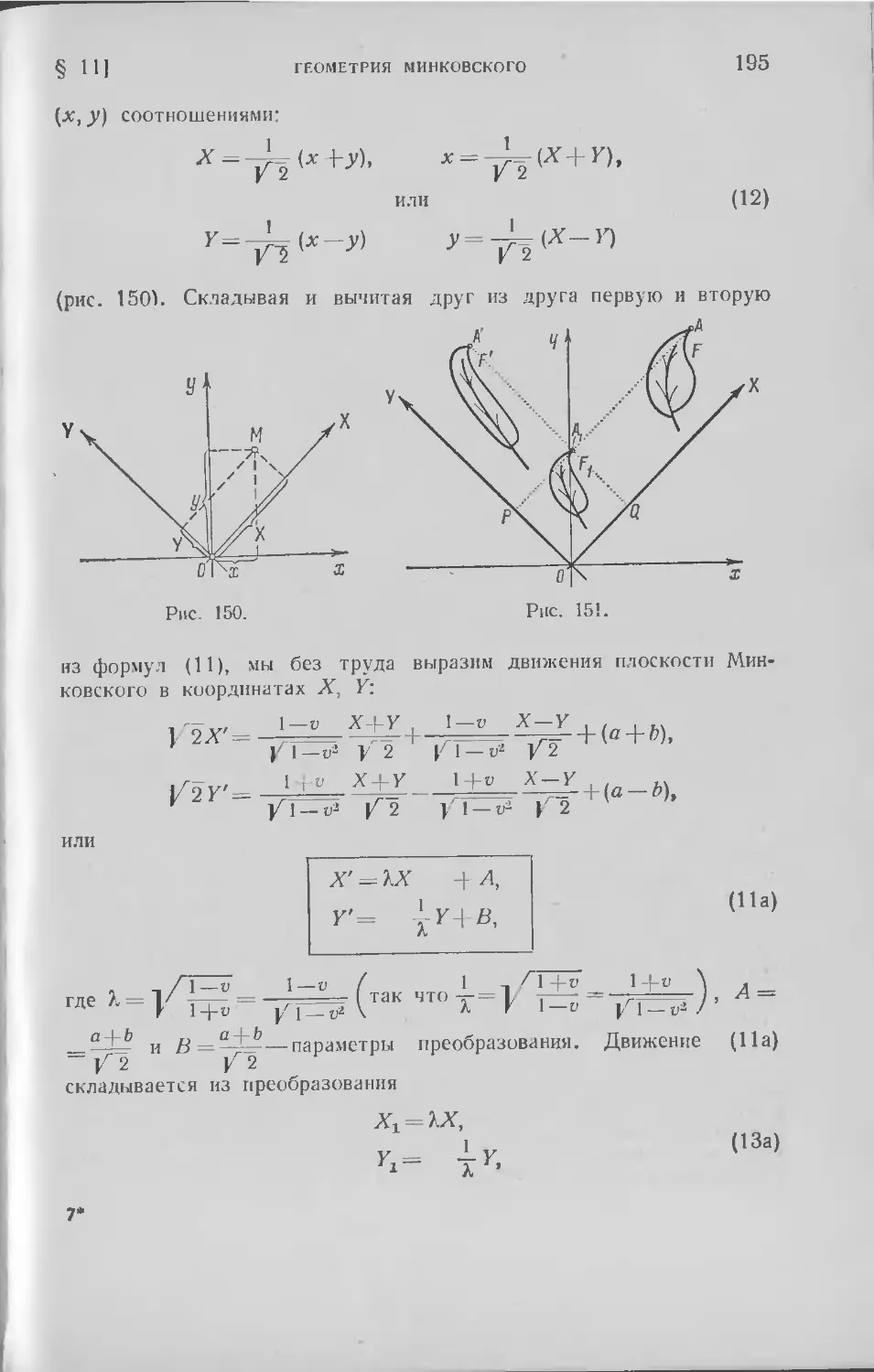
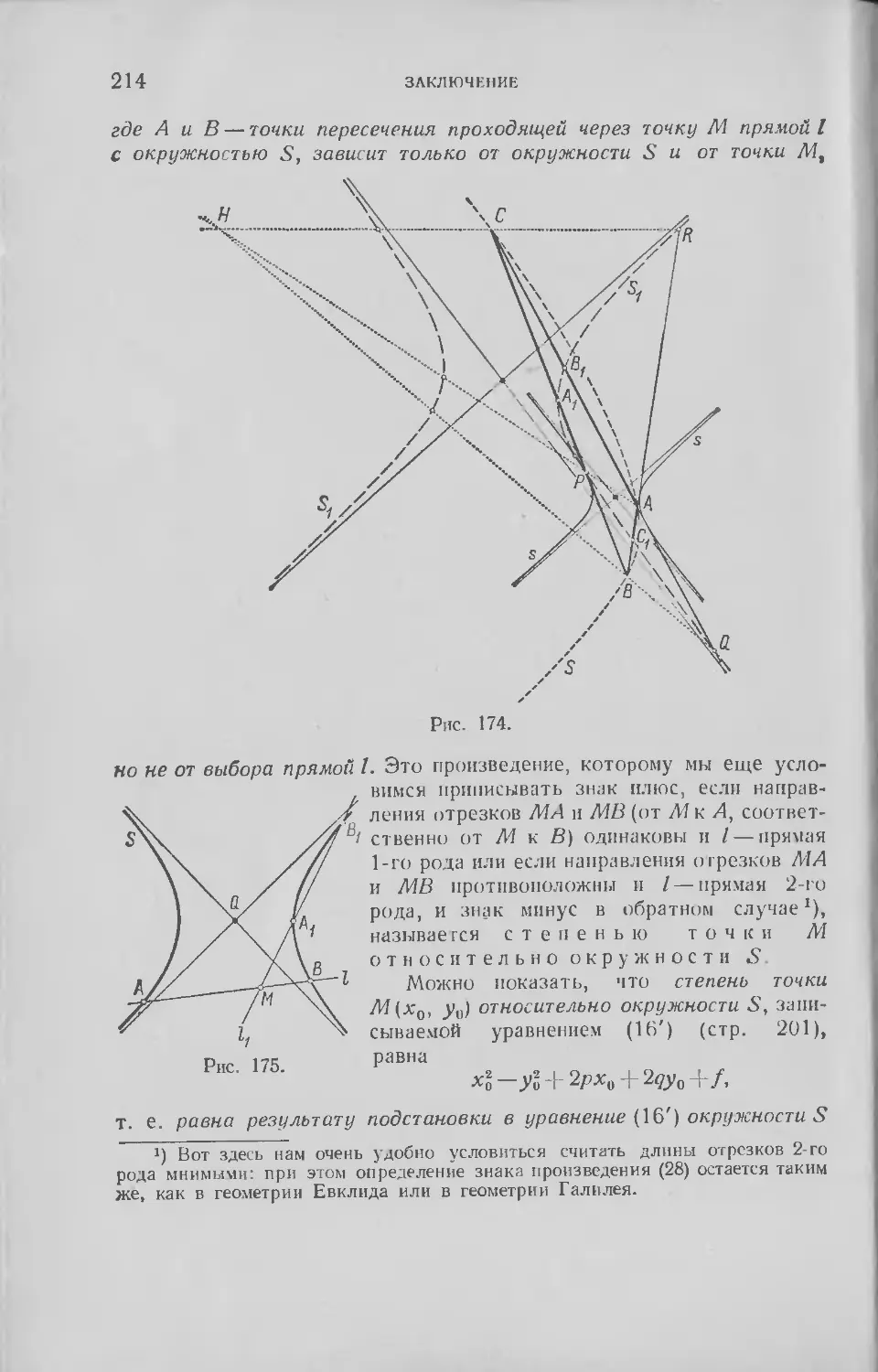
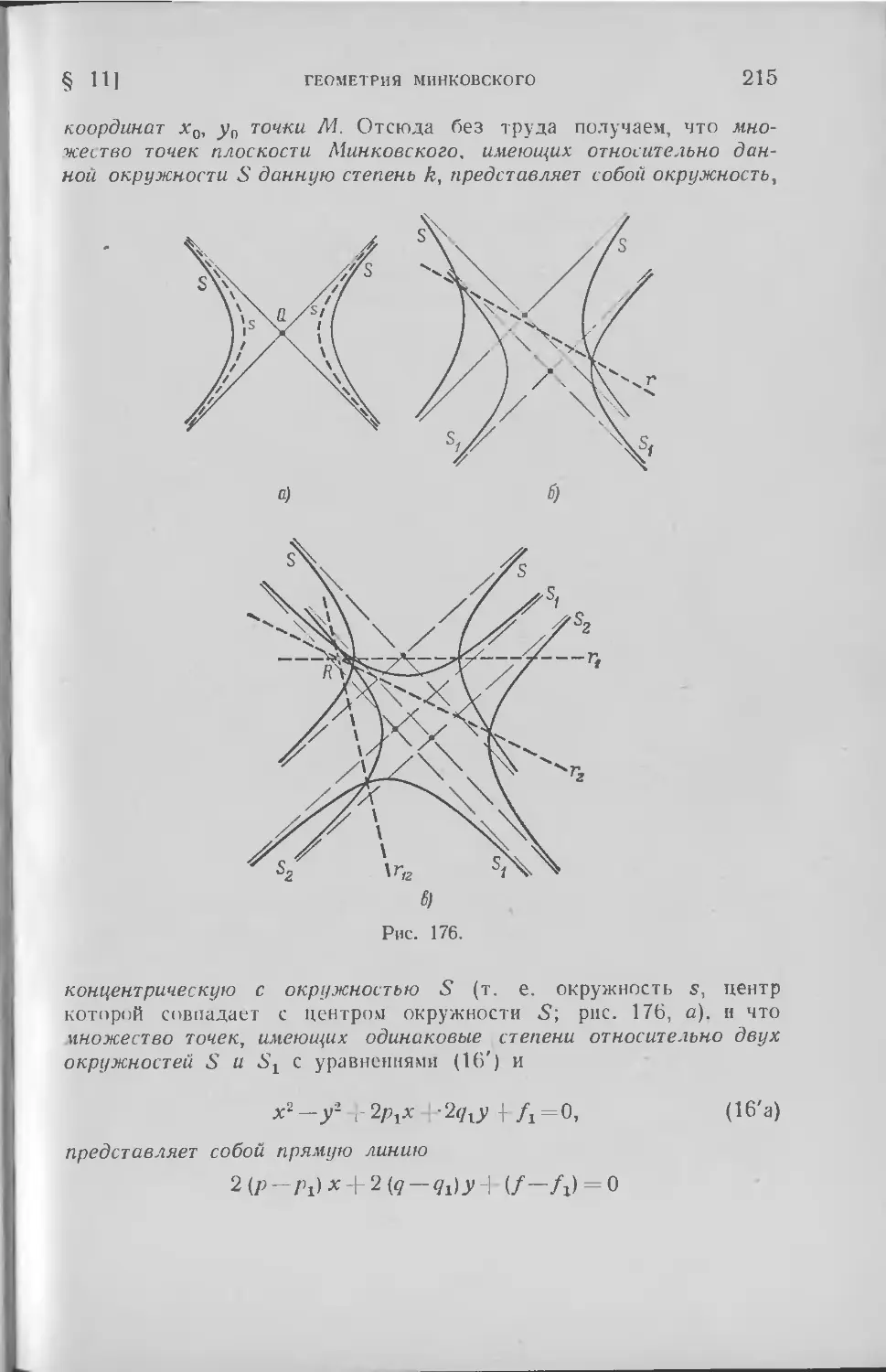
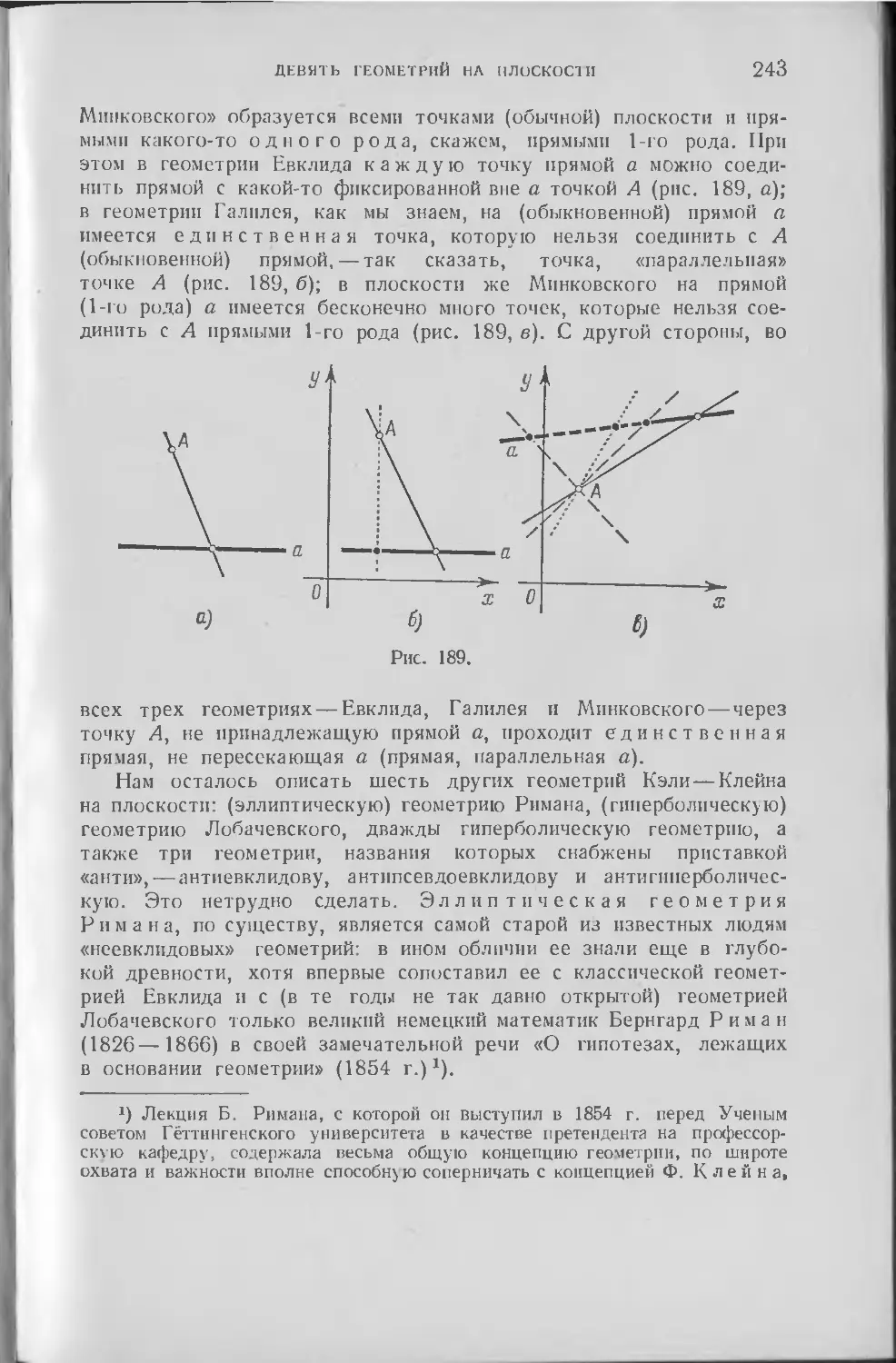
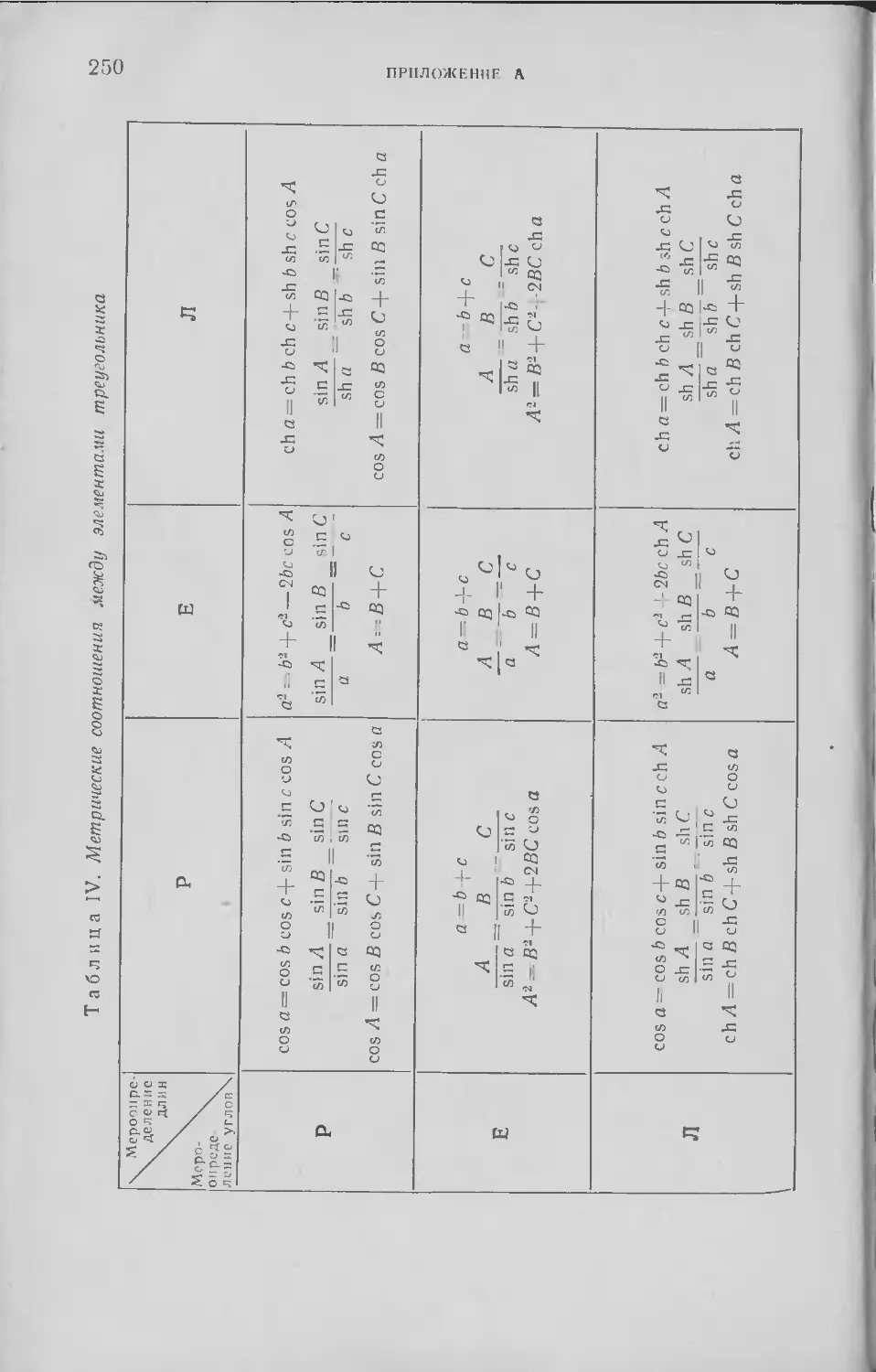
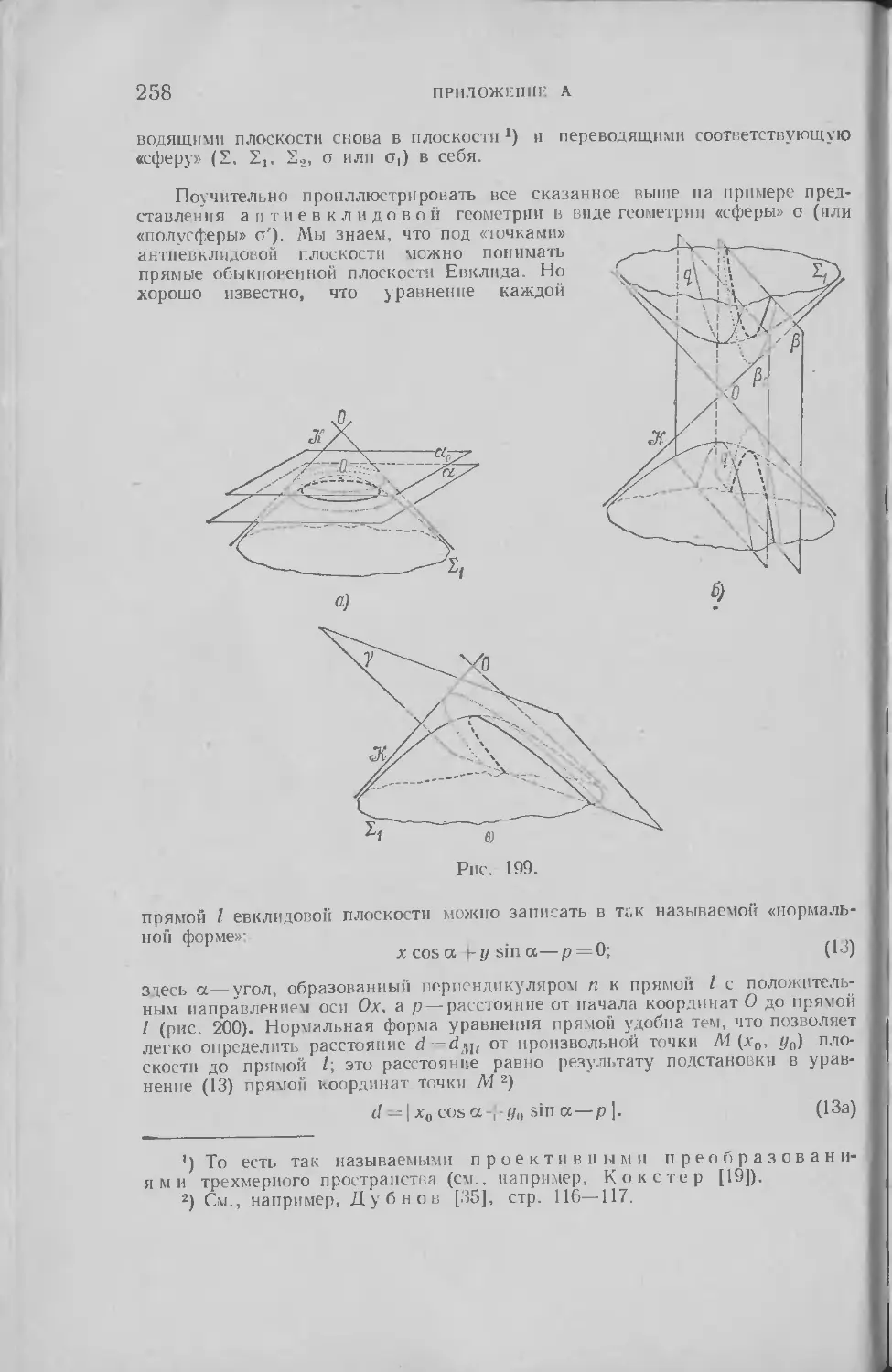
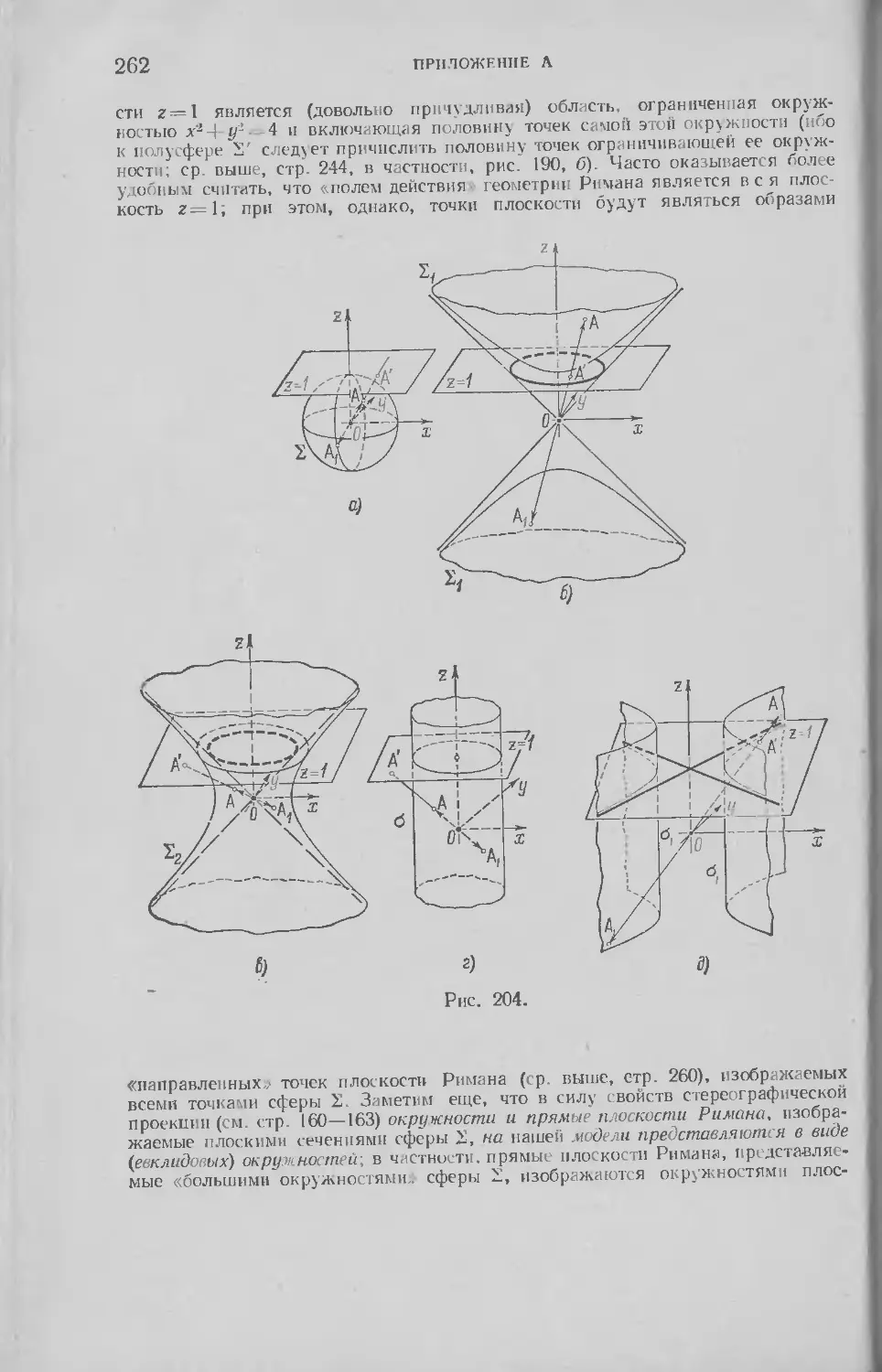
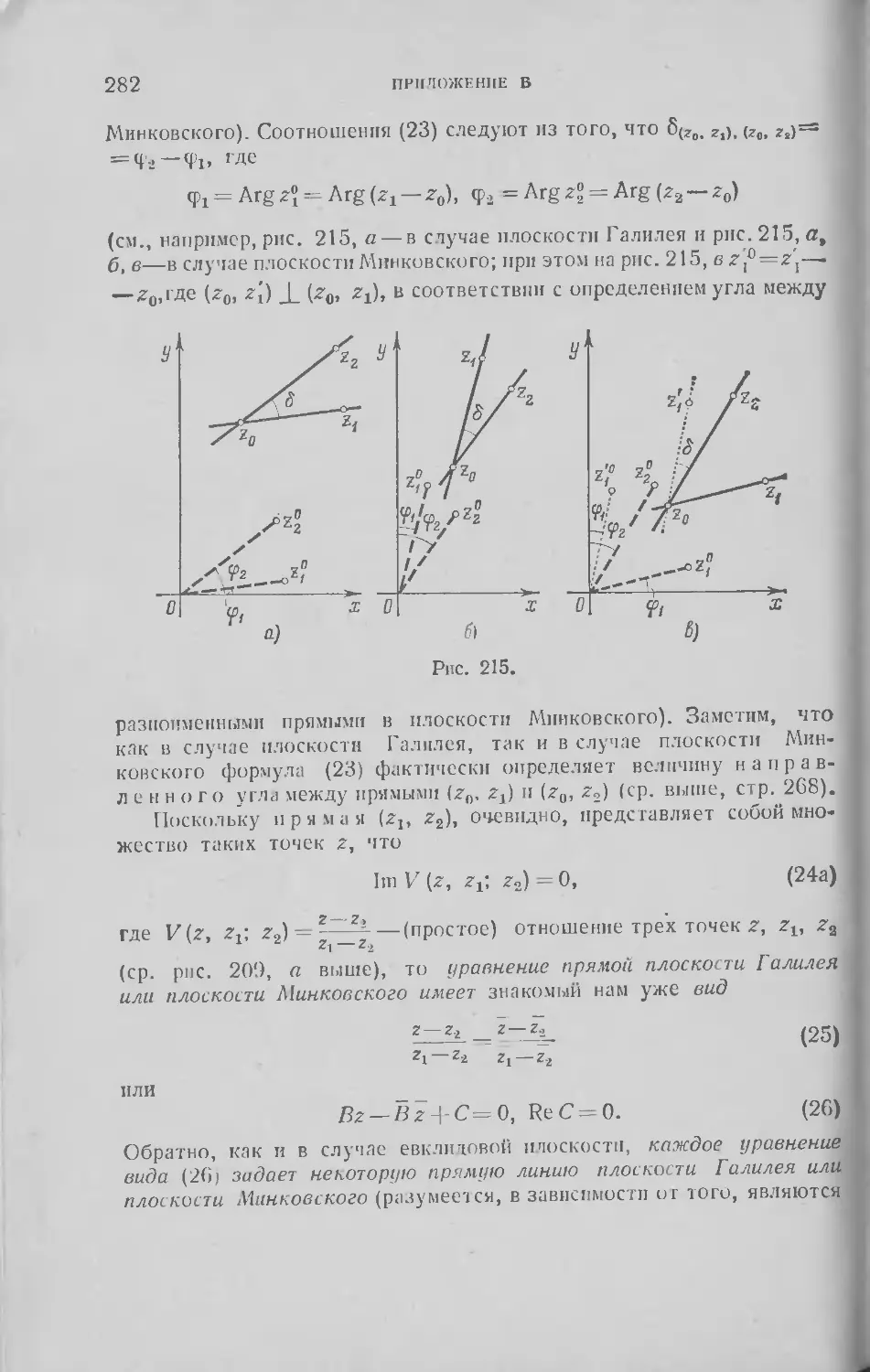
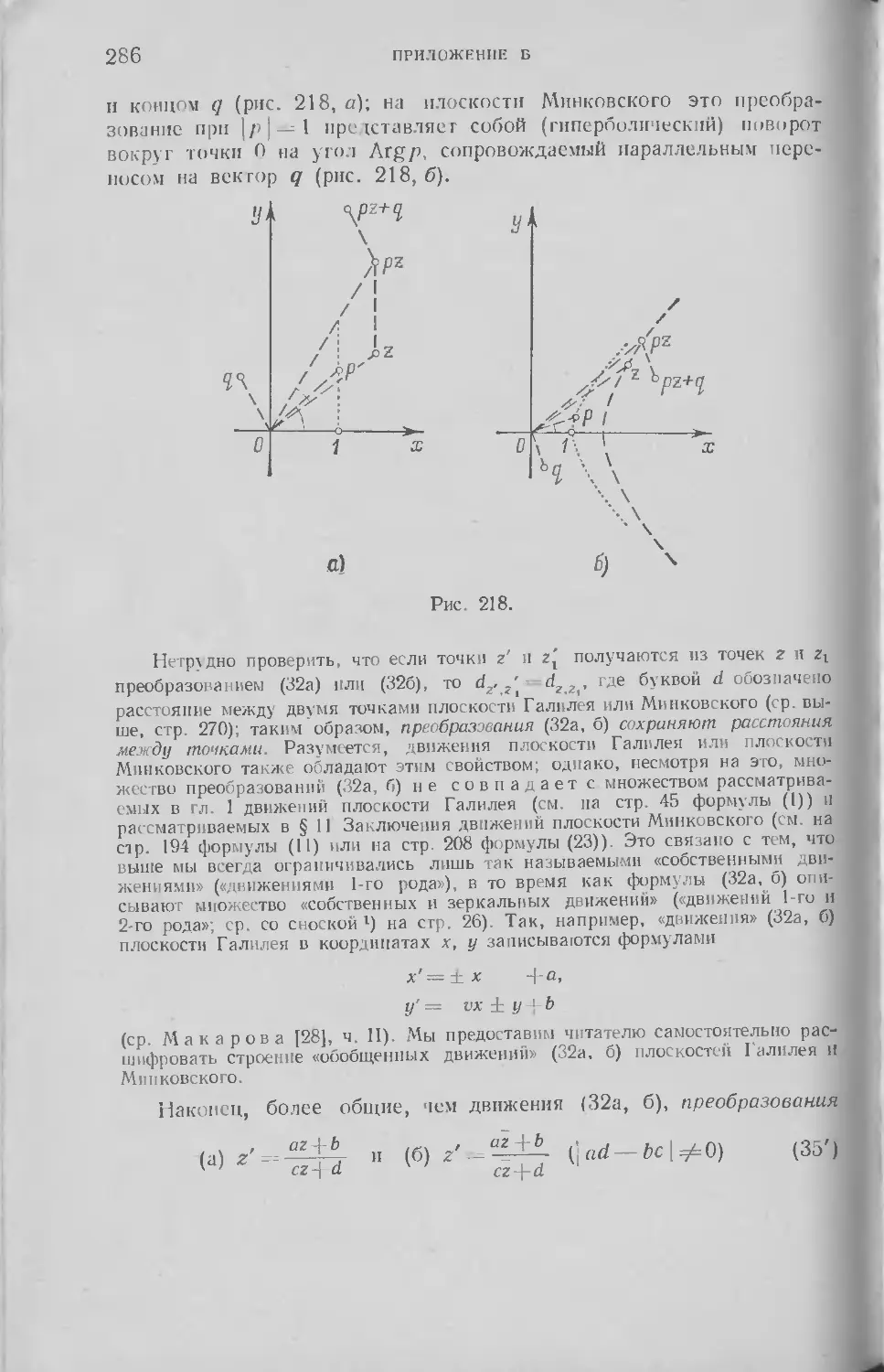
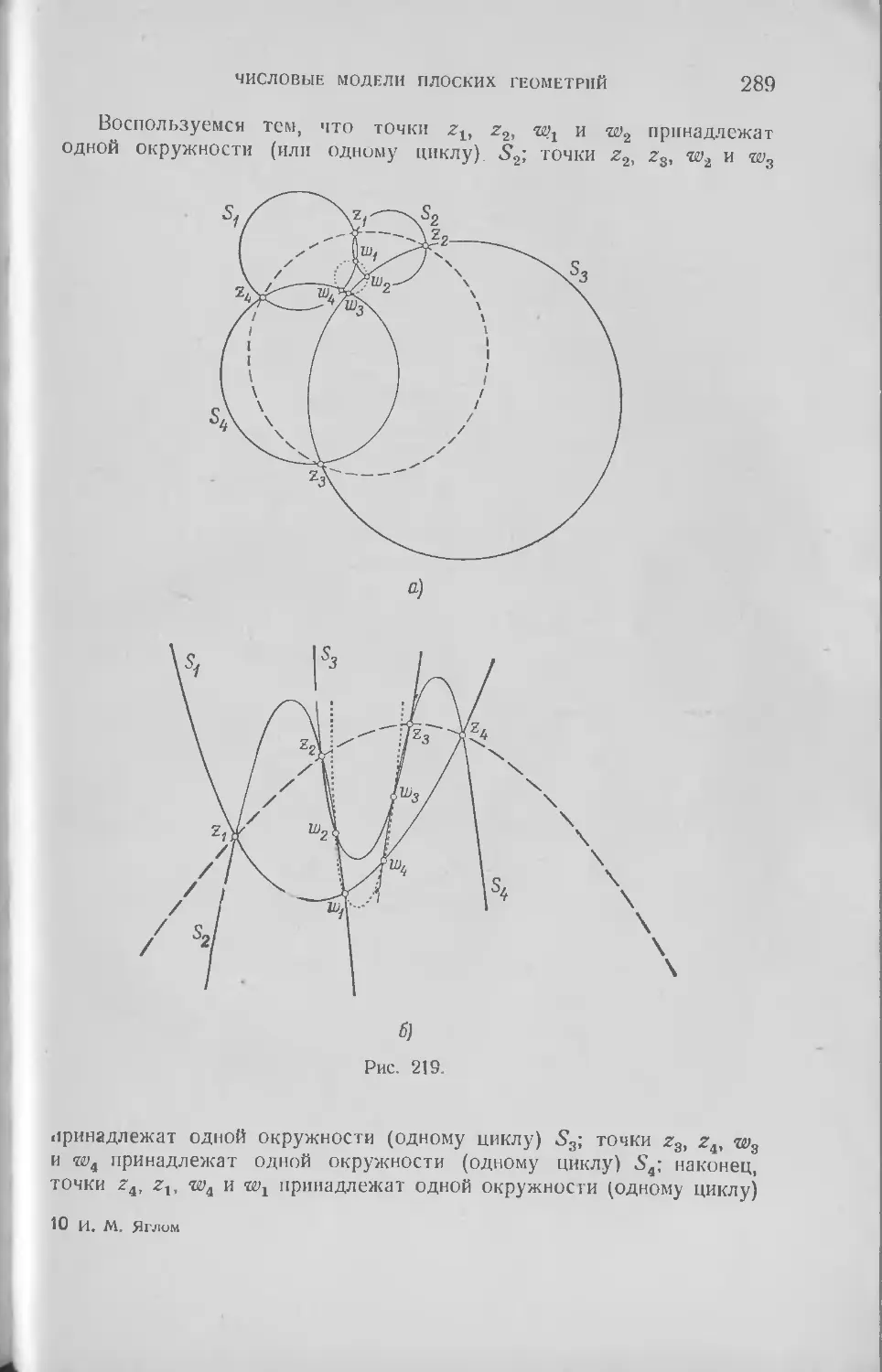
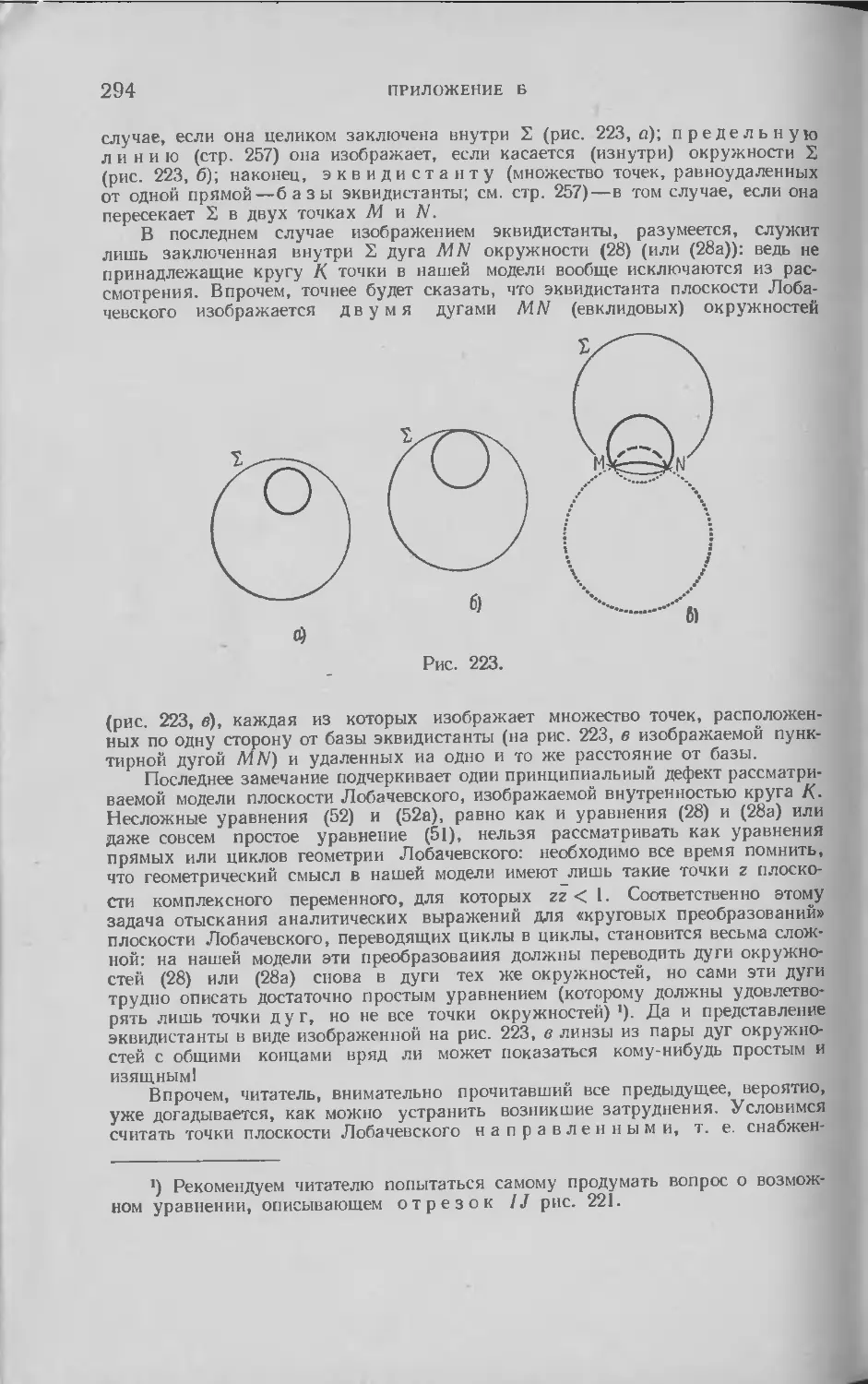
Текст

БИБЛИОТЕКА МАТЕМАТИЧЕСКОГО КРУЖКА
ВЫПУСК И
НМ.Яглом
ПРИНЦИП
ОТНОСИТЕЛЬНОСТИ
ГАЛИЛЕЯ
И НЕЕ ВИЛ И ЛОВА
ГЕОМЕТРИЯ
ИЗДАТЕЛЬСТВО «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
MOCK ВА 19 6 9

517.5
Я 29
УДК 513.81
Исаак Моисеевич Я алом
Принцип относительности Галилея и неевклидова геометрия
(Серия: «Библиотека математического кружка»)
М., 1969 г., 304 стр. с илл.
Редактор Ф. И. Кчзнер
Техн редактор К. Ф. Брудио Корректоры С. И. Емельянова, И. А. Шагес
Сдано в набор 15/1V 1969 г. Подписано к печати 27'Х 1969 г. Бумага 6С^-0С1 0.
Физ. печ. л. 19 Условн. печ. л. 19. Уч.-изд. л. 18,52.
Тираж 50 СОС экз. T-I3 293. Цена книги 56 коп. Заказ 84.
Издательство «Наука»
Главная редакция физико-математической литературы
Москва, В-7 1, Ленинский проспект, 15
Ордена Трудового Красного Знамени
Первая Образцовая типография имени А. А. Жданова
Главполиграфпрома Комитета по печати при Совете Министров СССР
Москва, М-54, Валовая, 28
2-2-2
167-09

ОГЛАВЛЕНИЕ
Предисловие . 4
Введение ... .13
§ 1. Что такое геометрия? . 13
§ 2. Что такое механика? 27
Глава 1. Расстояния и углы; треугольники и четырехугольники . 45
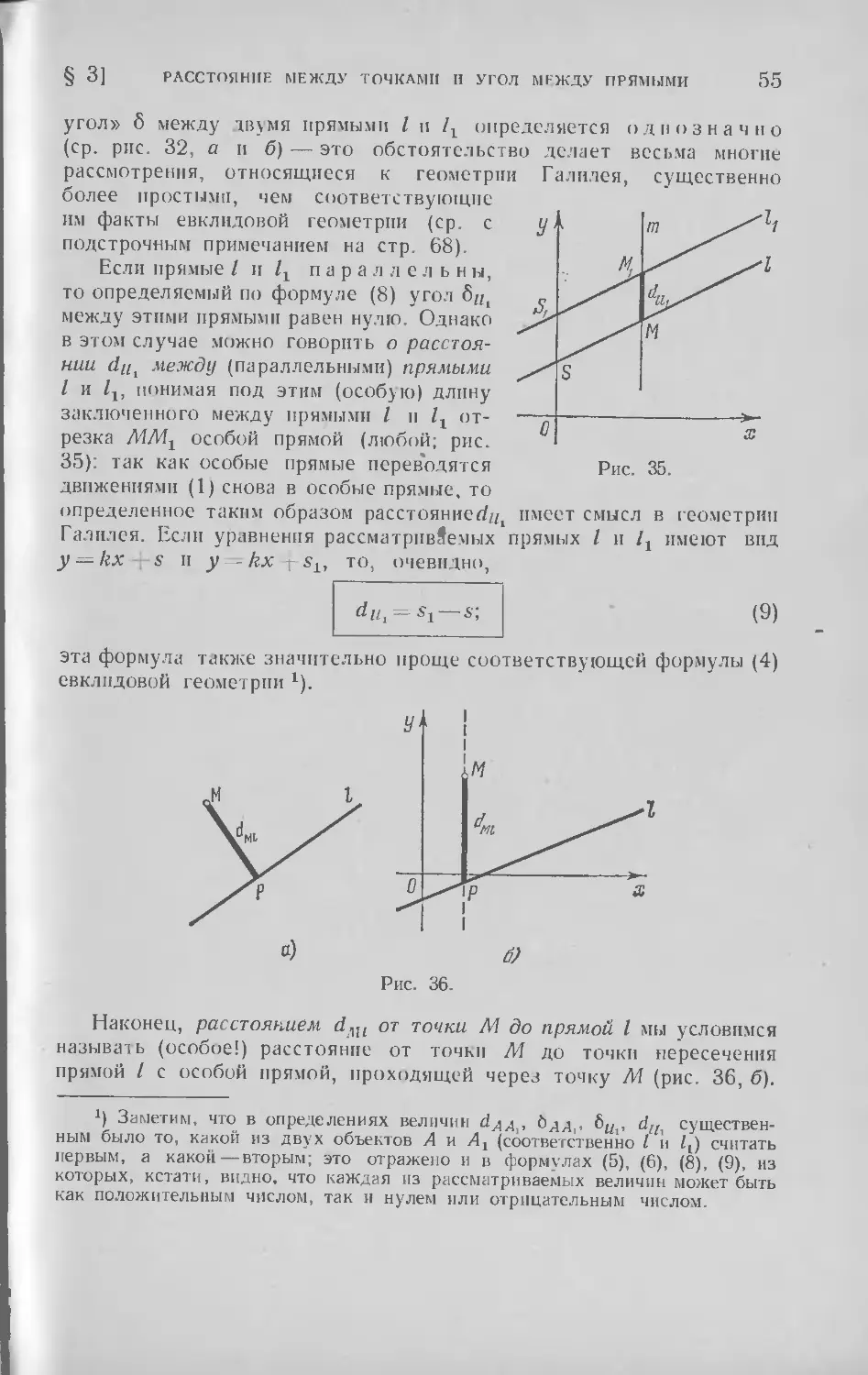
§ 3. Расстояние между точками и угол между прямыми 45
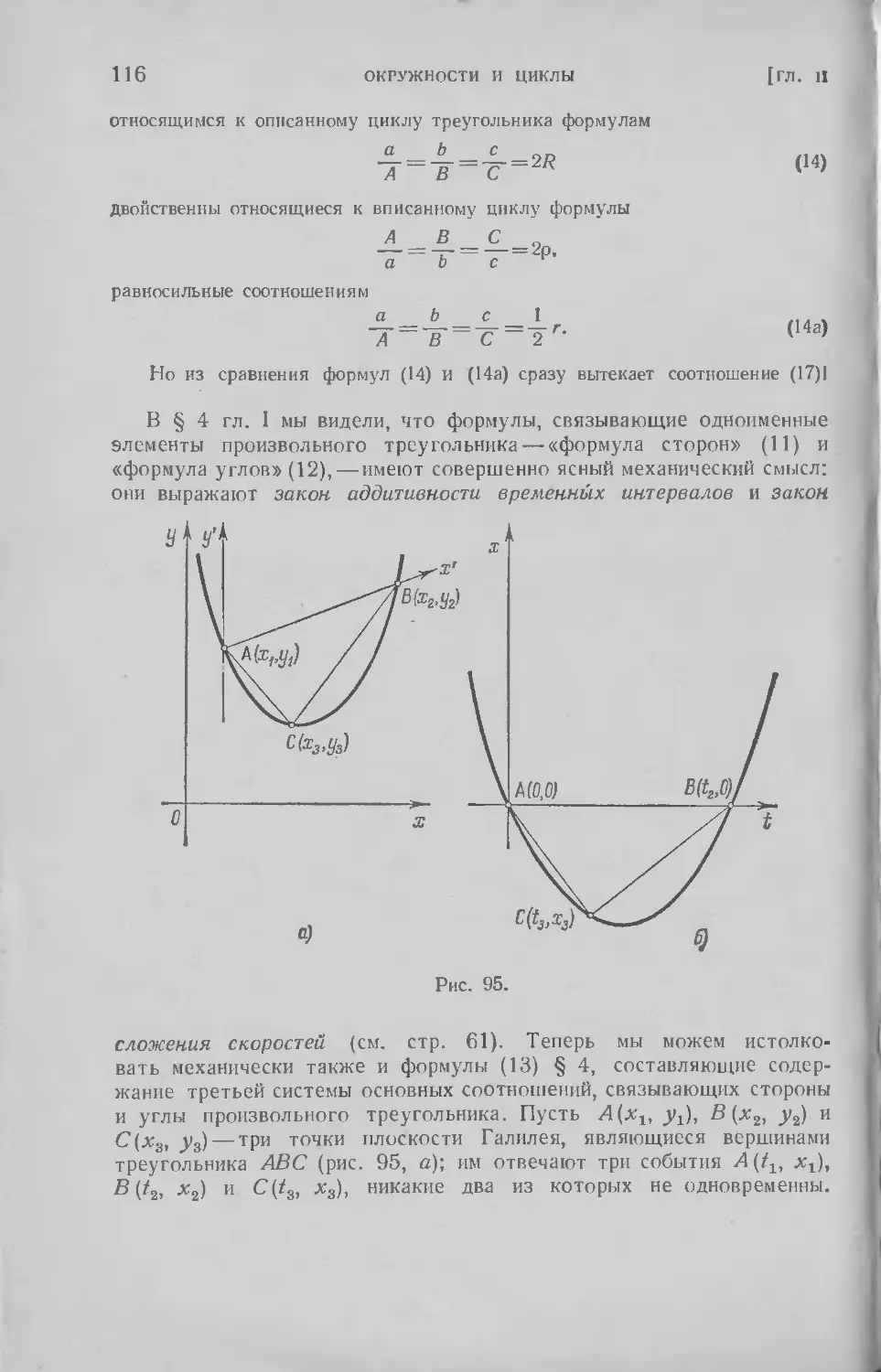
§ 4. Треугольник . ... 60
§ 5. Принцип двойственности; антипараллелограмм и антитрапецня 67
Глава П. Окружности и циклы ... .83
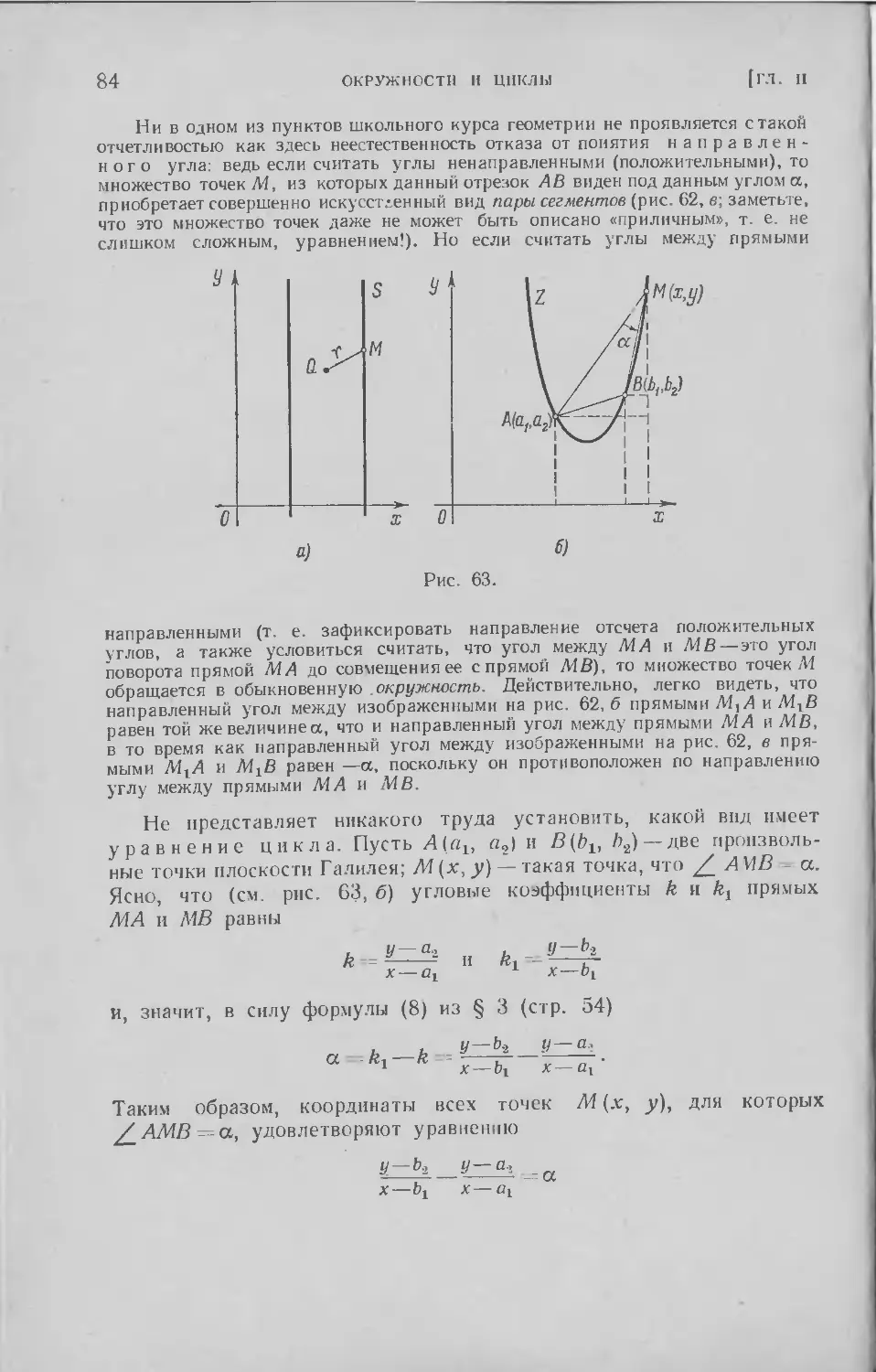
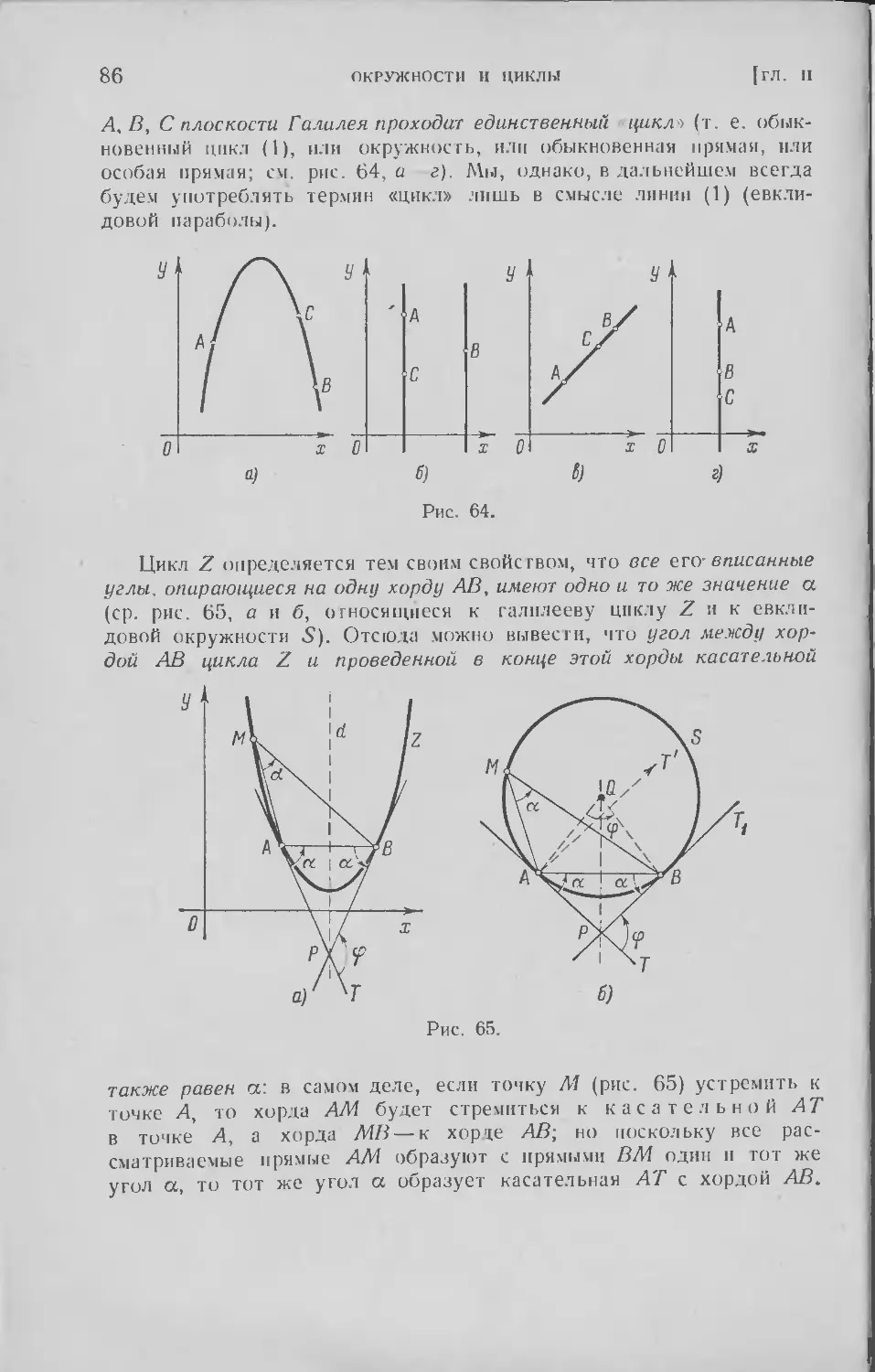
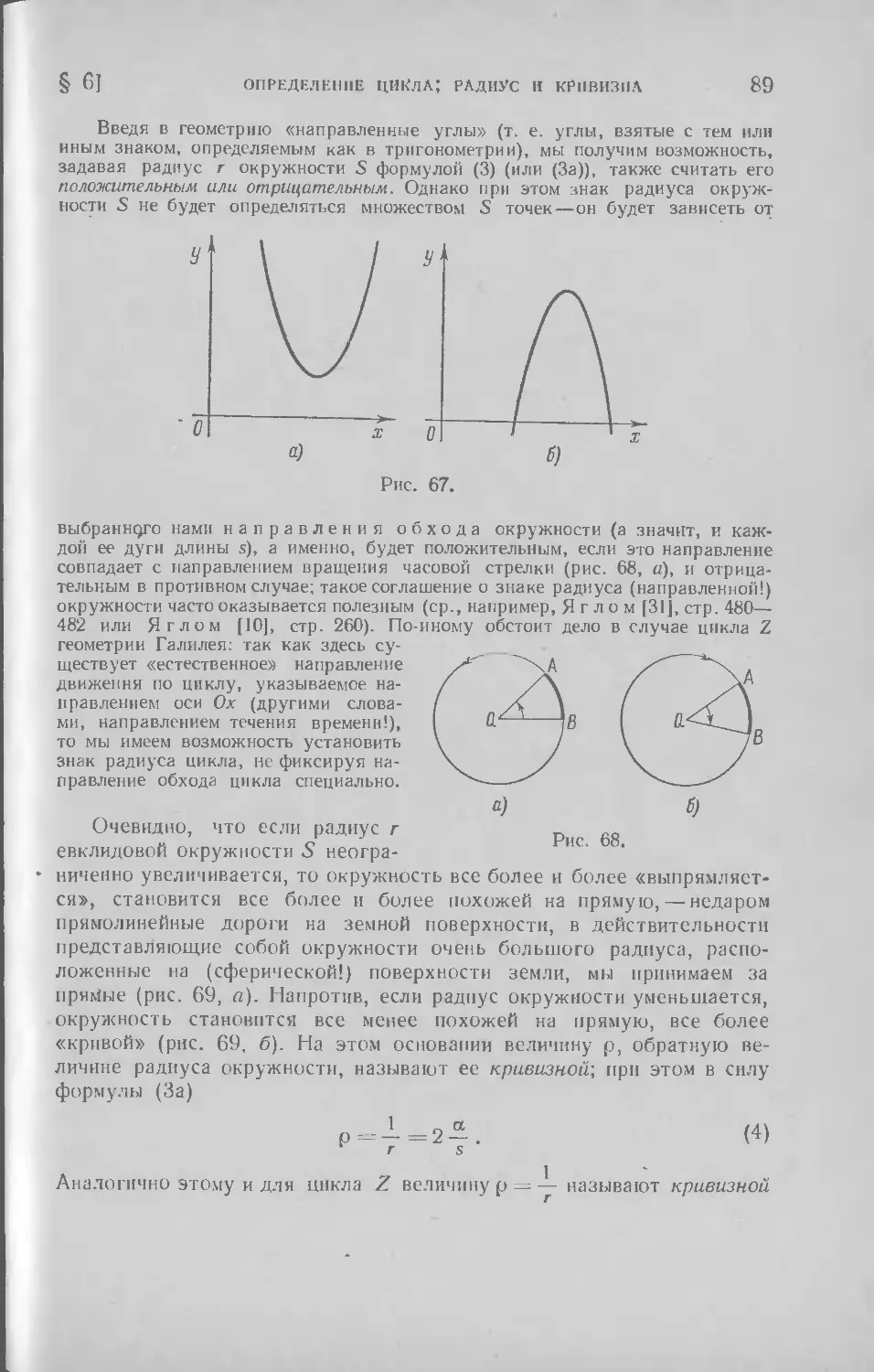
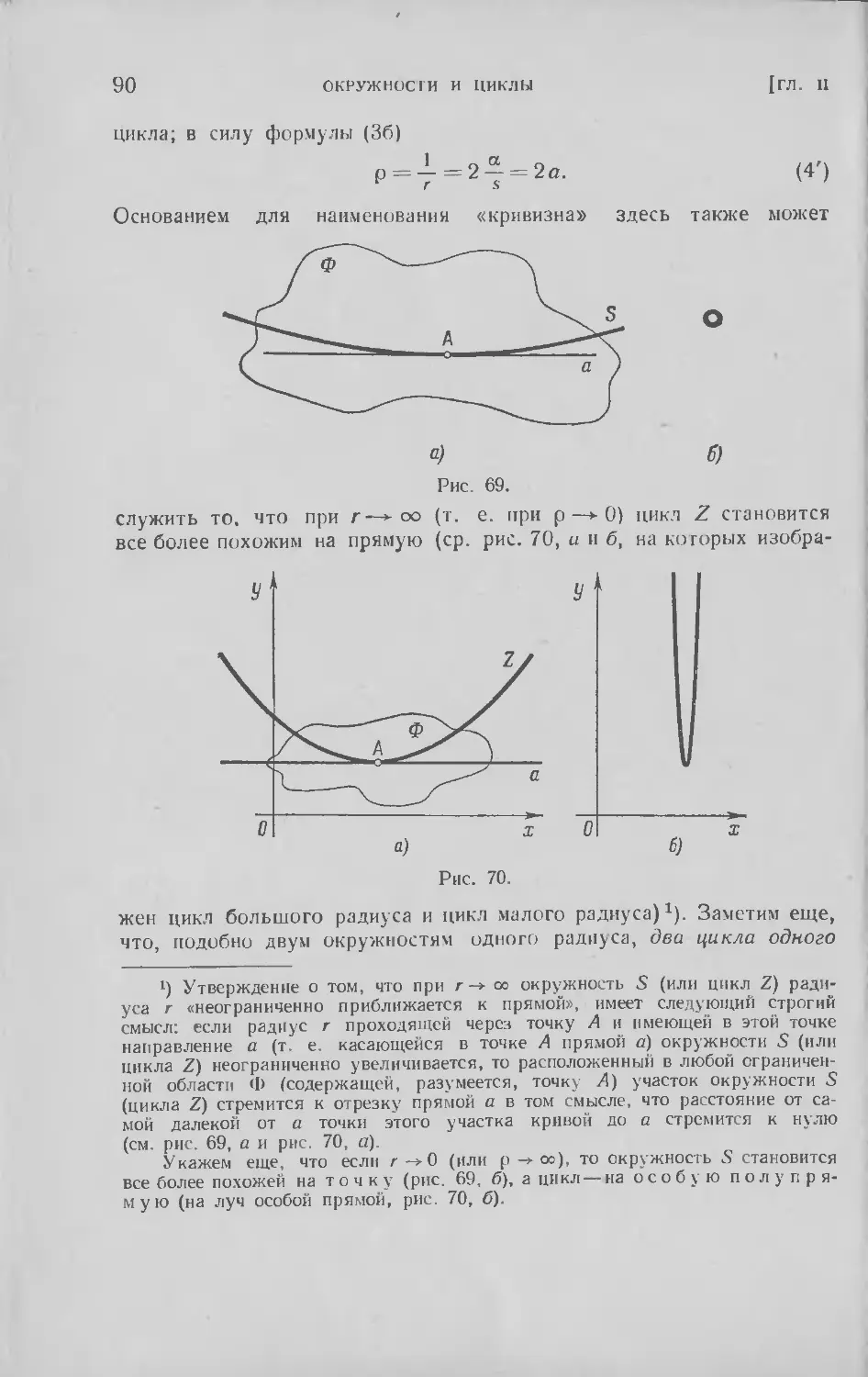
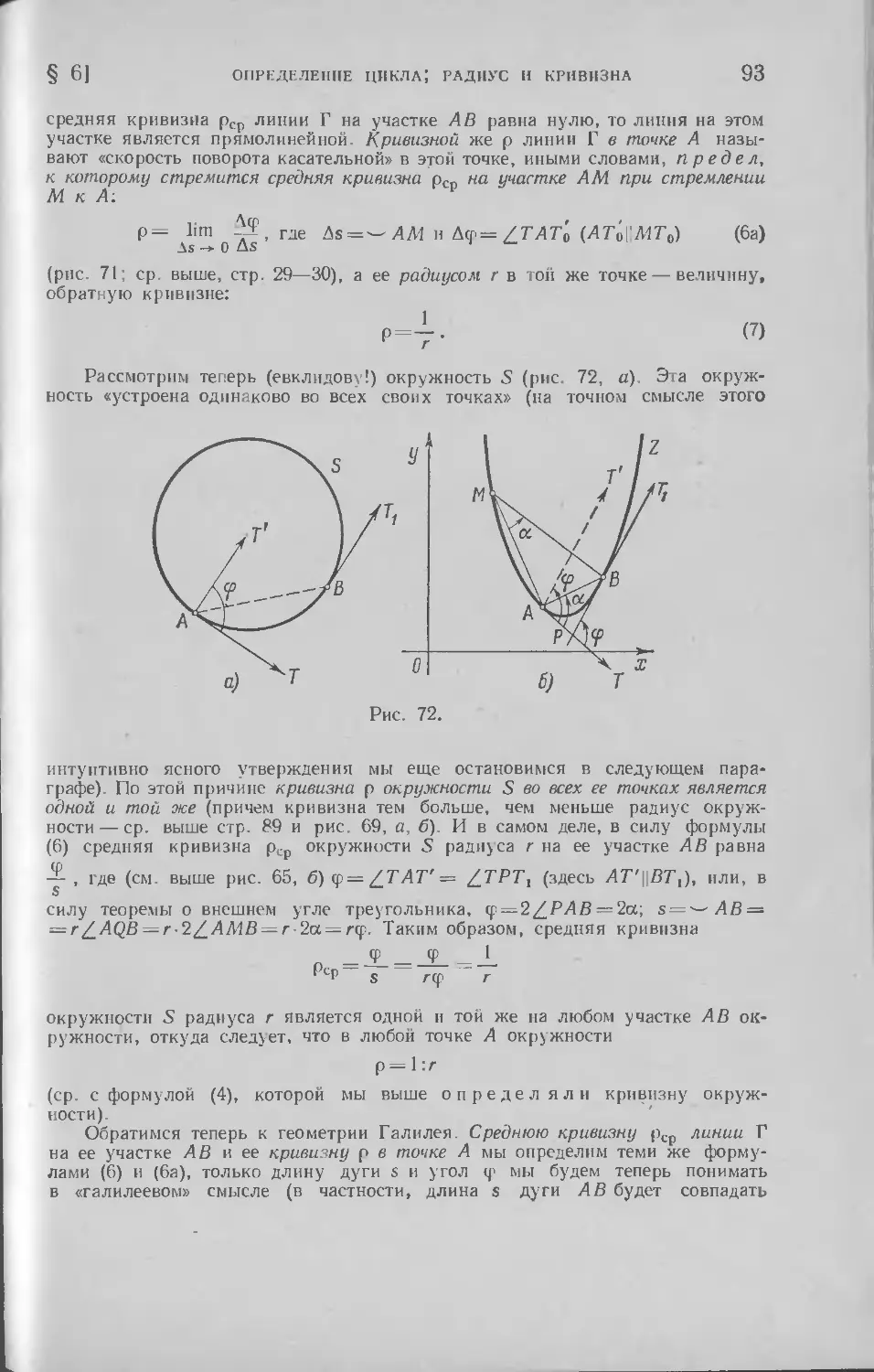
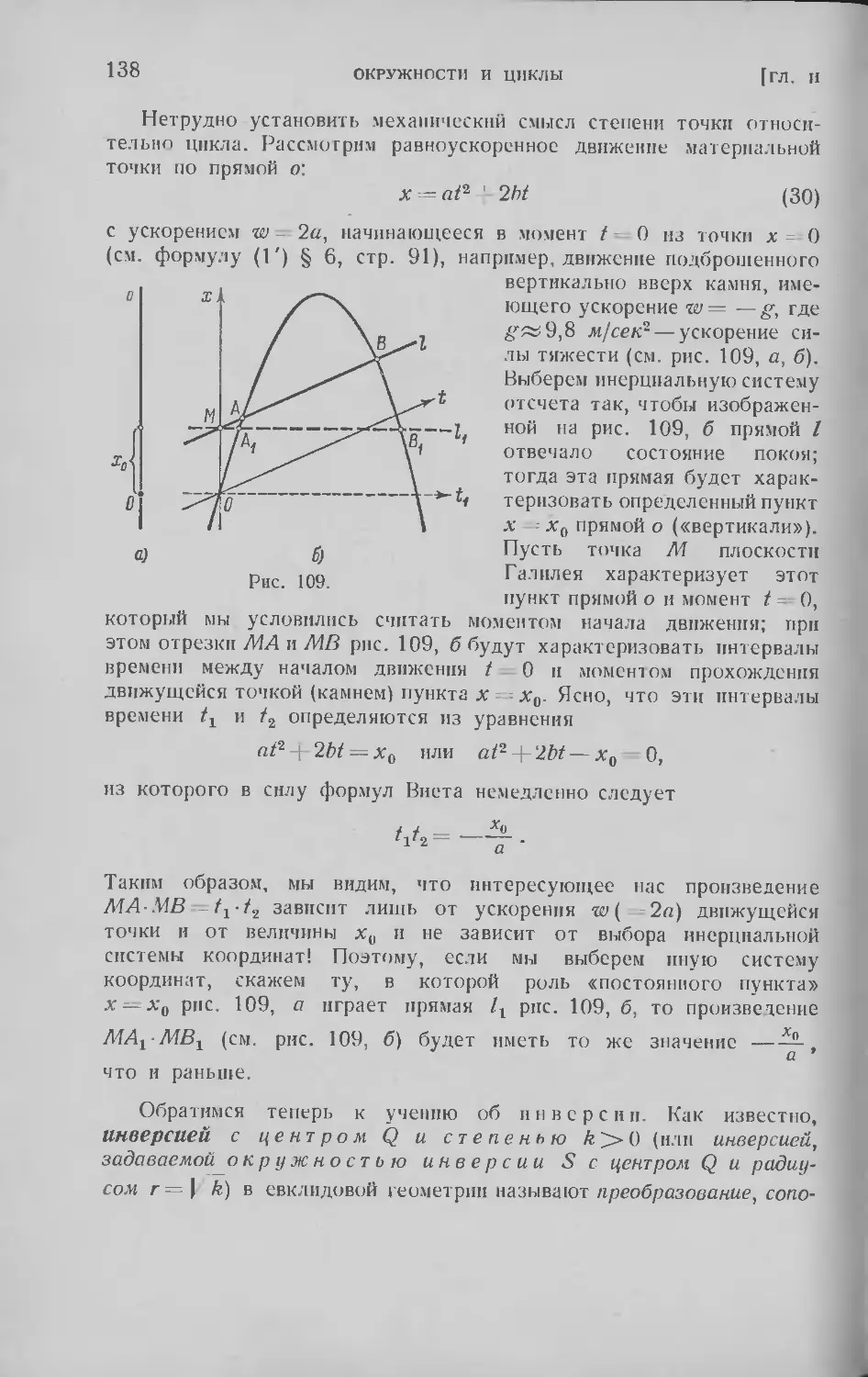
§ 6. Определение цикла; радиус и кривизна . 83
§ 7. Скольжение цикла по себе; диаметры цикла .... 98
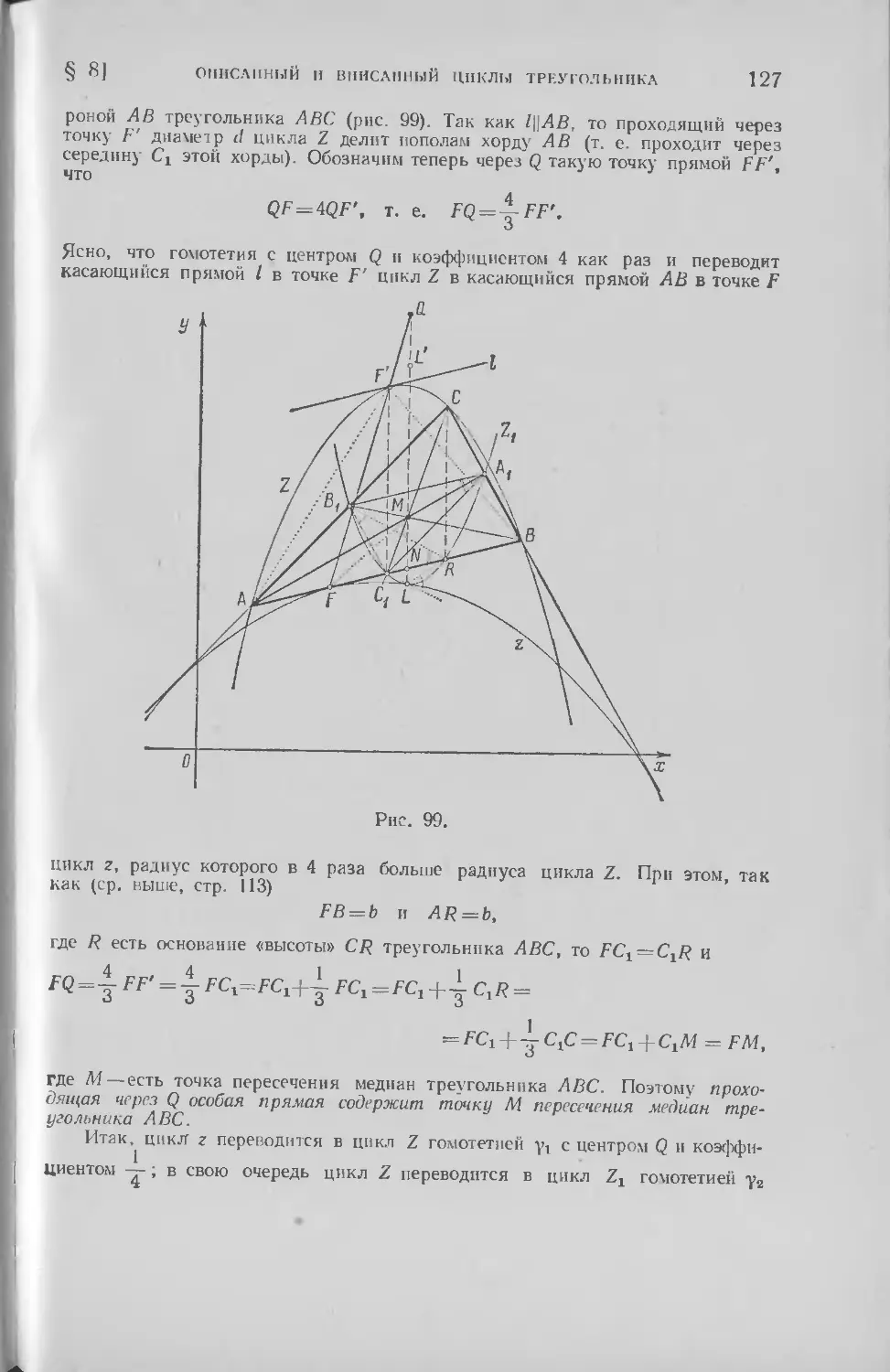
§ 8. Описанный и вписанный циклы треугольника . . .112
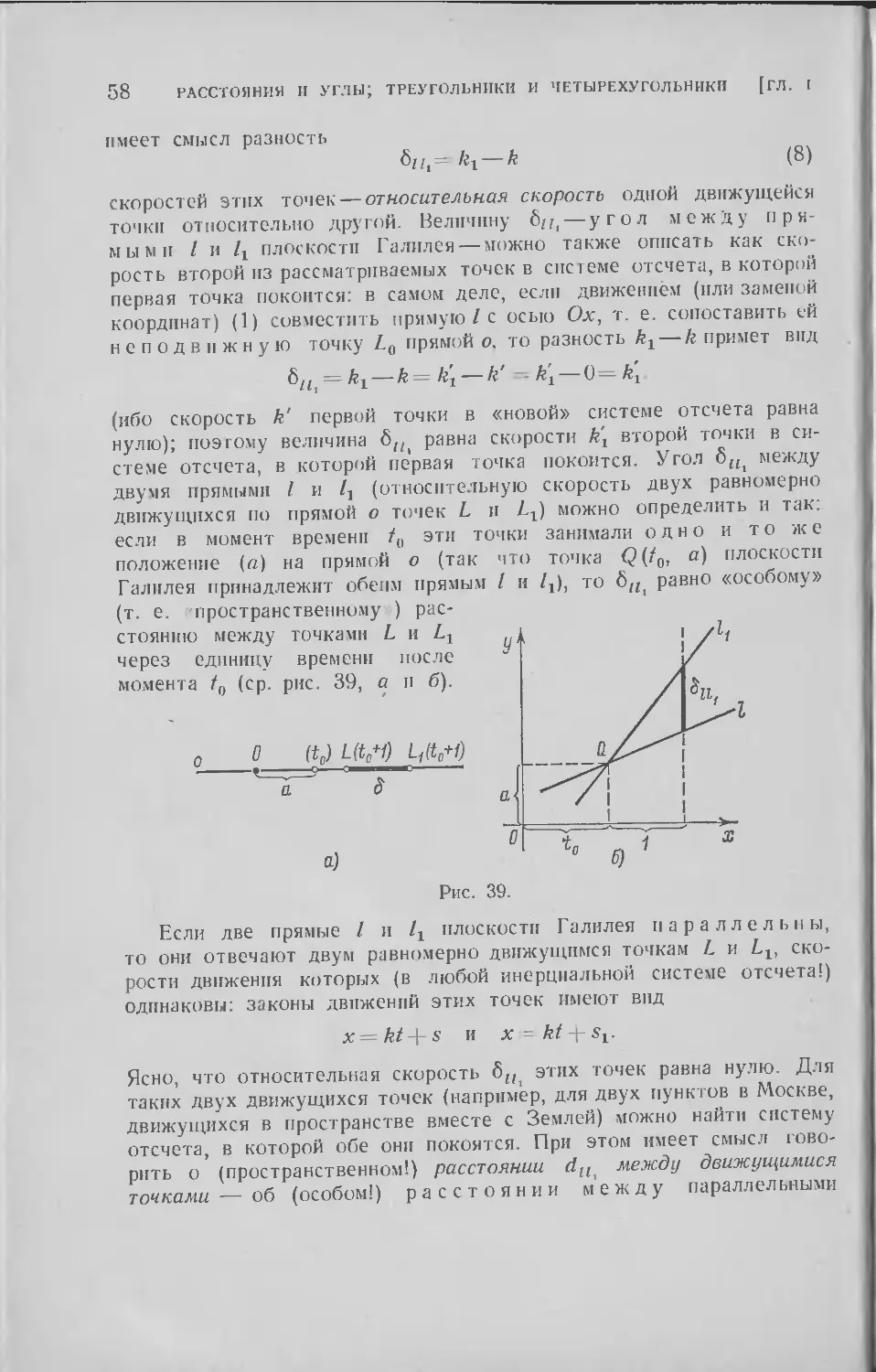
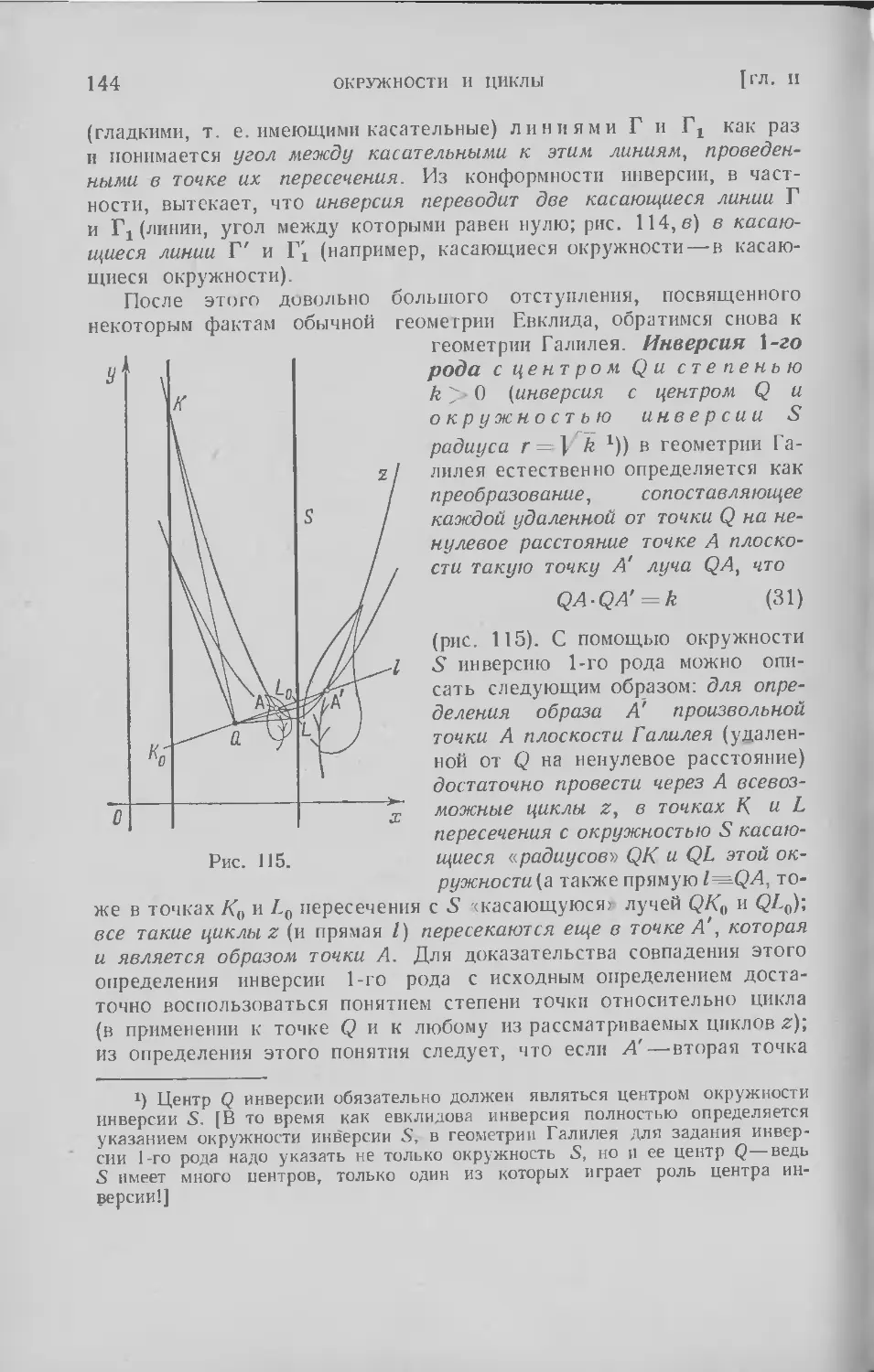
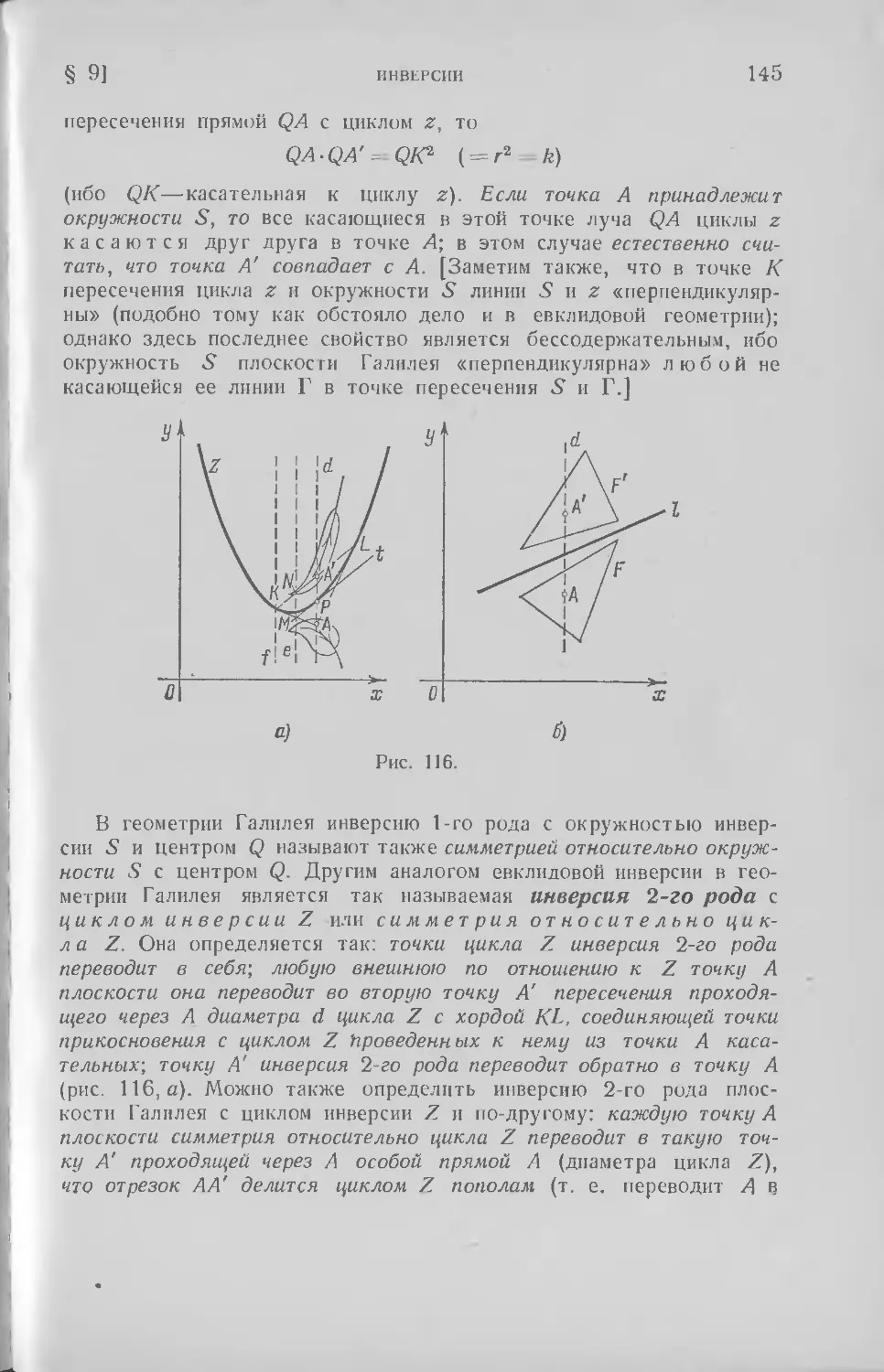
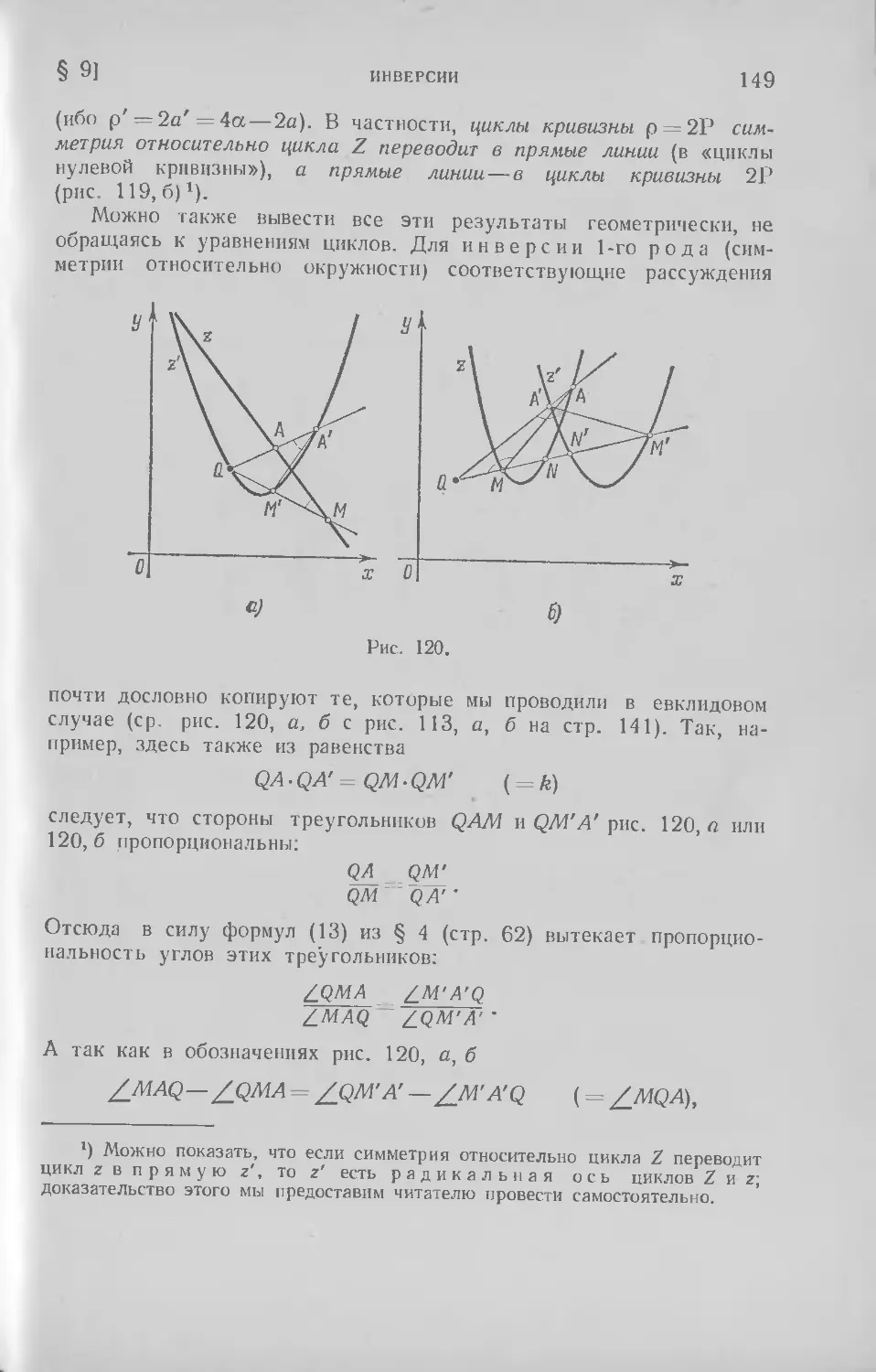
§ 9. Степень точки относительно окружности или цикла; инверсии 130
Заключение . 175
§ 10. Принцип относительности Эйнштейна и преобразования Ло-
Лоренца. . . . 175
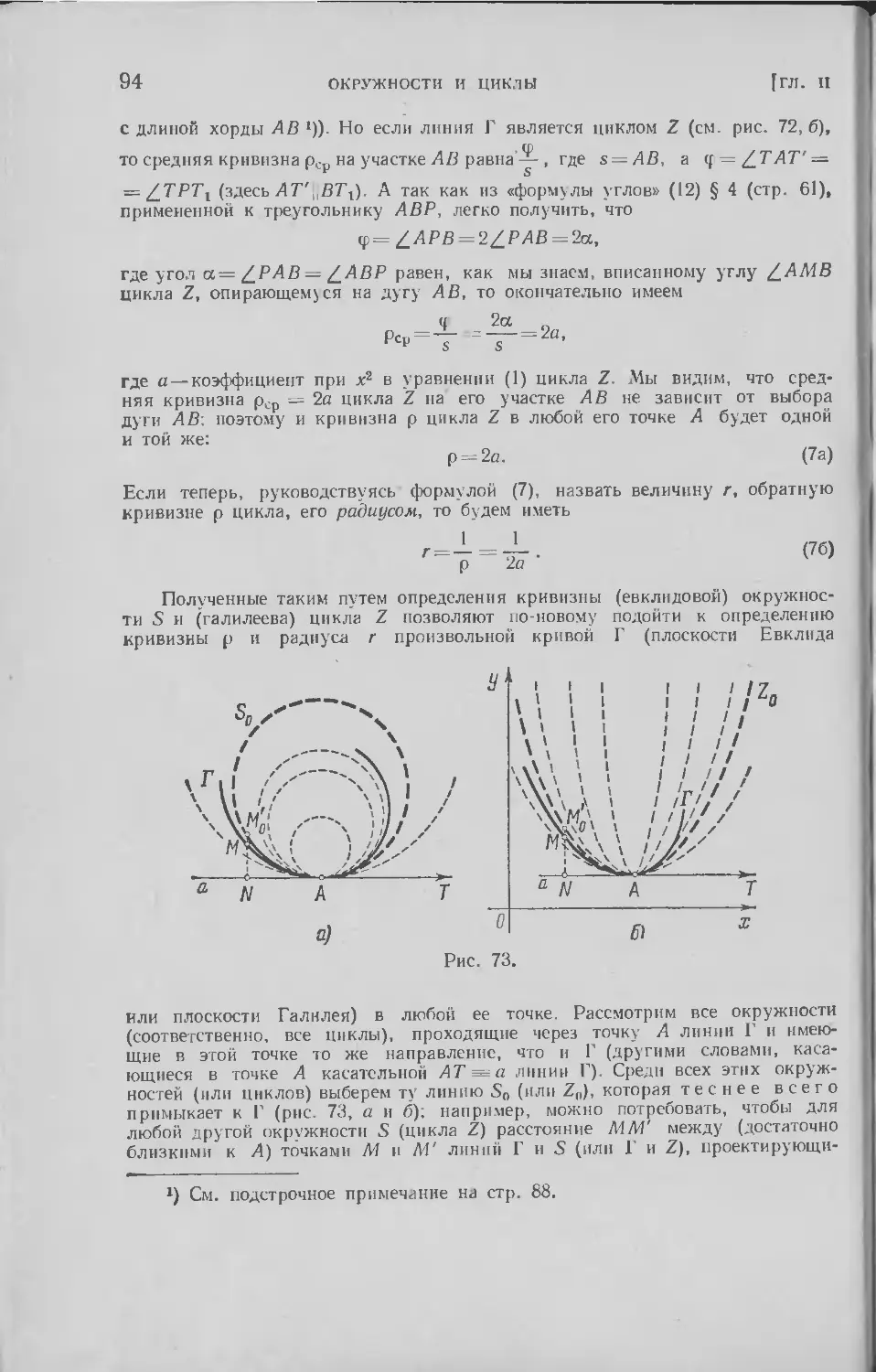
§ 11. Геометрия Минковского . . . . .... 193
§ 12. Геометрия Галилея как предельный случай геометрий Евкли-
Евклида и Минковского . 222
Приложение А. Девять геометрий на плоскости . . . 235
Приложение Б. Числовые модели плоских геометрий . . 266
Литература 300
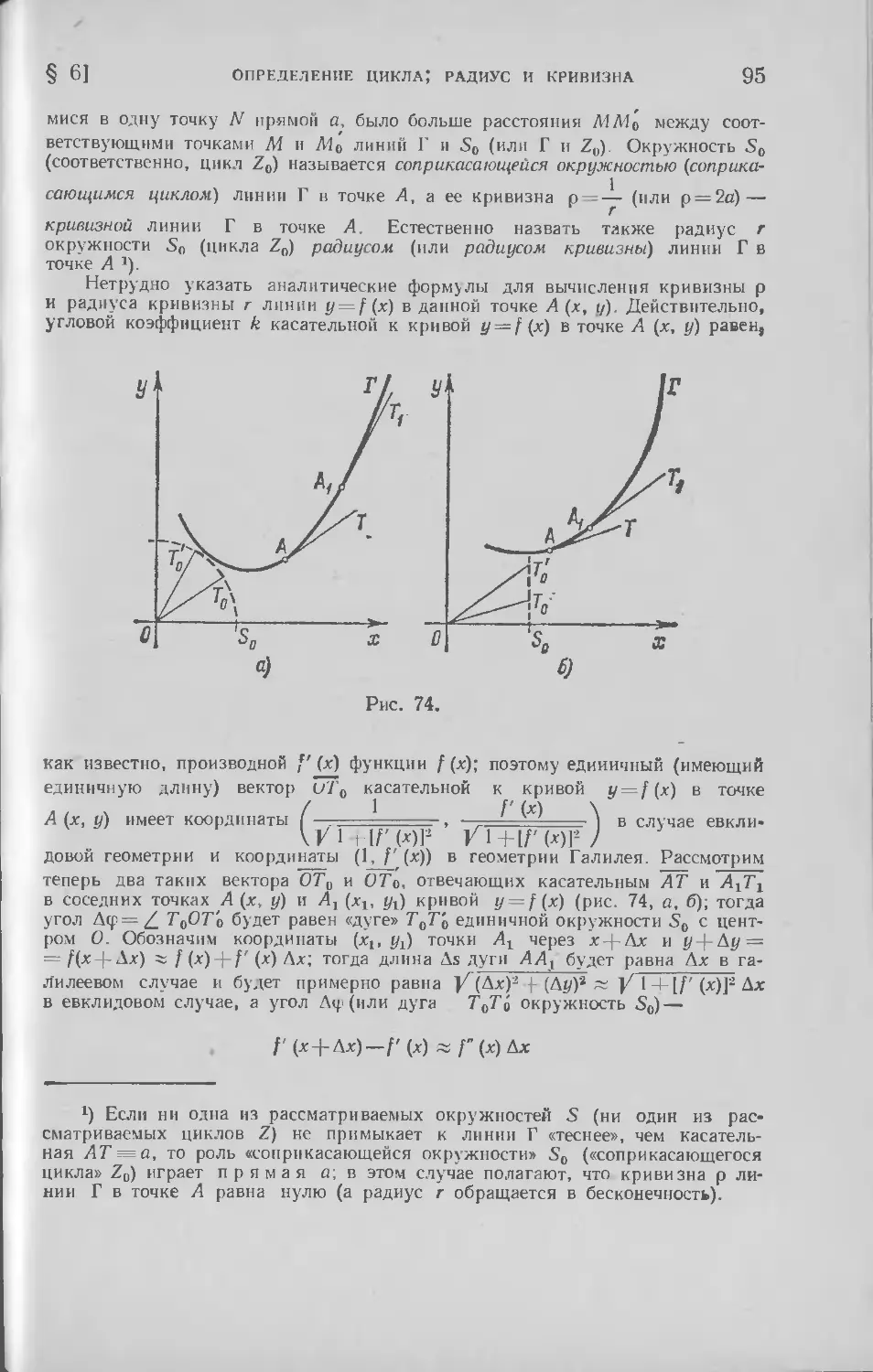
1*

ПРЕДИСЛОВИЕ
В русской научной и научно-популярной литературе, как и в
литературе многих других стран, имеется немало сочинений, посвящен-
посвященных неевклидовой геометрии Лобачевского; лишь некоторые из них
упомянуты в списке книг и статей на стр. 300—303. Изучение гео-
геометрии Лобачевского составляет обязательную часть программы ма-
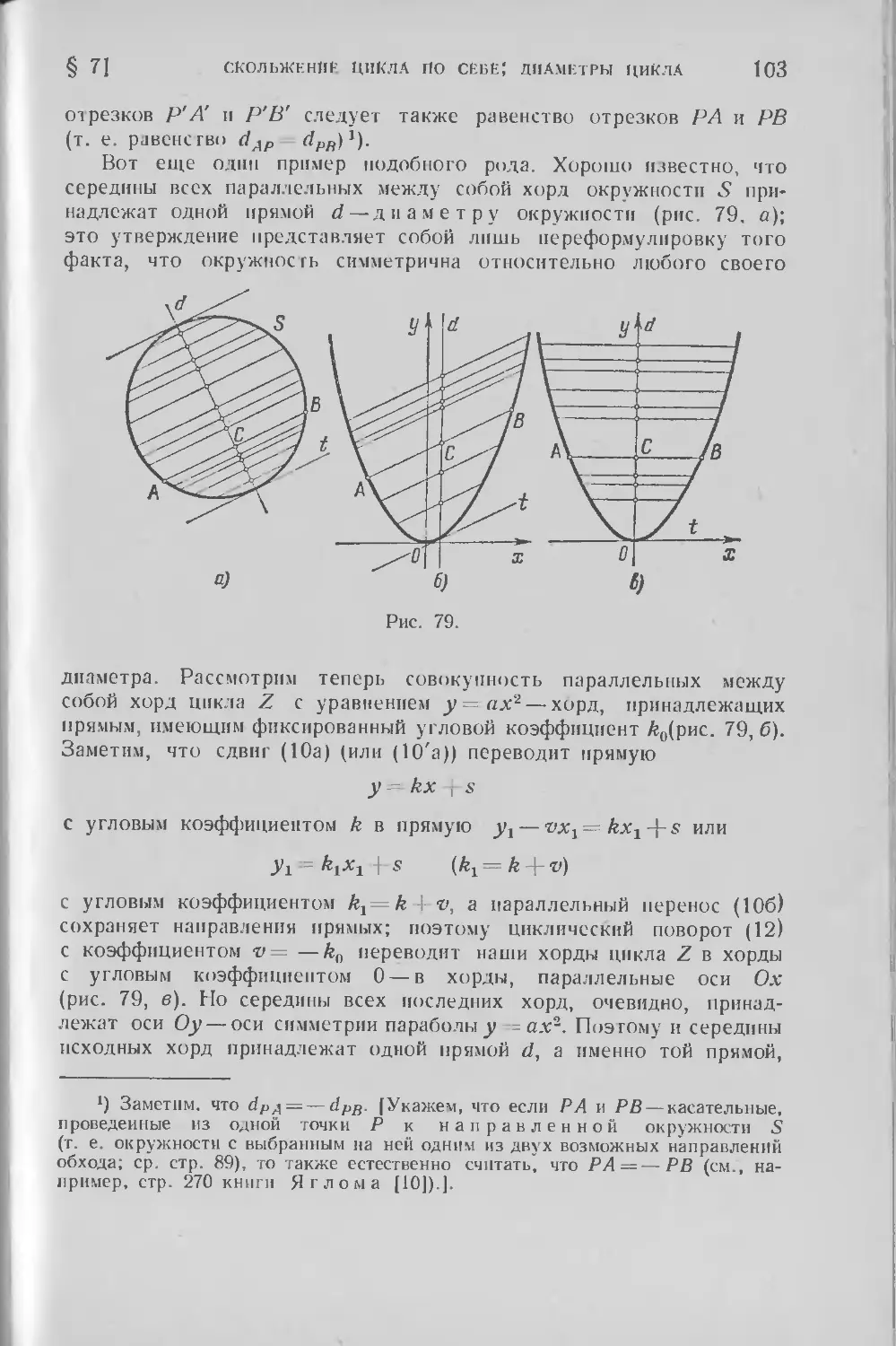
математических отделений большинства наших университетов и всех
педагогических институтов — ознакомление с основами этой геомет-
геометрической системы считается необходимой частью подготовки буду-
будущего учителя средней школы. Также и в школьных математических
кружках широко культивируются занятия геометрией Лобачевского.
При обсуждении путей перестройки математического образования в
средней школе некоторыми математиками и педагогами высказывалась
даже мысль о желательности включения элементов геометрии Лоба-
Лобачевского в общеобязательную школьную программу, а в рекомен-
рекомендуемые программы факультативных занятий математикой в средней
школе (т. е. необязательных занятий, которые, однако, должны
носить массовый характер) была включена тема, связанная с неевкли-
неевклидовой геометрией Лобачевского.
Причины столь широкого увлечения геометрией Лобачевского по-
понять нетрудно. Разумеется, увлечение это никак не связано с общема-
общематематическими или естественнонаучными приложениями геометрии
Лобачевского: приложения эти (к теории автоморфных функций,
например) носят достаточно специальный характер, и встретиться
с ними придется разве что одному из тысячи учащихся, добросо-
добросовестно изучающих (а затем излагающих экзаменатору) опреде-
определение параллельных по Лобачевскому и особенности взаимного рас-
расположения прямых на плоскости Лобачевского. Гораздо более важ-
важное и принципиальное значение имеет сам факт "неединственности»
геометрии, существования разных геометрических систем: он про-
проливает новый свет на основные особенности математической науки;
на роль идеализации в научном естествознании; на общее понятие
дедуктивной науки («выводной науки» по терминологии Аристотеля),
т. е. науки, развиваемой исходя из определенной системы аксиом;
на роль системы аксиом в математике и на предъявляемые к любой

ПРЕДИСЛОВИЕ 5
аксиоматике требования; на взаимоотношение двух аспектов геомет-
геометрии — геометрии как абстрактной математической дисциплины и
геометрии как естественнонаучной дисциплины, изучающей опреде-
определенную категорию свойств окружающего нас реального пространст-
пространства, так сказать, «геометрии-математики» и «геометрии-физики». Именно
это (и только это) обстоятельство и обусловливает вывод о том,
что наивное представление о «врож1енности», «единственности» и-ш
«естественности», чуть ли не о «богоданности» геометрической системы
Евклида должно быть у будущих учителей математики решитель-
решительнейшим образом разрушено.
Принимая этот вывод, мы, однако, забываем порой, что и са-
сама геометрическая система Лобачевского вовсе не является единст-
единственной a priori возможной ^неевклидовой» системой, что разных
«геометрий? мы знаем сегодня совсем не две только (Евклида и
Лобачевского), а очень и очень много.
Хорошо известно, что содержание геометрии в процессе ее
исторического развития неоднократно коренным образом менялось.
В течение столетий единственная цель геометрических исследова-
исследований виделась в возможно более полном исследовании свойств «обыч-
«обычного» трехмерного пространства Евклида. Несмотря на то, что
в рамках такого понимания геометрии созрели иные точки зрения, не
укладывающиеся в привычную схему (так, например, первой изучен-
изученной людьми «не евклидовой» геометрической системой, по существу,
является действующая на поверхности сферы так называемая «сфе-
«сферическая геометрия», хорошо известная еще в глубокой древности х)),
до дэздания неевклидовой геометрии Лобачевского не возникало
никаких сомнений в универсальности самого понятия евклидова про-
пространства. Относящиеся к первой трети XIX века революционные
открытия Карла Фридриха Гаусса. Николая Ивановича Лоба-
Лобачевского и Яноша Б о й а и 2) потому то и явились таким огром-
огромным событием в истории математики, что они нанесли непоправи-
непоправимый удар этим насчитывающим тысячелетия представлениям.
После появления неевклидовой геометрии Лобачевского укоре-
укоренилось мнение (а многие думают так еще и сейчас!), что возможны
всего две равноправные геометрические системы — Евклида и Лоба-
Лобачевского; сами творцы неевклидовой геометрии были в этом твердо
убеждены. Однако эта точка зрения просуществовала недолго:
*) С полной отчетливостью это было указано лишь Б. Риманом (см. ниже),
исследования которого во многом стимулировались фактом существования
неевклидовой геометрии Лобачевского.
2) О драматической истории открытия неевклидовой геометрии Лобачев-
Лобачевского см., например, указанную на стр. 303 книгу В. Ф. Кагана «Лобачев-
«Лобачевский». [Отметим, что фамилия венгерского математика Бойаи (Bolyai de Bolya)
транскрибируется в русской математической литературе весьма разнообразно —
см., например, книги [60], [72] и [73] из приведенного в конце книги списка
литературы.]

Ь ПРЕДИСЛОВИЕ
XIX век был периодом бурного развития геометрических учений.
В 1854 г замечательным немецким математиком Бернгаршч Р и м а-
ном был сформулирован чрезвычайно общий взгляд на геометрию,
сразу необычайно широко раздвинувший ее границы; Рнман же отметил
существование трех родственных друг другу геометрических систем,
близких к той геометрии, какую мы все изучали в средней школе:
«обычной» геометрии Евклида, «гиперболической геометрии Лобачев-
Лобачевского и 'эллиптической» геометрии, весьма близкой к геометрии на
поверхности сферы. Этот список геометрий был в 1870 г. продолжен
другим немецким математиком Феликсом К л е й н о м (см., например, его
книгу Неевклидова геометрия , указанную в списке литературы на
стр. 302): согласно концепции Клейна на плоскости существует
девять (!) родственных друг другу геометрий х), тремя из кото-
которых являются обычная геометрия Евклида, гиперболическая геомет-
геометрия Лобачевского и эллиптическая геометрия Римана (см. по этому
поводу приложение А в конце книги). Эти исследования Клейна,
которые возникли в результате своеобразного синтеза геометриче-
геометрических идей Лобачевского и заинтересовавших Клейна работ английско-
английского алгебраиста Артура К эли, привели к созданию в 1872 г. так
называемой "Эрлангенской программы, Клейна (см. его статью [8],
указанную в списке литературы на стр. 300), содержащей новый ши-
широкий взгляд на всю геометрию, по своей универсальности способ-
способный соперничать с концепциями Римана.
Таким образом, подобно тому как исключительное положение
геометрии Евклида было разрушено основополагающими исследо-
исследованиями Лобачевского, Бойаи и Гаусса, опубликованными еще
в 1829—1832 гг., исключительное положение геометрии Лобачев-
Лобачевского было разрушено классическими трудами Римана и ^Слейна
A854—1872 гг.). Однако еще и сегодня под неевклидовой геомет-
геометрией ; часто понимают одну только геометрию Лобачевского (реже
слова < неевклидовы геометрии во множественном числе употреб-
употребляют для обозначения гиперболической геометрии Лобачевского и
эллиптической геометрии Римана); существование же других гео-
геометрических систем остается известным лишь узким специалистам.
Причина этого, по-видимому, в значительной степени коренится во
влиянии дискуссий о природе окружающего нас реального простран-
пространства, в своей первоначальной постановке давно уже потерявших
всякое научное значение. Так, например, еще в «Неевклидовой гео-
геометрии» Ф. Клейна, вышедшей в свет в немецком оригинале в 1928 г.,
утверждается, что в окружающем нас мире должна реализовываться
*) Сам Клейн различал на плоскости семь разных геометрических сис-
систем (см., например, уже упоминавшуюся книгу Клейна «Неевклидова геомет-
геометрия»); дальнейшее членение «геометрий Клейна», в силу которого число
семь заменилось числом девять, было произведено в 1910 г. английским
геометром Д. М. И. Саммервиллем (D. M. Y. Sommerville).

ПРЕДИСЛОВИЕ 7
одна из трех «классических» геометрий Евклнвд, Лобачевского или
Римана1), хотя полная научная несостоятельность этой точки зре-
зрения била установлена «специальной теорией относительности» Аль-
Альберта Эйнштейна A905 г.) и, особенно, его же «общей теорией
относительности» A916 г.). Гипноз этих устаревших космологичес-
космологических дискуссий привел к тому, что в го время как геометрии Лоба-
Лобачевского в научной и научно-популярной литературе уделяется весь-
весьма большое внимание (так, например, даже столь частному вопросу,
как теория геометрических построений на плоскости Лобачевского,
посвящено несколько книг и бессчетное множество статей!), все
остальные «неевклидовы геометрии Клейна» освещены пока совер-
совершенно недостаточно. Настоящая книга и преследует своей целью
дать рассчитанное на широкого читателя изложение одной из этих
геометрических систем — системы, которая возникает, если принять
за «движения» двумерного многообразия «событий» (х, /) (где х —
координата точки на прямой, а / — время) преобразования Галилея
классической кинематики.
После этого исторического введения я позволю себе снова оста-
остановиться на вопросе о педагогической целесообразности увлечения
одной лишь неевклидовой геометрией Лобачевского. Важность озна-
ознакомления будущих учителей математики (а частично даже и инте-
интересующихся математикой учащихся старших классов средней школы)
с одной из геометрических систем, отличных от хорошо известной
им геометрии Евклида, сомнению, видимо, не подлежит. Но какую
геометрию выбрать для такого ознакомления? Этот вопрос, как мне
кажется, может служить предметом дальнейших дискуссий. Геомет-
Геометрия Лобачевского исторически является первой «неевклидовой» гео-
геометрической системой, — не считая это обстоятельство решающим,
я вовсе не склонен полностью его игнорировать. Кроме того, связь
этой геометрической системы с установлением недоказуемости акси-
аксиомы параллельности и с выяснением роли этой аксиомы в системе
Евклида сильно повышает педагогическое значение геометрии Лоба-
Лобачевского 2). С другой стороны, геометрия Лобачевского является
•) Книга Ф. Клейна, напечатанная уже после смерти ее автора, представ-
представляет собой обработку литографированного курса лекций, выпущенного Клей-
Клейном в 1892 г. и повторно в 1893 г. в качестве пособия для студентов Гёттин-
генского университета; модернизация, которой подвергли этот курс ученики
Клейна, подготовлявшие его к печати, кажется мне крайне недостаточной.
Также и в русском переводе «Неевклидовой геометрии», появившемся в 1936 г.,
к сожалению, отсутствует какое бы то ни было редакционное примечание,
предупреждающее читателя об архаичности идей, развитию которых посвяще-
посвящены многие страницы книги.
2) Особенно важно последнее соображение в условиях построения школь-
школьного курса геометрии в соответствии с общей схемой Евклида — Киселева
(см. указанные на стр. 300 учебники [1] — [7]). В случае же перехода на дру-
другую систему изложения (на чем настаивают многие математики и педагоги)
оно частично утратит свое значение.

О ПРЕДИСЛОВИЕ
относительно сложной; так, например, она определенно сложнее
обычной геометрии Евклида. Напротив, излагаемая в этой книге
геометрия является самой простой из всех геометрических
систем Клейна: можно даже сказать, что она настолько же проще
геометрии Евклида, насколько геометрия Евклида проще геометрии
Лобачевского. Относительная простота этой геометрии является ее
самым главным достоинством; она позволяет без большой затраты
времени и интеллектуальной энергии учащихся изучить ее со срав-
сравнительно большими подробностями —а ведь только развернутое
построение новой геометрической системы позволяет сопоставить
ее с евклидовой и только оно психологически способно по-настоя-
по-настоящему убедить в непротиворечивости рассматриваемой схемы! Другим
достоинством развиваемой в этой книге геометрической системы
является возможность ознакомления на ее базе со столь плодотвор-
плодотворным геометрическим инструментом, как принцип двойственности.
Наконец (последнее, но безусловно не наименее важное обстоятель-
обстоятельство!), очень глубокой и содержательной является иллюстрируемая
на примере рассматриваемой в настоящей книге геометрии общая
идея о связи «Эрлангенской программы» Клейна с физическими прин-
принципами относительности, по-новому раскрывающая как содержание
концепции Клейна, так и место принципов относительности в физике х).
Вот почему мне представляется заслуживающим серьезного внимания
вариант построения курса математики педагогического института,
содержащий параллельное освещение трех самых простых геомет-
геометрических систем — геометрии Евклида, «геометрии принципа относи-
относительности Галилея»и «геометрии принципа относительности Эйнштей-
Эйнштейна» (геометрии Минковского; см. § 11 этой книги) с одновременным
изложением основ (специальной) теории относительности.
Разумеется, настоящая книга, богатая, быть может и любопыт-
любопытными, но мало принципиальными деталями2) и рассчитанная на уча-
учащихся старших классов средней школы, на учителей -математики,
на студентов и преподавателей университетов и педагогических
институтов, готовящих учителей математики, никак не преследует
своей целью стиль серьезную реформу нашего высшего педагоги-
*) Достоинством геометрии Лобачевского часто считают возможности об-
обсуждения на ее базе различных космологических гипотез — однако уже сама
постановка вопроса о реализуемости во Вселенной геометрии Евклида или
геометрии Лобачевского способна затруднить восприятие идей теории относи-
относительности. С этой точки зрения мне кажется более ценной связанная с прин-
принципом относительности Галилея геометрия, способная сильно облегчить пони-
понимание соответствующих идей.
2) Так, например, здесь содержатся даже три доказательства аналога из-
известной из геометрии треугольника теоремы Фейербаха, в силу которой
окружность девяти точек треугольника касается вписанной и трех вневписан-
ных окружностей (см., например, пп. 44—45 указанной на стр. 301 книги
Зетеля [33]), между тем как научное значение этой теоремы ничтожно.

ПРЕДИСЛОВИЕ 9
ческого образования. Да сейчас определенно еще не время для та-
такой реформы: обсуждение поднятых здесь вопросов требует серьез-
серьезного знакомства с геометрическими системами, порождаемыми
принципами относительности Галилея и Эйнштейна, а эта книга,
видимо, является первым сочинением в научно-популярной литера-
литературе, в котором подробно анализируется «геометрия принципа отно-
относительности Галилея».
Да и в научной литературе эта геометрическая система была серьезно
изучена сравнительно недавно. Упоминание о соответствующей геометрической
системе можно найти уже у Ф. К лей на (см., например, указанную на
стр. 302 книгу «Неевклидова геометрия») и в излагающих идеи Клейна
учебниках (см., скажем, указанную на стр. 301 книгу В. Ф. Кагана
«Основания геометрии» — однако ссылки на эту геометрию имеют здесь эпи-
эпизодический характер, и содержание этой геометрической схемы, по существу,
остается нераскрытым. Более обстоятельной была трактовка той же темы в отно-
относящихся к 1913—1915 гг. научных статьях ряда немецких геометров (Г. Бек,
Ф. Бём, Л. Бервальд *)). В 1925—1928 гг. эта геометрия снова всплыла
в публикациях английского математика Л.Силберстейна, поляка С. Г л а-
с а, казанского геометра А. П. Котельникова и датчанина Д. Ф о г а 2);
в этих публикациях, видимо, впервые была отмечена связь рассматриваемой гео-
геометрии с принципом относительности Галилея. Однако обстоятельное изучение
рассматриваемой в настоящей книге геометрической системы, при котором
она в некоторых отношениях была проанализирована даже глубже евклидо-
евклидовой геометрии, относится к 50-м годам нашего столетия; это изучение связано
с именами замечательного голландского геометра Николааса К ей пера,
видного немецкого геометра Карла Штрубеккера, а также моей ученицы
Нели Михайловны Макаровой (см. список литературы в конце книги).
Отдельно приходится остановиться на вопросе о наименовании рас-
рассматриваемой в этой книге геометрической системы. В научной лите-
литературе эта геометрия именуется «полуевклидовой», «флаговой», «па-
«параболической», «изотропной» или «галилеевой»; однако ни одно из
этих названий нельзя признать полностью удачным. Термины «фла-
«флаговая геометрия», «параболическая геометрия» (или «дважды пара-
параболическая геометрия») и «изотропная геометрия» оправдываются
обстоятельствами, которые никак не могут быть раскрыты в элемен-
!) См. Н. Beck, Zur Geometrie in der Minimalebene, Sitzungsberichte
der Leipziger und Berliner Math. Gesellschaft 12 A913), стр. 14—30; F. В 6 h m,
Beitrage zum Aquivalenzproblem der Raumkurven, Sitzungsberichte der Acad.
zu Miinchen 2 A915), стр. 257—280; L. Berwald, Uber Bewegungsinvari-
anten und elementare Geometrie in der Minimalebene, Monatshefte fur Math.
und Phys. 26 A915), стр. 211—228.
2) Cm. L. Silberstein, Projective geometry of Galileian space-time,
Philos. Magazin 10 A925), стр. 681—696; S. Glass, Sur les geometries de
Galyley et sur une geometrie plane particuliere, Annales de la Societe Polo-
Polonaise de Math. 5 A926), стр. 20—36; А. П. Котельников, Принцип отно-
относительности и геометрия Лобачевского, Сборник «In memoriam Lobatschevskii»,
вып. 2, Казань, Главнаука A927), стр. 37—66; D. Fog, Den isotrope Plans
elementare Geometri, Math. Tidskrift, Сер. В A928), стр. 21—33.

10 ПРЕДИСЛОВИЕ
тарном сочинении, рассчитанном на лиц, не обладающих серьезной
математической подготовкой — поэтому зтесь они полностью отпа-
отпадают. Достоинством термина «полуевклидова геометрия» является
его близость к названию «псевдоевклндова геометрия», принятому для
геометрии, связанной с принципом относительности Эйнштейна; кроме
того этот термин звучит достаточно обыденно и не апеллирует
к неизвестным читателю этой книги понятиям вроде «флага», «изо-
«изотропной плоскости» или «параболической метрики». Однако первое
достоинство названия «полуевклидова геометрия» могут оценить лишь
лица, знакомые с «псевдоевклидовой геометрией Минковского»; вто-
второе же является одновременно и недостатком, поскольку для чита-
читателя, неискушенного в современной научной терминологии, наимено-
наименование «полуевклидова геометрия» будет звучать слишком уж «чудно»
(это нечто вроде «евклидовой полугсометрин»?). Наконец, наиболее
укоренившееся за последние годы название «геометрия Галилея»
исторически неточно— Галилео Галилей, творчество которого отно-
относится к началу XVII столетия, разумеется, не знал этой геометрии,
так как и чей о существовании рят.а равноправных геометрических
систем относится к числу наибольших научных достижений XIX века.
Более точным является наименование «геометрия, связанная с прин-
принципом относительности Галилея», близкое к названию этой книги,
однако оно слишком длинно для того, чтобы его можно было упо-
употреблять систематически. Вот почему мы все же остановились здесь
на названии «(неевклидова) геометрия Галилея», некоторым оправда-
оправданием которого может служить та блистательная ясность и полнота,
с которой сформулировал Галилей свой «принцип относительности»,
непосредственно приводящий к рассматриваемой (нсевклитовой!)
геометрии.
Наконец, несколько слов о структуре книги. Она является нестан-
нестандартной: наличие в книге обширного Введения, состоящего из двух
отдельных параграфов, Заключения, состоящего из трех цараграфов,
двух Приложений, обстоятельного списка литературы, даже непри-
непривычно (или здесь следует сказать «неприлично»?) большой объем
настоящего Предисловия — все это, конечно, не часто встречается
в сочинениях, рассчитанных на начинающего читателя, частично
даже на школьника. Эта сложная структура книги связана как
с необычностью темы (предпослать книге длинное Предисловие
меня вынудило то обстоятельство, что, как я убедился, даже само
ее название вызывает известное недоумение), так и (главным обра-
образом!) с ориентацией на разные категории читателей. Ясно, что
Литература (в которой, впрочем, собрано много доступных мало-
малоопытному читателю книг и статей) обращена в первую очередь
к преподавателю; учащийся средней школы может полностью ее
игнорировать. Также и текст, напечатанный мелким шрифтом (час-
(частично он обращен к учителю математики средней школы) может

ПРЕДИСЛОВИЕ 11
быть свободно пропущен без ущерба для понимания остальной
части книги. Ознакомление с Введением необходимо для понимания
всего последующего. В противоположность этому Заключение
вполне может быть при первом чтении и опущено; однако мне
кажется, что в дальнейшем, после некоторого перерыва быть
может, целесообразно вернуться к §§ 10 и 11 Заключения. При этом
следует иметь в виду, что написано Заключение довольно конспек-
конспективно— так, например, автор никакие имел своей целью увеличить
на единицу и без того достаточно обширный список существующих
в русской литературе популярных изложений основ (специальной)
теории относительности Эйнштейна, и весьма краткий § 10 бес-
бесспорно будет легче для тех читателей, которые предварительно озна-
ознакомились с какой-либо из перечисленных на стр. 301—302 книг [37]—
[53в](в первую очередь здесь хочется рекомендовать замечательные
книги Макса Борна[38] [38а]). Посвященный «неевклидовой геомет-
геометрии Минковского» § 11 также является довольно конспективным и не
рассчитан на быстрое чтение. В частности, он почти не содержит дока-
доказательств упоминаемых в нем теорем; инициативному читателю можно
порекомендовать попытаться найти эти доказательства самостоя-
самостоятельно (тут может оказаться полезной литература, указанная в конце
книги). Отмечу также, чго я всюду стремился сопоставлять феномены
«неевклидовой геометрии Галилея» с родственными им фактами обычной
(«школьной») геометрии Евклида; с этим параллельным изложением
двух геометрических систем частично связан сравнительно большой
объем книги.
Специального разговора заслуживают завершающие книгу При-
Приложения А и Б. Формально их можно считать рассчитанными на
того же читателя, что и основной текст книги: они также не тре-
требуют никаких предварительных знаний и поэтому доступны даже
достаточно настойчивому школьнику. Следует, однако, предупредить,
что слова «достаточно настойчивому» в предыдущей фразе никак
не являются лишними: крайне лаконичные по манере изложения
(и также почти не содержащие доказательств) Приложения состав-
составляют самую сложную часть книги — они заметно труднее для пони-
понимания, чем остальные разделы, и рассчитаны на вдумчивого читателя.
Мне кажется даже, что хотя в тексте Приложений и отсутствуют пря-
прямые ссылки на понятия и теоремы, незнакомые читателю с минималь-
минимальной подготовкой, на которую рассчитана эта книга, фактически Прило-
Приложения будут доступны лишь несколько более подготовленному чита-
читателю,— скажем, знакомому с аналитической геометрией и владеющему
основами неевклидовой геометрии Лобачевского. Понятно, что весь
предшествующий Приложениям материал от них никак не зависит, так
что эти Приложения можно и не читать Однако, хотя Приложения
А и Б и не составляют органической части книги, они представля-
представляются достаточно важными: изложив с большими подробностями

12 ПРЕДИСЛОВИЕ
содержание самой простой нз известных мне «неевклидовых» систем,
я счел уместным также слегка приоткрыть перед читателем дверь
в обширный мир иных, более сложных «геометрий», включающих
«геометрию Галилея» как простейший частный случай, — и в меру
своего умения выполнил это в Приложениях к настоящей книге.
Нумерация формул является независимой в пределах каждой
главы книги; иными словами эта нумерация начинается с формулы
A) во Введении и затем снова — в главе I. в главе II, в Заключе-
Заключении и в Приложениях. Поэтому ссылка на какую-либо формулу
в тексте книги, не сопровождаемая указанием страницы или номера
параграфа, отсылает читателя к формуле с соответствующим номером
в той же главе (причем самостоятельными главами считаются так-
также Введение, Заключение и Приложения); во всех остальных случаях
наряду с номером формулы обязательно указывается параграф книги,
в котором эта формула приведена, или страница, на которой она
напечатана.
В основу книги положено содержание лекции, которую я прочел
в 1956/57 учебном году учащимся двух старших классов московских
школ — участникам Школьного математического кружка при Москов-
Московском государственном университете. В 1963/64 учебном году эта
лекция в несколько расширенном виде была повторена в ряде высту-
выступлений перед учащимися восьмых классов, посещавшими Вечернюю
математическую школу при МГУ; эти выступления были подыто-
подытожены зачетом, который сдало несколько десятков школьников. Неко-
Некоторое отражение в настоящей книге нашел также (менее элементар-
элементарный и значительно больший по объему) специальный курс «Принципы
относительности и неевклидовы геометрии», прочитанный автором
некогда в МГПИ им. В. И. Ленина.
Приятная обязанность автора каждой книги состоит в том,
чтобы поблагодарить лиц, которые ему помогли. Я рад исполнить
здесь этот долг и выразить искреннюю признательность Г. Б. Гуре-
вичу, дружеская критика которого бесспорно пошла на пользу этой
книге. Традиционной уже для моих книг становится глубокая бла-
благодарность их редактору <?. И. Кизнер, помощь которой в подго-
подготовке окончательного варианта книги я склонен ценить весьма вы-
высоко. Наконец, я не могу не отметить того огромного труда,
который вложила М. С. Королева в изготовление эскизов чертежей —
без ее помощи и энтузиазма настоящая книга вряд ли бы смогла
увидеть свет.
И. М. Яглом
Март 1967 г.

ВВЕДЕНИЕ
§ 1. Что такое геометрия?
Геометрия, которую каждый из нас хорошо знает из курса сред-
средней школы, изучает те или иные свойства плоских фигур или про-
пространственных тел; при этом под фигурой (или телом) можно пони-
понимать просто множество точек плоскости (или пространства). Оста-
Остановимся теперь на вопросе о том, какие именно свойства фигур
и тел интересуют геометра. Этот вопрос допускает две различные
трактовки, приводящие, впрочем, к одним и тем же результатам;
обе эти трактовки будут нам впоследствии полезны и поэтому
заслуживают нашего внимания.
Первая трактовка связана с понятием равенства фигур1). Рав-
Равными (или одинаковыми) в геометрии называют те фигуры, которые
имеют одни и те же свойства и потому неразличимы: так,
все геометрические свойства изображенного на рис. 1 треугольника
Рис. 1.
ABC совпадают со свойствами изображенного на том же рисунке
треугольника MNP (равного треугольнику ABC, т. е. отличающе-
отличающегося от него лишь своим положением на плоскости, но не формой
2) В настоящей книге мы будем говорить главным образом о геометрии
на плоскости (планиметрии), изучающей свойства плоских фигур.

14 ВВЕДЕНИЕ
и нс размерами!): например, если мы знаем, что угол между ме-
медианой AD и биссектрисой АЕ треугольника ABC равен 15 , то
можем быть уверены, что и угол между медианой MQ и биссект-
биссектрисой MR треугольника MNP имеет ту же величину 15е. Именно
по этой причине в геометрии часто такие треугольники, как ABC
и MNP, принимают за один треугольник, а не за два: так, утверж-
утверждение о том, что по двум сторонам АВ = с и АС = Ь п упу
^.A = a, заключенному между ними, можно построить лишь один
треугольник (рис. 2, аI), означает лишь, что любые два треуголь-
треугольника ABC и А'В'С, имеющие одни п ге же стороны АВ = А'В'
( = с) и АС —А'С ( = Ь) и один и тот же угол /_А - /_А ( = а),
будут одинаковы, т. е. равны между собой. А 1ак как равные
фигуры (и только они) получаются одна из другой движением
(это утверждение равносильно определению движения!), то из сказан-
сказанного вытекает, ч го движение не меняет никаких свойств геомет-
геометрических фигур. Знаменитый немецкий математик конца XIX и начала
XX века Феликс Клейн A849—1925) предложил положить послед-
последнее обстоятельство в основу определения самого предмета геометрии:
содержание геометрии составляет изучение тех свойств фигур, кото-
которые сохраняются при всевозможных движениях2). Именно в силу
такого подхода к геометрии можно объяснить: почему угол меж чу
какой-либо стороной нарисованного на классной доске треугольника
') В противоположность этому по двум сторонам АВ—с и ВС = а и углу
?_ А —а, противолежащему одной из них, вообще говоря, можно
построить два треугольника ЛВС и АВСХ (рис. 2, б)
2) На самом деле определение геометрии по Ф. Клейну является несколько
более общим, чем приведенное нами (см. по этому поводу оригинальную
статью Клейна [8] или Введения к первой, второй и третьей частям
книги Яг л ома [9] —[10] и § 6 статьи Яглома и Атанасяна (И])",
однако для наших целей вполне достаточно ограничиться сказанным выше.
(Цифры в квадратных скобках отсылают читателя к списку литературы на
стр. 300—303.)

§ I]
ЧТО ТАКОЕ ГЕОМЕТРИЯ?
15
и другой его стороной представляет интерес i/ih геометра, в то время
как угол той же стороны с краем доски отношения к геометрии не
имеет: ведь первый угол сохраняется при любом движении тре-
треугольника, тогда как второй угол при таком движении меняется —
и значит, он характеризует лишь расположение треугольника па
доске, но отнюдь не его геометрические свойства.
Придирчивого критика выделенное курсивом определение геомет-
геометрии может не удовлетворить: он скажет, что вопрос о том, какие
свойства фигур заслуживают названия «геометрических», остается
открытым, пока мы не дамм «строго математического» определения
движения. То определение движения, кот орос было намечено
выше (движение — это преобразование плоскости, переводящее каж-
каждую точку А в новую точку А' так, что каждая фигура переходит
в равную ей), по-видимому, не удовлетворит такого критика: ведь
в школе равные фигуры обычно и определяются как такие,
которые можно перевести одну в другую движением. Однако равен-
равенство фигур можно также определить и не апеллируя к понятию
движения: две фигуры F и F' называются равным и, если между
их точками можно установить такое (взаимно однозначное) соответ-
соответствие, сопоставляющее каждой
точке А фигуры F вполне опреде-
определенную точку А' фигуры F' и на-
наоборот, что расстояние АВ между
каждыми двумя точками А и В
фигуры F равно расстоянию А'В'
между соответствую'цими им точ-
точками А' и В' фигуры F' (рис. 3).
Конечно, это определение являет-
является довольно громоздким и труд-
трудным для запоминания, но для по-
понимания оно, как нам кажется,
нисколько не трудно. А самое глав-
главное— это определение не евнзыва-
Рис. 3.
ет понятие равенства фигур с поня-
понятием движения; правда,вместо это-
этого оно ссылается на новое понятие — «расстояние между двумя точка-
точками». Разумеется, тот же вымышленный (пли, быть может, как раз
в этот момент читающий пашу книгу?) критик, в угоду которому мы
пустились в эти пространные объяснения, может спросить: а что
такое расстояние между двумя точками? Однако этот вопрос
не является очень трудным: для того чтобы определить расстояние
между двумя точками А и Л, плоскости, достаточно ввести на
плоскости какую-либо (какую угодно!) декартову прямоугольную
систему координат; при этом, если координаты точки А равны х и
у, а координаты точки Л, равны х1 и уг (рис. 4, а), то расстояние

16 ВВЕДЕНИЕ
d между точками А и Ал можно определить по формуле1)
Таким образом, понятие расстоянии между точками может быть све-
сведено к простой алгебраической формуле, которая уже не нуждается
в дальнейших пояснениях.
п
у
х
а)
Рис. 4.
Последнее замечание вплотную подводит нас ко второй трак-
трактовке вопроса о том, какие свойства фигур относятся к компетен-
компетенции геометрии. Хорошо известно—это было
установлено еще в XVII веке знаменитыми
французскими математиками Рене Декар-
томA596—1650) и Пьером Ферма A601—
1665), —что всю геометрию можно построить
на базе понятия числа, можно свести к алгеб-
алгебре: для этого достаточно только ввести на
плоскости какую-либо систему координат
(вроде изображенной на рис. 4, а). При этом
каждой точке А плоскости будет отвечать
пара чисел х и у — координат этой точки,
а каждой фигуре, т. е. совокупности точек,—
совокупность (множество) пар чисел.
Ряс. 5.
Так, например, множеству точек М, удаленных от фиксированной
точки Q(a, b) на постоянное расстояние г,— окружности 5 с
центром Q и радиусом г (рис. 5),— отвечает множество таких
5) Аналогично этому расстояние d между точками А (х, у, г) и Ах (xlt ylt
пространства равно
(рис. 4, б).
Aа)

§ 1]
пар чисел (х, у), что
ЧТО ТАКОЕ ГЕОМЕТРИЯ?
У(х — аJ + (у— Ь)*=г
17
или
т. е.
где
=—а, q=—b, f=a* + b*-
B)
B')
Bа)
Точно так же прямой /, пересекающей ось ординат Оу в точке
S @, s), удаленной от начала координат на расстояние OS = s и
образующей с осью абсцисс Ох такой угол ^_xQM=(pJ что
S(D,s\
Р(х,0) х
P(x,0)
Жв)
У\
9
о а
О P(x,0j
М(х,ф
Рис. 6.
МР
tg(P-=~Qp-^k (Рис- 6), отвечает совокупность всех таких пар чисел
(а-, у), что
C)
где как "свободный член» s, так и <угловой коэффициент) k могут
быть положительными, отрицательными или равными нулю, — отри-
отрицательность углового коэффициента & = tg<p означает лишь, что
^=\f (всегда отсчитываемый в направлении, противопо-

18 ВВЕДЕНИЕ
ложном направлению вращения часовой с т р е л к и)
тупой (ср. рис. 6, а—г). Аналогично этому прямой т, пара'пельной
оси ординат и пересекающей ось абсцисс в точке А (а, 0) (удален-
(удаленной от начала координат на расстояние ОА — а — положитечьнос
или неположительное), отвечает совокупность всевозможных пар
чнсет {х, у), гт,е
х- а D)
(рис. 7. а). [Прямой п, параллельной оси абсцисс (рис. 7, б) отве-
отвечает множество пар чисел (х. v), r'le
'у Ь;
последнее равенство представляет собой просто частный случай
равенства C^^—случай, отвечающий значению k 0.] Иногда говорят
также, что окружности 5 соответ-
соответствует уравнение B), а прямой
/ — уравнение C), пли что окружность
5 записывается уравнением B),
а прямая / — уравнением C).
^ Теперь естественно возникает
х вопрос о том, какие именно соот-
У ,
0
/77
А(а,0)
X
Гй(Л/>) п нгипен11Я между координатами то-
а) ' б) 1|(-'К имеют геометрический смысл,
„ ., а какие-—случайны, зависят лишь
Рис. 7. '
от выбора системы координат.
Так, например, в уравнении окружности B) величина г выражает
величину рачпуса — основную характеристику окружности; величина
же /; в уравнении B') не имеет геометрического смысла — нетрудно
найти две совершенно одинаковые (т. е. равные!) окружности, в урав-
уравнениях которых, имеющих форму B'), коэффициенты р будут раз-
разными, пли две различные (i. e. неравные!) окружности, записываемые
двумя уравнениями вида B') с одинаковыми коэффициентами/?1).
Отчего же проистекает это различие: почему одни величины в урав-
уравнениях линий имеют геометрический смысл, а другие нет?
Чшагель, вероятно, уже сам догадался, как ответить на по-
последний вопрос. Координаты (х, у) точки А зависят не только от
самой этой точки, но еще от чего-то, непосредственно с этой точкой
не связанного, — от выбора системы координат. Мы можем по-раз-
по-разному выбирать оси Ох и Оу системы (прямоугольных декартовых)
координат — и координаты одной и той же точки А кажтый раз будут
другими; в соответствии с этим н геометрическая фигура, например,
определенная линия, будет в разных системах координат описываться
разными совокупностями пар чисел. Если какая-либо величина, зада-
]) Ясно, что р——а зависит лишь от абсциссы а центра Q окружности;
но эта величина определяется не геометрическими свойствами окружности,
а лишь выбором системы координат.

§ 1]
ЧТО ТАКОЕ ГЕОМЕТРИЯ?
19
ваеман совокупностью пар чисел, отвечаюиигх опредетенной фигуре F,
не зависит от выбора системы координат, т. е. остается одной и
той же при переходе от одной системы координат к другой, значит,
эта величина имеет объективный характер, зависит лишь от фи-
фигуры F, связана с ее геомет-
геометрическими свойствами. Если же
при переходе от одной системы
координат к другой рассмат-
рассматриваемая величина меняется,
то она зависит от располо-
расположения фигуры F по отноше-
отношению к выбранной системе
координат, т. е является ха-
характеристикой не самой инте-
интересующей нас фигуры F (рис.
8, а), а гораздо более сложного
образа—фигуры F и коорди-
координатного креста>. образованно-
го осями Ох и Оу (рис. 8, б).
Сказанному выше можно придать такую форму, которая помо-
помогает реально отличать величины, имеющие геометрический смысл,
от тех, которые связаны лишь с выбором определенной системы
координат. Пусть точка А имеет в системе коортннат хОу (или
в системе координат {д:, у}, как мы будем писать в дальнейшем)
координаты х и у, а в иной
системе координат х'О'у' (пли
{Х',У'\)— координаты х' ку';
примем еще. что координаты
старого начала координат О
в новой системе координат
х'О'у' равны а и Ь, а угол
х^х' междУ осями Ох и О'х'
равен а (рис. 9) г). Наша задача
состоит в том, чтобы опреде-
определить новые координаты х',у'
точки А, зная ее старые
координаты д:, у, а также ве-
0(а Ь)
Рис. 9.
личины a, b и а.
Для решения поставтенной задачи полезно ввести в рассмотрение
угол /_ хОА (j (углы, как всегда, отсчптываются в том направ-
]) Мы здесь, как это принято в аналитической геометрии, ограничиваемся
«правыми» системами координат, т. е. такими, что поворот на 90° положи-
положите чыюго луча Ох оси абсцисс, переводящий его в положительный л\ч Оу оси
ординат, происходит в «положительном» направлении, т. е. в направлении,
протшюположноч направлению вращения часовой стрелки.

и,
Л?
Р(х,О) х
20 ВВЕДЕНИЕ
лении, которое в тригонометрии считается положительным), обра-
образуемый лучом ОА с положительным лучом Ох оси абсцисс, и рас-
расстояние ОА^г1); при этом координаты х и у точки А определятся
по формулам
x = rcosip, у — г sin ф E)
(рис. 10). Введем теперь «промежуточную»
систему координат х1Оу1 или {хъ yj, нача-
ло которой совпадает с началом «старой»
системы координат {х, у}, а оси параллельны
осям «новой» системы {х', у'} (см. рис. 9);
р 10 координаты точки А относительно этой си-
системы естественно обозначить через х1 куг.
Ясно, что с осью Ох1 луч О А образует угол фх = ф— а. (см. тот
же рис. 9); поэтому
хг = г cos Фх = /" cos (ф — а) = г (соз <р cos a -j- sin ф sin a) =
= г cos ф • cos a -f- /" sin ф • sin a = д; cos а +_у sin а
и
jx = r sin фх = г sia (ф — а) = г (sin ф cos а — cos ф sin a) =
= г sin ф-cosa—г совф- sin а= —д: sin a-\-y cos а.
С другой стороны, из того же рис. 9 следует:
где а = О'Р, Ь = РО.
Таким образом, окончательно получаем
х'— х cos а-{-у sin a + а,
у' = —х sin a-\-y cos a-J- Ь.
F)
Если нам известны «новые» координаты (х', у') точки, то, раз-
разрешив уравнения F) относительно «неизвестных» хну, мы полу-
получим формулы, выражающие «старые» координаты через «новые»:
х = (х' — a) cos а — (у'—b) sin a, -- *
у = (х' — a) sin а -f- {у' — b) cos a.
Последние формулы можно также записать в виде
х= х' cos a-\-y' sin a-'- а,
у — — х' sin а - у' cos a -\ b,
Величины лиф принято называть полярными координатами точки А.

§ 1] ЧТО ТАКОЕ ГЕОМЕТРИЯ? 21
где а и b — координаты точки О' в системе координат {х, у},
а сс = /_х'' Сх = —а — угол между осями О'х' и Ох1); это следует
из того, что мы, разумеется, имеем право считать |х', у'\ «старой»
системой координат, а {х, у\—«новой» и воспользоваться теми же
формулами F) (в которых следует только заменить величины a, b
и а имеющими аналогичный смысл величинами a, b и а).
Формулы F) мы заключили в рамку, чтобы подчеркнуть их важ-
важность: они играют в геометрии фундаментальную роль, поскольку
тишь с их помощью можно выяснить, имеет та или иная величина
(определяемая методами аналитической геометрии, т. е. с помощью
координат) геометрический смысл или не имеет. Например, рассто-
расстояние
d = \ (Xl-xf + (yi-y)z A)
между двумя точками А (х, у) и Ах (xv уг) имеет геометрический
смысл: в самом деле, если мы перейдем к новой системе координат
{х', у'}, то координаты точки А определятся формулами F), а коор-
координаты точки Ах — аналогичными формулами
х[= хгcosa,-{-y1 sin а,-\-а,
у\ = — xL sin a +_y I cos a-\-b.
Отсюда имеем
(y1—y) sin a]2 +
+ I — (*i — х) sin а + (уг— у) cos а]2 =
= (хг—л:J (cos2 а + s'm2a)-{-(y1—^J(cos2a+sin2a) =
= (х1-х)*+(у1-у)*,
что и доказывает независимость величины d от выбора системы
координат •
Аналогично этому, если уравнение окружности S в «старой»
системе координат \х, у\ имеет вид B'), то для того, чтобы полу-
получить ее уравнение в -новых координатах \х', у'}, надо в B')
вместе) х и у подставить их выражения через «новые» координаты
(Fа) или F6)). Таким образом, получаем
[х' cos a J-у sin a -(- а]2 -\- [ — х' sina-(- у' cosa+?]2 +
-\-2'р (х' cosa+y sina+ a)-\-2q( —х' sina+_y'
]) Точнее было бы положить a = 360° — а, так как мы условились отсчи-
отсчитывать углы в положительном направлении. Однако ясно, что эта неточность
здесь несущественна, так как она не влияет на вид формул F6).

22 введрние
или, по раскрытии скобок,
х'2-'-/Ч 2р'х'+2дУ+/'~- О,
где
р' — a cos а—b sin а j-p cos cc — q sin а,
q' = a sin a-'-b coscc-, p sin a-, ^cosa,
/'= a2-, 62 , 2pa-t-2qbif.
Отсюда видно, что величина р, в самом деле, геометрического смысла
не имеет (ибо, вообще говоря. p'=acosa—& sin cc+P cosa —
— q sin a^=p). А вот величина
имеет геометрический смысл, ибо, как нетрудно проверить,
р'г '-<7'2 = [(« cosa — Ь sin a) - (pcosa — q sin a)]'2 -\
+ [(« sin a ,- fc cos a) -\ (p sin a qcosa)]2-
a2 , *zi p2-tq2-\-2ap+2bq
и, следовательно,
И действительно, из формул Bа) (стр. 17) следует, что
где г—радиус окружности S.
Если уравнение прямой / в системе координат {х, {/} имеет вид C), то
в «новой» системе координат |х', {/'} эта прямая записывается уравнением
—х' sin a J- i/' cos a гЬ^/г(д;' cos a + {/' sin a ]-a) |-s.
Если cos a—k sin a ^ 0, то это уравнение можно переписать в виде
y' = k'x' -s'.
где
k cos a ,-sina , ka—b~ s
k = ¦ -. s =-
cosa—k sin a cosa—fcsina
если же cosa—fcsina = 0, то в виде
где _
b — ka — s
k cos a sin a
Отсюда следует, что ни величина k, ни величина s не имеют геометрического
смысла — они связаны лишь с особенностями расположения прямой / по отно-

§ 1]
ЧТО ТАКОЕ ГЕОМЕТРИЯ?
23
шению к системе координат. Однако тот факт, что для дв\х прямых—прямой
/ с уравнением C) и прямой 1г с уравнением
y = klx-,sl (За)
— справедливо равенство ft klt имеет определенный геометрический смысл,
ибо в этом случае при переходе к другой системе координат мы имеем
ft'
ft cos a- sin a
cos a-p sin a »
— = fti,
cosa—ft sin a cosa—ftLcosa
— и действительно, прямые с одинаковыми угловыми коэффициентами парал-
параллельны.
Рис. 11.
Далее, если прямые I и 1г параллельны, т. е. k = klt то геометри-
геометрический смысл имеет величина
в самом деле, очевидно,
, ka — b-t-s.
Si—S = —
У k--, -l
ka~\-b — s
—S
cosa—fesina cosa — fesina cosa—k sin a
/ft cos a sinaV (ft cos a j- si na)' -(cosa—ft sin a)'
Л ~ Z '¦ '
\cosa— ft sir
sin а
(cosa — ft sin aJ
(cos a—ft since)'2
так что
1- ft'2 1 ^ | cos a—ft sin a | [cosa—ftsma| у ft- -1
[Из рассмотрения уэображенного па рис. 11, а треуголышка SSj^P следует, что
\Sl— s
— расстояние между прямыми l и
= SSi cos <r=S1P=aJ

24 ВВЕДЕНИЕ
Если прямые I и 1Х с уравнениями C) и (За) не параллельны,
т. е. если k Ф kx, то геометрический смысл имеет довольно сложная величина
— ведь
bi ftx cos a + sin a ft cos a + sin a
cosa—kx sin a cosa—ft sin a
l a) (cos a—ft sin a)— (ft cos a+sin a) (cos a— kx sin a)
(cos a—kx sin a) (cos a—ft sin a)
(cos a—kx sin a) (cos a—ft sin a)
и
,-,, . ft. cos a + sin a ft cos a + sin a , ,
k\k + 1 = — = • —= = + 1 =
cos a—?i sin a cos a—fesina
(ftx cos a+sin a) (k cos a+sin a) + (cos a—?x sin a) (cos a—fcsina) _
(cos a—?i sin a) (cos a—k sin a)
(cos a—ki sin a) (cos a— k sin a)
так что действительно 1)
k\—k' kx—k
k[k' + 1 M+l '
и ^
[Нетрудно установить геометрический смысл величины и\\ '¦ если fc = tg
/?« +1
! +
и k1 = tg(p1, где ф и фг—утлы, образованные прямыми I и 1У с лучом Ох
(рис. 11,6), то
где б = ф1—ф — i/гол между прямыми 1г и /.]
_ _ _ _ ^
Если cosa—k sin a = 0 или cos a—kx sin a = 0, то в выражение -;
k
kxk'-\ 1
вместо ft', соответственно kx, надо подставить символ оо; другими словами,
если, например, cosa—ft sina = 0 (т. е. «новое» уравнение прямой / имеет
вид х'=а'), то мы считаем, что
fe'i-fe' fei-fe' ,. F~' 1
—i—l -= lim —j—i = lim —= ——
—в соответствии с правилами нахождения пределов. Но и в этом случае
ki — k' 1 —cosa + ^sina —ctga + ft, kx—k
k\k'+\ k\ kj cos a + sir.a fej
так как, очевидно, fe = ctga,

§ 1]
ЧТО ТАКОЕ ГЕОМЕТРИЯ?
25
Заметим еще, что на формулы F) можно также взглянуть
с несколько иной точки зрения. А именно, можно считать, что эти
формулы определяют переход от точки А{х, у) к точке А' (х', у'),
записанной в той же самой системе (прямоугольных декарто-
декартовых) координат {х, у}, т. е. определяют некоторое преобразование
С)
х О
Рис. 12.
б)
плоскости. Так как совокупность точек А и совокупность соответ-
соответствующих им точек А' обладают в точности одними и теми же
геометрическими свойствами (ведь это фактически одна и та же
совокупность точек, только записанная в разных системах коорди-
координат!), то ясно, что преобразование F) должно переводить каждую
фигуру F в точно такую же (т. е. равную первоначальной!)
фигуру F', откуда следует, что это преобразование есть движение.
И в самом деле, преобразование F) можно разбить на два преоб-
преобразования: преобразование
хх= х cos a +y sin а,
уг=—х sin а - г У cos cc,
выражающее поворот вокруг начала координат О на угол а (рис. 12, а),
и преобразование
х'=х1 + а,
(8)
У
выражающее параллельный перенос (рис. 12,6). Таким образом, мы снова
приходим к утверждению о том, что геометрия изучает свойства

26
ВВЕДЕНИЕ
фигур, сохраняющиеся при движениях (бI). Из сказанного вытека-
вытекает также следующее обстоятельство, которое часто оказывается
полезным: для того чтобы убедиться в том, что каждое движение F) со-
сохраняет некоторую величину, достаточно проверить, что эта величина
сохраняется при поворотах G) и при параллельных переносах (8).
Аналогично можно рассмотреть и вопрос о геометрии в прост-
пространстве. Каждую точку в пространстве мож1>о отнести к определенной
системе (декартовых прямоугольных) координат {х, у, г} (см. выше рис. 4, б);
при этом положение точки будет определяться тремя числами х, у и г (абс-
(абсцисса, ордината и аппликата). Переход от одной системы координат {х, у, г}
к другой системе координат {х', у', г'} задается весьма сложными формулами:
x' = (cos P cos a—cos у sin P sina)-* + (sin P cos a + cos V cos P sin а)-
+ sin у sina-г + ,
{/'= —(cos P sin a f cos у sin p cosa)-.v + (—sin p sin a + cos у cos P cos а)-у-\-
+ sin ycosa-z + b, (9)
z' = sin у sin p-x— sir. у cos $-y-{-CGsy-z 1-е,
где a, b, с—координаты «старого» начала О относительно «новой» системы
координат {х1, у', z'}, а а, р, у—так называемые углы Эйлера; эти \глы
изображены на рис. 13, на котором
{jCp ylt Z]}—это «промежуточная» си-
система координат (т. е. система, на-
начало которой совпадает с началом
«старой» системы, а оси параллельны
осям «новой» системы), а прямая ON —
линия пересечения плоскостей Оху и
Ох1у1. При этом можно утверждать,
что стереометрия изучает те соотно-
соотношения между координатами точек,
которые «выдерживают» преобразова-
преобразования (9). Можно также смотреть на
преобразования (9) и несколько по-
другому, считая, что система коорди-
координат фиксирована, а эти преобразова-
преобразования задают переход от точки А (х,у,г)
к новой точке А' (х', у', г'), т. е.
некоторое преобразование простран-
пространства. Поскольку описываемые фор-
мулами (9) преобразования представ
ляют собой не что иное, как движе
ния2), то при этом мы снова приходим к точке зрения Клейна, утверждаю-
утверждающей, что геометрия изучает те свойства фигур и тел, которые сохраняются
при движениях.
г) В соответствии с тем, что мы ограничиваемся рассмотрением лишь
«правых» систем координат (см. подстрочное примечание на стр. 19), фор-
формулы F) выражают не все без исключения движения плоскости, а лишь так
называемые «собственные движения» или «движения 1-го рода», переводящие
координатный крест, отвечающий «правой» системе координат, в координатный
крест, отвечающий также «правой» системе координат (см. по этому поводу
книги Перенелкина [5] или Яглома [9]).
2) Точнее, «собственные движения» или «движения 1-го рода» (см., на-
например, книгу Перепелки на [6]).
Рис. 13.

§ 2] ЧТО ТАКОЕ МЕХАНИКА? 27
§ 2. Что такое механика?
Основной целью настоящей книги является установление опре-
определенной связи между механикой и геометрией. В основе этой связи
лежит глубокая аналогия между ролью в геометрии движений (пони-
(понимаемых просто как преобразования плоскости или пространства,
сохраняющие расстояния между точками, вне всякой связи с такими
чисто механическими понятиями, как траектории точек при движении
или скорости отдельных точек) и ролью в механике равномерных
прямолинейных движений (вот тут уже понятие скорости — как о том
свидетельствует само слово «равномерный»—играет основную роль!),
или аналогия между ролью в геометрии декартовых прямоуголь-
прямоугольных координат н ролью в механике так называемых ннерцнальных
систем отсчета. Этой аналогии и будет посвящен настоящий
параграф.
Из трех основных разделов механики — кинематики, статики и
динамики — нас здесь в первую очередь будет интересовать кине-
кинематика, изучающая движения отдельных материальных точек и
материальных тел. При этом сам термин «движение» в механике
понимается совсем но-другому, чем в геометрии,— настолько по-
другому, что даже хотелось бы иметь здесь два разных названия,
что, однако, противоречит твердо укоренившейся традиции. Во вто-
второй фразе настоящего параграфа мы уже коснулись вскользь этого
различия; теперь остановимся на нем подробнее.
Под словом «движение» в геометрии понимается некоторое т о-
чечное преобразование, сопоставляющее каждой точке А
определенную точку А', и только это преобразование. Таким обра-
образом, вопрос о том, «каким образом» точка А перешла в точку А',
для геометра бессмыслен: само сопоставление А—> А'—это и есть
движение, и ни что, кроме этого сопоставления, его не интересует.
В противоположность этому в механике «движение» — это всегда
процесс, переводящий точку А в новую точку А'; при этом
здесь представляют интерес и траектории отдельных точек, и ско-
скорости или ускорения этих точек в отдельные моменты времени.
Наиболее принципиальное отличие механических движений от геомет-
геометрических как раз и состоит в том, что в механике учитывается
фактор времени, в то время как геометрия вообще не знает этого
понятия. Полное описание «механического» движения, переводящего
фигуру F в фигуру F', задается указанием того, как изменяет
положение каждая точка А фигуры F с течением времени;
используя привычные для^математнки термины и обозначения, можно
говорить о функциональней зависимости A=A(t) положения точки
А фигуры F от времени t. Эта функциональная зависимость задается
в некотором интервале времени: to^.t^.t1; при этом в момент t0
рассматриваемая фигура занимает исходное положение F (так что

28
ВВЕДЕНИЕ
A(to)=A — это точка фигуры F), а в момент t1—положение F'
(так что A(t1) = A'—точка фигуры F'; см. рис. 14).
Разумеется, главный интерес для механики как технической
дисциплины представляют движения трехмерных тел. Мы,
однако, наряду с этим будем рассматривать также плоские
движения, вроде того, которое изображено на рис. 14. Понятию
Рис. 14.
плоского движения можно придать следующий реальный смысл.
Рассмотрим некоторое тело Ф и так называемое плоско-параллель-
плоско-параллельное движение этого тела, т. е. движение, при котором все точки
тела Ф смещаются параллельно некоторой фиксированной плоскости
jt (рис. 15, а). Ясно, что при этом движение будет полностью харак-
характеризоваться процессом перемещения точек параллельного плоско-
плоскости л сечения этого тела, например движением по плоскости зх пло-
плоской фигуры F, по которой пересекает тело Ф плоскость л.
Наряду с этим мы будем также рассматривать прямолинейное дви-
движение, при котором все точки тела Ф двигаются с одинаковыми
скоростями в направлении определенной прямой о (рис. 15, б). Ясно,
что такое движение полностью характеризуется процессом движе-
движения произвольно выбранной точки А тела Ф. Скорость прямолиней-
прямолинейного движения можно характеризовать не вектором, а просто числом
(положительным или отрицательным, в зависимости от того, в какую
сторону вдоль прямой происходит движение)—ведь направление дви-
движения известно нам заранее. Также и положение точки А на пря-
прямой о характеризуется просто (положительным пли неположитель-
неположительным!) числом х, измеряющим (взятое с определенным знаком) рас-
расстояние точки А от фиксированного на прямой о начала отсчета О;

§ 2]
ЧТО ТАКОЕ МЕХАНИКА?
29
число х равно величине направленного отрезка ОА, т. е.
равно длине отрезка, если направление отрезка (от точки О к точ-
точке А) совпадает с заранее выбранным на прямой положитель-
положительным направлением, и числу, противоположному длине, в противном
случае. [Указанием на то, что отрезок считается направленным,
п)
будет впоследствии служить черточка над обозначающими отрезок
буквами; таким образом, ОА — это обычный (ненаправленный) отре-
отрезок, а ОА — направленный отрезок.] То обстоятельство, что как
скорость точки, так и положение точки на прямой характеризуются
одним числом, бесспорно является преимуществом; также и в других
отношениях прямолинейное движение значительно проще плоско-
плоскопараллельного движения, а тем более самого общего движения тел
в пространстве. Стремлением к простоте вызвано то, что в этой
книге основное внимание будет уделено прямолинейным дви-
движениям (материальной) точки А вдоль прямой о.
Выясним теперь, какие свойства движущихся тел интересуют
механика, какие понятия имеют механический смысл, а какие — не
имеют. На первый взгЛяд может показаться, что основными поня-
понятиями механики (точнее, кинематики) являются «траектория», «ско-
«скорость» и «ускорение»: траектория точки А — это просто линия,
вычерчиваемая точкой А в процессе ее движения (см., например,
рис. 14); средняя скорость точки А на интервале от момента t0 до
момента tx определяется как длина пути между точками A(t0)
и A (tj), деленная на разность tt—/0, а мгновенная скорость

30 ВВЕДЕНИЕ
в момент / — как предел средней скорости на малом интервале
времени от /до / Л/ при \t —»¦ 0 («производная от пути по
времени»); среднее ускорение на интервале от /0 до t1 опреде-
определяется как величина приращения скорости на этом интервале, делен-
деленная на tx — Z,,1), а мгновенное ускорение в момент /—как npeie.i
среднего ускорения на малом интервале от / т.о / \/ при V —»¦ 0
(«производная от скорости по времени»). Однако на самом деле
положение здесь оказывается совсем иным: ни траектории, ни ско-
скорости точек сами по себе никакого механического смысла не имеют
и рассматриваться механикой не могут.
Для того чтобы объяснить это положение, которое многим чи-
читателям сначала, возможно, покажется удивительным, мы предоста-
предоставим слово знаменитому Галплео Галилею A564—1642):
«Уединитесь с кем-либо из друзей в просторное помещение
под палубой какого-нибудь корабля, запаситесь мухами, ба-
бабочками и другими подобными мелкими летающими насекомыми;
пусть будет у вас там также большой сосуд с водой и пла-
плавающими в нем маленькими рыбками; подвесьте, далее, наверху
ведерко, из которого вода будет капать капля за каплей
в другой сосуд с узким горлышком, подставленный внизу. Пока
корабль стоит неподвижно, наблюдайте прилежно, как мелкие
летающие животные с одной и той же скоростью движутся
во все стороны помещения; рыбы, как вы увидите, будут пла-
плавать безразлично во всех направлениях; все падающие капли
попадут в подставленный сосуд, и влм, бросая какой-нибудь
предмет, не придется бросать его с большей силой в одну
сторону, чем в другую, если расстояния будут одни и те же;
и если вы будете прыгать сразу двумя йогами, то сделаете
прыжок на одинаковое расстояние в любом направлении. При-
Прилежно наблюдайте все это, хотя у нас не возникает никакого
сомнения в том, что пока корабль стоит неподвижно, все
должно происходить именно так. Заставьте теперь корабль
двигаться с любой скоростью, и тогда (если только движение
будет равномерным и без качки в ту и другую сторону) во
всех названных явлениях вы не обнаружите ни малейшего изме-
изменения и ни по одному из них вы не сможете установить, дви-
движется корабль или стоит неподвижно. Прыгая, вы переместитесь
по полу на то же расстояние, что и раньше, и не будете
делать больших прыжков в сторону кормы, чем в сторону носа,
на том основании, что корабль быстро движется, хотя за то
время, как вы бучете в воздухе, пол под вами будет двигаться
1) Здесь мы считаем, что интервал времени выбран так, что на протяже-
протяжении этого интервала скорость все время возрастает (точнее сказать, не убы-
убывает) или, наоборот, все время убывает (не возрастает).

§ 2] ЧТО ТАКОЕ МЕХАНИКА? 31
в сторону, противоположную вашему прыжку, и, бросая какую-
нибудь вещь товарищу, вы не должны будете бросать ее
с большей силой, когда он будет находиться на носу, а вы
на корме, чем когда ваше взаимное положение будет обратным;
капли, как и ранее, будут падать в нижний сосуд, и ни одна
не упадет ближе к корме, хотя, пока капля находится в воз-
воздухе, корабль пройдет много пядей; рыбы в воде не с боль-
большим усилием будут плыть к передней, чем к задней части
сосуда; настолько же проворно они бросятся к пище, положен-
положенной в какой угодно части сосуда; наконец, бабочки и мухи
по-прежнему будут летать во всех направлениях, и никогда не
случится того, чтобы они собрались у стенки, обращенной
к корме, как если бы устали, следуя за быстрым движением
корабля, от которого они были совершенно обособлены, дер-
держась долгое время в воздухе; и если от капли зажженного
ладана образуется немного дыма, то видно будет, как он восхо-
восходит вверх и держится напоаобие облачка, двигаясь безразлично,
в одн) сторону не более, чем в другую...»
(«Диалог о двух главнейших системах мира , день второй;
ср. также с «Посланием к Фраическо Инголи»1)).
В этом пользующемся заслуженной известностью и часто цити-
цитируемом отрывке содержится красочное, высокохудожественное опи-
описание одного из фундаментальнейших принципов механики, который
мы сегодня называем принципом относительности Гали-
Галилея и который можно кратко сформулировать в виде следующего
утверждения: никакие механические эксперименты, производимые
внутри физической системы, не могут позволить обнаружить равно-
равномерное и прямолинейное движение этой системы. Таким
образом, механические явления, проистекающие в двух «лаборато-
«лабораториях , одна из которой движется по отношению к другой равно-
равномерно и прямолинейно (например, на покоящемся и на движущемся
кораблях, о которых говорит в своем «Диалоге» Галилей), с точки
зрения наблюдателей, находящихся в одной и в другой лабораториях,
совершенно одинаковы, неразличимы. Из принципа относительности
Галилея вытекает, что все изучаемые механикой свойства тел сохра-
сохраняются при преобразованиях физической системы, состоящих
в придании ей постоянной ни величине и по направлению скорости
(эти преобразования называются преобразованиями Галилея).
Инымы словами, механиче'ский смысл имеют только такие свойства
(движущихся) тел, которые не меняются при преобразованиях Га-
Галилея (ср. с данным в § 1 Определением «геометрических свойств»
как таких, которые сохраняются при движениях!).
Галилей [13], стр. 286—287 (ср. также стр. 85—86 там же).

32
ВВЕДЕНИЕ
Принципу относительности Галилея можно придать '<геометризи-
рованную форму, совершенно непосредственно связывающую его
с определением геометрии по Клейну. Предположим, для простоты,
что мы ограничиваемся механическими явлениями, которые можно
считать происходящими в одной плоскости, например, изучаем дви-
движения физических тел на ограниченном участке земной поверхности,
который можно мыслить себе плоским. Рассматриваемую плоскость
мы, как обычно, отнесем к декартовым прямоугольным координатам
\х, у}; при этом, скажем, механическое движение произвольной
~)
1
V
D
AKWl (
У \'1
X M
Аи
^^\
-\А(г(У,у
X
-A)
\ \
1 /
F/ y
/
Г
v
A
F>
(
\.
Z'
л
r^ )
/ /*'
\ x
Рис. 16.
точки А будет описываться формулами, указывающими, как изме-
изменяются во времени координаты х, у этой точки:
x = x(t),
где / — время (а движение фигуры F будет задаваться подобными же
формулами, указывающими законы движения в с е х точек А=А(х, у)
этой фигуры !)). Но совершенно ясно, что переход к иной системе
координат {д;', у'}, которая получается из первоначальной системы
координат поворотом осей Ох и Оу на произвольный угол а и
сдвигом начала О системы координат в какую-то точку О' (рис. 16),
') По существу, здесь речь идет о плоско-параллельных движе-
движениях пространственных тел (см. стр. 28 и рис. 15, а): так как плоско-
плоскопараллельное движение тела Ф полностью определяется движением его
плоского сечения F, то мы можем ограничиться рассмотрением точек А тела
Ф, принадлежащих плоской фигуре F, т. е. определяемых указанием двух
координат х, у.

§ 2] ЧТО ТАКОЕ МЕХАНИКА? 33
разумеется, никак не может отразиться на содержании физических
законов, которые, следовательно, должны одинаково записываться
в координатах {х, у} и в координатах {х', у'}, связанных с коор-
координатами {х, у} формулами F) (стр. 20):
х' - х cos а +у sin a + а,
F)
у = — х sin a-\-y cosa + ft
где а = / хСх'— угол между осями Ох и О'х', а (а, Ь) — коорди-
координаты точки О в новой системе координат. Поэтому любое пред-
предложение, имеющее механический смысл, должно сохранять свою
форму при преобразованиях F). Принцип же относительности Галилея
утверждает, что, более того, все механические процессы будут
описываться в координатах х, у и в координатах х',у' совершенно
одинаково также и в том случае, когда начало и оси системы ко-
координат {л:', у'} движутся равномерно и прямолинейно по отноше-
отношению к системе координат {х, у} или, что то же самое, начало и
оси старой > системы координат {х, у} движутся равномерно и
прямолинейно по отношению к «новой системе координат {х', у'}.
Но если начало О системы координат {л;, у} движется со скоростью
v по прямой /, образующей с осью О'х' угол Р (см. рис. 16), то ко-
координаты a (t) и Ъ (/) начала О "старой» системы в новой,, системе
координат [х', у') в момент времени t будут равны
a (t)=a-^-vcos fW,
b+v sin p.^
(где а и b — координаты точки О в системе \х', у'} в момент /= 0),
и, следовательно, связь между координатами х', у' и х, у одной
и той же точки А в сновой и в < старой системах координат
будет описываться формулами
х' = х cos а {у sin а -f(wcos P) t -,-а,
у' = — х sin а -\ у cos а-1 (v sin P) t-\-b.
Таким образом, все имеющие механический смысл явления должны
записываться формулами, сохраняющими свой вид при преобразова-
преобразованиях A1) (или, как привыкли говорить математики, инвариантными
относительно преобразований A1)).
Формулы A1) можно ещё несколько дополнить. Заметим, что
как в формулы A0),"описывающие закон движения некоторой точки
А^=А(х, у), так и в сами формулы A1), кроме координат х и у,
входит также время 4—ведь основное отличие механических дви-
движений от геометрических как раз и состоит в том, что в физике
учитывается (игнорируемый геометрами!) фактор времени. Но ясно,
что выбор того или иного начала отсчета времени никак не может
отразиться на записи физических законов. Так, например, древние
2 И. М. Яглом

34 ВВЕДЕНИЕ
греки отсчитывали время от первой олимпиады A толя
776 г. до и. э.); древние римляне — от основания Рима B1 апреля
753 г. до н. э.); мы до сих пор отсчитываем время от рождения
Христа; мусульмане во многих странах отсчитывают время от дня
бегства «пророка» Мухамеда (пли Магомета) из Мекки в Медину
(так называемая «Хиджра»1)—16 июля 622 г. н. э.) и т.д., — и во
всех этих системах летосчисления (чаще всего берущих начало
от каких-то мифических событий!) все физические законы
записываются совершенно одинаково, так что переход от одной
календарной эры к другой никак не может отразиться на содержа-
содержании учебников по физике. Поэтому к формулам A1) следует доба-
добавить также формулу
означающую перенос начала отсчета времени; здесь d — время
«старого начала отсчета времени (т. е. момента / = 0) в новой
системе отсчета. Таким образом, имеем
A2)
Формулы A2) мы также заключили в рамку, чтобы подчеркнуть
их фундаментальную важность: математический смысл принципа
относительности Галилея и заключается в том, что все имеющие
механический смысл свойства (плоско-параллельных) движений за-
записываются формулами, сохраняющими свой вид при всех преобра-
преобразованиях A2).
Аналогично формулам F) предшествующего параграфа, формулы
A2) можно понимать двояко. С одной стороны, они описывают пе-
переход от одной системы отсчета {х, у, t\ к другой
системе {х', у', /'}; при этом все системы отсчета, связанные
друг с другом преобразованиями вида A2) (с разными параметрами
ее, Р, v, a, b, d), равноправны между собой и таковы, что механи-
механические законы записываются в этих системах отсчета наиболее
простым, «естественным» образом. Последнее утверждение имеет
следующий смысл. Рассмотрим наряду с исходной системой коорди-
координат {х, у) новую систему координат {х', у'}, движущуюся относи-
относительно системы координат \х, у} не равномерно и прямолинейно,
а каким-то другим более сложным образом, например вращающуюся
х' =
У' =
it
(cos a)
— (sin а)
X
х-
1 (sincc)j;-'
(coscc)^ т
(v cos |
(v sin \
i)ti
tл
-a
b,
d.
l) Арабское слово «бегство»; с переезда Магомета в Медину, по существу,
начался рост влияния его учения в арабском мире, в силу чего «хиджра»
является одним из главных религиозных праздников мусульман.

§ 2]
ЧТО ТАКОЕ МЕХАНИКА?
35
У>
X
Рис. 17.
с угловой скоростью (о вокруг начала О «старой системы коорди-
координат {х, у) (рис. 17). При этом на тела, покоящиеся по отношению
к подвижной системе координат \х', у'}, будут действовать посто-
посторонние силы, связанные с движением системы координат \х\ у'),
— так называемые силы инерции; в рассматриваемом случае это бу-
будет направленная от центра вращения
центростремительная сила действие
которой мы явственно ощущаем на
себе при поворотах трамвая, в котором
мы едем (с трамваем связана система
координат, по отношению к которой
мы покоимся). Те же системы отсчета,
в которых отсутствуют силы инерции
и все физические законы записываются
в своем естественном виде (не усло-
усложненном необходимостью учета < по-
посторонних сил инерции), называются
инерциальными системами отсче-
отсчета; таких инерциальных систем от-
отсчета существует бесконечно много,
и переход от одной из них к другой
осуществляется с помощью преобразований A2I). С другой стороны,
формулы A2) можно понимать как переход от одного события
А {х, у, t) (характеризуемого указанием места А (х, у) и времени /)
к другому событию А' (х', у', t'), причем точка А'(х', у') дви-
движется относительно точки А (х, у) равномерно и прямолинейно,
т. е. эти формулы можно понимать как некоторое преобразова-
преобразование в физическом пространственно-временном мире; эти преобразо-
преобразования A2) представляют собой не что иное, как преобразования
Г а л и л е я.
Теперь уже совсем просто объяснить, почему, казалось бы, столь
простые и важные понятия, как траектория движущейся точки или
ее скорость, на самом деле не имеют никакого физического смысла
и, стало быть, не могут фигурировать ни в одном физическом за-
законе. В самом деле, траектория движущейся точки очевидным
образом зависит от выбора той или иной из инерциальных систем
отсчета, движущихся друг относительно друга прямолинейно и рав-
равномерно. По этому поводу также хочется вспомнить Галилея, кото-
который сравнивал траекторию конца пера, которым рисует разные фи-
фигуры находящийся на- корабле художник, по отношению к быстро
движущемуся кораблю с траекторией того же конца пера по отно-
отношению к находящемуся на суше наблюдателю — последняя представ-
') По поводу всех затронутых здесь вопросов читателю можно пореко-
порекомендовать обстоятельные книги Хай к и на [14] — [15] или более краткую
брошюру Седова [16].

36
ВВЕДЕНИЕ
ляет собой почти прямую линию, направленную по пути следования
корабля, и лишь незначительно отклоняется от строгой прямолиней-
прямолинейности г). Точно так же и скорость точки А зависит от выбора
той или иной из ннерциальных систем отсчета: если корабль движется
в море прямолинейно и равномерно, то покоящееся по отношению
к кораблю тело может относительно земли двигаться весьма быстро.
Однако относительная скорость одного тела по отношению к дру-
другому, например скорость, с которой некоторый бегун приближается
к финишной ленте, имеет строгий механический смысл, поскольку
она не зависит от выбора инерциальной системы отсчета, в которой
рассматриваются оба эти тела: и в связанной с землей системой ко-
координат, и в системе координат, связанной с неподвижными звездами,
в которой и бегун и натянутая на финише лента перемещаются
с колоссальной, поистине космической) скоростгю, относитель-
относительная скорость бегуна, характеризующаяся тем, как быстро сокра-
сокращается расстояние между ним и лентой, имеет одно и то же зна-
значение. Еще более важно то, что абсолютный» смысл (не зависящий
от выбора той или иной инерциальной системы отсчета) имеет
ускорение каждой движущейся точки: ведь ускорение связано
с разностью скоростей (ср. выше, стр. 30), а переход от одной
инерциальной системы отсчета к другой системе сказывается лишь
в том, что все рассматриваемые скорости увеличиваются (или
уменьшаются) на одну и ту же величину, так что разность ско-
скоростей при этом никак не меняется.
Известно, что скорость точки выражается вектором, т. е. представляет
собой векторную величину; при этом скорость v произвольной
точки А в «старой» системе координат |л:, у\ (так называемая абсолютная
скорость точки) отличается от скорости v' той же точки относительно «новой»
системы координат {л:', у'} (от относительной скорости точки А) на векторную
величину а, совпадающею со скоростью начала О' системы координат {х', (/'}
относительно системы координат {х, (/} (так называемая переносная скорость
системы координат {х', </'} относительно системы координат {к, у)):
v = v' -j-a
(ср. ниже, стр. 61). Поэтому, если vx и v2—скорости двух^тел (например,
бегуна и финишной ленты) в одной системе отсчета, a v[ и v', — их скорости
в другой системе отсчета, то
v1 = v'1~, а и <v2 = vl>-', a,
так что
v1—v2 = v[ — v'2.
Совершенно так же обстоит дело и в том случае, когда vx и р2— скорости
одного тела в два разные момента времени tx и t2'- поскольку мы считаем,
что система 1х', у'} движется относительно {х, у] п р я м о л и н е й н о и равно-
равномерно и, значит, (векторная) величина а с течением времени не меняется,
то и тут
v1 = v[-{ а, р2 = <+а и v1—v-l = v'x— v'r
]) См. Галилей [13], стр. 270—272.

§ 2] ЧТО ТАКОЕ МЕХАНИКА? 37
Поэтому также и среднее ускорение «^ = —-—-? и мгновенное
* 1 — 'г
ускорение юмгнов = lim wcp не зависят от выбора инерциальной си-
стемы отсчета ').
До сих пор мы говорили о «двумерных» (точнее, плоскопарал-
плоскопараллельных) движениях, затрагивающих точки А (х, у) некоторой пло-
плоскости (плоскости хОу). Однако ничто не мешает нам ограничиться
еще более простыми прямолинейными движениями, при которых
приходится учитывать лишь движения точек А — А(х) некоторой
фиксированной прямой о (прямой Ох). При этом переход от одной
инерциальной системы отсчета на
прямой к другой задается форму- v
лами, указывающими, что начало О о •; •—— с >
системы координат {х\ движется щпю) А
относительно начала О' системы Рис. 18.
координат {х'\ с постоянной ско-
скоростью v (рис 18), т. е. что координата a (t) (подвижной!) точки О1
в «новой» системе координат {х'\ в момент времени t равна
где t — время, а а — координата точки О в момент времени / = 0.
А так как координаты х и х' одной и той же точки А в старой»
системе координат [х\ с началом О и в < новой:- системе координат
{х'\ с началом О' связаны, очевидно, зависимостью
(см. тот же рис. 182)), то мы имеем
х'= х -\-vt-\-a.
Присоединив к этой формуле еще формулу
') Мы рекомендуем читателю, знакомому с основами дифференциального
исчисления, самостоятельно проверить, что если г = г(х; у) — радиус-вектор
(движущейся) точки А (х, у), то ускорение r"=-jp- этой точки сохраняет
одно и то же значение при переходе от системы отсчета {х, у, t} к системе
отсчета \х', у', t'\ по формулам A2).
2) Мы здесь ограничиваемся рассмотрением, скажем, «правых» систем
координат, в которых положительное направление оси Ох (единствен-
(единственная ось координат на прямой!) заранее выбрано (например, является направ-
направлением вправо от точки О, если считать рассматриваемую прямую о горизон-
горизонтальной; ср. с подстрочным примечанием на стр. 19).

38 ВВЕДЕНИЕ
указывающую на возможность переноса начала отсчета времени,
мы окончательно получим следующие формулы:
A3)
указывающие, как записывается переход от одной инерциальной
системы координат к другой (т. е. преобразования Галилея),
если ограничиться только прямолинейными движениями.
Разумеется, строго прямолинейные движения встречаются в фи-
физике не так уж часто; поэтому механика таких движений представ-
представляет меньший интерес, чем механика плоско-параллельных движений
или, тем более, механика общих движений пространственных (т. е.
¦трехмерных ) тел. Однако изучение механики естественно начинать
с простейшего случая прямолинейного движения, где различие между
механическими и чисто геометрическими рассмотрениями, связанное
с фундаментальным принципом относительности Галилея, выступает
в наиболее отчетливом виде, не затушеванном техническими труд-
трудностями, возникающими, например,в связи с необходимостью учиты-
учитывать векторный характер основных механических величин (скоростей,
ускорений, сил). При этом изучение прямолинейных движений, вклю-
включающее, например, учение о (небольших) перемещениях материальных
точек под влиянием силы тяжести (эти перемещения направлены по
вертикали!), имеет и определенный «прикладной» интерес; с другой
стороны, сравнение, скажем, формул A3) с гораздо более сложными
формулами A2) (не говоря уже о формулах A6), стр. 42) хорошо
иллюстрирует выгоду в простоте изложения при рассмотрении только
прямолинейных движений.
Еще один важный аргумент в пользу рассмотрения одних лишь
прямолинейных движений связан с возможностью использования в этом
последнем случае весьма простых графических иллюстраций. Мы уже
знаем, что планиметрия изучает те факты, которые в координатах
\х, у) записываются формулами, сохраняющими свой вид при дви-
движениях F):
х' — л: cos a 4 у sin а 4- а, 1
у' ——л: sin а ^-у cosa-f- b. J
Аналогично этому в области прямолинейных движений механика ин-
интересуют те факты, которые в координатах {х, t) записываются
формулами, сохраняющими вид при преобразованиях Галилея 13
х' - - х -!-vt - a, \
\

§ 2]
ЧТО ТАКОЕ MKXAIIIIKA?
39
о
Условимся обозначать положение точки А(х) па прямой о в момент
времени / с помощью вспомогакелытй точки А(х, t) (двумерной)
плоскости xOt с коорчпнатами х и / (рис. 19, а, б). При этом мы
придем к своеобразной «геометрии», в которой «геометрический»
(точнее было бы сказать, механический!) смысл имеют лишь те факты,
которые записываются формулами, сохраняющим» свой вид при все-
всевозможных преобразованиях A3), играющих, таким образом, роль
движений этой геометрии, не ме-
меняющих ни одного из интересую- в-
щих нас свойств фигур. Этой-то ,4 а)
геометрии, которой можно ирлсво-
ить наименование геометрия прин-
принципа относительности Галилея пли,
короче, просто «геометрия Гали-
Галилея», и будут посвящены главы I и II -
настоящей книги. и х 6)
Геометрию Галилея мы будем р .„
рассматривать параллельно с обыч-
обычной геометрией или геометрией Евклида, называемой так по имени
великого греческого математика Евкшда, жившего (и преподавав-
преподававшего) в городе Александрия в Египте в III веке до и. э. и оста-
оставившего нам первый из дошедших до нас (и притом замечательный!)
учебник геометрии, по которому много веков подряд люди знако-
знакомились с этой наукой *). Геометрия Евклида отличается от геометрии
Галилея лишь тем, что в первой из них движения записываются
формулами F), в то время как в плоскости Галилея движения
имеют совсем иной вид A3). Для того чтобы облегчить сопоставле-
сопоставление этих двух замечательных геометрий , мы будем в дальнейшем
обозначать координаты точек плоскости Галилея теми же буквами
х и у, что и координаты точек плоскости Евклида (обычной плос-
плоскости); другими словами, мы условимся обозначать координату под-
подвижной точки А прямой о буквой у (а не х). а время — буквой х
(а не t). При этом геометрию Евклида и геометрию Галилея можно
будет охарактеризовать как изучение тех свойств фигур координат-
координатной плоскости {х, у}, которые сохраняются, -соответственно, при
преобразованиях (G) и при преобразованиях
A3а)
(ср. с формулами A3); заметим, что буквы а и b имеют в формулах
A3)и A3а) разный смысл). Эти две «геометрии» мы будем изучать
Учебник Евклида переведен и на русский язык (см. Евклид [1]—[3]).

40
ВВЕДЕНИЕ
параллельно; однако при использовании чисто геометрического подхода
к фактам геометрии Галилея мы рекомендуем читателю не терять из
виду возможности механического истолкования любого из этих фактов.
Заметим, наконец, что каждое преобразование Галилея A3а)
можно разбить на два преобразования: преобразование
Ху — X f ЛГГ = X-V- Vts
i или j. A4а)
уг= vx 4. у ty -= t)
отражающее равномерное движение со скоростью v начала Ог под-
подвижной :истемы координат {хг\ вдоль прямой о1), и преобразование
I или
\
A46)
отражающее перенос в другую точку О' начала отсчета координат
на прямой и изменение начала отсчета времени. Геометрический
смысл преобразования A46) (или преоб-
преобразования (8); см. выше, стр. 25) нам
уже известен — это есть параллельный
перенос (см. рис. 12, б на стр. 25). Что
же касается преобразования A4а), то оно
представляет собой так называемый сдвиг
в направлении оси Оу с коэффициен-
коэффициентом сдвига v, при котором все точки
оси Оу остаются неподвижными, а каждая
другая точка смещается в направлении
этой оси, причем величина смещения
пропорциональна (с коэффициентом про-
пропорциональности v) расстоянию точки от
оси Оу (при этом точки, расположенные
по одну сторону от оси Оу, сдвигаются
в одном направлении, а точки, располо-
расположенные по другую сторону оси Оу,—
в противоположном направлении; см. рис.
20J). Таким образом, для того чтобы
убедиться, что каждое преобразование
A3а) сохраняет значение некоторой величины, достаточно прове-
проверить, что значение этой величины сохраняют сдвиги A4а) и параллель-
параллельные переносы A46) — обстоятельство, которое нам ниже часто
будет полезно.
Рис. 20.
') Мы считаем, что в момент времени t =0 точка О1 совпадает с началом О
«старой» системы координат.
2) Ср. Яглом и Ашкинузе [56], стр. 37—39.

§ 2]
ЧТО ТАКОЕ МЕХАНИКА?
41
Аналогично этому изучение механики плоско-параллельных движений
сводится к своеобразной «геометрии» трехмерного пространства, отнесенного
к трем координатам {х, у, tj, «движения» которого описываются формулами A2).
Рис. 21.
Эта «геометрия», которую также можно было бы назвать (трехмерной) геомет-
геометрией Галилея (или стереометрией Галилея), представляет значительный инте-
интерес; однако она заметно слоЛнее геометрии Галилея на плоскости. «Движе-
«Движения» A2) можно «расщепить» на три преобразования: поворот
*!= я cos <х -\-y sin a,
У1——xsma-\-ycosa, A5a)
<!=- t
вокруг оси Ot (рис. 21, а); сдвиг
Уг =
(
i-t-(и sin
A56)

42 ВВЕДЕНИЕ
в направлении вектора v — (v cos р; v sin Р; 0) плоскости хОу, при ко-
котором точки самой плоскости хОу остаются па месте, а каждая плоскость я,
параллельная плоскости хОу, переносится параллельно в направлении век-
вектора v на расстояние vt J), пропорциональное расстоянию OQ — t плоскости л
от плоскости хОу (рис. 21, б), и, наконец, параллельный перенос
х' —х.2 -а,
У' ~- У-1 иЬ, A5в)
/' = t, , d
на ве к т о р с = (а; Ъ\ d) (рис. 21, в). Поэтому все имеющие смысл в «сте-
«стереометрии Галилея» величины должны сохранять свое значение (а все факты
«стереометрии Галилея» — сохранять свое содержание) при. поворотах A5а),
сдвигах A56) и параллельных переносах A5в).
Еще более сложной является «четырехмерная геометрия Галилея», адек-
адекватно отображающая все величины и факты, с которыми приходится сталки-
сталкиваться в механике при рассмотрении (самых общих!) движений пространствен-
пространственных тел. Эту «геометрию» можно описать как учение о тех свойствах четы-
четырехмерного2) пространства, отнесенного к координатам {х, у, г, <}, которые
сохраняются при общих преобразованиях Галилея
х' = (cos P cos a—cos у sin P sin a) x f (sin P cos а J-cos у cos P sin а) у~[
-г(sin у sin а) г-t (v cos 6t) t , a,
у' = —(cos P sin а Г cos у sin P cos a) x-*-(—sin p sin a T cos у cos P cosa)jh
I (sin у cos a) z (ycos 62) ' -*-b, A6)
z' =(sin у sin p) x — (sin у cos P) y-, (cos y) z- (v co.s 63) t -r c,
где cos2 6t '-cos2 6., + cos- 63 — 1 (ср. с формулами (9), стр. 26), играющими
в этой «геометрии» роль «движений». Мы не имеем возможности остановиться
здесь более подробно на содержании этой замечательной геометрии.
В заключение настоящего параграфа хочется коснуться еще одного вопроса.
Геометрия Галилея (трехмерная), «движения» которой задаются формулами A2),
возникает в результате попытки перевода на геометрический язык основных
фактов плоской кинематики. Совсем др\гая (но не менее интересная!)
геометрия получается при «геометризированном» описании феноменов плоской
статики — и нам трудно удержаться от соблазна дать здесь краткую харак-
характеристику и этой замечательной «геометрии».
Хорошо известно, что каждую систему сил в статике можно изменять,
сдвигая как угодно вектор каждой силы вдоль задаваемой этим вектором
прямой3), складывая приложенные в одной точке силы по правилу паралле-
•) Если величина vt отрицательна (т. е. отрицательна характеризующая
плоскость л координата /), то параллельный перенос производится в направ-
направлении, противоположном направлению вектора v.
2) Относительно понятия четырехмерного (и многомерного) пространства
см., например, Кокстер [19| или Розенфельд и Яглом [20].
3) Вектор, который позволено сдвигать как угодно вдоль прямой, по
которой он направлен, но нельзя переносить в точки, не принадлежащие
этой прямой, называется скользящим вектором; таким образом, система сил
в статике — это система скользящих некторов.

§ 2] ЧТО ТАКОЕ МЕХАНИКА? 43
лограмма или, наоборот, разлагая одну силу на несколько приложенных
в тон же точке сил, (векторная) сумма которых равна первоначальной силе >).
Такими преобразованиями (не меняющими механического действия системы
сил!) каждую систему сил можно привести к одной силе (т. е. к одному
«скользящему» вектору; см. примечание3) на стр. 42) или к так называемой
«паре» сил, т. е. к двум одинаковым по величине и противоположным по
направлению силам, направленным по двум параллельным прямым (но не
по одной прямой—в противном случае наши две
силы взаимно уравновесились бы!) Еще больший ин-
интерес представляет для нас возможность приведения
Рис. 22. Рис. 23.
любой системы сил к одному вектору F, прилож"нному в произвольно
фиксированном заранее «начале координат» О (главный вектор системы),
и к паре сил Л, =МЛН1 и h.,= —Л] Л1.,/У.,, которые можно считать прило-
приложенными в таких точках MY и М.,, что точка О является серединой отрезка
MtAi, (рис. 22); такая пара сил полностью характеризуется своим «моментом»
u = ft.OM,-sin / (ОМ[, Л,)ч h-OM.,-s\n /_ (ОЩ, h.^ = (OAT[xhi) ;-(ОЖ7хА2)
(главный момент системы) -). [В последней формуле косым крестом обо-
обозначено так называемое «косое», или «псевдоскалярное», произведение векто-
векторов: если векторы a -QA ( (xt; yj) и Ь = QB ( (х.,; ^.2)) приложены к одной
точке<2, тоа \b QA-QB sin/_AQB ( x^y^—x^,причем,каквсегда,угол AQB
считается положительным, если направление вращения, переводящего луч QA
в луч QB, противоположно направлению вращения часовой стрелки, и отрица-
отрицательным в противном случае (рис. 23) 3)]. При этом главный вектор системы сил
/ь /а- ,/,,, приложенных в точках Л1? А.,, Л„, равен сумме этих сил
а главный момент той же системы—сумме моментов всех сил
и @А[ /J-4OAI Л)+ \@А„ /„)¦
Так как вектор F определяется заданием двух своих координат х и у,
то множество всевозможных систем сил на плоскости «трехмерно», т. е. задается
\гказаннем трех чисел х, у>н и—«координат» этой системы4). При переносе
!) См., например, гл. III кни^-и Ландсберга [17].
-) См., например, гл. I книги Аппеля [21] или гл. IV (и, особенно,
§ 23 этой главы) книги Бухгольца [22].
3) См., например, § 4 статьи Болтянского и Яглома [23].
') Нетрудно понять, что если координаты системы сил j\, /2, ...,/,
равны хх, ух и и1у а координаты системы сил g-t, §•.,, ..., gm равны а'.,, у., и и.гп
то координаты X, Y uU новой системы включающей как все силы fi.f^, . -,fn,
так и все силы gi, g, .... g,n, равны суммам соответствующих координат
исходных систем сил: X = x1-j-jf2, Y ~ iJi-\-y.,, U =^ul-\-u2,.

44
ВВЕДЕНИЕ
начала системы координатор новую точку О' (а, Ь) (здесь а и Ъ — координаты
точки О' или вектора 00'- с по отношению к старой системе координат
\х, у\\ рис. 24) главный вектор F системы сил flt /2 /„, равный сумме
всех сил, очевидно, не изменится, а главный момент станет равным
... +(О'Л„ч/„) =
{(ОлГ-оо7)х/1}+{(бл;-оо7)х/2}+
Л)+(от2 ч/2) + + (ога х/„) -
= и — cv f" =
-оо7)- /„} =
t-/,:- +/„) =
u— (ay—bx)=bx—ay-j-u
(здесь мы -используем дистрибутивность косого произведения векторов по
отношению к сложению: (т-\-п)хр = (т р)-\-(п :р), а также то, что
с (а; &)) F (х\ у) = ау—Ьх). Наконец, при повороте осей координат на угол а
главный момент к, очевидно, не изменится (ибо и вообще не зависит от направ-
направления осей координат, а лишь от выбора «начала» О), а координаты х
и у вектора F преобразуются по следующим
формулам:
х'= х cos a + у sin а, \^
у'= —х sin a+i/cosa f
(ср. формулы G), стр. 25).
Таким образом, окончательно мы полу-
получаем, что при изменении системы коорди-
координат на плоскости «координаты» х, у. и си-
системы сил преобразуются следующим об-
образом:
Рис. 24.
х'= (cos а) л; + (sin a) у,
у' = —(sina)*-|--(cosa) у,
и'= Ьх —ау-\-и;
A7)
эти же формулы указывают, как меняются «координаты» (я, у, и) системы
сил, если плоскость со всеми приложенными к ней силами двигать как еди-
единое целое. Поэтому можно считать, что плоская статика сводится к изучению
трехмерного пространства {х, у, и}, в котором преобразования A7) играют
роль «движений», т. е. не меняют никаких свойств точек этого пространства
(систем сил).
Поскольку общая теория систем сил (приведение любой системы сил
к главному вектору и главному моменту) была впервые разработана замеча-
замечательным французским механиком Луи Пуансо A777—1859) в его книге
«Начала статики» A804), то «геометрию» трехмерного пространства, «движения»
которого задаются формулами A7), можно было бы назвать «геометрией
Пуансо». В дальнейшем мы не коснемся этой примечательной геометрии,
сосредоточив все наше внимание исключительно на геометрии Галилея.

ГЛАВА I
РАССТОЯНИЯ И УГЛЫ; ТРЕУГОЛЬНИКИ
И ЧЕТЫРЕХУГОЛЬНИКИ
§ 3. Расстояние между точками и угол между прямыми
Перейдем теперь к систематическому изучению геометрии Гали-
Галилея— геометрии плоскости хОу, «движения» которой задаются фор-
формулами
х'= х +а,
У' =vx+y+b.
A)
Таким образом, в дальнейшем нас будут интересовать лишь те свой-
свойства фигур плоскости хОу, которые сохраняются при преобразова-
преобразованиях A) (другими словами, сохраняются при сдвигах
х'= х,
у =
в направлении оси Оу и при параллельных переносах
х' = х + а,
A6)
у'=у + Ь;
см. выше, стр. 40): лишь такие свойства фигур имеют геометриче-
геометрический смысл в рамках рассматриваемой нами необыкновенной геомет-
геометрии. При этом мы не будем забывать, что сама эта геометрия есте-
естественно возникла из механических рассуждений, связанных с принци-
принципом относительности Галилея, так что слова «имеют геометрический
смысл» в нашем случае означают: «имеют механический смысл», т. е.
отвечают каким-то фактам «одномерной кинематики»—учения о дви-
движениях материальных точек вдоль фиксированной прямой о.
Прежде чем переходить к обсуждению содержания первона-
первоначальных понятий геометрии Галилея, полезно перечислить основ-

46
расстояния и углы; трнугольннкн и четырехугольники [гл. I
ные свойства «движений» A). Заметим, что преобразования A)
переводят
каждую прямую линию снова в прямую линию,
параллельные прямые снова в параллельные прямые,
два отрезка АВ и CD одной прямой в такие отрезки А'В' и CD',
CD' CD
410 W = AB>
каждую фигуру F в фигуру F' той же площади
(доказательство всех этих утверждений мы дадим несколько ниже);
поэтому понятия прямой линии, параллельных прямых,
отношения отрезков одной прямой, площади фигуры
имеют смысл не только в обычной геометрии Евклида, но и в геомет-
геометрии Галилея. Очень важно также то, что каждое преобразование A)
переводит любую прямую, параллель-
параллельную оси Оу, снова в прямую, парал- У
лельную оси Оу, — так что если в
геометрии Евклида понятие «прямая,
а)
Рис. 25.
параллельная оси Оу» является геометрически бессодержательным
(ибо обычным движением такую прямую можно перевести в любую
другую; см. рис. 25, а), то в геометрии Галилея параллельные
оси Оу н р я м ы е играют особую роль, отличную от роли всех
остальных прямых. [В противоположность этому «прямые, параллель-
параллельные оси Ох» не отличаются в геометрии Галилея от других «обык-
«обыкновенных» (т. е. не параллельных оси Оу) прямых: на рис. 25, б
показано, что сдвиг Aа) переводит прямую /, параллельную оси Ох,
в прямую Г, не параллельную этой оси.] В дальнейшем мы сохраним
термин «прямая», не сопровождаемый никаким прилагательным, только
за прямыми, не параллельными оси Оу; параллельные же оси Оу
прямые мы будем называть особыми прямыми.

§ 3]
РАССТОЯНИЕ МЕЖДУ ТОЧКАМИ II УГОЛ МЕЖДУ ПРЯМЫМИ
47
Для доказательства всех перечисленных свойств движений A)
достаточно проверить, что ими обладают сдвиги Aа), поскольку
параллельные переносы A6) заведомо всеми этими свойствами обла-
обладают (см. рис. 12, б на стр. 25).
То, что прямую, параллельную
оси Оу, сдвиг переводит также в
параллельную оси Оу,— а именно
в ту же самую прямую,— не-
непосредственно вытекает из опре-
определения сдвига Aа) (см. стр. 40,
в частности, рис. 20). Далее,
пусть сдвиг Aа) с коэффициентом
сдвига v переводит точку А пря-
прямой /, проходящей через начало
координат О, в точку А' (рис. 26). с-^
Обозначим прямую ОА' через /',
точки пересечения любой парал-
параллельной оси Оу прямой т с пря- i
мымн / и /' — через М и М', а точки %
пересечения прямых т и АА' с
осью Ох (которую мы всегда буадм
изображать перпендикулярной оси
Оу1)) —через Q и Р. Из рис. 26
Рис. 26.
легко получим
M'Q
А'Р
MQ АР
ки А сдвигом Aа), то
А'Р OP-v + AP
~АР ' ~АР
. Но так как точка А' получается из точ-
ОР
., „„ / OP OQ А'Р
Используя опять рис. 26 ^на котором -др = --щ " -Jp=
M'Q
имеем
т. е.
M'Q
MQ
АГР
~АР
_qp^ _
АР
OQ-v+WQ
MQ
M'Q OQ-v-, MQ.
Но это как раз и означает, что каждую точку М прямой / наш
сдвиг переводит в точку М' прямой Г, т. е. что он переводит прямую I
в прямую I'.
Пусть теперь 1Х — прямая, параллельная прямой / и не проходя-
проходящая через точку О (см. тот же рис. 26). Обозначим через d длину
') Это условие удобно нам в силу привычки к декартовым прямоугольным
координатам на плоскости, оси которых перпендикулярны, однако в рамках
геометрии Галилея оно бессодержательно: ведь в этой геометрии (евклидово)
понятие перпендикулярности прямых геометрического смысла не имеет.

48
расстояния и углы; треугольники и четырехугольники [гл. i
(обычную, т. е. измеряемую как в евклидовой геометрии!) равных
между собой вертикальных (т. е. параллельных оси Оу) отрезков
ААЪ ВВЪ ССЪ . . ., заключенных между прямыми / н 1Х. Вспомним,
что сдвиг Aа) сводится к переносу вдоль каждой прямой, параллель-
параллельной оси Оу, всех точек этой прямой на одно и то же расстояние
(но точек разных прямых — на разные расстояния); поэтому все
отрезки АА1=ВВ1=СС1 = .. . = й этот
сдвиг переведет в отрезки А'А[, В'В\,
С'С'1щ ... той же длины:
А'А[ = В'В[ = С'С[ = .. =d.
А так как концы А', В', С", ... этих
отрезков принадлежат прямой Г (в ко-
которую наш сдвиг переводит прямую/),
то вторые их концы А[, В[, С'ъ ... по-
попадут на прямую 1[, параллельную
прямой Г и отстоящую от Г на расстоя-
расстояние й в направлении оси Оу. Отсюда и
следует, что сдвиг Aа) переведет пря-
прямую 1Х в прямую 1[. Попутно мы убе-
убедились, что все прямые, параллельные
фиксированной прямой /, сдвиг Aа) пе-
переводит в прямые, параллельные пря-
прямой Г1), т. е. что параллельные
рис 27 прямые сдвиг переводит в параллель-
параллельные.
Еще проще доказать, что если отрезки АВ и CD какой-то пря-
прямой I сдвиг Aа) переводит в отрезки А'В' и CD' прямой I', то
CD'
А'В'
CD
'АВ'
доказательство этого факта, непосредственно вытекающее из рис. 27,
мы предоставим читателю провести самостоятельно. Заметим заодно,
что если АВ н EF—параллельные друг другу отрезки, то сдвиг
переводит их в такие отрезки А'В' и E'F' (также параллельные),
что
E'F' EF
А'В'~ АВ
(см. тот же рис. 27, где EF=CD и E'F'—CD', так как параллело-
параллелограмм CDFE переходит в параллелограмм C'D'F'E'); отсюда сле-
следует, что также и понятие отношения длин параллельных
отрезков имеет смысл в геометрии Галилея. Однако если
]) Нетрудно убедиться, что если прямая / образует с осью Ох угол а,
а прямая V — угол а', то tga' = tga+f.

§ 3]
РАССТОЯНИЕ МЕЖДУ ТОЧКАМИ И УГОЛ МЕЖДУ ПРЯМЫМИ
49
то сдвиг может перевести отрезки АВ и MN в такие отрезки А'В'
и M'N', что M'N':A'B'^MN:AB (см. рнс. 27, где АВ<А'В', но
MN>M'N').
Наконец, площадь фигуры F приближенно равна сумме площа-
площадей помещающихся внутри F «маленьких» квадратов, образованных
сетью прямых, параллельных осям Ох
и Оу и отстоящих друг от друга на
одно и то же «малое» расстояние е
(т. е. приближенно равно числу таких
квадратов, умноженному на площадь е2
одного квадрата, — рис. 28, наверху);
точное же значение площади опреде-
определяется как предел полученных таким
образом величин, отвечающих последо-
последовательности неограниченно уплотняю-
уплотняющихся сеток квадратов (т. е. таких,
что величина е неограниченно умень-
уменьшается). Сдвиг Aа) переводит фигуру
F в новую фигуру F', а сетку квадра-
квадратов— в сетку параллелограммов той
же площади (см. рис. 28, внизу) — ведь
параллельная оси Оу сторона паралле-
параллелограмма будет той же, что и сторона
квадрата, а опущенная на эту сторону
высота параллелограмма также равна
стороне квадрата. Поэтому приближен-
приближенное значение площади фигуры F', рав-
равное произведению числа помещающихся
внутри F' параллелограммов сетки на
площадь е2 одного параллелограмма,
будет тем ж е, что и приближен-
приближенное значение площади фигуры F.
А так как приближенное равенство
пл. F' яй пл. F имеет место при л го-
гобой точности определения площа-
площаРис. 28.
дей фигур
видно,
F и F' (зависящей от размера квадрата сетки), то, оче-
пл. F' =
После этих предварительных замечаний мы можем приступить
к обсуждению смысла понятий «расстояние между точками» и «угол
между прямыми» в геометрии Галилея. В евклидовой геометрии рас-
расстояние йААх между двумя точками А(х,у) и А1(х1,у1) определяется
формулой
=v?; B)

50
расстояния н углы; треугольники и четырехугольники [гл.
при этом равенство нулю расстояния между двумя точками означает,
что эти точки совпадают. Угол 6ц% между двумя прямыми I и 1Ь
записываемыми уравнениями
у = kx -\ s и у = kxx ~\- а1г
можно определить по формуле
/гг—k
tg б/г, =
**!+!'
C)
— это следует из того, что прямые / и 1} образуют с осью Ох
углы ф н фь определяемые равенствами tg<p = k и tgф1 = й1, так что
(см. выше, стр. 24 н рнс. 11,6).
Если k = kL, то прямые I и 1Х параллельны; в Этом случае
определенный по формуле C) «угол» 8^ между прямыми равен нулю.
Для параллельных прямых можно говорить о расстоянии йцг между
этими прямыми:
dn — ^~ , D)
ибо \s1 — s^
COS (f
есть высекаемый прямыми / и 1Х отрезок оси Оу,
1 ,• -.11
где ф — угол, образованный / н 1Х
с осью Ох (ср. выше, стр. 23, в
частности, рис. 11, а). При этом
следует иметь в виду, что хотя обе
величины 6//, и йц1 определяют «от-
«отклонение» прямых / и 1Х друг от
друга, они имеют совершенно разный
характер: угол 6 измеряется в «угло-
«угловых единицах» (в градусах или в ради-
радианах), а расстояние й — в единицах
длины (в метрах или сантиметрах).
Поэтому эти величины сравнивать
между собой нельзя: так, например, вопрос: «прямые I к 1Х образуют
угол в 30° (рнс. 29, а), а (параллельные) прямые от и т1 удалены друг от
друга на 15 см (рис. 29, 6); что больше — отклонение друг от друга пря-
прямых / н 1Х или отклонение друг от друга прямых т и /яг?»—явно бес-
бессмыслен. Заметим еще, что расстояние D) между прямыми может быть
определено лишь в том случае, если определяемый формулой C)
угол между этими прямыми равен нулю; прямые / и 1Х совпадают между
а)
Рис. 29.

§ 3]
РАССТОЯНИЕ МЕЖДУ ТОЧКАМИ II УГОЛ МЕЖДУ ПРЯМЫМИ
51
собой лишь в том случае, если угол б между ними равен нулю и,
кроме того, равно нулю и расстояние d между этими прямыми.
После этих предварительных замечаний, относящихся к геометрии
Евклида, можно перейти к нашей основной теме. Расстояние Aаах
между двумя точками А(х,у) и Л1(х1, уг) в геометрии Галилея
определяется по формуле
t = xl — х\
E)
оно равно проекции РРг отрезка АА1 на ось Ох (рис. 30, а). Так
как координата х точки А преобразуется при движении A) по фор-
формуле
х' = хЦ-а,
то ясно, что разность хх — х абсцисс двух точек Ах и А при дви-
движении A) не меняется. [Так же и из мисто геометрических соображе-
соображений нетрудно усмотреть, что проекция РР1 отрезка ААг на ось Ох
К
а)
б)
Рис. 30.
имеет смысл в нашей геометрии: ведь и параллельный перенос A6),
и сдвиг Aа), очевидно, сохраняют величину этой проекции.]
Если расстояние й^л, между точками А и Ах равно нулю, т. е.
х^-=х, то точки А и Ах принадлежат одной особой прямой (пря-
(прямой, параллельной оси Оу; рис. 30,6). Для таких двух точек можно
определить особое расстояние б^л, между точками:
F)
В самом деле, если абсциссы двух точек А(х, у) и Al(xl, yt) оди-
одинаковы (если х = jcj), то произвольное движение A) преобразует их
в точки А' (х'.у') и А[(х[,у'1), где х' — х\ ( = х + а) и

52 расстояния и углы; треугольники и четырехугольники [гл. i
поэтому
i'
т. е. разность у1—у не меняется при движении, а следовательно,
имеет на плоскости Галилея геометрический смысл. Однако если
расстояние Aаа, = х^—je между точками А и Ах отлично от нуля,
т. е. абсциссы этих точек различны, то разность уг—у ординат этих
точек не сохраняет своей величины при движении, ибо в этом случае
Да это и понятно — ведь сдвиг Aа) оставляет на месте начало О
системы координат и меняет ординату любой точки М, не принадче-
жащей оси Оу; поэтому он никак не может сохранять разность орди-
ординат точек М и О.
Очевидно, что две точки А и В плоскости Галилея совпадают
в том и только в том случае, когда равно нулю как расстояние dAB
между этими точками, так н особое расстояние 6ЛЙ между ними.
Окружностью S плоскости Галилея мы назовем множество
точек М{х, у), удаленных от фиксированной точки Q на постоян-
постоянное (по абсолютной величине) расстояние г; при этом точка Q{a, b)
называется центром окружности, а (неотрицательное) число г — ее
радиусом. Так как
(см. формулу E)), то уравнение
окружности .S имеет вид
d2QM =
или
х* + 2рх +д = 0, G)
где
р = — a, q — a2 — г2. Gа)
Ясно, что окружность 5 радиуса г с центром Q представляет собой
совокупность двух особых прямых, отстоящих от точки Q на рас-
расстояние г (рис. 31, а); если радиус г окружности обращается в нуль,
то эти две прямые сливаются в одну (рис. 31,6). Заметим еще, что
окружность 5 геометрии Галилея имеет строго определенный радиус
(равный половине расстояния между образующими эту окружность
прямыми), но бесконечно много центров: любую точку осо-
особой прямой, содержащей точку Q, можно принять за центр этой
окружности (см. тот же рис. 31).
Угол б/г, между прямыми I и 1Ъ пересекающимися в точке Q,
можно определить как длину заключенной между прямыми / и lt

§ 3]
РАССТОЯНИЕ МЕЖДУ ТОЧКАМИ И УГОЛ МЕЖДУ ПРЯМЫМИ
53
дуги NNX окружности 5 единичного радиуса с центром в точке Q
(ср. относящиеся к геометрии Евклида и к геометрии Галилея рис. 32, а
и 32, б; ясно, что под «длиной дуги» NNl окружности S геомет-
геометрии Галилея надо понимать «особую длину» 6,vw, отрезка AWb
У
S
V
Щх,у)
S
>М(х,у)
й(а,Ь)
х
Рис. 31.
т. е. особое расстояние между точками N и ./Vj содержащей их особой
прямой). Определенная таким образом величина бг/, угла, очевидно,
имеет смысл в геометрии Галилея, т. е. сохраняется при дви-
движениях A): ведь точку Q пересечения прямых I и 1Х движение
Рис. 32.
переводит в точку Q' пересечения полученных из / и /j движением
прямых /' и /]', а единичную окружность 5 и дугу TVA^ этой ок-
окружности— в единичную окружность S' с центром Q' и в дугу ЛГЛ^
окружности S' (рис. 33). Это определение угла между прямыми
в геометрии Галилея равносильно следующему: для того чтобы
найти угол 6^ между прямыми I и 1Ъ достаточно провести

54
расстояния и углы; треугольники и четырехугольники [гл. i
особую прямую т, удаленную от вершины Q угла на расстояние 1
и пересекающую стороны угла в точках N и Nx\ тогда
Если уравнения прямых I u А, имеют привычный вид _у= kx -\-s и
у = ktx <-slt а координаты точки Q равны х0 и у0, то уравнение
прямой m таково:
х-=хп , 1.
Поэтому точки А' и Nt будут иметь координаты
а следовательно,
6и,= 6л^= [*!(*
) — (Ад:,,
Aj — А = *! —
(ибо Q(x0, _у0)—общая точка прямых / и /t и поэтому kxo-\-s
= A1JC0-j-*1 = 0). Таким образом, окончательно имеем
бгг, = А1 — А;
(8)
эта формула значительно проще формулы C) для величины угла
между прямыми в евклидовой геометрии.
I'
Рис. 33.
0 I
Рис. 34.
Если одну из прямых / и /г, например 1г, поворачивать вокруг
точки Q устремляя ее к особой прямой ш, то угол б//( будет н е о г-
ран именно возрастать (рис. 34) —явление, которое противо-
противоречит нашим представлениям, заимствованным из геометрии Евклида.
Укажем еще, что в противоположность евклидову случаю га.шлеев

§ 3]
РАССТОЯНИЕ МЕЖДУ ТОЧКАМИ И УГОЛ МГЖДУ ПРЯМЫМИ
55
угол» б между 1в\мя прямыми I и /г определяется однозначно
(ср. рис. 32, а и б) — это обстоятельство делает весьма многие
рассмотрения, относящиеся к геометрии Галилея, существенно
более простыми, чем соответствующие
им факты евклидовой геометрии (ср. с
подстрочным примечанием на стр. 68).
Если прямые / л /х параллель н ы,
то определяемый по формуле (8) угол 8цг
между этими прямыми равен нулю. Однако
в этом случае можно говорить о расстоя-
расстоянии йц1 между (параллельными) прямыми
I и /j, понимая под этим (особую) длину
заключенного между прямыми I и 1Х от-
отрезка ММ1 особой прямой (любой; рис.
35): так как особые прямые перев'одятся
движениями A) снова в особые прямые, то
определенное таким образом расстояние^ имеет смысл в геометрии
Галилея. Если уравнения рассматриваемых прямых I и /j имеют вид
у = kx s ii у — kx f su то, очевидно,
У-
0
S—
S
ц
т ^^
dUy^
Н
X
Рис. 35.
s;
(9)
эта формула также значительно проще соответствующей формулы D)
евклидовой геометрии 1).
У
М
Р
Рис. 36.
Наконец, расстоянием йлп от точки М до прямой I мы условимся
называть (особое!) расстояние от точьн М до точки пересечения
прямой / с особой прямой, проходящей через точку М (рис. 36, б).
х) Заметим, что в определениях величин d^,, блл,. 6«,i d![t существен-
существенным было то, какой из двух объектов А и Аг (соответственно I и 1г) считать
первым, а какой—вторым; это отражено и в формулах E), F), (8), (9), из
которых, кстати, видно, что каждая из рассматриваемых величин может быть
как положительным числом, так и нулем или отрицательным числом.

56
расстояния и углы; треугольники и чртырехугольннки [гл. i
Это условие можно обосновать следующими соображениями: в евкли-
евклидовой геометрии расстояние от точки М до прямой /—эго рас-
расстояние от точки М до самой близкой к Ж точки Р прямой I
(рис. 36, а); в геометрии же Галилея "самая близкая к М точка Р
прямой/ удалена от М на нулевое расстояние, т. е. dMP = 0; поэтому
расстояние от точки М до прямой I приходится измерять особым
расстоянием между М и Р: dMl=bMp. Если прямая I записы-
записывается уравнением y=kx \-s, то координаты точки Р (точки пере-
пересечения I с проходящей через точку М (х0, у0) особой прямой т)
будут иметь вид (л:0, kxo-\-s); поэтому
МР
Таким образом,
A0)
т. е. расстояние от точки М до прямой / равно результату подста-
подстановки в левую часть уравнения
у — kx — s = 0
прямой I (уравнения C)из§ 1; см. стр. 17) координат л:0, _у0 точки Ж1).
Ясно, что определенное выше расстояние dnt между двумя парал-
параллельными прямыми / и 1г теперь можно описать как расстояние
от любой точки М прямой / до прямой lv
У'
0
«¦»
6)
X
Рис. 37.
Из определения расстояния от точки М до прямой I и расстоя-
расстояния между параллельными прямыми I и 1г следует, что роль перпен-
перпендикуляров к прямой в геометрии Галилея играют особые прямые
(ср. относящиеся к геометрии Евклида и к геометрии Галилея
рис. 37, а и 37, б). К этой аналогии между перпендикулярами к прямой
и особыми прямыми мы еще неоднократно будем возвращаться.
') Ср. ниже, стр. 258.

§ 3] РАССТОЯНИЕ МЕЖДУ ТОЧКАМИ И УГОЛ МРЖДУ ПРЯМЫМИ 57
Расшифруем теперь механический смысл всех введенных в этом
параграфе понятий. Ясно, что точке М (х, у) плоскости Галилея
в кинематике прямой о отвечает событие (t, x), характеризующееся
указанием места х на прямой о и времени t (рис. 38); при этом
роль «временной координаты» t события на плоскости Галилея играет
координата х, а роль «простран-
«пространственной координаты» х — коордн- О (t)
на га у. Расстояние d между "—v—'
двумя точками А и Аг плоскости х
Галилея есть не что иное, как Рис. 38.
временной интервал tt — t между от-
отвечающими этим точкам событиями А и At. Если этот интервал равен
нулю, т. е. если события А и Аг одновременны, то между этими
событиями существует пространственный интервал, равный расстоя-
расстоянию между отвечающими событиям А и А1 точками прямой о; этот
пространственный интерват совпадает с определенным выше особым
расстоянием б между отвечающими рассматриваемым событиям
точками плоскости Галилея. Заметим, что пространственньпЧ интервал б
можно определить только для одновременных событий, гак как
в противном случае расстояние ие^ду соответствующими точками
прямой о будет существенно зависеть от выбора той или иной
инерциальной системы отсчета и потому не будет иметь смысла
в геометрии Галилея. В самом деле, если в системе отсчета, свя-
связанной с Землей, расстояние между школой, где вы были днем, и
домом, в котором вы ужинаете вечером, сравнительно невелико, то
с точки зрения связанной с неподвижными звездами системы отсчета
вы днем были на громадном расстоянии от дома, где вы пьете чай
вечером, ибо за прошедшее между двумя рассматриваемыми собы-
событиями время Земля вместе с вами «ушла» очень далеко. Заметим
еще, что «обыкновенное расстояние rf» между двумя событиями и
«особое расстояние б» между (одновременными!) событиями —н е с р а-
в н и м ы е величины, так как измеряются они в совершенно разных
единицах: первое из них измеряется в единицах времени (сек, год,
век), а второе — в единицах длины (мм, м, км).
Прямая / плоскости Галилея с уравнением у-- kx-\-s отвечает
равномерному движению
точки по прямой о со скоростью А; впрочем, мы уже знаем, что
эта скорость существенно зависит от выбора инерциальной системы
отсчета и потому физического смысла не имеет. Зато для двух
прямых / и /[ с уравнениями y = kx '-s и у Aj.v-,-^, т. е. для
двух равномерно движущихся точек L и Lx прямой о с законами
движения
x = kt-\-s и jc=/s1/-fs1,

58
расстояния и углы; треугольники и четырехугольники [гл.
имеет смысл разность
6н,= K-k (8)
скоростей этих точек — относительная скорость одной движущейся
точки относительно другой. Величину t>nt — угол между пря-
прямыми / и 1Х плоскости Галилея — можно также описать как ско-
скорость второй из рассматриваемых точек в системе отсчета, в которой
первая точка покоится: в самом деле, если движением (или заменой
координат) A) совместить прямую / с осью Ох, т. е. сопоставить ей
неподвижную точку Lo прямой о. то разность kx — k примет вид
(ибо скорость k' первой точки в «новой» системе отсчета равна
нулю); поэтому величина 6/( равна скорости k\ второй точки в си-
системе отсчета, в которой первая точка покоится. Угол 6((i между
двумя прямыми / и /] (относительную скорость двух равномерно
движущихся по прямой о точек L и Lx) можно определить и так:
если в момент времени /0 эти точки занимали одно и то же
положение (а) на прямой о (так что точка Q(t0, а) плоскости
Галилея принадлежит обеим прямым / и /j), то 6п равно «особому»
(т. е. пространственному ) рас-
расстоянию между точками L и Lx
через единицу времени мосле ^
момента t0 (ср. рис. 39, а и б).
Рис. 39.
Если две прямые / и 1Х плоскости Галилея параллельны,
то они отвечают двум равномерно движущимся точкам L и Lx, ско-
скорости движения которых (в любой инерцпальной системе отсчета!)
одинаковы: законы движений этих точек имеют вид
x=kt-\-s и x = kt-\-sl.
Ясно, что относительная скорость б(/ этих точек равна нулю. Для
таких двух движущихся точек (например, для двух пунктов в Москве,
движущихся в пространстве вместе с Землей) можно найти систему
отсчета, в которой обе они покоятся. При этом имеет смысл гово-
говорить о (пространственном!) расстоянии dH] между движущимися
точками — об (особом!) расстоянии м'ежду параллельными

§ 3]
РАССТОЯНИЕ МЕЖДУ ТОЧКАМИ И УГОЛ МЕЖДУ ПРЯМЫМИ
59
прямыми; это расстояние равно, например, разности
sl — s
координат рассматриваемых точек на прямой о в момент t=0 (или в
любой другой фиксированный момент времени) Наконец, под расстоя-
расстоянием от точки (события) 7W до прямой / (т. е. равномерно дви-
движущейся вдоль прямой о точки L) естественно понимать расстояние
вдоль прямой о от пункта М этой прямой до движущейся точки L,
измеренное в момент времени t, фиксированный указанием события М.
Особая прямая m плоскости Галилея, описываемая уравне-
уравнением х= д, отвечает определенному моменту времени
t=a.
Ясно, что фиксирование в этот момент времени одновременно всех
точек прямой о (ибо особой прямой m плоскости Галилея отвечает
множество всех событий (а, х), где х произвольно) представляет
собой нечто вроде задания «движения с бесконечной скоростью»,—
это соответствует тому, %что «угловой коэффициент» особой пря-
прямой т, равный тангенсу угла, образованного прямой m с осью Ох
(т. е. tg90 ), следует считать бесконечным. Наконец, окружность
плоскости Галилея с центром*^ и радиусом г отвечает множеству всех
событий, удаленных от фиксированного события Q (t, а) на (времен-
(временной!) интервал г, т. е. множеству всех событий ~(t — г, х) и {t-\-r, x).
Все сказанное можно просуммировать в виде следующего «словаря»,
в котором слева записаны некоторые понятия геометрии Галилея, а
справа — отвечающие им понятия, относящиеся к кинематике прямой о.
Геометрические понятия
Точка
Прямая (обыкновенная)
Особая прямая
Расстояние d между точками
Особое расстояние б между точ-
точками
Угол б между прямыми
Расстояние d между параллель-
параллельными прямыми
Расстояние от точки до прямой
Окружность радиуса г
Механические понятия
Событие
Равномерное движение
Момент времени
Временной интервал между собы-
событиями
Пространственный интервал между
одновременными событиями
Относительная скорость
Расстояние между покоящимися
друг относительно друга точ-
точками прямой о
Расстояние (в заданный момент
времени) от фиксированной точ-
точки прямой о до равномерно дви-
движущейся точки
Совокупность всех событий, опе-
опережающих фиксированное со-
событие па время г и отстающих
от него на то же время.

60
расстояния и углы; треугольники и четырехугольники [гл. i
У
D
<^
^ч
s С4
XV
w
. Cv
^•\
\\
\\
\\N
V\
/
f>
чхч
w
s\^
ч\ч
Г
i\
\\
\\4
sX\
w
Lw
\\
\\-
\\x
\\
\\4
ч\\
w
w
_.
nV-
^\\
w
\\N
KV
¦a:
NV
\\
nV
\
1
i
X
Рис. 40.
Укажем еще кинематическое содержание понятия площади фигуры,
сохраняющего, как мы видели выше, смысл и в геометрии Галилея. Рассмотрим
произвольную фигуру F плоскости Галилея, т. е. какое-то точечное множе-
множество; этому множеству точек отвечает определенное множество событий,
каждое из которых задается указанием
места (на прямой о) и времени. По-
Попробуем оценить количественно это мно-
множество событий; при этом мы, естествен-
естественно, должны будем учитывать и простран-
пространственную протяженность множества F
событий и его длительность во времени.
Подобную оценку можно получить, раз-
размещая в множестве F событий «элемен-
«элементарные события», характеризующиеся не-
небольшой (но фиксированной!) протяжен-
протяженностью е в пространстве и какой-то за-
заданной наперед малой длительностью Т.
Но ясно, что подобному «элементарному
событию» на плоскости Галилея отвечает
малый прямоугольник со сторонами е и т;
поэтому размещение в множестве F со-
событий неперекрывающихся «элементарных событий» сводится к заполнению
фигуры F плоскости Галилея малыми прямоугольниками сетки, «шаг» кото-
которой в направлении оси Ох равен т, а в направлении оси Оу равен е (рис. 40;
ср. с рис. 28 на стр. 49). Полная же «пространственно-временная емкость»
множества F событий, оцениваемая количеством заключающихся в этом мно-
множестве «элементарных событий», приводит нас к понятию площади фигуры F
на плоскости Галилея.
§ 4. Треугольник
Простейшей фигурой плоскости Галилея является треугольник
ABC, образованный тремя точками А, В и С и тремя соединяющими
их (обыкновенными) прямыми ВС^^а, СА^Ь и АВ^^с (рис. 41).
При этом мы, как это принято и в геометрии Евклида, условимся
обозначать теми же буквами а, Ъ и с также и длины сторон тре-
треугольника, т. е. (положительные1)!) расстояния \dBC\=a, \dCA\ = b
и |^лв1=с; буквами А, В и С мы будем обозначать не только
точки плоскости — вершины треугольника, ной (положительные1)!)
величины его углов: |6Ьс|=Д \8са\ = В, |6аЬ| = С. Отметим еще,
что иногда для обозначения (положительной) длины |йлв| некото-
некоторого отрезка АВ мы будем употреблять ту же запись АВ, что и
для самого отрезка (например, такая запись будет встречать-
встречаться в некоторых равенствах, содержащих длины сторон треуголь-
треугольника).
Длины а, Ь, с сторон треугольника плоскости Галилея и величины
А, В, С его углов не независимы: они связаны некоторыми очень про-
простыми соотношениями. Прежде всего, очевидно, что если с — наи-
г) См. подстрочное примечание на стр. 55.

§ 4]
ТРЕУГОЛЬНИК
61
большая из трех сторон, то (см. рис. 41)
а-\-Ь — с.
A1)
Механический смысл этого равенства очевиден: если А, В и С—
какие угодно три события, то временной интервал между самым
ранним и самым поздним из них равен сумме интервалов между
первым и вторым событиями и ме-
между вторым и последним событи-
событиями (аддитивность времен-
временных интервалов).
С другой стороны, из того же
рис. 41, на котором CN\\AB и, сле-
следовательно, ?\ = Аи j/_2 = В, не-
непосредственно следует
= С.
A2)
х
Рис. 41.
Для того чтобы раскрыть механиче-
механический смысл этого соотношения, вы-
выберем (инерциальную) систему от-
отсчета так, чтобы стороне АС треугольника отвечал «покой» х);
при этом углы А и С будут выражать скорости равномерных
движений, изображаемых на плоскости Галилея прямыми с и а,
а угол В — относительную скорость движения а по отноше-
отношению к подвижной системе отсчета, задаваемой движением с (ины-
(иными словами: скорость движения а в такой системе отсчета, в ко-
которой прямая с изображает покой). Поэтому формула A2) выражает
классический закон сложения скоростей: абсолют-
абсолютная скорость С движения а равна сумме от носит ель-
ной скорости В того же самого движения по отношению
к движущейся системе отсчета с и переносной скорости,
т. е. скорости А подвижной системы отсчета. Пусть, например,
человек идет вдоль вагона движущегося поезда по направлению от
конца поезда к его головной части. Тогда скорость пассажира отно-
относительно железнодорожного полотна (т. е. его «абсолютная ско-
скорость») равна скорости движения пассажира по вагону (его «отно-
«относительной скорости»), сложенной со скоростью поезда («переносной
скоростью», характеризующей движение подвижной системы от-
отсчета, по отношению к которой отсчитывается относительная
скорость).
Другими словами: движением (I) совместим сторону АС с осью Ох.

62 РАССТОЯНИЯ II УГЛЫ, ТРЕУГОЛЬНИКИ И ЧРТЫРКХУГОЛЬНИК» [ГЛ. I
«Формула углов» A2) может быть выведена из «формулы сто-
«формулы сторон» A1) с помощью следующего соотношения, играющего в гео-
в геометрии Галилея роль, родственную роли теоремы синусов в гео-
в геометрии Евклида:
A3)
Таким образом, длины сторон любого треугольника плоскости Галилея
пропорциональны величинам противоположных углов:
а = Ы, Ь = КВ, с = 1С, A4)
где % — коэффициент пропорциональности, к которому мы еще вер-
вернемся ниже (в § 8); поэтому формула A1) получается из формулы A2)
умножением обеих частей формулы A2) на К.
Для доказательства формул A3) достаточно провести «высоты»
АР, BQ и CR треугольника ABC, т. е. особые прямые, проходящие
через вершины А, В и С треугольника и пересекающие его противо-
противоположные стороны в точках Р, Q и R. [Относительно соображений,
в силу которых особые прямые АР, BQ и CR в геометрии Галилея
уместно назвать «высотами» треугольника ABC, см. выше, стр. 56,
в частности, рис. 37.] Длины высот мы, как принято и в евклидо-
евклидовой геометрии, обозначим через ha, hb и hc:
ha = AP- \6Ap\,
hb = BQ^\beQ\,
K=CR=\bCR\.
В силу определения углов в геометрии Галилея, очевидно, имеем
he = B-a = A-b 115)
(рис. 42, а; напомним, что BR — BC=a и AR = AC=b); поэтому
а __ Ъ
А ~~ В '
Точно так же с использованием высот hb и ha доказывается, что
Й С
~А""С'
и
в ~ с •

§ 4]
ТРЕУГОЛЬНИК
63
Вот еще одно следствие соотношений A5). Нетрудно видеть,
что если 5 — площадь треугольника ABC (это понятие, как мы
знаем, сохраняет смысл и в геометрии Галилея!), то
= -naha = Tbhb=T chc.
A6)
В самом деле, «повернем» (при помощи некоторого движения A))
треугольник ABC в такое положение А'В'С, чтобы сторона В'С
Рис. 42.
треугольника А'В'С била параллельна оси Ох (рис. 42, б). При
этом «галнлеева длина» а' стороны В'С преобразованного тре-
треугольника и его «галнлеева высота» h'a станут равными ^евклидовой
длине» стороны В'С п «евклидовой длине» высоты А'Р\ так что
где S' — площадь треугольника А'В'С (одновременно «галилеева» и
«евклидова» — ведь в геометрии Галилея понятие площади имеет
тот же смысл, что и в геометрии Евклида!). Но поскольку величины
a, ha и 6" имеют смысл в геометрии Галилея, то они не меняются
при движениях A): а'~а, h'a = ha и S' = S (ср. рис. 42, а и б),
а значит,
S = у aha.
Аналогично доказываются и две другие из формул A6).
Подставляя теперь в первую из формул A6) ha = bC, а в
третью — значения A5) высоты hc, получим
6" = ~ аЪС= 1 асВ = ~ ЬсА.
A7)

64 РАССТОЯНИЯ И УГЛЫ; ТРЕУГОЛЬНИКИ И ЧЕТЫРЕХУГОЛЬНИКИ (ГЛ. I
Формулы A7) родственны формулам
? = -j-ас sin B = -—be sin A
A7')
Рис. 43.
евклидовой геометрии.
Из формул A3) сразу вытекает, что известное свойство равно-
равнобедренного треугольника евклидовой геометрии сохраняет силу и в
геометрии Галилея: если стороны
а и b треугольника ABC равны
между собой, то равны и противо-
противолежащие им углы. А и В и наобо-
наоборот ^ибо -^=-j; см. рис. 43^ .
Очевидно также, что высота CR
равнобедренного треугольника ABC
одновременно является также и
медианой, т. е. она делит про-
противоположную сторону АВ попо-
пополам (см. тот же рис. 43, на ко-
котором AR=AC=b, BR = BC=a).
Однако биссектрисой угла С
прямая CR уже, ' очевидно, не
является, ибо особая прямая делить угол пополам, разумеется,
никак не может. Отсюда сразу следует, что три биссектрисы
треугольника в геометрии Галилея не обязаны пересекаться в одной
точке1): так, на рис. 43 биссектрисы АК и BL углов А и В, оче-
очевидно, пересекаются в середине Q высо-
высоты CR, но прямая CQ (т. е. CR), как мы у
уже отмечали, не совпадает с биссектри-
биссектрисой CN угла С. В противоположность
этому три медианы AD, BE и CF тре-
уго гьника ABC обязательно пересекаются .
в одной точке М и делятся в ней в от-
отношении 2:1, считая от вершины:
AM:MD = BM:ME=CM:MF=2:\. Это
следует из того, что медианы треуголь-
ника ABC геометрии Галилея совпадают
с его евклидовыми медианами и отноше-
отношения, в которых делит медианы точка их
пересечения, имеют в геометрии Галилея и в геометрии Евклида
одно и то же значение (рис. 44; ср. выше, стр. 46).
У.
0
С
/l\
Я ¦
X
Рис. 44.
г) Можно показать, что в геометрии Галилея три биссектрисы треуголь-
треугольника никогда не пересекаются в одной точке; см. рис. 48,6.

§ 4]
TPFyrcmbHIIK
65
Отметим еще, что в геометрии Галилея не может быть треуголь-
треугольника, у которого все три стороны равны между собой: ведь если две
стороны треугольника очпнаковы, то третьи обязательно равна их
сумме! Аналогичное замечание справедливо и для углов; поэтому
равнобедренный треугольник можно также назвать равноугольным,
так как равечство двух углов (а только такая сравноугольность»
возможна в треугольнике) равносильно равнобедренности треуголь-
треугольника.
Если условиться обозначать a=dBC, b — dCA, с = йдв и Л=б,4д, .4с>
В~—?>вс,ВА' Cz ~&са,сн направленные (т.е. взятые с определенным
знаком)'стороны и углы треугольника ABC плоскости Галилея, то формулы
A1) — A3) этого параграфа примут следующий простой вид:
а- -Ь+с— О,
А • в ; с =о,
а Ъ с
А ВС'
A1')
A2')
A3')
таким образом, и здесь имеют место соотношения типа соотношения A4), где
также и знаку коэффициента пропорциональности Я можно придать опреде-
определенный геометрический смысл (ср. с подстрочным примечанием на стр. 118).
Остановимся еще на признаках равенства треугольников
в геометрии Галилея. Ясно, что два треугольника ABC и А'В'С. имеющих
0
*
/
АГ
1
1
I
А
I/
-v '
ь
•
>
а х
х
Б)
Рис. 45.
одинаковые стороны или одинаковые углы, не обязаны быть равными между
собой: ведь две стороны треугольника в геометрии Галилея позволяют найти
третью сторону, а два угла—третий угол, в то время как двумя сторонами
или двумя углами треугольник плоскости Галилея, очевидно, не определяется
(рис. 45, о, б). Также из того, что, скажем, две стороны а и b треугольника
ABC и заключенный между ними угол С или сторона а и два примыкающих
к ней угла В и С треугольника ABC равны сторонам а' и Ь' и углу С,
соответственно стороне а' и углам В' и С треугольника А'В'С, еще не
3 И. М. Яглом

66
расстояния и углы; треугольники и четырехуготьннки [гл. i
вытекает равенство треугольников ABC и А'В'С (так, у треугольников ABC и
АХВС на рис. 46, а сторона ВС =а и угол С—общие, а АС = АХС, но
АВ = а-\-Ь, а АхВ~а—Ь; у треугольников ABC' и АгВС на рис. 46, б сто-
сторона ВС = а и угол С—общие и ,/ ЛВС = /_АХВС, тогда как явно ЛВ > АХВ).
Однако если направленные (т.е. взятые со знаком -\- ил» —) стороны
a~=dBC и b = dCA треугольника ABC равны направленным сторонам a' =dB,c. и
' = dc,A> треугольника А'В'С' и С —бсв сл =
cA с л СЛ'==^> то треуголь-
треугольники ABC и ,4'б'С" равны; также треугольники ЛВС и Л'В'С" равны, если
= dBC -dB.c,-
И'С
.,= В', С- б,
СВ, С А —°С'В', С'А'~
= С". Доказательство этих теорем мы предоставим читателю.
6 Ь
а)
Заметим еще, что из соотношений A3) вытекает пропорциональность сто-
сторон треугольников А ВС и А'С'В', имеющих одинаковые углы (ср. выше, рис.
45, б): для таких двух треугольников
а' _Ь' с' _
Ь'' - - R-
с
В этом случае треугольник А'В'С можно получить из треугольника ABC
преобразованием подобия 1-го рода с коэффициентом
подобия k — отображением плоскости Галилея на себя, сохраняющим вели-
величины всех углов и увеличивающим все отрезки в одно и то же число k раз
(примером такого преобразования подобия может служить сжатие к
точке О или гомотетия — преобразование, переводящее каждую точку Л
О А'
плоскости в такую точку Л' л^ча О А, что _ —.fe; рис. 47, с). Аналогично
этому, если стороны треугольника А'В'С равны сторонам треугольника ABC
(ср. рис. 4г>, а), то в силу тех же соотношений A3) углы этих треугольников
пропорциональны:
А' В' _С__
А ~ В ~ С -*"

§ 5]
ПРИНЦИП ДВОЙСТВЕННОСТИ
67
В этом случае треугольник А'В'С можно получить из треугольника ABC
так называемым преобразованием подобия 2-го рода с коэф-
коэффициентом подобия х—отображением плоскости Галилея на себя,
сохраняющим величины всех отрезков плоскости Галилея и увеличивающим
а)
б)
-Р х
Рис. 47.
величины всех углов в одно и то же число у. раз (примером такого преобразо-
преобразования может служить сжатие к прямой Ох, переводящее каждую точ-
точку А плоскости в таьую точку А' луча РА\\Оу, что
РА'
см. рис. 47, б). Мы здесь не остановимся более подробно на весьма изящном
учении о подобных фигурах плоскости Галилея (т.е. о фигурах,
переводимых одна в другую преобразованием подобия 1-го рода, преобра-
преобразованием подобия 2-го рода или, наконец, преобразованием подобия 1-го ро-
рода, сопровождаемым преобразованием подобия 2-го рода).
§ 5. Принцип двойственности; антипараллелограмм
и антитрапеция
В предыдущем параграфе мы указали, что, в то время как меци-
аны треугольника в геометрии Галилея пересекаются в одной точке
(и делятся в этой точке в отношении 2:1, считая от вершины),
биссектрисы треугольника в одной точке не пересекаются Это
обстоятельство может разочаровать читателя, создать у него впе-
впечатление, что фигуры в геометрии Евклида устроены более 'пра-
внпьно-, более просто >, чем в геометрии Галилея: так, в геометрии
Евклида биссектрисы трех углов треугольника всегда сходятся
в одной точке (рис. 48, а), тогда как в геометрии Галилея никакая
из них никогда не попадает в точку пересечения двух других

68
расстояния и углы; треугольники и четырехугольники [гл. i
(рис. 48, бI)- Однако на самом деле геометрия Галилея проще
геометрии Евклида; в частности, и биссектрисы треугольника в гео-
геометрии Галилея обладают весьма простым и изящным свойством,
которое вполне может компенсировать нам то, что здесь нет теоремы
о точке пересечения биссектрис.
Рис. 48.
Вскоре это замечательное свойство биссектрис треугольника
геометрии Галилея будет нами раскрыто. Но вначале поговорим об
одной важной особенности геометрии Галилея, которая и помоет
нам найти требуемое свойство биссектрис. Хорошо известно, что
свойства прямых линий в геометрии Евклида во многом напоминают
свойства точек: так, например, через две точки проходит един-
единственная прямая (рис. 49, а) и две прямые могут пересекаться
только в одной точке (рис. 49, б); совокупность точек, принадле-
принадлежащих данной прямой а и расположенных между двумя точками М
и /V—отрезок MN (см. тот же рис. 49, а),— во многом родственна
совокупности прямых, проходящих через данную точку А и распо-
расположенных между прямыми т и п,—углу тАп (рис. 49, б); треуголь-
х) Впрочем, следует отметить, что сравнение рис. 48, с и б не яв-
является правомерным: ведь если в геометрии Галилея треугольник имеет
всего три биссектрисы, то общее число биссектрис углов треугольника
плоскости Евклида следует считать равным шести (три биссектрисы внут-
внутренних углов и три биссектрисы внешних углов треугольника!). Эти шесть
биссектрис треугольника образуют довольно сложную фигуру: они сходятся
по три в четырех точках—в центрах вписанной и трех вневписанных окруж-
окружностей треугольника; кроме того, из них можно составить четыре тройки пря-
прямых таких, что для каждой такой тройки точки пересечения биссектрис с
противоположными сторонами треугольника принадлежат одной прямой.

§ 5]
ПРИНЦИП ДВОЙСТВЕННОСТИ
69
ник можно описать, с одной стороны, как совокупность трех точек,
не принадлежащих одной прямой, и трех отрезков, соединяющих
эти точки (рис. 50, а), и, с другой стороны, как совокупность трех
прямых, не проходящих через одну точку, и трех углов, образо-
образованных этими прямыми (рис. 50, б), и т. д. Однако эта аналогия
а)
Рис. 49.
между свойствами точек и свойствами прямых не заходит, к сожа-
сожалению, особенно далеко; поэтому руководствоваться ею в выводе
новых свойств точек или прямых было бы довольно рискованно.
Основной причиной, нарушающей сходство между свойствами точек
Рис. 50.
и прямых, является существование параллельных прямых,
не имеющих ни одной общей точки: если бы свойства точек и прямых
были во всем одинаковы, то таким прямым должны были бы отвечать
«параллельные точки», т. е. пары точек, которые нельзя соединить
ни оцной прямой,— но «параллельных точек» в геометрии Евклида
нет. Другое различие между свойствами точек и прямых связано
с тем, что расстояние между точками Л и В может быть сколь
угодно большим; если же увеличивать угол между прямыми а
и Ь, поворачивая одну из этих прямых вокруг точки их пересечения,
величина угла поворота достигнет 180°, вращающаяся

70 расстояния и углы; треугольники и четырехугольники [гл.
прямая займет свое первоначальное положение, так что неограни-
неограниченно большим угол между двумя прямыми быгь не может1).
По-другому обстоит дело в геометрии Галилея. Прежде всего,
там имеются, так сказать, "параллельные точки ¦, т. е. такие точки,
которые нельзя соединить никакой (обыкно-
(обыкновенной!) прямой; правда, эгп точки (см.,
например, рис. 51) можно соединить особой
прямой, но особая прямая геометрии Галилея
существенно отлична от обыкновенной пря-
прямой, не равна ей. С другой стороны, угол
между двумя прямыми в геометрии Галилея
может быть сколь угодно велик: мы
можем провести через точку Q пересечения
прямых а и* b такую прямую Ьи что
/_aQb= /_bQb±, затем такую прямую Ь.,,
что /_bQbx— /_ЬЛС)К\ затем такую прямую
bs, что /biQb2= /_~b*Qb3, и т. д. —и каж-
х дый раз это будет новая прямая, более
'¦удаленная» от исходной прямой а (г. е.
Рис. 51. составляющая с прямой п больший угол),
чем все предшествующие (ср. рис. 52, п и б,
относящиеся к точкам одной прямой q и к прямым, проходящим через
одну точку Q). Все это создает новую ситуацию, характеризующуюся
I
|а
I
I
ь
I
I
почной аналогией свойств точек и свойств прямых —аналогией, про-
проявляющейся в том, что заменив в какой-либо теореме геометрии
Галилея слово «точка» словом «прямая» и наоборот, слово «.расстоя-
!) Правда, в тригонометрии рассматривают углы сколь угодно большом
величины; однако эти углы не определяются просто парой прямых —«сторон»
угла; поэтому они не аналогичны отрезкам, для задания которых достаточно
указать пару точек—«концов» рассматриваемого от-резка.

§ 5] принцип двойственности 71
ниеу> словом «(/гол», и наоборот, выражение «лежит На-» выражением
«проходит через-» и наоборот, мы придем к новой теореме, которая
тоже будет верной, если только была верна исходная теорема.
Выделенное курсивом утверждение (на вопросе о строгом обо-
обосновании которого мы остановимся ниже) носит название принципа
двойственности, а георемы, получаемые одна из другой с по-
помощью этого принципа,— двойственными друг другу георемами.
Это г принцип проливает новый свег на некоторые из известных нам
ранее фактов. Так, мы знаем, чго в геометрии Галилея, как и в
обычной геометрии Евклида, «отклонение» двух прямых друг от
друга оценивается величиной образованного этими прямыми угла;
если же этот угол равен нулю, т. е. прямые параллельны, то наряду
с углом возникает еще одна мера «степени отклонения» прямых,
а именно расстояние между ними. Аналогично этому «отклонение»
друг от ipyга двух точек характеризуется расстоянием между ними;
если же это расстояние равно нулю, т. е. точки принадлежат од-
одной особой прямой (этот случай родствен случаю параллельности пря-
прямых), в качестве новой меры «О1клоненпя» точек появляется особое
расстояние", измеряющееся совсем в других единицах, чем обыкно-
обыкновенное расстояние.
Но главным достоинством принципа двойственности является то,
что с его помощью можно выводить новые теоремы из уже известных.
Так, например, ясно, что относящиеся к произвольному треугольнику
формулы
a+h=c и А[В=С
двойственны друг другу, так что зная одну из них, мы могли бы
смело предсказать и другую. В некоторых случаях полученная таким
образом новая теорема может и совпасть с исходной: так, заменив
а Ь с
в соотношениях —г-- -Б"--рг стороны углами и наоборот, мы придем
/l D С
ABC .
к равенствам —=-г- = — , лишь формой отличающимся от первона-
первоначальных. Однако в большинстве случаев теорема, двойственная
какой-либо теореме геометрии, Галилея, будет выражать совершенно
новый факт, который без использования принципа двойственности
мог бы остаться незамеченным.
Ценность принципа двойственности легко продемонстрировать на
примерах. Мы уже знаем, что в равнобедренном треугольнике ABC,
в котором АС—-ВС, опущенная из вершины С высота (особая пря-
прямая) CF совпадает с проведенной из той же вершины медианой;
биссектриса же угла С отлична от медианы (и высоты). Последнее
утверждение можно еще уточнить. Совпадение медианы CF треуголь-
треугольника ABC с высотой означает, что прямая CF особая, т. е. что
середина F стороны АВ, так сказать, «параллельна» вершине С

72 расстояния и углы; треугольники и четырехуголЬннки [гл. i
(рис. 53). Но середине F стороны АВ треугольника по принципу
двойственности отвечает биссектриса / угла Г; поэтому «параллель-
«параллельности» точек С и F двойственно утверждеьие о параллельности
прямых с и /. Таким образом, мы приходим к следующему утвер-
утверждению: биссектриса / угла С при вершине
равнобедренного (пли равноугольного см.
выше, стр. 65) треугольника ABC, парал-
параллельна основанию АВ с этого треуголь-
треугольника. Для доказательства эюго утверж-
утверждения достаточно заметить, что биссек-
биссектриса /делит пополам заключенный между
сторонами угла С отрезок АР особой
прямой, и поскольку прямая FC является
средней линией треугольника АВР (ибо
FC\\AP и AF- FB), то прямая/ является
средн^р линией того же треугольника
АВР (так как она делит пополам его
стороны ВР и АР) и, значит, /\\ВА. "
В поисках дальнейших примеров мы
обратимся к свойствам параллелограммов и
трапеций. Ясно, что если противоположные
стороны четырехугольника ABCD плоскости Галилея параллельны
(такой четырехугольник мы и здесь будем называть параллело-
параллелограммом), то противоположные стороны его равны (рис. 54, а);
Рис.
У
_——¦
0
I
А
-— т
1
1
1
1
1
В)
i
i
i
1В
i
i
X
Рис. 54.
далее, диагонали АС и BD параллелограмма ABCD в точке пересече-
пересечения Q делятся пополам (заметим, что «галилеево» содержание послед-
последней теоремы ничем не отличается от содержания той же теоремы в
геометрии Евклида!). Двойственным параллелограмму объектом
геометрии Галилея является четырехугольник ABCD, противополож-
противоположные вершины А и С, В и D которого «параллельны», т. е. такой,
что АС и BD — особые прямые (рис. 54, б); обладающий таким
свойством (обязательно самопересекающийся!) четырехугольник ABCD

§ 5]
ПРИНЦИП ДВОЙСТВЕННОСТИ
73
со сторонами АВ==а, BC = h, CD^c, D/4 = rf мы назовем анти-
антипараллелограммом. Ясно, что противоположные углы анти-
антипараллелограмма равны (т. е. /4— С, В -D); этот факт, двойствен-
двойственный равенству противоположных сторон параллелограмма, с очевид-
очевидностью вытекает из самого определения величины угла в геометрии
Галилея. Далее, диагоналям АС и BD параллелограмма ABCD,
соединяющим противоположные вершины А и С, В и D, отвечают
я
Рис. 55.
точки Е \\ F пересечения противоположных сторон аи с, b и d
антнпаралле.шграмма ABCD; при этом длинам диагоналей АС и BD
параллелограмма в антипараллелограмме отвечают величины углов
аЕс и bFd. Точке Q пересечения диагоналей АС и BD параллело-
параллелограмма отвечает прямая q==EF; утверждению о том, что точка Q
делит диагонали АС и BD пополам, двойственна следующая теорема:
прямая EF, соединяющая точки Е и F пересечения противоположных
сторон антипараллелограмма, делит углы между противоположными
сторонами пополам. Для здказательства этой теоремы достаточно
провести особую прямую через • точку Е и заметить, что отрезок
UV этой прямой, заключенный между прямыми b и d, делится
в точке Е пополам (это следует из равенства противоположных углов
антипараллелограмма). Отсюда следует, что /^bFq = /_qFd\ но
тогда п /_aEq — /^qEc, так как /_ aEq = ^_ bFq-\- ^/_aBb и
ZqEc = /_ qFd , / dDc.
Тра иеи ией*мы, как обычно, будем называть четырехугольник
ABCD, противоположные стороны АВ и DC которого параллельны
(рис. 55, а). Так как трапеция плоскости Галилея является и евкли-
евклидовой трапецией, го средняя линия MN трапеции ABCD (соединя-
(соединяющая середины М и N боковых сторон AD и ВС) параллельна

74 расстояния и углы; треугольники и четырехугольники [гл. i
основаниям АВ и DC» равна их полусумме1). Четырехугольник ABCD
плоскости Галилея со сторонами АВ = а, BC = fr, CD =c, DA -s d,
две противоположные вершины В и D которого «параллельны»
(т. е. такой, что BD — особая прямая; рис. 55, б), мы назовем
а н т и т р а и е ц и е й. Боковым сторонам ВС и DA трапеции ABCD
отвечают вершины С и А антитрапеции ABCD, а серединам N и Л1
боковых сторон трапеции — биссектрисы /z==CS и m^AS углов С
и А антнтрапеции, пересекающиеся в точке 5". Параллельности сред-
средней линии MN трапеции ABCD ее основаниям АВ и CD двойственно
утверждение о том, что точка S пересечения биссектрис шип
углов А и С антитрапеции ABCD «параллельна» вершинам В и D,
т. е. принадлежит особой прямой BD, по это очевидно, ибо в силу
определения биссектрисы угла в геометрии Галилея прямые AS и CS
делят отрезок BD пополам. Утверждению же о том, что средняя
линия MN трапеции равна полусумме оснований АВ и DC, двойст-
двойственна теорема о том, что угол mSn равен полусумме углов аВЬ и
dDc антитрапецнн:
[Последнее вытекает из того, что в обозначениях рис. Г>5, б
здесь eiD1|iBD — особая прямая.] Частным случаем этой теоремы
является утверждение о том. что е треугольнике ABC (который
можно рассматривать как «вырожденную антнтрапецию» АВСР, где
ВР — высота треугольника) биссектрисы AS и CS углов А и С пере-
пересекаются в точке S высоты ВР (эта точка, очевидно, делит высоту
ВР пополам) и пбризуют угол, равный половине угла В треугольника
(ибо на рис. 56, a AS, -^ ABX\ ср. с теоремой о средней линии
треугольника, рис. .36, б).
Теперь нам уже нетрудно сообразить, какой теореме отвечает
в силу принципа двойственности теорема о точке пересечения медиан
г) Так как ММ \\AB\\CD, то это свойство трапеции является одновре-
одновременно «евклидовым» м «галнлеевым»: ведь оно равносильно утверждению, что
прямые KQ\\AD и LQ || С В, проведенные через середины К и L оснований А В
и CD трапеции, пересекаются на средней линии MN (ибо при этом, в силу
свойств параллелограмма, MN = A\Q-\-QN = AK-\-CL = — AB \-—DC), — a
все фигурирующие в этом утверждении понятия имеют и «Галилеев» смысл!

§ 5]
ПРИНЦИП ДВОЙСТВЕННОСТИ
75
треугольника. Серединам D, Е и F сторон ВС, СА и АВ треуголь-
треугольника ABC отвечают в силу принципа двойственности биссектрисы
d==AU, e BV и f=.CW его углов А, В и С (ср. рис. 57, а и б);
прямым AD, BE и CF—точки U, V и W пересечения биссектрис
х О
Рис. 56.
\JV
X
х О
Рис. 57.
треугольника ABC с его противоположными сторонами. Поэтому
теореме о гом, чго медианы AD, BE и СЕ треугольника ABC пере-
пересекаются в одной точке М (рис. 57, а), двойственно утверждение
о том, что точки U, V и W принадлежат одной прямой m (рис. 57, б).
При этом, так как

76 РАССТОЯНИЯ И УГЛЫ, ТРЕУГОЛЬНИКИ И ЧЕТЫРЕХУГОЛЬНИКИ [ГЛ. 1
то в силу принципа двойственное!и должно быть также
/_ aUm:/_тЩ= /_bVm:/_mVe - /_ cWm:/_mWf -2:1
— точки пересечения биссектрис (неравпобедренного 1I) треугольника
ABC с противоположными сторонами принадлежат одной прямой ш,
которая делит углы, образованные биссектрисами с противополож-
противоположными сторонами треугольника, в отношении 2:1, считая от стороны.
Это и есть то свойство биссектрис треугольника в геометрии Гали-
Галилея, с упоминания о котором мы начали этот параграф.
Для того чтобы доказать это свойство биссектрис треугольника,
вспомним доказательство теоремы о медианах 2). Прежде всего по-
покажем, что медианы AD и BE треугольника ABC делятся в точке
пересечения М в отношении AM-.MD ВМ:МЕ- 2:1. Для этого
соединим середины D и Е сторон ВС и СА с серединой N отрезка СМ
(рис. 58, а; пока мы не можем утверждать, что отрезок СМ при-
принадлежит медиане CF треугольника). Так как отрезки DN и EN
служат средними линиями треугольников ВМС и СМА, то DN\\BE
и EN\\AD, так что четырехугольник MDNE—параллелограмм. Отсюда
= NE - ~МА и ЕМ =
= —MB,
что и требовалось доказать. А так как эго рассуждение сохраняет
силу для любых двух медиан треугольника, то каждые две из них
делятся в точке пересечения в отношении 2:1, считая»от вершины;
отсюда уже вытекает, что все три медианы пересекаются в одной
1) Если треугольник ABC равнобедренный: АС—ВС, то прямая т, про-
проходящая через точки пересечения биссектрис AU и BV углов А и В с проти-
противоположными сторонами, параллельна основанию А В треугольника и биссек-
биссектрисе угла при вершине С (ср. выше, стр. 64, в частности, рис. 43).
2) См. Киселев [4], п. 143.

§ 5] принцип двойственности 77
точке (ибо обе медианы, BE и С/7, пересекают медиану AD в такой
точке М, что AM-.MD =2:1).
«Обратим» теперь это рассуждение, заменив в нем точки прямыми
и наоборот и отрезки углами и наоборот. Обозначим через т пря-
прямую UV, где U и V — точки пересечения биссектрис й -= AU и е = В1/
треугольника с противоположными сторонами. Пусть /г—биссектриса
угла mWjC, образованного прямой т со стороной АВ~с треуголь-
треугольника ABC (рис. 58. б: пока мы еще не можем утверждать, что точка Wl
совпадает с точкой W пересечения биссектрисы/ угла Ссо стороной с);
точки пересечения прямой п с биссектрисами й и е обозначим через R
и S. Так как точки R и S, будучи точками пересечения биссектрис
d и п, соответственно е и п, треугольников AVWX и BUWX, при-
принадлежат их высотам VP и 6'Q (ср. стр. 74 и рис. 56, а), то (само-
(самопересекающийся) четырехугольник RUVS— антнпараллелограмм; поэ-
поэтому /jnUd — /_eSn и /_mVe= /_dRn. А теперь, применяя к треу-
треугольникам AVW1 н Вб^У^! теорему о величине угла между биссек-
биссектрисами треугольника, без труда получаем, что
/_dUm-- /_nSe-~ mVa и /_ е\'т -/_nRd= j /_mVb,
т. е. что прямая т делит углы, образованные биссектрисами due
с противоположными сторанами треугольника в отношении 2:1, считая
от стороны. Наконец, так как прямая UW^^m^ где W — точка пе-
пересечения биссектрисы /= CW угла С со стороной АВ^^с, в силу
точно такого же рассуждения также обладает тем свойством, что
/_aUtnx:^_tnxUd =2:1, то она совпадает с прямой m = ?/l/, т. е.
точки U, V и W принадлежат одной прямой m такой, что
/_aUm:^ mUd -_ bVm: mVe =/_eWm:/mWf= 2:1.
Это доказательство «теоремы о биссектрисах» треугольника пло-
плоскости Галилея весьма поучительно—ведь оно представляет собой
совершенно точное «обращение» (в смысле принципа двойственности)
доказательства теоремы о медианах. Последнее обстоятельство
раскрывает новые черты самого принципа двойственности — оказы-
оказывается, что не только ф о р м у л и р о в к и двойственных друг другу
теорем можно получить очну из другой с помощью чисто словесных
«преобразований» (заменой слова «точка» словом «прямая» и т. д.),
но и доказательства двойственных теорем получаются одно
из другого точно таким же образом! Для того чтобы понять при-
причины этого, следует вспомнить, какой смысл имеет в геометрии сами
понятие «доказательства» (теоремы); обсуждение связанных с этим
вопросов не только поможет глубже понять обстоятельства, обусло-
обусловливающие принцип двойственности, но и позволит дать этому
принципу полноценное обоснование, в то время как до сих пор
мы ограничивались лишь иллюстрациями этого принципа,— правда,

78
расстояния и углы; треугольники и четырехугольники [гл.
иллюстрациями весьма выразительными, но доказательной силы,
строго говори, все же не имеющими.
Хорошо известно, что общий путь доказательства всех геомет-
геометрических теорем состоит в следующем. С помощью чисто логических
умозаключений интересующая нас теорема сводится к каким-то новым,
более просили, чем первоначальная; получаемые таким путем новые
теоремы также сводятся к более простым и т. д.— до тех нор, пока
У
х
мы не придем к простейшим геометрическим теоремам, называемым
аксиомами н принимаемым без доказательства. [В реальной прак-
практике доказательства теорем их чаще всего сводят не непосредственно
к аксиомам, а к известным ранее теоремам; но это ничего не меняет
в описанной схеме—просто здесь опускается, как уже известная,
некоторая часть всей цепочки дедуктивных умозаключений (выводов).]
Но в геометрии Галилея основные свойства точек и прямых, расстоя-
расстояний и углов совершенно равноправны; это означает, что,
заменив в формулировке любой аксиомы слово «точка-» словом
«прямая-» и т. д., мы получим также справедливое утверждение: так,
например, аксиоме «две прямые имеют не более одной общей точки-»
(рис. 59, а) отвечает утверждение «две точки можно соединить не
более чем одной (обыкновенной) прямой-» (рис. 59, б); аксиоме

§ 5] принцип двойственности 79
параллельности, утверждающей, что через каждую точку А,
лежащую вне прямой а, можно провести единственную прямую I,
не пересекающую а (рис. 59, е),—утверждение о том, что на каждой
(обыкновенной) прямой а, не проходящей через точку А, существует
единственная точка L, которую нельзя соединить с А (обыкновенной)
прямой (рис. 59, г), и т. д. Отсюда следует, что при такой же за-
замене одних слов другими каждая теорема геометрии Галилея
перехочнт в другую, также верную: в самом деле, эту новую теорему
можно доказать аналогично исходной, заменив во всем рассуждении
слово «точка» словом «прямая» и г. д. только это рассуждение
приведет не к тем же аксиомам, что и первоначальное доказательство,
а к 1войственным им предложениям (аксиомам), которые тоже спра-
справедливы. Причем это совершенно общее рассуждение избавляет нас
даже от необходимости доказывать отдельно двойственные друг
другу теоремы: доказав одну из них, мы автоматически
убеждаемся и в справедливости второй; поэтому все проведенные
выше доказательства теорем, двойственных известным теоремам
геометрии Галилея, можно считать излишними!
Вот еще одно доказательство сформулированной на стр. 76 теоремы
о точках пересечения биссектрис треугольника плоскости Галилея с проти-
противоположными сторонами. Хорошо известно, что теорема о точке пересечения
Рис. 60.
медиан (равно справедливая в геометрии Евклида и в геометрии Галилея!)
является непосредственным следствием так называемой теоремы Ч е в а, в
силу которой три прямые AU, BV и CW, проходящие через вершины треу-
треугольника ABC и пересекающие противоположные стороны в точках U, V
и Uv (рис. 60, а), в том и только в том случае пересекаются в одной точке
(или параллельны между собой), когда
AW BU СУ
Wb'Vc'va •
где отрезки AW n IV'fi, BU и UC, СУ и У А считаются направленными,
ср. выше, стр. 29]). [Из этой же теоремы вытекает и (евклидова) теорема
') См., например, § 73 книги Перепелки на [5] или задачу 57 б) книги
Я г лома [9]. (В дальнейшем мы во всех сл\чаях, где это не может вызвать
недоразумении, будем обозначать направленный отрезок с концами А н В
просто через АВ, без черточки сверху!)

80 расстояния и углы; треугольники и четырехугольники [гл. [
о точке пересечения биссектрис треугольника: ведь если AU, BV и СИ"—
евклидовы биссектрисы треугольника ABC с длинами сторон АВ—с, ВС —а,
СА=Ь, то AW:\X'B -b:a, BU:UC c:b, CV:VA -. =a:c и из равенства
А\Х_ В? ?V_^_ c_ а_
WB 'Ш' VA а ' b ' Т"
вытекает, что прямые AU, BV и CW пересекаются в одной точке ] Аналогично
этому принадлежность трех точек U, V и U" рис. 57, б одной прямой является
следствием теоремы Менелая, в силу которой точки U, V и W, при-
принадлежащие сторонам ВС, СА и АВ треугольника ABC (рис. 60, б), в том
и только в том, случае принадлежат одной прямой, когда
AW BU СУ
BW 'CU ' AV
(здесь также отрезки AW и BUT, BU и СИ, CV и AV считаются направ-
направленнымиI). В самом деле, если на рис. 57,6 АВ=AдВ = с, BC—dBC = a,
CA=dCA = b (где a-\-b-\-c=-Q; обратите внимание на знаки отрезков и углов!),
то в силу соотношений A3) из § 4 (стр. 62; ср. также стр. 65) из рассмотре-
рассмотрения треугольников ABU и ACU заключаем:
BU:AU=?BAU:?ABU и CU:AU = ? VAC:,/ UCA.
Но ?_BAU = ^_UAC (ибо AU—биссектриса угла А); поэтому
BU:CU=^UCA:Z. ABU = Z.C: Z В =c:b
(см. равенства A3) и A3'; из § 4). Аналогично доказывается, что
CV:AV = a:c и AT:B\V = b:a.
А
теперь
из
равенства
AW
B~W
BU
'си
CV
' AV~~
Ъ
а
с
'Т '
а
с
-A
сразу следует, что точки U, V и W принадлежат одной прямой.
Укажем еще один изящный пример двойственных друг другу теорем.
Хорошо известно, что прямая, соединяющая точку Р пересечений диагоналей
трапеции ABCD и точку Q пересечения ее непараллельных сторон, делит
попалам основания АВ и CD трапеции (рис. 61, а). [Для доказательства этого
достаточно заметить, что сжатие к точке Q (гомотетия; см. выше, стр. 66 и
рис. 47, а) с коэффициентом &1 = т^г переводит .46 в DC и, значит,
QA
переводит середину М отрезка АВ в середину N отрезка DC; поэтому точки
М и N лежат на одной прямой с центром Q рассматриваемого сжатия (го-
(гомотетии). Аналогично этому сжатие к точке Р (гомотетия) с коэффи-
циентом k.z = (здесь отрезки надо обязательно считать направленны-
РА
м и, так как й, отрицательно) переводит отрезок Лив отрезок CD и середину М
отрезка АВ в середину N отрезка CD; поэтому и точка Q лежит на одной
прямой с точками М и N.] Но точке Q пересечения боковых сторон трапеции
ABCD по принципу двойственности отвечает прямая q, соединяющая противопо-
противоположные (и не «параллельные») вершины А нС антитрапеции ABCD; точке Р пере-
пересечения диагоналей трапеции отвечает прямая р, соединяющая точки пересечения
1)См. §64 книги Перепелки на [5] или задачу 57 а) книги Я г л о м а [9].

5]
принцип двойственности
81
противоположных сторон антитрапецин; серединам М к N оснований трапеции
отвечают биссектрисы тип углов В и D антитрапеции (рис. 61, б). Таким
образом, в сил\ принципа двойственности мы можем утверждать, что (обыкно-
(обыкновенная) прямая q = AC. соединяющая противоположные вершины А и С антитра-
антитрапеции A BCD, прямая р, соединяющая точки пересечения противоположных сторон
антитрапеции, и биссектрисы тип углов В и D пересекаются в одной точке.
х
Доказательство этой теоремы вытекает из того, что, скажем, сжатие к пря-
прямой р (ср. выше, стр. 67, в частности, рис. 47,6), переводящее точку
В в точку D, переводит угол В антитрапеции в угол D и, следовательно,
переводит биссектрису т угла В в биссектрису п угла D; поэтому точка
пересечения прямых тип принадлежит прямой р («оси» рассматриваемого
сжатия). Аналогично устанавливается и факт принадлежности точки пересе-
пересечения прямых тип прямой q.
Мы рекомендуем читателю самостоятельно придумать другие примеры
двойственных друг другу теорем геометрии Галилея.
Заметим, наконец, что также и намеченное на стр. 77—79 доказатель-
доказательство принципа двойственности, в той форме, в какой оно было изложено-
вряд ли кто-либо сочтет полноценным: ведь равноправность основных свойств
точек и прямых в геометрии Галилея, на которой это доказательство бази-
базируется, была лишь проиллюстрирована на отдельных примерах, но не уста-
установлена с полной (математической) строгостью. Однако доведение эгого дока-
доказательства до конца невозможно без апелляции к полному списку аксиом
геометрии Галилея, который вряд ли уместно выписывать в книге, многие
читатели которой незнакомы даже с полной аксиоматикой геометрии Евклида
(обычно ведь опускаемой в элементарных учебниках — гм., например, книги
|4] или [7]1)!). Поэтому мы вынуждены ограничится здесь вышесказанным,
извинившись перед критически настроенным читателем за (неизбежную) не-
неполноту наших рассуждений.
В заключение этого параграфа скажем несколько слов о механическом
содержании принципа двойственности. К геометрии Галилея мы пришли,
') Образцы полной системы аксиом планиметрии Евклида читатель может
найти, например, в учебниках Перепелки на [5] и Погорелова [7а]
или в классической монографии Гильберта [76].

82 расстояния и углы; треугольники и чРтыРЕхугольники [гл. i
приняв за точки «события» одномерной кинематики, характеризуемые указа-
указанием места на прямой о и времени: роль движений в нашей геометрии играют
преобразования Галилея. При этом естественным образом определяется «рас-
«расстояние» между двумя событиями, измеряемое отвечающим этим событиям
интервалом времени; для одновременных событий, для которых это «расстоя-
«расстояние» равно нулю, можно определить новое «расстояние» — пространственное
расстояние между соответствующими пунктами прямой о. Далее, два (неодно-
(неодновременных!) события определяют «соединяющее» их равномерное движение
вдоль о, играющее роль прямой нашей геометрии,- - и на этой базе строится
содержательная теория, близкая, как мы видели, к евклидовой геометрии.
Но никто не мешает нам пытаться строить и другие геометрические системы,
принимая за точки не события, а дрчгие обьекты механики. В частности,
можно объявить «точками» новой геометрической системы всевозможные
равномерные движения но прямой о, отождествляя по-прежнему
с «движениями» получаемой таким образом «геометрии» преобразования
Галилея, состоящие в переходе от одной ннерциальной системы отсчета
к другой. При этом в множество равномерных движений также естественно
вводится «метрика»: за «расстояние» между двумя движениями (или «откло-
«отклонение» одного равномерного движения от другого) можно принять относи-
относительную скорость, имеющую, как мы знаем, «абсолютный» (т. е. не
зависящий от выбора системы отсчета) смысл; если же два рассматриваемых дви-
движения имеют одну скорость (т. е. относительная скорость одного из них по от-
отношению к другому равна нулю), то можно говорить об обычном расстоянии
между движущимися точками, которое в этом случае не меняется с течением
времени. Далее, два равномерных движения (с разными скоростями!) опре-
определяют единственное «событие», принадлежащее обоим движениям; это со-
событие в «геометрии равномерных движений» играет роль «прямой». Принцип
двойственности утверждает, что подобная «геометрия равномерных движений»
не будет ничем отличаться от той «геометрии событий», которой посвящена
основная часть этой книги.

ГЛАВА II
ОКРУЖНОСТИ И ЦИКЛЫ
§ 6. Определение цикла; радиус и кривизна
В элементарной геометрии рассматриваются свойства фигур
(обычной) плоскости Евклида, ограниченных отрезками прямых и д\гами
окружностей (примеры: треугольник, круг, круговой сектор). При
этом окружность плоскости Евклида чаще всего определяют как
множество («геометрическое место») точек, удаленных от фиксиро-
фиксированной точки Q ни постоянное расстояние г (рис. 62, а); реже исполь-
используется определение окружности как множества точек, из которых
данный отрезок АН виден под постоянным (направленным!) углом а
(рис. 62, б). В геометрии Галилея соотвегствуютие два множества
точек не совпадают. Выше мы уже видели, что окружность S
плоскости Галилея—множество точек, удаленных от фиксированной
точки Q на постоянное расстояние г,— является мало интересным
геометрическим образом: это есть просто пара особых прямых
(рис. 63, а). Гораздо больший интерес представляет множество Z
точек М, из которых данный («обыкновенный», т. е. принадлежащий
обыкновенной прямой) отрезок АВ виден под постоянным углом а;
это множество точек мы назовем ЦИКЛОМ.

84
Окружности и циклы
[гл. ii
Ни в одном из пунктов школьного курса геометрии не проявляется с такой
отчетливостью как здесь неестественность отказа от понятия направлен-
направленного угла: ведь если считать углы ненаправленными (положительными), то
множество точек М, из которых данный отрезок АВ виден под данным углом а,
приобретает совершенно искусственный вид пары сегментов (рис. 62, в; заметьте,
что это множество точек даже не может быть описано «приличным», т. е. не
слишком сложным, уравнением!). Но если считать углы между прямыми
У k
М
Рис. 63.
направленными (т. е. зафиксировать направление отсчета положительных
углов, а также условиться считать, что угол между МА и MB — это угол
поворота прямой МА до совмещения ее с прямой MB), то множество точек М
обращается в обыкновенную .окружность. Действительно, легко видеть, что
направленный угол между изображенными на рис. 62,6 прямыми Мл А и Л1гВ
равен той же величине а, что и направленный угол между прямыми МА и MB,
в то время как направленный угол между изображенными на рис. 62, в пря-
прямыми МХА и MjB равен —а, поскольку он противоположен по направлению
углу между прямыми МА и MB.
Не представляет никакого труда установить, какой вид имеет
уравнение цикла. Пусть А(аъ а2) и В(ЬЪ />2) —две произволь-
произвольные точки плоскости Галилея; М(х, у) — такая точка, что /_ АЧВ - а.
Ясно, что (см. рис. 63, б) угловые коэффициенты k и kt прямых
МА и MB равны
k =
У—а»
х—а.
k - y~bt
и, значит, в силу формулы (8) из § 3 (стр. 54)
а
—О,
Таким образом, координаты всех точек М (х, у), для которых
= а, удовлетворяют уравнению
х — Ь1 х—

§ 6] определение цикла; радиус и кривизна 85
или г)
Последнее уравнение можно переписать так:
Ф\ — «i)У -= а*2 + [(t>2 — Я2) — а (/7i + М * + ая А —
или
— ах~ 4- 2йл; - - с,
| j A)
где
с-
, поскольку прямая /IB является обыкновенной!). Но урав-
уравнение A) нам хорошо известно — оно выражает (евклидову) пара-
параболу
Таким образом, циклы плоскости Галилея изображаются пара-
параболами A). Иногда циклом называют множество точек, описываемое
уравнением
ах2 + 2Ьгх + 2Ъ2у + с = О, B)
несколько более общим, чем уравнение A) и приводимым к виду A),
если Ь.2=ф0, й=/=О. При этом частными случаями «цикла» оказы-
оказываются окружность (пара особых прямых), особая прямая,
обыкновенная прямая. Действительно, окружности соответст-
соответствует случай Ь.2=0, а=фХ), Ь\ — ас > 0: особой прямой —случай
Ь2=0, афО, Ь\ — ас = 02) или же случай a—bi=O, bt ^0; обыкно-
обыкновенной прямой — случай и = 0, Ь2^ф0. [Аналогично этому и уравне-
уравнение евклидовой окружности (уравнение B') из § 1 Введения, стр. 17)
можно записать в виде
a (.v2 H у2) ' - 21\х 4- 2Ь2у У- с = 0, B')
охватывающим наря!у с окружностями также и прямые линии (слу-
(случай обращения в нуль коэффициента а уравнения).] Понимание тер-
термина «цикл» в смысле «линия, записываемая уравнением B)» удобно
потому, что в таком случае верна теорема: через любые три точки
1) Заметим, что х — о, Ф 0 и х — ft, ,- 0, поскольку прямые МА и MB—¦
обыкновенные (ибо в противном случае «галилеева» углт между этими прямыми
просто не существует).
2) При b.,—0, a 5= 0 уравнение B) превращается в квадратное уравнение
ал:2-|-26,д:-|-с = 0. Если ft*—ас ¦ 0 (т. е. корни х1 и х2 уравнения—действительные
различные), то это уравнение равносильно совокупности двух уравнений х = х1, и
х — х2, т. е. действительно выражает окружность; если Ь*—ас = 0 (т. е. корни
уравнения совпадают), то рассматриваемое уравнение выражает особую прямую
(«окружность нулевого радиуса»); если же Ь\—ас < 0 (т. е. корни уравнения
мнимые), то уравнение ax'1-\-2blx-\-c = 0 вовсе не определяет никакого мно-
множества точек.

86
окружности и циклы
[гл. ii
А, В, С плоскости Галилея проходит единственный цикл-у (т. е. обык-
обыкновенный цикл A), пли окружное гь, или обыкновенная прямая, или
особая прямая; см. рис. 64, а г). Мы, однако, в дальнейшем всегда
будем употреблять термин «цикл» лишь в смысле линии A) (евкли-
(евклидовой параболы).
х О
х О х С
Ь)
Рис. 64.
Цикл Z определяется тем своим свойсгвом, что все его- вписанные
углы, опирающиеся на одну хорду АВ, имеют одно и то же значение а
(ср. рис. 65, а и б, относящиеся к галилееву циклу Z и к евкли-
евклидовой окружности S). Отсюда можно вывести, что угол между хор-
хордой АВ цикла Z и проведенной в конце этой хорды касательной
N
Рис. 65.
также равен а: в самом деле, если точку М (рис. 65) устремить к
точке А, то хорда AM будет стремиться к касательной AT
в точке А, а хорда MB — к хорч.е АВ; но поскольку все рас-
рассматриваемые прямые AM образуют с прямыми ВМ один и гот же
угол а, то тот же угол а образует касательная AT с хордой АВ.

§ 6] ОПРЕДЕЛЕНИЕ НИКЛА: РАТ.ИУС II КРИВИЗНА 87
Из последнего же факта в свою очередь следует, что касательные
РА и РВ, проведенные к циклу из одной точки Р, равны между со-
собой— вечь изображенный на рис. 65 треугольник РАВ равнобедрен-
равнобедренный, поскольку его углы при основании АН равны (см. сгр. бо).
Попытаемся теперь опречелнть «радиус» цикла Z. Поскольку ни-
никакого «центра» цикл плоскости Галилея не имеет, ми не можем ис-
исходить из определении радиуса евклидовой окружности как расстоя-
расстояния ог его центра до любой из точек — необходим какой-то иной
подхот. Радиус г окружности 5 можно также определить как коэф-
коэффициент пропорциональности между длиной 5 дуги АН окружности
и отвечающим этой дуге центральным углом ф = /_AQB, измеренным
в «естественной», т. е. раднанной1), мере:
(рис. 65, б); однако это определение радиуса также связано с по-
понятием центра окружности и потому не может бить перенесено на
случай цикла. Однако центральный угол ф можно заменить вписан-
вписанным углом ot, равным его половине; другими словами, можно сказать,
что радиус г окружности S равен отношению длины произвольной
дуги s - vj AB к удвоенной величине 2сс опирающегося на эту дугу
вписанного угла:
г = ^, (За)
а свойство вписанного утла окружности сохраняет силу и для цикла
(ведь этим свойством цикл и определяется).
Для того чтобы выделенное курсивом «определение радиуса»
можно было перенести на цикл Z плоскости Галилея, надо только
с
убедиться, что для любой дуги АВ данного цикла Z отношение — ,
где s есть длина рассматриваемой 1угн, а а — опирающийся па нее
вписанный угол, не зависит от выбора дуги. При этом под длиной 5
дуги АВ произвольной линии Г плоскости Галилея естественно по-
понимать предел, к которому стремится длина АА1 \- AyA., -f- . . .
. . . , All_lAn АпВ вписанной в АВ ломаной АА^А,. . .АпВ (рис. 66)
при неограниченном уменьшении всех звеньев ломаной. Однако такой
«евклидов» подхот. оказывается здесь довольно бессодержательным:
легко видеть, что (галилеева!) длина каждой вписанной в дугу АВ
ломаной ААхА.г. . .АпВ имеет о i н о и тоже значение, равное длине
1) Правда, в школьном курсе геометрии радианная мера угла опреде-
ляется равносильным C) равенством q =—; однако это определение отнюдь
не является единственно возможным: так, например, радианную меру угла
.. sin ф
можно определить условием lim — = 1.
4. -*о Ф

88
окружности и циклы
[гл. и
хорды АВ1). Поэтому н длину s дуги АВ кривой Г следует считать
равной длине s - d хв хорды АВ.
Заметим теперь, что в силу формул Aа) отношение
ве-
величины а вписанного в цикл Z угла, опирающегося на дугу АВ, к
длине s — dAB-bl — аг хорды АВ с концами в точках А(а1, а2) и
Рис. 66.
Рис. 66а.
b-т)' равно коэффициенту а в уравнении A) цикла. Поэтому,
условившись определять «радиус» г цикла Z как половину отно-
отношения длины s дуги АВ цикла (или отвечающей этой дуге хорды АВ)
к опирающемуся на АВ вписанному углу а (т. е. той же формулой
(За), которой можно определить и радиус евклидовой окружности!),
мы получим
s
а
Ъх—ах
1
2а
C6)
— радиус г цикла Z равен
1
2а
где а есть коэффициент при х- в
уравнении A) цикла. При этом, в противоположность радиусу окруж-
окружности S, радиус никла Z может быть и положительным и отрицатель-
отрицательным: циклы положительного радиуса изображаются (евклидовыми) па-
параболами, уходящими «вверх» (рис. 67, а), а циклы отрицательного
радиуса — параболами, уходящими «вниз» (рис. 67. б).
5) Здесь мы полагаем, что дуга А В кривой Г «нигде не поворачивает назад»
(по отношению к положительному направлению оси Ох, указывающему, как мы
знаем, направление течения времени), т. е. не имеет вида, изображенного на
рис. 66а. [Если кривая Г плоскости Галилея является «гладкой» в том смыс-
смысле, что в каждой ее точке существует касательная прямая (ср. с подстроч-
подстрочным примечанием1) на стр. 92), то такой вид кривой невозможен (напомним, что
особые прямые мы условились исключать из числа прямых).]

§ 6]
ОПРЕДЕЛЕНИЕ ЦИКЛА; РАДИУС II КРИВИЗНА
89
Введя в геометрию «направленные углы» (т. е. углы, взятые с тем или
иным знаком, определяемым как в тригонометрии), мы получим возможность,
задавая радиус г окружности S формулой C) (или (За)), также считать его
положительным или отрицательным. Однако при этом знак радиуса окруж-
окружности S не будет определяться множеством S точек—он будет зависеть от
выбранного нами направления обхода окружности (а значит, и каж-
каждой ее дуги длины s), а именно, будет положительным, если это направление
совпадает с направлением вращения часовой стрелки (рис. 68, а), и отрица-
отрицательным в противном случае; такое соглашение о знаке радиуса (направленной!)
окружности часто оказывается полезным (ср., например, Я г л о м [31], стр. 480—
482 или Яглом [10], стр. 260). По-иному обстоит дело в случае цикла Z
геометрии Галилея: так как здесь су-
существует «естественное» направление
движения по циклу, указываемое на-
направлением оси Ох (другими слова-
словами, направлением течения времени!),
то мы имеем возможность установить
знак радиуса цикла, не фиксируя на-
направление обхода цикла специально.
Рис. 68.
Очевидно, что если радиус г
евклидовой окружности 5 неогра-
неограниченно увеличивается, то окружность все более и более «выпрямляет-
«выпрямляется», становится все более и более похожей на прямую, — недаром
прямолинейные дороги на земной поверхности, в действительности
представляющие собой окружности очень большого радиуса, распо-
расположенные на (сферической!) поверхности земли, мы принимаем за
прямые (рис. 69, а). Напротив, если радиус окружности уменьшается,
окружность становится все менее похожей на прямую, все более
«кривой» (рис. 69, б). На этом основании величину р, обратную ве-
величине радиуса окружности, называют ее кривизной; при этом в силу
формулы (За)
1 п «
р —— =2— .
D)
Аналогично этому и для цикла Z величину р = — называют кривизной

90 окружноеги и циклы
цикла; в силу формулы C6)
[гл. н
Р = у=2^ = 2а. D')
Основанием для наименования «кривизна» здесь также может
служить то, что при г—*¦ оо (т. е. при р—>-0) цикл Z становится
все более похожим на прямую (ср. рис. 70, и и б, на которых изобра-
Рис. 70.
жен цикл большого радиуса и цикл малого радиусаI). Заметим еще,
что, подобно двум окружностям одного радиуса, два цикла одного
1) Утверждение о том, что при г -»¦ оо окружность 5 (или цикл Z) ради-
радиуса г «неограниченно приближается к прямой», имеет следующий строгий
смысл: если радиус г проходящей через точку А и имеющей в этой точке
направление а (т. е. касающейся в точке А прямой а) окружности 5 (или
цикла Z) неограниченно увеличивается, то расположенный в любой ограничен-
ограниченной области Ф (содержащей, разумеется, точку А) участок окружности S
(цикла Z) стремится к отрезку прямой а в том смысле, что расстояние от са-
самой далекой от а точки этого участка кривой до а стремится к нулю
(см. рис. 69, а и рис. 70, а).
Укажем еще, что если г -»¦ 0 (или р ->• оо), то окружность S становится
все более похожей на точку (рис. 69, б), а цикл — на особую полупря-
полупрямую (на луч особой прямой, рис. 70, б).

§ 6] определение цикла; радиус и кривизна 91
радиуса г = ~п~ могут быть совмещены параллельным переносом (ибо
хорошо известно, что все параболы у = ах2-+-2Ьх ->-с, где а фикси-
фиксировано, могут быть получены параллельными переносами из одной
параболы у=ах2).
Выясним теперь механический смысл понятия цикла. Произволь-
Произвольная кривая Г плоскости Галилея, записываемая уравнением
У^/(х), E)
отвечает движению (материальной) точки по прямой о, описываемо-
описываемому следующим законом изменения положения (а') точки на прямой
с течением времени f1):
E')
Циклу Z отвечает специальный вид движения E')."
c. (Г)
Но хорошо известно, что такая зависимость пути от времени ха-
характеризует равноускоренное (пли равнозамедленное) движе-
движение. В самом деле, скорость v движении A') в момент времени t,
очевидно, равна
v== ljm j?=
At ->¦ 0 ^ S
= Inn м = Iim Bat-\-a-kt-\-2b)
At->-0 At Д^ -» 0
а ускорение w этого цвнження
л= Ш„ ^= lim
Таким образом, уравнение A') описывает равноускоренное
движение точки по прямой о, причем ускорение этого движения
w = 2a
равно кривизне р отвечающего этому движению цикла Z плос-
плоскости Галилея: в частности, равноускоренные (в собственном смысле
слова) движения отвечают циклам положительной кривизны (рис. 67, я),
а равнозамедленные движения — циклам отрицательной кривизны
(рис. 67, б).
') Здесь, разумеется, снова надо потребовать, чтобы кривая Г нигде «не
возвращалась назади,—см. подстрочное примечание на стр. 88.

92 окружности и циклы [гл. и
Понятие «кривизны р (а также «радиуса» г) можно определить для
любой линии Г плоскости Евклида или плоскости Галилея. Вот как это
делается. Прямая линия характеризуется своей «прямизной», отсутствием
какого бы ни было «искривления». Последнее утверждение имеет следующий
точный смысл. Назовем касательной к линии Г в ее точке А предель-
предельное положение AT, к которому стремится секущая AM при стремлении точ-
точки М кривой к точке А (рис. 71; утверждение, что прямая AM стремится
к прямой AT, означает, что ^МЛГ-^-0). [Это
I определение касательной уже использовалось
^"/ выше при доказательстве теоремы об угле между
хордой цикла и касательной к циклу в конце
этой хорды 1).\ Естественно считать, что ка-
/J сательная AT указывает «направление» линии
Г в точке А. Последнее утверждение можно об-
обосновать следующими механическими сообра-
соображениями (ср ниже, стр. 97): если (материаль-
(материальная) точка двигается по (евклидовой) линии Г
под действием некоторых сил, причем в мо-
момент времени t, когда точка находится в
пункте А, на нее прекращают действовать
какие бы то ни было силы (в том числе силы,
«принуждающие» точку двигаться по линии Г),
то далее точка «по инерции» будет двигаться
по прямой AT 2).
«Прямизна» прямой линии / как раз и
выражается в том, что направление прямой во
всех ее точках остается одним и тем же; это означает, что во всех точках
будет одной и той же касательная к прямой (совпадающая, очевидно,
с самой прямой). Что же касается всех остальных линий, то они обладают
большей или меньшей «кривизной», т. е. их направление меняется, являясь
разным в разных точках линии. Количественную оценку «степени кривизны»
доставляет угол поворота касательной: если при сдвиге вдоль
линии Г из точки А в точку В на расстояние —'АВ =s касательная повора-
поворачивается на угол ф, т. е. угол между касательными AT и ВГ, в точках Л и В
равен ф3), то «средняя кривизна» рср линии Г на участке АВ принимается
равной
Г
V
л
А
;;
Аср
Рис.
/А

71.
/
\
Т
рср = -|-, где s = -AB и ц = 1ТАТ' (AT'UBTJ F)
(рис. 71). Ясно, что участки линии Г, которым отвечает большая средняя
кривизна рСр, более искривлены в наглядном смысле этого слова, чем участки
с меньшей средней кривизной (так, изображенная на рис. 71 линия Г име-
имеет большую среднюю кривизну на участке АВ, чем на участке ЛгВх); если
') Здесь и далее мы ограничиваемся Лишь рассмотрением достаточно «глад-
«гладких» линий Г, в каждой точке которых определена касательная AT (которой
ведь нет в «угловых точках» кривой) и кривизна р.
2) Другими словами, если закон движения материальной точки по линии Г
имеет вид r = r{t), где г = ОМ — радиус-вектор подвижной точки, a t — вре-
dr „ ,
мя, то мгновенная скорость "г>==~тг этои точки в момент t напрев-
и, Г
лена по касательной к линии Г.
3) Здесь мы считаем, что участок АВ линии Г выбран гак, что при дви-
движении точки по этому участку в направлении от А к В касательная к Г
поворачивается все время в одном и том же направлении (ср. с подстрочным
примечанием на стр. 30).

§ 6]
определение цикла; радиус и кривизна
93
средняя кривизна рср линии Г на участке АВ равна нулю, то линия на этом
участке является прямолинейной. Кривизной же р линии Г в точке А назы-
называют «скорость поворота касательной» в этой точке, иными словами, предел,
к которому стремится средняя кривизна рср на участке AM при стремлении
М к А:
Р= Km ^$, где
As —> 0 AS
= ~ AM н &<г=
(Ат'0[МТв)
Fа)
(рис. 71; ср. выше, стр. 29—30), а ее радиусом г в той же точке—величину,
обратную кривизне:
р=т-
G)
Рассмотрим теперь (евклидову!) окружность S (рис. 72, а). Эта окруж-
окружность «устроена одинаково во всех своих точках» (на точном смысле этого
а)
интуитивно ясного утверждения мы еще остановимся в следующем пара-
параграфе). По этой причине кривизна р окружности S во всех ее точках является
одной и той же (причем кривизна тем больше, чем меньше радиус окруж-
окружности— ср. выше стр. 89 и рис. 69, а, б). И в самом деле, в силу формулы
F) средняя кривизна рср окружности S радиуса г на ее участке АВ равна
— , где (см. выше рис. 65, б) <р=/_ТАТ' = ?ТРТ1 (здесь ЛГ'ЦВГ,), или, в
S
силу теоремы о внешнем угле треугольника, (р = 2/_РАВ — 2а; s = ~^ АВ =
/AQB = r-2/_AMB = r-2a = rq>. Таким образом, средняя кривизна
окружности 5 радиуса г является одной и той же на любом участке АВ ок-
окружности, откуда следует, что в любой точке А окружности
р=\:г
(ср. с формулой D), которой мы выше определ ял и кривизну окруж-
окружности).
Обратимся теперь к геометрии Галилея. Среднюю кривизну рср линии Г
на ее участке А В и ее кривизну р в точке А мы определим теми же форму-
формулами F) и Fа), только длину дуги s и угол ф мы будем теперь понимать
в «галилеевом» смысле (в частности, длина s дуги АВ будет совпадать

94
ОКРУЖНОСТИ И ЦИКЛЫ
[гл. н
с длиной хорды АВ ')). Но если линия Г является циклом 2 (см. рис. 72, б),
то средняя кривизна рср на участке АВ равна — , где s = AB, а ц = /_ТАТ' =
= ?7РТХ (здесь АТ'ИВТХ). А так как из «формулы углов» A2) § 4 (стр. 61),
примененной к треугольнику АВР, легко получить, что
ц>= ?АРВ = 2?РАВ = 2а,
где угол сс= ?РАВ= ?_АВР равен, как мы знаем, вписанному углу
цикла Z, опирающемуся на дугу АВ, то окончательно имеем
где а—коэффициент при х2 в уравнении A) цикла Z. Мы видим, что сред-
средняя кривизна рСр = 1а цикла Z на его участке АВ не зависит от выбора
дуги АВ: поэтому и кривизна р цикла Z в любой его точке А будет одной
и той же:
р = 2о. Gа)
Если теперь, руководствуясь формулой G), назвать величину г, обратную
кривизне р цикла, его радиусом, то будем иметь
__1___1_
~ р 2а
G6)
Полученные таким путем определения кривизны (евклидовой) окружнос-
окружности S и (галилеева) цикла Z позволяют по-новому подойти к определению
кривизны р и радиуса г произвольной кривой Г (плоскости Евклида
х
Рис. 73.
или плоскости Галилея) в любой ее точке. Рассмотрим все окружности
(соответственно, все циклы), проходящие через точку А линии Г и имею-
имеющие в этой точке то же направление, что и Г (другими словами, каса-
касающиеся в точке А касательной АТ = а линии Г). Среди всех этих окруж-
окружностей (или циклов) выберем ту линию So (или Zn), которая теснее всего
примыкает к Г (рис. 73, а и б); например, можно потребовать, чтобы для
любой другой окружности S (цикла Z) расстояние ММ' между (достаточно
близкими к А) точками М и М' линии Г и 5 (или Г и Z), проектарующи-
См. подстрочное примечание нг стр. 88.

§ 6]
определение цикла; радиус и кривизна
95
мися в одну точку N прямой а, было больше расстояния ММ0 между соот-
соответствующими точками М и Мо линий Г и So (или Г и Zv). Окружность 50
(соответственно, цикл Zo) называется соприкасающейся окружностью (соприка-
(соприкасающимся циклом) линии Г в точке А, а ее кривизна р = — (или р = 2а) —
кривизной линии Г в точке А. Естественно назвать также радиус г
окружности 50 (цикла Zo) радиусом (или радиусом кривизны) линии Г в
точке А г).
Нетрудно указать аналитические формулы для вычисления кривизны р
и радиуса кривизны г линии y = f(x) в данной точке А (х, if). Действительно,
угловой коэффициент k касательной к кривой y = f(x) в точке А (х, у) равен,
х О
X
Рис. 74.
как известно, производной ,*' (х) функции / (х); поэтому единичный (имеющий
единичную длину) вектор и'Г0 касательной к кривой y = f {x) в точке
А (х, у) имеет координаты ( , ) в случае евкли-
довой геометрии и координаты A, /' (х)) в геометрии Галилея. Рассмотрим
теперь два таких вектора ОТ0 и ОГо, отвечающих касательным AT и А1Т1
в соседних точках А (х, у) и Аг (х1г у{) кривой y = f(x) (рис. 74, а, б); тогда
угол A<p=Z Т0ОТ'о будет равен «дуге» ТОТ'О единичной окружности So с цент-
центром О. Обозначим координаты (хи (/х) точки А1 через х-\-Ах и у-{-Ау =
— f(x-{-Ax) ~ f (x)-\-f (х) Ах; тогда длина As дуги ААХ будет равна Ах в га-
лилеевом случае и будет примерно равна Y^(Ax)'2 { (AyI ~ j^l 4-[/' (х)\- Ах
в евклидовом случае, а угол Дф (или дуга Т0Тё окружность 50) —
*) Если ни одна из рассматриваемых окружностей S (ни один из рас-
рассматриваемых циклов Z) не примыкает к линии Г «теснее», чем касатель-
касательная ЛГ = а, то роль «соприкасающейся окружности» So («соприкасающегося
цикла» ZB) играет прямая о; в этом случае полагают, что кривизна р ли-
линии Г в точке А равна нулю (а радиус г обращается в бесконечность).

96 ОКРУЖНОСТИ II ЦИКЛЫ (ГЛ. II
в галнлеевом случае и гораздо более сложному выражению
U
в евклидовом случае1). Отсюда без труда получаем, что в геометрии Галилея
кривизна р = lim —51 и радиус кривизны г = — линии у = 1(х) в точке
As -» о As p
А (х, у) выражаются простыми формулами
б то время как в геометрии Евклида соответствующие формулы сложнее1):
Л (8')
Из формул (8') и (8) можно снова вывести, что кривизна окружности
х2-\ у2~г2 в любой ее точке равна—, а кривизна цикла y = ax2~\-2bx-{-c
равна 2а. Более того, исходя из этих формул можно установить, что
только окружности плоскости Евклида и циклы плоскости Галилея имеют
во всех своих точках одну и ту же кривизну; однако при этом к числу
окружностей (и циклов) в качестве их предельного случая линий нулевой
кривизны (или «бесконечно большого радиуса») надо причислять и (обыкно-
(обыкновенные) прямые. Так, например, ясно, что если для линии y = f(x) плоскости
Галилея.
р=/" (х) = const,
то уравнение линии имеет вид
где ct и с2—произвольные постоянные, т. е. эта линия является циклом.
Вообще, любая линия Г плоскости Евклида или плоскости Галилея полностью
(другими словами, «с точностью до положения на плоскости») определяется
заданием своей кривизны во всех точках линии, т. е. уравнением
p = p(s). (9)
где р—кривизна линии Г в (переменной) точке A, as—длина дуги QA линии Г,
отсчитываемая от произвольно выбранного на линии «начала отсчета длин
дуг» Q. Последнее утверждение составляет содержание теоремы о нату-
натуральном уравнении («натуральным уравнением» кривой Г называют
') Ср., например, Дубнов [35], п. 66, в частности, формулу C80')
и задачу 353.

§ 6] определении цикла: радиус и кривизна 97
уравнение (9)), которую по достоинству считают «самой главной» теоремой
теории (кривых) линий плоскости Евклида (или плоскости Галилея)г).
Нетрудно понять, что в механической интерпретации геометрии Галилея
кривизна р = у" (х) в точке А (х, у) кривой Г, определяемой уравнением у- -f (x),
соответствует мгновенному ускорению w- z~nr (B момент времени t)
материальной точки, движущейся по прямой о по закону x = f (t). Ясно также,
что соприкасающийся цикл ZB кривой Г в точке А соответствует равно-
равноускоренному движению материальной точки, причем (постоянное!) уско-
ускорение, мгновенная скорость и положение этой точки на прямой о в момент
времени t совпадают соответственно с мгновенным ускорением w (выражаю-
(выражающимся кривизной соприкасающегося цикла Zo, т. е. удвоенным коэффициентом
при Xй в уравнении этого цикла), мгновенной скоростью v и положением f (f)
на прямой о в момент времени t точки, движущейся по закону x = f (t). Здесь
уместно вспомнить, что касательная а к линии Г в точке А соответствует
равномерному движению со скоростью v, равной мгновенной скорости
в данный момент (выражаемой угловым коэффициентом касательной). Отсюда
следует, что угловой коэффициент fe = u касательной к линии Г не имеет
геометрического смысла в геометрии Галилея (ибо он, очевидно, меняется при
«повороте» кривой), а кривизна p = w и радиус г= 1 : р соприкасающегося цик-
цикла геометрический смысл имеют (ибо величина w имеет механический смысл).
В силу «3-го закона Ньютона»
/ = тш,
где т—масса материальной точки, а /—действующая на нее сила, «кривизна»
p = ffij лишь постоянным множителем т отличается от действующей на точку
силы. Таким образом, «теорема о натуральном уравнении» геометрии Галилея
сводится к утверждению о том, что движение материальной точки по прямой о
полностью определяется действующими на нее силами f (пропорциональными
«кривизне» р = Ы1 = —); фундаментальное значение этого факта в механике
проливает дополнительный свет на роль «теоремы в натуральном уравнении»
в теории кривых.
В заключение этого параграфа укажем, что поскольку кривизна
р= lim _? любой кривой Г определяется через отношение угла к длине
As -ю AS
дуги («расстоянию»), а радиус кривизны г = — = lim сводится к отно-
отношению длины дуги к углу, то любое преобразование подобия плоскости Евклида
*) Ср., например, п. 67 указанной выше книги Дубнова [35]. [В гео-
геометрии Галилея в силу формулы (8) линия y = f(x), задаваемая своим «на-
«натуральным уравнением» /"(х)=р = р (s) (или f"(x) = p (х), поскольку «длина
дуги» QA, где Q = Q (О, Ь), здесь измеряется значением абсциссы х точки А (х, у)),
определяется по формуле
w п
Р(*).
где постоянные С] и с2 произвольны; ясно, что все такие линии «равны между
собой» в смысле геометрии Галилея.]
4 И. М. Яг.пом

98
окружное in и циклы
[гл. и
(так же как и преобразование подобия 1-го рода плоскости Галилея ]) с коэф-
коэффициентом подобия It), сохраняющее величину всех углов и умножающее все
расстояния на k, в k раз уменьшает (т. е. при k < 1—увеличивает!) кривизну
любой кривой Г и в k раз увеличивает радиус кривизны; так, например, «сжа-
«сжатие к точке О» (гомотетия) с. коэффициентом k переводит окружность S или
цикл Z радиуса г в окр\жность S' (цикл 2") радиуса fer "(рис. 75, а, б).
Рис. 75.
Напротив, каждое преобразование подобия 1-го рода') плоскости Галилея
с коэффициентом подобия х, сохраняющее неличины ксех расстянин и \мно-
жающее величины всех углов на и, б я раз увеличивает (при я <. 1 — умень-
уменьшает!) кривизну любой кривой Г плоскости Галилея иву. раз уменьшает
радиус кривизны; так, например, «сжатие к прямой Oxi> с коэффициентом х
переводит цикл Z радиуса г в цикл Z' радиуса — (рис. 75, е).
§ 7. Скольжение цикла по себе; диаметры цикла
«Начала» Евклида (см. подстрочное примечание на стр. 39),
о роли которых в истории геометрии мы говорили выше, начинаются
с «определений» основных объектов геометрии вроде точки, примой,
линии и поверхности ). В частности, определение 4 Евклида
гласит:
Прямая есть линия, которая равно расположена по отношению
к точкам на ней.
Если как определение эта довольна туманная фраза совершенно
неудовлетворительна, то в качестве описания «самого важного»
2) См. выше, стр. 66—67.
2) Эти определения мы сегодня считаем самым слабым местом всего заме-
замечательного сочинения Евклида: автор «Начал» не понимал, что, не обладая,
еще никакими знаниями по геометрии, нельзя дать ни одного полноценного
определения, так что самые первые понятия геометрии мы должны восприни-
воспринимать исходя из нашей интуиции, без точных определений (подобно том\ как
самые первые геометрические предложения — аксиомы — мы должны принять
на веру, не доказывая их).

§ 7]
скольжение цикла по себе; диаметры цнктл
99
свойства прямой она вполне удачна: в самом деле, основным свой-
свойством прямой является ее «однородность», то, что любые два (рав-
(равные но длине) отрезка прямой совершенно одинаковы, равны: в этом
смысле ни одна точка прямой ничем не отличается от любой другой
ее точки. Однако это свойство прямой не является характеристиче-
характеристическим, не выделяет прямую из всех других линий (евклидовой) плос-
плоскости, поскольку наряду с прямой им обладает также и окружность,
которая ведь тоже «равно расположена по отношению к точкам
на ней», тоже однородна: любые две дуги окружности одной длины
одинаковы (равны), так что любые две точки окружности совершенно
равноправны. «Однородность» прямой или окружности находит свое
выражение в существовании «скольжений вдоль прямой или вдоль
окружности» — движений, совмещающих любую точку А прямой /
(или окружности S) с любой другой ее точкой А' и переводящих
прямую / (окружность S) в себя; роль эгих движений играет парал-
параллельный перенос в направлении прямой / (рис. 76, а) или по-
поворот вокруг центра Q окружности S (рис 76.6).
х
Ясно, что и прямая / плоскости Галилея допускает подобные
«скольжения но себе»: ведь параллельный перенос (рис. 76, а) яв-
является движением и в геометрии Галилея. Несложно показать, что
и цикл Z плоскости Галилея допускает такие «скольжения по себе».
В самом деле, сдвиг
х,=х
A0а)
(см. формулы A4а) из § 2, стр. 40), который можно также за-
записать так:
X Xv

100
окружности и циклы
[гл. и
переводит цикл Z с уравнением
у -- -- ахг
(И)
(рис. 76, в) в цикл Zx с уравнением
yx —
которое можно переписать так:
yx = ax\-\-
или, окончательно так:
— vxx=ax\,
= a (х\ + — хх-^-~ ]—
4а'
(Па)
Но ясно, что описываемый уравнением (Па) цикл Zx «равен» исход-
исходному циклу Z — он переводится в Z параллельным переносом
г'— X '
х ~2а'
A06)
Поэтому преобразование
A2)
складывающееся из сдвига A0а) и параллельного переноса A06),
переводит цикл Z в себя: сдвиг A0а) переводит точку А цикла Z
в точку Ах цикла Za, а параллельный перенос A06) — точку Ах
в точку А' исходного цикла Z (рис. 76, е). Движение A2) плоскости
Галилея, переводящее цикл Z в себя, называется (задаваемым циклом Z)
циклическим поворотом с коэффициентом v (или «циклическим
поворотом в направлении цикла Z»I). При этом поскольку при
сдвиге A0а) каждая точка А плоскости смещается «на нулевое рас-
расстояние» (т. е. переходит в такую точку Аъ что dAAi = 0), а парал-
параллельный перенос A06) смещает каждую точку на расстояние ^-
1т. е. переводит точку Ах в такую точку А, что «л,л' — ft), то
') Известно, что каждое (собственное!) движение плоскости Евклида пред-
представляет собой либо поворот, либо параллельный перенос (см., например,
книги Перепелки на [5] или Я г л о м а [9]). Аналогично этому можно
показать, что каждое движение плоскости Галилея (см. формулы A) из
§ 3, стр. 45) представляет собой либо циклический поворот, либо параллель-
параллельный перенос; доказательство этого утверждения мы предоставим читателю.

§ 7]
СКОЛЬЖЕНИЕ ЦИКЛА ПО СЕБЕ; ДИАМЕТРЫ ЦИКЛА
101
циклический поворот A2) смещает каждую точку на расстояние ^-:
точку А он переводит в такую точку А', что
v
АА'= 2а "
Но отсюда следует, что, подобрав соответствующим образом коэф-
коэффициент v циклического поворота, мы можем сдвинуть точку А
цикла Z на любое (положительное или неположительное!) рас-
расстояние d — для этого достаточно положить ;r-=d или v—2ad.
Рис. 77.
Таким образом, каждую точку А цикла Z можно подходящим цик*
лическим поворотом A2) перевести в любую другую точку А' этого
цикла. Можно доказать, что на плоскости Галилея такой «одно-
«однородностью» обладают только циклы и прямые линии, подобно
тому как на плоскости Евклида однородностью обладают только
окружности и прямые*).
При повороте плоскости Евклида, переводящем в себя окруж-
окружность 5", каждая точка плоскости смещается по концентрической с S
окружности (рис. 77, а). Аналогично этому при циклическом повороте
плоскости Галилея, задаваемом циклом Z, каждая точка этой пло-
плоскости смещается по циклу, «параллельному» Z, т. е. получаемому
из этого цикла «особым» параллельным переносом (т. е. параллель-
параллельным переносом в направлении особых прямых). В самом деле, цикл
у =ах2-\-с,
(ll'J
«параллельный» циклу Z, сдвиг A0а) (или A0'а)) переводит в цикл
уг—vxx = axl+c
Ср. выше, стр. 96.

102 ОКРУЖНОСТИ И ЦИКЛЫ
или (ср. с формулой A1а))
, v2 ., . . V1 .
'2а
[гл. п
а параллельный перенос A06) переводит последний цикл в цикл
т. е. снова в исходный цикл A1'). Таким образом, циклический пово-
поворот A2) переводит в себя не только цикл Z, но и любой цикл A1')
(где с произвольно!), откуда и следует, чго все точки плоскости при
этом преобразовании перемещаются по циклам
A1') (рис. 77, б). Аналогия между концент-
концентрическими окружностями и параллельными
циклами будет далее еще продолжена.
Циклические повороты очень удобны для
доказательства разнообразных свойств цик-
циклов. Мы начнем с уже знакомой нам теоре-
теоремы, утверждающей, что касательные РА и
РВ, проведенные к циклу Z из одной точки
Р, равны между собой (ср. выше, стр. 87).
Будем счита гь, что уравнение цикла Z (рис.78)
имеет вид A1); это условие не является
ограничением, поскольку каждый цикл имеет
уравнение A1)в некоторой специально подо-
подобранной системе координат 1). Произведем ци-
циклический поворот A2), переводящий цикл Z
в себя и совмещающий точку Р с точкой Р' оси Оу. [В общем случае
придется произвести циклический поворот, переводящий цикл Z
в себя и совмещающий точку Р с точкой Р' оси симметрии
(евклидовой) параболы Z.] При этом касательные РА и РВ цикла Z
перейдут в его касательные Р'А' и Р'В'\ поскольку понятие каса-
касательной цикла имеет смысл в геометрии Галилея, то движение
A2) плоскости Галилея, переводящее цикл Z в себя, переводит
касательную цикла Z в касательную того же никла. В силу симметрии
параболы у - ах2 относительно оси Оу отрезки Р'А' и Р'В' (где А'
и В' — точки соприкосновения касательных с параболой), очевидно,
равны между собой как в евклидовом смысле, так и в смысле гео-
геометрии Галилея (т. е. равны проекции отрезков Р'А' и Р'В' на ось
Ох). Но движение A2) плоскости Галилея не меняет (галнлеевых!)
длин отрезков; поэтому из равенства (в смысле геометрии Галилея)
!) Для дальнейшего нам надо, чтобы оси этой системы координат с точки
зрения евклидовой геометрии были взаимно перпендикулярны; поэтому наше
доказательство является «существенно не галилеевым», т. е. оно использует
факты и понятия, не имеющие геометрического смысла в геометрии Галилея
(ср. с подстрочным примечанием на стр. 47).

§ 71
СКОЛЬЖЕНИИ ЦИКЛА ПО СЕБЕ! Д11А.МКТРЫ ЦИКЛА
103
отрезков Р'А' и Р'В' следует также равенство отрезков РА и РВ
(т. е. равенство dAP dpftI).
Вот еще одни пример подобного рода. Хорошо известно, что
середины всех параллельных между собой хорд окружности S при-
принадлежат одной прямой d—диаметру окружности (рис. 79. а);
это утверждение представляет собой лишь переформулировку того
факта, что окружность симметрична относительно любого своего
X
диаметра. Рассмотрим теперь совокупность параллельных между
собой хорд цикла Z с уравнением у=ах2 — хорд, принадлежащих
прямым, имеющим фиксированный угловой коэффициент А0(рис. 79, б).
Заметим, что сдвиг A0а) (или A0'а)) переводит прямую
у = kx , s
с угловым коэффициентом k в прямую у^ — vx-^= kx1-\-s или
у1 = kxxx \ s (kx = k + v)
с угловым коэффициентом k1=k\v, а параллельный перенос A0б)
сохраняет направления прямых; поэтому циклический поворот A2)
с коэффициентом v= —kn переводит наши хорды цикла Z в хорды
с угловым коэффициентом 0 — в хорды, параллельные оси Ох
(рис. 79, в). Но середины всех последних хорд, очевидно, принад-
принадлежат оси Оу — оси симметрии параболы у =ах2. Поэтому и середины
исходных хорд принадлежат одной прямой d, а именно той прямой,
J) Заметим, что dPA = — dPB. [Укажем, что если РА и РВ —касательные,
проведенные из одной точки Р к направленной окружности S
(т. е. окружности с выбранным на ней одним из двух возможных направлений
обхода; ср. стр. 89), то также естественно считать, что РА =—РВ (см., на-
например, стр. 270 книги Я г лома [10]).].

104
ОКРУЖНОСТИ И ЦИКЛЫ
[гл. и
которую наш циклический поворот переводит в ось Оу. Так как
движение плоскости Галилея переводит d в особую прямую Оу, то
и сама прямая d является особой. Эта прямая называется диаметром
цикла Z (отвечающим хордам с угловым коэффициентом k0).
Таким образом, середины всех параллельных между собой хорд
цикла Z принадлежат одной особой прямой d — диаметру цикла.
При этом легко видеть, что все особые прямые являются диамет-
диаметрами цикла Z: в самом деле, особая прямая х=т переводится в ось Оу
циклическим поворотом A2) с таким коэффициентом v, что ^-= —т
или v= —lam; поэтому рассматриваемая прямая делит пополам
все хорды цикла Z, которые этот циклический поворот переводит
в параллельные оси Ох прямые. [Нетрудно проверить, что диаметр
х = т цикла у= ахг делит пополам все хорды, высекаемые циклом
на прямых с угловым коэффициентом k= 2am.]
Будем теперь сдвигать параллельно хорду АВ цикла Z, которую
делит пополам диаметр d, таким образом, чтобы длина хорды
уменьшалась. При этом, в конце концов, точки А, В и (принад-
(принадлежащая диаметру d) середина С хорды АВ сольются в одну
точку, и мы придем к утверждению:
касательная t в конце диаметра d цикла
Z параллельна хордам, которые делятся
пополам этим диаметром (ср. рис. 79, б, в
с рис. 79, а, относящимся к окружности).
Теорему о диаметрах цикла (т. е. утверж-
утверждение о том, что середины параллельных хорд
принадлежат одной особой прямой) легко до-
доказать и без использования свойств цикличе-
циклического поворота. В самом деле, пусть АВ и
CD—две параллельные хорды цикла Z, а РА
и РВ, QC и QD—касательные к циклу в кон-
концах этих хорд (рис. 80). Из равенства вписан-
вписанных углов ?ADC и ^_DAB цикла следует, что
AC = DB; с другой стороны, мы знаем, что
АР = РВ и CQ = QD. Отсюда получаем
0 = CQ—QD =
Рис. 80.
таким образом (обыкновенная!) длина отрезка
PQ равна нулю, т. е. прямая PQ особая.
Поэтому высоты РМ и QN равнобедренных треугольников РАВ и QCD
(являющиеся одновременно и медианами этих треугольников!) совпадают,
т. е. середины М и N любых двух параллельных хорд цикла Z принадлежат
одной особой прямой. Отсюда уже легко выводится, что середины всех парал-
параллельных между собой хорд цикла принадлежат одной особой прямой.
Теперь мы можем по-новому обосновать использование в гео-
геометрии Галилея особых прямых в качестве «перпендикуляров»

§ 7]
скольжениь цикла по себе; диаметры цикла
105
Рис. 81.
(ср. выше, стр. 56, и рис. 36—37). В геометрии Евклида диаметр
окружности перпендикулярен касательной, проведенной в конце
этого диаметра; поэтому для того, чтобы восстановить перпенди-
перпендикуляр к прямой а в ее точке А, достаточно построить окружность S,
касающуюся и в точке А, —
диаметр AQ этой окружности
и будет искомым перпендику-
перпендикуляром (рис. 81, а). Аналогично
этому уславливаются считать,
что и в геометрии Галилея
диаметр цикла «перпендикуля-
«перпендикулярен» касательной к циклу в
конце этого диаметра, т. е.
роль «перпендикуляра» к пря-
прямой а в ее точке А играет диа-
диаметр АР цикла Z, касающе-
касающегося прямой а в точке А
(т. е. проходящая через точку
А особая прямая; рис. 81, б). Понимая под углом между
прямой / и кривой линией Г у^ол между / и касательной /кГв точке
пересечения / и Г (рис. 82), мы можем сказать, что все диаметры
цикла Z «перпендикулярны» этому циклу (подобно тому как все
диаметры окружности 5 перпендикулярны окружности; ср.
рис. 81, а и б). Заметим еще, что диаметр й цикла Z, проходящий
через некоторую точку Р, делит пополам отрезок
АВ, соединяющий точки прикосновения с циклом
касательных РА и РВ, проведенных из точки Р
(ибо d является высотой равнобедренного тре-
треугольника РАВ; ср. рис. 65, а и б на стр. 86).
Сказанное проливает также новый свет на
аналогию между концентрическими окружностями
и параллельными циклами, о которой говорилось
выше. Назовем расстоянием от точки А до линии
Г расстояние от Л до самой близкой к Л
точки В линии Г. Можно доказать, что в ев-
евклидовом случае это расстояние (во всяком слу-
случае для гладкой линии Г без концов — замкнутой или бесконеч-
бесконечной) измеряется по перпендикуляру АВ к Г; другими словами,
прямая АВ перпендикулярна касательной t к линии Г в точке В
(рис. 83, аI). В геометрии Галилея наименьшее расстояние от
точки А до точек линии Г, вообще говоря, будет равно нулю; при
этом расстояние от А до Г надо будет измерять «особым расстоя-
расстоянием»" ЬАВ от точки А до точки В линии Г (рис. 83, б). Назовем
Рис. 82.
См., например, Болтянский и Яг лом [36], стр. 285—286.

106
ОКРУЖНОСТИ И ЦИКЛЫ
[ГЛ. II
теперь линию 1\ параллельной линии Г, если все точки Гх удалены
от Г на одно и то же расстояние (можно показать, что в этом
случае и Г «параллельна» Г\). В евклидовом случае «параллелью»
в этом смысле к прямой / будет прямая 1Х\\1 (рис. 84, а), а «па-
«параллелью» к окружности S — концентрическая с S окружность iSlt

§ 71 скольжение цикла но себе; диаметры цикла 107
причем расстояние от любой точки А окружности S} до S измеряется
по проходящему через А общему диаметру окружностей S и Sy
(рис. "84, б). В геометрии же Галилея «параллелью» к (обыкновен-
(обыкновенной) прямой / служит прямая /г || / (рис. 84, в), а «параллелью»
к циклу Z— цикл Zj, параллельный Z в определенном выше смысле,
причем расстояние от любой точки А цикла Zj до Z измеряется
по проходящему через А общему диаметру циклов Z и Zx (рис. 84, г).
Наконец, укажем, что теорема о диаметрах цикла имеет доста-
достаточно прозрачный механический смысл. Выберем такую систему
отсчета, в которой рассматриваемые параллельные прямые отвечают
фиксированным точкам прямой о (т. е. такую систему отсчета,
в которой эти прямые отвечают состояниям покоя); тогда
концы А и В хорды АВ цикла Z отвечают событиям, состоящим
в том, что двигающаяся равноускоренно материальная точка прохо-
проходит определенный пункт прямой о—тот пункт, для которого разным
моментам времени отвечают все точки прямой АВ. Нетрудно понять,
что каждый пункт прямой о (скажем, вертикали) равноускоренно
движущаяся точка (в качестве которой удобно представлять себе
подброшенный вверх камень, движущийся с ускорением —g, где
?¦^9,8 ж/сек2 — ускорение айы тяжести), вообще говоря, будет
проходить два раза: на пути «вверх» и на пути «вниз». При этом
середины всех определенных таким образом интервалов времени
(интервалов между двумя прохождениями «камнем» одного и того
же пункта) будут совпадать между собой и совпадать с моментом
достижения «камнем» крайней («самой высокой») точки прямой1).
Это и означает, чго соответствующие точки плоскости Галилея
принадлежат одной выделенной прямой.
Использование циклического поворота для доказательства относящихся
к циклам теорем, мы проиллюстрируем еще одним примером. Нетрудно
установить, что множество середин всех хорд (евклидовой) окружности S,
проходящих через фиксированную точку М, представляет собой окружность s
(или дугу окружности s); для того чтобы убедиться в этом, достаточно заме-
заметить, что прямая QP, соединяющая центр Q окружности S с серединой Р
проходящей через точку М хорды АВ, перпендикулярна АВ (и, следователь-
следовательно, точка Р принадлежит окружности s с диаметром MQ; рис. 85, а, б).
Однако это доказательство апеллирует к понятию центра окружности, и
потому возможность переноса его на циклы плоскости Галилея представляется
сомнительной.
Тот же самый факт можно установить еще и по-другому. На каждой
проходящей через точку М хорде АВ окружности S найдем такую точку N, что
AM = NB (или AN — MB); нетрудно понять, что все такие точки iV принад-
принадлежат концентрической с S окружности Slt проходящей через точку М (ибо
из соображений симметрии вытекает, что любая проходящая через М
хорда MN окружности St пересекает S в таких точках А, В, что AN = МВ;
]) Эта «крайняя» точка характеризуется тем, что мгновенная скорость
в ней равна нулю (т. е. касательная к циклу в соответствующей точке пло-
плоскости Галилея параллельна прямым, отвечающим состоянию покоя.)

108
ОКРУЖНОСТИ И ЦИКЛЫ
[гл. н
рис. 86, а, б). С другой стороны, середина Р хорды АВ является также и
серединой хорды MN, так что точка Р получается из точки Л' сжатием
к точке М (гомотетией) с коэффициентом 1/2; поэтому множество точек Р
принадлежит окружности s, гомотетичной S! с центром гомотетии М и коэф-
коэффициентом 1/2.
S)
Рис. 85.
Последнее рассуждение уже без труда переносится на циклы геометрии
Галилея. Прежде всего заметим, что если прямая / пересекает параллельные
циклы Z и Z\ с уравнениями у = ах- и у==ах2-\-с в точках А, В, соответ-
соответственно М, N (рис. 87), то AM=NB; для доказательства этого достаточно
Рис. 86.
с помощью подходящего циклического поворота A2) перевести прямую /
в параллельную оси Ох прямую V, в силу соображений симметрии, очевидно,
пересекающую Z и Zx в таких точках А', В' и М', Л", что А'М' = N'B'.
Теперь найдем на каждой проходящей через фиксированную точку М
хорде АВ заданного цикла Z такую точк) N, что АМ — .\В (или AN = МВ;

§ 7]
скольжение цикла по себе; диаметры цикла
109
рис. 88, а, б); в силу доказанного все полученные таким образом точки N
принадлежат проходящему через точку М циклу Zx, параллельному циклу Z.
Но середина Р отрезка АВ является также и серединой отрезка MN; поэтому
она получается из точки N сжатием к точке М (гомотетией) с коэф-
коэффициентом 1/2. Отсюда вытекает, что множе-
множество середин всех хорд цикла Z, проходящих ?
через фиксированную точку М, представляет Z
собой цикл (или дугу цикла) г (причем цикл г
гомотетичен циклу Zx с центром гомотетии М
и коэффициентом 1/2).
Обратимся теперь к принципу двойствен-
двойственности, которому был посвящен § 5 гл. I. В
силу этого принципа любой теореме геометрии
Галилея отвечает двойственная ей теоре-
теорема, получаемая из первоначальной заменой
слов «точка» и «расстояние» словами «пря-
«прямая» и «угол» и наоборот, выражения «па-
0
Рис. 87.
раллельные прямые» выражением «параллельные (принадлежащие одной
особой прямой) точки» и наоборот. При этом каждое понятие геометрии
Галилея, фигурирующее в исходной теореме, в формулировке двойственной
1 \
\ \
\
AV
-\
ч
и
1
1
/
0
У
'у?
У
и I
V 1
1А
1
/
г
X
Рис. 88.
теоремы заменяется «двойственным» понятием, получаемым из первоначального
той же заменой слов и выражений (пример: параллелограмм и антипаралле-
антипараллелограмм). Выясним теперь, какое понятие геометрии Галилея двойственно
понятию цикла.
Цикл Z мы определяли как множество точек М, из которых данный
отрезок АВ виден под постоянным углом а:
В определении двойственного циклу понятия роль отрезка АВ будет играть
угол aLb, образованный прямыми а и Ь\ точке М будет отвечать прямая т.
Прямые МА и MB заменяются теперь точками А и В пересечения т и а.

110
ОКРУЖНОСТИ II ЦИКЛЫ
[гЛ. II
соответственно т и Ь; угол буц^ ми (т.е. /_АМВ)— расстоянием АВ ( = Ays)
Таким образом, мы приходим к рассмотрению множества ? прямых т, на
которых данный угог aLb высекает отрезок АВ постоянной длины d:
(рис. 89).
Из существования «галилеева движения» (циклический поворот), перево-
переводящего в себя множество точек М (т. е. цикл Z), в силу принципа двой-
двойственности вытекает существование дви-
движения, переводящего в себя множе- „
ство прямых m (напомним, что дви- "
жение плоскости Галилея определялось
как преобразование в множестве точек
и множестве прямых, сохраняющее
У-
х
Рис. 89.
Рис. 90.
расстояния между точками и углы между прямыми; поэтому двойствен-
двойственным движению понятием будет снова движение). Отсюда уже можно вывести,
что прямые т являются касательными некоторого цикла; однако это можно уста-
установить и по-другому. Пусть т — произвольная прямая, пересекающая стороны
угла aLb в точках А и В, и пусть Z — цикл, касающийся прямых a, b и т
в точках D, Е и F (рис. 90) *). Так как касательные, проведенные к циклу
из одной точки, равны, то DA = AF и FB = BE. Но поскольку DE = DA +
-J- АВ-\-ВЕ (ср. с «формулой сторон» A1) § 4, стр. 61)), то отсюда следует2)
Таким образом, длина АВ ( = d) отрезка касательной т цикла Z, заключен-
заключенного между сторонами угла aLb, равна половине длины хорды DE цикла Z,
откуда следует, что на каждой касательной т цикла Z стороны угла aLb
1) Относительно существования такого цикла ср. ниже, стр. 112—113.
2) По существу, в этом рассуждении нсполья\ются направленные
(т. е. взятые с тем или иным знаком) длины отрезков (ср. прямые АВ и А^В^
на рис. 90).

§ 7]
СКОЛЬЖЕНИЕ ЦИКЛА ПО СЕБЕ; ДИАМЕТРЫ ЦИКЛА
111
высекают отрезок одной и тойже длины d
(=4-)-
Поэтому множе-
множество прямых т, на которых прямые а и b высекают отрезок фиксированной
длины d, совпадает с чножсством касательных цикла Z.
Теперь уже нетрудно сформулировать предложения, двойственные всем
известным нам свойствам цикла. Так, например, мы знаем, что касительные
РА и РВ, проведенные к циклу Z из одной точки
Р, равны между собой. Но циклу Z, понимаемому
как множество своих точек, двойствен цикл Z,
понимаемый как множество своих касательных ');
точке Р двойственна прямая р; проходящим че-
через точку Р касательным РА а и РВ = Ь цик-
цикла— принадлежащие прямой р точки А к В цикла;
расстояниям РА и РВ—утлы ^_аАр и /_рВЬ
(рис. 91). Поэтому из принципа двойственности
следует, что произвольная хорда А В (г р) цикла
Z образует с касательными а и Ь к циклу в кон-
концах этой хорды одинаковые углы,—теорема, лишь
формой отличающаяся от исходной теоремы.
Далее, множество середин параллельных между
собой хорд цикла принадлежит одной особой пря-
прямой. Параллельным прямым I и 1Х отвечают «па-
«параллельные» (т. е. принадлежащие одной особой
прямой) точки L и Lx\ точкам А, В и Alt Вл пересечения I и 1\ с циклом
Z — проведенные из точек L и Lx касательные с, b и а^Ь^, серединам .И и Mt
Рис.
отрезков АВ и А1В1—биссектрисы т и тг углов aLb и QiZ-ifej (ср. рис. 92,0
и б). Таким образом, теореме о диаметрах цикла отвечает утверждение о па-
параллельности биссектрис т и тх углов aLb и u^L^ (ведь точки М и Mt «па-
«параллельны», т. е. принадлежат одной особой прямой!). Доказательство этого
утверждения мы предоставим читателю.
') Строго говоря, следует считать, что циклу радиуса с двойствен цикл
кривизны с (т. е. раднчса 1/f), поскольку понятие ради)са цикла двойственно
понятию его кривизны.

112
ОКРУЖНОСТИ И ЦИКЛЫ
[гл. н
Наконец, мы знаем, что середины всех проходящих через одну точку М
хорд цикла Z принадлежат одному циклу г. Точке М в силу принципа двой-
двойственности отвечает прямая т; проходящей через точку М прямой /—точка L
прямой т; хорде А В—угол aLb, образованный проходящими через точку L
касательными а и b к циклу 2; середине Р хорды АВ—биссектриса р угла aLb
' С
а)
Рис. 93.
(ср. рис. 93, а и б). Таким образом, мы приходим к следующей замечательной
теореме, на доказательстве которой также здесь не остановимся: биссектрисы
всех углов, образованных проведенными из точек фиксированной прямой т
касательными заданного цикла Z, касаются одного цикла г.
§ 8. Описанный и вписанный циклы треугольника
Пусть ABC—треугольник плоскости Галилея со сторонами АВ=с,
^а, СА^ееЬ; буквами а, Ь, с мы будем обозначать как (обычные)
прямые АВ, ВС и СА, так и длины соответствующих отрезков.
Ясно, что через точки А, В и С проходит (единственный!) цикл,
который можно определить, например, как множество точек, из ко-
которых отрезок АВ виден под углом С; этот цикл Z (рнс. 94) мы
назовем описанным циклом треугольника ABC. Докажем, что
аналогично этому существует единственный цикл, касающийся трех
прямых а, Ь и с; этот цикл z мы назовем вписанным циклом
треугольника.
Нетрудно видеть, что вписанный цикл z треугольника ABC (если
только он существует!) должен касаться одной стороны треуголь-
треугольника и продолжений двух других сторон—пусть, например, он ка-
касается стороны АВ в точке Z7, а продолжений сторон СА и СВ

§ 8]
ОПИСАННЫЙ II ВПИСАННЫЙ ЦИКЛЫ ТРЕУГОЛЬНИКА
113
в точках Е и D (см. рис. 94). Так как треугольник DCE—равно-
DCE—равнобедренный (ибо касательные CD и СЕ, проведенные к циклу z из
точки С, равны между собой), то его высота СР является также
и медианой, откуда следует, что проходящая через точку С особая
прямая СР пересекает отрезки ED и АВ, что возможно лишь в том
случае, если АВ = с—наибольшая сторона треугольника ABC:
cab. Далее, поскольку
CD ' СЕ =(СВ \-BD)-r(CA+AE)= y
= СВ4 BF+CA+AF=CB+CA+
(В/7-! AF) = CB+CA + AB,
то
CD _ CF '
поэтому
АЕ=СЕ—СА = а,
А так как AF=AE и BF=BD, то
AF=a, BF=b. A36)
A3а)
Рис. 94.
Равенства A3)—A36) полностью определяют положение точек D,
Е и F на сторонах треугольника ABC. Докажем теперь, что опи-
описанный цикл z треугольника DEF (а этот цикл во всяком случае
существует!) касается в точках F, D и Е сторон АВ, ВС и С А
треугольника ABC (т. е. является вписанным циклом треугольника
ABC). В самом деле, вписанный угол /_DEF этого цикла равен раз-
разности углов /_DEC и /_FEA; но из равнобедренных треугольников
DEC и FEA с известными углами С и Л по «формуле углов» A2)
§ 4 (стр. 61) следует, что
и, значит,
С другой стороны, по той же «формуле углов», примененной к равно-
равнобедренному треугольнику DFB с известным углом В,
поэтому прямая DB = а, образующая с хордой DF цикла z угол
п
-=-, равный опирающемуся на эту хорду вписанному углу,

114 ОКРУЖНОСТИ И ЦИКЛЫ [ГЛ. II
является касательной цикла z. Точно так же доказывается, что
прямые ЕА -^ Ь и FA = с касаются цикла z в точках Е п F.
Радиусы описанного цикла Z и вписанного цикла z (которые,
как и стороны н углы треугольника, мы здесь считаем положитель-
положительными!) обозначим через R и г, а кривизны этих двух циклов — через
Р и р. В силу определения радиуса цикла мы имеем
— — — — — —2R A4)
А" В ~ С ~гК' U '
что позволяет нам по-новому трактовать коэффициент пропорцио-
пропорциональности X из соотношений A4) § 4 (стр. 62). Формулы A4) по-
позволяют вычислить величину радиуса R описанного никла Z
треугольника ABC no величинам его сторон и углов; они заметно
проще родственных им формул евклидовой геометрии, составляющих
содержание классической «теоремы синусов»:
А ? A4')
sin A sin В sin С
(где R—радиус описанной окружности евклидова треуголь-
треугольника ABC). Из формул A4) и формул A7) § 4 (стр. 63) вытекает,
что
г, а аЪс _ аЪс
2А~~ 2 (Abe) ~~ 2^2S '
где S — площадь треугольника ABC, или, окончательно,
Я-ll- 05)
Любопытно, что последняя формула в точности копирует соот-
соответствующую формулу евклидовой геометрии, получающуюся из
соотношений R=n f .- и S = -;rbcs\nA (см. формулы A4') и фор-
z sin /\ с.
мулу A7') из § 4). Однако в противоположность евклидовой гео-
геометрии величина радиуса R описанного цикла Z треугольника ABC
геометрии Галилея может быть просто выражена также и через
площадь S этого треугольника и величины его углов. В самом деле,
поскольку в силу A4)
а = 2AR, Ь = 2BR, с = 2CR,
то из A5) вытекает
Р- 2AR-2BR-2CR _ 2АВС р3
откуда получаем
пп О

§ 8] ОПИСАННЫЙ II ВПИСАННЫЙ ЦПК1Ы ТРЕУГОЛЬНИКА 115
Заме him также, что из формул A5) и A6) следует
^ A6а)
Обратимся теперь к вписанному циклу z треугольника ABC.
Мы вичелн, что этот цикл является описанным для изображенного
на рис. 94 треугольника DEF, стороны EF d, DF=e, DE f
и углы /_EDF D, /_DEF- E, /JDEF F которого легко найти.
Так, выше мы убедились, что Е = /_DEF = -^ ; аналогично вычисля-
вычисляются и величины двух других углов треугольника DEF:
Далее, из равнобедренных треугольников EAF (пе EA=AF=a),
DBF (пе DB- BF - />) и DCE (где DC CE=c) находим
й 2а, e=2b, f=2c.
А теперь из формул A4) получаем
d e f
г. е.
а Ь с г
Т--в^Т"^- A4а>
Таким образом, мы приходим к следующему замечательному соот-
соотношению:
г = 4/?, A7)
откуда следует также, что
Р -4р. A7а)
Заметим, что неожиданные с первого взгляда соотношения A7) и A7а),
не имеющие аналогов в евклидовой геометрии, являются непосредственными
следствиями принципа двойственности В самом деле, ясно, что понятию
описанного цикла Z треугольника ABC — цикла, содержащего точки А, В
и С,—двойственно понятие вписанного цикла г треугольника ABC—цикла,
для которого п р я м ы е а, Ьис являются касательными. Атак как величины
углов треугольника двойственны длинам его сторон и наоборот, а радиусу
цикла г — Inn _iL двойственно понятие его кривизны jj = lim L5C, то
As - о Аф Дф -> о As

116
ОКРУЖНОСТИ И ЦИКЛЫ
[ГЛ. II
относящимся к описанному циклу треугольника формулам
А~ В~ С ~ К
двойственны относящиеся к вписанному циклу формулы
п b с
равносильные соотношениям
A4)
а
1
A4а)
Но из сравнения формул A4) и A4а) сразу вытекает соотношение A7I
В § 4 гл. I мы видели, что формулы, связывающие одноименные
элементы произвольного треугольника — «формула сторон» A1) и
«формула углов» A2),—имеют совершенно ясный механический смысл:
они выражают закон аддитивности временных интервалов и закон
МОД
C(t3lx3)
Рис. 95.
сложения скоростей (см. стр. 61). Теперь мы можем истолко-
истолковать механически также и формулы A3) § 4, составляющие содер-
содержание третьей системы основных соотношений, связывающих стороны
и углы произвольного треугольника. Пусть А(хъ yj, В (х2, у2) и
С(х3, у3) — три точки плоскости Галилея, являющиеся вершинами
треугольника ABC (рис. 95, а); им отвечают три события A(tlf хг),
B(t2, x2) и C(t3, x3), никакие два из которых не одновременны.

§ 8] ОПИСАННЫЙ И ВПИСАННЫЙ ЦИКЛЫ ТРЕУГОЛЬНИКА И 7
Можно доказать (мы это сделаем чуть ниже), что существует един-
единственное равноускоренное (в широком смысле слова, т. е. равно-
равноускоренное, равномерное или равнозамедленное) движение, которое
«соединяет» эти три события; ускорение этого движения, имеющее,
как мы знаем, «абсолютный» (т. е. не зависящий от выбора инер-
цнальной системы отсчета) смысл, мы обозначим через w. Выберем
теперь инерциальную систему отсчета так, чтобы два из наших
событий, скажем А и В, отличались лишь временем, но не местом
на прямой о; кроме того, примем соответствующий событию А пункт
прямой о за начало отсчета координат (х), а время, отвечающее
событию А, — за момент начала отсчета времени. В таком случае
события А, В и С будут иметь следующие «пространственно-вре-
«пространственно-временные координаты»: Л @, 0), B{t2, 0) и С (ts, х3) (рис. 95, б; ср.
с рнс. 95, а, на котором изображены также оси новой системы
координат, отвечающей поставленным условиям).
Найдем теперь «соединяющее» наши три события равноускоренное
движение:
x = at2+2bt-{-c A8)
(ср. стр. 91). Так как условию A8) удовлетворяет событие х = 0,
t-О, то
с = 0; A8а)
так как ему удовлетворяет также событие х = 0, t = t2, то
аР2+2Ы2=0, т.е. 2b=—at2 A86)
(ибо t2=^=0). Для того чтобы определить последний неизвестный нам
коэффициент формулы A8)—коэффициент а, достаточно подставить
в уравнение A8) (для которого выполняются равенства A8а) и A86)!)
значения x=xs и t=t3. При этом мы получаем
xs=atl — at2ts,
откуда следует
а =
или, поскольку —= 2
'3—'2 '3 'зС'З — Т2>
A8в)
Итак, мы нашли (единственное!) искомое равноускоренное движе-
движение A8); коэффициенты а, Ь, с равенства A8) определятся усло-
условиями A8а)—{18в). А так как ускорение w движения A8) равно,
как мы знаем, 2а, то окончательно получаем
W = ( Х3 Х3\
=
2 U-*2 hj

118 ОКРУЖНОСТИ И ЦИКЛЫ [ГЛ. II
Но величина /2, очевидно, равна, (временному!) интервалу между
событиями В и А, т. е стороне АВ = с треугольника ABC. Далее,
скорость v., равномерного движения (материальной) точки, исходящей
в момент t — О из пункта д; = 0 и достигающей в момент времени t3
пункта х = xs, равна
а скорость vl равномерного движения материальной точки, исходя-
исходящей в момент времени ?2 из пункта х = 0 и достигающей в момент
времени t3 пункта х = xs, равна
Таким образом, разность
совпадает с относительной скоростью 2-го из рассматривае-
рассматриваемых равномерных движений относительно наблюдателя, совершающего
1-е движение (см. формулу (8) § 3, стр. 58 и 54), т. е. равна ве-
величине угла С треугольника ABC. Поэтому полученную нами фор-
формулу, выражающую ускореиие w через координаты t2, ts и д;а со-
событий А, В и С, можно переписать еще и такх):
А так как наше рассуждение не зависит от того, какое из рассмат-
рассматриваемых трех событий обозначено через А, какое — через В и ка-
какое— через С, то аналогично
\w\ _ A \w\ __ В
2 ~Т И 2 ~~ с
откуда и следует, что
(
а~ Ъ ~ с \ 2
Заметим еще, что (в системе единиц CGS) интервалы времени а, Ь и с
измеряются в сек, а скорости А, В и С — в см/сск, откуда вытекает, что от-
А В С
ношения —, —, — измеряются в см/сек2, в полном соответствии с тем,
что эти отношения выражают ускорение. Другими словами: поскольку стороны
!) Заметим, что если c—AB=dAR—н а п_р а в л е н н а я (т. е. взятая со
знаком + или —) длина стороны АВ, а С = 6сАсв—направленный
ш С
угол треугольника, то -^- = -=-.

§ 8]
ОПИСАННЫЙ И ВПИСАННЫЙ ЦИКЛЫ ТРЕУГОЛЬНИКА
119
треугольника ABC имеют размерность t времени, а углы—размерность
l/t скорости, то отношения углов к противолежащим им сторонам имеют
размерность lit'1 ускорения. А так как площадь 5 треугольника имеет
в геометрии Галилея размерность It (смсск) пространственно-временного
интервала (ср. выше, стр 60), то отношение
abc
имеет размерность (U):t3 — l/t2 ускорения (ср. формулу A5а)), а отношение
2А ВС
— размерность (lJtK:lt = P/t* квадрата ускорения (ср. формулу A6а)).
Рассмотрим теперь окружность Slt проходящую через середины
А±, В1 и С, сторон ВС, СА и АВ (евклидова!) треугольника ABC
(рис. 96, а) и цикл Zlt проходящий через середины А1г В± и Cj
а)
сторон (галилсева) треугольника ABC (рис. 96, б). Так как окруж-
окружность 51! и цикл Z1 описаны вокруг треугольника А1В1С1 со сторонами
/_ A1C1B1 = С, /_ С1В1А1 - В I треугольника, гомотетичного ABC
С центром гомотетии в точке М пересечения медиан треугольника

120 ОКРУЖНОСТИ И ЦИКЛЫ [ГЛ. II
ABC и коэффициентом гомотетии „-) , то радиус R± этой окруж-
окружности (цикла) равен
где R— радиус описанной окружности (цикла); поэтому в геометрии
Галилея /?]=-о-, где г — радиус вписанного цикла (ср. формулу A7),
стр. 115).
Окружность S1 геометрии Евклида проходит также и через
основания Р, Q и R высот АР, BQ и CR треугольника ABC, в силу чего
ее можно назвать окружностью шести точек1) треугольника ABC.
В самом деле, поскольку средняя линия А1В1 треугольника ABC
делит высоту CR треугольника пополам, то точки С и R симмет-
симметричны относительно прямой Аф^ Отсюда следует, что
/_ A1RB1 = /_ АСВ; B0)
поэтому точка R принадлежит St, ибо угол ^/ А1С1В1, вписанный
в S± и опирающийся на хорду АХВХ, тоже равен /_ АСВ (рис. 96, аJ).
[Аналогично доказывается и то, что точки Q и Р принадлежат Sv]
Но легко видеть, что проведенное здесь «евклидово» рассуждение
полностью сохраняет силу и для геометрии Галилея, в которой тоже
треугольники B1RA1 и В1САЪ «симметричные» друг другу относи-
относительно прямой Л1В1(ср. ниже, стр. 146), равны между собой, и, значит,
равенство B0), из которого вытекает, что точка R принадлежит Su
полностью остается в силе. [Здесь можно и не ссылаться на свойства
симметрии относительно прямой: так как очевидно (см. рис. 96, б),
что BlC=B1R и CA1 = A1R, т. е. треугольники BjCR и A±CR
равнобедренные, то
откуда (так же как и в евклидовом случае) и вытекает, что точка R
принадлежит циклу Zr] Цикл Zx называется циклом, шести точек
треугольника ABC.
1) Можно показать, что окружность St проходит также и через три точки,
делящие пополам отрезки высот треугольника от точки их пересечения до
вершин, в силу чего эту окружность обычно называют окружностью девяти
точек треугольника (см., например, § 29 книги Перепелкина [5] или
задачу 51а) книги Я г лома [9]).
2) Для того чтобы сделать все рассуждения независимыми от чертежа,
здесь (и далее!) следует воспользоваться понятием направленных)!, е.
взятых со знаком + или —) углов (ср. принадлежащие Д. И. Перепелкину
решения задач к книге Адам ара [7], стр. 488—489).

§ 8] описанный и вписанный циклы треугольника 121
В евклидовой геометрии имеет место замечательная теорема,
в силу которой окружность Sx шести точек (или девяти точек) тре-
треугольника ABC касается вписанной окружности s этого треугольника
и трех его вневписанных окружностей sa, sb и sc (рис. 97, а). Эта теорема
также переносится в геометрию Галилея: цикл Zx шести точек тре-
треугольника ABC касается вписанного цикла z (рис. 97, б). Отсюда
видно, насколько далеко заходит аналогия между геометрией Евклида
и геометрией Галилея!
Вот доказательство сформулированной теоремы, которое мы будем одно-
одновременно вести и для геометрии Евклида и для геометрии Галилея (ср. также
ниже, стр. 154—157); при этом в одном месте нам придется сослаться на резуль-
результаты нижеследующего § 9. Пусть СгТ — касательная к окружности шести то-
точек 5х(или к циклу шести точек Zx) в середине С1 стороны АВ (рис. 98, а, б).
Так как
?АС1Т = В—А.
Точки касания окружности s (цикла г) со сторонами АВ, ВС и СА
треугольника ABC мы обозначим через F, D и Е; точки касания окружности
sc с этими же сторонами — через Flt Dx и ?х. Проведем через вершину С
треугольника диаметр CWX окружностей s и sc, соответственно диаметр CR
цикла г1); здесь W и R—точки стороны АВ треугольника, К—точка на
продолжении CW за точку W. Из точек W и R проведем касательные WK,
WKi к окружностям s, sc, соответственно касательную RK к циклу г.
В силу теоремы о касательных к окружности и к циклу, проведенных из
одной точки,
WF и WK1 = WF1; FR = RK.
[Здесь в первых двух равенствах речь идет о совпадении «евклидовых длин»
Двух отрезков, а в третьем—о совпадении (положительных или неположи-
неположительных—ср. подстрочное примечание на стр. 103) «галилеевых длин» отрезков.]
Далее,-в евклидовом случае (рис. 98, а; напоминаем, что WC—диаметр
окружностей s и sc)
? AWK=18O°—2ZfiWC=180°—2(l80° — В
= 2B+C— 180° = 2B+C—(А + В+С) = В — А,
откуда вытекает, что KWKi — это одна прямая, параллельная СгТ.
Совсем по-другому доказывается аналогичное утверждение в галилеевом
случае. Здесь можно воспользоваться тем, что AR = AC = b и AF=CB = a,
!) Таким образом, в последующем рассуждении неожиданным образом
сходную роль играют биссектриса CW евклидова треугольника ABC и
высота CR треугольника ABC плоскости Галилея.

122
ОКРУЖНОСТИ II ЦИКЛЫ
[гл. И

§ 8]
ОПИСАННЫЙ И ВПИСАННЫЙ ЦИКЛЫ ТРЕУГОТЬНИКА
123

124 окружности и циклы [гл. п
_b-a 1 (Ъ а\_\ 9А,
~ AR ~ 4 \R~RJ~4 ^а~1 Л>
такчто FR = RK = b —аи, следовательно, FK. = FR + RK = 2(b— а) (рис. 98, б).
Поэтому хорде FK цикла г радиуса г отвечают вписанные углы величины
FK_2(b-a)_b-a
Чг~ Чг
(см. определение (За) радиуса цикла и формулы A7), A4)), а значит,
Таким образом, имеем
/.KRB = Z.KFR+IRKF = B — A (= /_АСХТ),
откуда и вытекает, что RK\fi\T¦
Проведем, наконец, прямую СХК и обозначим через L вторую точку пе-
пересечения этой прямой с вписанной окружностью s, соответственно с вписан-
вписанным циклом г; проведем также прямую СхКх и вторую точку пересечения
этой прямой с вневписанной окружностью sc обозначим через Lv Мы утверж-
утверждаем, что точка L принадлежит окружности Sx, соответственно циклу Zx;
точка Lx также принадлежит окружности St (более того, мы скоро убедимся
в том, что s и Sj, соответственно г и Zx касаются друг друга в точке L,
asc и S касаются друг друга в точке Z,x).
По теореме о секущей и касательной, проведенным к окружности s,
соответственно sc, из одной точки С1? имеем
CtK-CjL^CJ* B1а)
ClKvCiLl = C1F\m B16)
В силу аналогичной теоремы геометрии Галилея (см. ниже, стр. 134) равенство
B1а) сохраняет силу и в условиях рис. 98, б. Далее нам опять придется
вести доказательство для геометрии Евклида и для геометрии Галилея раз-
раздельно, причем во втором случае оно оказывается значительно проще.
Из равенств AF=a, ACl = -^- = -~- и AR = Ь (рис. 98, б), очевидно, вытекает
„_ а-\-Ъ Ь—а а-\-Ь Ь^а
FC1=-± а = —2~ и CiR = b ^— = ~y~ ;
поэтому равенство B1а) равносильно соотношению
CiKCiL^CiRt, B2)
из которого вытекает, что цикл Z, описанный вокруг треугольника KLR
(он изображен «мелким» пунктиром на рис. 98, б), касается в точке R прямой
АВ. Отсюда следует, что
= B — A
(вписанный в цикл угол равен углу между касательной и хордой); но, по-
поскольку ^_АС1Т==В — А, последнее равенство можно переписать так:
Это равенство означает, что точка L принадлежит циклу Zx (действительно,
угол /_ RLCX равен углу {_ ACjT между хордой АСг цикла Zx и касательной
С]Т к нему, а следовательно, угол /_ RLCy вписанный).
По существу, очень близки к проведенным рассуждения, касающиеся
рис. 98, а; однако они требуют несколько больших усилий. Обозначим

§ 8] ОПИСАННЫЙ И ВПИСАННЫЙ ЦИКЛЫ ТРЕУГОЛЬНИКА 125
основание опущенной из вершины С высоты треугольника ABC через R и
докажем, что
C1K-C1L = CXWC1R B2а)
и
C1/C1C1Z.1 = C1U7C1/?. B26)
[Заметьте, что роль двух точек W и R рис. 98, а играет одна точка R
рис. 98, б!] Длины сторон треугольника ABC обозначим, как всегда через
a, b и с. Так как
BF = BD и BD + BF = (a—CD) + (c—AF) = a + c— (
то BF = , а следовательно,
Cl/"~" 2 ~Т~
С другой стороны,
и
СЕХ + CDX = (b + Л ?х) + (а + SDj) =
откуда вытекает, что
и, значит,
Таким образом, произведения CxK-CtL ( = ClF2) к СуКх-С^ ( = C1/7f) равны
между собой, в силу чего достаточно доказать одно из равенств B2а) и B26),
скажем, равенство B2а).
Так как
=c и
с и
(ведь CW — биссектриса угла С треугольника АВС\), то
c+fc
и, значит,
™/_с _а (Ь-а)с
Несколько труднее вычислить длину х отрезка CrR. Так как

126 ОКРУЖНОСТИ И ЦИКЛЫ [ГЛ. II
то
откуда получаем
т. е.
и, следовательно,
Таким образом,
CWCR •
что и требовалось доказать.
Теперь заметим, что из равенств B2а) и B26) вытекает существование
окружностей S, соответственно Sx, проходящих через точки К, L, W и R,
соответственно Ki, Llt W и R (эти окружности изображены на рис. 98, а
«мелким» пунктиром). Из существования окружности S .следует, что
^ /?ZJC= 180° — ^/С№/? = 180 —?ТСЛВ=?ТС1А,
т. е. угол ,/ RLCi равен углу между хордой i?C\ окружности S! и касатель-
ной СХТ к этой окружности. Значит, этот угол является вписанным для
окружности Su т. е. точка L принадлежит окружности S,. Точно так же из
существования окружности Sx выводится, что окружности Sj принадлежит и
точка Lj.
Теперь мы уже находимся у самого конца нашего пути: осталось только
доказать, что пересекающиеся в точке L окружности s и S\, соответственно
циклы 2 и Zlt на самом деле касаются друг друга в этой точке и что окруж-
окружности sc и Sj касаются друг друга в точке Ц. Но это немедленно следует
из того, что касательные K.W и С,Т (соответственно KR и СХТ) окружностей
s и St (циклов г и Zt) в концах К и С\ хорд LK и LCX параллельны. В са-
самом деле, поскольку касательные к этим окружностям (циклам) во втором
конце L тех же хорд образуют с этими хордами те же самые углы, что и
касательные в точках К и Сх, то касательные к ним в точке L должны
совпасть, т. е. S, касается s (соответственно, Zt касается г) в точке L.
Точно так же из параллельности касательных K\W и С\Т к окружностям
в sc и St в точках К\ и Сл вытекает, что эти дне окружности касаются друг
друга в точке Z-j.
В заключение этого параграфа приведем второе доказательство
теоремы о том, что цикл шести точек треугольника плоскости Галилея каса-
касается вписанного цикла; это доказательство не переносится так непосредственно,
как первое в геометрию Евклида, однако оно несколько проще изложенного
выше и не апеллирует к содержанию последующих параграфов настоящей
книги. Найдем, прежде всего, «центр подобия» описанного цикла Z и вписан-
вписанного цикла г треугольника ABC, т. е. такую точку Q, что гомотетия с центром Q
и коэффициентом 4 (равным отношению радиусов циклов г и Z; см. формулу A7))
переводит цикл Z в цикл г Пусть прямая 1\\АВ касается цикла Z в точке F'\
через F мы, как и ранее, обозначим точку соприкосновения цикла г со сто-

ОПИСАННЫЙ II ВПИСАННЫЙ ЦИКЛЫ ТРЕУГОЛЬНИКА
127
роной АВ треугольника ABC (рис. 99). Так как 1\\АВ, то проходящий через
точку F' диаметр d цикла Z делит пополам хорду А В (т. е. проходит через
середину Сх этой хорды)- Обозначим теперь через Q такую точку прямой FF',
что
QF = 4QF', т. е. FQ = ^FF'.
Ясно, что гомотетия с центром Q и коэффициентом 4 как раз и переводит
касающийся прямой / в точке F' цикл Z в касающийся прямой АВ в точке F
X
Рис. 99.
цикл г, радиус которого в 4 раза больше радиуса цикла Z. При этом, так
как (ср. выше, стр. 113)
FB — Ъ и AR = b,
где /? есть основание «высоты» СЯ треугольника ABC, то /7С1 = С1/? и
= f Ci + ~ CtC = F
о
где М — есть точка пересечения медиан треугольника ABC. Поэтому прохо-
проходящая через Q особая прямая содержит точку М пересечения медиан тре-
треугольника ABC.
Итак, цикл г переводится в цикл Z гомотетией yt с центром Q и коэффи-
коэффициентом —; в свою очередь цикл Z переводится в цикл Ъх гомотетией у2

128
ОКРУЖНОСТИ И ЦИКЛЫ
[гл. и
с центром М и коэффициентом ^ (ибо последняя гомотетия переводит
треугольник ABC в треугольник Л1б1С1, вокруг которого описан цикл Zx).
Отсюда следует, что цикл г может быть переведен в цикл Zx гомотетией у
с коэффициентом тг; что же касается центра L гомотетии Yi то °н при-
принадлежит (особой) прямой QM и удален от точки М на такое расстояние LM,
что1)
В самом деле, точка L принадлежит прямой QM, ибо QM—«неподвижная
прямая» гомотетии Yi являющейся «произведением» гомотетии уг с центром Q
Рис. 100.
и коэффициентом — и гомотетии у2 с центром М и коэффициентом ——
(ведь обе эти гомотетии оставляют прямую QM на месте), а все неподвижные
прямые гомотетии у проходят через ее центр L. Равенство же LM=— MQ
о
вытекает из того, что определяемая им точка L есть «неподвижная точка»
преобразования у; действительно, ^ переводит L в такую точку V луча QM,
что QL' = j-QL, т. е.
МV = MQ—L'Q = 3LM —~ LQ = ЗШ —j (LM + MQ) =
=3IM— -^ LQ = iLM — -1 DШ) =
(рис. 99), а гомотетия у2 переводит U обратно в L.
Докажем теперь, что найденная точка L принадлежит, циклу Zx; отсюда
будет следовать, что цикл г, переводимый в Zx гомотетией с центром L,
касается Zx в этой точке (ср. рис. 100, а—г, на которых изображены два
Ср. § 1 гл. I второй части книги Я г лом а [9].

§ 8] ОПИСАННЫЙ II ВПИСАННЫЙ ЦИКЛЫ ТРЕУГОЛЬНИКА 129
цикла Z и Z' и их центр гомотетии Р). Очевидно, нам достаточно пока-
достаточно показать, что
l. B3)
Но /_RBiC1 вычислить легко: из рассмотрения треугольника RBiC1 следует,
что ?RB1C1 = ?B1C1R—/.B1RC1 = B— ^В^СХ\ с другой стороны, ZBi^ci =
= Z.B1A1Cl = A (как опирающиеся на одну хорду вписанные углы цикла Zx);
поэтому
-В —А.
Несколько сложнее подсчитывается величина ,/CjZ,/?. Пожалуй, короче
всего здесь рассуждать так: обозначим высоту F'C1 (равнобедренного!) тре-
треугольника ABF' через И, а высоту CR треугольника ABC через h (разумеет-
(разумеется, Н и h — это «особые» длины; H=bF,c , h=6cri); точку пересечения осо-
особой прямой QM с основанием АВ треугольника обозначим через N. Ясно,
4 1 4 1
H MN h б QMH
4 1 4 1
что QN = -^- H, MN = -Th; таким образом, QM—-7r-H—=-h, а значит,
о о о о
Но так как ?F''АСх = -^~, /_CAB = A и /_СВА=В, то (здесь достаточно
с С
вспомнить определение величины галилеева угла!) //=-=- •-к- и h = bA=aB;
таким образом.
сС—2ЬА — 2аВ _ (а + Ь) (А + В) — 2ЬА—2аВ
__ аА+ЬВ — ЬА — дВ _ (Ъ—а} (В — А)
"-" 9 ' "" 9
А теперь, вычислив величины углов /_NCXL и /_LRN:
с
(Ь-а)(В-А)шЬ-а 2 /D
~ 9 •~Т~'~Т(а~
получаем
ZC^R = ?NCXL + 1/LRN = B-A (=
— этим и завершается доказательстве!
Наконец, сформулируем теорему, двойственную теореме о цикле
шести точек; она гласит: цикл, вписанный в треугольник, образованный бис-
биссектрисами ах, fcj, ct треугольника ABC (этот треугольник двойствен тре-
5 И. М. Яглом

130
ОКРУЖНОСТИ И ЦИКЛЫ
[гл. и
угольнику А1В1С1, вершинами которого являются середины сторон треуголь-
треугольника ABC), касается также трех прямых р, q, r, проходящих через веричины
треугольника и параллельных противоположным сторонам; этот щикл шести
Рис. 101.
прямых» zx (радиус которого пдвос больше радиуса вписанного цикла г тре-
треугольника) касается описанного цикла Z треугольника (рис. 101).
Доказательство этой теоремы мы предоставим читателю.
§ 9. Степень точки относительно окружности или цикла; инверсии
Хорошо известно, что если проходящая через точку М прямая I
пересекает (евклидову) окружность S в точках А и В (рис. 102, а — в),
то произведение MA-MB зависит лишь от точки М и от окружнос-
окружности S, но не зависит от прямой I. Произведению МА-МВ принято
приписывать определенный знак, т. е. считать отрезки МА и
MB направленными: произведение МА-МВ считается поло-
положительным, если направления отрезков МА и MB (от М к А,

§ 9]
ИНВЕРСИИ
131
соответственно от Ж к В) совпадают, и отрицательным в противном
случае. Взятое со знаком + или — произведение
МА-МВ
B4)
называется степенью точки Ж относительно окружности S; ясно,
что эта степень будет положительна, если точка Ж лежит вне
окружности S (рис. 102, а); равна пулю, если М принадлежит 5
S
(рис. 102, б); отрицательна, если Ж лежит внутри 5 (рис. 102, в).
Если точка Ж лежит вне S, то степень Ж относительно ? равна
квадрату длины МТ касательной, проверенной к окружности .S из
точки Ж (ибо за прямую / можно принять МТ; при этом обе точ-
точки А и В сольются в одну точку Т).
Если MQ—d, где Q —центр окружности S радиуса г, а прямая /
проходит через точку Q и пересекает 5 в точках Ао и Во, то дли-
длина одного из отрезков МА0 и МВ0 равна d-\-r, а длина второго
равна \d — г\. Для учета знака произведения МА-МВ достаточно,
очевидно, взять со своим знаком разность (d — г), т. е. степень
точки М относительно окружности S всегда равна
d2 — r2. B5)
Поэтому если координаты точек М и Q равны (д:0,
степень точки Ж относительно .S равна
А так как уравнение окружности 5 имеет вид
(х — af + (y — bf — r2=0
или
и (а, Ь), то
B6)
B6')
где р=—а, <7=—b, /=a2 + fc2 — г2 (см. формулы B) — Bа) из
§ 1, стр. 17), то степень точки М (х0, у0) относительно окружнос-
окружности S равна результату подстановки в правую часть уравнения
окружности (B6) или B6')) вместо х и у координат л:0, у0 точки М.
5*

132
ОКРУЖНОСТИ И ЦИКЛЫ
[гл. и
Из сказанного сразу следует, что множество точек, имеющих отно-
относительно данной окружности S с уравнением B6) одну и ту же
степень k, описывается уравнением
или
т. е. представляет собой окружность, концентрическую с данной
(впрочем, это сразу вытекает из B5)); множество всех точек, име-
имеющих одинаковые степени относительно окружности S с уравнени-
уравнением B6') и окружности Sx с уравнением
X2 +У2 + 2рхх + 2qxy +Л = 0, B6")
описывается уравнением
X2 -гУ2 + 2рх A <lqy +/ = X2 +у* + 2Plx + 2q,y +/t
или
т. е. представляет собой прямую линию г—радикальную ось
окружностей .S и 5Х (рис. ЮЗI). [Исключение составляет случай,
когда р=рг и q = qt (т. е. когда окружно-
окружности .S и .Sj являются концентрическими!):
в этом случае искомое множество во-
вообще не содержит ни одной точки
(является пустым).] Нетрудно также
!г
Рис. 103.
Рис. 104.
понять, что попарные радикальные оси гъ г2 и г12 трех окруж-
окружностей S, .Sj и S2 либо параллельны, либо пересекаются в одной
точке R— радикальном центре окружностей S, St и .S^
(рис. 104; в самом деле, если две радикальные оси пересекаются,
то точка R их пересечения имеет одинаковую степень относительно
J) Теорема о радикальной оси легко доказывается и без использования
уравнения окружности (см., например, § 81 книги Перепелкина [5]
или § 3 гл. II книги Я г лома [10]).

§ 9]
ИНВЕРСИИ
133
всех трех окружностей, т. е. принадлежит и третьей радикальной
оси).
Обратимся теперь к геометрии Галилея. Совершенно ясно, что
если / — произвольная (обыкновенная) прямая, проходящая через
точку Ж и пересекающая окружность^в точках А и В, то произ-
произведение МА-МВ зависит лишь от точки М и окружности S, но не
от прямой I: ведь для всех прохоцящих через М прямых расстоя-
расстояния МА и MB будут одними и теми же (рис. 105). Произведение
МА-МВ B4)
(в котором отрезки МА и MB считаются направленными, так
что это произведение может быть положительным или неположи-
неположительным) называется степенью точки М относительно окружности S.
У
М
а)
х 0
&
Рис. 105.
в)
Ясно, что степень точки М относительно окружности 5 положи-
положительна, если точка М лежит вне 5 (рис. 105, а); равна нулю, если
М принадлежит 5 (рис. 105, б); отрицательна, если М заключена
внутри 5 (рис. 105, в). При этом если d=MQ — расстояние от
точки М до центра Q окружности .S (это расстояние будет одним
и тем же для всех центров Q окружности S), a r = AQ=QB —
радиус S, который здесь нам удобно считать совпадающим по зна-
знаку с d, то один из двух отрезков МА и MB будет равен d-\-r,
а второй будет равен d — г, так что и в геометрии Галилея степень
точки М относительно окружности S равна
d2—r2.
B5)
Несколько сложнее проводятся соответствующие рассуждения
для цик лов. Пусть / и/j—две прямые, проходящие через точку Ж
и пересекающие цикл Z в точках А и В, соответственно А, и Вх
(рис. 106). Ясно, что если точка Ж принадлежит Z (рис. 106, б),
то МА-МВ = МА1-_МВ1=0. Если же M не принадлежит Z, то
/_ АВВХ = /_ АА1В1 и j/_ АгАВ = /_ Афф как вписанные углы цикла,
опирающиеся на одну дугу; поэтому треугольники МААХ и МВХВ

134
ОКРУЖНОСТИ и ЦИКЛЫ
[гл. п
будут иметь одинаковые углы1). А так как стороны треугольников
пропорциональны противоположным углам (см. формулы A3) § 4,
стр. 62), то
^Ш или MA.MB-MAl-МВъ
что и доказывает независимость произведения B4) от выбора пря-
прямой /. Это произведение называется степенью точки М относительно
цикла Z. Ясно, что степень М относительно Z будет положительна,
если точка М лежит вне Z (рис. 106,а; в этом случае степень
точки М относительно цикла Z равна также квадрату длины МТ
Рис. 106.
касательной, проведенной к Z из Ж,— для доказательства этого
достаточно принять за / прямую МТ); равна нулю, если М принад-
принадлежит Z (рис. 106, б); отрицательна, если М лежит внутри Z
(рис. 106, в). [Точка М называется внутренней по отношению
к циклу Z, если через нее не проходит ни одна не пересекающая Z
прямая, и внешней в противном случае; при этом из внешней
точки к циклу Z можно провести касательную, а из внутренней
нельзя.]
Если координаты точки М суть л:0 и у0, а окружность 5 пред-
представляет собой пару (особых) прямых х~хг и х = хг, то отрезки
МА и MB равны хх — х0 и х2 — х0; поэтому степень М относи-
относительно .S равна
(*1 — X0) (*2 — *„) = (Хо — Xj) (Хо — Х2).
А так как уравнение окружности .S имеет в этом случае вид
или
B7)
B7')
2) Эти треугольники будут «подобны 1-м обр-азом»—они переводятся один
в другой преобразованием подобия 1-го рода (см. текст, напечатанный мел-
мелким шрифтом на стр. 66).

§ 9] инверсии 1.35
где 2b -—(х1 \ Хо), с ~хух.,, то степень точки М относительно
окружности S равна результату подстановки в правую часть урав-
уравнения B7) или B7') окружности вместо х и у координат х0, у0
точки М.
С другой стороны, пусть цикл Z имеет уравнение
х2 -; 2Ьгх ; 2Ь-2у Ь с = 0 B8)
(т. е. уравнение B) из § 6, стр. 85, где коэффициент а при л-2
равен 1), а прямая /, проходящая через точку М(х0, у0),— уравнение
У-Уо -k(x-x0). B9)
Тогда координаты {х1} ух) и (х2, у2) точек А и В пересечения пря-
прямой / с циклом Z определяются из системы B8)—B9) двух уравне-
уравнений с двумя неизвестными. Но из уравнения B9) следует
подставляя это значение у в B8), получим
** -; 2 (/^ + klh) х ; [2b, (уп - kx0) + с] =0,
откуда по формулам Виста имеем
х1 ; Хо = — 2 {bx r kb,), хгхг — 2Ь2 (уп — kx0) + с.
Поэтому степень точки М(х0, у0) относительно цикла Z
МА ¦ MB = (хг — х„) ¦ (л-., — д-0) -= xl — {х1Т Хо) хп +- д;гА-2
равна
хъ + 2 (/>! f kb,) х0 -f 2b, {у0 — kxn) с -- xl - - 2Ьгх0 ^ 2b.2x0 ' - с;
другими словами, степень точки М относительно цикла Z равна ре-
результату подстановки в уравнение B8) цикла вместо х и у коорди-
координат х0, у0 точки М.
Из доказанного непосредственно следует, что множество точек,
имеющих относительно окружности B7') или цикла B8) одну и ту
же степень k, описывается уравнением
х- -f 2Ъх + с = k, т е.
соответственно
x2-[-2bix4-2b2y + c^k, т.е. х2 ±2b1x + 2b2y-]- (с — k) = 0,
т. е. представляет собой окружность, «концентрическую» с данной
(имеющую ту же линию центров; это, впрочем, сразу следует и
из B5)), или цикл, параллельный данному. Далее, нетрудно видеть,
что множество точек, имеющих равные степени относительно данных

136 окружности и циклы
двух окружностей S и S1 с уравнениями B7') и
[гл. и
l = 0 B7")
или относительно окружности S с уравнением B7') и цикла Z
с уравнением B8), или относительно двух циклов Z и Z, с уравне-
уравнениями B8) и
представляет собой (обыкновенную или особую]) прямую г; эту пря-
прямую естественно назвать радикальной осью двух окружностей
Ь)
(или окружности и цикла, или двух циклов). Ясно, что радикальной
осью двух (неконцентрических) окружностей B7') и B7") будет
особая прямая
т. е. х=.
(а радикальная ось концентрических окружностей не существует
представляет собой пустое множество точек); также и радикальной
осью двух (непараллельных) циклов Z и Zx одного радиуса (для
таких циклов в уравнениях B8) и B8') frj^^111)) будет особая
прямая
т. е. х=
(рис. 107, а; радикальная ось двух параллельных циклов не
существует). Во всех остальных случаях радикальной осью (если она
существует) будет служить обыкновенная прямая (рис. 107, б, в);
!) Поскольку уравнение B8) можно, очевидно, переписать в виде
У~— 2ь~х2~^х~~2Ь~' то Радиус г цикла B8) равен ~Ь2,

§ 9]
ИНВЕРСИИ
137
так, например, уравнение радикальной оси циклов B8) и B8')
разного радиуса имеет вид
х2 + 2Ьгх + 2Ъ.гу + с = х2 + 2Ь™х
или
Ясно, что если две линии 2 и 2Х— цикл и окружность или два
цикла — пересекаются в двух точках Р и Q, то радикальной осью 2
и 2г служит прямая PQ (ибо точки Р и Q имеют относительно 2
и относительно 2Х одну и ту же степень 0, а потому принадлежат
радикальной оси 2 и 2Х).
л;
Аналогия между учением об евклидовых окружностях и учением
о циклах и окружностях геометрии Галилея может быть еще про-
продолжена. Так, например, в точности как в случае евклидовой гео-
геометрии, показывается, что если какие-либо две из попарных ради-
радикальных осей гъ г2 и г12 трех линий 2, 2Х и 22, каждая из
которых является окружностью или циклом, пересекаются в точке R,
то через эту точку (имеющую, очевидно, одинаковую степень отно-
относительно всех трех линий!) проходит и третья радикальная ось
(рис. 108, а, б); эту точку R естественно назвать радикальным
центром трех линий 2, 2Х и 22 *).
!) В геометрию Галилея можно без особого труда перенести все понятия
и теоремы той части евклидовой теории окружностей, которая базируется на
понятии степени точки относительно окружности (см., например, гл. X книги
Перепелки на [5] или раздел А статьи Яг лома [31]). Также и все
дальнейшее содержание теории окружностей, связанное с понятиями степени
прямой относительно окружности и степени окружности относительно окруж-
окружности (см., например, разделы Б и В статьи Я г лом а [31]), может быть
перенесено в геометрию Галилея; ср. ниже, стр. 174-

138
ОКРУЖНОСТИ И ЦИКЛЫ
[гл. и
I
Нетрудно установить механический смысл степени точки относи-
относительно цикла. Рассмотрим равноускоренное движение материальной
точки по прямой о:
x = ^2-' 2M C0)
с ускорением w - 2а, начинающееся в момент t - 0 из точки х = 0
(см. формулу A') § 6, стр. 91), например, движение подброшенного
вертикально вверх камня, име-
имеющего ускорение w= — g, где
?•^9,8 м/сек2 — ускорение си-
силы тяжести (см. рис. 109, а, б).
Выберем инерцнальную систему
отсчета так, чтобы изображен-
изображенной на рис. 109, б прямой /
отвечало состояние покоя;
тогда эта прямая будет харак-
характеризовать определенный пункт
Л' - х0 прямой о («вертикали»).
Пусть точка Ж плоскости
Галилея характеризует этот
пункт прямой о и момент t = 0,
который мы условились считать моментом начала движения; при
этом отрезки МА и MB рис. 109, б будут характеризовать интервалы
времени между началом движении t 0 и моментом прохождения
движущейся точкой (камнем) пункта х - = д:0. Ясно, что эти интервалы
времени tx и /2 определяются из уравнения
at2-[ 2Ы = х0 или аB + 2Ы — х0 0,
из которого в силу формул Виста немедленно следует
п)
Таким образом, мы видим, что интересующее нас произведение
МА-МВ -t1-t2 зависит лишь от ускорения w( 2a) движущейся
точки и от величины х0 и не зависит от выбора ннерциальной
системы координат! Поэтому, если мы выберем иную систему
координат, скажем ту, в которой роль «постоянного пункта»
х — х0 рис. 109, а играет прямая /г рис. 109, б, то произведение
МА1-МВ1 (см. рис. 109, б) будет иметь то же значение ——,
что и раньше.
Обратимся теперь к учению об и н в с р с и и. Как известно,
инверсией с центром Q и степенью ?>0 (или инверсией,
задаваемой окружностью инверсии S с центром Q и радиу-
радиусом r=\ k) в евклидовой геометрии называют преобразование, сопо-

§ 9]
ИНВЕРСИЙ
139
ставляющее каждой отличной от Q точке А пгоскости такую точку А'
луча QA, что
QA-QA'=k C1)
(рис. ПО). Несколько по-другому инверсию можно описать следую-
следующим образом: точки окружности S инверсия оставляет на месте;
каждую внешнюю по отношению к S точку А она переводит
в точку А' пересечения диаметра QA окруж-
окружности S с хордой KL, соединяющей точки К AKF
прикосновения с окружностью S проведенных
к ней из точки А касательных; точку А'
она переводит обратно в А. Последнее сле-
следует из того, что прямоугольные треуголь-
треугольники QKA' и QAK с общим острым углом Q
подобны между собой, так как из их подобия
вытекает
|*=^ или
с ПО.
Для определения образа А' произвольной (но отличной от Q)
точки А при инверсии с окружностью инверсии .S можно также
провести через А всевозможные окружности s (и прямую I), пер-
перпендикулярные окружности S, другими словами, такие, что
Рис. 111.
касательные к S и к s в точках К и L их пересечения перпенди-
перпендикулярны (т. е. окружность 5 должна касаться радиусов QK и QL
окружности S, проходящих через точки пересечения S и s, a прямая /
должна проходить через точку Q). Все такие окружности s и пря-
прямая I пересекаются еще в одной точке А', которая и является
образом точки А при инверсии (рис. 111, а). Для обоснования
последнего утверждения (оно может служить новым определением

140
ОКРУЖНОСТИ И ЦИКЛЫ
[гл. и
инверсии!) достаточно воспользоваться понятием степени точки отно-
относительно окружности (в применении к точке Q и к любой из рас-
рассматриваемых окружностей s); из определения этого понятия следует,
что если А' —вторая точка пересечения прямой QA с окружностью s,
то
QA-QA'=QK2 ( = r* = k)
(ибо QK—касательная к окружности s\). Если точка А принадлежит S,
то все проходящие через точку А и перпендикулярные 5 окружно-
окружности s (и прямая /) касаются друг
друга в точке А; в этом случае естест-
естественно считать, что точка А' совпадает
A'(xVj с А. Такое описание инверсии очень близко
к описанию симметрии относи-
относительно прямой ж, при которой каждая
точка А плоскости переходит во вторую
точку А' пересечения всех проходящих
через А окружностей s (и прямой /), пер-
перпендикулярных m (рис. 111, б); исходя из
этой аналогии, инверсию с окружностью
инверсии .S часто называют симметрией
относительно окружности S.
Самым важным из свойств инверсии является следующее: инвер-
инверсия переводит каждую окружность плоскости (где к числу окружно-
окружностей мы причисляем также и прямые, рассматриваемые как «окруж-
«окружности бесконечно большого радиуса») снова в окружность (или
в прямую). Проще всего доказать это свойство аналитически.
Инверсия с центром в начале координат О@, 0) и степенью k
переводит точку А(х, у) в такую точку А'(х', у') или А' (кх, ку)
(ибо А' принадлежит лучу ОА, рис. 112), что
Рис. 112.
OA-OA' =
т. е.
Ух'
Отсюда вытекает, что "к = 3 ., и, значит,
kx kx'
х =¦
*'г+</
'*'
или
C2)
(Последнее следует из того, что А' переводится в А той же
инверсией!) Поэтому окружность (или прямую) s с уравнением
= 0 C3)

§ 9]
ИНВЕРСИИ
141
(уравнение B') из § 6, стр. 85) инверсия C2) переводит в линию
с уравнением
kx' .„,.%' . __
х'^+у'* ш 1х'г+у'
т. е. снова в окружность (или прямую)
а' (
' = 0
C3')
(здесь мы отбрасываем ненужные нам более штрихи при х и у), где
а' = с, b\ = kbt, b'2 = kb2, с' = k2a. C3a)
При этом, если в уравнении C3)
а) а = 0, с —0 (т. е. 5 — прямая, проходящая через О);
(т. е. 5 — прямая, не проходящая через О);
5—окружность, проходящая через О);
б) а = 0, сфО
с = 0 (т. е.
в)
г) афО, сфО (т. е. 5 —окружность, не проходящая через О);
то в уравнении C3')
а) с' = 0, с' = 0 (т. е. s' — прямая, проходящая через О);
б) а'фО, с' = 0 (т. е. s' — окружность, проходящая через О);
в) с' = 0, с'фО (т. е. s' — прямая, не проходящая через О);
г) а'фО, с'ФО (т. е. s' — окружность, не проходящая через О).
Это чисто аналитическое рассуждение можно заменить следую-
следующим геометрическим. Проходящая через центр Q инверсии прямая s,
Рис. 113.
очевидно, переходит при инверсии сама в себя: ведь каждую точку А
прямой 5 инверсия переводит в точку той же прямой. Пусть
теперь s — прямая, не проходящая через центр инверсии Q; М и А —
какие-то две точки этой прямой, М' и А' — их образы (рис. 113, а).
Из равенства
QA-QA' - QM-QM' ( = k)

142 окружности и циклы [гл. и
следует, что
QA _QM'
QM QA '
Поэтому треугольники QA'M' и QM'A' подобны, и, значит,
C4)
Закрепим теперь точки М и М', а точку А заставим пробегать
прямую s. При этом множество точек А' будет определяться усло-
условием C4); другими словами, эго множество s' будет характеризо-
характеризоваться условием постоянства угла QA'M', под которым виден из
точки А' отрезок QM'. Но это и означает, что множество s' точек А'
представляет собой окружность, проходящую через точки Q и М'.
Обратно, если точка А рис. 113, а будет пробегать проходящую
через центр Q инверсии окруокность s', то множество точек А,
являющихся образами точек А', будет характеризоваться тем же
равенством C4), из которого видно, что /_AMQ ^QA'M'- const;
следовательно, это множество точек s представляет собой прямую,
образующую с прямой QM угол /_QMA, равный вписанному углу
окружности s', опирающейся на хорду QM'1).
Пусть теперь s — окружность, не проходящая через центр Q
инверсии; I — проходящая через Q прямая, пересекающая s в точках
М и N; Л —еще одна точка окружности s; М', N' и Л' —образы
точек М, N и А при инверсии (рис. 113, б). Из равенств
QA-QA' =QMQM' ( = k) и QA-QA' = QN-QN' ( = k)
вытекает пропорциональность сторон треугольников QAM a QM'A't
QAN и QN'A':
QA _ QM' QA _ QN'
QM ~ QA7' П QN~~ QA7' '
а следовательно, и равенство углов этих треугольников:
/_QA'M' = /_AMQ\ /_QA'N' = /_ANQ.
А отсюда в свою очередь вытекает, что
/N'A'M' = ZQA'M' —/_QA'N' = /_AMQ — /_ANQ= /_MAN
(здесь мы используем теорему о внешнем угле треугольника). Та-
Таким образом, когда точка А пробегает окружность s, характеризую-
характеризующеюся постоянством вписанного угла /_MANX), опирающегося на
]) Для того чтобы сделать это рассуждение совсем строгим, надо в соот-
соответствии со сказанным н5 стр. 83—84 ввести в рассмотрение направлен-
направленные углы (см. подстрочное примечание '-) на стр. 120; ср. на рис. 113, а
прямую QA с изображенной тонким пунктиром прямой QAr).

§ 9]
ИНВЕРСИИ
143
хор ту MN, точка А' пробегает линию s', характеризующуюся по-
постоянством угла ^/Л/М'ЛТ', т. е. тоже окружность.
Наконец, сходные рассуждения показывают, чго инверсия обла-
обладает свойством конформности, т. е. сохраняет углы между
линиями. В самом деле, пусть линию Г инверсия с центром Q и
степенью k переводит в линию Г'; А и А'—соответствующие
друг другу при инверсии точки этих линий; В — близкая к А точка
Г
Г' I
в) \-
^^^M^JA^=
а. т' А> А . .
Рис. 114.
линии Г, переходящая при инверсии в точку В' линии Г' (рис. 114, а).
Так как при этом
= k), т. е.
QB
то треугольники QAB и QB'A' подобны, т. е. /_BAQ--/_QB'А'.
Если теперь точка В стремится к точке А, то прямая АВ стремится
к касательной AT линии Г в точке А, а прямая А'В'—к касатель-
касательной А'Т линии Г' в точке А' (см. рис. 114, гг). Поэтому в пределе
равенство /_BAQ=/_QB'А' переходит в равенство
/_TAQ=
— линии Г и Г' образуют в точках А и А' с прямой QA одина-
одинаковые (но противоположно направленные, см. рис. 113, а) углы.
Отсюда следует, что если две пересекающиеся в точке А линии Г
и Г\ инверсия переводит в пересекающиеся в точке А' линии Г' и
Fj и AT, АТЪ соответственно А'Т', А'Т\ — касательные к Г и к Гх
в точке А и касательные к Г' и к Г, в точке А' (рис. 114,6), то
/_ТАТХ ?Г\А'Г.
Но последнее равенство и означает, что угол между Г и Гх равен
углу между Г' и Т\, поскольку под углом между двумя

144
ОКРУЖНОСТИ И ЦИКЛЫ
[гл. и
(гладкими, т. е. имеющими касательные) линиями Г и Гх как раз
и понимается угол между касательными к этим линиям, проведен-
проведенными в точке их пересечения. Из конформности инверсии, в част-
частности, вытекает, что инверсия переводит две касающиеся линии Г
и 1\ (линии, угол между которыми равен нулю; рис. 114, в) в касаю-
касающиеся линии Г" и Г'х (например, касающиеся окружности — в касаю-
касающиеся окружности).
После этого дивольно большого отступления, посвященного
некоторым фактам обычной геометрии Евклида, обратимся снова к
геометрии Галилея. Инверсия 1-го
рода с центром Q и степенью
k у 0 (инверсия с центром Q и
окружностью инверсии S
радиуса г = \ k х)) в геометрии Га-
Галилея естественно определяется как
преобразование, сопоставляющее
каждой удаленной от точки Q на не-
ненулевое расстояние точке А плоско-
плоскости такую точку А' луча QA, что
QA-QA'=k C1)
¦/
\
(рис. 115). С помощью окружности
.S инверсию 1-го рода можно опи-
описать следующим образом: для опре-
определения образа А' произвольной
точки А плоскости Галилея (удален-
(удаленной от Q на ненулевое расстояние)
достаточно провести через А всевоз-
всевозможные циклы z, в точках К и L
пересечения с окружностью S касаю-
щиеся «радиусов» QK и QL этой ок-
окружности^ также прямую /=фД то-
тоже в точках Ко и Lo пересечения с 5 хкасающуюся; лучей QK0 и QL0);
все такие циклы z (и прямая /) пересекаются еще в точке А', которая
и является образом точки А. Для доказательства совпадения этого
определения инверсии 1-го рода с исходным определением доста-
достаточно воспользоваться понятием степени точки относительно цикла
(в применении к точке Q м к любому из рассматриваемых циклов z);
из определения этого понятия следует, что если А'—вторая точка
а:
Рис. 115.
х) Центр Q инверсии обязательно должен являться центром окружности
инверсии 5. [В то время как евклидова инверсия полностью определяется
указанием окружности инверсии S, в геометрии Галилея для задания инвер-
инверсии 1-го рода надо указать не только окружность S, но и ее центр Q—ведь
5 имеет много центров, только один из которых играет роль центра ин-
инверсии!]

§ 9]
ИНВЕРСИИ
145
пересечения прямой QA с циклом z, то
QA-QA' = QK* ( =
k)
(ибо QK—касательная к циклу z). Если точка А принадлежит
окружности S, то все касающиеся в этой точке луча QA циклы z
касаются друг друга в точке А; в этом случае естественно счи-
считать, что точка А' совпадает с А. [Заметим также, что в точке К
пересечения цикла z и окружности .S линии S \\ z «перпендикуляр-
«перпендикулярны» (подобно тому как обстояло дело и в евклидовой геометрии);
однако здесь последнее свойство является бессодержательным, ибо
окружность .S плоскости Галилея «перпендикулярна» любой не
касающейся ее линии Г в точке пересечения .S и Г.]
U
f!
X
X
Рис. 116.
В геометрии Галилея инверсию 1-го рода с окружностью инвер-
инверсии 5 и центром Q называют также симметрией относительно окруж-
окружности S с центром Q. Другим аналогом евклидовой инверсии в гео-
геометрии Галилея является так называемая инверсия 2-го рода с
циклом инверсии Z или симметрия относительно цик-
цикла Z. Она определяется так: точки цикла Z инверсия 2-го рода
переводит в себя; любую внешнюю по отношению к Z точку А
плоскости она переводит во вторую точку А' пересечения проходя-
проходящего через А диаметра d цикла Z с хордой KL, соединяющей точки
прикосновения с циклом Z 'проведенных к нему из точки А каса-
касательных; точку А' инверсия 1-го рода переводит обратно в точку А
(рис. 116, а). Можно также определить инверсию 2-го рода плос-
плоскости Галилея с циклом инверсии Z и по-другому: каждую точку А
плоскости симметрия относительно цикла Z переводит в такую точ-
точку А' проходящей через А особой прямой А (диаметра цикла Z),
что отрезок АА' делится циклом Z пополам (т. е. переводит А в

146 ОКРУЖНОСТИ И ЦИКЛЫ [ГЛ. II
такую точку А' прямой d, что
АР - РА' или, точнее, бАР &ра',
где Р есть точка пересечения прямой d с циклом Z). В самом деле,
AK—AL, т. е. прямая d делит отрезок KL пополам; поэтому каса-
касательная t к циклу Z в точке Р пересечения цнкта Z с диаметром
d параллельна хорде KL (см. выше, стр. 102 и 104). Но если М
есть точка пересечения t и АК, то РМ = МЛ", как касательные к Z,
проведенные из одной точки М; другими словами, проходящая че-
через точку М особая прямая е равноудалена от й и от проходящей
через К особой прямой /. А отсюда в свою очеречь вытекает, что
если N есть точка пересечения особой прямой е с хордой KL, то
РА' -= MN = — А'А
(в силу теоремы о средней линии треугольника; все расстояния здесь
особые).
В последней интерпретации симметрия относительно цикла родст-
родственна симметрии относительно (обыкновенной) прямой / —
преобразованию, переводящему каждую точку А плоскости в такую
точку А' особой прямой d, проходящей через А, что отрезок АА'
делится прямой I пополам (рис. 116, б; ср. выше, стр. 56). И в
дальнейшем мы будем считать симметрию относительно прямой част-
частным случаем симметрии относительно цикла, подобно тому как (обык-
(обыкновенную) прямую иногда считают частным случаем цикла («цикл
бесконечно большого радиуса»).
Очевидно, что как инверсия 1-го рода (симметрия относительно
окружности), так и инверсия 1-го рода (симметрия относительно
цикла) каждую особую прямую р плоскости Галилея переводят
снова в особую прямую: инверсия 2-го рода оставляет прямую р
на месте, а инверсия 1-го рода переводит р в такую прямую //,
что произведение расстояний от центра Q инверсии до р и до р'
равно степени k инверсии. Поэтому окружность плоскости Галилея
(т. е. пару особых прямых!) каждая инверсия A-го или 2-го рода)
переводит снова в окружность. Гораздо более глубоким является
следующее свойство инверсии: каждая инверсия A-го или 2-го рода)
переводит любой цикл z (к числу которых мы причисляем здесь и
обыкновенные прямые, рассматриваемые как «циклы бесконечно
большого радиуса») снова в цикл (или прямую); к доказательству это-
этого свойства мы сейчас и перейдем.
Проще всего доказать это свойство инверсий аналитически.
Инверсия 1-го рот.а с центром в начале 0@, 0) координат
и степенью k переводит каждую точку А(х, у) плоскости в такую
точку А' (х', у') или А' (кх, %у) луча ОА, что
OA-OA'^k или х-Кх к

§ 9]
ИНВЕРСИИ
147
(рис. 117). Отсюда следует, что ^ —-т и, значит,
г' k
х =7'
х-
или
.А
х'
У-К
C5)
(ведь точку А' наша инверсия переводит в точку А). Поэтому цикл
(или прямую) z с уравнением
у -= ах2 4- 2Ьх 4- с A)
инверсия C5) переводит в линию z' с уравнением
~75" = G —7Т + 2?> — 4- С, "
х 2 л: 2 ' а; ' '
т.е. снова в цикл (или в прямую)
у = а'х2 + 2Ь'х + с', C6)
где
с'= ?-, &' =
Рис. 117.
' = kn. C6a)
В частности, если в уравнении A)
а) п = 0, с = 0 (т. е. z — прямая, проходящая через О);
б) « — 0, сфО (т. е. z — прямая, не проходящая через О);
в) афО, с= 0 (т. е. z — цикл, проходящий через О);
г) афО, с ФО (т. е. z — цикл, не проходящий через О),
то в уравнении C6)
а) а' = 0, с' = 0 (т. е. z'—прямая, проходящая через О);
б) а'фО, с' = 0 (т. е. z' — цикл, проходящий через О);
в) «' —0, с'ФО (т. е. z' — прямая, не проходящая через О);
г) а' фО, с'ФО (т. е. z'—цикл, не проходящий через О)
— см. рис. 118, ft, б; ср. выше, стр. 141.
С другой стороны, если цикл Z имеет уравнение
у ах2,
то симметрия относительно цикла Z (инверсия 2-го рода)
переводит точку А (х, у) плоскости Галилея в такую точку А' (х',у')
или А' (х, у') проходящей через точку А особой прямой д: = const,
что отрезок АА' делится пополам в точке пересечения Р(х, у^ или
Р(х, ах2) этой особой прямой с циклом Z (рис. 119, а). Отсюда
у' — ал-2= ах~—у,
т. е.
у' = ах2—у
= х'
или
у=2ах'2—у'
C7)

148
ОКРУЖНОСТИ И ЦИКЛЫ
[гл. II
(ведь и здесь точка А' переходит обратно в А). Поэтому цикл
(или прямую) z с уравнением A) инверсия 2-го рода C7) переводит
ъ\
а)
Рис. 119.
в линию z с уравнением
2ах'2—у' = ах'2 + 2Ъх + с',
т. е. снова в цикл или прямую
у^а'
где
о' = 2а — а,
(ЗС)
C66)
Таким образом, каждый цикл z кривизны р — 1а переводится сим-
симметрией относительно цикла Z кривизны Р = 2а в цикл z крлвизчы
р'-2Р-р C8)

§ 9]
ИНВЕРСИИ
149
(ибо p' = 2a'=4ot— 2а). В частности, циклы кривизны р = 2Р сим-
симметрия относительно цикла Z переводит в прямые линии (в «циклы
нулевой кривизны»), а прямые линии—в циклы кривизны 2Р
(рис. 119, бI).
Можно также вывести все эти результаты геометрически, не
обращаясь к уравнениям циклов. Для инверсии 1-го рода (сим-
(симметрии относительно окружности) соответствующие рассуждения
х D
fl**~M
Рис. 120.
почти дословно копируют те, которые мы проводили в евклидовом
случае (ср. рис. 120, а, б с рис. 113, а, б на стр. 141). Так, на-
например, здесь также из равенства
QA-QA'= QM-QM' ( = k)
следует, что стороны треугольников QAM и QM'A' рис. 120, а или
120,6 пропорциональны:
QA_ QjVT
QM ZZQA"
Отсюда в силу формул A3) из § 4 (стр. 62) вытекает пропорцио-
пропорциональность углов этих треугольников:
= /_MQA),
А так как в обозначениях рис. 120, а, б
/_MAQ—/_QMA = /_QM'A' —/_M'A'Q
l) Можно показать, что если симметрия относительно цикла Z переводит
цикл z в п р я м у ю г', то г' есть радикальная ось циклов Z и г;
доказательство этого мы предоставим читателю провести самостоятельно.

150
ОКРУЖНОСТИ И ЦИКЛЫ
[гл. и
то мы снова приходим к соотношению
/_QA'M' /_AMQ,
C4)
из которого вытекает, что изображенную на рис. 120, а прямую z
инверсия 1-го рода переводит в цикл z', а цикл г' —обратно впря-
впрямую z. Аналогично доказывается и то, что в случае, изображенном
на рис. 120,6, цикл z переходит в цикл z'.n наоборот. Наконец,
в точности как в евклидовом случае, показывается, что если инвер-
инверсия 1-го рода переводит (гладкую) линию Г в линию Г', то в со-
соответствующих друг другу при этой инверсии точках А и А эти
Рис. 121.
линии образуют с прямой QA одинаковые по величине (но обратные
по знаку!) углы, т. е. чю в обозначениях рис. 121, а
(ср с рис 114 а стр. 143). А отсюда уже выводится конформ-
конформность инверсии 1-го рода: если инверсия 1-го рода переводит пе-
пересекающиеся в точке А линии Г и 1\ в пересекающиеся в точке
А' линии Г и Г', и если AT, AT, и А'Г А'7\-соответственно ка-
касательные в точке А к Г и Г, и в точке А кТ и к 1\ (рис. 121, б),
то
В частности касающиеся между собой линии (например, касающиеся
циклы) инверсия 1-го рода переводит в касающиеся линии (в касаю-
касающиеся циклы).
Совсем по-другому приходится рассуждать в случае инверсии
2-го рода (симметрии относительно цикла Z). П)Сть симметрия
относительно цикла Z переводит точки А, М, N в точки А, М,

§ 9]
ИНВЕРСИИ
151
TV' и пусть Р, Q, R— точки пересечения особых прямых АА', ММ'
и NN' с циклом Z; точки пересечения прямых AM, A'M' n PQ с
особой прямой NN' обозначим через X, Y и U (рис. 122). Прямая
PQ, соединяющая середины Р и Q оснований АА' и ММ' трапеции
АА'М'М, делит, очевидно, пополам и параллельный основаниям
трапеций отрезок XV (ибо PQ есть медиана треугольника с осно-
основанием ММ' и боковыми сторонами М'А' и МА, если М'А'^МА;
если же М'А' || МА, то hPQ || ЛЖ || А'М').
Таким образом, имеем
N'Y = - N'U+ UY= (N'R— UR) + UY =
+ XU=- (XU+ UN) — 2UR = XN—
Разделив обе части равенства N'Y =
= XN—2UR на длину отрезка A'N'
(= AN - PR) и воспользовавшись тем, что
в силу определения углов в геометрии
Галилея
мы получаем
/_N' А' М' = /_MAN—2 /_QPR;
/_M'A'N'= 2/_QPR—/_MAN. ( '
Предположим теперь, что точки М п N
закреплены, а точка А пробегает прохо-
проходящий через М и N цикл (или прямую) Рис. 122.
z; в таком случае и точка А' будет
пробегать цикл (или прямую) z': ведь поскольку /MAN=a = const
(вписанный угол цикла z, опирающийся на хорду MN) и /_QPR =
= А = const (вписанный угол цикла Z, опирающийся на хорду QR),
У
0
\
\
\
\
\
\
А'
/z'
V\/z
\ г
.V
\
h
/
то и
/_M'A'N'- a' =2A — a = const.
Заметив затем, что кривизны р, р' и Р циклов z, z' н Z в силу
г/ г/' Д
определения D') из § 6 (стр. 90) равны 2 —, 2— и 2 —, где
s-= MN- M'N' QR, мы придем к соотношению C8). Наконец,
для того чтобы доказать конформность инверсии 2-го рода,
достаточно предположить, что в соотношении C9) точки А и N
закреплены, а точка М перемещается по какой-то линии у,

152
ОКРУЖНОСТИ И ЦИКЛЫ
[гл. и
стремясь к точке А (рис. 123,с); в пределе мы получим
/t'A'N' = 2 /TPR— /t AN,
где At, A't' и РТ—касательные в точках А, А' и Р соответственно
к линии у, к линии у' (в которую переводит наша инверсия линию у)
и к циклу Z. Отсюда вытекает, что если у и уг — две линии, пе-
пересекающиеся в точке Л, а у' и у'г — пересекающиеся в точке А'
У
х О
Рис. 123
линии, в которые инверсия 2-го рода переводит линии у и yv если,
далее, t, tt, соответственно t', t\ — касательные в точке А к у и к
yt и касательные в точке А' к у' и к у'} (см. рис. 123, б), то
'A'N' — /_ t\A'N' = B /_ TPR— /_ tAN) —
— B /_ TPR — /_ txAN) = /_ txAN — /_ tAN= /_ txAt
/_ t'A't[=
(на рис. 123, б прямые AN, A'N' и PR не изображены; ср. рис. 123, а).
В частности, касающиеся между собой линии (например, касающиеся
циклы) инверсия 2-го рода переводит в касающиеся линии (в каса-
касающиеся циклы).
Многочисленные применения, которые преобразования инверсии
имеют как в евклидовой геометрии1), так и в геометрии Галилея,
мы проиллюстрируем единственным простым примером. Пусть Бъ S.2,
S3 и Sit соответственно Zx, Z2, Z3 и Z4 — четыре окружности ев-
евклидовой плоскости или четыре цикла плоскости Галилея, причем
St и S3 (соответственно Zx и Z3) касаются S2 и St (Z2 и Z4);
относительно окружностей мы предположим еще, что Sx и S3, так же
J) Много примеров использования (евклидовой) инверсии собрано в гл. 2
книги Я г л о м а [10].

§ 9]
ИНВЕРСИИ
153
как S2 и Sit не имеют общих точек1) (рис. 124, а, б). Мы утвер-
утверждаем, что точки А, В, С и D касания этих четырех линий принад-
принадлежат одной окружности (соответственно одному циклу).
Для доказательства этого утверждения произведем инверсию
(соответственно, инверсию 1-го рода) с центром в точке А касания
а)
Рис. 124.
Sx и S2 (или Zx и Z2) и с какой угодно степенью k. Эта инверсия
переводит проходящие через центр инверсии окружности S1 и S.,
(циклы Zy и Z2) в прямые /j и /2; касающиеся окружности S3 и
•S4 (циклы Z3 и Z4) переходят при этом в касающиеся окружности
S'3 и ?4 (циклы Z'3 и Z4), причем S'3 (соответственно Z'3) касается /2,
a S^ (соответственно Z4) — 1г (ибо окружность S3 касалась S.2, a
окружность 54 касалась 5Х; соответственно цикл Z3 касался Z2,
а цикл Z4 касался Zj). Так как окружности St и S.2 (циклы Zx и
Z2) не имели отличных от А общих точек, а точка А не имеет
образа при инверсии, то прямые 1г и /2 не имеют общих точек,
т. е. /j || l2 (рис. 125, а, б). Проведем еще касательную t к S'3 и S'4
(к Z3' и Z4') в точке С их касания; точки касания окружностей S^
и 54 (циклов Z3 и Z4) с /2 и с /х естественно обозначить через В'
и /)'; точки пересечения прямой t с 1г л с 12 обозначим через М
и /V. Треугольники УИС/Э' и NCB' будут равнобедренными (ибо
!) Представляющееся не совсем естественным дополнительное условие,
требующее, чтобы рассматриваемые окружности не пересекались, связано с тем,
что, по существу, здесь рассматриваются направленные окружности (ср. выше,
стр. 89): если никакие две из наших окружностей не пересекаются, то им
можно приписать определенные направления с сохранением условия каса-
касания окружностей (касающиеся направленные окружности должны иметь
в точке соприкосновения одинаковое направлен11е); в противном случае
это не всегда можно сделать. На этом примере тоже видно, что геометрия
Галилея, циклы которой всегда являются направленными, проще геометрии
Евклида.

154
ОКРУЖНОСТИ И ЦИКЛЫ
[гл. II
касательные, проведенные к окружности пли циклу из одной точки
равны между собой); /_С'MD'' = /_С'NB' как соответственные углы,
образованные секущей t с параллельными прямыми 1Х и /., (легко
понять, что эгн углы равны н в геометрии Галилея). А отсюда вы-
вытекает, что /_D'С'М=- /_В'С'N—в геометрии Евклида эти углы
180 —а „ а
равны ^ » а в геометрии 1 алмлеп они равны -=-, гт,е а =
= /_СMD' = /_CNB'. Но из того, что /_D'C'M = /_B'C'N и
М
t Ч
х
Рис. 125.
в геометрии Евклида и в геометрии Галилея следует, что B'C'D'—
это одна прямая. Таким образом, наша инверсия с центром А пере-
переводит точки В, С и D в точки В', С" и D', принадлежащие одной
прямой, откуда вытекает, что исходные три точки В. С и D при-
принадлежат одной окружности (соответственно, одному циклу), про-
проходящей (проходящему) через центр А инверсии, т. е. что точки А,
В, С и D принадлежат одной окружности (одному циклу).
Вот еще один пример использования инверсии для доказательства теорем.
Покажем, что окружность шести (девяти) точек треугольника евклидовой
плоскости касается вписанной и трех вневписанных окружностей, а цикл шести
точек треугольника плоскости Галилея касается вписанного цикли треу-
треугольника (ср. выше, стр. 121). Пусть F—точка касания со стороной АВ тре-
треугольника ABC вписанной в этот треугольник окружности s, соответственно
вписанного цикла г; Fx—точка касания с АВ вневписанноп окружности sc;
Cl — середина стороны АВ (рис. 126, а, б; здесь и ниже сохранены обозначе-
обозначения стр. 119—126). Нетрудно убедиться, что в евклидовом случае CiF = C1Fl —
=—-—, где а, ?>, с—длины сторон треугольника (см. стр. 125); также и в

§ 9]
У
0
V
JV3
__——-
ИНВЕРСИИ
7 /
/ }
^__^/ а)
С /
^\
В)
Рис. 126.
\
155

156 ОКРУЖНОСТИ И ЦИКЛЫ [ГЛ. И
геометрии Галилея FC1= (см. стр. 124). Произведем теперь и н ве рс и ю
(инверсию 1-го рода) с центром в точке Ct и степенью k = ClFi
(=CxF\). Если проходящая через точку Сг прямая I пересекает окружность s
(цикл г) в точках М и N (а окружность sc—в точках Мх и N{), то в силу
определения степени точки относительно окружности (цикла)
поэтому рассматриваемая инверсия переводит точку М в точку N и наоборот
(а точку Мх—в точку Nx и наоборот). Отсюда следует, что окружности s
и sc (цикл г) наша инверсия переводит в себя. С другой стороны, окружность
шести точек ^.(цикл шести точек Zt) проходит через центр Сг инверсии и
через середины Bt и Лг сторон АС_ и ВС; поэтому инверсия переводит ок-
окружность Si (цикл Zi) в прямую А'^В^, проходящую через такие точки В'х и
А'х лучей CiB1 и С1Л1, что х)
Ь—а\'2 а _ф — а? п Л, k _(Ь—аJ Ъ (Ь—п)а
~2~ 2а И * 1-"СЙГ^~2 :У 26 '
т. е. что В^ и А'х—образы точек Bt и Ах при инверсии. Докажем теперь, что
прямая A'Ji^ касается окружностей s и sc (касается цикла г); отсюда и бу-
будет следовать, что окружность Si касается окружностей s и sc, соответственно,
что цикл Zx касается цикла г.
Точки пересечения прямой А'^В'^ со сторонами ВС и АС треугольника
обозначим через К и L. Из сравнения треугольников ЛХЛ^К и CiA^B^, BxB^L
и СхВ'А', очевидно, следует, что
BXL
А'А-ГА ГА'-Ь (Ь-аГ_е-ф-аР аBЬ-а) .
Я'Я Д'Г RC (fc~aJ a (Ь-аГ—а2 Ь(Ь-2а)
Таким образом, получаем
Ъ аBЬ-а) а. а Ь(Ь-2а) Ь
А^ = -а--~2Ь = Ь-У BlL==T-—2a~Y-a-
откуда вытекает, что
=~+[ь-^=Ь u LC = B1C-B1L=~(j~°) =
х) Здесь и далее длины а, Ь, с сторон треугольника считаются положи-
положительными; мы исходим также из рис. 126, а, б, где Ъ > 2а, так что все фигу-
фигурирующие ниже выражения (длины тех или иных отрезков) положительны
(для того чтобы сделать рассуждения полностью не зависящими от чертежа,
надо ввести в рассмотрение направленные отрезки).

§ 9] инверсии 157
Далее удобно вести доказательство по-разному для двух случаев, изобра-
изображенных на рис. 126, а и б. В евклидовом случае треугольники CAB и CKL
(где СА=СК = Ь и CB = CL = a) переходят один в другой при симметрии
относительно биссектрисы CW угла АСВ. Но ясно, что поскольку прямая CW
проходит через центры окружностей s и sc, то при рассматриваемой симмет-
симметрии обе эти окружности переходят в себя; поэтому прямая KL рис. 126, а
касается s и sc (ибо, скажем, прямую АВ и окружность s, касающиеся друг
друга, симметрия относительно CW переводит в прямую KL и окружность s,
которые также должны касаться).
В галилеевом случае можно воспользоваться тем, что прямые СВ и СА
касаются цикла г в таких точках О и ? и что CD — EC = c (см. формулу A3)
на стр. 113). Проведем теперь из точек К и L касательные КХ и LY к цик-
циклу г, отличные от KD и LE. Очевидно, что
XK = KD = CD—CK=c—b = a и LY = EL = EC—LC=c—a = b.
Но так как
откуда и следует, что точки X и Y совпадают (ибо эти точки не могут при-
принадлежать одной особой прямой — ведь каждая особая прямая является диа-
диаметром цикла и встречает цикл в единственной точке). Из доказанного
и вытекает, что прямая LK рис. 126, б касается в точке X = Y цикла z, чем
завершается доказательство.
В заключение остановимся еще на некоторых принципиальных
вопросах, связанных с преобразованием инверсии. Выше мы видели,
что евклидова инверсия переводит каждую точку А плоскости, от-
отличную от центра инверсии Q, в некоторую точку А'; при этом
центр Q инверсия не переводит ни в одну точку плоскости (ибо
равенство
QA-QA'=k C1)
при QA = 0 приводит к бессмысленному «равенству» QA' = оо). Таким
образом, строго говоря, инверсия не является преобразованием всей
(евклидовой) плоскости: на самом деле следует считать, что областью
определения («полем действия») преобразования инверсии является
плоскость с одной исключенной («выколотой») точкой — центром ин-
инверсии Q. Это обстоятельство сильно осложняет все связанные с
инверсией рассмотрения; выше мы просто закрывали глаза на все
эти трудности, отчего они, разумеется, вовсе не переставали су-
существовать. Так, например, мы не имеем права говорить, что пря-
прямая /, не проходящая через центр инверсии Q, переходит при ин-
инверсии в окружность s (ср. стр. 141—142, в частности, рис. 113, а):
ведь в точку Q окружности «не переходит никакая точка прямой /;
поэтому на самом деле следовало бы сказать, что прямая/переходит
в окружность s с выколотой точкой Q (рис. 127, а). Даже более
простое утверждение о том, что проходящая через Q прямая 1Х
переходит в себя, тоже является нестрогим: более правильно было

158
ОКРУЖНОСТИ II ЦИКЛЫ
[гл. и
бы сказать, что прямая 1Х с выколотой точкой Q переходит в себя
(рис. 127, б); точка же Q вообще никуда не переходит и при нс-
поль.юваиин инверсии ее следует считать «несуществующей». А если
в наших рассмотрениях используется несколько инверсий (довольно
частый случай в основанных на применении инверсии задачах!), то
геометрический образ, который должен быть положен в основу всех
а)
6)
Рис. 127.
построений, будет представлять собой совсем уж непривычную «ис-
«исколотую» плоскость — из плоскости надо будет исключить не только
центры используемых инверсий, но и точки, которые каким-нибудь
из применяемых преобразований переводятся в «несуществующие»
центры инверсий1).
Для устранения всех этих затруднений удобнее всего поступить
следующим образом. Вместо того чтобы исключать из плоскости
тс или иные точки, дополним плоскость еще одной (фиктивной,
т. е. с точки зрения элементарной геометрии несуществующей)
точкой Q — «бесконечно удаленной точкой» плоскости. Мы будем счи-
считать, что инверсия с центром Q переводит точку Q в бесконечно
удаленную точку Q, a Q переводит в Q; это хорошо согласуется
с равенством C1), в силу которого из QA=0 следует QA' = оо и
наоборот. Евклидова плоскость, дополненная одной бесконечно
удаленной точкой Q, и является «полем действия» инверсии —
каждую точку А «расширенной» плоскости (включая центр инвер-
инверсии Q и бесконечно удаленную точку Q) инверсия переводит в стро-
строго определенную точку А'; обратно, точку А' она переводит в
точку А. Так как инверсия обладает «круговым свойством» — окруж-
х) Так, например, приходится считать, что последовательность двух дей-
действующих друг за другом инверсий с центрами Q и Qt является преобразо-
преобразованием плоскости с тремя выколотыми точками: точкой Q (ведь первая ин-
инверсия не переводит Q ни в какую точку плоскости); точкой Q'y, которую
первая инверсия переводит в Qj (точку Qt не переводит ни в какую точку
плоскости вторая инверсия); точкой Q', которую вторая инверсия переводит
в (исключенную уже ранее, т. е., так сказать, «несуществующую») точку Q
(и в которую вторая инверсия переводит точку Q).

§ 91
HHBFPCHH
159
ности (точнее, обыкновенные окружности и «окружности бесконечно
большого радиуса», т. е. прямые) она переводит снова в окруж-
окружности,— то являющуюся полем действия инверсии плоскость с одной
бесконечно удаленной точкой Q намывают (евклидовой) круговой
плоскостью1). При этом, поскольку не проходящая через центр
инверсии Q прямая / переходит при инверсии и проходящую через
точку Q окружность S, а точка Q является образом бесконечно
Рис. 128.
удаленной точки Q, то естественно считать, что каждая прямая/
«проходит» через бесконечно удаленную точку Q; образом такой
дополненной точкой Q прямой будет полная окружность. Это согла-
соглашение снимает также и все затруднения, связанные с вопросом о
преобразовании при инверсии прямой 1Ъ проходящей через центр Q
этой инверсии: эта прямая переходит при инверсии сама в себя, при-
причем точка Q прямой 1г переходит в ее точку Q, а точка Q—-в
точку Q.
Наглядное представление круговой плоскости очень облегчает
стереографическая проекция — цен тральная проекция
плоскости л на сферу о из точки Q, принадлежащей сфере о; при
этом еще удобно считать, что сфера о* касается плоскости л в точ-
точке О, диаметрально противоположной точке Q (рис. 128). Ясно, что
каждой точке А плоскости л стереографическая проекция сопостав-
сопоставляет единственную точку А' сферы о; однако обратное соответствие
между точками сферы о и точками плоскости л не является полным,
ибо центру Q проекции не отвечает никакая точка плоскости.
Заметим теперь, что если мы будем двигаться по какой угодно
линии Г плоскости, удаляясь «в бесконечность», то образ А' точки А
линии Г будет стремиться к центру проекции Q; это обстоятельство
') См. по этому поводу Яглом п Атанасян [11], стр. 56—59.

160 ОКРУЖНОСТИ И ЦИКЛЫ [ГЛ. [I
делает уместным соглашение, по которому точке Q сферы а отве-
отвечает в силу стереографической проекции бесконечно удаленная точ-
точка Q, плоскости л. Таким образом, стереографическая проекция
осуществляет отображение круговой плоскости л на сферу о* и,
следовательно, сфера о* является естественным образом круговой
плоскости.
Стереографическая проекция обладает тем замечательным свой-
свойством, что она переводит окружности плоскости (к числу которых
здесь причисляются также и «окружности бесконечно большого ра-
радиуса»—прямые) в окружности сферы (т. е. в сечения сферы плоско-
плоскостями); при этом прямые переходят в окружности, проходящие через
точку Q—образ бесконечно удаленной точки Q. Последнее обстоятель-
обстоятельство проливает дополнительный свет на соглашение о том, что все
прямые («окружности» бесконечно большого радиуса») плоскости л
проходят через точку Q.
Это свойство стереографической проекции проще всего установить
аналитически. Пусть стереографическая проекция переводит точку
А (х, у) плоскости л (плоскости хОу) в точку А' (X, Y, Z) сферы а,
записываемой (в системе координат Oxyz) уравнением
— yY^T пли *2 ' У* + г2 —z =°. D0)
—сферы диаметра 1, касающейся плоскости хОу (совпадающей с плос-
плоскостью л) в начале координат О @, 0, 0); за центр проекции при-
примем точку Q @, 0, 1), диаметрально противоположную точке О
(см. тот же рис. 128). Так как (прямоугольные) треугольники QOA
и QA'O с общим углом Q подобны, то высоты ОА' и А'Р этих
треугольников пропорциональны их гипотенузам QA и QO. Но
Л'Р=1>2-, У2 и ОА' = У0Р°-\-А'Р2=УХ* +K2 +Z2;
далее
QO=\ и QA= VOA* + QO2 = Vx'2 +уг + 1.'
Таким образом, получаем
ИЛ" ~ Х
X'+Y* ~
или, наконец,
Заметим еще, что проекция луча РА' на плоскость л совпадает с лу-
лучом О А; поэтому Х- 'kx, Y=Xy. Подставив эти выражения в фор-
формулу D1), мы находим также
z = К(х2+П(х2+/-)=я

§ 9] ИНВЕРСИИ 161
А теперь из уравнения D0) сферы о, которому удовлетворяют коорди-
координаты X, Y, Z точки А', следует
2) = о, т. е. ь = #
Итак, окончательно получаем
поэтому
Но из формул D2)—D2а) вытекает, что окружность (или прямую) s
плоскости л с уравнением
а (х2 -\ у2) +- 2bj_x ^ 2Ь„у -.- с = 0 C3)
стереографическая проекция переводит в множество s' таких точек
А' (X, Y, Z) сферы о, что
т. е. в окружность, получающуюся в сечении сферы D0) плоскостью
az \-2b1x--2b2y [ c(\—z) = 0. D3)
При этом, если в уравнении C3) а = 0, т. е. рассматриваемая «окруж-
«окружность» s на самом деле является прямой линией, то и в уравне-
уравнении D3) а- 0, т. е. это уравнение имеет вид
2btx + 2b2y — cz-\-c = 0, D3а)
и, следовательно, соответствующая окружность s' содержит точку
Q@, 0, 1), принадлежащую как сфере D0), так и плоскости D3а).
Несколько более сложным является соответствующее.чисто геометрическое
рассуждение. Прежде всего совершенно ясно, что прямой I плоскости л в силу
стереографической проекции отвечает сечение сферы о плоскостью, проходящей
через центр проекции Q и через прямую /, т. е. проходящая через точку Q
окружность V сферы о (рис. 129; также каждой проходящей через точку Q
окружности V сферы о отвечает прямая / плоскости Я, являющаяся линией
пересечения плоскости окружности V с плоскостью я).
Пусть теперь s—о кружность плоскости п с центром К, А — произвольная
точка этой окружности. А'—отвечающая точке А точка сферы о (рис. 130).
Обозначим еще через Ki точку пересечения касательной плоскости т к сфере а
6 и. м. Яглом

162
ОКРУЖНОСТИ И ЦИКЛЫ
[гл. п
в точке А' с прямой QK (рис. 130, с; изображенный на рис. 130, б случай,
когда плоскость х параллельна прямой QK, мы рассмотрим отдельно).
Пусть л0 и лг — плоскости, параллельные плоскости я и проходящие через
точки Q и Ki соответственно; пусть, далее, Ко и А1~точки пересечения этих
Рис. 129.
плоскостей с прямыми
очевидно, следует
/си,
и QA. Ил подобия треугольников QKA и QKiAl
QKi " QK
т. е.
QK
QK
г.
Где г—радиус окружности s. С другой стороны, из того, что треугольник КХА' А±
подобен равнобедренному треугольнику KqA'Q (ведь КцА' и K0Q—касатель-
K0Q—касательные, проведенные к сфере о из одной точки Кп), вытекает, что треугольник К\А'Аг
также равнобедренный:
Таким образом, мы видим, что длина К\А' касательной, проведенной из точ-
точки К\ к сфере о, не зависит от выбора точки А окружности s; отсюда следует,
что и точка К\ будет одной и той же для всех точек А окружности s,
ибо при приближении точки Kt к о или удалении от о по прямой QK длина
проведенной из этой точки касательной к сфере меняется. Итак, отвечающие
точкам окружности s точки А' сферы о суть точки соприкосновения со сфе-
сферой о касательных, проведенных к ней из фиксированной точки К\- Ясно, что
множество всех таких точек представляет собой окружность, по которой сопри-
соприкасается со сферой а описанный вокруг о конус SfC с вершиной К\- Обращая
эти рассуждения, можно также показать, что (не проходящей через точку Q)
«малой окружностю s' сферы о, которую можно рассматривать как линию
соприкосновения со сферой о описанного вокруг нее конуса SfC с некоторой
вершиной Ki, отвечает в силу стереографической проекции окружность s плос-
плоскости я с центром в точке К пересечения прямой QKl с плоскостью я.
Пожалуй, еще проще случай, когда плоскость т параллельна прямой QK.
Обозначим точки пересечения прямой, проходящей через точку А' параллельно
KQ, с плоскостью лис фигурировавшей выше плоскостью я0 через В и С;
так как A'B"QK. то точка В принадлежит прямой КА (рис. 130, б). Из по-
подобия треугольника ВАА' и равнобедренного треугольника CQA' (ибо СА' и
CQ — касательные, проведенные к сфере о из одной точки С) следует, что
В А' = ВА; из подобия треугольника ABA' и треугольника AKQ вытекает,

§ 9]
ИНВЕРСИИ
163
что KQ=KA. Обратно, из равенства KQ = KA (не зависящего, очевидно, от
выбора точки А окружности s) вытекает, что если ВС — проходящая через
точку А' прямая, параллельная KQ, то СА'—CQ (см. рис. 130, б), т. е. С А' —
касательная к сфере о. Таким образом, в этом случае (характеризующем-
(характеризующемся равенством KQ = КА—г) множество s' точек А' представляет собой линию
а)
б)
Рис. 130.
соприкосновения сферы о с описанным вокруг о цилиндром Ц, образующие
которого параллельны QK; поэтому и здесь s'—окружность. Обращая эти рас-
рассуждения, можно точно так же показать, что стереографическая проекция пере-
переводит (не проходящую через точку Q) «большую окружность» s' сферы с, являю-
являющуюся линией соприкосновения сферы с описанным вокруг нее цилиндром Ц,
в окружность s плоскости Л с центром в такой точке К, что QK параллельно
образующим цилиндра, и радиусом r=QK-
6*

164 ОКРУЖНОСТИ И ЦИКЛЫ [ГЛ. II
Доказанное свойство стереографической проекции позволяет
использовать ее для представления «круговых преобразований» плос-
плоскости, т. е. преобразований, обладающих «круговым свойством», ана-
аналогичным свойству инверсий (см. стр. 158—159). Рассмотрим, например,
симметрию сферы о относительно горизонтальной диаметральной
Рис. 131.
плоскости б, т. е. преобразование, переводящее каждую точку Ах сферы
о в такую точку А[ сферы, что AXA[ J_ б (рис. 131). Ясно, что это
преобразование переводит окружности сферы снова в окружности;
поэтому порожденное им преобразование плоскости я— преобра-
преобразование, переводящее точку А плоскости л, отвечающую точке Alt
в точку Л', отвечающую точке А[, — будет обладать «круговым свойст-
свойством». Нетрудно выяснить, что представляет собой это преобразо-
преобразование плоскости я. Ясно, что точка А' принадлежит прямой ОА, являю-
являющейся линией пересечения плоскости п и проходящей через QO и АХА\
плоскости еХ л. Если Р1 и Р\ — проекции точек Ах и А[ на прямую QO,
то из подобия треугольников QA^ и QAO, QA'^ и QA'O, очевидно,
следует
(ибо QO=\, P'^^P^Ay и QP'y^Pfi). С другой стороны, поскольку
треугольник QA^O прямоугольный (ибо опирающийся на диаметр QO
сферы о угол QAXO прямой), то AlPf = QP1-P1O и, значит,
Таким образом, если точка А[ сферы о получается из точки А1 сим-
симметрией относительно плоскости б, то (отвечающая точке А\) точка А'
плоскости п получается из (отвечающей точке Аг) точки А инвер-
сией с центром О и степенью 1.
Представление инверсии в виде симметрии сферы о, на которую плоскость Л
отображена с помощью стереографической проекции, очень удобно для изуче-
изучения свойств инверсии; если (как иногда поступают) принять это представление
за определение инверсии, то как «круговое свойство» инверсии, так нее

§ 9]
ИНВЕРСИИ
165
конформность могут быть выведены из свойств стереографической проекции.
Стереографическая проекция очень полезна и для изучения свойств произ-
произвольных «круговых преобразований» — преобразований (круговой!) плоско-
плоскости л, переводящих каждую окружность или прямую линию снова в окруж-
окружность или прямую. Используя стереографическую проекцию, можно доказать
теорему: каждое круговое преобразование (круговой) плоскости л, отличное от
преобразований подобия, представляет собой инверсию, сопровождаемую еще,
быть может, преобразованием подобия. На доказательстве этой теоремы, иногда
называемой основной теоремой теории круговых преобразо-
преобразований, мы здесь не остановимся 1).
Перейдем теперь к геометрии Галилея. Здесь положение оказы-
оказывается еще более сложным, чем в случае евклидовой геометрии: ин-
инверсию 1-го рода с центром Q и какой угодно степенью k нельзя
X
считать преобразованием плоскости Галилея, поскольку существует
много точек, которые эта инверсия не переводит ни в какие точки
плоскости: таковы все точки, удаленные от точки Q на нулевое рас-
расстояние, т. е. все точки особой прямой q, проходящей через центр
инверсии Q. Это обстоятельство очень осложняет все связанные с ин-
инверсией 1-го рода рассуждения. Так, например, строго говоря, надо
считать, что эта инверсия, являющаяся преобразованием плоскости
Галилея с вырезанной из нее прямой q, переводит не проходящую
через центр инверсии Q (обыкновенную) прямую /, из которой исклю-
исключена точка L ее пересечения с прямой q, в цикл z, из которого
также исключена точка Q его пересечения с прямой q (рис. 132, а;
ср. с рис. 118, а на стр. 148). Аналогично этому проходящую через
точку Q прямую т с выколотой точкой Q рассматриваемая инверсия
переводит в ту же прямую с той же выколотой точкой; не проходя-
проходящий через точку Q цикл z, из которого исключена точка 7V его
пересечения с прямой q, — в цикл z', из которого также исключена
точка Р его пересечения с прямой q (ср. рис. 132, б с рис. 118, б).
См., например, Яглом [10], стр. 247—253.

166 ОКРУЖНОСТИ И ЦИКЛЫ [ГЛ. II
Еще сложнее будут выглядеть геометрические образы, с которыми
мы столкнемся в случае последовательного выполнения двух пли не-
нескольких инверсий.
После сказанного об евклидовой геометрии нам уже нетрудно
понять, как можно устранить возникшие затруднения. Дополним
плоскость Галилея «бесконечно удаленными точками» и условимся
считать, что в эти точки инверсия 1-го рода пе-
переводит точки прямой q; название «бесконечно
удаленные» хорошо согласуется с тем обстоя-
обстоятельством, что в силу соотношения
QA-QA' = k C1)
при приближении точки А к прямой q (при стрем-
стремлении к нулю расстояния QA) точка А' неограни-
неограниченно удаляется от точки Q (расстояние QA' не-
неограниченно растет). Поскольку все проходящие
через точку Q циклы (и прямые) наша инверсия
переводит в прямые, естественно считать, что
все (обыкновенные) прямые плоскости Галилея «проходят» через
бесконечно удаленную точку Q, в которую инверсия переводит
точку Q. Пусть, далее, цикл z пересекает прямую q в точке N,
где QN— п. Если центр инверсии Q совпадает с началом координат
О системы хОу (рис. 133), то цикл z описывается уравнением
у = ах2т2Ьх + с, A)
которому должна удовлетворять точка N@, п), т. е. уравнением A),
где с = я. Инверсия 1-го рода с центром О@, 0) и степенью k
переводит этот цикл z в цикл z' с уравнением
у =а'х2 + 2Ь'х + с', C6)
где
а = ~к—к
(см. формулы C6)—C6а), стр. 147), т. е. в цикл z' фиксированной
In
кривизны р'= —г- , а цикл z она переводит в z'. Поэтому уместно
И,
считать, что все циклы одной и той же кривизны р проходят через
определенную бесконечно удаленную точку Qo; при этом точку N
прямой q, удаленную от центра инверсии Q на расстояние ^qN— n,
инверсия степени k переводит в точку Q-zn -
Таким образом, галилееву плоскость оказывается удобным до-
дополнить множеством бесконечно удаленных точек, в которые пере-
переходят при инверсии 1-го рода с центром Q точки особой прямой q,
проходящей через Q; так как каждую особую прямую инверсия пере-
переводит снова в особую прямую, то можно говорить о «.бесконечно

§ 91
ИНВЕРСИИ
167
удаленной особой прямой». Точки этой прямой мы будем обозначать
через Qo, где р — произвольное (положительное или неположительное)
вещественное число; точку Qu можно обозначать также просто че-
через Q. При этом все циклы плоскости Галилея, имеющие кривизну р,
проходят через одну бесконечно удаленную точку, л именно, через
Точку Qf; в частности, «циклы кривизны 0», т. е. прямые, проходят
Рис. 134.
через точку Q0 = Q. Галилееву плоскость, расширенную введением
бесконечно учаленных точек йс, т. е. дополненную бесконечно уда-
удаленной особой прямой, естественно назвать циклической плос-
плоскостью Галилея; эта плоскость удобна в вопросах теории циклов.
Заметим, кстати, что инверсия 2-го рода — симметрия относительно
цикла Z кривизны Р — переводит цикл кривизны р в цикл кривизны
р' = 2Р — р (см. формулу C8), стр. 148); это означает, что бесконечно
удаленную точку Qo эта инверсия переводит в бесконечно удален-
удаленную точку ^2Р-р (в частности, точку Q,-2v 0Ha переводит в точку
О,- Ио, а точку Q — в точку ?1>р).
Наглядно представить себе цилиндрическую плоскость позволяет
стереографическая проекция — отображение точек плоско-
плоскости Галилея л на точки (кругового) цилиндра ?. Представим себе
круговой цилиндр ?, касающийся плоскости п вдоль особой прямой q,
и будем проектировать цилиндр ? на плоскость л из точки Q ци-
цилиндра ?, диаметрально противоположной какой-то точке О касания
цилиндра с плоскостью л и, следовательно, принадлежащей «верхней
образующей» о цилиндра (рис. 134). Каждой точке А плоскости л
наша стереографическая проекция сопоставляет единственную точку А'
цилиндра ?; однако обратное соответствие между точками цилиндра
и точками плоскости не является полным, так как точкам образую-
образующей о цилиндра ? не отвечают никакие точки плоскости л. По-
Поскольку при стремлении точки А' цилиндра ? к точке Q' образую-
образующей о образ А точки А' на плоскости л неограниченно удаляется
от прямой q, то можно условно считать, что точкам образующей о

168
ОКРУЖНОСТИ II ЦИКЛЫ
[гл. ц
отвечают в силу стереографической проекции «бесконечно удаленные
точки» плоскости Галилея. Так как каждая образующая цилиндра
переводится стереографической проекцией в особую прямую плос-
плоскости п, то можно сказать, что стереографическая проекция пере-
переводит цилиндр ? в плоскость я, дополненную одной «бесконечно
удаленной особой прямой» — образом образующей о цилиндра; таким
Рис. 135.
образом, стереографическая проекция устанавливает взаимно одно-
однозначное соответствие между точками цилиндра ? и точками цикли-
циклической плоскости Галилея п, в силу чего цилиндр ? является
хорошим образом циклической плоскости.
Стереографическая проекция плоскости п на цилиндр ?, переводит
окружности и циклы плоскости Галилея п в плоские сечения ци-
цилиндра ?. Проще всего доказать это свойство стереографической
проекции аналитически. Отнесем плоскость it к координатам х и у,
а пространство — к координатам х, у и z\ при этом условимся счи-
считать, что ось Оу совпадает с прямой q. Диаметр цилиндра Z, мы
примем равным 1; за центр проектирования примем точку Q@, 0, 1)
цилиндра, диаметрально противоположную точке О@, 0, 0) (рис. 135).
Уравнение
— 4-) = 1- или
— z = 0
D0')
окружности, получающейся в сечении цилиндра ? плоскостью xOz,
будет, очевидно, совпадать с уравнением цилиндра ?, поскольку
сечение цилиндра любой плоскостью у= const представляет собой
точно такую же окружность, как D0'). Пусть теперь стереографи-
стереографическая проекция сопоставляет точке А (х, у) плоскости п точку
А' (X, Y, Z) цилиндра ?; обозначим еще через В' (X, О, Z) точку
пересечения проходящей через точку А' образующей цилиндра с
плоскостью xOz, а через В(х, 0) — точку плоское!и п, отвечаю-

§ 9| инверсии 169
щую точке В' цилиндра (рис. 135). Из подобия прямоугольных тре-
треугольников QOB и QB'O с общим углом Q и опущенными на гипотену-
гипотенузы QB и QO высотами ОВ' и В'Р следует, что OR': PR' = QR: OQ,
или, так как OQ -- 1, РВ' X, QB = \ OB2 + OQ2 = \гх'1 + 1
/
и OB' y^PB'1^ OP2 j/.Y4 Z2(cp. выше. стр. 160),—что
x ~1
Отсюда мы заключаем, что
^¦ = х и Z=xX. DГ)
Теперь из уравнения D0') цилиндра, которому удовлетворяют коор-
координаты точки А' (К, Y, Z), без труда находим
Х2-\-х2Х2 — хХ=0 и, значит, Х=~—Х,
откуда также следует, что Z= хХ = х2/(х2-\-\). Наконец, поскольку
проекция луча Р±А' на плоскость it совпадает с лучом ОА и, значит,
X:Y= х:у, то Y = — • X — 2 .. . Таким образом, окончательно
получаем
Y = ^TT, Z = -^TT D2')
и, значит,
1-^ = ^+1 («'а,
Теперь ясно, что окружность или цикл
с = 0 B)
стереографическая проекция D2') переводит в сечение цилиндра D0')
плоскостью
az \-2b1x + 2b2y + c(\— z)=0. D3)
При этом, если в уравнении B) Ь2=-0, т. е. линия B) является
окружностью s (или особой прямой), то стереографическая про-
проекция переводит ее в сечение цилиндра ? плоскостью D3), где также
Ь2=0, т. е. плоскостью X, параллельной оси Оу (параллельной оси
цилиндра ?; см. рис. 136, а). Если же линия B) является циклом г
(или обыкновенной прямой; другими словами, если в уравнении B)
Ьг Ф 0), то стереографическая проекция сопоставляет этой линии

170
ОКРУЖНОСТИ И ЦИКЛЫ
[гл. и
сечение цилиндра t, плоскостью ц, не параллельной оси (рис. 136, б1)).
Всевозможным циклам фиксированной кривизны р, т. е. циклам,
6)
Рис. 136.
в уравнении B) которых можно положить Ь2= — 1 и я=р, отве-
отвечают сечения цилиндра ? плоскостями
пересекающими, очевидно, прямую о с уравнениями л: = 0, z=\
в точке /?@, -|-, 1 ), откуда следует, что эту точку R надо счи-
считать образом на цилиндре ? точки У, циклической плоскости Гали-
Галилея п, т. е. надо положить R Q'
= Q'. В частности, все прямые
') Линия пересечения цилиндра с такой плоскостью представляет собой
эллипс (см., например, п. 15 книги Я г лома и Ашкпнузе [56]).

§ 9]
ИНВЕРСИИ
171
плоскости Галилея — «циклы кривизны 0» — переходят в плоские
сечения цилиндра ?, проходящие через точку <?@, 0, 1)(e=QJ,).
Доказанное свойство стереографической проекции, отображающей
плоскость л на цилиндр ?, очень удобно для исследования с по-
помощью этой проекции «циклических преобразований» плоскости я,
т. е. таких преобразований (циклической1.) плоскости Галилея, ко-
которые переводят циклы плоскости (к числу которых здесь при-
причисляются также «циклы бесконечно большого радиуса» или «циклы
Рис. 137.
нулевой кривизны» — прямые) снова в циклы (или прямые). Рассмот-
Рассмотрим, в частности, какое преобразование плоскости отвечает в силу
стереографической проекции с и м м е т р и и цилиндра Z, относительно
горизонтальной диаметральной плоскости б, т. е. преобразованию,
переводящему каждую точку At цилиндра Z, в такую его точку
А[, что АгА[\_Ь (рис.137). Ясно, что эта симметрия переводит
плоские сечения цилиндра снова в плоские сечения цилиндра;
поэтому отвечающее ей преобразо-
преобразование плоскости л, — т. е. пре-
преобразование, переводящее точку А
плоскости л, соответствующую в
силу стереографической проекции
точке Аг цилиндра, в точку А', соот-
соответствующую точке А\ цилиндра,—
должно переводить циклы в циклы.
Поскольку ортогональная проек-
проекция обоих лучей QAX и QA[ на
плоскость jx совпадает с лучом ОА,
то точка А' принадлежит лучу О А. Далее, из сравнения рис. 137а,
изображающего сечение конструкции рис. 137 плоскостью xOz (точки
Вг и В\ рис. 137а суть точки пересечения проходящих через А1 и
Лх образующих цилиндра ? с плоскостью xOz, а В и В' — соответ-
В х
Рис. 137а.

172 окружности и циклы [гл. и
ствующие им в силу стереографической проекции точки плоскости jt)
с рис. 131 (стр. 164) следует, что
ОВОВ'= 1,
или, так как /4В||Оу и /4'В'||О_у (вспомним, что называется длиной
отрезка в геометрии Галилея!), что
ОА-ОА' = 1.
Поэтому преобразование, переводящее А в А', есть не что иное,
как инверсия 1-го рода с центром О и степенью 1
Рис. 138.
Рассмотрим теперь симметрию цилиндра ? относительно плоскости е,
параллельной плоскости xOz. Прежде всего, совершенно ясно, что
если Ах и А[—точки цилиндра ?, симметричные друг другу отно-
относительно плоскости xOz, то отвечающие им точки А и А' плоско-
плоскости л будут симметричны друг другу относительно оси Ох (рис.138,а);

§ 9]
(IHBFPCIIIi
173
таким образом, симметрии цилиндра относительно плоскости xOz
на плоскости п отвечает симметрия относительно прямой
Ох Пусть теперь точки А1 и А\ цилиндра Z, симметричны друг
другу относительно плоскости е с уравнением у = р, параллельной
плоскости xOz (рис. 138, б). Из сравнения формул D3) и B) (стр. 169),
следует, что сечению цилиндра t, плоскостью
У-9- О
0 или у = рх2-\-р
D4)
У-
отвечает линия
Р*2— У\ Р
плоскости jx, т. е. цикл Z кривизны 2р. Далее, если Вг есть точка
пересечения прямой AXA\ с плоскостью е, то тройка точек Аи В1
А\ сбразующей АХА'Х цилиндра Z, проектируется из центра проек-
проекции Q на плоскость jx в тройку точек А, В, А' прямой /4/4'||Оу,
причем, поскольку Аф^ - ВХЛХ, то и АВ = ВА'; таким образом,
отрезок АА' выделенной прямой плоскости jx делится пополам
точкой В пересечения этого отрезка с циклом D4). Таким образом,
симметрии относительно плоскости е отвечает инверсия 2-го
рода плоскости jx — симметрия относительно цикла Z.
Связь инверсии 1-го или 2-го рода на плоскости Галилея с симметрией
цилиндра ? относительно плоскости б или е очень удобна для изучения свойств
инверсии. Кроме того, подобное представление инверсий и «круговое свойство»
стереографической проекции плос-
плоскости Галилея на цилиндр позволя-
позволяют доказать следующую теорему,
которую можно назвать основ-
основной теоремой теории ци-
циклических преобразова-
преобразований: каждое циклическое преобра-
преобразование плоскости Галилея, от-
отличное от преобразования подобия,
представляет собой инверсию 1-го
или 1-го рода, сопровождаемую еще,
быть может, преобразованием по-
подобия. При этом под преобразова-
преобразованием подобия плоскости Галилея
с 1-м коэффициентом подобия k и
со 2-м коэффициентом подобия к
здесь понимается такое преобразо-
преобразование плоскости, переводящее
точки в точки и прямые в прямые, Рис. 139.
при котором все расстояния увели-
увеличиваются в k раз, а все углы увеличиваются в к раз, т. е. преобразование,
переводящее точки А и В в такие точки А' и В', а прямые а и Ъ в такие
прямые а' и Ь', что
А'В' йл-в- . Z (а1, Ь') да-ь-
с
АВ dAB
(a,
"аЬ
здесь числа k и к могут быть положительными или отрицательными. [Приме-
[Примером такого общего преобразования подобия может служить преобразование,

174
ОКРУЖНОСТИ II ЦИКЛЫ
[гл. и
получаемое в результате последовательного выполнения сжатия к точке О
(гомотетии) с коэффициентом k и сжатия к прямой Ох с коэффициентом к
(рис. 139).] На доказательстве этой основной теоремы те ори и цик-
циклических преобразований плоскости Галилея1) мы здесь не
остановимся.
Отметим еще в заключение, что принцип двойственности (см. § 5 гл. 1)
позволяет получить целый ряд новых результатов, двойственных тем, которые
были получены в этой главе. Так, например, понятию степени точки М
относительно цикла Z двойственно понятие степени прямой т относительно
цикла 2—произведения
?aLm-?bLm, B4а)
где а и b—касательные, проведенные к циклу Z из любой точки L прямой т
(рис. 140, а; произведение B4а) не зависит от выбора точки L прямой т.);
инверсии 1-го рода — осевая инверсия 1 го рода, т. е. преобразование, сопостав-
сопоставляющее каждой прямой с плоскости Л прямую с', проходящую через точку А
пересечения прямой с с фиксированной «осью инверсии» q и такую, что
= k, C1а)
где k—фиксированная «степень осевой инверсии» (рис. 140, б); инверсии 2-го
рода или симметрии относительно цикла Z — осевая инверсия 1-го рода или
осевая симметрия относительно цикла Z, переводящая каждую прямую а
плоскости в такую прямую а'\\а, что касательная t к циклу Z, параллельная
а и а', одинаково отстоит от прямых а и а' (рис. 140, в), и т. д. Мы не
У\
х О
X
а)
ft
станем развивать здесь всех этих построений, предоставив читателю сделать
это самостоятельно; отметим только, что соответствующая теория несравненно
проще той, к которой мы приходим в евклидовой геометрии при попытке рас-
рассматривать окружность не как множество точек, а как множество прямых2).
!) См. Макарова [28], ч. III.
2) См., например, § 5 гл. 11 книги Я г лома [10| или раздел Б статьи
Яглома [31]; по поводу соответствующих построений геометрии Галилея
см. Макарова [28], ч. III и Макарова [34].

ЗАКЛЮЧЕНИЕ
§ 10. Принцип относительности Эйнштейна
и преобразования Лоренца
В § 2 Введения к этой книге мы сформулировали принцип отно-
относительности Галилея как утверждение о том, что никакие физи-
физические эксперименты, производимые внутри механической системы,
не могут обнаружить равномерное и прямолинейное движение этой
системы (см. выше, стр. 31); таким образом, преобразование меха-
механической системы, состоящее в придании ей постоянной по величине
и направлению скорости, не меняет никаких экспериментально
наблюдаемых свойств этой системы. Однако кроме этого принципа
при выводе формул, выражающих преобразования Галилея, мы неявно
использовали еще одно чрезвычайно важное положение, на котором
теперь остановимся более подробно.
Принцип относительности Галилея полностью покончил с пред-
представлением о существовании какого-то «абсолютного», неподвижного
по самой своей сути пространства, по отношению к которому можно
определять положения и измерять скорости движения всех мате-
материальных тел. Все движущиеся друг относительно друга тела рав-
равноправны,— декларировал Галилей,—мы никогда не сумеем выяснить,
движется ли какое-нибудь из них или стоит на месте, а следова-
следовательно, само понятие «абсолютного» покоя лишено содержания.
«Абсолютное пространство но самой своей сущности,
безотносительно к чему бы то ни было внешнему, остается всегда
одинаковым и неподвижным»,—пишет Исаак Ньютон в своих бес-
бессмертных «Математических началах натуральной философии», — но
далее, почти цитируя Галилея, подчеркивает, что «совершенно не-
невозможно ни видеть, ни как-нибудь иначе различать при помощи
наших чувств отдельные части этого пространства... и вместо них
приходится обращаться к измерениям, доступным чувствам», т. е.
к измерениям в «относительном», движущемся пространстве, после
чего он наносит понятию «абсолютного» пространства последний
удар: «Может оказаться, что в действительности не существует
покоящегося тела, к которому можно было бы относить места и

176 ЗАКЛЮЧЕНИЕ
движения прочих»1). Таким образом, «абсолютное пространство»
Ньютона — это фикция: его нельзя обнаружить никаким прямым
наблюдением, никаким экспериментом и для точного описания зако-
законов природы оно совершенно не нужно.
По-другому обстоит дело со второй из основных категорий,
с которыми связано наше восприятие мира, — со временем. Правда,
Ньютон намеренно связывает эти две категории: «абсолютное,
истинное, математическое в р ем я, —говорит он, — само по
себе и по самой своей сущности, без всякого отношения к чему-
либо внешнему протекает равномерно и иначе называется длитель-
длительностью» (сравните с формулировкой, касающейся понятия «абсолют-
«абсолютного» пространства!) и почти сразу прибавляет: «возможно, что не
существует (в природе) такого равномерного движения, которым
время могло бы измеряться...»1). Однако на самом деле и Галилей,
и Ньютон всегда предполагали существование «абсолютного» вре-
времени, не связанного (если исключить произвольность в выборе «на-
«начального» момента, для которого /=0) ни с какой системой отсчета
и протекающего одинаково во всех
о A >~S В пунктах Вселенной. Теперь, следуя
? 1 ¦—¦о— а Эйнштейну, мы проанализируем пред-
предпосылки, на которых покоится убеж-
нис. 141. дение в «абсолютном характере» ка-
категории времени.
Предположим, что мы имеем два пункта А и В прямой о, не-
неподвижные друг относительно друга (рис. 141); покоятся они или
движутся относительно' выбранной инерциальной системы отсчета
—мы не знаем, да это и не важно, ибо сам выбор системы отсчета
произволен, не может быть мотивирован никакими физическими со-
соображениями. У находящихся в пунктах А и В наблюдателей есть
часы, позволяющие измерять время в этих двух пунктах; задача
состоит в том, чтобы установить «абсолютный», не зависящий от
выбора пункта (А или В) характер времени, добившись «абсолютной
синхронности» имеющихся у наших наблюдателей часов.
Сверку имеющихся в пунктах А и В часов можно осуществить
двумя различными методами. Можно сравнить, скажем, в точке А
ход двух часов, а затем перенести одни из них в точку В; так,
на каждом корабле имеется хронометр, ход которого был урегули-
урегулирован до выхода в море путем сравнения с имеющимися на суше
«эталонными» часами. Однако этот метод синхронизации часов прин-
принципиально мало удовлетворителен, поскольку он позволяет
лишь установить, что некогда, когда часы находились
в одном месте А, они шли синхронно; проверить, что также и в
разных пунктах А и В часы по-прежнему идут одинаково, он не
!) См. Ньютон [54], стр. 30,

§ 10] ПРИНЦИП ОТНОСИТЕЛЬНОСТИ ЭЙНШТЕЙНА 177
позволяет (а вдруг на ход часов влияет их механическое переме-
перемещение и в процессе переноса часов из точки А в точку В они от-
отстали или начали спешить?). Второй метод заключается в том,
чтобы настраивать часы в пункте В в соответствии с подаваемыми
из А сигналами — так, часы на корабле всегда проверяются по по-
подаваемым с суши радиосигналам «точного времени». Но для того
чтобы сигнал прошел путь от точки А до точки В, вообще говоря,
требуется некоторое время; это время можно было бы точно рассчи-
рассчитать, но для этого необходимо знать как расстояние между пунктами
А и В, так и скорость распространения сигнала, а эту скорость
нельзя определить совсем точно до тех пор, пока мы не имеем синхро-
синхронизированных часов, указывающих время в разных пунктах, т. е. пока
мы не имеем того, для чего нам только и нужно знание скорости рас-
распространения сигнала. Таким образом, и второй путь синхронизации
часов приводит к элементарному логическому кругу и, следоватечьно,
не позволяет прийти ни к каким удовлетворительным выводам.
Конечно, можно условиться подавать сигнал не из пункта А,
а из точки б1, расположенной точно посередине между пунктами
А и В; в момент поступления этого сигнала в оба пункта А и В
на расположенных в этих пунктах часах устанавливается одинаковое
время. Однако такая процедура явно предполагает, что пункты А
и В неподвижны; если же оба эти пункта двигаются, скажем,
в направлении, указанном стрелкой на рис. 141, то посланный из
«средней точки б1 сигнал дойдет раньше до точки А, чем до точ-
точки В, — ведь точка А движется навстречу сигналу, в то время как
точка В, напротив, от него удаляется. Но выше мы видели, что
утверждения ''точки А и В неподвижны» или «точки А и В (рав-
(равномерно и прямолинейно) движутся» не имеют физического смысла,
т. е. справедливость или несправедливость каждого из них не может
быть установлена никаким механическим экспериментом. А если так,
то мы опять оказываемся не в состоянии проверить, идут ли часы
в точках А и В одинаково или ход их несколько различен.
С этим же связана известная неопределенность в определении
временного упорядочивания событий, происходящих в двух разных
точках А и В прямой о. Ранее мы считали, что всем пунктам пря-
прямой о отвечают «оси времени t,,, которые можно считать параллель-
параллельными (см. рис. 142). При этом на отвечающей пункту В «временной
оси» ИВ1 можно указать отметку t^\ соответствующую определен-
определенному моменту времени t^ в пункте А; предшествующие этой от-
отметке t^) моменты в пункте В следует считать предшествую-
предшествующими и для момента tlQA\ а следующие за tW моменты—¦
следующими и за моментом И*К Однако, насколько обосновано
это предположение об абсолютной упорядоченности^ во времени
любых двух событий, даже относимых к разным пунктам прямой о?

178
ЗАКЛЮЧЕНИЕ
Рис. 142.
Конечно, если из пункта В в момент /'^ посылается какой-либо
сигнал (письмо, телеграмма) в пункт А, причем этот сигнал прихо-
приходит в Л в момент /(ол), то любое предшествующее /<jB) событие
в пункте В надо считать предшествующим и моменту /(ол): иначе
наблюдатель в пункте А мог бы получить информацию об относя-
относящемся к пункту В событии еще до того, как это событие про-
произошло, что явно противоречит
принципу причинности,
согласно которому следствие из
какого-либо события никак не
может иметь места раньше самого
события. Точно так же, если по-
посланный из А в момент /<ол> сиг-
сигнал приходит вйв момент Л2В), то
любое следующее за моментом
Л2В) событие в пункте В следует
считать последующим также и
для момента /<0Л). Таким образом,
лишь для событий в пункте В,
принадлежащих интервалу между
ЦВ) и f(B)^ их расположение во
времени по отношению к событию,
происшедшему в пункте А в момент /<0Л). остается нераскрытым.
Предположим теперь, что мы имеем в своем распоряжении сигналы,
распространяющиеся с большей быстротой, чем посланные ранее;
в таком случае мы сможем укоротить «интервал неопределенности»
(/<в>, tf>) (или t\B~> </<в><^2В)) в пункте В, отвечающий моменту <<л»
в пункте А (см. тот же рис. 142, где пунктирные линии /<В) /@Л) и
^(ол) /BВ> соответствуют этому более быстрому сигналу). Если
в принципе существуют сколь угодно быстрые сигналы,
то с помощью таких сигналов можно упорядочить во времени л ю б ы е
два события, происшедшие в разных пунктах А и В прямой о;
таким образом, в этом случае «интервал неопределенности» может
быть сведен к единственной точке /(()В), — и мы приходим к той
концепции одновременности событий, которая неявно подразумева-
подразумевалась во всей предшествующей части книги (см., в частности,
§ 2 Введения). Если же существуют какие-то «самые быстрые»
сигналы, то отвечающий этим сигналам «интервал временной неопре-
неопределенности» (t\B\ 7*2 ) (см. рис. 442, где изображенные жирным
пунктиром линии t\B)t{0A) и /оЛO2В> отвечают «самому быстрому»
сш налу) далее уже не может быть уменьшен, т. е. ..абсолютное»

§ 10J принцип относи пильное! и эЙнштейнл 179
(не зависящее от места) время Ныогона является такой же фикцией,
как и его «абсолютное» пространство.
Самым быстрым из известных нам сигналов является луч света,
—но является ли он принципиально самым быстрым из всех возмож-
возможных сигналов? На этот вопрос ответил физический эксперимент.
Совершенно ясно, что в рамках механики Галилея — Ньютона ника-
никакой сигнал не может быть «самым быстрым»: классический закон сло-
сложения скоростей (см., в частности, § 4 настоящей книги, стр. 61)
показывает, что имеющий скорость с сигнал, посланный из пункта А
в сторону движущегося ему навстречу с
со скоростью v «приемника сигнала» В : >- -*—
(рис. 143), имеет по отношению к В А В О
(большую с) скорость c-\-v. И част-
частности, и скорость света должна су- Рис. 143.
щественно зависеть от того, движется
ли приемник светового сигнала навстречу световому лучу, остается ли
он на месте, пли удаляется от источника света.
Эти соображения сделали сенсационными результаты тонких
экспериментов замечательного американского физика Альберга Абра-
гама Майкельсона A881 г.; в 1887 г. А. А. Майкельсон совмест-
совместно со своим другом, химиком Эдвардом Вильямом Мор.ми повторил
этот опыт, сделав его еще более убедительным), показавших, что
скорость света во всех инерциальных системах отсчета одна и та же
и не зависит от направления движения (подвижной) системы отсчета
по отношению к световому лучу1). Опыты Майкельсона—Морли
пробили глубокую брешь в классической картине мира, базирую-
базирующейся на принципах, положенных в основу механики Галилеем и
Ньютоном.
Объяснение экспериментов Майкельсона—Морли дал в 1905 г.
Альберт Эйнштейн A879 —1955), предложивший совершенно новое
обоснование всей механики. А именно, Эйнштейн полностью прини-
принимает принцип относительности Галилея в той его формулировке,
которую мы повторили в начале настоящего параграфа. Но вот
принцип существования «абсолютного» (т. е. не зависящего от
выбора места и системы отсчета) времени Эйнштейн решительно
отвергает, заменяя его принципом постоянства (т. е. неза-
независимости от выбора инерциальной системы отсчета) скорости
света; таким образом, так называемый принцип относитель-
относительности Эйнштейна состоит из двух постулатов, один из кото-
которых утверждает равноправность всех инерциальных систем отсчета
(этот постулат впервые выдвинул еще Галилей), а второй — посто-
') Описание опытов Манкельсона—Морли имеется буквально во всех кни-
книгах, посвященных специальном теории относительности Эйнштейна (см. спи-
список литературы, стр. 301—302).

180
ЗАКЛЮЧЕНИЕ
янстео скорости света во всех инерциальных системах отсчетаг).
Ясно, что с механикой Галилея — Ньютона, базирующейся на преоб-
преобразованиях Галилея, постулат постоянства скорости света несовме-
несовместим; поэтому механика Эйнштейна заменяет преобразования Галилея,
указывающие, как меняются координаты х, t (пространственно-вре-
(пространственно-временного!) события б1 при переходе от одной инерциальной системы
отсчета к другой, совершенно иными преобразованиями, указанными
впервые (исходя из других соображений) замечательным голландским
физиком Хендриком Антооном Лоренцом A853—1928) и по его
имени называемых преобразованиями Лоренца.
Наметим вывод преобразований Лоренца. Мы и здесь будем
использовать геометрические иллюстрации, послужившие основой
I
Рис. 144.
для перехода от преобразований Галилея классической механики
к геометрии Галилея. А именно, выбрав фиксированную систему
отсчета, сопоставим всевозможным «событиям» одномерной кинема-
кинематики (кинематики прямой о) точки плоскости, отнесенной к коорди-
координатам х (абсцисса точки прямой о) и t (время); при этом, анало-
аналогично тому как мы поступали прежде, условимся изображать
ось Ot горизонтальной, а ось Ох вертикальной (рис. 144). Выбе-
Выберем еще единицы измерения длины и времени ОХ0 и ОТ0 так, чтобы
скорость света (ее обычно обозначают буквой с) была равна 1;
таким образом, если время мы измеряем в секундах, то единицу
измерения длины придется взять близкой к 300 000 км (ибо скорость
света приблизительно равна 300 000 км!сек). При этом линия /
рис. 144 с уравнением
X = t ИЛИ X — t = 0
2) Аналогично этому и принцип относительности Галилея
на самом деле состоит из двух постулатов: постулата равноправности всех
инерциальных систем отсчета и постулата, утверждающего абсолютный
характер категории времени.

§ 10] ПРИНЦИП ОТНОСИТЕЛЬНОСТИ ЭЙНШТКИНА 181
будет изображать траекторию (или «мировую линию») светового
луча, распространяющегося со скоростью с=1 в направлении воз-
возрастания х от «события» О@, 0), отвечающего начальному моменту
времени /-Ои началу х = 0 отсчета координат х на прямой о.
Рассмотрим теперь наряду с первоначальной инерциальной сис-
системой отсчета {х, t) другую систему отсчета {х1, t'\, для которой
начало отсчета абсцисс х' в момент ^ = 0 совпадает с началом
отсчета абсцисс х, но далее двигается по прямой о с определен-
определенной скоростью v. Таким образом, в старой системе координат
начало х' = 0 новой системы координат описывается линией Of, урав-
уравнение которой имеет вид
х = vt.
В рамках механики Галилея — Ньютона переход от системы отсчета
{х, t) к системе отсчета {х', /'} характеризовался заменой осей
координат Ot, Ox осями Of, Ox' (рис. 144, а); при этом переход
от координат {х, t) к координатам {х', f) (где ось Ох' совпадает
с осью 0x1) записывался формулами Галилея
f= t y>
(здесь мы игнорируем постоянные а и b в формулах A3) из § 2,
отражающие изменение «начального пункта» х = 0 прямой о и «на-
«начального момента времени» t = 0). Однако при этом скорость све-
светового луча в новой системе отсчета («галилеев угол», образован-
образованный линией / рис. 144, а с осью Ох') будет равна уже не 1, а ве-
величине 1—w, что противоречит опыту Майкельсона — Морли.
Таким образом, для того чтобы наши преобразования не проти-
противоречили постулату постоянства скорости света, приходится отка-
отказаться от положения об «абсолютном» времени, геометрическим
выражением которого является неизменность направления оси Ох
(оси ^ = 0). Поэтому преобразования Лоренца геометрически должны
означать переход от системы координат {х, t) к системе координат
{х1, f), где уже. обе новые оси Of и Ох' имеют направления,
отличные от направлений старых осей Ot и Ох (рис. 144, б). При
этом, если единичные отрезки ОХ'0 и ОТ'В осей Ох' и Of по-преж-
по-прежнему имеют одинаковую (евклидову) длину и «мировая линия» светового
луча изображается той же прямой /, что и раньше, то оси Of и
Ох' будут образовывать с осями Ot и Ох одинаковые (евклидовы)
углы: /_tOf =/_ x'Ox — (f. Это следует из того, что прямая /
должна являться также биссектрисой и угла fOx', поскольку ее
уравнение в системе координат {х1, f\ по-прежнему имеет вид
x' = f или x' — f = 0,

182 ЗАКЛЮЧЕНИЕ
— ведь скорость света в системе отсчета \х', t'} тоже должна
равняться 1!
Найдем теперь формулы, связывающие старые координаты (дг, t)
некоторого события S и его новые координаты (xr, i') (рис. 144, б).
Ясно, что координата х равна длине длЖ5 отрезка MS, измерен-
измеренной в единицах длины, равных единичному отрезку ОА',, оси Ох;
координата же х' равна «новой длине» л,л M'S отрезка М' S, изме-
измеренного в единицах, равных единичному отрезку ОХ'0 оси Ох'. Но
(измеренная в единицах ОХ0) длина длуМх5 отрезка MXS, очевидно,
равна х — vt: ведь в координатах х, t прямая Of имеет уравнение
x = vt. Далее, отношение rji'M'S : длЛ^З зависит, очевидно, от
углов /_M'SMX = ?х'Ох (==ф) и /_N\XMS = /_t'Ox' и от еди-
единичных отрезков ОХ0 и ОХ'0 осей Ох и Ojc', но н е зависит от
выбора события 5. Поэтому, если мы обозначим коэффициент
пропорциональности дл ( т. е. ] через k, то буделг иметь1)
x' = k{x — vt). Ba)
Совершенно аналогично находится зависимость между новой вре-
временной координатой f события S и старыми координатами х, t
этого события. Из рис. 144, б следует
где длины отрезков NS и N'S измеряются в «единицах» ОТ0
( = ОА'П) и ОТ'0 (^ ОХ'о). Далее, из подобия (на рис. 144, б —пря-
—прямоугольных) треугольников OAW, и ОММ1 находим
длУИЛ/i
длОЛ' длОЛ/ '
где длины всех отрезков измеряются в одних и тех же единицах
ОХ0=ОТ0, или
R.nNNl vt
X =Т"
Таким образом,
vt_ _
. — х— v
и, следовательно,
, = t — vx.
1) Заметим, что формула Bа) отличается от первой из формул A), выра-
выражающих классические преобразования Галилея, лишь коэффициентом k
(вообще говоря, зависящим от скорости v движения «новой» системы отсчета
относительно «старой», определяющей «угол» ф между осями Ot и Of).

ПРИНЦИП ОТНОСИТЕЛЬНОСТИ ЭЙНШТКЙНА
183
А поскольку
угольнику
треугольник SN'N-l, как легко видеть, подобен тре-
тре'Mi (и 07; = ОХ'1 а ОТЬ = ОХЬ), то
jui'N'S_ju\'M'S
~ длЛ/iS
= k или
V
—tX
= k.
l\
Окончательно мы приходим ко второй из формул, выражающих пре-
преобразования Лоренца
t'=k(t — vx). B6)
Прежде чем идти дальше, заметим, что из формул Bа —б) вы-
вытекает одно довольно неожиданное следствие. Рассмотрим некото-
некоторый стержень длины d, покоящийся в системе отсчета {х, /};
пусть начало этого стержня совпадает
с точкой л; = 0 прямой о, а конец — с
точкой х = й; этим двум пунктам прямой
о будут отвечать «мировые линии», изо-
изображаемые на рис. 145 прямыми Ot и е,
где е || Of и е пересекает ось Ох в точке
Е (d, 0). Измерим теперь длину стержня
в системе отсчета \х', t'}, относительно
которой он, очевидно, движется с абсолют-
абсолютной скоростью v (со скоростью —v, если
учитывать и направление движения). Для
того чтобы определить «новую длину» это-
этого стержня, нам надо зафиксировать его
начало и конец в один и тот же момент
времени ?', скажем, в момент времени f =0 (точки О и Е' на рис. 145).
Ясно, что координаты (xf, t') точки Оимеют вид @, 0); что же касается
координат события ?", то (поскольку для этой точки i' — 0) в силу
формулы B6) t = vx\ с другой стороны, так как для этой точки
x = d (ибо x = d — это уравнение прямой е), то i = vd. Подставив
теперь эти значения х и t в равенство Bа), мы находим
х' = k {x — vt) = k (d — v2d) =- k A — v°) d.
Таким образом, в момент t'— 0 конец нашего стержня имеет про-
имеет пространственною координату x' = k{\—v'2}d; поэтому новая его
длина d' равна
d'=k(\— v-)d. C)
Итак, мы видим, что длина стержня существенно зависит от
выбора системы отсчета, в которой эта длина измеряется: если по
отношению к системе отсчета стержень перемещается с абсолют-
абсолютной скоростью v, то длина его умножается на величину k(\—v2),
где коэффициент пропорциональности k также зависит от v. Не-
Немного ниже мы раскроем характер зависимости k от v и увидим,
Рис. 145.

184 ЗАКЛЮЧЕНИЕ
что ?A—•а2) < 1, так что длина движущегося стержня оказывается
меньшей, чем длина того же самого стержня в состоянии покоя.
Так как предположение о сокращении длин движущихся предметов
впервые выдвинул ирландский физик Джордж Фрэнсис Фитцдже-
Фитцджеральд, который усмотрел в этом возможность чисто формального
оправдания результатов опыта Майкельсома—-Морли, то изменение
в k(\—v2) раз длин движущихся с абсолютной скоростью v пред-
предметов обычно называют фитцджеральдовым сокращением.
Вернемся теперь к формулам Bа—б). Выразим из них старые
координаты (х, t) события через его новые координаты (х', t');
для этого раскроем скобки в равенствах Bа) и B6), предварительно
умножив второе из них на v:
x' = kx — kvt; vt' = kvt — kvlx.
Сложив получившиеся уравнения, имеем
x'+vt' = k(\—v2)x,
откуда следует
Напротив, оставив без изменения равенство B6), а равенство Bа)
умножив на v, получим
vx' = kvx — kirt, t' = kt — kvx;
сложив, наконец, полученные уравнения, мы приходим к формуле
vx'+t' = /гA— v2)t,
откуда вытекает, что
Формулы B'а—б) и указывают правила перехода от новых коорди-
координат {х', t'} к старым координатам {х, t\.
Сравним теперь системы формул Bа—6) и B'а—б). Они отли-
отличаются друг от друга в двух отношениях. Во-первых, фигурирую-
фигурирующая в формулах B) скорость v заменяется в формулах B') на ве-
величину
v' = —v
(ибо x'-\-vt' = x'— v't' и t' -\ vx'=t'—v'x'), —этого, разумеется,
и следовало ожидать, поскольку, в то время как система отсчета {х\ t'\
движется по отношению к системе отсчета {л:, t) со скоростью v,
скорость v' системы отсчета {,v, t) по отношению к системе от-
отсчета {х', t'} будет равна —v. Во-вторых, множитель k формул B)
заменяется в формулах B') новым множителем

ПРИНЦИП ОТНОСИТЕЛЬНОСТИ ЭЙНШТЕЙНА
185
Из формулы D), в частности, следует, что покоящийся по
отношению к системе отсчета {х', t'} стержень длины d имеет
в системе отсчета {х, t) (по отношению к которой он движется
с той же абсолютной скоростью v, что и раньше) новую длину
d' = k'(\-v*)d = ±d. C')
Но ясно, что это «новое» фитцджеральдово сокращение по своей
величине никак не может отличаться от того, которое получается
в результате сравнения измеренных в системах отсчета {л:, t) и
\х', t'\ длин стержня, покоящегося в системе {х, t\: ведь против-
противное коренным образом противоречило бы основному принципу рав-
равноправия всех инерциальных систем отсчета, принципу, который
принимают и Галилей и Эйнштейн! Таким образом, мы вынуждены
считать, что
откуда
E)
При этом фигурирующие в формулах C) и C') «коэффициенты
фитцджеральдова сокращения» действительно оказываются одина-
одинаковыми (и меньшими единицы!):
k A — v2) = \ = Kl —v2,
так что длина стержня в движущейся системе отсчета действительно
оказывается меньшей длины того же самого стержня, пребываю-
пребывающего в состоянии покоя:
d' = VY^v2d. Fa)
Подставляя теперь значение E) коэффициента k в формулы B),
мы приходим к окончательным выражениям преобразований Лоренца:
х'
х—vt
—vx+t
G)
Формулы G) и были положены в 1905 г. Альбертом Эйнштей-
Эйнштейном в основу всей механики. При этом, однако, оказалось, что за-
замена преобразований Галилея A) преобразованиями Лоренца G)

186
ЗАКЛЮЧЕНИЕ
f'
приводит к многим совершенно неожиданным физическим феноменам,
настолько неожиданным, что довольно долгое время они серьезно
препятствовали признанию теории относительности. Об одном из
таких феноменов, так называемом «фитцджеральдовом сокращении»
Fа) движущихся предметов, мы уже говорили выше. Еще более
поражает воображение «удлинение (при движении) времени». Эта
гипотеза, на которой мы сейчас остановимся подробнее, принадле-
принадлежала Лоренцу, дополнившему ею идею Фитцджеральда о сокраще-
сокращении движущихся предметов, причем она также была высказана еще
до создания теории относительно-
относительности и внесла еще большую пута-
путаницу в умы физиков и философов:
ведь при сохранении «абсолютного
характера» фактора времени, от чего
впервые отказался только Эйнштейн,
формальные построения Фитцдже-
Фитцджеральда и Лоренца оставались, по
существу, совершенно необъясни-
необъяснимыми.
Для того чтобы пояснить эффект
«удлинения (или укорочения) време-
времени», рассмотрим двух наблюдателей
И и Н', связанных с системами
отсчета {х, t) и {х', t') и имею-
имеющих часы, фиксирующие время в этих
двух системах отсчета. Рассмотрим
определенный интервал @, т) времени длительности т в системе отсчета
{х, t\; момент t — О характеризуется «мировой линией» Ох рис. 146,
а момент t = т — мировой линией /\\Ох, пересекающей ось Ot
в точке F с координатами @, т). Пусть наблюдатель Н' в момент
^'=0 находится в пункте х = 0 прямой о; этому положению наблю-
наблюдателя в пространстве и во времени отвечает точка О рис. 146.
В системе отсчета {х', t'\ значению времени ^'=0 отвечает «ми-
«мировая линия» Ох'—точки этой линии отвечают всевозможным собы-
событиям, «одновременным» с точки зрения наблюдателя Н'. Аналогично
этому одновременными с событием F с точки зрения наблюдателя
Н' будут события, графически изображаемые точками проходящей
через F прямой /' || Ох'; сама точка F имеет в системе {х, f\ ко-
координаты @, т), а в системе отсчета \х', t'\ — координаты
Рис. 146.
X = ¦
—vr
и t =¦
(см. выше, формулы G)). Таким образом, с точки зрения наблюда-
наблюдателя Н' событие F произойдет в момент времени
У 1— it
>т, т. е.

§ Ю]
ПРИНЦИП ОТНОСИТЕЛЬНОСТИ ЭЙНШТЕЙНА
187
позже, чем для наблюдателя Н: интервал времени / = т, разде-
разделяющий происшедшие в одном пункте х= 0 прямой о события О
и F, для наблюдателя Н', движущегося со скоростью v относительно
рассматриваемого пункта (т. е. относительно системы отсчета,
в которой события О п F представляются происшедшими в одном
месте!), будет иметь длительность f, большую f.
Г = ' • t. F6)
Кажущуюся парадоксальной формулу F6) можно вывести еще и по-
другому. Рассмотрим тонкий стержень АВ длины t (этой буквой нам здесь
будет удобно обозначить длину стерж-
стержня), движущийся со скоростью v в на-
правлении прямой о, перпендикулярной
АВ (см. рис. 146а, на котором представ-
представлена плоскостью хОу, в которой проис-
происходит движение стержня; ось времени
здесь не изображена). Для наблюдателя
Н, неподвижного относительно стержня,
световой сигнал, направленный вдоль
стержня, пройдет путь АВ за время t
(ибо скорость света по нашему соглаше-
нию равна I). С другой стороны, для
наблюдателя Н', неподвижного относи-
относительно системы отсчета, в которой стер-
стержень движется, путь светового сигнала
от А до В (точнее, от А до пункта В', в- котором, с точки зрения этого
наблюдателя, будет находиться конец В стержня в момент поступления туда
светового сигнала) будет равен
[}
В v В'
Рис. 146а.
АВ'-
где ВВ' —vt' — путь, пройденный движущейся со скоростью v точкой В за вре-
время V, протекшее, по часам наблюдателя Н', между выходом сигнала из точки А
н поступлением его в пункт В (рис. 146а; заметим, что, поскольку стержень
не движется в направлении АВ, его длина для наблюдателей Н и Н' будет
одинаковой, — ср. с формулами A0) ниже). А так как скорость светового
сигнала будет равна 1 как в связанной с наблюдателем Н системе отсчета,
так и в системе отсчета, относительно которой покоится наблюдатель Н' (прин-
(принцип постоянства скорости света!), то (измеренное по часам наблюдателя //'!)
время V, за которое луч света пройдет путь
АВ'= ]
должно быть равно этому пути; отсюда получаем
или
т. е. Г =
1
t.
(бб)
Особенно удивительным представляется последнее рассуждение,
если облечь его в форму «парадокса близнецов», и сегодня еще

188 ЗАКЛЮЧЕНИЕ
иногда вызывающего споры и превратные толкования, хотя Эйн-
Эйнштейн исчерпывающим образом объяснил этот «парадокс» более чем
полвека тому назад. Предположим, что наши наблюдатели Н и Н' —
братья-близнецы, один из которых остается в точке х — 0 прямой о,
с которой связано начало системы отсчета \х, t}, а второй — дви-
движется относительно Н с большой скоростью v, например совер-
совершает космический перелет. «Мировой линией» наблюдателя Н' мы
первоначально объявим прямую Of рис. 146; это значит, что Н'
перемещается относительно Н с (положительной) скоростью v.
Затем, начиная с момента времени т по часам наблюдателя Н,
т. е. с точки /*\ пересечения прямых /и Of, «путешественник» Н'
изменяет направление своего движения, начиная приближаться
к (неподвижному) наблюдателю Н с той же абсолютной скоростью v.
Теперь он движется относительно Н со скоростью —v; это отве-
отвечает тому, что мировой линией наблюдателя Н становится прохо-
проходящая через точку Fx линия FXV, параллельная линии Otlt с им-
метричной Of относительно Ot. Через некоторое время оба
брата снова встретятся в пункте х = 0 прямой о; точке (и моменту!)
встречи отвечает точка V пересечения прямых Ot и FyV (рис. 146).
Ясно, что по часам наблюдателя Н между событиями О и V
пройдет
т | т -- 2т ед. времени;
выясним теперь, сколько времени займет путь между «мировыми
точками» О и V но часам его брата-близнеца Н'. Так как в систе-
системе отсчета {х, /} точка Ft имеет временную координату t - т, а в
системе отсчета \х', f\ — пространственную координату лг' = О, то
в силу первой из формул G) получаем
х = - in.
А теперь из второй формулы G) следует
т. е. в «мировой точке» Fx наблюдателю Н' отвечает «собственное
время» х'- х\ 1—vz. Далее, время движения от «мировой точки» F
до «мировой точки» V должно согласовываться с системой отсчета
{¦^li M (Рис- 146), относительно которой теперь покоится наблю-
наблюдатель Н'; при этом из соображений симметрии вытекает, что за
время движения между «мировыми точками» Fx и V наблюдатель Н'
«постареет» еще на
х\ 1 — v2 ед.времени
(подтвердите это прямой выкладкой!). Таким образом, все путеше-
путешествие наблюдателя Н' от «мировой точки» О до «мировой точки» V

§ 10] ПРИНЦИП ОТНОСИТЕЛЬНОСТИ ЭЙНШТЕЙНА 189
займет
%\^\—v2-\-r\ 1—•г>2=2т} 1—v2 ед. времени,
т. е. (поскольку 2т 1^1—v2 < 2т) Н' по возвращении из путеше-
путешествия окажется моложе своего брата-близнеца!
Конечно, этот результат (для практической реализации которого
мы должны располагать космическими кораблями, передвигающимися
со скоростью, близкой к скорости света, и должны суметь пере-
перенести нагрузки на организм, связанные с огромными ускорениями,
развиваемыми космическим кораблем в моменты пуска, остановки и
почти мгновенного изменения направления движения в мировой точ-
точке Fj) никак не может быть использован для удлинения жизни —
ведь все физические и физиологические процессы в «движущейся» г)
среде проистекают в полном соответствии со свойственным этой
среде «собственным временем»: так, Н' за время пути проживет
ровно 2т' = 2т]/1—v2 ед. времени, не больше и не меньше. Не-
Неправильные толкования этого результата чаще всего апеллируют
к равноправию любых инерциальных систем отсчета; «поэтому,—
говорят противники теории относительности, не давая себе труда
тщательнее продумать все рассуждение, — Н тоже двигался относи-
относительно Н' и, следовательно, при встрече он также должен оказать-
оказаться моложе своего брата Н'». Однако это рассуждение является
совершенно несостоятельным — ведь система отсчета, с которой свя-
связан наблюдатель Н', никак не является инерциальной, поскольку в
«мировой точке» Рг он резко изменил направление движения (ср. ска-
сказанное выше о возникающих ускорениях и связанных с ними пере-
перегрузках, вызванных силами инерции); поэтому ни о каком равноправии
системы отсчета {х, t), связанной с наблюдателем Н, и «системы
отсчета» {л;', t'\ — \хъ tt\, в которой живет его брат Н', здесь не
может быть и речи2).
Наконец, остановимся еще на эйнштейновском законе сложе-
сложения скоростей. Предположим, что система отсчета \x',t'\ дви-
движется относительно системы отсчета {х, t\, которую мы условимся
называть «неподвижной», с какой-то скоростью и; в системе отсчета
{х', t'} рассматривается некоторый объект А, движущийся со ско-
скоростью v. Нам требуется найти скорость w объекта А в системе
отсчета {х, t). Величины v, и и w играют здесь роль «относи-
«относительной скорости», «переносной скорости» и «абсолютной ско-
скорости»; поэтому в рамках классической механики Галилея — Ньютона
мы имели бы (ср. выше, стр. 61)
w=u \ v. (8)
*) Кавычки здесь призваны напомнить читателю, что без фиксирования
системы отсчета это прилагательное вообще не имеет никакого смысла; здесь
мы употребляем его с позиций брата Н.
2) Ср. также Скобельцын [53].

190
ЗАКЛЮЧЕНИЕ
Совсем по-другому обстоит дело в теории относительности Эйн-
Эйнштейна. Пусть прямая а (рис. 147)—-«мировая линия» движущегося
объекта Л; точки О и 5 — два положения этого объекта, в систе-
системе отсчета \х', Г) имеющие координаты @, 0) и (d', т'), где
d' = vi': ведь скорость объекта Л в этой системе отсчета равна v
и, следовательно, —— = v. В системе отсчета {х, t) точка (собы-
(событие) О имеет те же координаты @, 0); координаты же точки 5 в
системе отсчета {х, t) можно определить
.по формулам G), в которых надо только
вместо х' и 1' подставить л; и г1, а вместо
х и t — величины х' - - d' ii t' = т' и за-
заменить v на — и (скорость системы отсчета
\х, t\ по отношению к системе отсчета
\х', t'}). Таким образом, получаем
d' -\ их' _ ^ ud'-i-т'
и t = ¦
Рис. 147.
У 1-й*
откуда вытекает, что за время т =
(измеренное в системе отсчета
X 1— и2
{х, t\) наш объект А проходит по отношению к этой системе пугь
d==—-~^ и ¦ , т. е. его скорость и в этой системе отсчета равна
VT^Tfi '
d' - -их' _ ud'\ x' d'-{-их' vx'-\-ux' u-\-v
\г{— и*
ud' -| т' ичт'+т'
uv
Итак, формула (8) заменяется в теории относительности формулой
W =
u~\-v
uv+{ '
(9)
В частности, если рассматриваемый объект А— луч света, распро-
распространяющийся со скоростью v - 1 (ведь единицей скоростей явля-
является у нас именно скорость света!), то и
..I 1
¦ = 1
~ "и-1-.
— скорость света остается одной и той же во всех (инерциальных)
системах отсчета. Заметим также, что наличие в выражающих пре-
преобразования Лоренца формулах G) корня квадратного из вели-
величины 1—v" свидетельствует о невозможности существования сигна-
сигналов, распространяющихся быстрее света (т. е. имеющих скорость
В закчючение мы снова вернемся к вопросу об одновременности
и о понятиях «раньше — позже» в теории относительности. Так как

принцип относительности Эйнштейна
191
А
^абсолютное
скорость инерииальной системы {л:', t'} по отношению к системе
{л:, t) может быть любой (с тем лишь ограничением, что по абсо-
абсолютной величине она должна быть меньше скорости света, т. е.
меньше 1), то ось Of «подвижной» системы отсчета может зани-
занимать любое положение в угле тОп рис. 148; соответственно этому
ось Ох' должна располагаться в угле nOmv События S и 5, в
какой-то системе отсчета {л:', t'} являются «очновременнымн», если
они принадлежат прямой, параллельной оси Ох'. Поэтому любое
событие R, изображаемое ка-
какой-либо точкой одного из двух
вертикальных углов пОт1 и
nrOm, является «одновремен-
«одновременным» с О по отношению к
какой-то специально выбранной
(инерциальной) системе отсчета
{л:', t')\ при ином выборе си-
системы отсчета это событие
окажется предшествующим со-
событию О (так будет обстоять
дело в системе отсчета \хи /J
рис. 148) или будет следовать
за О (как, например, в системе
{д:2, t2) рис. 148). Что же ка-
касается событий, изображаемых
точками углов тОп и ту0пг,
то первые из них образуют
«абсолютное будущее» события О, а вторые — его «абсолютное
прошлое»; при этом причинная связь может связывать лишь
такие события R1 и R2, что одно из них («причина» /?j) является
«абсолютно предшествующим» второму («следствию» R2; см. тот же
рис. 148). В частности, если Ot и plp21| Ot— «оси времени», соот-
соответствующие в какой-то инерциальной системе отсчета {л;, t\ двум
пунктам прямой о — началу отсчета на прямой и некоторой точке
М, то все события, происходящие в пункте М, по отношению
к событию О делятся на три категории: луч Ргрг изображает мно-
множество событий, предшествующих О; луч Р.гр.г— множество
событий, следующих за О; наконец, отрезок РХР2 изображает
множество событий, «временно нейтральных» по отношению
к О: каждое из этих событий в зависимости от выбора ннерцнальной
системы отсчета может считаться происходящим «раньше» О, «одно-
«одновременно» с О или «позже» О (ср. рис. 148 с рис. 142 на стр. 178).
При этом, разумеется, лишь события, изображаемые точками луча Рхръ
могут служить «причинами» события О и лишь события, изображае-
изображаемые точками луча Р2р2, —являться его «следствиями».
Рис. 148.

192 ЗАКЛЮЧЕНИЕ
Экспериментальную проверку «релятивистских» (т. е. связанных
с теорией относительности) эффектов очень затрудняет то обстоя-
обстоятельство, что в случае «земных», т. е. встречающихся в обыденной
жизни на Земле, скоростей v (которые мы условились измерять
в такой системе единиц, что скорость света равна 1) коэффициент
& в формулах Bа — б) (стр. 182—183) или G) (стр. 185), так
У 1— i
же как и коэффициент ]/ 1 —v2 фитцджеральдова сокращения, очень
мало отличается от 1. Так, например, если
г» да 1000 км/час да 0,3 км/сек да 0,000001 скор, света
(такой порядок величины имеют скорости реактивных самолетов), то
/г=-^=]=^ да 1,0000000000005 и К1 —г;2 да 0,9999999999995.
Однако в явлениях, относящихся к «физике микромира» (т. е.
к физике ядра и элементарных частиц) или к «физике макромира»
(астрофизике и физике космоса), где приходится сталкиваться
с колоссальными скоростями, вполне сравнимыми со скоростью света,
пренебрежение теорией относительности Эйнштейна может привести
к серьезным ошибкам. К этому вопросу мы еще вернемся в § 12.
Следует иметь в виду, что в классической физике принцип относитель-
относительности Галилея применим только к механическим явлениям; это связано
с тем, что основные законы механики (знаменитые законы Ньютона,
известные каждому школьнику) «инвариантны относительно преобразований
Галилея A)», т. е. сохраняют свою форму при этих преобразованиях. Напро-
Напротив, основные законы теории электромагнитного поля — законы (или
уравнения) Максвелла, впервые выписанные в 1864 г. великим анг-
английским физиком Джеймсом Клерком Максвеллом A831—1879) и соста-
составившие основу его «Трактата об электричестве и магнетизме» A873), — инва-
инвариантны не относительно преобразований Галилея A), а относительно преобра-
преобразований Лоренца G); поэтому к явлениям электромагнетизма (в том числе
и к явлению распространения света, согласно теории Максвелла связанному
с электромагнетизмом!) принцип относительности Галилея неприменим. Эти
соображения легли в основу рассуждений замечательного французского мате-
математика и физика Анри Пуанкаре A854—1912), который пришел к идеям
специальной теории относительности одновременно с А. Эйнштейном (т. е.
в 1905 г.) и независимо от него.
Укажем, наконец, что до сих пор мы говорили о принципе относитель-
относительности Эйнштейна и о преобразованиях Лоренца только в применении к «одно-
«одномерной механике»—к кинематике прямолинейных движений в направлении
фиксированной прямой о. Однако принцип относительности Эйнштейна в той
его формулировке, которая указана на стр. 179—180, применим, разумеется, и
к плоско-параллельным (двумерным) или к произвольным (трехмерным) дви-
движениям; при этом переход от одной инерциальной системы отсчета к другой
будет задаваться более сложными преобразованиями Лоренца трехмерного
«мира событий» (х, у, t) (где (х, у)—координаты точки на плоскости, at —
время) или общего четырехмерного «мира» (х, у, г, t). Преобразования
Лоренца четырехмерного мира событий (х, у, г, /), оси координат в котором
выбраны таким образом, что направление движения «подвижной системы

§ 11]
ГЕОМЕТРИЯ МИНКОВСКОГО
193
отсчета» \х', у', z', t'\ относительно «неподвижной системы отсчета» \х, у, г, t\
совпадает с общей осью Ох = О'х' этих двух систем, а оси О'у' и О'г' «по:
движной» системы отсчета все время остаются параллельными соответствую-
соответствующим осям «неподвижной» системы отсчета (рис. 149), можно, разумеется,
записать так:
1
У 1—1>3
t.
A0)
г,
Jf
УХ—v'-
t.
У/
i
О1
Х,Х'
где г — скорость движения «подвижной» си-
системы отсчета относительно «неподвижной»;
однако в случае общего расположения ко- Рис. 149.
ординатных осей систем отсчета {х, у, z, t\
и ¦[*', у', z', t'\ эти формулы приобретают значительно более сложный вид.
Поскольку настоящая книга посвящена геометрическому истолкованию фактов
«одномерной кинематики», мы не останавливаемся здесь на этом вопросе.
§ 11. Геометрия Минковского
Выше мы видели, что переход от принципа относительности Га-
Галилея к принципу относительности Эйнштейна равносилен замене
элементарных преобразований Галилея классической кинематики
t'=
A)
задающих переход от одной инерциальной системы отсчета к дру-
другой, несколько более сложными преобразованиями Лоренца
х—vt
х =¦
— vx+t
G)
С другой стороны, основное содержание настоящей книги составляло
изучение геометрической системы, возникающей на координатной
плоскости {х, t\, где роль «движений» играют преобразования Га-
Галилея; соответствующую «геометрию», каждый факт которой может
быть интерпретирован в терминах кинематики прямой о, мы назвали
«геометрией Галилея». В этой связи также является совершенно
естественным изучение «геометрии» плоскости {л:, t\, роль «движе-
«движений» которой играют преобразования Лоренца. Эта геометрическая
система была указана выдающимся немецким математиком и физиком
7 И. М. Яглом

194 ЗАКЛЮЧЕНИЕ
Германом Мннковским A864-1909), который в 1907—1908 гг.
предложил использовать ее для «геометризпрованного» описания
феноменов релятивистской механики; ее обычно называют (псевдо-
(псевдоевклидовой) геометрией Минковского1).
Движениями плоскости Галилея служат преобразования:
у' = VX -\ у , Ь.
От записанных в форме A) преобразований Галилея эти движения
отличаются, во-первых, тем, что координаты точки на плоскости
теперь обозначаются не через /, л:, а через х, у, как обычно (при-
(причем координата .v играет роль времени /, а координата у заменяет
абсциссу д: точки на прямой о); далее, к числу движений причисля-
причисляются также и всевозможные параллельные переносы:
Х'ГХ + "' Aа)
у = у : ь,
отвечающие изменениям начала отсчета времени t и начала отсчета
координат \х\ на прямой о. Соответственно этому и под геометрией
Минковского мы будем понимать изучение тех свойств фигур коор-
координатной плоскости \х, у), которые сохраняются при движениях
х'
v'
У
1
У
1
1 — и3
V
V
>'
1—и*
1
1—tJ
-^ | а,
у+ь,
(И)
где v, а, Ъ — произвольные «.параметры» движения. От преобразо-
преобразований G) преобразования A1) отличаются тем, что координаты точки
на плоскости теперь обозначены через х, у (где можно считать,
что х — это время t, ay — абсцисса движущейся точки па прямой о),
а также тем, что к числу движений присоединены всевозможные
параллельные переносы Aа), отвечающие изменениям начала отсчета
времени и начала отсчета абсцисс на прямой о. В настоящем пара-
параграфе мы дадим краткий набросок геометрии Мннковского, почти пол-
полностью отвлекаясь здесь от механического истолкования фактов этой
замечательной геометрии в рамках теории относительности Эйнштейна.
Наряду с координатами (л;, у) точки в геометрии Минковского
используются также координаты (X, Y), связанные с координатами
') Происхождение термина «псевдоевклидова геометрия» свя-
связано с большой близостью геометрии Минковского к геометрии Евклида,
факты которой, впрочем, иногда в геометрии Минковского своеобразно иска-
искажаются (об этом см. ниже).

§ 11J
ГЕОМЕТРИЯ МИНКОВСКОГО
195
[х, у) соотношениями:
1
или
у
(х-у)
A2)
(рис. 1501. Складывая и вычитая друг из друга первую и вторую
\
Рис. 15!.
из формул A1), мн без труда выразим движения плоскости Мин-
ковского в координатах X, Y:
1~9Л" 1-и X+Y , 1-и X-Y
7-
или
A1а)
где /.
У 1+V лГ\~ф \
так что т=
1+v 1+v \ .
1—и |Л —и2/
._ ^JL и В = ~=—параметры преобразования. Движение (Па)
складывается из преобразования
v v
A3а)

196 ЗАКЛЮЧЕНИЕ
представляющего собой комбинацию сжатия к оси OY с коэффици-
коэффициентом сжатия X1) и одновременного сжатия к оси ОХ с коэффи-
коэффициентом -г- (см. рис. 151, где изображен случай Я,<1< -v-J и из па-
параллельного переноса
A36)
Y'= Y + B A3б)
Преобразование A3а) играет в геометрии Минковского роль пово-
поворота; такое преобразование евклидовой координатной плоскости
{X, Y\ называется гиперболическим поворотом (причины, обусловли-
обусловливающие это название, будут разъяснены ниже). В координатах {л:, у)
поворот A3а) записывается формулами
1 v
X = У У,
(ср. с формулами G), выражающими преобразование Лоренца).
Аналогично тому как это сделано было в § 3 гл. I для сдвига
(см. стр. 47), можно показать, что сжатие к прямой, а следовательно,
и преобразование A3а), переводит каждую прямую снова в прямую;
переводит параллельные прямые в параллельные прямые; сохраняет
величину отношения двух отрезков одной прямой (или параллельных
прямых),— следовательно, понятия прямой линии, параллельных
прямых, отношения отрезков одной прямой (или параллельных пря-
прямых) сохраняют смысл в геометрии Минковского. Далее, из формул
A1а) следует, что любая прямая, параллельная оси OY или оси ОХ:
Х= const или Y = const,
переводится движением A1) или (Па) в прямую того же направ-
направления. Таким образом, в геометрии Минковского мы имеем даже два
семейства «особых прямых», переводимых каждым движением
в прямую, параллельную первоначальной; через каждую точку плос-
плоскости проходит по одной особой прямой каждого семейства. Нако-
Наконец, квадрат, стороны которого параллельны осям ОХ и OY, пере-
переводится движением A1а) в прямоугольник той же площади (если
стороны квадрата равны е, е, то стороны прямоугольника равны
') Сжатие к оси OY с коэффициентом сжатия X переводит
каждую точку А (X, У) плоскости, удаленную от оси 0Y на расстояние X,
в такую точку Л, (XX, Y) перпендикуляра АР, опущенного из точки А на
прямую OY, которая удалена от OY на расстояние XX; при Х>1 слово
«сжатие» в названии этого преобразования лучше заменить словом «растяже-
«растяжение» (ср. выше, стр. 67, в частности, рис. 47, б).

§ 11]
ГЕОМЕТРИЯ МИНКОВСКОГО
197
Хе,у е ) ; поэтому сеть равный квадратов плоскости Мннковского
переводится движением A1а) в сеть равновеликих им прямо-
прямоугольников и, следовательно, каждая фигура F переводится движением
A1) или (Па) плоскости Минковского в фигуру F' той же площади
х
Рис. 152.
(рнс. 152, а, б; ср. выше, § 3 гл. I, в частности, рнс. 28 на стр. 49).
Таким образом, мы видим, что и понятие площади фигуры сохраняет
смысл в геометрии Минковского.
Рассмотрим теперь произвольный отрезок АВ, относительно ко-
которого нам пока будет удобно считать, что он не параллелен ни оси ОХ,
X
б)
Рис. 153.
ни оси OY. Пусть AKBL — прямоугольник с параллельными осям
ОХ и OY сторонами, диагональю которого служит отрезок АВ
(рис. 153, а). Преобразование A1) или (Па) переводит этот прямо-
прямоугольник снова в прямоугольник с параллельными осям ОХ и OY
сторонами; при этом площадь полученного прямоугольника A'K'B'L'

198
ЗАКЛЮЧГНИЕ
(рнс. 153,6) будет равна площади прямоугольника AKBL: движения
плоскости Минковского площадь прямоугольника AKBL не изменяют.
Ясно, что при близких точках А и В площадь прямоугольника AKBL
мала; поэтому можно считать, что величина u.nAKBL доставляет
своеобразную «меру отклонения» точек А и В друг от друга, стре-
стремящуюся к нулю при неограниченном сближении точек А и В и,
кроме того, одинаковую для двух «равных» (в смысле геометрии
Минковского) пар точек А, В и А', В'. Это как будто позволяет
принять величину urAKBL за «расстояние Минковского» между
точками А и В; однако поскольку площадь фигуры измеряется
в «квадратных» (а не в «линейных») единицах 1), то удобнее считать,
что в геометрии Минковского расстояние dAB между точками А и В
пропорционально корню квадратному из площади прямоуголь-
прямоугольника AKBL, т. е. равно k )¦ unAKBL. Выбор коэффициента пропор-
пропорциональности k, очевидно, определяется заданием единиц измерения
длин и площадей; нам будет удобно считать, что
A4)
dAB =
Ясно, что если точка С принадлежит отрезку АВ, то
(ибо площади изображенных на рис. 153, а подобных между собой
прямоугольников AKBL, AKlCLl и CK*BL2 пропорциональны ква-
квадратам диагоналей АВ, АС и ВС
этих прямоугольников).
Начнем теперь поворачивать отре-
отрезок АВ вокруг его конца А, сохраняя,
ГХ скажем, его евклидову длину (рис. 154).
Легко видеть, что по мере приближе-
приближения к положению АВ0\\ ОХ (или АВ°\\ OY)
площадь прямоугольника AKBL стано-
становится все меньше; для положения
АВ0\\ОХ (или AB°\\OY) отрезка АВ
0\
Рнс. 154.
х соответствующий ему «прямоугольник»
вырождается в отрезок АВа (или
АВ()), так что площадь его обращается
в нуль. Поэтому считают, что длина лю-
любого отрезка особой прямой равна нулю. Когда отрезок АВ в про-
процессе вращения вокруг точки А проходит положение АВ0\\ ОХ (или
АВ° || OF), площадь прямоугольника AKBL снова начинает расти;
при этом, однако, ориентация прямоугольника AKBL (направле-
(направление обхода его вершин А—>¦ К—>¦ В—у L; здесь АК \\ LB || ОХ и
*) Другими словами, площадь фигуры умножается на г'1 при увеличении
всех линейных размеров фигуры в г раз.

§ 11]
ГЕОМЕТРИЯ МПНКОВСКОГО
199
AL || KB || OK) меняется на противоположную (ср. прямоугольники
AKBL и AKiB1Ll на рис. 154). В силу последнего обстоятельства
расстояния между точками А и В и между точками С п D, так распо-
расположенными на плоскости, что отрезки ОМ\\АВ и ON\\CD принад-
принадлежат двум смежным углам, образованным прямыми ОХ и OY, удобно
считать качественно разными: два таких отрезка всегда несрав-
несравнимы между собой. Отрезки и прямые, параллельные проходящим
через начало координат прямым, заполняющим ту пару вертикальных
углов, образованных осями ОХ и OY, которая содержит ось Ох,
мы будем называть отрезками (соответственно прямыми) 1-го рода,
а отрезки и прямые, параллельные (проходящим через начало коор-
координат) прямым, заполняющим пару вертикальных углов, содержащих
ось Оу, — отрезками (прямыми) 1-го
рода; отрезки особых прям ы х (от-
(отрезки, параллельные прямой ОХ или
прямой OY), можно назвать отрезками
нулевого рода, а сами эти прямые —
прямыми нулевого рода. Каждый отре-
отрезок плоскости Мннковского движением
A1) пли (Па) переводи гея в отрезок
того же самого рода: необходи-
необходимым и достаточным условием равен-
равенства отрезков АВ и А'В' (т. е. воз-
возможности совмещения этих отрезков
движением A1) или (Па)) является
совпадение их длин и то, что оба отрезка суть отрезки одного
рода (если АВ и А'В' — отрезки нулевого рода, то оба они, кроме
того, должны принадлежать одному семейству особых прямых,
т. е. должны быть параллельны между собой).
Пусть теперь координаты точек Л и В в системе координат
{X, Y) равны (Хъ Yx) и (Х2, У2), а в системе координат {х, у} равны
(хг, уг) и (х2, у2)- Нетрудно видеть, что стороны прямоугольника
AKBL равны \Х„— Xt\ и | Y2 — Yx | (рис. 155); поэтому n.iAKBL =
= \(X2 — X1){Yi~—Y1)\ н, значит,
dAB--\ 2\(X2-X1)(Y2-Yl)\. A5)
Переходя с помощью формул A2) от координат X, Y к координатам
х, у, мы получим, что расстояние между точками A(xl,yl) и В (х2, Уъ)
равно
Рис. 155.
2 y[(*s-
т. е.
A5a)

200 заключение
(ср. с формулой A) на стр. 16, относящейся к евклидовой геометрии).
Легко видеть, что если отбросить знак абсолютной величины под
корнем, то подкоренное выражение в правой части формул A5) и A5а)
будет положительно, когда АВ— отрезок 1-го рода, и отрицательно,
когда АВ— отрезок 2-го рода; поэтому иногда также пишут
dAB=\ 2(X.2~X1)(Y.1-Y1) A5')
или
В этих формулах уже отражено то, чго длины отрезков 1-го и 2-го
рода измеряются в разных (причем несравнимых между собой!) еди-
единицах: длины отрезков 1-го рода — в действительных числах, а длины
отрезков 2-го рода — в мнимых.
Если ось Ох имеет механический смысл оси времени, а Оу есть ось,
характеризующая положение «события» на прямой о, то любой отрезок
1-го рода совпадает с интервалом между двумя событиями, которые в неко-
некоторой инерциальной системе отсчета (понимаемой так, как это принято в теории
относительности Эйнштейна) происходят в одном и том же месте, и длина
отрезка есть не что иное, как временной интервал между рассмат-
рассматриваемыми событиями в этой инерциальной системе отсчета. Аналогично, имея
отрезок 2-го рода, мы можем так подобрать инерцнальную систему отсчета,
что концы отрезка будут отвечать одновременным событиям; при этом изме-
измеренная в смысле геометрии Минковского длина отрезка совпадает с прост-
пространственным расстоянием между соотретствующими точками пря-
прямой о. Таким образом, можно считать, что длины отрезков 1-го рода изме-
измеряются в единицах времени (сек), а длины отрезков 2-го рода—в единицах
расстояния (еж). В соответствии с этим прямые 1-го рода геометрии Минков-
Минковского часто называют в р е м я п о д о б н ы м и прямыми, а прямые 2-го рода—
пространственноподобными прямыми.
Окружность S геометрии Минковского с центром Q и ра-
радиусом CD (где CD— какой-то отрезок 1-го или 2-го рода)
естественно определить как множество таких точек М, что отрезок
QM равен отрезку CD. Условимся обозначать координаты центра Q
окружности 5 в системе координат \Х, Y\ через (А, В), а в системе
координат {х,у}—через (а, Ь); координаты концов С и D отрезка
CD обозначим через {Хи Кх) и (Х2, К2), соответственно через (хъ ух)
и (х2, у2). Величину
2[Xt-X1){Ya-Y1) = {x%- xx? - (у2 -У1)*
(она может быть и положительной и отрицательной!) назовем квад-
квадратом радиуса окружности S и обозначим через + г2 (где г ^ 0). Ясно,
что уравнение окружности S с центром Q и квадратом радиуса ± г2
будет иметь вид
2(X-A)(Y-B) = ±r\ A6)
соответственно
(х-а)--(у-Ь)°--±г2 A6а)

§ 11]
ГЕОМЕТРИЯ ЫИНКОВСКОГО
201
(ср. с уравнением B) на стр. 17, т. е. с уравнением евклидовой
окружности!). Последнее уравнение также можно переписать следую-
следующим образом:
Х*--у*\2рх 2qy\f=0, A6')
где
р^—а, д =*, /=«2_й2=рл2
В частности, окружность с центром в начале координат О@, 0)
имеет в геометрии Мииковского уравнение
ЛТ^ const A7)
или
х2—/ = const. A7a)
Ясно, что с точки зрения обычной евклидовой геометрии окруж-
окружность A6) или A6а) представляет собой гиперболу, асимптотами
которой являются проходящие че-
через центр окружности особые пря-
прямые (рис. 156). Окружность S мы
назовем окружностью 1-го
рода или окружностью 2-го
рода, в зависимости от того,
является ее радиус отрезком 1-го
или отрезком 2-го рода. На рис. 156
сплошной линией и пунктиром изо-
изображены окружности S и S A-го
и 2-го рода) с общим центром Q
и квадратами радиуса -+ л2 и —л2;
такие две окружности мы будем называть сопряженными. «Крест»,
образованный проходящими через точку Q особыми прямыми QU и
QV, представляет собой множество точек, удаленных от точки Q
на нулевое расстояние; это множество точек иногда называют
окружностью нулевого радиуса (или окружностью нулевого рода).
Нетрудно видеть, что через любые три точки плоскости Минковского
проходит единственная прямая A-го, 2-го или нулевого рода) или
единственная окружность A-го, 2-го или нулевого рода).
С тем обстоятельством, что окружности плоскости Минковского
с евклидовой точки зрения являются гиперболами, связано евклидово
название преобразований A3а) или A3): эти преобразования называют
«гиперболическими поворотами», так как они переводят в себя окруж-
окружности A7) или A7а) с центром О, т. е. евклидовы гиперболы
(см. рис. 157 — гиперболы S м S z уравнениями АТ=±с преобра-
преобразование Х1 = ХХ, Yt = Y переводит в гиперболы Sx и Sx; последую-
последующее преобразование Х'=А'1, Y' = -=- Yx переводит, очевидно, гипер-
гиперболы S^ и S1 в исходные гиперболы 5 и S).
Рис. 156.

202
ЗАКЛЮЧЕНИЕ
Обратимся теперь к вопросу <>б угле м е ж д у прям ы м и. Углом
6гг между прямыми I и /х плоскости Минковского, пересекающимися
в точке Q, естественно назвать длину заключенной между прямыми I
и 1Х дуги NN1 «единичной окружности» S с центром Q; под еди-
единичной окружностью здесь понимается окружность, квадрат
радиуса которой равен 4 1 или —1.
Однако это определение угла имеет
смысл лить в том случае, когда обе
прямые /х и /2 суть прямые 1-го рода
(рис. 158, а) или когда обе они — пря-
прямые 2-го рода (рис. 158, б): лишь в
этих случаях обе прямые пересекают
одну и ту же «единичную окружность»
и, следовательно, высекают некоторую
дугу NNj этой окружности. Длину
дуги NN1 можно определить как предел
длины вписанной в NNt ломаной
ЫМгМя. . .MnNly все звенья которой не-
неограниченно уменьшаются; при этом лю-
любопытно отметить, что все звенья лома-
ломаной, вписанной в окружность 1-го рода,
будут отрезками 2-го рода и, наоборот, звенья ломаной, вписанной
в окружность 2-го рода, являются отрезками 1-го рода (на рис. 158
эти ломаные не обозначены). Поскольку такое определение величины
У
Ч
Рис. 157.
Рис. 158.
угла, связывающее ее с длиной дуги, вычисляемой с помощью не-
некоторого бесконечного процесса, является довольно слож-
сложным, то его удобно заменить следующим: величина f)Ui угла, обра-
образованного двумя пересекающимися в точке Q прямыми I и 1Ъ равна
удвоенной площади сектора NQNX единичного круга с центром Q

§ 11]
ГЕОМКТРИЯ МИНКОВСКОГО
203
(см. те же рис. 158, а, бI). Угол fi/(] между прямыми / и /: можно
считать также направленным, приписывая ему знак -j- или —-
в зависимости от того, происходит вращение, переводящее луч QN
в луч QNX, в направлении, обратном направлению вращения часовой
стрелки, или оно совпадае г с направлением вращения часовой стрелки.
Два угла АРВ и CQD, оба образованные прямыми одного и того же
A-го или 2-го) рода, равны в смысле геометрии Минковского
(т. е. переводятся один в другой движением A1) или A1а)) в том
и только в том случае, если все отрезки РА,
РВ, QC и QD — отрезки одного рода и если
— ^
qa,qc- О «величинах» углов, образо-
образоРис. 159.
j q,q
ванных прямыми разного рода, и об условиях
равенства таких углов мы еще скажем ниже.
Пусть теперь I и /j— две прямые, скажем,
1-го рода, пересекающиеся в точке Q; — NN1 —
дуга единичной окружности S с центром в
точке Q, высекаемая прямыми / и lt (рис. 159).
Произведем «гиперболический поворот», перево-
переводящий луч QN в луч С?Л\; луч QNX этот поворот
переведет в некоторый луч QN2; луч QN2 —
в луч QN3; луч QN3—в луч QNt и т. д.; здесь
N, Nt, N2 Ns, N4,.. —точки окружности S.
Поскольку все прямые QN (. ¦/"), QNt (_ /Д
QN2, QNS, QN^,...—прямые 1-го рода, то
все лучи QN, QNk (гдеб - 1, 2, 3,.. .) заключе-
заключены внутри угла UQV, ограниченного проходя-
проходящими через точку Q особыми прямыми QU и QV, отделяющими
прямые 1-го рода от прямых 2-го рода. Поэтому в геометрии Мин-
Минковского мы можем «неограниченно» вращать луч QN вокруг точки Q,
поворачивая его на сколь угодно большой угол (ибо
&qn. QNk = k-boN. qn,),~u ПРН этом мы никогда не достигнем осо-
особой прямой QU, образующей с прямой QN «бесконечно большой
угол». Точно так же показывается, что и прямую 2-го рода можно
повернуть на угол любой величины: особые прямые образуют с этой
прямой угол, который следует считать «бесконечно большим».
Оставив временно без внимания вопрос об угле между «разно-
«разноименными» прямыми (прямой 1-го рода и прямой 2-го рода), обра-
обратимся к определению расстояния от точки до прямой,
а затем и расстояния между параллельными прямыми.
Для того чтобы иметь возможность измерить эти расстояния, необ-
необходимо указать, какие прямые плоскости Минковского мы будем
называть перпендикулярными. Однако определение периенди-
*) Напомним, что обычное ("евклидово)' или «аффинное;*) понятие пло-
площади сохраняет свой смысл и в геометрии Мннковского (см. выше, стр. 197).

204
ЗАКЛЮЧЕНИЕ
I) lit
кулярных прямых не составляет затруднения: условимся, по образцу
(обычной) геометрии Евклида, называть все проходящие через центр
окружности прямые ее диаметрами и считать, что каждый диаметр d
окружности S перпендикулярен проведенной в конце этого
диаметра касательной t к окружности S (т. е. прямой 1-го или
2-го рода, имеющей с этой окружностью единственную общую
точку1)). Поэтому естественно считать, что прямая /г перпендику-
перпендикулярна прямой I, если для произвольной
окружности 51 с диаметром d \\ l касатель-
касательная, проведенная к этой окружности в кон-
конце диаметра d, параллельна lt (см. рис. 160).
Легко видеть, что перпендикуляром к пря-
прямой 1-го рода всегда будет прямая 2-го рода
и наоборот.
Если прямая / поворачивается вокруг
принадлежащей ей точки Q, приближаясь
к особой прямой QU, то проходящая через Q
прямая lt _|_ / (знак перпендикулярности
прямых в геометрии Минковского мы сохра-
сохраним таким же, как в геометрии Евклида)
поворачивается вокруг Q не в том же на-
направлении, что и Z, как в евклидовой гео-
геометрии, а в противоположном направ-
направлении (рис.160); при этом обе прямые, / и /j,
одновременно приближаются к прямой QU.
[Последнее вытекает также из того, что каждые две перпендику-
перпендикулярные (в смысле геометрии Минковского!) прямые I и 1г симметричны
(в евклидовом смысле!) относительно проходящих через точку Q их
пересечения особых прямых QU и QV (докажите!) 2).] В силу этого
естественно считать, что каждая особая прямая плоскости Мин-
Минковского перпендикулярна сама себе.
Заметим, чго из нашего определения перпендикулярности сим-
симметричность отношения перпендикулярности двух прямых (т. е.
то, что из /х _]_ / вытекает /J_/x) автоматически не следует. Однако
на самом деле эта симметричность имеет место: если прямая 1Х
перпендикулярна прямой I, то и I перпендикулярна /х (рис. 161). При
этом нетрудно показать, что если I J_lx, то имеющий направление
прямой I диаметр окружности S делит пополам все хорды окруж-
окружности, параллельные прямой 1Х; это обстоятельство также отражено
на рис. 161.
Рис. 160.
') Каждая особая прямая (проведенная в конце диаметра d) также имеет
с S единственную общую точку; эти прямые мы, естественно, не будем
называть кг сдельными к S.
2) Отсюда j же вытекает симметричность отношения перпендикуляр-
перпендикулярности (ср. ниже).

§ 11]
ГЕОМЕТРИЯ МИНКОВСКОГО
205
Теперь расстоянием dMi от точки М до прямой I 1-го или 2-го
рода естественно назвать длину йМР перпендикуляра МР, опущенного
из точки М на прямую / (рнс. 162). Расстоянием dij между двумя
параллельными прямыми 1г и I 1-го или 2-го рода мы назовем
Рис. 161.
Рис. 162.
расстояние с?м/ от произвольной точки М прямой 1г до прямой /;
легко видеть, что это расстояние не зависит от выбора точки М
(см. тот же рис. 162). Расстояние diif между прямыми 1г и / можно
также определить как длину dfjiN отрезка NtN, высекаемого пря-
прямыми 1Х и I на произвольной пер- ,
пендикулярной к ним прямой р; ^v \h 'Л у>М
ясно, что это определение равно-
равносильно первоначальному. Величина
расстояния между параллельными
особыми прямыми k и kx или
расстояния от точки М до осо-
особой прямой k в геометрии Минков-
ского никак не определяется1).
Заметим, что в геометрии Мин-
ковского нельзя уже, разумеется,
говорить, что перпендикулярные
прямые образуют между собой //у' ^^\5
л
угол _-,—напротив, так как эти
две прямые всегда будут разного
рода, то ни о какой «величине» угла между ними мы пока не можем
говорить. Однако сам факт наличия перпендикулярных прямых уже
2) Это связано с тем, что если k, kY—две произвольные (параллельные
между собой) особые прямые и М, М1—две произвольные точки (либо
одновременно принадлежащие k и kt, либо одновременно не принадлежащие
этим прямым), то существует движение A1) или (Па), переводящее А в А* и
М в Mi.
Рис. 163.

206
3AIU1IO4FHHE
позволяет сопоставить двум разноименным прямым (т. е. пря-
прямым, одна из которых 1-го рода, а другая — 2-го) / и 1г некоторое
число так, что совпадение этого числа для двух пар прямых равно-
равносильно «равенству» этих пар (т. е. возможности перевести одну из
них в другую движением A1) или (Па)): это число равно (направ-
(направленному!) углу б/'/,, где /' _1_ / (рис. 1G3). Разумеется, определен-
определенную таким образом величину мы должны считать несравнимой
с величиной угла между двумя прямыми 1-го рода или с величиной
угла между двумя прямыми 2-го рода.
Укажем еще, что если А, В, Мо— три точки плоскости Минков-
ского и прямые АВ, АМ0, ВМ0 — все неособые (т. е. прямые 1-го
или 2-го рода), то множество всех таких точек М, что (направлен-
(направленный) угол между МА и MB равен углу между М0А и Л?0В ^десь
считается, что МА — прямая того же рода, чго и Л1ОА, a MB — того
же рода, что и М0В; если же прямые МА и М0А, а также MB и
М0В — разного рода, то надо требовать, чтобы угол между МА
и MB был равен углу между М0А' и МйВ', где М0А' А_М0А,
М0В' J_МйВ), представляет собой окружность S, проходящую
через точки А, ВиМ0 (рис. 164, а). В частности, еслиточки Аи В фикси-
фиксированы, то множество всевозможных точек М таких, что МА J_ MB,
представляет собой окружность с диаметром АВ (рис. 164, б).
Рис. 164.
Далее нам понадобятся некоторые сведения, касающиеся «триго-
«тригонометрии гиперболы». Пусть 51 — «единичная окружность»
**-/=1 A8)
плоскости Мниковского с центром О@, 0) и пусть ОА — неподвиж-
неподвижный радиус окружности 5 (причем А(\, 0) — вершина гиперболы
A8)), а ОМ — подвижный радиус (ср. рис. 165 с рис. 165а, на

§ 11]
ГЕОМЕТРИЯ МННКОВСКОГО
207
котором изображены евклидова окружность
х2-\ у2 =¦ 1
A8а)
и два ее радиуса ОА и ОМ). Направленный угол 6Ол.ом=ф (пони-
(понимаемый в смысле геометрии Минковского, т. е. равный взятой со
Рис. 165.
Знаком-j-или — удвоенной площади заштрихованного на рис. 165
сектора АОМ гиперболы S) называют также гиперболическим
углом между прямыми ОА и ОМ; координаты х = ОР^>0 и у = РМ
подвижной точки М называют гиперболическим косинусом и гипер-
гиперболическим синусом угла ф и обозначают сЬф и ship. Отношение
РМ shq>
=——2—
г—
...
по аосолютнои величине равное длине отрезка AN,
высекаемого «подвижным радиусом» ОМ на касательной AT к гипер-
гиперболе 5 в ее вершине Л, называют гипер-
гиперболическим тангенсом утла ф и обозна-
обозначают через th ср.
Из рис. 165 видно, что при неогра-
неограниченном увеличении ума ц. величины
ch ф и sh<р также растут неограниченно,
a thф стремится к 1; далее, при ф—0
имеем сЬф=1, shф = 0 и Шф=0. На-
Наконец, из того же рис. 165 вытекает, что
ch(— ф) =
A9а)
(подобно тому как cos (—ф) = cos ф);
sh(— ф) = — ьЬф A96)
sh,
Рис.166.
(подобно тому как sin (— ф) = —sin ф); в силу этого и
th( —ф)=—Шф A9в)
(подобно тому как tg (— ф) = —tgф). Графики функций и = сЬф,
н = БПф и н = Шф изображены на рис. 166.

208 ЗАКЛЮЧЕНИЕ
Гиперболические функции обладают многими свойствами, род-
родственными свойствам тригонометрических функций sin ср, соз ф и tg cp;
эти свойства могут быть несложно доказаны с использованием пово-
поворотов A3а) или A3) х). Так, например, из уравнения A8) гипер-
гиперболы 5 следует, что при любом угле ср
сЬ2ф — sh2cp=l. B0)
Далее, при любых значениях углов ф и ч|)
Бп(ф ± ч|з) = sh ф ch ч|) + ch©shi|) B1а)
и
ch (ф ± -ф) = ch ф ch ф ± sh cp sh т]з, B16)
откуда в свою очередь следует, что
^ B1в)
Из формул B1а)—B1в) легко получаем также, что
sh 2ср= 2 sh ф ch ср,
2th|
I+th-f 2thf
th
и т. д.
Заметим, наконец, что фигурирующие в формулах A1) коэффи-
1 —v _. „
циенты . и . связаны между собой соотношением
У 1 1J yfy y2 J
» / -v У_!
сходным с равенством B0), связывающим гиперболические функции
сЬф и БЬф. Поэтому если мы подберем такой гиперболический
. — v , . 1
угол а, что sh гу, = то будем иметь спп= в силу
чего формулы A1) можно переписать так:
у' = х sh a-\-y ch a + b
1) См., например, книгу Шерватова [57], гл. IX книги Н о р-
дена [62] или п. 27 книги Я г лома и Ашкинузе [56].

''1 геометрия минковского 209
евкли-
т)
Обратимся теперь к учению о треугольниках плоскости
Минковского; при этом всегда будем считать, что стороны АВ ^ с
#с=« и LA = b рассматриваемого треугольника ABC являются
неособыми прямыми. Если все эти стороны являются прямыми одного
рода, то отрезки АВ = с, ВС = а и СА = Ь (длины сторон треуголь-
треугольника мы оудем обозначать теми же буквами а, Ь, с, что и соответ-
соответствующие прямые) можно сравнивать между собой; при этом еспи
только точки А, ВпС не принадлежат одной прямой то большая
сторона треугольника ABC обязательно будет больше сцммы децх
других сторон (см. рис. 167, гце АМ=АС = Ь и BN=BC=a так
Рис. 167. Рис ]67а>
что a + b = BN+AM<AB = c; ср. с рис. 167а, иллюстрирующим
известное неравенство а + Ь>с, связывающее стороны треуголь.
ника в геометрии Евклида).
Неравенство
а-\-Ь<с
(где с-наибольшая сторона треугольника ABC), можно также вы-
вывести и из так называемой «теоремы косинусов,, геометрии
Минковского: если все стороны треугольника ABC-прямые одного
роба, то
a2 = b* + c*-2bcchA, B4a)
где А=ЬАВ Ас~ (ненаправленный, т. е. положительный) угол между
сторонами АВ и АС треугольника ABC (понимаемый, разумеется в
смысле геометрии Минковского1)). Далее, площадь треугольника
может быть определена по формуле
плАВС = -1 ab sh С. B5)
») Выше у нас были определены лишь функции chq>, shrc и then ne
ф-угол между двумя прямыми 1-го рода; функции сЛ. sh* и Д где
4>-угол (в смысле геометрии Мннк)
фу ду двумя прямыми 1го рода; функции сЛ. sh* и Д где
4>-угол (в смысле геометрии Мннковского) между прямыми m и т, 2-г о
^^ТГГГХТ^ РаВеНСТВМИХ ™ - функция-м угла

210
ЗАКЛЮЧЕНИЕ
Из формулы B5), в частности, следует, что
-н- ab sh С = ^ (ic sh В = -у
откуда без труда получаем
"shC
B46)
(«теорема синусов»). Формулы B4а, б) и B5) можно также
перенести и на случай треугольника ABC, имеющего стороны раз-
разного рода; мы, однако, здесь на этом не остановимся.
Скажем еще несколько слов о «равнобедренных» и «пря-
«прямоугольных» треугольниках плоскости Минковского (из неравен-
неравенства с^>а-\-Ь следует, что «равносторонний» треугольник, все
Рис. 168.
стороны которого равны между собой, в плоскости Минковского
существовать не может). Если стороны АС и ВС треугольника ABC
равны (и, значит, АС и ВС—прямые одного рода), то вершины А
и В треугольника принадлежат окружности 5 с центром С и радиу-
радиусом СА — СВ (рис. 168, а). Примем точку С за начало координат;
тогда с помощью «поворота» A3а) или A3) медиану СМ треуголь-
треугольника (где М— середина стороны АВ) можно совместить с осью Ох.
Стороны СА' и СВ' полученного таким образом треугольника А'В'С
расположатся симметрично (в евклидовом смысле!) прямой Ох
(рис. 168, б), откуда следует, что медиана СМ равнобедренного
треугольника одновременно является его биссектрисой и «высотой)».
[Из того, что CM J_ АВ, вытекает, что основание АВ равнобедрен-
равнобедренного треугольника всегда является прямой другого рода, чем его
боковые стороны.] Нетрудно вывести из рис. 168, б также и аналог

§ 11]
ГЕОМЕТРИЯ МИНКОВСКОГО
211
теоремы о равенстве углов при основании равнобедренного тре-
треугольника.
Пусть теперь ABC—«прямоугольний» треугольник, т. е. АС_]_ВС
(рис. 169, а). При этом катеты АС и ВС треугольника обязательно
Рис. 169.
будут прямыми разного рода; предположим, что «гипотенуза» АВ
является прямой того же рода, что и катет ВС. В таком случае,
как нетрудно показать (ср. рис. 169, а с рис. 169, б, где точка
С — вершина гиперболы S),
c=cchB, b = cs\\B, b = athB. B6)
Из первых двух формул B6) и соотношения B0)
вытекает «теорема Пифагора»:
а2 —?2 = с2. B7)
Заметим также, что из сравнения второй из фор-
формул B6) и формулы B5) следует, чго площадь
произвольного треугольника ABC можно также
определить так:
уа-Лв, B5')
Рис. 170.
где ha = bshC—длина йАР «высоты» АР треугольника ABC, опу-
опущенной на сторону ВС=а (рис. 170).
Теорема о точке пересечения медиан треугольника переносится
на случай геометрии Мннковского без всякого изменения: (евклидово)
доказательство этой теоремы (ср. § 4 гл. I, в частности, стр. 64)
полностью сохраняет силу и в плоскости Минковского. Также и три
перпендикуляра, восставленных к сторонам треугольника ABC

212
ЗАКЛЮЧЕНИЕ
в его серединах, пересекаются в одной точке О — в центре опи-
описанной окружности 5 треугольника (рис. 171, а). [Заметим,
что если стороны треуготьника ABC одного рода и длина радиуса
Рис. 171.
описанной вокруг треугольника окружности равна R, то
shB shC
(докажите!).] Отсюда, в точности как в случае евклидовой геомет-
геометрии, устанавливается, что также и три высоты треугольника ABC
пересекаются в одной точке (рис. 171, б).
Треугольник плоскости Минковского имеет три биссектрисы лишь
в том случае, когда все стороны его — прямые одного рода: ведь
угол, образованный разноименными прямыми / и llt никак не может
иметь биссектрисы, т. е. прямой, образующей с / и с /L равные

§ 11]
ГЕОМЕТРИЯ МИНКОВСКОГО
213
углы1). Однако, если треугольник ABC имеет три биссектрисы (мы
знаем, что, например, в случае равнобедренного или прямоугольного
треугольника дело обстоит заведомо не так), то они пересекаются
в одной точке; эга точка о является центром вписанной окруж-
окружности s, касающейся всех сторон треугольника (рис. 171, в).
[Ясно, что если не все стороны треугольника являются прямыми
одного рода, то окружности, касающейся всех сторон треугольника,
существовать не может, ибо, например, все касательные окружности
1-го рода являются прямыми 2-го рода.]
Нетрудно видеть, что в геометрии Минковского, как и в геометрии
Евклида, касательные РА и РВ, проведенные к окружности S с центром Q
из одной точки Р, равны между собой и что прямая QP (т. е. проходящий
через точку Р диаметр окружности S) делит пополам отрезок АВ и перпен-
перпендикулярна прямой АВ (рис. 172). Укажем еще, что середины всех проходящих
Рис. 172.
Рис. 173.
через фиксированную точку М хорд окружности S принадлежат одной окруж-
окружности s (гр. рис. 173, где точка М принадлежит S). Наконец, середины сторон
треугольника ABC и основания его высот (а также точки, делящие пополам
отрезки высот, заключенные между точкой пересечения высот и вершинами
треугольника) принадлежат одной окружности S-i, радиус которой равен по-
половине радиуса описанной окружности S треугольника. Окружность Sx можно
назвать окружностью шести (девяти) точек треугольника ABC
плоскости Минковского; если треугольник ABC имеет вписанную окружность
s, то окружность шести (девяти) точек Sx треугольника ABC касается его
вписанной окружности s (рис. 174).
Рассмотрим теперь окружность 5 плоскости • Мннковского
и точку М (рис. 175). Нетрудно показать, что произведение
МА ¦ MB = dMA ¦ dMR, B8)
J) Биссектрису угла, образованного прямыми / и lt, можно описать как
множество точек, равноудаленных от I и от /х (отсюда, кстати сказать, сразу
вытекает сформулированная ниже теорема о точке пересечения биссектрис
треугольника). Но если прямые /и /х разноименные, то равноудален-
равноудаленных от / и 1\ точек не С}ществует вовсе, ибо расстояние от точки до прямой
1-го рода и расстояние от точки до прямой 2-го рода принципиально не-
несравнимы: первое из них измеряется в единицах длин отрезков 2-го рода
(так сказать, в «мнимых» единицах; ср. выше, стр. 200), а второе—в единицах
длин отрезков 1-го рода (в «действительных» единицах).

214
ЗАКЛЮЧЕНИЕ
где А и В — точки пересечения проходящей через точку М прямой I
с окружностью S, зависит только от окружности S и от точки М,
Рис. 174.
но не от выбора прямой 1. Это произведение, которому мы еще усло-
условимся приписывать знак плюс, если направ-
направления отрезков МЛ н MB (от Мк Л, соответ-
Dl ственно от М к В) одинаковы и / — прямая
1-го рода или если направления отрезков МА
и MB противоположны и / — прямая 2-го
рода, и знак минус в обратном случае1),
называется степенью точки М
относительно окружности ?
Можно показать, что степень точки
М(х0, у0) относительно окружности S, запи-
записываемой уравнением A6') (стр. 201),
Рис. 175. Равна „ .
т. е. равна результату подстановки в уравнение A6') окружности S
J) Вот здесь нам очень удобно условиться считать длины отрезков 2-го
рода мнимыми: при этом определение знака произведения B8) остается таким
же, как в геометрии Евклида или в геометрии Галилея.

§ 111
ГЕОМЕТРИЯ МИНКОВСКОГО
215
координат х0, уп точки М. Отсюда без труда получаем, что мно-
множество точек плоскости Минковского, имеющих относительно дан-
данной окружности S данную степень k, представляет собой окружность,
Рис. 176.
концентрическую с окружностью S (т. е. окружность s, центр
которой совпадает с центром окружности S; рис. 176, а), и что
множество точек, имеющих одинаковые степени относительно двух
окружностей S и S1 с уравнениями A6') и
A6'а)
представляет собой прямую линию

218
ЗАКЛЮЧЕНИЕ
ЧТО
kx
'х--у-
ky
У Х- — У1
или
B9)
V =
2Х
Отсюда, используя уравнение A6') окружности плоскости Мннковского,
без труда устанавливаем, что прямую 1-го или 2-го рода, проходящую
(соответственно, не проходящую) через центр инверсии Q, это пре-
преобразование переводит в ту же самую прямую (в окружность, про-
проходящую через центр инверсии; рис. 179, а), а окружность, прохо-
проходящую (не проходящую) через центр инверсии,— в прямую, не
Рис. 179.
проходящую через центр инверсии (в окружность, также не прохо-
проходящую через центр инверсии; рис. 179, б); особые прямые инверсия
переводит снова в особые прямые. Можно также показать, что
инверсия является конформным преобразованием плоскости
Мннковского: две линии Г и Гъ пересекающиеся в точке А, инвер-
инверсия переводит в две такие линии Г' и Г',, пересекающиеся в точке А',
что угол, образованный проведенными в точке А касательными t
и t1 к линиям Г и Гх, равен (в смысле геометрии Мннковского)
углу, образованному проведенными в точке А' касательными f
и t\ к линиям Г' и Т\. Все эги свойства инверсии могут быть
использованы для доказательства многочисленных теорем геометрии
Минковского; примеры этого (ср., например, выше, стр. 152—157) мы
предоставим читателю отыскать самостоятельно.
Остановимся еще в заключение на некоторых важных общих моментах,
связанных с преобразованием инверсии. Ясно, что определение B8а) инвер-
инверсии не позволяет найти образ А' такой точки А, расстояние <1qa которой от
центра инверсии Q равно нулю (ибо в этом случае соотношение B8а) приво-
приводит к нелепому выводу: ^„^, = 00). Но множество точек М плоскости

§ 11] ГЕОМЕТРИЯ МИНКОВСКОГО 219
Минковского, определяемое равенством
QM = dQM = 0, C0)
представляет собой совокупность двух проходящих через точку Q особых
прямых ql и q.,, т. е. оно еще более богато точками, чем в случае плоскости
Галилея *). Поэтому положение здесь оказывается даже более сложным, чем
в геометрии Галилея: строго говоря, следует считать, что на плоскости Мин-
Минковского инверсия представляет собой преобразование, «полем действия»
которого является не вся плоскость Минковского, а плоскость с исключенными
из нее двумя прямыми q^ и q.,; если точка Q совпадает с началом системы
координат {х, (/}, то уравнения прямых qY и q» имеют вид х = у, х=—у.
Ясно, что столь сложный характер «поля действия» инверсии в геометрии
Минковского влечет за собой многочисленные осложнения, с которыми мы
сталкиваемся при изучении свойств инверсии и при всех применениях этого
преобразования.
Устранить все эти затруднения можно тем же путем, каким мы шли
в случае геометрии Евклида ил» геометрии Галилея. Условимся считать, что
«полем действия» инверсии с центром инверсии О @, 0) является плоскость
Минковского я, дополненная множеством «бесконечно удаленных точек» —
образов точек особых прямых qx и q.2, проходящих через начало координат;
иными словами, будем считать, что каждой точке М (т, т) особой прямой qt
отвечает некоторая бесконечно удаленная точка fij^', а каждой точке N (п,—п)
особой прямой q, — бесконечно удаленная точка Qjf', в которые переводит
точки М и N инверсия с центром О и степенью 1; самому же центру инвер-
инверсии О сопоставим бесконечно удаленную точку Q = йо"Е Qo2', в которую
переводится точка О любой инверсией с центром О. Плоскость Минковского,
дополненную бесконечно удаленными точками От , Q'n\ й (где т и п пробе-
пробегают множество всех действительных чисел), можно назвать круговой пло-
плоскостью Минковского'2); эта круговая плоскость представляет собой естест-
естественное поле действия инверсии и других «круговых преобразований»,
т. е. преобразований, переводящих каждую окружность A6') плоскости Мин-
Минковского (в частности, прямую — при о = 0 в A6')) снова в окружность (или
в прямую).
Наглядно представить себе круговую плоскость Мимковского позволяет
стереографическая проекция (ср. § 9 гл. II, стр. 159—173). Пред-
Предположим, что наша плоскость Минковского я, отнесенная к координатам х, у,
совпадает с плоскостью г -0 трехмерного пространства {х, у, г}. Рассмотрим
однополостный гиперболоид у с уравнением
=Х или *2-j/2 + z*-z = 0, C1)
касающийся плоскости я (плоскости 2 = 0) в точке 0@, 0, 0) и одновременно
пересекающий ее по (особым) прямым qY и q2 с уравнениями у = х и (/ = — х
J) Это множество точек мы выше назвали «окружностью нулевого радиуса»
или «окружностью нулевого рода» с центром Q.
2) Некоторые соображения, па которых мы здесь не остановимся, застав-
заставляют дополнять круговую плоскость AliiHKOBCKoro еще двумя фиктивными
«бесконечно удаленными точками» 2Х и 2.,, переводимыми в себя инверсией
с центром О (ср. ниже, стр. ?87; см. также, например, § 5 книги Я г лома
[77] или статью Я г л о м а [78]).

218
что
ЗАКЛЮЧЕНИЕ
§ И]
ГЕОМЕТРИЯ МИНКОВСКОГО
л — w »
или
B9)
у/ Д
Г ~2Х '
Отсюда, используя уравнение A6') окружности плоскости Минковского,
без трут,а устанавливаем, что прямую 1 -го или 2-го рода, проходящую
(соответственно, не проходящую) через центр инверсии Q, это пре-
преобразование переводит в ту же самую прямую (в окружность, про-
проходящую через центр инверсии; рис. 179, а), а окружность, прохо-
проходящую (не проходящую) через центр инверсии,— в прямую, не
Рис. 179.
проходящую через центр инверсии (в окружность, также не прохо-
проходящую через центр инверсии; рис. 179, б); особые прямые инверсия
переводит снова в особые прямые. Можно также показать, что
инверсия является конформным преобразованием плоскости
Минковского: две линии Г и Г\, пересекающиеся в точке А, инвер-
инверсия переводит в две такие линии Г" и Т\, пересекающиеся в точке А',
что угол, образованный проведенными в точке А касательными t
и t1 к линиям Г и Г\, равен (в смысле геометрии Минковского)
углу, образованному проведенными в точке А' касательными f
и t\ к линиям Г" и Т[. Все эти свойства инверсии могут быть
использованы для доказательства многочисленных теорем геометрии
Минковского; примеры этого (ср., например, выше, стр. 152—157) мы
предоставим читателю отыскать самостоятельно.
Остановимся еще в заключение на некоторых важных общих моментах,
связанных с преобразованием инверсии. Ясно, что определение B8а) инвер-
инверсии не позволяет найти образ А' такой точки .4, расстояние d^.4 которой от
центра инверсии Q равно нулю (ибо в этом случае соотношение B8а) приво-
приводит к нелепому выводу: UqA, = оо). Но множество точек М плоскости
Минковского, определяемое равенством
219
C0)
представляет собой совокупность двух проходящих через точку Q особых
прямых цх и Цл, т. е. оно еще более богато точками, чем в .случае плоскости
Галилея 1). Поэтому положение здесь оказывается даже более сложным, чем
в геометрии Галилея: строго говоря, следует считать, что на плоскости Мин-
Минковского инверсия представляет собой преобразование, «полем действия»
которого является не вся плоскость Минковского, а плоскость с исключенными
из нее двумя прямыми qx и q.,; если точка Q совпадает с началом системы
координат {х, у}, то уравнения прямых qt и qt имеют вид х = у, х ——у.
Ясно, что столь сложный характер «поля действия» инверсии в геометрии
Минковского влечет за собой многочисленные осложнения, с которыми мы
сталкиваемся при изучении свойств инверсии и при всех применениях этого
преобразования.
Устранить все эти затруднения можно тем же путем, каким мы шли
в случае геометрии Евклида или геометрии Галилея. Условимся считать, что
«полем действия» инверсии с центром инверсии 0@, 0) является плоскость
Минковского л, дополненная множеством «бесконечно удаленных точек» —
образов точек особых прямых qx и q.2, проходящих через начало координат;
иными словами, будем считать, что каждой точке М (т, т) особой прямой q1
отвечает некоторая бесконечно удаленная точка Qm\ а каждой точке N (п,—п)
особой прямой q.2 — бесконечно удаленная точка Oj,2), в которые переводит
точки .И и N инверсия с центром О и степенью 1; самому же центру инвер-
инверсии О сопоставим бесконечно удаленную точку Q = йо" = йо2), в К0Т0РУЮ
переводится точка О любой инверсией с центром 0. Плоскость Минковского,
дополненную бесконечно удаленными точками Qm\ Qn2), Q (где тип пробе-
пробегают множество всех действительных чисел), можно назвать круговой пло-
плоскостью Минковского'1); эта круговая плоскость представляет собой естест-
естественное поле действия инверсии и других «круговых преобразований»,
т. е. преобразований, переводящих каждую окружность A6') плоскости Мин-
Минковского (в частности, прямую —при а- -О в A6')) снова в окружность (или
в прямую).
Наглядно представить себе круговую плоскость Минковского позволяет
стереографическая проекция (ср. § 9 гл. II, стр. 159—173). Пред-
Предположим, что наша плоскость Минковского л, отнесенная к координатам я, у,
совпадает с плоскостью г=-0 трехмерного пространства {х, у, г}. Рассмотрим
однополостный гиперболоид у с уравнением
—к- =-г или
2 — </2 + 2а — 2 = 0,
C1)
касающийся плоскости л (плоскости 2 = 0) в точке 0@, 0, 0) и одновременно
пересекающий ее по (особым) прямым q^ и q2 с уравнениями у = х и у — — х
1) Это множество точек мы выше назвали «окружностью нулевого радиуса»
или «окружностью нулевого рода» с центром Q.
2) Некоторые соображения, на которых мы здесь не остановимся, застав-
заставляют дополнять круговую плоскость Минковского еще двумя фиктивными
«бесконечно удаленными точками» 2j и 22, переводимыми в себя инверсией
с центром 0 (ср. ниже, стр. ?87; см. также, например, § 5 книги Я г лома
[77] или статью Я г л о м а [78]).

218
что
ЗАКЛЮЧЕНИЕ
§ И]
ГЕОМЕТРИЯ МИНКОВСКОГО
л — w »
или
B9)
у/ Д
Г ~2Х '
Отсюда, используя уравнение A6') окружности плоскости Минковского,
без трут,а устанавливаем, что прямую 1 -го или 2-го рода, проходящую
(соответственно, не проходящую) через центр инверсии Q, это пре-
преобразование переводит в ту же самую прямую (в окружность, про-
проходящую через центр инверсии; рис. 179, а), а окружность, прохо-
проходящую (не проходящую) через центр инверсии,— в прямую, не
Рис. 179.
проходящую через центр инверсии (в окружность, также не прохо-
проходящую через центр инверсии; рис. 179, б); особые прямые инверсия
переводит снова в особые прямые. Можно также показать, что
инверсия является конформным преобразованием плоскости
Минковского: две линии Г и Г\, пересекающиеся в точке А, инвер-
инверсия переводит в две такие линии Г" и Т\, пересекающиеся в точке А',
что угол, образованный проведенными в точке А касательными t
и t1 к линиям Г и Г\, равен (в смысле геометрии Минковского)
углу, образованному проведенными в точке А' касательными f
и t\ к линиям Г" и Т[. Все эти свойства инверсии могут быть
использованы для доказательства многочисленных теорем геометрии
Минковского; примеры этого (ср., например, выше, стр. 152—157) мы
предоставим читателю отыскать самостоятельно.
Остановимся еще в заключение на некоторых важных общих моментах,
связанных с преобразованием инверсии. Ясно, что определение B8а) инвер-
инверсии не позволяет найти образ А' такой точки .4, расстояние Uqa которой от
центра инверсии Q равно нулю (ибо в этом случае соотношение B8а) приво-
приводит к нелепому выводу: UqA, = оо). Но множество точек М плоскости
Минковского, определяемое равенством
219
C0)
представляет собой совокупность двух проходящих через точку Q особых
прямых цх и q», т. е. оно еще более богато точками, чем в .случае плоскости
Галилея 1). Поэтому положение здесь оказывается даже более сложным, чем
в геометрии Галилея: строго говоря, следует считать, что на плоскости Мин-
Минковского инверсия представляет собой преобразование, «полем действия»
которого является не вся плоскость Минковского, а плоскость с исключенными
из нее двумя прямыми qx и q.,; если точка Q совпадает с началом системы
координат {х, у}, то уравнения прямых qt и q.> имеют вид х = у, х ——у.
Ясно, что столь сложный характер «поля действия» инверсии в геометрии
Минковского влечет за собой многочисленные осложнения, с которыми мы
сталкиваемся при изучении свойств инверсии и при всех применениях этого
преобразования.
Устранить все эти затруднения можно тем же путем, каким мы шли
в случае геометрии Евклида или геометрии Галилея. Условимся считать, что
«полем действия» инверсии с центром инверсии 0@, 0) является плоскость
Минковского л, дополненная множеством «бесконечно удаленных точек» —
образов точек особых прямых qx и q.2, проходящих через начало координат;
иными словами, будем считать, что каждой точке М (т, т) особой прямой q1
отвечает некоторая бесконечно удаленная точка Qm\ а каждой точке N (п,—п)
особой прямой q.2 — бесконечно удаленная точка Oj,2), в которые переводит
точки .И и N инверсия с центром О и степенью 1; самому же центру инвер-
инверсии О сопоставим бесконечно удаленную точку Q = йо" = йо2), в К0Т0РУЮ
переводится точка О любой инверсией с центром 0. Плоскость Минковского,
дополненную бесконечно удаленными точками Qm\ Qn2), Q (где тип пробе-
пробегают множество всех действительных чисел), можно назвать круговой пло-
плоскостью Минковского'1); эта круговая плоскость представляет собой естест-
естественное поле действия инверсии и других «круговых преобразований»,
т. е. преобразований, переводящих каждую окружность A6') плоскости Мин-
Минковского (в частности, прямую —при а- -О в A6')) снова в окружность (или
в прямую).
Наглядно представить себе круговую плоскость Минковского позволяет
стереографическая проекция (ср. § 9 гл. II, стр. 159—173). Пред-
Предположим, что наша плоскость Минковского л, отнесенная к координатам я, у,
совпадает с плоскостью г=-0 трехмерного пространства {х, у, г}. Рассмотрим
однополостный гиперболоид у с уравнением
—к- =-г или
2 — </2 + 2а — 2 = 0,
C1)
касающийся плоскости л (плоскости 2 = 0) в точке 0@, 0, 0) и одновременно
пересекающий ее по (особым) прямым ql и q2 с уравнениями у = х и у — — х
1) Это множество точек мы выше назвали «окружностью нулевого радиуса»
или «окружностью нулевого рода» с центром Q.
2) Некоторые соображения, на которых мы здесь не остановимся, застав-
заставляют дополнять круговую плоскость Минковского еще двумя фиктивными
«бесконечно удаленными точками» 2j и 22, переводимыми в себя инверсией
с центром 0 (ср. ниже, стр. ?87; см. также, например, § 5 книги Я г лома
[77] или статью Я г л о м а [78]).

220
ЗАКЛЮЧЕНИЕ
(рис. 180). Условимся теперь сопоставлять каждой точке А (х, у) плоскости я
точку А' (х, у, г) пересечения гиперболоида у с прямой QA (отличную от А),
где Q @, 0, 1)—точка гиперболоида у, «диаметрально противоположная» точке О
(т. е. симметричная с точкой О относительно центра симметрии гиперболоида);
нетрудно видеть, что при этом
х-—{/2+1
У
C2)
(ср. с формулами D2) и D2'), стр. 161 и 169). Стереографическая проекция C2)
сопоставляет каждой точке плоскости я единственную точку гиперболоида у;
Рис. 180.
однако обратное соответствие между точками гиперболоида и точками плоскости
не является полным, поскольку точкам проходящих через центр проекции
(через точку Q) прямых ot и о2 с уравнениями у=х, г=\ и у = —х, z = l,
параллельных плоскости я, не отвечают никакие точки плоскости п.
Таким образом, оказывается удобным считать, что гиперболоид у является
образом плоскости л, дополненной двумя фиктивными «прямыми», так сказать,
«проектирующимися» в прямолинейные образующие ot и о, гиперболоида Y1)-
*) Нетрудно убедиться, что прямолинейные образующие
x—y=c(\—z), x+y=—z
x+y=d(l—z), x—y=-j
гиперболоида у отвечают в силу стереографической проекции C2) особым
прямым
у = х—с и г/ — —x-\-d
плоскости Минковского л; поэтому следует считать, что прямолинейным обра-
образующим ох и о2 отвечают «бесконечно удаленные особые прямые» плоскости л.
Это словоупотребление хорошо отвечает тому факту, что инверсия плоскости
Минковского переводит каждую особую прямую снова в особую прямую;
поэтому уместно считать, что особые прямые qx и q^ она переводит в «беско-
«бесконечно удаленные особые прямые» круговой плоскости Минковского.

§ 11] ГЕОМЕТРИЯ МИНКОВСКОГО 221
Сопоставив точки прямых ох и о2 бесконечно удаленным точкам Q^J' и ^«2>
плоскости я, а центр проекции Q — точке Q, мы сможем говорить, что стерео-
стереографическая проекция C2) представляет собой отображение гиперболоида у
на круговую плоскость Минковского Я, что позволяет рассмат-
рассматривать (однополостный) гиперболоид как «модель» круговой плоскости Мин-
Минковского.
Из формул C2) следует, что точки окружности (или прямой) A6')
плоскости Минковского стереографическая проекция отображает на точки
сечения гиперболоида у плоскостью
oz + 261x+2&2</+c(l— z) = 0; A6")
обратно, каждому плоскому сечению гиперболоида V отвечает окружность
(или прямая) плоскости я. При этом прямым отвечают сечения гипер-
гиперболоида у плоскостями, проходящими через точку Q (О, 0, 1); особым пря-
м ы м — сечения у плоскостями, проходящими через Q и содержащими прямо-
прямолинейную образующую гиперболоида у (ср. со сноской на предыдущей
странице); окружностям нулевого радиуса — сечения гипер-
гиперболоида у плоскостями, касающимися у (и в силу этого содержащими пару
прямолинейных образующих). В самом деле, например, точкам прямой, за-
записываемой уравнением A6'), где а = 0, стереографическая проекция сопостав-
сопоставляет точки сечения гиперболоида у плоскостью
очевидно, проходящей через точку Q (О, 0, 1). Поскольку в силу нашего со-
соглашения точка Q @, 0, 1) отвечает точке Q круговой плоскости Минковского,
то приходится считать, что все прямые «проходят» через бесконечно удаленную
точку Q. Произвольная же окружность A6') «содержит» одну бесконечно
удаленную точку Q',\' и одну бесконечно удаленную точку Q/,2'; эти точки
изображаются точками пересечения плоскости A6") с прямыми ог и о2-
То обстоятельство, что стереографическая проекция C2) переводит окруж-
окружности (и прямые) плоскости Минковского в плоские сечения гиперболоида,
позволяет использовать эту проекцию для представления «круговых преобра-
преобразований» (круговой) плоскости Минковского я. Рассмотрим, например,
столь простое преобразование гиперболоида у как симметрию относитель-
относительно горизонтальной плоскости 6 — плоскости г=1/2, т. е. преобразование, пере-
переводящее каждую точку Лх гиперболоида у в такую его точку Alt что
i4!i4i_L6 (рис. 181). Ясно, что эта симметрия переводит каждое плоское
сечение гиперболоида снова в плоское сечение. Поэтому отвечающее нашей
симметрии в силу стереографической проекции преобразование плоскости я,
т. е. преобразование, переводящее точку А плоскости я (соответствующую
точке Ai гиперболоида у в силу стереографической проекции) в точку А'
плоскости я (соответствующую точке Лх гиперболоида у), должно быть круго-
круговым. Нетрудно обнаружить, что это преобразование плоскости Минковского
является не чем иным, как инверсией с центром О и степенью 1 (инвер-
(инверсией с окружностью инверсии S, отвечающей в силу стереографической проек-
проекции сеченик гиперболоида у плоскостью 6),— это обстоятельство может быть
принято за определение инверсии и позволяет вывести все свойства
этого преобразования из свойств стереографической проекции. Использование
стереографической проекции позволяет также установить, что все круговые
преобразования плоскости Минксвского я, отличные от преобразований подобия
(т. е. от преобразований, переводящих каждые две точки А и В плоскости Я
в такие точки А' и В', что ——— = — = ?, где k—фиксированный коэффи-
А" ЯАВ

222
ЗАКЛЮЧЕНИЕ
циент подобия), можно представить в виде инверсии, сопровождаемой преобра-
преобразованием подобия; на доказательстве этой основной теоремы теории
Рис. 181.
круговых преобразований плоскости Минковского мы
здесь не остановимся.
§ 12. Геометрия Галилея как предельный случай
геометрий Евклида и Минковского
Итак, нам уже известны три различные геометрические системы,
действующие на обычной (аффинной) плоскости: геометрия Евклида
(школьная геометрия), геометрия Галилея, которой и была посвящена
основная часть этой книги, и геометрия Мннковского, с которой
мы вкратце познакомились в предыдущем параграфе. В процессе
всего изложения мы неоднократно обращали внимание на большую
близость эгих трех «геометрий». Многие теоремы формулируются
во всех трех геометриях совершенно одинаково; сюда относятся,
например: теорема о точке пересечения медиан треугольника; тео-
теорема об окружности (цикле) шести точек; теорема о степени точки
относительно окружности (или цикла); определение и свойства инвер-
инверсии (инверсии 1-го рода) и т д. Другие теоремы видоизменяются
при переходе от одной геометрии к другой, сохраняя, однако, какие-то
общие черты,— трудно, например, не признать «родственниками»
евклидову теорему синусов:
Ь с (ЪЪг)
а
sin A
sin В sin С

§ 12] ГЕОМЕТРИИ ГАЛИЛЕЯ, ЕВКЛИДА И МННКОВСКОГО 223
«теорему синусов» геометрии Галилея (см. формулу A3) на стр. 62):
а - Ь - с mi
и соответствующую теорему геометрии Мннковского (формула B46)
на стр. 210):
При этом в тех случаях, когда те или иные факты выглядят в трех
геометриях различно, геометрия Галилея, зачастую, оказывается
как бы «промежуточной» между геометриями Евклида и Мннковского:
так, например, если а^й^с — стороны (невырожденного, т. е. не
обращающегося в отрезок) треугольника, то
а \ Ь>с C4а)
в геометрии Евклида,
а' Ь^с C4)
в геометрии Галилея (см. формулу A1) на стр. 61) и
а ! Ь < с C46)
в геометрии Мннковского (стр. 209)г); уравнение окружности имеет
в геометрии Евклида в «естественных» (т. е. в декартовых прямо-
прямоугольных) координатах вид
а (х" - _у2) ;- 2Ьхх + 2/vy {- с =- 0 C5а)
(см. выше, стр. 85), в то время как уравнение цикла геометрии
Галилея имеет вид
ах2~\~2Ь1х + 2Ь.лу+с^0 C5)
(см. формулу B) на той же стр. 85), а уравнение окружности плос-
плоскости Мннковского — вид
а(х2— у2) + 2Ь1х + 2Ьгу+с = 0 (Зоб)
(ср. с формулой A6') на стр. 201) и т. д.
Вот еще один выразительный пример того же рода. При представлении
круговой плоскости Евклида весьма полезной была стереографическая
проекция — центральная проекция плоскости z = 0 трехмерного простран-
пространства {х, у, г) из точки Q @, 0, 1) на сферу о с уравнением
22_z = 0 C6a)
') Разумеется, уже неравенства a<ib^c предполагают, что все стороны
рассматриваемого треугольника плоскости Мннковского сравнимы между собой,
т. е. суть отрезки одного рода.

224 ЗАКЛЮЧЕНИЕ
(см. формулу D0) на стр. 160 и рис. 128). В случае геометрии Галилея сход-
сходную роль играет отображение плоскости г = 0 на цилиндр ?:
—у] =-j- или x2+z3—z = 0 C6)
(формула D0') на стр. 168 и рис. 134), а в случае геометрии Минковского —
отображение той же плоскости на (однополостный) гиперболоид у:
—9~) =Т или *'~~У' + г2 —2 = 0 C66)
(формула C1) на стр. 219 и рис. 180). При этом само понятие круговой (или
циклической) плоскости связано с наличием на плоскости «особых» точек, не
переводимых инверсией с центром Q ни в какие точки плоскости; это
множество точек («окружность нулевого радиуса» с центром Q) в геометрии
Евклида состоит из единственной точки Q, в то время как в гео-
геометрии Галилея оно представляет собой одну прямую, проходящую
через точку Q, а в геометрии Мннковского—две прямые, проходящие
через Q.
Связь геометрии Евклида (и геометрии Минковского) с геометрией
Галилея можно пояснить следующим образом. Выше (см. стр. 192) мы
уже указывали, что в случае земных скоростей, весьма малых по
сравнению со скоростью света, принцип относительности Эйнштейна
почти не отличается от классического принципа относительности
Галилея. В «геометризнрованной» форме это утверждение означает,
что если единица измерения длин вдоль оси Оу плоскости Минков-
Минковского (оси, указывающей положение точки на прямой о в терминах
«одномерной кинематики») является очень большой по сравнению
с единицей измерения длин вдоль оси Ох (оси времени; выше мы так
выбирали единицу измерения длин вдоль прямой о, чтобы скорость
света была равна 1, т. е. принимали за единицу длины расстояние,
которое свет проходит в единицу времени,— брали ее равной
300 000 км, если за единицу времени принята 1 сек), то геометрия
Минковского оказывается весьма близкой к геометрии Галилея.
В физике с этим обстоятельством связана возможность использования
классической механики Галилея—Ньютона во всех физических за-
задачах, не связанных с рассмотрением космических скоростей, близких
к скорости света (см. конец настоящего параграфа); в геометрии же
оно проливает дополнительный свет на близость псевдоевклидовой
геометрии Минковского к геометрии Галилея.
«Промежуточный» характер геометрии Галилея по отношению
к геометриям Евклида и Мннковского определяется аналогией формул
для расстояния й между точками А(х,у) и А1(х1,у1) в плоскости
Евклида
—уJ C7а)
(ср. с формулой A) на стр. 16), в плоскости Галилея
d- = (xx-xf C7)

§ 12]
ГЕОМЕТРИИ ГАЛИЛЕЯ, ЕВКЛИДА И МННКОВСКОГО
225
(см. формулу E) на' стр. 51) и в плоскости Минковского
<Р={Х1-х)*-{У1-у)*
C76)
единица
(формула A5'а) на стр. 200). Предположим теперь, что в геометрии
Евклида или в геометрии Мннковского единица О?'2 измерения длин
вдоль оси Оу заменяется новой единицей ОЕ'„ = — ОЕ2, а
О?\ = ОЕ[ измерения длин вдоль оси
Ох не меняется (рис. 182). В таком слу-
случае, если х, у — старые координаты точек
на плоскости, в которых расстояние меж-
между двумя точками определяется по фор-
формуле C7а),соответственно C76), а х ,у —
новые координаты, возникающие после j
указанного изменения единицы измерения
длин вдоль оси Оу, то .
X — X И у
или
: = х и у =
су
У= TJ
C8)
D
1\
I
I
I
I
I
Рис. 182.
Отсюда следует, что в координатах х', у' расстояние d между двумя
точками А(х, у) и А1(х1,у1) или А(х',у') и Ах {х\, у[) записывается
так:
или, если снова отбросить штрихи, обозначая новые координаты
по-прежнему через х и у, так:
t Q ж ¦ О I / V О
соответственно
(З7'а)
(З7'б)
Если теперь устремить с к бесконечности, т. е. считать «натураль-
«натуральную» единицу ОЕ1 измерения длин вдоль оси Ох исчезающе малой
по сравнению с единицей ОЕ% измерения длин вдоль оси Оу, то мы
придем к знакомой формуле
(P = {Xl — x)*, C7)
выражающей расстояние между двумя точками плоскости Галилея,
8 И. М. Яглом

226
ЗАКЛЮЧЕНИЕ
Мы и далее будем обозначать «новые» координаты, в которых
расстояние между двумя точками А и Ах измеряется по формулам
(З7'а)— (З7'б), теми же буквами х, у, что и раньше; на чертежах мы
будем изображать принятые единицы ОЕ[ и ОЯ2' измерения длин
вдоль осей Ох и Оу по-прежнему равными и даже будем применять
для них обозначения ОЕХ и ОЕп, помня, однако, что «равноцен-
«равноценная» ОЕ1 единица ОЕ2 измерения длин вдоль осп Оу представляет
У
Ё2.
0
[
д
В
~т~
i
I
I
w
д
i
i
i
X
-«-**,
Рис. 183.
собой с-кратное от единицы ОЕ2 (см. рис. 183, с, б, где с = 5). При
этом (измеренная по формуле (З7'а), соответственно (З7'б)) длина
отрезка ААХ будет совпадать с понимаемой в смысле геометрии Евк-
Евклида или геометрии Мннковского (т. е. измеренной по формуле C7а)
или C76)) длине отрезка ААЪ имеющего ту же, что и отрезок ААи
проекцию на ось Ох, но в с раз меньшую проекцию на ось Оу.
Устремляя с к бесконечности, мы в пределе как раз и приходим
к концепции геометрии Галилея, где длина отрезка определяется
исключительно его проекцией на ось Ох.
Заменим теперь отрезок А4Х отрезком АВ, параллельным оси Оу.
1
В этом случае отрезок АВ будет попросту составлять ¦—ю часть
с
первоначального отрезка АВ (см. тот же рис. 183); неограниченно
увеличивая с, мы придем к сравнению отрезка АВ с и с ч е з а ю щ е
малым отрезком АВ геометрии Евклида или геометрии Мннковского

§ 12] ГЕОМЕТРИИ ГАЛИЛЕЯ, ЕВКЛИДА И МННКОВСКОГО 227
с одинаковыми единицами измерения длин вдоль обеих осей, откуда
и следует, что при с—*-оо длина й подобного отрезки стремится
к нулю: d—>0. Последнее обстоятельство особенно легко усмотреть
в случае предельного перехода к геометрии Галилея от геомет-
геометрии Мин ко веко го. Рассмотрим две прямые
у = ±сх, C9)
любой отрезок которых имеет в геометрии Минковского нулевую
длину; выше (стр. 199) мы назвали такие прямые (а также и парал-
параллельные им прямые) особыми прямыми геометрии Мннковского.
Из рис. 183, б, на котором изображены «особые» прямые, пересекаю-
пересекающиеся в точке А, видно, что при с —>~ оо такие прямые неограниченно
приближаются к вертикали (т. е. к прямой, параллельной оси Оу);
в пределе их можно считать совпавшими с вертикалью, которая тем
самым обращается в (единственную при закрепленной точке А)
прямую нулевых длин отрезков.
Последнее обстоятельство можно проиллюстрировать еще и по-
другому. На рис. 183, а, б изображена также «единичная окруж-
окружность» 5 с центром А, т. е. множество точек, удаленных от точки А
(координаты которой мы теперь обозначим через а, Ь) на расстоя-
расстояние 1. Из формул (З7'а) и (З7'б) следует, что уравнение этой «окруж-
«окружности» имеет вид
(*-«J + ^=1. D0а)
соответственно
(х-«J-^1=1, D06)
т. е. что линия 5 представляет собой эллипс или гиперболу с полу-
полуосями 1 н с. Ясно, что при возрастании с линия 5 все более «вы-
«вытягивается» в направлении оси Оу; можно считать, что при с —*¦ оо
линия 5 обращается в пару (параллельных) прямых
(х — аJ=1 D0)
— единичную окружность плоскости Галилея. [На рис. 183, б имеется
также линия St с уравнением
D0в)
представляющая собой множество точек, тоже удаленных от А на
расстояние 1, но на качественно иное расстояние 1, отвечающее
длинам отрезков оси Оу. При с —>¦ оо эта «окружность» St сжимается
в соответствии с уменьшением того угла между особыми прямыми
(пересекающимися в точке А), внутри которого она расположена,
и, кроме того, неограниченно удаляется от точки А,
8*

228 ЗАКЛЮЧЕНИЕ
неизбежно исчезая из пределов сколь угодно обширного чертежа —
это соответствует исчезновению отрезков ненулевой длины, имею-
имеющих иную природу, чем отрезок ОЕХ.]
Перейдем теперь к вопросу о трансформации (евклидовых) углов
при описанном изменении единиц измерения длин. Мы знаем, что
(евклидов) угол б между прямыми
y = kx-\-s и y = k1x-\-sl D1)
определяется по формуле
(см. формулу C) на стр. 50). Замена переменных по формулам C8)
обращает уравнения D1) в следующее:
у' = ckx' -\-cs и у' = ckxx' -\- csx или у' —k'x'-\-s' и у' = k'xx' -j- sj,
D1')
где, в частности, k' = ck и kt = cklt т. е.
k —k' и k-.= — k\.
с * с
Подставляя теперь эти значения угловых коэффициентов k и kx
в исходную формулу D2а) и условившись не только обозначать
новые координаты х', у' по-прежнему через х и у, но также и но-
новые угловые коэффициенты k', k\ по-прежнему записывать симво-
символами k и kx, мы получим, что после изменения координат по форму-
формулам C8) угол б между прямыми D1) определится по формуле
D2')
±
Но при с—>- оо правая часть формулы D2'), очевидно, обращается
в нуль; другими словами, мы имеем tg б—>¦ 0, а следовательно, и
б—>¦ 0 — неожиданный и неприятный результат!
Впрочем, постигшая нас беда не принадлежит к числу особенно
серьезных. Из формулы D2') видно, что при очень большом с вели-
величина '~ тангенса угла б между прямыми D1) является очень
с 1 | 1
малой—она имеет порядок величины —1). Но известно, что при
С
х) Другими словами, при с-> со как tg6-»-0, так и > 0, причем
с
отношение tg6 : — стремится к конечному числу а Ф 0.
С

§ 12] ГЕОМЕТРИИ ГАЛИЛЕЯ, ЕВКЛИДА И МИНКОВСКОГО 229
малом угле б величина tg6 близка к величине самого угла б, изме-
измеренного, разумеется, в «естественной», т. е. в радианной, мере:
в самом деле, поскольку, как известно, lim . = 1 и lim cos6= I,
то, очевидно,
lim -^г- = 1. D3)
Таким образом, и величина (измеренного по формуле D2')!) угла б
между прямыми D1) при большом с является весьма малой: она
имеет порядок величины — .
С
Изменим теперь единицы измерения величин углов в новых коор-
координатах х', у', связанных со старыми формулами C8): примем, что
новая единица е' измерения углов связана со старой единицей е
(радианом!) равенством е' =— б. При этом новая величина б' угла ока-
окажется в с раз большей, чем прежняя величина угла б:
б' = сб пли 6=^-6'. D4)
Подставляя теперь это значение б в формулу D2') и заменяя затем
обозначение б' «новой» величины угла на прежнее обозначение б
(к этой операции мы, кажется, уже привыкли!), получаем
to-i = -i kl~k
с с '
или
ctZT = 7hT]b- D2">
Наконец, переходя к пределу при с —>- оо и учитывая, что
г , • . ¦• ^ . , .
lim ctg — =о lim —т- = о-1=б,
с-*» с 6с->0 ?
окончательно получаем
b = kl — k, D2)
т. е. получаем формулу для угла б между прямыми D1) плоскости
Галилея (см. формулу (8) на стр. 54). Совершенно аналогично можно
получить формулу D2) подстановкой C8) и из формулы
th8 = ?^ D26)

230 ЗАКЛЮЧЕНИЕ
для величины угла б между двумя (одноименными) прямыми D1)
плоскости Мннковского; (формулу D26) легко вывести нл формулы
B1в), стр. 208).
Заметим теперь, что из проведенного рассуждения слетует, что
описанная выше процедура изменения единиц измерения длин, при-
приводящая в результате последующего предельного перехода с —>¦ оо
к замене геометрии Евклида (или геометрии Мннковского) геомет-
геометрией Галилея, сопровождается уменьшением всех углов, так что
только лишь в результате изменения D4) единицы измерения углов
мы получаем конечные выражения для величин углов. Соответственно
этому при переходе от геометрии Евклида к геометрии Галилея мы
должны во всех формулах, в которых фигурируют углы, произвести
подстановку
б^А D4')
(см. вторую из формул D4)) и, кроме того,
sin б —>-sin — « — , cos б —> cos — ж 1 и tgS-^-tg — ^ — D3')
ее с п "ее
(ср. выше формулу D3) и родственные ей). В соответствии с этим
из евклидовой теоремы синусов
предельным переходом
а
sin Л
получаем
а
А/т
0
sin б
Ъ
В,т
с
sinC
с
С/т
C3а)
(здесь мы временно, вплоть до вывода формулы D6), употребляем
букву т в том значении, которое ранее имела буква с, к сожале-
сожалению, «занятая», для обозначения длины стороны АВ треуголь-
треугольника ABC), т. е. «теорему синусов» геометрии Галилея:
Аналогично из евклидовой теоремы косинусов
ao- = b2 + c' — 2bccosA D5а)
выводим:
а2 = Ь2 + с~—2Ьс-\ (=(c—bf),
т. е. известную формулу
с = а+Ь C4)
геометрии Галилея (здесь мы считаем, что с > а, с > Ь); из формулы

§ 12] ГЕОМК1РПН 1АЛНЛКЯ, КВКЛПДА II МЦНКОВСКОГО 231
длн площади треугольника в гео-метрии Евклида
С S
заменой sin С—>—, а также заменой «S1—»¦— (изменение единицы
измерения площадей!) получаем формулу
S=~abC D6)
для площади треугольника в геометрии Галилея (см. формулы A7')
и A7) на стр. 63—64) и т. д. Наконец, из формул
х'= х Qosa-\-y s\na-\- а,
D7а)
у' = — х sin а -{-у cos a -f- b
для евкчидовых движений (формулы F), стр. 20) с помощью под-
подстановки
1 . а ,
х —»¦ х, у —> — у, sin а —* — , cos а —с 1
С С
(см. C8) и D3'^ получаем
х =х-\ -f- \-a,
с с
или
-' — 4- —
у' = — ах -\-у + cb,
откуда, обозначая cb просто через Ь, величину —а—через г> и уст-
устремляя с к бесконечности, имеем
''°' D7)
т. е. формулы движений плоскости Галилея (формулы A) из § 3,
см. стр. 45). Аналогично могут быть получены формулы C3), C4),
D6) и D7) из соответствующих им формул геометрии Мннковского
(например, формулы D7) из формул B3), стр. 208); при этом только
приходится учитывать легко доказываемые соотношения
1- sh б ... t с ii. th б - ,ап>\
hm-g-=l, lim ch8= 1, lim -*- = 1. D3)
Обратимся теперь к вопросу об отношенпи евклидовой окружности
к циклу плоскости Галилея. Цикл мы определяли как множество
точек, из которых данный отрезок АВ виден под постоянным углом а

232
ЗАКЛЮЧЕНИЕ
(см. § 6 гл. II); поэтому и окружность мы здесь вынуждены пони-
понимать как множество S точек М(х,у) плоскости Евклида, из которых
данный отрезок АВ виден под постоянным {направленным) углом а
(рис. 184). Обозначив, в соответствии
У | | ^ ! с § 6, координаты точек А и В
через (аъ а2) и (blt b2), мы по-
получим, что угловые коэффициенты
k и k1 прямых AM и ВМ равны
k = ——- и &, = г1—-
«! — X Х Ъ^ — Х
(см. выше, стр. 84). В силу фор-
формулы D2а) для (евклидова) угла
между прямыми получаем отсюда,
что уравнение рассматриваемого
множества S точек М(х,у) имеет
вид
h — V "а—У
bt — х
bl—x
Ь-1—У _ пг—l
bx—x
а, —х
+ 1
¦ = tga,
или
— у) (а1 — х) — (Ь1—
2— у)—
"ft //
К/
Рис. 184.
или, наконец,
tg a (x2 +y*) + [(b2—a2) —tg a (
—tg«(«2 +
Ясно, что это есть уравнение окружности (на рис. 184 она
изображена жирным пунктиром).
Произведем теперь в нашем уравнении замену переменных:
x —>¦ x, у -+ f .
тогда получим

§ 12] ГЕОМЕТРИИ ГАЛИЛЕЯ, ЕВКЛИДА II МИНКОВСКОГО 233
или
=0, D86)
т. е. уравнение эллипса (на рис. 184 он изображен тонким пунк-
пунктиром). Наконец, предельный переход с —*- оо переводит уравнение
D86) в уравнение
—а.г)— ^
D8)
(евклидовой или аффинной) параболы, которая играет роль цикла
плоскости Галилея (она изображена на рис. 184 точками; ср. выше,
стр. 84—85). Также и все относящиеся к геометрии Галилея резуль-
результаты § 9 гл. II могут быть получены предельным переходом из
соответствующих предложений геометрии Евклида (доказанных в том
же параграфе!) или геометрии Минковского (см. § 11).
После всего сказанного не вызывает никаких затруднений и
вопрос о взаимоотношении «классической» и «релятивистской» меха-
механики, другими словами, принципов относительности Галилея и Эйн-
Эйнштейна. В § 10 мы всюду выбирали единицы длины и времени таким
образом, чтобы скорость света была равна 1; именно при таком
выборе единиц геометрическую картину кинематики прямой о, бази-
базирующейся на принципе относительности Эйнштейна, доставляет гео-
геометрия Минковского в той форме, как она строилась в § П. Однако
более обычным является иной выбор единиц измерения длин, при
котором единица длины в с раз больше рассматриваемой ранее еди-
единицы; это отвечает следующей подстановке, которую надо произ-
произвести во всех формулах из § 10:
t-+t,x-+±,v^Z. D9)
(ср. с формулами C8), стр. 225). В частности, равенство v=\ из
§ 10 сейчас заменяется следующим
-=1, т. е. v=c;
таким образом, с — это скорость света в рассматривае-
рассматриваемой (вообще говоря, произвольной) системе единиц длины и вре-
времени.
Произведя подстановку D9) в основных формулах G) из § 10,
|яы получим более распространенную запись преобразований

234
Лоренца:
ЗАКЛЮЧЕНИЕ
fi
или
E0)
— именно так записываются преобразования Лоренца вг> всех кни-
книгах [37] — [39] и [46] — [536] *). Ясно, что предельный переход
с —> оо переводит формулы E0) в формулы, выражающие преобра-
преобразования Галилея:
x' = x — vt, t' = t. E0')
Коэффициент 1 1 j фнтцджеральдова сокращения длин (стр. 185),
так же как и коэффициент 1,1/ 1—± (релятивистского) замедления
времени (стр. 187) при с —>¦ оо, обращаются в 1, т. е. в класси-
классической механике соответствующие эффекты не имеют места. Наконец,
формула
u-\-v
/W+1
E1)
сложения скоростей (формула (9), стр. 190) при нашей подстановке
переходит в формулу
или
W =
u-\-v
с с
которая при с —»¦ оо обращается в классическую формулу сложения
скоростей в механике Галилея — Ныогона:
w = u + v E1')
(формула (8), стр. 189).
х) Элементарные книги [40] — [43] вообще почти не содержат формул,
а авторы книг [44], [45] и [53в] принимают скорость света за 1 и записы-
записывают преобразования Лоренца формулами G).

ПРИЛОЖЕНИЕ А
ДЕВЯТЬ ГЕОМЕТРИЙ НА ПЛОСКОСТИ
Основное содержание настоящей книги составляло параллельное
рассмотрение двух геометрических систем, которые можно опре-
определить на (обычной или аффинной) плоскости,—хорошо известной
геометрии Евклида и более простой, но в ряде отношений неожи-
неожиданной для незнакомого с ней читателя геометрии Галилея. Однако
в Заключении (см. § 11) мы познакомились с третьей геометри-
геометрической системой — с геометрией Минковского, очень близкой к двум
предшествующим; с другой стороны, большинство читателей этой
книги, видимо, знает о существовании неевклидовой геометрии 'Лоба-
'Лобачевского (четвертая геометрия!) или даже знакомо с ее осно-
основами.
В настоящем Приложении мы поставим своей целью кратко оха-
охарактеризовать ряд плоских геометрий, включающий, в частности,
как геометрии Евклида, Галилея и Минковского, так и геометрию
Лобачевского. Все рассматриваемые в настоящем Приложении гео-
геометрии часто называют «неевклидовыми геометриями»; однако это
название, бесспорно уместное в отношении геометрий Галилея, Мин-
Минковского или Лобачевского, никак не подходит к самой геометрии
Евклида. Кроме того, современная наука знает множество геомет-
геометрических систем, отличных как от классической геометрии Евклида
(т. е. бесспорно «не евклидовых»), так и от всех геометрий, о кото-
которых мы здесь будем говорить; это обстоятельство также делает
термин «неевклидовы геометрии» довольно неудобным. Так как те
геометрии, о которых будет идти речь в настоящем Приложении,
были впервые указаны в 1871 г. знаменитым Феликсом Клейном1),
опиравшимся на несколько более ранние исследования англичанина
Артура К эли A821—1895J), то для их наименования мы будем
х) См. указанную в списке литературы статью Клейна [76] (немецкий
оригинал этой статьи вышел в свет в 1871 г.) или книгу Клейна [55].
2) Относительно истории открытия рассматриваемых здесь геометрий см.
краткий § 7 гл. X книги Клейна [55], обстоятельный учебник Кагана
[25] или стр. 184—193 очень интересной, но довольно трудной книги Клей-
Клейна [81], посвященной истории математики.

236 ПРИЛОЖЕНИЕ А
использовать тоже часто употребляющийся в литературе термин
геометрии Кэли—Клейна.
Согласно схеме Кэлн и Клейна на прямой линии о мы имеем
три существенно различные геометрии: (обычную) геометрию Евк-
Евклида, «.эллит ическую» геометрию Римана и «гиперболическую» гео-
геометрию Лобачевского. Евклидова геометрия на прямой
возникает при знакомом нам еще из средней школы правиле
В . А
а)
измерения длин отрезков: на прямой фиксируется «единица длины»
ОЕ и расстояние йдв между точками А я В прямой о определяется
формулой
(E) AB
Ш A)
(рис. 185, оI). При этом все «евклидовы движения» прямой о, т. е.
преобразования прямой, сохраняющие евклидово расстояние йлв
между точками, сводятся к
а) параллельным переносам (в направлении прямой о);
б) центральным симметриям (относительно точек прямой о).
Эллиптическую геометрию Римана можно воссоздать
на прямой о, если фиксировать вне о некоторую точку Q и поло-
положить, что «риманово расстояние» йлв между точками А и В пря-
прямой о равно (обычному, т. е. евклидову) углу /_AQB:
d%=/_AQB (la)
(рис. 185, б). Ясно, что если А, С, В — три последовательные
точки прямой о, то
(см. тот же рис. 185, б). Роль «эллиптических движений» прямой
о, сохраняющих «римановы расстояния» d^s между точками будут
играть:
АВ
х) Отношение -^= двух отрезков прямой о можно определить и не раз-
вивая полностью всю геометрию Евклида; мы здесь на этом не остановимся.

ДЕВЯТЬ ГЕОМЕТРИЙ НА ПЛОСКОСТИ 237
а) преобразования, порождаемые поворотами проходящих через
точку Q прямых—прямых пучка с центром Q, как мы будем гово-
говорить впоследствии,—на фиксированный угол а; такое преобразо-
преобразование переводит точку А прямой о в точку А', для которой
/_ AQA' = а;
б) преобразования, порождаемые осевыми симметриями в пучке
прямых с центром Q относительно проходящей через Q фиксиро-
фиксированной прямой /; это преобразование переводит точку А прямой о
в такую точку А', что прямая / является биссектрисой угла AQA'.
Наконец, гиперболическая геометрия Лобачев-
Лобачевского определяется на прямой о несколько более сложным обра-
образом. Для определения «расстояния Лобачевского» йдв между двумя
точками А и В прямой о надо зафиксировать две точки / и J этой
прямой; тогда
(рис. 185, е). Число k в этой формуле можно выбирать произвольно;
замена одного k другим (при сохранении одного и того же основа-
основания системы логарифмов, равного, скажем, 10) означает изменение
единицы измерения расстояний (длин отрезков). В «двойном отно-
отношении»
W(A, В;/, У) = ^:§1 B)
четырех точек А, В, I и J все фигурирующие в правой части
равенства B) отрезки удобно считать направленными; при
этом, для того чтобы двойное отношение W всегда было положи-
положительно (а неположительные числа логарифмовг) не имеют!), необ-
необходимо условиться, скажем, о том, что обе точки А и В принад-
принадлежат отрезку IJ. Таким образом, «гиперболическая прямая-» (или
«прямая Лобачевского») изображается отрезком IJ. Нетрудно
проверить, что если А, С, В—три последовательные точки отрезка
IJ (см. тот же рис. 185, е), то
в самом деле, очевидно,
W[A, С; I, J).W[Ct В; I, 7)= (^:g
и, следовательно,
log W(A, С; /, /) + log W(C, В; I, J) = \ogW{A, В; I, J).
Во всяком случае действительных.

238
ПРИЛОЖЕНИЕ А
Дллее, поскольку двойное отношение четырех точек прямой равно
двойному отношению четырех других прямолинейно расположенных
точек, полученных из первых четырех точек центральным проекти-
проектированием1), то «гиперболические движения» прямой о (точнее, «пря-
«прямой Лобачевского», т. е. отрезка IJ), сохраняющие «расстояния
Лобачевского» d^B, порождаются
а) симметрией относительно середины 5 отрезка IJ (ясно, что
эта симметрия не меняет двойных отношений четверок точек: если
точки А, В она переводит в точки А', В', то W(A, В; I, J) =
= W(A', В'; J, /));
б) центральными проектированиями отрезка IJ на отрезок IJX
из некоторой точки Оъ сопровождающимися обратным проектиро-
проектированием IJX на IJ из некоторой точки О2 прямой JXJ (рис. 186, а).
Рис. 186.
На рис. 186, б изображены полученные описанным методом «рав-
«равные» (в смысле геометрии Лобачевского) отрезки АВ, ВВг, BXB2,
В2ВЯ, ... Из этого рисунка видно, что, откладывая последовательно
от произвольной точки А «прямой» IJ любое число равных отрезков
АВ = BBX = Вфг = В2В3 = ...
(где равенство отрезков понимается в смысле геометрии Лобачев-
Лобачевского!), мы никогда не выйдем за пределы IJ, т. е. «прямая Лоба-
Лобачевского» IJ имеет бесконечную длину. [Последнее следует также
и из того, что если на рис. 185, е точка В стремится к /, то
W(A, В; I, J) = %--jj-+°° ("б0 В/-*°): поэтому d<$ — оо.]
Аналогично трем геометриям на прямой о можно ввести три
«геометрии» в пучке прямых с центром О, иными словами,
') См., например, книги Кокстера [19], Я г лома [10], Нордена
[62] или статью Яглома и Атанасяна [II].

ДЕВЯТЬ ГЕОМЕТРИЙ НА ПЛОСКОСТИ
239
ввести три системы измерения углов между прямыми пучка. Обыч-
Обычное «мероопределение углов» в пучке с центром О
Ь(^ = /_аОЪ (За)
(рис. 187, а; символ /_ мы здесь и дальше употребляем лишь
в смысле обычного—евклидова—-угла) называется эллиптическим.,
или римановым. Евклидово мероопределение углов, напротив, не
[О
вГ*
I /в 1 аГТ
совпадает с принятым в евклидовой геометрии; его можно опреде-
определить, зафиксировав не проходящую через точку О прямую q и
положив
где А н В — точки пересечения прямых а и b с q (рис. 187,6).
Ясно, что в пучке прямых имеется единственная прямая со||<7, обра-
образующая с любой другой прямой «бесконечно большой угол». Нако-
Наконец, гиперболическое мероопределение, или мероопределение Лоба-
Лобачевского, вводится в пучке прямых следующим образом: фиксируются
две прямые i н j пучка и для любых двух других прямых а и b
полагается
i ?_ (a, i) m sin
ab = k l°g
(«./Г sin
(Ь, i)\
(b, I))
C6)
(рис. 187, e); постоянная k здесь зависит от выбора единицы изме-
измерения углов. В «двойном отношении четырех прямых» a, b, i и j
W(a
w (а,
b, О
B')
все участвующие в образовании правой части равенства B') углы
удобно считать направленными; для того чтобы это двойное
отношение было положительным, надо, скажем, условиться, что
все прямые а, Ь,... принадлежат какой-то одной определенной паре

240
ПРИЛОЖЕНИЕ А
образуемых / и / вертикальных углов. Поскольку двойное отноше-
отношение B') четырех прямых пучка равно двойному отношению B) четы-
четырех точек пересечения этих прямых с произвольной пятой прямой
q (не проходящей, разумеется, через центр пучка)*), то величину
можно также определить равенством
где А и В — точки пересечения произвольно фиксированной прямой
q с прямыми а и Ь (см. тот же рис. 187, е). Из равенства (Зв),
в частности, следует, что каждая из прямых i и j образует с любой
другой прямой «бесконечно большой угол» (в смысле мероопреде-
мероопределения Лобачевского).
Теперь мы можем уже описать девять геометрий, которые,
согласно схеме Кэли — Клейна, определяются на плоскости. Пред-
Предположим, что мероопределение расстояний на любой прямой плос-
плоскости имеет какой-то один наперед указанный тип из трех возмож-
возможных типов «мероопределения длин» на прямой, т. е. оно может
быть евклидовым, эллиптическим (римановым) или гиперболическим
(мероопределением Лобачевского). Точно так же и мероопределение
углов в пучке прямых с центром в любой точке О плоскости будем
считать имеющим фиксированный тип — это мероопределение углов
также является евклидовым, эллиптическим или гиперболическим.
Комбинируя все возможные типы мероопределения расстояний и
мероопределения углов, мы получим 3-3 = 9 вариантов; в таблице I
перечислены все эти варианты с указанием названий соответствую-
соответствующей геометрической схемы.
Таблица
\. Тип мероопре-
^ч. деления длин
Тип мероопре-^4^^
деления углов ^\
Римана
Евклида
Лобачевского
I. Девять геометрий Кэли—Клейна на плоскости
Римана
Эллиптическая
геометрия
Римана
Антиевклидова
геометрия
Антигиперболи-
Антигиперболическая геомет-
геометрия
Евклида
Геометрия
Евклида
Геометрия
Галилея
Псевдоевклидова
геометрия
Минковского
Лобачевского
Гиперболическая
геометрия
Лобачевского
Антипсевдоевкли-
дова геометрия
Дважды
гиперболическая
геометрия
г) См. подстрочное примечание на стр. 239.

ДЕВЯТЬ ГЕОМЕТРИЙ НЛ ПЛОСКОСТИ
241
Знакомые нам геометрии Евклида, Галилея и Минковского зани-
занимают средний столбец этой таблицы. Во всех этих трех геомет-
геометриях метрика длин на прямой является евклидовой: длина отрезка АВ
АВ
определяется как отношение -qw , где ОЕ — «единичный отрезок»
этой прямой. При этом в евклидовой геометрии концы отложенных
от одной точки О отрезков единичной длины заполняют (обыкно-
(обыкновенную или евклидову) окружность 5 (рис. 188, а); мероопреде-
мероопределение углов в любом пучке прямых является «обычным», т. е. эллип-
эллиптическим (или римановым) и совпадает с исчислением длин дуг
единичной окружности 5, высекаемых соответствующими прямыми:
так, в обозначениях рис. 188, а, ЪаЪ = /_аОЬ=^- АВ.
В случае геометрии Галилея длины единичных отрезков,
отложенных от одной точки О, С привычной нам «евклидовой» точки
зрения будут различны: концы этих отрезков заполнят «окружность» 5
геометрии Галилея (рис. 188,6), представляющую собой пару
параллельных («особых») прямых (о таких прямых мы еще
будем говорить ниже). Мероопределение углов в любом пучке пря-
прямых будет евклидовым, т. е. не обычным: величина ЬаЬ угла
между прямыми а и b будет равна (евклидовой!) длине отрезка АВ,
высекаемого этими прямыми на «окружности», т. е. на прямой q
рис. 188, б (ср. этот рисунок с рис. 187, б). Заметим еще, что
«окружность» 5 не позволяет определить единичный отрезок на
прямой со || q; сравнивая отрезки этой прямой с иными отрезками,
мы вынуждены считать, что все они имеют нулевую длину. Но
такая «метрика» (определяемая тождеством dPQ= 0 для любых
точек Р и Q прямой со) не принадлежит ни к одному из трех
указанных выше типов «мероопределения длин»; между тем при
определении плоских геометрий Кэли — Клейна мы специально тре-
требовали, чтобы мероопределения длин на всех прямых имели один
и тот же характер. Однако при рассмотрении геометрии Галилея

242 ПРИЛОЖЕНИЕ А
мы, строго говоря, должны вообще исключить «особые прямые»
(т. е. прямые, параллельные д) из числа прямых (выше мы часто
так и поступали!): ведь в геометрии естественно требовать, чтобы
все прямые плоскости бьпи одинаковыми (или «равными»), в то
время как «особая прямая» плоскости Галилея существенно отли-
отличается от обыкновенной и не может быть совмещена с ней никаким
движением. Поэтому надо считать, что объектом изучения геометрии
Галилея является плоскость (ее можно назвать «плоскостью Гали-
Галилея»), состоящая из всех точек плоскости и всех обыкновен-
обыкновенных прямых (ср. выше, стр. 70). Эта «плоскость» полностью удо-
удовлетворяет наложенным нашей таблицей условиям.
Перейдем теперь к (псевдоевклидовой) геометрии Минков-
ского. В этой геометрии «единичная окружность» 5 — множество
концов всех отложенных от одной точки О отрезков единичной
длины — с евклидовой точки зрения представляет собой гипер-
гиперболу (рис. 188, в). Угол боЬ между двумя прямыми а и b мы выше
определяли равенством
где sA0R—площадь заштрихованного на рис. 188, в сектора «окруж-
«окружности Мннковского» 5" 1). Однако зту величину можно определить
и равенством
-к\ос
- « log
sjn z (а й • sjn z (fc>
где / и j—асимптоты гиперболы 5, или равенством
(Зв)
где Ао, Во, /0 и Jo — точки пересечения прямых о, b, i и j с фикси-
фиксированной прямой q, например, с касательной t к гиперболе в ее
вершине (докажите это!) 2); число k в формулах C6) и (Зв) опре-
определяется выбором основания системы логарифмов. Таким образом,
в плоскости Минковского «мероопределение углов» в пучке прямых
с центром в любой точке О плоскости является гиперболическим.
Заметим еще, что в соответствии с требованием «равенства»
любых двух прямых плоскости естественно считать, что «плоскость
') Заметим, что в евклидовой геометрии и в геометрии Галилея угол 6а(,
между прямыми а и Ь, пересекающимися в точке О, можно тоже определить
формулой
6
где s^ob — площадь высекаемого прямыми а и Ь сектора единичной евклидо-
евклидовой окружности, соответственно ^окружности Галилея1».
2) Величина 6„ь равна также (понимаемой в смысле геометрии Минков-
Минковского!) длине дуги АВ .единичной окружности'» S, где А и В—точки пере-
пересечения с S прямых а и Ъ.

ДЕВЯТЬ ГЕОМЕТРИЙ НЛ ПЛОСКОСТИ
243
Минковского» образуется всеми точками (обычной) плоскости и пря-
прямыми какого-то одного рода, скажем, прямыми 1-го рода. При
этом в геометрии Евклида каждую точку прямой а можно соеди-
соединить прямой с какой-то фиксированной вне а точкой А (рис. 189, о);
в геометрии Галилея, как мы знаем, на (обыкновенной) прямой а
имеется единственная точка, которую нельзя соединить с А
(обыкновенной) прямой, — так сказать, точка, «параллельная»
точке А (рис. 189, б); в плоскости же Мннковского на прямой
A-го рода) а имеется бесконечно много точек, которые нельзя сое-
соединить с А прямыми 1-го рода (рис. 189, е). С другой стороны, во
всех трех геометриях — Евклида, Галилея и Мннковского — через
точку А, не принадлежащую прямой а, проходит единственная
прямая, не пересекающая а (прямая, параллельная а).
Нам осталось описать шесть других геометрий Кэли — Клейна
на плоскости: (эллиптическую) геометрию Рнмана, (гиперболическую)
геометрию Лобачевского, дважды гиперболическую геометрию, а
также три геометрии, названия которых снабжены приставкой
«анти»,—антиевклидову, антнпсевдоевклидову и антигпперболичес-
кую. Это нетрудно сделать. Эллиптическая геометрия
Рим а на, по существу, является самой старой из известных людям
«неевклидовых» геометрий: в ином обличий ее знали еще в глубо-
глубокой древности, хотя впервые сопоставил ее с классической геомет-
геометрией Евклида и с (в те годы не так давно открытой) геометрией
Лобачевского только великий немецкий математик Бернгард Риман
A826—1866) в своей замечательной речи «О гипотезах, лежащих
в основании геометрии» A854 г.I).
*) Лекция Б. Римана, с которой он выступил в 1854 г. перед Ученым
советом Гёттингенского университета в качестве претендента на профессор-
профессорскую кафедру, содержала весьма общую концепцию геометрии, по широте
охвата и важности вполне способна ю соперничать с концепцией Ф. Клейна,

244
ПРИЛОЖЕНИЕ А
Рассмотрим единичную сферу 2 трехмерного евклидова прост-
пространства (т. е. сферу радиуса 1) и условимся называть прямыми
«большие окружности» сферы 2, т. е. сечения сферы 2 плоско-
плоскостями, проходящими через ее центр О (рис. 190, а). Если при
этом назвать «точками» просто точки сферы 2, то некоторым не-
неудобством явится то, что каждые две прямые будут пересекаться
в двух, а не в одной точке. Для того чтобы устранить это неу-
неудобство, мы назовем точкой эллиптической плоскости Римана сразу
Рис. 190.
пару диаметрально противоположных точек сферы; таким образом,
роль эллиптической плоскости будет играть не вся сфера 2, а
полусфера 2', причем надо еще отождествить между собой
(«склеить») диаметрально противоположные точки окружности, огра-
ограничивающей 2' (ср. рис. 190, б). Далее, под расстоянием йАВ
между двумя точками А к В прямой плоскости Римана (большой
окружности или, точнее, большой полуокружности) мы будем пони-
понимать длину дуги -—' АВ; ясно, что это «мероопределение» является
эллиптическим. Под углом ЬаЬ между двумя прямыми а и b эллип-
эллиптической плоскости Римана мы будем понимать просто двугранный
угол между плоскостями, содержащими большие полукруги а и b
(рис. 190,в); при этом, как нетрудно видеть, мероопределение
развитой последним в 1872 г. в лекции [8], произнесенной в аналогичной
обстановке в Эрлангенском университете; выделение эллиптической геометрии
является лишь одним (и притом весьма частным) результатом исследований
Римана (по этому поводу см., например, стр. 210—212 книги Клейна [81]).

ДЕВЯТЬ ГЕОМЕТРИЙ НА ПЛОСКОСТИ
245
углов в пучке прямых эллиптической плоскости будет «обычным»,
т. е. эллиптическим. Роль «движений» определенной таким образом
плоскости" Римана играют всевозможные повороты сферы 2 (рас-
(рассматриваемой как множество пар диаметрально противоположных
точек) вокруг ее центра О х).
Сходным образом можно также описать гиперболическую
геометрию Лобачевского и дважды гиперболичес-
гиперболическую геометрию. Заменим
(обычное) трехмерное пространство
Рис. 191.
Евклида псевдоевклидовым пространством, в котором
расстояние d между двумя точками А(х, у, z) и Al(xl, yx, zx) (где
х, у, z—обычные декартовы координаты в пространстве) измеря-
измеряется по формуле
di = (xl — хJ 'г(Ух—уJ — (z1 — zJ, D)
в то время как в евклидовом пространстве расстояние d между точ-
точками А(х, у, z) и А1(х1, уъ zt) вычисляется по формуле2)
-yf+(z1 — z)'\ D')
J) Таким образом, эллиптическая геометрия Римана оказывается очень
близкой к так называемой «сферической геометрии», изучающей геометричес-
геометрические образы на поверхности сферы (см. по этому поводу, например, статьи
Розенфельда [79] и Розенфельда и Яглома [24]).
2) Ср. подстрочное примечание на стр. 16.

246
ПРИЛОЖЕНИЕ Л
Из формулы D) вытекает, что в трехмерном псевдоевклидовом
пространстве имеются «единичные сферы» двух родов: «сфера» ?г
с центром в начале координат О@, 0, 0) записывается уравнением
х2+у2 — z~= — 1 E)
(с евклидовой точки зрения это будет двуполостный гиперболоид,
рис. 191, а); «сфера» 22 записывается уравнением
-г*=\ E')
(она представляет собой одноиолостный гиперболоид, рис. 192, а).
Условимся теперь называть точками гиперболической плос-
плоскости Лобачевского пары диаметрально противоположных
«ж
Рис. 192.
точек сферы ?х (так что вся плоскость Лобачевского совпадает
с одной «полостью» 2] двуполостного гиперболоида, рис. 191, б),
а прямыми — «большие круги сферы» 2^, т. е. сечения гипербо-
гиперболоида Zt плоскостями, проходящими через его центр О. Ясно, что
каждая такая «прямая» будет представлять собой гиперболу (точнее,
одну ветвь гиперболы; см. те же рис. 191, а, б), «метрику расстоя-
расстояний» на которой можно определить подобно тому, как определяется
метрика углов в пучке прямых плоскости Мннковского, — эта «мет-
«метрика» будет, разумеется, гиперболическойх). «Пучок прямых»
J) Расстояние d^g между двумя точками А и В можно также определить
как «псевдоевклидову длину» отрезка АВ соответствующей «прямой», т. е. как
предел длин вписанных в —-АВ ломаных, где под длиной ломаной понима-
понимается сумма длин всех ее звеньев, причем длина отрезка с концами в точках
(х, у, г) и (*!, ylt Zj) определяется по формуле

ДЕВЯТЬ ГЕОМЕТРИЙ НА ПЛОСКОСТИ 247
определенной таким образом гиперболической плоскости Лобачевского
(изображаемый сечениями поверхности —^ пучком плоскостей, про-
проходящих через одну прямую; ср. рис. 191, в) будет иметь такой
же характер, как и пучок прямых на плоскости Евклида; в этом
пучке можно ввести эллиптическое (т. е. обычное) «мероопределение
углов», что совпадает с указанными приведенной выше таблицей
признаками плоскости Лобачевского—первой «неевклидовой» плос-
плоскости, на существование которой указал в 1829 г. замечательный
казанский геометр Николай Иванович Лобачевский A792—1856) х).
«Движения» плоскости Лобачевского определяются как «вращения
сферы» 2Х (или «полусферы» -,[), т. е. как такие преобразования
трехмерного пространства {х, у, z}, которые оставляют на месте
начало координат О и сохраняют расстояния D) между точками
(ясно, что эти преобразования переводят сферу 2^ в себяJ).
Обратимся теперь к «сфере» 23 (рис. 192, а). Отождествим и
здесь диаметрально противоположные точки, т. е. рассмотрим «по-
«полусферу» 2» с отождествленными диаметрально противоположными
точками ограничивающей ее «окружности» (рис. 192, б). Условимся
точки этой «полусферы» И'„ называть точками конструируемой
«плоскости»; прямыми же мы назовем сечения «сферы» Z, (или
«полусферы» Ъ!г) плоскостями, проходящими через центр О и пере-
пересекающими 22 по гиперболе (не по эллипсу!). В таком случае на
каждой прямой (т. е. на гиперболе) можно будет ввести гиперболи-
гиперболическое мероопределение длин3). С другой стороны, пучок прямых
нашей геометрии, проходящих через одну точку Q, задается пучком
плоскостей, содержащих прямую OQ = q и пересекающих конус 'К
С уравнением
x2-]y°-z* = 0 Eа)
(см. рис. 192, а, в). Устроен этот пучок подобно пучку прямых в плос-
плоскости Мнпковского — так, например, определяющий его пучок плос-
плоскостей содержит две «предельные» плоскости i и у, касающиеся
конуса ЭС, и состоит из плоскостей, заключенных внутри двугран-
двугранного угла, образованного плоскостями / и j. В таком пучке можно
ввести «гиперболическое мероопределение углов», определив ЬаЬ
*) Почти одновременно с Н. И. Лобачевским и независимо от пего к но-
новой геометрической схеме пришли также знаменитый немецкий математик
Карл Фридрих Гаусс A777—1855) и венгерский офицер Янош Б ой а и
A802—1860) (см. подстрочное примечание -) на стр. 5).
-) Такой подход к геометрии Лобачевского позволяет, опираясь на ана-
аналогию между евклидовым и псевдоевклидовым пространством, развить эту
геометрию весьма широко (см., например, статью Розенфельда и Я г-
л о \i a [24] или написанное Б. А. Розенфельдом Дополнение к книге Ка-
Кагана [25]).
3) См. подстрочное примечание на стр. 246.

248
ПРИЛОЖЕНИЕ А
между двумя прямыми а \\ b знакомой уже нам формулой
'sin / (а, 0 sin / (b, i)\
(где, скажем, через ^/ (a, /) обозначен обычный, т е. евклидов,
двугранный угол между плоскостью i и плоскостью, определяющей
«прямую» и). «Плоскость» с введенными таким образом расстоя-
расстояниями и углами является дважды гиперболической плос-
плоскостью; ее «движения» и здесь порождаются «поворотами сферы»
22 псевдоевклидова пространства (понимаемой как множество пар
диаметрально противоположных точек!) вокруг ее центра О. Заме-
Заметим еще, что как в гиперболической геометрии Лобачевского, так и
в дважды гиперболической геометрии через точку, лежащую вне
прямой а, проходит бесконечно много не пересекающих а
прямых (рис. 193, а, б); при этом в геометрии Лобачевского через
любые две точки А и В проходит единственная прямая (так как
через три точки А, В и О пространства можно провести единствен-
единственную плоскость), в то время как в дважды гиперболической геомет-
геометрии на не проходящей через точку А прямой а можно указать бес-
бесконечно много точек, не соединимых никакой прямой с точкой А
(ибо не все плоскости АОВ, где В — переменная точка гиперболы а,
будут пересекать S2 по гиперболе; см. рис. 193, в).
Наконец, заметим, что из каждой известной нам геометрии можно
получить новую (но чрезвычайно близкую к исходной!) «геометрию»,
условившись называть точки «прямыми», а прямые — «точками» (и,
соответственно этому, расстояния между точками — «углами между
прямыми», а углы между прямыми — «расстояниями между точками»).
Такое, чисто словесное, «преобразование» переводит, как мы знаем,

ДЕВЯТЬ ГЕОМЕТРИЙ НА ПЛОСКОСТИ
249
геометрию Галилея в себя (см. § 5 гл. [); оно также переводит
в себя эллиптическую геометрию Рнмана и дважды гиперболическую
геометрию (в которых также справедлив принцип двойственности).
Каждую же из трех других известных нам геометрий — Евклида,
Мпнковского и Лобачевского — оно переводит в геометрию, «двой-
«двойственную» исходной, или «антнгеометрию»: геометрию Евклида —
в ант и евклидов у, геометрию Минковского — в а н тип се в до-
евклидов у, геометрию Лобачевского — в антигиперболи-
антигиперболическую.
В заключение приведем таблицы, характеризующие девять гео-
геометрий Кэли — Клейна с точки зрения свойств «параллельности»
прямых и точек, а также укажем без доказательства (см., впрочем,
ниже, стр. 290—292) основные зависимости, связывающие в каждой
из рассматриваемых геометрий элементы произвольного треуголь-
треугольника ABC. При этом буквы «Р», «Е» и «Л» в таблицах II — IV ука-
указывают соответственно на эллиптический (Рнман!), евклидов или
гиперболический (Лобачевский!) характер соответствующего меро-
мероопределения; буквы а и А обозначают в таблицах II и III произ-
произвольную прямую и произвольную точку, не принадлежащую пря-
прямой а; через А, В, С обозначены в таблице IV величины углов
треугольника ABC, а через а^ВС, Ь^СА, с=еАВ — длины его
сторон х).
Таблица II. Число проходящих Таблица III. Число принадлежащих
через точку А прямых, не пересекаю- прямой а точек, несоединимых прямой
щих прямую а с точкой А
^ч. Мероопре-
^ч. деление
^ч. длин
Мероопре- ^ч.
деление \^
углов ^ч.
р
Е
Л
Р
0
0
0
Е
1
1
1
Л
00
00
00
^^ Мерэопре-
^ч. деление
^~. длин
Мероопре- ^^^
деление ^^^
углов \^
Р
Е
Л
Р
0
1
00
Е
-
0
1
00
л
0
1
00
Истолкование геометрии Лобачевского на плоскости через посредство
псевдоевклидовой геометрии в пространстве определяет любопытную связь
геометрии Лобачевского с теорией относительности Эйнштейна, которая иногда
проходит незамеченной. Рассмотрим релятивистскую (т. е. связанную с идея-
!) В ряде отношений оказывается удобным считать фигурирующие в таб-
таблице IV величины а, Ъ, с; А, В, С снабженными знаком + или —, т. е.
считать стороны и углы треугольника направленными; мы здесь на этом не
остановимся. Также не остановимся мы на принятом в таблице IV истолко-
истолковании понятий «сторона» и «угол», позволяющем, например, утверждать, что
в евклидовой геометрии А = В-^-С (теорема о внешнем угле треугольника).

Таблица IV. Метрические соотношения между элементами треугольника
ел
о
ч Мероопре-
>* деление
ч. длин
Моро- \^
онрсдс \
луние углоп\
Р
Е
Л
Р
cos a = cos b cos c-\- sin b sin с cos A
sin Л sin В sin С
sin a sin ft sin с
cos A = cos В соь C + sin В sin С cos о
a =ft f-c
ЛВС
sin a sin 6 sine
A2 --- В2 + С-+2ВС cos a
cos a =- cos ft cos c+ sin b sin с ch A
sh Л sh В sh С
sin a sin 6 sin с
ch Л = ch В ch C+ sh В sh С cos a
E
a2= .6'2 + c2 — 26c cos Л
sin A sin В sin С
a b с
A-- --B + C
a — b-\-c
ABC
a b с
A = B+C
sh A sh В sh С
a b с
Л
ch a = ch ft ch c + sh ft she cos A
sin Л sin В sin С
sh a sh ft sh с
cos Л = cos В cos C+ sin В sin С ch a
a -b-\-c
ABC
sh a sh ft sh с
Л3 = В- + С:!- -2BCcha
sh Л sh В sh С
sh a sh 6 sh с
ch A = chBchC + sh BshCcha
3
g

девять сиомктрий нл плоскости 251
ми теории относительности) кинематику плоских (или, точнее, плоско-парал-
плоско-параллельных) движений (ср. выше, стр. 28). Нетрудно видеть, что геометрически
эта кинематика равносильна учению о трехмерном пространстве {х, у, t),
«движения» которого определяются формулами, родственными формулам G)
и A0) из § 10 (стр. 185 и 193); так, например, переход от системы отсчета
\х, у, t) к системе отсчета \х', у', t'\, движущейся относительно первона-
первоначальной системы отсчета в направлении осп Ох со скоростью v, определяется
формулами
*'= у — i-\-n,
+ Ь, F)
Но легко видеть, что если (х, у, t) и (хи ylt /^ — координаты двух «собы-
«событий» в первой системе отсчета, а (х', у', t') и (х[, у\, t\) — wx координаты во
второй системе, то
И вообще, можно показать, что двумерная релятивистская кинематика сво-
сводится к геометрии трехмерного псевдоевклидова пространства \х, у, г\ с мет-
метрикой
yy-{zl-z^, D)
где время обозначено не буквой t, а буквой г.
Рассмотрим, далее, множество равномерных движений по плос-
плоскости. Как выше, можно показать, что каждому такому движению отвечает
некоторая прямая линия в трехмерном псевдоевклидовом пространстве,
изображающем множество всех событий (характеризующихся двумя простран-
пространственными и одной временной координатами); таким образом, множество всех
равномерных движений по плоскости с точки зрения теории относительности
эквивалентно множеству всевозможных прямых трехмерного псевдоевклидова
пространства. При этом для каждых двух движений естественным образом
определяется «отклонение» одного из них от другого: это «отклонение» задается
скоростью одного из рассматриваемых движений по отношению к дру-
другому, принятому за состояние покоя («относительной скоростью» в терминах
§§ 3 и 10). Это "своеобразное «мероопределение» в множестве всех равномер-
равномерных движений заставляет отождествить между собой все движения с одной
и той же (по величине и направлению!) скоростью, поскольку «расстояние»
между двумя такими движениями оказывается равным нулю; таким образом,
множество всевозможных равномерных движений сводится к множеству
равномерных движений, включающих фиксированное «событие» О@, 0, 0)
(ибо для каждого равномерного движения можно найти движение с той же
скоростью v, «исходящее» из «пункта» О @, 0, 0)). Но такие равномерные дви-
движения изображаются прямыми трехмерного пространства, проходящими через
начало координат О и заключающимися внутри конуса Ж с уравнением Eа)

252
ПРИЛОЖЕНИЕ А
(рис. 194); последнее условие равносильно условию v< 1, где v — скорость
рассматриваемого движения в какой-то инерциальной системе отсчета (здесь
за единицу скоростей, как и в § 10, принята скорость света *)).
Заменим теперь каждую из рассматриваемых прямых точкой ее пересе-
пересечения с «полусферой» Sj—одной полостью (евклидова) гиперболоида
Если вспомнить, что скорость одного равномерного движения относительно
другого совпадает с «углом» между двумя изображающими эти движения
прямыми в смысле псевдоевклидовой геометрии, а этот угол в свою очередь
равен «расстоянию» между точками пересечения соответствующих прямых
с Si в смысле действующей на Si неевклидовой геометрии Лобачевского, то
мы придем к выводу, что с точки зрения тео-
теории относительности Эйнштейна множество
всевозможных равномерных движений по плоско-
плоскости совпадает с плоскостью Лобачевского, если
за «расстояние» между движениями а и Ь при-
принята относительная скорость движения а по
отношению к движению Ъ.
Точно так же показывается, что множе-
множество всевозможных равномерных движений в
пространстве с точки зрения теории относи-
относительности Эйнштейна совпадает с трехмерным
пространством Лобачевского (относительно ко-
которого см., например, книги Н орден а [62],
Рис. 194. Кагана [75] или статью Розенфельда
и Я г л о м а [24]), если за расстояние между
движениями а и Ь принята скорость движения а по отношению к движению Ь.
«Полем действия» геометрий Евклида, Галилея и Минковского
является (обычная или аффинная2)) плоскость; геометрии Римана,
Лобачевского и дважды гиперболическая геометрия определяются
на «единичных сферах» трехмерного евклидова пространства с мет-
метрикой
d2-_ (Xl-X
D)
и трехмерного псевдоевклидова пространства с метрикой
рассматриваемых как множество пар диаметрально противополож-
противоположных точек. Этот путь построения плоских геометрий Кэли — Клейна
с помощью стереометрических конструкций может быть еще про-
продолжен. Заметим, прежде всего, что «сферу» 22 псевдоевклидова
пространства с уравнением
х2 -\-у2— г2 = 1,
E)
*) В теории относительности, как мы знаем, движения со скоростью
¦ 1 считаются невозможными!
2) См. по этому поводу, например, книгу Яглома и Ашкинузе [56].

ДЕВЯТЬ ГЕОМЕТРИЙ НА ПЛОСКОСТИ 253
рассматриваемую как множество пар диаметрально противополож-
противоположных точек, можно принять также и за «поле действия» антигипер-
болической геометрии — достаточно только считать точками антиги-
антигиперболической плоскости точки «полусферы» 1!2 (рис. 192, б), а
прямыми — линии пересечения 2!2 с плоскостями, проходящими через
начало координат О и пересекающими гиперболоид 22 по эллипсу
(не по гиперболе!I). При этом под «движениями» антигиперболи-
антигиперболической плоскости по-прежнему понимаются преобразования, порож-
порождаемые «поворотами» псевдоевклидова пространства вокруг точки О.
Наряду с евклидовым пространством и псевдоевклидовым про-
пространством рассмотрим еще вырожденное евклидово про-
пространство (или полуевклидово пространство) — трех-
трехмерное пространство {х, у, z\, в котором расстояние d между
точками (х, у, z) и (хъ ylt zx) вычисляется по формуле
-.y)B, G)
и вырожденное псевдоевклидово пространство (или
полупсевдоевклидово пространство), в котором рас-
расстояние между теми же двумя точками определяется так:
# = (х1-хУ-(у1-уУ. (Г)
«Движения» вырожденных евклидова и псевдоевклндова пространств
записываются формулами
jc'= cos a- x-\-siaa-y -%-a,
у' = —sin а- A.' + coscc-_y -\-b, (8)
z'= их-\- vy-{-wz-\-c,
соответственно
х' = a\\a-x-{-%Va-y -\-a,
/ = sha-.Y + cha-_y _j_^ (8')
z'= ux-\- vy-\-wz -\-c.
В самом деле, легко видеть, что если, например, координаты
X', у', z' связаны с координатами х, у, z формулами (8), то
(*; - д:'J + {у[ -у'? = [(хг - х) cos a + [У1 -у) sin a]2 +
+ [— (*i — х) sin a + 0>i —у) cos a]2 = {xt — xf + (уг —yf
(ср. формулы (8) ii (8') с формулами F) из § 1 и B3) из § 11,
стр. 20 и 208, выражающими движения на плоскостях Евклида и
Минковского).
1 Другими словами, плоскостями, не пересекающими конуса Ж с урав-
уравнением Eа).

254
ПРИЛОЖЕНИЕ А
lit
л
-\—
41
I
б'
«Единичные сферы» а и о1 вырожденных евклидова и псевдо-
псевдоевклидова пространств записываются уравнениями
х2+/ = 1 (9)
и
*2-/ = 1, (9')
т. е. с евклидовой точки зрения они представляют собой круговой
и гиперболический цилиндры (рис. 195, а и 196, а). Точку 0@, О, О),
находящуюся на оси каждого из
этих цилиндров, будем считать
центром цилиндра; далее, усло-
условимся рассматривать каждый из
цилиндров (9) и (9') как множество
пар своих диаметрально противо-
противоположных (т. е. симметричных отно-
относительно центра О) точек. В таком
случае цилиндры а и ог (точнее,
полуцилиндры а' и а[ с отождеств-
отождествленными диаметрально противопо-
противоположными точками края полуцилиндра
а'; см. рис. 195, б и 196, б) можно
принять за изображение («модель»)
и ант и псевдоевклидовой плоско-
плоскостей. При этом роль точек рассматриваемых плоскостей играют
точки «полусфер» о' и о[, а роль прямых — сечения а' и о[ пло-
плоскостями, проходящими через точку 0@, 0, 0); расстояние между
Рис. 195.
антиевклидовой
Рис. 196.
точками А и В совпадает с измеренными в смысле вырожденной
евклидовой или псевдоевклидовой геометрии длиной отрезка АВ
«прямой», а «угол между прямыми» а и b — с углом между соот-
соответствующими плоскостями в смысле той же действующей в трех-
трехмерном пространстве вырожденной евклидовой или псевдоевклидовой

ДЕВЯТЬ ГЕОМЕТРИЙ НА ПЛОСКОСТИ 255
геометрии (мы здесь не останавливаемся на точном определении
содержания последнего понятия). «Движения» антиевктпдовой inn
антппсевдоевклпдовой плоскости порождаются движениями (8) или (8')
трехмерного пространства, оставляющими на месте центр О (О, 0, 0)
сферы а или аг.
Также н три оставшиеся геометрии Кэли — Клейна,— а именно
геометрии Евклида, Галилея н Мнпковского,— могут быть описаны
сходным образом. Наряду с евклидовой метрикой D') и псевдоевклн-
довой метрикой D), вырожденной евклидовой метрикой G) и вырож-
вырожденной псевдоевклндовой метрикой G') расстояние d между точками
А(х, у, z) и А1(х1, уъ zt) трехмерного пространства можно опре-
определить и по формуле
аналогичной формуле C7) из § 12, стр. 224, выражающей расстоя-
расстояние между точками А (х, у) и А1 {хъ ух) плоскости Галилея. Меро-
Мероопределению A0), которое нам будет удобнее записывать так:
d^ = (zx-zf, A0а)
отвечают три геометрии в пространстве; «движения» в этих трех
геометриях задаются формулами
х' — cos а • х -\- sin а -у -\- vxz + a,
у'=—sin а ¦ х + cos а -у -\- voz + b, A1)
z' = z + c
(трехмерное пространство Галилея; ср. формулы A1) с фор-
формулами A2) из § 2, стр. 34), соответственно
х' = ch а-лг + sh а-у h^^ + a,
у'= sha-x-\-cha-y-\-v2z + b, AГ)
г'= z + c
(псевдогалилеево пространство; ср. с формулами B3) из
§ 11, стр. 208) и
х' = х -f- uy -f- vz + 0,
/= у \-wz + b, (На)
z — г-{ с
(вырожденное галилеево или «флаговое» простран-
пространство). При этом во всех этих трех геометриях «единичная сфера»
сг0 задается уравнением
2-2=1 или z=±\; A2)
т. е. представляет собой пару параллельных плоскостей (рис. 197, а).

256
ПРИЛОЖЕНИЕ А
Рассмотрим теперь «сферу» о0 как множество пар диаметрально
противоположных, т. е. симметричных относительно начала координат
О@, 0, 0), точек; другими словами, ограничимся рассмотрением
одной «полусферы» о'0 (плоскости; рис. 197, б). Если принять сече-
сечения этой «полусферы» проходящими через точку О плоскостями за
«прямые» соответствующей геометрии и назвать «движениями»
а)
Рис. 197.
«повороты» A1), A1') или A1а), оставляющие на месте центр
0@, 0, 0) сферы а0, то мы придем к евклидовой геометрии,
псевдоевклидовой геометрии и к геометрии Галилея
на плоскости а'о.
Представление шести плоских геометрий Кэли—Клейна в виде сфер
в обыкновенном (евклидовом), псевдоевклидовом или вырожденном евклидовом
пространстве очень удобно для распознавания линий, ш рающнх в каждой из
этих геометрий роль (евклидовых) окружностей. Условимся называть циклами
такие линии плоскости Кэли—Клейна, которые «устроены одинаково в каж-
каждой своей точке>, иными словами, линии, допускающие «скольжения» по себе,
причем «скольжения», позволяющие совместить каждую точку линии с любой
другой ее точкой (ср. с § 7 гл. II). При таком понимании термина «цикл»
приходится считать циклами плоскости Евклида окружности и прямые линии
(записываемые ураввенлем C5а) из § 12, стр. 223); циклами плоскости Гали-
Галилея—линии, которые мы называли «циклами» раньше и которым теперь при-
придется присвоить какое-либо новое наименование, например «невырожденные
циклы», а также окружности и (обыкновенные и особые) прямые (все эти
линии записываются уравнением C5), стр. 223); циклами плоскости Минков-
ского—«окружности» и прямые (эти линии записываются уравнением C56),
стр. 223). Можно доказать, что все циклы каждой из шести геометрий К,эли—
Клейна—эллиптической (Римана), гиперболической (Лобачевского), дважды
гиперболической, антигиперболической, антиевклидовой и антипсевдоевклидо-
вой—изображаются плоскими сечениями соответствующей «сферы» B, 21? 22,
Oj или с2). Так, например, роль циклов (эллиптической) геометрии
Римана играют прямые и окружности, где окружность, как и в
евклидовой геометрии, определяется как множество точек, равноудаленных

ДЕВЯТЬ ГЕОМЕТРИЙ НА ПЛОСКОСТИ 257
от одной точки, называемой центром окружности; если плоскость Римана
изображает евклидова сфера 2, то циклы этой плоскости изображаются пло-
плоскими сечениями сферы 2— как проходящими через центр О@, 0, 0) сферы 2
(прямые плоскости Римана), так и не проходящими через О (окружно-
(окружности плоскости Римана, рис. 198). [Заметим, что в сферической геометрии
каждая окружность имеет два центра, изображаемых точками касания сферы
с плоскостями at и сц, параллельными содержащей окружность плоскости а;
однако соответствующие точки Qt и Q., сферы 2 служат образом одной точки
плоскости Римана, так что в геометрии
Римана окружность имеет только
один центр. ]
Обратимся теперь к (гипербо-
(гиперболической) геометрии Лоба-
Лобачевского. Список всевозможных
циклов геометрии Лобачевского хоро-
хорошо известен: это суть прямые, окружно-
окружности (о к р у жн ост ь радиуса г —
множество точек, удаленных на рас-
расстояние г от одной точки Q, называе-
называемой центром окружности), эквиди-
станты (эквидистанта шири-
н ы h—множество точек, удаленных на
фиксированное расстояние h от одной
прямой q, называемой базой эквиди- "ис- '""•
станты), предельные линии (предель-
(предельная лини я—предельное положение проходящей через фиксированную точку А
и касающейся в этой точке заданной прямой а окружности, радиус г которой
неограниченно увеличивается, или предел касающейся в точке А прямой а экви-
дистанты, ширина h которой неограниченно увеличиваетсяI). Мы уже знаем,
что в связанной со «сферой» 2t «модели» плоскости Лобачевского прямые
изображаются сечениями 2Х плоскостями, проходящими через центр О @, 0, 0)
«сферы» 2Х и пересекающими конус SV с уравнением Eа) (ибо иные плоско-
плоскости, проходящие через точку О, не пересекают «сферу» 2t). Можно также
показать, что окружности плоскости Лобачевского изображаются сечениями
«сферы» 2t плоскостями а, не проходящими через О и пересекающими конус
SK (и «сферу» 2t) по эллипсу (рис. 199, а); эквидистанты — сечениями 2t
плоскостями р, не проходящими через О и пересекающими Ж по гиперболе
(рис. 198, б); предельные линии —сечениями 2Х плоскостями у, не проходя-
проходящими через О и пересекающими SfC по параболе (рис. 199, в). Заметим также,
что в плоскости Лобачевского центром окружности, изображаемой сечением
«сферы» 2t плоскостью а, служит точка касания 2t с плоскостью a01| a
(рис. 199, а), а базой эквидистанты, изображаемой сечением 2t плоскостью
Р,— линия q пересечения 2Х с проходящей через точку О @, 0, 0) плоскостью
Ро I! P (эта линия изображает прямую плоскости Лобачевского).
Аналогично этому можно описать и циклы дважды гиперболической,
антигиперболической, антиевклидовой и антипсевдоевклидоаой геометрии; на
случае антиевклидовой геометрии мы еще остановимся несколько ниже. Заме-
Заметим еще, что из сказанного следует, что так называемые круговые пре-
преобразования каждой из шести перечисленных геометрий, т.е. такие
преобразования каждой из этих плоскостей, которые переводят циклы снова
в циклы, изображаются преобразованиями трехмерного пространства, пере-
2) См., например, Н орден [62], Каган ]75], Кокет ер [19],
Клейн [55], Розенфельд и Я г лом [24], Я г лом [10] или [77].
9 И. М. Яглом

258
ПРНЛОЖКППН А
водящими плоскости снова в плоскости
«сферу» (Z, 2[, S.,, о или о^) в себя.
и переводящими соответствующую
Поучительно проиллюстрировать все сказанное выше на примере пред-
представления а и ти е в к л и до в о й геометрии в виде геометрии «сферы» о (или
«полусферы» о'). Мы знаем, что под «точками»
антнесклидовой плоскости можно понимать
прямые обыкпонеиной плоскости Евклида. Но
хорошо известно, что уравнение каждой
Рис. 199.
прямой / евклидовой плоскости можно записать в тек называемой «нормаль-
«нормальной форме»-
х cos a +-i/ sin а—р = 0; A3)
зчесь а—угол, образованный перпендикуляром п к прямой / с положитель-
положительным направлением оси Ох, а р — расстояние от начала координат О до прямой
/ (рис. 200). Нормальная форма уравнения прямой удобна тем, что позволяет
легко определить расстояние d— й^ц от произвольной точки М (х0, у0) пло-
плоскости до прямой /; это расстояние равно результату подстановки в урав-
уравнение A3) прямой координат точки М 2)
d — \ х0 cos а-,-(/„ sin а — р \.
A3а)
*) То есть так называемыми проективными преобразовани-
преобразованиями трехмерного пространства (см., например, Ко к стер [19]).
2) См., например, Дубнов [35], стр. 116—117.

ДЕВЯТЬ TFOMEIPIIH НА ПЛОСКОСТИ
259
Если при этом каж ivio прямую / плоскости считать направленной,
т. е. снабженной стрелкой, указывающей то направление движения по прямой,
которое мы считаем положительным, то и перпендик\ ляр п можно будет
считать направленным, условившись, скажем, что поворот на 90'. переводящий
положительное направление / в положительное направление п, происходит
в направлении, противоположном направлению вращения часовой стрелки
(рис. 200а). В таком случае углу а можно будет придать любое значение:
Рис. 200.
Рис. 200а.
0°<а < 360°; с другой стороны, если условиться считать расстояние от точки
до (направленной!) прямой положительным или отрицательным, и зависимости
от того, лежит точка слева или справа от прямом, то и расстоянию р от О
до / можно будет придать люгое значение: —ее < р < ос. Таким образом,
множество всевозможных направленных прямых I (евклидовой) плоскости можно
сопоставить множеству всевозможных троек чисел
cos a, sin а, —р.
A4)
\
являющихся коэффициентами уравнения A3) пря-
прямой, т. г. множеству точек (cos a, sin а, —р) ци-
цилиндра о трехмерного пространства {#, (/, z} (рнс.
201). Уравнение этого цилиндра о имеет вид
х'-гУ1 1. (9)
т. е. о есть «сфера» вырожденного евклидова прост-
пространства (х, у, z}. При этом дге прямые / и /lt
отличающиеся только направлением,
характеризуются тропками чисел A4) и
((cos (а+180 ), sin (а+180), — ( — р)) =
= (—ее а, —sin а, р)
(см. рнс. 201), т. е этим прямым отвечают «диамет-
«диаметрально противоположные» (ф\гнмн слогами, симмет-
симметричные относительно начала координат О @, 0, 0))
точки цилиндра п; поэтому, если считать «точки»
антиевклндовой плоскости совпадающими с нена-
ненаправленными прямыми обыкновенной плоскости
Евклида, то каждая такая точка будет изображаться парой
противоположных точек «сферы» а.
X
Рис. 201.
диаметрально
9*

260 ПРИЛОЖЕНИЕ А
Однако в теории циклов антневклидовой геометрии удобнее считать
«точками» направленные евклидовы прямые *)! При этом если сохранить
принятое выше соглашение о знаке расстояния от точки до прямой, то
(направленное, т. е. взятое со знаком -\- или —) расстояние d = d/uj
от точки М (х0, y0) до прямой I с уравнением A3) будет равно
d = x0 cosa+г/о sin a—p. A36)
При этом сечение «сферы» о (т. е. цилиндра (9)) плоскостью
Ax + By+Cz = D A5)
или
d, A5')
А . В , D , , , .
Где а = -тг. Ь=-тг, d= -=.—это множество тех точек цилиндра, х2 ,-У" = 1'
С С С
которые изображают (направленные) прямые евкли-
евклидовой плоскости, удаленные от фиксированной точки
Q (а, Ь) на постоянное расстояние d (величина d может
быть и отрицательной). [Мы здесь исключаем из
рассмотрения плоскости, в уравнении A5) которых
С = 0, т. е. плоскости, параллельные оси цилиндра о.]
Таким образом, изображенные плоскими сечениями
«сферы» о циклы антиевклидовой геометрии суть не
что иное, как направленные окружности, понимаемые
^_ в смысле множества своих (направленных) касатель-
X ных (рис. 202, а); к числу этих окружностей отно-
относятся и точки (окружности радиуса нуль), точнее,
III \ I / пучки проходящих через одну точку прямых (рис.
' v » *' 202, б). Точки на нашей модели антиевклидовой
плоскости изображаются сечениями A5') цилиндра а,
где d = 0, т. е. сечениями о плоскостями, проходя-
проходящими через начало координат О @, 0, 0).
Круговые преобразования антиевклидовой плоско-
плоскости— это такие преобразования в множестве (направ-
(направленных) прямых евклидовой плоскости (совпадающих
с точками антиевклидовой плоскости!), которые пе-
*~ реводят окружности снова в окружности. Преобразо-
х вания евклидовой плоскости, обладающие этим свой-
5) ством, впервые рассмотрел замечательный француз-
Рис 202 скии математик Эдмонд Лагерр A834—1886);
поэтому их обычно называют преобразованиями Ла-
Лагерра2). Преобразования Лагерра изображаются такими преобразованиями ци-
цилиндра а, которые переводят плоские сечения цилиндра снова в его плоские
*) Соответственно этому в вопросах антиевклидовой геометрии, связанных
с теорией циклов и с учением о круговых преобразованиях, естественно счи-
считать точки антиевклидовой плоскости «направленным и», т. е. рассмат-
рассматривать каждую точку кал пару точек, совпадающих по положению на
(антиевклидовой) плоскости, но различающихся своим «направлением».
[«Направление» точки удобно задавать, например, указанием окружающей
точку дуги со стрелкой, выделяющей то из двух направлений вращения
вокруг этой точки, которое принимается за положительное; ср. рис. 224—226,
стр. 295—296.] Также и точки плоскостей Римана, Лобачевского, дважды
гиперболической, антигиперболической и антипсевдоевклидовой в ряде слу-
случаев удобно считать направленными; ср. ниже, стр. 295—296 или книги
Яг л ом а [10] и [77].
2) Ср. Я г лом [31], [10] или [77].

ПГВЯТЬ ГЕОМЕТРИЙ НА ПЛОСКОСТИ
261
сечения. Примером такого преобразования может служить центральное проек-
проектирование цилиндра о на себя из некоторого центра М, переводя-
переводящее каждую точку А цилиндра во вторую точку А' пересечения о с прямой МА
(рис. 203); если прямая MB касается цилиндра с1 (в точке В), то точка В'
считается совпадающей с В. Можно доказать, что описанное преобразование
^отвечающее так называемой «осевой инверсии», близкой к обычной инверсии)
переводит каждое плоское сечение цилиндра о снова в его плоское сечение.
От стереометрических «моделей» плоских геометрий Кэли — Клейна не-
нетрудно перейти к известным представлениям
этих геометрий на плоскости. Спроектируем каж-
каждую из сфер 2, 2], 23, о и ct трехмерного
пространства •[ х, у, г } из ее «центра» О @, 0, 0)
на плоскость z=l (рис. 204) 1). При этом каж-
каждая пара диаметрально противоположных точек
«сферы» перейдет в одну точку плоскости z=l
и мы сможем считать, что точки нашей «плоскости
Кэли—Клейна» изображаются точками (обыкно-
(обыкновенной 2)) плоскости. При этом эллиптиче-
эллиптическая плоскость Римана изобразится всей плоско-
плоскостью г= I (рис. 204, с), гиперболическая плоскость
Лобачевского—внутренностью круга х2 -\- у1 = 1
(рис. 204, б), дважды гиперболическая плоскость
и антигиперболическая плоскость — внешностью
того же круга (рис. 204, е), антиевклидова пло-
плоскость — плоскостью г = 1 без одной точки х = у=0
(рис. 204, г), наконец, антипсевдоевклидова пло-
плоскость— парой вертикальных углов \х/у\ < 1 пло-
плоскости г=1 (рис. 204, д). Ясно, что проходящие
через точку О @, 0, 0) плоские сечения любой
из «сфер» 2, 2lt 2.,, о и с1 центральная проекция
этой «сферы» на плоскость 2=1 из точки О
нии; поэтому в наших моделях шести плоских геометрий Кэли — Клейна
прямые этих плоскостей изображаются прямыми линиями плоскости 2=1.
Полученные таким путем < модели» плоских геометрий Кэлн — Клейна и яви-
явились исходным пунктом всех построений Кэли (алгебраических) и Клейна (гео-
(геометрических); они называются моделями Клейна этих геометрий3).
Иное представление тех же шести плоских геометрий Кэли — Клейна на плос-
плоскости можно получить, используя вместо центральной так называемую стерео-
стереографическую проекцию, отображающую точки «сфер» 2, 2Ь 2.2, о и ot
на точки плоскости (ср. выше, стр. 159, 167 и 219). «Сферы» 2 и 2Х содержат
точку Q @, 0, —1); спроектируем их из этой точки на плоскость 2=1, касаю-
касающуюся «сферы» в диаметрально противоположной Q точке Qt @, 0, 1)
(рис. 205, а. б). При этом мы получим отображение сферы 2 на (всю) плос-
плоскость 2=1; если же мы захотим ограничиться, скажем, верхней полусферой 2',
то нам придется считать, что «полем действия» геометрии Римана на плоско-
Рнс. 203.
переводит в прямые ли-
лиК Кй
х) Геометрия Евклида, Галилея и Минковского с самого начала были нами
определены как «действующие» на (обычной) плоскости; разумеется, эти пред-
представления также можно получить в результате центральной проекции «сферы» с0
на плоскость z = l, т. е. на «полусферу» о'0.
2) Точнее, проективной.
3) См. по этому поводу Клейн [55] или Каган [25]; по поводу модели
Клейна геометрии Лобачевского см. также Н орден [62], Александров
[64] или Яг лом [10].

262
ПРИЛОЖЕНИЕ А
сти z=l является (довольно причудливая) область, ограниченная окруж-
окружностью х2-\ у1- -4 н включающая половину точек самой этой окружности (ибо
к полусфере S' следует причислить половину точек ограничивающей ее окруж-
окружности; ср. выше, стр. 244, в частности, рис. 190, б). Часто оказывается более
удобным считать, что «.полем действия геометрии Рнмана является вся плос-
плоскость z=l; при этом, однако, точки плоскости будут являться образами
«направленных,,' точек плоскости Римана (ср. выше, стр. 260), изображаемых
всеми точками сферы 2. Заметим еще, что в силу свойств стереографической
проекции (см. стр. 160—163) окружности и прямые плоскости Римана, изобра-
изображаемые плоскими сечениями сферы 2, на нашей модели представляются в виде
(евклидовых) окружностей; в частности, прямые плоскости Римана, представляе-
представляемые «большими окружностями,, сферы ~, изображаются окружностями плос-

ДЕВЯТЬ ГКОМКТРНЙ НА ПЛОСКОСТИ
263
кости г=1, пересекающим» окружность х2±у- = 4 в диаметрально противо-
противоположных точках. Аналогично этому «верхнюю полусферу, 2i стереографиче-
стереографическая проекция переводит в круг x--\-ij'-<- 4 плоскости 2=1, являющийся
естественным «полем действия,, геометрии Лобачевского; однако в некоторых
случаях (например, при построении теории круговых преобразований геометрии
Лобачевского) приходится считать точки плоскости Лобачевского направлен-
направленными и полагать, что «область действия? геометрии Лобачевского совпадает
со всей плоскостью г=\, на которую стереографическая проекция отображает
Рис. 205.
всю «сферу^ 2Х. Так как стереографическая проекция «сферьсь 21 на плос-
плоскость г 1 переводит плоские сечения «.сферы-» 2] е окружности плоскости
(ср. выше, стр. 160—161), то в нашей модели геометрии Лобачевекого все прямые
линии и все циклы (окружности, предельные линии и эквидистанты) изобража-
изображаются (евклидовыми) окружностями.
"Сферы>, 2.,, о и ot содержат точку Р (—1, 0, 0); спроектируем их на плос-
плоскость х- 1, касающуюся сферы) в диаметрально противоположной* Р
точке Р1 A, 0, 0) (рис. 206, а — е). Полученное таким образом отображение
поверхностей So, о и а1 на плоскость позволяет построить на плоскости "мо-
"модели» дважды гиперболической, антигиперболической, антневклидовой и анти-
псевдоевклидовой геометрий, .(действующих» на поверхности рассматриваемых
«сфер»; при этом также удобно считать точки соответствующих геометрий
Кэлн — Клейна «направленными», ибо только в этом случае образами точек плос-
плоскостей Кэли—Клейна будут все точки «сфер» 2.,, о и Oi ]). Отметим еще, что
!) Заметим, что на самом деле «полем действия» получаемых описанным
путем «моделей» шести геометрий Кэлн — Клейна служит не хорошо знакомая
нам евклидова (или аффинная) плоскость, а более сложный геометрический
образ. А именно, стереографическая проекция сферы 2 и двуполостного
гиперболоида 2] на плоскость z—\ отображает 2 и 2t на евклидову
круговую плоскость (см. выше, стр. 159); стереографическая проекция
цилиндров о и О] на плоскость х - 1 отображает о и Oi на циклическую
плоскость Галилея (стр. 167); стереографическая проекция однополост-
ного гиперболоида 22 на плоскость *=1 отображает его на круговую
плоскость Минковского (см. стр. 219).

264
ПРИЛОЖЕНИЕ А
плоские сечения сферы 22 стереографическая проекция переводит в гипер-
гиперболы плоскости х = 1, а плоские сечения сфер о и ох стереографическая
проекция переводит в параболы; поэтому прямые и циклы дважды гипер-
гиперболической и антигиперболической плоскостей изображаются на нашей модели
Рис. 206.
гиперболами, а прямые и циклы антиевклидовой и антипсевдоевклидовой плос-
плоскостей—параболами.
Так как получаемые с помощью стереографической проекции модели
плоских геометрий Лобачевского и Римана (весьма, кстати сказать, близкие
к тем «моделям», изучение которых составляет предмет нижеследующего
Приложения Б) впервые рассмотрел знаменитый французский математик
Анри Пуанкаре A854 —1912), то все эти модели называются моделями
Пуанкаре геометрий Кэли — Клейна1).
В заключение укажем, что, подобно тому как на плоскости существует
32 = 9 геометрий Кэли — Клейна, в трехмерном пространстве существует 33 = 27
подобных геометрических систем, отвечающих всевозможным комбинациям
мероопределений расстояний между точками на прямой, плоских углов в пучке
прямых (совокупности прямых, принадлежащих фиксированной «плоскости
пучка» и проходящих через фиксированную точку—центр пучка) и двугран-
двугранных углов в пучке плоскостей (т. е. в совокупности всевозможных плоскостей,
проходящих через фиксированную прямую—ось пучка): каждое из этих
мероопределений может быть эллиптическим, евклидовым или гиперболическим!
При этом три типа мероопределений расстояний и три типа мероопределений
плоских углов были определены выше. Аналогично этому определяются и три
типа мероопределений двугранных углов: обычное (т. е. принятое в евклидо-
евклидовой стереометрии) мероопределение двугранных углов называется эллиптичес-
эллиптическим, или римановым; мероопределение, определяемое условием о том, что
величина угла между плоскостями а и р равна (евклидовой) длине отрезка
АВ, высекаемого плоскостями а и E на некоторой (не параллельной ребру
х) См. Я г лом [78] или [77]; по поводу моделей Пуанкаре геометрий Лоба-
Лобачевского и Римана см. также Клейн [55], Каган [25] или Я г лом [10].

ДЕВЯТЬ ГЕОМЕТРИЙ НА ПЛОСКОСТИ 265
двугранного угла) фиксированной прямой q, называется евклидовым; наконец,
мероопределение, задаваемое формулой
где знак /_ применяется в смысле обычного двугранного угла между плос-
плоскостями, а 1 и е — какие-то две фиксированные плоскости, принадлежащие
рассматриваемому пучку плоскостей, называется гиперболическим, или меро-
мероопределением Лобачевского.
Примерами пространственных геометрий Кэли —Клейна являются как
обычная геометрия Евклида, так и псевдоевклидова геометрия, вырожденная
евклидова и вырожденная псевдоевклидова геометрии, галилеева геометрия,
псевдогалилеева геометрия и вырожденная галилеева геометрия (см. выше,
стр. 252—253 и 255). Условившись характеризовать метрику на прямой, в пучке
прямых и в пучке плоскостей буквами «Р», «Е» и «Л» в зависимости от того,
является она эллиптической, евклидовой или гиперболической, и относя пер-
первую букву к метрике расстояний, вторую — к метрике плоских углов и третью —
к метрике двугранных "углов, мы сможем сказать, что евклидова геометрия
в пространстве относится к типу ЕРР, а псевдоевклидова — к типу ЕРЛ,
ЕЛР или ЕЛЛ в зависимости от того, считаем ли мы «плоскостями» нашей
«геометрии» плоскости, пересекающие конус Ж с уравнением
х*+у2—z2=0 Ea)
по эллипсам или по гиперболам, причем здесь следует отдельно рассмотреть
пространство, «прямыми» которого являются прямые, параллельные тем, ко-
которые заключены внутри конуса УС, и пространство, «прямые» которого
параллельны проходящим через точку О @,0,0) и лежащим вне SK прямым1).
Аналогично этому вырожденная евклидова геометрия относится к типу ЕРЕ,
а вырожденная псевдоевклидова геометрия — к типу ЕЛЕ; при этом «прямыми»
вырожденной псевдоевклидовой геометрии мы должны считать (евклидовы)
прямые, параллельные проходящим через точку О @, 0, 0) прямым, принад-
принадлежащим любой (но только какой-то одной!) паре вертикальных углов,
образованных плоскостями
х2 — у2 = 0 или (х + у) (х—у) = 0.
Наконец, галилеева, псевдогалилеева и вырожденная галилеева геометрии
относятся к типам ЕЕР, ЕЕЛ и ЕЕЕ.
Таким образом, выше мы уже встретились с девятью из двадцати семи
трехмерных геометрий Кэли"—Клейна, а именно с теми геометриями, в кото-
которых метрика расстояний является евклидовой. [Эти девять геометрий естественно
сравнить с тремя плоскими геометриями Кэли — Клейна, служащими основным
объектом изучения в настеящей книге: с геометриями Евклида, Галилея
и Минковского, в которых также метрика расстояний является евклидовой.]
Остальные 27 — 9=18 пространственных геометрий Кэли — Клейна можно
определить на сферах четырехмерных 2) обыкновенных и вырожденных евкли-
евклидовых и псевдоевклидовых пространств; однако эти построения3) уже выходят
за рамки настоящей книги.
*) Если все «плоскости» нашей геометрии Кэли — Клейна пересекают
конус SK по (евклидовым) эллипсам, то «прямыми» мы неизбежно должны
считать (евклидовы) прямые, параллельные проходящим через точку О пря-
прямым, лежащим вне Ж (ибо наши «плоскости» содержат только такие «прямые»).
2) См. К оке тер A9]; Розенфельд и Яглом [20].
3) См., например, книгу Розенфельда [82J.

ПРИЛОЖЕНИЕ Б
ЧИСЛОВЫЕ МОДЕЛИ ПЛОСКИХ ГЕОМЕТРИЙ
Хорошо известно, что точки евклидовой плоскости можно отож-
отождествить с комплексными числами, сопоставив точку с декартовыми
прямоугольными координатами (х, у) или с полярными координатами
(г, ф) комплексному числу
i sin ф) A6)
z = х Jriy = r{c
(рис. 207). Величины х и у называются соответственно действи-
действительной (вещественной) и мни-
мнимой частью числа z и обозначаются
символами Яег и Im^1); величины г и
ф называются модулем и аргумен-
аргументом числа z и обозначаются символами
\z\ и Arg z. [Аргумент числа гфО опре-
определен с точностью до произвольного сла-
слагаемого, кратного 2л, т. е. наряду с ф
аргументом z является любой угол
Ф + 2лй, где k — целое число; число
=0 не имеет аргумента.] Модуль \z\
ф
Рис. 207.
числа г можно определить по формулам
(a) H2 = j
или (б) \z\* =
A7)
где z — число, сопряженное числу г:
(a) Rez~Rez, \mz=—Im z или (б) |г| = |г|, Arg z——Arg z A8)
[т. е. если z= x-\-iy—r (cosф-(- i sin ф), то z=x — iy = r(cos( —ф) 4-
-f-isin(—ф))( = г(соБф — / sin Ф))]- Аргумент Aigz числа z задается
соотношениями
Rez , . . lm z ... . Im z . ,. .
-щ = cos (Argz), -yjj- = sin (Argz), -^ = tg (Argг), , ig)
!) Первые буквы французских слов reel—действительный л imaginnire —
мнимый.

ЧИСЛОВЫЕ МОДЕЛИ ПЛОСКИХ ГЕОМЕТРИЙ
267
которые уместно также переписать в более привычном большинству
читателей виде
(/ . X
Важно иметь в виду, что
Re (z±zx) = Re z+Re гъ Im (z±zx) = Im z±\m zx
(т. e. (x + iy) + (x1 \-iy1) = (x±x1)-\-i(y±y1)),
(т. e. r(cos(p
= ш'Arg
Г (COS№ + 1 Sin ф)
A9a)
B0)
B0a)
-f / sin фх) =
= /T1[c0S(<p+<p1) + i 5Ш(ф+ф1)]),а
= kxgz — kxgzx B06)
p,) +/ sin ((p — CPi)l). Из cooTHO-
шений A8) — B06) гакже следует, чго
=4- B1)
и что сумма z -z( = 2Rez) и произведение гг ( = [ z |2) двух соп-
сопряженных чисел будут числами вещественными, а разность
z — z ( — 21хп z-i) — числом чисто мнимым (т. е. имеющим вид ib,
где b вещественно). Равен-
Равенство z = z имеет место лишь
для вещественных чисел z, для
которых Im z = 0, Arg г~= 0 пли
л, а равенство z = —z— лишь
для чисто мнимых чисел z, для
которых Re z — 0, a Axgz =
- nzT.
Расстояние dZZi между °)
двумя точками евклидовой плос-
плоскости, отвечающими комплекс-
комплексным числам z и zlt—между точками z и гъ как мы б^дем говорить
в дальнейшем,— определяется формулой
Рис. 208.
\z — zx\
или
B2)
(рис. 208, а). Угол 8(Z(]- Zl) (Z(|, ?2> между прямыми, соединяющими точки
^! и 22 с одной и той же точкой z0,— между прямыми (г0, zx) и {z0, z2).

268
ПРИЛОЖЕНИЕ В
как бы будем дальше говорить,— задается равенством
„, г,) и.,
= Arg V (гг,
г0) = Arg
B3)
где выражение V(z2, zx; z0) —\
i—z0
можно назвать (простым) отно-
отношением трех точек 22, zx и z0. Формула B3) следует из того, что
^(zc,z1),(zo,z2)~92—фь гДе Фг и Ti — аргументы комплексных чисел
z\= z2 — z0 и z°1 — z1—z0 (рис. 208,6). При этом следует иметь в
виду, что угол 8(z > z }) (z Zj) — это направленный угол между
направленными прямыми (z0, zx) и (zn, z2), т. е. угол, на кото-
который надо повернуть положительный луч направленной прямой (z0, zx)
(луч, ведущий от z0 к гх) для совмещения его с положительным
лучом второй направленной прямой (z0, z2).
•• 6)
Ясно, что прямая (ненаправленная) (гъ z2) — это множество
таких точек z, что
Arg V (z, zx\ z2) = Arg ^=^- = 0 (или = л) B4)
(рис. 209, а). Отсюда следует, что прямую (zlt z2) можно опреде-
определить как множество таких точек z, что
Im V (z, z-,; z9) = Im z~z'2 — о B4а)
т. е. что число V(z, zx\ z2) вещественно. Последнее условие можно
также записать так:
г—z2 z—z2
B5)
Другими словами, уравнение прямой (zx, z2) имеет вид B5),
т. е. имеет вид
(гхгг — ггг2) = 0

ЧИСЛОВЫЕ МОДЕЛИ ПЛОСКИХ ГЕОМЕТРИЙ 269
или
Bz — Bz + C=0, ReC-=0, B6)
тд.еВ = г1— z2 и С~гхг% — z±z2, т. е. С—чисто мнимое число.
Обратно, можно показать, что каждое уравнение вида B6) задает
некоторую прямую линию, а именно прямую, проходящую через такие
точки zx и z2, что zt—z2 = В, z1z^ — z1z2 -С.
Окружность с центром z0 и радиусом г представляет собой
множество таких точек z, что
\г — го\ = г или (z-z0) (z — 70)= r* B7)
(рис. 209, б). Таким образом, уравнение окружности имеет вид
zz — zoz — zoz + (zozo—г2) = 0,
или вид
azz~-\-bz-\-h~I+c = 0, Im a = Im с = и. B8)
Верно и обратное: всякое уравнение вида B8) определяет некоторую
окружность, а именно окружность, центр z0 и радиус г которой
определяются равенствами 20 = , zozo—r2 = — Ясно, что
уравнения B6) и B8) можно записать в единой форме B8), где
только в случае уравнения B6) надо считать, что
а = 0 B9)
(для того чтобы придать уравнению B6) вид B8), надо умножить
все члены уравнения B6) на мнимую единицу i). Можно также при-
придать уравнениям B6) и B8) единый вид
Azz + Bz—Bz \-C=0, ReA=ReC=0, B8a)
причем в случае прямой линии (уравнение B6))
Л-=-0. B9а)
Окружность, проходящую через три точки гъ z2 и z3, можно
Также описать как множество таких точек z, что
8(г ,11, ,\—8,, ,,,, ,, = 0 (или = я)
(здесь углы и прямые — направленные; рис. 209, в) или что
ArgJ=fe-Arg^=|= 0 (или= я). C0)
Но (двойное) равенство C0) равносильно, очевидно, условию
lm(W{Zl,z2; ,»*)) = lm^$ = Im(|=|:g)=0, C0a)

270 прнложкннр б
где выражение W (гъ zn; гя, z) = ——г': ——- можно называть (слож*
ным пли двойным) отношением четырех точек гг, z2, гя и z. Таким
образом, условие принадлежности четырех точек zx, z2lz3 и z4 одной
окружности (или одной прямой) имеет вид
\mW(zlt z2; z3, zt) = lm 'z^;z±^f)=Q. C1)
z.. — z3 z.> — z4
Уравнение C0а) окружности, проходящей через точки zlt z2 и z3,
можно еще записать так:
i— z:l.Z|— г _ zt — г:, , г,
г, z3 гг —г гг~г3 г,—г
или так:
Azz + Bz—Bz^ С- 0, Re-4=ReC=0, B8а)
Т. е. в том же виде, что и раньше; теперь в уравнении B8а)
A=(z1 — z3)(z2—z3) — (z1—z3)(z2—z3),
B^z2(z1—z3){z2 — z3)—z1(zl—z3)(z2 — z3), B86)
С= ггг2 (z1—z3) {z2—z3)—z1zo {гг —z3) (z.2 —z3).
Движения евклтовой плоскости представляют собой' такие
преобразования плоскости, переводящие точку z в точку z', что1)
(a) z'=pzA-q или (б) z' —pz-\-q (pp — 1). C2)
В самом деле, легко показать, что если z' и z\ связаны с z и zlt
скажем, соотношением C2а), то
(z\-z')Cz\-~z') = [(pzj \-g) — (pz
= /; B-j — z)¦ p ( z1 — z) pp izl—z) (z1 —z) = {z1—z) (z1 —z),
Т. е. преобразование C2а) сохраняет расстояние B2) между точками:
В частности, простейшие преобразования
(a) z' = — z и (б)г'=г C4)
1) Нетрудно видеть, что формулой C2а) записываются так называемые
«собственные движения» («движения 1-го рода»), а формулой C26) — «зеркаль-
«зеркальные движения», или «движения 2-го рода» (ср. Перепелкин [5], Я г лом [9]).

ЧИСЛОВЫЕ МОДКЛН ПЛОСКИХ ГЕОМЕТРИЙ
271
выражают симметрию относительно т о ч к и 0 (рис. 210, а)
и с и м м е т р и ю о т и о с и т с л ь н о и р я м о й Jtn z 0 (рис. 210, б),
а общее преобразование C2а) представляет собой поворот вокруг
-z
I х
а)
(У
1 х
Рис. 210.
Рнс. 211.
точки 0 на угол Argp, сопровождаемый параллельным переносом на
вектор д с началом 0 и концом q (рис. 211).
Заметим, наконец, что преобразования
ил"
C5)
(которые родственны движениям C2), если с—О), обладают тем
свойством, что сохраняют значение двойного отношения W{zlt z.2; z3, г4)
четырех точек (случай преобразований C5а)) или заменяют его ком-
комплексно сопряженным (случай преобразований C56)). В самом деле,
если, например, точки z[, z'2, z's и z\ связаны с точками гг, z.z, z3 н г4
формулой C5а), го
W(z[, z'2;
Zl—Z-Л Zl~
— \(azi+b flz3
cza-\-d)'
az^j-bог,-|-г
\-b azt + b\ .
id czA-\-dj'
Jaz^j-b
W, + d
(ad—be) (гг—z3). (ad —fee) (г.,—z3)
. Г (ad—fee) (zl~ z4). {ad—be) (z2 — z4)"| __
¦ |_(cz, -d) (cz4 + d) • (cz., + d) (czi + d)J
Z, —Z4 CZij + di _Zj_—Zg.Zi—?4= ^, ^_ ^ ^^
~d\ Zo — z3 z2 — z4
Поэтому, если для четырех точек zx, z2, z3 и zt отношение
W{zlt z2; z3, z4) вещественно, то вещественно также н число
W(z[, z'2; z'3, г'л), где z\, г'„, z'3 и z\ — точки, полученные из zx, z2,
Z3 и г4 преобразованием C5а) пли C56); другими словами, четыре

272 ПРИЛОЖЕНИЕ Б
точки, принадлежащие одной окружности (или прямой), преобразо-
преобразование C5) переводит в четыре точки, также принадлежащие одной
окружности (или прямой). Таким образом, преобразования C5) евкли-
евклидовой плоскости переводят окружности (и прямые линии) снова
е окружности (и прямые линии), т. е. являются круговыми
преобразованиями (см. выше, стр.
.V,, 164). Более того, можно показать,
^_^<j>Z что каждое круговое преобразование
-^ ' евклидовой плоскости можно представить
в виде C5а) или C56). В частности,
_^_ инверсия с центром 0 и степенью 1
О ^--. 1 | х (ср. стр. 138—139) записывается следую-
следующим образом:
^2 г'= 4- C6)
Рис. 212 Z
(рис. 212; равенство C56) обращается
в C6), если в нем положить a = d = 0, fc = c=l).
Ясно, что преобразования C2) переводят каждую точку г евклидовой
плоскости в новую точку г'. Однако для преобразований C5а, б), где с ф 0.
это уже неверно — такие преобразования не являются взаимно однознач-
однозначными преобразованиями (евклидовой) плоскости. В самом деле, точку
d d
z= , соответственно z = — , обращающую в нуль знаменатель дроби,
с с
стоящей в правой части равенства C5), преобразование C5а) (соответственно
C56)) не переводит ни в какую точку плоскости.
Последнее обстоятельство связано с тем, что, в то время как операции
сложения, вычитания и умножения в области комплексных чисел всегда
осуществимы, операция деления осуществима не всегда: частное — не имеет
смысла, если z.2 = 0. Для того, чтобы устранить возникшее затруднение, иногда
условно полагают
и считают, что
= °°, z—оо = оо, z-oo = oo, —=оо, — = 0,
z оо
где z—произвольное комплексное число (причем в 3-м равенстве z Ф 0, а
во 2-м, 4-м и 5-м z Ф оо). Поэтому, если дополнить «плоскость комплексного
переменного» одной фиктивной «бесконечно удаленной точкой» оо, то на рас-
расширенной таким образом плоскости преобразования C5а, б) будут уже
взаимно о д н о-з н а ч н ы м и; в частности, преобразование C5а) переводит
d
точку z = в точку
й , , ad —be
_fl._+b _
Z= g =—^— = «9

ЧИСЛОВЫЕ МОДЕЛИ ПЛОСКИХ ГЕОМЕТРИЙ 273
и точку г=оз в точку
—
,_ о-оо+6 ___°° c + 0_a
2 с-оо +d = d с+О~~с~*
с-]
оо
Таким образом, естественным «полем действия» круговых преобразований
C5а, б) является не обычная плоскость Евклида, а круговая пло-
плоскость, получаемая из евклидовой плоскости пополнением последней одной
«бесконечно удаленной точкой» оо.
Намеченные выше построения могут быть еще расширены. Наряду
с комплексными числами математика знает две другие системы «чисел»—-
так называемые «дуальные числа» и «двойные числа». Дуальное
число определяется как выражение z — x-\-ey, где х, у— числа
вещественные, а «дуальная единица» е удовлетворяет условию е'2=0;
при этом, разумеется, «дуальная единица» е, подобно «комплексной
единице» i, является «числом особого рода», никак не сравнимым
с обыкновенными (вещественными) числами. Аналогично этому под
двойным числом понимается выражение z = x-\-ey, где х, у — веще-
вещественные, а «двойная единица» е (это тоже есть «число особого
рода», несравнимое с вещественными числами) удовлетворяет условию
е2= +1.
Дуальные числа, как будто, впервые рассматривал известный не-
немецкий геометр Эйген Штуди A862—1930), в силу чего в лите-
литературе их зачастую называют «дуальными числами Штуди»; двойные
числа, по-видимому, впервые ввел современник Штуди, видный
английский математик Вильям Клиффорд A845—1879)х).
Сложение и вычитание дуальных и двойных чисел определяется
аналогично сложению и вычитанию комплексных чисел:
(х + еу) ± (jcj + еУ1) = (x + Xl) + e (у ±У1), C7')
(х + еу) ±(х + еУ1) = (x±Xl) + e(y +уг), C7")
а умножение производится так:
(х + еу) (хг + еуг) = ххг + е (хуг) + е (ухг) + е2 (ууг) =
= xXl l-eixyi+yxj, C8')
(х + еу) (Xj + еУ1) = xxt + e (хуг) + е (ухг) + е2 (ууг) =
1) C8")
1) Заметим, что иногда выражение «комплексные числа» употребяют, так
сказать, в «обобщенном смысле», т. е. имея в виду сразу три системы
чисел —(обычные) комплексные, дуальные и двойные числа. Мы, однако, далее
будем употреблять термин «комплексные числа» лишь в его обычном смысле.

274 ПРПЛОЖИННЕ Б
(ср. с равенством (.v-1 iy)(xl iyl) — (xx1—yyl)-i~i{xy +¦ ухх)). Та-
*кпм образом, если и тля чисел z — х , еу и z = х - еу условиться
писать х--Мег, у- Im z, то, как н в случае комплексных чисел,
Re (г ± г у) = Re г ± Re гг, lm(z zkzj^lmz ±lmz1. B0)
Кроме того, для всех трех типов чисел (комплексных, дуальных и
двойных)
IrnB-2i)= Re z-lmZi \ \тг-Ясгг; C9)
однако, в то время как дпя комплексных чисел
Re (z ¦ zj -- Re z • Re zx — Im z ¦ Im zu D0)
для дуальных н двойных чисел соответственно
Re(z-^1) = Rez-Rc^1 D0')
и
Rc(z-zl) = Rez-Rez1 ^Imz-lmz^ D0")
Операция деления в множестве дуальных п двойных чисел тесно
связана с операцией образования числа z, сопряженного к дан-
данному числу z; эта операция для всех трех типов чисел определяется
единообразно:
если z = x-\ Iy, то z = x — Iy, где / = /, е, е D1)
(обозначение / мы будем применять и в дальнейшем). Таким образом,
для всех трех типов чисел
Re2=Re2 и Imz = — \mz. A8a)
Сумма двух сопряженных чисел (для любого типа чисел) является
числом вещественным, т. е. таким числом z, чго Im z- 0;
разность же сопряженных чисел является числом «чисто мни-
мнимым», т. е. таким числом z, что Rez = 0:
z -+-Z---2RCZ, z—z — 2\mz-I, I—i, e, e. D2)
Условие 2 = z характеризует вещественные числа, а условие 2 = —z —
чисто мнимые числа. Еще важнее, что также и произведение zz двух
сопряженных чисел всегда является числом вещественным:
(x+iy)(x — iy) = .vM /, (x-t ву)(х—ву)= х2,
)(х — су) = х-—у2. D3)
Поэтому для определения значения дроби — достаточно домножить
ее числитель и знаменатель на число z; при атом знаменатель zz

ЧИСЛОВЫЕ МОДЕЛИ ПЛОСКИХ ГЕОМЕТРИЙ
275
полученного выражения
zz
будет уже числом вещественным,
и для того, чтобы разделить на него число zxz, будет достаточно
полечить на zz отдельно Re (ztz) и \m(zxz):
х + iy (x + iy) (x—iy)
—fУ) _хх^ + г (xyl —xly)=_
• D4")
Из формул D4) — D4") следует, что, в то время как в области
комплексных чисел невозможно деление лишь на такое число
z = x-\-iy, что ,v2+y2 = 0, т. е. на число 0 ( = 0+/0), в области
дуальных или двойных чисел имеется больше чисел, деление на
которые невозможно. А именно, в области дуальных чисел невоз-
невозможно деление на такое число z = x-\-ey, что л: = 0, т. е. на все
числа вида еу ( = 0 + еу); в области двойных чисел невозможно деление
на такое число z=x-\-ey, что х2—_у2 = 0 (т. е. (х-\-у)(х—_у) = 0),—
другими словами, на числа вида х-\-ех и х — ex.
Мы знаем, что первое из равенств D3) кладется в основу опре-
определения модуля |z | комплексного числа z:
где
(см. A7)). Аналогично этому в области дуальных и двойных чисел
(сохраняя то же обозначение | z \ для модуля z) положим соответ-
соответственно
ы* = **=*«,
= zz= + {x2— у2).
A7а)
A76)
Точнее, для дуального числа z = x-\-ey мы условимся считать,
что
\z\ = x A7')

276 ПРИЛОЖЕНИЕ Б
(таким образом, модуль дуального числа может быть как положи-
положительным, так и отрицательным!), а для двойного числа z = x-\-ey
. I +1/^7 при и>|Н
\ ±КУ2*8 пи |*|<|jf|
\
при
Кроме того, удобно считать, что знак модуля двойного числа сов-
совпадает со знаком большего по абсолютной величине
из чисел х и у (таким образом, модуль двойного числа также мо-
может быть отрицательным!).
Теперь мы можем утверждать, что во всех трех системах чисел
(комплексных, дуальных и двойных) невозможно деление лишь на
числа нулевого модуля (на такие числа г, что |г| = 0). Такие числа
называют также делителями нуля, ибо для каждого подобного
числа z существует такое отличное от нуля число zlt что 22^ = 0:
0; (ey)-
(л: +ех) (а — еа) = A + е) A —е) (ха) = A — е2) (ха) = 0.
Пусть z — число ненулевого модуля: |г| = /"^=0. Вынесем
в выражении z = x-]-ey или z = x-\-ey числа z модуль |г|=/-этого
числа за скобку как множитель:
В случае дуального числа z = x-\-sy модуль |.г[ = /" числа z,
как мы знаем, равен х; поэтому можно написать
Отношение — = ф называют аргументом дуального числа z= x-\-ey
ненулевого модуля и обозначают через Argz; таким образом, каж-
каждое дуальное число ненулевого модуля можно записать так:
z — х + еу = г(\ +еф), где /• = |г| и cp = Argz, A6')
причем модуль \z\ и аргумент Argz числа z определяются по
формулам
|г| = л: = Кег A7')
ktgz = l. = J-=]BI = ^l. A9')
6 х \z\ \z\ Rez v/
В случае двойного числа z = x-\-ey надо отдельно рассмот-
рассмотреть случаи |х| > \у\ и |л:| < \у\. В случае Jjc^I^I модуль г

ЧИСЛОВЫЕ МОДЕЛИ ПЛОСКИХ ГЕОМЕТРИЙ 277
Числа z определяется по формуле
(a) r = \z\ = ±V*^f A7")
(где знак числа г совпадает со знаком числа х). Поэтому
и, следовательно, существует такое число ф (которое можно пони-
понимать как некоторый угол в геометрии Минковского; см. выше,
стр. 207), что
, . , х Rez , у \тг ,. shcp у Imz /1Г1„,
(a) ch ф = — = , shcp = — =-p-ri ^ю = -г-=-= —= й— A9 )
v ' ^ r z T r |zj Y сЬф х Re z v '
Г причем, естественно, сЬф ==— > 0; см. стр. 207 J. Если же |л:| < |_у[,
то
(б) /- = |г| = +КуГ=Г2 A7")
(где знак числа г совпадает со знаком числа у); поэтому
8— х2 _у2—х2«
1
( У V (х \а_
\г ) [г ) ~
г* —у*—х*~1ш
В этом случае существует такое число ф, что
,„. , х Re г . у Im z ,, ship Jt Rez лп»\
(о) 8Ьф = — =-т—r, chro= — = -т—т-, Шш=-г-1 = —= т— A9 )
v/ Y /• |z|' T /• |z|' т сЬф у Imz '
у
(и здесь ch ф = —> 0). Определенное формулами A9"а, б) числоср
называется аргументом двойного числа z и обозначается через kxgz.
Таким образом, каждое двойное число z = x -\-еу ненулевого модуля
можно записать в одной из форм
(a) z = г (ch ф -\- е sh ф) или (б) z = r(s\\q-\-e ch ф), A6")
где /" = |^| и ф = Агдг, причем модуль \z\ числа г = л:4-еу опре-
определяется формулами A7") (где знак числа \z\ совпадает со знаком
х для чисел вида A6"а) и со знаком у для чисел вида A6"б)), а ар-
аргумент Arg2 этого числа задается соотношениями A9"а, б). Числа
вида A6"а) (числа х-\-еу, где | х \ > \у |) мы условимся называть
двойными числами 1-го вида, а числа вида A6"б) (числа z = x-\-ey,
где |л:|<|_у|)—двойными числами 2-го вида.
Заметим еще, что
если z = х -\- еу = г A + еф), то z = х — еу = гA+е (—ф));

278 ПРИЛОЖЕНИЕ В
таким образом, для дуальных чисел также справедливы формулы
|г|-|*|, Argz = — Argz. A86)
Эти формулы сохраняют" силу и для двойных чисел 1-го вида, ибо
если z — x-\-ey=r (ch ф + esliq:), то z = x—ey = r(cl\{—(p)-|-esh(—ф))
(ср. с формулами A9а, б) из § 11, стр. 207). Однако для двойных
чисел 2-го рода они заменяются формулами
|F| = — И, Arg2 = — Arg*. A8в)
ибо
если z = х -f- еу = г (sh ф -\- е ch ф),
то z~-x— еу = —/-(sh(—ф) + ест1(—ф))
(см. те же формулы A9а, б) из § 11).
Составим теперь произведение двух дуальных чисел г = г(\-\-щ>)
и zl = r1{
= r(l-\-eq>)-r1(\+ еф^ -= ггх [A + еф) A + еф1)] =
= гг1A-;-8ф
Таким образом, для дуальных чисел выполняются (знакомые нам по
комплексным числам) формулы
B0a)
(соотношения B0а) для комплексных чисел называются форму-
формулами Муавра; их можно так назвать и в области дуальных
чисел). Следствиями B0а) являются правила
B06)
(т. е. т \еУ\=— A4-е (ф — фх))). Аналогично этому, если
ri (I + ?<|'i) ri
и г1 = г1(с11ф1 + е511 фх), то
zzx = г (ch ф + е sh ф) • rx (ch фх + е sh ф,) —
= rrx [(ch ф + е sh ф) (ch фх + е sh фг)] =
= rrx [(ch ф ch фх + sh ф sh фх) + е (ch cp sh ф, -L sh ф ch <pt)]

ЧИСЛОВЫЕ МОДЕЛИ ПЛОСКИХ ГЕОМЕТРИЙ 279
(ср. с формулами B1а, б) из §11, стр. 208); если z = г (sh ф -\ е ch ф)
и z1 = r1 (sh ф1-',-ес11 ф1), то
zzx -г(ъЪ.у \ е chф)¦ rt (sh ф1-)-еchф!) =
= rrx [(sh ф ¦+¦ е ch ф) (sh фх 4- е ch ф^] =
— rrx[(sh ф sh фх + ch ф ch фх) -(- е (sh ф ch ф1 -f ch ф sh фх)] —
= "Ч [ch (q -1- ф^) - е sh (ф f фх)];
наконец, если г = г (сЬф-)- еяЬф) и z1 = r1(sh фх -fe ch фД то
гг1 = г (ch ф -1- ^ sh ф) • rx (sh ф-j + е ch фх) =
= r^ [(ch ф ,- е sh cp)(shq)j -f ech фх)] =
= rrx [(ch ф sh фх -(- sh ф ch ф>х) -|- e (ch ф ch фх + sh ф sh фг)] =
(см. те же формулы B1а, б) из § 11). Таким образом, для двойных
чисел также справедливы формулы М у а в р а
| ^-гх I = ] -г" | -1 ^!!, Arg (zzj — Argz-\- Argz^, B0d)
однако здесь надо еще помнить, что произведение двух одноимен-
одноименных двойных чисел (двух чисел 1-го вида или двух чисел 2-го вида)
является двойным числом 1-го вида, а произведение двух разно-
разноименных двойных чисел (г. е. числа 1-го вида и числа 2-го вида) —
двойным числом 2-го вида. Из формул B0а) также следует, что
=--ПЛ- Arg(~)=htgz-Avgz1; B06)
I г1 I V г1 /
однако и здесь важно учитывать, что частное двух одноименных
двойных чисел всегда. является числом 1-го вида, а частное двух
разноименных двойных чисел — числом 1-го вида:
/•(chcp + eshcp) r (shrp + t'ch го) г , , . . , ,,
—) и i—iT=—. . , гг-Ц=— ГсЬ (ф — ф^+esh (ф —с
= —) ч ^ ^L. = _ [sh (ф — ф,) + e ch (ф — ф,I.
Заметим, наконец, что, как следует уже из формул B0), C9)
и D0) — D0"), D4) — D4") и определения D1) сопряженного числа
(или из формул B0а, б) и A8а—в), если речь идет об умножении
и делении), для всех трех типов чисел
/ _ \ _
— )-=:. B1)

280
ПРИЛОЖЕНИЕ Б
Укажем еще, что в области дуальных чисел для вещественных чи-
чисел Arg2 = 0, а для чисто мнимых чисел kxgz не существует;
в области же двойных чисел и для вещественных чисел и для чисто
мнимых чисел Argz = 0 .(причем первые из этих чисел являются
числами 1-го вида, а вторые — числами 2-го вида).
После этого аналитического введения перейдем к геометрии.
Условимся сопоставлять точке плоскости Галилея (см. §§ 3—9)
с декартовыми координатами х, у или с полярными координатами
г, ф (т.е. такой точке М, что ОМ = d0M = г и /_ хОМ = ЬОх, ом = ф;
разумеется, расстояния и углы здесь понимаются в смысле геометрии
Галилея!) дуальное число
z = x + ey = r{\+eq) A6')
(рис. 213, а). Далее, полярными координатами точки М
плоскости Минковского (см. § 11) мы будем называть (пони-
(понимаемое в смысле геометрии Минковского!) расстояние d
D
у
г
I
\v
1
<ч
1
1
1
1 ^
л:
%
Рис. 213.
и один из углов ?хОМ = box, ом = ф и ^уОМ=ЬОу, ом = Ф,
в зависимости от того, является ОМ прямой 1-го или 2-го рода
(ср. выше, стр. 209); затем условимся сопоставлять точке плоскости
Минковского с декартовыми координатами х, у или с полярными
координатами г, ф двойное число
Z — x-\-ey = г(с11ф-|-е8Пф) или г = л: + еу = г (sh ф -]-е ch ф) A6")
в соответствии с тем, какое из равенств ф = / хОМ или ф — /уОМ
имеет место (рис. 213, б). Сопоставим еще точкам «особой прямой»
х — 0 плоскости Галилея («прямой нулевой длины»; ср. выше, стр. 46
и 51) делители нуля в области дуальных чисел, а точкам двух «особых

ЧИСЛОВЫЕ МОДЕЛИ ПЛОСКИХ ГЕОМЕТРИЙ
281
прямых» х=у и х = —у плоскости Минковского («прямым нулевой
длины»; ср. выше, стр. 196 и 198) делители нуля в области двойных
чисел. Таким образом мы отождествляем точки плоскости Галилея
с дуальными числами (и поэтому в дальнейшем будем говорить
«точка z плоскости Галилея», понимая под этим ту точку плоскости
Галилея, которой сопоставлено дуальное число z), а точки пло-
плоскости Минковского — с двойными числами (и здесь мы тоже будем
свободно употреблять выражения типа «точка г»).
Расстояние йг< г, между двумя точками г и г1 плоскости
Галилея или плоскости Минковского будет определяться той же
формулой
или
B2)
к которой мы пришли, отождествляя точки евклидовой плоскости
с комплексными числами (рис. 214, а, б),— это следует из опреде-
определения A7а, б) модуля числа и из формул E) из § 3 (стр. 51) и
у.
D
z
1
1
1
d
\
1
X
о
У
/*'
\
\
\
я
Рис. 214.
A5)—A5'а) из § 11 (стр. 199—200). Далее, угол б(?0> 2i) (г§. ,,, между
прямыми (z0, z±) и {z0, z2), соединяющими точки zx и z2 с одной и
той же точкой z2 (если этот последний угол существует; ср. выше,
стр. 54 и 203), выражается уже знакомой нам формулой
„, г,), (г.. г,) = Arg F(z2, zx
B3)
Где величину V(z2, zx\ zo)=-r по-прежнему называют (простым)
zi— zo
отношением трех точек z2, zx и z0 (плоскости Галилея или плоскости

282 ПР1П0ЖЕННЕ б
МИНКОВСКОГО). Соотношения B3) СЛеДуЮТ ИЗ ТОГО, ЧТО б(г„. г,), (г„, г,) —
(см., например, рис. 215, а — в спучае плоскости Галилея и рис. 215, at
б, в—в случае плоскости Минковского; при этом на рис. 215, в z'®=z\—
— го,где (z0, z[) J_ (z0, zt), в соответствии с определением угла между
х О
/V
х О
х
6)
Рис. 215.
разноименными прямыми в плоскости Минковского). Заметим, что
как в случае плоскости Галилея, так и в случае плоскости Мин-
Минковского формула B3) фактически определяет величину направ-
направлен н о го утла между прямыми (.?„, z{j n (z0, г2) (ср. выше, стр. 268).
Поскольку прямая (zu z2), очевидно, представляет собой мно-
множество таких точек z, что
Im V (z, z{-, z2) = О,
B4a)
где V(z, zx\ z2) = ——^ — (простое) отношение трех точек z, гъ z%
2г — zi
(ср. рис. 20'.), а выше), то уравнение прямой плоскости Галилея
или плоскости Минковского имеет знакомый нам уже вид
г — г.,
или
Bz —
B5)
B6)
Обратно, как и в случае евклидовой «носкости, каждое уравнение
вида B(i) зидает некоторую прямую линию плоскости Галилея или
плоскости Минковского (разумеется, в зависимости иг того, являются

ЧИСЛОВЫЕ МОДЕЛИ ПЛОСКИХ ГЕОМЕТРИЙ
283
числа z И коэффициенты В и С 'цнльными числами или двойными),
а именно прямую, соединяющую такие точки zl n z2, что zx — z2 Б,
zxz2— ZyZ* = C.
Окружность с центром z0 и квадратом радиуса р, пе р = га
в случае геометрии Галилея и р = + г2 в случае геометрии
I
У
а)
х О
Рис. 216.
X
Мннковского, причем г > 0 (рис. 216, а, б; ср. выше, стр. 200),
представляет собой множество таких точек z, чго
— zo\ = r или (z — zo){z — zo) =
B7)
при этом в случае геометрии Минковского надо еще потребовать,
чтобы все разности z — z0 были числами одноименными (числами
одного вида). Таким образом, уравнение окружности имеет вид
или вид
azz-\-bz
(zozo — р) = 0
с =0, Im a = Im с = 0.
B8)
Обратно, каждое уравнение вида B8) определяет окружность пло-
плоскости Галилея или плоскости Минковского, центр 20 и квадрат
радиуса р которой определяются из соотношений
~~ _ _ ъ ~ _ с
zo — "^f 1 ^о^о Р ~~ ~~? •
Цикл плоскости Галилея, проходящий через три точки zx, z2 п z3
(рис. 217, «), и окружность плоскости Минковского, проходящая
через точки zx, z2 и z3 (рис. 217, б), — это множество таких точек z,
чго
°W г,),(г8, гг) = б(г. г,).(г, z.)

284 приложение в
(ср. выше, стр. 83 и 206), т. е. что
Im W(zlt zt: zs, z)=]mV^^ = lm
=0, C0a)
=——— : ?1~г
Zn Z3 Z2 Z
шение четырех точек zlt z2, zs, z плоскости Галилея или плоскости
где W(zlt z2: z3, z)=——— : ?1~г—{сложное или двойное) отно-
Zn Z3 Z2 Z
х
N
У
/I N.^
/ J S
0
N. \ \
Рис. 217.
Минковского. Таким образом, уравнение рассматриваемого цикла или
рассматриваемой окружности имеет вид
г2 —z3
zi — z zi —?.ч . zi—г
или вид
C06)
B8а)
где коэффициенты А, В и С записываются теми же формулами B86),
стр. 270, что и в случае евклидовой геометрии. Однако, в то время
как в геометрии Минковского, так же как и в геометрии Евклида,
уравнения B8) и B8а) равносильны (для того чтобы обратить от-
относящиеся к случаю геометрии Минковского уравнение B8) в уравне-
уравнение B8а) или наоборот, достаточно умножить все члены уравнения
на «двойную единицу» е), в геометрии Галилея эти уравнения раз-
различны (ибо сокращать все члены уравнения на «дуальную еди-
единицу» е нельзя, поскольку е является делителем нуля, деление на
который является незаконным). Это отвечает тому, что в геометрии
Гапилея окружность B8) и цикл B8а) представляют собой две
существенно различные линии, в то время как на плоскостях
Евклида и Мннковского линии B8) и B8а) не отличаются одна от
другой.
Уравнение B6) прямой в случае геометрии Минковского можно
считать частным случаем обоих уравнений B8) и B8а), которые

ЧИСЛОВЫЕ МОДЕЛИ ПЛОСКИХ ГЕОМЕТРИЙ 285
принимают форму B6) (или эквивалентную B6) форму), если
а = 0, B9)
соответственно если
А = 0. B9а)
Однако в геометрии Галилея прямую B6) можно считать частным1)
случаем цикла B8а) (уравнение B8а) обращается в уравнение B6),
если имеет место равенство B9а)), но не окружности B8). [Уравне-
[Уравнение окружности плоскости Галилея B8) в случае выполнимости
условия B9) принимает вид
= 0, Imc = O;
если положить здесь Ь = Ь1\еЬ.2, г=х-\-гу, то мы получим
(Ъ1 -f еЬ2) (х-\- гу) -f (bx — eb2) (х — еу) -+- с — 0 или 2Ьхх + с = 0, т.е.
с
¦— уравнение «особой прямой» плоскости Галилея.]
Соотношение
(Zz^) 0 C1)
представляет собой (необходимое и достаточное) условие принад-
принадлежности четырех точек хъ z2, z3, г4 плоскости Галилея одному
циклу {или прямой) или принадлежности четырех точек гъ z%, z3, z4
плоскости Минковского одной окружности (или прямой).
Движения плоскости Галилея или плоскости Минковского
можно описать как такие преобразования, переводящие точку z в
точку z', что
(a) z'=pz-'-q или (б) z' =pz + g (pp = \). C2)
В частности, преобразования
(a) z' = — z и (б) z'=~z, C4)
как и в случае евклидовой плоскости, представляют собой с и м-
метрик» относительно точки 0 и симметрию относи-
относительно прямой 1ги2---0 (см. выше рис. 210, а, б). Общее же
преобразование C2а) на плоскости Галилея при |р| = 1 есть нечто
иное, как сдвиг с коэффициентом сдвига Argp (ср. выше, стр. 40),
сопровождаемый параллельным переносом на вектор q с началом 0
Точнее, предельным (ср. выше, стр. 90).

286
ПРИЛОЖЕНИЕ Б
и концом q (рис. 218, а); на плоскости Мннковского это преобра-
преобразование при |/'|—1 приставляет собой (гиперболический) поворот
вокруг точки О на угол Arg/), сопровождаемый параллельным пере-
переносом на век гор q (рис. 218,6).
У
я
\
\
0
/
А
/ •
Л^ ;
^ ' 6
1
QpZ+Q
\
}PZ
I
X
У
С
•
Ар
н \
/Xpz
i
Рис. 218.
Нетрудно проверить, что если точки г' и z[ получаются из точек г и гг
преобразованием C2а) или C26), то йг. г'- d22|, где буквой d обозначено
расстояние между двумя точками плоскости Галилея или Мннковского (ср. вы-
выше, стр. 270); таким образом, преобразования C2а, 6) сохраняют расстояния
между точками. Разумеется, движения плоскости Галилея или плоскости
Мннковского также обладают этим свойством; однако, несмотря на это, мно-
множество преобразований C2а, б) не совпадает с множеством рассматрива-
рассматриваемых в гл. 1 движений плоскости Галилея (см. па стр. 45 формулы A)) и
рассматриваемых в § 11 Заключения движений плоскости Минковского (см. на
стр. 194 формулы A1) или на стр. 208 формулы B3)). Это связано с тем, что
выше мы всегда ограничивались лишь так называемыми «собственными дви-
движениями» («движениями 1-го рода»), в то время как формулы C2а, 6) опи-
описывают множество «собственных и зеркальных движений» («движений 1-го и
2-го рода»; ср. со сноской 1) на сгр. 26). Так, например, «движения» C2а, б)
плоскости Галилея в координатах х, у записываются формулами
х'— ± х +а,
у' = vx ± y-*-b
(ср. Макарова [28], ч. II). Мы предоставим читателю самостоятельно рас-
расшифровать строение «обобщенных движений» C2а, б) плоскостей Галилея и
Мннковского.
Наконец, более общие, чем движения C2а, б), преобразования
C!У)

ЧИСЛОВЫЕ МОДЕЛИ ПЛОСКИХ ГЕОМЕТРИЙ 287
переводят четыре точки пчоскости Галилея, принадлежащие одному
циклу (или одной прямой) в четыре точки, также принадлежащие
одному циклу (или одной прямой). Преобразования C5') плоскости
Мннковского переводят четыре точки, принадлежащие одной окруж-
окружности (или одной прямой) в четыре точки, также принадлежащие
одной окружности (или одной прямой). Эти утверждения, равносиль-
равносильные теореме о том, что (З5'а, б) суть круговые преобразо-
преобразования плоскости Галилея или плоскости Мннковского, следуют
из критерия C11 принадлежности четырех точек идиому циклу или
одной окружности и из того, что если точки z[, z.[, г'ъ, z\ полу-
получаются из точек zlt Zo, z3, 2 преобразованием (З5'а). то
W(z[, г'„\ z'3, г4') = W(zu z.2\ zs, г4), а если они получаются из
точек zlt z2, zs, ,?4 преобразованием (З5'б), то W[z[, г'г; z'3, г^) =
= W(z1, z2; zs, z4). В частности, преобразование
z' I, C6)
z
являющееся частным случаем преобразования (З5'б), представляет
собой инверсию A-го рода) с центром 0 и степенью 1 на плос-
плоскости Гатился, если z и z'—дуальные числа (ср. выше, стр. 138—
139), и инверсию с центром О и степенью 1 на плоскости Мин-
ковского, если z и z' двойные числа (ср. стр. 216).
При с ф 0 преобразования C5') в области дуальных чисел и в области
двойных чисел не являются взаимно однозначными: так^ю
точку г, что cz-\-d (пли cz , d) является делителем нуля, преобразование
(З5'а) (соответственно (З5'б)) не переводит ни в какую точку г' (ибо деление
на делитель нуля невозможно). Последнее обстоятельство заставляет расши-
расширить множество д\альных и двойных чисел, введя и рассмотрение фиктивные
(или «идеальные») числа
1
(и -Ч)-
соответственно
1 1
/ 1 — е 1 +е \ \
п
где Я, ц—всевозможные вещественные числа, и положив
со =со, оо = со,
соответственно
0^ = 0J, 0J = 0)!, О1 = О2, G.2—G! И СО = 00.

288 ПРИЛОЖЕНИЕ Б
После такого расширения области дуальных и двойных чисел можно, напри-
например, положить
QM+6 _ е __а+6е ,
соответственно
ащ-
ССОо-
или
aoi~\-b
coj-J-d
f-d 1
1 — е , t
4+d
2A— e) + t
o(l— e) + d
[1-е)
>d+e)
Ч1 +e)
(a+b)—be
(c-\-d)—de
(a-\-b)—(a—b) e
c+d — (c—d)e
В расширенном таким образом множестве дуальных или двойных чисел ото-
отображения C5') являются уже взаимно однозначными: каковы бы ни
были (дуальные, соответственно двойные) коэффициенты а, Ь, с, d преобразо-
преобразования (такие, что \ad—Ьс\фй, т.е. ad—be не является делителем нуля),
, az+b (
каждому числу г отвечает единственное число г =—-j—-, I илн г =
az + b \ „
==—=¦ ). Таким образом, круговые преобразования естественно рассматри-
cz + dj
вать как преобразования циклической плоскости Галилея, соответственно
круговой плоскости Минковского; эти плоскости получаются из «обыкно-
«обыкновенных» плоскостей Галилея и Минковского дополнением последних «идеаль-
«идеальными» или «бесконечно удаленными» точками, отвечающими числам Яю, со,
соответственно Кыг, (ш>2, оъ о2, со. На более детальном изучении «расширен-
«расширенных» множеств дуальных и двойных чисел и отвечающих этим числам геомет-
геометрических образов мы здесь не остановимся.
Сходство свойств комплексных чисел, дуальных чисел и двойных
чисел часто позволяет доказывать с помощью единой выкладки
(фигурирующие в которой числа можно считать числами любого из
рассматриваемых трех типов!) теоремы, относящиеся как к евклидо-
евклидовой геометрии, так и к геометрии Галилея или Минковского. Пусть,
например, Slt Sz, Ss, S4 — четыре окружности плоскости Евклида
или Минковского, соответственно четыре цикла плоскости Галилея;
точки пересечения S1 и S2, S2 и S3, S3 и St, 54 и S± мы обозна-
обозначим через z1 и wly соответственно zz и w2, z3 и w3, z4 и и>4. Дока-
Докажем, что если точки zlt z2, z3 и z4 принадлежат одной окружности
или прямой (соответственно одному циклу или прямой), то также и
точки wly w2l w3 и и>4 принадлежат одной окружности или прямой
(соответственно одному циклу или прямой; см. рис. 219, а, б, отно-
относящиеся к геометриям Евклида и Галилея).

ЧИСЛОВЫЕ МОДЕЛИ ПЛОСКИХ ГЕОМЕТРИЙ
289
Воспользуемся тем, что точки гъ z2, щ и w2 принадлежат
одной окружности (или одному циклу). S2; точки гъ z3, w2 и w3
а)
б)
Рис. 219.
¦финадлежат одной окружности (одному циклу) S3\ точки z3, г4, w3
и wt принадлежат одной окружности (одному циклу) S4; наконец,
точки z4, zx, wi и wx принадлежат одной окружности (одному циклу)
10 И. М. Яглом

290 ПРИЛОЖЕНИЕ Б
S±. Отсюда вытекает, что четыре двойных отношения
, щ; zs, W2) = ^|:J=
вещественны (ср. C1)). Поэтому и выражение
W (zt, w2; z^w^-Wjz^Wj, г„, и>3)_/zt —гг zt—г
W (гг, w3; г3, шг)-Г (г4, и^; гь и>4) \г3—г2'г3 —г4
= ^7^, z3; z2, zJ-W(wlt ws; w2, w4)
вещественно. Следовательно, из вещественности двойного отношения
W(zlt z3; z2, z4) вытекает вещественность и двойного отношения
W(wlt w3; w2, иL), и, значит, четверки
точек zlt z2, zs, z4 и та»!, w2, ws, tw4
одновременно принадлежат или не при-
принадлежат одной окружности (одному
циклу)!
X Вот более важный пример подобного
рода. Пусть ABC—треугольник плоскости
Рис. 220. Евклида, Галилея или Минковского; как
обычно, длины сторон этого треугольника
обозначим через а, Ь, с, а величины углов—через Л, В, С. Пусть вершины
этого треугольника соответствуют числам (комплексным, дуальным или двой-
двойным!) гь г2 и г3 (рис. 220). Очевидно, что если
ш1 = г3—г2> w2 = z1— г3, 413 = 22—2!,
то1)
|ш,| = а, \w2\ = b, |ш3|=с. D5)
Поэтому, обозначив
(откуда следует, что
t= —<fu Arg шг= —фг, Arg ^3= —Фз.
см. формулы A86) и A8в), стр. 266 и 278) и предположив для простоты, что
в случае геометрии Минковского wlt w2 и ws—двойные числа 1-го вида, будем
иметь
ш2 = 6 (Cos фа + / Sin ф2), ю3 = с (Cos ф3 + / Sin ф3),
1) Таким образом, в случае геометрий Галилея и Минковского а, 6, с
суть направленные длины сторон треугольника (ср. выше, стр. 65).

ЧИСЛОВЫЕ МОДЕЛИ ГГЛОСКИХ ГЕОМЕТРИЙ 291
где l = i, е или е, а символами Cos(p и Sin (f обозначены обыкновенные
(«евклидовы») тригонометрические функции cos ф и sin ф, соответственно «гали-
леевы тригонометрические функции» Со5ф=1, Б1пф = ф (ср. выше, стр. 276
и 229) или гиперболические функции («тригонометрические функции Минков-
ского») Совф=:сЬф, 5тф=5Ьф. Наконец, заметим еще, что
«Ра — фз = Д Чз — Ф1=б. ф1 —фг = С D6)
(см. тот же рис. 220 г)), так что в силу формул B0а) (стр. 267 и 278—279)
w2w3—bc (Cos A-}-/ Sin А),
г = са (Cos В + / Sin В),
j = ab (Cos С + / Sin С),
соответственно
з = Ьс (Cos А — / Sin A),
= са (Cos В—/ Sin В),
2 = ab (Cos С—I Sin С).
Воспользуемся теперь тем, что
[ = (г3—г
и, значит,
—w
Отсюда получаем
а2 = | w-l |2 = ш,^ = (ш2 + и>3) (№ + w3) = 2г + 3Щз + 23 + 23
= \ w2 \2 +\ w3 \3-{-bc(Cos A +1 Sin A)+bc(Cos A —I Sin А) = Ь* + с2-\-2bcCos А.
Но это есть не что иное, как теорема косинусов геометрий Евклида,
Галилея и Минковского, в геометрии Евклида имеющая вид
ф = Ь2 + с2 + 2Ъс cos A D7)
(заметим, что в обозначениях рис. 220, который мы теперь считаем относя-
относящимся к евклидовой геометрии ^ /1 = 180°—?_ ВАС, и поэтому формула D7)
равносильна соотношению a2 = b'1-\-c2 — 2fcccos ?. ВАС), в геометрии Галилея —
вид
. 1 = (?, + сJ
(ср. с формулой A1) из § 4 стр. 61) и в геометрии Минковского — вид
Образуем, далее, три выражения:
w2w3—w2w3 = bc (Cos A-\-l Sin A)—fcc(Cos A — / Sin A) = 2bcSin A-I,
w3wi — Шз^! = со (CosS+ / Sin B)—со (Cos В — / Sin B) = 2coSin B-I,
Wiw2 —wxw2 = ab (CosC+ / Sin C)—ab (CosC—f Sin C) = 2ofc Sin Cl.
Ho
W2W3—W2W3 = (Z1 — Z3){Z2 —Zrf — iZ! —Z3) {Z2— Zt) =
= 2i z.2 + г.гг3 + г3г, — ztz2—г2г3 — г3г,
l) Таким ойразом, А, В, С суть направленные углы треугольника
(ср. выше, стр. 65).
10*

292 приложение в
и, как легко показать, также
[Заметим, что стоящее справа выражение симметрично относительно гг,
г, и 2gl] Таким образом, имеем 2bc Sin A -I — 2ca Sin B-/ = 2obSinC-/ или
be Sin A~ca Sin B = obSinC,
откуда без труда получаем
a b с
Sin A Sin В SinC
— теорему синусов геометрий Евклида, Галилея и Минковского:
а _ b _ с
sin Л sin В sin С
(геометрия Евклида);
а Ь с
D8)
(геометрия Галилея; ср. выше, стр. 61) и
sh/l~shB shC K '
(геометрия Минковского, стр. 210).
Известно, что и точки неевклидовой геометрии Лобачев-
Лобачевского можно представить в виде комплексных чисел (см., например, М а р-
кушевич [80] или Яглом [77]). Для этого на плоскости комплексного
переменного выделяется круг К, определяемый условием гг< 1; точки этого
круга сопоставляются точкам плоскости Лобачевского. Расстояние dZ)Zl
между точками z и гх круга К, понимаемое в смысле геометрии Лобачевского,
действующей внутри /(, измеряется по формуле
а роль движений Лобачевского играют «дробно-линейные преобразо-
преобразования» C5), переводящие круг К в себя, т. е. преобразования
(a) z'=^±± и (б) г' = ??±1 (pp-qq^O). E0)
qz + p qz + p
Простейшими частными случаями движений E0а, б) являются преобразования
(а) г'=— г и (б) г'=г C4)
— симметрия относительно точки 0 плоскости Лобачевского (ср. выше
рис. 210, а) и симметрия относительно прямой Imz = 0 (рис. 221).
Дуга ММ' на рис. 221 изображает отрезок «прямой» плоскости Лобачев-
Лобачевского, «перпендикулярной» «прямой» Iniz = 0; при этом кавычки в последней
фразе указывают, что соответствующий термин понимается в смысле геометрии
Лобачевского, отличном, разумеется, от того, какой имеют те же самые поня-
понятия в геометрии Евклида. Образцом «неевклидовой прямой» может служить

ЧИСЛОВЫЕ МОДЕЛИ ПЛОСКИХ ГЕОМЕТРИЙ
293
отрезок IJ прямой Im г = 0—диаметр круга К; расстояние D9) между двумя
точками А и В этого отрезка совпадает с «гиперболическим расстоянием» A6)
(стр. 237) между точками «прямой Лобачевского» (отрезка) IJ. Все остальные
«прямые» плоскости Лобачевского могут быть получены из отрезка IJ прямой
Im z = 0 или прямой
2—1=0 E1)
движениями E0а, б); отсюда следует, что общее уравнение «.прямой» плоскости
Лобачевского имеет вид
E2)
E2а)
или
azz-\-bz + bz-\-a =
Azz+Bz— Вг'+А=0, Re/1 = 0.
Геометрически «прямые» плоскости Лобачевского изображаются диаметрами
круга К и заключенными внутри К Дугами окружностей, перпендикулярных
Рис. 221.
Рис. 222.
окружности 2, ограничивающей круг К (рис. 222; под углом между двумя
пересекающимися окружностями понимается угол между касательными к окруж-
окружностям в точке их пересечения).
Произвольные окружности
или
= 0, Ima=Imc =
Azz+Bz — Bz+C = 0, Re/l=ReC =
B8)
B8a)
(точнее, дуги окружностей, заключенные внутри К) изображают циклы
неевклидовой геометрии Лобачевского (т. е. линии, «устроенные» в каждой
своей точке одинаково, линии, допускающие «скольжения» по себе, с помощью
которых любую точку линии можно перевести в любую другую ее точку). Мы
уже знаем, что в «прямую» цикл B8) или B8а) обращается, если
а=с
А=С
E3)
E3а)
(ср. выше уравнения E2) и E2а)). «Окружность» плоскости Лобачевского
(т. е. множество точек, равноудаленных от одной точки—«центра окруж-
окружности»; см. стр. 257) евклидова окружность B8) или B8а) изображает в том

294 ПРИЛОЖЕНИЕ Б
случае, если она целиком заключена внутри 2 (рис. 223, о); предельную
линию (стр. 257) она изображает, если касается (изнутри) окружности 2
(рис. 223,6); наконец, эквидистанту (множество точек, равноудаленных
от одной прямой—базы эквидистанты; см. стр. 257)—в том случае, если она
пересекает 2 в двух точках М и N.
В последнем случае изображением эквидистанты, разумеется, служит
лишь заключенная внутри ? дуга MN окружности B8) (или B8а)): ведь не
принадлежащие кругу К. точки в нашей модели вообще исключаются из рас-
рассмотрения. Впрочем, точнее будет сказать, что эквидистанта плоскости Лоба-
Лобачевского изображается двумя дугами MN (евклидовых) окружностей
(рис. 223, в), каждая из которых изображает множество точек, расположен-
расположенных по одну сторону от базы эквидистанты (на рис. 223, в изображаемой пунк-
пунктирной дугой MN) и удаленных иа одно и то же расстояние от базы.
Последнее замечание подчеркивает одни принципиальный дефект рассматри-
рассматриваемой модели плоскости Лобачевского, изображаемой внутренностью круга К.
Несложные уравнения E2) и E2а), равно как и уравнения B8) и B8а) или
даже совсем простое уравнение E1), нельзя рассматривать как уравнения
прямых или циклов геометрии Лобачевского: необходимо все время помнить,
что геометрический смысл в нашей модели имеют лишь такие точки z плоско-
плоскости комплексного переменного, для которых zz < I. Соответственно этому
задача отыскания аналитических выражений для «круговых преобразований»
плоскости Лобачевского, переводящих циклы в циклы, становится весьма слож-
сложной: на нашей модели эти преобразования должны переводить дуги окружно-
окружностей B8) или B8а) снова в дуги тех же окружностей, но сами эти дуги
трудно описать достаточно простым уравнением (которому должны удовлетво-
удовлетворять лишь точки дуг, но не все точки окружностей) '). Да и представление
эквидистанты в виде изображенной на рис. 223, в линзы из пары дуг окружно-
окружностей с общими концами вряд ли может показаться кому-нибудь простым и
изящным!
Впрочем, читатель, внимательно прочитавший все предыдущее, вероятно,
уже догадывается, как можно устранить возникшие затруднения. Условимся
считать точки плоскости Лобачевского направленными, т. е. снабжен-
') Рекомендуем читателю попытаться самому продумать вопрос о возмож-
возможном уравнении, описывающем отрезок IJ рис. 221.

ЧИСЛОВЫЕ МОДЕЛИ ПЛОСКИХ ГЕОМЕТРИЙ
295
ными указанием того, какое направление вращения вокруг точки принимается
за положительное; на чертежах положительное направление вращения вокруг
точки задается окружающей точку маленькой дугой со стрелкой (рис. 224).
Далее будем считать, что две точки плоскости Лобачевского, отличающиеся
только направлениями, изображаются такими
комплексными числами z и г', что
, 1
г =—
г
C6)
т. е. г' получается из г инверсией с окруж-
окружностью инверсии 2 (инвгрсией с центром 0 и
степенью 1; см. тот же рис. 224). Кроме того,
условимся причислять к точкам плоскости Лоба-
Лобачевского также все точки окружности 2 с уравне-
уравнением гг=\; эти точки мы будем называть «бес-
«бесконечно удаленными точками» пло- Рис. 224.
скости Лобачевского и будем считать их нена-
ненаправленными (последнее условие можно объяснить тем, что вокруг такой
«точки» нельзя нарисовать кружок, так как она является в известном смысле
«граничной» точкой плоскости Лобачевского). «Бесконечно удаленную точку»
плоскости Лобачевского можно представлять себе как пучок («сходящихся
в этой точке») параллельных между собой (в смысле геометрии Лобачевского)
прямых, подобно тому как «бесконечно удаленную точку» евклидовой плоско-
плоскости часто понимают как пучок евклидовых параллелей.
Таким образом, теперь у нас множество всех (направленных и бесконечно
удаленных) точек плоскости Лобачевского изображается множеством всех
Рис. 225.
комплексных чисел z (включая и «число» оо, отвечающее взятой с «отрицатель-
«отрицательным направлением обхода» точке 0). Циклы плоскости Лобачевского мы также
будем считать направленными, т. е. снабженными указанием положи-
положительного направления движения по циклу; при этом направленную точку А
мы только в том случае будем считать принадлежащей направленному циклу S,
если направление вращения вокруг А «согласовано» с направлением движения
вдоль S (см. схематический рис. 225, а, где точка А считается принадлежа-
принадлежащей циклу S, а точка В—не принадлежащей ему). Далее, под (направлен-
(направленной!) эквидистантой с базой / мы будем понимать множество точек, удален-
удаленных от / на одно и тоже расстояние А, причем точки, расположенные по
разные стороны от /, по условию имеют разное направление (рис. 225, б;
таким образом, эквидистант с данной базой / и данной шириной h > 0 суще-
существует две и им можно условиться приписывать разные ширины h и —И).
Прямые плоскости Лобачевского уместно считать ненаправленными;
для сравнения напомним, что в антиевклидовой геометрии (см. выше,

296
ПРИЛОЖЕНИЕ Б
стр. 258—261) мы нашли удобным считать основным образом геометрии направ-
направленные прямые евклидовой плоскости: при этом окружности антиевклидовой
плоскости («циклы») мы также считали направленными, однако точки — нена-
ненаправленными (негде поставить стрелку!). При этом все точки прямой плоско-
плоскости Лобачевского рассматривают как «сдвоенные» (рис. 225, б), т. е. счи-
считают, что прямой / принадлежат точки обоих направленийх). Наконец, к
числу циклов плоскости Лобачевского причисляют и (ненаправленную) «окруж-
«окружность бесконечно удаленных точек», изображаемую окружностью 2 (окруж-
(окружностью zz=l) нашей модели. При этом совокупность всех (направленных)
циклов и всех прямых плоскости Лобачевского изображается совокупностью
всех вкружностей и прямых плоскости (обыкновенных) комплексных чисел
(см., в частности, рис. 226, на котором
изображена прямая / плоскости Лобачев-
Лобачевского и эквидистанта S с базой /). Урав-
Уравнение каждой прямой плоскости Лобачев-
Лобачевского будет иметь вид E2) (или E2а)), а
уравнение цикла — B8) (или B8а)).
Условие принадлежности четырех (на-
(направленных) точек гъ zx, z3 и г4 плоскости
Лобачевского одному циклу или одной пря-
прямой будет иметь хорошо знакомый нам вид:
lm W(zlt z2; г3) z4) = 0. C1)
Отсюда следует, что преобразования
az-\-b ,,. , az-\-b
= ^-!— и (б) г' = ^—
cz+d cz+d C5)
(ad—be Ф 0)
(a)
Рис. 226.
переводят четыре точки, принадлежащие
одной прямой или одному циклу, в четыре
точки, также обладающие аналогичным свой-
свойством, т. е. что C5) суть круговые пре-
преобразования плоскости Лобачевского.
Это обстоятельство позволяет геометрически описать все возможные круговые
преобразования плоскости Лобачевского2).
Выше мы видели, что точки плоскостей Евклида, Галилея и Минковского
можно представлять в виде «чисел» разной природы: комплексных чисел
z — x-\-iy, где i'2 = — 1, дуальных чисел г = х-\-еу, где е2 = 0 и двойных чисел
\ где е2=+1- С другой стороны, и (направленные) точки плоскости
!) Понятие направленного цикла было введено для того, чтобы установить
направление принадлежащих этому циклу точек: направление стрелки на
окружающей точку дуге, проведенной со стороны выпуклости цикла,
должно совпадать с направлением цикла (рис. 225, а). Однако для прямой
понятие «стороны выпуклости» теряет смысл; поэтому мы не имеем возмож-
возможности указать направление принадлежащих ей точек и, следовательно, все
точки прямой следует считать обладающими обоими возможными направле-
направлениями (рис. 225, в). [Также и из представления о прямой как об «эквидис-
танте нулевой ширины», обе ветви которой совпадают с «базой» эквидистанты,
следует, что точкам прямой надо приписывать оба возможных направления;
ср. рис. 225, б и в.]
2) См., например, Я г лом [77] или [78].

ЧИСЛОВЫЕ МОДЕЛИ ПЛОСКИХ ГЕОМЕТРИЙ 297
Лобачевского можно представлять в виде комплексных чисел. Эта система
истолкований плоских геометрий Кэли — Клейна может быть еще продолжена:
(направленные!) точки (эллиптической) плоскости Римана тоже можно пред-
представлять в виде комплексных чисел z = x-\-iy; с другой стороны, (направлен-
(направленные) точки антиевклидовой и антипсевдоевклидовой плоскостей можно изобра-
изображать дуальными числами z = x-\-ey, а (направленные) точки дважды гипербо-
гиперболической и антигиперболической плоскостей—двойными числами z — x-\-ey.
Таким образом, точки трех, плоскостей Кэли — Клейна с эллиптической (рима-
новой) метрикой углов—плоскостей Римана, Евклида и Лобачевского — изоб-
изображаются комплексными числами; точки трех плоскостей с евклидовой метри-
метрикой углов—плоскостей антиевклидовой, Галилея и антипсевдоевклидовой —
изображаются дуальными числами; точки трех плоскостей с гиперболической
метрикой углов (метрика Лобачевского) — плоскостей антигиперболической,
Минковского и дважды гиперболической—изображаются двойными числами.
При этом расстояние &z z между точками z и zr плоскости с эллиптической
(римановой) метрикой расстояний (т. е. плоскости Римана, антиевклидовой
или антигиперболической) определяется формулой
D9')
на плоскости с евклидовой метрикой расстояний (плоскости Евклида, Галилея
или Минковского) оно определяется более простой формулой
dlZi=(z-Zl)(z-z^), B2)
а на плоскости с гиперболической метрикой расстояний (метрика Лобачев-
Лобачевского; иными словами, на плоскости Лобачевского, антипсевдоевклидовой или
дважды гиперболической) расстояние dz, г, определяется (знакомой нам уже)
формулой
th ^i
2 -(l_2Zl)(l_z2l)- D9)
Движения на плоскости Кэли—Клейна, на которой расстояние определяется
формулой D9'), задаются как преобразования
Z'=E1±1 или г. = ^±? (Ipp+w^O); E0')
qz—p qz—p
на плоскости, где метрика расстояния указывается формулой B2), движения
имеют вид
z' = pz+q или z' = pz+q (pp=l), C2)
а на плоскости, где расстояние между точками z и гх указывается формулой
D9), движения имеют вид
г'=^±Я ил„ z-=U±3: (|pp-wl*0). E0а)
qz+p qz+p

298 ПРИЛОЖЕНИЕ Б
Уравнение прямой линии в этих трех случаях, отвечающих формулам D9),
B2) и D9') для расстояния между точками, имеет вид')
Azz-\-Bz—Вг+Л=0, Re/4=0, E2а)
соответственно
Вг—Вг+С = 0, ReC = O B6)
Агг + Bz—Ъг—Л = 0, Re /1=0. E26)
Однако уравнение цикла во всех трех случаях имеет один и тот же вид1)
г—~Вг+С = 0, ReA = ReC = 0. B8а)
Таким образом, в соответствии с тремя видами D9), B2) или D9') формулы
для расстояния между точками, условие обращения цикла E2а) в прямую
имеет вид
А— С = 0, E3а)
Л=0 B9а)
или
А+С = 0 E36)
(ср. с § 12 Заключения).
Используя уравнение B8а) цикла или условие принадлежности четырех
точек Zj, z2, г3, г4 одному циклу
Im«7Bl, г2; г3, г4) = 0, C1)
можно установить, что во всех девяти плоскостях Кэли—Клейна преобразо-
преобразования
переводят циклы плоскости снова в циклы, т. е. являются круговыми
преобразованиями соответствующей плоскости Кэли — Клейна.
1) Если фигурирующие в формулах E2б), B6), E2а) и B8а) числа явля-
являются комплексными или двойными, то эти уравнения можно также записать
в виде B8) или в виде аналогичных вариантов равенств E26), B6) или E2а)
(см., например, формулу E2)); однако если коэффициенты А, В, С я пере-
переменные г являются дуальными числами, то формулы B8а) и B8) перестают
быть равносильными.

ЧИСЛОВЫЕ МОДЕЛИ ПЛОСКИХ ГЕОМЕТРИЙ
299
Все сказаннное выше просуммировано в следующих таблицах:
Таблица VI. Расстояние йг,г.
Таблица V. Числа, изображающие между точками z и zt плоскости
точки плоскостей Кэли—Клейна Кэли —Клейна
Мероопре-
Мероопределение
углов
Р
Е
Л
Тип чисел
Z = X-\-iy, l= —1
г=х+гу, е2 = 0
г=х-\-еу, е2 = +1
Мероопре-
Мероопределение
расстоя-
расстояний
р
Е
Л
а
th2
2
2
2
(z_2i)(-_-}
A -«,)(! -zz,)
Таблица VII. Движения плоское- Таблица VI11. Уравнения прямых
ты Кэли—Клейна плоскости Кэли—Клейна
Мерооп-
ределе-
ределение
расстоя-
расстояний
Р
Е
Л
Движения
.,. Рг+Я
qz—p
z' = pz + q, pp=l
,/ Pz+Q
qz + p
Мероопре-
Мероопределение
расстоя-
расстояний
P
E
Л
Уравнение прямой
Azl + бг— В F— /1=0,
Re/1=0
Bz — Bz + C = 0,
ReC = 0
Azz + Bz — Bi + i4=0,
Re/1=0
Мы не остановимся здесь на применениях развитого аппарата к доказа-
доказательству конкретных теорем, ограничившись лишь в качестве единственного (и
весьма простого) примера указанием на то, что проведенные на стр. 288—290
выкладки доказывают сразу для всех девяти геометрий Кэли —
Клейна на плоскости следующую теорему: если циклы Sj и S2 пере-
пересекаются в точках zx и wlt циклы S2 и S3—в точках z2 и w2, циклы S3 и
S4—в точках z3 и w3 и циклы St и St—в точках z4 и wt, причем точки zlt
z2, zs и г4 принадлежат одному циклу (или одной прямой), то и точки щ,
w2, w3 и wt принадлежат одному циклу (или одной прямой).
Иные примеры подобного рода можно порекомендовать читателю отыскать
самостоятельно.

ЛИТЕРАТУРА
Учебники евклидовой геометрии
[1] —[3] Евклид, Начала, тт. I—III, M.— Л., Гостехиздат, 1948; 1949;1950.
[4] К и се лев А. П., Геометрия, ч. 1, М., Учпедгиз, 1962.
[5]—[6] Перепелкин Д. И., Курс элементарной геометрии, чч. 1—2,
М.—Л., Гостехиздат, 1948; 1949.
[7]Адамар Ж-, Элементарная геометрия, ч. 1, М., Учпедгиз, 1957.
[7а] Погорелов А. В., Элементарная геометрия (планиметрия), М.,
«Наука», 1969.
[76] Гильберт Д., Основания геометрии, М.—Л., Гостехиздат, 1948.
См. также кннгн Кокстера [19] и Яглома [9] - [10].
Литература к § 1 Введения
[8]Клейн Ф., Сравнительное обозрение новейших геометрических иссле-
исследований (Эрлангенская программа). Сборник «Об основаниях геометрии»,
М., Гостехиздат, 1950, стр. 399—434.
[9]—[10] Я г лом И. М., Геометрические преобразования, тт. 1—II, М.,
Гостехиздат, 1955; 1956.
[11] Я г лом И. М. и Атанасян Л. С, Геометрические преобразования,
Энциклопедия элементарной математики (ЭЭМ), кн. IV, М., Физматгиз,
1963, стр 49—158.
Основы аналитической геометрии на плоскости
[12] Дуб нов Я. С., Введение в аналитическую геометрию, М., Физматгиз,
1959.
Литература к § 2 Введения
[13]Галилей Галилео, Избранные сочинения в двух томах, т. I, M.,
«Наука», 1964.
[14]—[15] Хайкин С. Э., Что такое силы инерции, М.—Л., Гостехиздат,
1939; Силы инерции и невесомость, М., «Наука», 1967.
[16]Седов Л. И., Галилей и основы механики, М., «Наука», 1964.
[17]|Л а ндс бе р г Г. С. (ред.), Элементарный учебник физики, т. 1, М.,
«Наука», 1969.
[18]Хайкин С. Э., Механика, М. — Л., Гостехиздат, 1948.
См. также книгу Шварца [40].
Что такое четырехмерное пространство?
[19]Кокстер Г. С. М., Введение в геометрию, М., «Наука», 1966.
[20] Розе н фе л ь д Б. А. и Яглом И. М., Многомерные пространства,
ЭЭМ, кн. V, М., «Наука», 1966. стр. 349-392.

ЛИТЕРАТУРА 301
Системы сил в статике и скользящие векторы
[21]Аппель П., Теоретическая механика, т. 1, М., Физматгиз, 1960.
[22]Бухгольц Н. Н., Основной курс теоретической механики, ч. 1, М.,
«Наука», 1965.
[23] Бол т я н с к и й В. Г. и Яг лом И. М., Векторы и их применения
в геометрии, ЭЭМ, кн. IV, стр. 291—381.
См. также книги Ландсберга [17] н Ха йкнна [18].
Геометрия Галилея
[24]Розенфел ь д Б. А. и Яг лом И. М., Неевклидовы геометрии,
ЭЭМ, кн. V, стр. 394—476.
[25] К а г а н В. Ф., Основания геометрии, ч. II, М., Гостехиздат, 1956.
[26]Кёйпер Н. (Kuiper N.), Одна геометрия на плоскости (Ееп vlakke
meetkunde), Simon Stevin 30, 1954, стр. 94—105.
[27] Шт р у бек ке р К. (Strubecker К.), Геометрия в изотропной плоскости
I—III (Geometrie in einer isotropen Ebene I—III), Der mathematische
und naturwissenschaftliche Unterricht 15 A962—1963), стр. 297—306;
343—351; 385—394.
[28]Макарова Н. М., Геометрия Галилея — Ньютона I—III, Ученые за-
записки Орехово-Зуевского пединститута 1, вып. 1 A955), стр. 83—95; 7,
вып. 2 A957), стр. 7—27; 29—59.
[29]Макарова Н. М., Кривые второго порядка в плоской параболической
геометрии. Вопросы дифференциальной и неевклидовой геометрии (Уче-
(Ученые записки Моск. гос. пед. ин-та им. Ленина), М., 1963, стр. 222—251.
[30]Макарова Н. М., Двумерная неевклидова геометрия с параболиче-
параболической метрикой длин и углов. Кандидатская диссертации, Л., 1962.
См. также книгу Клейна [55].
Литература к гл. II
[31]Яглом И. М., Окружности, ЭЭМ, кн. IV, стр. 448—517.
[32]Кулидж Дж. Л. (Coolidge J. L.), Трактат об окружности и сфере
(A treatise on the circle and the sphere), Oxford, 1916.
[33]3етель С. И., Новая геометрия треугольника, М., Учпедгиз, 1962.
[34]Макарова Н. М., К теории циклов параболической геометрии на
плоскости, Сибирский матем. журнал 2, № 1 A961), стр. 68—81.
См. также книги Перепелкнна [5], Ада мара [7], Кок стера
[19], Яглома [10] и [77] и статьи Кёйпера [26], Штрубеккера [27],
Макаровой [28].
Общие свойства плоских кривых
[35] Дубнов Я. С, Основы векторного исчисления, ч. I, M.—Л., Гостех-
Гостехиздат, 1950, гл. V.
[36] Б о лт я нск и й В. Г. и Яг лом И. М., Геометрические задачи на
максимум и минимум, ЭЭМ, кн. V, стр. 270—348.
Литература к § 10 Заключения1)
[37] Эйнштейн А., О специальной и общей теории относительности (обще-
(общедоступное изложение), Петроград, Научное книгоиздательство, 1923;
Физика и реальность, М., «Наука», 1963, стр. 167—235; Собрание сочи-
сочинений, т. I, M., «Наука», 1965, стр 530—600
•) См. также (более полные) аннотированные списки литературы, прило-
приложенные к книгам [47] и [536].

302 ЛИТЕРАТУРА
[38]—[38а] Борн М., Эйнштейновская теория относительности, М., «Мир»,
1964; Теория относительности Эйнштейна и ее физические основы, М.—Л
ОНТИ, 1938.
[39] Д юре л л К., Азбука теории относительности, М., «Мир», 1964
[40] Шварц Дж., Как это произошло, М., «Мир», 1965.
[41]Ландау Л Д. и Румер Ю. Б., Что такое теория относительности,
М., «Сов. Россия», 1963.
[42] Г а р д н е р М., Теория относительности для миллионов, М., Атом-
издат, 1966.
[43] БлохинцевД. И. и Драбкина С. И., Теория относительности
Эйнштейна, М.—Л., Гостехиздат, 1940.
[44] С о ко л о в с к и й Ю. И., Теория относительности в элементарном изло-
изложении, М., «Наука», 1964.
[45] Б о н д и Г., Относительность и здравый смысл, М., «Мир», 1967.
[46]Эдд и н гто н А. С, Пространство, время и тяготение, Одесса, «Мате-
зис», IQ23.
[47] Н е в а н л и н н а Р., Пространство, время и относительность, М.,
«Мир», 1966.
[48] С м и л г а В. П., Очевидное? Нет, еще неизведанное М., «Молодая
гвардия», 1966.
[49] Ж у к о в А. И., Введение в теорию относительности, М., Физматгиз,
1961.
[50) Румер Ю Б. и Р ы вки н М. С, Теория относительности, М., Учпед-
Учпедгиз, 1960.
[51]Бергман П. Г., Введение в теорию относительности, М., ИЛ, 1947.
[52] Б о м Д., Специальная теория относительности, М., «Мир», 1967.
[53] С к обе л ьц и н Д. В., Парадокс близнецов в теории относительности,
М., «Наука», 1966.
[53а] К у р г а н о в В., Введение в теорию относительности, М., «Мир», 1968.
[536] Угаров В. А., Специальная теория относительности, М., «Наука», 1969.
[53в] Тейлор У. и Уилер Дж., Физика пространства — времени, М.,
«Мир», 1969.
[54] Ньютон И., Математические основы натуральной философии, в книге:
Крылов А. Н., Собрание трудов, т. VII, М.—Л., Изд-во Академии
наук СССР, 1936.
Литература к § 11 Заключения
[55] К лей и Ф., Неевклидова геометрия, М.—Л., ОНТИ, 1935.
[56] Яг лом И. М. и Ашкинузе В. Г., Идеи и методы аффинной и
проективной геометрии, ч. I, M., Учпедгиз, 1963.
[57]Шерватов В. Г., Гиперболические функции, М., Гостехиздат, 1958.
См. также книги Кагана [251, Б о р и а [38] — 138а] и статью Розен-
фельда н Яглома [24].
Пособия по неевклидовой геометрии Лобачевского1)
[58] Л обачевс к и й Н. И., Геометрические исследования по теории па-
раллельнь с линий, М.—Л., Изд-во Академии иаук СССР, 1945; Полное
собрание сочинений, т. 1, М.—Л., Гостехиздат, 1946, стр. 29—176.
[59] Л об а чев с к и й Н. И., Отрывки из работ «О началах геометрии»,
«Воображаемая геометрия», «Новые начала геометрии с полной теорией
параллельных», Сборник «Об основаниях геометрии» (см. [8]), стр. 27—70.
') Значительно более полный список литературы по этой теме (впрочем,
также совсем не претендующий на полноту и на сегодняшний день частично
устаревший) приложен к книге [75].

ЛИТЕРАТУРА
303
[60] Бол ья и Я., Appendix. M.—Л., Гостехиздат, 1950; Сборник «Об осно-
основаниях геометрии», стр. 71—100.
[61] Га у ее К. Ф., Отрывки- из писем и черновые наброски, относящиеся
к неевклидовой геометрии, Сборник «Об основаниях геометрии»,
стр. 101—120.
[62)Норден А. П., Элементарное введение в геометрию Лобачевского, М..
Гостехиздат, 1953.
[63]Делоне Б. Н., Элементарное доказательство непротиворечивости гео-
геометрии Лобачевского, М., Гостехиздат, 1956.
[64] А л е кса н д р о в П. С, Что такое неевклидова геометрия, М., Учпед-
Учпедгиз, 1950.
[65] Ал е кса нд ров П. С. и Колмогоров А. Н., Николай Иванович
Лобачевский, М.—Л., Гостехиздат, 1943.
[66] Широко в П. А., Краткий очерк основ геометрии Лобачевского, М.,
Гостехиздат, 1955.
[67] Каган В. Ф., Лобачевский, М.—Л., Изд-во Академии наук СССР, 1948.
[68] Kara и В. Ф., Лобачевский и его геометрия, М., Гостехиздат, 1955.
[69]Смилга В. П., В погоне за красотой, М., «Молодая гвардия», 1968.
[70] Каган В. Ф., Очерк геометрической системы Лобачевского, Одесса,
«Матезис», 1900.
[71] Б о нол а Р., Неевклидова геометрия, Спб., «Общественная польза», 1910.
[72] У с п е н с к и й Я-, Введение в неевклидову геометрию Лобачевского—
Болиаи, Пг., «Сеятель», 1922.
[73] Л у к ь я н ч е н ко С, Элементы неевклидовой геометрии Лобачевского—
Болье, М.—Л., Гостехиздат, 1933.
[74]Бальдус Р., Неевклидова геометрия, М.—Л., Гостехиздат, 1933.
[75] Каган В. Ф., Основания геометрии, т. 1, М.—Л., Гостехиздат, 1949.
См. также книги: Кокстера 119], Клейиа [55], Кагана [25],
Яглома [10] и [77] и статью Роэенфельда и Яглома [24].
Литература к Приложениям
[76] Клейн Ф., О так называемой неевклидовой геометрии, Сборник «Об
основаниях геометрии», стр. 253—303.
[77]Яглом И. М., Комплексные числа и их применение в геометрии, М.,
Физматгиз, 1963.
[78] Яг л ом И. М., Проективные мероопределения на плоскости и комп-
комплексные числа, Труды семинара по векторному и тензорному анализу
при МГУ, вып. 7, М.—Л., Гостехиздат, 1949, стр. 276—318.
[79] Роз е н фе л ь д Б. А., Основные понятия сферической геометрии и три-
тригонометрии, ЭЭМ, кн. IV, стр. 518—557.
[80] Ма р к у ш е в и ч А. И., Элементы теории аналитических функций, М.,
Учпедгиз, 1944, § 4, гл. V.
[81] Клейн Ф., Лекции о развитии математики в XIX столетии, ч. 1,
М.—Л., ОНТИ, 1937.
[82] Розенфельд Б. А., Неевклидовы пространства, М., «Наука», 1969.
См. также книги Кагана [25], Клейна [55] и статью Роэенфельдв
и Яглома [24].

ИЗДАТЕЛЬСТВО «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
Москва В-71, Ленинский проспект, 15.
БИБЛИОТЕКА МАТЕМАТИЧЕСКОГО КРУЖКА
Вып. 1. Д. О. Шклярский, Н. Н. Ченцов, И. М. Яглом, Избранные
задачи и теоремы элементарной математики, ч. 1. Арифме-
Арифметика и алгебра.
Вып. 2. Д. О. Шклярский, Н. Н. Чеицов, И. М. Яглом, Избранные
задачи и теоремы элементарной математики, ч. 2. Геометрия
(планиметрия).
Вып. 3. Д. О. Шклярский, Н. Н. Ченцов, И. М. Яглом, Избранные
задачи и теоремы элементарной математики, ч. 3. Геометрия
(стереометрия).
И. М. Яглом и В. Г. Болтянский, Выпуклые фигуры.
А. М. Яглом и И. М. Яглом, Неэлементарные задачи в эле-
элементарном изложении.
Е. Б. Дыикин и В. А. Успенский, Математические беседы
И. М. Яглом, Геометрические преобразования, I. Движения
и преобразования подобия.
Вып. 8. И. М. Яглом, Геометрические преобразования, [I. Линейные
и круговые преобразования.
Вып. 9. М. Б. Бал к, Геометрические приложения понятия о центре
тяжести.
Вып. 10. Г. Радемахер и О. Теплиц, Числа и фигуры. Опыты матема-
математического мышления.
Вып. 11. И. М. Яглом, Принцип относительности Галилея и неевкли-
неевклидова геометрия.
Вып.
Вып.
Вып.
Вып.
4.
5.
6.
7.

М глом